И. Л.Повх
г1 ТЕХНИЧЕСКАЯ Г Л ИДРОМ ЕХ АНИК А
Издание 2-е, переработанное и дополненное
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов машиностроительных специальностей втузов
ЛЕНИНГРАД.
«МАШИНОСТРОЕНИЕ» ЛЕНИНГРАДСКОЕ ОТДЕЛЕНИЕ
1976
605
П42
УДК 532.5 + 533.6 (07)
РЕЦЕНЗЕНТ КАФЕДРА «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕПЛОТЕХНИКИ» ЛЕНИНГРАДСКОГО ПОЛИТЕХНИЧЕСКОГО ИНСТИТУТА им. М. И. КАЛИНИНА
Повх И. Л.
П42	Техническая гидромеханика. 2-е изд., доп.
Л., «Машиностроение» (Ленингр. отд-ние), 1976.
• 504 с. с ил.
В учебном пособии рассмотрены основные вопросы современной гидромеханики: статика, кинематика и динамика. Приведены выводы общих уравнений движения сплошных сред. Даны законы переноса импульса, тепла н вещества. Изложена теория потенциального движения как для плоских, так и для пространственных потоков. Рассмотрена сжимаемость газа при дозвуковых и сверхзвуковых течениях. Освещены вопросы теории движения вязкой жидкости, подробно рассмотрены ламинарное и турбулентное движения в трубах и в пограничном слое. Дан метод расчета трубопроводов.
Во втором издании (1-е изд. 1969 г.) дополнительно изложены вопросы снижения сопротивления в трубах. Приведены сведения о теоретических и экспериментальных достижениях электромагнитной гидродинамики.
20303—032
П 038(01)—76
32-76
605
© Издательство «Машиностроение», 1976 г.
ПРЕДИСЛОВИЕ
При конструировании многих типов современных машин необходимы глубокие знания механики жидкостей и газов. Гидроаэромеханика, являясь общенаучной дисциплиной, так же как и теория упругости, должна быть связующим звеном между общетеоретическими предметами — физикой, математикой и теоретической механикой — и специальными курсами, посвященными изучению процессов в машинах.
Движение жидкостей и газов определяется процессами переноса импульса, тепла и вещества, поэтому в книге показывается общность уравнений этих переносов, рассматриваются тёория подобия, движение в трубах, а также изучается не только динамический пограничный слой, но и тепловой, и диффузионный. Такое изложение приближает курс к механике сплошных сред.
Ряд глав посвящен вопросам прикладной гидромеханики. Уделено внимание электромагнитной гидродинамике, так как быстро расширяется область практического использования электромагнитных насосов, магнитогидродинамических генераторов электроэнергии, электромагнитных расходомеров и других устройств.
Во втором издании учебного пособия переработана глава «Электромагнитная гидродинамика» и добавлены два параграфа о турбулентном пограничном слое.
Эффективность всех машин и сооружений в большо’й мере зависит от структуры потоков, в них происходящих. Это прежде всего относится к энергетическим машинам (турбины, насосы, компрессоры, вентиляторы, двигатели, генераторы и др.), химическим (сепараторы, фильтры, ферментеры, ректификаторы, адсорберы), транспортным (корабли, самолеты, железнодорожный и автомобильный транспорт), горным и сельскохозяйственным машинам.
Так как в машинах преобладают турбулентные потоки, характеристики которых определяют не только гидродинамику, но 1*
4	Предисловие
и тепломассоперенос и акустику, то изучению законов турбулентного движения следует уделить особое внимание. В связи с этим во втором йздании также добавлен параграф о методах снижения сопротивления добавками, получивших широкое распространение в последнее время. -
В настоящем учебном пособии не приводятся описания лабораторных работ и задач по курсу, так как они освещены в соответствующих книгах.
За помощь в переработке главы «Электромагнитная гидродинамика» и в подготовке книги выражаю благодарность доценту Донецкого государственного университета Н. И. Болонову.
ВВЕДЕНИЕ
1.	Предмет механики жидкостей и газов
Механика, являясь частью физики, изучает общие закономерности, связывающие механические движения и взаимодействия тел, находящихся в трех состояниях: твердом, жидком и газообразном. Различное состояние тел способствовало разделению механики на отдельные области.
В механике твердого тела рассматриваются абсолютно твердые и деформируемые тела; последние, в свою очередь, разделяются на тела упругие и пластические. Изучением законов движения абсолютно твердых тел занимается теоретическая механика, а упругих и пластических — теория упругости и теория пластичности.
Законы движения жидкостей и газов изучает механика жидкостей и газов, или гидромеханика.
Механика жидкостей и газов, так же как и другие области механики, разделяется на статику, кинематику и динамику. Часть гидромеханики, изучающая условия равновесия жидкостей и газов, называется гидростатикой. Кинематика жидкостей и газов изучает их движение во времени, не интересуясь причинами, вызывающими это движение. Предметом изучения гидродинамики являются движения жидкостей и газов в связи с их взаимодействием.
Гидромеханика пользуется в качестве основного метода исследований строгим математическим анализом. Вначале независимо, а затем параллельно гидромеханике развивалась гидравлика — прикладная инженерная наука о равновесии и движении жидкостей, основанная преимущественно на экспериментальных данных и разрабатывающая приближенные методы расчета течений жидкости в трубах, каналах и реках.
Жидкости и газы, являющиеся объектом изучения гидромеханики, обладают двумя основными свойствами: сплошностью и легкой подвижностью, или текучестью.
Известно, что все тела состоят из движущихся и взаимодействующих между собой молекул. Механика не занимается изучением движения отдельных молекул, а исходит из допущения, что все пространство непрерывно (сплошным образом) заполнено веществом.
6
Введение
Условие сплошности для жидкостей и газов выполняется, если характерные линейные размеры области течения (диаметр трубы, размах крыла и др.) велики по сравнению с параметрами, характеризующими движение молекул. Для газов, у которых длина свободного пробега молекул существенно зависит от температуры и давления, условие сплошности выполняется, когда линейные характерные размеры области течения велики по сравнению с длиной свободного пробега молекул.
Для выполнения условия сплошности в жидкостях необходимо, чтобы характерные линейные размеры области течения были достаточно большими пр сравнению с амплитудой колебаний молекул.
Из этих же условий определяется понятие элементарного объема жидкости или газа. Линейные размеры элементарного объема должны быть достаточно большими по сравнению с длиной свободного пробега молекул газа или амплитудой колебаний молекул жидкости и достаточно малыми по сравнению с характерными линейными размерами области течения.
Легкая подвижность, или текучесть, позволяет ввести понятие вязкости как свойства жидкостей и газов оказывать сопротивление при их перемещении. Текучесть есть величина, обратная вязкости. По сравнению с жидкостями газы обладают довольно большой текучестью и, следовательно, малой вязкостью.
Гидромеханика изучает законы движения так называемых ньютоновских жидкостей, для которых напряжения, вызываемые наличием вязкости, выражаются линейно через скорости деформаций .
Для неныотоновских жидкостей эта зависимость значительно сложнее. Законы движения неньютоновских жидкостей изучает реология.
Некоторые реологические тела и сыпучие среды обладают внутренним трением, аналогичным сухому трению между твердыми телами. Последнее проявляется в том, что при трогании с места необходимо преодолеть начальное сопротивление, называемое трением покоя.
В жидкостях и газах, изучаемых в гидродинамике, сухого трения нет, поэтому любая сколь угодно малая касательная сила вызывает смещение одного слоя относительно другого. Газы и особенно жидкости оказывают значительное сопротивление деформации всестороннего сжатия.
В гидромеханике иногда пользуются моделью идеальной жидкости, для которой вязкость принимается равной нулю, а следовательно, ее текучесть бесконечно большой. Такой подход к изучению некоторых движений жидкости возможен, когда силами вязкости можно пренебречь по сравнению с другими действующими силами.
Некоторые сведения из истории развития гидромеханики t
2.	Некоторые сведения из истории развития гидромеханики „
Гидромеханика прошла большой и сложный путь развития. Ее предыстория уходит в древние времена.
Постепенно в процессе труда человека накапливались отдельные наблюдения, открывались определенные закономерности движения жидкости и газа, которые затем обобщались и превращались в систему знаний—науку.
Отдельные результаты таких наблюдений были изложены в трудах древнегреческого философа Аристотеля (384—322 до н. э.). Некоторые законы гидростатики были сформулированы величайшим математиком и механиком древней Греции Архимедом (277—212 до н. э.).
Большой вклад в .развитие основ'гидромеханики был сделан Леонардо да Винчи (1452—1519), Стевином (1548—1620), Галилеем (1564—1642), Паскалем (1623—1662) и Гюйгенсом (1629— 1695).
Ньютон (1642—1727) в своем известном, труде «Математические начала естественно-научной философии», основываясь иа собственных опытах, установил, что сопротивление тел при движении в жидкости пропорционально квадрату скорости.
Начало гидромеханике как науке было положено в XVII столетии трудами академиков Российской Академии Наук М. В. Ломоносова (1711—1765), Леонарда Эйлера (1707—1783) и Даниила Бернулли (1700—1782).
Работы величайшего русского ученого М. В. Ломоносова по металлургии, горному делу, водяным двигателям и метеорологии  внесли крупный вклад в создававшуюся гидромеханику. Среди его трудов в этом направлении можно назвать: «О вольном движении воздуха, в рудниках примеченном», «Слово о явлениях воздушных, от электрической силы происходящих», «Попытка теории упругой силы воздуха» и др. Он разработал и построил прибор для измерения скорости и направления ветра, создал «аэродрольную» машину — прообраз современного вертолета.
Леонардом Эйлером были выведены уравнения равновесия и движения жидкостей и газов, указаны некоторые интегралы этих уравнений и сформулирован закон сохранения массы применительно к жидкости. Эйлер исследовал также некоторые вопросы движения к практическим задачам судостроения и конструирования гидравлических машин.
Даниил Бернулли впервые ввел термин «гидромеханика». Он установил зависимость между удельными энергиями при движении жидкости, которая в настоящее время называется уравнением Бернулли. Кроме того, он исследовал задачу о давлении струи жидкости на пластину.
8
Введение
Дальнейший этап в истории развития гидромеханики, объединяющий конец XVIII и начало XIX веков, характерен математической разработкой гидродинамики идеальной жидкости. В этот период вышли труды французских математиков Лагранжа (1736— 1813) и Коши (1789—1857), посвященные потенциальным плоским потокам, теории, волн малой амплитуды и др.
Основы теории движения вязкой жидкости были заложены французским ученым Навье (1785—1836) и английским физиком и математиком Стоксом (1819—1903). Поэтому уравнения движения вязкой жидкости называются уравнениями Навье—Стокса.
В 1881 г. профессор Казанского университета И. С. Громеко (1851 —1889) опубликовал работу «Некоторые случаи движения несжимаемой жидкости», в которой дал новую форму уравнений движения жидкости, удобную для получения энергетических зависимостей. Им же впервые было проведено теоретическое исследование нестационарного движения жидкости в капиллярах.
Из многочисленных экспериментальных исследований движения жидкости в трубах укажем на опыты с трубками малого диаметра французского врача и испытателя Пуазейля (1799—1869), изучавшего движение крови в сосудах, и опыты английского физика Рейнольдса (1842—1912), установившего в 1883 г. закон подобия течений в трубах. Целую эпоху в истории развития гидромеханики составляют исследования по воздухоплаванию, включающие разработку теории полета самолетов и ракет. Результаты этих исследований были изложены в трудах выдающихся русских ученых Д. И. Менделеева (1834—1907), Н. Е. Жуковского (1849—1921) и С. А. Чаплыгина (1869—1942).
В 1880 г. Д. И. Менделеев опубликовал работу «О сопротивлении жидкостей и воздухоплавании», в которой были высказаны важные положения о механизме сопротивления движению тел в жидкости и даны основные представления о пограничном слое. В XX в. эта работа получила большое развитие.
Созданию теории крыла и воздушного винта были посвящены исследования Н. Е. Жуковского. В 1906 г. он разработал теорию подъемной силы крыла, имеющую большое значение не только для авиации, но и для современного турбомашиностроения. Н. Е. Жуковский, как Эйфель (1832—1923) во Франции и Прандтль (1875—1950) в Германии, был создателем экспериментальной аэромеханики в России. Он создал известный всему миру Центральный аэрогидродинамический институт (ЦАГИ), ныне носящий его имя.
С. А. Чаплыгин посвятил свои исследования дальнейшему развитию теории обтекания крыла и решеток профилей. Он разработал теорию разрезного крыла, крыла с подкрылком'и закрылком; разработал основы теории определения сил, действующих насамо-лет при полете его с переменной скоростью. Работы С. А. Чаплыгина
Техническая гидромеханика
9
положили начало новому разделу гидромеханики — теории не-установившегося обтекания крыла потенциальным потоком. Важные исследования в этой .области впоследствии выполнили Н. Е. Кочин, А. И. Некрасов, М. В. Келдыш, М. А. Лаврентьев, Л. И. Седов и др.
Крупный вклад в теорию реактивного движения тел был сделан К- Э. Циолковским (1857—1935), И. В. Мещерским (1859— 1935) и А. А. Фридманом (1888—1925).
К. Э. Циолковский всю свою жизнь посвятил разработке проблем освоения космического пространства. Он установил основные принципы реактивного движения, обосновал возможность применения реактивных аппаратов для межпланетных сообщений и, в частности, разработал теорию многоступенчатой ракеты. К- Э. Циолковский является основоположником теории межпланетных сообщений.
И. В. Мещерский сформулировал законы движения тел с переменной массой, которые широко используются при решении многих проблем реактивного движения.
А. А. Фридман выполнил ряд фундаментальных исследований в области теории относительности и динамической метеорологии. Им получены также важные результаты при изучении законов движения сжимаемой жидкости.
Современный этап развития гидромеханики характеризуется появлением ее новых разделов: физико-химической, электромагнитной и космической гидродинамики, связанных с развитием многих областей техники.
3.	Техническая гидромеханика
Механика жидкостей и газов имеет чрезвычайно большой круг возможных технических приложений. Законы движения жидкостей и газов в трубах и каналах, в проточных частях машин, воды в реках и океанах, воздуха в атмосфере — вот далеко не полный перечень проблем, решение которых связано*с развитием механики жидкостей и газов.
Развитие авиации’ и судостроения привело к созданию соответствующих разделов гидромеханики. Таковы теория гидродинамического сопротивления среды, теория винта и крыла, проблемы устойчивости и управляемости самолета и др.
Интенсификация химических процессов невозможна без знания законов движения жидкостей и газов, без знания процессов перемешивания в потоках. Поэтому в последние годы гидродинамика получает широкое применение в химической технологии, возникают разделы так называемой физико-химической гидродинамики, начинается изучение потоков при наличии химических реакций.
10
Введение
Стремление к получению непрерывных металлургических процессов приводит к необходимости углубления знаний по гидродинамике жидких металлов; интенсификация технологических процессов в доменных, мартеновских и других металлургических печах требует изучения потоков газа при наличии тепловых и химических явлений.
Движение проводящий сред, таких, как жидкие металлы, слабо и сильно ионизированные газы (последние называются плазмой), расплавы солей и электролитов при наличии магнитных и электрических полей изучается в магнитной гидродинамике. Движение непроводящих жидкостей и газов (а точнее, сред с очень низкой электропроводностью) в электрическом поле изучает электрогидродинамика.
Заметим, что полное исследование взаимодействия заряженных частиц в ионизированном газе, так же как и взаимодействие частиц нейтрального, т. е. обычного газа, может быть произведено только на основе уравнений кинетической теории газов.
Гидродинамика получила .широкое применение при изучении атмосферы. Раздел метеорологии, который использует законы гидродинамики при исследовании атмосферы и ее движения, называется динамической метеорологией.
Усовершенствование машин стало невозможным без тщательного изучения происходящих в них газогидродинамических процессов. Почти во всех машинах имеются элементы, в которых происходит движение жидкостей или газов. В одних потоки жидких или газообразных сред связаны с выполнением основного назначения машин, в других — они лишь обеспечивают условия ее нормальной работы. К первым надо отнести двигатели, турбомашины и большую часть химических, обогатительных, бумагоделательных и других машин. Эффективность их полностью определяется совершенством элементов, обычно называемых проточной частью машин, в которых движется жидкая или газообразная среда.
Такие машины, как станки, краны и т. п., также имеют элементы, в которых имеет место движение жидкостей и газов. Это — подшипники, регуляторы и пр., от работы которых существенно зависит к. п. д. машины.	‘
Механику жидкостей и газов применительно к технике будем называть технической гидромеханикой. В основе технической гидромеханики лежат теоретические закономерности, созданные и проверенные на опыте. Необходимость ясного понимания законов течения жидкостей и газов при конструировании сложных современных машин и разработка технологических процессов производства настоятельно требует изучения технической гидромеханики.
Плотность и сжимаемость
11
4.	Плотность и сжимаемость
Для характеристики распределения массы в пространстве, занятом жидкостью или газом, обычно пользуются величиной, называемой плотностью. Среднее значение плотности среды в некотором малом объеме определяется как отношение массы Д/п, заключенной в этом объеме, к самому объему Д£7
А«	...
Pci’ “ ДУ	( )
Часто пользуются не средним значением плотности вещества в некотором объеме, а величиной плотности среды в данной точке М, в которой
При этом предполагается, что точка М при стремлении малого объема к нулю должна все время оставаться внутри объема Д(/. Иногда для характеристики распределения массы в пространстве применяют величину, обратную плотности, называемую удельным объемом v
v =	(3)
Плотность движущейся среды зависит от температуры и давления, а последнее — от характера движения среды. В общем случае плотность можно представить в виде функции от координат н времени
р = / (X, у, 2, f).
Поверхности равных значений плотности в пространстве и соответствующие им линии на плоскости называются соответственно изостерическими поверхностями и линиями.
Значения плотности для воды и воздуха в зависимости от температуры при давлении, равном 1 кгс/см2, приведены в табл. 1.
В технике пользуются понятием удельный вес у, определяемой силой тяжести F единицы объема вещества
&Р g&n ~ ~ьй “АТТ ~
(4)
Так как ускорение силы тяжести g зависит от координат точки, в которой производится измерение, то удельный весне может являться постоянной величиной. Определять ее надо по формуле (4), пользуясь табл. 1 и значением ускорения свободного падения g в данном месте.
Способность жидкости или газа под действием внешнего давления изменять свой объем и, следовательно, плотность называется сжимаемостью. Количественно сжимаемость среды определяется изменением ее плотности Др, отнесенной к единице при_
12
Введение
Таблица t
Температура, °C	р, кг/м3	
	воды	воздуха
— 10	—	1,42
0	1019	1,34
20	1017	1,25
40	1011	1,16
00	1000	1,10
80	9910	1,03
<. 100	9780	1,0
ложепного давления Др. В физике обычно пользуются обратной величиной, равной квадрату скорости звука а в данной среде, , \р а- = -т— • Др
Для малосжимаемых жидкостей и газов при больших изменениях давления Др изменение плотности будет малым, а скорость звука — большой, а для сильно сжимаемых жидкостей при малых Др изменение плотности Др будет большим, а скорость звука— малой. Следовательно, характеристикой сжимаемости жидкостей и газов в состоянии покоя служит скорость звука в данной среде. Чем больше скорость звука, тем меньше сжимаемость этой среды. Очевидно, что сжи-• маемость воды, скорость звука в которой 1500 м/с значительно меньше сжимаемости воздуха, в котором скорость звука около 300 м/с. В несжимаемой среде (Др = 0 пр_и Др =/= 0) а = оо, т. е. малые возмущения распространяются мгновенно.
Если жидкость или газ движется, то для оценки сжимаемости
обычно пользуются не абсолютным значением скорости звука, а отношением скорости потока V к скорости звука. В гидромеханике
это отношение называется числом М
М = —. а
(5)
В случае когда во всей области движения скорость жидкости мала по сравнению со скоростью звука в этой среде, число М будет мало по сравнению с единицей и независимо от абсолютного значения скорости звука жидкость или газ при таком движении можно считать несжимаемыми.
Сжимаемость газа начинает сказываться уже при дозвуковых скоростях. Влияние сжимаемости возрастает с увеличением числа М и становится большим при околозвуковых и сверхзвуковых скоростях. Часть гидромеханики, занимающаяся изучением движения сжимаемого газа, называется газовой динамикой.
5.	Законы переноса
В отличие от идеальных жидкостей и газов, у которых вязкость равна нулю и отсутствует перенос тепла и вещества, в реальных вязких жидкостях имеют место процессы и теплопереноса,
Законы переноса
13
и диффузии. Заметим, что процессы переноса тепла и вещества могут происходить как в покоящихся, так и в движущихся средах, в то время как перенос количества движения, являясь следствием проявления вязкости, имеет место только в движущихся жидкостях и газах.
При изучении законов переноса в потоках жидкостей и газов рассматриваются три величины: векторная — импульс, или количество движения, и две скалярные — тепло и вещество. В движущемся потоке в общем случае наблюдается неоднородность таких величин, как скорость, температура и концентрация вещества. Вследствие этой неоднородности в среде возникают явления переноса импульса, тепла и массы.
Если в потоке выделить некоторый элементарный объем, то на его поверхности будут действовать касательные и нормальные силы. Касательные силы возникают вследствие внутреннего трения или вязкости. Как известно, Ньютон сформулировал закон, согласно которому касательное напряжение трения между двумя слоями прямолинейно движущейся вязкой жидкости пропорционально отнесенному к единице длины изменению скорости по нормали к направлению движения
dV т = II — . r dn
(6)
Закон Ньютона позже был сформулирован в кинетической теории газов как закон переноса импульса молекул. Из уравнения (6) видно, что, когда V= const, перенос количества движения отсутствует и касательное напряжение равно нулю, т. е. т = 0.
Коэффициент пропорциональности в уравнении (6) называется динамическим коэффициентом вязкости
, , н
[и] = —
lr J м2
1 Нс
с ~ м2
Динамический коэффициент вязкости не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и ее температурой.
Наряду с динамическим коэффициентом вязкости, в дальней--шем часто будем иметь дело с кинематическим коэффициентом вязкости
v=-y’> М = м2/с.	(7)
В табл. 2 приведены значения динамических и кинематических коэффициентов вязкости для воды и воздуха при различных значениях температур.
14
Введение
Следует отметить, что для жидкостей с повышением температуры величина вязкости убывает, а для газов — растет.
Законы переноса тепла и массы имеют вид, аналогичный закону Ньютона. Перенос тепла характеризуется законом Фурье
Таблица 2	dT	\ dpcP? .. _.	п — 'к —— ~		— =					
СбО О.0	Вода		Воздух		7	ап	ап dptpT
। Темп* тура,	Ц • 10-	V-IO"	ц-10*	v-iO4	= а —1— ,	(8) dn ’	' ' а перенос вещества — законом Фика de w = D~.	(9) dn	v ’ В этих формулах q и w — количество тепла и вещества, переносимого через единицу площади в еди-
0 20 40 60 80 100	0,179 0,1 0,066 0,047 0,036 0,028	1,792 0,087 . 0,66 0,477 0,367 0,296	0,171 0,181 0,19 0,2 0,209 0,248	0,132 0,15 0,169 0,188 0,209 0,2	
ницу времени; 1 и с—температура и концентрация вещества; К и D—соответственно коэф- фициенты теплопроводности и диффузии; а = ——коэффи-рСр циент температуропроводности.'					
Эти законы можно сформулировать следующим образом: количество тепла, переносимого через единицу площади в единицу времени, пропорционально градиенту температуры, а количество вещества, переносимого через единицу площади в единицу времени, пропорционально градиенту концентрации этого вещества в по-
токе.
Так как в системе единиц СИ размерности q и wсоответственно раВНЫ
м2-с м2	м2-с
то размерность коэффициентов переноса будет следующей:
. Вт	1ГП м2	.	, . м2
л — —,	[О] = —	и	[а] — —	.
м-°С	1 J с	1 J с
Коэффициенты X и D зависят от физических свойств среды и температуры. Из молекулярной физики известно, что для газов все коэффициенты переноса (ц, X и D) возрастают вместе со средней тепловой скоростью молекул, т. е. с абсолютной температурой среды.
6.	Структура потоков. Турбулентность
По структуре все существующие потоки реальной вязкой жидкости делятся на ламинарные и турбулентные. При ламинарном или слоистом движении жидкости подкрашенные струйки
Структура потоков. Турбулентность
15
остаются резко выделенными во все время движения, т. е. отдельные частицы движутся по определенным траекториям. При турбулентном движении отдельные частицы жидкости совершают беспорядочное движение по хаотически переплетенным и быстро изменяющимся траекториям.
От структуры потока существенно зависят величины, характеризующие процесс переноса количества движения, тепла и вещества. Законы переноса, приведенные выше, пригодны лишь для ламинарных потоков, при турбулентном движении эти законы значительно сложнее.
Существование двух принципиально различных режимов течения вязкой жидкости было установлено экспериментально в конце прошлого века для труб и каналов.
Движение воды в реках и в трубах, движение газа в трубопроводах и в проточной части машин, движение воздуха в атмосфере и многие другие виды движения жидкости и газа в природе и технике являются преимущественно турбулентными.
Турбулентное движение жидкости сопровождается интенсивным перемешиванием ее частиц. Следовательно, там, где выравнивание концентрации раствора, тепла или количества движения необходимо произвести в более короткие сроки, турбулентность потока будет являться положительным фактором. Как будет показано далее, сопротивление жидкости движению телапри наличии турбулентности в потоке в одних случаях увеличивается, в других — уменьшается.
Величиной, определяющей изменение структуры потока, является число Рейнольдса
VI Re = —, V
где V и I — скорость и линейный размер, характерные для данного движения.
> Опыты показали, что переход ламинарного движения в турбулентное происходит при определенном значении числа Рейнольдса, называемом критическим числом Рейнольдса. Для’гладкой круглой трубы при острых краях входного сечения критическое число Рейнольдса, подсчитанное по средней скорости и по диаметру трубы, приблизительно равно 2300. Критические числа Рейнольдса для всех других потоков определяются экспериментально. При движении проводящих жидкостей в трубах в поперечном магнитном поле критическое число Рейнольдса может значительно превышать 2300.
Основным методом изучения закономерностей турбулентного движения до сих пор служат экспериментальные исследования; различные теории~турбулентности все еще имеют лишь вспомогательное значение.
ГЛАВА I
ОСНОВЫ ГИДРОСТАТИКИ
§ 1. Силы, действующие в жидкости. Гидростатическое давление
В гидростатике изучается теория равновесия жидкостей и газов. Для выяснения условий равновесия необходимо рассмотреть силы, действующие на некоторый объем жидкости.
Существует много различных принципов классификации сил, приложенных к частицам сплошных сред. В зависимости от области приложения силы делятся на внутренние и внешние. По своей природе или по характеру действия силы делятся на массовые (или объемные) и поверхностные.
Массовые, или объемные, силы пропорциональны массе выделенного объема или при постоянной плотности среды пропорциональны объему, они действуют на все частицы среды этого объема. Массовыми силами являются силы веса, все электромагнитные объемные силы, в том числе силы Лоренца и силы электростатического напряжения, и различные силы инерции (кориолисова сила, центробежная сила и др.).
Поверхностные силы действуют лишь на поверхность выделенного объема. Обычно поверхностные силы складываются из поверхностных сил, направленных по нормали к выделенной площадке, и поверхностных сил, направленных по касательной к этой площадке.
В покоящейся жидкости поверхностные силы направлены по нормали к элементу поверхности выделенного объема. В движущейся вязкой жидкости имеют место и нормальные, и касательные составляющие поверхностных сил. Последние определяют силы трения.
Распределение массовых сил в некотором объеме AU задается вектором плотности массовой силы, равным пределу отношения главного вектора массовых сил AF', приложенных к частицам некоторого объема с массой Ат, к этой массе при стремлении последней к пулю, т. е.
। • ДГ' г lim — = г.
Силы, действующие в жидкости. Гидр астатическое давление
17
Для характеристики распределения массовых сил обычно пользуются осредненным значением вектора плотности массовых сил, равным отношению главного вектора массовых сил к величине массы, т. е.
Am ~ Гср*
Размерность плотности массовой силы совпадает с размерностью ускорения
 сч  [ДГ']   Н   кг-м   м
I	[Дтг]	кг	кг-с2	с2
В отличие от объемных сил, вектор которых для частицы среды определяется однозначно, величина поверхностной силы в точке в общем случае зависит от выбора направления элементарной площадки. Обычно рассматриваются не сами поверхностные силы, а их напряжения, т. е.
где Др'— главный вектор поверхностных сил, приложенных к некоторой площадке As.
Размерность напряжений будет
- _ [Др'] =_Н =Д^_.
— [as| м2 м-с2
В практике часто пользуются единицей измерения давления, называемой технической атмосферой, которая равна 1 кгс/см2 — = 736 мм рт. ст. — 10 м вод. ст. = 10 000 мм вод. ст.
В технике пользуются размерностью кгс/м2 и давление выражают в миллиметрах водяного столба,
1 кгс/м2 = 10ч кгс/см2 = 1 мм вод. ст.
В международной системе единиц СИ за единицу давления принимается давление силы в 1 Н на 1 м2
1 Н/м2 = 98 066,5 кгс/см2= 9,80665 кгс/м2-
Так как эта единица очень мала, то можно применять укрупненные единицы давления: кН/м2, 1 МН/м2 и внесистемную единицу давления бар, равную 105 н/м2, а также дольные единицы бара — мбар и мкбар
1 кН/м2 = 1000 Н/м2 = п0 кгс/см2.
98,0665
Рассмотрим условие равновесия элементарного жидкого объема, находящегося под действием поверхностных и массовых сил.
§ И. л. Нов*
18
Основы гидростатики
Для этого в покоящейся жидкости выделим некоторый элементарный тетраэдр с длиной ребер dx, dy, dz (рис. 1.1). Три грани тетраэдра лежат в координатных плоскостях, а четвертая — наклонная грань — является замыкающей. Пусть площади соответствующих граней будут s(, Sy, sz и sn.
Поверхностные силы элементарного тетраэдра пропорцио
нальны произведению двух длин сторон тетраэдра, а массовые — объему. Следовательно, массовыми силами как величинами третьего
Рис. 1.1.
порядка малости можно пренебречь по сравнению с поверхностными силами — величинами второго порядка малости. -
Согласно основному свойству жидкостей, находящихся в равновесии, поверхностные силы, заменяющие действие отброшенной части жидкости при выделении тетраэдра, будут направлены по нормали к граням тетраэдра. Таким образом, эти силы являются силами давления. Если обозначить величины сил давления, приложенных к граням Рх, Ру, Рг и Рп (рис. 1.1), то для сохранения условий равновесия, известных из статики твердого тела, необходимо,
чтобы сумма всех внешних сил или сумм проекций всех внешних сил на координатные оси была равна нулю. Для рассма-
триваемого тетраэдра это условие можно записать в виде:
Рх = Рп cos (п х); Ру = Рп cos (п г/);
Рг = Рп cos (п г),
где п — орт нормали к наклонной грани.
Если первое уравнение системы разделим на величину площадки sx, а второе и третье соответственно на и sz, то получим условие равновесия в величинах напряжении сил давления:
Рх - ~ cos (пх); ьх sx
Ру Рп
Ри=-Г = — cos(n у ;
sy sy
рг — ~= ^ъп(пг).
Основное уравнение гидростатики. Условие Существования равновесия 19
Но из рис. 1.1 видно, что sx, su и s7 — проекции наклонной грани соответственно на плоскости yOz, xOz и хОу, т. е.
sx = sn cos (п х); Sy = sn cos (n у); sz — sn cos (n г).
Подставив эти величины в правые части предшествующих уравнений, окончательно получим:
рх = Рп, Ри = Рп, Pz = Рп, или
Рх = Ру = Рг = Рп = Р-	0-1)
Так как при выделении элементарного тетраэдра никаких ограничений относительно его положения в неподвижной жидкости не накладывалось, то из последнего уравнения следует, что в покоящейся жидкости величина напряжения силы давления, называемая гидростатическим давлением в точке, не зависит от ориентации площадки, к которой приложено давление. Этот вывод является выражением известного закона Паскаля, гласящим, что «. . . давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях». Очевидно, что если давление не зависит от ориентации площадки, проходящей через данную точку, и определяется только положением точки в жидкости, то давление р есть функция только координат х, у, г, т. е. р = f (х, у, г).
§ 2. Основное уравнение гидростатики. Условие существования равновесия
Для вывода основного уравнения гидростатики, устанавливающего зависимость давления в точке от характера действующих в жидкости массовых сил, рассмотрим равновесие элементарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости (рис. 1.2).
Пусть на единицу массы параллелепипеда действует массовая сила F с ее составляющими X, Y и Z. Если на три грани, пересекающиеся в точке О, будет действовать давление р, то на соответствующих противоположных гранях (рис. 1.2) давления будут равны:
р -|-	dx\ р + 4^- dy, р + ~ dz.
И 1 дх ’	1 ду и ' 1 dz
Тогда уравнение равновесия в проекции на ось х будет иметь вид
[р — (р “Ь d-x\] dy dzXpdxdydz = O,

Ьсновы гидростатики.
ИЛИ
др дх
= рХ.
Соответствующие уравнения в проекциях на оси у и z будут:
^ = pY и >=PZ. ду 1 дг '
Три последних уравнения являются основными, уравнениями гидростатики и часто называются уравнениями Эйлера равновесия жидкости или газа.
Эта система уравнений иногда записывается в виде:
Х~ — -^=0; р дх ’
—-^ = 0
Р ду
Z-------^=0.
р дг
(1-2)
Так как и
Xi-\- Y~j 4- Zk = F
4^- 1 + 4^ ! + & — §rad Р> дх 1 ду 1 1 дг 6
то, очевидно, система уравнений (1.2) может быть представлена в векторном виде -
£=j-gradp.	(1.3)
Равновесие тяжелой несжимаемой жидкости. Сообщающиеся сосуды 21
Если систему (1.2) умножим последовательно на dx, dy, dz и сложим, то получим
p(Xdx + Ydy + Zdz)=^dx + ^dy+^ dz. (1.4)
Так как правая часть последнего уравнения есть полный дифференциал
dx -}- dy + dz — dp, дх 1 ду J 1 дг
то уравнение (1.4) будет иметь вид
р (X dx + Y dy + Z dz) = dp.	(1.5)
Следовательно, при наличии равновесия полным дифференциалом должна быть и левая часть уравнения (1.4). В частности, при постоянной плотности (р = const) получим
(X dx + Y dy + Z dz) — d<Y>.
Из этого уравнения видно, что массовые силы имеют потенциал и проекции массовых сил можно выразить в виде:
Х = -^-; Y = ^~- Z = ^.	(1.6)
дх	ду	ду	'	'
Тогда уравнение (1.5) запишется таким образом: рс!Ф = dp.
Из этого следует, что жидкость может находиться в равновесии только в том случае, когда массовые силы, действующие в ней, имеют потенциал, т. е. проекции массовых сил удовлетворяют условию (1.6).
Поверхность, в каждой точке которой давление постоянно, называют поверхностью уровня. Если в уравнении (1.5) положить р = const, то уравнение поверхности уровня будет
Xdx + Y dy + Z dz — О, или ЛФ = 0.
Из последнего уравнения следует, что поверхность уровня одновременно является и поверхностью равного потенциала или так называемой эквипотенциальной поверхностью.
§ 3. Равновесие тяжелой несжимаемой жидкости. Сообщающиеся сосуды
Для несжимаемой тяжелой жидкости при отсутствии других массовых сил, кроме сил тяжести, имеем (ось z направлена вертикально вниз)
X = Y = 0 и Z = g,
22
Основы гидростатики
уравнения равновесия (1.2) в этом случае принимают вид:
-^=0; -^ = 0; %-=Pg. дх	ду	dz '°
Первые два из этих уравнений выражают независимость давления от координат х и у, т. е. поверхностями равного давления или поверхностями уровня являются горизонтальные плоскости. Интегрирование третьего уравнения
(1-7)
dp — Pg dz npi£ постоянных значениях g и р приводит к результату
Р = Pgz + С. (1.8)
Если начало координат поместить на свободную поверхность покоящейся жидкости, на которой постоянное давление р0 задано или атмосферному давлению, то, как Подставив зна-
равно
(1.8), при z = 0 С = р0.
для открытого сосуда следует из выражения чение постоянной С в уравнение (1.8) и имея в виду, что pg" = у, окончательно получим величину
гидростатического давления
в виде
Р = Ро + У*.	(1.9)
Это соотношение является выражением общего гидростатического закона, который формулируется следующим образом: давление в любой точке покоящейся жидкости равно внешнему давле-
Рис. 1.4
нию, сложенному с весом столба жидкости высотой от поверхности до данной точки и с площадью основания, равной единице.
Заметим, что закон в такой редакции верен как для несжимаемой, так и для сжимаемой жидкостей, т. е. для всех жидкостей
и газов и их смесей.
Размерность всех слагаемых в уравнении (1.9) будет иметь размерность давления — н/м2.
Закономерности, определяемые уравнением (1.9), широко используются в различных гидростатических машинах и приборах. К таким машинам можно отнести гидравлический пресс, гидравлический аккумулятор, различные системы объемных передач и пр.
Большая часть гидростатических машин и приборов использует свойства сообщающихся сосудов. Общее свойство сообщающихся сосудов заключается в том, что если на свободных поверх-
Равновесие тяжелой несжимаемой жидкости. Сообщающиеся сосуды
23
ностях сообщающихся сосудов давление одинаково и они заполнены одинаковой жидкостью, то во всех сосудах уровни будут одинаковыми.
Легко показать, что в сообщающихся сосудах, заполненных жидкостями с различными плотностями, высота столбов жидкостей над уровнем раздела обратно пропорциональна плотностям. Из рис. 1.3 видно, что давления в обоих сообщающихся сосудах будут одинаковы на плоскости, проведенной через поверхность раздела 00. Приравняв давление в этом сечении в правом и левом
—р0 может быть легко измерена с по-
мощью U-образной трубки, частично запол- Рис. 1.5 ненной некоторой жидкостью.
Из рисунка видно, что в сечении АВ давление в обоих коленах U-образной трубки одинаково. Так как в левом колене оно равно а в правом р0 + yh, получим
Pi = Ро + yh,
(1.11)
т. е.
Pi— Ро = yh.
Когда давление в баке рг будет меньше атмосферного (рис. 1.4, б), столб жидкости будет больше в левом колене, и разность давлений составит р0—pi — yh.
Очевидно, что измеряемая разность давлений определяется плотностью жидкости, налитой в U-образную трубку. При малых разностях давлений для получения легко измеряемой высоты столба необходимо брать жидкость с малой плотностью (вода, спирт и др.), а при больших — соответственно с большой (ртуть).
В измерительной практике часто применяют манометры, в которых, одно из колен U-образной трубки заменяется широ'ким сосудом (рис. 1.5). Тогда, пренебрегая изменением уровня в широком сосуде, величину давления можно определять по высоте столба h в калиброванной трубке.
При измерении очень малых давлений создают различные приспособления для более точного определения высоты столба.
24
Основы гидростатики
Так, калиброванную трубку иногда делают наклонной. В последнем случае величина разности давлений будет равна
pi — Ро = yl sin а, где I — длина столбика жидкости в наклонной трубке; а — угол между осью трубки и горизонтом.
§ 4. Равновесие весомого газа. Барометрическая формула
При малой высоте столба газа его плотность можно считать во всех точках одинаковой и величину давления определять по формуле (1.8).
При большой высоте столба воздуха, исчисляемой километрами, величину плотности надо считать зависящей от высоты, поэтому указанная формула будет неверна. Для получения формулы, справедливой в этом случае, используем уравнение (1.7), которое перепишем в виде dp = у dz.
Для интегрирования полученного выражения необходимо предварительно установить связь между давлением р и плотностью р. Простейшую зависимость дает закон Бойля—Мариотта, который верен при условии постоянства температуры. По этому закону плотность есть линейная функция давления, т. е.
Р = 7 = Р Ро То Ро '
Подставив значение в предыдущее выражение и проинтегрировав его, получим
Ро
2 = до (•	= ^1пДо .	(Г.12)
То j Р То Р
р
Решим уравнение (1.12) относительно р и найдем зависимость давления газа от высоты при постоянной температуре,
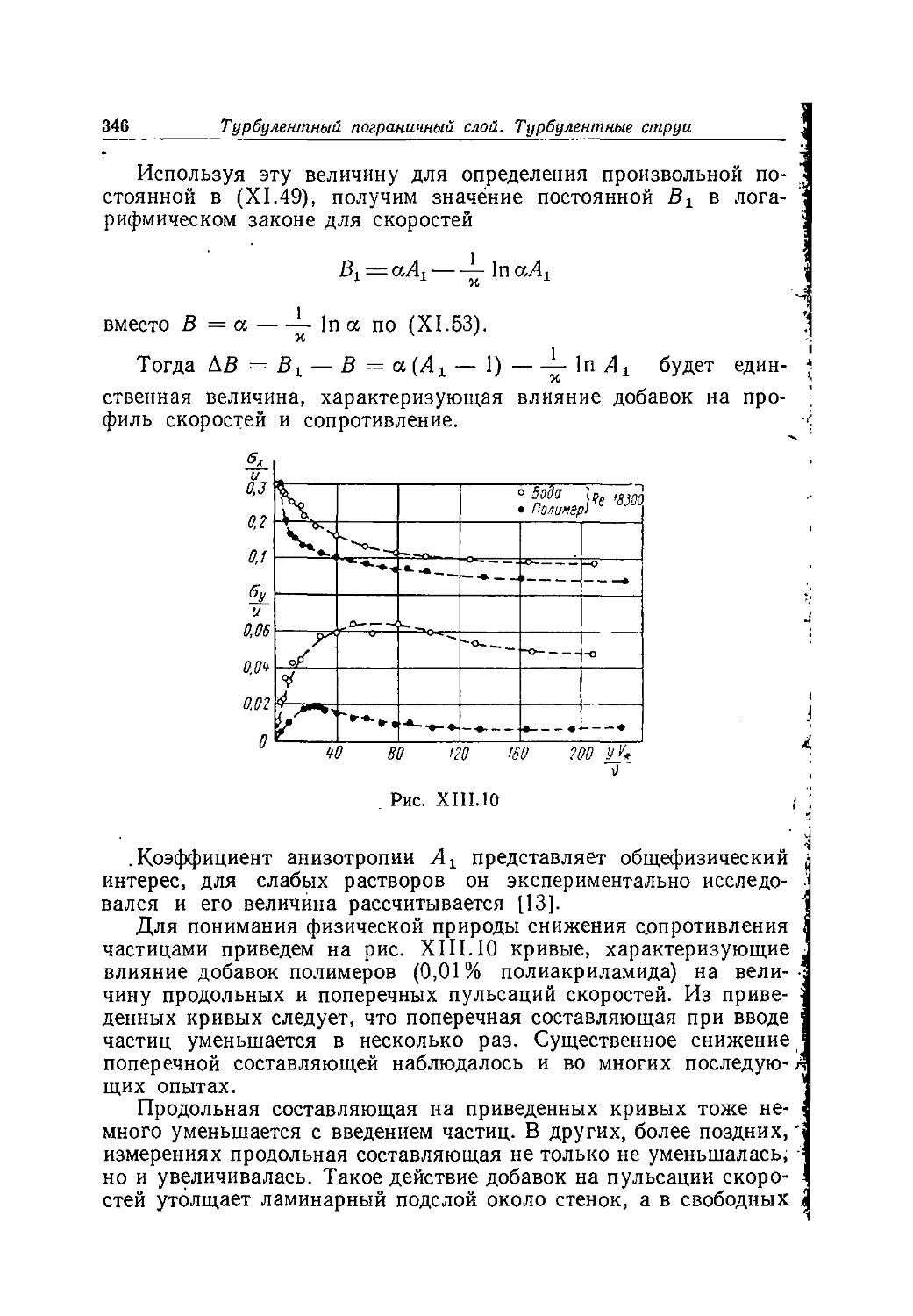
2
р = роъ~\	(1.13)
где
Применив уравнение (1.12) к двум высотам zx и z2, будем иметь соотношения:
z1 = /ioln— и z2 = /i0ln —.
Р\	Pi
Равновесие жидкости при наличии негравитационных массовых сил 25
Вычтя из Zj величину z2, получим так называемую барометрическую формулу, служащую для измерения разности высот по заданным значениям давлений р± и р2 в виде
Zj — z2 = Zi0ln	(1-14)
По формуле (1.14) гидростатическое давление р., в точке будет равно
p2=pxe "° .
Приведенные формулы для изотермической атмосферы будут тем точнее, чем меньше будет разность высот zr и г2. Существуют и более точные зависимости, учитывающие изменение температуры газа с изменением высоты.
§ 5. Равновесие жидкости при наличии негравитационных массовых сил
До сих пор мы рассматривали равновесие жидкостей и газов при наличии лишь гравитационных массовых сил — сил тяжести.
В практике имеет место равновесие жидкостей и газов при наличии негравитационных массовых сил — сил инерции и электромагнитных сил, действующих на
Рис. 1.6
двух случаях равновесия
проводящие среды.
Общее условие возможности существования равновесия, заключающееся в том, что массовые силы должны иметь потенциал, относится и ко всем негравитационным массовым силам. Равновесие жидкостей при наличии электромагнитной объемной силы будет рассмотрено в гл. XV.
В этом параграфе остановимся на
при наличии сил инерции.	is-s
Пример 1. Пусть сосуд, наполненный жидкостью, движется равноускоренно (или равнозамедленно) в горизонтальном направлении (рис. 1.6). Из теоретической механики известно, что задачу динамики можно рассматривать как задачу статики, если к внешним силам прибавить силы инерции.
Если сосуд движется равноускоренно с ускорением а, то при выбранной системе координат проекции напряжений массовых сил будут
X = a; Y = 0; Z = g.
Уравнение (1.5) после интегрирования примет вид р = pax + pgz + С.
26
Основы гидростатики
Произвольная постоянная С определится из условия, что при х = х0 и z = z0 давление будет р0, т. е.
С = р0— рах0 — pgz0,
следовательно, давление в любой точке жидкости определится по формуле
р — р0 = ра (х — х0) + pg (z — z0), а уравнение поверхностей уровня (р = const) будет иметь вид ра (х — х0) + pg (z — z0) = const.
Если равноускоренное движение с ускорением а направлено
вертикально вниз, то массовые силы, отнесенные к единице массы, будут
Х=У = 0и2 = § — а, а интеграл уравнения (1.5) будет равен р = р (g — a) z + С. , Постоянная определится из условия, что при z = z0 р = р0, т. е.
С = р0— Р (g — a) z0, тогда давление в любой точке жидкости равно
Р = Ро + Р (g— a) (z — z0). (1.15) Уравнение поверхностей уровня будет	j
z = const.
Из сравнения соотношения (1.15) с формулой (1.9) видим, что при таком движении уменьшается суммарное ускорение, а при а = g жидкость будет невесомой.
Очевидно, что, изменив направление движения на обратное, при том же ускорении получим эффект обратный, как бы утяжеление жидкости. Это явление наблюдается при взлете ракеты.
Пример 2. Рассмотрим равновесие жидкости, покоящейся относительно сосуда, равномерно вращающегося вокруг вертикальной оси с угловой скоростью со (рис. 1.7). Тогда проекции сил на оси координат будут
X — со2х, Y = а>2у и Z = —g, а уравнение (1.5) после интегрирования примет вид
Произвольная постоянная определится из условия, что при z — z0 и х = у = 0 р = р0 и С = р0 + yz0.
Давление жидкости на плоские и криволинейные стенки
27
Следовательно, гидростатическое давление равно
Р — Ро =	(*2 + у2) — у (z — z0),
уравнение поверхностей уровня будет
*2 + f/2 = ^ + C-
Это уравнение есть уравнение параболоида вращения.
§ 6. Давление жидкости на плоские и криволинейные стенки
В общем случае на поверхность s, погруженную в жидкость, будет действовать совокупность сил гидростатического давления,
которая в соответствии с законами статики твердого тела может
быть приведена к одной силе, равной главному вектору сил давления,
Р = — j pnds s
и к одной паре с моментом, равным
М = — j (г X pn)ds. S
Найдем величину главного вектора, приложенного к некоторой криволинейной поверхности (рис. 1.8), погруженной в жидкость. Вначале рассмотрим элементарную силу dP, действующую
видно, сила dP будет направлена по нормали к площадке ds и равна
dP — —рп ds.
Проекции этой силы на оси х, у и z представляют собой горизонтальные и вертикальную составляющие, величины которых соответственно равны:
dPx = р cos (n х) ds-, dPy — р cos (п у) ds-,
dPz = p cos (n z) ds,
так как проекции орта нормали на оси координат равны косинусам углов между нормалью и соответствующей осью координат.
28
Основы гидростатики
Из рис. 1.8 видно, что
dsx = ds cos (и x); dsu = ds cos (n y)\ ds2 — ds cos (n z).
Тогда составляющие силы давления, действующей на площадку ds, можно представить в виде:
Рис. 1.9
dPx = р dsx\ dPu = р ds,/, dP2 = р ds2.
Если воспользоваться формулой (1.9) и пренебречь атмосферным давлением, то последние зави-chmqcth примут вид dPx = yz dsx, dPu = yz dsy, dP2 = yz ds2.
Напомним, что индекс у буквы s означает ось, перпендикулярную плоскости, на которую проектируется площадка.
Компоненты сил давления на всю рассматриваемую криволинейную поверхность, погруженную в жидкость, будут равны:
Рх = j yz dsx = у J z dsx-, sx	sx
Pu=^\yzdsu = y\zds/, s</
P2 = у J z ds2 — yU,
(1-16)
где U — объем жидкости, заключенный между рассматриваемой криволинейной поверхностью и поверхностью жидкости.
Таким образом, вертикальная составляющая суммарного давления жидкости на криволинейную стенку равняется массе жидкости в объеме цилиндрической поверхности с вертикальными образующими, ограниченной снизу криволинейной стенкой и сверху поверхностью жидкости.
Горизонтальные составляющие суммарной силы давления на криволинейную стенку, как видно из формул, тоже определяются через массу некоторых объемов.
Давление жидкости, на плоские и криволинейные стенки
29
Главный вектор сил давления на стенку по величине равен
p=Yp2x + p2, + pI
Точка приложения главного вектора, называемая центром давления, определяется для криволинейной стенки довольно сложно.
Найдем главный вектор и центр давления для плоской стенки s, расположенной под некоторым углом к горизонту (рис. 1.9). Для этого проведем плоскость Q, включающую стенку s, до ее пересечения с поверхностью жидкости и расположим две системы координат,-имеющих общее начало в точке 0, так, чтобы плоскость хОу одной системы лежала на поверхности жидкости, а плоскость системы х'Оу' совпадала с плоскостью Q. Если оси у и у' совместим с прямой, образованной от пересечения плоскости Q с поверхностью жидкости, то угол между осями х,и х’ будет равен углу а наклона плоскости стенки. Ось г' будет нормалью к Q и s.
Тогда в соответствии с выражениями (1.16), так как dsx — cos (n х) ds; dsy = cos (n y) ds-, dsz = cos (n z) ds, получим
Px = у j z cos (n x) ds = —у sin a j z ds\ s	s
Py = у j z cos (n y) ds = 0; s
Рг — у j z cos (n z) ds — у cos a j z ds, s
откуда величина главного вектора будет равна Р =	= у f z ds.
S
Последний интеграл равен площади стенки s, умноженной на координату zc центра инерции или центра тяжести этой площадки. Следовательно, окончательно получим
P=yszc.	(1.17)
Так как yzc = рс, то Р — pcs.
Это означает, что сила давления жидкости на плоскую стенку определяется массой столба этой жидкости с площадью основания, равной площади стенки, и высотой от поверхности до центра тяже
30
Основы гидростатики
сти стенки. Из последней формулы следует, что главный вектор сил давления на плоскую стенку по величине равен произведению гидростатического давления в центре тяжести стенки на ее площадь.
Точка приложения главного вектора, называемая * центром давления, в общем случае не совпадающая с центром тяжести, может быть определена на основании законов статики твердого тела. Известно, что момент главного вектора системы сил равен сумме моментов составляющих сил. Если обозначить координаты центра давления хд, уД и гд, то уравнения моментов относительно осей координат будут:
РхД = j рх ds = у j xz ds-, s	s
Руд — \ РУ ds = у yz ds\ s	s
Pz* = | pz ds = у j z2 ds.
s	s
Из системы этих трех уравнений можно найти три неизвестные величины: хд, уЛ и гд. Нетрудно доказать, что центр давления расположен ниже центра тяжести. Если в последнем соотношении заменим р по формуле (1.17) и разделим обе части на у sin2 а, то получим гсгд	г 2г ’
—S— s = -Г-Ъ— ds. sm2a	J sin2a
s
Как известно, интеграл, стоящий в правой части, называется моментом инерции площади относительно оси Оу. Если представить соответствующий момент инерции относительно параллельной этой оси прямой, проходящей через центр тяжести, в виде ф
--^2^- и вспомнить, что момент инерции относительно оси, проходящей через центр инерции, меньше момента инерции относительно любой другой параллельной оси, то можно написать неравенство
ZcS< J z2 dS^Z^ZpS.
Сократив обе части неравенства на zcs, окончательно получим 2д zc-
Закон Архимеда. Плавание тел
31
§ 7. Закон Архимеда. Плавание тел
Закон Архимеда гласит: всякое тело, погруженное в жидкость, теряет в, своем весе столько, сколько весит вытесненная телом жидкость.
Вес тела можно определить как произведение объема тела U на его удельный вес ут, т. е. Gr = yrU, а вес жидкости, вытесненной телом при его полном погружении в жидкость, будет равен произведению объема тела на удельный вес жидкости = yU.
Величина бж направлена в сторону, противоположную силе тяжести, и называется гидростатической подъемной силой, или силой Архимеда. Сила Архимеда приложена к точке, которая является центром тяжести вытесненной телом жидкости. Эта точка называется центром водоизмещения, или центром давления.
Главный вектор сил, действующих на тело, погруженное в жидкость, и отнесенный к единице объема, равен
=	(1-18)
т. е. равен разности удельных весов тела и жидкости, в которую оно погружено.
Таким образом, сила, действующая на тело, погруженное в жидкость, равна
G = Gt-Gk = [/(Vt-7).
Для сферы
С = -|-лго(ут —	—	(1-19)
Очевидно, что если рт>р, то тело будет погружаться в жидкость, пока не достигнет дна. Если рт < р, то тело будет всплывать до тех пор, пока вес тела и вес жидкости, вытесненной погруженной частью тела, не станут одинаковыми. После этого тело будет плавать на поверхности жидкости.
При рт = р тело будет плавать внутри жидкости на любой глубине, т. е. оно может внутри жидкости занимать любое заданное телу положение.
Если плоское тело с плотностью рт <С р положить плоскостью на дно сосуда, заполненного жидкостью, то, несмотря на наличие неравенства рт <С р, тело останется лежать на дне сосуда. Это явное противоречие закону Архимеда объясняется тем, что тело, таким образом помещённое на дьо сосуда, испытывает гидростатическое давление лишь сверху. Снизу это давление на тело не действует, так как жидкость не проникает между дном сосуда и телом. При малейшем наклоне жидкость проникнет между дном и телом, и тело начнет всплывать.
Для многих случаев плавания, например плавания кораблей и подводных лодок, весьма важным является вопрос об устой
32
Основы гидростатики
чивости их равновесия. Условия устойчивости различны для тел, полностью погруженных в жидкость, и для тел, плавающих на поверхности.
Рассмотрим вначале случай полностью погруженного в жидкость тела. Если центр давления (ЦД) находится выше центра тяжести (ЦТ), то при наклоне тела относительно оси, нормальной
Рис. 1.10
плоскости чертежа, как видно на рис. 1.10, а, сила тяжести и гидростатическая сила образуют пару сил, которая будет возвращать тело в исходное положение. При обратном расположении центра тяжести и центра давления наклон тела (рис. 1.10, б) вызовет момент противоположного знака, который будет увели-
чивать угол наклона и, следовательно, поворачивать тело дальше от положения равновесия.
Таким образом, при полностью погруженном теле плавание будет устойчивым всегда, когда центр давления выше центра тяжести. Если
р j н	центр давления ниже центра
тяжести, то равновесие будет неустойчивым.
Для тел, плавающих на поверхности жидкости, условие устойчивости сложнее, чем для полностью погруженных тел, так как при наклоне тела (например, корабля) изменяется форма вытесненного объема и, следовательно, положение центра давления. Из рис. 1.11 видно, что при наклоне корабля вправо в ту же сторону отклоняется центр давления. При положении корабля, показанном на рис. 1.11, а, гидростатическая сила с силой тяжести образуют пару сил, которая будет восстанавливать равновесие; в случае, показанном на рис. 1.11, б, создается пара сил, которая будет увеличивать наклон корабля.
Капиллярные поверхностные силы
33
Если точку М, образованную пересечением средней линии с вертикалью, проходящей при наклоне корабля через центр давления, назовем метацентром, то условия равновесия будут определяться положением метацентра относительно центра тяжести. Когда метацентр выше центра тяжести, плавание тела будет устойчивым. При положении метацентра ниже центра тяжести равновесие будет неустойчивым.
Степень устойчивости (остойчивость) корабля определяется величиной расстояния между центром тяжести и метацентром, называемой метацентрической высотой. Чем больше метацентрическая высота, тем больше остойчивость корабля и тем быстрее он возвращается в положение равновесия, когда выводится из этого состояния внешними силами.
В практике судовождения для улучшения остойчивости часто прибегают к искусственному понижению положения центра тяжести судна. Так, в яхтах применяют тяжелый киль, а все тяжелые грузы на торговых судах никогда не размещают на верхних палубах и т. п.
§ 8. Капиллярные поверхностные силы
Многие процессы в природе и технике определяются наличием капиллярных поверхностных сил. В качестве примера проявления капиллярных сил рассмотрим сообщающиеся сосуды, один из которых представляет собой трубку очень (рис. 1.12). Сосуды А и В соединены резиновой трубкой. Установим конец трубки В на уровне жидкости в сосуде А. При этом, как видно из рис. 1.12, а, поверхность воды в трубке В будет горизонтальной. Если затем осторожно очень немного опускать трубку В, то ее конец станет ниже уровня воды в сосуде А, а поверхность
малого диаметра •<?
Рис. 1.12
воды примет выпуклую сфери-
ческую форму (рис. 1.12, б). Дальнейшее опускание трубки В приведет к увеличению радиуса сферы, образованной жидкостью на конце трубки В.
Очевидно, это явление противоречит закону сообщающихся сосудов, и так как атмосферное давление одинаково для обеих трубок, то для сохранения равновесия необходимо, чтобы на поверхность воды в трубке В действовало некоторое добавочное давление yh. Это добавочное давление, появляющееся на.криво-линейной (в данном случае выпуклой) поверхности жидкости,
вызывается молекулярными силами поверхностного натяжения.
3 И.Л. Понх
34
Основы гидростатики
Опыт показывает, что жидкость стремится уменьшить свою свободную поверхность. Это вызывается тем, что молекулы жидкости, расположенные на границе жидкости и газа, почти не притягиваются молекулами газа и, следовательно, силы, действующие на них со стороны молекул, расположенных внутри жидкости, притягивают их внутрь.. Такая поверхностная капиллярная сила отсутствует на горизонтальной поверхности (рис. 1.12, а). На криволинейных поверхно- _ стях с уменьшением радиуса кривизны поверхности она растет.
Для определенйя поверхностной силы рассмотрим более общий случай. Пусть элемент поверхности жидкости или поверхностей раздела двух жидкостей образует криволинейный прямоугольник со сторонами dlx и dl2 (рис. 1.13). Вследствие разности давлений pY—р2 на рассматриваемую площадку будет действовать сила (рг — р2) dlrdlz, которая должна быть уравновешена поверхностным натяжением.
Величину поверхностного натяжения на единицу длины обычно называют коэффициентом поверхностного натяжения или капиллярной постоянной и обозначают буквой о. Величина о зависит только от природы жидкости и от ее температуры.
Из рис. 1.13 видно, что сила (рх — р2) dl^dl^ будет уравновешена четырьмя составляющими поверхностных сил. Две из них, равные образуют между собой угол dp, а две других, равные adl2, образуют между собой угол da.
Так как углы da и dp очень малы, можно положить da = ^- и dP = -^-.
Al	К3
Тогда равнодействующие сил odl± и adl2 будут равны gdpd/1 = adllDdl2 и <sdadl2= adl'dl* , Rz	2 Ri
а условие равновесия всех сил, приложенных к площадке, будет
Поле скоростей и ускорений
35
Rx и /?., являются радиусами кривизны кривых dlt и dl2 или, точнее, взаимно перпендикулярных кривых, проведенных через центр элементарной площадки d^dl^.
Для цилиндрических поверхностей один из радиусов обращается в бесконечность и рг— Ръ = -^-i\
Для сферических поверхностей, которые имеют место при рассмотрении задачи о мениске воды в трубке (рис. 1.12),	= R2,
тогда
..	< 2а
Л — P2 = yh = ^-.
Заметим, что результирующая поверхностных сил для выпуклой поверхности (рис. 1.12) направлена внутрь жидкости, а для вогнутой поверхности — наоборот и что форма мениска в манометрической трубке будет зависеть от взаимодействия жидкости с трубкой. Если жидкость будет смачивающая (вода в стеклянной трубке), то мениск будет вогнутый и, следовательно, результирующая поверхностных сил будет направлена наружу. При несмачивающей жидкости (ртуть в стеклянной трубке) мениск будет выпуклым и результирующая сила направлена внутрь жидкости.
Если мениск в тонких трубках будет иметь сферическую форму с радиусом сферы, равным радиусу трубки г0, то, очевидно, капиллярные силы будут поднимать столб воды и уменьшать столб ртути в стеклянных’ трубках на величину, равную
Для воды эта величина в зависимости от радиуса трубки будет равна: при г0 = 10 см h = 0,1 мм вод. ст., при r0 = 1 мм h — 10 мм вод. ст. и r0 = 1 мкм h = 1,4-104 мм или 14 м вод. ст.
Для ртути, коэффициент поверхностного натяжения которой й 6,5 раза больше, чем для воды, столб будет опускаться на соответствующие величины, уменьшенные примерно в два раза.
ГЛАВА II
ОСНОВЫ КИНЕМАТИКИ СПЛОШНЫХ СРЕД
§ 1. Поле скоростей и ускорений
Часть механики, в которой рассматриваются общие свойства движения тел без выяснения причин его возникновения, называется кинематикой. В кинематике жидкостей и газов изучается
36
Основы, кинематики сплошных сред
положение частиц жидкости и газа в пространстве в зависимости от времени. По образному выражению Н. Е. Жуковского кинематика есть геометрия движения.
В отличие от теоретической механики, в которой изучается движение абсолютно твердого тела, а также движение отдельной точки или системы точек с фиксированным расстоянием между ними, в кинематике сплошных сред изучается движение деформируемых тел. В процессе движения таких тел изменяется первоначальная их форма и расстояние между двумя любыми частицами. Деформируемость является главной кинематической особенностью сплошных сред вообще и жидкостей и газов в частности.
Рассматриваемые здесь понятия и законы кинематики относятся не только к жидкостям и газам, но и ко всем сплошным или деформируемым средам. Таким образом, кинематика сплошных сред изучает геометрию движения жидких, газообразных и деформируемых твердых тел, имеющих одно общее свойство — сплошность, или непрерывность, среды.
Существует два метода изучения движения частиц. Один из них, называемый методом. Лагранжа, изучает движение в пространстве каждой индивидуальной частицы, другой, называемый методом Эйлера, изучает движение, происходящее в каждой точке пространства в любой момент времени, а поведением отдельных частиц не интересуется.
В первом случае положение каждой частицы будет определяться ее координатами х0, у0 и z0, заданными в некоторый момент времени t = /0. Следовательно, в любой другой момент времени t, не совпадающий с t0, координаты частицы определяются функциями:
х =	(х0, у0, г0, /); у = f2 (х0, у0, z0, /);
. Z = f3 (х0, у0, z0, t).
Аргументы х0, у0, z0 и t называются переменными Лагранжа.
При использовании метода Эйлера все векторные и скалярные элементы движения изучаются как функции от координат и времени, т. е. от четырех аргументов х, у, z и t, называемых переменными Эйлера. Например, скорость частиц будет представлена в виде
V = <Р (*. у&;$.
В общем случае исследования удобнее вести в переменных Эйлера, а в некоторых частных задачах может иметь преимущества метод Лагранжа.
В настоящем курсе метод Лагранжа не применяется; все изучение построено на методе Эйлера.
Будем считать, что все кинематические величины непрерывны в пространстве и времени и дифференцируемы. В отдельных слу
Поле скоростей и ускорений
37
чаях непрерывность некоторых величин может нарушаться, могут появляться поверхности разрыва таких величин, как скорости, ускорения и пр.
Движение сплошной среды характеризуется прежде всего скоростями ее частиц. В каждый момент времени каждая частица имеет определенную по величине и по направлению скорость.
Если поле скоростей остается неизменным во времени, то движение называется стационарным, или установившимся. Если же оно зависихдт времени, то движение будет нестационарным. В некоторых случаях характер движения будет зависеть от выбора системы координат. Так, в координатной системе, связанной с телом, движущимся с постоянной скоростью, обтекание этого тела (поезд, автомобиль и пр.) будет стационарным, в то время как в неподвижной координатной системе (для неподвижного наблюдателя) движение среды, обтекающей тело, будет нестационарным.
В практике часто пользуются понятиями средних скоростей. Обычно усреднение скорости производится либо по времени, либо по площади некоторого сечения потока. Среднее значение величины скорости за промежуток времени /0 представляет собой интеграл
f 1“Н(>
Г=А. J Vit.
Средняя величина скорости по некоторой площади s определяется следующим образом:
S
Вектор ускорения жидкой частицы, движущейся со скоростью V, является индивидуальной производной по времени от
-> dy	.
вектора скорости, т. е. W =
Так как вектор скорости в общем случае зависит от времени и координат, т. е. V = V (х, у, г, /), то по правилу дифференцирования сложной функции найдем
_dV_ = дР_ . dV_ _дх_ ЗУ ду_ _dV_ Зг	ш ..
dt	dt ' дх dt ' ду dt ' дг dt '	* ’ '
Так как производные от координат движущейся точки по времени есть соответствующие проекции скоростей, т. е.
дх	ду	дг
— =и; -£ = v; -Sr=w, dt ’ dt ' dt ’
38
Основы кинематики сплошных сред
получим
dV	dV	,	dV	,	dV	.	dV	/TT o.
-щ-=-з7-+«-5------------h^-5— •	(П.2)
dt	dt	'	dx	'	dy	'	dz	'	7
Используя оператор Гамильтона \7, равный
„ д •* , д -i , д ->
— I Н-Л— 1 ”1-л-
dx 1 dy 1 dz
ускорение жидкой частицы можно представить в виде 4—4-+$-v)v.
Первое слагаемое правой части равенства выражает изменение скорости во времени в некоторой фиксированной точке пространства; т. е. местное изменение, и поэтому называется локальной составляющей ускорения. Второе слагаемое характеризует изменение скорости частицы при ее перемещении и называется конвективной составляющей ускорения.
В проекциях на оси координат х, у, z уравнение (II.2) будет иметь вид
du ди . ди , ди , ди
= -зг + w-з-4-v-=- + w;
dt	dt	'	dx	1	dy	1	dz	’
dv	dv	,	dv	,	dv	,	do
dt	dt	1	dx	1	dy	1	dz	’
dw	dw	.	dw	,	dw	.	dw
-dt=:-dF+u^ + vd^ + wW
При стационарном движении локальное ускорение всегда равно нулю. При нестационарном движении оно может обращаться в нуль лишь тогда, когда в данной точке скорость имеет максимальное или минимальное значение во времени.
Конвективное ускорение может быть при стационарном и нестационарном движениях. Оно обращается в нуль лишь тогда, когда средняя скорость не зависит от координат.
Заметим, что индивидуальная производная по времени может быть взята не только от скорости или других векторных величин,-но и от скалярных величин, таких, как температура, плотность, концентрация и др. Тогда в общем случае индивидуальную производную можно представить в виде
^ = Чг + <У ?>	<п-3>
Например, для температуры она-будет иметь вид dT	дТ .	д¥	,	дТ ,	dT ,	dT
~тг = ~яГ + (tZ-V)T=-57+«-3- + a-5-+®-7r--dt	dt 1	v ' dt	1	dx 1	dy 1	dz
Линия тока и трубка тока
39
§ 2. Линия тока и трубка тока
При изучении векторных полей, встречающихся в механике сплошных сред, пользуются некоторыми характерными линиями и поверхностями. Прежде чем перейти к их определению, рассмотрим некоторые общие понятия, относящиеся к любым векторным полям.
Векторной линией в поле векторов называется линия, в каждой
точке которой в данный момент времени вектор касателен к ней Совокупность векторных линий, проходящих через все точки не
которого контура, образует векторную поверхность. Если контур, через все точки кото
рого проходят векторные линии, замкнутый, то часть пространства, заключенная внутри векторной поверхности, образует векторную трубку.
Исходя из определения векторной линии, нетрудно получить ее уравнение. Так как в каждой точке контура (рис. II. 1) вектор а касателен к контуру, то, следовательно, вектор а и элементарный вектор dr совпадают по направлению и их векторное произведение равно нулю
а X dr — 0.
Из условия равенства нулю проекций этого векторного произведения следует, что
dx ___ dy __________ dz .	(11 4)
ax(x, у, г) аИ(х, у, г) аг(х, у, г) ‘	V '
Приведенные понятия можно применить к любым векторным полям. Применительно к наиболее распространенному в гидромеханике векторному полю — полю скоростей — векторная линия называется линией тока, а векторная трубка — трубкой тока (рис. II.2).
Очевидно, уравнение линии тока будет
=	(II.5)
40
Основы кинематики сплошных сред
Если рассматривать движение жидкой частицы во времени, то линия, по которой двигалась частица в некоторый промежуток времени, называется траекторией. Для стационарного движения линия тока и траектория совпадают, при нестационарном движении они отличаются друг от друга.
Как следует из определения, линия тока есть линия, в каждой точке которой нормальная составляющая скорости равна нулю, т. е. через линию тока нет перетекания. Таким образом, между двумя произвольными линиями тока количество протекающей жидкости постоянно. Поэтому для несжимаемой жидкости в местах, где линии тока сближаются, величина скорости увеличивается и, наоборот, там, где они расхо-' дятся, скорости убывают.
Если через поверхность обтекаемого тела жидкость не про-
А'
Источник	Сток
Рис. П.З
Рис. II.4
текает, то эта поверхность есть поверхность тока. Для плоского обтекания (рис. П.З) это будет линия тока, которая в отличие от других называется нулевой линией тока.
В общем случае через любую точку движущейся среды в данный момент времени можно провести лишь одну линию тока, но существуют некоторые особые точки, в которых это правило нарушается. В особых точках линии тока пересекаются, следовательно, в этих точках вектор скорости должен иметь разные направления, что при конечном значении скорости невозможно. Поэтому в особых точках величина скорости должна быть равна либо нулю либо бесконечности.
При обтекании тела нулевая линия тока, образующая непроницаемый контур, имеет особые точки А и А' (рис. П.З). В этих точках, называемых критическими, величина скорости равна нулю.
Особая точка другого типа получается при рассмотрении задачи о вытекании среды из одной точки или, наоборот, при ее втекании в точку (рис. II.4). Первое движение будем называть точечным источником, а второе — стоком. В обоих случаях в точках пересечения линий тока величина скорости обращается в бесконечность.
Так как трубка тока образована совокупностью линий тока, то очевидно, что количество вещества, протекающего в любом сечении трубки, будет одним и тем же.
Градиент скалярной функции. Расхождение и циркуляция вектора 41
Далее рассмотрим понятие о потоке вектора скорости. В векторном анализе потоком любого вектора через поверхность называется интеграл по этой поверхности от проекции вектора на нормаль п в каждой точке, т. е.
j ап ds = j (a-ri) ds — j (ax dy dz + dx dz + az dx dy). (II.6) 3	3	s
В соответствии с этим поток вектора скорости через поверхность s есть скалярная величина, равная
Q — j Vn ds = j (V-ri) ds = j (u dy dz +’v dx dz + w dx dy). 3	8	3
Поток вектора скорости физически представляет собой секундный объемный, расход некоторой жидкости (среды) через поверхность s. Размерность потока вектора скорости будет
[<21 = (И [s] = 4 
Если поверхность s замкнута, то при отсутствии внутри поверхности источников и стоков поток вектора скорости через замкнутую поверхность будет равен нулю
J Vn ds = 0. 5
При наличии источника
J Vn ds > 0,
S
а при наличии стока
J Vn ds < 0.
§ 3. Градиент скалярной функции. Расхождение и циркуляция вектора скорости
Напомним некоторые операции векторного анализа, используемые в гидромеханике.
Из векторной алгебры известно, что скалярное произведение ортов будет
i • i = j j' = k • k = 1;
i’• j = j • i = i• k — k-i = j -k = k • ) .= 0,
42
Основы кинематики сплошных сред
а их векторное произведение равно
i х = J х j = k X k = 0;
i X j = k; j x £ = i; k x i = /;
j X i = —k; k x j — —i; i X k = —j,
поэтому, воспользовавшись оператором yz', чисто формально по
лучим следующие известные из векторного анализа формулы.
1. Действие оператора на скалярную функцию ср, равное
=	grad ср, (II.7)
определяет градиент скалярной функции-, grad ср есть вектор, который обладает, как будет показано далее, некоторыми особенностями и называется потенциальным вектором.
Для определения физического смысла величины вектора рассмотрим поле любой скалярной величины, встречающееся в механике (температура, плотность, давление и пр.). В скалярном поле характерными ли
ниями, определяющими поле, являются ли-
нии равных значений рассматриваемой величины. Для температуры — это изотермы, для давлений — изобары, для проекций скоростей — изотахи и т. д.
На рис. II.5 приведены изотахи для расходных составляющих скоростей в выходном сечении патрубка турбины. <•
В непрерывном поле скалярной величины через любую точку пространства можно провести^линию постоянного значения этой скалярной величины. При этом в каждой точке скалярного поля значение производной от рассматриваемой величины будет зависеть от выбора направления. По направлениям касательных к ли-
ниям постоянного значения производные равны нулю, а по нормали к этой линии производные будут иметь наибольшие значения. Градиент скалярной функции есть вектор, направленный по нормали к линии постоянного значения скалярной функции в сторону увеличения этой функции и равный по величине производной по направлению указанной нормали.
Градиенты скалярного поля составляют векторное поле.
Градиент скалярной функции. Расхождение и циркуляция вектора 43
2. Скалярное произведение оператора v на вектор а
v “ =	+ aJ'^=
дах дх
. да„ . да, ,. * +	+ № = diva
1 ду 1 dz
(II.8)
есть величина скалярная и называется дивергенцией или расхождением вектора.
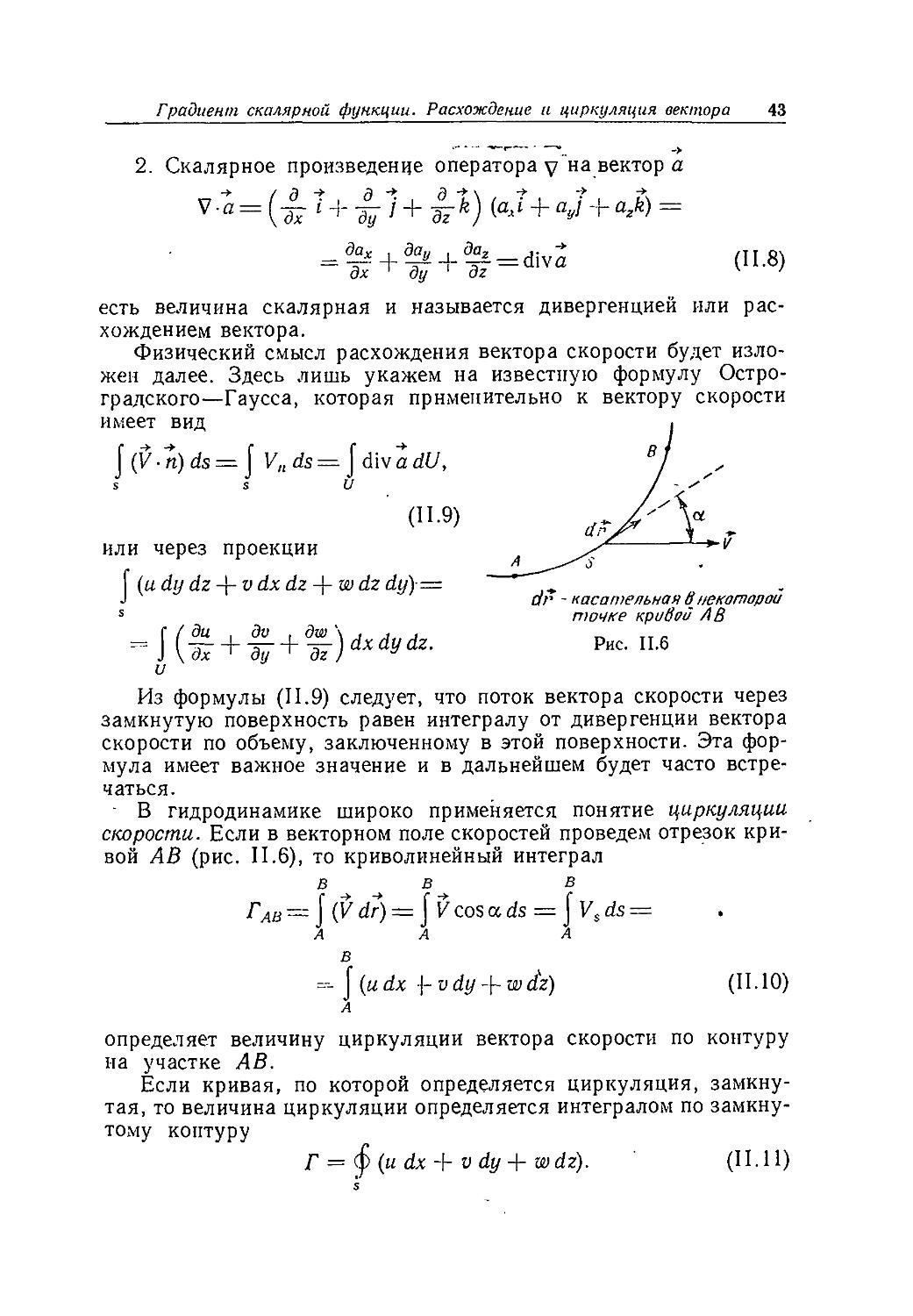
Физический смысл расхождения вектора скорости будет изложен далее. Здесь лишь укажем на известную формулу Остроградского—Гаусса, которая применительно к вектору скорости имеет вид
J (7 • п) ds = J Vn ds = J div a dU, s	st/
•9) или через проекции
I (и dy dz 4- v dx dz -j- w dz dy)•==
J	dr - касательная в некоторой
s	точке кривой AB
Из формулы (II.9) следует, что поток вектора скорости через замкнутую поверхность равен интегралу от дивергенции вектора скорости по объему, заключенному в этой поверхности. Эта формула имеет важное значение и в дальнейшем будет часто встречаться.
 В гидродинамике широко применяется понятие циркуляции скорости. Если в векторном поле скоростей проведем отрезок кривой АВ (рис. II.6), то криволинейный интеграл
в	в	в
ГАВ — j (Г dr) = j V cos a ds = j Vs ds =
A	A	A
В
=-- j (« dx \-vdy-)~wdz)	(II. 10)
A
определяет величину циркуляции вектора скорости по контуру на участке АВ.
Если кривая, по которой определяется циркуляция, замкнутая, то величина циркуляции определяется интегралом по замкнутому контуру
Г = (и dx -f- v dy + wdz).	(11.11)
44
Основы кинематики сплошных сред
§ 4.	Вихрь вектора скорости
Векторное произведение оператора V на вектор а
(V ха] = [(^Л-|-^/ + ^4) X (aJ+aJ+a2fe)] =
= (д^ _ да^\ 1	_ да^Х - fda^ _ да*\	- j J2)
\ ду dz J \ dz дх / 1	\ дх ду /	'
есть величина векторная и называется она вихрем или ротором вектора.
Заметим, что скалярное произведение оператора V на V
V7V7 /д'?’,	д	.	д ?\	/ д ? . д .	д t\
V • V — I “z I "	д	/ _ _	— k )	( “х i -I— -z— 1 -I- "ч k ) —
\ dx	dy	dz /	\dx 1 dy J	dz )
— 32 I d2 ,	_ V2 _ Л
dx1 "i dy- "T” dz2
есть оператор Лапласа. Применяя этот оператор к скалярной функции, получим
V • V<p = div grad ср = V2<p =+ ^ + •
Для всякого поля справедливы следующие правила
rot grad ср = v X v<P = О	(11.14)
и
div rot а = V • (V X а) = 0.	(11.15)
Очевидно, что первое выражение обращается в нуль потому, что векторное произведение параллельных векторов у и УФ равно нулю, а второе—потому, что здесь имеет место скалярное произведение взаимно перпендикулярных векторов
V и [у х а].
Рассмотрим физический смысл вихря вектора скорости. Из определения (И. 12) следует, что
rot V =	+	(11.16)
\ ду dz /	1 \ dz dx / ' 1 \ дх ду) v '
Напомним уже известное понятие вращения твердого тела. Пусть некоторое тело вращается с угловой скоростью <oz вокруг оси z (рис. II.7). Величина скорости точки тела М будет равна V — <огг, а ее проекции на оси х и у соответственно
и — —<огу, v = ®гх; к> = 0.
Вихрь вектора -скорости
45
~	ди dv
Определив значения и , получим
, Л dv	ди п
rot, V = -5----5- — 2<о,,
2 дх.	ду 2
т. е. -у rot2 V = ®2.
Если аналогичным образом рассмотрим вращение твердого
Рис. II.7
Физически неравенство нулю
значения rot V в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема.
Иногда вихревое движение отождествляют с турбулентным. Это разные понятия. Вихревое движение может быть и ламинарным, и турбулентным, а ламинарное и турбулентное (осредненное) движения в свою очередь могут быть как'вихревыми, так и безвихревыми.
->
Особое значение имеет безвихревое течение, когда rot. V = 0. При этом, как следует из формулы (11.16), должно выполняться условие
dw	dv	ди	dw	dv	ди	q
ду	dz	dz	дх	дх	ду ’
что возможно, если существует функция <р (х, у, z), удовлетворяющая условиям:
дФ	Э<р	Эф
= Щ — V, — W. дх	ду	дг
Действительно, при этом ди dw  Э2ф Эгф _________________________q
дг дх дх дг дхдг
46
Основы кинематики сплошных сред
Такое течение называют потенциальным. При этом, согласно формуле (П.7), вектор скорости можно представить в виде
V = ui-\-vj-Ywk=	-5-fe = grad<p...	(11.18)
Функцию ср называют потенциалом вектора скорости.
Очевидно, что если вектор скорости имеет потенциал, то в соответствии с формулами (11.18) и (II. 14) будем иметь
rot V = rot grad <p = 0.	(11.19)
Легко видеть, что при наличии потенциала скоростей в векторном поле циркуляция скорости на участке Л В (см. рис. II.6) определяется разностью значений потенциала скоростей в точках Л и В. Действительно, учитывая выражения (11.18), получим
j (и dxv dyw dz) — J -^-dx-j-^dy + ^dz =
А	А	У
В
= jdq> = cpB —Фд. A
§ 5. Основная теорема кинематики (первая теорема Гельмгольца)
Из теоретической механики известно, что скорость любой точки М твердого тела определяется геометрической суммой скорости поступательного движения вместе с некоторым полюсом О и скорости вращения вокруг мгновенной оси, проходящей через полюс О,
^1 = Vo + (® X Го),	’	(П.20)
где со — угловая скорость вращения; г0 — радиус-вектор точки М.
Аналогичная теорема, являясь основной теоремой кинематики, имеет место и для скоростей движения элементарных жидких объемов. Она гласит: скорость движения V любой точки жидкой частицы складывается из скорости квазитвердого движения и скорости деформации Уд,
Скорость квазитвердого движения, как следует из формулы (11.20), в свою очередь, складывается из поступательной скорости и скорости вращения.
Основная теорема"кинематики (первая теорема Гельмгольца)
47
Для доказательства этой теоремы определим в данный момент времени поле скоростей в окрестности точки Мй (рис. II.8). Пусть в точке Мо с координатами х0, уй и z0 скорости будут иметь значения и0, v0 и ау0.
Используя разложение в ряд Тейлора, можно найти значение скоростей и в точке М (х, у, г), расположенной в окрестности точки УИ0. С точностью до малых первого порядка они будут равны:
(П-21)
где Xi = х — х0, У1 = у — у0, Zi = г —г0 Прибавляя и вычитая в первом уравне нии (П.21) величину
<и-22>
получим
. ( ди	\	.	1	( ди .	ди \ .	.
U — Ил *4“ (	-л-5"	( “ч— -]	— | Цл -г-
° 1 \ дх jo	11	2	\ ду 1	дх /о
1 ( ди dw \	,
+ Т Ьт+аГЛ21^
^ 2 [дг дх Jo 1	2 \ с
Для дальнейших преобразований воспользуемся уравнением (П.17) и введем следующие обозначения:
( ди \	• ( до \	• ( dw \	•
\ ~дх)о — S11 \~ду/о ~ Si2 ч дг )в “ 33’
1 / ди . до \		•
Т \ а7 + дх )о Sl2 ~ Sn’
.4-0+^).=’»=^
4('£'+w)0=®2з=%-
Тогда уравнение (11.22) будет
« = «о + (0)у?1 — 0>гУ1) + (S11X1 + Я21У1 + SjjlZj), (11.23)
48
Основы кинематики сплошных сред
а остальные два уравнения (II.21) после аналогичных преобразований примут вид:
V = v0 + (®2Х! — cOxZj) + (s12xx +	+ SgaZj);
w = w0+ (®ЛУ! — ©^xj + (s13X! + s23J/! + s33Zj).
Первые два слагаемых правой части полученных уравнений можно рассматривать как скорости квазитвердого движения, третьи слагаемые являются скоростями деформации элементарного объема.
Так как, согласно рис. II.8,
г = xj + у J + Zjk, то
©^Zj — югг/! = (® х г)А.; (ozx1 — ©,(Zi = (® X г)у,
ЫхУ! — ^хх = (® X r)2.	(11.24)
Для характеристики скорости деформации введем функцию F, равную
F = -у (*пх1 'I- w'i + 4з2!) + ^12х1^14- s’i3xizi -l- yw
аг •	, •	, •
— SjiXj -j- S12z/j — S^Zp
ar •	. 	. •
— S^Xj^ S32l/1 + SogZj,
(11.25)
— SjgXj -|-	SgijZp
Используя выражения (11.24) и (11.25), окончательно получим:
. л , аг . ,•* •* . аг
и = w0 + (© х r)x +	; V = и0 4- (® х г)у +
-*	-> QP
w = w0 -Н (© X Г)г + 57 >
или в векторном виде
У = Vo + (“ X г) + grad F, -> -> -> где ]/0 — скорость поступательного движения; (® X г)—скорость вращательного движения вокруг мгновенной оси с угловой скоростью w; grad F — скорость чистой деформации.
Кубичеасое расширение
49
Скорость деформации жидкой частицы в точке М можно записать в следующей матричной форме:
S11	S21	S31 S12	s22	S32	= s	(11.26)
S13	S23	S33		
Матрица s называется тензором скоростей деформации, a s,7 — компонентами или составляющими тензора скоростей деформации.
Компоненты тензора скоростей деформации (II.26) можно представить в виде
где i и j принимают значения 1, 2, 3.
Такое представление компонентов тензора скоростей деформации нам понадобится при установлении их связи с тензором напряжений.
Покажем далее, что диагональные компоненты тензора s,7 характеризуют скорости относительного удлинения (сжатия) жидких отрезков, недиагональные компоненты sif —скорости перекосов элементарного объема, а сумма sxl + s22 + s33 —относительное изменение объема в единицу времени.
§ 6. Кубическое расширение
Если объем U сферической частицы радиуса R через бесконечно малый промежуток времени изменится и станет равным U то форма частицы либо останется сферической с радиусом либо, в общем случае, превратится в трехосный эллипсоид с полуосями а, b и с.
Величина полуосей будет равна:
а = Я(1 + *Л); 6=Р(1 +^<U\,
С = й(1+^Л).
Тогда относительное изменение радиуса по направлению оси х определится из соотношения
а — R _ ди
Rdt ~~дх ~ S1V
По осям у и z соответственно:
Ь — R   ди • _ с — R dw
Rdt ~~ду ~ $22 И Rdt ~~дг ~ S')3'
4 И. Л. Пов
50
Основы кинематики сплошных, сред
Если частица осталась сферической, то а = b = с = R, и соответственно
' _ ' • 1 R
S11 — S22 — S33 —	•
Очевидно, что относительное изменение элементарного объема в единицу времени будет равно
4	4
,, г, -тгЛаЬс------5-лй3	,
Uj^ = —= div 7. (11.28)
Udt	^R*dt дх ' ду ' дг
О
Таким образом, каждая диагональная составляющая тензора скоростей деформации характеризует скорость.относительного изменения длины отрезка, а их сумма — скорость относительного изменения элементарного объема жидкости, выражаемую через расхождение вектора скорости.
§ 7. Скорость деформации сдвига
Для характеристики компонентов тензора скоростей деформации s23, s12 и s13 рассмотрим детально один из них, например s12. Эта величина характеризует скорость деформации сдвига жидкой частицы в плоскости ху.
Рис. II.9
Пусть в некоторый момент времени жидкая частица будет иметь в плоскости ху форму квадрата со сторонами dx и dy (рис. II.9, а).	•	'
Так как скорости в вершинах квадрата будут неодинаковы, то через единицу времени рассматриваемый квадрат примет форму параллелограмма (рис. II.9, б). При этом угол сдвига между осью у и стороной О'С будет равен
, ди
Вихревая линия и вихревая трубка. Теоремы о вихрях
51
а угол между осью х и стороной О' А' соответственно
. Sv
y2^tgV2 = ^.
Так как мы рассмотрели изменение прямого угла СОА за единицу времени, то у = будет характеризовать скорость изменения первоначального угла СОА. Следовательно,
1 / ди . dv \
V ~~2 \'ду"^~дх) ~ S12’
т. е. s12 характеризует скорость деформации скоса угла или сдвига в плоскости ху.
Аналогичным образом можно показать, что s23 и s13 характеризуют скорости деформации сдвига в плоскостях yz и xz.
§ 8. Вихревая линия и вихревая трубка.
Теоремы о вихрях
Вихри скоростей образуют векторное поле, в котором могут быть найдены векторные линии и векторные трубки.
Линия, в каждой точке которой вихри вектора скорости или вектора угловых скоростей вращения частиц касательны к ней, называется вихревой линией.
Уравнение вихревых линий, как следует из выражения (II.4), будет
dx _ dy __ dz
шх ~	~	"
Если в пространстве, заполненном вихрями, взять некоторый замкнутый контур (не являющийся вихревой линией) и через каждую точку этого контура провести вихревые линии, то образуется вихревая поверхность. Часть жидкости, ограниченная этой поверхностью, называется вихревой трубкой. Когда замкнутый контур бесконечно мал, вихревая трубка называется элементарной.
Из определения вихревой линии и вихревой поверхности следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.
Следовательно, если ввести понятие о потоке вектора вихря скорости, равном по формуле (II.6)
j rot„ V ds, s
то поток вектора вихря скорости через вихревую поверхность будет равен нулю.
Из векторного анализа известно, что поток любого вектора через любую замкнутую поверхность, внутри которой нет особенностей, равен нулю. Из этой теоремы векторного анализа вытекает, 4*
52
Основы кинематики сплошных сред
что и поток вихря сквозь любую замкнутую поверхность тоже равен нулю
J rot„ V ds = 0.	(11.29)
Выделим в вихревой трубке (рис. 11.10) некоторую замкнутую поверхность, образованную двумя любыми поперечными сече-
ниями Sj и s2 и боковой поверхностью s6.
Так как поток вихря по боковой поверхности равен нулю, то, согласно формуле (11.29), j rot„ V ds — | rotn V ds2.
st	s2
Из полученного равенства вытекает следующее свойство вихревых трубок, известное в кинематике как вторая теорема Гельмгольца: поток вектора вихря скорости сквозь произольно проведенное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки.
Из этой теоремы следует, что поток вихря есть величина, характерная для всей вихревой трубки. Поэтому поток вихря принимают за характеристику вихревой трубки и называют интенсивностью вихревой трубки,
i — J rot„ V ds. s
Иногда интенсивность вихревой трубки выражают через угловую скорость со следующим образом:
i = J rot„ V ds = 2 j co„ ds. s	s
Если величина вихря постоянна по поперечному сечению вихревой трубки, то вторую теорему Гельмгольца можно записать в виде
Sj(Oni 52СОЛ2 $i®ni COnst.
Из этой теоремы вытекают очень важные следствия:
1) сечение вихревой трубки нигде не может стать равным нулю, так как в этом случае скорость вращения частиц должна стать бесконечно большой, что физически невозможно;
2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца (рис. П.П), либо «опираются» на стенку или на свободную поверхность.
К последнему типу вихрей принадлежат наблюдаемые в природе водяные и воздушные смерчи. Прибор, иллюстрирующий об
Вихревая линия и вихревая трубка. Теоремы о вихрях
53
разование вихря, показан на рис. 11.12. Вращение шкива, имеющего несколько радиальных перегородок, закручивает воздух. В области разрежения, создаваемого воздушным вихрем, вода поднимается и образует искусственный смерч.
В дальнейшем (см. гл. IV, п. 6) будет показано, что в идеальной жидкости при наличии массовых сил, обладающих однознач
ным потенциалом, интенсивность вихря не меняется со временем. Таким образом, вихри идеальной жидкости не могут менять в пространстве и во времени своей
Рис. Н.п
интенсивности. Они должны существовать вечно, они пе могут возникать и вырождаться.
В действительности в реальной жидкости из-за наличия вязкости вихри зарождаются и затем диффундируют, т. е. вырождаются.
Второй важной кинематической теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, один раз опоясывающему вихревую трубку. Докажем эту теорему для более общего случая с такой формулировкой: поток вектора вихря скорости через любую поверхность, опирающуюся на некоторый замкнутый контур, равен циркуляции скорости по этому контуру.
Вначале определим величину циркуляции скорости по некоторому бесконечно малому контуру, который находится в движущейся жидкости, имеющей непрерывно распределенные вихри. Пусть контур ОСВАО (рис. II.9, а) лежит в плоскости ху и имеет стороны dx и dy. Если в точке О проекции скоростей будут и и v, то в точках С и А величины скоростей, совпадающих по направлению со сторонами СВ и АВ, равны соответственно:
(u)c = u-l--^ dy; (и)л = v + dx.
54
Основы кинематики сплошных сред
Тогда циркуляция по контуру ОСВАО будет равна ЛГосвао = vdy -J-	dy) dx— (^ + 77 dx) dy — u dx,
или, раскрывая скобки и производя сокращение, получим drOCi3Ao —	~ 77) dx dy = г<Лг V dxdy.
Так как rot, У является проекцией вихря на ось z, нормальную к площадке dx dy, то правая часть последнего равенства является
ные вычисления для площадок dx dz и dy dz и распространив эти результаты на элементарную площадку ds, произвольно расположенную в пространстве, получим
df — rot„ V ds.
(11.30)
Соотношение (11.30) означает, что циркуляция по бесконечно малому прямоугольному контуру равна потоку вихря через площадку, ограниченную этим контуром, или интенсивности элементарной вихревой трубки.
Если теперь возьмем произвольный плоский контур с любой конечной площадью, то, разбив (как это показано на рис. 11.13) всю площадь на элементарные прямоугольники и вычислив циркуляцию по контурам этих прямоугольников, в результате суммирования по всей площади получим циркуляцию вдоль всего контура, равную
Г = j rot„ V ds. s
Полученную формулу можно применить не только для плоской площадки, а и для некоторой произвольной поверхности (рис. 11.14). Разбив эту поверхность на бесконечно большое коли
Вихревая линия и вихревая трубка. Теоремы о вихрях
55
чество бесконечно малых площадок cis, получим величину циркуляции для каждой площадки (считая ее плоской), равную
dr — rot,, V ds.
Суммируя циркуляции по элементарным площадкам, получим циркуляцию по поверхности
Г = J rot,, V ds.	(11.31)
s
Таким образом, теорему Стокса можно считать доказанной для произвольного контура, а следовательно, и для контура, опоясывающего вихревую трубку.
• Формула (11.31) после подстановки в нее выражения-для циркуляции (11.10) будет иметь вид
г-Ji?*.
Заменив вектор скорости на некоторый вектор а, получим известную из векторного анализа формулу Стокса, связывающую интеграл по контуру с интегралом по поверхности, опирающейся на этот контур,
Ja-dr = j roin a ds,	(11.32)
L	s
где
a-dr — at dl.
При дальнейшем изучении механики жидкостей и газов будет применяться известная в математике формула Остроградского— Гаусса, связывающая интеграл по замкнутой поверхности sc интегралом по заключенному в ней объему U. Напомним, что в векторной форме эта формула имеет вид
J а-п ds = j ап ds = j div a dU,	(11.33)
s	s	U	*
а в проекциях
J (ax dy dz ay dx dz -J- az dx dy) == s
= f	dU.	(11.34)
J \ dx 1 dy 1 dz )	v '
Используя формулу (11.33) для вектора скорости, получим важное в гидромеханике соотношение
jv„ds= f divVdt/,	(11.35)
56
Основы кинематики сплошных сред
говорящее о том, что поток вектора скорости через замкнутую поверхность равен расхождению вектора скорости в объеме, заключенном в этой поверхности.
§ 9. Поле скоростей, вызванное вихрями. Формула Био—Савара
Для нахождения поля скоростей при .пространственном обте-каппи тел, наряду с методом особенностей (применение источников, стоков и диполей), широко пользуются полями скоростей, созда-. ваёмыми вихревыми линиями.
Рис. II.15 нормальной оси вихря (рис.
Изучим поле скоростей, вызываемых или индуцируемых вихревыми линиями.
Наиболее простой является задача об индуцировании скоростей прямолинейным вихрем. Величина циркуляции скорости Г, индуцируемой прямолинейным вихрем в плоскости, 11.15), будет
Г = (|) V ds = V (f ds = 2лг V. S	S
Отсюда скорость V, индуцируемая вихрем, равна
‘'“i	(11.36)
и направлена по касательной к окружности радиуса г.
Рассмотрим наиболее общий случай. Пусть в некотором ограниченном пространстве U в каждой точке имеются вихри с компонентами rotx V — 2<£>х, roty V = 2<£>у и rotz V = 2гог, зависящими от координат х, у и г (сох, и coz — угловые скорости вращения частиц). Необходимо найти в каждой точке этого объема скорость или проекции скоростей и, v и w, индуцируемые зтими вихрями.
Компоненты угловых скоростей, как известно из формулы (11.17), выражаются через компоненты скоростей
_ 1 / дш до \ .	__ 1 / ди dw \	__ 1 / до ди \
х "Г ^,17 — J “ Т klz “ ~дх ) ’ ®г —	'ду)'
Ранее было показано [см. выражение (11.15)], что расхождение вихря равно нулю
div rot V = 0.
(11.37)
Поле скоростей, вызванное вихрями. Формула Био—Саеара	57
Обычно для нахождения поля скоростей вводят вспомогательный вектор а с проекциями ах, ау и аг, который относительно скоростей и, v, w имеет такое же значение, как скорости относительно проекций угловых скоростей сол., wr/ и сог. Это условие можно записать в векторном виде 1/ = rot а и в проекциях:
	даг	дау
и —	ду 	дг
	дах	даг
V —	дг	дх
—	дау	dav
	дх	ду
(11.38)
Будем считать, что расхождение введенного вектора а, называемого векторным потенциалом, равно нулю, т. е.
div а =	= 0.	(11.39)
дх ' ду ' Ог	'	7
Подставив значение вектора скорости, выраженного через векторный потенциал по (11.38), в (11.17), получим в векторном виде га = -^- rot rot V.
Проекция сох будет
•	1 / дю	до \
л 2 \ ду	дг J
Проделав аналогичные операции с остальными компонентами и имея в виду выражение (II.39), получим три уравнения с тремя неизвестными ах, ау и аг:
д'2ах _j_	д*ах	д*ах _	„	.
дх* 1	ду*	дг* ~	х’
д*аи	д*аи	д*а„
+ ТГ +	= — 2®„;
дх2 1 ду2 1 дг1	и
д2аг . д2аг d2az о дх* + ду* + дг* — — 2®г-
58
Основы кинематики сплошных сред
Приведенные дифференциальные уравнения в частных производных известны в математике как уравнения Пуассона. Решения этих уравнений имеют вид:
1 f dU
ах — -7J—	—
х 2л .1 х г
и
1. f аи
аи
и
г dU
(П.40)
и
При этом интеграл берется по всему объему U, заполненному вихрями. Вне области, занятой вихрями, <о = 0 и уравнения Пуассона становятся уравнениями Лапласа.
Таким образом, задачу можно считать решенной. По заданным соА (х, у, z), (йу (х, у, z) и <в2 (х, у, z) находим с помощью выражения (II.40) ах (х, у, z), а~{х, у, z) и аг (х, у, г), затем по соотношению (II.38) определяем и, v и w.
Применим этот метод к нахождению поля скоростей, индуцируемого произвольным вихревым, шнуром. В случае когда в рассматриваемом неподвижном пространстве имеется вихревой шнур, объем U будет равен площади поперечного сечения s шнура, умноженной на его длину. Следовательно, как видно из рис. 11.16, а, dU = s dL.
Составляющие вектора вихря скорости, стоящие под интегралом в выражения (П.40), можно представить в виде сох = ю cos (юх) = ю ;
Поле скоростей, вызванное вихрями. Формула Био—Савара
59
= со cos (сос/) = со ;
сог = со cos (coz) = со ,
где т| и £ — координаты точек вихревого шнура (в отличие от координат х, у и z вне вихревого шнура).
Имея в виду, что cos = Г, получим выражения (11.40) для
рассматриваемого случая в виде:
х 4л J г
L
Г f dr)	Г f dt
аи = -г- — и аг=-т— —.
Ч 4л J г г 4п J г
L	L
Для определения поля скоростей подставим найденные значения в выражения (11.38). Тогда для проекции скорости на ось х получим
L
Произведя аналогичные подстановки для других проекций и имея в виду, что расстояние между точкой вне вихря с координатами х, у и z и точкой вихревого шнура с координатами г| и £ (рис. 11.16, а) будет равно
г = V (х— ?)2 + (У — < + (z — С)2.
получим подынтегральные выражения:
jLf-LX— *. dr \ г J г3 ’
jL/JA — Ус и д f 1 \ _ гг ду \ г )	г3- dz \ г ) г* ’
где Xj = § — х; уi = f\ — у, zr — С — z — проекции радиус-вектора г на оси х, у и z.	*
60
Основы кинематики сплошных сред
Окончательно поле скоростей, индуцируемое вихревым шнуром, определится выражениями:
L	У1 Г	d'Q dL	zt dr) r dL /	dL	
L	Z1 r	dt, dL	r dL )	dL . r2 ’	(11.41)
L	r	dr\ dL	r dL /	1^-	
Отложив на направлении радиус-вектора г единичный вектор е (рис. 11.16, а), запишем его выражение в виде
Единичный вектор т на направлении касательной будет
Из формулы видно, что подынтегральные выражения в скобках будут соответствующими проекциями векторного произведения ортов т и е.
Следовательно, подставив в выражения (И.41) соответствующие проекции ортов, окончательно получим дифференциал вектора скорости, индуцируемой вихревым шнуром,
.Л Г * dL
= it [т х ’
или р
dV =-т—j-sinadL,
где а — угол между радиус-вектором г и касательной.
Полученное выражение называется формулой Био—Савара. Впервые она применялась для определения магнитного поля, возникающего вокруг электрического проводника.
Рассмотрим поле скоростей, вызываемых вихревой нитью с постоянной циркуляцией Г в точке М (рис. 11.16, б).
Если 1г — кратчайшее расстояние от точки М до вихревой нити АВ, то
г = —^-—ц dL = — d (h ctga) = h d(X2 , sin a	vs/ sin2a
Поле скоростей, вызванное вихрями. Формула Био—Савара
61
и формула Био—Савара примет вид
Г sina-sin2a hda	Г	.	,
dv = --------rj---,  sin а  da.
4л Л2	sin2a	4nh
Интегрирование по длине отрезка АВ дает значение V в виде «-₽
Г г	Г
V = -^—г sin a-da = -r-tr (cos0 -I- cos В).
4nh J	4n/i v 1
0
Для вихревой нити бесконечной длины
0 = Р = О; cos0 = cosB=l и У = -^-. г	1	2nd
Для вихревого луча, исходящего вверх или вниз от точки М,
₽=А и 0 = 0
и
V =	(11.42)
4n/i	v 2
Аналогичным методом можно получить поле скоростей при любых других размещениях вихрей в пространстве, например для круговой вихревой нити, вихревого слоя и пр.
ГЛАВА III
ОБЩИЕ УРАВНЕНИЯ ДЛЯ СПЛОШНЫХ СРЕД, ЖИДКОСТЕЙ И ГАЗОВ
Естественно, что на движение сплошных сред распространяются общие законы механики. Среди этих законов особенно важное и наиболее общее значение имеют законы сохранейия.
Наиболее общими законами сохранения, пригодными как в классической физике, так и в физике микро- и макромира, а следовательно, в квантовой механике и теории .относительности являются законы сохранения следующих .величин: энергии, количества движения или импульса и момента количества движения или момента импульса.
В классической физике, где обычно рассматриваются движения лишь со скоростями, значительно меньшими, чем скорость света, считается, что сохраняется также и величина массы вещества.
Применение законов сохранения массы, импульса, момента импульса и энергии к движущимся жидкостям и газам дает систему основных уравнений механики жидкостей и газов.
62	Общие уравнения для сплошных сред, жидкостей и газов
Законы сохранения, записанные для конечных произвольных объемов, составляют систему общих уравнений или общих теорем.
Использование законов сохранения для бесконечно малых объемов приводит к получению системы основных дифференциальных уравнений механики сплошных сред.
При выводе основных уравнений законы сохранения могут применяться как для изолированных, так и для неизолированных объемов.
Изолированными объемами называются объемы, не взаимодействующие с внешней средой, т. е. через их поверхность не происходит переноса вещества, импульса и энергии.
§ 1. Закон сохранения массы. Уравнение неразрывности
Закон сохранения массы для изолированной системы выражается в том, что масса т такой системы остается постоянной во все время движения. Следо-( х.	вательно, полная производная от
____L---- Ч-------------- массы по времени равна нулю
V ------/---- \------------*	dm п
\.	/	Если система не изолирована
х----'	и имеет постоянный по величине
' Рис. III. 1	объем V, то через ее поверхность
будет входить или выходить жидкость. Изменение массы этого объема в единицу времени будет равно
Am = f ^-dU,
J dt ’ и
Эр
где ----изменение плотности в единицу времени в единице
объема.
Для получения уравнения неразрывности движения, которое является выражением закона сохранения массы, рассмотрим/поток вектора рУ сквозь некоторую неподвижную замкнутую поверхность s произвольной формы (рис. III. 1) постоянного объема U.
Если количество втекающей жидкости не будет равно, количеству вытекающей жидкости, то изменение массы этого объема будет равно
Д/и = j pV„ ds, s
где Vn — проекция вектора скорости на нормаль к площадке ds.
Закон сохранения массы. Уравнение неразрывности
63
Так как при постоянном объеме изменение массы может произойти только за счет изменения плотности жидкости или газа, то можно написать равенство
Am = jpj/„ds = -	(П1.1)
s	и
Очевидно, положительному значению интеграла по поверхности соответствует некоторое количество вытекающей жидкости, при этом интеграл по объему должен быть отрицательным, так как при уменьшении массы ее плотность будет убывать.
Для перехода от интеграла по поверхности к интегралу по объему воспользуемся формулой Остроградского—Гаусса в виде (II.33). Тогда
j pVn ds — j diypH dU =
s	и
J L dx 1 dy 1 dz J
U
и (Ш.1) примет вид
Jdiv(pV) dU = -и	и
или
J (j|- + divpV)dt/ = O.	(III.2)
и
Интеграл по произвольному объему будет равен нулю в случае, если подынтегральная непрерывная функция равна нулю. Использовав это свойство, получим из уравнения (III.2) так называемое уравнение неразрывности в виде
-^- + divpi/ = 0.	(Ш.З)
Для стационарного движения уравнение неразрывности будет
div (рЙ) = 0 или (ри) 4-	(ри) + ~ (рда) = 0. (III.4)
Если жидкость несжимаема, т. е. р = const, то уравнение неразрывности примет вид
div V=	=°-	(III.5)
дх * ду * dz	'	7
Для несжимаемой жидкости
j Vn ds = 0,	(III.6)
64
Общие уравнения для сплошных сред, жидкостей и газов
т. е. поток скорости через любую замкнутую поверхность равен нулю.
Легко видеть, что уравнение (III.3) можно записать в виде р div V + V grad р = 0.	(III.7)
Уравнение неразрывности легко получить другим путем. Используя закон сохранения массы для элементарного объема did, получим
^(m) = 4(pdI/) = 0,
или после дифференцирования будем иметь
,-^^ + р4-(«У)=о.
Второе слагаемое, деленное на pdU, согласно формуле (11.28), есть величина относительного изменения объема dU, равная
Подставив последнее уравнение в выражение (III.8), получим уравнение неразрывности в виде
-f- р div V = 0. at '
§ 2. Силы, действующие в жидкости
Для определения величины поверхностных сил, действующих в движущейся жидкости, применим законы сохранения импульса и момента импульса к элементарному объему жидкости. Из физики известно, что
dK dmV dV £ ==—dr~==m~dt~ = R-
Для неизолированной системы закон сохранения импульса может быть представлен в виде
т. е. разность векторной производной от количества движения некоторого объема и главного вектора внешних сил, приложенных к нему, равна нулю во все время движения.
Применим этот закон к элементарному тетраэдру движущейся жидкости (рис. III.2). Тогда производная от количества движения элементарного тетраэдра будет
dK dVc , ^r = ^rdm’
(III.8)
(III.9)
(III.10)
Силы, действующие в жидкости
65
где Гс — вектор скорости центра инерции тетраэдра; dm — масса тетраэдра.
Главный вектор внешних сил можно представить как сумму главных векторов массовых и поверхностных .сил, т. е.
R — Rm + Rp-
Для тетраэдра вектор массовых сил будет равен F — вектор силы, отнесенный к единице массы.
Главный вектор поверхностных сил, действующих тарный тетраэдр, будет равен геометрической ных сил, действующих на боковые грани в координатных плоскостях с площадями dsx, dsy, dsz и на наклонную грань площадью dsn. Величина главного вектора поверхностных сил будет равна
Rр — Рп dsn	Рх dsx	Ру dsy	pz dsz,
F dm, где
на элемен-сумме поверхност-
где pi — векторы напряжения поверхностных сил, приложенных к элементарным площадкам, перпендикулярным соответственно осям х, у, z и боковой грани.
Подставив значения поверхностных сил в уравнения (III. 10), получим закон
сохранения импульса применительно к элементарному тетраэдру в виде
d^dtn — F dm + рп dsH — pxdsx —pydsy—pz dsz — 0. (III. 11)
. В последнем уравнении первые два слагаемых/ содержащие элемент массы, есть величины третьего порядка малости и ими можно пренебречь по сравнению с остальными слагаемыми — величинами второго порядка малости. Тогда вместо уравнения (III. 11) получим
Рп dsn — рх dsx -{- ру dSy pz dsz,	(111.12)
Из рис. II1.2 видно, что
dsx — dsa cos dSy —• dsn cos ds~z = dsn cos
(n, x) — nx dsn; (n^y) = ny dsn; (n^z) = nz dsn)
5 И. Л. Повх
(III.13)
66
Общие уравнения для сплошных сред, жидкостей и газов
после подстановки этих равенств в уравнение (III.12) и сокращения на d'sn получим
+	(III. 14)
или в проекциях на оси декартовых координат:
Рпх — ПхРхх + ПуРух + пгргх, Рпу = пхрху + ПуРуу + пгргу,
(III.15)
Риг — пхРхг + ПуРуг + nzPzz> 
где пх, Пу, п2 — соответствующие косинусы углов.
Величины рхх, руу, р2г называют нормальными напряжениями, а рху, рхг, рух — касательными напряжениями (первый индекс при напряжении р указывает ориентацию площадки — ее плоскость перпендикулярна обозначенной оси, а второй индекс — ось, на которую спроектировано это напряжение). Например, рху обозначает проекцию на ось у напряжения, приложенного к площадке, перпендикулярной к оси х.
Из системы (III. 15) видно, что проекции напряжения, приложенного к любой наклонной площадке, на оси координат линейно зависят от проекций напряжений, действующих на три взаимно перпендикулярные площадки, лежащие в координатных плоскостях. Следовательно, напряжение в любой точке в матричной форме может быть представлено в виде
Р =
РххРхуРхг PyxPyyPyz PzxPzyPzz
(III.16)
Матрица (III. 16) называется тензором напряжений.
Составляющие pXXJ рху. . . будем называть компонентами тензора напряжений или просто компонентами напряжений. Далее будет показано, что
'— Рух, Pxz — Pzx, Pyz------Pzy
(III.17
Эти равенства выражают условия взаимности касательных напряжений и делают тензор напряжения (III. 16) симметричным.
§ 3. Закон сохранения импульса. Уравнение движения в напряжениях
Для получения уравнения движения применим закон сохранения импульса к некоторому движущемуся произвольной формы объему жидкости, который можно записать_в виде
—К = 0.
dt
(III.18)
Закон сохранения импульса. Уравнение движения в напряжениях 67
Закон сохранения импульса в такой форме можно сформулировать следующим образом: разность векторной производной от количества движения жидкого объема и всех внешних сил, приложенных к нему, равна нулю во все время движения.
Для конечного объема жидкости U с поверхностью s закон сохранения импульса (III. 18) можно записать следующим образом:
-^r\pVdU—\pFdU—\pnds = Q, (III. 19) и	U	s
где, имея в виду, что pdU = dm = const,
= 4 1 № = 1 е 4м = I ё&ли. и	и	и
Воспользовавшись формулой Остроградского—Гаусса (II.9) для выражения интеграла по поверхности через интеграл по объему и имея в виду соотношение (III.13), получим
J рп ds = J (пхрх + ПуРу + пгрг) ds = s	S
и
при этом уравнение (III. 18) примет вид
+	+	= (III.21)
Так как величина объема U произвольна, то, приравнивая подынтегральную функцию нулю, получим закон сохранения импульса в векторной форме в виде
р^-р^-(# + 4- + ^-)=о-	<I,L22>
или
= +
(III.23)
где
div Р =
дх 1 ду 1 дг
(III.24)
5*
68
Общие уравнения для сплошных сред, жидкостей и газов
Очевидно, в проекциях на оси координат уравнение (III.22) можно записать
du ___ р । ( дрхх । друх । дргх \ .
Р dt Р х г \ дх ду г дг / ’ n dv_____\ (^Рху । дрду . дргу \ .
1	dt	Р	'J \ дх	1	ду	' дг	/	’
р = Р^г +	•
r	dt	г	2	1 \ дх	1	ду дг	/
(Ш.25)
Уравнения (III.22), (III.23) и (III.25), выражающие закон сохранения импульса, называются дифференциальными уравнениями движения в напряжениях.
§ 4.	Закон сохранения момента импульса. Симметрия тензора напряжения
Закон сохранения момента импульса можно сформулировать в следующей форме: разность (или векторная сумма) векторной производной от момента импульса L и момента внешних сил М относительно выбранной точки некоторого произвольного объема жидкости равна нулю во все время движения, т. е.
— М = 0.	(Ш.26)
Если обозначим г радиус-векторы центров элементарных объемов dU и площадок ds, к которым приложены векторы импульса, массовых и поверхностных внешних сил, то уравнение (II 1.26) примет вид
j pr X (W—~F)dU—J (rxp„)ds = 0.	(III.27)
и	s
Замечая, что г = ix -|- jy + kz, а согласно (III. 12) рп = п^х + + п2ру + п3рг, и вновь воспользовавшись формулой Остроградского—Гаусса для преобразования поверхностного интеграла в объемный, запишем уравнение (III.27) в виде
j{;x(f-w)p+(4-+^+>) +
-j- i X Рх 4~ j! X Ру + k X dU = 0.
Исходя из произвольности объема U и учитывая уравнение (III.21), получим
iX Px + i х py + k х рг = о.	(III.28)
Обобщенный закон Ньютона	69
Подставив в (III.28) значения напряжений через проекции и произведя векторное умножение, будем иметь
* {руг — Ргу) + 1{ргх — Рхг) + * {Рху ~ Рух) = О, откуда получим условие симметрии компонентов тензора напряжений, приведенное в п. 2 гл. III без доказательств
Рху — Рух у Рхг = Ргх И ру2 — ргу - (П1.29)
Таким образом, закон сохранения момента импульса не приводит к новому уравнению. Он лишь накладывает ограничения на слагаемые уравнения, выражающего закон сохранения импульса, т. е. делает тензор напряжения симметричным.
§ 5. Обобщенный закон Ньютона
Механические свойства сплошных сред, а-следовательно, и их классификация определяются видом связи между тензором напряжений и кинематическими и физическими характерными величинами среды. Такое соотношение между тензором напряжений и другими переменными носит название определяющего уравнения.
Жидкости и газы отличаются от всех других деформируемых сплошных сред тем, что в положении равновесия касательные напряжения на границе раздела двух смежных частей всегда равняются нулю.
Гидродинамика изучает законы движения большого класса жидкостей, у которых компоненты тензора напряжения связаны с компонентами тензора скоростей деформации линейно по закону, называемому обобщенным законом Ньютона.
Для нормальных компонент тензора напряжений рИ эта зависимость имеет вид
р(.(. = -р + 2р4£- +^divi/,	(Ш.ЗО)
где ц и X — коэффициенты вязкости; р — нормальное давление в жидкости при отсутствии вязкости.
Второй коэффициент вязкости А, который имеет место, как видно из формулы (Ш.ЗО), только для сжимаемой жидкости выбирается из условия, что давление в вязкой жидкости равно взятому с обратным знаком среднему арифметическому из трех нормальных напряжений, приложенных к трем взаимно перпендикулярным площадкам, т. е.
р = — Рхх + Руу + Ргг ,	(Ш.31)
О
где
Рхх + Руу + Ргг = — Зр -]- (2,и -{- ЗА) div V.
70
Общие уравнения для сплошных сред, жидкостей и газов
Отсюда следует, что. для удовлетворения допущения (III.31) необходимо, чтобы % = —2/3ц. Тогда нормальные составляющие тензора напряжений будут:
‘	„ ди 2	,. Л
рхх = — Р + 2|Л	- -у Ц div V;
Руу — Р 4“ 2ц ду
2 j- Л у pdiv V;
О
(III.32)
„	. „ dw 2 Л
Ргг = — Р -t- 2Ц - -уЦ dlV V.
Для касательных напряжений определяющим является соот-
ношение	
которое можно	записать в виде:
Р У---Рух
(III.34)
Руг — Ргу
Указанными свойствами обладают вода, воздух, спирты и многие другие жидкости и газы. Жидкости, удовлетворяющие обобщенному закону Ньютона, назыврются жидкостями Ньютона.
Жидкость, в которой
Рхх — Руу — Ргг—Р> а Рху — рхг — Руг — О,
иногда называют жидкостями Паскаля. Очевидно, к жидкостям Паскаля’относятся идеальные жидкости и вязкие жидкости в состоянии покоя. Таким образом, гидродинамика изучает закон движения жидкостей Ньютона и Паскаля. Течения других жидкостей и сплошных деформируемых сред при различных видах определяющих уравнений изучаются реологией.
§ 6. Уравнение движения сжимаемых жидкостей и газов
Если в уравнение движения в напряжениях (III.25) подставить значения компонентов тензора напряжений, согласно обобщенному закону Ньютона (III.33) и (III.34), то получим уравнение движения сжимаемой жидкости или газа в проекции на ось х
о	=₽Х +	[ - р + 2»	i И Iv £] +
+-^(т+»+42|Ц<+т)-
Уравнение движения сжимаемых жидкостей и газов
71
После элементарных преобразований правой части и аналогичных действий с другими проекциями будем иметь систему уравнений:
du v др , о д ( ди \ , Р = РХ dL. 2 —— ц —— ) -L ' dt г дх 1 дх у дх J '
д	Г	/ ди до \ I д Г	/ ди	. • dw \ 1
ду	L	\ ду	‘ дх / J	‘ дг |.	\ дг дх ) J
-4^(pdivV);
do	др , д Г ( ди . ди \ 1 .
, дГ /ду . dw \ I . п д / dw \ ~ду~ (,~дГ "dy/J 2 дг \^~дг~)~
-44-^divy>-
К трем уравнениям движения добавим уравнение неразрывности, или сплошности, движения в виде:
4- + div(pi/) = 0.
Эти четыре уравнения справедливы и для жидкостей, и~для газов.
Так как в сжимаемой жидкости неизвестными являются не только скорости и давления, но такие физические свойства, как плотность и вязкость, то для замкнутости системы уравнений необходимо ввести еще два соотношения: зависимость плотности от давления и связь вязкости с температурой. Рассмотрим эти соотношения раздельно для газов и жидкостей.
Для совершенного газа плотность выражается через давление по уравнению состояния
^- = RT = ~^~ i,	(III.36)
где i — энтальпия; k — показатель изэнтропы.
Уравнение состояния можно выразить уравнением Ван-дер-Ваальса и другими уравнениями.
72
Общие уравнения для сплошных сред, жидкостей и газов
Связь вязкости с температурой может быть выражена различными законами. Наиболее простым является степенной закон
Показатель степени п для воздуха при температурах 90— 300 К равен %, а при температурах 300—400 К п = 8/4.
В технике все чаще встречаются задачи, в которых необходимо учитывать влияние сжимаемости в жидкостях (например, при изучении взрывов в воде, движении жидкостей в гидропушках и гидромониторах и пр.). В этих случаях давление может достигать десятков тысяч атмосфер, поэтому величины платности и вязкости нельзя считать постоянными.
Зависимость плотности от давления для жидкостей представляется следующим обобщенным уравнением изэнтропы:
Р.+^. = const.	(III.38)
Для воды значения В и п, определенные опытным путем, равны: В = 3045 кгс/см2 и п = 7,15.
Величина вязкости может быть определена по одному из соотношений, известных из физики, например по формуле А. И. Бачинского
с
Т-ь ’
(III.39)
где с — постоянная для каждой жидкости; v — удельный объем; b — величина, близкая к постоянной, в уравнении Ван-дер-Ваальса.
Таким образом, получена замкнутая система из шести уравнений с шестью неизвестными (и, v, w, р, р, т|).
§ 7. Уравнения движения вязкой несжимаемой жидкости
Рассмотрим изотермическое движение вязкой несжимаемой жидкости. В этом случае плотность и вязкость будут величинами постоянными.
Подставим выражения компонент напряжений рхх, руу. . . в соответствии с формулами (III.32) и (III.34) в уравнения в напряжеиих (III.25) и, учитывая, что для несжимаемой жидкости
,. Л ди , ди . dw п div V = -з-Ь -з—F -а— = 0,
дх 1 ду 1 дг ’
(111.40)
Уравнения движения вязкой несжимаемой жидкости
73
получим уравнение движения вязкой несжимаемой жидкости. Так, для проекции на ось х найдем
др	,	/ д2и	.	д2и	.	д2и \	! д / ди	.	до dw \	_
дх	'	\ дх'2	'	ду2	1	дг2 ) дх \ дх	'	ду	"Г" dz )
Проделав аналогичные преобразования с двумя другими уравнениями (III.25) и имея в виду (III.5), будем иметь систему уравнений:
du  у 1 др . ^,2 -ТГ- = Л----------4— 4- vV(Z',
*dt	р дх 1
dy ,z 1 др .	„2
-77-	= Y---------4- vV2y;
dt	р ду 1
dw „	1 др .
-г?- = Z —--------4- -4- vV-ш,
dt	р дг 1	’
(III.41)
д2 , д2 . д2	„
где V2 =	— оператор Лапласа.
•Уравнения (III.40) и (III.41) представляют собой замкнутую систему с четырьмя неизвестными и, v, w и р. Величины р и v, а также проекции массовых сил X, Y и Z должны быть заданы. Аналогично уравнению (II.2) уравнения (III.41) представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. В векторной форме эти уравнения имеют вид
= F — у grad р -|- vVV.	(111.42)
Уравнения (III.41) впервые были получены в 1845 г. Стоксом и называются уравнениями Стокса.
Для решения системы (III.41) следует задать граничные условия. При наличии же локальных составляющих ускорения, т. е. для нестационарного потока, необходимы и начальные условия. Они задаются так же, как и для идеальной жидкости, в виде распределения скоростей во всей рассматриваемой области в момент времени t = 0, т. е. функциями: и (х, у, z, 0); v (х, у, z, 0) и W (х, у, z, 0).
Граничные условия как с математической, так и с физической точки зрения имеют весьма важное значение. Различие между движением идеальной и реальной жидкостей определяется не
74
Общие уравнения для сплошных сред, жидкостей и газов
только различием самих уравнений, но и видом граничных условий. Обычно граничные условия задаются на поверхности обтекаемого тела и на бесконечности, в невозмущенной жидкости. На бесконечности, как правило, считают известными величины скорости и давления, а для внутренней задачи — расход жидкости.
Вид граничных условий на поверхности зависит от того, движется ли тело в потоке или оно неподвижно, а поток на него набегает. Рассмотрим отдельно значение нормальной и касательной составляющих скоростей на поверхности обтекаемого тела.
Граничные условия для нормальной составляющей скорости определяются непроницаемостью твердой стенки. Так как через твердую стенку тела жидкость не перетекает, то эту стенку можно считать нулевой-линией тока при движении как идеальной, так. и реальной жидкостей. Отсутствие перетекания через линию или поверхность тока и есть граничное условие для нормальной составляющей скорости, Vn = 0.
Граничное условие для касательной составляющей скорости определяется прилипанием к стенке частиц жидкости или газа вследствие вязкости. Таким образом, скорость жидкости на поверхности неподвижного обтекаемого тела должна равняться нулю, а для движущегося тела она должна быть равна скоростям соответствующих точек движущейся поверхности.
Для разреженных газов длина свободного пробега молекулы I' не очень мала по сравнению с характерным размером b обтекае-мого тела, т. е. --1, что наблюдается в некоторых вакуумных
установках и в атмосфере на высоте 100—140 км. В этом случае на поверхности тел происходит не полное прилипание, а течение со скольжением. Следовательно, граничные условия для касательной составляющей будут другими.
При длинах свободного пробега, больших, чем линейные размеры тел, уравнения гидродинамики неприменимы. В этом случае пользуются уравнениями кинетической теории газов.
§ 8. Перенос тепла
Если в точках пространства, заполненного твердыми, жидкими или газообразными физическими телами, в некоторый момент времени имеют место различные температуры, то от точек с более высокими температурами тепло будет переноситься к точкам с более низкими температурами.
Процесс переноса тепла может осуществляться тремя путями: кондуктивным, конвективным и лучистым теплообменами.
Кондукциёй называется процесс передачи тепла при непосред- • ственном соприкосновении частиц тела, имеющих разные температуры. Отличительной чертой этого процесса является атомно
Перенос тепла
75
молекулярный характер переноса энергии, не связанный с макроскопическими перемещениями. Этим способом осуществляется перенос тепла в твердых телах и частично в жидкостях и газах. В покоящихся' и движущихся жидкостях и газах молекулы, не заггимая фиксированного положения и непрерывно перемещаясь, также передают тепло от молекулы к молекуле.
Кроме того, в жидкостях и газах перенос тепла осуществляется перемещением макрообъемов жидкостей и газов. Размеры этих частиц во много раз превосходят размеры молекул. Такой процесс называется конвективным теплообменом. Обычно различают два типа конвективного теплообмена: естественную конвекцию и вынужденную.
Естественной конвекцией будем называть такой перенос, при котором перемещение жидкостных и газообразных частиц, несущих тепло, вызывается только действием разности плотностей среды, возникающей из-за наличия разности температур. Когда перемещение частиц жидкости и газа, переносящих тепло, происходит не под воздействием разности плотностей, а в результате вынужденного движения (например, вентилятором), конвекция называется вынужденной.
Лучистый теплообмен — передача тепла между нагретыми телами, обусловленная процессами испускания, переноса, отражения, поглощения и пропускания лучистой энергии. В отличие от указанных выше переносов тепла, лучистый теплообмен между телами может происходить при отсутствии промежуточной среды (в вакууме).
Природа и закономерности радиационного переноса имеют волновой характер, такой же, как имеют любые другие электромагнитные волны (радио, свет, рентгеновские лучи). Все они отличаются лишь длиной волны. Тепловые излучения — это электромагнитные волны длиной 0,76—4000 мкм, в то время как видимые человеческим глазом световые лучи имеют длину волны 0,35— 0,75 мкм.
Если поверхности равных температур в некотором пространстве назвать изотермическими, то общее количество тепла Q, проходящего через площадку, составляющую часть изотермической поверхности с площадью s, за время t будет равно, согласно закону переноса,
О = — Л-т- st,
дп
где Т — температура; п — нормаль к площадке; X — коэффициент теплопроводности.
Количество тепла q, проходящего через единичную площадку в единицу времени, будет равно
76
Общие уравнения для сплошных сред, жидкостей и газов
или в векторной форме
~q = — X grad У.	' (III.43)
->
Величина q называется вектором теплового потока или плотностью теплового потока; его направление совпадает с нормалью к изотермической поверхности.
Проекции вектора q на декартовы оси будут:
« дТ	. дТ	, дТ
q*~	Х ду И Яг~ Х дг ’
Коэффициент теплопроводности имеет размерность в системе единицы СИ
а в системе МКС
[11 — [*?] _ «кал
1/4 -	- м.с.оС
L дп j
ккал т т	< ккал < «гол Вт
• или------отг. Известно, что 1-----= 1,1630 —•
м-ч- С	м ч* С	м- С
Значения X для разных веществ существенно различны и зависят от их температуры. Лучшими проводниками тепла являются металлы, хуже всех проводят тепло газы.
В табл. III. 1 приведены значения X [ "м^чАз] для Различнь1х веществ в зависимости от температуры х.
Таблица IIIЛ
Вещество	Л при т, °C					
	20	40	*	100	200	400	600
Вода	0,514	0,540	0,585	0,571	—	—
Масло машин-	0,125	0,124	0,118	0,112	—	—
ное						
Железо	62,5	—	58,0	53,6	41,7	34,2
Ртуть	7,47	8,00	9,03	10,61	—	— 
Серебро	—	359,0	357,0	321,0	310,0	—
Воздух	0,020	0,021	0,023	0,028	0,036	0,057
1 Для выражения в системе СИ приведенные в табл. III. I значения надо умножить на 1,1630.
Закон сохранения анергии. Уравнения энергии и переноса тепла
77
Из табл. III. 1. видно, что теплопроводность некоторых металлов с повышением температуры убывает. Для воздуха, водорода и других газов, наоборот, теплопроводность с повышением температуры растет.
Коэффициенты теплопроводности большинства жидкостей уменьшаются при повышении температуры, исключением являются вода и ртуть.
При конвективном переносе в практических расчетах количество тепла, переносимого от поверхности обтекаемого тела, имеющей температуру Тст, в поток с температурой Т, определяют по Ф°Р“Уле	D (Т . г„1 а.
которую часто называют формулой Ньютона. Здесь а — коэффициент теплоотдачи.
Величина плотности теплового потока q, согласно вышеприведенной формуле, будет-
<7 = а (Т - Тст).	(II 1.44)
Коэффициент теплоотдачи а зависит от скорости движения тела, его формы, размеров и физических свойств (коэффициента теплопроводности, теплоемкости, плотности и вязкости), а также от температуры жидкости или газа и стенки.
Зависимость а от скорости может быть представлена в виде а = а0 + cVn,
где а0 — коэффициент теплоотдачи, когда скорость тела V равна нулю; сип — постоянные.
Коэффициент теплоотдачи а характеризует собой условия теплообмена между поверхностью твердого тела и жидкостью. Численно он равен количеству тепла, переданного в единицу времени через единицу поверхности обтекаемого тела при разности температур между этой поверхностью и жидкостью в 1° С.
Размерность а в технических единицах будет
ккал
~тл	- м2-ч-°С’
а в системе СИ
г, Вт . ккал .	Вт
1а1—м2-°С И м'--ч-°С
Экспериментальному определению величины а посвящено много работ. Величина коэффициента теплоотдачи меняется в весьма широких пределах.
§ 9.	Закон сохранения энергии.
Уравнения энергии и переноса тепла
При движении жидкостей и газов должен соблюдаться закон сохранения энергии, который можно сформулировать следующим образом: изменение во времени полной энергии объема жидкости
78
Общие уравнения для сплошных сред, жидкостей и газов
или газа равно сумме работ в единицу времени внешних массовых и поверхностных сил, приложенных к этому объему и его поверхности, сложенной с отнесенным к единице времени количеством тепла, подведенного извне,
-^- = An + 4, + Q.	(III.45)
Полная энергия объема U складывается из суммы кинетической Ек и внутренней Ео, которые равны
£к=	и £о = J pedU = \pcvTdU,
и	и	и
где е = cvT — внутренняя энергия, отнесенная к единице массы. Работа массовых Ат и поверхностных Ап сил за единицу времени, или мощность этих сил, будет
Ат = j Р^7 • V dU и Ап = j рп • V ds, и	s
где F -V и рп- V — мощности сил, отнесенных первая—к единице массы и вторая — к единице поверхности.
Подведение тепла к объему извне в самом общем случае может складываться из молекулярного и конвективного переносов через поверхность этого объема QK и радиационного переноса Qr, равных:
QK = J ds = j (% grad Т)„ ds и QR = | pqR dU, s	s	U
где q& — плотность радиационного переноса тепла.
Прежде всего рассмотрим случай, при котором Ек = const и Ат — Ап = q% = 0. В этом случае внутренняя энергия будет изменяться только за счет переноса тепла через поверхность. Тогда уравнение энергии (III.45) будет
~ f pcvT dU = [ % grad Т ds.
1 U	s
Преобразуя по формуле Остроградского—Гаусса интеграл в правой части, получим
J [4	Г)—div % grad Т] dU = 0,
и
или, имея в виду произвольность объема и постоянство р, cv и X, получим уравнение переноса тепла в виде
=adivgrad Т,	(III.46)
Закон сохранения энергии. Уравнения энергии и переноса тепла
79
дТ , дТ . дТ . дТ t д*Т . д*Т . ^Г\ /Т1Т
dt + U дх ду + W дг ~а\ дх2 + ду* дг* ) ’	(111[-47)
где а — ------коэффициент температуропроводности.
При наличии только молекулярного переноса, когда и = v = = w — 0, последнее уравнение примет вид
дТ	/д*Г ,	д2Г .	д*Т	\	/ттт ло\
•дТ" - d- ( Д д’ “|-д“_о' “|-я 2	)	•	(II 1.48)
at	\ ах2 *	ду2 ‘	az2	/	v 7
Подставив найденные значения Ат и Ап в (III.45), получим уравнение, выражающее закон сохранения энергии в виде
^-±^cvT + ^-'\dU=\pF.VdU+\pn.Vds + и	U	s
+ f^ds + Jp^d{/.	(III.49)
s	U
Далее вывод уравнения будет таким же, как и в предыдущем случае. Интегралы по поверхности представляются через интегралы по объему, и подынтегральная функция приравнивается нулю. Имея в виду (III. 12), согласно формуле Остроградского— Гаусса, мощность поверхностных сил будет равна
J рп• Vds = J (пхрх-V + Пуру-V + п£г V)ds = S	S
= J Й (Px-V) + i (PyV) +i(Pz-V)] dU = J div (P-У) dU, и	и
где P, как это показано в (III.16) и (III.24), есть тензор напряжений.
Приток тепла через поверхность можно выразить как
J ‘k^-ds — j X(grad Т)п ds= j div (Я grad T) dU. s	s	U
Подставим значения преобразованных интегралов в уравнение энергии (III.49). Так как все члены уравнения будут интегралами по одному и тому же произвольному объему, то, считая подынтегральную функцию непрерывной, окончательно получим
Р -I- -у- = pF • V + di v (Р • V) + div (X grad Т) + pq^ (111.50)
Это уравнение энергии должно замыкать систему уравнений гидроаэродинамики для сжимаемых газов.
80
Общие уравнения для сплошных сред, жидкостей и газов
Используя уравнение движения в напряжениях (II 1.22), получим
p4”=l/p< = i/(pF+*	+
r dt 2	dt у ' dx ' dy 1 dz /
Подставив последнее уравнение в (III.50) и имея в виду, что
_ dV -* dV . -* dV
Px dx 1 рУ ду ' Рг dz ’
уравнение энергии запишем в следующем виде:
Рс» W Т 2=2 рх + Р'-Г^Г + 'S’ + div grad + рС1{<’
'	’ ' . Л  '	. (Ш.51)
s	у	-	•
где рх = pxxi pxs/j + pxzk и т. д.
Заменив векторы напряжений компонентами скоростей деформации (II 1.30) и (II 1.33), согласно обобщенному закону Ньютона, и сделав преобразования, получим уравнение энергии в скалярном виде
р cvT — Ф — р div У-----1- р (div У)2 div (X grad Т) pq$,
(III.52) где функция Ф, равная
Ф =2ц ($11 -|- $22 + 8зз -{- $12 + S 13 И" 82з),
характеризует величину диссипации энергии и называется функцией диссипации, а $г;- — компоненты тензора скоростей деформации (11.26).	, .	, ,
§ 10. Диффузия. Уравнение переноса вещества
Если в некотором объеме жидкости или газа имеются какие-либо частицы другого вещества, то перенос этого вещества, или его диффузия, обусловленная тепловым движением, будет происходить в направлении убывания его концентрации.
Способностью к диффузии обладают мельчайшие частицы вещества (отдельные молекулы, атомы или ионы), а также более крупные частицы, хорошо видимые в микроскоп, находящиеся среди молекул газа или жидкости и участвующие в броуновском движении.
Диффузия. Уравнение переноса вещества	81
Диффузионные процессы имеют большое значение во многих областях науки и техники. Особенно большую роль они. играют в химических явлениях, в металлургии. Например, при термической обработке металлов различные процессы поверхностного насыщения металла (цементация, азотирование, борирование, бе-риллизация и пр.) полностью определяются диффузией.
Диффузия происходит в газах, жидкостях и твердых телах, причем диффундировать могут как растворенные в веществе посторонние частицы, так и частицы самого вещества. Последнее явление называется самодиффузией.
Процесс диффузии так же, как и перенос тепла, обусловлен двумя совершенно различными причинами. Во-первых, при наличии разности концентраций возникает перенос вещества через поверхности, непосредственно соприкасающиеся. Такая диффузия называется молекулярной и наблюдается в твердых телах, а также в покоящихся жидкостях и газах и при их ламинарном движении.
Во-вторых, частицы вещества, растворенного в движущейся жидкости или газе, увлекаются и переносятся макрочастицами, размеры которых значительно больше размеров молекул. Такая диффузия называется конвективной диффузией вещества. Процесс диффузии в турбулентных потоках и частично в ламинарных полностью подчиняется механизму конвективной диффузии вещества.
Рассмотрим количественные закономерности процесса диффузии. Если с — концентрация одного вещества в другом, выраженная в кг/м3, в долях или процентах, то перенос массы в направлении наибольшего изменения концентрации с будет, согласно закону переноса массы (закону Фика), пропорционален площади поверхности s, через которую переносится вещество, и времени переноса t, т. е.
W = —D^st,	(III.53)
где D — коэффициент диффузии.
Знак минус означает, что перенос массы направлен в сторону, противоположную направлению наибольшего увеличения •концентрации.
Обычно рассматривается не общий перенос, а количество переносимого вещества через единицу площади в единицу времени
Величина w называется плотностью переноса вещества, которую можно назвать скоростью диффузии через единицу площади.
В общем случае, когда концентрация есть функция всех трех координат, плотность потока вещества, аналогично плотности потока тепла, будет векторной величиной, равной
w = —D grad с = wxi + wyj + w2k. (III.54)
6 И. Л . Повх
82
Общие уравнения для сплошных сред, жидкостей и газов
При этом величина проекции будет „ дс	гл дс	п дс
wx — — D -д-; wu = — D -д-; w2 — — D -д-. *	дх ' и	ду	дг
Размерность коэффициента диффузии равна
г П1 = W = кг'м4 = м* .
Гдс .1 кг-мг-с с tars,J
Приведенные формулы для диффузии вещества верны в случае, если в рассматриваемых средах имеют место лишь разности концентрации при постоянных или очень мало меняющихся температурах и давлениях. Если кроме разностей концентрации в среде существуют градиенты температур Т и давлений р, то перенос вещества определяется следующей формулой:
w^ — d(vc + -^- V?+y-Vp).	(III.55)
Диффузию, возникающую лишь из-за разности концентрации, называют обычной, или чистой, диффузией.
Перенос вещества, происходящий из-за разности температур, называется термодиффузией, а из-за существенного градиента давления, вызванного, например, внешним полем, называется бародиффузией. Величины Dkt и Dkp называются соответственно коэффициентами термо- и бародиффузии.
Баро- и термодиффузии наблюдаются при постоянной концентрации вещества с = const, когда обычная или чистая диффузия отсутствует. Если коэффициент диффузии D всегда положителен, то величины kt и kp могут быть как положительными, так и отрицательными. При малых концентрациях вещества kt = kp = 0.
В электролитах и ионизированных газах (плазме) при наличии разности электрических потенциалов будет происходить диффузия ионов, называемая электродиффузией.
Можно назвать и многие другие виды диффузии веществ, возникающей в жидкостях и газах под влиянием внешних сил.
Из формул (III.53) и (III.54) видно, что скорость диффузии определяется значением коэффициента диффузии D. Величина коэффициента диффузии возрастает с повышением температуры, когда тепловое движение частиц становится более быстрым.
Наибольшее значение коэффициента диффузии имеет место в газах. Если бы диффузия в газах определялась только скоростью теплового движения, то она протекала бы почти мгновенно, так как эта скорость составляет сотни метров в секунду. Процесс диффузии происходит значительно медленнее, потому что молекулы газа перемещаются из одной точки в другую, не слишком близкую к первой, не прямолинейно, а зигзагообразно вследствие столкновений с другими молекулами. Таким образом, скорость
Диффузия. Уравнение переноса вещества	83
диффузии в газах определяется как скоростью теплового движения молекул, так и длиной их свободного пробега, т. е. средней длиной тех прямолинейных отрезков пути, которые проходят молекулы газа от столкновения до столкновения. Чем больше длина свободного пробега, тем больше скорость диффузии молекул газа.
Диффузия в жидкостях идет значительно медленнее, чем в газах. Диффузия в твердых телах протекает особенно медленно. Например, если сложить и сильно сжать два куска различных металлов (медь и цинк или олово и свинец), то процесс взаимной диффузии при комнатной температуре продолжается месяцы и годы. При температуре 100—200° С уже через год в месте контакта меди и цинка образуется слой твердого сплава толщиной в 0,25 мм. При этом куски металла вследствие диффузии оказываются спаянными.
Коэффициент диффузии газа в газе имеет величину порядка 10"Б м2/с, для жидкостей (НС1 и NH8 в воде) 10"® м2/с, для твердых тел он составит 10"1Б м2/с.
Аналогично зависимостям для теплообмена величина плотности потока вещества w в задачах по обтеканию тел может быть выражена формулой
w — ад (с — сСТ),	(III.56)
где си сст — соответственно концентрации вещества в потоке и на поверхности обтекаемого тела; ад — коэффициент массооб-мена.
Размерность коэффициента массообмена
г ,	м	м
!<*„]=— или — . х AJ	Ч	С
Величина коэффициента ад редко применяется самостоятельно, чаще она входит в совокупность величин, определяющих процессы переноса вещества (см. п. 5 гл. X).
Уравнение молекулярной диффузии по аналогии с теплопроводностью можно записать в виде
При наличии конвективной диффузии, так же как и при конвективном переносе тепла, уравнение диффузии будет иметь вид
> = ^2с, или
+	—	(111.57)
dt 1 дх 1 ду 1 дг	'	'
Так же как и для переноса тепла и переноса количества движения, дифференциальное уравнение диффузии является уравне
84
Общие уравнения для сплошных сред, жидкостей и газов
нием второго порядка в частных производных с переменными коэффициентами. Точные решения этих уравнений могут быть получены лишь для наиболее простых случаев.
В задачах о диффузии граничные условия существенно зависят от процесса, происходящего на поверхности тела: 1) если поверхность тела не растворяется в обтекаемой жидкости, то на по-дс
верхности = 0; 2) если тело растворяется в обтекающей жидкости, то вблизи его поверхности быстро устанавливается равновесие, при котором концентрация в примыкающей к поверхности тела жидкости равна концентрации насыщенного раствора, с = с0. Очевидно, диффузия вещества из этого слоя должна происходить медленнее, чем процесс растворения; 3) когда твердая поверхность поглощает попадающее на нее диффундирующее вещество, тогда и на поверхности с — 0.
Из уравнений переноса тепла (III.47) и переноса вещества (III.57) видно, что оба уравнения совершенно одинаковы. Если в первом заменить температуру Т на концентрацию с, то получится второе уравнение.
Следовательно, если обозначить переносимую скалярную величину количества тепла и вещества буквой В, то уравнение переноса скалярной величины, согласно выражениям (II 1.47) и (II 1.57), будет иметь вид
дБ . дВ . дВ . дВ r-r I д2В , д2В , д2В \ ,TII -Q.
-47- 4- U-ч- Ч-и-а- + &У-Г- = тг + тт+ “TF I > (П1.&8) dt 1 дх 1 ду 1 дг 1 1 \ дх2 1 ду2 1 дг2 )	4	'
ИЛИ
4?=nv2B, at	’
где П — коэффициент молекулярного переноса скалярной величины (для переноса тепла П — коэффициент температуропроводности, а для диффузии — коэффициент диффузии).
Аналогичным образом можно написать единое выражение для потока скалярной величины вне зависимости от того, является скалярная величина теплом или веществом. В соответствии с выражениями (III.44) и (III.56) плотность потока скалярной величины Г от стенки будет равна
Г = а (В — ,ВСТ),	(II 1.59)
где а — коэффициент переноса скалярной величины.
Согласно (III.43) и (III.54), эта же величина может быть представлена в виде
Г = — П grad В.	(III.60)
Напряжения в идеальной жидкости
85
ГЛАВА IV
УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
§ 1. Напряжения в идеальной жидкости
Из всех моделей жидкости, рассматриваемых в гидромеханике, наиболее простой является модель идеальной жидкости. Как уже указывалось ранее, идеальной называют жидкость, в которой отсутствуют внутреннее трение и теплопроводность. Таким образом, при движении идеальной жидкости касательных сил трения нет и взаимодействие между соприкасающимися объемами жидкости сводится к действию нормальных поверхностных сил.
Допущение об отсутствии касательных поверхностных сил означает, что недиагональные компоненты напряжений в точке движущейся жидкости, приведенные в выражении (III.17), обращаются в нуль
Рху -= Рух Рхг Ргх == руг == Ргу —~ О»
Это допущение относится не только к площадкам, нормальным к осям произвольно выбранной системы координат, но и к любой наклонной к координатным осям площадке. Тогда, согласно выражениям (III. 15), можно написать проекции напряжений сил давления, нормальных к произвольно направленной площадке,
Рпх Рхх^х Н- Рух^у Ргх^г== Рхх^х* Рпу—^РууПу И Рпг:~~ Ргг^-zt
где рпх, рпу и рпг — проекции напряжения рп на координатные оси, равные
Рпх — Рп^х, Рпу— Рп^у, Рпг — Рп^г-
Из приведенных соотношений следует
Рхх'==Рп> Руу—^Рп, Pzz7=Pn> откуда
Pxx — Pyy — pzz = Pn = — P-	UV-1)
Равенство (IV. 1) означает, что при движении идеальной жидкости, так же как при состоянии равновесия любой сплошной среды, нормальное напряжение в данной точке не зависит от направления площадки, к которой оно приложено.
В гидростатике и гидродинамике скалярную величину нормального напряжения в данной точке потока идеальной жидкости будем называть гидродинамическим давлением или давлением в данной точке. Знак минус означает, что гидродинамическое давление направлено в сторону, противоположную внешней нормали площадки.
86
Уравнения движения идеальной жидкости
Модель идеальной жидкости существенно упростила математическую постановку задач гидромеханики, поэтому долгие годы классическая гидромеханика занималась лишь изучением движения идеальной жидкости.
Несмотря на то что идеальной жидкости в действительности не существует, многие теоретические решения, полученные в предположении идеальности жидкости, имеют большое практическое значение. Пригодность модели идеальной жидкости для многих задач обтекания тел объясняется прежде всего тем, что идеальная жидкость сохраняет основные свойства реальных жидкостей (непрерывность, или сплошность). Кроме того, при обтекании хорошо обтекаемых тел (крыла самолета, ракеты, лопатки турбины и пр.) влияние вязкости на распределение давления по поверхности этих тел сказывается лишь в очень слабой степени. Однако влияние вязкости оказывает решающее значение при подсчете сопротивлений тел в движущейся жидкости.
§ 2. Уравнение Эйлера движения идеальной жидкости.
Для вывода уравнения движения воспользуемся уравнением в напряжениях (II 1.25). При этом достаточно рассмотреть одну из его проекций, например на ось х,
п йи__z V , дрхх j друх , др2Х
Р dt—?*— —дГ +	I	>
где — проекция ускорения; рХ — проекция массовой силы, отнесенной к единице объема. Остальные три слагаемых представляют собой производные от нормальных и касательных напряжений в жидкости.
Так как в идеальной жидкости вязкость отсутствует, а касательные напряжения равны нулю, то величина нормальных напряжений будет рхх — рт = ргг = —р. Поэтому уравнения движения идеальной жидкости в проекциях на оси координат имеют вид:
du v др dv	др
р -т- = рХ —	р-тг — рУ--к-',
*dt 1 дх ’ r dt 1 ду ’
dw rr др P~dt=PZ-^-
(IV.2)
Полученную систему уравнений можно представить в векторной форме
(IV.3)
dV 2	1	,
-jt- = F---grad р.
dt	р &	'
Это уравнение движения идеальной жидкости часто называют уравнением Эйлера.
Уравнение Эйлера в ферме Громека
87
Для жидкости, находящейся в покое, из уравнения (IV.3) можно получить известное уравнение гидростатики, приравняв к нулю производные скорости по времени. В этом случае жидкость находится в равновесии под действием только массовых и поверхностных сил, а уравнения примут вид:
рХ = -^; рГ = -^; pZ = -^.
г дх ’	' ду ’	1 dz
В общем случае скорость движения жидкости зависит как от координат, так и от времени. Напомним, что зависимость для полного ускорения жидкости имеет вид
т-т	du dv dw
Подставив соответственно выражение для	в урав-
нения (IV.2), получим следующий вид дифференциальных уравнений движения (уравнений Эйлера):
ди . ди . ди . ди v	1 др
+ «-5 Г	----Ь W -д— = Х-------5^-J
dt	1	дх	1	ду	1	dz	р	дх ’
dv	,	ди	,	dv	.	до	1	др
dt	1	дх	1	ду	1	дг	р	ду ’	(IV.4)
дю	.	дю	.	дю	.	dw v 1	др
-4- и-х-к О-д---к йУ-з— =Z--------
dt	1	дх	1	ду	1	дг	р	дг
Для интегрирования этих уравнений необходимо иметь начальные и граничные условия. Пусть обтекаемое тело будет неподвижным. Так как поверхность этого тела является поверхностью тока и через нее жидкость не течет, то нормальная составляющая скорости в точках поверхности тела равна нулю, т. е. Vn — 0.
Идеальная жидкость не имеет вязкости, поэтому при обтекании тела частицы ее скользят по поверхности и касательная составляющая скорости в точках поверхности тела не равна нулю, т. е. Vt =h 0.
Начальные условия могут быть заданы в виде значений составляющих скорости в потоке в момент времени t = t0.
В какой-либо точке потока должна быть известна также величина давления, а в случае сжимаемой жидкости — и значение плотности.
§ 3. Уравнение Эйлера в форме Громека
Уравнениям движения идеальной несжимаемой жидкости можно придать вид, отличный от уравнений Эйлера. Для этого формально преобразуем левую часть уравнения Эйлера.
88
Уравнения движения идеальной жидкости
Ускорение жидкости в проекции на ось х записывалось в уравнении Эйлера в виде du __________________ ди
dt dt
ди дх
ди ду
ди дг
Добавлением и вычитанием величины о+ ау-^-правой части этого выражения можно придать вид ди , ди . до , dw
Так как
dw "дх
И
ди   I ди2
U дх	2 дх ’
до
1 до2 .	dw   1 dw2
2 дх ’	дх	2 дх
до ди дх ду левая часть уравнения Эйлера будет иметь вид ди . 1 { ди2 . до2 . dw2 \ , , , Л , Л . Т + 2 Ъ? Ы + (rot* Vw~ Г01г Vv} =
= 4г+4 4- (“2+у2++(rot^=
ди 1 dV2 . , , Л , Л,
= -дГ — -X-—Р (rotVxVY, dt 2 дх  4	' ’
rot2V;
ди dw , Л -------5- = rot,у, дг дх и
где (rot V X V)x — проекция векторного произведения двух векторов на ось х.
Преобразуя аналогично остальные уравнения Эйлера, запишем уравнения движения идеальной жидкости в форме Громека:
44+^+(го^х^ ^+44+(rot'^=z-
1 др ф 1 р дх ’
1 др
1 др*
р дг
(IV.5)
Предположим, что массовые силы, проекции которых на оси координат обозначены через X, Y и Z, имеют потенциал, т. е. что существует такая функция координат Ф, которая удовлетворяет следующим условиям:
Интегралы Коши—Лагранжа и Бернулли для потенциального движения 89
или
—йФ = Xdx н- Ydy -|- Zdz..
Это предположение можно сделать потому, что в практике массовой силой большей частью является сила тяжести, а сила тяжести, как известно, имеет потенциал.
Тогда, считая р постоянной величиной, уравнения (IV.5). можно записать в виде:
т + ^(-гТф I f)+(rotVxV), = 0;
-Я- + 4-(тГ-1 ф । f)-|-(roti?xV), = 0;
^ + ^(4 + ®+f) + (rotVxV), = 0 или в векторном виде:
-I- grad + Ф + •£-) + (rot Vx V) = 0.	(IV.6)
Уравнение (IV.6), так же как и уравнения (IV.5), называется уравнением Эйлера в форме Громека. Граничные и начальные условия для этих уравнений будут такими же, как и для уравнения Эйлера.
Особенность уравнения Эйлера в форме Громека заключается в наличии в явном виде члена, содержащего вихрь вектора скорости.
При равенстве нулю слагаемого (rot V X V) система уравнений (IV.5) сильно упрощается. Последнее слагаемое обращается в нуль в трех случаях: 1) скорость потока равна нулю; 2) векторы скорости и вихря скоростй параллельны, и поэтому векторное произведение равно нулю (это случай так называемого винтового движения, весьма редко встречающегося в практике); 3) вихрь скорости равен нулю (безвихревой или так называемый потенциальный поток).
§ 4. Интегралы Коши—Лагранжа и Бернулли для потенциального движения
Если во всей области движения rot V = 0, то существует потенциал скорости ср,	т. е.	по	формуле	(11.18):
dtp	dtp	dtp
u —	V =	; W = -д2- ,
dx	dy	dz
(IV.7)
ИЛИ
V = grad cp.
90	Уравнения движения идеальной'жидкости
Тогда уравнение Эйлера в форме Громека (IV.6) примет вид
Следовательно, выражение в скобках зависит только от времени, а от координат не зависит. Интеграл этого уравнения будет 4+4+®+f=№
где f (/) определяется из граничных условий. Этот интеграл уравнения Эйлера называется интегралом Коши—Лагранжа для потенциального движения идеальной несжимаемой жидкости.
Когда массовые силы являются только силами тяжести, потенциал этих сил равен Ф = gz, а интеграл Коши—Лагранжа принимает вид
4+4+«г+т=?«.	(iv.8)
В уравнении (IV.8) имеются два неизвестных ср и р, поэтому для решения задачи следует воспользоваться уравнением неразрывности ди , до , dw _ п ~ ду + ~дг —
Подставляя в это уравнение значения проекций скорости по формуле (IV. 7), получим
-д2ср . д-\р . д*^_— q	(IV 9)
дх* ду* дг*	Ilv-y?
Уравнение (IV.9) является уравнением Лапласа, решая которое можно найти ср. Подставив значение ср в уравнение (IV.8) и имея в виду, что
1/2— V I f_^P.\2 i ( дф V
определим давление р. Произвольная  функция f (/) будет найдена по величине р (Z) в некоторой точке.
Если движение стационарно, т. е. = 0, то уравнение (IV.8) примет вид
4+^г+т=с1-	<IV-10>
у
Этот интеграл уравнений Эйлера называется интегралом Бернулли для потенциального стационарного потока идеальной несжимаемости жидкости. Постоянная Сг будет одной и той же для всей области потенциального потока. Этот интеграл, часто
Интеграл Бернулли для линии тока
91
называемый уравнением Бернулли, имеет большое значение для всей гидромеханики. Из уравнения Бернулли видно, что во всей области безвихревого потока энергия жидкости в единице массы остается постоянной. Первое слагаемое выражения (IV. 10) является кинетической энергией, второе — потенциальной и третье характеризует работу сил давления.
Умножив все слагаемые уравнения (IV. 10) на величину плотности, получим интеграл Бернулли в виде суммы слагаемых, имеющих размерность давления,
-ф? + 2 + р = С = р0.	(IV.11)
где р — пьезометрический напор; --------скоростной или дина-
мический напор; yz — геометрический напор; р0 — полный напор.
В соответствии с уравнением (IV. 11) сумма динамического, пьезометрического и геометрического напоров во всей области потенциального потока остается величиной постоянной.
Разделив обе части уравнения (IV. 11) на g, получим уравнение Бернулли в виде
£ + г + Х=С.	(IV.12)
размер-— пьезо-
Каждый член, входящий в уравнение (IV. 12), имеет j/a	р
ность длины. Величину называют динамической, -у-метрической и г — геометрической высотами. Из уравнения (IV. 12) видно, что сумма этих высот во всей области потенциального потока остается величиной постоянной.
При отсутствии массовых сил интеграл Бернулли запишется
в виде
4 р
или
-^ + Р = с.
Если в уравнении (IV. 11) скорость V будем считать равной нулю, то получим интеграл уравнения Эйлера для случая гидростатического равновесия жидкости р + yz = const.
§ 5. Интеграл Бернулли для линии тока
Для того чтобы проинтегрировать уравнение Эйлера (IV.3) вдоль линии тока при вихревом движении, проделаем некоторые преобразования.
92	Уравнения движения идеальной жидкости
Умножив скалярно уравнения Эйлера (IV.3) на элементарное перемещение жидкой частицы Vdt, получим
^-.Vdt = F-Vdt — -J-gradp-m dt	р °- r
или для стационарного движения
d^-(Xdx + Ydy + Zdz) + ±(^dx + ^dy + ^dz)=O.
Допуская, что массовые силы имеют потенциал, т. е.
v___ дФ . v_____ дФ 7_______ дФ
— л ,	*	1	-> И	,
дх	ду	дг
и так как dx -Y -- dy -Y ~ dz есть полный дифференциал dp, окончательно уравнение (IV.3) имеет вид:
d(4-V2 + O + f)=0.	(IV. 15)
Это уравнение можно легко проинтегрировать. Интегралом будет
^+Ф + Д = С,	(IV.16)
или, имея в виду выражение потенциала сил тяжести, приведенное в § 4, запишем
Выражение (IV. 16) называется интегралом или уравнением Бернулли для линии тока.
Это уравнение получено при отсутствии предположения о потенциальности потока. Уравнение (IV. 16) тождественно уравнению Бернулли для потенциального потока. Различие состоит в том, что при потенциальном потоке постоянная С сохраняет значение для всей области потока, а при вихревом потоке каждая линия тока имеет свое значение постоянной С. Если все линии тока начинаются в области,' в которой жидкость покоится или движется равномерно и прямолинейно, постоянная С будет одинакова для всех линий тока. В случае вихревого движения постоянная С сохраняет свое значение и вдоль вихревой линии.
Все преобразования уравнения Бернулли и названия слагаемых, приведенные в предыдущем параграфе для потенциального потока, полностью относятся и к уравнению Бернулли для вихревого движения.
Теорема Томсона
93
§, 6. Теорема Томсона
Рассмотрим здесь некоторые вопросы, связанные с динамикой вихрей в идеальной жидкости. Докажем прежде всего теорему Томсона, имеющую большое значение в динамике идеальной жидкости. Она гласит: если массовые силы имеют однозначный потенциал и идеальная жидкость баротропна, то циркуляция скорости по замкнутому жидкому контуру будет постоянна во все время движения.
Движение жидкости будем называть баротропным, если плотность жидкости является функцией одного давления. В частности, движение воздуха или другого газа можно считать баротропным, если изменение его состояния происходит изотермически или адиабатически.
В первом случае температура постоянна и давление зависит только от плотности, а во втором — приток и убыль тепла отсутствуют и плотность можно также однозначно связать с давлением Р = f (₽)•
Рассматривая неустановившееся движение, представим слагаемые левой части уравнения Эйлера (IV. 14) в виде:
dx=~- (и dx) — и-^г (dx) — -£r(u dx) —
— ud(Y= -4- (u dx) — и du =— (u dx) — d(;
\ dt J dt '	1	dt x	1	\ 2 )
dv j d/j\	j / u2 \
dw . d ,	, / w2 \
-drdZz=z-di^d^-d\-r)-
Уравнение (IV. 14) при наличии потенциала массовых сил запишем в следующем виде:
—(udx -]-vdy -|- wdz) —	•
Так как выражение в скобках, согласно выражению (11.10), есть циркуляция по элементу дуги жидкого контура, то
J-dT = d^-=d(^ — (D—P\,	(IV.17)
dt	dt \ 2	j	'	'
где
р р= Г-^.
J р
Р9
94
Уравнения движения идеальной жидкости
Интегрируя уравнение (IV. 17) по всей длине замкнутого контура, получим
£ = (^_Ф_р)л-(4-ф_р)д1=о, (iv.i8)
так какщнтеграл по замкнутому контуру от правой части в силу однозначности величин, заключенных в скобки, равен нулю.
Из теоремы Томсона можно сделать два важных вывода. Первый — если в какой-либо части движущейся или неподвижной идеальной баротропной жидкости в некоторый момент времени циркуляция по замкнутому контуру равна нулю, то она остается равной нулю и в последующие моменты времени, или иначе — если движение было безвихревым, то и в последующие моменты времени оно останется безвихревым. Это положение часто называется теоремой Лагранжа.
Второй вывод — так как, согласно теореме Стокса, интенсивность вихревой трубки определяется циркуляцией скорости по контуру, окружающему вихревую трубку, то очевидно, что интенсивность вихревой трубки не изменяется с течением времени. Последнее следствие известно в гидромеханике как третья теорема Гельмгольца.
Следовательно, по теореме Томсона вихрь существует вечно. Он не может возникнуть и не может исчезнуть в идеальной и баротропной жидкости. В действительности из-за наличия вязкости жидкости или нарушения баротропности (например, зависимость плотности атмосферы от температуры, влажности и пр.) вихри возникают и вырождаются, т. е. теорема Томсона не верна. Несмотря на это, теорема Томсона и теоремы Гельмгольца о вихрях имеют большое значение для решения многих практических задач.
Для примера рассмотрим схему, объясняющую причину появления циркуляции, а следовательно, согласно теореме Н. Е. Жуковского, и возникновения подъемной силы на крыле самолета или на лопасти турбомашины.
Пусть крыло в некоторый момент времени начинает свое движение. До начала движения крыло находилось в состоянии покоя и, следовательно, циркуляция вокруг него равнялась нулю, но по теореме Томсона она должна остаться равной нулю в течение всего времени движения крыла. В действительности при полете самолета циркуляция вокруг крыла всегда существует так же, как и вокруг лопатки работающей турбины.
Совмещение двух как будто бы противоречивых явлений объясняется следующим образом: в начале движения крыла на верхней и нижней поверхностях возникают различные скорости, в результате чего на задней кромке образуется поверхность разрыва скоростей, которая приведет к появлению начального вихря (рис. IV. 1, а). Этот вихрь, интенсивность которого определяется
Основные понятия и уравнения
95
некоторым значением циркуляции, отрывается от крыла и остается на месте. Согласно теореме Томсона, на крыле должен остаться вихрь с циркуляцией, равной циркуляции сошедшего с крыла вихря, но противоположной по знаку (рис. IV. 1, б).
Рис. IV. 1
Таким образом, если взять контур, охватывающий положение крыла до начала движения и его положение в данный момент времени, то суммарная циркуляция по этому контуру во все время движения должна быть равна нулю. Циркуляция же «на крыле» может быть сколь угодно большой, но равной по величине и противоположной по знаку циркуляции в следе за крылом. Такая схема верна лишь для крыла бесконечного размаха.
ГЛАВ А V
ОДНОМЕРНОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ (ЭЛЕМЕНТЫ ГИДРАВЛИКИ)
§ 1. Основные понятия и уравнения
Одномерным будем называть движение, при котором скорость, давление, плотность, температура и другие параметры зависят от одной координаты, направление которой совпадает с направлением вектора скорости.
В действительности одномерного движения не существует, но при движении жидкостей и газов в трубопроводах и элементах проточной части машин и сооружений с большими скоростями, а точнее с большими числами Рейнольдса, максимальная скорость в любом поперечном сечении потока, как правило, мало отличается от средней скорости. Поэтому приближенно в этих случаях движение можно рассматривать как одномерное с некоторой средней по сечению скоростью. Если параметры одномерного движения пе зависят от времени, движение является стационарным, если зависят — нестационарным.
Введение понятия одномерного движения позволяет упрощенно решать многие задачи. Таким представлением движения широко
Sg Одномерное движение- несжимаемой жидкости (элементы гидравлики)
пользуются в гидравлике. Поэтому некоторые ученые называют гидравлику наукой об одномерном движении. Еще Л. Праидтль указывал, что «. . .совокупность задач о движении жидкости, рассматриваемых путем одномерного представления, принято называть гидравликой. Задачи же, рассматриваемые путем трехмерного или двухмерного представления, составляют предмет гидродинамики».
В настоящей главе рассмотрим одномерное движение несжимаемых жидкостей, т. е. собственно жидкостей, а также и газов, но при скоростях движения малых по сравнению с соответствующими скоростями звука.
Основными уравнениями одномерного движения несжимаемых жидкостей являются уравнение сохранения массы, уравне? ние импульса, моментов
импульсов и уравнение энергии, или уравнение Бернулли.
Для вывода первого уравнения рассмотрим движение жидкости в трубке тока (рис. V.1). Как известно, через боковую поверхность трубки тока жидкость не перетекает, и поэтому масса жидкости, а при постоянной плотности и объемный расход по длине трубки остаются постоянными
pViS, = pV2s2, или
V jSj = V 2s2.
Это уравнение и есть уравнение сохранения массы или уравнение неразрывности движения для трубки тока.
В соответствии с последним уравнением скорость в поперечном сечении трубки обратно пропорциональна площади поперечного сечения. Из анализа размерности видно, что
pVs=m [-^J ;

(V.l)
Таким образом, в первом случае секундная масса жидкости, а во втором — объем в единицу времени остаются постоянными по всей длине трубки тока.
Если весь поток разделим на трубки тока, то в местах потока, где скорости больше, поперечные сечения трубок тока будут меньше и, следовательно, трубки будут расположены гуще, а в ме-
Основные понятия и уравнения
стах с малыми скоростями — наоборот. Продифференцировав равенство (V.1), получим
1 dV	1 ds _n
V dx -г s dx ~
В случае постоянной площади поперечного сечения трубки тока и, в частности, для одномерного движения в цилиндрической трубке будем иметь
dV п	,
—— = 0 и V = const.
dx
Если скорость зависит не только от координаты, но и от времени, то уравнение неразрывности движения в дифференциальном виде будет
V dt ' V дх ' s dx
Вторым основным уравнением одномерного движения является уравнение изменения количества движения для трубки тока. Применим к трубке тока известную в механике теорему о том, что изменение главного вектора количества движения К во времени равно результирующей всех внешних сил, приложенных к рассма-
триваемому объему — R.
Рассмотрим движение жидкости в трубке тока с меняющейся по длине площадью поперечного сечения (рис. V. 1). Проведем поперечные сечения 1—1 с площадью Sj и 2—2 с площадью s2. Пусть средние скорости в соответствующих сечениях будут Vi и V2.
Вычислим изменение количества движения или импульса выделенного объема за время dt. Очевидно, за время dt частицы жидкого объема переместятся, заняв в трубке тока пространство между сечениями Г—Г и 2'—2'. Если движение стационарно, то между сечениями 1—1 и 2—2 объем жидкости и импульс останутся теми же, что и прежде. Изменение импульса произойдет лишь за счет потерь импульса между сечениями 1—1 и Г—Г и увеличения его между сечениями 2—2 и 2'—2'.
Следовательно, изменение вектора импульса dK за время dt будет
~dR = р$!VjVi dt — ps2V2V2 dt, или
7 И. Л. Повх
98 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Таким образом, в соответствии с теоремой об изменении импульса окончательно получим
d^ — m(VL— V2) = R или mVr — mV2 — R.
Теорема об изменении импульса для трубки тока при стационарном течении может быть сформулирована следующим образом. Разность векторов импульса жидкости, входящей и выходящей из некоторого выделенного объема трубки тока в единицу времени, равна главному вектору внешних сил, приложенных к этому объему.
Доказательство этой теоремы становится еще проще при использовании теоремы об изменении импульса, полученной для сплошных сред.
В соответствие с этой теоремой
J VpVnds = R. S
Для трубки тока этот интеграл, по боковым поверхностям образующийся в нуль, примет вид
\vipVlnds — \v2pV2nds = R. s,	s2
Так как при одномерном движении все параметры потока не меняются в поперечном сечении трубки тока, т. е. их можно вынести за знак интеграла, то
Pl^lnSl = P2^2nS2 = окончательно получим прежнее выражение CV1—V2)m = R.
Теорема моментов импульсов гласит, что производная по времени от главного момента импульса некоторой массы относительно какой-либо точки равна главному моменту относительно той же точки всех внешних сил, приложенных к массе.
Применим эту теорему к трубке тока, образованной межлопаточным каналом колеса турбины (рис. V.2).
Если секундная масса воды т' втекает в канал с абсолютной скоростью во входном сечении, расположенном на расстоянии от оси, то секундный момент импульса жидкости, входящей в межлопаточный канал, относительно оси О будет равен
m'V-f! cos
Обозначая радиус, угол и скорость в выходном сечении канала
Основные понятия и уравнения	99
соответствующими буквами с индексом 2, получим в выходном сечепии
/п'У2г2 cos р2.
Следовательно, на колесо, согласно теореме о моменте импульса, будет действовать момент, равный разности моментов импульса на входе и на выходе из межлопаточного канала, т. е.
| М' | = т' (VVi cos Рх — V2r2 cos Р2)-
Величина суммарного вращающего момента,’передаваемого водой турбине, будет равна
| М | = т (ViTj cos Pj — V2r2 cos p2),	(V.3)
где tn — суммарная секундная масса воды, протекающей через все межлопаточные каналы колеса турбины.
Уравнение (V.3) часто называют турбинным уравнением, или уравнением Эйлера для турбин. Это уравнение получено в предположении, что скорости на входе и выходе постоянны, а в* меж-лопаточпом канале скорость в каждом сечении зависит только от площади этого сечения. Такое допущение весьма приближенно отражает действительную картину потока.
Уравнение (V.3) можно применить для анализа движения в неподвижной спиральной камере. Пусть в спиральной камере (рис. V.3) поток входит в капал с поперечным сечением А—А и после вращения по спирали (показано штриховой линией) выходит из центрального отверстия неподвижной камеры. Если через р обозначить углы между вектором скорости и нормалью к радиусу, то из-за малости этого угла cos р 1, и условие (V.3) примет вид
7*
М = (Vxz-x — У2г2) т.
100 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Так как жидкость идеальна, то момент внешних сил относительно центра можно считать равным нулю; тогда окончательно получим
IVi = Vzrz = Vr = const.
Далее будет показано, что такое вращательное движение жидкости будет безвихревым движением.
Главная особенность теоремы импульса при установившемся движении сплошных сред заключается в том, что ее применение к некоторому объему, ограниченному контрольной поверхностью, не требует знания того, что происходит внутри выбранного объема. Все изменения определяются переносом импульса через контрольную поверхность.
Третьим основным уравнением является уравнение сохранения энергии, или уравнение Бернулли для трубки тока. В предыдущей главе уравнение Бернулли для линии тока было получено интегрированием дифференциального уравнения движения.
Используя закон сохранения энергии, приведем для одномерного движения вывод .уравнения Бернулли для трубки тока.
Выделим участок трубки тока, расположенный между сечениями 1—1 и 2—2 (рис. V.1). Определим количество энергии, перенесенной за время dt через эту трубку.
Считая скорость движения в поперечном сечении трубки постоянной, можно видеть, что за время dt жидкость из первого сечения переместится в сечение Г—1' на расстояние V±dt, а из селения 2—2 в сечение 2'—2' на расстояние V2dt. Массы вошедшей и вышедшей жидкости будут одинаковы и равны
— т dt.
Энергия потока, прошедшего через сечение 1—1 за время dt, будет складываться из следующих составляющих:
1)	кинетической энергии массы т dt, движущейся со скоростью
эта энергия равна —1 dt',
2)	потенциальной энергии давления, равной произведению силы давления ptst на перемещение Vidt, т. е.
dt = pSjVj dt = т dt\
3)	потенциальной энергии веса жидкости, определяемой относительно условно выбранной плоскости отсчета. Если обозначим расстояние от плоскости отсчета до центра тяжести сечения 1—1 через z, то располагаемая потенциальная энергия будет равна произведению веса жидкости gmdt на высоту zlt т. е. gmz^dt.
Истечение из отверстия
101
Следовательно, полная энергия потока, прошедшего через сечение 1—1, равна сумме
—Y~dt + mdt 4- gtnzx dt.
Для энергии потока, прошедшего через сечение 2—2 за время dt, аналогичным образом получим
dt ~ mdt 4- gmz2 dt.
Если жидкость идеальна, то никаких потерь в трубке тока не должно быть и полная энергия на входе и выходе должны быть равны между собой. Разделив полученные выражения на gmdt, окончательно получим уравнение Бернулли для несжимаемой жидкости
-g- + 4 + ^=-g- + f+ ^..	(V.4)
Так как сечения трубки тока были выбраны произвольно, то полная энергия, выраженная тремя составляющими: динамической „ V2	„	„ р	„
высотой , пьезометрической высотой -у и высотой уровня г, остается величиной постоянной по всей длине трубки тока.
Если жидкость не идеальная, то на участке от сечения 1—1 до другого произвольного сечения имеются потери энергии, и уравнение Бернулли принимает вид
V2 , о, , V% , р2 ,	, .
о-14- — 4- Zi = -Н- 4- — 4- z2 4- Дг, 2g у 1 2g 1 -у 1 2 1
(V.5)
где Дг — потери энергии, отнесенные к единице массы.
Величина потерь Дг для заданного потока будет зависеть от расстояния между выбранными сечениями. Она будет тем больше, чем длиннее выбранный участок.
§ 2. Истечение из отверстия
Рассмотрим задачу об истечении жидкости из сосуда через малое круглое отверстие, расположенное в днище сосуда (рис. V.4). Будем считать, что диаметр отверстия мал по сравнению с диаметром сосуда и высотой столба жидкости h.
Если отверстие выполнено в центре дна, то жидкость подтекает к нему со всех сторон одинаково, т. е. трубки тока внутри сосуда будут, как видно из рис. V.4, приближаясь к отверстию, сужаться. Струйка, пройдя плоскость отверстия, постепенно уменьшает свое поперечное сечение и лишь на некотором определенном расстоянии от стенки становится цилиндрической.
102 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Наиболее узкого поперечного сечения струйка достигает на расстоянии I, равном примерно половине диаметра отверстия. Сжатие поперечного сечения струи при истечении жидкости из отверстия происходит потому, что жидкость внутри сосуда притекает к отверстию в радиальном направлении и, достигнув края отверстия, не может внезапно изменить своего направления. Величина этого сжатия, определенная как отношение площади
поперечного сечения струи в наиболее узком ее сечении se к площади отверстия s, называется коэффициентом сжатия
Величина коэффициента сжатия, всегда меньшая единицы, определяется экспериментально. Численное значение коэффициента зависит прежде всего от формы сечения отверстия, места его расположения относительно стенок сосуда, величины критерия подобия Рейнольдса и др.
На рис. V.5 приведены четыре формы отверстий.’ Наибольшее значение коэффициента сжатия, близкое к единице, имеет йослед-нее по порядку отверстие с закруглениями по линиям тока и наименьшее— первое по порядку отверстие с острыми кромками внутри сосуда. В последнем случае величина е достигает значения 0,6.
Для определения скорости истечения из сосуда будем считать жидкость идеальной и применим уравнение Бернулли для трубки тока между сечениями 0—0 и 1—1 (рис. V.4) в самом узком месте струйки. Тогда уравнение будет иметь вид
I/2	у2
До । 7 । Ро _ Д1 । z _i_ Р»
2g г о Г т	I 1 । у
Истечение из отверстия
103
Предполагая, как указывалось ранее, что поперечное сечение отверстия очень мало по сравнению с площадью сосуда s0, можно положить Vo = 0. тогда скорость истечения будет
V1 = Узфо-^ + С7^)] • (V.6)
Считая ро = Р1 = ратм (Ратм— атмосферное давление) и производя отсчет уровня от плоскости сравнения (сечение 1—/), т. е. Z! = 0, az0 = й, окончательно получим величину скорости истечения
V, = /Ж	(V.7)
Эта формула, часто называемая формулой Торичелли, показывает, что скорость истечения идеальной жидкости не зависит от физических свойств жидкости и определяется лишь высотой столба h.
В действительности скорость истечения жидкости будет зависеть, как указывалось ранее, от геометрических характеристик отверстия, его расположения на стенке, числа Re. Поэтому в формулу Торичелли обычно вводится поправка, называемая коэффициентом скорости ср. При учете указанной поправки скорость истечения будет = cp]/2g/i.
Величина ср в общем виде как функция числа Рейнольдса может быть представлена ср = ср (Re). Ее величина изменяется в пределах 0,94—0,99. Таблицы значений ср можно найти в гидравлических справочниках.
Так как в практике представляют большой интерес не скорости, а объемные расходы жидкостей, вытекающих из сосуда, формула для расхода легко может быть получена в виде
Q = IZ1sc = cpes]/2g/z,
если pr Ро (сосуд с крышкой), то
Q = cpes 2g (h 4- Ро~Р1-) = <p8S V2gH, (V.9)
где H = h + Рь-Р'-.
У
Обычно произведение двух коэффициентов заменяют одним коэффициентом р, т. е. сре = р, называемым коэффициентом расхода.
Существует много эмпирических формул для определения коэффициентов расхода в зависимости от числа Re. Большинство из них имеют вид
р — а
I^Re
где а и В — постоянные.
104 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Для Re 106 а — 0,584-0,59 и В = 0,89. Число Re равно
R 4/^77 V где v — коэффициент кинематической вязкости; d — диаметр отверстия.
При числах Re > 105 можно считать все коэффициенты независящими от Re. Эту область чисел Re обычно называют квадратичной. Для характеристики потерь энергии при истечении жидкости пользуются понятием к. п. д. отверстия, определяемого
как отношение удельной кинетической энергии струи в узком сечении к напору h. Тогда из формулы (V.8) следует, что к. п. д. равен
Не рассматривая истечение тяжелой жидкости из насадков типа пожарных стволов и насадков гидромониторов, дадим краткую характеристику насадков, используемых для опорожнения сосудов. В качестве таких насадков применяют цилиндрические, сходящиеся и расходящиеся насадки. На рис. V.6 показаны типы цилиндрических насадков. Первые два (а и б) называются внешними, а, вторые (в и е) — внутренними цилиндрическими насадками. Течение в относительно длинных насадках (длина более 3—4 диаметров) при небольших напорах происходит так, как показано на рис. V.6, а ив. В этом случае, хотя и существует суженное сечение потока, истечение происходит при полном заполнении всего поперечного сечения насадка, т. е. коэффициент сжатия такого насадка е = 1.
Истечение, показанное на рис. V.6, б и г, происходит в коротких насадках при больших напорах. При этом струя пролетает насадок,
Истечение из отверстия
105
не касаясь его стенок, и коэффициент сжатия будет таким же, как и в тонкой стенке без насадка (е 0,62).
В качестве насадков применяются сужающиеся и расширяющиеся трубки. На рис. V.7 показаны три типа Насадков. Первые два: коиоидальный (рис. V.7, а) и конический (рис. V.7, б) сходя-
щиеся насадки, для которых коэффициент сужения равен единице, а коэффициент скорости близок к единице для коно-идальпых и значительно меньше (0,8—0,9) для конических сходящихся насадков. Течение жидкости в расходящихся насадках (рис. V.7, в) значительно отличается от одномерного. Оно будет рассмотрено в главе, посвященной движению в диффузорах.
Основные характеристики различных видов отверстий дл'я истечения тяжелой жидкости из сосудов приведены в табл. V.I.
Из табл. V.1 видно, что наи
лучшим по расходу и к. п. д.
является коиоидальный насадок. В относительно больших отверстиях, расположенных в вертикальной стенде, плоскость сравнения, от которой производится отсчет высоты напора, проводится
через центр тяжести поперечного сечения отверстия.
Таблица V.1
Форма отверстий	расхода ц	Коэффициент полезного действия <р*	сжатия 8
Круглое отверстие в тонкой стенке	0,625	0,93	0,6—0,7
Внешний цилиндрический иасадок	0,82	0,67	0,6—1,0
Внутренний цилиндрический насадок	0,71	0,50	0,6—1,0
Конический сходящийся насадок с углом 12°	0,94	0,91	0,99
Коиоидальный насадок	0,98	0,96	1,0
106 Одномерное движение несжимаемой жидкости (элементы гидравлики)
§ 3. Интеграл Бернулли для неустановившегося движения
Если в уравнении (IV. 14) не отбрасывать слагаемые, содержа-’ щие частные производные от проекции скоростей по времени, т. е. считать, что движение неустановившееся, то уравнение Бернулли для линии тока примет вид
I.
+	const,	(V.10)
о
где I—расстояние вдоль линии тока от начального сечения. Уравнение (V.10) пригодно и для трубки тока, если считать, что скорость постоянна в каждом поперечном сечении трубки и зависит только от I, изменяясь от се- чения к сечению. Если трубка тока будет иметь постоянное сечение по всей длине, то скорость не будет
fi
' h 
Л
А ________________1о
Рис. V.8
зависеть от' координат, и уравнение примет вид
+-у-+ -^-7 = const,	(V.11)
где V — функция только времени.
Полученное выше уравнение можно использовать для изучения нестационарных движений жидкости в цилиндрических трубах.
I В качестве примера рассмотрим истечение жидкости из сосуда через трубу длиной /0 (рис. V.8) в начальный момент движения. Применим уравнение (V.11) жк горизонтальному участку трубы .длиной /0. Тогда для сечения —А, проведенного внутри бака (при t = 0), уравнение (V.11) примет вид
р 1	2 “С-
Это же уравнение для некоторого сечения на расстоянии I от сечения А—А будет
р '2	1 dt
Интеграл Бернулли для неустановившегося движения 107
Приравняем левые части двух последних уравнений. Считаем, что Va <£ поэтому величиной Va можем пренебречь. Используя уравнение гидростатики для рА
Ра = Ро+ gph, получим
Р	}	V2	I	dV	I— Ро	\ „и
р	'	2	'	dt	р	Г £«•
Отсюда разность между давлением в любом сечении трубы р и давлением атмосферным р0 будет равна
p-p0=gh-(~ + ~l).	(V.12)
Если формулу (V.12) написать для сечения в конце трубы, где I = 10 и р = р0, то получится
=	(V..3)
Отсюда видно, что в начальный момент при наибольшем зна-чейии скорость V = 0, а при установившемся движении, когда
= 0, скорость Vi = V"2gh. Наибольшее значение производной, согласно выражению (V.13), равно
dV	h
dt	l0 '
Таким образом, в начальной стадии истечения скорость изменяется от нуля до постоянного значения, равного V = V 2gh, а ускорение— от наибольшего значения до нуля. Величина наибольшего ускорения пропорциональна напору и обратно пропорциональна длине трубопровода. Следовательно, чем длиннее трубопровод, тем меньше величина наибольшего ускорения.
Для грубой оценки времени, необходимого для перехода к приблизительно установившемуся движению, можно считать, что наибольшее ускорение остается постоянным до перехода к установившемуся движению, т. е. будем определять ускорение как частное от деления наибольшей скорости на время установления движения
dV _ п h _ Vi V^h dt ~ & l0 ~ T ~ T ’
откуда
'p__ EjZo _~i/~ 2 . _ ~i/~ 2 l0
gh — V gh V g //Г’
108 Одномерное движение несжимаемой жидкости (элементы гидравлики)
т. е. время установления обратно пропорционально ускорению или прямо пропорционально длине трубопровода и обратно пропорционально квадратному корню из величины напора.
§ 4. Внезапное расширение и сжатие потоков. Потери энергии
Когда поток жидкости, текущей в круглой цилиндрической трубе со скоростью Vlt внезапно переходит, как показано на рис. V.9, а, в цилиндрическую трубу со значительно большим диаметром, то образуется струя, постепенно заполняющая все поперечное сечение большей трубы. При этом на некотором рас-
Рис. V.9
стоянии устанавливается поток с некоторой скоростью V2, меньшей, чем скорость V],. Давление р2 в сечении 2—2 (рис.^У.Э, а) будет больше, чем давление рг в сечении 1—1.
При этом изменение давления произойдет по двум причинам. Во-первых, из-за увеличения поперечного сечения. Это изменение произойдет как в идеальной, так и в вязкой жидкости. Во-вторых, при внезапном расширении вязкой жидкости часть энергии будет потеряна на интенсивное перемешивание жидкости.
Для нахождения разности давлений в сечениях 1—1 и 2—2 воспользуемся уравнением импульса, который в сечении 1—1 равен
Ki = pVisi> а в сечении 2—2
Кч — рИ^г-
Изменение импульса в контрольном объеме между сечениями 1—1 и 2—2 должно равняться внешней силе, приложенной к данному объему. Внешняя сила равна разности давлений, умноженной на площадь поперечного сечения s2,
psiVi— PS2V2 = (р2— pi) s2.
Имея в виду, что масса жидкости остается постоянной
Р31У1 = ps2IZ2,
Внезапное расширение и сжатие потоков. Потери энергии
109
и сокращая на величину площади поперечного сечения s, получим
Р2-Р1 = pVHV,-V2).	(V.14)
Если внезапное расширение происходило бы без потерь энергии н часть кинетической энергии превращалось бы в потенциальную энергию давления, то изменение давления можно определить по уравнению Бернулли для идеальной жидкости
Р2—pi =-|-(И—vi).	(V.15)
Следовательно, изменение давления, происшедшее из-за потерь энергии, т. е. необратимое превращение механической энергии в тепловую, будет равно разности выражений (V. 15) и (V.14)
Др — р' — р2 = _1_ р	_ у2)2.
По такой же формуле в теоретической механике определяется потеря кинетической энергии при неупругом ударе твердых тел. Поэтому потери давления при внезапном расширении обычно называют потерями давления на удар. В действительности при этом никакого удара не происходит. В гидравлике эта формула часто называется формулой Борда.
Для установления закономерностей в гидромеханике необходимо знать не абсолютное значение потерь давления, а безразмерные коэффициенты, характеризующие потери. Так как внезапное расширение происходит на очень коротком участке, то потери энергии, происходящие при этом, называются местными потерями.
При внезапном расширении потери могут быть выражены в долях кинетической энергии жидкости в трубе с малым диаметром или в долях кинетической энергии в трубе с большим диаметром, т. е.
Л -Г pV> — Г pV2
Др —	2 — ^2 2
Очевидно, что численные значения коэффициентов £ и £2 будут различны.
Если формулу Борда представить в виде
то, принимая во внимание, что SjIZj = з2У2, получим коэффи-центы потерь при внезапном расширении
-4У-.
ПО Одномерное движение несжимаемой жидкости (элементы гидравлики)
В табл. V.2 приведены численные значения коэффициентов
и £, в зависимости от степени расширения п = —. Из таблицы "	.	si
следует, что для одних и тех же потерь давления численные значения коэффициентов потерь могут быть весьма различны. Поэтому при использовании коэффициентов потерь необходимо
Таблица V.2
п	ъ	
1	0	0
2	0,25	1
5	0,64	16
10	0,81	81
100	0,9801	9801
сю	1	сю
обращать внимание на то, к какой кинетической энергии относят данный коэффициент.
При истечении жидкости в сосуд с неограниченной емкостью (га —» ©о) коэффициент = 1, т. е. при этом теряется кинетическая энергия на входе. ,
Результаты опытов свидетельствуют о применимости формулы Борда для расчета потерь давления при внезапном расширении. Получить теоретическую формулу при внезапном сужении потока, аналогичную формуле Борда, не представляется возможным, так как природа по
терь в этом случае принципиально отлична
от потерь при внезапном расширении, а сама величина потерь значительно меньше, чем в первом случае.
Классическим примером сужения потоков является рассмотренное ранее истечение из сосуда. При этом, как хорошо видно из рис. V.9, б, главной особенностью является сужение потока за острой входной кромкой до некоторого поперечного сечения s и последующее затем его расширение до полного поперечного сечения трубы Sj.
При сжатии потоков, так же как и при расширении, можно пользоваться двумя коэффициентами потерь
Др=С1’
pvl
2
, рИ
>2 2
Потери и коэффициенты потерь можно представить в виде суммы: потери при сужении до поперечного сечения $0 и потери на расширение потока от з0 до Для коэффициента потерь
С>1 ^1сж Н~ С1расш*
Следует отметить, что по величине потери на расширение значительно превосходят потери на сжатие.
Интересно сравнить потери при внезапном расширении с соответствующими (при одинаковом соотношении площадей) потерями при внезапном сжатии. Первые подсчитаны по формуле Борда, а вторые получены из эксперимента. В табл. V.3 приведены коэф-
Дроссельные расходомеры. Трубка Вентури
111
фпциснты потерь, отнесенные к скоростному напору в широком сечении.
Коэффициент потерь при внезапном сжатии с учетом потерь при последующем расширении, а также коэффициент потерь ?еж> учитывающий потери только при сжатии, получены из эксперимента для турбулентных потоков при Re — 105.
Таблица V.3
s2	£2 при расширении	^2 при сжатии и расширении	Ьсж при одном сжати и
1	0	0	0
0,8	0,04	0,09	0,02
0,6	0,16	0,20	0,02
0,4	0,36 ‘	0,28 '	0,02
0,2	0,64	0,35	0,02
0,1	0,81	0,3'9	0,02
0,01	0,98	0,45	0,02
Если по направлению движения провести ось х (рис. V.9), то как при внезапном расширении, так и при внезапном сжатии скорость изменяется не скачкообразно, а постепенно. При расширении величина скорости убывает и, следовательно, производная от скорости по х отрицательна, а от давления — положительна, т. е.
dV , п dp п -т—<0 и -^>0, dx	Цх
а при сжатии
dV n dp п -j— >0 и -у- < 0.
dx	dx
Из вышеизложенного видно, что потери энергии при убывании скорости потока значительно больше потерь, имеющих место при увеличении скорости вдоль потока.
Этот вывод относится и к неодномерным потокам с постепенным расширением (диффузор) и сжатием (конфузор).
§ 5. Дроссельные расходомеры. Трубка Вентури
Если на некотором участке трубопровода от выбранного сечения 1—1 до сечения 2—2 происходит изменение площади поперечного сечения от sx до s2 и имеется некоторое местное сопротивление,
112 Одномерное движение несжимаемой жидкости (элементы гидравлики)
то уравнение Бернулли для этого участка примет вид pV?	pVo
откуда
рИ>	Р^
Pi Рч — 2~ (1 + Сг) 2~ •
Пользуясь получим
законом неразрывности движения
V2s2,
(V.16)
откуда средняя скорость потока в сечении 1—1 будет
у^ ____________J__________ j/~ 2(Р1 —Рг) _ j/~ 2(Р1—Рг)
Г	s2 -|"2	* Р	Р
S4
и соответственно объемный расход жидкости определится по формуле
Vxsx = psx ]/ 2(Pt ~р*> 3= pS1 VTg	(V.17)
Таким образом, любая разность давлений, -возникающая на некотором участке трубопровода, может быть использована для вычисления расхода жидкости в трубопроводе. Практически измерять достаточно точно любую разность давлений не всегда возможно. Поэтому надо, чтобы в диапазоне измеряемых расходов разность давлений на выбранном участке была бы настолько велика, чтобы ее можно было достаточно точно измерить обычными приборами.
Рассмотрим, от чего зависит величина перепада давления. Из уравнения (V.16) видно, что если £2 = 0 и sx = s2, то при любой большой скорости Рх разность давлений будет равна нулю. Поэтому необходимо, чтобы величина, заключенная в квадратные скобки выражения (V.16), т. е.
(i+e2)4-i=*.
S2
была отличной от нуля и находилась в определенных пределах.
В зависимости от того, каким путем может быть получена необходимая разность давлений, расходомеры могут быть разделены на два типа. В одних разность давлений создается местным сопро-
Дроссельные расходомеры. Трубка Вентури
113
тивлеипем, а в других — только изменением поперечного сечения трубопровода. Конечно, могут существовать расходомеры, в которых поперечное сечение изменяется и коэффициент местного сопротивления довольно велик.
При sx = s2 величина h может быть значительной лишь при достаточно большом коэффициенте потерь £2, в то время как при Si s2 это условие сохраняется и при отсутствии потерь, когда
=: О-
В цилиндрической трубе = s2, следовательно, разность давлений получается достаточной Только при значительной величине коэффициента сопротивления t2, чего можно достигнуть установкой в трубопроводе специального приспособления, увеличивающего местное сопротивление.
Процесс понижения давления в потоке жидкости называется дросселированием потока. Любое дроссельное устройство (колено, задвижка с фиксированным открытием и пр.) можно использовать для измерения расхода.
Проще всего пользоваться дроссельными устройствами, в которых в измеряемом диапазоне расходов величина коэффициента потерь £2 не зависит от скорости потока или, точнее, от числе Re Re — Zil = _
v nd
~v
где d — диаметр трубопровода.
Следовательно, во всем интервале измеряемых расходов коэффициент расхода дроссельного расходомера будет постоянным. Наиболее распространенными дроссельными расходомерами являются диафрагмы (рис. V. 10) и сопла (рис. V. 11).
8 И. Л. Повх
114 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Расходомером, в котором разность давлений создается не за счет дроссельного эффекта, а уменьшением поперечного сечения на измеряемом участке ($! > s2), является трубка Вентури (рис. V.12).
Для всех указанных расходомеров величина расхода определяется по формуле (V.17). Существующие теоретические методы расчета коэффициента расхода не дают возможности учесть всех факторов, влияющих па его величину. Поэтому коэффициент расхода часто определяется экспериментально.
Рис. V. 12
Так как во многих случаях- экспериментальное определение коэффициента расхода затруднено, разработаны нормали иа’из-готовление диафрагм, сопел и трубок Вентури. Коэффициенты расходов указанных приборов, изготовленных и установленных в трубопроводе по нормали Комитета стандартов, мер и измерительных приборов, в зависимости от числа Re приводятся в соответствующих правилах.
Нормальные расходомеры устанавливаются на прямолинейном участке трубопровода так, чтобы до прибора длина трубы была не менее десяти диаметров и за прибором— более пяти диаметров.
Отбор давлений у диафрагм и сопел осуществляется непосредственно у стенок приборов при помощи кольцевых камер через просверленные отверстия. Отбор давлений в трубках Вентури производится через несколько отверстий, просверленных в различных сечениях (рис. V.12).
Как видно из рис. V.11, существуют два обвода нормальных сопел: один для т=	0,45 и другой для т >0,45.
Геометрические характеристики и допуски на изготовление диафрагм и трубок Вентури приведены в соответствующих правилах.
Зависимости коэффициентов расхода от числа Re, определенных для нормальных диафрагм и сопел при различных значениях параметров, показаны на рис. V.13 и V.14. Из кривых, приведенных на рис. V.13 nV. 14, видно, что при некоторых значениях чисел Re,
Дроссельные расходомеры. Трубка Вентури
115
называемых далее предельными, коэффициенты расходов становятся постоянными и при дальнейшем увеличении чисел Re определяются лишь значением параметра т. Кривые зависимости коэффициента расхода от числа Re для трубок Вентури имеют такой же вид, как и для сопел.
Рис. V.13
Потери энергии при установке нормальных расходомеров могут быть оценены отношением постоянного давления к полному перепаду давлений Др. Величины этих потерь в процентах приведены в табл. V.4.
Потери в трубках Вентури составляют лишь небольшую часть общего перепада давлений, в то время как в соплах и особенно в диафрагмах они довольно велики и при т = 0,1 превышают 80% от измеряемого перепада.
Кроме рассмотренных расходомеров, измеряющих расход по разности давлений, в практике
Таблица V.4
m = ~D~	Диафрагма	Сопло	Трубка Вентури
0,1	88	83	14
0,2	78	66	12
0,3	68	52	8
0,4	57	39	7
0,5	46	28	6
0,6	36	—	—
116 Одномерное движение несжимаемой жидкость (элементы гидравлики)
широко применяются объемные расходомеры, механические с вращающимися крыльчатками, электромагнитные и др.
Принцип работы электромагнитных расходомеров будет рассмотрен в гл. XV.
§ 6. Кавитация
При движении жидкости в сужающейся трубе типа трубки Вентури в наиболее узком сечении ее скорость достигает наибольшего значения, а давление будет минимальным. Обозначим наибо-
лее узкое сечение цифрами 2—2 (рис. V. 15), тогда величина давления в соответствии с уравнением Бер- ! нулли будет равна
Рг^Рх —	И).
Давление р2> уменьшаясь с увеличением поджатия, не может обра- 1 щаться в нуль. Предел уменьшений s величины давления р2 зависит прежде всего от того, что течет по трубопро- \ воду: газ или капельная жидкость.
Кипение капельной жидкости (вода, спирт, масло и др.) при заданной температуре может быть получено понижением давления. Давле-.' ние, при котором происходит кипение
рис- уд5	жидкости, называется давлением па-
рообразования рк.
Величину давления парообразования рк д-ля различных жидкостей можно найти в физических справочниках. В качестве примера приведем величину рк для воды:
t, °C.............................. 200	100	40 20 4
Рк, мм рт. ст.................,.	11660 760 55,3 17 4
Из приведенных данных видно, что при температуре 20° С вода закипает при давлении 17 мм рт. ст. Если давление в наиболее узком сечении трубопровода достигнет давления парообразования, то жидкость в этом месте начнет кипеть и в трубе при этом образуются полости, заполненные паром, — каверны.
Закипание жидкости при пониженном давлении, возникающем в результате возрастания скорости потока, и образование в текущей жидкости полостей, заполненных паром или газом, называется кавитацией.
Кавитация
117
Кавитация может происходить во всех капельных жидкостях, в том числе и в жидких металлах. Последнее иногда наблюдается при использовании жидких металлов в качестве теплоносителей па атомных электростанциях.
Если после наиболее узкого сечения (рис. V.15), в котором происходит кавитация, последует расширение трубы, то основная масса жидкости на этом участке будет двигаться в виде свободной струи, окруженной пенообразной смесыб пузырьков пара и жидкости. Далее, ниже по течению, в некоторой точке паровая зона замкнется на стенке, и поток жидкости заполнит все сечение трубы.
На рис. V-15 показано распределение давлений, измеренных на стейке сначала сужающейся и затем расширяющейся трубы. Во всех случаях расход воды остается одинаковым. Давление изменялось на выходе из трубы при помощи дроссельного крана. При достаточно больших противодавлениях (кривые а и б) происходит обычное движение жидкости: в наиболее узком сечении давление достигает минимального значения, а затем вновь восстанавливается. Когда противодавление становится настолько малым, что в наиболее узком сечении наступает кавитация (кривая в), давление не восстанавливается. Дальнейшее понижение противодавления (кривые г и д'), как и следовало ожидать, не вызывая понижения давления в наиболее узком сечении, приводит к расширению области кавитации. При противодавлении, равном давлению парообразования, кавитацией охвачена вся расширяющаяся часть трубы (кривая е).
При отсутствии кавитации в наиболее узком сечении трубы (кривые а и б) изменение противодавления вызывает соответствующее изменение давления по всей длине трубопровода, в том числе и в сужающейся части. При наличии кавитации в горле трубы изменение давления на выходе с трубы (противодавление) распространяется лишь до конца области кавитации и никак не влияет на давление в сужающейся части. Следовательно, область кавитации является как бы запретной зоной, через которую изменение противодавления не может проникнуть в сужающуюся часть трубы.
Кавитация возникает не только при движении жидкости в трубопроводах, но и при внешнем обтекании тел, в частности, на лопастях гребных винтов, рабочих колес гидравлических турбин и насосов. Желательное увеличение скоростей вращения рабочих колес насосов, гидравлических турбин и гребных винтов приводит к тому, что скорости становятся настолько большими, что в некоторой области давление падает до давления парообразования, и возникает кавитация.
Появление кавитации всегда вызывает увеличение сопротивления, т. е. добавочную потерю энергии. Кроме этого, она приводит
118 Одномерное движение несжимаемой жидкости (элементы гидравлики)
к разрушению металла и появлению кавитационных шумов. Последствия кавитации настолько существенны, что обычно при проектировании насосов, турбин и винтов лопасти рассчитывают так, чтобы на них не возникала кавитация.
В качестве критерия, определяющего кавитационные свойства профилей, применяют так называемое число кавитации о
2
где р и V — соответственно давление и скорость в набегающем потоке.
Улучшение кавитационных свойств лопастей, т. е. уменьшение кавитационного числа, является одной из важнейших задач коп-
Рис. V.16
структорских бюро по проектированию насосов, турбин и винтов. Очевидно, что на лопастях кавитация возникает в точках, где давление наименьшее, а следовательно, скорость наибольшая. На рис. V. 16, а показана область возникновения кавитации на профиле. •
Кавитационная коррозия металла обычно происходит в местах, где кавитационная каверна замыкается (в точке К, рис. V.16). Природа разрушения металла еще недостаточно изучена, но можно утверждать, что разрушение происходит под действием очень мощных механических ударов пузырьков пара и жидкости, химического воздействия богатого кислородом воздуха, содержащегося в воде, и, как утверждают некоторые авторы, электрических полей, возникающих в каверне.
В результате всего этого воздействия почти все металлы разъедаются, их поверхность приобретает губчатый вид, и лопасти ломаются. Иногда процесс разрушения и поломки лопастей происходит очень быстро.
Шумы, возникающие при появлении кавитации, настолько велики, что они могут служить причиной вибрации отдельных элементов машин, приводящих к неустойчивой работе их и даже разрушению.
На рис. V.16, б показан так называемый суперкавитирующий профиль лопатки корабельного винта. У таких винтов область кавитации не замыкается на поверхности лопасти, а уходит в бес-
_______Гидравлический удар. Распространение малых возмущений	119 конечность. Поэтому они не подвергаются интенсивной кавитационной коррозии. Суперкавитирующие винты применяются на некоторых быстроходных судах.
§ 7. Гидравлический удар.
Распространение малых возмущений
Если при движении воды или другой капельной жидкости в трубопроводе резко изменить скорость течения (закрыть или открыть задвижку, выключить насос и пр.), то в трубопроводе возникает гидравлический удар, вызванный изменением давления. Гидравлический удар иногда вызывает даже разрушение трубопровода. Долгое время гидравлический удар наносил большой вред трубопроводам для воды, нефти и других жидкостей.
Наиболее полное изучение гидравлического удара и мер борьбы с ним было выполнено в 1899 г. Н. Е. Жуковским при изучении работы московского водопровода. Сейчас существует много методов устранения вредного действия гидравлическиого удара.
Однако гидравлический удар может приносить не только вред, но и пользу. На основе этого явления, в частности, создан специальный насос, называемый гидравлическим тараном.
Гидравлический удар можно рассматривать как частный случай одномерного неу стан овившегося движения жидкости.
Физическую картину явлений, возникающих при закрытии задвижки на трубопроводе, можно представить следующим образом. После закрытия задвижки не вся масса жидкости прекращает течение мгновенно. Вначале прекращает движение слой жидкости, непосредственно соприкасающийся с шибером^адвижки; затем последовательно прекращают движение слои жидкости на увеличивающемся со временем расстоянии от задвижки. При этом уплотняется (сжимается) ранее остановившаяся масса жидкости, и в результате повышения давления несколько расширяется труба. Вследствие этих обстоятельств в трубу войдет дополнительный объем жидкости.
Граница области повышенного давления будет распространяться по трубопроводу в направлении, противоположном первоначальному движению жидкости; с течением времени волна повышенного давления достигает начального сечения трубопровода. Если имеется резервуар большой емкости (рис. V.17), так что уровень жидкости в нем можно полагать неизменным, то давление в начальном сечении будет сохраняться примерно постоянным (ре = const). Поэтому при достижении волной давления начального сечения заканчивается первая фаза—фаза распространения повышения Давления в трубе.
Во второй фазе начнется течение жидкости по трубе из зоны более высокого давления в резервуар, а от резервуара к задвижке
1 20 Одномерное движение несжимаемой жидкости (элементы гидравлики)
будет перемещаться волна понижения давления. Вторая фаза заканчивается при достижении волной понижения давления задвижки в трубе. Давление в трубе, понижаясь, не достигает, однако, ве-
личины ре.
В третьей фазе продолжается течение жидкости по трубе в направлении к резервуару; в течение второй и третьей фаз из трубы обратно в резервуар выльется объем жидкости, вошедший в трубу в первой фазе. В третьей фазе поэтому продолжается снижение давления у задвижки, вдоль по трубе в направлении к резер-
вуару распространяется волна понижения давления, при этом по всей длине трубы давление станет меньше ре.
Рис. V. 17
При достижении этой волной начального сечения начнется четвертая фаза, которая сопровождается распространением по трубе волны повышения давления в направлении к задвижке; при этом жидкость вновь потечет в трубу. К концу четвертой фазы в трубопроводе создаются условия течения, близкие к началу первой фазы. Весь процесс повторяется.
В результате в каждом сечении трубы будут возникать колебания давления; вследствие .наличия сопротивления эти колебания будут затухающимй.
При эксплуатации трубопроводов необходимо уметь определять максимальное повышение ударного давления в случае внезапной остановки потока или безопасное время закрытия задвижки, соответствующее предельно допустимому повышению давления.
Это максимальное повышение давления называется гидравли-. ческим ударом.
Гидравлический удар может возникать не только при полном, но и при частичном закрытии заслонки.
Рассмотрим основные характеристики этого явления.
Пусть из некоторого объема (рис. V.17) жидкость движется по трубе длиной I со скоростью Уо. На конце трубопровода имеется задвижка А. Если в момент времени t заслонка Л будет частично прикрыта, то скорость протекания воды уменьшится и станет равной V = Го— ДР. Это уменьшение скорости в первый момент
Гидравлический удар. Распространение малых возмущений	121
времени произойдет лишь в непосредственной близости у заслонки и затем будет постепенно и непрерывно распространяться по трубопроводу.
В некоторый момент это изменение скорости достигнет сечения 1—1, а через весьма малый промежуток времени А/— сечения 2—2. Очевидно, что вместе с изменением скорости будут изменяться и другие параметры потока (давление, плотность и пр.). Пусть давление при этом возрастает на Др и станет равным р +
Ар. Тогда величина плотности также изменится и будет равной р + 'Ар.
Если за очень малый промежуток времени возмущение распространилось от сечения 1—1 до сечения 2—2 на расстояние Ах, то скорость распространения возмущений а, вызванных закрытием заслонки, будет
“=£	(V. 18)
Выразим Ах и А/ через параметры, определяющие величину возмущения. Если обозначим площадь поперечного сечения трубопровода через s, то в момент времени масса жидкости т, находящаяся между сечениями 1—1 и 2—2, равна
т = ps-Ax.	(V.19)
Через время А / эта масса увеличится и станет равной
т + Дт = (р + Ар) s-Ax,	(V.20)
откуда Ат будет определена как разность выражений (V.20) и (V.19)
Am = Aps-Ax.	(V.21)
С другой стороны, Ат может быть определена как разность масс жидкости, втекающей через сечение 1—1. со скоростью Ео и через сечение 2—2 со скоростью Vo—ДЕ, т. е.
Am = ps-AE-A/.	(V.22)
Приравнивая выражения (V.21) и (V.22) и сократив на s, получим
р-ДЕ-А/ = Др-Дх
или, подставив значение Дх из выражения (V.18), будем иметь я=р4р	га
Для нахождения величины ДЕ применим к массе жидкости, заключенной между сечениями /—1 и 2—2, принцип Далам-бера, гласящий, что если к внешним силам, действующим на некоторую массу, прибавитьсилу инерции, то задачу динамики можно
122 Одномерное движение несжимаемой жидкости (элементы гидравлики)
рассматривать как задачу статики. Внешняя сила, под действием которой частицы жидкости приходят в движение между сечениями 1—1 и 2—2, равна разности давлений Др, умноженной на площадь поперечного сечения трубы, т. е. s-Др. Сила инерции равна произведению массы на ускорение. Масса жидкости будет pc„s-Ax, а ускорение равно изменению скорости ДУ, деленному на время Д/, т. е.
Таким образом, получим дополнительное уравнение для исключения ДV из выражения (V.23). Оно имеет вид
Л	ДУ А
5-Др = Рср8-др Д^,
Дх
откуда, заменив на а и разделив на s, получим
ду = ^.
й'рср
Предположим, что изменение плотности Др весьма мало по сравнению с р, поэтому величину средней плотности рср заменим на р, тогда последнее соотношение примет вид
ДУ = 4г‘	(V-24)
Подставив выражение (V.24) в уравнение (V.23), окончательно получим выражение для определения скорости распространения возмущения, вызванного изменением положения заслонки в трубопроводе, в виде
При выводе этого соотношения никаких условий в отношении величины изменения скорости и никаких ограничений на физические свойства жидкости не накладывалось. Поэтому эта важная формула верна для любого малого возмущения, возникшего в потоке любой жидкости или газа.
Из физики известно, что есть квадрат скорости звука в данной среде при заданных температуре и давлении. Следовательно, малые возмущения в потоках жидкостей и газов распространяются со скоростью звука. Тогда скорость звука в потоке будет определять упругие свойства жидкостей и газов, а число М может быть определено как отношение скорости потока к скорости распространения малых возмущений, возникающих в сжимаемой упругой жидкости.
Известно, что упругость капельных жидкостей характеризуется величиной коэффициента объемного сжатия р, равного относи
Гидравлический удар. Распространение малых возмущений
123
тельному изменению объема жидкости U под действием изменения давления Др, т. е.
в=__1_
р и Ьр
Уравнение упругогосостояния жидкости будет At7 Др ' 0 .
—<г = v=iw
Так как относительное изменение объема равно относительному изменению плотности, величину (3 можно представить в виде
₽=-!Ж
откуда	р р
^- = 4- =—,	(V.25)
Др р₽ р	v ’
где Е = ---величина, обратная коэффициенту объемного сжа-
тия, называемая модулем объемной упругости.
Имея в виду уравнение (V.25), окончательно получим выражение для скорости распространения малых возмущений в капельных жидкостях	___
° = /<=Ут-	<v-26>
Величина модуля объемной упругости Е зависит от температуры жидкости и давления. Среднее значение Е можно взять равным: для воды — 19,6-108 Н/м2, для нефтепродуктов — 13,2-10Н/м2.
Зная модуль объемной упругости Е и плотность жидкости, можно найти скорость звука в данной жидкости; для воды при комнатной температуре она равна 1435 м/с.
Величина давления в трубопроводе после закрытия задвижки Pl = Р + Ар определяется из соотношения (V. 24)
Pl = р + Др = р 4- ар ДУ = р + ар (Уо — У).
При полностью закрытой задвижке (V = 0) изменение давления будет небольшим
Р1~Р = Др = арУ0.	(V. 27)
Выражение (V.27) называется формулой Жуковского.
Таким образом, вдоль трубопровода от задвижки к баку давление в виде удара будет распространяться со скоростью а. Волна повышенного давления дойдет до бака через время, равное t —	.
Тогда в баке установится давление более высокое, чем в трубопроводе, и затем уже от бака к задвижке пойдет волна давления с той же скоростью а.
124 Одномерное движение несжимаемой жидкости (элементы гидравлики)
Если жидкость считать идеальной и трубопровод недеформи-руемым, то процесс колебания давления в трубе будет бесконечным. Хотя сами возмущения малы, изменения давления в трубопроводе могут быть настолько велики, что трубы иногда сильно деформируются и даже разрушаются. В действительности из-за наличия вязкости и деформируемости трубопровода давление будет затухать.
Если принять во внимание деформацию трубы, возникающую при гидравлическом ударе, то уравнения (V. 19) и (V.22) останутся без изменений, а уравнение (V.20) примет вид (рис. V. 17)
* т + Am = (р + Ар) (s + As) Дх.	(V.28)
Величина Ат, определенная как разность выражений (V.28) и (V. 19), будет
Am = (р + Др) (s + Де) Дх — ps-Дх —
= Дх (s • Др 4- р • As + Др • Дз)
или, пренебрегая слагаемыми второго порядка малости, получим •' Am = (s-Ap 4- р-As) Дх.
Приравнивая последнее выражение к (V.22) и имея в виду (V.18), получим
ps • Д V • Д/ = Дх (s • Др 4- р  Дз) = a-&t (s • А р 4- р • Д/) > откуда величина а равна
_ ДУ а Др As
р" + ~
Подставив значение ДУ из формулы (V.24), окончательно получим выражение для скорости распространения малых возмущений в деформируемом трубопроводе в виде
Др
аа = -Л- р . .	(V.29)
Др As	4	'
Т + —
Определим величину относительного изменения площади попе-речного сечения трубы — . Так как площадь круга s = -j-, то приращение площади As, согласно правилам дифференцирования, будет
. ги/Д4
Окончательно получим — = 2^-.	(V.30)
s d	'	'
Гидравлический удар. Распространение малых возмущений
125
С другой стороны, относительное изменение диаметра можно выразить через механические свойства материала трубопровода. Растягивающие напряжения, возникающие в поперечном сечении стенок тонкостенной трубы под действием давления Др, будут
_Ap-d е— fi ,
где б — толщина стенок трубы.
Одновременно растягивающие напряжения могут быть определены как произведение относительного удлинения окружности трубы на модуль упругости материала. Так как относительное удлинение равно
л (d -f- Ad) — nd	Ad	Ad „
——!--------- = —r-, то e = —г-
nd	d	d c
Подставляя сюда из формулы (V.30), получим
Д^ __ Дй'	ооч
d ~ 2б£с •
Имея в виду формулу (V.31), найдем относительное увеличение площади поперечного сечения
As   Apd s	6£с
Подставив полученное выражение в формулу (V.29), будем иметь скорость распространения малых возмущений в трубе при наличии деформации труб
Др
'	G2 —----------
Ар Apd р £с6
Определяя по формуле (V.25) г
Др _ Др р - Е
и сокращая на Др, окончательно получим
а = .	!_^	.	(V.33)
Ур (4 + jk)
Из формулы (V.33) видно, что первое слагаемое в знаменателе характеризует сжимаемость жидкости (£ — модуль упругости жидкости), а второе — упругие свойства трубопровода (Ес —модуль упругости материала трубы). При увеличении толщины
126 Одномерное движение сжимаемого газа, (газовая гидравлика)
стенки 6 скорость распространения возмущений увеличивается. То же происходит и при повышении модуля упругости стенки трубы Ес.
Если подставить значение модуля для стали (Ес = 20,6 X X Ю10 Н/м2) и взять скорость звука в воде 1430 м/с, то скорость распространения малых возмущений будет
1 а — —	— ------.
у 1 -|- 0,021 -у
Величина, обратная второму слагаемому в знаменателе формулы (V.33), имеет размерность скорости
Она характеризует скорость распространения возмущений (волн), вызванных упругими свойствами материала трубопровода или любого обтекаемого тела. Поэтому при моделировании действия упругих свойств материала на поток жидкости обычно требуется соблюдение одинаковости числа Коши (Са), равного отношению скорости потока к указанной выше величине, т. е.
ГЛАВА VI
ОДНОМЕРНОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА (ГАЗОВАЯ ГИДРАВЛИКА)
§ 1. Основные формулы. Скорость звука
При движении воздуха и других газообразных сред с большими скоростями плотность газа будет зависеть от скорости движения. Изучением законов такого движения газа занимается газовая динамика.
Известно, что термодинамическое состояние газа определяется тремя величинами: давлением р, плотностью р и температурой Т. Зависимость между этими параметрами газа в широком диапазоне температур и давлений определяется уравнением состояния
А = ЯТ,
Р
где R — газовая постоянная.
Основные формулы. Скорость звука	127
Размерность R в системе единиц СИ определяется из соотношения
[ D1 _ [р] Дж
1 (РИЛ кг-°C •
Газовая постоянная для некоторых газов составляет:
кг-’С
287,14
259,97
296,85
519,95
4126,1
Воздух . .  ...............
Кислород.....................
Азот ........................
Метан •......................
Водород .....................
Изменение состояния газа может произойти при тепловом или механическом, или совместном тепловом и механическом воздействии. Тепловое воздействие осуществляется подводом или отводом тепла от газа, механическое — в совершении данным объемом газа некоторой работы или в приложении к нему некоторой внешней работы, например при сжатии газа.
В системе единиц СИ универсальной единицей работы (любого вида энергии), а также количества теплоты является джоуль (Дж), равный работе силы в 1 Н на пути в 1 м. В технике из-за малости величины джоуля часто пользуются кратными единицами: килоджоуль (кДж), мегаджоуль (МДж) и др.
Эквивалентность тепла и работы является частным результатом более общего первого закона термодинамики, который утверждает, что тепло, подводимое к покоящемуся газу, расходуется частично на повышение его температуры, т. е. на увеличение внутренней энергии газа Wlr и частично на совершение внешней работы L. Первый закон термодинамики можно записать в дифференциальном виде
dQ — dW; -J- dL.
Изменение внутренней энергии 1 кг массы газа может быть определено по формуле
dW( = cvdT,
где с.. — удельная теплоемкость при постоянном объеме. Тогда
dQ = cvdT-]-dL.	(VI.1)
Величину dQ можно рассматривать как количество тепла, подведенного при постоянном давлении,
dQ = ср dT,
где ср — удельная теплоемкость при постоянном давлении.
Тогда в соответствии с первым законом термодинамики следует, что работа, совершенная подведенным теплом, равна
128
Одномерное движение сжимаемого газа (газовая гидравлика)
разности между подведенным к газу теплом при его нагревании при постоянном давлении и теплом, которое пошло на увеличение внутренней энергии, т. е. dL = (ср — cv) dT.
Если работу расширения газа представить в виде произведения давления на изменение объема dL = р0 dU, то первый закон термодинамики будет иметь вид
dQ = L (ср — cv) dT + р0 dv.
Далее, пользуясь уравнением состояния в дифференциальной форме
р dv — R dT, получим
dQ = (R + cv) dT H- Cp dT, t. e.
RdT= (cp - cv) dT.
В результате получим соотношение
cp-c„^R.	(VI.2)
Из соотношения (VI.2) следуют две зависимости:
Ср _ k .
R k— 1 ’
где k =	.
cv
Если газ будет двигаться, то часть тепла затрачивается на изменение кинетической энергии. Тогда уравнение баланса энергии вместо выражения (VI. 1) будет иметь вид
dQ = cv dT + dL -f- V dV,
где V dV — d -у-.
Используя выражения (VI.3), будем иметь
dQ — (R-\-cv) dT ±VdV = R
A-VdV^j^RdT ^VdV.	(VIA)
При всем разнообразии процессов перехода газа из одного состояния в другое все они могут быть разделены на наиболее характерные, происходящие: а) при неизменном объеме — изохорические; б) неизменной температуре — изотермические; в) постоянном давлении — изобарические; г) при отсутствии теплообмена между газом и окружающей средой — ади абатические.
Основные формулы. Скорость звука
129
Так как газовая динамика имеет дело с быстро проходящими процессами, при которых теплообмен с внешней средой не успевает происходить, то, следовательно, в ней особо важное значение имеют адиабатические процессы.
При адиабатическом процессе давление р и плотность газа р связаны следующим соотношением:
ИЛИ
(VI.5)
р = Ср*, где k = —------показатель адиабаты;
cv
С = ?%-= const. Ро
Используя уравнение состояния, легко получить отношение температур при адиабатическом процессе. Оно будет равно
— — _Р_£о. = f-Po'f-1
Т0 Ро Р \ Р /
или
откуда получим:
т т0
fc-I
(VI.6)
Ро X Ро
о /
k
\ k—
(VI.7)

Известно, что формула для скорости звука имеет вид а2 = ^-. dp
При распространении звука без отвода тепла, т. е. при адиабатическом процессе, получим
а2 = %- = d У) = kCpk~' ~ k . dp dp	'	p
Следовательно, адиабатическая скорость звука равна
= V~kRT.	(VI .8)
Если рассматривать изотермический процесс, при котором р = Ср,
а
9 И. Л. Повх
130
Одномерное движение сжимаемого газа (газовая гидравлика)
то
следовательно, изотермическая скорость звука определится по формуле	___
аиз =]/-£•	(VI.9)
' г
В действительных газодинамических процессах имеет место адиабатическая скорость звука, так как тепло, выделяемое при сжатии газа звуковой волной, не успевает перейти в соседние слои газа.
Из формулы (VI.8) следует, что скорость звука в совершенном газе зависит только от абсолютной температуры и от его физических свойств.
Если газовую постоянную R выразить через молекулярную массу т и ускорение силы тяжести g по формуле
^=^М2/С2.°С, т	’
то скорость звука определится выражением
(VI. 10)
Из формулы (VI. 10) видно, что при увеличении молекулярного веса газа скорость звука уменьшается.
Зависимость (VI. 10) используется при определении скорости звука в экспериментальных установках. Так, для числа М — 2 необходимо иметь скорость потока, в два раза большую скорости звука. Для воздуха при Т = 288 К (/ = 15° С; т = 28,96; k = 1,41) а = 341 м/с; для фреона-12 при той же температуре а = 120 м/с. Следовательно, при числе М = 2 в воздухе необходимо создать поток со скоростью 682 м/с, а для фреона-12 достаточно иметь скорость 240 м/с.
§ 2. Основные уравнения. Интеграл Бернулли
Основными уравнениями для одномерного движения газа так же, как и для жидкости, являются: уравнение неразрывности, количества движения и энергии, или уравнение Бернулли, заменяющее уравнение энергии при адиабатическом движении идеального газа.
Уравнение неразрывности движения для трубки тока имеет вид Pl V iSi = р2У 2SZt
т. е. отличается от соответствующего уравнения несжимаемой жидкости тем, что плотность газа меняется от сечения к сечению.
Основные уравнения. Интеграл Бе.рнулли
131
Иногда в газовой динамике пользуются понятием плотности тока / = pV, равной массовому расходу газа через единицу площади. Тогда уравнение неразрывности примет вид
/1S1 = 12S2-
Это значит, что в местах сужения трубки тока плотность тока увеличивается, а при ее расширении — убывает.
Уравнение количеств движения имеет тот же вид, что и для несжимаемой жидкости, но при этом плотность будет неодинаковой для различных сечений
P1V1V1S1 = p2V2^2S2-
Когда плотность жидкости непостоянна, вид интеграла Бернулли определяется зависимостью плотности жидкости от параметров потока. Наиболее простым с точки зрения математики является движение, при котором плотность есть функция только давления. Жидкости, плотность которых есть функция давления, называются баротропными. Для баротропных жидкостей плотность равна р = Ф (р).
Тогда уравнение (VI. 15) для стационарного потока при наличии потенциала массовых сил будет
d (^- -1-ф) + -4т = °-\ 2	1	) 1 <р (р)
Если ввести интеграл в виде
P=fA,	(VI.11)
J Ф(Р)	'	'
Ро
то получим
d(-^ + <D4-P)=0, или
22_|_ф + Р = С.
Последнее выражение есть интеграл Бернулли для баротроп-пого движения.
Интеграл Бернулли для одномерного баротропного движения при отсутствии массовых сил имеет вид
где Р — так называемая функция давления, значение которой определяется из выражения (VI. 11) при заданной связи между плотностью и давлением.
132 Одномерное движение сжимаемого газа (газовая гидравлика)
Для изотермического процесса (Т = const, = С) функция' давления равна	J
р	р
[	= [ р° £р — -£о.]п_£_
j	Р	J	Ро Р Ро Ро ’
Ро	Ро
следовательно, интеграл Бернулли будет иметь вид
^ + ^ln-^-=C.	(VI.12)$
Ро Ро	У
Найдем	функцию Р при	адиабатическом движении идеального	;!
газа	(VI. 11)	j
Л 1 Л	1	'$
I	fell	fe / —1	fe—1\	
Р = Ьр = \p-Tdp= k Р^_[ — _ —).
J Р Ро J н fe—1 р0	Ро 7	:
Ро	Ро
Так как	j*
Л = (Л)‘,	ятрТ=р^^,	J
то окончательно	'j
р— k ( Р_______Р_\	;|j
fe— 1 к р Ро Г	.
Следовательно, интеграл Бернулли для адиабатического движе- j ния применительно к трубке тока будет равен	3
-9- + Г-Ц— +	— = (VI.13) S
2	1 k — 1 рх 2	1 fe — 1 р2	4	' -j
Интеграл Бернулли является одним из основных уравнений •• газовой гидравлики и широко применяется в различных своих з формах. Так, если воспользоваться уравнением состояния, то уравнение (VI. 13) будет иметь вид	;
+	+	^2 = const.	(VI.14)
Подставив вместо kPT квадрат адиабатической скорости звука а2, , получим	-	i
4 + А-4 + А—‘-	^.15) '
Если воспользоваться тепловой функцией, или энтальпией, определяемой формулой i = срТ, и подставить в эту формулу величину ср в соответствии с первой из формул (VI.3), получим
Параметры заторможенного газа. Энтропия
133
выражение энтальпии
Тогда интеграл Бернулли можно представить в виде
4 + CpT1==4 + CpT2 = const	(VI.16)
или 1/2	1/2
-у-4-ii	= const.	(VI.17)
Уравнения (VI. 13)—(VI. 17) далеко не исчерпывают всех возможных видов интеграла Бернулли для адиабатического процесса движущегося газа, но указанных форм достаточно для понимания последующего материала.
§ 3. Параметры заторможенного газа. Энтропия
Параметры газа в состоянии покоя при адиабатическом процессе без потерь энергии будем называть параметрами заторможенного газа. Определим температуру, давление, плотность, энтальпию и скорость звука заторможенного газа.
Если в уравнении (VI. 16) отбросить индексы, характеризующие сечения, й положить скорость в одном из сечений равной нулю, то получим
2 "Ь Ср-* — Ср/ о,
следовательно,
-^ = 14-2^-.	(VI.18)
Второе слагаемое уравнения (VI. 18) можно представить в виде
V2 _ 1 V2 _ k - 1 У2 = /г — 1 М2 2срТ ср kRT 1 й2 2М’
2 kR
Тогда безразмерная температура заторможенного газа будет равна
То = 4 = 1	(VI.19)
Используя соотношения адиабатического процесса ( VI.7), получим величины давления и плотности заторможенного газа
k
^1 = (1 -I-LzlL	(VI.20)
Р 1 •
4 = (1	(VI.21)
134
Одномерное движение сжимаемого газа (газовая гидравлика)
Имея в виду, что скорость звука а пропорциональна корню квадратному из абсолютной температуры, получим величину скорости звука в заторможенном газе в виде
1
^- = (1 +Ц11м2)2 .	(VI.22)
Так как энтальпия пропорциональна абсолютной температуре, то
А = ^-=1 +^м2.
В газовой динамике и в физике широко используется понятие об энтропии, характеризующей состояние газа. Энтропия может быть представлена в виде дифференциального соотношения
dS=-^-.	(VI.23)
В соответствии с первым законом термодинамики элементарный приток тепла, отнесенный к единице массы, равен
dQ = cvdT-£ dp = cvdT—£-&, г	г г
откуда
_ dQ dT __p_dp_ ао Т —cD Т рт р ’
Р т>
но из уравнения состояния — = R, следовательно, энтропия будет равна
dS==c0^P — R ^- = cvd\n-^- — Rdlnp Kip	р
или
dS =R (-^-dln-^---dlnp).
Подставив значение из выражения (VI.3), получим
[dln^----(^— l)dlnp]
или окончательно
dS=J-5-rdln-^-k— 1 pk
Проинтегрировав последнее выражение, получим разность зн^ений энтропии
= (Vt24)
Истечение из бака. Максимальная и критическая скорости 135
Если адиабатический процесс будет идеальным Р -2 _ Р1 _ Р Р2 Pi Р* ’
то изменение энтропии равно нулю.
Если воспользоваться параметрами заторможенного газа и заменить отношение плотностей на отношение температур, согласно (VI.7), то изменение энтропии можно представить в виде k
Pol \ 1 02 /
Температура заторможенного газа характеризует собой полную энергию, которая в случае изолированной системы во всех сечениях одинакова, следовательно, Т01 = Т02,. Поэтому уравнение для разности энтропий будет иметь вид
S2 — 31==/?1п^-.
Рп
Если в потоке нет потерь, то давление торможения постоянно, т. е. р01 = р02, и изменение энтропии отсутствует. Процесс, при котором энтропия газа остается неизменной, называется изэнтропическим. Из уравнения (VI.24) следует, что идеальный адиабатический процесс будет процессом изэнтропическим.
При наличии потерь в потоке р02 < р01 правая часть в последнем уравнении будет положительной, поэтому S2 > Si, т. е. энтропия возросла.
Таким образом, при всяком реальном процессе в изолированной системе энтропия увеличивается. Так как во всех машинах, в том числе компрессорах и турбинах, имеют место потери, то энтропия всех реальных процессов в машинах возрастает, т. е.
S2 — Si >0.
§ 4. Истечение из бака. Максимальная и критическая скорости
Рассмотрим истечение газа из бака (рис. VI. 1). Будем считать, что размеры бака настолько велики по отношению к размерам выходного отверстия, что можно полностью пренебрегать скоростью газа внутри бака по сравнению со скоростью в выходном сечении 1—1.
Следовательно, давление, температура и плотность внутри бака будут иметь значения параметров заторможенного газа, т- е- Ро> Ро и Тп. Для определения скорости истечения воспользуемся уравнением Бернулли (VI. 13)
V3 , k р _ k р0
2 ' fe — 1 р k— 1 Ро ’
136 Одномерное движение сжимаемого газа (газовая гидравлика) . )
откуда
17—1/' 2/г ( Ро	Р~Л
— У k—\ \ро	Р )
Вынося за скобки — и считая процесс адиабатическим и изэн
тропическим, т. е., имея в виду, что — = (—) k , окончательно
получим для определения
скорости истечения известную в газодинамике формулу
тЛ 2fe ро V k — 1 р0
(VI.25)
Из формулы (VI.25) видно, что при заданных параметрах заторможенного газа величина скорости истечения будет расти с уменьшением давления вне бака. Очевидно,
что скорость будет максимальной при истечении газа в абсолютный вакуум, т. е. когда р=0 и Т=0. Как будет видно из дальнейшего, сверхзвуковая скорость, близкая к максимальной, на практике может быть получена лишь
при истечении через насадок, поперечное сечение которого вначале уменьшается, а затем возрастает (сопло Лаваля).
Вначале рассмотрим истечение газа через сужающийся насадок.
Используя выражение для адиабатической скорости звука, получим
= У й =КА- <VI-26)
Если воспользуемся уравнением Бернулли (VI. 15), то °2 _ k Ро _
2 "’ft — 1 /г — 1 ро k— Г
Из последнего уравнения вытекает следующая зависимость ско« рости звука от скорости течения
a2 = a§_*zJp.	(VI.27)
Отсюда следует, что при заданных параметрах заторможенного газа с увеличением скорости истечения скорость звука будет убывать. Следовательно, при сужающемся насадке и достаточно большом перепаде давлений в баке и вне его скорость истечения может достигнуть величины, равной местной скорости звука.
Истечение ив бака. Максимальная и критическая скорости
137
После того как на выходе из насадка скорость достигла скорости звука, дальнейшее уменьшение противодавления (давление вне бака) 'не может привести к увеличению скорости истечения, так как, согласно теории распространения малых возмущений, внутренний объем бака станет недоступен для внешних возмущений: он будет заперт потоком со звуковой скоростью. Все внешние малые возмущения не могут проникнуть в бак, так как им будет препятствовать поток, имеющий ту же скорость, что и скорость распространения возмущений.
В этом главная особенность звуковых и сверхзвуковых течений.
Скорость потока, равная местной скорости звука, называется критической скоростью и обычно обозначается а*, т. е. V — = а = а*.
Подставив это значение в выражение (VI.27), найдем
„ч__	р0 _ 2fe р™	-„
a*~~k+l fe-j-1 Ро	(VI.28)
Воспользовавшись формулой (VI.26), ^получим
=	(VI.29)
Для воздуха (k = 1,4) а* = 18,3)/То. Если в уравнение Бернулли
V2 а2
-2-+CT = COnSt
подставить V = а = а*, то оно примет вид
V2 , a2	k J-1	2	/Лгг 2 । fe — 1	2 (fe — 1) а*'	(VI.30)
Имея в виду, что из выражения (VI.28)
(vr3l)
и используя условия адиабатичности процесса, получим величины критических параметров газа:
Z* - 2 •
Т о	k -j-1 ’
k
Р* _ / 2
Ро	\^ + 1/	’
1
Р* = / 2 \ Ь-1
Ро \ k 1)
(VI.32)
138 Одномерное движение сжимаемого газа (газовая гидравлика)
Определим расход газа через сужающееся сопло, присоединенное к баку с параметрами газа р0, р0 и Т^-При докритическом режиме масса газа, вытекающая из бака за одну секунду, будет равна т = pKs.
Критическое значение этой массы газа будет m* = Тогда безразмерный массовый расход газа может быть представ-
лен в виде
т  рУ т* Р*^*
Не производя дальнейших вычислений, приведем на рис. VI.2 график зависимости безразмерного расхода — от — (р' — про-тиводавление в области, окружающей бак). Пока давление р на выходе из • сопла меньше критического, проти- -водавление р' совпадает с давлением р на выходе. При дальнейшем уменьшении р', т. е. при р' < р*, наступает явление «запирания» выходного сечения. При этом расход не будет меняться, оставаясь критическим, несмотря на то, что'противодавление уменьшается. Как только — достиг-
Ро нет значения 0,528 (для воздуха), т
кривая — примет вид горизонталь-секундный массовый расход при
ной линии. Максимальный заданных параметрах газа в баке равен
= т* = p^s и, согласно выражению (VI.32), будет fe-H ^шах = (ял)2 (ft-I) ^PoPoS-
В газовой динамике наряду с числом М часто пользуются безразмерными числами Хит. Число X, называемое скоростным коэффициентом, равно отношению скорости потока в данной точке к величине критической скорости, общей для всего потока, т. е.
Х =
— М—= М ——, О'* «о ««
V
а*
или, имея в виду выражения (VI.22) и (VI.31),окончательно получим
(VI.33)
Движение газа в трубе переменного сечения. Сопло Лаваля
139
Из формулы (VI.33) видно, что при М = 1 скоростной коэффициент X = 1, а при увеличении числа М до бесконечности будет иметь максимальное значение 
(VL34)
.В табл. VI. 1 приведена зависимость скоростного коэффициентах от числа М для воздуха (й = 1,41). Легко видеть, что при изменении числа М от нуля до бесконечности X меняется от нуля до
Таблица VI. 1
м	X	т	м	X	%
0	0	0	1,0	1,0	0,408
0,2	0,218	0,089	2,0	1,633	0,667
0,4	0,431	 0,176	3,0	1,964	0,802
0,6	0,635	0,259	4,0	2,138	0,873
0,8	0,825	0,337.	СО	2,45	1
Число т, называемое числом Чаплыгина, есть отношение
скорости потока в данной точке к максимальной скорости, определяемой параметрами заторможенного газа. Используя формулы (VI.29) и (VI.33), получим
V _ V а* _* 1 f k— 1 _ -j /k— 1
Vшах	а* Vmax	V k -J- 1 r k -j- 1
1+Ц^Ма’
(VI.35)
При подстановке значения Хтах из формулы (VI.34) будем иметь ^max = I •
В табл. VI. 1 приведено изменение числа Чаплыгина в зависимости от числа М для воздуха. При изменении М от нуля до бесконечности и соответствующем изменении числа X от нуля до некоторого конечного значения число Чаплыгина для всех газов изменяется от нуля до единицы.
§ 5. Движение газа в трубе переменного сечения. Сопло Лаваля
Рассмотрим вначале одномерное движение идеального сжимаемого газа в трубе переменного сечения. Уравнение неразрывности такого движения будет иметь вид pVs = const. В ка
140 Одномерное движение сжимаемого газа (газовая, гидравлика)
честве второго уравнения используем уравнение Эйлера 3
dx р dx ‘	j
Продифференцировав первое уравнение по х, получим
j
откуда после деления на pVs получим
1	। 1 QL _r__L ______0	।
s dx ' V dx ' p dx '
Считая движение изэнтропическим и баротропным и имея 1 dp о	i|
в виду, что — а*, найдем	]
dp	_ dp	dp _ 1	dp	•
dx	dp	dx	a2	dx	’	i
Следовательно, предыдущее уравнение примет вид	J
1	ds	,	1	dV	,	1	dp	_ n	J
s	dx	‘	V	dx	'	pa2 dx
или, подставив значение из уравнения Эйлера и произведя. ' некоторые преобразования, получим	1
/ V2____A = v	;
\ а2 ) dx s dx
или окончательно
(VI.36) -
Уравнение (VI.36) позволяет провести важный качественный анализ характера движения сжимаемого газа в трубе переменного сечения. Прежде всего рассмотрим движение при числе М < 1, т. е. при дозвуковом потоке. .В этом случае величина М2 — 1 <0 и знак будет зависеть от знака производной скорости. Как видно из табл. VI.2, в сужающемся канале, или конфузоре, скорость растет, а в расширяющемся канале, или геометрическом диффузоре, она убывает. Эта закономерность общеизвестна и широко наблюдается в практике (русла рек, трубопроводы и пр.).
При числах М > 1, т. е. при сверхзвуковом потоке газа, имеем М2 — 1 >0, и, как видно из табл. VI.2, в сужающейся трубе скорость убывает, а в расширяющейся ^рубе она растет.
Из формулы (VI.36) следует, что для идеального газа получить в трубе переменного сечения скорость потока, равную скорости звука, т, е. число М, равное единице, можно только в минимальном
Движение газа в трубе переменного сечения. Сопло Лаваля
141
Таблица VI.2
—-		 Число М	Производная скорости	Изменение сечення	
-—			 М < 1	-^>0 dx	-^<о dx			r. конфузор W—-—J
	-^-<0 dx	-#->0 dx	V	—D Диффузор1 —
М> 1	-£->0 dx	4->0 dx	\	д		 Диффузор
	-^-<0 dx	-J-<0 dx	V~  	—> Конфузор'-1 "
сечении трубы. В максимальном сечении, в котором площадь , тоже имеет экстремальное значение, нельзя получить число М = 1, так как максимальному значению поперечного сечения трубы предшествует расширяющийся участок, в котором при дозвуковом потоке скорость убывает, а при сверхзвуковом — растет, что исключает возможность получения звуковой скорости в наибольшем сечении трубы.
Очевидно, что поперечное сечение может быть экстремальным и при = 0, т. е. скорость будет наименьшей (дозвуковой) в самом узком сечении и наибольшей (сверхзвуковой) в самом широком сечении трубы.
На рис. VI.3 показаны возможные случаи движения газа в трубе переменного сечения. Здесь приведены изменения скорости и давления вдоль трубы. Если скорость на входе дозвуковая, то возможны два случая (кривые 1 и 2).
В первом случае давление за соплом довольно велико и скорость в узком сечении не достигает скорости звука. Тогда в расширяющейся части скорость будет убывать и на выходе из сопла будет дозвуковой.
Во втором случае (кривые 2 и 2') скорость в наиболее узком ' сечении будет достигать скорости звука и в зависимости от величины давления за соплом либо дальше, в расширяющейся части трубы, становится сверхзвуковой (кривая 2), либо, если давление па выходе из трубы сверхкритическое, скорость в диффузоре убывает и при выходе из трубы становится дозвуковой (кривая 2').
142 Одномерное движение сжимаемого газа (газовая гидравлика)	j
Труба переменного сечения, рассчитанная так, что дозвуковая > скорость на входе становится сверхзвуковой на выходе, обычно называется соплом Лаваля. Наиболее узкое сечение сопла назы-
вается критическим сечением, а соответствующие параметры потока— критическими (скорость, давление, плотность и температура)..
Если скорость на входе сверхзвуковая, то, убывая в сужающейся трубе, она достигает наименьшего значения в наиболее узком сечении. Если это наименьшее значение остается больше
скорости звука, то в расширяющейся части трубы скорость газа растет и на выходе будет так же, как и на входе, сверхзвуковой
1 .i ч
4 i
Когда сверхзвуковой поток достигает в наименьшем сечении скорости звука (кривая 4), то так же, как и для кривой 2, возможны два случая. Если давление на выходе меньше критического, то в диффузоре скорость будет расти и на выходе она станет сверхзвуковой (кривая 2). При давлении больше критического скорость в диффузоре убывает и на выходе она достигает дозвуковой (кривая 2'). Расчет сопла Лаваля в соответствии с теорией одномерного движения идеального газа можно легко произвести, воспользовавшись формулами (VI. 19)—(VI.21) и (VI.32). Разделив параметры заторможенного газа (VI.19)—(VI.21) на параметры потока в критическом сечении, получим
4-1 V 2
Р р*
k fe-i
Р	Г	2
Р*	L	k	4-	1
Т____Г	2
Т *	l	k	1
k— 1 2
k — 1 2
fe—I
(VI.37)	•
Движение газа в трубе переменного сечения. Сопло Лаваля	143
—— ___
Площадь поперечного сечения сопла можно определить, обращаясь к уравнению неразрывности. Тогда, применяя соотношения (VI.33) и (VI.37), получим
- s _ р*У* __ Р. 1 _ 1 Г 2 (	ь-\ 2\iW=iy
s "" 7? “ ДК” ~	~ дг Lt+t V + ~2~ М Л
(VI.38)
Из формулы (VI.38) видно, что необходимое безразмерное значение площади сечения определяется для данного газа только числом М.
На рис. VI.4 показано изменение безразмерной площади поперечного сечения в зависимости от числа М в данном сечении (для воздуха).
Как видно из кривой, данному значению s соответствуют два значения числа М. Одно число М < 1, а другое число М > 1. Однозначное решение имеет место только для М = 1.
Приведенные формулы для одномерного движения идеального газа могут быть приближенно использованы для практических расчетов сопла Лаваля. При выводе этих формул не учитывались наличие вязкости в реальной жидкости, неоднородность поля скоростей в каждом поперечном сечении, теплоотдача через стенки сопла, нарушающая адиабатичность процесса, и пр.
Рассмотрим влияние вязкости па характер течения газа в трубе переменного сечения. Наличие вязкости приводит к добавочному перепаду давления в трубе. Перепад давления в круглой цилиндрической. трубе можно определить по формуле
А 1 I РР
где X — коэффициент сопротивления; I и d — длина и диаметр рассматриваемого участка трубы.
Для трубы переменного сечения эту формулу можно представить в дифференциальном виде
,, ,	- dx рУ2
(“Р)вязк	2 ’
где (<Д>)ВЯЗК — перепад давления из-за вязкости. Отсюда
/^р\	= й, рУ2
\ dx /вязк d 2 ’
или
_AZ!_ р \ dx /вязк d 2
144
Одномерное движение сжимаемого газа (газовая гидравлика}
С учетом потерь давления, обусловленных вязким трением, урав-\ нение движения можно записать в виде
vdV =______:'!(
dx р dx d 2 '
Данное уравнение с использованием уравнения неразрывности ji движения приводится к виду
(Др—1)	%_Км2,	'(!
v ' dx s dx 4r	'3
где г — радиус трубы в данном сечении.	.!
Так как для круглого поперечного сечения	"
Таблица VI.3
Число М	Производная скорости	dx
М< 1		4—м<0 dx	1 <
	-F<°	dx
М> 1	-4>о dx	4—%х>0 dx
	-^-<0 ах	dx
, ds п dr s — лг , а -7-=2лг-Г~, dx	dx
то последнее уравнение после простых преобразований будет иметь вид
(М2-1)^=.
(VI-39>
где = 4М2.
Уравнение (VI.39) позволяет установить ряд особенностей течения газа в трубах переменного сечения (табл. VI.3).
Из формулы (VI. 39) видно, что скорость пото-
ка станет равной скорости звука в том сечении трубы, где — — т. е. в расши-
ряющейся части — диффузоре, в то время как при отсутствии трения скорость, равная звуковой, была в минимальном сечении трубы.
Из табл. VI.3 видно, что при М < 1 скорость растет не только
в конфузоре, но и в слабом диффузоре, т. е. при
При М > 1 скорость растет только в некотором определенном диффузоре, т. е. при
В слабом диффузоре, когда 0 <	скорость при
М > 1 будет убывать.
Получение сверхзвукового потока в цилиндрических трубах
145
Аналогичные выводы, качественно отличные от выводов при движении идеального газа, можно сделать и для процесса уменьшения скорости.
Из уравнения (VI.39) легко получить закон одномерного адиабатического движения газа в цилиндрической трубе при наличии трения. Для цилиндрической трубы (г = const) уравнение (VI.39) будет
Из приведенной формулы видно, что при дозвуковом потоке (М < 1) на участке трубы постоянного сечения поток ускоряется, а при сверхзвуковом потоке (М. > 1), наоборот, замедляется.
§ 6.	Получение сверхзвукового потока в цилиндрических трубах
Существуют различные способы получения сверхзвуковой скорости потока. Кроме сопла Лаваля (геометрическое сопло) имеются расходные, тепловые, механические и другие сопла (негеометрические).
Рассмотрим теоретические основы некоторых негеометрических сопел и прежде всего расходного сопла. Пусть имеем цилиндрическую трубу с пористыми стенками, так что масса движущегося газа в трубе будет переменной величиной
т = pVs.
Тогда, дифференцируя уравнение по х и деля на pVs, йолучим
— 4^ + 1 4L + _L41 = _L^..	(vi.4O)
р dx ' V dx ' s dx m dx	'	1
Далее, используя уравнение Эйлера
ydV _______1_ dp
dx , p dx
и имея в виду, что
dp _ dp_ dp __ 2 dp
dx dp dx dx '
перепишем уравнение (VI.40) в следующем виде:
/___V	.	1 \	1	rfs	_ 1 dm
\	а*	'	V )	dx ' s	dx т dx
или окончательно
'	’ dx s dx m dx
Ю И. Л. Повх
146 Одномерное движение сжимаемого газа (газовая гидравлика)
Если труба цилиндрическая, то ~ = 0 и уравнение примет вид
Рис. VI.5
^->oj ах <
=	(VI.41) ..
Из уравнения (VI.41) следует, что при дозвуковом движении газа в трубе (М < 1) скорость потока при подаче газа в трубу | будет расти, а при удалении газа из трубы — убывать. В сверх- ) звуковом потоке (М > 1) явле-  ние будет обратным: при подаче' газа в трубу, т. е. при скорость потока уменьшается,/ а при удалении газа она растет. Кроме того, из формулы (VI.41) j видно, что число М = 1 будет : иметь место только в сечении, ’ dm п в котором = 0.
Используя полученную зависимость, можно создать так называемое расходное сопло. Если в цилиндрическую трубу : (рио. VI.5) с дозвуковой ско- | ростью на входе подавать через 1 стенки газ, то скорость потока 1 будет расти и в некотором (кри-тическом) сечении, в котором i скорости звука. Если за этим 1
dm Л
-^- = 0, она может достигнуть сечением газ отсасывать из трубы, сверхзвуковая скорость будет расти, достигая заданного значения.	,1
Таким образом, управляя изменением расхода, можно в одной ? и той же цилиндрической трубе получать на выходе из трубы различные сверхзвуковые потоки, в то время как геометрическое j сопло на расчетном режиме может быть использовано для полу- ’ чения потока только с одним заданным числом М. Для каждого числа М на расчетном режиме надо иметь свое геометрическое J сопло. Расходные сопла применяются в лабораторной практике [15).
Принцип работы теплового сопла можно установить, исходя из следующего.	" j
Из условия постоянства расхода в цилиндрической трубе j будем иметь
1	 1 _п
р dx V dx ’
так как pV = const.
Получение сверхзвукового потока в цилиндрических трубах 147
Дифференцируя уравнение состояния по х, получим ^-=r (’р4-+7'4£У dx V dx ' dx J
„	dp
После подстановки из предыдущего уравнения получим
dp _ _ dT RpT dV dx & dx V dx
Исключив с помощью уравнения Эйлера и проделав элементарные преобразования, имея в виду, что kRT = а2, получим уравнение в виде
’	(X —= R ^r-	(VI.42)
\fer2 / dx dx	'	’
Если правую часть выражения (VI.42) заменить уравнением энергии (VI.4)
R — — k~X dQ k~ly dV dx k dx k dx ’
то последнее уравнение примет вид
/.____V dV_ _ _ 1 —fe dQ
\ V2 ) k dx	fe dx ’
V2
умножив на k = M2£, окончательно получим
. (M2-l)7^-=-(£-l)M2-g-.	(VI.43)
Так как коэффициент при правой части уравнения (VI.43) всегда положителен, то скорость будет расти > 0 при М < 1 и > 0, т. е. когда приток тепла возрастает по длине трубы, а при М > 1 увеличение скорости будет при наличии dQ ~
неравенства <0, т. е. когда тепло отнимается от газа, движущегося в цилиндрической трубе.
В критическом сечении, в котором V = а и число М = 1, dQ Л приток тепла должен отсутствовать, т. е. = 0.
Следовательно, принцип работы расходных и тепловых сопел одинаков, так как подвод и отвод тепла оказывает действие, аналогичное притоку и отводу массы в цилиндрической трубе. На рис. VI.5 показана схема действия расходного и теплового сопел. 10*
148 Одномерное движение сжимаемого газа (газовая гидравлика)
Таким же образом, используя уравнения состояния, условие • постоянства массы и уравнение энергии, можно получить условие работы механического сопла в виде
где — изменение механической работы по длине трубы.
Из уравнения (VI.44) видно, что скорость растет при М < Г, когда > 0, т. е, когда поток в цилиндрической трубе совер-

Рис. VI.6
 ;
шает работу, например на колесе турбины. При М > 1 скорость: растет, когда < 0, т. е. когда механическая работа пере-; дается потоку газа, например, с помощью компрессора илинагне-!
тателя. В критическом сечении трубы М = 1 и — 0.
Кроме геометрического, расходного, теплового и механи-1 ческого сопел для получения сверхзвуковых скоростей можно1 воспользоваться комбинированными соплами. Примером могут^ служить комбинации геометрического и теплового или расход- * ного сопла, приведенные на рис. S VI.6. В схеме рис. VI.6, ал дозвуковой поток достигает критического сечения в сужающемся канале. После критического сечения сверхзвуковая скорость рас-, тет за счет отвода тепла q или массы т вещества.	.
В схеме рис. VI.6, б, наоборот, дозвуковой участок представ-,’ ляет собой цилиндрическую трубу с подводом тепла или газа, а сверхзвуковой — расширяющуюся трубу, в которой поток уско-;я ряется без теплообмена с сохранением постоянства массы газа.Л
В некоторых случаях движение газа может регулироваться.^ совместным действием указанных факторов (подвод тепла, веще-’j ства, механической работы и пр.).
Способы получения сверхзвуковых потоков с помощью элек- j тромагнитных полей будут рассмотрены в гл. XV.	i
Естественно, что рассмотренные выше соотношения могут быть применены не только для сверхзвуковых потоков, но и для плав- ’ ного перехода сверхзвукового потока к дозвуковому. Оказы-; .вается, что последняя задача не менее трудна, чем первая.
Распространение конечных возмущений. Скачок уплотнения 149 _____________________________ ’
§ 7. Распространение конечных возмущений.
Скачок уплотнения
В п. 7, гл. V было показано, что малые упругие возмущения в жидкостях и газах распространяются со скоростью, равной скорости звука в данной среде. Все результаты, полученные в п. 7 для жидкости, полностью относятся и к газам. В механике жидкостей и газов, так же как в других разделах физики, кроме малых возмущений имеют место сильные или так называемые конечные возмущения. Обычно при малых возмущениях величина приращения какого-либо параметра мала по сравнению с его значением до появления возмущения. Например, малое возмущение давления в жидкости может быть характеризовано безразмерной величиной
Д^=Д=^= ^-« 1,
Ро Ро
где р0 — давление в жидкости до появления возмущения; р — наибольшее значение давления после появления малого возмущения.
При конечном возмущении величина Др может быть порядка единицы и значительно больше.
Основное отличие этих двух видов возмущений заключается в поведении параметров потока, определяющих движение. При малых возмущениях все параметры потока являются непрерывными функциями координат и времени, в то время как при конечных возмущениях параметры потока (скорость, плотность, давление, температура) претерпевают конечные разрывы. В этом главное отличие малых возмущений от конечных.
Возмущения, вызванные в сжимаемых жидкостях и газах, в том числе и распространение звука, могут быть в зависимости от условий либо малыми, либо конечными возмущениями. Известно, что в обычных условиях акустические возмущения являются малыми возмущениями и распространяются со скоростью звука, а при сильных взрывах они будут конечными и скорость их распространения может значительно превосходить скорость звука.
Движение при малых возмущениях и движение при конечных возмущениях математически описываются совершенно различными уравнениями. Первое определяется линейным дифференциальным уравнением в частных производных, называемым в математике волновым уравнением. Обычно это уравнение имеет вид
92f — .,2 dt2 ~~ дх2 '
Движение же при наличии конечных возмущений описывается нелинейными дифференциальными уравнениями, решение которых представляет большие трудности.
150 Одномерное движение сжимаемого газа (газовая гидравлика)
Рассмотрим вначале качественную картину образования конечного разрыва в газах, называемого скачком уплотнения.
Пусть в бесконечной трубе (рис. VI.7) с неподвижным газом в некоторый момент времени tQ мгновенно начинает двигаться поршень П с некоторой конечной скоростью V. Тогда в момент времени tlt мало отличающийся от t.-, параметры газа на беско-нечности останутся неизменными, а в непосредственной близости *. перед и за поршнем они будут существенно отличаться от пара- ' метров газа, имеющих место до начала движения поршня. Если-' труба теплоизолирована от внешней среды и движение газа будет

адиабатическим и изэнтропическим, то перед поршнем газ, ежи--, маясь, вызовет увеличение плотности, давления и температуры, а за поршнем образуется разрежение и указанные параметры^ газа уменьшатся. Скорость потока в непосредственной близости] от поршня как перед, так и за ним будет равна скорости движения 1 поршня.	~	]
В каждый момент времени все параметры газа в трубе изме-няются непрерывно от их значения на поршне (перед и за поршнем) 3 до их значений на бесконечности. Тогда к этой системе можно ] применить закон распространения малых возмущении, считая, ’ что в каждой точке скорость распространения возмущений равна местной скорости звука. Так как в указанный момент времени  температура перед поршнем убывает вдоль трубы (х > 0, ’ рис. VI.7, а), а за поршнем она растет при удалении от поршня (х < 0), то местная скорость звука, пропорциональная корню квадратному из абсолютной температуры, перед поршнем убывает вдоль трубы, а за поршнем (при удалении от него) растет.
Если распределение скоростей вдоль трубы (перед и за пор-, шнем) в момент времени представить кривой 1 (рис. VI.7, б), то соответствующие кривые в моменты времени i2, t3, будут иметь вид кривых 2, 3 и 4. Кривая 2 перед поршнем (в зоне ежа-тия) может быть получена из кривой 1 путем добавки в каждой
Распространение конечных возмущений. Скачок уплотнения 151
точке соответствующего значения скорости звука. За промежуток времени /2 — точки кривой 1 сместятся по горизонтальному направлению на отрезки тем меньше, чем больше ординаты кривой 1. Таким образом, наклон кривой скорости возрастает. В последующие моменты времени это увеличение крутизны будет продолжаться, и в момент времени ti в некотором сечении кривая станет перпендикулярной оси х, т. е. произойдет скачок скорости. Очевидно, аналогичные изменения будут происходить и с другими параметрами потока. При этом в сече-
нии, в котором происходит скачкооб-	Скачок
разное уменьшение скорости, давление, к р, ( к, р, температура и плотность увеличатся.	т, р; т2
Такой скачок называется скачком уплот-
нения.
Следует отметить, что в действительности параметры потока изменяются не скачкообразно, а на некоторой весьма малой длине, имеющей величину порядка пути свободного пробега молекулы.
За поршнем в области разрежения картина будет обратной. Так как скорость звука по длине растет, то к точкам кривой 1 с меньшими скоростями будут добавляться большие отрезки и кривая будет вытягиваться; наклон кривых уменьшается, образуя волны разрежения, и, следовательно, в этой области скорости и другие параметры изме
няются непрерывно, а скачки и ударные волны не образуются.
Рассмотрим качественное изменение параметров потока в скачке, образованном от перемещения поршня в трубе. В этом случае плоскость скачка будет перемещаться вдоль оси трубы, т. е. на-
правление перемещения скачка и плоскость скачка перпендикулярны друг другу. Такие скачки называются прямыми скачками.
В системе координат, связанной с трубой, движение ударной волны вдоль трубы будет нестационарным, так как параметры потока в любой точке трубы будут зависеть от времени. Для приведения задачи к стационарной введем систему координат, связанную с плоскостью ударной волны. Тогда ударную волну можно считать неподвижной, параметры потока перед и за скачком постоянными величинами, скачкообразно изменяющимися в плоскости ударной волны.
На рис. VI.8 показаны параметры потока перед и за скачком. Так как при .движении поршня образовавшаяся ударная волна
152
Одномерное движение сжимаемого газа (газовая гидравлика)
перемещается в невозмущенной среде, то в системе координат, связанной с ударной волной, скорость перед скачком будет равна скорости перемещения ударной волны.
§ 8. Изменение параметров потока в прямом скачке. Ударная адиабата
Для установления Количественной зависимости параметров потока за скачком У2, р2, Ра’и Тг от параметров потока до скачка Vi, Pi, Pi и Ti воспользуемся общими уравнениями: уравнением сохранения массы, уравнением изменения количества движения и уравнением энергии.
Уравнение сохранения массы для движения в цилиндрической трубе, в которой площадь поперечного сечения постоянна, будет
рА = р272.	(VI.45)
Уравнение изменения количества движения при отсутствии объемных сил и поверхностных сил вязкости примет вид
Р! + Р1И? = р2 + рЛ	(VI.46)
Уравнение энергии может быть представлено в виде
/Т^Т т + 41 =	(VI-47)
ИЛИ
V? , . VI , .
~2 Ь 11 —~2---Ь f2 — 1о>
= ^RT = C”T-
Найдем вначале соотношение между скоростями перед и за скачком. Для этого уравнение (VI.46) разделим на piVj = р2У2 и напишем
Рг Pi
Рг^г P1V1
У1-У2-
(VI.48)
Записав уравнение энергии (VI.30) до и после скачка в виде k Pl |	1 z,2
k — 1 pi ' 2	2(k — i)
получим
Pl _ M-l 2 k — 1 v2
Pi 2k a* 2k и
P2 _ fe + 1 _2	k — 1 T/2
p2 2k	2k k2'
Изменение параметров потока в прямом скачке. Ударная адиабата 153
Подставив последние выражения в уравнение (VI.48), получим
Так как Vj =f= V2, то, разделив на (Vj — У2) и выполнив обычные преобразования, окончательно найдем
У,У2 = а2.	(VI.49)
Таким образом, мы получили весьма простую формулу, из которой следует, что при прямом скачке произведение скорости потока перед скачком на величину скорости за скачком равно квадрату критической скорости звука.
Если перейдем к скоростным коэффициентам и %2, получим
% Аг = 1-	(VI.50)
Используя равенства (VI.49) и (VI.30) и учитывая, что > У2,’ получим Vi > и У2 <а2.
Последние неравенства означают, что перед прямым скачком скорость всегда сверхзвуковая, а за скачком—дозвуковая.
Рассмотрим количественное изменение параметров потока в прямом скачке.
Скачок скорости ДУ = Уг — У2 можно определить, восполь-зовавшись формулой (VI.49), из которой следует, что У2= откуда
а2	/ д2 \	/	1 \
Ar = V',-Vs=V1--.= VI(l-lt)=V1(l-Jr).
(VI.51)
Величину- скачка давления Др = р2 — рх можно найти, используя выражение (VI.46), откуда
Др — Pi — pi — piVi — P2V2 = Р1^1 (Pi— У2) — PiVi дк ,
Имея в виду ранее полученное значение скачка скорости, получим
Др = Р1П (1 — А-).	(VI.52)
Для нахождения скачка плотности Др = р2 — Р1 воспользуемся соотношением (VI.45), из которого следует
>°2 = Р177 ’
Скорость V2 можно найти из формулы (VI.49), тогда
Др = р2 —P1 = P1	lj = Pi (М—1).	(VI.53)
154
Одномерное движение сжимаемого газа (газовая гидравлика)
Наконец, скачок температуры находится из уравнения энергии
M°=T2-Ti = ^(Vl—Vl)
или, определив V2 из формулы (VI.49) и вынеся VI за скобки, окончательно получим
<VL54)
Приведенные метров потока в перед скачком.
Имея в виду число М в виде
формулы выражают величину изменения пара-прямом скачке через коэффициент скорости
выражение (VI.33), можно % выразить через
1 _ k — 1	2	1
“ k + 1 -i" k + 1 М2 '
Заменив на Мх в формулах для скачков скоростей, давлений, плотностей и температур, получим:
2 ’	2 izjl—(VI.51)'
1 \ k + 1 k -|- 1 Mf J k +1 1 \ Mf / ’	4	1
<VL52>'
др=р, гЛ!~' 	<VL53)'
-I- 1
Скачок температур определится выражением
Д/о=^ г.м, [1 _(^=_! + _2__Цу].	(VI.54)'
Из всех приведенных формул видно, что скачок параметров потока возможен только при М± > 1 или > 1. При = = A.J = 1 и Mj < 1 или %! < 1 скачок физически невозможен. Скачок уплотнения возможен только при сверхзвуковом потоке; при звуковом и дозвуковом потоках скачок невозможен.
В табл. VI.4 приведены значения ДУ, ДТ и для воздуха (k =1,4) в зависимости от величины скорости Vj или числа Mj перед скачком при температуре Т х — 288 К (15° С) и нормальном атмосферном давлении.
Величины и — относительные изменения давления и
Pi Pi
плотности, отнесенные к соответствующим значениям перед скач-
Изменение параметров потока в прямом скачке. Ударная адиабата 155
Таблица VI.4
МЛ	V,, м/с	Г2, м/с]	ДГ, м/с	ДТ, °C	Ар Pi ктс/см*	Ар Pi
1	340	340	0	0	0	0
1,18	400	307	93	33	0,47	0,30
1.47	500	276	224	86,8	1,39	0,81
2,94'	1000	266	734	465	9,2	2,77
4,40	1500	319	1181	1075	22,2	3,74
5,90	2000	389	1611	1925	40,3	4,20
8,80	3000	540	2460	5940	92,3	4,58
11,8	4000	700	3300	7750	165	4,72
ком. Относительное изменение плотности в скачке, как видно из выражения (VI.53)', может быть записано следующим образом:
Др _	1 М?
Pi	1 ’
2 М?
Из приведенной формулы видно, что при стремлении числа М2 к бесконечности относительное изменение плотности имеет предел, равный
Для воздуха относительное изменение плотности при Мх —> оо будет равно = 5.
Указанные соотношения не учитывают диссоциацию и ионизацию газа при высоких температурах. При наличии диссоциации и ионизации газа величина относительного изменения плотности может быть больше пяти. .Так, при 7\ = 2260° С	= 6,04;
при 7\ = 14 000° С = 11,1, а при 7\ = 50 000° С = 8,97.
Pi	Pi
Известно, что при адиабатическом непрерывном движении идеального газа связь между давлением и плотностью определяется изэнтропической адиабатой
P^.= (P^\k.	(VI.55)
Pi \ Pi /
Из формулы (VI.55) видно, что при увеличении давления плотность растет неограниченно.
156
Одномерное движение сжимаемого газа (газовая гидравлика)
Установим зависимость плотности от давления в скачке уплотнения. Для этого воспользуемся уравнением изменения количества движения (VI.46) и уравнением энергии (VI.47). Из уравнения (VI.47) получим
VI — VI (&--&-}.	(VI.56)
«	1 \ Р1 Р2 /
Приведем уравнение изменения количества движения к виду Pi — р2 = РгИ — Pi W = Pi Vi (V2 — Ki).
, ,	+ Г2
Умножая правую часть равенства на —, а левую часть на равное значение, представленное в виде
= _1_ _1_	= 1 + _Ь_ = 1 j. Д_
Pl^l Pl	Pl р2^2 Pl Р2 ’
получим
Ц_И = (₽.-й)(^ + ^).
Приравнивая правую часть уравнения (VI.56) к правой части последнего выражения, найдем связь между давлением и плотностью
га (т “ тг) ==(Р1~Р2) (г + т) •
« — 1 \ pi р2 /	\ Pi Рг /
Группируя слагаемые с рг и р2, найдем
P1 U — 1 Pi Pi Р2 ) ~ pi \k — 1 р2 Р1 р2 ) '
Приведя полученное выражение к общему знаменателю и умножив на (k — 1) Р1Р2, окончательно получим
Pi __	4~ 1) Р2 — (& — 1) Pi _ (	) Р1 (_zyj
Р1 (k + 1)Р1- (k- 1)р2	(й+1)_(/г_1) Р2. ’
Р1
Уравнение (VI.57), устанавливающее зависимость давления от плотности в скачке уплотнения, в отличие от обычной изэнтропической адиабаты или адиабаты Пуассона (VI.55) называется ударной адиабатой, или адиабатой Гюгонио.
Решив уравнение (VI.56) относительно —, найдем
Pi
(Й4 1)4(6-1)21-Рг Рг Р1 (6—1)4(6 4 1)21-
Изменение параметров потока в прямом скачке. Ударная адиабата 157
Из последнего уравнения видно, что при у—> оо получается уже известное соотношение
Рг __> fe + 1 '
Pl “’Л— 1’
(VI.58)
Если, пользуясь уравнением состояния, заменить в выражении (VI.57) отношение плотностей отношением температур и давлений и затем написать "Полученное соотношение относительно Г *	•
получим
1 2 _ ______Р1_________\ Р1 /
Т1	(*4-1)-^+ (6-1)
Р1
На рис. VI.9 приведены обычная 1 и ударная 2 адиабаты и соответствующие зависимости температуры от давления. Из
рисунка видно, что при прямом скачке газ нагревается больше, чем при соответствующем изменении давления по обычной адиабате.
Если воспользоваться уравнением Бернулли (VI.47), заменив плотность и давление через температуру и подставив в него значение температуры за скачком, то большей температуре будет соответствовать меньшая скорость. Это значит, что при одном и том же изменении давления при обычном адиабатическом сжатии получаемая конечная скорость будет больше, чем скорость при соответствующем изменении давления .. в прямом скачке. При бесконечном увеличении давления в скачке плотность газа, как ранее было показано, остается величиной конечной.
158
Потенциальное движение идеальной несжимаемой жидкости
ГЛАВА VII
ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ
ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
§ 1. Комплексный потенциал и комплексная скорость
Ранее отмечалось, что идеальной жидкости в действительности не существует, однако приближения, связанные с ее введением в гидромеханику, значительно упрощают уравнения движения жидкости.
Теория движения идеальной жидкости широко разработана и во многих случаях дает вполне удовлетворительную картину движения реальной жидкости. Часто при изучении обтекания тех или иных тел пользуются последовательными приближениями, рассматривая вначале обтекание данного тела идеальной жидкостью, и затем вносят поправки на влияние вязкости.
Рассмотрим безвихревое движение идеальной жидкости.
Напомним, что в общем случае трехмерного движения течение будет безвихревым (потенциальным), если во всем потоке выполняется условие rot V = 0.
Это условие позволяет ввести функцию ср, называемую потенциалом скоростей; при этом проекции скорости определяются следующими соотношениями:
v =	w=-(VII.1)
дх ’ ду ’ дг	'	'
Вектор скорости будет V = grad ср.
Предполагаем, что потенциал скоростей ср и его две первые производные по координатам будут непрерывны.
Равенствам (VII. 1) удовлетворяет не только потенциал скорости <р, но и любая другая функция, отличная от ср на некоторую постоянную, т. е. <рх = <р + С. Следовательно, можно сказать, что потенциал скоростного поля определяется с точностью до постоянной.
Для установившегося безвихревого движения в общем случае <р = ср (х, у, г). Положив функцию ср (х, у, г) равной некоторой постоянной, т. е. ср (х, у, z) = С, получим уравнение поверхности, которую обычно называют эквипотенциальной поверхностью, или поверхностью равного потенциала.
Из векторного анализа известно, что если вектор а есть градиент некоторой скалярной функции f (х, у, г), то во всех точках поверхности f (х, у, z) = С вектор а нормален к поверхности
1
Комплексный потенциал и комплексная скорость
159
f (х, у, z) = С. Отсюда видно, что вектор скорости во всех точках эквипотенциальной поверхности ортогонален к ней. Так как вектор скорости всегда касателен к линии тока, то линии тока всегда нормальны к эквипотенциальным поверхностям.
Наибольший практический интерес имеет плоское стационарное безвихревое движение несжимаемой жидкости. Плоским будем называть такое движение, при котором все частицы жидкости перемещаются параллельно некоторой плоскости. При этом движение во всех плоскостях, параллельных этой плоскости, одинаково.
Выберем оси координат таким образом, чтобы определяющая течение плоскость совпадала с координатной плоскостью хОу. Тогда, считая, что от координаты z ничего не зависит, определим потенциал скорости для плоского движения:
v = ^-	(VII.
дх	ду	'
или так же, как и для пространственного движения V = grad ср.
В этом случае уравнения ср (х, у) — С будут уравнениями эквипотенциальных линий в плоскости хОу.
Уравнение неразрывности для несжимаемой жидкости в плоском движении имеет вид
4—4-4— = О или divIZ = 0.
дх 1 ду
Если ввести функцию ф, связанную с проекциями скоростей равенствами:
и =-тг~’> V— — ду	дх
(VI 1.3)
то функция ф тождественно удовлетворяет уравнению неразрывности, так как при подстановке в него значений и и v из выражений (VI 1.3) получим
д2Ф _ дгФ „
дх ду дх ду ~	•
Функция ф называется функцией тока, а выражение ф (х, у) = С является уравнением линий тока. Последнее легко доказывается подстановкой равенств (VII.3) в уравнение линий тока (II.5). Так же, как и потенциал скоростей, функция тока определяется с точностью- до постоянной.
Учитывая, что течение является безвихревым, т. е.
, Л ди	ди г,
rot V — ----— = 0,
дх	ду '
получим
Э2ф ___________
дх* + ду*
160
Потенциальное движение идеальной несжимаемой жидкости
Подставляя значения и и v из равенств (VI 1.2) в уравнение неразрывности, получим
д2ф  д2ф _ „
дх2 ду2
Эти уравнения показывают, что как функция тока, так и потенциал скорости удовлетворяют уравнению Лапласа, т. е. являются гармоническими функциями.
Из сравнения равенств (VII.2) и (VII.3) следует:
_дф_аф. дф___дф	vn
дх ~ ду ’ ду ~ дх ‘
Связь между двумя функциями <р (х, у) и ф (х, у), выраженная соотношениями (VI 1.4), имеет очень важное значение и в теории комплексного переменного называется условиями Коши—Римана. Известно, что если две функции ф и ф от х и у удовлетворяют условиям Коши—Римана, то комплексная величина
ф (х, у) + 1ф (х, у)
не просто зависит от х и у, а является функцией от одной комплексной переменной, z, равной z = х + iy = re1’0. Таким образом, существует функция комплексной переменной W (z), вещественная и мнимая части которой будут <р и ф, т. е.
W (z) = ф (х, у) + 1ф (х, у).	(VII.5)
Функция W (z) имеет очень большое значение в теории безвихревого плоского потока и называется комплексным потенциалом, или характеристической функцией течения.
Так как комплексный потенциал есть аналитическая функция от z, то производная от W (z) не зависит от направления дифференцирования и полностью определяется положением точки в плоскости хОу, заданной координатой z, т. е.
или
dW _ dW = dW дг дх ~~ d(iy)
д\У __ dW _ дф,  дф . дг дх дх ' дх ’
dW __ dW _ . dW _ . dtp . дф дг ~ д (it/)	1 ду 1 ду ду
Если использовать выражения (VI 1.2) и (VII.3), получим
aw? _ dW _ dW дг дх д {iy)
(VI 1.6)
Величина и направление скорости V в комплексной плоскости (рис. VII. 1) определится формулой
V = и + iv.
Комплексный потенциал и комплексная скорость
161
Сравнивая полученное выражение с формулой (VI 1.6), видим, что производная от комплексного потенциала по координате равна по величине скорости, но по направлению совпадает с зеркальным отображением вектора скорости относительно вещественной оси.
Так как в теории комплексного переменного величины z — = х + iy и z — х — iy .называют сопряженными, то
V = и — iv
можно назвать сопряженной скоростью.
Плоскость uv называется плоскостью годографа скорости, или плоскостью годографа.
Вычислим значение контурного интеграла, dz = (j) V dz = (j) (и— iv) (dx -f- idy) =
= Cp [(u dx 4- vdy) -|- i (u dy — v dx)],
(j) (u dx + v dy) = Г,
(j) (u dy — v dx) = dy -j- dx} - (f)	= Q.
Здесь Г — циркуляция скорости по замкнутому контуру; Q — объемный расход через замкнутый контур.
Таким образом, получим для действительной части (д. ч.)
§~dz = d.4. §Vdz = V
и для мнимой части (м. ч.)
§^dz = M.4.<$Vdz = Q,	(VII.7)
т. е. действительная часть интеграла определяет циркуляцию скорости по замкнутому контуру, а мнимая — объемный расход жидкости через этот контур.
Таким образом, для изучения плоских безвихревых движений идеальной жидкости можно широко пользоваться теорией комплексного переменного. При этом комплексному потенциалу определенного вида соответствует некоторое движение жидкости и, наоборот, каждое движение может быть представлено некоторым комплексным потенциалом. Соответственно можно поставить две задачи: 1) по заданному комплексному потенциалу построить движение, т. е. найти <р и ф и поле скоростей; 2) зная контур обтекаемого тела и значение скорости на бесконечности, найти
11 И, Л. Повх
162
Потенциальное движение идеальной несжимаемой жидкости
соответствующий комплексный потенциал. Вторая задача значительно труднее первой. В последующих параграфах рассмотрим примеры первой задачи для некоторых простых и важных для гидромеханики комплексных потенциалов.
§ 2. Некоторые простейшие потенциальные потоки
Плоскопараллельный поток. Наиболее простым примером комплексного потенциала является выражение
W (z) = az = а (х 4- iy).	(VI 1.8)
Рассмотрим последовательно это выражение для вещественного, мнимого и комплексного значений числа а.
Если а = вещественно, то
W (z) = a1z = aYx 4- iayy.
Так как W (z) = ср 4- 1ф, то <p = a±x и ф = агу, откуда получим, что эквипотенциальные линии ср = const имеют вид
ср = arf = С,
т. е. будут семейством прямых, параллельных оси у, а линии тока Ф = агу = С
будут семейством прямых, параллельных оси х.
На рис. VI 1.2, а показаны эквипотенциальные линии и линии
тока в плоскости хОу. <
Проекции скоростей можно найти по формула^ (VI 1.2) и
u=^- = ^- = a-	= —^1 = 0
дх ду	1 ’	ду	дх
Некоторые простейшие потенциальные потоки
163
Если совместить плоскость годографа с плоскостью хОу (рис. VI 1.2, а), то вектор скорости этого движения будет совпадать по направлению с линиями тока.
Если число а мнимое, т. е. а = iax (а1 — вещественное число), то
W (z) = az = iaY (х + iy) = —а^У + ia Yx,
тогда ф = —агу и ф — ахх.
Эквипотенциальные линии и линии тока соответственно будут: Ф = —агу = С и ф = агх = С.
По сравнению с предыдущим случаем линии тока и эквипотенциальные линии при умножении комплексного потенциала на мнимую единицу меняются местами.
Проекции скоростей будут
• и—	л и <?Ф__	п
дх ду\	ду дх 1
Если а — комплексное число, равное а = аг + ia2 (ах и а2 — вещественные положительные числа), то комплексный потенциал будет
W (z) = az = (aY + ia2) (х + iy) = (а3х — a2y) +
+ i (a2x + aYy) = ф + 1ф.
В этом случае потенциал скорости ф й функция тока ф имеют вид:
Ф = aYx — а$ и ф = а2х + a3y,
а2.
а проекции скоростей равны
dtp дф	dtp	chp
W* ” • *	г	1 И	~~ — -ч	 1	-ч
дх ду 1	ду дх
Уравнениями линий тока и эквипотенциальных линий соответственно будут:
а2х -{- агу — С\ или у = — у- х + С2;
«1% — а2у = С3 и ли у — — х -ф- С4.
а2
Полученные равенства представляют собой уравнения взаимно перпендикулярных прямых, показанных на рис. VII.2, б. Если комплексный потенциал W (z), представляющий собой плоскопараллельный поток, умножить на мнимое число i, то линии тока и эквипотенциальные линии поменяются местами.
Источник и сток. В качестве второго примера рассмотрим комплексный потенциал вида
W (z) = a In z — ф -f- £ф.	(VII.9)
11*
164
Потенциальное движение идеальной несжимаемой жидкости
Пусть а — вещественное число. Тогда
W (z) = a In z = a In re1’9 = a In г + a In е‘» = = a In г + iaQ.
Очевидно, потенциал скорости и функция тока такого движения будут- иметь вид
ср = a In г и Ф = аО.
Линии тока и эквипотенциальные линии, выраженные уравнениями:
аО — С и a In г = С,
будут соответственно семейством прямых, проходящих через начало координат, и семейством окружностей с центром в начале координат (рис. VI 1.3).
Рис. VII.3
Составляющие скоростей можно определить согласно выражениям в цилиндрической системе координат:
,, да> оф д - а
Уг=~^:=-7дО-=дГа[пг = -
У =-^- = 0.
° rdQ
(VII.10)
Знак Vr определяется знаком числа а. Если а положительно, то направление линий тока будет соответствовать источнику (рис. VII.3, а); при отрицательном а—стоку (рис. VII.3, б).
Следует отметить, что начало координат является особой точкой, в которой величина скорости обращается в бесконечность.
Зная поле скоростей, можно найти объемный расход источника или стока 2Л	2Л
Q = j Vгг d0 — j add = 2ла.
Некоторые простейшие потенциальные потоки
165
Следовательно, число а можно выразить через объемный расход Q, определяющий мощность источника или стока, и комплексный потенциал такого потока можно представить в виде
r(z) = A]nz.	(VII.11)
Вихрь. Если в комплексном потенциале (VI 1.9) число а мнимое, т. е.
а = icty,
W (z) = iar In z = ф + гф,
(VII.12)
то по сравнению с предыдущим линии тока и эквипотенциальные линии поменяются местами, так как
W (z) = in rei9 = —+ ia-i In r,
где «j — вещественное число.
Тогда ф = —аД и ф = аг In г, а уравнения линий тока и эквипотенциальных линий ф = «! In г = С и ф = —о^б = С будут
Рис. VII.4
соответственно выражать семейство окружностей с центром Ё начале координат и семейство прямых, проходящих через начало координат (рис. VII.4, а). Составляющие скоростей имеют значения
V —	— Г) и V — д(<>
дг ° и где
а-1. г
Для определения физического смысла вещественного числа аг найдем величину циркуляции Г вдоль любой замкнутой линии тока, содержащей внутри начало координат Г = 2лгУ0, после подстановки найденной величины V0 получим Г = —2лах, откуда
Г
166 Потенциальное движение идеальной несжимаемой жидкости
Следовательно, комплексный потенциал (VII. 12) потока с циркуляцией Г будет иметь вид
г, г
Величина скорости
обратно пропорциональна радиусу г, т. е. = const.
Такое движение жидкости соответствует циркуляционному потоку вокруг вихревой нити. В случае плоского движения имеем поток вокруг точечного вихря, находящегося в начале координат.
Вихресток и вихреисточник. При комплексном значении числа а, равном ф- iblt комплексный потенциал (VII.9) будет иметь вид
W (z) = (а± + ibj) In z = («j + ibj) In reze = = (at + ibj) (In r + In e1'0) =
= («! In r — bjQ) + i (bY In г 4- ах0), откуда потенциал скорости <р и функция тока ф равны
ср = у In г — &19; ф = bY In г + аг0.
Это движение можно рассматривать как сумму двух предшествующих потоков: источника или стока и вихря.
Линии тока такого движения, называемого вихреисточником, показаны на рис. VII.4, б.
Диполь. В качестве последнего примера рассмотрим комплексный потенциал
<VIL14)
После подстановки z = х + iy- получим гу,  т х — iy ______________________ т (х — iy)
2л (х + iy) (х— iy)	2л х'2 -|- у2 ’
откуда потенциал скорости ср и функция тока ф будут иметь вид т х ,	т и
<р = -х- -sn—з- И ф = — ----, "	.
1 2л хг у2 1	2л х2 -|- у2
Уравнения линий тока (ф = const) и эквипотенциальных линий (ср = const) запишем так:
X2 ф- у2 = су, х2 + у2 = сх.
Обтекание круглого цилиндра
167
Первое уравнение дает семейство окружностей, проходящих
через начало координат, с центрами, расположенными на оси у,
а второе — такие же окружности, но с центрами, расположенными
на оси х. Линии тока и эквипотенциальные линии диполя показаны на рис. VI 1.5.
§ 3. Обтекание круглого цилиндра
Рассмотрим комплексный потенциал W, представляющий собой сумму комплексных потенциалов плоскопараллельного потока, параллельного оси х, и диполя
Г(г) = ^г + ^1. (VII.15)
Рис. VII.5
Определим мнимую и вещественную части функции W (z)
tz । /п x \ . . IIZ m и \
VcX ‘4 Z---------3—i o" | “H ( VC£>y --------- о---2—i 2 1 •
1 2л . x2 -|~ у2 J \	2л x2 + у2 J
Тогда выражения для потенциала скорости и функции тока получим в виде:
, т 1	\
ф — \Vm -|-+ у2 j х;
ф—	2^ у2 J У'
Следовательно, уравнение линий тока будет
Приравнивая константу нулю, получим уравнение нулевой линии тока, которое разбивается на два
Первое уравнение представляет собой ось абсцисс, а второе — окружность радиуса а =	с центром в начале коор-
динат.
168
Потенциальное движение идеальной несжимаемой жидкости
На рис. VI 1.6 показаны линии тока движения жидкости, выраженного комплексным потенциалом (VII. 15).
Известно, что при движении идеальной жидкости из-за отсутствия в ней трения замена любой линии тока твердой стенкой не меняет характера движения. Поэтому, если в рассматриваемом потоке заменим нулевую линию тока твердой стенкой, то, как видно из рис. VI 1.6, получим обтекание круглого цилиндра плоскопараллельным потоком с вектором скорости на бесконечности,
ТО
перпендикулярным оси цилиндра. । Для определения поля скоростей и давлений представим по- < тенциал скорости <р в цилиндрических координатах. Так как
х = г cos 6, у = г sin О, х2 4- у2 = г2 и
,, __ т 1
2л ’
Зная выражение для <р, легко найти проекции скорости:
На поверхности цилиндра г = а и
Vr = 0, a Ve = —2Vra sin 9.	(VII.16)
Таким образом, скорость на поверхности цилиндра при его обтекании потенциальным потоком изменяется по синусоиде, достигая своего максимального значения в точках 9 = 90 и 270°.
Точки, в которых скорость равна нулю, обычно называются критическими. Очевидно, что при обтекании плоскопараллельным потоком круглого цилиндра такими точками будут 9 = О.и 9 = = 2л. Первая точка А называется передней критической точкой, а вторая В — задней.
i Из уравнения Бернулли, написанного для нулевой линии тока, можно найти распределение давления- на поверхности круглого цилиндра.
Обтекание круглого цилиндра
169
Если обозначим величину давления в любой точке на поверхности цилиндра через р, то уравнение Бернулли для нулевой линии тока примет вид
р17! -	, pv*
Р'~ Н 2 -----Р I 2 ’
откуда
В практике наибольший интерес представляет не абсолютное значение величины давления, а безразмерный коэффициент давления р
Р —. V2 со	и со
Р~2~
Так как из выражений (VII. 16) следует, что
1/2
—7-= 4 sin2 9,
(VII.17)
22 и2 г т
то коэффициент давления будет равен
Р
на поверхности круглого цилиндра
Р =
1—4 sin2 9.	(VII. 18)
На рис. VII.7 показано изменение р в зависимости от угла 9. Из рисунка видно, что р = 1 при 9 = 0 и 180°, pmln = — 3 при 9 = 90 и 270°.
170
Потенциальное движение идеальной несжимаемой жидкости
Из распределения скоростей и давлений видно, что и поле скоростей, и поле давлений симметричны относительно декартовых осей координат, проведенных через центр окружности. Следовательно, при обтекании круглого цилиндра потенциальным потоком идеальной жидкости на цилиндр никакие силы действовать не будут.
При обтекании круглого цилиндра реальной жидкостью распределение давлений, как видно из рис. VII.7, существенно отли? чается от теоретического. Оставаясь симметричной относительно оси абсцисс, кривая давлений для действительной жидкости будет несимметричной относительно оси ординат. Такая несимметрия вызовет появление проекции силы на направление движения — силы сопротивления. Следует отметить, что вид кривой распределения давлений будет зависеть для данного цилиндра от скорости потока, а точнее — от числа Re. Причем с увеличением числа Re распределение давлений будет приближаться к распределению давления на цилиндре, обтекаемом идеальной жидкостью.
Равенство нулю равнодействующей сил давления, приложенных к цилиндру при его обтекании идеальной жидкостью, можно легко доказать, определив проекции этой равнодействующей.
Проекции сил давления, действующего на элементарную площадку ds-1 (рассматриваем площадку единичной длины) будут равны:
dY = —р sin 0ds; dX = —р cos 0 ds.
Из предыдущих формул имеем
pV2
Р =	+	4sln20).
Но так как ds = a d6, то
2л	2л
Р	р/2 ('
Y = — рка j sin О А) — а —1(1 — 4 sin'2 0) sin 0 dd.
о	о
Учитывая, что
2 л	2 л
j sin0dO = O и Jsin30dO = O, о	°
получим Y = 0.
Аналогичным образом легко показать, что и величина силы сопротивления тоже равна нулю, т. е. X — 0.
Заметим, что сила сопротивления при потенциальном потоке идеальной жидкости равна нулю не только при обтекании круглого цилиндра, но и для любого другого тела, независимо от его формы.
Отсутствие силы сопротивления для тел, обтекаемых потенциальным потоком идеальной жидкости, в гидродинамике называется парадоксом Эйлера—Даламбера.
*
Циркуляционное обтекание круглого цилиндра
171
§ 4. Циркуляционное обтекание круглого цилиндра
Рассмотрим плоский потенциальный поток, определяемый комплексным потенциалом
№(г) = 7да(г + 4)+-2&-1пг-	<VIL19)
Этот потенциал описывает наложение параллельного оси X плоскопараллельного потока, обтекающего круглый цилиндр (VII. 15), и циркуляционного потока вокруг точечного вихря (VII. 13).
Для .нахождения потенциала скорости ср и функции тока ф найдем веществ.енную и мнимую части комплексного потенциала W. Так как
у = и. [(х + ад +	] - £ in re»,
то, имея в виду, что
х = г cos 9; у = г sin 9 и х2 + у2 = г2, получим в полярной системе координат:
ср = У- (1 + -^-)rcos9 + -^9;
ф = Vro (1 —	г sin 9—	In г.
Зная ф и ф, легко найти линии тока и эквипотенциальные линии, а также поле скоростей. Величины скоростей будут:
cos 9.
(VI 1.20)
v __д<р = Эф
г дг г об
На поверхности цилиндра (г — а) получим: г V0 = -2yOTsin9 + -^;
Vr = 0.
Уравнение линий тока будет иметь вид
Уоо (1---\ Vsin 9---In г — const.
\ г2 /	2л
Чтобы лучше представить себе такие линии тока, найдем точки на цилиндре, в которых скорость обращается в нуль, т. е. критические точки. Их можно определить, приравняв скорость У0 нулю. Из выражений (VII.20) имеем Г
2v“sin9=^’
172
Потенциальное движение идеальной несжимаемой жидкости
откуда
 о Г
Sin 0 = -г-г;------.
AiiVcoa
(VII.21)
Из формулы (VII.21) видно, что возможно следующее распо- . ложение критических точек.
I.	При Г = 0 будет иметь место бесциркуляционное обтекание. При этом углы, соответствующие критическим точкам, будут равны 0КР1 = 0 и 0кр2 = 180°.
2.	При Г < 4лУ^а (рис. VII.8) обе критические точки будут располагаться на окружности цилиндра симметрично относительно оси у в диапазоне 0 < < 0кр < я при выбранном знаке циркуляции.
3.	При стремлении величины циркуляции к значению 4л1/ета критические точки будут приближаться к оси ординат, а при Г = 4лУта получится одна критическая точка при 9кр = = -5- (рис. VII.8).
Линии тока (рис. VII.8) во всех случаях симметричны относительно оси у и несимметричны относительно оси х. Следовательно, при циркуляционном обтекании цилиндра проекция главного вектора сил давления на ось х равна нулю, т. е. X = 0, а проекция на ось у не равна нулю и может быть вычислена по формуле
2л
Y — — a j psinOdO. о
Величина давления р может быть найдена из уравнения Бернулли для нулевой линии тока
+~- = р	f (-2Н7— 2Vcx> sm е)2,
Д	Z \ 4,JiU	/
откуда
р = р<о 4- —К2------о2-	----2sin0 ) = C4-C1sin0 — C2sin20.
X.	Z \ Zjlu V 00	/
Подставив величину давления под знак интеграла, получим
2л
Y ~ —a j (С 4- Сг sin 0 — Сг sin2 0) sin 0 dO. о
 Простейшие пространственные потенциальные потоки
173
Известно, что интегралы от первого и третьего слагаемых равны нулю, и тогда
2л
У = _р£^ fsi^0de. я J
о
Но так как
2л	2л	2л
f  о 70 f 1 — cos 20 ,л	10 sin 20 I
j Sin-0^0 = j-----=	| = 3t,
0	0	0
то окончательно получим, что главный вектор сил давления при циркуляционном обтекании цилиндра будет направлен перпендикулярно скорости на бесконечности и
равен
Y = -р]/гоГ. (VII.22)
Формула (VII.22) является частным случаем формулы Жуковского, пригодной для любого контура, обтекаемого плоскопараллельным потоком. Вывод более общей формулы Жуковского будет приведен далее
о сила-
Рис. VI 1.9
(см. стр. 214).
Движение, аналогичное рассматриваемому, можно наблюдать при обтекании реальной жидкостью вращающихся тел. Возни-
кающая в этом случае сила, направленная перпендикулярно скорости на бесконечности, используется в некоторых устройствах. Так, например, в Италии были построены суда, которые перемещались от действия ветра на вращающийся цилиндр. Если, как это показано на рис. VI 1.9, на вращающийся цилиндр будет набегать поток ветра, то к цилиндру, а следовательно, и к кораблю будет приложена сила, направленная по нормали к направлению ветра. Таким образом, корабль может переме
щаться.
Действие поперечной силы может проявляться и при вращающемся движении футбольного мяча и пр.
§ 5. Простейшие пространственные потенциальные потоки
Задачи о пространственном обтекании тел в общем случае очень сложны. Даже в безвихревом потоке найти потенциал скорости трехмерного потока намного труднее, чем для плоского.
В общем случае трехмерного безвихревого движения потенциал скорости существует, т. е. имеется функция <р, удовлетворяющая условию (VI 1.1). В то же время функция тока в обычном представлении может существовать только для осесимметричных
174
Потенциальное движение идеальной несжимаемой жидкости
потоков. Из-за сложности трехмерных потоков рассмотрим лишь продольное обтекание осесимметричных тел.
Для нахождения потенциала скорости и функции тока осесимметричных потоков большое значение имеет выбор системы координат. Для большинства осесимметричных потоков написать функцию тока в удачно выбранной криволинейной системе координат не представляет больших трудностей. В прямоугольной же системе координат получить выражение функции тока чрезвычайно сложно, а иногда невозможно.
Следовательно, возможность отыскания функции тока зависит не только от формы движения, но и от выбора системы координат, в которой представляется движение тела. Наибольшее применение получили цилиндрическая и сферическая криволинейные системы координат.
Если в цилиндрических координатах, (г, z и [3) ось z совместить с осью симметрии осесимметричного тела, то при обтекании тела потоком, направление скорости которого будет совпадать с осью симметрии, все параметры потока полностью определяются координатами г, z и не будут зависеть от угла (3.
Проекции скоростей Vr и Vz в выбранной системе координат определяются через потенциал скорости <р:
^=4?;	(VIL23>
Уравнение неразрывности движения
+	= °	(VI 1.24)
позволяет утверждать, что существует функция тока ф (г, г), через которую проекции скоростей определяются следующим образом:
Ег = - — 4^; Уг = —(VII.25) г г дг г г дг	'	'
что можно проверить подстановкой этих равенств в уравнение (VI 1.24).
Скорость продольного осесимметричного потока в сферических координатах выражается через проекции и V0, определяемые потенциалом скорости:
и«=-Й-; П=4-аг-	<VI1-26)
Уравнение неразрывности в этом случае будет
-^-(W«sine) + ^(7?V9sin8) = 0,	(VII.27)
________Простейшие пространственные потенциальные потоки	17*5
и соответственно проекции скоростей определятся через функцию тока:
V —	1	££•
Л У?2 sin 0 <?0 ’
т/ ___________}_____^4
0 R sin 0 dR
(VIL28)1
Поверхности, заданные уравнениями <р = С и ф — С, как прежде указывалось, называются соответственно эквипотенциальными поверхностями и поверхностями тока.
Очевидно, что векторы скоростей будут касательны к поверхности тока, а следовательно, через нее так же, как и через линию тока, жидкость не течет. Поэтому расход жидкости, текущей между двумя поверхностями тока и ф2, будет постоянным.
На примере осесимметричного потока можно показать, что секундный расход жидкости через сечение, ограниченное окружностью радиуса г2, будет определяться функцией тока в точке этой окружности. Секундный расход через кольцевое сечение с радиусами rY и г2 будет равен
Q = 2л J V/ dr = 2л j dr --- 2л (ф2— ipi).
Если Tj = 0, то Q = 2лф2.
Рассмотрим простейшие примеры пространственных потенциальных потоков.
Однородный поток. Рассмотрим однородный поток с постоянной скоростью V-, направленной вдоль оси г. В этом случае в цилиндрической системе координат будет:
^ = ^ = -±41 = 0;
Г dr	г dz
I/ — дф _ 1 дф ,. дг ~ г дг —
откуда (с точностью до постоянной) потенциал скорости такого потока равен
Ф =	(VI 1.29)
а функция тока
ф = 1угаА	(VI 1.30)
Иточник (сток). Если поместить источник (или сток) в начале координат, то жидкость будет течь во все направления с одинаковой скоростью и секундный расход, называемый мощностью источника (стока) Q-, будет равен поверхности сферы
176
Потенциальное движение идеальной несжимаемой жидкости
радиуса 7?, умноженной на величину скорости, одинаковой во'',' всех точках сферы <2 = 4л УТ?2.
В сферических координатах VR = V, а
VR и Vq через потенциал скорости, получим:
(/ _1/— д(Р - Q •
VR—V — dR 4nR2 , v —— о vt>— r де —
V9 = 0;
выражая
(VII.31)
3
скорости 1 запишем | (VII.32) |
Интегрируя выражения (VII.31), найдем потенциал источника. Пренебрегая постоянной интегрирования,
<2
Аналогичным образом, выражая VR через функцию тока ф, J
получим в соответствии с выражением (VII.28)	|
у у  	*	дф  Ч	|
*	У?2 sin 6 66	4л/?2 ’	.3
поэтому функция тока источника будет иметь вид	j
ф = —^-cos0.	(VII.33) 1
Сток отличается от источника противоположным направлением движения^жидкости; для источника Q > 0, а для стока Q < 0. 1 Имея в виду, что связь сферических координат с цилиндри-ческими устанавливается формулами:	!
'7?2 = z2г2; cose = y=L==,	(VI 1.34)
получим, что потенциал скорости источника, находящегося в начале координат, в цилиндрической системе имеет вид
(VIL36)
а функция тока соответственно будет
ф = -^---Й=.	(VII.36)
Т 4jl /z2 f2	V ’
Если источник (сток) поместить не в начале координат, а в точке z = а, то потенциал скорости и функция тока.ф будут: ф=_^—2_-;	(VII.37)
V (г + а)2 г2
Q z —1~ а
(z -f- а)2 г2
(VI 1.38)
Простейшие пространственные потенциальные потоки	\П
Рассмотрим несколько примеров наложения пространственных потенциальных потоков.
Аналогично плоскому диполю (VII. 14) можно получить диполь пространственный. Если возьмем источник и сток равной мощности и расположим их на равных расстояниях от начала координат ±а и затем начнем их приближать к началу координат так, чтобы предел lim Qa = т оставался постоянным, то получим а~>0 Q->co .
пространственный диполь. Потенциал скорости и функция тока диполя будут соответственно равны:
(P = --4^COS0;	(VIL39)
(VIL4°)
Практический интерес представляет обтекание так называемого полутела (рис. VII. 10). Потенциал скорости полутела будет складываться из потенциала прямолинейного потока (VII.29) и потенциала источника (VII.35)
1/	<2	1
Соответственно функция тока из выражений (VII.30) и (VII.33) будет
или, имея в виду формулу (VI 1.34) и что г2 = R2 sin2 0, получим в сферических координатах
^ = 1^ 51^0 —A cos 9.	(VII.41)
Следует отметить,! что форма полутела обычно придается носику трубки для измерения скорости (трубка Пито—Прандтля), поэтому геометрическая форма полутела представляет большой интерес. Очевидно, обвод полутела можно получить положив Ф = 0.
Из (VII.41) при ф = 0 следует, что обвод полутела (рис. VII. 10) определится уравнением
_0_____1_
41/о	0 '
COSj
12 И. Л. Повх
178
Потенциальное движение идеальной несжимаемой жидкости
При 9 = 0, т. е. в критической точке, имеем
Найдя значение скоростей на поверхности полутела по выражениям (VII.26), можно, воспользовавшись уравнением Бернулли, определить распределение давлений по поверхности.
На рис. VII. 10 приведено расчетное распределение безразмерного давления р, равного
Р Pit
2
§ 6.	Обтекание шара
В качестве примера наложения потоков рассмотрим обтекание потенциальным потоком сферы, которое получается как совокупность однородного потока и диполя. Потенциал скорости такого потока выражается как сумма потенциалов однородного потока и диполя с обратным знаком
<p = l/0R (1 + cos9,	(VII.42)
а функция тока определится суммой величин ф из равенства (VI 1.30) и ф из равенств (VI 1.40) с обратным знаком
ф = (1V0R2— -^) sin29.	(VII.43)
Приравняв последнее выражение нулю, найдем нулевую поверхность тока
(4v«RI-4Msln’e=0'
Решая последнее уравнение, получим два корня. Первый корень sin2 0 = 0, откуда 0 = 0; ±л. . . есть уравнение оси г; второй корень — уравнение сферы с центром в начале координат и радиусом, равным
У ZHy о
Заменив сферическую поверхность тока твердой стенкой (рис. VII. 11), получим картину обтекания сферы параллельным потоком идеальной жидкости.
Величина момента диполя т определится из последнего равенства и будет равна т = 2л7?о17о.
Обтекание шара
179
Подставив значение т в формулы (VII.42) и (VII.43), получим выражения для потенциала скоростей и функции тока:
<p = V0R [1 + 4 (4г)3]cos6; = С1 ~(^)3]sin20-
Зная потенциал скорости или функцию тока, нетрудно найти проекции скорости VR и ]/0:
,'>=®=ЧЧт)']с“е;
(VI 1.44)
видно, что величина скорости на по-
Очевидно, что на поверхности шара при R = Ro будет V# = 0. Это естественно, так как нормальная составляющая скорости на линии тока всегда равна н;
На бесконечности при R имеем
]/Л= ]Z0 cos 9 и Уе = — Уо:
следовательно,
. v=yvb + v%=v0.
Таким образом, получим скопараллельный поток со ростью Vo.
Из выражений (VI 1.44) верхности сферы равна’
V = Ve = --f-Vosin9.
Точки, в которых скорость обращается в нуль, т. е. критические точки (но не линии, как в случае поперечного обтекания цилиндра), будут при 9 = 0 и 9 = л. На рис. VII. 11 критическими точками являются точки А- и В.
л 3
Максимальное значение скорости будет при 9 = -% ; у л, т. е. в миделевом сечении сферы. Абсолютное значение этой ско-з
рости равно Vmax = у Vo-
Зная поле скорости и используя уравнение Бернулли в форме
Ра+41 = р + 4!=₽ + ||и8з1п’е,
180
Потенциальное движение идеальной несжимаемой жидкости
легко найти распределение безразмерного давления по сфере
^=^r=1~^sin20-	(VIL45)
2
Минимальная величина давления будет в сечении, в значения ^при 0 =	;
скорость достигает максимального
котором она
равна р = —7.
При поперечном обтекании цилиндра (VII. 18) минимальное р = —3, а максимальная скорость в два раза больше скорости . на бесконечности. Следовательно, возмущения, вызываемые движением цилиндра, намного больше, чем при движении сферы. Это естественно, так как при поперечном движении цилиндра даже с длиной, равной диаметру цилиндра, количество вытесняе-' мой жидкости больше, чем при движении сферы того же диаметра.
При обтекании сферы реальной вязкой жидкостью поле скоростей и давлений на поверхности сферы существенно отличается от приведенного выше, или р (0) при обтекании сферы вязкой числа 'Re = и числа' М.
При больших числах Re сфера плохо Поток реальной жидкости срывается с поверхности Re'< ReKp этот срыв происходит при 9 = 82°, а для Re > ReKp при 0 > 120°. Критическое число Re зависит от степени турбулентности потока и изменяется в пределах от 1,2 • 10е при большой степени турбулентности; до 3-10® — при малой степени турбулентности.
На рис. VII. 12 приведены кривые распределения давлений по сфере, полученные экспериментально на шаре диаметром 150 мм при числах Re = 157 200-ь424 500.
Из сравнения приведенных кривых с зависимостью (VII.45) можно установить следующие отличия при обтекании сферы вяз-
Рро
1.0
0.8
0,6
0.4
0.2
0
-0,2
-0.4
-0.6
-0,8
' -1,0
-1.2
0 20 4/7 60 80 100 120140 160 180V,.. °
Рис. VII.12
Характер жидкостью
обтекается
кривых ]/0 зависит от
жидкостью, сферы. Для
Обтекание шара
181
кой жидкостью для больших чисел Re от соответствующего обтекания идеальной жидкостью:
1) поле давлений при обтекании идеальной жидкостью симме-
трично относительно миделевого сечения, в то время как при обтекании вязкой жидкостью оно несимметрично и существенно зависит от числа Re, особенно за миделевым сечением. Вблизи передней критической точки (примерно от 40—45°) кривые давления не зависят от числа Re;
2) минимум давления	Таблица VII. 1
при обтекании вязкой жидкостью всегда расположен до миделевого сечения;
3) при.стремлении числа Re к бесконечности кривые давления приближаются к кривым давления в идеальной жидкости.
Если допустить, что отрыв потока происходит в точке установления посто-
Re	сх		
	Формула Стокса	Формула Озеена	Опытные данные
0,0531	451,2	465,5	476,6
0,2437	98,5	103,1	109,6
- 0,7277	32,98	38,23	38,82
1,493	16,07	22,32	19,40
10,000	2,4	7,2	4,6
янного давления, то, как видно из кривых рис. VII.12 (точка О),
с увеличением числа Re область отрыва уменьшается.
Из симметрии кривой давления, построенной по уравнению (VI 1.45), следует, что главный вектор сил давления равен нулю. Это означает, что при равномерном движении сферы в идеальной жидкости она не испытывает никакого сопротивления. Оказы-
вается, что полученный результат для сферы верен для всех конечных тел, обтекаемых пространственным потенциальным потоком. Это явление называют в гидродинамике парадоксом Даламбера.
Теория обтекания сферы вязкой жидкостью при больших числах Re не разработана, поэтому в этом случае сопротивление сферы может быть определено только из опыта.
Задача о движении сферы при малых числах Re решена тёоре-тически. В этом случае закон сопротивления сферы представляется
в виде ряда
с»=  иР2=4(1	®oR'!+- ) <VIL46>
-g- р V0n7?0
где Сх — коэффициент сопротивления; X — сопротивление сферы.
Решение, учитывающее только первый член ряда, приводит к известной формуле Стокса, а решение, учитывающее два первых члена ряда, — к формуле Озеена. О точности решения и области применения этих формул можно судить, сравнивая результаты расчета с опытными данными (табл. VII.1).
182
Потенциальное движение идеальной несжимаемой жидкости
Формулы Стокса и Озеена верны для чисел Re порядка единицы и меньше. Зависимость Сх от числа Re в широком диапазоне чисел Re, полученная из опыта, приведена на рис. VI 1.13.
При изменении числа Re от 1,57 • 10е до 2- 10е коэффициент сопротивления убывает от 0,45 до 0,15, т. е. уменьшается в три раза.
После тщательного изучения экспериментальной зависимости^ коэффициента сопротивления сферы (рис. VII.13) оказалось воз-j можным представить эту зависимость в степенном виде
С*=^- (VIL47)<
Очевидно, что для закона Стокса, согласно (VII.46), а = 24 и т — 1. Значения величин а и т для различных диапазонов чисел Re приведены в табл. VI 1.2.
Таблица VI 1.2
Re	а	гп	в	ь	С	п
0-1	24	1	0,54	2	—1	1
1-50	25	3	0,52	7	1	4
		4		5	15	5
50-1 000	4	3	3,30	13	1	10
		10		17	51	17
1 000—200 000	0,45	0	30,0	1 2	0	1 2
Основные уравнения
183
Если приравнять полное сопротивление сферы архимедовой силе (1.19), то легко получить скорость установившегося движения сферы под действием силы Архимеда.
Из соотношения
aRe-m tcRq = nR30 (ух—у) =	(у— 1)
определим скорость
V = Bdbvc 1)", где Vi и у — удельные веса тела и жидкости, в которую оно погружено; d. = 2R0.
Значения постоянных В, Ь, с и п для различных диапазонов чисел Re приведены в табл. VII.2. При Re sg 1, т. е. для закона Стокса, имеем
ГЛАВА VIII
ПЛОСКИЙ ПОТЕНЦИАЛЬНЫЙ ПОТОК ГАЗА
§ 1. Основные уравнения
Если в покоящемся газе (воздухе) имеется некоторый источник слабых возмущений, то, как было показано ранее (п. 7, гл. V), эти возмущения будут распространяться во все стороны со скоростью, равной скорости звука. При периодических возмущениях все пространство вокруг источника через достаточно большой промежуток времени будет заполнено сферическими волнами.
Если такие возмущения производить в движущемся газе, • то область распространения возмущения будет зависеть от величины скорости движения потока по сравнению со скоростью распространения возмущений. Если скорость потока меньше скорости звука (рис. VIII. 1, а), то волны возмущений распространяются во всей области движения как по потоку, так и против него. На рис. VIII. 1 показана совокупность эксцентрических сфер, которые при значительном времени возмущения займут все рассматриваемое пространство.
При скорости движения газа, равной или большей скорости звука, волны не могут распространяться против течения. Следовательно, в этих случаях картина распространения возмущений будет принципиально отлична от двух выше рассмотренных слу
184
Плоский потенциальный потоп газа
чаев (V = 0 и V < а) и область возмущения может занимать лишь часть пространства, в котором происходит движение.
Если скорость потока равна скорости звука (рис. VIII. 1, б), то» слабые возмущения будут концентрироваться и через некоторое^ время образуют поверхность, которая на достаточно большом?' участке будет нормальна к скорости движения. При сверхзвуко-1 вой скорости потока концентрация малых возмущений будет про-ч исходить на некоторой конической поверхности, называемой кону-\
Рис. VIII.l	J
1
сом возмущения. Из рис. VIII.1, в видно, что угол раствора конуса,: равный 2а, может быть определен из соотношения^
sin а =.	(VIII.l)
Очевидно, чем больше число М набегающего потока, тем меньше угол а.
Покажем далее, что указанные выше два принципиально отличных процесса распространения возмущений при дозвуковых и сверхзвуковых скоростях газа описываются двумя совершенно различными типами дифференциальных уравнений.
Для получения этих уравнений представим уравнение неразрывности (III.3) в случае плоского течения сжимаемого газа в виде д , . , д , \	/ ди . до \ , др , др
17 (р«) н- — р(д7+д7)+ u д?+ D д7'
Но так как плотность зависит непосредственно от давления, то:
др _	др др	_ 1 др .	др	_ др др	_ 1 др
дх	др дх а2 дх ’	ду др ду а2 ду
Основные уравнения
185
Производные От давления можно найти из уравнения Эйлера (IV.4):
Тогда
др __ дх	р(	ди ,	ди \ и -д- + и-ч- ; дх 1	ду /
др. — _ ду	-pl	(dv	dv \ U -s—к U-ч- . дх 1 ду /
дР —_ дх	Р а2	( ди . ди \ ( U -ч—к и-ч- ) \ дх 1 ду )
дР —_ ду	Р а2	( dv , dv \ U -ч—к и-ч- , \ дх 1 ду } 
п
и уравнение неразрывности будет
+
или
ди	.	dv	1 /	ди ,	, dv	,	ди	,	dv \	п
-ч--к -ч-----Г и л----к -5------Г- UV-S-kUV-5— =0.
дх	1	ду	а2 \	дх 1 ду	'	ду	1	дх)
Считая движение потенциальным, будем иметь
д(р	5<р
и ----- -Xх; и = -чх дх ’	ду .
и, следовательно, частично выразив скорости через потенциал, получим
<?2Ф I д2<р___1_ Г 2 д2<р
дх2 ' ду2	а2 [и дх2
или окончательно
/._____и2 \ д2ц>
V	И2 ) ~д^
ду2 дх ду J и
4m_24^- = 0. (VIII.2)
а2) ду2 а2 дхду	'	’
Предположим, что движение газа происходит вдоль оси х. Тогда параметры возмущенного обтекаемым телом потока можно представить в виде:
и = Уоо + и'; р = рх + р';
v == v’; р = р« + р'>
где 1/ю', рсо . . . — параметры невозмущенного потока; и', и'   .— величины возмущений этих параметров.
186
Плоский потенциальный поток газа
Считая величины возмущений и их производные малыми, можем пренебречь их квадратами и произведениями. Используя это допущение, а также подставляя в уравнение (VIII.2) потенциал скоростей в виде суммы потенциала однородного потока, параллельног^ оси х, и потенциала возмущения <р' в виде
Ф = Усох + Ф',	(VIII.3)i
получим
(l-Ml)^ + ^-=0	(VIII.4)!
или
+-----Цт4гг- = 0’	(VIII.5)!
дх2 1 j__ду2	I
где Мто =	.
и<х>
Уравнение (VIII.5) есть линейное дифференциальное уравнение, в частных производных второго порядка с постоянными коэффи-’ циентами. В записанной форме это уравнение используется при, рассмотрении дозвукового потока (Мот < 1). Такое уравнение относится к так называемым уравнениям, эллиптического типа. Оно легко может быть сведено к уравнению Лапласа.	:
Так как при сверхзвуковом потоке Мот >1, то уравнение! (VIII.5) удобнее представить в виде	.<
(VIH.6)'
Уравнение (VIII.6) относится к уравнению гиперболического типа, и его решение может существовать лишь в области, ограниченной конусом возмущения.
Далее будут рассмотрены простейшие случаи дозвукового и сверхзвукового потоков. Движение газа при околозвуковой скорости (значения числа М близкие к единице) в настоящем курсе не изучаются.
§ 2. Дозвуковое обтекание тонкого профиля
При дозвуковых скоростях обтекания любого профиля обычно различают два случая: 1) когда скорость на бесконечности довольно велика, но во всех точках обтекаемого профиля она меньше звуковой; 2) когда дозвуковая скорость потока настолько велика, что в некоторых точках профиля возникает скорость, равная скорости звука. Число Мо,, соответствующее скорости потока, при которой на профиле появляется местная скорость звука, называется критическим и обозначается Мкр. Появление местной скорости звука на профиле обычно вызывает резкое увеличение его .коэффициенте сопротивления.
Дозвуковое обтекание тонкого профиля
187
Обтекание профиля при наличии на профиле местной скорости звука в книге не рассматривается. Изложим в этом параграфе простейшую теорию (Прандтля—Глауэрта) обтекания топкого профиля при малом угле атаки и числах Мот, меньших Мкр. Влияние сжимаемости можно установить путем сравнения потенциалов скоростей при обтекании профиля сжимаемой ф и несжимаемой ф0 жидкостями.
Предположим, что эти потенциалы линейно связаны между собой
Ф = е.ф0,	(VIII.7)
где е — коэффициент пропорциональности.
Пусть координаты в плоскости несжимаемого потока будут Xj и уг. Тогда, чтобы потенциал скорости ф удовлетворял уравнению (VIII.5), а ф0 — соотношению для несжимаемой жидкости
2!Фс_|__^ = 0,	(VIII.8)
дх; ду;
необходимо иметь связь между координатами в несжимаемом и сжимаемом потоках в виде
Уг	.
При X = %!	У Х
Ух = $У-	(VIII. 9)
Подставив в уравнение (VIII.5) выражения (VIII.7) и (VIII.9), получим
„ д2(Ра , кР <Э2<Ро _ А
М 'Г 1-М2те ду[ ~ 
Это уравнение тождественно совпадает с уравнением (VIII.8) только при условии, когда
р2=1 — М2„, или
₽ = ]Л1—Mt,	(VIII*. 10)
откуда следует, что при Мто = 0, £ = 1 и уг = у. При Mffi, большем нуля и меньшем единицы, коэффициент р всегда меньше единицы и уг < у, т. е. поперечная протяженность у при обтекании профиля в сжимаемом потоке больше, чем соответствующие величины y-х в несжимаемом потоке. При х = хх имеем
И = к =___________Ул.
(VIII.11)
Найдем соответствующее изменению толщины профиля изменение местных скоростей потока, которое происходит из-за влияния
188 Плоский потенциальный поток газа
сжимаемости. Величины скоростей в плоскостях х, у и можно найти через производные от потенциала скоростей <р п<(
координатам	, откуда
следовательно,
ц0 = v ]/" 1 — М^> , или	.	i
t> =	(VIII.12)
/1-м1
Следовательно, составляющие скорости по оси х остаются оди-J наковыми в потоках сжимаемой и несжимаемой жидкостей, а со-, ставляющие по оси у в сжимаемой жидкости увеличиваются!
Такому изменению скоростей должно соответствовать измене-' ние угла атаки. Из-за малости а получим	’
— А 1	__ «о
и, следовательно, будем иметь пропорциональное изменение коэффициента подъемной силы
Си = —5”		(VIII. 13)
Таким образом, для тонких профилей, обтекаемых при малых углах атаки сжимаемой жидкостью (при М«> < Мкр), влияние сжимаемости сводится как бы к утолщению профиля и увеличению угла атаки, а следовательно, и к увеличению подъемной силы в соответствии с формулой (VIII. 13).
Коэффициент давления в любой точке контура тонкого профиля, обтекаемого сжимаемой жидкостью, можно определить через коэффициент давления р в соответствующей точке при обтекании профиля несжимаемым потоком по формуле
У 1-М2го ‘
(VIII. 14)
Кроме приведенных формул, полученных на основе линеари-
Сверхзвуковое обтекание клина. Косой скачок уплотнения 189
зании уравнений, существуют и более точные решения. Более точным приближением является соотношение
полученное Т. Карманом.
Таким образом, зная характеристики тонкого профиля в несжимаемом потоке, легко, пользуясь приведенными формулами, найти эти характеристики для профиля в сжимаемом потоке при М < Мкр.
§ 3. Сверхзвуковое обтекание клина. Косой скачок уплотнения
Рассмотрим задачу о продольном обтекании сверхзвуковым потоком плоского клина с углом раствора 20 (рис. VIII.2, а). Если число Mj (Mi > 1) характеризует набегающий поток, то при малых
в	а
Рис. VHI.2
значениях угла 0 от острия клина будут отходить линии возмущения под углом а, синус которого согласно (VIII.1) будет равен 1 sin а = -г;—.
Mi
При замене нулевой линии тока твердой стенкой поставленную задачу можно свести к задаче о течении газа внутри тупого угла (рис. VIII.2).
Сверхзвуковой поток, параллельный стенке ВА, в точке А изменяет свое направление и двигается дальше вдоль AD.
Обозначим параметры потока до изменения направления индексом 1, а после изменения направления—индексом 2. Величина скорости V2 будет меньше, чем У^, и, следовательно, Mj >М3, так как при поджатии линии тока в сверхзвуковом потоке скорость убывает.

190
Плоский потенциальный поток газа
В соответствии с выражением (VIII. 1) линия возмущений АС]? для числа Mj должна быть направлена под углом
а. = arcsin-г-i—,
в то время как линия АС2 для М2 должна быть расположена под углом	]
а, = arcsin -гт— .
М2
Так как М2 < М1( то а2 > av Из последнего условия получаем, что линия возмущения АС2 для М2 (рис. VIII.2, б) должна пред-
шествовать линии возмущения АС] для Мг Такое расположение линий возмущения невозможно, следовательно, переход от М2 к М2 происходит скачком по линии АС под некоторым углом р. В отличие от прямого скачка, в котором направление скорости не меняется, в рассматриваемом скачке, называемом косым скачком уплотнения, скачкообразно изменяется не только абсолютное значение скорости, но и ее направление.
Для нахождения количественных изменений параметров потока в косом скачке напишем основные уравнения. Если индексами п vi t обозначим нормальные и касательные к линии скачка составляющие скоростей (рис. VII 1.3), то получим:
1)	уравнение сохранения массы
Pl^ln = Р2^2п‘>
2)	уравнение изменения количества движения в направлении нормали к линии скачка
pluhi 4“ Pl — p2w2n 4“ ₽2>
3)	уравнение изменения количества движения для продольной проекции
Р1^1ЛИ1/ — P2V2llV2t’
Сверхзвуковое обтекание клина. Косой скачок уплотнения
191
4)	уравнение энергии запишется в виде
°1л + vlt I k Pl ~ °2n + °2< .	6 р2
2	' k — I pi “	2	г k— ! p2 ’
Из уравнений сохранения массы и изменения количества движения следует, что vlt — vzt, т. е. в косом скачке касательная составляющая скорости не претерпевает разрыва.
Тогда уравнение энергии примет вид
2	2
। k pt   v2n - k p<>	/VI IT
а полное изменение скорости в скачке будет определяться изменением нормальной составляющей скорости AV = Vi— V2 = vln — — v2n.
Последний вид уравнения энергии и уравнения, приведенные выше, представляют собой систему уравнений для косого скачка. Эта система имеет тот же вид, что и для прямого скачка, с той лишь разницей, что вместо полной скорости в систему для косого скачка входят нормальные составляющие скорости.
Воспользовавшись решением, полученным для прямого скачка (п. 8, гл. VI), найдем:
Av — vj„ — о2„—
А	2Р1°1п / ,	1 \ .
Лр — Рг Pi — k + Ц М|„ ) ’
Ар = р2~- pi = pi (^in 1);
м = т2 - Т1 = 4=zl (&—4,),
(VIII.17)
гдеМ1ге=^; 4==-^-
Из уравнения энергии следует, что так же, как и в прямом скачке, в косом скачке уплотнения параметры заторможенного потока не меняются, т. е. величины заторможенных скоростей и температур, а также их критических значений до и после скачка одинаковы.
Если представить уравнение энергии в виде (VI.30)
9	9	9
и1п + иИ । al _ k 4-1	2
2	' k— 1 ~ 2(6 — 1) °*’
то получим
. а1 = _1±2_ (а2____	1 7,2 \
2 + k— 1	2(6—1)V*	6+1 V,tJ'
192
Плоский потенциальный поток газа
< (VIII.18)1
V]nV2„ =а
Так как vlt v2t — vh то „2 k — 1 2 а‘~ T=VVil
тоже не изменяется при прохождении через скачок. При косом скачке эта величина заменяет собой квадрат критической скорости в формулах для прямого скачка. Используя (VIII. 18), можно полу-) чить по аналогии с прямым скачком (VI.49) очень важное соотно-* шение для нормальных составляющих скоростей до и после скачка*
(VHI.19);
Так как косой скачок является прямым для нормальных составляющих скоростей,, и, следовательно, vln всегда больше скорости?; звука, то из формулы (VIII. 19) видно, что v2n всегда меньше ско- j рости звука, хотя полная скорость за косым скачком может быть' и сверхзвуковой. Далее, вновь рассматривая обтекание к-лина (рис. VIII.2), установим связь между углом клина 0 и углом наклона косого скачка 0.
Из рис. VIII.3 видно, что tg (0 — 0) =	, но так как по
формуле (VIII. 19)
V'2 cos2 0
a vln = Vi sin 0 и Vi = Vx cos 0, то a2-^l
tg(0 — 0) = —--Ш
V2 sin 0 cos 0
Разделив числитель и знаменатель правой части на квадрат скорости звука аг и произведя некоторые преобразования, получим
— 1) М2 sin2 0
tg(0 —0) =---------.----------.
(k -|- 1) Mj sin 0 cos 0
Воспользовавшись известными соотношениями тригонометрии и решая после подстановки уравнение относительно tg 0, окончательно получим
tg 0 = ctg 0
М2 sin2 0 — 1
(VIII.20)
2
- График зависимости 0 от 0 при различных значениях числа Мх для воздуха показан на рис. VIII.4. Из уравнения (VIII.20) и рис. VIII.4 видно, что при заданном угле конусности 0 угол 0 зависит от числа М;; при увеличении последнего угол 0 растет,
Сверхзвуковое обтекание клина. Косой скачок уплотнения 193
достигая некоторого предельного значения. Так как уменьшение угла конусности 0 не может привести к увеличению 0 до 90° (прямой скачок), то верхние ветви кривых, проведенные штрихами, в действительности не существуют.
Из кривых рис. VIII.4 видно, что для каждого газа углы конусности клина 0 не могут быть сколь угодно большими. Так, для воздуха при Мх = со максимальный угол конусности, при котором
возможно существование присоединенного к конусу косого скачка, будет равен 46°. При этом, как видно из графика, 0 = 68°. При обтекании клина с большим углом 0 так же, как и при обтекании тупоносых тел, скачок уплотнения отрывается от острия клина и становится криволинейным (рис. VIII.5).
Центральная часть поверхности скачка перпендикулярна к направлению скорости поэтому в этой области за скачком скорости будут обязательно дозвуковыми. При удалении от оси симметрии угол между направлением скачка и направлением скорости уменьшается, и в этой области так же, как и в косом скачку, за скачком скорость может быть сверхзвуковой.
На рис. VIII.5 показаны возможные области дозвуковых и сверхзвуковых потоков. Теории отсоединенных криволинейных скачков до настоящего времени еще нет.
. Так как расчет косых скачков по формулам (VIII. 19) и (VIII.20) довольно громоздкий, то в практике часто пользуются номограммами. Одна из таких номограмм приведена на рис. VIII.6. По этой номограмме при заданных значениях угла клина 0 и числа Мх находим точку, через которую проходят кривые с определенными значениями угла 0, числа М2 и отношения давлений ~. Так^при
0 = 12° и М= 2,8 получим М2 = 2,2, 0 = 31° и = 2,2,
13 И. Л. Повх
194
Плоский потенциальный поток газа
Начальное число М,
Ю !5	20	25	3.0	35	i.0	Ь.5	5.0	55
_________j________1 ______J________1________1-	---1________L- ,	,1____—J
§ 4. Сверхзвуковое обтекание внешнего угла
При сверхзвуковом обтекании внешнего угла (рис. VIII.7) поток расширяется и, следовательно, скорость потока после поворота будет больше, чем перед поворотом. В отличие от предыдущего случая, где скорость убывает скачком, при обтекании внешнего угла скорость будет расти непрерывно.
Если индексом 1 обозначим параметры потока перед поворотом, а индексом 2 — в области после завершения поворота, то, очевидно, Мг < М2. Так как вершина угла О есть источник возмущений, то углы наклона линий возмущения, проходящих через вершину О, к векторам скорости до и после поворота будут определяться следующими соотношениями:
sina1 = -r^-;	81па2 = -т^-.
Сверхзвуковое обтекание внешнего угла
195
точке
полярного угла
Тогда линии возмущений 0Сг и 0С2 будут отделять области невозмущенных потоков до и за поворотом, а сектор Сх0С2, называемый сектором возмущения, будет включать поток с непрерывно изменяющимися параметрами.
Задача о сверхзвуковом обтекании внешнего угла сводится к тому, чтобы по параметрам потока до линии возмущения ОСг и углу поворота 02 найти параметры потока за линией возмущения 0С2 и в секторе возмущения Сх0С2.
Для решения последней задачи введем полярные координаты г и 8 с началом координат в производить от вертикали вправо. Предполагая поток потенциальным, составляющие скорости vr и vs, зависящие только от угла е, можно выразить через потенциал скорости ср:
vr=* = уЛе):
Так как
dvr   д / д<р \  де	де \ дг )
= д ( д(Р \ дг \ де ) ’
<?Ф
а из предыдущего — rvs, то получим
доГ	д ,	,	.	dvs
-а— = -5—	~ V. 4- Г =. V.
де	dr '	s''	s 1	dr	s
(VIII.2I)
(вследствие того, что vs не зависит от г).
Имея в виду, что составляющие, направленные по нормали к линии возмущения, всегда равны скорости звука, запишем
(VIII.22)
vs = a = ]/.
Подставив в уравнение (VIII.22) величину — , найденную из уравнения Бернулли (VI. 13),	р
Р - k~l (у21 у2) — k~ 1 у2 р + 2k т — 2k max’ получим следующее дифференциальное уравнение: *4-1 (	2
+4- ^тах
13*
196
Плоский потенциальный поток газа
или, введя обозначение	= п, получим 	-==~ п de.
V ymax vr
Интегрируя это уравнение, получим выражение скорости
Vr = ^max sin п (8 + 80) = t>max sin ns*, (VIII.23) где 80— постоянная интегрирования, а 8* = 8 + 80.
Из выражения (VIII.23) видно, что проекция скорости vs равна ys = -§- = «Ушах cos П8*.	(VIII. 24)
Таким образом, значения скоростей в секторе возмущения определены. Найдем связь между углами 0 и е. Из рис. VIII.7 видно, что а = -£ + 0 — 8, или, введя 0* = 0 + е0, получим 05 = -у- + °* — е*-
Из рис. VIII.7 видно, что tg а =	. Подставив значение скоро-
стей из выражений (VIII.23) и (VIII.24), окончательно получим связь между 0 и 8 или 8* и 0* в виде
tg(v + 0*-e*)=«ctgn8*.	(VIII.25)
Таким- образом, задаваясь 8*, можно получить по формуле (VIII.25) значение 0* и по выражениям (VIII.23) и (VIII.24) величину скорости v2 = Vs + v2 в зависимости от vmax или Мх. Очевидно, что изменение скорости будет происходить в секторе СХОС2, т. е. при изменении угла от а = ах до а = а2 — 02. При а — а2 — — 02 получим установившиеся параметры потока за поворотом.
Величина постоянной интегрирования 80 определится по заданному значению Мх.
В частности, при 8* = О из формулщ*(УШ.25) следует, что 0* = О, а величины скоростей по выражениям (VIII.23) и (VIII.24) будут равны:
&г~’О» У5 =~ ^Ущах == Утах j/ । == У><р'
Последняя зависимость показывает, что вдоль стенки АО поток течет со скоростью звука, т. е. Мх == 1.
Из-за относительной сложности полученных формул обычно зависимость числа М от 0 и а выражают в виде графика (рис. VIII..8) и таблиц (табл. VIII.1).
Ниже приведена таблица для воздуха (k = 1,4).
Из таблицы и рис. VIII.8 видно, что поток не может совершать поворот на произвольно большой угол. Для воздуха предельным углом поворота 0тах является угол 129°,32. Такой поворот может
Сверхзвуковое обтекание внешнего угла
197
осуществляться только при полном расширении газа до абсолютного вакуума. Углы поворота 0° для каждого числа М определяются давлением за поворотом.
Давления и все другие параметры потока в секторе возмущения и за поворотом также могут быть рассчитаны и обычно приводятся в таблицах. Нарис. VIII.8 показана кривая давлений в зависимости от угла 0. Так как число М при увеличении утла поворота потока растет, то давление падает. Аналитическое выражение для р (е)
имеет вид k
р = ро (тутcos
(VIII.26)
Расчет параметров потока производится следующим образом: по заданному начальному числу М из таблицы или графика находят угол 0, к найденному значению 0 прибавляют угол поворота 02. Тогда
0 = 0 + 02
и затем по 0 определяют все параметры потока за поворотом.
Например, при начальном числе М = 2,778 и 0 = 9° находим (по таблице или графику) 02 = 45° и, следовательно, 0 = 54°.
Значению 0 = 54° соответствуют конечное число М'= 3,25,
0,019 и т. д.	„ ,	.
Таблица VI11.1
е,... °	е, ... °	а, ... °	м	е,... °	е, ...	а, ... 0	м •
0	0	90	1	20	75,74	34,26	1,779
1	23,72	67,28	1,1084	40	106,88	23,12	2,55
5	42,34	52,66	1,258	50	120,71	19,29	3,021
10	55,84	44,16	1,435	129,32	219,32	0,00	оо
Имея формулы для скоростей и давлений, нетрудно получить уравнение линии тока в секторе возмущения. Так как массовый расход между стенкой и любой линией тока будет постоянным, то можно для произвольной линии тока написать условие сохранения
,	т	С
массы т = ро/ = const, откуда г —----------- =-----.
' s	pt's	pt's
198
Плоский потенциальный поток газа
Подставляя значение v в соответствие с (VIII.22) и имея в виду, что движение изэнтропическое, т. е.
1
а также используя выражение для р (VIII.26), получим уравнение линии тока
' = ------~Т+Т '	(vni.27)
(cos ле,) k_ t
Задаваясь произвольной постоянной С, по уравнению (VIII.27) можно построить линии тока в секторе возмущения, а следовательно, и по всей области движения.
Так как здесь, как и во всех предыдущих случаях, газ считается идеальным, то можно любую линию тока заменить твердой стенкой. В рассматриваемом случае все линии тока, кроме нулевой, будут криволинейными, следовательно, приведенный расчет можно распространять и на криволинейные стенки.
§ 5. Обтекание пластины сверхзвуковым потоком
В случае малых возмущений, наблюдающихся при обтекании относительно тонких профилей при малых углах атаки, нелинейное дифференциальное уравнение (VIII.2) может быть линеаризировано и для сверхзвукового потока будет иметь вид (VIII.6).
Рассмотрим решение этого уравнения в случае обтекания тонкой пластинки сверхзвуковым потоком при малом угле атаки (рис. VIII.9). На верхней поверхности пластины из-за расширения потока сверхзвуковая скорость увеличивается по сравнению со скоростью на бесконечности, а давление падает по сравнению с дав
Обтекание пластины сверхзвуковым потоком
199
лением на бесконечности. На нижней поверхности, наоборот, происходит поджатие линий тока и скорость уменьшается, а давление возрастает.
Так как давление рв на верхней поверхности одинаково по всей длине пластины и по величине оно меньше, чем рт, а давление рн иа нижней поверхности больше, чем ра>, и одинаково по всей {длине, то результирующая аэродинамическая сила приложена к пластине в ее середине х = ~ и направлена перпендикулярно к пластине, а величина этой силы равна
i
R = \(pa~pB)dx.	(VIII.28)
о
Величина подъемной силы Y из-за малости угла 0 будет приближенно равняться /?, а величина силы сопротивления X будет равна X = R sin 0 ъ RQ.
Найдем рн — рв из линеаризованного уравнения Бернулли.
Так как скорость на верхней поверхности ив =	+ и', на
нижней иа = ит— и', причем и' Ua>, то
2
Р^СО О / j	f
рв — р«> = —2-----тг («со+ « )2 = —pu«,u ;
р ,	,ч2
Рн —Роэ=-2---------£-(««> — « )2 — рити
ИЛИ
ра — рв — 2pUa,u'.	(VIII.29)
Величину возмущенной скорости можно найти, предварительно определив потенциал этой скорости из линеаризованного уравнения (VIII.6), имеющего вид
d2<p'	1 . <92(р'  п
дх2 ы2 дуг	’
где о? = Ml — 1.
Общее решение этого уравнения может быть представлено в виде ф' = Ф1 (.У — х tg а) + ф2 (у + х tg а).
После подстановки этого решения в выражение (VIII.6) получим
Очевидно, что потенциал возмущенной скорости вне области возмущения обращается в нуль, т. е. ср' = 0. Примем одно из частных решений за значение ср' в области возмущения
ф' = с (у — х tg а,).
200
Плоский потенциальный поток газа
Тогда величины проекций возмущенной скорости будут , _ ду	и , _ ду_
дх	v ь ’	ду
Тангенс угла 0, на который отклоняется линия тока при переходе через сектор возмущений (рис. VIII.9), будет равен
, п ‘ о'	о'	с
tg 0 =-------:—- =-----=-------->
6	и„ + и'	U	II
откуда
С = ---Ueo tg 0 И и’ — Uco tg 0 tg а.
Подставив найденное значение и' в выражение (VIII.29), получим
рн—Рв = 2pul tgatg 0, следовательно,
Y == 2/р«1 tg a tg 0; X = 2/рм^ tg а tg2 О,
где I — длина пластинки.
Коэффициенты подъемной силы и сопротивления по этому упрощенному приближенному методу (методу Аккерета) будут соответственно равны;
(VIII.30)
Формулами (VIII.30) можно пользоваться и для расчета тонких профилей. В этом случае 0 (угол атаки) есть угол между хордой и набегающим потоком.
Заметим, что в отличие от обтекания тел идеальной жидкостью при малых скоростях, когда сопротивление полностью отсутствует, при больших сверхзвуковых скоростях возникает сила сопротивления (VIII.20), называемая волновым сопротивлением.
В заключение рассмотрим качественную картину обтекания пластины, расположенной в потоке под значительным углом атаки.
У передней кромки пластины поток разделяется на две части. В верхней части нулевая линия тока и пластина образуют внешний угол, обтекание которого было рассмотрено в предыдущем параграфе. При обтекании внешнего угла скорость непрерывно возрастает и образуется семейство линий возмущения, лежащих в секторе возмущений. Далее поток достигает конца пластины, где линии тока сгущаются и вновь приобретают те же направления и густоту, что и на бесконечности перед пластиной. Верхний поток
Геометрические и аэродинамические характеристики профилей	201
у задней кромки пластины соответствует течению внутри тупого угла, и в этом случае сверхзвуковая скорость убывает скачкообразно на линии, являющейся косым скачком уплотнения.
В нижней части пластины, наоборот, поток в передней точке соответствует обтеканию тупого угла, и здесь также образуется косой скачок; в районе же задней кромки скорость непрерывно растет в секторе возмущений, достигая значения скорости потока на бесконечности.
При решении задачи о таком обтекании уже нельзя применять линеаризированных уравнений.
ГЛАВА IX
ЭЛЕМЕНТЫ ТЕОРИИ ПРОФИЛЯ, РЕШЕТОК ПРОФИЛЕЙ И ТЕОРИЯ КРЫЛА
§ 1. Геометрические и аэродинамические характеристики профилей
Форма профилей, применяемых для крыльев и винтов самолета, корабельных винтов, лопаток паровых, газовых и гидравлических турбин, лопаток компрессоров, насосов и вентиляторов, а также других машин, в большой мере определяет эффективность их работы. В зависимости от назначения имеется большое разнообразие форм профилей. Иногда форма профиля определяется в значительной степени требованиями прочности, качеством материала и пр.
На рис. IX. 1 показаны четыре типа профилей. Форма первого профиля, относительно нетолстого и мало изогнутого, с закругленной передней кромкой, типична для крыльев и винтов дозвуковых самолетов, для компрессорных и гидротурбинных лопаток, второго профиля с острыми передними и задними кромками, —* для крыльев сверхзвуковых самолетов; форма третьего и четвертого профилей, довольно толстых и достаточно изогнутых — для лопаток реактивных и активных ступеней паровых турбин.
Основными геометрическими характеристиками профиля являются: хорда, средняя линия или осевая дуга, максимальные толщина и вогнутость и их абсциссы.
Хордой называют отрезок прямой, соединяющий две наиболее удаленные точки-профиля А и В (рис. IX.1). Для сильно изогнутых профилей хорда может быть проведена иначе.
Контур профиля обычно задается относительными координатами уй и уа в зависимости от х. При этоместь расстояние от носика, отнесенное к длине хорды b, а упи уа — ординаты верхнего
202
’Элементы теории профиля, решеток профилей и теория Крылй
(ув) и нижнего (ул) обводов профиля, также отнесенные к длине хорды Ь.
Средняя линия есть геометрическое место точек, равноотстоящих от верхнего и нижнего обвода по перпендикуляру к хорде (рис. IV. 1). Координаты средней линии можно найти по формуле ,. _ I Ув I ~~ । У» I г/ср	2	*
Расстояние от верхней до нижней части контура профиля
в каком-либо сечении,
Рис. IX. 1
перпендикулярном к хорде, называется абсолютной толщиной профиля. Толщина профиля переменна по хорде; максимальная толщина в обычных профилях располагается на расстоянии от передней кромки, составляющем 0,2— 0,4 длины хорды, т. е. хс = -у- =0,2 -5--=0,4.
Относительной толщиной профиля называется отношение максимальной толщины к длине хорды с —
В зависимости от назначения профиля относительная толщина обычно выбирается в пределах 8—15%.
Отношение максимальной ординаты средней линий (стрелы прогиба) к длине хорды называется относительной во-, Мер \ гнутостью /=	•
Безразмерная координата xf положения максимальной ординаты средней линии обычно составляет 0,2—0,5 от хорды.
Иногда характеристика профиля дополняется радиусами кривизны носика гнос и хвостика гхв.
Формы профилей крыльев современных самолетов, а также лопаток турбин и насосов, как правило, окончательно отрабатываются экспериментально. Исходными формами профилей для создания серий часто служат теоретические профили, полученные методом конформных отображений.
При изучении аэродинамических характеристик профилей обычно пользуются не самими силами и моментами, а их коэффициентами.
Для профилей вводят коэффициент подъемной силы Су, коэффициент сопротивления Сх и коэффициент момента Ст:
Су—
Y ~(>V*b
Сх — ~ j и Ст
±(>v*b
м
4-pvw’
Геометрические и аэродинамические характеристики профилей 203
где X и У — проекции равнодействующей аэродинамической силы R на оси х и у, причем ось х совпадает с направлением скорости на бесконечности; М — момент силы R относительно выбранной оси; b— длина хорды профиля.
Обычно силы X и У, а также момент М определяются экспериментально. Пользуясь формулой Жуковского, величину подъемной силы можно найти теоретически.
Силы и момент зависят от угла атаки а, величина которого обычно определяется углом между скоростью и хордой профиля.
Кривые зависимости Су от угла атаки, рассчитанные теоретически и найденные экспериментально, показаны на рис. IX.2. Из рисунка видно, что на всех углах атаки теоретические значения коэффициента подъемной силы больше соответствующих величин, определенных экспериментально. Такое снижение коэффициента подъемной силы объясняется влиянием вязкости.
В практике часто пользуются величиной качества профиля, равной К = 7Г--^•х
Из рис. IX.2 видно, что теоретическая кривая Су (а) в диапазоне небольших углов атаки есть линейная функция от а, в то время как экспериментальная кривая Су (а) имеет при некотором угле а, называемом критическим углом атаки, максимальное значение Су.
На этом же графике приведена зависимость коэффициента сопротивления от угла атаки. Наименьшее сопротивление профиля имеет место при бесциркуляционном угле атаки, т. е. при угле атаки а0, соответствующем нулевой подъемной силе. Сильно растет сопротивление вблизи критического угла атаки, т. е.
204
Элементы, теории профиля, решеток профилей и теория крыла
около Сугт*. Аэродинамические характеристики различных профилей помещены в атласах профилей. В практике часто пользуются так называемыми полярами крыла в виде Су (Сх), одна из которых показана на рис. IX.3.
Для получения теоретических профилей используют многие математические методы. Наиболее распространенным является метод конформных отображений.
§ 2. Конформные отображения. Теоретические профили
Метод конформных отображений, или преобразований, широко применяется для решения многих технических задач. Основой данного метода является отображение одной фигуры на другую и установление соответствия между точками этих фигур.
Рис. IX.4
В технике применяются разнообразные профили и обтекаемые контуры. Непосредственное получение комплексного потенциала для всех профилей и обтекаемых контуров представляет большие трудности. Поэтому естественно желание использовать хорошо изученное обтекание одного контура для нахождения параметров обтекания любого другого. Для этого необходимо установить соответствие между точками интересующего нас профиля и точками изученного эталонного контура. Установлением такого соответствия и занимается теория конформных отображений.
В качестве эталонного хорошо изученного контура можно взять круглый цилиндр с центром, расположенным в начале координат.
Найдем обтекание профиля, комплексный потенциал Wz которого в физической плоскости — плоскости расположения профиля— неизвестен (рис. IX.4). Рассмотрим вспомогательную плоскость £ = £ + й] с окружностью радиуса г0 и центром в начале координат.
Комплексный потенциал (£) обтекания цилиндра в плоскости £ нам известен. Тогда можно найти комплексный потенциал
Конформные отображения. Теоретические профили
205
обтекания профиля Wz, а следовательно, и поле скоростей вокруг профиля в физической плоскости, если известна функция комплексного переменного
z=№	(IX.I)
осуществляющая конформное отображение внешности контура С исследуемого профиля в плоскости z на внешность контура круга в плоскости £. При этом отображающая функция должна быть подобрана так, чтобы бесконечные точки в плоскости переходили в бесконечные точки в плоскости £ и направление скорости на бесконечности в обеих плоскостях было одинаковым.
Рассмотрим простейшие примеры отображающих функций z = f (£). Очевидно, что при z = t, контур в плоскости z остается таким же и в плоскости £, т. е. получается тождество.
Наиболее простыми являются преобразования: 1) z = t, + а;
2) z = at, и 3) z -g-, смысл которых покажем далее.
Первое преобразование (преобразование переноса начала координат)
z = С + а = (g + in) + a.	(IX.2)
Если а — комплексное число (а = аг 4- ia2), то
z = х + iy = (g + fli) + (г] + а2) i.
Следовательно,
х = g + «1 и у = п + а2.
Таким образом, преобразование (IX.2) приводит к переносу начала координат. При этом все кривые в плоскости t, остаются такими же, какими они были в плоскости г, и изменяется лишь начало координат при неизменном направлении осей.
В качестве примера рассмотрим, в какую, кривую в плоскости z преобразуется окружность, уравнение которой в плоскости t, будет (g + fej2 + (n + 62)2 = #2-
Если преобразующая функция
z = (Е- + if)) + (ai +	= х + iy,
то •>
I = х — fli и 1) =(/- а2
и уравнение кривой в плоскости г будет
(х - CJ2 + (у - С2)2 = R*.
Это уравнение выражает окружность того же радиуса, что и в плоскости £, с центром, не совпадающим с началом координат.
Второе преобразование
г = at,.	(IX.3)
206
Элементы теории профиля, решеток профилей и теория крыла
Если а — комплексное число, то
z = (fli — iaj (| + й) = х 4- iy
и, следовательно, х =	— а2т[-, у —	4- «2g.
Выясним геометрический смысл этого преобразования. Имеем £ = g 4- Й — Re1^ и а = aypia, следовательно,
z = aYe.ia Rel<p — 6е'0,
где 6 = axR; 0 = <р 4- а.	_
Очевидно, что рассматриваемая функция преобразует окружность радиуса R в плоскости £ в окружность с радиусом a^R в плоскости г, причем все точки окружности повернуты вокруг центра на угол а.
Третье преобразование возьмем в виде
z =	(IX.4)
где а — вещественная величина.
Выражение можно записать следующим образом:
£ = —.
ъ г
Если z = х 4- iy, то
__6 1-   а2   а^х	 а2У
Ь — Ь-rtT] —^ГТу— Х2 + у2	1 х2_у2 ’
<. а2х	а2у
откуда 1 = -^^ и П =
Рассмотрим, в какую кривую окружность в плоскости £ преобразуется на плоскости z.
Уравнение окружности в плоскости £ в общем виде будет A (£2 + n2) + Bl + Cn + D = 0.
Если подставим сюда значения £ и т], то получим
Да4 Г> 2J2-2-i2 -ь -^2 1 4- 2Вй2х„ - ~у.2 4- D = 0
L (х2Ч у2}2 у2У\ х-2~.-у2 х~ + у2
или, умножив на (х2 4- у2) и произведя элементарные преобразования, получим Да4 4- Ва2х — С а1 у 4- D (х2 4- у2) = 0.
Последнее уравнение есть уравнение окружности.
Заметим, что когда окружность в плоскости £ проходит через начало координат, т. е. в плоскости £ величина D = 0, то окружность в плоскости $ отобразится на плоскость z в виде прямой, заданной уравнением
Да4 4- Ва2х — Са2у = 0.
Последнее преобразование представим в виде суммы двух предшествующих
2==4-(^+т)-	<1Х-5)
'онформные отображения. Теоретические профили
20?
Это преобразование можно записать как часть более общего + + + •••
Преобразование (IX.5) называется преобразованием Жуковского. Подставив в выражение (IX.5) значение г-и £, получим г = х -F . . __ 1 Г,6 . . . . a1 2g ia2n
+	2 [ ®	g2 4- г}2	g24-n2 r
откуда
1=4- (5+рт?) •«=4- (i -	<1Х6)
Рассмотрим некоторые частные случаи преобразования* окружности, расположенной в плоскости £.
1. Пусть в плоскости £ будет задана окружность с радиусом а <(рис. IX.5) с центром в начале координат. Тогда уравнение этой окружности примет вид: £2 + Я2 = fl2-
Подставив это равенство в выражения (IX.6), получим: х — £ и у = 0. Но так как£ в плоскости £ меняется от —а до а, то уравнение х = £ определяет, отрезок прямой длиной 2a (рис. IX.5).
2. Пусть в плоскости $ будет задана окружность с центром в на-
чале координат, но с радиусом R > а. Подставив значение £2 +
-|- л2 — R* в выражение для х и у, получим
откуда
g /. .. а2 \	т) /, a2 \
х— 2\^~Я2)Иу—2\	R2)’
Тогда уравнение окружности в плоскости £ будет иметь в плоскости z следующий вид:
х2	1
a? Ы~1’
где
Z?2 -4- a3 * ai ~ 2R ’
R2 — as 2R
208
Элементы теории профиля, решеток профилей и теория крыла
Полученное уравнение в плоскости z дает эллипс с полуосями ах и Ьг.
3. Если в плоскости зададим окружность с радиусом R > а, но с центром на мнимой оси (рис. IX.6), то в плоскости г получим
Дугу круга с концами, опирающимися на ось х, причем расстояние от оси х до вершины этой дуги равнд расстоянию от оси £ до центра отображающей окружности.
Прогиб дуги f равен величине смещения центра окружности в плоскости £.
Рис. IX.7
Окружность радиуса Я 4= а с центром, помещенным на действительной оси не в начале координат (рис. IX.7), отображается преобразованием Жуковского на плоскость z в симметричный профиль (рис. IX.7, а). На этом рисунке плоскости z и £ совмещены.
Если центр отображающей окружности радиуса R =£= а поместить в некоторую точку, не лежащую на осях координат, то, как видно из рис. IX.7, б, в плоскости z получим изогнутый профиль с острой задней кромкой. Таким образом, при заданных значениях
Скорость и циркуляция в преобразованном потоке
209
величин:^ в формуле (IX.5), радиуса отображающей окружности R и координат центра отображающей окружности £0 и т]0 — можно получить в плоскости £ некоторый профиль крыловой формы, который называется профилем Жуковского.
§ 3.	Скорость и циркуляция в преобразованном потоке. Постулат Жуковского—Чаплыгина
Пусть в физической плоскости z (см. рис. IX.4) заданный крыловой профиль с угловой точкой на задней кромке будет обтекаться плоским потенциальным потоком со скоростью на бесконечности Усо2и с циркуляцией Ггпо контуру,охватывающему профиль.
Если известна функция, отображающая внешнюю область цилиндра в плоскости £ на внешнюю область профиля в плоскости г, т. е. дана зависимость z = /(£), то можно написать
W (г) = W [/(£)] = W, (£),
где W (г) — комплексный потенциал потока в плоскости г (его следует определить); (£) — комплексный потенциал потока во вспомогательной плоскости С (он считается заданным).
Пусть W1 — комплексный потенциал обтекания цилиндра с циркуляцией. Связь между комплексными скоростями 7 и Vz во вспомогательной и физической плоскостях может быть представлена в виде
dW =
dWx dW dz dz Vt	,TV
~ dz d£~ d£ ~	(IX>7)
dz dz
Следует отметить, что для единственности преобразования z = / (С) необходимо, чтобы при этом бесконечно удаленная точка в плоскости z переходила в бесконечно удаленную точку в плоскости $ и чтобы направления скорости на бесконечности были одинаковыми для обеих плоскостей.
Из уравнения (IX.7) видно, что скорость на бесконечности равна
(dz \
-7^ ) в соответствии с вышеуказанным условием “Ь / 00
сохранения направления скорости должна быть положительной.
Так как, согласно выражению (VII.7), действительная часть контурного интеграла от сопряженной скорости равна циркуляции скорости по этому контуру
д. ч.$7Е</£ = ГЕ,
14 И. Л. Повх
2t0 Элементы теории профиля, решеток профилей и теория крыла-
то, используя формулу (IX.7), получим
д. ч. jVd^=d. ч. §Vz-^dZ = d. ч. $V2dz = rz. . CS	сг
Следовательно, при конформном отображении циркуляция по 4 любому замкнутому контуру, охватывающему обтекаемый про-/: филь, не изменяется, т. е. ГЕ = Гг.	•
Комплексный потенциал (£) обтекания цилиндра с циркуля-/! цией будет в плоскости £ иметь следующий вид:	Л'
— V ггп Г	'Я
Vi =	In	(IX.9>|
Отметим, что в первом члене правой части равенства (1Х.9)| берется сопряженная скорость, так как здесь плоскопараллельный^ поток, обтекающий цилиндр, не параллелен оси х, а направлен подя некоторым углом к ней.	4
Ранее было отмечено, что характер обтекания цилиндра зави? сит от величины циркуляции. Как видно из рис. IX.4, каждому! значению циркуляции соответствуют свои критические точки.!: Следовательно, если в физической плоскости z не наложить каких-| либо ограничений, то критические точки могут разместиться в про-| извольных точках обвода профиля. Если заднюю критическукЭД точку расположить не на задней кромке, а на профиле выше илиЧ ниже точки Дх, то на острой кромке* в точке Аг будут возникать^ бесконечно большие скорости. С. А. Чаплыгин и Н. Е. Жуковский,/! имея в виду невозможность возникновения бесконечно большовд скорости в какой-либо точке профиля, предложили считать пракА тически осуществимым лишь такое обтекание, при котором поток', плавно с конечной скоростью сходит с заостренной задней кромки^ профиля. Это предложение было впоследствии названо постулатом/ Жуковского—Чаплыгина. Опыт показывает, что такое обтекание' профиля может происходить не при одном значении угла атаки," а в некотором интервале углов атаки, а следовательно, и цирку-’ ляции.
При очень больших углах атаки поток будет отрываться от: поверхности профиля и плавность обтекания будет нарушаться?. В данной главе рассматривается лишь плавное, или так называемое хорошее, обтекание профилей.	-	;
Крыловые профили, удовлетворяющие постулату Жуковского—<•! Чаплыгина, являются хорошо обтекаемыми. В действительности,/ условия обтекания определяются не только формой, т. е. геометр рией профиля, но и другими чисто гидродинамическими характер ристиками потока (угол атаки и числа подобия).	..
Постулат Жуковского—Чаплыгина накладывает ограничения на величину циркуляции. Циркуляция должна быть выбрана так, чтобы скорость на задней кромке профиля была конечной.
Скорость и циркуляция в преобразованном потоке
211
Задней критической точке Аг на профиле соответствует точка /12 на окружности (рис. IX.4). Как видно, в этих точках нарушается конформность отображения (отсутствует равенство углов).
Из теории функций комплексного переменного известно, что в таких точках
=00 или	=0.
X dz )а,	\ dt, ) л2
Таким образом, учитывая связь между скоростями в плоскостях £ и z, получим
7л, (z) = — ?л2 (£) =	= 00 •
\%)а,
Для того чтобы всоответствии с постулатом Жуковского—Чаплыгина величина VA, (z) была конечной, необходимо иметь V Аг (£) — 0. Отсюда следует, что точка Д2 на окружности в плоскости С является критической. Так как в плоскости С будет
Vа, £ fTl&Vсо z, то по формуле (IX.9) найдем
^1 (^)  ШаУ а, Л Н--г---
2ш’ I0
откуда
mmV,
= тА/а
а  Г 1 	'	l 2—L — л л2___________________+2шЧЛг
Так как координаты £л2 можно выразить через полярный угол е0 точки А2 на окружности, т. е. через £л2 = ае‘8°, а скорость на бесконечности через 2 = | V& г [ е‘°, последнее условие примет вид е—ее»
тх |	21 е- « - тт |	2 | е‘ + Г -1—- = О,
откуда величина циркуляции будет
ei (0-ео) _e-i <0—е0)
ч Г = — 4латм | Иа, г [--------,
где 0 — угол между вектором Vm г и осью х.
Используя равенство pice _________________pia
-—— = sina, 2г	’
где a = 0 — е0, окончательно получим значение циркуляции, соответствующее постулату Жуковского—Чаплыгина
Г = — 4лата, | Va, I sin a.
(IX. 10)
14*
212
Элементы теории профиля, решеток профилей и теория крыла
При а = 0 или 0 = е0 будет бесциркуляционное обтекание профиля. Следовательно, угол а определяется направлением скорости набегающего потока и направлением бесциркуляционного обтекания профиля. Этот угол часто называют теоретическим углом л атаки. Если профиль не имеет острой задней кромки, то постулат Жуковского—Чаплыгина может быть использован только при дополнительном допущении о расположении задней критической точки.
В п. 5 настоящей главы было показано, что окружность с цен- . тром в начале координат в плоскости с помощью преобразования Н. Е. Жуковского (IX.5) переходит в плоскости z в отрезок дли- j ной 2а (см. рис. IX.5), где а — радиус окружности.
Комплексный потенциал W (z) обтекания окружности в плоскости £, согласно выражению (VII. 19), будет
= КЛ2 г
Найдем комплексный потенциал обтекания пластинки (z) в плоскости z, для чего определим из формулы (IX.5) величину £ и подставим ее в выражение W (£); получим квадратное уравнение относительно £
£2 -2£z + a2 = О, откуда
= Z +
Дополнительный анализ показывает, что второй знак (минус) перед корнем учитывать не следует.
Подставив £ в W (£), получим выражение комплексного потенциала обтекания пластинки в плоскости-z
(г) = 4 Р» (г -1- ГЛ=^2) +	2 +
z |	г 4- V г2 —а2
+ 2^ 1п (z + К*2 —а2)
или, освобождаясь от иррациональности в знаменателе, имеем
07, (г) = 4 <г + Г'гЧ7?) + 4 <г~	+
т. е.
(г) = 4 + У“)2 +	+
+ £1п(г + 1/22 —а2)-
Скорость и циркуляция в преобразованном потоке
213
Имея в виду,.что = ит + iv^ и	— iv^, оконча-
тельно получим выражение для комплексного потенциала в физической плоскости z
Wi(z) = uOTz— ivm У z2~ a2 -j- ~ In (z -j- У z2— a2). (IX. 11)
Зная комплексный потенциал, легко найти вещественную и мнимую части; приравняв их константам, получим линии тока и эквипотенциальные линии. Линии тока для бесциркуляционного обтекания пластинки (Г = 0) показаны на рис. IX.8.
Для нахождения линий тока циркуляционного обтекания пластины необходимо воспользоваться постулатом Жуковского— Чаплыгина, гласящим, что на задней кромке (z = а) скорость должна быть конечной. Сопряженная скорость в плоскости z будет
равна
й dW\	. г , Г
V = —У ---------Woo 	4- к—
dz	j<22_aa 1 2ni
1 _!_
' Уг2~а2
г -j-Уг2 —а2
lV™Z 2ш
(IX.12)
Из выражения (IX. 12) видно, что при произвольной величине циркуляции на обоих концах пластины (z = ±а) скорость достигает бесконечно большой величины. Для того чтобы скорость на задней кромке имела конечное значение, необходимо, чтобы числитель второго слагаемого при z = а тоже обращался в нуль
Г л ^а-2?й = 0’ тогда Г = —2лаиот.
Подставляя найденное значение циркуляции в формулу (IX.8), получим величину сопряженной скорости
V----Поэ
214
Элементы теории профиля, решеток профилей и теория крыла
Так как значение координат на переднем и на заднем концах^ пластины z = ±а, то получим, что на заднем конце скорость будейя равна «со, а на переднем конце пластины скорость обращается! в бесконечность. Как видно из рис. IX.9, при циркуляционном! обтекании пластинки передняя критическая точка А не лежит н|а передней кромке, и, следовательно, на передней кромке скорое®! будет равна бесконечности. Таким образом, обеспечить в решенной задачи конечность скоростей как на задней, так и на переднеи| кромках пластины мы не можем.	Я
§ 4. Теорема Жуковского
Докажем теорему Жуковского для случая обтекания идеальной жидкостью произвольного тела. Формулировка теоремы, а такжЯ способ ее доказательства приведены такими, какими они были опубя линованы в книге Н.-Е. Жукова ского «Теоретические основы возЯ духоплавания» (1911 г.). Д Теорема. Если поток, имеюя щий в бесконечности скорость У^Я обтекает контур и циркуляция скорости по этому контуру равная Г, то равнодействующую силу даВа ле*ния жидкости на контур полу$ чим, если умножим вектор, предан ставляющий собой скорость потоЯ ка в бесконечности, на циркуляра цию скорости и на плотностй} жидкости и повернем полученный! вектор на прямой угол в сторону! обратную циркуляции.	J
Для доказательства теоремы рассмотрим обтекание некоторого» произвольного контура АВ (рис. IX. 10) установившимся потен^ циальным потоком со скоростью на бесконечности У^, направлец^ ной противоположно оси х.	£
Тогда потенциал скорости такого потока будет
где Ф1 — потенциал возмущенного движения.
Проекции скоростей в любой точке плоскости равны:
« = ?=	+
дх	1 дх
d<f __ Йф!
ду ~ ду ’
Теорема Жуковского
215
При значительном удалении от контура АВ, т. е. на круге бесконечно большого радиуса, и = —Уот и v = 0, так как производные и выражающие проекции скорости возмущения на бесконечном расстоянии от обтекаемого тела, равны нулю. Можно доказать, что величина проекций скорости возмущения обратно пропорциональна кубу расстояния от обтекаемого тела т. е.
dji _ _L и ______L
дх R3 ду Ra ’
Вокруг контура АВ проведем окружность С с достаточно большим радиусом R и применим к жидкому объему, заключенному между окружностью С и обтекаемым контуром, теорему об изменении количества движения.
Если обозначить через аир углы между осями координат и внутренней нормалью к элементу окружности ds, то секундная масса жидкости, протекающая через ds', будет
р (u cos а ucosp) ds — р — ]/«, + ^7) cos а +
+ cos р j ds — т ds,
а проекции переноса количеств движения через площадку ds па оси х и у соответственно равны
и m~Sy ^s'
Внешними силами'будут: сила, действующая со стороны обтекаемого контура АВ, с проекциями X и Y и сила давления р, приложенная к окружности С. Применяя теорему количества движения к контуру С, получим в проекциях на оси:
т^~ ds = Y. ду
(IX.13)
Величину давления, согласно уравнению Бернулли, можно представить в следующем виде:
р — с 2 ~С	2 [ \	'Z“ “I дх J “I \ ду ) J 
Подставив значения т и р в уравнения (IX. 13) и отбро-
/5<р,\2 /йфЛ2	1
сив члены -Л1 и Т2) как величины малости-5г> а также
216
Элементы теории профиля, решеток, профилей и теория крыла
интегралы с подынтегральным выражением С cos a ds, так как (|) cos a ds = 0, получим для проекции силы на ось х выражение
X — pVm cos ads — рУот J cos a ds — С	с
— рКо(р [( — Ko + ^cosa + ^cosp] ds = 0. С
Последний интеграл при отсутствии источников и стоков равен нулю, так как он определяет разность вошедшего в рассматриваемый объем и вышедшего из него количества жидкости.
Проекция силы на ось у будет равна
У = рУ<п ^^cospds — pVoo^^cosa ds — С
= — pV» (j)	COS a —	cos p J ds =
c
= —pVco (£ (wcosa — и cosP) ds. c
Очевидно, что v cos a и и cos P есть циркуляция скорости no ds. Таким образом, последний интеграл определяет циркуляцию скорости по окружности С. Но так как в области, заключенной между контуром АВ и окружностью С, никаких особенностей (вихрей) не содержится, то циркуляция по окружности С равна циркуляции по обтекаемому контуру АВ.
Следовательно,
У=—рКоГ,	(IX.14)
что и требовалось доказать.
Формула Жуковского для подъемной силы имела фундаментальное значение для развития теории крыла самолета
§ 5. Обтекание решетки профилей
В 1889 г. Н. Е. Жуковский предложил для изучения движения рабочих колес турбомашин воспользоваться обтеканием эквивалентной решетки профилей.
На рис. IX. 11 показана плоская прямолинейная решетка профилей, имитирующая сечение рабочего колеса. Геометрические характеристики профилей остаются теми же, что и для профилей крыльев. Основными геометрическими величинами, определяющими решетку, являются расстояние между соответствующими точками профилей — шаг решетки t — и угол между осью решетки и хордой р, называемый углом установки профиля в решетке.
Обтекание решетки профилей
217
Обычно пользуются не абсолютным значением шага t, а его значением, отнесенным к величине хорды -у- или обратной величиной Первая величина t = называется относительным шагом. В турбомашинах t изменяется в широких пределах. В турбинах I, как правило, меньше единицы (0,4—0,8), в компрессорах 7 может быть значительно больше (1,0—2,0), а для воздушных вйн-
тов еще больше. Очевидно, у всех колес и винтов, в сечениях, удаленных от втулки, шаг соответствующих решеток будет больше, чем в сечениях, близких к втулке.
Обозначив параметры потока перед решеткой (скорость, давление и угол входа) соответствующими буквами с индексом 1 (У1( рг и Pj), а за решеткой —индексом 2 (У2, р2 и (J2), введем так называемую величину скорости на бесконечности (рис. IX. 11)
. v<»=4&+^)-	(1Х-45)
Для получения основных закономерностей обтекания решеток профилей воспользуемся законами сохранения массы, импульса и энергии.
Закон сохранения массы для несжимаемой жидкости дает у12 = v22 = vz.
Последнее означает, что проекции скоростей перед и за решеткой на направление, перпендикулярное к оси решетки, равны.
Из закона сохранения энергии для случая идеальной жидкости получим соотношение
pV? рИ	/ТУ
Pi — Р^ = ^~2'	(1Х-
218
Элементы теории профиля, решеток профилей и теория крыла
Закон сохранения импульса, примененный к замкнутому коЯ туру ABCD, в проекциях на оси и и z дает следующие уравнения!
Ри = ptVz (У1а - V2a); Рг = ЦР1 -рг),	(IX.11
где Ри и Рг — проекции внешних сил на оси и и z.	д
Имея в виду, что	Я
и=+ VI п V?=vL + vL
и, следовательно, из (IX. 16)
pi - р.=4-	- у и = 4- (^«+vla) (v2a - vla) 1
или	.?
А-Р2 = 4	(1Х-^
где Г = t (У2а — У1а) — циркуляция скорости по контуру ABCD-, (рис. IX. 11).
Подставив (1Х.18) в (IX. 17), получим:	'
Ри = рУгГ, P2 = _9V^j\	(IX. 19)
Введя главный вектор внешних сил в виде Рг = Р'1 + Р1Л получим		3
(IX.20);
Формула (IX.20), являющаяся выражением теоремы Н. Е. Жу-ij ковского для решетки, благодаря введению фиктивной средней-векторной скорости (IX.5) не отличается по форме от соответствую-) щей формулы (IX. 14) для изолированного профиля.	»
Направление силы Р получим путем поворота вектора скорости^ Vn на 90° против направления циркуляции. Силы Ри и Рг назы-'j ваются соответственно окружными и осевыми усилиями.	:
Влияние вязкости сказывается в появлении потерь полногс^ напора р’ при движении жидкости от сечения DA до СВ. Тогда-;закон сохранения энергии будет	'
Р1—р2=	—И„)—(IX.21);
а величины окружного и осевого усилий примут вид: р,;=рУ2Г, р;=_руотаг'-	(1^.22):!
Значение циркуляции Г' в результате действия вязкости оказы-,) вается намного меньше циркуляции Г, определяемой для идеальной; жидкости.
Заметим, что в компрессоре и насосе давлениеза колесом больше;, чем до колеса. Следовательно, в компрессорной решетке скорость за решеткой согласно (IX. 16) будет меньше, чем до решетки, т. е, ’ компрессорная решетка должна быть диффузорной-
Элементы теории крыла конечного размаха
219
В реактивных ступенях турбин, наоборот, решетка конфузорная-. В активных ступенях турбин, где скорость лишь меняет направление, сечение межлопаточного канала будет сохраняться постоянным.
Очевидно, в насосе и компрессоре лопатки будут оказывать силовое воздействие на жидкости или газы, а в турбинах — наоборот, поток путем силового воздействия на лопатки будет вращать рабочее колесо.
§ 6. Элементы теории крыла конечного размаха
Теория крыла конечного размаха основана на допущении возможности замены крыла эквивалентными вихревыми системами, создающими в идеальной жидкости поля скоростей, аналогичные тем, которые наблюдаются вне пограничного слоя при обтекании л) _________
данного крыла реальной вязкой (	. )*
жидкостью.	---—Л------------
При изучении обтекания крыла бесконечного размаха было установлено, что действие вязкости жидко- б) 1 } j , сти, приводящее к образованию вих- /Т' рей, может быть искусственно заме-	5	~
пено одним присоединенным вихрем.
Было показано, что подъемная сила	Рис- 1Х-12
крыла бесконечного размаха по фор-
муле Жуковского (IX. 14) пропорциональна циркуляции, определяющей интенсивность присоединенного вихря.
Метод замены подъемной силы крыла действием лишь одного вихря используется в так называемой теории вихревой несущей линии (рис. IX. 12, а). Подъемную силу крыла можно создать не одним присоединенным вихрем, как это сделал Н. Е. Жуковский, а системой вихрей, непрерывно распределенных по контуру профиля крыла (рис. IX. 12, б). Теория, имеющая в своем основании такую схему, значительно сложнее первой; она называется теорией вихревой несущей поверхности.
В самом определении крыла бесконечного размаха предполагается, что интенсивность присоединенного вихря постоянна по всей длине крыла.
Очевидно, что при обтекании крыла конечного размаха подъемная сила, имеющая на крыле конечного размаха конечное значение, на концах крыла должна обращаться в нуль. Так как по теореме Гельмгольца вихревая линия не может заканчиваться в жидкости, то, следовательно, присоединенный вихрь должен сходить с крыла, образуя свободные вихри, уходящие на бесконечность за крылом.
220
Элементы теории профиля, решеток профилей и-теория крыла
По теории вихревой несущей линии крыло конечного размаха заменяется П-образным вихрем, состоящим, как показано на рис. IX. 13, а, из присоединенного вихря постоянной интенсивней сти, переходящего на концах крыла в свободные вихри той же ий! тенсцвности. Очевидно, по такой схеме подъемная сила крыла! а следовательно, и циркуляция не постоянны по размаху крыла; их распределение определяется только интенсивностью присоединен^ ного вихря. В середине крыла они имеют наибольшее значение, п<з мере приближения к концам убывают и у концов обращаются! в нуль.
Схема вихрей, соответствующая реальному распределению^ подъемной силы по крылу, показана на рис. IX. 13, б. От присоединенного вихря вдоль всего размаха отходят элементарные свобод-ные вихри с циркуляцией'<УГ. Таким образом, циркуляция убывает ,, от Г о в середине крыла до нуля на концах, а позади крыла обра-1 зуется сплошная вихревая пелена свободных вихрей, которая! по мере удаления от крыла сворачивается в два вихревых жгута. ;
Для простоты рассмотрим вначале схему крыла с П-образным > вихрем. На рис. IX. 14 показаны две проекции прямоугольного ? крыла длиной I и с хордой Ь. Отношение размаха или длины крыла . I к хорде Ь называется удлинением крыла А, =
Присоединенный вихрь поместим так, чтобы его ось совпадала 1 с осью z, а свободные вихри расположим на расстоянии = = I + 2е (е — расстояние между осью свободного вихря и концом крыла).	*
Если начало координат поместим, как показано на рис. IX. 14, • в точку пересечения оси левого свободного вихря и ось х направим '
перпендикулярно плоскости крыла вверх, то величина скорости, индуцируемая левым свободным вихрем в точке с координатой z, будет равна
г
v =— —
4лг
(IX.23)
Элементы теории крыла конечного размаха	221
Эта скорость направлена в сторону, противоположную оси х. Среднее значение скорости, индуцированной левым свободным вихрем, равно
, г+е
— J vdz. в
Имея в виду, что действие правого вихря будет таким же, как и действие левого, получим среднее значение скорости, индуцированной свободными вих-
рями,
Ы-е
^ср = 4- f vdz. (IX.24) в
Подставив под интеграл значение v из формулы (IX.23), получим
1-\-г 2 f Г , w,.D —----r j— dz =
‘-Р	/	J 4лг
.8
Г , /-(-е = 5—: 1П —!-- . 2л/ е
'Г
Так как е =	, то
(IX.25)
г 1 /i-Н г
УсР ~	2л/ П /j — I ~	2л1
Величина х, равная In обычно называется коэффициентом 11 Z самоиндукции крыла.
Если принять, согласно опытным данным и более строгой теории, I, — 1,04/, то х =In у-Ц- = 4, а средняя скорость (IX.25) ZjL Z будет равна
=	=	(IX.26)
СР 2л,/ л/	'	'
По формуле для подъемной силы и формуле Жуковского получим равенство
У = Сг/ф&/ = рШ
из которого следует так называемое уравнение связи
V = ^Vb.	(IX.27)
222 Элементы теории профиля, решеток профилей и теория крыла д
.	.	л
Подставив это выражение в формулу (IX.26), окончательной получим	у
^ = -^-JrV = -^v-	(1Х.28>3
II
Появление индуктивной скорости уср изменит действительный:)! угол атаки. Если при' ее отсутствии угол атаки крыла был бы, j как показано на рис. IX. 15, равен а, то появление индуктивной';
Рис. IX.15
скорости вызвало бы уменьшение его на угол скоса Да. Истинный угол атаки а„ будет равен ан = а — Да.
Величина угла скоса в связи с его малостью определится из соотношения
tg(Aa)^ Да = —(IX.29)
Подставив в формулу (I&.29) выражение цср из (IX.28), полу-. чим
(1Х.30)
Изменение угла атаки перед крылом на величину Да приведет' к изменению сил, действующих на крыло. Величина подъемной силы в соответствии с теоремой Жуковского будет направлена перпендикулярно местной скорости на бесконечности (Еместн), т. е. скорости, расположенной по отношению к набегающему потоку под углом Да. В связи с этим появится проекция силы Жуковского на направление набегающего потока V. Эта»»проекция является силой сопротивления Х;, называемого индуктивным.
Вычислим коэффициент индуктивного сопротивления. Если буквами без штриха обозначим подъемную силу и ее коэффициент, соответствующие углу атаки, определенному по скорости набегающего потока на бесконечности (рис. IX. 15), а со штрихами — силу и ее коэффициент, соответствующие истинному углу атаки,
Элементы теории крыла конечного размаха
223:
то между коэффициентами будут соблюдаться следующие соотно.-шения:
Су = Су cos Да; Cxi — Су sin Да,
где Cxi — коэффициент индуктивного сопротивления.
Ввиду малости Да cos Да 1 и sin Да «=* Да, откуда
Су^С'у; Сх1^Су^.	(1Х.ЗД)>
Учитывая формулу (IX.30) и опуская штрих, из выражения (IX.31) окончательно получим значение коэффициента индуктивного сопротивления в виде
С„=>.	(IX.32)
Таким образом, СХ1 изменяется прямо пропорционально квадрату коэффициента подъемной силы и обратно пропорционально удлинению. Следовательно,, индуктивное сопротивление обращается в нуль при Су = 0 и при бесконечном удлинении.
Если отказаться от довольно грубой П-образной схемы и считать, что величина циркуляции переменна по размаху, то скорость, индуцированная в точке z элементарным вихрем, сбегающим с с крыла в точке zr (рис. IX. 13, б), определится из равенства dv = __ dr
4л (zx — z)
Величина скорости, индуцированная в точке z всей вихревой пеленой, будет равна
i	i
2	2
С	С	dr л
11 dr 1 I dZj 21
V = T- 1 ----- =	1 --4----•
4л , I z, — z 4л J z, — z _2	_2
2	2
Величина индуктивного сопротивления может быть вычислена по формуле
i
2
Xi = p J T(z)vdz. i 2
После подстановки значения v в эту формулу получим i	i
=	( r(z)dz ( -^Г	,	(IX.33)
' 4л J 4 ' J dz, (z, — z)	'	'
___i_	I
2	~ ?
224
Подобие процессов переноса
Вся трудность вычисления полного индуктивного сопротивления заключается в нахождении функции Г (г).	j Расчеты, произведенные для; Таблица IX.1 крыльев с различной формой в пла-' не. показали, что коэЛЛипиент wwnvw.l		
Форма крыла в плане	6	тивного сопротивления следует определять по следующей формуле: c^==-ir(1 + 6)- (1Х-34) При 6 = 0 получаем формулу (IX.32). Значения 6 для различных форм крыльев в плане при X = 5 ч-8 даны в табл. IX. 1.
Эллипс Прямоугольник Трапеция Ромб	0 0,052 0 0,140	
ГЛАВА X
ПОДОБИЕ ПРОЦЕССОВ ПЕРЕНОСА
§ 1. Значение теории подобия
При изучении явлений, происходящих в природе, технике и обществе, наука широко пользуется методом моделирования этих явлений.
Смысл моделирования заключается в том, чтобы по результатам опытов на модели судить о явлениях, происходящих в натурных условиях. При этом изучение явлений на модели можно осуществить значительно проще и полнее, чем в натуре.
Рассматривая физиологические явления, акад. И. П. Павлов писал \ что «наблюдение собирает то, что ему предлагает природа, опыт же берет у природы то, что он хочет . . . Опыт как бы берет явления в свои руки и ... в искусственных, упрощенных условиях определяет истинную связь между явлениями».
Однако результаты опытов на модели могут быть использованы для решения задач практики только в случае, если при проведении опытов соблюдаются определенные законы моделирования.
Моделирование является весьма большой и ответственной научной задачей. Иногда исследование с помощью моделей является единственно возможным способом экспериментального изучения некоторых практически важных процессов. Так, процессы, которые длятся в течение многих лет или даже тысячелетий, нельзя исследовать в натуре, но можно в течение короткого про-
1 Павлов И. П. Собр. соч. Т. 2, 1951, с. 274
Значение теории подобия
225
межутка времени (часы, дни) изучать на моделях. К таким процессам можно отнести фильтрацию нефти в земле, образование русел рек и пр. Могут быть и обратные случаи, когда быстро протекающие во времени процессы изучаются на моделях в течение более длительного времени.
Моделирование различных физических процессов исходит из подобия рассматриваемых явлений.
Два явления называются подобными, если по характеристикам одного можно получить характеристики другого путем простого пересчета, аналогичного переходу от одной системы единиц к другой. Условиями подобия двух явлений являются равенства некоторых безразмерных параметров, называемых числами подобия.
Определение чисел подобия при моделировании изучаемых процессов требует глубокого знания механизма этих процессов и в общем случае является сложной задачей. При решении этой задачи следует все изучаемые процессы разделять на две существенно отличные группы. К первой надо отнести процессы и явления, которые можно описать уравнениями. Ко второй, представляющей наибольший интерес, относятся процессы и явления, еще не имеющие математического описания.
В случаях, когда уравнения исследуемых процессов неизвестны, единственной теорией, позволяющей найти числа подобия, является теория размерностей. При наличии дифференциальных уравнений исследуемых процессов числа подобия легко определяются как коэффициенты уравнений, представленных в безразмерном виде. Заметим, что степень сложности уравнений при этом не имеет никакого значения, так как для нахождения чисел подобия процесса, описываемого данным уравнением, его решения не требуется.
Естественно, что получение чисел подобия при наличии уравнений значительно проще, чем при отсутствии их. Поэтому теорию размерностей следует применять при получении критериев подобия лишь для процессов, не имеющих математического описания.
Числа подобия при использовании одних и тех же уравнений могут иметь совершенно различный вид. Если к этому добавить многообразие существующих процессов, то можно понять существование чрезвычайно большого количества чисел подобия.
В настоящей главе на основе анализа уравнений процессов переноса количества движения, тепла и вещества дается систематизация основных чисел подобия процессов переноса в жидкостях и газах.
Изучение любого процесса сводится к тому, что по заданным величинам находятся неизвестные, определяющие этот процесс, численные характеристики. Числа подобия, полученные из величин, заданных для данного процесса, обычно называют критериями подобия.
15 И. Л. Повх
226
Подобие процессов переноса
§ 2. Гидродинамическое подобие
Для выяснения условий, при соблюдении которых уравнения ] движения будут одинаковы, или движения подобны, напишем  уравнения Стокса (III.41) для случая плоского потока в безраз-; мерном виде. В качестве масштаба длины выберем какой-либо характерный размер тела I (хорда крыла, диаметр или радиус трубы и др.1), а в качестве масштабов скоростей, давлений, плотностей, температур и пр. — их характерные значения (на бесконечности, средние по объемным, массовым расходам и пр.).
Обозначив безразмерные величины теми же буквами, что и размерные, но с черточкой, произведем следующую замену:
х = 1х, у = 1у, р = рор;
и = Vou, v = Vov, v = vov;
t = tot, X - gX-, Y = gY, p = pop.
За масштаб времени принято время, характерное для данного движения, а за масштаб массовых сил, отнесенных к единице, массы, — ускорение силы тяжести.
После подстановки написанных выражений в уравнение (III.41) получим уравнение плоского движения и уравнение неразрывности для несжимаемой жидкости в безразмерной форме:
*0 dt
— ди , - ди \ и —— -4- и—^г = дх ду /
Ро/ р дх ' I* V ’
Vo dv .	(- dv , - dv \
v «-+ — (“ S’=
Poz p dy 1
Vo ( du . dv \ _ q
* \ dx dy J
(Х.1)
V,
I
Разделив первые два уравнения на а третье на —~ и опу- ; стив для простоты черточки над безразмерными величинами, ; получим:
I ди ди
Voto dt +
дУ j vl -povl P dx val v
Гидродинамическое подобие
227
I dv
Vo^o dt
1 dy )	1/2	p0i/2 p dy Fo/ V ’
du , dv ____л
~dx~ *" ~dy~ ~ U’
Из этой системы следует, что если два потока подобны, т. е. они описываются одинаковыми уравнениями с одинаковыми граничными и начальными условиями, представленными в безразмерном виде, то для них должны быть одинаковы по величине следующие безразмерные величины:
1 .	е1 .	Ро „ vo
iVo ’	’	pi/2 vai. •
Обычно в теории подобия пользуются комбинациями указанных величин, каждая из которых имеет свое название:
— = Sh— число Струхаля;
^0*0
1Л т_
—=	— число- Фруда;
V gl
—= Eu— число Эйлера;
PV'o
-^- = Re— число Рейнольдса.
(Х.2)
Условие одинаковости чисел подобия обозначается значком idem, т. е. Sh = idem, Re = idem и т. д.
Число Эйлера для сжимаемой жидкости
Ец_ Ро _ 1	_ 1 1
tU“ рИ* ~ * У* ~ * М* ’
где а = 1/ k —----скорость звука; k = —----показатель ади-
Т Р	со
абаты; М — отношение скорости потока жидкости к скорости звука, называемое числом Маха.
Следовательно, число Ей для сжимаемой жидкости выражается через k и М. Используя уравнение энергии в безразмерном виде, можно показать, что каждая из этих величин в отдельности должна быть одинакова для двух подобных потоков, т. е. k = idem и М = idem. Таким образом, потоки сжимаемой жидкости будут подобны при условии:
Sh = idem, Re = idem, Fr — idem, M = idem и k = idem.
Физический смысл чисел подобия можно установить, рассмотрев физическое содержание каждого слагаемого уравнения движения. Из анализа уравнения следует, что число Re выражает 15*
228
Подобие процессов переноса
отношение сил инерции к силам вязкости, поэтому для большинства технических задач числа Re довольно велики. Число Fr выражает отношение сил инерции к силам тяжести, или гравитационным силам. Число Ей характеризует отношение нормальных сил давления к силам инерции, а число Sh — отношение конвективной составляющей сил инерции к локальной составляющей тех же сил.
Если уравнения движения в безразмерном виде (X. 1) разделить не на размерный коэффициент при конвективной составляющей сил инерции, как это сделано выше, а на соответствующий коэффициент при локальной составляющей сил инерции, то получим числа подобия в виде: .
^2—= Sh; -2- = Ge; -£2K = Pu и -^-=Fu.	(Х.З)
VVo	e(t	P<A	v 7
Эти числа подобия характеризуют отношение конвективной составляющей сил инерции, сил тяжести, нормального давления и сил вязкости к локальной составляющей сил инерции. Каждое из них должно соблюдаться при нестационарных движениях, происходящих под действием соответствующих сил.
При изучении движения жидкостей в условиях, близких к невесомости, важное значение приобретают силы поверхностного натяжения. Если представить уравнения (Х.1) в одноразмерном виде и выделить размерные коэффициенты, то при наличии сил поверхностного натяжения они будут иметь вид
Ро + " ' ’ + Ро "у- + ’ • • —
= Ро£+—	....!-^+ •••+-£-•• •
Чтобы выяснить, каково влияние сил поверхностного натяжения на движение жидкости, необходимо разделить каждое выражение на последнее слагаемое справа. Полученная совокупность чисел подобия характеризует отношение соответствующих сил (локальные и конвективные силы инерции, силы тяжести, нормальные силы давления и силы вязкости) к силам поверхностного натяжения. Эти числа подобия будут равны:
р __ PoVoZ2 . р _ Ро^о^ _ р _ pogZ . р __ р01 и р __ ЛоК)
1 at ’	2	а’3 а ’	4 а 6 а ‘
Число Р3, характеризующее отношение сил тяжести к силам поверхностного натяжения, используется при моделировании процессов невесомости и называется числом Боде.
Интересно установить абсолютное значение чисел подобия и пределы их изменения в практических задачах техники.
Гидродинамическое подобие
229
Число Re, характеризующее отношение сил инерции к силам вязкости, может быть представлено в виде
Ре Уа1 _ ^оФо
vo Ro
Если за линейный размер для корабля взять его длину и для самолета — хорду крыл'а, то числа Re в обоих случаях изменяются в пределах 105— 109. В гидротурбинах за характерный линейный размер обычйо берут диаметр рабочего колеса. Тогда число Re для турбин изменяется в пределах 104—10е.
Подобие' нормальных сил давления определяется равенством чисел Мий или при малых скоростях потоков — числом Ей. Если скорость звука
a = V~kRT = 1/ г т
где т — молекулярный вес, то число М будет иметь вид
М = 848kgT '
Из формулы (Х.4) видно, что при одной и той же скорости движения и мало меняющихся k и g значение числа М пропорционально корню квадратному из величины относительной молекулярной массы среды и обратно пропорционально корню квадратному из абсолютной температуры.
При полете современных самолетов числа М = 0,2 4-3,0, снарядов — М = 2 4-4, ракет — М = 5 4-8. В проточной части турбомашин обычно число М < 1, т. е. потоки являются дозвуковыми, лишь в некоторых случаях имеют место потоки с М > 1.
Число Ей характеризует отношение нормальных поверхностных сил давления к силам инерции и равно отношению перепада давлений в двух точках потока к скоростному напору.
В большинстве задач гидродинамики (внешнее обтекание тел, движение жидкостей и газа в трубах и др.) величины давления и скорости в любой точке потока однозначно определяются числом Re. Следовательно, число Ей в этих случаях не является критерием подобия и его значение полностью зависит от других чисел подобия. Например, при движении жидкости в трубах число Ей представляет собой безразмерную величину сопротивления и зависит лишь от числа Re
Eu = ^ = /(Re).
Р^о
В некоторых задачах величина перепада задана и не связана однозначно с величиной скоростного напора в любой точке потока.
230
Подобие процессов переноса
В таких потоках число Ей не зависит от других чисел подобия I и является критерием, соблюдение которого обязательно. Приме- J ром'потока, при моделировании которого числа Ей должны быть i строго одинаковы, является поток в проточной части любой '1 турбомашины, в частности гидравлической трубины. В последнем случае величина перепада задана разностью уровней воды в верх- .> нем и нижнем бьефах и скорость в любой точке потока зависит ; не только от числа Re, но и от числа Ей.
Число Sh характеризует составляющие инерционных сил, 1 зависящих от времени. При этом может быть два случая: 1) когда нестационарность движения задается граничными условиями (машущее крыло, винт, колесо турбины и пр.); 2)-когда неста-ционарность может являться следствием стационарного обтекания какого-либо тела. В первом случае число Sh полностью определяется заданными условиями. Так, при исследовании работы винтов за характерное время принимается время одного оборота, 30
т. е, период Т = за характерный линейный размер —диаметр винта D, тогда число Sh определяет величину, называемую отно-
. V
сительнои поступью, А — 
Для судовых винтов X лежит в пределах 0,03—3. Во втором случае число Sh является зависимым критерием подобия, т. е. число Sh есть функция числа Re. Так, при стационарном обтекании цилиндра с его поверхности периодически отрываются вихри, частота отрыва которых заранее неизвестна и определяется режимом обтекания, т. е. числом Re.
Число k = — в отличие от других чисел подобия явно не cv
зависит от параметров потока. Оно полностью .определяется физическими свойствами газов, и зависимость его величины от параметров газа довольно сложна. При некоторых упрощениях можно считать, что k зависит от числа атомов в молекуле. Для одноатомных газов k = 1,66, двухатомных k — 1,4, трехатбмных k = 1,27; для молекулы с бесконечным числом атомов k стремится к единице.
Значение числа k слабо зависит от температуры.-Так, для воздуха при изменении температуры от 0 до 1500° С оно убывает от 1,4 до 1,28. Действительные значения показателя изэнтропы для различных газов в зависимости от температуры можно найти в термодинамических таблицах. Влияние числа k на обтекание существенно лишь при числах М, значительно больших единицы.
Для полного моделирования необходимо полное подобие процессов, т. е. равенство 'чисел подобия. Но- обычно пользуются приближенным моделированием, при котором подобие сохраняется по числам, наиболее характерным для данного процесса. Так, для стационарных процессов числа Sh не имеют значения. При
Гидродинамическое подобие
231
изучении движения жидкости в трубе самым существенным будет число Re. При испытании моделей турбомашин (турбины, насосы, компрессоры) необходимо равенство чисел Sh и Ей.
Число Re приобретает решающее значение при определении структуры потока. Все потоки делятся на ламинарные и турбулентные. Структура потока определяет процесс переноса массы, количества движения и тепла.
Выясним, как величина чисел подобия влияет на величину сопротивления тел. Сопротивление X любого тела можно представить в виде
X = CxP-^-S,
где Сх — безразмерный коэффициент сопротивления; S — хдрак-
Зависимость Сх от числа Re для шара показана на рис. Х.1. Из рисунка видно, что число Re существенно влияет на коэффициент сопротивления шара. Аналогичные кривые будут иметь место и для других плохо обтекаемых тел. Число Re, при котором происходит резкое падение сопротивления, называется критическим числом Рейнольдса и обозначается ReKP.
Число М также существенно влияет на величину сопротивления и на другие аэродинамические характеристики. Для обычных самолетов существует так называемый звуковой барьер, который характеризуется тем, что при приближении скорости самолета к скорости звука коэффициент лобового сопротивления резко возрастает и дальнейшее увеличение скорости сопряжено с необходимостью значительного увеличения мощности двигателя. Число М, при котором где-либо вблизи обтекаемого тела скорость газа достигает местной скорости звука, что приводит к резкому увеличению сопротивления, называется критическим числом М и обозначается Мк„ (рис. Х.2). Значение Мкр для крыла меняется в пределах 0,7—0,8. Для уменьшения лобового сопротивления строят самолеты со стреловидным крылом. При этом Мкр возрастает до 1,5—2,0 и несколько больше.
232	Подобие процессов переноса
--------------------------------------------------------------- ;
§ 3. Тепловое подобие
Аналогично гидродинамическому подобию рассмотрим условия j теплового подобия. Вначале разберем случай чистой теплопровод- 1 ности, т. е. переноса тепла молекулярным способом без конвекции. В этом случае уравнение переноса тепла имеет вид
дТ , С₽Р — М?'>
где ср — удельная теплоемкость жидкости.
Приведем это уравнение к безразмерному виду, для чего введем следующие безразмерные величины:
ср = СрСр,,-, р = рро; Т — ТТо;	х = xl, t — lt0,
где х, р, Т, X и Ср — безразмерные величины; I, р0, Тй, Хо, сРо — характерные размерные величины (масштабы).
Рассмотрим одномерное движение, т. е. Т = T(t, х), тогда дт — 1 дЧ
Ср$  dt дх2
Подставив принятые соотношения в уравнение переноса тепла, получим
сРоРоЛ) -; - дТ _ %0Т0 г д2Т - - дТ _ Хо t0 у д2Т
-Г-СрР1Г-~1^Х~^ ИЛИ С₽Р7Г“ W7 * дх2 
Как было указано ранее а = называется коэффициентом температуропроводности".
Число, равное называется числом Фурье. Оно характеризует нестационарность процесса молекулярного переноса.
Далее рассмотрим случай конвективного переноса тепла. Для одномерного установившегося движения соответствующее уравне-дТ	д2Т
ние имеет вид и — а 3 „ .
дх	дх2	х
Введя безразмерные величины, получим ' • '	'
КЛ ~ _дТ_ = срТр - д*т
I дх	дх2
или
- дТ	а0 ~ д2Т
и-=-= -гД- а -=-  дх	К/ дх2
Следовательно, для подобия процессов необходимо соблюдать равенство числа °°1 , характеризующего конвективный перенос; обратная величина называется числом Пекле (Ре): Ре = -^
(Х.5)
а
Тепловое подобие
233
Перенос тепла с поверхности при разности температур в потоке и на стенке 7\ — Tw можно представить в виде
Q = -X-^^ = a(T1-Ta,)F/,
где Т\ — температура окружающей среды; Tw — температура стенки; а — коэффициент теплоотдачи (теплопереноса).
Для плотности теплового потока имеем
=	=	(Х.6)
Воспользуемся выражением (Х.6) и получим еще одно число подобия. Если уравнение в безразмерном виде
- X	= аоТоа (Л - Tw)
1 дп
Vo разделим на —получим
дп ло
Число называется числом Нуссельта и обозначается Nu
Nu = -^-.	(Х.7)
ло
Так как коэффициент теплоотдачи а, входящий в число Nu, меняется от точки к точке, то это число является локальным.
Если в выражение для числа Nu подставить среднее значение коэффициента а
acp = -J-j adx, о
то полученное значение будет называться средним значением числа Нуссельта.
Количество тепла, которое снимается со стенки, имеющей длину I и ширину, равную единице, будет
Q = X (Г1- Тст) = NU X (7\— Тст).
Физически число Nu можно рассматривать как отношение действительного теплового потока, определяемого величиной коэффициента теплоотдачи а, к удельному тепловому потоку, который имел бы место в условиях чистой теплопроводности в слое толщиной I, т. е. Nu =
Др
I
234 Подобие процессов переноса
Если разделим число Ре на число Re, то получим число Рг -Я Ре _ vo _ voPocP _ _£рЛо______________pj.	w q\
Re a Xq	л
Число Pr характеризует отношение двух характеристик моле- Д кулярного переноса: кинематической вязкости v и коэффициента '-J температуропроводности а. Перенос импульса, связанный с вели-чиной v, определяется разностью скоростей, а перенос тепла, связанный с величиной а,— разностью температур. Следова-тельно, число Рг, явно содержащее лишь величины, определяющие
физич₽ские свойства среды, в дей- •' ствительности характеризует отноше-ние между полями скоростей и тем- . ператур. Тогда зависимость Nu = ; = f (Re, Рг) можно трактовать еле- * дующим образом: количество перено-симого тепла (Nu) зависит от вида  скоростного поля (Re) и его связи ' с полем температур (Рг).
Для идеальных газов число Рг, однозначно определяемое числом атомов в молекуле и не зависящее от температуры и давления, приведено в табл. Х.1
Таблица Х.1
Число атомов	cv	Pr
1	1,66	0,67
2	1,4	0,73
3	1,3	0,8
4 и более	—	1
Для реальных газов число Рг зависит от температуры и давле-йия и определяется экспериментально. Его значения несколько меньше единицы. Для большинства жидкостей числа Рг значительно больше единицы. Для жидких металлов число Рг имеет очень малые значения (-—10"2).
Числа Рг для некоторых сред приведены в табл. Х.2.
Зависимость числа Рг для жидких металлов от температуры показана на рис. Х.З.
Очевидно, что малые значения числа Ре соответствуют очень малому конвективному переносу в общем переносе тёпла. Следовательно, при значениях чисел Ре < 1 наблюдается только молекулярный перенос, т. е. теплопроводность, в то время как при больших значениях числа Ре роль молекулярного переноса будет ничтожна.
Так как Ре — RePr, то для газов, у которых обычно число Рг = 0,7 -т-0,9, можно считать Ре Re.
Последнее означает, что большим числам Ре будут соответствовать большие числа Re, а следовательно, при некотором достаточно большом числе Re перенос тепла будет осуществляться путем турбулентной конвекции.
При турбулентном течении жидких металлов отношение потока тепла, переносимого молекулярной теплопроводностью, к потоку
Диффузионное подобие
235
Таблица Х.2
Среда	Рг при температуре, °C			
	20	60	100	400
Воздух	0,7	—	0,690	0,661
Вода	7,02	3,02	1,74	—
Масло	10 400	1050	276	.—
Ртуть	0,0249	—	0,0162	—
Водяной пар	—	—	1,12	0,876
тепла, переносимому за счет турбулентного перемешивания, может быть приближенно оценено следующим образом.
порядка 1000 роль молекулярного и турбулентного механизмов переноса приблизительно одинакова, лишь при Ре 50 000, т. е. при очень высоких скоростях течения, в ядре потока преобладает турбулентный перенос тепла.
§ 4. Диффузионное подобие
Числа подобия для диффузионных процессов можно легко получить из уравнения диффузии вещества. Для одномерного движения уравнение молекулярной диффузии будет иметь вид дс__________________________р. дгс
dt ~ дх* "
236
Подобие процессов переноса
Заменим в этом уравнении все величины безразмерными .и характерными значениями (масштабами):
с = сос, t = t~t, X — Xl',
с0 дс	Dca д2с	дс	Dt0 д2с
dt	I2 дх2	at	I2 дх2
Т?	Z)^(J	АД,
Безразмерное число называется диффузионным числом
Фурье. Очевидно, что оно аналогично тепловому числу Фурье. При конвективном переносе вещества для одномерного движения воспользуемся уравнением
Проделав аналогичные преобразования, получим
— дс ‘ D д2с дх Vol дх2
Число p°Z называется диффузионным числом Пекле.
Число Ред подобно числу Re определяет структуру потока. По тому, велико ли число Refl по сравнению с единицей или мало, можно судить о том или ином характере переноса вещества. В первом случае молекулярной диффузией можно пренебречь по сравнению с конвективным переносом вещества, во втором — наоборот, молекулярная диффузия является определяющей.
Поделив число Ре на число Re, получим диффузионное число Прандтля Ргд, равное отношению кинематической вязкости к коэффициенту диффузии
т£?-=ТГ = Рг»'	(Х.9)
Во многих работах число Ргд называется числом Шмидта. Напишем теперь уравнение переноса вещества применительно к разности концентраций на стенке и в окружающей среде,
где ад — коэффициент переноса массы; Cj — концентрация вещества в окружающей среде; cw — концентрация вещества на стенке.
Запишем это уравнение в безразмерном виде
Dc0 дс	.
~	— °Vo (ci
или
Диффузионное подобие
237
Тогда получим локальное число Nu, равное
-^- = Nua.	(Х.10)
Аналогично тепловому числу Nu можно, воспользовавшись средним коэффициентом переноса вещества аср д, ввести среднее диффузионное число Нуссельта.
Для газа числовое значение коэффициентов диффузии и вязкости имеет один порядок, поэтому Ргд — 1. Иначе обстоит дело в жидкостях. Коэффициент кинематической вязкости подвижных жидкостей типа воды составляет около I0-2 см2/с. Коэффициент диффузии молекул и ионов в водных растворах имеет порядок D = 10’5 см?!с, макромолекул —D = 10-0 см2/с. Поэтому в воде и сходных жидкостях будет Ргд — 10s. При возрастании вязкости коэффициент диффузии уменьшается по закону
р const v
(X.U)
поэтому число Ргд растет с увеличением вязкости пропорционально квадрату последней. В вязких жидкостях число Ргд достигает значения 10е и более. Для жидких металлов число Ргд значительно меньше единицы. Значения Ргд для некоторых сред приведены в табл. Х.З.
Таблица Х.З
Диффундирующее вещество	Среда, в которой происходит диффузия	Температура среды, °C	D мг/с	Ргд
Hg	№	.19	3,25-Ю-з	0,000424
со2	На	18	6,05-IO'5	0,158
NH3	Воздух	0	2,17-10-»	0,634 •
02	Na	12	2,03-Ю-з	0,681
НС1	Н2О	0	2,23-Ю-з	0,81
свн„	Воздух	0	7,5-10-»	1,83
свнв	На	0	2,94-Ю-з	3,26
Следует отметить, что для газов тепловое и диффузионное числа Рг имеют одинаковый порядок, поэтому процессы переноса тепла и вещества в газах аналогичны, но процессы переноса тепла и вещества в жидкостях сильно отличаются друг от друга, так как сильно отличаются числа Рг и Ргд.
238
Подобие процессов переноса
§ 5. Подобие некоторых частных случаев переноса J
Известно, что на тело, погруженное в жидкость, действует J сила, называемая гидростатической или архимедовой. Ее величина j равна весу вытесненной телом жидкости и направлена в сторону, ; противоположную направлению сил тяжести. Архимедова сила .имеет важное значение не только при плавании твердых тел ; в жидкостях и газах, но и в случаях, когда в жидкостях и газах имеются частицы с удельным весом, отличным от удельного веса ' среды.
Неодинаковость плотностей частиц и среды может возникнуть по различным причинам. Прежде всего, частицы по своим . физическим свойствам могут отличаться от жидкости, в которую они погружены (капли масла в воде). В этом случае плотности, а следовательно, и удельные веса частиц и жидкости различны и критерием подобия будет общеизвестное число Архимеда, равное.
Ar = ^gJ^ = 4g-^,	(Х.12)
где р и Рх — плотность частиц и жидкости. Если в жидкости изменение плотности вызвано изменением температуры, то критерием подобия в этом случае будет так называемое число Грасгофа
Gr = ^-gpAT,	(Х.13)
К1 v где р — коэффициент объемного расширения, определяемый из '	о 1 Др
[соотношения р -----
:	р ДТ - 	।
: Для общности наименований целесообразно число Грасгофа ^называть тепловым’ числом Архимеда^	- -- -	,
। Гидростатическая-сила может появиться и при различии кон--’центрации примеси в-некоторой, среде. В этом случае критерием щодобия будет диффузионное число Архимеда
;	; Агд=^дс,	(х.14)
|где Ас — разность’концентраций вещества в среде и на стенке'; — коэффициент (аналогичный р), характеризующий относительное-изменение плотности ^-зависимости от концентрации;
t = 1 Др р- Дс	-
В литературе иногда это число называют диффузионным числом Грасгофа.
-Динамическое, тепловое и диффузионное числа Архимеда могут- быть получены из соответствующего анализа уравнения
Подобие некоторых частных случаев переноса
239
движения в форме
р-^- = ^Ар — PgpAT’ — pg£Ac + p.v2V.	(Х.15)
Проделав соответствующие операции с последним уравнением, получим динамическое число Нуссельта
Nu = -^-.	(Х.16)
В тех случаях, когда в жидкости велики силы поверхностного натяжения, основным критерием подобия является число Вебера
We =	(Х.17)
где о — коэффициент поверхностного натяжения.
Число Вебера выражает собой отношение сил инерции к силам поверхностного натяжения-.
Примером задачи, в которой число Вебера является определяющим параметром, может служить задача о форме и устойчивости струи жидкости, вытекающей из центробежной форсунки. Если взять за характерный размер радиус выходного отверстия г, а за характерную скорость — скорость истечения в выходном сечении V, то число Вебера будет иметь вид
We = -^L. а
Исследования формы факела- показали, что с уменьшением числа We угол конусности факела растет и расстояние от форсунки до точкй распада жидкости на капли убывает.
Число We имеет существенное значение при изучении процессов перемешивания взаимно, нерастворимых жидкостей. Вероятность дробления капель в мешалках определяется в зависимости от числа We, представленного в виде
We==pnV а
где п и d — частота вращения и диаметр мешалки; о — межфазное натяжение.
С увеличением числа We диаметр капель уменьшается и межфазная поверхность растет.
При изучении потоков в различных вакуумных установках и в разреженных газах определяющим параметром при моделировании является число Кнудсена. Оно равно отношению средней длины свободного пробега молекулы I к характерному линейному размеру модели b
кп=4- .	(х-18)
240
Подобие процессов переноса
Известно, что длину свободного пробега молекул можно определить по формуле
1= 1,225 /Г	(Х.19)
Следовательно, при постоянном k
(Х.20)
b Re	v '
т. е. число Кп пропорционально числу М и обратно пропорционально числу Re.
Область возможного применения законов обычной аэродинамики с использованием граничного условия' о равенстве нулю касательной составляющей скорости на поверхности обтекаемого тела характеризуется неравенством
Кп = -£-< 0,001.
В области чисел Кнудсена 0,001—0,1 следует рассматривать задачу о течении со скольжением.
При числе Кп >1,0 нарушается сплошность среды и имеет место свободное молекулярное течение, в которой применимы законы кинематической теории газов.
§ 6. Некоторые обобщения
Легко видеть, что тепловое и динамическое числа Пекле по. физическому смыслу и по форме аналогичны числу Рейнольдса. Следовательно, можно ввести три числа Рейнольдса: динамическое, тепловое и диффузионное,- равные:
Re = -^-;
Vo
ReT=pe = -^-; Кед=Ред=-^.
(Х.21)
В знаменателе этих формул находятся соответственно кинематическая вязкость, температуропроводность и коэффициент диффузии, т. е. величины, зависящие от вязкости. Поэтому при уменьшении вязкости все числа Рейнольдса будут расти, а при стремлении величины вязкости к нулю динамическое, тепловое и диффузионное — числа Рейнольдса будут стремиться к бесконечности.
Аналогично можно получить динамическое, тепловое и диффузионное числа Фурье.
Некоторые обобщения
241
При изучении тепловых и диффузионных процессов существенное значение имеют полученные выше числа Прандтля. Эти числа можно получить как отношение соответствующих чисел Рейнольдса:
Ргт =	ReT Re		 V a ’
	Кед Re	
Ргс =	Кед ReT		 a
(Х.22)
Первое число Прандтля называется тепловым, второе—диффузионным (или числом Шмидта), третье — смешанным (или числом Льюиса).
Тепловое число Прандтля представляет собой отношение кинематической вязкости (перенос импульса) и коэффициента температуропроводности (перенос тепла). Следовательно, тепловое число Прандтля, содержащее явно лишь величины, определяющие физические свойства среды, характеризует соотношение поля скоростей и поля температур. Следовательно, только при числе Рг = 1 такие поля будут подобными.
Аналогичные рассуждения можно полностью перенести на диффузионное число Прандтля. Оно характеризует соотношение между полем скоростей и полем концентраций, а смешанное число Прандтля, равное отношению a kD —отношение температурного поля к полю концентраций.
Так как для газов тепловые и диффузионные числа Прандтля при обычных температурах порядка единицы, то при этом динамические, тепловые и диффузионные числа Рейнольдса будут одного порядка: Re — ReT — Refl. Последнее означает, что профили скоростей температур и концентраций в потоках в этом случае будут подобными.
Все числа подобия можно представить в виде отношений величин, характерных для данного процесса: сил, длин, времен, скоростей и пр. Например, число Re, которое обычно имеет вид
о Vl
Re = p----= —,
Г Т] V
можно представить (как и число Маха) в виде отношения скорости V к величине -у, имеющей размерность скорости, или в виде отношения длины I к величине -р-, имеющей размерность длины,
I V
или в виде отношения времени -у к -у и т. д.
16 И. Л. Повх
242 Ламинарное и турбулентное стабилизированное движение в трубах
Если учесть, что в инженерной практике вместо безразмерных критериев подобия часто пользуются эквивалентными им размерными величинами и что количество наименований чисел подобия продолжает расти, то становится очевидной необходимость упорядочивания критериев подобия.
В заключение приведем сводную табл. Х.4 чисел подобия процессов переноса количества движения, тепла и вещества в жидкостях и газах.
Таблица Х.4
Число подобия	Прандтля	Архимеда	Нуссельта	Фурье	Рейнольдса
Динамическое	—	Аг == _ /з др 8 v2 р	—	г	vt Fu= ^2-	Re = -"_ V
Тепловое		Агт = /з • = g-^T	XT NuT = —	_	at Fut — p	Re
Днффу-знойное		>"	Nu =^L д D	r	Dt Fufl=~	о	VI Re«=-D-
ГЛАВА XI
ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ СТАБИЛИЗИРОВАННОЕ ДВИЖЕНИЕ В ТРУБАХ И ВДОЛЬ ПЛАСТИНЫ
§ 1. Структура потока в трубах.
Переход ламинарного движения в турбулентное
Опыты Гагена (1839 г.) по изучению движения воды в трубах и более обширные опыты Пуазейля по исследованию движения крови в капиллярных сосудах (1841 г.) впервые позволили установить некоторые общие закономерности движения жидкостей в трубах малого диаметра.
Уже Гагеном было замечено, что скорость и расход воды в трубах (диаметром 1,4—3,0 мм) при постоянном уровне воды в напорном резервуаре зависят от температуры. При повышении температуры скорость течения сначала возрастала до максимума, потом падала до минимума и затем вновь начинала расти. Следовательно, при некоторой температуре резко увеличивалось сопротивление.
Структура потока в трубах. Переход ламинарного движения в турбулентное 243
Гаген заметил, что при этом изменялась физическая картина потока. При низких температурах струйка воды, вытекающая из трубы, была как* бы неподвижной и своим видом напоминала стеклянный стержень. Повышение температуры приводило к появлению резко выраженных колебаний струйки, которые при дальнейшем увеличении температуры ослабевали, но не исчезали. Оказалось, что наибольшие колебания струйки имели место при
уменьшении скорости течения, т. е. при увеличении сопротивления. Тогда Гаген предположил, что повышение сопротивления происходит из-за изменения структуры потока и появления вихрей. Пропуская воду, смешанную с опилками, через стеклянную трубку, он заметил, что при малых скоростях опилки двигались только в направлении, совпадающем с осью трубы, а при больших скоростях появлялись поперечные состав-
ляющие скорости.
Окончательное выяснение структуры потока в трубах и п'ричин изменения ее было выполнено Рейнольдсом в 1883 г. Независимо от опытов Гагена с целью проверки своих теоретических исследований Рейнольдс провел опыты по изучению движения воды в трубах.
На рис. XI. 1 приведена схема экспериментальной установки. В бак длиной 183 см, шириной и высотой 46 см вставлялась стеклянная труба, на выходе из которой установлен специальный кран для регулирования скорости движения. На входное отверстие трубы был надет воронкообразный насадок с плавным переходом от стенок воронки к стенкам трубы. К воронке была подведена тоненькая трубка, через которую поступал раствор кр’аски; приток ее регулировался краном. Наполняя бак водой с различными температурами и меняя диаметры трубы от 0,8 до 2,7 см, Рейнольдс по поведению окрашенных струек в воде установил два резко отличающихся режима течения.
При малых значениях некоторых чисел (впоследствии названных числами Рейнольдса), равных Re —, окрашенная струйка текла- приблизительно параллельно стенкам трубы (рис. XI. 1, а), на всем ее протяжении, т. е. наблюдалось струйное, или так называемое ламинарное движение.
При числах Re, больших некоторого критического значения ReKP, структура потока в трубе резко менялась. Струйка раствора 16*
244 Ламинарное и турбулентное стабилизированное движение в трубах
краски по выходе из трубки начинала пульсировать и на некотором расстоянии от входа полностью размывалась, не оставляя даже следов (рис. XI. 1, б). В отличие от струйного движения Рейнольдс назвал это движение извилистым. Впоследствии оно было названо турбулентным, что означает бурный или возмущенный. Можно считать установленным, что во многих практически важных случаях (трубопроводах, внешних обтеканиях тел, в океанах и реках) имеет место перемежаемое движение, т. е. в потоках имеются и ламинарные и турбулентные участки.
В то время как физика ламинарного движения достаточно хорошо изучена, о турбулентном и перемежаемом движениях этого сказать нельзя. Известный физик Р. Фейнман, говоря об отсутствии теории турбулентных потоков в трубе, указал, что ее создание является центральной проблемой, задачей номер один всей современной физики. Еще Г. Галилей указал, что «легче изучать движение светил небесных, чем познать законы движения воды в ручейке».
В опытах Рейнольдса переход от ламинарного движения к турбулентному происходил при средних значениях критического числа Re1<p = 2300. В дальнейшем были выполнены многочисленные исследования по определению критических чисел Re самыми различными путями. При этом критические значения чисел Re определялись в большинстве опытов либо визуальными наблюдениями за структурой потока, либо по изменению величины сопротивления.
Особо следует отметить-Экспериментальное определение ReKP по росту теплоотдачи жидкости, движущейся в трубе, при переходе от ламинарного движения к турбулентному.
Так как число Ре = RePr, то аналогично существованию критических чисел Re существуют для данного числа Рг соответствующие тепловые и диффузионные числа Ре, при которых происходит резкое изменение процесса переноса тепла и вещества.
Таким образом, переход к турбулентному движению вызывает увеличение переноса количества движения, следовательно, и сопротивления, а также переноса всех других субстанций, таких, как примеси, тепло и др.
Опыты последних лет показали, что переход к турбулентному движению происходит постепенно. Вначале по мере приближения числа Re к критическому в ламинарном потоке образуются лишь отдельные очаги, или -так называемые «облачки», «пятна» или «пробки», имеющие турбулентный характер. Затем их количество увеличивается и при числах Re больше критических весь поток становится полностью турбулентным. Это явление, имеющее место не только в трубе, но и во всех других потоках, как указывалось выше, называется перемежаемостью.
Ламинарное движение в трубах
245
Мерой перемежаемости в любой точке является коэффициент перемежаемости у, равный доле времени существования турбулентного режима в этой точке, т. е.
где тт — время прохождения турбулентных пробок за рассматриваемый промежуток т0.
Следовательно, при полностью ламинарном движении коэффициент перемежаемости будет равен нулю, а при полностью турбулентном — единице.
В результате многочисленных опытов было установлено, что переход от ламинарного к турбулентному движению в трубах может происходить при различных значениях чисел Re. Величина критического числа Re зависит от многих причин и, прежде всего, от условий на входе в трубу. Чем меньше возмущения при входе в трубу, тем больше значение ReKp. Созданием особенно спокойных условий на входе удалось «затянуть» ламинарное движение до Re = 50-10®. Такое ламинарное движение весьма неустойчиво и при малейшем возмущении переходит в турбулентное. Так же как переохлажденная вода при малейшем возмущении превращается в лед, так и затянутое ламинарное движение при небольшом колебании потока или ударе по трубе мгновенно перейдет в турбулентное. Таким образом, можно утверждать, что верхней границы критического числа Re не существует. Опыты и теоретические исследования нижнего предела показали, что, каковы бы ни были условия на входе в трубу, движение будет оставаться ламинарным, если число Re будет меньше 2000. Следовательно, нижнее критическое значение числа ReKp = 2000.
Если труба будет иметь не круглое сечение, т. е. будет не цилиндрическая, то критические числа ReKP будут отличными от указанных выше для круглой трубы. Известно, что в сходящихся трубах ReKP значительно превышает ReKp для цилиндрических труб, а в расходящихся, наоборот, оно существенно меньше,‘чем в цилиндрических. Так как структура потока в трубах определяет такие важные величины, как сопротивление, теплоотдачу, характеристики перемешивания частиц, химические процессы и пр., то опыты по нахождению критических чисел Re для отдельных спефицических потоков в прямолинейных и криволинейных трубах продолжаются до настоящего времени.
Рассмотрим ламинарное и турбулентное движения несжимаемой жидкости в гладких и шероховатых трубах.
§ 2. Ламинарное движение в трубах
В качестве примера интегрирования уравнения Стокса рассмотрим ламинарное стабилизованное движение несжимаемой жидкости в круглой цилиндрической трубе.
246 Ламинарное и турбулентное стабилизированное движение в трубах
Под стабилизованным движением будем понимать такое стационарное движение, при котором скорость потока и профиль скоростей не зависят от продольной координаты. Следовательно, если направление движения совпадает с осью х, то проекции' скоростей на оси у и z будут равны нулю, а проекция скорости на  ось х будет зависеть только от у и г. Такое движение будет иметь место и в цилиндрической трубе на значительном расстоянии от входа.
Если направление потока в трубе произвольного сечения совме- s. стить с осью х и считать, что для стабилизованного движения со-, ;: ставляющие скоростей v и w отсутствуют, то в общем случай получим:
и =.и (х, у, z); v = w = 0; р (х, у, z).	jK
Используя уравнение неразрывности движения, получим, что;®
•^ = 0 и, следовательно, скорость в трубе не зависит от коор?!я| динаты х. Последнее является условием стабилизованного дви-;-л жения.	.';®
Уравнение Стокса после подстановки значений и (у, z), v =;$ = w = 0 и р (х, у, г) и отбрасывания массовых сил будет иметь вид;^
( д2и . д2и \ _ I др . др _ п др ______	' £
Из последних уравнений следует:	j.
1) величина давления не зависит от поперечных координат у и г и есть функция только координаты х, т. е. в частности, в круг- ". лой трубе давление меняется только вдоль оси, а следовательно,  постоянно в каждом сечении и не зависит от радиуса;
2) так как левая часть первого уравнения зависит только от у : и г, а правая часть не зависит ни от у, ни от z,. то, следовательно, правая и левая части этого уравнения должны быть равны одной и той же постоянной величине, т. е.
%-= const.	(XI. I)
Таким образом, уравнение Стокса для стабилизованного движения жидкости в цилиндрической трубе произвольного сечения или в более общем случае для прямолинейного параллельного стабилизованного движения вдоль оси х будет иметь вид
(XI,2) ;
ду2 ' dz2 ц dx	v 7
Если прямоугольную систему координат заменить на цилиндр^-ческую, в которой х = х, у — г cos q> и z == г sin ср, то уравнение "ijj (XI.2) в цилиндрической системе координат будет следующим:
д2и ।. 1 ди ’ 1 д2и _ 1 dp	/VT ill
дг2 "т" г dr \ г2 д<р2 |х dx	'	.
Ламинарное движение в трубах
247
Предполагая, что поток обладает осевой симметрией
^ = 0, ' дф ’
получим уравнение (XI.3) в виде 
d2u . 1 du ___ 1 dp-
dr2 "i” г dr dx ‘
(XI.4)
Так как
d2u \ du _ \ d dr2 ' r dr r dr
то уравнение (XI.4) окончательно примет следующий вид:
— ~	= — %-.	(XI.5)
г dr \ dr) ц dx	v '
После последовательного двойного интегрирования получим общее решение уравнения (XI.5)
u=^r-^r2+cilnr+^	(Xi.6)
Произвольные постоянные С1п Сг определяются из граничных условий. Для круглой трубы с радиусом г0 они могут быть записаны так: при г = г0 и = 0, а при г = 0 и — конечная величина.
Подставив г = 0 в уравнение (XI.6), получим при Сг = О бесконечное значение скорости на оси. Следовательно, для удовлетворения второго граничного условия необходимо положить = = 0. Используя первое граничное условие, найдем
__	1 dp г2
4i?Wr°-
Таким образом, для круглой трубы распределение скоростей по сечению будет параболическим, т. е.
Можно написать
=	= const,	(XI.8)
dx I	’	'	'
где Др — перепад давления в трубе длиной /.
Определим среднюю расходную и максимальную скорости в круглой трубе. Объемный расход Q равен
Q = 2n^urdr.	(XI.9)
о
248 Ламинарное и турбулентное стабилизированное движение в трубах 1
Используя формулу (XI,7) и выражение (XI.8), получим
даю».
Формула (XI.10) выражает известный закон о том, что секундный объемный расход жидкости при установившемся ламинарном • движении несжимаемой жидкости в цилиндрической трубе круглого сечения пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса (или диаметра). Этот закон часто называется законом Пуазейля, исследовавшего законы движения крови по капиллярным сосудам.	4
Величина средней расходной скорости «ср будет
Ucp~^T = ~8]1ГГ°-	(XI.11) J
Наибольшее значение скорости umax, как видно из выражения (XI.7), будет на оси трубы, т. е. при г = 0,
=	(XI. 12)
Из анализа формул (XI. 11) и (XI.12) вытекает очень важное свойство ламинарного установившегося движения жидкости в круглой трубе: максимальная скорость на оси трубы в два раза больше средней расходной скорости, т. е.
wmax —- 2ucp.	(XI. 13)
Это свойство можно использовать при нахождении объемного расхода, определяя не весь профиль скоростей, что необходимо по формуле (XI.9), а лишь значение скорости на оси трубы. Тогда формула для расхода будет
q —и
Ч — 2 umax’
Если отнести значение скорости в любой точке к максимальной на оси трубы, то можно из выражения (XI.7) получить формулу для безразмерного профиля скоростей
и j_______Г2
wmax	го
(XI.14)
в виде параболоида вращения-с меридиональным сечением в форме параболы.
Найдем величину сопротивления при движении жидкости, в трубе. Для установившегося движения в цилиндрических трубах сопротивление на данном участке определяется перепадом давления на этом участке, либо по формуле
2
Др = лЛ-Р^,	(XI.15)
Ламинарное движение в трубах
249
ИЛИ
2
Др = ф±2^д	(XI.16)
где X и ф — коэффициенты сопротивления.
Приравнивая правые части равенства (XI.15) и (XI.16) и имея в виду, что umax = 2ucp, получим отношение между коэффициентами
Х =	(XI.17)
Определив Др из формулы (XI. 11) и приравняв полученное значение правой части (XI. 15), найдем
о
Н I Р“ср
2
д __ л / Р^ср 8ц/	__
\р=К—-----—- = —исп — 64---- j —,--;г
н d 2 Гц р Р«ср^ d 2
откуда следует, что величина коэффициента сопротивления равна
(XI.18) Re ’
где Re =	—число Рейнольдса, составленное по расход-
ной скорости иср и диаметру трубы d.
Выражение коэффициентов сопротивления как функций числа Рейнольдса X (Re) или ф (Re) называется законом сопротивления ламинарного движения вязкой жидкости в цилиндрической трубе. Зная X или ф, легко найти перепад давления по выражениям (XI. 15) и (XI. 16), а следовательно, и величину мощности, необходимой для обеспечения заданного расхода Q (м3/с). Формула мощности имеет вид
N = QAp.
Для решения задачи о продольном движении жидкости между двумя соосными цилиндрами с радиусами гх и г2 постоянные Сх и С2 в уравнении (XI.6) определим исходя из следующих граничных условий:, величина скорости на стенках цилиндров равна нулю, т. е. и = 0 при г — гх и г = г2. Тогда, считая г2 > гх, получим формулу распределения скоростей
и = 4Ег(г2, — + In—	(XI.19)
М 1	JnZL fi
\	'I	/
Величину расхода и средней скорости найдем в виде
<2 =
nucpOi—г*);

250 Ламинарное и турбулентное стабилизированное движение в трубах
откуда	величина	перепада	давления	Др будет	1
Др =------—~уг •	(XI.20) 1
In—	ЧЯ
n.	а
Для	очень	узких	кольцевых	щелей, т.	е.	при малой разности, а
радиусов, допустимо щель считать ограниченной параллельными ^ плоскостями. Тогда формула (XI.20) значительно упростится; $ и Примет вид, удобный для практических расчетов,
Ap = agf£P,	(XI.21) |
где b = г2 —	— ширина щели.
Принимая для потока между соосными трубами выражение перепада давления	по	формуле	'!;
9	' 1
А 1	1	Р“ср	,	>
получим из выражения (XI.21) закон	сопротивления для ламинар- '.:1
ного движения в щели между соосными цилиндрами	
Л — Re ’
где Re =	.
V
Существует также точное решение для щели, образованной неконцентрическими цилиндрами. Не рассматривая здесь довольно громоздких решений, приведем лишь приближенную формулу для потерь давления при щилиндрах с мало отличающимися радиусами:
а„— 'W I
где е — эксцентриситет; b — ширина щели, которая была бы при отсутствии эксцентриситета.
Результаты многочисленных опытов при ламинарном установившемся движении в трубах круглого и кольцевого поперечного сечений хорошо совпадают с соответствующими данными, получен- -ными по вышеприведенным формулам.
Уравнение (XI. 12) было решено и для труб с эллиптическим, прямоугольным и треугольным поперечными сечениями. Приведем без доказательства некоторые формулы для ламинарного стабилизованного движения в трубах эллиптического и прямоугольного сечений.
Ламинарное движение в трубах
251
Если а и Ь — полуоси эллипса, а контур трубы в плоскости уг представить в виде	= 1, то формулы распределения
скоростей в сечении трубы
__ Др а2&2	/ < у2 z2 \
U 2р1 а* + Ь* V ’о2 ~ ~Ь*)
(XI.22)
дает уравнение эллиптического параболоида, а изотахи (линии равных скоростей) — подобные друг другу эллипсы, т. е. эллипсы с одинаковыми отношениями полуосей.
Из уравнения (XI.22) видно, что скорость будет максимальной на оси трубы, т. е. при у — г = О,
______ 1 Др a2fe2 «max— 2^— а2 + 62‘
Зная итах, можно скорость по формуле (XI.22) представить в безразмерном виде
и ____.____у2___Z2
"max	а2 '
Величина объемного расхода через трубу эллиптического сечения легко определяется интегрированием скорости (XI.22) по сечению, т. е.
a b	а Ъ
Q = 4 j j«dt/dz = «max4 J J (1 —	— ^-) dydz.
00	00
После вычисления интеграла получим
л 1	,	ла3&3Др
,	Q — j aabumax — 4{il (а2 +	.
Разделив объемный расход на площадь поперечного сечения трубы s = лаЬ, определим среднюю величину скорости
__ Др а2&2 _____ 1
“ср — ~4рГ а* + Ь* ~ Т “и””1.
Следовательно, так же как и для круглой трубы, средняя скорость равна половине максимальной.
Из последней зависимости можно найти выражение для потерь давления Др и, используя выражение (XI. 15), получить закон сопротивления. Оказывается, что формула сопротивления (XI. 15) для эллиптической трубы остается такой же, как и для круглой трубы, если величину диаметра для эллиптической трубы найти из следующих соотношений:
1 _ 1 г 1 > 1 1_ 1
d2 ~ 2 L (2а)2 + (26)2 J — 8 а2Ь2 '
252 Ламинарное и турбулентное стабилизированное движение в трубах
Легко видеть, что все формулы, полученные для трубы эллип- ; тического сечения при а = Ь, совпадают с соответствующими i зависимостями для круглой трубы.
Если рассматривать трубу прямоугольного сечения со стрро- , нами а и & и задать форму сечения в плоскости yz уравнениями ’ у — и z = то профиль скоростей и величина средней скорости, полученные из решения уравнения, будут:
. (2п —1)лг ~
2а	(2п—1)лу.
ch (2n — 1) л/>	2а
16 Ара2
U =4-----<гг~
(- 1)дЪ (2л — 1)»
со .1 (2п —- I ) 710
_ Ара2 .	192а VI Ш 2а
“СР — 3p.Z 1 зг6Ь / ।	(2/г—I)6
бра2 г / Ь \ 3р1 ' \ а / "
Расчетные значения функции f приведены, в табл. XI.1.
Таблица XI.1
а	1	1,25	1,5	2	3	4	5	10	СО
О | <3	0,422	0,515	0,585	0,686	0,789	0,824	0,874	0,938	1
Ряд, входящий в выражение для средней скорости, быстро сходится, поэтому для практических расчетов достаточно ограничиться удержанием его первого члена. В этом случае функция f может быть определена по следующей формуле:
( ( Ь \	.	192а ,, ( лЬ \
Потери на вязкое трение определяются следующей зависимостью:
Др =
Зр/Иср
Измерения потерь давления в трубах прямоугольного сечения с различным отношением сторон дали результаты, очень близкие к теоретическим.
Перенос тепла при установившемся ламинарном движении в трубе 253
§ 3. Перенос тепла при установившемся ламинарном движении в трубе
Рассчитаем величину теплообмена при стабилизованном ламинарном движении жидкости в круглой цилиндрической трубе с заданной температурой стенки 7’ст и температурой на оси Т±. Введем понятие температурного напора между двумя произвольными точками. Обозначим:
в = Т1 — Т^	= T — Тст,
где 9 — температурный напор между осью и стенками трубы; Ф — температурный напор между любой точкой и стенкой.
Так как мы рассматриваем стабилизованное движение, т. е. движение за начальным участком, то температура, так же как и величина скорости, будет зависеть только от радиуса. Не зная действительного профиля температур, предположим, что зависимость температурного напора О' от поперечной координаты можно представить в виде полинома .
О = а0 -|- аху а^у2, -|- а3у® -(-•••,	• (XI.23)
где у — расстояние от стенки.
Число членов полинома и величина коэффициентов а0, а1г а2 . . . определяются граничными условиями. В данном случае используем следующие четыре граничных условия.
‘ Первые два условия поставим на оси трубы: п р и у = гоО = О, а= 0—из условия симметрии профиля температур.
На стенке при у = 0 получим остальные два условия. Первое •& = 0, второе— для значения производных можно найти из следующих соображений. Считая, что теплообмен в непосредственной близости от стенки происходит только из-за теплопроводности, можно количество тепла, проходящего через цилиндрическую поверхность с радиусом г и длиной I, представить в виде
Q = — №лг1	.
ду
Тогда, подставив сюда значение г = г0 — у, а затем решив это уравнение относительно температурного градиента и продифференцировав по у, получим
d2T _ Q I	_	1 dT
dy* ~ 2л/Х (г0 — у)2 ~~ г0 — у dy '
Следовательно, на стенке при у = 0 получим условие для производных
\ dy2 ) ст	Го \ dy ) ст
254 Ламинарное и турбулентное стабилизированное движение в трубах
Использовав приведенные граничные условия, получим следующую замкнутую систему уравнений для нахождения коэффициентов полинома (XI.23):
ао=О;
щ/о а2Го -ф-	= 0;
а\ 2а2го + Зауо — 0;
2а2 = ^-.-2
После решения приведенных уравнений окончательно получим выражение для безразмерного профиля температурного напора
д __ Т Т'ст __ 6 у .' 3 / у \2	4 / у \3 „j _
Зная ft (у), легко найти тепловой поток на единицу поверхности стенки
q = —	= 1^ —.	(XI.25)
.	\ ду ) ст	\ dy / QT 5	г о
Количество тепла, подводимое к жидкости через поверхность трубы длиной I, будет
Q = 2лг0 lq — ^L лМ0.
При изучении переноса количества движения (при рассмотрении сопротивления тел) и переноса тепла законы представляются обычно в виде зависимости безразмерных величин. Для переноса тепла такой величиной является число Нуссельта.
Найдем коэффициент теплообмена а, рассчитанный по разности между средней температурой жидкости и температурой стенки. В этом случае величина теплового потока будет
q = а (Гер — Лт) = «дср.
Среднее значение температуры определим по уравнению
Га
J uTrdr
Ч	/тт _ О
1 ср ~0	’
J иг dr
о
Подставив сюда значения и (г) и Т (г) из уравнений (XI.24) и (XI. 14), а также имея в виду, что
©ср Т’ср -- Т'ст
-0-= Л-тст ’
получим 'О’ер = 0,5830.
Перенос тепла при установившемся ламинарном движении в трубе 255
' Следовательно, q =	— О,583а0.
Сравнивая величину теплового напора с (XI.25), определим коэффициент теплообмена
Используя выражение для числа Нуссельта (§ 6, гл. X), окончательно получим закон переноса тепла для стабилизованного ламинарного движения жидкости в трубе
(XI.26)
Если не пользоваться приближенным выражением поля температур в виде полинома (XI.23), а находить его из решения дифференциального уравнения переноса тепла (III.49), то Nu = 3,65.
Законы распределения скоростей (XI.7)
и температур (XI.24) получены в предположе- И	VA
нии, что коэффициенты вязкости, теплопровод- W ности и величина плотности постоянны. В дей- [__________
ствительности они зависят от температуры.	I
Особенно велика эта зависимость для жидкостей с большой вязкостью (например, для машинного масла).
Если учитывать зависимость физических г „„ — жидкостей от температуры, то характер всех	”
процессов переноса будет существенно опреде- Рис. XI.2 ляться направлениями тепловых потоков: от стенки,трубы к потоку или, наоборот, от потока к стенке. На рис. XI.2 показаны кривые распределения скоростей в нагреваемой и охлаждаемой трубах.
Очевидно, что в нагреваемой трубе температура стенки вь!ше, чем температура на оси, и профиль скоростей (кривая 2) становится у стенки более заполненным, а скорости на оси меньше, чем у параболы (кривая /). В случае "охлаждаемой трубы (кривая 5), т. е. когда температура стенки ниже температуры потока, скорость на оси больше, а у стенки меньше, чем в соответствующих точках параболы.
Такую деформацию параболического профиля скоростей можно легко понять, если учесть, что при одном и том же массовом расходе жидкости объемный расход будет увеличиваться в точках с повышенной температурой и убывать в точках потока с пониженной температурой. Приведенное рассуждение можно распространить и на турбулентные потоки.
256 Ламинарное и турбулентное стабилизированное движение в трубах
Так как температурное поле и теплообмен в некоторой степени зависят от профиля скоростей, то, следовательно, значение коэф- ; фициента теплообмена тоже должно зависеть не только от величины .j теплового потока, но и от его направления.
:	j
§ 4. Основы гидродинамической теории смазки
Одним из наиболее важных для техники случаев ламинарного  течения является движение смазочной жидкости между цапфой i и подшипником или между шейкой вала и вкладышем подшипника. « Толщина слоя смазки обычно мала, поэтому даже при значитель- ;
ных скоростях вращения цапфы или вала в таких потоках числа Рей-нольдса малы.	J
fflrfyyyyyy/y^	Задача определения течения ’
Щу0у^еу%у\ уА жидкости в смазочном слое впервые ^¥%У/Л\Ло,/У/УЛ t кч была поставлена русским ученым
Н. П. Петровым. В 1883 г. он опуб- ' У^^у^/ууууу	ликовал работу, в которой высказал ,
^^уу/УУ/УУ^Су^Ш важное предположение о том, что
в трении подшипника основную роль играет внутреннее трение в смазоч-ном слое. В этой же работе было дано
Рис. XI.3	первое теоретическое решение по-
ставленной задачи для простейшего случая, когда нагрузка очень мала и цапфу и подшипник можно рассматривать как соосные цилиндры.
Более общее решение можно получить, если принять, что цапфа расположена относительно подшипника эксцентрически (рис. XI.3). В этом случае между рабочими поверхностями цапфы и подшипника (или шейки и вкладыша подшипника) образуется клинообразный слой смазки.
Рассмотрим приближенное решение задачи о смазке для случая, когда жидкость заполняет все пространство между цапфой и подшипником, длину которых будем считать большой, а толщину слоя смазки малой по сравнению с радиусом цапфы. Принятые допущения на практике, как правило, выполняются, так как в технических устройствах стремятся уменьшить зазор между цапфой и подшипником, с тем чтобы расход смазочной жидкости был небольшим.
На рис. XI.3 приняты следующие обозначения: О — центр цапфы /; О' — центр подшипника 2; 00' — эксцентриситет; г0 и /?0— соответственно радиус цапфы и внутренний радиус под- , шипника.
Примем ось 00’ за ось полярных координат г, 9, а точку О — за центр этих координат. Внутренний радиус подшипника с цен-
Основы гидродинамической теории смазки	257
тром в точке О будет величиной переменной. Его можно представить как г0 + 6, где 6 — толщина слоя смазки.
Поскольку толщина слоя смазки мала, то с достаточной для практики точностью можно принять, что vr =	= 0 во всех
точках потока. Полагая также, что объемные силы в слое смазки малы по сравнению с силами вязкости, уравнение движения в полярных координатах можно представить в виде
=	(XI.27)
г дд ‘ дг2	'	'
Так как в уравнении (XI.27) г изменяется в пределах от г0 до г0 + 6, причем 6 <$( г0, то в этом уравнении можно заменить
77 =
или, полагая г = г0 + у, получим
=	(XI.28)
г0 ди ду2	'	'
Левую часть этого уравнения можно считать не зависящей от у. При этом условии уравнение (XI.28) легко интегрируется
^’»=27гa^^ + л^' + ,,	<х|-29>
ZZq]A ии
Постоянные интегрирования А и В могут быть найдены из следующих граничных условий:
при у = 0 ve = Vo; при у — 6 г>0 = 0.
После определения постоянных интегрирования решение (XI729) примет следующий окончательный вид:
(XL30>
Из выражения (XI.30) следует, что профиль скорости течения жидкости от сечения к сечению меняется в зависимости от величины и знака . В сечении = 0 распределение скоростей является линейным. Обозначим толщину слоя в этом сечении через 60 и вычислим расход жидкости в этом сечении на единицу длины подшипника
бо	бо
q = ^Vedy = \^^dy = ^,
0	Q
(7 И. Л. Повх
258 Ламинарное и турбулентное стабилизированное движение в трубах
Поскольку жидкость является несжимаемой, расход через всякое сечение между цапфой и подшипником должен оставаться.,» постоянным	'Л
е	в	$
q = \vQdy^\[^-^y(y-^V-^^-]dy=	j
0	0	'll
1 др , 63 , и06 _ v060	ZVT	;
= — '2^'> + v + ~ “"I-’	(XL31> i
i
Средняя скорость течения жидкости в любом сечении слоя :1 смазки будет соответственно равна
7. __ Я _	__1 в8 др	/ут
6	2 u 12г„ де '	-	(Л1.32)
Из (XI.32) следует, что средняя скорость изменяется по длине'; слоя смазки в зависимости от его толщины и величины и знака . 'I
Из (XI.31) легко определить, как изменяется давление по длине : слоя смазки
др __ 6цг0(6 —60) Ув
де	б3
Интегрируя (XI.33) в пределах от 0 до 0, получим -е	0-
p(0) = p(O) + 6proVo	-60J-J 
(XI.33)
(XI.34)
L.0	о
В случае замкнутого слоя смазки давление р должно быть непрерывной функцией 0, поэтому р (2л) = р (0). Следовательно, 2л	2л
Г dd _- f dd
J 63 —' °0 J d3 ’ 0	0
откуда -2л f d9 J 62 6o=4r-•	(XI.35)
г de . J 6s о
Для вычисления интегралов, входящих в (XI.34), целесообразно воспользоваться следующим соотношением:
6 = е cos 0 + (Ro — ги).
Основы гидродинамической теории смазки
259
Введем следующие обозначения:
6	_ 6 ___ . е _________ е___о
го	' Ro — го Лр
Первое из этих отношений можно назвать относительной толщиной слоя смазки, второе — относительным эксцентриситетом.
После вычисления интегралов зависимость (XI.34) принимает следующий окончательный вид;
р(9)-р(0) =
__ бцгрУр р sin 9(2 +р cos 0) ,ут (2 + Р2) (1 + р cos О)2'
Из (XI.36) следует, что приращения давления распределяются по окружности цапфы симметрично относительно оси оо' (рис. XI.4). При изменении угла 0 от 0 до л эти приращения положительны, а при его изменении от л до 2л — отрицательны.
Касательные напряжения могут быть определены из следующего уравнения:
дер	ор \
дг	г ) ’
Так как на поверхности цапфы у0 = Уо, a vr — 0, это уравнение принимает вид

(тг0)г==Го — р| df |r=ro Рг“-
Подставив сюда (XI.30), получим
(тгв)|-=г, = — А	— и Vo (-у -I- —) •
Учитывая, что г0 > 6, и используя (XI.36), после соответствующих преобразований получим окончательно
/т \	____ 2р.У0 Г 2________________3 (1 — Р2)___1 (XI 371
Н,еЛ-=/-о — ha [ 1 у р cos 0	(2 + Р2) (1 + pcos9)2 J ’
Из формулы (XI.37) видно, что касательные напряжения распределяются по окружности цапфы так же, как и напряжения давления, симметрично относительно оси 00'. В симметрично расположенных относительно оси 00' точках они одинаковы по величине, но противоположны по направлению.
Сравнивая формулы (XI.36) и (XI.37), нетрудно видеть, что приращение давления обратно пропорционально ho, а касательное напряжение обратно пропорционально h0.
260 Ламинарное и турбулентное стабилизированное движение в трубах
При полученном распределении давлений и касательных напряжений главный вектор всех поверхностных сил отличен от нуля, и потому цапфа в состоянии воспринять соответствующую
нагрузку.
В рассматриваемом случае течение жидкости вызывается не перепадом давлений, а увлекающим действием вращающейся цапфы. Иными словами, движение жидкости вызывается каса
тельными силами, приложенными по всей поверхности соприкаса
ния смазки с цапфой. Через эти касательные силы жидкости сообщается энергия и, таким образом, кинетическая энергия вращающейся цапфы передается жидкости в слое смазки. При этом, если кинетическая энергия от цапфы подводится равномерно по всей поверхности соприкасания со слоем смазки, то расходуется она в слое неравномерно: где толщина слоя смазки больше, там, согласно (XI.37), сопротивление вращению меньше, и наоборот.
Определим силовое воздействие смазки на единицу длины
цапфы.
На элементарную площадку цапфы rodQ-1, во-первых, будет действовать нормальная сила, направленная к центру цапфы и равная prodQ, и, во-вторых, будет действовать касательная сила,
направленная в сторону, противоположную вращению, и равная т;0госЮ-1 (рис. XI.5)? Так как касательные напряжения тг0 по поверхности цапфы распределены симметричноотносительно оси оо', то на элементарных ее площадках rod9-l, симметрично расположенных относительно той же оси, эти силы по величине будут равны, а сумма их проекций на ось оо' будет равна нулю. Приращения давлений в этих точках тоже равны по величине, но противоположны по знаку.
Отсюда следует, что главный вектор сил R, приложенных к поверхности цапфы, имеет направление, перпендикулярное к оси оо'. Чтобы найти его значение, необходимо перечисленные силы спроектировать на направление, перпендикулярное оси оо', и просуммировать по всей поверхности цапфы. Таким образом, главный вектор сил R, приложенных к цапфе, будет равен
2я	2я
R = | pr0 sin 0 d0 — j Tf0ro cos 0 dd.
о	0
Основы гидродинамической теории смазки
261
Учитывая, что
2л	2я
j р sin 0 dQ = — J pd (cos 0) = | — p cos 0 |o" -]-о	о
2n	2Л
+ f cos 0 dQ f cos 0 4т dQ, J ao J ai 0	0
получим
0
(XI. 38)
В подынтегральной функции выражения (XI.38) величиной тгб по сравнению с можно пренебречь. Учитывая это и подставляя в (XI.38) давление по (XI.36), после некоторых преобразований получим
_ 126^0 ______₽______
~ ft* (2 + ₽2)KT=₽S ‘
(XI.39)
Анализ выражения (XI.39) показывает, что главный вектор сил прямо пропорционален коэффициенту динамической вязкости жидкости и окружной скорости движения цапфы.
Определим главный момент сил, приложенных к цапфе.
Поскольку гидродинамическое давление направлено по радиусам, то главный момент сил определяется только касательными силами, действующими на поверхности цапфы. Считая положительным направление, противоположное вращению, главный момент мож^о представить следующим интегралом:
2л
М = — j UrQtodQ. о
Подставляя сюда (XI.37), получим
(2р2 + 1) h° (2-f-р2) /1 - р2
Из (XI.40) следует, что момент сил трения, так же как и главный вектор сил, прямо пропорционален коэффициенту динамической вязкости жидкости й окружной скорости движения цапфы.
Полученные формулы позволяют рассчитать трение в хорошо смазанных подшипниках при плоском течении жидкости в слое смазки, так как обычно задаются следующие параметры: р, г0, Vo, h0 и нагрузка R.
(XI.40)
262 Ламинарное и турбулентное стабилизированное движение в трубах
Из (XI.30) и (XI.40) вытекает следующая формула для коэф-. фициента жидкого трения:
f — М - h* (1+2R	/УТ4П
'ж — Rra ~ га Зр	•	(XI.41)
Коэффициент нагрузки, выдерживаемой подшипником, определится следующей формулой:
~ (2 + 0*) /Г=Гр2 •
(XI.42)
Из этих формул видно, что с уменьшением окружной скорости Уо относительный эксцентриситет 0 увеличивается и приближается к единице. Коэффициент жидкого трения при этом уменьшается и достигает величины /ж 0 = — • г о
Наоборот, с ростом окружной скорости относительный эксцентриситет уменьшается, а коэффициент жидкого трения возрастает. Минимальное его значение, как видно из (XI.41), будет при 0	0,71. При этом:
min = о,94/ж 0 = 0,94 А; £	= ! 5 08.
/ Л4 llllU л / Ж. U ’	»	2 О	’
В тех случаях, когда в сечениях, расположенных на диаметре, перпендикулярном к направлению действующей на подшипник нагрузки, производится подвод и отвод смазочной жидкости, как это имеет место в опорных подшипниках турбин, задача по определению трения в подшипниках решается аналогично.
§ 5.	Турбулентное движение. Уравнение Рейнольдса
Если в установившемся турбулентном потоке измерять скорость не пневмометрическим насадком, а безынерционным измерителем скорости, например термоанемометром, то действительная скорость будет беспорядочно пульсировать около своего среднего значения (рис. XI.6). Таким образом, турбулентный поток, в котором по измерениям пневмометрическими насадками скорость потока оказывается постоянной, т. е. движение установившимся, в действительности является нестационарным. Заметим, что при турбулентном движении пульсируют не только скорости, но и все величины, характеризующие поток: температура, давление, плотность, концентрация примесей 41 др.
Для исследования турбулентного течения его разлагают на осредненное по времени движение и на пульсационное движение.
Обозначив осредненное по времени значение составляющей скорости и через и, а пульсационную скорость через и' и т< д.,
Турбулентное движение. Уравнение Рейнольдса
263
получим следующие уравнения для составляющих скорости и для давления:
и — и + и'; v = v + v’;
W — w + р = р + р'-
Осредненное значение скорости определяется как интеграл по достаточно большому промежутку времени от действительного
значения скорости
и = -— и dt.
Z0 I
Тогда осредненные по времени значения пульсационных величин будут равны нулю:
и' = 0; v' = 0; w' = 0; р' =0.
Рис. XI.6
Операция осреднения проводится по определенным правилам. Пусть f и g суть зависимые переменные, которые необходимо осред-нить, и пусть q есть одна из четырех независимых переменных х, у, г, t. Правила осреднения обладают следующими четырьмя свойствами:	_	____
Г=Л f + g = 'f + g> fg=~fg> = \fdq = \'fdq.
Пульсационные составляющие скорости, как и все другие периодически изменяющиеся величины, могут быть охарактеризованы частотой и амплитудой. При турбулентном движении частоты и амплитуды скоростей пульсации изменяются в очень широких пределах. В каждой точке турбулентного потока имеют место пульсационные скорости с целым спектром частот: от низких (5—10 Гц) до очень высоких (50—100 кГц). Преобладают всегда низкочастотные колебания.
Средняя амплитуда пульсации характеризуется величинами, равными:
ах = 4- f
о„ = у'2; <yz = w'2.
Обычно степенью интенсивности турбулентности называютсреднюю квадратичную величину скорости пульсации, отнесенную к средней скорости потока,
(XI.43)
где V = У и2 + t)2 + w2-
264 Ламинарное и турбулентное стабилизированное движение в трубах
Интенсивность турбулентности изменяется от 0,3% в атмосфере до 7—8% и более в машинах.
В технике чаще всего имеет место турбулентное движение, однако законы его изучены еще недостаточно. Некоторые важные выводы можно сделать из анализа дифференциальных уравнений осредненного турбулентного движения, впервые предложенных Рейнольдсом. Допуская, что дифференциальные уравнения Стокса (Х.7) и уравнение неразрывности применимы и для турбулентного движения, можно в эти уравнения подставить действительные скорости движения и, произведя осреднение, получить уравнения осредненного движения.
Система дифференциальных уравнений движения при отсутствии массовых сил имеет вид:
ди । ди . ди	1 др .' г-,2
«з- 4-»т- + ш3- =----------4- vV2u;
дх	1	ду	дг	р	дх	1
до	.	до	.	до	1	др	.	„о
и -г- + и-□—=---------------4- 4- "vV2v;
дх	'	ду	1	дг	р	ду	1
dw	.	dw .	dw	1 др	.
U -5--k V -%-P W =-------------- + vvlw,
dx	1	dy 1	дг	p дг	'
du , do . dw ____л
dx ' dy * дг
Пользуясь уравнением неразрывности, левые части уравнений подставим в виде:
ди . ди	,	ди	д	, , . д	,	.	, д ,	,
и -Д- 4- V-Z-	+	ОУ-а-	=	(««) + -5“	1	-V (uwh
дх 1 Лу	дг	дх	' ’ 1 ду	'	’	1	дг 4	’
do	. до	, до	д	.	,	,	д ,	,	,	д	,	,
U ----b »-5---F = Т- (ии) + ~я~ (W) + "5- (У®);
дх	1 ду	1 дг	дх	4	’	г	ду '	’	1	дг	'	'
dw .	dw ,	dw	д ,	\	,	д ...	д	,	.
и д—\-v -д—Н w -ч— = д- (uw) + -5- (тал + -з- (адау). дх 	ду 1	дг	dx '	'	'	ду х	'	'	дг	'	’
Подставив полученные выражения в предыдущую систему и произведя операцию осреднения уравнений, получим:
д — , д — , д —	1 др ,	Г72--
-	д- ии 4- -д— uv 4- -д- uw —--4- + vv и,
дх	1	dy	1	дг	р	дх	1
д —	।	д	—	,	д	—	1	др	.	„о-.
-	д- UV 4- -a- vv-i--~-vw =----4--I- vv V,
дх	1	ду	1	дг	р	dy	'
д —	।	d —	. d	—	1 dp	।
-	a- uw -4- -^-vw 4- -a- ww —--4- 4- vv w,
dx	1	dy	1 dz	p dz	1
Турбулентное движение. Уравнение Рейнольдса
268
Подставим в эти уравнения вместо составляющих скорости их выражения через осредненные значения и пульсации:
ии = (и -j- и') (и + и’) = и2 + 2и и' -J- и'2; uv = (и -j- и') (и + и') = uv и v' + v и> + UW = (и -J- и') (w + w') — UW + и w’ -J- w и' + u’w", vw — (y + w') “h ^z) — vw -j- v w’ + w v' + v'w'\
VV = (v 4“ v') (V + u') = U2 + 2v v' + u'2;
WW = (w + w’) (w w') = WW + w'w' + 2w w'.
Пользуясь тем, что и' = v' = w' = 0, получим:
ии — и и + и'2;
VV = vv -j- v'2', ww = w w + ay'2; uv = uv-\- u'v'’, uw = uw-{- u'w", VW = VW -J- v'w'.
Тогда окончательно после подстановки и некоторых простык преобразований система уравнений осредненного турбулентного движения будет иметь вид:
i?66 Ламинарное и турбулентное стабилизированное движение в трубах
Такую систему часто называют системой уравнений Рейнольдса. Видно, что уравнение неразрывности движения остается таким же, как и для действительных скоростей, в то время как в уравнениях движения появляются новые слагаемые.
Если уравнение Рейнольдса сравнить с уравнениями в напряжениях (III.25):
5и .	ди	,	ди	дрхх	.	дрих	,	др^
дх 1	ду	1	dz	дх	1	ду	1	дг
до .	до	,	до	дрху	друу	дргу
и-г-4-и-з-4-№-з- = -=--Н —5---н
дх 1	ду	1	dz	дх	1	ду	1	дг ’
dw ,	dw	.	dw	дрхг	।	дРуг	,	др„
dx 1	dy	1	dz	dx	1	dy	'	dz
то соответствующие компоненты, определяющие напряжения в точке жидкого объема, будут:
— , П ди	—Т~г.
Рхх — — р + 2р-^-—рии,
— о до	-7-7.
Руу= — P + 2V-fy— PVV ’
— . п dw -7—;.
Pzz = — p-l-2P-dr—Pww>
(ди . до \	—у—,.
РХу = РуХ = Р{-^ +fa)—Puv’
( ди . dw \
Рхг — Ргх = Р[-^ + -g^J — puw ,
( до . dw \ Pyz = Pzy=P[-^ + -^) — pVW.
Тогда очевидно, что новые слагаемые в уравнении Рейнольдса есть дополнительные напряжения поверхностных сил, возникающих из-за наличия турбулентности. Совокупность турбулентных напряжений так же, как и вязких напряжений (III. 15), можно свести в .таблицу, называемую тензором турбулентных напряжений,
ри'и' pu'v' pu'w' pv’u' pv'v' pv'w'
pw'u' pw'v' pw’w'
Турбулентное движение вдоль безграничной пластины
267
Для того чтобы система уравнений Рейнольдса стала замкнутой, необходимо ввести дополнительные шесть уравнений, связывающих компоненты турбулентного напряжения с осредненными составляющими скоростей.
Если проделать аналогичные операции осреднения с уравнениями переноса тепла (III.47) и вещества (II 1.57), то получим векторы турбулентного переноса тепла и вещества.
§ 6. Турбулентное движение вдоль безграничной пластины. Ламинарный подслой
Прежде чем перейти к изучению турбулентного потока в трубе, рассмотрим установившееся движение жидкости вдоль безграничной пластинки. Расположим ось координат так, чтобы ось х была направлена вдоль пластинки, а ось у— по нормали (рис. XI.7). Будем полагать, что v = w — 0, а составляющая скорости зависит только от у. Вначале рассмотрим ламинарное движение. Так как давление во всей области можно считать постоянным, то уравнение Стокса для этого случая будет иметь вид
интегрируя его, найдем
Отсюда величина скорости и после повторного интегрирования будет
и=^у + С1.
Постоянная = 0, так как при у = 0 и — 0, т. е. на стенке скорость обращается в нуль, и, следовательно, для ламийарного потока вдоль безграничной пластинки имеет место линейное распределение скоростей
и=^У-	(XI.45)
При получении зависимости для профиля скоростей при турбулентном движении воспользуемся уравнениями Рейнольдса, считая, что для безграничной пластинки все параметры потока не зависят от х и г. Тогда уравнение (XI.44) будет иметь вид (черточки над осредненными величинами скоростей отбрасываем)
^[н-^ + (-Р^)]=°>
268 Ламинарное и турбулентное стабилизированное движение в трубах или
d Г du , ,1	л
-г- U-j—hт = 0, dy Lr dy 1	J
где т' = —pu'v'.
После интегрирования по у получим ди , , И "ду + Т —
Для определения постоянной С2 воспользуемся граничными условиями на стенке, т. е. при у = 0. На стенке скорости пульсаций, а соответственно и турбулентное напряжение трения т' обращаются в нуль. Тогда при у = 0
С2 = ^ = Н^|г/=0, следовательно, получим
^^+т' = т-	(Х1Л6>
Рассмотрим отдельно каждое слагаемое. Напряжение вязкого трения будет иметь значительную величину в непосредственной близости от стенки, и с увеличением расстояния оно будет убывать. Напряжение турбулентного трения, наоборот, вблизи стенки мало и по мере удаления от стенки растет. Область вблизи стенки, в которой величина т полностью определяется вязким трением, а турбулентное трение пренебрежимо мало, будем называть ламинарным подслоем (рис. XI.7).
В целях изучения профиля скоростей в области преобладания турбулентных напряжений трения рассмотрим область, в которой Нстановится, пренебрежимо малой величиной по сравнению с т'. Тогда в соответствии с выражением (XI.46)
т' = т(И = — puV.	(XI.47)
По аналогии с вязким трением турбулентное напряжение можно представить в виде
.du A du du т = Д — = р----— = ре -5- ,
dy	г р dy	г dy
где А и е — аналоги абсолютного и кинематического коэффициентов вязкости будем называть соответствующими коэффициентами турбулентного переноса.
По своей физической сущности А и е, являясь аналогами коэффициентов молекулярного переноса р, и v, существенно отличаются от последних.
В то время как коэффициенты молекулярного переноса однозначно определяются физическими свойствами жидкостей и газов
Турбулентное движение вдоль безграничной пластины	269
и их состоянием (температурой и давлением), но не зависят от динамических свойств потоков, коэффициенты турбулентного переноса определяются прежде всего статистическими свойствами движения. По величине последние могут превосходить коэффициенты молекулярного переноса (всегда положительные) в тысячи и сотни тысяч раз, но они могут быть одинакового порядка, а в некоторых случаях имеют отрицательные значения.
Когда турбулентность получает энергию только за счет неустойчивости больших градиентов средних скоростей движения, тогда коэффициенты турбулентной вязкости всегда положительны. В случаях, когда турбулентные вихри возникают не от кинетической энергии потока, а за счет тепловой, электромагнитной или других видов энергии, коэффициенты турбулентной вязкости могут становиться отрицательными и кинетическая энергия движения при этом может увеличиваться.
Турбулентные движения с отрицательной вязкостью, которые наблюдались в атмосфере и океане, ещенедостаточно изучены, хотя им посвящено ряд исследований1.
Формула (XI.47) для турбулентного напряжения трения в приведенном виде не может иметь практического значения, так как до настоящего времени ничего не известно о строгой связи скоростей пульсаций с осредненными скоростями потока. В таких случаях естественно воспользоваться некоторыми физическими предпосылками и затем для установления характера указанных связей использовать теорию размерностей.
Можно считать, что по аналогии с вязким трением величина х	du
турбулентного трения зависит от градиента скорости , а из формул (XI.46) и (XI.47) видно, что она является функцией расстояния у от стенки и зависит от плотности жидкости р.
Предположим, что величина турбулентного напряжения трения может быть представлена в самом общем виде степенным одночленом, зависящим от плотности жидкости р, градиента скорости ~ й некоторой характерной длины I, называемой длиной перемешивания, т. е.
г а / du \Ь .с
т=р Ш '
Тогда, подставляя размерности входящих в формулу величин» получим
Д = Г“]“Г±1‘ м., м2 L м3 J L с J 1	’
1 Старр В. Н. Физика явлений с отрицательной вязкостью. М., «Мир», 1971.
260 с.
270 Ламинарное и турбулентное стабилизированное движение в трубах
или
кг-м 1 Г кг То Г 1 16 . .с
—т- -	—=-	--- Гм1 .
Л* "* I Л I I 1 I	г Iе
С2-М2 J L м3 J [с]
Сравнивая показатели степени при кг, м и с, будем иметь следующую систему уравнений:
для кг а = 1; ’ для м — 1 = —За + с\ для с — 2 = —Ь.
Единственное решение этой системы дает значение а = 1, b = с = 2. Следовательно, турбулентное напряжение трения т' окончательно будет-равно
т'-т^рр^)2.
(XI.48)
Формула (XI.48) впервые, хотя и другим путем, была получена Л. Прандтлем и поэтому называется формулой Прандтля.
Длина перемешивания I характеризует собой масштаб турбулентности, т. е. средний размер связанных объемов жидкостей, участвующих в турбулентном переносе. Из большого разнообразия предложенных для I выражений наиболее простым является: I = ky. Подставив его в формулу (XI.48), получим
T^T^Fpt/2 (-^)2 •
Решая уравнение (XI.48) относительно-^- и интегрируя по у, получим профиль скоростей при турбулентном движении
““v/ftai' + C,
(XI.49)
Полученный так называемый логарифмический профиль скоростей в турбулентном потоке существенно отличается от ламинарного линейного распределения скоростей.
Так как формула (XI.49) выведена в предположении, что исследуется движение на некотором расстоянии от стенки, то она может не удовлетворяться при у = 0 и, следовательно, нельзя находить произвольную постоянную С3 из граничных условий на стенке. Действительно, при у = 0 скорость и = 0, а по уравнению (XI.49) при у = 0 будет и —> —оо. Поэтому для" определения Са необходимо воспользоваться понятием ламинарного подслоя.
Согласно прежним рассуждениям, будем искать такое расстояние от стенки у = бл, для которого при у < бл существенно преобладает вязкое трение, а при у > 6Л — турбулентное трение, т. е. при у < 6Л движение будет ламинарным, а при у > 6Л — турбулентным. Величина 6Л называется толщиной ламинарного подслоя или толщиной ламинарного фильма.
Турбулентное движение вдоль безграничной пластины
27 i
В действительности такой резкой границы между пристеночным подслоем ламинарного движения и областью турбулентного движения не существует. С физической точки зрения весь поток следует разделить по вертикали к пластинке на три области: 1) область непосредственно прилегающую к стенке с резким преобладанием вязкого трения; 2) область на некотором удалении от стенки с преобладанием турбулентного трения; 3) промежуточную, или переходную область, в которой вязкое (молекулярное) и турбулентное трение 'соизмеримы.	1
Эксперимент подтверждает наличие этих трех областей. Если ограничимся наличием лишь области ламинарного подслоя и воспользуемся методом размерностей, считая толщину подслоя степенной одночленной функцией от величин, ее определяющих — вязкости, плотности среды и напряжения трения на стенке тш, то получим
бл = аг)арЧ.	(XI.50)
Используя размерности величин ц, р итщ и имея в виду, что а есть безразмерная константа, будем иметь уравнение для размерностей в следующем виде:
г . Г Н-сПа г кг V ГН у
М - [ м2 J L мз J L м2 J или
КГ-М-С ~]а Г КГ 1 ь |" кг-м ~|с С2-М2 J [ м3 J 1 с2-м2 J
Приравнивая слева и справа в уравнении показатели степени при м, кг и с, получим следующую систему:
для м 1 = —а — ЗЬ — с;
для кг 0 = а + b + с;
для с 0 = —а — 2с.
Единственное решение этой системы дает а = 1 и & = с =--
Отсюда окончательно получим, что толщина ламинарного подслоя равна
Т1	V
V ртш 1/
(XI.51)
Для получения общепринятых обозначения:
формул введем следующие
и
— = /
У, *’
272 Ламинарное и турбулентное стабилизированное движение в трубах
Величина V*, имеющая размерность скорости и определяемая трением на стенке и плотностью жидкости, обычно называется динамической скоростью, а имеющая размерность длины,— динамической длиной. Заметим, что число Re, основанное на динамической скорости и динамической длине, всегда равно единице
v I у *1*  I V
Если воспользуемся вновь введенными значениями, то толщина подслоя 6Л будет равна
6Л -Ct у* -
Предполагая, что в подслое величина скорости есть линейная функция от у, и пользуясь формулой (XI.45), получим значение скорости на границе подслоя ил, равной
u =	6 — а I» —2^=,	(ХГ.52)
11 11 или
' г
Таким образом, получены граничные условия (при у = 6Л = — а/*, и = ил = aV*), используя которые можно найти в равенстве (XI.49) постоянную интегрирования С3. После подстановки указанных граничных условий в формулу (XI.49) имеем
у
ил = — In бл -j- С3, откуда
С3 = ил — 1п6л = 1/#(а — -l-Jna-j^-) =
= V* (а----— Ina) —— 1п-^~.
* \	« у х И*
Подставив значение С3 в формулу (XI.49), окончательно получим
Tr- = 4lnJVt+(“-T1"“)’	(Х1-53>
или, переходя от натуральных к десятичным логарифмам, будем иметь
и 2,303, yV* , /	2,303,	\
Таким образом, учитывая то, что а и к — константы, получим закон распределения скоростей в турбулентном потоке
^_ = Л1§^ + В,	(XI.54)
Профили скоростей при турбулентном движении в круглой трубе 273 где А и В — некоторые постоянные, определяемые через универсальные постоянные турбулентного движения а и х следующим образом:
Л 2,303 D 2,303 , Л =---- и В = а-------1g а.
х	• х ь
§ 7. Профили скоростей при турбулентном движении в круглой трубе	»
Как уже говорилось, при ламинарном движении полученные теоретические решения для труб с различными поперечными сечениями хорошо совпадают с результатами опытов. Для турбулентного движения в трубах точного теоретического решения не существует и все формулы и закономерности получены либо непосредственно из опыта, либо имеют полуэмпирич^ский характер.
Как будет показано дальше, между законом сопротивления и характером профиля скоростей в трубе существует однозначная связь, т. е. каждому профилю скоростей соответствует свой закон сопротивления, и наоборот. В настоящем параграфе рассмотрим лишь профиль скоростей.
Для получения закона распределения скоростей ио радиусу трубы будем полагать, что так же, как и для бесконечной пластинки в непосредственной близости от стенки трубы, имеет место ламинарный подслой, в котором скорость — линейная функция от у
и =	=	=	(Х1.55Ц-
и что профиль скоростей в остальной части трубы подчиняется ! х закону	л_
«	+ Д	(XI.56) Ч
у*	S v I	к 
где А и В выражаются через универсальные постоянные турбу-. лентности а и к.
Никурадзе из анализа весьма тщательно выполненных опы-
Ucpd тов в турбулентном потоке круглой трубы при числах Re =	,
достигавших 3,24-Ю6, нашел численные значения универсальных постоянных х = 0,45 и а = 11,5. Таким образом, был получен логарифмический профиль скоростей
-±-= 5,75 1gЬу-j-5,5,	(XI.57)
или в натуральных логарифмах
-£- = 2,5 In -^- + 5,5.
13 И. Л. Повх
274 Ламинарное и турбулентное стабилизированное движение в трубах
На рис. XI .8 показаны результаты опытов в диапазоне чисел Re от 4-103 до 3,2-10е. Здесь же приведена кривая 1 по формуле (XI.55) для ламинарного движения в непосредственной близости от стенки и кривая 2 для турбулентного движения по формуле (XI.57).
Из анализа приведенных кривых следует прежде всего вывод о том, что в действительном движении переход от ламинарного движения к турбулентному происходит не в точке, как это мы
предполагали при рассмотрении ламинарного под-';  слоя, а в некоторой обла- ч сти. При этом нижний .  предел —равен приб- | лизительно 5,0, а верхнее. ^ предельное значение — около 70. Это означает, что „4 в пределах 5 -С —- 	70
v	к •<!
имеет место переходная об’ ласть, в которой вязкое
и турбулентное трения соизмеримы. При < 5
будет только вязкое или
ламинарное трение, а при
>70 — только турбулентное трение. Отсюда следует, что
толщина ламинарного подслоя может быть определена из условия

(XI.58)
Так как выражения для логарифмического профиля скоростей (XI.56) или (XI.57) получены в предположении, что ламинарные касательные напряжения пренебрежимо малы по сравнению с турбулентными, то логарифмический профиль будет иметь место только на некотором удалении от ламинарного подслоя. Очень тщательные измерения показали (это видно и на рис. XI.8), что вблизи центра трубы распределение скоростей несколько отлично от логарифмического, но оно не очень существенно и в практических расчетах не учитывается. Можно считать, что логарифмический профиль скоростей является универсальным, пригодным для широкого диапазона чисел Re.
Вычислим далее так же, как для ламинарного движения, максимальную и среднюю скорости и расход жидкости при логарифмическом законе распределения скоростей. Очевидно, макси
Профили скоростей при турбулентном движении в круглой трубе 275
мальная скорость wmax будет на оси трубы, т. е. при у — г0. Подставив у = г0 в формулу (XI.57), получим
-^• = 5,75 1g ^2- + 5,5.	(XI.59)
Зависимости -у25- от 1g построенная по формуле (XI.59) и полученная из эксперимента, как это видно из рис. XI.9, очень хорошо совпадают.
Рис. XI.9
Вычтя из' формулы (XI.59) значение , по выражению
У * (XI.57), получим так называемый дефект скорости
= - 5,751g
5 Го или
« =^ + 5,751g-^=^- + 4-ln^-.	(XI.60)
и ♦ и	у * Ъ л0
Величина средней скорости может быть определена как отношение. объемного расхода Q к площади поперечного сечения трубы, т. е.
Го	1
ucp= -X- =	Г и(г0 — y)dy — 4 [ и (1-— } d(—\.
ср	лг§ J 4 и у J \ г0 ) \ го /
О	О’
Подставив под интеграл величину скорости по формуле (XI.60), получим
=	+	[ inJL (1 _ JLWJL\ =	—3,75.
У* v* ' X j г0 \ г0 / \ го / У*
°	(XI.61)
18*
276 Ламинарное и турбулентное стабилизированное движение в трубах
wcp	у г
Изменение — в зависимости от 1g * °, показано на рис. XI.9. Результаты эксперимента практически совпадают с расчетной прямой.
Разделив выражение (XI.59) на (XI.61), получим отношение максимальной скорости к ее расходной величине. При ламинарном движении в круглой трубе максимальная скорость в два раза больше средней, а при турбулентном движении это отношение
значительно меньше и с увеличением числа Re убывает, изменяясь от 1,3 при Re = 5000 до 1,15 при Re = 3 • 10е. При .Re —> оо указанное отношение как бы стремится к единице.	•	<
Такое изменение объясняется тем, что профиль скоростей при переходе от ламинарного движе-  ния к турбулентному (рис. XI. 10) становится более полным, а при турбулентном движении увеличение числа Re приводит к дальнейшему его заполнению.
Универсальность логарифмического профиля объясняется прежде всего тем, что во все его формулы входит динамическая скорость V*, определяемая через трение на
и
11 таг
Рис. XI. 10
стенке, которое, в свою очередь, зависит от числа Re. Отсутствие данных о величине трения на стенке осложняет применение полученных формул.
Более простым, но далеко, не универсальным профилем скоростей при турбулентном движении в трубе является так называемый Т*гепенной профиль. Этот профиль при числах Re ?«5-104
имеет вид
или в более общем виде
и “max
(XI.62)
Экспериментально было показано, что величина показателя степени п зависит от числа Re и с его увеличением убывает. Оказалось возможным каждому числу Re подобрать показатель степени п, так чтобы полученный профиль скоростей наилучшим образом совпадал с результатами эксперимента. На рис. XI. 11 при-
Профили скоростей при турбулентном, движении в круглой трубе 277
ведена зависимость (—— ) — — . Значение п подобрано при \ “max / ro	г
данном значении числа Re так, чтобы обеспечивалось-хорошее совпадение с опытом.
по сечению скорости при найдено. Определив ыср
Таблица XI.2
Отношение максимальной к средней степенном профиле может быть легко по формуле
1
или окончательно
(XI.63)
^в за-
“шах   (и ~г~ 1) (п -Ь 2) “ср	2
В табл. XI.2 даны значения
“ср висимости от показателя степени п.
Как й следовало ожидать, отношения
, полученные по степенному и логарифмическому законам, практически сов-
п	“шах “ср
1 6 1 7 1 8 1 9 1 10	1,264 1,224 1,194 • 1,173 1,156
падают.
Аналогично обычному степенному закону можно ввести степенное распределение скоростей в виде
Т^=л(^)"-	<ХГ64>
Значение коэффициента А можно определить из граничных
278 Ламинарное и турбулентное стабилизированное движение в трубах
= а. -	;
п, можно получить '' при п — -j- будет i
Sv
1
и обычный степей- .-я
условий на границе ламинарного подслоя: при у = 6Л скорость и = ил и постоянная А равна
л и* ( v Y
v* W*' ’
но = а и так как 6 =	, то £-
V*	V* v
Следовательно, А = аа~п = а1-п.
Зная величину а и задаваясь показателем значение постоянной А. Если а =^11,5, то А = 8,74, следовательно, ~ г 1 -^- = 8,74	.
V,	\ v )
Оказывается, что этот закон так же, как
ной, далеко не универсален. Такое распределение скоростей при п = — хорошо совпадает с экспериментом лишь в области ,« Re 105.
Следовательно, в отличие от логарифмического профиля ско-ростей, который является универсальным законом, дающим в турбулентной области хорошее совпадение с экспериментом во_ ' всем диапазоне скоростей, степенные законы являются далеко не* универсальными.
§ 8. Законы сопротивления при турбулентном движении в трубах
Между профилем скоростей в трубе и законом сопротивления существует однозначная связь, т. е. каждому профилю скоростей соответствует свой закон сопротивления, и наоборот.
В результате обработки опытов, выполненных при числах ReKp < Re < 5-104, Блазиус предложил степенной закон сопротивления в виде
* =	’Ь (XI.65)
где а = 0,3164; т = 0,25.
Более поздние опыты показали, что численные значения в законе сопротивления зависят от числа Re. Покажем, что степенному закону распределения скоростей (XI.62) соответствует ' степенной закон сопротивления (XI.65) и численные значе- ' ния постоянных а и т однозначно связаны с показателем степени п.
Рассмотрим вначале связь динамической скорости V* с коэффициентом сопротивления %. Так как при установившемся движении в трубе перепад Др полностью определяется величиной тре
Законы сопротивления при турбулентном движении в трубах
279
ния на стенке тш, то безотносительно к характеру движения жидкости в трубе можно написать следующее равенство:
лго Др = 2лго/ти, = лгоА, -j-	,
откуда получим величину напряжения на стенке тш т^-^Др	(XI.66)
' или puj;
(XI.67)
Из формулы (XI.66) видно, что напряжение трения на стенке в трубе равно перепаду давления на участке длиной, равной половине или
радиуса, из формулы	следует, что
__т/2 __	,,2
V * “ Т ср
«ср _ 21<2 .	У„. _
V» УК ’ «ср 2 К2 ’
применим формулу (XI.62) для границы ламинарного где при у = 6Л = а -X- скорость и = ил = aV*, то и А
(XI.68)
Если подслоя, получим аУ*   / а-v \п «max	\	)
После преобразования найдем
.' У, «ср = 2ПаП^ /	\п
“ср “max	\2ucpr0/ \V* /
И
=	1 L-M" (“ср Y!+1.
“шах	\ 2“срго / \ V* /
Воспользовавшись выражениями (XI.68) и (XI.63), окончательно получим
5п+1 2 (n—1)	2
2n+1a'!+1 [(n+ 1)(«4-2)] "+1 Л = ------------------------------
'2п Re^1
Сравнивая найденное выражение с формулой (XI.65), получим 5п-Н 2 (п—1)	2 )
a = 2"+1an+1 ((n+ 1)(»4-2)1	’
2п т — —гт •
(XI.69)
280 Ламинарное и турбулентное стабилизированное движение в трубах
Имея в виду, что каждому значению числа Re соответствует свой показатель степени п. в законе распределения скоростей, получим для закона сопротивления следующие значения пока- .• зателя степени (табл. XI.3).
Таблица XI .3
Re	п	т Гиз формулы (XI.69)]	Re	п	т [из формулы (XI -69)]
4-Ю8	1 6	2 7	4- 10s	1 8,5	2 9,5
[ 9-103	1 6,6	1 3,8	1,5- 10е	1 "эТ	2 10,5 '
J.1-106	1 7	1 4	3,2-10®	1 . 10	2 11
На рис. XI. 12 показано изменение коэффициента сопротивления X в зависимости от числа Re, полученное из многочисленных экспериментов. Здесь же нанесены прямые, соответствующие
закону сопротивления для ламинарного движения (кривая /) и степенному закону (кривая 2) при т = и а = 0,3164. Из рисунка видно, что при ламинарном движении закон сопротивления блестяще совпадает с результатами эксперимента, в то время как степенной закон сопротивления дает хорошее совпадение с экспериментом лишь при числах Re < 105. При значениях чисел Re > 105 надо подбирать другой показатель степени в степенном законе.
Законы сопротивления при турбулентном движении в трубах 281
Более универсальным, пригодным для всего диапазона чисел Re, является логарифмический закон сопротивления. Этот закон соответствует логарифмическому профилю скоростей и легко может - быть получен.
Представим формулу (XI.59) для максимальной скорости в виде
= 5,75 1« — + 5,5 = 5,751g (/-) + 5.S,
И, V*	V '	’	’ to\ v 2uc„J 1	’
(XI.70)
Так как по формуле (XI.61)
“шах — “ср о _с ---у----= 3,75
и по формуле (XI.68)
“ср _ 2
V* ~	’
то, очевидно, логарифмический закон сопротивления будет иметь вид
‘ =41lg(Re/i) + B1.
V Л
Никурадзе после тщательной обработки результатов своих опытов и многочисленных экспериментов других авторов пришел к выводу, что наилучшее приближение к опыту дает закон сопротивления в виде
’ =2 lg (ReУТ) —0,8.	(XI.71)
V Л
Формула (XI.71) неудобна, так как зависимость X от числа Re здесь дана в не явном виде. Формула (XI.71) была достаточно точно выражена Никурадзе следующей явной зависимостью:
% = 0,0032 + -^.	(XI.72)
Кривые, соответствующие последним формулам, показанЪ! на рис. XI. 12. Кривая 3 соответствует логарифмическому закону (XI.71), а кривая 2— степенному (XI.65). Видно, что кривая 2 дает хорошее совпадение с экспериментом в довольно широких пределах чисел Re, а кривая 3 практически совпадает во всем диапазоне чисел Re. Следовательно, логарифмический закон (XI.71) действительно является универсальным законом сопротивления.
Другой закон, который дает явную зависимость % (Re), хорошо соответствует эксперименту и выражает логарифмическую зависимость, был предложен П. К- Конаковым. Он имеет вид
%___________1
Л — (1,81gRe— 1,5)2 '
282 Ламинарное и турбулентное стабилизированное движение в трубах
Таким образом, получены законы сопротивления, соответствующие степенному и логарифмическому профилям скоростей. Аналогичным путем можно найти закон сопротивления, соответ-. ствующий степенному профилю (XI.64)
Напишем приведенную зависимость для оси трубы
Umax  д / ГрУ* \п д / Umaxr0 / V* \п \ V /	\ V / \ Ищах /
откуда, вспоминая выражение для V*, получим п+*
/ V* \П~Н _ / Та, \ 2 _ 1 / ИтахЛ) \~~п   ^ет
\ “шах /	— \Р“тах) “ Л \ V / ~ А
или окончательно
V’	(XI.73)
Wmax-р—
где Rem=^L; С = —V-Л"+’
Для наиболее распространенного профиля скоростей при п = — получим А = 8,7, а закон сопротивления будет иметь вид cf=—^—= 0,045 Re;^.	(XI.74)
Л umax р 2
В отличие от предыдущих законов сопротивления, в которых дана зависимость % (Re), в формуле (XI.74) дается зависимость так называемого местного коэффициента сопротивления Cf = _ ---Tw--- от числа'
max  р—
Кроме рассмотренных, существует много других чисто эмпирических формул для коэффициента сопротивления. Все они по своему существу являются некоторыми модификациями либо степенного, либо логарифмического закона.
Практика показывает, что законы сопротивления при турбулентном движении в трубах круглого сечения можно использовать и для расчета потерь в трубах любого другого поперечного сечения, если число Re выражать не через диаметр трубы, а через гидравлический радиус.
Движение жидкости в шероховатых трубах
283
R
Гидравлическим радиусом часто называют отношение площади поперечного сечения к его периметру. Если поперечное сечение трубы или. канала не полностью занято жидкостью, то для расчета гидравлического радиуса берут лишь так называемую живую площадь сечения, т. е. только ту часть, которая занята потоком.
Для круглой трубы гидравлический радиус R будет
aip _ г0 2пг0 2
Следовательно, величина сопротивления в трубе с заданным поперечным сечением будет иметь вид
л а I Р“ср 4^	2	’
и коэффициент % при этом будет функцией числа Re, построенного по гидравлическому радиусу, т. е. Re^=—.
Иногда в качестве гидравлического радиуса принимают отношение площади поперечного сечения трубы к полупериметру. Тогда при переходе к круглой трубе гидравлический радиус совпадает с ее радиусом.
§ 9. Движение жидкости в шероховатых трубах
Все рассмотренные закономерности получены для труб с абсолютно гладкими стенками. В практике, как правило, используют трубы, имеющие шероховатые стенки. Даже в том случае, когда в начале эксплуатации трубы являются гладкими, по истечении некоторого времени они обычно становятся шероховатыми из-за взаимодействия поверхности труб со средой.
Шероховатости бывают волнистыми и зернистыми, некоторые являются следствием выбранной технологии обработки схенок, другие — результатом химического воздействия и пр. В общем случае .количественно характеризовать шероховатость довольно трудно. Зернистую или бугорковую шероховатость можно определять ро средним размерам высоты бугорков и по их густоте, т. е. количеству бугорков на единице поверхности стенки. Обычно ограничиваются лишь средней высотой бугорка Д в мм, а еще чаще относительной шероховатостью, равной отношению средней вы-
,	Т А
соты бугорка к радиусу трубы, т. е. Д = —.
Абсолютная шероховатость для некоторых труб приведена в табл. XI.4.
Рассматриваемые далее результаты относятся к трубам с относительной шероховатостью менее 7—8%. Кривые зависимости
284 Ламинарное и турбулентное стабилизированное движение в трубах
Таблица XI .4
Материал	А, мм
Чугунные новые трубы	0,1—1,0
Стальные цельнотянутые трубы	0,02—0,1
Резиновые рукава	0,006—0,01
Тянутые из латуни и стеклянные трубы	0,0015—0,01
коэффициента сопротивления % от числа Re при различных значениях -у- показаны на рис. XI.13.
Из рисунка видно:
1)	при ламинарном потоке величина шероховатости стенок трубы не оказывает никакого влияния на коэффициент сопротивления, т. е. коэффициент сопротивления в этой области не зависит от шероховатости;
2)	значение критического числа Re также не зависит от шероховатости, • т. е. при любой относительной шероховатости переход от ламинарного потока к турбулентному начинается при одном и том же Re;
3)	величина относительной шероховатости почти не оказывает влияния на переходный режим от ламинарного, к турбулентному движению;
при турбулентном движении су- .
4)	поведение кривой К (Re) щественно зависит от величины относительной шероховатости.
При больших значениях относительной шероховатости кривая X (Re) пересекает кривую % (Re) для гладких труб, и при дальнейшем увеличении числа Re коэффициент сопротивления
Движение жидкости в шероховатых трубах
ж
становится постоянным, т. е. не зависит от числа Re. При малых относительных шероховатостях (менее 2%) в некотором диапазоне чисел Re кривая X (Re) совпадает с кривой для гладких труб. Затем при дальнейшем увеличении числа Re величина К достигает такого значения, при котором кривая К (Re) отходит от кривой для гладких труб, и коэффициент сопротивления становится независимым от числа Re.
Область, в которой К — функция только относительной шероховатости и не зависит от числа Re, называется областью квадратичной зависимости сопротивления от скорости, так как в этом случае Др ~ «?р.
Рис. XI. 14 .
Таким образом, влияние шероховатости наибольшим образом сказывается лишь при больших числах Re. Природа такой зависимости % (Re) для шероховатых труб объясняется характером обтекания бугорков шероховатости. При рассмотрении обтекания бугорков шероховатости можно различать два существенно отличных режима.
Первый режим наблюдается при малых числах Re. В этом случае бугорки шероховатости намного меньше толщины ламинарного подслоя, поэтому бугорки будут обтекаться полностью безотрывно (рис. XI. 14, а). Следовательно, в этом случае шероховатость не приводит к увеличению сопротивления, и никакой разницы между течениями в гладкой и шероховатой трубах не будет. При таком режиме шероховатая труба является гидродинамически гладкой.
Второй режим имеет место при достаточно больших значениях чисел Re. Здесь высота бугорков шероховатости значительно больше толщины ламинарного подслоя, т. е. Д бл. Как видно из рие. XI. 14, б, бугорки обтекаются турбулентным потоком как плохо обтекаемые тела с образованием отрывных зон. Коэффициент сопротивления плохо обтекаемых тел не зависит от числа Re, и при этом в трубах устанавливается режим, который можно назвать режимом развитой шероховатости или областью квадратичной зависимости сопротивления от скорости. Коэффициент сопротивления при этом режиме зависит только от относительной шероховатости.
286 Ламинарное и турбулентное стабилизированное движение в трубах
Между этими предельными режимами существует промежуточный, при котором высота бугорков шероховатости Д имеет порядок ламинарного подслоя.
Промежуточная область ограничивается, с одной стороны, > числом Re, до значения которого законы сопротивления шероховатой и гладкой труб совпадают, а с другой — числом Re, после котор.ого имеет место квадратичный закон сопротивления. При промежуточном режиме коэффициент сопротивления зависит и от числа Re, и от шероховатости.
Если воспользоваться толщиной ламинарного подслоя, определяемой при изучении турбулентного движения в гладких трубах (см. рис. XI.7), то рассмотренные режимы можно характеризовать следующими величиндми:
режим гидродинамически гладкой стенки
5
V
при этом коэффициент сопротивления является функцией только от числа Re, т. е. X = X (Re);
режим развитой шероховатости с квадратичной зависимостью сопротивления от скорости
— ^70, V	’
в этом случае коэффициент сопротивления является функцией только относительной шероховатости, т. е. X = X (у-);
промежуточный режим
5 sS с 70, V
при этом коэффициент сопротивления зависит как от числа Re, так и от относительной шероховатости, т. е. X = X f Re, — V
Гидродинамически гладкие стенки трубы иногда называют тех
нически или практически гладкими. В случае равномерно зернистой шероховатости стенку трубы можно считать гидродинами-
чески гладкой при относительной шероховатости, меньшей предельного значения Дпр
Дпр = 17,85Re~0>875.
Изменение сопротивления из-за наличия шероховатости вызывает соответствующее изменение профиля скоростей. На рис. XI. 15 показаны в безразмерном виде четыре профиля скоростей: один — для гладкой трубы и три — для труб с различной шероховатостью при режиме развитой шероховатости. Видно, что при увеличении
Движение жидкости в шероховатых трубах
287
шероховатости профили становятся менее заполненными, а градиент скорости вблизи стенки уменьшается. При дальнейшем увеличении шероховатости скорость будет обращаться в нуль вблизи -вершин бугорков.
Оказалось, что так же как и для гладких труб, профили скоростей можно в аналитическом виде представить степенной функцией
с показателем степени п, т. е.
Показатель степени п в области развитой шероховатости будет зависеть только от величины относительной шероховатости, т. е. п = f (у-) • Для приведенных на рис. XI. 15 кривых он изменяется в пределах от 1/i до 1/6. При режиме гидродинамически гладкой шероховатости величина п зависит только от числа Re, т. е. п =
= п (Re), а в промежуточной
Для шероховатых труб так
области п = <р ( Re, — \ го
же, как и для гладких, можно
получить универсальный так называемый логарифмический профиль скоростей. Для этого воспользуемся уравнением, полученным при рассмотрении турбулентного движения вдоль пла-
стины '
“ =±1пг/ + С. V *	Л
Однако произвольную постоянную определим не на границе ламинарного подслоя, а из более общих физических возможных условий для шероховатых стенок. Будем считать, что при некотором значении у = уД скорость обращается в нуль. Тогда
С =----1пуД.
Логарифмический профиль скоростей для шероховатых труб будет иметь вид
-Д- = — (In -Д- -J- In у)
V* и \ Д 1 г /
или в более общем виде
=	+ В.
(XI.75)
288 Ламинарное и турбулентное стабилизированное движение в трубах
Значение универсальной постоянной х остается неизменной и для шероховатых труб (х = 0,4), а постоянная у и, следовательно, величина В будет зависеть от режима движения, определяемого числа Re обтекания бугорков
Тогда формула (XI.75) примет вид
-±_ = 2,51n-f+	(XI.76)
Результаты опытов по определению величины В приведены на рис. XI.16.
V
Рис. XI. 16
ТЛ	г, 1
Из кривых видно, что зависимость В от 1g — полностью определяется режимом потока. При гидродинамически гладкой шероховатости и в промежуточной области величина В есть некоторая функция 1g , а при развитой шероховатости В = = 8,5 = const.
Следовательно, уравнение профиля скоростей для режима развитой шероховатости будет
-у-= 2,5 In-^-+8,5.	(XI.77)
Так как при гидродинамически гладкой шероховатости можно пользоваться профилем скоростей для гладких труб (XI.41), то величина В в этом случае может быть получена из равенства
-^ = 2,5 In -^- + 5,5 = 2,5 In -£- -|- В,
’ v	’ А 1
рткуда для гидравлически гладкой шероховатости
£ = 2,5 In + 5,5.	(XI.78)
Турбулентный перенос тепла и вещества при стабилизированном обтекании 289
На рис. XI. 16 приведены графики для функции В, рассчитанные в соответствии с уравнением (XI.78) (прямая 1) и уравнением (XI.77) (прямая 2). Значения 1g , в которых экспериментальные точки начинают отходить от прямых 1 и 2, можно считать границей режимов течения.
По заданному профилю скоростей нетрудно получить так же, как и для гладкой трубы, закон сопротивления. Рассмотрим закон сопротивления во второй области, для чего, используя уравнение (XI.77) на оси трубы
-^ = 2,51п-^4-8,5, представим его в виде -
“^-_^+^_ = 2,-51п^-4-8,5.
Согласно выражениям (XI.61) и (XI.68), имеем
“max —«ср „ - “ср _ Кв — о.7 о и .. 	-__ •
К.	Кь
Подставляя эти выражения в предыдущее уравнение, получим закон сопротивления для режима развитой шероховатости
% = 7------?----гг-.	(XI .79)
(216^+1.«)2
Все рассмотренные формулы пригодны лишь для так называемой песочной шероховатости. Применять полученные формулы для расчета труб с другими типами шероховатостей можно в случае, если вместо значения А пользоваться величиной, эквивалентной относительной шероховатости As, которая, определяется экспериментально. Величина эквивалентной относительной шероховатости «может сильно отличаться от геометрической. «Так, волнистой шероховатости с высотой всего 0,5 мм (пр'и диаметре трубы 500 мм) соответствует эквивалентная песочная шероховатость с высотой бугорка 10—20 мм. Это означает, что волнистая шероховатость вызывает значительно большее сопротивление, чем песочная с такой же высотой бугорков шероховатости.
§ 10.	Турбулентный перенос тепла и вещества при стабилизированном обтекании пластины
Если осреднения, аналогичные тем, которые использовались ранее, применить к уравнению переноса тепла и вещества (III.47) и (III.57), введя соответственно пульсации температур Т' и коц-19 И. Л. Повх
290 Ламинарное и турбулентное стабилизированное движение в трубах
центраций с', то получим рсредненные уравнения:
д [ дТ	. д ( дТ —ПгЛ
J- — а—-------v Т N- -V а-=--wT ;
ду \ ду	/ 1 дг \ дг	)
- дс	.	-	дс	,	—	дс	д (г,	дс	~~ry\ .
U “S--Г	"4“	 Т“	I	”5-W- С I -р
дх	‘	ду	1	дг	дх \	дх	/ '
.	д	(г-,	дс	~7~г\ । di^dc	——\
1	ду	\	ду ) 1 дг \ дг )
Из сравнения полученных уравнений с соответствующими уравнениями для ламинарного переноса тепла (III.47) и вещества (III.57) видно, что при турбулентном движении возникают добавочные составляющие переноса тепла:
и'Т'; v'T' и w'T'
и переноса вещества
м'с'; v'c' и w'c'.
Теория не дает выражений этих составляющих турбулентного или молярного переноса тепла и вещества, так же как и составляющих тензора турбулентных напряжений через осредненные характеристики потока. Следовательно, система уравнений оказывается незамкнутой, так как. число уравнений остается тем же, а количество неизвестных увеличивается.
Заметим, что добавочный перенос импульса (вектор), возникающий из-за наличия турбулентного движения, определяется тензором, а добавочные переносы тепла и концентрации — векторами.
Рассмотрим перенос тепла и вещества в случае установившегося или так называемого стабилизованного движения вдоль безграничной пластинки. В этом случае можно считать, что величины, входящие в осредненные уравнения: температура, концентрации и их пульсации, будут зависеть только от поперечной координаты у и не будут зависеть от продольной координаты.
Осредненные уравнения переноса будут иметь вид:
-A —— 7с'\ = 0.
dy \ dy	)	' dy \ dy	)
Интегралы этих уравнений равны:
d'T /*т\ de t f a -----v T = Ci, D —j----vc =C2.
dy	11 dy
Турбулентный перенос тепла и вещества при стабилизированном обтекании 2Й1
Если воспользоваться соответствующими уравнениями для переноса импульса
du —г~, Р~^~ — Ри v = Хи>
и иметь в виду, что на самой стенке турбулентные составляющие переноса тепла и вещества отсутствуют, то произвольные постоянные можно выразить через соответствующие значения ламинарного переноса на стенке:
%^-—pcp7r = qw-	(XI.80)
0-^—7? = ^.	(XI.81)
Так как о величине турбулентных или молярных составляющих переноса никаких достоверных теоретических или экспериментальных сведений пока нет, то можно предположить, что так же, как и для молекулярного переноса, величины молярного переноса пропорциональны соответствующим градиентам:
— pu'v' == А-~- = т';	(XI.82)
_рСрТГ = Лт-^- = 9';	(XI.83)
-М = АЛ-^- = м'	(XI.84)
или
(р + Д)_^- = та);
(D + A^=^>
где А, АТ и Ад по аналогии с ц, А, и D будем называть коэффициентами турбулентного, или молярного, переноса (обмена) импульса, ^епла и вещества.
Очевидно, что коэффициенты молярного обмена по своей величине и по физической сущности не имеют ничего общего с соответствующими коэффициентами молекулярного обмена. В частности, из выражений (XI.48) и (XI.82) следует '
т' = у WI I — 4 Ти
“ РУ I ду | ду dy ’
19*
262 Ламинарное и турбулентное стабилизированное движение в трубах
поэтому коэффициент турбулентного обмена А будет
А = x2pz/2 — у2, dy 3
Таким образом, коэффициент А, а также.другие коэффициенты зависят от координаты у. Докажем это с помощью метода размерностей, ранее примененного для нахождения коэффициента турбулентного обмена импульса.
Положим, что коэффициент молярного, или турбулентного, обмена Ат есть некоторая степенная .зависимость от у и -^-,т. е.
A^yya(w}b •
Размерность величины Ат будет
[41_ w _гД]_X [Al] [РМ —— с
тогда
. и, следовательно, а = 2; b = 1, т. е.
= <XL85)
Если аналогичные рассуждения применим для определения коэффициента турбулентного обмена вещества Лд, то получим Ла = Й2-|--	(XL86>
Значения постоянных х, у и 0 отличны от единицы.
Потоки тепла и вещества в турбулентном ядре течения будут иметь вид:
(XI.87)
<XL88)
При рассмотрении поля скоростей при турбулентном стабилизированном обтекании безграничной пластины может быть получено выражение du 1 dy ~ х у ’
Пограничный слой и его характерные толщины
293
Таким образом,
	/ =	?	iz dT'	(XI.89)
и	ш' -	= у uJL, к	dy	(XI.90)
откуда	df	_ к q' 1	
	dy	Y pepV'* У ’	
	de	у. w' 1	
	dy	~ P V» У ’	
После интегрирования последних выражений получим профили осредненных температур и концентраций в турбулентном ядре:
(XL91)
?=ТТГ1пу + с'2-	(XL92)
Таким образом, для температур и концентраций в турбулентном ядре потока так же, как и для скоростей, получены логарифмические законы распределения.
Произвольные постоянные и С2 можно определить, применив формулы (XI.91) и (XI.92) на границе ламинарного подслоя.
ГЛАВА XII
ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
§ 1. Пограничный слой и его .	характерные толщины
Известно, что реальная жидкость при обтекании тела из-за наличия вязкости как бы прилипает к его поверхности. Поэтому скорость потока на поверхности тела равна нулю. При удалении от тела по"' нормали к его поверхности скорость будет увеличиваться. На некотором расстоянии от тела она будет близка к той, которая была бы при обтекании этого тела идеальной жидкостью (рис. XII.1).
Расстояние, на котором происходит изменение скорости от нуля (на стенке) до величины, имеющей место в идеальной жидкости, характеризует область влияния вязкости. Назовем это расстояние
294
Ламинарный пограничный слой
толщиной области влияния вязкости. При внешнем обтекании рассматриваемая толщина, которую обозначим б, по мере удаления от передней критической точки к задней кромке будет расти. Введем безразмерную толщину влияния вязкости, равную значению б, деленному на характерный продольный размер I обтекаемого тела. Для крыла таким размером обычно является хорда
Прандтль еще в 1904 г. заметил, что величина б зависит от числа Re. При малых числах Re она может быть очень большой, следовательно, б будет б 1.
При больших, числах Re влияние вязкости сосредоточивается в небольшой области около тела, т. е. б < 1. В этом случае Прандтль предложил разделить поток, который обтекает тело, на три участка (рис. XII.1). Первый — непосредственно прилегает к обтекаемому телу и обычно называется пограничным слоем. Это очень тонкий слой, в котором сосредоточено все влияние вязкости. Второй участок — след за обтекаемым телом, третий — вся остальная область, в которой влияние вязкости не сказывается, и, следовательно, ее можно рассматривать как область потенциального потока идеальной жидкости.
По аналогии с полем скоростей можно рассматривать поля температур и концентраций вещества при наличии диффузии. Если температуры тела и потока будут различны, то величина области, в которой происходит изменение от температуры тела к температуре потока, будет зависеть от теплового числа Рейнольдса (Х.21). Обозначив толщину области изменяющейся температуры бт и введя безразмерное Д., равное бт = получим, что при малых значениях ReT величина б будет значительно больше единицы, а при больших ReT область изменяющейся температуры очень мала и бт < 1.
Область, непосредственно прилегающая к обтекаемому телу, в которой при больших ReT происходит изменение от температуры тела до температуры потока, называется температурным пограничным слоем.
Пограничный слой и его характерные толщины
295
Если концентрация вещества на поверхности обтекаемого тела отлична от концентрации вещества в потоке во все время движения, то аналогично тепловому пограничному слою при больших значениях диффузионного числа Рейнольдса (Х.21) установится диффузионный пограничный слой с толщиной бд 1.
При возникновении теплового и диффузионного пограничных слоев по аналогии с динамическим появляются тепловой и диффузионный следы и области постоянных значений температур и концентраций.
Рис. хп.2
При обтекании тела могут быть одновременно все три пограничных слоя, толщины которых в общем случае различны. Далее будет показано условие одинаковости этих толщин.
Скорости внутри пограничного слоя, как правило, монотонно увеличиваются от нуля на стенке до значения на границе слоя (рис. ХП.2). Температура же и концентрация в зависимости от их значений на стенке могут либо расти внутри слоя, либо убывать, как это показано на рис. ХП.2.
Так как практически величины скорости, температуры и концентрации к своим значениям на внешней границе стремятся асимптотически (рис. ХП.2), то при эксперименте толщина слоя определяется условно. Обычно за толщину слоя принимают такое значение координаты у, при котором скорость, температура или концентраций в точке отличаются от соответствующей величины вне слоя на 1—2% (например, и = 0,98(7). В механике жидкостей и газов часто пользуются более строго определенными толщинами пограничного слоя. Рассмотрим физический смысл некоторых других характерных толщин пограничного слоя.
Выясним прежде всего, как влияет вязкость на кинематику потока, т. е. на положение линий тока.
296
Ламинарный пограничный слой
На рис. XII.3 штриховыми линиями обозначены линии тока для идеальной жидкости, а сплошными — для реальной. Так как линии тока есть линии равных расходов, то, очевидно, линия тока АВ в идеальной жидкости должна соответствовать линии тока А'В' в реальной жидкости, расположенной несколько дальше от стенки. Определим величину смещения линий тока за счет влияния вязкости. Для этого найдем расход Qp реальной жидкости
Рис. XI 1.3
через поперечное сечение между стенкой и линией тока, удаленной от стенкй тела на расстояние у. Он будет равен
у
Qp = J н dy.
О
Соответствующая линия тока для идеальной жидкости будет расположена ближе к стенке на расстояние Д, найденное из условия равенства расходов. Запишем это условие в виде
у
Q,w = У {у — Д) = QP = ( « dy, но	о
У и (у — Д) = и j dy — U\, о
откуда у	и
г/Д = J (U~ U)dy и Д = J fl dy. о	о
Максимальное значение величины смещения Д будет при у = б. Оно равно
с
Дтах = 6*=|(1—^-\dy.	(XII.1)
О
Пограничный слой и его характерные толщины
29?
Величина Дшах обозначается б* и называется толщиной вытеснения. Толщина вытеснения, показанная на рис. XII.3 в виде заштрихованной площадки, практически не зависит от того, как определена толщина пограничного слоя. Из рис. XI 1.3 видно, что даже значительная неточность в определении толщины б мало сказывается на величине толщины вытеснения.
Вторая характерная толщина пограничного слоя определяется при выяснении динамического влияния вязкости на обтекание тел. Если тело обтекается потоком идеальной жидкости, то результирующая внешних сил, приложенных к телу, будет направ-
лена, согласно теореме Н. Е. Жуковского, перпендикулярно направлению движения. Никакой силы сопротивления (составляющей на направление движения) при этом не будет. Если же жидкость будет реальной,то из-за наличия вязкости появится сила сопротивления, которую можно определить, применяя теорему импульсов к некоторому контуру, включающему обтекаемое тело (рис. XII.4).
Найдем изменение количества движения в проекции на направление потока, совмещенное с осью х. Количество движения жидкости, проводящее через сечение АВ, будет qr — 2phU2.
Так как количество втекающей жидкости через АВ приближенно равно количеству вытекающей через А'В', то
л
„ 2phU = J ри dy,
—h
следовательно,
л
= pU Ju dy.
298
Ламинарный пограничный слой
Количество движения жидкости, выходящей через сечение А'В', будет равно h
q2 = р f и2 dy.
—h
Тогда в соответствии с теоремой об изменении количества движения проекция силы на направление движения, т. е. сила сопротивления, будет
Л	h
X — pU j и dy — р j и2 dy -J- q',
-h	—h
где q’ — количество движения жидкости, протекающей через боковые стенки АА' и ВВ' контура.
При стремлении h к бесконечности q' стремится к нулю. Окончательно получим со
X=pL/J «(1— ^)dy.
—<х>
Коэффициент сопротивления при этом будет равен +га	о»**
=	= Л	(ХП.2)
р —о
где
СО
s:=j	(хп.з)
—со
есть линейная величина, характеризующая динамическое влияние вязкости и называемая толщиной потери импульса.
В пограничном слое на поверхности обтекаемых тел формула толщины потери импульса имеет вид
6
(XII.4) о
В теории пограничного слоя важное значение имеют отношения толщин и, в частности, величина
Я*
н = -^.	(XII.5)
В тепловом и диффузионном пограничных слоях, как будет показано далее, применяются аналогичные характерные толщины и их отношения.
Уравнения ламинарного пограничного слоя
299
§ 2. Уравнения ламинарного пограничного слоя
Так как пограничный слой образуется лишь при больших числах Re, то уравнения движения в нем можно получить из общих уравнений движения вязкой жидкости, написанных в безразмерном виде, оценкой порядка величины слагаемых, входящих в уравнение.
Главная особенность такого анализа математических уравнений заключается в том, что масштабы, да и сами величины (линейные размеры и скорости), характеризующие продольные и поперечные составляющие движения, существенно различны. Для размеров это следует из ранее приведенного соотношения б< 1, что эквивалентно б I, т. е. поперечные размеры в пограничном слое значительно меньше продольных. Такое же соотношение будет и для поперечной и продольной составляющих скоростей.
Исходя из предположения, что силы инерции и вязкости внутри пограничного слоя одинакового порядка, и учитывая, что порядок сил вязкости на единицу объема внутри пограничного слоя будет
U /	,	т ди 1 \
равен р, -gj- ( по формуле -у = р, -д—	, а порядок сил инерции —
и2 (	У ди \
р —j— (в соответствии с выражением ри получим
откуда
<52____у _ _1_
I2	Ul ~ Re ’
где знак — означает порядок величины.
В результате получим очень важное для пограничного слоя соотношение
я	б	1
О   «"	у-, . , )
1 /Re
ДХП.6)
т. е. безразмерная толщина пограничного слоя обратно пропорциональна корню квадратному из числа Рейнольдса.
Уравнения Стокса для плоского стационарного движения реальной несжимаемой жидкости при отсутствии массовых сил имеют вид:
ди	. ди	\	др	.	( д2и	. д2и \ ,
U дх	_ V ду	р	дх V \ дх2 ду2 ) '
dv	. dv __	1	dp	.	/ d2v	, d2v \ .
U dx	' V. dy	' p	dy v \ dx2 dy2 ) ’
du . dv  Л dx ' dy
300
Ламинарный пограничный слой
Представим их в безразмерном виде, полагая:
х = хГ, у = у&, и = v = vV; р — рр0,
где черточками отмечены безразмерные величины, а I, 6, U, р0— характерные масштабы длины, скорости и давления. Подставляя эти величины в систему уравнений, получим:
U2 -	ди	.	UV -	ди	р0	др	,	(U	д^й	.	U	д*й \
/	дх	6	ду	Р1.	дх	\ 1	дх2	62	ду2 )
UV -	dv	,	V2 -	до	Ро	др	,	{ V	д2о	,	V	д2и \
I дх 6 ду Р?> ду \ I* дх2 5 ду2 )
U	ди	,	V	до „
—;-----=----5--=- = U.
I	дх	$	ду
Разделив безразмерные уравнения на коэффициенты при первых слагаемых, найдем:
-du . VI - du U —=- 4- -77T-V—-dx '	dy
-до	.	VI	- do
——---1--77я~	—~~	— ~
dx	Ud	dy
= _ Ро	+	(ХП.7)
pl/2 дх UI дх2 U& ду2 v
Ро /	I	• ZYTT
pU W ду 'Г Ul д~х2 W2 d~y2 ’ (	'
du . VI do ________p,
' W dy
удовлетворялось уравнение неразрывности,
Для того чтобы необходимо соблюдение условия
U8 -
(XII.9)
Имея в виду, что -у- выражается по формуле (XI 1.6), получим другое важное в теории пограничного слоя соотношение
(ХПЛ0)
Оценим теперь порядок величин слагаемых уравнения (XII.7).
Учитывая (XII.9) и полагая, как обычно, что давление р0 имеет v/ “V /2
порядок pt/2 и что -ygf	~ 1> перепишем уравнение
(XII.7) в виде
- ди . - ди	др . 1 д2и . д2и
дх ду	дх	дх2 ду2
Уравнения ламинарного пограничного слоя.
301
При стремлении числа Re к бесконечности уравнение (XII.7) примет вид
4+-4=_«+« (хил)
дх ду	дх ду2
Воспользовавшись уравнениями (XII.7), (XII.9) и (XII.10), уравнение (XII.8) можно представить в виде
- dv . — dv п др .	1 d*v , d2v
и -^4-	= Re—-Ь -и-----— 4-^-.
дх ду	ду Re дх2 ду2
Разделив последнее уравнение на число Re и устремив Re к бесконечности, окончательно получим важное в теории пограничного слоя отношение
др ду
= 0-
(XII.12) ’
Таким образом, давление внутри пограничного слоя не зависит от у, т. е. оно не меняется по нормали к стенке. Это соотношение сближает задачи о пограничном слое и о стабилизированном движении жидкости в трубе (XI. 1), где давление также не зависит от радиуса трубы.
Так как = 0, то частная производная —- может быть заменена полной, т. е. дх dx
Применяя уравнение Бернулли для потенциального потока вне пограничного слоя и дифференцируя его, получим в размерном виде соотношение
• dx r dx
где U — скорость на границе слоя.
Если представим уравнения (XII. 11) в размерном виде, то окончательно получим систему уравнений пограничного слоя:
ди	. ди j,	dU ,	д2и
и ~5---h у-л— = и	-т— 4-	V-5-?	;
дх	1 ду	dx 1	ду2
ди ] dv ____п
~&Г~Г ~ду~ ~
(XII.13)
Граничные условия на стенке останутся такими же, как и для уравнения Стокса, т. е.^при у — 0u = v = Q. Другое граничное условие, характерное для пограничного слоя конечной толщины, будет и = U (х) при у = 6.
На рис. XII.5 показаны профили скоростей в потоке, обтекающем тело. Точки А и В находятся в конфузорной области, где
302
Ламинарный пограничный слой
отрыв невозможен, так как здесь U’ > 0, а < 0, т. е. давление по потоку убывает. Следовательно, давление в каждой последующей точке будет меньше, чем в предыдущей. Такой градиент давления на стенке будет содействовать движению жидкости в пограничном слое. В диффузорной же части потока U' < 0, а > > 0, следовательно, давление на стенке растет, и в каждой последующей точке оно больше, чем в предыдущей. Такой градиент давления противодействует потоку, а вблизи стенки, где скорости
очень малы, он содействует движению жидкости в противоположном направлении и может служить причиной отрыва пограничного слоя.
Математически точка отрыва С определяется как точка, в которой трение на стенке равно нулю, т. е.
= ^wl=0 = ° ИЛИ Пр0СТ0 <1=0= °- (XIL14)
Аналогично уравнению для динамического пограничного слоя можно получить уравнение для теплового и диффузионного пограничных слоев.
Для вывода уравнения теплового пограничного слоя воспользуемся уравнением теплопроводности (II 1.47)
дТ , дТ	/ д2Т , д*Т\
дх ' dy	\ дх2 1 dyi J
Обозначив безразмерные величины соответствующими буквами с черточками, т. е. х = xl, у = у8, Т = ТТ0, и - uU, v = vV и вводя их в последнее уравнение, получим
ито - дТ , VT0 - дТ аТ0 д*Г . аТ0 дгТ
~~Г~ и~Г + v	7=г + "6^ тт •
1 дх 0 ду * дх 0 ду2
Уравнения ламинарного пограничного слоя
303
Разделив все слагаемые на коэффициент при первом члене, будем иметь уравнение в безразмерном виде
- дТ . VI - дТ _ а дЧ . а I д*Г
“ д~х +	д~у ~ UI дх2 + U8 6 д~у2 '
Оценим порядок величины коэффициентов слагаемых дифференциального уравнения.
г Согласно выражению (XI 1.9),	имеет порядок единицы.
при числах Рг порядка единицы, при боль-
ших Re стремится к нулю. Коэффициент последнего слагаемого a I2 Re 1
равен ut б2 — ReT — рг .
Очевидно, что после возвращения к размерным величинам получим уравнение для теплового пограничного слоя в виде
дТ .	дт	д2Т
и -л---= <2 лТ-
дх 1	ду	ду2
(XII.15)
Для вывода уравнения диффузионного пограничного слоя воспользуемся уравнением
дс .	дс	п / д2с . д2с \
дх 1	ду \ дх2 1 ду2 /
Представим его в безразмерных величинах, используя прежние обозначения и введя с — сс0, тогда
Uc0	— дс	.	Vc0	-	дс	Dc0 д2с	.	Dc0 d2c
I	дх	6	ду	I- дх2	б	ду2
Поделив обе части уравнения на получим
-	дс .	VI	-	дс	_	D	д'гс .	D	I	д2с
U	дх	ду	~	UI	дх2 +	U	82	ду2
и оценим весомость членов уравнения. Коэффициент при первом члене в правой части уравнения можно представить в виде
D _ 1 _	1
Ul ~ Refl ~ RePi-д '
Если числа Re достаточно велики, то —> 0 и этим членом можно пренебречь.
Коэффициент при втором члене, учитывая (XII. 10), будет равен
DI	D I2	1 р	1
U62 ~ Ul 62	Re Ке	Л
304
Ламинарный пограничный слой
Следовательно, учитывая (XII.9), дифференциальное уравнение диффузионного пограничного слоя запишем в виде
+	=	(XII.I6)
дх 1 ду ду2	'	'
§ 3.	Интегральные соотношения для динамического пограничного слоя
Для вывода интегральных соотношений в динамическом пограничном слое воспользуемся уравнениями ламинарного слоя в виде: j и
+ +	<XIL17)
> + < = 0.	(XII.18)
Учитывая, что ди ди2 ди ди д (uv) dv и -т- = -д------------u-д—, a v— и -т—,
дх дх дх ду ду	ду ’
левая часть уравнения (XII. 17) может быть представлена в виде
ди2 ди . д (uv) dv ___________ du2 . d (uv) _ / du . dv \
dx U dx ' dy U dy dx ‘ dy U \ dx ' dy / ’
Величина в скобке по уравнению (XII. 18) равна нулю, поэтому уравнение (XII. 17) запишем в виде
(XII.19)
дх 1 ду	1 ду2	'	>
Преобразуем также уравнение (XII. 18) следующим образом:
т, ди	.	т, dv	d(Uu)	dU	.	д (Uv)	dU	n
U “5 k U Т~ =  к—'-------« -5----5“^-----V “5— = 0>
дх	1 ду	дх	дх	1 ду	ду
но U = U (х) не зависит от у, следовательно, = 0, и уравне-
ние (XII. 18) будет
dWV-—u—- + d^v} — 0.	(XII.20)
дх	дх 1 ду	.v '
Вычтя из уравнения (XII.20) уравнение (XII. 19), получим
Интегрируя это уравнение по у от 0 до 6, найдем 6	б б
J[u(U — u)] dy + v(U — u) + U' (U— u)dy = —v о
6 ди I ду I • о
о
Интегральные соотношения для динамического пограничного слоя 305
Упростим это уравнение. Первый член будет равен б	б 	б
ООО
б
о
Учитывая условия на стенке (при «/ = 0 о = 0;	= и
на границе пограничного слоя (при у — 8 и = U; =0^ , будем иметь
б	б	б
v(U—u) |=0 и — v 4^ I = — 4^ | = —• k	ду <-р ду I р
Далее, преобразуя, получим б	б
-£-7/2 f-^(i — 4) dy-i-uu' f	•
dx J U \ U ) v ' J \ U / v p
о	о
6
Величина J (1 —dy является толщиной вытеснения 6*. о
б
Величина |-^(1 —dy является толщиной потери им-о
пульса 6**.
Окончательно уравнение перепишется в таком виде
+	=	(ХП.21)
или	х	р
J^ + _^(26** + 6*) = _^.	(XII.22)
Уравнение (XII.22) есть интегральное соотношение для динамического пограничного слоя, называемое уравнением импульсов.
Все задачи о пограничном слое могут решаться двумя путями. В одном случае пользуются не дифференциальными уравнениями, а интегральными соотношениями. При этом задаются некоторой формой профиля скоростей в пограничном слое и, используя интегральное соотношение, определяют напряжение трения Тц, на обтекаемой поверхности, а также такие интегральные величины, как толщина пограничного слоя 6, толщина вытеснения 6* и толщина потери импульса 6**. Такой способ решения называют приближенным методом. .
20 и. Л. Повх
306
Ламинарный пограничный слой
В другом случае решают дифференциальные уравнения с соответствующими граничными условиями и обычно получают значение скоростей во всей области пограничного слоя, т. е. и (х, у) и v (х, у), а следовательно, и трение на стенке. Будем называть такой способ точным методом.
§ 4. Точные решения
Первое точное решение для ламинарного пограничного слоя при скорости на внешней границе слоя, заданной в виде степенного ряда
U (х) = агх + а3х3 + а6х5 + • • •>
и при постоянном значении U получено Блязиусом в 1908 г.
Заметим, что задание U (х) таким образом соответствует обтеканию некоторого осесимметричного профиля при нулевом угле атаки, а постоянное значение скорости соответствует продольному обтеканию пластинки.
Рассмотрим здесь точное решение, полученное Фолкнером и Сканом в 1930 г. для степенного распределения скорости вдоль внешней границы слоя, заданного в виде
U (х) = схт.	(XII.23)
Если взять производную от U (х) по х, то U' = тсхт~х, откуда следует, что при т = 0 скорость U = с tywx соответствовать обтеканию пластинки; при т > 0 течение будет конфузорным, а при т <0 — диффузорным. Таким образом, зависимость для распределения скорости (XII.23) является достаточно универсальной.
Для точных'решений можно уравнения пограничного слоя (XII. 13) привести к виду, удобному для интегрирования, введя функцию тока ф, удовлетворяющую уравнению неразрывности. Для чего, положив и=~ и v = — и подставив значение скоростей и их производных в уравнения пограничного слоя (XII. 13), получим одно дифференциальное уравнение третьего порядка
_______________________i gp ।	_ и I у /хп 941 ду дх ду дх ду2 р дх ‘ ду3 дх ду3 ‘	’
Граничными условиями при внешнем обтекании тел будут: на поверхности обтекаемого тела (т. е. при у = 0) ф = 0; так как поверхность тела есть нулевая линия тока,
л
-4- = U = 0; ду
при значительном удалении от поверхности (у —> оо)
ду
Точные решения
307
Для того чтобы дифференциальное уравнение в частных производных (XII.24) привести к обыкновенному, вводятся новые переменные
=	и % = У]/С^т+^Х,П~\ (XII.25)
(XII.26)
Подсчитав значение величин, входящих в уравнениеЗ(ХП.24)
U - - тс2х^ ,	= слтФ' (£),
дх	' ду	къ/’
$ = «"-Ф- ©,	= А"	Ф' ©,
~s^И' © +	S'®"©]
и произведя простые преобразования, получим обыкновенное дифференциальное уравнение в виде
</3Ф । ф 4^
о 2т где 0 = ——:.
г т -|- 1
Приведение к уравнению (XII.26) свидетельствует о том, что его решение будет подобным, или автомодельным и безразмерный профиль скоростей в зависимости от новых безразмерных координат будет одинаков для значений х.
Граничными условиями в этом случае будут следующие:
при £ = 0, Ф = 0 и — 0; с.	d(t> ,
при ?-> оо,	1.
Уравнение (XII.26) при указанных граничных условиях было проинтегрировано на машине, и получены таблицы значений Ф (£); Ф' (£); Ф" (|) для девятнадцати значений п.
Координата у, скорость и ее производная определяются через новые переменные следующим образом:
ап
и = -^сх-Ф'(£, 0) = [/Ф' (Е-, 0);
Т/Р^£ф''(г ft) ду ду2 V	W-
На рис. XII.-6 приведены значения -р- = Ф' (гц, 0), построенные по результатам расчета. Очевидно, величина j]x, при которой 20*
308
Ламинарный пограничный слой
и
-ц равна единице или отличается от единицы на некоторое малое значение, будет соответствовать толщине слоя. Из характера кри-. вых (рис. XII.6) видно, что в конфузорных потоках (Р > 0) толщина слоя меньше, а в диффузорных (Р < 0) больше, чем на пластине (Р = 0).
В табл. XII. 1 приведены значения £6, соответствующие значению и = 0,981/, в зависимости от р. Толщина слоя 6, т. е. соответствующее значение у, выражается зависимостью
2v —---r—rvX 2 .
с (т 4-1)
Толщину вытеснения и толщину потери импульса можно представить в виде:
со	со
о	о
со	•	со	:
6** =	Р)[1 —Ф'(£; р)]<}(
J '	'	1/ тех! J	'!
0 * °
Интегралы могут быть вычислены по известным величина!^ Ф' Q) для каждого значения р. Обозначив первый интеграл через* А (Р), а второй через В (Р), получим:
_________________ т—1	______ т—1	, б* = Д(Р)У^х 2 ; б** = В(Р)]/^х 2 .
Точные решения
309
Таблица ХП.1
₽	—0,1988	—0,18	—0,14	—0,10	0	0,2
£6	4,6	4,0	3,8	3,6	3,2	2,8
А	2,359	1,871	1,597	1,444	1.217	0,984
В	0,585	0,568	0,539	0,515	0,470	0,408
Ф" (0)	0,0000	0,1285	0,2395'	0,3191	0,4696	0,6869
₽	0,4	0,6	0,8	1,0	1,6	2,0
?б	2,6	2,4	2,2	2,1	1,8	1,7
А	0,853	0,764	0,699	0,648	0,544	0,498
В	0,367	0,336	0,312	0,292	0,250	0,231
Ф" (0)	0,8542	0,996	1,120	1,2326	1,521	1,687
Легко видеть, что все характерные толщины 6, 6* и 6** одинаково зависят от х. Так как во всех случаях коэффициенты перед х положительны, то знак производной от толщины по х будет определяться величиной 1 — т. При т < 1, что соответствует области диффузорного потока (т < 0) и слабого конфузорного (0 < т < < 1), все толщины, как обычно, увеличиваются вдоль оси х. При т = 1 они постоянны, а при т > 1 (такие течения можно назвать сильно конфузорными) толщины убывают. Значения А (0) и В (0) приведены в табл. XII.1.
Величина трения на стенке, представляющая большой практический интерес, может "быть вычислена по формуле
т« ~ И |у=0 = У	НреЗх3'”-1®" (0, 0).
Из табл. XII. 1, в которой приведены Ф" (0, 0), видно, что при 0 = —0,1988 Ф" (0) = 0 это значит, что в таком диффузоре
310
Ламинарный пограничный слой
трение на стенке равно нулю, что возможно только при
ди I di/lz/=o
= 0.
Из этого следует, что на стенке должен существовать всегда отрывной профиль скорости. Создать такой поток трудно, так как отрывной профиль очень неустойчив. При продольном обтекании пластинки т = 0; U = с и для и = Q,99U величина £б = 3,6. Характерные толщины такого слоя будут равны:
6*=1,73	в*»=0,664 У^-. (XII.27)
Имея в виду, что Ф" (0, 0) = 0,4696, получим величину трения на стенке и местный коэффициент сопротивления соответственно
равными:
тда = 0,332]/-^-; Н = 2,6;
Ти> А	"V 0,664
Cf =----775-= 0,664 I/ -77— = —
f pU2	V Ux
• 2
(XII оа\
§ 5. Ламинарный пограничный слой на пластине
Изложим приближенный метод для продольного обтекания бесконечно тонкой пластины.	1
/Очевидно, в этом случае давление во всей области потока,; так же как и величина скорости вне пограничного £лоя, будут ве-; личинами постоянными, и уравнение импульсов (XI 1.22) при-' мет вид
(XII.29)
d6** __ Тш
dx ~ pU2 
Для решения этого уравнения зададимся выражением скорости' в виде полинома
и = а0 + агу 4- а2у2 + а3у3 . -j- апуп.	;
Значения коэффициентов а0; ах; а%. . . могут быть найдены и® граничных условий, причем для определения одного коэффициента! полинома требуется одно граничное условие. Таким образом, ко-j личество членов полинома должно соответствовать количеству! поставленных граничных условий.	1
В данном случае воспользуемся тремя граничными условиями.5 На стенке при у = 0 и = 0, на границе слоя при у = 6 и = VJ ди	п	1
а также	-=	=	0.	j
ду	j
Ламинарный пограничный слой на пластине
311
Подставив в полином, в котором берем три первых члена, указанные граничные условия, получим:
а0 = 0;
аг8 + а262 = U;
ах 4- 2а26 = 0,
о U	U
откуда = 2 -у и а2 =-^ и, следовательно,
• о \ о /
Зная и (у), легко найти 6*, 6** и xw е	1
О	о
1
Отсюда видно, что 6 > 6*-> 6**, т. е. толщина слоя больше толщины вытеснения, а последняя, в свою очередь, больше толщины потери импульса.
Из полученных значений 6* и 6** определим:
Л	Л*
-4г = 3 и Н = £*=2,5.
о*	о
Напряжение трения на стенке определяется формулой ди I n U
Xw—~д^ L=o—•
Тогда уравнение импульсов (XI 1.29) будет иметь вид
2 <Л _п |х
или	-	15 W
6 d8 = 15 dx,
откуда 62 = 30—+ С, a 6 = ]/з0^+ Cx.	' -
312_________________Ламинарный пограничный слой__________
' i Считая, что при х — 0 6 = 0, получим С2 = 0. Окончательно бу( дем иметь
г 1 / о a vx Ь 5,48	'	, ’
8= I/ ЗО-ту или — =
V и * Йе/
Ux	’
где Rez = —----местное значение числа Рейнольдса.	.’!
Воспользуемся четырьмя граничными условиями: при у — Q дъи '	?
и — 0 и — 0 (последнее следует из уравнения погранично^
слоя) и при у = 8 и — U и ~ = 0. Тогда, взяв четыре члена полинома для и, получим:
и 3 и 1 / у \2.
77~ ТТ ~"2 \ 6 ) ’
Таким образом, толщина пограничного слоя, а следовательно^ толщина вытеснения и толщина потери импульса для ламинарной^ пограничного слоя на пластинке увеличиваются пропорционально, корню из х, т. е. 6 ~ Ух', 6* ~ Ух и 6** — Ух.	,'i
Располагая выражением для толщины пограничного слоя,;! можно найти зависимость для напряжения трения на стенке j]
(XII. 31)!
т/ 4 t/3u.a	1 / 2 4/3цр	0,36IpU3
У 30 vx ~ |/ 15 х ~	’
I т. е. Тщ, .... • у х Полное сопротивление (в данном случае полное сопротивление' трения) можно определить для одной стороны пластины по формуле^
о	•;
где I — длина пластины; b — ширина пластины.
Для пластины в целом величина трения будет определяться^ удвоенной величиной (две стороны пластины), т. е.	.<
или
Хпп = 2b j xw dx, о
Ламинарный пограничный слой на крыловом профиле
313
Обычно интересуются не абсолютной величиной общего сопротивления, а значением коэффициентов. При этом пользуются двумя коэффициентами сопротивления трения: местным
„  ТИ>
Р 2 п общим
где S = 2Ы — площадь поверхности с двух сторон пластинки. Тогда в соответствии с формулой (XII.31) сх будет равно
__	_ 0,722
f 2 а полный коэффициент сопротивления трения для пластины выразится формулой
г _ 1,444
D Ul	х /Re ’
где Re = —. V
Подчеркнем, что Сх — -pLx.
Следовательно, коэффициент сопротивления обратно пропорционален корню квадратному из числа Re.
§ 6. Ламинарный пограничный слой на крыловом профиле произвольной формы
Существующие методы приближенного решения задачи о пограничном слое на профиле произвольной формы основаны на решении уравнения импульсов (XII.22). Не рассматривая всех известных способов решения, остановимся на более простом, получившем довольно широкое применение методе, предложенном Н. Е. Кочиным и Л. Г. Лойцянским.
Так как в уравнение импульсов входят три неизвестных: 6*, 6** и тда, то все приближенные методы сводятся к тому, чтобы прийти к уравнению с одним неизвестным путем выбора семейства профилей скоростей, зависящего от одного параметра. Выбрав такие профили, можно выразить 6*, 6** и rw через один параметр и таким образом получить обыкновенное дифференциальное уравнение относительно .^выбранного параметра.
В качестве такого параметра можно ввести величину f, называемую формпараметром, определяемую выражением
314
Ламинарный пограничный слой
Тогда семейство профилей в ламинарном пограничном слое будет выражаться зависимостью
6*, 6** и Тщ можно представить в виде
S* = J (1 “ 77 ) ЛУ = S** J[ 1 - M = 8**H
где H (f),
=	=р,Г-^-1	= -Й^-ф'(0, f).
\dy )y=o ‘ L дгц Jn1=o 6**	6** 1 ' ’ ''
T 6**
Если обозначить ф' (0, f) = £ (f) = 	, то уравнение импуль-
сов (XII.22) будет иметь вид
б**	а	‘
Умножив	его на	—	,	получим
или,	учитывая, что	коэффициент при	втором члене равен	".
(/'6**2 _ [	(
Uv ~~й’	1
и обозначив
2 [£(/)- (2 + H)f] =F (f),
приведем уравнение импульсов к виду	
d / 6**2 \_d / / \	F(f)
dx \ v /	dx \ U') U
Так как
J-(-L\UL
dx \ U' ) W dx 1 U'2 ’
то окончательно это уравнение примет вид
^=irf+-irF^. <X1L333
Зная F (f), можно при заданном U (х) решить это уравнение и найти f (х), а следовательно, 6** и Тц, (х).	i
Ламинарный пограничный слой на крыловом, профиле
315
Из точных решений, подтвержденных экспериментом, было установлено, что F ([) можно приближенно представить в форме линейной функции, имеющей вид
F (J) = а - bf.
На рис. XII.7 приведены кривые Н ([), £ (f) и. F (f), соответ-
ствующие точному решению уравнения для ламинарного погра-
ничного слоя при скорости на границе слоя U = схп. При этом
а = 0,45 и b = 5,35.
После подстановки значения F (/) в уравнение (XII.33) окончательно получим уравнение импульсов в виде
Это линейное дифференциальное уравнение первого порядка имеет следующее решение:
X
(XII.34)
J м	U
0
Постоянная С определяется из граничных условий. Считая, что при х = 0 {/ = = 0 и f конечна, получим С = 0. Выражая 6** через формпараметр f по формуле (XI 1.32), будем иметь
Рис. XII.7
6** = j/j Ub-' (С) dg. о
 (XII.35)
Зная f (х) и 6**, легко по кривым на рис. XII.7 найти Н (/) и С (/), а следовательно, 6* — 8**Н и xw по формуле
TK,(x) = p-^>rU/)-	'	-
Координата точки отрыва, как было указано ранее, определится из условия (XII. 14) Тщ = 0.
Последнее условие соответствует £ (/) = 0. Из рис. XII.7 видно, что £ (/) равно нулю при значении формпараметра fs = = —0,0681. Знак минус свидетельствует о том, что отрыв происходит в области диффузора.
Расчеты, выполненные по приведенной теории, хорошо совпадают с результатами эксперимента при f > 0 и дают некоторое расхождение лишь вблизи f =
318
Ламинарный пограничный слой
§ 7. Интегральное соотношение для теплового ламинарного пограничного слоя. Тепловой слой на пластине
Аналогично уравнению импульсов для динамического погра ничного слоя можно получить интегральное соотношение и ддг теплового слоя. Преобразуем уравнение теплового погранично^ слоя (XI 1.15) и	запишем	левую его часть	в виде	j
дТ	, дТ	диТ , доТ	( ди - ,	до \
W-ч =—5------------Ь -5----Т -5 ha-)-
дх	' ду дх ' ду	\ дх 1	ду )	,
По уравнению неразрывности последний член равен нулю, и урав нение (XII. 15) запишется следующим образом: -	j
диТ , диТ д2Т	,утт „л
В свою очередь, уравнение неразрывности представим так: « диТ doTm	J
+ —=	(XII.37
дх 1 ду	v
Если из уравнения (XII.37) вычтем (XII.36) и затем проинт^ грируем по у от нуля до бесконечности или до толщины слоя, получим
4 J и (7. - Т) dy + | vT^ - П = - а	f.
дТ
Так как при у = 6Т Т — Тт и = 0, а при у = О
то второе слагаемое обращается в нуль, а уравнение примет ви!
6Т
Разделив уравнение-на U^T^, получим

V
(XII.3I
Т
Т 4 rf
о
Если обозначим
а дТ I ^еотсо дУ Ь=о
6Т
f^-h-/-\dy = 8
J со \	1 оо /
О
то окончательно уравнение примет вид
di£* = а дТ I dx и^тт дУ Ь=о
“Я
*т >
Интегральное соотношение для теплового Ламинарного пограничного слоя 31?
Уравнение (XII.38) можно представить в другом виде, воспользовавшись следующим преобразованием:
Та- Т = (Тт- Тст) - (Т — Тег) = 0 - О,
тогда
т	т
j и (Тю - Т) dy =	± J (1 -dy, (XI 1.39)
о	о
п окончательно, введя обозначение
получим
d&** _ а дЬ I
dx ~	ду|у=0’
(XII.40)
Это уравнение теплового потока через пограничный слой. Оно может быть получено также из рассмотрения баланса тепла в пограничном слое.
Определим теплоотдачу от плоской пластины, имеющей постоянную температуру поверхности Тст, ламинарному потоку жидкости, движущемуся с постоянной скоростью.
Чтобы использовать интегральное соотношение (XI 1.40), необходимо знать профиль температур и скоростей в пограничном слое. Как и в ранее рассматриваемых случаях, представим Т (у) в виде полинома
Т (у) =	+ Ь1У + Ь# + Ь3у3 + • • • + bnyn. (XII.41)
Количество членов такого полинома и значение коэффициентов b0,	Ь3, . . ., ЬП можно определить по выбранным граничным
условиям. Используем.для данного случая два граничных условия на стенке и два на границе слоя.
На стенке при у = О Т = Tct и, учитывая, что тепловой поток q постоянен, будет = 0. Но так как
? ду L=o ’
то при у = О
^ = 0
ду2
На границе слоя при у = 6Т
318
Ламинарный пограничный слой
Подставив указанные граничные условия в (XII.41), получим! систему уравнений для bi, Ь2,
Ь3:
Tct = bo‘, 2й2 = 0
нахождения четырех коэффициентов
^о>,
т. е.
Т1 = Ь0 + Мт + М? + Ьз6?;	,
и Ь1 + 2Ь26т + ЗЬ36? = 0.	j
Решая эту систему, найдем, что	j
h	— Т	•	h	—	%	Т — Т'ст .	— а.	—	1	Л — Т'ст	1
О0 —/ст,	01 —	у	,	02 —и,	03—	2	6з	’	3
ит	|
или, используя соотношения для 0 и О', окончательно получим
I =	.	<хп^
Профиль скоростей представим также в виде многочлена и = а0 + агу 4- а3у* + а3у3	]
и используем аналогичные граничные условия. Имеем при у = 0] и = 0 и 5^ = 0, dy —о-— U’ на границе слоя при у = 6
и = U и -5— = 0. ду

Таким образом, получим систему уравнений, из которой найдем значение коэффициентов:
п 3 и
ао —°; О1 = т-ё-;
— п. —	1 и	<
й2 — и, 6Z3—	2 63 *	1
1
Следовательно, профиль скоростей будет иметь вид	:
,хп-43
Зная О (у) и и (у), можно написать интегральное соотношение дл5 теплового слоя (XI 1.40) в таком виде вт	.	;
А Г Г1_£X_i__L('X\2]x
dx J L 2 6T 2 \ 6T / J A 0
Интегральное соотношение для теплового ламинарного пограничного слоя 319
Приведенный интеграл легко вычислить, если положить, что тепловой пограничный слой меньше динамического или равен ему, т. е. бт 6.
В этом случае интеграл в интервале 6—6Т всегда обращается в нуль, так как # = 0 и, следовательно, значение подынтегральной- функции в выражении для б** в этой области всегда равно нулю.
Если положим -у = h, т. е. 6Т = ft6, то интеграл в уравнении (XII.44) будет равен
бт
f 0	б") 77 ~ 6 ( 20	280 Л*) = 20 S/l2 ( 1 Tf. ft2) '
о
Второе слагаемое мало по сравнению с первым, так как мы предположили, что 6Т 6, т. е. h 1. Пренебрегая вторым слагаемым, окончательно получим дифференциальное уравнение
3 а 3 а
20~dxn — Т 77б? = У 7Ж ИЛИ
ft26-^ + 2ft26222 —Ю-£-.
ах 1 ах U
Если значение величин б и 62 подставить из решения задачи о ламинарном пограничном слое, т. е. из (XII.30),
§	_ 140 v „ §2 — 4 С42
0 dx ~ 3 U и 0 “4,04 и ’
то последнее уравнение примет вид
21X (& 4- 4xft2 —= 1 13 а \п r dx) 11
Приняв дробь 21 приблизительно равной единице и помня,* что 1 о
у - Рг, получим
Если сделать подстановку <р — ft3, то . 4 dq> 1 ф+зхЛс ~ Рг ’
и очевидным частным решением этого уравнения будет 1	и 1
(₽=PF> т- е- h = —т> Рг3
320
Ламинарный пограничный слой
ИЛЯ
Рг3
Из выражения для толщины динамического ламинарного no-j граничного слоя (XII.30)
6 = 4,64/^,
окончательно получим
6Т = 4,64
(Х11.46)|
Следовательно, так же, как и для динамического пограничного^ слоя, 6т~]/х.	.]
Безразмерная толщина теплового ламинарного слоя на пла*Я стине равна	'я
(XI 1.47:
6Т __	4,64
~~ j/T^ypT ‘
Так как для каждого выбранного вещества можно считать, что^ „	, 6Т 1	'!
число Рг = const, ТО —-------
х /Re*
При решении уравнений предполагается, что h 1; это эквин; валентно тому, что число Рг 1. Следовательно, полученные^ решения непригодны для жидких металлов, у которых Рг<^Ц рассматрм пластин®
. Найдем величину коэффициента теплообмена для ваемого случая. Тепловой поток от пластины или можно представить в виде
к

откуда, пренебрегая знаком, получим
_ А. аг I
а 6 ду |у=о
А. 6$ или а = -s- -у-
6 ду h/=o
Из (XII.42) имеем	;i
I	=	_3	6	j
ду	|у=о	2	6Т	‘	4
Учитывая (XII.46),	получим	окончательно для локальноЯ
переноса тепла	Я
а = 0,32ЗХ p/'Pr	.	(XII.Ш
Дифузионный ламинарный пограничный слой на пластине
321
Приведенная на рис. XII.8 зависимость локального коэффициента теплообмена а от х показывает, что у переднего края пластины значение а очень велико, а затем по мере удаления от переднего края оно убывает.
В практике обычно интересуются не локальным, а средним значением коэффициента теплообмена аср, равным
X
аср = 1 j adx = 0,646%^Pr]/-^ = 2а.	(XII.49)
о
Таким образом, среднее значение коэффициента теплообмена всегда равно удвоенной величине локального коэффициента на данной длине пластины.	а
Часто законы переноса тепла выражают через критерии подобия в виде	.
Nu = f (Re, Pr).	!
_	,,	1 a
Если величину локального коэффи-	*--
циента в уравнении (XII.48) умножить на	i	X
~ , то уравнение примет вид	р XII 8
= Nux = 0,323/Рг]/^,	(XII.50)
Л/
или для полного числа Nu
Nu =	= 0,646 F Pr VRex.
Количество тепла, отдаваемого в единицу времени с одной стороны пластины единичной ширины, будет
Q=a(T„—— T1) = №Nu. (XII.51)
§ 8. Диффузионный ламинарный пограничный слой на пластине
Покажем, что дифференциальные уравнения и граничные условия для диффузионного слоя имеют такой же вид, как и для теплового. Тогда для диффузионного слоя можно воспользоваться полученными решениями.
Напомним, что уравнение для теплового слоя имеет вид
<50 .	50	52О	/VTT
и =- 4- v-д— = а -т-т-.	(XII.52)
дх 1	ду	ду2	4	'
Граничные условия:
при у — 0 0' = Т — Т„ = 0;
при у = 6Т О = 0 = 7\— Тст.
21 И. Л. Повх
322
Ламинарный пограничный слой
Если для диффузионного слоя по аналогии с тепловым ввести Фд= с — сст и 0Д = сх— сст, где сст и сх есть концентраций вещества соответственно на стенке обтекаемого тела и на границу слоя, то уравнение диффузионного пограничного слоя
дс .	дс	д2с
и -5“ + v ~5~ — D -5-5-
дх 1	ду	ду2
примет вид	;
+	' <XIL53i
а граничные условия будут следующими:	|
при у = 0 О'д = 0;	1
*• при у = бт = 0д.	I
Уравнения (XII.52) и (XII.53) по форме одинаковы; одинаковы] также их граничные условия, уравнение неразрывности является! общим. Тогда для получения основных зависимостей для ламинар-Я ного диффузионного слоя достаточно в известных решениях для>; теплового слоя произвести замену тепловых величин на соответ-i ствующие диффузионные. Например, интегральное соотношение’ для диффузионного слоя запишется в виде	i
д
= I £ (1 — о
dfiS*	D ^д I
dx	ивД ду |//=о ’
(XII.54)'

Как и для теплового слоя, предположим, что толщина диффу-

зионного слоя меньше или равна толщине динамического слоя, т. е. 6Д 6, тогда для пластины получим
_5д
“• 6
6Д=4,64-^Х
1 д /Ргд
РГД3
Если коэффициенты обмена вещества и диффузионное число' Нуссельта, как было показано ранее, записать в виде
да = ад(С1_Сст) = _р^|у=о,
т. е.
ZX	7-. д& I
w = ад0 — — D -т-А	dy 1^=0
а число
Nufl
«д* D ’
Диффузионный ламинарный пограничный слой на пластине
323
то получим формулы для локального и среднего коэффициентов переноса и для закона переноса:
«„ = 0,323^
ад ср — 2сс
(XII.55)
аах
Nu« = -g-
0,323 p'P^Re,.
Общее количество вещества, снимаемого потоком со стенки на единицу ее ширины в единицу времени, будет
М = ад (cCT — Cj) I • 1 = D (ост— сх) Nufl.
Сравнивая выражения (XII.50) и (XII.55), можно сделать вывод, что перенос тепла и вещества при равенстве теплового и диффузионного чисел Прандтля (это возможно) ' аналогичны друг другу.
Рассматривая величины, характеризующие динамический, тепловой и диффузионный пограничные слои, можно сделать вывод и о том, что параметры последних двух могут быть выражены через соответствующие величины динамического слоя; для толщины слоя о 6 о 6 от — -р и Од £ ’
Рг3	Рг3
Для профиля безразмерных концентраций а —	= с- с1 _____________L (JL\3
Од	Сет - Сх	2 6д 2	/ 
На рис. XII.9 показаны кривые безразмерных концентраций в зависимости от расстояния от стенки в мм, подсчитанные по последним формулам и полученные из эксперимента при числе Re = 2000. Из рассмотрения этих кривых видно, что теоретические формулы хорошо подтверждаются опытом.
21*
324
Турбулентный пограничный слой. Турбулентные струи
ГЛАВА Xllj
ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ;, ТУРБУЛЕНТНЫЕ СТРУИ
§ 1. Переход ламинарного пограничного слоя в турбулентный
При внешнем продольном обтекании пластины и любого дру-? того тела на стенке в непосредственной близости от критической? точки всегда будет существовать ламинарный пограничный слой. На некотором расстоянии от критической точки он становится' турбулентным. Переход, как правило, совершается в некоторой’ области; однако часто для простоты считают, что переход осу-?
.ществляется в точке.
Так как величина трения различна в ламинарном и турбулент-
УРбу-з
ном пограничных слоях, то вопрос о нахождении точки перехода.] имеет большое практическое значение. Однако надежных методов? расчета точки перехода ламинарного пограничного слоя в т лентный до настоящего времени нет.
Существующие методы можно разделить на теоретические?!
(в основе их — теория устойчивости движения, различные*йолу-<; эмпирические способы) и экспериментальные. Экспериментально? точка перехода определяется так же, как и для круглых труб, • по критическому значению чисел Re. Критические числа Re >. для точки перехода обычно выражаются либо через координату1! точки перехода, либо через одну из характерных толщин погра-,' ничного слоя б, б* или б**. Для пластинки	;
ReKP = f-^-') =3-105-и 5-105.	J
Имея в виду зависимость б(х) [формула (XII.27)] и выражения^ 6* = -^-б и б** =-^-б*, получим критические значения чисел Я Re соответственно:	д
= 300 000,	=2740;	'	.1
\ V /кр	\ V /кр	Я
=910 „	=36О.	I
\ V /кр	\ V /кр	Я
Для гладкой пластины при малой степени турбулентности набе- я тающего потока критическое значение Re^ достигает величины 
ReKP = 3-10e.	-Я
Экспериментальное определение точки или области перехода^ производят с помощью микротрубки полного напора, перемещая.™
Переход ламинарного пограничного слоя в турбулентный	325
ее от критической точки по потоку при постоянном расстоянии ее носика от обтекаемой поверхности. Зная давление в соответствующих точках, можно по показаниям трубки построить поле скоростей на одинаковом расстоянии от поверхности. Очевидно, что носик трубки при таком перемещении как бы все больше погружается внутрь пограничного слоя, переходя к точкам все с меньшими скоростями. В конце ламинарного слоя скорость достигнет минимума. В области перехода она быстро растет, а внутри турбулентного пограничного слоя скорость по мере перемещения трубки вдоль поверхности вновь убывает. Точкой перехода можно считать точку минимума скорости.
Теория устойчивости пограничного слоя, основанная на изучении влияния малых возмущений на профиль скоростей, дает координату нарушения устойчивости ламинарного пограничного слоя. Можно ожидать, что точка перехода лежит недалеко за точкой нарушения устойчивости.
Не касаясь деталей этой теории, укажем, что с ее помощью получена кривая зависимости 1g Re**p от f , показанная на рис. XIII. 1. Найдя зависимость формпараметра f от х для ламинарного пограничного слоя, как это показано в предыдущем параграфе, можно по известным б** и U найти соответствующие числа Re** и затем для данного крылового профиля построить зависимость 1g Re** от f. Пересечение кривой для данного профиля (показано штрихами) с основной кривой дает координату точки нарушения устойчивости. Если кривая Re**(f) не пересекается с основной кривой, то на всем профиле ламинарный слой устойчив и перехода не будет.
С помощью теории устойчивости были подсчитаны критические числа Re, соответствующие точкам нарушения устойчивости. Так, для распределения скоростей потенциального потока, заданного уравнением
U — U о — ах,
были найдены значения в зависимости от параметра х* = х dU х
= ~nr~dx' ~	• ОчевиДно, что при х* >0 U < 0 и поток
будет диффузорным, а при х* < О U' > 0 — конфузорным. В табл. XII 1.1 приведены критические значения чисел, соответствующие точке нарушения устойчивости.
Аналогичные результаты, полученные для потока со скоростями U = схт в зависимости от показателя степени т, даны в той же таблице.
Многочисленные опыты показали, что при переходе ламинарного слоя в турбулентный важное значение имеет вид функции [/(х).
326
Турбулентный пограничный слой. Турбулентные струи
В конфузорной части потока ламинарный слой намного устой нее, чем в диффузорной. Практически можно считать, что в д; фузорной области ламинарное движение неустойчиво.
Для грубых расчетов в случае обтекания крыловых профи; считают, что при Re = 10вн-10’ точка перехода совпадает с т кой максимума скорости. При Re < 106 точка перехода пере вдается в диффузорную часть, а при Re > 10’ она перемещав1 в конфузорный участок.
Кроме характера потока, на координату точки перехода щественно влияет число Re и степень турбулентности набей
щего потока, шероховатость поверх: стн обтекаемого профиля и др.
С увеличением числа Re набегающего потока участок ламина ного пограничного слоя уменьшается, т. е. точка перехода пр ближается к носику. Влияние степени турбулентности набега! щего потока на положение точки перехода в пограничном сл< продольно обтекаемой пластины показано на рис. XII 1.2. Вел: Ux
чина Rex = составленная для значений х, отделяющих лам
Таблица XIHl
Критические величины		Диффузор			Пластина	Конфузор	।	
х* = — X	U' и	0,075	0,05	0,025	0	—0,05	—0,104
/ 1/6*		120	206	364	575	1230	2630 1 j
\ V							
т		—	—	—0,048	0	0,2	1,0 ‘1
/ U8*				126	660	3200	12 600j
	/кр						
Механизм турбулентного слоя. Профили скоростей	327
парный участок III от переходной области II и области с развитой турбулентностью I, растет при понижении степени турбулентности до некоторого предела. Дальнейшее снижение степени турбулентности е (менее 0,08%) не приводит к возрастанию Rex И) следовательно, к увеличению ламинарного участка слоя.
Отметим также, что с увеличением шероховатости обтекаемой поверхности точка перехода приближается к носику, т. е. ламинарный участок слоя убывает.
§ 2. Механизм турбулентного слоя. Профили скоростей
Строгой теории турбулентного движения ввиду его сложности пока не существует. Это полностью относится к движению в пограничном слое. Из анализа уравнения Рейнольдса (XI.44) можно получить уравнения турбулентного движения в пограничном слое. К сожалению, решить эти уравнения даже для наиболее простого случая не удается.
Основная трудность создания теории турбулентного движения заключается в невозможности получения замкнутой системы уравнений, т. е. в невозможности'выразить компоненты тензора турбулентных напряжений (XI.44) через осредненные скорости движения. Как показано ранее, по аналогии с ламинарными потоками вводят коэффициенты переноса при турбулентном движении, складывающиеся из коэффициентов молекулярного и молярного или турбулентного переносов.
Современными экспериментами показано, что турбулентный пограничный слой по толщине довольно неоднороден. Структура слоя определяется характером стенки обтекаемого тела и свойствами набегающего, или внешнего, потока, поэтому условно всю толщину пограничного слоя можно разделить на две области: внутреннюю и внешнюю.
Внутренняя область полностью определяется стенкой и не испытывает прямого воздействия внешних условий, в то время ‘как на внешнюю область оказывает воздействие не только характер внешнего потока, но и движение жидкости около стенки.
В свою очередь обе области делятся еще на две подобласти: собственно турбулентных движений (внутренняя и внешняя) и четурбулентные; внутри — ламинарный подслой и вне — надслой перемежаемости. В табл. XIII.2 приведены характеристики областей турбулентного пограничного слоя. По структуре слой мож'йо разделить на три области: собственно турбулентное ядро (внутреннее и внешнее); подслой и надслой. Никаких резких границ между областями не существует.
Наиболее тонкой, составляющей около 1% от толщины слоя, является область ламинарного подслоя. В этом тонком слое про-
328
Турбулентный пограничный слой. Турбулентные струи
Таблица Xi
Область		Структура	Толщина, %	Интенсивность турбулентности, %	Доэд э нерка
Внутренняя	Подслой	Ламинарная перемежаемость	1,0—1,5	0	нЯ 58 75—-8 ''1 (И
	Турбулентный Внутренний Логарифмический	Турбу-лентная	15—20	Десятки	
Внешняя	Турбулентный Внешний След		50—40	Единицы	до-|
	Надслой Перемежаемость	Перемежаемость	36—40	2—3 Перемежаемость	
исходит изменение ламинарного потока на стейке до полное! турбулентного на внешней границе. Естественно, что эта г ница размыта и через нее происходит пульсация молей. Турбул? кые движения проникают внутрь подслоя почти до стенки, ос ваясь по своей природе полностью вязкими.
В ламийарном подслое процессы переноса определяются ко фициентами молекулярного переноса v, а и D. В остальной ча< турбулентного пограничного слоя коэффициенты молекуляра переноса пренебрежимо малы по сравнению с соответствуют^ коэффициентами турбулентного, или молярного, переноса.
Заметим, что иногда рассматривают также промежуточн! так называемый буферный участок, в котором коэффнцие! молекулярного и молярного переносов одного и того же поряд Этот участок расположен между ламинарным подслоем и тур; лентной частью пограничного слоя.
Профиль скоростей в подслое, как показано в (XI.6), лин ный, т. е.
и - у =	-2- у Р 4-,
(л s р р. 3	» И ’
или в безразмерном виде fn_____________________ “ . ^*У — Da*
(Х1Г1
Механизм турбулентного слоя. Профили скоростей	329
— ---------------------------------------------------_----
Внутренняя турбулентная область занимает около 15—20% толщины слоя. В этой области наибольшая степень турбулентности, достигающая нескольких десятков процентов, очень ве-дика диссипация энергии, составляющая около полной диссипации. Профиль скоростей в ней строго логарифмический, т. е.
Ф = -^- = Л ln-^-4-В,	(XIII.2)
НО л и В отличны от значений, полученных для потока в трубе (XI.57), соответственно равны А = 2,4 и В = 4,9. Поэтому эту область турбулентного ядра можно назвать логарифмической.
Во внешней турбулентной области степень турбулентности существенно снижается, коэффициенты переноса становятся постоянными, а профиль скоростей отличен от логарифмического. На рис. XII 1.3 показано изменение безразмерной скорости внутри слоя в зависимости от безразмерной координаты Re*, представленной в логарифмическом масштабе. Результаты многочисленных экспериментов, обозначенные кружками, хорошо совпадают вблизи стенки с линейным профилем (XII 1.1), с удалением от стенки с логарифмическим профилем (XIII.2), а при подходе к внешней границе слоя экспериментальные точки существенно отличаются от логарифмического профиля.
Кривая изменения коэффициента перемежаемости у в пограничном слое (рис. XIII.4) свидетельствует о том, что в области надслоя у сильно .убывает от единицы до нуля.
Отклонение профиля скоростей во внешней области слоя от логарифмического закона (XIII.2), показанное на рис. XIII.4, делает необходимым видоизменить этот закон, введя в него дополнительное слагаемое в виде
l?-=-1l"JV- + 8+vr(f)>
330
Турбулентный пограничный слой. Турбулентные струи
где П — так называемый параметр профиля для пластины, ный 0,55; W (-у) — универсальная функция следа, = 2sin2
Очевидно, вблизи стенки W (-у) очень мала, а на rpai слоя равна двум.
Из других попыток получения профиля скоростей для тур лентного пограничного слоя приведем выражение, предложен! Ван-Драйстом:
Re*	__________________________
J [14- ]/ 1 4-4z2Re* [1—ехр(^)]2) dRe*.
* о
Эта формула дает хорошее совпадение с опытом от стенки границы слоя.
Между турбулентным движением в пограничном слое и в тр имеются некоторое сходство и некоторое различие. Сходе заключается в наличии ламинарного подслоя и участка с ло рифмическим профилем скоростей, вместе составляющих 1 называемую внутреннюю пристеночную область, которая за; мает небольшую часть течения в трубе и в слое; течение в I не зависит от условий течения вдали от стенки. Следователь: во внутренней пристеночной области никакой разницы мел течением в трубе и в пограничном слое не существует.
Течения во внешней области существенно различны. В тр; нет взаимодействия с нетурбулентным потоком, нет области пе межаемости. При стабилизированном движении отсутствуют ; перечные составляющие скоростей, и скорости не зависят от п: дольной координаты х; в пограничном слое это не соблюдает
§ 3. Турбулентный пограничный слой на пластине
Вид уравнений движения и импульсов в турбулентном пог ничном слое остается таким- же, как и для ламинарного пог ничного слоя, но значения б, б*, б** и тш будут иными.
d&** _ ти dx ~ риг ’
В основу полуэмпирической теории турбулентного погран: ного слоя положена аналогия между турбулентным движенй жидкости в трубе и в пограничном слое. При рассмотрении зада о движении жидкости в трубе и в ламинарном пограничном щр было установлено: 1) давление зависит только от продольн координаты и не зависит от радиуса трубы и от расстояния нормали к стенке в пограничном слое; 2) скорости на стей
Турбулентный пограничный слой на пластине
331
Б обоих случаях раны нулю; 3) в трубе скорость достигает наибольшего своего значения на оси, а в пограничном слое — на его границе.
Из приведенного анализа можно установить следующие соответствия между параметрами потока в трубе и в пограничном слое.
Радиусу трубы и скорости на оси в трубе соответствует толщина слоя 6 и скорость на границе в пограничном слое. Эти соотношения можно применить к турбулентному движению. Тогда профили скоростей в турбулентном слое могут быть представлены в виде степенного или логарифмического законов, полученных ранее для труб.
Найдем сопротивление продольно обтекаемой пластины, воспользовавшись степенным законом
Введя обозначения t)j = получим величину 6**, необходимую для уравнения импульсов, 1 1 о	о
П'Л1
п -Ь 1
^"+1 I1 = п Л 2п -j- 1 |о (п -|- 1) (2п	1)' °
1 при п — —
6** =^6.
(XIII.4)
Для установления связи между т и 6 воспользуемся степенным законом, полученным для турбулентного движения в трубе (XI.74). Заменив в этом уравнении г0 на 6 и umax на U, получим
___
тда = 0,0225р6/2(-^^ 4.	(XIII.5)
Подставив полученные выражения в уравнение импульсов Для пластины, будем иметь
~	= 0,0225 (—бГ~.
72 dx ’	\ v )
Проинтегрируем это уравнение, используя для простоты гранич-ное условие: при х = 0 6 — 0, означающее, что турбулентный
332
Турбулентный пограничный слой. Турбулентные струи
пограничный слой начинается с передней кромки пласти! Получим 6 = 0,37х	5 или, имея в виду (XIII.4),	।
6** = 0,036х(-^) 5 .	(XIII
Видно, что для турбулентного пограничного слоя характ 4
ные толщины слоя пропорциональны х 5, в то время как для ; минарного (XI 1.26) они пропорциональны ]/х: Следователь турбулентный слой растет по координате х более интенсив чем ламинарный.
Зная 6, легко по (XIII.5) найти tw и,
следовательно,
величи
полного сопротивления трения (двух сторон) пластины. Оно ра:
i	_j_
Х=2|т[е,</х = 0,072р£/26/(^-) 5 о
Коэффициенты местного и полного сопротивлений пластины будут:
1 1
= 0,0576	5 =0,0576 Rex s;
cf — —(P p —
\	_1_	_2
C.=—~— = 0,072 (—\ 5 =0,072 Re 5
Сравнение с экспериментом показывает, что в последней ф муле лучше взять коэффициент не 0,072, а 0,074, т. е.
_ 1
Cf = 0,074 Re s.	(XII
На рис. XIII.5 в логарифмическом масштабе приведена по ценная зависимость С. от Re (кривая 2); здесь же (кривая /) пр
Турбулентный пограничный слой на пластине
333
дена зависимость Cf от Re для ламинарного пограничного слоя. Результаты многочисленных экспериментов нанесены точками. Из рис. XIИ.5 видно: 1) при одинаковых числах Re коэффициент полного сопротивления при турбулентном пограничном слое намного больше, чем при ламинарном; 2) формула (XIII.7) хорошо совпадает с экспериментом при небольших значениях чисел Re в пределах от 5-Ю5 до 107. При больших значениях Re приведенная формула дает заниженные результаты.
Из первого вывода следует более общий практический вывод: для уменьшения сопротивления трения хорошо обтекаемого тела необходимо добиваться увеличения участка ламинарного пограничного слоя ' и  уменьшения участка турбулентного.
Из многих опытов с длинными пластинами Фолкнер получил другой чисто эмпирический закон сопротивления в виде
_ 1
=	= 0,00655 Re** 6,	(XIII.8).
z/Л**
где Re**=-^—.
Если уравнение импульсов для пластины (XIII.2) представить в виде
d6** _ d Re** _ Тц,
dx d Rex pU2
и воспользоваться равенством (XIII.8), то получим уравнение импульсов в виде
_ 1
-^7 = 0,00655 Re** 6.	(XIII.9)
Это уравнение легко интегрируется. Произвольная постоянная определится из условия, что турбулентный пограничный слой начинается с носика пластины, т. е. при х — 0 6**=0. .Интегралом последнего уравнения с использованием указанных гра-6 ничных условий является выражение Re** =0,0153ReJ или, имея в виду, что
6
окончательно получим 6** = 0,0153х7 .
Из последней формулы видно, что толщина потери импульса и, следовательно, две другие характерные толщины турбулент-кого пограничного слоя пропорциональны х 7 .
334 Турбулентный пограничный слой. Турбулентные струи
Зная б** или Re**, легко по (XII.8) найти местный коэффи
Т/	7
циент сопротивления cf = —= 0,0263 Re* и полный коэф
₽Т
фициент сопротивления	'
1 _ 1
Cf= f -х^х- =0,0307 Re 7,	(XIII.10*
Р-^-м
Ul	0
где Re = —.
Последний закон сопротивления хорошо совпадает с экспери^ ментом и для чисел Re, значительно больших 107.
Логарифмический профиль скоростей для турбулентного по*, граничного слоя, полученный по аналогии с турбулентным двш жением в трубе имеет вид	;
 х ш <5 -
(XIII. 11]
Закон сопротивления, соответствующий
логар ифм ическому
профилю скоростей, довольно сложен. Местный коэффициент со*
противления в этом случае выражается зависимостью
Cf U2 (5,75 lg Re** + 3,8)2 '	(XIII. 12);
Р 2 }
Существуют и другие эмпирические законы сопротивления^ например формула Прандтля—Шлихтинга, имеющая вид
С; = 0,455(lg Re)-2-58.
Кривая 3 (рис. XIII.5), соответствующая этой формуле, лучшее совпадает с экспериментом, чем кривая,' соответствующая фор’ муле (XIII.7).	?
Хорошо соответствует опытным данным формула Шультца—•
Грунова (кривая 4 на рис. XIII.5)	•	j
Cf = 0,427 (lg Re —0,407)-2’64.	(XIII. 13),
§ 4» Турбулентный пограничный слой на произвольном профиле	;
Отсутствие строгих теоретических основ турбулентного движения привело к появлению значительного количества полуэмпи-; рических методов расчета турбулентного пограничного слоя н$ профиле. Изложим здесь разработанный Л. Г. Лойцянским та^ называемый однопараметрическиий метод расчета. Он выгодно отличается своей простотой и глубокой связью с методом таког^ же расчета ламинарного пограничного слоя.	!
Турбулентный пограничный слой на произвольном профиле
335
В турбулентном пограничном слое, так же каки в ламинарном, вводится формпараметр. Уравнение импульсов здесь имеет такой же вид, как и для ламинарного пограничного слоя. Допуская, что кривые зависимостей H(f) и £(/) подобны в ламинарном и турбулентном пограничных слоях, получим простое решение задачи.
В отличие от ламинарного слоя, в котором формпараметр f., (XII.30) и параметр £ имели вид:
U'6**2 v _rws** t\U
Re**,
(XIII.14)
— Тц) I
~ pU2 Ке ’
для турбулентного пограничного слоя в целях большей независимости решения от числа Re введен более общий вид указанных
величин:
/ = ^6**6 (Re**); £ = ^G(Re**),
(XIII.15)
где G(Re**) — некоторая функция от Re**, выбор которой будет произведен далее.
Выразим уравнение импульсов (XII.22) через / и £:
6** (2 + Н) =	.
dx 1 U 41	’ pU2
Умножив ' уравнение на G(Re**), получим
G (Re**)	-И (2+ #) = £•	(XIII. 16)
Преобразуем первое слагаемое, представив его через производную от произведения G(Re**)6**. Тогда
G(Re**)-^ = Л FG(Re**)£^^-l — 6**G' (Re**)	=
иХ иЛ |	t/ С/ J	м-Л
S..O' (Re..) ( Д	+ "2Д \.
dx \' U )	'	' \ v dx 1 у )
Так как
И ЯХ** 7/'Л**2
6**G' (Re**)	~— G' (Re**) =
_ Re**G' (Re**) Г **-. d&** n^fG' (Re**) _
~ G(Re”) x > dx	1 G(Re’*) —
= m (Re**) G (Re**) + tn (Re**) f,
336
Турбулентный пограничный слой. Турбулентные струи
где
m(De**4 — Re**G'(Re**) m(Ke ) —-------g (&**)—
{XIII. 17?
то
6 (Re**)	(f -mG(Re**)	-m(Re**) f
G (Re**)	\4- (f yjr ) — tn (Re**) f 1.
4	' dx 1 + m (Re**) L dx \1 U J 4 "J
Подставив полученное выражение в (XIII. 16), запишем
или, раскрывая производную, окончательно получим	,
£ =	(/)+-£ A	(XIII.1S
где	)
F (f) = (H-m)£- [3 + m + (l	(XII.1S
;
Зависимость F(f) определяется величинами G(Re**), H(f) ,i £ (/). Для нахождения G(Re**) сравним выражения f и £ дл; ламинарного (XIII. 14) и турбулентного (XIII. 15) пограничнц слоев. Из этих формул видно, что функция G(Re**) для ламинар ного слоя и для пластины (j — 0), и для произвольного профил| равна Re**. Из (XIII. 14) получим	4
' G(Re**) = Re**=^£(f) = (e^-) £(0).
Чтобы можно было воспользоваться экспериментальными дан) ными, полученными для турбулентного пограничного слоя щЯ пластине, необходимо ограничиться областью изменения формЯ параметра, мало отличающейся от нуля. Далее будет показано» что положительное значение формпараметра f может быть скольйЦ угодно большим, а отрицательное значение f должно быть близЯ ким к нулю. Таким образом, решение пригодно для любых koi™ фузорных потоков и потоков со слабой диффузорностью.
Такое ограничение позволяет представить функцию G в видЯ G(Re**)~(^)	1
V	/f=o’	(Я
причем значение коэффициента пропорциональности здесь несу» щественно, так как из (XIII. 17) видно, что его величина не поЯ влияет на функцию т, определяющую вид/7 (/). Следовательно» можно воспользоваться любым эмпирическим законом для турбуЯ лентного слоя на пластине. *	,’Н
Турбулентный пограничный слой на произвольном профиле 337
Если воспользуемся законом (ХШ.8), то получим
G(Re**) = (P^-)f=o= 153,2 Re**V.	(XIII.20)
Следовательно, теперь формпараметр и параметр будут иметь вид:
f = 153,2	6** Re**’5' = 153,2 ~ Re**’5';
£ =153,2 Re**’5'
(XIII.15)
(XIII.21)
а при f = 0, как следует из (XIII.20), £ (0) = 1.
Так как т при выбранном G (Re**) равно
•	_ Re**G' (Re**) _ 1
т~ G(Re**)	6 ’
то, согласно (XIII.19), получим
р=4е-(4+т//)л
(XIII.22)
Теоретических зависимостей Н([) и £(/) не существует. Полу- . ченные экспериментальные данные (некоторые из них показаны на рис. XIII.6) говорят о том, что в диффузорной области, близкой к отрыву, функции H(f) и £ (f) явно нелинейны, а одного формпараметра недостаточно для характеристики движения, т. е. вблизи отрыва однопараметрический метод .не пригоден.
22 И. Л. Повх
338
Турбулентный пограничный слой. Турбулентные струи
В слабых диффузорных потоках (f < 0) на пластинке (/ = 0) и в конфузорной области (f > 0) экспериментальные tohki! ложатся на одни кривые. Для простоты расчета можно Н и | в указанной области брать постоянными. Тогда F(f) по (XIII.22) будет линейной функцией F = а — bf, такой же, как и для ламинарного слоя, но с коэффициентами, равными а = 1,17, b = = 4,84-5,0 [при Н = 1,33-5-1,41 и £(0) = 1]. Используя эти коэффициенты, по (XIII.22) получим выражение для функции’ F (f), которое подставим затем в уравнение (XIII.18).	'
Получим уравнение импульсов, отличающееся от соответствую^ щего уравнения для ламинарного пограничного слоя (XI 1.33)) лишь значением коэффициентов а и Ь, в виде
df	U' f U" ,U' \ .
dx — а U \ U' Ь -U )f'
Интегралом этого уравнения является выражение
+	(XIII.23)^
Если турбулентный пограничный слой начинается с критиче-ской точки, т. е. ламинарный участок отсутствует, то С = 0 й
X
=	(ХШ.24^
Так как в числитель и знаменатель правой части равенства входит скорость, то, следовательно, критическая точка (х = 0), в которой скорость равна нулю, есть особая точка. Раскрывая неопределенность, получим
(0)	j
При наличии участка ламинарного пограничного слоя выражен ние для f(x) будет
X
а
' w — Ub (x)
ub
xt
u't
(XIII.25;
где индексом t обозначены соответствующие величины в точке перехода ламинарного слоя в турбулентный. Значение формпараметра f(t) находится по формуле (XIII.21).
Таким образом, при наличии ламинарного участка формпй! раметр f будет определяться по формуле	;
Дх)
_U'(x)
Ub (х)
’ х	L'
a j Ub-' (?) dl 4- 153,2vt/»-2 Re"6
- xt
(XIII.26}
Турбулентный пограничный слой на произвольном профиле 339
Число Рейнольдса Ref в точке перехода находится по теории ламинарного слоя. Зная f(x), можно по (XIII.21) найти Re**, а затем по (XIII.20) G(Re**). Учитывая, что в принятом приближении £ = 1, по формуле (XIII.5) найдем напряжение трения на стенке.
Местный коэффициент трения с, получим из соотношения
£, = -^ = 0(1^ = 0,0131 Re** б.	(XIII.27)
р ~
Таким образом, все параметры потока, в том числе полное сопротивление трения и полный коэффициент сопротивления трения, могут быть определены. Так как при безотрывном обтекании сопротивление будет определяться почти полностью трением, то, очевидно, в этом случае для уменьшения сопротивления необходимо увеличивать участок ламинарного пограничного слоя. Иначе обстоит дело с плохо обтекаемыми телами. Из кривых рис. XIII.6 видно, что отрыв турбулентного слоя происходит в точках (£ = 0) при значении формпарметра fs = —(3 -5- 6). Опыты с обычными авиационными профилями дают fs — —2, так что общий интервал значений fs в турбулентном слое находится в пределах fs = —(24-6).
Заметим, что по опытам лаборатории аэродинамики ЛПИ величина fs зависит от интенсивности диффузорного участка обтекаемого тела. Чем медленнее убывает скорость в диффузорном участке, тем дальше от носика находится точка отрыва и тем больше абсолютное значение формпараметра fs.
В ламинарном слое отрыв происходит при значении формпараметра fs = —0,089. Очевидно, для всех указанных случаев отрыв турбулентного слоя происходит значительно позже, чем ламинарносо.
Затягивание точки отрыва турбулентного слоя существенно влияет на величину полного сопротивления плохо обтекаемых тел, таких, как шар или поперечно обтекаемый цилиндр. На рис. XIII.7 показана кривая коэффициента сопротивления шара в зависимости от числа Re набегающего потока. Видно, что при некотором значении Re, называемом в дальнейшем критическим числом Рейнольдса (ReKP), происходит резкое падение коэффициента сопротивления. Это явление называется кризисом обтекания плохо обтекаемых тел. Сущность кризиса обтекания состоит в следующем.
Сопротивление плохо обтекаемых тел определяется прежде всего сопротивлением давления, которое зависит от величины области отрыва: чем больше область отрыва, тем больше сопротивление. При докритических числах Re отрывается ламинарный
340
Турбулентный пограничный слой. Турбулентные струи
слой, и точка отрыва в этом случае расположена под углсц Ф 82° (рис. XIII.7). Оторвавшийся слой переходит в турбУ лентный лишь на некотором расстоянии от тела.	J
При увеличении числа Re точка перехода приближается к тел; и при значении числа Re, равном критическому, достигает точй отрыва. Таким образом, при Re Re^ отрывается уже не лами парный слой, а турбулентный. Наличие турбулентных пульс! ций приводит к более интенсивному обмену энергией между по граничным с'лоем и внешним потоком. Поэтому кинетическая энергия частиц жидкости в пограничном слое увеличивается Последнее обстоятельство является причиной затянутого отрыва
турбулентного пограничного слоя по сравнению с ламинарным; т. е., если Re ReKP, точка отрыва расположена при ф = = 110-ь 120° (рис. XIII.7).
Таким оразом, величина области отрыва меньше при Re
RKP. Этим и объясняется резкое уменьшение сопротивлений плохо обтекаемого тела при достижении числом Re критической значения.	Ji
Величина ReKp сильно зависит от степени турбулентности н$ бегающего потока: большей степени турбулентности соответствуй меньшее значение ReKp.
Кризис обтекания можно вызвать искусственно и при докри тических числах Re, если искусственно турбулизировать погр.| ничный слой. Таким образом, для уменьшения сопротивленв^ плохо обтекаемых тел надо уменьшать величину ламинарной участка с тем, чтобы отрывался турбулентный слой.	и
§ 5. Профильное сопротивление	3
Во многих случаях даже при безотрывном обтекании сопро тивление трения не составляет основную часть профильного ей противления. Поэтому в большей части задач при безотрывной обтекании необходимо знать профильное сопротивление, т. es сопротивление трения плюс сопротивление давления.	J
Профильное сопротивление	341
Формулы, позволяющие определять профильное сопротивление крыла (ХП.2) и тела вращения, не могут быть использованы для расчета ввиду невозможности определения толщины потери импульса 6** на бескрнечности за обтекаемым телом.
Существующие методы определения сопротивления сводятся к выражению 6^* через параметры потока на задней кромке обтекаемого тела. Эти параметры могут быть найденв! как теоретическим, так и экспериментальным путем.
Для установления указанной связи применим к следу за обтекаемым телом интегральное соотношение пограничного слоя (XI 1.22). Так как в следе тю = 0 ввиду отсутствия стенки, то уравнение (XI 1.22) будет иметь вид
+	+	0.	(XIII.28)
Разделив это уравнение на 6** и проинтегрировав его по х от задней кромки до бесконечности за телом, получим
, С , <4 , Т 8* U' , _Л
In п у2 + J §** и dx — 0.
°° *к
Для вычисления последнего интеграла необходимо знать за-5*
висимость gjv = Н от х в следе.
Ряд исследований показал, что Н(х) зависит от формы профиля и его обтекания. Наиболее простой является линейная зависимость Н от х, для которой
Hcp=-L(HK + Hm).
После подстановки найденного значения в интеграл последнее уравнение будет иметь вид
1п-ё—1п^ + 4-(Як + Ясо)1п^=0
8К	2
или
, С , /ук\2+4("к+"«>) 1ПГ-=1ПЫ ик
Освобождаясь от логарифмов, запишем
=	.	(XIII.29)
\ С/со/
Если найденное значение 6^* подставить в (ХП.2), то коэффи-
342
Турбулентный пограничный слой. Турбулентные струи
циент профильного сопротивления будет выражаться следующей -
формулой:
, _ 26^ _2б’’	+
'ХР~ Ь Ь \Ua)
(ХШ.ЗО)
Так как на бесконечности за телом поле скоростей будет вы- ! равниваться, можно считать, что разность U — и = uL будет , всегда малой величиной; пренебрегая квадратом этой малой величины, найдем:
б	б	‘	.
6 » = J (1 - ТГ ) “f = J V (1 - т-) “ч=
о	о	!
б
= J (1 —^dy-=^. о
Таким образом, имеем 6^* = и — 1.
Значение Нк на задней кромке зависит от характера обтекания и меняется в пределах 1,3—1,4 для продольно обтекаемой пластины и 1,8—2,0 для толстых профилей.
Так как величина мало отличается от единицы, то неточность определения показателя степени может существенно повлиять на результаты расчета. Обычно берут Нк = 1,4. ТогДа формула (ХШ.ЗО) окончательно будет иметь вид
с«=2(й;Г-Т' (хш.зо
Экспериментальная проверка показала пригодность этой фор-, мулы для широкого класса обтекаемых профилей.
Если воспользоваться для определения 6,** формулой (XIII.26), • предполагая, что а = 1,17 и b = 5 и что имеет место ламинар- ; ный участок с координатой перехода xt, то получим	;

Величина у находится путем интегрирования по верхней и' нижней поверхностям профиля до х — 1 и затем сложения полученных значений. При подстановке определенной таким образом величины 6к* (при этом U = 77к) в формулу (XIII.31) выражение;
Снижение сопротивления добавками
343
для коэффициента профильного сопротивления может быть представлено в виде
1	1	25 / «»* \
r 0,G306	7
с*р = —г: JUW13IRe \й^) \ь)
Re7 Lx<
(XIII.32)
Определение Схр по этой формуле не требует знания величин UK пНк, необходимо лишь найти величину в квадратных скобках в степени 6/7 для обеих поверхностей крыла отдельно и. затем их сложить. Координата точки перехода xt и соответствующее значение 6** могут быть найдены теоретически (см. п. 1). Для обычных чисел Рейнольдса приближенно можно считать, что точки перехода и минимума давления совпадают. При этом допущении все расчеты упрощаются.
§ 6. Снижение сопротивления добавками
Разработка методов снижения сопротивления являлась важнейшей задачей с первых дней существования науки о движении жидкостей и газов. В настоящее время в связи с развитием дальних нефтепроводов и газопроводов, совершенствованием энергетических машин, увеличением скоростей водного и воздушного транспорта снижение сопротивления становится одной из важнейших научно-технических проблем.
Решение этих задач одинаково важно как при внешнем обтекании (крыло, корабль, ракета и пр.), так и при внутренних потоках (трубы, машины, реакторы и пр.).
Так как большинство практически важных потоков происходит при больших числах Re, то, следуя Прандтлю, можно утверждать, что воздействие вязкости, как показано в п. 2Д наиболее существенно сказывается не во всей толщине турбулентного пограничного слоя, а лишь в небольшой внутренней .части ее (составляющей 10—15%), непосредственно прилегающей’к поверхности обтекаемого тела.
В табл. XIII.2 показано распределение потерь энергии по высоте слоя. Если напомнить (XII. 1) о том, что динамическое влияние вязкости выражает толщина потери импульса 6**, то, пользуясь степенным законом скоростей на пластине и соотношением (XIII.4), получим 6**, отнесенную к 6, в зависимости от числа Re в следующих величинах:
106	1 06	3- 10°
1	1	1
7	9	10
0,097	0,091	0,083
Re ............ 4-10»
344
Турбулентный пограничный слой. Турбулентные струи
Поэтому все методы снижения сопротивления обычно сво- 'j дятся к воздействию на внутреннюю область турбулентного по- т граничного слоя, т. е. на область наиболее существенного изме- ;• нения скоростей.	'
Среди ряда методов снижения сопротивления, таких, как от- i; сос и сдув пограничного слоя, колебание обтекаемой поверх- г ности с определенными частотами и амплитудами и др., ! в последние годы большое распространение получил метод доба-  вок различных частиц в область потока вблизи стенки. .!
Не имеях возможности рассмат- j ривать здесь историю развития ; этих исследований и довольно большое количество различных > теоретических обоснований и мето- : дов, изложим лишь физические ‘.‘1 соображения и методику расчета1 *. •’1, Добавляя в пристеночную об-ласть турбулентного потока воды 1 g или воздуха (жидкости или газа) -3 соответствующим образом подоб- 1 ранные частицы, можно, как по- , казывает эксперимент, существен- J ным образом (на 60—80%) снизить ’ гидродинамическое сопротивление. Заметим, что введение таких час-; тиц в струи, след и другие потоки г в которых нет стенок) также сильно J например пожарная струя делается

свободной турбулентности влияет на их структуру, более компактной и более дальнобойной и пр.
Действие добавок при снижении сопротивления проявляется ’! в увеличении толщины ламинарного подслоя при сохранении -' линейного профиля скоростей в нем и логарифмического в тур- i булентной области. На рис. XIII.8 приведены кривые зависимо-^ сти скорости, отнесенной к V*, от логарифма для чистой'; воды и воды с добавками полимеров при концентрации их;, (1,44-2,5)  10"4. “ слоя филе
Видно, что добавки утолщают толщину под-,й и увеличивают значение В на ДВ в логарифмическом npo-jj скоростей (XIII.2), представленном в виде	 i
“ =_Lln^4-B + AB = -LlnRe*+Вх.	:;i
V* % v 1	1	х	1	1
$ многочисленных опытах с водой и воздухом при различных! добавках величина универсальной постоянной х оставалась |
В
1 Повх И. Л., Ступин-А. Б. О влиянии упругости растворов полимеров на $
снижение сопротивления. — «ПМТФ», 1972, № 1, с. 63—68.	•
Снижение сопротивления добавками
345
такой же, как и в потоках без добавок. Значение В, равное для чистой воды и воздуха 4,9—5,0, увеличивается при введении добавок до 10—12.
Зависимость коэффициента сопротивления X от числа Re для течений в трубе с добавками полимера (полиакриламида) при концентрации от 10~5 до 5-Ю"4 приведена на рис. XIII.9. Легко видеть, что добавки полимеров приводят к снижению коэффициента сопротивления, которое начинается в точках 77(-, называемых пороговыми точками. Видно, что с увеличением концентрации пороговые значения /7, и, следовательно, пороговые скорости уменьшаются.
Природа снижения сопротивления при внесении частиц может быть объяснена следующим образом. Частицы, попадая в область больших градиентов скоростей, которые имеют место в пристеночной области, создают анизотропию вязкости, увеличивая поперечную составляющую по сравнению с Продольной. Так как из-за малой концентрации добавок плотность жидкости или газа можно считать не изменяющейся, то коэффициент анизотропии вязкости' А х можно представить в виде
A =&-=%!- = 1 Их V, v ’
Увеличение вязкости в непосредственной близости от стенки должно привести к утолщению ламинарного подслоя. Принимая, как это видно в формуле (XI.51), линейную зависимость толщины ламинарного подслоя от вязкости и считая неизменной вторую универсальную постоянную турбулентности а, получим значение толщины ламинарного подслоя 61( при наличии добавок в виде
6i = «V-A-
346	Турбулентный пограничный слой. Турбулентные струи	.j
Используя эту величину для определения произвольной по- “ стоянной в (XI.49), получим значение постоянной в лога- ' рифмическом	законе	для	скоростей	1
Вх	= аА± — In ос/11	(
х	ч
вместо В	= а----—	In а	по (XI.53).	’’
1	i
Тогда ЛВ =	— В = а (Л г — 1)-----— In будет един- *
ственная величина, характеризующая влияние добавок на про-  филь скоростей и сопротивление.	<
.Коэффициент анизотропии Лг представляет общефизический интерес, для слабых растворов он экспериментально исследовался и его величина рассчитывается [13].
Для понимания физической природы снижения сопротивления частицами приведем на рис. XIII. 10 кривые, характеризующие а влияние добавок полимеров (0,01% полиакриламида) на вели- ' чину продольных и поперечных пульсаций скоростей. Из приве- : денных кривых следует, что поперечная составляющая при вводе 1 частиц уменьшается в несколько раз. Существенное снижение поперечной составляющей наблюдалось и во многих последую-/ щих опытах.	1
Продольная составляющая на приведенных кривых тоже не- i много уменьшается с введением частиц. В других, более поздних, измерениях продольная составляющая не только не уменьшалась, • но и увеличивалась. Такое действие добавок на пульсации скоро- : стей утолщает ламинарный подслой около стенок, а в свободных |
Снижение сопротивления добавками
347
струях уменьшает их поперечное сечение и делает их более дальнобойными.
Опыты с трубопроводами, кораблями и турбомашинами показывают, что соответствующим образом подобранные добавки
могут существенно снижать сопротивление и повышать к. п. д. машин. В качестве примера приведем на рис. ХИПП кривые к. п. д. насоса, работающего на чистой воде и с добавками полимеров. Видно, что при концентрации добавок от (1 -=-2)  10“3%
к. п. д. растет, увеличиваясь на 3—5 %. Последующее увеличение концентрации до 8-10-3% не приводит к дальнейшему росту к. п. д., но оно при этом всегда выше к. п. д. насоса, работающего на чистой воде. Аналогичные результаты имеются и по другим машинам, а также по элементам проточной части.
Какие же добавки надо вносить в поток для получения снижения сопротивления? Пока строгой теории о выборе типа добавок нет. Из анализа выполненных исследований следует, что все хорошо подобранные добавки могут существенно снижать сопротивление. При оптимально подобранных концентра
Рис. XIII.11
циях величина снижения со-
противления достигает 70—80%. Увеличение концентрации добавок более оптимальной приводит к снижению эффекта. Из двух добавок, используемых для снижения сопротивления в воде, полимеры и поверхностно-активные вещества (ПАВ), первые дают наибольшее снижение при концентрации 0,01%, а вторые
дают примерно такое же снижение при концентрации на один порядок больше, т. е. 0,1%.
Для потоков воздуха в качестве добавок использовались частицы графита, цинка, алюминия, стекла размером 10—30 мкм
при различных концентрациях.
Так как наилучший эффект снижения сопротивления дают полимеры, которые в области больших градиентов скоростей вытягиваются в нити, то и при подборе других частиц для снижения сопротивления следует выбирать такие, которые вблизи стенки образовывали как бы подвижную пленку, уменьшающую поперечную пульсацию скоростей.
348 Турбулентный пограничный слой. Турбулентные струи j
Имеются мнения по генерированию таких частиц (существуют1 щих даже ограниченное время) в морской воде или других движу-? щихся жидкостях с помощью электромагнитных полей или хими-;
ческих катализаторов.
Заметим, что различного рода добавки, изменяя сопротивле- -д ние, существено влияют на процессы переноса тепла и вещества, 1 а также на акустические эффекты, возникающие при обтека-J нии тел.	;|
§ 7. Свободная турбулентность. Турбулентные струи. 1
Ранее рассматривались задачи, относящиеся к турбулент- 1 ному движению вдоль твердых стенок или к так называемой '
пристеночной турбулентности. В
Рис. XIII.12
Картина взаимодействия двух
технике имеются потоки,'от-..’ носящиеся к области свобод- | ной турбулентности, глав- •] ная особенность которой — полное отсутствие стенок, | ограничивающих течение $ жидкости.	Д
К свободной турбулентно- 1 сти обычно относятся три ТИ- ч! па потоков (рис. XIII. 12): ' • а — два взаимодейству- 4 ющих параллельных потока, движущихся с различными j скоростями;	?
б — затопленная струя; . й в — след за неподвижным телом, обтекаемым безгранич-. 1 ным потоком, или спутное ч течение за движущимся те-. ’ лом.	ii;
При очень малых скоро- -1 стях все указанные потоки., и могут быть ламинарными, ho J для технических задач пос-1'ii ледние не имеют практиче- ( ского значения и поэтому 1 в книге не описываются. j параллельных потоков пока-I
зана на рис. XIII. 12, а (стенка, два потока с разными скоро-,; стями).
Из-за наличия турбулентного перемешивания поверхность раз- . рыва размывается и образуется зона перемешивания, ширина .1 которой в направлении движения увеличивается.
Свободная турбулентность. Турбулентные струи	349
Спутное течение, или аэродинамический след, возникает за движущимся в неподвижной жидкости телом. Частицы жидкости увлекаются движущимся телом, и по мере его удаления в некотором фиксированном сечении все больше расширяется область возмущения. Поэтому, рассматривая картину потока в данный момент времени, за телом можно видеть расширяющийся след с убыванием скорости движения в нем.
При обращенном движении, т. е. при обтекании потоком жидкости неподвижного тела, также образуется след.
Свободная затопленная струя возникает при истечении жидкости из отверстия или насадка. Вследствие турбулентности свободная струя частично смешивается с окружающей ее неподвижной-жидко-стыо и увлекает прилегающие слои жидкости за собой. Поэтому расход через поперечное сечение струи по мере удаления от источника возрастет. Так как во всей области затопленной струи давление всюду одинаково, то количество движения по длине струи остается постоянной величиной.
Все рассматриваемые течения обладают свойствами, характерными для пограничного слоя, а именно: линейные размеры поперечных сечений рассматриваемых потоков малы по сравнению с протяженностью в продольном направлении; скорость поперек потока изменяется значительно интенсивнее, чем вдоль потока. Следовательно, для изучения потоков со свободной турбулентностью можно воспользоваться дифференциальными уравнениями пограничного слоя. В частности, для плоского течения такие уравнения будут иметь вид:
ди ,	ди	1 дх ди	,	до	Л
«-5---=	"5--=
дх 1	ду	р ду	’ дх	1	ду
где т — касательное напряжение, обусловленное турбулентным и вязким трением.
Слагаемое, зависящее от давления, опущено, так как можно считать, что давление во всей области потока постоянно.
Не приводя здесь решения уравнений для свободной турбу1 лентности, в частности для струй, рассмотрим лишь основные результаты теоретических и экспериментальных исследований плоских и осесимметричных затопленных струй.
Под затопленными понимают струи, физические свойства вещества которых одинаковы или мало отличаются от физических свойств среды, в которую они втекают. Очевидно, струя воды в воздухе и воздуха в воде — незатопленные струи. Теория не-затопленных струй нами не рассматривается.
Схема движения жидкости в затопленной струе показана на Рис. XIII.13.
Предполагается, что в начальном, или выходном, сечении струи величина и направление скорости постоянны по всему
350 Турбулентный пограничный слой. Турбулентные- струи
сечению. Далее по потоку ядро струи с постоянной скорости убывает, а с краев образуется область заторможенной жидкост! Эту область часто называют пограничным слоем струи. Участ^ от начального сечения до окончания ядра струи, т. е. до nepexd
ного сечения, называется начальным участком. За переходны сечением идет основной участок, в котором область постоянна! скоростей отсутствует и пограничный слой занимает все попере’
ное сечение. Как видно из рис. XIII. 13, в основном участке стр' с ростом продольной коодинаты х по-прежнему расширяете а скорость на оси струи убывает.
Поле продольных скоростей воздушной струи, вытекающей5 прямоугольного отверстия 0,03x0,65 м, показано на рис.XIIIЛ Как видно из кривых, скорость при выходе была постояннс равной 35 м/с. Уже на расстоянии 0,2 м и более ядро плос:
Свободная турбулентность. Турбулентные струи
351
струи отсутствует, скорости на оси убывают, а ширина струи растет, достигая на расстоянии 0,75 м от начального сечения величины 0,3 м. На этом же рисунке построены безразмерные профили скоростей. На оси ординат отложены продольные скорости, отнесенные к осевой скорости, а по оси абсцисс расстояние от оси, отнесенное к расстоянию до точки, в которой скорость равна половине максимальной1. Видно, что в таких безразмерных координатах все кривые совпадают, т. е. существует полное подобие безразмерных профилей скоростей в основном участке струи. Приведенный вывод верен и для струй круглого сечения.
Таким образом, если обозначить ширину плоской струи буквой b и радиус границы круглой струи—ггр, то соответствующие безразмерные профили скоростей можно представить в виде:
и max \ b )
(XIII.33)
“max	V гр /
, Эти безразмерные профили скоростей универсальны.
Теоретически и на основании многих экспериментальных исследований можно считать, что граница плоской и осесимметричной струй — линейная функция от х. Следовательно, если х отсчитывать, от так называемого полюса струи, образованного пересечением продолжения границ струи (рис. XIII. 13), то b — = ах и г,.р = агх и, следовательно, безразмерные профили скоростей (XIII.33) могут быть представлены в виде
^max \ х / ^max \ х J
Условие постоянства количества движения вдоль струи
J рм2 ds = const, s
при этом для круглой струи элементарная площадка ds будет ds = 2лг dr, для плоской струи на единицу длины ds = 1 • dy.
Имея в виду последние равенства, получим количество движения Для осесимметричной струи
ггр
2л j рм2гdr = лгоРо^о,	(XIII.34)
.	о
1 Выбор такого характерного расстояния вызван трудностями экспериментального определения у, при котором скорость становится равной нулю.
352
Турбулентный пограничный слой. Турбулентные струи
в то время как для плоской струи оно равно ь
j ри2 dy = pdUpb0, о
где индексом 0 обозначены значения величин чении.
Представив оба интеграла в безразмерном что р — ро, получим соотвественно: ггр Го
1.
(XIII,
(XIII;
в начальном се;
виде и, считая.
ь
Ьо
Г / и \2
2
1;
Так как безразмерные величины, ные выражения, можно
представить
г ____ г ггр е
ra	г гр га
о 4 “°
в
входящие в подынтеграль; виде двух сомножителей’
у _ у ь
^0	60
и _ Ц ит. ит ио '
то интегралы получат вид:
г .. \ й / Г—	/•
1;
(ХШД
о
1
1.
-о
о
Согласно (XIII.33), оба интеграла будут равны некото числам, значение которых может быть определено теоретичес* или экспериментально. Теоретически полученные значения й тегралов равны:
(	= 0,0464;
J \ ит /
0
1
2
= 1,65, (XIII.3
о
где т)1 = — ' гр
Тогда окончательно из (XIII.35) получим величину мак мальной скорости на оси круглой струи в виде  const const X
U-m — Г г гр
и на оси плоской струи'
const
const
Уь Ух
Осесимметричные струи
353
Это означает, что скорость на оси круглой струи обратно пропорциональна расстоянию от полюса, в то время как для плоской струи она обратно пропорциональна корню квадратному из того же расстояния. Следовательно, скорость на оси круглой струи затухает быстрее, чем на оси плоской струи.
§ 8.	Осесимметричные струи
Рассмотрим основные характеристики осесимметричных струй, получивших широкое распространение в технике. После подстановки значения первого из интегралов (XIII.36) в равенство (XIII.35) получим
2	о,0464= 1,
откуда
-Г± = 3,3-£-.	(XIII.39)
В переходном сечении, где кончается ядро струи, ц0 = «тах и, следовательно, безразмерный радиус в переходном сечении всегда имеет постоянное значение, равное
= 3,3.	(XIII.40)
\ г О ]п
Объемный расход жидкости в поперечном сечении струи можно определить по формуле
ггр	'	1
Q = 2л j urdr = 2nwmr?p J тц dr^ — о	0
= 2лг^0-^-(^)
Согласно (XI11.39), имеем
(\ 2
In.) = 10,8 (-^2-У.
rQ /	\	/
Так как лго«о = Qo есть расход в начальном сечении, а интеграл
1
J = 0,0985, о
то окончательно величина объемного расхода будет
Q = 2,13Q0-^- или Q=# = 2,13^.	(XIII.41)
llm	Чо	Urn
23
И. Л. Повх
3
354	Турбулентный пограничный слой. Турбулентные струи	1
Если напомнить, что в переходном сечении ит = и0, то оковд чательно получим	;
ёп = -^=2,13,	(XIII.42$
Чо
т. е. безразмерная величина расхода жидкости в переходно^ сечении так же, как граница струи в этом сечении (XIII.40)^ имеет постоянное значение.
Приняв, как ранее было указано, границу струи на всем ее< протяжении, включая начальный участок, линейной функцией* от х, или г,.р = а^х, учитывая, что угол расширения струи—вели-чина не постоянная, так как его величина зависит от структуры^ потока в начальном сечении струи, можно ввести некоторый j коэффициент а, выражающий влияние структуры потока на угол । расширения струи. Тогда радиус границы струи можно пред- : ставить в виде	’*
ггр = а±х = фгрох,	(XIII.43).'
где фгр — безразмерная граница струи, равная фгр =
Известно, что фгр зависит только от формы поперечного се- . чения струи и для круглой струи ф,.р = 3,4. Величина а опре-деляется экспериментально и изменяется от 0,066 для потока •' с малой турбулентностью до 0,27 для потока за турбулизирующей 1 решеткой.
Если положить фгр = 3,4, то из (XII 1.43) следует
— ггр 3,4ах Лгр — ~ ~ '
Воспользовавшись (XIII.39), получим соотношение и:п _ 3,3го __________________ q дб
и0 3,4ах	’ ах ’
позволяющее определять скорость на оси основного струи и подтверждающее ранее установленную зависимость^ (XIII.37).	;
Положив в (XIII.45) ит = и0, получим формулу для нахожде^ ния абсциссы переходного сечения в виде	s
xn=0,96-J-.	(ХШ.4И
Абсциссу начального сечения струи х (отсчитывая от полюсай можно найти из (XIII.44), подставив туда ггр = г0. Она будёя
хо = О,29-у-.	(XI ПАЯ
(ХШ.44)
(ХШ.45$
Осесимметричные струи
355
Следовательно, расстояние от начального сечения до переходного (хп—х0) равно
х1 = хп —xo = 0,67-J-.	(XIII.48)
Если ввести абсциссу, отсчитываемую от начального сечения, и учитывать (XIII.47), то формулы (XIII.41) и (XIII.45) после подстановки х = х± + 0,29 -у примут вид:
Q = 2,22	+0,29^; ~ = ———. (XIII.49)
'	“»	0,29 + ^1
Гц
В технике часто встречаются струи, температура которых отлична от температуры окружающей среды. Струи, температура которых выше температуры среды (например, у ракетного двигателя), называемые горячими, распространяются в более плотной среде. В то же время холодные струи, наоборот, распространяются в менее плотной среде. Поэтому скорость первых должна убывать быстрее, чем у вторых.
При рассмотрении горячих и холодных струй соблюдаются условия сохранения не только количества движения (XIII.35), но и постоянства избыточного теплосодержания.
Если рассматривать разность между температурой в точке струи Т и температурой в окружающей среде Тя
ЬТ = Т — Тя,
разность между температурой на оси струи Тт и Тн
АТ = Тт - Та
и разность между постоянной температурой в начальном сечении и Тн	'
АТ 0 = Ао — Тн, то можно записать
'гр
2л J ри г dr — проио	(XIII.50)
0 /
Это означает, что избыточное теплосодержание массы жидкости в любом сечении струи равно избыточному теплосодержанию в начальном сечении ее.	*
Из уравнения состояния следует, что при р = const будет р _ Ро ~ Т •
23*
356
Турбулентный пограничный слой. Турбулентные струи
Заменив отношение плотностей на отношение температур получим (XIII.34) и (XIII.50) в виде
гр
Та
1;
О ггр
f2L ^L-L-d (_L.\ = 1
J Т и0 ДТ0 r0 U k гс J • о
(XIII.51
Если заменить, как в обычных изотермических струях, и _ и Um “о “т «о
Г Ггр 	и ггр	г о
и отношение температур представить в виде
Тв _ То Т Т„+-ДТ
где 6 = -^-;
1 н .
дт Тн ''
__L_
Th ' Th
____АТт ДТ0. ыm &Та Тн ’
ДТ
___п_________________J	 । । га_______________^Т
дт0 Тн
т0-тн Тн
=6—1,
то условия (XIII.51) примут вид:
26
о
2
,Л1 *11
ДТт ДТ
ДТ0 ДТщ
= 1;
no и'п	Г""
щ> ДТ0
(• ггр
и ДТ .
—-д7-Л1*11
1 1 । г fl п Ы J 1 + (6- 1) ДГо ДТте
(XIII.52;
(XIII.53J
Интегралы могут быть легко найдены для двух предельны^ случаев: 1) когда струя подогрета слабо; 2) для бесконечно сил! ного подогрева.
В первом случае можно считать,, что Т0 — Ти, а 0 = 1 следовательно, знаменатели подынтегральных выражений буд$ равны единице. Во втором случае То Тн, а 6 = оо и, сл'' довательно, в знаменателе можно пренебречь единицей.
Осесимметричные струи
357
Уравнения (XIII.52) и (XIII.53) могут быть решены при наличии следующих предположений:
1) профиль безразмерных избыточных температур связывается с безразмерным профилем скоростей формулой
<хш-54>
и, как следует из теоретического решения, 45>=0,32-^;	(XIII.55)
ДТ0 ’ и0 ’	'	'
2) угол раскрытия границ струи не зависит от степени нагрева, и, следовательно, сохраняется соотношение (XIII.44)
ггр _g ах_
г0 ’ го
Подставив в (XIII.52) значения (XIII.54), (XIII.55) и (XIII.44), получим уравнение ах   и0 го	ит
(XIII.56)
где
4=2-з>42
з
•*11^1
о	Г “/п
(/=(6-1)-^.
.	' “о
Расчетные значения А в зависимости от табл. XIII.3 или определяют по уравнению
A = 0,5d 4-0,95.
находят по
d
Таблица XIП.З
d	0	1	2	4	6	8	 10
А	0,34	1,45	1,95	2,94	3,94	4,95	5,95
Пользуясь последней зависимостью, можно (XIII.56) заменить более простой достаточно точной формулой
— Mg д т/ 526/0_п2<2_ (XIII.57)
г0	ит г I > v > и0 ’	'
358
Расчет трубопроводов. Местные сопротивления
с учетом (XII.55) формулу (XIII.57) можно привести к виду';
7? = W ^7 /1+0,72(0-1)^ .	(XIII.58^
Обе последние зависимости представлены графически н& Т
рис. (XIII. 15). Очевидно, что при < 1 струя будет холодной,;
1 'а
Т	I
а при > 1 — горячей. Из рис. XIII. 15, а видно, что при охлаж-. дении струи осевая скорость увеличивается и начальный участок „ = w0 растет, а при нагревании струи, наоборот. Такие же.^ выводы можно сделать из анализа кривых на рис. XIII. 15, б. J
ГЛАВА XIV'
РАСЧЕТ МЕСТНЫЕ
ТРУБОПРОВОДОВ. СОПРОТИВЛЕНИЯ
§ 1. Простые трубопроводы	;
j
Трубопроводы широко применяются для транспортировку жидкостей, газов, различных пульп и смесей. Существующий водопроводные, нефтепроводные, газовые, паровые и прочие сети можно разделить на два типа: магистральные трубопрОз воды, подающие ту или иную среду от источника до потребителя на большие расстояния, и разветвленные сети труб, обеспечиваю™ щие распределение этой среды непосредственно потребителям. Я
Магистральные и все длинные трубопроводы, не имеющими ответвлений, назовем простыми трубопроводами, а сеть труЙИ с различными разветвленными и параллельными участками -Ц сложными. И те и другие могут иметь различные диаметры трубИ
Простые трубопроводы
359
и большое количество участков местных сопротивлений (колена, краны, участки внезапного расширения и сужения трубопроводов и пр.).
Примеры простых трубопроводов — нефтепровод «Дружба», соединяющий СССР с рядом социалистических стран, газопровод Ставрополь—Ленинград и др. Пример сложных трубопроводов — системы, обеспечивающие население городов и сел водой, газом и теплом. Интересно отметить, что наиболее сложный трубопровод с упругими трубками различных диаметров — это система кровеносных сосудов человека.
Одна из задач расчета трубопровода — определить минимальную мощность, необходимую для доставки данного количества жидкости или газа в заданную точку, т. е. на определенное расстояние. Мощность, необходимая для транспортировки жидкостей и газов по трубам, равна
N = QAp.	(XIV.1)
Если Q и Ар выражать в системе СИ, то размерность [Q] равна м3/с, а [Др] = Н/м2, тогда мощность будет выражаться в Н-м/с или Вт и кВт
N = QAp Вт = 10-3<2Ар кВт.
Так как расход обычно задается, то расчет мощности сводится к нахождению перепада Ар, необходимого для транспортировки среды на заданное расстояние I. Этот перепад давления складывается из перепада, необходимого для преодоления сопротивления при стабилизированном движении Арт и местных сопротивлений Ары, т. е. Др = Арт + Дрм.
Потери при стабилизированном движении, согласно (XI. 15), для трубопровода круглого сечения с заданным объемным расходом Q и	заданным	диаметром d	можно	представить	в	виде
л	I “ср 8А.	pQ2 I	8 .-г Q2
—	d Р 2 ~ л2	d4 d	— л2 d4	’	(XIV*2)
nd2 — I
где Q = ucp -j- ; I = -д-безразмерная длина.
Коэффициент сопротивления % зависит от режима движения жидкости, который, как известно, определяется числом Re, равным
Re=^ v Jiva
Если число Re, подсчитанное по заданным значениям Q, d и v, меньше критического, то движение будет ламинарным и коэффициент сопротивления X (XI. 18) можно представить в виде
Х=§. = -^- = 16л^.	(X1V.3)
*\“ “еря	Ч
360___________Расчет трубопроводов. Местные сопротивления____
(
При турбулентном движении, согласно (XI.65),	и
V	1
х = ^!£1_ = 0)з164(-^) 4. (XIV-4)j Re^
Тогда окончательно, использовав (XIV.3) и (XIV.4), получим-;!
для ламинарного движения	'
аРт = ^-^	(Xiv.5)$
1
и для	турбулентного	j
Арт = 0,0246 pQ-4^	 	(XIV-6)|
Подставив значения перепадов давления в формулу для мош*л ности,	потребной	для перекачки жидкости,	получим	важные|1
расчетные зависимости. Потребная мощность при ламинарной^ движении	-	|
^л = Др(2 = 40,8-е^£.	(XIV.7J?
Таким	образом,	мощность пропорциональна	квадрату объем*!
ного расхода, абсолютной вязкости, длине трубопровода и об$ ратно пропорциональна диаметру трубы в четвертой степени;!
Для турбулентного движения	'
-/)2,75 0,25,
jVT =zAPQ = 0,0246-PQ d^75 1 ,  (XIV.Bf t. e. потребная мощность пропорциональна почти кубу объему ного расхода, длине трубопровода и плотности жидкости ил| газа в первой степени и обратно пропорциональна диаметру в сте| пени 4,75.	•;«
Для трубопроводов с развитой шероховатостью, когда коэ®| фициент сопротивления А не зависит от числа Re, а определяется лишь величиной относительной шероховатости, потребная мощ! ность будет пропорциональна расходу в кубе и обратно пропои циональна диаметру в пятой степени.	я
Приведенные формулы верны для горизонтального трубопрба вода. Если начало й конец трубопровода имеют разные уровИ zt и z2, причем zx < z2, то к вычисленным значениям ira| терь надо прибавить Ар = у(2! — z2). Тогда потребная мойи ность определится как произведение объемного расхода жидйя сти на сумму перепадов на трение и преодоление разности уровней.	, Я
Когда трубопровод будет иметь участки с разными диаметрами! то потери можно подсчитать для каждого участка и затем слЯ iM 11 л
Сложные трубопроводы
361
жить. Сумма потерь в этом случае может быть определена по следующей формуле:
при этом выбирается коэффициент сопротивления соответствующий режиму движения жидкости на участке с данным диаметром трубопровода.
Если при проектировании трубопровода будет задана не величина расхода, а значение располагаемого перепада давления, то объемный расход можно получить из уравнений (XIV.5) и (XIV.6). Тогда получим при ламинарном режиме
<2 = 0,241 ^4- — pl V
(XIV.9)
и для турбулентных потоков
4	19
«=8’34(v)' =
(XIV. 10)
При расчете и проектировании трубопроводов с различной шероховатостью обычно пользуются справочниками, в которых приводятся необходимые таблицы и номограммы.
§ 2. Сложные трубопроводы
В качестве примера сложного трубопровода рассмотрим разветвленный (рис. XIV. 1, а) и параллельный трубопроводы (рис. XIV. 1, б). В первом случае жидкость от насосной станции Л подается с секундным объемным расходом <20 двум потреби-
4
7
Рис. XIV. 1
телям в точках Сг и Сг, удаленным от точки разветвления В на расстояния Zj и /г, по трубопроводам с диаметрами dj и d2. Требуется узнать величину объемных расходов жидкости Qi и Qit проходящих по каждому трубопроводу в отдельности. Для простоты будем считать, что точки В, Cj и С2 находятся на одном уровне и режим движения (ламинарный или турбулентный) в обеих трубах один и тот же.
362
Расчет трубопроводов. Местные сопротивления
Так как в начале и в конце трубопроводов ВСг и ВС2 давлен ния одинаковы, то, следовательно, при любых режимах дви-жения перепады давлений по всей длине трубопроводов одина-ковы. Тогда, используя (XIV.2) и приравнивая перепады, можно; написать уравнение
откуда
1
(XIV.lLj
Если движение в обоих трубопроводах турбулентное, то
= / «ср 1^1 \ 4 = /Д\ 4	4
^1	\ «Ср 2^2 )	\ Qi /	\ ^1 /
’и по.(XIV.II)
19	4
<?! = /Д \ 7 /Д\ 7 .
<?2	\ ^2 /	\ К /
(XIV. 12);
соответственна
(XIV. 13)/
Для ламинарного движения в обеих трубах будет:
^2 Q1 ^2 . Q1 _ / ^1 V. ^2 ^1	Qi Qi \ ^2 )
Имея в виду, что Qi + Q2 = Qo> и подставив значение в соответствующие формулы, окончательно получим для турбу-д лентного движения	]
Qi=-------------------z;	(XIV.14)!
для ламинарного	-
«=—>  <X1V-15> ‘ + Ш Т7
•
Если обе трубы шероховаты и величины относительной шеро-. ховатости одинаковы, то при режиме развитой шероховатости?
• Xi = %2,	 j
тогда из (XIV.И) следует, что
Qi =----------%
Начальные участки труб
363
Последняя формула справедлива независимо от режима движения во всех случаях, когда Л.! = %2.
Из приведенных формул видно, что в равных по длине и диаметру гладких трубах при одинаковых режимах движения и в трубах с одной и той же относительной шероховатостью (при режиме развитой шероховатости)
Qi = Qz ~ 0>5Q0.
Аналогичные зависимости можно получить, используя (XIV. 11) и для случая, когда режимы движений в параллельных трубопроводах различны.
В качестве сложного трубопровода рассмотрим также параллельный трубопровод, показанный на рис. XIV. 1,6. Будем считать, что для такого трубопровода заданы общие расходы Qo, длина и диаметр каждой трубы между точками А и В.
Найдем распределение расходов по трубам 7, 2, 3, . . ., п и перепад давления между точками А и В.
Воспользовавшись (XIV.2), можно получить систему уравнений, определяющих расход через 'каждую параллельную трубу в виде
Задаваясь Л. и имея в виду, что для всех труб Др будет одинаковым, получим систему с количеством уравнений п, равным количеству параллельных труб. Так как Др тоже неизвестная величина, то для решения задачи необходимо иметь количество уравнений п + 1. Дополнительным уравнением будет задание суммарного расхода жидкости, т. е.
Qi + Q2 + • • • "i~ Qn — Qo-
Решая совместно эту систему уравнений, можно найти и Др.
Решения технических задач с разветвленными трубопроводами, с многими параллельными линиями (водопроводные и газовые линии в городах, вентиляционные каналы в шахтах и пр.) ве’сьма громоздки и требуют большой затраты времени.
Часто требуется знать, как перераспределится расход, если выключится тот или иной участок сети; что сделать с сетью, чтобы на некотором участке увеличить или уменьшить расход. Для быстрого решения таких задач широко применяется электрическое моделирование сетей.
§ 3. Начальные участки труб
При рассмотрении простых и сложных трубопроводов движение жидкости в трубах считалось стабилизированным и, следовательно, одинаковым во всех сечениях по длине трубопровода.
364
Расчет трубопроводов. Местные сопротивления
В действительности же при входе жидкости в трубопровод из резервуара большой емкости профиль скоростей, образующийся в начале трубы, на некотором входном участке будет изменяться} принимая форму, соответствующую режиму движения при дащ ном числе Re. Этот участок трубопровода назовем начальным} Очевидно, что сопротивление здесь всегда больше, чем при уста’ новившемся движении.
Для длинных магистральных трубопроводов изменение со-: противления из-за начального участка очень мало и влияний его не существенно. Но в машинах, установках и сооружениях с короткими участками труб начальные участки определяют весь процесс их работы и пренебрегать ими нельзя.	j
В теории начальных участков следовало бы рассматривать задачу о развитии произвольного профиля скоростей до устано^ вившегося. Ввиду крайней сложности общей задачи большая часть существующих решений посвящена изучению развития профиля скоростей в трубах с постоянной скоростью на входе по всему сечению. В этом случае длина начального участка и! процесс развития профиля скоростей будет зависеть от числа Rds или, точнее, от того, каким будет поток — ламинарным или турЗ булентным. В обоих случаях эту задачу можно рассматривать как задачу пограничного слоя. При однородном профиле скоро-стей на входе скорость непосредственно на внутренней стенку трубы равна нулю. Следовательно, при движении жидкости в трубе образуется тонкий пограничный слой, толщина которого постепенно увеличивается по мере увеличения расстояния ота входа. Сечение, в котором пограничные слои смыкаются, являетсяй! концом начального участка.	(Я
Для ламинарного начального участка существует несколько» теоретических решений. В некоторых из них, используя уравнечя ние импульсов и задаваясь профилем скорости, находят линяет суммарные характеристики (сопротивление и длину начального! участка); в других, используя дифференциальные уравнения^ определяют, как развивается Профиль скоростей.
Рассмотрим метод, использующий уравнение импульсов. На рис. XIV.2 приведены основные обозначения. Система включает;
I. Уравнение постоянства расхода б nroUo = 2л иг dr + л (г0 — б)2 U. о
2. Уравнение импульсов с
Д/ = /о — 1 = Пг1и1— 2л J«2rdr + n(r0 — 6)2t/2 о
где Д/ — разность количества движения.
(XIV.
— ЯГо(Ро — Р1Ц (XIV. 17)
Начальные участки труб
365
Имея в виду, что давление не-зависит от радиуса, и применив теорему Бернулли для ядра потока, правую часть последнего уравнения представим в виде
а/ о
дх — цТц,
3. Уравнение
(XIV. 18)
справледливо в конце начального участка, где количество движения будет изменяться только за счет сил трения.
Уравнения (XIV. 16)—(XIV. 18) пригодны как для ламинарного, так и для турбулентного потоков, все зависит от вида функций и(у) и rw {у).
Для ламинарного потока задача решена при заданном параболическом профиле скоростей и
7Г
2
(XIV. 19)
и напряжении сил трения
Тщ,
dy )у=й ’
(XIV.20)
представленному на
Решение уравнений (XIV. 16) и (XIV. 18) при указанных условиях приводит к довольно сложному аналитическому выражению, графически рис. XIV.3. Здесь по оси абсцисс отложено относительное изм&-нение скорости ядра течения в виде
U-Uo _ U	,
Uo Uo	1ф
При параболическом профиле скоростей (XIV. 19) в конце начального участка имеем: U = umax = 2U0 и 0 = 1. Следо-
Л1
366
Расчет трубопроводов. Местные сопротивления
вательно, при 0 = 1 координата х будет равна длине начального, участка I. Из кривой видно, что
-y- = 0,12Re = 0,12(XIV.21);-или	0
0,03= 0,03Rerf.	;
Сопротивление Ар определяется формулой
Ы6)-^-.	(XIV.22)
которая для установившегося движения в круглой трубе примет' хорошо знакомый вид (гл. XI, § 2)
д _ 16 X РЦ) 64 X ри2о	’
&Р ~ Re г0 2 - Red d 2 ’	‘
г> u*d где Red = -^-.
Решение уравнений (XIV. 16) и (XIV. 17) для турбулентного,, движения в трубе при предположении, что
1
_2L_=/'_£_V,	(XIV.23);
и при напряжении трения, полученном для турбулентного движения жидкости в трубе (XI.74), дает относительную длину начального участка,
4- = 0,693(Re(Z)T,	(XIV.24),
и относительную величину сопротивления
Др =	= 1,16 + -^.	(XIV.25)
Pllmax
Эксперименты показывают, что действительная длина начального участка как для ламинарного, так и турбулентного движе-' ния значительно больше, чем теоретическая. Так, по опытам' Кирстена, длина турбулентного начального участка при Re =, = (9-j-10)-103 в 4—5 раз больше величины, определенной пй) формуле (XIV.24).	<
§ 4. Потоки в диффузорах
Задача о течении в диффузоре — одна из наиболее сложных»; в аэродинамике. Необходимость изучать потоки в диффузорах? определяется не только тем, что в машинах, сооружениях и экс*’ периментальных установках имеются многочисленные расширяю-
Потоки в диффузорах
367
щиеся трубопроводы, но и наличием значительного диффузорного участка при наиболее интересных случаях внешнего обтекания единичного крыла и особенно решеток крыльев (компрессор, насос и активная турбина).
Необходимость изучения потоков в диффузорах определяется и тем, что потери в них значительно больше, чем в цилиндрических и конфузорных участках. Так, в паровых и газовых турбинах весьма значительную долю составляют потери в диффузорах выхлопных патрубков, а в гидралических — во всасывающих трубах. То же наблюдается в аэродинамических трубах (до 30% всех потерь — в диффузоре), вентиляционных- установках и других машинах.
Основное назначение диффузоров — постепенно уменьшать скорость потока и, следовательно, восстанавливать давление при наименьших потерях. В диффузорах движение как в ядре потока, так и в пограничном слое значительно менее устойчиво, чем в цилиндрической и тем более в сужающейся трубе. Поэтому в расширяющихся трубах переход ламинарного движения в турбулентное происходит прц значительно меньших числах Re, чем в цилиндрических. В цилиндрической трубе при любом характере движения и произвольных числах Re поток никогда не может отрываться от стенки. В диффузорах же такой отрыв может произойти на некотором расстоянии от входа даже при малых углах расширения.
Как было показано, в цилиндрической трубе существуют два участка. Первый — начальный, второй — участок стабилизованного движения (от конца начального участка на всем протяжении остальной длины трубы).
В диффузорах нет участка стабилизованного движения. Профили скоростей непрерывно деформируются до тех пор, пока поток не оторвется от стенки. Практически при малых углах расширения отрыв потока будет происходить лишь на очень большом расстоянии от входа. Если при' небольшой длине диффузора отрыва не происходит, то диффузор является безотрывным.
Причина отрыва потока, как указывалось, — наличие градиента давления на стенке. Он приводит к тому, что в каждой последующей точке по потоку давление больше, чем в предыдущей. Следовательно, вблизи стенки, где скорости потока из-за вязкости и так очень малы, градиент давления еще больше тормозит движение частиц жидкости. Это может привести к остановке жидкости в пограничном слое и даже вызвать движение в обратном направлении. При этом основной поток как бы оттесняется от стенки — происходит отрыв.
При углах расширения диффузоров примерно до 40° отрыв происходит не по всей поверхности, а лишь на некотором ее участке. Следовательно, на части внутренней поверхности диффузора
368
Расчет трубопроводов. Местные сопротивления
>!
поток движется безотрывно, лишь к концу он может полностью оторваться от всей стенки. Иногда область отрыва бывает весьма^ неустойчивой и перемещается на противоположную стенку диф-* . фузора. При углах более 40° поток полностью отрывается от всем] поверхности диффузора.
Отрыв значительно снижает эффективность диффузора (не до^’ пуская соответствующего увеличения давления) и повышает по.^ тери в нем. Поэтому при проектировании диффузора очень важщ). заранее определить расположение точки отрыва и по возможности уменьшить отрывную область. Для приближенных расчетов точк£|я отрыва в диффузоре может бытья определена (см. гл. XII) по знай! чению формпараметра f пограничЦ ного слоя. Напомним, что фом| мула для формпараметра записый! ,	L/'б**2	Я
вается так: г =----.	.яя
• V	vffl
При ламинарном движениа| жидкости в диффузоре значение формпараметра f в точке отрыва! равно fs — —0,089, а при турбуД лентном —значение формпараме'вЯ ра зависит от степени диффузорЦ
ности. В сильных диффузорах, когда среднее значение производя ной от скорости в ядре	1,5, величина формпараметрЦ
в точке отрыва fs = —1,0, а в слабых диффузорах это значениЦ достигает fs =. —4,0. В . средних диффузорах рекомендуется! брать = —2,0.	W
Для грубых расчетов можно воспользоваться результатами! опыта с плоским диффузором, приведенными на рис. XIV.4)$| Здесь показаны кривые начальной координаты отрыва поток в зависимости от угла расширения и площади того сечения, в ко-$ тором начинается отрыв, отнесенной к площади входного отвер-1 стия диффузора у Кривая 1 ограничивает справа области значений и а, при которых зона отрыва толщиной в 5 мь|| имела периодический характер; кривая 2 — область, в которой! была устойчивая зона отрыва толщиной 5 мм, а кривая 3 — обч ласть устойчивого отрыва толщиной нё менее 15 мм.	$
Степень совершенства диффузора определяется потерями энер*$ гии: чем их меньше, тем диффузор совершеннее. Потери энергию в диффузоре складываются из потерь: на трение жидкости о стенки-
и на расширение потока. Последние вызываются увеличением^ роста толщины пограничного слоя по сравнению с цилиндриче2; ским или сужающимся (конфузорным) потоками, что приводит;
Потоки в диффузорах
369
к заметному обратному влиянию пограничного слоя на распределение давления на стенках диффузора. Кроме этого, значительно возрастет коэффициент турбулентного обмена, определяющего напряжение турбулентного трения во всем потоке и^_ наконец, могут возникнуть потери, вызванные отрывом.
В обычных диффузорах потери на трение значительно меньше потерь на расширение даже при отсутствии отрыва.
Коэффициент потерь, или коэффициент сопротивления, для диффузора определяется как отношение потерь напора к скоростному напору на входе.
В цилиндрической трубе потери определяются как полная разность статических давлений по длине трубы. В диффузоре же статическое давление изменяется за счет падения скорости и наличия потерь, так что действительная (измеряемая) разность давления р2 — будет равна
Р2 — Р1 — (рг — Р1)ид—Ар — -у (V1 — И) — Ар,
где (р2 — Р1)Ид — увеличение статического давления в идеальном диффузоре, т. е. только за счет разности скоростных напоров.
Коэффициент потерь £ можно определить по формуле
др __Р2 —Р1_1	/ Ki V
рУ1 ~ .PEL \	‘
2	2
Иногда потери напора относят не к скоростному напору на входе, а к теоретическому приросту давлений, тогда коэффициент потерь £ определяется по формуле
С =	=------—------•	(XIV.26)
(р2 Р1/ИД	Р (у2 _у2)
Коэффициент потерь может быть представлен как сумма коэффициентов потерь на трение и расширение, т. е.
С = Стр + Ср-
Оба коэффициента потерь обычно определяются из эксперимента, хотя существует ряд методов теоретического расчета главным образом коэффициента трения.
Коэффициентом полезного действия диффузора называют отношение действительной разности давлений (р2 — Pi) либо к разности давлений в идеальном диффузоре, либо к скоростному
^4 И. Л. Првх
370
Расчет трубопроводов. Местные сопротивления
напору на входе в диффузор, т. е.
или
(Х1У.27У
Если воспользоваться уравнением постоянства расхода V±Fг = = V2F2, то между коэффициентом потерь и к. п. д. можно установить зависимость
£=(1—t]i) (1------иЛ ’ или£=1--------!----'
» V II/ у /па ]	ь	/п2 ’
F2	. .	'
где т =	----степень расширения диффузора.	!
В практике часто пользуются отношением потерь на расширен; ние в диффузоре к потерям, которые теоретически могут быть получены при внезапном расширении струи от узкого к широ-; кому сечению, т. е.
__ дРр	Дрр	'
Друд _L(V1-V2)2’
J
Эта величина называется коэффициентом полноты удара и ч характеризует собой степень несовершенства диффузора. Оче-1 видно, чем больше срр, тем больше угол расширения диффузора, и при внезапном расширении Дрр = Друд, а <рр = 1. От степени .! расширения т диффузора коэффициент <рр почти не зависит, . так как при любом большом т теоретически всегда можно выбрать ' сколь угодно малый угол расширения а.
Иногда коэффициентом, аналогичным <рр, пользуются и при оценке общих потерь и потерь на трение, т. е. вводят коэффициенты:
Др	ДРтр
т=-7-----------; <ртР=-^------------•
-^(^-V,)2	-^-(V1-V2)2	I
Тогда общий коэффициент полноты удара <р можно представить в виде суммы, т. е. <р = <рр + <ртр.
Все существующие диффузоры отличаются друг от друга? формой стенок (прямолинейные, криволинейные или ступенчатые),; поперечным сечением (круглые, квадратные, прямоугольные^ кольцевые и пр.) или углом раствора, длиной, степенью рас ши-' рения и другими признаками.
Потоки в диффузорах
371
Наиболее часто используется в практике простой прямолинейный диффузор круглого поперечного сечения. Его исследованию посвящено много экспериментальных и теоретических работ.
Приближенный расчет градиента давлений по длине такого диффузора может быть произведен следующим образом.
Рассмотрим очень короткий диффузор, такой, в котором можно пренебречь толщиной пограничного слоя 6 по сравнению с его радиусом г. Тогда уравнение постоянства расхода при степенном законе распределения скоростей с показателем степени п будет иметь вид
V Ft___________________1_______________
И ? , + А( 2 _2')+ei(1-------------2 ) ’
Г \ П + О ) Г2 \ Л -р о /
при б С г получим
V _ А.
Vt ~ F •
Следовательно, скорость в некотором сечении диффузора равна
V — Vt — и — -- — К . 1 F dF 1 F
Так как, дифференцируя уравнение Бернулли по х, получим dp	dV
—г~ = — ри -з— > dx r dx
а
dV _dV_dF___v Fi dF dx dF dx	1 F2 dx ’
то в общем случае для диффузора любой формы поперечного сечения градиент давления по длине будет ,
dp  . n pVi га 1 dF dx ~~	2	1 Fs dx •
Если ввести безразмерные величины — р — х И pVj	/ Ft
2
то последнее уравнение примет вид
dp  оря 1 dF dx ' F* dx •
Для круглого сечения
р пР* . р— лР2 dF = л р-— 4 ’ Л — 4 И dP 2 и'
24
372
Расчет трубопроводов. Местные сопротивления
следовательно,
4?- = 4D1 dx
dD dx
или, так как D =	+ 2х tg ,
dx	+ *tg-j-Y
\ V л 2 /
Потери на трение могут быть определены аналитически. Р& бота сил трения в единицу времени равна	'
Д£тр = т0 У,
где т0 — сила трения, которая может быть определена по фор;
муле
3
Здесь S — площадь стенок диффузора; X — коэффициент трения] отнесенный к участку длиной один диаметр; для цилиндрической трубы определяется по формуле (XI. 18) или (XI.74) или по крйЗ вым на рис. XI.9.
После подстановок получим	1
=.[ Т s
Зная энергию, потерянную на трение Д£тр, нетрудно полу-| чить коэффициент потерь на трение в диффузоре £тр, разделив! Д£тр на величину кинетической энергии на входе в диффузор;^
<. __ д£тр _ 1 г X ( V \з	J
^т₽ —	— F J 4	V]. ) а ’	S
2	5	J
где Шу = pFiVx — секундная масса потока.	' J
V F	J
Так как по уравнению неразрывности V = —т0 коэф^
фициент потерь на трение для диффузора с любой формой’попереч^ ного сечения будет
j- __рг X Г dS	f
Ьтр — г 1 4 j рs .	I,
Для круглого сечения
dS = ^-а smT
_ НХ ? dF
~ . . а J F3 ‘
4 sin р
Потоки в диффузорах
373
После интегрирования получим коэффициент потерь на трение для диффузора круглого сечения
или
«. __ X т3 — 1
о , а т3 8 s п Т"
Используя выражение
получим
X о .	®
8Sif>T
т 4- 1
Фтр —
Вторая составляющая потерь — потеря от расширения — определяется по ранее полученным эмпирическим формулам или" непосредственно по экспериментальным материалам.
Лучшее совпадение с опытом для диффузоров с углом расширения а от 0 до 40° дает формула
Фр=з,2 (te^)'-25-
Используя последние формулы, нетрудно получить суммарный коэффициент потерь <р в виде
Ф = фтр+Фр="я— а- +3,2 (tg-y) .
8 sm -у	'	'
Изменение коэффициента <р в зависимости от угла расширения а по опытным данным показано на рис. XIV.5. Несмотря на то чтофр растете увеличением угла а, общий коэффициент ф внача'ле, с увеличением угла, падает и только при а = 8-т-10° начинает сильно увеличиваться.
Зная аналитическое выражение для ф, можно найти угол расширения, соответствующий минимальному значению коэффициента общих потерь ф. Взяв производную по а от ф и приравняв ее к нулю, получим оптимальный угол расширения
4
аопт = 0,43(х^Ц-) 9 . опт ’	\ т — 1 /
Для X = 0,015 и т = 2,25 аопт — 6°. Отметим, что приведенная формула дает значения а в радианах.
374	Расчет трубопроводов. Местные сопротивления
Основываясь на многочисленных примерах, можно рекомен-^ довать для круглых диффузоров оптимальный угол расширения,^ отличающийся от расчетного, а именно аопт = 8°. Оказывается,'^ что для не очень длинных диффузоров при а = 8° и т — 2-=-4^ отрыв еще не происходит и поле скоростей на выходе из диффу, , зора еще достаточно однородно.	j
°3 i 5 618910 /4 18 20 30 00 50 6010ЮО 120l60d,...°
Рис. XIV.5
При одинаковых углах а и степенях расширения т длина диффузора прямоугольного сечения будет короче, чем круглого. Это объясняется интенсивным наращиванием пограничного, слоя; в углах диффузора с прямоугольным или квадратным сечением.
Опыт показывает, что существуют криволинейные диффузоры, в которых потери значительно меньше, поле более однородно, а поток устойчивее, чем в прямолинейных диффузорах.
§ 5. Поворотные устройства
В энергетических и других машинах используется большое'; разнообразие различных устройств для поворота потоков жидкостей и газов.	4
Независимо от формы поперечного сечения канала поворот/ потока осуществляется либо в канале, изогнутом под прямым' углом, либо в криволинейном канале, либо в таком, контур которого состоит из отрезков прямой.
Поворотные устройства
375
Задача о движении турбулентного потока реальной жидкости в колене до сих пор теоретически не решена. Поэтому анализ явлений, происходящих при повороте, можно производить, используя уравнения идеальной жидкости и результаты эксперимента.
Рассмотрим потенциальный поток идеальной жидкости в колене, показанном на рис. X1V.6. Частицы жидкости, движущиеся по криволинейным траекториям, находятся под влиянием центробежных сил инерции. На любой элементарный объем жидкости будет действовать сила, равная
dF = — dm, Г
где dm = pcpr dr — масса элементарного объема в канале единичной ширины; г — радиус кривизны.
Давление, вызванное этой силой, будет
dp = ^ = pl/2^.	(XIV.28)
Ввиду отсутствия потерь (считаем жидкость идеальной) полная энергия будет постоянной по всей
длине трубы и, следовательно, изменение давления может происходить только за счет изменения скоростного напора.
Уравнение Бернулли в дифференциальном виде будет
dp = — р]7 dV.
Следовательно, подставив значение dp из (XIV.28), получим дифференциальное уравнение
= — рУ dV или dr ___________________________ dV_
— — V'
Интегрируя последнее, получим Vr = const, т. е. скорость тем больше, чем меньше радиус. Из этого следует, что при движении по криволинейному каналу скорости частиц жидкости убывают с увеличением радиуса по гиперболическому закону. Следовательно, давление у внутренней стенки меньше, чем у внешней.
376 Расчет трубопроводов. Местные сопротивления
Внешняя стенка
Внутренняя стенка
Рис. XIV.7
Отсюда ясно, что при входе в криволинейное колено у вну4 тренней стенки образуется как бы конфузорный участок, а у внеш-j ней —диффузорный. При выходе же из криволинейного коленаа в прямую трубу, наоборот, у внутренней стенки образуются диффуЛ зорный, а у внешней—конфузорный участки.	i|
Полученная закономерность для идеальной жидкости являетс?$ определяющей и при движении реальной жидкости в криволиней-! ных каналах. Основной фактор, изменяющий картину потока, -J| прилипание реальной жидкости! к стенке.	- Я
Из теории пограничного слоя; известно, что в диффузорной обла^ сти он растет очень интенсивно$ мало устойчив и может легко отор-' ваться от стенки. Последнее явле-; ние и наблюдается в диффузорных^ областях криволинейного колена,' . Фотографии потока в колене отчету] либо показывают области местного* отрыва у внешней и внутренней! стенок. Схематически поток в ко-'| лене показан на рис. XIV.6. ВидЛ но, что имеют место отрывы мест-i; ные, так как диффузорные обла^ сти занимают небольшие участки.^
Если рассматривать для простоты колено с квадратным no-.J; перечным сечением, то на внешней стенке давление будет больше, чем на внутренней, в силу этого вдоль боковых стенок, вблизи;' поверхности которых скорость мала, жидкость будет перетекать^ от внешней стенки к внутренней. Схема перетекания показана нш рис. XIV.6.	1
Такое поперечное перетекание жидкости возникает в колена® не только прямоугольного, но и любого другого сечения и обычней называется вторичными токами. Их можно без особого труда нал блюдать и даже измерять составляющие скоростей, образующий парный вихрь. На рис. XIV.7 показано поле тангенциальных^ скоростей в выходном сечении колена.	$
Таким образом, структура потока в криволинейном канал^ определяется увеличением давлений и уменьшением скоростей^ в направлении от внутренней к внешней стенке колена. Это прИ-J водит к местному отрыву пограничного слоя, а следовательно^ появлению вихревых областей у внешней стенки колена вблизи входа и у внутренней стенки при выходе из колена и, наконец^ к образованию в колене парного вихря.	‘S
Указанные явления в различных количественных соотноше^ ниях имеют место во всех случаях поворота потока. Они опредок
Поворотные устройства
377
ляют природу потерь в колене и те качественные нарушения однородности потока; которые происходят при наличии колена в трубопроводе.
Потери в колене складываются из потерь на трение, на образование парных вихрей и потерь из-за наличия местных отрывов' потока. Последние имеют наибольшую относительную величину, вторые — меньшую и, наконец, потери на трение составляют наименьшую долю общих потерь. Таким образом, для уменьшения потерь в колене, так же как и во всех других потоках, прежде всего надо устранять или ослаблять местные аэродинамические диффузоры, часто приводящие к местным отрывам потока. Затем надо уменьшить интенсивность вторичных токов, образующих парные вихри, и только после этого заботиться об уменьшении сил трения.
Проведенный анализ указывает конструктивные пути уменьшения потерь в коленах. Из большого разнообразия таких путей приведем два наиболее распространенных — увеличение относительного радиуса закругления для криволинейных поворотных колен и установка в коленах направляющих лопаток. Первый путь весьма прост, но неизбежно ведет к большому увеличению радиуса закруглений, а следовательно, и общих габаритов колен. Это весьма нежелательно по конструктивным соображениям. Второй путь—установка направляющих лопаток—широко .применяется в аэродинамических трубах и все больше используется в промышленных установках и машинах.
Для криволинейных поворотов потока существенны: радиусы кривизны внешней и внутренней стенок, форма поперечного сечения, соотношение площадей входного и выходного поперечных сечений и др.
На рис. XIV.8 показана экспериментальная кривая зависимости коэффициента потерь от радиуса кривизны, отнесенного -к высоте канала Ь, т. е. £ = / (4г)1
Кривая / показывает изменение коэффициента потерь £ в зависимости от величины относительного внутреннего радиуса закругления квадратного нормального колена при наличии выходного участка, равного десяти калибрам. Нормальным коленом будем считать такое, у которого внутренняя и внешняя стенки очерчены радиусами, проведенными из-общего центра. Как и следовало ожидать, увеличение радиуса приводит к уменьшению потерь в нормальном колене.
Следует отметить, что £ очень сильно падает при изменении -у-от 0 до 1, в то время как при изменении от 1 до 2 значение £ изменяется от 0,17 до 0,14, а при -£- > 2£ достигает постоянного
378	Расчет трубопроводов. Местные сопротивления	j

значения. Отсюда следует, что увеличивать радиус кривизны нормальных колен имеет смысл только до определенного значения.
Кривая 2 характеризует функцию С \~ь~) ПРИ наличии прямого внутреннего угла и закругленной внешней стенки.
Кривая 3 справедлива при внешней стенке колена в виде прямого угла и закругленной внутренней.
Из кривых видно, что скругление внешней стенки менее эффективно, чем внутренней. Увеличение радиуса кривизны в от
дельности внешней или внутренней стенок (при г » Ь) вызывает даже некоторый рост коэффициента сопротивления.
Для труб прямоугольного сечения на сопротивление в колене значительно влияет ширина канала Н. На рис. XIV.9 показано изменение потерь в колене в зависимости от ширины трубы Н при различных значениях среднего радиуса закругления, отне-
гСр 2	4	5
сенного к высоте трубы, а именно -г- = -5-; 1; и -5-. о 3	3.3
С увеличением относительной ширины трубы коэффициент сопротивления падает, а ее уменьшение приводит к резкому возра
станию потерь, особенно в области, где -у- мало.
Существенное увеличение потерь при уменьшении объясняется тем, что при повороте потока, вокруг широкой стороны вторичные тоКи локализируются у боковых стенок и их роль в общих потерях в колене мала. В то же время при повороте потока вокруг малой стороны вторичные токи занимают все поперечное сечение и общие потери при этом сильно возрастают.
Поворотные устройства
379
Многочисленные опыты и некоторые теоретические соображения говорят о том, что соотношение площадей поперечного сечения перед и за коленом существенно влияет на его сопротивление.
Фотографии спектров обтекания в сужающихся и расширяющихся коленах показывают, что отрыв потока у внешней стенки, имеющийся при выходе из колена постоянного сечения, в случае сужающегося колена уменьшается или вовсе отсутствует, а при расширяющемся он в значительной степени увеличивается, сильно возмущает поток и приводит к дополнительному вихре-образованию. Естественно, что в сужающихся коленах потери меньше, чем в коленах постоянного сечения. По мере увеличения расширения растут и потери.
Изменение потерь в зависимости от соотношения площадей ~-за и перед коленом при повороте потока под прямым углом в колене с прямоугольным поперечным сечением (-у- = 4^ видно из следующих результатов эксперимента:
fa ....0,5 0,8 1,0 1,5
' 1
£.....................0,7	1,0 1,2 2,2
Видно, что влияние степени расширения канала в колене очень велико. Наиболее интенсивный рост потерь происходит в диффузорных коленах.
Расчленим потери в колене с расширением на два слагаемых. Первое слагаемое определяет потери на поворот в колене без расширения, второе — потери с расширением. Оказывается, что потери энергии в расширяющемся колене больше, чем суммарное сопротивление последовательно расположенных обычного колена и участка трубы с внезапным расширением потока.
При необходимости уменьшить габариты, а следовательно, радиусы кривизны поворотных колен часто прибегают к сильно изогнутым или даже прямоугольным и остроугольным коленам. В целях уменьшения значительно возрастающих при этом потерь и улучшения однородности поля скоростей за коленом широко используются различные профилированные и непрофилированные направляющие лопатки, устанавливаемые на повороте.
Опыты показывают, что правильное размещение тонких не-профилированных лопаток в криволинейных и прямоугольных коленах дает значительное снижение сопротивления.
На рис. XIV. 10 показано изменение величины £ квадратного колена при у = 0 в зависимости от положения лопаток.
Для того чтобы оценить роль направляющих лопаток в снижении потерь, приведем сводную таблицу результатов опытов, произведенных с самыми разнообразными поворотами потоков.
380 Расчет трубопроводов. Местные сопротивления	ЭД
Таблица XIЙ
Модель		ьа ~е	Г1 »*	га ьа	Тип лопаток	(без лопаток)	^de (с лопатками)	xioo% !|
Т-]		1	0	0	б	1,647	0,358	78,3 -
		1	0	1	б	2,705	0,560	79,3
		1	0,25	1	б	1,374	0,179	86,9
— /У ]		1	0,25	0	б	0,996	0,216	78,3
V ] ]		1	0,0834	0,0834	б а	1,485	0,307 0,405	79,3 72,7
—		1	0	0	в	4,01	0,702	82,5
у		1	0	0	в	4,25	0,653	84,6
УШ		1	0	0	в	4Л1	0,783	82,6
ц
"Я
Поворотные устройства
381
В табл. XIV. 1 даны результаты опытов с поворотом потоков на 90 и 180° (/—V///) при сохранении входных и выходных площадей поперечных сечений, с лопатками на повороте и без них. Схемы расположения лопаток показаны в конце таблицы. В последней ее графе указано понижение коэффициента сопротивления колена после установки лопаток. Коэффициент потерь £ отнесен к скоростному напору на выходе после поворота. Числа Рейнольдса при опытах, вычисленные -по расходной скорости и стороне ba, были равны 2,55-105. Из таблицы видно, что установка лопаток £ весьма сильно снижает потери в колене.
Однако потери в колене с на- 0,90 правляющими лопатками, распо- OgQ ложенными наилучшим образом, никогда не будут меньше потерь 0,70 в криволинейном канале со сколь угодно большим радиусом кривизны. Поэтому для получения 0,50 минимума потерь установку на-правляющих лопаток можно ре-  ' комендовать только в том случае, 0,30 когда по каким-либо причинам 02о
нельзя использовать колено с боль- ' 0	50	100
шим радиусом.	10
Рассмотрим изменение коэффициента потерь в зависимости от радиуса кривизны для нормального колена. Видим, что постановка направляющих лопаток особенно эффективна лишь в том случае, когда безразмерный радиус кривизны не может быть больше единицы, т. е. когда ~ < 1. О
В случае же, когда 1, постановка лопаток и любое изменение формы колена не могут привести к сколькощибудь значительному снижению потерь.
В коленах с уменьшающейся площадью сечения этот предел может быть существенно снижен. Так, при поджатии (т = 2) не следует устанавливать лопатки с 0,25.
Такой вывод естествен. Любые направляющие лопатки, поставленные в колено, увеличивают сопротивление трения, но при сильных поворотах они значительно снижают сопротивление давления, имеющее большое значение из-за наличия местного отрыва. При малых поворотах, т. е. больших радиусах кривизны, местные отрывы отсутствуют. В этом случае сопротивление тре-
382
Расчет трубопроводов. Местные сопротивления
ния является существенной составляющей полного сопротивл ния, поэтому, увеличивая радиус кривизны и вводя направляй щие лопатки, нельзя уменьшить сопротивление колена.
Профилированные лопатки, обычно применяемые в аэродин; мических трубах, строятся из двух сопряженных дуг окруд ностей по радиусам и координатам их центров, приведенным и рис. XIV. 11. Причем хх = 0,519/; хг = 0,489/; ух = 0,463 у г = 0,215/; zx = 0,139/; z2 = 0,338; rx = 0,663/; r2 = 0,553/; s = 0,035/.
Величина хорды лопатки / може быть определена из соотношения
Рис. XIV. 11
В
Относительный радиус закруглена рекомендуется брать в предела: 0,2—0,25.
колене может быть определено по одно:
Число лопаток из следующих формул
(XIV.29
(XIV.3^
Если задаться величиной хорды, то число лопаток будет соот ветственно:	_	_
п=—(----1; n = l,4r-y—; n=0,9r-y—.
Количество лопаток, определенное по формуле (XIV.29). обычно называют нормальным, по формуле (XIV.30) —оптималь ным и по формуле (XIV.31) —минимальным.
В первом случае при наибольшем числе лопаток они обычй* размещаются равномерно, т. е. на одинаковом расстоянии одн от другой.
Во втором и третьем случаях лопатки размещаются по арифме тической прогрессии в соответствии с формулой
at- = ах + (i — 1) d,
где ах — расстояние между хордой первой лопатки и хордо: дуги внутреннего закругления колена; /—порядковый номе; лопатки; d — разность прогрессии; at — расстояние между /• и (i — 1)-й лопатками.
Поворотные устройства
383
Для’ определения расстояний между всеми лопатками обычно решают совместно два уравнения:
S==ZL+l(2ai + nd); d =
где S — сумма арифметической прогрессии.
Величиной —, т. е. отношением расстояний между хордами
первой и последней лопаток и хордами соответствующих закруглений, обычно задаются. На основании опытов можно брать
ап
ai
Количество лопаток, рассчитываемое по формуле (XIV.30), и их равномерное распределение в колене применялось в первых трубах и по последним опытам не имеет преимущества по сравнению с коленом, рассчитанным по формуле (XIV.31).
На рис. XIV. 12 по данным ЦАГИ приведены кривые зависимости коэф-
фициента сопротивления £ от-£- для ко-
лена без лопаток и для колен с нор- I I I I I Г! I I I I 1_1 мальным, оптимальным и минимальным О %2 °>3 у числом лопаток.	п „шю
Из рассмотрения кривых следует:
а)	для нормального и оптимального ’числа лопаток наивыгоднейшим радиусом закругления будет — 0,25;
б)	при радиусе закругления 0,5b потери в колене с нормальным и оптимальным числом лопаток имеют одинаковое значение с потерями в колене без лопаток;
в)	при больших радиусах закругления (-£- > 0,25^ наивыгоднейшее число лопаток — минимальное, т. е. рассчитанное по формуле (XIV.31);
г)	коэффициент потерь в оптимальном случае имеет порядок 0,2.
Во многих случаях существенное требование к колену — однородность поля скоростей за ним. На рис. XIV. 13 показаны поля скоростей за коленами аэродинамической трубы на расстоянии от 200 до 1000 мм.
Поле скоростей за коленом без лопаток (рис. XIV. 13, а) неоднородно, а с лопатками (рис. XIV. 13, б) —уже на расстоянии Ю00 мм становится вполне однородным. Наивыгоднейшие углы
384	Расчет трубопроводов. Местные сопротивления
между хордой лопаток и осью трубы перед коленом находятс^ в пределах 45—51°. Увеличение и особенно уменьшение углад ухудшает поток.	'о
§ 6. Сопротивления при слиянии и разделении потоков. Дроссели и клапаны
Рассмотрим местные сопротивления, часто встречающиеся^ в технике, возникающие вследствие слияния и разделения пото-$ ков, установки различных дроссельных устройств и-некоторых^ конструкций клапанов.
Примеры слияния потоков показаны на рис. XIV. 14, а их разделение в тройниках круглых трубопроводов —нН рис. XIV. 14, б. Для характеристики потерь в тройниках пользу^ ются обычно тремя коэффициентами сопротивления: £ — полный коэффициентом сопротивления; £б и £п—коэффициентами со против^
Сопротивления при слиянии и разделении потоков
385
ления бокового ответвления и прямого прохода тройника, приведенными к скоростному напору в сборном трубопроводе, т. е.
r _ ДЯ «.	ДЯб . г _ АЯП
Ь - р|/2 > Ьб — pV2 > €п pV2 >
~ ~ ~
и, следовательно, так как сумма потерь давления в боковом ответвлении Д/7б и в прямом проходе Д/7П равна полным потерям ДЯ, то С = £б + с„.
Основными параметрами, определяющими потоки в тройниках, являются: геометрические —угол а и соотношение площадей Fc, Fa и F„ (последние выражаются величинами отношений F6 и Fn и Fc и величиной суммы F6 + Fn S Fc) и гидравлические, выраженные отношением соответствующих расходов Q6 и Qn к Qc; при этом для расходов будет всегда соблюдаться соотношение
<2б + <2п = <2с. или •^ + ^г=::1-
Потери при слиянии в тройнике происходят за счет турбулентного смешения двух потоков и потерь на поворот, иногда вызывающих местный отрыв (рис. XIV. 14, в). При этом струя с большими скоростями теряет часть своей кинетической энергии, в то время как струя с малой кинетической энергией ее приобретает.
Следовательно, разность между полными давлениями в ответвлении с меньшей скоростью и в трубе после воссоединения потоков может иметь отрицательное значение. Это относится и к коэффициенту сопротивления ответвления. Поэтому коэффициенты и £п могут быть или оба положительными, или один отрицательным, а другой положительным; полные потери всегда положительны.
Существуют различные громоздкие эмпирические формулы для нахождения коэффициентов потерь £б и £п. Для того чтобы получить представление о структуре таких формул, приведем выражения:
[! + (£У-2£(£У-2£(£У cos а] + К<.
где значения А, и Кп находятся по таблицам. -
Для характеристики потерь приведем в табл. XIV.2 значения коэффициентов и £п для тройников с различными параметрами.
Из таблицы видно, что £б с увеличением а и растет, а при а.
увеличении ----убывает. Как £б, так и ?п могут иметь отрица-
тельные значения.
25 И. Л. Повх
386
Расчет трубопроводов. Местные сопротивления
Таблица XIV.2
6	а, ... °	1 С О	' О’ О’	I	,	F6	| 5 при ~в—				
			0,2	0,4	0,6	0,8	1,0
	30	0,3 0,7	1,50 8,5	0,90 . 1,77	0,05 0,76	—0,08 0,50	—0,10 0,40
	' 45	о,з 0,7	1,64 9,2	0,30 2,15	0,08 0,85	0,00 0,60	—0,03 0,53
?п	30	0,3 0,7	—0,25 —3,40	0,10 —1,20	0,22 —0,50	0,30 —0,15	0,35 +0,10
	45	0,3 0,7	—0,13 —2,6	0,20 —0,85	0,28 —0,25	0,32 0,08	0,40 0,25 ’
Таблица XIV.3
	Р6. Fc	s при А-чс				
		0,2	0,4	0,6	0,8	1,0
	0,27	0,00	2,18	5,10	11,3	18,4
	0,55	—0,48	0,53	1,89	4,0	6,6
	1,0	—0,40	+0,10	0,83 .	1,47	2,3
Sn	—	0,64	0,65	0,85	0,96	1,0
При а — 90° (прямоугольный тройник) Сп почти не зависит от -у- и слабо зависит от-^~-. Для стандартного тройника из ковкого чугуна на резьбе при а = 90° и Fn = Fc коэффициенты потерь приведены в табл. XIV.3.
При разделении потоков (рис. XIV. 14, б) потери складываются из потерь на поворот в боковое ответвление и потерь на внезапное расширение в месте разделения потока. Последние сильно растут при увеличении площади отвода.
Сопротивления при слиянии и разделении потоков	387
Так, для прямоугольного тройника, изготовленного из ковкого чугуна, при а = 90° и Fn = Fc коэффициент потерь прямого прохода не зависит от величины и весьма слабо зависит ’ п
от в то время как коэффициент потерь бокового ответвления
существенно зависит от обеих указанных величин. Для сравнения со слиянием потока в прямом тройнике приведем соответствующие цифры для разделения потока в таком же тройнике (табл. XIV.4).
Видно, что коэффициенты
Рис. XIV. 15
потерь для больших значе-
ний при слиянии больше, чем при разделении. Для малых Чс	Чс
наоборот, коэффициенты потерь при слиянии потоков меньше,
чем при разделении.
Таблица XIV.4
1	с и IX. К	,	Q6 1 при —-— или			«с	
		0,2	0,4	0,6	0,8	1.0
	0,27	1,81	2,83	4,07	6,00	8,90
	0,55	1,20	1,59	1,77	2,20	3,30
	1,0	1,0	1,20	1,50	1,80	2,30
	—	0,64	0,57	0,51	0,55	0,70
Приведем несколько значений коэффициентов сопротивления для задвижек и клапанов.
Для простой задвижки (рис. XIV. 15) величина коэффициента сопротивления £, равного
г — А/у
Q ~ рИ; ’
2
в зависимости от значения относительного открытия задвижки приведена ниже:
К~. . . 0,125	0,2	0,3	0,4	0,5	0,6	0,8	0,9	1,0
t, . . . 97,8	35,0	10,0	4,6	2,06	0,98	0,17	0,06	0
25*
388
Электромагнитная гидродинамика
Для дроссельного клапана (рис. XIV. 16, а) и пробочного крана ’j (рис. XIV. 16, б) коэффициенты сопротивлений £ от угла 6 . ..° . Дроссель Кран
в зависимости?
15
30 3,91
40
10,8
5 0,24
50 32,6
10 0,52 0,90
открытия б следующие: 20 1,54
67	70
—	751
I
90
оо '(
Коэффициенты сопротивления конусного (рис. XIV. 17, а) ч и шарового (рис. XIV-17, б) клапанов могут быть определены по j
эмпирическим формулам. ,ji Для конусного клапана J
i=°’6 + TT^’ \ Do )
для шарового
С = 2,7-
0,8 .	0,14
h	/ Л У'
Do	\ Do)
Наиболее полно коэффициенты местных ставлены в гидравлических справочниках.
сопротивлений пред-,$
ГЛАВА XV
ЭЛ ЕКТРОМАГН ИТН АЯ
ГИДРОДИНАМИКА

Д

§ 1. Предмет электромагнитной гидродинамики
Законы движения жидкостей и газов при наличии сил электро? магнитного происхождения, или так называемых пондеромотор-у ных сил (п. с.), являются предметом изучения электромагнитной гидродинамики.
Электромагнитную гидродинамику можно разделить на три 'Й части: магнитную, электро- и феррогидродинамику.
Предмет электромагнитной гидродинамики	389
Магнитная гидродинамика изучает движение электропроводящих жидкостей и газов в электромагнитном поле. Движение непроводящих сред, при которых пондеромоторные силы возникают только под действием электрического поля, изучает электрогидродинамика. При этом в обоих случаях имеется в виду известное в обычной гидродинамике приближение сплошной среды. Кроме того, считается, что жидкость является немагнитной, она действует па магнитное поле не просто своим присутствием, а благодаря текущим в ней электрическим токам. Эти токи обладают собственным магнитным полем, благодаря чему напряженность магнитного поля в среде изменяется. С другой стороны, движущаяся электропроводная среда испытывает со стороны магнитного поля действие некоторых сил, зависящих от напряженности магнитного поля и скорости движения среды. Таким" образом, можно сказать, что движение воздействует на магнитное поле, а магнитное поле оказывает воздействие на движение.
Действие электромагнитных сил на твердые проводники широко используется для создания различных электрических машин и приборов. Принципиальная возможность использования пондеро-моторных сил в некоторых технических схемах с жидкими проводниками также не нова. Она известна со времен Фарадея. Но практическое использование этих сил в жидкостях и газах началось лишь в последние годы.
Электромагнитная гидродинамика, зародившаяся как наука о движении проводящих сред космического пространства, сейчас получает все большее применение в различных областях техники.
Плазменные движители для космических кораблей, прямое преобразование тепловой энергии в электрическую, транспортировка и измерение параметров течения проводящих жидкостей, электромагнитные способы обогащения — вот далеко не полный перечень проблем, решение которых связано с развитием магнит* ной гидродинамики.
Законы электрогидродинамики лежат в основе различных способов электрического обогащения и разделения полезных ископаемых, электрофильтров очистки газов и пр.
Феррогидродинамика рассматривает движение жидкостей и газов при воздействии сил магнитного происхождения.
§ 2. Уравнения электромагнитной гидродинамики
Система -уравнений электромагнитной гидродинамики представляет собой совокупность уравнений гидродинамики и электродинамики.
Уравнения электромагнитного поля. Взаимодействие между заряженными частицами осуществляется посредством электромагнитного поля, которое они создают вокруг себя.
390
Электромагнитная гидродинамика
Электромагнитное поле в самом общем случае определяется ; полем четырех векторных величин И, Е, В и D. Первые две величины называются напряженностями, а две другие — индукциями ] магнитного и электрического полей. Величины индукций связаны с соответствующими напряженностями соотношениями:
D = е£ и В = р.Я,	(XV. 1) ;
где 8 и р —диэлектрическая и магнитная проницаемости среды.
В большой части практических задач для изотропного вещества величины 8 и р — константы и, следовательно,, векторы Н и Е отличаются от В и D постоянными коэффициентами. Поэтому можно считать, что электрические и магнитные поля определяются не четырьмя векторами, а лишь двумя: Е или D для электрического  поля и Н или В для магнитного. Для анизотропного вещества 8 । и р надо рассматривать как тензорные величины и тогда векторы D | В не параллельны векторам Е и Н.	1
Источниками электрических и магнитных полей являются j электрические заряды и токи. Будем считать, что распределение 1 зарядов определяется скалярной величиной объемной плотности ' зарядов рс, а распределение токов —вектором плотности тока J.
Фундаментальными уравнениями электродинамики являются j четыре уравнения Максвелла \ которые включают закон Ампера, .: закон индукции Фарадея и уравнения сохранения для электрических и магнитных полей:
rot Н =	+ J;	(XV. 2)
rot£ = —	(XV.3)	*
divD = pc;	(XV.4)	’
divB = 0.	(XV.5)	:
Уравнение (XV.2) показывает, что вихревое магнитное поле создается при движении зарядов и при изменении во времени' электрического поля. По аналогии с электрическим током вели-
дЪ	.	:
чину называют током смещения, а сумму обоих членов — пол-ным током.
1 Теория электромагнитного поля была изложена Максвеллом в труде «Трактат об электричестве и магнетизме» (1873 г.).
Уравнения электромагнитной гидродинамики
391
Уравнение (XV.3) показывает, что в каждой точке магнитного поля его изменение по времени создает вихревое электрическое поле.
Источником электрического поля являются заряды. Это следует из третьего уравнения Максвелла.
Уравнение (XV.5) показывает, что вектор магнитной индукции соленоидален, т. е. расхождение этого вектора равно нулю.
Уравнения Максвелла являются обобщением опытных факторов и представляют фундаментальные постулаты электродинамики. Правильность этих постулатов проверена тем, что все выводы, следующие из них, согласуются с известными экспериментальными данными.
Система уравнений Максвелла является незамкнутой. Число уравнений в ней меньше числа неизвестных.
Кроме уравнений Максвелла в электродинамике существенное значение имеют закон сохранения заряда, или уравнение неразрывности (сплошности), и обобщенный закон Ома.
Закон сохранения заряда легко получить из уравнений Максвелла. Применив операцию div к уравнению (XV.2), будем иметь
div rot Н = Лг div D 4- div J = О, ut	1
а после подстановки значения D из уравнения (XV.4) получим закон сохранения заряда в виде
+ div J = 0.	(XV.6)
Замыкающим систему уравнений Максвелла для неподвижной проводящей среды векторным соотношением может служить закон Ома. Он устанавливает связь между плотностью тока проводимости и характеристиками электромагнитного поля. Эта связь зависит от свойств проводника. Во многих важных случаях для неподвижных проводников опытный закон Ома имеет вид
J = <з~Е.	(XV.7)
Коэффициент о называется проводимостью. Для изотропных проводников проводимость о —скаляр, причем о = где 7? — сопротивление проводника. Для анизотропных проводников проводимость о является тензорной величиной.
В движущемся проводнике входящая в уравнение Максвелла плотность электрического тока определяется из закона Ома, который выражает зависимость плотности тока J не только от проводимости о и напряженности электрического поля Е, но и от других параметров поля, определяющих свойства и движение рассматриваемой среды.
5	Электромагнитная гидродинамика
Если среда и условия задачи таковы, что векторы плотности тока и напряженности электрического поля параллельны, то такая) среда называется изотропно проводящей и закон Ома для нее имее^ простейшую форму
J = а [В + (V X В)1 + р/,	(XV.8)
где оЕ — ток проводимости; о (V X В) — ток индукции; peV — ток конвекции.	‘
Уравнения (XV.7) и (XV.8) хорошо описывают процессы про-текания тока в обычных твердых и жидких проводниках (металлы;; электролиты и т. д.), а также в слабо ионизированном газе, если напряженность магнитного поля невелика.	
Наряду с изотропно проводящими, могут рассматриваться^ анизотропно проводящие	среды,	для	которых	закон Ома имеет
более сложный вид	1
J=.v[E + (yx	В)—-L(JxB)] +	peV,	(XV.9)I
Pei	ч
где Pel —плотность заряда электронов;-p[(J X В) —ток Холла J При этом анизотропия в законах протекания тока связана с нали-| чием магнитного поля, при В = 0 анизотропно проводящая^ среда ведет себя как изотропно проводящая.	;
Уравнения гидродинамики. Приведенные уравнения электро?' динамики составляют часть системы уравнений электромагнитно^ гидродинамики. Другой частью этой системы являются уравнения гидродинамики, рассмотренные в гл. III. Для несжимаемой жидкости они имеют вид:	.:
+	(XV.10|
div V = 0.	(XV. Ш
В уравнении Навье—Стокса (XV. 10) отнесенная к единице массы объемная сила F представляет собой сумму всех внешних объемных сил, из которых можно выделить силы электромагнит* ного происхождения, т. е. пондеромоторные силы. Таким образом^
F = Fo + B9M,	’I
где Fo —объемные силы неэлектромагнитного происхождений! (силы тяжести и др.).	;|Ц
Если пондеромоторные силы разделить на электромагнитный FM и электрические F3, tq, как известно из электродинамики, они!
Уравнения электромагнитной гидродинамики	393
будут соответственно равны:
^м = (</ х В)--Я2grad р + -i-grad	; (XV.12)
Л = рЛ 1^Е2 grad 8 + -1- grad (f2p ,	(XV. 13)
где последние слагаемые обеих сил, называемые стрикционными силами, учитывают зависимость магнитной проницаемости р и диэлектрической проницаемости е от плотности среды р.
Для однородных сред эти силы могут быть представлены в виде:
A. = (J х В) + VB2;	(XV. 14)
F3 = РеЕ + VB2.	(XV. 15)
—
Величины р0 и е0 характеризуют магнитную и диэлектрическую проницаемости вакуума. Они равны:
р0 = 4л • 1(Г’	1,257 • 10"6 Гн/м; е0 8,85 • 10~12 Ф/м.
Для любого вещества е > е0, поэтому второй член правой части выражения (XV. 15) всегда является положительным.
Для парамагнитных веществ (кислород, литий; натрий, алюминий и др.) р >> р0. Это означает, что сила
grad В>
увлекает парамагнитные вещества в области, где индукция поля В имеет максимальное значение.
Для диамагнитных веществ (висмут, медь, ртуть, гелий,, водород, азот и др.) р < Ро и сила FM будет выталкивать эти вещества из области максимального значения магнитной индукции.
Для ферромагнитных веществ (железо, никель и др.) всегда Н » Ио-
Соотношением, определяющим тепловой баланс в движущейся электропроводной жидкости, является уравнение возрастания энтропии, которое для несжимаемой жидкости имеет вид
рс0 J -1 АТ + f	)2 + v • <XV-16)
В уравнении (XV. 16) два последних члена характеризуют вязкие и джоулевы потери соответственно,.
Уравнение индукции. В магнитной гидродинамике часто пользуются так называемым уравнением индукции
^-=rot(V ХВ) + ^ДВ,	(XV.17)
которое легко может быть получено подстановкой в уравнение (XV.3) величины В из закона Ома, a J —из уравнения (XV.2).
394	Электромагнитная гидродинамика
Учитывая, что
rot (V X В) = V div В — В div V + (BV) V — (VV) В, a div В = 0 и div V = 0, и вводя обозначение = vm, выражение (XV. 17) запишем в виде	!
+ (VV) В = (BV) V + vm АВ.	(XV. 18) \
Граничные условия. Для решения задачи о движении электро- . проводной жидкости в магнитном поле к приведенным уравнениям должны быть добавлены начальные и граничные условия.
Уравнения Максвелла или эквивалентные им уравнения справедливы только в таких точках пространства, в окрестности которых физические свойства среды изменяются непрерывно. На границах поля течения физические свойства могут претерпевать разрывы. Например, на твердой границе электромагнитные свойства жидкости будут скачком переходить в электромагнитные свойства твердого тела. При переходе через такую поверхность разрыва электромагнитных свойств должны выполняться следующие условия.
1. Нормальная составляющая вектора магнитной индукции остается непрерывной при переходе через поверхность раздела,
т. е. (В2—В^-п = 0, где п —единичный вектор нормали к по: верхности разрыва. Индексы 1 и 2 относятся к величинам, связанным непосредственно с каждой из сторон этой поверхности.
2.	Изменение магнитного поля Н на этой поверхности удовлетворяет условию п х (#2—= Js, где J s —плотность '; поверхностного тока (плотность тока на границе сред). При . конечной электропроводности о =/= оо и даже при о — 0 значе- j ние Js равно нулю, т. е. тангенциальные составляющие напряженности магнитного поля по обе стороны границы раздела равны между собой: п X Н2 = п х Нг. При бесконечной элек- : тропроводности о = оо J, может быть отлично от нуля.
3.	Касательная составляющая напряженности электрического • поля Е остается непрерывной при переходе через поверхность • разрыва, т. е. п х (В2—— 0.	
4.	Изменение электрической индукции на этой поверхности удовлетворяет условию п (О2—Ох) = pes, где pes —плотность свободного поверхностного заряда.	)
В большинстве задач магнитной гидродинамики можно пре- ' небречь плотностью поверхностного тока Js и плотностью свобод- •
Электромагнитная гидростатика	395
кого поверхностного заряда. Следовательно, граничные условия сведутся к условию, что касательные составляющие Н и Е и нормальные составляющие В и D должны быть непрерывными при переходе через поверхность, разделяющую тело и жидкость или две жидкости. Здесь следует иметь в виду различие в поведении Н, В нЕ, D, так как значения р и е могут быть различными по обе стороны границы.
§ 3.	Электромагнитная гидростатика
Большой интерес представляют уравнения электромагнитной гидростатики. Не имея возможности проанализировать вопрос о всех состояниях равновесия жидкости при наличии различных пондеромоторных сил, рассмотрим здесь лишь один частный случай. Будем считать, что векторы всех пондеромоторных сил лежат на линии действия сил тяжести. Тогда жидкости и газы, на которые действуют пондеромоторные силы, будут как бы утяжеляться, т. е. фактический вес их будет больше физического веса. При противоположном направлении пондеромоторных сил жидкости и газы в поле действия их будут как бы терять свой вес, так как фактический вес их будет меньше физического. В частном случае равенства пондеромоторных и гравитационных сил жидкости и газы будут в невесомом состоянии.
Рассмотрим раздельно уравнения магнито- и электрогидростатики.
Уравнения магнитной гидростатики получим, приняв в уравнениях (XV.8), (XV. 10) и (XV. 12) скорость равной нулю и магнитную проницаемость постоянной. Тогда будем иметь
g —-^-gradp +-^-[Е X В] = 0.	(XV.19) 
Совместив ось z с радиусом Земли и приняв
[£ X В]Х = [Е х В] = 0; -2-[Е х В]г = -^-<р = £1,
Р	р
вместо (XV. 19) получим
pg dz — dp 4- EiP dz = 0.
Обозначив давление на поверхности жидкости ра, а глубину погружения z0— z — h, получим, что давление в жидкости при наличии силы Лоренца, отнесенное к единице объема, будет равно
Р = Pa + (g + gi) ph = pa + 40h,	(XV.20)
где у 0—сумма физического веса и электромагнитной составляющей,
Yo = V + Vi = Р (g + £i)-	(XV.21)
398
Электромагнитная гидродинамика
Зависимость (XV.21) удобно представить в безразмерном виде-7=^ = 1 + л=1+-^ф,
где А —увеличение веса за счет электромагнитного поля.
Так как значение gr может быть выбрано произвольно, то из. уравнения (XV.20) следует, что электромагнитным полем в npo-J водящих средах можно легко менять их фактический вес. Так,  для определения условий невесомости достаточно в последнем ‘ соотношении принять, что у = 0 или сир = —у.	"
Выражение (XV.21) справедливо для любой проводящей среды,; в том числе и для частиц твердого тела, помещенного в проводя-! щую жидкость.
Если пренебречь локальными изменениями поля в непосред-1 ственной близости от частицы, то на нее будет действовать сила, я равная	"
G = Уо — Уо1 = (У — 7т) + (о — от) <Р,	(XV.22)1
где у 0 = у о<р и у01 = ут + от<р — фактические веса жидкости j и тела, погруженного в жидкость при наличии электромагнитного Я поля. Он складывается из составляющих, обусловленных физи-1 ческим весом и пондеромоторными силами.	'!>
Величина у — ут является гравитационной составляющей, j а (о — от) Ф = G3M — составляющей пондеромоторных сил, кото- ; рая‘ равна	<
Сэм = (о-от)ВЕ = ^/В,
где Ао = о — от, / = о£.	J
Это соотношение существенно изменяет условия плавания тел. ?
Если без пондеромоторной силы тело плавает при ут < у, то при.; наличии пондеромоторных сил это условие может не выполняться,?,! так как в этом случае для плавания требуется, чтобы у0 <y01.J
При одинаковых весах жидкости и тела (у = ух)	?
О = Оэм = (о—от) ф = "V- iB-
Если тело не проводник (от = 0), то
G = (у — ут) + Оф = (у + Оф) — ут, а при у — ух и от = 0
G = Оф = /В.
Так как значение ф может быть выбрано произвольно, то,; следовательно, при у—ух и от = 0 можно сделать Оф > 0 (тело;; будет плавать), либо Оф < 0 — (тело будет тонуть).	3
Электромагнитная гидростатика	387
Удобно вместо (XV.22) и (XV.23) использовать безразмерные соотношения:
5=:-Т=1+ т<₽ = 1 + А;
Q =2.0T-Y.oi.	1 + .£-g.T ф == 1 + д
У — Ут	у — Ут	1
где А = — <р и Ах = а~°1- <р. Т _	У~ Vi
Величины G характеризуют относительное влияние электромагнитного поля.
Если тело, находящееся в проводящей жидкости, будет иметь магнитную проницаемость, отличную от магнитной проницаемости жидкости, то кроме силы Лоренца (XV.23) на единицу массы тела, согласно (XV. 12), будет действовать сила
01 = 4“ Я2 grad ц.
На единичное тело, имеющее форму шара и погруженное в проводящую жидкость с отличными от тела проводимостью и магнит-„	о—ат	Да ц—цт
нои проницаемостью, в предположении, что ——г = —— и 51—=
Ди.
= —-----малые величины или что проводимости и магнитные
проницаемости жидкости и тела близки, можно получить
Описанные явления могут быть использованы для электромагнитного обогащения, сепарации, выделения шлаков и неметаллических включений из жидких металлов и т. д.
Если в уравнениях (XV. 10) и (XV. 13) примем скорость равной нулю и диэлектрическую проницаемость постоянной, то, считая, что вектор напряженности электрического поля Е совпадает с g, получим уравнение электрогидростатистики в виде
g +	(XV.24)
Г	Г
или
гДе g3 = Е.
После интегрирования уравнения (XV.24) получим Р = Р (g + £э) * = (V + Р£э) z = уог-
398
Электромагнитная, гидродинамика
Таким образом, видно, что при помощи объемных зарядов можно изменять фактическую плотность непроводящей жидкости : у0, равную	!
Yo = Y + Рёэ = Т + РеЕ,	(XV.25)
или в безразмерном виде
То = —= 1 + —+Д.
го т pg	1
где А = Е.	i
Pg	:
Если в непроводящую жидкость поместить диэлектрик с от-  личными от жидкости диэлектрической постоянной е и магнитной ; проницаемостью р,, то на тело будет действовать сила, опреде- j ляемая по формулам (XV. 12) и (XV. 13).	'
Для сферы при условии, что -~е- = и ~|1т- = I малы, а электрические и магнитные поля одинаковы по частоте < и фазе, было получено, что сила, отнесенная к единице объема, ; равна	’
+	<XV.26)i
Формулы (XV.25) и (XV.26) выражают возможность гравита- .] ционного разделения (в непроводящей жидкости) частиц, имеющих одинаковый физический вес, но различные диэлектрические и магнитные свойства.
1
§ 4. Проводимость жидкостей и газов	’
Численные значения проводимости различных сред лежат i в широких пределах. Для жидких металлов она довольно велика, ’ а для чистой пресной воды и воздуха при обычных температурах ч практически равна нулю. Так, проводимость меди равна 6-107 1/Ом-м, натрия ~107 1/Ом-м (100° С) и ртути ~10® 1/Ом-м j (20° С), в то время как проводимость пресной воды 2 — 5 X 1 X 10~5 1/Ом-м, а проводимость морской воды 3—5 1/Ом-м. j
Большое влияние на проводимость воздуха оказывает темпе- 1 ратура. Ее повышение приводит к увеличению скорости движения 1 молекул, а соударение молекул, обладающих большой кинетиче- 4 ской энергией, вызывает повышенную ионизацию газа. Зто при-водит к увеличению его проводимости. Напомним, что величина а ; меняется от нуля для неионизированного газа до единицы для; полностью ионизированного газа. При малых значениях степени .
— -1— : ионизации проводимость пропорциональна а и Т 2 , т. е. о —: ~аТ~т.	']
Проводимость жидкостей и газов
399
При больших значениях а проводимость не зависит от сте-з	з
пени ионизации и будет пропорциональна Т2, т. е. о — Т2 .
Использовав таблицы термодинамических свойств воздуха для температуры до 24 000 К, можно записать следующую эмпирическую зависимость проводимости от температуры:
а = о0е01’084 У7'-4300 при Т > 4300 К;
о = йое“'11084 ^430°-7' при Т < 4300 К,
6.(Ом м)'1
6 8 f2 !6 м Рис. XV.1 .
где о0 — проводимость воздуха при Т = 4300 К и заданном давлении.
При движении тел в воздухе с большими скоростями образуются скачки уплотнения, в которых газ сильно нагревается, ионизируется и становится проводником. Проводимость воздуха за скачком уплотнения (рис. XV. 1) сильно растет в интервале чисел М = 10-4-16.
Во многих практических задачах, например для непосредственного превращения тепловой энергии в электрическую, необходимо получить как можно большую проводимость газа. Ее можно повышать, не только увеличивая температуру газа, но и с помощью присадок щелочных металлов (калий, натрий, цезий). У этих металлов низкий потенциал ионизации, и они значительно увеличивают степень ионизации газов. Наиболее эффективен цезий, но он дефицитен, поэтому применение его ограничено. Калий и натрий весьма распространены и могут быть широко
использованы.
На рис. XV. 1 приведена расчетная кривая проводимости воздуха за скачком уплотнения при добавке 0,1% калия. Примесь калия особенно эффективна при числах М = 104-14. Так, при М = 10 проводимость в случае добавки 0,1% калия выше, чем без добавки, в 100 раз и более. При дальнейшем увеличении числа М эффективность добавок понижается.
Проводимость воды существенно зависит от находящихся в ней примесей. Например, проводимость морской воды определяется преимущественно наличием в ней солей хлористого натрия.
Проводимость водных растворов кислот и щелочей (рис. XV.2, а) значительно превышает проводимость морской воды и достигает 60—70 1/Ом-м.
400
Электромагнитная гидродинамика
На проводимость растворов сильно влияет температура. Так, для КОН (рис. XV.2, б) при изменении температуры от 12 до 65° С (массовая доля 20%) проводимость увеличивается почти в три раза.
Проводимость жидких металлов с увеличением температуры убывает. Так, например, проводимость олова при изменении тем-
Рис. XV.2
пературы от 300 до 900° С убывает примерно от 2 • 106 до 1,5 Х::! X 105 1/Ом-м. У натрия и некоторых других металлов с ростом' температуры проводимость убывает еще сильнее.
§ 5. Подобие электромагнитных явлений	"
-''i
Для нахождения чисел подобия, определяющих магнито-;, гидродинамические процессы, запишем уравнение движения с уче£;! том силы Лоренца в безразмерном виде. Обозначим масштабы,,;! к которым относятся все размерные величины, соответствующими;! буквами с индексом 0; масштабы, к которым относятся безраз-' мерные величины, — теми же буквами. с чертой:
v = VOV; р =рор; В = вов	J
и т. д. Масштабом длины для всех трех координат выберем неко^ торый характерный размер 10. Тогда указанное уравнение поел® деления на размерную величину при конвективном ускорений® примет вид
+ Л-В.-bj-Z.lixB) + Д4(PxB)xi. (XV.27J Р	Р Vq
Подобие электромагнитных явлений
401
В уравнении (XV.27) имеются знакомые числа гидродинамического подобия: числа Струхаля, Эйлера, Фруда и Рейнольдса.
Комбинации размерных величин при электромагнитных членах можно представить в таком виде:
° f Р-о#о z _ Нояо „ Ео , .
~^-(Ио//о)2/о = -^аУ0/о(л0.
и •'о	Р^О
Нетрудно убедиться в том, что безразмерные величины. Будем
-^5-, а-тг1о и а]/о/оро есть Р^о "о
величину, характеризующую
отношение магнитного давления к динамическому давлению, называть магнитным числом Эйлера

= Еим.
Число	называется магнитным числом Рейнольдса
VQl0 _ Volo___Пл
1	“ vm — Ке“’
ПЦо
1 а величина vm =----------магнитной вязкостью.
Е Ио<Т
Число -^-2- Zo можно назвать электрическим числом Рей-По
нольдса
aZ0-^- = Re3. П о
Если магнитное число Рейнольдса разделим на динамическое число Re, то получим величину
= сгр,0^ = —— = Ргм, Re	vm м
которую можно назвать магнитным числом Прандтля. Из формул видно, что динамические и магнитные числа Прандтля определяются только физическими свойствами вещества.
Следует отметить, что между vm и v имеется глубокая аналогия. Кинематическая вязкость v характеризует степень превращения кинетической энергии среды в тепло в результате действия сил трения; магнитная вязкость определяет диссипацию энергии электромагнитного поля в среде с конечной проводимостью, т. е. характеризует степень превращения электромагнитной энергии среды в тепло.
26 и. д. Повх
402 Электромагнитная гидродинамика
Из приведенного анализа следует, что если числа EuMJ ReM, Res, 'Ртм Для ДвУх различных магнитогидродинамиче-i ских явлений одинаковы, то эти явления подобны. Иногда! подобие может соблюдаться при совпадении лишь части ука-1 занных чисел.	j
Рассмотрим далее влияние указанных чисел подобия на дви-1 жение проводящей жидкости.	1
Магнитное число Эйлера равно отношению магнитного давле-: ния к динамическому или отношению плотностей магнитной и ки-^ нетической энергии и служит мерой относительного влияния ма-i гнитного поля на движение среды. Очевидно, при числах Еим Г влияние магнитного поля на движение проводящей жидкости1 будет мало; при больших числах Еим роль магнитной энергии будет велика. При значениях Еим порядка единицы энергия равномерно распределена между полем и движением, так что влияние; магнитного поля на движение и, наоборот, влияние движения на. поле являются одинаковыми.	'<
Число ReM имеет такую же форму, как обычное число Re,,j однако в физическом смысле чисел Re и ReM имеется большое: различие. Обычное число Re получается из динамических сообра*' жений кай отношение инерционной силы к силе вязкости, а число; ReM получается из кинематических соображений, учитывающих, как движение жидкости влияет на магнитное поле. Число Re,*' определяется как отношение.индуцированного тока к тому току^ который необходим для создания внешнего магнитного поля за-< данной напряженности, или как отношение напряженности инду-;' цированног» магнитного поля к напряженности приложенного^ извне магнитного поля.	Т-
В случае малых ReM < 1 среду можно рассматривать как?, слабо проводящую, вследствие чего наводимые в ней индукцион-н ные токи будут невелики. Среда при этом легко протекает (сколь*; зит) сквозь внешнее магнитное поле, мало'возмущая и искажая;’ его. Наоборот, при ReM > 1 магнитная вязкость становится очень® малой, и среда ведет себя как идеальный проводник, в которой^ легко могут возникать сколь угодно большие токи. Вследствие^! этого среда при своем движении вызывает сильное искажение и;, деформацию внешнего магнитного поля вплоть до полного его! выталкивания.
Следует отметить, что хотя перечисленных параметров доста-« точно для описания магнитогидродинамического движения, онН.' не являются единственными. Комбинируя их, можно получить" другие важные параметры.	;
.Известно так называемое число Гартмана	’
На = В0Е01/^-.
'	г
Подобие электромагнитных явлений
403
Зто число характеризует соотношение между электромагнитными силами, действующими на единицу объема движущейся среды со стороны магнитного поля, т. е. силами магнитной вязкости, и обычными вязкими силами.
Легко убедиться, что между Re, ReM, EuM и На выполняется следующее соотношение: На = ]/ Re ReMEuM.
Число Стюарта может быть легко получено как отношение квадрата числа Гартмана к числу Рейнольдса:
ci _ На2 ___ °ово£о
~	“ Ро1/о ‘
Число St характеризует меру влияния магнитного поля на движение электропроводной среды и определяется отношением электромагнитной силы, действующей на единицу объема среды, к силе инерции. При St 1 движение полностью определяется магнитным полем, и, наоборот, при St < 1 магнитное поле почти не влияет на движение.
Еще одни критерий можно получить, заменив в числе На о	X.
динамическую вязкость q одноразмерной величиной —: ________________________________________	ср
HaT = B0L0
Этот критерий можно назвать тепловым числом Hav Он характеризует отношение джоулева тепла, выделяющегося в единице объема движущейся электропроводной среды, к теплу, поступающему в единичный объем вследствие теплопроводности.
При магнитогидродинамическом подобии единственным числом, величина которого определяется через напряженность электрического поля Е, является электрическое число Re3. Из уравнения (XV.27) видно, что электрическое число Re3 характеризует величину электрической объемной силы, полученной за счет электрического поля с напряженностью Е при наличии магнитного поля с индукцией В.
Число Re3 можно представить в виде
Re3 = cqi0V3/0,
где V3 = -в- — величина, имеющая размерность скорости, вы-•^О
раженной в м/с; а — в 1/Ом-м; 10 — в м.
Для некоторых случаев движения тел в морской воде число Re3 может в зависимости от характерной длины меняться от сотых долей единицы до нескольких десятков.
Отношение электрического и магнитного чисел Рейнольдса можно представить в следующем виде:
м   Ибэ   Уэ   Е(, 1 9~ ReM “ Vo	Во Го ’
404
Электромагнитная гидродинамика
Эта величина определяется как отношение скоростей и можед быть названа электромагнитным числом М.
Магнитное число Прандтля характеризует собой отношение диссипации механической энергии (за счет вязкости) к диссипа; ции электромагнитной энергии (за счет наличия магнитной вяз* кости).	:
Величина Ргм для морской воды Ргм ~ 10"12, а для жидкий металлов с большой проводимостью число Ргм ~ 10"5.
Во многих технических задачах джоулево тепло значительней превосходит тепло, образованное действием вязкости, илиимеет одинаковый порядок с последним.	
Числа, или критерии подобия,' в электрогидродинамике можнб также получить из безразмерных уравнений.
Введем следующие
8 =—; Га
8о 0
безразмерные величины:
=-fe; 7=^ v=V!«-
При подстановке этих величин в уравнения электродинамики; и гидродинамики для стационарного движения получим уравнения* электрогидродинамики в безразмерной форме:
rot Е — 0;
div Е = Re3-~-;
8
1 = ре (Мэ V + £) —	div ре; (3)
(Г V) V= F^- Eu Vp + J- V2V + ЕиэрД(4)
(XV.28)i
div V = 0.	(5)
В системе безразмерных уравнений Re, Fi и Ей — критерии? гидродинамического подобия, а
______ Рео^о  М   Ер  г>_   МрЕр . р,   Рео^р/р Кбэ— 8р£0 - Мэ— уэ > KeZ D > LU3- pl/g
критерии подобия электрические. При этом число Rez, определяе-j мое через коэффициент подвижности ионов k, можно назвать ион-я ным числом Рейнольдса.	i
Если в качестве характерных величин выбрать другие, то изк' соответствующих безразмерных уравнений можно получить дру-,. гие критерии подобия, характеризующие отношение соответствуй ющих сил.	<й''.
Классификация уравнений электромагнитной, гидродинамики 405
§ 6.	Классификация уравнений электромагнитной гидродинамики
Рассмотрим вид уравнений, описывающих движение жидкости в электромагнитной гидродинамике и электрогндродинамике.
Магнитная гидродинамика. Система уравнений магнитной-гидродинамики включает уравнения Максвелла, закон Ома и уравнения гидродинамики.
Уравнения Максвелла в этом случае отличаются от (XV.2) — (XV.6) лишь тем, что в магнитной гидродинамике плотностью зарядов пренебрегают, положив рс = 0. Тогда в законе Ома для проводящих жидкостей можно пренебречь конвективным током и представить его в виде
J = о [Е + (V х В)].	(XV.29)
Учитывая, что ток смещения имеет тот же порядок, что и конвективный ток, уравнение (XV.2) запишем в виде
-i-rotB = J.	(XV.30)
Уравнения гидродинамики для несжимаемой жидкости (II 1.41) состоят из уравнения движения и уравнения неразрывности. Первое, имея в виду (XV. 14), можно записать:
=	+	^-(JxB)+ VB*. (XV.31)
Если, как принято в магнитной гидродинамике, рассматривать немагнитные среды, то величина магнитной проницаемости р будет равна р0, и последний член в уравнении (XV.31) будет равен нулю. Учитывая (XV.30), электромагнитную силу можно записать в виде
= (J х В) = -L rot В X в = 4- (BV) В - J- VB2.	(XV. 32)
D	1Л	1Л	£[Лг
Член имеет размерность давления и по аналогии с динамическим называется магнитным давлением.
Уравнение движения с учетом (XV. 32) примет вид
4- + (fc) И = —1- V ( Р +	) + -L F. + V ДУ +	(BV) В.
(XV.33)
Вид уравнения непрерывности (XV. 11) и уравнения индукции (XV. 17) или (XV. 18) остается неизменным.
В зависимости от причин движения основного потока проводящей среды в магнитной гидродинамике различают два предельных случая.
406
Электромагнитная гидродинамика
1. Основной поток проводящей жидкости создают внешний для рассматриваемого поля силы. За счет пересечения основного потока с силовыми линиями заданного магнитного поля возникаем электрический ток. Все установки, создающие электрический toi таким образом, будем условно называть генераторами. К ни$ прежде всего относятся собственно магнитогидродинамическщ генераторы, преобразующие тепловую энергию в электрическую и, кроме того, различного рода электромагнитные расходомеры; лаги и другие измерители скоростей жидкости.	;
2. Все движение проводящей жидкости полностью определяется только пондеромоторными силами, возникающими в рассматриваемом-электромагнитном поле. В этом случае и магнитное#] и электрическое поля задаются извне. Установки такого типа! будем называть насосами. К насосам можно отнести большое коли-! чество различных электромагнитных устройств, прежде всего соб-з ственно электромагнитные насосы для перекачки проводящих! сред и ряд других устройств, в которых проводящие среды пере-! мещаются или, в частном случае (в гидростатике), увеличивают! или уменьшают свой вес.	1
Принцип действия и схемы насосов и генераторов приведены в конце главы.
Тензор магнитных напряжений Максвелла. Так же как! и в обычной гидродинамике (II 1.22), в магнитной гидродинамике' уравнение (XV.33) может быть записано в напряжениях. При: этом в уравнении (II 1.25) сила F (Fx, Fy-, Fz) представляет собой сумму объемных сил электромагнитного и неэлектромагнитного происхождения. Электромагнитную силу (XV.32) так же, как и вязкие силы, можно выразить через систему эквивалентных напряжений, состоящую из нормальных ахх и касательных аху и т. д. компонент. При этом, очивидно, проекция этих напряжений на ось х будет иметь вид
_ д д -	д
Рх дх хх ~J~ fly ®ху “г dz &хг'
Запишем проекцию уравнения (XV.32) на ось х
Fx = -(BX4- + By4- + Вг4-}вх — 4~^-х р. \ х дх 1 tJ ду 1 г dz / х дх 2р
Принимая во внимание, что div В = 0, это уравнение запишем в виде
fx = — Г~ (в2х—1д-в2\ + 4- bxbv + 4- вхв2].
х р L дх \ х 2	/ 1 ду х у 1 дг х ZJ
Учитывая условие, что действие электромагнитной силы и эквивалентных напряжений одинаково, можно записать, что
охх =—— ( В2 и-В2У, ох„ = — BVBW; охг = — ВхВг. хх Н \	2 / XIJ [л * * xz р, х z
Классификация уравнений электромагнитной гидродинамики
407
Аналогично можно получить другие компоненты напряжений. Из этих компонент можно составить тензор так называемых максвелловских напряжений, который имеет вид, аналогичный тензору вязких (III. 16) и турбулентных напряжений (XI.5)
TiK = — В,ВК —
‘к ц ' к 2ц ‘к
где oI K = 1, если i = k или 0, если i =k k — символ Кронекера. Тогда для электромагнитной силы получим выражение в виде

'хк
Если ось х направить параллельно магнитному полю, то касательные напряжения исчезнут и будут иметь место только нормальные напряжения. Одно из них будет растягивающим вдоль силовых линий ахх = Вх и два других — снижающих в попе-
речных направлениях = огг = — Вх.
Электрогидродинамика. Как в магнитной гидродинамике, в электрогидродинамике система уравнения состоит из уравнений Максвелла, законов сохранения заряда, закона Ома и уравнений
гидродинамики.
Уравнения Максвелла с учетом отсутствия магнитных полей и слабой проводимости будут:
rotE = 0, div Е =----
8
(XV.34)
Закон сохранения заряда
-^ + div/ = O
и закон Ома
1 = Рг (У + kE) —D div ре,
(XV.35)
(XV. 36)
где k — коэффициент подвижности ионов; D — коэффициент диффузии.
Уравнения гидродинамики будут:
+ [VV] V = -Lf0—L Vp + vVV + E + VE*;
(XV.37)
div V = 0.	(XV.38)
Уравнения (XV.34)—(XV.38) составляют систему уравнений электрогидродинамики. В отличие от системы уравнений магнитной гидродинамики она не содержит величин, характеризующих
408
Электромагнитная гидродинамика
магнитное поле, так как при движении слабопроводящих жидкое стен токи невелики. Конвективный перенос зарядов и диффузия^ несущественные в магнитной гидродинамике, во многих электрод гидродинамических задачах имеют определяющее значение и прей небрегать ими нельзя.
При е — е0 уравнение (XV.37) будет иметь вид
*1
+ (VV) V = v - т grad р++ пН- (XV-39>]
Так же как и в магнитной гидродинамике, в электрогидроди-'' намике можно различать два противоположных процесса. Первый.'! процесс — когда пондеромоторные силы, действуя на жидкие и | газообразные диэлектрики, вызывают их перемещение. По ана-) логии с электромагнитными насосами установки, в которых про-^ исходит такое движение, будем называть электрогидродинами-j ческими насосами.	-
Второй процесс, обратный первому, состоит в том, что, пере- f мещая внешними силами жидкости или газы, содержащие заряды, ’ можно при помощи электродов снимать эти заряды и таким обра- ; зом создавать во внешней цепи электрический ток. Установки, в которых происходит такой процесс, можно называть электро-гидродинамическими генераторами. Существуют также и комби- ’J нированные установки, в которых одновременно имеют место оба процесса.
В качестве непроводящих сред, на которые воздействуют пон- I деромоторные силы и которые используют в указанных установ-.,] ках, применяют: воздух, дистиллированную воду, керосин, д фреоны, четыреххлористый углерод, трансформаторное и другие^ легкие минеральные масла и пр. Уравнения феррогидродинамики.11 „могут быть получены аналогично уравнениям магнитной гидро-динамики и элёктрогидродинамики.	j
Вмороженность и диффузия магнитного поля. Для больших;| чисел ReM, т. е. когда проводимость жидкости велика или велики! линейные размеры поля течения, имеет место так называемое;^ вмороженное магнитное поле. В этом случае вторым членом^ в левой части (XV. 17) можно пренебречь и записать его в виде |
_g_ = rot(VxB).	(XV.40)|
Условие вмороженности магнитного поля следует понимать^ так, что магнитные силовые линии как бы приклеены к частицами жидкости или вморожены в жидкость, т. е. если в какой-либо| момент времени магнитная силовая линия совпадает с линией^ тока жидкости, то она совпадает с ней все время. Например, если:| в пространство, где имелось магнитное поле, втекает среда с до-4 статочно большой электропроводностью, ненамагниченная вна’.<
Классификация уравнений электромагнитной гидродинамики
409
чале (т. е. в ней напряженность магнитного поля равна нулю), то эта среда выталкивает магнитное поле и последнее деформируется так, что силовые линии будут направлены вдоль отделяющей ее поверхности, нигде не проникая в нее. При этом необходимо иметь в виду, что понятие магнитных силовых линий является математической абстракцией. В действительности взаимодействие между движущейся средой и связанным с ней магнитным полем является более сложным. При движении в магнитном поле в среде индуцируются токи, магнитное поле которых, складываясь с "имеющимся полем, изменяет его таким образом, что силовые линии как бы смещаются вместе с веществом среды.
При малых числах ReM имеет место так называемый случай диффузии (затухания) магнитного поля, при этом оно практически не зависит от движения жидкости. Условие диффузии магнитного поля может быть легко получено из уравнения индукции в предположении ReM < 1 в виде
(XV.41)
Уравнение (XV.41) по виду аналогично уравнению теплопроводности
—— = аДТ dt
или уравнению молекулярной диффузии вещества
Здесь Тис — температура и концентрация вещества; а и D — коэффициенты температуропроводности и диффузии.
Из уравнения (XV.41) следует, что в покоящейся среде магнитное поле со временем будет затухать, т. е. оно будет «просачиваться» сквозь вещество от точки к точке. Скорость просачивания, или скорость выравнивания магнитного поля, отнесенная к единице площади, определяется коэффициентом vm. По аналогии с молекулярной диффузией он может быть назван коэффициентом диффузии магнитного поля или коэффициентом переноса магнитной субстанции. Из уравнения (XV.41) видно, что время затухания поля имеет следующий порядок: t ~
В технических задачах, где линейные размеры тел невелики, время затухания магнитного поля мало. Так, для сферы диаметром 1 м, выполненной из высокопроводящего материала (медь, серебро), t0 10-7 с; для морской воды такого же объема t0
10~7 с. Для космических тел время затухания магнитного поля очень велико. Для магнитного поля Земли оно равно 1,5-104 лет, для Солнца — 1010 лет, для звездных систем — еще больше.
410
Электромагнитная гидродинамика
§ 7. Одномерное движение невязкого газа
Рассмотрим задачу о стационарном течении невязкого провод дящего газа в канале с заданным поперечным сечением А (х)Я При этом будем считать, что параметры потока в любом сечении] канала одинаковы, т. е. являются функциями лишь координаты хЛ направленной вдоль оси канала; магнитное и электрическое поля] приложены к потоку извне, причем направлены они перпендику-Я лярно движению газа и друг к другу (рис. XV.3).	I
Система уравнений, описывающих] такое движение, имеет вид:	j
риА = const; (XV. 42)-'
РмДг+-£- = а(£-ыВ)В; (XV-43) :
( dT , du \
= а(£ — uB)E + Q; (XV.44)
• р = pRT. (XV. 45)

Первое из уравнений выражает постоянство массового расхода газа вдоль канала, второе — изменение количества движения, третье — изменение энергии движущегося газа, четвертое — уравнение состояния газа, величина Q означает отнесенное к единице массы тепло, полученное потоком (исключая джоулево тепло). Из этих уравнений найдем изменение скорости и числа М вдоль оси канала. Для этого продифференцируем уравнения (XV.42) и (XV.45) по х:
р и ' А
= 0;
EL _ -----— = 0.
Р Р Т
Здесь штрих означает производную по х. Исключая с помощью
этих соотношений из уравнения (XV.44), получим
₽'=-ж- = “ ” (4 + 4) -	[<>»“' - 4 (£- “В) £-7] 
Подставив это выражение в (XV.43), получим du 1 г А'	о в2 (6—1 Е2
и ~ dx ~ М2—1 [и А р \ k В2
6—1 6
Е и~в~и
В ' и )	6 р
(XV.46)
Одномерное движение невязкого газа
411
Уравнение (XV.46) удобно записать в виде
,	1 Г Л' аВ2	..	.
« = MS- ) ~А-------(U ~
Vvh <xv-47>
k— [ Е	Е
где И1	и3 = -д.
Подобным же образом, используя (XV.47), получим изменение числа М вдоль канала
k— 1 l-f-Ж2 Q /, . k— 1 м2\ аВ2	. .	.3
(XV.48) где
__	г-1-Ж2 „	_ kp
“2—2+ (fe — l)M2 Ыъ а°— р ‘
Заметим, что если в уравнениях (XV.47) и (XV.48) отбросить тепловые и МГД-члены, то получим хорошо известные в обычной газовой динамике соотношения Гюгонио
du 1 и dA ,,,, —j— = -Т75-Г—Г—Г~ ИЛИ (М2 1)
dx	М2 — Л dx . v	>
du   dA
~й	Т
И
1 -- ( ~ 1 М2
, dM =	1 к 2 У М ЛЛ
Л dx	М2—1 Л dx
ИЛИ (М2— 1) dM _ ЛЛ
Зти соотношения показывают, что в расширяющемся канале скорость и число М уменьшаются по сечению канала при дозвуковых скоростях и увеличиваются при сверхзвуковых.
Здесь нас интересует главным образом влияние МГД-членов на течение газа в канале.
Из уравнений (XV.47) и (XV.48) видно, что направление влияния МГД-членов на течение газа определяется знаком правых частей этих уравнений. Вклад, вносимый этими членами, может быть и положительным, и отрицательным в зависимости от отношения скорости потока к характерным скоростям ult u2, и3. Так, если М < 1, при А' = 0 и Q = 0 величина будет отрицательна, если выполнено неравенство < и < и3. Величина dM
будет отрицательна, если иъ < и < и3.
412
Электромагнитная гидродинамика
Это явление служит основой весьма эффективного и гибкой способа управления потоком газа в канале с помощью магнитнь! и электрических полей.
Как было показано выше, характерная скорость и2 являет^ функцией приложенных полей и числа М. Задавшись постоянный Е и В, нетрудно определить, что с изменением М величина и
меняется монотонно, при этойЯ и2 =-у-, если М = 0; . л «2 <	Л1»	если	М <	1;	-Я
и2 =	«1,	если	М =	1;	79
\и2 >	«1»	если	М >	1;	1
и2 =	«з>	если	М =	оо.	|
К сожалению, уравнений! (XV.47) и (XV.48) невозможнее проинтегрировать в общем виде? Однако их можно с успехов использовать для качественного рассмотрения течения в канале^ :учай течения газа в канале поу гз подвода тепла (Q = 0). Возу
Рис. XV.4
Рассмотрим более подробно стоянного сечения (Л = const)
можные случаи течения удобно проиллюстрировать диаграммой^! представленной на рис. XV.4.
Здесь линии и = ult и = и2, и = и3, М — 1 разбивают пло-jj скость (u, М) на восемь областей:	|
^15 Bi, Cjj Di,	|
^2! B2, C2> D 2.	1
Пусть в некотором сечении скорость и число М принимают не^ которые значения и0 и Мо. Характер течения будет определяться тем, в какую из областей попадают эти параметры потока. Рассмо^ трим по порядку все возможные случаи течения.	7
1. Область Ai, Мо <1; и0 > и3 >	> и2, в этом случае^
вначале > 0 и > 0. Тогда М приближается к единице,-а знаменатель в уравнении (XV.47) становится все меньше, и ско-j рость и при достаточной близости М к 1 возрастает очень быстро,] Когда М становится равным 1 (рис. XV.5, а), возникает запирани^ канала. Это значит, что параметры газа во всем канале, в том числет и на входе в него, изменяются так, что М = 1 достигается на выходе^ из канала.	'I
2. Область Bi, Мо < 1; и2 <	< и0 < и3;
область Cf, Мо < 1; u2 < ио < и\ < из>
Одномерное движение невязкого газа
413
вначале в обоих этих случаях < 0, т. е. М —> 0. Однако du . п	du г,
в первом случае < 0, т. е. и —> и1г а во втором > 0, т. е.
также и —> и2 в обоих случаях стремится к Этот случаи движения характерен тем, что скорость потока приближается к постоянному значению и ~	— g-, а число М = стре-
мится к 0 за счет неограниченного роста температуры потока (рис. XV.5, б и в).
3. Область Di, Мо < 1; и0 < и2 < «1 < «з>
du dM	о
начальные значения -т— и —т— положительны. Здесь имеются dx dx
три возможных случая дальнейшего развития потока, зависящие от начальных значений и0 и Мо.
Первый случай (рис. XV.5, а) приводит к запиранию канала. Это может произойти тогда, когда Мо становится достаточно близ-,	du	„	,
ким к 1, так что -т— становится бесконечно большим.
dx
Во втором случае (рис. XV.5, д) происходит ускорение потока с плавным переходом через скорость звука. Это возможно при таком задании начальных и0 и Мо, когда и достигает значения иг в том же сечении, в котором достигается значение М = 1.
Третий случай (рис. XV.5, е) может возникнуть при и0, близком к и2, когда кривые и и и2 пересекаются, что приводит к изменению знака Нетрудно видеть, что в дальнейшем течение развивается так, что числоМ стремится к 0, характерная скорость и2— к своему предельному значению-^-, а скорость потока, так же как и в областях Bj'h С1г приближается к значению и = иг — _ fe — 1 Е k В ‘
Теперь рассмотрим возможные случаи течения на сверхзвуковом режиме.
1.	Область Л2; Мо > 1; и0 > us > и2 > ult для этого du dM	о
случая и вначале отрицательны. Здесь снова возможны три случая течения, определяемые соответствующим выбором начальных значений скорости и числа М. В первом случае при приближении М к 1 торможение потока происходит очень быстро (XV.47) и в канале возникает скачок уплотнения (рис. XV.5, ж).
Во втором случае, для которого характерны другие начальные значения и0 и Мо, величина и может монотонно уменьшаться, приближаясь к и3, а М стремится к пределу, большему единицы (рис. XV. 5, з).
414
Электромагнитная гидродинамика
Рис. XV.5
Одномерное движение невяэкого газа
415
Наконец, возможно такое задание начальных значений и0 и Мо, при котором одновременно М становится равным 1, а и принимает значение, равное и3; этот случай доказывает теоретическую возможность плавного замедления сверхзвукового потока с плавным переходом через скорость звука (рис. XV.5, и).
2.	Область В2\ Мо >1; «1 < иг < и0 < и3; здесь—- > О и > 0. Это соответствует асимптотическому приближению и к «з по мере возрастания числа М от своего начального значения до некоторого предельного значения, большего единицы; и2, хотя и возрастает, не может достичь величины и, так как в этом случае все время положительно (рис. XV.5, к).
3.	Область С2; Мо > и; «1 < и0 < и2 < и3, вначале в этом случае > 0 и < 0. Скорость и, возрастая, принимает значение «2, которое, в свою очередь, уменьшается от своего начального значения. При этом, как видно из (XV.48), достигает некоторого минимального значения (рис. XV.5, л), после чего меняет свой знак на противоположный, и течение переходит в область В2, представленную на рис. XV.5, к, D2 : Мо > 1; и0 < их < < и2 < и3. В этом случае (рис. XV.5, м) < 0 и < 0. Согласно (XV.47), при приближении М к единице происходит быстрое торможение потока, приводящее к возникновению ударной волны.
Здесь поток не может плавно перейти через звуковую область, ибо для этого было бы необходимо иметь положительные du	dM.
начальные -т— и —т—. dx	dx
На основании рассмотренных возможных случаев движения газа можно отметить, что если в некотором сечении канала задайы величины и0 и Мо, то при смещении вдоль оси х эти параметры меняются таким образом, что точка с координатами (u, М) смещается в областях Alt В2, Dr направо вверх, в областях Л», Ви D2 — налево вниз, в областях Сг и С2 — налево вверх (рис. XV.5). Кроме того, из уравнений (XV.47) н (XV.48) видно, что переход через значение М = 1 в точках со значением скорости, отличным от иг и и3, невозможен (рис. XV.5). Следовательно, течение может переходить через скорость звука только в случае, когда М = 1 одновременно с и = их или и — и3.
Приведенный анализ показывает возможность создания широкого разнообразия режимов течения газа в канале при помощи подходящего подбора магнитного и электрического полей.
416
Электромагнитная гидродинамика
§ 8. Магнитогидродинамическое течение в трубах
Большой интерес в магнитной гидродинамике представляй стационарное движение вязкой проводящей жидкости с прямолй нейными линиями тока. Такому течению в некоторой степени сос! ветствует движение жидкости в соплах, диффузорах и канала различных МГД-устройств. К таким устройствам относятся, н;
пример, расходомеры, используемые при исследовании теченй проводящих сред, а также МГД-насосы и генераторы.	J
Ниже приводится несколько примеров стационарного движ
ния проводящей жидкости
при наличии электрического и магнии ного полей.	|
Течение между неподвижны^ параллельными стенками (плоска! труба). Рассмотрим плоское стации парное течение несжимаемой элео z ропроводящей вязкой жидкое® между параллельными бесконечны»® изолированными стенками в однород ном внешнем магнитном и электро ческом полях.	1
Будем считать, что скорость
внешнее электрическое поле £& и внешнее магнитное поле Во не меняются вдоль линий тока, кото рые будем считать параллельными продольной оси х (рис. XVJ$ В этом случае все параметры потока зависят только от коордй наты у, кроме давления, которое линейно меняется вдоль оси$ Система исходных уравнений имеет вид:	-'i
(i/v)i>=—Lvp + vav+_L[jxb);	(i)]	'I
div V — 0;	(2)	Уй
1	-> ->	д
J1	(3)
div В = 0;	(4) (XV.4®
rot Е = 0;	'	(5) J
J =	о IE +(У х	В)];	(6)	|
+	+	+ ст|
Рассмотрим граничные условия, необходимые для решенгйн задачи. Для скорости, справедливо известное условие прилипанИЖ V = 0 при у = ±а. Для температуры можно задать два варианта
Магнитогидродинамическое течение в трубах
417
граничных условий. В первом температура стенки постоянна: t = То при у = ±а, во втором — тепловой поток через стенку постоянен, т. е. -4^- = const при у = ±а.
Граничные условия для индуцированного магнитного поля определяются режимом работы канала. В частности, в режиме холостого хода, когда полный ток через канал равен нулю, справедливо условие Вх — 0 при у = =±а. При работе канала в режиме насоса или генератора это граничное условие не выполняется. Более общим является условие равенства нулю индуцированного магнитного поля в центре канала, т. е. Вх — 0 при у = 0.
Неизвестными являются V, р, В, Е и J. В данной постановке, очевидно,- V,. = Vz = 0, а из уравнения неразрывности Ух = = Ух (у).
Уравнение (XV.49, 4) в данном случае означает, что компонента вектора В по оси у постоянная, т. е. Ву — const — Во.
Уравнение (XV.49, 3) дает div J = 0, т. е. компонента вектора плотности тока по оси у постоянная; она должна равняться нулю, так как нижняя и верхняя стенки изолированы (Jy = const = 0).
Тогда для несжимаемой жидкости уравнение (XV.49, 1) в проекциях на х и у запишется в виде
дх dy* +
др ду
(XV.50)

где Jz — компонента вектора плотности тока в направлении оси z;
Vx —.скорость жидкости в трубе; г;— в этой главе вязкость.
Проектируя на координатные оси уравнение (XV.49, 6), получим, что компоненты вектора плотности тока по осям х и у равны нулю, а компонента на оси z определяется следующим образом:
Л = о (Ео - VXBO),	(XV.51)
где Ео — постоянная составляющая напряженности электрического поля по оси z, определяемая из условий на границах потока.
Проектируя уравнение (XV.49, 3) на ось z, получим уравнение для индуцированного магнитного поля в виде
<xv-52)
Проекция уравнения (XV.49, 7) на ось у запишется в форме
,(iy + ,"+A=o.	(XV.53)
1 \ dy J 1 dy* 'с	'
27 И. Л. Повх
418
Электромагнитная гидродинамика
Преобразуя уравнения (XV.50) и (XV.51), получим следующее дифференциальное уравнение для Vx:
_^._£Ё1ух = __2_В0£0 + —	(XV.54
dy2 ц х ц 1 г, дх ’	'
„	др
где р — постоянный градиент давления
Введем следующие безразмерные переменные: Vx = V0V5
у = ау\ х = ах и обозначим К. = Р = Vo = —а !
®« = вДг; 0=2w- Тогда система урава^ ний (XV.51)—(XV.54) запишется в виде:	)
_ Ha2V = Re р — /(На2; dy2
J2 = K -V;
(XV.55^ (XV.56)jj (XV.57)/ (XV.58)^
Решение уравнения (XV.55) при условии V = 0 при у = др п
и допущении, что = 0, имеет вид	/
V = (к —	) (1 -	(XV.59).;i
\ naz / \ сп На )	4	1 Д
1	-Я
или, имея в виду, что j V dy = 2, получим	j
-1	_	)
77	Re р	_	На	1
Л	На2	~ На —th На ’	.1
и, следовательно,
_ На ch На
V ~~ На ch На —sh На
ch На у ch На
(XV.60).
Подставляя полученное решение в уравнение (XV.56), получим ;
На (ch На — ch На ~у)
На ch На — sh На
(XV.61):
Магнитогидродинамическое течение в трубах
419
Интегрируя уравнение (XV.57) по у и используя решение (XV.61), получим
В, = Re„ [(К- 1)-й +	]• <XV. S2)
Дважды интегрируя уравнение (XV.58) при граничных условиях Т = То при у = ±1, получим выражение для профиля температуры в виде
0 = С1Рг[-^-(1—?)+-Ь (ch 2На — ch 2На #) +
+ <ch На ~ ch На ’	(XV.63)
где = ( На ch На-sh На У’ С* = На - 1) ch На - tfsh На.
Некоторые результаты расчета профилей скорости, тока, индуцированного магнитного поля и температуры приведены ниже.
Рис. XV.7
Из рис. XV.7, а видно, что профиль скоростей становится тем более заполненным,, чем больше число На, при этом градиент скорости у стенок растет, а в ядре потока — уменьшается. При На < 1, т. е. когда вязкие силы много больше электромагнитных сил, решение (XV. 60) приводится к виду
V = (1 —/).	(XV.64)
27*
эд
420	Электромагнитная гидродинамика
Если На 1, то уравнение (XV.60) в пределе может быть пред* ставлено в виде
V = 1 — ехр [—На (1 — у) ].	(XV.65V
На рис. XV.7, б приведено распределение тока в канале, соот-‘ ветствующее трем режимам течения. При этом, как уже отмеча-.;! лось, режим К = 1 соответствует холостому ходу.	j
Профили индуцированного магнитного поля для трех режимов" течения приведены на рис. XV.7, в.
Распределение температуры в функции координаты у для раз-^ личных значений чисел К и На показано на рис. XV.7, г. Из ри*,( сунка видно, что в режиме холостого?) хода число На почти не влияет на рас-;{ пределение температуры в канале. При ]
У
Во
Уо
*7777 777/7/7/7/.
z
Рис. XV.8
работе канала в режиме генератора или.^ насоса влияние числа На на распреде-'З ление температуры существенно.
Течение между параллельными'^ стенками, одна из которых движется.» (течение Куэтта). Рассмотрим еще Одинга пример плоского стационарного течениям
несжимаемой электропроводной-вязкой жидкости в однородном-» внешнем магнитном и электрическом полях. Это течение ограни-1 чено с одной стороны неподвижной плоскостью (у = 0), с дру-'jj гой — плоскостью, движущейся со скоростью Уо (риа. XV.8)<J Движение жидкости описывается системой уравнений (ХУ.49)ЛЯ Задача будет отличаться от рассмотренной ранее только rpa-ifl НИЧНЫМИ УСЛОВИЯМИ. ГраНИЧНЫе УСЛОВИЯ ДЛЯ СКОРОСТИ МОЖНО;:! записать в виде	.•а
VxVo при у = а и Vx = 0 при у — 0.	(XV.66) J
Граничное условие для индуцированного магнитного поля за-J пишется в форме Вх — const при у = 0. Записав проекции урав-а нений (XV.49, 2), (XV.49, 3), (XV.49, 6) на оси координат для рас-:| сматриваемой задачи, получим
d*Vx г>^ = dp ____
dy ~~
Jx = a (Ег - VxBoy,
(XV.67)3
J гВ0',
(XV. 68)"
(XV.69),'
’ — 1 dB* z dy '
(XV.70)^
Подставляя уравнение (XV.69) в уравнение (XV.67), получим^ - тW В°’	(XV-713
Магнитогидродинамическое течение в трубах
421
или, имея в виду принятые в предыдущей задаче безразмерные переменные, будем иметь
-^2-= На2 (7— Д);
dy2
Л = Д- 7;
dy
(XV.72)
(XV.73)
(XV.74)
Решение уравнения (XV.72) при указанных граничных условиях запишется в виде
у	(1 — K)shHay — KshHa(l —у)
(XV.75)
sh На
Используя решение (XV.75), получим выражение у _ (1 — K)shHay — KshHa(l — у)
для тока
sh На
(XV.76)
Подставляя решение (XV.76) в уравнение (XV.74) руя полученное выражение, будем иметь
g ____ К ch На (1 — у) + (1 — К) ch На у
интегри-.
Hash На
(XV.77)
и
Если упростить граничное условие для ВХ) приняв Вх = О при у = 0, получим
р- ch На —ch Нау Hash На
(XV.78)
Рассмотрим влияние числа На на распределение скорости и индуцированного магнитного поля в канале при Д = 0.
Из рис. XV.9, а видно, что с ростом числа На градиент скорости у нижней стенки уменьшается, а у верхней — растет. При этом напряжение трения у верхней стенки растет, а у нижней — уменьшается.
Действительно, т = ц -2-.
dy
При отсутствии магнитного поля
v - dv .
V = y и = 1;
dy
422
Электромагнитная гидродинамика
при наличии магнитного поля
dV _ (1 — К) На ch На у -|- К На ch На у —	sh На
Тогда трение на нижней стенке
_ dV |	_ На
T,,~Y1 dy L=o " shHa
(XV.79)
на верхней стенке
dv
тв = т1
dy у—а
На ch На shHa
Результаты расчета Вх показаны на рис. XV.9, б.
(XV.80)
I
Течение в трубе круглого сечения. Для описания этого течения воспользуемся системой уравнений магнитной гидродинамики (XV.49), дополнив ее уравнением (XV. 18), которое для стационарного режима течения будет
(l>V)B = (VV)B + -^rAB.
(XV.81).
Направим ось х вдоль трубы, а магнитное поле — по оси у. . Будем считать, что скорость жидкости имеет везде одинаковое , направление, совпадающее с направлением оси х, т. е. Vу — V? = = 0, a Vx = Vx (у, z). То же самое относится и к магнитному полю, * индуцированному вследствие движения проводящей жидкости, т. е'
Вх = Вх (у, г); Ву = О- Вх = 0.	]
Магнитогидродинамическое течение е трубах
423
При этих предположениях уравнения движения (XV.49, 1) и индукции (XV.81) в проекциях на оси координат примут вид:
_!_ДВХ = _В оро х « ду
1 \ ду* r дг* )
(XV.82)
В уравнении (XV.82, 2) -%— (р -|- —) = —/G = const — UX \	Х1Л/ 1
заданный постоянный вдоль оси х перепад давления.
Действительно, из уравнения (XV.82, 3 и 4) получим
р + -^ = Р(х),
(XV.83)
а в уравнении (XV.82, 2) все члены являются функциями лишь у и z. Следовательно, — const. Уравнение (XV.83) служит для определения давления в потоке, если В задано.
Как видно из уравнения (XV.49, 3), составляющими индуцированного тока будут
Л = 0; Л = —Jz = —	(XV.84)
х ’ у Но дг ’ г р0 ду.	v '
Пусть задано однородное магнитное поле Во в направлении у. Тогда составляющая напряженности магнитного поля по оси у будет
By = By инд + Во = Во.
В соответствии с этим первые два уравнения системы (XAZ.82) запишутся в форме
ар0 х 1 и ду
л |	| J_R _^ = _
* \ ду* ‘ дг*- ) ро 0 ду
(XV.85)

т. е. для определения Vx и Вх получилась система двух уравнений в частотных производных второго порядка.
Граничными условиями будут
Vx (D) = Вх (О) = О,	(XV.86)
где D — контур трубы.
424
Электромагнитная гидродинамика
Граничные условия для магнитного поля соответствуют изолж рованным стенкам трубьь
Введем новые неизвестные функции:
v = Vx-\---W — Vx-----------т==^-
Но Кчо	Но К П0
Используя эти функции, получим новую систему уравнений:
+	=	»(О) = 0;
»Р)=0.
(XV.87]
,1
(XV.88)-
Перейдем в первом из этих уравнений к безразмерным величий нам:	'!
7,*__£о 1/ g и .
2 У . ч А/?2 ’
у* — Л. •
Z* = -L-R ’
На = В0 j/^7?; г
~ R9
(XV.89)
(XV.90),|
j где 7? — радиус трубы; г — текущий радиус. В результате замены переменных получим = — 1;' 1 ду* у* (1,0)= о,
где 0 — полярный угол, отсчитываемый от оси у*.	,=
Решение неоднородного уравнения (XV.90) запишем как сумму;! решений однородного уравнения и частного решения неоднород--;1'; ного уравнения	J
причем на границе должно соблюдаться условие
(v0),.=1 =	(XV.91H
В качестве частного решения неоднородного уравнения возьмем^

й1
Магнитогидродинамическое течение в трубах
425
Тогда по условию (XV.91) для v0 получим краевую задачу:
?Ч + На|^ = 0;
/ \	У* COS 0
^)^=-йГ = -нГ-
(XV.93)
Чтобы упростить переход в последнем уравнении к полярным координатам, будем искать решение в виде
На , v0 = u (г*, 0) е 2 J .
При такой замене в уравнении пропадает член с первой производной по #*. В полярных координатах (у* — г* cos 0, г = = г* sin 0) имеем:
д-и , 1 ди , 1 дги	/ На \2„ а.
5г*2	г* дг* г*2 502	\ 2 ) “ —и>
«(1, 0)=5gleacos0.	(XV.94)
Решение (XV.94) будем искать в виде разложения в ряд Фурье по cos п0 на отрезке [—л, л ]
и = и0 (г*) + Ui (г*) cos 0 ---ип (г*) соз nQ 4---- (XV.95)
Для определения функций ип (г*) получим уравнение Бесселя чисто мнимого аргумента
ип + ±и'п- [уй- +	] «„ = 0.	(XV.96)
Общее решение этого уравнения запишется в виде
а„(г*) = Л„/„	г*) + ВпКп >	(XV.97)
где	’	' 2	'	' 2	'
г ( На _____.—пт / • На *\	, ( На -Л _ л -п4-1 „ / • На
ln\~r )—1 1п\1~г )' k"\~Tr )~Т1
Для того чтобы избавиться от особенности в точке г* = 0, надо положить Вп = 0.
Значение Ап находим из граничного условия (XV.91):
426
Электромагнитная гидродинамика
Очевидно, что
_На ,
и* ~ ц, = и (г*, 0) е 2
_ _На
= е 2
у* _
На “ На
И (Г*. е) —е2 У •
(XV.99)
Подставляя сюда и и (г, 0) из (XV.95) и раскладывая выражена .
у* п U
ние На-6 в Ряд ФУРье п0 cos ПОЛУЧИМ
(XV. 100) ;
где 7п(-у-г } — производная по всему аргументу.
Теперь, согласно (XV.87) перейдем к Vx и получим
Если подобным же образом рассмотреть второе уравнение системы (XV.88), то получим выражение для Н в виде
Магнитогидродинамическое течение в трубах
427
п=1
cos (2п—1)0.
(XV. 102)
Заметим, что при г* = 0 уравнение (XV. 101) имеет вид Г (—\
^(0) = ДйаА-	(XV.103)
На/о(,“/
На рис. XV. 10, а приведен график распределения скорости по сечению трубы в плоскости 0 = 0- при различных числах На. Здесь, как и в предыдущей задаче, видно, что наличие магнитного
поля приводит к торможению потока. Случай На —> 0 соответствует течению Пуазейля в круглой трубе. В самом деле, перейдя в выражениях (XV. 101) и (XV. 102) к пределу при На —♦ 0, получим limt£ = ^-(l—г*2); ПтЯх = 0.
На->0	4	На-»0
На рис. XV. 10, б показано распределение индуцированного магнитного поля по сечению трубы в плоскости 0 = 0.
В заключение отметим, что в рассматриваемом случае в отличие от обычной гидродинамики при На > 1 течение в трубе не является осесимметричным.
Течение в прямоугольной трубе. Рассмотрим стационарное, полностью развитое течение электропроводной жидкости в прямо
428
. Электромагнитная гидродинамика
угольном канале со сторонами 2а и 26 (рис. XV. 11), помещенном я в однородное магнитное поле. Система уравнений (XV.49) в проек-1 циях на оси координат запишется в виде:
JL-в/ । » ( I d*v> дх с0'г "Г ТЦ ду2 + dz-z
(1)
др_ = В I  ду
дР.—В I •
dz Dx‘y'
I — aE —_____L2?£-
1У —	gQ dz >
dEz _ dEy dy dz
(2)
(3)
(4)
(5)
(6)
(XV. 104) 3
•1
Из уравнений (XV. 104, 1 и 4) получим
Но ду \ дуг 1	3z2 ) 1	1	> ft
(XV. 105)1 ''л Из уравнений (XV. 104, 4, 5 и 6)" tj имеем	:?
BaadVx 1 (д*Вх 1 д2Вх
ОоНо” ду + (^ ду2 + дг2
Рис. XV. 11	(XV. 106), |
'  И
Рассматривая течение между стенками, изготовленными из изо-'ffl ляционного материала, граничные условия запишем в виде:
Вх = 0 при у = =±=а и z = ±Ь;
Vx — 0 при у — И 2 = ±Ь.
Введем новые переменные, аналогично тому, как это сделан<Й| в.предыдущей задаче:	;';и
v = Vx + —(XV.107)?|
Но v <”)
=	(XV. 108)1
Магнитогидродинамическое течение в трубах
429
Используя эти функции, уравнения (XV. 105), (XV. 106) запишем в форме
(т5> + -&) + -т->+^=°:	(XV.J09)
O + ^b-^w + ^o. . (XV.H0)
с граничными условиями v = w = 0 при у — ±а, г — ±Ь.
Уравнения (XV. 109) и (XV. НО) отличаются только знаком при числе На. Тогда естественно предположить, что функция w удовлетворяет тому же уравнению и тем же граничным условиям, что и функция V, т. е. достаточно найти решение только для v.
Решение для v можно найти, представив в области —Ъ < < z < b в виде косинусного ряда Фурье, т. е.	.
 К - V (-1)" — (2n+l)nz-
A1 л 2n+ 1 C0S 26
n=0
Тогда решение уравнения (XV. 109) имеет вид
__ 16К01Ь2 VI (—1)п Г. . em‘y sh тга — е.тгУ sh mta	(2n + 1) лг
V л3 (2n + I)3 L ' sh («j — /п2) а С0 26	’
л=о
(XV. 111)
где /пх и /п2 являются корнями квадратного уравнения
+ m  (?n + ip	= Q-	(XV. 112)
Решением для w будет то же самое выражение (XV. 111), но тг и т2 будут корнями другого^ уравнения:
щ2— — т-------^2-1гУ2я2=0. (XV. 113)
а	462	'	'
После того как. найдены выражения для v и w из уравйений (XV. 107) и (XV. 108), можно вычислить значения Vx и Вх.
Существенным отличием этой задачи от рассмотренных ранее является наличие тока не только по оси z, но и по оси у.
Экспериментальные исследования. Коэффициент трения магнитогидродинамических потоков в трубах. Число экспериментальных работ, посвященных изучению течения вязкой несжимаемой проводящей жидкости в магнитогидродинамических трубах, сравнительно невелико. Первой из них принято считать работу Гартмана и Лазаруса, хотя отдельные экспериментальные результаты были известны раньше. В этой работе были изложены результаты, полученные при течении ртути в трубах прямоугольного и круглого сечений малого диаметра при наложении на поток попе-
430
Электромагнитная гидродинамика
речного магнитного поля. В процессе исследований измерялись перепад давлений в активной части трубы и расход ртути. Экспериментальные и теоретические результаты для плоской трубы совпадали, когда число Re было достаточно мало, а напряженность магнитного поля — велика. Когда же эти условия не соблюдались, обнаруживалось значительное расхождение теории с экспериментом. Это объясняется нарушением одной из основных предпосылок теории — предположения о ламинарности течения. Весьма показателен график, представленный на рис. XV. 12. Здесь дана зависимость перепада давления в канале от напряженности магнитного поля.
При сравнительно малых числах Re с увеличением Н перепад давления увеличивается при постоянном числе Re (или расходе Q). Однако при достаточно больших числах Re и небольших значениях Н перепад давления с увеличением Н при постоянном Re вначале уменьшается и лишь потом возрастает.
Опыты Гартмана были повторены В. Маргетройдом при значительно больших размерах поперечного сечения экспериментальной трубы (у Гартмана— 0,0291 х 0,508 см2 и 0,06 х X 0,372 см2, у Маргетройда — 0,675 х 10 см2). Благодаря этому Маргетройд имел возможность получить гораздо большие значения числа Re. При этом напряженность магнитного поля была настолько велика, что позволяла подавлять турбулентные пульсации даже при наибольших числах Re (—105), осуществляемых в этом опыте.
Многократное повторение опыта показало, что ламинарный ре- . Re
жим течения существует тогда, когда -75— < 900, а начиная с На
Re
> 900 наблюдается турбулентное течение.
Удовлетворительное совпадение опытных и расчетных данных было также получено при проведении исследований ламинарного течения ртути в магнитогидродинамических трубах с сечением, отличным от плоского.
Магнитоеидродинамическое течение в трубах
431
На рис. XV. 13 приведены опытные данные, полученные Хожаи-новым при течении ртути в магнитогидродинамическом канале прямоугольного сечения с отношением сторон 1 : 2,5 (0,78 X X 1,9 см2). В области ламинарного режима течения они удовлетво-рительно согласуются с точным решением Шерклифа. На этом же рисунке для сравнения приведены опытные данные Никурадзе, полученные при течении воды в аналогичной трубе, что соотвег-ствует случаю течения ртути при отсутствии магнитного поля. В об* ласти перехода ламинарного режима течения в турбулентный данные Никурадзе дополнены опытными данными Шиллера, полученными в трубе прямоугольного сечения с- отношением сторон 1 : 2,8.
На рис. XV. 14 приведены опытные данные Гартмана, Лазаруса и Хожаинова, полученные при течении ртути в магнитогидродинамической трубе круглого сечения, диаметр которой соответственно составлял 0,116 и 1 см. В области ламинарного течения ртути эти опытные данные удовл'етворительно согласуются с точным решением, приведенным в предыдущем параграфе.
В магнитной гидродинамике при течении жидких металлов в магнитогидродинамических трубах вследствие сильного стабилизирующего действия поперечного магнитного поля область ламинарного режима течения существенно расширяется. Поэтому изучение таких течений представляет не только теоретический, но и большой практический интерес.
Как отмечалось ранее, важной интегральной характеристикой течений жидкости в трубах является коэффициент трения, который позволяет связать потери давления в канале со средней скоростью течения или расходом
=	=	(XV.114)
2F где = ---------гидравлический радиус, равный отношению
площади поперечного сечения трубы к половине смоченного .периметра.
Такое определение гидравлического радиуса для труб произвольного профиля при переходе к трубе круглого сечения обеспечивает совпадение гидравлического радиуса с радиусом круглой трубы. Для плоской трубы гидравлический радиус получается равным ее ширине, а для квадратной — полуширине.
Определяющие критерии, приведенные на рис. XV. 13 и XV. 14, основаны на гидравлическом радиусе.
Как было показано в гл. XI, в обычной гидродинамике при ламинарном режиме течения и заданном числе Re, коэффициент трения X зависит только от поперечного сечения канала. В магнитной гидродинамике этот коэффициент зависит еще и от магнитного поля,
432
Электромагнитная гидродинамика
Рис. XV. 13
Магнитогидродинамическое течение в трубах
433
Y 001) S2
Рис. XV.14
28 И. Л. Повх
4з4
Электромагнитная гидродинамика
а. точнее от числа На. Поэтому его удобно представить в виде
=	(XV.115)
В общем случае безразмерный параметр k (Г, На) может быть представлен следующим образом:
k(F, На) = ^ j J V2uds.	(XV.116)'
(S)
В выражении (XV.116) все величины безразмерные:	’
и = ~-, V2 = V/?I; s = -4-. «ср
Для вычисления интеграла по площади необходимо располагать точным решением для распределения скорости по сечению трубы и (У, z).
Используя точное решение Шерклифа для случая ламинарного; течения проводящей жидкости в магнитогидродинамическом канале прямоугольного сечения с произвольным отношением сто-
/	, х	, Ь \
рон [у = ±	, 2 = ± J , получим:
k(F, Ha) = ^f A

n=l
chHa-X-
(2n — I)4 ‘	2(2n— l)2v2shW
(XV. 117)]
Здесь у =	; Х = 1 + | у; № = На2 + 4 (2п - 1)М
При На —> 0 выражение (XV. 117) приводится к виду	s
w=—---------------;
,V_1	Г, №<2»-1)Т1	’
X (2n— I)4 L (2n—l)y J h=l	*
Отметим, что последнее выражение вытекает также из решения^ приведенного ранее в гл. XI.
При b —» оо выражение (XV. 117) принимает вид:
На)=4На—тент-
0,5На
(XV. 118*
Магнитогидродинамическое течение в трубах
435
Зависимость (XV. 118), справедливая для плоской трубы, может быть получена непосредственно путем подстановки решения (XV.60) в (XV. 116).
При больших числах На (На > 1), что всегда выполняется для жидких металлов, выражение (XV. 118) принимает вид
£(Г, На)~4На.	(XV. 119)
Для случая течения жидкости высокой проводимости (На 1) в магнитогидродинамической трубе прямоугольного сечения с произвольным отношением сторон и изоляционными стенками зависимость для параметра k (Г, На) может быть получена из решения для пограничного слоя:
k (Г, М)	----5-т-. (XV. 120)
v	% j 0,765у	2 1	'	'
/На% На%]
Нетрудно видеть, что при b » со (у 0) выражение (XV. 120) совпадает с (XV. 119).
Используя решение (XV. 101), можно получить выражение для k (Г, На) применительно к случаю течения проводящей жидкости в магнитогидродинамической трубе круглого сечения:
2На
Ь(Г, На) =
(XV. 121)
и=0
В формуле (XV. 121)	= 1 при /1 = 0 и 6„ = 2 при п > 0.
Выражение (XV. 121) с высокой степенью точности аппроксимируется следующей зависимостью:
й(Г, На) = (11 -|-5е-0’92На)На.
(XV. 122)
При На —> 0 зависимость (XV. 122) точно соответствует полученной в обычной гидродинамике.
Приведенные зависимости могут быть использованы для расчета потерь на вязкое трение при ламинарном течении проводящей жидкости в каналах МГД-устройств постоянного тока с гладкими стенками. Однако для этого необходимо знать, когда режим течения является ламинарным.
Анализ опытных данных показывает, что в гладких магнитогидродинамических трубах переход ламинарного режима течения проводящей жидкости в турбулентный происходит примерно при
436
Электромагнитная гидродинамика
одном и том же значении коэффициента трения (Хкр «=< 0,0177); Это обстоятельство позволило для определения величины Re^ в магнитогидродинамических трубах предложить следующий крщ терий:
Re“p~Awr--	(xv.r
Подставив (XV. 119) в (XV. 123), нетрудно убедиться, что для плоских магнитогидродинамических труб полученный результат точно совпадает с формулой Маргетройда.	;
При На —> 0 для трубы круглого сечения критерий (XV. 123)' принимает вид	1
ПрО	(Г) — 16    ЛЛС	j
к кр~ 00177 о,0177 уоэ.	я
'/Я
Если в качестве характерного размера выбрать диаметр трубы,! то Re°p будет равен 1810, что также удовлетворительно согла-Я суется с опытными данными.	|
Зависимость для коэффициента трения (XV. 115) в логарифмиЦ ческом масштабе представляется прямыми линиями (рис. XV. 131 и XV. 14). Отклонение опытных данных от этих прямых свидетель^ ствует о разрушении ламинарного режима течения.	|
Влияние поперечного магнитного поля на турбулентный поток! проводящей жидкости в трубах сводится к изменению распреде-| ления скорости течения по сечению трубы и подавлению турбулент-1 ных пульсаций. При малых и умеренных числах На профиль скойЯ рости по своей форме близок к обычному логарифмическому, т. eJ магнитное поле существенно не увеличивает градиента скоростей у стенок, ио подавляет турбулентные! пульсации. Поэтому при заЦ данном числе Re в опытах наблюдается уменьшение коэффициента! трения по сравнению с его величиной в обычной гидродинамике, а
При больших числах На эффект увеличения градиента скорости у стенок превалирует над эффектом подавления турбулентный пульсаций. Поэтому в данном случае в определенном диапазона чисел Re в опытах наблюдается увеличение коэффициента трении по сравнению с его величиной в обычной гидродинамике.	и
В литературе предложено несколько зависимостей для расчета! коэффициента трения при турбулентном течении проводящей жидкости в магнитогидродинамических трубах. Подавляющее боль-:' шинство из них ограничено определенным диапазоном чисел Re, и На.
Наиболее универсальной является зависимость, предложенная Рябининым и Хожаиновым,
^ = -Ц^ + М1~Ч'(Ке’Г)]- (ХУЛ24>
Ламинарное течение заряженной жидкости в плоской трубе
437
Здесь	-
_ 0,133	k(T).	„г_ На2	Re
т"“ Re0-25 Re ’	Re _ На2 ,	/ Ha^\2 '
P° + Pi Re *г°Ч Re )
Зависимость (XV. 124) правильно отражает физическую картину влияния магнитного поля на течение проводящей жидкости в магнитогидродинамических трубах. При Re — const и На —» со IF —> 1, т. е. режим течения становится ламинарным. При ТТ	X r-1	w A	k (Г, М) „ k<D а	г>
На = const и Re —> со	Т —> 0,	—Ц,—- —> 0	и ——> 0.	В	этом
Re	Re
случае формула (XV. 124) совпадает с известным законом Блазиуса для коэффициента трения в обычной гидродинамике.
Применительно'к случаю течения проводящей жидкости в плоской магнитогидродинамической трубе коэффициенты а, ро и соответственно равны:
а =	; Ро = 0,1 thj(2,45-10-BRe)£P1= 1 — 0,2e_(3'7'IC-‘Re>.
Зависимость (XV. 124) справедлива для гладких магнитогидродинамических труб. Влияние шероховатости стенок в рассматриваемом случае является сложным. Достаточно сказать, что в отличие от обычной гидродинамики шероховатость стенок трубы может оказывать существенное влияние на коэффициент трения ламинарных магнитогидродинамических потоков. Некоторые данные по такому влиянию приведены в литературе, однако их недостаточно для получения надежных расчетных зависимостей.
заряженной жидкости под
У
_ f
и
§ 9. Ламинарное течение заряженной жидкости в плоской трубе
Для решения уравнений электрогидродипамики рассмотрим установившееся ламинарное движение действием внешнего электростатического поля в плоской трубе с непроводящими стенками и с расстоянием между ними 2а (рис.' XV. 15). Будем считать, как и в соответствующей гидродинамической задаче, что ско- . рость и другие искомые функции, кроме давления р, зависят только от одной координаты у. Тогда из уравнения (XV.28, 1,3 и 5) следует, что
Vу = jy = const и Ех = const.	_	_
Ограничимся решением, для которого Vy = jy — 0, Ех — 1 -и V = и (у), а градиент по оси х — постоянная величина
₽ = >% + /(;,).	(XV.125)

-1
7777777/7777777Т77777777777
Рис. XV. 15
438
Электромагнитная гидродинамика
Полагая силы тяжести равными нулю, т. е. Fo = 0, а число Fr =* = 1, т. е. р = рVo, и опустив черточки над безразмерными величи-. нами, систему уравнений (XV.28) можно переписать в виде:	j
_Ре_.
dy —Кэ в ’
о Е — 1 dpe •
Re; dy ’
ix = Рг <№эи + 1);
др	1 d2u . с
= ~п—л—h Еиэре; дх	Re dy ' эг е
— pu 0 р
(1)
(2)
(3)
(4)
(5)
(XV. 126)'
Граничные условия, если координата у безразмерна и отнесена к полуширине канала (рис. XV. 15), будут:
на стенке, т. е. при у = 1, « (±1) = 0;
на оси, т. е. при у = 0, и (0) = 1; ре = p«o и Еу (0) — 0.
Последнее следует из условия симметрии потока и изменения знака Еу при у = 0.
Из уравнений (XV. 126) можно найти электрические Еу и ре, гидродинамические и (у) и р (х, у) характеристики потока.
Первый интеграл системы уравнений (XV. 126, 1 и 2) будет
Используя граничные условия на оси трубы ре (0) = ре0 и Еуо = 0
и определив из (XV. 126, 1), найдем постоянную С
C=-2TS>'
Следовательно,
R^7 (~di~^3pe0)’
второй интеграл будет иметь вид
Е>= V ’’•"‘ф +
Используя те же граничные условия, получим С\ = 0;
= ]/2^-Рг0 tg Re3Re^ • (XV. 127)
Ламинарное течение Заряженной жидкости в плоской трубе 439
Или, обозначив у RegRe^o = В, окончательно получим
£,= j/2-g-peotgB//.
Величина заряда ре (у) определится из (XV. 126) и (XV. 127). Она будет равна
ре =------, р<!0	-	= —р(?5-.	(XV. 128)
ге т 7 1	cos2 By	'	'
cos2 I/ у ResRe;pe0 у
Первый интеграл (XV. 126, 4) с учетом (XV. 126, 1) можно записать в виде
i =	+	(XV. 129)
и.у	их	1\“э v
После его интегрирования получим значения скорости
+ (XV-130>
где <р (у) = In cos (сх-f-'K — С~ Re,). После подстановки произвольных постоянных <р (у) будет равно
<р (у) = In cos у Re3 Re^peo у = In cos By.
Постоянные C2 и C3 находятся из граничных условий: и ( — 1) = = '0; С2 = 0; С3 = —"ТГ'^7. С учетом этого выражение для скорости течения жидкости примет окончательный вид
и==„^^(1_у2) + 2 «Ц^-1пс-^.	(XV.131)
2 дх ' s ' 1 Re3Re; cos В '	, '
Значение давления, исходя из (XV. 125), (XV. 126) будет равно
р = ^Р	= ^Lx_i_-£«0-tg2By	(XV.132)
Р дх Х 2 Re3 дх Х Re; ё у'
Если введем обозначение
Re др	о ReEu3 , „ „ D
«1=-----7Г-Г- И	= 2 -75—=7^- In cos В,
1	2 дх 2 Re3 Re(-
то скорость потока, согласно (XV. 131), можно представить в виде
0 = 0i(1-!,>) + „!(1-^).	(XV.133)
440 Электромагнитная гидродинамика
Первое слагаемое соответствует ламинарному движению, rosM пикающему из-за наличия перепада давления, а второе предстакЯ ляет собой составляющие скорости потока, вызванные поилерпмД торными силами; их и м2 — соответствующие максимальные сксМ рости (при у = 0).	Я
Найдя значение заряда на оси ре0 из условия, что средняя плотность тока в сечении трубы равна единице, получим  Я
А = Re^ez =	,	(XV. 134.1
так как kpeE0 = /. На рис. XV. 16 и XV. 17 приведены кривый распределения скоростей и плотностей зарядов по сечению трубь|
при чисто пондеромоторном течении и следующих значениях пара-1 метра А: 1— 106; 2 — 104; 3— 102; 4 — .10; 5 — 1 и 6— 0,1.j Видно, что при малых значениях А, пропорциональной плот')' ности тока/, заряды распределяются равномерно по сечению трубы;) (кривые 5 и 6), а при больших (кривые 1 и 2) они почти полностью';) сосредоточены у стенки. Следовательно, по мере увеличения пара-.1! метра А пондеромоторные силы у стенки резко растут, что приводит^' к выравниванию профиля скорости в ядре потока и увеличению ее-градиента у стенок.
При турбулентном движении коэффициент диффузии резко возрастает, что должно привести к выравниванию поля зарядов и уве-. личению действия пондеромоторной силы на расходную составляющую скоростей.
§ 10. Магнитогидродинамический пограничный слой
Рассмотрим в качестве примера ламинарный пограничный слой-на пластине при наличии поперечного однородного магнитного поля. Этот случай приобретает практическое значение лишь тогда,
Магнитогидродинамический пограничный слой
441
когда будут найдены эффективные способы увеличения электропроводности в пограничном слое. Если ориентироваться на электропроводность, возникающую при высокой температуре газа, то ожидать сильного влияния магнитного поля на характеристики потока не приходится. Так, при числе М = 25, температуре пластины 1600° С, высоте полета 30 км, магнитной индукции В приложенного извне поля 10 Гс и характерной длине L = 1 м параметр
аВЧ. На2 электромагнитного взаимодействия	, определяю-
щий отношение магнитных сил к гидродинамическим, имеет порядок 0,002, т. е. магнитные силы очень малы по сравнению с гидродинамическими.
Рассмотрим пограничный слой на пластине в электропроводной жидкости в присутствии магнитного поля, приложенного нор-мально.к пластине. При этом предполагается, что индуцированное в результате движения магнитное поле мало и им можно пренебречь по сравнению с приложенным полем. Кроме того, внешнее элект
рическое поле считается отсутствующим. В этих предположениях объемная плотность пондеромоторной силы, входящей в первое уравнение системы (XV.49), согласно закону Ома, представляется в виде
f =j х B = G(V X Во) X B0) = or[B0(B0-V)—V (В0>В0)].
В рассматриваемой задаче пограничного слоя на пластине направление местной скорости весьма мало отличается от направления невозмущенной скорости, т. е. B0V = 0. Исходя из этого, получим
7 = —оВ20У.
Тогда уравнение (XV.49,1) запишется в виде
dV . 1 „	пВо Л
—+ —Vp = W2V- — -V.
(XV. 135)
(XV. 136)
Рассмотрим задачу, в которой анализируется течение в пограничном слое, возникающем на полубесконечной плоской пластине, обтекаемой несжимаемой вязкой жидкостью при наличии магнитного поля (рис. XV. 18). Магнитное поле направлено перпендикулярно скорости свободного потока и связано с пластиной.
442
Электромагнитная гидродинамика
Уравнение (XV. 136) для плоского стационарного погранична слоя в системе координат, связанной с пластиной, записываете в виде
ди . ди ,	д2и	/v,7 ,_1
u-d^ + vl^ + m^=vW (XVJ^
<тВ?	•
Здесь	.
Граничные условия:	>
v = и = 0 при у = 0;
^-=о,	I
ду	1
ди	при у = оа.
На внешней границе пограничного слоя, как это следует иа до
уравнения неразрывности, необходимо иметь = т1.	,
, Заметим, что уравнение (XV. 137) отличается от уравнения не-сжимаемого пограничного слоя на пластине в классической гидрб-динамике лишь членом т^и, который представляет собой тормозя^ щую силу, действующую на жидкость, втекающую в магнитное поле. Вследствие действия этой силы скорость жидкости на верх-; ней границе пограничного слоя, т. е. при у = оо, изменяется пей закону и = Uco — т1х1 (и,. — скорость, с которой жидкость вхо-< дит в магнитное поле пластины).	J
Используем в нашей задаче введение новых переменных, пред-' ложенных Блязиусом,
g =	=	'	(XV.138):
Функцию тока ф представим в виде
з
Ф _ у umvx + у7пх^ + mxf2 + (тх)2 /3 + (тх)2 /4 +
(XV. 139)
где /0, /х, f2, . . . являются функциями только т]х и т =	. 
Составляющие скорости и их производные определяются еле-,; дующим образом:	’
__5ф _ 5ф дф dt]i .	i ду д^ ду	ду ’
дф дтц
v дх <?£ дх <Ь]х дх ’
Магнитогидродинамический пограничный слой
443
откуда
и = ию [fo + mxf2 + (wx)2 Д Ч-];	(XV. 140)
0 = 4 ]/"-у- [fo + mxf2 + (mxff4 Ч-] —
-4]Л^[/°+3тхЛ+5(тх)2л+	(XV‘14I>
4 = — -у- -у- [to Ч- mxh Ч- (М2й Ч- • • •] Ч-
Ч- [2mxf2 + 4 (mx)2 f4 Ч- •••]'»
~g^ = Um j/"[/о 4~ m*h Ч~ (wx) А Ч-  • • ]>
> - [fo + mxf2 + (mx)2fU  • •]•	(XV.142)
Подставив выражения проекций скорости и их производных по (XV. 140)—(XV. 142) в уравнение (XV. 137) и приравняв коэффициенты при одинаковых степенях параметра
ctBq	стВдХ2	1	На2
тх =---х =-----------= -к—,
Р“оо	П	V<x>x
V
получим систему обыкновенных дифференциальных уравнений для определения функций fn и их производных:
2f"o=-fyo,	(XV. 143)
/2=/^2-4-/оЛ-4^Ч-/о;	(XV.144)
=2/оАч- /2^-4	—г+f'2 <XV-145)
И т. д.
Граничные условия:
/о = /г = Л = • • • = 0 при ти = 0;
fo = h = f'i =  • • = 0 ПРИ П1 = °;
fo = 1 Н f2 = —1 при T]1 = оо;
Л = /б = • • • = 0 ПрИ Т]1 = оо.
444
Электромагнитная гидродинамика
Система полученных дифференциальных уравнений интегрИ руется численно. Расчетные профили скорости при различных зна чениях параметра тх представлены на рнс. XV.19.
Сплошные кривые соответствуют ряду (XV.140), в котором о>1 ражены члены старше первой степени тх. Штриховые кривые соо$ ветствуют следующему приближению, когда ряд оканчиваете! членом со второй степенью тх. Если в выражении (XV. 140) огра кичиться членом с первой степенью тх, то, как видно из график^
6
4
2
тх-0
Рис. XV.19
0,4 О 0,4 0,8 f.2$
такой ряд будет достаточно точна представлять действительное распрё! деление скоростей лишь для парад метра тх < 0,2. Очевидно, что еслц тх > 0,2, то в выражении ряда (XV. 140) необходимо брать больше^ число членов.
Приведенные данные свидетель^ ствуют о существенном влиянии по-; перечного магнитного поля на рас-) пределение скорости в пограничном; слое при тх > 0,1, причём с увели-" чением магнитного поля градиент: скорости у стенки уменьшается.
Местный коэффициент трения и толщина вытеснения запишутся в виде
0,664 — 1,789/пх + 0,706m2x2 j-----
Cf =-------------------------------!-----’
(ХУ.146|;.

6* = rnxy + (1,73 + 0,54/nx -j- 1,34т2х2 + • •
Из формул (XV. 146) и (XV. 147) следует, что при наличии поперечного магнитного поля, неподвижного относительно пластины,,) с увеличением параметра т коэффициент поверхностного трения’ уменьшается, а толщина вытеснения увеличивается.
Полученные решения приближенно характеризуют влияни^ магнитного поля на пограничный слой, образующийся на поверх-^ ности снаряда, движущегося с большой скоростью. При этом про-*! водимость может быть обусловлена термической ионизацией,' а также испарением металла, из которого сделан корпус снаряда.). Если магнитное поле движется вместе с потенциальным пото-) ком относительно неподвижной пластины, то в силу скольжения-j жидкости в пограничном слое относительно магнитного поля и из-’! менения направления действия пондеромоторных сил градиент’) скорости у стенки будет возрастать с увеличением напряженности.^ магнитного поля, что будет приводить к повышению коэффи-' циента трения.	)
Внешнее обтекание в магнитной гидродинамике
445
§ 11. Внешнее обтекание в магнитной гидродинамике
Решение задачи об обтекании твердого тела проводящей жидкостью в присутствии магнитного поля представляет значительный интерес для аэродинамики больших скоростей. Известно, что при сверхзвуковых скоростях полета перед телом образуется сильная ударная волна. Вследствие сильного нагрева газа за ударной волной происходит ионизация, т. е. газ становится электропроводящим. Если с движущимся телом связано магнитное поле, то с этим полем будет взаимодействовать газ, находящийся между телом и головной ударной волной. Такое взаимодействие изменит характер обтекания тела и-приведет к изменению теплового потока от газа к телу.
Рассмотрим обтекание диэлектрического тела, находящегося в потоке проводящей жидкости. При этом будем считать, что внутри обтекаемого тела имеется источник магнитного поля. Для простоты будем считать, что тело обтекается несжимаемой жидкостью. Учет сжимаемости не внесет никаких изменений в постановку задачи, если только не рассматривать течений с ударными волнами.
Используем систему уравнений (XV.49), описывающую движение проводящей жидкости в электромагнитном поле. С помощью уравнения (XV.49, 3) этой системы выражение для электромагнитной объемной силы можно записать в виде
7=7 X B = p0(rottf X Н).	(XV. 148)
В свою очередь, уравнение (XV.49, 3) на основании закона Ома запишется в форме
rot Н = а [Е + ц0 (V х Н}].	(XV. 149)
Дзяв операцию rot от обеих частей этого уравнения, получим rot (V х Н) + — V2# = 0.	(XV. 150)
Таким образом, рассматриваемая в нашей задаче система урав нений примет вид:
(V-V) V -h -1- Vp = vV2V + -^-rot Н хН;
div Н = 0; div V = 0;
rot (V X Д)-f-vMV2H = 0.
(XV. 151)
446
Электромагнитная гидродинамика
Запишем на основании уравнения (XV. 149) выражение длг| напряженности электрического поля в потоке	-1
E = -^-rotH— р0(Кх Я).	(XV. 1521
Очевидно, что для напряженности магнитного поля внутри тела справедливы уравнения:
rot Н = 0; div Н = 0; Н = —grad ф или \72ф = 0, (XV. 153) где ф— скалярный потенциал магнитного поля.
Аналогично этому для напряженности электрического пола, внутри тела имеем
Е = —grad <р; V2cp = 0,	(XV.154):!
где ф—потенциал электрического поля.	|
Сформулируем теперь граничные условия. На бесконечности-^ должны быть	
V = р = Ра>- Н = 0; Е = 0.	(XV.155)^
На поверхности тела задаем условие непроницаемости стенкиз (Vn = 0, где индексом п обозначена внешняя к поверхности тела,] нормаль) и условие прилипания (V = 0, если жидкость вязкая)..) Для магнитного поля на границе жидкость — тело имеем
Я„2 = 0,	(XV.156)ij
где индексы 1 и 2 относятся к области внутри тела и к потоку соот?’ ветственно. Кроме того, на границе
1 = (п х Н2) — (п х Я,),	(XV. 157):
где i — плотность поверхностных токов (не отождествлять с плотностью объемных токов /); п — орт внешней нормали.	\
Рассмотрим последнее уравнение системы (XV. 151). Записав, это уравнение	в	безразмерном виде, получим	:
rot (V* х Я*) +	72Я* = 0,	(XV. 158)’
Кем	,
где ReM ----------магнитное число Рейнольдса.
Vm
Как было отмечено, магнитная вязкость vm в последнем урав-' нении играет ту же роль, что и кинематическая вязкость v в пер-; вом уравнении системы (XV. 151), т. е. vm характеризует влияние: диссипации магнитной энергии на общую картину течения. В том
Внешнее обтекание в магнитной гидродинамике
447
случае, когда ReM —> оо, уравнение (XV. 158) записывается (в размерных величинах) в виде
rot(Vxtf)=0,	(XV. 159)
т. е. электрическим сопротивлением среды и связанными с ним джоулевыми потерями и диссипацией энергии магнитного поля можно пренебречь (точно так же, как и в обычной гидродинамике можно пренебречь эффектом вязкости при больших числах Рейнольдса). Если проводимость жидкости а бесконечно велика (ReM = оо), то набегающий на тело поток не может проникнуть в область, занятую полем, т. е. обтекаемую область можно рассматривать состоящей из намагниченного тела и каверны — области, в которой находится магнитное поле.
Если же проводимость жидкости большая, но конечная, то каверна постепенно будет заполнена жидкостью. Считая, что находящаяся внутри каверны жидкость покоится, и полагая в уравнениях (XV. 151) V = 0, получим, что магнитное поле в каверне должно удовлетворять уравнениям:
VpK = Por°t Н X	(XV.160)
div Н = 0,
где рк — давление в каверне.
На границе каверны с потоком должны выполняться условия:
Яп2—Ялк = 0;	(XV. 161)
Р2 = Рк + ^-	(XV. 162)
Если применить операцию rot к первому уравнению системы (XV. 160), то внутри каверны вектор Н должен удовлетворять уравнениям:
rot (rot Н х Я) = 0, div И = 0.
Если ток не протекает сквозь поверхности тела [/„=(rot Я)л2=0], т. е. когда оно электрически изолировано, задачу можно упростить, потребовав отсутствия объемных токов и в каверне.
Тогда
rot Н = -0,	(XV. 163)
(если в каверне отсутствует проводящая жидкость, то это условие выполняется автоматически). Из первого уравнения системы (XV. 160) при этом получим
рк = const,	(XV. 164)
а форма каверны находится из условия (XV. 162),
448
Электромагнитная гидродинамика
Для примера рассмотрим обтекание несжимаемой невязкой жидкостью плоского магнитного диполя, вектор момента которого перпендикулярен к направлению скорости набегающего потока: Для этой задачи существует решение, когда обтекаемая поверху ность представляет собой цилиндр радиуса а (рис. XV.20).
Магнитное поле внутри цилиндра и скорость вне его выражаются формулами:
Я — Но grad у (1 + - а у, );
V = Vogradx (1 +	) ,
где Va и Но—постоянные, связанные соотношением
причем На определяется через момент диполя q из соотношения q — HgC^.	.	''
Давление внутри каверны рк постоянно и связано с давлением! в критической точке р0 следующим образом:
Ро—Рк = % РоНо-
Рассмотрим задачу о вычислении силы, действующей на магнит-, ную проводящую сферу радиуса а при ее равномерном движении-в проводящей вязкой несжимаемой жидкости, находящейся в продольном внешнем магнитном поле Яо.
Используем для решения этой задачи систему уравнений ! (XV. 151). Ее можно записать в виде:
р (V. V) V = - V (р +	) + ц0 (Я • V) Н + TJVT;
divV = O; 61уЯ = 0;
(У-7)Я = (Я-¥)У + -^?2Я.
(XV. 167):
Внешнее обтекание в магнитной гидродинамике	449
Вводим связанные со сферой прямоугольную и сферическую системы координат, имеющие начало в ее центре, причем ось z направим вдоль внешнего магнитного поля (рис. XV.21).
Представив магнитное поле в виде
Н=^Н0 + У~т]1г,	' (XV. 168)
будем рассматривать лишь медленное движение сферы, т. е. скорость и индуцированное в результате движения магнитное поле можно считать малыми и пренебречь в системе уравнений (XV. 167) членами, содержащими (V-V) и (/i-V).
Подставляя теперь выражение для полного магнитного поля (XV. 168) в систему (XV. 167), получим уравнения:
w=_«* + Tv [р+;
divV —0; divh = 0; V<= — a	(XV.169)
где a = Яо р0.
Применяя далее операцию rot к уравнениям системы (XV. 169) и обозначая rot V = со, rot h = / (/ — пропорциональна плотности тока), будем иметь:
(XV.170)
Для решения задачи воспользуемся следующими граничными условиями:
на бесконечности V — Va>;	171)
на поверхности сферы V = 0.
Кроме того, вследствие осевой симметрии обтекания можно положить
^=°- 	<xv-173>
Перейдем теперь от граничных условий для V и h к условиям для со и /.
На основании уравнения (XV. 171) легко видеть, что на бесконечном удалении от сферы должны быть выполнены условия
со = 0 и / = 0,	(XV. 173)
а из условий (XV. 172) будем иметь
ior = coe = O,	(XV.174)
29 И. Л. Повх
450
Электромагнитная гидродинамика
что при подстановке в (XV. 170) дает	'fl
/г = /о = 0.	(XV. 175»
Из последних соотношений видно, что ток через поверхность» сферы отсутствует. Если принять к тому же, что относительное» движение сферы и магнитного поля отсутствует, то индуцирован-» ные токи внутри сферы не возникают. Следовательно, движение» проводящего шара в направлении внешнего однородного магнит-» ного поля не зависит от его электрических свойств, в частности от ] электропроводности.	Я
Приняв ток внутри сферы равным нулю и пользуясь известным условием непрерывности касательных составляющих плотности  тока на его поверхности, получим условие на границе
/ф = 0.	(XV. 176)
Далее, принимая во внимание (XV. 169) и (XV. 171), можно * найти, что на границе сферы соблюдаются условия:
-^ = 0; 4|- = 0; ^=0. (XV. 177) 1 д'д,	дг	'	’
Используя теперь третье и четвертое уравнения системы (XV. 169) и условия (XV. 177), получим
cosft-^-l =— rot# / I dr |r=a a u 1 lr=a
Принимая во внимание принятые ранее обозначения со = , = rot V и j = rot А, будем иметь граничное условие
= —<xv.l78)
I
Подобным же образом, используя условие (XV. 176), можно получить второе граничное условие	;
~д$ |r=a = °’	’
ф Воспользовавшись далее четвертым уравнением системы (XI. 169) 1 и соотношением rot h = j, получим уравнение
5	1,.	'
-^-vr =— rot./.
дг r a г 1
Так как при О = 0	легко получить соотношение,
связывающее величины j и Vm,
4-iroV/|„./r = AVe. (XV. 179)-
Внешнее обтекание в магнитной гидродинамике
451
Задача свелась к решению системы уравнений (XV. 169) при граничных условиях (XV.173), (XV.176), (XV.178) и (XV.179).
Уравнения (XV.170) при условиях (XV.176) удовлетворяются решением:
со / ar cos Ф	ar cos О \
0>Ф = £ Лп 2	- (-1)" е	х
Л=1
со /	ar cos О	аг cos О \
Ч> = £ ЛД-е ~-(-1)"е	~) х
п=1
1 (-^ДлДсозй), (XV.180)
где /<	1 (-7г) — цилиндрические функции мнимого аргу-
n + V Х 2 7
мента; Рп (cos Ф) — присоединенные функции Лежандра.
Для определения бесконечного множества неизвестных коэффициентов Лп используем систему уравнений, получаемую путем подстановки в (XV. 176) и (XV. 178) /ф и Юф cos 6', разложенных в ряд по системе ортогональных функций Рт (cos 6'). Приравнивая далее коэффициенты при Рт (cos 6') друг другу [члены с Р' (2т + 1) X х (cos Ф) в этих уравнениях отсутствуют], получим искомые коэффициенты Ап. Практически это достигается разложением ar cos О
е 2 по степеням cos Ф и использованием рекуррентных соотношений для Р'п (cos 6'), что позволяет получить коэффициенты уравнении в виде степенных рядов по параметру —К полученной системе добавляется уравнение, получаемое подстановкой решения (XV. 180) в условие (XV. 179). Заметим, что коэффициенты полученных таким образом уравнений зависят только от параметра
за исключением свободного члена, равного—Д. Поэтому коэффициенты Ап можно записать в виде
V
Л„ = --ДФ„(На),
где Фп (На) — функция, зависящая только от числа Гартмана.
452
Электромагнитная гидродинамика
(XV. 181'
Перейдем к вычислению действующей на сферу силы, выраж^ ние которой записывается в виде
F = — J pds + ^-^rVds, s -	s
где s — поверхность сферы.
Учитывая тот факт, что вследствие осевой симметрии задач® единственной составляющей силы, отличной от нуля, будет ее проекция на ось z и, используя условия (XV. 177), можно записав
дУг I	|,а
“aZ = — ®<р sin ft.
or lr=a	T |r=a
(XV. 18^
Представим далее давление, входящее в (XV. 181), в виде суммы двух слагаемых	3
Р = Pi + Pi,
причем
VP1 = an # - V (Но + V^h )2;
Vp2 = T)V2V = — т) rot ю.
(XV.183J
’I
J
Подставляя теперь рг в выражение (XV. 181) и переходя поверхностного интеграла к объемному, можно показать, что р‘| не дает вклада в общую силу.
На основании второго выражения (XV. 183) можно записать’
 р2 = — От] j rote со |^_e dft = ат] j 5ft. (XV. 184^ о г~	о г~а
Подставляя теперь (XV. 182), (XV. 184) в (XV. 181) и принимав во внимание (XV. 180) и (XV. 183), получим выражение для сил®
Fz = отепУсоОф (На),
где ф (На) — функция, зависящая только от На.
Если принять параметр На малым, то при вычислении Fz с точ-j ностью до членов На2 достаточно определить первые четыре коэф;? фициента Ап. Зная величины А1У А2, Л3 и Л4, можно найти, чтй выражение для силы запишется в виде	;]
.	Л=1 + ТНа + ^оНа*+'"-	1
где Fo = cm^Vcoa — выражение стоксовой силы сопротивлениям действующей на сферу.	1
Электромагнитные насосы. Магнитодинамическое генерирование энергии 453
§ 12. Электромагнитные насосы. Магнитодинамическое генерирование электрической энергии
Из предыдущих параграфов видно, что электромагнитную силу ([ = / х В), возникающую при движении проводящей жидкой или газообразной среды в электромагнитном поле, можно использовать для управления потоком этой среды. При этом, очевидно, соответствующей ориентацией электрического и магнитного полей электромагнитную силу можно направить так, что она будет либо ускорять поток, либо препятствовать его движению.
Пусть по каналу, образованному двумя проводящими
Рис. XV.22
полезная мощность. Эта схема
бесконечными пластинами, движется проводящая среда, имеющая скорость V а проводимость о.
Перпендикулярно движению потока в направлении оси z приложено однородное магнитное поле Во (рис. XV.22, а).
При движении проводящей среды в таком поле индуцируется электрический ток, направленный перпендикулярно пластинам вдоль отрицательной оси у. Если пластины соединены с некоторой внешней нагрузкой RH, то на последней может быть получена определенной величш
представляет собой генераторный режим работы рассматриваемого магнитогидродинамического устройства.
Можно представить и другую простую модель магнитогидродинамического устройства (рис. XV.22, б), в которой к жидкости, движущейся в магнитном поле, подводится энергия внешнего электрического поля. Это осуществляется присоединением к пластинам источника электрического тока. Подводя к жидкости или газу энергию электрического поля извне, можно ускорить поток. Таков насосный режим работы рассматриваемой нами модели.
Наконец, можно представить некоторое комбинированное устройство (рис. XV.22, в), в котором пластины соединены внешней цепью, имеющей нагрузку и источник тока. При этом замедляющее
454
Электромагнитная гидродинамика
действие электромагнитной силы будет свойственно генераторному режиму, ускоряющее — режиму потребления энергии (или насос^ ному).	-I
В насосном режиме энергия электромагнитного поля расход
дуется на нагрев и ускорение проводящей среды.	1
В генераторном режиме возможно ускорение газа, если одновременно его охлаждать.	;
Таковы принципиально возможные варианты работы простого рассматриваемого магнитогидродинамического устройства.	;
Рассмотрим несколько конкретных моделей магнитогидродина^ мических устройств.
Кондукционный насос. В последние годы интерес к электро*; магнитным насосам значительно возрос. Этому способствовало; быстрое развитие ядерной энергии, нуждавшейся в эффективных^ методах отвода жидкометаллических теплоносителей от реактора! к теплообменнику. Из-за высокой температуры теплоносителя! электромагнитные насосы—наиболее приемлемое средство для! его транспортировки. Весьма эффективно электромагнитные на-jj сосы могут быть использованы в металлургии для непрерывной i! транспортировки расплавленного металла.
Работу кондукционного насоса проиллюстрируем на примере’1 насоса постоянного тока (рис. XV.23). Он состоит из канала /,^j сечение которого в рабочей части имеет прямоугольную форму,'; электромагнита 2 и двух металлических полос 3, присоединенных' к двум противоположным сторонам канала. С помощью полос; (электродов) к проводящей среде, протекающей по каналу насоса, подводится электрический ток. Электроды включаются либо; последовательно с обмоткой электромагнита, либо питаются неза-, висимо. Взаимодействие электрического поля с магнитным полем; (создаваемым электромагнитом) приводит к появлению объемной электромагнитной (пондеромоторной) силы, которая заставляет проводящую среду двигаться.
Электромагнитные насосы. Магнитодинамическое генерирование энергии 455
Электромагнитные кондукционные насосы на постоянном токе конструктивно просты и могут служить для перекачивания металла с температурой до 800° С без специального охлаждения. Но у них имеется существенный недостаток — потребность в специальных источниках постоянного тока на десятки и сотни тысяч ампер.
Лишены этого недостатка однофазные кондукционные насосы переменного тока. Один из практически используемых типов такого насоса схематически показан на рис. XV.24.
В зазор шихтованного магнитопровода 2 (первичная обмотка 1 которого питается переменным током промышленной частоты) помещен канал 3. Две противоположные стенки его — электроды, к которым подключена вторичная обмотка 4.
Магнитный поток, получаемый в сердечнике, пронизывает зазор, создавая в нем некоторую индукцию В. В то же время этот поток возбуждает во вторичной обмотке э. д. с. и ток, замыкающийся через жидкий проводник, находящийся в канале. Взаимодействие совпадающих по фазе тока и магнитной индукции создает электромагнитную объемную силу, заставляющую проводящую жидкость двигаться вдоль канала. Однофазные электромагнитные насосы на промышленной частоте имеют низкий коэффициент полезного действия и потому получили распространение лишь в лабораторной, практике.
Индукционный насос. Впервые в 1915 г. Л. Чабб в патентной заявке описал индукционный насос, в котором вращающееся и бегущее магнитные поля использовались для перемещения жидких металлов. В 1927г. Тряпицын предложил применять для перекачки щелочных металлов индукционный насос. Аналогичный патент был получен в 1931 г. Эйнштейном и Сциллардом.
Советские ученые провели большую теоретическую и экспериментальную работу по исследованию индукционных насосов. Отметим Г. Штурмана, который в 1941—1948 гг. предложил и испытал ряд конструкций трехфазных насосов для жидкого металла, П. Я польского и др.
Принцип действия индукционного насоса рассмотрим на примере трехфазного насоса. Работает он аналогично асинхронному электродвигателю. Трехфазная обмотка, расположенная на плоском или цилиндрическом магнитопроводе, создает бегущее или вращающееся магнитное поле, возбуждающее токи в жидком проводнике. Взаимодействие индуктированных в жидкости токов с магнитным полем приводит к появлению в потоке электромагнитной объемной силы, заставляющей проводящую среду двигаться в осевом направлении.
По конструктивному исполнению индукционные насосы подразделяются на три основных вида: спиральный, плоский, линейный и цилиндрический линейный.
456 Электромагнитная гидродинамика
Устройство спирального индукционного насоса показано на рис. XV.25. Он состоит из индуктора 2 (выполненного так же, ка| и статор асинхронного двигателя), сердечника 1 и двух тонкостей! ных цилиндров, расположенных в зазоре между индуктором и сердечником. Между цилиндрами навита узкая лента 4, образую^
щая однозаходныи (или многозаходный) спирал^ ный канал <3, в котором находится жидкий металл!
Схема плоского линем ного индукционного на» coca представлена на рис| XV.26. Насос состоит из двух плоских индукторов 1, между которыми pacnoj ложен канал 2, имеющий в сечении прямоугольную
4
Рис. XV.25
форму. Каждый из индукторов представляет собой развернутый в плоскости статор обычного асинхронного двигателя.$	)
Отметим, что плоские линейные индукционные насосы из-за простоты их изготовления и высокой производительности широкб применяются для перекачки жидких металлов. Например,1, при нагнетании щелочных металлов к. п. д. этих насосов составляет примерно 25—40%.
/
Рис. XV.26
Схема цилиндрического линейного индукционного насоса по-4 казана на рис. XV.27. Насос состоит из рабочего канала 1 (выполз ценного в виде двух коаксиальных цилиндров, между которыми прогоняется жидкий металл), плоского индуктора 3 (свернутого] в цилиндр вокруг оси, перпендикулярной пазам) и внутреннегс| сердечника 2 (магнитопровода). В пазах цилиндрического индукз тора располагается трехфазная обмотка, создающая бегущее под оси магнитное поле. Оно индуцирует токи, бегущие по жидкому^ металлу. От взаимодействия индуктированных токов с бегущим, магнитным полем появляется пондеромоторная сила, заставляю^ щая металл перемещаться вдоль канала.	‘
Электромагнитные насосы. Магнитодинамическое генерирование анергии 457
Возможны и другие типы индукционных насосов.
Так, Ватт предложил применять однофазный индукционный насос, в котором жидкий металл в кольцевом канале образует вторичную обмотку трансформатора. В области кольцевого канала с помощью дополнительного магнитопровода создается магнит-
Рис. XV.27
ное поле, перпендикулярное индуктированному току. Насосы этого типа обладают высоким к. п. д., но весьма сложны по своей конструкции.
Магнитогидродинамические генераторы. Рассмотрим некоторые конкретные схемы магнитогидродинамических генераторов (МГ Д-генер аторов)..
На рис. XV.28 показана одна из возможных схем магнитогидродинамического генератора. Он состоит из канала 1 (по которому протекает ионизированный газ), катушек 3 (создающих направленное поперек канала магнитное поле) и электродов 2, расположенных на верхней и нижней стенках канала.
В ионизированном газе, протекающем по каналу, в поперечном магнитном поле индуцируется электрический ток, который снимается посредством электродов на внешнюю нагрузку 4. Подобное устройство представляет собой МГД-генератор.
458	Электромагнитная гидродинамика
Эффективность работы такого типа МГД-генератора може4 быть оценена электрическим к. п. д., показывающим, какая част] генерируемой мощности выделяется на нагрузке и какая рассей вается на внутреннем сопротивлении генератора.
Кроме омических потерь на внутреннем сопротивлении гене? ратора имеются потери тепла через стенки, и джоулевы потери в обмотках, создающих магнитное поле.	(
Электропроводность газа — одна из важнейших величин, опре-з деляющих эффективность МГД-генератора. Как известно, газ
300
Рис. XV. 29
становится проводящим, если часть его атомов или молекул иони-4; зируется. В МГД-генератор ах ионизация создается термически^ способом. При этом газ должен быть нагрет до температуры в не4 сколько тысяч градусов.	}
Когда газ ионизирован на 0,1%, он практически становится? хорошим проводником. Подобную невысокую степень ионизации,, как уже отмечалось, можно получить и при относительно низко^ температуре, но с добавлением к газу от 0,1 до 1% легкоионизи^ руемого элемента (калий, натрий и др.).	' ।
О роли проводимости газа в эффективности МГД-генераторй можно судить по расчетным кривым, приведенным на рис. XV.29.; Здесь представлена зависимость наибольшего характерного раз*, мера генератора определенной мощности (в данном случай! 100 000 кВт) в функции проводимости газа и напряженности маг-i нитного поля.	I
Из графика видно, что при небольшой степени ионизации для> снятия заданной мощности требуется генератор очень больших^ размеров.
Если взять в качестве характерной длины генератора 10 м; и выбрать магнитное поле с индукцией, равной 10 000 Гс, то необходимой для этих условий проводимостью газа будет о 1
Электромагнитные насосы. Магнитодинамическое генерирование энергии 459
(Ом-м)-1 и, следовательно, температура газа должна быть около 2000 К.
Рассмотрим теперь возможные варианты МГД-генераторов.
Простейшей является схема линейного МГД-генератора, экспериментальная модель которого показана на рис. XV.30. Он состоит из узкого канала 6, в который через вход 2 вдувается
ионизированный газ, предварительно нагретый в камере 3 дугой,
создаваемой электродами /. В дуговую камеру подаются легкоионизирующиеся добавки 4 в виде соединений щелочных металлов. К двум противоположным стенкам канала подводится магнитное поле, создаваемое электромагнитом 7. Индуктированный в проводящем газеток снимается с электродов, смонтированных на двух других стенках канала. Газ поступает в генератор из ресивера 5.
Можно показать, что выходная мощность на единицу объема потока пропорциональна произведению он2. Поэтому при конструировании конкретного типа МГД-генератора необходимо стремиться получить эту величину возможно большей.
Естественно, что мощность линейного
МГД-генератора ограничивается длиной, Рис xv.30 на которой происходит взаимодействие
ионизированного газа с магнитным полем. Один из способов увеличения длины взаимодействия — использование спирального
вихревого течения газа в поперечном магнитном поле.
Существуют две схемы генератора, в котором вихревое течение можно использовать для генерирования электрической энергии.
1. МГД-генератор, в котором магнитное поле 2 приложено радиально, а электродами 4 служат параллельные^плоские диски, ограничивающие поток (рис. XV.31).
Газ через входное сопло 1 подается в канал 3, а ток, снимаемый с электродов, замыкается на нагрузку 5.
2. МГД-генератор, в котором магнитное поле направлено по оси, а электроды представляют собой два (внешний и внутренний) коаксиальных цилиндра (рис. XV.32). Этот генератор представляет собой полый цилиндр, в который через сопла 3 вдувается ионизированный газ. Далее газ течет в канале 1 по спирали к оси цилиндра, проходит сквозь щели во внутреннем электроде 4 и выбрасывается через выходные патрубки 2. Все устройство помещается в осевое магнитное поле, создаваемое внешним магнитом 5. Разность потенциалов создается на двух электродах 4, представляющих собой коаксильные цилиндры, скрепленные двумя
460
Электромагнитная гидродинамика
пластинами из непроводящего материала. Ток, снимаемый с электродов, подается на' нагрузку 6.	;
Рассмотренные схемы МГД-генераторов предусматривают те-, чение газа как от периферии к центру, так и наоборот. К пре--имуществам вихревого МГД-генератора следует отнести компактность его конструкции (относительно большую удельную мощность, на единицу массы) и высокий к. п. д., а также эффективное исполь-.
Staff вазо
Рис. XV.3I
Рис. XV.32

зование магнитного поля. Кроме того, в таком генераторе можно получить более высокие выходные напряжения.
В последние годы большое внимание уделяется жидкометаллическим МГД-генераторам, которые рассматриваются как перспективные источники электроэнергии для транспортных объектов.
§ 13. Электрогидродинамические насосы и генераторы
Принцип действия и основные элементы одноступенчатого, многоточечного насоса для перекачки непроводящих сред пока-: заны на рис. XV.33. В трубу, заполненную непроводящей средой, 1 помещены генератор ионов (ионизатор) и коллектор. Под дей- ’ ствием разности потенциалов U, созданной на расстоянии z, ионы i стекают с концов ионизатора и перемещаются к коллектору. , Число точек, с которых стекают ионы, может изменяться от одной 1
Электрогидродинамические насосы и генераторы
461
до ста и более. Для повышения давления, создаваемого насосом, в трубе можно поставить последовательно несколько ступеней.
Коэффициент полезного действия насоса т]н, определенный по формуле
где Q — количество жидкости, перекачиваемой насосом в единицу времени; I — сила тока, достигает 10—20% и более.
Давление, создаваемое такими насосами, достигало: для воздуха 98,1 Н/м2, для жидкостей 1,96 Н/м2 при очень высоких разностях потенциалов (15—20 тыс. В) и очень малых токах (0,5 — 0,8 мА).
Электрогидродинамические насосы могут быть использованы для создания выключателей, реле, регуляторов напряжения, измерителей тока и напряжения и т. д.
Принципиальная схема электрогидродинамического генератора показана на рис. XV.34, а, а генератор наиболее распространенной конструкции приведен на рис. XV.34, б. Жидкость, подаваемая насосом, со скоростью проходя через ионизационную камеру, переносит ионы на коллектор, вызывая во внешней сети, имеющей сопротивление R, ток I с разностью потенциалов U.
Величина тока I, определяемая по формуле
пропорциональна квадрату скорости потока V.
Коэффициент полезного действия т]г генератора
IU
Т1г Q Др
в действующих установках достигает 10—15%.
462
Аэродинамический эксперимент
)
Электрогидродинамические генераторы могут найти широкое j применение в технике для различных целей. В частности, они-J могут быть использованы для измерения параметров течения,। непроводящих сред.	(	1
Комбинированное использование насоса и генератора позво4Я ляет создать трансформатор постоянного тока. Существующая мо-я дель трансформатора (на керосине) изменяет входные параметры^ от 15 000 В при 20 мА до 100 000 В при 3 мА.
ГЛАВА XVfj
АЭРОДИНАМИЧЕСКИЙ ЭКСПЕРИМЕНТ
§ 1.	Экспериментальные установки
Среди экспериментальных исследований, без которых невоз-'.-можно развитие науки, особое место занимают опыты в лаборато-J рии. Изучение физических явлений на модели может быть осуще-J ствлено проще, полнее и дешевле, чем в натуре. Но только еслиг будут соблюдаться законы моделирования и подобия (гл. X),’ результаты опытов с моделью можно использовать для решения^ задач практики.
В зависимости от взаимодействия тела и среды все встречаю-]! щиеся в практике задачи можно разделить на три категории,;!) Первая, когда тела движутся в неподвижной среде. Вторая, если’) тела неподвижны, а среда движется относительно их. Третья —1 смешанные явления, когда движутся и среда, и тело.
Пример обтекания первой категории — движение самолета*;!! в неподвижной атмосфере, лодки в неподвижной воде; второй —г| обтекание устоев моста в реке, потоки газа и воды в трубах)]! третьей — движение колес гидравлической, паровой или газовой^ турбин.	4
В основу экспериментальной аэродинамики положен принциш обратимости указанных явлений. В конце прошлого века опыты; французских ученых Дюбюа и Дюшмена показали, что сопротивле-J ние пластинки, обтекаемой потоком, почти на 30% больше, чей движущейся в неподвижной жидкости. Н. Е. Жуковский в 1891 щ с помощью разработанного им прибора показал, что разности в сопротивлении, полученная Дюбюа и Дюшменом, объясняется влиянием стенок канала, в котором они производили опыты| а также турбулентностью движущегося потока, которая умень^ шает ламинарный участок пограничного слоя на пластинкеЭД Таким образом, причина разности сил «происходит не от самож пластинки, а от разницы в движении жидких масс, в которые! мы погружаем пластинку».	S
Экспериментальные установки
463
После опытов Жуковского принцип обратимости явлений начал применяться еще более широко как в экспериментальных, так и теоретических исследованиях. Рассмотренные три категории движения в опытах всегда могут быть приведены к одному из первых двух.
В зависимости от того, движется исследуемая модель или она неподвижна, все методы аэродинамического эксперимента можно разделить на две группы. К первой отнесем методы, при которых объект исследования движется в покоящейся среде, ко второй — при которых, наоборот, изучаемый объект неподвижен, а среда движется.
Первая группа, в свою очередь, делится на три категории.
1.	Методы, основанные на изучении прямолинейного движения. К ним можно отнести изучение сопротивления при падении тел и исследование моделей при полете и при горизонтальном перемещении их по тросу или по рельсовому пути. Последний способ1 получил широкое применение в гидравлических каналах и судовых бассейнах, а также при изучении движения моделей ракет и снарядов на баллистических установках и ракетных тележках.
2.	Методы, основанные на изучении кругового движения тел с помощью использования ротативных машин, применяемых для исследования как в воздухе, так и в воде.
3.	Натурные испытания самолетов, судов, ракет и снарядов, получившие в последнее время широкое распространение в технике.
Методы, относящиеся ко второй группе, можно разделить на две категории.
I. Методы, использующие естественные потоки воздуха (ветер) или воды (река, канал и пр.). Эти методы шире применялись-в ранние годы развития экспериментальной аэродинамики. В отдельных случаях ими пользуются и теперь.
2. Методы, использующие искусственные потоки газа или жидкости, создаваемые вентилятором, насосом или каким-лрбо другим путем. Сюда можно отнести аэродинамические, гидродина-. мические и ударные трубы, почти все установки для исследования работы элементов проточной части энергетических машин, большую часть экспериментальных водяных и газовоздушных установок лабораторий заводов и конструкторских бюро. В зависимости от того, действует ли созданный искусственный поток постоянно (в течение длительного времени) или кратковременно, все установки последнего типа могут быть установками (трубами) постоянного либо кратковременного действия.
Основное преимущество применения труб постоянного действия по сравнению с трубами кратковременного действия, ракетными тележками и опытными бассейнами является возможность-длительных измерений и наблюдений изучаемых моделей.
464
Аэродинамический эксперимент
ото преимущество настолько велико, что для исследования; моделей кораблей все чаще применяются гидродинамические-трубы. Такие трубы строят, несмотря на то, что для их работы-необходимы насосные установки с потребными мощностями, в сотни и тысячи раз превосходящими потребляемые в бассейнах. Это объясняется тем, что на перемещение небольшой модели в неподвижной воде требуется значительно меньше мощности, чем на перемещение всего объема воды при неподвижной модели. При малых дозвуковых скоростях в экспериментальной аэродинамике не применяется используемый в опытовых бассейнах метод, при которых объект исследования движется в покоящейся среде.
Аэродинамические трубы постоянного действия. Цель исследования в обычных аэродинамических трубах (за исключением труб специального назначения) — изучение законов движения тел в однородных средах. Следовательно, труба проектируется так, чтобы в ее рабочей части могло быть смоделировано изучаемое обтекание тела. При этом поле скоростей и давлений в рабочей части должно быть одно-  родным во всем сечении. Динамическое подобие обеспечивается одинаковостью критериев подобия вообще и в частности — главным образом чисел Re и М.
В зависимости от скорости потока в рабочей части аэродинамические тру-
бы делятся на трубы: малых скоростей с числом М порядка 0,1— 0,2 и меньше; дозвуковые с числом М от 0,2 до 1,0; сверхзвуковые с числом М от 1 до 10—12; гиперзвуковые с числом М свыше 12.
В зависимости' от потока (замкнутый он или незамкнутый) все аэродинамические трубы делятся на два типа: прямые с незамкнутым потоком (рис. XVI ,1,а иб) и замкнутые с потоком, циркулирующим в замкнутом канале (рис. XVI. 1 в, г, д).
Главный недостаток незамкнутых труб — необходимость для них больших помещений. Надо, чтобы скорость воздуха в помещении была минимальной; для этого поперечное сечение помещения должно во много раз превосходить площадь сечения трубы.
Другой недостаток первого типа труб — низкий к. п. д., так как вся кинетическая энергия потока теряется при выходе воздуха из трубы в помещение. Этот недостаток устраняется в трубах замкнутого типа. Однако замкнутость цикла приводит к тому
Рис. XVI. 1
Экспериментальные установки	465
что возмущения, возникающие за винтом, а также на поворотах, распространяются по потоку в обратном канале и достигают рабочей части, делая профиль скоростей в ней неоднородным. Этот дефект можно ликвидировать расширением потока в обратном, канале, размещением лопаток на повороте, значительным поджатием потока перед рабочей частью и другими способами.
В зависимости от наличия в рабочей части твердых стенок, все аэродинамические трубы делятся на трубы с закрытой и открытой рабочей частью.
По состоянию среды в рабочей части трубы могут быть: с нормальным (атмосферным), повышенным, пониженным и, наконец, с переменным давлением. В последних в зависимости от задач может быть создано разрежение', т. е. некоторый вакуум, или повышенное давление.
Аналогично можно классифицировать трубы и по другим физико-химическим свойствам заполняющей их среды; трубы со средами, отличными от воздуха (гелий, фреон и др.), с переменными температурой и влажностью.
Соблюдение динамического подобия требует знания характера, сил, действующих на изучаемое тело, для того чтобы определить, каким из критериев можно пренебречь в изучаемом явлении. В экспериментальной аэродинамике чаще всего имеют существенное значение силы вязкости и поверхностные силы, возникающие из-за сжимаемости жидкости при скоростях движения, достигающих скорости звука и более. Следовательно, при проектировании, труб требуется, чтобы числа Re и М, получаемые при опытах, были равны их значениям в натурных условиях.
Получить большие числа Re можно только в трубах с большим: диаметром рабочей части или при значительном снижении величины кинематической вязкости среды. Кинематическую вязкость воздуха можно уменьшить, либо понижая температуру, либо по-выш ая давление.
Увеличение числа Re путем уменьшения кинематической вязкости послужило основанием для проектирования аэродинамических труб переменной плотности, точнее, с увеличенным давлением. Число Re, которое можно получить в такой трубе, прямо, пропорционально давлению. У существующих труб такого типа давление до 25 кгс/см2, скорость до 40 м/с и диаметр рабочей, части около 2 м. Считая, что в такой трубе длина модели 2 м, число Re будет иметь величину 1,38 -108, в то время как при нормальном давлении оно равно 5,5-106. При сохранении давления в данной трубе можно еще увеличить число Re за счет повышения скорости потока.
Труба переменного давления показана на рис. XVI. 1, д. Внешний корпус ее должен быть очень прочным. Толщина стальных стенок наружного кожуха достигает 50 мм.
30 И. Л. Повх
466
Аэродинамический эксперимент
Получение в аэродинамических трубах больших чисел М дик-,-1 тует необходимость создания труб с большими скоростями, а еле-.I) довательно, и с огромными потребными мощностями.
Моделирование явлений в трубах при значительных числах ! Re и М пока неизбежно приводит к постройке гигантских труб ’ с огромными скоростями. Вот почему уже в 1941—1945 гг. име- ? лись трубы с диаметром рабочей части 10—20 м, скоростью по-тока до 7 скоростей звука и потребляемыми мощностями около J 100 тыс. кВт.	*
Для оценки эффективности использования располагаемой энергии в аэродинамических установках обычно пользуются величиной качества, равной отношению кинетической энергии потока в рабочей части установки к энергии, расходуемой на 1 вращение вентилятора или компрессора.
Кинетическая энергия в рабочей части равна
E = -±-mV2 — -±-pV8s,	’
где tn, р, V — секундная масса, плотность и скорость в рабочей j| части; s — площадь рабочей части.	j
Следовательно, качество установки будет	,Й
у. _ Е . . Р^3
л ~	~ 2jV ’	1
где N — мощность привода.	,1
Аэродинамические трубы кратковременного действия. Основ-ной недостаток сверхзвуковых аэродинамических труб непрерыв-ного действия в том, что мощности, потребные для их работы,J чрезвычайно велики. Уже сейчас для относительно небольших?! чисел М потребные мощности таких труб достигают сотен тысяча киловатт. Стоимость и конструктивная сложность труб непрерывна ного действия почти полностью определяются их энергетическим^ оборудованием (двигатели, компрессоры, холодильники и пр.)Л
Поэтому трубы кратковременного действия последние foam's получают все большее распространение. Размеры рабочей часто современных труб уже превосходят I м, а числа М, получаемые^ в них, достигают М = 6 н- 10. Освоение быстродействующей! аппаратуры для измерения сил давлений и скоростей содействует^ все более широкому применению таких труб.	••
По схеме двигательного привода существующие конструкции? могут быть разделены на два типа: с истечением из баллонов? сжатого воздуха и с истечением в вакуумную емкость. j.
Первая схема (рис. XVI.2, а) включает в себя компрессор ,1»! устройство для отделения воды, масла и осушки воздуха 2, емкост^ для сжатого воздуха 3, быстродействующий кран 4, подогрева^ тель 5 и рабочий участок трубы, состоящий из коллектора 'О
Экспериментальные установки
467
сопла 7, рабочей части 8 и диффузора 9. Выбрасывание воздуха в атмосферу и глушение шума производится в выхлопной шахте 10.
В вакуумной установке (рис. XVI.2, б) воздух из атмосферы, пройдя осушитель 1, попадает в рабочий участок, состоящий из коллектора 2, сопла 3, собственно рабочей части 4 и диффузора 5. Впуск воздуха производится быстродействующим краном 6. Разрежение в вакуумной емкости 7 создается эксгаустером 8.
В качестве емкостей для труб первого типа используются баллоны, широко применяемые в различных отраслях промышлен-
Рис. XVI.2
ности. В качестве вакуумных емкостей используются специально изготовляемые стальные сварные шары с диаметром до 20 м. Отношение диаметра шара к толщине стальной стенки шара сохраняется равным около 670.
Ударные трубы. Для изучения движения при больших числах М в последние годы широко применяются ударные трубы различных конструкций. Они использовались для изучения процессов возникновения ударных волн, отражения и преломления их, процессов детонации в горючих газах, явлений конденсации и поведения газов при высокой температуре. Ударные трубы могут также применяться для исследования нестационарных явлений в машинах, изучения гашения возмущений при электрических разрядах, распространения взрывных волн в горных разработках, действия взрывных волн на элементы конструкций машин и сооружений.
Устройство ударной трубы очень несложно. Обычно она представляет собой трубу (рис. XVI.3, а) прямоугольного сечения, разделенную перегородкой (диафрагмой) на две неравные части: меньшую — камеру высокого давления и большую — камеру низкого давления.
Площадь поперечного сечения современных труб меняется в широком диапазоне — от нескольких квадратных сантиметров 30*
•bi
i
468
Аэродинамический эксперимент
Рис. XVI.3
1
роль и служит
звука, возни-при разрыве
до квадратного метра и больше. Длина труб достигает десяти и .а более метров. Из расчета на работу при высоких давлениях для 1 изготовления корпуса трубы используются достаточно прочные 3 материалы, чаще всего сталь. Разделяющая трубу диафрагма л изготовляется обычно из фольги, тонких металлических пластин -1 и т. п. В некоторых случаях (при получении ударных волн малой ] интенсивности) в каче- 5 стве диафрагмы можно j применять фотопленку и даже кальку.
Присоединяемый к камере низкого давления бак играет вспомогательную главным образом для гашения кающего диафрагмы.
Для запуска трубы ; в камеру высокого дав- ’ ления подают сжатый  (часто до нескольких десятков атмосфер) газ 1 либо создают в ней рез- j кое повышение давления 1 за счет взрыва какой- „ либо горючей смеси или i мощного электрического ,1 разряда. При этом в ка- ; мере низкого давления j оставляют нормальное -давление или даже соз- <; дают некоторое разре- } жение.	i
Действием созданно- '4 го высокого давления J или каким-либо другим способом диафрагма разрывается, и по J трубе низкого давления распространяется волна сжатия, которая, быстро увеличивая свою крутизну, превращается в ударную волну. Ударная волна, бегущая по частицам невозмущенного .< газа в камере низкого давления, создает за собой спутный поток газа, имеющий вполне определенную (но меньшую, чем у волны) • скорость.	j
Вслед за частицами газа, находившегося до разрыва диаф- 1 рагмы в камере низкого давления, в спутном потоке движутся « частицы газа из камеры высокого давления. Перемещающаяся *
Экспериментальные установки
469
поверхность, разделяющая в процессе движения частиц эти две области, называется контактной поверхностью. Передвижение частиц газа из камеры высокого давления приводит к возникновению непрерывной системы волн разрежения, в которой происходит плавное изменение от давления в спутном потоке до давления в газе, не возмущенном движением, в камере. высокого давления.
Таким образом, всю длину трубы в некоторый произвольный момент времени t можно разделить на пять участков (рис. XVI.3, б). Первый — камера низкого давления до распространяющейся в ней ударной волны; в этой области все параметры газа остались такими же, как и до разрыва диафрагмы. Второй участок занимает область от ударной волны до контактной поверхности; в этой области скорость движения частиц, давление и температура, возросшие в ударной волне, а также и число М остаются постоянными.
Третий участок расположен между контактной поверхностью и началом области разрежения. Сравнивая этот участок со вторым, можно установить, что давление и скорость здесь имеют такие же величины, температура резко падает, а число М возрастает.
Четвертый участок — это область, в которой происходит расширение газа. Здесь давление, плотность и температура падают (от их значений в камере высокого давления), а скорость и числом растут от нуля до соответствующих величин в третьем участке. Наконец, в камере высокого давления будет еще область невозмущенного газа — пятый участок, в котором все параметры газа останутся такими же, какими они быри до разрыва диафрагмы. Характер изменения параметров газа по всем участкам трубы в момент времени t показан на рис. XVI.3, в.
Весь процесс, происходящий в трубе, удобно представить в координатной системе х—t. На рис. XVI.3, г приведен процесс перемещения границ’ всех пяти участков от момента разрыва диафрагмы (/ = 0) до времени t. Такие диаграммы широко "используются для изучения одномерных движений газа. Для каждого момента времени t = пользуясь этой диаграммой, можно найти ширину каждого участка трубы, а для каждой точки трубы х — Xi за диафрагмой вправо — момент времени прохождения ударной волны контактной поверхности t2 и начала четвертого участка t3. Очевидно,, что разность — t2 = Д/2 определяет время, в течение которого второй участок проходит точку трубы с координатой х = xit а разность t2 — /3 = Д<3 — время прохождения третьего участка.
Установки для исследования решеток профилей. Все экспериментальные исследования работы элементов турбомашин могут быть разделены на две группы: первая — статические испытания,
470
Аэродинамический эксперимент
производимые над отдельными элементами на неподвижных уста- ’ новках, вторая — испытания на вращающихся моделях экспери- : ментальных турбин или даже на натурных турбинах.	Ч
Окончательные количественные заключения о работе того или ; иного элемента с учетом его взаимодействия с другими частями  машины дает только вторая группа исследований.	i
Однако наличие экспериментальных машин не исключает необ- 3 ходимость применения статических испытаний. Постановка слож- я ных, трудоемких и дорогостоящих опытов на вращающихся j установках предполагает проведение многочисленных предвари- 1 тельных испытаний на неподвижных моделях.	1
Преимущество статических испытаний не столько в относи- / тельной дешевизне опытов, сколько в том, что они позволяют ' более глубоко вскрывать сущность главных явлений, происходя- j щих в любом элементе машины. Тем самым можно получить более : глубокий анализ причин, вызвавших изменения суммарных харак-теристик работы того или иного элемента.	j
Объектом изучения на статических установках может быть- ! любой элемент проточной части турбины. Возможность полного j или частичного переноса на натурную турбину результатов, полу- : ченных на статической установке, будет зависеть от особенностей j данного элемента и от условий постановки опытов. Сейчас уже ; широко и достаточно успешно применяется изучение на непод-  вижных установках работы выхлопных патрубков, диффузоров, j рабочих и направляющих лопаток, клапанов и других элементов. J
Наиболее важный элемент турбомашины, требующий весьма ; тщательного изучения, — рабочее колесо. Работа колеса и на- < правляющего аппарата, как было указано ранее, имитируется < на статических установках с помощью решеток профилей. Основ-ные требования, определяющие конструкцию установок для , статического испытания плоских решеток профилей, следующие: j 1) поле скоростей и давлений в непосредственной близости перед 1 решеткой должно быть полностью однородным или иметь перио- i дичность с периодом, равным шагу; 2) установка должна позволять j легко менять параметры решетки: шаг, угол установки профиля ’1 в решетке и угол установки решетки, т. е. угол атаки; 3) измери- « тельная аппаратура должна обеспечить измерение величины и я направления скорости в каждой точке перед и за решеткой; 4j 4) поток за решетками должен быть ограничен стенками сравни-тельно небольшой длины и не иметь препятствий, расположенных Л в непосредственной близости по направлению движения.	1
Выполнение указанных требований представляет значитель- £ ные трудности. На рис. XVI.4 показаны схемы четырех типов установок для исследования плоских решеток. На рис. XVI.4, a g приведена схема установки с жесткими фиксированными боко- ] выми стенками. Между этими стенками устанавливается решетка,
Экспериментальные установки
471
состоящая из 4—8 лопаток. На такой установке при небольшом количестве лопаток невозможно получить в непосредственной близости перед решеткой периодический по шагу поток.
Опыт показал, что при внесении в поток под некоторым углом к нему небольшого числа лопаток сам поток перед решеткой деформируется и направление скорости на входе сильно меняется вдоль оси решетки. Выполнение первого требования наиболее удобно осуществить в аэродинамической трубе. Такая схема установки, созданной ЛПИ в 1948 г., показана на рис. XVI.4, б.
Рис. XVI.4
Существенная особенность установки — подвижность направляющих боковых стенок. Их перемещением создается перед решеткой поток, периодический по шагу. Как видно из рисунка, к конфузору аэродинамической трубы с открытой рабочей частью примыкает переход от круглого сечения (диаметром 1400 мм) на квадратное со стороной 900 мм. Для устранения влияния замкнутости потока за решеткой диффузор трубы был снят. Труба была фактически разомкнута и работала как вентилятор иа выхлоп.
Решетка монтировалась на двух металлических балках, опирающихся на опоры, расположенные по концам так, что ось решетки располагалась горизонтально. Решетка состояла из десяти лопаток с внешней хордой профиля, равной 200 мм, и высотой 900 мм. Лопатки изготовлены из дерева или металла. На середине одной из лопаток имелись дренажные отверстия, при помощи которых производилось измерение распределения давлений. Количество лопаток в решетке определялось величиной относитель
472
Аэродинамический эксперимент
ного шага t и углом установки Поля скоростей и давлений перед и за решеткой измерялись насадками, которые перемеща
лись вдоль оси решетки с помощью каретки, скользящей по верхней балке установки.
На рис XVI.4, в показана схема установки ЦКТИ, в которой формирование потока на входе производится с помощью продольно перемещающихся стенок (/, Г, 2 и 2'), а организация по
тока на выходе — стенкой 3. Поток, набегающий на решетку, формируется камерой, образованной стенками 2—2', 4—4' и5—5'.
Во всех рассмотренных схемах установок обычно можно легко изменять угол установки, шаг и высоту лопатки. Организацию по тока на входе в решетку можно производить также отсосом пограничного слоя и поворотом крайних лопаток в решетке.
Схема установки для исследо-вания решеток в сверхзвуковом потоке на входе показана на рис. XVI.4, г. Как обычно, решетка 1 смонтирована между двумя поворотными дисками 2. Несимметричное сопло Лаваля, состоящее из двух вставок 3 и 4, обеспечивает подвод потока со сверхзвуковой скоростью. Вставка 3 профилиро
вана и закреплена неподвижно, вставка 4 может перемещаться
и, оставляя неизменными размеры выходного и критического сечений сопла, изменять угол входа потока на решетку. Вели-, чину скорости меняют, изменяя сечение сопла с помощью j вставок 5. Для организации потока за решеткой служат под-.-; вижные стенки 6.
Плазмотроны. Для исследования обтекания моделей при очень, высоких температурах используются электродуговые установки;' и плазмотроны. Схема одного из плазмотронов, в котором полу*) чали струи плазмы с температурой до 12 000 К, показана над рис. XVI.5. Между цилиндрическим анодом / и катодом 4 обра-| зуется электрическая дуга, в область которой через тангенцн-; ально расположенные сопла 2 подается вода под давлением. 1 Вода, охлаждая внешнюю поверхность столбика плазмы, за-] ставляет уменьшать его поперечное сечение и тем самым увели,41 чивать плотность тока. Магнитное поле тока, текущего по струе| плазмы, еще больше сужает ее сечение и еще более увеличивает!
Методы аналогий
473
плотность тока. Таким образом, модель 3 обтекается струей, имеющей высокую температуру и большие числа М (до 25). Остаток пара выбрасывается через трубку 5. Иногда вместо воды применяют азот и другие газы.
§ 2. Методы аналогий
Если два или несколько явлений, различных по сйЪей физической природе, могут быть выражены одним и тем же дифференциальным уравнением с сохранением граничных условий, то эти явления называют аналогичными. Метод аналогий, расширяя возможности изучения явлений, уже давно получил широкое распространение в механике.
Н. Е. Жуковский еще в 1900 г. в своей речи на заседании Московского математического общества говорил, что «установление математической аналогии между двумя явлениями приносит нашему знакомству с ними пользу с двух сторон. Мы можем на основании найденной аналогии все разрешенные задачи в одной области физических явлений преобразовать в соответственные задачи в другой и получить таким образом решение последних. С другой стороны, если одно из двух математически аналогичных явлений сложно и трудно наблюдаемо, а другое может быть осуществлено на простом приборе, позволяющем измерить параметры, характеризующие явления, то опытное изучение второго явления может расширить наше знакомство с первым, несмотря на то, что явления могут представлять неразрешимую математическую задачу».
Сейчас во многих частях технической механики вообще и в механике жидкостей и газов, в частности, успешно используются электрические, газогидравлические, акустические, магнитные, тепловые и другие аналогии. В механике аналогиям посвящена обширная литература.
В технической гидродинамике используются следующие аналогии: электрогидродинамическая (ЭГДА); газогидравлическ^я (ГАГА); гидромагнитная (МАГА); мембранная; ламинарная; тепловая и диффузионная. Существуют и другие аналогии. Рассмотрим сущность указанных аналогий и область их применения. Вначале напишем уравнения для аналогов и затем произведем сравнение с уравнениями гидродинамики.
Первые пять аналогий относятся к аналогиям безвихревого движения идеальной несжимаемой жидкости, потенциал скорости и функция тока которого удовлетворяют уравнению Лапласа:
+ о- +	(xvi.i)
дх2 ду2 ~и’ дх2 ду2	v ’
Граничные условия для тела, обтекаемого потенциальным потоком идеальной жидкости, будут:
474
Аэродинамический эксперимент
1) на поверхности тела вследствие непроницаемости твердой стенки нормальная составляющая скорости равна нулю, т. е.
V _	_ дф __ п.
v,l~ дп ~ ds
2) на бесконечности при плоскопараллельном потоке, направленном вдоль оси х,
Vx==j3L=W=v и х дх ду 1	« ду	дх
Электрогидродинамическая аналогия (ЭГДА). Она основывается на том, что электрический потенциал <рэ и функция тока фэ удовлетворяют уравнению Лапласа (XVI. 1).
Граничные условия в электрическом поле зависят от того, является ли тело проводником или диэлектриком. Если тело, находящееся в электрическом поле, диэлектрик, то граничные условия будут:
на поверхности тела
дфэ _ дфэ _____
ds дп ’
на бесконечности
д<рэ _ дфэ  	дфэ   дфэ  ~
дх ду	ду ' дх ’
где qY — напряженность электрического поля на бескнечности.
Если модель изготовлена из электропроводящего материала, то граничные условия будут:
на поверхности
д<р3 _ дфэ _ _
дп ds ’
на бесконечности
д<рэ _ дфэ _ _	дфэ _ дфэ _
дх ' ду	ду	дх
Сравнивая приведенные граничные условия, можно легко видеть, что для осуществления аналогии должны соблюдаться следующие соответствия.
1. Если в электрическом поле поместить тело из непроводящего материала, то гидродинамическим величинам — потенциалу скорости, функции тока и скорости на бесконечности — соответствуют электрический потенциал, функция тока и напряженность электрического поля на бесконечности.
Будем называть эту аналогию аналогией А. Очевидно, что при аналогии А линии тока электрического и гидродинамического полей совпадают, а векторы электрического тока имеют то же направление, что и векторы скорости.
Методы аналогий
475
2. Если тело проводник, то потенциалу скоростей в гидродинамическом поле будет соответствовать функция тока в электрическом поле, а функция тока соответствует электрическому потенциалу. Соответствие скорости и напряженности электрического поля на бесконечности остается прежним.
Будем называть эту аналогию аналогией Б. При соблюдении ее векторы электрического тока и скорости во всем поле-ортогональны.
Однородное электрическое поле, в котором изучается обтекание профиля, может быть создано в жидком электролите, налитом
в ванну с помощью электропроводной бумаги, фольги, тонкого слоя электропроводящей краски, желеобразного электропроводящего материала и пр. В практике машиностроительных заводов чаще всего используются ванны, заполненные обычной чистой водопроводной водой, растворами медного купороса, серной или соляной кислоты,- Концентрация растворов должна быть очень малой (0,002—0,005%), так как в противном случае происходят электрохимические процессы и состав электролита меняется.
На рис. XVI .6 приведены схемы электролитических ванн для моделей, изготовленных из проводящих и непроводящих материалов.
При изучении потоков в патрубках, коленах и других элементах машин форма ванны определяется формой исследуемого элемента.
На рис. XVI.7 показаны схемы ванн для исследования потока в колене (а), диффузоре или конфузоре (б) и для изучения поля скоростей, вызываемых радиальными вихрями в области между двумя цилиндрами (в). Последнее имеет значение при изучении пространственных потоков в турбомашинах. Для этого, как видно из рисунка, достаточно ванну сделать в форме секторального выреза из цилиндров и один электрод поместить иа плоскость А, а другой — иа плоскость В. Аналогичные ванны можно построить и для изучения потоков в вентиляторах и насосах.
476
Аэродинамический эксперимент
ЭГДА для сжимаемого газа. Когда плотность является переменной величиной, уравнение для потенциала скоростей принимает вид
д2ф "дх2
д2ф __________1	/ дф	др	.	дф	др \
дг/2	р	\ дх	дх	'	ду	ду )'
(XVI.2)
Уравнение (XVI .2) можно решать приближенным методом. Правая часть уравнения будет тем ближе к нулю, чем меньше число М. За нулевое приближение берут решение уравнения, когда правая часть его равна нулю. Затем по найденному таким
Рис. XVI.7
образом значению ф (х, у) можно определить скорость в каждой точке"й плотность р (х, у). Найденные ф (х, у) и р (х, у) можно подставить в правую часть уравнения (XVI.2) и затем найти новое приближение для ф (х, у), а следовательно, р (х, у) и т. д. Решение уравнения таким методом представляет большие трудности.
Используя метод последовательного приближения, можно решать поставленную задачу с помощью ЭГДА. Тогда, очевидно, нулевым приближением будет потенциал скоростей, определенйый без учета влияния сжимаемости, т. е. в обычной электролитической ванне.	''
При получении первого и последующих приближений заметим, ' что проекции скоростей в сжимаемой жидкости можно определить ’ по формулам:
У __ дф ____ 1 дф у _______ дф _	1	дф
х	дх	р ду	’ ‘J	ду	р	дх
Для электрического поля электрический потенциал и тока связаны с составляющими напряженности поля q мулами:
с__ 1	дфэ	_ 1	дфэ _______ 1	дфэ	__ 1	дфэ
а	ду 6	ду	’ У а	ду 6	дх
где о — удельное сопротивление электролита; б — толщина слоя электролита.	и
(XVI.3)
функция ’! и f фор-
, (XVI.4) 'j
Методы аналогий
477
Если между потенциалом и функциями тока электрического и гидродинамического полей существует соответствие, то из выражений (XVI.3) и (XVI.4) следует,’ что
Vx = fo=-^-f', Vy = qa = -^-q, отсюда б = ро.
Таким образом, при постоянной величине о толщина слоя электролита в ванне_ пропорциональна плотности. Очевидно, в этом случае модель не будет являться проводником, и граничные условия будут:
на поверхности модели дфэ _ д^э  п. дп дг	’
на значительном расстоянии от модели
д<Рэ __ <Ж _ 6 с. дд>э   дф  q дх ду р ' ’ ду	дх
Для того чтобы гидродинамический потенциал соответствовал функции тока электрического поля, модель должна быть изготовлена из проводника, а измерения нужно производить по схеме для несжимаемой жидкости (рис. XVI.6). Теоретически преимущества этого способа те же, что и для несжимаемой жидкости: можно производить измерения скоростей и потенциалов не только при бесциркуляционном обтекании модели, но и при наличии любой конечной величины циркуляции.
Для измерения поля скоростей вокруг профиля, обтекаемого сжимаемым газом как при первом, так и при втором методе может быть полностью использована установка ЭГДА для несжимаемой жидкости.
Изменения, которые должны быть внесены в обычную установку, заключаются в том, что при использовании первого метода дно ванны должно быть изготовлено из легко деформируемого материала (парафина, парафина с воском и др.). Электрическая схема и остальные детали установки остаются без изменений.
Гидромагнитная аналогия (МАГА). Она основана на том, что скалярный потенциал магнитного поля <рт удовлетворяет при постоянном значении магнитной проницаемости уравнению Лапласа
д2<?т । д2<рот _а
дх* ' ду*
Так как компоненты напряженности магнитного поля равны гг   дгрт . J,   д<Рт Пх~ ~ дх ’ У ~ ду ’
478
Аэродинамический эксперимент
то, следовательно, при выполнении одинаковых граничных уело- < вий магнитному потенциалу будет соответствовать гидродинами- -ческий потенциал, а проекциям скорости в потоке жидкости будут | соответствовать проекции вектора напряженности магнитного поля.
Эта аналогия была разработана проф. А. Н. Патрашевым, но из-за сложности измерений параметров магнитного поля пока не получила широкого распространения.
Мембранная аналогия. Эта аналогия основана на том, что прогиб ненагруженной мембраны z удовлетворяет уравнению Лапласа
<Э2г . d2z __„
дх2 "г ду2 ~и’
т. е. прогиб соответствует гидродинамической функции ф. Тогда скорость плоского потока несжимаемой жидкости можно определить через прогиб в виде
Уравнение нагруженной мембраны является уравнением Пуассона и имеет вид d2z д2г _ _р_ дх2 ' ' ду2 т ’
где р — избыточное давление на мембрану; т — натяжение мембраны.
Последнее уравнение имеет в гидродинамике своим аналогом уравнение для функции тока плоского вихревого движения идеальной несжимаемой жидкости во вращающейся системе координат
дх2 1 ду2
где со — угловая скорость вращения системы координат.
При использовании мембранной аналогии чаще всего применяют мыльные, белковые и резиновые пленки. Аппаратура и методика мембранной аналогии хорошо разработаны.
Ламинарная аналогия. Эта аналогия основана на том, что, как показано в гл. X, для ламинарного движения вязкой жидкости между двумя близко расположенными пластинками существует потенциал средних скоростей. Следовательно, если.’ между пластинками поместить какое-либо тело (цилиндр), то , спектр обтекания его будет соответствовать обтеканию этого тела идеальной жидкостью.
Методы аналогий
479
Ламинарная аналогия по сравнению с ранее перечисленными имеет то преимущество, что она дает визуализацию линий тока, в том числе и для неустановившихся процессов. Ее недостаток — меньшая точность измерений и некоторое отклонение за счет прилипания жидкости к обтекаемым телам.
Газогидравлическая аналогия (ГАГА). Аналогия между движением газа при больших скоростях потока и движение жидкости на мелководье разработана для двух случаев: аналогия между одномерным движением газа и потоком жидкости по руслу, имеющему заданную форму поперечного сечения; аналогия между двухмерным движением газа и движением жидкости в канале прямоугольного сечения. Для пространственного потока газа такой аналогии пока нет. Не останавливаясь на первом, рассмотрим второй случай.
Выпишем систему уравнений двухмерного движения идеального газа и соответствующую систему уравнений движения идеальной жидкости в прямоугольном канале малой глубины. Рассматривая эти две системы, можно найти условия, при соблюдении которых будет существовать аналогия между указанными движениями.
Уравнение неразрывности стационарного движения плоского потока, газа имеет вид
а соответствующее уравнение движения воды в широком лотке глубиной h при наличии свободной поверхности будет
Т W+-^(to) = 0,
где и и V — составляющие средней по высоте скорости.
Из сравнения приведенных уравнений следует, что указанная аналогия будет иметь место, если плотности в потоке газа соответствует глубина воды в лотке, т. е. р ~ h.
Для изэнтропического течения газа имеем
Р __!.
Ро	— ’
для воды
— — 1 _ V2 = 1
2<?/i0	1__рг?
480
Аэродинамический эксперимент
Уравнения будут одинаковыми, если числу М в газе будет соответствовать число Fr в потоке воды, т. е.
M-~Fr, т. е. — ~	,
а Ygh
и показатель изэнтропы будет k — 2.
Граничные условия одинаковы для обеих систем, так как стенки геометрически подобных тел, обтекаемых жидкостью н газом, непроницаемы, т. е. нормальные составляющие скоростей на поверхности обтекаемых тел равны нулю.
Если воспользоваться известными зависимостями между плотностью, температурой и давлением при адиабатическом процессе в газах, то условия наличия аналогии между двухмерным движением газа и движением жидкости в прямоугольном канале могут быть представлены величинами, которые приводятся ниже:
Газ
Р
Pi
м = -Г а
Р Pi
Т
У\акР
Гкр Го
MZ	h г- г / h V h ,r-r 2
Жидкость . . . -г— Fr = —( — ) -т— V gh hr	уgh	\ hi ) ь 3
Несуществующий газ с показателем изэнтропы k = 2 называют гипотетическим, а иногда гидравлическим газом.
Эта аналогия может применяться как при дозвуковом, так и сверхзвуковом обтекании тел. Наибольший интерес. представляет аналогия при сверхзвуковом обтекании.
Однако рассмотренная аналогия не позволяет получить достаточно достоверных количественных характеристик обтекания тел плоским потоком реального газа. Основные причины этого: различия величин показателя изэнтропы воздуха или газа и его--аналога; отсутствие учета влияния вязкости и теплопроводности; 1 несоответствие между гидравлическим прыжком и скачком уплотнения; пренебрежение вертикальными составляющими скоростей и ускорений; пренебрежение капиллярными волнами.	'<!
Принципиально возможны и практически осуществимы два,; типа конструкций установок ГАГА: 1) жидкость неподвижна, J а модели движутся; 2) жидкость движется, а модели неподвижны (рис. XVI.8).
Преимущество установок первого типа —отсутствие на по- ' верхности воды посторонних волн, а недостаток их —необходи- J мость наличия зазоров между движущейся моделью и дном,,.:| трудность измерений на подвижной модели. Этого недостатка м лишены установки второго типа, зато в них при движении воды"1 на поверхности образуется рябь, т. е. большое количество мелких' я возмущений, которые могут искажать результаты измерений.'а Создание гладкой поверхности движущейся жидкости весьма $
Измерение Скоростей. в потоках
481
затруднительно. Для решения задач, связанных с интерференцией между моделями, применяют установки, в которых движутся и вода, и одна из моделей. Так, при изучении взаимодействия направляющего аппарата и рабочего колеса решетка, имитирующая направляющий аппарат, располагается неподвижно в движущейся воде, а решетка рабочего колеса перемещается парал-
лельно оси направляющего аппарата.
Все перечисленные аналогии относятся к изучению потоков идеальной жидкости. Для изучения сил трения при движении вязкой жидкости вдоль стенки применяют тепловую и диффузионную аналогии. Основанием для применения их служит общность уравнений переноса количества движения, тепла и вещества.
Эта общность позволяет находить напряжение трения на стенке- через величины, характеризующие перенос
тепла и вещества в данной
точке. Не приводя всего вывода, укажем, что напряжение трения на стенке т может быть определено через тепловые и диффузионные числа Нуссельта по формулам:
т — qa ( Nu \з_. N -
I2 \ 0,807 ) ~ 1	’
т —Л£ f Nua y_/,Nu3 I2 \ 0,807 ) —
(XVI.5)
где а и D — коэффициенты температуропроводности и диффузии. Коэффициенты kv и обычно определяются экспериментально. Таким образом, по числам Nu и NuA можно найти напряжение трения.
§ 3.	Измерение скоростей в потоках
Измерения скоростей и давлений являются наиболее важными и широко применяемыми в экспериментальной механике жидкостей и газов. Разработано много методов определения скоростей и давлений, создано для этого огромное количество.приборов различных конструкций. Из всех методов, применяемых для измерения скоростей, отметим следующие.
1.	Механический метод, при котором используются приборы типа вертушек, анемометров, доски Вильда и пр. В основе этого метода лежит непосредственное механическое воздействие потока на приемный элемент прибора.
31 И. Л. Повх
482
Аэродинамический эксперимент.
2.	Пневматический способ, при котором применяется большое число различных насадков (трубки, цилиндрические и шаровые зонды и др.). В этих приборах принимающим и передающим элементом является некоторый объем жидкости или газа, а значение скорости вычисляется по величине измеренного давления.
3.	Метод измерения, основанный на определении скорости движения частиц среды или субстанции, так называемый кинематический метод. Сюда надо отнести приборы, позволяющие определять скорость переноса ионизированных или нагретых объемов среды, освещенных или светящихся частиц и др.
4.	Способ измерения скоростей по количеству тепла, снятого с приемника. К приборам, основанным на этом методе, относятся прежде всего различного вида термоанемометры.
5.	Определение скоростей измерением давлений электриче- । скими датчиками. Здесь используются пьезоэлектрические, индуктивные, емкостные, магнитострикционные и другие датчики.
6.	Акустические методы, позволяющие измерять скорость потока по распространению звука в потоке.
7.	Оптические методы измерения.
Каждый из этих способов имеет свои преимущества и недостатки. Выбор метода измерения зависит от особенностей поставленной задачи. Так, для измерения местных скоростей, быстро изменяющихся во времени, нельзя использовать приборы, работающие по первым трем способам. Акустический и оптический методы наиболее эффективны при изучении потоков со сверхзвуковыми скоростями. Кинематический метод может с успехом применяться как абсолютный метод при тарировке приборов.
Среди применяющихся на практике различных методов опре^ деления скоростей и давлений наибольшее значение в экспериментальной аэродинамике имеет пневматический способ, основанный на измерении давления в определенных точках поверхности внесенных в поток измерительных приборов. Такие приборы называются насадками или зондами.
В этом параграфе рассмотрим методы измерения скорости трубками, цилиндрическими и шаровыми зондами.
Трубки для измерения скорости. Теория пневматических приборов для измерения скоростей основана на использовании уравнения Бернулли.
Если в некоторой точке потока необходимо знать значение скорости, то в эту точку потока устанавливают продольно обтекаемую трубку (рис. XVI.9). Поверхность такой трубки можно рассматривать как поверхность полутела (IX.20). Тогда нулевая линия в точке А образует так называемую критическую точку, в которой скорость потока обращается в нуль. В последующих точках по поверхности трубки скорость будет расти и затем вновь падать (как показано на рис. XVI.9), достигнув на некотором уда
Измерение скоростей в потоках
483
лении от носика скорости на бесконечности, т. е. скорости, которая была бы в этом месте при отсутствии трубки.
Уравнение Бернулли для двух сечений 1—1 и 0—0 нулевой линии тока будет иметь вид
PKL , п __РЦ , п 2 + Р1 2	' Ро'
Так как Vo = 0, то скорость равна
= у 2(Ро~Р1) .
(XVI.6)
Полное давление р0 может быть определено, если в критической точке сделать отверстие и тонкой трубочкой соединить его
с микроманометром. Давление рх определяют с помощью щели или нескольких отверстий, размещенных в сечении 2—2, в котором величина скорости из-за подтормаживающего влияния Ножки трубки равна скорости Из уравнения Бернулли, написанного для сечений 1—1 и 2—2, очевидно, что рг = р2. Отверстия в сечении 2—2 часто называют статическими.
Обычно разность давлений р0—рх измеряют дифференциальным микроманометром в миллиметрах водяного столба.
Впервые трубки для измерения скорости потока воды в реке были применены в 1732 г. французским ученым Пито. Он показал, что обычная стеклянная трубка, опущенная в поток (рис. XVI. 10), позволяет определить полный напор и величину скорости. Поэтому часто трубки, имеющие лишь одно отверстие в критической точке, т. е. трубки для измерения полного напора, называют трубками Пито. Трубки, имеющие отверстия
31*
484 Аэродинамический эксперимент
в критической точке и статическое отверстие, иногда называют трубками Пито—Прандтля.
При измерениях в потоках газа с большими скоростями плотность его будет переменной, и для расчета скорости надо пользоваться формулой Сен-Венана (VI.2б)
2k k—l
k-i -
Pt \ k
Po /
(XVI.7)
Формула (XVI.7) пригодна лишь для дозвуковых скоростей. При скоростях потока порядка скорости звука и при сверхзву-
Рис. XVI. 10
ковых скоростях надо учитывать появление скачка уплотнения, и поэтому приведенной формулой пользоваться нельзя.
Ограничение верхнего предела скорости, которую допустимо считать поформуле (XVI.6), можно определить, если представить ее в виде
Ро —Рх = -£г-(1+8)>
где е — поправка на сжимаемость. ' Значения поправки для обычных температур приведены ниже:
V, м/с...................... 34	68	102	136	170	204
е, %	.................... 0,25	1,0	2,25	4,0	6,2	9,0
Видно, что при допустимой погрешности в 1 % формулу можно применять до 68 м/с, а при 2,25% —до 100 м/с.
Нижний предел скорости, определяемой скоростными трубками, зависит от точности измерения разности давлений. Обычно он равен 6—8 м/с.
Цилиндрические зонды. Для измерения вектора скорости в плоском потоке применяются различные насадки. Их широкое распространение объясняется не столько достаточно высокой точностью измерения направления скорости (0,06—0,1°), сколько возможностью одновременно измерять давление, скорость и полный напор. Наиболее часто применяются цилиндрические (рис. XVI.11, а), рожковые (рис. XVI. 11, б) и хоботковые (рис. XVI.11, в) зонды.
Первый из них представляет собой цилиндрическую трубку с тремя отверстиями, расположенными на некотором расстоянии от ее конца в плоскости, перпендикулярной к образующей цилиндра. Два боковых отверстия расположены симметрично отно-сительно^центрального.
Измерение скоростей в потоках
485
У рожковых и хоботковых зондов отверстия расположены на
концах трех тонких трубок. В хоботковом трубки расположены так, что^их приемные близко друг от друга.
Существенный недостаток рожковых и хоботковых насадков —значительное перемещение их приемных отверстий при повороте насадка вокруг оси державки. Для устранения этого недостатка державку насадка изгибают так, чтобы при вращении приемные отверстияJ находились на оси вращения.
Преимущество цилиндрических зондов по сравнению с другими насадками в том, что у них взаимное расположение отверстий строго фиксировано (следовательно, тарировка зонда обладает большим постоянством). Кроме того, благодаря большой разности давлений в центральном и боковом отверстиях повышается точность измерений.
насадке две или три отверстия находятся
Рис. XVI. 11
Все три типа насадков позволяют измерять направление и величину скорости, полный напор, давление. Для измерения
только направления потока можно пользоваться зондами с двумя боковыми отверстиями и различными флюгерками. Нд рис. XVI. 12 показаны некоторые типы насадков-угломеров.
Рис. XVI.12
При измерении давления и скорости зондами с трем?Г отверстиями один микроманометр с небольшим наклоном присоединяется к двум боковым отверстиям, а другой — к центральному и боковому отверстиям зонда. Если зонд вращением вокруг оси державки установить так, чтобы первый микроманометр давал первоначальное нулевое показание, то критическая точка совпадает с центральным отверстием. Следовательно, давление в центральном отверстии будет равно полному напору
Р. = Л + К,-ф-:.	(XVI.8)
где Кц — коэффициент, введенный для учета ошибки при измерении полного напора за счет неточности изготовления централь
486
Аэродинамический эксперимент
ного отверстия. Обычно Кц =1. В боковом отверстии давление (Рб) будет меньше, чем в центральном отверстии, и его можно формально представить в виде суммы, состоящей из давления набегающего потока и некоторой части скоростного напора,
Рб = Р1-|-Кб-ф-	(XVI.9)
Так как показания (Л—а) второго микроманометра, присоединенного к центральному и боковому отверстиям, пропорциональны разности р0— рб, то из формул (XVI.8) и (XVI.9) следует, что
(Р1 + Кц-ф-) - (pi + Кб-ф) = (А—а)ту,
где т — масштаб микроманометра; у — плотность спирта, налитого в микроманометр.
Отсюда можно получить следующую формулу для определения скорости:	___________
<XVL10>
Давление можно определить, включив в схему третий микроманометр, один из штуцеров которого присоединен к центральному отверстию зонда. Тогда показания (Л-[— at) этого микроманометра дадут разность между полным напором (XVI.8) и атмосферным давлением, т. е.
Pi + Лц ф - ра = (Л1 — flj) т.у,
откуда
Рх-ра = ^-а^туу-К^. (XVI.11)
Подставив в формулу (XVI. 11) значение скорости Vx, измеренное вторым микроманометром,' получим окончательную формулу для определения давления
Pi — Ра — (/11— fli) туу —	ц^- (Л — а) ту. (XVI. 12)
Коэффициенты Кц и Кц — Кб, необходимые для вычисления скорости и давления, определяются в результате тарировки.
Этим способом можно определить направление, величину скорости и давление в потоке любым из трех указанных насадков.
Шаровой зонд. Шаровой зонд представляет собой шарик с пятью отверстиями, просверленными в двух перпендикулярных друг к другу диаметральных плоскостях. Шарик помещен на цилиндрической державке (рис. XVI. 13). Угол между осями центрального и каждого из боковых отверстий шарика составляет
Измерение скоростей в потоках
487
40°. Каждое отверстие соединяется тонкими трубками, проходящими внутри державки, со штуцерами, имеющимися на противоположном конце зонда. Обычно применяемые зонды имеют шарик диаметром 5—10 мм.
Наиболее удобный и широко распространенный способ измерения углов — смешанный, при котором один из углов ср определяется вращением, а второй угол б — по показаниям манометров.
Вращая шарик вокруг оси державки, при любом направлении потока в пространстве можно получить такое положение шарика, при котором давления в точках 4 и 5 одинаковы. Очевидно, что при этом вектор скорости потока будет лежать в плоскости, про-
ходящей через отверстия 1, 2 и 3, и задача сведется к определению его величины и направления в этой плоскости, положение которой определяется по лимбу.
В зависимости от угла б, образованного вектором скорости с осью отверстия 2 в плоскости /, 2, 3, в каждом из указанных отверстий возникает давление, которое может быть формально представлено в виде суммы, составленной из давления в потоке и части скоростного напора,
Рп = Р1 + Кп£^->
где Кп—безразмерный коэффициент давления п-го отверстия, зависящий от угла б.
Если присоединить n-е отверстие к баку микроманометра, трубка которого соединена с атмосферой, то получим
' — Ра 4-Р1Н- Kn^- = yhn,	(XVI.13)
где hn — высота вертикального столба жидкости в трубке микроманометра.
Для любого i-ro отверстия имеем
Л-Л+К,-Ф- = Л-	(XVI.14)
488
Аэродинамический эксперимент
Из этих двух уравнений можно определить скорость и давление. Вычитая уравнение (XVI. 14) из (XVI. 13), получим
(Кп~К^ = v(hn~ U	(XVI.15}
откуда

2т(^п—/г.)
V f>(Kn-Kt)
И
Pl Pa — v(hn Кп —
Коэффициенты Kt и Кп в этих формулах являются неизвестными функциями от не определенного еще угла 6.
Для определения угла б нужно найти связь между показаниями манометров и этим углом. Функция, выражающая эту связь, должна быть ограниченной, однозначной и независимой от скорости и давления. Этим условиям удовлетворяет функция
=	(xvi.16)
Второе равенство в формуле (XVI. 16) следует из формулы (XVI. 15).
Таким образом, если тарировкой заранее установить зависимость /(в от угла б, то при эксперименте, получив по показаниям манометра, можно легко найти угол б.
В формуле для определения скорости должны быть выбраны такие п и i, чтобы разность hn — h; имела бы значение, не равное нулю. Такому условию удовлетворяет разность h2—h.^
Тогда
V, = 1/	(XVI.17)
г Р (Дг—Д«)
И
p1-Pa = y{h2-K2^^')-	(XVI.18)
При больших б для определения скорости можно пользоваться также формулой
v _ 1/ 2Т — hj) V1~ V рСКз-Кх)’
Тогда при отсутствии ошибок измерения hj — hj __________________ hs — hj
Ks-Ki-
'-.Измерение скоростей в РотбкМ
489
При наличии расхождении, не превышающих 2—3%, скорость может быть вычислена по средней величине	+
*	\^2—А4
Х8-Х1/
При расхождениях более 3% следует произвести повторные измерения и расчет. Эти же результаты контроля могут быть использованы и при определении давления.
Если начало координат расположить так, чтобы ось у была
направлена по оси державки, ось z — перпендикулярно плоскости исследуемого сечения, ах — перпендикулярно плоскости yz, то для определения проекций вектора скорости на эти оси получим формулы:
Vw= Vicos в sin ср; Vly=ViSin6;
Vlz == Vj cos 6 cos ср.	Рис> XVI-14
Рис. XVI. 15
Тарировочные кривые для зонда показаны на рис. XVI. 14, а установка для тарирования зондов и схема подключения отверстий зонда к микроманометрам—на рис. XVI. 15. Тариро-
4дб
Аэродинамический эксперимент
вочная установка должна обеспечить поворот шарика в заданном потоке вокруг двух осей у и z с фиксацией углов.
ii Тарировка зонда производится в однородном потоке с известным и постоянным по всему сечению направлением скорости. В такой поток с известной величиной скорости и давления (обычно это поток аэродинамической трубы) помещается зонд с помощью специального . координатаика. Он позволяет установить зонд под любым углом к потоку. Пользуясь схемой присоединения- " микроманометров и вычислив соответствующие коэффициенты для каждого значения угла б, легко построить тарировочные. кривые, т. е. кривые изменения К6; К3 —К,2 — Ki и К2 в за- •’( висимости от б.	, •
Таким образом, для определения направления и величины скорости, а также давления в данной точке пространства достаточно измерить ha—hi, h2—и h2, затем рассчитать К6 по форт муле (XVI. 16) и по кривой (б) определить угол б. Далее по кривым К2— К^= f (б) и К2= f2 (б), полученным при тарировке зондов, найти К2—Kt и К2 и по формулам (XVI.17) и (XVI.18) определить Vr и. рг—ра.
§ 4. Микроманометры
Для определения давлений пользуются большим количеством различных приборов. Необходимость изучать нестационарные давления привела к широкому использованию различных физических и, в частности, электрических способов измерения.
Рассмотрим лишь наиболее простые, так называемые жидкостные микроманометры, которые работают на принципе сообщающихся сосудов. Конструктивно самым простым жидкостным микроманометром является U-образная трубка (рис. XVI. 16). ' t ) U-образная трубка. Она применяется для измерения стационарных или весьма мало меняющихся давлений. Разность давлений & мм вод. ст., что соответствует, как ранее указывалось, кгс/м2, или 9,8 Н/м2, выражается формулой
Др = рг—р2 = уН,
где Н — разность уровней в коленах трубки; у — плотность.
Если колена U-образной трубки наклонены, то измеряемая разность давлений определится формулой
Др = Лу sin а,
где А —отсчет по шкале трубки, мм; а —угол между горизонталью и осью трубки.
В зависимости от величины разности давлений U-образную трубку заполняют жидкостями с различными плотностями. Нан-
М икроманометры
491
более употребительные жидкости — ртуть, вода и спирт. При употреблении воды следует учесть, что она обладает значительным поверхностным натяжением. В трубке, диаметр которой равен d мм, вода вследствие капиллярности поднимается на дополнитель-ную высоту Дп = -^-мм. Величина эта меняется в зависимости от температуры жидкости и степени загрязнения стенок трубки-В этом отношении спирт лучше воды, так
Д ГП	11
как для него Д/i = -г- мм. а
Рис. XVI. 16
Для выяснения верхнего предела частот колебания давления, измеряемого U-образной трубкой, применим к жидкости, колеблющейся в изогнутой трубке (рис. XVI. 17), ранее полученное уравнение Бернулли для нестационарного движения (V. 10). Пусть в трубке постоянного сечения столб жидкости отклонится от положения равновесия на величину х. Величина ускорения, входящего в уравнение (V.10)
i
. у + §2 + ~ 4- J ds = const, (XVI. 19) о
будет равна
dV._,, dV . dV .
dt ds ' ' dt ’
так как по закону сохранения массы скорость во всех точках трубки одинакова, то.
Если отсчет длины столба жидкости I производить по оси. трубки от левого колена (рис. XVI. 17), то, имея в виду, что на поверхности трубки давление в обоих коленах будет одинаковым
492
Аэродинамический эксперимент
и интеграл в уравнении (XVI. 19) на конце левого колена равен нулю, получим уравнение Бернулли для обоих концов трубки •
, о ,	। d?x ,
— gx sin р = gx sin a 4-	1
или
1 + §x (sln a +sin ₽) — °-
Это уравнение хорошо известно из теории колёбаний. Его решение имеет вид
х — a cos (at + у), где со — круговая частота колебаний, a=j/ g(sin ю+ sin Р) .
для вертикальной U-образной трубки sin a = sin 0 = 1 и
»=/?•
Если принять во внимание при качании столба жидкости сопротивление трения по ламинарному закону (XI. 18), то круговая частота из-за влияния вязкости уменьшится и будет равна
'	1/ 2g	I6v2
I	г* •
Для трубки длиной I = 50 см и радиусом г- = 0,2 см для ,: спирта или воды круговая частота будет около 6 1/с.
Так как частота измеряемых процессов должна быть в 5—10 раз меньше собственной частоты прибора, то жидкостный манометр. .. может измерять давления с очень малыми частотами колебания.
Микроманометры с вертикальной шкалой. Чтобы избежать необходимости делать отсчет по двум менискам, одно из колен U-образной трубки делают значительно шире другого, так чтобы изменением уровня в широкой трубке можно было пренебречь (рис. XVI. 18).
Изменение уровня жидкости в широком колене при особо точных измерениях можно легко учесть. Обозначив площадь поперечного сечения широкого колена через Flt а площадь поперечного сечения узкого колена через F2, получим, что изменение уровня в широком колене ДЯ и перемещение мениска в узком колене Н связаны следующим соотношением:
F^H = F2H.
Измеряемая разность давлений будет
Р1_ра = (я + дя)у
Микроманометры
493
ИЛИ
Pl—Рг = Т#(1 +7J-) = Y# (1 +n2)>
где n —отношение диаметров узкого и широкого колен. Существуют микроманометры с оптическим приспособлением для точного отсчета положения мениска в узком колене. р
Такой прибор сострит из бачка и жестко связан- р ной с ним стеклянной трубки. Параллельно трубке укреплена стойка с миллиметровыми делениями и зуб- —► - — чатой рейкой. По рейке с помощью колеса перемещается каретка, несущая оптическое приспособление для на-	* —
блюдения мениска, зеркало, нониус и лупу (для от-	?
счета по нониусу). Последняя укреплена на двух шаровых шарнирах, что позволяет рассмотреть любое место нониуса. При помощи этой лупы отмечается положение н мениска с точностью до 0,05 мм.
При проведении измерений каретку ставят в такое положение, чтобы наблюдаемый через оптическое приспособление мениск соприкоснулся с его перевернутым отображением в зеркале. Наличие оптического приспособления позволяет измерять разности давлений" в пределах от 4 до 200 мм вод. ст. с погрешностью, не превышающей 1%.
Если приходится измерять осредненное значение пульсирующего давления, то можно при помощи особого крана включить демпфирующие приспособления, состоящие из системы капилляров.
Недостаток микроманометра — требуется сравнительно много времени для производства отсчета (что утомительно для глаза). Неудобства эти усугубляются, когда приходится одновременно снимать показания нескольких приборов.
У таких приборов величина п2 около 0,005—0,001; следовательно, поправка на изменение уровня очень мала.
Микроманометры с наклонными трубками. Большое распространение получили микроманометры, в которых увеличение точности при измерении давления достигается не с помощью оптического приспособления, а применением конструкции с наклонными трубками.
Принципиальная схема микроманометра с наклонной трубкой приведена на рис. XVI. 19.
Увеличение чувствительности и точности отсчета достигается тем, что вертикальный столб жидкости Н, соответствующий измеряемой разности давлений (рх—р2), заменяется наклонным стол
494
Аэродинамический эксперимент
бом А, причем Л = s?a . Обычно sin а называют масштабом микроманометра и обозначают буквой т.
Угол а должен быть тем меньше, чем меньше разность давлений, подлежащая определению. Зависимость между отсчетом на трубке микроманометра А и измеряемым-давлением выражается формулой
Р1—Р2 = Y И — а) т,
где а—начальный отсчет на трубке.
Диаметр трубки микроманометра должен быть порядка 3— 4 мм, так как применение более узких трубок приводит к сильному влиянию капиллярных сил; при использовании более широких трубок положение отсчета неопределенно вследствие большой протяженности мениска.
Практически микроманометры такого типа выполняются в виде приборов самых разнообразных конструкций. Опцшем только два из них: микроманометр аэродинамической лаборатории ЛПИ и микроманометр типа ЦАГИ.
Микроманометр ЛПИ (рис. XVI.20) состоит из бачка 1 и присоединенной к нему измерительной трубки 2. Трубка может вращаться вокруг поперечной оси и с помощью штифта и дуги 3 фиксироваться в определенных положениях, соответствующих масштабам микроманометра (т = 0,5; 0,2; 0,1; 0,04). Измерительная трубка снабжена демпфером 7, который позволяет производить измерения давлений при наличии пульсации. Весь прибор установлен на металлическом основании 4, горизонтальное положение которого обеспечивается установочными винтами 6 и уровнями 5. Микроманометр заливается спиртом-ректифика-том. Для облегчения отсчета спирт подкрашивается фуксином (бактериологическим) или каким-либо другим веществом, не дающим в течение продолжительного времени осадка.
По миллиметровой шкале можно делать отсчет с точностью до 0,5 мм, поэтому микроманометр ЛПИ позволяет измерять давления от 2 мм вод. ст. с точностью до 1%. В этом микроманометре п2 = -^2- = 0,0009, т. е. изменения уровня спирта в бачке можно не учитывать, ибо поправка меньше 0,1%.
Микроманометры
495
Ввиду того, что трубка не строго прямолинейна, сечение ее по длине не постоянно и отверстие в дуге не всегда достаточно точно просверлено, прибор необходимо тарировать.
Остальные конструкции микроманометров с поворачивающейся трубкой существенно не отличаются от описанной.
В некоторых приборах наклон трубки осуществляется с помощью микрометрического винта, а отсчет угла производится по
шкале, нанесенной на дугу. Отдельные приборы снабжены переключателями, позволяющими удобно производить измерения знакопеременных разностей давлений. Есть приборы, где масштаб доводится до 0,01. Осуществление таких углов наклона требует
4Й6
Аэродинамический эксперимент
тщательной тарировки и весьма чувствительных уровней (с точностью не ниже 10").
Микроманометр ЦАГИ (рис. XVI.21) отличается от всех перечисленных конструкций тем, что у него измерительная трубка скреплена с баком неподвижно. Наклон трубки производится вращением бака 1 в обойме 2. Такая конструкция позволяет избежать пробки в месте соединения трубки с баком. Недостаток этой системы заключается в том, что практически трудно уничтожить некоторый люфт между баком и обоймой и, следовательно, нельзя гарантировать точности установки малых масштабов. В микроманометре ЦАГИ наименьший масштаб равен 0,125.
Здесь рассмотрены лишь методы измерения величин, характеризующих стационарные или слабо меняющиеся процессы. Для измерения нестационарных скоростей, давлений и.сил, действующих на тела, находящихся в потоках, а также определения характеристик турбулентного движения используют различные физические методы [11].
Наиболее распространенным и хорошо изученным прибором для измерения быстро меняющихся скоростей газов и жидкостей и их пульсаций является термоанемометр. Принцип работы термоанемометра заключается в том, что скорость движения жидкости или газа определяется по количеству тепла, снимаемого с тонкой нити или пленки, температура которых выше температуры потока, в котором они помещены.
Нить или пленка подогревается электрическим током. При некоторой скорости количество тепла, снимаемого потоком с датчика, должно равняться количеству тепла, подводимому с помощью электрического тока. При изменении скорости надо изменять количество тепла нагрева. Если оно меняется изменением силы тока при сохранении температуры, т. е. сопротивления, то величина скорости будет функцией тока, т. е. V = <р (i). Такой метод называется методом постоянной температуры. Если сила тока остается постоянной, а равновесие достигается изменением сопротивления, т. е. V = ф (/?), то такой способ называется методом постоянного тока.
Последние годы наибольшее распространение получают термоанемометры с постоянной температурой.
Для измерений в проводящих жидкостях, таких как большинство технических и питьевых вод, морская вода и пр. в Донецком университете разработан электромагнитный кондукционный анемометр, измеряющий средние и мгновенные значения скоростей.
Работа этого прибора основана на известном законе физики — при пересечении магнитного поля проводником в нем возникает э. д. с., пропорциональная скорости движения проводника, его проводимости и напряженности магнитного поля. Значит, если в потоке создать - постоянное магнитное поле,, перпендикулярное
Микроманометры
497
скорости потока, то на электродах ортогональных гидродинамическим и магнитным линиям тока получим э. д. с., пропорциональную величине скорости.
Такие приборы [11] могут работать с локальным магнитным полем или полем, пересекающим весь поток. Освоенные в университете образцы измеряют скорости от 0,5 до 20 м/с, а пульсации скоростей от 0,5 до 2000 мм/с.
При изучении потоков с большими до- и сверхзвуковыми скоростями широкое применение получили оптические и акустические методы. Их основное преимущество заключается в возможности производить локальные измерения без ввода в поток каких-либо датчиков. В принципе и оптические, и акустические приборы работают либо за счет изменения параметров при прохождении волн через заданную область, либо при их рассеивании на инородных частицах в потоках. Применение лазеров и голографии, а также доплеровского эффекта в оптике и акустике открывает большие перспективы в изучении полей скоростей и турбулентных характеристик.
32 И. Л. ПОВ)С
СПИСОК ЛИТЕРАТУРЫ
1. Абрамович Г. Н. Прикладная газовая динамика. М., «Наука», 1969. 824 с.
2. Берд Р., Стюарт В., Лайтфут Е. Явление переноса. М., «Химия», 1974. 686 с.
1^3. Дейч М. Е. Техническая газодинамика. М.—Л., Госэнергоиздат, 1961. 671 с.
4.	Кириллов И. И. Теория турбомашин. Л., «Машиностроение», 1972. 535 с.
V5. Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика.
; 2. М.—Л., Физматгиз, 1963. 535 с; 612 с.
. / 6. Краснов Н. Ф. Прикладная аэродинамика. М., .«Высшая школа», 1974. 739 с.
7.	Краснов Н. Ф. Аэродинамика. М., «Высшая школа», 1971. 630 с.
8.	Лабораторный курс гидравлики насосов и гидропередач. Под ред. С. С. Руднева и Л. Г. Подвидза. М., «Машиностроение», 1974. 416 с.
и 9. Лойцянский Л. Г. Механика жидкости и газа. М., «Наука», 1973. 847 с.
10.	Монин А. С., Яглом А. М. Статистическая гидромеханика. Т. 1; 2. М., «Наука», 1967. 639 с.; 720 с.
11.	Повх И. Л. Аэродинамический эксперимент в машиностроении. Л., «Машиностроение», 1974. 480 с.
12.	Повх И. Л., Капуста А. Б. н Чекин Б. В. Магнитная гидродинамика в металлургии. М-, «Металлургия», 1974. 240 с.
13.	Повх И. Л., Ступин А. Б. Двухслойная модель пристенной турбулентности k слабых растворах полимеров. —«Бионика», 1975, № 9, с. 69—74.
\1Д	. Седов Л. И. Метод подобия и размерности в механике. М., «Наука», 19677 428 с.
15.	Сверхзвуковые течения газа в перфорированных границах. М., «Машиностроение», 1967. 143 с. Авт.: Г. Л. Гродзовский, А. А. Никольский, Г. П. Свищев, Г. И. Таганов.
16.	Шлихтннг Г. Теория пограничного слоя. М., «Наука», 1974. 711 с.
ОГЛАВЛЕНИЕ
Предисловие......................................................... 3
Введение............................................................ 5
1.	Предмет механики жидкостей и	газов............ 5
2.	Некоторые сведения из истории	развития гидромеханики ...	7
3.	Техническая гидромеханика ................................ 9
4.	Плотность и сжимаемость ................................. 11
5.	Законы переноса ......................................... 12
6.	Структура потоков. Турбулентность........................ 14
Глава I. Основы гидростатики....................................... 16
§ 1.	Силы, действующие в жидкости. Гидростатическое давление	—
§ 2.	Основное уравнение гидростатики. Условие существования равновесия .................................................. 19
§ 3.	Равновесие	тяжелой	несжимаемой	жидкости.	Сообщающиеся
сосуды .................................................. 21
§ 4.	Равновесие	весомого	газа.	Барометрическая	формула	...	24
§ 5.	Равновесие жидкости при наличии негравитационных массовых сил.................................................... 25
§ 6.	Давление жидкости на плоские и криволинейные стенки . .	27
§ 7.	Закон Архимеда. Плавание тел............................ 31
§ 8.	Капиллярные поверхностные силы ......................... 33
Глава II. Основы кинематики сплошных сред ......................... 35
§ 1.	Поле скоростей и ускорений............................... —
§ 2.	Линия тока и трубка тока................................ 39
§ 3.	Градиент скалярной функции. Расхождение и циркуляция вектора скорости ........................................•.	41
§ 4.	Вихрь вектора скорости..............................;	•	44
§ 5.	Основная теорема кинематики (первая теорема Гельмгольца) 46
§ 6.	Кубическое расширение................................... 49
§ 7.	Скорость деформации сдвига.............................. 50
§ 8.	Вихревая линия и вихревая трубка. Теоремы о вихрях ...	51
§ 9.	Поле скоростей, вызванное вихрями. Формула Био-Савара	56
Глава III. Общие уравнения для сплошных сред, жидкостей н газов 61
§ 1.	Закон сохранения	массы. Уравнение неразрывности	...	62
§ 2.	Силы, действующие в жидкости..................... 54
§ 3.	Закон сохранения импульса. Уравнение движения в напряжениях ...................................................... 56
§ 4.	Закон сохранения	моментов импульса. Симметрия	тензора
напряжения ............................................. 58
§ 5.	Обобщенный закон	Ньютона....................... 59
SOO
Оглавление
§ 6.	Уравнение движения сжимаемых жидкостей и газов . . . .
§ 7.	Уравнения движения вязкой несжимаемой жидкости . . .
§ 8.	Перенос тепла .......................................
. § 9. Закон сохранения энергии. Уравнения энергии и переноса тепла .......................................................
§ 10. Диффузия. Уравнение переноса вещества...............
Глава IV. Уравнения движения идеальной жидкости..................
§ 1.	Напряжения в идеальной жидкости......................
§ 2.	Уравнение Эйлера движения идеальной жидкости.........
§ 3.	Уравнение Эйлера в форме Громека .....................
§ 4.	Интегралы Коши—Лагранжа и Бернулли для потенциального движения...................................................
§ 5.	Интеграл Бернулли для линии тока.....................
§ 6.	Теорема Томсона ......................................
Глава V. Одномерное движение несжимаемой жидкости (элементы гидравлики) .....................................................
§ 1.	Основные понятия и уравнения..........................
§ 2.	Истечение из отверстия ..............................
§ 3.	Интеграл Бернулли для неустановившегося движения . . .
§ 4.	Внезапное расширение и сжатие потоков. Потери энергии . .
§ 5.	Дроссельные расходомеры. Трубка Вентури..............
§ 6.	Кавитация.............................................
§ 7.	Гидравлический удар. Распространение малых возмущений
Глава VI. Одномерное движение сжимаемого газа (газовая гидравлика) .......................................•................
§ 1.	Основные формулы. Скорость звука.....................
§ 2.	Основные уравнения. Интеграл Бернулли................
§ .3.	Параметры заторможенного газа. Энтропия..............
§ 4.	Истечение из бака. Максимальная и критическая скорости
§ 5.	Движение газа в трубе переменного сечения. Сопло Лаваля ......................................................
§ 6.	Получение сверхзвукового потока в цилиндрических трубах
§ 7.	Распространение конечных возмущений. Скачок уплотнения
§ 8.	Изменение параметров потока в прямом скачке. Ударная адиабата ..................................................
Глава VII. Потенциальное движение идеальной несжимаемой жидкости .............................................................
§ 1.	Комплексный потенциал и комплексная скорость.........
§ 2.	Некоторые простейшие потенциальные потоки............
§ 3.	Обтекание круглого цилиндра..........................
§ 4.	Циркуляционное обтекание круглого цилиндра...........
§ 5.	Простейшие пространственные потенциальные потоки . . .
§ 6.	Обтекание шара.......................................
Глава VIII. Плоский потенциальный поток газа.....................
§ 1.	Основные уравнения...................................
§ 2.	Дозвуковое обтекание тонкого профиля.................
§ 3.	Сверхзвуковое обтекание клина. Косой скачок уплотнения
§ 4.	Сверхзвуковое обтекание внешнего угла................
§ 5.	Обтекание пластины сверхзвуковым потоком .............
Оглавление
501
Глава IX. Элементы теории профиля, решеток профилей и теория крыла............................................................ 201
§1.	Геометрические и аэродинамические характеристики профилей —
§ 2.	Конформные отображения. Теоретические профили........	204
§ 3.	Скорость и циркуляция в преобразованном потоке. Постулат Жуковского—Чаплыгина....................................... 209
§ 4.	Теорема Жуковского..................................... 214
§ 5.	Обтекание решетки профилей............................. 216
§ 6.	Элементы теории крыла конечного размаха............... 219
Глава X. Подобие процессов переноса............................... 224
§ 1.	Значение теории подобия................................. —
§ 2.	Гидродинамическое подобие.............................. 226
§ 3.	Тепловое подобие ..................................... 232
§ 4.	Диффузионное подобие.................................. 235
§ 5.	Подобие некоторых частных случаев переноса............ 238
§ 6.	Некоторые обобщения................................... 240
Глава XI. Ламинарное и турбулентное стабилизированное движение в трубах и вдоль пластины ........................................ 242
§ 1.	Структура потока в трубах. Переход ламинарного движения в турбулентное .............................................. —
§ 2.	Ламинарное движение в трубах......................... 245
§ 3.	Перенос тепла при установившемся ламинарном движении в трубе ................................................... 253
§ 4.	Основы гидродинамической теории смазки............... 256
§ 5.	Турбулентное движение. Уравнение Рейнольдса.......... 262
§6.	Турбулентное движение вдоль безграничной пластины. Ламинарный подслой ............................................ 267
§ 7.	Профили скоростей при турбулентном движении в круговой трубе .............................г....................... 273
§ 8.	Законы сопротивления при турбулентном движении в трубах 278
§ 9.	Движение жидкости в шероховатых трубах............... 283
§ 10.	Турбулентный перенос тепла и вещества при стабилизированном обтекании пластины.................................. 289
Глава XII. Ламинарный пограничный слой............................ 293
§ 1.	Пограничный слой и его характерные толщины...........*	—
§ 2.	Уравнения ламинарного	пограничного	слоя................ 299
§ 3.	Интегральные соотношения для динамического пограничного слоя ...................................................... 304
§ 4.	Точные решения......................................... 306
§ 5.	Ламинарный пограничный	слой	иа	пластине .............. 310
§ 6.	Ламинарный пограничный слой на крыловом прсфиле произвольной формы .............................:............. 313
§ 7.	Интегральное соотношение для теплового ламинарного пограничного слоя. Тепловой слой на пластине...................  316
§ 8.	Диффузионный ламинарный пограничный слой на пластине 321
Глава XIII. Турбулентный пограничный слой. Турбулентные струи 324
§ 1.	Переход ламинарного пограничного слоя в турбулентный . .	—
§ 2.	Механизм турбулентного слоя. Профили скоростей . ; . • •	327
§ 3.	Турбулентный пограничный слой на пластине.............. 330
502
Оглавление
§ 4.	Турбулентный пограничный слой на произвольн
§ 5.	Профильное сопротивление...................
§ 6.	Снижение сопротивления добавками ..........
§ 7.	Свободная турбулентность. Турбулентные струи
§ 8.	Осесимметричные струи .....................
Глава XIV. Расчет трубопроводов. Местные сопротивлен
§ 1.	Простые трубопроводы.......................
§ 2.	Сложные трубопроводы.......................
§ 3.	Начальные участки труб.....................
§ 4.	Потоки в диффузорах .......................
§ 5.	Поворотные устройства......................
§ 6.	Сопротивления при слиянии и разделении потоко и клапаны .......................................
Глава XV. Электромагнитная гидродинамика..............
§ 1.	Предмет электромагнитной гидродинамики . .
§ 2.	Уравнения электромагнитной гидродинамики .
§ 3.	Электромагнитная гидростатика.............
§ 4.	Проводимость жидкостей и газов ...........
§ 5.	Подобие электромагнитных явлений..........
§ fr.	Классификация уравнений электромагнитной мики ,.........................................
§ 7.	Одномерное движение невязкого газа ....
§ 8.	Магнитогидродинамическое течение в трубах .
§ 9.	Ламинарное течение заряженной жидкости в пл<
§ 10.	Магнитогидродинамический пограничный слой
§ 11.	Внешнее обтекание в магнитной гидродинамика
§ 12.	Электромагнитные насосы. Магнитодинамическо' вание электрической энергии ...................
§ 13.	Электрогидродинамические насосы и генератор!
Глава XVI. Аэродинамический эксперимент...............
§ 1.	Экспериментальные установки ...............
§ 2.	Методы аналогий ...........................
§ 3.	Измерение скоростей в потоках..............
§ 4.	Микроманометры.............................
Список литературы.....................................
ИЗДАТЕЛЬСТВО „МАШИНОСТРОЕНИЕ"
В 1976 г. будут выпущены следующие книги:
1,Пановко Я. Г. Основы прикладн рии колебаний и удара. Изд. 3-е, перераб, 2. Троицкий В. А. Оптимальные пр колебаний механических систем.
3. Дроздович В. Н. Газодинамическ шипники.
4. Коновалов Г. Ф., Конова л енн Системы автоматического управления с э. магнитными порошковыми муфтами.
б. Пневматика и гидравлика. П и системы управления.
Иван Лукич ПОВХ
ТЕХНИЧЕСКАЯ
ГИДРОМЕХАНИКА
Редактор издательства И. 3. Симоновский Переплет художника О. И. Цыплакова Технический редактор Т. П. Малашкниа
Корректор Р. Г. Солодкииа
Сдано в производство 26/XI 1975 г.
Подписано к печати 27/IV 1976 г. М-22232
Формат бумаги 60X90'/  Бумага типографская Xs 3.
Печ. л. 31,5- Уч.-изд. л. 28,5. Тираж 17 500 экз.
Зак. № 636. Цена I р. 23 к.
Ленинградское отделение издательства «МАШИНОСТРОЕНИЕ> 191065, Ленинград, Д-65, ул. Дзержинского, 10
Ленинградская типография Nt 6 Союэполиграфпрома при Государственном комитете Совета Министров СССР по делам издательств, полиграфии и княжной торговля |9§144;1Денидград, С-144, ул. ^Овсеенко, 19
	ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.	Строка	Напечатано	j	Должно быть
47 । 6-я снизу	/ ди \ _ • С dv \ __	\( ди \ _  , / dv \ _• \ дх )q ~ Su \ ду /о ~	\ дх )о ~ S“’ \ ду /о — $22’ 22\'<Эг /о 3S’	\ <3z Л-*33’
476 [ 3-я	> ।	. _ 1 <Э<рэ =	1	, _ _1_ Зфэ _ о ду	।	' ~ о дх 1
И. Л. Повх. Техническая гидромеханика Зак. 636.