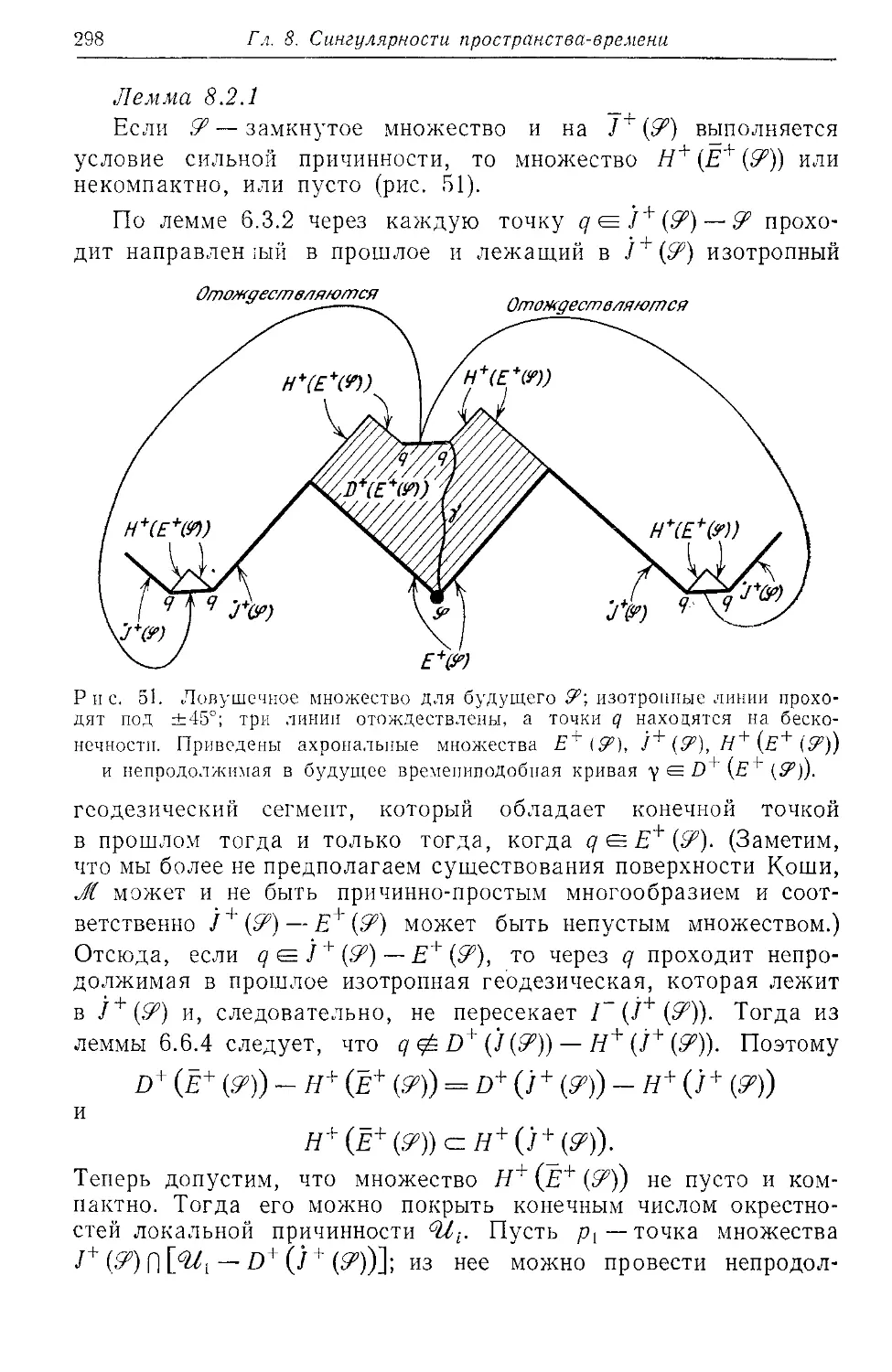
Text
С. ХОКИНГ. ДЖ. ЭЛЛИС
КРУ П НОМАСШТАБ НАЯ
СТРУКТУРА
ПРОСТРАНСТВА-ВРЕМЕНИ
Перевод с английского
Э. А. ТАГИРОВА
Под редакцией
Я. А. СМОРОДИНСКОГО
ИЗДАТЕЛБСТВО «МИР»
МОСКВА 1977
THE LARGE SCALE STRUCTURE
OF SPACE-TIME
S. W. HAWKING, F. R. S.
Institute of Astronomy
and Gonville and Caius College, Cambridge
and
G. F. R. ELLIS
Department of Applied Mathematics,
University of Capetown
CAMBRIDGE UNIVERSITY PRESS
1973
УДК 52 + 53
Книга посвящена новому подходу к теории относительности
и ее астрономическим приложениям, основанному на использова-
нии методов современной дифференциальной геометрии. Приме-
нение их оказалось исключительно плодотворным при исследова-
нии свойств пространства-времени в особых условиях, а именно
проблем сингулярности в космологии, черных дыр и т. п.
Авторы рассмотрели роль гравитации, методы дифферен-
циальной геометрии и общую относительность, физический смысл
кривизны пространства-времени, точные решения и задачу Коши
в общей теории относительности, проблему сингулярности и ее
приложения к выяснению природы черных дыр и различных
этапов расширения Вселенной.
Книга рассчитана на широкие круги физиков, математиков
и астрономов, интересующихся проблемами релятивизма, и может
служить учебным пособием для студентов.
Редакция космических исследований, астрономии и геофизики
х 20605-114
041(01)-77
114-77
© Cambridge University Press, 1973
© Перевод на русский язык, «Мир», 1977
Предисловие к русскому изданию
В книге С. Хокинга и Дж. Эллиса общая теория относитель-
ности изложена как математическая теория геометрии простран-
ства-времени. Задача авторов — описать на современном мате-
матическом языке свойства решений уравнений Эйнштейна.
Язык, которым пользуются авторы, пока мало привычен для фи-
зиков и может показаться многим слишком абстрактным. Но
развитие науки всегда приводит к изменению ее языка. Это про-
исходит тогда, когда новые задачи оказываются слишком запу-
танными, если их пытаться исследовать, применяя лишь старый
привычный аппарат.
Когда в книгах по электродинамике в 30-х гг. появились
формулы векторного анализа, то говорили о потере наглядности
и физического смысла формул. Столь же непривычен и труден
был аппарат квантовой механики. Ясно, что для решения старых
задач, таких как движение перигелия Меркурия, старые методы
проще и нагляднее. Новый язык понадобился тогда, когда фи-
зики от поисков конкретных решений уравнений Эйнштейна пе-
решли к качественному исследованию этих уравнений.
Особенно «тяжелой» оказались проблемы сингулярностей,
или «особенностей». Всякое ли решение уравнения Эйнштейна
имеет истинную (не устранимую координатным преобразова-
нием) особенность или нет? После многих работ, среди которых
надо отметить фундаментальные работы Лифшица, Халатнико-
ва, Белинского, исследовавших поведение решений вблизи осо-
бенности (старыми методами), необходимость новой точки зре-
ния на всю проблему стала очевидной.
Новую точку зрения — по существу новое направление — от-
крыли работы Пенроуза, а вслед за ними работы Хокинга.
Именно это направление — от основ до трудных обобщающих
теорем — изложены в предлагаемой книге последовательно и
очень четко. Читатель, преодолевший трудности освоения языка
современной дифференциальной геометрии, будет вознагражден
той красотой, которая откроется в последующих главах, когда
речь пойдет уже о конкретных типах пространства-времени,
представленных в виде карт и атласов, и увидит, как далеко
можно уйти от классических моделей.
Книга построена так, что в ней изложен весь необходимый
математический материал. Однако некоторая общая подготовка
6
Предисловие к русскому изданию
читателя, в рамках элементарных курсов топологии, все же не-
обходима. Изучение книги убедит читателя в том, что новые ма-
тематические средства, вводимые авторами в общую теорию от-
носительности, необычайно сильны и необходимы для дальней-
шего развития теории.
В переводе книги мы старались следовать установившейся
русской математической терминологии, но иногда приходилось
изобретать и новые термины; для объяснения их полезно поль-
зоваться словариком-указателем в конце книги.
Я. Смородинский
Посвящается Д. Шаме
Предисловие
Предмет этой книги — структура пространства-времени в
масштабах длин от радиуса элементарной частицы (~ КН13 см)
до радиуса Вселенной (~ 1023 см). По причинам, указанным в
гл. 1 и 3, наш подход основан на общей теории относительности
Эйнштейна. Эта теория ведет к двум следующим предсказаниям
относительно Вселенной: во-первых, конечной участью массив-
ной звезды является коллапс за горизонт событий; при этом
образуется «черная дыра», внутри которой заключена сингуляр-
ность; во-вторых, в нашем прошлом существует сингулярность,
которая представляет собой в некотором смысле начало наблю-
даемой Вселенной. Наше изложение в основном направлено на
обоснование двух указанных выше результатов. Это связано
прежде всего с двумя областями исследований: с теорией пове-
дения семейств времениподобных и изотропных кривых в про-
странстве-времени и с изучением характера различных отноше-
ний причинности в пространстве-времени. Мы подробно обсудим
эти проблемы. Кроме того, в книге излагается теория развития
во времени решений уравнений Эйнштейна с заданными началь-
ными данными. Параллельно мы исследуем глобальные свойства
разнообразных точных решений уравнений поля Эйнштейна,
многие из которых обнаруживают неожиданные свойства.
Частично эта книга основывается на обзорном докладе, пред-
ставленном в связи с награждением одного из нас (С. X.) пре-
мией Адамса. Многие из идей, изложенных здесь, принадлежат
Р. Пенроузу и Р. Героку; мы благодарим их за помощь и реко-
мендуем читателям их обзорные статьи [58, 59, 128, 131]. Боль-
шую пользу мы извлекли из дискуссий со многими нашими кол-
легами, особенно с Б. Картером и Д. Шамой. Им мы также
приносим благодарность.
Кембридж с. Хокинг
Январь 1973
Дж. Эллис
Глава 1
Роль тяготения
Согласно общепринятому в современной физике взгляду, изу-
чение Вселенной можно разделить на две части. Первая — это
установление локальных законов, которым удовлетворяют раз-
личные физические поля. Эти законы обычно формулируются в
виде дифференциальных уравнений. Вторую часть составляют
проблема граничных условий для этих уравнений и глобальные
свойства их решений. Она в том или ином смысле содержит в
себе идею о крае пространства-времени. Эти две части не обяза-
тельно независимы. Действительно, уже была высказана мысль,
что локальные законы определяются крупномасштабной струк-
турой Вселенной. Эту точку зрения обычно связывают с именем
Маха, а в менее отдаленном прошлом ее развивали Дирак [41],
Ша ма [155], Дикке [39], Хойл и Нарликар [82] и др. Мы не будем
придерживаться столь возвышенной точки зрения: мы просто
начнем с локальных физических законов, установленных экспе-
риментально, и посмотрим, к каким выводам относительно круп-
номасштабной структуры Вселенной они могут привести.
Конечно, предположение о том, что физические законы, уста-
новленные в лаборатории, применимы во всех других точках
пространства-времени, где условия могут быть совсем иными —
это далеко идущая экстраполяция. Если эти законы перестанут
выполняться, мы скажем, что имеется еще какое-то поле, кото-
рое повлияло на локальные законы, однако существование его
до сих пор не было обнаружено в наших экспериментах из-за
того, что оно мало меняется в пределах такой области, как Сол-
нечная система. На самом деле большая часть наших резуль-
татов не будет зависеть от конкретного характера рассматри-
ваемых физических законов: они окажутся связанными лишь с
определенными общими свойствами, такими, как описание про-
странства-времени посредством псевдоримановой геометрии и
положительная определенность плотности энергии.
Фундаментальные взаимодействия, известные сейчас в физи-
ке, можно подразделить на четыре класса: сильные и слабые
ядерные взаимодействия, электромагнетизм и тяготение. Среди
перечисленных тяготение намного слабее остальных: Gm2/e2, от-
ношение силы тяготения между двумя электронами к силе их
электростатического взаимодействия, по порядку величины
10
Гл. 1. Роль тяготения
равно 10-40. Тем не менее тяготение играет доминирующую роль
в формировании крупномасштабной структуры Вселенной. Это
происходит из-за того, что сильное и слабое взаимодействия об-
ладают весьма коротким радиусом действия (~10~12 см и ме-
нее), а электромагнетизм хотя и является дальнодействующим
взаимодействием, но для тел макроскопических размеров оттал-
кивание одноименных зарядов почти полностью компенсируется
притяжением разноименных. Напротив, тяготение, по-видимому,
всегда является силой притяжения. Следовательно, гравитацион-
ные поля всех частиц тела складываются и создают поле, кото-
рое для достаточно больших тел преобладает над всеми другими
силами.
Тяготение не только доминирует на больших расстояниях, но
и является силой, которая одинаковым образом действует на все
частицы. Эту универсальность тяготения впервые выявил Гали-
лей, который обнаружил, что два любых тела падают с одина-
ковой скоростью. Позднее это было проверено с очень большой
точностью опытами Этвеша и Дикке с сотрудниками [39]. Было
обнаружено также, что свет отклоняется гравитационными по-
лями. Поскольку принимается, что нет сигналов, распространяю-
щихся быстрее света, это означает, что именно тяготение опре-
деляет причинную структуру Вселенной, т. е. определяет, какие
события пространства-времени могут быть причинно связаны
друг с другом.
Эти свойства тяготения служат источником серьезных труд-
ностей: если бы в некоторой области сконцентрировалось доста-
точно большое количество вещества, то последнее могло бы от-
клонить свет, испускаемый из этой области, настолько, что свет
был бы втянут обратно в эту область. Эта возможность была
осознана в 1798 г. Лапласом, который отметил, что тело такой
же плотности, как и Солнце, но с радиусом в 250 раз большим
создало бы столь сильное гравитационное поле, что свет не мог
бы уйти с его поверхности. Тот факт, что это было предсказано
так давно, настолько поразителен, что мы приводим в приложе-
нии перевод статьи Лапласа.
Втягивание световых лучей массивным телом можно предста-
вить более точно, используя идею Пенроуза о замкнутых лову-
шечных поверхностях. Рассмотрим сферу ?Г, окружающую неко-
торое тело. Пусть в какой-то момент от РГ исходит импульс све-
та. В некоторый последующий момент t фронты сходящихся и
расходящихся от 2Г волн образуют сферы и РГ г соответ-
ственно. В нормальных условиях площадь РГi (поскольку она
представляет собой сходящийся свет) будет меньше, а площадь
?Г2 (поскольку она представляет собой расходящийся свет) (см.
рис. 1)—больше, чем площадь ST. Однако если внутри РГ за-
ключено достаточно много вещества, то и площадь РГ\, и пло-
Гл. 1. Роль тяготения
11
щадь 5G будут меньше площади .'7~. В этом случае поверх-
ность называют замкнутой ловушечной поверхностью. По
мере возрастания времени t площадь £Г2 будет становиться все
меньше и меньше (при условии, что тяготение остается силой
притяжения, т. е. при условии, что плотность энергии не станет
отрицательной). Поскольку вещество внутри сферы ?Г не может
иметь скорости, превышающей световую, оно окажется запертым
Рис. 1. В некоторый момент времени сфера излучает вспышку света.
В более поздний момент свет, излученный в точке р, образует сферу У’ во-
круг р, и огибающие поверхности i и 2 образуют соответственно фронты
сходящихся и расходящихся волн. Если площади обеих поверхностей ?Г \ и
3~1 меньше площади , то 3~ представляет собой замкнутую ловушечную
поверхность.
в области, граница которой стягивается к нулю за конечный
промежуток времени. Это наводит на мысль, что наша модель в
чем-то ошибочна.
Однако мы покажем, что при выполнении некоторых разум-
ных условий здесь на самом деле возникает сингулярность про-
странства-времени. Можно думать, что сингулярность — это ме-
сто, где ныне известные нам физические законы нарушаются.
В качестве альтернативы можно считать, что сингулярность
представляет часть границы пространства-времени, которая, од-
нако, находится не на бесконечности, а на конечном расстоянии.
Тогда сингулярности перестают быть чем-то порочным с точки
зрения физики; но и при таком взгляде на вещи нам еще остает-
ся решить проблему граничных условий. Другими словами, нам
не известно, что именно выходит из сингулярности.
12
Г л. 1. Роль тяготения
Предполагается, что в двух случаях концентрация материи
будет достаточно для возникновения замкнутых ловушечных по-
верхностей. Первый случай — гравитационный коллапс звезд с
массой больше двух масс Солнца; этот случай должен иметь
место после выгорания ядерного горючего звезды. При этом
звезда, как считают, коллапсирует к сингулярности, которая не-
видима для внешних наблюдателей. Второй случай — это сама
Вселенная как иелое. Недавние наблюдения микроволнового
фонового излучения свидетельствуют, что Вселенная содержит
достаточное количество материи для возникновения замкнутой
ловушечной поверхности при обращении времени. Это означает,
что в прошлом, в начале нынешней эпохи расширения Вселен-
ной, существовала сингулярность. Эту сингулярность мы можем
в принципе наблюдать, и ее можно было бы интерпретировать
как начало Вселенной.
В данной книге мы рассматриваем крупномасштабную струк-
туру пространства-времени на основе общей теории относитель-
ности Эйнштейна. Выводы из этой теории находятся в согласии
со всеми выполненными до сих пор экспериментами. Однако
наша трактовка предмета будет достаточно общей и для того,
чтобы охватить такие модификации теории Эйнштейна, как тео-
рия Бранса — Дикке.
Хотя мы ожидаем, что большинство наших читателей знако-
мы с общей теорией относительности, мы все же пытались напи-
сать книгу так, чтобы от читателя не требовалось иных знаний,
кроме математического анализа, алгебры и топологии точечных
множеств. Вот почему мы посвящаем гл. 2 дифференциальной
геометрии. Наш подход является в разумной мере современным
в том отношении, что мы даем наши определения в форме, не
зависящей явно от координат. Однако для удобства вычислений
временами мы пользуемся индексами; большей частью мы избе-
гали также употребления расслоенных пространств. Читатель,
немного знающий дифференциальную геометрию, может при же-
лании пропустить эту главу.
В гл. 3 дана формулировка общей теории относительности
в виде трех постулатов математической модели пространства-
времени. Эта модель представляет собой многообразие JL вместе
с метрикой g лоренцевой сигнатуры. Физический смысл метрики
раскрывается в первых двух постулатах — локальной причинно-
сти и локального сохранения энергии-импульса. Эти постулаты
общие для специальной и общей теорий относительности, и, сле-
довательно, основанием для них может служить эксперименталь-
ное подтверждение первой из этих теорий. Третий постулат —
полевые уравнения для метрики g — экспериментально обосно-
ван не столь хорошо. Однако большинство наших результатов
будет зависеть лишь от того следствия уравнений поля, что для
Гл. 1. Роль тяготения
13
положительной плотности материи тяготение является силой
притяжения. К этому свойству тяготения приводят как общая
теория относительности, так и некоторые ее модификации, на-
пример теория Бранса — Дикке.
В гл. 4 устанавливается физический смысл кривизны, для
чего мы изучаем ее влияние на семейства времениподобных и
изотропных геодезических. Указанные линии представляют пути
малых частиц и световые лучи соответственно. Кривизну можно
интерпретировать как приливную силу, которая вызывает отно-
сительные ускорения между «соседними» геодезическими. Если
г
Рис. 2. Линия рг не может быть кратчайшей линией от р до гР, поскольку
между р и г имеется фокальная точка q. На самом деле кратчайшей линией
от р до У будет рх или ру.
тензор энергии-импульса удовлетворяет условиям положитель-
ной определенности, то результирующее действие приливной
силы на невращающиеся семейства геодезических всегда оказы-
вается собирательным. Используя уравнение Райчаудхури (4.26),
можно показать, что это приводит к существованию фокальных
или сопряженных точек, в которых соседние геодезические пере-
секаются.
Чтобы выявить роль этих фокальных точек, рассмотрим одно-
мерную поверхность 9? в двумерном евклидовом пространстве
(рис. 2). Пусть р— точка, не лежащая на 17. Тогда найдется
кривая, соединяющая 9Р и р, которая будет короче (или не длин-
нее) любой другой кривой от 9? до р. Ясно, что эта кривая будет
геодезической, т. е. прямой линией и будет пересекать 9? ортого-
нально. На самом деле, в ситуации, изображенной на рис. 2,
имеется три геодезические, ортогональные к 9> и проходящие
через р. Геодезическая, проходящая через точку г, очевидно, не
14
Гл. 1. Роль тяготения
есть кратчайшая линия от 9> до р. В этом можно убедиться [103],
например, заметив, что соседние геодезические, ортогональные
к 9} в точках и и v, пересекают геодезическую, проведенную из г,
в фокальной точке q, лежащей между РР и р. Тогда, присоединяя
к отрезку uq отрезок qp, мы получим кривую от -Р до р, длина
которой такая же, как у прямой гр. Но поскольку uqp не есть
прямая линия, можно было бы срезать угол у точки q и полу-
чить кривую короче, чем гр. Отсюда видно, что гр не есть крат-
чайшая кривая от 9? до р. Значит, кратчайшей кривой будут или
хр, или ур.
Эти соображения можно перенести на случай четырехмерного
пространственно-временного многообразия Л с лоренцевой мет-
рикой g. Вместо прямых линий тогда нужно рассматривать гео-
дезические, а вместо кратчайшей кривой искать времениподоб-
ную кривую наибольшей длины между точкой р и простран-
ственноподобной поверхностью 9> (ввиду лоренцевой сигнатуры
метрики здесь не будет кратчайшей времениподобной кривой, но,
возможно, найдется такая кривая наибольшей длины). Эта кри-
вая должна быть геодезической, пересекающей 9> ортогонально,
и между 9? и р не может быть какой-либо фокальной точки гео-
дезических, ортогональных к РР. Аналогичные результаты можно
получить для изотропных геодезических. Эти результаты исполь-
зуются в гл. 8 для доказательства существования сингулярно-
стей при определенных условиях.
В гл. 5 мы описываем ряд точных решений уравнений Эйн-
штейна. Эти решения не являются реалистическими в том смыс-
ле, что все они обладают точными симметриями. Однако они
служат полезными примерами для последующих глав и иллю-
стрируют различные возможные поведения решений. В частно-
сти, космологические модели, обладающие высокой симметрией,
почти все имеют пространственно-временные сингулярности.
Долгое время думали, что эти сингулярности, возможно, обус-
ловлены именно высокой степенью симметрии и они будут от-
сутствовать в более реалистических моделях. Показать, что это
на самом деле не так — одна из основных наших целей.
В гл. 6 мы исследуем причинную структуру пространства-
времени. В частной теории относительности те события, которые
могут причинно влиять на некоторое данное событие, и те, на
которые это событие само может причинно влиять, образуют
внутренние части световых конусов прошлого и будущего соот-
ветственно (рис. 3). В общей теории относительности метрика g,
которая задает световые конусы, вообще говоря, меняется от
точки к точке, а топология пространственно-временного много-
образия Л не обязательно совпадает с топологией евклидова
пространства /?4. Это приводит к большему разнообразию воз-
можностей. К примеру, можно было отождествить соответствую-
Гл. 1. Роль тяготения
15
щие точки на поверхностях 9\ и Х2 на рис. 3, чтобы получить
пространство-время с топологией /?3 X 51. В нем есть замкнутые
времениподобные кривые. Однако существование таких кривых
Рис. 3. В специальной теории относительности световой конус события р
является множеством всех лучей света, проходящих через р. Прошлое собы-
тие р — это внутренность светового конуса прошлого, а будущее событие
р — внутренность светового конуса будущего.
привело бы к нарушению причинности: можно было бы путеше-
ствовать в собственное прошлое. Большей частью мы ограни-
чимся рассмотрением пространственно-временных многообразий,
в которых такого рода нарушения причинности исключены.
Тогда в пространстве-времени для любой данной пространствен-
ноподобной поверхности существует максимальная область
16
Гл. 1 Роль тяготения
пространства-времени — назовем ее областью Коши (Cauchy de-
velopment*)),— в которой можно делать предсказания по из-
вестным начальным данным на д’. Область Коши обладает
тем свойством («глобальная гиперболичность»), что при нали-
чии в ней двух точек, которые можно соединить времениподоб-
ной кривой, между ними существует такая кривая наибольшей
длины; она будет геодезической.
Причинная структура пространства-времени может быть ис-
пользована для определения границы или края пространства-
времени. Эта граница включает в себя как бесконечность, так и
те части края пространства-времени, которые находятся на ко-
нечном расстоянии, т. е. сингулярные точки.
В гл. 7. мы рассматриваем задачу Коши для общей теории
относительности. Будет показано, что начальные данные на про-
странственноподобной поверхности определяют решение одно-
значно в области Коши для этой поверхности и что в некото-
ром смысле это решение зависит непрерывно от начальных дан-
ных. Эта глава включается для полноты изложения, а также
потому, что в ней используется ряд результатов предыдущей
главы, но чтение ее не обязательно для понимания последующих
глав.
В гл. 8 обсуждается определение пространственно-временных
сингулярностей. Это представляет известную трудность, по-
скольку нет возможности рассматривать сингулярные точки как
часть пространственно-временного многообразия Л.
Затем мы доказываем четыре теоремы, которые устанавли-
вают наличие сингулярностей при определенных условиях. Эти
условия распадаются на три категории. Во-первых, требуется
чтобы тяготение было силой притяжения; это может быть вы-
ражено в виде некоторого неравенства для тензора энергии-им-
пульса. Во-вторых требуется, чтобы количества материи, содер-
жащегося в некоторой области, было бы достаточно для того,
чтобы ничто не могло покинуть эту область. Это произойдет,
если имеется замкнутая ловушечная поверхность или если вся
Вселенная сама пространственно замкнута. Третье требование
состоит в том, чтобы не было никаких нарушений причинности.
Однако в одной из доказываемых теорем это требование не яв-
ляется необходимым. Основная идея доказательства состоит в
том, чтобы с помощью результатов гл. 6 показать, что между
определенными парами точек должны существовать временипо-
добные кривые наибольшей длины. Тогда можно доказать, что
если бы сингулярности отсутствовали, то были бы фокальные
*) В пашей литературе термин «Cauchy development» иногда переводят
как «область зависимости». — Прим, перев.
Гл. 1. Роль тяготения
17
точки, а, следовательно, не было бы кривой наибольшей длины
между этими парами точек.
После этого мы даем описание предложенной Шмидтом про-
цедуры построения границы пространства-времени, отображаю-
щей его сингулярные точки. Эта граница может отличаться от
той части причинной границы (ее определение дано в гл. 6),
которая соответствует сингулярностям.
В гл. 9 показано, что второе условие теоремы 2 гл. 8 должно
выполняться вблизи звезд с массой 1,5 массы Солнца на конеч-
ных стадиях их эволюции. Сингулярности, которые возникают
при этом, вероятно, находятся за горизонтом событий и нена-
блюдаемы извне. Там, где когда-то была звезда, внешний на-
блюдатель видит «черную дыру». Мы рассмотрим свойства этих
черных дыр и покажем, что вероятным итогом процесса образо-
вания их является установление в пространстве-времени метрики
из семейства решений Керра. В предположении, что так на са-
мом деле и происходит, можно наложить определенные ограни-
чения сверху на количество энергии, которое можно извлечь из
черной дыры. В гл. 10 показано, что второе условие теорем 2 и 3
гл. 8 выполнено при обращении знака времени для Вселенной
в целом. В этом случае сингулярности были в прошлом по отно-
шению к нам и представляют собой начало развития всей на-
блюдаемой Вселенной или ее части.
Существенная часть вводного материала содержится в раз-
делах 3.1, 3.2 и 3.4. Читателю, желающему понять лишь тео-
ремы, предсказывающие существование сингулярностей во Все-
ленной, достаточно затем прочитать только гл. 4 и разд. 6.2—6.7,
8.1, 8.2. Применение этих теорем к коллапсирующим звездам
дано в разд. 9.1 (где используются также результаты приложе-
ния Б); в разд. 10.1 эти теоремы на основе некоторого истолко-
вания моделей Робертсона — Уокера применяются к Вселенной
в целом. Обсуждение характера сингулярностей содержится в
разд. 8.1, 8.3—8.5 и 10.2; важную роль при этом играет пример
пространства Тауба — НУТ (разд. 5.8). Определенный интерес
представляет также модель Вселенной типа I Бианки (разд. 5.4).
Читателю, желающему ознакомиться лишь с вопросом о чер-
ных дырах, необходимо прочитать гл. 4 и разд. 6.2—6.6, 6.9,
9.1—9.3. Здесь мы основываемся на определенной интерпретации
решения Шварцшильда (разд. 5.5) и решения Керра (разд. 5.6).
Наконец, читатель, который в первую очередь интересуется
свойствами эволюции во времени уравнений Эйнштейна, может
ограничиться чтением разд. 6.2—6.6 и гл. 7. Для него окажутся
интересными примеры, приведенные в разд. 5.1, 5.2 и 5.5.
Мы старались сделать указатель полезным путеводителем по
всем введенным определениям и связям между ними.
Глава 2
Дифференциальная геометрия
Структура пространства-времени, о которой пойдет речь в
следующей главе и которая является основной для изложения
во всей остальной части книги, — это структура многообразия,
наделенного лоренцевой метрикой и определяемой ею аффин-
ной связностью.
В настоящей главе, в разд. 2.1, мы введем понятие много-
образия, а в разд. 2.2 — векторы и тензоры, являющиеся есте-
ственными геометрическими объектами, определяемыми на
многообразии. В разд. 2.3 будут рассмотрены отображения мно-
гообразий, что приведет нас к понятиям подмногообразий и ин-
дуцированных отображений тензоров. Производная индуциро-
ванного отображения, определяемого векторным полем, дает
производную Ли; она вводится в разд. 2.4. Там же мы даем
определение внешнего дифференцирования — другой дифферен-
циальной операции, зависящей только от структуры многообра-
зия. Эта операция встречается в обобщенной форме теоремы
Стокса.
В разд. 2.5 вводится дополнительная структура — связность;
это позволяет ввести ковариантную производную и тензор кри-
визны. В разд. 2.6 рассмотрено соотношение между метрикой
и связностью и дано выражение для тензора кривизны через тен-
зор Вейля и тензор Риччи, которые связаны между собой тожде-
ствами Бианки.
В оставшейся части главы мы обсудим ряд других вопросов
дифференциальной геометрии. В разд. 2.7 рассмотрены метрика
и связность, индуцированные на гиперповерхности, и выведены
уравнения Гаусса — Кодацци. В разд. 2.8 вводится задаваемый
метрикой элемент объема, который затем используется для дока-
зательства теоремы Гаусса. Наконец, в разд. 2.8 мы вкратце
остановимся на расслоенных пространствах, уделяя особое вни-
мание касательным и реперным расслоениям. Это позволит пере-
формулировать многие из введенных ранее понятий на красивом
геометрическом языке. Сведения из разд. 2.7 и 2.9 в дальнейшем
используются только в одном или двух местах и несущественны
для понимания основного содержания книги,
2.1. Многообразия
19
2.1. Многообразия
По существу многообразие есть пространство, локально по-
добное евклидову пространству в том смысле, что оно может
быть покрыто кусками координатных сетей. Такая структура
позволяет ввести дифференцирование, но не позволяет разли-
чить внутренним образом разные координатные системы. Сле-
довательно, структурой многообразия определяются такие по-
нятия, которые не зависят от выбора системы координат. Мы
дадим точную формулировку понятия многообразия, введя
предварительно некоторые определения.
Обозначим через R'1 евклидово пространство п измерений,
т. е. множество всевозможных наборов п чисел (х1, х2, ...,хп),
(—оо < х{ < оо) с обычной топологией (открытые и замкну-
тые множества определены, как обычно). Пусть уRn означает
«нижнюю половину» Rn, т. е. область Rn, в которой х1 0. Ото-
бражение ф открытого множества О cz Rn (соответственно
•|- Rn^ на открытое множество О' сг Rn (соответственно у Rn^
называется отображением класса Сг, или, короче, ^-отображе-
нием, если координаты (х'1, х'2, х'т) точки ф(р) в О', яв-
ляющейся образом точки р в О, есть r-кратно непрерывно диф-
ференцируемые функции (т. е. их r-е производные существуют
и непрерывны) координат (х1, х2, ..., х11) точки р. Если отобра-
жение является отображением класса Сг для любого г 0, то
говорят, что это отображение класса С°°, или С°°-отображение.
Под С°-отображением мы подразумеваем непрерывное отобра-
жение.
Говорят, что функция / на открытом множестве О ozRn ло-
кально удовлетворяет условию Липшица, если для каждого от-
крытого множества 'U сс О с компактным замыканием суще-
ствует постоянная R, такая, что для любой пары точек р, q
|f(P) — f(q) | R\P — <?|, где \р\ означает
{(х>« + (х2(р))2+ ... + (хп(р))2}'\
Отображение ф будем называть удовлетворяющим локально ус-
ловию Липшица и обозначать это как С1-, если координаты
точки ф(р) как функции координат точки р локально удовлетво-
ряют условию Липшица. Аналогично, будем говорить, что ф
есть ^-отображение, если оно класса Сг и производные
(г—I)-го порядка координат ф(р) являются функциями коор-
динат р, локально удовлетворяющими условию Липшица.
В дальнейшем мы обычно рассматриваем функции класса Сг,
НО аналогичные определения и результаты справедливы и для
функций класса Сг~.
20
Гл. 2. Дифференциальная геометрия
Пусть З3 есть произвольное множество в Rn (соответственно в
; тогда отображение ф из 3 в некоторое множествоЗ3'czRm
^соответственно у /?т) называется Сг-отображением, если ф яв-
ляется сужением на З3 и З3' Сг-отображения некоторого откры-
того множества О, содержащего З3, на некоторое открытое мно-
жество О', содержащее З3’.
п-Мерное многообразие Л класса СГ, или (^-многообразие,
есть множество Л вместе с атласом {°Иа, фа} класса Сг, т. е.
с набором карт фа}, где — подмножества Л, а фа —
взаимно-однозначные отображения соответствующих °Ма на такие
открытые множества в Rn, что
1) <^а образуют покрытие Л, т. е. Л = 33^
а
2) если 31 а П не пусто, то отображение
^М'ШАЧНШАЧ)
есть Сг-отображение некоторого открытого подмножества Rn на
открытое подмножество Rn (рис. 4).
Каждое -II., есть локально-координатная окрестность в том
смысле, что в ней определены локальные координаты х'1, а =
= 1, ..., п, заданные отображением фа [т. е. если p^.°Ua, то
координатами точки р являются координаты точки ф-Др)^ R,n}.
Условие (2) требует, чтобы в пересечении двух координатных
окрестностей координаты одной окрестности были функциями
класса Сг координат другой окрестности, и наоборот.
Какой-либо другой атлас называется совместным с данным
Сг-атласом, если их объединение есть атлас класса Сг для всего
многообразия Л. Атлас, состоящий из всех атласов, совместных
с данным, называется полным атласом многообразия. Таким об-
разом, полный атлас есть множество всех возможных систем
координат, покрывающих Л. Топология в Л определяется тре-
бованием, чтобы все открытые множества Л состояли из объеди-
нений множества вида принадлежащих полному атласу.
В такой топологии каждое отображение фа становится гомео-
морфизмом.
Определение дифференцируемого многообразия класса Сг
с краем получается заменой «/?”» на «у/?п». Тогда край мно-
гообразия Л, обозначаемый дЛ, определяется как множество
всех точек многообразия Л, образы которых при отображении фа
лежат на границе области у/?п в Rn. дЛ представляет собой
(п— 1)-мерное многообразие без края.
Эти определения могут показаться излишне сложными, од-
нако простые примеры показывают, что описание пространства
2.1. Многообразия
21
единственной координатной окрестностью, вообще говоря, невоз-
можно. Очевидно, двумерная евклидова плоскость, R2, является
многообразием. Декартовы координаты (л, у; —со <р х < оо,
—оо < у < оо) покрывают всю плоскость как одну координат-
ную окрестность, в которой ф является тождественным отобра-
жением. Полярные координаты г, 0 покрывают координатную
окрестность (г > 0, 0 < 9 < 2л); нужны по меньшей мере две
такие координатные окрестности, чтобы покрыть R2. Двумерный
Рис. 4. Там, где кооординатные окрестности б2/а и пересекаются, коор-
динаты связаны Сг-отображением ФаОФр-1.
цилиндр С2 представляет собой многообразие, получающееся из
R2 отождествлением точек (х, у) и (х + 2л, у). Тогда (х, у) яв-
ляются координатами в окрестности (0 2л; —oo<;?/<;oo),
и, чтобы покрыть С2, нужны две такие координатные окрестно-
сти. Лист Мёбиуса является многообразием, которое получается
подобным же образом: отождествляются точки (х, у) и
(х4-2л, —у). Двумерную сферу (2-сферу) S2 единичного радиуса
можно определить как поверхность в R3, задаваемую уравнением
(х1)2 + (%2)2 + (х3)2 = 1. Тогда
х2, х3; —— 1 < х2 < 1, — 1<х3<1,
будут координатами в каждой из областей х1 > 0, х1 < 0, и по-
надобится шесть таких координатных окрестностей, чтобы по-
крыть всю сферу. В действительности S2 вообще невозможно
покрыть только одной координатной окрестностью. Аналогично,
n-мерную сферу (/г-сферу) S” можно определить как множество
точек
(х')2 + (х2)2 + ... +(х«+>)-’ = 1
в Rn+'.
22
Гл. 2. Дифференциальная геометрия
Многообразие называется ориентируемым, если в полном ат-
ласе есть такой атлас {Л,,, фа}, что в каждом непустом пересе-
чении (1 якобиан \дхфдх'>\, где х\ ..., хп п х'1, . . ., х'п —
соответственно координаты в и °U$, положителен. Примером
неориентируемого многообразия является лист Мёбиуса.
Пока мы дали самое общее определение многообразия. В боль-
шинстве случаев полезно наложить еще два условия, а именно,
что Л хаусдорфово и паракомпактно. Это гарантирует нам
обычные локальные свойства.
Топологическое пространство называется хаусдорфовым, если
оно удовлетворяет аксиоме разделения Хаусдорфа: для любых
двух различных точек р, q е Л существуют непересекающиеся
открытые множества °U, Т с Л, такие, что р е с2/, q s Т.
Ь а,
<-----------« • Г» гг
.Г4) (XI)'
b' а'
------• •-------------=*~у
(У~Уь)-----------------------------(У = О)
Рис. 5. Пример нехаусдорфова многообразия. Эти две линии отождествлены
при х = у < 0. Однако точки а (х = 0) и а' (у — 0) не отождествлены.
Нельзя считать, что всякое многообразие — непременно хаусдор-
фово. Рассмотрим, например, ситуацию, изображенную на рис. 5.
На двух прямых отождествим те и только те точки b и Ъ', для
которых хь — уь, < 0. Тогда любая точка содержится в некото-
рой (координатной) окрестности, гомеоморфной открытому под-
множеству в R1. Однако не существует непересекающихся от-
крытых окрестностей °U, Т, удовлетворяющих условию а е °U,
а' е Т, где а — точка х = 0 и а' — точка у — 0.
Атлас фа} называют локально-конечным, если для лю-
бой точки р е Л найдется открытая окрестность, которая пере-
секается лишь с конечным числом множеств °Ua. Л называют
паракомпактным, если для любого атласа [Ua, Фа} существует
локально-конечный атлас {Ур, фр}, каждое Та которого содер-
жится в некотором <2/а. Связное хаусдорфово многообразие па-
ракомпактно тогда и только тогда, когда оно обладает счетным
базисом, т. е. существует такая счетная система открытых мно-
жеств, что любое открытое множество можно представить как
объединение множеств из этой системы ([91], р. 271).
Если не оговаривается иное, все рассматриваемые далее мно-
гообразия предполагаются паракомпактными связными хаусдор-
2.2. Векторы и тензоры
3
Новыми многообразиями класса С°° без края. Позднее мы уви-
дим, что при наделении Л дополнительной структурой (о суще-
ствовании аффинной связности см. разд. 2.4) требование пара-
компактности выполняется автоматически в силу прочих огра-
ничений.
Функция f на (^-многообразии Л есть отображение из Л
в У?1. Говорят, что она класса Cr (г k) в точке р е Л, если ее
представление в некоторой локально-координатной
окрестности CU., есть функция класса Ст ((Хфункция) локаль-
ных координат точки р\ f называется Сг-функцией на множестве
f с Л, если f есть О-функция в каждой точке р еТ.
В дальнейшем мы воспользуемся следующим свойством па-
ракомпактных многообразий (см. [91], р. 272). Пусть {74,, ф,,}—
любой локально-конечный атлас на паракомпактном (^-много-
образии; всегда можно найти систему функций ga класса Ck,
таких, что
1) 0 X ga. 1 на Л при любом а;
2) носитель ga, т. е. замыкание множества {ре
3= 0}, содержится в соответствующем
3) У ga (р) = 1 для всех р е Л.
а
Такую систему функций будем называть разложением еди-
ницы. Этот результат справедлив, в частности, для функций
класса С°°, но он, очевидно, не имеет места для аналитических
функций (аналитическую функцию можно представить в виде
сходящегося степенного ряда в некоторой окрестности каждой
точки р е Л, причем если она равна нулю в некоторой открытой
окрестности, то она равна нулю всюду).
Наконец, прямое произведение .X X & многообразий .X, 3
есть многообразие со структурой, которая естественным образом
определяется структурой Л и для произвольных точек р^Л,
q 3 существуют координатные окрестности Л, Т, содержащие
соответственно р и q, такие, что точка (р,д)^Л/(3 содер-
жится в координатной окрестности ЛУЛ"1 Л/^3 и имеет
в ней координаты (хг, у^, где X — координаты р в и yi — ко-
ординаты q в Т.
2.2. Векторы и тензоры
Тензорные поля представляют собой множество геометриче-
ских объектов на многообразии, которые определяются есте-
ственным образом структурой многообразия. Тензорное поле
эквивалентно заданию тензора в каждой точке многообразия.
Поэтому в первую очередь мы определим тензоры в точке много
образия. а начнем с основного понятия вектора в точке.
24
Г л. 2. Дифференциальная геометрия
Кривая Х(0 класса Ch, или, короче, Сй-кривая на Ж, есть
отображение класса С'1 некоторого интервала вещественной пря-
мой R1 в Ж. Вектор (контравариантный вектор) {dldt\ , каса-
тельный к С4-кривой Х(0 в точке Ц/q), есть оператор, который
ставит в соответствие каждой С’-функции f в X(fo) число
(dfldf)K |;. Иначе говоря, (dfldt)y, есть производная f в направле-
нии по параметру t\
(#), I, = lim Т « + s»~f (W- (2- D
\ Ot /К It s -»0 s
Сам параметр t вдоль кривой, очевидно, удовлетворяет соотно-
шению (d/dt)rf = 1.
Пусть (х1, ..., хп)—локальные координаты в некоторой
окрестности точки щ тогда
/ д[ \ _V1 (Л ВР д[ I _____________ dH df I
At dxJ Lu dz дх! I <f/
(Здесь и повсюду в книге мы пользуемся правилом суммирова-
ния, согласно которому по повторяющемуся индексу подразуме-
вается суммирование по всем значениям этого индекса.) Таким
образом, любой касательный вектор в точке р можно предста-
вить в виде линейной комбинации производных по координатам.
Обратно, пусть дана линейная комбинация Vi(didxi) |р, где Vi —
какие-то числа; рассмотрим кривую Х(£), определяемую уравне-
нием хЦЩ)) = х3'(р) + tV} для t из некоторого интервала
[—е, е]; тогда касательным вектором в этой кривой точке р яв-
ляется Vi(d/dxi)P. Следовательно, касательные векторы в р об-
разуют векторное пространство над R\ натянутое на координат-
ные производные (d/dxi)\P; структура векторного пространства
задана соотношением
(aX + ₽Y)f = a(Xf) + ₽(Yf),
справедливым для всех векторов X, Y, чисел а, |3 и функций f.
Векторы (д/дх^р линейно независимы. (Допустим, что они за-
висимы, т. е. существуют числа Vi, не все равные нулю, такие,
что Vi(d/dxj) |р = 0; тогда, применив это соотношение к каждой
координате, мы получим равенство
= у* = о
дх'
т. е. противоречие.) Таким образом, пространство всех касатель-
ных к Ж в точке р векторов, обозначаемое ТР(Ж) или просто Тр,
есть и-мерное векторное пространство. Это пространство, пред-
ставляющее собой множество всех направлений в р, называется
2.2. Векторы и тензоры
25
касательным к Я векторным пространством в р. Можно пред-
ставлять себе вектор V е Тр в виде стрелки в р, направленной
здоль кривой А.(/), т. е. вдоль касательного вектора V в то чке р;
зри этом «длина» V зависит от выбора параметра t вдолзь кри-
зой и определяется соотношением V (ф) — 1. [Жирным шрифтом
отмечено, что V — оператор; его компоненты V-* и V (/) — р> езуль-
гат действия V на функцию f, — являются числами и печат-аются
курсивом.]
Пусть {Еа} (а = 1, ..., п)—какая-либо совокупность п ли-
нейно независимых векторов в точке р. Тогда любой изектор
V е Тр можно записать в виде V = УаЕа, где числа {Va } суть
компоненты V относительно базиса {Еа} векторов в р. (В ч астно-
:ти, в качестве {Еа} можно выбрать координатный базис (д/фдхф р;
тогда компонентами V‘— V(хф = (dx*)di) \ р будут произвводные
координат xi в направлении V.)
Линейная форма*) (ковариантный вектор) ю в р есть веще-
ственная линейная функция на пространстве Тр. Число, кюторое
линейная форма ю ставит в соответствие вектору X в тоочке р,
будем записывать в виде (ю, X); тогда из линейности следует,
что при всех а, р е R1 и X, Y е Тр выполняется равенство
<<о, аХ + 0Y) = а <<о, X) ф- 0 (о, Y).
Подпространство в Тр, определяемое при заданной лижзейной
форме ю уравнением (о, X) = const, линейно. Поэтому . линей-
ную форму в точке р можно представлять себе как пару гилоско-
стей в Тр, таких, что вектор X лежит в одной плоскости, если
(w, X) = 0, и касается концом другой, если (со, X) = 1.
Пусть дан базис {Еа} векторов в р; тогда можно построить
такую единственную систему {Е“} из п линейных форм, щто ли-
нейная форма Е; отображает любой вектор X в число Ж* (i-ю
компоненту X относительно базиса {Еа}). При этом, в частности,
(Еа, Еь) — 6%. Определив линейные комбинации линейны: х форм
равенством
(а® + 0П, X) = а (о), Х> + 0 (п, X)
для любых линейных форм w, q и произвольных а, е R1,
X е Тр, можно рассматривать {Е“} как базис для литейных
форм, ибо любую линейную форму можно записать в виде
© = coiE, где со; = (ю, Ег). Таким образом, множество всех ли-
нейных форм в точке р образует n-мерное векторное простран-
ство Т*р, дуальное касательному пространству. Базис литейных
*) В оригинале «one-form» (1-форма). Мы пользуемся здесь бо1лее при-
вычным термином «линейная форма», по после введения на стр. 30 термина
ър-форма.-», мы тоже будем называть линейную форму 1-формой. — Прим,
перев.
26 Гл. 2. Дифференциальная геометрия
форм {Еа} есть базис, дуальный базису векторов {Еа}. Для лю-
бых (о е Т*р, Х^Тр число (о, X) можно выразить через компо-
ненты Ыг и X’ в дуальных базисах {Еа}, {Еа}:
<<0, = ГЕ/) = ®Х
Любая функция f на Л определяет в р линейную форму df
по правилу: для произвольного вектора X
<df, X) = Xf.
df называется дифференциалом f. Пусть х1, ..., хп — локальные
координаты; совокупность дифференциалов (dx1, dx2, . .., dx”)
в точке р образует базис линейных форм, дуальный базису век-
торов (д/дх1, б/бх2...д)дхп) в р, поскольку
(dxf, д[дх!} = = 6‘,.
дх‘
Дифференциал df произвольной функции f записывается в этом
базисе в виде
J £ df А I
df ——7- dx .
дх
Если df ф 0, поверхности f = const являются (п— 1)-мерными
многообразиями. Множество всех векторов X, для которых
<^df, X) = 0, образует подпространство Тр, состоящее из всех
векторов, которые касательны в точке р к кривым, лежащим на
поверхности f = const. Следовательно, df можно рассматривать
как нормаль к поверхности f = const в р. Если а =И= 0, то adt
также будет нормалью к этой поверхности.
Из пространства Тр векторов ври пространства Т*р линей-
ных форм в р мы можем образовать прямое произведение
Пг = ЛхЛХ ХЕР х ТрХТрХ ... х Тр,
г сомножителей s сомножителей
т. е. упорядоченное множество векторов и линейных форм
(т]1, ..., т/, YJ, где Y — произвольный вектор, т] — про-
извольная линейная форма.
Тензор типа (г, s) в точке р есть функция на Пр, линейная
по каждому из аргументов. Пусть Т — тензор типа (г, s) в р;
он ставит в соответствие элементу (л1, Лг, Y1( ..., Ys) про-
странства Пр число, которое запишем в виде
Пг, Y1( .... УЛ
2.2. Векторы и тензоры
27
Тогда линейность означает, что
ГСП1....«Х + pY, Y2..........Ys) =
= а-7’« ...» X, Y2) .... Ys) +
+ ₽• W, .... Пг, Y, Y2, Ys)
при любых а, ре/?’ и X, Y e Tp.
Пространство всех таких тензоров называется тензорным
произведением
Trs (р) = ТР® ... ®ТР®ГР® ... ®ГР.
г сомножителей s сомножителей
В частности, Т\(р) = Тр и Т®(р) — 'Г*р.
Сложение тензоров типа (г, s) определяется следующим обра-
зом: (Т + Т') есть тензор типа (г, s) в точке р, такой," что для
произвольных Y; е Тр, е 1*р
(Т + Т')№, ..., if, Y„ ..., Ys) =
= ..., rf, Yb ..., Ys) + r(n', if, Yl_______Ys).
Аналогично определяется умножение тензора на скаляр а: аТ есть
тензор, такой, что для любых Y, е Тр, ту е Т*р
аТ(п', Ч2, Y„ ..., Ys) = a-T(n‘, .... rf, Y„ Ys).
В сочетании с этими правилами сложения и умножения тензор-
ное произведение Trs(p) является векторным пространством раз-
мерности nr+s над R1.
Пусть X, е Тр (Z = I, ..., г) и о е Г„ (/ = I, . .., s). Тогда
мы будем обозначать через Х[ ® ... ®Хг®(о'® ... ® (0s такой
элемент из Trs (р), который ставит в соответствие элементу
(ч', ..., rf, Yi, ..., Ys) из Пг число
К х,><П2, х2) . •. (пг, хг><0)', Y,) ... W, Y,}.
Аналогично, если ReTs(p) и Ss7''"(p), будем обозначать
через R®S такой элемент пространства ТР+з(р), который ста-
вит в соответствие элементу (г)1...rf, Yb ..., Ys+<7) из Пр+,
число
•••. 4s, Y1; ..., Yr)S(qs+1, ..., ns4 Yr+„ ..., Yr+p).
Тензорные пространства в p вместе с операцией умножения ®
образуют алгебру над R1.
Если {ЕД {Е«} — дуальные базисы соответственно в Тр
и Т*р, то
{Eaj® ... ®Ea(.® E6‘ ® ... ® E6s}, at, bj—X, ..., п,
28
Гл. 2. Дифференциальная геометрия
будет базисом в Trs (р). Произвольный тензор Т <=Trs(p) можно
записать в этом базисе как
Т = Г',"\ . Е ® ® Е g Е&>® . . . ®еЧ
... Ds аГ
где 7,ai---ar& ь —компоненты Т относительно дуальных бази
еоч (Е„), (Е“): '
„...“’'(Е'1. Е“'. Е,,, .... E(j).
Соотношения тензорной алгебры в р можно написать для ком-
понент тензоров:
(т _1_ т'\а\ аг _та1---аг д_т/а1’--вг
^a'-arbi,„b=a-T^-arbt_ b-,
(T®T')a'---a^+ph . =T^---ar T'ar+i‘"ar+p '
V 1 bf- bs + q bi---bs bs+t...bs + (j
Обычно мы будем представлять тензорные соотношения именно
в такой записи ввиду ее удобства.
Если {Еа'} и {Еа} —другая пара дуальных базисов в^и Т*р,
их элементы можно записать в базисах {EJ, {е“} в виде
Еа- = Фа-аЕа, (2.2}
Еа' = Ф\Еа, (2.3)
где Фа-а и Ф“а — несингулярные матрицы яХп. Поскольку
{ЕЛ, {ЕЛ — дуальные базисы,
6Ь'а' = (еЛ Еа-> = (ф^Е6, Фа'“Еа) = ФЛФЬ'ьд? = ФЛФЬ'а,
т. е. ФЛ, Фа а — взаимно-обратные матрицы и 6ab = Ф^Ф6 ь-
а ...а
Компонентами Т ] г , , тензора Т относительно дуаль-
1 s
НЫХ базисов {Еа'}, {Еа} являются
, = р(е“1, ..., е“г Е,, ...,Е,\
b ... b I ’ ’ ь, ь I
Г S \ 1 S/
Они связаны с компонентами pai---arb .ь относительно бази-
сов {Еа}, {Е°} соотношением
, = Га1-аг ф< ... ф< ф ?• ... ф (2.4)
Ь, ... b b, ... b a a b Ь
\ s 1 s 1 г 1 s
Свертка тензора Т типа (г, s) с компонентами ТаЬdef... g
относительно базисов {Еа}, {Ев} по первому контравариантному
2.2. Векторы и тензоры
29
и первому ковариантному индексам есть по определению тен-
зор С'(Т) типа (г — 1, s — 1), компоненты которого относительно
тех же базисов равны ТаЬ daf... g, т. е.
C\(T) = Tab-daf ...gEb® ... ®Ed®Ef® ... ®Ег.
Если {Еа-}, {Еа} — другая пара базисов, то определяемая ею
свертка равна
С'} (Т) = Г*'6'-•d'a7'...g'E6'® ... ®Е^®ЕГ® ... ®Eg' =
= ••• Ф<АЛ ... Фвг-Еб® ...
... ®Ed®E?® ... ®Ег =
= Tab--daf...gEb® ... ®Ed®Ef® ... ®Eg = C;(T),
так что свертка тензора С} не зависит от базиса, использован-
ного при ее определении. Подобным же образом можно сверты-
вать Т по любой паре контравариантных и ковариантных индек-
сов. (Если бы мы свернули по двум контравариантным или по
двум ковариантным индексам, то полученный тензор зависел бы
от базиса.)
Симметричная часть тензора Т типа (2,0) есть тензор
S(T)(m, П2) = 4-<Г^’ Ъ) + Т(ъ, П1)}
при произвольных т][, г)2 е Т*р. Будем обозначать компоненты
3(Т)аЬ этого тензора через Т<аЪ'1; тогда
Аналогично, компоненты антисимметричной части Т будем обо-
значать через
Вообще для обозначения компонент симметричной или антисим-
метричной части тензора по данной совокупности ковариантных
или контравариантных индексов мы будем заключать эти индек-
сы в круглые или квадратные скобки. Так,
Т(а, ... аг) f = yj-{сумма по всем перестановкам индексов
at, ..., аг в Tai... ab "f}
и
^[“i ••• аг} = уг{альтернированная сумма по всем переста-
новкам индексов alt .... аг В Та{ ... аЬ f}
30
Гл. 2. Дифференциальная геометрия
Например,
- 4 {Kabcd + K°dbc + Kacdb - Kabdc - Kacbd - Kadcb}.
Тензор симметричен по данной совокупности контравариантных
или ковариантных индексов, если он равен своей симметричной
части по этим индексам, и антисимметричен, если он равен своей
антисимметричной части. Так, например, тензор Т типа (0,2)
симметричен, если ТаЬ ~ -% (ТаЬ -ф ТЬа); это свойство иначе можно
выразить равенством Т[аь] — 0.
Особый интерес представляют тензоры типа (0, q), антисим-
метричные по всем q индексам (при этом необходимо q^n')\
такой тензор называется q-формой. Если А и В соответственно
р- и 7-формы, можно из них построить (р -ф q) -форму А А В,
где А означает антисимметризованное тензорное произведение
®; иначе говоря, А Л В есть тензор типа (0, р -ф q) с компонен-
тами
(А А В)а _ bc ,,.f~ ^[а ... Ь^с ... р-
Из этого следует, что АЛВ=(—1)р^(ВЛА). Пространство
внешних форм (т. е. пространство всех р-форм при всех р, вклю-
чая линейные формы в качестве 1-форм и скаляры в качестве
0-форм) вместе с операцией умножения образуют грассманову
алгебру (внешних) форм. Пусть {Е“}— базис линейных форм;
тогда формы Ea> Д ... Д Еар (а{ = 1, .... п) образуют базис
р-форм, поскольку любая р-форма А может быть представлена
в виде А = Аа ... ьЕ“ Л ... Л Е6, где Аа ... ь = А[а ... Ь].
До сих пор мы рассматривали тензоры, определенные в не-
которой фиксированной точке многообразия. Система локальных
координат {А} на открытом множестве к Ж задает базис век-
торов {(д!дх1)\р} и базис линейных форм (1-форм {(dA)|p}),
а следовательно, и базис тензоров типа (г, s) в каждой точке 01.
Такой базис тензоров называется координатным базисом. По
определению мы имеем тензорное поле Т типа (г, s) класса Ch
(тензорное Ск-поле) на множестве ТслЖ, если в каждой точке р
множества У задан элемент пространства Trs(p}> такой, что ком-
поненты Т относительно любого координатного базиса, опреде-
ленного на У, являются функциями класса Ck.
Вообще говоря, в использовании координатного базиса тен-
зоров нет необходимости: вовсе не обязательно, чтобы на У для
заданного базиса векторов {ЕД и дуального ему базиса линей-
ных форм {Е“} нашлось такое открытое подмножество, в кото-
ром существовали бы локальные координаты {л;а}, удовлетво-
ряющие условию Еа = д/дха и Е“ — dxa. Однако использование
координатного базиса приводит к некоторым упрощениям, в част-
2.3. Отображение многообразий
31
ности,для любой функции f выполняется соотношение Ea(Ebf)~
= Eb(Eaf), эквивалентное равенству д2Цдхадхъ — d2f/dxbdxa.
При переходе от координатного базиса Еа — д/дха к координат-
ному базису Еа’ = д!дха' в силу (2.2) и (2.3) имеем
Ясно, что базис общего вида {Еа} можно получить из коорди-
натного базиса {djdx1-}, задав функции Еа1, компоненты Еа
в базисе {d/dv'}; тогда (2.2) и (2.3) запишутся соответственно
в виде Еа = Е'ад1дх1 и En — Eaidxl, причем матрица Eat дуальна
матрице Е„.
2.3. Отображение многообразий
В этом параграфе, пользуясь общим понятием отображения
(^-многообразия, мы дадим определение понятий вложения, по-
гружения и индуцированного отображения тензоров. Первые два
из них будут полезны позднее при рассмотрении подмногообра-
зий, а третье играет важную роль при исследовании поведения
семейств кривых и при установлении свойств симметрии много-
образий.
Отображение ф из «-мерного (^-многообразия Л в «'-мерное
(^'-многообразие называется отображением класса Сг или
О’-отображением (г k, r^fe'), если для каких-либо локаль-
ных координатных систем в Л и Л’ координаты точки-образа
е Л' суть Сг-функции координат точки ре Л. Поскольку
такое отображение, вообще говоря, не является взаимно одно-
значным (например, оно не может быть таковым, если «>«'),
то в общем случае оно не имеет обратного. Даже, если некото-
рое Сг-отображение имеет обратное, то последнее, вообще го-
воря, не будет класса Ст (пусть, например, ф есть отображение
Я1-*#1, устанавливающее соответствие х—>х3; тогда ф~1 недиф-
ференцируемо в точке х — 0).
Пусть f — функция на Л'. Отображение ф задает на Л функ-
цию ф*, значением которой в точке р является значение f в точ-
ке ф(р), т. е.
= (2.5)
Таким образом, когда ф отображает точки из Л в Л’, ф* линей-
но отображает функции из Л' в Л.
Если Х(()—кривая, проходящая через точку р<=Л, то кри-
вая ^>(Л(()) в Л', на которую отображается Л((), проходит через
точку Ф(р). При г 1 касательный вектор к этой кривой! в точ-
ке ф(р) будем обозначать как ф* (d/dt) Д ф ( ; его можно рассма-
тривать как образ вектора (d/dt)}\p при отображении ф.
32
Г.i. 2. Дифференциальная геометрия
Очевидно, <£* есть линейное отображение из ТР(Ж) в Тф [р) (Ж').
Из (2.5) и определения вектора как производной по направле-
нию следует, что отображение векторов </>* можно охарактеризо-
вать соотношением
x(Olp==-M(J)U
для каждой Сг-функции (г 1) в точке ф(р) и вектора X в р.
Используя отображение векторов <£* из Ж в Ж', можно при
т 2^ 1 определить линейное отображение 1-форм ф* изТ*ф(Р) (Ж')
в Т*р (Ж), требуя, чтобы свертка вектора и 1-формы при этих
отображениях сохранялась. Тогда 1-форма А е Т*ф (Р> отобра-
жается в 1-форму <£*А е Т*р, причем для произвольного век-
тора X е Тр имеем
{ф*Ь, Х>|р = <А, ФХ)\ф{рУ
Следствием этого является равенство
</►* (df) = d (</>*/). (2.7)
Отображениям ф* и ф* можно придать более широкий смысл
отображений контравариантных тензоров из Ж в Ж' и ковари-
антных тензоров из Ж' в Ж соответственно, если задать следую-
щие правила:
Фгт ^т°г(р)->фд ^НШрУр
ф*:Т^Гй (</>(p))->^TeT°s(p),
причем для любого г\1^Т*ф(Р')
т(Ф^...,Ф*у)\р = ф,тм........
и для любого
П(хи...,хд = тхн...,^дд(р).
При г 1 говорят, что (^-отображение ф из Ж в Ж' имеет
ранг s в точке р, если размерность ф*(Тр(Ж)) равна s. Оно на-
зывается инъективным в р, если s = п (и, следовательно, п^п')
в р\ тогда в Тр нет вектора, который обращается отображением
ф* в нуль, ф» называется сюръективным, если s = п' (и, следова-
тельно, п п').
(^•отображение ф (г 0) называют погружением, если оно
и обратное ему отображение локально также являются Сг-отоб-
ражениями, т. е. если у каждой точки р Ж существует такая
ее окрестность °U, что обратное отображение ф~1, ограниченное
на ф(°Ы), тоже принадлежит классу Сг. Это означает, что п^2п'.
В силу теоремы о неявной функции ([161], р. 41), при 1 ф
тогда и только тогда будет погружением, когда оно инъективно
в каждой точке р е Ж\ в этом случае ф„ есть изоморфизм Тр на
2.3. Отображение многообразий
33
его образ ф„(Тр) с: ТФ(Р). В этом случае говорят, что образ ф(Л)
является «-мерным погруженным подмногообразием в Л'. Это
подмногообразие может иметь самопересечения, т. е. ф может не
быть взаимно-однозначным, если ограничиться малой окрест-
ностью в Л'.
Погружение является вложением, если оно представляет со-
бой гомеоморфизм на свой образ по индуцированной топологии.
Таким образом, вложение есть взаимно-однозначное погружение;
Рис. 6. Взаимно однозначное погружение Р1 в R2, не являющееся вложе-
нием. Оно получено гладким присоединением части кривой у = sin (1/%)
к кривой {(у, 0); — со < у < 1}.
однако не всякое взаимно-однозначное погружение есть вложе-
ние, см., например, рис. 6. Отображение ф называется собствен-
ным, если образ любого компактного множества У£ сг Л' при
обратном отображении (Ж) компактен. Можно показать, что
собственное взаимно-однозначное погружение есть вложение.
Образ ф{Л} многообразия Л при отображении ф называется
п-мерным вложенным подмногообразием Л'.
Отображение из Л в Л' называют Сг-диффеоморфизмом,
если оно является взаимно-однозначным Сг-отображением и об-
ратное отображение ф~1 есть С'-отображение из Л' в Л. В этом
случае п — п' и при г~^г-1 ф одновременно и инъективно, и сюръ-
ективно. Обратно, из теоремы о неявной функции следует, что
если ф* и инъективно, и сюръективно в точке р, то р имеет от-
крытую окрестность °U, такую, что ф:Л -> ф(^1) есть диффео-
морфизм. Таким образом, ф есть локальный диффеоморфизм в
окрестности р, если ф.„ является изоморфизмом из Тр в ТФ(Р).
2 Заказ 381
34
Гл. 2. Дифференциальная геометрия
Если отображение ф является (/-диффеоморфизмом (г^1),
то ф* отображает ТР(Л() в Тцп](.ТС) и (Ф~‘) отображает Г‘р(./А)
в Т*ф(р)(Л'). Следовательно, мы можем определить отображе-
ние ф* пространства Trs (р) в Trs (ф (р)) при любых (г, s) равенством
Ttf......rf, Х„ .... Хг)|р =
= Ф*т ((</>-')* < . . , (</>-')* VIs, ^Х1, • • •, ФЛ) \фМ,
где Хг е Тр и г\’'е^'Гр произвольны. Это отображение тензоров
типа (г, s) на М в тензоры типа (г, s) на М' сохраняет симмет-
рии и соотношения тензорной алгебры; например, свертка фЛТ
равна отображению ф* свертки Т.
2.4. Внешнее дифференцирование и производная Ли
Теперь нам предстоит рассмотреть три дифференциальных
оператора на многообразии, два из которых полностью опреде-
ляются структурой многообразия, а определение третьего
(разд. 2.5) связано с введением дополнительной структуры.
Оператор внешнего дифференцирования d линейно отобра-
жает поле r-формы в поле (г + 1)-формы. Его действие на поле
0-формы (т. е. на функцию) f дает поле 1-формы df по правилу
(ср. с разд. 2.2):
(df,X) = Xf (2.8)
для всех векторных полей X; действие d на поле г-формы
А = АаЬ... d dxa Д dxb Д ... Ad/
дает поле (г + 1)-формы dA:
dA = dAab... d A dxa A dx6 A A dxd. (2.9)
Чтобы убедиться, что это поле (г + 1)-формы не зависит от вы-
бора координат {ха}, использованных при его определении, рас-
смотрим другую систему координат {№'}. Тогда
А = Aa'v ,,.d' dxa' A dxb' A • • dxd',
где
Л _ дха дхъ dxd „
Л а’Ъ' ... d' а, ь, • • d, Aab ... d~
дх дх dx
2.4. Внешнее дифференцирование
35
Следовательно, (г + 1)-формой dA, определяемой этими коор-
динатами, является
dA = dAa-i' ...d' dxa' Д d?' Д ... Д dxd’ =
= d (-r^ tv- • • • Aab ••• Л dxa'л dx'6'л • • dx"' =
\ dx dx" dx /
- Adx“' да?' л ... A dxd' +
dxa dx dxa
/)2 а ъ b д d
+ -4^— ^Aab...d dx?' Д dxa' A dx1?' Д... л dxd'+
dx dx dx dxa
= dAab... d Д dxa Д dxb A ... A dxd
ввиду симметрии д2ха!дха' дх?' и антисимметрии dx?' Д dxa' по
а' и е'. Отметим, что такое определение подходит только для
внешних форм: оно не будет независимым от выбора координат,
если внешнее умножение Л заменить тензорным произведением.
Используя равенство d (fg) — gdf + fdg, справедливое для про-
извольных функций f, g, для любых r-формы А и 1-формы В
получим, что d(A Л В) = dA Л В + (—l)rAAdB. Согласно
(2.8), локально-координатное выражение df имеет вид df —
= (df/dx^dx^, отсюда следует, что d(df) = (d2f/dxidx^)dxi Л
д Ах1 = 0, поскольку первый множитель симметричен, а второй
антисимметричен. Аналогично, из (2.9) следует, что
d(dA) = 0
для любого поля r-формы А.
Оператор d коммутирует с отображениями многообразия в
следующем смысле: пусть $-.Я -> Л' есть Сг-отображение (г^2)
и А — некоторое С^-поле внешней формы (А Зд 2) на Я’\ тогда,
согласно (2.7),
d (^>*А) = </•* (dA)
(что эквивалентно правилу дифференцирования сложных функ-
ций) .
Оператор d естественным образом появляется в общей фор-
мулировке теоремы Стокса на многообразии. Сначала мы опре-
делим интегрирование n-формы. Пусть Л — компактное ориен-
тируемое n-мерное многообразие с границей дЯ и пусть {fa} —
разложение единицы для конечного ориентированного атласа
Тогда интеграл по Я поля n-формы А на Я опреде-
ляется как
$а = £ $ М12 .„d.r'd.r ... d.A, (2.10)
м а *a(^a)
2*
36
Гл. 2. Дифференциальная геометрия
где Л12... п — компоненты А относительно локальных координат в
координатной окрестности °Urx, а интегралы в правой части — это
обычные кратные интегралы по открытым множествам фа.(аИа')
в Rn. Таким образом интегрирование га-формы по Л сводится
к отображению формы в Rn (путем введения локальных коорди-
нат) и обычному кратному интегрированию в Rn\ существова-
ние разложения единицы гарантирует глобальную справедли-
вость этой операции.
Интеграл (2.10) является хорошо определенной величиной,
поскольку, выбирая другой атлас {Тр, фр} и разложение еди-
ницы {gp} для этого атласа, мы получили бы интеграл
Е S ёЛт ...nAxV ••• d^'-
где х'1' — соответствующие локальные координаты. Из сравнения
этих двух величин в пересечении П координатных окрест-
ностей, принадлежащих двум атласам, видно, что первую из них
можно представить в виде
ЕЕ 5 1а8&А12...пйх]йх2 ... dx",
« 15 ^а(^аПГр)
а вторую в виде
ЕЕ 5 UA2'...„'d*''d*2' ixn'-
а ₽ Ч’р^аПГр)
В силу законов преобразования n-формы А и кратных ин-
тегралов в Rn эти выражения равны в окрестности любой точки,
и, следовательно, А не зависит от выбора атласа и разложе-
м
ния единицы.
Подобным же образом можно показать, что этот интеграл ин-
вариантен относительно диффеоморфизмов: если ф есть ^-диф-
феоморфизм (г 1) из Л в Л', то
= 5 А.
М' м
Обобщенную теорему Стокса можно сформулировать теперь
с помощью оператора d следующим образом: пусть В — поле
(п — 1)-формы на Л, тогда
В = п dB,
ЗМ <М
2.4. Внешнее дифференцирование
37
в чем можно убедиться (см., например, [161]), используя данные
выше определения; по существу мы получили общую формули-
ровку этой фундаментальной теоремы анализа. Чтобы выпол-
нить интегрирование в левой части, нужно задать ориентацию
границы дЛ многообразия Л. Это делается следующим обра-
зом. Пусть — такая координатная окрестность из ориентиро-
ванного атласа многообразия Л, что °ил пересекает дЛ\ тогда,
согласно определению дЛ, фл(Ша П dj?) лежит в плоскости
х1 — 0 в Rn и Фа^а П Л) лежит в нижней половине х1 0.
Координаты (х2, х3, ..., хп) являются тогда ориентированными
координатами в окрестности ‘З/д П дЛ границы дЛ. Можно убе-
диться, что таким путем получается ориентированный атлас
на дЛ.
Структурой многообразия естественным образом опреде-
ляется другой вид дифференцирования — производная Ли. Рас-
смотрим произвольное векторное Сг-поле (rljs 1) X на Л.
Согласно фундаментальной теореме для систем обыкновен-
ных дифференциальных уравнений [18], через каждую точку
р е Л проходит единственная максимальная кривая %(/), такая,
что 2,(0) = р и ее касательный вектор в точке Х(0 есть вектор
Пусть {лч} — локальные координаты, так что кривая Х(/)
имеет координаты х’(0, а вектор X — компоненты X1. Тогда ло-
кально эта кривая есть решение системы дифференциальных
уравнений
dx'/d/ = Х‘ (х' (I), ..хп(/)).
Эта кривая называется интегральной кривой векторного поля X
с начальной точкой р. Для каждой точки q^-Л найдется ее от-
крытая окрестность °U и е > 0, такие, что X задает семейство
диффеоморфизмов фрЛ1 -> Л, если |/|< е, которые получаются
переносом каждой точки на параметрическое расстояние t
вдоль интегральных кривых X. В самом деле, отображения ф(1)
образуют однопараметрическую локальную группу диффеомор-
физмов, поскольку <фt+s Ф± Фз=ФзОф1 ДЛЯ |/l, |5|, П + «1<
<8, так что ф-л~(ф^ *» а ф0 есть единица группы. Этот
диффеоморфизм отображает в <^*Т | (р) в точке р любое тензор-
ное поле Т типа (г, s).
По определению производная Ли Т тензорного поля Т от-
носительно X есть взятое с обратным знаком значение в точке
t = 0 производной семейства тензоров Ф^Л | по t, т. е.
Из свойств </>* следует
1) Lx сохраняет тип тензора, т. е. если Т — тензорное поле
типа (г, $), то LxT — тензорное поле того же типа;
38
Гл. 2. Дифференциальная геометрия
2) Лх — линейное отображение и сохраняет свертку.
Можно доказать, что как и в обычном анализе справедливо
правило Лейбница;
3) для произвольных тензоров S, Т Lx (S ® Т) = LXS ® Т ф-
+ S ® ТХТ.
Из предыдущих определений непосредственно следует
4) Lxf = Xf, где f — любая функция. При отображении
точка q = Ф-tip) отображается в р. Поэтому есть отображе-
ние из Тд в Тр. Следовательно, в силу (2.6)
В локальных координатах {%'}, введенных в окрестности точ-
ки р, координаты компоненты $t*Y в р равны
\Р = № \Рxi = yi \<, ттлу!
х > / ip ip W дх‘ (</) дх‘ (q)
Поскольку
dx1 _ „г .
dt “Л 'W
TO
d Гдх{(ф{(д))\ __ dX‘
d/ \ dxTq) ) t = o dxi p'
и, следовательно,
P Л = - ^ I. - -> X’ -^Y>. (2.11)
Для любых С2-функций f последнее равенство можно переписать
в виде
(LxY)f = X(Yf)-Y(Xf).
Иногда мы будем обозначать LxY через [X, Y], т. е.
Z.XY = — TYX = [X, Y] = [Y, X].
Когда производная Ли двух векторных полей X, Y равна
нулю, говорят, что эти векторные поля коммутируют. В этом
случае, если из точки р двигаться вдоль интегральной кривой
поля X на расстояние t (по параметру кривой), а потом вдоль
интегральной кривой Y на расстояние s, то конечная точка будет
той же, как при движении сначала на расстояние s вдоль инте-
гральной кривой Y, а затем на расстояние I вдоль интегральной
кривой X (см. рис. 7). Таким образом, множество всех точек,
которых можно достичь, двигаясь из данной точки р вдоль инте-
гральных кривых X и Y, образует погруженное двумерное под-
многообразие, содержащее р.
2.4. Внешнее дифференцирование
39
Компоненты производной Ли 1-формы о можно получить
сверткой равенства
Lx (о ® Y) = Lx® ® Y 4- со ® LxY
[свойство (3) производной Ли]; в результате имеем
Lx («), Y) = (Lx<o, Y) + (co, LxY)
[по свойству (2) производной Ли], где X, Y — произвольные век-
торные С4-поля. Выбирая в качестве Y базисный вектор Е; =
Рис. 7. Преобразования, порождаемые коммутирующими векторными по-
лями X, Y, переводят точку р соответственно в точки 0zx(p), 0sY (₽)•
= djdx\ получим, что координатные компоненты равны
, - (да. X , (дл’ \
(Lx<>>)i = I —— ) X1 + ®/ ( —— ),
\ dXj ) \дх1 J
поскольку из (2.11) следует, что
k laxUJ дх1
Аналогично, применяя правило Лейбница к выражению
Lx (Т ® Е" ® ... ® Erf ® Ее ® ... ® Eg)
и затем свертывая по всем индексам, можно найти координат-
ные компоненты производной Ли любого тензорного С'-поля
40
Гл. 2. Дифференциальная геометрия
Т типа (г, s); они равны
(W)ab-de/...g
... d
ef
дх1
(2.12)
В силу (2.7) любая производная Ли коммутирует с d, т. е.
для любого поля р-формы ю
d (Lxft>) = Ах (do).
Как из этих формул, так и из их геометрической интерпрета-
ции вытекает, что производная Ли АхТр тензорного поля Т типа
(г, s) зависит от направления векторного поля X не только в
точке р, но и в соседних точках.
Таким образом, введенные нами два дифференциальных опе-
ратора, определяемые структурой многообразия, имеют слишком
ограниченный характер для того, чтобы служить обобщением
понятия частной производной, которое необходимо для задания
уравнения полей физических величин на многообразиях. В са-
мом деле, d действует только на внешние формы, а производная
Ли отличается от обычной частной производной тем, что послед-
няя (как производная по направлению) зависит только от на-
правления в рассматриваемой точке. Нужное нам обобщение
производной — ковариантную производную — можно получить
при введении на многообразии дополнительной структуры. Это
будет сделано в следующем параграфе.
2.5. Ковариантная производная и тензор кривизны
Дополнительная структура, которую мы введем, — это (аф-
финная) связность на JI. Связность V в точке р е Л есть пра-
вило, по которому любому векторному полю X ставится в точке р
в соответствие дифференциальный оператор Vx, который отобра-
жает произвольное векторное Сг-поле (г 1) в векторное поле
VXY и обладает следующими свойствами:
1) VxY есть тензор по аргументу X, т. е. для произвольных
функций f, g и векторных С'-полей X, Y, Z
Vfx+gYZ = fVxZ + gVYZ
(это эквивалентно условию зависимости Vx только от направле-
ния X в р);
2) VXY линейно по Y, т. е.
Vx(aY + pZ) = aVxY + pVxZ
для любых векторных (Д-полей Y, Z и a, f; е
2.5. Ковариантная производная
41
3) для любой О-функции f и векторного О-поля Y
Vx(/Y) = XfY + /VxY.
При выполнении всех этих условий Vx У есть ковариантная про-
изводная (относительно связности V) векторного поля Y в на-
правлении X в точке р. Согласно условию (1), ковариантную
производную векторного поля Y можно определить как такое
тензорное поле типа (1, I), которое при свертке с X дает вектор
VXY. Тогда имеем
3) OV(fY) = df ® Y+fVY.
Связность V класса Сг (Сг-связность) на ^-многообразии
(k г + 2) есть правило, по которому в каждой точке задается
связность V, такая, что, если Y — векторное Сг+1-поле на аХ, то
VY — тензорное Сг-поле.
Пусть в некоторой окрестности °U даны произвольный базис
С'+1-векторов {Еа} и дуальный базис 1-форм {Е“}; будем запи-
сывать компоненты VY как Уа-ь, тогда
= Еа.
На связность задают я3 Сг-функций Г%С) определяемые ра-
венствами
Г%с = (Еа, VEftEc)OVEc = Г%СЕ& ® Еа.
Для любого векторного С'-поля Y
VY = V (ГЕ.) = dYc 8 Е. + УТ%.ЕЬ 8 Еа.
Таким образом, компонентами VY относительно координатных
базисов {д/дха} и {dx6} являются
уа ___ dYa ।
1 -,ь — —у + 1 ь?У •
Трансформационные свойства функций ГаЬс задаются свойствами
связности (1) —(3):
Га'ь,с, = <Еа', Ve^Ec') = <Фа'аЕа, V®y6Es (Ф/Е.)) =
= фа аф/ (еь (ф/) + ф/ПД
поскольку Еа/=Фа“Еа, Еа =ФааЕа. Это равенство можно пе-
реписать в виде
= фД (ЕУ (ф/) + фДф/ГД).
В частности, если базисами являются координатные базисы, оп-
ределяемые координатами {ха}, {ха'}, закон преобразования
42
Гл, 2. Дифференциальная геометрия
имеет вид
Га' ___ дха' С д2ха , дхь дхс \
-1 Ь'С' _ п I h' л с' • h' л с’ ЬС I *
дха \ дх° дх дх дх /
Из-за члена Еь- (ФС'а) функции ГаЬс не преобразуются как ком-
поненты тензора. Однако если ковариантные производные VY и
VY получены с использованием двух различных связностей, то
VY - VY = (Га6с - Гabc) YcEb ® Ед
будет тензором. Таким образом, разности (Г%с — Га6с) являются
компонентами тензора.
Более широкое понятие ковариантной производной произ-
вольного тензора Сг-поля (г 1) можно ввести, задав следую-
щие правила (ср. со свойствами производной Ли):
1) если Т — тензорное Сг-поле типа (7, s), то VT — тензорное
Сг-1-поле типа (q, s -ф 1);
2) V — линейный оператор, коммутирующий со сверткой;
3) для произвольных тензорных полей S, Т выполняется пра-
вило Лейбница
V (S ® Т) = VS ® Т + S ® VT;
4) Vf = df для любой функции f.
Запишем компоненты VT в виде (^E.T}a’"d =Ta"'de...8-h-
\ « / е ... g
Согласно правилам (2) и (3), имеем
Ve„Ec = - Гс6аЕа,
где {Еа} — базис, дуальный {Еа}. Методом, аналогичным выводу
равенства (2.12), можно показать, что координатные компо-
ненты VT равны
rrdb ... d
™ab ... d Ui ef ... g I т-iCt ... d ।
1 ef ... g;h — Г 1 hjI ef ... g T
+ rVa/’-def...g+ ... +r\Ta6-/ef...g- (2.13)
т-if rr.cib ... d тп/ rpdb ... d тч/ rpab ... d
he* !f~-g 1 hji ej ... g~~ 1 hgl ef...
Интересным примером является единичный тензор E6®Ea, имею-
щий компонентами 6%; его ковариантная производная равна
нулю, и, следовательно, нулю равны также и ковариантные
производные обобщенных единичных тензоров с компонентами
s[VV--6ap4
Пусть Т —тензорное Сг-поле (г^1), заданное вдоль ^-кри-
вой Л(0; тогда можно ввести DT/й, ковариантную производ-
ную Т вдоль Л (2), как V5/5;T, где f — любое тензорное Сг-поле,
2.5. Ковариантная производная
43
расширяющее Т на некоторую открытую окрестность кривой k(t).
DT/dt является тензорным Сг-1-полем, которое определено вдоль
кривой Л. (О и не зависит от расширения Т. Пусть X — касатель-
ный вектор к Л. (/), тогда в записи через компоненты имеем
Y)Ta de... s/dt = Та de,.. ,g; hXh. В частности, можно выбрать
такие локальные координаты, в которых координаты кривой Л(/)
равны xa(t), Ха = d,ve/d/, и тогда для векторного поля
Y)Ya/dt = dYa/dt + YabcYc d?/dt (2.14)
Говорят, что тензор Т параллельно переносится вдоль кри-
вой Y, если DT/dl = 0. Пусть дана кривая a(Z) с концами в точ-
ках р и q, тогда из теории обыкновенных дифференциальных
уравнений при условии, что связность V — по меньшей мере
класса С1-, следует единственность тензора, получаемого в точ-
ке q параллельным переносом вдоль кривой л(^) тензора, задан-
ного в точке р. Таким образом, параллельный перенос вдоль К
есть линейное отображение из Trs (р) в Trs(q), сохраняющее все
тензорные произведения и тензорные свертки. В частности, из
этого следует, что параллельный перенос базиса векторов вдоль
данной кривой из р в q задает изоморфизм из Тр в Тд. (Если
у кривой есть самопересечения, то р и q могут быть одной и той
же точкой.)
Важное понятие возникает при рассмотрении ковариантной
производной вдоль К самого касательного вектора. Кривая Х(0
называется геодезической кривой, если вектор
^Х“4(4)Л
параллелен вектору (d/W)?., т. е. если найдется такая функция f
(возможно, равная нулю), что Ха-, ьХь — fXa. В этом случае
можно ввести новый параметр v (t) вдоль кривой, так что будет
выполняться равенство
— ( —) =. 0
dv \dvh
Такой параметр называется аффинным параметром. Связанный
с ним касательный вектор V — (d/dv)\ параллелен X, но мас-
штаб определяется условием К(ц)= 1; V подчиняется уравне-
ниям
Va.bvb + у- °;- =0, (2.15)
’ Gt>2 'ОС dy ’ х ’
причем второе (локально-координатное) выражение получается
применением (2.14) к вектору V. Аффинный параметр геодези-
ческой кривой определен с точностью до аддитивной и мульти-
пликативной постоянных, т. е. с точностью до преобразования
44
Гл. 2. Дифференциальная геометрия
v' = av + b, где а, b — постоянные; свобода в выборе b соответ-
ствует свободе выбора новой начальной точки 7.(0), свобода в
выборе а — возможности перенормировки масштаба вектора V
умножением на постоянную: V/ = (l/a)V. Будем называть гео-
дезическую кривую просто геодезической, если эта кривая па-
раметризуется каким-либо аффинным параметром.
Пусть задана Сг-связность (гГ^гО); тогда из известных тео-
рем для обыкновенных дифференциальных уравнений следует,
что для любой точки р е Л и для любого вектора Хр в р суще-
ствует максимальная геодезическая 7.x (v) в Л с начальной точ-
кой р и начальным направлением Хр, т. е. Кх(0)=р и
(d/dv)%| г-=0 ~ Хр. Если г 1, то эта геодезическая единственна
и ее зависимость от р и ХР непрерывна. Это означает, что при
г 1 можно определить такое Сг-отображение еху.ТрЛ, что
для каждого Хе Тр, ехр(Х) есть точка в Л, находящаяся на
единичном расстоянии по параметру вдоль геодезической 7.х,
начинающейся в р. Это отображение не обязательно определено
для всех Хе7'я, поскольку геодезическая 7.x (и) может не быть
определена для всех и. Если же v может принимать все значе-
ния, то говорят, что геодезическая Xx(v)—полная. Многообра-
зие Л называется геодезически полным, если все геодезические
на Л полны, т. е. если отображение ехр определено на всем про-
странстве Тр каждой точки р е Л.
Независимо от того, полно или нет многообразие Л, отобра-
жение ехрр имеет ранг п в р. Поэтому в силу теоремы о неявной
функции [161] существует открытая окрестность Дф начала в ТР
и открытая окрестность ДД точки р е Л, такие, что ехр есть
Сг-диффеоморфизм Д’о на Л’р. Такая окрестность Л’р назы-
вается нормальной окрестностью точки р. Далее, Л’р можно счи-
тать выпуклой, т. е. такой, что всякая точка q е Л’р может быть
соединена с любой другой точкой геодезической, начи-
нающейся в q и целиком лежащей в Л’р. Внутри выпуклой нор-
мальной окрестности Д’ координаты (х1, ..., хп) можно ввести
следующим образом: выбираем какую-либо точку q е Д’, базис
{Еа} в Тч и координаты точки геД’ задаем соотношением
г = ехр (л:“Ео) (т. е. точке г приписываем координаты в базисе
{Еа} точки exp-I(r)e Тд). Тогда (д/дх{)\д=Е{ и, согласно
(2.15), Г* (Ik) —0- Такие координаты называются нормальными,
координатами с началом в q. Герок [55] использовал существова-
ние нормальных окрестностей для доказательства наличия счет-
ного базиса у связного хаусдорфова С3-многообразия с С-связ-
ностью. Таким образом паракомпактность С3-многообразия можно
связать с существованием на нем С'-связности. «Нормальное»
локальное поведение геодезических в этих окрестностях контра-
стирует с поведением геодезических в большом в общем случае,
2 5. Ковариантная производная 45
когда, с одной стороны, две произвольные точки, вообще говоря,
не могут быть соединены какой-либо геодезической, а, с другой,
некоторые геодезические, исходящие из одной точки, могут со-
браться как фокусе в некоторой другой точке. Позднее мы столк-
немся с примерами и того и другого поведения.
Если задана С'-связность V, то равенство
Т (X, Y) = VXY - VYX - [X, Y]
определяет некоторое тензорное С',-1-поле типа (1, 2), где X,
Y — произвольные векторные Сг-поля. Такой тензор называется
тензором кручения. В координатном базисе его компоненты
равны
mi ___-pi т-н
1 Ik — A & — 1 £/•
Мы будем иметь дело лишь со связностями без кручения-, иначе
говоря, мы предполагаем, что Т = 0. В этом случае координат-
ные компоненты связности удовлетворяют условию — Г1^-,
и поэтому такую связность часто называют симметричной. Связ-
ность тогда и только тогда является связностью без кручения,
когда f-:ij = f-л Для всех функций f. Из уравнения геодезической
(2.15) следует, что связность без кручения полностью опреде-
ляется заданием геодезических на Л.
В отсутствие кручения ковариантные производные произволь-
ных векторных О-полей связаны с их производными Ли соотно-
шением
[X, Y] = VxY -VYX^(LxY)a ~Ya-bXb - Xa-bYb, (2.16)
а для любого тензорного С’-поля Т типа (г, s)
/ т m\ab «•« d __rpCib ... d vh mlb •«. d xrci
x^xJ ) ef...g— ef g',hX 1 ef... gX ;/ ‘
mdj .d xrb rpdb ... / -trd t
— / ef ... gA / ef...gA ;/ +
+ mob ... d vr/ । mob ... d у/ । t mcib d -yi
* !f-..gX-e + l ei.<.gX-f + ... +1
(2.17)
Легко проверить также, что внешняя производная связана с ко-
вариантной следующим образом:
dA=4...c;dd/Adx*A ... Adx^(dA)e...c</ = (-l)pAra...c;dJ,
где А — произвольная р-форма. Таким образом, уравнения, со-
держащие внешнюю производную или производную Ли, всегда
можно выразить через ковариантную производную. Однако в
силу своих определений производная Ли и внешняя производная
не зависят от связности.
46
Гл. 2. Дифференциальная геометрия
Если вектор X,., из данной точки р перенести параллельно
вдоль некоторой замкнутой кривой у снова в ту же точку р, то
получится вектор Хр, вообще говоря, отличный от X,.,; если вы-
брать другую кривую у', то полученный при этом новый вектор
в р будет, вообще говоря, отличен от ХР и от Х'р. Эта неинтегри-
руемость параллельного переноса соответствует тому, что кова-
риантные производные в общем случае не коммутируют. Меру
этой некоммутативности дает тензор (кривизны) Римана. Пусть
даны векторные Сг+1-поля X, Y, Z, а векторное Сг-1-поле R(X, Y) Z
определено Сг-связностью V следующим образом:
R (X, Y) Z = Vx (VYZ) - V¥ (VxZ) - V[x, yjZ. (2.18)
Тогда поле R(X, Y)Z линейно no X, Y, Z, и можно убедиться,
что значение R(X, Y)Z в р зависит только от значений X, Y, Z
в р, т. е. R(X, Y) Z есть тензорное Сг '-поле типа (3, 1). Чтобы
записать (2.18) в компонентах, определим вторую ковариантную
производную VVZ вектора Z как ковариантную производную
V (VZ) тензора VZ; ее компоненты равны
Z®c = (Za®;c.
Тогда (2.18) можно записать в виде
RabcdXcYdZb = (Za-,dYd).c Xе - (Za-dXd).c Yc -
- Za-d (Yd-cXc - X\fYc) = (Za.,dc - Za.cd) XcYd,
где компоненты тензора Римана Rabcd относительно дуальных
базисов {Еа} и {Еа} определяются как Rabcd = (Еа, R(EC, Ed)Eb).
Поскольку X, Y — произвольные векторы, равенство
Za-dc — Za-<cd —RabcdZb (2.19)
выражает некоммутативность вторых ковариантных производ-
ных Z через тензор Римана.
Поскольку для любых векторных С2-полей X, Y, Z и любого
С2-поля 1-формы т; выполняется равенство
Vx (fl ® VyZ) = Vxi) ® VyZ 4- Ц ® VxVyZ (тр VXVYZ) =
= X«n, VYZ»-(Vxn, VyZ),
то из (2.18) следует, что
(Ea, R(EC, Ed)E6) = Ec((Ea, VErfE6)) - Ed ((Ea, V^E*))-
-<VEEa, VErfEft) + (VEX, VEcb)-(E*, V[Ec. Ed]E4
Выбрав в качестве {Ea}, {Ea} координатные базисы, можно вы-
разить координатные компоненты тензора Римана через коор-
2.6. Метрика
47
динатные компоненты связности:
Rabed = + г (2.20)
Пользуясь этими определениями, можно убедиться, что кроме
симметрии
R bcd~ R bdc^e^R b(cd) == 0 (2.21 а)
тензор кривизны обладает также симметрией вида
R^bcdi ^0^Rabed + Radbe + Racdb = 0. (2.216)
Подобным же образом можно убедиться, что первые ковариант-
ные производные тензора Римана удовлетворяют тождествам
Бианки-.
Rab\cd-,e} = 0^Rabcd-,e + Rabec.d + R^de'.c = 0. (2.22)
Теперь мы видим, что параллельный перенос произвольного
вектора вдоль произвольной замкнутой кривой локально инте-
грируем (т. е. Хр необходимо совпадает с Хр в каждой р^Л),
только если Rai,cd — 0 во всех точках в этом случае мы гово-
рим, что связность плоская. Свертывая тензор кривизны, можно
определить тензор Риччи как тензор типа (0, 2) с компонентами
Rbd — Rabad-
2.6. Метрика
Метрический тензор g в точке р е Л есть симметричный тен-
зор типа (0, 2) в р, так что Сг-метрика на Л есть Сг-поле сим-
метричного тензора g. Метрика g приписывает каждому век-
тору Xsy, его «длину» |g(X, X) р и задает «косинус угла»
g(X,Y)
( I g (X, X) g (Y, Y) I P
между любыми двумя векторами X, Ye Тр, для которых
g(X, X) g(Y, Y) =/= 0. Будем говорить, что векторы X, Y ортого-
нальны, если g(X, Y) = 0.
Компонентами g относительно базиса {Еа} являются
gab = g<Ea, Eb) = g(£b, Ee),
т. е. компоненты g равны просто скалярным произведениям ба-
зисных векторов Еа. Если пользоваться координатным базисом,
то а
g = ® <Б?. (2.23)
Длины касательного пространства, определяемые метрикой,
связаны с длинами на многообразии следующим образом. Длина
пути между точками р = у(а) и q — y(b) вдоль кривой у(/)
48
Гл. 2. Дифференциальная геометрия
класса С°, кусочно класса С1, с касательным вектором d/dt, та-
ким, что g(djdt, d/dt) имеет один знак во всех точках у(0> равна
ь
L =^\g (d/dt, д/dt) \'l2dt. (2.24)
a
Выражения (2.23), (2.24) можно символически представить в
форме
ds2 — gtj dx1 dx!,
используемой в классических руководствах для выражения дли-
ны «бесконечно малой» дуги, задаваемой смещением координат
х{ -> х* + dx1.
Метрика называется невырожденной, если не существует та-
кого ненулевого .вектора для которого g(X, Y) = О при
всех Y е= Тр. В терминах компонент метрика не вырождена, если
матрица (gab) из компонент g неособенна. Далее мы всегда бу-
дем предполагать, что метрический тензор не вырожден. Тогда
соотношением
gabgbe =
мы можем однозначно определить симметричный тензор типа
(2,0) с компонентами gab относительно базиса {Еа}, дуального
к базису {Е“}. Иначе говоря, матрица (gab) тоже неособенна, и
тензоры gab, gab можно использовать для установления изомор-
физма между любым ковариантным тензорным аргументом и
любым контравариантным аргументом, иначе говоря, для «под-
нятия» и «опускания индексов». Таким образом, если Ха— ком-
поненты контравариантного вектора, ему однозначным образом
сопоставляется ковариантный вектор с компонентами Ха, причем
Ха = gabXb, Ха = gabXb. Аналогично, тензору Таъ типа (0, 2) мы
можем однозначно сопоставить тензоры Таъ~gacTcb, Ta=gbcTac,
Tab — gacgbdTcd. Вообще мы будем рассматривать подобные
взаимосвязанные ковариантные и контравариантные тензоры как
различные представления одного и того же геометрического объ-
екта; в частности, gab, 8аь и gab можно считать представлениями
(относительно дуальных базисов) одного и того же геометриче-
ского объекта g. Однако в некоторых случаях, когда мы будем
иметь дело более чем с одной метрикой, нужно будет тщательно
различать, какая из метрик используется для поднятия или опу-
скания индексов.
Сигнатура g в точке р есть число, равное разности числа по-
ложительных и числа отрицательных собственных значений мат-
рицы (gab) в р. Если метрика g не вырождена и непрерывна, то
сигнатура постоянна на ЛС Подходящим выбором базиса {Еа}
компоненты метрического тензора в любой точке р можно при-
2.6. Метрика
49
вести к виду-
gab = diag(+1, +1, • +1, -1, -1, , -1),
(п + s)/2 членов (п — s)/2 членов
где s — сигнатура g, п— размерность Л. В этом случае базис-
ные векторы {Еа} образуют ортонормированную систему в р,
т. е. каждый из них есть единичный вектор, ортогональный ко
всем остальным базисным векторам.
Метрика, сигнатура которой равна п, называется положи-
тельно определенной-, для такой метрики g(X, X) = 0 => X = О,
а ее каноническая форма имеет вид
gab = diag(+1, +!)
п членов
Положительно определенная метрика является «метрикой» в
пространстве в топологическом смысле этого слова.
Метрика с сигнатурой, равной п— 2, называется лоренцевой
метрикой; ее каноническая форма:
gab = diag (+1, ..+1, -1).
(n— 1) членов
Если Л наделено лоренцевой метрикой, нулевые векторы в
р<=Л можно разделить на три класса: вектор ХеГ- назы-
вается времениподобным, изотропным или пространственноподоб-
ным в зависимости от того, отрицателен, равен нулю или поло-
жителен скалярный квадрат g(X, X). Изотропные векторы обра-
зуют в Т-р двухполостный конус, отделяющий времениподобные
векторы от пространственноподобных (рис. 8). Если X, Y — ка-
кие-либо два непространственноподобных (т. е. времениподобных
или изотропных) вектора, лежащие в одной и той же полости
изотропного конуса точки р, то g(X, Y) <Д 0, причем равенство
имеет место, только когда X и Y — параллельные изотропные
векторы [т. е. при X — aY, g(X, X) = 0].
Любое паракомпактное Сг-многообразие допускает положи-
тельно определенную Сг-,-метрику (т. е. такая метрика опреде-
лена на всем Л). Чтобы убедиться в этом, возьмем разложение
единицы {/yj для локально-конечного атласа {°иа, фа}. Тогда g
можно задать равенством
g(x, Y) = Ef,W.x,
а
где ( , ) — естественное скалярное произведение в евклидовом
пространстве Rn; таким образом атлас используется для задания
метрики путем отображения евклидовой метрики в Л. Ясно, что
50
Гл. 2. Дифференциальная геометрия
такое введение метрики неинвариантно относительно изменения
атласа и, следовательно, на JI имеется много подобных положи-
тельно определенных метрик.
В противоположность этому паракомпактное Сг-многообразие
допускает лоренцеву Сг-1-метрику тогда и только тогда, когда
Времениподобные
векторы (внутри
изотропных
конусов)
Изотропный конус
Гиперплоскость,
натянутая на
Рис. 8. Изотропные конусы, определяемые лоренцевой метрикой.
Изотропный конус
Изотропные векторы
(на изотропных конусах)
Пространственноподобные
векторы (вне изотропных
конусов )
оно допускает неисчезающее С',-1-поле линейных элементов; под
полем линейных элементов подразумевается сопоставление каж-
дой точке р е Л пары равных и противоположно направленных
векторов (X, -X), т. е. поле линейных элементов подобно век-
торному полю, но не имеет определенного знака. Чтобы убе-
диться в этом, введем на многообразии положительно опреде-
ленную Сг-1-метрику g. Тогда в каждой точке р можно следую-
щим образом определить лоренцеву метрику g:
g(Y, Z) = g(Y, Z) —2 Z)~’
2.6. Метрика
51
где X — один из векторов пары (X, —X) в р. (Отметим, что X
появляется в этом выражении четное число раз, и поэтому
несущественно, подставлять X или —X.) Очевидно, g(X, Х) =
— — g(X, X), и если Y, Z — ортогональны к X относительно g,
то они ортогональны к X также относительно g, причем
g(y, Z) = g(Y, Z). Следовательно, ортонормированный относи-
тельно g базис будет ортонормированный и относительно g.
Поскольку метрика g не единственна, то на Ж имеется множе-
ство лоренцевых метрик, если есть хотя бы одна. Обратно, пусть
дана лоренцева метрика g; рассмотрим уравнениеgabXb = ),gabXb,
где g — какая-либо положительно определенная метрика. При
этом получим одно отрицательное и (п— 1) положительных соб-
ственных чисел А. Поле собственного вектора X, соответствую-
щего отрицательному собственному значению, будет локально
определено с точностью до знака нормирующего множителя; его
можно нормировать, наложив условия gabXaXb = —1, и полу-
чить таким образом поле линейных элементов на Ж.
В действительности любое некомпактное многообразие допу-
скает поле линейных элементов, а чтобы такое поле допускало
компактное многообразие, необходимо и достаточно, чтобы ха-
рактеристика Эйлера многообразия равнялась нулю (т. е. тор Т2
допускает, а сфера S2 не допускает поле линейных элементов).
Позднее будет установлено, что многообразие может быть раз-
умной моделью пространства-времени, только если оно неком-
пактно и в силу этого на нем существует множество лоренцевых
метрик.
До сих пор мы рассматривали метрический тензор и связ-
ность как две не зависимые друг от друга структуры на Ж.
Однако при заданной метрике g на Ж имеется единственная
связность без кручения, для которой ковариантная производ-
ная g равна нулю, т. е.
= 0- (2-25)
При этой связности параллельный перенос векторов сохраняет
скалярное произведение, задаваемое метрикой g; поэтому, в
частности, длины векторов инвариантны. Например, если d/dt~
вектор, касательный к геодезической, то вдоль этой геодезиче-
ской g(d/dt, d/dt) = const.
Из (2.25) следует, что для производных векторных С’-по-
лей X, Y, Z
X(g(J, Z)) = Vx(g(Y, Z)) = Vxg(Y, Z) + g(VxY, Z)+
+ g(Y, VxZ) = g(VxY, Z) + g(Y, VXZ).
Складывая это выражение с аналогичным выражением для
Y(g(Z, X)) и вычитая аналогичное выражение для Z(g(X, Y)),
52
Гл. 2. Дифференциальная геометрия
получим
g(Z, VxY) = l{-Z(g(X, Y)) + K(g(Z, X)) + X(g(Y, Z)) +
+ g(Z, [X, Y]) + g(Y, [Z, X])-g(X, [Y, Z] )}•
Выбирая в качестве X, Y, Z базисные векторы, выразим компо-
ненты связности через производные компонент метрики gab =
= g(Ee, E6) и производные Ли базисных векторов:
Гй&с = £(Еа, %Ес) = ^с.
В частности, при использовании координатного базиса эти про-
изводные Ли равны нулю и получаются обычные соотношения
Кристоффеля для координатных компонент связности:
г -1 Г 1 Z99RZ
abc 2 l дхс ' dxb дха г { 2 )
Далее мы везде будем предполагать, что на Л введена эта един-
ственная Сг-1-связность без кручения, определяемая Сг-метри-
кой g. С ее помощью можно ввести нормальные координаты
(разд. 2.5), используя, например, ортонормированный базис в q.
Впредь под нормальными координатами мы будем подразуме-
вать нормальные координаты, заданные с помощью ортонорми-
рованного базиса.
Тензор Римана для связности, задаваемой метрикой, есть
Сг-2-тензор, обладающий свойством симметрии
R(ab) cd 0 Rabcd == Rbacd (2.27а)
в дополнение к симметриям (2.21). Из равенств (2.21) и (2.27а)
следует, что тензор Римана симметричен также по парам индек-
сов {а&}> {с^}'.
Rabcd ~ Rcdab- (2.276
Отсюда видно, что тензор Риччи симметричен:
Rab^Rba- (2.27в)
Свертка тензора Риччи есть по определению скалярная кри-
визна:
п__ па __ па ЛА
X i\ а X badS •
Вследствие этих симметрий Rated имеет (Vi2)ft2(fi2— 1) алге-
браически независимых компонент, где п — размерность Л. Из
них /г(п+1)/2 компонент можно выразить через компоненты
тензора Риччи. Если п = 1, то Rated = 0. При п = 2 Rated имеет
одну независимую компоненту, которая по существу совпадает
с R. При п = 3 тензор кривизны полностью определяется тензо-
ром Риччи. Если п > 3, остальные компоненты тензора кривизны
2.6. Метрика
53
можно выразить через тензор Вейля Саъс<1, определяемый равен-
ством
2 2
Сabcd R-abcd п — 2 {^a[d^c]b + gb[c^d]a} — 1) (п — 2) ^^a[cSd]b ‘
Из того, что последние два слагаемых в правой части обладают
свойствами симметрии тензора кривизны, следует, что Cabcd так-
же обладает этими свойствами. Легко убедиться, что в дополне-
ние к этому
cabad = o,
т. е. тензор Вейля — это та часть тензора кривизны, все свертки
которой равны нулю.
Иначе тензор Вейля можно охарактеризовать тем, что он яв-
ляется конформным инвариантом. Две метрики g и g назы-
ваются конформными, если можно подобрать некоторую ненуле-
вую функцию Q, такую, что
g = Q2g. (2.28)
Тогда для любых векторов X, Y, V, W в точке р
g (X, Y) ё (X, Y)
g(V, w) g(V, w) ’
т. е. углы и отношения длин при конформных преобразованиях
сохраняются; в частности, конформные преобразования сохра-
няют структуру изотропного конуса в Тр, поскольку
g (X, X) > 0, =0, < 0 g- (X, X) > 0, =0, <0
соответственно. Поскольку компоненты метрики связаны соотно-
шениями
gab = & gab, ё g ,
то координатные компоненты связностей, определяемых метри-
ками (2.28), связаны между собой равенством
Г%с = Г%с + Q"1 + С - gbcgad -^\. (2.29)
\ дх дх дх J
Вычисляя тензор Римана для g, получаем
г,аЬ —2 паЬ г Д&
R cd = Q R ed + O[CQd},
где
Qa6 = 4Q“‘ (Q-%e gae - 2 (Q"1).^ (Q~');d gcdtfb,
54
Гл. 2. Дифференциальная геометрия
причем ковариантные производные в этом уравнении взяты от-
носительно метрики g. Отсюда (при условии п > 2)
Rbd = + («- 2) Q’1(fi"1);dcg6c-(n-2)-1Q-'I(^"2);aCg“c6^
и
____ у-уО,
bed bed'
Это последнее равенство выражает тот факт, что тензор Вейля
конформно-инвариантен. Из полученных соотношений следует,
что
R = QXR — 2 (п — 1) Qr\l-cd§.cd — (гс — 1) (п — 4) Q,c^gcd. (2.30)
Расщепив тензор Римана на две части, выражаемые соответ-
ственно через тензор Риччи и тензор Вейля, можно с помощью
тождеств Бианки (2.22) получить дифференциальные соотноше-
ния между тензором Вейля и тензором Риччи; свертывая (2.22),
имеем
Rabcd-,a = Rbd\c— Rbc-.d, (2.31)
а после вторичной свертки
Rac-.a=^R-,c
Пользуясь определением тензора Вейля (при м>3), можно
переписать (2.31) в виде
Cabcd-,a = 2 2 — 2 (и- 1) ;с]) • (2.32)
Если п 4, равенство (2.31) содержит всю информацию, имею-
щуюся в тождествах Бианки (2.22) и, таким образом, при п ~ 4
соотношение (2.32) эквивалентно этим тождествам.
Диффеоморфизм ф:Л -+ Л будем называть изометрией, если
он переводит метрику в себя, иначе говоря, если отображенная
метрика ф*£ равна g в каждой точке. Тогда отображение
фд.ТР-^ТФ (р) сохраняет скалярные произведения
S (X, Y) 1„ = ф£ (ФЛ, ФХ I. (р) = g (ФХ ФХ I, (р)-
Если данная локальная однопараметрическая группа диффео-
морфизмов ф[, порожденная векторным полем К, есть группа
изометрий (т. е. при каждом t преобразование ф1 есть изомет-
рия), то К будем называть векторным полем Шиллинга. Произ-
водная Ли метрики относительно К равна нулю:
LKg = 1 im у (g - фи§) = 0,
так как g = фи§ при каждом но, согласно (2.17), LK gab = 27((a.6)
и, следовательно, векторное поле К Киллинга удовлетворяет
2.7. Гиперповерхности
55
уравнению Киллинга
Ка-ь +Кь-.а = О. (2.33)
Обратно, если К~ векторное поле, удовлетворяющее уравнению
Киллинга, то LKg~ 0 и
t i
K.S Ip = g Ip + 5 7Г №'*g) Ip df = g Ip + S i (^гЛлХ=о Ip df =
о 0
t
^1л№Лй=о1л==
0
t
= g Ip — ^r*(LKgl^r(p)) di' = S\p‘
0
Итак, для того, чтобы К было векторным полем Киллинга,
необходимо и достаточно, чтобы оно удовлетворяло уравнению
Киллинга. Тогда локально можно выбрать координаты ха —
= (х\ t) (v= п — 1), в которых Ка = dxafdt = 6а„; в этих
координатах уравнения Киллинга принимают вид
dgabldt == ОО gab = gab (xv).
В общем случае пространство не обладает какими-либо сим-
метриями и поэтому не допускает никаких векторных полей Кил-
линга. Пространства частного вида могут допускать г линейно-
независимых векторных полей Кя (а = 1, .... г). Можно пока-
зать, что совокупность всех векторных полей Киллинга на таких
пространствах образует r-мерную алгебру Ли над R, 0 г
п (n + I) (верхний предел может быть меньше, если мет-
рика вырождена), причем умножение в этой алгебре задается
скобками Ли [ , ] [см. (2.16)]. Локальная группа диффеоморфиз-
мов, порожденных этими векторными полями, есть г-мерная
группа Ли изометрий на многообразии Я. Полная группа изо-
метрий на Я может включать некоторые дискретные изометрии
(такие, как отражения в плоскости), которые не порождаются
векторными полями Киллинга; свойства симметрии пространства
целиком определяются этой полной группой изометрий.
2.7. Гиперповерхности
Пусть 9 есть (п— 1)-мерное многообразие и Q:9Я— не-
которое вложение; тогда образ 0 (9) многообразия 9 называют
гиперповерхностью в Я. Если р е 9, образ Тр в при отоб-
ражении 0* будет (п— 1)-мерной плоскостью, проходящей через
56 Г л. 2. Дифференциальная геометрия
начало. Следовательно, существует ненулевая линейная форма
n е T’stp), такая, что для любого вектора X е Тр (п, 0*Х) = 0.
Форма п единственна с точностью до знака и нормировочного
множителя, и если локально задать 0(^) уравнением f = 0, так
что df ф 0, то в качестве п можно локально взять df. Если
0(^) — двустороннее подмногообразие в Ж, то п можно выбрать
так, что полученное поле 1-формы на 0(6^) будет всюду отлично
от нуля. Это будет иметь место, если и 5К и Ж — ориентируемые
многообразия. В таком случае выбор направления п связывает
ориентации 0(^) и Ж\ пусть {%'} — такие локальные координаты
из ориентированного атласа на Ж, в которых локально уравне-
ние 0(^) имеет вид х’ = 0ип = adx1, где а > 0, тогда (х2, ...
..., хп) будут ориентированными локальными координатами
на 0(^).
Если g есть метрика на Ж, вложение индуцирует метрику
0*g на так что для X, Y е TpG*g(X., Y) |р = g(0*X, 0*Y) |е(».
Иногда эту метрику называют первой фундаментальной формой
на 5^. Если g — положительно определенная метрика, то и 0*g
будет положительно определенной. Если же g — лоренцева мет-
рика, то 0*g будет
а) лоренцевой при gabnanb > 0,
б) вырожденной при gabnanb = 0,
в) положительно определенной при gabnanb < 0.
В случае (а) гиперповерхность 0(^) называется временипо-
добной, в случае (б)—изотропной и в случае (в) простран-
ственноподобной.
Чтобы убедиться в существовании этих возможностей, рас-
смотрим вектор Nb = nagab\ он ортогонален ко всем векторам,
касательным к 0(^), т. е. ко всем векторам подпространства
Н — в*(Тр) в Ге(Р). Предположим сначала, что сам вектор N не
лежит в этом подпространстве. Тогда, если (Е2, .... Еп) обра-
зуют базис в Тр, векторы N, 0*(Е2), . . . , 0*(ЕП) линейно незави-
симы и составляют базис в Т^. Компоненты g относительно
этого базиса равны
_/g(N, N) 0 /g(N, N) 0 \
0 g(ME(.), 0t(E;.))J“l 0 0*g (Ег, Е;-) / ‘
В силу предположения о невырожденности g отсюда следует,
что g(N, N) #= 0. Если g положительно определена, то g(N, N) > 0
и, следовательно, индуцированная метрика 0*g тоже должна
быть положительно определенной. Если g лоренцева и g(N, N) =
= gabnanb < 0, то 0*g необходимо положительно определена, так
как матрица из компонент g имеет только одно отрицательное
собственное число. Аналогично, если g(N, N) = gabnanb > 0, то
0*g — лоренцева метрика. Предположим теперь, что вектор N
2.7. Гиперповерхности
57
касателен к 0 (У). Тогда найдется ненулевой вектор X <= Тр,
такой, что 0„(X) = N; но g(N, 0„Y) = 0 для всех YsJp, и, сле-
довательно, 0*g(X, Y) = 0. Таким образом, метрика 0*g вы-
рождена. Кроме того, полагая Y = X, имеем g (N, N) = gabnanb = 0.
Если gabnanb 0, нормальную линейную форму и можно
нормировать так, чтобы она имела единичную „длину", т. е.
= ± 1. В этом случае отображение 0*:7’*е (р) -> Т*р будет
однозначным в (п—1)-мерном подпространстве Я*(е, 0) простран-
ства Т*0(Р), состоящем из всех линейных форм « в ©(/?), для
которых gabnaab = 0; это следует из того, что 0*п==О и и не
лежит в Я*. Поэтому обратное отображение (0*)~' будет ото-
бражением 0, пространства Т*р на Н*е^ и, таким образом,
на Т*е<р).
Это отображение можно расширить обычным образом до
отображения ковариантных тензоров в У в ковариантные тен-
зоры в 0($?)с поскольку у нас есть отображение 0„ контра-
вариантных тензоров в в ковариантные тензоры в 0(^), мы
можем расширить 0, до отображения 0, произвольных тензоров
в 7/ в тензоры в 0 (^). Это отображение обладает тем свойством,
что свертка 0Д с п по любому индексу равна нулю, т. е.
(0Д)а-ьс...^а = о И (0j)a-6c...dgc4 = o
для любого тензора Т
Рассмотрим тензор h на 0(^), определяемый как h = 0*(0*g).
Его можно записать через нормированную линейную форму п
(напомним, что gabnanb — ±. 1) в виде
^ab '~~ gab Я ПаПь,
поскольку отсюда следует, что 0*h = 0*g и habgbctic = 0.
Тензор hab = gachcb есть оператор проектирования, т. е.
habhbe — hac. Он проектирует вектор ХеГеад на ту его часть,
которая лежит в подпространстве Н = 0ДГр) касательного к 0(^)
пространства Тв(ру.
Ха = habXb ± папьХъ,
где второе слагаемое представляет собой часть вектора X,
ортогональную к 0(^). Тензор 1гаь проектирует и линейную форму
сдеГ*е(р) на ее часть, лежащую в подпространстве Н*в(Р):
со^ h p^b _1_ сор.
58
Гл. 2. Дифференциальная геометрия
Подобным же образом можно спроектировать любой тензор
Те77(0(р)) на его часть, принадлежащую пространству
Hrs (0 (р)) = Яо (р) ® ... ® Нв (р) ® Яд <Р) ® ... ® Не (р),
г множителей s множителей
т. е. часть, ортогональную к п по всем индексам.
0* является взаимно однозначным отображением из Тр в Яе(Р>.
Поэтому отображение 0* из Теуру в Тр можно задать, проекти-
руя сначала Те{Ру на Не <Р) посредством hab и выполняя затем
обратное отображение (0)7'• Поскольку мы уже определили
отображение 0* линейных форм в 0(^), можно расширить опре-
деление 0* до отображения 0* тензоров на 0(^) любого типа в
тензоры на многообразии ПР. Это отображение обладает тем
свойством, что 0*(0Д) = Т для любого тензора ТеГДр) и
0Д0*Т) = Т для любого тензора Т е Hrs(fi{p)). Мы будем ото-
ждествлять тензоры на д’ с тензорами из Hrs на 0(^), если они
переходят друг в друга при отображениях 0„, 0*. В частности,
h можно рассматривать как индуцированную метрику на 0(Д).
Пусть и есть какое-либо расширение единичной нормали п
на некоторую открытую окрестность гиперповерхности 01Д);
тогда тензор X, определенный на 0(^) формулой
'Pai а!1 b^c-,d’
называется второй фундаментальной формой на Поскольку
проектирование с помощью hab ограничивает ковариантные про-
изводные касательными к 0(5Д направлениями, X не зависит от
способа расширения. Локально поле можно представить в виде
n = adf, где f и а —функции на JP, причем на 0(^) f — О. По-
скольку
U = U и ^ = 0,
тензор ХаЬ симметричен.
Индуцированная на метрика h — 0*g задает на 5^ связ-
ность. Ковариантное дифференцирование относительно этой связ-
ности мы будем обозначать двойной чертой ||. Для любого тен-
зора ТеЯ( справедливо равенство
Та - ьс... № = Г -Л... ... /г6М ... hldhme,
где Т — любое расширение Т на некоторую окрестность 0(^).
Это определение не зависит от выбора расширения, так как свер-
тывание с hat ограничивает ковариантное дифференцирование
направлениями, касательными к 0(^). Чтобы убедиться в пра-
27. Гиперповерхности
59
вильности приведенной формулы, достаточно показать, что ко-
вариантная производная индуцированной метрики равна нулю
и кручение отсутствует. Это следует из равенств:
hMc = + ^f\g heahfbhSc = 0
И
f _ ye ,g г = h° h4 r
h\ab n aH b‘-.eg a1 b' ;ge I ||6a'
Тензор кривизны R'abed относительно индуцированной мет-
рики можно следующим образом связать с тензором кри-
визны Rabcd на 0 (^) и второй фундаментальной формой Z. Пусть
Y е Н — векторное поле на 0(5^); тогда
p/а yb уа уа
bed1 1 ||dc 1 lied'
Имеем
Ya\\dc = (ИДС = haghldhkc =
= Ye-,tkhaehfdhkc + Ye-dn.ene.khf dhaghkc + Ye-fnfnf,khaehit}hk
и, поскольку на 0 (t?) Yene — 0,
Ye-jnehfd = (Yene).fhfd - Yene-fhfd = - Yene.}hfd.
Отсюда
R'abcdYb = (Rebkfhaehkchfd ± XbMae T Yb,
и так как это равенство справедливо для всех УеЯ, то
R'abcd = Refgtlhaehfbhgchhd ± (2.34)
Это соотношение называют уравнением Гаусса.
Свертывая это уравнение по а и с и умножая на hbd, полу-
чаем скалярную кривизну R' относительно индуцированной
метрики
R' = я + 2Rabnan1’ ± (хаау + %а\аь- (2.35)
Можно вывести иное соотношение между второй фундаменталь-
ной формой и тензором кривизны Rabed на 0(^), если из равен-
ства
Wa\b = ^a^da\ehSb
вычесть равенство
^ab\a=={nc-,dhachde\fhfaheb.
В результате получаем уравнение
^a-tfa^RepdlTb. (2.36)
называемое уравнением Кодацци.
60
Гл. 2. Дифференциальная геометрия
2.8, Элемент объема и теорема Гаусса
Пусть {Е“}-~ базис 1-форм; из него можно образовать
«-форму
е = «!Е’ Д Е2 Д ... ДЕ".
Если {Еа} — другой базис, связанный с {Еа} соотношением
Еа = ФавЕа, то е и «-форма е', определяемая базисом {Еа},
связаны равенством
е' = det (фа а) 8,
и, следовательно, эта форма не единственна. Однако наличие
метрики можно использовать для введения «-формы
I |’/2
11 = 1 £Г е,
где g = det (gOb). Компоненты этой «-формы равны
= б“д.
Согласно закону преобразования g, определитель det®ac со-
кращается при условии, что он положителен. Поэтому, если Я
ориентируемо, «-формы ц, определенные координатными бази-
сами некоторого ориентированного атласа, будут тождественны.
Иначе говоря, если задана ориентация Я, можно однозначно
определить поле n-форм ц (каноническую «-форму) на Я.
Контравариантный антисимметричный тензор
h
имеет компоненты
где s — сигнатура g (и, следовательно, число («— s)/2 равно
числу отрицательных собственных значений матрицы {gab} из
компонент метрики). Поэтому эти тензоры удовлетворяют соот-
ношениям
ilab-%ef...ft=(-l)^!6a[e66f (2.37)
Из соотношений Кристоффеля следует, что ковариантные произ-
водные т)а&. _ d и T\ab---d относительно связности, определяемой
метрикой, равны нулю, т. е.
d — 0 = n h , .
1 \е 1ао ... d',e
С помощью канонической «-формы можно определить объем (от-
носительно метрики g) «-мерного подмногообразия ^Н^-Я. как
2.8. Элемент объеме и теорема Гаусса
61
уг]. Таким образом, т| можно рассматривать как положительно
<U
определенную меру объема на Я. Мы будем часто пользоваться
ею в этом смысле, обозначая ее du. Отметим, что здесь d не
означает оператор внешнего дифференцирования; du есть про-
сто мера на Я. Если f — функция на Я, можно определить ее
интеграл по °Н относительно этой меры:
f du = ft).
<U <и
Относительно локальных ориентированных координат {хя} этот
интеграл можно представить в виде кратного интеграла
J flgpdx’dx2 ... dx",
<u
который инвариантен относительно замены координат.
Свертка векторного поля X на Я с т] будет полем 1-формы
Х-т|, причем
Эту (n—1)-форму можно интегрировать по любому (п—1)-
мерному компактному ориентируемому подмногообразию У3.
Этот интеграл запишем в виде
$ Xadaa = Jx-n,
т/>
причем мы считаем, что форма т|, являющаяся мерой на Т, опре-
деляется канонической формой daa. Если ориентация Т задана
направлением нормальной формы па, то daa можно представить
в виде nada, где da — положительно определенная мера объема
на подмногообразии Т. Пока нормаль па не нормирована, мера
объема da определена неоднозначно. При нормировке на па на
единицу по метрике g на Я, т.е. если naribgab = ±1, da стано-
вится равной мере объема на У, которую задает на У индуциро-
ванная метрика (чтобы убедиться в этом, достаточно выбрать
ортонормированный базис с nagab в качестве одного из базисных
векторов).
С помощью канонической формы из теоремы Стокса можно
вывести формулу Гаусса: для любого компактного «-мерного
подмногообразия <2/ сд Я
J X°daa= J X-ij = n Jd(X-n)-
tfU °и
62
Гл. 2. Дифференциальная геометрия
Однако
=(-1ГЧ... О"л....<*'»=
, .((г-1)-7~ (/1-S) 1
= (-D ^-ns-'“na,..dengs... ле.и =
= na..,de6sts... ^б“г]х% = ^Ч...Л>
где дважды использовано равенство (2.37). Отсюда для любого
векторного поля X
J Xadoa= J Xe,gAv\
д°и <й
это и есть теорема Гаусса. Отметим, что эта теорема справед-
лива при такой ориентации в °U, задаваемой нормальной фор-
мой т|, при которой (п, X) > 0 для вектора X, направленного
наружу <U. Если метрика g такова, что gabnanb <_ 0, вектор gabnb
направлен внутрь 7/.
2.9. Расслоенные пространства
Некоторые из геометрических свойств многообразия Ж легче
всего рассматривать, построив многообразие, называемое рас-
слоенным пространством. Локально оно представляет собой пря-
мое произведение Ж и некоторого подходящего пространства.
В этом разделе мы дадим определение расслоенного простран-
ства и рассмотрим четыре примера, которые будут полезны в
дальнейшем: касательное расслоение Т(«<), тензорное расслое-
ние Trs (Ж), расслоение линейных реперов ЦЖ} и расслоение
ортонормированных реперов О(.<).
Ск-расслоение над (^-многообразием Ж (s k) есть (^-мно-
гообразие S и сюръективное О-отображение n:S ->Ж. Много-
образие S называется пространством расслоения, Ж—базой и
л — проекцией. Там, где это не приведет к путанице, мы будем
обозначать расслоение просто через S. Вообще говоря, образ
л-1(р) точки р е Ж при обратном отображении не обязательно
гомеоморфен л-1 (q) для другой точки q е Ж. Простейший при-
мер расслоения — прямое произведение {Ж Ж, Ж, п}, я кото-
ром Ж—некоторое многообразие, а проекция л определяется
как л(р, v) = р для всех р Ж, v е Ж. Например, выбирая в
качестве Ж окружность и в качестве Ж действительную пря-
мую 7?1, мы получим прямое произведение над S1 — цилиндр С2.
Расслоение называется расслоенным пространством, если оно
локально является прямым произведением. Следовательно, рас-
2.9. Расслоенные пространства
63
слоение есть расслоенное пространство со слоем если су-
ществует такая окрестность ‘2/ каждой точки q е Л, что окрест-
ность л-1 (£?/) изоморфна °U X ST в том смысле, что для каждой
точки />£'?/ найдется диффеоморфизм <f>p точки л-1 (р) на 3^,
такой, что отображение ф, определяемое как ф (и) = (л (u),
есть диффеоморфизм ф:л_| -> °U X ST- Поскольку Л пара-
компактно, мы можем выбрать локально конечное покрытие Л
такими открытыми множествами °Ua. Если 'Т/ц и с11^ — два мно-
жества такого покрытия, отображение
есть диффеоморфизм SK на себя для каждого р е Q ^р).
Поэтому образы л-1(р) точек р^Л все необходимо диффео-
морфны (и, значит, друг другу). Например, лист Мёбиуса
есть расслоенное пространство на S1 со слоем У?1; нужны два
открытых множества °Ui, <U?.-, чтобы получить покрытие множе-
ствами вида X R1- Из этого примера видно, что многообра-
зие, являющееся локально прямым произведением двух других
многообразий, в общем случае тем не менее не будет прямым
произведением многообразий. Именно по этой причине понятие
расслоенного пространства столь полезно.
Касательное расслоение Т(Л) есть расслоенное пространство
над (^-многообразием, получающееся при наделении множества
К — J Тр естественной для него структурой многообразия и
р s М
естественной проекцией на Л. Таким образом, проекция л ото-
бражает каждую точку Тр на р. Структура многообразия на <5
определяется локальными координатами {zA} следующим обра-
зом. Пусть {/} —- локальные координаты на открытом множестве
<U ст Л. Тогда любой вектор VeT, можно представить в виде
V = V'dldx1 |р. Координатами {zA} в л_1(^/) будут {zA) = {x£, Еа}.
Если выбрано покрытие Л некоторыми координатными окрест-
ностями Ла, соответствующие карты задают Сй-1-атлас на ё",
при этом ё становится Сл~'-многообразием (п2-мерным). Чтобы
убедиться в этом, нужно только заметить, что в любом пере-
сечении сг/аП^|5 координаты {хга} некоторой точки являются
С^-функциями координат {Хр} той же точки, а компоненты {Еаа}
некоторого векторного поля будут С®-’-функциями компо-
нент {1/ар} того же поля. Тогда координаты {гла} будут
в л-1 (°Ua П С6-'-функциями координат {глр}.
Слой л~’(р) есть Тр и, следовательно, является векторны
пространством размерности п. Структура векторного пространства
64
Гл. 2 Дифференциальная геометрия
сохраняется при отображении <f>a, р:Тр--> Rn, которое определяется
как фа,р(ц) = Vaa(u), т. е. р отображает вектор в точке р
на его компоненты относительно координат {хаа}. Если {xap} —
другая система локальных координат, отображение р) о (^>р< .П1
есть линейное отображение Rn на себя и, следовательно, оно
является элементом общей линейной группы GL(n, R).
Тензорное расслоение типа (г, s) над Л, обозначаемое через
Trs{JC), определяется подобным же образом. Строим множество
s= U ^(р)> задаем проекцию л как отображение каждой
р S
точки Ts(p) на р и для любой координатной окрестности °U cz Л
вводим в л-1^) локальные координаты {zA} как {гл} =
= {х‘, Таьс... </}, где {/} — координаты точки р, {Та ьс... —
координатные компоненты Т (т. е. Т—Та "'ьс... dd/dxa ®...® dxd |р).
Этим мы превращаем <F в ^“’-многообразие размерности rtr+s+I;
любая точка и<^Т$(Л) соответствует единственному тензору Т
типа (г, $) в точке л (и).
Расслоение линейных реперов ЦЛ) есть расслоенное О-1-
пространство, определяемое следующим образом. Полное про-
странство <У состоит из всех базисов во всех точках Л, иначе
говоря, из всех множеств систем п линейно независимых нуле-
вых вектором {Е0}Еа е Тр для каждого р^Л (а — 1, ..., п).
Проекцией л является естественная проекция, отображающая
базис в точке р в саму эту точку. Пусть {х!}—локальные коор-
динаты на открытом множестве Л, тогда
{zA} = {ха, Е/, ЕД .. ., Епт],
где Ej есть /-я компонента вектора Еа в координатном ба-
зисе д)дх\ являются локальными координатами в л-1 (<U). Общая
линейная группа GL(n, R) действует на ЦЛ) следующим обра-
зом: если {Еа} — базис в р^Л, то AeGL(n,/?) отображает
и = {р, Еа} в
А{и) = {р, АаЬЕь}.
Если Л наделена метрикой g с сигнатурой з, можно ввести
подпространство расслоения ИЛ)—расслоение ортонормиро-
ванных базисов О (Л), которое состоит из ортонормированных
(относительно g) базисов во всех точках Л. На О (Л) действует
подгруппа О (у(п + з), y(n—s)} группы GL(n,R). Эта под-
группа состоит из несингулярных вещественных матриц Ааъ, удо-
влетворяющих условию
AabGbfArfc Gad>
2.9. Расслоенные пространства 65
где Gbc ~ матрица вида
diag (+ 1, + + 1, — 1, — 1, —1).
п + S п — S
—2— членов —-— членов
Матрица АаЬ отображает (р, Еа) (= О (Ж} в (р, Даг>Еь) с= О (Л\
В случае лоренцевой метрики (т. е. s = п — 2) группу O(n — 1, 1)
называют ц-мерной группой Лоренца.
Сг-сечение расслоения есть С'-отображение Ф:Ж-+$, такое,
что л ° Ф есть тождественное отображение на Ж\ таким образом,
сечение есть установление Сг-соответствия между каждой точкой
реЖ и некоторым элементом Ф(р) слоя я~1(р). Сечение каса-
тельного расслоения Т(М) есть векторное поле на Ж; сечение
Tsp/) есть тензорное поле Т(Ж) типа (г, s) на Ж; сечение ЦЖ)
есть набор п ненулевых векторных полей {Еа}, которые линейно
независимы в каждой точке; наконец, сечение О (Ж) есть набор
ортонормированных векторных полей на Ж.
Поскольку нулевые векторы и тензоры задают сечения в
Т (Ж) и Trs (Ж), эти расслоенные пространства всегда допускают
сечения. Если Ж ориентируемо и некомпактно или компактно с
характеристикой Эйлера, равной нулю, на нем будут везде суще-
ствовать ненулевые векторные поля и, следовательно, везде не-
нулевые сечения Т(Ж). Расслоения Ь(Ж) и О (Ж) могут как
допускать, так и не допускать сечений; например, L(Rn) их до-
пускает, a L(S2) —нет. Если Ь(Ж) допускает сечение, Ж назы-
вается параллелизуемым. Герок показал [55], что некомпактное
четырехмерное лоренцево многообразие Ж допускает спинорную
структуру в том и только в том случае, когда оно параллели-
зуемо.
В терминах расслоенного пространства Ь(Ж) можно дать
изящное геометрическое описание связности на Ж. Ее можно
рассматривать как правило параллельного переноса векторов
вдоль любой кривой у(Т) в Ж. Таким образом, если {Еа} есть
базис в точке р = у(/0), т. е. {р, Еа} есть точка и в Ь(Ж), то
параллельным переносом {Ея} вдоль у(/) можно однозначно по-
строить базис в любой другой точке кривой у (0, т. е. указать
единственную точку у(/) в слое л-1(у(^)). Следовательно, суще-
ствует в Ь(Ж) единственная кривая у(0. называемая лифтом
у(0, для которой
1) у(/0) = и;
2) л (у (0) = у (/);
3) базис, изображаемый точкой у(/), в Ж переносится па-
раллельно вдоль кривой у (/).
3 Заказ 381
66
Гл. 2. Дифференциальная, геометрия
В терминах локальных координат {zA} кривая у(/) записы-
вается как {xa(y(7)), при этом
dEml (i) i i dxa (у (i)) _ n
di "г m a‘ dt
Рассмотрим касательное пространство Ти(Е(Л)) к расслоен-
ному пространству Ь(Л) в точке и. Его координатным базисом
является {д/дгА | и}. n-мерное подпространство, натянутое на ка-
сательные векторы {(d/dtp щ к лифтам всех кривых, проходя-
щих через р, называется горизонтальным подпространством Ни
пространства Ти(Е(Л)). Через локальные координаты
/_а_\ _ dxa (у (/)) д . dEml д _
\ dt /у di дха di дЕт‘
_ dxa (у (i)) / д _ р jri д \
di т а1 дЕт1)'
так что координатным базисом в Ни является {д[дха —
— Ет'Г‘ajd/dEP}. Таким образом, связность в Л определяет
горизонтальные подпространства в касательном пространстве
каждой точки L(Jl\ Обратно, в Л можно ввести связность,
задав для этого в ГИ(Е(М)) при каждой иеА(,.#) п-мерное
подпространство со свойствами:
1) если А е GL (п, R1), то отображение Ти(Е(Л))->
—>• Та (и) (Р (Л)) переводит горизонтальное подпространство Ни
в На («);
2) Ни не содержит ненулевых векторов, принадлежащих
вертикальному подпространству Vu.
По определению вертикальное подпространство Vu есть
п2-мерное подпространство в TU(L(JO)), натянутое на векторы,
касательные к кривым в слое (л («)); в терминах локальных
координат Vи натянуто на векторы {д[дЕт1}. Свойство (2) озна-
чает, что Ти есть прямая сумма Ни и V и.
Проектирующее отображение л: индуцирует
сюръективное линейное отображение лд Ти(Ь(Л))->ТпыЦЛ),
такое, что л„ (’/„) = 0, а сужение л* на Ни есть взаимно одно-
значное отображение Ни на Tnw- Следовательно, л*-1 есть
линейное отображение ТпыЦЛ) на Ни. Поэтому для любого
вектора Х^.ТР{Л) и точки существует такой един-
ственный вектор X е Ни, называемый горизонтальным лифтом
вектора X, для которого лДХ) = X. Пусть даны кривая у (/)
в Л и начальная точка и в л-1(у(^0)), тогда в можно
построить единственную кривую у(/), проходящую через и,
касательный вектор которой есть горизонтальный лифт каса-
тельного вектора кривой у (/). Таким образом, зная горизонталь-
ные подпространства в каждой точке можно определить
2.9. Расслоенные пространства
67
параллельное перенесение базисов вдоль любой кривой у (?) в Л.
Затем можно определить ковариантные производные вдоль кри-
вой у (/) для любого тензорного поля Т как обыкновенные про-
изводные по t компонент Т относительно параллельно перене-
сенного базиса.
Если на Л введена метрика, ковариантная производная ко-
торой равна нулю, то ортонормированность параллельно перено-
симых реперов сохраняется. Следовательно, горизонтальные под-
пространства касательны к О(Л')^ИЛ) и задают связность
в О(Л\
Аналогично, через параллельный перенос векторов и тензо-
ров связность на Л задает «-мерные горизонтальные подпро-
странства в касательных пространствах к расслоениям Т(Л) и
ТГ3(Л). Координатными базисами этих горизонтальных подпро-
странств являются соответственно
____verf д •>
W ае dVf J
И
{"йх5--" ьс... dVaef + (и т- Д- для каждого нижнего индекса)—
— Та ” bf... dTfec — (и т. д. для каждого верхнего индекса)
у___________________________________________________д 1
дТа-Ьс... J'
Как и в случае ЦЛ), л„ взаимно однозначно отображает эти
горизонтальные подпространства в 7’л:(и)(М). Таким образом,
снова можно обратить л, так, чтобы для любого вектора
ХеГЯ(1|) получить единственный горизонтальный лифт Xs'^.
В частном случае Т (Л) единственному вектору W Тп (и) (Л)
соответствует сама точка и и, следовательно, в Т (Л) связностью
внутренним образом определено горизонтальное векторное
поле W; в локальных координатах {ха, У6}
Это векторное поле можно интерпретировать следующим обра-
зом: его интегральная кривая, проходящая через и = (р, X) е
Т(Л), есть горизонтальный лифт той геодезической в Л, ка-
сательный вектор которой в р есть X. Значит, векторное поле W
представляет все геодезические в Л. В частности, семейство
всех геодезических, проходящих через р^Л, есть семейство ин-
тегральных кривых W, проходящих через слой лы1 (р) с Т(Л);
кривые в Л имеют пересечения по крайней мере в р, а кривые
в Т (Л) нигде не пересекаются.
3*
Глава 3
Общая теория относительности
Чтобы понять появление сингулярностей и возможное круше-
ние общей теории относительности, нам важно иметь точную
формулировку этой теории и установить, в какой степени она
единственна. Поэтому мы представим теорию в виде нескольких
постулатов, касающихся математической модели пространства-
времени.
В разд. 3.1 мы введем эту математическую модель, а в
разд. 3.2 сформулируем первые два постулата — локальной при-
чинности и локального сохранения энергии. Эти постулаты яв-
ляются общими и для специальной и для общей теорий относи-
тельности, и поэтому можно считать, что они экспериментально
обоснованы теми опытами, которые проводились для проверки
специальной теории относительности. В разд. 3.3 мы выведем из
лагранжиана уравнения материальных (т. е. негравитационных)
полей и получим из него тензор энергии-импульса.
Третий постулат, определяющий уравнения поля, приведен
в разд. 3.4. Экспериментально он обоснован не так хорошо, как
первые два, но, как мы увидим позднее, любые иные уравнения
приводили бы по крайней мере к одному или даже нескольким
нежелательным следствиям или же требовали существования
дополнительных полей, которые экспериментально не обнару-
жены.
3.1. Пространственно-временное многообразие
Математическая модель пространства-времени (т. е. совокуп-
ности всех событий), которой мы будем пользоваться, есть пара
(_#, g), где Л— связное четырехмерное хаусдорфово С°°-много-
образие, g—лоренцева метрика (т.е. метрика сигнатуры + 2)
на Л.
Две модели (Л, g) и (Ж, g') будем считать эквивалентны-
ми, если они изометричны, иначе говоря, если существует диф-
феоморфизм Ъ'.Л -> Л'', который переводит метрику g в метри-
ку g', т. е. 0*g = g'. Тогда, строго говоря, моделью простран-
ства-времени является не просто одна пара (Л, g), а весь класс
эквивалентности пар (Ж, gz), эквивалентных (Л, g). Обычно
мы будем иметь дело только с одним представителем (Л, g)
3.1. Пространственно-временное многообразие 69
данного класса эквивалентности, но тот факт, что эта пара опре-
делена лишь с точностью до эквивалентности, важен в некото-
рых ситуациях, в частности при рассмотрении задачи Коши
в гл. 7.
Многообразие берется связным, поскольку нам недоступна
никакая информация относительно несвязных частей. Мы счи-
таем его хаусдорфовым, поскольку это, по-видимому, согласуется
с накопленным опытом. Однако в гл. 5 мы рассмотрим пример,
в котором можно поступиться этим условием. Вместе с условием
лоренцевости метрики условие хаусдорфовости означает, что Я
паракомпактно [55].
Понятие многообразия естественным образом отвечает нашим
интуитивным представлениям о непрерывности пространства и
времени. К настоящему времени такая непрерывность установ-
лена до расстояний порядка 10~15 см экспериментами по рассея-
нию пионов [49]. Наверное, будет трудно распространить понятие
непрерывности до много меньших расстояний, поскольку для
этого понадобится частица такой большой энергии, что родится
несколько других частиц, и они исказят эксперимент. Возможно
поэтому, что модель, в которой пространство-время рассматри-
вается как многообразие, неприемлема для расстояний меньше
10-15 см, и нам следовало бы пользоваться такой теорией, в ко-
торой в таких масштабах пространство-время обладает какой-то
иной структурой. Однако можно ожидать, что подобные откло-
нения от описания пространства-времени как многообразия не
повлияют на общую теорию относительности до тех пор, пока
характерный гравитационный масштаб длины не станет такого
же порядка. Это могло бы случиться лишь при плотности по-
рядка I058 г/см3, т. е. в таких предельных состояниях вещества,
относительно которых в настоящее время ничего не известно.
Тем не менее, рассматривая пространство-время как многообра-
зие и делая определенные разумные предположения, мы пока-
жем в гл. 8—10, что какое-то нарушение общей теории относи-
тельности должно иметь место. Им могли бы быть или несостоя-
тельность уравнений поля, или необходимость квантования мет-
рики, или нарушение структуры многообразия.
Метрика g позволяет делить ненулевые векторы в точке
р^Я на три класса; именно, ненулевой вектор Хе Тр назы-
вается времениподобным, пространственноподобным или изо-
тропным, смотря по тому, является ли g(X, X) отрицательным,
положительным или нулевым (ср. рис. 5).
Порядок г дифференцируемости метрики выбирается доста-
точным для того, чтобы уравнения поля были определены. Они
могут быть определены в смысле обобщенных функций, если ко-
ординатные компоненты метрики gab и gab непрерывны, имеют
локально квадратично-интегрируемые обобщенные первые
70
Гл. 3. Общая теория относительности
производные по локальным координатам. Набор п функций f.a
на Rn называются обобщенными производными функции ф на
Rn, если для любой функции С°°-функции ф на Rn с компакт-
ным носителем
f-,a^dnx = — f (dty/dxa) &пх.
Однако это условие слишком слабое, поскольку оно не гаранти-
рует ни существования, ни единственности геодезических; для
этого требуется метрика класса С2- (С2--метрика по определе-
нию обладает первыми производными координатных компонент,
удовлетворяющими локальному условию Липшица; см. разд. 2.1).
Фактически в большей части книги мы будем предполагать, что
метрика принадлежит по крайней мере классу С2. Это позволяет
определить уравнения поля (а они содержат вторые производ-
ные метрики) в каждой точке. В разд. 8.4 мы ослабим требова-
ния к метрике до класса С2- и покажем, что это не влияет на
наличие сингулярностей.
В гл. 7 мы пользуемся иным условием дифференцируемости
для того, чтобы показать, что развитие во времени полевых
уравнений определяется подходящими начальными условиями.
Мы потребуем, чтобы компоненты метрики и их обобщенные
первые производные до порядка m (m 4) были локально
квадратично-интегрируемы. Это условие заведомо выполняется,
если метрика принадлежит классу С4.
Фактически порядок дифференцируемости метрики с точки
зрения физики, скорее всего, не имеет значения. Поскольку мет-
рику никогда нельзя измерить точно, а лишь в пределах некото-
рой ошибки, то никогда нельзя установить, существует ли дей-
ствительно разрыв в производных того или иного порядка. Та-
ким образом, всегда можно представить результаты измерений
как С°°-метрику.
Если предполагается, что метрика принадлежит классу Сг, то
атлас многообразия должен быть порядка С’+1. Можно, однако,
всегда найти аналитический податлас в любом О-атласе (s^l)
([174], цит. в [112]). Поэтому, не ограничивая общности, можно с
самого начала предположить, что атлас аналитичен, даже в том
случае, когда из-за того, что метрика класса С’’, физически мож-
но задать только Сг+1-атлас.
Чтобы гарантировать включение в нашу модель („#, g) всех
несингулярных точек пространства-времени, мы должны нало-
жить на нее определенные условия. Будем говорить, что Сг-пара
(J(', g') является Сг-расширением (Л, g), если существует изо-
метрическое Сг-вложение ц: ,/7- > Л’. Если бы такое расширение
существовало, то нам пришлось бы рассматривать в качестве
точек пространства-времени также и точки Л’. Поэтому мы
3.2. .Материальные (негравитационные) поля
71
потребуем, чтобы модель (Я, g) была Сг-нерасширяемой, т. е.
чтобы не существовало ее Сг-расширения (Я', gz), при ко-
тором ц(Я) не совпадает с Я'.
В качестве примера пары (Л-,, gj), которая не является не-
расширяемой, рассмотрим двумерное евклидово пространство
с осью х, вырезанной между Xi — —1 и Xi = +1. Очевидным
способом его расширения является «возвращение на место» вы-
резанных точек, но можно также расширить его, взяв еще один
экземпляр (./A, g2) такого пространства и отождествив нижний
берег разреза при |%i|< 1 с верхним берегом разреза при
|х21 < 1, а верхний берег разреза при |лу | < 1 с нижним бере-
гом разреза при | х21 < 1. Полученное таким образом простран-
ство (Яг, £з) нерасширяемо, но не полно, поскольку мы остались
без точек (яд = ± 1, г/i = 0). Мы не можем поместить эти точки
обратно, так как мы стеснены условиями продолжения верхней
и нижней части оси х на различные листы. Однако, если взять
подмножество 01 ст Я$, определенное условиями 1 < Xi < 2,
— 1 < z/i < 1, то можно расширить пару (01, g3и поместить
обратно точку х< = 1, щ = 0. Это побуждает к более строгому
определению нерасширяемости: пара (JC g) называется локаль-
но Сг-нерасширяемой, если не существует какого-либо открытого
множества 00 ст Я с некомпактным замыканием в Я, такого,
что пара (01, g 1^) имеет расширение (00', g'), в котором замы-
кание образа 00 компактно *).
3.2. Материальные (негравитационные) поля
Мы будем рассматривать на Я различные поля, например
такие, как электромагнитное поле, нейтринное поле и т. д., кото-
рые описывают «материальное содержимое» пространства-вре-
мени. Эти поля будут подчинены уравнениям, которые можно
представить в виде таких соотношений между тензорами на Я,
что все производные по положению будут ковариантными произ-
водными относительно симметричной связности, определяемой
метрикой g. Этот вывод следует из того, что только тензорные
соотношения определяются структурой многообразия, а связ-
ность, задаваемая метрикой, — пока единственная связность, ко-
торую мы вводили. Если бы была задана другая связность на Я,
то разность двух связностей была бы тензором, и его можно
было бы рассматривать как новое физическое поле. Аналогично,
другую метрику на Я можно было бы рассматривать как еще
одно физическое поле. Уравнения полей иногда выражаются в
виде соотношений между спинорами на Я. В этой книге мы не
*) Если .// — одномерное многообразие, т. е. Л==Л\, то пару (Л. g),
удовлетворяющую указанному условию, будем называть локально С’-непро-
должимой (ем. стр. 205).— Прим перев.
72
Г л. 3. Общая теория относительности
будем иметь дела с такого рода соотношениями, поскольку для
тех задач, которые мы собираемся рассматривать, в них нет на-
добности. В действительности все спинорные уравнения можно
заменить несколько более сложными тензорными уравнениями
(см., например, [143]).
Мы получим ту или иную форму теории в зависимости от
того, какие материальные поля включим в нее. Можно ввести в
теорию все поля, которые экспериментально наблюдаются, при-
чем можно было бы постулировать и существование полей, кото-
рые еще не обнаружены. Так, например, Бранс и Дикке ([39],
приложение 7) постулировали существование дальнодействую-
щего скалярного поля, которое связано слабо со следом тензора
энергии-импульса. В форме, приданной ей Дикке ([39], приложе-
ние 2), теорию Бранса — Дикке можно рассматривать просто
как общую теорию относительности с дополнительным скаляр-
ным полем. В настоящее время идут споры о том, обнаружено
экспериментально такое поле или нет.
Мы будем обозначать материальные поля, включаемые в тео-
рию, через ЧТв c...d> где индекс (i) нумерует рассматривае-
мые поля. Следующие два постулата относительно природы тех
уравнений, которым подчиняются поля W/2 bc ...d, являются об-
щими для частной и общей теорий относительности.
Постулат (а). Локальная причинность
Пусть °U — выпуклая нормальная окрестность, р, q — любые
две точки уравнения, описывающие материальные поля,
должны быть такими, чтобы передача сигнала от одной из этих
точек до другой была возможна тогда и только тогда, когда р
и q могут быть соединены О-кривой, лежащей целиком в и
имеющей касательным вектором всюду ненулевой времениподоб-
ный или изотропный вектор; такую кривую мы будем называть
непространственноподобной. (Наша формулировка теории отно-
сительности исключает возможность существования частиц вроде
тахионов, движущихся по пространственноподобным кривым.)
Идет ли сигнал от р к q или от q к р, зависит от направления
времени в °И. Вопрос о том, можно ли во всех точках простран-
ства-времени непротиворечивым образом задать направление
времени, будет рассмотрен в разд. 6.2.
Более точную формулировку этого постулата можно дать че-
рез формулировку задачи Коши для материальных полей. Пусть
точка р ^.‘U такова, что каждая непространственноподобная
кривая, проходящая через р, пересекает пространственноподоб-
ную поверхность х4 = 0 в пределах °И. Пусть — множество
тех точек на поверхности х4=0, которых можно достигнуть, дви-
гаясь из р в пределах Т/ по непространственноподобным кривым.
Тогда мы потребуем, чтобы значения материальных полей в точ-
3.2. Материальные (негравитационные) поля 73
ке р однозначно определялись значениями на З2" этих полей и их
производных до некоторого конечного порядка и в то же время
не определялись однозначно значениями на любом собственном
подмножестве множества ST, к которому З2" может быть непре-
рывным образом стянуто. (Более полное обсуждение задачи
Коши см. в гл. 7.)
Именно этот постулат выделяет метрику g среди других по-
лей на Jt и придает ей четко выраженный геометрический ха-
рактер. Если {ха}— нормальные координаты в 'ТС вблизи р, ин-
туитивно довольно очевидно (доказательство см. в гл. 4), что
точками, которых можно достигнуть из р по непространствепно-
подобным кривым в ‘2/, являются точки с координатами, удовле-
творяющими условию
(х1)2 + (х2)2 + (х3)2 - (О2<0.
Граница этих точек представляет собой образ изотропного ко-
нуса в р при экспоненциальном отображении, т. е. множество
всех изотропных геодезических, проходящих через р. Таким об-
разом, установив, какие точки могут сообщаться сигналом с р,
можно определить изотропный конус Лд> в Тр. Коль скоро из-
вестно NP, то с точностью до конформного множителя опреде-
ляется метрика в р. В этом можно убедиться следующим обра-
зом. Пусть X, Y е Тр соответственно времениподобный и про-
странственноподобный векторы. Уравнение
g (X + XY, X + XY) = g (Х,Х) + 2kg (X, Y) + k2g (Y, К) = О
имеет два действительных корня Xi и Х2, поскольку g (X, X) < О
и g(Y, Y) > 0. Если мы знаем Np, то можем определить Х[
и Х2; но
X1X2 = g(X,X)/g(Y, Y)-
Таким образом, по изотропному конусу можно установить отно-
шение величин времениподобного и пространственноподобного
векторов. Тогда, если W и Z—-любые два неизотропных вектора
в р, то
g (W, Z) = j (g (W, W) + g (Z, Z) - g (W + z, w + Z)).
Каждую величину в правой части можно сравнить с «длиной» X
или Y и таким способом найти g (W, Z)/g (X, X). (Если вектор
W + Z изотропен, то можно использовать соответствующее вы-
ражение, содержащее W + 2Z.) Итак, существование локальной
причинности позволяет измерить метрику с точностью до кон-
формного множителя. На практике это измерение удобнее всего
осуществить, используя тот экспериментальный факт, что не об-
наружено никакого сигнала, который распространялся бы быст-
рее электромагнитного излучения. Это означает, что свет должен
74
Г л. 3. Общая теория относительности
распространяться по изотропным геодезическим. Однако такое
свойство света является следствием конкретных уравнений, кото-
рым подчиняется электромагнитное поле, а не самой теории от-
носительности. Дальнейшее рассмотрение причинности мы про-
должим в гл. 6. Среди прочих результатов мы получим, что от-
ношения причинности могут быть использованы для определения
топологической структуры Л. Конформный множитель метрики
можно определить, пользуясь постулатом (б), который формули-
руется ниже; тогда все объекты теории будут физически наблю-
даемыми.
Постулат (б): локальное сохранение энергии и импульса
Уравнения, описывающие материальные поля, таковы, что
существует симметричный тензор ТаЬ, называемый тензором
энергии-импульса, который зависит от полей, их ковариантных
производных и метрики; он обладает следующими свойствами:
1) ТаЬ обращается в нуль на открытом множестве в том и
только в том случае, когда материальные поля исчезают на бИ.
2) ТаЪ подчиняется уравнению
ТаЬ-ь = ®. (3.1)
Условие (1) выражает тот принцип, что все поля обладают
энергией. Не исключены возражения против формулировки
«только в том случае» на том основании, что могут оказаться
два ненулевых поля, тензоры энергии импульса которых компен-
сируют друг друга. Такая возможность связана с допустимостью
существования отрицательной энергии и обсуждается в разд. 3.3.
Если метрика допускает векторное поле Киллинга К, то урав-
нение (3.1) можно проинтегрировать и получить закон сохране-
ния. Чтобы убедиться в этом, введем вектор Ра, компоненты ко-
торого равны Ра = ТаЬКъ- Тогда
Ра-а = ТаЬ-аКь + ТаЪКъ-а.
Первый член есть нуль по уравнению сохранения (3.1), а второй
обращается в нуль, так как тензор ТаЪ симметричен и для век-
тора Киллинга К 2Ка. b = LKgab = 0- Поэтому, если <&— ком-
пактная ориентируемая область с границей дФ, то по теореме
Гаусса (разд. 2.7)
J Pftdoy,= Jp&;6dt) = O. (3.2)
dS> S>
Это равенство можно описать словами как равенство нулю пол-
ного потока К-й компоненты энергии импульса через замкнутую
поверхность.
Когда метрика плоская, как это имеет место в частной теории
относительности, можно выбрать координаты {л"'}, в которых
3.2. Материальные (негравитационные) ноля
75
компоненты метрики равны gab — еа5аъ (суммирования нет!),
где 6пЬ — символ Кронекера, е — +1, если а = 1,2, 3, и еа = —1,
если а = 4. Тогда векторами Киллинга будут
L = —(а=1,2, 3, 4)
а дха
(они порождают 4-трансляции) и
д д
М — е„ха —-(суммирования нет; а, 8=1, 2, 3, 4)
а|3 Щ р <)х!'
(порождающими шесть «вращений» в пространстве-времени).
Эти изометрии образуют 10-параметрическую группу Ли изомет-
рий плоского пространства-времени, называемую неоднородной
группой Лоренца. Их можно использовать для определения де-
сяти векторов Ра и Ра, подчиняющихся уравнению (3.2). Можно
а а|3
считать, что вектор Р описывает поток энергии, а Р, Р, Р — по-
4 12 3
ток трех компонент импульса; Р можно интерпретировать как
а 13
поток момента импульса.
Если метрика не плоская, то в общем случае нет ни одного
вектора Киллинга, и подобных законов сохранения не суще-
ствует. Однако в подходящей окрестности точки q можно ввести
нормальные координаты {х“}. Тогда в точке q компоненты мет-
рики gab = еаЬаъ (суммирования нет!), а компоненты связности
Г%с = 0.
Можно взять такую окрестность 3) точки q, в которой gab и
Гаьс отличаются от их значений в q на произвольно малую вели-
чину; тогда £(й; ь) и ЛГ(в; 6) не будут в 2) точно равны нулю, но
rz.fi
будут отличаться от нуля сколь угодно мало.
Таким образом, интегралы
Pb d<уь и Рь бой
dS> а dSj “р
в первом приближении по-прежнему будут равны нулю; иначе
говоря, в малой области пространства-времени в этом приближе-
нии энергия, импульс и угловой момент импульса все еще сохра-
няются. Используя это, можно показать, что малое изолирован-
ное тело приближенно движется по времениподобной геодезиче-
ской линии независимо от своей внутренней структуры, если
только плотность энергии неотрицательна (расчет движения ма-
лого тела в теории относительности см. в [42]). Этот факт можно
рассматривать как галилеевский принцип падения всех тел с
одинаковой скоростью. В ньютоновских терминах можно было
бы сказать, что для всех тел инертная масса (т в F = та)
76 Гл. 3. Общая теория относительности
равна пассивной гравитационной массе (массе, на которую дей-
ствует гравитационное поле). Справедливость этого была уста-
новлена с высокой точностью экспериментами Этвеша и Дик-
ке [39].
Постулат (а) позволяет измерить метрику в каждой точке
с точностью до конформного множителя. Пользуясь постулатом
(б), можно связать между собой эти множители в различных
точках, так как уравнения сохранения ТаЬ-ь = О, вообще говоря,
не выполняются для связности, полученной из метрики g = Q2g.
Это можно было бы осуществить, наблюдая пути малых «проб-
ных» частиц и определяя времениподобные геодезические. Пусть
у(0—одна из таких линий иК = (d/dt)y— ее касательный век-
тор; тогда из (2.29) имеем
~ ка ка + гй-’й; ькька - сг1 (кькс$ J gadQ.d.
Поскольку у(/)—геодезическая относительно пространственно-
временной метрики g, то Д[ь (D/<3/)/(“1 = 0. Следовательно,
К[Ь 1^а] = - (KKdgcd) Klbga] е (In Q);e. (3.3)
Зная конформную структуру, мы можем выбрать какую-либо
метрику g, представительницу данного класса конформно-экви-
валентных метрик, и вычислить левую часть в (3.3) для любой
пробной частицы. Тогда по правой части (InQ);6 определяется
с точностью до множителя Ка£аъ- Рассмотрев другую кривую
у'(/), касательный вектор которой К.'а не параллелен вектору Ка,
можно найти (1п й);г> и таким образом определить Q везде с точ-
ностью до постоянного множителя. Этот постоянный множитель
зависит от используемых единиц измерения и может быть вы-
бран произвольно.
Конечно, на практике конформный множитель измеряется не
таким способом; обычно используется тот факт, что существует
большое число подобных друг другу систем (например, элек-
тронных состояний атомов), движение которых вдоль времени-
подобных геодезических сопровождается рядом событий, обу-
словленных внутренними движениями. Эти события отмечают
положения систем в пространстве-времени. Интервалы между
этими событиями, по-видимому, не зависят от предыстории си-
стем в том смысле, что интервалы, измеренные для двух сосед-
них систем, находятся в соответствии друг с другом. Если воз-
можна эффективная изоляция подобных систем от внешних
материальных полей (так что они должны будут двигаться по
геодезическим) и если предположить, что их внутреннее дви-
жение не зависит от кривизны пространства-времени, то мет-
3.3. Лагранжева формулировка
77
рика —- единственное, от чего оно может зависеть. Следователь'
но, длина дуги между двумя последовательными событиями на
кривой должна быть одинаковой для каждой пары последова-
тельных событий на любой такой кривой. Если принять эту
длину дуги в качестве единицы измерения, можно определить
конформный фактор в любой точке пространства-времени.
В действительности может оказаться, что изоляция системы
от внешних материальных полей невозможна. Так, например,
в теории Бранса — Дикке присутствует скалярное поле, которое
везде отлично от нуля. Однако конформный множитель все же
можно определить, если потребовать, чтобы уравнение сохране-
ния ТаЬ-ь—О удовлетворялось. Таким образом, зная тензор
энергии-импульса ТаЬ, мы можем узнать и конформный множи-
тель.
3.3. Лагранжева формулировка
Условия (1) и (2) постулата (б) ничего не говорят ни о спо-
собе построения тензора энергии-импульса для данной системы
полей, ни о его единственности. На практике в основном пола-
гаются на интуитивные представления о том, что такое энергия
и импульс. Однако в тех случаях, когда уравнения полей могут
быть выведены из некоторого лагранжиана, для тензора энер-
гии-импульса существует определенная и однозначная формула.
Пусть L, некоторая скалярная функция полей Ч’ц® ьс... щ
их первых производных и метрики, есть лагранжиан. Уравнения
полей получаются из требования, чтобы действие
I = L du
s>
было стационарно при вариации полей внутри компактной че-
тырехмерной области 2). Под вариацией поля ^ц)а“‘ье...л. в 3) мы
подразумеваем однопараметрическое семейство полей Wypfu, г),
где и е (—8, е) и г е Л. такие, что
1) W(f, (0, r) = T(0(r),
2) T(i) {и, г) = Ч**(г) (г), когда г^Л — 2).
Обозначим дЧ^ (ц, г)/ди |и=0 через ДЧ*‘((-); тогда
+ ЛГЛ^-------------Л... Л du,
г(i) с ... /
где 4f(j)a " ьсd-.e — компоненты ковариантных производных 4r(f);
но д(чгц)а"Л...^е) = (ДЧ\г)а %... и потому второй член
78
Гл. 3. Общая теория относительности
можно записать в виде
~(~лгт~ь—) w4—
\ Оil с ... d;e ).е J
Первый член в этом выражении может быть представлен как
$Qa;edu = J Q°doa,
S> dS>
причем Q —вектор, компоненты которого равны
<г'=£т5г^—
ц) ° (О с ... d'.e
Этот интеграл равен нулю, ибо условие (2) эквивалентно утвер-
ждению, что АЧ’Д) обращается в нуль на границе дЗ). Таким
образом, чтобы дЦди 1И==О = 0 при всех вариациях в любой обла-
сти 3), необходимо и достаточно, чтобы при всех i удовлетво-
рялись уравнения Эйлера — Лагранжа
-----------------) =0- <зл)
от(1) c...d \0Tu) c..-d;e/;e
Мы получили уравнения полей.
Тензор энергии-импульса мы выведем из лагранжиана, рас-
сматривая изменение действия, индуцированное изменением
метрики. Предположим, что вариация geb(«, г) оставляет поля
М(0 с ... d неизменными, но изменяет компоненты метрики gab-
Тогда
д!
ди
;,W а ... b
c...d;e
dL
АТ(ц с ,.. d;e + --AgaiT du -|-
dSab J
+ \L^-bgab. (3.5)
J ugab
S)
Последний член возникает из-за того, что мера объема du зави-
сит от метрики. Для вычисления этого члена вспомним, что du
есть каноническая 4-форма г] с компонентами т]аьса =
= (— g)-'2 4!6|aIdb2dcddd]4, где g = det(gaiJ). Отсюда
drived _ 1 I dg ... 1.2.3. 4_
T (- g) w 4!6la dc bd] -
=- 4 (- gr'12 g^AMc3^=
1 ef
2 S ^labcdi
3.3. Лагранжева формулировка
79
и, следовательно,
4 sa4v.
dgab 2 s
Первый член в (3.5) появляется из-за того, что член
ДЧДД&с... не обязательно будет равен нулю, несмотря на
то, что ДЧ/ц®’” с...</ = 0: вариация метрики индуцирует вариа-
цию компонент связности Г%с. Поскольку разность двух связно-
стей преобразуется как тензор, ДГ%С можно считать компонен-
тами тензора. Они связаны с вариацией компонент метрики со-
отношениями
ЛГ%, = I s“ Р, + (Лг.д, -
(Вывести эту формулу проще всего, замечая тот факт, что она
является тензорным соотношением и, следовательно, должна
быть справедлива в любой системе координат. В частности,
можно выбрать нормальные координаты с началом в точке р.
В этих координатах в р обращаются в нуль компоненты Гаьс и
производные компонент gab по координатам. Тогда можно убе-
диться, что данная формула справедлива в р.) Используя это
соотношение, можно выразить ДЧД® ьс... ц,е через (Agbc);d,
после чего обычное интегрирование по частям приводит к по-
дынтегральному выражению, содержащему только &gab- Итак,
мы можем записать д!/ди в виде
J(r6Agab)du,
з>
где ТаЪ — компоненты симметричного тензора, который мы при-
мем за тензор энергии-импульса рассматриваемых полей. (Отно-
сительно связи между этим тензором и так называемым канони-
ческим тензором энергии-импульса см. [142].)
Этот тензор энергии-импульса удовлетворяет уравнениям со-
хранения вследствие полевых уравнений, которым подчинены
bc.-.d‘ Действительно, предположим, что имеется диффео-
морфизм который отличается от тождественного пре-
образования только внутри Ф. Тогда вследствие инвариантности
интегралов относительно дифференцируемого отображения
имеем
I = L du = Ьц — Lt| = \^ф‘ (Li]).
S> S) ф (S>) s>
Следовательно,
J(Tn-^(b1)) = 0.
з>
80
Гл. 3. Общая теория относительности
Если диффеоморфизм ф порожден векторным полем X (отлич-
ным от нуля только внутри 3)), то отсюда следует, что
Lx(Eti) = O;
s>
однако
------(-^гй—) >
S> (<•)£) c...d \0T(i) c...d;e/\ej
\TabLxgabAv.
so
Первый член обращается в нуль в силу полевых уравнений.
Во втором члене CKgab — 2Х(в.&). Таким образом,
S Щ’М..) <1» = 2 S ((Т‘>ХЩ - T“;iXa) do.
s> 3>
Вклад первого члена можно представить в виде интеграла по
границе 3), который равен нулю из-за того, что X = 0 на дЗ).
Отсюда следует, что Tab.b = 0, поскольку второй член должен
обращаться в нуль при произвольном X.
Теперь мы приведем в качестве примеров лагранжианы для
некоторых полей, которые представляют интерес для последую-
щего.
Пример 1. Скалярное поле ф
Это поле может соответствовать, например, л°-мезону. Его
лагранжиан является
где tn, й — константы. Уравнение Эйлера — Лагранжа (3.4)
имеет вид
«а6-пй==о.
Тензор энергии-импульса равен
Tab = - 4 g«b Ф2 ) • (3.6)
Пример 2. Электромагнитное поле
Оно описывается 1-формой А, называемой потенциалом. По-
тенциал определен с точностью до добавления градиента какой-
либо скалярной функции. Лагранжиан имеет вид
L-~-^FabFcdgac&bd,
3.3. Лагранжева формулировка
81
где тензор электромагнитного поля F по определению равен 2dA,
т. е. Fаь — 2А\ь-,а]. Варьируя по Аа, получаем уравнения Эйле-
ра— Лагранжа (3.4) в виде
Fab;cgbC = 0.
Эти уравнения и уравнение = 0 (т. е. уравнение dF =
= d (dA) = 0) представляют уравнения Максвелла для электро-
магнитного поля без источников. Тензор энергии-импульса имеет
вид
Tob - (FocFbdgcd - 4 gabFijFklgikgil) . (3.7)
Пример 3. Заряженное скалярное поле
Оно является фактически объединением двух вещественных
скалярных полей и фг в одно комплексное скалярное поле
ф = -ф[ Л- гф2, которое может соответствовать, например, л+- и
«“-мезонам. Полный лагранжиан заряженного скалярного и
электромагнитного полей равен
L = ~ + ieAa^ §аЬ (tb “ ieAi$) - Й - i FabFcdgaCgM,
где е — постоянная и ф — поле, комплексно сопряженное ф.
Варьируя независимо по ф, ф и Аа, имеем уравнение
+ ieAagab (2ф,6 + геЛ.ф) + ieAa.bgab^> = 0,
получаемое отсюда комплексным сопряжением, и уравнение
i Fab-cgbC ~ - ieAaty + М (Ф;а + = 0.
Тензор энергии-импульса равен
таь = 4 ОМ-Л + + 4 (~ +
+ ~ + 4т F<>cFbdgcd + е2АаАь^ + LSab-
Пример 4. Изэнтропическая идеальная жидкость
Здесь подход несколько отличается от предыдущих случаев.
Жидкость описывают функцией р, называемой плотностью, и
конгруэнцией времениподобных кривых, называемых линиями
тока. Под конгруэнцией кривых подразумевается такое семей-
ство кривых, что через каждую точку Л проходит одна кривая.
Если Зд достаточно малая компактная область, то конгруэнцию
можно представить в виде диффеоморфизма у:[а, й]ХЛ° -> 3),
где [а, Ь] — некоторый замкнутый интервал из R1 и AF — некото-
рое трехмерное многообразие с краем. Кривые называют време-
ниподобными, если их касательные векторы W= (<3/d/)Y, [a, b]
82
Гл. 3. Общая теория относительности
всюду времениподобны. Вектор потока жидкости определяет-
ся как j = р¥, где V — касательный вектор вида V =
= (—g(W, W) и, следовательно, g(V, V) = — 1. Требуется,
чтобы поток сохранялся, т. е. ja-a = 0. Поведение жидкости опре-
деляется заданием потенциала упругих сил (или внутренней
энергии) е в функции р. Лагранжиан берется в виде
£ = -2р(Ц-е),
и требуется, чтобы действие было стационарным при вариации
линий тока, а р подбирается так, чтобы обеспечить сохранение
потока ]а. Вариация линий тока есть дифференцируемое отобра-
жение
у: (- б, б) X [a,
удовлетворяющее условиям
у (0, [а, б], Л’) = у([а, b] Л*),
и
у (и[а, б], Л’) = у ([а, б], Л9) на JI — S), (ые(—б, б)).
Следовательно, AW = AKW, где К = (<?/ди)у. К можно пред-
ставить себе как вектор, задающий смещение некоторой точки
линии тока при вариации. Отсюда следует, что
АГ = уа.ъ^ь -
Используя тот факт, что А = 0 = (A/a).o, имеем
(Ар);аГ + АрГ;а + p;a LVa + р (АV% = 0.
Подставляя сюда AVa и интегрируя вдоль линий тока, получаем
Ар^(р^);й + рГ;с1/йГ.
Следовательно, вариация интеграла действия равна
т? L=-2 5 (1 +
Ф
После интегрирования по частям
L“2 ИМ1 + Ж) т«+р ) tte“+i/т-)) к.} а»,
«0
где Va ^Va-.bVb. Если это выражение равно нулю при всех К, то
(р+ p)Va = ~P,b(gba+VbVa),
3.3. Jiагранжева формулировка
83
где ц — р(1 + е)— плотность энергии и р — p2(de/dp) — давле-
ние. Итак, ортогональный к линиям тока градиент давления за-
дает Г"', ускорение линий тока.
Чтобы получить тензор энергии-импульса, проварьируем мет-
рику. Вычисления можно упростить, если заметить, что сохра-
нение тока может быть выражено в виде равенства
Если линии тока заданы, то из уравнений сохранения величи-
на ja однозначно определяется в каждой точке данной линии
тока через свое начальное значение в некоторой фиксированной
точке той же линии тока. Поэтому д/— gia не изменяется при
вариации метрики. Но
Р2 = gab,
и, следовательно,
2р Др = (/V - jcjcgab) Agab,
а отсюда
Tab = {р (1 + е) + р' VaVb + Р2 §аЬ =
= (p + p)VaVb + pga&. (3.8)
Любую форму материи, тензор энергии-импульса которой имеет
вид (3.8) (независимо от того, выведен он из некоторого лагран-
жиана или нет), будем называть идеальной жидкостью. Уравне-
ние сохранения энергии и импульса (3.1) в приложении к (3.8)
дают
И;а1/я + (р + р)Уя;а = 0, (3.9)
(p + p}Va + (gab+ VaVb)p,<b=Q. (3.10)
Эти уравнения совпадают с полученными из лагранжиана. Бу-
дем называть идеальную жидкость изэнтропической, если дав-
ление р является функцией одной лишь плотности энергии ц.
В этом случае можно ввести сохраняющуюся плотность р и вну-
треннюю энергию е и вывести эти уравнения и тензор энергии
импульса (3.8) из некоторого лагранжиана.
Можно также рассмотреть заряженную жидкость с сохра-
няющимся электрическим зарядом е (т. е. 7а.а = 0, где J = eV —
электрический ток). Лагранжиан заряженной жидкости и элек-
тромагнитного поля имеет вид
L = -i F«bFcdgacgbd - 2р (1 + в) - JaAa.
84 Гл. 3. Общая теория относительности
Последний член задает взаимодействие между жидкостью и по-
лем. Варьируя А, линии тока и метрику соответственно, получаем
Fab.b = 4л/а,
(И + р) Va = - p.ib {gab + VaVb) + FabJb,
Tab = (И + p) VaVb + pgab + (rcFbc - 1 gabFcdFcd) .
3.4. Уравнения поля
До сих пор мы не конкретизировали метрику g. В специальной
теории относительности, которая не рассматривает гравитацион-
ные эффекты, принимается, что метрика плоская. Однако наблю-
дения показали, что лучи света, проходящие вблизи Солнца, от:
клоняются от своего первоначального направления. Поскольку
световые лучи представляют собой изотропные геодезические,
отсюда следует, что пространственно-временная метрика не мо-
жет быть плоской или хотя бы конформной плоской метрике.
Поэтому нам нужно иметь какой-то рецепт вычисления кривизны
пространства-времени. Оказывается, его можно сформулировать
так, чтобы в пределе малой, медленно изменяющейся кривизны
воспроизводились результаты ньютоновской теории тяготения.
Поэтому нет необходимости во введении какого-либо дополни-
тельного поля для описания тяготения. Это не означает, что до-
полнительного поля, ответственного за часть гравитационных
эффектов, вообще не может быть. Такого рода скалярное поле
было введено Иорданом [86] и Брансом и Дикке [39]. Причем,
как отмечено выше, такое дополнительное поле можно было бы
рассматривать просто как еще один вид материального поля и
включить в полный тензор энергии-импульса. Поэтому мы при-
держиваемся того взгляда, что поле тяготения описывается
только пространственно-временной метрикой. Тогда возникает
проблема нахождения полевых уравнений, связывающих метри-
ку с распределением материи.
Эти уравнения должны быть тензорными уравнениями, учи-
тывающими материю только через ее тензор энергии-импульса,
т. е. они не выявляют различий между двумя различными мате-
риальными полями, которые имеют одинаковые распределения
энергии и импульса. Данное условие можно рассматривать как
обобщение ньютоновского принципа равенства активной грави-
тационной массы тела (массы, создающей поле тяготения) пас-
сивной гравитационной массе (массе, на которую действует поле
тяготения). Экспериментально это равенство было проверено
Крейцером [93].
3.4. Уравнения поли 85
Чтобы установить, какими должны быть искомые уравнения
поля, рассмотрим предельный ньютоновский случай. Поскольку
в ньютоновское сравнение 1равигационпого поля время не вхо-
дит, соответствие с ньютоновской теорией нужно устанавливать
в статической метрике. Под статической метрикой подразуме-
вается метрика, которая допускает времениподобное векторное
поле Киллинга К, ортогональное к семейству пространственно-
подобных поверхностей. Эти поверхности можно рассматри вать
как поверхности постоянного времени и отмечать их пара мет-
ром t. Введем единичный времениподобный вектор V — ^-1К,
где р=-КаКа. Тогда Г:й= - VaVb, где Va = Va.,bVb = Г%§аЬ
описывает отклонение от геодезпчпости интегральных кривых
вектора V (которые, конечно, одновременно являются интеграль-
ными кривыми вектора К). Заметим, что КйКа = 0.
Эти интегральные кривые определяют статическую систему
отсчета; иными словами, для частицы, история которой представ-
лена одной из этих кривых, пространственно-временная метрика
кажется не зависящей от времени. Частица, выведенная из со-
стояния покоя и движущаяся по геодезической, выглядела бьп так,
как будто она получила начальное ускорение —V относительно
этой статической системы отсчета. Если / лишь незначительно
отличается от единицы, начальное ускорение выведенной из по-
коя свободно движущейся частицы приблизительно равно гра-
диенту f, взятому со знаком минус. Это наводит на мысль, что
в качестве величины, аналогичной ньютоновскому гравитацион-
ному потенциалу, следует рассматривать f— 1.
Уравнение для этого потенциала можно вывести, рассматри-
вая дивергенцию V"':
Ё“ а = (Va-,bVb\a = Va-b-,aVb + Va-bVb-a =
= RabVaVb + (V “Д* Vb + (VbVb)2 = RabVaVb.
Однако
Va;a = (r]f:bgab\a = - r2f;af;bgab +
И
UvV = - f,ava-bvb = - r'U-.bg*1’,
так что имеем
f.,ab(§ab + VaVb) = fRabVaVb.
Левая часть есть лапласиан f относительно метрики, индуциро-
ванной на 3-поверхности {t — const}. Если эта метрика почти
плоская, то мы получим ньютоновский лапласиан потенц нала.
Таким образом, мы получим согласие с теорией Ньютона bs пре-
дельном случае слабого поля (т. е. когда f « 1), если правая
часть будет равна плотности материи, умноженной на 4nG плюс
86 Г л. 3. Общая теория относительности
члены, которые малы в предельном случае слабого поля. Это
будет иметь место при условии, чго существует соотношение
вида
Rab~ КаЬ, (3.11)
где Каь — тензорная функция тензора энергии-импульса и мет-
рики, такая, что (inG)-lKabVaVb равно плотности материи плюс
члены, которые малы в ньютоновском приближении. Допустим
на время, что имеется соотношение такого вида.
Поскольку Rab удовлетворяет свернутым тождествам Бианки
Ra -b = у R;a, ИЗ (3.11) следует
V;6=y/<:6. (3.12)
Отсюда видно, что кажущееся естественным уравнение КаЬ =
= 4nGTab не может быть правильным, так как из(3.12) и урав-
нений сохранения Таь-,ь = О мы получили бы, что T-a = Q. Для
идеальной жидкости это означало бы, что р — Зр = const во
всем пространстве-времени — условие, которому в общем слу-
чае жидкость удовлетворять не может.
В действительности из тех тождеств, которым удовлетворяет
тензор энергии-импульса, законами сохранения являются в об-
щем случае только тождества первого порядка. Отсюда следует,
что тензорной функцией Rab тензора энергии-импульса и мет-
рики, для которой тождества (3.12) выполняются при любом
тензоре энергии-импульса, может быть только функция
Kab = ^(jab Тgab^ Agab, (3.13)
где х и Л — некоторые постоянные. Значения этих постоянных
можно определить из ньютоновского приближения. Рассмотрим
идеальную жидкость с плотностью энергии р и давлением р, ли-
нии тока которой являются интегральными кривыми вектора
Киллинга (т. е. жидкость покоится в статической системе отсче-
та). Ее тензор энергии-импульса имеет вид (3.8). Подставляя
его в (3.13) и (3.11), получим
f;ab (§ab + = f (4 х (И + Зр) - л) . (3.14)
В ньютоновском пределе давление р обычно весьма мало в срав-
нении с плотностью энергии. (Мы пользуемся единицами, в ко-
торых скорость света равна единице. Если единицы таковы, что
скорость света равна с, выражение р + Зр следует заменить на
р + Зр/с2.) Следовательно, приближенное согласие с ньютонов-
ской теорией будет достигнуто, если х — 8пб, а постоянная | А |
очень мала. Мы будем пользоваться единицами массы, в кото-
3.4. Уравнения поля
87
рых G == 1. В этих единицах масса 102S г соответствует длине
1 см. Из наблюдений удаленных галактик, выполненных Сендей-
джем [145, 146], вытекают ограничения на |Л| порядка 10-56 см-2.
Обычно мы будем принимать Л = 0, но следует помнить о воз-
можности иных значений.
Теперь можно проинтегрировать (3.14) по компактной обла-
сти ST 3-поверхности {t = const} и преобразовать левую часть в
интеграл от градиента f по граничной 2-поверхности д^~:
J f (4л (ц + 3/9)) da - J f.ab (gab + VaVb) da =
= 5 f:a(ga4 W)dT6,
dff-
где da — элемент объема 3-поверхности {t = const} в индуциро-
ванной метрике и dr& — элемент площади 2-поверхности д9~ на
этой 3-поверхности. Это приводит к аналогу формулы Ньютона
для полной массы, заключенной внутри 2-поверхности. Есть, од-
нако, два важных отличия от ньютоновского случая:
1. В интеграле в правой части появляется множитель f; это
означает, что материя, находящаяся в области, где } значительно
меньше единицы (большой отрицательный ньютоновский потен-
циал), дает меньший вклад в полную массу, чем материя из
области, где f почти равно единице (малый отрицательный нью-
тоновский потенциал).
2. Давление дает вклад в полную массу; это означает, что в
определенных условиях оно может способствовать, а вовсе не
препятствовать гравитационному коллапсу.
Уравнения
Rab = 8л — у Тgat)^ + i\gab
называются уравнениями Эйнштейна, и часто их записывают в
следующей эквивалентной форме:
(Rab — jRgab) + Agab = 8nTab. (3.15)
Поскольку тензоры в обеих частях симметричны, эти уравнения
образуют систему десяти связанных нелинейных дифференциаль-
ных уравнений в частных производных для метрики и ее первых
и вторых производных. Однако ковариантные дивергенции левой
и правой частей тождественно равны нулю, т. е.
(Rab - | Rgab + = О
И
88
Гл. 3. Общая теория относительности
независимо от уравнений поля. Таким образом, в действитель-
ности уравнения поля содержат только шесть независимых диф-
ференциальных уравнений для метрики. Это как раз то число
уравнений, которое нужно для задания геометрии пространства-
времени: четыре из десяти компонент метрики могут быть при-
ведены к произвольным значениям при использовании четырех
степеней свободы в виде координатных преобразований. К этому
выводу можно прийти и другим путем: две метрики gi и g2 на
многообразии Л задают ту же самую геометрию, если суще-
ствует диффеоморфизм 0, переводящий gi в g2; поэтому уравне-
ния поля должны определять метрику с точностью до класса
эквивалентности относительно диффеоморфизмов, в выборе ко-
торых имеются четыре степени свободы.
В гл. 7 мы рассмотрим задачу Коши для уравнений Эйн-
штейна и покажем, что последних вместе с уравнениями для ма-
териальных полей при подходящих начальных данных доста-
точно для определения эволюции пространства-времени и что
они удовлетворяют постулату причинности (а) (стр. 72).
Уравнения Эйнштейна могут быть выведены из требования
стационарности действия
1= ^(A(R-2A.) +L)dv (3.16)
з>
при вариации §аь- Здесь L — лагранжиан материи и А — подхо-
дящая постоянная. Действительно,
Д ((R - 2Л) du) = ((7? - 2Л) | gabAgab + Rab Agab + gab ARab) cl v;
последний член можно переписать в виде
gab ARab du = gab ((ДГ%ь);с - (дгас);&) du =
= (ArW&“ArWC);Cdu.
Отсюда интеграл от этого члена можно преобразовать в инте-
грал по границе д0, который обращается в нуль потому, что
ДГа(,с = 0 на д£>. Поэтому
^L= Н^((|я-л)«->-Л'”)+7'“''}^И», (3.17)
s>
и если dlldu обращается в пуль при всех Aga.b, мы получаем
уравнения Эйнштейна, положив А = (8л)”1.
Может возникнуть вопрос, нельзя ли, варьируя действие, по-
лученное из какой-либо другой комбинации метрического тен-
зора и тензора кривизны, получить другую разумную систему
уравнений. Однако скалярная кривизна R — единственный ска-
ляр, который линеен по вторым производным метрического тен-
3.4. Уравнения поля
89
зора, так что только и этом случае можно выделить поверхност-
ный интеграл и получить уравнение, содержащее производные
метрики не выше второго порядка. Если же исходить из какого-
либо другого скаляра, например RabRab или RabcdRabcd, то полу-
чится уравнение, содержащее четвертые производные метриче-
ского тензора. Это обстоятельство нежелательно, ибо все прочие
уравнения физики первого или второго порядка. Если бы урав-
нения были четвертого порядка, то для описания эволюции .мет-
рики пришлось бы задавать начальные значения не только мет-
рики и ее первых производных, но также значения вторых и
третьих производных.
Мы будем предполагать, что уравнения поля не содержат
производных метрики выше второго порядка. Если эти уравне-
ния выводятся из какого-либо лагранжиана, то действие обяза-
тельно должно иметь вид (3.16). Однако можно получить си-
стему уравнений, отличную от эйнштейновской, если наложить
ограничения на вид вариаций Д§аь, при которых мы требуем
стационарности действия. Скажем, можно было бы ограничиться
метриками, конформными к плоской метрике, т. е. положить
gab = Q2riab,
где г]оь -— плоская метрика специальной теории относительности.
Тогда
А^^СГ'ДЙ^,
и действие будет стационарным при условии, что
{(л(4/?-д)^--/?а°)+7'аЬ}АС^ = О
при всех AQ, т. е. если
R + A-'T = 4A.
Из (2.30)
R = - 6Q“3Q|bcn6c = - QQ~'Q.bcgbc + i2Q-2Q.cQ.dgcd,
где | означает ковариантное дифференцирование относительно
плоской метрики т]аб. Для статической метрики Q = const вдоль
интегральных кривых вектора Киллинга К (т. е. Q не будет за-
висеть от времени t). Модуль К будет пропорционален Q.
Поэтому
(g^ + V^Q-1^
= - | R + 2й~2й;ай;6/& - -bVb =
90
Г л. 3. Общая теория относительности
Таким образом, лапласиан f будет равен — ~R плюс член, про-
порциональный квадрату градиента f. Этим последним членом
в слабом поле можно пренебречь. Согласно уравнениям поля
Для идеальной жидкости Т = —ц 4- Зр. Следовательно, согла-
сие с ньютоновской теорией достигается, если Л мало или равно
нулю и Д-1 = —24л.
Эта теория, в которой на метрику наложено условие, чтобы
она была конформно-плоской, известна как теория Нордстрема.
Ее можно переформулировать как теорию, в которой метрика i]
плоская, а гравитационное взаимодействие представлено доба-
вочным скалярным полем ф. Как упоминалось ранее, такого рода
теория не согласуется с наблюдаемым отклонением луча света
массивными объектами и не может объяснить измеренное сме-
щение перигелия Меркурия.
Наблюдаемые значения этих величин (отклонения луча и
смещения перигелия Меркурия) можно было бы получить при
следующем ограничении на вид метрики:
gab = ^^ab + WaWb),
где 1Га— произвольное поле 1-формы. В этом случае ньютонов-
ский предел имел бы место в статической метрике, в которой Wa
параллельно времениподобному вектору Киллинга. Однако
могла бы существовать и другая статическая метрика, в ко-
торой не параллельно вектору Киллинга, и она нс приво-
дила бы к ньютоновскому пределу. Кроме того, это ограничение
выглядит довольно искусственным. Представляется более есте-
ственным не накладывать иных ограничений на метрику, кроме
требования, чтобы она была лоренцевой.
Поэтому в качестве нашего третьего постулата мы примем:
Постулат (в): Уравнения поля
На многообразии Л удовлетворяются уравнения поля Эйн-
штейна (3.15).
Предсказания этих уравнений согласуются в пределах оши-
бок эксперимента с выполненными до настоящего времени на-
блюдениями отклонения луча света и сдвига перигелия Мерку-
рия. В то же время пока остается открытым вопрос, существует
ли дальнодействующее скалярное поле, которое нужно было бы
включить в тензор энергии-импульса.
Глава 4
Физический смысл кривизны
В этой главе мы рассмотрим, как сказывается кривизна
пространства-времени на семействах времениподобных и изотроп-
ных геодезических. Эти семейства могут изображать соответ-
ственно линии тока жидкости и (или) мировые линии фотонов.
В разд. 4.1 и 4.2 мы выведем формулы для скорости вращения,
поперечного сдвига (sheer) и расхождения (expansion) таких
семейств кривых; уравнение для скорости расхождения (уравне-
ние Райчаудхури) занимает центральное место в доказатель-
ствах теорем о сингулярностях в гл. 8. В разд. 4.3 обсуждаются
общие неравенства для тензора энергии-импульса, из которых
вытекает, что гравитационное воздействие материи всегда стре-
мится вызвать сближение времениподобных и изотропных геоде-
зических. Из результатов разд. 4.4 видно, что следствием этих
энергетических условий будет появление сопряженных или фо-
кальных точек в невращающихся семействах времениподобных
или изотропных кривых общего вида. В разд. 4.5 показано, что
из наличия сопряженных точек следует существование таких ва-
риаций кривых между двумя точками, которые переводят изо-
тропную геодезическую во времениподобную кривую или вре-
мениподобную геодезическую во времениподобную кривую боль-
шей длины.
4.1. Времениподобные кривые
Мы видели в гл. 3, что при статической метрике существует
связь между длиной времениподобного вектора Киллинга и нью-
тоновским потенциалом. Находится ли тело в гравитационном
поле, можно узнать по тому, ускоряется ли оно или нет, если его
вывести из состояния покоя относительно статической системы
отсчета, задаваемой этим вектором Киллинга. Однако в общем
случае в пространстве-времени может не быть ни одного вектора
Киллинга, и тогда не будет и какой-либо выделенной системы
отсчета для измерения ускорения. Все, что еще можно сделать,—
это взять два близких друг к другу тела и измерить их относи-
тельное ускорение. Такое измерение позволяет определить гра-
диент гравитационного поля. Если рассматривать метрику как
аналог ньютоновского потенциала, то градиенту ньютоновского
поля будут соответствовать вторые производные метрики. Они
92
Гл. 4. Физический смысл кривизны
определяются тензором Римана. Поэтому можно ожидать, что
относительное ускорение двух соседних тел будет связано с ка-
кими-то компонентами тензора Римана.
Чтобы установить эту связь более строго, изучим поведение
конгруэнции времениподобных кривых с единичным касательным
вектором V (g(V, V) = —1). Эти кривые могут представлять ли-
нии тока жидкости или (в том случае, когда они являются гео-
дезическими) истории малых пробных частиц. В случае идеаль-
ной жидкости, согласно (3.10),
(ц + р) Va = -- p.bhab, (4.1)
где Va = Va-,bVb — ускорение линий тока, а Наь — Ьаь + VaVb —
тензор, который проектирует вектор X е Тч в подпространство
Hq пространства Тд, ортогональное к V. Можно рассматривать
ha.b и как метрику в Нд (ср. с разд. 2.7).
Пусть 7(0—некоторая кривая с касательным вектором Z =
= (d/dt)b- Тогда можно построить семейство кривых сме-
щая каждую точку кривой 2. (f) на расстояние s вдоль интеграль-
ных кривых V. Если определить теперь Z как (д/д/)Л(г s), то из
определения производной Ли (см. разд. 2.4) следует, что
Z,VZ = 0, или, иначе говоря,
-^-Ze = V’%Z6. (4.2)
Величину Z можно интерпретировать как вектор, представляю-
щий относительное расположение указанных выше двух точек
на двух соседних кривых, которые находятся на равном расстоя-
нии от некоторых произвольных начальных точек. Если к Z до-
бавить вектор, кратный V, то полученный вектор будет изобра-
жать относительное расположение точек тех же двух кривых, но
находящихся на различных расстояниях. В действительности нас
интересуют лишь девиация соседних кривых (separation of
neighbouring curves), а не расположение отдельных точек на
них. Поэтому нам приходится иметь дело с Z с точностью до
компоненты, параллельной V, т. е. только с проекцией Z в каж-
дой точке q на пространство Qg, которое состоит из классов экви-
валентности векторов, отличающихся только добавлением век-
тора, кратного V. Это пространство можно представлять себе
как подпространство Нд пространства Тд, состоящее из векторов,
ортогональных к V. Проекцию Z на Нд будем обозначать через
xZ° = habZb. В случае жидкости можно рассматривать ^Z как
расстояние между двумя соседними частицами жидкости, изме-
ренное в их системе покоя.
Из (4.2) следует, что
= (4.3)
4.1. Времениподобные кривые
93
Эта формула дает скорость изменения девиации двух бесконечно
близких кривых, измеренную в Hq. Применяя к (4.3) операцию
D/ds еще раз и проектируя на Нч, получаем
= hab (v\cd iZcVd + Vb-,cVc.dVeZeVd +
(J о \ (J -J z
+ Vb.cVcVs.,dZeVd + Vb.,chceZe.dVd).
Изменяя порядок дифференцирования в первом члене и исполь-
зуя (4.2), приводим это равенство к виду
U9 (Ус ~1Гьы ^СуЬуС!+
+ habVb-cd.Zc + VaVbtZb. (4.4)
Это уравнение, известное как уравнение девиации или уравнение
Якоби, дает относительное ускорение, т. е. вторую производную
по времени девиации двух бесконечно близких кривых, изме-
ренную в Hq. Мы видим, что если эти кривые — геодезические,
то девиация зависит лишь от тензора Римана.
В ньютоновской теории ускорение каждой частицы опреде-
ляется градиентом потенциала Ф, и поэтому относительное уско-
рение двух частиц на расстоянии Za равно <&-abZb. Таким обра-
зом, член с тензором Римана Ra.bcdVbVd аналогичен ньютонов-
скому Ф-,ас- Действие этой «приливной силы» хорошо демонстри-
рует пример сферы, составленной из свободно падающих на
Землю частиц. Каждая частица движется по прямой, проходя-
щей через центр Земли, но более близкие к Земле частицы па-
дают быстрее тех, которые находятся дальше. Это означает, что
сфера не сохраняет свою форму, а деформируется в эллипсоид
того же объема.
Чтобы исследовать уравнение девиации, мы введем в произ-
вольной точке q интегральной кривой y(s) вектора V дуальные
ортонормированные базисы Е1( Е2, Е.3, Е4 и Е1, Е2, Е3, Е4 про-
странств Tq и T*q, причем возьмем Е4 = V. Было бы желательно
перенести затем эти базисы вдоль кривой y(s), чтобы получить
такие же базисы в каждой точке y(s). Однако при параллельном
переносе базисов вдоль y(s) (т. е. когда D/ds для каждого век-
тора обращается в нуль), Е4 не будет оставаться равным V, а
Ei, Е2, Е3 не останутся ортогональными к V, если y(s) — не гео-
дезическая. Поэтому мы введем новую производную вдоль y(s),
так называемую производную Ферми th/ds. Для векторного
поля X вдоль y(s) она определяется формулой
DP (XI DX С DV \ DV
-^— = -5—g(x, -v- V + g(X, Vн-
ds ds 6 \ ’ ds J 1 ° ' ’ ' ds
94
Гл. 4, Физический смысл кривизны
и обладает следующими свойствами:
df D
1) = ~^< если у (s) — геодезическая;
DFV
2) = 0;
’ ds
3) если X и Y — векторные поля вдоль y(s), такие, что
Dfx DfY
—— - о = ——
ds ds
TO g(X, Y) = const вдоль у (s);
4) если Xе — векторное поле вдоль у (s), ортогональное к V, то
(Последнее свойство показывает, что производная Ферми явля-
ется естественным обобщением производной D/ds.)
Итак, если перенести ортонормированный базис пространства
Tq вдоль y(s) так, чтобы производная Ферми каждого базисного
вектора была равна нулю, получится ортонормированный базис
в каждой точке y(s) с Е4 — V. Векторы Еъ Е2, Е3 можно интер-
претировать как орты невращающейся системы координатных
осей вдоль y(s). Физически их можно реализовать с помощью
маленьких гироскопов, оси которых направлены вдоль каждого
из векторов.
Определение производной Ферми для векторных полей вдоль
y(s) можно распространить на произвольные тензорные поля
обычным образом, а именно:
I. Dp/ds представляет собой линейное отображение тензор-
ных полей типа (г, s) вдоль y(s) на тензорные поля типа (г, s),
которое коммутирует со свертками;
Dp DfK DfL
II. -^(K®L) = ^-®L + K®^-;
DFf df
HI- =
ds ds
где f — произвольная функция.
Из этих правил следует, что над дуальным базисом Е1, Е2,
Е3, Е4 пространства Tq также совершается перенос Ферми
вдоль y(s). Используя производные Ферми, можно переписать
(4.3) и (4.4) в виде
^±Za = Va;btZb, (4.5)
^-^Za = -RabcdLZcVbVd + habVb-cxZc + VaVbiZb. (4.6)
4.1. Времениподобные кривые
95
Эти соотношения можно выразить через дуальные базисы, полу-
ченные переносом Ферми. Поскольку ±Z ортогонален к V, у него
есть компоненты лишь относительно Е1( Ег, Ез. Следовательно,
его можно представить как ZaEa, если мы условимся, что грече-
ские индексы пробегают только значения 1,2,3. Тогда (4.5) и
(4.6) можно записать через обыкновенные производные:
= (4.7)
^Z“ = (-7?%4 + V“;b + V“Ve)Ze, (4.8)
где и — те компоненты Va-,t, для которых а = а и b — р. По-
скольку компоненты Z“ удовлетворяют линейному обыкновен-
ному дифференциальному уравнению 1-го порядка (4.7), эти
компоненты можно выразить через их значения в некоторой
точке:
Za(S) = 4ap(S)zX (4.9)
где (s)— матрица 3X3, которая в точке q равна единичной
матрице и удовлетворяет уравнению
-т^- Дир (s) = Ха;уИу|3 (s). (4.10)
В случае жидкости можно считать, что матрица Дар задает
форму и ориентацию малого элемента жидкости, сферического
в точке q. Эту матрицу можно записать в следующем виде:
Tlap — OapSa|j, (4.11)
где Оа|з — ортогональная матрица с положительным определите-
лем, а Sa|3 — симметричная матрица. Оар и Sap могут быть вы-
браны в точке q равными единичной матрице, причем Оар мож-
но рассматривать как матрицу, характеризующую вращение со-
седних кривых относительно базиса, полученного переносом
Ферми, а 5а|з — как матрицу, описывающую смещение этих кри-
вых относительно y(s). При этом определитель Sap, который ра-
вен определителю Дар, характеризует трехмерный объем выре-
заемого соседними кривыми элемента поверхности, ортогональ-
ной к y(s).
В точке q, где Дар — единичная матрица, производная
dOa$/ds антисимметрична, а dSag/ds симметрична. Таким обра-
зом, антисимметричная часть дает скорость вращения со-
седних кривых в точке q, симметричная часть дает скорость из-
менения девиации от y(s), а скорость изменения объема опреде-
ляется следом Va;p. Поэтому мы введем тензор вращения
®ab =hahb“V\c-d], (4-12)
96
Гл. 4. Физический смысл кривизны
тензор расхождения
0аЬ = (4.13)
и объемное расхождение
Q^Qabhab = Va.bhab = Va-,a- (4.14)
Далее мы определим тензор поперечного сдвига как часть 0а&
с нулевым следом:
Cab = — у habQ (4.15)
и вектор вращения как
«а = 4 ^abcdVb&cd = Д ^abcdvbVc-d- (4.16)
Ковариантную производную вектора V можно выразить через
эти величины:
V + aab + ^Qhab~V aVb- <4'17)
Это разложение градиента вектора скорости жидкости анало-
гично соответствующему разложению в ньютоновской гидроди-
намике.
В ортонормированием базисе, полученном переносом Ферми,
вращение и расхождение можно записать с помощью матрицы
Аа, и и обратной ей матрицы А 'ар:
<£»сф = — А \[а Лз]7> (4.18)
9а|3 А у(а Д|3)у> (4.19)
6 = (det А)-1(det А). (4.20)
Из уравнения девиации (4.8) следует, что
Да0 — (— Raiyi + V а.у + ЙаЙу) Ayg. (4.21)
Если известен тензор Римана, то это уравнение позволяет вычи-
слить распространение вращения, сдвига и расхождения вдоль
интегральных кривых V.
Умножив (4.21) на /К'щ и взяв антисимметричную часть,
получим
17 ®а(3 = 2юу[а6Ыу + ^Га;|ЗГ (4-22)
Таким образом, распространение вращения зависит от антисим-
метризованного градиента ускорения, но не от «приливной силы».
4.1. Времениподобные кривые
97
Запишем это уравнение в другой форме:
w.23)
Отсюда видно, что Дуасоу6Д6р— постоянная матрица, если рас-
сматриваемые кривые — геодезические; в частности, если, вра-
щение обращается в нуль в одной точке какой-либо кривой, то в
случае геодезических оно равно нулю во всех точках этой кри-
вой. Если эти кривые представляют линии тока идеальной
жидкости, то из (4.1) следует, что
! dp
^ = -7477®*^.
Если жидкость изэнтропическая, то отсюда следует закон со-
хранения:
1ЕЛуао)у6Лб,. = const, (4.24)
где
Этот закон сохранения представляет собой релятивистскую фор-
му ньютоновского закона сохранения момента количества дви-
жения. В геодезическом случае или при отсутствии давления он
сводится к обычному утверждению, что величина вектора мо-
мента количества движения обратно пропорциональна площади
сечения элемента жидкости, ортогонального к этому вектору.
Когда давление не равно нулю, появляются дополнительный ре-
лятивистский эффект, возникающий из-за того, что давление со-
вершает работу над жидкостью, вследствие чего возрастает
масса, а следовательно, и инерция элемента жидкости [ср. с
(3.9)]. Это означает, что вращение жидкости под давлением воз-
растает медленнее, чем можно было бы ожидать без учета дав-
ления.
Умножив (4.21) на и взяв симметричную часть, нахо-
дим
0а0 — — -Яа4|34 ““ СОауССур — баубуР + Ё(а;|3) + Va(4.25)
Уравнения (4.25) и (4.23) можно записать в общем базисе (не
ортонормированном и не обязательно полученном путем пере-
носа Ферми) при помощи замены обыкновенных производных на
производные Ферми и проектированием на подпространство, ор-
тогональное к V.
След уравнения (4.25) равен
77 0 = - RabVaVb + 2сУ - 2а2 - 1 92 + Va-,a) (4.26)
4 Заказ 381
98
Гл. 4. Физический смысл кривизны
где
2<в2 — йаг,со°6 О,
2<т2 = GabGab >0.
Это уравнение, впервые полученное Ландау и независимо Рай-
чаудхури, в дальнейшем будет играть весьма важную роль. Из
него видно, что вращение порождает расхождение, как и следо-
вало ожидать из аналогии с центробежной силой, в то время
как сдвиг приводит к схождению. Согласно уравнениям поля
для идеальной жидкости, касательным вектором линий тока ко-
торой является Va, имеем
RabVaVb = 4K(v + 3p).
Поэтому можно ожидать, что этот член также приводит к схо-
ждению. Общее исследование знака этого члена будет прове-
дено в разд. 4.3.
Вычитая из (4.25) его след, получим
®аЬ = СacbdV И ha hb Red b b
~ f 9<Ta6 + hachbdV{e-,d) -jhab (2й2 - 2a2 + Va-.a + ~Rcdhcd\ (4.27)
где Cabcd — тензор Вейля. Поскольку этот тензор имеет нулевой
след, он не входит непосредственно в уравнение расхождения
(4.26), но из-за присутствия члена —2о2 в правой части этого
уравнения тензор Вейля, индуцируя сдвиг, косвенно вызывает
схождение кривых. Тензор Римана выражается через тензор
Вейля и тензор Риччи:
^abed С abed ga[d^ c]b §b[c^d]a 3 g a[cg d]b‘
Тензор Риччи определяется уравнениями Эйнштейна
Rab jT gabR “Ь А-gab ЗпТаЬ.
Следовательно, тензор Вейля представляет собой ту часть кри-
визны, которая локально не определяется распределением мате-
рии. Однако он не может быть совершенно произвольным, по-
скольку тензор Римана должен удовлетворять тождествам
Бианки:
Rab{ed’,e\ = 0.
Последние можно переписать в виде
seabed rabc
В ;d = J
где
rabc nclaib] . 1 c[bD;a]
— A T "g g X
(4.28)
(4.29)
4.2. Изотропные кривые
99
Эт<о соотношение похоже на уравнения Максвелла в электроди-
намике:
r>ab та
Г -,Ь = J ,
где Fab — тензор электромагнитного поля, a J'1 — ток источников.
Таким образом, тождества Бианки (4.28) в определенном смысле
можно считать уравнениями поля для тензора Вейля, являюще-
гося той частью кривизны в данной точке, которая зависит от
распределения материи в других точках. (Этот подход был ис-
пользован для анализа поведения гравитационного излучения в
работах [71, 113, 116].)
4.2. Изотропные кривые
Как и в случае времениподобных кривых, тензор Римана бу-
дете влиять на скорость изменения относительного расположения
изотропных кривых. Для простоты мы рассмотрим только изо-
тропные геодезические. Они могут отображать мировые линии
фотонов; влияние тензора Римана будет состоять в искривлении
или фокусировке малых пучков световых лучей.
Чтобы исследовать это явление, рассмотрим уравнение де-
виации для конгруэнции изотропных геодезических с касатель-
ным вектором К (g(K,K) = 0). Здесь имеются два важных от-
личия от случая времениподобных кривых, рассмотренного в
предыдущем разделе.
Во-первых, там мы располагали возможностью нормировать
касательные векторы V к времениподобным кривым при помощи
услювия g(V, V) =—1. В сущности это означает, что кривые
бы.ли параметризованы длиной дуги s. Ясно, что это невозможно
для изотропных кривых, так как дуги их имеют нулевую длину.
Самое большее, что можно сделать, — это воспользоваться аф-
фшнным параметром и; тогда касательный вектор К подчиняется
уравнению
-£-/С = /саХ = о.
(W
Од.нако v можно умножить на функцию f, постоянную вдоль
каждой кривой. Тогда fv будет другим аффинным параметром,
и соответствующим касательным вектором будет f-1K. Таким об-
разом, если кривые заданы как точечные множества на много-
образии, то касательный вектор будет однозначен лишь с точ-
ностью до множителя, постоянного вдоль каждой конвой.
Во-вторых, еще одно различие состоит в том, что Qq, фактор-
пространство Тд по К, теперь не изоморфно Нд, т. е. подпро-
странству Тд, ортогональному к К: из-за того, что g(K, К) = О,
сам: вектор К тоже содержится в Hq. На самом деле, как будет
показано ниже, реальный интерес представляет не пространство
100
Гл. 4. Физический смысл кривизны
Qq в целом, а только его подпространство Sq, состоящее из клас-
сов эквивалентности векторов из Нд, которые отличаются лишь
на вектор, кратный К. В случае лучей света элемент Sg можно
рассматривать как вектор, описывающий девиацию двух близ-
ких лучей, излученных источником в одно и то же время.
Как и прежде, введем дуальные базисы Еь Е2, Е3, Е4 и Е1,
Е2, Е3, Е4 пространств Тq и в некоторой точке q на кривой у (у).
Однако не будем брать их ортонормированными: выберем Е4
равным К, в качестве Е3 возьмем некоторый другой изотропный
вектор L, скалярное произведение которого с Е4 равно — 1, т. е.
g(E3, Е3) = 0, g(E3, Е4) = — 1, а Е, и Е2 пусть будут единичными
пространственноподобными векторами, ортогональными друг
другу и векторам Е3, Е4:
g(Eb E,)=g(E2> E2) = l, g (Е,, E2)=g(Eb E3) = g(E1, Е4)=0 и т. д.
Отметим, что в силу неортонормированного характера этого
базиса форма Е3 будет равна форме —K.agab, а Е4 = —Lagab.
Можно убедиться, что Еь Е2, Е4 образуют базис в Hq, в то время
как проекции векторов Еь Е2, Е3 на Qq образуют базис в Qy,
наконец, проекции Е4 и Е2 образуют базис в Sq. Как правило,
мы не будем различать вектор Z и его проекции на Qq или Sq.
Базис Ei, Е2, Ез, Е4, обладающий указанными свойствами, будем
называть псевдоортонормированным. Параллельным переносом
этих векторов вдоль геодезической у (у) мы получим псевдоорто-
нормированный базис в каждой точке у (у).
Мы используем этот базис для анализа уравнения девиации
изотропных геодезических. Если Z — вектор девиаций, изобра-
жающий относительное расположение соответствующих точек
на соседних кривых, то, как и прежде, имеем
Z-kZ = 0,
так что
-~Za^Ka.bZb (4.30)
и
^Za=~RabcdZcKbKd. (4.31)
В псевдоортонормированном базисе Ка,4 — 0, поскольку вектор
К — касательный к геодезической. Поэтому при а = 1, 2, 3 урав-
нение (4.30) можно представить как систему обыкновенных диф-
ференциальных уравнений:
4-Za = Ка-aZ15,
do ,р ’
где, как и прежде, греческие индексы принимают значения 1,2,3.
Отсюда видно, что проекция Z на пространство Qq подчиняется
4.2. Изотропные кривые
101
уравнению распространения, содержащему только саму эту про-
екцию, без компоненты, параллельной К. Далее, К3-с = 0, по-
скольку (Ка§аьКЬУ.с = 0. Отсюда следует, что компонента Z3 —
= —ZaKa постоянна вдоль геодезической y(v). Это можно ин-
терпретировать следующим образом: девиация лучей света, ис-
пущенных одним и тем же источником в разное время, остается
постоянной во времени. Коль скоро это так, наибольший интерес
представляет поведение соседних изотропных геодезических с
чисто пространственным вектором девиации, т. е. Z с Z3 = 0.
Проекции таких векторов на Qq будут лежать тогда в подпро-
странстве и будут подчиняться уравнению
4 __ TSfTl уп
7? 2 - К >
где т, п принимают только значения 1, 2. Оно подобно уравне-
нию (4.7) для времениподобного случая, за тем исключением,
что теперь мы имеем дело с двумерным пространством векто-
ров Z, соединяющих соседние кривые.
Как и в предыдущем разделе, Zm можно выразить через его
значения в некоторой точке q:
Zm(v) = Amn(v) Zn'\q,
где Amn (v) — матрица 2X2, удовлетворяющая уравнениям
-^-Amn(v)=Km;pApn(v), (4.32)
Ати(у) — RmiPiAph (у)- (4.33)
Как и прежде, будем называть ытп = К[т-П} вращением, 6тп =
— К(т-,п) — скоростью девиации, 9, след 0т„ — расхождением;
сдвиг дтп определим как бесследовую часть Qmn. Уравнения для
них подобны уравнениям для аналогичных величин в предыду-
щем разделе:
(4'34)
0 = - RabKaKb + 2й2 - 262 -102, (4.35)
®тп = С mini ^&тп- (4.36)
Уравнение (4.35) является аналогом уравнения Райчаудхури
для времениподобных геодезических. Снова мы видим, что вра-
щение вызывает расхождение, в то время как сдвиг приводит
к схождению. В следующем разделе мы покажем, что в нормаль-
ных условиях член с тензором Риччи (Rai>KaKb) отрицателен и,
102
Гл. 4. Физический смысл кривизны
следовательно, порождает фокусирование. Как и прежде, тензор
Вейля непосредственно не влияет на расхождение, но вызывает
искривление, которое в свою очередь приводит к схождению (ср.
[127]).
4.3. Энергетические условия
В реальной Вселенной тензор энергии-импульса будет со-
стоять из вкладов большого числа различных материальных по-
лей. Поэтому, даже если нам были бы известны точный вид
вклада каждого поля в отдельности и его уравнения движения,
было бы слишком сложно выписать точное выражение для тен-
зора энергии-импульса. В самом деле, мы весьма смутно пред-
ставляем поведение материи в условиях предельно высоких дав-
лений и плотностей. Таким образом, может показаться, что мало
надежды на предсказание существования сингулярностей во Все-
ленной по уравнениям Эйнштейна, поскольку их правая часть
нам неизвестна. Однако, по-видимому, имеются основания для
того, чтобы потребовать выполнения определенных неравенств
для тензора энергии-импульса. В этом разделе мы собираемся
рассмотреть эти неравенства. Оказывается, что во многих си-
туациях их достаточно для того, чтобы независимо от вида тен-
зора энергии-импульса доказать наличие сингулярностей.
Первым из этих неравенств является
Слабое энергетическое условие
Тензор энергии импульса в каждой точке р е Я удовлетво
ряет неравенству TabWaWb 0 при любом времениподобном
векторе Вследствие непрерывности это условие будет
справедливо и для любого изотропного вектора We7f„
Наблюдателю, мировая линия которого имеет единичным ка-
сательным вектором V, локальная плотность энергии кажется
равной TabVaVb. Следовательно, наше неравенство эквивалентно
утверждению, что локальная плотность энергии, измеренная ка-
ким-либо наблюдателем, неотрицательна. С точки зрения физики
это представляется весьма разумным. Для дальнейшего выясне-
ния смысла этого неравенства воспользуемся тем обстоятель-
ством, что в точке р компоненты тензора энергии-импульса ТаЬ
в базисе Еь Е2, Е3, Е4 (с времениподобным Е4) можно предста-
вить в одной из четырех канонических форм.
Тип I
4.3. Энергетические условия
103
Это тот общий случай, когда тензор энергии-импульса обладает
времениподобным собственным вектором Е4, и притом единствен-
ным, за исключением случая, когда у. = —ра (а = 1, 2, 3). Соб-
ственное значение у представляет собой плотность энергии по
измерениям наблюдателя, мировая линия которого в точке р
имеет касательным вектором Е4; собственные значения ра (а =
= 1, 2, 3) являются главными значениями давления в трех про-
странственноподобных направлениях Еа. Таков вид энергии-им-
пульса для всех наблюдаемых полей с ненулевой массой покоя,
а также и для всех полей с нулевой массой покоя, за исключе-
нием одного особого случая, когда мы имеем каноническую фор-
му типа II.
Тип II
Pi о
0
0
V V -ф X
В этом особом случае тензор энергии-импульса имеет дву-
кратный собственный вектор Ез -ф Е4. Единственный наблюдае-
мый случай такой формы — когда безмассовое поле представ-
ляет собой излучение, целиком распространяющееся в направле-
нии Е3 -ф Е4. В этом случае pi, рг и х равны нулю.
Тип III
/ р 0 0 Ох
. | 0 — v 1 1 |
срао _ I I
I О 1 -v О Г
X О 1 О V /
Это — особый случай, в котором тензор энергии-импульса обла-
дает трехкратным изотропным собственным вектором Е3 -ф Е4.
Полей, обладающих тензором энергии такого вида, не обнару-
жено.
Тип IV
Pl 0 0
'раЬ __ 0 Р-2 — X V , х2 < : 4v2.
0 v 0
104
Гл. 4. Физический смысл кривизны
Это — общий случай, когда у тензора энергии-импульса нет вре-
мениподобных или изотропных собственных векторов. Наблюдае-
мых полей с тензорами энергии-импульса такого вида тоже не
существует.
Для типа I слабое энергетическое условие будет выполняться
при ii^O, р, + ра 0 (а=1, 2, 3). Для типа II оно будет
выполнено, если р\ 0, р2 0, х > 0, v — +1- Эти неравен-
ства являются весьма разумными, и им удовлетворяют все экс-
периментально обнаруженные поля. Для физически нереализую-
щихся типов III и IV слабое энергетическое условие не выпол-
няется.
Этому условию удовлетворяет также скалярное поле ф, по-
стулированное Брансом и Дикке [39]. От этого поля требуется,
чтобы оно всюду было положительным. Его тензор энергии-им-
пульса имеет вид (3.6), причем т = 0. Тензор энергии-импульса
всех других полей отличается в ф раз от того, что было бы, если
бы это скалярное поле не существовало.
Слабое энергетическое условие не выполняется для «С-поля»,
предложенного Хойлом и Нарликаром [82], которое также яв-
ляется скалярным полем с т = 0; только на этот раз тензор
энергии-импульса имеет противоположный знак и, следователь-
но, плотность энергии отрицательна. Ввиду этого возможно одно-
временное рождение квантов полей с положительной энергией и
С-поля с отрицательной энергией. Этот процесс происходит в
стационарной модели Вселенной, предложенной Хойлом и Нар-
ликаром, в которой по мере разлета частиц вследствие общего
расширения Вселенной непрерывно рождается новое вещество,
так что поддерживается постоянная средняя плотность. Однако
подобный процесс вызывает трудности с точки зрения кванто-
вой механики. Даже если сечение такого процесса очень мало,
наличие бесконечного фазового объема для квантов положи-
тельной и отрицательной энергии привело бы к рождению
бесконечного числа пар в конечной области пространства-вре-
мени.
Такой катастрофы не случится, если выполняется слабое
энергетическое условие. Существует также несколько более силь-
ное условие, при котором невозможно рождение материи в том
смысле, что пространство-время остается пустым все время, если
оно пустое в какой-либо момент времени, и никакая материя не
поступает из бесконечности; наоборот, материя, имеющаяся в
какой-то момент времени, не может исчезнуть и, таким образом,
присутствует всегда. Этим условием является
Условие энергодоминантности
Для любого времениподобного WaTabWaWi> 0, а ТаЬ^а —
непространственноподобный вектор.
4.3. Энергетические условия
105
Это условие можно интерпретировать следующим образом:
любой наблюдатель видит, что локальная энергия неотрицатель-
на, а локальный поток энергии непространственноподобен. Экви-
валентным этому является утверждение, что в любом ортонор-
мированном базисе энергия доминирует над другими компонен-
тами Tab, т. е.
Т°°'^\ТаЬ\ для любых а, Ь.
Это условие выполняется для типа I при ц 0, —и Ра Ц
(а = 1, 2, 3) и для типа II при v = +1, х Js 0,
Рис. 9. Компактная область <Н пространства-времени с невремениподоб-
ными границами прошлого и будущего (d°Up, (Ш), и времениподобной
границей (<Ж)3. °U (t')~ часть ‘U, лежащая в прошлом поверхности Ж (t')
(определяемой значением t = i').
(i = 1, 2). Другими словами, условие энергодоминантности пред-
ставляет собой слабое энергетическое условие, дополненное тре-
бованием, чтобы давление не превышало плотности энергии. Ему
удовлетворяют все известные формы материи и имеются серьез-
ные основания предполагать, что оно выполняется во всех си-
туациях. Дело в том, что скорость звуковых волн, распростра-
няющихся в направлении Еа, равна скорости света, умноженной
на (dpa/d;i)адиаб- Значит, должно быть справедливо неравенстве
(dpa/dg) С 1, ибо, согласно постулату (а) разд. 3.2, никакой сиг-
нал не может распространяться быстрее света. Отсюда следует,
что ра и, поскольку для любой известной формы материй дав-
ления малы, когда малы плотности. (Блудман и Рудерман [8. 9]
показали, что могут быть поля, для которых перенормировка
массы может привести к тому, что давление будет больше
105
Гл. 4. Физический смысл кривизны
плотности энергии. Однако, на наш взгляд, это скорее говорит
против теории перенормировок, чем в пользу возможности такой
ситуации.)
Рассмотрим теперь ситуацию, изображенную на рис. 9, когда
имеется С2-функция t, градиент которой всюду времениподобен.
(В разд. 6.4 будет показано, что такая функция существует, если
только пространство-время не слишком близко к нарушению
причинности.) Граница д°И компактной области состоит: 1) из
части (d^i, нормальная форма п которой непространственно-
подобна и такая, что на nat-bgab > 0; 2) из части (<Ж)г, нор-
мальная форма п которой непространственноподобна, но
nat-bgab <0 и 3) из остальной части (<Ж)з (которая может быть
пуста). Знак нормальной формы п получается из требования,
чтобы (n, X) было положительным для всех векторов X, которые
направлены наружу SZZ (ср. с разд. 2.8); 5^(7') означает поверх-
ность t = Г, a — область в <2/, в которой t <_ t'. Для даль-
нейшего использования в разд. 7.4 мы установим одно неравен-
ство, которое выполняется не только для ТаЪ, но и для любого
симметричного тензора Sab, удовлетворяющего условию энерго-
доминантности. В приложении к тензору энергии-импульса это
неравенство будет означать, что он обращается в нуль всюду
в CU, если он равен нулю на (<Ж)з и на начальной поверхности
Лемма 4.3.1.
Существует некоторая положительная постоянная Р, такая,
что для любого тензора Sab, удовлетворяющего условию энерго-
доминан гности и обращающегося в нуль на (сШ)3,
Sabt-a dffb Sabt-adGb +
t t
+ J SaVadobW+$ ( J Sa*;ada6W.
Рассмотрим интеграл по объему
7(0= J (Sabt.a).b dv = J Sabt-ab&v+ J Sab-bt-a&v.
(0 <U (t) CU (0
По теореме Гаусса его можно преобразовать в интеграл по
границе области ‘U (/):
/(0= Sa4adcT6.
4.3. Энергетические условия
107
Граница <U(f) состоит из (t) f] &U и 'U П 7Г (/). Поскольку
Sab = 0 на (<Ж)3, то
I (t) — j
<U </)п(а^)1 (/)п(Ж)2 cUn3f(t}
В силу условия энергодоминантности Sabt-a существует непро-
странственноподобный вектор и Sabt-at-b 0. Так как нормаль-
ная форма на (<Зб2/)2 непространственноподобна и nat-bgab < 0,
то второй член в правой части неотрицателен. Следовательно,
Sabt-,a dCb Sabt;ad(Jb +
'г/пдаю «)п(<э^)1
+ j (Sabt.ab + Sab.,bt-,a)<iv.
<U (t)
В силу компактности 01 в любом ортонормированием базисе
с времениподобным вектором, направленным по t-ab, существует
некоторая верхняя граница для компонент t-a. Значит, сущест-
вует такое Р > 0, что в
Sabt-ab^PSabt.at.b
для любого Sab, удовлетворяющего условию энергодоминант-
ности. Интеграл по “2/(0 можно представить в виде поверхно-
стного интеграла по ^(Г)(~|^ с последующим интегрированием
по f:
t
J (PSabt,at.b + Sab;bt.a) du = И J (PSabt.b 4- Sab.b) d<ral dr,
(i) *'ЭГ(Г)П<^
где daa — элемент поверхности (Г). Итак,
J Sabt,a dab^- J Sabt-a dcr6 +
t t
+ $ Sa4a dcrA d/+$ f Sa6;a ФщЛ dr. □
'да(Г)п^ ' 'да (t')n^ '
Из этого результата сразу следует
Теорема сохранения
Если тензор энергии-импульса удовлетворяет условию энерго-
доминантности и равен нулю на (<9<2/)з и на начальной поверх-
ности тогда он равен нулю всюду в (U.
108
Гл. 4. Физический смысл кривизны
Допустим, ЧТО
t
x(t) = j Tabt-at-,b dv— ( j TaZ7;a do^d/' 2>0.
‘Um '43f(/')n^ '
Тогда по лемме 4.3.1 получаем dxf&t Px. Но при достаточно
малых значениях t 3@(t) не пересекает Pl и, следовательно,
х — 0. Тогда х=0 при всех t и, следовательно, ТаЬ=0 в Pl. □
Из теоремы сохранения следует, что тензор энергии-импуль-
са, равный нулю на множестве 9\ равен нулю также на обла-
сти Коши будущего, Z)+(^), которая по определению есть
множество всех точек, обладающих тем свойством (рис. 10), что
Рис. 10. Область Коши будущего D+ (S’) пространственноподобного мно-
жества (S’).
любая проходящая через них непространственноподобная кри-
вая, направленная в прошлое, пересекает РР (ср. с разд. 6.5).
Действительно, если q—-какая-нибудь точка £)+(<?’), то область
Д+(5г'), расположенная в прошлом q, компактна (предложение
6.6.6), и ее можно взять в качестве Pl. Этот результат можно
интерпретировать в том смысле, что из условия энергодоминант-
ности следует невозможность движения материи быстрее света.
Значение слабого энергетического условия для нашего иссле-
дования сингулярностей состоит в том, что из него следует
вывод о фокусирующем (точнее недефокусирующем) действии
материи на конгруэнции изотропных геодезических. Если нет
вращения, расхождение 0 подчиняется уравнению
4 9 = - RabKaKb - 2d2 -4 02.
Таким образом, 0 в этом случае монотонно убывает вдоль изо-
тропной геодезической, если RabWaWb 0 для любого изотроп-
ного вектора W. Назовем это условие условием изотропного схо-
ждения. Из уравнений Эйнштейна
Rab 2 Agab Вл7'
4.3. Энергетические условия
109
следует, что условие изотропного схождения независимо от зна-
чения Л содержится в слабом энергетическом условии.
Из (4.26) можно получить, что расхождение 9 времениподоб-
ной геодезической конгруэнции будет монотонно убывать вдоль
геодезической, если RacWa U"6 jjs б для любого времениподобно-
го W. Это условие назовем условием времениподобного схожде-
ния. В силу уравнений Эйнштейна оно удовлетворяется, если
для тензора энергии-импульса выполняется неравенство
TabWaWb > WaWa Т - g^A) .
Для типа I это имеет место при
Н + Ра>0, — 4^-Л>0,
а для типа II — при
V = +1, х>0, р2^о и Р1 +/’2 — тур Л >0.
Будем говорить, что тензор энергии-импульса удовлетворяет
сильному энергетическому условию, если приведенное неравен-
ство выполняется при Л = 0. Это требование сильнее слабого
энергетического условия, и все же в приложении к полному тен-
зору энергии-импульса оно физически обосновано. Действитель-
но, в общем случае (тип I) оно нарушается только наличием
отрицательной плотности энергии или большого отрицательного
давления (например, для идеальной жидкости плотностью
I г/см3 нарушение может произойти только при р < —1015 атм).
Это условие выполняется для электромагнитного поля и безмас-
сового скалярного поля (в частности, для скалярного поля Бран-
са— Дикке). Для скалярного поля с ненулевой массой m тензор
энергии-импульса имеет вид (разд. 3.3)
Tab = <ha<hb — у gab (f-.cf-.dg^ + W2</>2).
Отсюда, если Wa — единичный времениподобный вектор, имеем
TabWaWb - | WaWaT = ау- - 4 (4-37)
т. е. это выражение может быть отрицательным. Однако из урав-
нений скалярного поля следует
1 m3 ,2 1 , ,
-2-^^=^^-.abgab.
Учитывая это соотношение в (4.37) и интегрируя по некоторой
области °U, получаем
4 J {gab + 2WnWb) ф;аф-ь do + 4 J dw .
41 Q°U
но
Гл. 4. Физический смысл кривизны
Первый член неотрицателен, ибо g'-111 + 2WaWb есть положитель-
но-определенная метрика, а второй член мал по сравнению с пер-
вым, если область °11 велика по сравнению с длиной волны him.
Для л-мезонов, которые классически можно описывать скаляр-
ным полем, т = 6- 10~25 г, fi/m = 3-10~13 см. Итак, хотя тензор
энергии-импульса л-мезонов может и не удовлетворять сильному
энергетическому условию в каждой точке, это не будет влиять
на схождение времениподобных геодезических на расстояниях,
превышающих 10~12 см. Возможно, такое нарушение сильного
энергетического условия привело бы к тому, что теоремы о син-
гулярностях (гл. 8) теряли бы справедливость при радиусе кри-
визны меньше 10~12 см, но при этом кривизна столь велика, что
ее можно было бы с успехом принять за сингулярность
(разд. 10.2).
4.4. Сопряженные точки
В разд. 4.1 мы видели, что компоненты вектора девиации, ха-
рактеризующего взаимное расположение y(s) и соседней кривой
в конгруэнции времениподобных геодезических, подчиняются
уравнению Якоби:
-^Za = -T?a4p4Zs (а, р=1, 2, 3). (4.38)
Решение этого уравнения будем называть якобиевым полем
вдоль y(s). Поскольку решение может быть охарактеризовано
заданием Za и dZ“/ds в некоторой точке у(з), то вдоль y(s) бу-
дет шесть якобиевых полей. Существует три независимых яко-
биевых поля, равных нулю в некоторой точке q е y(s). Их мож-
но записать следующим образом:
Лз) = у*)|Я
где
Аа. (s) = - 7?a4vMvp (s), (4.39)
и (s)— матрица 3X3, равная нулю в q. Можно считать, что
эти якобиевы поля описывают девиацию (взаимное разделение)
соседних геодезических, проходящих через q. Как и прежде,
можно определить вращение, поперечный сдвиг и расхождение
якобиевых полей вдоль у($), обращающихся в нуль в q-.
®сф ~ 41 ‘v IB 41a]Y, (4.40)
°aP = 41 7(641a)v y“6ap0, (4.41)
0 = (det A)-'-j-(det A). (4.42)
4.4. Сопряженные точки
111
Они будут подчиняться выведенным в разд. 4.1 уравнениям с
ро = 0. В частности, матрица
^1уа®у6-^63 ~2 (^Y“’d? ^V|3 ^Y|3 "ds" ^Y“)
будет постоянной вдоль y(s). Однако она равна нулю в q, где
Аар = 0. Следовательно, <оар = 0 везде, где Аар неособенна.
Будем говорить, что точка р на y(s) сопряжена точке q вдоль
y(s), если найдется якобиево поле, не равное тождественно нулю,
которое исчезает в q и р. Можно представлять себе р как точку,
в которой пересекаются бесконечно близкие геодезические, про-
ходящие через q. (Отметим, однако, что в р будут пересекаться
только бесконечно близкие геодезические; не обязательно, чтобы
две различные геодезические, выходя из q, проходили через р.)
Якобиевы поля, обращающиеся в нуль в q, определяются матри-
цами Лар. Поэтому точка р сопряжена точке q вдоль y(s) тогда
и только тогда, когда Аа$— особенная матрица в р. Объемное
расхождение 0 определяется как (det A)-1d(det A)/ds. Поскольку
Aap подчиняется уравнению (4.39) с конечным Ra^i, d (detA)/ds
должно быть конечно. Следовательно, р будет сопряжена q вдоль
y(s), если 9 становится бесконечным в р. Обратное тоже верно,
ибо 0 = d In (detA) /ds, а матрица Aap может быть особенной
только в .изолированных точках, иначе она была бы особенной
всюду.
Предложение 4.4.1
Пусть в некоторой точке y(si) (si > 0) объемное расхожде-
ние 0 принимает значение 0t < 0 и пусть всюду RabVaVb 0;
тогда между y(si) и y(si + (3/—91)) [при условии, что y(s) мож-
но продолжать до этих значений параметра] существует точка,
сопряженная q вдоль y(s). (Это последнее условие может ока-
заться невыполненным, если пространство-время геодезически
неполно. В гл. 8 такая неполнота интерпретируется как проявле-
ние сингулярности.)
Объемное расхождение 0 матрицы Аар подчиняется уравне-
нию Райчаудхури (4.26):
-^0 = -Т?аЛ/а1/й-2а2-|о2.
(Здесь мы пользуемся тем, что вращение отсутствует.) Все чле-
ны в правой части отрицательны. Следовательно, при s > Si
3
s-(s, + (з/ — 00)'
Отсюда следует, что 0 обращается в бесконечность, так что су-
ществует точка, сопряженная q, при значении $0, заключенном
между Si и sj + (3/—0i). п
112
Гл 4. Физический смысл кривизны
Другими словами, если выполняется условие времениподоб-
ного схождения и если соседние геодезические, выходящие из q,
начинают сходиться к y(s), то некоторые бесконечно близкие
геодезические пересекут y(s), если только можно провести у(д)
до достаточно больших значений параметра s.
Предложение 4.4.2
Если Rat>VaVb и если в некоторой точке p = y(st) при-
ливная сила RabcdVbVd не равна нулю, найдутся такие значения
so и s2, что 7 = y(s0) и r = y(s2) будут сопряжены вдоль y(s)
при условии, что y(s) можно продолжить до этих значений s.
Решение уравнения (4.39) вдоль y(s) однозначно опреде-
ляется значениями Aa!i и d/1ap/ds в точке р. Рассмотрим множе-
ство Р, состоящее из всех таких решений, для которых Дар | р =
= бар, a (dyl^p/ds) | р — симметричная матрица со следом
(-) ,) >0. Для каждого решения из Р найдется некоторое s3 > s1(
при котором Ла|з (s3)—особенная матрица, поскольку или
О р < 0, и тогда это следует из предыдущего результата, или
0 р= 0, и тогда (doy^/ds) | Р =И= О, а, значит, о2 > 0, и вследствие
этого 0 становится отрицательным при s > s4. Элементы множе-
ства Р находятся во взаимно-однозначном соответствии с про-
странством S всех симметричных матриц 3 X 3 с неположитель-
ным следом [т. е. со всеми (d/l^g/ds) |р]. Следовательно, имеется
отображение q из S в y(s)> которое каждому начальному зна-
чению (d/lap/ds)|р ставит в соответствие ту точку на y(s)> в ко-
торой Да|з в первый раз становится особенной. Это отображение
непрерывно. Далее, если какая-либо из компонент (d/l^/ds) | р
очень велика, соответствующая точка на у(«) будет находиться
близко к р, поскольку член Ratyi в (4.39) в пределе становится
пренебрежимо малым и решение приобретает тот же вид, что и
в плоском случае. Таким образом, найдутся такие постоянные
С>0 и s4 > Si, что если какая-либо компонента (d/lap/ds) |р
больше С, то соответствующая точка на у(«) ближе к р, чем
y(s4). Но в пространстве S подпространство, состоящее из всех
матриц, элементы которых меньше или равны С, компактно.
Отсюда видно, что существует такое s5 > sb что r|(S) содер-
жится в сегменте [y(«i), y(ss)]- Рассмотрим теперь точку г —
= y(s2), причем s2 > s5. Если между г и р нет точек, сопряжен-
ных г, якобиевы поля, равные нулю в г, должны иметь в точке р
положительное расхождение 0 (иначе они принадлежали бы
множеству Р, представляющему собой все семейства якобиевых
полей без вращения с неположительным объемным расхожде-
нием в р). Тогда из предыдущего предложения следует, что най-
дется точка q = y(s0) ($0<Si), которая сопряжена г вдоль
y(s). □
4.4. Сопряженные точки
113
Для реалистического с точки зрения физики решения уравне-
ний Эйнштейна можно ожидать, что каждая времениподобная
геодезическая проходит сквозь какую-то материю или гравита-
ционное излучение и, следовательно, содержит точку, где
RabcdVbVd =И= 0 (хотя этого может и не быть в точном решении
с высокой симметрией). Было бы разумно предположить, что
в таком решении каждая времениподобная геодезическая содер-
жит пары сопряженных точек, при условии, что эта линия может
быть продолжена достаточно далеко в обоих направлениях.
Мы рассмотрим также конгруэнцию времениподобных геоде-
зических, нормальных к пространственноподобной трехмерной
поверхности 2ё. Пространственноподобной 3-поверхностью мы
называем вложенное трехмерное подмногообразие, определенное
локально уравнением / = 0, где f есть С2-функция и gabf-,af-,b < О
при f = 0. Введем N, единичный нормальный вектор к Ж: № =
= (— gbcf;bf-,c)~'/2 gadf-,d и второй фундаментальный тензор х на
Xab = hachbdNc-d, где hab = gab + NaNb называется первым
фундаментальным тензором (или индуцированным метрическим
тензором) на 3$ (ср. с разд. 2.7). Из этого определения следует,
что тензор х симметричен. Конгруэнция времениподобных геоде-
зических, ортогональных к 2ё, будет состоять из времениподоб-
ных геодезических, у которых единичные касательные векторы V
на 2ё равны N. Тогда имеем
Va;6 = xa& на Ж (4.43)
Вектор девиации Z, изображающий расположение относительно
y(s) соседних геодезических, нормальных к Зё, будет подчи-
няться уравнению Якоби (4.38). На y(s) Zb точке q ее %ё удо-
влетворяет начальному условию
4za = Xa,3Z₽. (4.44)
Мы представим якобиевы поля вдоль y(s), удовлетворяющие
этому условию, в виде
Za(S) = /la3(S)Z0|<7,
где
'^$2 (4.45)
а в точке q Лар — единичная матрица, и
77 Лх|3 = Хау-^ур* (4.46)
Будем говорить, что точка pey(s) сопряжена поверхности Уё
вдоль y(s), если существует якобиево поле вдоль у(з), не рав-
ное тождественно нулю, удовлетворяющее в q начальному
Ill
Г л. 4. Физический смысл кривизны
условию 4.4.4 и обращающееся в нуль в р. Другими словами, р
сопряженно Ж вдоль y(s), если и только если Аа$ особенна в р.
Можно представлять себе р как точку, в которой пересекаются
соседние геодезические, нормальные к Ж. Как и прежде, Аа$
будет особенна там и только там, где расхождение становится
бесконечным. Начальное значение в q равно нулю, и
поэтому соар = 0 на y(s). Начальное значение 0 равно Хаь<7аЬ-
Предложение 4.4.3
Если RabVaVb >0 и %abgab < 0, найдется точка, сопряжен-
ная Ж вдоль y(s) на расстоянии от Ж не более 3/(—%аьёаЬ), при
условии, что y(s) можно продолжить на такое расстояние.
Для доказательства можно использовать уравнение Райчауд-
хури (4.26), как и при доказательстве предложения 4.4.1. п
Будем называть решение уравнения
Zm = - RminiZn (т, п=1, 2)
вдоль изотропной геодезической у(п) якобиевым полем вдоль
у(а). Компоненты Zm можно рассматривать как компоненты век-
тора в пространстве Sq каждой точки q относительно базиса Ei,
Е2. Будем говорить, что р сопряжено q вдоль изотропной геоде-
зической у(у)> если существует не равное тождественно нулю
якобиево поле вдоль у(и), обращающееся в нуль в q и р. Если
Z — вектор, соединяющий соседние изотропные геодезические,
проходящие через q, компонента Z3 будет равна нулю всюду.
Таким образом, р можно представлять себе как точку, в которой
пересекаются бесконечно близкие геодезические, проходящие че-
рез q. Опишем обращающиеся в нуль в q якобиевы поля вдоль
Y(s) матрицами 2 X 2Amn:
Zm(v) = Ami±Zn\q.
Как и прежде, имеем Atm&>tkAkn = 0, и поэтому у якобиевых по-
лей, равных нулю в р, вращение отсутствует. И снова р будет
сопряженно q вдоль y(s), если и только если
0 = (det АГ14 (det А)
обращается в р в бесконечность. Аналогично предложению 4.4.1
имеем
Предложение 4.4.4
Если всюду RabKaKb 0 и если в некоторой точке у (Vi) рас-
хождение 0 имеет отрицательное значение 0Х < 0, тогда между
y(vi) и y(vi + (2/—61)) найдется точка, сопряженная q вдоль
4.4. Сопряженные точки
Ш
у(у), при условии, что у(у) можно продолжить на такое рас-
стояние.
Расхождение 0 матрицы Атп подчиняется уравнению (4.3.5):
±е =-RabK“Kb-
и, следовательно, доказательство проводится, как прежде. □
Предложение 4.4.5
Если всюду RabKaKb > 0 и если p = y{vi), a KcRdK[aRb]cdieRf]
отлично от нуля, то найдутся такие а0 и v2, что q = у (у0) и
г = У(а2) будут сопряжены вдоль у (а) при условии, что у (а)
можно продолжить до этих значений а.
Если KcKdK\aRb}cd{eKn отлично от нуля, то же верно и для
Pm4n4- Тогда доказательство аналогично доказательству предло-
жения 4.4.2. п
Как и во времениподобном случае, условие KcKdK[aRb]cdleRf]¥=
=£ 0 выполняется для изотропных геодезических, проходящих
сквозь некоторую материальную среду, за исключением случая,
когда эта среда есть чистое излучение (тензор энергии-импульса
типа II, разд. 4.3), распространяющееся в направлении векто-
ра К, касательного к геодезической. В пустом пространстве это
условие выполняется, если рассматриваемая изотропная геоде-
зическая содержит точку, в которой тензор Вейля отличен от
нуля, а К не принадлежит ни к одному из направлений, для ко-
торых KcKdK[aCb]cdieKf\ — 0 (таких направлений самое большее
четыре). Поэтому представляется разумным предположить, что
в физически реалистическом решении уравнений Эйнштейна
каждая времениподобная или изотропная геодезическая содер-
жит точку, в которой KaKbK(cRd]ab\eKf] отлично ог нуля. Будем
говорить, что пространство-время, в котором выполняется это
условие, удовлетворяет типовому условию (generic condition).
Подобным же образом мы можем рассмотреть изотропные
геодезические, ортогональные к пространственноподобной 2-по-
верхности SP. Под пространственноподобной 2-поверхностью RP
мы имеем в виду вложенное двумерное подмногообразие, опре-
деляемое локально уравнениями fi = О, fz = 0, где fi и f2 суть
такие О2-функции, что при Д — 0, f2 — 0 векторы fVa и /2.0 не
равны нулю, не параллельны и
для двух разных действительных значений ц = и ц =
Тогда каждый вектор, лежащий на этой двумерной поверхности,
обязательно пространственноподобен. В качестве изотропных
116
Гл. 4. Физический смысл кривизны
векторов, нормальных к ЗР, введем N“ и N2a, пропорциональ-
ные соответственно gab (ft.b + p,J2.&) и gab (f1;b + ц2)2;6), и затем
нормируем их так, чтобы
Введя еще два единичных пространственноподобных вектора Yta
и У2°, ортогональных друг к другу и к А)0 и N2a, можно по-
лучить псевдоортогональный базис. Определим два вторых фун-
даментальных тензора на 17:
„U = - N nc.d (YfY^ + У2Т2а) (Г/У1й + У2%й),
где га = 1, 2; i/ab и 2Хаь симметричны.
Существуют два семейства изотропных геодезических, нор-
мальных к 17, соответственно двум изотропным нормалям N“ и
NY1- Рассмотрим то семейство, касательный вектор которого К
на ЗР равен N2. Мы можем фиксировать наш псевдоортогональ-
ный базис Е7 Е2, Е3, Е4, приняв, что на 17 Ej = Y1( E2 = Y2,
E3 = Nb E4 = n2, и перенеся его параллельно вдоль изотропных
геодезических. Проекция на пространство Sg вектора девиации Z,
описывающего взаимное разделение соседних изотропных геоде-
зических относительно изотропной геодезической у(у), будет
удовлетворять уравнению (4.30) и начальным условиям
^-^m = YLm^n (4-47)
в точке q е ST А у (у). Как и прежде, вращение этих полей будет
равно нулю; начальное значение расхождения 6 равно гХаб£“ь.
Аналогично предложению 4.4.3 имеем
Предложение 4.4.6
Если всюду RabKaКь ^0 и 2%abgab < 0, то существует точка,
сопряженная ЗР вдоль у (у), в пределах афинного расстояния
2/(— 2Xabgab) от ЗР. °
В силу определения сопряженных точек их существование
означает наличие в семействах геодезических самопересечений
или каустик. Дальнейшее обсуждение роли сопряженных точек
будет дано в следующем разделе.
4.5. Вариация длины дуги
В этом разделе мы рассмотрим времениподобные и непро-
странственноподобные кривые, которые кусочно класса С3, но
могут иметь точки, где их касательные векторы терпят разрыв.
Мы будем требовать, чтобы в таких точках два касательных
4.5. Вариация длины дуги
117
вектора ((?/<?/) и (d/dt) |+ удовлетворяли условию
««о—.
т. е. чтобы они были направлены внутрь одной и той же полости
изотропного конуса.
Предложение 4.5.1
Пусть SZZ — выпуклая координатная окрестность точки <?.
Тогда те точки в <2/, которых можно достичь из q по времени-
подобным (соответственно непространственноподобным) кривым,
имеют вид ехр9 (X), Хе Tq, где ^(Х, Х)<0 (соответственно
sp/O). (Здесь и в остальной части раздела мы полагаем, что от-
ображение ехр ограничено такой окрестностью начала в Tq, ко-
торая диффеоморфна под действием ехр9.)
Другими словами, изотропные геодезические, выходящие из q,
образуют границу той области в SZZ, которую можно достичь из q
по времениподобным или пространственноподобным кривым в TtZ.
Интуитивно это утверждение достаточно очевидно, но поскольку
оно является фундаментальным для понятия причинности, мы
докажем его строго. Начнем с доказательства следующей леммы:
Лемма 4.5.2
В времениподобные геодезические, проходящие через q,
ортогональны к трехмерным поверхностям о = const (о<0),
где по определению при ре'?/ а (р) = g (ехр?-1р, ехр7-1Р)-
Доказательство опирается на тот факт, что вектор девиации
точек равного расстояния вдоль соседних геодезических, перво-
начально ортогональный к этим геодезическим, остается ортого-
нальным к ним. Точнее, пусть X(t) означает кривую в Tq, причем
g(X(/)> Х(0) = —1. Нужно показать, что соответствующие кри-
вые Z.(t) = ехр?($0Х(/)) (so : const)—там, где они определе-
ны,— ортогональны к времениподобным геодезическим
y(s)= expe(sX(/0)) (to — const). Следовательно, для двумерной
поверхности а, определяемой a(s, t) = exp?(sX(/)), нужно дока-
зать, что
«((£)„• (Я)-»
(см. рис. 11). Имеем
АЛА = +
ds ° У ds ’ dt ) ° \ ds ds ' dt ) ~ ® v, ds ’ ds di )
Первый член в правой части равен нулю, потому что d/ds — еди-
ничный касательный вектор к времениподобной геодезической,
выходящей из q. Во втором члене согласно определению
118
Гл. 4. Физический смысл кривизны
производной Ли имеем
D д D д
ds dt dt ds
Итак,
d / d jL\ = a(jL D a "1 = 1 19 (Д_ д У — п
ds \ ds ’ dt / ® \ ds ’ dt ds ) 2 dt \ ds ’ ds ) ’
и, следовательно, g(d/ds, d/dt) не зависит от s. Но при s = 0
(d/dt) а = 0; поэтому g(d/ds, dfdV) тождественно равно нулю. □
Рис. 11. В нормальной окрестности поверхности постоянного расстояния
от q ортогональны к геодезическим, проходящим через q.
Доказательство предложения 4.5.1
Пусть Ся означает множество всех времениподобных векто-
ров в q. Они заполняют внутренность конуса в Tq с вершиной
в начале. Пусть у(?)—некоторая времениподобная кривая в
от q до р и пусть дана кусочно С2-кривая в 7',:у(/) =
= ехр<;”1 (у(0). Тогда, отождествляя касательное пространство
к Tq с самим Т9, имеем
(д/д^\^(д/д!Ц.
4.5. Вариация длины дуги
119
Поэтому вектор (д/dt)^ времениподобен в q. Отсюда видно, что
кривая у (/) входит в область Cq, но ехр9(С9)— это та область <2/,
в которой о< 0 и в которой, в силу предыдущей леммы, по-
верхности ст = const пространственноподобны. Таким образом, ст
должно монотонно убывать вдоль у(0> поскольку вектор (<3/dt)v,
будучи времениподобным, никогда не может быть касательным
к поверхности cr = const и поскольку в любой точке разрыва про-
изводных у(0 два касательных вектора направлены в одну и ту
же полость изотропного конуса. Поэтому /?еехрДС,;), что за-
вершает доказательство для времениподобных кривых.
Чтобы доказать, что непространствепноподобная кривая у(7)
остается в exp7(Cg), рассмотрим такую малую вариацию у(0,
которая переведет ее во времениподобную кривую. Пусть Y —
векторное поле на Tq, такое, что индуцированное на 'II векторное
поле exp9*(Y) всюду времениподобно, и g(Y, {djdt) q) < 0.
Пусть при каждом е^О Р(г, е) есть кривая в Tq, которая выходит
из начала, причем ее касательный вектор (д/дг)& — (d/dt). |/=г +
+ eY |е (r g). Тогда р(г, е) — дифференцируемая функция г и е.
Для каждого е > 0 ехр9(Р(г, е)) является времениподобной кри-
вой на и, таким образом, содержится в ехр9(С9). Следова-
тельно, непространственноподобная кривая expg(p(r, 0)) = у(г)
содержится в expg(C(7) = ехрд (С9). □
Следствие
Если рЕ ?/ можно достичь из q по непространственноподоб-
ной, но не по времениподобной кривой, то р лежит на изотроп-
ной геодезической, проходящей через q. □
Длина непространственноподобной кривой y(t) от q до р равна
р
Ш q, 4)]'2d/’
<7
где интеграл взят по дифференцируемым частям этой кривой.
При положительно определенной метрике можно искать крат-
чайшую кривую между двумя точками, но в лоренцевой метрике
нет никакой кратчайшей кривой, поскольку любую кривую мож-
но деформировать в изотропную, длина которой равна нулю.
Однако при определенных условиях между двумя точками или
между точкой и пространственноподобной трехмерной поверх-
ностью найдется непространственноподобная кривая наибольшей
длины. Сначала мы будем иметь дело с ситуацией, когда две
точки близки друг к Другу. Затем мы выведем необходимые
условия для общего случая, когда две точки не обязательно
близки. Достаточное условие для этого случая будет рассмотре-
но в разд. 6.7.
120
Гл. 4. Физический смысл кривизны
Предложение 4.5.3
Пусть q и р принадлежат нормальной выпуклой окрестно-
сти 01. Тогда, если можно соединить q и р непространственно-
подобной кривой в 01, то кривая наибольшей длины единственна
в 01 и является непространственноподобной геодезической от q
до р. Более того, если ввести функцию p(q, р), равную длине
этой кривой, когда она существует, и равную нулю, если такой
кривой нет, то р(</, р) непрерывна в 01 X 01.
По определению выпуклой нормальной окрестности (разд. 2.5)
в 01 существует единственная геодезическая у(0, Для которой
у(0)= q, у(1)= р. Поскольку эта геодезическая есть дифферен-
цируемая функция своих концов, интеграл
а(<7, P)=pO)v. (4)v>
будет дифференцируемой функцией на Oiy^U. (Это та же функ-
ция о, что и в лемме 4.5.2.) Таким образом, функция р(д, р) не-
прерывна в О1\О1, поскольку она равна [—ст((/, р)при а < 0
и нулю в иных случаях. Остается теперь показать, что в случае
существования в 01 времениподобных кривых, соединяющих q
и р, времениподобная геодезическая между ними имеет наиболь-
шую длину. Пусть, как прежде, a(s,t) = expg(sX(/)), причем
g(X(/), Х(/)) =—1. Если А(/)—времениподобная кривая в О/
от q до р, ее можно представить в виде Х(/)= Тогда
( = Л0 (зг)а + ( аг)а-
Поскольку два вектора в правой части взаимно ортогональны
в силу леммы 4.5.2 и g( (d/ds)a, (d/ds)a)= —1, то
s((4)r (4)>-(f'™’+s((4V (£)>-(fw.
причем равенство имеет место тогда и только тогда, когда
(d/dt) а = 0, т. е. если и только если А,— геодезическая кривая.
Итак,
р
L (A,, q, р) < J Г (/) d/ = р (q, р),
причем равенство имеет место тогда и только тогда, когда А.—
геодезическая кривая в 01 от q до р (она единственна). □
Теперь мы перейдем к случаю, когда q и р не обязательно
принадлежат выпуклой нормальной окрестности 01. Необходи-
мые условия для того, чтобы времениподобная кривая у(£), со-
4.5. Вариация длины дуга
121
единяющая q и р, была кривой наибольшей длины от q до р, мы
выведем из рассмотрения малых вариаций. Вариация а кривой
y(t) есть С1--отображение а:(—е, е) X [0. 1р\ со следующи-
ми свойствами:
1) а(0,0= у(П;
2) существует такое подразбиение 0 = В < t2. . . < tn = tp
отрезка [0, tp], что а является С3-отображением на каждом
(—е, е) X [h, ^i+i];
3) а(и, 0) = q, а(и, tp) = р\
4) для любой постоянной и а(и,Г)—времениподобная кри-
вая.
Вектор Z = (д/ди)а |и„0 будем называть вектором вариации.
Обратно, если вдоль y(t) задано непрерывное векторное поле Z
кусочно класса С2, обращающееся в нуль в q и р, мы можем
определить вариацию а, для которой Z будет вектором вариации:
а (и, 0 — expr (hZ |г),
где и е (—е, е) при некотором е > 0 и г = у (/).
Лемма 4.5.4
Вариация расстояния от q до р при отображении а равна
п-1 { i + I
dL I V С ( д ( ,-i D д ( df \ d ) \ ,, .
du |H=0 “ L J g I du ' { f dt dt f \ dt ) dt J ) +
> = 1 t.
n-1
где f2 = g(d/dt,d/df)—квадрат касательного вектора, a
[f~ld/dt]— разрыв в одной из сингулярных точек у(/).
Имеем
4)f'd/=
Интегрируя по частям, получаем нужную формулу.
□
Эту формулу можно упростить, выбирая в качестве парамет-
ра t длину дуги s. Тогда g (д/dt, d/dt) = —1. Обозначив через V
122
Гл. 4. Физический смысл кривизны
единичный касательный вектор d/ds, имеем
V)d»+ “fs(Z, IV]).
f = l ti 1=2
где V = DV/ds — ускорение. Отсюда следует необходимое усло-
вие того, чтобы у(0 была кривой наибольшей длины от q до р:
она должна быть геодезической кривой без изломов, в противном
случае можно выбрать вариацию, которая даст более длинную
кривую.
Можно также рассмотреть времениподобную кривую у(/) от
некоторой пространственноподобной 3-поверхности 3$ до точ-
ки р. Вариацию а этой кривой определим, как прежде, за тем
исключением, что свойство (3) заменим на следующее:
3) а (и, 0) лежит на 3%, а (и, /Р) = р.
Отсюда следует, что на поверхности 3$ вектор вариации
Z = д/ди лежит в
Лемма 4.5.5
П—1 4i + l п-1
= S 5 £(V> Z) ds + £g(Z, [V]) + g(Z, V)|s=0.
i = l tt 1 = 2
Она доказывается так же, как и лемма 4.5.4. □
Отсюда следует необходимое условие для того, чтобы y(t)
была кривой наибольшей длины от 3$ до pi она должна быть
геодезической кривой без изломов, ортогональной к 3№.
Путем варьирования а мы убедились, что первая производ-
ная длины времениподобной геодезической равна нулю. Следую-
щим нашим шагом будет вычисление второй производной. Опре-
делим двухпараметрическую вариацию а геодезической линии
у(0, соединяющей q и р, как О-отображение
а: (—sj, eJXC—е2, е2) X [0,
с такими свойствами:
1) а(0, 0, о= y(0;
2) существует такое подразбиение 0 = ti < t2 <3. . <3tn =
— tp отрезка [0, tp], что а является С3-отображением на каждом
(—е); ei) X (—-ег, е2) X [ti. C+t];
3) а(и}, и2, 0) = q, а(и}, и2, tp) = р;
4) для любых постоянных Ui, и2 a(ut, и2, t) является време-
ниподобной кривой.
4.5. Вариация длины дуги
123
В качестве двух векторов вариации мы вводим
1 \d«i/alu.=o ' \<5zz27alM;=o
м2=0 м;=0
Обратно, если вдоль у(() заданы два непрерывных векторных
поля Zi и Z2, кусочно класса С2, можно определить вариацию,
для которой они будут векторами вариации:
a(ut, и2, 0 = expr (h,Z| + u2Z2),
r = y(t).
Лемма 4.5.6
При двухпараметрической вариации геодезической кривой
у(0 вторая производная длина равна *)
n-l ff + l
U; = 0 ti
n-l
-R(V, Z2)v})ds + £g(z„ [^-(Z2+g(V, Z2)V)]).
i=2
Согласно лемме 4.5,4, имеем
Ui=;
Отсюда
d2L I = у C ( D _d_ ff-iJLJ?________________f-2 (d 1 'l л/
ди-2 диу |U|=o Z—t J ® \ du2 dui ’ t dt dt \ dt ) dt ) J
u2=o
Первый и третий члены равны нулю, так как у (/) — геоде-
зическая кривая без изломов. Во втором члене можно восполь-
*) Напомним, что векторное поле R(X, Y)Z определяется формулой
(2.18). — Прим, перед.
124
Гл. 4. Физический смысл кривизны
зоваться тем, что
_p__D__d__ р z а а \ а . d р д
ди2 dt dt \ dt ’ du2 ) dt ' dt du2 dt
d2f
du2 dt
д \ д . D- d
du2 J eJi ' dt2 du2 ’
£))=
dt dt ) J’
В четвертом члене
-D-Tr'^-Wr1—^- + rW—J-AA1
du2 L' dt J L dt du2 ' ° \ dt du2 ’ dt J dt J'
Затем, выбирая в качестве t длину дуги s, получим требуемый
результат. □
Из определения второй производной следует, что она симмет-
рична по двум векторам вариации Zj и Z2, хотя это и не видно
сразу из полученного выражения. Мы видим лишь, что оно зави-
сит от проекций Zi и Z2 в пространство, ортогональное к V. Сле-
довательно, мы можем ограничиться рассмотрением вариаций,
для которых Zi и Z2 ортогональны к V. Пусть TY — (бесконечно-
мерное) векторное пространство, состоящее из всех непрерыв-
ных, векторных полей кусочно класса С2 вдоль у(0, которые
ортогональны к V и равны нулю в q и р. Тогда д2Ь1ди%дщ будет
симметричным отображением Ту X Ту на /?!. Его можно рассма-
тривать как симметричный тензор в 7\ и записать в виде
£<2ьад=а5т|В1.0. Z„ Z2erv.
U2s?a0
Мы можем вычислить также вторую производную длины от
Ж до р геодезической кривой у(0, нормальной к Зв. Восполь-
зуемся прежним методом, только теперь один из концов кривой
у(/) не закреплен, а может перемещаться по Ж
Лемма 4.5.7
Вторая производная длины у(0 от Зв до р равна
п-1 Z2 + 1
5 «(z„{-^z2-R(v,z2)v})ds +
2-1 t{
+ £ г (z- [£ z>]) + е (z., £ z2) |к - z (z„ z2) |ж,
4.5. Вариация длины дуги
125
где Zi и Z2 взяты ортогональными к V, a x(Zb Z2) есть второй
фундаментальный тензор на Зё.
Первые два члена такие ясе, как в лемме 4.5.6. Добавочные
члены имеют вид
Второй член обращается в нуль, поскольку д/дщ ортогональ-
но к d/dt. Если принять, что t — длина дуги s, то d/dt будет
равно единичной нормали N к Ж Поскольку изменения одной
конечной точки у(/) ограничены перемещениями по Зё, d/dui
будет всегда ортогонален к N. Таким образом,
Z_D____д_
& к ди2 dui
J du2 ° k dUi J ° k dut du? J
/ д 0 \
k <3«i ’ du? ) '
□
Будем говорить, что времениподобная геодезическая линия
у(/), соединяющая q с р, максимальна, если функционал
L(Zi, Z2) отрицательно полуопределен. Иначе говоря, если кри-
вая у(/) не максимальна, то существует малая вариация а, ко-
торая дает более длинную кривую от р до q. Аналогично, будем
говорить, что времениподобная нормальная к Зё геодезическая
кривая от Зё до р максимальна, если функционал L(Zi, Z2) отри-
цательно полуопределен; следовательно, если кривая y(t) не ма-
ксимальна, существует малая вариация, которая дает более
длинную кривую от Зё до р.
Пpedлoжeнue 4.5.8
Времениподобная геодезическая линия у(0, соединяющая q
с р, максимальна тогда и только тогда, когда в (q, р') нет точек,
сопряженных q вдоль у (О-
Предположим, что в (q, р) нет сопряженных точек. Введем
ортонормированный базис вдоль у (О, полученный переносом
Ферми. Якобиевы поля вдоль у(/), равные нулю в q, можно оха-
рактеризовать матрицей Aag(7), которая неособенна в (q, р), но
особенна в q (и, возможно, в р). Ввиду изолированности сопря-
женных точек величина d(lndetA)/ds будет бесконечна там, где
матрица особенна. Следовательно, векторное поле Z е Ту
класса С° и кусочно класса С2 можно представить в [q, р] как
2'! = .4aJ6,
Up »
126
Г л. 4. Физический смысл кривизны
где IF0 — векторное поле класса С° и кусочно класса С1 в [q, р].
Тогда
sp
цг, Z) = £ J | (ЛабГб) + RaiyiAувГб} ds _
О
+ £4вг»[^(Л,и] =
5
Р
= lim У ( Л„ГВ{ 2ЛабIF15 + АабIF61 ds +
g^o^Z-1 J аР I ds ao ds 1 ao ds2 J 1
e
+ £x4U7M4-ir»] =
s
p
= ~У\ [Aaf.4-W^Aa6~W& +
/Л/ J ( ap ds ao ds 1
о
+ if0 (4- лаАв - Axr 4- Лв') 4~
1 \ ds ap ao ap ds a07 ds J
(Мы ввели предельный переход, поскольку вторая производ-
ная IF6 в точке q не определена.) Однако
( js ^аб) 2Лар(ОауД^в О-
Отсюда следует, что L(Z, Z)^0.
Обратно, допустим, что существует точка г е (д, р\ сопря-
женная q вдоль у (/). Пусть W — якобиево поле вдоль у (/),
обращающееся в нуль в q и г, и пусть К = П-такой вектор, что
Kagab wb = ~ 1 в точке г-
Продолжим W до р, положив его равным нулю в [г, р]. Поло-
жим Z = еК + е-'К, где е — некоторая постоянная. Тогда
L (Z, Z) = е2Т (К, К) + 2L (К, W) + 2e~2L (W, W) = e 'L (К, К) + 2.
Следовательно, взяв достаточно малое е, мы можем сделать
L(Z, Z) положительным. □
Аналогичный результат можно получить для времениподоб-
ной геодезической линии y(t) от Зв до р, ортогональной к Зв:
Предложение 4.5.9
Времениподобная геодезическая линия y(i) от Зв до р ма-
ксимальна тогда и только тогда, когда в (Зв, q) нет точек, со-
пряженных Зв вдоль у. □
4.5. Вариация длины дуги
127
Исследуем теперь вариации непространственноподобных кри-
вых от q до р. Выясним условия, при которых можно найти ва-
риацию а кривой у(/), приводящую к условию g(dfdt, dfdt) < О
всюду, иначе говоря, переводящую у(/) во времениподобную
кривую от q до р. При вариации а
А'Й = о 0 ( D а / р _д_ д \ _
ди \dt ' dt ) J у ди dt ' dt ) k dt ди ’ dt ) ~
Чтобы получить времениподобную кривую от q до р, требуется,
чтобы это выражение было меньше или равно нулю на всей кри-
вой y(t).
Предложение 4.5.10
Если р и q соединены непространственноподобной кривой
у(/), которая не есть изотропная геодезическая, то их можно со-
единить времениподобной кривой.
Если у(/) не является изотропной геодезической от р до q, то
должна быть точка, в которой касательный вектор имеет разрыв,
или должен существовать открытый интервал, на котором век-
тор ускорения (D/5/) (5/5/) отличен от нуля и не параллелен djdt.
Рассмотрим сначала случай, когда нет разрывов. Имеем
o-f—— _LA__L d f ( д d _n
® I dt dt ' dt J~ 2 dt I dt ’ dt ) J ~ U’
Отсюда видно, что (D/5/) (dldt) является пространственноподоб-
ным вектором там, где он отличен от нуля и не параллелен dldt.
Пусть W — времениподобное векторное С2-поле вдоль у(/), при-
чем g(W, d/dt) < 0. Тогда мы получим времениподобную кривую
от р до q, варьируя вектор вариации
где
t
х — c~1ebt e~bt (1 —уа2^ dt,
*ч
2_ / D д D <5 \
a~~s ~dt ’ ~dt~di)'
»=-«(* •£)•
6 = max(—e-'g(w, Л-)) на [д, </],
128
Гл. 4. Физический смысл кривизны
а у — неотрицательная функция на [р, qj, такая, что ур — yq — 0 и
t
р
— y//<r)cU = 0.
Предположим теперь, что существует некоторое подразбиение
tq < ti < t2 < . . . < tp, такое, что касательный вектор d/dt не-
прерывен на каждом сегменте [ti, ^+)]. Если сегмент [ti, Z,+i] не
является изотропной геодезической кривой, его можно варьиро-
вать так, чтобы получить между концами сегмента временипо-
добную кривую. Поэтому нужно только показать, что мы можем
получить времениподобную кривую из непространственноподоб-
ной кривой, составленной из сегментов изотропных геодезиче-
ских, касательные векторы которых не параллельны в точках
разрыва y{ti). В качестве t можно выбрать аффинный параметр
на каждом сегменте //+1]. Разрыв [d/dt] \t будет простран-
ственноподобным вектором, будучи разностью двух непарал-
лельных изотропных векторов на одной и той же половине изо-
тропного конуса. Следовательно, вдоль [£г—i, /,+1] можно по-
строить такое векторное С2-поле W, для которого
g(W, d/dt) < О на [/,-], ti]
и
gtW, d/dt) >0 на [tit /г+1].
Тогда времениподобную кривую между у(/,-1) и y(^+i) получим,
варьируя с вектором вариации Z = xW, где
x = c“I(^+1 — ti)(t — t^i)
При ti—1 t ti И
x = c-‘l(ti — ti-l)(ti+i — t)
при ti < £ < ti+i, где с = —g(W, d/dt). □
Итак, если y{t) не является геодезической кривой, то из нее
вариацией можно получить времениподобную кривую. Если у (О
является геодезической кривой, то в качестве t можно взять
аффинный параметр. Тогда видно, что необходимым (но не до-
статочным) условием получения в результате вариации времени-
подобной кривой является ортогональность вектора вариации
д/ди к касательному вектору d/dt на всей y{t), ибо в противном
случае производная {d/dt)g{d/du, d/dt) была бы положительна
где-нибудь на у(0- Для такой вариации {d/du) g {d/dt, d/dt) = О
и надо исследовать вторую производную.
Рассмотрим поэтому двухпараметрическую вариацию (х. изо-
тропной геодезической y{t), соединяющей q и р. Ее определение
будет прежним, за тем исключением, что мы ограничимся (по
4.5. Вариация длины дуги
129
причинам, приведенным выше) варьированием с векторами ва-
риации
-Ч и -/-I ,
Л'1 lU1=.o ди2 |М1=0
1Г = 0 «; = 0
ортогональными к касательному вектору (d/dt) на у(/).
Исследовать поведение L при таких вариациях затруднитель-
но ввиду того, что (—g(d/dt-, d/dt))1/2— недифференцируемая
функция, если g(d/dt, d/dt) = 0. Вместо этого мы рассмотрим
вариацию
Ясно, что необходимым (но не
ния времениподобной кривой от
положительность Л.
Имеем
достаточным) условием получе-
q до р при вариации а является
откуда
1 Р-Л I ______ у С / д ( D- д ___р Z Л Л \ д ) \ ,
2 ди2 diii |„ Д-> J \ dui ’ ( dt- ди> у dt ’ ди2 J dt J )
+2ДД- [т. Д])- ,449>
Эта формула очень похожа на формулу для вариации длины
времениподобной кривой. Можно показать, что вариация Л рав-
на нулю, если вектор вариации пропорционален касательному
вектору d/dt, поскольку он изотропен, a R(d/dt, d/dt) (d/dt) = 0
в силу антисимметричности тензора Римана. Такая вариация
эквивалентна перспараметризации у (t). Итак, если мы хотим
получить вариацию, приводящую к времениподобной кривой,
нужно рассматривать только проекции вектора вариации в про-
странство S,, в каждой точке q кривой у (О. Другими словами,
при введении вдоль y(t) пссвдоортонормированного базиса Е|,
Е2, Е3, Е4 с Ен — d/di вариация Л будет зависеть только от
компонент Z,n вектора вариации (т — 1,2).
5 З.'кяз VI
130
Гл. 4. Физический смысл кривизны
Предложение 4.5.11
Если в (<?,/?) нет точек, сопряженных q вдоль уД), т0
d2A/du21 и=0 < 0 для любой вариации а. кривой y(t), вектор ва-
риации которой <5/ди|и=() ортогонален к касательному вектору
d/dt к у(0> не равен всюду нулю и не пропорционален всюду
д/dl. Иначе говоря, если в (q, р) нет точек, сопряженных q
вдоль y(t), то не существует малых вариаций, переводящих
у(0 во времениподобную кривую от q до р.
Доказательство аналогично доказательству предложения 4.5.8
с использованием вместо Аар матрицы 2X2 Атп из разд. 4.2. □
Предложение 4.5.12
Если в (q, р) есть точка г, сопряженная q вдоль у(0, то най-
дется вариация у(/), которая дает времениподобную кривую от
q до р.
Доказательство предложения будет несколько громоздким
из-за того, что необходимо показать времениподобность каса-
тельного вектора всюду. Пусть Wm — компоненты в простран-
стве S (см. разд. 5.2) якобиева поля, равного нулю в q и г. Оно
удовлетворяет уравнению
где для удобства в качестве t взят аффинный параметр. По-
скольку W является по крайней мере векторным полем класса С3
и (dlFm/dO =/= 0 в q и г, можно написать Wm = fWm, где —
единичный вектор, причем f и I?7—поля класса С2. Тогда
-^/ + «=0,
где
h = Wт + RmMWm Wn.
Пусть точка х £ [г, р] такова, что Wm ^=0 в [г, х] и hi есть мини-
мальное значение h в [г, х]. Тогда, если а > 0 и а2 Ц- hi > 0 и
если b — {—f (eat — I)-1} |х, поле
Zm = {b(eat — 1) +
равно нулю в q и х и удовлетворяет в (<?, х) неравенству
Z'n^Zm + RmMZn)>Q.
Выберем вариацию а (и, t) кривой у (t) от q до х так, что ком-
поненты ее вектора вариации (д/ди) |и_0 в S равны Zm и выпол-
4.5. Вариация длины дуги
131
няется условие:
/Ра —^1 -I- (~ ——^1 =
& \ ди ди ’ dt ) |а=о "г” & \ ди ’ dt ди ) |ц-о
— е/ при
е (tx — t) при
где tx — значение t в точке х и е > 0, но меньше наименьшего
значения величины Zm(d2Zm/tW2 + T?m4n4Zn) в области ~^tx / С
<3у tx. Тогда, в силу (4.49), (d2/du2) g(d/dt, d/dt) < 0 всюду в
(q,x) и в этом интеравле достаточно малые и, а дают времени-
подобную геодезическую. Если мы присоединим эту кривую к
куску у(0 от х до р, то получим непространственноподобную
кривую от q до р, которая не будет изотропной геодезической
кривой. Следовательно, существует вариация, которая приводит
к времениподобной кривой, соединяющей q и р.
Подобным же методом можно доказать
[IpedAOtHceHue 4.5.13
Если y(t)—изотропная геодезическая кривая 2-поверхно-
сти д’ до р, ортогональная к S’, и если в р) нет точек, со-
пряженных S’ вдоль у, то не существует малых вариаций у,
дающих времениподобную кривую от S’ до р.
ПpedAOOiceHue 4.5.14
Если в (S, р) имеется точка, сопряженная S вдоль у, то су-
ществует вариация у, дающая времениподобную кривую от S
до р.
Результаты, касающиеся вариаций времениподобных и не-
пространственноподобных кривых, будут использованы в гл. 8
для доказательства отсутствия геодезических наибольшей длины.
5*
Глава 5
Точные решения
Любое пространство-время можно в определенном смысле
считать решением уравнений поля Эйнштейна
Rab 2 R-Sab ^Sab 8л1 аЬ (5-1)
(мы пользуемся единицами, принятыми в гл. 3), поскольку, вы-
числив по метрическому тензору пространства-времени левую
часть (5.1), мы можем ввести, тензор энергии-импульса Т аь как
правую часть (5.1). Определенный таким образом тензор мате-
рии будет, вообще говоря, обладать неприемлемыми физиче-
скими свойствами, тогда как решение уравнений (5.1) будет
иметь смысл лишь при разумном характере распределения ма-
терии.
Под точным решением уравнений Эйнштейна мы будем под-
разумевать пространство-время (Ж, g), в котором уравнения
поля удовлетворяются тензором энергии-импульса ТаЬ какой-то
конкретной формы материи, причем выполняются постулат (а)
(«локальной причинности») гл. 3 и одно из энергетических усло-
вий (разд. 4,3). В частности, можно искать точные решения для
пустого пространства (7фь = О), для электромагнитного поля
[Tab вида (3.7)], для идеальной жидкости [Та1, вида (3.8)] или
для пространства, содержащего электромагнитное поле и иде-
альную жидкость. Ввиду сложности уравнений поля получить
точные решения можно только в пространствах достаточно вы-
сокой симметрии. Кроме того, точные решения являются идеали-
зацией в том смысле, что любая область пространства-времени,
по-видимому, содержит разные формы материи, в то время как
точные решения можно получить лишь при довольно простом
материальном содержимом. Тем не менее точные решения слу-
жат источником идей о качественно новых явлениях, которые
могут возникнуть в общей теории относительно и, таким обра-
зом, указывают на возможные свойства реалистических решений
уравнений поля. Примеры, которые мы приведем, демонстри-
руют многие интересные для последующих глав типы поведения
решений. Мы рассмотрим эти решения, обращая особое внима-
ние на их глобальные свойства. Многие из этих свойств были
обнаружены только недавно, хотя сами решения в локальной
форме уже известны давно.
5.1. Пространство-время Минковского
133
В разд. 5.1 и 5.2 мы рассматриваем простейшие лоренцевы
метрики — те, для которых кривизна постоянна. Пространствен-
но-однородные и изотропные модели описаны в разд. 5.3, а их
простейшие анизотропные обобщения — в разд. 5.4. Во всех этих
простых моделях мы видим наличие сингулярного начала, если
только Л не принимает больших положительных значений. Сфе-
рически-симметричные метрики, описывающие поле массивного
заряженного или нейтрального тела, и аксиально-симметричные
метрики, описывающие поле тяготения вне массивных вращаю-
щихся тел конкретного типа, рассмотрены соответственно в
разд. 5.5 и 5.6. В них показано, что появление некоторых сингу-
лярностей в явном выражении для метрики вызвано лишь не-
удачным выбором координаты. В разд. 5.7 дано описание модели
Вселенной Геделя, а в разд. 5.8 — решение Тауба — Ньютона —
Тамбурино — Унти (Тауба — НУТ). Последние модели, вероят-
но, не описывают реальную Вселенную, но они интересны свои-
ми патологическими глобальными свойствами. Наконец, ряд дру-
гих интересных точных решений приведен в разд. 5.9.
5.1. Пространство-время Минковского
Пространство-время Минковского (^, i]) является простей-
шим пустым пространством-временем в общей теории относи-
тельности и в действительности представляет собой простран-
ство-время специальной теории относительности. Математически
оно есть многообразие R4 с плоской лоренцевой метрикой 1].
В естественных координатах (х1, х2, х3, х4) на Д'* метрику ц мож-
но записать в виде
ds2 = - (dx4)2 + (dx1 )2 + (dx2)2 + (dx3)2. (5.2)
Если используются сферические полярные координаты (t, г, 0, <£),
где xk = t, х3 = г cos 0, х2 = г sin 0 cos ф, х1 = г sin 0 sin ф, то
метрика принимает вид
ds2 = — dt2 + dr2 + г2 (d02 4- sin2 0 d^2). (5.3)
Очевидно, эта метрика, сингулярна при г — 0 и sin 9 = 0, однако
это происходит из-за того, что используемые координаты не яв-
ляются допустимыми в этих точках. Чтобы получить регулярные
координатные окрестности, необходимо на координаты наложить
ограничения, например 0 < г <_ оо, 0 < 0 < л, 0 < <£ < 2л.
Для покрытия всего пространства Минковского нужны две такие
координатные окрестности.
Другая координатная система получается при выборе опере-
жающей и запаздывающей изотропных координат v, w.
v = 1 + г, w = t — г (=$ v w).
134
Гл. 5. Точные решения
Тогда метрика имеет вид
ds2 = — du day + j (w — w'y (d02 + sin2 0 d</>2), (5.4)
где —oo < t) < oo, —oo < w <z оо. Отсутствие в метрике чле-
нов df2, dtw2 отражает тот факт, что поверхности {ay = const},
а
Рис. 12. Пространство Минковского. Изотропные координаты о (да) можно
представить себе в виде сходящихся (расходящихся) сферических волн, рас-
пространяющихся со скоростью света; они являются опережающими (запаз-
дывающими) временными координатами. Пересечение поверхности {о = const}
с поверхностью {да = const} является 2-сферой, а — координатные поверхности
о, w (одна координата опущена), б — плоскость (/, г); каждая точка изо-
бражает 2-сферу радиуса г
{v — const} изотропны (т. е. w-aw-bgab = 0 = v-av-bgnb}, см.
рис. 12.
В системе координат, в которой метрика выражается в виде
(5.2), геодезические имеют вид xa(t»)= bav-\-ca, где Ьа и са —
постоянные. Таким образом, экспоненциальное отображение
ехрр:Тр -> Л определяется формулой
xa(expp Х) = Ха + ха (р),
где Ха — компоненты X относительно координатного базиса
{д/дха} пространства Тр. Поскольку ехр является взаимно одно-
значным отображением на все многообразие Л, оно представ-
ляет собой диффеоморфизм между ТР и Л. Следовательно, лю-
5.1. Пространство-время Минковского
135
бые две точки Л' можно соединить единственной геодезической
линией. Отображение ехр определено всюду на Тр для
всех р, и в силу этого пространство-время (Л, i]) геодезически
полно.
Область Коши (Cauchy development) будущего, прошлого)
£>+(^) (соответственной-^)) пространственноподобной гипер-
поверхности 9Р определяется как множество всех точек в Л, ко-
Р и с. 13. Поверхность Коши (х4 = const} в пространстве-времени Минков-
ского и пространственноподобные поверхности Р’п. Р’р., которые не являются
поверхностями Коши. Все нормальные к поверхностям 9^, геодезические
пересекаются в точке О.
торые обладают тем свойством, что все непродолжимые в про-
шлое (будущее) непространственноподобные кривые, проведен-
ные из этих точек, пересекают 9е1 (ср. с разд. 6.5). Если
D+iJP) U D-(^) = Л, т. е. если каждая непродолжимая непро-
странственноподобная кривая пересекает 9?, то такую 9? будем
называть поверхностью Коши. В пространстве-времени Минков-
ского поверхности {x4=const} образуют семейство поверхностей
Коши, покрывающих Л полностью. Можно, однако, построить
нерасширяемые пространственноподобные поверхности, которые
13В
Гл. 5. Точные решения
не будут поверхностями Коши; например, поверхности
,7'а: {— (х4)2 + (х1)2 4- (х2)2 + (х3)2 = а = const},
где о < 0, х4 < 0, пространственноподобны, но лежат целиком
внутри изотропного конуса прошлого начала О и потому не яв-
ляются поверхностями Коши (см. рис. 13). В самом деле, об-
ласть Коши будущего поверхности —это область, ограничен-
ная 5Д и световым конусом прошлого точки О. В силу лем-
мы 4.5.2, времениподобные геодезические ортогональны к по-
верхностям Э’о. Если г е D+^a) U то времениподобная
геодезическая, проходящая через г и О, является времениподоб-
ной геодезической наибольшей длины между г и Если же г
не лежит в О+(^о) U D-(^o), то времениподобной кривой наи-
большей длины между г и не существует, поскольку или г ле-
жит в области а 0, и тогда вообще нет времениподобных гео-
дезических, проходящих через г и ортогональных о, или г лежит
в области о < 0, х4 О, и тогда времениподобная геодезиче-
ская, проходящая через г и ортогональная к существует,
но она не будет кривой наибольшей длины между г и ибо
на ней имеется точка О, сопряженная к (ср. с рис. 13).
Для исследования структуры бесконечности в пространстве-
времени Минковского воспользуемся интересным представлением
этого пространства, принадлежащим Пенроузу. От изотропных
координат у, w перейдем к новым изотропным координатам, в
которых бесконечности v и w преобразованы к конечным значе-
ниям. Для этого введем соотношениями tg р = v, tg q = w ко-
ординаты p и q, причем —л/2 < р < л/2, —л/2 < q < л/2 (и
p'^-q'). Тогда метрика пространства (dt, ц) принимает вид
ds2 = sec2 р sec2 7 ( — dp dq 4~ у sin2 (f — <?) (^92 + s'n2 ® ^</’2)) -
т. e. физическая метрика конформна метрике g, для которой
ds2 = — 4dp dq -ф sin2 (p — q) (d02 4- sin2 0 dp2). (5.5)
Эту метрику можно привести к более привычному виду, если
ввести
t' = p + q, г' = р — q,
где
— л < t' + г' < л, —п<1'— г' < л, (5.6)
тогда вместо (5.5) имеем
ds2 — — (df )2 ф- (drz)2 4- sin2 г' (d02 4- sin2 0 d<f>2). (5.7)
Таким образом, все пространство-время Минковского изобра-
жается областью (5.6) метрики
ds2 = sec2 (у (/' 4- г')} sec2 (у (f — г')) ds2,
5.1. Пространство-время Минковского
137
где ds определяется из (5.7); координаты (/, г) из (5.3) связаны
с t', г' соотношениями
2^ = tg(|(f + r')) + tg (4
2r=tg (4 (/'+и)—tg (4 <t'—и) •
Метрика (5.7) локально совпадает с метрикой статической мо-
дели Эйнштейна (см. разд. 5.3), пространство-время которой пол-
ностью однородно*). Можно аналитически продолжить (5.7) на
всю статическую модель Эйнштейна, т. е. можно продолжить
координаты t', г' так, чтобы они покрывали все многообразие
7?1 XS3, где —оо <; t' < оо и г', 0, ф рассматриваются как ко-
ординаты на S3 (с координатными сингулярностями при г' = О,
г' = л и 0 = 0 и 0 = л, подобными тем, что были в (5.3); эти
сингулярности устраняются переходом к другим локальным ко-
ординатам в окрестности точек, где метрика (5.7) особенна).
Опуская два измерения, можно представить статическую вселен-
ную Эйнштейна в виде цилиндра x2 + z/2=l, вложенного в
трехмерное пространство Минковского с метрикой ds2 =
= — d/2 + dx2 + dz/2 (полностью статическую модель Эйнштей-
на можно получить вложением цилиндра х2 + у2 -ф г2 -ф w2 = 1
в пятимерное евклидово пространство с метрикой ds2 =
= —d(2 -ф dx2 -ф di/2 -ф dz2 -ф dw2, ср. c [141]).
Итак, мы имеем следующую картину: все пространство-время
Минковского конформно области (5.6) статической модели Эйн-
штейна, т. е. заштрихованной области на рис. 14. Можно считать,
что граница этой области отражает конформную структуру бес-
конечности пространства-времени Минковского. Она состоит из
изотропных поверхностей р = л/2 (обозначенной 57+) и q——л/2
(обозначенной У-) и включает в себя точки р = л/2, q — л/2
(обозначенную i+), р = л/2, q = —-л/2 (обозначенную i°) и р =
= —л/2, q — — л/2 (обозначенную М). Любая направленная в
будущее времениподобная геодезическая в пространстве Мин-
ковского достигает i+ (М) при бесконечно большом положитель-
ном (отрицательном) значении своего аффинного параметра, и
можно считать, что любая времениподобная геодезическая начи-
нается в М и кончается в i+ (ср. с рис. 15, а). Аналогично можно
считать, что изотропные геодезические начинаются на У- и кон-
чаются на 57+, в то время как пространственноподобные геодези-
ческие начинаются и кончаются в i°. Таким образом, 1+ и можно
*) Под однородностью пространства-времени здесь имеется в виду су-
ществование группы изометрий, преобразованиями которой каждую точку про-
странства-времени можно перевести в любую другую точку; обычно такая
группа преобразований называется транзитивной (см. стр. 188). — Прим
не пев.
138
Гл. Г. Точные решения
рассматривать как изображения времениподобной бесконечно-
сти будущего и прошлого Т7+ и — изотропной бесконечности
будущего и прошлого и t° — пространственноподобной бесконеч-
ности. (Однако эти утверждения не относятся к негеодезическим
Рис. 14. Статическая вселенная Эйнштейна, представленная как вложен-
ный цилиндр; координаты 0, Ф опущены. Каждая точка изображает половину
2-сферы площадью 4л sin2 г'. Заштрихованная область конформна всему
пространству-времени Минковского; ее границу (часть изотропных конусов
точек z+, i®, t-) можно рассматривать как конформную бесконечность про-
странства-времени Минковского.
кривым: негеодезическая времениподобная кривая может начи-
наться, например, на и кончаться на 5^+.) Поскольку любая
поверхность Коши пересекает все времениподобные и изотропные
геодезические, то она должна выглядеть как сечение всего про-
странства-времени, достигающее границы (°. Конформную струк-
туру бесконечности можно представить также, начертив диа-
грамму плоскости (К, г') (см. рис. 15, б). Как и на рис. 12, а, каж-
дая точка этой диаграммы изображает сферу S2, а радиальные
изотропные геодезические изображаются прямыми, идущими под
углом ±45°. Такого рода диаграммой может быть представлена
т — О
i'(p=-jn)
Пространственно-
подобная геодезичес-
кая
времениподобная
геодезическая
Изотропная геодезическая
& (г— оо, Z=+°O_)
I
р =. const
1~
2-ссрерь'
const
г °
&~(Г — оо,
t~-оо)
Поверхность
д = const
д — const
Поверхности
t — const
1°(рассматри- г
вается как одна
точна)
Поверхность
р = const
а
Рис. 15. а — заштрихованная область на рис. 14 (теперь опущена только одна координата), изображающая пространство-
время Минковского и его конформную бесконечность; б — диаграмма Пенроуза пространства-времени Минковского. Каждая
точга изображает 2-сферу, за исключением точек i+, i°, i~, каждая из которых является единственной точкой, и точек
на линии г — 0 (где полярные координаты сингулярны).
140
Гл. 5. Точные решения
структура бесконечности любого сферически симметричного
пространства. На таких диаграммах бесконечность будет изо-
бражаться одной линией, начало полярных координат — пункти-
ром и неустранимые особенности метрики — двойной линией.
Конформная структура пространства Минковского, описанная
здесь, представляет собой то, что можно было бы считать «нор-
мальным» поведением пространства-времени на бесконечности;
другие типы поведения встретятся нам в следующих разделах.
Упомянем, наконец, что можно построить пространства, ло-
кально совпадающие с {Л, t]), но с иными (крупномасштабны-
ми) топологическими свойствами; это достигается отождествле-
нием в Л точек, которые эквивалентны относительно дискретной
изометрии без фиксированной точки (например, отождествление
точки (х1, х2, х3, х4) с точкой (х1, х2, х3, х4 -ф с), где с — постоян-
ная, меняет топологическую структуру 7?4 на R1 X S1 и приводит
к появлению в пространстве-времени замкнутых времениподоб-
ных линий). Очевидно, (Л, 1]) представляет собой универсаль-
ное накрывающее пространство для всех таких производных
пространств; последние подробно рассмотрены в [3].
5.2. Пространство-время де Ситтера 1-го и 2-го рода
Пространственно-временные метрики постоянной кривизны
локально характеризуются условием Raba} = (Viz)/? (gaegbd —
—gadgbc). Ему эквивалентно равенство CabCd = O — Rab — Rlb)Rgab,
и, следовательно, тензор Римана определяется одним лишь ска-
ляром Риччи R. Из свернутых тождеств Бианки сразу следует,
что R = const во всем пространстве-времени; действительно, эти
пространства однородны. Тензор Эйнштейна имеет вид
Rab Rgab = Rgab 't
поэтому эти пространства можно считать решениями уравнений
поля в пустом пространстве с Л = R/4 или решениями для иде-
альной жидкости с постоянной плотностью /?/32л и с постоянным
давлением — R/32n. Однако последняя трактовка, по-видимому,
неприемлема, поскольку тогда или давление, или плотность
должны быть отрицательными; кроме того, уравнение движения
(3.10) для такой жидкости становится неопределенным.
Пространство-время Минковского является пространством
постоянной кривизны с R — 0. Пространство постоянной кривиз-
ны с R > 0 есть пространство-время де Ситтера 1-го рода, кото-
рое обладает топологией Rl X S3 (см. интересное описание
свойств этого пространства в [152], принадлежащее Шрединге-
ру). Оно наиболее просто реализуется в виде гиперболоида
— v + w‘ + х2 -|- у2 + z2 = а2
5 2. Пространство-время де Ситтера
141
в плоском пятимерном пространстве Г<Ф с метрикой
— do2 -4- dee12 + dx2 -+- dy2 dz2 = ds2
(рис. 16). На этом гиперболоиде можно ввести координаты
(t, X, 9, ф), определяемые соотношениями
a sh (а~Ч) = v, a ch (a“’t) cos % = w,
a ch (ст'?) sin х cos 0 = х, a ch (а'Ч) sin х sin 9 cos ф — у,
а ch (а"’1/) sin х sin 9 sin ^> = z.
В этих координатах метрика имеет вид
ds2 = — d/2 + a2 ch2 (а-1/) • {dx2 + sin2x(d02 4- sin2 0 d<£2)}.
Особенности метрики при х = О, X = л и 9 = 0, 0 = л обуслов-
лены лишь полярными координатами; за исключением этих три-
виальных сингулярностей, координаты t, %, 9, Ф покрывают все
пространство при —оо <с t <С <х>, 0 х л> 0 0=С л,
0 ф :< 2л. Пространственными сечениями постоянного t яв-
ляются сферы S3 постоянной положительной кривизны, и они
представляют собой поверхности Коши. Их геодезические нор-
мали представляют собой линии, монотонно сходящиеся до не-
которого минимального пространственного расстояния и затем
снова расходящиеся до бесконечности (см. рис. 16, а).
На гиперболоиде можно ввести также координаты
а , w + а Л ах л ац ~ az
t=aln-------, х = j—, й=—р—, z =----------i—.
u w + a ' J w v w + v
В этих координатах метрика принимает вид
ds2 = — d?2 + exp (2a ~ ’/) (dx2 + dy2 dz2),
однако они покрывают лишь половину гиперболоида, так как f
не определены при w -(- v 0 (см. рис. 16,6). Область про-
странства де Ситтера 1-го рода, для которой v -|- w > 0, обра-
зует пространство-время стационарной модели Вселенной, пред-
ложенной Бонди и Голдом [12] и Хойлом [80]. В этой модели
предполагается, что материя движется по геодезическим норма-
лям к поверхностям {f = const}. Поскольку при этом происхо-
дит «разрежение» материи, то для поддержания постоянного
значения плотности предполагается непрерывное рождение по-
вой материи. Бонди и Голд не пытались вводить уравнения поля
для этой модели, но Пирани [135] и Хойл и Нарликар [82] заме-
тили, что метрику стационарной модели можно рассматривать
как решение уравнений Эйнштейна (с Л = 0 ), если в дополнение
к обычной материи ввести скалярное поле с отрицательной плот-
ностью энергии. Это «С-поле» вызывало бы также и непрерыв-
ное рождение материи.
142
Ул. 5. Точные решения
Стационарная модель обладает тем достоинством, что ее
предсказания просты и определенны. Однако с нашей точки зре-
ния у нее имеются два неудовлетворительных свойства. Пер-
вое — существование отрицательной энергии, о чем говорилось
в разд. 4.3. Второе—-возможность расширения пространства-
времени, связанная с тем, что оно является только половиной
х - О
X =О
Поверхности
t=const
t= О;расстоя-
ние между
геодезически-
ми нормаля-
ми мини-
мально
Геодезические
нормали
Изотропные поверхноети
(граница сети
координат)
геодезическая, не
Геодезические
нормали
Поверхности
i= const
Времениподобная
пересекающая поверхности
t = const
а
5
Рис. 16. Пространство-время де Ситтера 1-го рода, представленное в виде
гиперболоида, вложенного в пятимерное плоское пространство (на рисунке
два измерения опущены); а — координаты (Л %, 6, </>) покрывают весь гипер-
болоид; сечения {/ = const} являются поверхностями кривизны k = -р 1.
б — координаты (t, х, у, i) покрывают половину гиберболоида; поверхности
{t = const} являются плоскими 3-пространствами; их геодезические нормали
расходятся из точки в бесконечно удаленном прошлом.
пространства де Ситтера 1-го рода. Несмотря на эти возраже-
ния, по-настоящему справедливость стационарной модели опре-
деляется тем, насколько ее предсказания согласуются с наблю-
дениями. Согласия в настоящее время, по-видимому, нет, но на-
блюдения еще не дают достаточно оснований для окончатель-
ного вывода.
Пространство де Ситтера 1-го рода геодезически полно, но в
нем существуют точки, которые нельзя соединить никакой геоде-
зической. Этим оно сильно отличается от пространств с положи-
тельно определенной метрикой, где геодезическая полнота гаран-
тирует возможность соединения любых двух точек по крайней
мере одной геодезической. Половина пространства де Ситтера,
S.2. Пространство-время де Ситтера
143
соответствующая стационарной модели, не полна в прошлом
(существуют геодезические, которые полны во всем пространстве
и пересекают границу области стационарной модели, поэтому
они неполны в этой области).
Чтобы исследовать бесконечность в пространстве-времени
де Ситтера 1-го рода, определим временную координату t' сле-
дующим образом:
£' = 2arctg(expa-1/) —л, (5.8)
где
1 4' 1
2 Л t 2 •ГС*
Тогда
ds2 — a2 ch (a-1/7) • ds2,
где ds2 дается формулой (5.7) после замены г' на %. Таким обра-
зом, пространство де Ситтера 1-го рода конформно части стати-
ческой вселенной Эйнштейна, определенной неравенством (5.8)
(рис. 17, а). Диаграмма Пенроуза для пространства де Ситтера
1-го рода изображена на рис. 17,6. Половина этого рисунка,
представленная на рис. 17, в, изображает ту часть простран-
ства-времени де Ситтера, которая соответствует стационарной
модели.
Мы видим, что в отличие от пространства Минковского
в пространстве де Ситтера 1-го рода для времениподобных и
изотропных кривых существует как в будущем, так и в прошлом
пространственноподобная бесконечность. Это различие соответ-
ствует существованию в пространстве-времени де Ситтера гори-
зонтов частиц и событий для геодезических семейств наблюда-
телей.
Рассмотрим в пространстве де Ситтера 1-го рода семейство
частиц, историями которых являются времениподобные геодези-
ческие. Эти линии начинаются на пространственноподобной бес-
конечности Д'- и кончаются на пространственноподобной беско-
нечности Д+. Пусть р — некоторое событие на мировой линии
частицы О этого семейства, т. е. некоторый момент ее истории
(собственное время, измеренное вдоль мировой линии О). Све-
товой конус прошлого события р — это множество событий в
пространстве-времени, которые может увидеть наблюдатель, на-
ходящийся на частице в это время (наблюдатель О). Мировые
линии некоторых других частиц могут пересекать этот конус, и
эти частицы наблюдатель О может увидеть. Но могут существо-
вать частицы, мировые линии которых не пересекают этот изо-
тропный конус и, таким образом, еще не видны наблюдателю О.
В более поздние моменты времени наблюдатель О может уви-
деть большее число частиц, но и в эти моменты будут существо-
вать частицы, невидимые О,
144
Гл. 5. Точные решения
Мы будем говорить, что частицы, которые наблюдатель О в
событии р может увидеть, отделяются от частиц, не видимых О
в это время, горизонтом частиц наблюдателя О в событии р\
—$ * (t’-л/г), apepa S3
-9t'= const
t'=0
Л/2), apepa S3
Рис. 17. а — пространство-время де Ситтера I-го рода конформно области
— л/2 < t' < л/2 статической вселенной Эйнштейна; б — диаграмма Пенроуза
пространства-времени де Ситтера 1-го рода; в — диаграмма Пенроуза ста-
ционарной модели Вселенной. На диаграммах а и б каждая точка изобра-
жает 2-сферу площадью 2л sin 2%; изотропные линии проходят под углом 45°;
% = 0 и % = л отождествляются.
этот горизонт определяется мировыми линиями частиц, лежащих
на пределе видимости наблюдателя О. Отметим, что горизонт
частиц определен, только если мировые линии всех частиц се-
мейства известны. Если некоторая частица лежит на этом гори-
зонте, то р — это событие, в котором изотропный конус момента
«рождения» этой частицы пересекает мировую линию О. С дру-
гой стороны, в пространстве Минковского is любом событии р
5.2. П ространство-время де Ситтера
145
на мировой линии О можно увидеть все другие частицы, если
они движутся по времениподобным геодезическим. Пока мы
рассматриваем только семейства геодезических наблюдателей,
Частица, видная О
в р
Горизонт частиц
для 0 в р
Мировая линия О
Мировые
линии
частиц
Частицы, которые
еще не видны О вр
Изотропный конус прошлого О в р
б
Рис. 18. а — горизонт частиц, определяемый конгруэнцией геодезических
кривых при пространственноподобпой бесконечности прошлого 3 изотропных
геодезических; б — отсутствие такого горизонта при изотропной 3~.
существование горизонта частиц можно считать следствием
пространственноподобности бесконечности прошлого (рис. 18).
Все события вне изотропного конуса прошлого невидимы из р
и до события р никогда не были видимы. Мировая линия О
имеет предельную точку на ГГ+. В пространстве-времени де Сит-
тера 1-го рода изотропный конус прошлого этой точки (получае-
мый предельным переходом в реальном пространстве или непо-
средственно пз конформного пространства-времени) является
границей между событиями, которые хотя бы в какой-то момент
146
Гл. 5. Точные решения
времени станут видимы наблюдателем О, и событиями, кото-
рые О никогда не увидит. Такую поверхность мы называем гори-
зонтом событий будущего данной мировой линии. Это граница
Мировая линия О
Горизонт событий
прошлого О
Изотропный конус
будущего О в р
Мировая линия
Горизонт событий прошлого О ср
События, колю-
ры е О никогда
не увидит
Горизонт событий
будущего О
События, на кото-
рые О никогда не
сможет повлиять
а
Мировая линия геодезического
наблюдателя О
Мировая линия негеодезического
наблюдателя R
Изотропный конус прошлого
О в р; в конечном итоге он охватит Твризонт событий будущего для R
все пространство-время я
Рис. 19. а — горизонт событий будущего для частицы О, который суще-
ствует, когда бесконечность будущего У+ пространственноподобна; анало-
гично горизонт событий прошлого, который существует, когда пространственно-
подобна бесконечность прошлого б — если бесконечность будущего со-
стоит из изотропной поверхности Sf+ и из г°, для геодезического наблюда-
теля О не существует горизонта событий будущего. Однако у ускоряющегося
наблюдателя может быть горизонт событий будущего.
мировой линии прошлого. Напротив, в пространстве-времени
Минковского предельный изотропный конус любого геодезиче-
ского наблюдателя включает все пространство-время и, следо-
вательно, в нем нет событий которых геодезический наблюдатель
никогда не сможет увидеть. Однако, если наблюдатель движется
равноускоренно, его мировая линия может иметь горизонт собы-
тий будущего. Существование горизонта событий будущего для
5.2. Пространетво-время де Ситтера
147
геодезического наблюдателя можно рассматривать как следствие
пространственноподобности (рис. 19).
Рассмотрим горизонт событий для наблюдателя О в про-
странстве-времени де Ситтера и предположим, что в некоторый
момент собственного времени (событие р на его мировой линии)
его изотропный конус пересекает мировую линию частицы Q.
После этого наблюдатель О всегда может видеть частицу Q. Но
на мировой линии Q имеется событие г, которое лежит на гори-
зонте событий будущего частицы О; О никогда не увидит тех
событий на мировой линии Q, которые расположены позднее г.
Более того, любое данное событие на мировой линии О отделено
бесконечным промежутком собственного времени от события,
когда он сможет увидеть г, но вместе с тем между любым собы-
тием вдоль мировой линии Q и событием г, представляющим со-
бой обычное событие на этой линии, проходит конечное время.
Таким образом, наблюдатель О за бесконечное время видит ко-
нечную часть истории Q; выражаясь более физично, при наблю-
дении частицы Q наблюдателем О происходит красное смеще-
ние, которое стремится к бесконечности по мере приближения
наблюдаемых на мировой линии Q событий к точке г. Соответ-
ственно с частицы Q никогда нельзя будет увидеть событий, сле-
дующих за некоторой точкой на мировой линии О, а близлежащие
к ней точки наблюдаются с очень большим красным смещением.
Изотропный конус будущего любой точки мировой линии яв-
ляется границей множества таких событий в пространстве-вре-
мени, на которые О может влиять начиная с данного момента.
Чтобы получить максимальное множество тех событий в про-
странстве-времени, на которые О может влиять хоть в какой-то
момент, возьмем изотропный конус будущего предельной точки
мировой линии О, расположенной в бесконечности прошлого 3>'~;
иначе говоря, возьмем границу будущего этой мировой линии
(ее можно рассматривать как изотропный конус момента рожде-
ния частицы О). Такая нетривиальная область существует для
геодезического наблюдателя только тогда, когда бесконечность
прошлого пространственноподобна (и тогда она фактически
является горизонтом событий прошлого частицы О). Из приве-
денных рассуждений ясно, что в стационарной модели, где бес-
конечность прошлого для изотропных и времениподобных геоде-
зических изотропна, а бесконечность будущего пространственно-
подобна, любой фундаментальный наблюдатель имеет горизонт
событий будущего, но не имеет горизонта событий прошлого.
Отождествлением точек пространства де Ситтера 1-го рода
мы можем получить другие локально-эквивалентные ему про-
странства. Простейший случай — отождествление антиподаль-
ных точек р, р' (см. рис. 16) на гиперболоиде. Полеченное про-
странство не ориентируемо во времени: если в р время течет
Н8
Гл. 5. Точные решения
в направлении стрелки, то антиподальное oi ождоснмепне тре-
бует, чтобы оно в р' текло в направлении против стрелки, по
такое отождествление будущей прошлой половины изотропного
конуса нельзя распространить на весь гиперболоид. В работе
[19] подробно изучены пространства, получающиеся при таких
отождествлениях; в частности, в ней показано, что произволь-
ная точка в полученном пространстве может быть соединена
геодезической с любой другой точкой, если и только если про-
странство не ориентируемо во времени.
Пространство постоянной кривизны с R < 0 называется про-
странством де Ситтера 2-го рода. Оно обладает топологией
S1 X R3 и может быть представлено в виде гиперболоида
— U2 — V2 + X2 + у2 + Z2 = — 1
в плоском пятимерном пространстве R5 с метрикой
ds2 = — (dn)2 — (dn)2 + (dx)2 + (dy)2 + (de)2.
В этом пространстве существуют замкнутые времениподобные
линии, однако оно не является односвязным, и если мы развер-
нем круг S1 (чтобы получить его накрывающее пространство А?1),
то будем иметь универсальное накрывающее пространство про-
странства де Ситтера 2-го рода, в котором пет замкнутых време-
ниподобных линий. В дальнейшем под пространством де Сит-
тера 2-го рода мы будем подразумевать это универсальное на-
крывающее пространство; оно имеет топологию Ri.
Метрика этого пространства может быть записана в виде
ds2 — — df2 + cos2t {d%2 + sh2 x (d02 + sink 9 d</>2)}- (5.9)
Эта система координат покрывает лишь часть пространства и
имеет кажущиеся сингулярности при t = ±л/2. Пространство
целиком может быть покрыто координатами (С, г, Q, ф), в кото-
рых метрика принимает статическую форму:
ds2 = — ch2 г dt'2 + dr2 + sh2 r (d92 + sin2 0 d^2).
В таком представлении пространство покрывается поверхностя-
ми {f = const} с негеодезическими нормалями.
Для исследования структуры бесконечности введем коорди-
нату г'.
г' = 2 arctg (ехр г) — л/2, 0^г'<л/2.
Тогда получаем ds2 = ch2rds2, где ds2 определяется формулой
(5.7); иными словами, все пространство де Ситтера 2-го рода
конформно области О X R X л/2 эйнштейновского статического
цилиндра. Соответствующая диаграмма Пенроуза приведена на
рис. 20. Изотропную и пространственную бесконечности в этом
случае можно представлять себе как времениподобную поверх-
ность. Топология этой поверхности эквивалентна Д1 X S2.
Гг ~ Л/2
г'=0
б
Р и с. 20. а — универсальное пространство де Ситтера 2-го рода конформно
половине статической вселенной Эйнштейна. Координаты (/, / 0. Ф) покры-
вают лишь изображенную на рисунке ромбовидную область тогда как коор-
динаты (/. г, 0, Ф) покрывают все пространство. Все геодезические, ортого-
нальные к поверхностям {t = const}, сходятся в точках р и q и затем расхо-
дятся в новую такую же ромбовидную область и т. д.; б — диаграмма
Пенроуза пространства де Ситтера 2-го рода. Бесконечность состоит из вре-
мениподобной поверхности У и отдельных точек г+, 1~. Приведены проекции
некоторых времениподобных изотропных геодезических.
150
Гл. 5. Точные решения
В пространстве де Ситтера 2-го рода нельзя построить кон-
формное преобразование, переводящее временную бесконечность
в конечную область, если не сжимать статическую вселенную
Эйнштейна в точку (если при конформном преобразовании вре-
менная координата бесконечности становится конечной, то мас-
штаб пространственного сечения умножается па бесконечный
множитель), и поэтому мы изображаем времениподобную бес-
конечность отдельно стоящими точками i+, i~.
Линии {/_, 0, ф = const} являются геодезическими, ортого-
нальными к поверхностям {t = const}; они все сходятся в буду-
щем (соответственно в прошлом) в точках q (соответственно р)
пространства-времени, и этим схождением объясняется наличие
кажущихся (координатных) особенностей в первоначальном
виде метрики. Этими координатами покрывается область между
поверхностью t = 0 и изотропными поверхностями, на которых
геодезические нормали становятся вырожденными.
Это пространство обладает двумя другими интересными чер-
тами. Во-первых, вследствие времениподобности бесконечности
в нем нигде нет поверхности Коши. Хотя и можно построить
семейства пространственноподобных поверхностей (например,
поверхности {К = const}), которые покрывают пространство пол-
ностью, все же для любой данной поверхности такого семейства
существуют изотропные геодезические, которые ее нигде не пере-
секают. Если задать начальные данные на какой-либо из этих
поверхностей, за пределами ее области Коши нельзя что-либо
предсказать; таким образом, с поверхности {t=0} можно делать
предсказания лишь в области, покрытой координатами t, %, 8, Ф-
Любой попытке предсказаний вне этой области препятствует по-
ступление «свежей» информации из времениподобной бесконеч-
ности.
Во-вторых, в соответствии с тем, что все геодезические нор-
мали из t = 0 сходятся ври?, все геодезические из р в про-
шлое расходятся (нормально к поверхности {t = const}) ненова
сходятся в q. В действительности все времениподобные геодези-
ческие из любой точки этого пространства (и в прошлое, и в бу-
дущее) фокусируются в точку-изображение, от нее снова расхо-
дятся и снова фокусируются во вторую точку-изображение и т. д.
Поэтому времениподобная геодезическая из р в будущее никогда
не может достичь 3 в отличие от изотропной геодезической в бу-
дущее, которая доходит до J и образует границу будущего точ-
ки р. Как следствие такого различия между времениподобными
и изотропными геодезическими в будущем точки р (т. е. там,
куда могут быть проведены из р направленные в будущее вре-
мениподобные линии) существуют области, которых нельзя
достичь из р по какой-либо геодезической. Множеством точек,
которых можно достичь по направленным в будущее времени-
5.?. Пространство Робертсона—Уокера 151
подобным линиям из р, будет множество точек, лежащих выше
изотропного конуса будущего точки р; множество точек, кото-
рых можно достичь из р по направленным в будущее времени-
подобным геодезическим, образует внутренность бесконечной
последовательности ромбообразных областей, подобных той, ко-
торая покрывается координатами (t, %, 0, ф). Заметим, что лю-
бую точку в области Коши поверхности t = 0 можно достичь
с этой поверхности по единственной геодезической нормали, но,
вообще говоря, до точек вне области Коши нельзя провести
геодезическую нормаль к t = 0.
5.3. Пространство Робертсона — Уокера
До сих пор мы не интересовались тем, как связаны с реаль-
ной физической Вселенной точные решения. Следуя Эйнштейну,
мы можем спросить: найдется ли пространство-время, которое
является точным решением для какой-либо подходящей формы
материи и при этом хорошо описывает крупномасштабные свой-
ства наблюдаемой Вселенной? Если таковое найдется, то мы мо-
жем утверждать, что имеем разумную «космологическую мо-
дель», т. е. модель физической Вселенной.
Однако мы не можем построить космологическую модель, ко-
торая была бы свободна от некоторой примеси философии. В са-
мых ранних космологиях человек приписывал себе господствую-
щее положение в центре Вселенной. Начиная с времен Копер-
ника, мы постепенно спустились на среднего размера планету,
обращающуюся вокруг среднего размера звезды на окраине до-
вольно обычной галактики, которая сама является всего лишь
членом Местной группы галактик. Мы стали теперь столь демо-
кратичны, что не возьмемся утверждать, будто наше положение
в пространстве хоть как-то выделено. Вслед за Бонди [10] будем
называть предположение о невыделенности нашего положения
принципом Коперника.
Этот несколько туманный принцип можно интерпретировать
следующим образом: при выборе подходящего масштаба Все-
ленная приблизительно пространственно однородна.
Под пространственной однородностью мы подразумеваем су-
ществование действующей на JI группы изометрий, поверхности
транзитивности *) которой являются пространственноподобными
3-поверхностями; другими словами, любая точка на одной из
этих поверхностей эквивалентна любой другой точке той же по-
верхности. Конечно, Вселенная не в точности пространственно
однородна; в ней существуют локальные неоднородности, такие,
*) Поверхностью транзитивности группы преобразований называется по-
верхность, каждая точка которой может быть переведена преобразованием
группы в любую другую точку этой поверхности. — Прим. ред.
152
Гл. 5. Точные решения
как звезды и галактики. Тем не менее представляется разумным
предположить, что Вселенная пространственно однородна в до-
статочно больших масштабах.
Хотя мы и можем построить математические модели, удовле-
творяющие этому требованию однородности (см. следующий раз-
дел), по непосредственно проверить однородность с помощью
наблюдений трудно вследствие того, что нет простого способа
измерения расстояний до удаленных объектов. Эта трудность
смягчается тем обстоятельством, что в принципе мы довольно
легко можем обнаружить путем наблюдений внегалактических
объектов изотропию (т. е. проверить, совпадают ли результаты
наблюдений в различных направлениях), а изотропия тесно
связана с однородностью. Выполненные до сих пор наблюдения
по проверке изотропии подтверждают вывод о приближенной
сферической симметрии окружающей нас Вселенной.
В частности, было показано, что внегалактические радиоис-
точники распределены приблизительно изотропно, а обнаружен-
ный недавно фон микроволнового излучения в исследованной
области спектра в высшей степени изотропен.
Записать и исследовать метрики для всех случаев сфериче-
ски-симметричиого пространства-времени вполне возможно. Кон-
кретными примерами пространств с такой симметрией являются
решения Шварцшильда и Райснера—Нордстрема (см. разд. 5.5),
которые, однако, являются асимптотически плоскими простран-
ствами. Вообще говоря, в сферически-симметричных пространст-
вах есть самое большее две точки, из которых пространство
представляется сферически-симметричным. Такие пространства
могут служить моделями пространства-времени вблизи массив-
ного тела, но если принять их в качестве моделей Вселенной, то
это согласуется с изотропией по данным наших наблюдений
лишь при условии, что мы расположены вблизи какой-то весьма
специфической точки. Исключением являются те модели, в ко-
торых Вселенная изотропна относительно каждой точки в про-
странстве-времени; поэтому мы будем трактовать принцип
Коперника как утверждение о приближенной сферической сим-
метрии Вселенной относительно каждой точки (поскольку она
приближенно сферически-симметрична вокруг нас).
Как было показано Уокером [171], точная сферическая сим-
метрия относительно каждой точки означает, что Вселенная про-
странственно однородна и допускает 6-параметрическую группу
изометрий с поверхностями транзитивности в виде простран-
ственноподобных 3-поверхностей постоянной кривизны. Такого
рода пространства называются пространствами Робертсона —
Уокера (или Фридмана); пространство Минковского, простран-
ства дс Ситтера обоих родов являются частными случаями про-
странства Робертсона —Уокера общего вида. Отсюда мы заклю-
5.3. Пространство Робертсона — Уокера
153
чаем, что пространства Робертсона — Уокера даюг хорошее при-
ближение к крупномасштабной геометрии пространства-времени
в области, доступной нашим наблюдениям.
В пространстве Робертсона — Уокера координаты можно
выбрать так, чтобы метрика имела вид
ds2 = — df + S2 (/) do2,
где do2— метрика трехмерного пространства постоянной кривиз-
ны, причем она не зависит от времени. Геометрия этого трехмер-
ного пространства существенно зависит от того, положительна,
отрицательна или равна нулю его кривизна К’, подбором функ-
ции S можно нормировать К так, чтобы в первых двух случаях
она была равна +1 или —1. Тогда метрику do2 можно записать
в виде
где
da2 = d/2 + f2 (%) (d02 + sin2 0 d^2),
' sin%
sh%
при
при
при
+ 1,
К = 0,
Л = - 1.
f(x) = 1
Если К = 0 или К = —1, координата % пробегает значения от О
до оо, а при К = +1 имеем 0 sC -/ sC 2л. При К=0 или К—— 1
трехмерное пространство диффеоморфно R3 и, таким образом,
«бесконечно»; когда К = +1, оно диффеоморфно трехмерной
сфере S3 и, следовательно, компактно («закрыто» или «конеч-
но») . Можно было бы отождествить подходящие точки в этих
трехмерных пространствах и получить иные глобальные тополо-
гии; в случае отрицательной и нулевой кривизны это можно сде-
лать даже так, чтобы в результате получилось компактное трех-
мерное пространство [102]. Однако такая компактная поверх-
ность постоянной кривизны не допускает никакой непрерывной
группы изометрий [175]: хотя в каждой точке существуют век-
торы Киллинга, они не задают какое-либо глобальное векторное
поле Киллинга, и локальные группы изометрий, определяемые
ими, нельзя объединить в одну глобальную группу. В случае ну-
левой кривизны компактное пространство может обладать толь-
ко 3-параметрической группой изометрий. Ни в одном случае
полученное пространство-время не будет изотропным. Мы не бу-
дем делать подобных отождествлений, поскольку поводом для
изучения пространств Робертсона — Уокера была их изотропия
(и, следовательно, наличие 6-параметрической группы изомет-
рий). В действительности единственным отождествлением, кото-
рое не приводит к анизотропному пространству, является ото-
ждествление антиподальных точек на S3 в случае постоянной
положительной кривизны.
154
Гл. 5. Точные решения
Симметрия решений Робертсона — Уокера требует, чтобы
тензор энергии-импульса имел вид, соответствующий идеальной
жидкости, плотность ц и давление р которой являются функ-
циями только временной координаты t, а линии тока описы-
ваются кривыми %, 0, ф — const (так что %, 0, ф — сопутствую-
щие координаты). Можно считать, что эта жидкость описывает
материю во Вселенной в приближении равномерного «размазы-
вания»; тогда функция S(?) характеризует девиацию соседних
линий тока, т. е. «близких» галактик.
Уравнение сохранения энергии (3.9) теперь принимает вид
ц = — 3 (ц + р) S/S. (5.10)
Уравнение Райчаудхури (4.26) выглядит следующим образом:
4л (ц + Зр) — Л = — 3S/S, (5.11)
уравнения поля сводятся к одному уравнению [по существу, это
соотношение (2.35)]:
3S2 = 8л (ц53)/5 + AS2 - ЗК. (5.12)
Когда S =К= 0, соотношение (5.12) можно получить (с произволь-
ным значением К) как первый интеграл уравнений (5.10), (5.11);
таким образом, оно фактически служит для отождествления по-
стоянной К с кривизной трехмерного пространства {t = const}
с метрикой do2.
Разумно предположить (см. энергетические условия, разд. 4.3),
что и >0 и р >0. (В действительности по современным оцен-
кам 10-29 г/см3 Цо 10~31 г/см3, цо ро 0.) Тогда, если
Л = 0, то из (5.11) видно, что S не может быть постоянной;
иначе говоря, из уравнений поля следует, что Вселенная должна
или расширяться, или сжиматься. Наблюдения показывают (это
впервые обнаружили Слайфер и Хаббл), что галактики уда-
ляются от нас, т. е. что в настоящее время вещество во Вселен-
ной расширяется. Последние наблюдения дают для современ-
ного значения S/S значение
// = (S/S)lo« 10“10 лет-'1
(по-видимому, с точностью до множителя ~2). Отсюда, соглас-
но (5.11), следует, что при Л = 0$ должна обратиться в нуль
за некоторый конечный интервал времени Ф в прошлом (время
to измеряется вдоль мировой линии нашей Галактики), причем
t0 < Я-' « Ю10 лет.
Из (5.10) следует, что по мере расширения Вселенной плотность
уменьшается; в прошлом, наоборот, она была выше и принимала
сколь угодно большие значения при S -> 0. Поэтому точка, где
5.3. Пространство Робертсона — Уокера
155
5 = 0, не является только координатной особенностью, как при
введении координат (5.9) во вселенной де Ситтера 2-го рода; тот
факт, что плотность обращается при 5 = 0 в бесконечность,
означает, что некоторый скаляр, определяемый тензором кривиз-
ны, тоже бесконечен. Это делает подобную сингулярность даже
серьезней, чем та, которая возникает в соответствующей ньюто-
новской ситуации; в обоих случаях мировые линии всех частиц
пересекаются в одной точке и плотность становится бесконечной,
но здесь становится сингулярным в точке 5 = 0 само простран-
ство-время. Мы должны исключить эту точку из пространствен-
но-временного многообразия, поскольку в ней не могут выпол-
няться никакие известные физические законы.
Эта сингулярность — наиболее удивительное свойство реше-
ний Робертсона — Уокера. Она возникает во всех моделях, в ко-
торых ц + Зр > 0 и Л отрицательна, равна нулю или имеет не
слишком большое положительное значение. Сингулярность озна-
чает, что у Вселенной (или по крайней мере у той ее части,
о физике которой мы имеем некоторое представление) имеется
начало, отдаленное от нас конечным промежутком времени. Од-
нако этот результат основан на предположении о строгой про-
странственной однородности и сферической симметрии. Хотя это
предположение может оказаться разумным приближением для
достаточно больших масштабов в настоящее время, оно, конеч-
но, не выполняется локально. Можно допустить, что при про-
слеживании эволюции Вселенной назад во времени местные
неоднородности настолько возрастут, что они смогут воспрепят-
ствовать появлению сингулярности, приводя к «упругому отра-
жению» частей Вселенной. Может ли подобное произойти и
содержатся ли сингулярности в реалистических решениях с не-
однородностями— это центральные вопросы космологии; их об-
суждение составляет основной предмет этой книги. Как мы
увидим, имеются веские основания считать, что физическая Все-
ленная действительно была сингулярной в прошлом.
Если задана какая-либо разумная связь между р и щ урав-
нение (5.10) можно проинтегрировать и получить р в функции 5.
Давление в настоящую эпоху очень мало. Если р и Л положить
равными нулю, то из (5.10) находим
4 л М
3 В — 5з .
где М — постоянная; при этом (5.12) имеет вид
35! = = (5.13)
Первое уравнение выражает сохранение массы при нулевом дав-
лении, а второе (уравнение Фридмана) представляет собой урав-
нение сохранения энергии для сопутствующего объема материи:
156
Гл. 5. Точные решения
постоянная Е — это сумма кинетической и потенциальной энер-
гий. Если Е < 0 (т. е. К > 0), то S будет возрастать до неко-
торого максимального значения и затем спадет до нуля; если же
Е 0 (т. е. К -С 0), то S возрастет неограниченно.
Явные решения уравнения (5.13) примут простой вид, если
их записать через новый временной параметр r(t), определяе-
мый равенством
dr dr (5.14)
тогда имеем
5 = (у) (chr — 1), t = 4-(sh т — t) u при 1;
t — 1 3 -3 х при /< = 0;
S = — у (1 — cost), t = —- у-(т — sin t) при 1.
(Случаю /\ = 0 соответствует вселенная Эйнштейна — де Сит-
2
тера; очевидно, тогда S ~ i3 .)
При р > 0 поведение качественно такое же. В частности, для
р — (у — 1)ц, где у = const, 1 si- у sE 2, получаем 4лц/З — Л4 /S3v,
и решение (5.12) вблизи сингулярности имеет вид
2
S ~ t3'1.
Если Л < 0, то решение свидетельствует о расширении от
начальной сингулярности к некоторому максимуму с последую-
щим коллапсом во вторую сингулярность. Если Л > 0, то для
Е = 0 или —1 расширение продолжается вечно, и асимптоти-
чески решение приближается к стационарной модели. При К= 1
существует несколько возможностей. Если Л больше некоторого
значения ЛКрПт (при p — Q ЛКрпт = (—Е/ЗЛ4)3/(ЗЛ1)2), реше-
ние начинается с сингулярности и описывает вечное расширение
с асимптотическим приближением к стационарной модели. При
Л = ЛкрИТ имеем статическое решение — статическую вселенную
Эйнштейна. [Метрическая форма (5.7)—это частный случай ста-
тического решения Эйнштейна с ц 4- Р = (4л)'1, Л = 1 + 8лр.]
Существует еще решение, начинающееся с сингулярности и
асимптотически приближающееся к вселенной Эйнштейна, и ре-
шение, начинающееся со вселенной Эйнштейна в бесконечном
прошлом и все время расширяющееся. Если Л < Лкрпт, имеется
два решения: одно описывает расширение от начальной сингу-
лярности и затем коллапс во вторую сингулярность; второе—
сжатие, начинающееся при бесконечном радиусе в бесконечном
прошлом, до некоторого минимального радиуса с последующим
5.3. Пространство Робертсона — Уокера
157
расширением. Только это последнее решение и решение, которое
в бесконечном прошлом асимптотически приближается к стати-
ческой вселенной, могли бы соответствовать наблюдаемой Все-
ленной и не иметь при этом сингулярностей. Однако в этих
моделях всегда S > 0, что, по-видимому, противоречит резуль-
татам наблюдений красных смещений далеких галактик [145,
146]. Кроме того, максимальная плотность в этих моделях, ока-
зывается, не. слишком сильно отличается от современной плот-
ности, что приводит к трудностям в объяснении таких явлений,
как микроволновой фон излучения и распространенность гелия
в космосе: перечисленные явления скорее всего свидетельствуют
об очень горячей плотной фазе в истории Вселенной.
Так же как и в предыдущих случаях, мы можем построить
конформные отображения пространств Робертсона — Уокера в
статическое пространство Эйнштейна. В качестве временной ко-
ординаты будем использовать параметр г, определяемый соотно-
шением (5.14); тогда метрика принимает вид
ds2 = S2(r){ — dr 4- d%2 + f2(x)(d02 + sin2 0 d^2)}. (5.15)
В случае К = 4-1 она уже конформна статическому простран-
ству Эйнштейна [для согласования с обозначениями формулы
(5.7) нужно положить т = У, % = г']. Таким образом, это про-
странство отображается точно на ту часть статического про-
странства Эйнштейна, которая определяется областью значе-
ний т. Когда р = Л = 0, т меняется в пределах 0 < т < л и
все пространство отображается на эту область статического про-
странства, а его граница — на трехмерные сферы т = 0, т = л.
(Если р > 0, оно отображается на область, в которой 0 < т <
< а < л, где а — некоторое число). В случае К = 0 простран-
ство в тех же координатах оказывается конформно-плоским [см.
(5.15)], так что после конформных преобразований (см. разд. 5.1)
мы получим отображение рассматриваемого пространства на об-
ласть, представляющую пространство-время Минковского в ста-
тической вселенной Эйнштейна (см. рис. 14); конкретный вид
области отображения снова определяется значениями, которые
принимает т. При Л = 0 имеем 0 < т < оо, и, следовательно,
это пространство (которое при р = 0 представляет собой про-
странство Эйнштейна — де Ситтера) конформно половине обла-
сти, изображающей пространство-время Минковского. В случае
К = —1 получаем метрику, конформную части той области ста-
тического пространства Эйнштейна, для которой л/2 t' 4- г'
Р> —л/2, л/2 Г f — г' р> —л/2, причем
f = arctg (thy (т 4-х)) 4-arctg (thy (т — %)} ,
г' == arctg (thy (т 4- х)) — arctg (th у (т — х)) •
158
Гл. 5. Точные решения
Какая именно часть этой области покрывается, зависит от обла-
сти изменения т; при Л = 0 рассматриваемое пространство отоб-
ражается па верхнюю половину.
%=л/г
5 6
Рис. 21. а — пространства Робертсона — Уокера (р = Л = 0) конформны
изображенным на рисунке областям, которые соответствуют трем случаям:
/( = + 1, 0, —1; б — диаграмма Пенроуза пространства Робертсона — Уокера
при 7( = -|-1 и р = Л = 0; в — диаграмма Пенроуза пространства Роберт-
сона — Уокера при К = 0 или /< = —1 и р = Л = 0.
Итак, мы установили, что эти пространства и их границы кон-
формны некоторой (вообще говоря, конечной) области статиче-
ского пространства Эйнштейна (рис. 21, а). Однако имеется важ-
ное отличие от предыдущих случаев: часть границы теперь не
!> 3. Пространство Робертсона — Уокера
159
является «бесконечностью» в прежнем смысле, а представляет
собой сингулярность, в которой 5 = 0. (Можно считать, что кон-
формный множитель переводит бесконечную область в конечную
путем бесконечно сильного сжатия, а сингулярную точку 5 = 0
превращает в конечную область бесконечно сильным растяже-
нием.) Вносимые при этом в конформные диаграммы отличия
по существу невелики: мы по-прежнему можем построить диа-
граммы Пенроуза (рис. 21,6 и в). В каждом случае, когда р^О,
сингулярность при t=Q изображается пространственноподобной
поверхностью. Это соответствует существованию горизонтов ча-
стиц (определяемых точно так же, как в разд. 5.2) в простран-
ствах Робертсона — Уокера. Когда К= +1, граница в будущем
также пространственноподобна, из чего следует существование
горизонтов событий для фундаментальных наблюдателей. Если
Л = 0, а /\ = 0 или К — —1, то бесконечность будущего изо-
тропна, и в этих случаях нет никаких горизонтов событий буду-
щего для фундаментальных наблюдений.
На этом этапе нам следует разобраться в таком вопросе:
пространство де Ситтера 2-го рода можно представить в роберт-
сон-уокеровском виде (5.9) и затем отобразить конформно на
часть статической вселенной Эйнштейна. Если это проделать, то
мы обнаружим, что координаты Робертсона — Уокера покры-
вают только малую часть всего пространства-времени. Иначе
говоря, пространство-время, описываемое координатами Роберт-
сона— Уокера, можно расширить. Поэтому нам нужно показать,
что вселенные Робертсона — Уокера, в которых имеется мате-
рия, на самом деле нерасширяемы.
Это действительно так, поскольку при ц > 0 и р 0 для
любого вектора X в произвольной точке q можно показать, что
геодезическая у (у), проходящая через q = у(0) в направле-
нии X, удовлетворяет одному из двух условий:
1) у (у) можно продолжить на произвольные положительные
значения v или
2) существует некоторое значение v = v0 > 0, такое, что ска-
лярный инвариант
(>,-/ -- 4Rgn) (к11 - 4 Rgu) -= (ц + Лф + 3 {р - Л)-
не ограничен на у ([О, у0])-
Ясно, что поверхности {t — const} являются поверхностями
Коши в этих пространствах. Далее, мы видим, что сингулярность
в них универсальна в следующем смысле: все времениподобные
и изотропные геодезические, проходящие через какую-либо точку
пространства, приближаются к сингулярности при некотором
конечном значении своего аффинного параметра. (Поскольку
160
Гл. 5. Точные решения
изотропные геодезические образуют границу прошлого кажцой
точки, все непродолжимые времениподобные кривые также стре-
мятся к сингулярности.)
5.4. Пространственно-однородные космологические модели
Как мы видим, в любом пространстве-времени Робертсона —
Уокера, в котором р > 0, р 0 и постоянная Л не слишком ве-
велика, имеются сингулярности. Однако из этого нельзя делать
вывода о существовании сингулярностей в более реалистических
моделях мира, учитывающих тот факт, что Вселенная не одно-
родна и не изотропна. Конечно, никто не надеется получить точ-
ное решение, которое бы описывало Вселенную во всех деталях.
Однако можно найти точные решения с меньшими ограниче-
ниями, чем в решениях Робертсона — Уокера, которые могли бы
служить приемлемой моделью Вселенной, и посмотреть, имеются
в них сингулярности или нет; тот факт, что эти модели действи-
тельно содержат сингулярности, указывает на то, что существо-
вание сингулярностей, возможно, является общим свойством
всех пространств, которые можно принять в качестве разумных
моделей Вселенной.
Мы получим простой класс таких решений, если, сохраняя
требование пространственной однородности (строгий принцип
Коперника), откажемся от требования изотропии (в настоящее
время Вселенная кажется приблизительно изотропной, но могла
быть значительная анизотропия в более ранние эпохи). Таким
образом, в этих моделях предполагается существование группы
изометрий 6г, орбитами которой в некоторой части модели яв-
ляются пространственноподобные гиперповерхности. (Орбита
точки р под действием группы Gr есть множество точек, в кото-
рые переводится точка р под действием всех элементов группы.)
Такие модели локально можно построить известными методами;
случай г = 3 рассмотрен в [76], случай г = 4 — в [87] (если
г >4, пространство-время по необходимости является простран-
ством Робертсона — Уокера).
Наиболее простой случай пространственной однородности —
это когда соответствующая группа изометрий абелева; тогда
пространство относится к типу I по классификации Бианки [7];
так что пространство-время с такой группой изометрий будем на-
зывать пространством типа I Бианки. Мы рассмотрим некоторые
свойства этих пространств и затем сформулируем теорему, ут-
верждающую, что сингулярности имеют место во всех непустых
пространственно-однородных моделях, в которых удовлетворяет-
ся условие времениподобного схождения (разд. 4.3).
Допустим, что пространственно-однородное иросгранство-
время обладает абелевой группой изометрий; для простоты
5.4. Пространственно-однородные модели
161
предположим, что Л = 0 и что материальное содержимое Все-
ленной представляет собой идеальную жидкость без давления
(«пыль»). Тогда существуют сопутствующие координаты
(t, х, у, г), в которых метрика имеет вид
ds2 == - &t'2 + X2 (/) dx2 + Y2 (t) dу2 + Z2 (0 dz2. (5.16)
Если соотношением S'2 = XYZ ввести функцию S(t), то из за-
конов сохранения видно, что плотность материи определяется
равенством 4лц/3 = М/S3, где М — подходящим образом вы-
бранная постоянная. Общее решение полевых уравнений можно
записать в виде
/ \2 sin а / ^’/s \2 sin (а+2л/3)
X = -д—J , Y = S (^—J
/ //, \2 sin (а+4п/3)
2=44-)
причем
s3=4w + 2);
2(>0)—постоянная, характеризующая степень анизотропии
(мы исключаем изотропный случай 2 = 0, совпадающий со
вселенной Эйнштейна—де Ситтера (разд. 5.3)), а постоянная
а (—л/6 < а л/2) задает направление наиболее быстрого
расширения. Средняя скорость расширения определяется равен-
ством
S _ 2 ^ 2
S ” 3/ t + 2 ’
скорость расширения в направлении х равна
2 z + y20+2sina)
Х = Щ /4-2 ’
а скорости расширения У/У, 2/Z в направлениях у и z даются
выражениями, в которых а заменена соответственно на «+2л/3,
а + 4л/3. Такое решение описывает расширение из сильно ани-
зотропного сингулярного состояния при t = 0, приводящее при
больших t к почти изотропной фазе, в которой пространство-
время такое же, как во вселенной Эйнштейна — де Ситтера.
Средняя длина S монотонно возрастает по мере возрастания I;
первоначально высокая скорость ее изменения (S— i11 при ма-
лых 0 постоянно убывает (S — /2/’ при больших t). Следова-
тельно, в ранние периоды анизотропная Вселенная эволюцио-
нирует быстрее, чем ее изотропный эквивалент.
Допустим, что мы рассматриваем эту модель назад во вре-
мени и приближаемся к сингулярности. Первоначальное почти
6 Заказ 381
162
Гл. !i. Точные решения
изотропное сжатие станет сильно анизотропный и ранние пе-
риоды. При общем значении а, т. е. при а ф л/2, член
1 + 2 sin (а + 4л/3) будет отрицательным. Следовательно, кол-
лапс в направлении осп z должен прекратиться и сменится рас-
ширением, причем скорость расширения в достаточно поздние
моменты времени стремится к бесконечности. Напротив, в на-
правлении осей хи у коллапс будет монотонно стремиться к син-
гулярности. Таким образом, при развитии рассматриваемой
модели в обычном направлении времени мы имеем «сигарооб-
разную» сингулярность: вдоль оси z материя коллапсирует из
бесконечности, затем коллапс прекращается и начинается рас-
ширение, в то время как в направлениях осей х и у материя
монотонно расширяется во все моменты времени. Если в такой
Вселенной можно было бы принять какой-либо сигнал, испу-
щенный в достаточно ранние моменты времени, то в направле-
нии оси z наблюдалось бы максимальное красное смещение;
материю в более ранние моменты времени мы наблюдали бы
со все уменьшающимся красным смещением, которое перехо-
дило бы по мере удаления в прошлое в фиолетовое смещение.
Несколько иначе происходит развитие в специальном случае
а = л/2. Тогда оба множителя 1 ф- 2 sin (а ф- 2л/3) и
1 2 sin (а + 4л/3) обращаются в нуль и скорости расширения
имеют вид
X 2^2 У __ Z __ 2 1
X ~~ 3t / ф S ’ У ~ Z ~ 3 / + 2 ’
Если рассматривать обращенную во времени модель, то ско-
рость коллапса в направлениях у и z асимптотически замед-
ляется до нуля, а в направлении х бесконечно возрастает. При
обычном направлении времени мы имеем «блинообразную» син-
гулярность: материя монотонно расширяется во всех направле-
ниях с бесконечно большой начальной скоростью расширения в
направлении оси х и без начальной скорости в направлениях
осей у и z. Красное смещение в направлении оси х будет сколь
угодно большим, а в направлении у и z — конечным.
Дальнейшее исследование показывает, что в общем («сигаро-
образном») случае, несмотря па анизотропию расширения, суще-
ствуют горизонты частиц в каждом направлении. В специальном
(«блйнообразном») случае в направлении осп х нет никаких го-
ризонтов; действительно, координаты часгиц, которые видны в
момент /о из начала координат (х, у, г), лежат внутри бесконеч-
ного цилиндра
х2 + у'2 < р\
где
р-тН(Т*+эГ-(Т*Л-
5.4. Пространственно-однородные модели
163
Хотя мы рассмотрели пространственно-однородные модели толь-
ко при пулевом давлении и Л = 0, легко можно получить свой-
ства этих пространств при более реалистическом материальном
содержимом; если, например, мы возьмем идеальную жидкость
с р = (у — 1)р, у — const(1 < у < 2) или смесь фотонного газа
и вещества с р мб ц/3, поведение вблизи сингулярности будет
таким же, как и в случае пыли.
Интересным следствием отсутствия горизонта частиц в на-
правлении оси х в специальном («блинообразном») случае яв-
ляется возможность непрерывного продолжения решения за син-
гулярность. Покажем это в случае решения для пыли.
Метрика имеет вид (5.16), причем теперь
= +2))Л У(0 = 2(0 = (4лП(/ + 2))'3. (5.17)
Введем новые координаты т, ц, удовлетворяющие уравнениям
Тогда получаем, что метрика (5.16), (5.17) в новых координатах
имеет вид
ds2 = Л2 (0 (- dr" + dt]2) + В2 (/) (dz/2 + dz2), (5.18)
где
A (t) = exp ( - ) (4 M (t + 2))_1/3. В (/) = (4 M (t + I))2'3;
(5.19)
при этом все пространство (при t > 0) отображается на об-
ласть У, определяемую неравенствами т > 0, т2 — г]2 > 0. Функ-
ция Нт, г]) теперь задана как решение уравнения
т2 — -/И/- ехр—М=----, (5.20)
2 2-
где t > 0. На плоскости (т, ц) введены конформно-плоские ко-
ординаты. Проекция области Т, ограниченной поверхностью
t > 0, на эту плоскость изображена на рис. 22. На этой диа-
грамме мировые линии частиц изображаются прямыми линиями,
расходящимися от начала.
Функции Л(0, -^(0 непрерывны при t -> 0 сверху. Поэтому
решения можно продолжить непрерывно из верхней полупло-
скости па всю плоскость (т, ц), положив, что (5.19) выпол-
няется всюду (5.20)—внутри Т и что вне области Т имеет
место равенство
ЦП П) = 0.
6*
Галактики, которые не видны
О из р
Мировые линии
галактик-, О в р
видит эти
галантина
Сингулярность
Мировая линия
t=0
Поверхности
t— const
Изотропный конце прошлого
врг^ДО)
Рис. 22. Пространство типа I Бианки с пылевидной материей, обладающее
«блинообразной» сингулярностью, а — плоскость (т, Г]); изотропные линии
проходят под углом ±45°; б — поперечный разрез пространства в координа-
тах (т, Г], у) (координата z опущена), на котором виден световой конус
прошлого точки р = (т0, 0, 0). В направлении оси у имеется горизонт частиц,
но его нет в направлении оси х (т. е. т]).
5.4. Пространственно-однородные модели
165
Тогда формула (5.18) дает С°-метрику, которая внутри F экви-
валентна (5.16), (5.17), а вне Т является метрикой плоского
пространства-времени. Однако это решение не принадлежит
классу С1 при переходе через границу 7°, и плотность материи
становится на этой границе бесконечной (поскольку на ней
S—>0). Из-за того, что первые производные квадратично-неинте-
грируемы, уравнения Эйнштейна на этой границе невозможно
трактовать даже в смысле обобщенных функций (см. разд. 8.4).
Хотя продолжение решения на границу единственно, нет способа
сделать его однородным вне области Т. Итак, мы получили про-
должение для случая пыли; подобным же образом можно про-
должить решение в случае смеси вещества и излучения.
Вернемся теперь к рассмотрению непустых пространственно-
однородных моделей общего вида. Существование сингулярности
в таких моделях прямо следует из уравнения Райчаудхури, если
материя движется по геодезическим без вращения (как это бу-
дет, например, в случае ортогональности геодезических к поверх-
ностям однородности и при выполнении условия времениподоб-
ного сближения). Однако существуют пространства, в которых
вещество обладает ускорением и турбулентностью; возможно,
какой-либо из этих двух факторов может воспрепятствовать по-
явлению сингулярности. Следующий результат, являющийся
усовершенствованным вариантом теоремы Хокинга и Эллиса [74],
показывает, что в действительности ни ускорение, ни вращение
не могут помешать существованию сингулярностей в этих мо-
делях.
Теорема
Модель {Я, g) не может быть времениподобно геодезически
полной, если;
1)ЯаьКаКь > 0 для всех времениподобных и изотропных век-
торов К (это справедливо, если тензор энергии-импульса типа I
(разд. 4.3) и ц 4- pi > 0, ц + £ pt — 4лЛ > 0) ;
2) существуют уравнения движения материальных полей,
для которых задача Коши имеет единственное решение (см.
гл. 7);
3) данные Коши на некоторой пространственноподобной
3-поверхности <34? инвариантны относительно группы диффеомор-
физмов <3^, которая транзитивна на Уё.
Поскольку внутренняя геометрия <34? инвариантна относитель-
но транзитивной группы диффеоморфизмов, последние являются
изометриями и многообразие <34? полно, т. е. не может иметь
края. Можно показать (см. разд. 6.5), что из существования
непространственноподобной кривой, пересекающей <34? более
одного раза, следует существование для Я накрывающего
166 Гл. 5. Точные решения
многообразия Л, в котором каждая связная компонента образа
поверхности Ж будет пересекаться по более одного раза с лю-
бой непространствешюподобной кривой. Допустим, что Л—
времениподобное геодезически полное многообразие, и пока-
жем, что это противоречит условиям (1) — (3).
Пусть Ж — связная компонента образа Ж в Л. Согласно
условию (3), данные Коши па Ж однородны. Поэтому по усло-
вию (2) область Коши какой-либо области Ж изометрична об-
ласти Коши любой другой подобной области Ж. Вследствие
этого однородны и поверхности {s = const}, где s есть расстоя-
ние от Ж, измеренное вдоль геодезических нормалей к Ж, если
они лежат внутри области Коши поверхности Ж. Эти поверхно-
сти должны лежать или целиком внутри или целиком вне обла-
сти Коши Ж, ибо в противном случае на Ж> существовали бы
эквивалентные области, которые имели бы неэквивалентные об-
ласти Коши. Поверхности {s = const} будут лежать в области
Коши постольку, поскольку они остаются пространственнопо-
добными, ибо граница (если она существует) области Коши
поверхности Ж> должна быть изотропной (разд. 6.5).
Геодезическая, ортогональная к Ж, будет ортогональной и
к поверхностям {s = const}, поскольку вектор девиации точек,
отстоящих на равном расстоянии от Ж вдоль соседних геодези-
ческих, сохраняет ортогональность к этим геодезическим, если
он был ортогонален к ним первоначально. Как и в разд. 4.1,
пространственное разделение соседних геодезических, ортого-
нальных к Ж, можно охарактеризовать матрицей А, которая
единична на Ж. Пока А не вырождена, отображение из Ж на
поверхности {s = const}, задаваемое нормальными геодезиче-
скими, будет ранга 3, так что эти поверхности будут простран-
ственноподобпыми 3-поверхностями, находящимися в пределах
области Коши Ж. Расхождение
0 = (det А)-1-^||^-
этих геодезических подчиняется уравнению Райчаудхури (4.26)
с нулевыми вращением и ускорением. По условию (1)
> 0 для всех времениподобных векторов Va. Следовательно, 0
становится бесконечным, а матрица А — вырожденной при неко-
тором конечном положительном или отрицательном значении s0
параметра $. Отображение из Ж на поверхность s = su может
иметь самое большее ранг 2, поэтому на Ж найдется по крайней
мере одно векторное поле Z, для которого AZ == 0. Интеграль-
ные кривые этого векторного поля являются теми кривыми на Ж,
5.5. Решение Шварцшильда
167
которые отображаются геодезическими нормалями в одну точку
на поверхности s = s0. Таким образом, эта поверхность будет
самое большее двумерной. Поскольку при |s|<|so| геодезиче-
ские лежат в области Коши поверхности 5^, поверхность s = s0
будет лежать или внутри или на границе этой области. Согласно
условию (1), тензор энергии-импульса имеет единственный вре-
мениподобный собственный вектор в каждой точке. Эти соб-
ственные векторы образуют времениподобное векторное С'-поле,
интегральные кривые которого можно рассматривать как линии
тока вещества. Все линии тока, проходящие через s = s0, долж-
ны пересекать Но тогда в силу однородности Ж все линии
тока, проходящие через должны проходить и через s = s0.
Следовательно, линии тока задают диффеоморфизм между 3$ и
поверхностью s = s0. Это невозможно, так как <3^— трехмерная
поверхность, a s = s0 — двумерная. п
В самом деле, если все линии тока должны проходить через
двумерную поверхность, то следует ожидать, что плотность ве-
щества станет бесконечной. Таким образом, мы убедились, что
крупномасштабные вращение или ускорение не могут сами по
себе воспрепятствовать появлению сингулярностей во вселенной,
подчиняющейся строгому принципу Коперника. Из последующих
теорем мы увидим, что неоднородности также не могут запре-
тить существование сингулярностей в моделях мира.
5.5. Решения Шварцшильда и Райсснера—Нордстрема
Хотя пространственно-однородные решения могут служить
хорошими моделями для крупномасштабного распределения ма-
терии во Вселенной, они непригодны, например, для описания
локальной геометрии пространства-времени в Солнечной систе-
ме. Эту геометрию в хорошем приближении можно описать ре-
шением Шварцшильда, которое представляет собой сфериче-
ски-симметричное пустое пространство-время вне сферически-
симметричного массивного тела. Все эксперименты по проверке
различия между ньютоновской теорией и общей теорией отно-
сительности, выполненные до сих пор, фактически основаны на
предсказаниях, связанных с этим решением.
Метрику пространства Шварцшильда можно представить в
виде
ds? = — (1—у'-') dt2 + (1 •—dr2 + г’ (d02 + sin2 0) d$2,
(5.21)
где г > 2/n. Очевидно, что это пространство-время — статиче-
ское (т. е. d/dt представляет собой градиентный времениподоб-
ный вектор Киллинга) и сферичсски-симметричное, т. е.
168
Гл. 5. Точные решения
инвариантно относительно группы изометрий 50(3), действую-
щей на 2-сферах {/ = const, г = const} (ср. с приложением Б).
Координата г задана в этой метрической форме внутренним об-
разом требованием, чтобы площадь этих поверхностей транзи-
тивности была равна 4лг2. Решение Шварцшильда — асимпто-
тически плоское, поскольку метрика при больших г имеет вид
gab — Лаь + ^(1/г). Сравнение с ньютоновской теорией (ср. с
разд. 3.4) показывает, что т имеет смысл гравитационной массы,
измеренной на бесконечном удалении от тела, создающего дан-
ное поле. Следует подчеркнуть, что это решение единственно:
если какое-либо решение уравнений поля в пустом пространстве
сферически-симметрично, то локально оно изометрично решению
Шварцшильда (хотя в какой-то другой координатной системе
оно, конечно, может выглядеть совсем иначе; см. приложение Б,
а также [6]).
Обычно метрику Шварцильда при г, превышающих некоторое
значение га > 2т, можно рассматривать как решение вне неко-
торого сферически-симметричного тела, внутри которого (г < rq)
метрика имеет иной вид, определяемый тензором энергии-им-
пульса вещества этого тела. Однако интересно посмотреть, что
получится, если рассматривать эту метрику как решение в пу-
стом пространстве при всех значениях г.
Тогда метрика особенна при г — 0 и г = 2т (имеются также
тривиальные сингулярности полярных координат при 9 = 0 и
0 = л). Следовательно, мы должны вырезать точки, в которых
г ~ 0 и г = 2m, из многообразия, задаваемого координатами
(t, г, 0, ф), поскольку в разд. 3.1 мы приняли, что пространство-
время должно представлять собой многообразие с лоренцевой
метрикой. Вырезав поверхность г = 2т, мы разделим многооб-
разие на две непересекающиеся компоненты, в которых 0<r<2m
и 2m < г < оо. Поскольку мы приняли, что пространственно-
временное многообразие должно быть связным, мы должны
брать в рассмотрение только одну из компонент и, очевидно,
выбрать при этом ту, в которой г > 2m, т. е. соответствующую
внешнему полю. После этого мы должны задаться вопросом,
расширяемо ли многообразие Л со шварцшильдовой метри-
кой g, т. е. существуют ли большее многообразие Л', в которое
можно было бы вложить Л, и нужное число раз дифференцируе-
мая лоренцева метрика g' на Л', совпадающая с g на образе Л.
Ясно, что расширение можно осуществить в области, где г~>2т.
Вычисление показывает, что, несмотря на особенность метрики
в шварцшильдовых координатах t, г, 0, ф, при г = 2m ни один
скалярный полином тензора кривизны и метрики не расходится
при г -> 2m. Это наводит на мысль, что особенность при г = 2m
не является истинной физической сингулярностью, а скорее всего
оказывается следствием неудачного выбора координат.
5.5. Решение Шварцшильда
169
Чтобы подтвердить это и показать, что (Ж, g) можно расши-
рить, введем
r* ~ S ' == / + 2m In (г — 2m).
Тогда
v^t + г*
— опережающая изотропная координата и
w^t — г*
— запаздывающая изотропная координата. Используя координаты
(о, г, 0, ф), получим метрику gz в форме Эддингтона — Финкель-
стейна:
ds2 = — (1 — 2m/r) du2 + 2 do dr + r2 (d02 + sin20 d$2). (5.22)
Многообразием Ж является область 2m < г < оо, но метрика
(5.22) не сингулярна и даже аналитична на большем многооб-
разии Ж', для которого 0 < г < оо. Та область модели {Ж', g'),
для которой 0 < г < 2m, фактически изометрична области мет-
рики Шварцшильда, для которой 0 < г < 2m. Итак, используя
другие координаты, т. е. вводя иное многообразие, мы расши-
рили метрику Шварцшильда так, что она перестала быть особен-
ной при г = 2m. Как видно из диаграмм Финкельстейна, в мно-
гообразии Ж' поверхность г — 2m изотропна (рис. 23). Она
является сечением 0 = const, ф = const пространства-времени,
каждая ее точка изображает 2-сферу площади 4лг2. На этой
диаграмме изображены некоторые изотропные конусы и ради-
альные изотропные геодезические; изображены также поверхно-
сти {t = const}, и видно, что t становится бесконечным на по-
верхности г — 2т.
Подобное представление решения Шварцшильда обладает
тем необычным свойством, что оно не симметрично во времени.
Этого можно было бы ожидать из-за наличия перекрестного
члена (du dr) в (5.22); качественно асимметрия видна на диа-
грамме Финкельстейна. Ярче всего она проявляется в том, что
поверхность г — 2т ведет себя как полупроницаемая мембрана,
пропуская направленные в будущее времениподобные или изо-
тропные кривые только извне (г > 2m) внутрь (r<2m). Ни
одна направленная в прошлое времениподобная или изотропная
кривая изнутри г — 2т не может приблизиться к г — 0. Однако
любая направленная в будущее времениподобная или изотроп-
ная кривая, пересекшая г = 2m, достигает г — 0 в пределах ко-
нечного аффинного расстояния. При г-> 0 скаляр RabcdRabcd рас-
ходится как т21гъ. Поэтому г = 0 является истинной сингуляр-
ностью; пространство (Ж', g') не имеет С2-расширения через
г — 0 (на самом деле оно не имеет даже С°-расширения).
Т-2т
Р и с. 23. Сечение постоянных 0 и Ф в решении Шварцшильда, а — кажу-
щаяся сингулярность для г = 2/;г при использовании координат (Z, г); б— диа-
грамма Финкельстейпа, полученная переходом к координатам (а, г) (липин
под углом 45° являются линиями а). Поверхность г = 2т — изотропная по-
верхность, на которой t = со.
б.б. Решение 1Uппрцшильдп
171
Если вместо и использовать координаты w, то метрика при-
мет вид g77
ds’ = — (1 — 2т/г) — 2 dco dr + r ' (dQ 4- sin- 0 d^2).
Она аналитична на многообразии Я", задаваемом координата-
ми (то, г, 0, ф) при 0 < г < оо. Снова мпогобразием Я является
область 2т < г < оо, и новая область 0 О < 2т изометрична
области 0 < г < 2т метрики Шварцшильда, но эта изометрия
обращает направление времени. В многообразии Я” поверх-
ность г = 2т снова является изотропной поверхностью, дей-
ствующей как полупепроницаемая мембрана. Однако на этот
раз она проницаема в противоположном направлении времени;
пропускает извне (г > 2т) внутрь (г < 2т) только направлен-
ные в прошлое времениподобные или изотропные кривые.
На самом деле можно осуществить оба расширения {Я', g')
и (Я", g") одновременно, т. е. существует еще многообразие Я*
с метрикой g*, в которое и (Я', g'), и (Я", g") могут быть изо-
метрично погружены так, что они совпадут в области г > 2m,
которая изометрична пространству (Я, g). Такое расширенное
многообразие было построено Крускалом [95]. Чтобы получить
его, рассмотрим (Я, g) в координатах (о, w, 0, ф)\ тогда мет-
рика имеет вид
ds2 = — (1 — 2m/r) dv с!ю -К г2 (d&2 + sin2 0 d^2),
где г определяется равенством
у (о — w) = г 4- 2т In (г — 2m).
Таким образом, 2-пространство 0 = const, ф = const представ-
лено в изотропных конформно-плоских координатах, поскольку
пространство с метрикой ds2 — do с!ш плоское. Самое общее ко-
ординатное преобразование, оставляющее метрику этого 2-про-
странсгва конформно-плоской, а обе координаты изотропными,
имеет вид v'= v'(v), w'==w'{w), где v' и w'—произвольные
О-фупкции. Получающаяся при этом метрика имеет вид
ds2 = — (1 —-S'K da7 day7 4- r2 (d02 4- sin2 0 d<£2).
\ r ) dv dw । \ । < >
Чтобы привести ее к виду, который соответствует тому, что
было получено ранее для пространства-времени Минковского,
положим
х7 = у (о7 — w'), С==у(о74-щ7)
и придем к следующему окончательному выражению:
ds2 = Г2 (1', х') (— d/72 4- dx72) + г2 (f, х') (d02 ф- sin2 0 d ф2). (5.23)
172
Гл. 5. Точные решения
Конкретный вид этой метрики определяется выбором функций
v', w'. Крускал выбрал
v' = exp(t'/4m), to'= ехр — (—w/4m).
Тогда для г имеем уравнение
(К)2 — (х')2 = — (г — 2т) ехр (r/2m), (5.24)
а для F — формулу
(5.25)
На многообразии Я*, определяемом координатами (/', х', 0, ф)
при (t')2— (х')2<2т, функции г и F [задаваемые (5.24),
(5.25)] положительны и аналитичны. Пусть метрика g* дана
формулой (5.23); область I пространства (Я*, g*), определен-
ная неравенством х’ >|К|, изометрична (Я, g), т. е. области
решения Шварцшильда, для которой г > 2т. Область х' > —t'
(области I и II на рис. 24) изометрична опережающему рас-
ширению Финкельстейна (Я', g'). Аналогично, область х' > V
(области I и II' на рис. 24) изометрична запаздывающему рас-
ширению Финкельстейна (Л"', g"). Имеется также область
определяемая неравенством х' <—|К|, которая тоже оказы-
вается изометричной внешнему решению Шварцшильда. Ее
можно рассматривать как другую асимптотически-плоскую все-
ленную по ту сторону шварцшильдовской «горловины». (Рассмо-
трим сечение t = 0; 2-сферы {г = const} выглядят при боль-
ших г так же, как в евклидовом пространстве; однако при ма-
лых г их площадь убывает к минимальному значению 16лт2 и
затем вновь возрастает, словно эти 2-сферы расширяются в дру-
гом асимптотически-плоском 3-пространстве). Из рис. 24 видно,
что области I' и II изометричны опережающему, а области Г и
II'— запаздывающему расширению Финкельстейна области I'.
Из области I в область /' не проходит ни одна времениподобная
или изотропная кривая. Все направленные в будущее времени-
подобные и изотропные кривые, которые пересекают часть по-
верхности г = 2т, описываемую теперь уравнением t' = [x'f,
стремятся к сингулярности при t' = (2m-)-(x')2)'h, для которой г—0.
Подобно этому направленные в прошлое времениподобные и
изотропные кривые, пересекающие t' — — |х'|, стремятся к дру-
гой сингулярности при t' = —(2т 4- (х')2)1'2, где снова г = 0.
Расширение Крускала (Я*, g*)—единственное аналитиче-
ское и локальное нерасширяемое расширение решения Шварц-
шильда. Вводя новые опережающие и запаздывающие изотроп-
ные координаты
v" = arctg (и' (2т)~'1г), w" == arctg (w' (2m)~‘f2),
— л < v" + w" < л, — 4- л < v" < 4- л, — 4 л < w" < 4 л,
а Л Л 2»
Рис. 24. Максимальное аналитическое расширение решения Шварцшильда.
Координаты 0, Ф опущены; изотропные линии проходят под углом ±45°.
Поверхности {г = const} однородны, а — диаграмма Крускала, на которой
изображены асимптотически плоские области I и 1' и области II, II', для
которых г < 2m; б — диаграмма Пенроуза, изображающая конформную бес-
конечность и две сингулярности.
174
Гл. 5. Точные решения
можно построить диаграмму Пенроуза для расширения Кру-
скала (рис. 24,6). Ее можно сравнить с диаграммой для про-
странства Минковского (см. рис. 15,6). Теперь мы имеем беско-
нечности будущего, прошлого и изотропную бесконечность для
каждой из асимптотически-плоских областей I и Г. В отличие
от пространства Минковского конформная метрика теперь не-
прерывна, по недифференцируема в точках г°.
Если мы рассмотрим изотропный конус будущего какой-либо
точки вне г — 2т, то радиальная геодезическая, направленная
по радиусу наружу, достигает бесконечности, а направленная
внутрь достигает сингулярность в будущем; если точка лежит
внутри г = 2т, то обе эти геодезические попадают на сингуляр-
ность, и все будущее этой точки кончается этой сингулярностью.
Таким образом, любая точка вне г = 2т может избежать сингу-
лярности (и, следовательно, сингулярность не «универсальна»
в отличие от пространства Робертсона — Уокера), но как только
частица оказалась внутри г = 2т, она обязательно достигнет
сингулярности. Оказывается, этот факт тесно связан с тем об:
стоятельством, что каждая точка внутри области II изображает
2-сферу, которая является замкнутой ловушечной поверхностью.
Это означает следующее: рассмотрим какую-либо 2-сферу р (на
рис. 24 опа изображается точкой) и две 2-сферы q и s, образо-
ванные фотонами, которые испущены с поверхности р в один и
тот же момент времени от центра и к центру поверхности р.
Площадь q (она равна 4№) будет больше, а площадь s будет
меньше площади р, если все три сферы лежат в области г > 2т.
Если же все они лежат в области II, где г < 2т, то площади
обеих сфер: и q, и s будут меньше площади р (на рис. 24 значе-
ние г убывает в области II при движении снизу вверх). В таком
случае мы говорим, что р является замкнутой ловушечной по-
верхностью. Каждая точка внутри области II' является замкну-
той ловушечной поверхностью при обращении времени (суще-
ствование замкнутых ловушечных поверхностей — необходимое
следствие того обстоятельства, что поверхности г = const про-
странственноподобны), и соответственно все частицы в обла-
сти II должны быть «пришельцами» из сингулярности в про-
шлом. В гл. 8 мы увидим, что само существование сингулярно-
стей тесно связано с существованием замкнутых ловушечных
поверхностей.
Решение Райссиера — Нордстрема описывает пространство-
время вне электрически заряженного сферически-симметричпого
тела (которое, однако, не обладает ни спином, пи магнитным
дипольным моментом, вследствие чего это решение не может
служить хорошим описанием поля тяготения вокруг электрона).
Следовательно, тензор энергии-импульса такой же, как у элек-
тромагнитного поля, созданного зарядом этого тела. Решение
5.5. Решение Шварцшильда
175
Райсспера — Нордстрема — единственное асимптотически-пло-
ское сферически-симметричное решение уравнений Эйнштейна —
Максвелла н локально оно напоминает решение Шварцшильда:
существуют координаты, в которых метрика имеет вид
- (1 - + ~) d/2 + (1 - + 4)^ +
+ г2 (d02 4- sin2 0 d</>2), (5.26)
где т — гравитационная масса и е — электрический заряд тела.
Это асимптотически-плоское решение естественно рассматривать
как решение только вне тела, а внутри должна быть какая-то
другая метрика; но интересно посмотреть, что получится, если
мы будем считать, что решение имеет смысл для всех г.
Если е2 > т2, метрика неособенна везде, за исключением не-
устранимой особенности при г = 0, которую можно рассматри-
вать как точечный заряд — источник поля. Если е2 т2, метри-
ка имеет особенности также в г+ и г_, где г± = т ±(т2— е2)|/2;
она регулярна в областях оо > г > г+, г+ > г > г_ и г_> г > О
(если е2 = т2, существуют только первая и третья области). Как
и в случае Шварцшильда, эти сингулярности можно устранить
введением подходящих координат и расширением многообразия
до получения максимального аналитического многообразия [21,
64]. Главные отличия возникают из-за того, что множитель пе-
ред d^2 имеет два пуля, а не один, как в случае Шварцшильда.
В частности, это приводит к тому, что первая и третья обла-
сти — обе статические, тогда как вторая область (если она суще-
ствует) — пространственно-однородна, но не статична.
Чтобы получить максимально расширенное многообразие, мы
будем действовать аналогично шварцшильдову случаю. Введем
координату г*:
* С dr
Г J , 2m е2 ’
1 - —+ —
тогда для г > г+
г* = г ф- ~ 'п (г “ гт) — г+ 2Г 'п (г — г~) ПРИ б2 < т\
г = г + 'п In (г — т)"'—г _ 1П при е~ = т!,
г*' = г + т In (г' — Чтг + е2) + —varctg , при е2 > т2'
Вводя опережающие и запаздывающие координаты v, ш
v = t 4-
w = t — г*.
176
Гл. 5. Точные решения
приведем метрику (5.26) к изотропному виду
ds2 = — (1 — + -yr) da dte> + г ’ (d02 + sin2 0 d^2). (5.27)
В случае е2 < т2 определим новые координаты a", w" следую-
щим образом:
а" == arctg exp fr+^ 2~- aA , w" == arctg Г— exp f—r~- .
Тогда метрика (5.27) принимает вид
/ 2т е2 \
ds2 = I 1------1—г ) 64 cosec 2а" cosec 2w" dv" dw" 4-
\ r 1 r2 ) (r+ — г-}2 1
+ r2(d02 + sin20c/^2), (5.28)
где г определяется неявно уравнением
tg a" tg w" = — exp (
\ 2Г .
-а/2
и а = (г+)-2(г_)2. Максимальное расширение мы получим, если
примем (5.28) в качестве метрики g*, а в качестве Л*— макси-
мальное многообразие, на котором g* принадлежит классу С2.
Диаграмма Пенроуза этого максимального расширения при-
ведена на рис. 25. Имеется бесконечное число асимптотически-
плоских областей, где г> г+; они обозначены цифрой I. Эти об-
ласти соединены промежуточными областями II и III, где
г+ > г > г- и г_ > г > 0 соответственно. По-прежнему в каж-
дой области III имеется неустранимая сингулярность при г = О,
но в отличие от решения Шварцшильда она времениподобна, и
направленная в будущее времениподобная кривая из области I,
пересекающая поверхность г = г+, может избежать этой сингу-
лярности. Такая кривая может пройти через области II, III и II
и появиться в другой асимптотически-плоской области I. Возни-
кает захватывающая возможность совершить путешествие в дру-
гие вселенные через «ходы», проделанные зарядами. К сожале-
нию, скорее всего такой путешественник не сможет вернуться
обратно в нашу Вселенную и рассказать о том, что же он видел
«по ту сторону».
Метрика (5.28) аналитична всюду, за исключением поверхно-
сти г = г_, на которой она по меньшей мере класса С2. Можно
ввести другие координаты v"’ и w'"\
v'" = arctg exp ( r+% ~~2r— a^ ,
W
—--------W
2пг'_„
поверхности
t — const
Рис. 25. Диаграмма Пенроуза для максимально расширенного решения Райс-
снера — Нордстрема (е2 < т2). Бесконечная цепь асимптотически плоских
областей 1 (со>г>г+) соединяется областями II (г+>г>г-) и
III (г— > г > 0); каждая область III ограничена времениподобной сингу-
лярностью при г = 0.
178
Гл. 5. Точные решения
где п — целое число, причем п 2(г+)2(г_)2. В этих координа-
тах метрика аналитична всюду, за исключением г — г+, где она
по меньшей мере класса С2. Координаты v"', w"'—аналитиче-
ские функции координат и" и w" всюду вне поверхностей г = г+
иг — Г-. Таким образом, многообразие Л* может быть покрыто
аналитическим атласом, состоящим из локальных координатных
окрестностей, определяемых координатами v", w" при г =/= г_ и
координатами v’", w"' при г г+. В этом атласе метрика ана-
литична.
В случае е2 = т2 расширение осуществляется подобным же
образом; в случае е2 > т2 модель нерасширяема уже в исход-
ных координатах. Диаграммы Пенроуза для этих двух случаев
приведены на рис. 26.
Во всех этих случаях сингулярность времепиподобпа. Это
означает, что в отличие от решения Шварцшильда временипо-
добные и изотропные кривые всегда могут избежать встречи с
сингулярностью. Фактически это выглядит так, словно сингуляр-
ности отталкивают частицы: времениподобные геодезические не
могут столкнуться с сингулярностью, хотя это может произойти
с радиальными изотропными геодезическими и негеодезическими
времениподобными кривыми. Следовательно, эти пространства
времениподобны (по не изотропны) и геодезически полны. Вре-
мениподобный характер сингулярности означает также, что в
этих пространствах нет поверхностей Коши: для любой данной
пространственноподобной поверхности можно найти временипо-
добную или изотропную кривую, которая достигает сингулярно-
сти, не пересекая эту поверхность. Например, в случае е2 < т2
можно найти пространственноподобную поверхность У?, которая
пересекает две асимптотически-плоские области I (см. рис. 25).
Она будет поверхностью Коши для этих двух областей I и со-
седних областей //; но в соседних более поздних областях III
существуют направленные в прошлое непродолжимые времени-
подобные и изотропные кривые, которые подходят к сингуляр-
ности, но не пересекают поверхность г = Г— Поэтому можно
сказать, что эта поверхность представляет собой горизонт Коши
будущего для 5К Расширение решения за пределы г = г_ не
определяется данными Коши на If. Продолжение, которое мы
произвели, является единственным локально нерасширяемым
аналитическим продолжением, но существуют другие, неанали-
тические С°°-продолжения, удовлетворяющие уравнениям Эйн-
штейна-Максвелла.
Наблюдатель О, чья мировая линия остается вне г = г+ и
продолжается до бесконечности будущего i+ (см. рис. 25), на-
блюдал бы частицу Р, пересекающую поверхность г = г+, с бес-
конечным красным смещением. В области II между г — г+ и
г = г- поверхности г = const простраиственпоподобны и, следо-
б
I и е. 26. Диаграмма Пенроуза для максимально расширенных решений Райс-
спера — Нордетрема: еI 2 = т2 (а), е2 > т2 (о). В первом случае имеется бес-
конечная цепь областей / (со > г > т), связанных областями Ill (т > г > 0).
Точки р не являются частью сингулярности г = 0, а представляют собой
исключительные точки на бесконечности.
180
Гл. 5. Точные решения
вательно, каждая точка рисунка изображает 2-сферу, которая
является замкнутой ловушечной поверхностью. Наблюдатель Р,
пересекающий поверхность г = г_, обозрел бы всю историю од-
ной из асимптотически плоских областей за конечное время.
Объекты этой области поэтому были бы видны с бесконечным
фиолетовым смещением по мере приближения к i+. Это дает
основание думать, что поверхность г = г_, возможно, неустой-
чива относительно малых возмущений начальных данных на
пространственноподобной поверхности д’ и что такие возмуще-
ния, вообще говоря, приведут к сингулярности на г — г—
5.6. Решение Керра
Обычно астрономические объекты вращаются, и поэтому
нельзя считать, что поле вне их в точности сферически-симмет-
рично. Решение Керра — единственное известное точное реше-
ние, которое может служить для описания стационарного осе-
симметричного асимптотически-плоского поля вне массивного
вращающегося объекта. Оно будет внешним решением только
для массивных вращающихся полей с конкретным набором
мультипольных моментов; для тел с другими мультипольными
моментами внешние решения будут иными. Однако решение
Керра является, по-видимому, единственно возможным внешним
решением для черных дыр (см. разд. 9.2 и 9.3).
Это решение можно записать в координатах Бойера и Линд-
квиста (г, 0, ф, t), в которых метрика имеет вид
ds2 = р2 + d02) + (Н + a2) sin2 9 d<£2 — d^-j-
+ -^-(asin2 0 с1ф — dt2)2, (5.29)
где
p2 (г, 0) s г2 + a2 cos2 0 и A (r) =s r2 — 2mr + a2,
m и a — постоянные, причем m является массой, а та — момен-
том количества движения, которые как бы измерены в бесконеч-
ности [16]; при а = Г) это решение переходит в шварцшильдово.
Ясно, что эта метрика инвариантна относительно одновремен-
ного обращения t и ф, т. е. относительно преобразовайия
ф-*—ф, хотя она и не инвариантна относительно обращения
одного только t (за исключением случая а = 0). Этого следо-
вало ожидать, поскольку при обращении времени вращающийся
объект меняет направление своего вращения на противополож-
ное.
Если а2 > т2, то А > 0, и приведенная метрика особенна
только при г = 0. Эта сингулярность в действительности яв-
ляется не точкой, а кольцом; в этом можно убедиться при пере-
5.6. Решение Керра
181
ходе к координатам Керра — Шильда (х, у, z, t), где
х + iy = (г + id) sin 0 ехр i (d</> ф аД-1 dr),
z = rcos0, t = j (dt + (r2 + а) A-1 dr) — r.
В этих координатах метрика принимает вид
ds2 = dx2 + dr/2 + dz2 — di2 -ф
, 2mr3 [" r (x dx + у dz/) — a (x dy — у dx) , z dz , ,r
+ r* + a^' L----------K+T2------------+ ~T + d/J ’ (5-3°)
где г как функция x, у, z определяется с точностью до знака
уравнением
г4 — (х2 + у2 + z2 — а2) г2 — а2г2 = 0.
При гфО поверхности {г — const} на плоскости х, у, г явля-
ются конфокальными эллипсоидами, вырождающимися при г=0
в диск z2 ф у2 si a2, z — 0. Кольцо х2 -ф у2 = а2, z = 0 этого ди-
ска является истинной сингулярностью кривизны, поскольку на
нем расходится скалярный полином RabcdRabcd• Но на самом ди-
ске (вне кольца) любой скалярный полином конечен. Чтобы по-
лучить максимальное аналитическое расширение этого решения,
можно аналитически продолжить функцию г от положительных
к отрицательным значениям через открытый диск х2 -ф у2 < а2,
z = 0.
Для этого присоединим другую плоскость, определяемую ко-
ординатами х', /, z', так что точки на верхней стороне диска
х2 -ф у2 < a2, z = 0 в плоскости (х, у, z) отождествляются с точ-
ками с теми же координатами х и у на нижней стороне соответ-
ствующего диска в плоскости (х', у', z'). Аналогично, точки с
нижней стороны диска в плоскости (х, у, z) отождествляются
с точками с верхней стороны диска в плоскости (х', у', z')
(рис. 27). Метрика (5.30) очевидным образом распространяется
на это расширенное многообразие. В области (х', у', z') она по-
прежнему имеет вид (5.29), но значения г не положительны, а
отрицательны. При больших отрицательных г пространство сно-
ва асимптотически-плоское, но теперь масса отрицательна. При
малых отрицательных г вблизи кольцевой сингулярности вектор
д/дф времениподобен, так что окружности t = const, г = const,
0 = const являются замкнутыми времениподобными кривыми.
Эти кривые можно деформировать так, чтобы они проходили
через любую точку расширенного пространства [23]. Решение
Керра геодезически неполно ввиду кольцевой сингулярности;
однако ее достигают только те времениподобные и изотропные
геодезические, которые лежат на экваториальной плоскости в
той части, где г > 0 [23].
Ось симметрии
Плоскость л/z Плоскость x'z'
Р и с. 27. Максимальное расширение решения Керра при а- > т- получается отождествлением верхней поверхности диска
х" У~ <. а-, 2 = 0 в плоскости (х, у, z) с нижней поверхностью соответствующего диска в плоскости (х', у', д'), и на-
оборот. На рисунке приведены сечения у = 0 и у' — 0 этих плоскостей. Двойной обход вокруг сингулярности х- + у- = а2,
2 = 0 переводит из плоскости (х, у, z) в плоскость (х', у', z') (где г < 0) и обратно в плоскость (х, у, г), где г > 0.
5.6. Решение Керра
183
Расширение в случае а2 < т2 несколько сложнее из-за суще-
ствования двух значении г-. r+ = т 4- (т2 — а2)1/2 и г_ =
= т — (т2 — а2)'-'-’, при которых А (г) обращается в нуль. Эти
поверхности подобны поверхностям г — г+ и г = г_ в решении
Райсснера — Нордстрема. Для продолжения метрики через эти
поверхности перейдем к координатам Керра (г, 0, ф+, и+), где
du+ = dt 4- (г ф- а2} А '1 dr, d<£+ •= d^> + аА“1 dr.
Тогда на многообразии, определяемом этими координатами,
метрика имеет вид
ds2 — р2 d0- — ‘2а sin2 0 dr d^+ + 2 dr du+ ф-
4- p"2 [(r2 + a2)2 — Aa2 sin2 0] sin2 0 d^+2 —
-- 4ap~2mr sin2 0 d</>+ d«+ —- (1 — 2/nrp~2) d«+2, (5.31)
она аналитична при г = г+ и г = г~. Снова мы имеем сингуляр-
ность при г = 0, которая имеет ту же форму кольца и описан-
ную выше геодезическую структуру. Метрику Керра можно рас-
ширить и на другое многообразие, определенное координатами
(г, 0, ф-, и-), где
du_ = dt — (г2 + a2) dr, dA_ = d^> — aA~‘ dr,
а метрика имеет вид (5.31) с заменой ф+, на —ф_, —и~. Ма-
ксимальное аналитическое расширение получается комбинацией
этих двух расширений, как в случае Райсснера — Нордстрема
[15, 23]. Его глобальная структура очень похожа на структуру
решения Райсснера — Нордстрема, за тем исключением, что те-
перь возможно продолжение через кольцо к отрицательным зна-
чениям г. На рис. 28, а показана конформная структура решения
вдоль оси симметрии. Области I соответствуют асимптотически-
плоские области, в которых г > г+. Области II (г_ < г <г+)
содержат замкнутые ловушечные поверхности. Области III
(—оо < г < г_) содержат кольцевую сингулярность, в любой
области III через каждую точку можно провести замкнутую вре-
мениподобную кривую, в других двух областях (I и II) нет ни-
каких нарушений причинности.
В случае а2 = т2, г+ и г_. совпадают и области II отсутствуют.
Максимальное расширение похоже на расширение решения
Райсснера — Нордстрема при е2 = т2. О конформной структуре
вдоль оси симметрии для этого случая можно судить по рис. 28, б.
Решение Керра, будучи станционарпым и осесимметричным,
имеет двухпараметрическую группу изометрий; она необходимо
абелева [26]. Следовательно, существуют два независимых ком-
мутирующих векторных поля Киллинга. Имеется только одна их
184
Гл. 5. Точные решения
линейная комбинация №, которая времениподобна при произ-
вольно больших положительных и отрицательных г. Кроме того,
можно составить линейную комбинацию К'1 этих полей, равную
Рис. 28. Конформная структура решения Керра вдоль оси симметрии
О < а2 < т (а); а2 = т2(б). Пунктирные линии соответствуют линиям
г — const; области I, II и III в случае (а) разделяются поверхностями
г = г+ и г — г-, а области I и III в случае (б) — поверхностью г — т.
В обоих случаях структура пространства вблизи кольцевой сингулярности
такая же, как на рис. 27.
нулю на оси симметрии. Орбиты вектора Киллинга Ка опреде-
ляют станционарную систему отсчета: объект, движущийся вдоль
одной их этих орбит, из бесконечности выглядит станционарным.
Орбиты вектора Киллинга К'-' представляют собой замкнутые
кривые, что соответствует вращательной симметрии решения
Керра.
В решениях Шварцшильда и Райсснера — Нордстрема век-
тор Киллинга, времениподобный при больших г, времениподобен
всюду в области I и становится изотропным на поверхностях
г =• 2т и г = г+ соответственно. Эти поверхности изотропны.
Отсюда следует, что частица, которая пересекает одну из этих
S.6. Решение Керра
185
поверхностей, в направлении будущего не может вернуться в
прежнюю область. Эти поверхности являются границей той об-
ласти решения, из которой частицы могут достичь бесконечно-
сти Д+ данной области I, и они называются горизонтами собы-
тий этой (/+. Для наблюдателя, движущегося в области / по
какой-либо орбите вектора К", они являются фактически гори-
зонтами событий в смысле, установленном в разд. 5.2.
Ось симметрии
(0=0)
Пальцевая
сингулярность
Рис. 29. Решение Керра при 0 < а2 < т-\ эргосфера лежит между предель-
ной поверхностью стационарности и горизонтом г — г+. Частицы могут уйти на
бесконечность из области / (вне горизонта событий г = г+), но не из обла-
стей II (между г = г+ и г = г_) и III (г < г_; эта область содержит коль-
цевую сингулярность).
Экваториальная
плоскость
(0=Л/2)
Поверхность
предела стацио-
нарности
Эргосьрера
Горизонт
событий
Наоборот, для решения Керра вектор Киллинга К“ простран-
ственноподобен в некоторой области вне г = г+, называемой
эргосферой (рис. 29). Внешней границей этой области является
поверхность r = m-j-(m2— a2cos0)1/2, на которой Л'а изотропен.
Она называется предельной поверхностью стационарности, так
как является границей области, в которой частица, движущаяся
по времениподобной кривой, может находиться на орбите век-
тора Киллинга и таким образом оставаться в покое относитель-
но бесконечности. Предельная поверхность стационарности вре-
мениподобна, за исключением двух точек на оси, в которых она
изотропна (в этих точках она соприкасается с поверхностью
г —Гр). Там, где она времениподобна, ее могут пересекать и
входящие, и выходящие частицы. Поэтому она не является го-
ризонтом событий для Д+. Горизонтом событий в действитель-
ности является поверхность г = r+ = m + (m2 — а2),/г. Из рис. 30
I8G
Гл. 5. Точные решении
видно, почему это так. На нем изображена экваториальная пло-
скость 0 = л/2; каждая точка на этом рисунке представляет со-
бой орбиту вектора Киллинга Л?', т. е. стационарна относитель-
но 17+. Малые круги изображают положение фронта светового
Поверхность
предела ста-
ционарности
Рис. 30. Экваториальная плоскость решения Керра при т2 > а2. Круги изо-
бражают положение через короткое время вспышек света, излученных источ-
никами, которые обозначены жирными точками.
импульса через короткое время после излучения из точек, изо-
браженных черными кружками. Вне предельной поверхности
стационарности вектор Киллинга Л? времениподобен, т. е. ле-
жит внутри светового конуса. Это означает, что точка на рис. 30,
изображающая орбиту точки вспышки, лежит внутри фронта
волны света.
На предельной поверхности стационарности вектор изо-
тропен, и точка, изображающая орбиту точки вспышки, лежит на
фронте волны. Однако фронт волны лежит частью вне, а частью
внутри предельной поверхности стационарности, поэтому части-
ца, движущаяся по времениподобной кривой, может с этой по-
верхности уйти в бесконечность. В эргосфере между предельной
57 Модель вселенной Гёделя
187
поверхностью стационарности и поверхностью г—г+ вектор Кил-
липга К" ппострапственнопотобеп, и точка, изображающая ор-
биту испускания, лежит вне фронта волны. В этой области вре-
мениподобное пли изотропное движение не может происходить
по орбите вектора Киллинга и поэтому частипа не может оста-
ваться в покое относительно бесконечности. Однако положения
волновых фронтов таковы, что частицы по-прежнему могут пере-
сечь предельную поверхность стационарности и уйти на беско-
нечность. На поверхности г = г+ вектор по-прежнему про-
странствеппоподобен, по фронт волны, расходящийся ст частицы
на этой поверхности, лежит целиком внутри этой поверхности.
Это означает, что частица, движущаяся по времениподобной
кривой из какой-либо точки па или внутри поверхности г = г+,
не может выйти из области, охватываемой этой поверхностью, и
достичь бесконечности. Поэтому поверхность г = г+ является
горизонтом событий для £/+ и изотропна.
Хотя вектор Киллинга К" пространствепноподобен в эргосфе-
ре, модуль К'Ч\ьК[пКЪ] бивектора Киллинга К[аКм отрицателен
всюду вне г = г+, за исключением оси = 0, где он равен нулю.
Поэтому на № и Л"' натягивается 2-поверхность и, следователь-
но, в каждой точке вне г = г+, за исключением оси, имеется
линейная комбинация К'" и Ка, которая времениподобна. Таким
образом, решение в эргосфере в некотором смысле локально ста-
ционарно, хотя и не станционарно относительно бесконечности.
Одной линейной комбинации Ка и /<", которая была бы времени-
подобна всюду вне г = г+, не существует. Величина бивектора
Киллинга на г = г+ обращается в нуль и положительна внутри
этой поверхности. На г = г+ оба вектора Ка и Ка простран-
ственноподобпы, но существует их линейная комбинация, изо-
тропная всюду па этой поверхности [25].
Рассмотренные нами свойства эргосферы и горизонта собы-
тий будут играть важную роль при рассмотрении черных дыр
в разд. 9.2 и 9.3.
Подобно тому как решения Райсснера — Нордстрема можно
рассматривать как решение Шварцшильда при наличии заряда,
имеется семейство аналогичных решений Керра [23]. Их глобаль-
ные свойства весьма похожи па свойства решения Керра без
заряда.
5.7. Модель Вселенной Гёделя
В 1949 г. Курт Гёдель опубликовал статью [62], которая за-
метно стимулировала изучение точных решений, более сложных,
чем рассмотренные выше. Он дал точное решение уравнений
Эйнштейна с материей в виде идеальной жидкости без давления.
(То„ = QU„ub, где р — плотность материи и иа — нормированный
188
Гл. 5. Точные решения
вектор 4-скорости.) Многообразием Л является /?4, а метрика
записывается в виде
ds2 = — df + dx2 — у ехр (2 д/2 мх) dy2 + dz2 —2 ехр(д/2 <ох) di dy,
где а > 0 — постоянная. Уравнения поля удовлетворяются, если
и = д/дхР (т. е. ма = д%) и
4лр = а>2 = — Л.
Постоянная ю фактически является угловой скоростью вращения
вектора потока иа.
Это пространство-время обладает 5-параметрической транзи-
тивной группой изометрий, т. е. это пространство-время пол-
ностью однородно. (Группа транзитивна на Жесли она отобра-
жает любую точку Л на любую другую точку Л.} Данная мет-
рика является прямой суммой метрики gp
ds2 — — dt1 4~ dx2 — у ехр (2 д/2 мх) dy2 — 2 ехр (д/2 <вх) dt dy
на многообразии определяемом координатами (/, х, у),
и метрики g2:
ds22 = dz2
на многообразии Лг = R1, определяемом координатой г. Чтобы
описать свойства этого решения, достаточно рассмотреть M'bgi) .
Введем на Л1 новые координаты ф):
ехр (д/2 <ох) = ch 2r + cos ф sh 2г,
ау ехр (д/2 <ох) = sin ф sh 2г,
tg 4 = ехР (“ 2r) tg 4
тогда метрика gj принимает вид
ds.2 = 2ю-2 (— df2 + dr2 — (sh4 г — sh2 г) d</>2 -f- 2 д/2 sh2 г dф df),
где —oo <z t' <Z оо, Q r <Z оо и О Ф 2л, причем ф = О
отождествляется с ф = 2л; вектор потока в этих координатах
равен и (ю/V2)<3/<3f • В этом выражении для метрики видна
вращательная симметрия этого решения относительно оси г = 0.
Путем того или иного выбора координат можно любую линию
тока вещества сделать осью симметрии.
Поведение модели (Л\, gi) иллюстрирует рис. 31. Световые
конусы на оси г = 0 содержат направление d/dt' (вертикальное
направление на диаграмме), но не содержат горизонтальных на-
правлений д/дг и д/дф. По мере удаления от оси световые ко-
нусы раскрываются и поворачиваются в направлении_координат-
ной линии ф, так что при радиусе г = r0 = In (1 + V2) д/дф яв-
ляется изотропным вектором, а окружность радиуса Го вокруг
начала оказывается замкнутой изотропной кривой. При больших
г—о
(координатная осб)
Мировая линия
вещества (га
Ф постоянны)
Изотропный конус р (фокус в р')
Рис. 31. Вселенная Гёделя (опущена координата г). Это про-
странство обладает вращательной симметрией вокруг любой
точки; на диаграмме корректно представлены вращая-ельная сим-
метрия вокруг оси г = 0 и временная инвариантность. По мере
роста г световой конус раскрывается и переворачивается (это
Изотроп-
касатель-
ныиконр.
Изотропный но-
нус, содержащий
окружность
r>in(f+Y2)
Изотропный Изотропный
конурсоуер- телййыйн~
/мс//опо'и п
^окружноств окружности
амннутая +
времена л одоб- кинутая
I изотропная)
rein (1+Я)
(замкнутая прострси
ственнолбдобная)
Изотропный конце будущего
р'(фокус в р")
Изотропные Наустика на изотропном
_у\~2еодездуеские конусе будущего р
ный конус,
Изотроп- V _
ный конус с — и
будущего
t vo\- 1V11VI1 ftVJIJV 1 Ч-Zl „ 11^ Cl т Л DU V1
изображено на линии L), что приводит к замкнутым времени-
подобным кривым. Диаграмма не отображает наглядно тот факт,
что в действительности все точки пространства эквивалентны.
190
Гл 5. Точные решения
значениях г д/дф становится времениподобным вектором, и
окружности постоянных г и f представляют собой замкнутые
времениподобные кривые. Поскольку (Jh, g() обладает 4-пара-
метричсской транзитивной группой изометрий, то получается,
что через каждую точку (./6, gi), а следовательно, и через каж-
дую точку решений Гёделя (Л, g) проходит замкнутая времени-
подобная геодезическая.
Все это дает основание думать, что решение Гёделя не имеет
физического смысла. Существование замкнутых времениподоб-
ных кривых означает, что в Л нет вложенных трехмерных по-
верхностей без края, которые были бы всюду пространственно-
подобны, ибо замкнутая времениподобная кривая, пересекшая
такую поверхность, пересекает ее нечетное число раз. Это озна-
чает, что кривая не может быть непрерывным образом стянута в
точку: непрерывная деформация может изменить число пересе-
чений лишь на четное число. Это в свою очередь противоречит
тому, что многообразие Л, будучи гомеоморфно Д4, односвязно.
Существование замкнутых времениподобных линий означает так-
же невозможность в Л какой-либо космической координаты вре-
мени t, которая возрастала бы вдоль любой времениподобной
или изотропной кривой, направленной в будущее.
Решение Гёделя геодезически полно. Поведение геодезиче-
ских может быть описано с помощью разбиения на (Лу, gi) и
(Лг, £г). Поскольку метрика g2 на Л2 плоская, компонента
в Л2 вектора, касательного к геодезической, постоянна, т. е.
координата z зависит линейно от аффинного параметра на
геодезической. Поэтому достаточно описать поведение геоде-
зических в (Л\, gi). Изотропные геодезические, проходящие
через точку р на оси координат (рис. 31), первоначально
расходятся (у оси), доходят до каустики г = In (1 + д/2) и за-
тем сходятся к точке р' на оси. Поведение времениподобной
геодезической аналогично: они достигают некоторого максималь-
ного значения г, меньшего чем 1п(1 + д/2), и снова сходятся
к р'. Точку q с г > In(1 + д/2) можно соединить с р некоторой
времениподобной кривой, но не времениподобной или изотроп-
ной геодезической.
Дальнейшие детали свойств решения Гёделя можно найти
в работах [62; 96].
5.8. Пространство Тауба— НУТ
В 1951 г. Тауб получил пространственно-однородное решение
уравнений Эйнштейна в пустом пространстве с топологией /?XS3
и метрикой
ds'= — U~' dt2 -Г (2/)2П (dip + cos 0 Аф)2 +
+ (Ф + Z2) (dO2 + sin2 0 d<2), (5.32)
5.8. Пространство Тауба — НУТ
191
где
2 (mt + /-)
t2 + r-
m и I — положительные постоянные. Здесь 9, ф, гр — координаты
Эйлера на S3 и, следовательно, 0 гр 4л, 0<0 Д л,
О ф 2л. Эта метрика особенна при t = t+ — (rn ± (rtv 4- /2) ",
где U = 0. Ее можно продолжить через эти поверхности и полу-
чить пространство, найденное Ньюменом, Тамбурино и Унти
[Л 15], но прежде чем перейти к обсуждению этого расширения,
рассмотрим простой двумерный пример с похожими свойствами,
принадлежащий Мизнеру [105]. Это пространство обладает топо-
логией S1 Х^1, а метрика g определяется формулой
ds2 = — С1 dt2 + t dip2,
где 0 о" гр 2л. Эта метрика особенна при t — 0. Если принять,
что многообразие Л определяется координатами гр и t, причем
О < t < оо, то (v<, g) можно расширить, вводя гр' = гр — In t.
Тогда получаем метрику g':
ds2 = + 2 dip' di + t (dip')2.
Метрика g' аналитична на многообразии Л' с топологией
S’X-R1, которое определяется координатами гр' и t, причем
—оо < t < оо. Область t > 0 пространства (Л', g') изометрич-
на (v<, g). Основные черты пространства (Л', g') можно понять
из рис. 32. В области t < 0 имеются замкнутые времениподоб-
ные линии, но их нет там, где t > 0. Одно семейство изотропных
геодезических изображается на рис. 32 вертикальными линиями;
они пересекают поверхность t = 0. Другое семейство прибли-
жается к t — 0 по спирали, но никогда не пересекает эту поверх-
ность. Аффинные длины этих геодезических всегда конечны. Та-
ким образом, расширение (XZ', g') не симметрично относительно
двух семейств изотропных геодезических, хотя исходное про-
странство (Л, g) было симметричным. Однако можно задать
другое расширение {Л", g"), в котором эти два семейства ме-
няются ролями. Для этого определим гр" как г]/' = гр Ц- In t. Ин-
тервал, определяющий метрику g", равен
ds2 = - 2 dip" dt + t (dip")2.
Метрика g" аналитична на многообразии Л" с топологией
S1 X определяемом гр" и неравенством — оо <у t <2 оо. Об-
ласть t > 0 пространства (Л”, g") изометрична (Л, g). Опре-
делив так гр", мы в некотором смысле «раскрутили» второе се-
мейство изотропных геодезических так, чтобы они превратились
в вертикальные линии, и теперь их можно продолжить через
t = 0. Однако при этом мы «намотали» первое семейство, так
Рис. 32. Двумерный пример Мизнера. а — расширение области I за гра-
ницу t == 0, в область II. Вертикальные изотропные геодезические полны,
но закручивающиеся — нет; б — универсальное накрывающее пространство
является пространством Минковского. Относительно дискретной подгруппы G
группы Лоренца точки s эквивалентны. Аналогично, точки р, q, г эквива-
лентны. Рисунок (а) получается отождествлением эквивалентных точек
в областях 1 и II.
5 8. Пространство Тауба — НУТ
193
что его геодезические стали спиральными, и их уже нельзя про-
должить через t = 0. Таким образом, мы имеем два неэкви-
валентных локально нерасширяемых аналитических расширения
пространства {Л, g), причем обе геодезических неполны. Связь
между этими двумя расширениями хорошо видна при переходе
к накрывающему пространству пары {Л, g).
Оказывается, что таким накрывающим пространством явля-
ется область I двумерного пространства Минковского {Л, q),
содержащаяся внутри светового конуса будущего точки р
(рис. 32,6). Изометрии (Я, т)), оставляющие неподвижной точ-
ку р, образуют однопараметрическую группу (группа Лоренца
для метрики т)), орбитами которой являются гиперболы {о =
— const}, где п = ? — х2, a t, х — обычные координаты Минков-
ского. Пространство (Л, g) есть фактор-пространство простран-
ства (7, т)) по дискретной подгруппе G группы Лоренца, которая
состоит из Ап (п целое), причем А отображает (?, х) в
(t ch л + х sh л, х ch л + t sh л),
иначе говоря, отождествляются точки
(? ch пл + х sh пл, х ch п л +1 sh пл)
при всех целых п, и в Л они соответствуют точке
/ = у(? — х2), i|: = arth(4-).
Действие группы изометрии G в области I — собственно раз-
рывное. Действие группы Н на многообразии Л2 называется соб-
ственно разрывным, если:
1) у каждой точки q е Я имеется окрестность '?/, такая, что
A {°Ll) П °U = 0 для любого А е Н, который не является едини-
цей группы;
2) точки которые при любом А^Н удовлетворяют
условию Aq — г, обладают соответственно окрестностями °U и
°U', такими, что В(°и) П <№ =А= 0 при любом В е Н.
Условие (1) означает, что фактор-пространство ABIH явля-
ется многообразием, а условие (2)—что это многообразие хаус-
дорфово. Таким образом, фактор-прострайство (7, t\)IG есть ха-
усдорфово пространство {Л, g). Действие G собственно разрыв-
но также в областях 7-ф77(?>—х). Следовательно,
(7-(-77, t\)IG — тоже хаусдорфово пространство; на самом деле
оно совпадает с {Л', g'). Аналогично т])/б — хаусдор-
фово пространство {Л", g"). Отсюда видно, почему одно семей-
ство изотропных геодезических может быть выбрано полным в
расширении {Л', g'), а другое семейство — в расширении
7 Заказ 381
194
Гл. 5. Точные решения
{Л", g”). Казалось бы, можно осуществить оба расширения
одновременно. Однако действие группы G в области (/H-/7-J-ZZZ),
т. е. при t > —|х|, удовлетворяет лишь условию (1), а условие
(2) для точек q на границе между / и II точек г на границе
между I и /// не выполняется. Поэтому фактор-пространство
(/ + II + III, t])/G не хаусдорфово, хотя и является многообра-
зием.
Этот тип нехаусдорфова поведения отличается от примера,
приведенного в разд. 2.1. Там можно было провести непрерыв-
ные кривые, которые разветвляются так, что две ее ветви уходят
в разные области. Такое поведение мировой линии наблюдателя
представляется крайне неудобным. В многообразии (/ + II ф-
-\-HI)IG нет разветвляющихся кривых. Кривые из области I
можно продолжить в II или в III, но не в обе эти области одно-
временно. Это могло бы служить отправной точкой для такого
ослабления требования хаусдорфовости модели пространства-
времени, при котором допускаются ситуации описанного здесь
типа, но исключаются те, которые приводят к бифуркации кри-
вых. Дальнейшие результаты по нехаусдорфовым моделям про-
странства-времени можно найти в работе [66].
Можно убедиться, что условию (1) удовлетворяет действие G
на Л—{р}. Следовательно, пространство (Л—{p},r))/G яв-
ляется в некотором смысле максимальным нехаусдорфовым рас-
ширением пространства (Л, g). Однако и оно геодезически не-
полно, ибо есть геодезические, которые проходят через точку р,
которую надо удалить. Если же р оставить, то действие группы
не удовлетворяет условию (1) и поэтому фактор-пространство
Л/G не будет даже нехаусдорфовым многообразием. Рассмо-
трим, однако, расслоение линейных реперов Ь(Л), т. е. совокуп-
ность всех пар (X, Y) X, Ye Tq, линейно-независимых векторов
во всех точках q <=Л. Действие элемента .4 группы изометрий G
на Л индуцирует операцию Л» на Ь(Л), которая переводит ре-
пер (X, Y) в точке q в репер (А*Х, /4*Y) в точке A (q). Эта опе-
рация удовлетворяет условию (1), поскольку даже для (X, Y)e
е Тр, Л*Х =^= X и 4*Y =f= N, если, конечно, А не есть тождествен-
ное преобразование; она удовлетворяет также условию (2), если
даже X и Y лежат на изотропном конусе р. Таким образом, фак-
тор-пространство Ь(Л)/О — хаусдорфово многообразие. Оно
является расслоенным пространством над множеством Л/G, ко-
торое само не хаусдорфово и даже не многообразие. В опреде-
ленном смысле Ь(Л)1С можно было бы рассматривать как рас-
слоение линейных реперов для пространства Л/G. Тот факт, что
расслоение линейных реперов может иметь нужные свойства,
даже если само пространство ими не обладает, приводит к мыс-
5.8. Пространство Тауба — НУТ 195
ли о полезности изучения сигулярпостей с точки зрения расслое-
ния линейных реперов. Общий подход к этому указан в разд. 8.3.
Вернемся теперь к четырехмерному пространству Тауба
(^, g), где Л— это У?1 X S3, а метрика g дана формулой (5.32),
Поскольку Л односвязно, мы не можем, как в двумерном при-
мере, построить накрывающее пространство. Однако можно по-
лучить похожий результат, рассматривая Л как расслоенное
пространство над S2 со слоем X S1; проекция расслоения
п\Л —► S2 определяется как (t, ф, 0, ф)-+(в, ф). Фактически это
произведение оси t на расслоение Хопфа S3—> S2 [162], у кото-
рого имеется слой S1. Пространство (Л, g) допускает 4-пара-
метрическую группу изометрий, поверхностями транзитивности
которой являются 3-сферы {t = const}. Эта группа изометрий
отображает слои расслоения п'.Л —*S3 снова в слои, так что
изометричны все пары (,Х, gj, где ST является слоем w
w /ф X S1) и g — метрика, индуцированная в слое четырехмер-
ной метрикой g на Л. Слой можно рассматривать как пло-
скость (t, ф), а метрика g на 3~ получается из (5.32) отбрасы-
ванием членов с d0 и (1ф, т. е. g определяется квадратичной фор-
мой
ds’ = -t7Id/’ +4/2Щс!ф)2. (5.33)
Касательное пространство Tq в точке q е Л можно разло-
жить на вертикальное подпространство Vq, которое касательно
к слою и натянуто на векторы d/dt и <Э/с?ф и на горизонталь-
ное подпространство Hq, которое натянуто на векторы d/dQ и
д/д</>— cos 0<3/<3ф. Любой вектор X <= Tq можно представить как
сумму векторов Ху, лежащего в Vq, и Хн, лежащего в Hq.
Тогда метрику g в Tq можно записать так:
g (X, Y) = gv (Х7, Yy) + (f + /2) gH КХ, л J„), (5.34)
где gt =g, a gH — обычная метрика на 2-сфере: ds2 = d02 +
4- sin2 0 dj>2. Итак, хотя метрика g и не является прямой сум-
мой gv и У2-\-Р)ён (поскольку /?'Х53 не есть прямое произ-
ведение S2 и Rl X S1), все же локально ее можно рассматривать
в виде такой суммы.
Интересующая нас часть метрики g содержится в gv, и по-
этому мы рассмотрим аналитические расширения пары (^", gr).
Взяв их в такой же комбинации с метрикой gH 2-сферы, как в
(5.34), мы получим аналитические расширения пространства
(X g).
Метрика gv, определяемая формулой (5.33), имеет особенно-
сти при t = t±, в которых U = 0. Однако, если взять многообра-
зие &~0, задаваемое ф и t- < t < t+, gy) можно расширить,
7*
196
Гл. 5. Точные решения
введя координату
Тогда получаем метрику g'v, для которой
ds2 == 4/ d t| z (LU (t) dip' — df).
Эта метрика аналитична на многообразии 9~' с топологией
S1 X/?, определяемой координатами гр', t, причем —оо < t <; оо.
В области t- < t < t+ (ST', gy,) изометрична (£Го, gv). В этой
области нет времениподобных кривых, но они есть при t <Z t_
и Z > t+.
Это очень похоже на свойства рассмотренного ранее про-
странства {Л', g'), за исключением того, что теперь возникают
два горизонта (при t — Z_ и t = t+) вместо одного горизонта
(при t = Q). Одно семейство изотропных геодезических пересе-
кает оба горизонта t == Z_ и t = t+, а другое семейство описы-
вает спирали вокруг этих поверхностей и неполно.
Как и прежде, можно произвести иное расширение введением
координаты
При этом получаем метрику g", для которой
ds2 = 4/dip"(Zt7(/W' + dZ)
и которая аналитична на многообразии £Г”, определяемом коор-
динатами гр" и t, — оо < / < оо. Эта метрика тоже изометрична
(ZT0, Sv) в области t- < t < t+. Связь между разными расшире-
ниями снова можно продемонстрировать, перейдя к накрываю-
щему пространству. Накрывающим пространством Л(! является
многообразие ZT0, определяемое координатами — оо < гр < оо и
Z- < t < t+. На о метрика gy может быть записана в изотроп-
ной форме
ds2 = 4/47 (/) dip'dip", (5.35)
где — оо < гр' < оо, — оо < гр" < оо. Ее можно расширить по-
добно тому, как это было сделано в случае решения Райсснера —
Нордстрема. Выберем на £Г0 новые координаты (ы+, v+) и
(ы_, V-):
u± = arctg(exp-J-), v± = arctg(- exp ,
где
t+ — t- t+ — t~
a+ ~ 41 (mt + Г-) И a“ — 4nl (mt + /2) ’
5.8. Пространство Тауба — НУТ
197
Здесь п > (mt+ + -f- /2) — некоторое целое число. Тогда
метрика gv, полученная из (5.35) этим преобразованием, анали-
тична на многообразии ST, изображенном на рис. 33, причем
t~°O
t ~-oo
III
II
.t=t
III-
III
II
III-
Однородные поверхности
t-const (времениподоб-
ные орбиты группы)
Рис. 33. Диаграмма Пенроуза максимально расширенного накрывающего
пространства для двумерного сечения пространства Тауба — НУТ; изобра-
жены орбиты группы изометрии. Пространство Тауба — НУТ и его расши-
рения получены из части этого пространства отождествлением точек при
действии дискретной подгруппы группы изометрии.
t ~-оо
II
Одиороунв/е поверхности
t= const (пространственно -
подобные орбиты группы)
координаты и+, v+ аналитичны везде, кроме поверхности t — t_,
а координаты ы_, V- — везде, кроме t = t+; на своих поверхно-
стях неаналитичности (и+, и+) и («_, п_) принадлежат по край-
ней мере классу С3. Здесь имеется определенное сходство с рас-
ширением плоскости (/, г) решения Райсснера — Нордстрема.
Пространство (&", gv) обладает однопараметрической груп-
пой изометрий, орбиты которой изображены на рис. 33. Вблизи
точек р+, р- эта группа действует подобно группе Лоренца в
двумерном пространстве Минковского (см. рис. 32,6). Пусть
198
Гл 5 Точные решения
G — дискретная подгруппа группы изометрии, порожденная не-
тривиальным элементом А последней. (&~0, gy) представляет со-
бой фактор-пространство одной из областей (Il+, gv-) по G.
(^'.g/) и (,Т", g/') являются соответственно фактор-простран-
ствами (/_ +//++///_, gv)/G и (/+ + П+ + 1Н+, gy)/G. По-
строив фактор-пространство области (/+ + П+ -ф /_), мы могли
бы получить хаусдорфово многообразие: это соответствует тому,
чтобы расширять у поверхности t — t+, как при построении
(£Г', g/), а У поверхности t = С, как при построении (SF", g/').
Так же как в примере Мизнера, взяв фактор-пространство всего
пространства ТАГ без точек р+ и р~, получаем нехаусдорфово мно-
гообразие, а взяв фактор-пространство получим простран-
ство, которое не хаусдорфово и не многообразие. Аналогично
примеру Мизнера, фактор-пространство расслоения линейных ре-
перов над ST образует хаусдорфово многообразие.
Комбинируя эти расширения плоскости ф, ф) с координатами
(0, ^), можно получить соответствующие расширения четырех-
мерного пространства („<, g). В частности, два расширения
, g/) и , приведут к двум различным локально не-
расширяемым расширениям пространства (JI, g), которые оба
геодезически неполны.
Рассмотрим одно из этих расширений, скажем , g').
3-сферы, являющиеся поверхностями транзитивности группы изо-
метрии, пространственноподобны в области С < t < t+ и вре-
мениподобны при t Д> t+ и t < Поверхности транзитивности
t = и t = t+ изотропны и образуют горизонт Коши для лю-
бой пространственно-подобной поверхности, содержащейся в
t- < t < t+, поскольку в областях t <Zt- и t > t+ имеются
времениподобные кривые, которые никогда не пересекают со-
ответственно t — С и t — t+ (в этих областях существуют, в
частности, замкнутые времениподобные кривые). Область про-
странства-времени С t t+ компактна, и все же имеются
времениподобные и изотропные геодезические, которые все
время остаются внутри нее и неполны. Такого рода поведение
будет рассмотрено позднее, в гл. 8.
Более подробное описание пространства Тауба — НУТ можно
найти в работах [103, 109].
5.9. Прочие точные решения
В этой главе мы рассмотрели ряд точных решений и исполь-
зовали их для того, чтобы дать примеры различных глобальных
свойств, более общее исследование которых мы хотим провести
позднее. Хотя локально известно много точных решений, лишь
относительно малое число их изучено глобально. В заключение
5.9. Прочие точные решения
199
этой главы отметим вкратце два других интересных семейства
точных решений, глобальные свойства которых известны.
Первое из них составляют решения в виде плоских волн в пу-
стом пространстве-времени. Они гомеоморфны Р4, и можно вы-
брать такие глобальные координаты (у, г, и, и), пробегающие
значения от —оо до 4*оо, в которых метрика имеет вид
ds2 = 2 du dv -|- dy2 + dz2 -j- H (z, y, u) du2,
где
H = (y2 — z2) f (it) — 2yzg (u),
и /(«), §(«)—произвольные С2-функции, характеризующие ам-
плитуду и поляризацию волны. Эти пространства инвариантны
относительно пятипараметрической группы изометрий, которая
кратно-транзитивпа на изотропных поверхностях {и = const};
особый подкласс, в котором f(u) = cos 2«, g(u) — sin 2и, допу-
скает еще одно векторное поле Киллинга, т. е. такие однородные
пространства инвариантны относительно 6-параметрической
группы изометрий. Эти пространства не содержат замкнутых
времениподобных или изотропных кривых, однако в них не мо-
жет быть поверхностей Коши [124]. Локальные свойства этих
пространств детально изучены Бонди, Пирани и Робинсоном [13],
а глобальные — Пенроузом [124]. Оцват и Шюкинг [118] иссле-
довали глобальные свойства такого пространства с более высо-
кой симметрией. В работе [89] Хан и Пенруоз рассмотрели, как
рассеиваются две ударные плоские волны и как это приводит к
сингулярности.
Во-вторых, мы отметим 5-параметрическое семейство точных
решений уравнений Эйнштейна — Максвелла без источников,
найденное Картером [24] (см. также [37]). В это семейство в ка-
честве частных случаев входят решения Шварцшильда, Райссне-
ра — Нордстрема, Керра, решение Керра с зарядом, решение
Тауба — НУТ и де Ситтера 1-го и 2-го родов. Описание неко-
торых их глобальных свойств дано в [22]. Несколько конкретных
решений, тесно связанных с этим семейством, рассмотрены в
[45, 90].
Глава 6
Причинная структура
Согласно постулату (а) разд. 3.2, из одной точки многообра-
зия Л к другой можно послать сигнал только в том случае, если
эти точки могут быть соединены непространственноподобной гео-
дезической. В этой главе мы займемся дальнейшим исследова-
нием такого рода причинных отношений и получим ряд резуль-
татов, которые будут использованы в гл. 8 для доказательства
существования сингулярностей.
В разд. 3.2 отмечалось, что изучение причинных отношений
эквивалентно изучению конформной геометрии многообразия Л,
т. е. множества всех метрик g, конформных физической метри-
ке g (g = Q2g, где Q — ненулевая Сг-функция). При такого
рода конформном преобразовании метрики геодезическая кри-
вая, вообще говоря, не останется геодезической, если только она
не изотропная, но даже в последнем случае аффинный параметр
вдоль кривой перестанет быть аффинным. Таким образом, в
большинстве случаев геодезическая полнота (т. е. возможность
продлить все геодезические до любых значений их аффинных
параметров) будет зависеть от конкретного конформного множи-
теля; следовательно (исключая специальные случаи, описанные
в разд. 6.4), полнота не является свойством конформной геомет-
рии. Кларке [33] и Зейферт [157] показали, что при выполнении
некоторых физических разумных условий причинности любая ло-
ренцева метрика конформна метрике, в которой все изотропные
геодезические и все направленные в будущее времениподобные
геодезические полны. Геодезическую полноту мы рассмотрим
позднее, в гл. 8, где она служит основой для определения сингу-
лярности.
В разд. 6.1 мы занимаемся вопросом ориентируемости време-
ниподобных и пространственноподобных базисов. В разд. 6.2
даны определения основных причинных отношений и более ши-
рокое определение непространственноподобной кривой, допу-
скающее не только кусочную дифференцируемость, но и просто
непрерывность. Свойства границы будущего некоторого множе-
ства рассмотрены в разд. 6.3. В разд. 6.4 обсуждается ряд усло-
вий, которые исключают нарушение или близость к нарушению
причинности. Тесно связанные между собой понятия области
6 ! Ориентируемость
201
Коши и глобальной гиперболичности введены в разд. 6.5 и 6.6,
а в разд. 6.7 они использованы для доказательства существова-
ния непространственноподобных геодезических максимальной
длины между определенными парами точек.
В разд. 6.8 излагается метод построения причинной границы
пространства-времени, принадлежащий Героку, Кропхеймеру
и Пенроузу. Конкретный пример такой границы дает класс
асимптотически плоских пространств, который исследуется в
разд. 6.9.
6.1. Ориентируемость
В ближайшей к нам области пространства-времени «стрела»
времени четко задана направлением роста энтропии квазиизоли-
рованных термодинамических систем. Однако не вполне ясно,
какова связь между этой «стрелой» времени и другими «стре-
лами» времени, которые определяются расширением Вселенной
и условием излучения в электродинамике; интересующийся, этим
читатель может найти обсуждение этого вопроса в работах [63,
79, 81, 83]. Представляется физически разумным предположить,
что существует локальная термодинамическая «стрела» времени,
заданная непрерывным образом в каждой точке; но мы ограни-
чимся требованием, чтобы имелась возможность задать непре-
рывно разделение непространственноподобных векторов на два
класса, один из которых, по нашему выбору, назовем классом
векторов, направленных в будущее, а другой — классом векто-
ров, направленных в прошлое. Если такое деление возможно, то
будем говорить, что пространство-время ориентируемо по вре-
мени.
В некоторых типах пространства-времени задать такую ори-
ентацию по времени невозможно. Примером служит простран-
ство-время, построенное из пространства де Ситтера (разд. 5.2)
отождествлением точек, получаемых отражением относительно
начала пятимерного объемлющего пространства. В этом про-
странстве существуют замкнутые кривые, не гомотопные нулю,
при обходе по которым направление времени меняется на обрат-
ное. Однако ясно, что эта трудность могла бы быть устранена
просто снятием отождествления точек, и это фактически всегда
возможно: если пространство-время (Л, g) не ориентируемо по
времени, то оно имеет двукратное накрывающее пространство
(Л, g), которое ориентируемо. Л можно определить как множе-
ство пар (р, а), где р е Л, а а — одна из ориентаций времени
в р. Тогда вместе с естественной структурой и проекцией
л:(р, а)-*рЛ является двукратным накрывающим многообра-
зием для Л. Если Л двусвязно, то (Л, g)ориентируемо по вре-
мени. Если Л односвязно, то (Л, g) неориентируемо по времени.
202 Гл 6 Причиннпл структура
но (Л, g)—ориентируемо. В последующих разделах мы будем
предполагать, что имеет место одно из двух: либо (Л, g) ориен-
тируемо по времени, либо мы рассматриваем ориентируемое по
времени накрывающее пространство. Если мы сможем доказать
наличие сингулярностей в накрывающем пространстве, то они
должны быть и в (Л, g).
Можно задаться таким вопросом: является ли пространство-
время пространственно-ориентируемым, т. е. можно ли разделить
непрерывным образом базисы из трех пространственноподобных
осей на левые и правые? Герок [51] указал на интересную связь
между пространственной и временной ориентируемостью, сле-
дующую из того факта, что некоторые эксперименты в физике
элементарных частиц не инвариантны относительно зарядового
сопряжения или пространственного отражения (или того и дру-
гого вместе). Вместе с тем имеются теоретические основания для
уверенности в том, что все взаимодействия инвариантны отно-
сительно комбинации зарядового сопряжения, отражения и обра-
щения времени (СРГ-теорема, см. [164]). Если считать, что нару-
шение инвариантности относительно зарядового сопряжения и
пространственного отражения в слабых взаимодействиях — не
локальное явление, а происходит во всех точках пространства-
времени, то из этого следует, что при обходе по любой замкну-
той кривой такие характеристики, как знак заряда, ориентация
базиса пространственноподобных осей и ориентация времени
могут измениться или остаться неизменными лишь все три вме-
сте. (Обычная теория Максвелла, в которой электромагнитное
поле имеет определенный знак в каждой точке, не допускает из-
менения знака заряда при обходе по замкнутой кривой, не гомо-
топной нулю, без изменения ориентации времени. Однако можно
было бы построить теорию, в которой поле двузначно и меняет
свой знак при обходе по такой! кривой. Такая теория была бы в
согласии со всеми имеющимися экспериментальными данными.)
В частности, если предположить, что пространство-время ориен-
тируемо по времени, то оно должно быть и пространственно-
ориентируемым. (Фактически этот вывод следует из одних лишь
экспериментальных данных без использования СРТ-теоремы.)
Герок [55] показал, что из возможности задать двухкомпо-
нентные спинорные поля в каждой точке с необходимостью сле-
дует параллелизуемость пространства-времени, т. е. возможность
ввести непрерывную систему базисов касательного пространства
в каждой точке. (Дальнейшие следствия существования спинор-
ных структур получены в [56].)
6.2. Причинные кривые
Принимая, что пространство-время ориентируемо по времени
в смысле, разъясненном в предыдущем разделе, мы в Каждой
6 2. Причинные кривые
203
точке можем разделить непрострапственпоподобиы^ векторы на
направленные в будущее и в прошлое. Тогда для м пожеств 9 и
можно определить хронологическое будущее 1+(9&щи) множе-
ства 9 относительно 99 как множество всех точек в любую
из которых можно достичь из 9 по направленно^ в будущее
времениподобной кривой в 99. (Под кривой мы в сегда имеем
в виду кривую ненулевой протяженности; одна точ ка 11е счита-
ется кривой. Таким образом, 1+{9, 99} не может со держать 9.)
1+{9,Л} будем обозначать 1+{9}~, 1+(9) являете^ открытым
множеством: если р^Л можно достичь из 9 по н аправленной
в будущее времениподобной кривой, то имеется м^дая окрест-
ность р, которую тоже можно достичь по такой крив ой.
Для этого определения существует дуальное, в Е^отором «бу-
дущее» заменяется на «прошлое» и + на —; чтоС5ы не повто-
ряться, мы будем считать дуальные определения результаты
самоочевидными.
Обозначим через J+(9, 99} причинное будущее ^множества 9
относительно 91\ оно определяется как объединен не 9 С\91 с
множеством всех тех точек в 99, которых можно Достичь из 9
по направленным в будущее непространственнопо/цобным кри-
вым в 99. В разд. 4.5 мы видели, что непространствещцоподобная
кривая между двумя точками, которая не является; изотропной
геодезической кривой, может быть деформирована вер временипо-
добную кривую между этими точками. Поэтому, е<рли 99— от-
крытое множество и р, q,r 99, то как из условия
q е 7+ (р, 99},
так и из условия
q <= 1+ (р, 99}, rt=J+(,q,9l}
следует, что ге^ГГ(р, 99}. Отсюда 1+ (р, 99}Г'(р^99) и
1 + (р, 99} = j + (р, 91}, где для любого множества Л, Ж озна-
чает замыкание, _ _______
Ж = Ж П И - Ж')
означает границу Ж.
Будем снова вместо J+(9, Л} писать просто i^-{9}. J+(9)
представляет собой область пространства-времени, в которой
события из 9 могут причинно влиять: как видно из рис. 34,
J+(9} не обязательно замкнутое множество, даже если 9 пред-
ставляет собой одну точку. Кстати, этот пример иллюстрирует
полезный способ построения пространства-времени е заданными
свойствами причинности: начинаем с некоторого пространства-
времени (при отсутствии других указаний это будет простран-
ство Минковского), вырезаем из него какое-либо замКНуТОе мно-
жество и, если нужно, склеиваем его подходящим образом (т. е.
204
Гл. 6. Причинная структура
отождествляем точки Л}. В результате получаем снова много-
образие с лоренцевой метрикой, т. е. пространство-время, хотя
оно и выглядит несколько неполным, поскольку некоторые точки
вырезаны. Однако выше было отмечено, что эта неполнота мо-
жет быть «исправлена» подходящим конформным преобразова-
нием, которое передвинет вырезанные точки в бесконечность.
ческае, проходящие
дерезУ и образующие
прошлое множества
УЧУ)
Рис. 34. При удалении из пространства Минковского одной точки причин-
ное будущее 7+ (РР замкнутого множества У не обязательно замкнуто. На-
ходящиеся за этой точкой части границы будущего /+ (^) могут быть обра-
зованы изотропными геодезическими сегментами, не имеющими в Ж ко-
нечных точек в прошлом.
Контур будущего (horismos) для множества У относительно
°И, обозначаемый через Е+(^, 4/), определяется как /+(^, Л)—
— I+(9!,,aU)\ будем писать Е+(&) вместо £+(^, Л}. (В некото-
рых работах отношения ре/+(</), ре/+(</)) и реE+(q) обо-
значаются соответственно как q р, q < р и q р.) Если 'U —
открытое множество, согласно предложению 4.5.10, точки
£+(^, aU} должны лежать на направленных в будущее изотроп-
ных геодезических из 91', если же °U—нормальная выпуклая
окрестность точки р, то из предложения 4.5.1 следует, что
Е+{р,°1Е) состоит из направленных в будущее изотропных геоде-
зических в с началом ври образует в °U границу как хроно-
логического /+(р, “2/), так и причинного 1+(р,°11) будущего точ-
ки р. В частности, это имеет место в пространстве Минковского,
где такую границу образует изотропный конус точки р. Но в бо-
лее сложных случаях такое не обязательно.
Для последующего изложения удобно расширить определе-
ние времениподобных и непространственноподобных кривых,
ослабив требование кусочной дифференцируемости до требова-
6.2 Причинные кривые
205
ния лишь непрерывности. Хотя в таком случае кривая может и
не иметь касательного вектора, мы все же сможем говорить, что
она непространственноподобна, если локально любые две точки
кривой можно соединить кусочно дифференцируемой непростран-
ственноподобной кривой. Точнее, будем говорить, что непрерыв-
ная кривая Jft, где ЗГ — связный интервал из 7?1, направ-
лена в будущее и непространственноподобна, если для каждой
t е существует ее окрестность G в ST и нормальная выпуклая
окрестность <U точки у(0 в Л, такие, что для любого е Gi
у(/1)е/~(у(0, ^)-Y(0,
если /i < t, и
если t < G. Будем говорить, что у направлена в будущее и вре-
мениподобна, если те же самые условия выполняются при за-
мене J на /. Впредь, если не оговаривается иное, под времени-
подобной или непростраиственноподобной кривой мы будем под-
разумевать именно такую непрерывную кривую, а две кривые,
которые получаются одна из другой перепараметризацией, будем
считать эквивалентными. После такого обобщения мы можем
доказать утверждение, которое неоднократно используется в
оставшейся части главы. Сначала дадим несколько новых опре-
делений.
Точка р будет называться конечной точкой в будущем непро-
странственноподобной кривой направленной в буду-
щее, если для каждой окрестности Т этой точки существует та-
кое значение что у (Б) для каждого при
Непространственноподобная кривая непродолжима в будущее
(соответственно непродолжима в будущее в множестве 9), если
у нее нет конечной точки в будущем (соответственно нет конеч-
ной точки в будущем в множестве 5^). Точка р будет называться
предельной точкой бесконечной последовательности непростран-
ственноподобных кривых Хп, если любую окрестность р пересе-
кает бесконечное число этих кривых. Непространственноподобная
кривая будет называться предельной кривой последовательно-
сти },п, если имеется подпоследовательность последователь-
ности такая, что для каждой ре/., А' сходится к р.
Лемма 6.2.1
Пусть 9 — некоторое открытое множество и пусть — бес-
конечная последовательность непространственноподобных кри-
вых в 9, которые непродолжимы в 9. Если р ^9 — предельная
точка последовательности то через р можно провести непро-
странственноподобную кривую X, которая непродолжима в буду-
щее в 9 и является предельной кривой последовательности Хп.
206
Гл. 6. Причинная структура
Достаточно рассмотреть случай У = Л, поскольку S' можно
считать многообразием с лоренцевой метрикой. Допустим, что
% — нормальная выпуклая координатная окрестность точки р
Рис. 35. Проходящая через точку р непространственноподобная предельная
кривая % для семейства непространственноподобных кривых для этого
семейства р является предельной точкой.
и что ^(<7, а)—открытый шар координатного радиуса а с цен-
тром в q. Пусть постоянная b > 0 такова, что <%(р,Ь) суще-
ствует, и пусть 2.(1,0)га— последовательность лп A ^Ux, сходя-
щаяся к р. Так как $(р,Ь)—компактное множество, оно содер-
жит предельные точки последовательности 2.(1,0)п. Любая такая
предельная точка должна лежать либо в J'(р, либо в
/+(р, поскольку в противном случае существовали бы
6.3. Ахрональные границы
207
окрестности Т\ точки у и точки р, которые нельзя было бы
соединить непространственноподобной кривой в °И\. Пусть
.гне/+(р, <U^(p, Ь)
— одна из этих предельных точек (рис. 35) и 7(1, 1)п — сходя-
щаяся к Хц подпоследовательность из 7(1, 0)п. Точка Хц будет
точкой нашей предельной кривой 7. Продолжая по индукции,
определим точку
как предельную точку последовательности 7(г— 1, i— 1)п при
j = 0 и подпоследовательности 7(i, / — 1) при i j г; пусть
также 7(t,/)п— подпоследовательность подпоследовательности
7(1, 1), сходящаяся к Хц. Другими словами, мы делим интервал
[0, Ь] на все меньшие и меньшие отрезки и получаем точки нашей
предельной кривой на соответствующих сферах с центром в р.
Поскольку любые две точки Хц (j г) разделены непростран-
ственноподобно, замыкание объединения всех Хц (j i) даст не-
пространственноподобную кривую 7 от р = хго до Хц = Хц. Те-
перь остается построить такую подпоследовательность 7,'г после-
довательности 7П, чтобы для каждого q е 7 7„ сходилась к q.
Это мы сделаем, выбирая в качестве 7m член подпоследователь-
ности 7(zn, п), который пересекает каждый из шаров
&(xmj, m^b) при 0 т. Таким образом, 7 будет предель-
ной кривой последовательности 7„ от р до Хц. Пусть теперь
— нормальная выпуклая окрестность вокруг Хц; повторим
построение, используя теперь последовательность 7^. Поступая
таким образом, можно продолжить 7 неограниченно. □
6.3. Ахрональные границы
Из предложения 4.5.1 следует, что в нормальной выпуклой
окрестности °U граница множеств J+^p,^) или I+(p,°U) образо-
вана направленными в будущее изотропными геодезическими с
началом р. Для установления свойств границ более общего типа
введем понятия ахронального множества и множества будущего.
Множество 9 называется ахрональным (в литературе его
иногда называют «полупространственноподобным»), если
/+(^) П & пусто, иначе говоря, если никакие две точки д’ не раз-
делены времениподобно. д’ называется множеством будущего,
если 9? тз 1+Отметим, что если д’—множество будущего,
то Ж — д’— множество прошлого. Примерами множеств буду-
щего служат ЛДЛ3) и 7+ (Л3), где Л3— любое множество. При-
меры ахрональных множеств дает следующий фундаментальный
результат.
208
Гл. 6. Причинная структура
Предложение 6.3.1
Если 5^ — множество будущего, то д’ (граница (?) представ-
ляет собой замкнутое вложенное ахрональное трехмерное
(^-многообразие.
Если q е д’, то любая окрестность q пересекает д’ и М— У.
Если ре/+(<7)> то у точки q существует окрестность в /~(р).
Следовательно, /+(д)с!7. Аналогично I~(cf)^dt— д’. Если
r^.l+(q), то существует такая окрестность точки г, что
Т с= 1+ (<?) сд д’.
Таким образом, г не может принадлежать д’. В некоторой
окрестности °Ua точки q можно ввести нормальные координаты
(х1, х2, х3, х4) с времениподобным вектором <3/дх4 так, чтобы кри-
вые {х‘ = const, z = 1, 2, 3} пересекали и I+ (q, и Г (q, Qla).
Тогда каждая из этих кривых должна содержать точно одну
точку д’. Координата х4 этих точек должна быть функцией
Липшица от х‘ (Z = 1, 2, 3), поскольку никакие две точки д
не разделены времениподобно. Поэтому взаимнооднозначное
отображение ф:д Л дда —> R3, задаваемое равенством фа (р) = х‘ (р)
(г = 1,2,3) для p(=dQd/a, есть гомеоморфизм. Таким обра-
зом, {д’<д1б11а. фа) есть С*-атлас для д’. □
Множество со свойствами д’, перечисленными в предложе-
нии 6.3.1, будем называть ахрональной границей. Такое мно-
жество можно разбить на четыре непересекающихся подмно-
жества dN, д\, д’-, д0 следующим образом: для точки q е д’
найдутся или не найдутся точки р, г д’, такие, что р е
е Е~ (у) — q, r^E+(q) — q и различные возможности опреде-
ляют эти подмножества множества д’ по следующей схеме:
Зр Зр
Эг
Если q^dN, то г е Ет (р), поскольку г = /+(р) и согласно
предложению 6.3.1 г е /+ (р). Это означает, что в д’ имеется
изотропный геодезический сегмент, проходящий через q. Если
q е д’+ (соответственно д’2), то q является конечной точкой
в будущем (соответственно прошлом) изотропной геодезиче-
ской в д’. Подмножество пространственноподобно (точнее
непричинно). Это разбиение иллюстрируется рис. 36.
6.3
Ахрональные границы
209
Полезнее условие, определяющее принадлежность точки
одному из множеств дает следующая лемма, при-
надлежащая Пенроузу [128]:
Лемма 6.3.2
Пусть Ж — некоторая окрестность q е Ф, где &— множество
будущего. Тогда
1) из 1+ (<у) с /+ (S? — Ж) следует, что q^9’N[]9,+ ,
2) из Г (q) cz Г (Ж — 91 — 1Г) следует, что q е & N U
Достаточно доказать пункт (1), поскольку можно считать
также и границей множества прошлого Ж— 91. Пусть {хп}—
бесконечная последовательность точек в I+(q~) Л Ж, сходящаяся
Рис. 36. Ахроналы'ая граница & может быть разделена на четыре множе-
ства: пространствепноподобное изотропное & N и SP (соответственно S’-) —
конечная точка будущего (соответственно прошлого) изотропной геодезиче-
ской в 5А
к q. Если /+(<7)cz/+(^ — Ж), от каждого хп до Л1— Ж можно
провести направленную в прошлое времениподобную кривую.
По лемме 6.2.1 существует направленная в прошлое предельная
кривая А от q до (S?— Ж). Поскольку /“(</)—открытое множе-
ство и содержится в Ж — д’, I~(q) П & пусто. Отсюда Ъ должна
быть времениподобной геодезической и лежать ъ 9>. □
В качестве иллюстрации предыдущих результатов рассмо-
трим , границу замкнутого множества будуще-
го Ж. Согласно предложению 6.3.1, она является ахрональным
многообразие1М, и по лемме 6.3.2 каждая точка множества
S {Ж}— Ж принадлежит [/+(Х)].у или [/+((%/’)]+. Это означает,
что J (Ж) — Ж порождается изотропными геодезическими сег-
ментами, которые могут иметь конечную точку в будущем в
/+(Х)—Ж, но если они имеют конечные точки в прошлом, то
обязательно только в самом Ж. Как видно из рис. 36, может су-
ществовать изотропная геодезическая, порождающая сегменты,
210
Гл. 6. П ричинная структура
которые вообще не имеют конечных точек в прошлом, а уходят
в бесконечность. Очевидно, что это несколько надуманный при-
мер, но Пенроуз [124] показал, что аналогичное поведение имеет
место в таком простом случае, как плоские волны; другими при-
мерами служат решения де Ситтера 2-го рода (разд. 5.2) и Райс-
спера — Нордстрема (разд. 5.5). В разд. 6.6 мы увидим, что та-
кое поведение связано с отсутствием поверхностей Коши для
этих решений.
Будем говорить, что открытое множество °И — причинно-
простое, если для каждого компактного множества
Г (Ж) fl <U = Е+ (Ж) П и Г (Ж) Л <U = Е~ {Ж Л °И).
Это эквивалентно утверждению, что ЕГ(Ж) и 1~(Ж) замкнуты
в
6.4. Условия причинности
Постулат (а) разд. 3.2 требует только локальной причинно-
сти; глобальные вопросы остаются при этом открытыми. Следо-
вательно, мы не исключили такую возможность, что в больших
масштабах могут найтись замкнутые времениподобные геодези-
ческие (т. е. времениподобные окружности S1). Но существова-
ние таких кривых, по-видимому, привело бы к возможности ло-
гических парадоксов: можно представить ситуацию, когда космо-
навт на звездолете может совершить круг по такой кривой и,
возвратившись обратно к своему старту, помешать самому себе
стартовать в первый раз. Конечно, здесь есть противоречие
только с позиций элементарных представлений о свободе воли,
но их не так легко отбросить, поскольку эти представления опи-
раются на уверенность, что мы вольны осуществить любой воз-
можный эксперимент. Не исключено, что можно построить тео-
рию, в которой допускались бы замкнутые времениподобные
кривые, а представление о свободе воли было бы как-то измене-
но (см., например, [150]), но проще представить себе, что про-
странство-время удовлетворяет требованию, которое мы назы-
ваем хронологическим условием, а именно, чтобы в простран-
стве-времени не было замкнутых времениподобных кривых.
Однако мы должны иметь в виду возможность существования
точек (может быть, там, где плотность или кривизна очень ве-
лики), в которых это условие не выполняется. Множество всех
таких точек будем называть множеством, нарушающим хроноло-
гию-, оно характеризуется следующим предложением:
Предложение 6.4.1 (Картер)
Множество многообразия Ж, нарушающее хронологию, есть
объединение пересекающихся множеств вида I+(q) Г) I~(q),
q
S.4. Условия причинности
211
Если q принадлежит множеству многообразия Ж, нарушаю-
щему хронологию, то должна существовать направленная в бу-
дущее времениподобная кривая X с конечными точками в про-
шлом и будущем в q. Если г е I~(q) П I+(q), то найдутся напра-
вленные в прошлое и будущее времениподобные кривые щ и р2,
соединяющие q и г. Тогда ц, будет направленной в
будущее времениподобной кривой с конечными точками в про-
шлом и будущем г. Более того, если
г е [/- (?) П /+ (?)] Л [/~ (р) П /+ Ш
то
р^Г (?) П /+ (7) = Г (р) Л 1+ (р).
Для завершения доказательства заметим, что каждая точка г,
в которой нарушается хронология, принадлежит множеству
/+(г)Л/+(г). □
Предложение 6.4.2
Если Ж компактно, то множество, нарушающее хронологию
в Ж, является непустым.
Ж может быть покрыто открытыми множествами вида /+(</),
q <= Л. Если хронологическое условие выполняется в q, то
Таким образом, если бы хронологическое условие
выполнялось в каждой точке, нельзя было бы покрыть Ж конеч-
ным числом множеств вида /+(7). □
Из полученного результата, по-видимому, разумно сделать
вывод, что пространство-время некомпактно. Другой аргумент
против компактности состоит в том, что никакое компактное че-
тырехмерное многообразие с лоренцевой метрикой на нем не
может быть односвязным. (Существование лоренцевой метрики
означает, что характеристика Эйлера х(^<) = 0 ([162], р. 270).)
4
Как известно, %= У (— Вп, где Вп^0 —n-е число Бетти
п = 0
многообразия Ж. В силу дуальности ([160], р. 297) Вп=В^-п. Так
как Во = Bi. — 1, это означает, что В> У= 0, откуда в свою оче-
редь следует, что Л1(^<)^ 0 ([160], р. 398). Таким образом, ком-
пактное пространство-время является в действительности ком-
пактным многообразием, в котором отождествлены некоторые
точки. Представляется физически разумным не отождествлять
точки, а считать, что пространством-временем является накры-
вающее пространство.
Мы будем говорить, что выполнено условие причинности,
если не существует замкнутых непрострапственноподобных кри-
вых. Аналогично предложению 6.4.1 имеем
212
Гл. 6. Причинная структура
Предложение 6.4.3
Множество точек, в которых нарушается условие причинно-
сти, есть объединение непересекающихся множеств вида
П 7+(у), q е Л. □
В частности, если в точке q е Л условие причинности нару-
шено, а хронологическое условие выполняется, должна суще-
ствовать замкнутая изотропная геодезическая кривая у, проходя-
щая через q. Пусть v — аффинный параметр на у (рассматри-
ваемый как отображение открытого интервала из У?"1 на Л} и
пусть .... f-i, v0, Vf, v2, ... — последовательные значения v и q.
Тогда мы можем сравнивать в точке q касательный вектор
dldv |о и касательный вектор d[dv |0=С1, полученный парал-
лельным переносом при обходе по у. Поскольку оба вектора
имеют одинаковое направление, то они должны быть пропорцпо-
нальны djdv |D=Oi — adjdv |с . Множитель а имеет следующий
смысл: аффинное расстояние vn+i — vn, покрываемое при n-м об-
ходе по у, равно а-п(щ— п0)- Отсюда при а > 1 v никогда не
достигает значения (t»i — п0) (1 — а-1)-1, и, таким образом, кри-
вая у геодезически неполна в будущем, несмотря на то, что
можно совершить бесконечное число оборотов. Аналогично, если
а < 1, то у неполна в прошлом, в то время как при а = 1 она
полна в обоих направлениях. В двумерной модели пространства
Тауба — НУТ, описанной в разд. 5.7, существуют замкнутые изо-
тропные геодезические, которые служат примером случая с
а > 1. Поскольку множитель а является конформным инвариан-
том, эта неполнота не зависит от конформного множителя. Од-
нако такого рода поведение может встретиться лишь при нару-
шении причинности в том или ином смысле; если выполняется
условие сильной причинности (см. ниже), подходящее конформ-
ное преобразование метрики превращает все изотропные геоде-
зические в полные [33].
Множитель а приобретает более широкий смысл в силу сле-
дующего результата.
Предложение 6.4.4
Пусть у — замкнутая изотропная геодезическая кривая, кото-
рая неполна в будущем; тогда найдется вариация у, которая
сдвигает каждую точку у в будущее, и при этом получается за-
мкнутая времениподобная кривая.
Согласно разд. 2.6, на Л можно построить поле линейных
элементов (V, —V), нормированное так, что g(V, V) = —1. По-
скольку мы предполагаем, что Л ориентируемо во времени,
можно согласованным образом выбрать одно из направлений
(V, -V) и получить в результате направленное в будущее вре-
мениподобное векторное поле V. Тогда можно ввести положи-
6.4. Условия причинности
213
тельно-определенную метрику g':
g' (X, Y) = g (X, Y) + 2g (X, V) g (Y, V).
Пусть t — неаффинный параметр на у, который равен нулю в не-
которой точке б/еуи для которого g(V, d/dt) = — 1/д/2. Тогда
t измеряет собственное расстояние вдоль у в метрике g' и пробе-
гает значения —оо < t < оо. Рассмотрим вариацию у с векто-
ром вариации д/ди, равным xN, где х— функция x(t). Согласно
разд. 4.5,
1 <3 / д <3 \ d / д <3 \ / д D <3 \
2 ди k dt ’ dt ) dZ @ \ ди ’ dt ) & к, ди ’ dt dt ) ~
= Т).
где f(d/dt) = (DO) (d/dt). Допустим теперь, что v— аффинный
параметр на у. Тогда d/dv будет пропорционален d/dl: d/dv —
= hd/dt, где h~ldh/dt = —f. После одного обхода по у вектор
d/dv умножается на а > 1. Следовательно,
ф f dt — — In а О 0.
Поэтому, если мы возьмем функцию x(t) равной
exp I f (f ) dt' + b~1 Лп a j,
'0 '
где b = ф dZ, то получим вариацию у в будущее и замкнутую
времениподобную кривую. □
IlpedAOM:entie 6.4.5
Если
а) НаьКаК.ь О 0 для любого изотропного вектора К;
б) выполняется типовое условие: каждая изотропная геоде-
зическая с касательным вектором К содержит точку, в которой
K.[aR.b\ cd [eKf]KCKd У= О',
в) в Л выполняется хронологическое условие,
то в Л выполняется условие причинности.
Если бы существовали неполные замкнутые изотропные кри-
вые, то в силу предыдущего предложения их можно было бы
варьировать так, чтобы получить замкнутые времениподобные
кривые. Если бы существовали полные замкнутые изотропные
линии, то по предложению 4.4.5 они содержали бы сопряженные
точки и, согласно предложению 4.5.12, их снова можно было бы
варьировать к замкнутым времениподобным кривым. □
214
Гл. 6. Причинная структура
Из этого видно, что в физически реалистических решениях
условие причинности и хронологическое условие эквивалентны.
Отождествляются
Изотропная
геодезическая
вь/резается
поноска
Рис. 37. Пространство, в котором всюду выполняются условие причинности
и условие, выделяющее прошлое, но условие, выделяющее будущее, в р
или q не выполняется (действительно, /+ (р) = 1+ (<?)). Наклон изотропных
конусов на цилиндре увеличивается, пока одно изотропное направление
не станет горизонтальным, и затем конусы снова выпрямляются; из про-
странства удалена полоса, так что она разрывает эту изотропную геодезиче-
скую, которая иначе была бы замкнута.
Подобно отказу от замкнутых времениподобных линий, пред-
ставляется разумным исключить ситуации, в которых будут су-
ществовать непространственноподобные кривые, возвращающие-
ся сколь угодно близко к своей исходной точке или проходящие
сколь угодно близко от таких непространственноподобных кри-
вых, которые в свою очередь проходят бесконечно близко от
исходной точки первой кривой и т. д. Картер [27] указал, что в
6.4. Условия причинности
215
действительности имеется более чем счетная бесконечная иерар-
хия таких условий причинности более высокого порядка; они за-
висят от числа и порядка рассматриваемых предельных процес-
сов. Мы опишем первые три из этих условий и затем сформули-
руем предельно-сильное условие причинности.
Говорят, что в p<=Jl выполняется условие, выделяющее буду-
щее (соответственно прошлое) [94], если в каждой окрестности р
Вырезается
Изотропная
геодезическая
Отождествляются
Вырезается
Рис. 38. Пространство-время, которое удовлетворяет условию причинности
и условиям, выделяющим проштое и будущее, но в точке р не удовлетво-
ряет условию сильной причинности. С поверхности цилиндра удалены Две
полоски; световые конусы проходят под углом ±45°.
содержится такая окрестность р, которую никакая направленная
в будущее (соответственно в прошлое) из р непространственно-
подобная кривая не пересекает более одного раза. Эквивалент-
ное утверждение состоит в том, что из равенства /+(<?)= 1+{р)
(соответственно из /“(<?) = 1-(р)) следует, что q=p. На рис. 37
дан пример ситуации, когда условие причинности и условие, вы-
деляющее прошлое, выполнены всюду, но условие, выделяющее
будущее, не выполняется в точке р.
Говорят, что в р выполняется условие сильной причинности,
если каждая окрестность р содержит такую окрестность р, ко-
торую никакая непространственноподобная кривая не пересекает
более одного раза. Пример нарушения этого условия дан на
рис. 38.
Предложение 6.4.6
Если условия (а) —(в) предложения 6,4.5 выполнены и, кро-
ме того,
216 Гл. 6. П ршшнная структура
г) Ж— изотропно геодезически полное многообразие, то на
Ж выполняется условие сильной причинности.
Допустим, что в р е Ж условие сильной причинности не вы-
полняется. Пусть Ж— нормальная выпуклая окрестность точ-
ки р и пусть Vn cz -Ll — бесконечная последовательность окрест-
ностей р, таких, что любая окрестность р содержит все Vn с
достаточно большими га. Тогда для каждого Vn будет существо-
вать направленная в будущее непространственноподобная кри-
вая Ап, которая выйдет за пределы °U и затем вернется в Vn.
По лемме 6.2.1 найдется непродолжимая непространственнопо-
добная кривая А, которая будет предельной кривой для после-
довательности Ап- Никакие две точки А не могут иметь вре-
мениподобное разделение, иначе их можно было бы соединить
некоторой Ап, так чтобы получилась замкнутая непространст-
венноподобная кривая. Таким образом, А должна быть изотроп-
ной геодезической. Но по условиям (а), (б) и (г) А должна
содержать сопряженные точки и, следовательно, точки с време-
ниподобным разделением. □
Следствие
На Ж будут выполняться также условия, выделяющие про-
шлое и будущее, ибо они содержатся в условии сильной при-
чинности.
С этими тремя условиями причинности более высокого поряд-
ка тесно связано явление захвата. При построении направленной
в будущее непространственноподобной кривой у, которая непро-
должима в будущее, возможны следующие варианты:
1) кривая войдет и останется в компактном множестве
2) кривая не будет оставаться внутри какого-либо компакт-
ного множества, но будет постоянно возвращаться в компактное
множество
3) кривая не останется внутри какого-либо компактного мно-
жества SP и не будет возвращаться более конечного числа раз
в любое такое множество.
В третьем случае можно считать, что у уходит к краю про-
странства-времени, т. е. или на бесконечность, или в сингуляр-
ность. В первом и во втором случае мы будем говорить, что бу-
дущее у соответственно полностью или частично захвачено мно-
жеством У. Может показаться, что захват имеет место только
при нарушении условия причинности, но пример, принадлежа-
щий Картеру (рис. 39), показывает, что это не обязательно. Тем
не менее справедливо следующее предложение:
Предложение 6.4.7
Если условие сильной причинности выполняется на компакт-
ном множестве д’, то не может быть непродолжимых в будущее
6.4. Условия причинности
217
непространственноподобных кривых с будущим, полностью или
частично захваченным множеством 9.
У можно покрыть конечным числом выпуклых нормальных
координатных окрестностей <Ui с компактным замыканием, та-
ких, что любую °Ui любая непространственноподобная кривая
пересекает не более одного раза. (Такие окрестности мы будем
а
5
Рис. 39. Пространство с захваченными непространственноподобными линиями
но без замкнутых непространственноподобных линий. Многообразие пред-
ставляет собой Rl X S1 X S1 и описывается координатами (t, у, г), причем
(/, у, z) отождествляется с (I, у, z + 1) и с (у, у + 1, z + а), пде а — ирра-
циональное число. Лоренцева метрика имеет вид
ds2 — (ch t — I)2 (d t- — d y~) + dt dy — d z~.
a — сечение {z = const}, показывающее ориентацию изотропных конусов;
б —сечение t = 0, показывающее часть изотропной геодезической.
называть окрестностями локальной причинности.) Любая непро-
должимая в будущее непространственноподобная кривая, кото-
рая пересекает одну из этих окрестностей, должна ее покинуть и
не возвращаться в нее. □
Предложение 6.4.8
Если на компактном множестве 9* выполняются условия, вы-
деляющие будущее или прошлое, то не может существовать не-
продолжимая в будущее непространственноподобная кривая, бу-
дущее которой полностью захвачено 9. (Этот результат приве-
ден здесь, поскольку он интересен сам по себе, но в дальнейшем
он нам не понадобится.)
Пусть {Та}, (а = 1, 2, 3)—счетный базис из открытых мно-
жеств в Л' (т. е. любое открытое множество в Ж можно предста-
218
Гл. 6. Причинная структура
вить как некоторое объединение множеств Поскольку на 9~!
выполняется условие, выделяющее будущее или прошлое, любая
точка р е 91 будет иметь нормальную выпуклую координатную
окрестность °U, такую, что никакая направленная в будущее (со-
ответственно в прошлое) непространствешюподобная кривая,
выходящая из р, не пересекает 91 более одного раза. Введем
функцию f(p), равную наименьшему значению а, при котором
Та содержит р и сама содержится в некоторой окрестности °U.
Допустим, что имеется непродолжимая в будущее непро-
странственноподобная кривая с будущим, полностью заключен-
ным в 91. Пусть точка q е л такова, что А/ = ЛП7+(<7) содер-
жится в 9\ Определим как замкнутое непустое множество,
состоящее из всех точек SK которые являются предельными точ-
ками Ъ. Пусть р0 е Ж»— та точка, в которой f(p0) равна наи-
меньшему значению /(р) на Тогда через р0 можно провести
непродолжимую непространственноподобную кривую у0, каждая
точка которой будет предельной точкой //. Никакие две точки у0
не могут иметь времениподобное разделение, иначе некоторый
сегмент V можно было бы деформировать так, чтобы получить
замкнутую непространственноподобную кривую. Следовательно,
уо будет непродолжимой изотропной геодезической, которая пол-
ностью захвачена в 9> и в направлении будущего, и в направле-
нии прошлого. Пусть — замкнутое множество, состоящее из
всех предельных точек области уо П /+(ро) (или, в случае выпол-
нения на 9* условия, выделяющего прошлое, уоГ1/_(ро))-
с: ^0, поскольку каждая такая точка будет также и предель-
ной точкой V. Ввиду того что не может содержать каких-
либо предельных точек множества уо П /+(ро) (соответственно
уо П (/?о)), будет точно меньше ^о- Так мы получим беско-
нечную последовательность замкнутых множеств Д Д
••• . Каждое л^р не пусто, ибо является множе-
ством всех предельных точек изотропной геодезической с буду-
щим (соответственно с прошлым), полностью захваченным в
Ур-1 П/+(^р-1) (соответственно в ур—i П /~(рр-1))• Пусть
Ж = Г| Поскольку 9? компактно, Ж — непустое множество:
пересечение любого конечного числа множеств «s/р непусто. До-
пустим, г ^Ж. Тогда f(r) = f(pp) для некоторого р. НоУ’цр^П
П c^p+i пусто, и поэтому г не может принадлежать множеству
i9/p+i, а значит, и не может принадлежать Ж. Отсюда ясно, что
существование непродолжимой в будущее непространственнопо-
добной кривой с полностью захваченным в 9Р будущим невоз-
можно.
Причинные отношения в (Jt, g) можно использовать для вве-
дения на Ж топологии, называемой топологией Александрова,
6.4. Условия причинности
219
Эта топология, в которой по определению множество открыто
в том и только в том случае, если оно является объединением
одного или больше множеств вида /+(/?) П I~ (q), р,д<=Л.
I+(p) открыто в топологии многообразия; поэтому любое
множество, открытое в топологии Александрова, будет откры-
тым и в топологии многообразия, хотя обратное не обязательно
верно.
вырезаете»
вырезается
----Изотрот/б/е геодезические
Вырезается
I6
I
f
Рис. 40. Пространство, удовлетворяющее условию сильной причинности,
в котором, однако, малейшее изменение метрики может привести к появлению
замкнутых времениподобных линий, проходящих через р С поверхности ци-
.линдра удалены три полоски; световые конусы проходят под углом ±45°.
Допустим, однако, что на Л выполняется условие сильной
причинности. Тогда вокруг любой точки г е Л найдется окрест-
ность локальной причинности aLL. Топология Александрова пары
(<2/, g|<2/), которая сама рассматривается как пространство-вре-
мя, очевидно, совпадает с топологией многообразия в окрестно-
сти °И. Отсюда следует, что топология Александрова многообра-
зия Л совпадает с топологией многообразия, так как Л можно
покрыть окрестностями локальной причинности. Это означает,
что при выполнении условия сильной причинности топологиче-
ская структура пространства-времени может быть установлена
изучением причинных соотношений.
Как видно из рис. 40, даже наложение условия сильной при-
чинности не ликвидирует все причинные патологии; простран-
ство-время находится на грани нарушения хронологического
условия в том смысле, что малейшее изменение метрики может
220
Гл. 6. Причинная структура
привести к появлению замкнутых кривых. Такого рода ситуация
не выглядит физически реалистической, поскольку общая теория
относительности, по-видимому, является классическим пределом
еще неизвестной квантовой теории пространства-времени, а в
Рис. 41. Открытое множество °U в открытой С°-топологии на про-
странстве (X) симметричных тензоров типа (0,2) на Я.
этой теории принцип неопределенности должен воспрепятство-
вать тому, чтобы метрика имела точное значение в каждой точ-
ке. Поэтому, чтобы быть физически осмысленным, то или иное
свойство пространства-времени должно обладать определенного
рода устойчивостью, т. е. этим свойством должны обладать и
«близкие» пространства. Для придания точного смысла слову
«близкий» необходимо задать некоторую топологию на множе-
стве всех пространств-времен, т. е. всех некомпактных четырех-
мерных многообразий и лоренцевых метрик на них. Мы не будем
касаться проблемы объединения многообразий с различными
топологиями в односвязное топологическое пространство, а рас-
смотрим лишь введение топологии в множество всех лоренцевых
Сг-метрик (r^ 1) на данном многообразии. Это можно сделать
разными способами в зависимости от того, требуем ли мы, чтобы
6.4. Условия причинности
221
«близкая» метрика была близка только по своим значениям
((/-топология) или же еще и по производным до й-го порядка
((/-топология), а также от того, требуется ли близость везде
(открытая топология) или только на компактных множествах
(компактная открытая топология).
Для наших целей интересна открытая С°-топология. Ее можно
определить следующим образом. Пространства Т5°Др) симмет-
ричных тензоров типа (0, 2) в каждой точке р е Ж обра-
зуют многообразие (с естественной структурой). Г$°(^)— рас-
слоение симметричных тензоров типа (0, 2) над Ж. Лоренцева
метрика g на Ж есть установление соответствия Между некото-
рым элементом Тк-ЛЖ} и каждой точкой р^.Ж, и, следова-
тельно, ее можно рассматривать как такое отображение или
сечение Тs02 (Ж), для которого n?g=l, где л — проек-
ция Тз2(Ж)^-Ж, переводящая хеДрл в р. Пусть — от-
крытое множество в Г$°(.<), и пусть О (^ — множество всех
лоренцевых С°-метрик g, таких, что £(Ж) содержится в
(рис. 41). Тогда открытое множество лоренцевых (/-метрик
в открытой (/-топологии определяется как объединение одного
или более множеств вида О
Будем говорить, что на Ж выполняется условие устойчивой
причинности, если пространственно-временная метрика g имеет
такую открытую окрестность в открытой (/-топологии, что в лю-
бой метрике, принадлежащей этой окрестности, нет замкнутых
времениподобных кривых. Использование (/-топологии не при-
вело бы к отличиям, но компактная открытая топология недопу-
стима, так как в ней каждая окрестность любой метрики содер-
жит замкнутые времениподобные кривые. Другими словами,
условие устойчивой причинности означает, что в каждой точке
можно слегка расширить световой конус, не получая при этом
замкнутых времениподобных кривых.
Предложение 6.4.9
Условие устойчивой причинности выполняется всюду в Ж,
если и только если существует функция f на Ж, градиент кото-
рой всюду времениподобен.
Замечание. Функцию f можно мыслить как род космического
времени в том смысле, что она возрастает вдоль каждой направ-
ленной в будущее непространственноподобной кривой.
Доказательство. Из существования функции f с везде време-
ниподобным градиентом следует условие устойчивой причинно-
сти, поскольку замкнутые времениподобные линии невозможны в
любой метрике h, которая близка к g настолько, что изотропный
конус каждой точки р е Ж в метрике h пересекает проходящую
222
Гл. 6. Причинная структура
через р поверхность {/ — const} только в р. Чтобы показать
справедливость обратного утверждения, введем на Л объемную
меру ц (она не связана с объемной мерой, задаваемой метри-
кой g), по которой полный объем Л равен единице. Один из
способов введения этой меры состоит в следующем: выберем для
Л счетный атлас фа), в котором фсА^а) компактно в /?4.
Пусть цо — естественная евклидова мера на А’4, и пусть fa — раз-
ложение единицы для атласа ^а). Тогда ц можно опреде-
лить как
Z fa2-a [Цо(^а)]“‘ фа^а.
а
Теперь, если выполняется условие устойчивой причинности,
найдется семейство лоренцевых Сг-метрик h(a), а е [0, 3] со
следующими свойствами:
1) h(0) является пространственно-временной метрикой g;
2) для каждого а е [0, 3] в метрике h(a) нет замкнутых вре-
мениподобных кривых;
3) если «1, Яг е [0, 3] и di < az, то каждый вектор, непро-
странственноподобный в метрике h(a1), будет времениподобным
в метрике h (а2) •
Пусть 0(р, а), р <= Л — объем области 1~(р, Л, h (а)) по
мере ц, где через °U, h) обозначено прошлое относитель-
но в метрике h. Для данного значения а е(0, 3) 0 (р, а) будет
ограниченной функцией, возрастающей вдоль каждой непро-
странственноподобной кривой. Однако эта функция может не
быть непрерывной: как видно из рис. 42, может оказаться, что
небольшое изменение положения позволяет наблюдателю уви-
деть прошлое за «ширмой» и таким образом увеличить объем
прошлого. Следовательно, нам нужно каким-то образом сгла-
дить 0(р, а) так, чтобы получить непрерывную функцию, воз-
растающую вдоль каждой направленной в будущее и непро-
странственноподобной в метрике h(0) кривой. Это можно сде-
лать, проводя усреднение по области изменения а. Пусть
9
0 (р) = 0 (р, a) da;
1
покажем, что 0 (р) непрерывна на Л.
Сначала нужно показать, что 0(р) полунепрерывна сверху.
Зададим е > 0; пусть $ — шар с центром в р, такой, что объем
по мере ц меньше, чем е/2. По свойству (3) для а{, а2 е [0, 3]
с й] < а2 в найдется окрестность & а2) точки р, для
которой
[Г (ад), h (aj) П ш [/" (р, Я h (а2)) Л $].
6.4. Условия причинности
223
Пусть п — положительное целое число, большее чем 2е-1. Тогда
мы определим множество = Д (1 + у At’1, 1 + у («+1) п-1) ,
i
i — Q, 1, 2п. $ является окрестностью р и содержится в
ST (а, а + /г-1) при любом а (= [1, 2]. Поэтому /“ (q, Л, h (а)) — $
Р и с. 42. Небольшой сдвиг точки из р в q приводит к большому изменению
объема прошлого этой точки. Световые конусы проходят под углом ±45°;
удалена полоска.
будет содержаться в I (р, Л, h (а + п ')) — если q е S’ и
а е [1, 2]. Отсюда
6 (р, а) < 6 (р, ° + у е) + у е
и, следовательно, 0(р)^ 9(р)+е, из чего видно, что 0 полуне-
прерывна сверху. Аналогично доказывается, что она полунепре-
рывна снизу. Чтобы получить дифференцируемую функцию,
можно усреднить 0 с подходящей сглаживающей функцией по
окрестности каждой точки. Выбирая достаточно малую окрест-
ность, можно получить функцию f, градиент которой везде вре-
мениподобен по метрике g. Детали этой процедуры сглаживания
можно найти в работе [167]. □
Пространственноподобные поверхности {f = const} можно
рассматривать в качестве поверхностей одновременности в про-
странстве-времени, хотя они, конечно, не единственны. Если эти
поверхности компактны, то они все диффеоморфны одна другой,
но это не обязательно справедливо, если некоторые из них не-
компактны.
224
Гл. 6. Причинная структура
6.5. Области Коши
В теории Ньютона имеется мгновенное дальнодействие; по-
этому, чтобы предсказать события в будущих точках простран-
ства-времени, мы должны знать состояние всей Вселенной в
настоящий момент времени, а также наложить некоторые гранич-
ные условия на бесконечности, вроде того, что потенциал стре-
мится к нулю. Напротив, из постулата (а) разд. 3.2 следует, что
в теории относительности события в различных точках простран-
ства-времени могут быть причинно связаны только в том случае,
если их можно соединить непространственноподобной кривой.
Таким образом, знание соответствующих данных на замкнутом
множестве д (если данные известны на открытом множестве, то
на его замыкании они получаются в силу непрерывности) позво-
лит устанавливать события в области D+(^) будущего д, назы-
ваемой областью Коши будущего множества д и определяемой
как множество всех таких точек р <^Л, для которых каждая не-
продолжимая в прошлое непространственноподобная кривая,
проходящая через р, пересекает д (отметим, что О^(д)^ д).
Пенроуз [127, 128] определяет область Коши множества д
немного иначе, а именно как множество всех точек р^.Л, та-
ких, что каждая непродолжимая в прошлое времениподобная
кривая, проходящая через р, пересекает д. Такое множество мы
будем обозначать /5+(^). Справедлив следующий результат:
Предложение 6.5.1
£>+ (^)=5т(п
Очевидно, D+ (д) D+ (д’). Если точка q Л — Ь+ (д’), то
у нее есть окрестность с2/, не пересекающая д. Из q можно
провести непродолжимую в прошлое кривую Л, которая не
пересекает д. Если г е Л f| I~ (q, <U), то /+ (г, °И) является
открытой окрестностью q в Л—D+(d). Следовательно,
Л — D+ (д’) — открытое множество, a D+ (д’) — замкнутое. До-
пустим, что существует точка р <= П+ (д’), у которой имеется
окрестность У, не пересекающая D+ (д). Выберем точку х е
^I~(p, Т). Из нее можно провести непродолжимую непро-
странственноподобную кривую у, которая не пересекает д’.
Пусть уа — последовательность точек на у, которая не сходится
к какой-либо точке, причем у„+1 лежит в прошлом уп. Пусть
ТК’п. — нормальные выпуклые окрестности точек уп, причем УКп+\
не пересекается с 7fn. Пусть, наконец, zn есть последователь-
ность точек, такая, что
zn+x е 1+ (уп+1, Гя+1) П Г (zn, Л - д’).
6.5. Области Коши
225
Тогда должна существовать непродолжнмая времениподобная
кривая с началом в р, которая проходит через каждую точку
и не пересекает 9’. Но это противоречит условию, что р е Ь+ (9’).
Следовательно, Ь+(S?) содержится в замыкании D+(У), и по-
этому Ь+ (5Р) = D+ (З’). □
Граница области £>+(^) в будущем, т. е. D+(9}) — I~(D+ (.9’)),
очерчивает пределы области, которая может быть предсказана
Рис. 43, Область Коши будущего D+ и горизонт Коши в будущем Н+ (S’)
замкнутого множества S’, которое частично изотропно и частично простран-
ственноподобно. Отметим, что горизонт Н+ (S) не обязательно связен. Изо-
тропные линии проходят под углом ±45°; удалена полоска.
по известным данным на З’. Это замкнутое ахрональное множе-
ство мы будем называть горизонтом Коши в будущем множе-
ства SP и обозначим его через Н+(^); как видно из рис. 43,
Я+(97) пересекает 9^, если множество 3 изотропно или имеет
«границу». Чтобы придать этому выражению точный смысл,
определим границу (9’) ахронального множества 3 как множе-
ство всех точек ее:/', в каждой окрестности 91 которых есть
точки р е I~(q, 9Z) и г е I+(q, ‘U), которые можно соединить не-
пересекающей 3 времениподобной кривой в 91. В силу аргу-
ментов, аналогичных тем, что были приведены в доказательстве
предложения 6.3.1, получаем, что 3 является трехмерным вло-
женным (^-подмногообразием, если непустое ахрональное мно-
жество 3 не имеет границы.
8 Заказ 381
226
Гл. 6 Причинная структура
Предложение 6.5.2
Для замкнутого ахропального множества 17 граница (Я+(^))
совпадает с границей (9}).
Пусть -2Ж — последовательность окрестностей точки q, при-
надлежащей границе (Я+(1?)), такая, что любая окрестность q
содержит все °Un с достаточно большим п. В каждой окрестно-
сти <Ып найдутся точки р е I~(q, и rn<= I+(q, 9/п), которые
можно соединить времениподобной кривой не пересекающей
Н+(9>). Это означает, что Ж не может пересечь £)+(17). По пред-
ложению 6.5.1 q^D C/) и, следовательно, Г (</) с 1~ (П+ (^))с:
ст Г (17) (J D+ (9^. Таким образом, рп должна лежать в
Кроме того, каждая непродолжимая в направлении прошлого
времениподобная кривая с началом в q должна пересечь 17. По-
этому при каждом п на каждой времениподобной линии в 92п,
соединяющей q и рп, должна быть точка множества 9> и, значит,
q должна принадлежать 9?. Так как кривые лп не пересекают 9\
q лежит на границе (17). Аналогично доказывается обратное
утверждение. □
Предложение 6.5.3
Пусть 9?— замкнутое ахрональное множество. Тогда Я+(^)
порождается изотропными геодезическими сегментами, которые
или вообще не имеют конечных точек в прошлом, или имеют ко-
нечную точку в прошлом на границе (9?).
Множество 9~ = является множеством про-
шлого. Следовательно, в силу предложения 6.3.1, 9~— ахрональ-
ное ^-многообразие. Я+(^) —замкнутое подмногообразие мно-
гообразия 3~. Пусть q <= [Н+(9>')— граница (17)). Если q ф 9Р, то
q£/+(17), поскольку q^D0'9}. В силу ахрональности 9> най-
дется нормальная выпуклая окрестность Ж точки q, которая не
пересекает 7“ (17). Пусть теперь q <= 9?, и пусть Ж— нормальная
выпуклая окрестность q, такая, что ни одна точка из 7+(^, Ж)
не может быть соединена с какой-либо точкой из l~(q, Ж) вре-
мениподобной кривой, не пересекающей 17. В любом случае, если
р — какая-либо точка в /+(7), должна найтись направленная в
прошлое времениподобная кривая от р до некоторой точки из
JI — 9~— Ж, поскольку иначе р лежала бы в £)+(^). Отсюда,
согласно условию (1) леммы 6.3.2, примененному к множеству
будущего JI — 9~, имеем q 9~ 90.. °
Следствие
Если граница (9’) = 0, то Н+(9), когда он не пуст, является
ахрональпым трехмерным вложенным С’-многообразием, кото-
рое порождено изотропными геодезическими сегментами, не
имеющими конечных точек в прошлом.
6.5. Области Коши
227
Непричинное множество без края мы будем называть ча-
стичной поверхностью Коши. Иначе
ность Коши — это пространственно-
подобная гиперповерхность, кото-
рую ни одна непространствснвопо-
добная кривая не пересекает б зее
одного раза. Допустим, что суще-
ствует связная прострапственнопо-
добная гиперповерхность (без
края), пересекаемая непростран-
ственноподобной кривой в точках pi
и рг- Тогда р\ и р2 можно соединить
кривой ц, лежащей в д, и ц U I
будет замкнутой кривой, которая
пересекает д только один раз. Эту
кривую нельзя непрерывным обра-
зом стянуть в нуль, поскольку такая
деформация может изменить число
пересечений кривой с д только на
четное число. Таким образом, Ж не
может быть односвязным. Это озна-
чает, что мы могли бы «развер-
нуть» Ж, перейдя к односвязному
универсальному накрывающему
многообразию для Ж, в котором
каждая связная компонента образа
д является пространственноподоб-
ной гиперповерхностью (без края),
а следовательно, частичной поверх-
ностью Коши в Ж (рис. 44). Однако
переход к универсальному накры-
вающему многообразию может «раз-
вернуть» Ж больше, чем требуется,
Р и с. 44. SP — связная про-
страпственноподобпая гипер-
поверхность без края в Л.
Опа не является частичной по-
верхностью Коши, однако
каждый образ д-1 (^) поверх-
ности SP в универсальном на-
крывающем многообразии Ж
многообразия .// представляет
собой частичную поверхность
Коши в .1!.
и дать в результате такую частич-
ную поверхность Коши, которая бу-
дет некомпактной даже тогда, когда
д компактно. Для целей последую-
щих глав было бы желательно иметь
накрывающее многообразие, кото-
рое развертывает ,// так, чтобы каж-
дая связная компонента образа д
была частичной поверхностью Коши,
но при этом оставалась гомеоморф-
ной д. Такое накрывающее много-
образце можно построить по крайней мере двумя различными
способами.
8*
228
Гл. б. Причинная структура
Напомним, что универсальное накрывающее многообразие
можно определить как множество всех пар (р, [л]), где р еЛ и
[?.] — класс эквивалентности кривых в Л от некоторой фиксиро-
ванной точки q е Л до р, гомотопных по модулю q и р. Накры-
вающее многообразие Лц определяется как множество всех пар
(р, [Л.]), где [л]—класс эквивалентности кривых от г? до р,
гомотопных по модулю 9 и р (т. е. концы на поверхности 9 мо-
гут сдвигаться по ней). Можно сказать, что Лн — это наиболь-
шее накрывающее многообразие, в котором каждая связная
компонента образа 9 гомеоморфна 9. Накрывающее многообра-
зие Ла [52] по определению— это множество всех пар (р, [X]),
где на этот раз [А] является классом эквивалентности кривых от
фиксированной точки q до р, которые пересекают 9 одинаковое
число раз, причем пересечение в направлении будущего счита-
ется положительным, а в направлении прошлого — отрицатель-
ным. Можно сказать, что Ла является наименьшим накрываю-
щим многообразием, в котором каждая связная компонента
образа 9 делит Ла на две части. В обоих случаях топологиче-
ская и дифференциальная структура накрывающего многообра-
зия фиксируется требованием, чтобы проекция, отображающая
(р, [X]) в р, локально была диффеоморфизмом.
Введем D (9) — D+ (9) U D~ (9). Частичная поверхность
Коши 9 называется глобальной поверхностью Коши (или про-
сто поверхностью Коши), если О(9) = Л. Таким образом, по-
верхность Коши — это пространственноподобная гиперповерх-
ность, которую каждая непространственноподобная кривая пере-
секает точно один раз. Примерами поверхности Коши в
пространстве Минковского служат поверхности {х4 = const}, но
гиперболоиды
{(х4)2 — (.г3)2 — (%2)2 — (.К)2 = const}
являются только частичными поверхностями Коши, поскольку
изотропный конус будущего или прошлого в начале системы ко-
ординат будут горизонтами Коши для этих поверхностей (см.
разд. 5.1 и рис. 13). То, что данная поверхность является поверх-
ностью Коши, — это не только свойство самой поверхности, но
также и свойство объемлющего пространства-времени в целом.
Например, достаточно вырезать из пространства Минковского
только одну точку, как полученное пространство-время вообще
не будет допускать ни одной поверхности Коши.
Если для рассматриваемого многообразия Л существует по-
верхность Коши, то, имея нужные данные на ней, мы могли бы
определить состояние Вселенной в любой момент прошлого или
будущего. Однако мы не можем собрать такие данные, не побы-
вав в будущем каждой точки поверхности, что в большинстве
случаев невозможно. Мы не располагаем вескими физическими
6.6. Глобальная гиперболичность
2Э
доводами для уверенности в том, что Вселенная допускает по-
верхность Коши; имеется целый ряд известных точных решений
уравнения Эйнштейна, которые ее не допускают. Среди них опи-
санные в гл. 5 пространство де Ситтера 2-го рода, плоские вол-
ны, пространство Тауба — НУТ, решение Райсснера — Норд-
стрема. Последнее представляет собой особо интересный случай:
поверхность & на рис. 25 позволяет предсказать события во
внешних областях /, где г > г+, и в соседних областях II, где
< г < г+, но при этом существует горизонт Коши г = г_.
Точки соседней области III не лежат в £)+(^’), ибо в этой обла-
сти имеются непространственноподобные кривые, которые непро-
должимы в направлении прошлого и не пересекают г = г_, а
стремятся к точкам i+ (их можно считать расположенными на
бесконечности) или к сингулярности г — 0 (которую нельзя рас-
сматривать как часть пространства-времени, см. разд. 8.1). В эту
область может поступать дополнительная информация из беско-
нечности или сингулярности, которая нарушит любые предсказа-
ния, сделанные на основе одних только данных на 5*’. Итак, в
общей теории относительности наша способность предсказывать
будущее ограничена как трудностями, связанными с необходи-
мостью знать данные на всей пространственноподобной гиперпо-
верхности, так и тем, что даже такого знания может оказаться
недостаточно. Однако, несмотря на эти ограничения, все же мож-
но предсказать, правда, при определенных условиях существо-
вание сингулярностей.
6.6. Глобальная гиперболичность
С областями развития тесно связано свойство глобальной ги-
перболичности [99]. Множество Л9 называется глобально гипер-
болическим, если на Л9 выполняется предположение о сильной
причинности и если для любых двух точек р, 7+(р)А
A J~(q) компактно и содержится в Л9. В некотором смысле мож-
но считать, что это определение говорит о том, что ни одна точка
из /+(/?) А /~(д) не принадлежит краю пространства-времени,
т. е. бесконечности или сингулярности. Термин «глобальная ги-
перболичность» возник в связи с тем, что волновое уравнение
с источником в виде б-функции аре..Т имеет в Л9 единственное
решение, обращающееся в нуль вне Л9— 7+(р, Л9) (см. гл. 7).
Напомним, что Л9 называют причинно-простым, если для лю-
бого компактного множества Ж, содержащегося в Л9, 7+(^)А
А Л9 и 1~(^) А Л9 замкнуты в Л9.
Предложение 6.6.1
Открытое глобальное гиперболическое множество Л9 — при-
чинно простое.
230
Гл. 6. Причинная структура
Пусть р — любая точка множества Л9. Допустим, что есть
точка
q е= (7+ (р) — Г (р)) Г1 Л’.
Поскольку Л9 открыто, должна быть точка ге(/ДДД). Но
тогда q е J+ (р) Л .Г (г), что невозможно, так как J+ (р) П Д (г)
должно быть компактным и поэтому замкнутым. Таким образом,
/+ (р) Л Л9 и Ж (р) П Л9 замкнуты в Ж. _______
Допустим теперь, что существует точка qe.(j+(JH’) —
— J+ (J^)) П Л9. Пусть qn — бесконечная последовательность точек
/+(ДЛЛ9, сходящаяся к q, причем qn+i е/“ (рд). Для каждого п
Г (qn) П Ж будет компактным непустым множеством. Поэтому
П{Д(^)П^} будет непустым множеством. Пусть р — точка
п
этого множества. Тогда qn при всех п будут лежать в J+ (р).
Но J+ (р) замкнуто. Поэтому J+ (р) содержит q. □
Следствие
Если Жх и Ж,- компактные множества в Л9, J+ (Xi) Л Ж (.7zf'2)
компактно.
Можно найти конечное число точек pt е Л9, для которых
{U 1+ (рг)}=эХ,.
Аналогично, существует конечное число точек qf, таких, что Ж^
содержится в
и/’(<?/)•
/
Тогда J+ (Ж{) Л Ж содержится в
U У+ (Pi) Л Г (q,)}
i. i
и замкнуто. □
В работе [99] Лере дал иное, но эквивалентное введенному
выше определение глобальной гиперболичности; сейчас мы его
сформулируем. Для точек p,q <=Jl, для которых в У+(р) П /“(<?)
выполняется условие сильной причинности, мы введем С(р, р) —
пространство всех (непрерывных) непространственноподобных
кривых, соединяющих р и q\ при этом принимается, что две кри-
вые уД) и Z(«) представляют одну и ту же точку пространства
С(р, р), если они получаются одна из другой перепараметриза-
цией, т. е. если существует непрерывная монотонная функция
f(«), такая, что y(f(zz)) = Z(zz). (Пространство С(р, 7) можно
6.6. Глобальная гиперболичность
231
ввести, даже если на 7+(р)П /“(<?) условие сильной причинности
не выполняется.) Топология C(p,q) определяется заданием
окрестностей кривой ус С(р, q), состоящих из всех тех кривых
в С(р, q), точки которых в Ж лежат в окрестности Ж9 точек у
(рис. 45). Определение Лере [99] состоит в том, что множество Л
называется глобально гиперболическим, если C{p,q) компактно
для всех р, q <=Л\ Эквивалентность этих определений видна из
следующего результата:
Рис. 45. Окрестность точек кривой у в Л. Окрестность у в С (р, q) со-
стоит из всех кривых от р до q, точки которых лежат в Ж,
Предложение 6.6.2 (Зейферт [/55], Герок [52])
Пусть на открытом множестве Л = /_(Л5)П 7+(Л9) выпол-
няется сильная причинность. Тогда для глобальной гиперболич-
ности Л необходимо и достаточно, чтобы пространство С(р, q)
было компактно для всех p,q е Л.
Предположим сначала, что С(р, q) компактно. Пусть гп—•
бесконечная последовательность точек /+(р) П/“(<?), и пусть
Гп — последовательность непространственноподобных кривых от
р до q, проходящих через соответствующую гп. Ввиду компакт-
ности C(p,q) существует кривая Г, к которой в топологии
С(р, q) сходится некоторая подпоследовательность Г'п. Пусть
— такая окрестность кривой Г в Ж, что Щ компактно. Тогда
'Т/ будет содержать все Г'п, а значит, и все Гп при достаточно
больших га; следовательно, имеется точка г е 'U, которая явля-
ется предельной точкой последовательности Очевидно, г ле-
жит на Таким образом, любая бесконечная последователь-
ность в /+(/?) Г) /“(<?) имеет предельную точку в 1+(р) П /“(<?)•
Поэтому /+(р)П J~(q) компактно.
232
Гл. 6. Г1 ричинная структура
Обратно, допустим /+(/?) П 7-(<?) компактно. Пусть /,п — бес-
конечная последовательность непространственноподобных кри-
вых от р до q. По лемме 6.2.1, примененной к открытому множе-
ству Л — q, в нем существует направленная в будущее непро-
странственноподобная кривая X с началом в р, которая непро-
должима в Л—q и для которой найдется подпоследователь-
ность л'п, сходящаяся к г при каждом г е X. Кривая Л должна
иметь конечную точку q в будущем, поскольку, согласно предло-
жению 6.4.7, она не может быть полностью заключена в буду-
щем в компактном множестве 7+(р) П 7"(р) и не может покинуть
это множество иначе как в q.
Пусть °U — любая окрестность л в Л, и пусть /у (1=£Д’^й)—
конечное множество точек на Z, таких, что г\ = р, — q и каж-
дая rt имеет окрестность F/, удовлетворяющую условию П
П 7~(F>)c: З/. Тогда для достаточно больших п г'п ст °И. Следо-
вательно, Vп сходится к ?. в топологии С (£,<?), и пространство
компактно. □
Связь между глобальной гиперболичностью и областями Ко-
ши устанавливается следующими утверждениями:
Предложение 6.6.3
Если — замкнутое ахрональное множество, то
если оно не пусто, является глобально гиперболическим множе-
ством.
Докажем сначала несколько лемм.
Лемма 6.6.4
Если p^D+fP1) то каждая непродолжимая в про-
шлое непространственноподобная кривая, проходящая через р,
пересекает
Пусть p^D+(ff>)—и у — непродолжимая в будущее
непространственноподобная кривая, проходящая через q. Тогда
можно найти точку q е Д+(5г’) П /+(р) и непродолжимую в про-
шлое непространственноподобную кривую X, проходящую через
нее, такие, что для каждой точки А' е /. найдется точка у е у,
лежащая в области 1~(х). Так как X пересекает & в некоторой
точке xlt то существует ^еуП/Д!?). □
Следствие
Если р е int(Z)(S^)), то любая непродолжимая непростран-
ственноподобная кривая, проходящая через р, пересекает
и /+(3*).
Имеем int(D(^’))=Z)(Sp) — {H+(^)U Если ре/+(^)
или /“(^), результат получается сразу. Если —/+(^),
6.6. Глобальная гиперболичность
233
то р е 9* с, D~ (9’), и отсюда снова следует то же утвержде-
ние. □
Лемма 6.6.5
В int(£>(^)) выполняется условие сильной причинности.
Допустим, что через р е int D (9) проходит непространствен-
ноподобная кривая X. Согласно предыдущему результату, долж-
ны существовать точки у е/. П/ДМ) и г /. Л /+(^). Посколь-
ку точка геМ(у), то она принадлежит также и что
противоречит ахрональности ‘Т’. Таким образом, в int D (9) вы-
полняется условие причинности. Теперь допустим, что в р нару-
шается условие сильной причинности. Тогда, как и в лемме 6.4.6,
должна существовать бесконечная последовательность направ-
ленных в будущее непространственноподобных кривых Гп, кото-
рая сходится к проходящей через q непродолжимой изотропной
геодезической у. При этом существовали бы точки q е у Л 7~(^)
и геуЛ /+(tZ), и, следовательно, нашлась бы некоторая л„, ко-
торая пересекает /+(^), а значит, и Это противоречит
ахрональности 9. □
Доказательство предложения 6.6.3. Мы хотим показать, что
С(р, q) компактно, если р, q е int(Z) (9)). Рассмотрим сначала
тот случай, когда р, q е I~ (9), и предположим, что pe=J~(q).
Пусть Гп — бесконечная последовательность непространственно-
подобных кривых, соединяющих р и q. Согласно лемме 6.2.1, бу-
дет существовать направленная в будущее непространственно-
подобная предельная кривая с началом в р, которая непродол-
жима в Л — q. Она должна иметь конечную точку в будущем
в q, так как иначе она пересекла бы 9, что невозможно, посколь-
ку Рассмотрим теперь случай, когда p^J~(9),
q е /+(^)Л 1+{р) Если конечной точкой предельной кривой X
является q, то она и есть искомая предельная точка в С(р, q).
Если q не является конечной точкой Г, то на ней должна быть
точка у^1+(9), поскольку Г непродолжима в Л— q. Пусть
Г'п — подпоследовательность, которая сходится к г для любой
точки г s /. между р и q. Пусть Г — направленная в прошлое
предельная кривая подпоследовательности Г'п с началом в q.
Если конечной точкой в прошлом кривой Г является точка р, то
она и будет искомой предельной точкой в С(р, у). Допустим, что
р не является конечной точкой кривой К и она не проходит че-
рез у. Тогда на ней должна быть некоторая точка ге/-(^).
Пусть Т"п — подпоследовательность Г'п, сходящаяся к г для лю-
бой точки rsi. между q и z. Пусть У — открытая окрестность
кривой Г, не содержащая у. Тогда для достаточно больших п все
Г"п П J+(9) должны принадлежать Т. Однако это невозможно,
234
Гл. 6. Причинная структура
ибо у — предельная точка А"п. Поэтому должна существовать
непространственноподобная кривая от р до q, которая будет пре-
дельной точкой последовательности Кп в пространстве С(р, q).
Случаи, когда и p^J-fJ?), q е £+(5^), вместе
с дуальными им случаями, исчерпывают все возможные комби-
нации. Следовательно, во всех этих случаях мы получаем непро-
странственноподобную кривую от р до q, являющуюся предель-
ной точкой последовательности в топологии пространства
С(р, q). □
Подобными же рассуждениями можно доказать
Предложение 6.6.6
Если q int(£)(S?’)), то £+(^’)П£_(7) или компактно, или
пусто. □
Чтобы показать, что глобально гиперболична вся область
£>(^), а не только ее внутренняя часть, необходимо наложить
некоторые дополнительные условия.
Предложение 6.6.7
Если 9?— замкнутое ахрональное множество, такое, что в
/+(^) П одновременно удовлетворяются и условие сильной
причинности, и одно из следующих условий:
1) непричинность (что имеет место, если и только если 9Р
непричинно);
2) компактность —
тогда £>(^)— глобально гиперболическое множество.
Допустим, что в какой-то точке ?е£>(^) условие сильной
причинности не выполняется. Тогда в силу утверждения, анало-
гичного лемме 6.6.5, через q должна проходить непродолжимая
изотропная геодезическая, в каждой точке которой нарушена
сильная причинность. Но это невозможно, поскольку такая кри-
вая пересекала бы 9>. Следовательно, на выполняется
сильная причинность.
Если р, то выполняется условие предложения 6.6.3.
Когда p^J~(^), q <= /+(^), можно, как и при доказательстве
предложения 6.6.3, провести из р направленную в будущее пре-
дельную кривую А, а из q — направленную в прошлое предель-
ную кривую А и выбрать подпоследовательность Х"п, которая
сходится к г для каждой точки г на К или А. В случае (1) X пе-
ресекает д’ в единственной точке х. В любой окрестности х будут
точки кривых Н'п с достаточно большими п и, следовательно,
ввиду ахрональности д’ в ней будет точка х"„ = 'К"'п П 9Г От-
сюда, х"п будет сходиться к х. Аналогично, х"п будет сходиться
к % а= £ Г) Таким образом, х = х и можно соединить X с А, что
приводит к непространственноподобной предельной кривой в
6.6. Глабильная гиперболичность
235
В случае (2) предположим, что q не является конечной точ-
кой в будущем кривой Л. Тогда I покинет область по-
скольку она пересекает и в силу предложения 6.4.7 должна
выйти из компактного множества /-('Z). Поэтому на 7
можно найти точку х, которая не лежит в /~(^). Для каждого п
выберем точку х"п е 3 П . Поскольку компактно, найдутся
некоторая точка у е ЗР и подпоследовательность 7/"п, такие, что
соответствующие точки х"' п сходятся к у. Допустим, что у не
лежит на X. Тогда при достаточно больших п х'"п будет лежать
в будущем любой окрестности точки х. Это означает, что
хеЛ(^). Однако последнее невозможно, поскольку х нахо-
дится в /+(^), но не в компактном множестве /+(5г’) П .
Поэтому Л пройдет через у. Аналогично, Л тоже пройдет через у.
Итак, эти кривые можно соединить и получить предельную кри-
вую. □
Из предложения 6.6.3 следует, что существование поверхно-
сти Коши для открытого множества Л9 означает глобальную ги-
перболичность Л9. Из следующего предложения видна справед-
ливость обратного утверждения.
Предложение 6.6.8 (Герок [57])
Если открытое множество Л9 глобально гиперболично, то оно,
рассматриваемое как многообразие, гомеоморфно Rl X ЗР, где
ЗР— трехмерное многообразие и {а}Х^ есть поверхность Коши
в многообразии Л9 для каждого а е R1.
Как и при доказательстве 6.4.9, введем на Л9 меру у так,
чтобы полный объем Л9 по этой мере был равен единице. Для
р е Л9 введем функцию f+(p)—объем области /+(р, Л9) по
мере ц. Ясно, что f+(p)—ограниченная функция на Л9: она убы-
вает вдоль любой направленной в будущее непространственно-
подобной кривой. Мы покажем, что глобальная гиперболичность
означает непрерывность /+(р) на Л9, так что нам не нужно, как
при доказательстве предложения 6.4.9, «усреднять» объем буду-
щего. Достаточно лишь доказать, что /+(р) непрерывна на лю-
бой непространственноподобной кривой 7.
Пусть геА, и пусть хп — бесконечная последовательность
точек на А, лежащих строго в прошлом относительно г. Пусть
ЗГ — П /+ (хп, Л9). Допустим, что f+(p) не полунепрерывна свер-
п
ху в ге?.. При этом должна существовать точка
Тогда r^J-J_q, но каждая точка хп Л9) и, следова-
тельно, re J~(q, Л9), что невозможно, поскольку, согласно пред-
ложению 6.6.1, J~(q, Л9) замкнуто в Л9. Подобным же образом
доказывается полунепрерывность снизу.
236
Гл. 6. Причинная структура
По мере движения точки р в будущее вдоль непродолжимой
непространственноподобной кривой 7 на Л9 значение f+(p) долж-
но стремиться к нулю. Предположим, что имеется некоторая
точка, которая лежит в будущем любой точки. Тогда направлен-
ная в будущее кривая л войдет в компактное множество /+(г)П
J~(q) и останется внутри его при любом г е/«, что невоз-
можно в силу предложения 6.4.7, так как на Л9 выполняется
условие сильной причинности.
Рассмотрим теперь определенную на Л9 функцию f(p) =
= f~ (р) /1'+ (р) Любая поверхность f = const будет непричинным
множеством и, согласно предложению 6.3.1, вложенным в Л9
трехмерным С1--многообразием. Она будет также поверхностью
Коши для Л9, потому что вдоль любых непространственноподоб-
ных кривых f~ и f+ стремятся к нулю в прошлом и в будущем
соответственно. На Л9 можно ввести времениподобное векторное
поле V и задать непрерывное отображение 0, которое переводит
точки Л9 вдоль интегральных кривых поля V на пересечения
этих кривых с Тогда (lnf(p), р(р)) есть гомеомор-
физм Л9 на Д!Х^, который можно превратить в диффеомор-
физм, если сгладить f, как при доказательстве предложения 6.4.9.
□
Таким образом, если все пространство-время глобально ги-
перболично, оно обладает весьма скучной топологией.
6.7. Существование геодезических
Важность глобальной гиперболичности для гл. 8 связана со
следующим результатом:
Предложение 6.7.1
Пусть р и q лежат на глобально гиперболическом множе-
стве Л9, причем q е /+(р). Тогда р и q можно соединить непро-
странственноподобной кривой, длина которой не меньше длины
любой другой непространственноподобной кривой от р до q.
Мы дадим два доказательства этого утверждения: первое,
принадлежащее Авезу [4] и Зейферту [156], основано на исполь-
зовании компактности С(р, q), а второе (применимое лишь при
открытом Л9) представляет собой метод построения самой этой
геодезической.
Пространство C(p,q) содержит плотное подмножество
С'(р, <?), состоящее из всех времениподобных О-кривых от р
до q. Длина одной такой кривой определяется (ср. с разд. 4.5)
как
иМ(-Д^4)У".
р
6.7. Существование геодезических
237
где t есть С’-параметр на 2.. Функция L не является непрерыв-
ной на Cz(p, <?), поскольку любая окрестность Л содержит зигза-
гообразную кусочно почти изотропную кривую произвольно ма-
лой длины (рис. 46). Эта потеря непрерывности возникает от
того, что мы пользуемся С°-топологией, согласно которой две
кривые близки, если в Л близки их точки, но не требтется бли-
зости их касательных векторов. Можно было бы наделить
Ри с. 46. °11 — открытая окрестность времениподобной кривой % от р до q.
В CU существуют времениподобные кривые от р до q, которые приближенно
являются ломаными изотропными кривыми и имеют сколь угодно малую
длину.
C'(p,q) С’-топологией и таким образом придать L непрерыв-
ность, но мы не делаем этого, ибо С'(р, q) некомпактно; ком-
пактное пространство получается только после присоединения
всех непрерывных непространственноподобных кривых. Вместо
этого мы пользуемся С°-топологией и распространим определе-
ние L на С(р, q).
Из-за сигнатуры метрики увеличение извилистости времени-
подобной кривой сокращает ее длину. Таким образом, L не полу-
непрерывна снизу. Однако имеет место
Лемма 6.7.2
L полунепрерывна сверху в С°-топологии на С'(р, q).
Рассмотрим времениподобную СР-кривую 2.(0 от р до q, при-
чем в качестве параметра выберем длину дуги от р. В достаточ-
но малой окрестности °U кривой 7 можно найти функцию f, кото-
рая равна t и такова, что поверхности {f=const} пространствен-
ноподобны и ортогональны к d/dt [т. е. gnbf.b |% = Один
способ задания такой функции состоит в построении простран-
ственноподобных геодезических, ортогональных к Л. Для
238
Гл. 6. Причинная структура
достаточно малой окрестности ЯЛ кривой 7. они дают однознач-
ное отображение Л на 2., и значение / в некоторой точке р окре-
стности ЯЛ можно определить как значение I в той точке 2., на
которую отображается р. Любую кривую р в Л° можно парамет-
ризовать функцией ). Касательный вектор к р. можно
представить в виде
где к — пространственноподобный вектор, лежащий на поверх-
ности {/ = const}, т. е. kaf.a — O. Тогда
е О)„ Ш,) -
Однако на A, gabf.af.b = — 1. Отсюда, при данном 8>0 можно
выбрать настолько малую окрестность ЯЛ' сс ЯЛ, что в ЯЛ’
gabf.af.b> — 1 +е. Поэтому для любой кривой ц в ЯЛ'
L [р] <(1 + 8)'/° L [X]. □
Теперь мы определим длину непрерывной непространственно-
подобной кривой 7. от р до q следующим образом. Пусть 'ЯЛ —
окрестность А в JL и пусть ПЯЛ}—наименьшая верхняя грань
длин времениподобных кривых в ЯЛ от р до q. Тогда мы опреде-
лим L [?„] как наибольшую нижнюю грань ПЯЛ) для всех окрест-
ностей Я1 кривой а в Это определение длины применимо ко
всем кривым от р до q, в каждой окрестности которых суще-
ствует времениподобная ^-кривая, т. е. оно применимо ко всем
точкам в С (р, q), которые принадлежат замыканию С (р, q). Как
мы знаем (разд. 4.5), пепространственноподобная кривая от р
до q, если она не является изотропной геодезической кривой без
изломов, может быть деформирована во времениподобную ку-
сочно С'-кривую от р до q, а изломы этой кривой можно округ-
лить так, чтобы получить времениподобную С^кривую от р до q.
Следовательно, точки в C(p,q)—C'(p,q)—это изотропные гео-
дезические без изломов (не содержащие сопряженных точек), и
мы положим, что их длина равна нулю.
Такое определение L превращает ее в полунепрерывную
сверху функцию на компактном пространстве C'(p,q). [На са-
мом деле, пока непрерывная непространственноподобная кривая
удовлетворяет локальному условию Липшица, она дифференци-
руема почти всюду. Поэтому длину все еще можно было бы
определить как
6.7. Существование геодезических
239
и это не противоречило бы введенному выше определению.] Если
C'(p,q) — 0, но C(p,q)—непустое множество, то р и q соеди-
няются изотропной геодезической без изломов; кроме нее между
р и q не существует иных непространственноподобных кривых.
Если С'(р, q)^=0, это множество содержит некоторую точку,
в которой L достигает своего максимального значения, т. е. най-
дется непространственноподобная кривая у от р до q, длина ко-
торой больше или равна длине любой другой такой кривой. Со-
гласно предложению 4.5.3, у должна быть геодезической кривой,
поскольку иначе можно было бы найти точки х, у е у, которые
лежали бы в нормальной выпуклой координатной окрестности
и могли бы быть соединены геодезическим сегментом большей
длины, чем часть у между х и у. □
Для другого, конструктивного доказательства мы введем
функцию d(p, q) от p,q е Я, равную нулю, если /+(р), а в
противном случае равную наименьшей верхней грани длин, ку-
сочно непространственноподобных кривых от р до q, направлен-
ных в будущее. [Отметим, что d (р, q) может быть бесконечной.]
Для множеств Д’ n -Д' введем d(0, равную наименьшей
верхней грани d (р, q} при р <= 0, q Я.
Допустим, что q е /+(р) и d (р, q) конечно. Тогда для любого
б > О можно подобрать времениподобную кривую X от р до q
длиной d(p, q)~ у б и такую окрестность <U точки q, что X мож-
но деформировать во времениподобную кривую длины d (р, q) — б,
соединяющую р с любой точкой г е °U. Следовательно, функ-
ция d(p, q) там, где она конечна, полунепрерывна снизу. В об-
щем случае d(p, q) не полунепрерывна сверху, но имеется
Лемма 6.7.3
Функция d (р, р) конечна и непрерывна по р и q, когда р и q
принадлежат глобально гиперболическому множеству Л.
Сначала мы докажем, что d(p, q) конечна. Поскольку на ком-
пактном множестве 7+(р)П/~(q) выполняется условие сильной
причинности, его можно покрыть конечным числом таких ло-
кально-причинных множеств, каждое из которых не содержит
непрострапственноподобные кривые длиннее некоторого 8. По-
скольку любая непространственноподобпая кривая от р до q мо-
жет войти в каждую окрестность не более одного раза, она
должна иметь конечную длину.
Предположим теперь, что р, q е Л; существует такое по-
стоянное б > 0, чго каждая окрестность q содержит точку г&/Е.
для которой
d(p, r)>d(p, q) + 6.
240
Гл. б. Причинная структура
Пусть хп — бесконечная последовательность точек в Л, сходя-
щаяся к q, для которой d (р, хп) > d (р, q) + б. Тогда из каж-
дой хп до р можно провести непространственноподобную кри-
вую длина которой больше, чем d(p, </)+б. По лемме 6.2.1
существует направленная в прошлое непространственноподобная
кривая X, которая проходит через q и является предельной кри-
вой последовательности Хп. Пусть °U — локально-причинная
окрестность точки q. Тогда X не может пересечь I-(q){\ <U, ибо
в этом случае одну из кривых Кп можно было бы деформировать
в непространственноподобную кривую от р до q с длиной больше
d(p,q). Поэтому X П Л обязательно будет изотропной геодези-
ческой с началом в q, и в каждой точке х е К П функция
d(p,x) будет иметь разрыв больше, чем б. Повторением этих
же аргументов можно показать, что X — изотропная геодезиче-
ская и что в каждой точке хе/, функция d(p, х) имеет разрыв
больше, чем б. Отсюда видно, что р не является конечной точ-
кой кривой X, так как по предложению 4.5.3 d (р,х) непрерывна
в локально-причинной окрестности точки р. С другой стороны,
1 должна быть непродолжимой в М — р, п поэтому, если бы р
не была его конечной точкой, то она должна была бы, согласно
предложению 6.4.7, выйти из компактного множества /+(р)П
ПЭто доказывает, что d (р, q) полунепрерывна сверху
на Л. □
Используя функцию расстояния, легко построить геодезиче-
скую максимальной длины от р до q в случае открытого Л.
Пусть ст Л — локально-причинная окрестность р, не содержа-
щая <7, и пусть х <= /+(р) П /“(</) такова, что функция d(p, г) +
+ d (г, q), г е °U максимизируется при г = х. Проведем из р че-
рез точку х направленную в будущее геодезическую у. Для всех
точек г на у между р и х будет выполняться соотношение
d (р, г) + d (г, q) = d (р, q). Допустим, что имеется точка у е
е —q, являющаяся последней точкой на у, в которой это
соотношение выполняется. Пусть Т ст Л — локально-причинная
окрестность точки г/, не содержащая q, и пусть точка ге Д(?)П
П/”(</) такова, что d(y, r)-|-d(r, 7), г достигает сво-
его максимального значения d (у, <?) при г = z. Если г ф у, то
d(p, z)> d(p, y) + d(y, z) и d(p, z) + d(z, q)>d(p, q).
что невозможно. Отсюда видно, что соотношение
d(p, r) + d(r, <y) = d(p, q)
должно выполняться для всех reyfl J~(q)- Ввиду компактности
/+(р)П/“(<?) кривая у должна покинуть J~(q) в некоторой точ-
ке у. Допустим, у Л q; тогда у должна лежать на направленной
в прошлое изотропной геодезической с началом в q. Соединив у
б 8 Причинная граница пространства-времени
241
с %, мы получили бы непространственноподобную кривую от р
до q, варьируя которую, можно было бы получить кривую более
длинную, чем d(p, q\, но это невозможно. Следовательно, у—
геодезическая кривая от р до q длины d (/?,<?). □
Следствие
Если 9— частичная С2-поверхность Коши, то к каждой точке
q е £>+(^) можно провести направленную в будущее времени-
подобную геодезическую кривую длины d(9, q), ортогональную 9
и не содержащую между 9 и q сопряженную к 9 точку.
Согласно предложению 6.5.2, Н+(9) и Я~(^) не пересекают
9 и, следовательно, не принадлежат D(9).
Поэтому и в силу предложения 6.6.3 D (9) = int 0(5?) — гло-
бально гиперболическое множество. По предложению 6.6.6
9C\J~(q) компактно, и, следовательно, d(p, q), р е 9 достиг-
нет своего максимального значения d(^, q) в некоторой точке
г ^9. При этом между г и q будет существовать геодезическая
кривая у длины d(9, q), которая, согласно лемме 4.5.5 и пред-
ложению 4.5.9, должна быть ортогональна к 9 и не должна
иметь между 9 и q точку, сопряженную к 9. □
6.8. Причинная граница пространства-времени
В этом разделе мы изложим в общих чертах метод присоеди-
нения границы к пространству-времени, предложенный Героком,
Кронхеймером и Пенроузом [60]. Это построение зависит только
от причинной структуры (Ж, g), т. е. в нем не различаются гра-
ничные точки, находящиеся на конечном расстоянии и на беско-
нечности. В разд. 8.3 мы дадим описание другого построения,
при котором присоединяется граница, представляющая лишь
сингулярные точки. К сожалению, похоже, что между этими по-
строениями нет явной связи.
Будем предполагать, что (Ж, g) удовлетворяет условию при-
чинности. Тогда любая точка р в (Ж, g) однозначно определя-
ется ее хронологическим будущим /+(р) или прошлым 1~(р), т. е.
Г (р) = Г (q) ОI+ (р) =I+(q)^P= q-
Хронологическое прошлое Ж == 1~(р) любой точки р е Ж обла-
дает следующими свойствами:
1) Ж — открытое множество;
2) Ж — множество прошлого, т. е. /_(Ж)сд Ж;
3) Ж не может быть представлено в виде объединения двух
собственных подмножеств, обладающих свойствами (1) и (2).
Множество со свойствами (1) — (3) мы будем называть не-
разложимым множеством прошлого, сокращенно НП. (Опреде-
ление, данное в [60], не включает свойства (1), тем не менее оно
эквивалентно нашему определению, поскольку в [60] под «мно-
242
Гл. 6. Причинная структура
жеством прошлого» подразумевается множество, которое равно
своему хронологическому прошлому, а не только содержит его.)
Рис. 47. Диаграммы Пенроуза пространства Минковского и пространства
де Стр л 2-го рода (ср. рис. 15 и 20). на которых изображены: ГНП,
представляющее на точку р пространства Минковского (а), и ГНП и
ГНБ, представляющее на Н точку р пространства де Ситтера 2-го рода (б).
Аналогично определяется неразложимое множество будущего
(НБ).
Все НП делятся на два класса: собственные НП (СНП), кото-
рые являются прошлым каких-либо точек в Ж., и граничные НП
6.8. Причинная граница пространства-вргмеки
243
(ГНП), которые не являются прошлым каких-либо точек в Л.
Идея состоит в том, чтобы рассматривать эти ГНП и соответ-
ствующим образом определенные ГНБ в качестве представите-
лей точек, лежащих на причинной границе (с-граница) про-
странства (Л, g). Например, в пространстве Минковского
заштрихованную область на рис. 47, а можно рассматривать в
качестве представителя точки р на 5'+. Заметим, что в этом при-
мере многообразие Л в целом само является и ГНП, и ГНБ,
причем эти НП и НБ можно считать представителями точек i+ и
i~ соответственно. Всем точкам конформной границы простран-
ства Минковского, за исключением i°, могут быть поставлены в
соответствие ГНП или ГНБ. В некоторых случаях, таких, как
пространство де Ситтера 2-го рода, где конформная граница
времениподобна, представителями одной и той же точки гра-
ницы могут быть и ГНБ и ГНП (рис. 47,6).
ГНП можно охарактеризовать и как прошлое непродолжи-
мых в будущее времениподобных кривых. Это означает, что про-
шлое 7~(у) непродолжимой в будущее кривой у можно рассма-
тривать в качестве представителя конечной точки у в будущем
на с-границе. Другая кривая у' в будущем будет иметь ту же ко-
нечную точку, если и только если /~(у) = 1~(у').
Предложение 6.8.1 (Герок, Кронхеймер и Пенроуз)
Множество УП есть ГНП тогда и только тогда, когда суще-
ствует непродолжимая в будущее времениподобная кривая у,
для которой /_(у)= УП.
Предположим сначала, что имеется кривая у, для которой
/-(у) = УГ1. Пусть УП = Hl U Т, где HI и Т — некоторые откры-
тые множества прошлого. Нам нужно показать, что или Hl с Т,
или Т cz HI. Предположим противное: П1 не содержится в Т и
F не содержится в HI. Тогда можно найти точку q е Hl — У° и
точку г — HI. Поскольку q, r^I~(y), должны найтись такие
точки q', г' Еу, что qt=I~(q') и г^1~(г'). Но независимо от
того, какое из множеств, HI или Т, содержит более позднюю из
точек q', г', она будет содержать также и q, и г, что противоре-
чит первоначальному определению q и г.
Обратно, допустим, что УП есть ГНП. Тогда можно построить
времениподобную кривую у, для которой /~(у) = Ж. При этом,
если р — какая-либо точка множества УП, то
уп = Г (УП П /+ (р)) и Г (Ж - /+ (р)).
Однако Ж неразложимо, и потому или УП = 1~(УП П 1+(р)), или
УИ = 1-(УИ — 1+(р)). Точка р не содержится в 1~(УП — 1+(р)),
так что вторая возможность исключается.
Этот вывод можно переформулировать следующим образом:
в Ж найдется точка, находящаяся в будущем относительно
244
Гл. 6. Причинная структура
любой данной пары точек из Ж. Выберем теперь счетное плотное
семейство точек рп е Ж. Возьмем некоторую точку qo Ж, на-
ходящуюся в будущем ро. Поскольку q0 и pi принадлежат Ж,
в будущем обеих этих точек можно подобрать точку q2 е Ж
и т. д. Так как каждая точка qn, полученная таким способом,
лежит в прошлом последующей точки, в Ж можно построить
времениподобную кривую, проходящую через все точки последо-
вательности.
Для каждой точки р е Ж Ж И /+(р)— открытое и непустое
множество и оно должно содержать по меньшей мере одну из рп,
поскольку эти точки плотны. Но для каждого k точка рь лежит
в прошлом qh, поэтому сама р лежит в прошлом у. Отсюда ясно,
что каждая точка Ж лежит в прошлом у, и> поскольку у принад-
лежит открытому прошлому множеству Ж, должно иметь место
равенство Ж = /“(у). °
Обозначим через Л множество всех НП пространства (.Ж, g).
Тогда Л представляет все точки Л вместе с точками будущей
с-границы; аналогично, Л, множество всех НВ пространства
{Л, g), представляет Л вместе с прошлой с-границей. Причин-
ные отношения I, J и Е можно распространить на Л и Л сле-
дующим образом. О множествах (U, У сд Л будем говорить, что
<U^r (Г, Л} при <U с У,
°Н е 1~ (У, Л) при с= (q) для некоторой точки q Е У,
°U^E~ (У, Л) при (У, Л), но <U(£T {У, Л).
С учетом этих отношений НП-пространство Л является причин-
ным пространством [94]. Существует естественное инъективное
отображение Л->Л, которое переводит точку р^Л в
1~(р) е Л. Это отображение является изоморфизмом причинного
отношения J~, поскольку p<^J~(q) тогда и только тогда, когда
/- (/?) е J~ (I~ (q), Л). Причинное отношение 1~ сохраняется толь-
ко в одну сторону, т. е. р Г (q)^I~ (р) е Г (/- (q), Л). По-
добным же образом можно определить причинные отношения
на Л.
Теперь наша цель состоит в том, чтобы как-то составить из
Л 'л Л пространство Л*, которое имело бы вид Л U А, где А
можно было бы назвать границей пространства {Л, g). Для
этого нам нужен метод отождествления соответствующих НП и
НБ. Начнем с построения пространства Л^, представляющего
собой объединение Л и Л, в котором каждое СНБ отождествле-
но с соответствующим СНП. Другими словами, Л^ соответ-
ствует точкам Л вместе со всеми ГНП и ГНБ. Однако, как по-
6.9. Асимптотически простые пространства
245
казывает пример пространства де Ситтера 2-го рода, необходимо
еще и отождествление некоторых ГНП с определенными ГНБ.
Один способ такого построения состоит в наделении ЖЖ тополо-
гией и в последующем отождествлении некоторых точек ЛЖ та-
ким образом, чтобы эта топология стала хаусдорфовой.
Как было упомянуто в разд. 6.4, базисом такой топологии в
топологическом пространстве Ж могут служить множества вида
1+(р) П /“(д). К сожалению, подобный метод не может быть при-
менен для задания базиса топологии Ж#, поскольку в Ж* могут
быть точки, которые не принадлежат хронологическому прошло-
му какой-либо точки Ж*. Однако топологию Ж можно получить
также исходя из подбазиса, который состоит из множеств вида
1+ (р), /~(р), Ж —1+(р) и Ж — Г (р). Следуя этой аналогии,
Герок, Кронхеймер и Пенроуз показали, как можно задать топо-
логию на Я*. Для НБ Л е Ж определяем множества
и 0},
и
= и У = Г (Г) 1+ (Ж)
для НП .5? е Ж множества ^?int и Х?ехр определяются аналогично.
Открытые множества пространства Ж^ определяются тогда как
объединения и конечные пересечения множеств вида л-/'111, л/ех*‘,
^int и ^?ext. Множества л/"1* и ^?int являются аналогами мно-
жеств /+ (р) и Г (q) в Ж*. Если, в частности, Л = 1+ (р) и
Т — (р), то тогда и только тогда, когда q е 1+ (р).
Эти определения позволяют, однако, включить ГНП в ^lnt. Мно-
жества ^ext и Жх‘ являются аналогами Ж — 1+(р) и Ж — Г (q).
Окончательно мы получаем пространство Ж*, отождествив
в Ж* наименьшее число точек, необходимое для превращения Ж*
в хаусдорфово пространство. Точнее Ж* — фактор-пространство
Ж^1Н!г, где Rh — пересечение всех отношений эквивалентности
R <= ..Г:Х.;Г:-, для которых Ж^/R хаусдорфово. Пространство Ж*
обладает топологией, индуцированной из .<* и согласующейся
с топологией многообразия Ж на подмножестве Ж сдЯ*. Вообще
говоря, дифференцируемую структуру многообразия Ж нельзя
распространить на с-границу А, хотя можно это сделать для
части Д в частном случае, который будет описан в следующем
разделе.
6.9. Асимптотически простые пространства
При изучении таких конечных физических систем, как звезды,
приходится рассматривать асимптотически плоские простран-
ства, т. е. пространства, метрика которых стремится к мет-
рике пространства Минковского на больших расстояниях от
246
Гл. 6. П ричинная структура
рассматриваемой системы. Примерами пространств, имеющих
асимптотически плоские области, служат решения Шварцшильда,
Райсснера — Нордстрема и Керра. Как мы видели в гл. 5, кон-
формная структура изотропной бесконечности этих пространств
и пространства Минковского одинакова, что дало Пенроузу [123,
125, 128] основание использовать это обстоятельство в качестве
своего рода определения асимптотически плоского пространства.
Хотя Пенроуз не накладывал требования сильной причинности,
мы будем рассматривать только сильно причинные пространства.
Такое ограничение упрощает дело и не приводит к потере общ-
ности в тех ситуациях, которые мы хотим исследовать.
Ориентируемое во времени пространственно-ориентируемое
сильно причинное пространство (Ж, g) назовем асимптотически
простым, если существует пространство (Ж, g) и вложение
Q-.Ж-^-Ж, при котором Ж становится многообразием с гладким
краем дЖ в Ж и выполняются следующие условия:
1) на Ж существует гладкая (скажем, по меньшей мере клас-
са С3) функция й, такая, что на 9{Ж} функция Й положительна
и Q2g = 0*(g) [т. е. g конформна g на 9 (Ж)];
2) на дЖ й = 0 и dQ. 0;
3) каждая изотропная геодезическая в Ж имеет две конечные
точки на дЖ; _
Мы будем обозначать Ж (J дЖ = Ж.
На самом деле приведенное определение — несколько более
общее, чем нам необходимо: ему удовлетворяют и космологиче-
ские модели, например пространство де Ситтера 1-го рода. Что-
бы сузить его до асимптотически плоских пространств, мы будем
говорить, что пространство {Ж, g) асимптотически простое и пу-
стое, если в дополнение к условиям (1)—(3) оно удовлетворяет
еще и условию _
4) Rab — 0 на открытой окрестности дЖ в Ж. (Это условие
можно видоизменить так, чтобы вблизи дЖ разрешалось присут-
ствие электромагнитного излучения.)
Край дЖ можно считать находящимся на бесконечности в
том смысле, что в метрике g любой аффинный параметр на изо-
тропной геодезической в Ж достигает неограниченно большого
значения вблизи дЖ. Это происходит потому, что аффинный па-
раметр v в метрике g связан с аффинным параметром v в мет-
рике g соотношением do/da = Й-2. Поскольку на дЖ й = О, J da
расходится.
Из условий (2) и (4) следует, что край дЖ является изотроп-
ной гиперповерхностью. Действительно, тензор Риччи Rab для
метрики gab связан с Rab для gab равенством
Ra = tr2Rab - 2Й-1 (Q)|ac t + {- + Зй’2й|0Q|d}
6.9. Асимптотически простые пространства
247
где | означает ковариантное дифференцирование относительно gab.
Отсюда
R = Q-2/? - + ЗЙ_^|сЙ|й§с<г.
Поскольку метрика gab класса С3, то на дЖ, где Q = 0, /? при-
надлежит классу С1. Это означает, что QicQ]dgcd = 0. Но по
условию (2) й|с у= 0, т. е. Q\cgcd — изотропный вектор, а поверх-
ность дЖ (Q = 0) — изотропная гиперповерхность.
В случае пространства Минковского дЖ состоит из двух изо-
тропных поверхностей 3^+ и каждая из которых имеет топо-
логию /?* X S2. (Заметим, что ей не принадлежат точки i°, t+, i~,
так как вблизи этих точек конформная граница не является
гладким многообразием.) Мы покажем, что в действительности
для любого асимптотически простого и пустого пространства дЖ
имеет такую структуру.
Поскольку дЖ— изотропная поверхность, локально Ж лежит
в ее прошлом или будущем. Из этого видно, что дЖ должна со-
стоять из двух несвязных компонент 3^+ и З2-, на которых рас-
положены соответственно будущие и прошлые концы изотропных
геодезических в Ж. дЖ не может состоять более чем из двух
компонент, ибо тогда нашлась бы некоторая точка р ,= Ж, из ко-
торой одни направленные в будущее изотропные геодезические
шли бы к одной компоненте, а другие — к другой. Множества
изотропных направлений в р, ведущие к каждой из компонент,
были бы при этом открытыми, что невозможно ввиду связности
множества изотропных направлений в будущее в точке.
Теперь мы установим одно важное свойство рассматривае-
мых пространств.
Лемма 6.9.1
Асимптотически простое и пустое пространство (Ж, g) при-
чинно простое.
Пусть УЛ —• компактное множество Ж. Нужно показать, что
каждая изотропная геодезическая образующая поверхности
/(Ж’, Ж} имеет прошлый конец в УЛ. Допустим, что имеется та-
кая изотропная геодезическая, которая не имеет конца в УЛ.
Тогда у нее не может быть какого-либо конца в Ж и она должна
пересечь З2-, что невозможно.
Предложение 6.9.2
Асимптотически простое и пустое пространство (Ж, g) яв-
ляется глобально гиперболическим.
Доказательство аналогично доказательству предложения 6.6.7.
На Ж вводится элемент объема так, чтобы полный объем Ж по
этой мере был равен единице. Ввиду причинной простоты (Ж, g)
248
Гл. 6. Причинная структура
функции /^(р), представляющие собой объемы областей М(р),
непрерывны на Л. Поскольку на Л выполняется условие силь-
ной причинности, f+(p) будет убывать вдоль каждой направлен-
ной в будущее непространственноподобной кривой. Пусть %—
непродолжимая в будущее времениподобная кривая. Допустим,
что множество = ["] (р) — не пустое. Тогда должно бьт
р «= к
будущим множеством и изотропные, порождающие границу &
в Л, не могут иметь прошлых концов в Л. Таким образом, они
должны пересечь У~, что снова ведет к противоречию. Отсюда
видно, что f+(p) стремится к нулю, когда р устремляется в буду-
щее по А. Из этого следует, что каждая непродолжимая непро-
странственноподобная кривая пересекает поверхность
^{р :/+(р) =Х(р)}, которая поэтому является поверхностью
Коши для Л. □
Лемма 6.9.3
Пусть W— компактное множество асимптотического про-
стого и пустого пространства [Л, g). Тогда каждая из изотропных
геодезических образующих поверхности Д+ пересекает 7+(Ж, Л)
один раз; точка над J означает границу в Л.
Пусть реХ, где Л — одна из изотропных геодезических
образующих Д+. Тогда прошлое множество (в Л) J~ (р, Л)(]Л
должно быть замкнуто в Л, ибо каждая из изотропных геоде-
зических образующих границы этого множества, должна иметь
будущую конечную точку в в точке р. Поскольку на Л
выполняется условие сильной причинности, Л — Г~(р, Л) будет
непустым. Теперь предположим, что Хе /+(Ж, Л). Тогда прош-
лое множество Р| (j~ (р, Ж) П Л} должно быть непустым. Од-
р «= Л
нако это невозможно из-за того, что изотропные образующие
границы этого множества пересекли бы при этом $+. Теперь
допустим обратное, что X не пересекает J+ (7f, Л). Тогда
Л — [J (Л (р, Л} П Л) будет непустым. Но это снова ведет
реЛ
к противоречию, потому что изотропные образующие границы
прошлого множества U (/~ (р, Л} П X) пересекли бы при
этом . р1=К □
Следствие
Поверхность &+ топологически совпадает с /?’ X
Х(/+(Ж, дЛ).
Теперь мы покажем, что 3± и Л обладают такой же топо-
логией, как и в случае пространства Минковского.
6 9. Асимптотически простые пространства
249
Предложение 6.9.4 (Герок [59])
В асимптотически простом и пустом пространстве (Ж, g)
поверхности Д+ и 3~ топологически эквивалентны /?' X S2,
а Ж топологически эквивалентно /Д.
Рассмотрим множество N всех изотропных геодезических к Ж.
Поскольку они все пересекают поверхность Коши 5$?, локальные
координаты на W можно задать с помощью направлений этих
геодезических на 36 и локальных координат из точек пересечения
с 36. Этим мы превращаем N в расслоенное пространство на-
правлений на 36 со слоем S2. Однако каждая геодезическая пе-
ресекает также 3+. Поэтому N является расслоенным простран-
ством и над 3+. В этом случае слоем является S2 без одной
точки, которая соответствует изотропной геодезической образую-
щей 3+, не принадлежащей Ж. Другими словами, слоем являет-
ся R2. Следовательно, пространство N топологически эквивалент-
но 3+ X R2- Однако поверхность 3+ эквивалентна Rl X
X ЛЗГ, Ж} П дЖу. Это согласуется с тем, что П ~ 36 /. S2
лишь при условии, что 36 л: R2 и 3+ & Rl X S2. □
Как показал Пенроуз [125], из этого результата следует, что
тензор Вейля для метрики g равен нулю на 3+ и 3~. В качестве
объяснения можно сказать, что компоненты тензора Вейля для
метрики g вырождаются, т. е. вблизи 3+ и 3~ они убывают как
различные степени аффинного параметра на изотропной геодези-
ческой. Далее, в работах [114, 122] были получены в виде инте-
гралов по 3+ законы сохранения для энергии-импульса, как бы
измеренных с поверхности 3+.
Изотропные поверхности 3+ и 3~ составляют почти всю
с-границу А (см. определение в предыдущем разделе) простран-
ства (Ж, g). Чтобы убедиться в этом, заметим, во-первых, что
любая точка р е 3+ задает ГНП 1~~ (р, ЖУ Г\ Ж. Допустим, что
X,— непродолжимая в будущее кривая в Ж. Если будущей ко-
нечной точкой Г является р е 3+, то ГНП 1~(}.у совпадает с
ГНП, которое определяется точкой р. Если у кривой л нет конеч-
ной точки в будущем на 3+, то Ж — /~(Х) должно быть пустым,
так как в противном случае изотропные геодезические образую-
щие пересекали бы 3\ что невозможно: л не пересекает
3+. Таким образом, на каждую точку из 3+ приходится одно
ГНП, и еще одно ГНП, связанное с i+, есть само многообразие Ж\
других ГНП нет. Аналогично, множество всех ГНБ составлено
теми ГНБ, которые соответствуют каждой точке 3~ и одним
ГНБ, соответствующим г-, которое снова совпадает с самим Ж.
Теперь требуется проверить, не отождествляем ли мы какие-
нибудь ГНП или ГНБ, т. е. установить, что Ж* хаусдорфово.
Ясно, что никакие два ГНП или ГНБ, соответствующие 3+ или
250
Гл. 6. Причинная структура
3~, не являются неразделимыми по Хаусдорфу. Если р е 3+, то
можно найти такую q Л, что р ф I+(q, Л). Тогда (/+ (q, Л))ех1
является окрестностью в Л* для ГНП 1~ (р, Л) Л Л, а
(/+(<?,.<) )int будет непересекающейся окрестностью ГНП, соот-
ветствующего i+. Таким образом, i+ отделимо по Хаусдорфу от
любой точки поверхности У+. Аналогично, i~ отделимо по Хаус-
дорфу от любой точки 3'~. Таким образом, с-граница любого
асимптотически простого и пустого пространства (Л, g) такая
же, как у пространства Минковского, т. е. состоит из 3+, и
двух точек i+, i~.
К числу асимптотически простых и пустых пространств отно-
сятся пространство Минковского и асимптотически плоские
пространства, в которых есть только ограниченные объекты, на-
пример звезды, не испытывающие гравитационного коллапса. Од-
нако решения Шварцшильда, Райсснера — Нордстрема или Кер-
ра не входят в этот класс, потому что в них имеются изотропные
геодезические, у которых конечные точки не лежат на <7+ или.7~.
Тем не менее у этих пространств имеются асимптотически пло-
ские области, подобные тем, которые существуют у асимптоти-
чески плоских и простых пространств. Из этого видно, что сле-
дует ввести еще понятие слабо асимптотически плоского и пу-
стого пространства (Л, g) как пространства, для которого най-
дутся асимптотические простое и пустое пространство (Л', g')
и окрестность °U' края дЛ’ многообразия Л’, такие, что °И' Л Л'
изометрично некоторому открытому множеству Л с: Л. Под это
определение подходят все упомянутые выше случаи. В решениях
Райсснера — Нордстрема и Керра существуют бесконечные по-
следовательности из асимптотически плоских областей Л, кото-
рые изометричны окрестностям <№ асимптотически простых и пу-
стых пространств. Таким образом, в них изотропные бесконеч-
ности образуют бесконечные последовательности. Однако мы
будем рассматривать в этих пространствах только одну асимпто-
тически плоскую область. Тогда можно считать {Л, g) конформ-
но-вложенным в пространство {Л, g) так, чтобы окрестность °11
края дЛ в Л была изометрична °W. Край дЛ состоит только из
пары изотропных поверхностей 3+ и 3~.
Обсуждение слабо асимптотически простых и пустых про-
странств будет продолжено в разд. 9.2 и 9.3.
Глава 7
Задача Коши в общей теории
относительности
В этой главе вкратце рассмотрена задача Коши в общей тео-
рии относительности. Мы покажем, что при задании определен-
ных данных на пространственноподобной 3-поверхности ЗР суще-
ствует единственная максимальная область Коши £>+(^) и что
метрика на множестве °ll cz £)+(£?) зависит только от начальных
данных на П 3?. Мы установим также, что эта зависимость
непрерывна, если °И обладает компактным замыканием в Д+(^').
Обсуждение этого вопроса включено сюда как потому, что он
интересен сам по себе, так и потому, что при этом используются
некоторые результаты предыдущей главы, и, наконец, для того
чтобы показать, что уравнения поля Эйнштейна действительно
удовлетворяют постулату (а) разд. 3.2, согласно которому сиг-
нал может быть передан из одной точки в другую, только когда
эти точки можно соединить непространственноподобной кривой.
Однако в последующих трех главах результаты данной главы
фактически не используются, и поэтому читатель, больше инте-
ресующийся сингулярностями, может ее пропустить.
В разд. 7.1 обсуждается специфика рассматриваемой задачи
и дана ее точная формулировка. Для того чтобы связь между
тензором Риччи и метрикой, установленную в области покрытой
одной координатной системой, представить в форме, справедли-
вой на всем многообразии, в разд. 7.2 вводится глобальная фо-
новая метрика g. На ковариантные производные физической мет-
рики g относительно фоновой метрики g мы налагаем четыре
калибровочных условия. При этом исключаются четыре степени
свободы, соответствующие возможности диффеоморфизмов ре-
шений уравнений Эйнштейна, и мы приходим к приведенным ги-
перболическим уравнениям Эйнштейна второго порядка для мет-
рики g относительно фоновой метрики g. В силу уравнений со-
хранения эти калибровочные условия выполняются во все
моменты времени, если они и их первые производные удовлетво-
ряются в начальный момент.
В разд. 7.3 будет показано, что существенную часть началь-
ных данных для g на трехмерном многообразии д’ можно выра-
зить через два трехмерных тензорных поля /гаЬ, /аЬ на ЗР. При
этом трехмерное многообразие ЗР вкладывается в четырехмерное
многообразие Ж, а метрика g определяется на ЗР так, что hab
252
Гл. 7. Задача Коши в общей теории относительности
и %аЬ становятся соответственно первой и второй фундаменталь-
ными формами на 9 в метрике g. Это можно сделать так, чтобы
на 9 выполнялись калибровочные соотношения. В разд. 7.4 мы
установим некоторые основные неравенства для гиперболических
уравнений второго порядка. Они связывают интегралы от квад-
ратичных выражений по первым производным решений с началь-
ными данными для этих решений. В разд. 7.5 мы докажем суще-
ствование и единственность решений приведенных уравнений
Эйнштейна с Та$ = 0 (пустое пространство) в виде малых воз-
мущений какого-либо заданного решения в пустом пространстве.
После этого существование и единственность локальных реше-
ний для произвольных начальных данных доказываются путем
деления начальной гиперповерхности на малые почти плоские
области и последующего соединения полученных решений.
В разд. 7.6 будет показано, что при фиксированных началь-
ных данных существует единственное максимальное решение в
пустом пространстве и что его зависимость от начальных данных
в определенном смысле непрерывна. Наконец, в разд. 7.7 мы на-
метим путь для распространения этих результатов на решения
при наличии материи.
7.1. Характер задачи
Задача Коши для гравитационного поля в некоторых важных
аспектах отличается от той же задачи для других физических
полей.
1. Уравнения Эйнштейна нелинейны. Правда, в этом отноше-
нии они не слишком сильно отличаются от других полей: хотя
электромагнитное, скалярное и прочие поля в заданном про-
странстве-времени сами по себе подчиняются линейным уравне-
ниям, они образуют нелинейную систему при учете их взаимо-
действий. Отличительным свойством гравитационного поля яв-
ляется то, что оно представляет собой поле с самодействием:
оно нелинейно даже в отсутствие других полей. Именно поэтому
гравитационное поле характеризует пространство-время, в кото-
ром оно распространяется. Для получения решений нелинейных
уравнений обычно пользуются методом последовательных при-
ближений такими линейными уравнениями, относительно реше-
ний которых известно, что они сходятся к решению нелинейного
уравнения в определенной окрестности начальной поверхности.
2. Две метрики gi и ga на многообразии Л физически экви-
валентны, если существует диффеоморфизм ф-.Л -*Л, который
переводит gi и gz — £г); ясно, что gi удовлетворяет урав-
нениям поля, если и только если им удовлетворяет g2. Поэтому
решения уравнений поля могут быть единственны лишь с точ-
ностью до диффеоморфизма. Для того чтобы из этого класса
7.2. Приведенные уравнения Эйнштейна
253
эквивалентности метрик выделить определенный член, описы-
вающий пространство-время, вводят фиксированную «фоновую»
метрику и накладывают четыре «калибровочных условия» на ко-
вариантные производные физической метрики относительно фо-
новой метрики. Эти условия устраняют четыре степени свободы,
соответствующие указанным диффеоморфизмам, и обеспечивают
единственное решение для компонент метрики. Все это аналогич-
но наложению условий Лоренца на электромагнитное поле для
устранения свободы в выборе калибровки.
3. Поскольку метрика определяет структуру пространства-
времени, мы не знаем заранее, какова область Коши начальной
поверхности, а следовательно, не знаем и области, в которой
должно быть определено решение. Дается только трехмерное
многообразие с некоторыми начальными данными ы на нем и
требуется найти четырехмерное многообразие Ж, вложение
-> Ж и метрику g на Ж, удовлетворяющую уравнениям Эйн-
штейна, начальным данным на 0(^) и требованию, чтобы вло-
жение 0(5?) было поверхностью Коши в Ж. Мы будем говорить,
что {Ж, 0, g), или просто Ж, есть развитие пары (9>, и). Другое
развитие (Ж', 0Z, g') той же пары (<?’, ®) назовем расширением
развития Ж, если существует диффеоморфизм а многообразия
Ж на Ж', который оставляет образ д’ точечно неподвижным и
переводит g' в g (т. е. ©-‘а-1©' — id на 9>, и a*g' = g). Мы пока-
жем, что при выполнении на определенных уравнений связи
развития (^, и) существуют и, далее, что существует развитие,
которое максимально в том смысле, что является расширением
любого другого развития пары (5Ф и). Заметим, при такой фор-
мулировке задачи Коши учтена возможность производить диф-
феоморфизмы, поскольку всякое развитие представляет собой
расширение любого своего диффеоморфизма, сохраняющего не-
подвижными точки образа поверхности У.
7.2. Приведенные уравнения Эйнштейна
В гл. 2 тензор Риччи был выражен через частные производ-
ные компонент метрического тензора по координатам. Для целей
этой главы удобно получить выражение, применимое во всем
многообразии Ж, а не только по отдельности в каждой коорди-
натной окрестности. Для этой цели введем наряду с физической
метрикой g фоновую метрику g. При двух метриках требуется
осторожность в обращении с ковариантными и контравариант-
ными индексами. (Во избежание путаницы мы откажемся на
время от обычного правила поднятия и опускания индексов.)
Ковариантные и контравариантпые формы g и g связаны соот-
ношением
gabgbc = = gabgbc-
(7.1)
254
Гл 7. Задача Коши в общей теории относительности
Удобно принять контравариантную форму метрики gab за основу
и считать, что ковариантная форма выводится из (7.1). Исполь-
зуя альтернирующий тензор f|a&ccz, определенный фоновой метри-
кой, можно представить связь между gab и gab в следующем яв-
ном виде:
gab = Scdgelg‘' (det g) f]aCeiflbdfj, (7.2)
где
(det g)-1 = ^gabgedgefgl%cerfbdff
есть определитель из компонент gab в базисе, ортонормированием
относительно метрики g.
Разность связности Г, определяемой метрикой g, и связ-
ности Г, определяемой g, является тензором и может быть выра-
жена через ковариантную производную g относительно Г (ср.
с разд. 3.3):
= гд - г д = 4 г'Д (g„,gc,g“ - - г,ЛД (ТЗ)
где вертикальной чертой обозначена ковариантная производная
относительно Г, а символом 6 — разность величин определенных
относительно gag. Тогда из (2.20) следует, что
t>Rab = 6rdabid-dYdad\b + ^rdabbrede -№daef>rebd. (7.4)
Отсюда
6 1gab*) = gaigbiMa + 2 tgiiagb)1Rii - &gai bgblKii ~
-1 bgabR - j gab (^‘Rii + gil =
=4 g11 t>gab}il - g^ +4 gab (ф1; - gcdgii ^1;/)+
+ (члены, содержащие ^gcd^ и (7.5)
Ф6 g\ - Tgbc£d£de\c = (det ((det g) Sbc\c =
= (detg)-1^c|c (7.6)
^c-(detg)6gbc.
Наш план состоит в следующем. Выберем подходящую фоно-
вую метрику g и представим уравнения Эйнштейна в виде
Rab - 4 Rgab = 6 (Rab - 4 Rgab) + Rab - 4 SabR = 8nTab. (7.7)
7.2. Приведенные уравнения Эйнштейна
255
Это уравнение будем рассматривать как нелинейное дифферен-
циальное уравнение второго порядка для определения g через
его значения и значения его первых производных на некоторой
начальной поверхности. Разумеется, чтобы эта система была
полна, нужно задать уравнения, которым подчиняются физиче-
ские поля, входящие в тензор энергии-импульса ТаЬ. Однако
даже тогда, когда это сделано, мы еще не имеем системы, кото-
рая однозначно определяет развитие во времени через началь-
ные данные. Причина этого уже упоминалась: решения уравне-
ний Эйнштейна могут быть единственны лишь с точностью до
диффеоморфизма. Для получения определенного решения этот
произвол устраняется наложением четырех калибровочных усло-
вий на ковариантные производные g относительно фоновой мет-
рики g. Мы будем пользоваться так называемыми «гармониче-
скими» условиями:
грь = фьус = О,
которые аналогичны калибровочному условию Лоренца Лг;, = 0
в электродинамике. Вместе с этим условием получим приведен-
ные уравнения Эйнштейна
gi!i>abltj + (члены с и фаЬ)= 16лГ& — 2Rab + gabR. (7.8)
Мы обозначим левую часть уравнения (7.8) через Д^сД^), где
ЕаЪcd — оператор Эйнштейна. Таким образом, при подходящем
выборе тензора энергии-импульса мы получаем гиперболические
уравнения второго порядка и в разд. 7.5 продемонстрируем су-
ществование и единственность его решений. Но до этого нужно
еще проверить совместность гармонических условий с уравне-
ниями Эйнштейна. Поясним это: мы получили (7.8) из уравне-
ний Эйнштейна, положив фЬа\с= 0. Теперь мы должны убедить-
ся, что решение, к которому приводит (7.8), действительно обла-
дает таким свойством. Для этого продифференцируем (7.8) и
свернем. Получим уравнение вида
+ Bbi^ + CcV = 16ЛГ6;а, (7.9)
где точкой с запятой обозначена производная относительно g,
а тензоры Bcbi и Ссь зависят от gab, Rabcd, gab и gab\c- Уравнение
(7.9) можно рассматривать как линейное гиперболическое урав-
нение второго порядка для фь. Тогда, поскольку правая часть
обращается в нуль, можно воспользоваться теоремой единствен-
ности решения для таких уравнений (предложение 7.4.5) и пока-
зать, что фд = 0 всюду, если значения этой величины и ее пер-
вых производных равны нулю на начальной поверхности.
В следующем разделе мы увидим, что подходящим диффео-
морфизмом начальные данные для -фь можно обратить в нуль.
256
Гл. 7. Задача Коши в общей теории относительности
Остается еще показать, что единственное решение, полученное
наложением гармонического калибровочного условия, связано
диффеоморфизмом с любым другим решением уравнений Эйн-
штейна с теми же начальными данными. Это будет сделано в
разд. 7.4 путем специального выбора фоновой метрики.
7.3. Начальные данные
Поскольку (7.8) является гиперболической системой второго
порядка, может показаться, что для получения решения следует
задать значения gab и gab\cuc на начальной гиперповерхности
0(5?), где ис — некоторое векторное поле, касательное к 0(^).
Однако эти 20 компонент не все существенны или независимы;
при произвольном изменении некоторых из них решение самое
большее претерпевает диффеоморфизм, в то же время другие
должны удовлетворять определенным условиям совместности.
Рассмотрим диффеоморфизм р:.У7->.У7, оставляющий 0(^)
точечно неподвижным. Он индуцирует отображение р», перево-
дящее gab в точке р е 0(^) в новый тензор p*gab в той же точке.
Если вектор па е Т*р ортогонален к 0(^) [т. е. naVa = 0 для
любого VrieTJ: касательного к 0(^)] и нормирован так, что
nagabnb = —1, то подходящим выбором ц вектор na\ugab можно
сделать равным любому не касательному к б(^) вектору в точ-
ке р. Следовательно, компоненты nagab не существенны. С дру-
гой стороны, поскольку р оставляет 0 (д’) точечно неподвиж-
ным, метрика hab — Q*gab, индуцированная на д, будет оста-
ваться неизменной. Поэтому только та часть g, которая лежит
на 0(^), необходима для получения решения. Остальные компо-
ненты nagab можно задавать произвольно; решение при этом
самое большее претерпит диффеоморфизм. Чтобы прийти к этому
выводу иным путем, вспомним, что мы сформулировали задачу
Коши для начальных данных, определенных на абстрактном
трехмерном многообразии д, и затем искали вложение его в не-
которое четырехмерное многобразие. На самой поверхности д
нельзя задать четырехмерное тензорное поле вроде g, а можно
ввести только трехмерную метрику h, которую мы будем считать
положительно определенной. Контравариантная и ковариантная
компоненты h связаны соотношением
habhbc = bac, (7.10)
где теперь б“с — трехмерный тензор на д’. Вложение 0 преобра-
зует hab в контравариантное тензорное поле O../iab на Q(d), обла-
дающее свойством
naQJi“b = 0.
(7.11)
7.3. Начальные данные
257
Ввиду произвольности nagab мы теперь можем на 0 (9') задать
тензорное поле g:
gab = QJiab — uaub, (7.12)
где ua — произвольное, не касательное к 9 (9?) и всюду отличное
от нуля векторное поле на 0 (^). Определяя из (7.1), имеем
hai> = 8*gab, nagab = — nauaub, gabuaub = —1. (7.13)
Отсюда hab — метрика, индуцированная на 9> метрикой g,
а иа — единичный вектор, ортогональный к 0(^) в метрике g.
Положение с первыми производными gab\c uc аналогичное:
tiagab\c uc можно привести соответствующим диффеоморфизмом
к любым наперед заданным значениям. Однако здесь имеется
дополнительная сложность, состоящая в том, что gab\c зависит
не только от g, ио и от фоновой метрики g. Чтобы выразить су-
щественную часть первой производной g только через тензорные
поля, заданные на 9\ мы поступим следующим образом. Введем
на 9? симметричное контравариантное тензорное поле %аЬ. При
вложении отображается в тензорное поле 9*%аЬ на 0(^). По-
требуем, чтобы Од"'-' было равно второй фундаментальной фор-
ме (см. разд. 2.7) подмногообразия 0(^) в метрике g. Тогда по-
лучим
e^ = 9^a4^(«Wd =
= 0Лас9ЛМ ^egec\d - №fcdusgefr (7.14)
Используя (7.3), находим
0Дйй = 4 ОЛЙС0ЛМ (- gcigdsgi!^k + gbiu\c + gciu\by (7.15)
Обращением этого равенства можно получить выражение для
ga\ctic через Од"6:
~ga\ctic^ - 0да6 + ^ha%hbdgi(culw + u^aWb\ (7.16)
где Wb— некоторое векторное поле на Подходящим диф-
феоморфизмом ц ему можно придать любое нужное значение.
Тензорные поля hab и %аЬ нельзя задать на 9? совершенно не-
зависимо, поскольку свертка уравнений Эйнштейна (7.7) с па
дает четыре уравнения, которые не содержат gab]cducud, т. е. вто-
рых производных g, имеющих ненулевые проекции на нормаль
к 0(^). Таким образом, должны существовать четыре связи ме-
жду gab, gab\ciic и паТаЬ. Используя (2.36) и (2.35), их можно
9 Заказ 381
258
Гл 7. Задача Коши в общей теории относительности
представить в виде уравнений на трехмерном многообразии 9>:
lC\dhce-^d.ehcd = ^(Tdeud\ (7.17)
| {R' + (Х%)2 - f’fkJy = 8л0* (Tdeudue), (7.18)
где двойной вертикальной чертой || обозначена ковариантная
производная на относительно метрики h, a R' есть скалярная
кривизна, полученная из h.
Таким образом, данные w на S?, необходимые для получения
решения, состоят из начальных данных для материальных полей
(например, в случае скалярного поля ф они состояли бы из двух
функций на —значения ф и ее нормальной производной) и
двух тензорных полей hab и %аЬ на S?, которые подчиняются урав-
нениям связи (7.17), (7.18). Последние представляют собой эл-
липтические уравнения на поверхности д’ и накладывают четыре
связи на 12 независимых компонент (ЛаЬ, %аЬ). При этих усло-
виях можно показать, что восемь из этих компонент задаются
независимо, а оставшиеся четыре находятся решением уравне-
ний связи (см., например, [17]). Пару (17, со), удовлетворяющую
этим требованиям, будем называть комплектом начальных дан-
ных. Следующим нашим шагом будет вложение в подходящее
четырехмерное многообразие Л с метрикой g и задание gab на
0(17) соотношением (7.12) при некотором выборе вектора иа.
Положим иа = gabnb. Тогда иа будет ортогонален к 0(^) в обеих
метриках: g и g. Воспользуемся также свободой выбора Wa в
выражении gab[cuc из (7.16) для того, чтобы обратить фь в нуль
на 0(^). Это приведет к требованию
wb=- gb\dgcewd+4 gcd^^b +
+ <7-19)
[Заметим, что все производные в (7.19) касательны к 0(17), как
и требуется тем обстоятельством, что рассматриваемые поля
должны быть заданы на одной только поверхности 0(^).] Для
выполнения всюду в Л условия фь — О нужно, кроме того, чтобы
вектор фь[с ис обращался в нуль на 0(17). Но это сразу следует
из уравнений связи, если на 0(17) удовлетворяются приведенные
уравнения Эйнштейна (7.8). Следовательно, мы можем присту-
пать к решению уравнений (7.8) как нелинейной гиперболиче-
ской системы второго порядка на многообразии Л с метрикой g.
[Заметим, что для фЪа мы имеем 10 уравнений; при доказа-
тельстве существования решений этих 10 уравнений мы не будем
делить их на систему уравнений связи и систему уравнений, опи-
сывающих развитие во времени, и, следовательно, не возникает
вопроса об удовлетворении уравнений связи вне 0(^).]
7.4 Гиперболические уравнения
259
7.4. Гиперболические уравнения второго порядка
В этом разделе мы воспроизведем некоторые результаты от-
носительно гиперболических уравнений второго порядка, приве-
денные в [40]. При этом мы обобщим их так, чтобы они были
применимы ко всему многообразию, а не только к одной коор-
динатной окрестности. Эти результаты будут использованы в по-
следующих разделах для доказательства существования и един-
ственности развитий комплекта начальных данных (^, со).
Введем сначала ряд определений. Мы будем пользоваться
прописными латинскими буквами для обозначения совокупностей
контравариантных или ковариантных индексов; так, тензор типа
(г, s) будем записывать как Ктт, а число индексов, которые
представляют собирательный индекс /, обозначим через |7|, т. е.
|/| = г. Введем на Ж положительно определенную метрику еаъ и
ец = еаЬесй ... epq, erJ = e^ecd . . .
г сомножителей г сомножителей
где 111 = | J | — г. Затем определим | K.’j I (или просто | К I), норму
тензора К.1 j : | К1 j I = {К1 jKLMeiL.eJM}'l2> где П°Д повторяющимися
собирательными индексами подразумевается свертка по всем
индексам, которые они представляют. Через | DmKlj | (или просто
|DmK I) будем обозначать | К1 til I, где \L\-m, а черта | озна-
чает, как и прежде, ковариантное дифференцирование относи-
тельно g.
Пусть Л9 — некоторое вложенное подмногообразие с компакт-
ным замыканием в Ж. Тогда || К7./, Л9 ||„г определяется как
Г m ]’/2
] £ $(|ZWy|)2da[ ,
х р = о eV '
где do — объемный элемент на Л9, индуцированный метрикой е.
Зададим еще ЦК, Л’Цт в виде такого же выражения, но с произ-
водными, взятыми в касательном к Л9 направлении. Очевидно,
ПК, лх>iiк, л9!.
Тогда векторные пространства тензорных полей К1.) типа (г, s)
являются по определению пространствами Соболева
если их значения и значения их производных (в смысле обоб-
щенных функций) определены почти всюду на Л9 (т. е. всюду,
исключая, быть может, множество меры нуль; в оставшейся части
этого раздела почти всюду утверждения следует понимать
в смысле «почти всюду») и если || К.1 j, Л9 Ik — конечная величина.
Пространство Соболева с нормой || , Л9 Ik является банаховым
9*
260
Гл. 7. Задача Коши в общей теории относительности
пространством, в котором тензорные Ст-поля типа (г, s) обра-
зуют плотное подмножество. Если е' — другая непрерывная по-
ложительно определенная метрика на Ж, то найдутся такие
положительные постоянные Ct и С2, что
на Л
и
Сх II K'j, Jflm < II K’j, ЛЧ'т < с2 II K‘j,
Следовательно, || , Л9!^ будет эквивалентной нормой. Анало-
гично другая фоновая Ст-метрика g' будет давать эквивалент-
ную норму. В действительности из двух лемм, приведенных ниже,
следует, что для g" е Wm (Л9) и размерности Л9, меньшей 2m,
норма, полученная с помощью ковариантных производных отно-
сительно g", снова эквивалентна исходной.
Теперь мы приведем три фундаментальных результата для
пространств Соболева. Их доказательства можно получить,
пользуясь книгой Соболева [159]. При этом потребуются слабые
ограничения на вид Л9. Будет достаточно потребовать, чтобы
в каждой точке р края дЛ’ можно было вложить в Л5 поло-
вину «-мерного конуса с вершиной в р, где п — размерность Jf.
Это требование выполняется, в частности, когда край д№
гладкий.
Лемма 7.4.1
Существует положительная постоянная (зависящая от Л9,
е и g), такая, что | К IPi II К, N\\m на Л9 для любого
е И’’'’1''(Л’) с 2т > п, где « — размерность Л9.
Если KJ j (.№) и 2т > п, то отсюда и из того, что век-
торное пространство всех непрерывных полей Krj на Л9 с нормой
sup|КI является банаховым пространством, следует непрерыв-
ность К,1 j на А°. Аналогично, если К1j eWm+p, то будет
Ср-полем на Л9.
Лемма 7.4.2
Существует положительная постоянная Р2 (зависящая от Л9,
е и g), такая, что для любых полей Ipq^- Wm(AP) с 4т^п
выполняется неравенство
IIAWq, л Но < Р2II К, Л9!Ы1 L, N\\m.
Если га ^4 и 2m > га, то из этой и предыдущей лемм сле-
дует, что для любых двух полей K!j, LpQ^Wm(Л9) их произ-
ведение K‘jLpq также принадлежит Wm{AP).
7.4. Гиперболические уравнения
261
Лемма 7.4.3
Если N' есть (п—1)-мерное подмногообразие, гладко вло-
женное в Л', то существует положительная постоянная Р3 (за-
висящая от Л, Л', е и g), такая, что для любого поля К1 j е
^1Уш+1(Л'’) выполняется неравенство
ПК, л’щ,.
Мы докажем существование и единственность развитий ком-
плекта (^, ю), когда hab е 1У4+“ (<?) и %ab W3+a (IP), где о —
любая неотрицательная целая. [Если поверхность ЗР не компакт-
на, то /zab е Лт(Л) означает, что hab е Лт(Л) при каком-либо
открытом подмножестве Л с & с компактным замыканием.] Для
этого достаточно, чтобы на 3? hab принадлежала классу С4+а и
ХаЬ — классу С3+а; необходимым условием, согласно лемме 7.4.1,
является принадлежность hab классу С24'1 и %аЬ — классу С{+а.
Решение для gab, которое при этом получается, будет принадле-
жать пространству IT4+a(J^) для каждой гладкой простран-
ственноподобной поверхности Л и, следовательно, производные
до (2Д- а) -го порядка включительно будут ограничены, т. е. gab
будет класса С(2~а)~ на ,Л.
Эти условия дифференцируемости можно ослабить для слу-
чаев, подобных ударным волнам, когда решение на вполне «хо-
роших» гиперповерхностях уже не принадлежит пространству IT4
(см. [29, 83, 120, 127]). Однако не найдено доказательства тео-
ремы существования и единственности для общего случая, когда
решение не принадлежит IF4. Условие принадлежности решения
к классу IT4 уже само по себе является улучшением результатов
предшествующих работ [29], и тем не менее оно несколько силь-
нее, чем хотелось бы, ибо для определения уравнений Эйнштей-
на в смысле обобщенных функций достаточно непрерывности
метрики и локальной квадратичной интегрируемости ее обобщен-
ных производных (т. е. при g класса С° и принадлежащем l^1).
С другой стороны, всякое условие принадлежности классу УЛ
при р < 4 не гарантирует единственности геодезических, а при
р < 3 — их существования. Сами мы стоим на той точке зрения,
что эти различия в условиях дифференцируемости не существен-
ны, поскольку, как было объяснено в разд. 3.1, для модели про-
странства-времени можно принять, что метрика принадлежит
классу Сх.
Чтобы доказать существование и единственность развитий,
мы установим сейчас ряд фундаментальных неравенств (леммы
7.4.4 и 7.4.6) для гиперболических уравнений второго порядка,
используя метод, подобный доказательству теорем сохранения в
разд. 4.3.
262 Гл. 7. Задача Коши в общей теории относительности
Рассмотрим многообразие Л вида X X Х‘, где <2^ —трех-
мерное многообразие. Пусть 2/ — открытое множество Л с ком-
пактным замыканием, у которого имеется граница 62/ и которое
пересекает X (0), причем через (i) обозначена поверхность
Ув X {t}, Пусть 2/+ и 2/(Л) —те части 2/, для которых
Рис. 48. 2/ — открытое множество с компактным замыканием в многообра-
зии Л — <№ X К}- °U+ — область множества °U, для которой t Дз 0, и °И (Г) —
область °U между t = 0 и t — t' > 0.
соответственно /^0 и (рис. 48). Пусть g — фоновая
С2_-метрика на 2/+, а е — положительно определенная ^--ме-
трика. Рассмотрим тензорные поля KJ j, подчиняющиеся гипер-
болическому уравнению второго порядка вида
L (X) AabRl1[ab + B^qjK^ + ClllQJKQP = Frit (7.20)
где A — лоренцева метрика на 2/+ (т. е. симметричное тензорное
поле сигнатуры +2), В, С и F — тензорные поля типов, обозна-
ченных их индексами, и вертикальная черта означает ковариант-
ное дифференцирование относительно метрики g.
7.4. Гиперболические уравнения
263
Лемма 7.4.4
Если
1) d(U{\aU+ ахронально относительно А,
2) существует некоторая постоянная Q, > 0, для которой на “2/+
Aabttat[b<-Q{
и
AabWaWb>Q{eabWaWb
для любой 1-формы W, удовлетворяющей равенству Aabt\aWb = О,
3) существует некоторая постоянная Q2, такая, что на °U+
|A|<Q2, |DA|<Q2j |B|<q2, |C|<Q2,
то найдется некоторая положительная постоянная Р4 (зависящая
от (U, е, g, Qi и Q2), такая, что для любого решения К} } урав-
нения (7.20) справедливо неравенство
|| К, ж (0 Л 2/+ 111 < л {II К, Ж (0) л <U+ II, -ф || F, <2/ (/)1|0}.
Для тензорного поля К1 j по аналогии с тензором энергии-им-
пульса для скалярного поля единичной массы (разд. 3.2) обра-
зуем «тензор энергии» Sab:
Sab = _ 1 AabAcd^ a^k'jK.Pq} eJQe.IP.
(7.21)
Тензор Sab подчиняется условию энергодоминантности (разд. 4.3)
относительно метрики А (иными словами, если вектор Wa вре-
мениподобен относительно А, то SabWaWb 0, а вектор SabWa
непространственноподобен относительно А). Более того, в силу
условий (2) и (3) будут существовать такие положительные по-
стоянные Q3 и Q4, что
Q3 (I К I2 + I DK I2) < Sabtlat}b < Q4 (| К I2 + I DK I2). (7.22)
Теперь мы применим лемму 4.3.1 к Sab, выбрав в качестве <2/+
компактную область £7* и пользуясь объемным элементом dv
и ковариантным дифференцированием, которые определяются
метрикой g:
J s%do6< J so6/|addd +
^(/)f|^4- ^(0)0^4-
t
+ U 5 (T’S% + Sa&la)daJ df, (7.23)
0 I Э€(П П 27+ J
где P — положительная постоянная, не зависящая от Sab.
(В первом слагаемом правой части по сравнению с леммой 4.3.1
264
Г л. 7. Задача Коши в общей теории относительности
изменен знак из-за того, что элемент dad поверхности 2$(t)
взят с той же ориентацией, что и t\b, т. е. dd;, = t\b da, где da-
положительно определенная мера на 5®(Z).) Ввиду непрерыв-
ности eng найдутся такие положительные постоянные Qs и Q6,
что на будет выполняться неравенство
Q5da^ da $4Q6 da, (7.24)
где da —элемент площади на 2^(Z), индуцированный метрикой е.
Таким образом, в силу (7.22) и (7.23) существует некоторая по-
стоянная Q7, такая, что
ЦК, ^(0n^+lli2<Q7{llK, ^(0)(W+lli24-
+ J || К, Ж (Z') П 114 dZ' 4- J {Sa\bt\a da) dZ' |. (7.25)
О О '
Из (7.20) следует, что
= А^К1 j\cFpqeJQeip + члены, квадратичные по K'j и
Kpq\c, с коэффициентами, содержащими Acd, Acd\e,
Rcdef, BcP,QJ и CPIQJ. (7.26)
Поскольку все коэффициенты на °И+ ограничены, существует
такая постоянная Q8, что
Sa\bt\a < Q8 {I F |2 + 1 к I2 + I DK I2}. (7.27)
Следовательно, найдется постоянная Q9, при которой в силу
(7.25) и (7.27) будет выполняться неравенство
ЦК, ЗДП^+lli <Q9{иК, Ж0)П^+11.2 +
+ $ || К, Ж(Z') п 111 dZ' 4- IIF, (Z) Но21
о '
это неравенство можно представить в виде
>«?9{х4-!/}, (7-28)
где
x(f) = II К, W^^II/dZ'.
о
Отсюда
х^е^1 е~Му (t') dt'. (7.29)
и
7.4. Гиперболические уравнения
265
Поскольку у — монотонно растущая функция t и поскольку t
ограничено в <U+, существует такая постоянная Qlo, которая
обеспечивает выполнение неравенства
x<Q,or/.
Итак,
|| К, Ж (0 П 111 {II К, (0) П II, 4- IIF, <U (/) ||0},
где
Ра = (Q9 + □
С помощью этого неравенства мы немедленно можем доказать
единственность решений линейных гиперболических уравнений
2-го порядка, т. е. уравнений, для которых А, В, С и F не зависят
от К- В самом деле, пусть Л11/ и будут решениями уравне-
ния L(K)= F, причем начальные значения как их самих, так и
их первых производных на ^(0)П£2/ совпадают. Тогда преды-
дущий результат можно применить к уравнению £(К4 — К2) = О
и получить, что
|| К1-К2, Ж (t) п Hi = 0.
Отсюда К1 = К2 на °U+- Таким образом, мы имеем
Предложение 7.4.5
Пусть А — лоренцева С1--метрика на М и пусть В, С и F ло-
кально ограничены. Пусть Ж с: JI — некоторая пространственно-
подобная и непричинная относительно А З-поверхпость. Тогда
решение линейного уравнения (7.20) однозначно определено на
множестве T^D+фё, А) его значениями и значениями его пер-
вых производных на Зв П А).
Согласно предложению 6.6.7, О+(Зв, А) имеет вид Зв X R1.
Если (?е7, то по предложению 6.6.6 множество 7—(<?) П 7+(2^)
компактно и может быть взято в качестве °П+. □
Итак, физическое поле, подчиняющееся линейному уравнению
вида (7.20), будет удовлетворять постулату причинности (а)
разд. 3.2 при условии, что изотропный конус в метрике А совпа-
дает с изотропным конусом пространственновременной метрики g
или лежит внутри него.
Чтобы доказать существование решений уравнений (7.20),
нам понадобятся неравенства для производных К более высо-
кого порядка. Мы примем теперь, что фоновая метрика g по
крайней мере класса С5+а, где а — неотрицательное целое число,
а множество возьмем таким, чтобы область 5^(0) П aLl имела
266
Г л. 7. Задача Коши а общей теории относительности
гладкую границу и чтобы при этом существовал диффеоморфизм
H^(0)fW)X[0, Л] <2/+,
обладающий тем свойством, что для всякого /е[0,/J
X {(^ (0) П ^), t} = П ^+-
Сделаем этот выбор так, чтобы на поверхности 3^(t)(]6U+ су-
ществовали верхние границы Д, Р2, Р3 для постоянных Pit Р2, Р3
в леммах 7.4.1—7.4.3.
Лемма 7.4.6
Если выполнены условия (1) и (2) леммы 7.4.4 и если
4) существует такая постоянная Q3, при которой
||А, ^+||4+a<Q3, ||В, ^+||3+a<Q3> II С, °И+ ||3+а < <2з
[в силу леммы 7.4.1 здесь содержится и условие (3)], то суще-
ствуют такие положительные постоянные Р^а (зависящие от
е, g, a, Qi и Q3), что выполняется неравенство
IIК, 5W)lW+IU</\a{IIK, ^(0)(W+ll4+a-HF, ^(ОИз+Д
(7.30)
Из леммы 7.4.4 мы имеем неравенство для
НК,
Чтобы получить неравенство для
IIK, ^(OlW+lb,
образуем тензор «энергии» Sab для первых производных K!j\c и
поступим, как прежде. Дивергенцию Sat\b можно при этом вы-
числить дифференцированием уравнений (7.20):
Sa%, = AnaKpj\cdFPQ\eeeceJQeIP + (члены, квадратичные по K.'j\c и
К1 !\си с коэффициентами, зависящими от Acd, Acd\e,
RCdef, RCdeflg, BCP‘qj, B°P1Qj\d, CP,QI, CP!QJ\d)', (7.31)
Все эти коэффициенты (за исключением, быть может, BcP!Qj\d
и CP!Qj\d) ограничены на °йщ. в случае а = 0. При интегриро-
вании по поверхности <Ж(ОП^+ в (7-31) член, включающий
ВсР1си\а, имеет вид
- АаЬК! ЦсъВ1'рт\щеК5Кщесее^еР1<\6а. (7.32)
PC (Г) П ‘U-4-
7.4. Гиперболические уравнения
267
Существует некоторая постоянная Q., для всех t', при которой
интеграл (7.32) меньше или равен величине
Q4 $ | DB 11 DK 11 D2K I da С
3W'lncU+
<-|q4 J !D'JK:2 + |DBr|DK7dG. (7.33)
3t(tyncU +
Согласно лемме 7.4.2,
J |DB|2|DK|-d<r<
c p/ll В, Ж it') П II/ IIK, Ж (Г) П -И II/,
где по условию (4) и лемме 7.4.3
|| В, W) (W+П2 </^з-
Ограничение на член, включающий CP1Qj\d, можно получить
подобным же образом. Таким образом, согласно лемме 4.3.1,
найдется постоянная Q5, такая, что выполняется неравенство
J (|D2KH|DKI2)d<j<Q5 Г j (| D2K I2 + I DK I2) da +
ЗС(ОП^+ 1зс(0)лОД+
+ ^||K, 5W(W+ll/df+ $|DF|2dal. (7.34)
о <W) j
Из леммы 7.4.4 следует, что
J |KI?da^||K, ^(0П^+1112<
3C{t)p<U+
< 2Р/ {|| К, Ж (0) П U II/ + || F, <U (О II/}. (7.35)
Складывая это неравенство с (7.34), получаем
ЦК, ^(0(W+ll/^QejjIK, ^(O)(WII/ +
+ $ II К, Ж (П П II/ df 4- I! F, (0II/1 (7.36)
о )
где Q6 = Q54~2f>4. Из рассуждений, аналогичных ходу доказа-
ельства леммы 7.4.4, следует существование некоторой постоян-
ной Qi, при которой
ПК, ь ||2<Q7 {II к, ^(0)^Z||2 + ||F, ^(Ollij- (7-37)
268
Гл, 7. Задача Коши в общей теории относительности
Тогда из леммы 7.4.1 следует, что на <2/+ справедливо нера-
венство
IKK P}Q7 {II К, (0) |!2 + IIF, <Ы (0||0}. (7.38)
Используя это неравенство, можно подобным же методом по-
лучить неравенство для ЦК, % (t) fl <U+ Из- Дивергенция тензора
«энергии» приводит к выражению вида
Q8 j (| D3K I2 + I D2B |21 DK I2) da. (7.39)
Согласно лемме 7.4.2, второе слагаемое ограничено величиной
QsK1| В, (/') П ||321| К, Ж (О П К- 1122,
где по условию (4) множитель ||В, (t) f| ||3 определен почти
всюду и квадратично-интегрируем поСледовательно, мы можем
получить неравенство для || К, (/) f| К- ||3 тем же способом,
что и для || К, 5^(0 П Иг- Процедура получения неравенств
для производных более высокого порядка аналогична. □
Следствие
Существуют постоянные Р6,а и Р7<а, при которых
ЦК, ^(OIW+lk+a^.UlIK, 5^(0) 0^4^ +
+ II K'jlatP, ^(0)ПШ+д4-||Р, ^lis+a}
И
II К, Ik+a Р7,а (тот же множитель),
где иа — некоторое векторное С3+а-поле на Уё (0), причем оно
нигде не касательно к 3>ё (0).
Согласно (7.20), производные К второго и более высоких по-
рядков могут быть выражены через поле F, его производные в
направлении иа, К1 j\a иа и производные К в направлениях, каса-
тельных к поверхности <3^(0). Из леммы 7.4.3 следует, что
||А, ^(0)n^ll3+a<^3Q3,
|| В, ^(0)n^||2+a<P3Q3,
(7.40)
||С, Ж0) П ||2+й < P3Q3,
|| F, ^(0)П ||2+а < Р3Н F, %.||3+а.
Итак, должна существовать некоторая постоянная Q4, такая, что
UK, W)(Wll4+a<Q4{IIK, Ж0)ПШ+й4-
+ II Ж (0) П <7/ j|3+a 4- IIF, <U+ ||3+а}. (7.41)
7.4. Гипербо.шческие уравнения
269
Второй результат непосредственно следует отсюда, так как
координата t ограничена на cUJr. □
Теперь мы можем приступить к доказательству существо-
вания решений линейных уравнений вида (7.20). Сначала пред-
положим, что компоненты А, В, С, F, и и g являются анали-
тическими функциями локальных координат х‘, х2, х3 и х4
(х4 = /) в некоторой координатной окрестности Т, а в качестве
начальных данных KIj = aK,i и К1 j\aua = \К'j возьмем аналити-
ческие функции координат х1, х2, х3 на Ж (0) П Тогда из (7.20)
можно вычислить частные производные компонент тензора К
в направлении, не касательном к Ж (0): д2 (К1 j)/dt2, д3 (К7j)/dt2 дх1,
о3(K!j)/dt3 и т. д. через 0K!j и 1К7У на <Ж(0). Таким образом,
К!j можно представить в виде формального степенного ряда
по х’, х2, х3 и t вокруг начала координат р. По теореме Коши —
Ковалевской [36, р. 39] этот ряд будет сходиться в некотором
шаре Т(г) координатного радиуса г и даст решение
уравнений (7.20) с заданными начальными условиями. После
этого мы выберем аналитический атлас из С°°-атласа многообра-
зия М, покроем Ж(0) П координатными окрестностями вида
}С(г) из этого атласа и в каждой координатной окрестности по-
строим решение так, как это было сделано выше. Таким образом
мы получаем решение в области ^(/г) для некоторого t2 > 0.
Затем повторяем этот процесс, используя По теореме
Коши — Ковалевской отношение последовательных интервалов/,
для которых степенной ряд сходится, не зависит от начальных
данных, и, следовательно, решение можно продолжить на всю
область %1+ за конечное число шагов. Этим доказывается суще-
ствование решений линейных уравнений вида (7.20), когда коэф-
фициенты, правая часть и начальные данные, аналитичны. Те-
перь мы снимем требование аналитичности.
Предложение 7.4.7
Если выполнены условия (1), (2), (4) и если
5) F е !F3+“ (<2Z+),
6) 0К е W4+a (^ (0) П ^), iK е W3+a (Ж (0) П ^),
то уравнение (7.20) имеет единственное решение К IF4+a (с?/+)>
для которого на ^(0) K7z=oK/z и KTj\aua = iK7/.
Для доказательства этого утверждения мы аппроксимируем
коэффициенты и начальные данные аналитическими функциями
и покажем, что получающиеся при этом аналитические решения
сходятся к полю, которое является решением данного уравнения
с заданными начальными условиями. Пусть А„ (п= 1,2,3)—
последовательность аналитических полей на CU+, сильно сходя-
щаяся в W4+a{aU+) к А. (Говорят, что А„ сильно сходится к А
270
Гл 7. Задача Коши в общей теории относительности
в Wm, если || А„ — А ||,„ сходится к нулю.) Пусть В„, С„ и F„ —
аналитические поля на <U+, на которые сильно сходятся соот-
ветственно к В, С и F в пространстве IF3+a(£?Z+), и пусть ОКП
и jKn — аналитические поля на Ж (0) П CU, сильно сходящиеся к 0К
и [К соответственно в Ц74+« (Ж> (0) f) 4/) и W/3+a (Ж (0) f] <U). При
каждом значении п будет существовать аналитическое реше-
ние Ki уравнения (7.20) с начальными значениями Кп! j = оКп'
Кп j\aiia = \Kni- Согласно следствию леммы 7.4.6, норма
|| К„, <U+ Ik+a ограничена при п-> оо. Тогда по теореме Рисса [140]
существует поле К Wi+a (sll+) и подпоследовательность КП'
последовательности К,,, такая, что для каждого Ь, 0 b 4 Ц- а,
DbKn’ слабо сходится к (Последовательность полей lnJj
на Ж называется слабо сходящейся к I1 j, если
j -> p^/^dcr
для любого С°°-ПОЛЯ J1 J.)
Поскольку Ai7, B„ и C„ сильно сходятся в IF3(<2/+) к А, В
и С, sup | А — Ал |, sup ] В — Brt | и sup | С — Сп | будут сходиться
к нулю. Следовательно, L^(Km') будет слабо сходиться к Т(К).
Но Ln' (Км') = F^ и F„' сильно сходится к F. Отсюда L(K) = F.
На ^())n^Z Кп'1! и К.п’1ПаЦ'а будут слабо сходиться к K!j и
К^раЖ1, которые поэтому должны быть равны соответственно
и xK‘j. Таким образом, К является решением данного урав-
нения с заданными начальными условиями. Согласно предложе-
нию 7.4.5, оно единственно. Поскольку каждый тензор Кп удо-
влетворяет неравенству из леммы 7.4.6, ему будет удовлетво-
рять и К- о
7.5. Существование и единственность решения задачи Коши
для уравнений Эйнштейна для пустого пространства
Результаты предыдущего раздела мы используем теперь в
задаче Коши в общей теории относительности. Сначала рассмо-
трим уравнения Эйнштейна для пустого пространства (ТаЬ — 0),
а влияние материи исследуем в разд. 7.7.
Приведенные уравнения Эйнштейна
Eabcd ($cd) = 8лТаЬ - (£а6 - ~ Rgab) (7.42)
представляют собой квазилинейные гиперболические уравнения
второго порядка, т. е. имеют вид (7.20), причем коэффициенты
А, В и С являются функциями К и DK (в нашем случае Aab — gal>
является на самом деле функцией <j>ab и не зависит от фаЬ\с).
Чтобы доказать существование решений этих уравнений, мы
7.5. Существование и единственность решения 271
поступим следующим образом. Возьмем некоторое подходящее
пробное поле ф'аЬ и используем его для определения значений
коэффициентов А, В и С в операторе Е. Затем будем решать
(7.42) при этих значениях уже как линейное уравнение с на-
чальными данными, определяемыми полем <]>', и получим новое
поле ф"аЬ. Тем самым мы получим отображение а, переводящее
ф' в ф", и покажем, что при определенных условиях это ото-
бражение имеет неподвижную точку (т. е. существует ф, для
которого а(ф) = ф). Эта неподвижная точка и будет искомым
решением нашего квазилинейного уравнения.
Возьмем в качестве фоновой метрики решение уравнения
Эйнштейна в пустом пространстве и выберем поверхности
5^(0 П^+ и Д/ГНД так, чтобы они были пространственно-
подобными в метрике g. Тогда по лемме 7.4.1 найдется такая
положительная постоянная Qa, что коэффициенты А', В', С',
определяемые функцией ф', будут удовлетворять условиям (1),
(2) и (4) леммы 7.4.6 с заданными значениями (Д и Q3, если
только
110', U+\\i+a<Qa. (7.43)
В этом случае из (7.41) имеем
|| ф", ||4+а < Д, а { II уф, Ж (0) П Ш+а + II хФ, Ж (0) П Ш+Л
Следовательно, отображение a:IF4+a((2/+)->lF4+aC2/+) преобра-
зует замкнутый шар IF (г) радиуса r(r<Qa) в lF4+a(c?/+) в себя
при условии, что
И
||^,Ж0)ПШ+а<4'Л.Г’- (7.44)
Покажем, что а имеет неподвижную точку, если выполняется
(7.44) и радиус г достаточно мал.
Допустим, что ф' и ф', принадлежат пространству W (г).
Поля ф'' = а(ф\^ и = удовлетворяют равенствам
= Д'(0") = О, где Д' —оператор Эйнштейна с коэф-
фициентами А(, В( и С(, которые определяются функцией ф\.
Следовательно,
= (7.45)
Поскольку коэффициенты АД В/ и С/ дифференцируемым
образом зависят от ф{' и D0j' при ф( из W (г), то существует
272
Гл. 7. Задача Коши в общей теории относительности
такая постоянная Q4, что на %+
IВ' 1 “ R г I < <3< (IФ | “ Ф 'г I + I °*' 1 ~ D’S': !) С? .46)
I С', - С'21 < Q, (| Ф\ - ф', | + | D*', - Оф'г
Поэтому, в силу лемм 7.4.1 и 7.4.6,
WT - Е’ЩФ",) I < 3rQ,P,p-'Pt.. МФ'-Ф'А + \°Ф'~ I»'. I).
Теперь применим лемму 7.4.4 к 7.4.5, чтобы получить неравенство
«д. (ШТ)
где Q5 — некоторая постоянная, не зависящая от г. Таким обра-
зом, для достаточно малых г отображение а будет стягивающим
по норме II II! (т. е. II а (0,) — а (02) Ik < || 0, — 02 Hi) и последова-
тельность о.п(ф'^ будет сильно сходиться в Wl (01 к некото-
рому полю ф. Но по теореме Рисса из а'1 (ф'J можно выбрать
подпоследовательность, слабо сходящуюся к некоторому полю
ф е W (г). Следовательно, поле ф должно совпадать с ф и при-
надлежать пространству 1F (г). Поэтому отображение а(0) будет
определенным и для него
При п->оо правая часть стремится к нулю. Из этого следует,
что || а (ф) — ф, 01+ К) = 0 и потому а(ф) = ф. Поскольку а —
стягивающее отображение, эта неподвижная точка единственна
в W (г). Следовательно, мы доказали
Предложение 7.5.1
Если g — решение уравнений Эйнштейна в пустом простран-
стве, то приведенные уравнения Эйнштейна в пустом пространстве
имеют решение ф^д^+а (01+) при достаточно малых ||о0, (0) П
(Wik+a и ||,0, WWU Норма ||0, ^(0)fW+||4+a огра-
ничена, и, следовательно, поле ф по крайней мере класса
С(2+а)~. □
Локально это решение единственно даже среди решений,
которые не принадлежат пространству IE4 (с?/+).
Предложение 7.5.2
Пусть 0 является С1--решением приведенных уравнений
Эйнштейна в пустом пространстве с теми же начальными дан-
ными на открытом множестве F сл X (0) П<2/. Тогда 0 = 0 в не-
которой окрестности множества У в
7.5. Существование и единственность решения 273
Ввиду непрерывности ф в найдется окрестность <Н' мно-
жества Т, в которой для А, В и С выполняются условия
леммы 7.4.4. Как прежде, имеем
£(0-0) = -(£-£)(£). (7.48)
Аналогично, будет существовать постоянная Q6, обеспечивающая
выполнение неравенства
и(£-£)(^), адгж+и,.
Применяя к (7.48) лемму 7.4.4, получим неравенство вида
где
t
х=\\\ф-ф,
О
Отсюда ф — ф на <U'+. □
Из предложения 7.5.1 видно, что при наложении достаточно
малых возмущений на начальные данные для решения уравне-
ний Эйнштейна в пустом пространстве мы снова получаем неко-
торое решение в области °U+. Однако в действительности тре-
буется доказать, что решение существует для любых начальных
данных hab и хад, которые удовлетворяют уравнениям связи на
трехмерном многообразии 9С Для этого мы поступим следую-
щим образом. Будем считать, что многообразием Л является /?4,
что е — евклидова метрика, a g — плоская метрика, т. е. метрика
Минковского ('она является решением уравнений Эйнштейна в
пустом пространстве). Область <и выберем так, чтобы в обыч-
ных координатах Минковского х1, №, х3 и %4 (%4 = t) поверхность
д°И П °U+ была пространственноподобна, а область ^(0)П<2/
состояла из точек, для которых (х1)2 + (х2)2 + (з:3)2 1, xi — 0.
Теперь мы будем руководствоваться идеей, что любая метрика
выглядит почти плоской, если ее рассматривать в достаточно ма-
лых масштабах. Поэтому при отображении достаточно малой
области поверхности на 5^(0) П можно учесть предложе-
ние 7.5.1 и получить решение в £2/+. Затем можно повторить эту
процедуру для других частей У и объединить полученные реше-
ния так, чтобы образовалось многообразие Л с метрикой g, ко-
торое и будет развитием комплекта начальных данных (93, и).
Пусть F| — координатная окрестность а с координатами у1,
у2, у3, в которой в начале координат р координатные компо-
ненты hab равны ЬаЪ. Пусть (/у) — открытый шар координатного
радиуса fi с центром в р. Зададим отображение 0: Ti(fi)
274
Гл. 7. Задача Коши в общей теории относительности
соотношениями х1 = fi~Xy (* = 1, 2, 3), х4 = 0. По обычному за-
кону преобразования базиса компоненты 9Jza& и 9даЬ в коорди-
натах {х} равны компонентам hab и /а6 в координатах {у}, умно-
женным на fi~2. Введем в Т\ новые поля h'ab и %ab : h’ab =
= f2hab и %ab = f\%ab Тогда, поскольку Л на непрерывна
(фактически принадлежит классу С2+а), выбором достаточно ма-
лого f, можно величины g'ab — gab и g'a\uc сделать сколь угодно
малыми на 3*ё (0) П где g'ab и g'ab]cuc получаются из h'ab
и %'аЬ, как в разд. 7.3. При этом производные g'ab и g,ab[cuc
на поверхности <?6(0) тоже убывают по мере убывания f
Следовательно, ||о0', (0) П ||4+0 и || , <Ж(0) П IL+а могут
быть приведены к настолько малым значениям, что можно
будет использовать предложение 7.5.1 и решение для полу-
ченное в °U+. Тогда g^b = fr2g'ab будет решением приведенных
уравнений Эйнштейна с начальными данными, определяемыми
тензорами hab и /аЬ. Аналогично можно получить решение <2/_,
той части CU, в которой t 0.
Теперь мы можем покрыть Г? координатными окрестностями
y°a(fa) виДа ^i(fi), отобразив их вложениями 97 на окрестно-
сти вида <2/, и получить решения gaab в °Ua. Тогда задача
сведется к тому, чтобы отождествить соответствующие точки в
пересечениях окрестностей и тем самым превратить набор
окрестностей ^2/?. в многообразие JT с метрикой g. Это можно
сделать, используя гармонические калибровочные условия
= ёЪсщ - I gbcgdeg% = 0. (7.49)
По определению 6Гаьс (7.3) оно эквивалентно условию gdei)Vb d&=^-
Поэтому для любой функции z
Z-tabg '—Z\ab§ vl abZ\cg —2\abg • (7.50)
Если фоновой метрикой является метрика Минковского, az —
одна из координат Минковского х1, х2, х3, х4, то правая часть
(7.50) обращается в нуль. Допустим теперь, что на некотором
многообразии Л мы имеем произвольную лоренцеву 1174+а-мет-
рику g. В некоторой окрестности сд Jt мы можем получить
такие четыре решения z1, z2, z3, z4 линейного уравнения
2;<ngft& = 0, (7.51)
градиенты которых линейно независимы в каждой точке
Тогда мы можем задать диффеоморфизм >,.# вида ха = га
(а=1, 2, 3, 4). Этот диффеоморфизм будет обладать тем
свойством, что метрика \xtgab на Л будет удовлетворять гармо-
7.5. Существование и единственность решения 275
ническому калибровочному условию относительно метрики Мин-
ковского g на Л. Таким образом, если метрика g является ре-
шением уравнений Эйнштейна на Л, метрика p„g будет решением
приведенных уравнений Эйнштейна с фоновой метрикой g.
Процедура отождествления точек в пересечении двух окрест-
ностей и сводится таким образом к решению (7.51) в 'Ua
для координат хф, -vp2, г.'1, Л'ф с использованием начальных
данных для хщ и х$а ьиь, определяемых пересечением коорди-
натных окрестностей У' а и Fр на 9>. В действительности
х^\аи.а = 0 ('= 1> 2, 3) и х^иа = 1, где иа = д/дхаа — единичный
вектор в <?/а, ортогональный к 5^(0) в метрике g. Таким обра-
зом, х^ — ха4, хотя х^ вообще не будет совпадать с ха‘. По
предложению 7.4.7 координаты x-f будут в С(2+а)-функциями.
[В предложении 7.4.7 фоновая метрика, относительно которой
берутся ковариантные производные, должна была принадле-
жать классу С<5+а)_. Поэтому предложение 7.4.7 нельзя было
применить к (7.51), где ковариантные производные берутся от-
носительно метрики g, принадлежащей только пространству
Wi+a. Однако мы можем ввести фоновую С5+“ метрику g и пред-
ставить (7.51) в виде
z\\abgab + Z\laBa — 0,
где || означает ковариантное дифференцирование относительно g.
После этого Можно воспользоваться предложением (7.4.7).]
Поскольку градиенты х,>а на Ж (0) П линейно независимы,
они будут линейно независимы и в некоторой окрестности
поверхности Ж (0) в с?/а. Метрика |\£аа6 на р в будет
по меньшей мере класса С1-. Ввиду того что она подчиняется
приведенным уравнениям Эйнштейна и имеет те же начальные
данные на 0 П ^в), °на должна совпадать с gp в некоторой
окрестности cz <U области 0р (Та П Fp). Отсюда видно, что
можно соединить и и получить развитие области
Выбрав покрытие {Уа} поверхности & локально ко-
нечным, мы можем поступить подобным же образом, соединить
подмножества других окрестностей {'Тсф} и получить развитие
т. е. построить такие многообразия Л с метрикой g и вложе-
ние &ЛР-+Л, что метрика g удовлетворяет уравнениям Эйн-
штейна в пустом пространстве и согласуется с имеющимися
начальными данными со на поверхности 0 (S?), которая является
поверхностью Коши для Л. Если {Л', g') — другое развитие
комплекта (^, со), то аналогичная процедура устанавливает диф-
феоморфизм ц между некоторой окрестностью поверхности 0'(^’/)
276 Гл. 7. Задача Коши в общей теории относительности
в Ж и некоторой окрестностью поверхности 0 (^) в Ж, для
которого №tg'ab — §“Ь' Следовательно, нами доказана
Теорема о локальном решении задачи Коши
Если hab е Wi+a(!P) и %аЬ s W3+a(!P) удовлетворяют уравне-
ниям связи для пустого пространства, то существуют решения
(Ж, g) уравнений Эйнштейна в пустом пространстве, такие, что
gs №^а(Ж) и®е 1Е4+-'- на любой гладкой пространственнопо-
добной поверхности Рё. Эти решения локально единственны в сле-
дующем смысле: если (Ж', g') —другое развитие того же ком-
плекта начальных данных (^, и), принадлежащее пространству
Wl+a, оба развития (Ж, g) и (Ж’, g') являются расширениями
некоторого общего развития комплекта (ГР, и).
Утверждение, что ge 1Г4+а(^), следует из леммы 7.4.6 и из
того, что поверхности постоянного f можно выбрать произвольно.
□
7.6. Максимальное развитие и устойчивость
Итак, мы показали следующее: если начальные данные удо-
влетворяют уравнениям связи для пустого пространства и при
этом можно найти некоторое развитие начальных данных (т. е.
можно распространить решение на некоторое расстояние в буду-
щее и прошлое от начальной поверхности, если эти данные удо-
влетворяют уравнениям связи), то это развитие, вообще говоря,
можно продолжить дальше в будущее и прошлое, что даст более
протяженное развитие комплекта начальных данных (ГР, со). Од-
нако, следуя ходу рассуждений в [33], мы докажем существова-
ние единственного (с точностью до диффеоморфизма) развития
(Ж, g) комплекта (ГТ, и), являющегося расширением любого
другого развития этого комплекта.
Напомним, что (Ж\, gj — это расширение пространства
(Ж2, g2), если существует вложение р.:.<2-> Жх, при котором
P'*&2 = gi и 01-1Ц02 суть тождественное отображение на ГР. Если
даны точка q е ГР и расстояние $, мы можем однозначно задать
точки /?! s Жх и р,е Л2 путем смещения q на расстояние s
вдоль геодезических, ортогональных к 01(5^) и 02(^) и прохо-
дящих через 0^7) и 02(д) соответственно. Поскольку р,(р2) должно
совпадать с р\, вложение и будет единственным. Поэтому можно
частичнэ упорядочить множество всех развитий комплекта (ГР, и),
положив (Ж2, g2)^(J7i, gj, если (Лъ gj является расширением
(Л2, g2). Пусть теперь (Жа, ga} — вполне упорядоченное мно-
жество (множество Ж- называется вполне упорядоченным, если
для каждой пары различных элементов а, b е Ж или а^Ь
или Ъ^а) развитий комплекта (ГР, и); тогда можно построить
многообразие JC как объединение всех Жа, причем при
7.6. Максимальное развитие и устойчивость
277
(v<a, ga) 'С (л#р, gp) каждая точка ра е Жа отождествляется
с pa(1(pa) е гДе Паркер—> Ж^ — вложение. Многообразие Ж'
будет иметь индуцированную метрику g7, равную pa,ga на
каждой pa(^a), гДе И а- а~^ ^1' — естественное вложение. Ясно,
что (Ж', g7) тоже будет развитием комплекта , и); поэтому
любое вполне упорядоченное множество имеет верхнюю грань,
и, таким образом, по лемме Цорна (см., например, [88], р. 33)
существует максимальное развитие {Ж, g) комплекта (^, и),
расширением которого является только оно само.
Теперь мы покажем, что {Ж, g) является расширением любого
развития комплекта (^, ю). Допустим, что (Ж', g7) — некоторое
другое развитие (^, со). Согласно локальной теореме Коши, су-
ществуют развития (^, и), для которых как (Ж, g), так и {Ж', g7)
являются расширениями. Множество всех общих для них раз-
витий также частично упорядочено, и снова по лемме Цорна
найдется максимальное расширение (Ж", g77) с вложениями
улЖ"-> Ж и р!’.Ж''->Ж' и т. д. Пусть Ж' будет объедине-
нием Ж, Ж' и Ж", в котором каждая точка р" е Ж" отожде-
ствляется с р(/?") е/ и с |г'(/?") е Ж'. Если мы сможем по-
казать, что многообразие Ж^ хаусдорфово, то тем самым до-
кажем, что пара {Ж+g+) является развитием комплекта (^, и).
Она будет расширением как (Ж, g), так и (Ж', g'). Однако
единственным расширением пространства {Ж, g) является оно
само и, таким образом, (Ж, g) должно совпасть с (Ж+, g+) и
быть расширением пространства {Ж', g7).
Допустим, что Ж+ — не хаусдорфово многообразие. Тогда
существуют точки р с J и p7e(|i/(.#")l‘c,/', для
которых каждая окрестность точки р обладает тем свойством,
что р7(р_|(Д/)) содержит р'. Далее, поскольку пространство
{Ж", g") является развитием, оно, как и его образ р (Ж") в Ж,
будет глобально гиперболическим. Поэтому граница множества
р (Ж") в Ж должна быть ахрональной. Пусть у — времениш -
добная кривая в Ж с конечной точкой будущего р'. Тогда р'
должна быть предельной точкой в Ж' кривой р7р~'(у). На са-
мом деле она должна быть конечной точкой будущего, так как
в {Ж', g7) выполняется сильная причинность. Следовательно,
для данной точки р точка р' единственна. Далее, в силу непре-
рывности векторы в р' можно однозначно связать с векторами
в р. Таким образом мы можем подобрать такие нормальные
координатные окрестности <й для р в Ж и W для р' в Ж',
точки °11 П р {Ж") которых при отображении р7(р-1) будут ото-
бражаться в точки <%' П р7 (Ж") с теми же значениями координат.
278
Гл 7. Задача Коши в общей теории относительности
Отсюда следует, что множество всех „нехаусдорфовых*1 точек
из (ц (Л7')) открыто в (ц (Л7'))’- Мы предположим теперь, что
^"--непустое множество, и придем затем к противоречию.
Пусть А — направленная в прошлое изотропная геодезическая
в Ж, проходящая через тогда, используя возможность
связать направления в р с направлениями в р', можно провести
в Ж' в соответствующем направлении изотропную геодезическую
в прошлое А\ проходящую через р'. Каждой точке множества
А П (ц (Ж"))’ будет соответствовать точка из К' П (р/ (Ж"))’, и,
следовательно, каждая точка, принадлежащая А |~| (jl (Ж"У}',
будет точкой из ST. Поскольку 0 (^) является поверхностью
Коши для Ж, кривая А должна покинуть (ji в некоторой
точке q. В некоторой окрестности q найдется точка г е ЯГ, через
которую можно провести пространственноподобную поверх-
ность Ж, обладающую тем свойством, что (<Ж — г) cz й (Ж"').
В Ж’ существует соответствующая пространственноподобная по-
верхность Ж = (р'р-1 (Ж — г)) U г', проходящая через г'. Поверх-
ности Ж и Ж можно рассматривать как образы трехмерного
многообразия Ж при вложениях Ур. ЖЖ и ф:<Ж -> Ж', для
которых ф“1р.|/~1ф является тождественным отображением на
Ж — ф-1(р). Индуцированные на Ж> метрики ф (g) и i|/(g') со-
гласуются одна с другой, поскольку Ж — р и Ж' — р' изо-
метричны. Согласно локальной теореме Коши, они принадлежат
пространству Wi+a (Ж). Аналогично, вторые фундаментальные
формы также согласуются и принадлежат №3+а(Ж). Окрестности
поверхностей Ж в Л и Ж' в Ж' будут 1К4+а-развитиями Ж.
По локальной теореме Коши они должны быть расширениями
одного и того же развития (Ж*, g*). Присоединяя {Ж*, g*)
к {Ж", g"), мы получили бы большее развитие комплекта на-
чальных данных (3, <о), причем (Ж, g) и (Ж', g') были бы рас-
ширениями этого развития. Однако это невозможно, ибо (Ж", g")
уже является наибольшим общим развитием. Из этого следует,
что многообразие Ж+ должно быть хаусдорфовым, а следова-
тельно, и пространство (Ж, g) должно быть расширением про-
странства (Ж', g').
Итак, нами доказана
Теорема о глобальном решении задачи Каши
Если hab е №4+а(<?) и хаЬ е \Ж+п(Ж) удовлетворяют уравне-
ниям связи для пустого пространства, то для уравнений Эйн-
штейна в пустом пространстве существует максимальное разви-
тие {Ж, g) cgE К4~-'-(.>#) iige Wz4+°(Ж) комплекта начальных
7.6. Максимальное развитие и устойчивость
279
данных для любой гладкой пространственноподобной поверхно-
сти 5^. Это развитие является расширением любого другого
такого развития.
Пока мы доказали лишь то, что полученное нами развитие —
максимальное среди развитий, принадлежащих пространству
№4+а (Ц74+а-развитий). Если а>0, то существуют также 1Г4+а-1-,
UZ4+a~2-, ..., ^-развития, которые являются расширениями по-
лученного развития. Однако Шоке-Брюа показал [30], что все эти
расширения должны совпасть с 1Г4-развитием. Это происходит
вследствие того, что мы можем дифференцировать приведенные
уравнения Эйнштейна и затем рассматривать их как линейные
уравнения на ^-развитии для первых производных gab. Затем,
пользуясь предложением 7.4.7, можно показать, что gab е IT5 на
1Г4-развитии, если начальные данные принадлежат простран-
ству W5. Следуя этому рецепту, мы можем показать, что при
начальных данных класса С00 будет существовать С°°-развитие,
которое фактически совпадает с 1Г4-развитием.
Мы доказали существование и единственность максимальных
развитий только для случая, когда метрика не «хуже», чем клас-
са IT4. В действительности можно доказать существование раз-
витий для начальных данных из IT3, но в этом случае мы не
сможем доказать единственность. Не исключено, что максималь-
ное Ц74-развитие может быть расширено или так, чтобы метрика
перестала принадлежать пространству W1, или так, чтобы 0(^)
перестала быть поверхностью Коши. В последнем случае по-
явится горизонт Коши; примеры этого были даны в гл. 6. С дру-
гой стороны, возможно присутствие сингулярности того или
иного рода, и тогда развитие нельзя расширить так, чтобы поря-
док дифференцируемости метрики был достаточен для ее физи-
ческой интерпретации. Действительно, как мы увидим в следую-
щей главе (теорема 4), если множество X компактно и xab/ia&<0
всюду на развитие нельзя расширить так, чтобы оно было
геодезически полным и обладало С2~-метрикой (т. е. локально
ограниченной кривизной).
Мы показали, что существует отображение из пространства
пар тензоров (h'lb, %аЪ) на X, удовлетворяющих уравнениям
связи, в пространство классов эквивалентности метрики g на
многообразии jt, которое, согласно предложению 6.6.8, диффео-
морфно & X R1- Если две пары (hab, и (h'ab, %'аЬ) эквива-
лентны относительно диффеоморфизма —* д? (т. е. k*hab — h'ab
и Х*хаЬ = х/<гЬ), т0 они порождают эквивалентные метрики g. Та-
ким образом, мы имеем отображение классов эквивалентности
пар (hab, %аЬ) в классы эквивалентности метрик g. hab и хаЬ вме-
сте имеют 12 независимых компонент. Уравнения связи накла-
дывают на них четыре соотношения, а эквивалентность
280
Гл. 7. Задача Коши в общей теории относительности
относительно диффеоморфизмов можно использовать для исклю-
чения еще трех произвольных функций; остается пять независи-
мых функций. Можно считать, что одна из этих функций харак-
теризует положение поверхности 9(^) в развитии („#, g). Сле-
довательно, максимальные развития, удовлетворяющие уравне-
ниям Эйнштейна, в пустом пространстве определяются четырьмя
функциями трех переменных.
Было бы желательно показать, что отображение из классов
эквивалентности пар (hab, %аЬ) в классы эквивалентности мет-
рик g в каком-то смысле непрерывно. Подходящей для этого
топологией на классах эквивалентности является компактная
открытая Н^-топология (ср. с разд. 6.4). Пусть g — лоренцева
С'-метрика на Л, а Л — открытое множество с компактным за-
мыканием. Пусть V — открытое множество в Wr(°U), и пусть
О (Л, V)—множество всех таких лоренцевых метрик на Л, су-
жения которых на °U принадлежат V. Открытые множества ком-
пактной открытой 1Гг-топологии в пространстве всех ло-
ренцевых !^г-метрик на Л определяются как объединения и ко-
нечные пересечения множеств вида O(U, V). Тогда топология
пространства S*r (Л) классов эквивалентности ^-метрик на Л
индуцируется проекцией
которая ставит в соответствие метрике ее класс эквивалентности
[т. е. открытые множества в ЗЛг (Л) имеют вид л (Q), где Q —
открытое множество в 3?Г(Л)]. Аналогично компактная открытая
1Гг-топология в пространстве Qr(^) всех пар (hab, %аЬ), удовлетво-
ряющих уравнениям связи, определяется множествами вида
О)'?/, V, V'), состоящими из пар, для которых hab <= V и %ab ^V',
где V и V'— открытые множества соответственно в Wr(3>)
и С°°-метрики на Л образуют подпространство З^Л)
пространства 3? (Л) всех лоренцевых метрик на Л. Так как
С°°-метрика принадлежит пространству W при любом г, 3?^ (Л)
обладает рассматриваемой №""-топологией. Мы можем ввести
в ЗКЛЛ} топологию, задавая ее всеми открытыми множествами
в 3?т(Л) в 1Гг-топологиях при каждом г. Аналогично опреде-
ляется С°°-топология на Л‘гг (Л) и на
Желательно также показать, что отображение Дг из про-
странства йг(^) классов эквивалентности пар (hab, %ab') в про-
странство 3?*(Л) классов эквивалентности метрик нег р рывно
по открытой компактной ’^-топологии в обоих пространствах.
Другими словами, предположим, что имеются начальные данные
hab е Wr (З’) и уай е ЦД-1 (<?), которые на Л дают решение
g ^Wr (Л). Желательно показать, что для е>0 и для области
7.6. Максимальное развитие и устойчивость
281
fC-Jt с компактным замыканием существуют д>0 и некото-
рая область cz г? с компактным замыканием, такие, что
||g' — g, V ||r < е при всех начальных данных (h'ab, %'аЬ), удо-
влетворяющих условиям || h' — h, (у]\г<~Ь и ||х'~ X, "ViTr-i <
Это утверждение, возможно, справедливо, но доказать
мы его не в состоянии. Что мы действительно можем доказать —
это справедливость данного утверждения для метрики, при-
надлежащей классу С(г+1)“. Оно сразу следует из предложе-
ния 7.5.1, если взять g в качестве фоновой метрики и некоторую
подходящую окрестность из (Z) [~| J+ (0 (^)) в качестве с2/.
Если мы обратимся к лемме 7.4.6, то обнаружим, что в дей-
ствительности можно ослабить требования к фоновой метрике:
вместо С1г+1)--метрики можно взять №г+ ’-метрику, но ^-ме-
трика уже недопустима ввиду присутствия производных г—I
порядка тензора кривизны для фоновой метрики. (Под словами
„фоновая Wr+ ’-метрика" мы имеем в виду принадлежность этой
метрики пространству W+i относительно какой-то другой фо-
новой Сг+1-метрики.) Итак, отображение Дг:йг (j?) -> 2!г (Л) из
классов эквивалентности начальных данных в классы эквива-
лентности метрик будет непрерывным в открытой компактной
1Кг-топологии для всякой !Кг+’-метрики. Хотя 1Кг+’-метрики
образуют среди !Кг-метрик плотное множество, возможно, что
отображение Дг не будет непрерывно на и7г-метрике, если она не
является одновременно и Wr+ ’-метрикой. Однако оо1 = оо и
соответственно отображение Д^Й^ (^) -> (Л) будет непре-
рывным по Сго-топологии в обоих пространствах.
Этот результат может быть сформулирован так:
Теорема об устойчивости решения задачи Коши
Пусть (Л, g) — максимальное !Кэ+“-развитие начальных дан-
ных и ХеГ'фД 0<а<оо, Г-область из
/ЦЭСТ1)) с компактным замыканием, Z—окрестность g в
и cz 0 (9?) — открытая окрестность J+ (У) П 0 (£”) с компактным
замыканием. Тогда в Q.5+aKU) существует окрестность Y пары
(h, X), в которой для всех (hz, X') е Y, удовлетворяющих уравне-
ниям связи, существует диффеоморфизм р:Л' -> Л со свойствами:
1) отображение 0~’р,0' является тождественным на 0~ ’ (с2/),
2)
где (Л’, g') — максимальное развитие пары (hz, Xz). □
Утверждение этой теоремы сводится примерно к следующему:
если возмущение начальных данных на поверхности Коши 0 (^')
282
Гл. 7. Задача Коши в общей теории относительности
мало в области / (К) U 0 СК), то мы получим новое решение,
близкое к исходному в Г В действительности возмущение из-
начальных данных должно быть малым на несколько большей
области поверхности Коши, чем / (У) |"| 0 (^), так как изотроп-
ные конусы в новом решении будут немного иными, чем прежде,
и может оказаться, что Т" не лежит в области Коши мно-
жества J~ П 0
7.7. Уравнения Эйнштейна при наличии материи
До сих пор мы для простоты рассматривали уравнения Эйн-
штейна только для пустого пространства. Однако аналогичные
результаты получаются и при наличии материи, если уравнения,
которым подчиняются материальные поля удовлетворяют
определенным, физическим разумным условиям. Схема получения
этих результатов такова. Решаем уравнения движения мате-
рии с заданными начальными условиями в заданном простран-
стве-времени с метрикой g'; затем решаем приведенные уравнения
Эйнштейна (7.42) как линейные уравнения с коэффициен-
тами, которые определяются метрикой g', и с правой частью Т'аЬ,
которая определяется g' и решением для материальных полей.
При этом получаем новую метрику g" и повторяем все снова,
взяв g" вместо g'. Для того чтобы показать, что такая процедура
сходится к решению системы из уравнений Эйнштейна и урав-
нений движения материи, на последние необходимо наложить
определенные условия. Мы их сформулируем следующим обра-
зом:
а) если {(/Ч^)} е 1К4+а(Ж) и {ДСДе 1КНДК^) — начальные
данные на ахрональной пространственноподобной поверхно-
сти Ж в 1К4+“-метрике g, то существует единственное реше-
ние материальных уравнений в некоторой окрестности Ж в обла-
сти О+(Ж), причем {'Ко} е 1К4+а (Ж'} для любой гладкой про-
странственноподобной поверхности Ж' и
^(i) = o'T(i), = ДДХ на Ж
б) если {Ч’ф)} — !К5+а-решение в области с2/+ в !К5+а-ме-
трике g, существуют такие положительные постоянные Qj и Q2,
что для любого 1К4+а-решения {'Р'ц)} в метрике g', для которой
||g' —g, ||4+а < Qo
и
X ^(0)fW44a +
(»)
+ 11,4%) - ,4%, WXWlUXQ,,
7.7. Уравнения Эйнштейна при наличии материи
283
выполняется неравенство
2 11 **"(/) - Ч'п), Г Il4+a < Q2 { II g' - g, Ika +
(О
+ S II 'П) - o^G), (0) n w4+a +
w
+ SlIi^G)-!*^), ^(O)n^l+J;
(0
в) тензор энергии-импульса Таь является полиномом по
И gab.
Условие (а) представляет собой локальную теорему Коши
для материальных полей в заданной пространственно-временной
метрике. Условие (б) представляет теорему об устойчивости ре-
шения задачи Коши для материальных полей при вариациях
начальных данных и пространственно-временной метрики g.
Если уравнения движения материи — это квазилинейные гипер-
болические уравнения второго порядка и их изотропный конус
совпадает с изотропным конусом метрики g или лежит внутри
него, то выполнение этих условий можно установить так же, как
это было сделано для приведенных уравнений Эйнштейна.
В случае скалярного поля или электромагнитного потенциа-
ла, удовлетворяющих линейным уравнениям, эти условия выпол-
няются в силу предложения 7.4.7. Мы можем рассмотреть также
скалярное поле, взаимодействующее с электромагнитным потен-
циалом: зададим метрику и электромагнитный потенциал, решим
уравнение скалярного поля как линейное уравнение в этой мет-
рике и с этим потенциалом и затем решим уравнения электро-
магнитного поля в заданной метрике со скалярным полем в ка-
честве источника. Можно показать, что итерации этой процедуры
при.достаточно малых начальных данных сходятся на множестве
вида к решению уравнений скалярного и электромагнитного
полей с их взаимодействием в заданной метрике; затем, изменяя
масштабы метрики и полей, покажем, что при достаточной ма-
лости (по измерениям в пространственно-временной метрике g)
можно получить решение для любых допустимых начальных
данных. Эта же процедура действует при любом числе связан-
ных квазилинейных гиперболических уравнений второго порядка,
если связь не содержит производные выше первого порядка.
Уравнения движения идеальной жидкости не являются гипер-
болическими уравнениями второго порядка, а образуют квазили-
нейную систему первого порядка. (Определение гиперболической
системы первого порядка см. в [36], р. 577.) Для такой системы
можно получить аналогичные результаты при условии, что конус
лучей совпадает с изотропным конусом пространства-времени
284 Гл. 7. Задача Коши в общей теории относительности
с метрикой g или лежит внутри него. Требование, чтобы уравне-
ния движения материи были гиперболическими уравнениями
второго порядка или составляли гиперболическую систему пер-
вого порядка и чтобы их конусы совпали с конусом простран-
ственно-временной метрики g или лежали внутри него, можно
считать более строгой формулировкой постулата локальной при-
чинности из гл. 3.
При выполнении условий (а), (б) и (в) можно доказать
предположения 7.5.1 и 7.5.2 для системы приведенных уравнений
Эйнштейна и уравнений движения материи; из этих предложе-
ний следуют локальная и глобальная теоремы о решениях за-
дачи Коши и теорема об устойчивости.
Глава 8
Сингулярности пространства-времени
В этой главе мы используем результаты гл. 4 и 6 для того,
чтобы установить основные свойства пространственно-временных
сингулярностей. Астрофизические и космологические следствия
будут рассмотрены в последующих главах.
В разд. 8.1 мы обсудим вопрос об определении самого поня-
тия сингулярности в пространстве-времени. Мы введем понятие
6-неполноты — развитие представления о геодезической неполно-
те — как признак того, что из пространства-времени вырезаны
сингулярные точки; при этом мы намечаем два возможных спо-
соба связать 6-неполноту с определенным типом сингулярности
кривизны. В разд. 8.2 даны четыре теоремы, которые говорят
о наличии неполноты в самых разнообразных ситуациях.
В разд. 8.3 мы излагаем предложенный Шмидтом метод
построения 6-границы, изображающей сингулярные точки про-
странства-времени. В разд. 8.4 доказывается, что сингулярности,
предсказываемые по крайней мере одной из упомянутых теорем,
не могут в точности совпадать с разрывами тензора кривизны.
Мы покажем также, что неполные геодезические не бывают
изолированными, а составляют трехпараметрическое семейство.
Ситуация, в которой неполные кривые полностью или частично
заключены в компактной области пространства-времени, обсуж-
дается в разд. 8.5. Мы показываем, что это связано с нехаусдор-
фовым поведением 6-границы и что в характерном пространстве-
времени наблюдатель, движущийся по одной из этих неполных
кривых, испытывал бы действие бесконечных сил, вызванных
кривизной. Мы показываем, также, что свойства, подобные тем,
которыми обладает пространство Тауба — НУТ, не могут воз-
никнуть у пространства-времени, содержащего какую-либо ма-
терию.
8.1. Определение сингулярностей
Аналогия с электродинамикой могла бы привести к мысли,
что пространственно-временную сингулярность разумно опреде-
лить как точку, в которой метрический тензор не определен или
недифференцируем нужное число раз. Однако при этом мы на-
толкнемся на ту неприятность, что эти точки можно просто вы-
резать и сказать, что оставшееся многообразие представляет все
286
Гл. 8. Сингулярности пространства-времени
пространство-время, которое, согласно предлагаемому определе-
нию, будет уже несингулярным. Конечно, рассматривать такие
сингулярные точки, как часть пространства-времени, было бы
неразумно, ибо в них не удовлетворялись бы обычные уравнения
физики и нельзя было бы производить какие-либо измерения.
Поэтому в разд. 3.1 мы определили пространство-время как пару
(Л7, g), в которой метрика g лоренцева и нужное число раз диф-
ференцируема, и, потребовав, что (^, g) нельзя расширить с
сохранением нужной степени дифференцируемости, гарантиро-
вали, что из пространства-времени вместе с сингулярными точ-
ками не была выброшена ни одна несингулярная точка.
Вопрос о наличии сингулярностей в пространстве-времени
превращается в вопрос о том, были ли вырезаны из простран-
ства-времени какие-либо сингулярные точки. Есть надежда, что
это можно установить по факту неполноты (в том или ином
смысле) пространства-времени.
В случае многообразия Л с положительно определенной мет-
рикой g мы можем ввести функцию расстояния р(х, у), которая
равна точной нижней грани длин кривых, соединяющих х и у.
Функция р(х, у) является метрикой в топологическом смысле,
т. е. базисом для открытых множеств многообразия Л служат
множества ^(х, г), состоящие из всех точек у е Л, для которых
р(х, г/)< г. Пара (Л, g) называется метрически полной (m-пол-
ной), если любая фундаментальная по функции расстояния р
последовательность сходится к точке, лежащей в Л. (Фундамен-
тальной последовательностью называется бесконечная последо-
вательность, для которой при любом е > 0 существует число N,
такое, что р(хп, хт) < е для любых п и т, больших N.) Имеется
альтернативная формулировка: (Л, g) является га-полной, если
каждая С4-кривая конечной длины имеет конечную точку в смыс-
ле разд. 6.2 (заметим, что эта кривая не обязательно должна
быть класса С1 на конце). Отсюда следует, что m-полнота обес-
печивает геодезическую полноту (g-полноту), т. е. возможность
продолжить каждую геодезическую до произвольных значений
ее аффинного параметра. Действительно, было доказано [92], что
для положительно-определенной метрики g-полнота и т-полнота
эквивалентны.
Лоренцева метрика не определяет какую-либо топологиче-
скую метрику, поэтому у нас остается только g-полнота. Можно
различать три типа g-неполноты: времениподобную, изотропную
и пространственноподобную. Если вырезать из пространства-вре-
мени регулярную точку, то получившееся многообразие будет
неполно во всех трех смыслах и можно было бы надеяться, что
полнота одного из упомянутых типов свидетельствует о полноте
других двух типов. К сожалению, это не обязательно так [97],
что видно из следующего примера, найденного Героком [54]. Рас-
8.1. Определение сингулярностей
287
смотрим двумерное пространство-время с координатами х, t и
метрикой gab. Введем новую метрику gab = Q,2gab, где положи-
тельная функция Q обладает следующими свойствами:
1) £2 = 1 вне области между вертикальными линиями х—— 1
И X — 1
2) Q симметрична относительно оси t, т. е. Q(7, х) = £2(/, —х).
3) На оси t t2Q. -> 0 при t -> оо.
В силу свойства (2) ось t — времениподобная геодезическая,
которая, согласно (3), неполна при t оо. Однако каждая изо-
тропная или пространственноподобная геодезическая покидает
область между х = —1 их = ф1 и не возвращается в нее. Сле-
довательно, в силу свойства (1) данное пространство изотропно
и пространственноподобно полно. Можно построить примеры, ко-
торые неполны в любом из трех указанных выше смыслов и
полны в оставшихся двух.
Времениподобная неполнота имеет непосредственное физиче-
ское истолкование: из нее следует возможность существования
свободно движущихся наблюдателей, мировые линии которых
имеют начало или конец на конечном интервале собственного
времени. Такое поведение мировой линии может вызвать даже
более сильное возражение, чем бесконечная кривизна, и, по-ви-
димому, пространство, в котором имеются такие линии, следует
рассматривать как сингулярное. Хотя аффинный параметр на
изотропной геодезической не совпадает по своему физическому
смыслу с собственным временем на времениподобной геодезиче-
ской, тем не менее изотропно геодезически неполные простран-
ства, вроятно, тоже нужно считать сингулярными, как из-за того,
что изотропные геодезические представляют собой истории ча-
стиц с нулевой массой покоя, так и по причине существова-
ния примеров (например, решение Райсснера — Нордстрема,
разд. 5.5), которые, надо думать, сингулярны и при этом вре-
мениподобно полны, но изотропно геодезически неполны. По-
скольку по пространственноподобным кривым ничто не движется,
смысл пространственноподобной геодезической неполноты не
столь ясен. Поэтому мы будем придерживаться той точки зрения,
что времениподобная и изотропная геодезическая полнота яв-
ляется минимальным условием, при котором пространство-время
можно считать свободным от сингулярностей. Отсюда, если про-
странство-время времениподобно или изотропно геодезически не-
полно, мы скажем, что в нем есть сингулярность.
Преимущество принятия времениподобной и (или) изотроп-
ной неполноты в качестве индикатора сингулярности состоит в
том, что, исходя из этого, мы можем доказать ряд теорем об
условиях, при которых сингулярность появляется. Однако класс
времениподобно и (или) изотропно неполных пространств не
включает в себя все пространства, которые было бы желательно
288
Гл. 8. Сингулярности пространства-времени
считать в том или ином смысле сингулярными. Например, Герок
[54] построил пространство-время, которое геодезически полно,
но содержит непродолжимую времениподобную кривую (не гео-
дезическую) конечной длины с ограниченным ускорением. Такую
кривую мог бы пролететь наблюдатель на каком-нибудь косми-
ческом корабле, обладая конечным запасом топлива. По истече-
нии конечного промежутка времени его нельзя было бы изобра-
жать точкой этого пространственно-временного многообразия.
Если мы собираемся утверждать, что пространство-время, в ко-
тором жизнь свободно падающего наблюдателя преждевременно
обрывается, содержит сингулярность, то, очевидно, мы должны
быть готовы к тому же выводу и в случае наблюдателя на кос-
мическом корабле. Для этого нам требуется какое-то обобщение
понятия аффинного параметра на случай любых О-кривых —
геодезических и негеодезических. Тогда можно было бы ввести
понятие полноты, требуя, чтобы в полном пространстве любая
С’-кривая конечной длины, в смысле измерения по такому пара-
метру, имела бы конечную точку.
Идея, которой мы собираемся воспользоваться, была, по-ви-
димому, впервые высказана Эресманом [46] и сформулирована
в более изящной форме Шмидтом [148].
Пусть %(/)—^-кривая, проходящая через р е Л, и {EJ
(t — 1, 2, 3) — базис в Тр. Мы можем параллельно перенести {Ег}
вдоль %(/) и получить базис в T^t) при каждом значении t. Тогда
касательный вектор V = (d/dt) ад можно будет выразить через
этот базис: V —У'(/)Ег— и мы сможем посредством формулы
S (Svlv^2
ввести обобщенный аффинный параметр и на А. Параметр и зави-
сит от точки р и от базиса {EJ в р. Если {Ег} —другой базис
в р, то существует некоторая несингулярная матрица Ар, такая,
что
Е, = S Ат'Еу.
г
Поскольку {Ег} и {EJ переносятся вдоль k(t) параллельно,
это соотношение выполняется при постоянных Я/'. Таким обра-
зом,
Ввиду несингулярности матрицы Я/' найдется постоянная С > О,
для которой
с£ v‘V <c~l X v!vl.
8.1. Определение сингулярностей
289
Следовательно, длина кривой К по параметру и конечна тогда и
только тогда, когда опа конечна по параметру и'. Если X — гео-
дезическая кривая, то и— аффинный параметр на Л; красота же
этого определения состоит в том, что и можно задать на любой
С‘-кривой. Мы будем говорить, что пространство-время {Ж, g)
b-полное (сокращение от bundle-complete, см. разд. 8.3), если
у каждой С^-кривой конечной длины, измеренной по обобщен-
ному аффинному параметру, существует конечная точка. Если
эта длина конечна при одном обобщенном аффинном параметре,
то она будет конечна при всех таких параметрах, так что мы ни-
чего не теряем, если ограничимся лишь ортонормированными
базисами. Когда метрика g положительно определена, обобщен-
ный аффинный параметр, определяемый ортонормированны.м ба-
зисом, является длиной дуги и потому ft-полнота совпадает с
m-полнотой. Однако понятие ft-полноты можно ввести, даже если
метрика не является положительно-определенной; фактически
для ее определения достаточно наличия связности на Ж. Ясно,
что из ft-полноты следует g-полнота, но приведенный выше при-
мер показывает, что обратное утверждение неверно.
Итак, мы будем называть пространство-время свободным от
сингулярностей, если оно ft-полное. Это определение согласуется
с высказанной выше точкой зрения, что времениподобная и изо-
тропная геодезическая полнота является минимальным условием
для того, чтобы пространство-время можно было считать сво-
бодным от сингулярностей. Может появиться желание слегка
ослабить это условие и называть пространство-время свободным
от сингулярностей только тогда, когда оно непрос "ранственно-
подобно ft-полное, т. е. если все непространственноподобные
(^-кривые конечной длины, измеренной по обобщенному аффин-
ному параметру, имеют конечную точку. Однако это определение
выглядело бы довольно громоздким при формулировке ft-полно-
ты через расслоенные пространства; такую формулировку мы
дадим в разд. 8.3. Фактически в каждой из теорем, доказывае-
мых нами в разд. 8.2, подразумевается, что пространство-время
(Ж, g) времениподобно или изотропно g-неполное и, следова-
тельно, содержит сингулярность по обоим из вышеприведенных
определений.
Интуитивно чувствуется, что с сингулярностью должна быть
связана неограниченно большая кривизна вблизи сингулярной
точки. Но мы исключили сингулярные точки из определенного
нами пространства-времени, и поэтому возникает трудность с тем,
что такое «вблизи» и что такое «неограниченно большая». Мож-
но сказать, что точки ft-неполной кривой находятся вблизи сингу-
лярности, если им соответствуют значения обобщенного аффин-
ного параметра, близкие к верхней грани этого параметра. Труд-
нее придать точный смысл «неограниченно большой кривизне»,
ю Закат 3,41
290
Гл. 8. Сингулярности пространства-времени
поскольку численные значения компонент тензора кривизны
зависят от базиса, в котором они измеряются. Один из подходов
состоит в том, чтобы рассматривать скалярные полиномы по
gab, Tjabcd И Rabed- БуДвМ ГОВОРИТЬ, ЧТО 6-НеПОЛНЭЯ КОНВЭЯ СООТ-
ветствует сингулярности скалярных полиномов кривизны, если
любой из этих скалярных полиномов неограничен на данной не-
полной кривой. Однако, когда метрика лоренцева, эти полиномы
не определяют полностью тензор кривизны: Пенроуз заметил,
что для решений в виде плоской волны все скалярные полиномы
равны нулю, тогда как тензор Римана отличен от нуля (подобно
тому как ненулевой вектор может иметь нулевую длину). Таким
образом, кривизна может в определенном смысле быть очень
большой, даже если скалярные полиномы малы. С другой сто-
роны, можно измерить компоненты тензора кривизны в базисе,
параллельно перенесенном вдоль кривой. Будем говорить, что
^-неполная кривая соответствует сингулярности кривизны в па-
раллельно перенесенном базисе, если любая из компонент тен-
зора кривизны на этой кривой не ограничена. Ясно, что суще-
ствование сингулярности скалярных полиномов означает также
существование сингулярности в параллельно перенесенном ба-
зисе.
Можно было бы надеяться, что в физически реалистических
решениях 6-неполнота кривой соответствует обоим видам сингу-
лярности кривизны. Однако пространство Тауба — НУТ
(разд. 5.8) служит примером решения, где, по-видимому, эта на-
дежда не оправдывается. В этом пространстве неполные геоде-
зические полностью заключены в некоторой компактной окрест-
ности горизонта. Метрика в этой компактной окрестности вполне
регулярна, и потому скалярные полиномы тензора кривизны ко-
нечны. Ввиду особого характера этого решения компоненты тен-
зора кривизны в базисе, параллельно перенесенном вдоль за-
ключенной геодезической, остаются ограниченными. Поскольку
заключенная геодезическая содержится в компактном множестве,
многообразие Л нельзя расширить до такого большого четырех-
мерного хаусдорфова паракомпактного многообразия Л', в кото-
ром неполные геодезические можно было бы продолжить. Сле-
довательно, эта неполнота возникла не от удаления сингулярных
точек. Тем не менее движение по одной из этих неполных вре-
мениподобных геодезических доставило бы наблюдателю мало
удовольствия: хотя его мировая линия не имеет конца, она кру-
жится и кружится внутри компактного множества, и наблюда-
тель никогда не перейдет через определенный момент своей
жизни. Поэтому представляется разумным считать такого рода
пространство-время сингулярным, хотя в нем и нет сингулярно-
сти скалярных полиномов кривизны или сингулярности кривизны
в параллельно перенесенном базисе. Согласно лемме 6.4.8, не-
8.2. Теоремы о сингулярностях 291
полнота, состоящая в полном заключении, может возникнуть
лишь при нарушении условия сильной причинности. В § 8.5 мы
покажем, что в типовом пространстве-времени частично или
полностью заключенная ^-неполная кривая соответствует сингу-
лярности кривизны в параллельно перенесенном базисе. Мы по-
кажем также, что полностью заключенная неполнота такого
рода, как в пространстве Тауба — НУТ, не появляется, если в
пространстве-времени имеется хоть какая-либо материя.
8.2. Теоремы о сингулярностях
В разд. 5.4 было показано, что при определенных разумных
условиях в пространственно-однородных решениях будут сингу-
лярности. Аналогичные теоремы можно доказать для ряда
других классов точных симметрий. Тем не менее вовсе не обяза-
тельно было бы придавать этим результатам какой-либо физиче-
ский смысл, поскольку они все-таки обусловлены ограничением,
чтобы симметрия была точной, чего, конечно, не будет ни в ка-
кой реальной физической ситуации. Поэтому многие авторы
полагали, что сингулярности являются лишь следствием симмет-
рии и не появятся в общем решении. Эта точка зрения была под-
держана Е. М. Лифшицем, И. М. Халатниковым и их сотрудни-
ками, которые показали, что определенные классы решений с
пространственноподобными сингулярностями не содержат того
числа произвольных функций, которое предполагается у общего
решения уравнений поля (эта работа подытожена в [101]). Как
считали авторы [101], это свидетельствует о том, что данные
Коши, приводящие к таким сингулярностям, имеют меру нуль
в множестве всех возможных данных Коши и, значит, не должны
иметь отношения к реальной Вселенной. Однако впоследствии
В. А. Белинский, И. М. Халатников и Е. М. Лифшиц [5] нашли
иные классы решений, которые, по-видимому, содержали полное
число произвольных функций, причем в этих решениях были син-
гулярности. Поэтому они отказались от утверждения, что в об-
щих решениях нет сингулярностей. Их методы интересны тем,
что проливают свет на возможную структуру сингулярностей, но
не ясно, сходятся ли используемые ими степенные ряды. Никто
еще на нашел общего вида условий, при которых возникновение
сингулярности неизбежно. Тем не менее мы рассматриваем ре-
зультаты Белинского, Лифшица и Халатникова как свидетель-
ство в пользу нашей точки зрения, согласно которой сингулярно-
сти, предсказываемые теоремами этого раздела, вообще говоря,
связаны с бесконечностью кривизны.
Первая теорема о сингулярностях, не содержащая каких-либо
предположений о симметриях, была доказана Пенроузом [126].
Он ставил целью доказать, что в звезде, коллапсирующей внутрь
10*
292 Гл. 8. Сингулярности пространства-времени
своего шварцшильдова радиуса, появится сингулярность. Если
коллапс строго сферически-симметричен, решение можно полу-
чить прямым интегрированием, и сингулярность всегда возникает.
Однако далеко не очевидно, что так будет и тогда, когда суще-
ствует неоднородность или хотя бы небольшой момент количе-
ства движения. В самом деле, в ньютоновской теории самый
незначительный момент количества движения может воспрепят-
ствовать появлению бесконечной плотности и вызвать у звезды
переход от сжатия к расширению. Однако Пенроуз показал, что
в общей теории относительности ситуация совсем иная: если
коллапсирующая звезда ушла внутрь своей шварцшильдовой
поверхности (поверхность г = 2m), то она уже не сможет из-под
нее выйти. Шварцшильдова поверхность в действительности
определена лишь для строго сферически-симметричного решения,
но Пенроуз использовал более общий критерий, который эквива-
лентен в случае решения Шварцшильда существованию шварц-
шильдовой поверхности и приложим к решениям, не обладаю-
щим строгой симметрией. Этим критерием является существова-
ние замкнутой ловушечной поверхности ТГ, которая представляет
собой такую замкнутую (т. е. компактную, без края) простран-
ственноподобную 2-поверхность класса С2 (обычно S2), что два
семейства ортогональных к ?Г изотропных геодезических у по-
верхности ?Г сходятся (т. е. \%л£аЬ и 2%abgab отрицательны, где
1Хаь и Ааъ — Две изотропные вторые фундаментальные формы
на (В последующих главах мы обсудим обстоятельства, при
которых появляется такая поверхность.) Это можно представить
себе следующим образом: J7” находится в столь сильном грави-
тационном поле, что даже расходящиеся лучи света затягиваются
обратно и превращаются в сходящиеся. Поскольку ничто не мо-
жет двигаться быстрее света, материя, заключенная в после-
довательно запирается внутри 2-поверхностей все меньшей и
меньшей площади, и все выглядит так, словно должно случиться
что-то «плохое». Что это так и есть, строго доказывает теорема
Пенроуза.
Теорема 1
Пространство-время (Л, g) не может быть изотропно геоде-
зически полным, если
1) RabKaКъ 0 для всех изотропных векторов (ср. с
разд. 4.3);
2) в ,/# существует некомпактная поверхность Коши
3) в Л существует замкнутая ловушечная поверхность <3~.
Замечание. Идея доказательства такова. Нужно показать,
что граница будущего поверхности будет компактной, если
Л — изотропно геодезически полное многообразие. Затем дока-
зывается, что это несовместимо с некомпактностью
8 2 Теоремы о сингулярностях
293
Доказательство. Из существования поверхности Коши сле-
дует, что Л—глобально-гиперболическое (предложение 6.6.3) и
потому причинно простое (предложение 6.6.1) многообразие. Это
означает, что границей множества /Ч.Т) будет поверхность
E+(fF) и ее образующими будут ортогональные ЕГ геодезические
Рис. 49. Двумерное сечение геодезически полного пространства с компакт-
ной поверхностью Коши Ж Будущее Z+ (^") 2-сферы 3~ имеет компактную
границу j + (SiT), поскольку расходящиеся изотропные геодезические встре-
чаются, обойдя цилиндр кругом.
сегменты с конечными точками в прошлом на . Допустим, что
Л—изотропно геодезически полное многообразие. Тогда, со-
гласно условиям (1) и (3) и предложению 4.4.6 вдоль любой на-
правленной в будущее изотропной геодезической, ортогональной
к 3~, в пределах аффинного расстояния, 2с"1 должна
быть точка, сопряженная ЕГ, причем с равно значению n%abgab
в точке, где данная изотропная геодезическая пересекает ЁГ. Со-
гласно предложению 4.5.14, те точки такой изотропной геодези-
ческой, которые лежат за точкой, сопряженной ЁГ, принадлежат
области /+(^"). Таким образом, каждый образующий сегмент
поверхности /+(^~) должен иметь конечную точку в будущем
в сопряженной к точке или до нее. Вблизи Т" на каждой орто-
гональной к .7" изотропной геодезической можно задать непре-
рывным образом аффинный параметр. Рассмотрим непрерывное
294
Гл. 8. Сингулярности пространства-времени
отображение X [0, b] X Q ->Л (Q — дискретное множество
1,2), определяемое переносом точки р е на аффинное расстоя-
ние v е [О, Ь] вдоль одной из двух направленных в будущее изо-
тропных геодезических, проходящих через р ортогонально к ГГ.
Ввиду компактности поверхности будет существовать некото-
рое минимальное значение с0 величин (—и (—Mabgab) •
Тогда, j+(,X)c: X [ОА] X Q) при Ьо = 2ссГ'-Следовательно,
7(£7~), будучи замкнутым подмножеством компактного множест-
ва, компактно. Это было бы возможно, если бы поверхность Коши
Зё была компактной, потому что тогда граница могла бы замк-
нуться и образовать компактную поверхность Коши, гомеоморф-
ную Зё (рис. 49). Однако ясно, что мы встретим затруднения,
если потребуем, чтобы поверхность Уё была некомпактной. Что-
бы доказать это строго, мы можем воспользоваться тем фактом
(см. разд. 2.6), что Л допускает направленное в прошлое, вре-
мениподобное векторное (Ч-поле. Каждая интегральная кривая
этого поля будет пересекать 3/ё (поскольку это поверхность
Коши) и пересекает /+(^~) самое большее один раз. Таким об-
разом, эти интегральные кривые задают непрерывное взаимно-
однозначное отображение /+(^")->5^. Если множество /+(£Г)
компактно, его образ а(7+(^")) тоже компактен и поэтому го-
меоморфен /(^). Однако ввиду некомпактности Ж множество
ос)/4-)^-)) может и не содержать всю поверхность Ж и в таком
случае должно иметь границу в Ж. Это, однако, невозможно,
поскольку, согласно предложению 6.3.1, 7+(£Г), а следовательно,
и а (7+(И) должны быть трехмерными многообразиями (без
края). Отсюда видно, что допущение изотропной геодезической
полноты Л (оно было сделано для доказательства компактности
7+(^")) неверно. □
Условие (1) этой теоремы (именно, что RabKaKb 0 для лю-
бого изотропного вектора К) обсуждалось в разд. 4.3. Чтобы оно
выполнялось, не имеет значения, какого порядка величины по-
стоянная Л, лишь бы плотность энергии была положительной
для любого наблюдателя. В гл. 9 будет показано, что условие (3)
(существования замкнутой ловушечной поверхности) должно
удовлетворяться по крайней мере в некоторой области простран-
ства-времени. Остается рассмотреть условие (2) (существова-
ния некомпактной пространственноподобной поверхности ^ё, яв-
ляющейся поверхностью Коши). Согласно предложению 6.4.9,
если допустить устойчивую причинность, то существование про-
странственноподобных поверхностей обеспечено. Условие ком-
пактности пространственноподобной поверхности — не слишком
серьезное ограничение, поскольку единственный пункт, в котором
2. Теоремы о сингулярностях
295
мы его использовали, это когда показывали, что а(7+(5г)) не
•может совпадать со всей поверхностью Ж Однако можно дока-
зать то же самое, если вместо некомпактности 26 потребовать,
чтобы с поверхности 3^ можно было провести направленную в
будущее непродолжимую кривую, которая не пересечет/+(^").
Другими словами, теорема была бы справедлива даже тогда,
когда поверхность 3$ компактна, если при этом существуют на-
блюдатели, которые могут избежать падения на коллапсирую-
щую звезду. Это было бы невозможно, если бы коллапсировала
сама Вселенная; но и при этих условиях, надо думать, сингуляр-
ности имеются, и это мы скоро покажем. Действительно тонкий
пункт теоремы — это требование, чтобы 3$ была поверхностью
Коши. Оно используется в двух местах: во-первых, при доказа-
тельстве того, что Jff—причинно простое многообразие, из чего
следовало наличие у образующих поверхности 7+(^~) конечных
точек и, во-вторых, когда мы проверяли, что при отображе-
нии а каждая точка 7+(^ ) отображается в точку поверхности Ж
Что это условие (чтобы была поверхностью Коши) необхо-
димо, видно из примера, данного Бардином. Глобальная струк-
тура в нем такая же, как у решения Райсснера — Нордстрема,
за тем исключением, что реальные сингулярности при г = О
устроены так, что они становятся в точности началом полярных
координат. Это пространство-время удовлетворяет условию
RabKaKb 0 для любого изотропного, но не времениподобного
вектора К, и в нем имеются замкнутые ловушечные поверхности.
Единственно, чем это пространство-время не удовлетворяет усло-
виям теоремы 1, тем, что в нем нет поверхностей Коши.
Следовательно, теорема 1, по всей видимости, утверждает,
что в коллапсирующей звезде будет или сингулярность, или го-
ризонт Коши. Это очень важный результат, ибо в любом случае
мы теряем возможность предсказывать будущее. Однако он не
дает ответа на вопрос, появляются ли сингулярности в физиче-
ски реалистических решениях? Для того чтобы разрешить его,
нам нужна теорема, в которой не предполагается существование
поверхностей Коши. Одно из условий такого рода теоремы
должно состоять в том, что RabKaKb 0 не только для изотроп-
ных, но и для всех времениподобных векторов, поскольку невы-
полнение этого условия — единственная возможность для того,
чтобы пример Бардина перестал быть аргументом. Теорема, ко-
торую мы приведем ниже, включает это условие и, кроме того,
хронологические условия (условие отсутствия замкнутых време-
ниподобных кривых). С другой стороны, она приложима к более
широкому классу ситуаций, поскольку существование замкнутых
ловушечных поверхностей является теперь только одним из трех
возможных условий. Другое из этих альтернативных условий
296
Гл. 8. Сингулярности пространства-времени
состоит в том, чтобы существовала компактная частичная по-
верхность Коши, а третья — в том, чтобы существовала точка,
световой конус прошлого (или будущего) которой начинает
сходиться снова (рис. 50). Первое из этих двух последних усло-
вий выполняется в пространственно замкнутых решениях, тогда
как второе тесно связано с существованием замкнутых ловушеч-
ных поверхностей, но его формулировка лучше подходит для на-
ших целей: например, в том случае, когда сходящийся вдали све-
Р и с. 50. Точка р, изотропный конус прошлого которой начинает сходиться
вторично.
товой конус — это наш собственный световой конус прошлого;
тогда мы можем непосредственно установить, выполняется ли
это условие. В последней главе будет показано, что наблюдения
микроволнового фона свидетельствуют о его выполнении.
Точная формулировка такова:
Теорема 2 (Хокинг и Пенроуз [75])
Пространство-время (jft, g) не является времениподобно или
Изотропно геодезически полным, если
1) Rat>KaKb 0 для любого непространственноподобного век-
тора К (ср. с разд. 4.3);
2) выполняется типовое условие разд. 4.4, т. е. если каждая
нелространственноподобная геодезическая содержит точку, в ко-
торой K[aRb\cd[eKf\KCKd ¥= о, где К — касательный вектор к этой
геодезической;
8.2. Теоремы о сингулярностях
297
3) на Л выполняется хронологическое условие (т. е. нет
замкнутых времениподобных кривых);
4) справедливо по меньшей мере одно из трех следующих
утверждений:
а) существует компактное ахрональное множество без гра-
ницы;
б) существует замкнутая ловушечная поверхность;
в) существует такая точка р, что на любой направленной
в прошлое (или на любой направленной в будущее) изотропной
геодезической из точки р расхождение 0 изотропных геодезиче-
ских из р становится отрицательным (т. е. изотропные геодези-
ческие, выходящие из р, фокусируются материей или кривизной
и начинают сходиться).
Замечание. Приведем альтернативную формулировку тео-
ремы.
Следующие три условия не могут выполняться одновременно:
I) каждая непродолжимая непространственноподобная гео-
дезическая содержит пару сопряженных точек;
II) на Л выполняется хронологическое условие;
III) имеется ахрональное множество 9?, для которого £'+(^’)
или Е-)^) компактны. (Будем говорить, что такое множество —
соответственно ловушечное для будущего или ловушечное для
прошлого.)
Мы докажем теорему 2 именно в этой формулировке. Дока-
зательство первого варианта отсюда следует непосредственно,
поскольку, если бы многообразие Л было времениподобно и изо-
тропно полным, то из условий (1) и (2), в силу предложений 4.4.2
и 4.4.5, следовало бы условие (I); условие (3) — то же самое,
что и (II), а из (1) и (4) вытекало бы условие (III): в случае (а)
9Р было бы компактным ахрональным множеством без границы и
£+ (^Р) = Е- (9>) =
а в случаях (б) или (в) множество 9? будет соответственно замк-
нутой ловушечной поверхностью или точкой р; тогда, согласно
предложениям 4.4.4, 4.4.6, 4.5.12 и 4.5.14, соответственно Е+(9>)
или E-fJ?) будут компактны как пересечения замкнутых мно-
жеств j+(9>) и /~(^) с компактными множествами, состоящими
из всех изотропных геодезических некоторой конечной длины
от 9’.
Доказательство. Поскольку доказательство довольно длинное,
мы разделим его на части и докажем сначала лемму и следствие
из нее. Отметим, что из рассуждений, аналогичных доказатель
ству предложения 6.4.6, вытекает, что в силу условий (I) и (II
на Л имеет место сильная причинность.
298
Гл. 8. Сингулярности пространства-времени
Лемма 8.2.1
Если 1?— замкнутое множество и на 1+ (S?) выполняется
условие сильной причинности, то множество Н+ (£+ (9?)) или
некомпактно, или пусто (рис. 51).
По лемме 6.3.2 через каждую точку q^j+(9?)~ 9Р прохо-
дит направлен 1ый в прошлое и лежащий в 1 +изотропный
Рис. 51. Ловушечное множество для будущего ЭЕ изотропные линии прохо-
дят под ±45°; три линии отождествлены, а точки q находятся на беско-
нечности. Приведены ахрональные множества Е + (Р7), j + (ST), Н+ (Е + (^))
и непродолжимая в будущее времениподобная кривая у е D+ (Е + (9’)).
геодезический сегмент, который обладает конечной точкой
в прошлом тогда и только тогда, когда q е Е+ (17). (Заметим,
что мы более не предполагаем существования поверхности Коши,
Jt может и не быть причинно-простым многообразием и соот-
ветственно J+(S’) — Е+(9?) может быть непустым множеством.)
Отсюда, если q е J + (1?) — Е+ (9}), то через q проходит непро-
должимая в прошлое изотропная геодезическая, которая лежит
в J+ (1?) и, следовательно, не пересекает (7+(.7)). Тогда из
леммы 6.6.4 следует, что q ф. D+ (J (9?У) — Н+ (j+ (9’’)). Поэтому
D+ (Ё+ (^)) - Н+ <£' (^)) = D+ (j+ (^)) - Н+ (j + (^))
и
Н+ (£+ (Я) <= Н+ (j+ (^)).
Теперь допустим, что множество Н+ (£+ (1?)) не пусто и ком-
пактно. Тогда его можно покрыть конечным числом окрестно-
стей локальной причинности Пусть р{— точка множества
1+ (^) A [^i — D+ (j+ (S^))]; из нее можно провести непродол-
8.2. Теоремы о сингулярностях
299
жимую в прошлое непространственноподобную кривую, которая
не пересечет ни J+ (^), ни D+ (Ё+ (У)). Поскольку окрестности Щ
имеют компактные замыкания, выходит из Пусть —
Точка на вне <?<. Тогда, поскольку q. (= ]+ (3?), найдется не-
пространственноподобная кривая щ от </! до . Эта кривая
пересечет D+ (е+ (^)), а значит, и некоторые из окрестностей
отличные от ‘У/, (скажем, (U^. Теперь пусть р2— точка из
Mi п[Х-п+(/ + (^))]> поступим, как и прежде, и т. д.
Эта процедура ведет к противоречию, ибо окрестностей ло-
кальной причинности предполагалось лишь конечное число, и в
то же время мы не можем вернуться в предыдущие 33,, посколь-
ку ни одна непрострапственноподобная кривая не может пересечь
31, больше одного раза. Следовательно, множество Я+(£+(5’))
должно быть или некомпактным, или пустым. □
Следствие
Если 3?— ловушечное множество для будущего, существует
непродолжимая в будущее времениподобная кривая, которая
целиком содержится в D+ (Е+ (3’)).
Введем на М времениподобное векторное поле. Если каждая
интегральная кривая этого поля, пересекающая £+(£?), пересе-
кает также и Я+(Е+(^)), то эти кривые задают непрерывное
взаимно-однозначное отображение Ё+(7’) на Я+(Е+(^)), и по-
тому область Я+(Е+(^)) будет компактной. Пересечение /+(6^)
с кривой, которая не пересекает Я+(Е+(S?)), дает искомую
кривую у (рис. 51 изображает одну из возможных ситуаций).
□
Рассмотрим теперь компактное множество ЗГ, определяемое
как Е+(3’) П /“(у) Поскольку у содержится в int/+(Е+(^’)),
Е~(^) будет состоять из и части /~(у). Поскольку кривая у
непродолжима в будущее, изотропные геодезические образую-
щие сегменты поверхности J_(y) не могут иметь конечных точек
в будущем. Но по условию (а) всякая непродолжимая непро-
странственноподобная геодезическая содержит пару сопряжен-
ных точек. Следовательно, в силу предложения 4.5.12 непродол-
жимое в прошлое продолжение v' каждого образующего сегмен-
та v поверхности /~(у) должно войти в область (у). При этом v
должна иметь конечную точку в прошлом в первой точке р мно-
жества v' П /-(у) или до нее. /_(у)~ открытое множество, и не-
которая окрестность точки р должна содержать точки области
(у), лежащие на соседних геодезических. Следовательно, аф-
финное расстояние до точек р от 3~ должно быть полунепрерыв-
но сверху, а множество Е~(3~) должно быть компактным как
пересечение замкнутого множества /~(у) с компактным множе-
300
Гл. 8. Сингулярности пространства-времени
ствол, которое образовано проведенными из геодезическими
сегментами некоторой ограниченной аффинной длины. Тогда из
леммы следует, что найдется непродолжимая в прошлое време-
ниподобная кривая к, содержащаяся в int D~(Е~ (ST)) (рис. 52).
изотропных образующих сегментов поверхности Е (ГГ). Кривая Л — непро-
должимая в прошлое времениподобная кривая, содержащаяся в int D~ (Е~ (У))
Пусть ап — бесконечная последовательность точек на А, обла-
дающая следующими свойствами:
I. ап+1 е= /-(а„).
II. Любой компактный сегмент А содержит лишь конечное
число точек ап.
Пусть Ьп—аналогичная последовательность на у, но с заме-
ной 1~ в свойстве 1наЛпс '>1Е /+(ai).
Из того что у и А должны содержаться в глобально гипербо-
лическом множестве int D (Е~(&~)) (предложение 6.6.3), следует
существование непространственноподобной геодезической ма-
ксимальной длины между каждой точкой ап и соответствующей
точкой Ьп (предложение 6.7.1). Любая из этих геодезических
будет пересекать компактное множество Е+(9>). Следовательно,
должна существовать q Е+(9’), которая будет предельной точ
8 2. Теоремы о сингулярностях 301
кой кривой на рп А Е+(^) и непространственноподобное напра-
вление в <7, которое будет пределом направлений геодезиче-
ских |лп. (Точка q и направление в q задают точку в расслоении
направлений над Л. Такая предельная точка существует в силу
компактности той части расслоения, которая является расслое-
нием направлений над £+(^’).) Пусть у'п — подпоследователь-
ность ц», такая, что П £+(./) сходится к q и направления р.'
в Е+(^) сходятся к предельному направлению. (Точнее, точки,
определяемые кривой р.' в расслоении направлений над £+('?’),
сходятся к предельной точке.) Пусть р будетнепродолжимой гео-
дезической через q в предельном направлении. По условию I тео-
ремы, на р существуют сопряженные точки х и у, причем
у^1+(х). Пусть точки х' и у' расположены на р соответственно
в прошлом и будущем точек х и у. Согласно предложению 4.5.8,
найдутся б > 0 и некоторая времениподобная кривая а от х'
до у', длина которой равна б плюс длина р от х' до у'. Пусть °U
и У — нормальные выпуклые координатные окрестности точек х'
и у' соответственно, причем в каждой из них нет ни одной кри-
вой длины ’Де. Пусть х" = А а и у” = Т А а, а х’п и у' п —
точки на p\i, сходящиеся соответственно к х' и у'. При доста-
точно больших п длина р'та от х'п ДО у'п будет меньше, чем е/4
плюс длина р от х' до у'. Кроме того, при достаточно больших п
х'п и у'п будут лежать соответственно в I~{х", CU) и 1+(у'',У').
Тогда, двигаясь от х'п к х" вдоль а до у” и затем от у” до у'п,
мы получим непространственноподобную кривую, более длин-
ную, чем р'„. Но в силу свойства II при достаточно больших п
а'п и Ь'п будут лежат на р'п соответственно в прошлом точки х'п
и в будущем точки у'п- Следовательно, р'та должна быть непро-
странственноподобной кривой наибольшей длины от х'п до у'п-
Мы приходим к противоречию, доказывающему теорему. □
Хотя эта теорема устанавливает существование сингулярно-
стей при весьма общих предположениях, у нее есть один недо-
статок: она ничего не говорит о том, где эта сингулярность —
в прошлом или в будущем. В случае (б) условия (4), когда
имеется компактная прострапственноподобная поверхность, нет
никаких оснований считать, что будущее в этом отношении пред-
почтительнее прошлого, но в случае (а), когда имеется замкну-
тая ловушечная поверхность, можно думать, что сингулярность
находится в будущем, а в случае (в), когда изотропный конус
прошлого начинает стягиваться, можно полагать, что сингуляр-
ность— в прошлом. Если условие (в) несколько усилить, а имен-
но потребовать, чтобы все направленные в прошлое временипо-
добные и изотропные геодезические начинали сходиться в преде-
лах компактной области в то можно показать, что сингу-
лярность находится в прошлом.
302 Гл. 8. Сингулярности пространства-времени
Теорема 3 (Хокинг [73])
Если
1) RabKaKb 0 для любого непрос'Гранственноподобног о век-
тора К (ср. разд. 4.3);
2) на (Л1, g) выполняется условие сильной причинности;
3) существуют направленный в прошлое единичный вектор W
в точке р и положительная постоянная Ь, такие, что если V —
единичный касательный вектор к направленной в прошлое, про-
ходящей через р времениподобной геодезической, то на каждой
такой геодезической расхождение 0 = Va-a этих геодезических
становится меньше, чем —Зс/b на расстоянии b/с от р, где с =
= —
тогда через р проходит неполная в прошлое, непростран-
ственноподобная геодезическая.
Пусть /(“ — параллельно перенесенный касательный вектор
к направленной в прошлое, проходящей через р непростран-
ственноподобной геодезической со следующей нормировкой:
KaWa = —1. Тогда для упомянутой в условии (б) временипо-
добной геодезической К°- = с~1Уа, откуда Ка;а = с-1Еа;а. По-
скольку функция Ка-а непрерывна на непространственноподобной
геодезической, она становится меньше, чем —З/b на изотропной
геодезической, проходящей через р, в пределах аффинного рас-
стояния Ь. Если Yb Y2, Y3 и Y4— псевдоортонормированная тет-
рада на этих изотропных геодезических, причем Yi и Y2 — еди-
ничные пространственпоподобные векторы, a Y3 и Y4 — изотроп-
ные векторы, для которых У3аУ4а =—1 и Y4 = К, то расхожде-
ние 0 изотропных геодезических в р определяется формулой
0 = Ка-.Ь (У/У? + Y2aY2b) = Ка;а + Ка-.b ^3%' + У4°У36).
Второй член равен нулю, так как Ка переносится параллельно.
Третий член можно представить в виде 1/a(KaKa):ьУ3ь; эта функ-
ция отрицательна, ибо — 0 на изотропных и КпКа <0 —
на времениподобных геодезических. Отсюда видно, что 0 стано-
вится меньше —З/b в пределах аффинного расстояния b вдоль
каждой изотропной геодезической из точки р. Таким образом,
если бы все направленные из р в прошлое изотропные геодезиче-
ские были бы полны, то контур (horismos) Е~(р) был бы ком-
пактен. Любая точка q е J~(E~(p))—Е~(р) при этом будет ле-
жать в 1~(р). Следовательно, опа не может находиться в
J+(E~(p)), поскольку Е~(р)—ахрональное множество. Отсюда
Т(ГС<Г (Е- (р)) = Е~ (р),
т. е. будет компактным множеством. Тогда по предложению 6.6.7
Е>-(Е~(р)) будет глобально гиперболической областью. Соглас-
но предложению 6.7.1, каждую точку г е D~(E (p) ) можно со-
8.2. Теоремы о сингулярностях
303
единить с р непространственноподобной геодезической, на кото-
рой между г и р не будет ни одной точки, сопряженной р. Отсюда
в силу предложения 4.4.1 область D~(Е~(р)) должна содер-
жаться в expp(F), где F— компактная область в Тр, которая
состоит из всех направленных в прошлое пепространствепнопо-
добных векторов Ка, удовлетворяющих условию KaWa —2Ь.
Если бы все непространственноподобные геодезические из р в
прошлое были полны, множество ехрр(№) было бы определено
для любого № е F и было бы компактно как образ компакт-
ного множества при непрерывных отображениях. Однако, со-
гласно следствию леммы 8.2.1, D~(E~(p)) содержит непродол-
жимую в прошлое времениподобную кривую. По предложению
6.4.7 она не может быть полностью заключена в компактном
множестве ехрр(Е), и, следовательно, предположение, что все
направленные в прошлое из р непространственноподобные гео-
дезические полны, не может быть верным. □
Теоремы 2 и 3 являются наиболее полезными теоремами
о сингулярностях, ибо можнопоказать, что их условия удовле-
творяются в ряде физических ситуаций (см. следующую главу).
Однако не может ли оказаться, что эти теоремы свидетельствуют
не о сингулярности, а о замкнутой времениподобной кривой, на-
рушающей условия причинности? Это было бы много хуже, чем
просто потеря возможности делать предсказания, что является
альтернативой теореме 1; по нашему мнению, такое нарушение
причинности более неприемлемо, чем сингулярность. Тем не ме-
нее хотелось бы знать, может ли нарушение причинности вос-
препятствовать появлению сингулярностей? Из нижеследующей
теоремы следует, что в определенных ситуациях не может. Это
означает, что сингулярности нужно принимать всерьез, и при-
дает нам уверенность, что вообще нарушение причинности не
является выходом из положения.
Теорема 4 (Хокинг [73])
Пространство-время не является времениподобно геодезиче-
ски полным, если
1) RahKaKb 0 для любого непространственпоподобного
вектора К (ср. с разд. 4.3);
2) существует компактная прос^ранственноподобная гипер-
поверхность (без края);
3) единичные нормали к всюду на годятся чли расхо-
дятся.
Замечания. Условие (2) можно трактовать как утверждение
о пространственной замкнутости Вселенной, а условие (3)- как
утверждение о том, что она расширяется (сжимается). Как было
объяснено в разд. 6.5, мы можем взять накрывающее многообра-
304
Гл. 8. Сингулярности пространства-времени
зие Л, в котором каждая связная компонента образа поверхно-
сти диффеоморфна 9? и является частичной поверхностью
Коши в Л. Мы будем работать с многообразием Л и обозначим
через одну связную компоненту образа 9?. Рассматривая за-
дачу Коши в Л, мы видим, что наличие сингулярностей (но не
обязательно их характер) является устойчивым свойством дан-
ных Коши на 9Р, поскольку достаточно малые вариации данных
на 9? не нарушают условия (3). Это служит контрпримером к
предположению Лифшица и Халатникова, что сингулярности по-
являются лишь для множества данных Коши меры нуль, хотя
следует помнить, что определение сингулярности, которому мы
следуем здесь, не совпадает с тем, которым пользуются Лифшиц
и Халатников.
Доказательство. По условиям (2) и (3) свертка второй фун-
даментальной формы поверхности 9? имеет на У отрицательную
верхнюю грань. Таким образом, если бы Л (и значит, Л) было
времениподобно геодезически полно, то на каждой направленной
в будущее геодезической, ортогональной к Д в пределах конеч-
ной верхней грани b расстояния от 9Р (предложение 4.4.7) суще-
ствовала бы точка, сопряженная Д. Но, согласно дополнению
к предложению 6.7.1, до каждой точки можно про-
вести направленную в будущее геодезическую, ортогональную
к д’, на которой между q и 9Р нет ни одной точки, сопряженной
поверхности Д. Пусть X [0, 6] -> Л — дифференцируемое
отображение, которое смещает точку реХ и расстояние s е [0, Ь]
вдоль направленной в будущее геодезической, ортогональной
к д в точке р. Тогда множество ₽:^Х[0, Ь] компактно и содер-
жит О+(Х). Отсюда компактны В+(д) и Н+(д). Если бы мы
предполагали выполнение условия строгой причинности, то иско-
мое противоречие следовало бы из леммы 8.2.1. Однако даже и
без этого условия можно прийти к противоречию. Рассмотрим
точку реЯ+(Х). Поскольку каждая направленная в прошлое
непространственноподобная кривая от q до д’ будет состоять из
(возможно, нулевого) изотропного геодезического сегмента в
Н+(д) и из непространственноподобной кривой в D+td), функ-
ция расстояния d(d, q) будет меньше или равна Ь. Отсюда, по-
скольку d полунепрерывна снизу, можно было бы найти беско-
нечную последовательность точек rn<=D+{d), сходящихся к q,
для которых d(d, гп) будет сходиться к d(d, q). Каждой гп бу-
дет соответствовать по крайней мере один элемент р-1(г„) из
XX [0, Ь]. Ввиду компактности XX [0> Ь] найдется элемент (р, s),
8 2. Теоремы о сингулярностях
305
который будет предельной точкой последовательности (/«).
В силу непрерывности s = d(d, q) и 0(р, s) — q. Таким образом,
к каждой точке q е Н+ (<?’) можно будет от д провести геоде-
зическую длиной d(d, q). Теперь пусть 71 е Я+(£?) лежит в про-
шлом точки q на той же изотропной геодезической образующей X
поверхности Я+(^). Соединив геодезическую длиной d(d, qt)
от д’ до 71 с сегментом Z между qt и q, мы получим непростран-
ственноподобную кривую d (d^qd) от д’ до q, которую можно
варьировать так, чтобы получить более длинную кривую между
теми же конечными точками (предложение 4.5.10). Следователь-
но, d(d, q), q.<= H+(d) будет строго убывающей функцией
вдоль каждой направленной в прошлое образующей Н+{д). Но
это ведет к противоречию, так как в силу полунепрерывности
снизу функции d(d, q) она должна иметь минимум на компакт-
ном множестве Н+(д). □
Условие (2) компактности д необходимо, так как в про-
странстве Минковского (Jt, я) некомпактная поверхность
^(х1)2 + (х2)2 + (х3)— (х4)2 = —1, х4 < 0 является частичной по-
верхностью Коши с = — 3 во всех точках. Если возьмем
область пространства Минковского, задаваемую неравенствами
х4 < 0, (х1)2 + (х2)2 + (х3)2 + (х3)2 — (х4)2 < 0,
мы можем отождествить точки, полученные действием дискрет-
ной группы изометрий G, так, что d’lG будет компактно [102].
Согласно теореме 4, пространство (^/С, т]) будет времениподоб-
но геодезически неполным, поскольку отождествление относи-
тельно действия группы G не может быть распространено на все
многообразие Jt [ни условие (1), ни условие (2) разд. 5.8 не
выполняются в начале координат]. В этом случае сингулярность
в смысле неполноты возникает из плохих глобальных свойств и
не сопровождается сингулярностью кривизны. Этот пример был
предложен Пенроузом.
Условия (2) и (3) можно заменить на следующие:
2Z) д’ есть поверхность Коши для J(\
3') х“а имеет на д грань, отличную от нуля.
Хотя в этом случае не может быть горизонта Коши, однако
длины всех направленных в будущее времениподобных кривых
из д’ должны иметь некоторую конечную верхнюю грань.
Герок [50] показал, что при сохранении условия (2) и замене
условий (1) и (3) на условия
1") RabKaKb 0 для любого непространственноподобного
вектора, причем равенство имеет место лишь при Яаъ = 0;
306 Гл. 8. Сингулярности пространства-времени
3") существует такая точка р е 9, что любая непродолжи-
мая непространственноподобная кривая, пересекающая 9’, пере-
сечет также J+(p) и имеет место одно из двух: либо об-
ласть зависимости поверхности 9 плоская, либо многообразие^
времениподобно геодезически неполно.
Условие (3") требует, чтобы наблюдатель в точке р мог уви-
деть любую частицу, которая пересечет 9 и чтобы он сам был
видим с нее. Метод доказательства состоит в том, чтобы рас-
смотреть прострапственноподобные поверхности без края, кото-
рые содержат точку р. Из этих поверхностей можно построить
топологическое пространство S(p) подобно тому, как мы строили
топологическое пространство из всех непространственпоподоб-
ных кривых между двумя точками. Условия (2) и (3") означают
тогда, что S(p) компактно. Можно показать, что площади по-
верхностей являются полунепрерывными сверху функциями в
S(p) и должна быть некоторая поверхность У, проходящая че-
рез р, площадь которой больше или равна площади любой дру-
гой поверхности. Из вариационных соображений, аналогичных
тем, что приводились в случае непространствепноподобных кри-
вых, следует, что /'У обращается в нуль всюду па 9', за исклю-
чением, быть может, точки р, где поверхность может и не быть
дифференцируемой.
Рассмотрим однопараметрическое семейство пространствен-
ноподобных поверхностей 9(и), где 5^(0) = 9'. Вектор вариации
W = д/ди можно представить как fn, где п — единичная нор-
маль к поверхностям, f — некоторая функция. Используя уравне-
ние Райчаудхури для конгруэнции интегральных кривых вектор-
ного поля W, можно показать, что
f { - j 02 - 2о2 - Rabnan + Г^,аЬИаЬ },
(JLL О J
где
0 == X 7-аЬ 3" ^ab ёаЪ “Ь ratlb
И
> 1 ab
= у ОаЬО •
Если существует точка q 9', в которой Rabnanb9=0 или хий=^0,
мы можем подобрать такую функцию f, при которой (дВ/ди) < 0
всюду на 9'. Если Rabnanb = 0, %ab = 0 всюду на 9', но при
этом имеется некоторая точка q е 9’, в которой Cabcdnbnd 9= 0,
то тогда д<у/ди 9= 0 и можно найти такую функцию f, что
дВ[ди = 0 и д-В/ди2 < 0 всюду на 9’. В любом случае можно
построить поверхность 9", на которой всюду %аа < 0 и, следо-
вательно, многообразие Л будет изотропно геодезически не-
8.3. Описание сингулярностей 90?
полным в силу теоремы 4. Если Rab, %ab и Cabcdnhnd равны нулю
всюду на ,7'., то из тождеств Риччи для па видно, что Cabcd~Q
на 7', т. с. в области D(7) пространство-время является пло-
ским. Примером, в котором условия (1"), (2) и (3") выполнены,
а область D(7) плоская, служит пространство Минковского
с отождествлением {х1, х2, х3, х4} с {х1 + 1, х2, х3, х4}, {х1, х24~ 1,
х3, х4} и {х1, х2, х3+1, х4}. Оно геодезически полно. Однако
приведенный ранее пример тоже удовлетворяет этим условиям
и свидетельствует о том, что область D(7) может быть одно-
временно геодезически неполной и плоской.
8.3. Описание сингулярностей
Приведенные выше теоремы свидетельствуют о наличии син-
гулярностей в широком классе решений, но содержат мало ин-
формации о природе этих сингулярностей. Чтобы исследовать
этот вопрос более детально, нужно определить, что подразуме-
вать под размерами, формой, местонахождением и прочими ха-
рактеристиками сингулярности. Это было бы совсем легко, если
бы сингулярные точки включались в пространственно-временное
многообразие. Однако установление структуры многообразия
в таких точках физическими измерениями было бы невозможно.
В самом деле, может существовать много структур многообра-
зия, совпадающих в регулярных областях, но различающихся
в сингулярных точках. К примеру, в решении Робертсона —
Уокера многообразие в окрестности сингулярности t = 0 можно
описать координатами
{t, г cos 0, rsin0cos</>, г sin 0 sin $}
или координатами
{t, Sr cos 0, Sr sin 0 cos <j>, Sr sin 0 sin <f>}.
В первом случае сингулярностью будет трехмерная поверхность,
а во втором — единственная точка.
Выход заключается в том, чтобы разработать рецепт по-
строения некоторой границы д многообразия Ж, которая одно-
значно устанавливается измерениями в несингулярных точках,
т. е. структурой (.<, g). Затем было бы желательно задать по
меньшей мере топологию, а может быть, и дифференцируемую
структуру в пространстве Л+ Л U д. Одним из подходов мог
бы служить метод неразложимых множеств для бесконечности,
описанный в разд. 6.9. Но этот метод зависит лишь от конформ-
ной метрики и потому не позволяет отличить бесконечность от
сингулярных точек па конечном расстоянии. Чтобы такое раз-
личие существовало, по-видимому, нужно при построении Л+
ЗС8 Гл. 8. Сингулярности пространства-/’ пемени
исходить из того критерия, которым мы пользовались при дока-
зательстве существования сингулярностей, а именно из Ь-непол-
ноты. Изящный метод такого построения был разработан Шмид-
том. Этим методом перекрываются более ранние конструкции
Хокинга [72] и Герока [53], в которых сингулярные точки опре-
деляются как классы эквивалентности неполных геодезических.
В этих конструкциях не требуется, чтобы все //-неполные
кривые (скажем, неполные времениподобные кривые с ограни-
ченным ускорением) обязательно имели конечные точки. В опре-
делении классов эквивалентности имеется некоторая неоднознач-
ность. Конструкция Шмидта не страдает этими недостатками.
Метод Шмидта состоит в задании положительно определен-
ной метрики е на расслоении ортонормированных реперов
jt : О(^)->Здесь О(Л7)—множество всех ортонормирован-
ных четверок векторов {Еа}, Еа е Тр для каждого р е Л (а про-
бегает значения от 1 до 4), а л — проекция, которая отображает
базис в точке р в саму точку р. Оказывается, что множество
О (Л) неполно по метрике е, если и только если многообразие
Л b-неполно. Если О {Л} /«-неполно, можно с помощью фунда-
ментальных последовательностей образовать пополнение О (Ж)
до метрического пространства. Проекция л может быть продол-
жена на О (Л), и тогда фактор-пространство О (./7) по л есть по
определению многообразие Л+, которое является объединением
Л с множеством дополнительных точек д. Множество д состоит
из сингулярных точек многообразия Л в том смысле, что оно
является множеством конечных точек всех ft-неполных кривых.
Чтобы выполнить построение, вспомним (разд. 2.9), что
связность на Л, задаваемая метрикой g, определяет четырех-
мерное горизонтальное подпространство Ни десятимерного ка-
сательного пространства Ти в точке we О(Л). Таким образом,
Ти представляет собой прямую сумму подпространства Ни и
вертикального подпространства Vu, состоящего из всех векторов
в Ти, которые касательны к слою л-1 (л(и)). Теперь мы по-
строим базис {Ga} = {Еа, FJ для Ти, где А пробегает значения
от 1 до 10, a i от 1 до 6; {Ё,,} есть базис для Ни, и {F,}— базис
для Vu.
Для данного вектора Хе Тл(иу(Л) существует единственный
вектор Хе Ни(О (Л)), удовлетворяющий условию л*Х = X.
Следовательно, на О (Л) однозначно определены четыре гори-
зонтальных векторных поля Ео, которые являются горизонталь-
ными лифтами ортонормированных базисных векторов Еа для
каждой точки ие О (Л). Интегральные кривые поля Еа в О (Л)
соответствуют параллельному перенесению базиса {Еа} в Л
вдоль геодезической в направлении вектора Е3. Группа 0(3, 1),
мультипликативная группа всех несингулярных действительных
8 3. Описание сингулярностей
309
лоренцевых 4 X 4-матриц АаЬ, действует в слоях 0 множества
О {Л}, переводя точку и — {р, Еа)<=О(Л) в точку А(и) =
-= {р, AabEb} О (Л). Можно рассматривать О (3,1) как ше-
стимерное многообразие и при этом описывать касательное про-
странство Tj (0(3, 1)) к 0(3, 1) в единице группы / векторным
пространством всех 4 X 4-матриц а, обладающих свойством
dabGbc = —a,.bGim. Тогда при аеГ/(0(3,1)) мы можем опре-
делить кривую в 0(3, 1) через At = exp(ta), где
п=0
Отсюда, если и<=0(Л), то в л_|(л(«)) можно задать кривую,
проходящую через и, полагая Лаи (/) = At (и). Поскольку кри-
вая Xau(t) лежит в слое, ее касательный вектор (Pldt)K верти-
кален. Поэтому для каждого можно определить верти-
кальное векторное поле F (а):
F(a) \u = (d/dt)^ii]u
для всякого иеО(^). Пусть {а,} (1=1, 2, ..., 6) есть базис
в Tj, тогда Fi=F(ai) представляют собой шесть векторных
полей на 0(Л) и могут служить базисом для Vu в каждой
точке ие О(^£).
Матрица Be 0(3, 1) задает отображение 0(Л}^-0{Л')
вида и-* В (к). При индуцированном отображении В*: Т'и-+Твм
вертикальные и горизонтальные векторные поля преобразуются
следующим образом:
В,(Ёа) = Ва-г,1Ё&,
BJF/) = C/F;,
где Сi = ВabaibcB^}cda’da и {а*}— базис в T*h дуальный базису
{aj в Т] (следовательно, alabajab = б1;, a’abajcd = 6ac6bd). Для
дальнейшего будет важна не конкретная форма этих индуци-
рованных отображений, а их свойство быть постоянными на О (Л).
Теперь у нас есть базис {Ол} = {Ёа, FJ (А = 1, ..., 10)
в Ти в каждой точке и <= О (Л). Поэтому мы можем задать
положительно-определенную метрику е на О (Л) соотношением
е(Х, Y) = У, XAYA, где X, Y Т (и) и ХА, YA — компоненты X
А
и Y в базисе {Gx}. Используя метрику е, можно ввести функ-
цию расстояния р(и, v), где и, как нижнюю грань
длин кривых от и до v (измеренных по метрике е). Тогда можно
поставить вопрос: является ли О (Л) полным множеством отно-
сительно функции расстояния р?
31(1 Гл. ft Сингулярности пространства-времени
Предложение 8.3.1
(О (Л), е) является //z-полным пространством тогда и только
тогда, когда пространство-время g) Zz-полно.
Пусть у(0 — некоторая кривая в Л. Тогда, если задана точка
иыл_'(д). где реу, можно построить горизонтальную кривую
у(П, которая проходит через и и для которой л(у(/)) = у(/).
Из определения положительно-определенной метрики е следует,
что длина дуги y(Z), измеренная по этой метрике, равна обоб-
щенному аффинному параметру у (/), определяемому тем базисом
в точке р, изображением которого является точка и. По-
этому, если у у(V) нет конечной точки, но длина ее, измеренная
по обобщенному аффинному параметру, конечна, то у у(t) тоже
нет конечной точки, но конечна длина по метрике е. Таким
образом, m-полнота множества О (Л) означает b-полноту в мно-
гообразии Л.
Чтобы доказать обратное, нужно показать, что для С’-кри-
вой X (/) конечной длины в О (Л), не имеющей конечной точки,
л(Х(0) является С'-кривой в Л со следующими свойствами:
1) у нее конечная аффинная длина;
2) у нее нет конечных точек в Л.
Свойство (1) доказывается следующим образом. Пусть
Тогда через и можно провести горизонтальную кривую
Х(0, такую, что л (%(/)) = л(%(^)). Для каждого значения t X(t)
и Z (t) будут лежать в одном и том же слое, так что в 0(3, 1)
будет единственная кривая B(t), для которой l(t) ==
Это означает, что
где В = dB/dt. Отсюда
(М)=2Ж (ЯКД’+
ь
+ (.ВаЬВ 1 Ьса‘са)2'»
i
где {ЁД — базис Я*„, дуальный базису {ЁД (т. е. (Ёа, Ё6> = 6%),
и а1аЪ — базис Т/, дуальный базису а, аЬ (т. е. at аЬа! аЬ = 6/).
Матрица ВаЬ удовлетворяет равенству BabGbcBdc = Gad. От-
сюда
Bab^acBcd ^bdi
так как Gab = G~\b. Дифференцируя по t, имеем
BabB bficd:== GacBdbB Ьс‘
8.3. Описание сингулярностей
311
Таким образом, ВаЪВ ' Ьс <= Т, (О (3, 1)). Поскольку матрицы а1а1
образуют базис T*h существует такая постоянная С, что
X (ваЬВ~'Ьса1са)2 > С (BabB~{bcBadB~idc').
Любая матрица S е 0(3, 1) может быть представлена в виде
В = QAQ, где
z chg О 0 sh g, \
I ° 10 0 |
Л=1 00101
V sh g 0 0 ch с, '
и Q и О — ортогональные матрицы вида
причем О и О — ортогональные 3 X 3-матрицы, а векторы ба-
зиса {ЕД пронумерованы так, что Е4 — времениподобный вектор.
Матрица А соответствует изменению скорости в направлениих\
а матрицы Q и Q соответствуют вращениям. При таком разло-
жении
BabB~'bcBadB^de^2^.
Для любого векторного поля X е Ти
£((Ёй, X>Qab)2 = £((E“, X))2.
b а
Следовательно,
Отсюда
и поэтому
Пусть оо — наименьшая верхняя грань для ||| на Л(/).
Тогда
£(Х)>|£(Х)е-^ + С'Ч0,
312 Гл, 8. Сингулярности пространства-времени
где L (л)— длина кривой 7. по метрике е. Так как она конечна,
должны быть конечны g0 и Л(Л). Следовательно, аффинная
длина кривой я(?.(/)) в Л, равная L(2v), будет конечна.
В завершение доказательства предложения 8.3.1 мы должны
показать, что нет такой точки р е Л, в любую окрестность СН
которой входит и остается там кривая л(2«(0). Поскольку точка
р обладает нормальной окрестностью, это вытекает из следую-
щего утверждения:
Предложение 8.3.2 {Шмидт [147])
Пусть Л’ — компактное подмножество многообразия Л. До-
пустим, что в О (Л) имеется кривая % (/) конечной длины и без
конечных точек, которая входит в л-1 (Ж) и остается там.
Тогда существует непродолжимая изотропная геодезическая у,
целиком содержащаяся в Л.
Пусть K(t)— горизонтальная кривая, проходящая через не-
которую точку «ек(/), причем п(/(г)) = Кривая 7.(t)
не имеет конечной точки. Допустим, что есть точка е^О(Л),
которая является конечной точкой горизонтальной кривой 7{t).
Тогда должна существовать такая открытая окрестность Ж
точки v с компактным замыканием, что 7.(t) входит в нее и
остается там. Пусть УП'— множество {х е О {Л): Вх е Ж для
всех матриц Вс |g| go}- В силу компактности Ж и ограничен-
ности go множество Ж7 должно быть компактным. Кривая 7.(t)
войдет в Ж' и останется в нем. Но любое компактное множество
m-полно относительно положительно определенной метрики е.
Следовательно, кривая ?.(/), обладая конечной длиной, должна
будет иметь конечную точку в Ж7. Из этого видно, что у кривой
!(/) нет конечной точки.
Пусть {хп}—последовательность точек на 7.(t), не имеющая
какой-либо предельной точки. Поскольку Л3— компактное мно-
жество, найдется точка хеЛ1, которая является предельной точ-
кой л(х„). Пусть СП— нормальная окрестность точки х с ком-
пактным замыканием, и пусть о:^/—*О(Л)—сечение О {Л)
над °U, т. е. о (р), р <=йИ, — ортонормированный базис в р. Пусть
X(t) = а(л (7.(t))) при 7.(1) е л-1 (°U). Тогда, как и в предыду-
щем предложении, будет существовать единственное семейство
матриц Л(1)е0(3, 1), такое, что 7.(t) ~ A(t)X(t) и матрицы А
можно представить в виде А = QAQ. Допустим, что
имеет конечную верхнюю грань gi, где хп' = X (Ж) — подпосле-
довательность последовательности х„, сходящаяся к х. Тогда
точки хп’ должны принадлежать множеству °W — {v е О (Л):
: Д-1е ед а(<2/) при некоторой матрице Ле 0(3, 1) с |g|<gi}.
8.3. Описание сингулярностей
313
Однако множество сЦ' должно быть компактным и потому дол-
жно содержать предельную точку последовательности {хп>}, что
противоречит нашему выбору {х„}. Таким образом, |£(Д)| не
имеет конечной верхней грани. Поскольку ортогональная группа
компактна, мы можем выбрать такую подпоследовательность
{хп"}> чт0 &п" будет сходиться к некоторой матрице й', а й„» — к
некоторой й' (здесь Йге// = Й(Д) и т. д.); и
^>n"+l > а > ® (8.1)
для некоторой постоянной а.
Пусть
V(/) = (Q')-‘^(0 и д(0^АД‘(аТ^(0-
Тогда Лга"(Д) стремится кх = Qzo(x). Поскольку длина кривой
k(t) конечна, кривая к' (t) тоже имеет конечную длину. Это
означает, что стремится к нулю интеграл
zn"+l
J ((Xй)2 + (Х7 + (X2)2 + (Х3)2)’4 dt,
где _
(Д,\ 4=“,”'2-3
и
Ё“ =—^=г (Ё4 + Ё1), Ё* =(Ё4 - Ё1).
Следовательно,
{п' + 1
J | ХЛ | dt
tn"
стремится к нулю при каждом А. Компоненты У„”А касатель-
ного вектора к горизонтальной кривой Д (t) равны
У„Л = е-?«"Х“, Y^v = ein''Xv, Yn? = X2, Yn3 = X3.
Поэтому
tn"+1
J |Y„"X|d^ (Л = «, 2,3) (8.2)
tn"
стремится к нулю.
Пусть ц — интегральная кривая горизонтального векторного
поля Е”, проходящая через х. Тогда л(ц) будет изотропной гео-
дезической в Л?. Допустим, что п(,и) выходит из JY как в
314
Гл. 8. Сингулярности пространства-времени
направлении будущего, так и в направлении прошлого. Тогда най-
дется некоторая окрестность У точки х с компактным замыка-
нием и с тем свойством, что в каждом из этих направлений ц
покидает множество Т', где F = {а е О (Л} : существует Д,
для которой AcsTJ. Окрестность Т можно выбрать настолько
малой, чтобы она обладала упомянутым свойством для любой
интегральной кривой векторного поля Ер, которая пересекает Т,
т. е. так, чтобы любая такая кривая выходила из п-1 (Л9) в обоих
направлениях. Пусть —трубка, состоящая из всех точек на
интегральных кривых поля Е”, пересекающих Т. Тогда множе-
ство П л-1 (Л9) компактно. При достаточно больших п" кривая
А.П"(^п") будет содержаться в Т. Согласно (8.2), поперечные
к направлению Е1 компоненты касательного к Zfl" вектора
настолько малы, что при достаточно больших п" и t > tn» кри-
вая Хп" (/) нигде не сможет выйти за пределы трубки
П яг1 (Л9), за исключением ее концов, т. е. там, где выхо-
дит из д-ЦЛ9). Однако Хп" (/) не может покинуть лжЧЛ9), по-
скольку %(/) не выходит из л-1 (Л9). Следовательно, ХП" дол-
жна лежать в Ч/ П л-1 (Л9) при Это ведет к следую-
щему противоречию. Кривая An"+i(^"+i) содержится в Т\ од-
нако, согласно (8.1), окрестность можно выбрать настолько
малой, что
Хп" (^я"+1) — Дге"+1А»1" 1^-/г"+1 (6г" + 1)
будет лежать в У, но не в F. Отсюда следует, что наше пред-
положение о том, что изотропная геодезическая л(ц) выходит
из Л9 в обоих направлениях, ложно. Следовательно, должна
быть какая-то точка р е Л9, которая является предельной точ-
кой л(ц). Тогда по предложению 6.3.1 существует непродолжи-
мая изотропная геодезическая у, проходящая через р, которая
содержится в, Л9 и является предельной кривой для л(ц). □
Если расслоение О (Л) m-неполно, можно построить его по-
полнение по метрике О (Л). Оно по определению есть множе-
ство классов эквивалентности фундаментальных последователь-
ностей из точек расслоения О (Л). Если х = {хт} и у = {ут} —
две фундаментальные последовательности в О (Л), расстоянием
р(х, у) между х и у является по определению lim р{хп,уп),
п -> оо
где р — функция расстояния на О (Л), определяемая положи-
тельно определенной метрикой е; будем говорить, что х и у
эквивалентны, если р (х, у) — 0. О (Л) можно разложить на
часть, гомеоморфную О {Л), и множество граничных точек д
(т. е. О(Л) = О (Л) U d). Функция расстояния р задаст топологию
8.3. Описание сингулярностей
315
на О (Л). Из (8.1) следует, что эта топология на О не зависит
от выбора базиса {а,} в Т{. ____
Действие группы 0(3,1) можно распространить на О (Л).
В самом деле, преобразование базиса {GA} под действием
Де0(3, 1) не зависит от положения в О (Jr). Значит, суще-
ствуют такие положительные постоянные Ci и С2 (зависящие
только от Л), что
С{р(и, и)^р(Л(м), Л(р)) <С,о (и, v).
Это означает, что под действием А последовательности Коши
будут отображаться на фундаментальные последовательности
и классы эквивалентности фундаментальных последовательно-
стей будут отображаться на такие же классы эквивалентности.
Поэтому действие 0(3, 1) распространяется на 0(^<) единствен-
ным образом. Тогда Л+ можно определить как фактор-про-
странство 0(Д/) по группе 0(3, 1). Поскольку О (Л)/О (3, 1) =
= Л и поскольку под действием 0(3, 1) неполная фундамен-
тальная последовательность остается неполной, мы можем
представить Л+ как объединение многообразия Л и множества
д, называемого ^-границей Л. Точки д можно считать изображе-
ниями конечных точек классов эквивалентности b-неполных кри-
вых в Л. ___________
Проекция л : О (Л)^> Л+, которая относит точку в О (Л)
к ее классу эквивалентности относительно действия группы
0(3, 1), индуцирует топологию на Л+ по топологии на О (Л).
Однако л не индуцирует на Л+ функцию расстояния, ибо функ-
ция р не инвариантна относительно 0(3,1). Таким образом,
хотя топология пространства О (Л) — метрическая и соответ-
ственно хаусдорфова, топология на Л+ не обязательно хаусдор-
фова. Это означает, что могут найтись такая точка р~Л и
такая точка q е д, что любая окрестность р в Л+ будет пересе-
кать любую окрестность q. Это случится, когда точка q будет
соответствовать неполной кривой, которая полностью или ча-
стично захвачена в Л. Мы обсудим неполноту, связанную с за-
хватом, позднее, в разд. 8.5.
Если g— положительно определенная метрика на Л, то Л+
гомеоморфно пополнению (Л, g) фундаментальными последо-
вательностями. Конструкция Шмидта обладает, в частности, тем
желательным свойством, что при вырезании из пространства
замкнутого множества Л для каждой точки из Л возникает по
меньшей мере одна точка в ^-границе, которая окажется конеч-
ной точкой для некоторой кривой в Л — Л. Примером появле-
ния более одной точки ^-границы для одной точки из Л служит
двумерное пространство Минковского, в котором в качестве Л
взят отрезок оси t между — 1 и +1. Тогда при — 1 < t < 1
316
Гл. 8. Сингулярности, пространства-времени
для каждой точки (0, t) будут две точки ^-границы. Примером,
когда точка на st не может быть достигнута какой-либо кривой
из Л — st-, служит множество
st = р — sin у , /=5^о| и {— 1 С 1, х = 0}.
В Л— st нет ни одной кривой, которая имела бы конечную
точку в начале координат, и, следовательно, эта точка не может
лежать в {Л — Л)+, хотя она и принадлежит st.
Несмотря на изящную формулировку, метод Шмидта, к со-
жалению, крайне трудно применить на практике. Единственным
решением, для которого можно найти Л+, помимо пространств
постоянной кривизны является двумерное решение Робертсона —
Уокера с обычной материей. В нем доказывается, что д —
это пространственноподобная I-поверхность, как и можно было
бы ожидать из конформной картины. В этом случае можно на-
делить д естественной дифференцируемой структурой и превра-
тить Л+ в многообразие с краем. Однако, видимо, не суще-
ствует какого-либо общего способа введения структуры много-
образия на д. Конечно, естественно думать, что в типовых
ситуациях д будет в высшей степени иррегулярным и на нем
нельзя будет ввести гладкую структуру.
8.4. Характер сингулярностей
В этом и следующем разделах мы исследуем характер сингу-
лярностей, предсказываемых теоремой 4. Мы рассматриваем
именно эту теорему, а не другие, потому что из нее можно полу-
чить больше информации о сингулярности. Однако сингулярно-
сти, предсказываемые остальными теоремами, обладают сход-
ными свойствами.
Сразу встает вопрос: сколь сильное нарушение дифференци-
руемости метрики допустимо? Теоремы предыдущего раздела
утверждают, что пространство-время должно быть геодезически
неполным, если метрика принадлежит классу С2. Это условие
необходимо для того, чтобы были хорошо определены сопря-
женные точки п вариации длин дуг; иными словами, чтобы ре-
шения уравнения геодезических зависели от начальных положе-
ний и направлений дифференцируемым образом. Однако о гео-
дезической неполноте можно говорить при условии, что решения
уравнения геодезических существуют. Они существуют, когда
метрика принадлежит классу С1; единственность решений и их
непрерывная зависимость от начальных положений и направле-
ний имеет место, если метрика класса С2~ (т. с. если связность
локально липшицева). Фактически можно обсуждать Ь-непол-
чоту, опираясь лишь на существование положительно-опреде-
8 4. Характер сингулярностей
317
ленной метрики е в расслоении реперов О(^£), которая почти
всюду определена и локально ограничена. Это имеет место, если
компоненты связности Г%с определены почти всюду и локально
ограничены, т. е. если метрика класса С1-.
Итак, может показаться, что содержание теорем о сингуляр-
ностях не связано с неограниченным ростом кривизны, а свиде-
тельствует лишь о наличии разрыва кривизны (т. е. метрика ста-
новится класса С2- вместо С2). Мы покажем, что это не так:
при выполнении условий теоремы 4 пространство-время должно
быть времениподобно геодезически неполным (и, следовательно,
^-неполным), даже если потребовать, чтобы метрика была клас-
са С2~. Метод доказательства состоит в том, чтобы аппроксими-
ровать С2--метрику С2-метрикой и произвести вариацию длины
дуги в этой метрике.
Предположим, что данное пространство-время нерасширяемо
при метрике класса С~ ~ и что выполнены условия теоремы 4.
Теперь требуется, чтобы условие времениподобного схождения
Rra,K:'Kb 0 выполнялось «почти всюду», причем тензор Риччи
Rab определяется через обобщенные производные. Единственный
пункт в доказательстве теоремы 4, который теряет силу в С2--
метрике, — это тот, где используется вариация длины дуги для
того, чтобы показать, что не может существовать точка р е
е О+(^), для которой (ИЗ3, р)'> — 3/0о, причем 0О — максималь-
ное значение на 93. Итак, если бы многообразие Jt было гео-
дезически полным, то нашлись бы такая точка р и ортогональ-
ная к 93 геодезическая от (.Р до р длиной d(&, р). Пусть CU— от-
крытое множество с компактным замыканием, которое содержит
1~(р) П /+ (5^), и пусть е и g— соответственно положительно
определенная и лоренцева С°°-метрика. Для е > 0 можно найти
лоренцеву С°°-метрику ga&b, удовлетворяющую на --U условиям
1) \?УЬ -gabl<£,
2) | - gab!c | < е-
3) |§ea6|cd | <' гдс C — постоянная, зависящая от QI, e, g, g,
4) RzabRaRb > — e | Ka |2 для любого вектора К, для которого
gzabRaRb 0. (Метрику g^ab можно построить, покрывая СН ко-
нечным числом локальных координатных окрестностей (Fa, фа),
интегрируя координатные компоненты gab с подходящей сгла-
живающей функцией ре(х) и суммируя интегралы с разложе-
нием единицы {фа}, т. е.
£еай (</) = £ $ ёаЬ d4M
<! Фа (z«)
где \ рЕ (,r) = 1. )
318 Г л. 8. Сингулярности пространства-рремени
Свойство (1) означает, что при достаточно малых значениях е
точка р будет лежать в D+ (д’, gE) и J~ (р, gE) П gB)
будет содержаться в (U. Поэтому в метрике gE будет существовать
геодезическая уе от д’ до р длиной dE(^, р). Кроме того,
| de (&, р) — d^P, р) | будет стремиться к нулю при е-»0.
В силу свойств (1), (2), (3) и стандартных теорем для обык-
новенных дифференциальных уравнений при е—>-0 касательные
векторы к геодезическим в метрике ge будут стремиться к каса-
тельным к геодезическим в метрике g с теми же начальными
точками и направлениями. При этом, если ^“-единичный каса-
тельный вектор к геодезической в метрике g, ортогональной к д’,
то на
^л₽(^Х[о, 2d (д’, р)])
величины | V'11 будут ограничены сверху. Следовательно, для
любого б > 0 найдется такая постоянная ei > 0, что при е < ei
будет удовлетворяться неравенство Rt,abVeaVeb>—б. Теперь
мы можем установить противоречие, показав, что достаточно
малое изменение энергетического условия не будет препятство-
вать появлению сопряженных точек в метрике ge на расстоянии,
меньшем ds(g, р). В самом деле, расхождение 0е геодезических
в метрике ge подчиняется уравнению Райчаудхури:
' 0е2 _ 2os2 - RsabVe°Vsb.
QS О
Отсюда
+ РейП/ОК';0г-2.
Поэтому, если бы начальное значение 0ЁО было отрицательным,
а Зб9е,“2 было меньше единицы, то величина 0tX стала бы отри-
цательной на расстоянии от д, не превышающем 3/0О(1—Зб9о~2).
Но 08а —> 0о при е—>0. Отсюда видно, что при достаточно малых
е в метрике gE на любой геодезической, ортогональной д’, будет
сопряженная точка на расстоянии от д’, меньшем чем р).
Поэтому многообразие Л должно быть временпподобно геоде-
зически полным, даже если мы требуем от метрики лишь при-
надлежности классу С2п
Из этого результата вытекает, что при попытке расширить
пространство-время с целью сделать неполные геодезические
полными или метрика перестанет быть лоренцевой, или кри-
визна должна быть локально неограниченной, т. е. должна быть
сингулярность кривизны. Однако, даже если кривизна локально
не ограничена, все же метрику можно интерпретировать как
решение уравнений Эйнштейна в обобщенных функциях при
условии, что объемные интегралы компонент тензора кривизны
8.4. Характер сингулярностей
319
по любой компактной области будут конечны. Последнее будет
справедливо, если метрика лоренцева, непрерывна и обладает
квадратично интегрируемыми первыми производными. В част-
ности, это будет выполнено, если метрика лоренцева и класса
С1- (т. е. локально липшицева). Примерами таких С1--решений
служат гравитационные ударные волны (кривизна имеет пове-
дение типа 6-функции на изотропных 3-поверхностях; см., на-
пример, [29, 130]), массивные тонкие оболочки (где кривизна
ведет себя как 6-функция на времениподобных 3-поверхностях;
см., например, [83]) и решения, содержащие вещество без дав-
ления («пыль»), в которых геодезические линии тока обладают
двумерными и трехмерными каустиками (см. [65, 120]).
Ввиду нелинейной зависимости кривизны от метрики не все-
гда возможно аппроксимировать (^“'-решение в обобщенных
функциях С2-метрикой, подчиняющейся условию схождения или
хотя бы нарушающей это условие на не слишком большую ве-
личину, как в предыдущем случае (свойство 4). Однако во всех
упомянутых выше примерах это возможно. Для этого в сущ-
ности есть физическое оправдание: их надо рассматривать как
математические идеализации С2- или С°°-решений, которые под-
чиняются условию сближения и в которых кривизна велика в
малых областях. К этим С2-решениям можно было бы приме-
нить теоремы разд. 8.2 и доказать существование в них непол-
ных геодезических. Из этого ясно, что предсказываемые сингу-
лярности не могут быть лишь гравитационными ударными вол-
нами или каустиками линий тока, а должны представлять собой
более серьезные нарушения метрики. (С обычными гидродина-
мическими ударными волнами связаны лишь разрывы плотно-
сти и давления, и в этом случае метрика может быть класса
С2-.) Хотя мы и не можем доказать это строго, мы уверены, что
сингулярности должны оказаться такими, чтобы метрику нельзя
было расширить даже как решение уравнений Эйнштейна в
обобщенных функциях, т. е. наряду с неограниченностью в син-
гулярной точке компонент тензора кривизны их объемные
интегралы в любой окрестности такой точки должны быть не ог-
раничены. Так обстоит дело во всех известных примерах сингу-
лярностей, за исключением особого случая решения Тауба —
НУТ, которым мы займемся в следующем разделе. Если эта
догадка верна для «характерных» особенностей (т.е. для всех
особенностей, кроме тех, начальные условия для которых обра-
зуют множество меры нуль), то мы можем рассматривать син-
гулярность как точку, в которой уравнения Эйнштейна (и, на-
верное, остальные известные законы физики) теряют силу.
Другой вопрос, на который хотелось бы иметь ответ: каково
число неполных геодезических, если есть сингулярность? Если
только одна, то может создаться впечатление, что эту сингуляр-
320
Гл. 8. Сингулярности пространства-времени
ность можно игнорировать. Из доказательства теоремы 4 мо-
жно видеть, что при отсутствии горизонта Коши, т. е. если 91 —
поверхность Коши, ни одну времениподобную кривую с поверх-
ности (неважно, геодезическая она или нет) нельзя продол-
жить до длины, превышающей — 3/0и, где Оо — максимальное
Рис. 53. Точка р удалена из пространства-времени, поскольку па ней на-
ходится сингулярность. Соответственно для поверхности SP существует гори-
зонт Коши Н+ (^).
значение метрики на На самом деле этот результат спра-
ведлив даже тогда, когда поверхность 91 некомпактна, если %“о
при этом имеет отрицательную нижнюю грань. Однако это не
обязательно свидетельствует о том, что любая времениподобная
кривая должна встретиться с сингулярностью. Скорее, сингуляр-
ность будет сочетаться с горизонтом Коши, и потому мы ли-
шимся возможности предсказывать будущее. Пример этого дан
на рис. 53. Здесь метрика сингулярна в точке р и соответственно
эта точка вырезана из пространственно-временного многообра-
зия. Существует горизонт Коши, расходящийся от этой дыры.
Этот пример показывает, что самое большее, на что можно на-
деяться,— это доказать существование трехмерного семейства
геодезических, которые неполны и остаются в пределах обла-
сти Коши поверхности (в нашем примере это — геодезиче-
ские, которые проходят через р). Могут быть иные геодезиче-
8.5. Захваченная неполнота
321
ские, которые уходят из области Коши 9 и которые не-
полны, но мы не можем предсказать их поведение по условиям,
заданным на 9.
Ясно, что в £>+(<?) должно быть более одной неполной гео-
дезической. Действительно, из теоремы 4 следует, что должна
быть геодезическая у, ортогональная к 9, которая остается в
Д+(^), но неполна. Пусть р — точка, в которой у пересекает 9.
Тогда можно слегка изменить поверхность 9 в окрестности
точки р так, чтобы получилась новая поверхность 9, для кото-
рой по-прежнему < 0, но которая не ортогональна к у. То-
гда по теореме 4 должна найтись другая, ортогональная к 9'
времениподобная геодезическая у', которая неполна и не пере-
секает горизонт Н+(9'), совпадающий с Н+(9).
В действительности можно доказать, что имеется по меньшей
мере трехмерное семейство времениподобных геодезических (по
одной через каждую точку некоторой ахрональной поверхности),
которые остаются в D+(9) и неполны. Все эти геодезические
соответствуют одной и той же точке границы в смысле нераз-
ложимых прошлых множеств (разд. 6.8), т. е. все они имеют
одно и то же прошлое. Однако в силу построения предыдущего
раздела они не могут соответствовать одним и тем же точкам.
Схема доказательства такова. В теореме 4 было показано, что
должна существовать направленная в будущее ортогональная
к 9 времениподобная геодезическая, которую нельзя продол-
жить до длины 3/0Q. Можно высказать более сильное утвержде-
ние: должна существовать такая геодезическая у, которая
остается в пределах D+(9) и в каждой своей точке является
кривой максимальной длины, т. е. для каждой q^y длина у от
9 до q равна d(9, q). Идея теперь состоит в том, чтобы рас-
смотреть функцию d(r, у) при ге/_(у). Ясно, что она ограни-
чена на /+ (9) П(у). Из того факта, что у — кривая макси-
мальной длины от 9, следует, что в окрестности у функция
d(r, у) непрерывна, и поверхности d(r, у) = const являются про-
странственноподобными поверхностями, пересекающими у орто-
гонально. Тогда времениподобные геодезические, ортогональные
к этим поверхностям, остаются внутри /“(у) и, следовательно,
неполны.
8.5. Захваченная неполнота
В разд. 8.1 мы предложили использовать ^-неполноту в ка-
честве определения сингулярности. Наш замысел состоял в том,
чтобы поставить 6-неполную кривую в соответствие сингуляр-
ной точке, которая удалена из пространства-времени. Допустим,
И Заказ 381
322
Г л. 8. Сингулярности пространства-времени
однако, что имеется Ь-неполная кривая у которой существует
предельная точка р е т. е. К частично или полностью захва-
чена в компактной окрестности р. Тогда мы не можем вложить
Л в большее четырехмерное хаусдорфово паракомпактное мно-
гообразие Л' так, чтобы Л продолжилась в Л'. Действительно,
если q — точка, в которой л пересекает границу Л в Л', то лю-
бая окрестность q должна пересекать любую окрестность р, что
невозможно, поскольку Л' хаусдорфово и q ф р. По существу,
захваченную неполноту в Л+ можно охарактеризовать нехаус-
дорфовым поведением пополнения Л+ из конструкции Шмидта.
Предложение 8.5.1
Точка р е Л не отделена по Хаусдорфу в Л+ от точки red,
если в Л существует неполная кривая X, для которой р служит
предельной точкой, а г — конечной точкой в Л+.
Допустим, что р^Л — предельная точка Ь-неполной кривой
X. Можно построить горизонтальный лифт X кривой X в расслое-
нии ортонормированных реперов О (Л). Некоторая точка
х е л~‘ (г) cz д = О (J?) — О (Л)
будет служить для Л. конечной точкой. Если Т — некоторая
окрестность точки г в Л+, то является открытой окрест-
ностью х в О (Л). Таким образом, ля'ДТф содержит все точки
на Л. после некоторой точки у. Поэтому все точки на X после
л (у) будут лежать в Т и Т будет пересекать любую окрест-
ность точки р, так как р — предельная точка кривой %. □
Пространство Тауба — НУТ (разд. 5.8) служит примером, в
котором существуют неполные геодезические, причем все они
полностью захвачены в компактных окрестностях горизонтов
прошлого и будущего U(t) — 0. Поскольку в этих компактных
окрестностях метрика вполне регулярна, неполные геодезиче-
ские не соответствуют сингулярностям скалярных полиномов
кривизны. Рассмотрим неполную в будущем замкнутую изотроп-
ную геодезическую Х(и) на горизонте будущего У(/) = 0. Пусть
р = и пусть Vi — первое положительное значение V, для
которого h(v) = p. Тогда, как и в разд. 6.4, параллельно перене-
сенный касательный к X вектор будет удовлетворять равенству
mi =йт| ,
\ до ) |р_0, \5p7Ip_o’
где а> 1. Л(и„) = р для каждого п, где
V |_г
г-1
8 5. Захваченная неполнота 323
И
Таким образом, если на 2.(и) взять параллельно перенесенный
псевдоортонормированпый базис {Еп), где Е4 = d/dv, то для
другого изотропного базисного вектора Е3 выполняется равен-
ство Ез Uv = а“”Ез Uo- П₽и каждом обороте вдоль замкнутой
изотропной геодезической Z вектор Е4 становится больше, а век-
тор Ез — меньше. Векторы Ei и Е2 не меняются. Поэтому если
тензор Римана имеет ненулевую компоненту, которая включает
Е4 и, возможно, Е] и Е2, то она будет казаться все больше и
больше при каждом обороте по X и, следовательно, будет иметь
место сингулярность кривизны в параллельно перенесенном ба-
зисе. Однако в пространстве Тауба—НУТ вектор Е3 можно вы-
брать так, что у тензора Римана будет только одна независимая
компонента, а именно Р(Е3, Е4, Е3, Е4). Она включает Е3 и Е4
одинаковым образом и поэтому не меняет своего значения с обо-
ротами по X. Поскольку такой же вывод, по всей вероятности,
справедлив для любой захваченной кривой, похоже, что в про-
странстве Тауба — НУТ нет никакой сингулярности кривизны,
хотя оно, согласно нашему определению, сингулярно. Хотелось
бы знать, может ли случиться нечто подобное в физически реа-
листических решениях, содержащих вещество, или же простран-
ство Тауба — НУТ является особым патологическим случаем.
Этот вопрос важен потому, что в следующей главе мы будем
обосновывать такую интерпретацию предыдущих теорем, со-
гласно которой они свидетельствуют не о том, что непременно
должна быть сингулярность, а о том, что в сильных гравитаци-
онных полях общая теория относительности теряет силу. Таких
полей нет в ситуации, подобной пространству Тауба — НУТ.
Этот вывод основан на весьма специальном виде тензора Ри-
мана в пространстве Тауба — НУТ. Следует ожидать, что в об-
щем случае на захваченной кривой будут отличны от нуля не-
которые другие компоненты тензора Римана и соответственно
появятся сингулярности кривизны в параллельно перенесенном
базисе, хотя сингулярности скалярных полиномов могут и отсут-
ствовать. Действительно, можно доказать
Предложение 8.5.2
Если р<^Ж— предельная точка ^-неполной кривой X и если
в р для всех нспространственноподобных векторов К
RabKaKb=£V,
то кривой 7. соответствуют сингулярности кривизны в парал-
лельно перенесенном базисе. (Условие RabKaKb =¥= 0 может быть
11*
324
Гл 8 Сингулярности пространства-времени
заменено условием отсутствия каких-либо изотропных направ-
лений Ка, ДЛЯ которых KaKCCabc[dKe\ — 0.)
Пусть —выпуклая нормальная координатная окрестность
точки р с компактным замыканием, и пусть {Y,}, {Y’}— поле
дуальных ортонормированных базисов в с2/. Пусть {ЕД, {ЕД —
параллельно перенесенные дуальные ортонормированные базисы
на кривой Х(/), a t — параметр на К, такой, что в
где X' — компоненты касательного вектора d/dt в базисе {УД.
Тогда параметром t измеряется длина дуги в положительно
определенной метрике в °U, в которой базисы {Y,}, {YQ ортонор-
мированы.
Поскольку в р RabKaKb Ф 0 для любого непространственно-
подобного вектора №, существует окрестность Т с <U, в которой
Rab = CZaZb + R'ab,
где С ф 0 — постоянная, Za— единичный времениподобный век-
тор и R' аЬ удовлетворяет неравенству CR'abKaK.b > 0 при любом
непространственноподобном векторе Ка. Допустим, что после
некоторого значения ?о параметра t кривая X пересечет Т. По-
скольку у "К нет конечных точек, а р — предельная точка X, та
часть X, которая лежит в Т, будет иметь бесконечную длину,
если она измерена по параметру ?. Однако обобщенный аффин-
ный параметр дается формулой
где Y’ — компоненты касательного вектора (<?/<??)>,, так что
У \:-Х1 = 1 и Еу— компоненты базиса {ЕД в базисе {Y1}. По-
i
скольку параметр и конечен на кривой 7., модуль вектора-стол-
бца Еа^Х{ должен стремиться к нулю и соответственно преобра-
зования Лоренца, определяемые компонентами Еу, должны
стать неограниченно большими. Z — единичный времениподоб-
ный вектор, и поэтому компоненты Z в базисе {ЕД будут не-
ограниченно расги, а следовательно, и некоторые компоненты
тензора Риччи в базисе {ЕД станут сколь угодно велики. □
Из этого результата видно, что наблюдатель, чья история
представляет собой ^-неполную, захваченную непространствен-
поподобную кривую в характерном пространстве, будет сбро-
шен с этой кривой за конечный промежуток времени, тогда как
другой наблюдатель может путешествовать в том же районе, не
8.5. Захваченная неполнота
325
испытывая ничего подобного. Интересным примером в этом от-
ношении служит такое пространство Тауба — НУТ, у которого
метрика умножена на конформный множитель Й, отличающийся
от единицы лишь в малой окрестности точки р на горизонте. Это
конформное преобразование не меняет причинной структуры
пространства и не влияет на неполноту замкнутой изотропной
геодезической, проходящей через точку р. Однако, вообще го-
воря, RabKaKb 0, где — касательный вектор к этой замкну-
той изотропной геодезической. После каждого цикла RabKaKb
умножается на а2, и поэтому имеет место сингулярность кри-
визны в параллельно перенесенном базисе. Все же метрика
вполне регулярна в компактной окрестности горизонта, и потому
с этой неполнотой не связана никакая сингулярность скаляр-
ных полиномов кривизны.
Было бы желательно исключить ситуацию такого рода, ко-
гда неполные кривые полностью захвачены в компактной об-
ласти. Однако такое могло бы произойти в бесконечном счет-
ном множестве различных областей пространства-времени. По-
этому при рассмотрении ее нельзя ограничиться случаем, когда
все неполные кривые полностью заключены в каком-то одном
компактном множестве. Вместо этого правильно будет сказать,
что мы хотим исключить ситуацию, когда множество неполных
кривых, которое в каком-то смысле компактно, полностью за-
хвачено в компактной области многообразия Л. Чтобы выра-
зить это в более строгой форме, мы введем следующее опреде-
ление ^-ограниченности.
Определим пространство В (Л) как множество всех пар
(X, и), где и —точка в расслдении линейных реперов ЦЛ) и
А— С’-кривая в Л, имеющая только одну конечную точку, ле-
жащую в л(ц). Пусть <U— открытое множество в Л и Т — от-
крытое множество в Ь{Л}. Мы определим открытое множество
Т) как множество всех элементов из В {Л}, таких, что А
пересекают °U и и е Т. Множества вида 0(01, Т) при всех
°U, Т образуют подбазис для топологии В {Л). Напомним, что
отображение exp : Т(Л)-+ Л определяется заданием вектора X
в точке р и смещением из р вдоль геодезической в направле-
нии X на единицу расстояния, измеренного по аффинному пара-
метру, который определяется вектором X. Аналогично мы мо-
жем задать отображение Ехр: В (Л) -> Л, следуя из л (и) вдоль
кривой Z на единицу расстояния, измеренного по обобщенному
аффинному параметру, который определен точкой «е £(.<).
Отображение Ехр определено непрерывным образом для лю-
бого В (Л), когда Л — полное многообразие. Будем говорить,
что пространство (Л, g) ^-ограничено, если для любого ком-
пактного множества №а:В(Л) Ехр(IE) обладает компактным
замыканием в Л. Ввиду непрерывности Ехр пространство {Л, g)
326 Гл %. Сингиляпности пппстранствп-еременп
Ь-ограничено, если оно b-полно. Однако пространство Тауба—
НУТ, например, ^-ограничено, но b-неполно. Мы покажем, что
это оказалось возможным только из-за того, что пространство
Тауба — НУТ везде пустое. Присутствие любой материи на по-
верхности 53 (теорема 4) будет означать, что пространство и
^-неполно, и ^-неограниченно.
Теорема 5
Пространство-время ^-неполно, если выполняются условия
(1) — (3) теоремы 4 и, кроме того,
4) тензор энергии-импульса не равен нулю где-либо на
5) тензор энергии-импульса подчиняется условию энергодо-
минантности (разд. 4.3) в несколько более сильной форме
(разд. 4.3): если № — непространственноподобный вектор, то
ТаЬКа равен нулю или непространственноподобен и ТаъКаКь О,
причем равенство имеет место лишь при ТаЬКь — 0.
Замечание. Условие (4) можно заменить типовым условием
(см. теорему 2).
Доказательство. Рассмотрим накрывающее пространство Ла
(разд. 6.5), определенное как множество всех пар (р, т[Х]), где
л — кривая от q до р, р, q е Л и i[л]— разность чисел пересе-
чений поверхности Д кривой X в направлении будущего и в на-
правлении прошлого. Для каждого положительного а множе-
ство
да^{(Р,1тр^, /[%]=«>
диффеоморфно поверхности Д и является частичной поверх-
ностью Коши в Лв. Вообще, если многообразие Л й-ограниче-
но, Лв еще не обязательно является таковым, но в рассматри-
ваемой ситуации справедливо следующее утверждение:
Лемма 8.5.3
Пусть выполнены условия (1) — (3), и пусть Д+(^о) не об-
ладает компактным замыканием в Ла', тогда, если ф— накры-
вающая проекция, ^.Ла,—*Л, ф(Д+(^о)) не будет иметь ком-
пактного замыкания в Л.
Многообразие Л диффеоморфно или многообразию Ла, или
той части Ла многообразия Ла, которая лежит между Да и
^а+ь в последнем случае Да и Дл+\ отождествляются. Если
для любого Ла П Д+(5’о) не имеет компактного замыка-
ния в Ла, то ф (D+До)) не будет иметь компактного замыкания
в Л. Если, однако, множество Ла П Д+(Д0) обладает компакт-
ным замыканием для всех а 0, в силу некомпактности О+(^0),
оно должно быть также и непустым для всех а 0. Но для
р е Да собственный объем Ла-\ ограничен снизу неко-
торой постоянной с. Следовательно, для любого а 0 собствен-
8.5. Захваченная неполнота
327
ный объем области Яа A не должен быть меньше с. Но
это невозможно, поскольку, в силу условий (1) — (3) и предло-
жения 6.7.1, собственный объем ZJ+^o) меньше, чем 3/(—Оо)Х
X (площадь поверхности 91), где 0и — отрицательная верхняя
грань %% на У. □
Используя этот результат, можно доказать такое утвержде-
ние:
Лемма 8.5.4
Если D+^o) не имеет компактного замыкания, многообра-
зие Я не является ^-ограниченным.
Пусть Ж— подмножество пространства В (ЯЛ}, состоящее
из всех пар (Л, и), где 7;— любая непродолжимая в будущее,
ортогональная к 9^ времениподобная геодезическая кривая в Яъ
с конечной точкой и и е л-1 (г) —любой базис в г, один
из векторов которого касателен к 7» и имеет длину —3/0О, а
остальные векторы образуют ортонормированный базис в
Пусть {£Ра} — набор открытых множеств, покрывающих Ж.
Каждое будет объединением конечного числа пересечений
множеств вида О(с2/, У). Достаточно рассмотреть случай, ко-
гда Ф можно представить в виде
^а = ПО(^аРДЛ)>
8 1
где при каждом а — набор некоторого конечного числа от-
крытых множеств в Яс и Уа_— открытое множество в ИЯо).
Пусть (ц,и)еЖ. Тогда существует значение а, при котором
(ц, v)e^a. Это означает, что геодезическая р. пересекает от-
крытое множество при каждом значении р и что v е Та.
Поскольку геодезические непрерывно зависят от их начальных
значений, найдется окрестность точки л (у), такая, что ка-
ждая непродолжимая в будущее геодезическая, проходящая
через и ортогональная к будет пересекать при
каждом значении р. Пусть с: Жг — открытое множество, та-
кое, что л(Жа) с Тогда
(и, У)еО(л(Жа),П)
содержится в &а. Таким образом, множества {О (л(Жа)Жа)}
образуют измельчение покрытия
Рассмотрим подмножество 2? расслоения ЦЯв), состоя-
щего из всех базисов над в которых один из базисных век-
торов ортогонален к Д'о и имеет длину — 3/0О, а остальные
векторы образуют ортонормированный базис в &?0. В силу
компактности 3?, оно может быть покрыто конечным числом
множеств Уа. Следовательно, компактно и Ж, поскольку его
можно покрыть конечным числом множеств О(л(Жа), У
328
Гл. 8. Сингулярности пространства-времени
По предложению 6.7.1 каждая точка области £>+(17’о) лежит
в пределах собственного расстояния —3/0о вдоль направленной
в будущее времениподобной геодезической, ортогональной к ^0.
Это означает, что Ехр (Ж) содержит D+^o). Пусть ф, : В{Яа}-^
-*B(JC) есть отображение, переводящее (Х,и)еВ(^е) в
(ф (Л), ф» (и)) е В(Ж\I. Тогда ф»(Ж) будет компактным под-
множеством пространства В (.Ж), для которого
Ехр(ф+Ж)дэ ф(П+ (^0).
Таким образом, если D+ (^0) не компактно, ф(£)+(17’0)) тоже
не компактно и, следовательно, пространство (Л", g) не является
^-ограниченным. □
Отсюда видно, что достаточно доказать некомпактность
D+t&o). Допустим, что оно компактно. Тогда горизонт
тоже должен быть компактным. Ниже мы покажем, что отсюда
вытекает равенство нулю расхождения изотропных геодезиче-
ских всюду на H+(9’o). Это невозможно, если плотность мате-
рии где-либо на Н+^о) отлична от нуля.
Лемма 8.5.5
Если 3?— частичная поверхность Коши и если горизонт
Я+(27) компактен, то изотропные геодезические сегменты-обра-
зующие Д+(2’) геодезически полны в направлении прошлого.
Из предложения 6.5.2 следует, что сегменты-образующие не
имеют конечных точек в прошлом. Следовательно, они должны
образовывать «почти замкнутые» кривые в компактном множе-
стве Если бы они образовывали настоящие замкнутые
кривые, то можно было бы воспользоваться предложением 6.4.4
и показать, что при их неполноте в направлении прошлого ва-
риацией в направлении прошлого из них можно получить
замкнутые времениподобные геодезические. Однако это оказы-
вается невозможным из-за того, что такие кривые должны
были бы лежать в D+(S>). В случае, когда изотропные геодези-
ческие образующие горизонта Н+(2’) только «почти замкнуты»,
доказательство аналогичное, хотя несколько более тонкое.
Введем направленное в будущее единичное векторное поле V,
геодезическое в некоторой окрестности °И с компактным за-
мыканием горизонта Н+(2?). Введем, как в предложении 6.4.4,
положительно определенную метрику
g' (X, Y) = g (X, Y) + 2g (X, V) g (Y, V).
Пусть г —параметр, измеряющий собственное расстояние в ме-
трике g' вдоль изотропной геодезической, образующей сегмент у
горизонта Н+(2?), причем t = Q в некоторой точке q е у. Тогда
8.5. Захваченная неполнота
329
g(\, d/dt) = — 1 / д/2 . Поскольку у у нет конечной точки в прош-
лом, параметр t не ограничен снизу. Пусть f и h даны равен-
ствами
г д D / д \ д , д
' dt ~~ dt к ДГ ) ’ ~dv ~~ П ~дТ ’
где v — некоторый аффинный параметр. Допустим, что у гео-
дезически неполна в прошлом, тогда аффинный параметр
t
v = j h~} At'
u
при t—>—оо должен иметь нижнюю грань v0. Рассмотрим те-
перь вариацию а кривой у с вектором вариации д/ди = —%V.
Тогда
— g(—+ л:/г-1 — 1 (8.3)
ди \ dt dtj\u^o "V2 \ At At)
Поскольку h—>оо при t—>—оо, можно найти такую ограничен-
ную функцию х(1), что выражение (8.3) будет отрицательным
при всех t 0. Однако этого не будет достаточно для уверен-
ности в том, что вариация дала всюду времениподобную кри-
вую, поскольку может случиться, что область значений и, для
которой (8.3) остается отрицательным, стремится к нулю при
t—>—оо. Чтобы учесть это, рассмотрим вторую производную
при вариации:
д2 / д d \ ____ д / ( d D д \ \ _
ди2 & \ dt ’ dt ) ди \ dt ’ dt du ))
__ / D d D d \ . / d DP d \ .
& k dt du ’ dt du ) ' & \ dt ’ dt du du )
/ d ( d d \ d \
+ S k dt ' K k du ’ dt ) du ) ’
Выбирая (дх/ди) = 0 и пользуясь тем фактом, что V — геоде-
зическое векторное поле в окрестности °11 горизонта Я+(2’), по-
лученное выражение при О и е можно привести к виду
^)v)].
В любом ортонормированном относительно метрики g' базисе
компоненты тензора Римана и ковариантных производных (от-
носительно g) V будут на °U ограниченными. Таким образом,
существует такая постоянная С > 0, что
а- / <э Q,/a а \
ди2 ё k. dt ’ dt ) С Х ё к dt ’ dt J •
330
Гл. 8. Сингулярности пространст ва-времеии
Далее,
dx
dt ’
так что
1 dx
-7= — и —.
р2 df
Отсюда при
2 д/2 и
где d — 2 д/2 еС, + 2е2С12 + 1 и Cj —верхняя грань для | d.r/df1.
Таким образом, имеем
и
где
— I = —ft 1 — (ftx), у lu-o-o,
du l„_o V2 df У '“-0-0’
у = g (d/dt, d/dt). Поэтому
у C d (ch Cxu — 1) + a sh Cxu sh Cxu (d th у Cxu -f- a) ,
a = (l/A/2')C-|d(lnftA:)/dft
Возьмем теперь
где
о
х — h 1
t
где
о
ft-1 df;
тогда a = — (1/д/2) C "'ftx. Поскольку функция f = — h 1 (dh/dt)
ограничена на компактном множестве Я+(^) и поскольку пред-
полагается, что интеграл
о
ft“’ dt' — — v
t
сходится при /-> —- оо, х и | dx/dt | должны иметь верхнюю грань,
a ft при — оо </^ 0 — положительную нижнюю грань. Тогда
для 0 < и < min (е, 2C~2d~ '^2) у < 0, если — оо < t 0.
Другими словами, вариация а должна дать непродолжимую
в прошлое времениподобную кривую, лежащую в intZ)+(27)
8.5. Захваченная неполнота
33!
и полностью заключенную в компактном множестве °11. Но это
невозможно, поскольку по лемме 6.6.5 в int О+(27) выполняется
условие сильной причинности. Следовательно, кривая у должна
быть геодезически полной в направлении прошлого. □
Рассмотрим расхождение 0 касательных векторов djdt к
изотропным геодезическим образующим поверхности /7+(До).
Допустим, что 0> 0 в некоторой точке q образующей у и пусть
ЗГ — пространственноподобная 2-поверхность в некоторой
окрестности q на /7+(До), проходящая через q. Образующие по-
верхности //+($%) будут ортогональны к ?Г и будут сходиться
в прошлое. Тогда по условию (1) и доказанной выше лемме
должна быть точка г е у, сопряженная -Т вдоль у (предложе-
ние 4.4.6). Точки у, лежащие за точкой г, могли бы быть со-
единены с времениподобными кривыми (предложение 4.5.14).
Но это невозможно в силу того, что /7+(До)— ахрональное
множество. Следовательно, 0 «у 0 на 77+(До).
Рассмотрим теперь семейство дифференцируемых отображе-
ний
₽г:Я+ (5CW/Г (Д',),
определяемых как перенос точки r/e/Ci'^,,) на расстояние z
(измеренное в метрике gz) в прошлое вдоль изотропной геоде-
зической, проходящей через q. Пусть d.4— площадь малого
элемента поверхности Н+^о), измеренная в метрике gz. При
отображении р2
4-dH= -0 dH.
dz
Следовательно,
A J ал = ~ J о ал. (8.4)
Но pz отображает Я+(Д’О) в H+i&o} [и на Н+(9РЬ'), если обра-
зующие сегменты не имеют будущих конечных точек]. Таким
образом, интеграл (8.4) должен быть меньше или равен нулю.
Вместе с предыдущим результатом это означает, что на /7+(До)
0 = 0. Согласно уравнению распространения (4.35), это воз-
можно лишь тогда, когда RabRaRb = Q всюду на H+f&’o), где
К — касательный вектор изотропной геодезической образующей.
Однако, согласно теореме сохранения (разд. 4.3), из условия
(5) следует, что величина ТаЬК.аК.ь где-нибудь на /7+(Д’) от-
лична от нуля и, согласно уравнениям Эйнштейна (с А-членом
или без него), ТаЬКаКь = RabKaKb.
[Строго говоря, требуемая форма теоремы сохранения не-
сколько отличается от приведенной в разд. 4.3. Поскольку нет
332
Гл. 8. Сингулярности пространства-времени
каких-либо подходящих пространственноподобных поверхностей,
пересекающих Н+(9^о), мы используем семейство поверхностей,
одной из которых является /7+(^0), а остальные — простран-
ственноподобные. Эти поверхности можно задать, взяв значение
функции t в точке р В+ЦРо) равным собственному объему
J+(p) П D+^o), взятому со знаком минус. Поскольку вектор t-a
становится изотропным на Я+(^о), утверждение о существова-
нии такой постоянной С > 0, при которой на D+(S^o) выпол-
няется неравенство
-Z 1;аЬ^Ы t-tat;b,
более не является обязательно справедливым. Однако, если
Va — времениподобное векторное поле на D+(J?0), существует
постоянная С, для которой
TabLab^CTab (t-atb + t-.aVb')
И
TabVa-,b<CTab(t.at.b-Vt.aVb).
Затем можно поступить, как в разд. 4.3, используя ТаЬ (t;ab "+ Уа-,ь)
вместо Tabt.ab и доказывая, что величина Tab (t-,at-,b + t-aVb) не
может быть равной нулю на Н+($Р0), если она отлична от нуля
на 9^0. Тогда наше утверждение следует из условия (5).] □
Глава 9
Гравитационный коллапс и черные дыры
В этой главе мы покажем, что звезды массой более «1,5 Мо
должны претерпеть коллапс после того, как их ядерное топливо
иссякнет. Если начальные условия не слишком асимметричны,
то будут выполнены условия теоремы 2 и, следовательно, будет
иметь место сингулярность. Однако эта сингулярность, по всей
вероятности, скрыта от глаз внешнего наблюдателя, который ви-
дит только «черную дыру» там, где когда-то была звезда. Мы
выведем ряд свойств таких черных дыр и покажем, что в ре-
зультате их эволюции, по-видимому, устанавливается ситуация,
описываемая решением Керра.
Коллапс звезд рассмотрен в разд. 9.1, в котором показано,
как может возникнуть замкнутая ловушечная поверхность во-
круг любой достаточно большой сферической звезды на поздних
стадиях ее эволюции. В разд. 9.2 мы исследуем горизонт со-
бытий, который, по-видимому, образуется вокруг такого кол-
лапсирующего тела. В разд. 9.3 рассматривается конечное ста-
ционарное состояние, к которому приводит решение вне гори-
зонта. Вероятно, это должно быть одно из решений семейства
Керра. В таком случае можно наложить определенные ограни-
чения на количество энергии, способное выделиться в рассмат-
риваемом процессе.
Для более глубокого изучения черных дыр см.: Black Holes.
Les Houches 1972, В. Dewitt, cd. Gordon a. Breach, 1973.
9.1. Коллапс звезды
Вне статического сферически симметричного тела, такого,
как звезда, решением уравнений Эйнштейна с необходимостью
является та часть одной из асимптотически плоских областей
решения Шварцшильда, для которой г больше некоторого зна-
чения Го, соответствующего поверхности звезды. Это решение
можно сшить при г < Го с решением, которое зависит от кон-
кретного радиального распределения плотности и давления в
звезде. Даже когда звезда не статическая, но сохраняет свою
сферическую симметрию, внешнее решение будет фактически
частью решения Шварцшильда, обрезанного на поверхности
звезды. (Это и есть теорема Биркгофа, доказательство которой
дано в приложении Б). Если звезда статическая, то г0 должно
334
Гл. 9. Гравитационный коллапс и черные дыры
быть больше 2/и (радиус Шварцшильда). Это следует из того,
что поверхность статической звезды должна соответствовать
орбите времениподобного вектора Киллинга, а в решении
Шварцшильда времениподобный вектор Киллинга существует
только при г > 2ш. Если /0 меньше 2ш, то поверхность звезды
должна расширяться или сжиматься. Чтобы дать представление
о величине радиуса Шварцшильда, отметим, что для Земли он
равен ~ 1 см, а для Солнца 3,0 км. Отношения шварцшильдова
радиуса к радиусу для Земли п Солнца равны соответственно
~10-9 и 2-10 6. Таким образом, радиусы нормальных звезд
далеки от соответствующих шварцшильдовых радиусов.
Эволюция типичной звезды включает длительную ( ~109 лет)
квазистатическую фазу, в которой расходуется ядерное топливо,
а тепловое давление и давление излучения уравновешивают
силу тяжести. Но когда ядерное топливо выгорает, звезда на-
чинает остывать, давление падает, и вследствие этого звезда
сжимается. Предположим теперь, что давление не может оста-
новить это сжатие, прежде чем радиус звезды не станет меньше
ее радиуса Шварцшильда (ниже мы увидим, что это, по всей
видимости, возможно для звезды с массой больше некоторого
определенного значения). Тогда, поскольку решение вне звезды
шварцшильдово, вокруг звезды будет существовать замкнутая
ловушечная поверхность Ж (рис. 54) и, согласно теореме 2,
должна существовать сингулярность, если только не нарушается
причинность и выполняются соответствующие энергетические
условия. Существенно, однако, что если звезда не является в
точности сферически симметричной, при некотором не слишком
большом отклонении звезды от сферической симметрии замкну-
тая ловушечная поверхность все равно возникает. Это следует
из доказанной в разд. 7.5 устойчивости решения задачи Коши.
В самом деле, мы можем рассматривать данное решение как
развитие из некоторой частичной поверхности Коши 5^
(рис. 55). Если теперь мы изменим начальные данные на малую
величину в компактной области /“(У") П Ж то новое развитие
из поверхности Ж в области /+(<2^) П /“(S'-) будет достаточно
близким к прежнему, так что в возмущенном решении вокруг
звезды по-прежнему будет существовать замкнутая ловушечная
поверхность. Таким образом, мы показали, что имеется множе-
ство начальных данных ненулевой меры, которые приводят
к замкнутой ловушечной поверхности и, следовательно, согласно
теореме 2, к сингулярности.
Звезда может вращаться или обладать магнитным полем,
и это две главные причины, по которым ее сферическая сим-
метрия может быть нарушена. Изучая решение Керра, мы мо-
жем составить некоторое представление о том, каким быстрым
должно быть вращение без того, чтобы оно воспрепятствовало
б
Рис. 54. Коллапс сферической звезды, а — диаграмма Финкельстейна [пло-
скость (г, /)] коллапсирующего сферически симметричного жидкого шара.
Каждая точка изображает 2-сферу; б — диаграмма Крускала коллапсирую-
щего жидкого шара; в — диаграмма коллапса, на которой опущена только
одна пространственная координата.
336 Гл. 9 Гравитационный коллапс и черные дыры
появлению ловушечной поверхности. Предполагается, что реше-
ние Керра можно рассматривать как внешнее решение для тела
массы m с моментом количества движения L = ат. При а < т
имеются замкнутые ловушечные поверхности, а при а > т они
Рис. 55. Коллапс сферической звезды (как па рис. 54, в). Изображена ча-
стичная поверхность Коши Ж. Начальные данные в компактной области
J~ Л Ж поверхности Ж ведут к появлению замкнутой ловушечной поверх-
ности ?Г в компактной области (^") П J+ (Ж).
отсутствуют. Поэтому можно ожидать, что при моменте коли-
чества движения звезды больше квадрата ее массы вращение
может прекратить сжатие звезды еще до появления замкнутой
ловушечной поверхности. Подобный вывод следует из того,
что при L = т2 и сохранении момента количества движения в
течение коллапса скорость вращения поверхности звезды при-
ближается к скорости света, когда радиус звезды близок к ее
радиусу Шварцшильда. В настоящее время у многих звезд
моменты количества движения больше квадратов их масс (для
Солнца L~m2). Однако, по-впдимому, есть основания ожи-
дать, что в результате торможения магнитным полем и грави-
9 1. Коллапс звезды
337
тационного излучения некоторая часть момента количества дви-
жения теряется. Поэтому положение таково, что в некоторых
звездах, а вероятно в большинстве, момент количества движе-
ния не препятствует появлению замкнутых ловушечных поверх-
ностей, а значит п появлению сингулярности.
При почти сферическом коллапсе магнитное поле В, вморо-
женное в звезду, будет расти как р2/з, где р — плотность веще-
ства звезды; следовательно, магнитное давление будет пропор-
ционально р4/з. Эта скорость роста настолько мала, что, если
магнитное поле оказалось несущественным для поддержания
равновесия звезды в исходном состоянии, оно никогда не станет
достаточно сильным, чтобы заметно повлиять на коллапс.
Чтобы понять, почему звезда с массой больше некоторого
значения, в которой выгорело ядерное топливо, не может про-
тивостоять собственному тяготению, проведем качественное ис-
следование (основанное на неопубликованной работе Картера)
уравнения состояния вещества при нулевой температуре.
В горячем веществе существуют давление, вызванное тепло-
вым движением атомов, и давление излучения. Однако в холод-
ном веществе при плотностях, меньших ядерной плотности
(~1014 г/см3), существенную роль играет только давление, свя-
занное с принципом Паули. Чтобы оценить величину этого дав-
ления, рассмотрим концентрацию фермионов п массы т. По
принципу Паули каждый фермион будет эффективно занимать
объем п-1. Таким образом, согласно принципу неопределенно-
сти, фермион будет иметь пространственную компоненту им-
пульса порядка W'3. Если фермионы нерелятивистские, т. е.
если йп,/з < т, то их скорость будет порядка если же
они релятивистские (т. е. йп,/з>т), то их скорость практиче-
ски равна единице (т. е. скорости света). Давление будет по-
рядка произведения импульса на скорость и плотность числа
частиц, т. е. ~й2п3/зт-1 при fin'11 <2 т и ~?ш’3 при йп,/з > т.
Когда вещество нерелятивистское, главный вклад в давление
вырождения вносят электроны, поскольку величина т~х для
них больше, чем для барионов. Однако при высоких плотностях,
когда частицы становятся релятивистскими, давление не зави-
сит от массы частиц, вызывающих его, а зависит только от их
числа в единице объема.
Для малых холодных тел собственным тяготением можно
пренебречь, и давление вырождения вещества будет уравнове-
шено электростатическими силами притяжения между сосед-
ними частицами, образующими ту или иную решетку. (Мы пред-
полагаем, что имеется равное число положительно и отрица-
тельно заряженных частиц и приблизительно равное число
электронов и барионов.) Эти силы вызывают отрицательное дав-
ление порядка е^п'11. Таким образом, плотность холодного тела
338 Гл. 9. Гравнсарионный коллапс и черные дыры
малых размеров будет равна по порядку величины
e6tne»intl~6 1 г/см3), (9.1)
где тс— масса покоя электрона и тп — масса покоя нуклона.
Для больших тел самогравитация становится существенной.
Чтобы получить точное решение, необходимо проинтегрировать
соответствующие уравнения Эйнштейна. Однако важные осо-
бенности можно установить более простым путем, проводя ка-
чественные расчеты на основе ньютоновской теории. В звезде
массы М и радиуса г0 сила тяготения, действующая на типичный
единичный объем, имеет порядок (Л1/г20) птп, где птп ж М/г30—
плотность. Эта сила уравновешена градиентом давления
где Р— среднее давление в звезде. Таким образом,
Р = _М2/г04 ж М'и'т''.
Если плотность достаточно мала и основной вклад в давление
дают вырожденные нерелятивистские электроны, то
Р = = T1V тга4/з,
так что
п = М тп те п .
Эта формула верна для таких тел, для которых она дает зна-
чение п больше, чем величина (9.1), и меньше, чем пт/fi-3, т. е.
при е3тп~2 < М <. 1^тп-2. Такие звезды называются белыми
карликами.
Если плотность настолько велика, что электроны являются
релятивистскими, т. е. п > mftr3, то давление будет опреде-
ляться релятивистским соотношением; следовательно,
Теперь формула для давления не содержит п. Таким образом,
можно было заключить, что мы получаем звезду массы
МL = ~ 1,5A1©,
которая может иметь любую плотность выше /?ге3тпй-3, т. е.
любой радиус меньше те-1. Давление вырожденных
электронов не может предотвратить сжатие звезды массой боль-
ше ML.
В действительности, когда электроны становятся релятивист-
скими, они стимулируют обратный бета-распад, образуя ней-
троны
е~ + р -> ve + п.
При этом содержание электронов в звезде уменьшается и дав-
ление вырожденных электронов падает, что вызывает сжатие
9 /. Коллапс звезды
339
звезды, и электроны становятся еще более релятивистскими.
Такая ситуация неустойчива, и процесс будет продолжаться до
тех пор, пока почти все электроны и протоны не превратятся
в нейтроны. На этой стадии может вновь наступить равновесие:
звезда будет поддерживаться давлением вырожденных нейтро-
нов. Если нейтроны нерелятивистские, получаем
п —
если же они релятивистские, то звезда по-прежнему должна
иметь массу ML, а радиус, меньший или равный Однако
ML/fi'l2rrr2n = 1, и, следовательно, такая звезда находится
вблизи общерелятивистского предела MJR х 2.
Итак, мы приходим к выводу, что сжатие звезды массы,
большей ML, не может быть предотвращено давлением вырож-
дения электронов или нейтронов. Чтобы показать это строго,
рассмотрим ньютоновское уравнение равновесия
_ рЛ/ (г) г
(9-2)
где
М (г) = 4л pr" dr
о
— масса, заключенная внутри сферы радиуса г. Умножим обе
части равенства (9.2) на г4 и проинтегрируем по частям от О
до r0. С учетом того, что р = 0 при г = г0, получим
\pr3 dr = (M2(,r0))'!/8n.
О
Поскольку р никогда не превышает
Го , Го х’/з
pr3 dr < h [ nr~ dr | = h (Л4 (r0)) ” (4лтп)~ /’.
о \o /
Отсюда масса Л1 (r0) должна быть меньше (8Й) ' (4л)-1''2 тп~2, т. е.
М (г0) < 8/i hmn~2.
340
Гл 9 Гравитационный коллапс и черные дыры
Мы подытожили эти результаты на рис. 56. На диаграмме
нанесена средняя концентрация нейтронов в зависимости от
массы тела М. Жирная линия изображает приближенно равно-
весную конфигурацию холодных тел. В горячих телах помимо
давления вырожденного вещества будут существовать тепло-
Плотность числа нуклонов п
Звсзаы. в которых идут
ядерные
Полная ргасса
Рис. 56. Плотность числа нуклонов в зависимости от полной массы стати-
ческого тела М. Жирная линия — равновесное состояние холодных тел; го-
рячие тела при соответствующих температурах могут быть в равновесии
выше этой линии. Общая теория относительности запрещает статическое со-
стояние любых тел в заштрихованной области.
вое давление и давление излучения, поэтому такие тела могут
быть в равновесии в области выше жирной линии. Жирная
штриховая линия справа соответствует равенству
Af/r0(=MV3mp'/s) = 2.
В области справа от этой линии вообще нет равновесных со-
стояний, и эта область соответствует звезде, ушедшей внутрь
своей сферы Шварцшильда. Далеко влево от этой линии разли-
чием между ньютоновской теорией и общей теорией относи-
тельности можно пренебречь. Вблизи нее нужно учитывать
общерелятивистские эффекты. Для статического сферически
симметричного тела, состоящего из идеальной жидкости, эйн-
9 1. Коллапс звезды
341
штейновские уравнения поля можно свести (см, приложение Б)
к такому уравнению:
dp _ (н + р) [М (г) + 4лг3р]
dr г [г- 2М (г)]
(9.3)
где радиальная координата такова, что площадь 2-поверхности
{г = const, t — const} равна 4лг2. Величина 70 (г) теперь опре-
деляется как
г
4лг2ц dr,
о
где ц = р(1 + е)—плотность полной энергии, р — птп и е —
релятивистская добавка к массе, связанная со спином фермио-
нов. Величина 70(го) равна шварцшильдовой массе 70 для внеш-
него решения Шварцшильда при г > г0. Для звезды конечных
размеров она меньше, чем сохраняющаяся масса
где N — полное число нуклонов в звезде, так как разность
(М— 70) соответствует количеству энергии, излученной на бес-
конечность с момента образования звезды из диффузного пер-
воначально покоящегося вещества. Практически эта разность
никогда не превышает нескольких процентов и уж никак не
больше 270: Бонди [И] показал, что при р, > 0, р>0 и ц,
убывающем к поверхности звезды, (1—не может быть
меньше */3, а при р ц — меньше '/г- Отсюда 70 < М < 3 70.
Сравнивая соотношение (9.3) с (9.2), в которое вместо р и 70
подставлены соответственно ц и М, мы видим, что все дополни-
тельные члены в правой части уравнения (9.3) при и
р 0 отрицательны. Следовательно, так как в ньютоновской
теории сжатие холодной звезды массы M>ML неизбежно, то
и в общей теории относительности сжатие холодной звезды
шварцшильдовой массы 70 > Ml также неизбежно. Это озна-
чает, что холодная звезда, содержащая более 3 MLlmn нуклонов,
не может противостоять сжатию. Практически дополнительные
члены в (9.3) означают, что предельное число нуклонов меньше
ML/mn.
Говоря о нейтронных звездах, мы пренебрегали ядерными
силами. Учет их несколько изменит положение линии равнове-
сия для нейтронных звезд на рис. 56 [20, 68, 166, 167], однако
342
Гл. 9. Гравитационный коллапс а черные дыры
даже при учете ядерных сил звезда, содержащая больше ML/mn
нуклонов, не придет к какому-либо равновесию при нулевой
температуре. Это связано с тем, что точка, в которой нейтроны
в звезде массы ML становятся релятивистскими, почти совпа-
дает с релятивистским пределом М/R «з 2. Таким образом, звез-
да, содержащая несколько больше чем MLlmn нуклонов, достиг-
нет ядерных плотностей, уже оказавшись внутри своей сферы
Шварцшильда.
На рис. 56 эволюционный путь звезды будет лежать на вер-
тикальной линии, если только звезда не потеряет в том или
ином процессе значительное количество своего вещества. Звез-
да конденсируется из газового облака и разогревается вслед-
ствие сжатия газа. Если ее масса меньше некоторого значения
порядка 10 2 ML, то температура никогда не возрастает на-
столько, чтобы начались ядерные реакции; звезда в конечном
счете излучит свой запас тепла, и установится состояние, в ко-
тором ее тяготение уравновешивается давлением вырожденного
газа нерелятивистских электронов. Если масса больше
-~10~2 то температура достигнет значения, достаточного,
чтобы началась ядерная реакция превращения водорода в ге-
лий. Энергия, выделяемая в этой реакции, уравновесит потерю
энергии вследствие излучения, и звезда длительный период
[~ 1010(tWl//W)2 лет] будет пребывать в квазистатическом рав-
новесии. Когда водород в сердцевине звезды иссякнет, сердце-
вина сожмется и температура возрастет. При этом могут на-
чаться новые ядерные реакции, в которых гелий в недрах
звезды будет превращаться в более тяжелые элементы. Однако
энергия, выделяющаяся при этих превращениях, не очень ве-
лика, и сердцевина не может оставаться слишком долго в этой
фазе. Если масса меньше 7ИЬ, то звезда в итоге станет белым
карликом и будет удерживаться давлением вырожденных не-
релятивистских электронов или, возможно, превратится в ней-
тронную звезду и будет удерживаться давлением вырожденных
нейтронов. Но когда масса заметно больше ЛК, уже не суще-
ствует равновесного низкотемпературного состояния. Поэтому
звезда должна или уйти внутрь своей сферы Шварцшильда, или
каким-то образом сбросить столько вещества, чтобы ее масса
стала меньше ML.
Выброс вещества наблюдается в сверхновых и планетарных
туманностях, но в теории этого процесса еще много неясного.
Звезды с массой 20 ML, вероятно, способны сбросить большую
часть своей массы и превратиться в белые карлики или ней-
тронные звезды с массой меньше ML — вот все, что можно ска-
зать на основании расчетов [2, 35, 98, 172, 176]. Однако вряд ли
звезда с массой, превышающей 20 ML, способна потерять более
95% своего вещества, и следует полагать, что внутренняя об-
9 2. Черные deiphi 343
ласть этой звезды в любом случае должна сколлаиспровать
внутрь своей сферы Шварцшильда. (Последние вычисления дей-
ствительно указывают на то, что звезды с массой М > 5 ML не
в состоянии сбросить достаточное количество вещества, чтобы
избежать релятивистского коллапса.)
Обратимся к большим массам и рассмотрим тело массой
~ 108 Ml- Если оно сколлапсирует до своего шварцшильдова
радиуса, то плотность будет всего лишь порядка 10 ~4 г/см3
(меньше плотности воздуха). Если вещество первоначально бу-
дет холодным, рост температуры будет недостаточен ни для
уравновешивания сил тяготения, ни для «зажигания» ядерного
горючего. Поэтому невозможна потеря массы и нет никакой
неопределенности в выборе уравнения состояния. Кроме того,
из этого примера видно, что условия, при которых тело пересе-
кает свою сферу Шварцшильда, совсем нс обязательно должны
быть в том или ином смысле экстремальными.
Итак, по-видимому, некоторые тела с массой 2>ML (а, ве-
роятно, большинство) коллапсируют в конце концов внутрь
своих сфер Шварцшильда и порождают замкнутые ловушечные
поверхности. В нашей Галактике имеется во меньшей мере 109
звезд с массой, превышающей ML. Таким образом, существует
огромное число ситуаций, для которых теорема 2 предсказывает
существование сингулярностей. Наблюдаемые следствия коллап-
са звезды мы обсудим в последующих разделах.
9.2. Черные дыры
Как будет выглядеть коллапсирующее тело для удаленного
наблюдателя О? На этот вопрос можно дать ответ, если кол-
лапс строго сферически симметричен, так как тогда решение вне
тела будет шварцшильдово. В этом случае наблюдатель О' на
поверхности звезды уйдет в определенный момент времени
(скажем, в 1 ч по своим часам) внутрь сферы г = 2 т, причем
он не заметит в этот момент ничего особенного. Однако после
пересечения сферы г = 2 т он станет невидим наблюдателю О
(рис. 57), остающемуся вне этой сферы. Как бы долго наблю-
датель О ни ждал, он никогда не увидит О', после того как
часы последнего покажут 1 ч. Вместо этого О будет наблюдать,
как часы О' явно отстают и асимптотически приближаются к
моменту 1 ч. Это значит, что частота света, принимаемого на-
блюдателем О от О', становится все меньше и меньше и соот-
ветственно интенсивность света убывает все сильнее. Таким об-
разом, хотя поверхность звезды никогда по исчезает из поля
зрения наблюдателя О, она скоро становится столь слабой, что
практически перестает быть вищимой. Точнее, наблюдатель О
увидит сначала, как уменьшится яркость центра диска звезды,
Сингулярность
Горизонт ।
событий I
г --2т
Решение Шварцшильда
для пустоты
Начало ।
координат
Световой конус
прошлого
наблюдателя О
УСГ
Начало
координат
Сингулярность
г-О
Горизонт "
событий
Пустое
простра.
ство
У (г)
Световой
конус
прошлого
наблюдателя О
Рис. 57. Наблюдатель О, который никогда не упадет внутрь коллапсирующей жидкой сферы, никогда не увидит в исто-
рии наблюдателя О', находящегося на поверхности этой сферы, событий происшедших после определенного момента
(скажем, 1 часа), а — диаграмма Финкельстейна; б — диаграмма Пенроуза (вторая жирная точка па рисунке соответствует
наблюдателю О').
9 2 Черные дыры
345
а затем этот процесс падения яркости будет распространяться
к его краю [1]. /Характерное время этого спада интенсивности
равно по порядку величины времени, за которое свет проходит
расстояние 2 т.
Итак, остается объект, который во всех отношениях практи-
чески невидим. Однако он будет иметь ту же шварцшильдов-
скую массу и создавать такое же гравитационное поле, как и
до коллапса. Можно было бы обнаружить присутствие этого
объекта по его гравитационному действию, например по влия-
нию на орбиты близлежащих объектов или по отклонению луча
света, проходящего вблизи пего. Кроме того, возможно, что газ,
падающий на такой объект, будет порождать ударные волны,
которые будут служить источником рентгеновских лучей или
радиоволн.
Наиболее удивительное свойство сферически симметричного
коллапса состоит в том, что сингулярность оказывается в обла-
сти г < 2 т, откуда свет вообще не может уйти на бесконеч-
ность. Поэтому, если наблюдатель останется вне г = 2 т, то он
никогда не увидит сингулярность, предсказываемую теоремой 2.
Кроме того, нарушение физических законов, происходящее в
сингулярности, не может сказаться на нашей способности пред-
сказывать будущее в асимптотически плоской области про-
странства-времени.
Спрашивается, справедлива ли эта картина, если коллапс
не строго сферически симметричен? В предыдущем разделе мы
воспользовались теоремой об устойчивости решения задачи
Коши, чтобы показать, что малые отклонения от сферической
симметрии не помешают появлению замкнутых ловушечных
поверхностей. Однако эта теорема в приведенной форме утвер-
ждает лишь, что достаточно малое возмущение в начальных
данных приведет к возмущению в решении, которое мало в ком-
пактной области. Из этого не следует, что возмущение решения
останется малым сколь угодно долго.
Можно ожидать, что в общем случае наличие сингулярно-
стей приведет к горизонтам Коши (как в решениях Райсснера —
Нордстрема и Керра), а следовательно, к нарушению возмож-
ности предсказывать будущее. Однако если сингулярности не
видны извне, возможность предсказания сохраняется во внеш-
ней асимптотически плоской области.
Чтобы показать это строго, мы предположим, что в (J?\ g)
содержится область, асимптотически плоская в смысле слабой
асимптотической простоты и пустоты (разд. 6.9). Тогда суще-
ствует пространство (^, g), в которое (.#, g) может быть кон-
формно вложено как многообразие с краем Ж — Ж U дЖ, где
край дЖ многообразия Ж в Ж состоит из двух изотропных
346
Гл 9. Гр'аеитпципннып коллппс. и черные дыры
поверхностей J'4 н ,7~, которые соответствуют бесконечности в
будущем и прошлом. Пусть .7— частичная поверхность Коши
в JI. Мы будем говорить, что в пространстве („#, g) будущее
асимптотически предсказуемо с поверхности ГР, если ^7+ содер-
жится в замыкании множества £>4(<7) в конформном многооб-
разии Л. Примерами пространств, в которых будущее асимпто-
тически предсказуемо с некоторой поверхности ГР, являются
пространство Минковского, решение Шварцшильда при ш О,
решение Керра при m 0, | а | in и решение Райсснера —
Нордстрема при m 0, |e|=Cm. Решение Керра с |а|>т и
решение Райсснера — Нордстрема с не являются про-
странствами с асимптотически предсказуемым будущим, по-
скольку в них для любой частичной поверхности Коши ГР
существуют непродолжимые в прошлое непространственнопо-
добные кривые от поверхности Z7+, которые не пересекают ГР,
а стремятся к сингулярности. Асимптотическую предсказуе-
мость будущего можно рассматривать как условие отсутствия
в будущем от ГР «голых» сингулярностей, т. е. сингулярностей,
которые видимы с ^74.
При сферическом коллапсе мы получаем пространство с
асимптотически предсказуемым будущим. Вопрос в том, спра-
ведливо ли это и для песферического коллапса? Мы не можем
дать строгий ответ на этот вопрос. Расчеты по теории возмуще-
ний Дорошкевича, Зельдовича, Новикова [43] и Прайса [137]
свидетельствуют, по-видимому, о том, что малые отклонения от
сферической симметрии не приводят к появлению голой сингу-
лярности. Кроме того, Гиббонс и Пенроуз пытались, хотя и
безуспешно, обнаружить противоречия, которые показали бы,
что в некоторых ситуациях развитие пространства с асимптоти-
чески предсказуемым будущим не имеет смысла. Их неудача,
конечно, не доказывает, что асимптотическая предсказуемость
имеет место, но говорит в пользу этого. Если она невозможна,
то мы не можем сказать ничего определенного об эволюции
какой-либо области пространства, содержащего сингулярность,
поскольку из сингулярности может поступать новая информа-
ция. Поэтому мы будем придерживаться предположения о том,
что условие асимптотической предсказуемости будущего вы-
полняется по крайней мере при достаточно малых отклонениях
от сферической симметрии.
Можно ожидать, что частица на замкнутой ловушечной по-
верхности не в состоянии вырваться к поверхности <7+. Однако
если допускаются произвольные сингулярности, то можно все-
гда произвести нужные разрезы и отождествления, чтобы про-
ложить путь для «побега» частицы. Из следующего утвержде-
ния видно, что это невозможно в пространстве с асимптотиче-
ски предсказуемым будущим.
9 2 Черные дыры
347
Предложение 9.2.1
Если
а) в пространстве („#, g) асимптотически предсказуемо бу-
дущее с частичной поверхности Коши 9,
б) RabKnKb Л 0 для всех изотропных векторов /(“, то зам-
кнутая ловушечная поверхность 2Г в D^(9) не может пересечь
7~(б/+, „#), т. е. ее нельзя увидеть с 9+.
В самом деле, допустим, что Т П 1(.7\ Л) не пусто. Тогда
должна существовать точка р е .7 в 1ЛЛ, Л}. Пусть —
окрестность Л, изометричная окрестности <W границы дЛ'
асимптотически простого и пустого пространства {Л', g') в
конформном многообразии Л'. Пусть 9'— поверхность Коши
в Л', которая совпадает с 9 па CW П Л'. Тогда множество
9' — W компактно и, следовательно, по лемме 6.9.3 каждая
образующая поверхности 3+ покидает область 7+(5’/ — °U’, Л'}.
Отсюда видно, что для любого компактного множества Ж ст 9
каждая образующая 3+ выходит из J+(W, Л). Из этого сле-
дует, что любая образующая 3+ выходит из области
/+(^~, Л), так как она содержится в П 9, Л}. Поэтому
изотропная геодезическая образующая ц поверхности J(3~, Л)
должна пересечь 3+. Образующая ц должна иметь конечную
точку в прошлом на 9~, так как иначе она пересекла бы 3~(9).
Поскольку [х доходит до 3+, ее аффинная длина бесконечна.
Но по условию (б) любая изотропная геодезическая, ортого-
нальная к 9~, должна содержать на конечном аффинном рас-
стоянии точку, сопряженную 9~. Следовательно, она не может
оставаться в 1+(9~,Л) на всем пути к 3+. Этим доказывается,
что Л не может пересечь J~(3+, Л). □
Из всего этого следует, что замкнутая ловушечная поверх-
ность в D+(9) в пространстве с асимптотически предсказуемым
будущим должна лежать в Л — 1~(3^,Л). Следовательно,
должен существовать нетривиальный горизонт событий (буду-
щего) J~(3+, Л), являющийся границей области, из которой
частицы или фотоны могут уйти на бесконечность в направле-
нии будущего. Согласно определению (разд. 6.3), горизонт со-
бытий есть ахрональная граница, образованная изотропными
геодезическими сегментами, у которых могут быть конечные
точки в прошлом, но нет конечных точек в будущем.
Лемма 9.2.2
Если условия (а) и (б) предложения 9.2.1 удовлетворены
и если имеется непустой горизонт событий Л), то
расхождение 0 изотропных геодезических образующих этого
348
Г л 9 Г раеитационный коллапс и черные дыры
горизонта неотрицательно в области
г($+, ж)пп+(^).
Допустим, что есть открытое множество °U, такое, что 0 < О
на °11 П /~(<7+, Ж). Пусть — пространственноподобная 2-по-
верхность в °U Г) 7_(Д+, Ж). Тогда 0 = /2% = 0. Пусть Т — от-
крытое подмножество множества <2/, которое пересекает Ж и
обладает компактным замыканием, содержащимся в °U. В Т мы
можем немного изменить 2Г так, чтобы по-прежнему было
Х.2аа < 0, но чтобы при этом в °U поверхность Т пересекала
/-(Д+, Ж}. Как и прежде, это ведет к противоречию, поскольку
любая образующая поверхности Ж) в /_(<7+, Ж) должна
обладать конечной точкой в прошлом на Ж П Т, где она долж-
на быть ортогональна к 3~. Однако ввиду того, что х2“а < 0 в У,
любая выходящая из Т изотропная ортогональная к £Г в У гео-
дезическая будет содержать на конечном аффинном расстоянии
точку, сопряженную 2Г, и потому не может оставаться в
Ж} на всем пути к <7+. □
В пространстве с асимптотически предсказуемым будущим
/+(^) П Ж) содержится в Д+(^). Если на горизонте
событий найдется точка р &/+(!?), которая не принадлежит
£*+(5’), малейшее возмущение может привести к тому, что р
попадет в Ж), т. е. будет видна из бесконечности; это
означает, что данное пространство не является более асимпто-
тически предсказуемым. Ввиду этого, по-видимому, имеет смысл
несколько уточнить определение асимптотически предсказуе-
мого будущего: будем говорить, что в пространстве-времени бу-
дущее асимптотически сильно предсказуемо с частичной поверх-
ности Коши Ж если <7+ содержится в замыкании области
D+(9>) ъ Ж yl Г\ J~ (Ж , Ж) содержится в D+(&’y Дру-
гими словами, с поверхности 9Р можно делать предсказания еще
и относительно некоторой окрестности горизонта событий.
Предложение 9.2.3
Если (Ж, g)—пространство с сильно асимптотически пред-
сказуемым будущим с частичной поверхности Коши 5^, то су-
ществует гомеоморфизм
а:(0,
для которого при каждом т=(0, оо) поверхность ^(т)==
S(WX^) представляет собой частичную поверхность Коши
со следующими свойствами:
а) при т2 > ^(тг) сд /+(^(ti) );
9.2. Черные дыры
349
б) при каждом т граница поверхности ^(т) в конформном
многообразии Л является прострапственноподобной 2-сферой
£ (т) в <7+, такой, что при т2 > щ £ (тг) находится строго в
будущем сферы ЗДт]) ;
Рис. 58. Пространство (Jt, g) с асимптотически сильно предсказуемым с ча-
стичной поверхности Коши 7 будущим. Изображено семейство 93 (т) лро-
странственноподобных поверхностей, которые покрывают Z)+ (7) — 9? и пере-
секают 7+ по семейству 2-сфер S£ (т).
в) при каждом т множество £ (т) U (.7+ П 2(2 (т), Л}) есть
поверхность Коши в Л для D (Т').
Другими словами, Т’(т) есть семейство пространственнопо-
добных поверхностей, гомеоморфных <?, которое покрывает
D+{£) — £ и пересекает ,7+ (рис. 58). Эти поверхности можно
рассматривать как поверхности постоянного времени в асимпто-
тически предсказуемой области. Выберем их так, чтобы они
пересекали -7'; тогда при наличии гравитационного или иного
излучения какая-либо масса, расположенная на этих поверх-
ностях и измеренная из бесконечности, будет убывать.
350
Гл. 9 Гравигационпый коллапс и черные дыры
Построение ^(т) подобно доказательству предложения 6.4.9.
Выберем непрерывное семейство 2? (т) (оо > т > 0) простран-
ственноподобных 2-сфер, которые покрывают <7+ так, что при
Т2 > Xi S (хг) находится строго в будущем сферы S(xi). Вве-
дем на Л меру объема так, чтобы полный объем Л по этой
мере был конечен. В первую очередь докажем следующую
лемму:
Лемма 9.2.4
Величина £(т), объем множества /“(.!?(т), Л) П £>+(^’), есть
непрерывная функция т.
Пусть Т — какое-либо открытое множество с компактным
замыканием в
ПЖ jr)no+(n
Тогда из каждой точки множества Т можно провести времени-
подобную кривую до S’(t), которую можно деформировать так,
чтобы получить времениподобные кривые до Z (т — 6) при не-
котором б > 0. При данном 8 > 0 можно найти такое Т, объем
которого больше fe(r)—8. Следовательно, найдется 6 > 0, при
котором &(т— б)>&(т)—8. С другой стороны, допустим, что
существует открытое множество Ж, которое не имеет пересе-
чения с /-(S’(t), Л} Л £)+(£?), но содержится в {S? (/), Л} Л
Г) £>+(£?) при любом т' > х. Тогда, если р е Ж, должны суще-
ствовать направленные в прошлое времениподобные кривые
от каждой S3 (/) до р. Поскольку область <7+ между S£ (т) и
S’(ti) компактна для любых Ti > т, из Z(т) можно будет про-
вести направленную в прошлое непространственноподобную
кривую /., которая будет предельной кривой для {А,/}- Посколь-
ку {Ат'} не пересекают область Г~ (Z {х}, Л~), А тоже не будет
ее пересекать и, следовательно, будет изотропной геодезической,
лежащей в /"(S’(t), Л}. Она войдет в Л’ и потому должна
или иметь конечную точку в прошлом в р, или пересечь &. Пер-
вое невозможно, так как в этом случае Ж имеет пересечение
с /“(S’(r), Л}, а второе невозможно, поскольку ре.7+(У).
Следовательно, не существует такого открытого множества, ко-
торое лежало бы в Л} при каждом х' > т, но не
принадлежало бы /“(S’(t), X)I"IjD+(Sp). Таким образом, для
данной постоянной е найдется такая постоянная б, что
k (т 4- 6) < k (т) -J- 8,
т. е. k(x)—непрерывная функция. □
Доказательство предложения 9.2.3. Введем функции f(p) и
й(р, т), p^.D+(S), представляющие собой объем 1+(р) и
9 2. Черные дыры
351
/^(Й’(т), Л}. Так же как в предложении 6.4.9, функция /(р)
непрерывна на глобально гиперболической области D+(S?)—,'Т’
и стремится к нулю на каждой непродолжимой в будущее не-
пространственноподобной кривой. Поскольку /-(S’(x), Я) П Л
есть множество в прошлом, область
D ' (7)-Г(Х(т), Л)-д’
глобально гиперболична. Следовательно, при каждом значении
т функция h(p, т) непрерывна на D+{9’) — д’. Это означает, что
при данном е > 0 можно найти такую окрестность <2/ точки р,
что \h(q, т) — h(p, т) | < е/2 для любого q <= °Ц. По лемме 9.2.4
можно найти б > 0, такое, что |&(т')—&(т) | < е/2, когда
|т'— т|<б. Отсюда \h\q, X)—п(р, т) | < е, т. е. функция
h(p, т) непрерывна на (D+ (£’) — д’) X (0, оо). Поверхности д’(т)
можно определить, тогда как множества точек p^D+(g’)—д’,
для которых h(p, t)=t/(p). Ясно поэтому, что они представ-
ляют собой пространственноподобные поверхности, которые по-
крывают £>+(5’)—д’ и удовлетворяют условиям (а) — (в).
Чтобы задать гомеоморфизм а, нам понадобится временипо-
добное векторное поле на D+^g1) — д’, пересекающее каждую
поверхность ^(т). Построим такое поле следующим образом.
Пусть У — некоторая окрестность поверхности <7+ в конформном
многообразии Л и Xi — некоторое непространственноподобное
векторное поле на X, которое на <7+ касательно к образующим
SP+. Далее, пусть др 0 есть С2-функция, равная нулю вне Т и
отличная от нуля на SP+, Х2 — времениподобное векторное поле
на Л и, наконец, х2 О — С2-функция на Л, отличная от нуля
на Л, но равная нулю на Тогда векторное поле Х =
= Х]Х1 + х2Х2 обладает требуемым свойством. Гомеоморфизм
а:Д+(^)—д’-^^О, оо)Х^ отображает точку p^D+tg’)—д’
в пару (т, q), где т определяется тем, что ре1?(т), а инте-
гральная кривая поля X, проходящая через р, пересекает д’
в точке q. □
Если в области Z)+(^) пространства с асимптотически пред-
сказуемым будущим существует горизонт событий /(«7+ Л),
то из свойства (в) предложения 9.2.3 следует, что при доста-
точно больших т поверхности S^(t) пересекут этот горизонт. Оп-
ределим черную дыру на поверхности д’(т) как связную ком-
поненту множества ^(т)=^(т)—7~(.7+, Л). Другими сло-
вами, черная дыра — это область поверхности ^(т), из которой
ни частицы, ни фотоны не могут уйти на поверхность
По мере роста т черные дыры могут сливаться, и в резуль-
тате такого вторичного коллапса могут образоваться новые чер-
ные дыры. Вместе с тем из следующего утверждения видно, что
черные дыры никогда не могут распасться.
352
Гл. 9 Гравитационный коллапс и черные дыры
Предложение 9.2.5
Пусть ^?1(т1)—черная дыра на JT’(ti). Пусть ^2(т2) и
^з(т2)—черные дыры на более поздней поверхности ^(т2). Если
^2(т2) И ^з(т2) пересекают /+(^1 (и)), то ^2(т2) = (т2).
По свойству (в) предложения 9.2.3 каждая направленная
в будущее непродолжимая времениподобная кривая из
пересечет S^(t2). Следовательно, область
/+(^1(т1))П^(т2)
связная и будет содержаться в связной компоненте ^(т2). □
Для физических приложений в первую очередь интересны
черные дыры, образовавшиеся в результате гравитационного
коллапса из первоначально несингулярного состояния. Уточ-
ним это понятие. Будем говорить, что частичная поверхность
Коши 9Р обладает асимптотически простым прошлым, если об-
ласть /-(J?) изометрична области некоторого асимпто-
тически простого и пустого пространства-времени (Жг, g7), где
— поверхность Коши для (Ж, g7). Согласно предложению
6.9.4, поверхность 9” обладает топологией /?3, следовательно, 9
имеет такую же топологию. Тогда из предложения 9.2.3 сле-
дует, что каждая поверхность ^(т) обладает топологией /?3 и
объединение ^(т) с граничной 2-сферой Z (т) на <7+ гомео-
морфно единичному кубу /3, если {Ж, g)—пространство со
строго асимптотически предсказуемым с поверхности 9 буду-
щим и с асимптотически простым прошлым.
Хотя мы интересуемся главным образом пространствами,
имеющими асимптотически простые прошлые, будет уместно
рассмотреть в следующем разделе пространства с асимптоти-
чески предсказуемым будущим, которые не имеют асимптоти-
чески простого прошлого, но при больших временах служат
хорошим приближением к пространствам, имеющим его. Приме-
ром этого является сферически симметричный коллапс, рассмо-
тренный нами в начале раздела. Если поверхность звезды ушла
за горизонт событий, метрикой внешней области является мет-
рика решения Шварцшильда, и на ней не сказывается дальней-
шая судьба звезды. Поэтому при исследовании асимптотиче-
ского поведения уместно попросту забыть о звезде и рассма-
тривать решение Шварцшильда в пустом пространстве как
пространство, в котором будущее сильно асимптотически пред-
сказуемо с поверхности типа изображенной на рис. 24. Эта
поверхность не обладает асимптотически простым прошлым и
топологически она представляет собой S2 X 7?1, а не /?3. Однако
часть 9 вне горизонта событий в области I имеет такую же
топологию, как область поверхности ^(т) вне горизонта собы-
тий на рис. 57. Мы хотим рассматривать пространства, в кото-
9.2. Черные дыры
353
рых будущее сильно асимптотически предсказуемо с поверхно-
сти 9? и которые при этом таковы, что часть 9?, находящаяся
вне горизонта событий, обладает такой же топологией, как не-
которая поверхность ^(т) в пространстве с асимптотически
простым прошлым. Конечно, в более сложных случаях может
оказаться несколько компонент ^(т), соответствующих кол-
лапсу нескольких тел. Поэтому мы будем рассматривать про-
странства, которые сильно асимптотически предсказуемы с по-
верхности 9Р и обладают тем свойством, что
(а) множество 9Р П Ж} гомеоморфно пространству/?3
с вырезанным из него открытым множеством с компактным
замыканием.
(Отметим, что это открытое множество может и не быть
связным.) Кроме того, было бы удобно наложить такое требо-
вание:
(Р) поверхность 9? односвязна.
Предложение 9.2.6
Пусть (JL g)—пространство, которое сильно асимптотиче-
ски предсказуемо с частичной поверхности Коши удовлетво-
ряющей требованиям (к), (Р). Тогда
1) поверхность ^(т) также удовлетворяет требованиям (а),
(Р);
2) при любом т д$\ (т)—граница черной дыры ^i(r) в 9—
компактна и односвязна.
Поскольку поверхности 9^(т) гомеоморфны 9Р, они удовле-
творяют требованию (Р). Можно определить инъективное ото-
бражение
ж^д^'г О+, Ж)
как перенесение каждой точки ^(т) по интегральной кривой
векторного поля X, введенного в предложении 9.2.3, до ее пере-
сечения с 6Р. Пространство {Ж, g)—асимптотически простое
в слабом смысле, поэтому в ^(т)П Ж) вблизи /7+ можно
построить 2-сферу 3>. Часть ^(т), которая находится вне 9,
будет отображаться в область 9?, расположенную вне 2-сферы
у(^). Отсюда видно, что область множества Ж),
которая не содержится в у(^(т) Г) Ж)), должна иметь
компактное замыкание. Следовательно, множество у(^(т)П
П 7~(<7+, Ж)) должно быть гомеоморфным пространству /?3, из
которого вырезано открытое множество с компактным замыка-
нием. Поскольку поверхность гомеоморфна /?3 — У, где
7° — открытое подмножество пространства /?3 с компактным за-
мыканием, граница дЗНг) будет гомеоморфна дТ и в силу этого
]2 Заказ 381
354
Г л. 9. Гравитационный коллапс и черные дыры
компактна. Граница d$i (т), будучи замкнутым подмножеством
<3й?(т), также компактна.
Допустим, что d&i (т) состоит из двух несвязных компонент
<3^'1 (т) и Д^12(т). Тогда в ^(т) — й?(т) можно было бы прове-
сти кривые X] и 7.2 от 3? (г) до (З^Дт) и дЗ^2 (т) соответственно.
Можно было бы также в int (г) провести кривую ц от (Зй^Дт)
до d^i2 (т). Соединив все эти кривые, мы получили бы замкну-
тую кривую в ЗР (т), которая имела бы с д^Цт) только одно
пересечение. Эту кривую нельзя деформировать в ^(т) к нулю,
что противоречит тому факту, что &(т) односвязна. □
Нас интересуют лишь такие черные дыры, в которые реально
можно «провалиться», т. е. такие, граница которых дЗПт) со-
держится в /+(У~, Л). Поэтому к требованиям (а) и (|3) мы
добавим такое:
(у) для достаточно больших т ‘Т’(т) QJ~(3+, Л) содержится
в 7+(У- ЛУ.
Будем называть {Л, g) регулярно предсказуемым простран-
ством, если его будущее сильно предсказуемо с частичной по-
верхности Коши 9? и если оно удовлетворяет требованиям (а) —
(у). Все пространства, упомянутые в начале раздела, имея
асимптотически предсказуемое будущее, являются в то же
время и регулярно предсказуемыми. Из предложения 9.2.6 вид-
но, что когда мы имеем дело с регулярно предсказуемыми
пространствами, развивающимися из некоторой частичной по-
верхности Коши, существует взаимно-однозначное соответствие
между черными дырами ^(т) и их границами <ЗЙ?,(т) в ^(т).
Поэтому в такой ситуации можно было бы дать эквивалентное
определение черной дыры как связной компоненты множества
^(т)п му.
Приведем утверждение, в котором устанавливается важное
для следующего раздела свойство границы черной дыры.
Предложение 9.2.7
Пусть (Л, g)—регулярно предсказуемое пространство, раз-
вивающееся из некоторой частичной поверхности Коши <?, при-
чем RabKaKb 0 для любого изотропного вектора Ка. Пусть
^i(t)—черная дыра на поверхности ^(г), а №(/)} (« =
= 1, ..., М)—черные дыры на более ранней поверхности
^(т'), для которых (К)) П 3^\ (т) ф 0. Тогда площадь
Д1(т) границы (3^1 (т) больше или равна сумме площадей
ДДт') границ (З^Дт'), и равенство имеет место лишь при
N = 1.
Другими словами, площадь границы черной дыры не мо-
жет убывать со временем, и если две или более черные дыры
9.2. Черные дыры
355
сливаются в одну, площадь границы последней будет больше
суммы площадей границ исходных черных дыр.
Поскольку горизонт событий есть граница прошлого поверх-
ности <7+, его изотропные геодезические образующие будут об-
ладать конечными точками в будущем, только если они пере-
секают <7+. Это, однако, невозможно, так как изотропные гео-
дезические образующие не имеют конечных точек в будущем.
Таким образом, изотропные образующие горизонта событий не
имеют конечных точек в будущем. По лемме 9.2.2 их расхож-
дение 0 неотрицательно; следовательно, площадь двумерных
сечений этих образующих не может убывать по мере роста т.
В силу свойства (в) предложения 9.2.3 и согласно предложе-
нию 9.2.5, все изотропные геодезические образующие поверх-
ности /~(<7+, Ж}, пересекающие IT'(K) в одном из с^(т'),
должны пересечь ^(т) в Таким образом, площадь
d^i (г) больше или равна сумме площадей {дЗЪ(т')}. Когда
У > 1, (т) будет содержать У раздельных замкнутых под-
множеств, которые соответствуют образующим поверхности
/_(5Х+, Ж}, пересекающим каждую дЗЦ(т'). Поскольку d^i(r)
связна, она должна содержать открытое множество образую-
щих, которые не пересекают какую-либо из а имеют
прошлые конечные точки между 'Т’(т) и ^(т')- □
Определение черной дыры через горизонт событий Ж]
удобно тем, что он является изотропной гиперповерхностью и
обладает потому рядом привлекательных свойств. Однако это
определение зависит от поведения решения во все времена в бу-
дущем; при заданной частичной поверхности Коши ^(т) мы не
можем сказать, где расположен горизонт, не решив сначала
задачи Коши во всей области Коши будущего этой поверхности.
Поэтому будет полезно дать определение горизонта иного рода,
который зависит лишь от свойств пространства-времени на по-
верхности ^(т).
Из предложения 9.2.1 мы знаем, что в развивающемся из
частичной поверхности Коши ЗР регулярно предсказуемом про-
странстве любая замкнутая ловушечная поверхность на S?(r)
должна находиться в &(т). Этот результат связан только с тем
фактом, что входящие ортогонально к этой 2-поверхности изо-
тропные геодезические сходятся. При этом не важно, сходятся
или нет входящие изотропные геодезические. Поэтому мы бу-
дем говорить, что ориентируемая компактная пространственная
2-поверхность в D+(<P) есть внешняя ловушечная поверхность,
если расхождение 0 выходящих ортогонально к ней изотропных
геодезических неотрицательно. (Случай 0 = 0 включается сюда
для удобства.) Чтобы определить понятие семейства выходящих
12*
356 Гл. 9. Гравитационный коллапс и черные дыры
изотропных геодезических, воспользуемся свойством ((3) ча-
стичных поверхностей Коши Т’(т). Пусть X — времениподобное
векторное поле из предложения 9.2.3. Тогда любую компактную
ориентируемую 2-поверхность 5* в D+(7’) можно отобразить по-
средством интегральных кривых поля X на компактную ориен-
тируемую 2-поверхность ГР' в Т’(т) при любом данном значе-
нии т. Пусть % — кривая в Т'(т) US’(r) от 3? (т) до 9>', пересе-
кающая ГР' только в своей конечной точке. Тогда можно опре-
делить внешнее направление на ГР' и 5Дт) как направление, в ко-
тором X приближается к ГР'. Поскольку поверхность З'(т) одно-
связна, это определение однозначно. Семейством выходящих
изотропных геодезических, ортогональных 7s, является тогда се-
мейство, отображаемое полем X на кривые в З’(т), которые для
ГР' являются выходящими.
Зная решение на поверхности ^(т), можно найти все внеш-
ние ловушечные поверхности ГР, которые лежат в ^(т). Мы оп-
ределим ловушечную область ГГ (т) на поверхности Т'(т) как
множество всех точек через которые проходит внеш-
няя ловушечная поверхность ГР, лежащая в ^(т). Как показы-
вает следующий результат, существование ловушечной области
ГГ (т) приводит к существованию черной дыры ^(т), и при каж-
дом значении т ГГ (т) лежит в ^(т).
Предложение 9.2.8
Пусть (Л, g)—регулярно предсказуемое пространство, раз-
вивающееся из частичной поверхности Коши 3^, и пусть в этом
пространстве ЯаъКаК.ь 0 для всякого изотропного вектора №.
Тогда внешняя ловушечная поверхность ГР в №(^) не пересе-
кает №(<7+, Л}.
Это предложение доказывается подобно предложению 9.2.1.
Допустим, что ГР пересекает 7_(У+, Л\ Тогда 7+(^, Л} должна
пересекать <7+. К каждой точке из <7+Г1 Н(ГР, Л} можно про-
вести направленную в прошлое изотропную геодезическую об-
разующую поверхности /+(7’, Л}, имеющую конечную точку
в прошлом на .7, но не имеющую точек, сопряженных .№ В силу
(4.35), расхождение 0 этих образующих будет неположительно,
поскольку оно неположительно на поскольку RabK.aKb 0.
Таким образом, площадь двумерного сечения упомянутых обра-
зующих будет всегда меньше или равна площади £7. Это при-
водит к противоречию, так как <7+П/+(^, Л), находясь на
бесконечности, имеет бесконечную площадь. □
Внешнюю границу дЗ~\(х} связной компоненты ГГДт) лову-
шечной области .№(т) мы будем называть кажущимся горизон-
том. Согласно предыдущему результату, из существования ка-
9.2. Черные дыры
357
жущегося горизонта д?Гi (т) следует, что существует вне его
или совпадает с ним компонента d^i(r) горизонта событий. Об-
ратное, однако, не обязательно верно: внутри горизонта собы-
тий может и не быть внешних ловушечных поверхностей.
Рис. 59. Сферический коллапс звезды массы т, сопровождаемый сфериче-
ским коллапсом оболочки массы бот; внешнее решение будет решением
Шварцшильда для массы т после коллапса звезды и решением Шварц-
шильда для массы т = 6m после коллапса оболочки. В момент Т] имеется
горизонт событий, но нет кажущихся горизонтов событий; в момент т_> внутри
горизонта событий есть два кажущихся горизонта событий.
С другой стороны, внутри одной компоненты <Э^(т) гори-
зонта событий может быть более одной связной компоненты
ловушечной области Такая возможность иллюстрируется
рис. 59. Похожая ситуация возникает при рассмотрении столкно-
вения и слияния двух черных дыр. На начальной поверхности
358
Гл. 9. Гравитационный коллапс и черные дыры
^(п) имеются две ловушечные области £T](ti) и £T2(ti),
находящиеся соответственно в черных дырах и ^г(Т1).
Рис. 60. Столкновение и слияние двух черных дыр. В момент времени Ti
внутри горизонтов событий (Tt), дЗЗ (т2) существуют кажущиеся гори-
зонты д&\, д&~2. К моменту т эти горизонты событий сливаются и образуют
один горизонт событий; к этому моменту образуется третий кажущийся го-
ризонт, окружающий предшествующие кажущиеся горизонты.
По мере их взаимного сближения они сливаются и образуют
единую черную дыру ^3(т2) на более поздней поверхности
^(тг). Однако кажущиеся горизонты д°Гi(t) и д°Г2(т) не со-
льются немедленно, а появится третья ловушечная область
^з(т), окружающая первые две (рис. 60). В некоторый более
поздний момент ?Г,, Т2 и ?Г3 сольются воедино.
9.3. Конечное состояние черной дыры
359
Мы лишь набросаем схему доказательства основных свойств
кажущегося горизонта. Прежде всего имеем
Предложение 9.2.9
Каждая компонента д°Г (т) является такой 2-поверхностью,
что выходящие ортогональные изотропные геодезические имеют
на д°Г (т) нулевое схождение 0. (Такую поверхность мы будем
называть маргинальной внешней ловушечной поверхностью.)
Если бы 0 было положительным в некоторой окрестности
в д£Г(т) точки р дсГ (т), то была бы окрестность °U точки р,
такая, что любая внешняя ловушечная поверхность в ^(т), ко-
торая пересекает °U, пересекла бы также и д2Г(т). Следова-
тельно, 0 0 на д£Г (т).
Если бы 0 было отрицательно в некоторой окрестности
в д£Г (т) точки р е д^Г (т), то можно было бы растянуть д?Г (т)
в ^(т) так, чтобы получить внешнюю ловушечную поверхность
снаружи д°Г(т). □
Итак, изотропные геодезические, ортогональные к кажуще-
муся горизонту ОТ (т) на поверхности 5?(т), выходят из дЗ~(т)
с нулевым схождением. Однако если на их пути встретится ма-
терия или область, где тензор Вейля удовлетворяет типовому
условию (разд. 4.4), они начнут сходиться, поэтому их пере-
сечение с более поздней поверхностью ^{т') будет лежать
внутри кажущегося горизонта д?Г(т'). Иначе говоря, кажу-
щийся горизонт движется наружу по меньшей мере со ско-
ростью света и быстрее света, если на его пути попадется ве-
щество или излучение. Как видно из вышеприведенного при-
мера, это движение может быть еще и разрывным. Вследствие
этого с кажущимся горизонтом иметь дело труднее, чем с гори-
зонтом событий, который всегда движется непрерывным обра-
зом. Мы покажем в следующем разделе, что горизонт событий
и кажущийся горизонт совпадают, когда решение стационарно.
Поэтому надо ожидать, что оба горизонта очень близки друг
к другу, если решение почти стационарно в течение длитель-
ного времени. В частности, их площади в таких случаях, по всей
вероятности, одинаковы. Если имеется решение, которое из на-
чального почти стационарного состояния через некоторый пе-
риод нестационарности переходит к конечному почти стацио-
нарному состоянию, то можно использовать предложение 9.2.7,
чтобы связать площади начального и конечного горизонтов.
9.3. Конечное состояние черной дыры
В предыдущем разделе мы принимали, что в удалении от
коллапсирующей звезды можно предсказать будущее. Как было
показано, из этого предположения следует, что звезда уходит
360
Гл. 9. Гравитационный коллапс и черные дыры
за горизонт событий, который скрывает сингулярность от внеш-
него наблюдателя. Материя и энергия, пересекающие горизонт
событий, будут навсегда потеряны для внешнего мира. Поэтому
следует ожидать, что на бесконечность в виде гравитационных
волн будет излучено ограниченное количество энергии. Когда
подавляющая часть энергии будет излучена, вне горизонта ре-
шение, по-видимому, будет приближаться к стационарному со-
стоянию. Ввиду этого в данном разделе мы исследуем строго
стационарные решения для черных дыр в предположении, что
их внешние области будут довольно точно соответствовать ко-
нечным состояниям решений вне сколлапсировавших объектов.
Точнее, мы будем рассматривать пространство (J?', g), кото-
рое удовлетворяет следующим условиям:
1) (Л, g)—регулярно предсказуемое пространство, разви-
вающееся из частичной поверхности Коши
2) существует группа изометрии &р.Л -> Л, у которой век-
тор Киллинга К времениподобен вблизи и 2Г-,
3) [Л, g)—пустое пространство или содержит поля типа
электромагнитного или скалярного, которые удовлетворяют хо-
рошо определенным гиперболическим уравнениям и условию
энергодоминантности: TabNaLb 0 для направленных в буду-
щее времениподобных векторов N, L.
Будем называть пространство, удовлетворяющее этим усло-
виям, стационарным регулярно предсказуемым пространством.
Мы считаем, что при больших значениях т область 1~(2Г+, Л){\
П/+(2?(т)) регулярно предсказуемого пространства, содержа-
щая коллапсирующие звезды, будет почти изометрична анало-
гичной области некоторого стационарного регулярно предска-
зуемого пространства.
Условие (3) основано на том предположении, что любая
материя с ненулевой массой покоя в конечном счете «прова-
лится» за горизонт. Могут остаться лишь поля дальнодействую-
щих сил типа электромагнитных. Из условий (2) и (3) следует,
что пространство [Л, g) аналитично вблизи бесконечности, где
поле векторов Киллинга времениподобно [110]. Мы примем, что
решение в других местах является аналитическим продолже-
нием из этой наружной области. Рассматриваемые здесь ста-
ционарные решения не обладают асимптотически простыми
прошлыми, так как они соответствуют лишь конечному состоя-
нию системы, и не описывают более раннюю динамическую
стадию. Но нас интересуют свойства этих решений только в бу-
дущем, а не в прошлом. Свойства в будущем и прошлом могут
различаться, поскольку нет никакой априорной причины для
того, чтобы они были обратимы во времени; фактически такая
обратимость возникает как следствие результатов, которые бу-
дут получены ниже.
9.3. Конечное состояние черней дыры
361
В стационарном регулярно предсказуемом пространстве пло-
щадь двумерных сечений горизонта событий не будет зависеть
от времени. Это приводит к следующему фундаментальному ре-
зультату:
Предложение 9.3.1
Пусть (Л, g)—стационарное регулярно предсказуемое про-
странство-время. Тогда образующие горизонта событий буду-
щего /"(У+, Л) не имеют конечных точек в прошлом
в /+(.!7~, Л}. Пусть У1“—направленные в будущее касательные
к этим образующим векторы; тогда в /+ Л} вектор об-
ладает нулевыми сдвигом о и расхождением 0 и удовлетворяет
равенству
7?я6У1ПУ.й = 0 =
Чтобы не прерывать изложения, мы отложим доказательство
этого и других результатов до конца раздела. Из этого пред-
ложения видно, что в стационарном пространстве-времени ка-
жущийся горизонт совпадает с горизонтом событий.
Теперь мы приведем некоторые результаты, которые указы-
вают на то, что семейством решений Керра (разд. 5.6), вероят-
но, исчерпываются пустые стационарные регулярно предска-
зуемые пространства. Мы не будем приводить здесь доказа-
тельств теорем Израэля и Картера, а только сошлемся на
соответствующие статьи. Остальные результаты будут доказаны
в конце данного раздела. На основании этих результатов мы
полагаем, что для незаряженного коллапсирующего объекта
в конце концов устанавливается решение Керра. Если сколлап-
сировавшее тело обладает ненулевым полным зарядом, реше-
ние, как мы полагаем, будет стремиться к одному из решений
Керра для заряженного тела.
Предложение 9.3.2
В стационарном регулярно предсказуемом пространстве
каждая связная компонента горизонта <W(r) в /+(.7~, Л) го-
меоморфна 2-сфере.
Не исключено, что могут существовать несколько связных
компонент с^(т), соответствующих нескольким черным дырам,
расположенным на неизменных расстояниях друг от друга. Та-
кая ситуация может возникнуть в предельном случае, когда
каждая из этих черных дыр имеет заряд е, равный ее массе т,
и не вращается [69]. По всей вероятности, это единственный
случай, в котором могут возникнуть настолько значительные
сильные отталкивания, что они уравновесят гравитационное
притяжение между черными дырами. Поэтому мы будем
362
Гл. 9. Гравитационный коллапс и черные дыры
рассматривать решения, в которых сТ^(т) обладает только од-
ной связной компонентой.
Предложение 9.3.3
Пусть (Л’, g)—стационарное регулярно предсказуемое про-
странство. Тогда вектор Киллинга Ка отличен от нуля в одно-
связной области .<) Я/^(.7+, Л\. Пусть дано То, при
котором ^(т0) П Л} содержится в Z+(5r_, Л}. Если
д^(то) имеет только односвязную компоненту, то область
/+(.7^, .<) Л 7~ (.7+, .<) Л Л гомеоморфна [О, 1]XS2X/?1.
При дальнейшем изложении мы будем следовать одному из
двух возможных путей в зависимости от того, равен или не
равен нулю всюду ротор вектора Киллинга Ка, т. е. Ka-,bKp(\abcd-
Если он равен нулю, то мы будем называть решение статиче-
ским регулярно предсказуемым пространством-временем. Грубо
говоря, если черная дыра в некотором смысле не вращается, то
можно ожидать, что решение будет статическим.
Предложение 9.3.4.
В статическом регулярно предсказуемом пространстве-вре-
мени вектор Киллинга К времениподобен во внешней области
Д)П7“О+, Л), а на
7“О+, Х)Л7+О~, Л)
отличен от нуля и направлен вдоль изотропных образующих
поверхности / - Л).
Поскольку ротор вектора К равен нулю, он ортогонален
к некоторой гиперповерхности, т. е. существует некоторая функ-
ция е, такая, что вектор Ка пропорционален |;а. Тогда мы мо-
жем представить метрику во внешней области в виде gab —
— уИ<аКь + hab, где f = КаКа и hab — индуцированная метрика
на поверхностях {S = const}, причем она характеризует разде-
ление интегральных кривых поля №• Внешняя область, таким
образом, допускает изометрию, которая переводит точку на по-
верхности g в точку на поверхности —g, лежащую на той же
интегральной кривой векторного поля К. Эта изометрия обра-
щает направление течения времени; пространство, допускаю-
щее такого рода изометрию, будем называть симметричным во
времени. Таким образом, если аналитическое расширение внеш-
ней области содержит горизонт событий будущего Л),
то оно будет содержать и горизонт событий прошлого /+(5<_, Л}.
Эти горизонты событий могут как пересекаться, так и не пере-
секаться; решения Шварцшильда и Райсснера — Нордстрема
при е2 < /и2 служат примерами, когда эти горизонты Пересе-
9.3. Конечное состояние черной дыры 363
каются, а решение Райсснера — Нордстрема при е2 = т2—
примером, когда они не пересекаются. В последнем случае
f.a = 0 на горизонте. Важность этого положения вытекает из
того факта, что на горизонте будущего j~(3+, Л)
выполняется условие Ка-,ьКь = = 0Да, где 0^0— по-
стоянная вдоль каждой изотропной геодезической образующей
поверхности /_(Д+, Л}. Пусть v есть направленный в будущее
аффинный параметр вдоль каждой такой образующей. Тогда
К = ad/dv, где а — функция вдоль образующей, подчиняю-
щаяся уравнению da/dv = 0. Если 0 0 и образующая гео-
дезически полна в направлении прошлого, то функция а и век-
тор Киллинга К будут равны нулю в какой-то точке. Эта точка
не может лежать в 7+(.7щ Л) и потому будет точкой пересече-
ния горизонта событий будущего Л} и горизонта собы-
тий прошлого 7+(«7щ Л} [14]. Если 0 = 0, то вектор К всюду
отличен от нуля, и ни в одной точке горизонт не разветвляется.
Израэль [84] показал, что статическое регулярно предсказуе-
мое пространство-время должно быть шварцшильдовым, если:
а) ТаЪ = 0;
б) величина f = для вектора Киллинга Ка всюду в
Л)С\3^(д/+, Л) обладает ненулевым градиентом;
в) горизонт событий прошлого ]+(&-, Л) пересекает гори-
зонт событий будущего Л) по компактной 2-поверхно-
сти З2".
[Из условия (в) и предложения 9.3.2 следует, что З2" связна
и обладает топологией 2-сферы. Израэль не приводит условия
(а) — (в) в точно такой форме, но его и наша формулировки
эквивалентны.] Далее, он показал [85], что при замене условия
отсутствия материи (а) требованием, чтобы тензор Таъ был тен-
зором энергии-импульса электромагнитного поля, пространство-
время оказывается пространством Райсснера — Нордстрема.
В работе [111] условие (б) было снято для случая вакуума.
На основании этих результатов мы полагаем, что в случае
статичности конечного состояния решения вне горизонта собы-
тий метрика во внешней области должна быть метрикой Шварц-
шильда.
Теперь мы рассмотрим случай, когда конечное состояние
внешнего решения стационарное, но не статическое. Мы счи-
таем, что это имеет место, когда сколлапсировавший объект
в исходном состоянии вращался.
Предложение 9.3.5
В пустом стационарном регулярно предсказуемом про-
странстве, если оно нестатическое, вектор Киллинга Ка
364
Гл. В. Гравитационный коллапс и черные дыры
пространствепноподобен в некоторой части внешней области
J+(ST-,jT) П Я}.
Область в Я) Л J~(3r+, Я), в которой вектор Ка про-
странственноподобен, называется эргосферой. Из предложе-
ния 9.3.4 следует, что эргосферы не существует, если метрика
статическая. Значение эргосферы состоит в том, что в ней не-
возможно движение частицы по интегральной кривой вектора
Киллинга №, т. е. частица не может оставаться в покое при на-
блюдении ее с бесконечности. Поскольку эргосфера располо-
жена снаружи от горизонта, частица из нее все же может уйти
на бесконечность. Примером стационарного нестатического ре-
гулярно предсказуемого пространства с эргосферой служит ре-
шение Керра при а2 т2 (разд. 5.6). В работах [129, 133] по-
казано, что из черной дыры с эргосферой можно извлечь опре-
деленное количество энергии, бросив частицу из бесконечности
в эргосферу. Поскольку частица будет двигаться по геодезиче-
ской, величина Ео s ~рйаКа > 0 будет постоянна вдоль ее
траектории
р‘ = (?„>,’) + р,'КпЛ‘ = о,
гак как роа — геодезический вектор и № — вектор Киллинга;
здесь роа = mvoa— вектор импульса частицы, m — ее масса по-
коя и Vo — единичный вектор, касательный к мировой линии
частицы. Предположим затем, что частица распадается на две
частицы с импульсами pia и Pza, где роа = Р\а + Р2а- Поскольку
вектор Ка пространственноподобен, pia можно выбрать так,
чтобы он был направленным в будущее времениподобным век-
тором, для которого Ei = —Р1аКа < 0. Тогда будем иметь
Е = —Р2аКа > Ео. Это означает, что вторая частица может
уйти на бесконечность, где она будет иметь большую энергию,
чем первоначально брошенная частица. Таким образом, мы из-
влечем из черной дыры некоторое количество энергии.
Частица с отрицательной энергией не может уйти на беско-
нечность, а должна оставаться в области, где вектор № про-
странственноподобен. Допустим, что эргосфера не пересекает
горизонт событий /~(Д+, Я). Тогда эта частица должна будет
оставаться во внешней области. Повторяя описанный процесс,
можно продолжать извлечение энергии из черной дыры. При
этом решение, по-видимому, будет постепенно меняться. Однако
эргосфера не может исчезнуть, поскольку должно остаться
какое-то место для частиц с отрицательной энергией. Как мы ви-
дим, возможно одно из двух: или мы можем извлечь бесконеч-
ное количество энергии (что представляется невероятным), или
эргосфера должна в конце концов пересечь горизонт. Мы по-
кажем, что в последнем случае решение должно спонтанно пре-
9.3. Конечное состояние черной дыры
365
вратиться в аксиально симметричное или статическое и при
этом теряется возможность извлечения энергии с помощью про-
цесса Пенроуза. Как возможность извлечения бесконечного ко-
личества энергии, так и спонтанное изменение решения, по-ви-
димому, говорят о неустойчивости исходного состояния черной
дыры. Поэтому представляется разумным предположить, что
в любом реалистичном состоянии черной дыры эргосфера пере-
секает горизонт.
В работе [67] показано, что предельная стационарная по-
верхность, которая является внешней границей эргосферы, бу-
дет содержать по крайней мере две интегральные изотропные
геодезические кривые вектора №. Если на этих кривых f-a =И= О
и если они геодезически полны в прошлом, будут точки, в кото-
рых № — 0. Но во внешней области таких точек быть не мо-
жет (см. предложение 9.3.3); следовательно, в этом случае
эргосфера пересекает горизонт. Однако предположение о пол-
ноте в прошлом интегральных кривых векторного поля №, по-
видимому, неприемлемо, так как оно представляло бы собой
определенное предположение относительно прошлой области
решения, которая, как мы отмечали прежде, не является физи-
чески значимым; вместе с тем возможно и имеет смысл пред-
полагать, что эти кривые полны в будущем. В статическом слу-
чае можно было бы показать, что решение симметрично во
времени, но нет никакой априорной причины для того, чтобы
такой симметрией обладало стационарное нестатическое реше-
ние. Поэтому мы будем оправдывать предположение о пересе-
чении эргосферой горизонта не результатами [67], а рассужде-
ниями, связанными с извлечением энергии.
Смысл соприкосновения эргосферы с горизонтом можно
объяснить следующим образом. Пусть 2\ —- односвязная ком-
понента области /~(.7+, Л} Г) /+(№“, Л}, и пусть Эй— фактор-
множество Z относительно ее образующих. Согласно предло-
жениям 9.3.1 и 9.3.2, оно гомеоморфно 2-сфере. По предложению
9.3.1 пространственное разделение двух соседних образующих
постоянно вдоль них и потому может быть описано инду-
цированной на метрикой h. Изометрия 0г переводит образую-
щие в образующие и, таким образом, действует как группа изо-
метрии пространства (Эф h). Если эргосфера пересекает гори-
зонт, то вектор № где-то на горизонте пространственноподобен
и действие 0( в (^ь h) будет нетривиальным. Тогда оно должно
соответствовать вращению сферы Эд вокруг некоторой оси, и ор-
битами этой группы в j будут две точки, соответствующие по-
люсам, и семейство окружностей. Частица, движущаяся вдоль
одной из образующих горизонта, казалась бы тогда движу-
щейся относительно определяемой вектором № системы от-
счета, которая стационарна на бесконечности. Поэтому мы
366
Гл. 9. Гравитационный коллапс и черные дыры
могли бы сказать, что горизонт вращается относительно беско-
нечности.
Следующий результат показывает, что вращающаяся черная
дыра должна быть аксиально симметричной.
Предложение 9.3.6
Пусть (Я, g)—стационарное нестатическое регулярно пред-
сказуемое пространство, в котором эргосфера имеет пересече-
ние с Я} И /+(5Г_, Я}. Тогда существует однопараметри-
ческая циклическая группа изометрии 0ф(О^^<2л) этого
пространства, которая коммутирует с Qt и орбиты которой про-
странственноподобны вблизи Д+ и
Метод доказательства этого предложения состоит в исполь-
зовании аналитичности метрики g для того, чтобы показать су-
ществование изометрии 0Ф в некоторой окрестности горизонта.
Затем эта изометрия распространяется на все пространство пу-
тем аналитического продолжения. Этот метод был бы приме-
ним, даже если бы метрика была неаналитична в изолированных
областях вне горизонта, например, если бы вокруг черной дыры
существовало кольцо из вещества или какая-то рамка из стерж-
ней. В этом случае возникает следующий кажущийся парадокс.
Рассмотрим вращающуюся звезду, окруженную стационарной
квадратной рамкой, сделанной из стержней. Если черная дыра
приближается к стационарному состоянию, то из предложе-
ния 9.3.6 следует, что метрика g должна быть аксиально сим-
метричной везде, за исключением области, где она неаналитична
(на стержнях). Однако гравитационное воздействие стержней
помешает метрике стать аксиально симметричной. Разрешение
парадокса состоит, по-видимому, в том, что в этом случае чер-
ная дыра не может быть стационарной, пока она вращается.
Должно произойти следующее. Гравитационное воздействие
стержней слегка деформирует черную дыру. Обратное влияние
черной дыры на рамку вызовет ее вращение и, таким образом,
приведет к потере момента количества движения через излуче-
ние. В итоге вращение как черной дыры, так и рамки затормо-
зится, и решение будет приближаться к статическому состоя-
нию. Статическая черная дыра может и не быть аксиально
симметричной, если пространство вне ее не пустое, т. е. если
условие (а) теоремы Израэля не удовлетворяется.
Это рассуждение свидетельствует о том, что реальная чер-
ная дыра никогда не будет строго стационарной, пока она
вращается, так как Вселенная вокруг нее не будет строго ак-
сиально симметричной. Однако в большинстве случаев скорость
замедления вращения такой черной дыры будет крайне мала
[70, 136]. Поэтому в хорошем приближении можно пренебречь
9.3. Конечное состояние черной дыры
267
малой асимметрией, которую вызывает материя в удалении от
вращающейся черной дыры, и рассматривать такую черную
дыру как если бы она находилась в стационарном состоянии.
Поэтому мы будем изучать свойства вращающейся аксиально
симметричной черной дыры.
Из следующего результата Папапетру[119], обобщенного Кар-
тером [25], видно, что векторы Киллинга: соответствующий
временной трансляции, и Ка, соответствующий угловому вра-
щению ®ф, — оба ортогональны к некоторым семействам 2-по-
верхностей.
Предложение 9.3.7
Пусть (Л’, g)—пространство-время, допускающее 2-параме-
трическую абелеву группу изометрии с векторами Киллинга
и |2. Пусть Т с: Л — связное открытое множество, и пусть
Wab = ?1[аЬ&]. Тогда, если
a) wabRbcr\cdefwef == 0 на F,
б) wab = 0 в некоторой точке из Т, то W[ab-,cWd]e = О на Т.
В стационарном аксиально симметричном пространстве ус-
ловие (б) удовлетворяется на оси симметрии, т. е. на множестве
точек, где К.а = 0. Условие (а) удовлетворяется в пустом про-
странстве, а также в присутствии свободного (без источников)
электромагнитного поля [25]. По теореме Фробениуса [151] при
щ,/, =7^ 0 равенство нулю представляет собой условие
локального существования семейства 2-поверхностей, ортого-
нальных wab, т. е. любой линейной комбинации |i и |2- В слу-
чае аксиально симметричного стационарного пространства-вре-
мени это означает, что локально мы можем ввести координаты
[t, ф, х1, х2), в которых К = d/dt, R — d/d</> и Kaxm;a = 0 =
= Raxm.a при tn — 1,2. Тогда метрика локально допускает изо-
метрию (t, ф, х1, х2)->(—t, —ф, х1, х2), обращающую направле-
ние течения времени, т. е. метрика симметрична во времени. Та-
ким образом, если аналитическое расширение по метрике вблизи
бесконечности пустого стационарного регулярно предсказуемого
пространства-времени содержит горизонт будущего, то оно со-
держит и горизонт событий прошлого.
По аналогии с предложением 9.3.4 имеем предложение 9.3.8.
Предложение 9.3.8 [ср. с [2S])
Пусть (JZ, g) — стационарное аксиально симметричное регу-
лярно предсказуемое пространство-время, в котором W[ab-cWd]e — 0,
где wab = К[аКь\- Тогда h s wabwab < 0 в любой точке, лежащей
вне оси К ~ 0 во внешней области Г'(Л , ^')П7-(У+, Л).
На горизонтах j “ (У+, Л) П J+ Л) и J+ Л) П Г (.7, Л)
h — Q, но wab нигде не обращается в нуль, кроме оси.
368
Гл. 9. Гравитационный коллапс и черные дыры
Отсюда видно, что во внешней области в каждой точке вне
оси существует некоторая линейная комбинация векторов Кил-
линга Л'" и №, которая времениподобна. Снаружи эргосферы
времениподобен сам вектор Л'“, но чтобы получить временипо-
добный вектор между предельной стационарной поверхностью
и горизонтом, нужно к № добавить вектор, пропорциональ-
ный Л’“. На горизонте нет никакой времениподобной линейной
комбинации, но существует изотропная линейная комбинация,
направленная вдоль изотропных образующих горизонта. Вне
оси К = 0 горизонт можно локально охарактеризовать как мно-
жество точек, на котором h = wabwab = 0.
Тогда мы приходим к теореме Картера [28], которая указы-
вает на то, что объекты, описываемые решениями Керра, ве-
роятно, являются единственными стационарными черными ды-
рами в пустом пространстве. Картер рассмотрел стационарное
регулярно предсказуемое пространство, удовлетворяющее усло-
виям
а) ТаЪ = 0;
б) аксиально симметричное;
в) горизонт событий прошлого JI} пересекает гори-
зонт событий будущего /"(<9’'+, Ж} по компактной связной 2-по-
верхности 9~\. (Согласно предложению 9.3.2, она будет 2-сфе-
рой.) Картер показал, что такие решения распадаются на два
несвязных семейства, каждое из которых зависит от двух па-
раметров. В качестве этих двух параметров можно принять
массу m и момент количества движения L, измеренные с беско-
нечности. Одно из семейств известно — это решения Керра
си>0, й'Х гп2, где а — L/m. (Решения Керра с а2 > т2 со-
держат голую сингулярность и потому не являются регулярно
предсказуемыми пространствами.) Представляется маловероят-
ным, чтобы существовали какие-либо другие несвязные семей-
ства. Поэтому было высказано предположение, что вне незаря-
женного сколлапсировавшего объекта установится решение
Керра с а2 т2. Это предположение подтверждается анали-
зом линейных возмущений при сферическом коллапсе [43, 137,
139, 168].
В предположении, что эта гипотеза Картера — Израэля
справедлива, можно полагать, что площадь 2-поверхности
<3^(т) на горизонте событий будет стремиться к площади неко-
торой 2-поверхности на горизонте событий г = г+ в решении
Керра при такой же массе и таком же моменте количества дви-
жения, измеренных с поверхности ^(т) на J+. Эта площадь
равна 8nm(m-(-(m2— а2)72), где т— масса в решении Керра и
та — момент количества движения. (Если коллапсирующее
тело имеет электрический заряд е, то следует ожидать, что
9.3. Конечное состояние черной дыры
369
окончательно установится решение Керра с учетом заряда. Пло-
щадь 2-поверхности на горизонте событий такого решения
равна
4л [2m2 — е2 + 2m (m2 — а2 — е2)'/г].
Используя это выражение, можно обобщить наши результаты
на заряженные черные дыры.) Рассмотрим коллапс, в котором
к поверхности 91 (ti) устанавливается решение Керра с массой
гп.\ и моментом количества движения т\а,\. Предположим, что
затем в течение конечного времени черная дыра взаимодей-
ствует с частицами или излучением. В итоге к поверхности
^(тг) установится иное решение Керра с параметрами т2, аг-
Из рассуждений в разд. 9.2 следует, что площадь с^(тг)
должна быть больше или равна площади <3^(ti). В действи-
тельности она должна быть строго больше, так как 0 может
быть равно нулю лишь при условии, что никакое вещество или
излучение не пересекает горизонт. Это означает тогда, что
«2 [«2 + W — Я22)'/2] > [wi + W — <Я12)'А]- (9.4)
Если Я1 =# 0, то неравенство (9.4) позволяет, чтобы т2 была
меньше т\. Поскольку в асимптотически плоском пространстве-
времени [122] выполняется закон сохранения полной энергии и
импульса, неравенство т2 < тх должно означать, что мы ка-
ким-то образом извлекли из черной дыры определенное количе-
ство энергии. Один из способов извлечения энергии мог бы
состоять в том, чтобы построить вокруг черной дыры квадрат-
ную рамку из стержней и заставить момент силы, наводимый
вращающейся черной дырой на рамку, совершать работу.
С другой стороны, можно было бы использовать процесс Пен-
роуза: бросить в эргосферу частицу, разделить ее там на две
частицы, одна из которых уйдет на бесконечность с энергией,
большей чем у первоначальной частицы. Другая частица про-
валится через горизонт событий и уменьшит момент количества
движения черной дыры. Таким образом, этот процесс можно
рассматривать как процесс извлечения вращательной энергии
черной дыры. Кристодулу [32] показал, что при этом можно до-
стичь результата, сколь-угодно близкого к пределу, устанавли-
ваемому неравенством (9.4). Наибольшая энергия извлекается
при а2 — 0; в этом случае полученная энергия т\ — т2 меньше,
чем
mJl --UT1 +(1
( V2 L \ т,- J J )
Рассмотрим теперь случай, когда коллапсируют две звезды,
расположенные на значительном расстоянии друг от друга.
370
Гл. 9. Гравитационный коллапс и черные дыры
и возникают две черные дыры. Следовательно, найдется некото-
рое значение г', при котором д$(г') состоит из двух отдельных
2-сфер d$i(x') и д^2(т')- Поскольку они удалены друг от друга,
можно пренебречь их взаимодействием и предположить, что
решение вблизи каждой из черных дыр почти совпадает с ре-
шениями Керра с параметрами mt, ai и m2, а2 соответственно.
Отсюда площади и <?^f2(Tz) будут приблизительно
равны
8ЛЩ] [/щ + (пг2 — «12)'/2] и 8лш2 [m2 + (т2 — а22)72]
соответственно. Теперь допустим, что эти черные дыры сталки-
ваются и сливаются. При таком столкновении выделится опре-
деленное количество гравитационного излучения. В итоге у по-
верхности ^(т") эта система придет к решению, похожему на
одно решение Керра с параметрами ш3, а3. В силу тех же аргу-
ментов, что и выше, площадь д$(г") должна быть больше пол-
ной площади д$(г'), равной сумме площадей <Wi (-К) и <М2(т').
Итак,
т3 [т3 + (ш32 — а32)‘/2] > nil [mj + (mi2 — а^)72] +
+ т2 [т2 + (т22 — а22)*/2]-
Согласно закону сохранения для асимптотически плоских про-
странств, энергия, уносимая на бесконечность гравитационным
излучением, равна
nil + m2 — m3
и ограничена приведенным выше неравенством. Эффективность
превращения массы в гравитационное излучение
e. = (mi + m2 — т3) (mi + ш2)-1
всегда меньше ’/г- Если щ = а2 = 0, то е < 1 — 1/V2; следует
подчеркнуть, что это верхние пределы, истинная эффективность
может быть много меньше, хотя само существование предель-
ного значения может означать, что достижима заметная его
доля.
Мы показали, что доля массы, способная превратиться
в гравитационное излучение при слиянии двух черных дыр,
ограничена. Если бы, однако, первоначально было большое
число черных дыр, то они могли бы слиться попарно, возник-
шие при этом новые черные дыры снова могли бы слиться
и т. д. Из соображений размерности можно ожидать, что на
всех этапах эффективность будет одинаковой. Таким образом,
в гравитационное излучение могла бы превратиться очень боль-
шая часть первоначальной массы. (Этот аргумент выдвинули
Мизнер и Рис.) На каждом последующем этапе энергия, излу-
9.3. Конечное состояние черной дыры
371
ченная в виде гравитационных волн, будет больше, чем на пре-
дыдущем. Этот механизм мог бы объяснить наблюдавшиеся
Вебером всплески гравитационного излучения.
Теперь мы приведем доказательства предложений, выдвину-
тых в этом разделе. Для удобства мы повторим их формули-
ровки.
Предложение 9.3.1
Пусть (Л’, gj—стационарное регулярно предсказуемое про-
странство-время. _Тогда образующие горизонта событий буду-
щего Л) не имеют конечных точек в прошлом
в /+(Д_, Л}. Пусть Ун — направленные в будущее касатель-
ные к этим образующим векторы; тогда в /+(<7_, Л} вектор УН
обладает нулевыми сдвигом а и расхождением 9 и удовлетво-
ряет равенству
7?«ьУ 1°У1Ь = 0 = Y.^C^Y^Y^Y^.
Пусть ЯЗ — пространственноподобная 2-сфера на 3~. Тогда
5й- можно покрыть семейством 2-сфер $?(/), полученных дви-
жением ЯЗ в обе стороны вдоль образующих поверхности и
под действием 0/, т.е. ’₽’(/) = Qtffi). Введем теперь функцию х
в точке p^J+(7~, Л} как наибольшее значение t, при кото-
ром р е 1+(Я? (/), Л}. Пусть °11 есть окрестность .7+ и 3~, ко-
торая изометрична соответствующей окрестности асимптоти-
чески простого пространства-времени. Тогда функция х будет
непрерывна и будет иметь некоторую нижнюю грань х' на
7 П CU. Из этого следует, что х непрерывна в той области мно-
жества /_(Д+, Л), где она больше х'. Пусть p^J+(3/~, Л) П
П 7“(Д+, Л). Тогда под действием изометрии 0; точка р будет
переведена в область множества /-(.7Д Л), где х > х'. Од-
нако
xlef(p) = xl + /’
Следовательно, х непрерывна в р. _____ _
Пусть то > 0 таково, что Т’(то) Г)-Н(«7+, Л) содержится
в Л). Пусть X —образующая поверхности /_(7+, Л),
пересекающей ^(то). Допустим, что на К существует некоторая
конечная верхняя грань х0 функции х. Поскольку рассматри-
ваемое пространство асимптотически простое в слабом смысле,
х -> оо по мере приближения к 2"(то) на ^(то). Следовательно,
на
^(т0)ЛГ Л)
372
Гл. 9. Гравитационный коллапс и черные дыры
функция х должна иметь некоторую нижнюю грань. Под дей-
ствием группы 0( образующая Л преобразуется в другую обра-
зующую 9< (Л). Поскольку образующие поверхности Ж)
не имеют никаких конечных точек в будущем, продолжение
в прошлое кривой 9г (Л) все же будет пересекать & (т0) П J~ ,Л).
Это ведет к противоречию, поскольку тогда верхняя грань х
на О/ (Л) была бы меньше xlt если f — х0.
Пусть х2 есть верхняя грань х на 9? (т0) П 7 - (.!7+, Л). Тогда
каждая образующая Л поверхности_7 ~ (^Х+, Л\ пересекающая
^(т0), пересечет (/) = 7 + ('g2 (/), Ж) П j ~ (^+, Ж) при
Каждая образующая 7-(<7+, Л), которая пересекает (t'),
будет пересекать 0/(^(то)) при —хР Но поверхность
П 7“ (^+, „77) = 9Д.7 (т0) П 7“ (^7 \ Ж)) компактна. Сле-
довательно, компактна и ^(/).
Рассмотрим теперь, как меняется площадь (/) по мере
роста t. Поскольку 9^0, эта площадь не может сокращаться.
Если бы было 0 > 0 на некотором открытом множестве, пло-
щадь увеличивалась бы. Она увеличивалась бы также, если бы
образующие горизонта обладали конечными точками в прош-
лом на ^”(0- Однако, так как (t) движется под действием
изометрии 0«, площадь должна оставаться неизменной. По-
этому 0 — 0, и в той области поверхности Л), для ко-
торой х х2, нет конечных точек в прошлом, а поскольку
каждая точка из 7” (.7", Ж) П Л) может быть переве-
дена изометрией 9; в область, где х > х2, этот результат отно-
сится ко всей поверхности 7~(«7+, ^)П7+(7Х“, Л). Тогда из
уравнений распространения (4.35) и (4.36) получаем: дтп = 0,
RabYiaYib = о и УщС^ь^УщУ^Ур = 0, где Ун — направлен-
ный в будущее касательный вектор к изотропной геодезической
образующей горизонта. о
Предложение 9.3.2
В стационарном регулярно предсказуемом пространстве
каждая связная компонента горизонта д^(т) в 7+(<7~, Л) го-
меоморфна 2-сфере.
Рассмотрим, как ведет себя расхождение уходящих ортого-
нальных к дЖ(х) изотропных геодезических при малой дефор-
мации д$(х) наружу в J~(3+, Л}. Пусть Y2a— другой направ-
ленный в будущее изотропный вектор, ортогональный к д91(т)
и нормированный так, что УрУоа = — 1- При этом остается
свобода преобразований Yi->Y( — e^Yj, Y2-> Y' = e-v\2. Ин-
дуцированная метрика на пространственноподобной 2-поверх-
ности д$(х\ равна Наъ ~ gab + YlaY2b + Y2aYlb. Введем семей-
9.3. Конечное состояние черной дыры 373
ство поверхностей сдвигая каждую точку д&(х) на
расстояние w по параметру вдоль изотропной геодезической
с касательным вектором Y2a. Векторы Yia будут ортогональны
к ST(т, да), если они подчиняются уравнениям
/UYjW = - и Г,йУ2а .. ~1.
Тогда
(H%X^U J/О";-
= hsapa;bhbt + pspt - hsJ “h8eYle.bhbt + (9-5)
где ра s — hbaY-2^bY\c- Свертывая с АД получаем
^- = (У1^й);сГ/ =
= Pb-/bd ~ R^Y' + R^bY^Y.yh +
На горизонте Yia-cficdhbа — Q, поскольку сдвиг и расхождения
горизонта равны нулю. При масштабном преобразовании Y/ =
= e^YI; Y2 =е-&42 вектор ра заменяется на р,а = ра + haby.b и
поэтому изменение dO/Пда |шг=0 равно
•гН=. = Р«А“ + ~ +
+ RabebY^YWY? + р'ар'а. (9.6)
Член y.bdhbd есть лапласиан у на 2-поверхности cW(r). Согласно
теореме Ходжа [78], можно выбрать у так, что сумма первых
четырех членов в правой части (9.6) будет постоянной на 5,®(т).
Знак этой постоянной будет определяться знаком интеграла от
(- RacY,aY2C -h RadcbYdY2Y2'Yb)
по д.$(т) (интеграл от Pb.dhbd равен нулю как интеграл от ди-
вергенции). Этот интеграл можно вычислить, используя урав-
нение Гаусса — Кодацци для скалярной кривизны R 2-поверх-
ности с метрикой h:
R = Riiklhikhil — R~ 2RwY1iY^YlkY2l + 4/?(/У1Т/,
так как 6 = а = 0 на О(т). По теореме Гаусса — Бонне [92]
R dS — 2лх>
(т)
374
Гл. 9. Гравитационный коллапс и черные дыры
где dS — элемент площади и % — эйлерова характеристика по-
верхности д'/! (т). Итак,
$ (- RabYfY/ + RabcbYfY^Y^ dS =
6Й (т)
= -лх+ $ (уЯ- ^by,ay2")dS. (9.7)
бй? (т)
В силу уравнений Эйнштейна
у R + RabY 1 aY 2 = 8лТаЬУ,аУ2ь > 0;
последнее неравенство следует из условия энергодоминантно-
сти. Эйлерова характеристика / равна +2 для сферы, 0 для
тора и отрицательна для любой другой компактной ориентируе-
мой 2-поверхности (поверхность д^(х) должна быть ориенти-
руемой, поскольку она является краем). Отсюда правая часть
(9.7) может быть отрицательной лишь при условии, что
д$(х)— сфера.
Допустим, что правая часть (9.7) положительна. Тогда
можно выбрать у так, что d0/die/|w=o > 0 всюду на Д^(т).
При малых отрицательных значениях w' можно получить
в /_(Д+, Jt) такую 2-поверхность, что ортогональные к ней ухо-
дящие изотропные геодезические будут сходиться. Это противо-
речит предложению 9.2.8. Допустим теперь, что / = 0 и что
TabYfY2b = 0 на Д$(т). Тогда можно выбрать у так, чтобы
сумма первых четырех членов в правой части (9.6) была равна
нулю на Д^(т). При этом на
P'^ + Rabc^X^Y^
Если RabcdYiaY2bY1cY2d 0 где-либо на д&(х), то и член р'ар'а
в (9.6) должен быть где-то отличен от нуля; можно слегка из-
менить у так, чтобы было 6076и/|ю=о > 0 всюду. Так мы
снова приходим к противоречию.
Теперь допустим, что всюду на д$(х) RomYiaY2bY/Y2d — 0
и р'а = 0. 2-поверхность Д^(т) можно сдвинуть назад вдоль
Y2a, выбирая у на каждом этапе так, что
-2Ко1У1”Г/ = р-Х-1я=0.
Если бы TabYxaY2b или р'а не были равны пулю при w' < 0, то
можно было бы подобрать у так, чтобы получить в Т'(.7+,.О
2-поверхность с 0 < 0. Это противоречило бы предложению
9.3. Конечное состояние черной дыры
375
9.2.8. С другой стороны, если бы при w' < 0 всюду было
Таъ^\а^2ъ = 0 и р'а == 0, то мы получили бы 2-поверхность
с б = 0 в Ж}, что также противоречит предложению
9.2.8.
Противоречия не возникает только при % = 2, т. е. если
д$(т) есть 2-сфера. □
Предложение 9.3.3
Пусть {Ж, g) — стационарное регулярно предсказуемое про-
странство-время. Тогда вектор Киллинга К" отличен от нуля
в области 7+(77_, Jir/nT; Ж}, которая односвязна. Пусть
дано То, при котором £?(то) Л 7“(77+, Ж} содержится в Ж).
Если сШ(то) имеет только односвязную компоненту, то область
7+(77_, Ж)П^~(3/'+, Ж} П Ж гомеоморфна [0, ОХ^Х#1-
Функция введенная в предложении 9.3,1, непрерывна на
7+(.7~, Ж} П Ж'} и обладает тем свойством, что х |0 (р) =
==х| +/. Отсюда видно, что К не может равняться нулю в
Ж} Л Л). Интегральные кривые К устанавливают
гомеоморфизм между двумя из поверхностей
Л){\ Г О+, ^)Л.< (-оо</<оо).
Область Ж} П 7_(Т7+, Ж} П Ж покрывается этими по-
верхностями и, следовательно, гомеоморфна /?’ X /+('₽’(О> <^) А
А 7“(.7+, Ж} А Ж при любом f. Выберем t достаточно большим,
чтобы поверхность 7+(*<? (0, «т7) имела пересечение с ^(т0) в та-
кой окрестности HL поверхности 7Z+, которая изометрична соот-
ветствующей поверхности в асимптотически простом простран-
стве. Интегральные кривые К устанавливают гомеоморфизм
между
7 + (0, ..#) А г о+, Л) л Л И яо А /" О+, Я).
Последняя область односвязна в силу свойства (а) и предло-
жения 9.3.2. Если далее имеет только одну связную ком-
поненту, то __
(То) л г (ж, Л)
обладает топологией [0, 1)Х-$2. Отсюда топологически
/+(^-,^7) ГСТ~(ЗГ+, Ж} Л Ж есть [0, 1)Х32ХЯ‘- □
Предложение 9.3.4
В статическом регулярно предсказуемом пространстве-вре-
мени вектор Киллинга К времениподобен во внешней области
Ж) А /-(&+,Ж), а на 1~(Н'+,Ж) Л 3+(Л~,Ж) отличен от
376 Гл. 9. Гравитационный коллапс и черные дыры
нуля и направлен вдоль изотропных образующих поверхности
/~(.7+, Л}.
Горизонт событий /~(<7+, Л} изометрией 0; отображается
в себя. Следовательно, на (<7+, Л*) fl J+ Л} вектор К
должен быть либо изотропным, либо пространственноподобным.
Пусть при т = То ^(т0) П J~ (Д+, Л) содержится в /+(.7~, Л}.
Тогда функция f = КаКа должна равняться нулю на некотором
замкнутом множестве в J+ (т0)) Г) (^+, Л~).
Из того, что Ка есть вектор Киллинга и rot К — 0, следует
Kuf.M. (9.S)
Согласно пре_длож_ению 9.3.3, № 0 на односвязном множе-
стве /+(-^Д ^)П/“(^+, Л). По теореме Фробениуса из ус-
ловия rot К = 0 следует, что в этой области найдется функция g,
такая, что Ка — — ccg;G, где а — некоторая положительная
функция.
Пусть р — точка множества Л9 и X(v)—кривая, проходящая
через р и лежащая на поверхности постоянного Тогда в силу
(9.8),
1 ка A in f = JL
2 du ' ди
Если Л(и) выходит за пределы Л9, то левая часть этого урав-
нения будет не ограничена. Но правая часть непрерывна, по-
этому кривая Л(ц) должна лежать в Л9 и множество Л9 должно
содержать поверхность g = £|р. Однако на некоторой открытой
окрестности точки р функция f должна быть отлична от нуля,
потому что иначе она была бы равна нулю всюду. Следова-
тельно, связная компонента Л9, содержащая р, есть 3-поверх-
ность g = g|p. Допустим, что р е= J+ (<7^, л) П Л}.
Тогда найдется направленная в будущее времениподобная кри-
вая у (и) от ЗГ~ до ST+, проходящая через р. На g = g|p вектор
№ должен быть направлен в будущее. Отсюда (д/ди) > О
при | = ||р. Это ведет к противоречию: g = g|p не может иметь
пересечения с ЗГ+ или потому что Ка вблизи бесконечности
времениподобен. Таким образом, вблизи ,7+ и либо g > g|p,
либо £ < ||р. □
Предложение 9.3.5
В пустом стационарном регулярно предсказуемом простран-
стве-времени, если оно нестатическое, вектор Киллинга № про-
странственноподобен в некоторой части внешней области
i+&~, л)пг О+, л).
9.3. Конечное состояние черной дыры
377
Функция _х, введенная в предложении 9.3.1, непрерывна на
J+(s~, л)п/~(у+, Л) и притом дх/dt = 1 вдоль каждой
интегральной кривой. Поверхность х = 0 в 7+ (5r~, Jt) f]
П 7_(5<+, Л] можно аппроксимировать гладкой поверхностью X,
которая нигде не касается №• Затем на7+ J~(S+, Л)
можно ввести гладкую функцию х, обладающую тем свойством,
что х = 0 на Ж и х-аКа = 1. Градиент вектора Киллинга можно
представить в виде
К;6 = паЬЛс^ + ^Л1>
где f = К"Ка и
..а_. 1 ^.abcdjz /?"
<о KbKc-d-
Вторая производная К удовлетворяет равенству
2№;1йс] = RdabcKd-
Однако Ка-,ьс — К[а-,ь]с- Следовательно,
Ra-,bc — RdcbaK^ >
и отсюда
Ka'bb = - RadKd. (9.9)
Вектор qa = f~lKa = х-а ортогонален к №. Умножим (9.9) на
qa и проинтегрируем в 7"(У+, Л) по области S, ограниченной
поверхностями Л9! и Л^, которые заданы уравнениями х =
— х2 + 1 и х = Х2 + 2, где Х2 имеет тот же смысл, что и в при-
ложении 9.3.1; в результате получим
j RabKaqb dv = - J (№;6<?a);6 do + J Ka.bqa'b do =
% & %
= J Ra’bqadob~2 ^p2^a^adv. (9.10)
dz Z
Граница dS области S состоит из поверхностей
д&^Л\[\7~(_2Г+, Jt\ Л’2 П 7 'Ч^№<),
куска dSz поверхности 7_(dX+, Л} между Л91 и Л92 и куска
dSi, поверхности между и Поверхностный интеграл
по dS\ равен поверхностному интегралу по dS%, взятому с об-
ратным знаком, так как эти поверхности переводятся одна
в другую изометрией 0ь
Вблизи функция f — — 1 +(2m/r)+ О(г~2) и <вааа =
„0(г-6), Где г — некоторая подходящая радиальная коорди-
ната. Поэтому поверхностный интеграл по dSi на равен
378
Гл. 9. Гравитационный коллапс и черные дыры
нулю. Допустим теперь, что вектор № времениподобен всюду
на Z и изотропен на горизонте. Тогда со'1, будучи ортогональ-
ным к К, пространственноподобен всюду в Z. Отсюда, если
<в =И= О, т. е. решение нестатично, последний член в правой ча-
сти (9.10) будет отрицательным. Если рассматриваемое про-
странство пустое и интеграл по d3J равен нулю, то это ведет
к противоречию.
Чтобы вычислить этот интеграл, нужно прибегнуть к пре-
дельному переходу. Пусть z — функция на поверхности Л9!, та-
кая, что на горизонте она равна нулю, но ее градиент в на
горизонте отличен от нуля. Функцию z можно задать на S
условием z-aKa = 0. Градиент z можно представить в виде
2;а = X-bZ’b [Ка + fRa),
где Ra — вектор, касательный к поверхностям {х = const} и нор-
мированный так, что RaKa'= — 1- Возьмем теперь К.а'’ьдадоь
по поверхности {г = const} между и Тогда d<r& = daz;&,
где do — некоторая непрерывная мера. Итак,
j Ra-bqa dab = J (4 x-a (f);a - x.aKa.bRbf + | f.bRb) x-,bz'b do.
Поскольку горизонт представляет собой поверхность f = 0 и
поскольку Ка- направлен вдоль изотропных образующих гори-
зонта, вектор f-a на горизонте пропорционален №. Отсюда
J №;/T/ado6 = 0.
dXi
Это приводит к противоречию, которое доказывает, что № дол-
жен быть где-то в Z пространственноподобным, если простран-
ство пустое. □
Предложение 9.3.6
Пусть (Л', g)—стационарное нестатическое регулярно пред-
сказуемое пространство-время, в котором эргосфера имеет пе-
ресечение с № (у+, J+ , J(). Тогда существует однопа-
раметрическая циклическая группа изометрии 0Ф (0 ф сТ
су 2л) этого пространства, которая коммутирует с 0г и орбиты
которой пространственноподобны вблизи и 3~.
Пусть 3J есть односвязная компонента множества
7“(У+, Ж} П 7+ (J~, Ж}, и пусть Эу— фактор-множество по
ее образующим. Тогда орбитами изометрии 0( в горизонте Z\
будут винтовые линии, многократно пересекающие одни и те же
образующие. Пусть при некотором > 0 0/, есть один оборот
9.3. Конечное состояние черной дыры.
379
в S^i. Тогда, если р е Zто 0^(р) будет лежать на той же об-
разующей Z\ и притом в будущем точки р, так как
•Ч. (Р) = Ч + ^
н
Мы можем выбрать направленный в будущее изотропный век-
тор Y> так, чтобы он был касателен к образующим, и так, чтобы
он обладал следующими масштабными свойствами:
1) Г1а;йУ16 = 2еУ1а, где е;аУ1а = 0,
2) если v —• параметр вдоль этих образующих, такой, что
Yi = д/dv, то
Ч,(Р) = Ч + 'г
Векторное поле Yi, определенное таким образом, инвариантно
относительно изометрии 0/, т. е. LKYi = 0. Затем мы можем за-
дать в пространственноподобное векторное поле Y, = К —
— Y|; Z.KY3 = 0 и Лу,Уз = 0 (отметим, что Y3 — не единичный век-
тор, и в действительности он будет равен нулю на образующих
yi и у2, соответствующих полюсам Э']). Интегральные кривые
векторного поля Y3 в Z\ будут представлять собой окружности,
вырождающиеся на yi и у2 в точки.
Пусть ц— некоторая кривая в Z\ от yi до у2, ортогональ-
ная к Yi и Y3, причем такая, что орбиты Y3, пересекающие р,
образуют в Z\ гладкую пространственноподобную 2-поверх-
ность SP. Пусть ^(и)—’Семейство пространственноподобных
2-поверхностей в Z\, полученных сдвигом каждой точки поверх-
ности ZP вдоль образующих Z\ на параметрическое расстоя-
ние V. Z(v) совпадает также с 0г>(^). Введем Y2 — другой изо-
тропный, ортогональный к ^(и) вектор, нормированный так,
что У1аУ2а = — 1 (рис. 61); тогда ЛкУг = 0.
Пусть Y4 — пространственноподобный вектор на р, касатель-
ный к р. Тогда мы можем определить Y4 на Zi, увлекая его
вдоль векторных полей К и Yb т. е. LKY4 = 0 == TY, Y4.
(Эти равенства совместны, поскольку LKYi = 0.)- Y4 будет орто-
гонален к Y! на Zi ввиду того, что (iVgabY?) = 0; кроме
того,
ОТГ.аЬ К? = + YЛЬГ4аУЛ
Первый член равен нулю ввиду изотропности Yi, а второй член
равен 2еУ1аУ4а. Таким образом, если первоначально YiaY4a = 0,
то эта величина остается равной нулю. Y4 ортогонален к Y2 на
Z\, поскольку он лежит на поверхности ^(и), a Y2 нормален
к этой поверхности. На Z\ он будет также ортогонален к Y3,
потому что Тк (Т3ХьУ/) = 0 и
(V aV \ V b _V а V bV I V а V bv ___п
Ч 3 4 ЬаГ.Ь 1 1 — z 1 -л1 3 1 4a Т 1 I '.Ь* 4 1 За —
силу равенства Yia-bhacfibd = 0.
380
Гл. 9. Гравитационный коллапс и черные дыры
В некоторой окрестности З’у будет существовать единствен-
ная изотропная геодезическая Л, ортогональная к поверхности
^*(у), проходящей через данную точку г. При этом для точки г
Рис. 61. Изометрия 0; сдвигает точку р и поверхность Ф (о) в точку
0; (р) и поверхность ГР (о + Л) на горизонте Вектор Y; касателен к изо-
тропной геодезической образующей Z\, Y2 — изотропный вектор, ортого-
нальный SP (у) и Y3, лежит в Ф (а). К — поле векторов Киллинга на
порождающее группу изометрии 0;.
можно ввести координаты (у, w, где w — аффинное рас-
стояние вдоль ц, определяемое по Y2, а значения (у, 0, ф) взяты
в i-i Л Здесь 0 и ф— такие сферические полярные коорди-
наты для образующих поверхности S’i, при которых Уза0,а — 0,
У4<»<^а = 0. (Другими словами, мы выберем на Y3 =
= д/дф и Y4 = d/dQ.) Возьмем базис {Yi, Y2, Y3, Y4}, па-
раллельно перенесенный вдоль изотропных геодезических с ка-
сательным вектором Y2. Тогда Y2 = djdw. Определим вектор К:
9.3. Конечное состояние черной дыры
381
К = djdv. Это значит, что Ly2K = 0. Введем вектор
VT {(r3fer36)l/’ +1 (г?к46Р } •
Тогда
zaza = о, zaza = 1, zaza = о,
где чертой сверху обозначено комплексное сопряжение.
На £\ можно ввести следующее семейство тензорных полей
{gJ:
So = S и = Ly2(Ч(---(М)‘••))•.
п раз
Во введенных выше координатах gnab — dn(gab)/dwn. По-
скольку рассматриваемое решение аналитично, оно полностью
определяется семейством g„ на ^i. Мы покажем, что на £\
производные Ли всех gn по К равны нулю. Из этого следует,
что производные Ли полей gn относительно К = К — К также
равны нулю. Отсюда видно, что пространство-время допускает
однопараметрическую группу порожденную векторным по-
лем к. Для простоты мы ограничимся лишь случаем пустого
пространства, но аналогичные аргументы имеют силу и в при-
сутствии материальных полей, подобных электромагнитному и
скалярному, которые подчиняются хорошо определенным гипер-
болическим уравнениям.
При нашем выборе координат компоненты Lg-g являются
частными производными по v координатных компонент gab.
Последние постоянны на 3?\, так что Lgg =0. Мы покажем
ниже, что Lj^gj 1г1 = 0, и затем применим метод индукции. Пред-
положим, что
MA. = 0>
Из самого построения базиса следует, что Lg всех п-х кова-
риантных производных всех базисных векторов Y|, Y2, Z, Z
равны нулю. Имеем
Sn+l ab = Sn ab-Jz + ёп cbY2-,a + acY2 -,b‘
Производные Ли по К второго и третьего членов равны нулю.
Первый член включает в себя ковариантные производные Y2
порядка (ft-j-l) и более низких порядков. Производная Ли по
382
Гл. 9. Гравитационный коллапс и черные дыры
К всех членов низших порядков равна нулю. Члены, включаю-
щие (п + 1)-е ковариантные производные, равны
<Y2a-bef... Sbc + Y2bwf... ^Y/Y^ ... Y2Y2 =
= (Y№Y2e + Y2b.,aeY2e).{ ...ghcY2f ... У/ +
+(члены более низкого порядка)=
- ^Y2a-eY2e\b + RpabeY2pY2 + (У2й;еУ2е);а + RpbaeY2pY2e).f... gh X
X^2f ••• Y2 + (члены более низкого порядка).
Производные Ли по К от этого выражения будут равны нулю,
если равны нулю производные Ли по К тензора Римана и его
ковариантных производных до порядка (п—1).. Тогда полу-
чим, что LRg„+1 =0.
Чтобы показать, что производные Ли по К тензора gi и ко-
вариантных производных тензора Римана равны нулю, удобно
воспользоваться некоторыми обозначениями, введенными Нью-
меном и Пенроузом [113]. Они состоят в использовании псевдо-
ортонормированного базиса с двумя пространственноподобными
векторами Y3 и У4, скомбинированными в один комплексный
изотропный вектор Z, во введении для каждой компоненты связ-
ности и тензора кривизны особого символа и в явной (без сум-
мирования) записи всех тождеств Бианки и уравнений, опре-
деляющих тензор кривизны. Эти соотношения комбинируются
в пары, так что они образуют вдвое меньшее число комплекс-
ных уравнений. Символы для связности определяются так:
х = У!а;йУаУД п = -У2а;6УаУ1г',
р = Yia-bZaZb, К = - Y2a-bZjZb,
o = Yla-bZaZb, ц=- Y2a-bZaZb
т = Yla-bZaY2b, v = - Y2a-,bZaY2b,
8 = | (У1а;6У2аУ1Ь - Za.bZaY?), a = у (У1а;6У2аР - Za.bZaZb),
₽ = | (Yla-bY2aZb - Za.,bZaZb), у = 1 (У1а;йУ26У26 - Za-bZaY2).
Символы для тензора Вейля:
% = -ca6cdy1az6y2czd,
= - CabcdY{aYbYfZd,
1 Cabcd (У^У/У^У/ - YiaY2bZcZd),
^^CabcdY,aYbYjZd,_
XY$ —~ CabcdY2aZbY2Zd,
9.3. Конечное состояние черной дыры
383
Мы рассматриваем пустое пространство, и тензор Риччи равен
нулю (т. е. в формализме Ньюмена — Пенроуза Флв = 0 = Л).
Поскольку базис параллельно переносится вдоль Y2, имеем v =
= у = т = 0. Поскольку Y2 есть градиент координаты v, л =
— р + а и р = р. Более того, на 3?\ х = р = о — 0, е = ё,
У1(в) = 0 и То = 0.
Нужные нам уравнения имеют вид
/Да) — Z (е) = (р + ё — 2е) а + Ра — Ре — х% + (е + р) л, (9.11a)
Y1 (Р) — Z (е) = (а + л) а + (р — ё) Р — рх — (а — л) е + Ть (9.11 б)
Л (^) — Z (л) = р^. + ар + л2 + (а — Р) л — (Зе — ё)Х; (9.11в)
/Др) — Z (л) = рр + аЛ + лл — (е + ё) р — л (а — Р) + Т2, (9.11г)
Z (р) - Z(a) = р(а + р) - а(3а - р) - % (9.11д)
[эти уравнения получаются из уравнений Ньюмена — Пен-
роуза (4.2)] и
К1 (Tj) - Z (То) - - ЗхТ2 + (2в + 4р) % - (- л + 4а) То, (9.12а)
У, (Т2) - Z (Т,) = - 2хТ3 + ЗрТ2 - (- 2л + 2а) Tj - ХТ0, (9.126)
(Т3) - Z (Т2) = - хТ4 - (2е - 2р) Т3 + ЗлТ2 - 2ЛТ1; (9.12в)
У, (Т4) - Z (Т3) = - (4е - р) Т4 + (4л + 2а) Т3 - З^Т2, (9.12г)
У2 (То) - Z (ТО = - рТо- 2pTi + ЗаТ2 (9.12д)
[эти уравнения получаются из уравнений Ньюмена — Пен-
роуза (4.5)].
Из (9.11д) Т, = 0 на Тогда из (9.126) (Т2) = #(Т2) = 0
на 2\. Складывая (9.11а) с уравнением, комплексно-сопряжен-
ным (9.116), получим
У1(л) = У1(а + р) =
= Z (е) + Z (ё) + 2лр + 2ла — л (е — ё) — х/. — хр + Тр,
отсюда на ЗА _
У! (л) == Z (е) + Z (ё).
Следовательно, на Yx (Yj (л)) = Yj (Z (e) + Z (ё)). Но на
LYlZ = 0 и Y[(e) — 0. Поэтому на У1(У1(л)) = 0. Отсюда
Видно, что на л = Д-ф Bv, где А и В — постоянные вдоль
образующей горизонта Z\. Но л |р = л |0^ ( следовательно,
л = const вдоль образующих Вычитая из (9.11а) комплексно-
сопряженное выражение (9.116), находим, что (а — Р) = const
вдоль указанных образующих.
384
Гл. 9. Гравитационный коллапс и черные дыры
Затем с помощью подобных же рассуждений относительно
(9.11в) и (9.11г) можно показать, что вдоль образующих по-
верхности S7! |1 и X постоянны. Поскольку п, р, и X задают ко-
вариантную производную Y2, отсюда следует, что на2'1 LgY2a.b=
= 0, т. е. что i^g, == 0.
Таким же способом на основе (9.12в) и (9.12г) доказы-
вается, что на S’i ^1(^з) = Т1(ЧГ4)= 0. Отсюда следует, что
на S\ L$Rabcd = 0 и соответственно равны нулю производные
Ли по К вторых производных базисных векторов. В частности,
действие Y[Y2 на любую из компонент связности дает нуль.
Из (9.12д) ^(Т2(Т0))= ^/2(^0)= 0 на Подействуем
оператором YiY2 на (9.12а). Коммутатор Y1Y2 — Y2Y1 содержит
только первые ковариантные производные базисных векторов.
Таким образом,
Tg (Y. Y2 — Y„Y.) == 0 на Z..
1\ \ 1 2 J 1/ 1
Отсюда по аналогии с предыдущим доказательством Получим,
что
^(ШЬМВДЬО на %х.
Повторим наши рассуждения в применении к (9.106 — 9.10г),
чтобы показать, что К (Т2 0F2)) = К (Т2(¥3)) = KYY2 СР4)) = 0
на Sx. Отсюда видно, что производные Ли относительно К
первых ковариантных производных тензора Римана равны
нулю. Затем, следуя той же схеме, можно показать, что
Ж(у2(ад|^=оит,д. □
Предложение 9.3.7
Пусть (J(, g) — пространство-время, допускающее 2-параме-
трическую абелеву группу изометрии с векторами Киллинга
и S2. Пусть Т сд JI — связное открытое множество, и пусть
= ТогДа, если:
a) wabRbcT}cdefwef = 0 на X,
6) wab — 0 в некоторой точке из У, то
№[аЬ;Л]е = ° на
Пусть x7 = lXa,bwcdy\abQd И 27^l2a.^cdx\abcd. Тогда
naW1X==-4!g1,a^1V1 =
- з!£А2'%6;с’ ~ 3!ёЛА1М - 2 X 3!?ЛД1С1<
9.3. Конечное состояние черной дыры
385
Отсюда
(3!)-' + ^%[аМ'с} +
+^и%ь'с}-а - УМа^ь’с} - -
п?. [о с. be. c];d qc. [#о Ь о n«. [etc. be. c]\d /гх •< q\
"“Al ;<Й2 91 —^91 £2 \<&\ ”А1 £2 91 ;<й (9.13)
Первый и четвертый члены исчезают, поскольку и f2- век-
торы Киллинга; второй и пятый члены взаимно уничтожаются,
поскольку g] и g2 коммутируют. 6 = 0 в силу того, что
Si — вектор Киллинга, и потому равен нулю третий член. Ана-
логично L^a.b = Q вследствие того, что с2— вектор Киллинга,
коммутирующий с g[. Из этого вытекает, что сумма шестого
и восьмого членов равна нулю. Седьмой член исчезает в силу
симметрии и соотношение c,a’d-,d = — Каь£, которому
удовлетворяет всякий вектор Киллинга. Таким образом, равен-
ство (9.13) приводит к виду
na%)X;rf = 2.3!^[%V]^A
По условию (а) правая часть обращается в нуль на Т. Следо-
вательно, [% —const на Z; на самом деле i% = 0 на Т, по-
скольку эта величина обращается в нуль при wab — 0. Анало-
гично и 2% = 0 на Равенство нулю [% и 2Х необходимо и
достаточно для того, чтобы
W[ab-cWd]e = 0. □
Предложение 9.3.8.
Пусть {Л, g)— стационарное аксиально симметричное регу-
лярно предсказуемое пространство-время, в котором W[ab-cWd\e = 0,
где wab = К.[аКь]. Тогда h^wabwab <0 в любой точке, лежащей
вне оси К = 0 внешней области J+ , Л^ J~ (У+, Л\ На
горизонтах Г(У+, .#)Г|/+О~, .<) и j+O~, Л)
h = 0, но wab нигде не обращается в нуль, кроме оси симметрии.
По предложению 9.3.3 вектор Ка отличен от нуля в
7+ОД „<)П/~О+, Л\ Пусть л будет окружностью S1, ко-
торая является ненулевой интегральной кривой векторного поля
К в J+ , Л)[\]~{$\ Л). Действием изометрии 0( можно
переместить 7. в О+(^). Поскольку в О+(^) нет непростран-
ственноподобных замкнутых кривых, 2. должна быть простран-
ственноподобной кривой, а потому и вектор /<“ должен быть
пространственноподобным всюду в
7+(Д-, .1)п7"(Д+, Л),
13 Заказ 381
386
Гл. 9. Гравитационный коллапс и черные дыры
за исключением оси, где он равен нулю. Допустим, что сущест-
вует некоторая точка р, в которой Ка и Ка оба отличны от нуля
и одинаково направлены. Поскольку они коммутируют, инте-
гральные кривые Ка и Ка, проходящие через р, должны со-
впасть. Однако интегральные кривые 1\а замкнуты, а интеграль-
ные кривые № — нет. Следовательно, К!’- и Ка там, где они от-
личны от нуля, линейно независимы. Поэтому wab ¥= 0 всюду в
,#)п7'(.7+, Я), за исключением оси.
Ось представляет собой двумерную_поверхность. Пусть
есть множество из которого исклю-
чена ось, и пусть 3L есть фактор-множество по 9Ф. По-
скольку интегральные кривые Ка замкнуты и пространствен-
ноподобны в фактор-множество будет хаусдорфовым
многообразием. На 3L можно ввести лоренцеву метрику
hab = gab — КаКь, спроектировать с ее помощью век-
тор Киллинга Кй и получить в ненулевое векторное поле
habKb, которое будет векторным полем Киллинга для метрики hab.
Условие W[ab-,cWd]s = 0 в Я означает, что в ЗЕ, (Kbhb[C)\d he]fKf = О,
где вертикальной чертой обозначена ковариантная производная
относительно h. Оно как раз и означает, что на 3$ должна
существовать функция £ такая, что K.bhba = — а^а. Далее
будем рассуждать, как при доказательстве предложения 9.3.4.
Покажем, что при выполнении условия KaKbhab = 0 в точке
поверхность £ = £|р будет поверхностью в 33, изотропной
относительно метрики h. Функция £ .на S3 индуцирует функ-
цию | на <2/, обладающую свойством: lo№ = 0. Следова-
тельно, £ = £ |р будет поверхностью в Ж, изотропной относительно
метрики g.
Допустим, что р соответствует интегральной кривой А век-
торного поля К“, не лежащей в J~ (Д+, Я). Пусть q<^. Я — точка
на Л. Тогда должна найтись направленная в будущее времени-
подобная кривая у (ц) от через q до Д+. Если эта кривая
пересечет ось, ее можно будет слегка деформировать, чтобы
избежать такого пересечения. Отсюда можно прийти к проти-
воречию, аналогичному противоречию при доказательстве пред-
ложения 9.3.4.
Глава 10
Начальная сингулярность во Вселенной
Расширение Вселенной во многих отношениях подобно кол-
лапсу звезды, если не считать того, что направление времени
при расширении обратное. В этой главе мы покажем, что усло-
вия теорем 2 и 3, по-видимому, выполнены, и это указывает на
наличие сингулярности в начале современной фазы расширения
Вселенной; в связи с этим мы рассмотрим проявления про-
странственно-временных сингулярностей.
В разд. 10.1 мы покажем, что при условии частичной тер-
мализации микроволнового фонового излучения во Вселенной
в результате рассеяния существуют направленные в прошлое
замкнутые ловушечные поверхности; альтернативным условием
их существования является выполнение принципа Коперника,
согласно которому наше положение во Вселенной ничем не вы-
делено. В разд. 10.2 мы рассмотрим возможную природу этой
сингулярности и несостоятельность в самой сингулярности со-
временной физической теории.
10.1 Расширение Вселенной
В разд 9.1 мы показали, что многие звезды в конце концов
будут коллапсировать и при этом возникнут замкнутые лову-
шечные поверхности. Переходя к большим масштабам, можно
рассматривать расширение Вселенной как обращенный во вре-
мени коллапс. Поэтому можно надеяться, что в космологиче-
ском масштабе условия теоремы 2 будут выполнены при об-
ратном направлении времени, если материи во Вселенной
достаточно для того, чтобы возникли замкнутые ловушечные по-
верхности и если она в некотором смысле достаточно симмет-
рична. Мы приведем два довода в пользу того, что материи
действительно достаточно. Они оба основаны на данных наблю-
дений микроволнового фонового излучения, но исходные пред-
посылки несколько различны.
Наблюдения в радиодиапазоне между 20 см и 1 мм указы-
вают на существование фонового излучения, спектр которого
(представленный на рис. 62, а), по-видимому, близок к спектру
излучения абсолютно черного тела при температуре 2,7 К (см.,
13*
10* 10’ ю° 10~' 1О'г
Рис. 62. а — спектр микроволнового фонового излучения. Точки соответ-
ствуют наблюдаемым значениям «избыточного» фонового излучения. Сплош-
ная линия представляет собой спектр Планка, соответствующий темпера-
туре 2,7 К. б — изотропия микроволнового фонового излучения. Показано
распределение по температуре вдоль небесного экватора; для получения
этих точек усреднены данные более чем за 2 года. (Из книги Д. У. Шамы
«Современная космология», М., изд-во «Мир». 1973.)
10 1. Расширение Вселенной
389
например, [48]). Это фоновое излучение, по-видимому, изотропно
в пределах 0,2% (рис. 62,6; см., например, [155] и ссылки, при-
веденные там). Высокая степень изотропии свидетельствует
о том, что это излучение не может зарождаться в пределах на-
шей Галактики (Солнечная система расположена вне плоскости
Галактики), а должно быть внегалактического происхождения.
В этом диапазоне мы можем наблюдать дискретные источники,
причем расстояния до некоторых из них, как это установлено
по другим данным, порядка 1027 см; следовательно, мы знаем,
что на указанных длинах волн Вселенная прозрачна вплоть до
таких расстояний. Таким образом, излучение источников, на-
ходящихся на расстояниях больше 1027 см, должно было сво-
бодно распространяться по направлению к нам по крайней мере
на таких расстояниях.
Возможные объяснения происхождения этого излучения та-
ковы:
1) оно является излучением абсолютно черного тела, остав-
шимся от ранней горячей фазы Вселенной;
2) оно является результатом наложения очень большого
числа весьма удаленных неразрешенных дискретных источни-
ков;
3) оно генерируется межгалактической пылью, которая тер-
мализует другие виды излучения (вероятно, в инфракрасной
области).
Из этих объяснений наиболее приемлемым представляется
первое. Второе кажется невероятным, так как, по-видимому,
нет достаточного числа источников с нужным спектром, которые
могли бы создать заметную долю наблюдаемого излучения в
данном диапазоне частот. Далее, мелкомасштабная изотро-
пия излучения означает, что число дискретных источников
должно быть очень велико (порядка числа галактик), а боль-
шинство галактик, по-видимому, не имеет заметного излучения
в этой области спектра. Третье объяснение также представ-
ляется маловероятным, поскольку концентрация межзвездных
частиц, которая понадобилась бы для этого, слишком велика.
Хотя первое объяснение кажется наиболее вероятным, мы все
же не будем исходить из него, так как это означало бы, что
мы заранее предполагаем существование ранней горячей фазы
в эволюции Вселенной.
Первое объяснение включает в себя принцип Коперника,
согласно которому наше местонахождение в пространстве-вре-
мени ничем не выделено. По нашей интерпретации из этого
принципа следует, что микроволновое фоновое излучение дол-
жно выглядеть одинаково изотропным для любого наблюда-
теля, скорость которого относительно близлежащих галактик
мала. Другими словами, мы предполагаем существование
300
Г л. 10. Начальная сингулярность во Вселенной
расходящейся геодезической конгруэнции (расходящейся — по-
тому, что галактики удаляются друг от друга, геодезической —
потому что они движутся под действием одного лишь тяготе-
ния с единичным вектором 4-скорости Г“), представляющей
усредненное движение галактик, относительно которых это мик-
роволновое излучение выглядит почти изотропным. Из прин-
ципа Коперника следует также, что большая часть микровол-
нового излучения свободно движется к нам с больших расстоя-
ний (жЗ-1027 см). Это видно из того, что вклад в фоновое из-
лучение сферического слоя вокруг нас толщиной dr и радиуса г
в определенном приближении не зависит от г: количество излу-
чения, поступающего из этого слоя, будет пропорционально г2,
а уменьшение интенсивности — обратно пропорционально квад-
рату расстояния г2. Так будет до тех пор, пока не станет за-
метным красное смещение источников, не будет сказываться
эволюция источников или не станут значительными эффекты
кривизны. Однако все эти явления проявятся лишь на расстоя-
ниях порядка радиуса Хаббла, ~ 1028 см. Следовательно, по-
давляющая часть излучения будет свободно приходить к нам
с расстояния >1027 см. Из того факта, что, преодолев такое
большое расстояние, излучение остается изотропным, мы мо-
жем заключить, что в больших масштабах метрика Вселенной
близка к одной из метрик Робертсона — Уокера (разд. 5.3).
Этот вывод следует из результатов Элерса, Герена и Сакса [44],
к изложению которых мы переходим.
Микроволновое фоновое излучение можно описать функцией
распределения f(u, р) (и е Л, р^Ти), заданной на изотроп-
ных векторах в Т (Jt) (их совокупность можно рассматривать
как фазовое пространство фотонов). Если функция распределе-
ния строго изотропна для наблюдателя, движущегося с 4-ско-
ростью Va, то она будет иметь вид f(u, Е), где Е =— Vapa.
Поскольку это излучение распространяется свободно, функ-
ция f должна подчиняться уравнению Лиувилля в Т(Л). Это
означает, что функция f постоянна вдоль интегральных кривых
горизонтального векторного поля X, т. е. вдоль любой кривой
(и (ц), р (у)), где и (у)—изотропная геодезическая в Л ир =
= dfdv.
Поскольку /(и, Е) 0 и f должна стремиться к нулю при
Е -> оо (иначе плотность энергии излучения была бы бесконеч-
ной), должен существовать открытый интервал Е, в котором
д^дЕ =й 0. В этом интервале мы можем выразить Е как функ-
цию f: Е = g(u, f). Тогда уравнение Лиувилля означает, что на
каждой изотропной геодезической
(юл)
10 I
Расширение Вселенной
391
где g рассматривается как функция на Л при фиксированном f.
Кроме того,
W = - = - V^PaPb- (Ю-2)
Можно разложить ра на две составляющие: направленную
вдоль Va и ортогональную к Va, т. е. р — Е{Va + Wa), где
WaWa = 1, WaVa = 0. Тогда из (10.1) и (10.2) следует, что при
всех единичных векторах Wa, ортогональных к Va, выполняется
равенство
+ j eg + (gi>„ + V" + v-v‘ = о,
где dg/dt — скорость изменения g вдоль интегральных кривых V.
Отделяя сферические гармоники, имеем
<тй5 = 0, (10.3а)
= < (Ю.Зб)
I д _ d (In g) /,П
Т0---------jy— . (10.Зв)
Поскольку мы приняли, что КЛ = 0, из (10.36) следует, что
вектор Vа ортогонален к поверхностям {g = const), и это озна-
чает, что завихренность шаЬ равна нулю. В силу Уа = 0 имеем
V[a-,b] — 0. Следовательно, Va можно записать как градиент
функции I: Vа = — t-a.
Тензор энергии-импульса излучения будет иметь вид
ТаЬ ' "д' 4 д' №rSab>
где = jdf. Поскольку скорость галактик относительно
интегральных кривых вектора Va мала, их вклад в тензор энер-
гии-импульса можно аппроксимировать тензором энергии-им-
пульса непрерывной жидкости с плотностью цс, 4-скоростью Va
и пренебрежимо малым давлением. Тогда мы придем к выводу,
что геометрия пространства-времени такая же, как в модели
Робертсона — Уокера. Для этого заметим сначала, что
(Уа;Да = 4 (6 (&% + VaVb)).,a = (Va.a).,b + ^abaVg = 4- RbaVa-
Умножая это уравнение на hbc = gbc + VbVc, находим
hbcRcaVa = - у hbeec.
Левая часть равна нулю в силу уравнений поля, и, следова-
тельно, расхождение 0 постоянно на поверхностях t = const
392
Гл. 10. Начальная сингулярность во Вселенной
(которые являются также поверхностями постоянного g). По
функции 0(/) из уравнения S/S = у 0 можно определить функ-
цию S(t). Тогда уравнение Райчаудхури (4.26) принимает
форму
3S । . л л
-у—4л[л — Л — О,
откуда следует, что ц — ф- 2цй тоже постоянно на поверх-
ностях {t = const}. Из определения следует, что pG и по
отдельности постоянны на этих поверхностях.
Из той части равенства (4.27), след которой равен нулю,
видно, что Cabc<iVb V'1 — 0. Уравнения Гаусса — Кодацци
(разд. 2.7) приводят теперь к следующей формуле для тензора
Риччи на 3-поверхностях {t = const}:
Fab = hachdRcd + RacbdVcVd + O0ai> + Qac + 0% =
= 2AO6 (—g 92 + 8npi ф- a) .
На трехмерном многообразии тензор Римана полностью опре-
деляется тензором Риччи:
R3abcd = hab (- R3ef + i R3Hef) cd-
Отсюда каждая 3-поверхность {/ — const} есть трехмерное про-
странство постоянной кривизны R (/) = у ^8л[л + Л — у О2) .
Интегрирование уравнения Райчаудхури приводит к формуле
К(/) = 1(8лИ + Л--^)=^г, (10.4)
где k — постоянная. Нормируя S, можно положить k ==^1,0
или —1. Рассматриваемое четырехмерное пространственно-вре-
менное многообразие есть ортогональное произведение этих
3-пространств и линии t. Итак, наша метрика может быть за-
писана в сопутствующих координатах, как
ds2 = —'dt2 ф- S2 (/) dy2,
где dy2 — метрика 3-пространства постоянной кривизны !г, т. е.
метрика Робертсона — Уокера (см. разд. 5.3).
Теперь мы покажем, что в любом пространстве Робертсона —
Уокера с положительной плотностью энергии и Л = 0 имеется
замкнутая ловушечная поверхность в каждой 3-поверхности
{/ = const}. Чтобы убедиться в этом, представим dy2 в виде
dy2 = d%2 + f2 (х) (d02 ф- sin2 0 d^2),
гДе Их) равно sin/, х или sh х в зависимости от того, чему
равно k: ф-1, 0 или —1. Рассмотрим 2-сферу /7" радиуса хо, рас-
10 I. Расширение Вселенной
393
положенную в поверхности t = t0. Два семейства направлен-
ных в прошлое ортогональных к Д" изотропных геодезических
будут пересекать поверхности {/ = const} по двум 2-сферам ра-
диуса
t
% = Х»±^. (10.5)
о
Площадь поверхности 2-сферы радиуса % равна 4л52(t) f2(/).
Таким образом, оба семейства изотропных геодезических будут
сходящимися в прошлом, если при t — t0 неравенство
U))>0
выполняется для обоих значений х из (10.5). Это произойдет при
S (Д . I' (Хо)
So (to) S (t0) / (хо)
но, согласно (10.4), это неравенство выполняется, если
Г 8 _ (4 \ О? /1 X 1 f (Хо)
|_уЛ[л(г0)с> (г0)—«J >±-дт^-,
что в свою очередь справедливо, если S (to)%o взять большим, чем
(3/8лщ0)1/2 при k — Q или —1, и большим, чем min(V3/8np0, л/2)
при k = 4-1.
Этот результат интуитивно можно интерпретировать как
требование, чтобы в момент времени t0 сфера координатного
радиуса Хо содержала массу порядка 4/з лц053 (t0)Хо3 и, таким
образом, была внутри своего радиуса Шварцшильда, если
S (t0) Хо < 8/з гсроЗ (t0)3 Хо3, т. е. если S(t0)x по порядку величины
больше -у/3/8л[л0. Мы будем называть величину -у/8/8лцо шварц-
шильдовой длиной материи плотностью ц0.
До сих пор мы полагали, что микроволновое излучение
строго изотропно. Это, конечно, не так, поскольку Вселенная
не является в точности пространством Робертсона — Уокера.
Однако крупномасштабная структура Вселенной должна быть
близка к структуре модели Робертсона — Уокера по крайней
мере назад во времени, к моменту, когда микроволновое фоно-
вое излучение было испущено или претерпело последнее рас-
сеяние. (Отклонения микроволнового излучения от строгой изо-
тропии можно использовать для оценки того, сколь велики от-
клонения от геометрии Робертсона — Уокера.) Для достаточно
большой сферы существование локальных неоднородностей не
должно заметно влиять на количество материи в ней и потому
не должно сказываться на существовании замкнутых ловушеч-
ных поверхностей вокруг нас в современную эпоху.
394
Гл. 10. Начальная сингулярность со Вселенной
Приведенное выше рассуждение не зависит от спектра мик-
роволнового излучения, но подразумевает выполнение принципа
Коперника. Рассуждение, которое мы приведем теперь, не свя-
зано с принципом Коперника, но в определенной степени зави-
сит от формы спектра. Мы предположим, что приблизительно
равновесный характер спектра и высокая степень изотропии
фонового излучения являются свидетельством того, что оно, по
крайней мере частично, термализовано многократным рассея-
нием. Иначе говоря, на каждой направленной от нас в прош-
лое изотропной геодезической должно быть достаточно веще-
ства, чтобы прозрачность в этом направлении была не слишком
велика. Мы покажем затем, что этого вещества будет доста-
точно, чтобы наш световой конус прошлого оказался сходя-
щимся в прошлом.
Рассмотрим точку р, изображающую нас в настоящий мо-
мент времени, и пусть — направленный в прошлое единич-
ный вектор, параллельный нашей 4-скорости.
Аффинный параметр и направленных в прошлое изотроп-
ных геодезических, проходящих через р, можно нормировать
условием KaWa = —1, где К = djdv — касательный к этим
изотропным геодезическим вектор. Расхождение 0 в этих изо-
тропных геодезических будет подчиняться уравнению (4.35)
с й = 0. Таким образом, если RabRaKb О, то 0 < 2/и. От-
сюда следует, что при v = щ > v0
J RabKaKb du - > ё-
Vo
и поэтому 9 станет отрицательным, если найдется а0, такое, что
V1
^RabRaRb dv>2/v0.
Vo
Используя уравнения Эйнштейна сЛ = 0, получаем
V1
уи0 \8nTabKaKbdv> 1. (10.6)
На сантиметровых волнах наибольшее отношение непрозрачно-
сти к плотности вещества при разумных значениях последней
соответствует томсоновскому рассеянию на свободных электро-
нах в ионизованном водороде. Поэтому оптическая толща на
расстоянии v будет меньше
и
ир (Оф) du,
о
10.1. Расширение Вселенной
395
где х—непрозрачность вследствие томсоновского рассеяния на
единицу массы, р — плотность вещества и Va — локальная ско-
рость газа. Красное смещение вещества определяется формулой
z = KaVa—1. Поскольку вещество со значительным фиолето-
вым смещением не наблюдается, мы будем предполагать, что
на нашем световом конусе прошлого величина KaVa всегда
больше единицы вплоть до оптической толщи, равной единице.
Поскольку на этих длинах волн наблюдаются галактики с крас-
ными смещениями 0,3, большая часть рассеяния должна проис-
ходить при красных смещениях z > 0,3. (В самом деле, если
квазары — действительно космологические объекты, то рассея-
ние должно происходить при красных смещениях z > 2.) При
постоянной Хаббла порядка 100 км/(с-Мпс) ~ 1010 лет-1 крас-
ное смещение 0,3 соответствует расстоянию около 3-1027 см.
Принимая для это значение для вклада в интеграл (10.6) ве-
щества, которое вызывает рассматриваемое рассеяние, получим
3,7 • 1028
тогда как оптическая толща вещества между v0 и vx меньше
6,6- ю27 Jp(KaVa)dv.
Поскольку KaVa 1, легко убедиться, что неравенство (10.6)
будет выполнено при оптической толще меньше 0,2. При опти-
ческой толще Вселенной, меньшей 1, нельзя ожидать ни спек-
тра, близко совпадающего со спектром излучения абсолютно
черного тела, ни такой высокой степени изотропии в малых
угловых масштабах, если только не существует очень большого
числа дискретных источников, покрывающих лишь малую часть
неба (по площади), при этом каждый из них должен в грубом
приближении иметь спектр излучения абсолютно черного тела
с температурой 3 К, но значительно большей интенсивности.
Это представляется маловероятным. Поэтому мы уверены, что
условие 4.III теоремы 2 удовлетворяется и, следовательно, где-
то во Вселенной должна быть сингулярность, если конечно, вы-
полнены и остальные условия.
Ввиду своей общности теорема 2 не говорит нам, находится
ли сингулярность в нашем прошлом, или в будущем нашего
прошлого. Казалось бы, очевидно, что сингулярность должна
быть в нашем прошлом, однако можно построить пример, в ко-
тором она находится в будущем: рассмотрим Вселенную Ро-
бертсона— Уокера с k — +1, которая коллапсирует к син-
гулярности в некоторый момент t = t0, а при t->—оо
396
Гл. 10 Начальная сингулярность во Вселенной
асимптотически приближается к статической Вселенной Эйн-
штейна. В ней удовлетворяется энергетическое условие и имеются
точки, световые конусы прошлого которых начинают сходиться
(поскольку они пересекаются на «противоположной стороне»
Вселенной). Однако сингулярность находится в будущем. Ко-
нечно, это довольно искусственный пример, но из него видно, что
следует проявлять осторожность. Поэтому мы приведем рассуж-
дение, основанное на теореме 3, которое указывает на то, что
при выполнении принципа Коперника Вселенная содержит син-
гулярность в нашем прошлом. Теорема 3 подобна теореме 2, но
требует, чтобы вместо всех изотропных геодезических все вре-
мениподобные геодезические, направленные в прошлое из неко-
торой точки, начинали сходиться. Это условие не выполняется
в приведеннохМ выше примере, хотя ему удовлетворяют геоде-
зические, направленные в будущее из любой точки.
Рассуждая так же, как в случае изотропных геодезических,
получим, что схождение 0(s) направленных в прошлое из точ-
ки р времениподобных геодезических будет меньше
S
~~ \RabVaVbds,
s0 J
So
где s — собственное расстояние вдоль этих геодезических, V =
= d/ds и s > s0. Пусть W — направленный в прошлое времени-
подобный единичный вектор в точке р и с = — VaWa\p (и, сле-
довательно, с> 1). Тогда 0 станет меньше —с в пределах рас-
стояния Ri/c вдоль любой геодезической, если существует не-
которое Ro (Ri > Ro > 0), такое, что вдоль этой геодезической
j RabVaVb ds > с + е) . (10.7)
R 1с
Условие (3) теоремы 3 будет удовлетворено при b -----
— max(Pi, (Зе)-1).
Чтобы привести неравенство (10.7) к виду, подобному (10.6),
мы введем вдоль времениподобных геодезических аффинный
параметр v — s/c; тогда (10.7) приобретает вид
«I
4 7?0 RabKaKb dv > 1 + Roe, (10.8)
О J
я,
где К = d/dv и KaWa\p = — 1. В отличие от (10.6) мы не мо-
жем убедиться в выполнении условия (10.8) прямо по его яв-
ному виду, поскольку оно записано для времениподобных гео-
дезических. Поэтому мы обратимся к рассуждению, приведен-
ному в первой части настоящего раздела, где мы показали, что
10.1. Расширение Вселенной
397
Вселенная близка к модели Робертсона — Уокера по крайней
мере в прошлые времена до момента, когда микроволновое фо-
новое излучение претерпело последнее рассеяние.
Пусть W — вектор — dfdt в модели Робертсона — Уокера.
Вдоль направленной в прошлое времениподобной геодезической,
проходящей через р,
Ji (waKa) = wа..ьКаКь = 4-4г (- бИ •
UU О UI { С~ }
Отсюда, WaKa^.— 1, если dS/dt > 0. Однако
и, следовательно, при некотором е>0 условие (10.8) будет
удовлетворено для любой геодезической, если только суще-
ствуют моменты времени t2, h, t2 <Z h<. ip, такие, что
t _ t r
(Ю.9)
В силу уравнений поля сЛ = 0
RabKaK.b = 8л { (р + р) (Г аКа)2 - ~ (р - р) с-2} .
Поэтому при условии, что Р^О,
RabKaKb>^pWaRa)2.
Следовательно, (10.9) удовлетворяется, если
t — t
-р 3 -3 4лр d/ > 1. (10.10)
ti
Если принять, что микроволновое излучение имеет спектр
абсолютно черного тела при температуре 2,7 К, то в настоящее
время плотность его энергии порядка 1(Г34 г/см3. Если это из-
лучение — первичное, то плотность его энергии будет пропор-
циональна S-4. Поскольку 5-1 = 0(п/;) при стремлении t
к нулю, неравенству (10.10) можно удовлетворить, взяв t3 —
= tp/2 и достаточно малое t2. Насколько мало значение t2,
должно зависеть от конкретного поведения S, которое в свою
очередь зависит от плотности вещества во Вселенной. Это до-
вольно неопределенная величина, но она, по-видимому, лежит
между 10 22 и 5 10 29 г/см3. В первом случае f2 должно быть
таким, чтобы S (ZP)/S (/2) 30, а в последнем — таким, чтобы
S (/p)/S(/2) 300. Микроволновое излучение, по-видимому, за-
полняет всю Вселенную, поэтому любая направленная в прош-
лое времениподобная геодезическая должна проходить сквозь
398
Г л. 10. Начальная сингулярность во Вселенной
него. Таким образом, оценка, основанная на модели Роберт-
сона — Уокера, должна служить хорошим приближением для
вклада фонового излучения в (10.10), если оно возникло позд-
нее момента t2 и если сама модель Робертсона — Уокера яв-
ляется хорошим приближением для столь далекого прошлого.
Из рассуждений, приведенных в начале данного раздела, сле-
дует, что последнее справедливо при условии, что с момента t2
фоновое излучение распространялось к нам свободно. Однако
не исключено, что существует ионизованный межгалактический
газ плотностью порядка 5-10~29 г/см3, и в этом случае излуче-
ние могло претерпеть последнее рассеяние в момент времени /,
в который S(ZP)/S(Z)« 5. Оптическая толща в прошлое к мо-
менту t равна
О
ХЦгаз^, (10.11)
t
где к не превышает 0,5, если ц измерять в г/см3 и t в см.
В прошлом не может быть значительной непрозрачности до
t == tp— 1017 с, так как нам видны объекты на расстоянии по
крайней мере 3-1027 см. Принимая для /3 это значение, мы ви-
дим, что при такой плотности ионизованного газа соотношение
(10.10) будет удовлетворяться при значении t2, которое соответ-
ствует оптической толще, не превышающей 0,5.
Итак, сложилось следующее положение. Мы принимаем, что
выполняется принцип Коперника и что микроволновое излуче-
ние было испущено либо до момента t2, в который S (tp) /S (t2) m
» 300, либо до момента, в который оптическая толща Вселен-
ной равна единице, если этот момент более поздний, чем t2.
В первом случае условие (2) теоремы 3 будет удовлетворено за
счет плотности излучения, а во втором случае — за счет плот-
ности газа. Следовательно, если выполнены обычные энергети-
ческие условия и условия причинности, то мы можем заклю-
чить, что в нашем прошлом должна быть сингулярность (т. е.
должна существовать направленная от нас в прошлое непро-
странственноподобная геодезическая, которая неполна).
Пусть имеется пространственноподобная поверхность, пере-
секающая наш изотропный световой конус прошлого, и ряд то-
чек на этой поверхности; можно ли утверждать, что в прошлом
каждой из них есть сингулярность? Это было бы так, если бы
Вселенная была настолько однородна и изотропна в прошлом,
чтобы могло возникнуть схождение всех направленных в прош-
лое времениподобных геодезических из этих точек. Ввиду тес-
ной связи между схождением времениподобных геодезических
и замкнутыми ловушечными поверхностями можно ожидать,
что нужная степень однородности и изотропии в прошлом име-
10.1. Расширение Вселенной
399
лась, если Вселенная была однородна и изотропна на расстоя-
ниях порядка шварцшильдовой длины (3/8 лц) ,/2.
Измерения Пензиаса, Шрамля и Уилсона [134], обнаружив-
ших, что интенсивность микроволнового фонового излучения
изотропна в пределах 4% при телесном угле диаграммы
1 • 4 • 10-3 квадратных градуса, дают прямые свидетельства од-
нородности Вселенной в прошлом. В предположении, что мик-
роволновое излучение не генерировалось позднее поверхности,
соответствующей оптической толще, равной единице, получаем,
что наблюдаемая интенсивность пропорциональна Г4/(1 -ф z)4,
где Т — эффективная температура наблюдаемой точки на этой
поверхности и z — ее красное смещение. Вариации наблюдае-
мой интенсивности могут возникнуть по четырем причинам:
1) из-за доплеровского сдвига, вызванного нашим собствен-
ным движением относительно излучения абсолютно черного
тела [154, 163];
2) из-за вариаций гравитационного красного смещения, вы-
званных неоднородностями в распределении вещества между
нами и рассматриваемой поверхностью [138, 144];
3) из-за доплеровских сдвигов, вызванных локальными воз^
мущениями скоростей вещества на поверхности;
4) из-за вариаций эффективных температур поверхности.
(В действительности деление на пункты (1), (2) и (3) зависит
от способа отсчета и имеет только эвристическое значение.)
Таким образом, наблюдения свидетельствуют, что неоднород-
ности температуры с характерными угловыми размерами 3'
имеют относительные амплитуды меньше 1 % и что при тех же
характерных размерах не существует локальных флуктуаций
скорости вещества с 1 % скорости света. Область поверхности
с угловым диаметром около 3х будет соответствовать области,
которая сейчас имеет диаметр около 107 св. лет. Если поверх-
ность, соответствующая оптической толще, равной единице,
имеет красное смещение z = 1000 (максимально возможное),
то шварцшильдова длина в тот момент соответствовала бы об-
ласти с современным диаметром около 3- 10s св. лет. Таким об-
разом, каждая точка на поверхности единичной оптической
толщи, по-видимому, должна иметь в своем прошлом сингуляр-
ность.
Более косвенные данные о степени однородности Вселенной
на ранних стадиях основаны на том, что наблюдения содержа-
ния гелия в ряде небесных объектов согласуются с расчетами
образования гелия в предположении, что Вселенная была од-
нородна и изотропна в прошлом вплоть до температуры по-
рядка 109 К [121, 170]. С другой стороны, расчеты по анизотроп-
ным моделям дают совершенно иные количества гелия. По-
этому, если принять, что гелий распределен во Вселенной
400
Гл. 10. Начальная сингулярность во Вселенной
довольно равномерно (относительно этого есть некоторые сомне-
ния) и что этот гелий образовался на ранних стадиях Вселен-
ной, то можно сделать вывод, что Вселенная была эффективно
изотропна и однородна в эпоху с температурой 109 К- Следова-
тельно, можно ожидать, что в прошлом любой точки этого вре-
мени имеется сингулярность.
Мизнер [106] показал, что столкновения электронов и ней-
трино создают значительную вязкость, если температура дости-
гает 2-Ю10 К. Эта вязкость могла бы привести к затуханию не-
однородностей, размеры которых соответствуют в настоящее
время расстоянию 10 св. лет, и снизить анизотропию до срав-
нительно малой величины. Таким образом, если принять подоб-
ное объяснение современной изотропии Вселенной (такое объ-
яснение весьма привлекательно), то можно заключить, что
сингулярность должна быть в прошлом любой точки в эпоху
с температурой около 1010 К-
10.2. Природа и проявление сингулярностей
Есть надежда узнать кое-что о природе сингулярностей, ко-
торые, по-видимому, все же появляются, исследуя точные реше-
ния с сингулярностями. Но хотя мы и показали, что малые воз-
мущения начальных данных не препятствуют появлению син-
гулярности, все же не очевидно, что свойства сингулярности
будут столь же устойчивы. В разд. 7.5 мы показали, что задача
Коши устойчива относительно малых возмущений начальных
условий, но эта устойчивость относится только к компактным
подобластям области Коши, а область, содержащая сингуляр-
ность, не компактна, за исключением случая, когда сингуляр-
ность соответствует захваченной неполноте. Мы приведем
пример, в котором характер сингулярности действительно не-
устойчив. Рассмотрим однородное сферически симметричное
облако пыли, коллапсирующее к сингулярности. Метрика вну-
три облака будет подобна метрике части вселенной Роберт-
сона — Уокера, тогда как область вне облака будет описы-
ваться метрикой Шварцшильда. И внутри, и вне облака пыли
сингулярность пространственноподобна (рис. 63, а). Допустим
теперь, что к этой пыли мы добавили электрический заряд не-
большой плотности. Метрика вне облака пыли станет теперь
частью решения Райсснера — Нордстрема для е2 < т2 (рис.
63,6). Внутри облака появится сингулярность, так как доста-
точно малая плотность заряда не помешает ее возникновению.
Характер сингулярности внутри облака пыли, по-видимому, бу-
дет зависеть от распределения заряда. Важно, однако, следую-
щее: как только поверхность облака пыли пройдет точку р
внутри г = г+, что бы ни произошло внутри облака, это не по-
влияет на часть sq времениподобной сингулярности.
Сингулярность
(г =0)
Сингу/гяртстб
(г=О)
Рис. 63. а — коллапс сферического облака пыли; б — коллапс заряженного
облака пыли, в котором заряд слишком мал, чтобы помешать появлению
в облаке пыли сингулярности; в — коллапс заряженного облака пыли, в ко-
тором имеется заряд, достаточный для того, чтобы воспрепятствовать по-
явлению сингулярности в самом облаке; сингулярность появляется вне облака,
которое сжимается и снова расширяется в другое асимптотически плоское
пространство
1 1 Заказ 3?!
402
Гл. 10. Начальная сингулярность во Вселенной
Если теперь увеличить плотность заряда настолько, что она
станет больше плотности вещества, то облако может пройти
через два горизонта в точках г — г+ и г = г_ и вновь начнет
расширяться в другую вселенную, при этом внутри него не по-
явится никакой сингулярности, хотя вне его будет временипо-
добная сингулярность {Дж. М. Бардин, не опубликовано),
в полном согласии с теоремой 2 (рис. 63, в).
Этот пример очень важен, так как он показывает, что воз-
можны времениподобные сингулярности, что материя может
избежать сингулярного состояния и что она может проникнуть
сквозь «кротовую нору» в другую область пли в другую часть
той же области пространства-времени. Конечно, вряд ли кол-
лапсирующая звезда может иметь столь большую плотность
заряда, но поскольку решение Керра так похоже на решение
Райсснера — Нордстрема, можно ожидать, что момент количе-
ства движения способен создать подобную «кротовую нору».
Можно немного пофантазировать и предположить, что до со-
временной фазы расширения Вселенная находилась в фазе
сжатия, в течение которой росли локальные неоднородности и
возникали отдельные сингулярности; однако большая часть ма-
терии, избежав этих сингулярностей, перешла к расширению,
превратившись в нашу наблюдаемую Вселенную.
Существование сингулярностей в пределах прошлого каждой
точки в весьма ранний момент времени, когда плотность была
велика, накладывает ограничения на расстояние между сингу-
лярностями. В принципе можно было бы представить, что мно-
жество геодезических, которые «упираются» в эти сингулярно-
сти (т. е. неполны), имеет меру нуль. Тогда можно было бы
утверждать, что эти сингулярности физически несущественны.
Однако на самом деле это не так, потому что существование та-
ких сингулярностей приводит к образованию горизонта Коши и,
следовательно, к невозможности предсказывать будущее. Мы
могли бы получить таким образом путь к решению проблемы
энтропии в модели пульсирующей Вселенной, поскольку в каж-
дом цикле сингулярности могли бы вносить отрицательную эн-
тропию.
До сих пор мы исследовали математические следствия пред-
положения о том, что модель пространства-времени представ-
ляет собой лоренцево многообразие и что при этом удовлетво-
ряются уравнения поля Эйнштейна с Л = 0. Мы показали, что,
согласно такой теореме, в нашем прошлом должны быть
сингулярности, связанные с коллапсом Вселенной, а в нашем бу-
дущем — сингулярности, связанные с коллапсом звезд. Если
Л •< 0, то эти выводы остаются неизменными. Если же Д ~> 0,
то наблюдения скорости расширения Вселенной [145, 146] го-
ворят о том, что Л не может превышать 3 • 105- см-2. Это зна-
10.2. Природа и проявление сингулярностей
403
чсние эквивалентно отрицательной плотности энергии 3 X
X Ю 27 г/см3. Такое значение Л могло бы сказаться на расши-
рении Вселенной в целом, но оно бессильно повлиять на поло-
жительную плотность вещества коллапсирующей звезды. Та-
ким образом, Л-член, по-видимому, не дает нам возможности
избежать проблемы сингулярности.
Можно, конечно, сказать, что общая теория относительности
не дает правильного описания Вселенной. До сих пор эта тео-
рия проверялась только при весьма малых отклонениях от пло-
ского пространства (радиусы кривизны порядка 1012 см). По-
этому ее применение к явлениям типа коллапса звезды, когда
радиус кривизны становится меньше 106 см, кажется слишком
далеко идущей экстраполяцией. С другой стороны, теоремы
о сингулярностях зависят от уравнений Эйнштейна не во всей
полноте, а только от того, что RayKaKb 0 для любого непро-
странственноподобного вектора №; поэтому они будут справед-
ливы также и в любой модификации общей теории относитель-
ности (такой, как теория Бранса — Дикке), в которой тяготе-
ние всегда есть сила притяжения.
По-видимому, можно выдвинуть следующий разумный прин-
цип: если теория предсказывает сингулярность, то это указы-
вает на нарушение теории, т. е. она более не дает правильного
описания наблюдений. Возникает вопрос: когда нарушается об-
щая теория относительности? Можно ожидать, что в любом
случае она нарушается, когда становятся важны квантовые
эффекты; из соображений размерности следует, что этого
не должно случиться, пока радиус кривизны не станет порядка
10~33 см, что соответствует плотности 1094 г/см3. Однако мы
можем спросить: является ли лоренцево многообразие прием-
лемой моделью для пространства-времени при характерных
длинах такого порядка? В настоящее время эксперименты сви-
детельствуют, что предположение о структуре многообразия
при характерных длинах более 10~15 см приводит к предсказа-
ниям, согласующимся с наблюдениями [49]; но может оказаться,
что нарушение теории происходит при длинах между Ю '1' и
10~33 см. Радиус 10 27 см соответствует плотности 1058 г/см3, ко-
торую всегда практически можно рассматривать как сингуляр-
ность. Поэтому следует построить по методу Шмидта (разд. 8.3)
поверхность вокруг областей с радиусом кривизны меньше,
скажем, ИН7 см. С нашей стороны поверхности будет допу-
стимо рассматривать пространство-время как многообразие, но
внутри этой поверхности потребуется еще не известное нам
квантовое описание. Материю, пересекающую такую поверх-
ность, можно рассматривать как входящую во Вселенную или
покидающую ее, и нет причин, по которым количества входя-
щей и уходящей материи должны быть равны,
14*
404
Гл, 10. Начальная сингулярность оо Вселенной
Во всяком случае, теоремы о сингулярностях свидетельст-
вуют о том, что по предсказаниям общей теории относительно
сти гравитационное поле должно стать предельно сильным. Чтг
это имело место в нашем прошлом, подтверждается существо
ванием микроволнового фонового излучения со спектром абсо-
лютно черного тела, свидетельствующего о том, что у Вселен-
ной была очень горячая и плотная ранняя фаза.
Вероятно, теоремы о существовании сингулярностей можно
несколько усовершенствовать, но на наш взгляд они и в таком
виде достаточно хорошо отражают суть дела. Однако они мало
что говорят нам о характере сингулярностей. Хотелось бы
знать, какого рода сингулярности могут появиться в общей тео-
рии относительности в характерных ситуациях. Один из путей
к этому состоит в усовершенствовании предложенного Лифши-
цом и Халатниковым метода разложения в степенные ряды и
выяснении пределов его применимости. Может оказаться также,
что существует определенная связь между сингулярностями,
рассматриваемыми в общей теории относительности и в других
областях физики (см., например, теорию элементарных ката-
строф Тома [165]). С другой стороны, можно было бы попы-
таться решить проблему в лоб, численным интегрированием
уравнений Эйнштейна на вычислительной машине. Однако для
этого, вероятно, придется ждать появления нового поколения
вычислительных машин. Хотелось бы знать также, будут ли
голыми сингулярности, возникающие при коллапсе из несингу-
лярного асимптотически плоского состояния, т. е. будут ли они
видны с бесконечности или будут скрыты за горизонтом собы-
тий.
Другой важной проблемой является формулировка кванто-
вой теории пространства-времени, применимой к сильным по-
лям. Такого рода теория может исходить из некоторого много-
образия или может допускать изменения топологии. Некоторые
предварительные попытки в этом направлении уже были пред-
приняты Де Виттом [38], Мизнером [107, 108], Пенроузом [132],
Уилером [173] и другими. Однако интерпретация квантовой тео-
рии пространства-времени и ее отношение к сингулярностям
еще далеки от ясности.
Гипотезы и споры, касающиеся предмета этой книги, не
новы. По существу, еще Лаплас предсказал существование чер-
ных дыр: «Иные звезды появлялись внезапно и исчезали после
нескольких месяцев ярчайшего сияния... . Все эти звезды .. .
не изменяли своих положений, пока они светили. Поэтому
в беспредельных глубинах пространства существуют темные
тела, столь же значительные по величине и, возможно, столь
же многочисленные, как звезды». (П. С. Лаплас, «Изложение
10.2. Природа и проявление сингулярностей 405
системы мира»). Как мы видим, современное понимание поло-
жения вещей удивительно похоже на лапласовское.
С незапамятных времен высказывалась мысль о возникнове-
нии Вселенной из ничего; см., например, первую «Антиномию
Чистого Разума» Канта и комментарии к ней ([158], р. 117—123,
145—159 и [117], 389—406). Результаты, которые мы получили,
говорят в пользу идеи, что история Вселенной началась неко-
торое конечное время тому назад. Однако самый момент воз-
никновения— сингулярность — находится за пределами справед-
ливости известных сейчас законов физики.
Приложение А
Пьер Симон Лаплас*)
Доказательство теоремы о том, что сила притяжения небес-
ного тела могла бы быть столь велика, что от него не будет
исходить свет **)
1. Если v — скорость, t — время и s— расстояние, которое
равномерно проходится в течение этого времени, то, как из-
вестно, v = s[t.
2. Если движение не является равномерным, то для получе-
ния значения v в какой-либо момент нужно поделить пройден-
ное расстояние ds и интервал времени di одно на другое, т. е.
v = ds/dt, поскольку скорость на бесконечно малом интервале
постоянна и движение, таким образом, можно принять за рав-
номерное.
3. Непрерывно действующая сила будет стремиться изме-
нить эту скорость. Это изменение скорости, а именно du, яв-
ляется поэтому наиболее естественной мерой этой силы. Но по-
скольку любая сила вызывает двойной эффект за двойное
время, мы должны разделить изменение скорости du на время
d^, в течение которого это изменение вызывается силой Р; та-
ким образом, получается общее выражение для силы Р, т. е.
ds
р do di
dt dt
Теперь, если di есть постоянная,
, ds ___ d ds d ds
di d/ di ’
соответственно
n _ d ds
__________ “Ж- •
*) Allgemeine geographishe Ephemeriden. verfasset von Einer Gesell-
schaft Gelehrter, Weimer, IV, Bd. 1st, 1799, ed. F. X. von Zach. Мы благодарны
Д. У. Дьюхэрсту, снабдившему пас этой ссылкой.
**) Эта теорема о том, что во Вселенной светящееся тело той же плот-
ности, что и Земля, но диаметр которой в 250 раз больше диаметра Солнца,
может силой притяжения воспрепятствовать своим лучам света достичь нас
и, следовательно, самые большие тела во Вселенной могли бы остаться для
нас невидимыми, была приведена Лапласом в его «Изложении системы
мира», часть II, стр. 305, без доказательства. См. A. G. Е., Мау 1798, р. 603,
V. 1.
Приложение А
407
4. Пусть сила притяжения тела М; второе тело (например,
частица света) находится иа расстоянии г; действие силы М
на эту частицу света будет —Mlrr, отрицательный знак появ-
ляется из-за того, что действие М противоположно движению
света.
5. Теперь согласно (3) эта сила также равна d dr/d/2; сле-
довательно,
гг dz-
Умножая на dr, получим
после интегрирования
где С — постоянная величина, или
/ dr \2
=2С + 2Л4г-‘.
Теперь, в силу (2), Ar/dt— скорость v и соответственно спра-
ведливо равенство
v2 = 2C + 2Мг~1,
где v — скорость частицы света на расстояни i г.
6. Теперь для определения постоянной С допустим, что R —
радиус притягивающего тела и а — скорость света на расстоя-
нии R (следовательно, на поверхности притягивающего тела);
тогда из (5) получается
а2 = 2С + 2M/R,
поэтому
2С = а2 — 2M/R.
Подставляя это в предыдущее уравнение, получим
7. Пусть R' будет радиус другого притягивающего тела; его
сила притяжения будет iM, а скорость света на расстоянии г
составит v'-, тогда, согласно уравнению в (6),
8. Если сделать г бесконечно большим, последний член
в предыдущем уравнении обращается в нуль, и мы получаем
408
Приложение А
Расстояние до неподвижных звезд столь велико, что это
предположение справедливо.
9. Пусть сила притяжения второго тела так
свет не может удалиться от него; это можно
тически следующим образом; скорость света
Подставив такое значение v' в уравнение (8) для v', получим
уравнение, из которого можно вывести массу
это происходит. Следовательно, имеем
„ , 21М 2 2zA4
0 = а------— или
г R'
велика, что
выразить анали-
v' равна нулю.
1М, при которой
10. Чтобы определить а, допустим сначала, что этим при-
тягивающим телом является Солнце; тогда а — скорость света
Солнца на поверхности Солнца. Однако сила притяжения
Солнца в сравнении со скоростью света столь мала, что можно
эту скорость принять за равномерную. Из явления аберрации
следует, что Земля проходит 20"своего пути, в то время как
свет проходит от Солнца до Земли; следовательно: пусть V есть
средняя скорость Земли на ее орбите, тогда мы имеем
a:V = радиусу (выраженному в секундах); 20"= 1 : tg 20" .
11. Мое предположение в «Изложении системы мира», часть
II, стр. 305, состоит в том, что R' = 250 R. Далее, масса изме-
няется как объем притягивающего тела, умноженный на его
плотность, объем — как куб радиуса, соответственно масса —
как куб радиуса, умноженный на плотность. Пусть плотность
Солнца — 1, плотность второго тела = р; тогда
M:iM=iR3: pR'3 = 1Д3:р2503Д3,
или
1:г = 1 : р(250)3,
или
/ = (250)3р.
12. Подставляем значения i и R' в уравнение a2 — 2iM[R и,
таким образом, имеем
г__ 2 (250)3 рМ _р /о_Д_
а 250/? Л Р R ’
или
___ a2R
Р ~ Т(250)2 А/ •
13. Чтобы получить р, необходимо еще определить М. Сила
А4 Солнца на расстоянии D равна MjD2. Пусть D — среднее
расстояние до Земли, V — средняя скорость Земли; тогда эта
сила равна также (см. «Астрономию» Панде, III, § 3539\
Приложение А
409
Отсюда MjD'1 = V2/D, или М = V2D. Подстановка этого в урав-
нение (12) для р дает
a-R 8 / а \2 R
2 (250)= V-D ~~ (1000)2 tV) ~D ’
скорость света
скорость Земли
V
------р согласно (10),
tg 20" —
ь 4
/\ я и с. р а д и у с и“j I
— =-------------!----——------^ = 1е среднего видимого радиуса 0.
D среднее расстояние до у ar-' t j
Следовательно,
tg 16Z2"
1000 tg 20" ’
откуда следует, что плотность р приблизительно равна 4, или
такая же по величине, как и плотность Земли.
Приложение Б
Сферически-симметричные решения
и теорема Биркхофа
Мы хотим рассмотреть уравнение Эйнштейна в случае сфе-
рически-симметричного пространства. Существенным свойством
сферически-симметричного пространства-времени можно считать
существование мировой линии 3?, относительно которой про-
странство-время сферически-симметрично. Тогда эквивалентны
все точки на каждой пространственноподобной 2-сфере З’л
с центром в произвольной точке р е 3? и определяемой как
поверхность постоянного расстояния d вдоль всех геодезиче-
ских, ортогональных к S’ в точке р. Если изменить направле-
ние в точке р действием ортогональной группы 50(3), остав-
ляющей сферу 3 инвариантной, пространство-время по опре-
делению не меняется и соответствующие точки сферы 5Д
отображаются друг в друга; таким образом, пространство-время
допускает группу 50(3) в качестве группы изометрий, причем
орбитами группы являются сферы Sj. [Могут быть частные
значения d, при которых поверхность 3d превращается в точку
р'; тогда р’ будет другим центром симметрии. Точек (р' и сама
точка р), связанных таким образом, может быть самое боль-
шее две.]
Однако может быть так, что в некоторых пространствах,
которые хотелось бы рассматривать как сферически-симметрич-
ные, мировая линия, подобная 3, не будет существовать. На-
пример, в решениях Шварцшильда и Райсснера — Нордстрема
пространство-время сингулярно в точках, для которых г = 0;
иначе эти точки могли бы быть центрами симметрии. Поэтому
мы примем существование группы изометрий SO(3), действую-
щей на 2-поверхностях, подобных S’d, за характеристическое
свойство сферически-симметричного пространства-времени.
Итак, мы скажем, что пространство-время сферически-сим-
метрично, если оно допускает в качестве группы изометрий
группу 50(3) с орбитами в виде пространственноподобных 2-по-
верхностей. Тогда эти орбиты необходимо будут 2-поверхно-
стями постоянной положительной кривизны.
Для каждой точки q на любой орбите 3(q) существует од-
номерная подгруппа изометрий Д, оставляющая q инвариант-
ной (если есть центральная ось то это — группа вращений
вокруг р, оставляющая геодезическую pq инвариантной). Мно-
Приложение Б
411
жество (q) всех геодезических, ортогональных к ^(q), в точке
q образует локально 2-поверхпость, инвариантную относитель-
но [поскольку подгруппа Iq, которая меняет направления
в S₽(y) относительно q, оставляет неизменными направления,
перпендикулярные к (<?)]. В любой другой точке r^Viq)
группа Iq снова меняет направления, ортогональные к ^(q),
оставляя в то же время (7) инвариантной; ввиду того что
Iq должна действовать в групповой орбите ^(г), проходящей
через г, эта орбита ортогональна к ^(<7). Таким образом, груп-
повые орбиты ортогональны к поверхностям [147]. Далее,
эти поверхности локально определяют взаимно-однозначное ото-
бражение между орбитами группы, в котором f(q), образ
точки q в д’(г), является пересечением и ^(г). Поскольку
это отображение инвариантно относительно действия /д, век-
торы равной длины в 9? (q) в точке q отображаются в векторы
равной длины в ^(г) в точке /(7); и так как все точки ^(<7)
эквивалентны, при отображении векторов из любой точки !?(q)
в ее образ в ^(г) все длины получают один и тот же множи-
тель. Таким образом, ортогональные поверхности конформно
отображают орбиты 9? одну в другую.
Если выбрать координаты {/, г, 0, ф] так, чтобы групповыми
орбитами 9? стали поверхности {Т г = const}, а ортогональ-
ными поверхностями Y? — поверхности {0, ф = const}, то мет-
рика при этом примет вид ds2 = dx2(t, г) Y2(t, г) dfi2 (0, ф),
далее выбирать функции I, г так, чтобы {/ — const}, {г = const}
где dr2 — неопределенная метрика 2-поверхности и dQ2 — мет-
рика поверхности постоянной положительной кривизны. Если
были ортогональны в 2-поверхностях (ср. с [6]), метрику
можно записать в виде
ds2 = + X2 (t, г) dr2 + Y2 (t, r) (d02 + sin2 0 dф2). (Б. 1)
Г* \l, Г)
(Отметим, что на этих поверхностях все еще остается свобода
произвольного выбора г или А)
Допустим, что наблюдатель, движущийся вдоль линий t,
измеряет плотность энергии ц, изотропное давление, поток энер-
гии q, причем анизотропных давлений нет. Тогда уравнения
поля для метрики (Б. 1) можно записать в виде
= (Б.2)
8ли = 3? + Л(_2_)'_3(4_у +
+ 2г4г + г(т)7 ®-3)
412 Приложение Б
M К'ИШ. JU-- ' — ——... x.<, . J M и-*- , —*—.» - — -*, <_ ,r-j.jj.. ,,w ; •
- 8лр = ~ + 2F (f 4-)' + 3 (^-)2 F2 +
+ AIZ.„frV (Б4)
'A'- YF \XY ) ’ D J
4л (ц + 3p) = i (-4x)' - F (f4) - 2F (?r) -
где штрих означает д/'дг, а точка — d/dt.
Рассмотрим сначала уравнения поля в пустом пространстве
Яаъ = 0; это означает, что в (Б. 2) — (Б. 5) мы должны поло-
жить р = р = q = 0. Локальное решение зависит от рода
поверхностей {У = const}; эти поверхности могут быть врсменп-
подобны, пространственноподобны или изотропны; кроме того,
они могут быть не определены (если Y — постоянная). В исклю-
чительном случае, когда УаУ;а=0 на некотором открытом
множестве °U (сюда входит случай постоянного У), на <U вы-
полняется равенство
~ = FY. (Б.6)
Однако, если справедливо (Б.6), значение Y', получающееся
из (Б. 2), не согласуется с (Б.З). Следовательно, мы можем
рассматривать точку р, где Y’aYia < 0 или Y'aY-a > 0; такое не-
равенство должно выполняться в некоторой открытой окрест-
ности °U точки р.
Рассмотрим прежде всего случай, когда У’°У;а < 0. Тогда
в °И поверхности {У = const} времениподобны, и можно взять У
в качестве координаты г. (При этом г будет KoopdunaToii, оп-
pedeApeMoii площадью, так как площадь 2-поверхности {г, t =
— const} равна 4лг2.) Итак, У = 0, Y' = 1, а из (Б. 2) видно,
что X — 0. Далее, из (Б. 4) следует, что (F'/F)’ = О, и поэтому
можно выбрать новую временную координату t' (t) таким об-
разом, чтобы положить F = F(г). Тогда имеем F = F(r), X =
= Х(г), У = г и решение HeodxoduMO статическое. Из урав-
нения (Б.З) после этого получается, что d(r/X2)/dr = 1, так
что решение имеет вид X2 = (1 —2т/г)_], где 2m— постоянная
интегрирования. Уравнение (Б. 4) можно проинтегрировать; при
подходящем выборе постоянной интегрирования получим F2 —
= X2, и тогда (Б. 5) тождественно удовлетворяется. При таких
F и X метрика имеет вид
ds2 = — (1 — —dt2 4- -—+ г2 (dQ2 + sin2 6 d^2); (Б.7)
I г )
это — метрика Шварцшильда при г > 2m.
Приложение Б 413
Теперь предположим, чго У’аУ:11 > 0. Тогда поверхности
{У — const} пространствепионодобны в :JU. и мы можем выбрать
У в качестве координаты /. Теперь У— 1, У7 — 0, и из (Б. 2)
следует, что F' = 0. Можно выбрать координату г так, чтобы
было X — Х(ф)- тогда F — F(t), X — X(t), Y — I и решение —
пространственноподобно однородное. Теперь (Б.4) и (Б. 5)
можно проинтегрировать и получить следующее решение:
ds2 = - 2JZ'’ у + - 1) dr2 - F (d02 + sin2 0 d^>2). (Б.8)
Это часть решения Шварцшильда, относящаяся к области вну-
три шварцшильдова радиуса, ибо преобразование t -> г', г -> f
приводит эту метрику к виду (Б. 7) с г' < 2/и. Наконец, если
поверхность {У = const} в некоторой части открытого множе-
ства Т пространственноподобна, а в другой части временипо-
добна, можно в этих частях получить решения (Б.8) и (Б, 7)
и затем сшить их ла поверхности ¥;аУ:а — 0, как это было сде-
лано в разд. 5.5. Таким образом, получим ту часть максималь-
ного решения Шварцшильда, которая лежит в Т. В итоге мы
доказали теорему Биркхофа: любое С2-решение уравнений Эйн-
штейна в пустом пространстве, сферичсски-симметричное в от-
крытом множестве Т, локально эквивалентно в Т части макси-
мально расширенного решения Шварцшильда. (Это верно, даже
если пространство класса С° и кусочно класса С1, см. [6].)
Теперь мы рассмотрим сферичсски-симметричные решения
для статической идеальной жидкости. Можно подобрать такие
координаты {t, г, 0, ф}, в которых метрика имеет вид (Б. 1),
жидкость движется вдоль линий t (и, следовательно, q = 0)
и F — F(r), X = X(r), Y=Y(r). Из уравнений поля (Б.З),
(Б. 4) тогда следует, что ц + р = 0, если Y' = 0; такой слу-
чай мы исключаем как не имеющий смысла для реальной
жидкости и считаем, что Y' 0. Поэтому мы снова можем вы-
брать У в качестве координаты г; тогда метрика имеет вид
ds2 = + х2 dr2 + r2 <d02 + siir' ° О- И
Из свернутых тождеств Бианки ТаЪ-ь ~ 0 следует, что
р' — (р + р)-у = 0. (Б. 10)
Уравнение (Б.5) удовлетворяется тождественно, если справед-
ливы (Б.З), (Б. 4) и (Б. 10). Уравнение (Б.З) можно проин-
тегрировать явно и получить
^'2 = (1 (Б.П)
414 Приложение Б
где
А) (/•) = 4 л j [,ir dr,
о
И использовать граничное условие Х(0)= 1 (т. е. эта жидкая
сфера имеет регулярный центр). С учетом (Б. 10), (Б. И) урав-
нение (Б.4) приводится к виду
dp _ (ц + р) (Л1 + 4лрг3) /г,
’ г(г-2Л4) ’ (БЛ2’
которое определяет р как функцию г, если известно уравнение
состояния. Наконец, из (Б.10) имеем
р (.о
F(r) = Cexp f (Б.13)
J В1 I Р
р (0)
где С — постоянная. Уравнения (Б. И) — (Б. 13) задают мет-
рику внутри сферы, т. е. до г = г0, где г0— значение г на по-
верхности жидкости.
Обозначения
Числа указывают на страницы, где даны определения.
— определение
3 — существует
==> — следует
У — знак суммы
□ — конец доказательства
Множества
и A U В — объединение А и В
П А П В — пересечение А и В
с Ас В, Вс А — А содержится в В
— А~ В — В вычитается из А
е х^А —х есть элемент множества А
0 — пустое множество
Отображения
ф:41 , — ф отображает р е 41 в ф(р') е Z
ф(41) — образ 'U при отображении
ф~х — отображение, обратное к ф
fog —композиция, вслед за g производится отображе-
ние /
Ф^ Ф* ~ отображения тензоров, индуцированные отобра-
жением ф, 31
Топология
А — замыкание А
А — граница А, 203
int А — внутренность А, 232
Дифференцируемость
С°, Сг, Сг~, С°° -— условия дифференцируемости, 19
Многообразия
— п-мерное многообразие, 19—20
(<2ZU, фа) — локальная карта, задающая локальные коорди-
наты ха, 20
416
Обозначения
дЛ — край многообразия Л, 20
Rn — евклидово м-мерное пространство, 19
уТ?'1 — нижняя половина (%i 0) пространства R11, 19
Sn — /i-сфера, 21
X — прямое (декартово) произведение, 23
Тензоры
(d/dt)K, X
<о, d/
<®, X)
{Ей}, {Еа}
7 р> 1 р
Trs{p)
Trs(J()
Т (Л)
ЦЛ
— векторы, 24
— 1-формы (линейные формы), 25, 30
— скалярное произведение вектора и 1-формы,
25
— дуальные базисы векторов и 1-форм, 25
ь — компоненты тензора типа (г, s), 26—29
— тензорное произведение, 27
— внешнее произведение, 30
— симметризация (т. е. Т\аЬ}), 29
— антисимметризация (т. е. Т[а&]), 29
— символ Кронекера ( + 1, если а = Ь, и 0,
если а=£Ь)
— касательное пространство и дуальное про-
странство в точке р, 24
— пространство тензоров типа (г, s) в точке р,
27
— расслоение тензоров типа (г, s) на Л, 64
— касательное к Л расслоение, 63
— расслоение линейных реперов на Л, 64
Производные и связность
д/дх1 — частная производная по координате х{
(d/dt\ — производная вдоль кривой Z(Z), 24
d — внешняя производная, 26, 34
LxY, [X, Y] — производная Ли вектора Y по вектору X, 37
V, \ .\, Таь-,с — ковариантная производная, 40—41
D/d/ —ковариантная производная вдоль кривой, 42
rljk — компоненты связности, 41
ехр — экспоненциальное отображение, 44
Римановы пространства
g) — многообразие Л с метрикой g и связностью
Кристоффеля
Я — элемент объема, 60
Rabcd~ тензор Римана, 46
Обозначения
417
Rab — тензор Риччи, 47
Е — скалярная кривизна, 52
Cabcd ~ тензор Вейля, 52
О (р, q) — ортогональная группа, оставляющая метрику Gab
инвариантной, 64
йаь — диагональная метрика
diag (+1, +1, -1.....--1)
р членов q членов
О (.<) — расслоение ортонормированных реперов, 64
Пространство-время
Пространство-время есть 4-мерное риманово пространство
(Л, g) с нормальной метрической формой diag ( + 1, +1, —1,
— 1). В качестве локальных координат выбраны (х1, х2, х3, х4)
ТаЬ — тензор энергии-импульса материи, 74
\... d — материальные поля, 77
L — лагранжиан, 77
Уравнения поля Эйнштейна имеют вид
Rab 2 R^ab Н- -^ёаЬ 8л,Та1,,
где Л— космологическая постоянная.
(^, о) — комплект начальных данных, 258
Времениподобные кривые
± — ортогональная проекция, 92
~DF/ds — производная Ферми, 93
0 — расхождение, 96
гой, ®аЬ, ® — вращение, 96
оаЬ, ° — сдвиг, 96
Изотропные геодезические
0 — расхождение, 101
®а6, ® — вращение, 101
даЬ, о — сдвиг, 101
Причинная структура
1+, 1~ — хронологические будущее и прошлое, 203
/+, 7“ — причинные будущее и прошлое, 203
Е+, Е~ — контуры будущего и прошлого, 204
D+, D~ — области Коши будущего и прошлого, 135, 224
Я+, Н~ — горизонты Коши в будущем и прошлом, 178, 224
418
Обозначения
Граница пространства-времени
JC = Л и л, где А — с-граница, 224
3+, 3 ~, г+, i~ — с-граница асимптотически простого и пу
стого пространства, 138, 250
Л = Л\}дЛ, —когда Л"—асимптотически простое в ела-
бом смысле; граница дЛ многообразия Л
состоит из 3^ и 3~, 246, 250
Л+ = Л\^д, — где д есть ^-граница, 315
Литература
i. Ames IP. L., Thorne K. S., The optical appearance of a star that is col-
lapsing through its gravitational radius, Astrophys. J., 151, 659—670 (1968).
2 Arnett IF. D., Gravitational collapse and weak interactions, Can. J. Phys.,
44, 2553—2594 (1966).
3. Auslander L., Markus L., Flat Lorentz manifolds, Memoir 30, Amer. Math.
Soc. (1958).
4. Avez A., Essais de geometrie Riemannienne hyperbolique globale, Applica-
tions a la Relativite Generale, Ann. Inst. Fourier (Grenoble), 132, 105—190
(1963).
5. Белинский В, А., Лифшиц E. M., Халатников И. M., Колебательный ре-
жим приближения к особой точке в релятивистской космологии, Успехи
физ. наук, 102, 463—500 (1970).
6. Bergmann Р. G., Cahen М., Komar А. В., Spherically symmetric gravita-
tional fields, J. Math. Phys., 6, 1—5 (1965).
7. Bianchi L., Lezioni sulla teoria dei gruppi continui finiti transformazioni,
Spoerri, Pisa, 1918.
8. Bludman S. A., Ruderman M. A., Possibility of the speed of sound exceed-
ing the speed of light in ultradense matter, Phys. Rev., 170, 1176—1184
(1968).
9. Bludman S. A., Ruderman M. A., Noncausality and instability in ultradense
matter, Phys. Rev., DI, 3243—3246 (1970).
10. Bondi H., Cosmology, Cambridge Univ. Press, London, 1960.
11. Bondi EE, Massive spheres in General Relativity, Proc. Roy. Soc. London,
A282, 303—317 (1964).
12. Bondi H., Gold T., The steady-state theory of the expanding universe, Mon.
Not. Roy. Astron. Soc., 108, 252—270 (1948).
13. Bondi EE, Pirani F. A. E., Robinson /., Gravitational waves in General
Relativity, III. Exact plane waves, Proc. Roy. Soc. London, A251, 519—533
(1959).
14. Boyer R. Fl., Geodesic Killing orbits and bifurcate Killing horizons, Proc.
Roy. Soc. London, A311, 245—252 (1969).
15. Boyer R. EL, Lindquist R. IP., Maximal analytic extension of the Kerr met-
ric, J. Math. Phys., 8, 265—281 (1967).
16. Boyer R. EL, Price T. G., An interpretation of the Kerr metric in General
Relativity, Proc. Camb. Phil. Soc., 61, 531—534 (1965).
17. Bruhat Y., The Cauchy problem, in Gravitation: an introduction to current
research, ed. L. Witten, Wiley, New York, 1962, pp. 130—168.
18. Burkill J. C., The Theory of Ordinary Differential Equations, Oliver and
Boyd, Edinburgh, 1956.
19. Calabi E., Marcus L_, Relativistic space forms, Ann. Math., 75, 63—76
(1962).
20. Cameron A. G. W., Neutron stars, in Ann. Rev. Asti on. Astrophys., eds.
L. Goldberg, D. Layzer, J. G. Phillips, Ann. Rev. Inc., Palo Alto, Califor-
nia, 1970, pp. 179-208.
21. Carter B., The complete analytic extension of the Reissner — Nordstrom
metric in the special case e2 = m2, Phys. Lett., 21, 423—424 (1966).
420 Литература
22. Carter В., Stationary axisymmetric systems in General Relativity,
Ph. D. Thesis, Cambridge Univ., 1967.
23. Carter B., Global structure of the Kerr family of gravitational fields, Phvs.
Rev., 174, 1559-1571 (1968).
24. Carter B., Hamilton — Jacoby and Schrodinger separable solutions of Ein-
stein’s equations, Comm. Math. Phys., 10, 280—310 (1968).
25. Carter B., Killing horizons and orthogonally transitive groups in space-
time, J. Math. Phys., 10, 70—81 (1969).
26. Carter B., The commutation property of a stationary axisymmetric system,
Comm. Math. Phys., 17, 233—238 (1970).
27. Carter B., Causal structure in space-time, J. General Relativity and Gra-
vitation, 1, 349—391 (1971).
28. Carter B., Axisymmetric black hole has only two degress of freedom, Phvs.
Rev. Lett, 26, .331—332 (1971).
29. Choquet-Bruhat Y„ Espace — temps Einsteinies generau.x, chocs gravita-
tionnels, Ann. Inst. Henri Poincare, 8, 327—338 (1968).
30. Choquet-Bruhat У, Equations aux derivees partielles-solutions C“ d’equa-
tioris hyperboliques non-lineaires, Compt. Rend. Acad. Sei. (Paris), 1971.
31. Choquet-Bruhat У, Geroch R. P., Global aspects of the Cauchy problem in
General Relativity, Comm. Math. Phys, 14, 329—335 (1969).
32. Christodoulou D., Reversible and irreversible transformation in black hole
physics, Phys. Rev. Lett, 25, 1596—1597 (1970).
33. Clarke C. J. S., On the geodesic completeness of causal space-times, Proc.
Camb. Phil. Soc, 69, 319—324 (1971).
34. Colgate S. A., Mass ejection from supernovae, Astrophys. J, 153, 335—339
(1968).
35. Colgate S. A., White R. H., The hydrodynamic behaviour of supernovae
explosions, Astrophys. J, 143, 626—681 (1966).
36. Courant R., Hilbert D., Methods of Mathematical Physics, Vol. II: Partial
Differential Equations, Interscience, New York, 1962. (Русский перевод:
P. Курант, Уравнения с частными производными, изд-во «Мир», М,
1964.)
37. Demianski М., Newman Е., A combined Kerr — NUT solution of the Ein-
stein field equations, Bull. Acad. Pol. Sci. (Math. Astron. Phys.), 14, 653—
657 (1966).
38. De Witt B. S, Quantum theory of gravity: I. The canonical theory, Phys.
Rev, 160, 1113—1148 (1967); II. The manifestly covariant theory, Phys.
Rev, 162, 1195—1239 (1967); III. Applications of the covariant theory,
Phys. Rev, 162, 1239—1256 (1967).
39. Dicke R. H., The theoretical significance of Experimental Relativity, Blackie,
New York, 1964.
40. Dionne P. A., Sur les problemes de Cauchy hyperboliques bien poses,
J. d’Analyses Math, 10, 1—90 (1962).
41. Dirac P. A- M., A new basis for cosmology, Proc. Roy. Soc. London, A165,
199—208 (1938).
42. Dixon W. G., Dynamics of extended bodies in General Relativity: I. Mo-
mentum and angular momentum, Proc. Roy. Soc. London, A314, 499—527
(1970); II. Moments of the charge-current vector, Proc. Roy. Soc. London,
A319, 509—547 (1970).
43. Дорошкевич А. Г, Зельдович fl. Б., Новиков И. Д., Гравитационный кол-
лапс несимметричных и вращающихся масс, ЖЭТФ, 49, 170—181
(1965).
44. Ehlers I., Geren Р., Sachs R. К., Isotropic solutions of the Einstein — Lion-
ville equations, J. Math. Phys, 8, 1344—1349 (1968).
45. Ehlers J., Kundt IF, Exact solutions of the gravitational field equations,
in Gravitation: an Introduction to Current Research, ed. L. Witten, Wiley,
New York, 1962, pp. 49—101.
Литература 421
46. Ehresmann С., Les connexions infinitesima les dans un espace fibre diffe-
rentiable, in Colloque de Topologic (Espaces Fibres) Bruxelles 1950, Mas-
son, Paris, 1957, pp. 29—50.
47. Ellis G. F. R., Sciama D. W., Global and non-global problems in cosmo-
logy, in Studies in Relativity (Synge Festschrift), ed. L. O’Raiffeartaigh,
Oxford Univ. Press, London, 1972.
48. Fields G. B., Cosmic background radiation and its inter action with cosmic
matter, Rivista del Nuovo Cimento, 1, 87—109 (1969).
49. Foley R. J., Jones R. S., Lindebaum S. J., Love Iff Д, Ozaki S., Plai-
ner E. D., Quarles C. A., Willen E. H., Experimental test of the pion-nuc-
leon forward dispersion relations at high energies, Phys. Rev Lett., 19,
193-198, 622 (1967).
50. Geroch R. P., Singularities in closed universes, Phvs. Rev. Lett., 17, 445—
447 (1966).
51. Geroch R. P., Singularities in the space-time of General Relativity,
Ph. D. Thesis, Department of Physics, Princeton Univ., 1967.
52. Geroch R. P., Topologv in General Relativitv, J. Math. Phvs., 8, 782—786
(1967).
53. Geroch R. P., Local characterization of singularities in General Relativity,
J. Math. Phys., 9, 450—465 (1968).
54. Geroch R. P., What is a singularity in General Relativity, Ann. Phys.
(New York), 48, 526—540 (1968).
55. Geroch R. P., Spinor structure of space-times in General Relativity. I,
J. Math. Phys, 9, 1739—1744 (1968).
56. Geroch R. P., Spinor structure of space-times in General Relativity. II,
J. Math. Phys, 11, 343—348 ((1970).
57. Geroch R. P., The domain dependence, J. Math. Phys, 11, 437—439 (1970).
58. Geroch R. P., Singularities, in Relativity, eds. S. Fickler, M. Carmeli and
L. Witten, Plenum Press, New York, 1970, pp. 259—291. (Русский перевод
в сб. «Квантовая гравитация и топология», «Мир», М, 1973.)
59. Geroch R. Р., Space-time structure from a global view point, in General
Relativity and Cosmology, Proc, of Intern. School in Physics «Enrico Fer-
mi», Course XLVII, ed. R. K. Sachs, Academic Press, New York, 1971,
pp. 71 —103.
60. Geroch R. P., Rronheimer E. H., Penrose R., Ideal points in space-time,
Proc. Roy. Soc. London, A327, 545—567 (1972).
61. Gibbons G., Penrose R., в печати.
62. Godel R., An example of a new type of cosmological solution of Einstein’s
field equations of gravitation, Rev. Mod. Phys, 21, 447—450 (1949).
63. Gold T. (ed.), The Nature of Time, Cornell Univ. Press, Ithaca, 1967.
64. Graves J. C., Brill D. R., Oscillatory character of Reissner — Nordstrom
metric for an ideal charged wormhole, Phys. Rev, 120, 1507—1513
(1960).
65. Грищук Л. FI., Некоторые замечания об особенностях в космологических
решениях уравнений гравитации, ЖЭТФ, 51, 475—479 (1966).
66. Hajicek Р., Causality in non-Hausdorff space-times, Comm. Math. Phys,
21, 75—84 (1971).
67. Hajicek P., Exact Models of Charged Black Holes, II. Axysymmetric sta-
tionary horisons, Comm. Math. Phys, 34, 53—76 (1973).
68. Harrison В. R., Thorne R. S., Wakano Л4, Wheeler J. A., Gravitation
theory and gravitational collapse, Chicago Univ. Press, Chicago, 1965.
(Русский перевод: Дж. Уилер, Б. Гаррисон, М. Вакано, R. Торн, Теория
гравитации и гравитационный коллапс, изд-во «Мир», М, 1976.)
69. Hartle J. В., Hawking S. W., Solutions of the Einstein-Maxwell equations
with many black holes, Comm. Math. Phys, 26, 87—101 (1972).
70. Hartle J. B., Hawking S. W., Energy and angular momentum flow into
a black hole, Comm. Math. Phys, 27, 283—290 (1972).
422 Литература
71. Hawking S. W., Perturbations of an expandin'? universe, Astrophys. J 14S,
544—554 (1966).
72. Hawking S. IF., Singularities and the geometry of space-time, Adams Pri/e
Essay, 1906, не опубликовано.
73. Hawking S. IF., The occurrence of singularities in cosmology, III. Causa-
lity and singularities, Proc. Roy. Soc. London, A300, 187—201 (1967).
74. Hawking S. IF., Ellis G. F. R., Singularities in homogeneous world models
Phys. Lett., 17, 246—247 (1965).
75. Hawking S. IF., Penrose R., The singularities of gravitational collapse and
cosmology, Proc. Roy. Soc. London, A314, 529—548 (1970).
76. Heckmann 0., Schilcking E., Relativistic cosmology, in Gravitation: an
Introduction to Current Research, ed. L. Witten, Wiley, New York, 1962,
pp. 438—469.
77. Hocking J. G., Young G. S., Topology, Addison-Wesley, London, 1961.
78. Hodge IF. V. D., The Theory and Application of Harmonic Integrals, Cam-
bridge Univ. Press, London, 1952.
79. Hogarth J. E., Cosmological considerations on the absorber theory of radia-
tion, Proc. Roy. Soc. London, A267, 365—383 (1962).
80. Hoyle F., A new model for the expanding universe, Mon. Not. Roy. Astron.
Soc., 108, 372—382 (1948).
81. Hoyle F., Narlikar J. V., Time-symmetric electrodynamics and the arrow
of time in cosmology, Proc. Roy. Soc. London, A277, 1—23 (1963).
82. Hoyle F., Narlikar J. V., A new theory of gravitation, Proc. Roy. Soc.
London. A282, 191—207 (1964).
83. Israel IF., Singular hypersurfaces and thin shells in General Relativity,
Nuovo Cimento, 44B, 1 —14 (1966); erratum Nuovo Cimento, 49B, 463
(1967).
84. Israel IF., Event horizons in static vacuum space-time, Phys. Rev., 164,
1776—1779 (1967).
85. Israel IF., Event horizons in static electrovac space-time, Comm. Math.
Phys., 8, 245—260 (1968).
86. Jordan P., Schwerkraft und Weltall, Friedrich Vieweg, Braunschweig, 1955.
87. Kantowski R., Sachs R. K-, Some spatially homogeneous anisotropic rela-
tivistic cosmological models, J. Math. Phys., 7, 443—446 (1967).
88. Kelley J. L., General Topology, van Nostrand, Princeton, 1965.
89. Khan K- A., Penrose R., Scattering of two impulsive gravitational plane
waves, Nature, 229, 185—186 (1971).
90. Kinnersley IF., Walker M., Uniformly accelerating charged mass in General
Relativity, Phys. Rev., D2, 1359—1370 (1970).
91. Kobayashi S., Nomizu K-, Foundations of Differential Geometry, Vol. I,
Intersci., New York, 1963.
92. Kobayashi S., Nomizu K-, Foundations of Differential Geometry, Vol. II,
Intersci., New York, 1969.
93. Kreuzer L. B., Experimental measurement of the equivalence of active and
passive gravitational mass, Phys. Rev., 169, 1007—1012 (1968).
94. Kronheimer E. H., Penrose R., On the structure of causal spaces, Proc.
Camb. Phil. Soc., 63, 481—501 (1967).
95. Kruskal M. D.t Maximal extension of Schwarzschild metric, Phys. Rev.,
119, 1743—1745 (1960).
96. Kandt IF., Tragheitsbahnen in einem von Gddel angegebenen kosmologi-
schen Modell, Z. Phys., 145, 611—620 (1956).
97. Kundt IF., Note on the completeness of space-times, Z. Phys., 172, 488—
489 (1963).
98. Le Blanc J. M., Wilson J. R., A numerical example of the collapse of a ro-
tating magnetized star, Astrophys. J., 161, 541—552 (1970).
99. Leray J., Hyperbolic differential equations, duplicated notes, Princeton In-
stitute for Advanced Studies, 1952.
Литература
423
100. Lichnerowicz A., Theories Relativistes de la Gravitation et de 1’Electro-
magnetisme, Masson, Paris, 1955.
101. Лифшиц E. M., Халатников И. M., Investigations in relativistic cosmology,
Adv, in Phys. (Phil. Mag. Suppl.), 12, 185—249 (1963).
102. Ldbell F., Bcispiele geschlossener drei-dimensionaler Clifford-Kleinsche
Raume ncgativer Kriimmung, Ber. Verhandl. Sachs. Akad. Wiss. Leipzig,
Math, Phys. KI., 83, 167—174 (1931).
103. Milnor J., Morse Theory, Annals of Mathematics Studies No. 51, Princeton
Univ. Press, Princeton, 1963. (Русский перевод: Дж. Милнор, Теория
Морса, изд-во «Мир», М., 1966.)
104. Misner С. W., The flatter regions of Newman, Unti and Tamburino’s gene-
ralized Schwarzschild space, J. Math. Phys., 4, 924—937 (1963).
105. Misner C. W., Taub — NUT space as a counterexample to almost anything,
in Relativity Theory and Astrophysics, I: Relativity and Cosmology,
ed. J. Ehlers, Lectures in Applied Mathematics, Vol. 8, American Math. So-
ciety, 1967, pp. 160—169.
106. Misner C. W., The isotropy of the universe, Astrophys. J., 151, 431—457
(1968).
107. Misner C. 117, Quantum cosmology. I, Phys. Rev., 186, 1319—1327 (1969).
108. Misner C. Ж, Minisuperspace, preprint, Univ, of Maryland, 1971.
109. Мизнер Ч. В., Тауб A. X., Пустая Вселенная, не имеющая особенностей,
ЖЭТФ, 55, 233—255 (1968).
ПО. Milller zum Hagen Н., On the analyticity of stationary vacuum solutions
of Einstein’s equations, Proc. Camb. Phil. Soc., 68, 199—201 (1970).
111. Milller zum Hagen H., Robinson D. C., Seifert H. J., Black holes in static
vacuum space-times, in General Relativity and Gravitation (1972).
112. Munkers 1. R., Elementary Differential Topology, Annals of Math. Studies
No. 54, Princeton. Univ. Press, Princeton, 1954.
113. Newman E. T., Penrose R., An aproach to gravitational radiation by a me-
thod of spin coefficients, J. Math. Phys., 3, 566—578 (1962).
114 Newman E. T., Penrose R., New conservation laws for zero-rest mass
fields in asymptotically flat space-time, Proc. Roy. Soc. London, A305,
175—204 (1968).
115. Newman E. T., Tamburino L., Unti T. J., Empty space generalization of
the Schwarzschild metric, J. Math. Phys., 4, 915—923 (1963).
116. Newman E. T., Unti T. W. J., Behaviour of asymptotically flat empty spa-
ces, J. Math. Phys., 3, 891—901 (1962).
117. North J. D., The Measure of the Universe, Oxford Univ. Press, London, 1965.
118. Ozsvath I., Schilcking E., An anti-Mach metric, in Recent Developments in
General Relativity, Pergamon Press — PWN, 1962, pp. 339—350.
119. Papapetrou A., Champs gravitationncls stationnares a symmetric axiale,
Ann. Inst. Henri Poincare, AIV, 83—105 (1966).
120. Papapetrou A., Hamoui A., Surfaces caustiques degenerees dans la solution
de Tolman. La Singularity physique en Relativite Generale, Ann. Inst.
Henri Poincare, VI, 343—364 (1967).
121. Peebles P. J. E., Primordial helium abundance and the primordial fireball.
II, Astrophys. J., 146, 542—552 (1966).
122. Penrose R., Asymptotic properties of fields and space-times, Phys. Rev.
Lett., 10, 66—68 (1963).
123. Penrose R., Conformal treatment of infinity, in Relativity, Groups and To-
pology, eds. С. M. de Witt and B. de Witt, Les Houches Summer School,
1963, Gordon and Breach, New York, 1964. (Русский перевод в сб. «Гра-
витация и топология», изд-во «Мир», М., 1965.)
124. Peiuose R-, A remarkable property of plane waves in General Relativity,
Rev. Mod. Phys., 37, 215—220 (1965).
125. Penrose R., Zero rest-mass fields including gravitation: asymptotic beha-
viour, Proc. Roy. Soc. London, A284, 159—203 (1965).
424
''Литература
126. Penrose R., Gravitational collapse and space-time singularities, Phvs Rev
Lett., 14, 57—59 (1965).
127. Penrose R., General Relativity energy flux and elementary optics, in Per
spectives in Geometry and Relativity (Hlavaty Festschrift), ed. B. Hoff-
mann, Indiana Univ. Press, Bloomington, 1966, pp. 259—274.
128. Penrose R„ Structure of space-time, in Battelle Rencontres, eds., С. M. d
Witt, J. A. Wheeler, Benjamin, New York, 1968, pp. 121—235. (Русски'1
перевод.: P. Пенроуз, Структура пространства-времени, изд-во «Мир» М
1972.)
129. Penrose R., Gravitational collapse: the role of General Relativity, Rivish
del Nuovo Cimento, 1, 252—276 (1969).
130. Penrose R.. The geometry of impulsive gravitational waves, in Studies in
Relativity (Synge Festschrift), ed. L. O’Raiffeartaigh, Oxford Univ. Press.
London, 1972.
131. Penrose R., Techniques of differential topology in relativity, Lectures at
Pittsburgh, 1970, A. M. S. Colloquium Publications, 1972.
132. Penrose R., MacCallum M. A. H. A twistor approach to space-time quan-
tization, Phys. Rep. (Phys. Lett. Section C) (1972).
133. Penrose R., Floyd R. AL, Extraction of rotational energy from a black hole,
Nature, 229, 177—179 (1971).
134. Penzias A. A., Schraml J., Wilson R. W., Observational constraints on
a discrete source model to explain the microwave background, Astrophys.
J., 157, L49—L51 (1969).
135. Pirani F. A. E., On the energy — momentum tensor and the creation of
matter in relativistic cosmology, Proc. Roy. Soc., A228, 455—462 (1955).
136. Press W. H., Time evolution of a rotating black hole immersed in a static
scalar field, Astrophys. J., 175, 245—252 (1972).
137. Price R. FL, Nonspherical perturbations of relativistic gravitational col-
lapse, I. Scalar and gravitational perturbations; II. Integer spin, zero rest-
mass fields, Phys. Rev., 5, 2419—2454 (1972).
138. Rees M. J., Sciama D. Л4., Large-scaledensity inhomogeneities in the uni-
verse, Nature, 217, 511—516 (1968).
139. Regge T., Wheeler J. A.. Stability of a Schwarzschild singularity Phys.
Rev., 108, 1063—1069 (1957).
140. Riesz F., Sz-Nagy B., Functional Analysis, Blackie and Sons, London,
1955. (Русский перевод: Ф. Рисе, Б. Секефальви-Надь, Лекции по функ-
циональному анализу, ИЛ, М., 1954.)
141. Robertson Н. Р., Relativistic cosmology, Rev. Mod. Phys., 5, 62—90 (1933).
142. Rosenfeld L., Sur le tenseur d’impulsion — energie, Mem. Roy. Acad. Belg.
Cl. Sci., 18, No. 6 (1940).
143. Ruse FL S., On the geometry of Dirac’s equations and their expression in
tensor form, Proc. Roy. Soc. Edin., 57, 97—127 (1937).
144. Sachs R. K., Wolfe A. M., Perturbations of a cosmological model and an-
gular variations of the microwave background, Astrophys. J., 147, 73—90
(1967).
145. Sandage A., The ability of the 200-inch telescope to discriminate between
selected world models, Astrophys. J., 133, 355- 392 (1961).
146. Sandage A., Observational cosmology, Observatory, 88, 91 — 106 (1968).
147. Schmidt B. G„ Isometry groups with surface-orthogonal trajectories, Zs.
Naturforsch, 22a, 1351—1355 (1967).
148. Schmidt B. G., A new definition of singular points in General Relativity,
J. Gen. Rel. and Grav., 1, 269—280 (1971).
149. Schmidt B. G., Local completeness of the &-boundarv, Comm. Math. Phys.,
29,49—54 (1972).
150. Schmidt FL, Model of an oscillating cosmos which rejuvenates during con-
traction, J. Math. Phys., 7, 494—509 (1966).
151. Schouten J. A., Ricci Calculus, Springer, 1954.
Литература
425
152. Schrodinger Е., Expanding Universes, Cambridge Univ. Press London
1956.
153. Sciama D. W., On the origin of inertia, Mon. Not. Roy. Astron Soc 113,
34—42 (1953).
154. Sciamo D. W., Peculiar velocity of the sun and the cosmic microwave
background, Phys. Rev. Lett., 18, 1065—1067 (1967).
155. Sciama D. W., Astrophysical cosmology, in General Relativity and Cosmo-
logy, ed. R. K. Sachs, Proc, of the International School of Physics «Enrico
Fermi», Course XLVII, Academic Press, New York, 1971, pp. 183—236.
156. Seifert H. J., Global connectivity by timelike geodesics, Zs. Naturforsch.,
22a, 1356—1360 (1967).
157. Seifert H. J., Kausal Lorentzraume, Doctoral Thesis, Hamburg Univ., 1968.
158. Smart 1. J. C., Problems of Space and Time, Problems of Philosophy Se-
ries, ed. P. Edwards, Collier-Macmillan, London; Macmillan, New York,
1964.
159. Соболев С. Л., Некоторые применения функционального анализа в мате-
матической физике, Изд-во Сиб. отделения АН СССР, Новосибирск, 1962.
160. Spanier Е. Н., Algebraic Topology, McGraw-Hill, New York, 1966.
161. Spivak M., Calculus on Manifolds, Benjamin, New York, 1965. (Русский
перевод: M. Спивак., Математический анализ па многообразиях, изд-во
«Мир», М., 1968.)
162. Steenrod N. Е., The Topology of Fibre Bundles, Princeton Univ. Press,
Princeton, 1951. (Русский перевод: H. Стинрод, Топология косых произ-
ведений, ИЛ, М., 1953.)
163. Stewart J. М. S., Sciama D. W., Peculiar velocity of the sun and its
relation to the cosmic microwave background, Nature, 216, 748—753 (1967).
164. Streater R. F., Wightman A. S., P. С. T., Spin, Statistics, and All That,
Benjamin, New York, 1964.
165. Thom R., Stability Structurelie et Morphogenese, Benjamin, New York,
1969.
166. Thorne K. S., The General Relativistic theory of stellar structure and dyna-
mics, in High Energy Astrophysics, ed. L. Gratton, Proc, of the Interna-
tional School in Physics «Enrico Fermi», Course XXXV, Academic Press,
New York, 1966, pp. 166—280.
167. Tsuruta S., The effects of nuclear forces on the maximum mass of neutron
stars, in The Crab Nebula, eds. R. D. Davies, F. G. Smith, Reidel, Dor-
drecht, 1971.
168. Vishveshwara С. 1Л, Generalization of the «Schwarzschild Surface» to
arbitrary static and stationary Metrics, J. Math. Phys., 9, 1319—1322
(1968).
169. Vishveshwara С. V., Stability of the Schwarzschild metric, Phys. Rev., DI,
2870—2879 (1970).
170. Wagoner R. 1Л, Fowler W. A., Hoyle F., On the synthesis of elements at
very high temperatures, Astrophys. J., 148, 3—49 (1968).
171. Walker A. G., Completely symmetric spaces, J. Lond. Math. Soc., 19, 219—
226 (1944).
172. Weymann R. A., Mass loss from stars, in Ann. Rev. Astron, and Astro-
phys., Vol. 1, Ann. Rev. Inc., Palo Alto, 1963, pp. 97—141.
173. Wheeler J. A., Superspace and the nature of quantum geometrodynamics,
in Batelle Rencontres, eds. С. M. de Witt, J. A. Wheeler, Benjamin, New
York, 1968, pp. 242—307.
174. Whitney H., Differentiable manifolds, Annals Math., 37, 645 (1936).
175. Yano K., Bochner S., Curvature and Betti numbers, Annals Math., Studies
No. 32, Princeton Univ. Press, Princeton, 1953. (Русский перевод: К. Яно,
С. Бохнер, Кривизна и числа Бетти, ИЛ, М., 1957.)
176. Зельдович Я. Б., Новиков И. Д., Релятивистская астрофизика, изд-во
«Наука», М.. 1967
Предметный указатель
Атлас 20, 70
— локально-конечный 22
— ориентированный 35
— полный 20
• — совместный с данным атласом 20
Аффинный параметр 43, 287
---обобщенный 288, 289
Базис 25
— дуальный 26
— координатный 24
— ортонормированный
— псевдоортонормированный 100, 382
Бесконечность будущего (прошлого)
времениподобная 137, 138, 145
---изотропная 137, 145
--- пространственноподобная 137,
138
Бианки тождества 47, 54
Бранса — Дикке теория 72
Будущее асимптотически предсказуе-
мое 346
— сильно предсказуемое 348
— захваченное 216, 217
— причинное 203
— хронологическое 203, 241
Вариация кривой 121, 122
— метрики 78
— поля 77
— связности 79
Вектор вариации 121—123
— времениподобный 49, 69
— изотропный 49, 69
— касательный к С6-кривой 24
— Киллинга 55
— ковариантный 25
— поток 82
— пространственноподобный 49, 69
Вложение 33, 55
Вращение 95
— изотропных геодезических 101
Геодезическая 44
— изотропная 99
— полная 44, 212
Геодезическая кривая 43
---максимальная 125, 126
Гиперповерхность 55
— времениподобная 56
— изотропная 56
— пространственноподобная 56
ГНБ (граничное НБ) 243—245, 249,
250
ГНП (граничное НП) 243—245, 249,
250
Горизонт кажущийся 356, 357—359
— Коши 178, 198, 320
— событий 146
— — бесконечности в будущем 185
— частиц 144
Граница ахрональная 208
— пространства-времени 244
Группа изометрии 55, 153, 367
— транзитивная 137, 165, 188
Да вление 83
— вырожденных нейтронов 339
--- электронов 337
Девиация кривых 92
— геодезических 101
Диаграмма Пенроуза 138, 139
Диффеоморфизм 33, 34
Длина пути вдоль кривой 47, 48
Задача Коши для материальных по-
лей 72, 73
— — для уравнения Эйнштейна
253—258
— — устойчивость решения 281, 334
Захват 216
Захваченная неполнота 322, 323
Идеальная жидкость 81, 83, 92
— — изоэнтропическая 83, 85
Излучение космическое фоновое 387—
389
Изотропный конус 49, 53, 73
Карта локальная 20
Киллинга бивектор 187
— вектор 55
— векторное поле 55, 74, 153, 187
Предметный указатель
427
Коллапс звезды 333, 334
Компоненты тензора 28
Комплект (начальных данных) 258,
276, 278
Конгруэнция кривых 81
Контур будущего 201
Конформный множитель 53, 74, 76,
77
Координаты изотропные 133
- - локальные 20
— нормальные 44, 52
Коперника принцип 151, 152, 167, 168,
387, 389
Космологическая постоянная 86, 109,
154, 159, 402
Край многообразия 20, 246
Кривая времениподобная 81
— интегральная 37
— класса О (Сь-кривая) 24
— направленная в будущее 205
— иепродолжимая в будущее (про-
шлое) 205
— непространствснпоподобпая 72
— предельная 205
— с захваченным будущим 216, 217
Кристоффеля соотношения 52
Лагранжиан заряженного скалярного
поля 77, 81
— идеальной жидкости 81
— скалярного поля 80
— электромагнитного поля 80
Лифт 65
— горизонтальный 66
Локальная причинность (постулат)
72, 131, 210, 265
Локальное сохранение энергии и им-
пульса (постулат) 74
Метрика 47—55, 68 __
— индуцированная 56
— конформная 53, 73—77. 89. 90. 200
— лоренцева 49—52, 56, 68, 90, 119,
286
— невырожденная 48
— положительно-определенная 49
— пространственно-временная 68, 84
— статическая 85
— фоновая 253—255, 271—276, 280—
281
Многообразие 19, 69
— геодезически полное 44, 216, 286,
289, 292, 296
— класса Сг ((^-многообразие) 20
-------с краем 20
— накрывающее 228
Многообразие ориентируемое 22, 56,
60, 65
паракомпактное 22, 44, 49—50
— параллелизуемое 65, 202
— причинно простое 210, 229, 295
— связное 68
— универсальное накрывающее 228
— хаусдорфово 22, 44, 69, 193, 194
277, 278
Множество ахрональное 207, 225—
227, 232, 297
— будущего 207, 208, 209
— вполне упорядоченное 276
— глобально гиперболическое 229,
230—236
— ловушечное для будущего (про-
шлого) 297, 299
— нарушающее хронологию 210, 211
— непричинное 208, 227
— причинно простое 210, 229
Модель Вселенной Гёделя 187, 188—
190
— статическая Эйнштейна 137, 156
--- стационарная 141
Модель пространства-времени мате-
матическая 68
---— геодезически полная 33, 165
— — — изометричная 68
----------локально О-непродолжи-
мая 71
— —------- локально Сг-нерасширяе-
мая 71
—------— Сг-нерасширяемая 71
НБ (неразложимое множество бу-
дущего) 241, 242—245
НП (неразложимое множество про-
шлого) 241, 242—245
Область Коши 135, 150, 166, 224, 232
---будущего 224
— ловушечная 356
^-Ограниченность 325, 327
Окрестность выпуклая 44
— локальной причинности 217, 219
- - нормальная 44
Отображение инъективное 32
— класса С1' (Сг-отображение) 19, 31
- - конформное 53, 157
— собственное 33
— сюръективное 32, 62
— тензоров 32, 34
— экспоненциальное 44, 134
Перенос параллельный 213
— Ферми 94
428
Предметный указатель
Плоские волны (гравитационные) 199,
229
Поверхность внешняя ловушечная 355
— — — маргинальная 359
— замкнутая ловушечная 11, 174,
909 907 994
- Коши 135, 150, 199, 228, 295
— прострапственноподобная ИЗ, 115
— стационарности предельная 185
— транзитивности 151, 152
Погружение 32
Подмногообразие вложенное 33
— погруженное 33
Подпространство вертикальное 66
— горизонтальное 66, 308
Поле линейных элементов 50, 212
— скалярное 80, 109
— — заряженное 81
— электромагнитное 80, 81
— якобиево НО, 125
— — вдоль изотропной геодезиче-
ской 114
Полнота 289, 308
— геодезическая 286, 289
— метрическая 286, 308
Последовательность сильно сходя-
щаяся 269
— слабо сходящаяся 270
— фундаментальная 286
Произведение внешнее прямое (мно-
гообразий) 93, 62
— тензорное 27
Производная внешняя 34, 35, 45
— ковариантная 41, 42
--- вдоль кривой 42
— Ли 37—40, 45
— Ферми 93, 94
Пространство дуальное касательному
25
— евклидово 10
— касательное 25
— компактное 40
— /п-полное (метрически полное) 286,
308
— постоянной кривизны 140
— расслоенное 62
— Соболева 259, 260
— Тауба —НУТ 190, 191 — 198, 229,
322
— типа Бианки I 160
Пространство-время 68
— асимптотически простое 246, 247—
250
-------пустое 246, 247—250
— — — в слабом смысле 251, 345
--сильно предсказуемое 348,
353
— геодезически полное 286, 289, 292,
296
• - де Ситтера 1-го рода 140, 141 —
148
— — — 2-го рода 148, 149—151, 229
— компактное 189
— Минковского 133, 134—140, 247
— й-ограпиченное 325—327
— ориентируемое по времени 201
202, 212,'246
— й-полиое 289, 308, 310, 326
- -- цространственпо-ориеитируемое
202
— расслоенное 62, 63
— регулярно предсказуемое 354, 356,
360
— — — статическое 363
--------стационарное 360, 361, 366,
371
— Робертсона — Уокера 152, 153—
159, 390—398
Прошлое асимптотически простое 352
Развитие (начальных данных) 253,
273—277
— максимальное 276—281
Разложение единицы 23, 36
Расхождение 96, 98
— изотропных геодезических 101, 108
— объемное 91, 111
Расслоение 62
— касательное 63
— линейных реперов 64, 194
— ортонормированных базисов 64
— тензорное 64
Расширение многообразия 70, 169,
172, 177, 183, 253, 276—281
Сг-Расширение 70, 171
Решение (уравнений Эйнштейна) 132
— Керра 180
— пространственно-однородное 160
— Райсснера — Нордстрема 175,
176—186, 229
— точное 132
— Шварцшильда 167, 166—174, 363,
412
Свертка тензора 28
Связность 40, 41, 52, 53, 65
— без кручения 45
— класса Сг (С'-связность) 41
— плоская 47
Сигнатура метрики 48, 49
Сингулярность «голая» 346
— кривизны в параллельно перене-
сенном базисе 290, 323
Предметный указатель
429
— скалярных полиномов кривизны
290
Скалярная кривизна 52
СНБ (СНП) 243, 245
Собственно-разрывное действие груп-
пы 193, 194
Тензор 26
— антисимметричный 30
— Вейля 53, 54, 98, 102
— вращения 95
— кручения 45
— метрический 47
— параллельный перенос 43
— поперечного сдвига 96
— расхождения 96
— Римана (кривизны) 46, 47, 52—54,
93, 98, 99
— — на гиперповерхности 59
— Риччи 47, 52, 98
— свертка 28
— симметричный 30
— сложение 27
— умножение на скаляр 27
— фундаментальный второй 113
— — первый 113
— энергии-импульса 78—80, 102—НО
-------идеальной жидкости 83
—-------------канонические формы (типы)
102, 103
--- — скалярного поля 80, 81
—-------------- электромагнитного поля 81
Теорема Бпркхофа 413
— Гаусса 62
— Стокса 35
— — обобщенная 36
Теория относительности общая 68, 72,
403
---специальная 68, 72, 74, 133
Топология 19, 220
— Александрова 219, 220
— лоренцевых метрик 220, 280
— открытая 221
— пространства кривых 230, 231, 238
Точка конечная 205, 209, 226
— предельная 205, 207
— сопряженная поверхности 113, 131
---точке 111, 112—114, 125, 130
Уравнение Гаусса 59
— Кодацци 59
— Райчаудхури 97, 98, 101, 111
— Якоби (девиации) 93, НО
Уравнения поля (постулат) 90
Уравнения Эйлера — Лагранжа 78
— Эйнштейна 87, 88, 89, 131, 252
-----приведенные 255, 270—276
Условие, выделяющее будущее 215,
216
— времениподобного схождения 108,
319, 398
— изотропного схождения 108, 109,
319, 398
— Липшица 19, 70, 238
причинности 211, 212—216, 241,
398
— сильной причинности 215, 216—
219, 231—233, 302
— типовое 115, 213, 296, 359
— устойчивой причинности 221
— хронологическое 210, 297
— энергетическое сильное 109, 154,
334, 398
-----слабое 102, 103—105, 334
— энергодоминантности 104, 360
Условия калибровочные 255
— — гармонические 255
Устойчивость решения задачи Коши
281, 334
Форма линейная 25, 56, 57
—• каноническая 60
— фундаментальная вторая 58
1-форма 30
9-форма 30, 34
Функция иа многообразии 23
-------класса Сг (Сг-функция) 23
Черная дыра 351, 352—359, 368—370
-----вращающаяся 362—370
— — слияние 370—373
Шварцшильда радиус 334
Шварцшильдова длина 393
Эйлера характеристика 51, 65
Эйнштейна оператор 255
Эргосфера 185, 364—366, 369
Оглавление
Предисловие к русскому изданию......................................5
Предисловие.........................................................7
Глава 1. Роль тяготения.............................................9
Глава 2. Дифференциальная геометрия................................18
2.1. Многообразия..............................................19
2.2. Векторы и тензоры.........................................23
2.3. Отображение многообразий..................................31
2.4. Внешнее дифференцирование н производная Ли................34
2.5. Ковариантная производная и тензор кривизны................40
2.6. Метрика...................................................47
2.7. Гиперповерхности .........................................55
2.8. Элемент объема и теорема Гаусса...........................60
2.9. Расслоенные пространства..................................62
Глава 3. Общая теория относительности..............................68
3.1. Пространственно-временное многообразие....................68
3.2. Материальные (негравитационные) поля......................71
3.3. Лагранжева формулировка...................................77
3.4. Уравнения поля............................................84
Глава 4. Физический смысл кривизны.................................91
4.1. Времениподобные кривые....................................91
4.2. Изотропные кривые.........................................99
4.3. Энергетические условия...................................102
4.4. Сопряженные точки ........................................ПО
4.5. Вариация длины дуги......................................116
Глава 5. Точные решения...........................................132
5.1. Пространство-время Минковского...........................133
5.2. Пространство-время де Ситтера 1-го и 2-го рода........140
5.3. Пространство Робертсона—Уокера...........................151
5.4. Пространственно-однородные космологические модели........160
5.5. Решения Шварцшильда и Райсснера — Нордстрема.......167
5.6. Решение Керра............................................180
5.7. Модель Вселенной Гёделя..................................187
5.8. Пространство Тауба — НУТ.................................190
5.9. Прочие точные решения....................................198
Глава 6. Причинная структура......................................200
6.1. Ориентируемость..........................................201
6.2. Причинные кривые....................................... 202
Оглавление
431
6.3. Ахрональные границы........................................207
6.4. Условия причинности...................................... 210
6.5. Области Коши...............................................224
6.6. Глобальная гиперболичность.................................229
6.7, Существование геодезических................................236
6.8. Причинная граница пространства-времени.....................241
6.9. Асимптотически простые пространства........................245
Глава 7. Задача Коши в общей теории относительности.................251
7.1. Характер задачи ...........................................252
7.2. Приведенные уравнения Эйнштейна............................253
7.3. Начальные данные ..........................................256
7.4. Гиперболические уравнения второго порядка..................259
7.5. Существование и единственность решения задачи Коши для урав-
нений Эйнштейна для пустого пространства....................270
7.6. Максимальное развитие и устойчивость.......................276
7.7. Уравнения Эйнштейна при наличии материи....................282
Глава 8. Сингулярности пространства-времени.........................285
8.1. Определение сингулярностей.................................285
8.2. Теоремы о сингулярностях...................................291
8.3. Описание сингулярностей....................................307
8.4. Характер сингулярностей....................................316
8.5. Захваченная неполнота......................................321
Глава 9. Гравитационный коллапс и черные дыры.......................333
9.1. Коллапс звезды.............................................333
9.2. Черные дыры.............................................. 343
9.3. Конечное состояние черной дыры . ..........................359
Глава 10. Начальная сингулярность во Вселенной......................387
10.1. Расширение Вселенной......................................387
10.2. Природа и проявление сингулярностей.......................400
Приложение А (Пьер Симон Лаплас)....................................406
Приложение Б. Сферически-симметричные решения и теорема Биркхофа 410
Обозначения......................................................415
Литература.......................................................419
Предметный указатель.............................................426
Уважаемый читатель!
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и др. просим присылать по адресу:
129820, Москва, И-110, ГСП, 1-й Рижский пер., дом 2,
изд-во «Мир».
С. Хокинг, Дж. Эллис
КРУПНОМАСШТАБНАЯ СТРУКТУРА ПРОСТРАНСТВА-ВРЕМЕНИ
Редактор Л. В. Самсонеико. Художник П. М. Пучков
Художественный редактор В. М. Сафаров
Технический редактор Т. А. Максимова Корректор Н. И. Баранова
Сдано в набор 28/Х 1976 Подписано к печати 5/V 1977. Бумага тип. № 2 60X90716— 13,5 бум. л.
27 печ. л. Уч.-изд. л. 26,64. Изд № 27/8446. Цена 3 р. 40 к. Заказ № 381.
Издательство «Мир», Москва, 1-й Рижский пер.. 2
Ордена Трудового Красного Знамени Ленинградская типография М 2 имени Евгении
Соколовой Союзполиграфпрома при Государственном комитете Совета Министров СССР
ио делам издательств, полиграфии ц книжной! торговли
198052, Ленинград, Л-62, Измайловский проспект, 29