УЧЕБНОЕ ПОСОБИЕ
.
L для ВЫСШИХ УЧЕБНЫХ ЗАВЕДЕНИЙ
'1

r I .
u /
o


 IIШ
{ - I
..Q


:EJ у:
.....;,. (.
rz1 ..
t:: -l /f?",t:/I3
U :f;':?


:, vo""
 \
f%
\

/?)



 1
\ '}::


КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ ПРОЦЕССОВ В ПАКЕТЕ


IOPJIII31 ЛИ"ИI--lшеКОN с. В. Пор ш не 8


I




ББК 32.8
П 60
Поршнев С. В.
П60 Компьютерное моделирование физических процессов в па кете
MATLAB.  М.: rорячая линия  Телеком, 2003,  592 с., ил.
ISBN 5-935171287.
КНИI'а посвящена обучению основам компыотсрноrо МОДСJ1ИРОU;lНИЯ
фИЗИ'IССКИХ процессов, Каждая rлава содержит теоретический матсриал,
описание математических методов, используемых при рещCIIИИ соответст,
вующих задач, и задачи для самостоятелыюrо реШСllИЯ. 13 качсстве базо'
Boro проrрамшоrо проду".а использустея пакет MATLAB,
ДЛЯ студентов вузов, обучающихся по специалыюстям математика.
информатика. физика. может быть полезна для ПРСllодавателей COOTBeTCT
в)'ющих дисшшлин. СПСllиалиетов,
ББК 32.8
Адрес 113дательства вИнтернет WИ(W. TECHBOOK.RU
e'l1lQil: l'аdiоsЫ @тfu,nef.rи
у чебное издание
Поршнев Серrей Владимирович
Компьютерное моделирование фюических процессов
в па кете МА TLAB
Учебное пособие
Коррсктор В. С. Морозова
Обложка художника В. r. СИТlIIlкова
ЛР N 071825 от 16 Iapтa 1999 r.
ПОДllllСallO в псчать 14.04.04. Формат 60x84/L6.
УСЛ. IIСЧ. :1. 37.5. Тираж 2000 экз. ИЗ.1. N 128
Зак, [576.
Отпечатано с rOTo8blX диапозитивов в 000 ПФ .Полиrрафист>,
160001, r, Волоrда, ул, Челюскинцев, 3,
тел,; (8172) 72,55,31, 72,60,72
@ Поршнев С. В.. 2003
@ Оформление издательстш\
«rоря чая линия ТелеКОI». 2003
ISBN 593517-128-7
f
i
" .,'
:\
,
'I,( :
'1'
j,
"'1
.},
rлава 1
МОДЕЛИРОВАНИЕ ОТНОСИТЕЛЬНЫХ
ДВИЖЕНИЙ В КЛАССИЧЕСКОЙ
МЕХАНИКЕ
1.1. Введение
в классической механике, для описания механических явлений, в качестве
первоro шara необходимо выбрать ту или иную систему отсчета. В различных
системах отсчета законы движения имеют, вообще rоворя, различный вид. Если
взять произвольную систему отсчета, то может оказаться, что законы движения
даже простых явлений будyr выrлядеть весьма сложно.
для нахождения траекторий относительных движений в классической
механике используется предположение об абсолютности времени во всех
системах отсчета (как инерциальных, так и неинерциальных). Используя
данное предположение, рассмотрим движение одной и той же точки в двух
различных системах отсчета К и K из которых вторая движется относи
тельно первой с произвольной скоростью V(t) = R(t) (R(t)  радиусвектор,
описывающий'Положение точки начала системы координат К/относительно
системы отсчета К). Будем описывать движение точки в системе К/ радиу
COMBeктopOM 1"(1), направленным из начала координат системы К/в TeKY
щее положение точки. Тоrда движение рассматриваемой точки относитель
но системы отсчета К описывается радиусомвектором 1'(1)
1'(t) = 1"(t)+R(t),
а относительная скорость v(t)
v(t) = r(t) = r'(t)+R(t),
(1.1)
(1.2)
rде 1"(1)  скорость точки относительно системы отсчета K R(t)  скорость
движения системы отчета К / относительно системы отсчета К (рис. 1.1).
Таким образом, для нахождения закона движения точки в произвольной
системе отсчета К необходимо:
1) задать закон движения точки относительно системы отсчета -Т</(функ
цию 1"(1);

<!.-!!..п-':'?..!.'!:.!!!!'?!.!..о.Р.5'!!.':!'I:1:ll!!ескux nроцессов в nакете МА ТLAB
. ................................h""'","", 'h'h"...h' ..h.......'
1
I
I
i
i
2) задать закон движения системы отсчета К' относительно системы OT
счета К (функцию R(t);
3) определить закон движения точки относительно системы отсчета К
в соответствии с (1.1).
7:
к
х'
Рис, 1,1, К постановке задачи
об описании относительных
движений
о
х
Возможна дрyrая постановка данной задачи, в которой по известному
закону движения материальной точки r(t) относительно некоторой систе
мы отсчета К и по известному закону движения системы отсчета К' относи
тельно системы отсчета К. R(t) требуется найти закон движения материаль
ной точки в системе отсчета К' r'(t). Очевидно, что решение задачи в такой
постановке дается следующими формулами:
r'(t) = r(t) R(t), (1.3)
v'(t) = r'(t) = r(t) R(t) . (1.4)
Несмотря на то, что решение задачи о нахождении траектории относи
тельноrо движения исчерпывается формулами (1.1)  (1.4), построение KOH
кретных траекторий движения без использования ПК может вызвать опре
деленные трудности, а в ряде случаев привести к неправильным результа
там. Ниже мы рассмотрим две поучительные, на наш взrляд, задачи,
соответствующие обеим постановкам, и продемонстрируем в ходе их реше
ния возможности, заложенные в пакет МА ТLAВ дЛЯ построения rpафиков
функций, зависящих от одной переменной.
1.2. Построение орбиты Луны
в rелиоцентрической системе отсчета
С точки зрения кинсматическоrо подхода эта задача соответствует IIер
вой постановке задачи об относительном движении. В rелиоцентрической
системе отсчета (система к) Земля движется по окружности радиуса R I =
= 1.496,108 км (период обращения ТI = 3,156,107 с), Луна в свою очередь
4
';
.l.:..!40дел!!Е..ов'!.'.,!!:'..!!!!!.IIO!!,,!!':!IЫIЫХ дви.!.ий в k-!!.'!..СCUЧ-:СКО!!.!!-'=!l!!UТ:::
движется Boкpyr Земли (система К') по окружности радиуса R2 = 3.844.105
км (период обращения Т2 = 2,36,106 с. Как известно [1,2], при движении Ma
териальной точки по ОКРYJКности радиуса R с постоянной yrловой CKOpO
стью ro координаты радиусавектора, проведенноrо из начала координат к
текущему положению точки, меняются по закону
 (R cos(w t +- <7'0 )] R СО{ 2т" t +- <7'0)
R(t) = = (1.5)
R sin(w t +- <7'0) R sine;- t +- <7'0 )
rде <7'0  начальная фаза, характеризующая положение частицы в момент
времени t = О, которую в дальнейшем мы будем полаraть равной нулю. За
меняя в (1.5) R на R1, R2 и подставляя в (1.1), получаем зависимость радиуса
вектора Луны в rелиоцентрической системе координат от времени:
R2 со{ :t)+-Rl со{  t)
. (2") R . (2" )
R2sш Т2 t +- lsш 1j.t
 (X(t ))
r(t)= y(t) =
(1.6)
;
'}
Выражение (1.6) задает орби'I)' Луны (у = y(x(t») в параметрической
форме, rде параметром является время. Предваряя дальнейшее чтение пара
rpафа, rде орбита Луны построена с использованием пакета МА ТLAВ, pe
комендуем качеСТВI;ННО оценить ее вид.
Для построения искомой орбиты в пакете MAТLAВ в режиме непосред
cтвeHHoro вычисления необходимо передать пакету следующую последова
тельность команд. (В пакете МА ТLAВ часть строки, следующая за знаком
% является комментарием и при самостоятельном вводе команд может быть
опущена.)
» Rl=1.496*10Л8; % задание численноrо значеIfия радиуса
% орбиты Земли
» Тl=3.156*10Л7; % задание численноrо значения периода
% обращения Земли BOкpyr Солнца
» R2=3.844*10Л5; % задание численноrо значения радиуса
% орбиты Луны
» Т2=2.360*10Л6; % задание численноrо значения периода
% обращения Земли BOKpyr Солнца
» t=O:TlII000:Tl; % задание дискретной переменной, изменяющейся
% от О до тl с шarом Тl/I000
!
i

I
I
I
I
;)
1,'
5

,/
J-'!!..'!.'!ют!!!!!!!!.!!делUl!!!..ваlluе !!!!!3UЧ':.. '!!?'i,=.!'!..'!.e.'!'! М'!.!....L!:._,ш
% вычисление координат радиусавектора Земли
» Xz=Rl *cos(2*pi*tffl);
» Yz=Rl *sin(2*pi*tffl);
% вычисление координат радиусавектора Луны в системе координат,
% связанной с Землей
» Xm=R1*cos(2*pi*tff2);
» Ym=R,-*siп(2*рi*tff2);
% вычисление координат радиусавектора Луны в rелиоцентрической
% системе координат
» Xotn=Xz+Xm;
» Yotn=Yz+Ym;
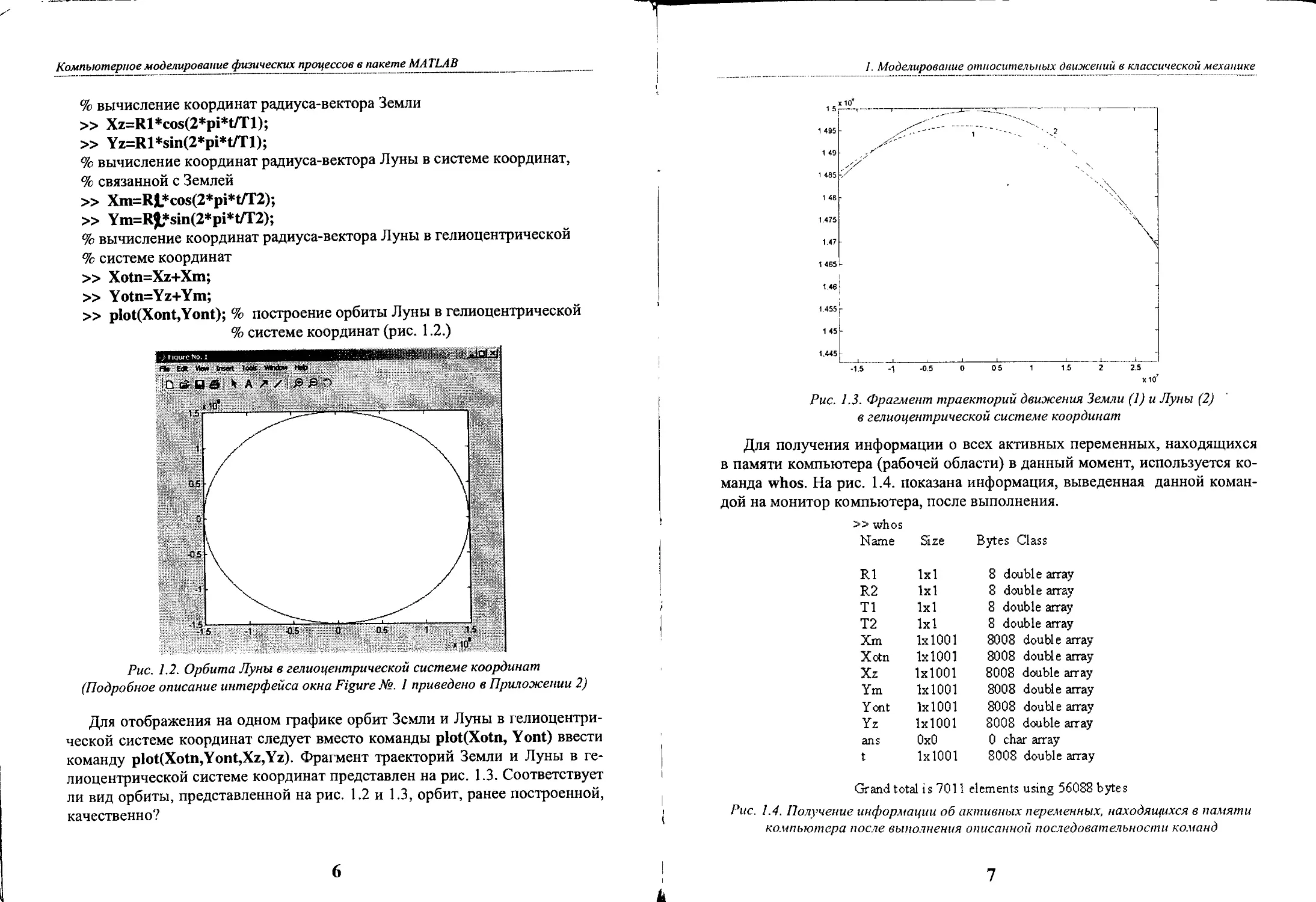
» plot(Xont,Yont); % построение орбиты Луны в rелиоцентрической
% системе координат (рис. 1.2.)
Рис. 1,2, Орбита Луны в zелиоцентрической системе координат
(Подробное описание интерфейса окна Figure Ng, 1 приведено в ПРWlOжении 2)
Для отображения на одном rpафике орбит Земли и Луны в rелиоцентри
ческой системе координат следует вместо команды plot(Xotn, У ont) ввести
команду plot(Xotn,Yont,Xz,Yz). Фраrмент траекторий Земли и Луны в re
лиоцентрической системе координат представлен на рис. 1.3. Соответствует
ли вид орбиты, представленной на рис. 1.2 и 1.3, орбит, ранее построенной,
качественно?
6
l
!
J:!'!.<:'.:!.?I!.'!.'.'!:!..:.!!.п:.II()':'IтеЛЬ1I);е.I.,!!!._-'!!..:'аlluке
15"0,:-:::::-==,- c.... _ш ШТШ1
1495 --::::::.  ,   ,....-..., ,2
/
149 r
" / I
1 485 ;;/ 
148
1.475
1.47
1 465
1
1.46f
I
1.455r
145L
1щL
,1.5 -\
05
1.5
,
2.5
х 107
-0.5
Рис, 1.3. ФраZAtеюn траекторий движения Земли (1) и Луны (2)
в zелиоцеюnрической систе.ме координат
Для получения информации о всех активных переменных, находящихся
в памяти компьютера (рабочей области) в данный момент, используется KO
манда whos. На рис. 1.4. показана информация, выведенная данной KOMaH
дой на монитор компьютера, после выполнения.
» whos
Name Size Bytes Class
Rl lхl 8 doub1e ал-ау
R2 lхl 8 dou ь1 е ал-ау
Тl lхl 8 double ал-ау
Т2 lхl 8 double ал-ау
Хm lх 1 00 1 8008 double ал-ау
Xotn lх 1 00 1 8008 doubl е а!ТЭ.у
Xz lхl001 8008 doub1e ал-ау
Уm lх 1 00 1 8008 double ал-ау
Yont lх 1 00 1 8008 double ал-ау
Yz lхl00l 8008 doub1e ал-ау
ans ОхО О char ал-ау
t lхl001 8008 doub1e ал-ау
Grand total is 7011 elements using 56088 bytes
Рис. 1.4, Получение информации об активных переменных, находяUfUХСЯ в памяти
компьютсра после выl1л//енияя от/санной последовательности ко.нанд
7


.l!:YM--'l_Ы?'.'.'l?fJ.!t..?I?.?I?l!!!.о.а.'Il!I?Р.l!'!.ч-.I?:'.'?:,Р"?"1j_е::?..I!.е.",-I?NJ..1.Т1:.f!
,(, ) = l ]  вектор скорости Л уны относительно Земли.
Для визуализации искомой зависимости необходимо выполнить сле
дующую последовательность команд:
» Rl=1.496*10Л8; % задание численноrо значения радиуса
% орбиты Земли
» Тl=3.156*10Л7; % задание численноrо значения периода
% обращения Земли BOкpyr Солнца
» R2=3.844*10Л5; % задание численноrо значения радиуса
% орбиты Луны
» Т2=2.360*10Л6; % задание численноrо значения периода обращения
% Земли BOKpyr Земли
» dt=Tl/2000;
» t=O:dT:Tl; % задание дискретной переменной, изменяющейся от О
% до т1 с шarом Т1/1000
% вычисление координат радиусавектора Земли
» Xz=Rl *cos(2*pi*t/Тl);
» Yz=Rl *sin(2*pi*t/Тl);
% вычисление координат радиусавектора Луны в системе координат,
% связанной с Землей
» Xm=Rt:cos(2*pi*t/Т2);
» Ym=Rsin(2*pi*t/Т2);
% вычисление координат радиусавектора Луны в rелиоцентрической
% системе координат
» Xotn=Xz+Xm;
» Yotn=Yz+Ym;
% вычисление значений проекций скорости движения Земли на
% соответствующие координатные оси в rелиоцентрической
% системе координат
» Vx=diff(Xz)/dt;
» Vy=diff(Yz)/dt;
о/с вычисление значений проекций скорости движения Луны
Я на соответствующие координатные оси в
О/С системе координат, связанной с Землей
» vx=diff(Xm)/dt;
» vy=diff(Ym)/dt;
'lc вычисление значений функции, задаваемой выражением (1.7)
I
I

10
!
&.
!:... Модel!'!'ров:''!.='.'.':'.!!.'!!:3I!..вuжеll,!!!.! класcuче:...<!!!!=.а.!!.'!..:
» V=(Vx. Л2+ Vy. Л2). ЛО.5-(Vх. *п+ Vy. *vy)J(Vx. Л2+ Vy. Л2). ЛО.5;
» tl::O:dt:Tl-dt;
% построение траектории движения Луны и траектории движения
% Земли в rелиоцентрической системе координат
» subplot(2,1,1); plot(Xm, Уm);
% построение rpафика функции, задаваемой выражением (1.7)
» subplot(2,1,2); plot(t1,V);
Результаты выполнения приведенной последовательности команд пред
ставлены на рис. 1.6. (R2 =3,844.107 км), рис. 1.7. (R2 =3,844.105 км).
Анализ зависимостей v оmн (t), представленных на рис. 1.6 и ].7, позволя
ет объяснить причину отличий орбит. Функция D(t) при R2 =3,844.]05 км
всеrда положительна, т. е. Луна всеrда движется в направлении движения
Земли и петли не образуются. При R2 = 3,844.]07 км величина D(t) прини
мает отрицательные значения, т. е. существуют моменты времени, в KOTO
рые Луна движется в направлении, противоположном направлению движе
ния Земли, а потому орбита имеет петли.
Рис, /,6. Траектория движения ЛУНЫ в zелиоцентрической системе координат при
R2 =3,844 ,/ 07 /Ш (верхняя зависимость), завиСUJ\fость мzновенных значений
разности .нежду модулем скорости Земли и nроекцией скорости движения JlYHbl
на liаправ,7ение скорости двuже//uя Зем1U
11

!!:!м._'?.!!'.:E!.!.oe м!!.!!..е::.!'.I?!!..!.:.и-:'.р!!.?!.Iч.:..,!!пJ!!!.!i:!!!.!...!!'5...е...n:.:А!..А.!!:_1.1!.ШШ_ШШ. ШШ
Отметим, что постоянные в пакете МА ТLAB трактуются как матрицы
размерности 1 х 1, Для сохранения значений переменных, находящихся в раш
бочей области, используется команда save имяфайла или функция
sаvе(имяфайла), Для заrpузки ранее проведенноrо сеанса работы с паке
том МА ТLAB используется команда lоаd(имяфайла) или функция
lоаd(имяфайла). Команда save имеет несколько различных форм:
save имяфайла  записываются все переменные рабочей области
в файле имя  файла с расширением ,mat;
save имяфайла Х  записывается только значение переменной Х;
save имяфайла Х У Z  записываются только значения переменных Х,
УиZ.
После записи команды save также можно указывать ключи, уточняющие
формат записи файлов:
шmаt  двоичный МА Тшформат, используемый по умолчанию;
шаsсii  ASCII формат единичной точности (8 цифр);
-ascii -dоubIе  ASCII формат двойной точности (16 цифр);
-ascii -dоubIе шtаЬs  ASCII формат двойной точности с разделителем и
метками табуляции;
V 4  запись МА Т-файла в стандарте версии МА ТLAВ 4.0;
-append  добавление в существующий МАТшфайл,
Приведенный выше протокол команд можно сохранить в виде файла
на диске для последующеrо анализа решения или использования как OCHO
вы проrpаммы сценария, используемой при решении подобных задач, кош
мандой diary имяфайла или функцией diary (имяфайла). Например,
для записи в файл МООП.m протокола приведенных выше команд необходи
мо ввести следующую команду:
» diary Мооп.m % открытие файла для сохранения протокола,
Затем каждая последовательно выполненная команда будет заноситься в
файл МООП.m, Для приостановки записи выполняемых команд в файл исш
пользуется команда diary off. Отметим, что данная команда также записы
вается в файл Мооп.m, Начиная с версии МА TLAB 6.0 и выше, данный на-
бор команд можно выполнить автоматически, набрав в командной строке
имя файла Мооп и нажав клавишу <Enter>,
Созданный нами документ позволяет расширить задачу и посмотреть,
какой будет орбита Луны при различных значениях радиуса и периода об
ращения, Например, на рис, 1,5 представлена орбита Луны в rелиоцеН1РИш
ческой системе координат при r = 3,844'107 км,
8
J
.ш....._..._ш:!!.':!.f!J..!!.I!!.'!!ш.!!.'!!.!'..о!!...."!.'!...ь-i!-е/1<3..I!..Ч::КОЙ !!.:'!!!._
05
--0.5
,
о
1.5
0.5
Рис, /,5, Орбита Луны в zелиоцентрической системе координат
при r = 3,844.107 /см
Сравнивая орбиты Луны, представленные на рис. 1.4 и рис. 1.5, обнару
живаем их существенные отличия. Для объяснения причины этих отличий
/ необходимо сравнить линейные скорости движения Луны в первом и во
втором случае и линейную скорость движения Земли. Так как направление
линейной скорости движения Земли относительно Солнца, как и направле
ние линейной скорости движения Луны относительно Земли, меняются во
времени, оставаясь постоянными по величине, в качестве количественной
характеристики соотношения линейных скоростей движения Луны в Земли
в rелиоцентрической системе координат следует выбрать разность между
модулем линейной скорости движения Земли и проекцией линейной СКОрОш
сти Луны на направление вектора линейной скорости Земли
( )=1"( (V(t)v(t))
v отн t I V t  : (  '
!V t 
(1.7)
(dX(t)]
еде \7(1) = d!!t)  вектор екорост движения Земли оrnОСl<reПоио Солица,
9

!!!.!5!.."!.:Е!!:!!!!.l!.!!I!!..I.':!:.рr:Ч:'!'!!!!!.lJ.:С:о.!!в..!!аке'!!..:fl!..1!.!:.!!....... 
Рис, /,7, Траектория движения Луны в zелиоцентрической системе КDopдиHaт при
R2 =3,844./rt км (верхняя зависимость), зависимость MZHoeeHHblX значений
разности между модулем скорости Земли и проекцией скорости движения Луны на
направление скорости движения Земли
'11
11
I
Задача 1.1
J. Определите предельное значение радиуса орбиты Луны, при котором не
происходит появление петель, Как выzлядит орбита Луны в 2елиоцен
три ческой системе координат в этом случае?
2. Зафиксируйте радиус орбиты Луны и постройте орбиту Луны при раз
личных значениях периода обращения, Что можно сказать о размере
петель в этом случае?
3. В заключение сделаем ряд замечаний по поводу некоторых операторов и
функций, использованных в данном разделе. Обратите внимание на способ
задания дискретных nеременных (векторов) (, t1, Здесь мы использовали
знак: , являющийся одним из важнейших синтаксических знаков nакета
MATLAB, Этот знак, поставленный между двУА-tЯ числами, задает вeK
тор, компоненты котОР020 nринимают значения от меньше20 числа до
большею с ша20М J, Например, оператор х = 0:9 задает целочисленный
вектор х = [О, 1,2,3,4,5, б, 7,8,9]. Oт'vtemuм, что в МАтив также дOnYCKa
ется явное задание вектора с nOA-toЩЬЮ квадратных скобок Если иШ2 uзме
нения дискретноЙ nерелtенной 011Vlичается от единиц, то при ее определе
Illlll следует указывать значение ша2а. аншlO2UЧНО mOA-tу, как это было
сде.7ано выше в llр02ра_шtaх, приведенных в настvящелt разделе,
12
шш......l.:..?!...е.!!!If!о:!.r:!.I!!.:."!.!!.()",с:.':!"!.:3.../!..ь-!.х..в!!.!..1!..'!..!!'!..I:!:I!.!!f!!!!!.I,:!:
4. Так как пакет MATLAB является пакетом, изначально ориентированным
на матричные вычисления, основные объекты, с которыми onepttpyem
пакет, являются векторами и матрицами. При обращении к функции,
например, у = cos(x), 2де х  вектор, значение котОРО20 определено вы
ше, MATLAB проводит вычисления для каждО20 элемента вектора ap
2умента и присваивает их соответствующи-м компонентам вновь соз
даваем020 вектора,
5. Для построения двух 2рафиков на одном чертеже были использованы KO
манда (2,1,1), subplot(2,1,2), позволившие разбить 2рафическое окно на
две отдельные части, В общем случае ко.мандаобращение к данной KO
манде имеет следующий вид: subplot(m,п,p) или subplot(m пр). Здесь
значение m  указывает, на сколько частей разбивается окно по вepти
кали, п  указывает, на сколько частей окно разбивается по 20ризонта
ли, р  порядковый номер подокна, считая слева направо и сверху вниз,
Команда subplot( ) используется как для создания новО20 подокна, так и
для перехода от одН020 подокна к дРУ20МУ, После вызова данной KOMaH
ды появляется команда plot( ) 2рафик и/или 2рафикu в соответствую
щем подокне.
6. ТехНОЛ02UЯ созданuя интерфейса пользователя, nозволяюще20 упростить
процедуру вычислений, описана в Приложении 3,
1.3. Построение орбиты Марса в системе отсчета,
связанной с Землей
с ТОЧКИ зрения кинематическоrо подхода эта задача соответствует BTO
рой постановке задачи об относительном движении. В rелиоцентрической
системе отсчета (система К) Земля движется по окружности радиуса R\ =
1.496.108 км, период обращения Т\ = 365.24 суток, Марс двиrается по эл
липсу, большая полуось KOToporo ам = 2.28.108 км, период обращения Map
са Т м = 689.98 суток, эксцентриситет орбиты е '" 0.093 [3]. Движение Земли
ОПИСывается радиусомвектором R(t), задаваемым выражением (1.5). В свя
зи С тем, что орбита Марса является эллипсом, зависимости x=x(t), y=y(t) от
времени задаются параметрически [4]: .
x() = ам (cos e), (1.8)
y() = ам .Jl  е2 sin  , (1,9)
(()= TM(e'sin), (1.10)
2, Ji'
13
.......

!!.:!.'!.!!.'!l!!.'.Р/'О=-!!.!!.е:!.'!?.!!.!!.'!!=-!Р.!!.l!..с.!5.'.'.I!.!!..'i5,ОВ B..!!aKell1.!.!!..A ТL!!........
I
,1
:111
1'1
11'1
i
:1
.
Полному оборо1)' по ЭШIШIсу соответствует изменеIШе параметра  от О до 21t,
Для построения орбиты Марса необходимо вычислить в одни и те же
моменты времени координаты радиусоввекторов, описывающих положе
ние Земли и Марса в rелиоцентрической системе отсчета, затем в COOTBeт
ствии с (1.3) вычислить координаты Марса в системе отсчета, связанной с
Землей. Запишем эту последовательность действий более четко в виде BЫ
числительноrо алrоритма.
1. Задание интервала изменения параметра .
2. Разбиение интервала изменения параметра  на N последовательных
интервалов.
3. ВычислеIШе для каждоro значения переменной  соответствующих зна
чений времеIШ и координат орбиты Марса х, у соrласно (1.1 О), (1.8), (1.9).
4. Для каждоrо значения времени вычисление координат Земли в COOT
ветствии с (1.5).
5. Вычисление для каждоrо значения времени координат орбиты Марса
в системе отсчета, связанной с Землей.
6. Построение орбиты Марса в системе отсчета, связанной с Землей.
Для построения искомой орбиты в пакете МА ТLAВ в режиме непосред
CТBeHHoro вычисления необходимо выполнить следующую последователь
ность команд.
» Rl=1.496*10Л8; % задание радиуса орбиты Земли
» Тl=365.24; % задание периода обращения Земли BOкpyr Солнца
% в сутках
» Аm=2.28*10Л8; % задание радиуса орбиты Марса
» Тт=689.98; % задание периода обращения Марса BOKpyr Солнца
% в сутках
»Е=О.О93; % эксцентриситет орбиты Марса
» Np=1000; % число точек на один оборот BOKpyr Солнца Марса
»dksi=(2*pi)lNp; % вычисление шаrа D. изменения переменной ;
» ksi=O:dksi:2*pi; % вычисление значений координат вектора ;;
% вычисление значений координат вектора Т; = t(J (формула (1.1 О»
» T=TmI(2*pi)*(ksi-Е*siп(ksi»;
% вычисление MrHoBeHHbIX значений проекции радиусавектора Марса
% на ось оХ (формула (1,8»
» Xm=Am*(cos(ksi)-Е); %
% вычисление MrHoBeHHbIX значений проекции радиусавектора Марса
о/с на ось оУ (формула (1,9»
» Ym=Am*((1-Е. Л2). ЛО.5)*siп(ksi);
14
.....
.'..:?!'Р.?Il!.I<:,!!IIи-.,!!'.Iь.'.:. !!.I'.в...1<!!.Ilи-.е1!..А!Il'IК-
% вьrчислеIШе мrнOBeнныx значеIШЙ проеющи радиусавектора Земли на ось оХ
» Xz=Rl *cos(2*pi*TIТ1);
% вычисление MrHoBeHHbIx значений проекции радиусавектора Земли
% на ось О У
» Yz=Rl *sin(2*pi*TIТ1);
» plot(Xz,Yz,Xm,Ym)
Результаты выполнения приведенной последовательности команд пред
ставлены на рис, 1,8,
х 10'
2 51-TI.
I 
2  /'''/ ,
I // ,
15 r /  ",
1, "  "-
1l, / // "' '
r/.1 \
05 I I \
I I
\ J
\ /
..
-----
', //

J
I
I
--j
о
05\
, \
1  \
I ",
15r 
i
-2 
.J
2.5
/
/
/
/
//
/
j
I
1
2.5
х 108
,
0.5
1.5
,
2
,
1

-1.5
-0.5
о
2
Рис, 1,8. Орбиты Марса и Земли в zелиоцентрической системе координат
Для построения орбиты Марса в системе координат, связанной с Землей,
необходимо выполнить следующую последовательность команд:
» Rl=1.496*10Л8; % задание радиуса орбиты Земли
» Тl=365.24; % задание периода обращения ЗеМJIИ Boкpyr Солнца
% в сутках
» Аm=2.28*10Л8; % задание радиуса орбиты Марса
» Тm=689.98; % задание периода обращения Марса BOKpyr Солнца
% в сутках
» Е=О.О93; о/с эксцентриситет орбиты Марса
15

!!.f!..l:!..'!!!!?'!!f!fJ.!!?'!._А!..?:Лr.P..о!.!!!!=-1!!!!._=:"':!::._'!.!!.f!..t=:"?..I!..!'!..'5..:'!!..e."!..1!:1J!."._ ,,ш .шш
11
'.Ii,
11
1':
11
",1
:11
il
I!I!
!
;
» Np=1000; % число точек на один оборот BOKpyr Солнца Марса
» К=9; % число оборотов Марса Boкpyr Солнца
»dksi=(2*pi)/Np*K; % вычисление шаrа д'; изменения переменной ,;
» ksi=O:dksi:2*pi; % вычисление значений координат вектора ';i
% вычисление значений координат вектора 1j = t(';i) (формула (1.1 О))
» T=TmI(2*pi)*(ksi-Е*siп(ksi));
% вычисление мrновенных значений проекции радиусавектора Марса
% на ось оХ (формула (1,8))
» Xm=Am*(cos(ksi)-Е); %
% вычисление мrновенных значений проекции радиуса-вектора Марса
% на ось оУ (формула (1.9))
» Уm=Ат*«1-Е. Л2). ЛО.5)*siп(ksi);
% вычисление MrнoBeHHЫx значений проекции радиуса-вектора Земли
% на ось оХ
» Xz=R1 *cos(2*pi*Trr1);
% вычисление MrHoBeHHbIx значений проекции радиуса-вектора Земли
% на ось о У
» Yz=R1*sin(2*pi*Trr1);
% вычисление мrновенных значений проекции радиусавектора Марса
% на ось оХ в системе координат, связанной с Землей
» Хоtп=Xm-Xz;
% вычисление MrнoBeHHЫx значений проекции радиусавектора Марса
% на ось о У в системе координат, связанной с Землей
» Уоtп=Уm-Уz;
»plot(Xotn,Yotn,.... % визуализация орбиты Марса
Xotn(1),Yotn(1),... % визуализация начальноrо положения Марса
'ks' ,... % режим рисования одних маркеров
'MarkerEdgeColor' ,'Ь' ,... % задание цвета rpаницы маркера
'MarkerFaceColor' ,'g' ,... % задание цвета закраски маркера
'MarkerSize' ,5); % задание размера маркера
Результаты выполнения приведенной последовательности команд пред
ставлены на рис, ] .9.
Отметим, что в пакете МА ТLAB имеются возможность продемонстри
ровать движение Марса в системе координат, связанной с Землей, в дина-
мике, Для этоrо достаточно заменить команду plot( ) командой
comet(Xotn,Y otn).
16
,..!Jo.:!'?:l!и-!!.й-с:!I!!..=-?,,!!I!'?:.!!'!!=л.ы
,ьI,.,ви-IuI;_вc...Cl!..."!.:/("?,,q =-:!.'I!,=-
х 10'
41 'т 'T--' ''-Т-''-Т-'-''T -- 'Ш'Т
:r:'jO3::C::,
/i)/(. // '7(" ,---\\--"\'\"\>,
1 !/ / .' ! /_-'-., 1, ,J--,--,.I", \ \ \'\
'11 '1 /'1 ,/, \ ,,'-../ " " 1'. ! -- \ , , '\
{I I I \ ./'\ \.; ....... " i \ I \ i \\
r v \/ \/ \ ':' / '. ;' \1 \1' I
0\\ 1\ (\ (".." //<--._<__, ,c;.. \, /'\ /\1 /1) 11
\\1\ .\! ! 'f' ,/ / ( . / " J 1/
1 V\' i '\. ; '..----+--/ /-,  - '-1 1/ '.'!; i!
 \. \'.... \"""'- 1 i \<; j ! /( //1 //:;
\''" ' " .. " J I /, ./ /'//
-2 '-,\,'\__' ':..':...._ />L,_  ",// //// /
'\,\, \ '.'.'. '--./--- /' /> .' /.:;/ J
,,--" , """'''''''''''''7L' .......;,:""' /::.../;/
L",,"c::: '---"'" / ,/' /",/--:,.<,,-
.3 _ . / ,.-.п /
-"::";::;;,:;;;/
.4 -3 .  4". 4
Х 10'
Рис. j,9. Траектория движения Марса в системе координат. связанной с Землей
Еще одной важной характеристикой движения Марса (в первую очередь,
для межпланетных космических полетов) является расстояние между Зем
лей и Марсом s(t), которое определяется модулем радиусавектора, описы
вающеrо положение Марса в системе отсчета, связанной с Землей, Для по-
строения данной зависимости следует выполнить следующую последо
вательность команд:
» Rl=1.496*10Л8; % задание радиуса орбиты Земли
» Тl=365.24; % задание периода обращения Земли ВОкру!' Солнца
% в сутках
» Аm=2.28*10Л8; % задание радиуса орбиты Марса
» Тm=689.98; % задание периода обращения Марса BOKpyr Солнца
% в сутках
» Е=О.О93; % эксцентриситет орбиты Марса
» Np=1000; % число точек на один оборот Марса ВОКру!' Солнца
» К=9; % число оборотов Марса Boкpyr Солнца
»dksi=(2*pi)/Np*K; % вычисление шаrа д'; изменения переменной ;
» ksi=O:dksi:2*pi; % вычисление значений координат вектора ';;
% вычисление значений координат вектора 1j = t(;; ) (формула (1,1 О))
17
...

К...?I!..I!!.ТI:':Е.'!':'!...й-.:'JlfJ..й-.с:!.'.:4:.:.U:.=К-I:.If'.():.=':'I!'!..l!.К--:ТI:'!...fl!..."!/3.. ..
........
I Моде.лuроваlluе оmllосumелыIх двuжеllUЙ в классuчек-i!.:х.3!!!!!,
..........:..........................,.....
» T=Tm/(2*pi)*(ksi-Е*siп(ksi»;
% вычисление мrновенных значений проекции радиусавектора Марса
% на ось оХ (формула (1,8»
» Xm=Am*(cos(ksi)-Е); %
% вычисление мrновенных значений проекции радиусавектора Марса
% на ось о У (формула (1.9»
» Ym=Am*«1-Е.Л2).ЛО.5)*siп(ksi);
% вычисление мшовенных значений проекции радиусавектора Земли
% на ось оХ
» Xz=Rl *cos(2*pi*Ttrl);
% вычисление мrновенных значений проекции радиусавектора Земли
% на ось о У
» Yz=Rl*sin(2*pi*Ttrl);
% вычисление мrновенных значений проекции радиусавектора Марса
% на ось оХ в системе координат, связанной с Землей
» Хоtп=Xm-Хz;
% вычисление мrновенных значений проекции радиуса-вектора Марса
% на ось о У в системе координат, связанной с Землей
» Уоtп=Уm-Уz;
% вычисление мшовенных значений расстояния между Землей и Марсом
» R=(Xotn. Л2+ У otn. Л2). ЛО.5;
» plot(T,R)
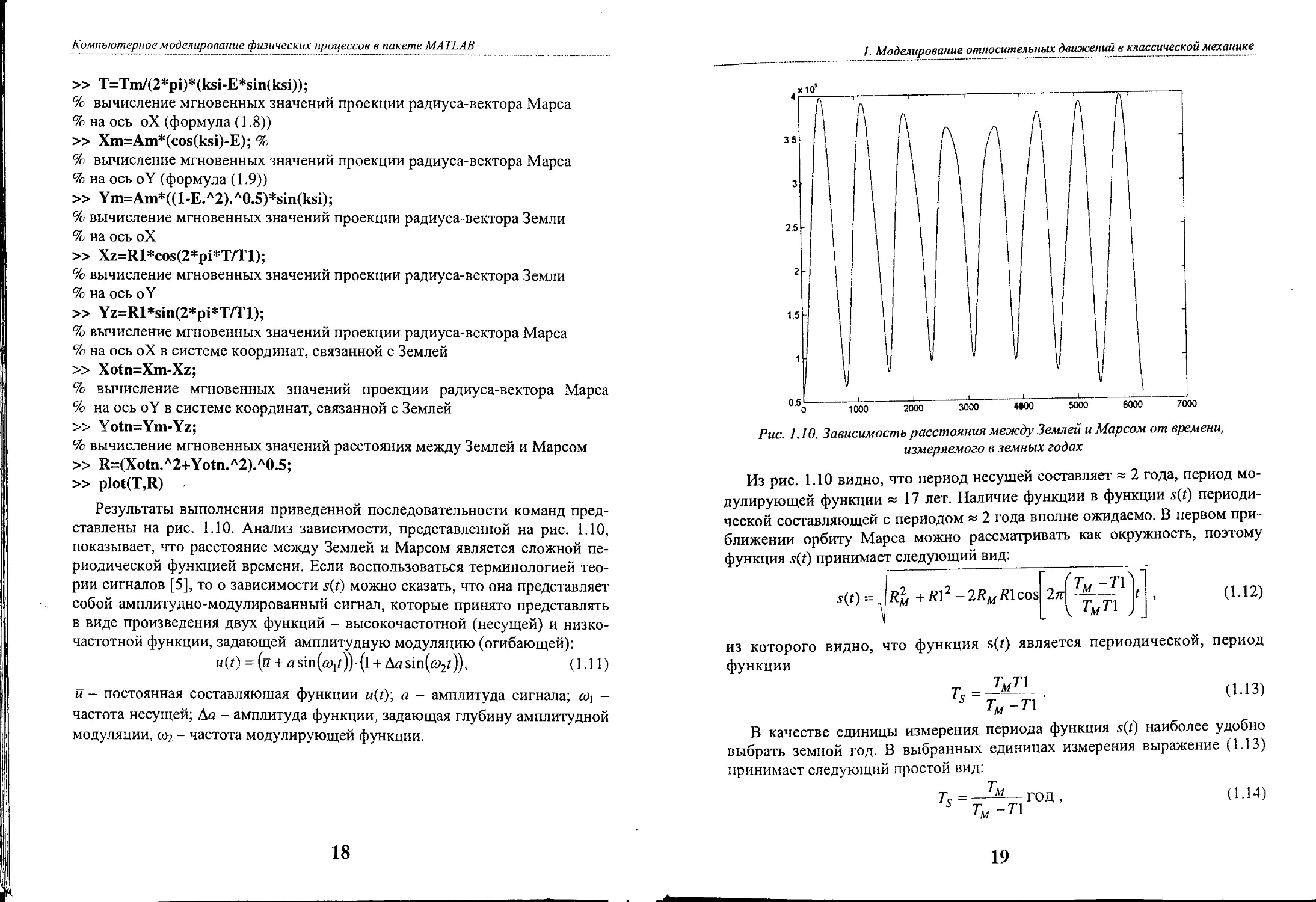
Результаты выполнения приведенной последовательности команд пред
ставлены на рис. 1.10. Анализ зависимости, представленной на рис. 1.10,
показывает, что расстояние между Землей и Марсом является сложной пе
риодической функцией времени. Если воспользоваться терминолоrией Teo
рии сиrналов [5], то о зависимости s(t) можно сказать, что она представляет
собой амплитудномодулированный сиrнал, которые принято представлять
в виде произведения двух функций  высокочастотной (несущей) и низко
частотной функции, задающей амплитудную модуляцию (оrибающей):
H(t) = (и- + а sin(lUlt )), (1 + Да sin(lU2t )), (1.1 1)
х10'
4 (\ (\

3.5 \ (\ \
3 !
\
2.5
I
2 I
\
 
1.5 ' I
\
, , , , ,
0.50 10'00 2000 3000 4t00 5000 6000 7000
Рис, 1.1 О, Зависимость расстояния между Землей и Марсом от времени,
измеряемО20 в земных 20дах
Из рис. 1.10 видно, что период несущей составляет  2 rода, период MO
дулирующей функции  17 лет. Наличие функции в функции s(t) периоди
ческой составляющей с периодом  2 rода вполне ожидаемо, В первом при-
ближении орбиту Марса можно рассматривать как окружность, поэтому
функция s(t) принимает следующий вид:
*) =Rk +R1' 2RMR1'O{2(TMTI}], (1.12)
из KOToporo видно, что функция s(t) является периодической, период
функции
и-  постоянная составляющая функции и(t); а  амплитуда сиrнала; iVI 
частота несущей; Да  амплитуда функции, задающая шубину амплитудной
модуляции, 0)2  частота модулирующей функции.
TMТl
Ts = .... .
ТМ Тl
В качестве единицы измерения периода функция s(t) наиболее удобно
выбрать земной rод, В выбранных единицах измерения выражение (1.13)
принимает следующий простой вид:
ТМ
Ts = rод ,
ТМ  тl
(1.13)
(1,14)
18
19

й-t:..Й-'!1!!!!.t.?:!!.'??...й-с:'!'!.е p'!.'!.,!eCKUX процессов в пакете МА ТLAB
......... -'. ''...h....... .... о.. . ...... .......... """"N..
позволяющий вычислять длительность периода в земных rодах, Для pac
сматриваемоrо случая Т, "" 2,1247 rода.
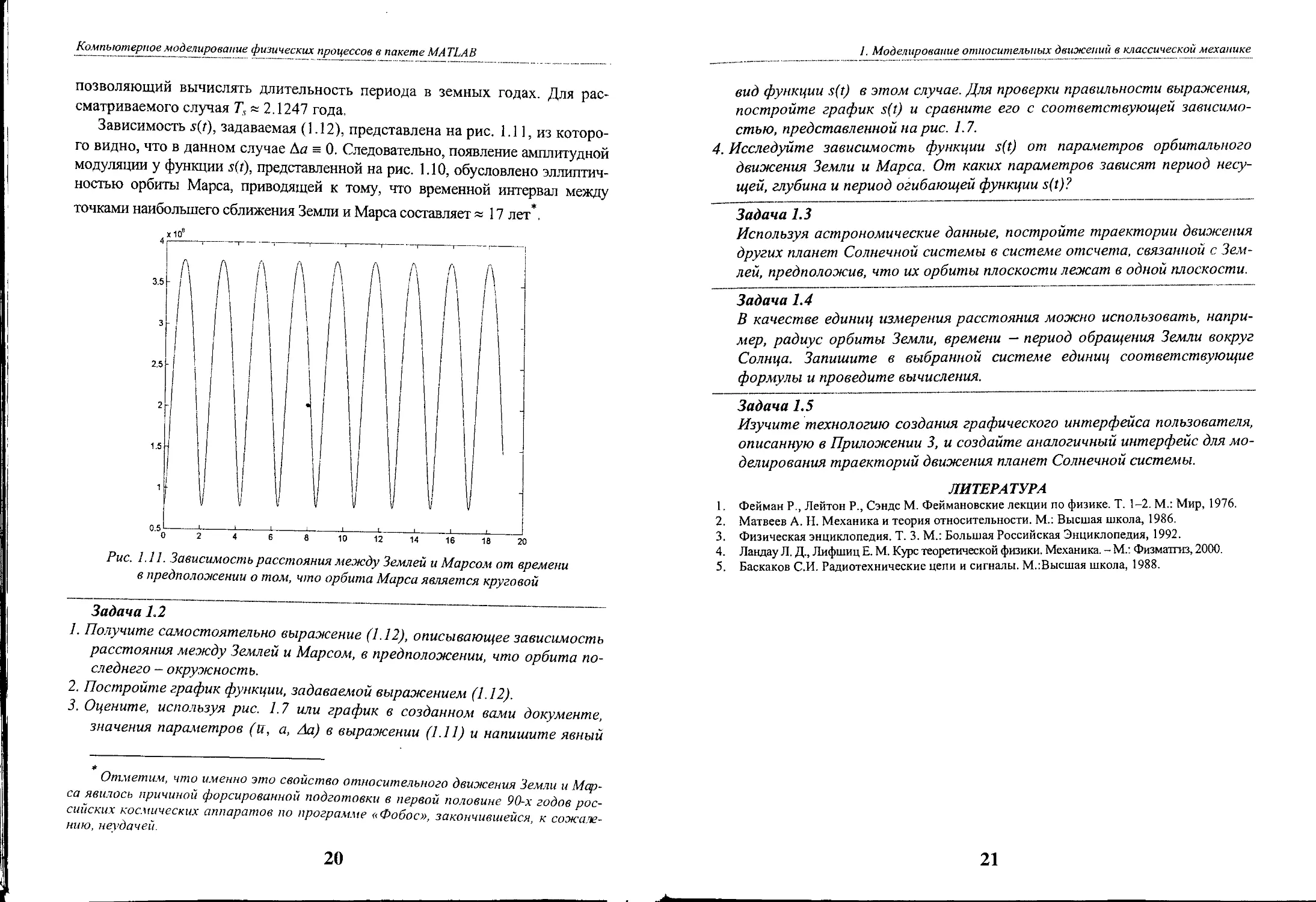
Зависимость s(t), задаваемая (] ,12), пред ставлена на рис. ].] ], из KOTOpO
ro видно, что в данном случае I1а == О. Следовательно, появление амплитудной
модуляции у функции s(t), представленной на рис, ].1 О, обусловлено эллиптич
ностью орбиты Марса, ПрИВОДЯщей к тому, что временной интервал между
точками наибольшеrо сближения Земли И Марса составляет "" 17 лет *.
х 10€
4J; (
"1 i \ r \ 1\
'[ i 11 \ I \
25 I I ,1
,:1 \ 1111
1l i
о 2
'''''''''''''!'i
1! 11 I
11 \ I I ' I \ I
  J  
i
, , J
10 12 14 16 18 20
Рис, 1.11. Зависи.мость расстояния J\lежду Землей и MapcOJ\l от времени
в предполо;жении о том, что орбита Марса является крусовой

.
Задача 1.2 .Ш
1. ПШI}'чите самостоятелыю выражение (1, 12}, описывающее зависимость
расстояния между Землей и Марсом, в предположении, что орбита пo
следнеzo  окружность,
2. Постройте 2рафик функции, задаваемой выражением (1,12),
З. Оцените, используя рис, 1,7 или 2рафик в созданном вами документе,
Значения паРаАlетров (и, а, L1a) в выражении (1,11) и напишите явный
*
От.метим, чт именно это cвйcтвo относительноzо движения Земли и Map
са вll.10CЬ I1Рllчинои форсированно и подсотовки в первой половине 90x содов oc
CUlICKUX кос.It:lческих аппаратов 110 просрамме « Фобос», заКОнчивиlейся к co 
НUЮ, неудачеll. ' /к!
20
............ш.. ... !"!.().:II?"'?'С:!.'!..:'Й-'!!й-5'.'!..,!!::Z!'.III..'I:':.='IJ.I;!lС:ш::с.к-й-:"!.:а"IJ.К-:
вид функции s(t) в этом случае, Для про верки правuльности выражения,
постройте 2рафик s(t} и сравните е20 с соответствующей зависимо
стью, представленной на рис, ],7.
4. Исследуйте зависимость функции s(t} от napa.,wempoe орбиталЬН020
движения Земли и Марса, От каких параметров зависят период Hecy
щей, 2Лубина и период 02ибающей функции s(t)?
.......................
Задача 1.3
Используя астрономические данные, постройте траектории движения
дРУ2их планет Солнечной системы в систе.ме отсчета, связаюlOй с Зе.м
лей, предположив, что их орбиты плоскости лежат в одной плоскости,
Задача 1.4
В качестве единиц измерения расстояния можно использовать, Haпpи
мер, радиус орбиты Земли, времени  период обращения Земли вОКРУ2
Солнца. Запишите в выбранной систе.lI1е единиц соответствующие
формулы и проведите вычисления.
.................
Задача 1.5
Изучите 'техНОЛО2ию создания 2рафичеСК020 интерфейса пользователя,
описанную в Прuложении 3, и создайте анал02ичный интерфейс для MO
делирования траекторий движения планет Солнечной системы.
ЛИТЕРАТУРА
1, Фейман Р., Лейтон Р" Сэндс М. Феймановские лекции по физике, Т, 12. М,: Мир, 1976.
2, Матвеев А, Н, Механика и теория относительности. М,: Высшая школа, 1986.
3. Физическая энциклопедия, Т, 3. М,: Большая Российская Энциклопедия, 1992,
4, Ландау Л, Д,, Лифшиц Е, М, Курс теоретической физики, Механика.  М,: ФИЗМа1тиз,2ОО0.
5, Баскаков С,И. Радиотехнические цепи и сиrналы, М,:Высшая школа, 1988,
21
....

r лава 2
МОДЕЛИ ФИЗИЧЕСКИХ ПРОЦЕССОВ,
ИСПОЛЬЗУЮЩИЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
l-rО ПОРЯДКА
2.1. Моделирование остывания наrретых тел
Природа переноса тепла от HarpeToro тела в окружающий ero воздух
весьма сложна и включает в себя механизмы конвекции, излучения, испаре
ния и теплопроводности. Однако при небольшой разности температур меж
ду HarpeTblM телом и окружающей средой для описания процесса остывания
можно использовать простую модель, впервые предложенную И. Ньюто
ном, В данной одели температура холодильника (окружающей) принима
ется постояннои, а скорость передачи тепла от Harpeтoro тела к холодиль
нику, пропорциональной разности температур между ними. Это утвержде
ние в математической формулировке записывается на языке дифферен
циальных уравнений (ДУ) в следующем виде:
dT
 =r(TT)
dt S '
(2.1)
т'де Т  температура HarpeToro тела, Т"  температура окружающей среды,
r  «коэффициент остывания». Значение «коэффициента остывания» зави
сит от механизма передачи, площади HarpeToro тела и тепловых свойств ca
Moro тела. Знак минус в (2,1) появляется во избежание физически ненаблю
даемои ситуации, коrда Т > Ts. Соотношение (2.1) называется законом теп
лопроводности Ньютона.
Так как в уравнение (2,1) входит только первая производная не известной
функции T(t), ero относят к ОДУ первоrо порядка. В связи с тем, что боль
шое количество физических процессов описывается данным классом ОДУ,
важно научиться находить их решения, По определению решением ОДУ
первоrо порядка, разрешенноrо относительно производной,
dy (
сь: = f х, у(х)) (2,2)
называется дифференцируемая функция у= rp (х), удовлетворяющая этому
уравнеНIIЮ, т. е. такая, что qJ'(x) == f(.\, ер (х)) тождественно на некотором
2. Мй-е).фиЗl!.ч:с}("и..!'рй-цеССО.:.!'СI10ЛЬ3УIOLЦие дифферe1lциа..л.ыlеe уравис!,ия 1 20 поря-дка
участке изменения х ll]. Задача нахождения решения уравнения (2,2), YДOB
летворяющеrо начальному условию rp (ха) = уа, называется задачей Коши,
В общем случае уравнение (2,2) аналитическоrо решения, выражающе
rося через элементарные функции, не имеет, Кроме Toro, даже при наличии
аналитическоrо решения представление ето в rpафическом виде существен
но облеrчает ero анализ. Отмеченные причины являются весьма важным ap
rYMeHToM в пользу нахождения приближенных численных решений ОДУ.
2.2. Алrоритм Эйлера
При численном решении ОДУ вместо исходноrо дифференциальноrо ypaB
нения ищется решение конечноразностноrо ОДУ, Переход к конечно.
разноC11IОМУ уравнению в уравнении (2,2) осуществляется следующим образом.
Вместо точноrо значения производной рассмюривает ее разностный аналоr
dy  у(х.:.: Llx )=.)'(х) , (2.3)
dx Llx
rде L1x достаточно малая величина, Тотда в конечных разностях уравнение
(2.2) принимает следующий вид:
)(,:,:"Llx) у(х) = f(x, у (х)) , (2.4)
Llx
Откуда сразу получаем формулу для нахождения значения функции у(х)
в точке x+Llx
у(х + Llx) = у(х)+ Llxf(x, у(х)). (2.5)
Из (2.5) видно, как построить алrоритм для решения задачи Коши,
1. Задать начальные условия (ха, Уа),
2. Вычислить значение функции у(х) в точке x]=xO+Llx, определяемое BЫ
ражением (2.5)
)'1 = уа + Llxf(xo, Уа) (2,6)
3, Повторить процедуру, описанную в п, 2, и найти значение функции
)'(х) в точке Х2 = хl -+- Llx и т, д, для всех значений переменной х" = ха + iLlx ,
Наиболее удобно записать данный алrоритм в виде итерационной формулы
)'; = Yi.1 + Llxf(XH' У(.\"1 )), i = 1,2,., (2,7)
Данный метод называется методом касательных или методом Эйлера. Из
(2.4) видно, что метод будет давать хорошее приближенlН к «истинному»
значению функции у(х), если приращение арт"умента Llx достаточно мало,
Величина шаrа Llx зависит от конкретной зада,\и. Т'еометрическая интерпре
тация (2.7) приведсна на рис, 2,1, из которото 'rlOНЯТНО, что значение в n.й
23
...

l'
к омп ыо mepll :I?д,?!':Р.?'I!:I:.ф"и-!!!=--:..к-х..?р':>"'iе..с:..в-.lllкете "!.Tli.
точке оценивается по значению функции и ее производной в п  1 й точке,
при этом принимается, что значение производной (т. е, yrол наклона
касательной) на отрезке [Xil; х;] остается неизменным. Не выполнение
данноrо условия приводит к отклонению численноrо решения от точноrо,
которое может быть уменьшено уменьшением &:
у
Yn
,
I
I
Yn..l
РиС, 2.1, rеометрическая
интерпретация метода Эйлера
xn Х
2.3. Проrрамма для решения дифференциальных
уравнений первоrо порядка методом Эйлера
Приступая к разработке проrpаммы вне зависимости от использованноrо
языка проrpаммирования, необходимо разбить всю задачу на последова
тельность независимых заданий, соответствующих аЛI'ОрИТМУ, описанному
в предыдущем разделе, Проrpамма должна состоять из следующих блоков:
1. Задание начальных условий.
2. Задание функции j(x,y(x)).
3, Задание отрезка, на котором Ищется решение, и шаrа интеrpирования.
(Отметим, что на практике оказывается более удобным задавать не шаr ин
теrpирования, а количество интервалов, на которые разбивается отрезок ин
теrpирования, а затем вычислять значение шarа),
4. Вычисление координат точек, в которых ищется решение дифферен
циальноrо уравнения,
5, Решение уравнения (2.2) методом Эйлера.
6. Вывод результатов.
Для примера рассмотрим решение задачи Коши дЛЯ ОДУ
, ?
y=y+x
с начальным условием у(О) = 1,
Для решения поставленной задачи в пакете МА ТLAB потребуется соз
даIlие двух файлов, называемых ш..файлами, потому что имена этих файлов
имеют вид <ИМЯ>,m, Отметим, что большая часть времени пользователя
24
2, Модели физических процессов, испОЛь-!?':'iеРР:l!...е:'.!!.':!...а:!.Ыlье..!.!!..авl/:!I!!3...-:!:?... пop!!.к-..
...............
пакета МА ТLAВ состоит в создании, редактировании и выполнении ш
файлов. В пакете МА ТLAB существуют два вида файлов: файлы
проrpаммы и файлыфункции. Файлыпроrpаммы состоят из последова..
тельности обычных операторов пакета MAТIJAB. Примером проrpаммы яв
ляется, например, файл сценария, содержащий последовательность команд,
выполненных в предыдущем разделе при моделировании относительных
движений. Переменные, используемые в проrpамме, являются rлобаль
ными  они изменяют значения переменных с аналоrnчным названием в pa
бочей области текущей сессии. Файлыфункции содержат описания специ
фических функций, созданных пользователем для решения конкретной за
дачи. Они дают возможность пользователю фактически расширить
возможности MATLAB, поскольку имеют тот же статус, как и дрyrие функ
ции пакета.
Любой модуль, содержащий функцию, возвращающую один выходной
параметр, имеет следующую структуру:
function var = паmеfuпсtiоп(списокпараметров)
% Комментрии
Блок команд, реализующих вычисление функции
var == выражение; % данная строчка вводится, если функция
% возвращает результат вычислений
Свойства mфайла, содержащеrо mфункцию,
1. mфайл начинается с объявления типа function, после KOToporo указь
вается имя переменной, являющейся параметром, возвращаемым функциеи,
имя самой функции и список формальных параметров, передаваемых
в функцию при ее вызове.
2. Если последняя строка функции имеет вид var == выражение, то в Ka
честве значения функции возвращается значение выражения занесенноrо
в переменную var.
З. Все переменные, используемые в теле функции, являются локальными
переменными, т. е. их определение действует только внутри данной функции.
4. Для использования rлобальных переменных их список приводится
В строке, предваряющей блок проведения вычислений:
function var = паmеJuпсtiоп(списокпараметров)
% Комментрии
global varl, var2, var3 % объявление rлобальных переменных
Блок команд, реализующих вычисление функции
var = выражение; % данная строчка ВRОДИТСЯ, если функция
% возвращает результат вычислений
25
...

l!..,?АlпЬ?.'!'!!Р.!.?!!..'о.л..!!Й-.r::''!!:Ф.!=!.Р'?н:LЙ-. «!1r::=rrl:1J!:.:!!!................
5. Функция является самостоятельным проrpаммным модулем, взаимо
действующим с дрyrими проrpаммными модулями через входные, BЫXOД
ные и rлобальные переменные.
6, В файле функции допускаются комментарии, начинающиеся симво
лом%.
7, При вызове файлафункции сначала происходит ero компиляция, а за
тем исполнение, Машинный код mфункции хранится в рабочей области
пакета MATLAB.
8. Обращение к функции осуществляется указанием ее имени и значений
переменных, перечисленных в списке формальных параметров:
имя  переменной == namefunction( список  параметров )
namefunction( список  параметров )
Любой модуль, который содержит функцию, возвращающую несколько
выходных параметров, имеет следующую структуру:
function [var1,var2,...] = патеfuпсtiоп(списокпараметров)
% комментарии
Блок команд, реализующих вычисление функции
varl == выражение1;
var2 == выражение2;
var3 == выражение3;
Обращение к функции, возвращающей несколько выходных параметров:
[varl,var2,...] = патеfuпсtiоп(списокпараметров)
После этоrо переменные var1,var2,... становятся определенными и их
можно использовать в последующих математических выражениях.
При обращении к функции, возвращающей несколько выходных пара
метров, в виде:
имя  переменной  namefunction( список  параметров )
в переменную имяпеременной возвращается только значение перемен
ной varl.
Создадим, следуя перечисленным выше правилам, функции, позволяю
щие найти численные решения задачи Коши для обыкновеННОl'О ДУ перво
ro порядка, ПервыЙ файл, создаваемый нами файл, будет содержать Функ
цию, стоящую в правой части уравнения, второй  реализацию вычисли
тельной схемы метода Эйлера, Для создания mфайла необходимо
запустить встроенный в пакет МА TLAB текстовый редактор, выбрав после
26
l'
,2, Mo!!!:!'. Р!!!.l!...ч::к-'!!..-пУУ.!j!!,,,?в.:...!!.с:!!.I!!!!:!.ОЩU! дu1!.1!ер:.!!.Н':!...а.!!./!!.!.l!..авlе:.:'?_'!..?!!.1!.'5.С::
овательно следующие пункты меню: File  New  M-File, приемы peдaK
ирования текста в котором аналоrичны любому редактору текстов, рабо
ющему под управлением операционной системы Windows. Затем набрать
та 
во вновь создаваемом mфайле следующии текст:
function F = f(x,y)
% f(x,y)  функция, стоящая в правой части дифференциальноrо
% уравнения
F = x-уЛ2;
и сохранить ero на жестком диске под имене f.m. 
Далее аналоrичным образом создаем фаил, содержащии следующие KO
мандЫ, реализующие метод Эйлера:
function [Х, Y]=Euler(yO,xO,x1,N)
% функция, возвращающая численные решения
% дифференциальноrо уравнения первоrо порядка
% методом Эйлера
dx=(xl-хО)IN; % вычисление шаrа интеrpирования
% начальные условия
x(l)=xO;
y(l)=yO;
% вычислительная схема метода Эйлера
for i=l:N
x(i+ l)=x(l)+dx*i;
y(i+ 1)=y(i)+dx*f(x(i),y(i»;
end; 
% возвращение результатов вычислении
Х=х;
У=у;
и сохраняем ero на диске под именем Euler.m, Функция Euler возвращает
дВа вектора: Х, У  ве1<ТОрЫ содержащие значения координат узлов сетки,
на которой ищется решение ОДУ, и значения решения ОДУ в данных узлах
соответственно.
После создания файлов f.m и Euler.m, для получения решения ОДУ и
ero визуализации следует в командном окне пакета ввести следующие KO
манды (для добавления новой строки в командном окне МА TLAВ слдует
o,r,HoBpeMeHHo нажимать клавиши Shift и Enter, для выполнения всеи по
следовательности команд нажать клавишу Enter):
» уО= 1 ;
хО = о;
27

...1

!!.':''I1.Р!.IО!:/.?,!!!II!.овCJ.I1!.!.!!. ",_СJ(!l..х.._Р"?__ес.с:,:,в_'l,!J(=-'I1.еIv!..1.?'!::l!.._ш_.___...._ ...._ ш____...
хl = 10;
N = 100;
[x,y]=Euler(yO,xO,xl,N);
plot(x,y)
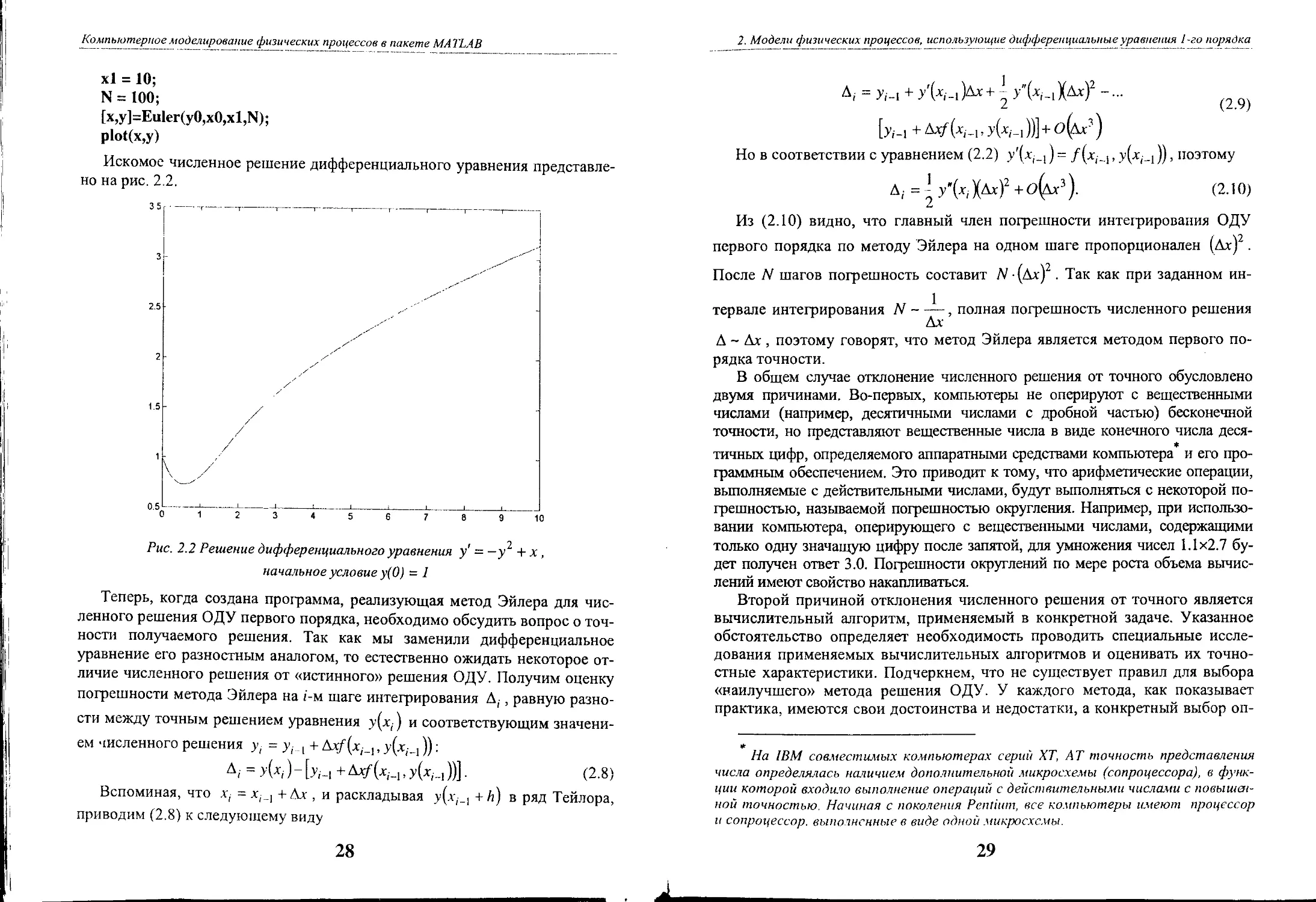
Искомое численное решение дифференциальноrо уравнения представле
но на рис, 2.2.
35r
I
з1-
", .T""""""'. T.-T,.........
/
/
./'
,/
//
"...---
2.5
I
1':11
1I1
I
1
1.5
/
//
/
/
I /
1 \ 
0.5l_,_.Lш...l..,_
О 1 2 3 4
..........l.....
7 8 9 10
6
j
1.
1::
Рис, 2,2 Решение дифференциальноzo уравнения у' = y2 + Х .
начальное условие у(О) = 1
Теперь, коrда создана проrpамма, реализующая метод Эйлера для чис
ленноrо решения ОДУ первоrо порядка, необходимо обсудить вопрос о точ
ности получаемоrо решения. Так как мы заменили дифференциальное
уравнение ero разностным аналоrом, то естественно ожидать некоторое OT
личие численноrо решения от «истинноrо» решения ОДУ, Получим оценку
поrpешности метода Эйлера на i-M шаrе интеrpирования 11; , равную разно-
сти между точным решением уравнения у(х;) и соответствующим значени-
ем 'шсленноrо решения У'. = У. 1+ 11x+(x. }'(х. )),
, ". :J ,l' . ,-1 .
11; = У(Х;)  [УН + Llxf(XH, У(ХН ))] ,
У(ХН + h) в ряд Тейлора,
(2,8)
Вспоминая, что Х; = ХН + l1x , и раскладывая
приводим (2,8) к следующему виду
28
. ...._._:_л.!?=.л--l:1!.!I..:."'_с/(х..!!!!.?.!!е..с.с:.: ..!l..С:.I.?:!.ХI.!l..I!I..=д-!l..Р.rJ!_е!!./lllrl!!..!1!'..= !.P.a...II=,":'!.. :':"0l!:'!.J(,!.
11; = УН + у'(х;ш,)I1x+  У"(Х;шlХI1x)2 ...
2 (2.9)
[Ун +l1xt(XH,Y(XH))]+O')
Но в соответствии с уравнением (2.2) у'(Хjш!) = t(X;__I' У(Х;ш!)), поэтому
11; =! у "(xJI1x )2 + o3 ).
2
(2.1 О)
Из (2,10) видно, что rлавный член поrpешности интеrриропания ОДУ
псрвоrо порядка по методу Эйлера на одном шаrе пропорционален (11x)2,
После N шаrов поrpешность составит N, (11x У . Так как при заданном ин-
1
тервале интеrpирования N  , полная поrpешность численноrо решения
l1x
11  11x, поэтому rоворят, что метод Эйлера является методом первоrо по-
рядка точности,
В общем случае отклонение численноro решения от точноro обусловлено
двумя причинами. Во-первых, компьютеры не оперируют с вещественными
числами (например, десятичными числами с дробной частью) бесконечной
точности, но представляют вещественные числа в виде конечноro числа деся
*
тичных цифр, определяемоro аппаратными средствами компьютера и ero про-
rpaмMHbIM обеспечением. Это приводит к тому, что арифметические операции,
вьmолняемые с действительными числами, будyr выполняться с некоторой по-
rpешностью, называемой поrpешностью окрyrления. Например, при использо
вании компьютера, оперирующеrо с вещественными числами, содержащими
только одну значащую цифру после запятой, для умножения чисел l.lx2.7 бу
дет получен ответ 3.0. Поrpешности окрyrлений по мере роста объема вычис-
лений имеют свойство накапливаться.
Второй причиной отклонения численноrо решения от точноrо является
вычислительный алrоритм, применяемый в конкретной задаче. Указанное
обстоятельство определяет необходимость проводить специальные иссле
дования применяемых вычислительных алrоритмов и оценивать их точно-
стные характеристики. Подчеркнем, что не существует правил для выбора
«lшилучшеrо» метода решения ОДУ, У каждоrо метода, как показывает
практика, имеются свои достоинства и недостатки, а конкретный выбор оп-
"'
На IВМ сов.нестимых компьютерах сериЙ ХТ, А Т точность представления
числа определялась наличием допОЛllителыюй микросхемы {сопроцессора}, в функ-
ции которой входtто выполнение операциЙ с действительными числами с повЫИ;(Ji
ной точностью. НаЧUlIGЯ с поколения Penfillll1, все !-;О.\tIlьютеры U.неюm процессор
u сопроцессор. выполнснные в виде одноЙ ,НИ!-;fIOсхс.НЫ.
29
.J

11 I
11 1
1I I
11 1
'"..!!l..'!!.9!!!?:о.е:!.!'Е?с:.'!!:1!'!':!.:.'5.'!:...'Р.'i:й-.!'с:.К:,!!: /!!A...т..:!:!!.
ределяется требованиями и квалификацией исследователя, а также xapaKTe
ром KOHKpeTHoro решения, который заранее неизвестен, Вот некоторые наи
более типичные вопросы, присущие численным исследованиям. На сколько
точным должен быть ответ? На каком интервале следует искать решения
задачи? Каковы возможности вашеrо компьютера?
На практике точность численноrо решения определяют, уменьшая шаr
интеrpирования ОДУ дО тех пор, пока численное решение не перестанет за
висеть от шаrа при заданно уровне точности, Выбирая величину шarа,
важно помнить, что выбор слишком малоrо шаrа приводит к увеличению
объема вычислений и, соответственно, поrpешности окрyrлений.
Дрyrой не менее важной характеристикой алrоритма является ero устой
чивость. В рЯде задач возникают ситуации, коrда численные результатыI Ha
ходятся в хорошем соответствии с «истинным решением» на коротких ин
тервалах, а на больших интервалах отклоняются от Hero. Это обусловлено
тем, что малые поrpешности алrоритма, MHoroKpaTHo перемножаясь, приво
дят к rеометрическому росту поrpешности. О таком алrоритме примени
тельно к данной задаче rоворят как о неустойчивом алrоритме. Очевидно,
что использование алrоритма, оказывающеrося неустойчивым в данной за
даче, приведет к неверным численным результатам. Поэтому при решении
конкретной задачи проводят специальные исследования, позволяющие oцe
нить точность и устойчивость выбранноrо вычислительноrо алrоритма.
I
I11
'1
2.4. Оценка коэффициента остывания
по экспериментальным результатам
,
!II'
1:
l'
Прежде чем при ступать к исследованию точности численноrо решения
уравнения (2.1), получаемоrо методом Эйлера, найдем оценку «коэффици
ента остывания» r. Для этоrо воспользуемся экспериментальными результа
тами, полученными при остывании чашки кофе [2]. В табл. 2.1 представле
ны результаты измерений температуры чашки кофе в последовательные
моменты времени (температура окружающеrо воздуха 22,0 ОС). Температу
ра реrистрировалась с точностью 0.1 ОС.
1
11
I
II11
I1
Таблица 2.1
Время, мин Т, ос Время, .нин Т, ос
О 83.0 8,0 64,7
1,0 77,7 9,0 63,4
2,0 75,1 ]0,0 62,1
3,0 73,0 1 ],0 61,0
4,0 71,1 12,0 59,9
30
2. Модели физических nроцессов, иС/10льзующие д':!.1).1):Р',!II':!.(J:?!!t>.I.:У.Р1!Iе!:llя.J:?.Il?РJ/дка
. ............ ..... ......... ...... ..................... о.. . .... ш......... ..... .... .....
Вре.\1Я, мин Т, ос Время, мин Т, ос
5,0 69,4 13,0 58,7
6,0 67,8 14,0 57,8
7,0 66,4 15,0 56,6
В связи с тем, что задача обработки экспериментальных данных присут
ствует во всех лабораторных физических практикумах, мы считаем целесо
образным на рассматриваемом примере продемонстрировать методику pea
лизации метода наименьших квадратов (МНК) в пакете МА ТLAB,
Напомним постановку задачи МНК и общий подход к ее решению. Для
HeKoToporo набора данных, заданных таблично, требуется найти формулу,
выражающую данную зависимость аналитически, Поставим здачу так,
чтобы с caMoro начала обязательно учитывался характер исходнои функции:
найти функцию заданноrо вида
y=F(x), (2.1])
которая в точках Xj, Х2"'" Х/1 принимает значения, как можно более близ
кие к табличным значениям Yj, .У2"'" .у 11' Предположим, что приближаю
щая функция F(x) в точках Xj, Х2'" " х" имеет значения
)'1' )'2,"" )'/1'
(2.12)
Требование близости табличных значений Yj,.Y2 ,"', У" И значений
(2,12) можно истолковать следующим образом, Будем рассматривать eOBO
купность значений функции f(x) и совокупность значений (2,12) как KOOp
динаты двух точек пMepHoro пространства. С учетом этоrо задача прибл
жения функции может быть переформулирована следующим образом: наи
ти такую функцию F(x) заданноrо вида, чтобы расстояние между точками
М (у У У ) и М ('\1 Y2 У.) было наименьшим, Воспользовавшись
l' 2'.'.' Il .11' ,..., II
метрикой евклидова пространства, приходим к требованию, чтобы величина
fGi= )'j)2 + (У2 . )'2)2 +... + (У1l  )'11)2 (2.13)
была наименьшей, что равносильно следующему: сумма квадратов
(Уl  )'1)2 + (У2  )'2)2 +"'+(YIl  у/У
(2,14)
должна быть наименьшей,
Окончательно задача приближения функции fi.x) теперь формулируется
следующим образом: ДНЯ функции ,j(x ), заданной табл. 2,1, найти функцию F(x
)определенноrо вида так, чтобы сумма квадратов (2,14) была наименьшей.
31
L

1\
li
! i
l'
1:
1I1
!I
111
1I

Ji?'':!'!.!?''1!!ер'!'()!!.().:f!.1!Р':!I:Ф--и-з.ич-=сих п-l!!!ljе.с:..?'!.='!.l1.т.l!......... .. ..
Эта задача называется приближением функции методом наименьших
квадратов.
Рассмотрим метод нахождения параметров приближающей функции в об
щем виде на примере приближающей функции, зависящей от трех параметров:
У = F(x,a,b,e). (2.15)
Имеем
F(x;,a,b,e)= y;,i = 1,2,...,п.
Сумма квадратов разностей соответствующих значений функций
F(x) имеет вид:
(2.16)
f(x) и
n
)Y; F(x;,a,b,e)Y =Ф(а,Ь,е).
;;1
Сумма является функцией Ф(а, Ь, с) трех переменных. Используя необ
ходимое условие экстремума:
дФ =0 дФ-=0 дФ =0
да 'дЬ 'де'
(2.17)
получаем систему уравнений
n
2)У;  F(x;,a,b,e,)]. F(x;,a,b,e)= о,
;;1
n
)Y;  F(x;,a,b,e,)]. [<-Ь(х;,а,Ь,е)= о,
;;1
(2.18 )
11
)Y;  F(x;,a,b,e,)]. F;(x;,a,b,e)= о.
;;1
, 1
, ,
,
Решив систему (2.18) относительно параметров а, Ь, с, получаем KOH
кретный вид функции F(x,a,b,c), Изменение количества параметров не
приведет к искажению сущности caMoro подхода, а выразится в изменении
количества уравнений в системе (2,18),
Значения разностей
11
11,
У;  Р(х;,{/,Ь.с)= &, (2.19)
называют отклонениями измеренных значений от вычисленных по формуле
(2,15),
I
,1
I
11
32
../t.!.!!!..:з!!1!!!.,!Ч-:!:I.х...!.У:'O}jес.св:!!.:'ll()f!.!'i()'!I'!=ф'р'el!:I'l!.'!(!!!.}'p"'!!'e.!.Z:':'!.. !'!...'!..()I!!!К-.
Сумма квадратов отклонений
11
(J' = I&?
(2.20)
в соответствии с принципом наименьших квадратов для заданноrо вида
приближающей функции должна быть наименьшей.
Из двух разных приближений одной и той же табличной функции
лучшим считается то, для KOmOpozo (2.20) имеет наиме1lьшее значение.
Для примера получим систему уравнений, для определения неизвестных
коэффициентов, при использовании линейной аппроксимации
F(x,a,b)=ax+b.
Найдем частные производные (2.16)
aF = х aF = I .
да ' дЬ
Составим систему вида (2.18)
I(y;ax;b)xi =0,
I(y; ax; b)=O.
(2.21 )
(2.22)
(Здесь и далее сумма ведется по переменной i = 1,2,...11.)
Далее имеем:
" х. v.  а " x  Ь" х. = О
I",l ' , ,
Iy; a Ix; bll=O.
Разделив каждое уравнение (2.18) на 11, получим
(1 2) (1 ) 1
Lx; .а+ Ix; .b=IX;y;,
(Ix}a+b=IY;'
Введем обозначения
(2.23)
(2.24)
1 " Х; = М х' l " У; =М l'
11 11 .
! " Xi)'; = М-п..!.. " х; = М "
11 . 11 х
2157б
33

1
l'
11'
1;1
1;;
111
il
!'
1/
'1
1I1
I
11 i
1 I
I
]l
k-.?-'!!.'!...й--т--:'fJ.1!?е.'!?е.Р.?в.(1llU:фи.:J.UЧ е./(I'.:Р'CIе.с,?в.в.шй-/(е.'!':..е. J.;J,-'!.тrlВ-ш.
Тоrда система (2.24) принимает вид:
М х"а + М А ,Ь == М АУ ,
МА'а+Ь==Му
(2.25)
или в матричной форме
(.: . X:)=(:)
Откуда
(:H J(:')
(2.26)
Вычислив значения параметров а, Ь в соответствии с (2,26), получим KOH
кретные значения и, следовательно, конкретный вид линейной функции (2.21).
Для аппроксимации экспериментальных данных, представленных в табл,
2.1, будем использовать экспоненциальную функцию вида
F(x, а, Ь) == ехр(Ь + а ,t ) , (2.27)
rде а и Ь  неизвестные коэффициенты, значения которых нужно оценить по
методу наименьших квадратов. Решение данной задачи может быть сведено
к рассмотренной выше задаче отыскания коэффициентов линейной функ
ции. Действительно, введем в рассмотрение функцию
Ф(х,а,Ь)==lп(F(х,а,Ь))==а+Ь.(, (2.28)
которая оказывается линейной функцией относительно неизвестных коэф
фициентов а, Ь. Таким образом, для решения задачи о нахождении аппрок
симирующей функции (2.27) можно использовать следующий алrоритм:
1. По известной таблице 2.1, построить таблицу, содержащую зависи
мость ln(T)==f(t).
2. Используя данные новой таблицы, найти значения неизвестных коэф
фициентов а, Ь линейной функции, решив систему уравнений (2,26).
3. Определить аппроксимирующую функцию, подставив найденные
значения коэффициентов а, Ь в (2.27),
Описанный алrоритм реализуется в пакете МА ТLAB следующей после
довательностью команд:
»х = :15; % задание моментов времени из табл, 2,1
»у = [83 77.7 75,1 73.071.169.4 67.8 66.4 64.7 63,4 62.1 61.059.958.757.8
56.6]; О/С задание значений температуры из табл, 2,)
» N = lengtblx);
34
.!!.!>'!3!'...U4!.':'.!.'!:!.е.!!..к-:!.::'Р..CI':!:..:!.в-:'!.:'!!!!'...Ь--:J.УIОl!!дuффе'р":'!!,:!!:.a.!!.'ыe !.Р...l!.в.!!.:!.?!!!!/(а
» у1 = log(y);
% вычисление элементов матрицы системы (2,25)
» Мх = sum(x)/N;
» Му = sum(yl)/N;
» Мх2 = sum(х.Л2)/N;
» Мху = x*yl'/N;;
» М = [Мх2 Мх; Мх 1]; % задание матрицы системы (2.25)
» d = [Мху Му]'; % задание векторстолбца свободных членов системы (2.25)
» s = М\d; % решение системы линейных уравнений (2.25)
» t = 0:0.01:x(N); % задание дискретной пере мен ной для вычисления
% значений аппроксимирующей функции
» Т = exp(s(1)*t+s(2»; % вычисление значений
% аппроксимирующей функции
»plot(x,y,'o',t,T,'MarkerSize',2) % визуализация исходных данных
% и аппроксимирующей функции
Результаты выполнения перечисленной выше последовательности KO
манд представлены на рис, 2.3.
Представляется целесообразным сделать небольшой комментарий к He
которым командам, использованным при решении задачи об аппроксима
ции исходных данных экспоненциальной функцией. При вычислении зна
чения выражения М Х)' ==! LX;Y; требуется вычислить скалярное произве
п
дение двух векторов, которые в пакете МА ТLAB по умолчанию
записываются в виде строк, поэтому выполнение команды х*у, приводит к
появлению следующеrо сообщения об ошибке:
??? Error using ==> *
Inner matrix dimensions must agree.
(ошибка в использовании ==> *
размерности матриц должны быть соrласованными)
Причина данной ошибки является следствием Toro, что в пакете MAТLAВ,
ориентированном на выполнение матричных операций, любой вектор также
рассматривается как матрица, В рассматриваемой задаче Х,у  векторы раз
мерности 1 х 1 6, По правилу умножения матриц число столбцов первой MaT
рицы должно равняться числу строк второй матрицы, Как очевидно, данное
условие для векторов х,у не выполняется, поэтому операцию умножения сле
дует предварить операцией транспонирования вектора у'.
35

1\, J ','I,O/Ul!j{ j 'J(,Jl .1.'('1 11'1 lJr".",,'--- '1 ".
,. ,,}"'-- "'"I''f"'"''' "'р'"'' ".... ,'1 .."", "'" , ,..
64.7000
63.4000
62.1000
61.0000
59.9000
58.7000
57.8000
5606000
."',5 !
I
1
80 i
,
I
60 I
I
55L .
о
"
Для вывода данных, представленных в табл, 2.1 в виде окружностей, в
команде plot после ввода имен векторов х, у указан тип маркера точек 'о',
Размер маркера точек задается в команде plot строкой 'MarkerSize' и сле
дующим за ней числом 2. Размер маркера точек задает'ся после перечисле
ния всех векторов, используемых для построения !рафиков,
Отметим, что можно использовать два друrих способа решения рассматри
ваемой задачи, Первый состоит в использовании встроенной в пакет МА T
LAB функции polyfit(x,y,n), возвращаюшей значения коэффициентon
I
65 
I
,. _, ...1. , 
'i
_, ......L.._.-. ,_
10
»у
у=
Columns 1 through 5
83.0000 77.7000 75.1000
Columns 6 through 10
69.4000 67.8000 66.4000
Columns 11 througll 15
62.1000 61.0000 59.9000
Colunm 16
56.6000
73.0000 71.1000
64.7000 63.4000
58.7000 57.8000
"
полинома пй степени р(х) = L aixNi в порядке уменьшения степеней,
;;0
который с наименьшей среднеквадратичной поrрешностью аппроксимирует
табличные данные, занесенные в векторы х, у, Данный метод реализуется
следующей последовательностью команд:
» х = о: 15; % задание моментов времени из табл, 2.1
» у = [83 77.7 75.1 73.071.1 69.467.866.464.763.462.1 61.059.958.7...
57.856.6];
» N = length(x);
» х1 = х';
» у1 = log(y)';
» s = polyfit(xl,y1,1); % вычисление коэффициентов полинома
» t = O:O.OI:x(N); % задание дискретной переменной для вычисления
% значений аппроксимирующей функции
» Т = exp(polyval(s,t)); % вычисление значений
'Ус' аппроксимирующей функции
» pJot(x,y,'0',t,T,'MarkerSize',2) % визуализация исходных данных
% и аппроксимирующей функции
Второй способ состоит в использовании функции lsqcurvefit, решаЮЩеЙ за
дачу нелинейноrо метода наименьших квадратов, :записанную в форме (2.17):
Рис. 2.3. Исходные дачные и аll!!рОА:си.1tl/р)'ющая их функция
Ниже показаны значения переменных у п у'
»у'
ans =
83.0000
77.7000
75.1000
73.0000
71.1000
69.4000
67.800fl
66.400IJ
36
37

: I
, 1
,1
I
jl
'i
11 i
K0A!...mfJ.!.I!!!.. моделUР5!ваIlU:" ФU:.!.!..J?!!.'i!':'!..!!.!'.f!.!!'!. MA!,!::!,
.... . ....2..:fo!..одел.и. rf)Зlческ.и::. !Р"О!!"-?lI.:.?ЗJ1.'?Ujеиq)q:"р""IIIIIа:! Ь!.Iе.У..I.).й-.в-',,'!..f!.J::?!l?Р..J/К-й-.
( n 2]
. а.х +Ь
mш t;[y; e ' ] .
Отметим, что существует возможность настроить пакет Optimization,
установив значения соответствующих опций пакета, Общий список опций
пакета можно получить, выполнив команду
» optimset
DerivativeCheck: [ оп I {off} ]
Diagnostics: [ оп I {оЩ ]
DiffМaxChange: [ positive scalar {le-l} ]
DiffМinChange: [ positive scalar {le-8} ]
Display: [ off I iter I notify I final ]
GoalsExactAchieve: [ positive scalar I {О} ]
GradConstr: [ оп I {off} ]
GradObj: [оп I {off} ]
Hessian: [ оп I {оЩ ]
HessMult: [function I {[]} ]
HessPattern:[sparse matrix
{sparse( ones(NumberOtV ariables))} ]
HessUpdate: [ dfp I gillmurray I steepdesc I {bfgs} ]
Jacobian: [оп I {off} ]
JacobMult: [function I ([]) ]
JacobPattern: [ sparse matrix I {sparse(ones(JrowsJcols))} ]
LargeScale: [ {оп} I off]
LevenbergMarquardt: [ оп I off]
LineSearchType: [cubicpoly I {quadcubic} ]
MaxFunEvals: [ positive scalar ]
MaxIter: [ positive scalar ]
MaxPCGIter:[positive scalar I
{max(l,floor(numberOtV ariables/2»}]
MeritFunction: [ singleobj I multiobj ]
MinAbsMax: [ positive scalar I {О} ]
PrecondBandWidth: [positive scalar I {О} I Inf]
TolCon: [ positive scalar ]
TolFun: [ positive scalar ]
ToIPCG: [positive scalar I {O.l} ]
ToIX: [ positive scalar ]
TypicalX: [ vector I {ones(NumberOtV ariables,l)} ]
Подробное описание каждой опции приведено в документации, постав
ляемой вместе с пакетом MATl.AB. Например, для Toro, чтобы включить
Вывод в командное окно значения функции, минимизирующей (2,29), на
каждом шаrе итерации следует выполнить следующую команду:
(2.29)
Данная функция входит в пакет Optimization, который расширяет воз
можности пакета МА ТLAB в области решения задач оптимизации, систем.
нелинейных уравнений и задач апроксимации.
Для 'решения задачи сначала создадим mфайл, содержащий определение
минимизируемой функции:
function Z = MNK(s,xdata)
% определение минимизируемой функции (2.29)
N=length(xdata);
k=1:N;
Z=exp(s(1)*xdata(k)+s(2) );
который сохраним на жестком диске в каталоrе, предлarаемом пакетом
МА ТLAВ, по умолчанию под именем MNK.m.
Далее необходимо выполнить в командном окне следующую последова-
тельность команд:
»xdata = 0:15; % задание моментов времени из табл. 2.1
» ydata = [8377.775.1 73.0 71.1 69.4 67.8 66.4 64.7 63.4 62.1 61.0 59.9...
58.757.856.6]; % задание значений температуры из табл. 2.1
»sO=[-0.13]; % задание начальноrо приближения
» [s,resnorm] = Isqcurvefit('MNK' ,sO,xdata,ydata)
После выполнения приведенной выше последовательности команд в pa
бочем окне будет выведена следующая информация:
Optimization terminated successfully:
Relative function value changing Ьу less than OPТIONS.ToIFun
s=
-0.0241 4.3749
resnorm =
21.8311
(Оптимизация успешно завершена
Относительное отклонение функции меньше, чем OPTIONS.ToIFun)
Здесь переменная s, содержит значения искомых параметров функции (co
ответственно а и Ь), resnorm  сумму квадратов отклонений, вычисляемых
в соответствии с (2.19), (2,20).
38
39

I
 '
11
11
1:
1
l!..?..ь.'!!.fI1!.fJ!а..е !!.?l!.'н?а.I..Ри-':.'l!.I5'Р..?Н.l!.:.?.в-.в-.пl5.fI1.А4:..А.х.I:..1..!!.... ...... .
... МО'I!:'з.>.!!ЗUч-!.U:'!!р"'?!!!!.?.!:.пО!!ь-!!:.<:"'!!.':!.l!..д-!!РР.:'fJ!!''iи-!1!!..e УI!!.!.:!..ю=?'2'?J!.1!..
» [s,resnorm] =
Isqcurvefit('MNK' ,sO,xdata,ydata,",' I ,optimset('display' ,'iter'»
Norm of First-order
Iteration Func-count f(x} step
1 4 50659 1
2 7 50659 2.74811
3 10 50659 0.687029
4 13 20192.1 0.171757
5 16 12355.5 0.343514
6 19 1885.55 0.687029
7 22 50.9973 0.34649
8 25 21.8404 0.0314554
9 28 21.8311 0.000625592
10 31 21.8311 5.9392е-006
Optimization terminated successfully:
Relative function value changing Ьу less than OPТIONS.ToIFun
s=
-0.0241 4.3749
, I
I
I
optimality CG-iterations
5.09е+ОО4 О
5.09е+ОО4 1
5.09е+004 О
8.05е+004 О
2.14е+004 1
5.35е+ОО3 1
4.55е+003 1
14 1
1.3 1
0.0179 1
Задача 2.2*
Для изучения точности метода Эйлера можно воспользоваться анали.
тическим решением ОДУ (2,1), которое записывается в виде
T(t)=Ts (Ts To)'eп, (2.30)
2де Ts  температура окружающей среды, То  начальная тeмпepaтy
**
ра тела .
1. Выберите значение коэффициента r, соответствующее реальному пpo
цессу, и внесите необходимые иЗJ.tенения в документ, описанный в раз
деле 2,3, чтобы найти численное решение уравнения (2.1). Задайте вpe
менной интервал, на котором будет находиться численное решение,
ша2 инте2рирования АЕ, те.«пературу окружающей среды и начальную
температуру жидкости в чашке, Постройте на одном чертеже точ-
ное и численное решения,
2. Вычислите разность между численным и точным решениями для сле-
дующих значений ша2а инте2рированuя At == 0.1, 0.05, 0.025, 0,01 и 0.005,
Зависит ли разность между численным и точным решениями от вpeмe
ни? Нарисуйте 2рафик разности как функцию АЕ. Будет ли эта раз
ность убывающей функцией АЕ? Если разность между точным и анали
тическим решениями при заданном значении t пропорциональна (АЕ)п, то
численный метод называется методом п20 порядка точности. Какой
порядок точности у метода Эйлера?
3. Какой ша2 необходимо выбрать, чтобы точность 0.1% дости2алась в
момент времени t == 1? Какой необходимо выбрать величину ша2а АЕ,
чтобы точность 0.1% дости2алась в момент времени t == 5?
Задача 2.3
Процесс зарядки изначально незаряжеНН020 электричеСК020 KOHдeHca
тора в RС-цепи (рис. 2.4), к которому в момент времени t == О прuложе-
но напряжение и, описывается ОДУ перв020 порядка
RdQ =VQ (2.31)
dt С
с начальным условием Q(O) = О.
1, Найдите численное решение уравнения (2,31), задав следующие xapaKтe
ристики цепи R == 2000 Од С == 10.6 Ф, V == 1 О В, Как зависит заряд
resnorm =
21.8311
Здесь использована функция optimset(' display' ,'iter'), позволяющая ус-
тановить значение опции display равным iter. Для отмены вывода в KO
мандном окне какойлибо информации о процессе вычислений следует на-
брать команду
» [s,resnorm] =
Isqcurvefit('MNK' ,sO,xdata,ydata,"," ,optimset(' display' " off'»
s=
-0.0241 4.3749
I
resnorm =
21.8311
1
1
l' 1
111 I
Задача 2.1
Постройте на одном чертеже аппроксимирующие функции, коэффици
енты которых вычислены каждым из трех вышеперечисленных J.temo
дов. Сравните сумму квадратов отклонений между табличными значе.
ниями и значениями атlроксиJ.tирующих функций, полученными при иc
пользовании функций polyfit и lsqcurvefit.
1
I
11
,
40
*
Задачи 2,],2.2,2.3 взяты авторо.н из [21-
** За.нети-н, что T(t = о) = Т':;  (Ts  То)= То ' а T(t  (0) = Ts .
41

 /
i
!I
,
111
!<,:?1.!?".!.:fJ..!!.?'!..л.!!!.:::':.fJ..?I!.!I'!..4:и.!...и..:.'!...'!.fJ..?У:.C?..'!.Cl.'!..'!.,!и!.1;!1...:!!!..___.
:!ure.:.и че!!.Р..й-.!:.с.!!..:':!.r:.'!...й-!!.ь-..:IJ..l?Uj,'!!.'!1!.tf!..'!.l!.!:.!I!..'!..ь-..!.'!..}'fJ..Cl/1!..'!..!11!!..'!..?.'!...Й-Р.!!15.Cl.
на конденсаторе от времени? Увеличивается ли заряд до бесконечноzо
значения или происходит есо насыщение?
R

fu ТС
Рис. 2.4. Элекmрическая схема зарядки
конденсатора
Несмотря на то, что не следует отдавать предпочтение одному KaKOMY
нибудь алrоритму, для наших дальнейших целей оказывается достаточным
оrpаничиться одним вычислительным алrоритмом, который позволяет по
лучать устойчивые решения, отвечающие требованиям по точности, во всех
рассмотренных нами задачах. Указанными свойствами обладает метод Pyн
reKyrra 4ro порядка, Данный метод реализуется следующей итерацион
ной формулой [3]:
Уn+! = Уn + (k!(уn)+2k2(Уn)+2kз(уn)+k4(Уn)), (2.32)
2, Один из методов определения точности численноzо решения заключает
ся в повторении вычислений с меньшим шаzом и сравнении полученных
результатов, Если в обоих результатах совпадают п десятичных цифр,
то можно предположить, что совпадают и следующие десятичные
знаки, Какой необходимо выбрать шаz, чтобы получить решение с тpe
мя правильными десятичными знаками в момент времени t = 0.005 с?
3. Каковы особенности численноzо решения уравнения (2.31) и значений ша
zoe!1t = 0,005, 0,004, 0.003? Приводит ли малое изменение шаzа к боль
шому изменению вычисляемой величины Q? Устойчив ли метод Эйлера
для любой величины шаzа?
rде k\, k2, kз, k4  поправки, вычисляемые по формулам
k!= t(xn, yJ,
k2 = t(xII + 1:ll/2, уn + I:llk!/2),
kз = t(xn + 1:ll/2, уn + I:llk2/2),
k4 = t(xn + I:ll, уn +!1у).
У словие. сходимости данноrо метода записывается в виде [3]
1:llЛ- ::; 2.78,
(2.33)
(2.34)
2.5. Решение дифференциальных уравнений
методом РунrеКутта 4ro порядка
rде л коэффициент, входящий в модельное уравнение
dy
 + Л-у = О, л- = const > О, х > О, у( О) = Уа .
dx .
Решение задачи Коши методом PYHreKyттa 4ro порядка в пакете
МА ТLAB реализовано в виде функции ode45. Данный метод рекомендуется
использовать при первой попытке нахождения численноrо решения задачи.
Помимо данной функции в пакете МА ТLAB реализованы и дрyrие Me
тоды решения дифференциальных уравнений и систем ОДУ:
ode23  функция реализует одношаrовые явные методы PYHreKyттa
(2 и 3) порядков. Функция используется при решении нежестких систем
ОДУ обеспечивает удовлетворительную точность при меньших, нежели
функция ode45 временных затратах.
ode113  функция реализует мноrошarовый метод АдамсаБашворта
Мултона переменноrо порядка, Функция используется при необходимости
обеспечить высокую точность ':!исленноrо решения,
ode15s  функция реализует мноrошаrовый метод переменноrо порядка
(от 1 до 5 по умолчанию), основанный на формулах численноrо дифферен
цирования, Данный метод следует использовать в том случае, если не yдa
ется найти численное решение с помощью функции ode45.
(2.35)
Задача 2.4
Предположим, что начальная температура кофе 90 "С, однако начи
нать пить кофе МОЖНО, КОсда температура опустится ниже 60 "С,
Предположим, что вы .можете добавить в кофе молоко, которое
уменьшает температуру кофе на 5 "С. Для т02О чтобы охладить кофе
до нужной температуры, вы можете поступить двумя способами:
1) добавить молоко при температуре кофе 90 "С;
2) добавить .молоко при температуре кофе 75 "С, В какO/t" случае охлажде
ние кофе до 60 "С произойдет быстрее? (Ответ необходимо получить,
выполнив численные расчеты.)
Изучив разделы 2.l2.3 и решив задачи 2.l2,2, можно убедиться в извест
ных оrpаничениях метода Эйлера по точности, а так же в возникновении в ряде
С1учаев неустойчивых решений, Эти недостатки определили необходимость
разработки новых вычислительных aлrоритмов, их подробное описание заин
тересованный читате.'1Ь может найти в списке литературы [2].
42
43

' l' 1
1I i /1
1:1
!1! '
i I 
1\
:1
I
i '
i
i

i i
i'li i
( I
I!'
i;i
111
l'
I, '
1111
i
11
, ,
1
1
f,
f
,1
!.:..С?'!.!:.rrJерJJа.'!.l!!!ваJ'!!.:...Рl!...1J!!!1j:::..а:!...!!!!I!!..!!..1.!LA!!.,
....'
"":!!..?€!.л..и1.}и!., i'le.I': I1р"?ес:.с:.?:ис:.I.?lз?!,,?U/ие д.!JР"Р"Р'!.'!.Уи.а..л..lз!'ь:. 'Рr:-./lи.f!.1 :?О.п--?Р.f!?I':r:-..
ode23s  функция реализует одношаrовый метод, использующий моди
фицированную формулу Розенброка 2ro порядка. Данной метод обеспечи
вает более высокую скорость вычислений по сравнению с дрyrими Meтoдa
ми при относительно .более низкой точности вычислений.
ode23t  функция реализует метод трапеций с интерполяцией. Данный
метод используют при решении уравнений, описывающих колебательные
системы с почти rармоническим выходным сиrналом.
ode23tb  функция реализует неявный метод PYHreKyrra в начале ин
тервала интеrpирования и далее метод, ИСпользующий формулы обратноrо
дифференцирования 2ro порядка. Данный метод обладает большей CKOpO
СТЬЮ. нежели метод ode15s при, соответственно, меньшей точности.
Все перечисленные выше функции, называемые в документации пакета
Solver (решатель), MOryт решать системы ОДУ явноrо вида у' = F(t, у).
Кроме Toro решатели odel5s, ode23s, ode23t и ode23tb системы дифферен
циальных уравнений неявноrо вида М (t, У )у' = P(t, у), а также все решате
ли, кроме ode23s, MOryт решать уравнения вида М (у )у' = P(t, у).
для реения дифференциальноro уравнения (2.1) сначала создаем mфайл,
содержащии определение функции, стоящей в правой части уравнения (2.1):
function Z=Tempr(t,T)
% определение функции, стоящей в правой части уравнения (2.1)
global Ts r
Z(I)=-r*(Т-Тs);
который сохраним на диске под именем Tempr.m.
Далее необходимо выполнить в командном окне следующую последова
тельность операторов:
» global Ts r % объявление rлобальных переменных
» Ts = 22 % задание значения температуры окружающей среды
» r = 0.024 % задание значения коэффициента остывания
» ТО = 80 % задание начальной температуры тела
» [t,T]=ode45('Tempr',[0:0.01:15],TO); % Tempr  имя файла,
% содержащеrо определение функции, стоящей в правой части
% уравнения (2,1); [0:0.01:15]  вектор, определяющий интервал
% интеrpирования, ТО  вектор начальных условий
» plot(t,T)
После выполнения приведенной выше последовательности команд будет
создано окно, содержашее rpафик зависимости температуры тела от BpeMe
ни. пrедставленный на рис. 2,5,
Во 'с;: 
78 
76
74.
,
'...."
721"
70
"-
....
......"
--.'......."
"---
.....
'.......
ба
66:
-'"
"---.
64"
1
'....
......,
62""""""'"
О 5

10 15
Рис. 2.5. Числеююе решение уравнения теплопроводности,
возвращенное функцией ode45
По умолчанию решатели систем ОДУ пакета МА ТLAB используют па
раметры, относительная поrpешность которых не превосходит перемен-
ной RelTol = 1 o3 , rpаница абсолютной поrpешности численноrо решения 
переменная AbsTol  равна 106. Для изменения значений этих переменных
используется команда
»options = odeset('ReITol' ,lе-4,' AbsTol' ,lе-4);
предваряющая команду вызова функции решателя системы ОДУ.
Задача 2.5
Решите задачи 2.1, 2.2, используя вместо функции, реализующей оиетод
Эйлера, функции оае45, оае23, ode15s, ode23s, ode23t, ode23tb, Проведи-
те сравнительную Qценку точности данных методов, сравнив числен-
ные и точнЫе решения,
2.6. Моделирование радиоактивноrо распада
Ядерный распад зависит только от внутренних свойств данноrо типа
aToMHoro ядра. Особенность атомных ядер состоит в том, что они MorYT
распадаться, Вероятность распада описывается выражением:
W  скорость распада  ] dN (2,35)
  кличетво ядр H' ,
44
45

I
1
1 11
j,!
:1
ii
1
'11
11,
1,
11
1'1'
!II
11'
;1
li
l!'?'!..!"!.:Р'!":.'.Л-р'О.!!I'!.1!.II!..'!.'!..IIР.й-.'!:'?..й-.l!в.'!..:!,::.:.!'!..TL.l!.
[де N(t)  количество ядер в образце в момент времени (,
ядер, распавшихся за время dt
dN = N(t)N(t +dt).
Тоrда скорость распада определяется как
dN
 =W,N.
dt
dN  количество
(2.36)
(2.37)
Уравнение (2.16) называется уравнением распада. Оно является ОДУ
первоrо порядка с разделяющимися переменными, которое может быть леr
ко проинтеrpировано, Ero решение имеет следующий вид
N(t) = N ое w '1 , (2.38)
[де N о  число ядер в момент времени t = О .
...,.......
Задача 2.6
Найдите численное решение уравнения (2,16), используя функции ode45,
ode23, ode15s, ode23s, ode23t, ode23tb, Сравните точные численные pe
шения уравнения (2,17), полученные разными методами, Как меняется
точность числеННО20 решения при изменении ша2а инте2рирования?
2.7. Моделирование цепной реакции
ядерноrо взрыва
1 '1
1
I ,1
Ji
1
I
i!
в 1938 [. было открыто деление aToMHoro ядра при попадании в Hero
нейтрона. При этом оказалось, что ядро распадается на две части с OДHO
временным вылетом 23 нейтронов, Осколки ядра под действием кулонов
ских сил приобретают кинетическую энерrию, которая затем переходит в
тепловую энерrию кристаллической решетки. В свою очередь, образовав
шиеся нейтроны Moryт попасть в друrие ядра, что опять приведет к делению
ядра с появлением дополнительных нейтронов и т. д. Данное явление полу
чило название цепной реакции, В том случае, если число нейтронов на каж
дом последующем шаrе больше числа нейтронов на предыдущем шаrе про
исходит рост числа осколков в rеометрической проrpессии, В результате
происходит ядерный взрыв.
Для описания цепной реакции используется следующая математическая
модель, Будем рассматривать ядро u235 как шарик радиуса R, Нейтрон,
двиrаясь со скоростью v, за время dt захватит цилиндрический объем V
V = ff' R2 . v' dt , (2,39)
'1
I
1
46
2.fo! й-.(' лurfJl/?U чес.: ..l1jJl./е.сс()вIс:.'!.. (),ЛЗ'уIOЩ1:(' д uффеfJе.'IЦU(lЛЬ'lье )lР.f1в.I/е.I/l!!:'!.(),ll()jJl!а
Нейтрон вызовет деление ядер, находящихся в данном объеме, Количе
ство делений, вызванных одним нейтроном, за время dt :
N ' V ' а = N ' ff ' R2 . \1 . а . dt , (2.40)
[де а  вероятность распада ядер, N  концентрация ядер,
Удобно преобразовать (2,19), введя величину CJ'r = а. ff,R2 (называемую
сечением деления), характеризующую способность ядер данноrо вещества к
делению под действием нейтронов:
N ,V 'а = N 'CJ', ,v.dt, (2.41)
Будем предполаrать, что при единичном акте деления образуется f--l ней
тронов и один нейтрон поrлощается, Тоrда, изменение числа неитронов за
время dt, определяется выражением
dn=п,N'CJ'r'v,dt'(f--lI), (2.42)
[де п  количество нейтронов.
Уравнение (2.43) является ОДУ первоrо порядка, Решение уравнения (2.43)
п(t) = по ,exp(N 'CJ'r 'v' (, (f--l  1)). (2.44)
Оценим порядок величины п(t) для образца со следующими параметра
/ 3 6 024 2  2 109
ми: плотность образца р = 182 СМ' , f--l = 2,5, CJ'r = 1. ,1 см, v .
см/с, Так как для выбранной плотности вещества концентрация ядер
р 22 3
N =NA :::;4.6,10 СМ ,
f--luш
(2.45)
то за время 1 06 с начальное количество нейтронов увеличивается
в :::;1026 раз, т. е. происходит ядерный взрыв, 
При построении модели мы предполаrали, что все образовавшиеся неи
троны участвуют в делении, поэтому даже один свободный нейтрон будет
ВЫзывать ядерный взрыв, Однако этот вывод не соответствует опытным
данным, которые показывают, что ядерный взрыв может происходить,
только при определенных у'словиях, Данное обстоятельство свидетельствует
о необходимости уточнения модели ядерноrо взрыва, Эт.о уточнение COCTO
ит в учете Toro обстоятельства, что часть образовавшихся нейтронов может
покидать образец, не участвуя в дальнейшем делении ядер,
Окончательно модель, учитывающая рождение и вылет нейтронов, опи
сывается следующим уравнением:
. dn
=(ab)'п, (2.46)
dt
здесь
п = N . CJ'J . \' . (р -1) .
(2.47)
47


,1
: 11
1,
II
'!i:
,11
11
I1
11 '
1,
'" 1
: I
11,.1" :
"
,1
il i
I I
(11
1I1
I
1
'1 I
11 I!'
;11\1
I1
"
!
1:1
1
1
'1', 1,1
11'
Н!
II
_K--а'!..I()'!.'ер'/()= .л:_()д-е:'!.l!.()!l!.!.'!.:РlllIЧ_ е.с::<..rХl1fJач.:?.._ !. !z.J(el1le.A1. А T1..
k.v
Ь = -- 
RU'-"
r лава 3
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
l2.48)
rде k  дополнительный множитель, учитывающий реальное уменьшение
плотности нейтронов, Ru'-"  характерный размер образца урана *,
Из (2.46) видно, что существует линейный размер образца, называсмый
критическим радиусом RKp' для KOToporo а  Ь = О ,
R = 
кр N'ar'Cul)'
3.1. Введение
Большинство задач, связанных (,; определением закона движения тела в
близи земной поверхности, имеют известные аналитические решения, He
смотря на зто, мы считаем полезным вновь вернуться к зтим задачам и по
лучить их решения с помощью пк. Так как на примере их решения можно
продеМОНСlрировать наиболее общие приемы и подходы к решению физи
ческих задач на пк. При решении данных задач используется простейшая
модель, в которой не учитываются ВОЗf>ЮЖ!lые вращения и внутренние дви
жения тела, Т, е, реальное физическое тело заменяется идеализированным
объектом, не обладающим внутренней структурой  материальной точкой.
Задача описания закона движения материальной точки lрадиционно pac
сматривается в кинематике, rде движение материальной точки рассматрива
б *
ется езотносительно причины ее вызывающеи , и в динамике, rде paCCMaT
риваются силы, действующие на тело, В соответствии со вторым законом
Ньютона ускорение ll, с которым движется тело, прямо нропорционально
действующей на Hero силе Р (а если сил, приложенных к материальной
точке, несколько, то их равнодействующей, т. е, векторной сумме сил) и об
ратно пропорционально ero массе т:
(2.49)
Масса образl1а, соответствующая критическому радиусу (критическая
масса), определяется как
4 
м "р =  1tR;p , Р , (2.50)
3
Для реальноrо U235 М кр == 50 Kr при критическом радиусе 8.5 см,
Задача 2.7
Считая образец, U320товленный из u235, сферическим, исследуЙте пo
ведение решений уравнения (2,46) при различных значениях массы образ
ца, (Указание, Изобразите на одном чертеже зависимости n(t), полу
чеНllые при различных значениях .массы образца).
ЛИТЕРАТУРА
1. Самойленко А, М" Кривошея С. А., Перстюк Н, А. Дифференциальные уравнения: приме
ры и задачи, М,: Высшая школа, 1989.
2. rулд Х., Тоболчник Я, Компьютерное моделирование в физике, М.: Мир, 1990,
3, Самарский А. А, Введение в численные методы. М.: Наука, 1987.
4. Бахвалов Н, С, Численные методы, М.: Наука, 1975,
5. Березин И С" Жидков НЛ, Методы вычислений. Ч, 1, М,: Наука, 1966,
6, Марчук [, И. Методы вычислительной математики, М.: Наука, 1980,
F
II =  .
т
(3.1)
в общем случае сила Р зависит от положения точки, характеризуемоrо
радиусомвектором f(t), скорости v(t) и времени F = F(r,v,t). Тот факт,
что силы, действующие на тело, не зависят от производных скорости, явля
ется свойством природы, но не следствием математическоrо описания, Это
свойство позволяет найти простые объяснения для мноrих наблюдаемых на
практике движений,
Так как по определению
*
Вид зависш.юсти коэффициента Ь от линейных размеров образца очевиден !13
следующих соображений, Количество нейтронов, выходящих из образца, пря.\Ю
Ilроnорционально скорости их движения и Ilлощади Ilоверхности образца и оориlllНО
nрОllорционально КО.1lI'lеству ядер, содержащихся в д,тНО.1I образце. Так как IlЮ
щадь Ilоверхности IlрОnОРЦllона.7ЬН<1 квадрату .7инейН020 раЗА/ера образца, а КОЛII
'1,,-('т60 ядер  е20 объе1tу, 111. е. кубу .1Uнейною peH1Iepa, то коэффициент h будет
оорт11l1O nрОllорционалсн ЛilllеЙIlО.If.1' раЗ,'\Iеру
dv
li = 
dt
d2f
=
? '
dt
*
Данный Ilодход )-',ж-е был иСI7О.7ьзова;{ на.\tlI в ZЛ. Z.
48

11
,11
111
11.',
'1
11:
11:
1\'
111 11I1
1.. ,.i.
'f
f 1"
1'11
комIJытери?"" моде:7ироваllие (IJUЗllчесКUХllроцессоввlJкеП1е 1i!/1 ТLA.В- .
3. Диllамика ,иатериалыlOU точки
................-.... ..... ... ..........
.....................
то зависимость скорости 01 времени описывается уравнt:нием
dv Р
dt т
у
(3,2)
а зависимость координаты 01 нремени 
d2r Р
dt2 т
то для описания движения материальной точки необходимо решить ОДУ
BToporo порядка относительно координаты (3,3), которое для тела с посто
явноЙ массоЙ эквивалентно системе ОДУ первоrо порядка
{ d
v(t) = !
dt
. dv' (3.4)
a(t)=
dt
h
(3,3)
Рис, 3,1. Система координат,
используемая для описания движения
тела в zравитационном поле Земли
Данное уравнение является ОДУ Bтoporo порядка, для KOToporo задача
Коши ставится заданием начальных условий: значений координаты
у(о) = уо и скорости v(o) = у'(О) = vo' Аналитический ответ получается по
следовательным интеrpированием (3.6):
v(t)=vog.t, (3.7)
y(t)=Yo+vo.t+g.t2. (3.8)
2
Рассмотрим последовательность действий, реализующих решение этой
задачи в пакете МА ТLAB с начальными условиями у(о) = 1 О, У 1(0) = 1.
Поскольку описанные выше решатели работают с системами ОДУ, при
веденными к форме Коши, то необходимо систему BToporo порядка привес
ти к системе ОДУ первоrо порядка, введя новую переменную
dy
dt = Z . (3.9)
Тоrда уравнение (3.6) принимает следующий вид:
dz
  g (3.10)
dt  .
Уравнения (3.9), (3.10), образующие систему ОДУ первоrо порядка,
можно записать в матричном виде
()=(zJ. (3.11)
Запись системы в виде (3.11), позволяет создать mфайл, содержащий
описание векторфункции, стоящей в правой части (3.11):
function dy=Angle(t,y)
global g
dy=zeros(2,1); % задание векторастолбца размерности 2хl
% задание координат векторфункции, стоящей
% в правой части (3,11)
у=о
Для описания движения тела с переменной массой необходимо решать
уравнения (3,2), (3,3), в которых т в данном случае является функцией
времени,
3.2. Движение тел в rравитационном поле Земли
без учета трения
Рассмотрим задачу об одномерном движении материальной точки с по
стоянной массой в rpавитационном поле Земли. В соответствии с законом
всемирноrо тяrотения сила, действующая на тело массы т, равна
уМl11 g111
F  . ..    (3,5)
 (R )')2  (1 + )'/ R)2 '
rде )'  расстояние от поверхности Земли, R  радиус Земли, у . rpавитаци
I 2
онная постоянная, М  масса Земли, g = уМ I R ,При этом на первом шаrе
будем считать силу тяжести постоянной, что справедливо, как видно из
(3,5), для y/R « 1,
Выберем систему отсчета, с положительным направлением координат
ной оси вверх (рис. 3,1),
Подставляя (3.5) в (3.3). получаем уравнение движения в выбранной сие
теме отсчета
d2y
' = g ,
dt"
(3.0)
50
51

1 i
!!!.-!!..r:..!71'!.l!.'!.?.е:!.и.F.'?..11.!!i!.: 4?II!.'.!..с:!.:.JХ./!Е.!!.I.в !!..'!..'!.п!(!./!!.__A:!!. ......
,
1,'
I
dy(1)=y(2);
dy(2)=-g;
и сохранить ero на диске под именем Angle.m.
Далее необходимо выполнить в командном окне следующую последова
тельность команд:
» global g % объявление rлобальной переменной
% задание начальных условий
» yO=lO;
» vO=l;
»[t,y]=ode45('Angle',[O:O.Ol:1.5],[yO vO]); % решение системы ОДУ (3.11)
»figure(l); plot(t,y(:,l»; % построение зависимости у = y(t)
% rpафическом окне N!! 1
»figure(2); plot(t,y(:,2»; % построение зависимости у' = y'(t)
% rpафическом окне N!! 2
После выполнения приведенной выше последовательности команд на
экране монитора появляются два независимых стандартных rpафических
окна. В окне с названием Figure К!! 1 отображается зависимость координаты
от времени (рис. 3.2), в окне с названием Figure К!! 2 отображается зависи
мость скорости от времени (рис. 3.3.)
'I!
1I
l' :
I!I
l' I
':
"
1
::
1 -----------------------------
81 ..
, 
''''

'-
'.
I
I
'1
1
I
J
I
1
I
J
I
i
"
4 i
r
I
2
 '
-- I
. I
-- l
'\\\1
'1
,
O ,
о 0.5 15
Рис. 3.2. 3ависимость координаты .l1атериальной точки от времени
52
ш ..!:&/fl'К--I1.!.а:.п:jJ1I(':.:?li.!I1.?'.'.К--!'
Задача 3.1
J. Сравните зависимости скорости и координаты от времени, задаваемые
выражениЯА--tU (3,7), (3,8), с а1шлоzичными '3ависимостя.wи, полученными
численным решением уравнения (3,6), Какова точность числснноzо ре--
шения?
2. Постройте завиСUAюсть скорости от координаты.
3. Постройте зависимость пройденноzо пути материальной точки от
времени.
4. Постройте зависимости кинетической и потенциальной энерzий от вре--
мени,
5. Одним из фундаментальных законов физики является закон сохранения
энерzии, в соответствии с котОРЫА1 полная энерzия материальной точ--
ки, дви:ж:ущейся в zравитационном поле Земли, должна оставаться по--
стоянной. Проверьте полученное численное решение ОДУ на соответ--
ствие этОJWУ закону. С какой точностью выполняется закон сохранения
энерzии и чем можно объяснить обнаруженные расхождения?
2f'--'-----Т------ "'---I
__ I
о "'" 1
J """ j
 I
'----, i
.........."', jl
"'.........."
--------,
 
 I
" I
'-----., '
--. I
" ,
',
   _  .._  .]
0.5 1 '.5
.4
6 .
.8
10
121
-14 L.....__. .
о
Рис, 3.3, Зависимость скорости материальной точки от времени
Задача 3.2
Точное уравнение движения, полученное подстановкой выражения для
силы тяжести, действующей на тело в zравитационном поле 3еД1ли,
(3,5) в выражение (3.3), имеет вид:
53


i 1
1
I
11
I1
1111
li:
l'
, I
 i
1
1
I
l'
111
1'1
11
!!?Af.ь.?".':J1!?i!.!!.t!..l?!!.IJ?!!I!!.:.1!....и:.!!l!...С!..'!.Р!!..LJ.=:..й-.!!.I!i!.'!'.i!.1:!..!!._.__ш
!f!II!_к-.I!ll!rI1ери-.а../I?Й точки
d2y
dt2
dx
= 21
dt
d2j =0
dt
dy
.= 22
dt
d22 
ш  g
dt
(3.12)
"'о
.у --""е о
g
(1 + y .
(3.14)
1. Постройте зависимость ускорения свободноzо падения от высоты
подъема материальной точки над поверхностью Земли,
2. Получите численное решение уравнения (3.12) и сравните ezo с cooтвeт
ствующим решением уравнения (3,6) для выбранных ранее начальных yc
ловиях, Сколь велико отличие этих решений?
3. Сравните решения уравнений (3.6) и (3.7) при различных значениях Ha
чальной высоты. Начиная с каких высот zравитационное поле Земли
нельзя считать однородным?
4. Постройте зависимости кинетической и потенциальной энерzий от вpe
мени,
5. Проверьте полученное численное решение ОДУ на соответствие закону
сохранения энерzии, С какой точностью выполняется закон сохранения
энерzии?
Ш_....Ш..Ш.
Задача 3.3 .
Шарик, имеющий небольшой радиус (по сравнению с чем?), падает
с высоты h на yпpyzo отражающую поверхность, '
1. Разработайте пpozpaммy, позволяющую исследовать движение шарика,
падаЮЩе20 с заданной высоты на отражающую поверхность, пpeдпo
лаzая, что удар является абсолютно упруzим,
2. Постройте зависимости координаты, скорости, перемещения от времени и
скорости от координаты,
3. Исследуйте движение шарика при неабсолютно упруzoм ударе,
Рассмотрим двумерное движение материальной точки в rpавитационном
поле Земли, описываемое уравнением (3.3). В системе отсчета, показанной
на рис. 3.4, уравнение (3.3) эквивалентно следующей системе ОДУ BToporo
порядка:
h
..................
...................
................... ..............
...................
.....................................
х
Рис, з.4. К задаче з.з
Для решения задачи Коши данной системы следует задать четыре Ha
чальных условия х( о), х'( о), у( о), у'( о), а также создать mфайл, coдep
жащий определение векторфункции, стоящей в правой части системы ОДУ
(13.14), состоящий из следующих строк:
function dy=Anglel(t,y)
global g % объявление rлобальной переменной
% задание векторастолбца размерности 4хl
dy=zeros( 4,1);
% задание координат векторфункции, стоящей в правой
% части (3.11)
dy(1)=y(2);
dy(2)=0;
dy(3)=y(4);
dy( 4)=-g;
который следует сохранить на диске в файле Anglel.m.
Далее необходимо выполнить в командном окне следующую последова
тельность команд:
» global g % объявление rлобальной переменной
% задание начальных условий
» хО = о;
» vxO = 2;
» уО = о;
» ууО = 5;
% решение системы ОДУ (3,14)
» [t,X]=ode45('Anglel',[O:O.Ol:1.019],[xO vxO уО vyO]);
% построение зависимости х = x(t) rpафическом окне N2 1
» figure(l); plot(t,X(:,l); title('x=x(t)');
d2x
=o
dt2
d2y
=g
dt2
(3,13)
dx
Система уравнений (3,13) заменой переменных dt = 21 '
ся К системе линейных уравнений первоrо порядка:
dy
 = 22 сводит
dt
54
55

111'
I1
i i
, .
1,
'!
I
I
, il,
!!..?,,:,:!bOlп!P''.I?!!...':!..?'!!!..?..'.I':!e..1!!!!.!!..:''C'!..rp,!!,,!?..!!.!.!!..aKe."!.!!!!..1!!:1!!._ ..... ........
. .. .,.!:.!!.':!!.Iи-.r:.!!.1!.l!.,:!!!!!.I'.?.!,!Й-,.'5..'!.
% построение зависимости у = y(t) rрафическом окне N2 2
» figure(2); plot(t,X(:,3»; title('y::y(t)');
% построение зависимости х' = x'(t) rpафическом окне N2 3
» figure(3); plot(t,X(:,2»; title('vx=vx(t)');
% построение зависимости у' = y'(t) rpафическом окне N2 4
» figure(4); plot(t,X(:,4»; title('vy=vy(t)');
% построение зависимости у = у(х) rpафическом окне N2 3
» figure(5); plot(X(:,1),X(:,3»; title('y=y(x)');
Fd(V)= k\v,
FAv)=k2v2,
(3.15)
(3.16)
.>_.........
rде параметры k\, k2 зависят от свойств среды и rеометрии тела. Особо OT
метим, что зависимости (3.15), (3.16) не являются точными законами физи
ки, а представляют собой феноменолоrические выражения, приближенно
описывающие функцию Fd (у) в некоторых диапазонах скоростей.
При относительно малых скоростях сила сопротивления описывается
выражением (3.15). Для тел, имеющих относительно простую форму, из
вестны аналитические выражения коэффициентов k1. Например, для шари
ка радиуса r коэффициент сопротивления задается формулой Стокса
k\ = 6щ..Jr , (3.17)
Задача 3.4
1. Выберите начальныеусловия и решите систему уравнений (3,10).
2, Постройте зависимости х = x(t) , у = y(t), ух = x'(t), Уу = y'(t),
ух = ух(х), Уу = уу(х), у = у(х).
3. Найдите аналитическое решение системы ОДУ (3,10).. Сравните зави
сuмости x=x(t), y=y(t), vx=x'(t), vy=y'(t), Ух=уАх), vy=vy(x),
у = у(х), задаваемые аналитическими выражениями, с аналО2ИЧНЫМИ
зависимостями, полученными численным инте2рированием,
4. Постройте зависимость перемещения материальноЙ точки и У2Ла меж
ду вектором скорости и осью оХ от времени.
5, Постройте зависимости кинетической и потенциальной энер2UЙ от вpe
мени,
6. Проверьте полученное численное решение ОДУ на соответствие закону
сохранения энер2ИИ, С какой точностью выпОЛ/-IЯется закон сохранения
энер2ИИ?
rде   динамическая вязкость среды. Числовые значения плотности и ди
намической вязкости различных сред при t = 20 ос и давлении 1 атм пред
ставлены в табл. 3.1.
Таблица 3.1
Воздух Вода rлuцерuн
кr 1,29 1.103 1,29.103
р, 3
м
Н.с 0.0182 1.002 1480
f.J,
м2 . I
Представляет практический интерес оценить величину предельной CKO
рости Vl движения шара, падающеrо вертикально, т. е. скорости движения
при которой сила тяжести будет равна силе трения. Подставив (3.17) в
(3.11), запишем данное условие в виде
6лf.J rv( = mg , (3.18)
3.3. Движение в rравитационном поле Земли
с учетом силы трения
в предыдущем парarpафе мы рассмотрели движение тел в rpавитационном
поле Земли без учета сил сопротивления, действующих на тело со стороны cpe
ды, через которую оно движется. При движении реальных тел в rазовой или
жидкой средах, как показьmают результать\ экспериментов, сила трения являет
ся шавным фактором, который определяет характер движения тела.
О силе сопротивления, действующей на движущееся в среде тело, из
вестно, что она (за исключением некоторых отдельных случаев) растет с
ростом скорости, Наиболее общими зависимостями силы сопротивления от
скорости являются
откуда
4/3p?  2r2 р3.
6лf.J r 9f.-1
mg
Уl = ,
6лf.J r
(3.19)
rде р  плотность тела.
Значения предельной скорости Vj для шара радиуса r
= 0,8,] 03 Kr/M3 (дерево) представлены в табл, 3,2,
0,1 м, р=
56
57


:1
I
i
I
i
1
'1
I i
1
I
! !
j,

Е<?11П' ,/о In ':[1:10еlfOеЛtl.р'О'Iе фuз!"{'!..с.К-l'::fJ?1! '!..cc.?в в пакете М А ПА В
 J.j:!..'!.!.'!..1<!! М.!J.!..z:.il!!.'!!.I!!.'!!.?'!..К--
Таблица 3.2
Значения предельной скорости V2 дЛЯ шара радиуса r == 0,1 м, Р ==
= 0.8'103 Kr/M3 (дерево) представлены в табл. 3.4.
[ Воздух Вода Тлицерин
V,M/C 960 17 0,012
Таблица 3.4
I
При больших скоростях сила сопротивления описывается выражением
(3,12), Из экспериментов о веЛИЧине k2 известно, что она пропорциональна
площади поперечноrо к потоку сечсния тела 5, плотности среды Р и зависит от
формы тела. Данную зависимость принято выражать следующей формулой
1
k2 ==  с5ро ,
2
Вода
rлuцерuн
Воздух
18.0
V,M/C
0.65
0.58
Сравнение результатов, представленных в табл. 3.2 и 3.4, показывает,
что при движении тела в воздухе и воде Vl« V2' Это означает, что при
движении тела в этих средах преобладающей будет сила сопротивления, квaд
ратичная по скорости, которая сделает движение тела равномерным при значи
тельно меньших скоростях, нежели линейная часть силы сопротивления.
Для дальнейшеrо анализа особенностей движения тел в rpавитационном
поле Земли при наличии силы сопротивления удобно измерять скорость
движения в единицах установившейся скорости Vl' V2 . В выбранных едини
цах измерения выражения (3.11), (3.12) принимают следующий вид:
Fd == k1V{ ) == mg( ). (3.24)
F, = k,v,(:')' = тg( J (325)
Рассмотрим падение тела вертикально вниз с нулевой начальной CKOpO
стью при наличии силы сопротивления. Так как сила сопротивления зависит
от скорости при аналитическом решении данной задачи, удобно использо
вать уравнения движения в форме (3.2)
mg  mg()  mg()2
dv == mgFd  Уl V2
Ш m m
(3,20)
rде  с  безразмерный коэффициент (коэффициент формы), характеризую
щии лобовое сопротивление, РО  плотность среды, Известные значения KO
эффициентов формы для некоторых тел, представлены в табл, 3.3.
Таблица 3.3
Диск Полусфе Полусфе «Капле «Капле
ра ра Шар видное видное
тело» тело»
D D o o o o
1,11 1.33 0,55 0.4 0,045 0.1
Проведем аналоrичные оценки предельной скорости V2 дЛЯ квадратич
Horo закона сопротивления, Приравнивая силу сопротивления и силу тяже
сти, имеем
5 РО 2
С v ==тg
2 2 ,
g(l :. {:,)'}
(3.26)
(3.21)
откуда
V2 == r}i
v Р
(3,22)
Которое, как очевидно, является уравнением с разделяющимися перемен
ными и может быть леrко проинтеrpировано аналитически, Повторным ин
теrpированием зависимости v=v(t) находят зависимость координаты MaTe
риальной точки от скорости, Дополнив уравнение (3.26) уравнением
dx
d/ == V, (3,27)
или
", = f;;З g .
(3,23)
58
59

11
I
l5..пI?п:.:Р..?:!й-?"'е:.tp,?'f!.I!_I!'.е1!.!:з.!:.:.с..К-l!х.rlfJ.?'!.:'=':..О!.'!.'!'!'.!:_1.l}_.юшш
З. Динамика материаЛbllOti точки
о.. ... .. о.. .... .... ....... ........... . ш .. . .. ...... .. ... .'' . о... . .......
получаем систему дифференциальных уравнений, которую можно решить в
шtкете МА TLAB численно.
В связи с тем, что выше мы подробно обсудили методы решения ОДУ
BToporo порядка в пакете МА ТIAB, далее мы приводим только текст ш
файла, содержащеrо описание вектор-функции, стоящей в правой части
системы уравнений (3.26), (3.27):
function Z=Friction(t,y)
global g,vl,v2
dy=zeros(2,1)j
% задание координат векторфункции, стоящей в правой части
% системы (3.26), (3.27)
dy(1)=y(2)j
dy(2)=-g*(1-y(2)/vl-(y(2)/v2) Л2) j
() (1. при х  О
sgll\x = , (3,28)
L-l,прих<О
При пРОШ60ЛЬНОМ направлении дви,жения вдо.7Ь оси о У выра:жение
(3,24), (3.25) для сил сопротивления прини.нает следующиЙ вид:
FJ =Sgll(V),/1lg(:J, (3,29)
Р,! = sgll(V)' тg( -;;)2 (3,30)
Подставив (3,29), (3,30) в (3,22) получаем уравнение движения тела
dv II1g  Fd ( v / l( v 12 J'
_ =,Ш=,g 1+sgn(v),+sgn\l')' ..шш). (3.31)
dt т у! У2
1. Для значений преде.7ЫЮЙ скорости, представлеННblХ в табл. 3,2, 3.4, pe
шит е численно уравнение дви,жения (3,31) и постройте зависимости
у = y(t h v = v(t), v = v(y) (в пакете MAТlAB функция, возвращающая знак
nереАtенной, имеет вид sign(uмяnере.менной),
2. Решите уравНСНllЯ движения (3,28), nредполаzая наличие в правой части
только линейноzо и квадратичноzо членов, Сравните полученные решеш
ния с nредыдущи-м решение.'W, Какие можно сделать выводы?
3. Сравните зависи.мости у = y(t), l' = (t), v = у(у), полученные без учета и
при учете силы сопротивленuя, На сколько оm7ичаются .максшwальные
высоты подъе.",ш тела при учете и без учета силы треllия?
Задача 3.5
1. Для значений предельной скорости, представленных в табл. 3.2, 3,4, реш
шите уравнение движения (3.26) и постройте зависимости у = y(t) ,
v = v(t), v = v(y)
2. РеИlUте уравнения движения (3.26), nредполаzая наличие в правой части
только линеUНО20 и квадратuчноzо членов. Сравните полученные реше
ния с предыдУЩИ.ltt решенuе.и. Какие можно сделать выводы?
3, Сравните завиСLНtOсти у = y(t), v = v(t), v = v(y), полученные без учета и
при учете силы сопротивления, Можно ли считать реалистичной MO
дель движения тела в zравитациОННOJ,1 поле Земли, не учитывающую Ha
личuе силы трения?
4, Решите уравнения движения, не предполazая постоянства силы тяжести.
у у
V)' р)'
рк V.

/. VK Х Х

/Н
Т'Т . )'
'-/mg
Рис. 3.5
Задача 3.6
3аА!етим, что уравнение движения (3.23) описывает только частный
случай  падение с нулевой начальной скоростью. ПОЛУЧШt более общее
уравнение движения, справедливое при любых начальных условиях. Так
как сила сопротивления всеzда направлена против направления CKOpO
сти, то при движении тела в пОЛОJlсительном направлении оси оУ сила
сопротивления отрицательна, и наобороm, при движении те.7а в отриш
цательном направлении оси оУ сила сопротивления положительна, в то'
время как сила тяжести всеzда направлена в отрицательном направле
нии оси о У. Эти условия наиболее просто выразить, используя знаковую
функцию sgп(x)
60
6]

15..'?1.':.!().'!.'.:l!!!.?.-!!!!z.!P.()а..'!!!.Ф_.:<:К:.r:.Р.()'}е..с()п!!'!...e.!!':.:.'!...1.т1.!! ....
Задача 3.7
При движении материальной точки массой т с начальной скоростью
iio, направленной под У2Лом ()о к 2Орuзонту (рис, 3.4), на материальную
точку действуют сила тяжести и сила сопротивления Fd' направлен
ная противоположно скорости v (рис, 3.5). Уравнения дви,жения тела в
данном случае имеют следующий вид:
d2x [IVi (Iv! )2)
dt2 = g  +  cos()
d2 у = g  g[ ivi + (M)2)sgn(v . )in ()'
dt2 Vj v2 )
r лава 4
ЗАДА ЧА КЕПЛЕР А
4.1. Введение
11
2де Ivl = f'v
Так как cos()=vx/lvl,sin()=vy/lvl, то уравнения системы (3.32)
преобразуются к виду
d2x = g[H+(J1)2).!. dx
dt2 Vj v2 Ivl dt
d2; =gg[H+(H)2)sgn(dY) dy
dt Vj v2 dt IVI dt
1. Выберите начальные условия и решите систему уравнений (3.33),
2.Постройте зависимости x=x(t), y=y(t), Vx=X'(I), vy=y'(t),
Vx = vx(x), vy = vy(x), у = у(х).
(3.33)
Задача о движении планет в поле тяжести небесных светил, являющаяся
частным случаем задачи о движении в поле центральных сил, известна на
протяжении нескольких тысячелетий истории человечества и в настояшее
время рассматривается как в школьных курсах физики, астрономии, так и в
вузовских курсах классической механики и астрономии.
Большую часть наших знаний о движении планет объединили в себе за
коны Кеплера, полученные на основе анализа данных астрономических Ha
блюдений, которые формулируются следующим образом.
1. Всякая планета движется по эллиптической орбите, в одном из фоку
сов которой находится Солнце,
2. Скорость планеты возрастает по мере удаления от Солнца таким обра
зом, что прямая, соединяющая Солнце и планету, в равные промежутки Bpe
мени заметает одинаковую площадь.
3. Для всех планет, вращщощихся BOKpyr Солнца, отношение T2/R3 оди
наково (Т  период обращения планеты BOKpyr Солнца, R  большая полуось
эллипса).
Отметим, что получить аналитическое решение задачи Кеплера удается
только в случае рассмотрения движения двух тел, взаимодействующих по
закону обратных квадратов. Это решение рассматривается во всех учебни
ках по классической механике, только малая часть из которых приведена
в списке литературы [13]. Задача Кеплера для трех и более тел аналитиче
CKoro решения не имеет, может быть решена только численно. Поэтому в
Этой rлаве основное внимание мы уделяем численному решению уравнений
движения тела в центральном поле.
(3.32)
3. Постройте зависимости nереJнещения материальной точки и У2ла меж
ду вектором скорости и осью оХ от времени,
4. Сравните полученные результаты с результатами задачи 3,1,
ЛИТЕРАТУРА
1. r'улд Х., Тобо'lНИК Я. Компьютерное моделирование в физике. Часть 1. М,: Мир. 1990.
2. Хеннер Е. К, Шестаков А. П. МатемаТИ'lеское моделирование. Пермь: Пермский rосудар-
ственный педаrоr И'lеский университет, 1995,
3. Матвеев А. Н. Механика и теория относительности. М,: Высшая школа, 1986.
4. Аппель П. Т еореl И'Iеская механика. М,: r-иФмл, 1960.
4.2. Уравнения движения планет
Ij r
в качестве отправной точки решения задачи Кеплера рассмотрим дви
жение двух тел, взаимодействующих друr с друrом, считая их при этом Ma
териальными точками. Функция Лаrpанжа такой системы имеет вид
.'" .2.2
[, =- mI'j' + тL!2  U(Р  r 1) = тIij + 1112'2
2 2 1 21 2 2
ymrfn
+  . ., 
ij  1'2
(4.1 )
62
i
:1

, I
[
l'
'!
I
[ I
I
I
'j
J?tl:.IO!!P.Ii()e.tO_J<:J. 1l!()ва!lI!е_1!I!:.!:: :':С:L:'хпРОl/_ес()в!lt!.!'.е.IrIе.Л!1 T1.B.
4 Задача Кеплера
.... ...... .. . ........... ........... ..
[де i], 1'2 - радиусывекторы первоrо и BToporo тела, соответственно,
U'i  '21)  потенциа!JЪНая взаимодействия тел, r  rpавитационная посто
янная. Введем вектор взаимноrо расстояния обоих тел
r =. 'i P2' (4.2)
Тоrда в системе отсчета с началом координат в центре масс, рассматри
ваемой системы тел,
Воспользовавшись уравнениями Лаrpанжа (здесь обобщенными коорди
натами являются координаты радиусавектора Р, обобщенными скоростя
ми  координаты вектора т)
d oL
dt а r
получим уравнение движения тела
d2r у т(т1 +т2)
т. = .;'
dt2 p3 '
, 1
oL
дР
(4,8)
т1'i +т2Р2 =0,
(4,3)
(4.9)
Из (4,2), (4,3) находим
m2
'i = .. .. Р,
т\ +т2
(4.4)
которое при 1111 » т2 принимает вид
d2r у т\т2
т =P,
2 dt2 [ri3
в полном соответствии с законом всемирноrо тяrотения Ньютона.
Отметим два важных свойства силы тяrоrения, вытекающих из (4.10):
1) сила зависит только от расстояния между телами; 2) сила направлена по
прямой, проходящей через центры взаимодействующих тел. Такие силы Ha
зываются центральными, Можно показать [1], что следствием указанных
свойств является сохранение момента импульса тела
L=[FXp], (4.11)
m1
'2 =.'P.
т1 +т2
Подставляя (4.4), (4.5) в (4.1) получаем
,2 . 2 ( )
L = т'  +u(rl)= -тP + Y1 т\ +,
2 2!'i P2[
(4,1 о)
(4.5)
(4.6)
rдe введено обозначение
т=\т2 (4.7)
тl +m2
Величину определяемую в соответствии с (4.7), принято называть при
веденной массой. Функция (4.6) формально совпадает с функцией Лаrpанжа
одной материальной точки с массой т, движущейся в поле с потенциалом
иP[), симметричным относительно начала выбранной системы отсчета.
Таким образом, задача о движении двух взаимодействующих теп сводится к
решению задачи о движении одноrо тела с массой 111 в заданном внешнем
поле U(Fi), создаваемом неподвижным центром с массой m] +m2' OTMe
тим, что если масса одноrо из взаимодействующих тел значительно меньше
массы друrоrо тела, последнее можно рассматривать как неподвижный при
тяrивающий центр, и найденная зависимость r(t) буде'! описывать тpaeKTO
рию движения более леrкor'о тела, В противном случае, решив задачу о
движении тела с массой т в потенциале иp[) по зависимости 1'(1) в COOT
ветствии с (4.4), (4.5), находя! траектории каждой частицы i](t) 12(')'
[де р = тР .
Сохранение момента импульса, в свою очередь, означает, что траектория
движения тела в центральном поле лежит в плоскости, которой перпенди
кулярен вектор L. Кроме Toro, движение тела оrpаничивается условиями
сохранения полной энерrии
E=mv2ym(+т2) .
2 !У!
(4.12)
и величины
[; х 1:] у m(т\т.1.P' = const ,
:r:
Для решения уравнений движения выберем прямоyrольную систему KO
ординат, начало которой находится в центре масс (рис, 4,1), (Отметим, что в
ОТличие от аналитическоrо решения, наиболее просто получаемоrо в поляр
Ной системе координат, численное решение задачи Кеплера более удобно
ПРОВодить в декартовой системе координат.)
(4.13 )
64
. 3\57б
65

I
,)1
}II
!!.A! ЬО!!lеJ!!I?1!!,.Л-"р"О..а.'t"..фI13" ч ec...иx IР?е..,:овI1е..т-п-е...},!1.L.rI,.
у
т
Рис, 4,1, Система координат.
используемая для описания движения
тел, под действием силы
М = т1 + т2 х 2равитациОННО20 взаимодействия
Уравнения движения (4,9) в выбранной системе координат имеют сле
дующий вид
d2x У т(щ +т2)
т х
d2t  11'13 '
d2y ут(тl +т2)
т  У
d2t  11'13 .
Введя обозначение М = тl + т2 и сократив общие множители, запишем
выражения (4.14), (4.15), составляющие систему ОДУ втoporo порядка, в виде
d2x у М
dt2 (  х,
x2+iJ-'-
(4.14)
(4.15)
(4.16)
d2y
dt2
уМ
3 у.
(х2 + у2 
Предваряя численное решение системы уравнений (4.16), (4.17), прове
дем обезразмеривание этих уравнений. Если в качестве единиц измерения
расстояния и времени выбрать радиус орбиты R и период обращения Т, co
ответствующие движению тела по окружности, то можно ввести безразмер
ные переменные Х = х/ R, У = у/ R ,Т = (/Т . Выполнив в (4.16), (4.17) за
мену переменных xx, yY, (T, получаем
d2X уМ т2
=.x ,
d 2 ( 
r R3 X2+y2J
d2y у М т2 ,
 = ,,.} ,
dr2 ( 
R3 х2 +y2,
(4.17)
(4.18)
(4,19)
66
.. н шш .l!ш:""!'!РС}
Как известно, при движении тела по окружности величина цeHтpocтpe
мительноrо ускорения а связана с радиусом крyrовой орбиты IRI и CKOpO
стью тела !уl соотношением
1\112
a=
iR; .
,
(4.20)
При движении в rpавитационном поле по окружности центростреми
тельное ускорение обусловлено rpавитационной силой. Следовательно,
1,2
т17!
lЛl
утМ
I 12 '
/
(4.21)
откуда находим
1'1 =( l )2
Выражение (4.21), являясь общим условием для любой крyrовой орбиты,
позволяет найти зависимость периода движения от радиуса орбиты. Период
движения
(4.22)
21l'1 Л[
Т=м,
(4.23)
поэтому, подставив в (4.22) выражение (4.21), получим.
r1l'21R13
T I
 уМ
Подставляя выражение (4.23) в (4.18), (4.19), получаем окончательно
обезразмеренную систему уравнений
d2x
dr2
(4.24)
41l'2
.. ..  Х
(х 2 + y2)i
d2y 41l'2
=зУ.
dr (x2+y2
Из уравнений (4.24), (4.25) видна их универсальность  они не зависят
Ни от периода обращения тела Boкpyr центра поля, ни от радиуса орбиты.
(4.25)
(4.26)
67

Ii и-л!.1Jы
illlер"'lоемM 00, e:7Ul'0'1111Ie Ipи1 '!.СК-'I;( Пf)0.llеL(}6. 1lак-. еп,  А!!:..Т-L,f!.
ш:,'!..а.?.f!ша.,l!п-Jl.'!.l!.f!
Следовательно, величина 1'21 R3 , входящая в (4,17), (4,18), одинакова для
всех тел, совершающих движение в rpавитационном поле по замкнутым
траекториям, Данный результат является доказательством справедливости
тpeTbero закона Кеплера,
При решении системы диф
ференциальных уравнений будем
считать, что в начальный момент
времени тело находилось в точке
с радиусомшвектором F = (R,o) ,
скорость тела была направлена Рис. 4,2, К выбору начальных УСЛIJвиu
вертикально вверх v ::: (О, v) числеllliО20 интеzрирования уравнении
( 4 2) движения
рис, . .
Так как система уравнений (4.24), (4.25) является безразмерной, необхош
димо также привести к безразмерному виду начальные условия, Выполнив,
как и выше, замену переменных F = Р . R, t::: r ' Т , приводим начальные усш
dZ2
dr
dZI
=Z2
dr
2
 ш 'ш
[ ]3
1 2 ш
Z, + Z3 2
dz--"
 ::: Z4
dr
( 4,30)
р:::(1,о),
V ::: ( О, v).
(4,27)
2
41Z' . Z3
3
[ 2 2]ш
Zl + Z3 2
Следуя общим правилам решения систем обыкновенных дифференциш
альных уравнений первоrо порядка в пакете МА TLAВ, создадим mфайл
Orbit.m, содержащий определение векторшфункции, стоящей в левой части
системы (4.30):
function dy=Orbit(t,z)
dy=zeros(4,1); % задание векторашстолбца размерности 4хl
% задание координат векторшфункции, стоящей
% правой части (4.30)
dy(1)=z(2);
dy(2 )=-4*pi л 2 *z(l )/(z(l) л 2+z(3) л 2) л (3/2);
dy(3)=z(4);
dy( 4)=-4*pi Л2*z(3)/(z(1) Л2+z(3) Л2У (3/2);
dZ4
dr
х
ловия К следующему виду:
(4.28)
rде Т определяется выражением (4,24).
Однако использовать конкретные числовые значения R, Т, М для про
верки законов Кеплера не требуется, так как безразмерные начальные усло
вия также обладают известным универсализмом, Для Toro, чтобы это покаш
зать, найдем безразмерную скорость тела, движущеrося в rpавитационном
поле по окружности. Подставив (4.23) в (4,28), получаем
V=(0,21Z'), (4.29)
Следовательно, для получения орбит, отличных от KpyroBbIx, достаточно
задавать значения начальной скорости, отличные от 211:,
4.3. Численное моделирование орбиты
Далее необходимо выполнить в командном окне следующую последова
тельность команд:
% задание начальных координат х(О), у(О)
» xO=l;
» уО=О;
% задание начальных скоростей х'(О) у'(О)
» vxO=O;
» vyO=2*pi*1.2;
» [t,У]=оdе45('ОrЫt',[О:lОЛ-5:2.5],[хО vxO уО vyO]);
» figure(l)j plot(t,Y(:,l»; % построение зависимости х::: x(t) (рис. 4,3)
» figure(2); plot(t,Y(:,2»; % построение зависимости х'::: x'(t) (рис, 4.4)
» figure(3); plot(t,Y(:,3»; % построенйе зависимости у = y(t) (рис, 4.5)
» figure(4)j plot(t,Y(:,4»j % построение зависимости у'::: y'(t) (рис, 4,6)
» figure(5)j plot(Y(:,1),Y(:,3»)j % построение траектории движения (рис, 4.7)
Предваряя нахождение численноrо решения системы уравнений (4,25),
(4.26), приведем ее эквивалентной системе уравнений первоrо порядка, выш
полнив замену переменных Х  Zl' Х'  Z2' У  Z3' У' Ш+ Z4 :
68
69

e=(1-(blа)Л2)ЛО.5
else
е=(1-(а/Ь )Л2)ЛО.5
end
I 1:
!..'!.!'lОт!!!!!!1!.!!..i>...е:!.':'.е'!!.':'.:..1!!!33:.!:I!!!!!..ессов в пакет! МА !и!!..
Зависимости кинематических характеристик от времени и траектория
движения представлены на рис. 4.3----4.7.
1.5
-0.5
\ (1
\ I
\ //
,/
е=
0.4386
0.5
1
1.5
.2
-2.5
...з .   .""""."....L.."
О М 1 U 2 U
I
I
1
I
l'
I
Рис, 4.3. Зависимость х = x(t)
Для отображения на одном чертеже траектории материальной точки и
притяrивающеrо центра необходимо выполнить следующую последова
тельность команд:
» ХО=О; УО=О; % задание координат притяrивающеrо центра
» plot(Y (:,l),Y (:,3),хО,УО, 'о' ,'MarkerSize',5};
Для вычисления эксцентриситета орбиты необходимо выполнить сле
дующую последовательность команд:
» MinX=min(Y(:,l»; % вычисление минимальноrо элемента
% в первом столбце матрицы У
» MaxX=max(Y(:,l»; % вычисление максимальноrо элемента
% в первом столбце матрицы У
» a=(MaxX-МiпХ)I2; % вычисление длины первой полуоси
»MinY=min(Y(:,3»; % вычисление минимальноrо элемента
% во втором столбце матрицы У
» MaxY=max(Y(:,l»; % вычисление максимальноrо элемента
% во втором столбце матрицы У
» b=(MaxY-МiпУ)I2; % вычисление длины второй полуоси
% вычисление эксцентриситета
» if Ь<=а
j,
70
/
/
/"
//
/
/
//
/
\ /
\ /
\ ./
:\ /
\ /
,./
-60
,
1.5
,
0.5
Рис, 4.4. Зависимость х' = x'(t)
т
15r //
J I \
J/
1/
v
°r
!
\
\
\
\.
\
\
\
\
\
\
'",
".
'-.
-o.5f
i
1
.1 L
1
!
1.5 
-2.  ,
О
,
05
 . 
1
I..
15
Рис, 4,5, Зависимость у = y(t)
71
........i>.....l!..ll1}e'p'a

2
2.5
/
. ..lш
2
2.5

11:
l'
.1
11
I1
11
I
il
1:
K?:п.ь.(},!:pl1(}e. -"!.o.(P.й-'!!.:P.и-..'!..K:'!.'3.p(}yeo.в. в п.a..I1I!vf..r1.Tr1.!!.
... 4:}Cl.9.Cl.Cl.l!.:1Jl'!..jJCl.
8'"""", ..... ... -.
'.
i\
6:
начинается с первоrо значения; значения x(t), x'(t ), у(1 ), Y'(I) содержатся co
ответственно в lM, 2M, 3M, 4,м столбцах матрицы,
Так как решение уравнений движения про водится на равномерной
временной сетке, то для задания начальноrо и конечноrо значений
BpeMeHHoro интервала, в течение KOToporo вычисляется площадь сектора,
заметаемоrо радиусомвектором, достаточно указать номер cooтвeTCT
вующей строки матрицы У и количество используемых точек (т, е, длину
BpeMeHHoro интервала),
При достаточно малом шаrе интеrpирования f:.t уравнений движения
(определяемым количеством точек N, в которых ищется решение системы
ОДУ, М = Tfinish/N) площадь, заметаемая радиусомвектором за время f:.t,
примерно равна площади треуrольника с вершинами в точках (0,0),
(У(п, 1), У(п, 3)), (У(п + 1,1), У(п + 1,3)) (см. рис, 4,8).
4 
2:
°t
, I
,
il
I
-2r
-4 L 
О
..   .
05
.
1
15

Рис, 4,6, Зависимость у' = y'(t)
!. УiЛ + 1,1 iY, n + 1,3!i
0.5
/
/
!
i
\
--
\
\"',-
"
\
\
i
/
Рис, 4,8, К объяснению вычислитеЛЬНО20
aлzориmма проверки втОр020 закона
Кеплера
Для вычисления площади треуrольника, у KOToporo заданы координаты
вершин, можно воспользоваться формулой repoHa
s =  p(paXp bXp c),

(0,0) а (YinJ i,Y(n,3 )',
1.5
/
/
//
''"'
'.
'-
',о
".5
.1
I
/
/
/
(4.31 )
-2 
3 -25 -2
L ....J . ......J_ ..I.-
-15 -, -05 О
I
. ..  ..!
05 15
rде р  полупериметр треуrольника, изсбраженноrо на рис. 4.8, а, Ь, с 
длины ero сторон:
,15
/
Рис, 4,7, Траектория движения
а = Y(п, 1)2 + У(п, 3) 2 ,
Ь = Y(п + 1.1)2+У(п,з)2 ,
с =  1, 1) Y(ni)]2TY(n + L3) У(п, з)]2 .
(4.32)
! 11
"
4.4. Проверка BToporo закона Кеплера
(4.33)
(4,34)
Для про верки BToporo закона Кеплера необходимо провести сравнение
площади, заметаемой радиусомвектором за равные промежутки времени,
используя значения кинематических характеристик движения тела в rpави
тационном поле, полученные численным решением системы ОДУ (4,30),
возвращенные в матрицу У. Напомним, что размерность матрицы У, содер'
жащей решения системы ОДУ, Nx4; нумерация столбцов и строк матрицы
Однако проrpамма вычисления площади сектора, заметаемоrо радиусом
вектором, получается более компактной, если использовать встроенную в
пакет МА ТLAB функцию cross, вычисляющую векторное произведение
трехмерных векторов, Как известно из аналитической rеометрии, площадь
треуrольника, изображенноrо на рис, 4,8, равна
! 
I ,
1
'1
72
73

  i
I 11
, !
,; 
!!.?:I_ь'.?п:.Е.l.?=.л:с:е!!.'!!!!>!.I!!.I!!=4:.?!,_чекuх пp?цeco :,,!'!.e!!'.!.!!..1ТLAB
4. Задача Кеплера
..................
s =  I [о х Б] I '
(4.35)
% t, У  переменные, возвращенные одним из решателей систем ОДУ
% Tstart  начальный момент времени
% dT  длительность BpeMeHHoro интервала
dt=t(2)-t(1); % шar интеrpирования ОДУ
Nstart=ceil(Tstartldt)+l; % вычисление номера начальной координаты
dN=ceil(dT/dt); % число шaroв
Nstop=Nstart+dN; % номер последней координаты
% вычисление значения Nm
i=length(Y);
while Y(l,l)<Y(i,l)
Nm=i-l;
i=i-l;
end;
Nlength=Nm;
% вычисление площади, заметаемой радиусомвектором
s=O;
for i=Nstart:Nstop
% проверка условий (4.30)
if i<Nlепgth-l
xl=[Y(i,l) Y(i,3) О];
x2=[Y(i+l,l) Y(i+l,3) О];
end;
if i==Nlength
xl=[Y(i,l) Y(i,3) О];
x2=[Y(l,l) Y(1,3) О];
end;
if i>Nlength
xl=[Y(i-Nlепgth,l) Y(i-Nlength,3) О];
x2=[Y(i+l-NIепgth,l) Y(i+l-Nlength,3) О];
end;
s=s+nonn( cross(xl,x2) )/2;
end;
z=s;
поэтому алrоритм ВIчисления площади сектора, заметаемоrо радиусом
вектором, реализуется следующей последовательностью действий:
1. Задание начальноrо момента времени и длины BpeMeHHoro интервала,
на котором вычисляется площадь, заметаемая радиусомвектором,
2, Присвоение координатам вектора О, соответствующих значений KO
ординат орбиты (У(п, 1) = о, У(п, 3) = 1, z = О) в момент времени t(n).
3, Присвоение координатам вектора О, соответствующих значений
координат орбиты (z = О), в момент времени t(n + 1),
4. Вычисление площади треуrольника М , заметаемоrо радиусомвекто
ром на временном интервале [t(п), t(n + 1)] ,
5, Нахождение площади, заметаемой радиусомвектором на временном
интервале [t(I),t(n + 1)], суммированием известной площади, заметаемой pa
диусомвектором на интервале [t(1),t(n)], и М .
При составлении проrpаммы, реализующей описанный вычислительный
алrоритм, мы исходили из следующих предположений:
1. Материальная точка в момент времени t(l) = О находится в точке с pa
диусомвектором (У(l,l) = 1, У(1,3) = о),
2, Длительность BpeMeHHoro интервала, на котором получено численное
решение системы ОДУ (4.30), такова, что материальная точка совершает не
более 1,25 оборота,
Так как нам заранее неизвестно точное значение периода одноrо оборота
материальной точки BOKpyr притяrивающеrо центра, в проrpамме мы Haxo
дим ero численно, определяя при этом номер Nm соответствующеrо элемен
та вектора. Кроме Toro, следует учесть, что периодичность движения при
водит к следующим правилам вычисления номера текущей координаты pa
диусавектора:
п, если п :<:; Nm
п  Nm, если п > Nm
Далее приводится листинr Illфайла KeplerLow2.m, содержащий
цию KeplerLow2, реализующую описанный выше алrоритм,
function z=KeplerLow2( t, У, Tstart,dT)
% функция, возвращающая площадь, заметаемую
,'O радиусом вектором
( 4,36)
функ
для обращения к функции KeplerLow2, после нахождения численных
решений системы ОДУ (4.30) следует ввести команду
» KeplerLow2(t,Y,2.0,0.5)
аOS=
1.8882
74
75

I
1
I i
I
К-о.М-.Й-'I1..:Е.'?:.М-?.l!..?!.'!.!'!:!:..1!!..':,::,:с.!.'!!.'!.l!..Й-:.с...й.. ...I!.:'!' 1,T/ll!..... ..ШШ..
4. Задача Кеплера
........ ...... ......... ........
Представляет определенный интерес, не только вычислить площадь ceK
тора, заметаемоrо радиусомвектором, но и изобразить данный сектор на
рисунке вместе с траекторией тела, Для этоrо необходимо модифицировать
функцию KeplerLow2 таким образом, чтобы она возвращала помимо зна
чения площади, заметаемой радиусомвектором, координаты притяrи
вающеrо центра и радиусавектора в соответствующие последователь
ные моменты времени и затем использовать функцию patch. Ниже при
веден листинr mфайла KeplerLow.m, содержащеrо модифицированную
функцию KeplerLow:
function [z,Xr, У r ]=KeplerLow( t, У, Tstart,dT)
% функция, возвращающая площадь, заметаемую радиусомвектором,
% и координаты соответствующих точек орбиты
% t,Y  переменные, возвращенные одним из решателей систем ОДУ
% Tstart  начальный момент времени
% дТ  длительность BpeMeHHoro интервала
dt=t(2)-t(1); % шаr интеrpирования ОДУ;
Nstart=ceil(Tstart/dt)+l; % вычисление номера начальной координаты
dN=ceil(dT/dt); % число шаrов
Nstop=Nstart+dN; % вычисление номера начальной координаты
x(l)=Oj y(l)=O; % координаты притяrивающеrо центра
% вычисление значения Nm
i=length(Y)j
while Y(i,l)<Y(i-l,l)
Nm=i-l;
i=i-l;
епд;
Nlength=Nm;
% вычисление площади, заметаемой радиусомвектором
s=O;
m=l;
for i=Nstart:Nstop
m=m+ 1;
о/с проверка условий (4,30)
if i<Nlепgth-l
xl=[Y(i,l) Y(i,3) О];
x2=[Y(i+l,1) Y(i+l,3) О];
епд;
if i==Nlength
xl=[Y(i,l) УО,3) О];
x2=[Y(1,1) Y(1,3) О];
епд;
if i>Nlength
xl=[Y(i-Nlепgth,l) Y(i-Nlength,3) О];
x2=[Y(i+l-Nlепgth,1) Y(i+l-Nlength,3) О];
епд;
s=s+norm( cross(xl ,х2) )/2;
x(m)=x1(l);
у(m)=х1(2);
епд;
х(m+ 1)=x2(1);
у(m+ 1)=x2(2);
z=s;
Xr=x;
Yr=y;
Для вычисления площади, заметаемой радиусомвектором, и визуализа
ции сектора необходимо выполнить следующую последовательность KO
манд:
»[z,Xr,Yr]=KeplerLow(t,Y,0.5,1/0); % обращение к функции KeplerLow
»plot(Y(:,1),Y(:,3)); % построение орбиты
» patch(Xr,Yr,'g'); % визуализация сектора
Результат выполнения описанной последовательности команд представ
лен на рис, 4,9.
2
I
1
15!'
I
1 
i
05[
о',

'"
"
\
\
\
,
!
-с 5-.
.,i
\.
,
'"
"'-"-"'-
I
I
I
,'5, ш,ш..шш=,..j
.:з 2 5 -2 -1 5 .1 .05 О 05 1 1 5
Рис. 4.9. Траектория движения и сектор. за.нетае.\tый радиус вeKтopo.'
1Ю вре.\1еIlНО.Н интервале {O.5.I]
76
77

1, В чем отличие орбиты тела, двИ2ающе20СЯ в новом потенциале, от op
биты тела, двИ2ающе20СЯ в потенциале 1/11' ? Убедитесь в том, что пo
лученный результат не зависит от ша2а инте2рирования,
2. При каких начальных условиях планета будет двИ2атьс вОКРУ2 цен!)"ра
притяжения по раскручивающейся или по закручивающеися спирали,
3. Один из способов описания траектории
движения тела  рассмотрение ее как Эk
липтической орбиты, которая ,медленно пo
ворачивается (прецессирует) в направлении
движения тела. Количественно прецесcuя
характеризуется У2ЛОМ между прямыми,
проходящими через последовательные пери
2елии и фокус эллипса (рис, 4,10). Оцените
величину этО20 У2Ла для выбранных пapa Рис, 4,1 О
метров орбиты и значения 8.
4. Предложите ал20ритм и составьте прО2рш,tМу, позволяющую aвтOMa
тизировать процедуру вычисления У2ла прецессии,
5. Используя составленную прО2рамму, зафиксируйте знач:ние 8 и иссле
дуйте зависимость У2Ла прецессии <р от длины большои поуоси а He
возмущеННО20 эллипса, Постройте 2рафик соответствующеи зависимо
сти, Оцените функциональную зависимость У2ла прецессии от длины
большой полуоси эллипса, (Указание, Постройте 2рафик зависимости
'"
ер = ер (а) в ЛО2арифмическом масштабе .)
6. Используя составленную прО2рамму, зафиксируйте длину большой полуоси
эллипса а и исследуйте зависимость У2Ла прецессии <р от величины 8, По
стройте 2рафик соответствующей зависимости, Оцените функционь
ную зависимость У2.ла прецессии <р от величины 8, (Указание, Построите
2рафик зависимости ер = ер( 8) в пОЛУЛО2арифмическом масштабе.)
'.?!.I1ер'l9....9.е.Л-l!Р?.':I1!!!:...1!.l1!..l!::'':..к.. I!!!.'!..е'}!!.!'!а.к.:.'!I.е..А!..1!..:!J!. ..
Задача 4.1
1, Проведите расчеты при различных значениях начальной скорости и убе
дитесь, что для безразмерных скоростей, незначительно меньших или
превосходящих 27r, орбита является замкнутым эллипсом, в одном из
фокусов котОРО20 находится Солнце, Это является иллюстрацией пpa
вильности первО20 закона Кеплера,
2. Убедитесь в том, что при задании начальных условий й(о) = (1,0),
9(0) = (0,21r) орбита является КРУ20вой,
3. Вычислите значения нормировочных переменных для системы Солнце Земля,
4. Реальные значения параметров движения орбиты Земли составляют:
период обращения Т = 3.156.107 с, линейная скорость движения по op
бите v = 29.75.1rY м/с, радиус орбиты Земли R = 1.496,]011 ](М, Исполь
зуя эти данные, определите эксцентриситет орбиты Земли е и сравни
те это значение со значением, известным из эксперимента (е = 0.0167).
Объясните обнаруженные отличия.
5. Определите значение начальной скорости, при которой происходит падение
тела на центр поля, Чему равно значение полной энер2Uи системы в этом
случае? Каковы значения этой скорости для системы Солнце  Земля?
6. Определите значение начальной скорости, при которой тело может
удалиться от притяzивающе20 центра на бесконечно большое расстоя
ние. Чему равно значение полной энеР2ии системы в этом случае? KaKO
вы значения этой скорости для системы Солнце  Земля?
7. Проведите численные эксперименты и найдите зависимость эксцентри
ситета орбиты и периода обращения от величины начальной скорости,
8. Изменяя номер начальной точки, убедитесь в выполнении третье20 за
кона Кеплера,
9. Оцените точность, с которой выполняется второй закон Кеплера, Ka
кой параметр определяет точность сохранения указанной величины?
10. Убедитесь в существовании инте2ралов движения, описываемых вы
ражениЯА-tU (4,12,4.13),
Задача 4.3
Для тела, совершающе20 движение в потенциале
U(T) \
;Fi
........................... H''"HH''HH"'H'.. ""'"''НННН''Нш
Задача 4.2
Рассмотрите динамические эффекты, обусловленные малым отклоне
нием силы притяжения от закона обратных квадратов (cooтвeтcт
венно потенциала от закона 1/'1'J), предположив, что
..!:'!.'!3:Ч-':I..К :'!Л-:'r':I..
U1'I) ,
IFIIб
'" Для построения 2рафика функции в ПОЛУЛО2ариф.иическоJИ масштае иСIlОЛЬ
ется функция seтilogy. НаПРlшер. для построения 2рафика функции e х. на интер.
вале [О,1.5] следует ввести G.1ед'ющую последовательность КОЛ1анд:
» x=0:O,01:J,5;
» sет;lщ:у(х,еХfJ(хЛ2));
2де 8 < < 1,
78
79

f( '.bl()rIp'1!..()=t()':.p"'O..a.l1.1',:1). '!='!.l!.>:"т:?.()l!(()ш па..К-ffl':.1'!..1Т.L1l!.
4. Задача Кеплера
.. . ... .............  ..... .шш........,......... .
1. Напишите систему уравнений движения тела.
2, Для безразмерных начальных условий х(О) = 1, у(О) = О, х'(О) = 1 анали.
тически получите значение безраз.мерной скорости, обеспечивающей
движение тела по окружности.
3. Получите численное решение уравнений движения, постройте зависиш
мость кинематических характеристик от времени и орбиту тела. Подш
берите ша2, обеспечивающий получение КРУ20вой орбиты в течение неш
скольких периодов,
4. Внесите несущественные иЗJl.lенения в значения начальной скорости,
обеспечивающей существование КРУ20вой орбиты. Какой будет новая
орбита? Чему равна величина полной энер2ии?
9, Будет ли орбита устойчивой, т. е. будет ли ма,7ЫЙ nередШlflЫЙ тансен.
циальный импульс вызывать малые вОЗJ,/ущения орбиты, а также будет
ли орбита оставаться периодической при отсутствии возмущений при
дальнейшем движении?
10. Исследуйте устойчивость орбиты 6 <:лучае движения тела в nоmенциаш
ле U1'I) . под действием таН2енциаЛhllЫХ сил.
I
rl
....... ... .. ..... ......
Задача 4.5
Известно, что от Солнца в направлении Зе.нли существует поток час..
тиц, называемый солнечным ветро.М, который при водит к возмущению
орбиты дви:-НСУЩС20СЯ тела, Воздействие солнечною ветра на движ)'ш
щеесЯ тело можно раСCJиатривать, как действие слабой постоянной
силы W, действующей на тело в 20рuзонталЬНОJl.l направлении.
1. Запишите уравнения движения, описывающие движение тела в 2равита.
ционноJ,/ поле при учете СОЛ1lеЧН020 ветра.
2. Промоделируйте орбиту при различных значениях величины и/
3. Как .меняется орбшnа тела?
4. Что происходит с инте2ралами движения при учете солнеЧНО20 ветра?
Задача 4.4
Используя описанную nр02рамму, проведите исследование влияния воз
мущений на орбитальную станцию, движущуюся по КРУ20вой орбите
вОКРУ2 Земли:
1, Как меняется орбита станции, если за счет включения на короткое вре.
мя дви2ателя пристыкованной к ней ракеты.носителя станция получиш
ла приращение скорости дv в радиальном направлении?
2, Как зависит это изменение от величины приращения скорости в радиш
альном направлении и е20 длительности?
3. Установите, меняется ли У2Ловой момент и полная энеР2ия под действи.
ем радиалЬН020 возмущения?
4. Будет ли орбита устойчивой, т, е, будет ли малый переданный радиаль
ный импульс вызывать малые возмущения орбиты, а также будет ли
орбита оставаться периодической при отсутствии возмущений при
дальнейшем движении?
5. Проведuте исследования устойчивости в случае движения тела в потен.
циале url) j!,2 под действием радиальных сил.
.1'
6, Как ,меняется орбита станции, если за счет включения на короткое вре.
J,lЯ двиzателя, пристыкованной к ней ракеты.носителя, станция полу.
чила приращение скорости дv в касательном (танzенциаЛЬНОJl.l)
направлении?
7, Как зависит это изменение от величины приращения скорости в танzенш
циальном направлении и ezo длительности?
8, Установите /l1еняется ли уzловой момент II полная энерzия под действиш
ем танzеНЦllйЛЫIOZО вОЗJl.fуще.чШi?
4.5. Пространство скоростей
Ранее в разд, 4,2 мы описали проrpамму, позволяющую строить орбиту
тела, двиrающеrося в потенциале url) II' т, е, rpафик зависимости
у = у(х).
О данной зависимости rоворят, что она построена в пространстве KOOp
динат {х, у}. Можно поступить совершенно аналоrично и построить rpафик
зависимости Vy = Vy (v х) (ряд последовательных значений вектора скорости
тела), который представляет собой траекторию движения тела в про стран.
стве скоростей {vx, \ }. Далее в этом разделе мы более подробно обсудим
вопрос о том, какую форму имеет орбита в пространстве скоростей, если в
пространстве координат орбита является эллипсом,
Для описания орбиты в пространстве скоростей воспользуемся интеrpа.
лом движения (4.] 3), который в предположении 1111» т2 имеет вид
80
81

!<.Й-М--?111.:Е.lltJ.е...10деl!.IIр"()',!!.I еф'll:tI:ск.х..'ljJоч-есо.,!ае111.= "!.1X:'!l!..
[ , [] у тМт  [ , L] у тМто
Ух   r. x. 
!тl о ITo!'
(4.37)
rде, как и ранее, М = т] + т2' т2 == т; То = (хо, Уо)  радиусвектор тела в
начальный момент времени. Запишем (4.37) в координатной форме:
( I утМХ] r II утМхо '1
JnV . LI   mv ,oll,  
.\ 1 ITI .\ , IT
l (4,38)
 mv 1[:  J11!A1Y = l mv 01 [i  yтMy...Q )1 .
х I 'I х, I
iT ITO
ИЗ (4,39) найдем
х = !. (mv \' 1[1  АуО)
утМ' .
у =(mv ILIA О)
утМ х, х
(4.39)
rде
А =mv ILIJ'ff!.'!!l. (4.40)
хО хО, I' I '
то!
I I утМхо 4
Ауо = mvyo LI+I I ' ( .41)
, . :
Возведя в квадрат выражения для х, у в (4.39), сложив их, и учитывая,
что !Ti2 = х2 + у2, получаем
2 2 ( )2
Ахо ( А,о  утМ
(Vx  ILI ) +lvy l)  III
у
(4.42)
Сравнив (4.42) с выражением для окруж
ности радиуса R, центр которой смещен OTHO
сительно начапа координат в точку с коорди
натами (хо' уо) (рис,4,[1)
(x хо)2 +(yyo)2 = R2,
(4.43)
х
приходим К выводу О том, что в пространстве
скоростей орбита тела представляет собой OK
ружность радиуса
Рис. 4.11
утМ
R, = .."C ,
L
(4.44)
82
.. : ClClч--а!<.е.п-:.1е.р..а.
центр которой находится в точке
(А,.о Ао)
',' . :, ,Поэтому скорость частицы
ILll,
можно записать в виде
v=u+w, ( 4.45)
rде
(А"о Ахо) (4.46)
u =,1:1 ' 1[1 '
й  вектор, проведенный из начала координат в центр окружности, w  Bpa
щающийся вектор, модуль Koтoporo равен радиусу окружности Rv'
Отметим, что в каждый момент времени радиусвектор планеты Т пер
пендикулярен вектору "'. Для доказательства данноrо факта достаточно
вычислить скалярное произведение векторов w и r
(r,w)=(r,v)(r.u). (4.47)
Используя (4.39), (4.46) найдем
 Irllll ( Ауо Ахо)
(r.v) = x.vx + Y'v), = ;mM щvх ЩVу , (4.48)
(У .й) = х,их + у 'иу ==  (E vy + 1f vx). (4.49)
Подставив (4.48), (4.49) в (4.47), находим, что скалярное произведение
векторов w и r равно нулю, т. е. вектора являются взаимно
перпендикулярными.
Так как в разделе 4.2. бьmо получено численное решение в безразмерных
nepeMeHHbIx, для проверки сделанных выше выводов необходимо найти BЫ
ражения для безразмерных значений момента импульса [, радиуса окруж
ности Rv, выражений (4.40), (4.41), и, подставив последние в (4.42), полу
чить уравнение окружности в безразмерных переменных.
Выбрав в качестве единиц измерения длины радиус круrовой орбиты R,
в качестве единиц измерения времени период движения по крyrовой орбите
Т, найдем
[= т[тхР]= m[(r 'R)X(V' :)] = т  [fxv]= т  [,
 Р::; Т
rде f = \' = V ,
R' R
(4.50)
83


!ОМl1ыотертlOс' М()UСЛUРОШlUе 1у!!!и:ескю; пpoцe('coв в-.п.аКt'J1.l.с.л!jJl'L:4i3. ..
Подставляя (4.46) в (4,50) и учитывая (422), (4,24), находим
4п-2
п\! = -I'=':
iJi
ПОC'I)'IIая анаJЮПIЧНО, про водим обезразмеривание выражений (4.40), (4.4]):
  4п-251о
А О  v () ' (4,52)
х  XFo1[1
(4,51 )
4п-2хо
А"о = \o + ...: .IO%:'
. , I ILI
,rol I
Более подробно рассмотрение параметров орбит в пространстве CKOpO
Сlей можно найти в [6]. Чисто rеометрическое рассмотрение происхожде
ния замкнуrых орбит при движении тел в IIОЛЯХ, обратно пропорциональ
ных расстоянию до центра, проведено в [7].
(4,53)
Задача 4.6
J, Получите самостоятельно выражения (4,51)(4,53),
2. Убедитесь в том, что орбита в пространстве скоростей является
окру.жностью, хотя в пространстве координат она является эллипсом.
], Дополните документ, в котором проводится решение уравнений движе
ния тела в центральном поле, выражениями, позволяющими вычислять
координаты центра окружности и ее радиус,
4, Используя ЧИС7енное решение уравнений движения, проверыпе справедли
вость выражениЙ (4,51)(4,53),
5, Убедитесь в том, что в каждыЙ момент времени радиусвектор r пла
неты перпендикулярен вектору скорости W. Как можно объяснить
данный факт?
6, Исследуйте, как изменяется орбита в пространстве скоростеЙ под
действием импУЛЬСН020 удара в таН2енциаЛЬНО.tt направлении,
7. Исследуйте, как изменяется орбита в пространстве скоростей под дей
ствие.lt U/vt11УЛЬСНО20 удара в радиальном направлении,
8, Используя представление о то.М, что в каждыЙ момент времени радиус
вектор r планеты перпендикулярен вектору скорости iv, объясните
наблюдаелtOе ИЗJltенение орбиты в системе пространственных коорди
нат под действие.М штульсных ударов в таН2енциальном и радиальном
направ,7еllИЯХ.
9, ИССlедуйте u],l/eHeHue орбиты в пространстве скоростей под деЙстви
e.tt СОЛНСЧНОZО ветра.
84
4. Задача J<еплсра
.. .... ..... ... ........ ....... .
4.6. Моделирование Солнечной системы
Ранее мы заНIIМались моделированием орбит, рассматривая задачу двух
сил. Однако реальные планетные системы не являются системами двух тел,
так как между всеми телами действуют силы rpавитационноrо взаимодейст
вия. Несмотря на то, что силы rpавитаЦИОIШОI'О взаимодействия маПbl по
сравнению с силой притяжения к uентральному светилу, в ряде случаев ('ни
приводят к реально наблюдаемым эффектам, Например, на основании He
совпадения экспериментальных данных 06 орбите- планеты Уран и теоретп
ческих расчетов было предсказано существование планеты Нептун,
Учет взаимноrо влияния друrих тел, находящихся в 11'авитационном по
ле, создаваемом телом большой массы (М), означает, что полная Сilла, дей
ствующая на планету, уже не является центральной, Кроме Toro, в деЙстви
тельности орбиты планет MOryT не лежать в одной плоскости (как, наIlрИ
мер, в Солнечной системе), поэтому для проведения точных расчетов
необходимо решать задачу в трехмерном пространстве, Однако для пони
мания последствий влияния сил rpавитационноrо взаимодействия между
движущимися телами оказывается достаточно рассмотреть двумерную MO
дель, состоящую из двух тел, имеющих массу п-l, ' т2'
Для описания движения тел этой у
системы выберем прямоyrольную
систему координат, представленную т2
на рис. 4,]2, В выбранной системе
координат в предположении, что
М » 1111 + 1112, функция Лаrpанжа
имеет вид:
х
Рис, 4,12
,) ,) м м
J. = !!l]r] + т2T2 + +[1112  +- у 11!, (4.54)
2 2 Ii]! IF21r]2
Воспользовавшись уравнениями Лаrpанжа (4,8) получим уравнения дви
жения тел:
)
dr] ут,М  у 11111112 
1111 ?='.-j.rl..,/i2'
dt Ir] - i1j2 .
( 4.55)
d21j
111? ,Ш
 d12
 l!!.2lv!  у 1111Jп? 
1"',13 rl + ..I'з" /'12'
" /'121
(4.56)
85


Кй-А!.1':..ТIl!Р!!?=..()l!е,!.I'!"-.1,!!!!==-К--,!!:.lр()'i,=:..?..в:'a.'.<.!:ТIl.!.!!:.!!.................
Для нахождения численноrо решения системы уравнений (4.58), (4,59),
как и было сделано выше, следует провести обезразмеривание уравнений
движения. Выбрав в качестве единиц измерения длины и времени величи
в rpa
ны, соответствующие движению по крyrовой орбите тела массой т,
витационном потенциале, создаваемом телом массой М, получаем
d2Xl 4к2
.? =  з XI ...
dr " -
,Х2  Xl)2 + (У2  п)2)
4к2б, 3 (X2 Xl)
X2  Xl)2 + (У2  Yl)2)
4к2
3 Yl  ...
X2  Xl)2 +(Y2 Yl)2 J
4к2б, 3 (Y2 П)
X2 Хl)2 + (У2  п)2)
4к2
 --'..'...'." ..----. Ш"..,.,"' Xl +
3 ...
X2  Хl)2 +(У2  Уl)2)
4к2д:
..'. ...----..... ......l.,.."..(X2 Хl)
X2  Хl)2 + (Y2 п)2 J
4к2
.. 3 П+...
X2Xl)2 +(У2п)2)
4к2б
. 2(Y2Yl)
X2Xl)2 +(У2п)2У
d2Yl
dr2
d2X2
dr2
d2Y2
dr2
=
(4.57)
(4.58)
(4.59)
(4.60)
ще д, = т! / м , д2 = т2 / м , Х 1, П, Х2, У2  координаты радиусов векторов
i\,1'2 соответственно,
При решении системы дифференциальных уравнений будем считать, что
в начальный момент времени тело массой т] находилось в точке с радиу
COMBeKTopOM Ij = (R,'o) , скорость тела была направлена вертикально вверх
" I!
" ,!
86
...............
4. Задача Ке1l.7ера
..... ....... ....... . ... ..... ....... Ш НО . ..... ... .... ......... .... ... Ю"'Ш"""'. . ..... . ".'-'"  ......... . . .... ..."...............
У, = (О, V,), тело массой т2 находилось
в точке с радиусомвектороМ 1'2 = (R2,0)
( R2 = R] i М), скорость тела была Ha
IJравлена вертикально вверх У2 = (О, V2)
(рис. 4,13),
Безразмерные начальные условия
имеют вид
у
У!
У.
R) t::.R
т! т2
Рис. 4,13
,0]=(1,0), ,o2=(H,0). V]=(O,V] :} V2=(0,V2 :). (4,61)
Задача 4.7
Найдите решение системы уравнений движения (4,57)  (4,60), считая,
что параметры орбит и 'daCCbl движущихся тел совпадают
С соответствующими параметрами Земли и Луны,
1. Постройте зависимости координат и скоростей движения обоих тел
от времени,
2. Используя вычисленные значения координат, постройте зависимости
координат от времени и орбиту Луны в систел;/е отсчета, связанной
Землей, Сравните полученные результаты с данными о движении Луны,
приведенными в 2Л, 1,
Задача 4.8
Исследуйте особенности движения системы трех тел, считая, что
М =0,6, д] =10.2, д2 =10.3, У] = (0,2к), V\ = (о,2к/l.б) ,
1. Постройте орбиты планеm, считая, что взаимодействием между ними
можно пренебречь, Чему равны их периоды обращения вОКРУ2 центра
поля?
2. Постройте орбиты планеrп, решив систему (4.57)  (4.60), В чен качест
венно проявляется их взаимодействие? Опишите форму орбит, Почему
влияние взаимодействия на одну u3 планет меНЬИlе, че.н на дРУ2УЮ?
3. Проверыпе, сохраняются ли инте2ралы движения отдельно для первой
и второй планет. Сохраняются ли полная энерzия и по.7НЫй MO.'deHm
обеих п7анет?
4. Используя реа.7ьные астронолtUческие данные, оцените степень в.7ияния
Юпитера на орбиту Земли.
87

i-!()\[ п ь JO iп.(?'l0: .мй-дсЛ ир,ив Й!luсrJ/?!'.ч '!ких.:р?цессов '1:!e,!, е _ т-.4!!..
ЛИТЕРАТУРА
i Ландау П. Д., Лифшиц Е М, Курс lеоретической физики, Механика. М.:Физматrиз, 1958.
2. ]'О."ЬДСlейн [. Классическая механика. М.: Мир, 1974.
3 Лппсль П, Теоретическая механика. М.: rиФмл, 1960,
4. ['улд Х., Тобочник Я. Компьютерное моделирование в физике, Часть 1, М.: Мир, 1990,
5. XCHHep, К., Шестаков. П. Математическое моделирование. Пермь: Пермский [ocyдap
Сl-венныи педаrоrичеСКИII университет, 1995.
(j. Abelson Н., di Sessa А., Rudolph L. Velocity Space the Geometry of Planetary Orbits// Ат. J.
Phys., 43, 579, 1975,
7 (1i Sessa, Orbits А. А minienvlrUHment for exploring orbital mechanicsJ/ Computers in Edication
eds. О. исaпmе, R.l,ewis, 359, NoI1hHolIand, 1975. '
r лава 5
МОДЕЛИРОВАПИЕСТАТИЧЕСКИХ
ЭЛЕКТРИЧЕСКИХ И МАrпитпых
ПОЛЕЙ
5.1. Электрическое поле системы
неподвижных зарядов
Как известно, электрическое поле, создаваемое неподвижным точечным
электрическим зарядом q в вакууме в данной точке пространства, xapaKTe
ризуется скалярным потенциалом
q1(R) = ШД, (5.1)
4п-со IR  1'1
!I
11
rде R  радиусвектор точки наблюдения, r  радиусвектор точки, в KOTO
рой находится электрический заряд, &0  8.85,}о'12 Ф/м, Векторной xapaKTe
ристикой данноrо поля является напряженность
Е = v q1(R) = - __'l (Л  1') .
4п-с'о IR  1'13
(5.2)
I
1 r
Скалярный потенциал электрической системы, состоящей из N электри
ческих зарядов, q1' q2 ... q N , И напряженность электрическоrо поля у довлет
воряют принципу суперпозиции:
N
q1(R)=-L'
4п-со i=1 ;Rljl
1 N .
Е(Л)= - - L qI1(Rlj),
4п-со i=l IR  'il-
(5.3)
I '1
(5.4)
rДе Ij  координата iro заряда,
При анализе электростатических. полей системы произвольно располо
женных зарядов, характеризующихся скалярной функцией  потенциал.ОМ
q1(R) и векторной функцией  напряженностью Е(Я) , возникает задача Ha
rЛЯДноrо представления этих величин. Один из возможных способов пред-
88

I
i I
l!..о..п--ь.lо.."!:..I!!.I?':..?'?!'!Р"()ва.!.,!е .1!ll.:,!е..с:.!IР.о..lf.:::о..в.I!:II!.:. .1!!1:.i!................
.._..!.!...о!.,!!Р"()!3./!!.:.:!!.'..а.II!.!!.':'и-!..1!..ектl!.!!....ч:.:..'!.!!I!..'!II!.!'..Ь!.:()!.'.:Е
ставления потенциала электростатическоrо поля tp(R) реализуется следую
щей последовательностью действий:
1) задание функции, которая возвращает значения потенциала, вычис
ляемые в соответствии (5.3) в узлах заданной координатной сетки;
2) задание дискретной координатной сетки;
3) вычисление в соответствии с (5.3) значения tp(R) в каждом узле KOOp
динатной сетки;
4) построение rpафика поверхности и карты эквипотенциалей.
Следуя последовательности действий, описанной выше, создадим т
файл, содержащий описание функции tp(R):
function Phi=Potential( q,xq,yq,X, У);
% задание функции, возвращающей значения потенциала в узлах
% координатной сетки, вычисляемых в соответствии с (5.3)
% q  вектор, содержащий значения электрических зарядов
% xq, yq  векторы, содержащие xe и ye координаты электрических зарядов
% Х, У  векторы, содержащие xe и ye координаты узлов сетки
еО=8.85*10Л-12; % диэлектрическая проницаемость вакуума
Nq=length(q); % число зарядов в системе
Nx=length(X); % число узлов по оси оХ
Ny=length(Y); % число узлов по оси оУ
% проход по каждому узлу сетки
for i=l:Ny
for j=l:Nx
s=O;
% суммирование по зарядам
for k=l:Nq
s=s+q(k)/( (X(j)-xq(k» Л 2+(У (i)-уq(k»Л 2) ЛО.5;
end;
M(iJ)=s1( 4*pi*eO);
end;
end;
РЫ=М;
Функция Potential возвращает матрицу размерности NyxNx, содержа
щую значения потенциала в соответствующих узлах координатной сетки.
Вычислим потенциал, создаваемый системой, состоящей из N == 50 электри
ческих зарядов, расположенных в точках с координатами (5 RO + } 0:0 . i} ,
У; =0, i=I,..,N (рис, 5,1), Для про ведения вычислений в качестве единиц
измерения заряда будем использовать заряд электрона е = ].б.} 016 Кл,
единиц измерения длины  RO = } 06 М .
у
х
....HH__H_ ... )
qqq qqq
Рис. 5.1
Решение данной задачи в пакете МА ТLAВ выполняется следующей по
следовательностью команд:
» е=1.6*10Л-16; % заряд электрона
» RО=10Л-6; % единица измерения расстояния
» N=50; % число зарядов
» i=l:N;
» q(i)=e; % заполнение вектора, содержащеrо значения зарядов
» xl=-5*RO; % хя координата левоrо конца системы зарядов
» x2=5*RO; % хя координата правоrо конца системы зарядов
»xq(i)=xl+(x2-xl)/N*i; % вычисление х-х координат системы зарядов
1» yq(i)=O; % задание у-х координат системы зарядов
» Nl=78; % число узлов прямоyrольной координаrnой сетки
»Xmin=-10*RO; Ymin=-10*RO; % задание координат нижнеrо левоrо уrла
% координаllЮЙ сетки
» Xmax=10*RO; Ymax=10*RO; % задание координат BepXHero правоrо
% yrла координаrnой сетки
» i=l:Nl+l;
»Х(i)=Xmiп+(Хmах-Хmiп)/Nl*(i+l); % вычисление xx координат
% узлов сетки
» j=l:Nl;
»У(j)=Уmiп+(Уmax-Уmiп)/Nl*(j+l); % вычисление yx координат
% узлов сетки
»M(iJ)=Potential(q,xq,yq,x,Y); % вычисление значений
% потенциала в узлах
% координаrnой сетки
» [Xl,Yl]=meshgrid(X,Y); % вычисление матриц х1 ,YI,
% используемых функциями
% визуализации двумерных и
90
91

/(0\1 IJ bl{)'/1 er)II()C/ OJ"7Uf){)BCJ jlи-e 1Jl' зичс K-1':!1f!.()!I'!.сс.{)ввl'CJ'!.!'.l: lv!lIA в-.
Ck трехмерных зависимостей
»surf(Xl,Yl,M); о/с визуализация IIоверXJЮСТИ rp =-: rp(x, у)
Результат выполнения приведснной выше последовательности KO
манп представлсн на рис, 5,2,
70
60
50
40.
зо
20.
10 '1
01
1 ",
:s,.
'-,
о  "'__________о
--0.5 .''-'::... /
,1 .1
,
х10
х 10
0.5
Рис, 5,2
70 l
::j
40]
:: '1
10 '1
0",,--
1 '.......
o;"""""'"
>---"
"
х 10
х 10
Рис. 5,3
Пакет МА ТСАВ представляет пользователям широкой спектр возмож
ностей для визуализации функций, зависящих от двух переменных, с HeKO
торыми из которых нам представляется целесообразным познакомить чита
теля.
Для построения отображения поверхности без изображения сетки и за
полнения поверхности с использованием интеРIIОЛЯЦИИ цвета дополнитель,
НО C:IC:1yt:T Rвести команды:
92

5.:..!;! oдe:иpo.вa1!.e С"!{lти-'1'!.с.к-и:, J':'K ':f!ЕI'!:l:.и--I!..:CJ<.'.!и-'!'!/ых.../)л.ей.
» figure(2);
» surf(Xl,Yl,M);
» shading interp
Результаты их выполнения представлены на рис. 5.3,
Для построения двумерной карты линий уровня (эквипотенциалей) функции
rp = rp(x, у) следует ввести команды:
» figure(3);
»contour(Xl,Yl,M,33) % здесь 33  число линий уровня
Результат вьmолнения приведенных выше команд представлен на рис, 5.4,
;.
;,,]
,   ", ,,"" 4
I

j
//
// l
//' 1
/-- -- I
L .J
8 10
х.10'"
/
//
...--'".....
/
J
[' ''-,-'" -, "- '
6' '-.... .......................
" ...,......
" '
 '-"""'--
"
i. .  C
-8 -6 -4
.....-..... .' /"
" 
. /"
/

о
.
4
-2
Рис. 5.4
для вывода значений, соответствующих каждой эквипотснциали, необ
ходи!\ю выполнить следующую последовательность команд:
» figure(4);
» [С,Ь] = contour(Xl,Yl,M);
» clabel(C,h)
» colormap c()ol
реЗУ::Iьтат выполнения которой представлен на рис. 5,5,
Здесь команда contour возвращает матрицу С, содержащую координаты
вершин ломаных, аппроксимирующих соответствующие эквипотенциаль
ные линии, вект()рстолбец h ,J,сскрипторов для каждой линии уровня, ис
пользуе\1ЫЙ далее командой clabel, II строит карту линий уровня. Дa.ae KO
93

!!!!>теР..'!!!"!.I!t!..е:'uРо.!!'!...1!и-!!!'!...скux пР!!.'i'!..f!.!'!.l!кет-'!!:!!...
_._"!..?"е:'.!!.t!'!...!!...'!!!!.'!!'!...Ч--'=--?"f!'5.'!!.Р.3'5.и-'!...2!!.'!...'!!..I!!":!..,!I,!!,f!.'!'!.-
манда clabel, используя данные, возвращенные функцией contour, подпи
сывает значения функции на каждой линии уровня. Команда colormap оп
ределяет цвет заливки карты линий уровня,
10'110"
11
11
li
8
6
4
..t>
Рис. 5.7
для построения трехмерной карты линий уровня (эвипотенциалей)
функции rp = rp(x, у) следует ввести команды:
» figure(6);
» сопtоur3(Хl,Vl,м);
Результаты выполнения данной последовательности команд представле
ны на рис. 5.8.
Рис, 5.5
. для отображения на одном чертеже поверхности и карты линий уровня
следует выполнить команды:
» figure(5);
» meshс(Хl,Vl,м)
70
ео
60
50
,,"*.....>
j/'
:;
щ
so
40
эо
30
20
20
10.
10
О.
1
о
10
-"->......
05 ......
------- О,.
о "--':
.5 ------..., 
';,>-<
-1 -1
.111"
х 10 
..-10.
Рис. 5,6
Рис, 5.8
94
95

КЙ--l!.II/(l!.п е.l!II?:(??71:J!?ваll!lе1:.и.!':с,:'--!!:. rp?!I..:?lae!'!.e..{1T1lJ  Ш .. . .. ШШШШШШШ Ш
1.
I I
в отличие от функции rp(й), напряженность элеКТРОСТilтическоrо поля
Е(Й) является векторной функцией, которая в каждой точке пространства
характеризуется величиной поля и направ.ттением, Для описания веКТорноrо
110.1Я будем использовать силовые линии  линии, касательные к которым в
каждой точке параллельны вектору напряженности электрическоrо поля,
В связи с тем, что СИ:lОвые линии несут информацию только о наПРJвпении
вектора напряженности электрическOI'О поля, но не ero величине, для анаш
лиза изменения величины напряженности электрическоrо поля в про(;транш
стве будем испОльзовать функцию IЕ(Й).
Таким образом, для исследования особенностей напряженности элекш
трическоrо поля, создаваемоrо произвольной конфиrypацией электрических
заРЯДОВ,следует:
1) задать в пространстве дискретную координатную сетку;
2) вычислить в узлах сетки координаты напряженности электрическоrо
поля E(R)=(EX'EJ;
3) построить в каждом узле сетки единичные векторы
ii = (E.. Еу) Ka
IE';E' '
I , , I
сательные к силовой линии электрическоrо поля;
4) построить rpафик поверхности и карту линий уровня функции iЕ(Й).
Данный алrоритм в пакете MAТLAB может быть реализован следующей
последовательностью команд:
» е=1.6*10Л-16; % заряд электрона
» RО=lОЛ-6; % единица измерения расстояния
» N=50; % число зарядов
» i=l:N;
» q(i)=e; % заполнение вектора, содержащеrо значения зарядов
» xl=-5*RO; % хшя координата левоrо конца системы зарядов
» x2=5*RO; % х-я координата правоrо конца системы зарядов
»хч(i)=хl+(х2-хl)lN*i; % вычисление хшх координат системы зарядов
1» yq(i)=O; % задание у-х координат системы зарядов
» Nl=23; % число узлов прямоyrольной координатной сетки
»Хшiп=шl0*RО; Ymill=-lО*RО; % задание координат нижнеrо
% левоrо уrла координатной сетки
»Хшах=10*RО; Ушах=10*RО; 0/.; задание координат Bi:pXHcr'o
% правоrо yrла координатноЙ сетки
» i=l:Nl+l;
»Х(i)=Хшiп+(Хшю(.Хшiп)lNl*(i+]); o/r Вычисление Х-1( коорпинат
96

шшш.!!'!??,е!'и.РшI!.'.Iи...е'!!й-"!и.чше:.и.!..:;7е.'!.."!Еи.'1: '--!!:.l1ш!:и..."!..I',:,! п<:.f!.:!!
% узлов сетки
» j=l:Nl+l;
» У(j)=Ушiп+(Ушах-Уmill)lNl*(j+l); % вычисление у-х координат
% узлов сетки
»M(iJ)=Potential(q,xq,yq,X,Y); % вычисление значений потенциала
% в узлах координатной сетки
»[Хl,Уl]=шеshgrid(Х,У); % вычисление матриц Xl,Yl, используемых
% функциями визуализации двумерных
% и трехмерных зависимостей
» [рх,ру ]=gradient( -М,О.l,О.l); % вычисление r-радиента функции rp(й)
% вычисление координат единичных векторов, касательных к СШlОвой линии
» pxl=pxJ(px. Л2+ру. Л2). ЛО.5;
» руl=ру.l(рх.Л2+ру.Л2).ЛО.5;
» figure(l);
» quiver(Xl,Yl,pxl,pyl,O.5) % построение BeKTopHoro поля единичных
% векторов, касательных к силовой линии
% в узлах координатной сетки
» шр=(рх.Л2+ру.Л2).ЛО.5; % вычисление абсолютных значений
% вектора напряженности
% в узлах координатной сетки
» figure(2);
» СОlltоur(Хl,Уl,шр,17); % построение линий равной напряженно(,"Ти
Результаты выполнения приведенной выше последовательности команд по
казаны на рис. 5.9 (векторное поле), рис. 5.10 (линии равной напряженности).
4ш--ш1576
i j'........
.,." '" j
.-- / , J
 \ \. ..... .....   .....  
I  \ \, ...... .... ......... 
 \ \, \,. " ...... ..... ..............
I \,...'-",............?-.
.t :jHHEE 1
. I .. \, \ \. " " '\, .... ....
':\ 
о 05 1_5
х 10
-0.5 . .,, /'
,. /....--. 
.' " ," .'
.,"
,1
; ,-.,/ *'
/ / .' I
.-
{
.(}:s
Рис. 5.9
97

1!<:А!.п--'<!'!.'е.[J!I?=_А!?дЛUfJ<:,,-е..1!.и.з..и..:._п--[J()у:?п--(l'!..:.'!.'e.A!...1Т:!!!.
х 10
10
8
6
Рис, 5,10
1:
Задача 5.1
Создайте докуменm, позволяющий строить потенциал и напря:ж:енность
элекmричеСК020 поля диполя, считая, что составляющие е20 электрические
заряды одинаковы по величине и противоположны по знаку,
], Имеет ли значение в данной задаче в каких единицах из/.!еряется заряд
и расстояние?
2. Как изменится электрическое поле, если заряды будут иметь одинако
вые знаки?
3. Убедитесь в том, что силовые линии НИК02да не заканчиваются на пo
ложительных зарядах и все2да идут к отрицательным зарядам, ПОЧе/ИУ
силовые линии НИК02да не пересекаются?
Задача 5.2
Создайте докуменm, позволяющий строить потенциал
и напря:ж:енность электричеСК020 поля квадроуполя,
т. е. электрическую систему, состоящую из четырех
равных по абсолютной величине электрических зарядов,
расположенных в вершинах квадрата, считая что
электрические заряды, расположенные в соседни.-" вep
шинах, имеют разный знак (рис. 5./1).
{)а
Рис. 5.11
98

.._.:.?д-е.l!.':'Е?!!.!.Iи..е.'!!.I_п-.':uх. J'1:'!..'!.'fJ..=-с. и..А!.Cl..'!.и-.п--2.I}:.по.!!_е
1. Как вЫ2лядит электрическое поле вблизи квадроуполя (ближняя зона)?
2, Как вЫ2Лядит электрическое поле на большом расстоянии от Kвaдpoyпo
ля (дальняя зона)?
3, Исследуйте зависимость электричеСКО20 поля в ближней и дальней зонах
от расстояния до центра системы и расстояния между зарядами,
Задача 5.3
Создайте докуменm, позволяющий строить потенциал и напряжен
ность электричеСК020 поля проmяжеНН020 диполя, т, е, диполя, co
стояще20 из N (>] О) зарядов, знаки которых последовательно череду
ются,
], Сравните электрическое поле при четном и нечетном числе зарядов, co
ставляющих диполь, в ближней и дальней зонах,
2. Сравните электрическое поле при четном и нечетном числе зарядов, co
ставляющих диполь, с электрическим полем точеЧН020 заряда,
3. Исследуйте зависимость электричеСК020 поля протяжеНН020 диполя в
ближней и дальней зонах от расстояния между зарядами,
Задача 5.4
Рассмотрите однородно заря
женную квадратную пластину со
стороной L и полным зарядом Q,
лежащую в плоскости xy
(рис, 5,12).
Как известно, в пределе при Loo
при постоянной плотности заряда
а = Q/ L2 вектор напряженности
электричеСК020 поля
по нормали к
!ЁI = а/2со .
Ё направлен
пластине,
Р(о,у, О) У
Рис, 5,12
Для нахождения электричеСК020 поля заряжетlНОй пластины конечных
раЗ.меров разбейте пластину сеткой из N х N ячеек так, чтобы каждую
ячейку />tOж'но было считать точеЧНЫ/>1 зарядо/>! величиной dq = Q.i '
N
], Создайте докуменщ позволяющиЙ вычислять потенциал электрическою
поля заряженной пластины конечных размеров.
2, Выберите точку и постройте зависи.ность потенциала электричеСК020
поля от числа ячеек. Оцените размер ячейки, начиная с котОР020 е20
99

l!.()MbIOl1}epltOe MO?elIp'Oall" 1)113.::'':':x...IlI!.()H"C()BBfl{l,,leA 7AB
уменьшение оказывает заметное влияние на точность вычислений. Как
зависит этот размер ячейки от координаты точки наблюдения?
3, Для выбранных размеров ячейки исследуйте электрическое поле на раз
личных расстояниях от пластины.
4, Проведите сравнение электричеСКО20 поля заряженной пластины конеч
ных размеров с электрическим поле'.1, создаваемым бесконечной пла
стuной и точечным зарядом,
5.2. Маrнитное поле витка с постоянным током
Изучение электрических полей систем неподвижных электрических за
рядов, проведенное нами в предыдущем разделе; было основано на законе
Кулона (5.2) и принципе суперпозиции (5.3), (5.4), Аналоrом закона Кулона
в электростатике в маrнитостатике является закон БI1ОСавараЛапласа, в
соответствии с которым напряженность маrнитноrо поля, создаваемоrо
элементом тока ldl , имеет вид
ро [d/ xR]
dB =  1 ,. (5.5)
41l' IRi3
I'де величина тока 1 измеряется в амперах (А), напряженность маrнитноrо
поля Jj  в теслах (Тл), J10 = 4л- ,] 07 ,Тл ,м/ А  маrнитная проницаемость
вакуума.
Закон БиоавараЛапласа имеет в маrнитостатике совершенно общий
характер и вместе с принципом суперпозиции используется для нахождения
напряженности мarнитноrо поля, создаваемоrо произвольной системой по
стоянных токов, В любой точке пространства, Действительно, так как Ha
пряженность мarнитноrо поля, создаваемоrо элементом тока /dl, распо
ложенном в точке с радиусомвектором 1', в точке с радиусомвектором R
равна
"
I ! I
I ,
I
dB = f.LQ 1 [сй.: х (Л 1' )]
41l' IЛ  1'13 '
(5,6)
I
I
i
: I
то для вычисления напряженности мю'нитноrо поля, создаваемоrо произ
вольной системой постоянных токов, следует задать ориентацию каждоrо
элемента тока /dT, ВХОДящеrо в структуру, If вычислить напряженности
маrнитных полей, создаваемых каждым элементом тока и в соответствии с
принципом суперпозиции произвести суммирование напряженностей Mar
нитных ПО,1ей:
100

шшш:fl1.()"qUI!.(J(l'.":',!!{l"'!. че..СК-lIХ :JЛ:К-I1IРU чеСКlIХ '.l.21IU"'!.IIIx.fl!!.Jle
dB = EQ 1 f  х (Л   )]
41l' ;=1 IЛ  13 '
(5,7)
rде N  число элементов, 1j  радиусшвектор, соответствующеrо элемента
Отметим, что вычислить маrнитное поле аналитически, используя (5.6),
(5.7), оказывается возможным, только для структур, имеющих достаточно
высокую степень симметрии (прямой провод, поле кольца на оси симметрии
и т. д,), Для большинства токовых конфиrураций расчет маrнитноrо поля
может быть проведен только численно, Наиболее важными rеометрически
ми конфиrурациями токовых структур, для которых необходимо знать pac
пределение напряженности маrнитноrо поля, являются: прямой провод,
петля, соленоид, тороидальная обмотка. Далее мы опишем документ, позво
ляющий вычислять маrнитное поле петли с постоянным током, и проведем
критический анализ известных моделей, используемых при расчете маrнит
ных полей соленоида и тороидальной обмотки с постоянным током.
Для расчета напряженности маrнитноrо
поля петли с током выберем систему KOOp
динат, в которой плоскость ХоУ совпадает с
плоскостью петли (рис. 5.13),
В выбранной системе координат поло
жение iro элемента тока ld,
z
(5,8)
у
rде
df, " /а[ e::, }
drp =  ' rpi = idrp, i = 0,1,... N  1 , N  число элементов тока, описыва
Рис, 5,13
ется радиусомвектором 1j,
r, " а[ :;; J (59)
Подставив (5.6), (5,7) в (5.5), нетрудно получить выражения для COCTaB
ляющих вектора напряженности маrнитноrо поля В Х' ВУ' В Z' однако для
расчета напряженности и визуализации маrнитноrо поля в пакете MATLAB
Этоrо не требуется, так как в пакет встроены функции для вычисления CTaH
дартных действий BeKTopHor'o анализа: вычисление скалЯРНОI'О произведе
ния, векторнOI'О про изведения и т. д,
101

!..?-"!..й..'!!рl!.?=!!l!.':Р.?..С:!I!.!1!!!.З-'!:п-J!о.1j:"п.с:'5!..'!!!.':!.!..1:f!шшш....шшш..
На примере вычисления и визуализации напряженности маrНИ1ноrо по
ля, создаваемоrо витком с током в плоскости х = О , опишем последователь
ность действий, позволяющих решить поставленную задачу, В рассматри
ваемой плоскости, как очевидно из соображений симметрии, составляющая
напряженности мarнитноrо поля вдоль оси оХ равна нулю, поэтому дале
мы проводим вычисления только составляющих напряженности вдоль осе и
о У, oZ. Так как далее нас будет интересовать форма силовых линий, но не
абсолютное значение напряженностей множитель (f.1-0/4;r)I будем полarать
равным единице.
Сначала необходимо создать файл Ring.m, содержащий описание функ
ции, возвращающей значения составляющих напряженности маrнитноrо
поля, листинr KOToporo мы приводим ниже:
function [By,Bz]=Ring(a,Y,Z)
% функция возвращающая значения проекций напряженности маrнитноrо
% поля на оси аУ, 02, вычисляемые в соответствии с (5.7)
Nstep=100; % количество элементов, аппроксимирующих кольцо
Х=О;
Ny=length(Y); % число узлов координатной сетки по оси о У
Nz=length(Z); % число узлов координатной сетки по оси oZ
deltaphi=2*piINstep; % шar по yrлу
п=1 :Nstep+ 1;
phi(n)=deltaphi*(n-l); вычисление вектора rpll = пdrp
% вычисление составляющих напряженности маrнитноrо поля
% в соответствии с (5.7)
for i=I:Nz
for j=I:Ny
s=[O О О];
for n=I:Nstep+l
dL=[ -a*sin(phi(n) )*deltaphi a*cos(phi(n) )*deltaphi О];
r=[a*cos(phi(n» a*sin(phi(n» О];
R=[X УШ Z(i)];
s=s+cross(dL,(R-r»./«R-r)*(R-r)').Л(З/2); % знак <' >  операция
0/0 транспонирования
end;
by(iJ)=s(2);
Ьz(iJ)=s(З);
end;
end;
102

,fl!..()еЛ-Р'!..l!./е сп.IС:lп.:':.!IХ 'JлекmР:':':.С:11U'-I.ь.z.: 1Iй..Jl.Й
Ву=Ьу;
Bz=bz;
Далее необходимо выполнить следующую последовательность команд:
Nl=21; % число узлов сетки
i=I:Nl+1;
Ymin=-5; Zmin=-5; % нижний левый yrол координатной сетки
Уmах=5; Zmax=5; % верхний правый уrол координатной сетки
% вычисление координат узлов сетки
Y(i)=Ymin+(Ymax- Ymin)/Nl *(i-l);
Z(i)=Zmiп+(Zmах-Zmiп)/Nl *(i-l);
а=l; % радиус кольца
[Ву Bz]=Ring(a,O,Y,Z); % вычисление проекций напряженности
% маrнитноrо поля
mр=(Ву.Л2+Вz.Л2).ЛО.5; % вычисление значений модуля напряженности
% маrнитноrо поля в узлах координатной сетки
% вычисление координат единичных векторов, касательных к
% силовой линии маrнитноrо поля, в узлах координатной сетки
Ьуl=Ву./mр;
bzl=Bz./mp;
quiver(Y,Z,byl,bzl); % визуализация BeKTopHoro поля
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 5.14.
61
4
\ , ! I I
\, \, ,.
t ! ,.
"""'--  ", ...... , '-, " "
;' Jf /' .'" ,. ,,'" 
..,.. ..... '" " "'- ... ",
/.  .. ... .. ..... ........
. .. ." ". ..... '. "-, ..,
" " ... ..
« .... ..... .., , .... " '\
. .. ,. .... .... .d-
.. ....... ...  ... 'О" ..... ",
/' / ........... ....... 
. ..   ..  ..... "-. .... "
l' "  .'"  .....
....> - ..... . .. ......... ,, ..... ..
; / ,/ .' ..... ..  ... ..... -.... .....
" ,,' ...  
.' t;' ,,' "' ..'" .  . '"-,
\, ,
\ \
 .  ........ ... ..... ' " '"
  " " '.. , '. '\ \
--- ,," ..
, .' I  ' ,,- ... ..
"
" 1 t
i i i : J / " . А'. I '
:,    ::::':'
' . ......... .. A , ./ ! t 
\ --." \ \ \ \ \  
, :  :  .l } : : :
" ", 
" ,.  :. - :: ",,' ".. ..' *
2
.,.1" /' J
". .... ...... 
.. -' ." ./" "  ., "' .,., ....
.""  ,,""
! r
, .." - ..., ......
4
, I , ,
,
" , '" ...
-6
.6

'4
.2
..........L............L......
О 2 4 6
Рис. 5.14
103

I!..0"'! п--I!1.,!,ер'!I'?=':'::Z':!.l?..о..ll':!.'!rf!.'-!!.':!.'!.=-.':'.'.'::rp,,:,уе.:с:.,:,в--'!к---e.'!!.= A:!L,:,!f!.. ... ..
Анализ рис, 5,14 показывает, что поле единичных векторов позволяет на Ka
чественном уровне получать информацию о форме силовых линий и направле
нии напряженности мarнитноrо поля в данной точке координаllЮЙ сетки.
Определенный недостаток технолоrии визуализации силовых линий
маrнитноrо поля состоит в том, что линия, являющаяся по своей физиче
ской сути непрерывной, заменяется набором векторов, касательных к дaH
ной линии. Для получения более адекватноrо изображения силовых линий
маrнитноrо поля необходимо использовать векторный потенциал маrнитно
ro поля А, связанный с напряженностью маrнитноrо поля следующим co
отношением:
В = rotA , (5,10)
Используя (5.10), можно показать [22], что силовая линия есть линия, на
которой IA(x, у, z = coпst. Следовательно, для построения силовой линии
маrнитноrо поля необходимо вычислить модуль BeKTopHoro потенциала в
узлах координатной сетки и затем построить карту эквипотенциалей.
Векторный потенциал мarнитноrо поля, создаваемоrо элементом тока
ld/ , равен
110 ld/
dA   .
 4л- !Rrl'
(5.11 )
rде R  радиусвектор точки наблюдения, r  радиусвектор элемеmа тока,
Векторный потенциал мarнитноrо поля А, создаваемоrо произвольной
системой токов ld в соответствии с принципом суп ер позиции равен
N N 
А = L>i\ = f.JO L !dl;, (5.12)'
;=1 4л- ;=1 IR  r;1
Так как далее нас будет интересовать форма силовых линий, но не абсо
лютное значение напряженностей, множитель (110/4л-)1 будем полаrать
равным единице,
Для практической реализации предложенноrо алrоритма, как и ранее,
сначала необходимо создать файл RingA.m, содержащий описание функ
ции, возвращающей значения составляющих напряженности маrнитноrо
поля, листинr KOToporo мы приводим ниже:
function A=RingA(a,Y,Z)
% функция возвращающая значения модуля векторпотенциала
% маr'нитноrо поля, вычисляемоrо в узлах координатной сетки,
% расположенной в плоскости У oZ, в соответствии с (5.12)
104

...... .........:.fl!...о..?eJl,!!р.,?аllи-.=l!.'!!.':!.'!.=c:.':'.и-. l!.=-':'.'!!.fll'!.=С':!..1!.I!!!..'!!.!!..'!.'?Л-=-
Nstep=lOO; % количество элементов, аппроксимирующих кольцо Х=О;
Ny=length(Y); % число узлов координатной сетки по оси о У
Nz=length(Z); % число узлов координатной сетки по оси oZ
deltaphi=2*pi/Nstep; % шаr по yrлу
n=l:Nstep+l;
phi(n)=deltaphi*(n-l); вычисление вектора rpn = пdrp
% вычисление модуля напряженности векторпотенциала
% маrнитноrо поля
for i=l:Nz
for j=l:Ny
s=[O О О];
for n=l:Nstep+l
dL=[-а*sin(рhi(п»*dеltaрhi a*cos(phi(n»*deltaphi О];
r=[a*cos(phi(n» a*sin(phi(n» О];
R=[X Уф Z(i)];
s=s+dLJ«R -r)*(R -r)'). Л(1/2);
end;
ax(iJ)=s(l) ;
ay(iJ)=s(2);
az(iJ)=s(З);
end;
end;
А=(Ьх. Л2+Ьу. Л2+Ьz. Л2). ЛО.5;
Далее необходимо выполнить следующую последовательность команд:
Nl=21; % число узлов сетки
i=l:Nl+l;
Ymin=-5; Zmin=-5; % нижний левый yrол координатной сетки
Утах=5; Zmax=5; % верхний правый yrол координатной сетки
% вычисление координат узлов сетки
Y(i)=Ymin+(Ymax- Ymin)/Nl *(i-l);
Z(i)=Zmiп+(Zmaх-Zmiп)/Nl *(i-l);
a=l; % радиус кольца
mp=RingA(a,Y,Z); % вычисление модуля BeKTopHoro потенциала
contour(Y,Z,mp,55) ;
Результаты выполнения приведенной выше последовательности команд
пред ставлен на рис, 5,15,
Анализ карты эквипотенциальных поверхностей, представленных на
рис, 5,5, [Jозволяет выявить два недостатка, Вопервых, на карте непраВИЛh
105

КОАтЫО'!.lер//Ое мй-.":f!.ровс:!.uе Фи--ч-.:К-'!.Е.й-.1j::'й-.!..Iк-:'!!.е MATLAB
но отображаются силовые линии, проходящие вблизи центра кольца, что
объясняется особенностями вычислительноrо алrоритма. BOBTOpЫX, сило
вые линии оказываются неrладкими, что обусловлено использованием KO
ординатной сетки с достаточно большим шаrом и использованием пакетом
МА TLAB при построении силовых линий маrнитноrо поля последователь
ных отрезков прямых,
5[--==
4 .// '-...
1
..
1
.2
.3
.4
 i
I
-5 ... .......L ........L_1. .J.... .. ....l. . J
 -4 -3  -, о 1 2 3 4 5
--........................
Рис, 5,15
Устранить второй недостаток достаточно просто, используя какойлибо тип
интерполяции исходных данных на координатную сетку меньшеrо размера:
С7с задание новой координатной сетки
» yi=Ymin: (Ymax-Уmiп)/I000: Уmах;
» zi=Zmiп:(Zmах-Zmiп)/I000:Zmaх;
о/с формирование матриц, используемых функцией interp2
» [уl zl]=meshgrid(Y,Z);
» [у2 z2]=meshgrid(yi,zi);
% вычисление значений BeKTopHoro потенциала на координатной сетке
% меньшеrо размера с использованием бикубической
% сплайнинтерполяции
» zi3 = interp2(yl,zl,mp,y2,z2,'bicubic');
» сопtоur(уi,zi,ziЗ,55); % визуализация силовых линий
Результат выполнения приведенной выше последовательности команд
представлен на рис, 5,16,
106
...............
 ..:!!делuрй---в:!!!.'!..:'!!'!!.':.ч-!!. Эl!:.'!!!!..=:.!5'!... Ma2.!!.'!..'!!..'!...."!!..!'.!!e:!
:/' .. //::-:-
../ ' //.- .........
/ // ш_-:--<', /  . _________
2 /'    '_':..
/ / .  %:;=,-=:",.,:-::;-, "- '\
/' / ///:::-;",?:,>" "'
1 I I 1, /?? ,'1$,'" ' , '
1, i f ( / !/!!/:" ",,;-\\\ \ \)' \ \
о \ \ \ \\ \S. /1&) I ) J)
1 .\\:.". :;:';./' / /
, -';"'-''-':::::----'O---' ,,':::i::::>:::/ / //
2 ' "'  ,----===- r I А '\ -::::,.<.././ / /
"'...." ----...:?// \ / /'
: ' ._ :// ../ 
...............  .
.5
5
..
3
.2
.1
о
Рис. 5.16
Таким образом, сочетание обоих описанных в настоящем разделе Meтo
дов визуализации силовых линий мarнитноrо поля позволяет получить aдe
кватное представление об их rеометрии.
Задача 5.5
Как известно, напря:женность поля, создаваемою ма21lитным диполем
& , описывается формулой
B(R):= 3(& .R)!L. (5.13)
IRI5 IRI3
1. Исследуйте особенности Ма2нитНО20 поля, создаваемО20 Ма2нитным дипо
лем, Рассмотрите Ма2нитные поля 1-ш различных расстояниях от диполя.
2. Сравните ма2нитные поля, создаваемые кольцом с током и ма2нитным
диполем, Какой вывод можно сделать?
5.3. Маrнитное поле соленоида
с постоянным током.
Вопрос о структуре маrнитноrо поля однослойноrо соленоида с посто
янным током обсуждается практически во всех учебниках  от школьных до
ставших в настоящее время классическими вузовских учебников по злек
..
Результаты данною раздела впервые получены автором совместно с В, И. Ха-
ритоновым в [15].
107

!!:!.r:::тер"''!f}!!.!!!!делuрованuе1!..U:!!!::'=--'5.'!!'!!!..I!1J...е.:::''',!!!'!''!!!!'5.!.!!..1!!:!!..... ..
тричеству, маrнетизму [l5] и электродинамике [610]. Расчет поля на оси
соленоида, допускающий решение в аналитическом виде, в случае беско
нечно длинноrо соленоида и соленоида конечной длины предлаrается в Ka
честве задач во мноrих задачниках [11  13].
Соленоид, соrласно устоявшейся точке зрения, рассматривается как ис
точник маrнитноrо поля. Один конец соленоида является северным полюсом,
дрyrой  южным, поле вне соленоида
считается аксиальносимметричным,
а внутри катушки в приближении
бесконечно длинноrо соленоида  ok
нородным. Общий вид силовых ли
ний данноrо маrнитноrо поля пока
зан на рис, 5.17, что подтверждается
элементарными опытами со стрелкой
компаса и мarнитными опилками,
располarаемыми на rоризонтальной
плоской поверхности с малым коэф
фициентом трения, проходящей че
рез продольную ось соленоида.
Известный метод расчета напряженности маrнитноrо поля однослойноrо
соленоида состоит в представлении соленоида набором последовательно
расположенных колец и суммировании в соответствии с принципом супер
позиции напряженностей маrниrnых полей, создаваемых каждым кольцом в
выбранной точке пространства. При таком подходе неявно предполarается,
что ток при плотной намотке вдоль продольной оси соленоида отсутствует
или исчезающе мал по сравнению с током вдоль кольца. Это послужило
причиной, по которой маrнитное поле, обусловленное составляющей тока
вдоль оси соленоида, считалось малым по сравнению с мarнитным полем,
обусловленным движением электрических зарядов вдоль кольца. Данное
допущение однако недостаточно корректно,
Доказательство высказанноrо утверждения про ведем в два этапа; на пер
вом построим качественную картину протекания тока по соленоиду, на BТO
ром этапе проведем количественные расчеты, Причем, в отличие от тради
ционноrо подхода, обсужденноrо выше, рассмотрим изменение условий
движения носителей заряда при последовательном усложнении rеометрии
токовой структуры (прямой ток  спираль  соленоид), Оставаясь в рамках
электронной теории, рассмотрим ток в проводе как последовательность
движущихся с постоянной скоростью зарядов, Очевидно, что намотка про
вода не меняет скорость движения носителей заряда вдоль про вода Vo (т, е,
абсолютную величину скорости), однако появляются составляющие CKOpO
5. МодеЛllр:!.ваlIU С'!!.'!.I!''1е'5.?е'5.'!'РЧ:СК':'.Х..':'.. Л:'!.211"!..п-Iхп-,!i:'
сти носителей заряда вдоль координатных осей (рис, 5,18), При этом дви
жение носителей заряда вдоль оси oZ будет движением с ПОС10ЯННОЙ CKOpO
стью V z ' В плоскости Хо у  с постоянной скоростью JJ по окружности,
у
"
v

Рис. 5,17
х//
j/ Рис, 5,18
Выразим данные скорости через радиус спирали а и шаr спирали h, для
чеrо рассмотрим развертку одноrо витка спирали в плоскости XoZ
(рис, 5.19),
2",.
r V1
 Vz
h
Рис, 5,19
Из рис, 5,19 очевидно, что
17
.'F;;::::':::'::. ,
,j(27r а)2 -+-/12
2п Q
JJ.  vO' F?c
(271 a) -+ 11
Vz = v'o cosa = Vo
(5.14)
(5,15 )
108
109

l!?-'!./.?'п-.(!Р.IIО: .-'!.()?(!Л'!.Р.()l1.'ltlеrptltI'!.'!К-t1;(п-Р.оч(!=? шп-ак-(!'п-.(! .1;!1TE1f!..
5. м oдe. U'р'()аlll.lесп-.l1.'l11Iчес:.К--t1:' .:)1 еюп-р t1че.К-1Iх..t1-'!.аII!Iп./:ь.;(I:?7е.
(5,17)
Для про верки рассуждений, приведенных выше, получим аналитическое
выражение для напряженности маrнитноrо поля соленоида на основе закона
БиоСавараЛапласа (5,6) и принципа суперIIОЗИЦИИ, проинтеrpировав (5,6)
по всем элементам тока,
Как известно [14], положение любой точки спирали полностью опреде
ляется заданием единичноrо вектора п, направленноrо вдоль оси спирали
(ось oZ), и вектора д, отмечающеrо положение точки спирали в плоскости,
перпендикулярной к вектору п (рис. 5,20), Тоrда положение любой точки
спирали определяется радиусомвектором R, зависящим от одноrо пара
метра  уrла поворота rp:
R(rp) = nh  + l'i cosrp + [п Х l'i]sin rp. (5.19)
2][
Элемент тока /dl выражается через вектор r(rp), касательный к спира
Учитывая, что шаr спирали h выражается через длину соленоида [js и
число витков N как h = Ls/ N , и переходя в (5.14), (5.15) к токам, получаем
L
/ z = Nee!o (2][ а;)2 + L; ,
2][ aN
/ = N e'o '
z е !1?1rf 2 2
'v(2][aN) +Ls
(5.16)
rде Ne  линейная плотность электронов в соленоиде (число электронов в
про воде, намотанном на соленоид, отнесенное к длине соленоида); е  заряд
электрона,
Кроме Toro, намотка провода приводит к увеличению длины провода с
током L, которая выражается через число витков и шаr намотки
L=N(2][a)2+h2 =(2][aN)2, (5,18)
Анализ выражений (5,16), (5.17) показывает, что поле соленоида с OДHO
слойной намоткой является суперпозицией полей двух токов, один из KOTO
рых является кpyroBbIM, второй  продольным, Увеличение числа витков
приводит, с одной стороны, к уменьшению шаrа спирали и, следовательно,
к уменьшению величины продольноrо тока (см, выражения (5.16), (5.18», с
дрyrой стороны, к увеличению длины провода, HaMoTaHHoro на соленоид,
что приводит к возрастанию количества носителей заряда, двиrающихся в
соленоиде, т. е. возрастанию линейной плотности заряда, Из выражений
(5.18) и (5.17) видно, что количество электричества, перемещающееся в Ha
правлении оси oZ в единицу времени остается неизменным при увеличении
числа витков соленоида, Таким образом, при любом количестве витков
(любом шаrе намотки) количество электричества, перемещающеrося в Ha
правлении продольной оси соленоида в единицу времени, оказывается paB
ным количеству электричества в прямо м проводе, Следовательно, соленоид
с однослойной обмоткой должен обладать аксиальносимметричным Mar
нитным полем в плоскости, перпендикулярной продольной оси соленоида,
подобным полю прямоrо тока, Учитывая аналоrию с маrнитным полем
прямоrо тока, естественно в дальнейшем называть ero поперечным полем 
в отличие от маrнитноrо поля, приведенноrо на рис, 5.17, При большом
числе витков соленоид можно рассматривать как проводящий цилиндр KO
нечных размеров, по которому течет продольный ток, следовательно, мож
но ожидать появления отличия поперечноrо маrнитноrо поля соленоида и
маrнитноrо поля прямоrо тока, которое должно проявляться при увеличе
нии числа витков,
ли, как
/dl = If(rp)drp,
(5.20)
rде
r ( rp) =  п д si n rp + [ fi Х й] cos rp .
2][
(5.21 )
tZ
I
/
I
/
/
C
o
// [n.з]
/:
-'
-'
:;-'
j!:C'
у
>-
Рис, 5.20
Обозначим вектор, направленный из начала координат в точку наблюде
ния, через Ro, тоrда вектор r = Ro  R(rp ) , Таким образом, напряженность
маrнитноrо поля в точке наблюдения записывается в виде
110
111

KO:tI_lbIvтeplloe модлu!?и-,!!lIе 4!з--и-к-х I1рVljе=с.CJ.в_ l1акете MALAB
Ё = f1-C! 2"fN [т(р) х (ЯС!.  tp ))] d
4п IR  Я( ,3 tp , (5.22)
о I о tp
Для вычисления интеrpала (5,22) перейдем к координатной записи, За
метив, что в выбранной системе координат векторы п. а, [п ха] , входящие в
(5,]9)  (5.22), имеют координаты n=(O,O.l), д=(],о,о), [пха]=(О.],О),
получим координаты векторов R(tp ). r(tp).   R(tp) в виде
R( tp) = (а cos ip.a sin tp. 2; tp ). (5,23)
r(tp)=(aSintp,acosip.), (5.24)
ЯО R(tp) = (Ха  acostp,yo  asin ip.Zo  t7l' tp ). (5.25)
Подставляя (5,23)  (5.25) в (5.22), получаем для составляющих напря
женности маrнитноrо поля соленоида вдоль соответствующих координат
ных осей:
2" N (( zorp }cosrp (уо asinrp»)
ВХ =  f -  2712 ''3;2drp ;(5.26)
о (RJ + а2 +l2:rp)  2(хоаСОБср+ауо sinrp+2: Zo ))
1101 2" N ((xoacosrp )2h; + aSin, Zo  il[ ср))
Ву = 4;' f - -/2drp; (5.27)
о (RJ +а2 +С: ср)  2( xoacosrp+ayo sinrp + 2: zo))
2"Н
В = 1101 f  «УQ..Cl.siПР)!1р+а50SЧ7.(Хо СОБср»), .  dm (528)
z 4п-' h 2 h '13/2 'f" .
О ( RJ + а 2 + ( 2 ср)  {toa cos rp + ауо sin rp + 21[ Zo ) j
в связи с тем, что соленоид имеет ЦIШиндрическую форму, представляется
целесообразным записать компонеюы поля в ЦIшиндрической системе коорди
нат. Для этоrо положение точки наблюдения будем хар3h.'Теризовать в плоско
СТИ, перпендикулярной продольной оси соленоида, радиусом,вектором "0 и
уrлом поворота 91 о ' положение относительно продольной соленоида  KO
ординатой 2(), ТOJ-да выражения для напряженности составляющих поля в IIИ
112
...... 
. .. ... ...:А!?cJё--':!.I:?,,!IIII_rп.'!.rп.'!..:с..КUХJ:к-rп.l!li'.!:!:К-uxi-Л1.'!../I':!.rп'lЬ>: I1CJ.Л
линдрической системе координат находятся соответствующей заменой пере
менных в (5.26)  (5,28): ХО r ocostp о. Уо  ro sil1 ер о' R6  ri + 26 и перехо
дом из декартовой в цилиндрическую систему координат, определяемым
матрицей поворота относительно оси oZ [] О}:
[Вт'1 (co,stpo sintpo
:J=l S)tp() cotpo
О'[В ]
J: .
(5,29)
Описанная выше замена переменных и выражение (5.29) позволяют леr'
ко получить окончательные выражения для составляющих напряженности
мarнитноrо поля в цилиндрической системе координат. В связи с тем, что
процедура нахождения составляющих напряженности мarнитноrо поля в
цилиндрической системе координат теперь является тривиальной, а оконча
тельные выражения весьма rpомоздки, автор их не приводит,
Отметим, что выражения (5.26)  (5,28) получены абсолютно cтporo, без
использования какихлибо приближений и позволяют проводить вычисле
ния для соленоидов с произвольными параметрами (длиной, поперечным
сечением и числом витков), Их анализ показывает, что интеrpалы в (5.26)
(5.28) всеrда отличны от нуля. Следовательно, однослойный соленоид имеет
поперечное маrнитное поле, аналоrичное полю прямоrо тока,
Так как интеrpалы (5.26)  (5.28) не берутся в элементарных функциях,
целесообразно, задавшись конкретными параметрами обмотки (шаrом, чис
лом витков и радиусом поперечноrо сечения), провести численное вычис
ление компонент вектора напряженности маrнитноrо поля и провести ero
визуализацию, как это было описано в предыдущем разделе, Так как далее
нас будет интересовать форма силовых линий, но не абсолютное значение
напряженностей, множитель (f10/4;r)/ будем полаrать равным единице в
(5.26)  (5.28),
Обсудим более подробно особенности вычисления интеrpалов (5.26) 
(5.28), В пакете MATLAB дЛЯ нахождения значения определенноrо инте
rpала от некоторой функции f(x) на интервале [а,Ь] необходимо выпол
нить следующую последовательность действий:
]) провести разбиение отрезка [а,Ь] интеrpирования на N отрезков и
сохранить координаты их концов в векторе Х;, i = ],.., N ;
2) вычислить значения подынтеrpальной функции f(x) в узловых точ
ках Х;: F; = f(x;);
113

i!.'?,r!r'.'?.'r:.еf..'.'.?е:':'(),!Лllроаlll',! 1!з.IIЧ,!k'II);11J1()li,!совв 11<1кеmе МА ПА В
3) использовать функцию trapz, реализующую метод трапеций:
trapz(x,F),
Таким образом, для вычисления и визуализации напряженности МaJ'НИТ
Horo поля соленоида нужно следующее,
1, Создать тфайлы, возвращающие значения составляющих
напряженности маr'нитноrо поля вдоль каждой из координатных осей:
% листинr файла ВХ.т
function z=Bx(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции напряженности
% маrнитноrо поля на ось оХ
phi=O:pi/50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h); % вычисление значений функции в узловых точках
z=trapz(phi,F); % вычисление значений интеrpала
function F=f(psi,xO,yO,zO,a,h)
% описание подынтеrpальной функции в (5,26)
F =( (zOpsi *ы (2 *pi»* а. *cos(psi)-h/(2 *pi)*(yOa *sin(psi» )J ...
(хОЛ2+уОЛ2+z0Л 2+а Л2+(hI(2 *pi)*psi). Л2...
2 *( хО* а *cos(psi)+a *yO*sin(psi)+hI(2 *pi)*zO*psi». л (3/2);
% листинr файла Ву.т
function z=By(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции
% напряженности мarнитноrо поля на ось о У
phi=O:pi/50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h,I); % вычисление значений функции в узловых точках
z=trapz(phi,F); % вычисление значений интеrpала
function F=f(psi,xO,yO,zO,a,h);
% описание подынтеrpальной функции в (5,27)
F=( (xO-а *cos(psi) )*hI(2*pi)+a*sin(psi). *(zO-рsi *Ы(2 *pi» )J...
(хО л 2+уО Л2+z0 Л2+а Л2+(hI(2*рi)*рsi). л 2-...
2 * (хО * а *cos(psi)+a *yO*sin(psi)+h/(2 *pi)*zO*psi». л (3/2);
% листинr файла BZ.m
function z=Bz(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции напряженности
% маrнитноrо поля на ось oZ
phi=O:pi/50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h,I); % вычисление значений функции в узловых точках
114
...............
,: fl1.?5!'!!!.t1f...О'!.'III(?t11'!.r:rtl,(?ск..IIJ:?l!(?к..'!':fJ.":!.(?к....lI'.'!.III.r:rI':);r:.°3.(?E
z=trapz(phi,F); % вычисление значений интеrpала
function F=f(psi,xO,yO,zO,a,h);
% описание подынтеrpальной функции в (5,28)
F=( (yOa*sin(psi) )*а. *sin(psi)+a*cos(psi). *(xOa*cos(psi» )J...
(хОЛ 2+уОЛ 2+z0Л 2+а Л2+(hI(2*рi)*рsi). Л2...
2 *( хО* а *cos(psi)+a *yO*sin(psi)+hI(2 *pi)*zO*psi». л (3/2);
2. Задать координатную сетку (вычислить координаты узлов сетки).
3. Вычислить в каждом узле сетки значение составляющих напряженно
стей маrнитноrо поля соленоида.
4. Построить векторное поле единичНЫХ векторов, касательных к сило
вым линиям маrнитноrо поля, выполнив последовательность действий, опи
санную в предыдущем разделе,
Для построения непрерывных силовых линий маrнитноrо поля, как было
показано выше, следует вычислить в узлах координатной сетки значения
BeKTopHoro потенциала А(х, у, z)
A=!!OIJ. d[(?) , (5.30)
4Л' iRoR(tp
rде d[, R  векторы, определенные соrласно (5.19)  (5.20), Ro  радиус
вектор точки наблюдения, и построить карту эквипотенциальных поверхно
стей функции !A(x,y,z.
Подставляя (5.19)  (5,20) в (5.30), получаем выражения для составляю
щих BeKTopHoro потенциала маrнитноrо поля соленоида вдоль COOTBeтcт
вующих координатных осей:
2"N
А  f10l J,  а sin tp d . (5 31)
х   1/2 tp , ,
4п- о ( RJ + а2 +(iIl' tp У  2( xoacostp + ауо sintp + i;. Zo ))
2"N
 Ро! J  ,acostp ,,d '(5 32)
А"  '4п- "'"'''2  1/2 tp, '
о ( RJ + а2 +( tp)  \xoacostp+ayO sin tp+ Irzo ))
2"N h
zO
Az = f14 J ,, . Ш,:;---' ШШlfidtp ,(5.33)
о (RJ+a2+( 1,tp) 2(xoacosrp+ayoSintp+'zoll
. 2п- 2п- / )
115

i!:пIOт-=Р'.!I(Jе. л.1 ()?e,:,p()1!!..11J1)U'!.:' e..CIJp'Oe.O ва.'5.т-::J!.1 Т-LАJ!.
Таким образом, для вычисления и визуализации силовых линий маrнит
Horo поля соленоида нужно следующее.
]. Создать шфайлы, возвращающие значения составляющих BeKTopHoro
потенциала маrнитноrо поля вдоль каждой из координатных осей:
% листинr файла АХ.т
function z=Ax(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции BeKTopHoro потенциала
% маrнитноrо поля на ось оХ
phi=O:pil50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h); % вычисление значений функции в узловых точках
z=trapz(phi,F); % вычисление значений интеrpала
function F=f(psi,xO,yO,zO,a,h);
% описание подынтеrpальной функции в (5.31)
F=-(а*siп(рsi)).I... .
«xO-а*соs(рsi)). Ч+(уО-а*siп(рsi». Ч+(zО-h.l(2*рi)*рsi). Ч). ЛО.5;
% листинr файла Ау,т
function z=Ay(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции
% BeKTopHoro потенциа.па маrНИТноrо поля на ось о У
phi=O:pil50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h); % вычисление значений функции в узловых точках
z=trapz(phi,F); % вычисление значений интеrpала
function F=f(psi,xO,yO,zO,a,h);
% описание подынтеrpальной функции в (5.32)
F=(a*cos(psi».I...
«xO-а *cos(psi». л 2+(yO-а*siп(рsi». л 2+(zO-h.l(2 *pi)*psi). л 2). ЛО.5:
%шфат .
function z=Az(xO,yO,zO,a,h,N)
% функция, возвращающая значение проекции BeKTopHoro
% потенциала мar'нитноrо поля на ось oZ
phi=O:pil50:2*pi*N; % вычисление координат узловых точек
F=f(phi,xO,yO,zO,a,h); % вычисление значений функции в узловых точках
z=trapz(phi,F); % вычисление значений интеrpала
function F =f(psi,xO,yO,zO,a,h);
% описание подынтеrральной функции в (5,33)
F=(h/(2*pi».I...
«xO-а*соs(рsi). л 2+(yO-а*siп(рsi». Л2+(zО-h.l(2*рi)*рsi). Л2), ЛО.5:
116
.........
шш ш шш:l>!=Uр'?{JII1J: т-i1т-:.еt::'!.х.эл-е.т-р:..е!:.К1Jх.1JАti1-'!'!.т-"ы /JОЛ-е.й
2. Задать координатную сетку,
3, Вычислить в каждом узле сетки значение проекций BeKTopHoro потен
циала маrнитноrо поля соленоида на соответствующие координатные оси,
4, Построить карту линий уровня функции !А(х, у, z) .
Для примера на рис, 5,2] и 5.22 показаны проекции силовых линий oд
нослойноrо соленоида с параметрами а = 0,5, [, = б, N = 200, нижний конеи
KOToporo расположен в плоскости z = О, на плоскости х = О и z = 3, COOTBeT
ственно. Проекция векторноrо потенциала на плоскость YoZ вычислялась на
квадратной координатной сетке со следующими параметрами: левый ниж
ний yrол (5,5), правый верхний уrол (5,5), число узлов N == 1 7 х 1 7 , Проек-
ция BeKTopHoro потенциала на плоскость Z=3 вычислялась на прямоуrоль
ной координатной сетке со следующими параметрами: левый нижний уrол
(5,5), правый верхний уrол (5,8), число узлов N==17x17, На рис, 5,21 и
5.22, более толстыми линиями показаны соответствующие сечения соле
ноида,
2
.4
................
.5 О
Рис. 5.2/
Для сравнения проекции напряженности маrнитнOJ'О поля на плоскость
Z == 3 и проекции напряженности маrнитноrо поля на ось oZ вычислено их
Отношение на различных расстояниях от оси oZ (рис, 5,23), Как очевидно,
данная величина есть TaHreHc уrла между силовой линией и осью oZ, KOTO
рый характеризует искривленность силовых линий,
117

.1!.?At'l.ы
111_е!:'.о:_At?<!..'::'l.lJЕ?'!'3!.и.:"рlJ!!':..ч.:/(_р?ц-:.=B_'!..'!.'5...:111:J!1T..!!_.... ....
.,
.2
,3
.4
.5
-5
Рис, 5,22
055
\
\
\

0.5
0.45
04
0.35
0.3
0.25
0.2
05
, 5
2.5
Рис, 5.23
3.5
Как показывает анализ зависимости, представленной на рис, 5.23, у со-
леноида с указанными размерами составляющая напряженности маrнитноrо
поля, лежащая в плоскости Z  3, т. е, достаточно далеко от обоих концов
соленоида, оказывается ОДНоrо порядка с составляющей напряженности,
параллельной оси oZ, Следовательно, силовые линии маrнитноrо поля, соз-
даваемые однослойным соленоидом, являются не плоскими, но пространст-
венными кривыми.
118
......
..шш... .5.. 1I!:..?:ли.ро..аllие:п-1(!,иuчес.кu?:к-.п.1РU че..: к!/хи .iI1а."и.п.l:I'Хш I)олей
Задача 5.6
Используя выражения (5,27), (5,28)  (5.30), исс.7едуйте MaZHumHoe поле
внутри и снару,жи пря.МОZО соленоида с постОЯННЫА/ током при различ-
ной длине соленоида и шаzе нш,ютки,
4Jl'uo f В 
], Сравните значения KOHnlypHOZO интеzрала .. .. . cil, вычисляе.моzо по
круzовы.м контурам, один из которых находится внутри, а друzой вне
соленоида.
2. Сравните значения радиальной Br и нор.мальной (т, е. перпендИКУ_7ЯРНОЙ
к радиусу-вектору точки наблюдения) Brp состав.1яющих напря;женно-
сти маzнитноzо поля,
3. Как зависит нормальная составляющая напряженности маzнитноzо по-
ля соленоида В от азимутальноzо уzла <р ?
rp
4. Вычислите зависимость напряженности поперечноzо маzнитноzо поля
от расстояния до продольной оси соленоида при неизменной длине соле-
ноида и различном шаzе намотки, Постройте полученные зависимости
и сравните их с аналоzичнОЙ зависимостью напряженности АшzнитlЮZО
поля, создаваемоzо постоянным прямым током,
5. Можно ввести еще один парmнетр 11, характеризующий маzнитное поле
соленоида с постОЯНl-lЫМ током,  отношение нормальной составляю-
щей напряженности Brp к продольной составляющей напряженности
маzнитноzо В в данной точке, Этот параметр определяет «степень
z
вертикальностш) силовой линии маzнитноzо поля, т, е, показывает,
можно ли пренебречь напряженностью поперечной составляющеЙ .1I1az-
нитноzо поля по сравнению с напряженностью ezo продольной состав-
ляющеи:
а) в выбранной точке пространства вычислите значения пара.метра 11
при различном шаzе намотки и фиксированных размерах соленоида,
Изобразите данную зависимость zрафически;
б) при выбранном шаzе намотки и длине соленоида вычислите зависи-
мость парсм/етра 11 от расстояния до продольноЙ оси соленоида,
Изобразите данную зависимость zрафически;
"? [1
в) АtОЖНО ли считать силовую линию вертикальнои. очему известные
опыты с металлическими опилками не позволяют выявить обнару-
женную особенность маzнитноzо поля прямоzо соленоида с nocтo
янны.'I1 токо.'I1?
119

'?WllblOIp"1I.0e моде.Л-.UР'О.Й-IIи-.:rjJuз'!.ескuх пp"?цec.c..?.в--'!.'!.K!.!.!..1 ТLAB
5.4. l\1аl'нитное поле тороидальной обмотки
с постоянным током.
Для нахождения маrнитноrо поля тороидальной обмотки с постоянным
током (рис, 5.24) принято использовать уравнение Максвелла:
rot В == J ,
имеющее в интеrpальной форме следующий вид [4]:
1I
fBdT = L(:tIk),
L. k=1
(5,34)
[де L  контур, охватывающий ток, 1 k  сила тока, oXBaTbIBaeMoro контуром,
J
l
2.............
J
Рис, 5.24
Следующий шаr в нахождении мarнитноrо поля состоит в замене об
мотки тора с протекающим по ней током поверхностным током с постоян
ной линейной плотностью i (рис, 5.25). При ИСПользовании данной модели
линии тока предполаrаются расположенными в меридиональных плоско
стях, про ходящих через ось симметрии тора, т. е, набором колец с током,
Циркуляция маrнитноrо поля тора В в (5,34), зависящеrо, из соображений
симметрии, тол!'ко от раСL'ТОЯНИЯ до центра тора, равна 2пRB, Полный ток,
пронизывающии площадь, оrpаниченную этой окружностью, равен NJ, [де
N  числ витков тороидальной обмотки, Откуда напряженность маrнитно
1'0 поля В внутри тора равна
в = J!Jl.. NJ ,
2л R
,.
Рез.1'.7ьтаты данно,'о p{j5(Je.?a впервые получены автором совместно с В И. Xa
!'/III1<JновыЛ/ в ! 19] .
]20
 ........
.. :(J':'l!!.l!..(Jв--й-н!,:с.'!!.й-.'!!.z:.. Ч.с..кu::?леК-Il1РIl ЧСК-:'Х.и-.. ' Й-.!!и-.mllI!.'!.?л-е.й.
Рис. 5,25
Рассмотрение контура, представляющеrо собой окружность, радиусом,
большим радиуса тора, показывает, что полный ток, протекающий через
данный контур, равен нулю, так как ток в каждом витке катушки пересекает
ее дважды в противоположных направлениях, Отсюда с неизбежностью
следует вывод о равенстве нулю напряженности маrнитноrо поля вне тора.
Однако количественное обоснование принятоrо выше допущения о воз
можности замены тороидальной обмотки повеРХНОСl1Ю распределенным током
либо не приводится, либо утверждается, что составляющей тока вдоль тора при
достаточно плотной намотке можно пренебречь [5,16]. Справедливость данных
подходов можно поставить под сомнение, так как они противоречат закону co
хранения заряда. Действительно, при протекании тока J через тор и подводя
щие провода количество электричества, проходящеrо в единицу времени через
выбранное сечение провода 1, должно равняться количеству электричества,
проходящеI'О через выбранное поперечное сечение провода 2 (рис. 5.24), Сле
довательно, количество электричества, перемещаемое в единицу времени
вдоль окружности радиуса R тора, одинаково при любой крymзне на.\10ТКИ.
Так как перемещение заряда вдоль оси тора есть продольный ток, величина KO
TOpOro равна J, то тор должен обладать внешним мапlИтным полем, аналоrич
ным мarнитному полю витка с током.
Для подтверждения проведеННОI'О качественноrо доказательства сущест
вования внешнеrо маrнитноrо поля тора проведем прямые вычисления
напряженности маrНИТНОI'О поля на основе закона БиоСавараЛапласа [4]:
dB = PJl lc!r
4 "
1L r'
(5.35)
[де Jdl  элемент тока, r  радиус вектор от элемента тока в точку наблю
дения, и принципа суперпозиции . интеrpированием (5.35) по всем элемен
там тока. Для однозначноrо описания положения элементов намотки введем
два радиусавектора. вектор R7, описывающий положение центра дaHHO
121

f(oMlIbIOтep/ive моделироваuие фюических I1роцессов в иакете MATLAB
............... ....... ..................
1'0 сечения тора меридиональной ПЛОСКОСТЬЮ с началом В точке О
  ' , и вектор
а , Оl1исывающии положение элемента спирали в меридиональной плоско
сти (рис. 5.26),
l
ii Рис, 5,26
Выберем систему координат XYZ так, что при нулевом yrле поворота веь.-тор
R.T имеет координаты (RT ,0,0), вектор II  (а,О,О), Положение каждой точ
ки тороидальной намотки в выбранной системе координат будем описывать
радиусомвектором r , который является суммой векторов Лт, ll:
r = ЛТ +ll, (536)
Очевидно, что при постоянном уrле намотки положение любой точки
спирали будет определяться одним параметром  уrлом поворота ер вектора
R т в плоскости ХоУ, Найдем связь yrла поворота вектора II в меридио
нальной плоскости ер 1 С уrлом поворота ПJ вектора R В П Х У
'f' Т лоскости О ,для
чеrо рассмотрим плоскост
ную развертку одноrо витка
тороидальной намотки, пред
стаВJ!ЯЮЩУЮ прямоуrольный
треуrольник, длины катетов
КОТОрOI'О равны длинам дуr
окружности радиуса R в
плоскости ХоУ и окружности
радиуса а в меридиональной
плоскости (рис, 5,27),
При Nвитковой намотке они
поэтому уrол намотки j3 равен
aN
j3 = arctg .
RT

у
21ta
R, ,2trfN
Рис. 5,27
равны RT. 2тrl N и 2тса, соответственно,
122
(5,37)
...
. .............:/':!.!!е:':!!.l!..?.аllи'r:.."!'!.ч.:.:.'!?'5."!Р...'!:.'5.'!!.:л.:..а'!.'!."!!'ь..?JI:.Р.
Рассмотрим развертку спирали при произвольном yrле поворота ер, l1ред
ставляющуЮ, как и для одноrо витка, прямоуrольный треуrольник. В этом
случае длины соответствующих катетов равны RT. ср, а'ер l' Используя из
вестные формулы, связывающие катеты прямоуrольноrо треуrольника че
рез уrол между катетом и rипотенузой, получим
Rr'ep,tgj3=a'ep], (5.38)
Подставляя выражение для yrла j3из (5.36) в (5.37), окончательно найдем
epl= N ер, (5.39)
Учитывая (5.35), (5.38), запишем зависимость координат радиуса
вектора f от уrла поворота ер в выбранной системе координат
r = ((RT+a cos N ер )cosep, (RT+a cos N ер )sin ер, asiпN ер) (5.40)
Элемент длины тороидальной обмотки dT выражается через вектор l ,
касательный к обмотке в данной точке, и уrjл поворота dep
dT = ldep, (5.41)
rде вектор l по определению равен [14]
 df
t = .
dep
(5.42)
Из (5.40), (5.42) найдем
[ (RT sin ер + а sin epcos Nep+ Nasin Nepcosep)]
l = RT cos ер  aN sin Nepsin ер + а cos Nepcosep .
aN cos Nep
Выражение для напряженности маrнитноrо поля, создаваемоrо ЭJIемен
том тороидальной обмотки в точке пространства, положение которой опи
сывается радиусомвектором Ro=(xo,Yo,zo), учитывая (5.35), (5.41), можно
(5.43 )
записать в виде:
 f1(}J [Тх(ЛоУ]
dB =  ,dep'
4п- ,"  13
,1\(} r
(5.44)
rде
R oy = (xo(R т +а cos N ер )cos ер, Уо  (R 7+а cos N ер )sin ер, Zoasill N ер) ,(5.45)
{ . .....  . ..,..... , ,.. ."'" ......
IRoFI= \j(XO(RT+acosNep)cosep)2 +...
;(;"':'(R; +a's' Nq;)i;y"'T"N;)'i
(5.46)
123

KOA<пЫ()I1Ip'lIoe А,одеf!.I'р'()вlIи=1)и!чеСk'их процессов в lIаксте MAТLAB
............................ .....
.. ........:!>!'!.'!'.I!р()в.а.'I.сl1!.i1..п.:.ч_=с:.".li?f!.к-п.:.l!.l!.:_е._К-l!._. А(1_IIи-f/lllь_zx..I1(Jл_е.
Составляющие маrнитноrо поля, создаваемоrо тороидальной обмоткой с
постоянным током в точке с радиусомвектором Ro, вдоль координатных
осей находятся непосредственным интеrpированием (5.44). Окончательные
выражения компонентов напряженности маI'НИтноrо поля через интеrpалы
элементарно получаются подстановкой выражений (5.45) (546) (5 43)
в (5.44)' . , ,
В, f.l 01 f (RТсОsqJаNsiпNqJCоsqJ+асОsNqJсОsqJ)(zоаsiпNqJ)+..,
4л- о l (хо (RT+acosNqJ )COSqJ)2 +(Уо (RT +acos NqJ )sinqJ)2 +.., --) (5.47)
 aNcosNqJ(Yo(RT+acosNqJ) cos qJ)
]3 dqJ,
+( zoasin NqJ)2
В =  f.l (/ f (RT sin qJ +asin qJcosNqJ + Nasin NqJcos qJ)( zoasin NqJ) + '"
у 4л- о [(Xo(RT+acosNqJ)cosqJ)2 +(Yo(RT+acosNqJ)sinqJ)2 +...  (5.48)
 +aNCosNqJ(xo(RT+acosNqJ) cos qJ)
]3 dqJ,
+( zoasinNqJ)2
В =f.l J f (RTsinqJ+asinqJcosNqJ+NasinNqJcos qJ)...,
7 4л- а [ (XO(RT+acosNqJ)cosqJ/ +(Ya(RT+acosNqJ)sinqJ)2 +... 
'(Уа (RT+aCOS NqJ )sin qJ)
 3 dqJ
( zoasin NqJ)2 ] .
(5.49)
Важно отметить, что несмотря на rpомоздкость выражений (5.47) 
(5.49), вычислительные средства пакета MATLAB позволяют записать pe
шение данной задачи в компактной форме. При составлении проrpаммы
можно использовать подход, описанный в предыдущем разделе при расчете
и визуализации маrнитноrо поля соленоида с постоянным током, Однако
соответствующая проrpамма показала, что для расчета напряженности Mar
нитноrо поля соленоида даже для сетки с небольшим числом узлов требует
ся неприемлемо MHoro времени, Как показала пошаrовая проrонка про
rpаммы, наибольших временных затрат требует операция вычисления BeK
TopHoro произведения, входящеI'О в выражение (5,35), которое приходится
вычислять MHoroKpaTHo для каждоrо значения переменной рЫ, По этой
причине мы отказались от использования встроенной в МА ТLAB функции
cross, записывая явные выражения для каждой координаты BeKTopHoro про
изведения, Ниже приводится листинr файла ATor.m, содержащий описа
ние функции, возвращающей значения составляющих напряженностей
вдоль соответствующих координатных осей,
% листинr файла ATor.m
function [Ах,Ау ,Az]=A Tor(xO,yO,zO,Rt,a,N);
% функция, возвращающая значение составляющих напряженности
% маrнитноrо поля вдоль соответствующих координатных осей
dphi=pil(5*N); % шаr интеrpирования
phi=O:dphi:2*pi; % вектор, содержащий значения узлов интеrpирования
[rx ry rz]=rTor(Rt,a,N,phi); % вычисление координат вектора R
% в соответствии с (5.40) в узлах
% интеrpирования
[tx ty tz]=CTor(Rt,a,N,phi); % вычисление координат вектора t,
% в соответствии с (5.4 3)
N2=length(rx); % длина вектора
% вычисление составляющих напряженности маrнитноrо поля
% в соответствии с (5.22)
ХО(1 :N2)=xO;
УО(1 :N2)=yO;
ZO(1:N2)=zO;
Rx=XO-rх;
Ry=YOl")';
Rz=ZOrz;
Z=(Rx. Л2+Rу. Л2+Rz. л 2). л (1/2);
f1=tx.lZ;
f2=ty.lZ;
12"
- f aNcosNqJ,...
4п- а [(Xo(Rl+acosNqJ)COS qJ)2 +(yO.(RT+acosNqJ)sinqJ/ +...
,( х a(RT+acos NqJ )cos qJ)
. 3 dqJ
+( z()asinNqJ)2J
Как видн из выражений (5.47)  (5.49), составляющие маrнитноrо поля
тороидальнои обмотки с ПОстоянным током не выражаются через элемен
тарные Ф!НКlJ,ИJ1, IIОЭТОМУ возможно только численное исследование oco
бенностеи ЭТОI'О поля.
124
125

!..?п'!!!!!():'_'''!..Й-:'l!.'Р.)I,!еrJ!.'!?'!.'!..':.К-'!;( _!'..й-'!..е.с.::й-в_к---е!!.l!!..1.1.Т!:!!.!!.__щ_ .. _.
tз=tzJZ;
Ax=trapz(phi,f1);
Ay=trapz(phi,f2);
Аz=trарz(рhi,tз) ;
function [rx,ry,rz]=rTor(Rt,a,N,phi)
% Функция, возвращающая координаты вектора R в соответствии с (5.40)
rx=(Rt+a*cos(N*phi)). *cos(phi);
ry=(Rt+a *cos(N*phi)). *sin(phi);
rz=a*sin(N*phi);
function [tx,ty ,tz]=t Tor(Rt,a,N,phi)
% функция, возвращающая координаты вектора t в соответствии с (5.43)
tx=-(Rt*sin(phi)+a *sin(phi). *cos(N*phi)+...
а *N*sin(N*phi). *cos(phi));
ty=Rt*cos(phi)- N* а *sin(phi). *sin(N*phi)+a *cos(N*phi). *cos(phi);
tz=a*N*cos(N*phi);
Далее для вычисления и визуализации напряженности мarнитноrо поля в
плоскости У 02 необходимо выполнить следующую последовательность KO
манд.
Nl=21; % число узлов
i=I:Nl+l;
Ушiп=-100; Zmin=-100; % левый нижний yrол координатной сетки
Уmах=100; Zmax=100; % правый верхний уrол координатной сетки
% вычисление координат узлов сетки
Y(i)=Ymin+(Ymax- Ymin)1N1 *(i-l);
Z(i)=Zmiп+(Zmах-Zmiп)1N1 *О-l);
Rt=l; % радиус большоrо кольца тора
а=О.5; % радиус малоrо кольца тора
N=lOO; % число витков
% вычисление составляющих напряженности маrнитноrо поля
% в узлах координатной сетки
for i=I:Nl+1
for j=1:Nl+1
[Ьх Ьу bz]=BTor(O,Y(i),Z(j),Rt,a,N);
Bx{iJ)=bx;
By(iJ)=by;
Bz(iJ)=bz;
end;
end;
126
.a..........
.._..'_!!.'!..1!'!.l!!.'..в'!.';'!e.:111'!.11!'!e.:к-и.x: Эl!:'К-11!fJ'!ч.'!..::.к-'!_л:..а.2!!'!111'!.х....'!!!!!.:'
% нормировка векторов
mр=(Ву.Л2+Вz.ЛZ).ЛО.5;
byl=ByJmp;
bzl=BzJmp;
quiver(Y,Z,byl,bzl,O.5); % визуализация aeKTopHoro поля
11'
100l
I
I

J
-1
.
 .  . .  ...... -. " , , ; I "  ' ... . .  -- ......
 ,-    .  '- . '. . : I  .- .   . -- .. -.
, . . .Ф .. . .. " \  . . .' ..". . .  . ....
ii),'!!!];U""j;\:'\:
 : " \ ' \  . ' ",. _.' r r . . r I ! ' ,
\ \ \ \ , ' > " "' .... .. .. '  , , f : .. .
" , \ . . ,. '" .... .. . . ,. " . / ' I -' ,
ttt j
.... ....   .. 4 . ." '" .,,', '. .   ....   ...
, ... . . .... ...'  .r "', ;"...... -  ...."
 ....  .  ." ' / .' " " " ,' -.  . ....
,
-100
,
,50
,

i
1
,
100
Рис, 5,28
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 5.28,
Отметим, что как и в случае с прямым соленоидом, использование MHO
rослойной тороидальной обмотки с числом слоев п, намотанной в одном
направлении, приведет к пропорциональному увеличению (в п раз) количе
ства электричества, перемещающеrося в единицу времени вдоль окружно
сти тора радиуса R, по сравнению с однослойной обмоткой. Следовательно,
напряженность маrнитноrо поля мноrослойной тороидальной обмотки В
будет в п раз больше поля однослойной обмотки В,:
=пB.
При использовании мноrослойной тороидальной обмотки, в которой Ha
правление намотки в каждом следующем слое противоположно предыду
щему, при четном количестве слоев суммарное количество электричества,
перемещающеrося в единицу времени вдоль окружности тора радиуса R,
равно нулю, при нечетном количестве слоев  равно количеству электриче
ства, перемещающеrося в единицу времени вдоль оси радиуса R, в OДHO
слойной тороидальной обмотке, Следовательно, тороидальная обмотка
с четным количеством слоев обмотки не имеет внешнеrо маrнитноrо поля,
127

l!..п-ЬЮ-ТI1.!!?.!!'!ЕС}!1!...и-:..1!.Ч-:'с.!5.'!!!.?,Н,в!!..к-..е.!!'i!.АВ . .
а тороидальная обмотка с нечетным числом слоев имеет внешнее маrнитное
поле, равное полю однослойной тороидальной обмотки.
.'-...
Задача 5.7
Как известно [J 3J, маснитное поле витка с током имеет нулевые co
ставляющие вдоль осей оХ; о У и ненулевую составляющую вдоль оси oZ,
зависящую от расстояния до центра витка В:
В  /l- о] 27r R2
z  47r (R2 + z2)12 '
rде R  радиус катушки, z  расстояние между точкой наблюдения и цeH
тром витка.
1, Вычислите зависимость напряженности ""aтитH020 поля тороидалыlOЙ
обмотки на оси oZ от расстояния до центра тора (радиус тора  5 см,
радиус поперечноzо сечения  0,5 см, число витков  N == 500) и cpaвHи
те с аналоzичной зависимостью для витка с током,
2. Объясните причину отсутствия проявлений внешнеzо матитносо поля
тороидальной обмотки в опытах по визуализации матитносо поля с
помощью матитных опшlOК [17]. (В этих опытах тороидальная об
мотка и подстШlaЮЩая поверхность с металлическими опШlками раз
мещались в одной плоскости.)
5.5. Численное решение уравнений Лапласа
и Пуассона
в предыдущих разделах мы находили потенциал и напряженность элек
трических полей, обусловленных стационарным распределением электриче
ских зарядов, используя принцип суперпозиции, Во мноrих случаях прихо
дится решать более сложные задачи, из которых наиболее типичными яв
ляются следующие:
1. Нахождение потенциала электрическоrо поля при неизвестном MeCTO
положении исходных зарядов, но заданном электрическом потенциале на
rpаницах области. (Например, задача о распределении потенциала электри
ческоrо поля, создаваемоrо системой неподвижных про водников, помещен
ных в вакуум и подключенных к батареям, Здесь можно измерить потенци
ал каждоrо проводника, но задать распределение электрических зарядов на
проводниках, зависящее от их формы, весьма сложно.)
2. Нахождение потенциала электрическоrо поля, создаваемоrо заданным
распределением электрических зарядов р(х, у, z) в пространстве.
128
...
.   ...J..:.!!.?i!.'!!!..и-l!.CJ.вl1'IUе.:"!I1Т11UЧ-:'5.?..ле'5.'!'-.I!.и-ЧС}5и-:.'.:.l1..,,!1и-'!'-!!! !'..?л-е..
Хорошо известно, что прямой метод вычисления потенциала электриче
CKoro поля tp(x, у, z) в этих задачах состоит в решении уравнения Лапласа
82 (fJ 82 tp 82 tp
tp(x у х) =  + . +, == о
, , / 8 х2 8 у2 8 Z2
(5.50)
и уравнения Пуассона
82tp 82tp a2tp
tp(x, у, х) == 2 +2 +  ::: p(x, у, Z),
дх ду az
соответственно. Уравнения (5.50), (5,51) относятся к классу диффереНIlИ
альных уравнений в частных производных эллиптическоrо типа.
В дальнейшем мы будем рассматривать только частный случай эллипти
ческих уравнений для поля tp, зависящеrо от двух пространственных пере
менных. Совершенно очевидно, что для полноrо решения задачи уравнения
(5.50), (5.51) необходимо дополнить rpаничными условиями, Различают три
типа rpаничных условий: 1) rpаничные условия Дирихле (значения tp зада
ются на некоторой замкнутой кривой в плоскости (х,у) и, возможно, на He
которых дополнительных кривых, расположенных внyrpи области
(рис. 5.29»; 2) rpаничные условия Неймана (на rpанице задается нормаль
ная производная потенциала tp); 3) смешанная краевая задача (на rpанице
задается линейная комбинация потенциала tp и ero нормальной производ
ной).
(5.51 )
у=l
у=l


"-
J
у=О
х=О
у=О
х= О
х=l
х=l
Рис, 5.29
Рассмотрим методы численнor'о решения более общеrо уравнения (5,51),
предполаrая, что решение ищется в единичном квадрате, В качестве первоrо
шarа получения численноrо решения преобразуем уравнение (5,5]) к виду,
удобному для численноrо решения. Для этоrо в плоскости (х,у) задаем сетку
51576
129

.rs.()м..!!ь.!(),!!еРl!<J.:'_А1..()':!и.Р...()с:.l1!-,::'4.)и.з..и-.ч.:.с!5._!!Р()У'!..<J.....'!:"tl:' л-!11J:'!l!
из (N + 1) х (N + 1) узлов, покрывающую рассматриваемую область. (Для
простоты выбираем шаr сетки h по каждой координатной оси равномерным
и одинаковым.) Узлы сетки будем обозначать парой индексов (i, Л, пробе
rающих значения от О до N. В выбранных обозначениях координаты точки
и, j) равны (Х; = ih, у j = jI7). Обозначив значения функций ер, Р в узловых
точках qJij = СР(Х;, у j ), Pij = Р(Х;, у j ), и используя для аппроксимации про
изводной 3точечную формулу [18,20], получаем разностную аппроксима
цию уравнения (5.51)
qJ;+lj + qJHj  2qJij qJ;j+l + qJij1  2еру  (5.52)
- + . P
h2 h2  ij .
Уравнение (5,52) может быть получено друrим способом, основанном
на вариационном принципе, Рассмотрим Функционал Е поля qJ следующеrо
вида:
1 1
Е = J dx J dY[ i (У' qJ )2  РСР] ,
а а
Так как величина (Y' ср) есть электрическое поле, а Р  плотность заря
да, то величина Е равна полной энерrии системы. Найдем вариацию функ-
ционала Е
(5.53)
! .
1 1
дЕ = f dxf dy[V ср' V бqJ рбrp].
а а
Интеrpируя по частям первый член (5.48), получаем
1 1
дЕ = J dlдqJ п, V qJ + J dx J dyJqJ[ v2qJ  Р],
с а а
[де криволинейный интеrpал берется по rpанице рассматриваемой области
(С), а if  единичная нормаль к rpанице, Для вариаций, удовлетворяющих
rpаничным условиям на rpанице (С) дср == О , поэтому криволинейный инте-
rpал в (5,55) также равен О, Требование равенства дЕ нулю для всех таких
вариаций, означает, что qJ удовлетворяет уравнению (5,51),
Для вывода дискретной аппроксимации уравнения в частных производ-
ных на основе вариационноrо принципа аппроксимируем Е через значения
поля в узлах сетки, используя двухточечную разностную формулу для про-
изводной И правило трапеций для вычисления интеrрала:
(5.54)
(5,55)
130
...
....._.___.л-!()'!.Л!!.l!...о.!!.'!!.:'I1!._:'!!!!..'!!.'!..ч:.:'t!.'5.'!!l!...!!..'?5UX U Ma2!!'!..'!!.'!...."!!3...():._
N N NN
Е =  L L [(qJij  qJHj У + (qJij  qJij-l y] h2 L LPijqJij .
;=1 j=1 ;=1 j=1
Накладывая условие
(5.56)
 O
дт..  ,
'f'IJ
(5.57)
для всех ij, приходим к разностному уравнению (5.52).
Предваряя решение двумерных уравнений Лапласа и Пуассона, paCCMOT
рим методы решения одномерной краевой задачи, которая может бьпь опи
сана уравнением BToporo порядка
d2qJ
 = p(x) (5,58)
ш2
с заданными значениями ср(О) и qJ(l). Соответствующий Функционал Е для
данноrо уравнения имеет вид
E=HH:)'p+
(5.59)
а ero дискретный аналоr на равномерной сетке с шarом h = 1/ N
N N-l
Е = 21,; L(qJ;  срн)2  h Lp;qJ; .
;=1 ;=1
.
Варьируя (5.60) по всем СР; , получаем разностное уравнение
СР;+1 + СР;-1  2ср; = h2 Р;,
(5.60)
(5.61)
[де СРа =ср(О), qJN =qJ(l).
Уравнение (5.61) задает систему линейных уравнений относительно He
известных переменных СР; (i = 1, N  1), причем матрица системы уравне-
ний является трехдиаrональной (т. е. в матрице отличными от нуля оказы
ваются только элементы, расположенные на rлавной диаrонали и двух диа
rоналях, расположенных выше и ниже rлавной диarонали). Для небольшоrо
числа точек (например, N:<; 100) данную систему уравнений можно решить
* в выражении для энерi?ИИ ({Ji встречается дважды: в членах (({Ji  ({Jil i и
(({J;; 1  ({J,)2
131

'?:И- пJ!!.'!1.:Р.!!'?:!!.'!Ей-_вl!!tи-: 1; UЗl<'/(!.Кl<;(J!Р'Й-.':!.:.с.й-f!. 15.:Jrlelv! A:.!:,!l!.... ..
прямыми методами [21] или использовать специальный прямой метод, раз
работанный для решения «трехдиаrональных» систем [20], Однако на прак
тике при численном решении эллиптических уравнений приходится исполь
зовать сетки, имеющие значительно большее количество узлов, поэтому мы
считаем целесообразным оrpаничиться рассмотрением только итерацион
ных методов (на примере метода релаксации), применяемых в случае боль
ших разряженных матриц.
Перепишем уравнение (5,61), разрешив ero 011ЮСИтельно переменной qJi:
ер; == 1 [qJi+l +СРн +h2 р;]. (5.62)
Несмотря на то, что значения СРН, qJi+l' входящие в правую часть ypaB
нения (5.62), нам не известны, ero можно интерпретировать как «уточне
ние» значений qJi через значения в соседних точках. Следовательно, метод
решения уравнения (5,62) (метод rауссаЗейделя) состоит в следующем:
1) выбрать некоторое начальное приближение для решения уравнения
(5.61); 2) продвиrаясь по сетке (например, слева направо), уточнить решс
ния уравнения в соответствии с (5.62). При MHoroKpaTHoM повторении опи
caHHoro процесса начальное приближение может сойти (<<срелаксировать»)
к точному решению.
На практике вместо уравнения (5.62) используют обобщенное ypaBHe
ние, в котором на каждом шаrе релаксации qJi заменяется линейной комби
нацией из cBoero cTaporo значения и «улучшенноrо» по формуле (5,62)
qJi cp; ==(1w)qJi + i+l +СРн +h2pJ (5.63)
Для исследования сходимости описанной процедуры вычислим измене
ние функционала энерrии Е. Подставляя (5.63) в (5.60), после ряда
преобразований найдем
, w(2W)[1 { 2 \ ]2
Е E==h '2 vP;+l +CP;1 h P;jqJi (5,64)
Из (5.64) видно, что при ]о,2[ энерrия не возрастает и, следовательно,
итерационный процесс будет сходиться к требуемому минимальному зна
чению. Существование посторонних минимумов энерrии свидетельствует о
плохой обусловленности линейной системы. Параметр w определяет CKO
рость сходимости итерационноrо процесса  скорость релаксации, Принято
различать два случая: при rv < I rоворят, что используется метод «нижней
релаксации», при OJ > I  метод «верхней релаксации»,
132
..........
.Й-f!!I!!.l!..ованuе С'!!!!..I!!.ск.!..лектрuческux u Ma2HuI!!.Hых п!!eй
в качестве примера, иллюстрирующеrо релаксационный метод, pac
смотрим одномерную краевую задачу для уравнения (5.58) с
p(x)=12x2,tp(O)=tp(I)=O, имеющую точное решение qJ(х)=х6хЗ) с
энерrией Е = 9/14 == -----0.64286.
для решения поставленной задачи необходимо создать mфайл, coдep
жащий описание функции, возвращающей матрицу, в nM столбце которой
находятся решения, полученные на nM итерационном шarе. Ниже приво
дится листинr файла Iteration.m, который содержит описание данной
функции.
% листинr файла Iteration.m
function z=interation(N,Omega,NumberoCIteration)
% функция, реализующая итерационный процесс
h=lIN; % шar сетки
i=l:N+l;
% начальные значения
x(i)=(i-l)*h;
f=ro(x);
phi(i)=O;
% интерационный цикл
for k=l:NumberoCIteration
for i=l:N-l % прохождение по узлам сетки
phi(i+ l)=(l-Omega)*phi(i+ 1)+Omega/2*(phi(i)+phi(i+2)-...
h.Л2*f(i+l»;
end;
if k==l
q=phi'; % сохранение решения на первом шarе итерации
eISe
q=cat(2,q,phi'); % сохранение каждоrо следующеro решения
% в новый столбец матрицы q
end;
end;
z=q;
function z=ro(x)
% начальное приближение
z=-12*х.Л2;
Здесь для сохранения решений уравнения, получаемых на каждом ите
рационном шarе, в соответствующем столбце матрицы q мы используем
133

Компьютерное моделирование физических процессов в nакете МА тив
ФУНКЦИЮ cat. Первый apryмeнт функции определяет способ размещения
добавляемоrо вектора. Если значение первоrо элемента установить равным
единице, то вектор будет добавлен к существующему вектору снизу, если
2  то новый вектор размещается справа от существующеrо, т. е. формиру
ется матрица.
для нахождения численных решений, а также отображения точноrо pe
шения и решений, полученных на выбранных итерационных шarax, на rpa
фике следует выполнить следующую последовательность команд:
N = 21; % число узлов сетки, в узлах которой ищется решение уравнения
i = I:N+l;
x(i)=lIN ;
Omega=l; % параметр итерационноro процесса
Niteration=200; % число итераций
у = Iteration(N,Omega,Niteration);
Nl=200; % число точек для построения rpафика ФУНКЦИИ
j = I:Nl+l;
хЩ) = G-l)/Nl; % координаты узлов сетки для вычисления
% значений точноrо решения
уЩ) = xl(i)*(I-хl(i).ЛЗ); % точное решение
plot(xl,yl,x,y(:,10),' , ,х,у( :,50),':' ,х,у( :,180),' -. ');
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 5.30.
0.5 . .. .:......
'-"",
//" . "'"
j , \
.(
;/ \
;1 \
/ \
/ .
/ . \
/ \.\
0.05 / 'Х
0.45
0.4
0.36
0.3
0.25
0.2
0.15
0.1
о ::...L:.. '..l. ..... .L ....... .... ... ......1. . ...l. .l ..... L. ..
О  U U U U м u u u 1
Рuс,5,ЗО
134
..........
ш. ....... _:А!.?:'.fшо.в.l!!ше..?_I_.fI'!1!:Ч-"-.I:'.'!.15.'!!!'...U.:.!."-95'!..х. (lI'!!..IbX.rz.?:'.'!..
Можно продемонстрировать сходимость итерационноrо процесса, по
строив зависимость функционала энерт'ии как функцию числа итераций,
Для решения поставленной задачи необходимо создать mшфайл, содержа
щий описание функции, возвращающей значения функционала энерrии на
nM итерационном шаrе. Ниже приводится листинr файла Iterationof
Energy.m, который содержит описание данной функции.
% листинr файла IterationoCEnergy.m
function z=InterationoCEnegy(N ,Omega,Number oCIteration)
% функция, возвращающая значения энерrии на каждом
% шаrе итерационноrо процесса
h=I/N; % шаr сетки
i=I:N+l;
% начальные условия
х(i)=(И)*h;
f=ro(x);
phi(i)=O;
% итерационный цикл
for k=I:NumberoCIteration %
for i=I:N-l % прохождение по узлам сетки для вычисления
% решения
phi(i+ 1)=(1 Omega)*phi(i+ 1 )+Omega/2*(phi(i)+phi(i+2)...
Ь. Л2*f(i+l»;
end;
е=О;
for i=2:N+l % прохождение по узлам сетки для вычисления энерrии
e=e+(phi(i)-phi(i -1». л 2/(2*Ь)+Ь *phi(i)*f(i);
end;
En(k)=e;
end;
z=En;
function z=ro(x)
% начальное приближение
z= 12*х. Л2;
ДЛЯ нахождения зависимости энерrии от номера шаrа итерации, а также
отображения данной зависимости на rpафике следует выполнить следуюш
щую последовательность команд:
» Ni = 200;
» i=I:Ni;
135

.l!..С?lI!.'!..'!l!'!!l!..,!...о'!.!!!!.елuроваl.'!:!:..1!!!!.'!.:!..'!.::.'.Р!!..'!..:':_о..!!!!!'5...'!'-!!1!...1.Ез!!.ш..._..
» z=InterationoCEnergy(Ni,l,2OO);
» z1(i)=-9/14;
» plot(i,z,i,zl,'--');
Результаты выполнения перечисленной выше последовательности KO
манд представлены на рис. 5.31.
о  T  .. т- ..
 Ш'Шl
1
.1
\
\
\
\
O.2 \
\
З \
\
\
\
.4 \
\
\
\
.5 \
\
"'.
.6
"0"
'.--::--:-;-----::::::..
==]
160 180 200
4).7  ш.....1...................L._ ... ..........L.........
О 20 40 60 80 100 120 140
Рис, 5.31, Зависимость энерzии от номера итерации
Задача 5.8
1. Используя выражения (5,60), (5.63), получите формулу (5.64).
2. Получите аналитическое решение рассмотренной выше краевой задачи
и найдите точное значение энерzuи,
3. Исследуйте зависимость скорости сходимости релаксациОННО20 пpoцec
са от значения пара.метра ()), Сравните скорость сходимости методов
верхней и нижней релаКсации.
В практических расчетах читателю МО2ут при20диться несколько по-
лезных советов, приведенных в [18J:
1. Выбор хороше20 началЬНО20 приближения у.:wеньшает необходимое число
итераций,
2. Необходимо использовать оптимальное значение пара.метра релаксации,
которое может быть оценено аналитически или получено эмпириче
ским путем.
3. Процесс может оказаться более эффективным, если несколько итера-
ций провести по некоторой сеточной подобласти, в которой сеточное
136

,...____.._._:..l::!...о.!.f!!!.'!Р..?..в--.а!!'!!!.!т'!..:'5..'!..:!/!!!!5..."'-.Е.и----ч--9!:....и::....'!...lI!.'!:::!!!!..'!'-!!ь.!..-:"'!.'?.1!.
решение известно наиболее слабо, что позволяет сэкономить затраты
на релаксацию уже отрелаксировавших частей решения,
4. Провести расчет на относительно 2рубой сетке, для которой объем вы-
числений невелик, а затем экстраполировать полученное решение на бо-
лее мелкую сетку и использовать эти значения в качестве началЬНО20
приближения для последующих итераций,
Для решения ДBYX и трехмерных задач также может быть использована
описанная выше итерационная процедура, В двухмерном случае аналоr
формулы (5.64) получается решением уравнения (5,52) относительно fPij и
заменой в (5.64) СР;  fPij :
fPij  fPij = (1 w)fPij + : [fP;+lj +fPHj +fPijtl +fPij1 +h2 Pij]' (5.65)
Если данный алrоритм применяется последовательно к каждому сеточ
ному узлу (например, все узлы пробеrаются последовательно слева направо
и сверху вниз), то можно показать, что Функционал энерrии (5.56), при yc
ловии, что w лежит в соответствующих пределах, всеrда уменьшается и
процесс сходится к искомому решению.
Продемонстрируем метод релаксации на примерах решения двумерноrо
уравнения Лапласа (5.50) и двумерноrо уравнения Пуассона (5.51).
Поставим следующую краевую задачу для уравнения Лапласа: найти
решение уравнения (5.50) в квадрапюй области (О  х  1 см, О  У  1 см)
при заданных значениях потенциалов на rpаницах и(х,о) = 10, u(x,l) = IO
( и(О, у) = u(l, у) = 5). Для решения поставленной задачи необходимо создать
т-файл, содержащий описание функции, возвращающей значения потен
циала на каждом шarе итерационноrо процесса. Ниже приводится листинr
файла IterationL.m, содержащий описание данной функции.
function z=interationL(N,Omega,NumberoCIteration,phi)
% функция, возвращающая значения потенциала на каждом шаrе
% итерационноrо процесса
h=llN; % шar сетки
% вычисление координат узлов сетки
i=l:N+l;
x(i)=(i-l)*h;
j=l:N+l;
y(j)=(j-l)*h;
% итерационнъrй цикл
for k=l:NumberoCIteration
137

.l5.'?-"!...,,!?"!..е.р.::'?:..'?'!..1!.Р"'?'!..'!.'.:е1!.l!'!.:::!5..'!!:...'!.!'..'?.Н':"9?.'!.'5!.'!!I:!.1:ТL..1:!!.ш
% прохождение по узлам сетки
for j=2:N
for i=2:N
phi(i,j)=(1-Оmеgа)*рhi(i,j)+Оmеgа/4*(рhi(i+ l,j)+phi(i-l,j)+...
phi(i,j+l)+phi(i,j-l)-h.А2*f(i+l,j+l»; % релаксация
end;
end;
if k==l
q=phi;
else
q=cat(2,q,phi);
end;
end;
z=q;
Далее необходимо выполнить следующую последовательность команд:
N=15;
i=l:N+l;
j=l:N+l;
mu(i,l)=lO; % потенциал на левой rpанице
mu(i,N+l)=-lО; % потенциал на правой rpанице
mu(1,j)=5; % потенциал на нижней rpанице
mu(N+l,j)=5; % потенциал на верхней rpанице
% задание начальноrо приближения
kx=2:N;
ky=2:N;
mu(kx,ky)=12; % параметр релаксации
Omega=l;
Niter=200; % число итераций
z=interationL(N,Omega,Niter,mu); % решение уравнения Лапласа
% вычисление векторов и матриц для построения карты линий уровня
x(i)=(i-l)/N ;
yG)=(j-l)/N;
[xl yl]=meshgrid(x,y);
K=lOO; % номер итерации для построения карты линий уровня
Nl=(N+l)*K+l;
N2=(N+l)*(K+l);
A=z(1:N+l,Nl:N2); % выделение Kro решения из общей матрицы решений
[С,Ь] = contour(xl,yl,A,17);
138

5, Моделирование статических электрических и Ma2HитHых полей
Результат выполнения приведенной выше последовательности команд
представлен на рис. 5.32.
1..
-"
0.9 \"'" -"--
'- ,..........._-...._-........
Q.8 ""-. 
'.
""'-,,
--------...
'\
\
\
0.7
'...
---........,
0,6
\
\
\
\
0.5
0.4
i
,/
...../
0.3
//
_.-""-- 
/
// -......
0,1 j<.'=,...
0,2
.. ......
О ..... ......
О  U U U U U U Q.8 М
Рис, 5,32, Карта эквипотенциалеи решения краевой задачи уравнения Лапласа
на 1О0-м шаzе итерации
для про смотра процесса релаксации решения уравнения Лапласа следу
ет выполнить следующую последовательность команд:
% последовательность команд для создания анимационноrо клипа
set(gca,'oextplot','replacechildreo'); % задание режима перерисовки
% карты в одном и том же окне
% создание кадров анимационноrо клипа
for K=2:Niter-l
Nl=(N+ l)*(K-l)+ 1;
N2=(N+l)*K;
A=z(1:N+l,Nl:N2);
[C,h]=contour(xl,yl,A,17);
F(K-l)=getframe; % создание одноrо кадра
eod;
МА ТLAВ, в процессе выполнения цикла по переменной К, выводит на
экран каждый вновь создаваемый кадр. для повторноrо воспроизведения
анимационноrо клипа используется команда movie(F,o), rде F  имя пере
менной, в которую помещены кадры клипа, о  число повторений клипа,
139

J5.-"!..I?'!.'!Р.!."!.'?Е.е:!.'!Р..'?!'!!'!:.1!'!:!:'!.Р'?!!.::.:..?...'!а.е..."!.!1...A.!.!:..1J!.......... ''"
.... :.?Е.e:z.!!Р.Й-l!."'!: '!!tl..f11U Ч--l!'!!..J/:'!..'!l1!.'!..Ч!!.:''5!!-''!..tl.:!!.'!f11!!..I!!.'?J/:'
если значение n не указано, то клип воспроизводится бесконечное число раз
(до закрытия rpафическоrо окна), Для получения стопкадра следует щелк
нуть по любому пункту меню rpафическоrо окна. Для продолжения воспро
изведения нужно щелкнуть мышью в поле rpафика. Можно сохранить соз
данный анимационный клип в файле, используя команду save. Например,
для созданноrо выше анимационноrо клипа данная команда имеет следую
щий синтаксис:
»save имяфайла F
для заrpузки и выполнения ранее созданноrо анимационноrо клипа ис
пользуется следующая последовательность команд:
»Ioad имяфайла имяпеременной
» mоviе(имяпеременной)
дическими rpаничными условиями. Как будет выrлядеть решение ypaBHe
ния в данном случае?
Рассмотрим решения краевой задачи двумерноrо уравнения Лапласа
(5.55) для квадратной области (О  х  1 см, О  У  1 см) с известными по
тенциалами на rpаницах (и(х,О)=10В, и(x,1)=10B, и(о,у)=5,
и(1, у) = 5В), полученноrо на сетке, состоящей из 15х 15 узлов (рис, 5,32),
Из рис, 5.32 видно, что линии, расположенные на карте эквипотенциальных
уровней оказываются неrладкими (имеют в некоторых точках изломы). Ha
личие изломов, в свою очередь, у линий равных потенциалов свидетельст
вует о наличии разрывов у производной функции  tp( х, у), описывающей
напряженность электрическоrо поля, С друrой стороны, как известно из
теории функций комплексноrо переменноrо, функция tp(x, у), удовлетво
ряющая уравнению Лапласа, является аналитической [22]. Необходимым и
достаточным условием аналитичности функции tp(x, у) является непрерыв
ность ее производных, которому, как очевидно, не отвечает полученное Ha
ми численное решение. Обнаруженный «дефект» численноrо решения свя
зан с большим шаrом сетки, на которой ищется решения уравнения (5.50).
Для ero устранения можно использовать два способа: 1) находить численное
решение на сетке с меньшим шаrом; 2) используя найденное числовое pe
шение на сетке, состоящей из 15х 15 узлов, находить значения в точках, не
совпадающих с узлами сетки, с помощью интерполяционной процедуры.
Подробное рассмотрение методов интерполяции функций и связанных с
этой задачей проблем ВIХОДИТ за рамки данноrо раздела, поэтому мы orpa
ничиваемся только одним методом, получившим в последние rоды наи
большее распространение в прикладных исследованиях  методом сплайн
интерполяции. Происхождение этоrо метода и caMoro термина «сплайю>
связывают с техническим приемом чертежников. При необходимости про
вести непрерывную кривую через сеточный rpафик { х", у" } на бумаrе Ha
носят точки { х }' } Около каждой из них втыкают две булавки и через
1l' п .
образовавшийся коридор пропускают rибкую и упруrую ста.пьную линейку
(<<сплайн»). Форма, которую принимает эта линейка, является решением за
дачи о сплайнинтерполяции сеточной функции { х", у" }, Можно показать,
что функция у(х), описывающая форму линейки, сводится к уравнению
y(IV) = О, Из уравнения Эйлера следует, что функция у(х) является куби
ческим полиномом, при этом на каЖ,Е\ОМ интервале [Х/1' Х,н 1] имеется свой
.......
Задача 5.9
1. Рассмотрите процесс эволюции карты эквипотенциальных пoвepXHO
стей в процессе итераций,
2, Исследуйте скорость сходимости методов нu:жней и верхней релаксаций,
3. Измените описанный выше документ, используя для разностной aппpOK
симации лапласиана 5точечную формулу, имеющую более высокий llO
рядок точности:
Л=( IH +16/;1 301; +16/;+1  1;+2)'
12h
Как uзме1lЯется решение при использовании более точной формулы,
а также эффективность расчетов?
4. Используя описанный выше документ, вычислите завиСШtOсть разности
потенциалов от расстояния между двумя линейными зарядами, Cpaв
ните полученные численные результаты с известным аналитическим
решением этой задачи, Исследуйте зависимость скорости сходимости
Аtетода релаксаций и точности числеННО20 решения от ша2а сетки,
5, ПОМlLWО 2раничных условий Дирихле можно задавать периодические 2pa
ничные условия, при которых потенциалы на правой и левой, а также на
верхней и нижней 2раницах задаются произволыiми,' но равными по вe
личине дРУ2 дРУ2У, т, е.
tp;o = tp; N ; tpOj = tpN j ,
Эти условия Moryт описывать пространственно периодическое распре
деление плотности заряда в кристалле, Модифицируйте соответствующим
образом описанный выше документ и решите уравнение Пуассона с перио
140
14]

ш .. . ш"" ..ш......'.А!'?'!!:.р"'?'!..С:li:1I.rrlU:(;,К-UХ Jl.е..'5.rrlР.u.'!.:.к-!!.х...1!....'!:.т-'.1!..т:'.'х..fl.'?!!.:Е
Компьютерное моделирование физических процессов в пакете МА ТИВ
кубический мноrочлен. для обеспечения rладкости интерполяционной про
цедуры накладывается требование непрерывности в узловых первой и BТO
рой производных функции у(х). Аппарат сплайнинтерполяции в настоя
щее время существенно развит (в частности, разработаны методы интерпо
ляции функций, зависящих от двух переменных) и доведен до уровня
стандарmых функции, включенных в современные проrpаммные средства
для математических вычислений.
для использования сплайнинтерполяции следует дополнить приведен
ную выше последовательность команд следующими командами:
% задание координатной сетки для вычисления значений сплайна
M=lOO;
n=l:M;
х2(п)=(п-l)lМ;
у2(п)=(п-l)lМ;
[х2 Y2]=meshgrid(x2,y2);
zi3 = interp2(xl,yl,A,x2,Y2,'splain'); % вычисление значений сплайна
[C,h]=contour(X2, Y2,zi3,17);
Результаты вьmолнения допоmnrreльных команд представлены на рис. 5.33.
Сравнение зависимостей, представленных на рис, 5.33, показывает, что,
используя сплайн"интерполяцию, удалось устранить недостатки численноrо
решения, проявляющиеся в наличии изломов линий paBHoro потенциала,
0,9 ::шшшш...' .'. шш.
\, ,............................
\" 
""
""---,
..........
'-
\
1
i
)
/
/
"
Задача 5.1 О
1. Используя Лlассив интерполировщтых значений решения уравнения Лап..
ласа, вычислите напряженность электричеСКО20 поля и постройте
карту нормированных векторов единичной длины, касательных к сuло
вой линии электричеСКО20 поля, (Указание, См, 5.1.)
2. Постройте карту эквипотенциалыlхх поверхностей функции Il(x, у ,
Сравните карты линий уровня функций tp(x, у) и IE(x, у ,
Последовательность действий, позволяющая найти и провести после..
дующую визуализацию числеННО20 решения уравнения Пуассона, анапо..
2ична описанной выше последовательности действий, Однако требует
ся внести некоторые изАlенения в тфайл, содержащий определение
функции, возвращающей численное решение, поскольку процесс релаксаш
ции не должен касаться области с заданной плотностью заряда. Ниже
приводится листиН2 файла IпteratioпP.m, содержащий модифицирован..
ную функцию, возвращающую численное решение уравнения Пуассона с
правой частью вида:
( )  {7, при х Е [0.4,0.6], у Е [0.4,0.6]
f х  .
О, при х (j!:: [0.4,0,6], у (j!:: [0.4,0.6]
(5.66)
0.8
-.....,,
"'/,....
//
;'
,/ /....
0.1 i
/'//_/' /
,.' ...-
!
I
I
i i \\1
\\ \
\\
'\
% листинr файла InterpolationP.m
СопсНоп z=interationP(N ,Omega,Number oCIteration,phi)
h=llN; % шаr сетки
% вычисление координат узлов сетки
i=l:N+l;
x(i)=(il)*h;
j=l:N+l;
yO)=O l)*h;
f=ro(N,x,y); % вычисление значений функции, описывающей
% заданное распределение заряда
for k=l:NumberoCIteration % итерационная процедура
for j=2:N % проход по узлам сетки
for i=2:N
% проверка, rде находится текущий узел
if (x(i»=0.4)&(x(i)<=O.6) &(уа»=О.4) &(уо )<=0.6)
0,3
............
'\
\
\
\
\
\
i
I
1
I
I
,
0,7
0,6
0.5
0.4
0,2
/
/
о . ш.' .
О 0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Рис, 5,33, Карта эквипотенциалей решения краевой задачи уравнения Лапласа
на 100M шаzе итерации при использовании сплайнинтерполяции
142
143

!.':!.-,,!п ':.'!':.е!!!!!!.:!!ш:.'!!?f!..I!!.:.и-:.1!!!!!!Ч:'С,!!!!!'i:..ов BI.'!.e'!'..A.!.!T1J!...
phi(iJ)=f(iJ)*hA2; % если в области с заданным распределением
% то равно значению потенциала
else
% если вне области, то релаксация
phi(iJ)=(1-Оmеgа)*рhi(iJ)+Оmеgа/4*(рhi(i+ lJ)+...
phi(i-lJ)+рhi(iJ+ l)+phi(iJ-l)-рhi(iJ»;
end;
end;
end;
if k==l
q=phi;
else
q=cat(2,q,phi);
end;
end;
z=q;
function z=ro(N,x,y)
% функция, описывающая плотность распределения заряда
for j=l:N+l
for i=l:N+l
if (x(i»=O.4)&(x(i)<=O.6)&(y(j»=O.4)&(y(j)<=O.6)
z(iJ)=700;
else
z(iJ)=O;
end;
end;
end;
..,.....,..
Задача 5.11
Найдите численные решения 2раничной задачи и(х,о) = u(x,l) = О,
и(О, у) = и(l, у) = о уравнения Пуассона с заданным распределением
плотности заряда (5,66) и проведите их визуализацию, аналО2ично тo
му, как это было сделано выше в данном разделе,
144

'ШшШ шшш :!:!.?f!!l'!Р.?I1...I1:!::.!l!.'11.'!.'!,:К---':К-!!.'Ри-'.!:(;к-их..'!..М-'!.'!.'!.'11.'!"!!..!.l!!.e!!.
ЛИТЕРА ТУРА
1. Калашников С. r, Электрические и маrнитные поля. М.: Наука, 1970.
2, Фриш С. Э., Тиморева А,В. Курс общей физики. М.: Физматrиз, 1961, Т. 11.
З, Фейман р" Лейтон р" Сэидс М. Феймановские лекции по физике, Вьш. 5,6. М,: НаУ'A!I, 1977.
4. Парселл Э, Электричество и маrнетизм. Берклеевский курс физики. М: Наука, 1975,
5. rOBOpK08 В. А. Электрические и маrнитные поля. Л.: rостехиздат, 1960.
6. Тамм И, Е, Основы теории электричества, М,: Наука, 1966,
7, Смай, В. Электростатика и электродинамика, М,: Иностранная литература, 1954,
8, Стрэттон ДЖ. А, Теория электромаrнетизма. М.: Иностранная литература, 1948.
9, Джексон Дж. Классическая электродинамика. М,: Иностраниая литература, 1965.
10, Зоммерфельд А. Электродинамика, М.: ИЛ, 1958,
11. Сбориик задач по общему курсу физики. Электричество и маrнетизм,тод ред, И, А. Яков
лева, М,: Наука, 1977,
12, Батыrин В, В., Топтыrин И.Н, Сбориик задач по электродинамике. М,: Наука, 1970,
13, Векштейи Е, r, Сборник задач по электродинамике, М,: Наука, 1966,
14, Смирнов В. И, Курс высшей математики, М,: Физматrиз, 1958, Т.3,
15. Поршнев С. В., Харитонов В,И, Особениости маrнитноrо поля соленоида с постоянным
током!/Электричество, 1998, N 6,
16, Сивухин Д, В, Общий курс физики, Электричество, М,: Наука, 1977, Т, Ш,
17, Поль р, В, Учение об электричестве. М.: Физматrиз, 1962,
18, Куиин С. Вычислительная физика. М,: Мир, 1992,
19, Поршнев С. В" Харитонов В.И, Маrнитное поле тороидальной обмотки/треподавание фиш
зики в высшей школе, 1998, N 14,
20, Федоренко р, П, Введение в вычислительную физику, М,:Издшво Моек. физ.штехи, инта, 1994,
21, Самарский А, А. Введение в численные методы. М,: Наука, 1987,
22, Морс Ф,М, Фешбах r, Методы теоретической физики, Т, 1, М,: ИЛ, 1958,
145

 М:!!.!!.!!в::.'!.'!!'!...'!..3!:!!!!'!!!.l!..е.,!!!?иче!.:!lЕ!..!.С:I!'!!!?..и..'!!.'!..!!!!.'!!..,!!.'!...Ь::...'!,5l!!!!!,
r лава 6
МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ
ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
В ЭЛЕКТРИЧЕСКИХ И МАrнитных
ПОЛЯХ
Аналитическое решение системы (6.3) может быть найденно для относи
тельно небольшоrо числа случаев, поэтому для описания движения заря
женных частиц в электромаrнитных полях необходимо проведение числен
ных расчетов.
6.2. Рассеивание частиц в центральном поле.
Опыт Резерфорда
F = q(E +[УХ В]).
В соответствии со вторым законом Ньютона
dp = d(mv) = F
dt dt '
(6.1 )
Как известно [1], задача об описании результата столкновения двух час
ТИЦ с массами т], т2 может быть сведена к эквивалентной задаче об ОТКЛО
нении одной частицы с массой т (т  приведенная масса) в поле U(Р) He
подвижноrо силовоrо центра, расположенноrо в центре инерции. Явление
рассеивания состоит в том, что частица с начальной кинетической энерrией
Е и прицельным расстоянием р (рис. 6.1) влетает в потенциальное поле на
большом удалении от ero центра. По мере прохождения через поле частица
отклоняется от пер во начальной траектории и после удаления от центра поля
на достаточное расстояние частица продолжает движение с той же энерrией
Е, но под yrлом Х К исходному направлению движения. Для полноrо опре
деления результата столкновения двух частиц необходимо решение ypaBHe
ний движения (6.2) с учетом KOHKpeTHoro закона взаимодействия частиц.
Так как потенциал зависит лишь от расстояния частицы до центра поля, yr
ловой момент частицы является интеrpалом движения, а вся ее траектория
будет лежать в одной плоскости. Поэтому система уравнений движения в
данном случае будет состоять из двух уравнений BToporo порядка или четы
рех уравнений первоrо порядка (для двух координат и двух скоростей).
6.1. Введение
Как известно, на электрический заряд q, движущийся в скрещенных
электрическом Ё и маrнитном В полях со скоростью У, действует сила
Лоренца
(6.2)
rде т  масса заряда, при нерелятивистском движении равная массе покоя
то, и зависящая от скорости по закону при движении со скоростями, близ
ким и К скорости света.
т= =mor. (6.2а)
I 1;1!2
]
 с2
Следовательно, для полноrо описания движения заряженной частицы
необходимо при заданных напряженностях электрическоrо и маrнитноrо
полей решить задачу Коши системы, состоящей из трех дифференциальных
уравнений BToporo порядка:
dp d(nlV) ( [
dtx= dt ),=q EAx,y,z)+ vхЁ(х,у,z)]х)
dpy d(mvy) ( [ ] )
d; = dT=qE,.(x,y,z)+ vxB(x,y,z), ' (6.3)
dp. d(mv,) (Ё ( ) [ ( )] )
-d'=d.=q zx,y,z+vxBx,y,z.
t t '
[де индексы х, )', Z обозначают проекции векторов на соответствующую ось
выбранной системы координат.
,
,
\
\
,
\
,
\
\
\
\. А
Ш(::\ Ш"ТШШ
_  !_. :,k,
о Рис, 6,1
Проведем подробное исследование движения альфа-частицы
(та = 6.65.] 0.-27 Kr; qa = +2е , е = 1.60 ,1 019 Кл) в окрестности ядра атома
золота (т Аи = 3,27 .1 02S Kr, q Аи = + 79е ) (ядро атома мишени в первом экс-
147

l!..?:,,,!!,.!:!..O'!!!.P!?!!...:.c:.'!.E..l!..'!!..'!!!!..1!.'!.:.'!:!!!!!..!'.l!.c:.'!!.c ,в!!.,!'.<...е.'!!.: 4. ТLr}.I!..шш '"ш
перименте Резерфорда по рассеиванию). Так как та« тАи' будем прини
мать при численных расчетах, что т == тАи и рассматривать ядро атома зо
лота в акте рассеяния как неПОДВИЖное. Поскольку альфачастица не I1рОНИ
кает в ядро, то можно считать, что взаимодействие между частицей и ядром
описывается законом Кулона
F =Ш!. qQ Л, (6.4)
4л-с IRiЗ
о ,
[де CO диэлектрическая проницаемость вакуума (со ::::: 8.85.1012 ф/ М), q,
Q  заряды рассеиваемой частицы и кулоновскоrо центра соответственно,
R  радиус-вектор заряда q.
Следовательно, система уравнений движения альфа-частицы в прямо-
уroльной системе координат, центр которой совпадает с зарядом Q, будет
иметь следующий вид:
d2x 1 qQ
т=x
dt2 4л-со (х2 + i )/2
d2y 1 qQ
тшш = ш. .'Ш'ШШ-. у
dt2 4л-со (х2 + i )/2
Для дальнейшеrо численноrо решения удобно записать (6.5) в виде сис
темы 4x уравнений первоro порядка
(6.5)
dx
v =
х dt
dv х 1 qQ
т.ш х
dt  4л-со (х2 + i )/2
dy
V.' = dt
dv l' 1 qQ
т , = . .Ш.. у
dt 4л-со (х2 + i )/2
Для однозначноrо вычисления траектории движения рассеиваемой час-
тицы необходимо также задать следующие начальные условия: х(О), у(О),
vx(O) , vy(O).
Для численных расчетов оказывается удобным записать систему уравне-
ний (6,6) в безразмерных переменных Т, х, у, i\, V-" т, q, Q, связан-
(6.6)
ных С размерными следующим образом:
148
........
Ш А!.:Л..!!.l!.о.,!I!..'!:шi!.'!.!!.'!..':'..'!.":'l!екmр!,.'!!,.!",,!р!!,<?.О!.!,.?,:'.:к-!!!'Р'.,!Ч-::К-'!.!!.J'!!.,!!!,:ш'!!l
t х у \'
Т' Х =  ' у =  ' УХ = (а/Т) ,
 \1,  т q  Q
v-' = (а/Т) , т = М ' q = Qo ' Q = Qo '
f
(6.7)
здесь Т, а, М, Qo  единицы измерений времени, расстояния, массы и заряда,
соответственно.
Подставив (6.7) в (6.6), найдем
dX
v =
х dТ
tn а dvx   шдQ ш- '"
 '. ,  ш   х
М т2 dT  4л-соа2 (х2 + )12 )/2
dy
v1'=
'dТ
tn а dv1' Q5 qQ
= )1
М т2 df 4л-соа2 (х2 + у2 )/2
Оставляя в левых частях уравнения только безразмерные
преобразуем (6.8) к следующему виду
(6.8)
величины,
dX
v =
х dr
tn dvx = К qQ Х
dT (х2 + )12 )/2
dy
v =шш
-'dТ
 dv" qQ 
т dT = К (х2 + )12 )/2 У
( 6.9)
rде
Q2 мт2
К .9 'шш (6.1 О)
 4л-соа3 .
Анализ выражения (6,10) показывает, что численное значение коэффи
циента К зависит от величин Т, а, М, Qo, Выбор величин М, Qo достаточно
очевиден: в качестве единиц измерения массы выбираем массу протона
(М = ],67.10.27 Kr), а в качестве единиц измерения заряда  заряд электрона
(Qo == е), Для выбора числовых значений величин Т, а заметим, что отношсш
149

;,
'1
.lir:__:':.'!!!!!Р.!.':!!.l!.делuР"!!'!!''!!..'!:...Р''!..ЗUЧ:95.5!!!..цессо!!.!!!аке!!!!.!!А ТLAB ..__....
 . __А!...о..i?!!.'!!.?в-.I!.'1!.(!в-.'!..!.и-f!..?!:'!!Р.и-'!.::?Р.f!.__?в-..в-..?!:е.К--'!'!!!:.'!.'::__К-'!...::!'!.!..1!:..'!!..'IIш'!..?:f!.X..
ние а/Т имеет размерность скорости. Поэтому их значения выберем так,
чтобы обеспечить выполнение условия
а
==c, (6.11)
Т
[де с  скорость света в вакууме (с == 3.108 м/с).
Из сравнения (6.7) и (6.11) очевидно, что сделанный выбор единиц изме
рения длины и времени автоматически обеспечивает измерение скорости
частицы в долях скорости света. Подставляя (6.11) в (6.1 О), найдем
Q5M
К ==T . (6.12)
41l'coc а
Подставляя в (6.12) числовые значения М, Qo, t.O, с, найдем
К::С 1.53.1018 М
 (6.13)
а
Из (6.13) очевидно, что выбирая значение а == 1018 м, мы обеспечиваем
численное значение коэффициента К близким к единице, т. е. записываем
систему (6.9) в виде, наиболее удобном для численноrо решения. Отметим,
что в выбранных единицах измерения размер ядра атома золота (10.1015 м)
составляет 104. Следовательно, при моделировании рассеивания альфа
частицы на ядре атома золота значения начальных координат частицы по
оси оХ нужно выбирать из условия х(О) »104. Таким образом, в выбран--
ных единицах измерения заряд рассеивающеrо центра Q == 79, заряд рассеи
ваемой частицы q == 2, ее масса  т == 4, значения начальной скорости дви
жения частицы находятся в интервале [0,1].
Весьма важным является вопрос о выборе длительности BpeMeHHoro ин
тервала, на котором находится численное решение системы ОДУ (6.9), так
как только при ero правильном выборе можно точно определить yrол pac
сеивания Х. Совершенно очевидно, что длительность BpeMeHHoro интервала
зависит от начальноrо положения частицы и начальной скорости, а также
величин электрических зарядов взаимодействующих частиц и должна под
бираться для конкретных параметров моделируемой системы. Для выбора
оптимальной длительности BpeMeHHoro интервала можно использовать сле--
дующий алrоритм, основанный на постоянстве yrла между вектором CKOpO
сти и осью оХ, в областях невозмущенноrо движения частицы:
1. Проводится численное решение системы ОДУ (6.9) на временном ин
тервале длительностью;::: 2x(O)/vx(0) .
2. Строится зависимость уrла между вектором скорости и осью оХ от
времени: хИ == arccosx(t)/ x(t))2--(vy(t)i}
3. При отсутствии участков, на которых хИ;::: coпs/ , ищется численное
решение на временном интервале большей длительности и анализируется
зависимость хИ.
В связи с тем, что в ходе решения рассматриваемой задачи приходится
решать систему дифференциальных уравнений на первом шаrе решения
следует создать т--файл, содержащий описание функции, возвращающей
значения правой части системы ОДУ (6.9). Далее приводится листинr соот--
ветствующеrо файла CenterPole.m.
% листинr файла CenterPole.m
function dy=CenterPole(t,z)
% описание функции, возвращающей значения правой части
% системы (6.9)
global q Q м % задание rлобальных переменных для получения
% их значений из вызывающей проrpаммы
A=1.53*q*QIМ;
dy=zeros(4,1); % задание вектор--столбца размерности 4х1
% задание координат векторфункции, стоящей в правой части (6.9)
dy(1)=z(2);
dy(2)=A *z(1)/(z(1)Л2+z(3)Л2)Л(3/2);
dy(3)=z(4);
dy( 4)=А *z(3)/(z(1)Л2+z(3)Л2)Л(3/2);
Для нахождения численноrо решения системы ОДУ (6.9) необходимо
выполнить следующую систему команд:
» global q m Q % задание rлобальных переменных
» q=2; % заряд рассеиваемой частицы
» m=4; % масса рассеиваемой частицы
» Q=79; % заряд рассеивающеrо центра
»xO=-lОЛ6; % х--я координата начальной точки
» уО=4*lОЛ4; % значение прицельноrо параметра
» vxO=O.l; % х--я составляющая начальной скорости
»vyO=O; % у--я составляющая начальной скорости
»Тmах=2*lОЛ6 % длительность BpeMeHHoro интервала, на котором
% ищется численное рещение системы ОДУ (6,9)
»dt=Tmaxl2000; % шаr интеrpирования системы ОДУ (6,9)
150
151

!!..?п-.?'!!Т1I:!!!.?:.!!?=:E?I,!:..p',!::,!e:<.. ,!!!!!,,!!.!!в в !!,К-!!!!,!!A!,!:!!,.......
.:'!...!!!!.1!.l!.?'!.'!!i!..'!?':.:'"3.l!...:'!!l!.''!.:!5!!-:!!!!!!!.?"':!!!'чес':.....'!.!!!!3:'!.!!.'!'!!::п-о!!.
..........  ..... ................ ..  .... ., ,... . ". . .... ...... ...,.......... ....  .. ......... ........ .... ......
0.3
Задача 6.1
1. Проведите численные расчеты и постройте на одном чертеже ce.Meй
ство траекторий и услов рассеивания альфачастицы при различных
значениях прицелЬНО20 параметра. Объясните полученные результаты.
2. Постройте зависимость У2ла рассеивания Х от прицелЬНО20 параметра,
(для этО20 можно выбрать диапазон изменения прицелЬНО20 пapaмeт
ра, выбрав ша2, разбить е20 на конечное число точек и для каждО20 зна
чения прицеЛЬНО20 параметра, решив уравнения движения, определить
У20Л рассеивания.) Объясните, почему У20Л рассеивания является воз
растающей или убывающей функцией nрицелЬНО20 параметра.
Задача 6.2
Для упрощения процесса вычислений и построения 2рафиков зависuмо
стей, характеризующих процесс рассеивания заряженной частицы на
неподвuжном центре, разработайте проект 2рафичеСКО20 интерфейса
пользователя и создайте е20 практичеСkУЮ реализацию, используя cpeд
ства визуалЬНО20 проектирования пакета MATLAB.
В физических применениях обычно приходится иметь дело не с индиви
дуальным рассеиванием одной частицы, но с рассеиванием целоrо пучка
одинаковых частиц, падающих на центр с одинаковой начальной скоростью
и различными прицельными параметрами. Различие в прицельных парамет
рах р обуславливает рассеивание частиц пучка под различными уrлами Х.
для характеристики исследуемоrо процесса принято вводить число частиц
dN, рассеиваемых в единицу времени на yrлы, лежащие в интервале X+dx.
Однако для характеристики процесса рассеивания более удобной оказыва
ется величина dст(называемая (<эффективным сечением рассеивания»)
dN
dcт = , (6.14)
п
% решение системы ОДУ
»[Т Y]=ode45('CenterPole',[O:dt:Tmax],[xO vxO уО vyO])j
» figure(l)j рlоt(У(:,l),У(:,З»j % построение траектории движения
»хi=асоs(У(:,2)J(У(:,2).Л2+У(:,4).Л2).ЛО.5)j % вычисление уrла наклона
% вектора скорости к оси оХ
»figure(2)j plot(t,xi) % построение зависимости yrла рассеивания
% от времени
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 6.2 и 6.3.
х ,о'
3.5 --
1.5
'1
1
, I
/
// j
/
/
/
/
/
/
,--/
2.5
.l--
-,
..::е .. ';;2' о
.. ..........L. .....--L.......
0.2 0.4 06
I
1
.J....____J
0.8 ,
"о'
Рис. 6.2. Траектория
движения частицы,
рассеиваемой
Itа Itеподвижltом ядре
0.5
0.35

i
02
(
(
I
I
I
I
,
I
I
I
!
i
/
rде п  число частиц, про ходящих в единицу времени через единицу площа
ди поперечноrо сечения пучка. Эта величина определяется видом рассеи
вающеrо поля.
Связь между Х и Р взаимно однозначна, в чем вы моrли убедиться, pe
шив задачу 6.1. Поэтому в заданный интервал yrлов между Х и X+dx pac
сеиваются лишь те частицы, прицельный параметр у которых лежит в ин
тервале между rXX) и Ax)+dp,x). Число рассеянных частиц равно произве
дению п на площадь кольца между окружностями с радиусами АХ) и
AX)+dAX), т. е. dN = 27rp dp' п. Подставив это выражение в (6.14), найдем
o;z,;
0'5
0.1
Рис. 6.3. Зависимость
Уела рассеивания
от времени
o05l
I
01
о
, , , ...... .......L....._..............._..............._...L.........
02 ::14 06 08 1 12 14 Н 18 2
х 10.
152
153

:;
 й-.мп IO /11 ер"'..й-.е А' од=l1Р.й-.I!.:Iе..Р..'!.з..'.IЧ-=К-l,!:If'й-.':!.=й-._. :11!.k-еl11!..,,!А.!.1/!.щ_ ..
А!..!?,,!!!!:!щ,!':!..е!.':!...!!.'.:.и-1!.!.l!..'!!.I!.'!.ч-=к-'!!.....з-.аРЯ?"'.!!.!.JI!.!:.I11J!!!.К--'!!..!!,!,!,'!.!!'!.'!!.:'.,!щО
d  ( Idp(x)1
СУ  2тrp dp = 2тrp Х )1-dхЩldх ' (6.15)
Разделив обе части выражения (6.15) на dx, получаем формулу для
дифференциа.пьноrо сечения рассеивания:
dCJ  2 ( )ldp(X)!'
dX  тrp Х 141' (6.16)
Анализ выражения (6.16) показывает, что для нахождения дифференци
альноrо сечения рассеивания необходимо знать зависимость р = р(х) ,
Выше мы научились, решая уравнения движения альфащчастицы в КУЛОНОВщ
ском поле ядра атома золота, вычислять зависимость Х = х(р) . В связи с
тем, что функция Х = х( р) является однозначной, нахождение функции
р = р( х) , обратной к данной, не вызывает затруднений. Однако в выражещ
ние (6.16) помимо функции Р = р(х) входит и ее производная, которая не
может быть вычислена без дополнительных действий, так как функция
р = р(х) определена на неравномерной по переменной Х сетке. Выход из
создавшейся ситуации состоит в решении классической интерполяционной
задачи: нахождении значений функции в промежуточных точках по извест
ным в конечном числе точек значениям функции (узловым точкам). Одним
из наиболее популярных в настоящее время подходов к решению данной
задачи является подход, основанный на использовании сплайнов (полином
третьей степени) [2]. В связи с тем, что подробное рассмотрение теории
сплайнщинтерполяции выходит за рамки нашей книrи, мы оrpаничиваемся
только описанием примера, демонстрирующеrо использование функции ОДщ
номерной сплайнинтерполяции,
Для вычисления дифференциальноrо сечения рассеивания нами исполь
зуется следующий алrоритм:
1. Задать интервал изменения прицельноrо параметра р.
2, Задать шаr изменения дискретноrо параметра I1p.
З. Вычислить для каждоrо значения прицельноrо параметра р; численщ
ные решения системы ОДУ (6.9) и определить соответствующие yrлы pac
сеивания Xi'
4, Решить задачи сплайнщинтерполяции для функции р; = P(Xi) на paB
номерной сетке по переменной Х,
5. Вычислить на равномерной сетке по переменной Х численным диффещ
ренцированием ПрОИзводную функции р = р(х) ,
6, Вычислить в соответствии с (6,16) дифференциальное сечение рассеи
вания.
Для реализации описанноrо алrоритма необходимо выполнить следую
щую последовательность команд:
» clear all % очистка рабочеro пространства
» global Q q м % задание rлобальных переменных
» Q=79j % заряд рассеивающеro центра
» q=2; % заряд рассеиваемой частицы
» М=4; % масса частицы
» Тmах=2*10Л7j % длительность BpeMeHHoro интервала, на котором
% ищется численное решение системы ОДУ (6.9)
» dt=Tmaxl2000; % шar интеrpирования
»xO=-10Л6; % хя координата начальной точки
» пО=О.1; % хщя составляющая начальной скорости
» vyO=O; % уя составляющая начальной скорости
» Ушiп=О; % минимальное значение прицельноrо параметра
» Уmах=10Л5j % максимальное значение прицельноro параметра
»N=100j % число интервалов разбиения отрезка [Ymin,Ymax]
» dy=(Ymax- Ymin)/N; % шar разбиения
% вычисление значений yrла рассеивания дЛЯ N+ 1 значения
% прицельноro параметра
»for i=1:N+1
y(i)=(i-1)*dyj
[Т Y]=ode45('CenterPole' ,[O:dt:Tmax],[xO пО y(i) vyO])j
M1=length(T);
xi(i)=acos(Y (M1,2)J(Y (М1,2). Л2+ У (М1,4). л 2). ЛО.5)j
end;
» figure(1); plot(y,xi)j % визуализация зависимости уrла
% рассеивания от прицельноrо параметра
% задание параметров сетки для вычисления интерполированных
% значений зависимости р = р(х)
» x1=min(xi)j
» x2=max(xi)j
» Nxi=1000j
» dxi=(x2-x1)/Nxij
» i=1:Nxi+ 1;
»Xi(i)=x1+dxi*(i-1)j % вычисление координат узлов сетки
» Yi=interpl(xi,y,Xi,'splain')j % вычисление интерполированных
% значений зависимости р = р( х)
» dro=abs(diff(Yi)Jdxi)j % численное дифференцирование
% зависимости р = р( х)
» j=l:Nxi;
154
155

l!. й-..'!Ь!<!.'!!!!!.'.'.<!..:."'?l!.'!!!.I!!'.lJ.Р!!!:!.:l!!.l!.'!:с:().'!'!!.:!!...!!:-!.
...ш:.fl.:".:'!!..'fJ.!!.I!..I!.lJд!.1!...':!!...lJ!I.?Лш'!!.l!..'!.:':С:К.!'.!!!Р..Я-'!I!..!..Э!!..:'5'!!l!.!!ч-:.С:'.!.l!и-'!!.1!..ь:::.'!!!!!.f}!,
3.51--Т--------
i
няется тем, что решt:ние системы дифференциальных уравнений, возвра
щенное функцией ode45, оказывается недостаточно точным, и, как следст
вие, с поrpt:шностью вычисляются :шачения уша рассеивания. Далее зави
симость Х = х(р) подверrается процедуре сплайнинтерполяции, которая
не может устранить присутствующую в исходных данных поrpешность, Дa
лее интерполированная последовательность подверrается процедуре чис
ленноrо дифференцирования, которая, как известно, при водит к обязатель
ному увеличению поrpешности, содержащейся в исходных данных. Следст
вием зтоrо и являются результаты, представленные на рис. 6.5. При
использовании решений системы ОДУ (6.9), полученных более точным
численным методом, реализуемым функцией odel13, отмеченной особенно
сти не возникает (рис. 6.6). Естественной платой за более точное решение
является примерно двукратное увеличение времени счета.
» dsigma(j)=2*pi*Yi(j). *dro(j); % вычисление дифференциальноrо
% сечения рассеивания
» xi1(j)=Xi(j);
» plot(xil,dsigma) % визуализация зависимости дифференциальноrо
% сечения рассеивания от уrла
Результаты выполнения описанной выше последовательности команд
представлены на рис, 6.4 и 6.5.
31;,
!\
2 5  1
;\
" ,
i \
i '
........
Рис. б.4. Зависимость
У2ла рассеивания
от nрицелЬНО20
параметра
х 1n"
6Ш,
1
I
5 I
i !
.1 \
I i
. I
3r \
J \
r \
,1 \
1 \
1 \
01 \..
о 0.5
,
1.5
1.5t
i
i
1f
i
1
o.5
I
I
oL 
о
\,
\
'-
  2 ш__._ ..- -k'.10
110'
т;'
8f i
7 I
I
6 I
2.5
3.5
5 I
I
Рис, 6. б, Зависимость дифференциалЬНО20 сечения рассеивания от У2Ла рассеивания,
вычисленная по числеН1IОМУ решению уравненuя фу/t/щией odel13
Анализ зависимостей дифференциальноrо сечения рассеивания от yrла,
представленных на рис. 6.5 и 6.6, показывает, что данная зависимость меня
ется в широком динамическом диапазоне. Для их представления удобно исш
пользовать rpафики, при построении которых на оси о У откладываются
значения In(O") (полулоrарифмический масштаб). Для построения данноrо
rpафика в пакете МА ТLAВ используется команда semilogx:
» semilogy(xil,dsigma);
ре-зультат выполнения которой представлен на рис, 6.7,
Рис. б,5. Зависи.lfость
дuфференциаЛЬНО20
сеченuя рассеивания
от У2ла рассеuвания
:, I
11 
ои "'ш
О 05
1 5 2.5 3.5
Зависимость дифференциальноrо сечения рассеивания от yrла рассеива
ния выrлядит на первый взrляд несколько неожиданно, так как в выражение
для вычисления дифференциальноrо сечения (6.16) входят две монотонные
Ф . ( ) dp( х)
УНКЦIIИ. р х , Ш;Тх . Причина присутствия колебаний на рис. 6.5 объясш
156
157

,I!..ОМ!!!!7!еР!!!?"'!Р!!!!..аllи1!..'!.з-':!!.'!2!'.l!!!.,!!?'!!''!!''''''!!!.'5:!!'А!'LA 
......
.  ?: !'!...""_иЕ.'!..вl!.!'.1!.,,.!!.!'.,,IUJl..J.,l!..,,'!.fJ.'-!.че:к:!Х?{l'рJ!й--?l!.'5.I!!fJ.1!.'!.."с:...К-:!l.....А!'!.':!.I!!.'!:.II!..!!.'!..
10"
1
I1X =Х '!]ОХ  !ТIiп
Nint
4. Вычислить количество частиц l1N i ' попавших в интервал [xi' Xi + I1X] .
5. Вычислить «экспериментальные» значения дифференциаЛЬНО20 сечения
рассеивания для кажд020 интервала У2лов
l1a-i 1 l1Ni
. .
I1X п I1X
6. Создайте в пакете Mathcad документ, реализующий описанный выше ал
2Оритм,
7. Постройте на одном чертеже «теоретическую» и «эксперuменталь
ную» зависимости дифференциаЛЬН020 сечения рассеивания от уела,
Сравните полученные результаты,
8. Исследуйте, как зависит величина отклонения между «теоретической»
и «экспериментальной» зависимостями от плотности потока частиц и
величины элементарною уела I1x.
9. Пересчитайте созданный ваАШ документ не менее 10 раз, сохраняя при
этом результаты вычислений в отдельных файлах. Проведите cpaвHи
тельный анализ полученных результатов. Проведите усреднение полу
ченных зависимостей и сравните отклонение между теоретической
и усредненной «экспери.«ентальной» зависимостями дифференциально
20 сечения рассеивания от уела рассеивания.
10'\
10:(
"о
10'
10'
-.........
10' (
1rfL
10'
о 0.5
.-.......................
'
,
1.5
"-
\
\
i
I
1
! 1
,
2.5 3 3 5
Рис. 6.7. Зависимость дифференциалыlOZО сечения рассеивания
от У2Ла рассеивания в nолулоzариф:мичеС1<ОМ масштабе
Задача 6.3. Численное моделирование опыта Резерфорда
В опытах Резерфорда происходило рассеивание потока альфачастиц
на ядре атома золота, значения прицельных параметров у которых Ha
ходились в некотором интервале значений [О;РтюJ, и затем проводился
подсчет числа частиц, попавших в интервал уелов [Х,Х+ДХ]. Если счи
тать, что распределение альфачастиц в потоке по llрицельно.«у пapa
.«етру было равномерным (т. е. любое значение llрицельнош параметра
из интервала [о; Ртах] является равновероятным), то можно построить
.математическую модель опыта Резерфорда, спедуя OJ/20ритму:
1. Задать Np чисел, имеющих значения прицельных пap(l};/empoe, равномерно
распределенных на интервале [О;Ртах] (плотность потока частиц
Np .
п =2')
"Ртах
2. Для каждой imou частицы вычислить У20Л рассеивания Х; .
З. 3адать число интервалов Nin на которые будет разбиваться отрезок
[Xmin' Хтах]
........-
Задача 6.4
Задача о рассеивании заряженной частицы в поле кулоновСКО20 центра
имеет аналитическое решение
da- (а )2 cos1 (6.17)
dX =" mv sin3 Х '
2
2де v",  скорость частицы на бесконечно БОЛЬШОАt удалении от pacceи
вающе20 центра; а = fJ.Q .
4"&0
1. Запишите формулу (6,17), используя введенные выше безразмерные пepe
менные,
2. Вычислите значения дифференциаЛЬН020 сечения рассеивания для различ
ных У2лов рассеивания Х, Постройте 2рафик зависимости дифференци
аЛЬН020 сечения рассеивания от У2ла Х.
.
Для 2e1lepatfllII .чатриl{Ы, содержащей случаЙ1lые числа. в пш:ете МАТ1АВ IIС11О.1ьзvется
ФУ1lКЦllЯ raпd(II,III), "де 11  чис.о строк матрицы. m . ЧllО1О столбцов матрzщы. HaпjJUMep,
д.7Я 2e1lepatfllll Сl11jlOЮi С(lСlll0ящеll из 5 :JЛе,'-1С1l11юв, 1Iеобходюю выпО-"lшm& KOMa1lJy» raпd(I,5)
Д,7Я ?C1lCpatfllll ве'I1,f)Р-СI1l0лбца K"Ha1lCY» raпd(5,1)
158
159

!5.l!п::.'!!"!!'.l!.!..?.l!Р...l!'!'!.=--1!.1!..:.и.:::к'!!.I1J!.?..1f.О!!.!.!!I!.!!!!!.. M1.!J!........... .....
З. Сравните результаты численных расчетов дифференциальною сечения
рассеивания и расчетов по формуле (6,17). Чем можно объяснить обна
руженные оmичия? (Указание, В связи с большu.;w динамическим диaпa
da-
зоно.« изменения функции  при сравнении результатов, полученных
dx
численным и аналитическим методами, испОЛЬ'3yUте пОЛУЛ02арифмиче
cкuй 2рафик, при построении котОР020 по оси ординат откладываются
значения loi da-).)
,dX
ДРУ20Й подход к решению рассматриваемой задачи основан на использо
вании закона сохранения У211ов020 ,момента
2 drp
L=mv P=mr  (6.18)
'" dt '
2де dX  У211овая скорость частицы, r  расстояние между частицей и
dt
рассеивающим центро.«, и закона сохранения энеР2ии:
mv2
2+U(r)=E ,
(6.19)
2
mv
2де Е = .... .
2
В цилиндрической системе координат выражение (6.19) принимает вид
 2 + r2ф2)+ U(r) = Е . (6.20)
2
Выразив drp из (6.18) и подставив в (6.20), получаем
dt
mt2 L2
..... +...... +U(r)= Е.
2 2mr2
Отсюда
r"""" ......... .... '....
/2 L2
t=  [Е U(r)]", m2;Z
или, разделяя в (6.22) переменные и инте?рируя:
t = f .... ,__.cir --.. .--.... +coпst.
.12: [Е ....щТ')] J:}.
 т т2r2
160
(6.21)
(6.22)
(6.23)
.............?:..!:!одел.'!Рl!fJ..с:.'!.z.!!!.. ..:'..!.l!е...'!!Р.!:..z.!::.:3.!?J!д....й-..в.!!..::.l!(!.!!!!!!..и.че'!.I}!'!!!!..x. п-l!l!'!!
Если в (6, J 8) в качестве независимой переменной использовать расстоя-
ние r, то можно записать
drp drp [dr]"'! L [dr]"'!
dr = dt dt = r2 dt (6.24)
Подставляя (6,22) в (6,24), разделяя переменные и инте2рируя, находим:
L
dr
rp = f I r2 L2 + coпst . (6.25)
,12m[E  U(r )]......
 r2
Формулы (6.23) и (6,25) решают поставленную задачу в общем виде.
Фор.«ула (6,25) определяет связь между У211ОМ поворота и радиус-
вектором, т. е, уравнение траектории, Формула (6.23) определяет
в неявном виде зависимость расстояния от времени,
В точке поворота, 2де t == О квадратный корень в (6.22), а вместе с ним
и подынте2ральные выражения в (6.23), (6.25) меняют знак, Если oт
считывать У20Л <р от направления paдиycaвeKтopa, проведеННО20
в точку поворота, то примыкающие с двух сторон к этой точке отрез
ки траектории будут отличаться только знаком У211а <р при одинаковых
значениях r, Это означает, что траектория движения рассеиваемой
частицы будет симметрична относительно выбраНН020 направления,
поэтому обе асимптоты орбиты пересекают указанную прямую под
одинаковыми У211ами (рис, 6.1). Обозначим У20Л между асимптотой и
указанной прямой rpo. Т02да, как видно из рисунка, У20Л отклонения час
тицы Х при ее пролете мимо центра есть
Х = Iл-  2rpol. (6.26)
У20Л rpo определяется С0211асно (6.25) инте2ралом
L
ос  dr
rpo = f .... r2 2 ' (6.27)
/;' J[E U(r)]!:-....
v r2
2де rmin  корень уравнения
. f ......--....--....
2 L2
...[EU(r)] =0.
т m2r2
(6.28)
б--------1576
161
..........

1"
11
1!.Й-:"fI./Й-'!1е.Р.й-е.:",й-.еl!.l}fJ.оа./е..Р.з..t.j ех..п.Ей-ц-ес:()в..в. п.е.'!1.:..Jv!1.l!
11
li
111
1;
111
1,1
11
Задача 6.5
]. 'Запишите уравнения (6.22), (6.23), (6.25), (6.27) в безразАtерном виде.
2. Используя обезразмеренные уравнения (6.23), (6,25), проведите вычисле
ния и постройте траекторию движения альфачастицы в электро
статическом поле ядра атома золота, Сравните траекторию движе
ния с аналО2ичной зависимостью, полученной выше решение;.! уравнении
движения. Объясните полученные результаты,
3. Используя уравнение (6,26) и обезразмеренное уравнение (6,27), вычисли
те зависимость р = р(х) и изобразите ее 2рафически, Сравните дaH
ную зависи.мость с анаЛО2ичной зависимостью, полученной выше реше
нием уравнений движения, Объясните полученные результаты.
4. Вычислите значения дифференциаЛЬНО20 сечения рассеивания для различ
ных У2Лов рассеивания Х, Постройте 2рафик зависимости дифферен
циаЛЬНО20 сечения рассеивания от У2ЛG Х.
5. Сравните результаты численных расчетов дифференциалЬНО20 сечения
рассеивания, полученных решение.м уравнений движения и пРЯМЫАl вы
числением У2ла рассеивания, с результатами, получаемыми по формуле
(6,17), Чем можно объяснить обнаруженные отличия? Какой метод
расчета оказывается более точным?
6.3. Моделирование движения электрических
зарядов в постоянном маrнитном поле
Для описания движения заряда в постоянном маrнитном поле при задан
ной зависимости напряженности мarнитноrо поля от координат необходимо
решить следующую систему ОДУ
d;: о d; х) о q[V х В(х, у, <)1
dPY = d mdV'.):;: q[v х В(х, у, z)], (6.29)
t t .
dl!:;: t!.Vz) :;: q[v х В(х, у, z)]
dt dt 
Далее в данном разделе рассмотрим моделирование движения электри
ческих зарядов в постоянном однородном маrнитном поле В при релятиви
стских и нерелятивистских скоростях,
При движении со скоростями мно,о меньшими скорости света система
ОДУ принимает вид
162

:Й-:l!.!!.Р.()в--а.'.!..!в.!!.':/и-!!.:!,е'5.'!1Р..'!....ч-:.з-..ар1!д.....в!,е.'!!Р..'!....ч-!!.':..к-'!!..'!..:"''!.'!!!!..Ь!..::..tl!!!!:'!!..
dx. :;:f{ [v х В]
dt mo Х
d\'y :;: [v Х В], ' (6.30)
dt mo .
t!. =f{ [vxB]
dt mo z
Предваряя численное решение системы ОДУ (6.30), введем безразмер
ные переменные (:;: t/T, В:;: BIIBI, 1f:;: v/c (с  скорость света), Я:;: R / сТ ,
в которых система ОДУ принимает следующий вид:
d,,: :;: qTIBI  х вl
dt mo
dv. :;: qT[B\ [1f х 111- ' (6.3])
dt mo .
t!Y :;: qTl [\1 х вl
dt mo
Для выбора единиц измерения времени заметим, что на электрический
заряд, движущийся в плоскости, перпендикулярной напряженности маrнит
Horo поля, действует сила, перпендикулярная ero скорости. Следовательно,
в данном случае заряд будет двиrаться по окружности (ларморовской OK
ружности) радиуса R, который можно найти из условия равенства цeHтpO
бежной силы и силы Лоренца
2
 :;: qv\Bi .
R
(6.32)
Откуда
mov
R= q!BI'
Вспоминая, что период обращения материальной точки, двиrающейся по
окружности с равномерной скоростью, равен длине окружности, деленной
на модуль линейной скорости, и используя (6.33), найдем
27rR 21l111o
Т :;:   :;: , .
v qBI
Из (6.34) видно, что выбор в качестве единицы измерения времени пе
риода обращения заряда по ларморовской окружности позволяет записать
систему ОДУ (6,3) в следующем виде
(6.33)
(6.34)
163

.l5.?..п-ЬЮ"!:"l!...!..<!.елUРОl!.аllu!!...1!."!..'!.:::,!!:'Р.!!..Ii=-t:!.!!.!!!!..'5.!!I!!.!:1A T!:..1.!!........
d: = 2л-[v х BL = 2л-(vуВz  VzBv)
dt .
d,,! = 2л-[v х В]у = 2л-(vzВх  "хВу).
dt . .
 = 2л-[v х Bl = 2л-(vхВу  t1yBJ
dt . .
Orметим, универсальность системы ОДУ (6.35), заключающуюся в том,
что в выбранной системе единиц коэффициенты системы не зависят от па
раметров заряда и напряженности мarнитноrо поля, которые входят в без
размерные начальные условия: радиусвектор начальноrо положения заряда
 = R/cT и вектор начальной скорости o = vo/c. Леrко видеть в OДHOpOД
ном поле система уравнений (6.35) является замкнутой, так как уравнения
зависят только от трех неизвестных функций Vx (t), Vy (t), Vz (t). Найдя чис
ленное решение (6.35), далее интеrpированием зависимостей Vx (t), Vy (t), Vz (t)
можно определить зависимости i(t),y(t),z(t). Однако оказывается более
удобным дополнить (6.35), тремя уравнениями для координат:
di  dy  dz  (6 36 )
=v =v =v . а
dt х' dt .у' dt z '
(6.35)
так как, решив более общую систему ОДУ, состоящую из 6 дифференци
альных уравнений одновременно, можно найти зависимости i(t),y(t),z(t)
и Vx (t), vy (t), Vz (t). Дополнительный apryмeHT в пользу данноrо подхода
состоит в том, что общая система уравнений распадается на две независи
мые системы только для однородноrо мarнитноrо поля, для неоднородноrо
поля следует решать систему ОДУ, состоящую из 6 дифференциальных
уравнений первоrо порядка.
для нахождения решения общей системы уравнений движения следует
создать mфайл, содержащий описание векторфункции, стоящей в правой
части системы ОДУ. Ниже приводится листинr соответствующеrо файла
LorenzForce.m
% листинr файла LorenzForce.m
function f=LorenzForce( t,z)
% задание функции, возвращающей значения первых производных
global Н
f=zeros(6,1); % задание векторстолбца размерности 6хl
164
11
l

il:.,,!оделUРО6!!.lIuе д-!!uже'!..uя ЭЛе:5.трuче.!!!l.дов !!..!!'...е!5!!!!!..."!....ческ-....'!..!!.uт'!..'!...о
% задание координат векторфункции, стоящей в правой части
% общей системы ОДУ
f(I)=z(2);
(2)=2 *рi*(Н(3)*z( 4)- Н(2 )*z( 6»;
f(3)=z(4);
С( 4)=- 2 *pi *(H(3)*z(2)- Н(1 )*z( 6»;
f(5)=z(6);
С( 6)=2*pi*(z(2)*H(2)-z( 4)*Н(I»;
Далее необходимо выполнить следующую последовательность команд:
» global Н;
» Н=[О О 1]; % напряженность мarнитноrо поля
% начальные условия
» хО=О;
» уО=О;
» zO::O;
» п=О.I;
» vy::O;
» vz::O.Ol;
% решение системы ОДУ
»[t R]=ode45('LorenzForce',[O:10/1024:10],[xO пО УО VYO zO vzO));
% построение траектории движения частицы
» plot3(R(:,I),R(:,3),R(:,5),xO,yO,zO, 'о' ,'MarkerSize' ,6);
» axis square; grid оп
Результат выполнения
приведенной последователь
ности команд представлен на
рис. 6.8.
/.../"----,
I ...... ______. . 
. ------:>....::,>}
V'>r--': 
R5 ::>-..'"""'''-::. ;.
' .' ,- >rv
х '--c-' 'x'1
)( >C . ::O< )(
&'':::XI
>< .,. ' 
 '>--". ..::Jxj
К:::';:.:::>1
Q<; "--... /'- . ,,:,!
\.х '::-><,
«'-'-.. . ..-;... ..Х J
о \"- --,...., /1
о " ,.,.........   .....:._...._/ _,/ .
..o.o '....."'.............-// ./O.02
-a.   0.01
_. -" / О
-аоз "x-/01
-а04 -а.02
0.1
0.08
0.06
004
0.02
Рис. 6.8
165

'1
! :
'i
.1!!!,:"!,fI!:!!!!!!!pIIOi!...e:!.,:!PO!!!.I!:!:"p.':!..!!!'!.!..,!!.!!!!'i:'I!..!!.'!.кет!.!1} Т!!.........ШШШ...ШШ..
... ...... ......... ... ................ ......_..... ..........................ш..
Задача 6.6
1. Постройте проекции траектории движения на соответствующие коорш
динатные плоскости,
2. Проекция траектории движения на плоскость, перпендикулярную вектош
ру напряженности ма2нитНО20 поля, является окружностью. Oпpeдe
лите ее радиус и период обращения по окружности. Объясните полу
ченные результаты,
3. Исследуйте зависимость величины ша2а спирали от скорости движения
заряда?
4. Постройте зависимости скорости и ее проекций на соответствующие
координатные плоскости от времени,
5. Исследуйте зависимость точности и устойчивости числеННО20 решения
системы ОДУ (6.36) от ша2а инте2рирования,
Обратимся к анализу особенностей движения заряда, дви2ающе20СЯ с
релятивистской скоростью, в постоянном электрома2нитном поле, Для
этО20 необходимо разрешить уравнение (6.2) с массой, зависящей от
скорости движения по закону (6.2а), относительно первой производной
скорости, Подставляя (6,2а) в (6,2) и выполняя дифференцирование пош
лучаем:
')!
11

("'oy v) ="'оу dv + тov dy = F ,
dt dt dt
2де сила F задается уравнением (6.1).
Так как
dy d ( 1 J 1 (vv) y3(vv)
dj= dt $=ivI2/c2 = lvI2/c2J/2 7=7'
то (6,37) принимает вид
. y3(vv)
тоу v + "'ov Ш-2 = F .
с
Умножая обе части выражения (6.38) скалярно на v, получаем
, 12
..... 1 Iv..... 3 .....
"'ОУ (vv)+ "'ОУ' z-ш(vv) ="'ОУ (vv) = (Fv).
с
Откуда
(6.37)
(6.38)
(vv) = (Fv .
тoy
Подставив (6,39) в (6.38), получае.М уравнение движения, разрешенное
относительно производноЙ
1
\1
1
11
ill
\\l
166
(6.39)
.-.........
ш-.:.А!..()'!Р()с:.!!и..д..tl.ЭI<:.IIи-:я:.f!.'5."!Р':'.".'5.tl.?с:.Ря..д..()в...в.f!.е'!.!!!Р....':'..".:"'5.и.:tl.::'i!!.!.':!'!'."!..()f!J/.:'
то dv = 1 (Р  v (Р V)), (6.40)
d/ У с с
Уравнение (6.40) описывает движение электрических зарядов в проuзш
вольном постоянном электрома2нитном поле, При движении в постош
янном ма2нитном поле сила Лоренца Р = q[vB] перпендикулярна скорош
сти, следовательно, все2да (Р v) = О, поэтому уравнение движения
принимает вид
"'o!. = .!.q[vB] = q[vB1  Ivl2 ,
dt у с2
или в координатной записи
dv,!, =[vxB]x1lvI2 /с2
dt то
ddVy =Д--Ш[vхВ1.iIVlilс2 (6.416)
t"'o .
dvz =Д--Ш[vхВ] 1lvI2/c2
dt"'o z
При выборе, как и ранее, в качестве единиц измерения времени периода
вращения заряда массой "'о по ларморовской окружности Т, СКОрОш
сти  скорость света с, расстояния  сТ, система ОДУ записывается
в виде:
(6.4Ia)
dv [ \ r:
d; = 2п: 17 х »1 = 2п:(v.Jlz Vzl1yN1lvI2
!. =2п:[vх»1. =2п:(vzl1хvхl1z)1:"'If.
 = 2п:[v х Bl = 2п:(vх11у  vyl1J1  11712
(6.42)
Задача 6. 7
1. Создайте тшфайл, содержащий описание функции, возвращающей значеш
ния правой части системы дифференциальных уравнений (6.42), и прош
моделируйте движение зарядов в постоянных однородных ма2нитных
полях с релятивистскими скоростями,
2, Постройте проекции траектории движения на соответствующие
координатные плоскости, Сравните траектории движения, полученные
при одинаковых начальных скоростях, решив нерелятивистские и
релятивистские уравнения движения.
167

.!!.?..А!...п-.!"!!..€!..:..!!.?'!.Е..I!!Iа:Р.'!.3!!J!!!",!!!3.!..!!.!!'!.теJ!}..!!:!!
3. Проекция траектории движения на плоскость, перпендикулярную вeKтo
ру напряженности MazнumHOZO поля, является окружностью. Oпpeдe
лите ее радиус и период обращения по окружности, Сравните получен
ные результаты с аналоzичными значениями, полученными для нереля
тивистскю: уравнений движения, Объясните полученные результаты.
4. Исследуйте зависимость величины шаzа спирали от скорости движения
заряда?
5. Постройте зависимости скорости и ее проекций на соответствующие
координатные плоскости от времени,
6. Исследуйте зависимость точности и устойчивости численноzо решения
системы ОДУ (6.42) от шаzа интеzрирования.
I,
I
I
6.4. Моделирование движения электрических
зарядов в постоянных электрических
и маrнитных полях
 i
I
В этом параrpафе мы рассмотрим особенности движения электрических
зарядов с нерелятивистскими и релятивистскими скоростями в скрещенных
постоянных однородных электрических и маrнитных полях. для описания
движения зарядов со скоростями MHoro меньшими скорости света необхо
димо найти решение систему ОДУ (6.3), считая, что масса заряда не зави
сит от ero скорости
то dvx =q(ЕхСх,у,z)+[vхЁ(х,у,z)]х)
dt
mo dvy = q(Ev(X.'y,z)+[vxВ(х,у, z)])'). (6.43)
dt '
mo dvz = q(Ez (х, у, z) + [v х В(х, у, z)]J
dt
Выбирая, как и ранее, в качестве единиц измерения времени период Bpa
щения заряда массой по ларморовской окружности Т, скорости
скорость света с, расстояния  сТзапишем систему ОДУ (6.43) в виде
d: = 2JZ'[ х »1 = 2JZ'Ex + 2JZ'(vxEz  VzE)')
dt .
. = 2JZ'[ Х »1. = 2JZ'Ey + 2JZ'( VzEx  VxEz), (6.44)
dv [ '" 1 ,р< (  р; )
 = 2JZ' V Х В 1: = 2JZ'Lz + 2JZ' vxB)'  t\Dx
dt . .
168
1,

:.?!!.1!...и-Е.о..в--.й-'!.и-'!..!!!..И!!..?J/...е'!!Р..II....ЧI!.!...аJ!?..О.!!ll..:z.'5.'!!Р..1I....:.с...к---"!'!.!!!!.l}!,'!!!!.ь!!'!I!.!!!!!.
rде Е; = E;/c:BI (i = х, у, Z ).
Для однозначноrо описания движения необходимо задать безразмерные
начальные условия: радиусвектор начальноrо положения заряда ЛО = Л/ сТ
и вектор начальной скорости Vo = vo/c.
Рассмотрим более подробно случай, допускающий аналитическое реше
ние: движение во взаимно перпендикулярных электрическом и маrнитном
полях. Направление вектора В выбираем за ось oZ, а плоскость, проходя
щую через векторы В и Е, за плоскость YoZ (рис. 6.2). Тоrда систему
уравнений движения (6.44) запишем в виде
{ :Х = 2JZ' jH z
у = 2JZ' хН z + 2JZ' Еу .
'f = 2JZ' Ez
Из тpeтbero уравнения видно, что вдоль оси oZ заряд двиrается paBHO
мерно ускоренно, т. е.
(6.45)
.J'!o 2
Z  JZ'Li + Voi . (6.46)
Умножая второе уравнение системы (6.45) и складывая с первым, Ha
ходим
d
(x +ij)+ 2JZ' i(.t +ij)= 2JZ' iEv, (6.47)
dt .
Анализ уравнения (6.47) показывает, что ero можно рассматривать как
уравнение относительно переменной .t + ij . Как известно, интеrpал этоrо
уравнения есть сумма частноro интеrpала уравнения (6.47) и частноrо инте
rpала однородноrо уравнения (уравнение (6.47) без правой части). Первый
из них есть
.t + ij = ae21f;t ,
второй равен Еу . Таким образом,
.t + ij = ае 21f (; + Е.у, . (6.48)
Постоянная а в (6.48) (в общем случае комплексная) находится из Ha
чальных условий. Рассмотрим далее случай, коrда в начальный момент
времени скорость заряда направлена вдоль оси оХ: Х(О) = VxO' j(O) = О,
В этом случае постоянная а оказывается вещественной:
а = Vxo  Еу . (6.49)
169

"
:1
!
',11
1
'1
'11
!
, '
1
. м..!!?"!Р.'.'.?!.м..!!.и-Р...?!!.Cl.!t':!!:.Р.':!.з-!'Ч-I!..'.<.'!.fJ!!..':!.:'?!..,Cl.к-.е"!1!..fl1.:!. !!:.1.!!. 
.... ....А!..?':!!!.6!!.!!.'!...е.....д---!!!!!!!.!/!:!."!!!..'!...'!!.9:!!!...з-!!.l!..JI?!!.I!.!.f!!.!!!!!!..'!...Ч!.:"к-'!!..'!..!!.'!.."!!!..'!?
Подставив (6.49) в (6.48) и отделив вещественную и мнимую часть,
найдем:
х =асоs(л:t)+Б\, у =аsiп(л:t). (6.50)
Из (6.50) видно, что компоненты скорости частицы в плоскости ХоУ яв
ляются периодическими функциями времени, средние значения которых
равны
2. Убедитесь в справедливости полученных выше аналитических результа
тов (формулы 6.49, 6,50  6.52, 6.54).
3. Постройте траекторию движения частицы в трехмерном пpocтpaHcт
ве и ее проекции на соответствующие координатные плоскости.
4. Проведите расчеты для значений начальной скорости, удовлетворяющих
условиям 1а! >IБуl,lаl =IБуl,lа( >IБу:, и сравните траектории движения и
их проекции на координатные плоскости,
5. Проведите расчеты для значений начальной скорости, удовлетворяющей
условию а = Бу' и проанализируйте вид траектории заряда, объясните
(х) = Бу, (у) = О,
(6.51)
т. е, частица в скрещенных электрическом и мarнитном полях движется со
средней скоростью в направлении, перпендикулярном плоскости YoZ. эту CKO
рость называют скоростью электрическоrо дрейфа. Вспоминая, что обезразме
ренный вектор напряженности мarнитноro поля есть единичнЫЙ вектор, можно
записать безразмерную скорость дрейфа в векторном виде как
Vd = [Ёil]. (6.52)
Все формулы данноrо параrpафа справедливы при условии малости CKO
рости заряда по сравнению со скоростью света, которое в безразмерном ви
де имеет вид 1vl« 1 . Аналоrичное требование справедливо и для скорости
дрейфа, которое выполняется при условии, что обезразмеренные напряжен
ности электрическоrо и маrнитноrо полей удовлетворяют условию
Бу « н z . (6.53)
Интеrpируя уравнения (6.50) еще раз и выбирая постоянные интеrpиро
вания так, чтобы при t = О х=у=о, получаем:
полученные результаты.
6. Проведите расчеты и проанализируйте особенности движения при yc
ловuи Vx:;:.O,Vy :;:.O,Vz :;:.0.
7. Исследуйте особенности движения заряда в параллельных однородных
постоянных электрическом и ма2нитном полях.
8. Запишите закон сохранения заряда для рассматриваеМО20 случая в без
размерном виде и оцените точность выполнения для полученных чис
ленных решений.
Для описания движения релятивистскою заряда в скрещенных электри
ческом и ма2нитном полях необходимо находить решение системы ОДУ
(6.40).
Выбрав, как и ранее, в качестве единиц измерения времени период вpa
щения заряда массой то по ларморовской окружности Т, скорости 
скорость света с, расстояния  сТ систему ОДУ запишем в виде:
РХ = 2тсБх + 2л:(v.Jlz  vJly)
Ру = 2тсБу + 2л:(vzl1х  Vxl1z)
РС = 2тсБz +2л:(vхl1у Vyl1J
Vx = [РХ  Vx (pxvx + PyVy + Р: vz)bl1  IV[2
\\ = [Ру  vy (Рх Vx + Ру vy + Pz Vz 1fl=.v12
r ,.. ,
Vz = [Рс  Vz (p,vx + pyv\' + Ре vJJ1 1jj'12
х = siп(2л: t)+ Е,'!
2л: .
а
у = (соs(л: t) 1)
2л:
Уравнения (6.54) задают в параметрическом виде кривую, называемую
трахоидой.
(6,54)
(6.55)
Задача 6.8
J. Запишите законы изменения координат заряда и выражения для CKOpO
сти дрейфа в размерных переменных,
2, Запишите условие (6,53) в размерных единицах.
Задача 6.9
Проведите моделирование в пакете МА TLAB движения нерелятивист
СКО20 заряда в скрещенных электрическом и ма2нитном полях:
J, ВЫl10лните численные расчеты при условии '\:;:' О, ''у = v z = О ,
Задача 6.10
ПРОАюделируйте движение релятивистСКО20 электрическою заряда,
описываемое системой ОДУ (6,55), в скрещенных электрических и АШ2.
нитных полях.
170
171

.l!::!!ь.!?"ft}z:..!'.?.:!?..?еlР..!l..с:.'."!!:.1!':!'!f!СК-,!!!'iСОвl!..К-'!!.=А:!-i:!:.f!...._..ш..
" !
r
I
J. IIроведите численные расчеты при условии v x;t О, v.1 = V z = О и сравните
с аналоzичными зависимостями, полученными при решении системы
ОДУ (6.45), С каких скоростей начинают проявляться отличия в зако
нах движения?
2. Опишите релятивистское движение заряда в параллельных однородных
электрическом и маснитном полях,
3. Опишите релятивистское движение заряда во взаимно перпендикуляр
ных однородных постоянных электрическом и MazнитHoM полях (pac
смотреть случаи 11.1' = Н z' 11.1' > Н z' 11.1' < Н z). в каком направлении пpo
исходит наиболее быстрое возрастание скорости движения заряда?
r лава 7
ФУРЬЕ-АНАЛИЗ НЕПРЕРЫВНЫХ
И ДИСКРЕТНЫХ ФУНКЦИЙ
7.1. Введение
ЛИТЕРАТУРА
1, Ландау Л, Д" Лифшиц Е, М, Механика, М,: Наука, 1958.
2. Носач В, В, Решение задач аппроксимации с помощью персональных компьютеров, М,:
МИКАП, 1994.
З. Ландау Л, Д" Лифшиц Е. М. Теория поля, М: Наука, 1988,
4, YrapoB В, А, Специальная теория относительности. М,: Наука, 1977,
5, Арцимович Л, А., Лукьянов С, Б, Движение заряженных частиц в электрических и маrнит
нъ1х полях, М,: Наука, 1978,
Одним из эффективных подходов решения задач из различных разделов
физики (в первую очередь теории колебаний и волновой оптики) является
подход, основанный на спектральном разложении функций, являющихся
решением тех или иных уравнений (метод Фурье). В то же время в традици
онных учебниках по физике использование данноrо метода оrpаничено дoc
таточно узким KpyrOM задач, имеющих аналитические решения. Выбранный
нами в данной книrе подход, основанный на нахождении численных реше
ний уравнений, описывающих поведение физических систем, и сущест
вующая возможность вычисления спектров таблично заданных функций
существенно расширяют ВОзможности данноrо метода и, как следствие, по
зволяют повысить наrлядность и физическую содержательность излarаемо
ro материала. Отметим, что в данном разделе мы не претендуем на абсо
лютную математическую cтporocTb изложения материала, которая, по MHe
нию Р. Хэмминrа, «скорее связана с внyrpенними потребностями MaTe
матики и эстетики, чем с нуждами физическоrо мирю> [1], но пытаемся,
в первую очередь показать полезность данных математических понятий для
решения реальных физических задач и научить применению их на практике.
I
7.2. Разложение периодических сиrналов
в ряды Фурье
По определению периодической функцией называют функцию, OTBe
чающую условию:
s(t) = s(t + пТ), 11 = 1,2,... ,
(7.] )
rде Т  период функции.
Для нахождения спектральноrо разложения функции s(t) введем в pac
смотрение следующие наборы функций:
1/ /т ,Ii/T siп(2л- (!Т), 2/T sin( 4л- (/Т),,, , .J2/T siп(2л- nt/n...
../57r соs(2л- t/n, .j2/T соs(2л-2t/Т),,,, fi7T соs(2л- nt/n",
(7,2)
172
, \

!<:.?.m-.'-'-'!!._".!Р...?.-=.:"!.I!..i!...':Р...и-: 1!.и--и-'!.!'..'-'-l!'.f:.:..'-'-.:!'.'.!-!..Т--'i!!._._..__...._..-.-... - .
!:cJ>.)lР...':..:f!If!:qи- J еl!.еРJI"!.Х.ши-!!:J(р".!ь!ш1!.)IIJ(ц-и-й
Любая функция из (7.2), которую для краткости обозначим um(t), YДOB
летворяет условию периодичности (7.1).
Рассмотрим три следующих интеrpала:
т {О, т :f; п
 J cos(2;r тt/T)cos(2;r nt/ndt = 1, т = п :f; О ;
О 2, т = п = О
т
 J cos(2;r тt/T)sin(2;r пt/T) = о; (7.3)
О
т {о, т :f; п
 J sin(2;r тt/T)sin(2;r nt/ndt = 1, т = п :f; О ,
О О, т = п = О
Функции, удовлетворяющие условию (7.3), называются ортоrональны
ми, а систему функций (7.2) называют ортонормированным базисом, обра
зованным rармоническими функциями с кратными частотами. У слови е op
тоrональности можно записать в компактной форме, используя символ
Кронекера:
т
Ck = J s(t )ukdt . (7.7)
О
Подставляя в (7,7) набор функций (7,2), найдем значения коэффициентов
ряда:
т
аО =  J s(t )dt ,
О
(7.8а)
т
а" = ffi J s(t )cos(2JZ" n/ndt , (7.8б)
О
т
Ь,! =  J s(t)sin(2;r n/T)dt . (7.8в)
О
Введя основную частоту йJ = 2;r/T последовательности, образующей пе
риодическую функцию s(t), запишем ряд Фурье для периодическоrо сиrнала
т
J и; (t)Uk (t)dt = <S;k ,
О
(7.4)

s(t) = а; + )a" cos(nйJt)+b" sin(пйJt)). (7.9)
,,=1
Анализ (7.9) показывает, что функция s(t) содержит независящую от
времени постоянную составляющую и бесконечный набор rармонических
колебаний, так называемых rармоник с частотами йJ" = пйJ (п = 1,2,... ),
кратными основной частоте последовательности. Можно показать, что
имеет место равенство
rде
{O,i :f;k
<S'k =
I 1,i = k .
Разложим произiюльную периодическую функцию s(t) в ряд:
, ,
i I
ос)
s(t) = Lc;u;(t).
;=0
Представление (7.5) называется обобщенным рядом Фурье функции s(t)
в выбранном базисе.
Коэффициенты данноrо ряда находятся умножением (7.5) на базисную
функцию uk(t) и интеrpированием по периоду функции s(t):
т о'; т
f S(t)Uk(t}:it = LC; f U'Ukdt , (7,6)
О ;=0 О
Откуда, используя свойство ортонормированности (7.4), найдем
(7.5)
т 2 ос)
 f s(t)2dt = + L[af +Ьп
т О 2 k=1
Если записать коэффициенты ряда Фурье в ВИДе
а" = А" cos ер", Ь" = А" sin ер",
(7.10)
rде
А" =  ;, +b, tg ер" = ь" / а" '
то получим эквиваJlентную форму ряда Фурье:
о';
s(t)= а; + LA" cos(nйJt epll)'
,,=1
(7,11 )
174
175

1!0!'1! Ь'!!'!!.:.р'Ir:!!r:..!!.'-!Е!!.'!.!.'!е...Р''!'!:..'!;(.,!'Р..l!..':!I!.п-.r::.'!!.! Y3..!!:.f!...
шшшШш Ш ....ш!.:.5!У.!!.ь-:.=--r:!'c:J/ши-:ш.'!:''!.l!..:'р'Ь.l.!..I.ь-!х.. '!....':!'5P.!"!'.!.."!':: ш1!.1!.'5'i':!..ш
I
1
Спектральное разложение периодической функции можно выполнить,
используя систему базисных функций в виде экспонент с мнимыми показа-
телями:
{ }  {XP(ik}  +
Иk  T ,k O,H,2,...,
которые, как леrко убедиться, вычислив интеrpал
т т
J .d 1 J imt шiktd s:
ИmИk t = Т е е t = Umk '
О О
являются ортоrональными.
Ряд Фурье в данном случае принимает вид
ос
(t)  1 '" il!юt
S .  JТ L.Jcl!e
tI:::::OO
(7.12)
Задача 7.1
J. Найдите аналитически коэффициенты ряда Фурье периодцческой послеш
довательности прямоу?Ольных видеои,tnульсов (рИС, 7, J) с известными
параметрами Т, Т, А .
U(t)
т
т
(7.13)
'1;
Рис. 7, J
2. В радиотехнике отношение q =Т/Т называют скваженностью последо-
вательности. Построите и сравните зависимости амплитуды cпeK
тральных zapMOHUK от частоты пйJ при различной скваженности пош
следовательности.
'1;
'1;
t
с коэффициентами
т
1 J () шil!юtd
СI! = Ji s t е t .
о
На практике принято использовать и друryю форму записи ряда Фурье:
(7.14 )
7.3. Эффект rиббса
ос
s(t) = L с,/I!юt ,
,,=OC;
т
С = J (') ш.il!юtd
I! s t е t.
Т
о
Выражения (7.13)  (7.16) представляют собой ряд Фурье в комплексной
форме.
Спектр функции s(t) в соответствии с формулами (7.15), (7.16) coдep
(7.1 б)
Эффект rиббса возникает при разложении в ряд Фурье разрывных
функций. Изучим основные ero проявления на примере разложения прямо
yrольной импульсной функции
( ) {1/2,0t T/2
s t  ,
1/2,Т/2 < t T
которая имеет скачок, равный 1 в точке разрыва Т /2 . Формальное разложе
ние в ряд Фурье находится подстановкой функции s(t) в формулы (7.8),
вычислением ИНТеrpалов, оказывающихся равными
ak =0,
bk = J. hш (1)] = f rc2'k ,k  четное,
rc k 1 о, k  нечетное
и подстановкой выражений для коэффициентов в (7.9):
(7.15)
rде
, I
жит компоненты на отрицательной полуоси частот, причем C11 = C, пош
этому слаrаемые с положительными и отрицательными частотами объеди
няются в пары, например:
С еil1юt + С е шillюt = IC I i(l1юt+.-р.) IC I шi(l1юt+.-р,) = 21С I ( t  )
11 шl! 11 е + I! е I! cos пйJ ерl1'
Таким образом, отрицательная частота является не физичеСЮfМ, а MaTe
матическим понятием, вытекающим из способа представления комплексных
чисел,
176
177

I
, :
i
:!
I
I
11
'1
' '
1:
()..:".!___п-,::к:.'!!.P!.o..e. ?дел.tp.().f!.'.I.'!.:Р.'!з---и-___ч.:к'!.х.п-роц-е.::()!!______п-:zе.'!!..е.!!..Т [А В
.ш.___!:.'!!!.Еь.:::'!!'!!l!!!..I!е.п-Р..=Р..'!-..f!!Ь!!и-___i!!!:'5.l!.I!.".!!х.Р./к-'!..'!.
2 [ , (21r) 1 ,(2те ) 1 ( 2те) J
s(t) = ---;; sш\ т t +- '3 sшт--- 31 +- 5 sin .T 51. +-.., =
2  1 ,( 2те )
=  L.J sш (2} +- 1)1
те k=O 2k +- 1 Т'
Несмотря на то, что полученное разложение позволяет познакомиться с
Основными особенностями эффекта rиббса, мы предварим дальнейшее pac
смотрение этоrо вопроса описанием последовательности команд, позво---
ляющей получить в пакете МА TLAB, разложение в ряд Фурье произволь
ных функций,
Для решения поставленной задачи необходимо создать следующие т
файлы: FF.m (содержит описание функции, разлаrаемой в ряд Фурье),
AF.m (описание функции, возвращающей значение заданноrо коэффициен---
та разложения в ряд Фурье по косинусам в соответствии с (7.8а), (7.8б),
BF.m (описание функции, возвращающей значение заданноrо коэффициен
та разложения в ряд Фурье по синусам в соответствии с (7.8в)). Далее при
водятся листинrи данных файлов.
% листинr файла FF.m
function z=FF(t,T)
% описание функции, раскладываемой в ряд Фурье
N=length(t);
for i=l:N
if t(i)<O
z(i)=O;
end;
if (t(i»=O)&(t(i)<=T/2)
z(i)=1/2;
end;
if (t(i»T/2)&(t(i)<=T)
z(i)=-1I2;
end;
if t(i» Т
z(i)=O;
end;
ещ\;
% листинr файла AF.m
function z=AF(k,T)
% описание функции, возвращающей значение k---ro коэффициента
dt=T/IOOO;
t=O:dt:T;
% вычисление значения подынтеrpальной функции
F=FF( t, Т). *cos(2*pi*kIТ*t);
z=2rr*trapz(t,F); % вычисление интеrpала
% листинr файла BF.m
function z=BF(k,T)
% описание функции, возвращающей значение k---ro коэффициента
dt=TI1000;
t=O:dt:T;
% вычисление значения подынтеrpальной функции
F=FF( t, Т). *sin(2*pi*kIТ*t);
z=2rr*trapz(t,F); % вычисление интеrpала
Далее необходимо выполнить следующую последовательность команд:
clear аН % очистка рабочей области
Nf=9; % число rармоник
k=l:Nf;
T=l; % длительность импульса
AO=AF(O,l); % вычисление А(О) в соответствии с (7.8в)
for k=l:Nf % вычисление коэффициентов A(k), B(k)
A(k)=AF(k,T);
B(k)=BF(k, Т);
end;
% вычисление значений усеченноrо ряда Фурье на временном
% интервале [0,1]
Np=lOOO;
t=O:TlNp:l;
for i=l:Np+-l
S=AO/2;
for k=l:Nf
S=S+-A(k)*cos(2 *pi *kIТ*t(i) )+-B(k)*sin(2*pi* k1Т*t(i));
end;
s(i)=S;
end;
% визуализация усеченноrо ряда Фурье и исходной функции
plot(t,s,t,FF(t,T),' -- ')
Результаты выполнения описанной выше последовательности команд
представлены на рис, 7.2,
Сравнение rpафиков исходной функции и функции, являющейся резуль
татом разложения в ряд Фурье, представленных на рис, 7.2, обнаруживает
их отличие. Обнаруженное отличие между исходной функцией и усеченным
рядом Фурье носит название эффекта rиббса,
178
179

f!.-Л-l'.!Ь?"!.l!.'..?:_.?е!!.IР..r:.в--f!'./u:1!'!.з-!!.'!.:::К-'-!!..!IJ!..'::::.?в п{lК':I!.:J!..1:.в...... _.
ш.!l!.!'.!.:.'!'.I!:!!::.'.:fI!!..:l!.,--в-.'!.а.':!..'!.::КР".:'!'..I::..1!)'IК-!i'!.
Обr1;;:-/:,:':Ш:,lУТШ- _H_ -[
0.41 I I ; I
Ii \ : I
О 2и 1: I
r \ l
О, I 
i \ .1
l\ n
'02i \ /Н)
., I
'041 , \ !,
-\I-:\_- /,:--",j '.._ j
\) ,/  '-/ \,/
Задача 7.2
Для количественных характеристик отличия между функциями j(t) и
s(t) при различном числе членов усеченною ряда Фурье можно исполь-
зовать максимальное значение функции S(t)  j(t) и дисперсию данной
функции,
1. Постройте при различных значениях числа членов усечеННО20 ряда Фурье Nf:
а) 2рафики функций j(t)  s(t);
б) оцените периоды колебаний функции и сравните е20 с периодами ко-
лебаний последне20 удержаННО20 члена ряда Фурье.
2, Постройте зависимости маКСUJ.1алЬНО20 значения функции j(t)s(t) и
ее среднеквадратиЧНО20 отклонения от числа членов усечеННО20 ряда
Фурье на временном интервале [0,05;0,045]. (Примечание: для вычисле-
ния среднеквадратичеСКО20 отклонения используйте функцию std(v),
v  вектор, содержащий значения функции j (t)  s(t) ,)
Решив задачу 7.2, вы определили, что период колебаний функции j (t) 
s(t) равен периоду либо первоrо отброшенноrо члена, либо последнеrо
удержанноrо члена. К. Ланцош предложил способ уменьшения эффекта
пульсаций за счет сrлаживания усеченноrо ряда
SN(t) = а; + t.(akco{ t)+bkSin(2 ()) (7.17)
.0.6 .
.o.aL............L..........L............L..........L...........J
о 0.1 02 03 O4 0.5 0.6 0.7 0.8 0.9 1
Рис, 7,2, Исходная функция u усеченный ряд Фурье М=9)
ДЛЯ ВЫявления причины обнаруженноrо эффекта следует изменить в
приведенном выше документе число rармоник рЯда Фурье и пересчитать
документ заново. rрафики исходной функции и ее ряда Фурье при исполь
зовании 18 rармоник (Nf = 27) представлены на рис. 7.3, Анализ получен
ных результатов позволяет сделать качественный вывод о том, что увеличе
ние числа членов усеченноrо ряда Фурье приводит к уменьшению отличия
между функциями f (t) и s(t).
0'6:'!'Ш'Шl
! \ i "'\..; \r"\"""-.r ',;-' 'j'<./"., '<..,,'\.! \.1 \,1.......
04 !' ' '\,
1',1 \.
u I 1
О[ ;. 
-О2[ !
I .
I
'04r
1
:]
о
,..',.-"- ,:>-'-;;
за счет интеrpирования (усреднения) по этому периоду.
При выборе в качестве интервала сrлаживания периода последнеrо чле
на усеченноrо ряда Фурье (здесь для Toro, чтобы продемонстрировать ис-
чезновение этоrо члена N  номер последнеrо удержанноrо члена, но на
практике N берется как номер первоrо отбрасываемоrо члена) сrлаженное
значение hN(t) получим как среднее от SN(t):
t+(T/2N)
hN(t)= - JSN()d, (7.18)
T/N
t(T/2N)
Подставляя (7.17) в (7.18), получим
L
0.1
02
  ....L
ОЗ 04
05

06
0.7
08
09
Рис. 7.3. Исходная функция u усеченный ряд Фурье (N=27)
180
181

.l!...:!!'!.?..е...:!!.I!..':!.rp!!'!.f!.'..':!.е...Р''!.З!!.':!:Р..'i()!...'!.l!.e...'!!.A!!.!............... ....
......... .!:...}'1!.{1II{1Jlll. 1'е.'!.!?.е...Р'Iт.,ll.':!.:У!:.'!!.,!I=. P'!!'!</.I':!.
I1
I
1+(T/2N)
( N J аа
hN t)= d+...
т 2
1(T/2N)
N [ 1+(T/2N) t+(T/2N) ]
+ L ak f co{2  )ц + bk f Sine } =
k=l 1(T/2N) 1(TI2N)
= '!JL + N [a {SiП[2лk/Т(t + Т/2N)]siп[2лk/Т(t T/2N)]} 
2 Т L...J k 2лk/Т '"
k=l
 Ь {СОS[2лk/Т (t + T/2N)]  соs[2лk/Т (t  T/2N)]}]
k 2лk/Т .
Применяя известные триrонометрические формулы, окончательно
получаем
7.4. Спектральный анализ непрерывных
неIlериодических сиrналов
Рассмотрим обобщение метода рядов Фурье на случай непериодических
сиrналов, позволяющее получать их спектральные характеристики. В Teo
рии обработки радиотехнических сиrналов она называется задачей анализа.
Пусть функция s(t) задана на временном интервале конечной длитель
ности [0,7]. Дополнив данную функцию такими же сиrналами, Периодиче
ски следующими через интервал времени Т, получим изученную в преды
дущем парarpафе периодическую последовательность s р (t), которая может
быть представлена в виде комплексноrо ряда Фурье
N
hN(t) =  + CТ(N,k{ ak COse t)+bk Sin(2 t)],
ос)
s p(t) = L CllejllwI
1l=
(7.21 )
(7.19)
с коэффициентами
rде cт(N,k) TaK называемые сиrмамножители
cт(N,k)= Sin{N) . (7.20)
Таким образом, сrлаженный ряд Фурье есть исходный ряд Фурье с KO
эффициентами, умноженными на соответствующие сиrмафакторы. OTMe
тим, что эффект сrлаживания достиrается за счет Toro, что при k = N сиr
мафактор Nro члена оказывается равным нулю.
С физической точки зрения формулу (7.19) можно трактовать как Ha
блюде ни е исходной функции S N (t) через узкое просвечивающее прямо
уrольное окно шириной Т / N . Наблюдаемая функция hN (t) есть средняя
интенсивность света от исходной функции SN(t). Она оказывается более
яркой, коrда функция SN(t) больше, и менее яркой, коrда функция меньше.
т
С" =  J S(t)ejllWldt. (7.22)
а
Для возвращения к одиночному интервалу устремим к бесконечности
период повторения Т, при этом:
1. Частоты соседних rармоник пш и (п + l)ш окажутся сколь уrодно
близкими, поэтому в формулах (7.21), (7.22) дискретную переменную пШ
можно заменить непрерывной переменной Ш.
2. Коэффициенты С1I станут неоrpаниченно малыми изза наличия вели
чины т в знаменателе формулы (7.22).
Для нахождения предельноrо вида (7.21) при Т  00 введем понятие
спектральной плотности мощности, воспользовавшись тем, что коэффици
енты ряда Фурье образуют комплексно сопряженные пары:
С  А i'l'.. С  А i'P"
1J  пе , IJ  пе ,
'''ММ'М''ММ'"м"'м"'ШМ'М""'ММ'М'"M"'MM'''M' ''M'M""MM'M'MM
Задача 7.3
Дополните описанный выше докумеюп блоком, позволяющим проводить
С2Лажuвание усеченною ряда Фурье, и проведите сравнительный анализ
отклонения между функциями j(t) и 11N(t), анаЛО2UЧНО тому, как это
было сделано в задаче 7.2.
а каждой паре отвечает простое rармоническое колебание
А е;(lIа.> 1 +'I'..} + А е i(llw 1+'1'..> = 2А cos(п Ш t + ПJ )
fl II II 'f'lJ
с комплексной амплитудой 2 А"ei'l'.. = 2С1l .
На малом интервале частот t'1Ш в окрестности HeKoToporo выбранноrо
значения частоты Ша будет содержаться N = t'1Ш/ Ш = t'1шТ 12п отдельных
182
183

.?':.'!!..'п.fJ!<!:":"!?!?!.'!?...r:!...:..Р.'!..з-!:!.п.l!.?..':!.С}!!..!!.паке'!l..fl,f!,!:!!,!!,,..............
........ . ..... Ш..  .?Р..::!::!!.'-'-{!:.?!}!..:'!Е..!!I!!,,1!..ь-!!.lIl!!.,!!!!Ь-!р'Х}IКlj':!..
пар спектральных составляющих, частоты которых отличаются сколь уrод
но мало, поэтому составляющие можно складывать, предполarая, что они
имеют одну и ту же частоту и характеризуются одинаковым комплексными
амплитудами
ох!
1 J .
s(t) = .. S(r.v)e'UJ1dr.v,
27r
(7,28)
oc
oc
Данная формула называется обратным преобразованием Фурье функции
s(t).
Полученный фундаментальный результат формулируется следующим
образом: функция s(t) и ero спектральная плотность связаны прямым и об
ратным преобразованиями Фурье:
2 JOC .
2Сп = т s(t}e IUJol dt .
Таким образом, комплексная амплитуда эквивалентноrо rармоническоrо
сиrнала, отображающая вклад всех спектральных составляющих, содержа
щихся внyrpи интервала дш, равна
ос
S(r.v) = J s(t)ejUJldt,
(7.29а)
ас ос
2N J . дш J .
МО) =  s(t)e'(J}otdt = s(t)el(J}oldt.
о Т 7r
oo oo
oo
(7.23)
ос
s(t)= JS(r.v)ejUJ1dr.v.
27r
(7.29б)
Из (7.22) видно, что можно ввести функцию, называемую спектральной
плотностью функции s(t):
ас
oc
В математике доказано, что соотношения (7.29) справедливы для абсо
лютно интеrpируемых функций, т. е. функций удовлетворяющих условию
S(r.v) = J s(t}ei(J}tdt.
ос
(7.24)
Jls(t)dt < 00.
(7.30)
oc
Обратной к задаче анализа является задача нахождения вида функции
s(t) по ero известной спектральной плотности, называемая в теории обра
ботки радиотехнических сиrналов задачей синтеза. Для ее решения предпо
ложим, что непериодический сиrнал получается из периодической последо
вательности, коrда ее период Т ---+ 00. Воспользовавшись формулами (7.21)
и (7.22), запишем
ос 1 '
s(t) = lim " S(пr.v}e/ll(J}1 .
Toc L.J Т
п=oo
(7.25)
oc
Данное условие существенно оrpаничивает класс допустимых функций, oд
нако, с одной стороны, в современной математике разработан аппарат так Ha
зываемых обобщенных функций, позволяющих разумным образом вычисляrь
спектральные плопюсти неинтеrpируемых функций, с дрyrой, все реальные
сиrналы, реrистрируемые в физических экспериментах, имеют конечную дли
тельность, а потому автоматически удовлетворяют условию (7.30).
Перечислим без доказательства основные свойства преобазоания Фурье.
1 . Линейность преобразования Фурье (спектр линеинои комбинации
функций si(t) Si(r.v) есть линейная комбинация спектров исходных
функций с аналоrичными коэффициентами: L ajs i(t) = L ajS(r.v).
;
2. Спектр вещественной функции s(t) является комплексной функцией:
Входящий в (7.25) коэффициент 1/Т при любом целом п пропорциона
лен разности между частотами соседних rармоник :
1 r.v 1
==[п(r.v+I)пr.v]. (7.26)
Т 27r 27r
Подставляя (7.26) в (7.25), получаем:
1 ос .
s(t) = lim  "S(пr.v)eтUJ1[r.v(п+I)пr.v] (7.27)
т ac 27r L.J
1l=CC
00 ас
S(r.v)= J s(t)cos(r.vt)i J s(t)sin(r.v t)= A(r.v)iB(r.v),
ac
ac
причем
Так как частотные интервалы между соседними rармониками неоrpани
ченно сокращаются, сумму в (7.27) можно заменить интеrpалом
ас ас
JA(r.v)sin(r.vt) = О, JB(r.v)cos(r.vl)=O.
(7,31 )
.Х,
184
185

5. (),\/ п '() '1JР"'Й--= t?,'!!!.'!р"?а!li=rjJ'!.!и-=:.и-п..fJ.?''!..'!Сс:.()€!.!:к--'!'!!=''!..ТI!,
. Ш...........ШШШ.Ш...ШШШШ..!.'::'!.!!I!3!!!ш.,!,!,!р"ер!!'!...к--р!.'!.'!!..?!:..rjJУ.'.t!.':!.и-ш
3, СпеК1ральная плотность функции, смещенной во времени sCt  (о),
связана со спектральной плотностью исходной функции (s(t)  S(O))
s(ttо)шш+S(О)ешiШI" .
4, Спектральная плотность произведения функций ( s(t)  S(O),
y(t)  V (О) ) есть свертка спектров исходных функций
ОС)
J o(xa)dx=l,
(7.37)
OC)
ОС)
J f(x)o(x a)dx = f(a)
(7.38)
шОС)
ос
S(t)y(t)H fS()V(O))d.
шОС
7.5. Спектральный анализ дискретных функций
ос
На практике наиболее часто приходится находить спектры функций, за
данных в дискретные моменты времени, к таковым относятся как реальные
сиrналы, реrистрируемые с помощью аналоrоцифровоrо преобразователя
(АЦП), так и любые зависимости, задаваемые таблично. Например, решения
дифференциальных уравнений и систем ОДУ, вычисляемые в дискретные
моменты времени. Далее мы будем рассматривать только задачу спеК1Раль
Horo анализа функций, заданных на равномерной временной сетке, т. е. че
рез равный промежуток времени /)., называемый интервалом дискретизации,
/). = tm tml = tmш1 tmш2 =..., (7.39)
так как любую дискретную функцию можно, используя процедуру интерпо
ляции привести к равномерной временной сетке.
Для нахождения спектральной плотности дискретной функции S d (О)
заметим, что переход от непрерывной функции s(t) к дискретной функции
sAt) можно описать, введя в рассмотрение обобщенную функцию,
5. Функция, спектр которой представлен в виде произведения
S(O) = Sl (О) )S2(0) , причем S[ (О) н s[ (t) и S2(0)  S2(1) является сверткой
сиrналов во временной области S(O)  JSl(t  )S2(}i .
шОС
6. Скалярное произведение двух функций s(t)  s(O), y(t) н V(O) с
точностью до коэффициента пропорциона.пьно скалярному произведению
их спектральных плотностей
I
\
I
(
ос; ос;,
(s, У) = Js(t)y*(t)dl = 2 JS(O)V*(O)}iO).
 
Отметим, что последнее свойство позволяет вычислить спектральную
плотность для есконечно протяженных неинтеrpируемых функций: функ
ции постояннои величины
s(t) = А = coпst н S(O) = 2лАо(0); (7.32)
монохроматической комплексной экспоненциальной функции
s(t) = Аехр(iШаI) н 2лАо(0)  0)0);
(7.33)
ОС)
1](t)= Lo(t k/),),
k=шОС)
(7.40)
спектральную плотность rармонических колебаний
s(t) = Acos(O)ol) Н s(O) = лА[о(О)  OJo)+ 0(0) + Ша)], (7.34)
s(l) = АsiП(ШаI) н S(O) = iлА[о(О)  0)0) + 0(0) + Ша)], (7.35)
rде д'(х  а)  дельташфункция Дирака, обладающая следующими
свойствами:
называемую дискретизирующей последовательностью.
Учитывая фильтрующее свойства дельтафункции (7.33), дискретная
функция, есть скалярное произведение непрерывной функции s(l) и функш
ции 1](1):
д'(xa)={o,x*a ,
00, х = а
(7.36)
ОС) ОС)
sd (1) = (S(I), 1](t» = J ф) L 0(1  M}il ==
ш<;LO k=oc
(7.41)
= С..., хС  2/),), х(  /).), х(о), х(/).), х(2/),),., ,)
186
187

. к- .?"-.ь.I?,,!!ер..'---?=-<:"'!...Iр"й.в-.с:.!:..Р..lI..з.u:к.lI..:'р',!'i:С::?'!'! Ilc:..:.".!.e.!!!....1:4J!..... ...............шш..
.. ...... !Рь-:й-ll1J/lJз l/епl!еР..ь.Ill,,!.. u ..uс:к.Р..:'!!!ы-.х.Ф-у'I!l{UЙ
Так как функция 1](t) определена лишь в точках tk = kI1 (k = 0,::!:I,::!:2,.,,)
интеrpирование в (7,36) можно заменить суммированием, при этом роль
дифференциала будет иrpать интервал дискретизации Д;
XJ
S А ш) = L S (ш  2пп/ д)
(7.47)
пOC:
XJ
sAt) = Д LSkO(tkI1),
k=XJ
(7,42)
Из (7.46) видно, что спектр дискретной функции представляет собой
сумму бесконечноrо числа «копий» исходноr"о спектра непрерывной функ
rщи, расположенной на оси частот через одинаковые интервалы
2л/ Д (рис. 7.4), Как видно из рис, 7.4, для действительных функций s(t),
имеющих спектр, симметричный ОТносительно точки ш = О и оrpаничен
ный верхней rpаничной частотой шu = 27ifu , условие отсутствия наложения
отдельных копий спектра записывается в виде
Jl' 1
0.) <  + <  (7 48)
u  Д , J u . 2д . . ..
т. е. с точностью до коэффициента Пропорциональности Д интеrpал (7.41)
равен произведению функции s(t) и дискретизирующей последовательно.
сти 1](t). Будем считать, что для функций s(t) и 1](t) известны их спекш
тральные плотности S(ш) и S'1(ш), соответственно. В соответствии со
свойством 4 (см. раздел 7.3) спектр про изведения двух функций равен
свертке спектров этих функций
XJ
SАш)=ш fS'1()S(Ш.)d.
2л
(7.43)
д
I
I

Для нахождения спектральной плотности функции 1](t) разложим дaH
ную функцию в ряд Фурье. В соответствии с (7.16)
!!"
С =fо(t)еi2Jl't/Дdt=. (7.44)
п Д Д
о
Подставляя (7.44) в (7.15), получаем
1 XJ
1](t) =  L ei2Jl' nt/ Д dt . (7.45)
Д
,,=oc:
 2тrjll тr/Д О тrjtJ. 21l/tJ.
Рис. 7.4. Спектральная плотность
модулированной импульсной
последовательности при различных
значениях верхней 2раничной частоты:
а  верхняя "раничная частота велика;
б  верхняя 2раничная частота ,мала
шXJ
Выражение для нахождения спектральной плотности функции sAt) по
ее дискретным значениям можно получить, подставив (7.42) в (7.24):
Подставив (7.45) в (7.29а) и учтя (7.33), найдем
00  00
S'1(ш) =..1 f Lеi2ппl/ДеiйJtdt = 21 LО(Ш2пп/д).
з:J"=rr;; 11=.....-.00
00 0000 ':fJ
sd(ш)= f Sd(t)eiйJtdt = Д f LSkO(tkI1}?iйJtdt = Д LSkeiйJk!!" (7.49)
X) XJk=XJ k=XJ
С дрyrой стороны спектральная плотность была найдена выше друrим
способом (см. выражение (7.46», поэтому справедливо соотношение
(7.46)
XJ XJ
Д LSkeiйJk!!" = LSАш2пп/д),
k=r:t::: п=OC:
(7.50)
Из (7.46) видно, что спектр дискретизируюшей последовательности СОш
стоит в частотной области из бесконечной совокупности дельтаимпульсов,
при этом функция S'1(ш) является периодической с периодом 2л/д cl.
Подставляя (7.46) в (7.43) и меняя порядок суммирования и интеrpиро
вания, находим
называемое формулой суммирования Пуассона.
Из (7.50) видно, чт() однозначно найти функцию SАш) по значениям
функции Sd (/), вообще rоворя, невозможно из,за эффекта Ш1Jюжения копий
спектра, Единственное исключение составляет случай, коrда исходная
функция S(/) имеет спектр, удовлетворяющий условию (7.48), тоrда оче.
188
189

.<!.I!!'::''!!.'!!:!!!:.I!..t!...:f!.'!Р..?f!.!..l!.1!.З!'::''!!:'Р..?'.i:..?....I!:!!'!.!!.1-!'!:!!.........
видно, что спектр дискретной функции SАш) совпадает со спеК1РОМ He
прерывной функции S( ш)
{ О,Ш<1r/11
S(ш) = 6. kt:ke iOJkI'1,  1r/11 s ш s 1r/6. .
О, ш > 1r/ ш
Полученный результат является следствием теоремы Котельникова,
имеющую следующую формулировку: nроuзволыlйй СUZ1lШl, сnектр KO
mopozo lIе содержиm часmоm выше fи rц, можеm быmь nОЛ1l0сmью вoc
сmаll0влеll, если uзвесmllЫ оmсчеmllые Зllачения эmоzо сиZIlШlа, взяmые
через рав1lые nроме:жуmки времени 1/2fи. (Здесь под восстановлением
имеется в виду вычисление значений функции в любой момент времени, не
совпадающий с моментами дискретизации,)
(7.51)
7.6. Спектральный анализ дискретных функций
конечной длительности
в предыдущем параrpафе при решении задачи о нахождении спектраль
ной плотности дискретной функции мы предполarали, что значения этой
функции заданы в неоrpаниченном числе точек на временной оси. На прак
тике получить столь обширные сведения о поведении функции оказывается
невозможным. Это обстоятельство приводит к тому, что всеI'да спектраль
ный анализ про водится на временном интервале конечной длительности.
Рассмотрим особенности спектральноrо представления дискретной
функции, заданной на временном интервале конечной длительности [0,7'] N
отсчетами SO'Sl'S2'''''SNI' взятыми соответственно в моменты времени
0,6.,211, ., ., (N  1)6. . Полное число отсчетов N = Т /6. .
Используя подход, развитый в предыдущем парarpафе, поставим
в соответствие исходной непрерывной функции s(t) ее дискретное пред
ставление
Nl
sAt)=I1>kJ(tk6.). (7.52)
k=O
Дискретная последовательность S<i (t) представима рядом Фурье
190

..... ....? ..<?!'Рь-е.:с:.!..l!.З..'Iе.'!.рерЬ-'IIЬ-t...!!.Р.!.'!!.Ь-t..1!.J!!.'il.
ос)
S (t) = 6. "'\' С ei21r1l1/T
<i  11 '
(7.53)
1l=ОС:
rде
т
С = J JS (t)ei21r1l1/T dt . (7.54)
11 ТI1 <i
О
Подставляя (7.52) в (7.54) и вводя безразмерную переменную 1;=1/11,
получим
NДN1
С" = JI1 J >kJ(t k6.)ei21rl/T d1 =
О k=O
N Nl Nl N
=  JLSkJ(1;  k)ei21r1l/N dl; = LSk J д(1; k)ei21r1l/N dl;.
о k=O k=O О
Используя фильтрующее свойство дельтафункции, получаем
Nl
С  1 "'\' i21r 1Ik/ N
11  ske .
N k=O
Формула (7.55) определяет последовательность коэффициентов, обра
зующих дискретное преобразование Фурье (ДПФ), которое имеет следую
щие свойства.
1. ДПФ есть линейное преобразование.
2. Число коэффициентов CO'Cl'C2""'CN1' вычисляемых в COOTBeTCT
вии с (7.55), равно числу отсчетов дискретной последовательности.
3. Коэффициент Со (постоянная составляющая) есть среднее значение
(7.55)
дискретной последовательности.
4. Если N  четное число, то
Nl
1 "'\' k
CN/2 = .. (l) sk .
N k=O
5. Для вещественной дискретной последовательности, коэффициенты
ДПФ, номера которых расположены симметрично относительно N /2 , обра
зуют сопряженные пары:
Nl Nl
С  J "'\' i21r(N1I)k!N   "'\' i2tmk!N  С.
N'1I  ske  ske  11'
N k=O N k=O
191

.li:'.!?'!!!.l!!.t..?:.:?..с:!.'!Ей-.С:_.:_р'':,!_:К-.l..!.t.jJ!!,.'iе.с:?_I!.в '!.с:.К-:.'!I!.Т f:!1..1!.
поэтому можно считать, что коэффициенты CN/241"",CNJ отвечают отри
цательным частотам.
Задача 7.4
Вычислите, используя пакет MATLAB, ДПФ дискретной последователь
ности, заданной восьмью равно отстоящими отсчетами
{Sk} = (1,1,1,1,0,0,0,0) и изобразите 2рафически абсолютные значения KO
эффициентов ДПФ, называемых спектром мощности,
1. Сколько различных 2армоник имеетДПФ данной последовательности?
2. Считая длительность интервала дискретизации равной 1 с. вычислите
частоты этих 2армоник и величины !'!.!; == 1i+!  1i (расстояние между
2армониками). Как изменится результаm, если интервал дискретизации
будет равен 0,1 с, 0,5 с, 2 с?
3. Какова верхняя 2раничная частота спектра дискретной последователь
ности при указанных длительносmяx интервала дискретизации?
Задача 7.5
Вычислите, используя пакет Mathcad, ДПФ дискретной последова
тельности, заданной восьмью равноотстоящими отсчетами
{Sk} = (1,1,1,1,0,0,0,0,0,0,0,0,0), и изобразите 2рафическu абсолютные
значения коэффициентов ДПФ,
1. Сколько различных 2армоник имеетДПФ данной последовательности?
2. Считая длительность интервала дискретизации равной 1 с, вычислите
частоты этих 2ар.МОНИК величины !'!.fi = fi+l  f; (расстояние между
2армониками)? Как изменится результаm, если интервал дискретизации
будет равен 0,1 с, 0,5 с, 2 с?
3. Какова верхняя 2раничная частота спектра дискретной последователь
ности при указанных длительностях интервала дискретизации?
4. Сравните полученные результаты с результатами задачи 7.3, К чему
приводит дополнение дискретноЙ последовательности нулями? Почему
2раничные частоты спектров дискретных последовательностей,
имеющих различное количество членов, но одинаковый интервал диc
кретизации, оказываются одинаковыми?
Если для дискретной последовательности SO'SI'S2""'SN1 найдены KO
эффициенты ДПФ CO'Cl'C2'''''CNI' то восстановление исходной дис
кретной последовательности /11Ожет быть осуществлено в caoтвeт
ствии с (7,53). При этом, как очевидно, бесконечный ряд Фурье cтaHO
вится ряда.1/ с кuнечным число.М членов:
192

..._:!:..<!J'.fJ.!:...e.=I!!!.'!!!!!?"'1} :.'!.Е:р"I!!!..Ь!!..,!,!рет-1!.."!.Р.У.!.!К-'i'!ii..
x(t) = СО + 21C1. соs(2Л' t/T + lf'l ) + 21С2! COs( 4л- t/T + lf'2) +...
+ 2: С N/2 j cos(N л- t/T + lf'N/2)
еде lf'i = arg( С; ), i = 1,2,..., N /2  фазовый У20Л коэффициента ДПФ,
Для нахождения формулы восстановления дискретноЙ последователь
ности SO'Sl'S2""'SN1 по известным коэффициентам ДПФ
CO,Cl,C2,,,,,CN1 умножаем (7.54) на базиснуюехр(i21mk/N) функцию и
проводим суммирование по индексу п:
N N N
LC i21f1!"/N  ..! L i21f1!"/N L ;21f1!m/N 
lIе  е Sme 
N
11=0 11=0 т=О
Nl Nl
=  LSmLei2J!'("m)n/N.
т=О 11=0
Так как базисные функции являются орт020Нальными
Nl
L ei2J!'("m)n/N = Nokт,
n=О
(7.56)
(7.57)
(7.58)
2де От"  символ Кронекера:
{lk=m
Okт =' .
O,k'i:-m
Подставляя (7,57) в (7.56), получаем
Nl Nl Nl
 LSmLei2J!'("m)1I/N = LSmNOkт =s".
т=О 11=0 т=О
Откуда
Nl
 "С i2J!'1I"/N
х"  L...J lIе .
11=0
(7.59)
Задача 7.6
Используя пакет MATLAB и коэффициенты ДПФ, полученные в задачах
7.3, 7,4, проверьте правильность формул (7.56) и (7.59),
7.7. Быстрое преобразование Фурье
Из формул (7.54) и (7.58) видно, что для вычисления ДПФ или обратноrо
ДПФ последовательности из N элементов требуется выполнить N2 операций
с комплексными числами. Если число элементов обрабатываемых массивов
7]576
193

l<:I!.':!?,'!!:р'/():,\1?:l!..f..'?f!..с:.I.:.4!.l!?'::.с.К-l1!.."fJ()'i:.с.c.c>в.в./a..к-.e,'!!.:"!....:,!!!,.. .
.......!<!2P.':!..'.!.'!3!!!:.':!!..P.!!.lвll и диc'2'.!!!!'!... ФУII!5.'iIl
составляет порядок тысячи и более, то время, необходимое на выполнение
этих преобразований резко возрастает и теряется возможность обработки
сиrналов в реальном масштабе времени,
В 60e rоды ХХ века Кули и Тьюки был предложен метод вычисления
коэффициентов Фурье, позволивший снизить объем вычислений до
N log2 N операций. Он получил название алI'оритма быстроrо преобразо
вания Фурье (БПФ). В настоящее время процедуры, реализующие алrоритм
БПФ, входят во все математические библиотеки, используемые при написа
нии проrpамм на языках проrpаммирования BbIcoKoro уровня, и специали
зированные пакеты для математических вычислений. В связи с тем, что
подробное рассмотрение алrоритма выходит за рамки нашей книrи, мы pac
смотрим только основную идею БПФ дЛЯ случая, коrда число отсчетов
N = 2Р , Р  целое число.
Разобьем входную последовательность {Sk} на две части с четными и
нечетными номерами:
;21f(п+N/2) ,i21f". i21rп
е N =el1fe N =e N
получаем выражение для второй половины множества коэффициентов ДПФ:
.2нп
I
C"+N/2 = С"Е  е N С"о, (7.64)
rде k =O,I,2,...N/21.
Это позволяет представить пй коэффициент ДПФ в виде
1 N/21( i21U12k i2m\2k+l)]
С" =  L s2ke N +s2k+le N =
N k=O
(N/21 ; 2тl k ,21U1 N/21 ; 21U1 k J.
1  N/2 IN  N/2
=  L..J s2kEe + е L..J s2k+lOe
N ЬО k
Из (7.60) видно, что первая половина коэффициентов ДПФ исходноrо
сиrнала с номерами от О до N /2  1 выражается через коэффициенты ДПФ
двух частных последовательностей:
(7.61)
rде п =0,1,2,...N/21.
Формулы (7.62), (7.64) лежат в основе алrоритма БПФ: последователь
ности отсчетов с четными и нечетными номерами вновь разбиваются на две
части. Процесс продолжается до тех пор пока не получается последователь
ность, состоящая из одноrо элемента. ДПФ данной последовательности
совпадет с сами элементом. Затем последовательно находят коэффициенты
ДПФ предыдущих последовательностей.
В пакете MAТLAВ быстрое одномерное преобразование Фурье реализо
вано парой функций, выполняющих прямое и обратное БПФ: fft/ifft. Данные
функции используются как для действительных, так и для комплексных по
следовательностей, при этом длина последовательностей может быть про
извольной.
Обращение к функциям:
fft(v)  возвращает дискретное преобразование Фурье 2mMepHOro Beктo
ра, apryмeHT KOToporo есть результат дискретизации через равные проме
жутки времени некоторой функции. Результат работы проrpаммы 
комплексный вектор размерности 2'"+ 1. Элементы вектора, возвращаемоrо
функциейfft, вычисляются по формуле
N1
  i21f"k/N
С"  L..J Vke ,
k=O
{Sk}E = {S2k},{Sk}0 ={S2k+l}'
(7.60)
. 21r"
'l
С" = С"Е + е N С"о, (7.62)
rде N  число элементов вектора v;
ifft(v)  обратное дискретное преобразование Фурье, комплексноrо BeK
тора, содержащеrо значения ДПФ. Вектор V должен иметь 2m+ 1 элементов.
Р б   2,"+1
езультат ра оты проrpаммы деиствительныи вектор размерности .
Элементы вектора, возвращаемоrо функцией ifft, вычисляются по формуле
N1
с = J  V ei21r"k/N
"NL..Jk '
k=O
rде N  число элементов вектора v. Отметим, что для всех векторов спра
ведливо соотношение ifft(fft(,))=v;
rде п =O,l,2,...N/21.
Так как последовательности коэффициентов массивов {Sk}E и {Sk}O яв
ляются периодическими с периодом N /2 , то
С"Е = C"+N/2E' С"О = C,IfN/20' (7.63)
Подставляя (7.63) в (7,62) и учитывая, что
194
195

.!!..<':-л-!l?'!!:rI!!!::!..??е!!.'!F...'!..в-.а..!I.U'!.1!.зu :CX:. p()'iec.':.'!...JC:'!'!'.'! !.!Т-1.в-. . ....
.....!:.<!!!Е':.'!.:с:'I,?r:'.'.е.!!.Е:Р..':.'!!.'!-..':!!....'!?liР.!.'!!!!.."!:.Х:...1!.J!!'i
//t(v,п)  возвращает дискретное преобразование Фурье 2nMepHoro BeK
тора, aprYMeHT KOToporo есть результат дискретизации через равные проме
жутки времени некоторой функции. Результат работы проrpаммы есть KOM
плексный вектор размерности 2n+ 1. Если п > leпgth( v) последовательность,
хранящаяся в векторе v, дополняется нулями;
if/t(v,п)  обратное дискретное преобразование Фурье, комплексноrо
вектора, содержащеrо значения ДПФ. Результат работы проrpаммы 
комплексный вектор размерности 2n+ 1. Если п > leпgth( v) последователь
ность, хранящаяся в векторе v дополняется нулями.
В качестве примера использования функций вычисления БПФ пакета
MAТLAB рассмотрим задачу о вычислении спектра функции, являющейся
суммой двух периодических функций
s(t) = А! siп(2л- Лt) + А2 siп(2л- /2t),
rде А! = 0.8, Л = 40 ТЦ, А2 = 0.4, /2 = 90 rц, заданной набором дискрет
ных значений в N==8192 точках на интервале [0,2] с. Для решения задачи He
обходимо выполнить следующую последовательность команд:
» N=8192; % число точек для вычисления функции
» i=1:N;
» Ттах=2; % длительность BpeMeHHoro интервала в секундах
»t(i)=Tmaxl(N-1)*(i-1); % задание временной сетки
» fl=40 % частота первой составляющей в rц
»f2=90 % частота второй составляющей в rц
% вычисление MrHoBeHHbIx значений функции
» f(i)=0.8*sin(2*pi*fl *t(i»+0.4*sin(2*pi*f2*t(i»;
» figure(1);plot(t,f);
% вычисление спектра
» с=ш(о;
% вычисление нормированноrо амплитудночастотноrо спектра
» j=2:N/2;
» Cm(j-1)=abs( c(j-1»/(N/2)j
»Freq(j-1)=(j-1)trmax; % вычисление вектора частот в rц
» plot(Freq,Cm);
» axis([O 100 О 1]);
Результат выполнения описанной выше последовательности команд
представлен на рис, 7.5 и 7,6.
0.5
.1
I
i i
1.5  I I I
О 0.2 0.4 0.6 0.8
.L............................
1.2 1.4 1.6 1.8
Рис. 7.5, Зависимость мсновенных значении функции! =f(t) от времени
0.9
0.6
0.7
0.6
05
0.4
03
I
1
1:
il
10 20 30 40 50 60 70 60 90 100
0.2
01
о
о
Рис, 7,6, Спектр функцииf=f(t)
........
Задача 7.7
Вычислите спектр функции s(t) = Asin(2;ifst + л-/S) А=3, f.=1O rц по
N=2JO известным значениям на интервале [О,2} с, Изменился ли вид
спектра по сравнению с ранее рассмотренны.'41 случаем? Сравните фазы
сармоник, имеющих частоту 1 О ТЦ, в первом и во втором случае,
196
197

.1!.?!,пЬIO!!!!!!!!.I!!!..f!.uров'!!.'!!.:1!.'!..!!!'!.роце,:!!!!!!!!акете М}!,!:!!.Ш......
ш_!:J:'.Р"=:I'-!.з.._='If!.е.Р..!:!.i!._U'!...'2!.:'!!.I!.:.1!J:'.Iуи.й
Задача 7.8
Вычислите спектр функции
s(t)=A,sin(21l' N+IJ.'J)+A2sin(21l' f2t+qJ2)'
2де А}=l, f}=1O rц, <f'}=лl8, А2=О,5, fi15 ТЦ, <f'2=лl3 по N=2JO извест
ным значениям на интервале (О,2] с, изобразите ею 2рафически и oпpe
делите фазы соответствующих спектральных 2армоник.
Задача 7.9
Для разделения функций, входящих в функцию s(t), заданную в пpeды
дущей задаче, можно использовать полосовую фильтрацию, которая
заключается в умножении спектра функции S(m) на весовую функцию
w{w)
.. ............ ..... .....
Задача 7.11ШШ--ШШШШ_Ш_Ш_-'
В первой 2Лаве нами была подробно рассмотрена задача построения
траектории движения Марса в системе координат, связанной с Зе.млей,
в которой была вычислена зависимость расстояния s(t) между Землей
и Марсом от времени. Проведите спектральный анализ функции s(!)
и определите значения: постоянной составляющей функции s(!), амш
плитуду несущей и ее частоту. 2Лубину амплитудной модуляции u час
тоту модулирующей функции,
.............
w{m)= {1,т Е [,]
О,ю [,]
и выполнении обратН020 преобразования Фурье. Используя полосовую
фильтрацию, проведите разделение функций, входящих в функцию s(t).
Сравните отклонение функций, значения которых определены в резУЛЬш
тате полосовой фильтрации функции s(t), от исходных функций.
ЛИТЕРАТУРА
1, Хемминr Р. В, Цифровые фильтры, М,: Советское радио, 1980,
2, Баскаков С. И, Радиотехнические цепи и сиrналы, М,: Высшая школа, 1988,
3. Марпл С. Л, Цифровой спектральный анализ и ero приложения, М,: Мир, 1990,
4. Оппенrейм А, В., Шафер Р,В, Цифровая обработка сиrналов. М,: Радио и связь, 1979.
5, Рабинер Л" rолд Б, Теория и применение цифровой обработки сиrналов, М,: Мир, 1978,
6, Бендат Дж, Пирсол А, Прикладной анализ случайных данных, М,: Мир, 1989.
7, Джекинс r" Ва1ТС д, Спектральный анализ и ero приложения. М,: Мир, Вып, 1, 1971,
Вып, 2, 1972,
Задача 7.10
Исследуйте численно спектральный состав функции вида
s(t) = и ",(1 + mcos(nt + Фо))соs(mоt + qJo),
которую в радиотехнике используют для описания си2налов с амплиш
тудной модуляцией, при различных значениях параметров. Проанализиш
руйте вид спектра при различных значениях параметров. Получите разш
ложение функции в ряд Фурье аналитически и сравните полученные pe
зультаты с результатами численною анализа.
Проведите аналО2Uчные исследования для функций вида
s(t) и .(1 + t т, cos(n,t +Ф, )}О'(Щ/ + 9\»,
s(!) = и 111 cos( то! + т sin nt) (си2Нал с частотной модуляцией),
s(t) = и 111 cos( то! + т, sin п,! + т2 sin п2!) ,
s(t) = и т cos(mo! + f-J t 2/2) (си2Нал с линейной частотной модуляцией),
198
199

...........Ш....:!:!<!..:.!}ll!'!.'!!!.I!'!..е....!!.ебательl/Р..(1.!!.:9!:..
r лава 8
МОДЕЛИРОВАНИЕ
КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
запишем уравнения движения линейноro rapмоническоrо осциллятора в виде
2
х+шох=о, (8.4)
rде %  циклическая частота.
Уравнение (8.4) является линейным дифференциальным уравнением
BToporo порядка. Аналитическое решение данноrо уравнения хорошо из
вестно:
8.1. Линейный rармонический осциллятор
x(t) = Acos(wot + 0'),
(8.5)
Один из наиболее распространенных типов движения механических сис
тем представляют собой малые колебания, которые система совершает
вблизи положения устойчивоrо равновесия. Наиболее простым с математи
ческой точки зрения оказывается описание движения систем, имеющих oд
ну степень свободы. Примером такой системы является тело массой т, pac
положенное на абсолютно rладкой rоризонтальной поверхности и прикреп
ленное к свободному концу пружины жесткостью k (рис. 8.1). Будем
описывать положение тела координатой х и примем за начало отсчета
( х = О ) точку равновесия rpуза на пружине. При смещении тела из положе
ния равновесия х = О на небольшое расстояние х со стороны пружины бу
дет действовать возвращающая сила, пропорциональная величине смещения
и направленная в сторону положения равновесия:
F = kx . (8.1)
rде А,О'  постоянные, называемые амплитудой и начальной фазой, опреде
ляются из начальных условий для координаты х и скорости v = dx/ dt .
По определению период периодической функции есть наименьшее Bpe
МЯ, через которое движение повторяется, т. е.
x(t + т) = x(t) . (8.6)
Так как период функции косинус равен 2п, то величина шот COOTBeTCT
вует одному периоду колебания:
%т = 2" ,
откуда находим связь между % и Т
Т = : = 7т = 2"И, (8.7)
Частота колебаний v представляет собой число периодов в одну секунду
и определяется выражением
х-о Рис. 8.1
Знак минус в (8.1) указывает на то, что сила стремится вернуть тело в
положение равновесия. На основании BToporo закона Ньютона
mX = kx .
Разделив обе части уравнения на массу m и введя обозначение
Jk
%= ',
т
1
v   (8.8)
T .
Необходимо отметить, что в соответствии с (8.7) период колебаний зави
сит от отношения k/m, но не зависит от А и Ii. Это означает, что период
колебаний линейноrо rармоническоrо осциллятора не зависит от амплитуды
колебаний.
Леrко показать, что полная энерrия линейноrо rармоническоrо осцил
лятора
1 2 1 2
Е = mv +kx
22'
(8.9)
(8.2)
(8.3)
rде первый член  это кинетическая энерrия, второй  потенциальная энерrия.
Предваряя рассмотрение более сложных случаев периодическоrо движе
ния физических систем, уравнения движения большинства из которых не
допускают аналитическоlО решения, продемонстрируем общий подход
________о
201

.l!?:."!.'.'..?".!.=l!!.Iо!..е.:z.'!.fl.!!f!..с:!..'!!.=1!.з-!!:.!.'='5..l!!.пр''!...?'т.zc:.".!.."!..1:..!.!!........ ...Ш.....
....... ......!..: М'!...елUl!.'!..f!.!.!'!..':.'5..0:'.=-б-!!.'!!!!!'..'!!!..ь-':.:"'!:Р.!!!i'=?!
Результаты выполнения приведенной последовательности команд пред
ставлены на рис. 8.28.4.
Рис, 8,3, Зависимость
скорости
2армоничесвКО20
осциллятора
от времени
к нахождению и анализу численных решений уравнения движения на при
мере линейноrо rармоническоrо осциллятора (8.4). Вычисленные зависимо
сти x(t), v(t) полностью описывают движение одномерноrо линейноrо
rармоническоrо осциллятора. С друrой стороны, пару значения функций
{x(tn), v(tll)} В выбранный момент времени [" можно рассматривать, как KO
ординаты некоторой точки в двумерном пространстве, называемом фазовой
плоскостью. Кривая, образованная на фазовой плоскости, при нанесении
точек {x(t;), v(t;)} в последовательные моменты времени, называется фазо
вой траекторий.
Для нахождения численноrо решения уравнения движения линейноrо
rармоническоrо осциллятора (8.4) и их визуализации следует привести ОДУ
BToporo порядка к системе дифференциальных уравнений первоrо порядка,
затем создать mфайл, содержащий определение функции, стоящей в правой
части системы ОДУ. Ниже приводится листинr соответствующеrо файла
Oscillator .т.
% листинr файла Oscillator.m
function dy=Oscillator(t,z);
% функция стоящая в правой части системы ОДУ первоrо порядка,
% эквивалентной ОДУ (8.4)
global omega; .
dy=zeros(2,1); % задание векторстолбца размерности 2х 1
dy(I)=z(2);
dy(2)=-оmеgаЛ2*z(I);
Далее необходимо выполнить следующую последовательность команд:
» global omega;
» k=9; % коэффициент жесткости
» т=1; % масса осциллятора
» Т=2*рi*(k/m)ЛО.5; % период колебаний
» omega=2*piff; % циклическая частота
» RO=[O.5 1]; % начальные условия
»[t Z]=ode45('Oscillator',[O:5*T/N:5*T],RO); % решение системы ОДУ
» figure(I); plot(t,Z(:,I»; % визуализация зависимости x=x(t)
» figure(2); plot(t,Z(:,2»; % визуализация зависимости v=v(t)
» figure(3); plot(Z(:,I),Z(:,2»; % визуализация фазовой плоскости
» figure(4);comet(Z(:,I),Z(:,2»; % визуализация движения на фазовой
% плоскости в динамике
202
',
1
, /\ / \ {\
, ,
; i ; ;
2 ; ; !
, i
, ; 1
; , I
1 I i
, i ;
i !
, '1
, ,
,1 ,
,
, !
.2 I j \
\ ! \ Рис. 8.2. Зависимость
, \) \)
координаты 2армоничеСКО20
"о 10 20 30 '" .. .. 711 00 90 100 осциллятора от времени
'.5r' r ,  .Т" .  , .  .....,-  "'T
i
i
1
,k
.\
l'
f \
f \
I i
, ,
1 i\
: I
! \
1 I
i \
I
I
/,
1\
I \
j \
; ,
\
i
i
\
I
"\
" "
! ')
!
i
I
I
i\
1,
l'
О.Ос \
1;
! \
: I
oL 
i \
\
\
;
\
,
\
1
\ !
\ f
!
\ !
1
I
I
i
1
I
.......J....._
80 90 100'
i
\
\
\./
;
,
i
i
. I
\ I
\/
;
-0.5  \ i
\ /
v
, ,
\/
i
.1,
i
i
.'5L
о 10
  _......L...
     ro
1.51
,1
r
,
/Ш  ШШ"
/ "
I '
I \
/
oof
ol
I
!
,
\
\
"-
,.,
j
/
..,.
.,.
Рис. 8.4. Фазовая
траектория 2арJ\lоническоi'О
осциллятора
15 ............... ..L . .- .
.4 .3 -2 -1 О 1 '2 3
203

.!!..<!:."!п--!!!.9!.!.I!!:!.:.:'.!Р..'!.I!..I!!:.Р.!!.::..!lF..<!.':!..е.:?!..!..I!.::'!Т1I.!:!!1:.T1...
... :"!'!....'!!'..Р..'!..Cl!!..z:.:'55!:'.с:..Т1I:..л-.Ь!!.'?!:..Р..'!..!!.::"?'!..
"'0 .. ....ш ......... ...... ......... .... ... . . ............ щ........... ...... ............... ШШ ....... ....
Задача 8.1
l. Вычислите полную энеР2ИЮ 2армоничеСК020 осциллятора для тех MO
ментов времени, в которые известны значения координаты и скорости,
Постройте 2рафик временной зависимости величины I1n = (Еп  Ео)/ Ео .
Как меняется данная величина во времени?
2. Постройте 2рафик зависимости отклонения между численными значе
ниями координаты и скорости и аналитическими, Как меняются дaH
ные величины во времени? Оцените точность получеНН020 числеНН020
решения по координате и по скорости,
3. Дополните описанный выше документ блоком, позволяющим проводить
спектральный анализ численных решений ОДУ (8.4): вычислять спектр
зависимостей x(t), v(t), строить 2рафики спектральных плотностей
SAf), Sv(f) и определять, используя данн'ые 2рафики, значения
циклической частоты шо = 2;r 10 и периода колебаний Т.
4. Для различных значений % вычислите соответствующее им значение
периодов Т Предположив, что величина Т пропорциональна (k/mY,
оцените показатель степени, построив 2рафик зависимости
т = Т(Чт) в дважды Л02арифмическом масштабе.
5. Вычислите значения амплитуды А и полной энеР2ИИ Е для начальных yc
ловий х(О) = 4, v(O) = О и х(О) = О, v(O) = 4, выбрав в обоих случаях значе
ния k, т, при которых шо = 2, Какая величина определяет значение
амплитуды А?
6. Постройте зависимости потенциальной и кинетической энеР2ИЙ от вpe
мени, В какие моменты времени эти зависимости достИ2ают свое20
наибольшею и наименьше20 значения? Тде находится в данный момент
осциллятор?
7. Вычислите и сравните средние значения кинетической и потенциальной
энеР2ИЙ за один период колебания.
8. Вычислите зависимости x(t) для различных значений амплитуды А и пo
кажите, что форма данной функции и ее период не зависят от А при
фиксированном значении отношения k/m. В каких единицах необходимо
113.1ерять вреJНЯ для т020, чтобы величина x(t)/ А не зависела от А и
k/ т ? Как будет вЫ2лядеть уравнение движения линеЙНО20 2арА10ниче
СК020 осциллятора (8.4) в данном случае?
9. Как видно из рис, 8.4, фазовая траектория линеЙН020 2армоничеСК020 oc
циллятора является эллипсOJН, Дополните документ блоком, позволяю
ЩИМ вычислять размеры е20 большой и малой полуосей. Будут ли отли
чаться фазовые траектории для различных начальных условий? Какие
физические величины определяют размеры большой и малой полуосей
эллипса? Запишите аналитическое уравнение эллипса, проведите ею
анализ и сравните свои выводы с результатами, полученными при чис
ленных расчетах,
Задача 8.2
Уравнения, описывающие поведение линеЙН020 2армоничеСК020 осцилля
тора получены в предположении малости амплитуды колебаний, что
позволяет записать силу, возвращающую осциллятор в положение paв
новесия в виде (8.l), Для описания движения с конечными амплитудами
выражение для возвращающей силы будет содержать члены, пpoпop
циональные второй и более высоким степеням х, а уравнение движения
примет следующий вид:
х+шJх=ах2 (8.10)
Проведите сравнительный анализ решений уравнения (8,] О) при различ
ных значениях параметра а и решений уравнения (8.4), используя зави
симости x(t), v(t) фазовую траекторию и 2рафик спектральной плот
ности,
8.2. Математический маятник
Рассмотрим движение rpуза массой т, прикрепленноrо к одному из KOH
цов жесткоrо стержня длиной L, друrой конец KOToporo закреплен в точке
подвеса. Такая система, как известно из опыта, будучи выведенной из по
ложения равновесия будет совершать колебания.
Для описания движения данной системы в первом приближении исполь
зуют модель, в которой пренебреrают трением в точке подвеса, массой
стержня по сравнению с массой rpуза, и считают, что вся масса rpуза при
ложена в одной точке. Данная модель называется математическим маятни
ком (рис. 8.5). Так как движение rpуза происходит по дyrе окружности pa
диуса L с центром в точке О, то положение rpуза характеризуется уrлом OT
клонения стержня от вертикали е. При движении по окружности линейная
скорость и ускорение rpуза равны
de
\1 = L (,8,11 )
dt'
204
205

l!.?."!"!:о.'!!:'f!1!?..el!.':Р...°!..l!!'I'!.'1!.'I!!.!!.:!5..'!!3.Ео..'-!...е::.:!!!.!!!.с:..A.!..!!..._._..__
Уравнение (8.14) оказывается нелинейным, ero решение, как и решения
большинства нелинейных уравнений, не выражается через элементарные
функции, что определяет необходимость получения ero численноro решения.
Однако при достаточно малых yrлах, при которых sin ()  () , уравнение
становится линейным
d2()
a==L..
dt2
В принятой модели на математический
маятник действуют две силы: сила тяжести
mg, направленная вертикально вниз, и
сила реакции стержня (рис. 8.5). Равнодей
ствующая этих сил, равная, как видно из
рис. 8.5, mg sin () , направлена в сторону
уменьшения yrла. Следовательно, ypaBHe
ние движения математическоrо маятника
записывается в виде:
d2()
mL  == mg sin () , (8.13)
dt
или
d2() g.
. ==  . SlП () .
dt2 L
d2() g
.==()
dt2 L.
Вводя обозначение
rg
%L
...ш..:..fl!.о.i>.Р"?(l!!.1!(l111.:"..I.Р..о.'i.о.в
(8.12)
Получим выражение для полной энерrии математическоrо маятника, яв-
ляющейся интеrpалом движения. Как видно из рис. 8.5, потенциальная
энерrия математическоr"о маятника и, отсчитываемая от точки равновесия
маятника,
(8.14)
и == mgh == mgL(1  cos ()) ,
( )2
1 2 1 2 d()
Кинетическая энерrnя равна  ntV ==  mL  , поэтому полная энерrnя
2 2 dt
1 ( d())2
Е == mL2 Ш + mgL(1 cos()).
2 dt
Уравнение (8.19) позволяет получить формулу, связывающую период
колебания математическоrо маятника и уrол начальноrо отклонения. Для
d()
этоrо разрешим уравнение (8.19) относительно :
dt
d() J 2 Ш" 'Ш.Ш.Ш..
Ш ==:t .(E mgL(1 cos())),
dt mL2
Из (8.20) видно, что переменные разделяются
d()
dt == :t
(E mgL(1 cos()))
mL
Интеrpируя (8.21), находим выражение для периода колебаний MaTeMa
тическоrо маятника
(8.18)
(8.19)
Рис, 8,5
(8.20)
(8.21)
(8.15)
8
" d()
Т=2 f f .
8" (E mgL(1 cos()))
mL2
(8.22)
(8.16)
rде ()о  начальный уroл отклонения маятника.
При движении маятника из начальноrо положения с нулевой начальной
скоростью Е == mgL(1  cos ()о) , поэтому
rШ' 8
!2L " d()
Т   i f J;eseo ' (8.23)
B()
и сравнивая уравнения (8.4) и (8.15), видим, что они оказываются одинако
выми. Следовательно, результаты, полученные в разделе 8,1 для линейноrо
rармоническоrо осциллятора, MOryт быть использованы при описании ма-
тематическоrо маятника, В частности, период малых колебаний математи
ческоrо маятника
27r (L
т == % == 27rg'
не зависит от амплитуды колебаний,
206
(8.17)
Задача 8.3
Создайте в пакете MATLAB документ, позволяющий находить численш
ное решение уравнения движения АштематичеСКО20 маятника (8.15).
Получите численное решение уравнения движения при различных наш
207

Iiомп-'!!!!!l!':С:! !I<?=,,!р.!!а!..'!I!!.IjJ,!!.:.к-,!! п-Eo.!/::?!! !!1!.:!._
._ .. _Ш ..... ...._J':!.="l!.!!(l!..'!:'..r:.КОЛ=?"(l::'..:Л..!!.':'!.!...f!р'О'!!'''---с.:с.!!
чальных уzлах отклонения и проведите их сравнительный анализ, иc
пользуя зависимости x(t), v(t) , фазовую траекторию и zрафик cпeK
тральной плотности,
1. Сравните спектральные плотности при малых и конечных уzлах откло
нения маятника от вертикали, В чем проявляется отличие линейных и
нелинейных колебаний математическою маятника?
2. Используя zрафики спектральных плотностей Sx(f). постройте зави
симость периода колебаний математическоzо маятника от начальноzо
уzла отклонения? Качественно объясните получаемые ре'3ультаты,
З. Используя формулу (8.23), постройте зависимость периода колебаний
математическоzо маятника от начальноzо уzла отклонения, Сравните
полученный результат с аналоzичными результатами, полученными при
анализе спектров S х и) .
4. Как выzлядят фазовые траектории математическою маятника при
различных значениях начальноzо уzла отклонения?
Возможности пакета MATLAB позволяют не только получить количе
ственные характеристики движения математическоzо маятника, яв
ляющиеся в известной мере статическими, но и получить дина.мическую
картинку, демонстрирующую есо движение.
Для создания анu}wации движения математическоzо Jwаятника необхо
димо в качестве первосо шаzа вычислить соответствующие декартовы
координаты по известной зависимости уzла отклонения маятника от
времени, хранящейся в матрице Z, возвращенной функцией ode4S. Как
видно из рис, 8,6, при нахождении маятника в nepBOAt, втором, третьем
и четвертом квадрантах координаты х. у соответственно по следую
щим формулам:
x(t) = Lsin(п  e(t )), y(t) = Lсоs(п  e(t))
x(t) = Lsin(п  e(t )), y(t) = Lсоs(п  e(t))
x(t) = IJsin e(t), y(t) = Lcos e(t)
x(t) = Lsin e(t), y(t) = L cos e(t)
l
208
у
Для создания анимационноrо клипа необходимо выполнить следующую
последовательность команд:
» clear аll % очистка рабочей области
» global omega
» g=9.8; % ускорение свободноrо падения
»L=I; % длина маятника
» Т=2*рi*(g/L)ЛО.5; % период колебаний
» omega=2*piff; % циклическая частота
» phiO=pi*0.995; % начальный уrол
»RO=[phiO О]; % начальные условия
» N=5000; % числов узлов временной сетки
»[t Z]=оdе45('ОsсШаtоr',[0:3*Т/N:3*Т],RО); % решение уравнения
% движения
% вычисление декартовых координат маятника
»for i=I:N+l
if Z(i,I»pil2
8 1 (i, 1 )=L*cos(Z(i,1 )-pil2);
81 (i,2)=L*sin(Z(i,1 )-pil2);
end;
if Z(i,I)<-pil2
81 О,1 )=- L *cos( abs(Z(i,l) )-pil2);
81 (i,2)=L*sin( abs(Z(i,l) )-pil2);
end;
if (-рil2<=Z(i,I))&(Z(i,I)<=рil2)
81(i,I)=L*sin(Z(i,l) );
8 l(i,2)=- L*cos(Z(i,I));
end;
end;
% визуализация MrнoBeHHЫx значений координат маятника (рис. 8.7)
»figure(I); plot(t,81(:,I),t,82(:,2));
% координаты подвеса
» 8а(I,I)=0;
» 8а(I,2)=0;
% координаты маятника
» 8а(2,1)=81(1,1);
» 8а(2,2)=81(1,2);
% отображение маятника в момент времени t=O (рис, 8.8)
» figure(2); plot(Sa(:,I),Sa(:,2),8a(2,1),8a(2,2),'o')j
»axis([-1.21.2 -1.21.2]);
у
х
1ш.. у
X{
Рис. 8.6
209

l!..?:!/!?!!j!'Р"''.'?А!.?i!...еl}Р...?.с:./I1!и-.!и-.'!...с.15.и-.х_ процессов в пакете МА ПАВ
. ....... ..... ........... ..... .................и...... .... ...........,
._..__.____!.:"!.?.l!!!.f..?..а..'.'!!._'!!!леб..'!'!!!.'!.Р.._'!.-=?..
»set(gca,'nextplot','replacechildren'); % включение режима перерисовки
% т-рафиков в одном и том же окне
r'r [''-, \ T"
i
I
1
» k=l;
» % создание анимационноrо клипа
» for i=l:lOO:length(Sl)
Sa(2,1)=Sl(i,1);
Sa(2,2)=Sl(i,2);
C=plot(Sa( :,l),Sa(: ,2),Sa(2,1),Sa(2,2),' о ');
F(k)=getframe;
k=k+l;
епд;
» movie(F,l) % однократное воспроизведение клипа
-За;;;;8.4-"-" .., -- ...._..-- .. .. .. -- -----..
Проанализируйте зависимости x(t), y(t) и убедитесь в правuльности
работы прО2раммы, вычисляющей завиСимости x(t), y(t).
-Заia---Ч-;8.5'--"----"'--...
Дополните созданный ранее дОКУhtент блоком, позволяющим одновре-
менно анимировать движения линеЙНО20 и нелинеЙНО20 математиче
ских маЯтников,
I I I I
-1 -0.8 --0.6 --0.4 --0.2
Рис, 8.8. Положение маятника в момент времени (=о
0.8
06
0.4
0.2
--0.2
-0.4
-0.6
0.8
-1 r
. ""T "''TTl
1
]
,,
0.2 0.4 0.6 0.8
8.3. Затухающие колебания
Из опыта известно, что в большинстве реальных колебательных систем
присутствует трение. Это приводит к тому, что в отсутствие подкачки энер
rии в колебательную систему амплитуда колебаний уменьшается до ее пол
ной остановки. Такие колебания называются затухающими. В качестве
примера колебательной системы, совершающей rармонические колебания,
рассмотрим движение rpуза на пружине (рис. 8.1). При движении с малыми
скоростями, как было подробно обсуждено в rл. 3, можно использовать MO
дель, в которой сила трения пропорциональна первой степени скорости
движения. В этом случае уравнения движения можно записать в виде:
d2x 2 dx
- = %x y (8.24)
dt2 dt
rде r  коэффициент затухания.
(\;' " /\
1\' ;! I
! \1 i
I i \
J. "
i:\ 1.
'i i.
i !:
, 11 i'
, I \ l'
,  ,
1: ; !
, \J
I\-
J \ . f \ '! \:' J
i \ i \ , , i \ i
1, I I J !
I \ J, I ! 1
; /\ 11' I i \ 1
. j i I J j
i: \ i ' \
J: .,
\ j : 1 l' : "
\' : j . ' \
/ :!! .. .1. \I
I \ I /\ . I
-0.2 1 I \ 1 1
:::l : i, '!:; ::, : j
J \ I I i f f I
08 l' I I 1 1 I \ 1 1 I '
. I i ! I \: iJ I J ' f
\ II '1 I J (; \ f
-1  j i_l J.... iL
о 10 20 30 40 50 60
Рис. 8. 7. ЗависиJ\lОсти координат от времени
(СI1.70итая кривая KoopдиHaтa х, пунктирная кривая координата у)
,'.'HH..,.'H'"'''.
Задача 8.6
], Создайте в пакете MATLAB тфаЙJl, содержащий описание функции,
стоящей в правой части системы дифференциальных уравнений, экви-
валентной уравнению (8,24),
2, Проведите расчеты и постройте зависимости x(t), v(t) для колебатель
ной системы с параметрами шо = 3, х(О) = 1, ,(o) = о, r = 0,5.
l
210
211

.'!..I!.!,!?'!'.е!!!.If!!...!:!..?-:!'!Р.!!<!..l!'l}!1!IЗ--и..'.!.u!'.?.'!!:С?.__1!./('!'.:'.:i!....._.._
.__._ш___шшш___________:fl!.e:zи..Р..CJ..'!!!.._!!.':.Б:!.'!'!!'!Ь!!':!'!Е?'.!.с.:._
3. Определите частоту и период колебаниЙ осциллятора, используя спектр
функции x(t) , Сравните спектры и частоту колебаниЙ со случаем
отсутствия затухания, Проведите расчеты для нескольких значений
r Е [0,5;4] и постройте zрафик зависимости частоты колебаний от ко-
эффициента затухания, Попробуйте определить аналитическое
выражения данной функции,
4. Можно определить амплитуду как маКСUJltальное значение функции x(t)
на одном периоде колебаний, Вычислите время релаксации т, оnределяе
мое как врел1Я, за которое амплитуда колебаний уменьшается в е::::: 2,72
раз относительно максимальноzо значения. Покажите, что значение т
неизменно в течение всею времени колебаний, Проведите расчеты для
нескольких значений r Е [0,5;4] и постройте zрафик зависиМости време-
ни релаксации от коэффициента затухания, Качественно объясните
полученную зависимость.
5, Постройте zрафик зависимости полной энерzии от времени для различ-
ных значений коэффициента затухания. Если энерzия маятника умень-
шается не монотонно, объясните причину это явления,
6. Вычислите средние значения кинетической, потенциальной и полной
энерzий по полному nериоду. Постройте zрафики зависимости этих
средних от номера периода, Проведите сравнительный анализ времен-
ных зависимостей этих средних от 't при различных значениях коэффи-
циента затухания у.
7. Проведите вычисления и постройте зависимости x(t), v(t) для у=4,5,6,7
и 8, Будет ли осциллятор совершать колебательные движения для всех
значениях у? Определим положение равновесия как точку, в которой
амплитуда колебаний становится меньше HeKomopozo заданноzо значе-
ния, наnри;иер, 1 o3. Дополните использованную вами последователь-
ность команд командами, позволяющим вычислять время достижения
равновесия, Постройте зависимость времени достижения равновесия
от коэффициента затухания,
8. Осциллятор называется критически затухающим при данном значении
Шо, если r равно наименьшему значению, при котором переход к поло-
жению равновесия происходит монотонно. Для каких значений у будет
юltеть место критическое затухание при шо = 3, шо = 2 ?
9. Постройте фазовые диаzраммы для случаев шо = 3, У = 0,5, 2, 4, 6, 8,
Ilроана.7Uзируйте особенности фазовых диаzрамм при различных вели-
чинах коэффициента затухания и объясните причину их качественных
отличий.
8.4. Вынужденные колебания линейноrо
rармоническоrо осциллятора
При воздействии на линейный rармонический осциллятор внешней пе-
ременной силы F(t) система будет совершать движение, которое от в отли-
чие от рассмотренных в предыдущих параrpафах называется вынужденны
ми колебаниями. Соответствующее уравнение движения имеет вид:
2 dx F(t)
X=%xy- +Ш, (8.25)
dt т
Задача 8.7
1. Создайте в nакете MATLAB документ, позволяющий находить численное
решение уравнения (8,25) для силы
f(t) = Аосоs(шt) , (8.26)
т
2. Проведите расчеты и постройте зависимости x(t), v(t) для колебатель-
ной системы с параметрами шо = 3, х( О) = 1, v( О) = о, r = 0,5, Ао = 1,
ffi = 2, Сравните полученные резулыпаты с результатами предыдущей
задачи, В чем состоит качественное отличие поведения функции x(t)
от случая невозмущенноzо движения? Чему равны период и частота и
функции х( t) после нескольких колебаний?
3. Проведите расчеты и постройте зависимости x(t), v(t) для начальных
условий х(О) = О, v(O) = 1. Чему равны период, частота и функции x(t)
после нескольких колебаний? Существует ли у функции x(t) предельная
форма, которая не зависит от начальных условий? Зависит ли поведе-
ние функции x(t) от начальных условий на коротких временах? Выдели-
те nереходную часть функции x(t), которая зависит от начальных ус-
ловий и затухает со временем, и установившуюся часть, определяющую
поведение функции на больших временах и независящую от начальных
условий,
4, Вычислите и сравните сnеюпры исходной функции x(t), части функции
x(t), соответствующей переходному периоду, части функции x(t), со-
ответствующей установившемуся движению.
5, Вычислите функцию x(t) и ее спектр для шо = 1 и шо = 4, Чему равны в
каждом случае период и частота установившихся колебаний ФУНЮJии
x(t) ? Какие параметры влияют на частоту установuвшихся колебаний?
212
213

с.!I!!:'.'!!!!!.:Р.!!..f!!:..!!.:!.'!Р.!!..!l!!..I!!:...1!.'!!.'!'::'.к-..':'.!..!!Р...о...'f.::.!...!!к-..!:..!f.!-.!!::!..
..ш. :fo!. (J,!еl}J1.(J<!...а.!!.uк-..й--л.б---а'!!!.l!.!I::'!?.ОLl.:=(J
Убедитесь в том, что установuвшееся движение описывается формулой
x(t) = Л(ш )соs(ш t + д-),
сде 8  разность фаз между приложенной силой и установившимися KO
лебанuями.
Вычислите 8 для <.00 = 3, r == 0,5, и значений <.о = о; 1,0; 2,0; 2,2; 2,4; 2,6;
2,8; 3,0; 3,2; 3.4. Повторите расчет для у = 1,5 и постройте zрафик за
висимости 8(<.0) для обоих значений у. Дайте качественное объяснение
полученной зависимости, (Указание. Для оценки 8 используйте спектр
стационарной части функции x(t).)
6. Постройте и проанализируйте фазовую диасрамму для случаев то = 3,
у = 0,5; 2; 4; 6; 8. Как выzлядят фазовые диасраммы при различных у?
Объясните обнаруженные отличия.
лебательной системы и внешней силы, Сравните резонансную частоту
кинетической энерzии и резонансную частоту амплитуды,
Задача 8.9
Исследуйте и опишите особенности движения линейносо zармоническо
со осциллятора под влиянием силы F(t) :
F(t) = coпst = Fo;
F(t) = Asin(pt);
F(t) = at ;
F(t) = ЕоеШ;
F(t)= Foeat cos(pt),
считая, что в начальный момент времени система находится в поло
жении равновесия (х(О) = О, у(О) = О), Рассмотрите случаи, КОсда
а,р«шо; a,p%; р=%; а,р»шо.
Задача 8.8
Результаты предыдущей задачи показываюm, что в установившемся
режиме характер колебаний линейносо zармоническоzо осциллятора с
трением зависит от частоты, приложенной к нему силы. Одна из xa
рактеристик этих колебаний  амплитуда, являющаяся некоторой
функцией частоты внешней силы.
1. Для начальных условий х(О) = О, v(O) = О вычислите значения функции
Л(т), называемой амплитудночастотной характеристикой, для
<.о = о; 1,0; 2,0; 2,2; 2,4; 2,6; 2,8; 3,0; 3,2; 3,4; 3,6; 3,8; 4,0; 5,0; 6,0 при
то = 3, r = 0,5, Постройте zрафик функции л( т) и качественно
объясните поведение этой функции. При наличии у функции А( ш)
максимума определите соответствующее данной точке значеН1fе
частоты <.от (резонансная частота). Сравните значение собственной
частоты zармоническоzо осциллятора <.00 и резонансной частоты <.от.
2. Вычислите значение функции А(т) в точке ш = шт и отношение
дт/ шт ' сде .<1<.0 является «шириной» резонанса, (Величина .<1<.0 определя
ется как ширина интервала частот между точками l1A-tплитудно
частотной характеристики, равными лт/J2.) Проведите вычисления
при то = 3, У == 0,1; 0,5; 1,0; 2,0 и оцените вид зависимостей Ат и
дт/ тт от у,
3, Вычислите среднюю за период колебаний кинетическую энерzию осцил
лятора в установившемся режи'J-1е при указанных выше параметрах KO
Задача 8.10. Демонстрация nринциnа суnерnозиции в динамике ли
нейных систем
1. Рассмотрите движение линейноzо 2армоническосо осциллятора с тpeHи
ем под действием периодической силы (8.10) при % = 3, х(О) = О,
v(O) = о, r = 0,5, <.о = 2 для двух случаев Ао = 1,2 Как соотносятся за
висимости x(t) в установившихся режимах? Какой результат будет
получен при Ао = 4 ? Удовлетворяют ли переходные режимы для различ
HblX внешних сил тем же соотношениям, что и установuвшиеся рe:ж:u.мы?
2. Вычислите отклики на внешние силы Fl, F2, F3 и Fl+ F2+ F3 при ш = 2,
Ао=0,5; <.о = 4, Ао=0,25; <.о = 6, Ао==0125, Сравните спектры ycтaHoвив
шихся режимов функций x(t) и сформулируйте принцип суперпозиции
для решений линейных уравнений,
3. Проведите расчеты, аналоzичные расчетам в п.2, для математичеСКО20
маятника, движение которосо описывает уравнением (8.14). Применим
ли nринцип суперпозиции к нелинейным системам?
ЛИТЕРАТУРА
1, Ландау Л, Д., Лифшиц Е. М. Механика. М,: Наука, 1958.
2. Мандельштам И. Л. Лекции по теории колебаний, М,; Наука, 1972.
3. Матвеев А. Н, Механика и теория относительности. М.: Высшая школа, 1986.
4. rулд Х" Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990. Ч. 1.
214
215

      _  !:..!1...0е.!!.'!Р...l!!'!!=-!!..с:..1!'!.().!.!:.!:1!!!:,.!'!..UU
Отмеченные обстоятельства определяют целесообразность рассмотрения
данных моделей в соответствующих курсах физики и компьютерноrо Moдe
лирования. Однако необходимо отметить два важных обстоятельства Bo
первых, аналитические решения уравнений движения длинных линеиных
цепочек ( N > 3 ) MOryr быть получены только для относительно небольшоrо
числа случаев [2]: 1) ko = k1 =... = kNI' то = т1 =... = mNI;
2)ko=k2=k4="" k!=kз=ks=",; mO=ml=...=mNl;
3) ko = k1 =... = kNI' то = т2 = т4 =..., тl = тз = ms =...;
4) ki = k -:1- kN,i =O,l,...,N 1, mo = тl =... = mNl' 5) kj = k, i = О, 1,...,N,
т; = т -:1- т NI' i = 0,1,..., N  2. BOBTOpЫX, большинство этих решений
оказываются весьма rpомоздкими и для их последующеrо анализа прихо
дится использовать ПК. 
Запишем уравнения движения для каждой массы колебательнои систе
мы, представленной на рис. 9.1:
{ moХо = koxo  k1 (хо  х1)
mjXj =k;(x; XH)kj+l(X Xj+l),=l...N 2.
mNIXN1  kN1 (XN1 XN2) kNxN1
для удобства дальнейшеrо решения запишем уравнение (9.1), введя обо
значение йJp = ka/mp, в следующем виде:
{. 2 2( )
ХО = йJOOXo  йJlO ХО  Хl
Х  йJ(x,  Х. 1 )йJ 1'(Х'  X"tl)' i = l...N  2.
i  11 , , 1+ I I
XN1 = йJ!NI(XN1 XN2)йJNIXN1
Следуя общему подходу к решению рассматриваемой задачи, изложенному
в [3], ищем решение системы дифференциальных уравнений (9.2) в виде:
х' = A-еjlLII, i = О, l..N  1. (9.3)
, ,
Подставив (9.3) в систему (9.2), сrpуппировав члены, пропорциональные
Ai, и записав систему в матричном виде, получим:
В.А=О,
rлава 9
МОДЕЛИРОВАНИЕ
ВОЛНОВЫХ ЯВЛЕНИЙ
9.1. Введение
в данной rлаве мы продолжаем рассмотрение колебательных движений,
начатое в rл. 8, в которой были рассмотрены raрмонический осциллятор,
линейный и нелинейный математические маятники. Здесь в качестве базо
вой математической модели выбрана линейная цепочка связанных raрмони
ческих осцилляторов. С помощью данной модели при достаточно большом
числе частиц оказывается возможным изучить основные особенности вол
новых движений (в первую очередь показать, что энерrия передается вдоль
цепочки, хотя каждый осциллятор колеблется вблизи cBoero положения
равновесия), осуществить в пределе непрерывной цепочки переход к ли
нейному волновому уравнению. Далее мы рассмотрим такие фундаменталь
ные понятия волновой теории, как беryщая волна, стоячая волна, волновой
пакет, фазовая скорость, rpупповая скорость, дисперсия, интерференция,
дифракция, рефракция, поляризация, принцип Ферма.
9.2. Моделирование свободных колебаний цепочки
связанных rармонических осцилляторов
Модели, представляющие собой линейные цепочки (рис. 9.1), состоящие
из конечноrо или бесконечноrо числа связанных осцилляторов, оказались
весьма эффективными и в настоящее время используются в различных об
ластях физики: физике твердоrо тела, физике сплошных сред, химической
физике, радиофизике и др. (Например, в [1] для описания системы трех свя
занных электрических колебательных контуров использована модель,
представляющая собой систему шариков с массами т/, mz, тз, связанных
между собой пружинками одинаковой жесткости k,) Используя модели ли
нейных цепочек, оказывается возможным естественным образом осущест
вить переход к волновым процессам и ввести такие понятия, как длина вол
ны, rрупповая скорость, фазовая скорость, дисперсия и др.
rде
[ .40 1
Аl
А= ,
AN 1
........
Рис. 9.1
217
(9.1)
(9.2)
(9.4)

I.lbl(J ".!.J1!(J.е.!:.'..е.л..1!:р'О,!111.'.1!и?и ческlV:
6 nакете МА ТLAB
9. МоделиРО6а1!!:!.'!.. 60:".!JIII
        
NI
.t(t) =  L СаЕ:а% sin(%t + СРа)'
а=О
Для решения задачи Коши системы дифференциальных уравнений (9.2)
необходимо задать значения координат х(О) и скоростей х(О) каждоrо тела
системы в начальный момент времени и решить систему уравнений
NI
х(о) = L СаЕ:а COS(CfJa)
а=О
NI
х(О) =  L СаЕ:аО)а sin(CfJa)
а=О
rде Z  нулевая матрица, размерности NlxN 9
[з&0) 3) ... 3&NI)]
,;:;,(0) ,;:;,(1) ,;:;,(NI)
I I I
Е>= . ,
(O) (I) ,;:;,(NI)
NI NI NI
[%3&0) 3) ... o)N13&NI)]
т...=(О) т.,;:;,(I) ... O)N 13(INI)
 u1 11 
Е> = . ,
V: :
(O) (1)  ,;:;,(NI)
 %NI  NI O)NINI
[Со cos(CfJo) J
С= CN]CS(CfJNI) ,
[ Cosin(CfJo) J
Cv = CN] Si(CfJN]) ,
Система уравнений (9.13) оказывается нелинейной, однако блочная
структура матрицы позволяет найти решение данной системы, не прибеrая к
в  трехдиаrональная матрица, элементы которой вычисляются по сле
дующим правилам:
В 2 2 2 В 2
00 = O) + тоо + тlО ' О] = mlO '
2 222 2'2N2
B;,I1 = O)ll ' В;; = O) + Ш;; + Ш;+];, В;;+I = O)i+I;' 1 = ".  ,
(9.5)
В 2 В 2 2 2
NIN,2 = O)N]N'I' N.IN] = O) + O)NIN1 + mNNl'
Необходимым и достаточным условием существования решения систе
мы уравнений (9.4) является равенство нулю определителя матрицы В
1тВ  т2: = О. (9.6)
Уравнение (9.6), называемое характеристическим уравнением, является
уравнением степени N  1 относительно 0)2. Оно имеет в общем случае
N  1 различных вещественных положительных корней O), а = 1,..N  1 .
Каждому собственному числу т соответствует собственный вектор За'
являющийся решением уравнения
n.';:;'  2,';:;'
 a  Ша a'
относительно неизвестных Са,ера .
Запишем (9.12) в матричном виде
(Х(О))=(Е> ) ( )
х(О) Z:v' v '
(9.7)
11I
111
l'
1.
1"
li
1'1
,'1
i!
1:1
il!
"
rде О  трехдиаrональная матрица элементы которой вычисляются по сле
дующим правилам:
222
.000 = тоо + 0)10, .001 = т]o,
2 2 2 2. N
.Qi.i1 = mii ' П;; = 0);; + Ш;+];, .Q;;tl = mi+li' t = 2,..  2,
(9.8)
.О = ф2 D. = 0)2 + 0)2
N]N2 NIN]' N]NI NIN] NNI'
Частоту т, а = 1,..N  1 называют частотой нормальных колебаний, а
вектор 3а  вектором нормальноrо колебания, отвечающеrо ай частоте.
Вектор нормальноrо колебания ra меняется во времени по закону
ra = 3а cos( O)at + сра).
Общее решение системы дифференциальных уравнений (9.2)
суперпозиция всех векторов нормальных колебаний ra:
Nl
x(t) = L СаЕ:а cos(ma1 + СРа)
а=О
(9.9)
x(t), есть
(9,10)
,
I
['де С а' СРа  произвольные постоянные, определяемые из начальных условий,
Скорость движения масс можно определить, продифференцировав (9.1 О)
по времени:
218
219
(9.11 )
(9.12)
(9.13)
(9.14)
(9.15)
(9.16)
(9,17)

l!.А!."!.:'Jl..I.й.еА!.й..i!!.l}.Р!!.l!/'!:р'!IЗ:,!!ш'.У!..й-':I:.(;.й-<!'.Il!:е"!..:fl.!.:!.Т:!.. Ш... ш''ш'"
ш шшшш9:fl!.й.!!.е.::IlР..?l!.'.'.Il.:в--й-:1!!.?..l!.lifI..:.'.'.и-
(9,18)
(9.19)
Предваряя описание решения задачи об описании колебаний цепочки
связанных осцилляторов, приведем алrоритм ее решения:
1. Задать число тел, образующих цепочку N.
2, Задать массы тел т;, i=O,1 ..., N9,
3, Задать значения коэффициентов жесткости пружин ki, i=O,I..., N.
(Отметим, что для описания движения цепочки со свободным концом дoc
таточно положить ko = О или kN = О.)
4. Вычислить элементы матрицы Q в соответствии с (9.8).
5. Найти собственные числа йJ матрицы а,
6. Найти собственные векторы =-а' соответствующие набору собствен
2
ных частот йJ а .
7, Задать начальные условия х(О), х(О).
8. Решить систему линейных уравнений (9.18), (9.19) относительно BeK
торов С] и С2 соответственно.
9. Вычислить координаты вектора Св соответствии с (9.20),
10. Вычислить значения начальных фаз нормальных колебаний ер; в co
ответствии с (9.21).
11. Определить законы движения тел, образующих колебательную сис
тему в соответствии с (9.10) и (9.11).
12. Провести анализ полученных законов движения.
Данный алrоритм в пакете МА TLAB реализуется следующей последова
тельностью действий:
»clear аН
» N=3; % число тел колебательной системы
» m=[1 2 1]; % массы тел колебательной системы
»k=[llll]; % жесткости пружин колебательной системы
»RO=[-0.2 0.0.3]; % смещения тел в момент времени t = О
» vO=[l .3 О]; % скорости тел в момент времени t = О
% вычисление элементов матрицы йJp = ka/mp
»for alpha=I:N+l
for beta=I:N
omega(alpha,beta)=k(alpha)/m(beta);
end;
end;
» i=l:N;
»j=l:N;
численным методам. Для этоrо, сначала, решив две линейные системы
уравнений
o 'С1 = х(О),
0уС2 = х(О) ,
найдем векторы C1, с2, затем координаты вектора С
с; = .JC? + Су;, i = O,l,...N 1,
и далее значения начальных фаз каждоrо нормальноrо колебания:
ер; = arctan( :. ).
(9.20)
(9.21 )
Отметим, что функция arctan на интервале [0;2тс] является двузначной
(рис. 9.2), поэтому для выбора правильных значений данной функции необ
ходимо контролировать знаки числителя и знаменателя дроби в выражении
(9.21). Как очевидно из рис. 9.2, правильное значение yrла выбирается по
следующим правилам:
1
1
О 0.4
l
2 О 1 :! 3 4 5 б
.9=
ж
Рис, 9.2, К выбору правUЛЫЮ20 значения У2Ла
arcta{ sin(x»)
cos(x)
1l' + at'ctan(!n(x?)
cos(x)
1l' + arctan(in(x) )
cos(x)
2ТС' -+- arctan( il1i2)
. cos(x)
при sin(x) ;:: О, cos(x);:: о
приsiп(х) < O,cos(x) > О
при sin(x) < O,cos(x) < О
при Sin(x) > О, cos(x) < о
220
1I
(9.22)
221

!l.?!'....п::!!!!'3.=l!!.i!!:..дел'2?с:.'!!..tE'!!!!:!.l!...с...!!Р...й...'!!:с!..!. '!..f!:..!'!:..!!..1?!:.1..f!.................
.. .:Л1..0Р"?!.!'?3.!!?..::!!.1Z:й.
% вычисление элементов матрицы ОМЕаА в соответствии с (9.8)
» OMEGA(iJ)=O;
»for i=l:N
if i==l
OMEGA(i,i)=omega(1,1)+omega(2,1);
OMEGA(1,2)=-omega(2,1);
eod;
if i> 1
if i<N
OMEGA(i,i-l)=-оmеgа(i,i);
OMEGA(i,i)=omega(i,i)+omega(i+ l,i);
OMEGA(i,i+ 1 )=-omega(i+ l,i);
else
OMEGA(i,i-l)=-оmеgа(i,i);
OMEGA(i,i)=omega(i,i)+omega(i+ l,i);
eod;
eod;
eod;
» [Sigma,Teta]=eig(OMEGA); % вычисление собственных значений и
% собственных векторов матрицы ОМЕаА
» Теtа=ТеtаЛО.5; % вычисление собственных частот
» for i=l:N
for j=l:N
Sigma VG,i)=- Teta(i,i)*SigmaG,i);
eod;
eod;
»Сl=SigmаЛ-l*RО'; % решение системы уравнений (9.18)
»С2=SigmаVЛ-l*vО'; % решение системы уравнений (9.19)
»С=(Сl.Л2+С2.Л2).ЛО.5; % вычисление координат вектора С
» clear alpha
% вычсление фазы нормальных колебаний в соответствии с (9.21), (9.22)
» for l=l:N
if C(i)==O
alpha(i)=O;
else
alpha(i)=a tao( С2( i)JC 1 (i»;
if Cl(i)<O
alpha(i)=pi+alpha(i);
eod;
if Cl(i»O
if C2(i)<O
alpha(i)=2 *pi+alpha(i);
eod;
eod;
eod;
eod;
» N=leogth(OMEGA);
»Nl=2Л13; % число узлов временной сетки
» j=l:Nl;
» Тmах=80; % правая rpаница BpeMeHHoro интервала
»1O)=G-l)/(Nl-l)*Тmах; % координаты узлов временной сетки
% вычисление значений координат тел в узлах временной сетки
»for j=l:Nl
s=zeros(N,l);
for i=l:N
s=s+C( i) *s igma(: ,i). *cos(T eta(i,i )*10 )+alpha(i»;
eod;
X(:J)=s;
eod;
% вычисление значений скоростей тел в узлах временной сетки
»for j=l:Nl
s=zeros(N,l);
for i=l:N
s=s+C(i)* Sigma(: ,i). *Т eta(i,i)*sio(T eta(i,i)*1O)+alpha(i»;
eod;
Xv(:J)=-s;
eod;
% визуализация зависимостей MrHoBeHHbIx значений смешен ий и скорости
% от времени
» figure(l);figure(l);plot(t,X(l,:),' -k' ,t,X(2,:),' --k' ,t,X(3,:),' :k')
» figure(2) ;plot(t,X v(l,:), '-k' ,t,X v(2,:), '..k' ,t,X v(3,:),': k')
% построение траектории движения тел на фазовой ПЛОСКОСПf
» figure(3);plot(X(1,:),Xv(1,:»
» figure(4);plot(X(2,:),Xv(2,:»
» figure(5) ;plot(X(3,: ),Х v(3,:»
% вычисление спектров зависимостей смещений тел системы от времени
» cl=fft(X(l,:»;
» c2=fft(X(2,:»;
» c3=fft(X(3,:»;
» j=2:Nl/2;
'* вычисление спектральной плотности смещений тел
» CmlG-l)=аЬs(сlG-l»/(Nl/2);
» Cm2G-l )=abs(c2G-l )/(Nl/2);
222
223

,1
1,
-Компьютерное моделирование физических nроцессов в nакете МА TLAB
.. ..._!______й-!!..e.-!'.,!poвaHиe !..ОЛllовых }!!!!.'.!.'!..ий
» Cm3(j-l)=abs(c3(j-l»/(Nl/2);
»Freq(j-l)=(j-l)lI'maх; % вычисление частот спектрaJ.IЬНЫХ rармоник
% визуализация спектральных плотностей смещений тел
»figurе(З);sеmilоgy(Frеq,Сml, '-k' ,Freq,lO*Cm2, t --k',...
Freq,500*Cm3,': k')
» эxis([О 2.5 10Л.З 2000])
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 9.39.8.
"
,1
.'
.1
. I
, .
, ,
, ,.
, .
, .
! .
 r .
.
"
"
"
, 1
, ,
, I
, I
. ,
, !
, i
,1
.,
':
-,
;
.
,
.
,
,
I 1
: '
-2 '
1
: :
,
.3 \,1
Рис. 9.4, Зависимость
мzновенных значений
скорости движения тел
от времени
. ''T'
;,
"
"
.,
, ,
11
,
,
,.
,
1.
1
,
I
I
,
:
I
I
1
:
1 1
1 1.
 :'
I ,
I :
!
.
:)
Рис. 9.3, Зависимость
МZHoвeHHЫX значений
смещений тел
от времени
3 .
,\ 1\ I .; 1\
J  !' :  !\ :  : :
I ,1 I ' '1 I 1: ' 
: :  : . I 1 I : :
: j t I I I
'.i" i J\   ! I!A '\, /,
-, J ,j,.; ,\./ ' li: '1'
1, I :  I V:: f
,\ J I j 
, : 11) \} 1,;, \\ \ i
.3' V' ':   \;
60
,
50
60
40
,
, ,
I i
,
,
,
,
1,
V
'.
"
,1
,1
-  
' ,! "
.1
1 ,
, '
,
\
"
IJ"
"
1,
/'
,
, ,
, ,
, ,
, I
. ; ,
-} : :
I I .'
; t ;  
[ f \ : :\,
1 . ,
1 I ! 1 :
I : :1 ,:
, ..,,:' .1
\ 1 \:: i :;: :.
f! : : I :. Ij
:.. 1: : ; i
:; :, 1; \ J
11 \ I :'
11 "1' 1_
I I I , I ,  :
l! V \] \1
 
.... .... ..............L._
О ro   40 Ю 60 ro
.4  
о 10 20 за
224
60
,
70
J
R157б
4 ............... ...............
I
3
2
о
-,
-2
-3
-4 , , ,
4 -3 -2 -, О 2 3 4
Рис, 9,5, Фазовая траектория первоzо тела
4
3
2
-2
-3
4 L...
-4

-3 2 -, О
2
,
3
Рис. 9,6. Фазовая траектория второzо тела
225

ш ...ш?':.1:!..?'_?:!'.'!J!I}!.с:.!!I!.?':'l!!.?в...I!..!!:l,!!,.:gш
.Компь,!!!!!!!р}!ое МО!р'а!!,!=-р',!!uчеСК3J!очесс::!!!..!!..!!.'!..кет!..!!!!-.!!:АВ ШШ.
I
'!I
4
ЗАМЕЧАНИЯ
1, Описанная последовательность команд позволяет проводить анализ
движения линейной цепочки с произвольным числом масс. Однако вводить
данные при больших значениях N недостаточно удобно. Поэтому для ана-
лиза колебаний длинных линейных цепочек нужно сначала создать файлы,
содержащие значения масс, коэффициентов жесткости пружин, начальные
смещения и координаты вектора начальной скорости, используя, например,
проrpамму электронных таблиц Excel. При этом следует расположить ис-
ходные данные в одном столбце и сохранить их в файле в формате «Тек-
стовый файл (разделителипробелы)>>. В этом случае, созданный файл бу-
дет иметь расширение txt. Обратите внимание, что файл нужно размещать в
папке, имеющей название, состоящее из букв анrлийскоrо алфавита, имя
файла также должно состоять ИЗ букв анrлийскоrо алфавита. Чтение данных
из файлов данных типов осуществляется командой dlmread. Например, ec
ли значения масс пружинок сохранены в файле mass.txt, находящемся на
диске С в папке Data, считывание данных осуществляется следующей ко-
мандой: m = dlmread('C:\Data\mass.txt'). Обратите внимание, что при соз-
дании файла необходимо использовать настройку, при которой для разделе
ния целой и дробных частей действительных чисел используется точка. Для
установки соответствующеrо стандарта ввода действительных чисел необ-
ходимо выполнить следующую последовательность команд операционной
системы Windows: Пуск  Настройка  Панель управления  Язык и
реrиональные стандарты  Настройка, затем в поле Разделитель целой
и дробной части установить «.».)
2. Для нахождения собственных чисел и собственных векторов матрицы
нами использовалась функция eig. При обращении
» d = eig(A)
функция возвращает вектор-столбец, содержащий собственные значения
матрицы А. При обращении
» [V,D] = eig(A)
функция возвращает две матрицы, диаrональная матрица V содержит соб
ственные значения матрицы А, матрица D  собственные векторы, записан-
ные в виде вектор-столбцов,
3
2
О.
.1
-2
-3
-4 2 3
-4 -3 .2 -1 О
Рис. 9.7, Фазовая траектория mpembezo тела
10'
10'
I
101 n
11
"
!\ f:
1\ ;-
100 / J\ ,: \
" '-" \..
'.
10" "'0""'__'____"""0 'Ш-'ш-ш. ......__.... -Ш-Ш.
10"
10.] ......L.
О 0.5
Задача 9.1
1. Исследуйте свободные колебания системы, состоящей из двух связанных
осцилляторов, Вычислите зависимости xo(t), '\'0(1), Х1 (t), х\ (t) для на-
чальных условий хо(о) = 0,5, хо(о) = О, х\(о) = О, х\(О)=О считая,
что {ko = k2 = l,k) = 0.8,п = т) = 1}, {ko = k2 = !,k] = l,то = т1 = 1}
2
2.5
1.5
Рис. 9.8. Спектры функций x(t;) (масштаб по оси оУ полулоzарифмический,
для большей наzлядности zрафики сдвинуты друz относительно друzа)
226
227

1!?(ь?.т-еl!!О=-"!?''??'l!..а!/:rJ!,!З-11'!с..К-.l':У !y?=c.c.?_в... :r:.':11=IT...L...1..l!......._ _ ...Ш.
ш.. ....... : 1v!...Оel!.lll!овl!..l!!!I!..?:1!.?l вл---:/:
на временном интервале [0;800}, выбрав вре.Аtенную сетку, состоящую
из i4 точек Что представляют собой изучаемые движения?
2, Проанализируйте удвоенные спеюпры зависuмостей xo(t), Х1 (t) (Здесь
множитель 2 учитывает тот факт, что в спектре функции одноЙ
частотной компоненте соответствуют две zapMOHUKll с положите.1Ь
ной и отрицательной частотами (CAt, раздел 7,7)) Как соотносятся /Ш...
ординаты экстремумов спектров зависимостей xo(t), Х1 (t) С собст---
венными частотами, значения которых возвращаются в вектор Е? Как
соотносятся значения экстремумов спектров зависимостей xo(t). Хl (t)
со Зllаченишtи коэффициентов, входящих в выражение (9.11)? (Указа---
lIие. В выбранных в описанном выше дОКУАlенте обозначениях завиСUJI1О'"
сти координат тел колебательной системы имеют вид:
xo(t) = 80,оСо cos (30t + ао) + 80,\С1 cos (3\t + а1)'
х\ (t) = 81,ОС1 cos (30t + ао) + 81,\С\ cos (3\t + а1)')
3. В че.м причина различий между значенUЯAtu коэффициентов, входящих
в выражения для xo(t), x\(t), и значениями экстРeJ.tумов cooтвeтcт
вующих спектров? Как />1еняется точность спектральной оценки коэф",
фициентов, входящих в выражения для xo(t), х\ (t), при изменении шаzа
временной сетки? Как меняется точность спектральной оценки коэф---
фициентов, входящих в выражения для xo(t), x\(t), при длитеЛЫlOсти
сиzнала? Объясните полученные результаmы.
Задача 9.4
Решите задачи 9,1, 9,2 для начальных условий Хо(О) = 0.5, Хо(О) = О,
Х1 (о) = O,5, Х1 (О) = О, Вычислите и изобразите zрафически энерzию
каждой частицы как функцию времени и качественно опишите ее пове-
дение, Проведите исследование и определите, как зависит частота ко...
лебаниЙ от жесткости пружин ko = k2, k1, Объясните полученные ре...
зультаты, Сравните полученное значение частоты с соответствую---
щим значением, найденным в предыдущей задаче,
Задача 9.5
Решите задачи 9,1  9.2, считая, что {ko = k2 = 1, k\ = 0.2,
то = 1, т2 = 2} . Как меняются частоты каждоzо колебания при k! = 1 ?
Исследуйте зависимость частот собствеНlIЫХ колебаний от массы тел
колебательной системы.
Задача 9.6
Дополниmе описанный выше документ модулем, позвОЛЯЮЩU/>1 решать
обратную задачу: по известным значениям собственных частот и со...
ответствующим им собственным векторам определять начальные yc
ловия, при которых возбуждается только одна мода колебаний. Про---
верьте правильность работы модуля, задав соответствующие началь---
ные условия, вычислив зависимости хо (t), Х1 (t) и проанализировав
спектр данных зависимостей,
Задача 9.2
Решите задачу 9.1, считая, что {ko = k2 = 1, k\ = 0.2, n'1J = m\ = l}, Как
меняются частоты каждоzо колебания при k\ = 0.1.
Задача 9.3
Решите задачи 9,1, 9.2 для начальных условий Хо(О) = 0,5, Хо(О) = О,
Х1 (О) = 0.5, Х1 (О) = О, Получите выражения для кинетической и потен...
циальной энерzий каждой частицы. Пользуясь законпн сохранения энер---
zuu, справедливоzо для всей системы, проверьте полученные выражения,
Вычислите и изобразите энерzию ка:)lCдоЙ частицы как функцию epCAte...
ни zрафически, и качествеюlO опишите ее поведение, ИсследуЙте, как
зависит частота колебаниЙ от жесткости пружин ko = k2, k[, Объяс
ните полученные результаты,
Задача 9.7
Как известно [4}, при сложении двух колебаний x\(t) = Acos(cqt) ,
Х2 (t) = А cos( Ш2t) с равными амплитудами и близкими частотами Ш1'
Ш2' отвечающим следУЮЩeJ.tу условию: Ш2 = Ш1 :t I1ш, zде I1ш« Ш[, Ш2'
в рассматриваемой системе всеzда возникают биения, т, е, зависи---
мость координаты от времени описывается зависимостью
x(t) = [2АСОS(ШmОdt)]СОS(Шmid/i),
zде Штill/ = (Ш1 + Ш2 )/2, Шmоd = IШj  Ш2 !/2 .
1. Используя результаты задачи 9,3, выберите значения коэффициентов же...
сткости прy:ж:uн, обеспечивающих возникновение в системе биений, Ис---
пользуя результаты задачи 9,6, опредШlllте начальные условия, при кото---
рых в системе связанных ОСЦllJU/Яторов возникают биения. Для найденных
начальных условий вычислите зависимости xo(t), xo(t) , х[ (t), х\ (t),
228
229

I!I
l!..Й-::'!!_'!!.fJ!Iй-!...?.е!!.'!.!'.:!f!..'.'!.!:.Р.!'.!..'!::к-'!:.п-Е.Й-I!е..й-__в_п-I!..п:..:!:,!.у...!1_
ш.._:.!!!!'!..:l!.'!!!..Й-!!!.'!.'!.=!!..й-!'!I?_,:?!:'.3!",l!..:'.!.'!.
2, Определите значения O)mid/' O)тod' задайте функцию x(t), вычислите
М2новенные значения смещения, описываеА-t020 данной функцией, и oтo
бразите их на 2рафике, Сравните полученные результаты с результа
тамирасчетов по формуле (9,10),
Таким образом, в результате решения задач 9.19.6 можно сделать сле
дующие выводы: движение колебательной системы, состоящей из двух свя
занных осцилляторов, всеrда представляет сумму двух движений, имею-
щих различные частоты (нормальные колебания). Существуют начальные
условия, при которых в системе возбуждается только одно нормальное ко-
лебание. При {ko = k2 =1= k1 ,то = т1 = 1} нижняя частота нормальных коле-
баний 0)1 = .)ko/m , верхняя частота нормальных колебаний
0)2 = -J( + 2k'I )/ т. При возбуждении нормальных колебаний с частотой
0)1 частицы колеблются в фазе, с частотой 0)2 частицы колеблются в про
тивофазе. При определенных значениях масс, коэффициентов жесткости
пружин и начальных условиях в колебательной системе возникают биения.
1. Сравните численные значения собственных частот 0)" с известным ана-
литическим результатом 0), = 2 r k Sin(), s = 1,2,.. ., N [2, зада-
, т 2(N + 1)
1rS
ча Н!! 7.1}, 2де к! = называют волновым вектором SЙ моды
2(N + 1)
колебаний, Постройте зависимость О)! = О)! (к).
2. Величину V f = О)! / к s называют фазовой скоростью колебаний. Пост
ройте 2рафик зависимости V f = V f (к s) и убедитесь в том, что при
S :::= 1 (длинноволновой предел) фазовая скорость не зависит от волново-
20 вектора.
Задача 9.11
1. Рассмотрите движение колебательной системы, состоящей из N свя-
занных осцилляторов (N  10), считая, что {т; = 1, i = 0,1,..., N  1,
kj =I,j=O,I,...,N}. Задайте начальные условия хо(О) = 0.5,
х;(О) = O,i = 1,2,.. .,N  1.
2. Вычислите М2новенные значения функций Х; (t), i = 0,1,..., N  1 .
3. Используя М2новенные значения функций x;(t), i =O,I,...,N 1, определи-
те скорость распространения возмущений в линейной цепочке, (Указа
ние. Для нахождения скорости распространения возмущения следует
определить временные интервалы (п (n=1,2,...,N  1), в течение которых
смещение п-20 тела превысит заданное значение (например, 102), затем
по зависимости п=f(t,J, используя линейную ре2рессию., оценить У2Л060Й
коэффициент лцнии ре2рессии.)

Задача 9.8
Рассмотрите движение колебательной системы, состоящую из трех
связанных осцилляторов, считая, что {ko = k4 = 1, kl = k2 = kз = 0.2,
т; = 1, i = 0,1,2}, с ненулевыми начальными условиями. Опишите зави-
симость смещения частиц от времени,
Задача 9.9
Решите задачу 9.8 с начальными условиями, приведенными в табл, 9.1,
пола2ая все начальные скорости равными нулю,
Таблица 9.1. Начальные условия для задачи 9.10
хо(О) xl(O) Х2(0)
Слvчай 1 0.5 0.5 0.5
Случай 2 0.5 O,5 0.5
Случай 3 0.5 О -0.5
Задача 9.1 О
Рассмотрите движение колебательной cucmeA-tbl, состоящей из N свя-
занных осцилляторов (N  1 О), считая, что {т; = 1, i = 0,1,. . ., N  1,
k j = 1, j = 0,1" .., N } , при различных начальных условиях.
. в пакете MAТI.в для нахождения наклона линии pezpeccuu в смысле наименьших
квадратов необходимо вьmолнить следующую последовательность команд:
% задание исходных данных
» (=[О 123 4)';
»у=[О.1 0.92.12.9 4.15}';
% решение системы уравнений метода наименьших квадратов
»X=[oпes(size(t)) t};
» а=х\у;
» Т=О:О.ОI :4;Т=Т'; % задание временной сетки для вычисления значений
% аппроксимирующей функции
» Y=[oпes(size(n) Tf*a; % вычисление значений аппроксимирующей функции
» plot(t,y, 'о', Т, Y,' 'у; % визуализация исходн. данных и аппРОКСlL'o1ирующей функции
230
231

{)'!"!:fJ!.О=I!..r?..е:!.,!?.!!.ваI}!I!..р''!..З---и.:.!.:'5..U'!.р'О':r:.{)!!.!!'!с:.=!'::.!!}J!::!!. ........._... ..'"'" . . .
.. ....?:_А:!{)I!!!.'!?овl!..'!':!_:{):'I!!{)l!.!!.!!..='!..'!!i
2 2 ( ) F(t)
ХО = ШооХо  ШlО Хо  Хl + 
то
Х; = Шi7(Х;  ХН)Шili(Хi  Xi+l)' i = 1...N  2.
XN1 =ШINI(ХN1 ХN2)ШNIХN1
(9,23)
2) задать вектор, содержащий начальные условия (xi(O), х';(О) ,
i=1,2...N1);
3) обратиться к одной из функций, возвращающих таблицу, содержа
щую численное решение системы ОДУ, например функции ode45;
4) провести визуализацию полученных численных решений.
Описание функции, возвращающей значения первых производных сис
темы ОДУ (9.23), мы разместили в файле Euler2.m, листинr KOToporo при
водится ниже.
% листинr файла Euler2.m
function z=euler2(t,x)
% описание функции, возвращающей значения первых
% производных
global k m А Omega
N=length(m); % число тел колебательной системы
z=zeros(2*N,I);
z(I)=x(2); .
z(2)=-(k(1 )/m(l) )*х( 1 )-(k(2)/m(l) )*( х(1 )-х(3))+ F( t,A,Omega);
К=3;
for i=2:N-l
z(K)=x(K+l);
z(K + 1 )=-(k(i)/m(i) )*(x(K)-х(К- 2) )-(k(i+ 1 )/m(i) )*(х(К)- х(к + 2»);
К=К+2;
end;
z(2*N-l)=х(2*N);
z(2*N)=-(k(N)/m(N) )*(х(2 *N -1)-х(2 *N-3))-k(N+ 1)/m(N)*x(2*N -1);
function f=F(t,A,Omega)
% функция, описывающая внешнюю вынуждающую силу
f=A *sin(Omega*t);
Далее для нахождения и визуализации численноrо решения системы
ОДУ (9.23), описывающих систему, совершающую свободные колебания,
необходимо выполнить следующую последовательность команд:
» clear аН;
» global k m А Omega
» N=16; % число тел колебательной системы
» n=I:N;
»т(п)=1; % задание масс тел
» i=l:N+l;
4. для тО20 чтобы убедиться в независимости вашей оценки скорости pacпpo
странения возмущений от N, повторите расчеты для б6льших значений N.
5. Проведите исследование и определите зависимость скорости pacпpo
странения возмущения от массы тел, образующих колебательную cиc
тему, и жесткости пружин,
6. Рассмотрите (<неупорядоченную» систему при помощи приписывания
телам колебательной системы различных масс (например, с помощью
2енератора случайных чисел). Как влияет беспорядок на скорость pac
пространения возмущения?
7. Рассмотрите (<неупорядоченную» систему при помощи приписывания
пружинам колебательной системы различных жесткостей (напршнер, с
помощью 2енератора случайных чисел). Как влияет беспорядок на CKO
рость распространения возмущения?
Задача 9.12
Используя описанный выше документ, решите задачу 7.4 из задачника [2].
9.3. Моделирование вынужденных колебаний
цепочки связанных rармонических осцилляторов
Для описания движения цепочки связанных rармонических осциллято
ров под действием вынуждающей силы следует добавить в правую часть
системы уравнений движения (9.2) соответствующие выражения для внеш
ней силы. Дальнейшее рассмотрение оrpаничим случаем, коrда сила прило
жена к точке А колебательной системы (рис. 9.1), что для достаточно длин
ных цепочек не при водит к потере общности.
Система дифференциальных уравнений в данном случае принимает сле
дующий вид:
Будем искать численное решения системы (9.23). Напомним, что ранее нам
уж приходилось решать системы дифференциальных уравнений BToporo по
рядка (см, rл, 4, 6), ДJIя этоrо нами использовался следующий aлrоритм:
1) задать векторфункцию, возвращающую значения первых производ
ных системы ОДУ (размерность функции 2М;
232
233

!
.?:.п!'.I?'!!:l!!.'!1'::!..?:l!.fJ.?I!..II'!I!..1!.'!..:l!!:..fJ.?l1.:I},!!.!!.l!..:!!!..:!!...А.!!:...шшш. ш'..ш..шш... "ш...
... :.J:!!!.:3.':!Е.?С:!!,!=?:1'.!?lшв!l.еl!...
»k(i)=l; % задание жесткостей пр ужин колебательной системы
» n=1:2*N;
% начальные условия
» RO(n)=O;
» RO(1)=0.5
» А=О; % амплитуда внешней вынуждающей силы
» Omega=O.O; % частота внешней вынуждающей силы
» Tfin=50*pi; % правая rpаница временной сетки
»Nр=2Л131; % число узлов временной сетки
» [Т ,M]=ode45('euler2' ,[O:Tfin/Np:Tfin],RO);
»subplot(4,4,1);plot(T,M(:,1»;axis([0 40 -0.5 0.5]);titIe('n=l');
»subplot(4,4,5);plot(T,M(:,3»;axis([0 40 0.5 0.5]);title('n=2');
»subplot(4,4,9);plot(T,M(:,5»;axis([0 40 -0.5 0.5]);title('n=3');
»subplot(4,4,13);plot(T,M(:,7»;axis([0 40 -0.5 0.5]);title('n=4');
»subplot(4,4,2);plot(T,M(:,9»;axis([0 40 -0.5 0.5]);titIe('n=5');
»subplot(4,4,6);plot(T,M(:,1l»;axis([0 40 -0.5 0.5]);title('n=6');
» subplot(4,4,10);plot(T,M(:,13»;axis([0 40 -0.5 0.5]);title('n=7');
»subplot(4,4,14);plot(T,M(:,15»;axis([0 40 -0.5 0.5]);title('n=8');
»subplot(4,4,3);plot(T,M(:,17»;axis([0 40 -0.5 0.5]);title('n=9');
»subplot(4,4,7);plot(T,M(:,19»;axis([0 40 -0.5 0.5]);title('n=10');
»subplot(4,4,1l);plot(T,M(:,21»;axis([0 40 -0.5 0.5]);title('n=1l');
»subplot(4,4,15);plot(T,M(:,23»;axis([0 40 -0.5 0.5]);title('n=12');
»subplot(4,4,4);plot(T,M(:,25»;axis([0 40 0.5 0.5]);title('n=13');
»subplot(4,4,8);plot(T,M(:,27»;axis([0 40 -0.5 0.5]);title('n=14');
»subplot(4,4,12);plot(T,M(:,29»;axis([0 40 -0.5 0.5]);title('n=15');
»subplot(4,4,16);plot(T,M(:,31»;axis([0 40 -0.5 0.5]);title('n=16');
Резулътат выполнения приведенной выше последовательности команд
представлен на рис. 9.9.
Одной из основных проблем численноrо решения ОДУ и систем ОДУ явля
ется проблема выбора шarа интеrpирования Ы, поскольку при достаточно
большом шarе интеrpирования возникают неустойчивые решения, т. е. реше-
ния, поrpешность которых начинает возрастать во времени экспоненциально
быстро. Один из способов проверки устойчивости метода заключается в кон-
троле величины полной энерrии, которая в случае свободных колебаний долж
на сохраняться, поэтому для проверки правильности выбора шarа интеrpироваш
ния Ы можно использовать следующий aлrоритм:
1, Задать начальные смещения и скорости тел цепочки связанных
осцилляторов.
2, Задать временной интервал, на котором ищется решение системы ОДУ.
3. Задать число точек, в которых ищется численное решение системы ОДУ,
4, Найти решение системы ОДУ.
5. Вычислить значения энерrии системы связанных осцилляторов в кажш
дый момент времени.
6. Проанализировать изменение энерrии системы во времени на задан..
ном временном интервале и оценить точность выполнения закона сохране-
ния энерrии.
7. При неудовлетворительной точности решения повторить пп. 36.
8. При удовлетворительной точности решения перейти к анализу выну-
жденных колебаний.
::8 ::В I;' ::8
:B :;8 '8 j3.
::'8 8 'B:B
':'  .. ':' ':'8 ':
.,Н, .', .. .',  .. .', ..
Рис, 9.9. Зависимость М2новенных значений смещения тел
колебательной системы от времени
Как очевидно, для реализации описанноrо выше алrоритма необходимо
уметь вычислять энерrии каждоrо из тел системы в заданные моменты вре-
мени. Для решения данной задачи можно использовать функцию Еп, описа
ние которой мы сохранили в файле Еп.m.
% листинr файла ЕП.т
function E=En(N,m,k,M)
K=length(M); % число строк матрицы решений
Кl=l;
for j=l:N
for i=l:K
if j> 1
234
235

Ko.ltl1bIoтep/{oe ЛIОе.:'!.РОll..й-./t1е.РlЗ-t1ч,:кu!роцессоll.. в l1акете MAJAB
... 9 !v!О"..t1Р"?!!:l!!:lI..'?:Z!Оll..lЯ-lI..3.!?1!t1
ifj<N
e(i)=0.5*m(j)*M(i,2*j), л 2+...
0.25*k(j)*(M(i,2*j-l)-М(i,2*j-3 »). Л2+...
0.25*k(j+ 1)*(M(i,2* j-l)-M(i,2*j+ 1». Л2;
end;
end;
if j==1
e(i)=0.5*m(I)*M(i,2)A2+0.5*k( 1)*М(i,I)Л2+.,.
О .25*k(2 )*(M(i,I)-M(i,3» Л2;
»for i=l:Np+l
s::.:E(i,:);
Efull(i)=SUlll(S);
elld;
» figure(l);plot(T,E(:,l),T ,Е( :,4),Т,Е( :,8),Т,Е( :,12»
» axis([O 30 О 0.25]);
» figUl'e(2);plot(T,Efull)
Результаты выполнения лриведенной выше последовательности команд
представлены на рис. 9.10 и 9.11.
0.251''''" ''T--'-- , с '"',--'
end;
if j==N
e(i)=0.5*m(N)*M(i,2 *N) Л2+0.5*k(N+ 1 )*M(i,2 *N -1) Л2+...
0.25*k(N)*(M (i,2*N  1)- M(i,2*N -3» Л2;
end;
end;
en(:,Kl)=e';
Kl=Kl+1;
end;
Е=еп;
Для вычисления MrHoBeHHblx значений энерrии тел колебательной сис-
т емы и ее полной энерrии необходимо выполнить следующую последова-
тельность команд:
» clear аН;
» global k m А Omega
» N=16;
» n=I:N;
» m(п)=1;
» i=I:N+l;
» k(i)=I;
» n=I:2*N;
» RO(n)=O;
» RO(1 )=0.5;
» А=О.О;
» Omega=O.O;
» Tfin=50*pi;
» Nр=2Л13-1;
» [Т ,M]=ode45( 'euler2' ,[0: TfinINp:Tfin],RO);
» E=En(N,m,k,M);
» plot(T,E(1,:),T,E(8,:),T,E(J6
".
02 / \
.. \ /1
r'
015
0.1
,/4
rf'
\ l' \ / е 12
\ (, \ / /
\1\1, //\, / J
\/ v \/у! \ (\ /<\ \ /\ /' I
1\ ! И, \) У I i '\r'/( ':,yf\ r--J "-" I
" '\'/""'\,' \.Х \ ,; \'
! '-- '.j \'.J, v  . -/....п v-f'Х;
/''-.) ';J....  \..::. ., - '-....<:..... ...,;
00"   10 15 20 25 зо
Рис, 9,1 О, Мzновенные
значения энерzuй
выбранных тел
колебательной
системы
0.05
O.2502....
J
i
!
i
l
I
1

Рис. 9,11. Зависимость
полной энерzии системы
от времени
0.2488
0.2486 
0.246J
0.2482 j
О
029
0.2496
0.2494
0.2492
20
40
6()
    
80 100 120
140
160
236
237
11

li?'!..Ы.!!.п-:.9??.!.1.?!!.и..fJ:.?С:'1и..1!и..з-.'!..е.к-.lv:..р"?е:ов....в.'!..к-.":.1v!...А.!!:::!l!..... ...
..... ?:...':!..?':!.и..Р.?в--С::ll.е.?Л-Il?в!!JlJ/.:Illl.
i
11
Анализ зависимоCПI мrновенной энерrии колебательной системы от BpeMe
ни, представленная на рис, 9.11, показывает, что полная энерrия отклоняется от
cBoero первоначальноro значения по линейному закону. При этом максималь
ная величина отклонения, характеризующая точность численноrо решения, на
выбранном временном интервале не превосходит 0.24%,
 -Задч 9.lT   .
Используя документ, описанный в разделе 9.2, найдите точные значения
зависимостей координат тел системы связанных осцилляторов от вpe
мени, совершающей свободные колебания, Сравните зависимости KOOp
динат тел системы связанных осцилляторов от времени, найденные
численным решением системы ОДУ (9,2), с точными значениями, Oцe
ните точность числеНН020 решения,
Для анализа движения системы связанных осцилляторов под действием
вынуждающей силы следует в приведенной выше последовательности KO
манд задать отличными от нуля значения переменных А и Omega.
 
 w  MM"M_M'  .'MM
Задача 9.14
Рассмотрите движение колебательной системы, состоящей из N свя
занных осцилляторов (N  10), считая, что {т; =1,i=0,1,.."N1,
k j = 1, j = 0,1,...,N}, при начальных условиях (х;(о) = О, х;(О) = О} под
действием внешней силы f(t) = Asin(nt), nриложенной в т. А,
1. Найдите частоты собственных колебаний OJ", S = 0,1,..., N  1 paCCMaт
риваемой системы связанных 2армоническux осцилляторов.
2. Исследуйте движение кажд020 из тел системы связанных осцилляторов
при n = OJs' S = 0,1,..., N  1. используя для этО20 зависимости Х; (t).
v;(t), E;(t) i=0,1,...,N1 иuxсnектры,
З. Исследуйте движение кажд020 из тел системы связанных осцилляторов
при условии (п Е [min(OJJ; mах(OJ. )], n * OJs,S = O,1,...,N 1}.
4. Опишите движение колебательной системы при п« min(OJs) и
n »max(OJs). Как зависит амплитуда колебаний от номера частицы
при п» max(OJs) ?
5. Опишите движение колебательной системы при n < min(OJ,,) и
n > mах(OJ,).
6. Исследуйте зависимость скорости распространения возмущений в ли
нейой цепочке от частоты возбуждающей силы, Объясните nолучен
ныи результат,
7. Исследуйте зависимость скорости распространения возмущений в ли
нейной цепочке от массы тел системы связанных осцилляторов,
8. Исследуйте зависимость скорости распространения возмущения в ли
нейной систeJt.tе от :JJCесткости nружин,
В результате решения задачи 9.14 можно сделать следующие выводы: в
линейной системе связанных rармонических осцилляторов происходит пе
редача энерrии вдоль цепочки от левоrо конца цепочки к правом)'. PaCCMaT
риваемая система обладает фильтрующими свойствами, не пропуская коле
бания с частотами п« min(OJ".} и п» max(OJs). При воздействии на сис
тему внешней вынуждающей силы с частотой п, отвечающей условию
п« min(OJs), система совершает колебания как единое целое с частотой, paв
ной частоте внешней вынуждающей силы, При воздействии на систему внеш
ней вынуждающей силы с частотой п, отвечающей условию п» max(OJs),
амплитуды колебаний частиц убывают к правому концу цепочки.
.M
Задача 9.15
Решите задачу 9.14, считая, что
т; =2,i=1,3,...,N kj =1,j=0,1,...,N}.
{т; = 1, i = 0,2,. . ., N  1,
M"""""""'
Задача 9.16
Решите задачу 9,14, считая, что
kj =1,j=0,2,...,N, kj =2,j=1,3,.,.,N1}.
{т; =1,i=0,1,...,N1,
MM'MMMMMM.M
Задача 9.17
Решите задачу 9,14, считая, что система, состоит из осцилляторов
различных масс (задавая массы, например, с помощью 2енератора слу
чайных чисел). Как влияет беспорядок на поведение системы и скорость
распространения возмущения?
.-...
i
11
Задача 9.18
Решите задачу 9,14. считая, что система состоит из осцилляторов с
одинаковыми массами, соединенными nрУЖИНGМи различной жестко
сти (задавая значения коэффициентов жесткости, например, с no
мощью ?енератора случайных чисел). Как влияет беспорядок на noвeдe
ние системы и скорость распространения вОЗАlущения?
238
239
11

В предыдущем разделе мы обнаружили, что в системе из N связанных
осцилляторов колебания отдельных тел приводят к распространению энер
['ии вдоль цепочки на произвольные расстояния, Данный факт указывает на
аналоrию между колебанием цепочки связанных осцилляторов и волнами,
распространяющимися в непрерывных средах. Для Toro, чтобы осуществить
переход от колебаний дискретной цепочки осцилляторов массой т, связан
ных пружинками одинаковой жесткости k, длина которых в равновесном
состоянии равна а, к волновому движению непрерывной среды, paCCMOT
рим уравнению движения iro тела
d2u. k
=(2и;и;+1 иH)' i=2,3,...N2, (9.24)
dt т
rде и;  смещение iI'O тела относительно положения равновесия.
При Noo, aO и постоянной длине цепочки, можно заменить в (9.24)
и; (t), rде i  дискретная переменная на функцию и( х, t), rде х  непрерывная
переменная. Данная замена позволяет записать (9.24) в следующем виде:
a2u(x,t) ka2 1
2  2[u(x+a,t)2u(x,t)+u(xa,t)].
д! т а
Разложив функцию u(x,t) в ряд Тэйлора в точках x:t а
( + )   + аи а2 д2и
u xa,! u(x,t)a++...,
ах 2дх
и подставив в (9.25), получим
a2u(x,t) ka2 д2и

д,2 т д х2 .
Вводя обозначения Jl = т! а , Т = k! а (Т  натяжение, Jl  линейная плот
ность массы), v2 = Т / Jl, запишем (9.26) в следующем виде:
2u(x,t)  . a2
а t2  v2 д х2 .
Уравнение (9,27) называется ВОЛновым уравнением. Непосредственной
подстановкой в (9,27) леrко убедиться в том, что любые функции вида
f(xvt), f(x+vt) являются ero решениями, При этом на прямых, опреде
ляемых уравнениями x:t 1'1 = coпst, решения уравнения остаются постоян
:'!!.':'!rr:.P'!oe?::'!.P..?I!!I'!.:.P'.U!'C:" Р.?II::?в'!1<::rr:..!'.!!LА в
9.4. Моделирование волновых движений
1,
 !
1'1
;11
I1
11
'11
J
ill
"1
;11
11
11
11'
1:
 I
240
. .. ?"!.?::'.ll??в1 /ll:'ОI!?вlХЯ-l!.I!I,q
ными, Так как нолновое уравнение (9.27) является линейным, решения вол
HOBoro уравнения удовлетворяют принципу суперпозиции, т, е. любая
функция вида
N
!jf(x,t)= )f;(XVl)+ ii(x+ vt)]
;=1
(9,28)
(9.25)
также является решением волновоrо уравнения (9.27), Следовательно, по
ведение волны произвольной формы можно описать, представляя ее в виде
набора синусоидальных волн (ряда Фурье), Данный подход мы используем
в дальнейшем для анализа движения волновOI'О пакета в среде с дисперсией.
Анализ особенностей решений волновоrо уравнения, следуя выбранному
в нашей книrе подходу, будем проводить численно. Для описания эволюции
решений волновоrо уравнения в пакете МА AВ в качестве первоrо шаrа
необходимо создать три файла: файл Wave.m, содержащий функцию, опи
сывающую решение волновоrо уравнения в момент времени 1 = о; файл
WaveP.m, содержащий функцию, описывающую волну, распространяю
щуюся в положительном направлении оси оХ; файл WaveN.m, содержащий
функцию, описывающую волну, распространяющуюся в отрицательном Ha
правлении оси оХ.
% листинr файла Wave,ill
function z=Wave(A,x)
% функция, решение волновоrо уравнения в момент времени t = О
z=A *ехр( -х. л 2/4);
% листинr файла WaveP.m
function z=WaveP(A,x,v,t)
% функция, описывающая волну, распространяющуюся в
% положительном направлении оси оХ
z=Wave(A,x-v*t);
% листинr файла W aveN.ill
function z=WaveN(A,x,v,t)
% функция, описывающая волну, распространяющуюся в
% отрицательном направлении оси оХ
z:Wave(A,x+v*t);
Затем для вычисления значений соответствующих функций и визуализа
ции решений волновоrо уравнения необходимо выполнить следующую
последовательность команд:
(9.26)
(9.27)
241

.!!.l!...мnь!!!!рно!r:..!!.'!!!.!!lI..l!!..'!:'.f!...Р'':!..,:!:!.:''С'5..'-!!l!l!..lfе':=-Й-lI..'!.'5I!!!'!.!1А Т--.....
.. _т.._... .ш.!..:!:..е.'!.'!Р.I}!!'!.нuе lI..?!'.!!..l!...3.!!!!!!еll':!!}ш
li:
li'
I1
'1'
'iil
l'
I
1...'11
,1
111
111
I
11'
1:
» clear аll;
% задание пространственной сетки
» xmin=-2*pi;
» xmax=2*pi;
» Nx=lOl;
» i=l:Nx;
» x(i)=xmin+(xmax-xmin)/(Nx-l)*(i-l);
% задание временной сетки
» tmin=O;
» tmax=50;
» v=0.05;
» Nt=lOl;
» j=l:Nt;
» t(j)=tmin+(tmax-tmin)/(Nt-l)*(j-l);
% вычисление значений функций, описывающих решение
% волновоrо уравнения
» for i=l:Nt
for j=l:Nx
Ml(iJ)= W aveP(l,x(j), v ,t(i);
M2(iJ)=W aveN (l,x(j), v,t(i»;
end;
end;
% визуализация решений волновоrо уравнения
» figure(1);plot(x,Ml(1,:),x,M1(40,:), ,_о' ,х,М1(80,:),': ');
» figure(2) ;рlоt(х,М2(l,: ),х,М2( 40,:),' _.' ,х,м2(80,:),': ');
»[X,Y]=meshgrid(x,t); % задание двумерных матриц, используемых
% для визуализации функций,
% зависящих от двух переменных
»figurе(З);surf(Х,У,Мl);соlоnnар gray
»figure(4);surf(X,Y,M2);colormap gray
» figure(5);contourf(Ml,15);colormap gray
»figure(6);contourf(M2,15);colormap gray
Результаты выполнения приведенной выше последовательности команд
представлены на рисунках 9.129.17.
о.: .ш.Ш' ШШ/Тf\\l
0.8 I , \
I! \
: ,
: 
. '
: .
, ,
: \
.: \
J \
! \
! \
: \
: \
/ \
/' \"
, ,
"'''c'''/' . ".......
0.6
0.7
0.3
О"'
Q.4
02
о..
-в
..
-2
Рис, 9,12. Функция up(x,t)
в фиксированные моменты
времени t=O, 40, 80
"
" '--х-
о .10
:r (, \
:: I \
05 ! \
u I \
I \
0.3
0.2
:1
Рис. 9.13, Функция иix,t)
в фиксированные моменты
времени t=O, 40, 80
-2
1.
i
o.a..j
О..
О..
o.
i
o...
О..
о
50
O
,g
" -----
30....................
'" -------...
,,
о 10
D2
I
Рис. 9,14, Поверхность, описываемая
функцией Up(x,t)
Рис. 9,15, Поверхность, описываемая
функцией иiX,t)
1"
'1

242
243

li?А(Ы'!.П1Р'!{(!,"- "(O?r::z.P"?ti<:'!III". rf;311ч-еСКIIХ пpoцe(:?в .aKelп.e .JI! !l:Al!.
9 ..1oelP?a..'!1!.'!.. .?л-,-,-оы?:.явл ell!f 11
"
"
ОтметИJl1, что наряду с длиной волны А и периодом (юлны Т в физИf.:е
также часmо используют величины: k= 2п/ А, называемую волновым
eeKmopOAt; f:::: 1/1', llазывае'Иую частотой вщны и (j):::: 21(1' :::: 21[/ f ' в
данных обозначениях функция, описывающая 2ЩЩОНИЧf>СКУЮ волну, за
пИСhlваf>тся в виде
.00
"
БС
"
30
и(х,t)=Асоs(kxО)t). (У,зо)
Используя (9,30), определите, какие волны (волновые числа и частоты
волн) представлены в формуле (9,29),
"
20
Рис. 9.16. Карта линии УрО6НЯ
функции Up(x,t)
Рис. 9,17, Карта линий JрО6НЯ
функции иiX,t)
Задача 9.21
Проанализируйте особенности распространения волны
и(x,t):::: sin(x  vt) + sin(x + и) ,
Опишите получающуюся в резулыnате волну.
"
Как видно из рис. 9.129.17 функции Up(x,t), ull(x,t) описывают волны,
распространяющиеся, соответственно, в положительном и отрицательных
направлениях оси оХ. (Такие волны называются беrущими.) Отметим, что
форма данных волн во времени остается неизменной.
Задача 9.19
Замените в описаюю.м выше дОКУА1енте функцuю ехр(х2 /2) на функцuю
l/ 21( ) П  д v
cos Т' х . роаналuзuрyuте пове ение решениu волновоzо уравнения
для разлuчных значенuй А. Расс.мотрите решенuе волновою уравненuя
nри t = О  функцuю и(х,о). Чему равен nериод функцuu и(х,о), назы
ваемый длuной волны? Рассмотрите решенuе волновоzо уравнения nри
х = О  функцuю u(O,t). Чему равен nериод функцuu u(O,t), называемый
nериодом волны? Убедuсь в том, что отношенuе nериода Функцuu
и(х,О) К периоду функциu u(O,t) равно скорости расnространенuя вол
ны v. Получuте этот же результат аналuтuческu.
Задача 9.22
Рассмотрите случай двух zармонuческuх волн одинаковой амплuтуды,
распространяющихся с одинаковой скоростью v = 1 в положитшtЬНО.il1
наnравленuи оси оХ, и имеющих разные частоты 0)1 == 1 u 0)2 =9.05,
Опuшuте форму u(x,t) для разлuчных времен {, Оцените скороапь pac
пространенuя мелкомасштабных zорбов амплuтуды (фазовую CKO
рость). Оцените скорость распространения низкочастотной 02uбаю
щей (zрупповую скорость). Сравните значенuя фаЗ060Й u срупповой CKO
ростей.
9.5. Фурьеаанализ волновых пакетов, движущихся
в среде с дисперсией
Задача 9.20
Проаналuзuруйте особенностu распространения волны, оnисываемой
функцией
u(x,t):::: 4 [1 +sin(xvt)+! sin3(xvt)+ !Sin5(xvt))]. (9.29)
1( 3 5
Какие значенuя длuн волн u nериодов представлены в (9,29)?
Анализ выражения (9.30) показывает, что можно ввести фазовую функ
цию косиносоидальной беryщей волны, распространяющейся в положи
тельном направлении оси оХ, как apryмeHT волновой функции cos( о) t  kx) :
ф(х,t)==О)tkx. (9.3])
Если мы хотим следить за какимлибо rpебнем волны (максимум
cos ф(х, ()) или за ее впадиной (минимум cos ф(х, ()), по мере увеличения
времени переходить к все большим значениям х так, чтобы фаза ф(х, () бы
ла постоянной, Условие постоянства фазы с математической точки зрения
означает, что полный дифференциал функции ф(х,t), имеющий вид
I
,
244
245

.?.п./Й-.'llРl?.'Н?':!./JЕ?I'!.!:1!.!!.з-!!_'!.'!. IIp!!..'!=:?..!!!!.!!!.1!..T.!!................................._
_ Ш __ __ _ ____}:!1'?,=,'!.р?вl!!.!'!.:_й-.лIoы' JlвЛII'!.!i_
dф ==(}t +(}x == wdt kdx,
(9.32)
Каждая rармоническая составляющая в (9.35) определяет собственную
rармоническую волну с частотой w == w(k) , т, е, каждая частотная COCTaB
ляющая беrущей волны распространяется со своей собственной фазовой
скоростью
равен нулю. Приравнивая (9.32) нулю, находим условие постоянства фазы:
dx w
dt == V f == k , (9.33)
rде vJ  фазовая скорость волны.
Выражение (9.33) дает связь между фазовой скоростью волны, частотой
волны и волновым вектором. Вообще rоворя, условия распространения вол
ны определяются свойствами среды. При этом йJ, а, следовательно, и фазо
вая скорость, MOryт зависеть от волновоrо вектора k. Волны, у которых фа-
зовая скорость зависит от волновоrо вектора, называются дисперrирующи
ми, В противном случае волны называются недисперrирующими. Дисперrи-
рующая волна, представляющая собой суперпозицию беryщих волн с
различными волновыми числами, будет менять свою форму по мере рас-
пространения в пространстве, так как составляющие с различными длинами
волн распространяются с различными скоростями.
Продемонстрируем влияние дисперсии на распространение волн на при-
мере задачи о движении волновоrо пакета в среде с дисперсией, под кото-
рым мы будем пони мать некоторую синусоидальную волну, имеющую ко-
нечную протяженность в пространстве или во времени. Решение данной за
дачи основано на представлении волновоrо пакета в виде суперпозиции
rармонических функций (метод Фурье) [6].
Рассмотрим задачу об описании движения волновоrо пакета, локализо-
BaHHoro в момент времени t == О в пространстве. Данное условие означает,
что оrибающая пакета является функцией, достаточно быстро стремящейся
к нулю при х  :!:оо . Введем обозначение
[(х) == и(х,О). (9.34)
Условие «быстроrо стремления функции к нулю» обеспечивает возмож
ность ее разложения в ряд Фурье. Если функция [(х) не периодическая
функция по координате, то ее суперпозиция составляющих ее функций He
прерывна по переменной k, и выражается через интеrpал Фурье
w(k)
Vf =-. (9,37)
k
Искомая функция u(x,t), описывающая беryщую волну, является супер
позицией rармонических беryщих волн, образующих начальное возмуще-
ние. Это означает, что найти u(x,t) можно заменой kx на (kxw(k)t) в Ka
ждой rармонической составляющей суперпозиции (9.35):
00
u(x,t) == J A(k)ei(kHO(k)t)dt.
(9.38)
oo
Таким образом, aлrоритм аналиrnческоrо решения задачи достаточно прост.
1. Задать функциюf(х), описывающую начальное возмущение при t = О.
2. Задать функцию w == w(k) .
3. Определить функцию A(k), вычислив интеrpал (9.36).
4. Определить функцию u(x,t), вычислив интеrpал (9.37).
Однако для Toro, чтобы использовать данный алrоритм при нахождении
численных значений функции и( х, t), требуется ero некоторая доработка,
связанная прежде Bcero с тем, что вычисление интеrpалов в (9.36), (9.37),
(9.38) приходится проводить на интервалах конечной длительности, т. е.
проводить разложение функции не в интеrpал, а в ряд Фурье. В данном слу-
чае, как было показано в rл. 7, вместо (9.36), (9.37), (9,38), следует исполь-
зовать следующие выражения:
Nl
[(х)== LA(n)ii(1lX , k = 21l (9.39)
п=О хтах  хт;п
[(х) = J A(k)eikxdk,
(9.35)
ХтаХ
A(п)== J f(x)e-ikllXdx, п == O,l,...,N  1,
хтах  xmin
xmin
(9.40)
ос
-00
N
( ()  "" А( ) i(kll(xxтiп ){IJ(k1l))
U Х,  L..J п е ,
11=0
(9.41 )
rде
00
A(k) == J f(x)e-ikxdx.
(9.36)
rде N  число значений функцииf(х).
для ускорения вычислений коэффициентов А(п) можно использовать БПФ,
-х
246
247

?:f /l.b!..?"! еР..'.'.?=h!?Р'.О.I!!I.l!=--:Р..'.?!!'!.=/(:z:!..!!РЙ--lJ!?.!.п.I!.=111=1':!1Т!:.ш ..  .
..ш .?: ivf Oe:!??c:./I1!=?l!!!?':!:!!.)'.='.I'!...
Таким образом, численное решение задачи о движении волновоrо пакета
может быть найдено в соответствии со следующим алrоритмом.
1. Задать функцию f(x), описывающую начальное возмущение при t = О.
2, Задать функцию ш = ш(k) .
3, Задать rpаницы пространственноrо интервала, на котором ищется
решение задачи.
4, Задать число узлов пространственной сетки,
5. Вычислить значения функцииf(х) в узлах пространственной сетки.
6. Вычислить коэффициенты разложения функцииf(х) в ряд Фурье.
7. Вычислить значения функции u(x,t) в заданный момент времени в co
ответствии с (9.41),
Описанный выше алrоритм в пакете МА ТLAB реализуется следующей
последовательностью действий:
» clear аН;
» Nx=1024;
% задание пространственной координатной сетки
» j=I:Nx;
» xmio=-10*pi;
» xmax=60*pi;
» x(j)=xmio+(xmax-xmio)/(Nx-l)*(j-l);
»А=I; % амплитуда волновоrо пакета
» k=0.5; % волновой вектора пакета
» z=A *exp(i*k. *х). *ехр( -(х/l0). Л2); % вычисление значений комплексной
% ФУНКЦИИ,описывающей пакет
% в момент времени t == О
su=O;
for 0=1 :Nx
su=su+s( o)lNx*exp( i * (k*o* (хо)- xmio )-Omega(k. *0 )*t1»;
eod;
psi(j)=su;
eod;
% вычисление мrHoBeHHЫx значений решений
% волновоrо уравнения в момент времени t = 90
» t1=90;
»for j=I:Nx
su=O;
for o=I:Nx
su=su+s( o)lNx*exp(i *(k *0 *(хо )-xmio)-Omega(k. *0) *t1»;
eod;
psi1(j)=SU;
eod;
% визуализация оrибающей волновоrо пакета
% в момент времени t = 0,50,90
> > figure( 4) ;plot(x,abs(z ),x,abs(psi),x,abs(psi1»;
Результаты выполнения приведенных выше команд пред ставлены на
рис. 9.189.21.
l'
% визуализация волновоrо пакета
» figure(1);plot(x,abs(z»
» figure(2);plot(x,real(z),x,imag(z),' -- ')
% вычисление и визуализация спектра волновоrо пакета
» s=fft(z);
» m=2:200;
» m=I:200;sl(m)=s(m+l);
» figure(3) ;plot(2*pi*m/(xmax-xmio),abs(sl»
» k=2*pil(xmax-xmio);
% вычисление мr'новенных значений решений
% волновоrо уравнения в момент времени t = 50
» tl=50;
» for j=1 :Nx
Тш rш 
1\
0.8 '\
0.6 ,
,
,
0.4 {, ,
,
" ,
,
" \
02 Л\ I
1\'
, ,
I: , ,
\' \ ' ,
-02 : :
1:1 ,
\" f:
,0.4 11
-0.6 \' \1
J U
8.
I
.1LH.
,50
 .......L   ....L..._ ....L  ... ..
50 iOO 150 200
i
Рис. 9.18. J.{Нlшая и действительная часть началЬНО20 80з.'W)'щения
248
249

.:'.I!.:':,!:[J!.I?:'.?..:l!.JР...й-il.:l:ф-:.:!!Ч :С'5.прй-.::,:.lJ вr:.:'!!:..fl!1:...!!:I!.......
.....""........ .MM"M....M'.... ШМ....'М...... .'M'M"MM ..M,,"M" М
.. ....,........?:.fl!й-.:.л..?'?.il.!!::..f!.?..л.:I?...в--:в-л.:::и.
1 ['' "'.. ...,...,...
оэr i \
I ; i
08[' i i
i I
07 I I
,.l i
I I
,
Рис, 9,20, Спектр
функции f
1   .   M
1\
1\
I I
I 1
i \
, '
I \
i
05
о.
O'f
0'2f
0.1
o
.50
,
I
,
!
,
"

о
0.9
08
07
о.
05
\
\
1.

50
; \
; \
! \
, I
,
\
i
... ............'l
100
._ ............L...._ 
150
901
1
!
80
(,
1\
1\
I
I \
\
\
\
\
\
70
I
I
60
I
50l
I
..l
I
зоL I
I I
20f I
,.11
f!
01/
о
(\
::1 I
"f ' i \
 cтM 5;)М .. \ , -;M 20(,
,1
250
Рис, 9,19 Оzибающая
волновоzо пакета в ."юмент
времени t = О
Анализ результатов, представленных на рис. 9 ,189 ,21, показывает, что
волновой пакет локализован на отрезке [20,20], Анализ спектра, представ
ленноrо на рис, 9.20. показывает, что в момент времени 1 '" О пакет пред
ставляет собой суперпозицию синусоидальных волн, волновые числа KOTO
рых находятся в диапазоне [0;1]. Спектр имеет максимальное значение при
km = 0.5, ширина спектра /!"k  1. В процессе движения меняется форма
волновоrо пакета: происходит уменьшение высоты оrибающей пакета при
одновременном увеличении ero ширины (расплывание волновоrо пакета в
пространстве). Изменение формы волновоrо пакета происходит в COOTBeT
ствии с законом сохранения энерrии
N
LU(1;,x,Y = coпs1 . (9.42)
п=О
200
.М.Ш
Задача 9.23
1. Оцените фазовую скорость сармоники с волновым числом, равным km.
2. Оцените фазовые скорости сармоник V f' волновые векторы kц Koтo
РЫХ удовлетворяют условиям IS(k,,2) = 0.5IS(km)[, IS(kц), = O.lIS(km) .
Оцените разброс фазовых скоростей в каждом из рассматриваемых
случаях.
3. Оцените zрупп(Jвую скорость движения пакета V (скорость движения
р
ею оzибающей), Сравните данную величину с ее точным значением, пo
лученным по известной формуле [5J,
Vp = dk)\k =km (9.43)
4. Оцените срупповые скорости сармоник V f ' волновые векторы kц которых
удовлетворяютусловuям IS(k,,2) = 0.5IS(kmY, !S(kц) =0.1:S(km)l.
Оцените разброс срупповых скоростей в каждом из раССllютриваеlltых
случаях,
...................,....
Рис, 9,21. Оzuбающuе
волново<,о пакета в моменты
времени (=О,50,90
Задача 9.24
Дополните описанный выше документ фра2Ментом, позволяющu.н вы..
числять М2новенные значения энерzиu волновоzо пакета, и проверьте
выполнение закона сохранения энерzии для пакета, локализованноzо при
1=0 в пространстве.
251

I:::.'?Aп!?.!!!ef..'1 ?еt'?е.Л-Uf..о.аtlи-:.. rf:.и-зu:.е..'::':'.Л!jJОlJ..:,:ов/с:..'!.и!.fl!...!..:!.!!..
9:..М:!д.r::..и-!!.<!.с:..Ilи-е?Л-'LOIi.Ь::'Ii.I=!'':'.
Задача 9.25
Дополните описанный выше доку.wент фра2Ментом, позволяющим oпpe
делять ширину волновО20 пакета Ди при заданнш./ значении е20 02И
бающей,
], Используя описанный выше документ, оцените закон из"wенения ширины
волновО20 пакета во времени (ди) t '
2. Сравнит: полученный результат с известной оценочной фОрА/УЛОЙ, при
веденнои в [5].
у.
f(t)= f А(ш)еiиХdш,
о
(9.48 )
rде
'lO
(ДU)t =(ДU)о+ДVрt,
(9.44)
А(ш)=Jf(t)е,iШl'dt. (9.49)
о
Каждая I'армоника, как и в рассмотренном выше случае, определяет соб
ственную I'армоническую беrущую волну с волновым числом k, значение
KOToporo определяется из дисперсионноrо соотношения
k=k(ш). (9.50)
Здесь каждая частотная составляющая беI'ущей волны распространяется
с фазовой скоростью
2де (дu)о  ширина пакета при t = О, дv р  разброс 2рупповых скоростей,
ЛVр =()I  ы =(1)' . Ы, (9.45)
dk Ik  km dk k  km
З. Убедuтесь в спра д д
ве ливости принципа неопре еленности для волновых
Ы(ди)!  2л.
(9.46)
ш
Vf=k(ш)'
Искомая функция и( х, t), описывающая беrущую волну, является
суп ер позициеЙ данных rармонических беrущих волн. Это означает, что
найти u(x,t) можно заменой шt на (ш(k)tkx) в каждой I'армонической
составляющей суперпозиции (9.48).
(9.51 )
пакеmов
.- .....,  -......._.......  ''"''"'"',   И   
Задача 9.26 . '"'" .
Решите задачи 9,249,26 для волновых nакетов с пряAtОУ20ЛЬНОЙ и тpe
У20ЛЬНЬШU формами 02ибающей,
Задача 9.27
Задайт: начальное вОЗ.wущение в виде двух nРЯМОУ20ЛЬНЫХ импульсов
ширинои Лх, разнесенных в пространстве на расстояние l1X , Oпpeдe
лите, через какое вре.мя (врс.wя nерекрыванuя. импульсов) разрешение
данных U},тульсов окажется невОЗМОЖIIЫ.М, Pacc.wompume случаu:
Д,.\'  l1X и лх < l1X . Как зависит данныйрезупьmат от значения k ?
т'
Рассмотрим друrую постановку задачи о движении волновоrо пакета.
Предположим, что передатчик, расположенный в точке х :::; О, действует на
непрерывную одномерную однородную открытую систему таким образом,
что функция, описывающая беrущую волну в точке х :::; О, имеет известную
зависимость от времениf(t):
f(t)=u(O,t). (9.47)
При этом будем считать, что волновой пакет локализован во времени,
т. е, оrибающая пакета является функций достаточно быстро стремящейся к
нулю при t  ос>. Сделанное предположение позволяет представить функ
IlИЮ f( 1) В виде интеrpала Фурье:
. ......
'lO
u(x,t) = J А(ш) еi(rvtk(ЙФ)dш, (9.52)
о
Таким образом, алrоритм аналитическоrо решения задачи, как и в пре
дыдущем случае, достаточно прост:
1. Задать функцию f(t), описывающую начальное возмущение при х = О,
2, Задать функцию k = k(ш) .
3, Определить функцию А(ш), вычислив интеrрал (9.49).
4. Определить функцию u(x,t), ВЫЧИСЛИR ИНТСI-рал (9.52).
Однако дЛЯ TOJ'O, чтобы использовать данный апrоритм при нахождении
численных значений функции и( х, t), требуется ero некоторая доработка,
связанная прежде Bcero с тем, что вычисление интеrpалов в (9.48), (9.49),
(9.52) приходится проводить на временных интервалах конечной длитель
ности Т, т, е, ПрОБОДИТЬ разложение функции не в интеrpал, а в ряд Фурье. В
данном случае, как было показано в rл. 7, вместо (9.48), (9.49), (9,52), необ
ходимо !IСПО.'1ЬЗ0вать слеllуюшие выражения:
252
253

1!'?..tt Ъ!?,,!I:l!.t?_:..-!!.'?еl}l!.fJ.<!...'!!.'.е...1!.'!.!'!.'!:К-!'!.!,,У!,,?l}:СС..?.. !!1!,К-:.ffl_:.fl!:!l! __
......??:3..l!?1!'l'!.:й-:'!!.'?z.!!:'.!...
Nl
f(t) = LA(n) ei(2;rmnt ,
пO
(9.53)
z=-1/(2 *alpha )+( (1/2*alpha). Л2+0mеgаJ(аlрhа *Nu) )ЛО.5;
end;
2) выполнить следующую последовательность команд:
» clear аН
% задание временной сетки
» tmin=O;
» tmax=300;
» Nt=1024;
» j=l:Nt;
» tG)=tmiп+(tmaх-tJniп)/(Nt-l)*G-l)j
% вычисление и визуализация значений функции, описывающей
% волновой пакет в момент времени t = О
» Omega=0.7j
» A=l;
» z=A *exp(i*Omega*t). *exp(-«t-40)/10). Л2)j
» figure(1);plot(t,real(z),t,imag(z»
% вычисление и визуализация спектра начальноrо возмущения
» s=fft(Z)j
» j=1:200j
» s1G)=sG+l);
» freq=2*pi/(tmax-tmin)*jj
» figure(2)jplot(freq,sl)
»v=lj % скорость движения пакета
» alpha=O.5j % коэффициент, входящий в дисперсионное соотношение
% вычисление значений функций, описывающих волновой пакет
% в выбранных точках пространства, и их визуализация
» omega=2*pi/(tmax-tmin);
» х=50;
»for j=l:Nt
su=O;
for n=l:Nt
su=su+s(n)/Nt*exp( -i*(К( omega *п, v ,alpha)*x-...
omega*n*tG»)j
end;
psiG>=su;
endj
» x=150;
»for j=l:Nt
su=O;
I!
il
I
I
]
l'
т
А( )  1 TJf() i(2;r/T)1l!d  О 1 N 1
п T t е t,lJ "..., ,
о
N
u(x,t) = LA(n)ei[(2;r/nlltk«2;r/nll)x] ,
п=О
(9,54)
(9,55)
rде N  число значений функцииfiх).
Для ускорения вычислений коэффициентов А(п) можно использовать
БПФ,
Таким образом численное решение задачи о движении волновоr'о пакета
может быть найдено в соответствии со следующим алrоритмом.
1. Задать функцию fit), описывающую начальное возмущение при t = О,
2, Задать функцию k = k(w). (Отметим, что при невозможности анали
тическоrо обращения дисперсионноrо соотношения w = w(k) , следует для
каждоrо заданноrо значения частоты ш" = 27rs/T,s=1,...N соответствую
щее значение волновоrо числа находить численно, как корень уравнения
ш" = w(k).)
3, Задать rpаницы BpeMeHHoro интервала, на котором ищется решение
задачи.
4. Задать число узлов временной сетки.
5. Вычислить значения функцииfit) в узлах временной сетки.
6. Вычислить коэффициенты разложения функцииfit) в ряд Фурье,
7. Вычислить значения функции u(x,t) в заданный момент времени в co
ответствии с (9.55).
Данный алrоритм для волновоrо пакета с дисперсионном соотношением
вида w(k) = k + а k 2 реализуется следующей последовательностью действий:
1) создать файл Кт, содержащий описание функции k = k( ш) :
% листинr файла Кт
function z=K(Omega,Nu,alpha)
% описание функции k =k(w)
if alpha==O
z=Omega/Nu;
else
254
255

!!!!Мп-!!!!!,!!!!р.!.lOе :!!..l!.елиРО!!с:!.!.'!1!.'!!..,-!чеС!5..,!!'Р!!.I!:..С!!.!.!I!'!!т..е. МА ТLAJ!..  ..
. .,.... . . . .,.:...!:!!!.e:'.!!.poв'.!..,!!!e воЛlIO'Х явлений
for n=l:Nt
su=su+s(n)/Nt*exp( -i*(К( omega*n, v ,alpha)*x-...
omega*n*t(j»);
end;
psil(j)=su;
end;
» plot(t,abs(z),t,abs(psi),t,abs(psi1»;
Результат выполнения описанной выше последовательности команд
представлен на рис. 9.229.25.
I1
11
1,1
:1
1I1
1!
;
08r. ! !
iiI
::1 1.\ 1\
0.2f л I'I[!'
i (i'l!
O'JI'I...I"..\
j 'li:j!'\/
I 'j!!\!
-o.2f 11'1 '/"
! [! i:
-О4[ i I i
.\Jel [:
! 1:
'Q8f 11
_1l. . j ......
О 50 100
15-,
t
Рис, 9.23. Оzи6ающая
начаЛЬНО20 вОЗ.иvщенuя
Анализ результатов, представленных на рис, 9,22, 9.23, показывает, что
волновой пакет локализован на отрезке [20,60], Анализ спектра, представ
ленноrо на рис. 9.24, показывает, что в точке х == О, пакет представляет co
бой суперпозицию синусоидальных волн, частоты которых находятся в
диапазоне [0,3;9.1]. Спектр имеет максимальное значение при Ют = 0.71,
ширина спектра /!"Ю 1':> 0.8 . В процессе движения меняется форма волновоrо
пакета: происходит уменьшение высоты оrибающей пакета при OДHOBpe
менном увеличении ero ширины (расползание волновоrо пакета в простран
стве). Изменение формы волновоrо пакета происходит в соответствие с за
коном сохранения знерrии (9.53).
.!
:
50 I \
I
40 I
зо I
20
I
10 i \
00 , ,'- , I
0.5 1 1.5 2.5 3.5 4,5
1

J
 .J......... 
200
1
j
ЗOQ
Рис, 9,22. Мнu.7;tая
и действительная
части начальноzо
возмущенuя
..L.
250
11
091
0.8
I
07[
oe
i
051
'\ I
1\
/.
1\
! I
I I
I \
I ;
I \
I i
! \
01" I I
I
/ \
o'..... . """""""'J...........
О  100 1
Рис, 9,24. Спектр функции, описывающей начальное возмущение
:1 X) ,
00 50 100 1 200
'300
о 4r
I
03:
o2l
Рис. 9,25, Оzuбающие волновоzо пакета в точках x=O,50,150
. ............... 
200
25с
300
256
9.1576
257

.?':'.?'!!.'!..l!'!:_!:!.?.:f..?'!.I:.p". Ч:(:J1.?"ц-::.:.,!п'!.:1!..:._J1!..iТ-:!:l!._щщщ___ ... Щ. ..__.
. .'.J1!..О_?:'Л'!.fJ..?li..,!!.I!!!:!..?:?!?.f!.t.:!l:.li..л-еll_U.
Задача 9.28
1. Оцените фазовую скорость 2армоники с частотой, равной Шт'
2, Оцените фазовые скорости 2армоник V f' волновые векторы k1,2 кото-
рых удовлетворяют условиям S({J)1,2) == o,51S( Шт )1. IS({J)I,2) == O.1iS( Шт)! .
Оцените разброс фазовых скоростей в каждом из ра ссматриваемых
случаях.
3. Оцените 2рупповую скорость движения пакета V f (скорость движения
е20 02ибающей), Сравните данную величину с ее точным значением, по-
лyчeHHыM по известной формуле [5J,
Vp==dk)lk==k({J)m)' (9.56)
Задача 9.31
Решите задачи 9,289,30 для волновых пакетов с пРЯМОУ20ЛЬНОЙ и тре-
У20ЛЬНЬLНИ формами 02ибающей.
Задача 9.32
Антенна, находящаяся в точке х  О, излучает два пРЯМОУ20ЛЬНЫХ И.Н-
пульса шириной /1Т, разнесенных во времени на интервал /1То, Опреде-
лите, на како.« удалении от антенны разделение данных импульсов
окажется невОЗJ1ЮЖНЫМ. Рассмотрите случаи: /1Т;2: /1То и /1Т < /1То '
Как зависит время перекрывания импульсов от значения Шт?
4. Оцените 2рупповые скорости 2армоник V f' частоты которых Ш1,2
удовлетворяют условиям iS({J)1,2) == O.5IS( Шт )1, IS({J)1,2) == O.1IS( Шт )1.
Оцените разброс 2рупповых скоростей в каждом из рассматриваемых
случаях,
Задача 9.33
Модифицируйте описанный выше документ, дополнив ею фра2Ментом,
позволяющим вычислять значения волновых чисел, для пакетов с произ-
вольным законом дисперсии, Используя модифицированный документ,
опишите распространение волн на поверхности слубокой воды (длина
волны мною меньше слоя воды), имеющих следующее дисперсионное со-
отношение
Задача 9.29
Дополните описанный выше документ фра2Ментом, позволяющим в ы
числять М2новенные значения энер2ИИ волнов020 пакета, и проверьте
выполнение закона сохранения энеР2ии для пакета, локализоваНН020 в
точке х == О во времени,
/1 ш( /1и ) [ ;2: 2л ,
(9.58)
т
(J) == gk + k3 , (9.59)
р
2де g = 980 см/с, р z 1,0 2/cAt3, Т z 72 дин/см (коэффициент поверхност-
ною натяжения),
1. Постройте 2рафики завиcu.мостей фазовой и 2рупповой скорости движения
волны от длины волны, При какой длине волны эти скорости ра вны?
2. Исследуйте движения волновых пакетов, распространяющихся по по-
верхности 2лубокой воды, анал02ично тому, как это было сделано в да H
ном разделе выше,
(Указание. Корни уравнения (9,59) в пакете MAТLAB можно найти сле-
дующей последовательностью действий:
1. Создать файл dispw.m, содержащий описание функции
f({J),k) == ш gk +!. k3
р
% листинr файла dispw.m
function z=dispw(k)
% описание функции f( ш, k )
global omega g Т ro
z=omega-g*k+ Т/rо*kЛЗ;
Задача 9.30
Дополните описанный выше документ фра2.ментом, позволяющим oпpe
делять ширину волнов020 пакета /1и при задаННОАl значении е20 02И
бающей,
1. Используя описанный выше документ, оцените закон изменения ширины
волнов020 пакета во времени (/1и)[.
2, Сравните полученный результат с известной оценочной формулой, пр и-
веденной в [5].
(/1и)[ ==(/1и)о +/1{J)t, (9.57)
2де (&)0  ишрина пакета при t == О, /1ш  ширина спектра пакета.
3. Убедитесь в справедливости принципа неопределенности для волновых
пакетов
258
259

1!..?МП10п.'.9!..:{?''! o.?e:ZP"?!,{Jl{I',! 1131IчеСКllХ 11Р"?цесс?вп<1.кеll1,! !:f:4TL1..
ш?i>!.??Z:Р?f!.{JII.':!.r:...f!.?I?.5!Л!.I':'.ш
2, Выполнить следующую последовательность команд,
» global omega g Т ro;
» g=980;
» т =72;
» ro=l;
» omega=1000;
» fzero('dispw',O)
ans =
1.1250
сивности волны, являющейся результатом интерференции волн, излученных
коrерентными точечными источниками,
Здесь для нахождения корня уравнения мы использовали функцию fze-
ros, обращение к которой может быть выполнено несколькими способами:
1, fzеrо('имяфайла',начальноеприбдижение)
2. fzеrо('имяфайла',[хl х2]) (здесь xI, х2  начальная и конечная точки
интервала, на котором ищется решение уравнения, выбираемые из условия
j(xl), j(x2) < О)
З. fzеrо('имя  файла' ,начальное  приближение,tоl)
fzеrо('имяфайла',[хl x2],tol)
(здесь tol  поrpешность вычисления корня уравнения)
4. options = optimset('Display' ,'iter');
а = fzеrо«('имяфайла',начальноеприближение,орtiопs)
а = fzеrо('имяфайла',[хl x2],options)
(вывод на экран значений корня уравнения на каждом шаrе итерационноrо
процесса)
j'
d!
......
r1
.
s
)'
L
х
Рис, 9,26. Схема опыта Юнzа
Для ответа на вопрос, какая картина будет наблюдаться на экране, полу
чим выражение, описывающее распределение интенсивности света от двух
точечных источников. Электромarнитная волна, излучаемая монохромати
ческим источником света, является сферической волной. Напряженность
электрическоrо поля E(r,t), в точке, удаленной от источника на расстояние r
определяется следующим выражением
А
Е(r,t)=соs(krliJt+ф), (9.60)
r
9.6. Интерференция и дифракция
[де А  амплитуда волны, Ф  начальная фаза волны, которую далее дЛЯ KO
[ерентных источников будем полаrать равной нулю.
Множитель 1/r отражает тот факт, что интенсивность света убывает с
увеличением расстояния между источником и точкой наблюдения. Из
принципа суперпозиции известно, что полное электрическое поле, созда
ваемое двумя источниками в точке Р, равно
А А
E(t) = Е] +Е2 = cos(kr] liJt)+cos(kr2 liJt). (9.61)
r] r2
Напряженность электрическоrо поля в точке Р, создаваемоrо N источни
ками света, положение которых в пространстве относительно системы KO
ординат ХоУ задано их радиусами-векторами Л;, i = 0,1, N  1 , определяется
по формуле
Под явлением интерференции понимают сложение волн, приходящих по
отдельности от одноrо и Toro же точечноrо источника, либо волн, испу-
щенных двумя точечными источниками и имеющих одинаковую частоту и
постоянную разность фаз, Классическим примером интерференции свето-
вых волн является опыт Юнrа с двойной щелью, схема KOToporo представ-
лена на рис. 9,26. Источник света S, излучающий свет только одной частоты
(монохроматический источник), помещен на одинаковом расстоянии от
двух одинаковых отверстий, имеющих координаты (0,0,d12), (0,0,d/2) соот-
ветственно, При этом размеры отверстий таковы, что их можно считать то-
чечными источниками света, излучающими волны с одинаковой частотой и
фазой (коrерентные источники). На расстоянии [. от точки с координатами
(0,0,0) расположен экран, на котором наблюдается распределение интен-
N-] А (2тr
E(t,F) = L cos IFRi
;;0 IFRil А
ЙH) ,
(9.62)
[де F  радиус-вектор точки наблюдения.
260
261

'j I
.1!..?п,:,--оп:=fJ!{(J=А1.?=l!.'!Р?iI!.'еР.'!?и-.ч.:.с.К--::,!р.й-lj=сс.?п.I!..:п:= !!:I..!:!:.B
...ш.....ш Ш... .Ш......_....... ...............!!iй-.!.1!!!,!!:й---I!?..в--"!.!!.л:.,-,--'!!!.
Наблюдаемая интенсивность волны Z в точке Р
Z=(E2),
(9.63)
%'в заданной точке пространства в соответствии с (9,66)
% арryменты функции:
% Lambda  длина волны
% N  число источников
% А  вектор, содержащий значения интенсивностей источников света
% RO  матрица, столбцы которой содержат координаты источников света
% r  векторстолбец, содержащий координаты точки наблюдения
su::O ;
ksi=0:10Л-3:1; % задание сетки для вычисления интеrpала в (9.67)
Ni=length(ksi); % число узлов сетки
% вычисление значений подынтеrpальной функции в (9.56)
for i=I:Ni
su=O;
for j=I:N
Rr=dot(r- RO(: ,j),r- RO(:,j» л 0.5;
su=su+A(j )1Rr*cos(2*pi/Lambda *Rr-2*pi *ksi(i»;
end;
f(i)=su.Л2;
end;
E=trapz(ksi,t); % вычисление интеrpала в (9.65) методом трапеций
2) выполнение следующей последовательности команд:
» N=2; % число источников света
% задание параметров и координат источников света
» А(I)=I;
» А(2)=I;
» LamЬdа=5000*10Л-7;
» RO=[O О -0.1];
» Rl=[O О 0.1];
»R=cat(2,RO',Rl'); % создание матрицы, столбцы которой
% содержат координаты источников света
% задание сетки для вычисления распределения интенсивности
% световой волны
» Np=200;
» i=I:Np;
» zmin=-5;
» zmax=5;
» z(j)=zmin+(zmax-zmin)/(Np-l)*(j-l);
» L=200;
[де ( ) означает усреднение по времени:
т
(E2)=fE(r,t)2dt. (9.64)
о
Для вычисления среднеrо оказывается удобным преобразовать
(9,63) следующим образом поскольку в соответствии с (9.60)
E=E(r,wt)=E(r, t).
можно ввести безразмерную переменную  = t /Т и записать интеrpал (9.64)
в следующем виде
1 l(Nl \2
(Е2)= IE(r,)2d= I t;lrRilco{2;lrRil2Jr)j d. (9.65)
Вычисление интеrpала в (9.64) для произвольноrо количества источни
ков не встречает принципиальных трудностей, однако получающиеся в pe
зультате выражения оказываются весьма rpомоздкими и для их анализа
приходится использовать пк. В этих условиях представляется оправданным
про водить вычисления интенсивности в соответствии с (9.65) сразу в чис
ленном виде. Алrоритм решения данной задачи достаточно очевиден.
1. Задать функцию, описывающую интенсивность световой волны, в co
ответствии с (9.65)
2. Задать количество источников света и длину излучаемой световой волны.
3. Задать расположение источников света (набор векторов Ri,i = 0,1,N  1).
4. Задать пространственную сетку, в узлах которой производится вычис
ление интенсивности световой волны.
5. Вычислить значения интенсивности в узлах пространственной сетки.
Реализация описанноrо алrоритма осуществляется в пакете МА TLAВ
следующей последовательностью действий:
1) создание файла Intensity.m, содержащеrо описание функции, возвра
щающей значение интенсивности в заданной точке пространства в COOTBeт
ствии с (9.65)
% листинr файла Intensity,m
function E=Intensity(Lambda,N ,A,RO,r)
% описание функции, возвращающей значение интенсивности
262
263

11
,
l'
I
I I
11
, :
?!;!",!'.'.ш'!!!Р!'.?':. МО!!!.l!!'..в--а.!.'!!:1!!!!!!.'!.::'5.шпl!.?lJ!:?!.!.ша.'5.='!I!..шА1А Т-!::!.!!..ШШШ..Ш.Ш.......Ш ".ш.шш..
...:. А1!!el},'!?й-.I!..I!!!..в--?..!?..в--I>!...х..l!..'!::!..'.!.ш
% вычисление и визуализация интенсивности световой волны на отрезке
% х = О, У = L, zE[zmin,zmax]
» for i=I:Np
r=[O L z(i)]';
l(i)=Intensity(Lambda,A,N,R,r );
end;
» рlоt(z,Иrnах);
Результаты выполнения описанной выше последовательности команд
представлены на рис. 9.27.
здесь л  длина волны, А  амплитуда волны, N  количество источников
света, RO  составной массив, содержащий радиусышвекторы источников
света, r  радиусвектор точки наблюдения, Nb  число точек усреднения,
Для реализации вычислений в соответствии с (9,66) необходимо создать
файл, названный нами Intensityl.m, содержащий описание соответствую--
щей функции.
% листинr файла Intensity1,m
function E=Intensity l(Lambda,A,N,RO,r,Nb)
% описание функции, возвращающей значение интенсивности
% в заданной точке пространства в соответствии с (9.66)
% apryмeHTЫ функции:
% Lambda  длина волны
% N  число источников
% А  вектор, содержащий значения интенсивностей источников света
% RO  матрица, столбцы которой содержат коорд, источников света
% r  екторшстолбец, содержащий координаты точки наблюдения
% Nb  число точек усреднения
su=O;
% вычисление значений подынтеrpальной функции в (9.65)
for i=I:Nb
su=O;
for j=I:N
Rr=dot(r- RO(: ,j),r- RO(:,j» ЛО.5;
su=su+A(j)lRr*cos(2*pi/Lambda*Rr-2*рi/NЬ*i);
end;
f(i)=su.Л2;
end;
Е=mеan(п; % усреднение значений подынтеrpальной функции
% в соответствии с (9,66)
Для вычисления распределения интенсивности в соответствие с (9.66)
необходимо выполнить следующую последовательность команд:
» N=2; % число источников света
% задание параметров и координат источников света
» А(I)=I;
» А(2)=I;
» LаmЬdа=5000*10Л-7;
» RO=[O О -0.1];
» R1=fO О 0.1];
Jp\ Ш"/I\ \ШIН 11 ! 111"111\11111\11\ I !il111 \ '
[1 I I \: I!\, 111 11
+ 11111, 11,1 \/111,,1 .
::1' ' II'I! 11 :: 1:11 I \
о.зr-\ \ \ I I I I \ I
021 I i I I 1 \ I '\ \ 1 I i \ 1/1
01 i \,  J i    '\  J I '
OLl.....L L..L l .I    L _....lj J
.5 .4 " .2 .1 О 1
Рис, 9.27. Распределение световой волны на оmрезке х  О, У = L, ztt [vпiп,vпax}
Как показывает практика работы с данным документом, на вычисление
интеrpала (9.65) даже вдоль одной прямой пакету MAТLAB требуется до с..
таточно большое количество времени, КОТорое, как очевидно, будет в Np раз
больше при анализе распределения интенсивности на плоскости у = L.
Можно устранить отмеченный недостаток, если вместо вычисления инте
rpала (9.65), проводить усреднение напряженности cYMMapHoro электриче
cKoro поля по конечному числу точек интервала [0,1]. Функция, реализую
щая данное усреднение, имеет следующий вид:
1
Еl(л, А, N, RO, r, Nb) = --'...
Nb+l
Nh [ N А . 2 2 )) 2 ,
L L Ш  I,eos( ,;r,rRO;I,;r '}
)=1 ;=] Ir RO;, А Nb+l
(9.66)
264
265

к- Obl?"![J! 1!!?'!!!.'!Ро.'!.'II:Р.'!..!lI':К--lIх..'!Р.?н::?в__Clк--'!.'!:'!.1.т.::!.I!...... ._
'._ .?:. JO,J, ?e'!.r?!.I!..'!..II'!.C?!'.:?.:x..!!I!!'.!..lI.
I 11'1
1I
,,1 11 11 I I /1\
'1 I'! I l' . 1 А '111 11
04 ! 1 iu\ ,\ 111 11\ i 1 1 \\ I\!\I/' 11111 11 : 1 1\ 11 ,111 !
I ' I ' 11 I \ 11 I  1 111 11 111 11 \
02 \ I i \ II!I \ I !I 111 I l' \ 1 I 11 [, 11 \  11 i II! 1 '1
О I j,1\ '{{,!11ilJ _!;ltll, :/ 1\} I  \!]
-5 .<4 -3 -2 -1 О , 2 3 4 5
Для анализа пространственноrо распределения интенсивности необхо
дим о выполнить следующую последовательность команд:
% задание пространственной сетки
» Np=200; % число узлов
» i=l:Np;
» xmin=-5;
» хmах=5;
» x(i)=xmin+(xmax-xmin)/(Np-l )*(i-l);
» i=l:Np;
» zmin=-5;
» zmax=5;
» z(i)=zmin+(zmax-zmin)/(Np-l)*(i-l);
» L=200;
% вычисление и визуализация распределения интенсивности
% в соответствии с (9.66)
» for i=l:Np
for j=l:Np
r=[x(j) L z(i)]'j
l1(iJ)=Intensity l(Lambda,A,N ,R,r,3);
end;
endj
»plot(z,I1(:,20)/max(I1(:,20») % распределение интенсивности
% на отрезке x=4.0452, y=L, ZE[5,5]
»plot(z,I1(20,:)/max(I1(20,:») % распределение интенсивности
% на отрезке XE[5,5], z=4.0452, y=L
,
,
I1
11
11
!I
I 
lil
11
i'
11
»R=cat(2,RO',Rl'); % создание матрицы, столбцы которой содержат
% координаты источников света
% задание сетки для вычисления распределения интенсивности световой
% волны
» Np=200;
» i=l:Np;
» j=l:Np;
» L=200j
» zmin=-5j
» zmax=5j
» z(j)=zmin+(zmax-zmin)/(Np-l)*(j-l)j
» Nb=3j % число точек усреднения
% вычисление интенсивности световой волны на отрезке
% х = О, У = L, zE[zmin,zmax]
» for i=l:Np
r=[O L z(i)]'j
l1(i)=Intensity 1 (Lambda,A,N ,R,r,Nb)j
endj
Анализ разности между значениями распределений интенсивностей 1, 11,
вычисленными на отрезке х = О, У = L, ZE[zmiп, zmax] (рис. 9.28), показыва
ет, что уже при усреднении по трем точкам абсолютное значение разности
не превосходит 1.10IO, поэтому далее при решении задач следует использо
вать функцию Intensityl.
::1
1:
1 :
0.8
» contourf(X,Z,I1)
» colonnap gray
» xlabel('x')j
» ylabel('z')
Результаты выполнения описанной последовательности команд пред-
ставлены на рис, 9 ,299 .31.
Рис. 9.28. Абсолюmное значение разносmи .нежду значениями распределении
интенсивносmеи 1, l1, вычисленными на отре1ке х = О, У = L, ZE[zmiп, zmax]
266
267

11
t
l<'О/I1ы()пlерllOе.:'l()?е.лuроа.l/l'е rpl'UЧСЮl):процессов в пакеmе f4!AB..
9. Моеq/.lрОf3<1flUевО1l10вых явл-е:ll'
1I1
ill
11
I
I
1
 I
'1  !I Т 1, ,1 ] (1 I  I  l'  1, Т 1  / j
I ,1, I I I I I ['I ,1 I "
09' " l' l' l' '1 1 1 'I[ ,1 11 11 '1" I 1I
1 1I '11 11 1I 11 1 I1 I! 11 1I 1, i 1 !I :\ I! 11 JI'
tJ 13  I! '11 ! '1 i 1
! 11 I :: 11 '1111 ,1 11111111111' i I111I '1'1 I1
" 1 1 ,1, 1 I '1'
111 1 1 111' 1I [11 i 11 11 1 i 11111 l' ,1
" 1, ! 111 ' I ч
" 1 ' ' i ! i 11 1, ' 11111 i I i I 11 i .1 i: I i 11 i 11 11
11' 1 11, I 11 1, I 1 1, 1
"11 11 1 I I ! 1 III! 11 !: 11 11 :! 111 !!
0'11111 [11/ [ l' I 11111111 11 [1 illl I111
1111 11 111.1 11 il 1 li \1 11 I ',I I 1.11..:.
0,.,1 1, 1, 11 11 I1 1[1 I1 11 III! 1111
," " ,;  '! ', 11 li f i l' \
o -_. ..l   ......1. l 1 J.
.5 -<4 .;, .2 -1 О 3
Задача 9.34
J, Используя описанный выше докуменщ проверьте, что координаты )ии
ниму.нов интенсивности волны для выбранных zеометрических размеров
систе.МЫ в 1/,юскости у = 1, находятся из условия
1( d sin 0 1(
),
2
(9,67)
\
\.
7
сде sin0;::; ,
L
2. Получите выражение (9,67) аналитически, проинтесрировав (9.65).
3. Исследуйте, как меняется положение первосо h1Uнимума при изменении
А в диапазоне [4 .10,4;6 .1O4J мон,
4. Зафиксируйте значение А и проварьuруйте L от 1 до 300 мм, Как зави
сит положение htaKcu.'o1YMa интенсивности от I. при L»(Xтax.......'<:тin)'
(yтaxyтin)?
Рис. 9,29. Распределе/ше
интеНСИ6l-IOсти на отрезке
x=4,0452. y=L, ZE{5,5]
1 0OO51"""""""'T"
,1
t,
Рис. 9,30, Распределение
интенсивности на отрезке
XE{5.5], z=4,0452. y=L
099.
'9751
I
oo,::r
о S96L..........L.....":"".......L......J..
-5 --4 з -2 .1 О 1
\
\
\
\
Задача 9.35
Проаналuзир)'Йте распределение интенсивности в lиlOскости У =L, для слу
чаев КОсда число щелей N == 3,4,..,,20, считая, что ).=5.104 ММ, 1_==200 мм,
d == 0,09, (Данная модель является моделью дифракционной решетки.)
1. Постройте зависимость макси.мальноzо значения интенсивности от
числа щелей N.
2. Как зависит расстояние между пиками от числа щелей?
3. Проварьируйте L от 1 до 300 мм, Как зависит положение максимума
интенсивности от L при L»(xтaxXтin),( Утах Yтin)?
09SЭ5
0999
\
\
0.9005
\
\
\
...J.....'
4 5
Задача 9.36
На практике ширина реальных щелей zораздо больше длины волны, пo
этому более адекватной является модель, в которой щель paCCMaтpи
вается как набор косерентных источников сферических волн (принцип
Fюйzенса),
1. Рассчитайте распределение интенсивности света с длиной волны
А = 5 ,] 0,4 мм от одной щели конечноzo раз.мера, за.меняя еzo N = 20 тo
чечными источника.ми, отстоящими друс от друса на 0.001 мм. Oпpeдe
лите ширину центра.%НОZO пика интенсивности при L == 200 мм, Как
соотносится ширина центральноzо пика с шириной щели? Как зависят
полученные результаты от числа источников N?
2. Как зависит положение первосо миниму.ма дифракционной картины от
длины волны, ширины щели и расстояния до экрана,
3. Проведите сравнительный аналuз распределений интенсивности для
l_ == 1.\1.11 и L == 50ALM.
.'
.'
Рис. 9,31. Распределение
интенсивности волны
в плоскости )'L
. о
.,
1
268
269

!!..А.!.п--?_'!!е..l!..II!?е..й--л..':!!.?'!.l!.!''!.е..Р..lI!:.е.К--lI!.Р?':I.е..'?6:1,!К--'!..'!!.е...fo!.._!:..!!!! ...___.  .... "''." ... 
.ш ?Jo!.й-cJ..'!..л..'!.J1.!!,!1!1Iе..f!..Й-l!.11Й-6ых..!!.!.'!1IЙ
Задача 9.3 7
Исследуйте распределение интенсивности света при интерференции на
системе дx щелей, используя модель щели конечной ширины, Для этоzо
замените каждую из щелей 20 точечны.ми истОЧНИКaJ.JИ, отстоящими друz
от друzа на 0,000] мм, расстояния между серединами щелей задайте paв
ными О,] .мм, Как соотносится распределение интенсивности в данной MO
дели с анало?Uчнымu распределениями для дx точечных щелей? Как зави
сит распределение интенсивности от длины волны?
/S1
z:
женность поля электромаrнитной волны в точке с координатами (о, L, z)
есть сумма 4 волн: 1) волны, излученной источником, расположенным в
точке (0,L."a,/2), и прошедшей через отверстие S]; 2) волны, излученной
источником, расположенным в точке (0,L,,,as/2), и прошедшей через OT
верстие S2; 3) волны, излученной источником, расположенным в точке
(0,Ls,a..l2), и прошедшей через отверстие S]; 4) волны, излученной ис
точником, расположенным в точке (0,L.,,as/2), и прошедшей через OT
верстие Sz. При этом фазы интерферирующих волн оказываются различны
ми, поэтому для нахождения напряженности cYMMapHoro поля следует учи
тывать начальную фазу, которую ранее для KorepeHTHoro источника мы
положили равной нулю (см, формулы (9.60), (9.64». Обозначим начальные
фазы этих волн 1)111, CfJ1z, <Р21, <Р22 соответственно. Как очевидно из рис. 9,32,
значения начальных фаз, зависящие от rеометрических размеров paCCMaT
риваемой системы, определяются следующими выражениями
С2Ш
1)1]] = 1)122 = (  а;) + L; , (9.68)
1)1]2 = 1)12] = (%  а; y; L; (9.69)
С учетом начальных фаз интерферирующих волн выражение для напря
женности поля в точке (о, L, z)
E(r,t) = II [со{ 2; liJl  о) 1 + 1)111) + со{ 2; 'Т11  О)! + 1)121)] +
II [со{2; Ir21  0)1 + 1)1]2 )+со{2; [Т21  О)! +1)122 Л
Используя известные триroнометрические формулы
cosa +cosb = co{ а b }о{ а ;Ь),
(9.70)
1,
jl
1I1
1111
111'
I!II
1111:
н
,:1
111
:1
1,:;
11
11
11'
"1,
11,
!
'
,'1
",i
Задача 9.38
Подход, использованный в задачах 9.36, 9.37, может быть применен для
вычисления распределения интенсивностей волн, прошедших через oт
верстия конечной ширины и высоты (дифракция), Для этоzо следует
представить соответствующее отверстие как набор N KozepeHlnHblX
источников сферических волн, равномерно распределенных по плоскости
отверстия, Рассчитайте распределение интенсивности для прямо
уzольноzо отверстия размером ] х3 мм, освещаемоzо светом длиной
волны л=5.} o4 ММ, Сравните распределение интенсивностей для раз
ЛИЧНЫХ значений LE[3,200) мм, определив предварительно для каждоzо
L минимальные значения N, начиная с которых распределение интенсив
ности не зависит от числа источников, Постройте зависимость числа
N от расстояния L.
S2
Ls L
Рис, 9,32, Красчету интерференционной картины от nротяжеННО20 источника
Рассмотрим влияние размеров ИСточника KorepeHTHoro излучения на
распределение интенсивности при интерференции на системе двух точеч
ных щелей (рис. 9.32). Предваряя численные расчеты, проведем качествен
ную оценку, позволяющую ввести величину, определяющую распределение
интенсивности света в плоскости у = L. Заменим протяженный источник
света двумя точечными источниками, расположенными соответственно в
точках (0,I."a,/2), (0,L.,,a,/2), и найдем распределение интенсивно
сти света в плоскости y=L, В соответствии с принципом rюйrенса напря

приводим (9.70) к виду
E(r,t) = [cos( 2Jl'ir.'  о) t+ I)1ll + 1)121 )cos( 1)111  1)121 )] +
liJl л] 2 2
ш [cos(2Jl' Т? I  о) t + Ри :t: I)12 )cos(p1J..  1)17.1 )],
I! л  2 2
(9.71)
1

270
271

Ii,:!,/(!..,,!!p.'!!!!??'!!!.fJ.?al.I., rJ!.!!.z.'::'.е'!!!..Оlf..е.:'!..в!!'!!.='!..А !..1:l!
9. М O?el}':'.!!.?!.a..'.l!.e..'!.?!':.'!?':..Z.f!.'!.Jl=':
Полаrая, что d, а.\ « L,,, из (9,68), (9,69) найдем, что
If'll  If'21 = 1f'12  If'22 = !!... da s
2 2 2ЛLs
Подставив (9,72) в (9.71), окончательно получим
( ) [А ( 2л. I 2лLs ) А ( 2л l' 2л:Ls )]
Е Р, t =  cos. ;1'11  й) t + . +  I cos . 1'2:  й) t + ... . .. .
1'11 л Л1'2i л л
cos(, a,. ).
лLs
Из (9.73) видно, что напряженность электрическоrо поля волны двух
разнесенных коrерентных источников отличается от напряженности элек
трическоrо поля точечноro источника множителем cos(Jr... das.), поэтому
2лL"
(9,72)
напря,жеююсть электрическоzо поля волны:
1 Nlr А (2Л ))
E(r,t) = LL 1':':lcos lrRm.r.vt+lf'm; .)
т=О ;=0 \ r Rml л
9.7. rеометрическая оптика
(9,73)
В общем случае для описания процесса распространения волн необхо
димо решить волновое уравнение, являющееся дифференциальным ypaBHe
нием в частных производных, с заданными начальными и rpаничными yc
ловиями. Методы ее решения, изучаемые в специальном разделе математи
ки, который называется «уравнения математической физики», в большин
стве случаев оказываются весьма сложными. Однако существует важный
частный случай, коrда длина волны MHoro меньше всех характерных разме
ров системы. В этом случае оказывается возможным использовать модель,
в которой волна распространяется аналоrично движению пучка частиц,
движущихся по определенным траекториям  лучам, поэтому данное при
ближение получило название rеометрической оптики. Распространение CBe
товых лучей подчиняется принципу Ферма (принцип наименьшеrо BpeMe
ни): луч света идет между двумя точками по такому пути, который
требует наименьшеzо времени.
А
i
условие, при котором отличия распределений данных интенсивностей HeBe
лико, можно записать в виде
I
11
.11
:11
,,!'
11
!i!'
!,
;1
'1
1:
'11
ilij
:11,
"
1,'
л das л
< (9.74)
2ЛLs  2 .
Выражение (9.74) устанавливает связь между yrловым размером источ
ника 0 s = а" / Ls и уrловым размером области волновоrо фронта 0 ео/! ' В KO
торой излучение протяженноrо источника KorepeHTHo [7]:
л
0ео/! ::;  (9.75)
0>
а
L
li1
11
"
1,'
'{'
I
Задача 9.39
Проведите в опыте Юнzа численные исследования распределения ин
mенсивности волны, создавае.МОЙ протяжеННЫ!>t источником KOёepeHт
Н020 излучения, представив еёО в виде набора N точечных исmочников.
положение которых задается набором радиусвекторов
Rs;,; = 0,1"" N  1, Подтверждают ли результаmы АtOделирования оцен.
ку размера области (9, 74)? (Указание, Фазы волн epOi' epl;' излучае/>lые
каждым точечным источником соответственно в точках 51 и 52. oпpe
деляются выражением
If'т; =.2; IRm  Rs;l,; = 0,1,.. ,N  1,т = О,],
 ь
J)
В Рис, 9.33
Применим принцlШ Ферма к задаче прелошения, в которой свет падает на
поверхность раздела двух сред, в которых скорость света различна (рис. 9.33).
Принято выражать скорость света в среде v через скорость света в Ba
кууме с и показатель прело мления среды п
с
V=.
п
Время прохождения света из т, А в т, В, как видно из рис, 9.33, равно
yT;'.;Z Jb2:( L  х /
t = ----,.. +.'--. --',
V! '2
х
(9.76)
(9,77)
!'де 'I = С I п1, '2 = С / 112 .

272
273

ш.ш::I.r.V'!.l!''..:.о.:'.'.'.?'!.I.JljJ':'.'U.
'?М-!Jь!о.Т/Jер!,о.е. .! о.дJ1.о.ва.'.I!'.Р'llз:кuх..п'ро.у:.:='!'!. п-l!.'5!'.Т/J.:А!..Т!:А I!.ш... .
в соответствии с принципом Ферма dl/dx == О, поэтому
1 х 1 Lx
Ш .Ш o
v]-J;?+x2 v2Jb2+(Lx)2 .
Так как x/faT2 == sша, (Lx)/ b2 +(Lx)2 == sin{J, то (9.78) мож
но записать в следующем виде (закон Снелла):
п] sina = П2 sin{J.
Рассмотрим задачу о распространении
луча в среде неоднородным коэффициен
том преломления. Будем считать, что луч
падает на прозрачную среду с коэффици
ентом преломления п, зависящим от у
(п == п(у», под малым yrлом к нормали в
точке у = о (рис. 9.34). Для нахождения
уравнения, описывающеrо форму луча,
рассмотрим луч света, проходящий через
несколько плоскопараллельных пластинок
с различными коэффициентами преломле
ния (рис. 9,35). В соответствии с законом
Снелла (9,79)
по sin а == пl sin Рl = П2 sin Р2 == пз sin {Jз =...
Так как соотношение (9.79) не "
зависит от числа и ширины отдель
ных слоев, оно будет справедливо и
при непрерывном изменении коэфш
фициента преломления в направле
нии оси о У:
n(y)sin{J(y)=nosina, (9.81)
rде р(у)  уrол между направлени
ем луча и осью оУ (рис. 9.36),
Как видно из рис, 9.36,
tga(y) = ctg{J(y) = dy/ dx ,
поэтому
у
(9.78)
/
(9,79)
о
по
х
Рис, 9,36, К получению уравнения, описывающеzо распространение луча
в неоднородной среде
п(у)
Под(,'тавляя (9,81) в (9,82) и учитывая, что а::=: л/2 , приводим (9.82) к виду
п(у) (9.83)
J1;(dy/dx)2 == по'
Решив (9.83) относительно dy/dx, получим дифференциальное ypaBHe
ние первоrо порядка с разделяющимися переменными
 =Kn))' l (984)
о
.
Рис, 9,34
(9.80)
Ero решение имеет вид
пз
\'
Х == J dy (9.85)
У. ,(y 2)2  1
 по
При произвольной зависимости п(у), вообще творя, интеrpал в (9.85)
может не выражаться через элементарные функции, поэтому для анализа
траектории движения луча будем вычислять ero численно. Для этоrо можно
использовать следующий алrоритм.
1. Задать функцию п(у).
2. Задать координату точки падения уа'
3. Задать максимальное значение координаты Утах'
4, Вычислить координаты Yi, i=O,I,... ,N 1 точек разбиения отрезка
[ уа ,Утах] на N частей,
5. Вычислить N значений интеrpала (9,85) на интервалах [Уа,У,].
6, Отобразить rpафически зависимость у=у(х) ,
пZ
п1
Рис, 9,35
sin{J(y)== Ш2JД;') ==Ji+(;,'/dX)2
274
(9,82)
275

к- Й-'1ь.'0'!.1р'1о!!е:!'Рова.Iе..Р.и-з.l/ек-uх f1Р.оче..сс.й-в !.lс:.ке'f1.е..lv!.Т'L1-.l!. .
Для реализации данноrо алJ'оритма необходимо выполнить следующую
последовательность действий,
1> Создать файл CoeffRefractiol1.m, содержащий описание функции, воз
вращающей значение функции п(у)/ по ' [де по  коэффициент преломле
ния в точке падения луча,
% листинr файла CoeftRefraction,m
f"nction z=CoeffRefractiOI1(Y)
% функция, возвращающая значение функции п(у)/ по = .Jl+4y
z=(1 +4*у). ЛО.5;
2, Выполнить следующую последовательность команд:
% задание координатной сетки по оси о У
» уmil1=10Л5;
» уmах=20;
» Np=100;
» i=I:Np;
» y(i)=ymin+(ymaxymil1)/(Np 1)*(i 1);
» Nk=1000; % число узлов для вычисления интеrpала
% с переменным верхним пределом
% вычисление значений интеrpала с переменным верхним пределом (9.85)
» for i=I:Np
5"=0;
for k=I:Nk
У (k)=ymil1+(y(i)-ymil1)/(Nk 1)*(k 1);
Z(k)=I/( CoeffRefraction(Y(k) )Л2 I)ЛО.5;
el1d;
Xb(i)=trapz(Y,Z);
Yb(i)=Y(Nk);
end;
» plot(Xb,Yb)
Результат выполнения описанной выше последовательности команд
представлен на рис, 9,37.
Полученный результат выrлядит достаточно неожиданно. Можно было
ожидать, что луч, падающий на rpаницу раздела, должен идти вдоль оси Х,
но не по искривленной траектории,
201
181
,,
"f
12
10
.'.А:..fй-д-е!!и-р"Й-.,!'.I.и-е..Й-I!'.Ь,я-вЧ-:'..и-.
/.
4 /
/
2 / J
/ ,
/. .
....>__.... I
О  ..........I........l..................J
О 1 2 3 4 5 6
Рис. 9,37, Траектория движения луча в среде с nере.менны.«
коэффициентом преломления
Полученный результат требует
дополнительноrо объяснения. В [eo
метрической оптике под лучом по
ни мается узкий пучок света, KOTO
рый с некоторым приближением
можно считать участком фронта
плоской волны (принцип rюйrен
са). При падении плоской волны на
оптическую неоднородность во
второй среде возбуждаются BTO
ричные волны (рис. 9.38). Вторич
ная волна движется в среде с Heok
нородным показателем преломле
ния с различными скоростями: тем Рис, 9,38, К объяснению причины
медленнее, чем больше 11, и наобо искажения луча при движении волны
рот. Это приводит К искажению в среде с неоднородным коэффициентом
фронта вторичных волн. преломления
Таким образом, лучи, рассматриваемые в rеометрической оптике, пред
ставляют собой пример математической модели, используемой для описа
ния ряда оптических явлений. Важно понимать, что в реальной природе
«лучей» не существует. При невозможности решения задачи с точки зрения
rеометрической оптики, следует представить луч как перпендикуляр к уча
стку фронта плоской волны, ширина KOToporo значительно больше длины
волны, и рассмотреть явление с точки зрения rеометрической оптики,
276
277

.А!?"'!!:'I!..I?':...?"::р'вl!.!,,::'!..rp!,!:'!...>:.!II!..?"Чe==I:'1!!'!..!!!..."!..!..:!l!........
. ... .....А1..?":'р'вl!.'lJl!.в--?Л!I?.вых явлеllИЙ
Задача 9.40
Используя описанный выше документ, проведите сравнительный анализ
траектории луча для различных законов изменения коэффициента пpe
ЛQ}\1ления f(y) == б + ауа f ' Почему в ряде случаев вычисление численно
20 значения инте2рала (9,85) оказывается невозможны_'d, НО при исполь
зовании в качестве нижней 2раницы инте2рирования некоторой велuчu
ны &«1 uнте2рал оказывается сходящuмся?
9.8. Поляризация
Ez(yJ)==E\ocos(27ry21l'n. (9,89)
Из выражений (9,88), (9.89) видно, что напряженности электричеСКОI'О
поля не зависят от длины волны, следовательно, поляризация элеКТРОМaI'
нитной волны также не зависит от ее длины,
Для изучения основных свойств поперечных волн вычислим в выбран
ный момент времени t составляющие напряженности электрическоrо поля
волны, распространяющейся в положительном направлении оси о У, Реше
ние рассматриваемой задачи в пакете МА ТLAВ находится выполнением
следующей последовательности команд:
» clear аН
% задание координатной сетки для вычисления составляющих
% напряженности электрическоrо поля
» Np=lOO;
» i=l:Np;
» ymin=O;
» утах=2;
» y(i)=ymin+(ymax-ymin)/(Np-l)*i;
% вычисление составляющих напряженности электрическоrо поля
» ExO=l;
» EzO=l;
»t=2.1; % выбранный момент времени
» Ex(i)=ExO*cos(2*pi*y(i)-2*рi*t+рil2);
» Ez(i)=EzO*cos(2*pi*y(i)-2*рi*t);
% визуализация напряженности электрическоrо поля
% в узлах координатной сетки
» compass(Ex(l),Ez(l»
» hold оп
» compass(Ex(lO),Ez(lO»
» compass(Ex(20),Ez(20»
» compass(Ex(30),Ez(30»
» compass(Ex( 40),Ez( 40»
Результат выполнения приведенной выше последовательности команд
представлен на рис. 9,39,
в предыдущих разделах при рассмотрении волновых явлений нас не
интересовало направление колебаний волны. В данном разделе мы pac
смотрим явления, зависящие от поляризации волны. Отметим, что поня
тие поляризации используется только для описания поперечных волн,
поскольку задание направления распространения продольной волны aB
томатически определяет направление колебаний среды. Для поперечной
волны единственным оrраничением направления колебаний является yc
лови е, в соответствии с которым они должны происходить В плоскости,
перпендикулярной направлению распространения, поэтому, например,
электрическое поле электромаrнитной волны, распространяющейся
в направлении оси о У, может быть представлено двумерной векторной
функцией E(y,t) = (Ex(y,t),Ez(y,t)). Если электромarнитная волна являет
ся монохроматической, то функции EAy,t), Ez(y,t) изменяются незави
симо дрyr от друrа с одинаковой частотой. Отмеченное обстоятельство по
зволяет представить данные функции в следующем виде
Ex(y,t) =Ехо cose; уwtФ). (9.86)
E,.(y,t) == Е\,О cos( 2л У  w t), (9.87)
. . л
rде ЕхО, Е,о  амплитуды соответствующих напряженностей,
Анализ выражений (9.86), (9.87), показывает, что оказывается удобным
ввести безразмерные переменные: координату у = у/л и время
r = t/(2Jr/W), используя которые можно представить выражения (9.86),
(9,87) в следующем виде
Е, (yJ) == Ехо cos(21l' У  2л r ф), (9,88)
278
279

. O пь.I?'!!.l!..fJ.!о..'!../.?<!.еl!.'!Р.!!_С:/.:'1!.!!зu l!.._с.'5..'!!:...':.fJ..':!'!.с..=-О!!!!,:е'!!..А!..1.!..:!.!!..._mmm....._m...
ттт ..._т?: r:! О<!.eJ!.'!Р!!'!.II::тв?l!!!?'Ы__::'Я_6Jl!'':'_
90
Результат выполнения приведенной выше последовательности команд
представлен на рис, 9.40,
180
.'\\.. .li
.....
;;.\> .
::
02-1
011
:l
-о.
-о.
. 2.5
-02 '_________... //'2
о-л.......... -< л 1.5
 .....----<;.-- 1
0.2 '-----, / 0,5
'---x О
О.. -0.5
270
РИС, 9.39, Визуализация проекции вектора напряженности матитнOi!О ПОЛЯ
на плоскость оУ в момент времени t=2.J
Для визуализации напряженности электрическоrо поля, вычисленной в
узлах координатной сетки, в трехмерном пространстве необходимо выпол
нить следующую последовательность команд:
» clear аН
% задание пространственной координатной сетки
» Np=53; % число узлов сетки
» i=1:Np;
» хщ=о;
» ymin=O;
» уmах=2;
» у(i)=уmiп+(уmахуmiп)/(Nр-1)*(i 1);
» z(i)=O;
% вычисление составляющих напряженности электрическоrо поля
» ЕхО=1;
» EzO=1;
» t=2.1;
» Ex(i)=ExO*cos(2*pi*y(i)-2*рi*t+рil2);
» Ez(i)EzO*cos(2 *pi *y(i)-2*pi *t);
» Ey(i)=O;
» quiver3(x,y,x,Ex,Ey,Ez)
»view([50 36])
Рис. 9.40, Визуализация в трехмерном пространстве вектора напряженности
маzнитноzо ПОЛЯ в момент времени t=2,J
Как видно из рис. 9.39 и 9.40, вектор напряженности электрическоrо поля
описывает окружность и поворачивается при движении вдоль оси аУ по часо
вой стрелке (если смотреть со стороны положиrеньноrо направления оси оУ). О
такой волне roворят, что она имеет левую крyroвую поляризацию.
Задача 9.41
Используя описанный выше документ,
трома2нитной для следующих случаев:
1) Ехо =1, Еуо =1, ф=О,;r;
2) Ехо =0.5, Еуо =1, ф=О,;r;
3) Ехо = 1, Е,.о = 1, Ф = л/4,л/2;
4) Ехо =0.5, Еуо =1, ф=;r/2.
определите поляризацию элек
Задача 9.42
Решите задачу 9,41 для электрома2нитной волны, у которой cocтaв
ляющие электРОJ'.Ш2нитно?0 поля изменяются по закона.м
Е Jv,t) = Е хО cos( йJ t  2; у  ф ),
280
281

f!.С?:I!?!'!е.I!.I?:,,:,:,е..UP?''!..Й-!I.:. .rJ!.'!е..:I'!..f.о..1f.:.::овш,!ш:.'!!.е....!'f:.l!..шш.......
Еу (y,t) = Е,о COS(OJ t !! У) ,
. . А.
При распространении электролщzнитной волны в среде, имеющей nокаш
затель преломления отличный от единицы, уравнения (9, 86}, (9,87)
nринимают следующий вид
Ex(y,t) = Ехо со{ 2; nу  OJ t ф j, (9.90)
Е,. (y,t) = Е,.о cos( 2л nу  OJ t), (9.9 1)
. . А.
zде А.  длина электромаzнитной волны в ваКу'уМе.
В некоторых веществах (например, кварц, кварцит), скорость расnрош
странения волны зависит от направления ее распространения, Такие
вещества называются веществами с двойным лучепреломлением, Если
nоказатели преломления вдоль осей оХ  nх и о У  nу различны, то уравш
нения для составляющих напряженности имеют вид
Ex(y,t) = Ехосо{2; пху OJt ф). (9.92)
E,.(y,t) = Еуо cos(2Jr nуу OJt), (9.93)
, , А.'
rлава 10
МОДЕЛИРОВАНИЕ СИСТЕМ,
СОСТОЯЩИХ ИЗ Большоrо ЧИСЛА
ЧАСТИЦ (МЕТОД МОЛЕКУЛЯРНОЙ
ДИНАМИКИ)
10.1. Введение
1
1,
,1
, I
1
1
1
Задача 9.43
Предположим, что на кристалл с двойным лучепреломлением падает
электромаzнитная волна с круzовой поляризацией. Задайте nоказатели
преломления пx=9.1, nу=9,2 и определите, при какой толщине кристалла
волна, имеющая на входе круzовую поляризацию, становится на выходе
линейно поляризованной, Как зависит ориентация вектора Еу от толш
щины пластины. Что получается, если через кристалл той же толщи
ны проnускать линейно поляризованную электромаzнитную волну?
в предыдущих разделах нами рассматривались системы, состоящие из
небольшоrо количества частиц (за исключением rл. 9), Однако большинство
реальных физических систем состоит из большоrо числа взаимодействуюш
щих дрyr с друrом частиц. Например, в 1 CM3 кислорода при Т=300 К,
р = 1,01.105 Па находится 2,5.1019 молекул. Вознкает естственный вопрос
как решить задачу об описании поведения этои сложнои моrочастичнои
системы? В этой rлаве рассматривается наиболее очевидныи подход к pe
шению данной задачи  прямое решение микроскопических уравнений
движения частиц, взаимодействующих дрyr с дрyrом (метод молекулярной
динамики). При этом наибольший интерес представляют не сами тpaeктo
рии, но вычисляемые с их использованием характеристики изучаемых сис
тем, например, термодинамических характеристик, вычисляемых усреднеш
нием по траекториям.
Необходимо отметить, что возможности современных компьютеров
оrраничивают метод молекулярной динамики (МД) по числу частиц MO
делируемой системы. Однако оказывается, что исследование поведения
систем с использованием метода МД даже для относительно небольшоrо
числа (от нескольких сотен до нескольких тысяч) дает достаточное KO
личество информации для понимания наблюдаемых свойств rазов, жидш
костей и твердых тел.
Отметим, что вопросы, рассматриваемые в настоящей rлаве, изучаются
в специальном разделе физике  статистической физике. Детальное pac
смотрение всех тем, традиционно включаемых в известные учебные курсы
[1 5], безусловно выходит за рамки нашей книrи, поэтому мы оrpаничиваш
емся рассмотрением некоторых наиболее принципиальных вопросов для
понимания поведения статистических систем и применения вычислительш
ных алrоритмов,

[,

I
,
ЛИТЕРАТУРА
1. ['етманова Е, [" Костарев Д. Б, Резонансные явления в системе связанных осцилляторов//
Электромаrнитные волны и электронные системы, 2009, Т. 6, N2 5.
2. Коткин r'. Л., Сербо В, [, Сборник задач по классической механике. М,: Наука, 1977,
3, Ландау Л. Д., Лифшиц Е, М, Механика. М.: Наука, 2000,
4, Крауфорд Ф. Волны, М.: Наука, 1974.
5, rулд Х" Тобочник Я, Компьютерное моделирование в физике, М,: Мир, 1990, С, 220.
6. Фарлоу С, Уравнения с частными производными для научных работников и инженеров.
М,: Мир, 1985.
7. Мешков И, Н., Чириков Б, В. Электромаrнитное поле, Ч, 2, Электромаrнитные волны и оп-
1Ика. Новосибирск: Наука, 1987.
282

I
)
:1"
!
!! ?IIJь/()т-.еР..lI()е '/.()e.:'!..P.(). 1I'!..:.rp'!.lt_ч-:.'!..:пр() е.5:с._()в.'.l_а:.'./::.1.Т..1:..11!.......
... ..' !9():.q 11Р.()?//и-.е[:и-./11.:.t с..().("!.lоя._Uj!llз-..?'()::':,!!?"()'l..:I5:л!ч3.с.т-и-.у
1 0.2. Математическая модель
статистической системы
V(r) = 4VOl(  )12 -( У J '
(10,3)
Ставя перед собой целью понимание качественных свойств систем, co
стоящих из большоrо количества частиц, упростим задачу, предположив,
что молекулы являются химически инертными, а их движение является.
классическим, Кроме Toro, будем считать, что СИJIа взаимодействия двух
молекул зависит тОлько от расстояния между ними, поэтому полная потен
циальная энсрrия и определяется суммой энерrий двух частичных
взаимодействий:
[де cr определяет «характерную); длину потенциала, а \10 , rлубину потен
циальной ямы, которые в дальнейшем мы выберем в качестве единиц изме
рения расстояния ( 1" = r/ ст) и энерrии (\7 = V(r )/V о ), Как видно из (10,3),
потенциал V (r) достиrает CBoero минимальноrо значения -Vo в точке
1
r . = 26 (j V(r) = О в точке ro = (j .
тт '
В выбранных единицах измерения потенциал ЛейнардаДжонсона имеет
вид
N
и =V('i2)+V('iз)+...+V(r2З)+"'= IV(r;j)
i<j=1
[де Vij) зависит только от абсолютной величины расстояния rij между
частицами i и j. Модель парноrо взаимодействия адекватно описывает «про
стые» жидкости, например, жидкий apr"OH.
Для электрически нейтральных атомов теоретически возможно, исполь
зуя законы квантовой механики, получить аналитическое выражение для
функции V(r). Однако, вопервых, такой расчет оказывается весьма rpo
моздким, BOBTOpЫX, для большинства задач оказывается достаточным ис
пользовать просryю феноменолоrическую формулу, учитывающую, что при
малых rсила взаимодействия между молекулами Р(Р) = Vи(i') является
силой оrrалкивания, а при больших r  силой притяжения. Оrrалкивание в
соответствии с квантовомеханическими представлениями обусловлено пра
вилом запрета Паули [6]. Слабое притяжение при больших r, rлавным обра
зом, обусловлено взаимной поляризацией каждоrо атома. Результирующая
сила притяжения называется силой ВандерВаальса. Таким образом, при
использовании модели двухчастичноrо взаимодействия, задача описания
поведения статистической системы сводится к выбору вида потенциала
V(r) и решению задачи Коши системы дифференциальных уравнений
d2'f N
т=V IV(rij)' (10.2)
dt i<j=1
Одной из наиболее употребительнь!х феноменолоrических формул для
описания потенциала межмолекулярноrо взаимодействия является потенци
ал ЛейнардаДжонсона
(10.1 )
V(r)={()'2 ( )6].
(10.4)
rрафик безразмерноrо потенциала ЛейнардаДжонсона преставлен на
рис. 10.1, из KOToporo видно, что потенциал является короткодеиствующим,
Т.е.ПрИ 1";:::2.5 V(r)=O.
05
V(r) о
25
05
l05
Рис, 10.1. Зависимость безразмер/Юi!О потенциала
ЛейнардаДжонсона от координаты
Для выбора переменной Т, используемой для обезразмеривания системы
уравнений движения (10.2), разложим потенциал V(r) в ряд Тэйлора вблизи
( . 21/б -""\ Сохранив члены ряда пропорциональны
минимума потенциала rmlП VJ'
ми первой и второй производным И приведя подобные члены, окончательно
получим
2
18,23 2
V(M);:: VO +  VоЛr
(j
(10.5)
[де Лrl« r rlllП
284
285

((o-л1.п.ы
l11ер1/0еe Аl0дел-!!..оваlll' фuч:.скх пр?Ц?!1аК-l11,J:!А Al!.
Сравнив (10,5) с известным выражением для потенциальной энерrии rap
моническOIО осциллятора
Е =: !.. kx2
2 '
(10.6)
приходим К выводу, что величина
,1
il
;!)
l'
I
l'
2
2.18,23
X=2VO
O
является аналоrом коэффициента жесткости пружины rармоническоrо oc
циллятора, т. е, частица, находящаяся в потенциале ЛейнардаДжонсона,
при малых смещениях от точки минимума будет совершать линейные rap
,.....-;
монические колебания с периодом 1'= 2л."jm/ Х . (Например, для ЖИДкоrо
aproHa, у KOToporo VO/kB =119.8 К (kB постоянная Больцмана),
o-=3.405.108cM, масса т = 6.69.102З r, Т = 1.14.10!1 с.) Далее будем ис
пользовать Т для обезразмеривания времени ( Т = t/1' ).
Перейдя в (10.2) к безразмерным переменным r = т/о-, V = V(r)/V о'
r = t/1', и учитывая выражение (10.7), получаем окончательное выражение
для безразмерной системы уравнений двиения
7
d2'f 2зл2  N
dr = 3 V,l)7(Y;J. (10.8)
I<J=1
Система дифференциальных уравнений (10.8), дополненная начальными
условиями 11(0), \7j(O), является математической моделью рассматриваемой
статистической системы.
(10.7)
10.3. ЧИСJIенный адrоритм решения системы
уравнений движения
После составления математической модели системы, состоящей из
большоrо числа взаимодействующих частиц, следует выбрать численный
алrоритм решения, от правильноrо выбора KOToporo напрямую зависит точ
ность решения, В rл, 9 при численном решении уравнений движения мы
убедились, что контроль за устойчивостью численноrо решения можно
осуществлять, следя за полной энерrией системы, величина которой в иде
286
.... ........щ!...9:J:!.'!!.:1!!!I!..()в--l!!!..'!!.Сl11:'!'.'.:'?:''!!.CJ..J/...!.':...'!!:'!:':!.'!'!!!.'!...:'!!...
альном случае должна оставаться постоянной, Отметим, что стандартные
функции пакета МА ТLAB, использованные нами в rл, 9 при моделировании
колебаний цепочек, в данной задаче оказываются неработоспособными
вследствие необходимости использования специальных rpаничных условий
(см, более подробнее ниже в настоящем разделе), Отмеченные обстоятель
ства определяют необходимость разработки собственных пользовательских
функций, реализующих решение уравнений движения в методе молекуляр
ной динамики. Анализ алrоритмов низкоrо порядка точности, таких как
аrоритм Эйлера и алrоритм ЭйлераКроммера. показывает, что данные ал
rоритмы не MOryт обеспечить сохранение энерrии на временных интерва
лах, рассматриваемых при моделировании молекулярной динамики. В этих
условиях приходится применять вычислительные алrоритмы, имеющие бо
лее высокий порядок точности, одним из которых является алrоритм Верле.
Про иллюстрируем суть данноrо алrоритма, следуя [7], на примере реше
ния системы уравнений одномерноrо движения частицы
dv  а (10.9)
dt  ,
dx
dt = V. (10.10)
Запишем разложение зависимостей хн! == X(tn + At) и v,,+1 == v(tn + At) в
ряд Тэйлора
Х,нl = Хп + x(tn)M +!.. x(tll Хм)2 + о[(м)з], (10.11)
2
vn+1 =vll +i{tll)M+O[cAt)2J (10.12)
Замечая, что x(tll)=V,1' x(tll)=J)(tll)=all перепишем (10.11), (10.12) в
следующем виде
ХIl+1 =ХIl + vllAt+.!all(At)2 +о[(м)3], (10.13)
2
VIl+! = V'l + allAt + O[cAt)2 J. (10.14)
По аналоrии с (10.13), (10.14) запишем разложение в ряд Тэйлора для
XIl1 == x(tll  At):
XII1 =ХIl VIlAt+all(At)2.
Сложив (10,13) и (10,15), получим
. )?
Xllt! +XIl! =2ХIl +all(At ,
(10.15)
(10,16)
287


1]

11
11:
1:
 '
i
.1!'.!':!?."!:I!/!'.!!?,,'!jJ?l!.I''!!:..1!из,?,,!еI5 npoye.:::.()al5.:.."!!.!TL11!
..... .........!.  Мо!!!!!!!!.,'!..в.l!.I':.е.:.!!.:1!!..С().'!!.?.JlU.!.U.!,?!!:,!О2(}l!. чап-:,:
откуда
Затем, повторяя описанную процедуру Х1I+1 из (10.17) и подставив X1It1
В (10.24), после очевидных выкладок окончательно получим
1
vlI+1 = vlI +2'(а1l+1 +а1l).11 . (10.25)
Вычислительная схема, задаваемая выражениями (10.21), (10.25), MaTe
матически эквивалентна алrоритму Верле, описанному выше. Данная схема,
называемая скоростной формой алrоритма Верле, является самостартую
щей, а потому не требует использования какихлибо дополнительных BЫ
числительных алrоритмов. Описание друrих вычислительных схем, исполь
зуемых для решения уравнений движения, приведено в [8].
При использовании метода МД для моделирования поведения raзов и
жидкостей, как правило, предполаrается, что рассматриваемая система Ha
ходится в некоторой кубической ячейке  МДячейке. Будем считать, что
МДячейка имеет линейный размер L, ее объем V = LЗ. Использование куби
ческой решетки порождает шесть нежелательных поверхностей. Частицы,
отраженные от этих поверхностей, будут возвращаться внутрь ячейки, по
этому rpани ячейки будут вносить значительный вклад в макроскопические
характеристики системы, особенно для систем с малым количеством час
тиц. для уменьшения описываемоrо эффекта принято вводить периодиче
ские rpаничные условия [8] (рис. 10.2), математическая формулировка KO
торых для любой наблюдаемой величины А имеет вид:
А(У) = А(У + nL), (10.26)
rде n = (п1' п2' пз) , а пl, п2, пз  произвольныецелые числа.
Х/Н 1 = 2х"  X1I1 + all(!l1)2 .
Вычитая (10,15) из (10.13), окончательно получим
(10.17)
V  XIlJ!.:-:- X1I1
/1  2Ы
rлобальная поrpешность алrоритма Верле, реализуемоrо формулами
(10.17), (10.18), имеет третий IlОрЯДОК для координаты и второй порядок для
скорости. Отметим, что скорость не участвует в интеrpировании уравнений
движения, поэтому в литературе, IIосвященной численным методам, данный
алrоритм называется «неявной симметричной разностной схемой», Очевид
ный недостаток неявной разностной схемы состоит в том, что он не являет
ся самостартующим, поэтому приходится использовать друrой алrоритм
для получения нескольких первых точек.
Отмеченный недостаток можно устранить, добавив и вычтя из обеих
частей равенства (10.17) величину X/I/2:.... t
 1( ) 1 1 2
X/I-t 1  X/I + 2' X/I+1  X/I1  2' X1I1.2' Xn.f1 + Х1I + а1l (!l1) =
 1( 2
X1I +VII!lt2' Х1I+1 2Xll +XIII)+all(!lt)
Из (10.17) найдем
(10.18)
(10.19)
 Х1I+1  2Х1l + Х1I4111
а  ---- . ,
11 (ы)2
поэтому (10.19) можно записать в виде
1 2
X/I+1 = Х1I + vlI!lt + a/I(!lt) . (10.21)
2
Поступая аналоrично, перепишем (10.18) для vlI+1 И (10.17) для Х/I-I2:
(10.20)
t-{!)
t-{!)
t-{!)
ер
ер
 x/I+2 x/I
v'1+1  t ,
Х/1-I2 = 2x1lt1 X1I +all+1(!l1)2
t-{!)
ер
t-{!) t-{!)
ер
ер . ер
t-{!)
(10.22)
(10.23)
ер ер
t-{!)
Рис, ] 0.2. Прuмер периодических
zраничных условий в двумерном
случае, Правило ближайшей
частицы означает, что расстояние
между частицами ] и 2
определяется длиной вектора,
обозначенною двунаправленной
стрелкой
соответственно.
Подставив (10,23) в (10,22), получаем
1 ,
Х1I-+ 1 + ,\111+ 1.11 + , а/н J (!l1)  х"
(10.24 )
\"11 f J ==
.1!
288
289
10-1576

.l!:.'!,:,'.'!:!'!!..l!.l!!!...'!.r!.'!.l!...'!l!!''::.p!.'..U'5.'!!.'!!!!!.!i.ec!:.<!!!!!п--'5...е'!!..е!..!!.ш.................ш
...........!.9:.. 1!!!!!.?..«!!.'!:'..!!.:'''!:!!'!!!'?''l!...'''!...'!!... болъ!!!.?.<:!?ч-!!5!'!! ча:.'!!.!'..!!
Данный алrоритм имеет следующую вычислительную реализацию: при
l1ересечении частицей rpани основной ячейки она возвращается в ячейку
через противоположную rpaHb с той же скоростью, Введением периодиче
ских rpаничных условий устраняется влияние rpаней и вводится квазибеш
сконечный объем для более точноrо описания макроскопической системы,
т. е. МДячейка оказывается «встроенной» в среду. Каждая компонента pa
диусавектора трансляции является числом между нулем и [, Для iй части
цы, находящейся в точке с радиусомвектором р;, имеются отображения
частицы в точках с радиусамивекторами р; + пL, [де п  целочисленный
вектор,
Для выбранных rpаничных условий потенциальная энерrия принимает
следующий вид
V(ij,...,rN)= Lv(rij)+ LLvrirj+пLI). (10.27)
i<j п i<j
для Toro, чтобы избежать вычисления бесконечной суммы в (10,27),
принимается следующее правило [8]: расстояние lF;jl между частицами,
расположенными в точках с радиусамивекторами 1j, Pj' соответственно,
определяется как Ip;jl = minri + P j :t пLI) по всем п. Данное правило ознаш
чает, что частица, находящаяся в базисной ячейке взаимодействует с кажш
дой из N 1 частицей в базисной ячейке или со своими ближайшими OTO
бражениями (рис. 10.2,). Важно понимать, что использование данноrо пра
вила приводит к «обрезанию» потенциала на расстояниях
L
rc >.
2
Это приводит К потере фоновоrо вклада удаленных частиц, поэтому для
устранения эффекта конечности системы значение L должно выбираться
достаточно большим, чтобы силы, действующие на расстояниях больших
Ц2, были пренебрежимо малы. Отметим, что более правильный подход со,.
стоит в учете взаимодействия каждой частицы со своим отображением,
Ссылки на ориrинальные работы, посвященные данному подходу и описа
нию вычислительных алrоритмов, ero реализующих, приведены в [8],
Сформулируем окончательно алrоритм метода МД:
1, Задать число частиц системы N,
2, Задать начальную конфиrурацию системы (совокупносrь координат
1j (о) 11 скоростей i'; (О) частиц)
3. Задать h  шаr интеrpирования системы дифференциальных ypaB
нений (10.8).
4. Задать Nh  число шаrов, в которых вычисляются решения системы
дифференциальных уравнений (10,8),
5. Вычислить в соответствии с (10.21), (10.25) и учетом периодических
rpаничных условий значения координат F; и скоростей Vi' i = 0,1,.. . N в по
следовательные моменты времени 111 ' i = 0,1,..., Nh .
10.4. Моделирование системы, состоящей
из большоrо числа частиц, методом молеку лярной
динамики
Рассматриваемая нами статистическая система является детерминиро
ванной, поскольку для описания ее поведения решается задача Коши систе
мы линейных дифференциальных уравнений с постоянными коэффициен
тами. При этом получаемые решения напрямую зависят от начальных усло
вий F;(O), v;(O) (начальной конфиrypации системы). Отметим, что их
правильный выбор оказывается далеко не простой задачей (например, зараш
нее совершенно неочевидно, как выбрать начальную конфиrypацию, чтобы
изучаемая система вела себя как жидкость с заданной температурой.), по
этому сначала мы обсудим особенности эволюции статистической системы
из произвольных начальных конфиrураций, Один из возможных вариантов
задания начальных условий  размещение частиц в узлах некоторой прямо
уrольной сетки (размер которой, как очевидно, должен быть меньше размеш
ра МДячейки) и задании векторов их скоростей случайным образом, Ha
пример, с помощью [енератора случайных чисел с равномерным законом
распредсления, 1I,анный подход использован ниже в задаче моделирования
статистической системы методом МД,
Для решения поставленной задачи оказывается удобным сначала создать
mфайлы, содержащие описания: 1) функции, возвращающей начаJIЬНУЮ
конфиr-урацию системы (файл init.m); 2) функции, возвращающей MrHoBeH
ные ускорения каждой частицы системы и MrHoBCHHoe значение потенци
альной энерrии (файл Асс.т); 3) функции, возвращаюшей значения KOOp
динат, составляющих скорости и ускорений вдоль соответствующих KOOp
динатных осеЙ (файл Verlet.m); 4) функции, возвращающей составной
массив, содержащиЙ значения координат, проекциii скоростей и ускорений
290
291

liOAfпl:!.rrl.e.I?!I'!.!.I?t!..i!.fJ...0c:.'Ii!: .rpi!.Зi!.'!.t!..:.'!.: ./У!? e:<.:?.  !,,"-r:i\!.1J!:/I!1 .... .... ..........
I I
на соответствующие координатные оси в узлах временной сетки (файл
Moldin.m),
% листинr файла init.m
function z=init(Lx,Ly,Nx,Ny,Vmax)
% функция, возвращающая начальную конфиrурацию системы
% Lx  ширина МДячейки
% Ly  высота МДячейки
% Nx  ширина начальной ячейки
о/с Ny  высота начальной ячейки
% Vшах  максимальное значение скорости
PosJow=Ly/(Ny+l)j
Poscol=LxI(Nx+l)j
N=Nx*Nyj % число частиц системы
i=lj
for Rows=l:Ny
for Col=l:Nx
% задание начальных координат частиц
х(i)=Роsзоl*СоV2j
y(i)=PosJow*Rowsj
% задание начальных скоростей частиц
Vx(i)= Vmax*(2 *rand(l)-l)j
Vy(i)= Vmax*(2*rand(1)-1)j
i=i+l;
end;
end;
% проекции скорости центра масс системы
Vxfull=mean(Vx);
Vy full=mean(VY)j
i=l:N;
Vx(i)=Vx(i)- Vxfull;
Vy(i)=Vy(i)- Vy full;
% возврат матрицы, содержащей начальные значения координат и
% проекций скоростей частиц статистической системы
z=cat(2,x' ,у' ,Vx', Vy');
% листинr файла Асс.т
function z=Acc(R V,Lx,Ly,N)
% функция, возвращающая мrиовенные ускорения каждой чаСТIIЦЫ
o/r системы 11 м['новенное значение потенцпальной энерпш
!1
I
1
292
J:i\!.??:и-Р..?<l.I.i!.:<':'!.:'"-'::?:rrr'!.l!.'!!.и.и.з---.'?!'!:.?.'!.'l}!с:.'!!'!...<l.С!'.Jи..!!.
% R V  матрица, возвращенная функцией Init
% Lx  ширина МД-ячейки
% Ly  высота МДячейки
% N  число частиц системы
Ер=О;
for i=l:N
Ax(i)=O;
Ay(i)=Oj
Pe(i)=Oj
end;
for i=l:N-l
for j=i+l:N
Dx=R V(i,l)-R VG,l)j
% про верка rpаничных условий
if abs(Dx»Lxl2
. Dx=Dx-sigп(Dх)*Lхj
endj
Dy=R V(i,2)-R VG,2);
% про верка rpаничных условий
if abs(Dy»Ly/2
Dy=Dy-sigп(Dу)*Lу;
end;
Ax(i)=Ax(i)+Fx(Dx,Dy); % проекция ускорения на ось оХ
AxG)=AxG)-Fх(Dх,Dу); % третий закон Ньютона
Ay(i)=Ay(i)+Fy(Dx,Dy); % проекция ускорения на ось оУ
AyG)=AyG)-Fу(Dх,Dу); % третий закон Ньютона
r = (DхЛ2+DуЛ2). ЛО.5;
Ер=Ер+4*(1/r.Л12-lIr.Л6)j % потенциальная энерrия
end;
end;
Pe(N)=Epj
z=cat(2,Ax' ,Ау' ,Ре');
% листинr файла Verlet,m
fur.ction z=Verlet(R V,Lx,Ly,N,dt)
% функция, возвращающая значения координат,
% составляющих скорости и ускорений частиц
% вдоль соответствующих координатных осей
% R V . мачшца, возвращенная функцией Init
293


компыоер//оеe моделuрова//uе Фuзu.'!.:с..'!!Р..'!.'i:.О.I!.'!...!!!!!!!.1!.!:::!!!.....
...............
I
11
1: i
,\
'1
I
I
% Lx  ширина МДячейки
% Ly  высота МДячейки
% N  число частиц системы
% dt  шаr интеrpирования
for i=l:N
% новое положение частицы
x(i)=R V(i,l)+R V(i,3)*dt+R V(i,5)*(dtЛ2)/2;
y(i)=R V(i,2)+R V(i,4)*dt+R V(i,6)*(dtЛ2)/2j
% перемещение при необходимости частицы
% в центральную ячейку
if x(i)<O
x(i)=x(i)+Lxj
end;
if x(i»Lx
x(i)=x(i)- LXj
end;
if y(i)<O
y(i)=y(i)+Lyj
endj
if y(i»Ly
y(i)=y(i)-Ly;
end;
end;
% изменение скорости с использованием «cTaporo» ускорения
for i=l:N
Vx(i)=R V(i,3)+0.5*R V(i,5)*dt;
Vy(i)=R V(i,4)+0.5*R V(i,6)*dt;
end;
% вычисление «HoBoro» ускорения
R Vnew=cat(2,x',y',Vx',Vy');
Accnew=Acc(R V new ,Lx,Ly ,N);
% вычисление скорости с использованием «HoBoro» ускорения
for i=l:N
Vx(i)= Vx(i)+O.5* Accnew(i,l)*dt;
Vy(i)= Vy(i)+O.5* Accnew(i,2)*dtj
endj
z=cat(2,x' ,у' ,Ух' ,Уу' ,Accnew);
function zl=Fx(x,y)
о/с проекuия силы, деЙствующеЙ на частицу, вдоль оси оХ
I
1 I
. I
294

.........9.!!.!!д-:!!!!Р..?'!!!!!.1:::!'!!...:.5.<?с..'!l<?.!tI.=-.?!!'!!!?':!?.:!!:'.c...:!c...'!!..'!H..
zl=-2Л(7/3)*(рiЛ2)/3*х. *( -2/(х. Л2+у. Л2). Л7+ l/(x. Л2+у. Л2). Л4);
function z2=Fy(x,y)
% проекция силы, действующей на частицу вдоль оси о У
z2=-2Л(7/3)*рiЛ2/3*у. *( -2/(х. Л2+у. Л2). Л7+ l/(x. Л2+у. Л2). Л4);
% листинr файла Moldin.m
function z=Moldin(Lx,Ly,N,Ni,dt,A)
% функция, возвращающая составной массив,
% содержащий значения
% координат, проекций скоростей и ускорений частиц
% на соответствующие координатные оси
% в узлах временной сетки
% Lx  ширина МДячейки
% Ly  высота МДячейки
% N  число частиц системы
% Ni  число МДшаrов
% dt  шаr интеrpирования уравнений движения
% А  массив, возвращенный функцией Init
Accold=Acc(A,Lx,Ly,N);
A2=cat(2,A,Accold);
A3=cat(3,A2)j
k=Oj
while k<Ni
А2= V erlet(A2,Lx,Ly ,N,dt)j
A3=cat(3,A3,A2)j
k=k+lj
end;
z=A3j
Далее необходимо выполнить следующую последовательность команд:
% размер начальной ячейки
» Nx=5;
» Ny=5;
»N=Nx*Ny; % число частиц системы
% размер МДячейки
» Lx=8j
» Ly=8;
» Уmах=О.2; % максимальное значения начальной скорости
» А=IпЩI.,х,I.у,Nх,Nу,VmаХ)j % начальная конфиrурация
295

!!OM'!!:!!!'!'...p"I!!!!!.!'!!!.'!.P...l!'!:.!!'!:!P.!!!.'!.'.!.:(;!.'!!...'P.!!.'ie.!!.!!!!.'5.тe !:!...1!.!!._ .'"
I !
» Ni=10Л4; % число МДшаrов
» dt=1 *10Л-4; % величина МДшаrа
» md=Moldin(Lx,Ly,N,Ni,dt,A);
% визуализация мшовенных конфиrypаций системы в выбранные
% моменты времени (рис, 1O.310,6)
»plot(md(:,I,I),md(:,2,I),'oK','Size',3);axis([0 Lx О Ly])
»plot(md(:,1,501),md(:,2,501),'oK','Size',3);axis([0 Lx О Ly])
» plot(md(:,1,5001),md(:,2,5001),'oK' ,'Size' ,3);axis([0 Lx О Ly])
»plot(md(:,1,10001),md(:,2,10001),'oK','Size',3);axis([0 Lx О Ly])
% вычисление числа частиц в левой половине ящика
for i=I:Ni+l
Nl(i)=O;
tmp=md(:,I,i);
for j=I:N
if tmp(j)<=Lxl2
Nl(i)=Nl(i)+ 1;
end;
end;
end;
% визуализация зависимости числа частиц, находящихся
% в левой половине ящика от времени (рис. 10.7)
i=I:Ni+l;
L(i)=12.5;
plot«i-l)*dt,Nl,'k' ,i*dt,L,' --k');
axis([O Ni*dt О 30])
% вычисление мшовенных значений кинетической и
% потенциальной энерrий системы
»for i=I:Ni+l
Sum=O;
tmрVх=md(:,з,i);
tmpVy=md(:,4,i);
for j=I:N
Sum=Sum+O.5*(tmp Vх(j)Л2+tmр Vy(j)A2);
end;
Ek(i)=Sum;
Ep(i)=md(N,7,i);
end;
% визуализация зависимостей кинетической, потенциальной
% и полной энерrий, приходящихся на одну частицу
296
\1',
..........!'!.!:!...о?.!!!'..!:!!!.?!..'!:.'!..'!!5..'!.:'-'-':.с:..й-.'!!!!.Jl...UJ...U::I!!..!5.?3..ъ.'!!.й-.ч-!!.Ч-'!:.!!
%, от времени (рис. 10.810.10)
» i=1 :Ni+ l;figure(1);plot«i-l)*dt,Еk/N,'k')
» i=1 :Ni+ 1 ;figure(2);plot«i-l)*dt,Ер/N,'k')
» i=l:Ni+ l;figure(3);plot«i-l)*dt,(Ер+Еп)/N, 'k')
Результаты выполнения описанной последовательности команд пред
ставлены на рис. I0.310.10.
00
Рис. /0.3. Начальная
конфиzyрацuя
статистической
системы
2
6
6.
Рис. /0.4. Конфиzурацuя
статистической
системы в момент
времени t=O,05
о ........L................L._.L.
0123' 567
297


11 ,1
! 111
: 11
111
1
I[
I
11'
:11
l'
!5..,:ь.'!!._'!I!'.Р"!!?!!.!!елu!!.'!!.'.!!!!.1!.r:!3..:_с..'!!....Р..'!н<!!!.! п!,,!,!:!,!!,_.,_.._.
._....!'!:."!!!!!!l..!!!!.'!!.!!!!..!'..!:.'!.:.."!..:....:..й-.!!''!.ЯЩ,!:?!,.!:!!!О20 ч-!!5!'!!сm
30 """Т'""'"I"'"-т.""""""",."""""""."""""",,,
7
25
20
5 о
,
1
111
'1'
111
111
111
'Ii
:1
I1
15
10
5
о
о
,
6
8
2
3
l .. J
ШШ__Ш
Рис, 10,5, Конфиzyрацuя статистической системы в момент времени (=0,5
о  1 I
О  U U м м u и м u 1
Рис, 10.7, Зависимость числа частиц, находящuxся в левой половине ящика,
от времени (Nleft=Nleft((})
50
"' ....... .. ..
о 0.1 0.2 0,3 0.4 0.5 0.6 0.7 0.8 0,9
Рис, 10.8. ЗавиСUJI1Ость кинетической энерzии, приходящейся на одну частицу,
от времени (Ek=Ek(tl)
:1111
11
1I
11 1
!I I1
III!I
i !
зое
6
250
5
200
150
100
i ljl
I
J
11
,
5
о
о
8
Рис, 10,6, Конфиzурация статистической системы в момент времени (=1,0
298

299

l!.?.Й-'!I!!!!?!.Й-.е::.l!..?I!.'!!.!!!Р!?..3.':.='5.'-!..,rp?:'С:?I!..'!.:'!!:"!1..!!:..1!!................
350
400 ................ . .
зоо
250
200
150
100
50
J{
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
о
-50
О
Рис, 10,9, Зависимость потенциальной энер2ии, прuxодящейся на одну частицу
от времени (EpEp(t))
380
11 1 360
340
320
300
280
260
О
j
1 IM,JJJCj
0.1
0.2
0.3
0.4
0.5
07
08
0.9
0.6
Рис. 10.10. Зависимость полной энер2ии, приходящейся на одну частицу
от времени (EE(t))
i
300
шш ...шшшJ:...I:!::':flfJ..?в.'!.!./шешс:с::.м...:.9!'?и.!!!::!..й-fl..1!:Iй--?Ч-Z::'Л.Ч'!..:''!!У
Анализ зависимостей, представленных на рис, 10,710.l0, показывает,
что с течением времени система стремится к состоянию равновесия (про
цесс релаксации), в котором примерно одинаковыми остаются число частиц
в левой и правой половинах МДшячейки и полная энерrия системы, (OTMe
тим, что поскольку значения начальной скорости задаются с помощью re
нератора случайных чисел, данные зависимости, полученные при пересчете
документа, будут всеrда отличаться от зависимостей, представленных на
рис. 10.7lO.lO, однако качественно они должны вести себя подобным об
разом),
..''....
Задача 10.1.'
Используя зависuмости Nleft=Nleft(t), Ek = Ek(t) , Ер = Ep(t) , Е = E(t) ,
оцените: 1) время релаксации статистической систeJI1Ы к состоянию
равновесия; 2) средние значения кинетической, потенциальной и полной
энер2UЙ системы в состоянии равновесия; 3) оцените величину фЛУКш
туаций кинетической, потенциальной и полной энерzuй системы в co
стоянии равновесия.
Задача 10.2
Опишите движение отдельной частицы в процессе релаксации,
проаналuзировав зависимости x(t), y(t), R(t)=  x(t)2 + y(t)2 , У = у(х),
v х = ,-,X<t) , vy = v.At) , v у = f( v J. Постройте зависимости хЩх(О),
уЩу(О), R(t)---R(O), (R(t)---R(О)i.
Задача 10.3
Опишите движение отдельной частицы после достижения системой в
момент времени tr равновеСН020 состояния, Постройте зависимости
хщх(ц, ущу(ц, R(t)R(r.), (R(t)R(tr)i. Вычислите средние значеш
ния <хщх(ц>, <ущу(ц>, <R(t)R(tr»' Считая, что среднеквадраш
тическое отклонение частицы от началЬН020 положения меняется во
времени по линейному закону «R(t)R(tr)i>=а{t-----tr), оцените с пOMO
ЩЬЮ метода наименьших квадратов значение коэффициента а, Провеш
дите анаЛ02ичный анализ для дРУ20Й частицы и сравните полученные
результаты,
· Во всех задачах данной 2лавы, 2де начальные Ilараметры статистической
систе.\1Ы не о?оворены Сllециа.1Ь1Ю, OHlI соответствуют параметрCLИ, указаННЫЛ1
в тексте ?лавы при oпllcaHUU соответствующе?о документа
301


J5,:?l<f...пЬIO.'!!!Р!:?:.й-е:!.12!.f!.!!с:/::..1!!!.з-..и...:с.f!.I!.!!.Н::':?.1!..!!'!:"'!':1.!.!!.ш..._.__...._...
Задача J 0.4
Рассмотрите обратный во времени процесс, выбрав в качестве началь
ных значений координат частиц, i = 0,1. .. N соответствующие коорди
наты из последней вычисленной КОНфИ2урации статистической систе
мы Ni (X;(O)=x;(dt,Ni),Y;(O)=y;(dt'Ni),i=O,l...N), в качестве Ha
чальных скоростей соответствующие значения скоростей из последней
конфиzyрации статистической системы, взятых с противоположным
знаком (Vx;(O) = VXi(dt, Ni), Vy;(O) = VYi(dt, Ni)), Каково состояние
статистической систеJ\tы в момент времени dtNi?
....
Задача 10.5
Используя описанный выше доку.нент, исследуйте поведение статисти
ческой системы с большИм количеством частиц, Как зависят от числа
частиц в состоянии равновесия: 1) время достижения равновесия;
2) ве.П.ичина флуктуаций числа частиц в левой половине МДячейки
(Nleft(t)N/2); 3) величина флуктуаций кинетической энер2ИИ, пpиxo
дящейся на одну частицу, ((Ek  Ek)2) , здесь уzловые скобки ( ) озна
чают усреднение по времени, Ek  среднее значение кинетической энер
zии), 4) величина флуктуаций потенциальной энерzии, прuxодящейся на
одну частицу, ((Ер  Ер )2); 5) величина флуктуаций полной энерzии,
прuxодящейся на одну частицу ((Е  Е)2)? (Прuмечание. Основной вe
личиной, определяющей точность полученных решений, является ша2 по
времени h. Однако уменьшение шаzа интеzрирования при фиксирован
ном интервале времени, на KomopOJW исследуется динамическая систе
ма, приводит к пропорциональному увеличению общеzо времени вычис
лений. Общеzо критерия выбора шаzа h, к сожалению, не существуеm,
поэтому ею величина определяется путе.м ЭJlтирическоzо подбора:
1) выбор определенноzо Иla2а, 2) расчеm, 3) анализ достоверности полу
ченных результатов, если полученные результаты недостоверны (пoвe
дение соответствующих величин качественно отличается от зависи
мостеu, представленных на рис. 1 О, 7 1 0,120), то выбирается меньший
ша2 и повторяются пп, 2,3.)
В статистической физике для характеристики систем, состоящих из'
большоrо числа чаСТИll, используют функции расиРi:деления по скорости
i I
l'
i I
: t
302

........!.9:.л.!..!!.g!:.!!.?в-..С!..I..:.. С.!:'.:'!'_:':.:ш:l!.Jlши.!!'.!ш_'!:!.!!.ш'!!!::!...ш!!:.с..'!'!:'!
Р( v) и энерrии Р( Е) . Функция Р( v) определяет вероятность Р( v )Ll V обна
ружить частицы, скорость которых находится в интервале [v;v+Llv).
Функция Р(Е) определяет вероятность P(E)LlE обнаружить частицы,
кинетическая энерrия которых находится в интервале [E;E+LlE]. Для вычис
ления функции распределения по скорости в равновесном состоянии может
быть использован следующий алrоритм:
1. Определить минимальное Vmin И максимальное Vmax значения CKOpO
сти на временном интервале [Т],Т2], на котором система находится в paвHO
весном состоянии.
2. Задать Nh  число отрезков, на которые разбивается отрезок [Vmin,Vmax],
3. Вычислить мrиовенные функции распределения, подсчитав в каждый
момент из интервала [Т],Т2], число частиц, попадавших в отрезки
[vmin + Llv .i; Vmin + Llv .(i + 1)], rде Llv = (vmax  vmin )/Np, i = O,l...,Nh 1.
4. Усреднить MrHoBeHHbIe функции распределения.
Для вычисления удобно создать файл Distr.m, содержащий описание
функции, реализующей приведенный выше алrоритм. Листинr данноrо
файла приводится ниже.
% листинr файла Distr.m
function z=Distr(md,N, Tstart,dt,Flag,Nh)
% функция, возвращающая вероятность нахождения
% проекций скорости частицы в интервале [v, v + Llv]
% md  массив, возвращенный функцией MoCdin
% N  число частиц системы
% Tstart  момент времени, начиная с KOToporo про водится
% вычисление мrиовенных распределений
% dt  шаr интеrpирования уравнений движения
% Flag  строковая переменная, значение которой по проекции
% на какую ось вычисляется вероятность распределения
% Nh  число интервалов разбиения интервала скоростей
» Np=length(md); % число МДшаrов
» k=l;
» if Flag=='x'
L=3;
else
L=4;
end;
Nstart=round( TstartJdt);
303

I
I
l!..f!.А1..'!1!!."!f!l!!!!!!!!!!J...l!!!.'!Е'!...в(/:!Р!!.:!!...СКl!!!!f.l!!!l!.пl!..е.'!I!ш!...LAВ ШШШШШШ .. ш
1I1
,
'1,'
I
, I
11
I
I
V=md(:,L,Nstart);
% создание матрицы, содержащей MrHoBeHHbIe значения
% проекций скорости частиц
for i=Nstart+l:Np
zl=md(:,L,i);
V=cat(2,V,zl);
end;
% нахождение минималъноro и максималъноro значений скороС1И чаС1ИЦ
Vl=min(V);
Vmin=min(Vl);
V2=max(V);
Vmax=max(V2);
dv=(Vmax-Vmiп)lNh; % длина интервала по скорости
m=l:Nh+l;
iпtеr(m)=Vmiп+dv*(m-l); % координаты узлов сетки
g(m)=O;
% вычисление мrновенных распределений
k=l;
for i=Nstart:Np
v=V(:,k);
k=k+l;
g=g+hist( v ,inter);
end;
g=gI«Np-Nstart)*Nh); % среднее распределение
z=cat(2,inter' ,g');
Отметим, что при использовании функций min, max для матриц возвра-
щаемый результат является вектором, содержащим, соответственно, мини-
мальные и максимальные значения по каждому столбцу матрицы. Данные
функции, будучи примененными к вектору, возвращают скаляр  мини-
мальное/максимальное значение. Для подсчета числа частиц, попадающих в
заданные интервалы, мы используем специализированную функцию пакета
МА 1LAВ hist, которая зависит от двух векторов: первый содержит значе-
ния анализируемой последовательности у, второй  координаты интервалов
разбиения отрезка [yrпin, ушах].
для вычисления распределения частиц по проекциям скорости на коорди
наrnые оси необходимо вьшолнить следующую последовательность команд:
% размер начальной ячейки
» Nx=5;
» Ny=5;
304

.Ш: О=!.IJl.f!.(/:!I.е.':':'!I..l!!!::Сш,,!? !!.._ ?'!..l!'!!!!;;!!Ч-!:!':!Ч-l!..:'!!.и--ц
» N=Nx*Ny; % число частиц системы
% размер МД ячейки
» Lx=8;
» Ly=8;
» Vmax=O.2; % максимальное значения начальной скорости
»A=Init(Lx,Ly,Nx,Ny,Vmax); % начальная конфиrypация
» Ni=lОЛ4; % число МД шarов
» dt=l *lОЛ-4; % величина МД шаrа
» md=Moldin(Lx,Ly,N,Ni,dt,A);
» Tstart=O.25;
» Nh=lO; % число интервалов
» z=Distr(md,N,Tstart,dt,'x' ,Nh);
» zl=Distr(md,N,Tstart,dt,'y' ,Nh);
% визуализация распределений частиц по проекциям скорости
% (рис. 10.1112)
» bar(z(:,1),z(:,2»;colormap white
» bar(zl(:,1),z1(:,2»;colormap white
Результаты выполнения описанной последовательности команд пред
ставлены на рис. lO.1110.12.
0.7  ..,..... ....... ._, -..,..... -.1.
0.6
0.5
0.4
0.3
0.2 '
0.1 x:r]
 !;!
о  ....J
-60 -40 2O 20 40 60
Рис, /0.11. Вероятность нахождения nроекции скоростей частиц на ось оХ
. [V V+Л,]
в интервале скоростеи .
305

!!...Й-I!й-п:.еJ!.,I!й-е!!..й-'!.Е..'!. .р'!..?'!.'!..::''!!..'11!й-::.с.CJ..!..'!!!е..."!.:Jo:!.1!/1.l!
о 7 . . -"""""''''-- -
06
[
05 I
04 I
03
I
02
0.1
О
,60 O
Рис, 10,12, Вероятность нахождения nроекции скоростей частиц на ось оУ
в интервале скоростей [v, v + v]
Задача 10.6
Создайте функцию, возвращающую вероятность обнаружить модуль
скорости частицы в интервале [v,v+LJv]. Чему равно наиболее вероят
ное значение скорости? Чему равно среднее значение скорости? Cpaв
ните вероятности обнаружить nроекцию скорости на соответствую
щие оси и вероятность нахождения модуля скорости в заданном диana
зоне скоростей,
Задача 10.7
Создайте функцию, возвращающую вероятность обнаружить КUHeти
ческую энерzию частицы в интервале [Е,Е+&]. Сравните вероятности
обнаружить nроекцию скорости на соответствующие оси, вероят
ность нахождения модуля скорости в заданном диапазоне скоростей с
вероятностью обнаружить кинетическую энерzию частицы в иHтepвa
ле [Е,Е+&].
[1
I
 0.5. Оценка макроскопических характеристик
статистической системы
в предыдущем разделе мы характеризовали состояние rаза числом час
тиц в левой части МДячейки. Известно, что в термодинамике равновесное
состояние характеризуется такими параметрами, как абсолютная темпера
тура Т, среднее давление Р, объем V, полная энерrия,
306

...... ........_..... ._ f!:.!:!..й--.!?!.!!.CJ..CJ..1l!.!:""!.':":"':'"!.Й-1l!'!.:,:и:.!!.'?.J/и-'_й-!!л..l!"':CJ..:!'::ll!!.
Для определения температуры можно использовать теорему о paBHopac
пределении, соrласно которой на каждую переменную, входящую в выра...
жение для энерrии равновесной классической системы, приходится по Т/2 в
ero энерrии, В том случае, если кинетическая энерrия частиц значительно
больше средней потенциальной энерrии их взаимодействия, можно считать,
что внутренняя энерrия системы обусловлена только движением частиц, по
этому
NT = L(!mV;),
2 . 2
1
(10.28)
rде d  размеренность системы, скобки ( ) означают усреднение по времени,
Отметим, что в (10,28) температура т измеряется в энерrетических еди
ницах, перевод которых в rpaдycbI Кельвина осуществляется делением тем...
пературы Т на постоянную Больцмана kB = 1,38 '1023 Дж/К.
.M
Задача 10.8
Оцените вОЗ.можность использования модели идеальноzо zаза для Ol1и
сания рассматриваемой системы, Дополните описанный выше доку:
мент функцией, позволяющей вычислять температуру равновеснои
статистической системы в соответствии с (10,27),

Задача 10.9
Выражение (10,27) устанавливает связь между средним знач:нием ки...
нетической энерzии, вычисляемой как сумма средних значении KиHeти
ческux энерzий частиц (среднее по траектории), Можно предложить
альтернативный способ вычисления температуры
 NT = (L ! mv;) . (10.29)
2 , 2
I
Дополните описанныЙ выше документ функцией, позволяющей вычис
лять телтературу равновесной статистической систе.мы в cooтвeт
ствии с (10.29). Сравните найденное значение температуры с резуль
татом, nолученныlM в предыдущей задаче. Объясните полученный ре...
зультат,
Способ вычисления давления рассматриваемой статистической системы
вытекает из теоремы вириала, в соответствии с которой
1 / N \
PV = NT + d\L1jFi /, (]о,зо)
, 1 ,
307

'/
.15.!!.л--'!'!!!.п-lер"IIlf.=1!.р'?ва',!I фU?Z:С;I:':);.!.'?!I:С(Jв-.I}3к-.:"'!.!!А пАВ
l'
['де ij  радиусвектор iй частицы, Р;  полная сила, действующая на iю
частицу со стороны остальных чаСТИIl (здесь сумма берется по всем N час
тицам), Вывод формулы (10,30) приведен в [7, С. ]79.180],
Для вычисления давления в соответствии с (10,30), сначала необходимо
вычислить MrHoBeHHbIe значения давления, затем провести усреднение на
временном интервале, на котором система является равновесной, Далее мы
приводим листинr файла Virial.m, содержащеrо описание функции, воз
вращающей MrHoReHHbIe значения давления,
% листинr файла Viria1,rn
function z=virial(md,E,Lx,Ly)
% функция, возвращающая мшовенные значения давления
% в соответствии с (10.30)
% шd  массив, возвращенный функцией Mo]din
% Е  вектор, содержащий MrHoBeHHbIe значения энерrии
% Lx  ширина МД ячейки
% Ly  высота МД ячейки
K=length(md); % число МД шarов
N=size(md,l); % число частиц системы
% вычисление мшовснных значений энерrии в соответствии с (] 0.30)
for i=l:K
Vl=E(i)/(Lx*IJY);
V2=O;
for j=l:N
V2= V2+md(j, 1,i)*md(j,5,i)+md(j,2,i)*md(j,6,i);
end;
V (i)= Vl +O.5*V2/(Lx*Ly*N);
end;
z=V;
Для вычисления и визуализации зависимости мшовенных значений
энерrии от времени необходимо выполнить следующую последователь
ность команд:
% вычисление MrHoBeHHhIx значений кинетической энерrии
»for i=l:Ni+l
Sum=O;
tmpVx=md(:,3,i);
tmpVy=md(:,4,i);
for j=l:N
Sum=Sum+O.5*(tmp Vх(j)ЛZ+tmр Vу(j)Л2);
end;
Ek(i)=Sum;
fi
11; I
i 11
308
ш ...1.:!':.!й-д.UЕ.?'6!!!'и.еС",:Л--t :.С(J"'.(JJllJ}.l:':);ш!!!.Й-1!.!'llJ.??!!::!.ч':..т-'!..
end;
% вычисление и визуализация MI'HoBeHHhIx :шачений давления
» Z=virial(md,Ek,Lx,Ly);
»i=1 :Ni+ 1 ;p]ot«i 1 )*dt,Z,'K')
Результаты выполнения описанной выше последовательности команд
прсдставлены на рис, 10.13,
110 I'Ш'Ш'ШШ'ШШ' , '---Т-Ш-----'Ш' --r''ш"''-  'Ш"Т'"-Т"'I
':II( lrП"1rN{lv\rУN\N,rr1"j 'Yi\"\'1/1
i
70 ,
60
50
40 '
зо
20 I
О 0.1 0.2
.......L...
04 0.5 0.6 0.7
,
0.8 0.9
О.З
Рис, 10,13, Зависимость М2новенных значений давления от времени
Задача 10.10
Задайте функцию, позволяющую определять средние значения давления,
Оцените точность вычисления давления, Исследуйте, как зависит вели
чина флуктуаций давления от числа частиц статистической системы,
Одна из проблем метода МД  проблема получения равновесных конфи
rypаций с заранее заданной температурой, знание которой необходимо для
оценки ряда ее термодинамических характеристик, так как данная величина
зависит от целоrо ряда параметров системы: начальной энерrии, числа час
тиц, размеров системы. Для преодоления отмеченных трудностей обычно
используют перенормировку кинетической энерrии  процедуру, с физиче
ской точки зрения эквивалентную добавлению в систему извне энерrии или
ее отводу из системы, Для ее реализации может быть использован следую
щий алrоритм.
1. Задание требуемой температуры Т} .
2, Задание начальной равновесной конфиrypации,
309


.l!.'!.lfl.Ь:О.п.lеI?'О.:!1!!...'!.Р..'?!.'3.!I':!:1!..'-!..3!'...::'5.'!..:flР.'!.If..е..::'?.в---'!...а.'!...:1т..:!.!!ш,...
I
I
111
' I
I i
I
1
 i
3, Задание числа шаrов по времени Nm, через которые производится HOp
мировка скорости.
4, Интеrpирование уравнений движения на временном интервале
[dt, j;dt(j + Nm)]
5, Вычисление средней кинетической энерrии
Ek = \/  f mv;), (10.31)
,N ;=1 2
6, Вычисление нормировочноrо коэффициента
т
р =  . (10.32)
Ek
7, Нормировка значений скорости
V; = pl/dv;. (10.33)
8. Повторение действий, описанных в пп. 47, на последующих BpeMeH
ных интервалах.
Ниже представлены листинr файла Moldinl.m, содержащеrо описание
функции, реализующей описанный алrоритм, и последовательность команд,
которую необходимо выполнить:
% листинr файла Moldin1.m
function z=Moldinl(Lx,Ly ,Nx,Ny ,N,Ni,dt,A, Tf,Nm)
% функция, возвращающая составной массив, содержащий
% значения координат, проекций скоростей и ускорений частиц
% статистической системы частиц с заданной температурой на
% соответствующие координатные оси в узлах временной сетки
% Lx  ширина МДячейки
% Ly  высота МДячейки
% N  число частиц системы
% Ni  число МДшаrов
% dt  шаr интеrpирования уравнений движения
% А  массив, возвращенный функцией Init
% Tf  температура системы
% число, задающее частоту применения процедуры перенормировки
Accold=Acc(A,Lx,Ly,N);
A2=cat(2,A,Accold) ;
А3=саt(З,А2) ;
k=O;
М=I;
310

J 9 М-()делuрова!uе cи:"!, сосltll?ЩI1Х':!. б'!.3':,-!!!!.2?. ч'-!..сла часпl1Щ
Na=length(A)
while k<Ni
А2= V erlet(A2,Lx,Ly,N ,dt);
ifM==Nm
for i=l:M
beta=O;
for j=l:Na
beta=beta+O .5*(А2О,3) л 2+ А2О,4) л 2);
end;
betal(i)=beta;
end'
, 
beta2=sum(betal)/(M*Nx*Ny); % среднее значение кинетическои энерrии
о/оперенормировкаскоростей
for j=l:Na
А2О ,З)=А2(j,3 )*(Tf/beta2) л 0.5;
А2О,4 )=А2О,4)* (Тf/Ьеtа2)ЛО.5;
end;
M=l;
else
M=M+l;
end;
А3=саt(З,А3,А2);
k=k+ 1;
end;
z=A3;
Далее необходимо выполнить следующую последовательность команд:
% размер начальной ячейки
» Nx=5;
» Ny=5;
» N=Nx*Ny; % число частиц системы
% размер МДячейки
» Lx=8;
» Ly=8; 
»Vmax=O.2; % максимальное значения начальнои скорости
» A=Init(Lx,Ly,Nx,Ny,Vmax); % начальная конфиrурация
» Ni=lОЛ4; % число МДшаrов
»dt=l *10Л-4; % величина МДшаrа
» md=Moldin(Lx,Ly,N,Ni,dt,A);
% вычисление MrHoBeHHbIX значений кинетической
311

I
i ,1
: ,1
'?л:п--I'?,!р'Iел:.,?д,!р,!!.: Р!!'!ч:с..к'!..х п--р'?'}ес:со!...!!!!.'5.:..'!I! L:!:!!
! l'
% и потенциальной энерrий системы
» for i= 1 :Ni+ 1
Sum=O;
tmрVх=md(:,З,i);
tmpVy=md(:,4,i);
for j=l:N
Sum=Sum+O.5*(tmp VxGY2+tmp VуG)ЛZ);
end;
Ek(i)=Sum;
Ep(i)=md(N,7,i),
end;
% визуализация зависимостей кинетической, потенциальной
% и полной энерrnй, приходящихся на одну частицу, от времени
» i=I:Ni;figure(I);plot«i-l)*dt,ЕkIN,'k')
» i=I:Ni;figure(2);plot( (i-l)*dt,Ер/N, 'k')
» i=1 :Ni;figure(3);plot( (i-l)*dt,(Ер+Еп)/N,'k')
% вычисление и визуализация мrHoBeHHЫX значений давления
» Z=virial(md,Ek,Lx,Ly);
» i=I:Ni+l;figure(4);plot«i-l)*dt,Z,'k')
Результаты выполнения описанной последовательности команд пред
ставлены на рис. IO.1410.l7.
,i
11:......'
!
i l'
, ,
ilj
l'
! i.1
: 1;
, 1I
1I
11'
11
I
, 1'1
l'
11
1
soo
450
400
350
300 
250
200
150
100
50
J
0,9
о __..............L ........J...................L.. '
О О 1 О 2 О 3 О 4 05 О,В
,
0.7
,
08
Рис, /0./4. Зависимость МёНовенных значений кинетической энерcuи,
nриходящейся на одну частицу, от времени
312

... .... .............' !!!!'?!::':!P"'?'!!!':c!c.. fI1.:' :?c..fI1!?,Ujt!'?!.'..'?,:!?.c..''? ч,!/.'.'}.
700 'r' _.,--, "-"",,,,,,'O  1'1
воо
500
400
300
200
I \
) LI\IAJl\лJLv!J\Аw
100
O
о
0.2 0.3
0.4
0.5
0.6
0.7 0.8 0.9
().1
Рис, 10,15, Зависимость мzновенных значений nоmеllциальной энерzии,
nрuxодящейся на одну частицу, от вре;'Иени
2()()
l
I
I
I
 
() ..,..1......L....,J
о 0.1 0.2 О 3 ().4 05 О.В 0.7 08 () 9 1
,-
18()
16()
14()
120
100
80
60
40
Рис, 10,16, 3ависиЛ1Ость мтовенных значений полной энер.?ии,
nриходящейся на одну частицу, от времени
313

i
,l!:.й-. IОl1I.ер"!й-.: .АI.й-.."!!z:.Р.CJ.I.':'.=р'I!?':'.=uх...IР"CJ.'!..:Й--'!:'!I..:.1v!.А ТLAB
I
l'
2001' '--"'T--- T'' '--''---Т""'----'T'" ...----, , ''----..--..J
160 r
1601 I
140 I

,L........J
0.6 0.9 1
60
60
40
20
о
о
,
0.5
,
0.6
0.1
0.2
0.3
0.4
0.7
11:
Рис, 10,17, Зависимость JI12новенных значений давленuя от времени
Анализ зависимостей, представленных на рис, 10.1410.17, показывает,
что в моменты времени, соответствующие перенормировке, происходит
скачок энерrии, Между моментами нормировки, коrда система не подверrа
ется внешним воздействиям, энерrия остается практически постоянной.
Флуктуации энерrии обусловлены периодическими rpаничными условиями,
которые обеспечивают сохранение только полноrо числа частиц в МД--
ячейке: при выходе частицы за пределы ячейки в нее вводится точно такая
же частица. Вновь введенная частица оказывается в друrом, нежели преды--
дущая, месте, следовательно, это приводит к изменению суммарной энерrии
взаимодействия частиц в системе,
Задача 10.11
Важной термодинаА1Uческой характеристикой систем, состоящих из
БОЛЬШ020 числа частиц, является их теплоемкость при постояннOJW
объе.не Cv == (aE/anv, 2де Е  полная энеР2ИЯ системы, Данная величи--
на еСIl1Ь мера количества тепловой энеР2ии !1Е, которое необходи.\ю
сообщить системе, чтобы увеличить температуру на !1Т, Так как те--
n.70емкость зависит от числа частиц системы, вводят удельную теn--
.70e-lIКОСll1lJ на одну частlЩУ Cv == (' v / N, Наиболее просто можно оце--
'I1III1Ь уде.7ЬН)'Ю теnлоеА1КОСIl1Ь, используя следующиЙ аЛ20ритм.
1, Rычи('.7ШI1Ь энерzию сиСIl1С\lЫ при различных температурах (не менее
-4 значеНl1й;.
314
...__.................__.__....9J:!з!!..Л-':'.Р.'?.?:!!..':'.:':'.:I1I..=. СCJ.:!?l.CJ..'!j!.Il!.'?л'?й-.__'?...:!?l.':'..
2, Отобразить зависимость Е == Е(Т) zрафически,
3, Проанализировав вид зависимости Е == Е(Т), выбрать вид аппрокси--
мирующей кривой и подобрать с помощью метода наименьших квадра--
тов соответствующие коэффициенты,
4. Вычислить значение первой производной аппроксимирующей зависимости,
Используя описанный алzоритм, вычислите удельную теплоемкость Cv
изучаемой системы, Как зависит теплоемкость от температуры?
Исследуйте, как зависит удельная теплоеАtкость Cv от числа частиц
и размеров системы,
........................HH..H..._.HHH
Задача 10.12
Плотные юзы.. и жидкости описываются приближенно уравнением
состояния Ван--дер--Ваальса:
P==Tap2, (10,34)
lbp
Феноменолоzически паршwетры а и Ь связаны с приn1Яzивающей и от--
талкивающей частями потенциала взаимодействия, соответственно,
и в первом приближении не зависят от тенпературы,
1. Проведите вычисления и постройте зависимость Р == Р(Т).
2. Используя зависимость Р == Р(Т), оцените значения коэффициентов а, Ь.
3. Измените размеры МДячейки, иЗАtенив тем самым плотность юза,
Оцените значения коэффициентов а и Ь для новых значений плотности,
Сравните значения коэффициентов а, Ь с соответствующими значе--
ниями, полученными в задаче 10,10,
10.6. Оценка коэффициентов переноса в методе
молекулярной динамики
Будем следить за траекторией движения i--й пробной частицы, ПУСТh в
некоторый произвольно выбранный момент времени (1 ее координата равна
ij (t[) , в момент времени (2  ij (t 2) , Torдa смещение iй пробной часПlЦЫ за
время 1 2  11 равно ij (12 )  li (1[ ), Среднее смещение частиц статистическоЙ
системы в состоянии равновесия за время 12 -- 11 определяется как среднее
по всем частицам системы и по всем временным интервалам, ДЛИТСJJhНОСТh
которых равна 12  11 :
315


/
I
I\o' 11 I т ep'I/:. .'.o::'. !lfJО,!/!I!.'!.4!!l3':'.Ч:'(:':И--Х !1fJ."..'!.C,! '!..aK'!.т-:.м-.T1:!!,
1\
I
1 N 1 N \
r= N'ij('2)ij(f])= N!1j(r2)ij(,])J'
Так как каждая частица взаимодеЙt:Твует с ДРУI'ИМИ частицами системы
направление скорости частиц меняется случайным образом, поэтому cpeд
нее смещение частицы оказывается равным нулю. В этих условиях более
информативной величиной является величина среднеrо квадрата смещения
R(f2 , определяемоrо формулой
iR(,2 =(lij('2)ij(,!)2), (10.36)
(10,35)
11
I
I
rде усреднение проводится по всем частицам и по временным интервалам,
длительность которых равна f = '2  '1' В состоянии равновесия средний
квадрат смещения частицы IR(,) 2 зависит только от разности времен '2  '1'
но не от выбора начала отсчета. Далее представлен листинr файла R2.m, co
держащеrо описание функции, возвращающей значения среднеrо квадрата
смещения, и последовательность команд, которую необходимо выполнить
для вычисления значений среднеrо квадрата смещения.
% листинr файла R2,m
function z=R2(md,Lx,Ly ,dt, Tstart,dk)
% функция, возвращающая значения среднеrо квадрата смещения
% md . массив, возвращенный функцией Moldin
% l.х  ширина МДячейки
% Ly  высота МДячейки
% dt  шаr интеrpирования уравнений движения
% Tstart  момент времени, начиная с KOToporo проводится
% вычисление среднеrо квадрата смещения
% dk  определяющее шаr вычисления среднеrо квадрата смещения
K=length(md);
Кstart=floor(Tstart/ dt);
Nm=floor( (К- Кstart)/dk);
N=size(md,l);
C(l,l)=O;
C(1,2)=O;
for nm=l:Nm
R=O;
il=O;
for k=Kstart:K-dk*пm
316
....-..........
.. ш/о ..fv!?дiC711ровШ/ll'!. СllСIПeAf.,состОЯ-llI':'.Х lJ.б?,1Ь!l!.,,?ш ':'.сла(1(:".!И--
for j=l:N
Dx=md(j, 1,k)-md(j,1,floor(k +dk*nm»;
Dy=md(j,2,k)-md(j,2,flооr(k+dk*Ilm) );
% периодические rраничные условия
if abs(Dx»IX/2
Dx=Dx-sigп(Dх)*Lх;
end;
if abs(Dy»Ly/2
Dy=Dy-sigп(Dу)*Iу;
end;
R=R+DхЛ2+DуЛZ;
i1=il+l;
eIld;
end;
С(пm+ l,l)=dt*nm*dk;
С(пm+ 1,2)=R/(il *N);
end;
z=C;
Последовательность команд:
% размер начальной ячейки
» Nx=5;
» Ny=5;
» N=Nx*Ny; % число частиц системы
% размер МДячейки
» Lx=8;
» Ly=8; 
»Vmax=O.2; % максимальное значения начальнои скорости
»A=Init(Lx,Ly,Nx,Ny,Vmax); % начальная конфш'урация
» Ni=lОЛ4; % числоМД шаrов
» dt=l *10Л-4; % величина МДшаrа
» md=Moldin(Lx,Ly ,N,Ni,dt,A);
% вычисление и визуализация среднеrо квадрата смешения
» Z=R2(md,Lx,Ly,dt,O.7,50);
» plot(Z(:,1),Z(:,2),'k')
Результат выполнения описанной последовательности команд представ
лен на рис, 10.18.
317

lil
11
I
1
1,
1,
:,
.l!.'!.А1..'!...Ь!!!''!!:Р''I!!!:.z:J!..?!'!.II}!:.1!и-з-и-.:с:...к-.'!р'!.е.'!. вI!.к-:fl:!1...!..!l!.м,, ........ .....
o:T' т ,  , , .. .. .. .. ,  1
1
озf
025f
i
021
о 15
I
I
011
I /
0.05 /
oL_:::</ . '.....J
О 005 01 015 02 025 ОЗ аЗ5
Рис, 10.18, Зависимость среднею квадрата смещения от вре.мени
...,....... .. И''.'Н'  .. _.............. .. .  >Ю
Задача, 10013
В соответствии с точным решением задачи о движении частицы под
действиеw случайных сил, полученным А. Эйнштейном, в равновесной
двумерной системе средний квадрат смещения частицы IR(t)2 Л1еняется
по закону
IR(t)2 =4,D./, (10,37)
сде D  коэффицеюn сш.юдиффузии,
1. Для вычисленной зависимости iR(I} 2, используя метод HaUJHeliblUUX Kвaд
ратов, оцените значения коэффициента са;нодиффузии D,
2, Используя зависимости [JJ(I)2, i =1,2,..,N, получите оценки коэффициен
тое СШ.10диффузии каждой чаСl1nЩЫ D;, Сравните значения коэффици
ентов самодиффузии D и Di. Оцените тОЧllOсmь оценки коэффициента
самодиффузии D,
Еще ОДНОЙ важной характеристикой поведения статистической системы
является автокорреляционная функция скорости Z(I), являющаяся количест'
венной хараюеристикой меры зависимоии значений скорости, сдвинутых
ДРУI' относите,lf,НО друr 11pyra на опреде.1t'ННЫЙ временной интервал.
Для вычисления значений автокоррспяционной функции Z(t) СПС.lует
взять 1начешы стсорос::!! каждоЙ чаСТИllЫ, Р:lщсленные временным ]1Нт<'рва-
.10М i '" i, . 1:. rкрс:,шожить 1нзчеНIIЯ l:КОРОСПI, усрс.'цппь JlО.1ученные про
И1веленшr <ll1 BPC\!(:HHЫ1 интеrRала1 .тJlIпеТТhНОСТЬЮ t 11 ткем частица".! pac
318
ш ....!!!.:J:!.'!.?eI!.р"('!.-ва IIU:C!!.:'!!:At..,c..?CI?:,!tЦ .и-З-.?'!.л-и..:!.:о'!..и-(:.:'!а '!..<l.п.!UН.
сматриваемой системы, Математическая форма записи JIaHHoro определения
имеет вид
Z(I) = (Vi (t,) . Vi (t2)) ,
(10,38)
rде 1 = 12  1[ .
Коэффициент самодиффузии [) и автокорреляционная функция ДBYMep
ной статистической системы связаны следующим соотношением
+00
D = l J Z(t )dl .
(10.39)
oo
Далее представлен листинr файла CorrV.m, содержащеrо описание
функции, возвращающей значения среднеrо квадрата смещения, и последо
вательность команд, которую необходимо выполнить для вычисления зна
чений среднеrо квадрата смещения,
% листию' файла СопV.m
function z=CorrV(md,dt,Tstart,dk)
% функция, возвращающая значения автокорреляционной
% функции скорости
% md  массив, возвращенный функцией Moldin
% dt  шаr интеrpирования уравнений движения
% Tstart  момент времени, начиная с KOToporo проводится вычисление
% автокорреляционной функции
K=length(md)j
Kstart=t1oor(Tstart/ dt) j
Nm=t1oor( (К - Kstart)/dk) j
N=size(md,l)j
for nm=l:Nm
V=Oj
i1=Oj
for k=Kstart:K-dk*пm
for j=l:N
V =V +md(j,3,k)*md(j,3,t100r(k+dk*nm))+...
md(j,4,k)*md(j,4,t100r(k+dk*nm)) j
i1=il+lj
endj
endj
C(nm,l)=dt*(l1m-1 )*dkj
C(nm,2)=V/(il *N)j
endj
z=C:
319
...............

.. i
111'
, I
i
!<.'?A!'!!:!?.'!':l!!e й.<?.РУ{l!!.:.р'!,:.с..  пfJ...ч--.::....а.:."!.:fl!...1.т-...:!.l!, .,...
i J
Последовательность команд:
% размер начальной ячейки
» Nx=5j
» Ny=5j
» N=Nx*Nyj % число частиц системы
% размер МДячейки
» Lx=8j
» Ly=8j
» Vmax=O.2; % максимальное значения нача.пьной скорости
»A=Init(Lx,Ly,Nx,Ny,Vmax)j % начальная конфиrурация
» Ni=lОЛ4j % число МДшаrов
» dt=l *lОЛ-4j % величина МДшаrа
» md=Moldin(Lx,Ly,N,Ni,dt,A)j
% вычисление и визуализация автокорреляционной функции скорости
» Tstart=O.7j
» dk=50j
» Z=CorrV(md,dt,Tstart,dk)j
» plot(Z(:,1),Z(:,2),'k')j
Результат выполнения описанной последовательности команд представ
лен на рис. 10.19,
Задача 10.14
Используя вычисленную зависимость Z(t}, оцените З1Iачение коэффици
ента СaJиодиффузии в соответствии с выражением (10,39).
I '
I
Задача. 10.15
Предположите, что зависилюсть Z(t} от времени описывается функци
ей вида
Z(t)=Aexp(t/r), (10.40)
еде ' время корреляции.
Подставьте теоретическую зависимость Z(t) в формулу (10,39) и oпpe
делите, ка" связан коэффициент диффузии D с времене.м корреляции r.
Используйте даЮlOе соотношение между D и r для вывода выражения
дляD,
Задача 10.16
Используя вычисленную зависимость Z(t), ОЦl:'ните по методу наи/l1ень
ших "вадртпов численные значения величин А и т. входящих в выражение
( 10.40),
320
.... .....!.::Л-::Р..й..<:!!с!'.с..'!':. .й.с..'!'й.'!i'!.:.!,!..fj?3.!:.'!!!!.:5::'.I!:.I!.:.'!2.U!!
Задача 10.17
Получите оценки коэффициента само диффузии D, используя результа
ты задач 10,16 и 10,17, Сравните найдеЮlOе значение коэффициента
самодиффузии с соответствующими значенuмщ полученными в зада
ча.:r: 10,14, 10,15. С какой точностью совпадают эти оценки?
::\ШШl
\
14 \
\
12 \
\
10 \
\
sr \
:l.  /
,.,/
о ..............L........L. I ,
О 0.05 0.1 0.15 0.2 0.25 0.3 0.35
Рис. 10,19. Зависимость автокореляционной функции скорости частиц
статистической системы Z(t) от времени t = t2  t1
10.7. Моделирование фазовых переходов
методом молекулярной динамики
Анализ потенциала ЛейнардаДжонсона, представленноrо на рис. 10.20,
позволяет сделать вывод о том, что в одномерном случае частица, находя
щая в этом потенциале, может совершать два вида движений: при Е < О фи
нитное (между точками остановки X1, Х2, являющихся корнями уравнения
U(х1, Х2) = Е), при Е ::::: о  инфинитное (имеется одна точка остановки х]).
Следовательно, если предположить, что при достижении точки остановки
частица получает извне дополнительную кинетическую энерrию (например,
за счет толчка), то с течением времени полная энерrия частицы будет воз
растать, Коrда ее значение станет положительным, произойдет качествен
ное изменение: движение из финитноrо станет инфинитным (произойдет
«фазовый переход»),
1I1576
321


{'
I
_?.t'!.!O.'!I.:l!! (=.А!lJ:Р"::I1.!_:_fj1ЗZ::_С':'.х...'!.ЕlJ'j:.:'?..!!lJк-.=-'!I.:..fl.!1т-.1.l!
Р(7')
Е>О
Е<О
r
7'
I
i I
Рис. 10.20, К объясненuю прuчuн фuнuтНО20 u uнфuнuтНО20 двuженuй
Проведя аналоrию между одномерным движением частицы в потенциале
ЛейнардаДжонсона и поведением статистической системы, состоящей из
большоrо количества частиц, можно предположить возникновение качест
венных изменений состояния рассматриваемой системы при изменении ее
внутренней энерrии, Движение частицы, полная энерrия которой положи
тельна, становится инфинитным, т. е. частица получит возможность пере
мещаться по всему объему статистической системы. Если движение всех
частиц системы, изначально совершавших финитное движение (кристалли
ческое состояние), становится инфинитным, можно rоворить о фазовом пе
реходе (система переходит из кристаллическоrо состояния в жидкость).
Полная энерrия статистической системы есть сумма кинетических энер
rий всех частиц и потенциальной энерrии, вычисляемой суммированием
энерrий парноrо взаимодействия частиц (10.1). Следовательно, ее величи
на зависит от двух параметров, задаваемых в момент времени t = о: вели
чины максимальной скорости и расстояния между частицами, т. е. началь
ной плотности системы. Для исследования зависимости полной энерrии
системы от указанных величин, можно использовать функцию initE, описа
ние которой сохранено в файле initE.m.
% листинr файла initE.m
function [z,E]=initE(Lx,Ly ,Nx,Ny ,Vmax,k)
% функция, возвращающая начальную конфиrурацию системы
% Lx  ширина МДячейки
% Ly  высота МДячейки
% Nx  ширина начальной ячейки
% Ny  высота начальной ячейки
% Утах  максимальное значение скорости
% k  коэффициент, определяющий начальную плотность системы
PosJow=Ly/(Ny+ 1);
Poscol=LxI(Nx+l);
N=Nx*Ny;
322
ш..ш_...__:!!о.д!:'!.I!.lJ..11.11:.с..и..:'!'.::lJ.'!'.lJZ:lJ!.!!.'?!!.':.':!!lJ.'!.'!Л-I1.'l!!.'!'.I'j
i=l;
for Rows=I:Ny
for Col=I:Nx
x(i)=Poscol*CoV2*k;
y(i)=Posrow*Rows/2*k;
Vx(i)= Vmax*(2*rand(I)-I);
Vy(i)= Vmax*(2*rand(I)-I);
i=i+l;
end;
end;
Vx3ull=mean(Vx);
Vу3uП=mеап(Vу);
i=I:N;
Vx(i)=Vx(i)- Vx3ull;
Vy(i)=Vy(i)- Vy full;
Ер=О;
for i=I:N-l
for j=i+l:N
Dx=x(i)-хG);
if abs(Dx»Lxl2
Dx=Dx-sigп(Dх)*Lх;
end;
Dy=y(i)-уG);
if abs(Dy»Ly/2
Dy=Dy-sigп(Dу)*Lу;
end;
r=(DхЛZ+DуЛ2).ЛО.5;
Ep=Ep+4*(I/r. л 12-1/r. Л6);
end;
end;
z=cat(2,x' ,у', Vx', Vy');
Ek=O;
for i=I:N
Ek=Ek+O.5*(Vx(i)A 2+ V у(i)Л2);
end;
E=Ep+Ek;
Задача 10.18
Исследуйте, как зависит полная энерzиЯ систеА1Ы в момент времени
t == О от плотности частиц и СУМJlЮРНОЙ кинетической энерzии,
323


'}' .
i .
!<...'?-л:.п-I?'!.('Р..llО=l()'!..л-z:.ЕCJ()!'!!=..Ф--и-З-U.'!.:..:.и-:..!1J!.()'jе.с.С..'?в-.в-.п-(lк-.е.11l=.!1. !1:..1J!..
i r
Задача 10.19
Исследуйте поведение статистической системы, имеющей следующие
параметры Nx=5, Ny=5, и=8, Ly=8, Vmax=2, k1,6. Выберите ша2 иH
те2рирования d r равныл1 5.]0..4 U нqйдите решение уравнений движения
на протяжении, по крайней лtере, 2.]04 ша20в по времени.
], Чему равно значение полной энеР2ии системы в момент времени t = О?
2, Проанализируйте форму М2новенных kонфи2ураций статистической
системы в различные моменты вреЛ1ени, Как ведет себя система при
данных начальных условиях?
3. Проанализируйте зависимости paдиycoввeKтopoв частиц от времени,
4, Оцените время достижения системой равновеСНО20 состояния. Какой
критерий достижения равновесия вы использовали?
5, Постройте зависимости iR(I2 и Z(I) в равновесном состоянии,
6. Сравните зависимости :R(I2, Z(I) с аналО2ичными зависимостями, пo
лученными в предыдущем разделе,
Задача 10.20
Исследуйте поведение статистической системы при увеличении
температуры, дости2аемом последовательныл1 увеличением значения
Vmax, ответив на вопросы, поставленные в задаче ] 0.20, Удалось ли
вам пронаблюдать фазовый переход кристаллическое состояние  жид
кость 2аз?
Задача 10.21
Решите задачи 10,20, ]0,2] для статистической системы, имеющей
следующие параметры Nx=7, Ny=7, Lx=20, Ly20, При каких значениях
начальной плотности и максимальной скорости Vmax рассматриваемая
система будет находиться в кристаллическом состояни? Как пpoтe
кает фазовый переход в рассматриваемой системе?
I I
10.8. Заключение
в данной rлаве даны основные сведения о методе молекулярной дина
мики, показано, что ero использование даже для двумерной системы с He
большим количеством частиц позволяет выявить на качественном уровне
ряд основных свойств статистических систем, ввести некоторые понятия
кинетической теории переноса в жидкостях и rазах, Для получения количе
ственных результатов требуется моделировать трехмерные системы, co
стоящие из большоrо числа частиц, что с неизбежностью при водит к увели
324
. ш Ш__ ... ш_ ш1':!.?,,!:uроваl1uеuст:.-л:.:СО<:''!I()и-!!.'.:х:..!!З-?Л-'!!()()'lIс.Л-(l'lIl.:и-!!.
чению времени счета, Наибольшие временные затраты приходятся на фор
мирование paBHoBecHoro состояния и расчет сил и энерrии, Для сокращения
временных затрат используются различные подходы, Их подробное обсуж
дение, выходящее за рамки нашей книrи, заинтересованный читатель может
найти в [8, 9]. Там же приведен обширный список литературы, посвященной
различным вопросам, связанным с методом мд.
ЛИТЕРАТУРА
1, Рейф ф, Статистическая физика, М,: Наука, 1972,
2, Матвеев Д, Н, Молекулярная физика, М.: ВысшЩl школа, 1981,
3, Ландау Л, Д" Лифшиц Е, М. Статистическая физика, Часть 1. М,: Наука, 1976,
4, Климонтович Ю, Л, Статистическая физика. М,: Наука, 1982,
5, Румер Ю, Б, Рывкин М, Ш. Термодинамика, статистическая физика и кинетика, М,:
Наука, 1977,
6, Ландау Л, Д" Лифшиц Е, М, Квантовая механика. Нерелятивистская теория, М,: Hay
ка, 1974,
7, rулд Х., Тобочник Я, Компьютерное моделирование в физике, М,: Мир, 1990,
8, Хеерман д, В, Методы компьютерноrо эксперимента в теоретической физике, М.:
Мир, 1990,
9, Лаrарьков Д, Н" CepreeB В, М, Метод молекулярной динамики в стаТИСТИЧесКОЙ физике//
Успехи физических наук, 1978, Т, 125, вып' 3, С, 40048,
325


(
1,
I
r
rлава 11
МЕТОДЫ МОНТЕ..КАРЛО
11.1. Введение
I i
Системы с большим числом степеней свободы, примеры которых мы
начали рассматривать в предыдущей rлаве, представляют значительный ин
терес для физики. Вычисление термодинамических характеристик таких
систем зачастую требует вычисления интеrpалов большой размерности. Ha
пример, классическая функция распределения неидеальноrо rаза, находяще
rося при температуре Т (измеряемой в энерrетических единицах) и состоя
щеrо из N частиц с потенциалом попарноrо взаимодействия U(iijl), про
порциональна 3NMepHoмy интеrpалу
1 N
Z JdЗ dЗ TuQr"I)
= rl'" rNe 0<1 (11.1)
За исключением очень малых значений N прямое вычисление интеrpала
(11.1) изза большоrо объема вычислительных операций не представляется
возможным. Отмеченное обстоятельство определило необходимость разра
ботки более эффективных методов вычислений MHoroMepHbIM интеrpалов, к
которым относятся методы МонтеКарло. Основная идея метода состоит в
замене вычисления подынтеrpальной функции в каждом узле пространст
венной сетки, число которых для достижения требуемой точности должно
быть велико, ее вычислением только для значений абсцисс, являющихся pe
презентативной случайной выборкой. (Ситуация в данном случае аналоrич
на ситуации с предсказанием результатов выборов путем опроса небольшо
ro количества избирателей). Метод МонтеКарло оказывается весьма эф
фективным при решении различных типов задач статистической физики и
квантовой механики.
I i
I
11.2. Численные методы интеrрирования функций,
зависящих от одной переменной
Предваряя обсуждение метода МонтеКарло, ознакомимся с известными
численными методами, применяемыми для интеrpирования функций, зави
сяших от одной переменной, Данные методы основаны на rеометрической
интерпретации определенноrо интеrpала
....J:.!!.."!!I..I!.fl!.?I'!'.'!..:l'.?
ь
F = f Лх)1х,
(11,2)
а
как площади фиrypы, оrpаниченной
rpафиком функции j(x) и прямыми
Х = а , х = Ь (рис. 11.1).
Разделим отрезок [а,Ь] на N paB
ных отрезков длиной Llx, rде
f(x}
ba
Llx=.
N
х
(11.3)
а
ь
Рис, J J,J, К определению
определеюlOZО интеzрала
Тоrда координата правоrо конца iro отрезка определяется по формуле
Х; = Ха + iLlx , (11 .4)
rде Ха = а, i =O,I,...N .
Простейшая оценка площади под кривой j(x) может быть получена,
как сумма площадей прямоуrольников, одна из сторон KOToporo совпадает с
[X;'X;+l] отрезком, а высота равна значению функции в точке х;(метод ле
вых прямоуrольников) (рис. 11.2) или в точке х;+l (метод правых прямо
уrольников) (рис. 11.3).
{М {(х)
х
х
Рис, J J,2, Метод левых
прямоуzолыtков.. Поzрешность
вычисления значения интеzрала
на каждом шаzе 1I0казана
закрашеННЫ.ми фиzурами
Рис, J J,3, Метод правых
пря]иоуzольников, Поzрешность
вычисления значения интеzрала
на каждом шаzе показана
закраиlеННЫJ,(и фиzурами
Значение определенноrо интеrpала вычисляется по формулам
Nl
FI. = Lf(xi)Llx,
;=0
( 11,5)
327


!..?Ь!!!..'!!.!!!.I!!!.:!i!..':!!.'.!Р'ува!!!!!.1!!!.'!.'!.::"l!.l!.:!'i.::::.?в.в!!!.!!,,!1...:!!!........... _...
N
FR = LJ(X;)Llx
;=1
(11.6)
ДЛЯ методов левых и правых прямоyrольников соответственно.
Задача 11.1
Вычислите значения оnределенныlx интеzралов на интервале [о, 7l/2] ,
выбрав в качестве nодынтеzральных функций функции Л(Х) = sin(x),
f2(X) = cos(x). Используйте метод левых и nравых nрямоуzольников.
1. Сравните численные значения определенных интеzралов, полученные Me
тодом левых и nравых nрямоуzольников.
2. Вычислите точное значения определенных интеzралов. Сравните точные
и численные значения определенных интеzралов, оцените nоzрешность
значений определенных интеzралов, найденных численно.
3. Исследуйте зависимость точности значения оnределенноzо интеzрала
от количества точек N. Постройте zрафики зависимости nоzрешности
от числа точек N и шаzа интеzрирования Llx. Объясните полученные pe
зультаты. Используя метод наименьших квадратов, попробуйте nодоб
рать функцию, описывающую зависимость nоzрешности от числа тo
чек N и шаzа интezрирования Llx.
I
!'
Задача 11.2
Решите задачу 11.1 для интервала интеzрирования [о, 7r]. Сравните no
лученные результаты с результатами задачи 11.1.
I 1
Задача 11.3
Одна из известных модификаций метода nрямоуzольника заключается в
вычислении j{x) в средней точке каждоzо отрезка, Получите вычисли
тельную формулу для данной модификации метода nрямоуzольника. Ис
пользуя найденную формулу, решите задачи 11,1, 11.2, Сравните no
zрешности вычисления оnределенноzо интеzрала методом nрямоуzоль
ников и методом средней точки,
Задача 11.4
Значение оnределенноzо интеzрала зависит от nодынтеzральной функ
ции и пределов интеzрирования, Если в и1l1пеzрале (11.2) нижний предел
остается постоянным, а в качестве верхнесо предела выбрана HeKoтo
рая nеременная У, то F является функцией от У (интеzрал с nepe.:weHHblM
верхним пределом)
I
I
1 
\'
F(y)= J f(x)dx.
(11.7)
а
328

...._...._......_шш_......ш.:А!...е..'!!!!.?!A!...f!!!"!.:!!!!.ll!!..
1. Для функций f,(x), f2(X) из задачи 11,/ вычислите на интервале [о; 7r ]знаш
чения функций Fl.2Cy) и отобразите их zрафически,
2. Для заданных функций!I(х),f2(Х) получите аналитические выражения для
функций FI.2(Y), вычислив интеzрал (J 1,7), Постройте zрафики функций
FI.2(Y)'
3. Сравните значения функций FI.2(Y)' найденные численно, с cooтвeтcт
вующими значениями, вычисленными по аналитической формуле, Оцеш
ните nоzрешность численноzо решения,
4. Постройте zрафик зависимости величины nоzрешности от переменной
}', Объясните полученный результат.
Можно повысить точность вычисления оnределенноzо интеzрала, если
заменять реальную функцию на каждом интервале [Х;, х;+,], i = 0,1, ...
N  1, отрезком прямой, проходящей через точки с координатами
(Х;, f(x;» , (Х;+" f(;;+,» (линейная интерполяция). искомыlй оnределен
ный интеzрал определяется как су.мма площадей всех трапеций:
N' [ N' ]
FN = L !(j(xi+,)+ f(x;»Llx = ! f(xo)+ Lf(x;)+! f(xN) Llx .(11.8)
;=0 2 2 ;=1 2
Задача 11.5
Решите задачи 11.1, 11.3, 11.4, используя для вычисления интеzрала
формулу трапеций (11.8), Сравните nоzрешности нахождения onpeдe
ленноzо интеzрала методом nрямоуzольников и методом трапеций,
Сравните nоzрешности нахождения значений интеzрала с nеременным
верхним пределом методом nрямоуzольников и методом трапеций.
Более высокая точность вычисления интеzралов обеспечивается при
использовании параболической интерполяции (полиномом второй cтe
nени) по трем соседним точкам:
у = ах2 + Ьх + с. (11.9)
Для нахождения коэффициентов а, Ь, с полинома, nроходящеzо через
точки (ха' Уа), (х"у,), (Х2'У2)' нужно найти решение следующей cиc
темы линейных уравнений:
уо = ахб +Ьхо +с
у, =ax +Ьх, +с, (11.10)
У2 = axi +ЬХ2 +с
относительно неизвестных а, Ь, с.
Решив систему (J /,1 О) относительно неизвестных а, Ь, с любым из
вестным методОАt (например, Крамера), подставив найденные выражеш
ния в (J /,9) и выполнив элементарные nреобразования, получаем
329

l' 1,
/ :
1
!5..:I_ь.п1fJ.!I!!е.?<:!Е:!.?.l'!..rf'!..!!!'5.'!.Р.'i:с..О!'I}!!.15.:.'!".!!J:!.1:'l:..1.!!.
 I
(х  х] )( х  Х2 ) (х  хо )( х  Х2 )
У = Уо --- + Уl .. + О,.
(хо  х, )( хо  Х2) (х]  Х2 )( х]  Х2)
(x Xo)(X х])
+ У2
(Х2  ХО)(Х2  х])
Площадь под параболой у = У( х) на интервале [хо' х2] находится
посредством элементаРН020 инте2рирования (11,11):
1
Fo = (Yo +4у] + Y2)Llx,
3
2де Llx = Х1  ХО = Х2  хl' ИСКОМЫй определенный инте2рал находится
как площадь всех параболических cez.мeHтoв (формула Симпсона):
]
FN = 3 и(хо) + 4f(x]) +2f(Х2)+4f(хз)+ 0.0
+2f(XN2)+4f(XN1)+ f(XN)]Llx
Обратите внимание на то обстоятельство, что в формуле Симпсона N
должно быть четным числом.
Аналитические оценки п02решностu описанных методов иHтe2pиpoвa
ния приведены в пРWlOжении 2.1.
(11.] 1)
(1].12)
1
l'
; I
(1 ].13)
,,1
l'
1,'
1:
i '1 I
I I I
1 '
1]1 li
, :1
;j
! I
:!i '
1111
111
11
Задача 11.6
Решите задачи 11.1, 11.3, 11.4, используя для вычисления инте2рала
формулу Симпсона (11.13). Сравните п02решности нахождения oпpeдe
ленною инте2рала методом трапеций и методом Симпсона. Сравните
пО2решности нахождения значении инте2рала С пере.менным верхним
пределом методом трапеции и методом Симпсона.
11.3. ОСНОВЫ метода Монте-Карло
Проиллюстрируем идеи метода МонтеКарло на примере вычисления
определенноrо интеrpала от функции, зависящей от одной переменной.
Пусть нам необходимо вычислить интеrpал (1] .2) от некоторой заданной
функции f(x) на интервале [а,Ь]. В предьщущем разделе мы рассмотрели
несколько различных формул интеrpирования, в которых использовались
значения функции f(x), вычисляемые в равно отстоящих точках. Однако
можно использовать и друrой подход, суть KOToporo леrко понять из сле
дующеrо примера.
1
I
1
I
i
",
330
11. Методы МОllтеКарло
......... . ..............................
Представим себе прямоуrольник
высотой Н и длиной Ь  а, такой, что
функция f(x) целиком лежит внутри
данноrо прямоуrольника (рис. 11.4),
Сrенерируем N пар случайных чисел
равномерно распределенных в данном
прямоyrольнике:
а::;' Х; ::;, Ь, О::;, У; ::;, Н .
н
о
а Ь
Рис, 11.4, К объяснению ал20ритма
вычисления определеНН020 инте2рала
методом МонтеКарло
Тоrда доля точек (Х;, У;), удовлетворяющих условию У; ::;, f(x;), являет
ся оценкой отношения интеrpала от функции f(x) к площади рассматри
BaeMoro прямоyrольни.ка. Следовательно, оценка интеrpала в данном методе
может быть получена по формуле
F =A
N N'
(11.14)
(11.15)
rде ns  число точек, удовлетворяющих условию Yi::;' f(x;), N  полное KO
личество точек, А  площадь прямоуrольника.
В пакете МА ТLAВ описанный алrоритм реализуется следующей
последовательностью команд:
% координаты нижнеrо левоrо уrла прямоyrольника
» Xmin=O;
» УIПiп=О;
% координаты правоrо BepxHero узла прямоуrольника
» Xmax=pil2;
» Ymax=1.5;
»N=1000; % число точек случайной последовательности
% вычисление последовательности случайных чисел равномерно
% распределенных на интервале [Xmin,Xmax]
» for i=l:N
х(i)=Хmiп+(Хmах-Хmiп)*rапd(l);
end;
% вычисление последовательности случайных чисел равномерно
% распределенных на интервале [Упllп,Уmах]
» for i=l:N
y(i)=Ymin+(Ymax- Ymin)*rand(l);
end;
»f=inline('sin(x)', 'х'); О/С задание подынтеI-Ральной функции
331


/1"
"
,
,
.п--!:!!!!!!.f.lое :'!!.:!.?!!.l!.J!Р.!!.'!..IР.'!.'!..е..К-'!.;о;,,:Р5!.'1!!.:.:.?!!..!.:!I!.'!..!!!.:.._!:1!.......
r 1
% подсчет точек, лежащих ниже rpафика функции [(х)
»for i=l:N
if f(x(i»>=y(i)
s(i)=lj
else
s(i)=Oj
endj
endj
»S=sum(s)j
» A=(Xmax-Хmiп)*(Уmах- Ymin)j % площадь прямоyrольника
» А *S/N % % вычисление значения интеrpала
ans =
1.0344
"
I 'i
i! :
1;:
в приведенной выше последовательности команд мы использовали
функцию inline, которая преобразует первый apryмeHT функции, являю
щийся строковым выражением, в описание функции, зависящей от пере
менных, стоящих на втором и последующих местах в списке формальных
параметров функции. Например, для задания функции F(x,y) = sin(x+y) He
обходимо ввести следующую команду:
»F=inline('sin(x+y) " 'х', 'у')
F=
Inline function:
f(x,y) = sin(x+y)

Задача 11.7
Дополните описанный выше доку.мент блоком, позволяющим отобра
жать на одном рисунке 2рафик функции и точки, распределенные слу-
чайным образом.
Задача 11.8
1. Сравните значение определеНН020 инте2рала, полученное с помощью опи-
саНН020 выше ал20ритма, с е20 точным значением и оцените п02реш
ность вычислений,
2, Не менее 10 раз пересчитайте документ, фиксируя при этом получаемые
значения определеННО20 инте2рала, Оцените среднее значение получен-
ной пОС.7едовательности значений и ее дисперсию, Сравните полученные
результаты с точным значением определеНН020 инте2рала,
3, Выполните задание 2 для раЗЛИЧН020 числа точек случайной последова-
тельности N. Постройте 2рафик зависщиости смещения значения опреде-
.7еНН020 инте2рала (СА1ещение  разность _"'tе:жду точньш и вычисленньш
"
't:
'1
332

11. Методы МО1/теКарло
.Ш.. ....................... ............ ...........Мю.... .... .. "0 ......ш..... ш . .........,.....  ". ........ ................. ......... .........
значением определеННО20 интezрала) от N. Постройте 2рафик зависимо-
сти дисперсии от N. Используя метод наименьших квадратов, попро-
буйте подобрать функцию, описывающую зависимость дисперсии от
числа точек N.
Можно предложить и дРУ20Й путь вычисления определеНН020 инте2ра-
ла, расс;иатривая е20 как среднее значение функции j{x) на отрезке
[а,Ь]:
N
FN =(ba).l Lf(x;),
N ;=1
2де Х;  последовательность случайных чисел с равномерным законом
распределения на отрезке [а,Ь].
Описанный ал20ритм реализуется в пакете МАТLЛВ выполнением сле
дующей последовательности команд:
(1].]6)
% Задание координат концов отрезка интеl1'ирования
» Xmin=O;
» Xmax=pil2;
» N=1000j % длина случайной последовательности
% rенерация случайной последовательности
» for i=l:N
х(i)=Хmiп+(Хmaх-Хmiп)*rапd(l);
endj
» f=inline('sin(x)')j % задание подынтеrpальной функции
% вычисление определенноrо интеrpала
» i=l:Nj
» s(i)=f(x(i))j
» (Xmax-Xmin)*mean(s)
ans =
0.9808
Задача 11.9
Решите задачу 11.9, используя для вычисления значения инте2рала
формулу (11,16),
Аналитическая оценка пО2решности формулы (11,16) может быть пo
лучена, если рассматривать последовательность значений fi = f(x;).
Дисперсия а2 последовательности fi определяется выражениеАl
а] =(2)и)2,
(11,17)
333

! I"!
11
, ,
.I!OM-Ь.!!!!l!!!?!!!..е:!.'!.1!!!.I!!_<:.1!..'!!..':!:.с.!5.'!!'!Е!!,lj::..?!!,.!!,,'!'!A!...1.!!::!!!... ...__..
сде
I
r I1
"1
I
I
I
1:1
:1
111
1 '1
1
l'
1 N
(1)= N L,f(Xi)
i=l
(11.18)
и
1"
'11
11
I
N
(12)= .. L,f(x;?
N i=l
Т02да в соответствии с централыюй предельной теоремой теории вe
роятностей дисперсия значения определенноzо интеzрала определяется
выражением
O'  o} = [ ff(x;)2 ( ff(Xi)]2]. (11.20)
N N N i=1 N i=!
Из (11.20) вытекают два следствия, весьма важных для практическоzo
вычисления инте2ралов методом МонтеКарло. Boпepвыx, ошибка
вычисления инте2рала о' F в оценке значения инте2рала уменьшается
как N!/2, т. е, очень медленно. (Сравните данный результат с вашими
результатами, полученными в задаче 11.9.) Изза отмеченной особенно
сти значения определенных инте2ралов от функций одной переменной,
вычисленные методом МонтеКарло, оказываются менее точными,
чем, например, результаты, получаемые методом трапеций, в котором
ошибка убывает как N2 (см. прШl. 2.1). Однако для МН020мерных и1l1пе
2ралов данное преимущество исчезает.
Второй важный момент, вытекающий из (11,19), состоит в том, что
точность оценки оnределеНН020 инте2рала зависит от дисперсии функ
ции о' f' т. е. функция по возможности должна изме1lЯться, как можно
меньше. Для уменьшения дисперсии, и, следовательно, повышения точ
ности метода умножим и разделим подынте2Ральную функцию на пo
ложительную весовую функцию w(x), нормированную условием
ь
fw(x)dx=l. (11.21)
(11.19)
,1
il
11,
:1;
l'
l'
1I1
111
:11
:1
1 1
I
' 1
а
в результате интеzрал (11,2) можно nереnисать в виде
r
I Ui,
334
...... .... .ш ...!!: NJ:'!!!!.':!.!t:!!?.!''!!:.:I!!!.tл-:!
ь
F = fl2W(X)dX,
. w(x)
II
(11.22)
Про ведем замену переменной х на
х
у(х) = J w(';)d'; ,
(11.23)
а
так что
dy = w(x), у(х = а) = О, у(х = а) = 1. (11.24)
dx
ТОсда интеzрал (11.22) становится равным
Ь
F=ff(x(y))dy. (11.25)
w(x(y))
II
Вычисление значения данносо интеzрала проводится так же, как это
было сделано выше, усреднением значений f(x(y ))/w(x(y)) по случайной
выборке точек у, равномерно распределенных на интервале [а,Ь]:
N
F   L f(X(Yi)) . (11.26)
N i=! w(x(y;))
Из (11.26) видно, что если выбрать такую функцию w, которая ведет
себя подобно функции f (т. е. она велика там, 2де велика f и мала там,
2де мала f), то подынте2Ральная функция f /w в (11,26) может быть
сделана «квазипостоянной». Описанная процедура позволяет YMeHЬ
шить дисперсию оценки иlllпе2рала (11.26) при условии правШlЬН020 вы
бора подходящей весовой функции w и возможности обратить cooт
ношение (11.23) для получения зависимости х(у).
Задача 11.10
1
1. Вычислите .методом МонтеКарло интеzрал от функции f(x) = '2
1 +х
на интервале [0,1], Сравните полученное значение интеzрала с е20 точ
ным значение,'>!.
1
2. Выберите в качестве весовой функцию w(x) = ......)' Убедитесь
3( 4  2х
в том, что данная функции удовлетворяет условию (1],21), Постройте
335


, f' '
'1'
1
КО'!!I1I.I?!!..й.'!Р.r:!!.Il!.!.."!..1!!!3...!'':!'./i'!!!!!!f!!..с:'!У113.е.!!'.!!1Т!:..1l!._.....ш..шшш
1
11
11
l'
11,1
zрафики функций w(x), f(x)/w(x). Сравните область значений функций
Лх), f(x)/w(x). Найдите явное выражение для функции у(х) , вычислив
интеzрал (11,23) для выбранной функции w(x), Найдите функцию
х:ох(у), обратив функцию у=:; у(х) , Получите аналитические выражеш
ния для функций f(x(y», w(x(y», Сzенерируйте последовательность
случайных чисел с равномерным законом распределения на интервале
[0,1], Вычислите значение определенноzо интеzрала в соответствии с
 (11,26), Оцените точность вычисленноzо значения интеzрала, сравнив
ezo с точным значение.м.
Для понимания с наиболее общих позиций, почему замена переменных
оказывается полезной, необходимо учесть, что равномерное распределение
точек по у, соответствует распределению точек по х с плотностью вероятно
сти dy / dx =:; w( х), при этом w( х)ш  вероятность Toro, что данное число
принадлежит отрезку [х, х +- ш]. Условие нормировки задается выражением
(11.20). Это означает, что точки сryщаются около наиболее «важных» зна
чений х, rде w (и, как ожидается, и f) велика, и что вычисление подынте
rpальной функции в «несущественных точках», rде w и f малы, составляет
малую часть от Bcero объема вычислений.
Применим описанный подход для rенерации чисел с заданным законом
распределения w( х) на ИIПepвале [а, Ь]. Обозначим через r случайное число,
равномерно распределенное на интервале [0,1] с IШотностью вероЯ'I1IОСТИ
Р (r):o {1, если r Е [0,1]
 (11.27)
и о, если r  [0,1]
Наша цель состоит в отыскании соопюшения между х и r тзкоro, что если r
распределена по закону (11.27), х будет распределена с IШотностью w(x).
Для получения данноro соотношения сначала вычислим интеrpал
х
Р(х) = f w()d .
(11.28)
а
Здесь функция Р(х)  интеrpальная функция распределения, равная Bepo
ятности получения числа меньшеrо или paBHoro х. В rеометрической интер
претации Р(х)  это часть площади фиrypы под кривой плотности вероят
ности слева от х.
Покажем, что обращение выражения
Р(х) = r
(11.29)
336
1 I
. .. !:А:!"!.'!'!!._й..'I!:!!.I!!.!..л-..
приводит К искомому соотношению
х :о Р \х) ,
(] 1.30)
Так как переменная r распределена на отрезке [0,1] равномерно, то
функция Р(х), связанная с r соотношением (11.29), также распределена
равномерно. Вероятность 1'oro, что Р(х) принадлежит отрезку
[p(x),P(x)+dP(x)], равна dP(x). С друrой стороны, в соответствии с
(11.29)
dP(x):odr. (11.31)
Соотношение между dP(x) и dx найдем, продифференцировав выражеш
ние (11.28):
dP(x) = р(х) (11.32)
dx
Отсюда, используя (11.27), имеем для О  r ]
dP(x) = w(x)dx = Ри (r )dr . (11.33)
Из выражения (11.33) видно, что переменная х распределена с требуемой
плотностью вероятности Р( х) .
Таким образом, rенерация чисел с заданным законом распределения
проводится в соответствии со следующим алrоритмом.
1. rенерация случайноrо числа r.
2. Нахождение соответствующеrо значения соrласно (11.30).
Применим описанный алrоритм для получения случайных чисел, paвHO
мерно распределенных на отрезке [а,Ь]. Требуемая плотность вероятности
равна
) {.!.,еСЛИХЕ[а,ь]
P = ba .
о, если х  [а,Ь]
Функцию интеrpальноrо распределения вероятности Р(х) на отрезке
[а,Ь] находим, подставив (11.34) в (11.28) и вычислив интеrpал. В результа
те получим
(11.34)
xa
p(x)= .
ba
Далее подставляем (11.35) в (11.29)
xa
r =  -- ,
ba
(11.35)
(11.36)
337
........

l' J
I I
J!..-'!.'!..Ь!!!rrl...е.!!!.'!I!..!.!i!.'!!!.'IlP...'!.с:!."!.1:?"!.:..с..':!.'!Е°'1.:''"'!.1!..:rrI.!J'!.1L...1.!!. ....._
'r I
1,
I!,
откуда находим искомое соотношение
х= pl(r)= а +(ba)' r. (11.37)
Несмотря на то', что метод неполноrо интеrpала действует безошибочно,
для ero применения приходится находить обратную функцию (см. (11.30»,
которая может быть получена только для сравнительно небольшоrо класса
функций. Кроме Toro, может оказаться, что интеrpал (11,28) не берется aHa
литически. Предположим, что нам известна таблица значений х(Л, при KO
торых неполный интеrpал от w(x) принимает ряд значений с равномерным
шаrомнаотрезке [а,Ь],т.е. y}=j/M; j=O,I,...,M. Тоrда
11
I:I
I
I
r
li!
;11
1,11
"
I
II!
,1
!I
Х.
УР  = J w()Ц.
о
В результате значения х} для целых j, выбираемых с равной вероятно
стью из набора чисел О,I,...М, будут аппроксимировать требуемое распре
деление. (Для концевых точек j = О и j = м требуется отдельное paCCMOT
рение.) Для нахождения Х}' проинтеrpируем численно дифференциальное
уравнение (11.32), применив простую дискретизацию
У }+1  У 1  ( )
w Х} .
Х}+1  Х}
Так как У }+1  у} = 1/ М , получаем удобное рекуррентное соотношение
(11.38)
(11.39)
для нахождения Х} :
'1
1
I1
1
Х}+I = Х} + () .
Mwx}
Друrим удобным методом
OДHO и MHoroMepHbIx случай
ных величин снеравномерным
законом распределения являет
ся метод отбораотказа (фон
Нейман), Ero rеометрическая
интерпретация представлена на
рис, ] 1.5.
(11.40)
, 1
:\'
О 1
Рис. ]],5. Теометрическая интерпретация
метода отбораотказа
i
(.:
338

...............ШШ..... .ш.... ......!,I:!е.,!,у'!!!!II,!,:!!..л-!!
Предположим, что необходимо сrенерировать случайную величину х,
распределенную на интервале [0,1] с вероятностью w(x), и пусть w'(x) 
положительная функция, удовлетворяющая во всей области интеrpирования
условию w'( х) > w( х). (Заметим, что в данном случае определенный инте
rpал от w' будет больше 1). Бывает удобно (хотя и не всеrда полезно) BЫ
брать w' константой, превышающей функции w'(x) в рассматриваемой об
ласти. Если теперь сrенерировать точки в двумерной области, равномерно
заполняющие площадь под кривой w'(x), а затем отобрать только точки,
лежащие под кривой w(x), то последние будут распределены с плотностью
вероятности w(x). На практике данный метод реализуется следующей по
следовательностьюдействий:
1. Берутся две случайные величины Х; , У}' определяющие. положение
расположения точки в двумерном пространстве под функцией v'( х) . Зна
чение Х; принимается в том случае, если У; < W(X;) .
2. Если точка отверrается, то rенерируется следующая пара чисел Х;, у} .
Отметим, что данный метод эффективен только в том случае, коrда
функция сравнения w'(x) выбирается близкой к w(x). В противном случае
на rенерацию бесполезных отброшенных точек будет затрачиваться MHoro
машинноrо времени.
Для rенерации множества точек, равномерно распределенных под кри
вой w'( х) , можно использовать следующий !lЛrоритм,
1. Взять два случайных числа Х; Е [0,1], У; Е [O,max(w'(x))].
2. Принять значение (Xj, У j ) , если у;  w'( Х;) .
Задача 11.11
С2енерирйте методом отбора-отказа выборку точек на отрезке [0,1],
распределенную по закону w(x) = (1 x2). и с помощью данной вЫ
1
борки оцените инте2рал от функции f (Х) = -------Z на интервале [0,1].
l+х
Рассмотренный выше метод вычисления одномерных интеrpалов леrко
обобщается для вычисления dMepHbIx интеrpалов вида F = J Лх; )dd Х:
339

l'
. Jofn. 1?'!'..e.I?!!..!.Jof!!.e)J!pal'u.1!,!:e':1!I?..?lf.e.:!п.1!!т-e.!:1.!!:!!. .
N
F =  L!(X;)'
N ;=1
(11.41)
rде все координаты случайных векторов Xi выбираются независимо дрyr
от друта.
В качестве примера расчета MHoroMepHbIx интеrpалов методом MOHTe
Карло раССМ01ИМ задачу о нахождении центра масс и момента инерции
двумерных твердых тел, для которых известен закон распределения плотно
сти Р( Х, у) . Масса dm малоrо элемента площади dxdy равна
dm=p(x,y)dxdy, (11.42)
а полная масса тела
,
,
, .
М = н p(x,y)dxdy. (11.43)
Пределы интеrpирования в (11.29) определяются rеометрией тела. Koop
динаты центра масс Х, У определяются в соответствии с формулами
Х =  ff хр(х, y)dxdy, (11.44)
У =  н ур(х, y)dxdy. (11.45)
Момент инерции при вращении двумерноrо тела относительно оси Z равен
1z = Н(х2 +y2)p(x,y)dxdy. (11.46)
Вычисление М, Х, У, 1 z осуществляется в соответствии с формулами
1 N
М N = (Х2 x1)(Y2  YI)N LP(x;, у;), (11.47)
;=1
1 N
ХН =(Х2 XI)(Y2  Yl) N LX;p(x;,y;), (11.48)
;=1
1 N
УН = (Х2 X1)(Y2  У1) N LY;p(x;, у;) , (11.49)
;=1
N
1;:,N =(Х2 x1)(Y2  У1)  L(X; + упр(х;,у;) , (11.50)
;=1
i
1
[
340

!!,:!.:! e.'!'..!'.<:!.!v!.I!lIe: p.?
rде последовательности случайных чисел Xj:::; Х; :::; Х2, у!:::; у; ::; У2 l'снери
руются независимо друr от друrа,
Задача 11.12
1. Для диска, изображенноzо на рис, 11,6, вычислиmе л,tеmодом MOHтe
Карло полную массу, центр масс и MO},teHm инерции диска оmносиmельно
оси oZ, ПРИJlJиmе внешний радиус диска r2 = 5, радиус круzовой полосmи
r1 = 1.5, Центр круzoвой полосmи находиmся в mочке с координатшни
(0,2,5), Счиmаmь плоmносmь диска однородной и равной 1,
2. Вычислиmе полную массу, центр масс и момент инерции диска oтHocи
mельно оси Z с помощью средств инmеzрированuя пакета МА TLAB.
Сравните полученные резульmаmы с резульmаmaJIJU, полученными .lИеmо
дом МонmеКарло.
З. Повmориmе расчеmы, выпол
ненные в пп, 1, 2, с плоmно
сmью р(х,у)=I+!(х2 +у2), сде
2
координаты х, у оmсчиmываюm
ся от центра большоzо диска,
у
х
Рис, 11.6, Диск, рассматриваемый
в задаче 11,12
Рассмотренный метод замены переменной также может быть обобщен и
на мноrомерный случай. При этом весовой функции w(x), нормированной
на единицу, будет соответствовать новая переменная интеrpирования у( х) с
якобианом преобразования IB у/д xi. В общем случае найти обратную
функцию х(у) трудно (если вообще возможно), поэтому удобнее представ
лять эту замену переменных в MHoroMepHoM случае как операцию rенериро
вания последовательности Х; (у;) с плотностью вероятности w(y).
Решив задачи 11.11, 11.12, можно убедиться, что метод МонтеКарло дa
ет результаты, достаточно близкие к результатам, получаемым традицион
ными методами. Однако для достижения заданной точности вычислений в
методе МонтеКарло приходится использовать значительно б6льшое коли
чество частиц, Преимущества метода МонтеКарло проявляются при BЫ
Числении MHoroMepHbIx интеrpалов. Зададимся общим числом точек N, в
которых проводится вычисление определенноrо интеrpала, и сравним эф
фективность детерминированных и случайных методов интеrpирования,
341

1'1
1
:!.l.!!l!р'!.С:_fС:<:!'':!РОl!!.':!:..1!.'!-з!'-:с...flр''''J._е:::'о.!.fll!.'5!!'!!.!!...1!!:.!!...............
r I
в традиционном методе, например, в MHoroMepHoM аналоrе метода трапе
ций при заданном числе точек N, проводится разбиение каждоrо отрезка,
параллельноrо соответствующей координатной оси dMepHoro пространст
ва, на N1/d интервалов длиной h  NI/d . При этом ошибка интеrpирования
по ячейке объемом hd оказывается пропорциональной O(hd+2) (см.
прил. 2,1), поэтому суммарная поrpешность интеrpирования по всем ячей
кам в традиционном методе равна
NO(hd+2)= O(N2/d). (11.51)
Из (11.48) видно, что при больших d эта поrpешность убывает очень
медленно. С дрyrой стороны, уравнение (11.20) показывает, что ошибка Me
тода МонтеКарло уменьшается как N1/2 и не зависит от d. Если предпо
ложить, что оба численных множителя в этих оценках порядка единицы, то
леrко увидеть, что точность метода МонтеКарло становится более эффек
тивным при d  4 . Конечно, точная оценка зависит от используемой тради
ционной схемы интеrpирования или от Toro, насколько удачно выбрана Be
совая функция в методе МонтеКарло. Однако основной результат состоит в
том, что при больших d скорости уменьшения ошибки с ростом N в дeтep
минированных и стохастических методах существенно различаются.
1;
l'
11;:1
111'!
1:,1
1.
I
j 11'1
I 1'1
'i 11'
11111"
l'
" 111;
I[
11
11
11.4. Алrоритм rенерации случайных чисел
с равномерным законом распределения
в предыдущем разделе мы обсудили вопрос о вычислении определен
ных интеrpалов методом МонтеКарло, который состоит из двух основных
операций: 1) rенерации точек, распределенных в области интеrpирования с
заданной плотностью вероятности w(x), 2) вычисления значения функции
j(x)/w(x) в этих точках. При этом алrоритм rенерации случайных чисел с
заданным законом распределения основан на использовании случайных чи
сел с равномерным законом распределения. Следовательно, точность BЫ
числения интеrpала зависит не только от количества точек, используемых
для вычисления значения интеrpала, но и от качества работы reHepaTopa
случайных чисел. В этом разделе рассматриваются основные алrоритмы и
характеристики rенерации случайных чисел.
Для применения в вычислительных экспериментах reHepaTop должен
обладать следующими характеристиками:
 хорошими вычислительными свойствами,
 эффективностью,
11
1
342
]], Методы МОllmеКарло
... ..Ю О'. .... ....... ........_.... .  "M"" ,"",,'"MMM....M.''''M'''M'MM'M_M''''М
 большим периодом,
 воспроизводимостью.
Первыми и наиболее важными из рассматриваемых характеристик явля
ются, конечно, статистические свойства. Известен пример, коrда использо
вание плохоrо reHepaTopa случайных чисел в методе молекулярной динами
ки привело к обнаружению особоrо поведения системы определенноrо раз
мера. Результаты независимоrо исследования, проведенноrо друrими
авторами, не подтвердили этой особенности. Это позволило сделать вывод о
том, что причиной обнаруженной особенности явилось плохое качество re
нератора случайных чисел [7].
Также очень важна вычислительная эффективность reHepaTopa. Про
rpaMMbI для компьютерных экспериментов требуют orpoMHoro числа
случайных чисел. Для получения порядка 1010 чисел за оrраниченное
время одно случайное число должно вычисляться очень быстро. Кроме
Toro, важно требование на размер необходимой для работы [енератора
памяти компьютера. reHepaTop должен быть достаточно быстрым и эко
номичным по памяти.
В действительности, rенерируются не случайные числа, а последова
тельности псевдослучайных чисел, поэтому последовательность rенерируе
мых чисел после определенноrо количества шаrов повторяет саму себя. Ее
период должен быть заведомо больше длины, необходимой для последова
тельности случайных чисел. Опасность представляет также исчерпание по
следовательности случайных чисел или даже приближение конца ее цикла,
Это также приводит к неверным результатам.
Существуют различные способы rенерации на компьютере случайных
чисел [8]. Далее мы рассмотрим, в первую очередь, наиболее широко pac
пространенные в настоящее время MTOДЫ, объединенные OO!1M названием
(<линейные конrpуэнтные reHepaTOpbI», Они производят определенным спо
собом при задании начальноrо целоrо числа последовательность случайных
чиел с равномерным законом распределения. Несомненным достоинством
reHepaTopoB данноrо типа является их воспроизводимость.
Линейный конrpуэнтный reHepaTop выдает последовательность произ
вольных целых чисел, которые можно привести к единичному интервалу
[0,1]. Для этоrо достаточно разделить все члены последовательности на
максимальное возможное целое число. Ненормированная последователь
ность целых чисел, однако, предпочтительнее по причине большей вычис
лительной эффективности алrоритма.
343
........

JII
!!.'!.b':)'!.'..E!_ !!е!!.'2!.,!!I'!l!.!Р!:!з'!.'!.:..с..'!Е!!,'i::"о.!!1I!!.:.."!..:А!...А !.!:.Ю...
Алr'оритм линейноrо конrруэнтноrо reHepaTOpa (Лемер, 1948)
Пусть т, а, с, Хо  причем т> Ха, т > а, т > с и Ха:2: О, а :2: О, с:2: О,
Тоrда псевдослучайное число последовательности Х; получается из
предшествующеr'о ему числа X;l как
Х; =(а.х; +c)modm.
(1 ] .52)
I
\
"1
11
11 '
11,1
(Здесь mod  функция деления по модулю, т. е. функция получения остатка
от деления одноrо числа на дрyrое. Например] 9 mod 4 == 3.)
При соответствующем выборе чисел т, а, с, Ха алrоритм N!! ] выдает по
следовательность случайных чисел. При этом rенерируемая последователь
ность имеет повторяющийся цикл или период, не превышающий т чисел.
Для получения достоверных результатов при моделировании физических
систем необходимо использовать rенераторы с максимально большим пе
риодом. Максимальный период достиrается при c:f:. О. Такой reHepaTop Ha
зывается смешанным. Однако, как показала практика, смешанные reHepaTo
ры дают плохие результаты по сравнению с rенераторами, у которых с = О
(мультипликативные rенераторы). Отметим, что для обеспечения макси
мальноrо периода мультипликативноrо конrpуэнтноrо reHepaTopa модуль т
и множитель а необходимо подбирать специально.
Алrоритм линейноrо конrpуэнтноrо reHepaTopa в пакете МА ТLAВ pea
лизуется выполнением следующей последовательности команд:
» а=7;
» с=7;
» т=55;
» х(1)=20;
» N=100;
» for i=1:N
x(i+ 1)=mod(a*x(i)+c,m);
end;
» i=1:N+ 1;plot(i,x,'-kS');
» axis([O 100 О 60»;
Результат выполнения приведенной выше последовательности команд
представлен на рис. 11.7.
Задача 11.13
Исследуйте зависимость периода последователыюсти случайных чисел,
получаемых при использовании различных алzориmмов, от их числовых
параметров (параметров: а, с, т).
J
)!jl
';'
l'
1I
1.;
1:1
II'k.
111
11
1
,
<.
344

   _  !...Me"!..I!t:!..'!'!'.:I!.!!.l!!!.
60 r.-T-T -"'Т.._,...
.1 
4011'
.fl

I
J
I
 1\ I
11  J 1,' I
11 о
1I
1
l j!i 9:! ']
I I 111! f /1 r ,1\,', I
1 '.! 11 ,i,' I 11 11 ' I I
/'I'P I!I 11'
\ 1 ' ,1 , L  о
   00 ro 00 00 
1
о
о
о
о
10 
Рис, 11.7.' Случайная последовательность, czенерированная в соответствии
с алzоритмом линейНО20 КОН2руэнтНО20 2енератора
Задача 11.14
1. Модифицируйте прozрамму так, чтобы в качестве начальною значения
в ал20ритме Лемера использовалось случайное число, выдавае.iwое 2eHe
ратОРОАl случайных чисел с равномерным законом распределения пакета
МА ПАВ, Проанализируйте, как это скажется на свойствах 2eHepиpye
мой последовательности.
2. С2енерируйте две последовательности, у которых начальные значения
выбираются случайным образом, Вычислите корреляцию между дaHHЫ
ми последовательностями. Можно ли считать их независиМblми?
З. Постройте и сравните cиCт02PaмJllЫ данных последовательностей. Ka
кой величU/юй можно охарактеризовать степень неравномерности
плотности распределения данных случайных последовательностей?
11.5. Алrоритм Метрополиса
Несмотря на то, что методы rенерации случайных чисел с заданным pac
пределением, рассмотренные в предыдущем разделе, Moryт оказаться в ряде
случаев весьма эффективными, в общем случае весьма сложно, а в боль
шинстве случаев невозможно, провести их обобщение для сложных MHoro
мерных весовых функций, Отмеченное обстоятельство определило необхо
дим ость разработки друr'их подходов, свободных от указанных недостатков,
345

l'
1
J!.?:\111.!?'11..P,,o.. A! ?<:'."!!??I!./"!'!1!.."!!!'...ч.:':/(!.Е?:'С':?'!..I!.".'!1:..'!..!!.......
r I
'1
11
I
I
I
'1,
I
jl
1
Один из общих методов получения произвольноrо HepaBHoMepHoro pac
пределен ия вероятности был предложен Метрополисом, Розенблатом и
Тэйлером в 1953 r, Метод Метрополиса представляет собой частный случай
процедуры выборки по значимости, в которой некоторые возможные BЫ
борки отбрасываются,
Для простоты рассмотрим одномерный вариант метода Метрополиса,
Предположим, что мы хотим сrенерировать случайные переменные с про
извольной плотностью вероятности р(х). В методе Метрополиса модели
руется «случайное блуждание» точек {xi}, распределение которых после
большоrо числа шarов асимптотически приближается к распределению Be
роятности Р( х). Случайное блуждание определяется заданием вероятности
перехода W(Xi  Х j) от одноrо значения Xi к дрyrому Х j , Можно показать,
что достаточным (но не обходимым) условием сходимости распределения
Хо, Х1' Х2"" к Р(Х) является выполнение условие «детальноrо баланса»
P(Xi)W(Xi xJ=p(X)'V(Xj xJ (11.53)
Отметим, что соотношение (11.53) не определяет W(i  Х J единствен
ным образом. Рассмотрим простейший вариант, удовлетворяющий условию
(11.53):
I11
1:
i:
I
I
I
W(Xi  Х j )= min[l' Р(Х J] .
P(Xi)
Предположим, что «пешехоД» находится в точке с координатой XIl' Для
формирования ХII+1:
1. Выбираем случайную координату Х[ =Х" +бll, rде бll случайное
число на отрезке [б,б].
2. Вычисляем W = Р(Х[)/ p(XIl) ,
3. Если W;::: 1, принимаем данный переход и полаrаем Xlltl = Х['
4, Если W < 1 , rенерируем случайное число r.
5, Если r::; w, принимаем данный переход и полаrаем XIlt1 = Х[ .
6. Если Пробный переход не Принят то полаrаем Х 1 = Х
, п+ 11 .
(11.54)
При практической реализации метода Метрополиса возникает законо
мерный вопрос о выборе величины пробноrо шаrа б. для ответа на этот BO
прос предположим, что «пешеход» находится в максимуме W, т, е, в точке
Х п наиболее вероятноrо нахождения, Если шаr бвелик, то значение и{х[),
346
  ! !:A!...:..т??,:! оltl11е.:!!...а.Ел-:!..
будет значительно меньше, чем значение w( Х Il ), И большинство пробных
шarов будут OTBeprHYТbI, т. е. выборка окажется неэффективной. Если шаr б
выбран не достаточно большим, то большинство шarов будет принято, но
пешеход не сдвинется достаточно далеко, поэтому выборка также окажется
неэффективной. На практике хорошим выбором является такая величина
пробноrо шаrа, при которой принимается около половины всех пробных
шarов.
Отметим, что алrоритм Метрополиса не лишен ряда недостатков, Bo
первых, последовательные точки выборки Хо, Х1" ,. не являются независи
мыми, что показывает анализ способа их получения: точка Xi+l вероятнее
Bcero оказывается в точке Х;. ЭТО приводит К тому, что точки, имеющие
правильное распределение, не будут статистически независимы. Например,
окажется неверной оценка дисперсии (11.20) значения интеrpала
f w(x)f(x)dx
F  
 f w(x)dx ,
вычисляемоrо путем усреднения значений функции f(x) по точкам слу
чайноrо блуждания. Данную зависимость можно оценить количественно,
вычислив авто корреляционную функцию
C(k) = ИJi+k)=fjl , (11.55)
(f/)ui
rде ( ) означает усреднение по случайным блужданиям, например,
Nk
UJi+k) =Nk L,f(Xi )f(xi+k), (11.56)
/=1
На практике для устранения этоrо эффекта следует вычислять интеrpал
и ero дисперсию, используя точки траектории случайноrо блуждания, раз
деленные таким временным интервалом, чтобы значение автокорреляцион
ной функции не превосходило 0.1,
BOBTOPЫX, существующее влияние стартовой точки на значения I'енери
руемой последовательности, несмотря на то, что в методе Метрополиса лю
бое начальное положение является приемлемым и ero результаты не долж
ны от Hero зависеть. Отмеченное обстоятельство приводит к необходимости
отбросить несколько начальных шаrов, в течение которых система прихо
ДИТ В «равновесное состояние» (термализуется), На практике стартовую
347


},
1
1!...'..OI1!H!.?":. ,,:,.о,,:'рс:.':'Р!':'Ч-":::..Р.'!.l!.'!..GCJ.. .../I'!.'!../':'.'':1:1!!.............шшш........ 'Ш"'ШШ
1
11
l'
il
11:
точку ха выбирают в точке максимума вероятности w( х). Затем делается
несколько термализационных ша!'Ов для устранения влияния стартовой точш
ки, и только после 3Toro rенерируется выборочная последовательность,
Продемонстрируем реализацию алr'оритма Метрополиса в пакете МА т.,
САВ на примере I'енерации последовательности случайных чисел, имеющих
х'
1 
[ауссово распределение р(х) = Ш е 2.5 Необходимо создать файл
,}2.л,5
Меtrороlis.щ содержащий описание функции Metropolis, возвращающей
значения случайной последовательности с требуемым законом распределения,
"
11
I ,
'!':
J
:!I:I
1;:11
.1 1)
I 1,
1:'
I"';i
'1'
1;
I
% листинr файла Metropolis.m
function z = Metropolis(x,Delta,p)
% функция, возвращающая случайное число, вычисленное
% в соответствии с алrоритмом Метрополиса
% х  координата начальной точки
% Oe1ta  максимальное значение пробноrо шаrа
% р  имя функции, описывающей распределение
% плотности вероятности
Xt=x +Delta *(2*rand(I) 1);
w=p(Xt)/p(x);
if w>=1
Xnew=Xt;
end;
ifw<1
r=rand(I);
if r<=w
Xnew=Xt;
else
Xnew=x;
end;
end;
z=Xnewj
Далее необходимо выполнить следующую последовательность команд:
% задание функции, описывающей закон распределения
» р=iпliпе('I/«2*рi*5)ЛО.5)*ехр( -хЛ2110)' ,'х');
» N=2*10Л4j % число точек случаЙной последовательности
»х(1)=О; % первый член случайной последовательности
% вычисление членов случайной последовательности
:!
j
11
, .

348
!.!:А!...'!..'!!.(;}шl л.-:.'!.'!п:,,:Rрло,
» for i=2:N
x(i)=Metropolis(x(i-l ),О.5,р 1;
end;
% визуализация случайной последовательности
» figure(1);i=I:N;plot(i,x,'k');
% вычисление распределения вероятностей
» Ni=50; % число интервалов rистоrpаммы
» k=I:Ni;
» dx=(max(x)min(x»/(NiI);
» Interval(k)=min(x)+dx*(k-l)j
» s=hist(x,lnterval);
» for j=I:Ni
z(j )=miп (х )+dx * (j -1 );
Z(j)=N*p(z(j»*dx;
end;
% визуализация экспериментальноrо и теоретическоrо
% распределения вероятности
» figure(2);bar(lnterval,s);colormap white
» hold оп
» plot(z,Z,'k')
» hold off
Результат выполнения описанной последовательности команд представ-
лен на рис, 11.8, 11,9.
6i"""""""''-"'""'"""""""'' !"''r. T""
,
i
6;
!
,,'
l'
-41
.6 
I
60- oT.'o." .."o ti' ..t -... 1""4 .
Рис. 11.8. Последовательность С.7учайных чисел, С2енерированная
в соответствии с методо.И МонтешКар.70
349


l' I
'I( 11I
I
j
I
!!?lI!.'!'.!?'!!tI!?еА!..?_е::.'!1!.CJ.'!.а!.I.U.:Р.!!.'!._uч..:.с!.'!..х..п-Р..?_'-!.=::...й-..в.в._п-(l'5.:..п:.:А.!...!:1! _Ш
12ОО[
I
 1
) I 1\ I
' I  \ 1
1 111 \ 1
11'111-;
,'. I
i 1" I
: 
1000
! 1
8001
I
600['
400
I
I
200f
I
J
-8
I,i
/1
Рис. J J,9, Теоретическая (сплошная кривая) и экспериментальная распределения
вероятностей случайной последовательности
ji
11  I
Задача 11.15
Вычислите авто корреляционную футщию C(k) в соответствии с (11.55).
Чему равно значение С(О)? Определите значение k, при которо;м
C(k):S; 0.1,
I '.111.',
)1
1:
,'11
Задача 11.16
Модифицируйте функцию Metropolis так, чтобы она возвращала пOMи
мо значения координаты общее число переходов при вычислении пepe
Аtещения на каждом ша2е. Подсчитайте отношение длины случайной
последовательности к полному числу ша20в. Как зависит данная вели
чина от величины проБН020 ша2а,
Задача 11.17
Примените алzoритм Метрополиса для 2енерации одномеРН020 HOp
маЛЬН020 распределения, Для различных значений проБН020 ша2а иссле
дуйте долю принятых пробных ша20в, корреляционную функцию (и, сле
дователыlO, nрие.нлемую частоту выборки) и суммарную эффектив
ность расчета, Воспользуйтесь С2енерированными случаЙНЫАtU числа/ии
для вычисления инте2рала
350
...............
. ........ ш...ш!!.:."::'!!?д-!?I'!.'.=:!<..(lр"f!О
+ ос: Xl
J x2e2 dx
oo
и оцените n02решность nолучеНН020 значения. Сравните эффектив
ность метода Метроnолиса с эффективностью расчета методами,
рассмотренными в предыдущем разделе,
Задача 11.18
1. Используя метод Метроnолиса, оцените значение инте2рала
4
J 2 xd
х е х.
а
Постройте 2рафик числа посещений «пешеходом» точек XO,xl,...Pas
номерно ли выбирается nодынте2Ральная функция, Если нет, то в какой
области изменения функции отсчеты производятся чаще?
2. Вычислите инте2рал
4
J 2 xd
х е х,
а
используя метод выборки по значимости,
ЛИТЕРАТУРА
1, Бахвалов Н. С" Лапин А. В" Чижонков Е, В, Численные методы в задачах и упражнениях,
М.: Высшая школа, 2000,
2. rулд Х" Тобочник Я, Компьютерное моделирование в физике, Т, 2, М,: Мир, 1990,
3, Кунин С, Вычислительная физика, М.: Мир, 1992,
4. Тейлор Дж, Введение в теорию ошибок, М,: Мир, 1985,
5, Метод статистическнх испытаний/Под ред, Ю. А, Шнейдера. М., rиФм, 1962,
6, Соболь И. М, Численные методы МонтешКарло. М,: Наука, 1973,
7, Хеерман д, В, Методы компьютерноrо эксперимента в теоретической физике, М,:
Наука, 1990.
8. Кнут Д. Искусство проrраммирования для ЭВМ, Т. 2. Получисленные алrоритмы. М.:
Мир, 1977,
351

11' I
..... ,",,',',.___  ..  .. !_ll}':!.t1lIылужj!!.'!..._
rлава 12
СЛУЧАЙНЫЕ БЛУЖДАНИЯ
[о, что после N шаrов пешеход окажется на расстоянии Х от начала отсчета,
Знание вероятности Р N (Х) позволяет вычислить среднее смещение
i=N
(xN)=[LiPN(X) (12,1)
i=N
12.1. Введение
и дисперсии
',1
1
11
Впервые задача о случайных блужданиях была сформулирована в 1906 [.
Пирсоном. В пер во начальной формулировке требовалось определить, на Ka
ком расстоянии от начальной точки будет находиться пешеход, сделав N
шаrов равной длины в произвольных направлениях. Отметим, что со BpeMe
ни постановки задачи в такой формулировке модели случайноrо блуждания
получили широкое распространение в физике, биолоrии, химии, общест
венных науках. Например, для описания диффузии молекул rаза, движения
коллоидных взвесей в жидкости, моделирования длинных полимерных цe
почек, решения ряда задач квантовой механики и др. В этой и последующих
rлавах рассматриваются модели, для реализации которых используется Me
тод случайных блужданий,
(дx) = (x) (XN)2 ,
( 12.2)
12.2. Одномерные случайные блуждания
[де (дx)  средний квадрат отклонения
N
(x)=[2 Li2PN(X),
x=N
В методе полноrо перебора количество и вероятность всех блужданий
для заданных N и Х вычисляются в явном виде. Начнем рассмотрение Meтo
да случайных блужданий со случая, коrда N = 1. Пешеход с вероятностью р
может сместиться на один шаr вправо, затем с вероятностью р сделать сле
дующий шаr вправо или с вероятностью q  влево (рис. 12.2).
.\"=-1 .\"=1
............... ...............
q р
(12.3)
Рассмотрим идеализированную одномерную задачу о движении пешехо
да, который в момент времени t = О находится в точке Х = О (рис, 12.1).
Рис, 12,2, Случайные одНОl>tерные блуждания пешехода при N  1

х
Рис, 12,1. К постановке задачи об одномеРIIОМ случайном блуждании
у
.
.
.
х=о
.
.
.
.
Значения (X1) и (Хп, вычисляемые по формулам (12.1) и (12.3), равны
1
(XI) = [Li(Xi)= [q +/р = (р q)[, (12.4)
i=I
Будем считать, что все шаrи имеют одинаковую длину [, а направление
каждоrо следующеrо шаrа не зависит от направления предыдущеrо шаra.
Предположим, что на каждом шаrе по времени пешеход делает шаr вправо
с вероятностью рили шаr влево с вероятностью q = 1  р. Обозначим общсе
количество шаrов, сделанных пешеходом, вправо n; , влево n, ТОI'да пол
ное число шаrов равно N = 11; + 11, Полное смещение пешехода после N
шат'ов равно Х = (11;  п)[ , [де N [ :<:; Х:<:; N [ , Зависимость Xi (i = О, , ' " N )
называют реа,'шзацией случайноrо процесс а, Совокупность зависимостей
Xi ' имсющих ОДИНаКОВУЮ длину и начинающихся из одной точки, нпзыва
ЮТ ансамблсм реализаций, Необходимо определиrъ вероятность PN(X) TO
1
(Хп = /2 Li2(Xi)= [2q + [2 Р = (р + q)[2 = [2.
i=1
(12.5)
Тоrда среднеквадратическое отклонение (дхп, вычисляемое в COOTBeT
ствии с(12.2), равно
(дхп=[2 [(pq)]2[2 =(1(pq))(J+(p+q))[2 =,..
= 2q. 2р .[2 = 4pq[2
Рассмотрим случай N = 2. Предположим, что пешеход, сделав шаr из
точки Х = О, оказался в точке Х = 1, Вероятность данноrо события равна р.
Так как направление следующеI'О шаrа пешехода не зависит от направления
(12.6)
1,
121576
353

(! I
CJ..tп.!:.'?ер"IICJ.. _t_?:I1Р..CJ..'!.С!'11:1l1!I1.:к.1J..'lfJCJ..чеСCJ..в..'!._п.(lк..е...111.: "iА_ТIЗ..
предыдущеrо, то он может оказаться с вероятностью р2 в точке Х = 2 или с
вероятностью pq в точке Х = о. Вследствие симметрии задачи анаJЮI-ИЧНЫЙ
вывод можно сделать для случая, коrда пешеход смещается влево от точки
Х = о. Следовательно, вероятность обнаружить пешехода, сделавшеrо два
шarа в точке Х = О, равна 2pq, в точках Х =:t2 вероятность равна р2, Для
дальнейшеrо анализа удобно изобразить рассматриваемые смещения пеше
хода rpафически (рис. 12,3).
х=-:1 х-""О Х"":!
......., ...." ..""",.,....... +.................,........

(1'
1,1
......
...............
lЩ
Рис, 12.3, Случайные одно. мерные блуждания пешехода при N = 2
Среднее значение (Х2) и средний квадрат отклонения (хn, вычисляе
мые в соответствии с (12.1) и (12.3), при N = 2
2
(Х2) = [LiP2 (Х;) == 2[q2  [qp + [pq + 2[р2 == 2(р2  q2)[ ==
;=2
==2(р q)(p + q)[ == 2(р q)[,
2
(x) == [2 Li2 Р2(х;) == [2 (4q2 + 4р2)= 4(q2 + р2 )[2.
;=2
Подставляя (12.7), (12.8) в (12.2), находим среднеквадратичное отклонение:
(t1x) == 8pq [2, (12,9)
Применим метод перебора для N == 3. Все возможные для данноrо случая
блуждания представлены на рис. 12.4.
(12.7)
(12.8)
x=31
+-----------+-----------+-----------
x=l1
+-----------+-----------
..............
: I
х=l1 .\'=31
............................ ........................................
+-----------

.............
+___________с I с ...............
q3 3 p(f1 3 Jl(f 1'3
Рис, 12.4. Случайные одномерные блуждания пешехода при N = 3
Осуществляя перебор всех блужданий, аналоrично тому, как это дела
лось для случаев N == 1,2 получаем
354
I
"

12,<?1..:(lg!tь:=б-.J.:!.!!!'.1!
з
(хз) == 1 LX/1(X;) = 1 (3q3 3pq2 + 3p2q + 3р3)== 31 (р2  q2)p + q) ==
i=,З
== 3(р + q)(p  q) == 3(р  q) ,
(12.10)
з
(xп==12Lx;1(xi)=12q2 +3pq2 +3qp2 +9р2)=
i=З
(12.11)
== [2 2pq + [3(р q)]2)
(t1xn == 12pq[2 , (12.12)
Сравнение выражений (12.4), (12.7), (12.10) показывает, что при произ
вольном N среднее смещение (XN) может быть вычислено по формуле
(XN)==(pq)NI. (12.13)
Сравнивая, аналоrично, (12.6), (12,9), (12.12), находим, что при произ
вольном N дисперсия (t1x) может быть вычислена по формуле
(t1x) == 4pqN [2.
(12.14)
.>......,.>...>..,
Задача 12.1
Найдите все возможные смещения частицы при N == 4, Вычислите Me
тодом перебора (Х N ), (t1x), Сравните полученные результаты с co
ответствующими значениями, вычисленными по формулам (12,13),
(12.14).
Так как полное число возможных Nшаrовых блужданий в одномерном
случае составляет 2N, то для реализации метода полноrо пере50ра
целесообразно использовать компьютер. (Отметим, что, даже в этом случае
метод полноrо перебора оrpаничен малыми значениями N.) Для реализации
данноrо метода на компьютере необходимо знать аналитическое выражение
функции, описывающей вероятность PN(X)' или рекуррентное соотноше
ние, позволяющее вычислять вероятность Р N (х) при Nшarовых блужда
ниях по значению вероятности при (N 1 )шаrовых блужданиях.
Для нахождения peKyppeHTHoro соотношения составим таблицу
(табл, 12,1), в каждую ячейку которой поместим число посещений пеиiехо
дом соответствующей точки при Nшаrовом блуждании (N == 1,2,...,5).
355

j' ,
l'
:й-."!.п--ь.!?!п--е.ЕCJ..:.л-!.?еЛ-UF!!.U 1!.r.:з.и-че.к: '!Eo.eCCO._'!.'!.:п:e. !:!.AT1:1!. ......
Таблица 12.1. Число посещений пешеходом точек с задаННЬL'lfи координатами
1
I
Число ша Координаты точек
?О8, N 5/ 4/ 3/ -2/ -11 О 11 2/ 3/ 4/ 5/
1 1 О 1
2 1 О 2 О 1
3 1 О 3 О 3 О 1
4 1 О 4 О 6 О 4 О 1
5 1 О 5 О 10 О 10 О 5 О 1
I ,
I
: \
! I
Анализ данных, представленных в табл. 12.1, показывает, что
Р2 (i:2l) =  (i:l) , 1 (i:3l) = Р2 (i:2l),
Р4(Ып = 1(i:3l), Ps(i:5l)= P4(i:4l);
Р2(0) =  (l)+  (п,
Рз(1) = P2(21}+ Р2(0), 1(п = Р2(0)+ Р2(2п,
Р4( 21} = Рз( зп + Рз(I}, Р4(0) = 1(п+ 1и), Р4(2п = Рз (п + Рз(31},
Рs(зl} = Р4( 4п + Р4( 2п, ps(l) = Р4( 21}+ Р4(0),
Ps(t) = Р4 (0)+ Р4 и), Ps(3l) = Р4 (21)+ Р4( 4l). (12.16)
Из (12.15), (12.16) видно, что число посещений пешеходом точки Х; при
Nшаrовом блуждании связано с числом посещений точек Хш при (NI)
шarовом блуждании следующим образом:
PN(Xi:N)= PNl(Xi:NI)'
PN(X;) = PN(XH)+ P(X;+I)'
(12.15)
11 :
1: I
11,
I
i
(12.17)
(12.18)
rде i=2,...,NI.
Для получения значений вероятностей нахождения пешехода в точках
Х; нужно умножить значение каждой ячейки из табл. 12.1. на значения co
ответствующей ячейки из табл, 12.2.
Таблица. 12.2.значения коэффициентов, используемых для вычисления вероят
ностей посещения пешеходом точек с задаННЬLJни координатами
i'
Число Координаты точек
шаi!О8, -11 11 21 31 41 51
N 51 41 -31 -21 О
1 q р

356
i
,
Щ__ !.:СЛУ'!../.ь.!.f!.л-r.._/и-.fl
Число Координаты точек
шаi!О8. -51 41 -31 -21 -11 О 11 21 31 41 51
N
2 q2 pq р2
3 q3 pq2 2 3
pq Р
4 q4 Р q3 v2a2 p3q р4
5 q5 pq4 p2q3 p3q2 p4q р5
Задача 12.2
Изобразите zрафически возможные блуждания пешехода при N=5. 6.
Найдите значения числа посещений пешеходом соответствующих тo
чек и сравните их с результатами, nолучаeJI1ыми по формулам (12,17),
(12.18).
Задача 12.3
Пользуясь соотношениями (12,17), (12.18), составьте npozpaммy для
перебора возможных блужданий при заданных значениях N Вычислите
точные значения PN(x), (XN).(!ll).
Задача 12.4
В одномерном случае оказывается возможным с помощью методов
теории вероятностей получить выражение для функции Р N(X) [1):
N! (+f) (f)
Р (х) Р q (12.19)
N = (Щ  )!(  )1 '
zде ( N +1'). (N ) число шаzов влево и вправо соответственно,
Используя формулу (12.19), проверьте полученные вами результаты в
задаче 12.3.
В методе МонтеКарло в отличие от метода полноrо перебора всех N
шarовых блужданий про водится rенерация достаточно большоrо количест
ва реализаций (ансамбля реализаций) (NТrial  число реализаций в ансамб
ле) с искомым законом распределения, При этом длина отдельных реализа-
ций NStep должна быть такой, чтобы обеспечить принадлежность каждой
реализации выбранных блужданий множеству, содержащему все допусти
мые блуждания, (Обычно длина реализации варьируется от 100 до I 000 ша
357


(' I
l'
1
: 
! 11
ill.'I.'
11,
1 ji:
,1 !
,С
i:
l
. '
ОtlI?п:ер'I'.:'!:!!.i!...:.р::.с:'!!!е.rJ!.ll!..llч-.е..:КРОУ.е..с:..?в'!.:.."!.е...АJ:!.!!.........ш... ... ..... .
ш.шшJ:.С::':J'.ч-.С:Й!Iе....?Л-У...,./lI,I!!
[ов.) Затем из каждой реализации выбираются значения смещения пешехода
на последнем шаrе, Это позволяет сформировать выборку длиной NTrial,
статистические свойства которой оказываются близкими к свойствам по
следовательности, получаемой методом прямоrо перебора.
Для реализации описанноrо выше вычислительноrо алrоритма на первом
этапе следует создать файл Walkm, содержащий описание функции, реали
зующей метод MOHTe Карло.
% листинr файла Wa!k,m
function z = Walk(NStep,NTrial,p)
% функция, реализующая метод МонтеКарло
% NStep  длина единичной реализации (число шаrов пешехода)
% NTria!  длина случайной последовательности, возвращаемой
% функцией Wa!k
% р  вероятность перехода вправо
for i=2:NTrial
х=О;
for j=l:NStep
if p>=rand(l)
x=x+l;
else
x=x-l;
end;
end;
X(i)=x;
end;
z=X;
Далее необходимо выполнить следующую последовательность команд:
» NStep=lOOO; % длина единичной реализации
» NTrial=lOOO; % число испытаний
» р=О.5; % вероятность перехода вправо
» M=Walk(NStep,NTrial,p);
% визуализация случайной последовательности
» i=l:NTrial;
» figure(l);plot(i,M,'k')
% вычисление и визуализация rистоrpаммы случайной последовательности
» Xmin=min(M);
» Хmах=тах(М);
» Ni=50; % число интервалов rистоrpаммы
» k=l:Ni;
»dx=(Xmax-Хmiп)/(Ni-l); % длина интервала rИСТОlраммы
» х(k)=Хmiп+dх*(k-l);
» s=hist(M,x);
» figure(2);bar(x,s); colormap white
Результаты выполнения данной последовательности команд представле
ны на рис. 12.5, 12.6.
100 ;. 'T'  '.T' T"r . ......,
Рис, 12,5, Случайная
последовательность,
возвращенная функцией
Walk
...
100 200
.........L.. "......L...... .................. I
400 500 600 700 800 900 1000
6Oi
i
50
I
1
<Ос
I
ЗО
i
20
i
!
10
, '
! I
I i
1
i
Рис. 12,6, ТистОi!раJlша
вычисленная для случайной
последовательности,
представленной на рис, 12,5
i
о'
.100
100
Анализ rистоrpаммы, представленной на рис, 12,6, позволяет высказать
rипотезу о том, что значения случайной последовательности распределены
по нормальному закону,
для проверки данной rипотезы будем использовать следующий aлrоритм:,
1, Вычислить среднее отклонение пешехода от начальной точки (XN) ,
358
359

/'1 I 
1
!!..?Ьl!.."!.ер!!..?:"!!!е::.I!.I!!!!!.'!.!..и-:...1!и.!.!!:.'!..'!!!..f!'j:с..с.f!.!!'5...ете !!..!-!!. ....   .. 
11
!
2. Вычислить среднеквадратичное отклонение пешехода от начальной
точки (Llx1).
3. Вычислить теоретические частоты попадания значений случайной по
следовательности в заданные интервалы в предположении о нормальном
законе распределения членов случайной последовательности:
Х,,+,
Freqkl= J NTria['пorтpdf(x,XO,o}ix;
Х"
(пorтpdf(x,XO,cт)= e(XXO)'/2и').
27rСТ
4. Вычислить критерий xквaдpaT для случайной последовательности
Х =  (Yi=!eqj )= .
;=0 Freqj
5. Вычислить теоретическое значение критерия XKBaдpaT
qchisq(O.995, rows(Y) 1  з).
6. Сравнить полученные критерии XKBaдpaT.
Описанный алrоритм реализуется следующей последовательностью KO
манд:
» NStep=1000; % длина единичной реализации
»NTrial=1000; % число испытаний
» р=0.5; % вероятность перехода вправо
» M=Walk(NStep,NTrial,p);
% вычисление и визуализация rистоrpаммы случайной последовательности
» Хmiп=miп(М);
» Xmax=max(M);
» Ni=50; % число интервалов rистоrpаммы
» k=I:Ni;
»dx={Xmax-Xmiп)/(Ni-l); % длина интервала rистоrpаммы
» х(k)=Хmiп+dx*(k-l);
» s=hist(M,x);
» ХО=mеап(М);
» sigma=std(M);
% вычисление теоретических частот
» Nf=20; % число узлов сетки для вычисления интеrpала
» k=I:Nf;
'(
360
. J:...J'.'!.g!!!>!.:'lIJ.'.:жд!!.,':!3
»for i=I:Ni-l
Xl=x(i);X2=x(i+ 1);
dx=(X2-Хl)/(Nf-l);
xl(k)=Xl +dx*(k-l);
yl=NTrial*normpdf(xl,XO,sigma);
Freq (i)=trapz(x l,у 1);
end;
% вычисление экспериментальноrо критерия XKBaдpaT
» Xi=O;
»for i=I:Ni-l
Xi=Xi+(s(i)-Frеq(i». Л2IFrеq(i);
end;
»Xi
Xi=
68.3450
% вычисление теоретическоrо критерия XKBaдpaT
» сhi2iпv(0.995,Ni-I-3)
ans=
74.4365
Сравнение критерия xквaдpaT (paBHoI'o 68.3450), полученноrо дЛЯ СЛУ
чайной последовательности, представленной на рис. 12.6, и rpаничноrо зна
чения критерия xквaдpaT (paBHoro 74.4365), определенноrо теоретически,
позволяет сделать вывод об отсутствии оснований для опровержения rипо
тезы о нормальном законе распределения рассматриваемой последователь
ности случайных чисел,
Отметим, что для случайной последовательности данных можно исполь
зовать не только, в известной мере, интеrpальную характеристику  rисто
rpaMMY, но и вычислять точные значения функции распределения, Для это
ro, как очевидно, следует подсчитать количество посещений пешеходом
К:lЖДОЙ точки отрезка [х min, х тах] и отнести их к ПОЛНОМУ ЧИСЛУ шаroв,
сделанных пешеходом, Для вычисления функции распределения необходи
мо создать файл DistrR, содержащий функцию, возвращающую значения
вероятности нахождения пешехода в данной точке,
% листинr файла DistrR,m
function z = DistrR(M)
% функция, возвращающая вероятность нахождения пешехода
% в данной точке
М l=шiп(М);
361


.1!""!/т-е[JlIО:..l>t...ef}':.'.1??(lI'':.'.:.1!..з.':.'..:.:':.'.Х:.прое:cв !!.(l.:'!l.:.1:TI:..!:l!........ ... ........ ., ,Ш...
I ,
III,! !.
I1
1:
'ii
М2=тах(М);
k=Ml;
K=l;
while k<=M2
0=0;
for i=l:length(M)
if k==M(i)
п=п+l;
end;
end;
S(K,l)=k;
S(К,2)=nЛепgth(М);
K=K+l;
k=k+l;
end;
z=S;
Далее необходимо выполнить следующую последовательность команд:
» Ml=DistrR(M);
» bar(Ml(:,1),Ml(:,2),Oo2);
»colormap gray
Результат выполнения данной последовательности команд пред ставлен
на рис. 12.7.
0.035
0.03
0.025
0.02
0.015
001
0005
шl1
о
.100
80 w60 .40
2O
20
40
60
80
100
Рис 12,7. Вероятность нахождения пеUlехода 6 заданных точках отрезка
362
............
... ...!l.:С;:::!'..с:..Iz.:'.?Jl!..аlz.':.'.я-
Задача 12.5
Сравните значения (XN)' (tu), получае/l'lые методом МонтеКарло с
точными значениями, вычисляемыми по формулам (J 2.13), (12,1 4), Oцe
ните точность определения (XN). (tu) методом МонтеКарло, Ис
следуйте, как зависят поzрешности (х N ), (tu) от числа шаzов pea
лизации NStep и размера ансамбля реализаций NTria/, Изобразите дaH
ные зависимости zрафически, Попробуйте подобрать функции,
аппроксимирующие зависимости (XN)' (tu),
Задача 12.6
Дополните описанный выше документ пакета MATLAB блоком, позво
ляющим вычислять среднее значение смещения пешехода и ezo cpeдHe
квадратическое отклонение в соответствии с (12,1)--{12,З) для случай
ной последовательности, zенерируемой методом МонтеКарло, Полу
чите численные значения этих величин, Сравните полученные значения
со значениями, найденными в описанном выше документе,
Задача 12.7
ВО MH02UX прuложенuяx моделей случайных блужданий величина (tu) при
достаточно больших N удовлетворяет степенному закону, например,
(tu1)  N2v. (12.20)
(Соотношение (J 2,20) является примером асимптотическоzо масштаб
HOZO закона.) Для одномерных случайных блужданий, как видно из
(12.14), v=1/2.
Постройте в лоzaрифмическом масштабе zрафик зависимости (tu)
от N и оцените, используя метод нашtеньших квадратов, показатель
степени v, определенный в формуле (12.20). Оцените поzрешность най
денноzо значения v, Исследуйте, как зависит поzрешность значения v
от числа шаzов реализации NStep и размера ансамбля реализаций NTria/,
Изобразите данную зависимость zрафически, Попробуйте подобрать
функцию аппроксимирующую данную зависимость,
Задача 12.8
Еще одной важной величиной, характеризующей случайные блуждания,
является (S N)  среднее число различных узлов решетки, посещае.II'IЫХ
363

{" !
1" '
1
.1!0:'!..!'?'.'!...:P..!?:.!'!.'?.<l..:::''!E.'?..C!.'!!'::1!l!.!'!.'!.:_'!l!. пl''?./!.:С:''ОI!.I!..!!.'!.'!..:'.'!...:л.-!...1.Т!:!!.I!......
во время Nша20вО20 блуждания. Вычислите методОАl МонтеКарло
(8 N) и определите асимптотическую зависимость (8 N) от N.
Задача 12.9
1. Рассютрите случай р = 0.7, N8tep == 1000, NTrial = 1000. Вычислите
(XN), (t:u:), Как можно интерпретировать (XN) в данно.м случае?
2. Решите задачи 12,512, 7 для случая р = 0.7.
12.3. Метод случайных блужданий на плоскости
;'1
i
: !
Рассмотрим обобщения метода одномерных случайных блужданий для
систем большей размерности. Их обсуждение совершенно естественно Ha
чать с рассмотрения случайных блужданий в двумерной плоскости. Стати
ческий характер задачи случайноrо блуждания означает, что следует pac
сматривать либо большое количество случайных блужданий одноrо пеше
хода, либо большое число пешеходов, движущихся одновременно. Далее
нами используется второй подход.
Рассмотрим rpуппу пешеходов, расположенных в момент времени t = О,
случайным образом в Kpyre единичноrо радиуса с центром в начале коорди
нат. Будем считать, что на каждом шarе по времени каждый пешеход дви
жется случайным образом равно вероятно в одном из четырех направлений:
в положительном направлении оси оХ, в отрицательном направлении оси
оХ, в положительном направлении оси оУ, в отрицательном направлении
оси оУ. При этом направление движения выбирается в соответствии с MeTO
дом МонтеКарло в зависимости от величины случайноrо числа и заданноrо
пороrовоrо значения.
Для моделирования двумерных случайных блужданий необходимо соз
дать два файла: файл Init2.m, содержащий описание функции, возвращаю
щей начальную конфиrypацию системы, и файл Move.m, содержащий опи
сание функции, возвращающей MrHoBeHHbIe значения координат пешеходов,
% листинr файла Init2.m
funetion z = Init2(NPartiele,R)
% функция, возвращающая начальную конфиrypацию системы
% NPartic1e  число пешеходов
% R  радиусвектор максимальноrо смещения
о/с от начала координат
for i=l:NPartiele
RO=(2*rand(1 )-l)*R;
1"
364
Ir
...............
.... .._ ... ?.С;:::')1.Ч'!.!..',:!:"J/!'!.lIия
teta=2*pi*rand(1);
ХУ (i,I)=RO*eos( teta);
XY(i,2)=RO*sin(teta);
end;
z=XY;
% листинr файла Моуе.m
funetion z = Move(A,NPartiele,NStep)
% функция, возвращающая MrHoBeHHbIe значения координат пешеходов
% А  массив, возвращенный функцией Init
% NParticle  число пешеходов
% NStep  число шаrов МонтеКарло
for j=I:NPartiele
ХУ(I,I)=Ау,I);
ХУ (1,2)=Ау,2);
for i=I:NStep-l
prob=rand(I);
if prob<=O.25
XY(i+ 1,1)=XY(i,I)+ 1;
XY(i+ 1,2)=XY(i,I);
end;
if (prob>O.25)&(prob<=O.5)
XY(i+l,I)=XY(i,I)-I;
XY(i+l,2)=XY(i,I);
end;
if (prob>O.5)&(prob<=O. 7 5)
XY(i+l,I)=XY(i,I);
XY(i+l,2)=XY(i,1)-I;
end;
if prob>O.75
XY(i+l,l)=XY(i,l);
XY(i+l,2)=XY(i,1)+I;
end;
end;
if j==l
Z=XY;
else
Z=eat(3,Z,XY);
365

; 1:,1,
I11
j
',1
!
Ком/! ыol::р'I!еe l>!.е:uр()в'!.1111:4JU3lJ'!.'!.'!.J(lJХ/!Р..lf.:ССО.в.в,./!аJ(е111е"!..1 TL..1!.
t
end;
end;
z=z;
Далее необходимо выполнить следующую последовательность команд:
» NParticle=2000; % число пешеходов
»NStep=400; % число шаrов МонтеКарло
» R=I; % радиусвектор максимальноrо смещения от начала координат
» A=Init2(NParticle,R); % вычисление начальной КОНфШ}lpации
% визуализация начальной конфиryрации системы
» Np=1000;
» i=I:Np;
» dрhi=2*рil(NрI);рhi(i)=dрhi*(i-l);
» x=cos(phi);y=sin(phi);
» figure(I);plot(x,y,'k');
» hold оп
» plot(A(:,I),A(:,2),'ok', 'Markersize' ,0.1);
» hold off
% вычисление координат каждоrо пешехода в заданное время
» Am=Move(A,NParticle,NStep);
% визуализация MrнoBeHHЫx значений координат
% и радиусоввекторов первorо и cOToro пешеходов
» figure(2);plot(i,Am( :,I,I),'k' ,i,Am(: ,1,100),' :k');
» figurе(З);рlоt(i,Аm( :,2,1), 'k' ,i,Am( :,2,100),' :k');
» R=(Am(:,I,I). Л2+Аm(:,2,1). Л2). Л05;
» RI00=(Am(:,1,100). Л2+Аm(:,2,100). Л2). ЛО.5;
» figure(4);plot(i,R,'k',i,RI00,':k');
% вычисление усредненных по ансамблю пешеходов значений координат
» Сос i=I:NStep
Сос j=I:NParticle
X(j)=Am(i,IJ);
Y(j)=Am(i,2J);
end;
x(i)=mean(X) ;
y(i)=mean(Y);
end;
% визуализация MrHoBeHHbIx значений координат и радиусавектора,
% усредненных по ансамблю пешеходов
I
'"
;;,.
'1'
'1
, ,
, I
, I
i
i I
1
i 1
i!,
366
'
"
.._.. ..,___._.....l:Z'!..,-,:..лz.?}С!!!lJ!!_
» i=I:NStep;figure(5);plot(i,x,'k')
» figure(6);plot(i,y,'k')
» Rm=(х.Л2+у.Л2).ЛО.5;
» figure(7);plot(i,Rm,'k');
% вычисление и визуализация квадратов координат и квадрата
% радиусавектора, усредненных по ансамблю пешеходов
»Сос i=I:NStep
Сос j=I:NParticle
X(j)=Am(i,IJ). л 2;
У (j)=Am(i,2J). Л2;
end;
xm(i)=mean(X);
ym(i)=mean(Y);
end;
% вычисление и визуализация мrнoBeHHЫX значений
% среднеквадратичноrо отклонения усредненной траектории
» i=1:NStep;figure(8);plot(i,xm,'k')
» figure(9);plot(i,ym,'k')
» R2=xm+ym-х.Л2-у.Л2;
» i=1:NStep;figure(10);plot(i,R2,'k')
Результаты выполнения описанной
ставлены на рис. 12.8 12.17.
'r-'T
0.8: /
0.8r
O.. I
02r
:\
::: ,
":1 .0:8 .0:6 ;
последовательности команд пред
............... ' .....,.
.......................-...........,

'\
\
\
/
/
/
/
---/
/
/
./
Рис, 12,8. Начальное распределение пешеходов
 I
02 04 06 О..
367

 I
1I
l'
,11
l'
:(
\
! ,1
Ком,!!:!!!!!!!!рное моделирование физическ-их процессов в пакете МА тив
20
wЛ\ r
N I v\j
н1 У
fJ V'
V .
< ,- .
. .
, l'
15
!:
1.
I
'101
о
,
..
,
100
,
150
,
200

,
300
,..
Рис. 12,10. Зависимость
MZHoeeHHЫX значений у-й
координаты пepeozo и comozo
пешеходов от номера шazа
Монте-Карло
i,
I
...
1:,
I\Pv
h ;м-. r{
(, ,л j \;/J  I
Ir \v \,1 W
I 1
0.05 f"
· i
О..
.З$
0.3
О.,.
02
0.15
.1
-O05
О
1
.....L.    .
 100 1     
368
I
...
Рис. 12.9. Зависимость
JlfZHOBeHHЫX значений х-й
координаты пepeozo и comozo
пешеходов от номера шazа
МонтеКарло
,
..
,
100
,..
,
150
.
200
,
250
300
Рис. 12,11. Зависимость
MZHoeeHHЫX значений paдиycoв
векторов первой и сотой
частиц от номера шаzа
МонтеКарло
...
0.45 ',..O''  -т"""""",,,,"'['.''T . \
 tJ\ )
0,4 . ,!lll i J 1
..35 '1 ';' if
'\ N \!
'\ ! \ l' )
!/.N 1.
!IL\, ,\ ' :1
{r'i1;'\\ I '
1 ,1 I
\ ./i ""\.J\i
\! 1I
t
1'"
............................... .
..3
....
,
J 1\ \ (
( \J\ I / ,n
; \1  1 '
.1 '1 J
'\1
о.: ('
..2
0.15
..омо '-tOO
.._
150
Рис. 12.13. Зависимость
MZHoeeHHblX значений yй
координаты, полученной
усреднением по ансамблю
пешеходов, от номера шаzа
МонтеКарло
07, 
i
,
o.sL
i
0.5:---
0.4;
0.3 
r'\1. ,./1. \ !r
, \ {1  f.'i \
r i\ .I!i "
\'\ I У\ l'  \ '!/\! ,.
, 1 "1 1 , 1"'1,1'1,
! у >J \1 \ ( : 
i 
02,
l'
01 Ij
A.....1) ,
Q  ....L.._ ._._ .
о '! 10С
150

. . _..........I.   
200 250 300
.
350
1
1
HJ
400
ш ,. .'ш шшJ!.:шЛ}!'Чl!.!!'!l:нсдl!!!':1!,
Рис. 12.12, Зависимость
MZHoeeHHblX значений ХЙ
координаты, полученной
усреднением по ансамблю
пешеходов, от номера шаzа
Монте-Карло
0.45 !
о · [ #\ J ,I!u\t 
озs[  , I  \II' \1'
.t !  Ij' (Ii  I
0.,5\ . 11i \ I! \i
01 r /I I! III
005iJ
I! '
o!I,1
оsL.. ,....,
. о 50
 
100 150
1\ fI I
11 1"1'" \ '!
! \ t,  \! ! i
) I l /V l
i\ , ! \.
jy\l; I
{ 
  -(!- 2-'
'00
3':.0
369
........L...L.... .  .
200 250 300 350
1
J
400
 1
1
I
I
i
1
I
.'"
400
Рис. 12,14.3aeucШlocmb
JfZHOBeHHblX значений
paдиycaвeKтopa,
получеНН020 усреднением по
ансамблю пешеходов, от
номера ша?а МонmеКарло

; 1
il
I
l'
l!:}I1.пЬ:l1I.р':I_?.ео.е..Л-l1'р[J,аll!'.е..4:uзuческuх процессов в пакете MAТLAB
.  ............. .............. . .... ..ш ...... о.. .......ш ............................ ш
250
l'
, '
!( I
200'
150'
,00'
/
/
/'
./
50, ///
./
//
oL ш.
о 50
..........L .
100 150 200
Рис, 12.16, Зависимость
MZHoeeHHb/X значений
усредненноzо по ансамблю
пешеходов квадрата
смещения вдоль оси о У от
номера шаzа МонтеКарло
:f
350f
1
3001

1
:[
,,,,,1
1 I
! I 501
1
,L'
о "
I
I I
/"
./
100 150 200
250
.. ..
300 350 <400
2501
I
I
i
200f
I
,)
1
1
1
1
100f
I
1
501 ,//
,/
./-
./
о 
о 50 100
250
;ос
350
370
Рис, 12,15, Зависимость
]I1ZHoeeHHb/X значений
усредненноzо по ансамблю
пешеходов квадрата
с.}l1ещения вдоль оси оХ от
номера шаzа МонтеКарло
,/,
/,,.,//
j'
//
/
/
/
j'/
//
.--
,
'50
200

300
350
400
'00
Рис, 12,17, Зависимость
MZHoeeHHb/X значений
среднеквадратичною
отклонения усредненной
110 ансамблю пешеходов
траектории от номера шаzа
МонтеКарло
...............
. ..!!:(::J!.'!.:!':!.е.__,j)':>!:11и--fl
Анализ зависимости, представленной на рис, 12.17, показывает, что с Te
чением времени происходит линейное увеличение площади окружности,
внутри которой находятся все пешеходы, т, е,
/ А о2 \  А '
\ til'i /  '1,
(12,21)
rде А ::::: 1  коэффициент пропорциональности.
Из (12.21) видно, что среднеквадратичное смешение Rj == .J(M!) , мсня
ется с увеличением числа шarов по закону
II--?-- .v
\M;)=JA'I, (12.22)
rде для рассматриваемой двумерной модели v = 1/2 .
Задача 12.10
Создайте анимационный /\Лип, демонстрирующий в динамике процесс
увеличения площади, занимаемой пешеходами.
.Ш.......Ш......Ш...... ,,,,,,,,,,ш'шN. ...N'N.......N
Задача 12.11
Оцените, используя .метод наименьших квадратов, значение коэффици
ента А в (12,21), Определите пО2решность найдеННО20 значения А, иc
пользуя метод оценки п02решностей коэффициентов линейной pe2pec
сии, изложенный в [2, 2лава 8].
и.и'.ИИ''ИИ .и'.' ........и. ...'и..
Задача 12.12
Предположим, что каждый пешеход расположен случайным образом
внутри единичной окружности и имеет случайную начальную скорость,
направленную в одном из четырех возможных направлений. При этом
каждый пешеход в единицу времени совершает один ша2 в направлении,
совпадающе.м с направление.м начальной скорости, Проведите исследо
вание движения данной 2руппы пешеходов и постройте зависимости
(х;), (у;), (х;), (уп, (дхп, (!J.yп, (М?), i=O,l,...,N,CpaBHumepe
зультаты, полученные для .модели случайной скорости, с аналО2ичными
резулыпатами, полученными для модели случайною блуждания. Имеют
ся ли качественные различия в поведении рассматриваемых моделей?
Отметим, что процесс движения пешеходов подобен процессу движения
молекулы в разреженном rазе, Действительно, предположим, что молекула
между столкновениями с друrими молекулами пробеrает расстояние [, Если
допустить, что последовательные смещения молекулы между столкнове
ниями статистически независимы, то ее движение будет аналоrично pac
смотренному выше движению пешеходов, Так как движени: молекулы в
371

I , '1
' '
'I( "
! 1
l!..ОIIЬlоп-zеjJ/?:"l>!..?,д-.=-"р',о..f!'.,!:!!:rjJ?и-:.с..к."!:.Р.?:ссо!! к-.:п-z!:,!'!..А.!.J:!!1!.  '".
разреженном rcвe является диффузионным процессом, возникает возмож
ность установить связь случайноrо процесса с диффузией, Зависимость
среднеквадратическоrо смещения (AR(t)2) диффундирующей частицы от
времени описывается известным Соотношением Эйнштейна
(AR(t)2)=2dDt, (12.23)
; ,
l'
11
I
:I
rде d  рсвмерность пространства, D  коэффициент самодиффузии молеку
лы. Если отождествить длину свободноrо пробеrа [ с длинной шаrа пейlехо
да и принять время между столкновениями равным т, то ; = t/T . Следова
тельно, формулу (12.23) можно переписать в виде
(AR(t)2) = 2dD т i. (12,24)
Сравнивая (12.21), (12.24) и учитывая, что в рассматриваемом случае d =
2, т = 1, [=], находим выражение для коэффициента диффузии пешехода в
двумерном случае
А 1
D=44' (12.25)
в общем случае для оценки коэффициента диффузии следует использо
вать формулу (12.14), которая с учетом сделанных выше предположений,
принимает вид
:,'
(Ах2) = 4Pq[2(;).
Сравнивая (12.26) с (12.23), получаем
2pq[2
D = d-; . (12.27)
КОЭффициент диффузии D в двумерном случае (при р = q = 1/2) равен
[2
D= ,
4т
Сравнение (12.25) и (12.28) показывает, что значения коэффициентов
самодиффузии D, получаемых в численных экспериментах с моделями, в
которых ['# 1, т '# 1 , Moryт быть вычислены умножением значения COOTBeт
ствующеrо коэффициента, найденноrо для Модели, в которой [= 1, т = 1 , на
коэффициент [2/ Т ,
(12.26)
(12.28)
 1
1,
1
: 
I!
372

1 :'лУЧ,!!!л.!..dа!'Jl
Задача 12.13
Перечислите все случайные блуждания на квадратной решетке с N = 4
, 2 )
И получите точные значения для (XN )'(YN) И \ARN . Сравните резуль
таты аналитических расчетов с результатами, полученными .методо,и
МонтеКарло.
Отметим, что рассмотренная выше
квадратная решетка, в которой число бли
жайших соседей равно четырем, не являет
ся единственно возможной формой решет
ки. На практике для моделирования ДBY
мерных плоских тел при меняется тpe
уrольная решетка (рис. 12.18), период
которой далее, если это не oroBopeHo oco
бо, будем считать равным единице.
.f\- ·
.\L
./\.
Рис, 12,18, Возможные
направления смещения пеиlехода
при блуждании
по треуzольной решетке
Задача 12.14
Исследуйте особенности движения 2руппы пешеходов, распределенных
в момент времени t = О случайным образом в КРУ2е едИНИЧНО20 радиуса,
на треУ20ЛЬНОЙ решетке, Проведите исследование движения данной
 f 2\ I 2\
2руппы пешеходов и построите зависимости (х;), (У;), \ Х; /' \}'; /,
(Ах;), (Ау;), (м;), i = 0,1,..., N. Сравните результаты, полученные
для треУ20ЛЬНОЙ решетки, с аналО2ИЧНЫМИ результатами, получеННЬLwи
для случаЙНО20 блуждания на квадратной решетки. Имеются ли каче
ственные различия в поведении рассматриваеJНЫХ моделей? По какому
закону меняется (м;) и чему равняется v в (12.21)? Зависит ли от
симметрии решетки коэффициент самодиффузии D?
Задача 12.15
Рассмотрите падение дождевой капли, начинающей движение из точки
с координатами (о, h), под действием случайных порывов ветра. Ис
пользуйте модель случайных блужданий на квадратной решетке, счи
тая, что вероятность Pd ша2а вниз больше вероятности Ри ша2а
вверх, а вероятность смещения капли влево равна P, вправо  p.
Так как Р,/ > Ри, то можно ожидать, что после некотОРО20 числа uш
20в капля достИ2нет земной поверхности. Выберите вероятности пepe
ходов равными Ра = 0,5, Ри = О,), P. = P = 0.2. Проведuте модели
373

К?М-I.l.ь_,отеР..'.'.?е.I?:'Л- fJ?'!.'I':!е..1)U!!I,!:.=К-I!fJ(JЦ:',СС?. .'!.I!.к-е.'!l.:..!.!...1: !!:.:!:.!!.. _
"
i "
r '
рование л,tетодО,11 Монте-Карло, Постройте траекторию движения ка-
пли, зависимости (х;), (у;), (хп. (уп, (l1xп, (мп, 2де () обозна-
чают усреднение по ансамблю реализаций, и определите среднее время
r, за которое капля достИ2нет поверхности земли, и функциональную
зависимость r = r(!z) , Как зависит (11x?) от h и <? Чему равняется
скорость падения капли? (Указание, Для моделирования движения пе-
шехода в 20рuзонтальном направлении используйте случайные числа с
равномеРНЫЛl заКОНОЛl распределения на отрезке [1,1].)
..,.">,.'H'''M'''M.." "''MM' MM.M'M"',,,
l'
1"
1 :!
11
Ij
,11
Задача 12.16
Рассмотрите двулtерную модель случайных блужданий, в которой
в единицу времени пешеход совершает ша2 единичной длины в случайном
направлении, Создайте, используя документ, описанный в разделе 12,2,
nр02рамму для вычисления методом Монте-Карло вероятности
PN(r)dr нахождения пешехода в интервале от r до r + dr, 2де r  рас-
стояние, отсчитываеАюе от начала координат, N  число ша20в, со-
вершаемых пешеходом,
1. Покажuте, что для достаточно больших значений N функции распреде-
ления пешеходов PN(X) , PN(y) вдоль осей оХ, оУ, соответственно, ап-
проксимируются нормальны,и законом распределения. Постройте зави-
сююсти (XN)' (x), (11x), (YN), (y), (!J.y). Предположив, что
(11x), (!J.Y)  aN2\' (12.29)
оцените, используя htетод наименьших квадратов, значения коэффици-
ента а и показателя степени v, входящих в (12,29),
Сравните значение v для одномерных и двумерных случайных блу.жданий,
2. Постройте зависимости (RN), (R) (M), Можно ли аппроксимиро-
вать зависимость (M) зависимостью вида (12,29)?
З. Постройте функцию, описывающую вероятность PN(r)dr нахождения
пешехода в интервале от r до r + dr , 2де r  расстояние, отсчитывае-
мое от начала координаm, N  число ша20в, совершаeJ.1ЫХ пешеходом,
Используя критерий х-квадрат, проверьте 2ипотезу о возможности ап-
проксимации функции PN (r) 2ауссовой кривой,
4. Перейдите к полярным координата)lt r = fx2 + у2 , rp = arctg(y/ х) и nо-
кажите, что распределение пешеходов по У2ЛУ <р близко к paeHOMepHO)lty.
I I
! 1
374
..............
12:?lучаЙ1lЫ' 7!:ж:.д..а1l!IЯ
Результаты исследования модели двумерных блужданий, использован,
ной в задаче 12.16, показывают, что функции распределения верОЯlностеи
пешеходов вдоль соответствующих координатных осей MOryT быть аппрок-
симированы нормальным законом распределения. Типичные результаты,
полученные при решении задачи 12.16, представлены на рис. 1.2.19 12:24,
(Здесь нами использовалась выборка, сформированая по NTпa! (NTпal=
=1000) независимым случайным реализациям длинои NStep (NStep=40O).!
В то же время функция распределения радиусов-векторов точек случаинои
последовательности, как видно из рис. 12.24 и как следует из результатов
задачи 12.16. часть 3, не описывается нормальным законом распределения.
200
100
хи) о
100
200 О
200
400
600
800
1000
Рис, 12,] 9. Xe координаты точек двумерной случайной последовательности
200
100
Рис. ]2,20, У-е координаты точек двумерной случайной последовательности
200
150
R(i) 100
50
j
Р 12 21 Ради,vсывекторы точек двумерноЙ случаЙной последовательности
IIС. . .
375

ii''!.l(JrIJеР.!()е..:,!!!!!..(J'!!!'!4!!!.!..':'..С'!::'!!!.?'!.(!й-!..!.1!!='!.'!м...!!:..1:!!.._...ш
40
зо
"Ir
,;' .11
 ...1.".'1" .'. ,
. 1'''' ,!
1:,"'; ,; .1
.'I,..' .... ,.! :.. '1..... ..1. '.' ...'1
I" "! I I '1' I " ,
,мJJfii;.;",I/' f
.. .. ,---,---L
20
10
150
50 О 50 100 150 200
Рис, 12.22, Теоретическая (СfUlOшная) и экспериментальная (столбчатая
диаzрамма) функции распределения х.х координат случайной последовательности
40
ЗО
,.
,
1I '1
'1 20
i
10
о
150 50 100 150
Рис. 12.23. Теоретическая (сплошная) и экспериментальная (столбчатая
диаzрамма) функции распределения Yx координат случайной последовательности
40
20
ul.d..... ,
50 100 150 200
Рис, 12,24, Экспериментальная функция распределения paдиycoввeК1пopoв точек
случайной последовательности
Для объяснения полученноrо результата найдем функцию распределе
ния вероятности двумерных случайных блужданий. Так как движение пе
шехода вдоль осей оХ и о У независимы, вероятность Р(х, у )dxdy обнару
жить пешехода в окрестности точки с координатами (х, у) равна произве
дению функций, описывающих функции распределения вероятностей
координат вдоль соответствующих координатных осей:
376
...............
....................'... """'"'" .
.... ._... шl:.1!Х:'!!'!!Л.I!'!!..
Р(х,у)= Px(x).Py(y)dxdy,
(12.30)
rде
PAx)='e(X(X))'/2O': ,
&ах
( )  _ (y(y))' /20':
Ру у   е ,
, "2,,ау
(12.31)
( 12.32)
Ах, Ау  нормировочные постоянные.
Подставляя (12.31), (12.32) в (12.30) и считая, что ах = ау = а получим
Р(х, у) = .3e(X' +.1" У20" dxdy, (12.33)
2"а2
rдеА  нормировочный коэффициент, определяемый из условия
Н P(x,y)dxdy= N,
(12.34)
s
здесь s  область, занятая пешеходами, N  число пешеходов.
Переходя в (12.33) к полярным координатам
х = rcosrp ,
у = rsinrp,
получаем
) А r' /20"
P(r,rp = e rdrdrp.
2"а
Orметим, что выражение, стоящее в правой части (12.35), не зависит от
переменной rp, что свидетельствует о равномерности распределения пеше
ходов по yrлу.
Проинтеrpировав (12.35) по уrлу, изменяющемуся от О ДО 2", получаем
вероятность нахождения частицы в интервале [r, r + dr]:
P(r) = 4er'/2O" rdr.
а
Значение нормировочной постоянной А найдем из условия (12.34)
R
J А .r'/20" d  N
-----те r r  ,
оа
( 12.35)
(12.36)
(12.37)
rде R  радиус окружности, занимаемой пешеходами,
377

f J
K(JnbIoтep!"'.(Je моделроа.'I ф"и:'/1ч-:..к:nроцессов в nакете М1.Т:4!!....__шш.
Вычислив в (12,37) интеrpал, получаем выражение для нормировочноrо
коэффициента А:
 i
N
А = .шшш, (12.38)
1 ешR2/2а2
Подставляя (12,38) в (12.36), окончательно найдем
P(r) = ..!'i.er'/2a' dr (12,39)
ст2 1  е шR' /2а' '
Результат вычисления вероятности по формуле (12.39) для случайной
последовательности, MrHoBeHHbIe значения радиусавектора которой пред
ставлены на рис, 12.21, показаны на рис, 12,25.
40
60 80 100 120 140 160 180
Рис, 12,25. Теоретическая (сплошная) и эксперu..wентальная (столбчатая
диаzрамма) функции распределения paдиycoввeKтopoв точек случайной
последовательности
.
.
Задача 12.17
Дополните созданный вами документ для решения задачи 12,16, фра2
ментом, позволяющим вычислять теоретическую функцию распределе
ния в соответствии с (12,39).
Для описания рассеяния частицы на неподвижных рассеивающих цeH
трах с анизотропным сечением рассеивания используют модель, в которой
СЧИТilется, что пешеход на Nшм шаrе с вероятностью р смещается в направ
лении перехода на N 1 шarе и с вероятностью (1  р) в противоположном
направлении (<<персистентное» случайное блуждание). Алrоритм моделиро
вания «персистентноrо» случайноrо блуждания методом МонтеКарло pea
лизуется следующей последовательностью действий.
1. Задать длину случайной последовательности (число шаrов пешехода)
NStep и размер ансамбля случайных реализаций NTrial.
2, Задать начальную координату пешехода и направление первоrо шarа,
i
I
,
11
,
:
378

.... .ш...J2 :шс;:,:'Q'ча'.'.ь'.: блуждания
3. Выбрать пороrовое значение вероятности перехода р.
4. Сrенерировать случайное число q с равномерным законом распредеш
ления на интервале [0,1],
5. Если q  р, осуществить переход в направлении, совпадающем с наш
правлением перехода на предыдущем шаrе.
6. Если q < р, осуществить переход в направлении, противоположном
направлению перехода на предыдущем шаrе,
7. После выполнения заданноrо числа шаrов NStep вернуть пешехода в
начальную, иначе повторять пп. 46, пока число шаrов меньше NStep.
8, Сrенерировать новую случайную последовательность, выполняя пп. 57.
9. Если число случайных последовательностей меньше NTrial, повторить
пп. 58,
Для моделирования персистентных случайных блужданий в пarете
МА TLAB в соответствии с описанным алrоритмом необходимо создать
файл Walk2.m, содержащий описание функции, возвращающей MrнoBeHHыe
значения координат пешеходов на каждом шаrе МонтешКарло.
% листинr файла Walk2,m
function z = Walk2(NStep,NTrial,p,xO,dx)
% функция, возвращающая MrHOBeHHbIe значения координат пешеходов
% NStep  число шаrов МонтешКарло
% NTrial  число пешеходов
% р  пороrовое значение вероятности перехода
% хО  координата пешехода в момент времени t=O
% dx  направление смещения пешехода на первом шаrе
for i=l:NTrial
х=хО;
d=dx;
K=l;
for j=l:NStep
if p<rand(l)
d=-d;
end;
x=x+d;
Z(K)=x;
K=K+l;
end;
if i==l
X=Z';
379

f
!..й.-,,!11Ь!?.I.:р"I:о.е:й.:l!.IIfJ.й..l!..lluе.rp!!3.че.СКUХ:ll?й.ll':'.с?в в!l'!.к-.::_ МА ТLAB
else
X=cat(2,X,Z')j
endj
endj
z=Xj
Далее необходимо выполнить следующую последовательность команд:
% вычисление MrHOBeHHbIx значений среднеrо по ансамблю
% пешеходов смещения
» for i=l:NStep
for j=l:NTrial
X(j)=M(iJ)j
endj
x(i)=mean(X)j
end;
% вычисление мrнoBeHHЫx значений среднеI'О по ансамблю пешеходов
% квадрата смещения
» for i=l:NStep
for j=l:NTrial
X2(j)=M(iJ). Л2j
endj
x2(i)=mean(X2)j
endj
% вычисление и визуализация мrиовенных значений
% среднеквадратичноrо отклонения пешехода от начальной точки
% cpeДHeHHЫX по ансамблю реализаций (рис. 12.26) ,
» 1=1:NStepjXs(i)=x2(i)-х(i).Л2j
» plot(i,Xs,'k')

Задача 12.18 - ---
Используя метод наименьших квадратов, оцените по зависимости
(Ах;), j =O,1,...,NStep1, значение v в (12,20) и значение коэффициен-
та самодиффузии D.
'Зд;"12:19    .
PaCMтpитe,---- используя описанный выше документ, два случая:
р  0.5 u р  0.75 , Используя метод наименьших квадратов, оцените
по зависимости (АХ 2 '/' J.  о N 1
, J'  ,..  значение v в (12,20) и значение коэф-
фициента самодиффузuи D. Дайте физическое объяснение, почеwу зна-
380
. ..._. .l_. С':1уча.,U!1 ,!:еf!,1}':JI<.а..".!я
чения коэффициента диффузии зависят от пОР020вО20 значения веро-
ятности перехода р, Постройте зависимость коэффициента caмo
диффузии от порО20вО20 значения вероятности р,
::I........... .........T.........
I
800f
8001
4J
200ll / //
/
о :::"----'-----'-.J 
О    а      
r'f'
,J
/
/"
/1'
/
/,,,,/'
///
,-
/
/
,//-
Рис, 12,26. Зависимость М2Новенных значений среднеквадратиЧНО20 отклонения
пешехода, усреднеННО20 по ансамбто реализаций, от номера иЮ2а Монте-Карло
,_'''H"'''...
Задача 12.20
Постройте зависимость J(!.x;), j = 0,1,.,., NStep  1, Постройте 2pa
фик зависимости скорости движения пешехода от времени, Оцените
предельную скорость движения пешехода, Как зависит предельная CKO
рость движения пешехода от пОРО20в020 значения вероятности р?
Задача 12.21
Для описания особенностей процесса диффузии в хро.чатО2рафической
колонке используется следующая модель случайных блужданий: пешеход
может с вероятностью р остаться на месте или с вероятностью l----p
сместиться на один ша2. Модифицируйте функцию Walk2 так, чтобы
данная функция возвращала ансамбль случайных последовательностей,
С2енерироваllНЫХ по задают,,,,у правилу, Определите коэффициенты ca
модиффузии [) при различных значениях пОрО20вой вероятности р.
Отобразите зависиАtOсть D = D(p) 2рафически.
В физике твердоrо тела и конденсированных сред важную роль СЫf-Рали
модели случайноrо блуждания при напичии ловушек. Рассмотрим более
подробно одну из таких моделей, используемых для изучения особенностей
381
J

.I!.?-'!..'1ь.'?.п:.еl!!?"-,:!?,!р"9IJ1J..1J_'JКl..IЧ!.?.lfс.о.ll__аК--11I !!.А..т--.l!.._.
переноса энерши в твердом теле, Твердое тело в данной модели представ
ляется в виде решетки, состоящей из двух типов узлов (подрешеток): узлов-
хозяев и узлов-ловушек, Падающий фотон поrлощается узлом-хозяином
(атомом), в результате чеrо происходит ero возбуждение. Затем энерrия
возбуждения (экситон) случайным образом передается ближайшим соседям
и возбужденный атом возвращается в основное состояние, Блуждание экси-
тона по решетке продолжается до тех пор,- пока он не встретится с узлом
ловушкой, при котором энерr'Ия поrлощается и происходит некоторый фи-
зический процесс, например, химическая реакция.
Рассмотрим один из наиболее простых вариантов описанной модели пе-
реноса энерrии: экситон распространяется в одномерной решетке, содер-
жащей периодическую подрешетку, содержащую узлы-ловушки, Отметим,
что, если расстояние межд:у узлами-ловушками одинаково, блуждание по
бесконечной решетке можно заменить случайным блужданием по окружно-
сти (рис. 12.27).
о . . . с . . . ------..-4)
Рис, 12,27. Эквивалентная замена
случайною блужда//ия на одномерной
решетке, содержащей подрешетку
узлов-ловушек с периодом равным 4,
блужданием на окруж//ости с N3
узла.;иихозяевами (закраиlенный
кружок) и одним узлти ловушкой
(незакраиlенный кружок)

()
......
Для оценки зависимости среднеrо времени жизни экситона " (время,
в течение KOToporo возбуждение распространяется из начальной точки до
узла-ловушки) используем метод Монте-Карло. Будем считатъ, что в одно-
мерной решетке имеются узлы ловушки, расположенные в точках х == О ,
х = а (а > О). Пешеход начинает движение из точки ХО Е [о, а] и с равной ве-
роятностью за время 1" = 1 переходит в один из ближайших соседних узлов
решетки. Для нахождения вида функциональной зависимости 1"! == 1"z(a,xo)
будем использовать следующий вычислительный алrоритм,
1. Задать расстояние между узлами ловушками а.
2. Задать число точек Ns, в которых ВЫЧИСляются значения функции
1"! ==1"z(a,xo).
3. Провести разбиение отрезка [О ,а] на Ns интервалов
(хо; == (а/ Ns)'i, i  0,1,...Ns).
382
. !.)!_ч!I.Ье_?JlJ:?!::?JI
4, Вычислить NTrial случайных реализаций, состоящих из NStep шаrов, в
каждом узле разбиения отрезка [о, а] хо;'
5, Определить время достижения узла-ловушки пешеходом для каждой
случайной последовательности '! . ==min(xO;,axO;), k==1,2,...,NTrial.
k,l
6. Вычислить среднее время жизни возмущения
NТr;aZ
('Z);=N;T]'-l L'Zk,i
па k=l
стартующеrо из точки хО; .
Для реализации описаннOI'О алrоритма создадим файл Time2.m, содер-
жащий описание функции, возвращающей два вектора: 1) вектор, содержа-
щий значения стартовой точки, 2) вектор, содержащий усредненное по aH
самблю реализаций время достижения узла-ловушки.
% листинr файла Time2.m
function [X,t] = Time2(NTrial,p,Ns,a)
% функция возвращающая значения зависимость 1"! == Tz(a,xo)
% NTria1  число испытаний
% р  rpаничное значение вероятности перехода
% Ns  число узлов разбиения отрезка [о,а]
% а  расстояние между узлами сетки
dx=a1(Ns+l); % шаI' изменения координат стартовых точек
for m=l:Ns
i=l;
while k=NTrial
j=O;
x=dx*m;
% перемещение i-ro пешехода до достижения узла-ловушки
while (х<а)&(х>О)
if p>ral1d(l)
x=x+l;
else
x=x-l;
end;
j=j+l;
end;
Ns(i)=j; % время жизни i-r'o пешехода
i=i+ 1;
el1d;
383


!'.!й.fII.р!!.и-!!и-е;!.UЕ<:..а.'.I':.1!.!!'ч-,:с.х. ,!роцеССО8 8 nакете МА ТLAB
.. . ..........-. .. .'-'
X(m)=dx*m;
t(m):::mean(Ns); % среднее время жизни для данноrо значения
% начальной точки
end;
Далее необходимо выполнить следующую последовательность команд:
»NTrial=2000; % число испытаний
»Ns=6; % число узлов разбиения отрезка [о,а]
» а=30; % расстояние между узлами сетки
» [Х T]=Time2(NTrial,0.5,Ns,a);
»plot(X,T:Sk') % визуализация зависимости '[ = ,(а,хо)
Результат выполнения описанной последовательности команд представ
лен на рис. 12.28.
240i
i
220l
I
1
I
2ОСс
!
180>
I
i
i
,501
I
140f
I
I
120l
О
2Q
,....L
25
,
30
._ ..1
10
15
Рис, 12,28, ЗавиСWllость '( = ,(30,хо)
.. .... .,.
Задача 12.22
Проверьте, используя метод наименьших квадратов, что зависимость
Т( = Тl (а, Хо) описывается формулоЙ
,=(2D)lxo(axo)' (12.40)
. ,e-=ициeп:!ии 6 oтcyиe :!!.и: .
Задача ]2,23
Структуре реа7ЬНЫХ твердых тел присуще наличие разнuобразных дe
фектов, простейшu.\1 из которых яв.7яется отсутствие ато.Ю в одном
384
!C;;:zra.!! f!..л-r?!:f},!
из узлов решетки Шlи наличие дополнительною атома на поверхности,
При конечной температуре кристалла вакансия диффундирует, меняясь
местами с соседними атомами случайным образом. Предположив, что
в _иомент времени t == О вакансия расположена в центре окружности
радиуса r, проведите моделирование движения вакансии и определите
время, за которое вакансия достиzает поверхности металла, находя
щейся на расстоянии r, Постройте распределение вероятности для
времени достижения вакансией zраницы, Какой функцией можно aп
проксимировать данное распреде.ление вероятности?
.......
Задача 12.24
Рассмотрите одномерную решетку с отражающими узлами,
расположенны}fu в точках х = :ta, Наличие отражающих узлов
означает, что пешеход, начавший случайное движение в момент
времени t = О из точки хо Е ]a, а[, попав на пM шаzе в точки Хп = :ta ,
на п+ 1 шazе окажется в точках х = :ta :+ 1. Исследуйте случайные
блуждания пешехода, используя ,нетод МонтеКарло, и определите
функцию распределения вероятности PN,xo (х). Сравните функции
распределения вероятностей при наличии и отсутствии отражающих
стенок. Начиная с каких значений N различия в рассматриваемых
распределениях становятся существенными?
12.4. Моделирование движения решеточноrо rаза
в модели решеточноrо rаза рассматривается случайное движение He
взаимодействующих дрyr с друrом частиц (пешеходов) на двумерной или
трехмерной решетках. Условие отсyrствия взаимодействия частиц означает
невозможность попадания двух частиц в один узел. (Данная модель исполь
зуется в физике твердоrо тела, так как в твердых телах (в первую очередь,
в металлах) диффузия обусловлена температурными вакансиями, KOHцeH
трация которых зависит от температуры.) Основной характеристикой, пред
ставляющей интерес с физической точки зрения, в д<;.нной задаче является
кuэффициент диффузии D. Метод МонтеКарло в данной задаче реализует
ся в соответствии со следующим алrоритмом:
1. Задать числа узлов решетки L,
1
2. Задать числа частиц N (N:5 L).
3. Задать начальное распределение частиц,
4. Перемещать частицы случайным образом в один из свободных соседних
узлов, (Если узел оказьmается занятым, то частица остается в текущем узле.)
tЗ1576
385


'11

1
Х::'!..М-IЫО теРI!.?'!..м-'!.?еЛ':':.Р.!!.(l!.I1!!I,!..':':.'!..С:!Iх...'I?оцесс.CJ.в- в па K'!..".l..e .}y!/J..T:tB
... !.:ЛJ'::..'!.й'!.'!!.'!..л!..д'!':':..f!
Для реализации описанноrо алI'оритма в пакете МА TLAB необходимо
создать файл IoitL.m, содержащий описание функции, возвращающей Ha
чальную конфиryрацию системы, и MoveL.m, содержащий описание функ
ции, возвращающей мrновенные (на каждом шаrе МонтеКарло) значения
координат частиц системы.
% листинr файла InitL.m
fuoctioo [x,y,Site] = IoitL(L,NParticle)
% функция, возвращающая начальную конфиrypацию системы
x=zeros(NParticle,l) ;
y=zeros(NParticle, 1);
Site=zeros(NParticle,NParticle) ;
i=l;
while i<=NParticle
% случайный выбор номера узла
Xadd=floor«L+ 1)*raod(I)+ 1);
У add=floor«L+ 1 )*raod(I)+ 1);
if Xadd==O
Xadd=l;
eod;
if У add==O
У add=l;
eod;
if Site(Yadd,Xadd)==O % если узел свободен, помещаем в Hero частицу
Site(Xadd, У аdd)=10Л307;
x(i)=Xadd;
y(i)=Yadd;
i=i+l;
eod;
eod;
% листинr файла MoveL.m
fuoctioo z = MoveL(L,NParticle,NTrial,x,y,Site);
% функция, возвращающая мrновенные значения координат частиц
Х=х;
У=у;
Sitel=Site;
z=cat(2,x,y);
for i=I:NTrial1
for j=l:NParticle
ITrial=floor(NParticle*raod(I)+ 1); % номер перемещаемой частицы
if IТrial==O
IТrial=l;
eod;
XTrial=X(IТrial) ;
YTrial= У (IТrial);
% перемещение в случайном направлении с учетом
% периодических rpаничных условий
Directioo=floor( 4*raod( 1)+ 1);
if Directioo==1
XTrial=XTrial+ 1;
if XTrial>L
XTrial=XTrialL;
eod;
eod;
if Directioo==2
XTrial=XTrial 1;
if XTriakl
XTrial=L-ХТriаl;
eod;
eod;
if Directioo==3
YTrial=YTrial+l;
if YTrial>L
YTrial= YTrial L;
eod;
eod;
if Directioo==4
YTrial= YTrial-l;
if YTriakl
YTrial=L- YTrial;
eod;
eod;
if Sitel(YTrial,XTrial)==O % узел свободен
Sitel(Y (ITrial),X(IТrial))=O;
X(IТrial)=XTrial;
У (ITrial)= YTrial;
Sitеl(УТriаl,ХТriаl)=10Л307; % новый узел занят
eod;
eod;
386
387

, I
,l!..'!.п-!!"!f}'рl10е моделuрй-а.I!''!..1!.!'..зuче::!!.'!! nе'!..'!!!!:.с:.!!.!!..!!. nаке"!!.!!.:!.!'...ш ''ШШ'Ш'
zl=cat(2,X, У);
z=саt(З,z,zl);
eod;
Далее необходимо выполнить следующую последовательность команд:
» L=50; % размер ячейки
» NParticle=2000; % число пешеходов
» NTrial=lOO; % число испытаний
» [Xi Yi Site] = IoitL(L,NParticle); % вычисление начальной
% конфиrypации
»figure(l);plot(Xi,Yi,'.k') % визуализация начальной конфиrypации
»C=MoveL(L,NParticle,NTrial,Xi,Yi,Site); % вычисление координат
% пешеходов на каждом
% шarе МонтеКарло
% вычисление MrHoBeHHbIx значений среднеквадратическоrо
% отклонения, усредненных по ансамблю пешеходов
» for i=l:NTrial
R2=O;
X=C(:,l,i);
Y=C(:,2,i);
for j=l:NParticle
дх=Ху)- Xi(j);
dy= У у)- Yi(j);
if abs(dx»U2
dx=dx-dxlаЬs(dx)*L;
eod;
if abs(dy»U2
dy=dy-dу/аЬs(dу)*L;
eod;
R2=R2+dx. Л2+dу. Л2;
eod;
dR(i)=R2INParticle;
eod;
» i=l:NTrial;plot(i-l,dR)
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 12.29 и 12.30.
50 ."7 ;.  .'---:  :" 
T  _._.. .,   
. .... . . . . .
. . .,0 .
. "0 ..,. . . . ..
45 :: .':'.::':::. ':: .
...... ....шш ШШ ш:S!:.!'.Й!!,:!:!..ЛУ.'!'!.l!
. . . " I
. . : :. :: i
. . . . .., . .. ... ..... . . . . .
40:: :..:',:,:'.:.:':, ::::':"':'::::.,::::- : ::
35::' :':..:,:....,:: ,:". . 1
<:::; ;: ::,::,::;::;: ::;'::.::-::::::::::::;:
25 :' ":.':: , ::' ":: '.: ::,::,:':-:,': : :,' :]
20 ,: ...:' ': ::':,: :::,::,":,:,:.-::::' ..":.:1
::!:р:,,:!
00 10 15 20 2s 30 35 40 4S 50
Рис, /2.30. Зависимость
MZHoBeHHЫX значении
среднеквадратическоzо
отклонения, вычисленных
усреднением по ансамблю
пешеходов, от номера шаzа //
Монте-Карло 00 ' ;. 3 '0 50 60 70 60 90 IОС
Сделаем два важных замечания, относящихся к рассматриваемой модели
и последовательности выполняемых команд для ее реализации.
1. Для описания движения частиц на решетке конечных размеров ис
пользуются периодические rpаничные условия, подобные rpаничным усло
виям, использованным в методе молекулярной динамики (см. разд. 10.)
2. «Время» в рассматриваемой модели измеряется в единицах, равных
длительности одноrо шаra метода МонтеКарло на частицу, т. е. за один шаr
метода МонтеКарло каждая частица совершает в среднем один переход
Коэффициент диффузии D может быть оценен как предел выражения
D(t) = ш1 j AR(t)2 j'
2dt'
388
Рис. /2.29, Расположение
пешеходов в начальный
момент времени
'5
///
///
/'
//
/
//,./
/
/
40
35
30
25
20
'5
10
(12,4])
389

!!.!!..А!...п-'!!!!!..l!.'..'?!...!?!.'.!!!'!.1!.'!--З..!.!с:!5.':!..tlf!.?.':I!.:'О!..!!.!!.f!..!'.!е м-...1!!:...........
при t  00 , Из рис. 12.30 видно, что коэффициент диффузии может быть
оценен как уrол наклона прямой, аппроксимирующей зависимость (мп
методом наименьших квадратов.
Задача 12.25
Вычислите коэффициент диффузии решеточноzо zаза на квадратной
решетке D для значений плотности р = 0.1, 0.2, 0.3., 0.4, 0.5, 0.6, 0.7, 0.8
(р = NParticle / L2), Постройте zрафик зависимости D = D(p), Попро
буйте подобрать аналитическую функцию, аппроксимирующую данную
зависимость. Почему D = D(p) является монотонно убывающей функ
цией плотности?
Задача 12.26
Для заданноzо значения плотности решеточноzо zаза вычислите He
сколько зависимостей (мп, определите параметры прямых aппpOK
сuмирующих данные зависимости, вычислите сумму квадратов разно
стей между точными значениями (мп и соответствующими aппpOK
симированными значениями (сумма квадратов отклонений), Как
зависит сумма квадратов отклонений от числа частиц решеточноzо
zаза N.
:1
Задача 12.27
Предложите алzоритм и вычислите зависимость вероятности пepexo
да частицы в момент времени t в некоторую свободную ячейку и ее воз
вращения в момент времени t + 1 назад в ту же ячейку от плотности
решеточноzo zаза. Определите качественно зависимость между значе
нием коэффициента диффузии D и данной вероятностью.
Задача 12.28
Рассмотрите модель случайных блужданий частиц на одномерной pe
шетке, в которой исключается попадание двух частиц в один узел. (Это
оzраничение означаеm, что частицы не МОёут проходить друё через
друёа.) Вычислите зависимость (дх2) от времени, Сравните зависи
.мость (дх?) с аналоzичными зависимостями, получаеМЬ/Jl1и в модели
одномерных случайных блужданий, Можно ли zoворить о процессе
диффузии в данном случае? Какова в рассматриваемой модели зависи
. 2)
мость (дх от t?
I
1:
I
I .
I '
390

.......... ..... ..ш.!l.:2'..'!.IЬ!.=J/!:'!IIl!
12.5. Непрерывная модель случайных блужданий
Рассмотрим переход от дискретной модели случайных блужданий, pac
смотренных нами в разделе 12,2, к непрерывной. Если предположить, что
направления шаrов пешехода равновероятны, то дискретное случайное
блуждание можно переписать в виде простоrо «порождающеrо» уравнения:
Р" (i) =  Pпl (i + 1) +  P,'1 (i  1), (12.42)
rде Р" (п  вероятность попадания пешехода после п шаrов в iй узел,
Для получения непрерывноrо аналоrа (12.42)  дифференциальноrо
уравнения для плотности вероятности P(x,t) положим t = пт, х = ia,
Рпи) = aP(x,t), rде -r  временной интервал между двумя последователь
ными шаrами, а  период решетки. Используя выбранные обозначения, IIе
репишем (12.42) в эквивалентной форме:
1 1
P(x,t) = '2 Р(х + a,t  ') + '2 Р(х  a,t  т) . (12.43)
Вычтя из обеих частей (12.43) P(x,t  т) и разделив на r, при водим к виду
1 а2
. [P(x,t) P(x,t  т)] =  [Р(х + a,t  T) 2P(x,t  т) +...
-r 2.
1
+P(xa,t-r)]2'
а
Считая а, -r малыми и перейдя к пределу а  О, -r  О при конечном OT
ношении D = а2/2т , получаем одномерное уравнение диффузии
(12.44)
aP(x,t)  D a2p(x,t)
at  ш дх2 ., .
Поступая аналоrично, можно получить уравнение диффузии в тpeXMep
номпространстве
(12.45)
P(x,y,z,t2 = DV2p( . t)
at х, }, Z, ,
(12.46)
rде v2 = д2 / д х2 + д2 / д / + д2 / д Z2  оператор Лапласа.
Уравнение (12.46) называется уравнением диффузии или уравнением
ФоккераПланка. Оно используется для описания динамики молекул rаза и
жидкости, Можно показать, что решением уравнения (12.45) для свободно
ro пространства является функция
391

!5.й-..'!.!().!!'!!!!I!!..'!.е:!.'!!!о.!!'!!.'!.!:Р':'!.!=с.и--х...."-l!!!..'i::.с:..й-.п-r!.:"-,!.!!!..1!..!'ш. .....Ш
х'
P(x,t) = .J2t е 4DI,
(12.47)
rде p(x,t)  плотность вероятности обнаружить частицу в момент времени
t в точке х, которая при t = находилась в точке х = О. Функция, стоящая в
правой части (12.47), для заданных моментов времени описывает нормаль
ное распределение, При этом с течением времени ero ширина меняется про
порционально (1/2 .
Задача 12.29
Убедитесь в том, что функция p(x,t), задаваемая выражением (12,47),
является решением уравнения (12.45):
ос
(x(t)) = f xP(x,t)dx = о;
(12.48)
oc
ос
(х2И) = fx2p(x,t}dx=2Dt.
(12.49)
oc
Анализ (12.49) показываеm, что (x2(t))  t, как и для случая одномерных
случайных блужданий на дискретной решетке, Обобщение (12.49) на d
мерный случай дает (R2(t)) = 2dDt, 2де (R2(t))  квадрат смещения
частицы,
Уравнения (12.45), (12.46) относятся к уравнениям параболическоrо ти
па. Численные (детерминированные) методы их решения будут paCCMoтpe
ны нами позднее в rл. 15. Отметим, что для решения данных уравнений
можно использовать не только детерминированные, но и случайные MeTO
ды, основанные на методе МонтеКарло. Для этоrо следует перейти от He
прерывных уравнений (12.45), (12.46) к их дискретным аналоrам и исполь
зовать случайные блуждания на дискретной пространственной сетке с дис
кретными временными шаrами. Так как асимптотическое поведение
решений уравнения в частных производных и модели случайноrо блужда
ния оказываются одинаковыми, то в данном случае метод МонтеКарло яв
ляется методом численноrо анализа. Если целью исследования является
изучение модели случайноrо блуждания на решетке, то метод случайноrо
блуждания является методом моделирования. Следовательно, в данном слу
чае различие между моделированием и численным анализом определяется
только точкой зрения исследователя,
I
I !
392

..........!.._____.9!?!.,!!!!..I'3..=.-Э!{;!!!.!.r..и-'!
Задача. 12.30
Обобщите, описанные в разделах 12,2, 12,3, методы случайных блужда
ний на случай трехмерной решетки, Вычислите зависимости (RN),
(R ), (M) для простой кубической решетки (z = б) и оцените значе
ние v. Зависит ли значение v от размерности пространства? Вычисли
те значение i<.оэффициента диффузии для трехмерных блужданий, Co
2Ласуется ли полученное вами значение с формулой (12.41)?
ЛИТЕРАТУРА
1, Рейф ф, Статистическая физика, М,: Наука, 1972,
2, Тейлор Дж, Введение в теорию ошибок. М,: Мир, 1985,
3. rулд х., Тобочник Я. Компьютерное моделирование в физике, М,: Мир, 1990, Ч, 2,
4, rросберr А, Ю" Хохлов А, Р. Физика в мире полимеров, М,: Наука, 1989.
5. rросберr А, Ю" Хохлов А, Р. Cra-rnстическая физика макромолекул, М.: Наука, 1989.
6. Соболь И, М, Численные методы МонтеКарло, М.: Наука, 1973,
7. Кун ин С. Вычислительная физика, М,: Мнр, 1992.
8. Пресс В, П" Фланнерн Б, П., Тьюкольски С. А" Веттерлинr В, Т, Чнсленные рецепты, М,:
Мир, 1990,
393

l'
11
I
:1
!
IJ
1
, I
11
I 
.... ............Ш..Ш.!.:....':!.!!..'!:?':!P.!!.!'!!:'!!.'!!!!..'!!.'!..e..:'!.!!.:'!:'!!.'!!1.'!!.
r лава 13
МОДЕЛИРОВАНИЕ СТАТИСТИЧЕСКОЙ
СИСТЕМЫ В ПРОЦЕССЕ РЕЛАКСАЦИИ
И СОСТОЯНИИ РАВНОВЕСИЯ
13.2. Моделирование "роцесса релаксации
статистической системы
13.1. Введение
Рассмотрим сосуд, в котором находится идеальный rаз, разделенный
переrородкой на две равные части, одна из которых в начальный момент
времени пуста (рис. 13.1). В левой половине сосуда находится N молекул.
После MrHoBeHHoro удаления подвижной заслонки молекулы начинают пе
реходить из заполненной части сосуда в пустую. Поскольку движение каж
дой частицы происходит независимо от всех остальных, вероятность про
хождения через отверстие для всех частиц одинакова. Будем полarать, что в
единицу времени через отверстие проходит одна частица.
В предыдущих rлавах мы смоrли убедиться в эффективности компью
TepHoro моделирования при изучении поведения систем, состоящих из
большоrо количества частиц (систем со мноrими степенями свободы). OKa
зывается, что в модельных экспериментах даже с относительно небольшим
числом частиц (по сравнению с реальными системами, содержащими по
рядка 10201025 взаимодействующих друr с дрyrом атомов и/или молекул)
можно выявить наиболее существенные особенности поведения статистиче
ских систем, понять механизмы, приводящие к такому поведению, Отметим
важную особенность рассматриваемых систем, состоящую в стремлении с
течением времени к беспорядку. В соответствии с современными представ
лениями именно данное свойство макроскопических систем определяет Ha
правление или «вектор времени».
В этой rлаве мы продолжаем рассмотрение свойств систем, с мноrими
степенями свободы, состояние которых может быть описано как путем за
дания координат, скоростей каждой частицы системы и законов их взаимо
действия (описание микроскопическоrо состояния), так и путем задания
некоторых усредненных параметров системы, например, средней темпера
туры макросистемы, средней концентрации молекул и т. д. (макроскопиче
ское описание). Для демонстрации понятий порядок и беспорядок, направ
ление времени, микроскопическое и макроскопическое описание системы
нами используется модель, состоящая из N тождественных частиц, взаимо
действием которых друr с друrом можно пренебре'fЬ (идеальный rаз) , Бу
дем также предполаrать, что rаз заключен в изолированный сосуд (т. е. не
подвержен влиянию внешней системы или силы) и пребывает в покое в Te
чение долrоrо времени. Адекватным аналоrом модели идеа.аьноrо rаза яв
ляется разреженный реальный rаз, в котором время одноrо пролета между
стенками сосуда MHoro меньше, чем время между столкновениями двух MO
лекул, Выбранная модель позволяет использовать для описания изменения
параметров микроскопических состояний системы, а через них и изменения
макроскопических параметров, вероятностные методы,
. . .
. . .
. . .
. . .
Рис, 13,1. К моделированию процесса
релаксации статистической системы
для идентификации микро и макросостояний рассматриваемой системы
предположим, что частицы изначально пронумерованы от 1 до N. Микросо
стояние будем описывать номерами частиц, находящиМися в левой полови
не ящика, поскольку знание номеров этих частиц позволяет однозначно оп
ределить номера частиц, находящихся в правой половине ящика. В качестве
макроскопической характеристики рассматриваемой системы будем ис
пользовать число молекул, находящихся в левой половине ящика. Основная
цель исследования состоит в определении численности частиц в левой п и
правой п' половинах ящика (п + п' = N) в заданные моменты времени. Оче
видно, что для получения однозначноrо ответа на данный вопрос требуется
знание функции PN(n,t), определяющей вероятность нахождения в момент
времени t в левой половине ящика п частиц.
Один из методов нахождения функции PN(n,t)  метод точноrо перебо
ра, уже рассматривавшийся нами в rл. 12 при обсул;дении метода случай
ных блужданий, Рассмотрим метод перебора для случая, коrда при t = О
п = 6 и п' = О . При t = 1 возможна единственная комбинация: п = 5, п' = 1 ,
отсюда Р(п = 5,t = 1) = 1. При t = 2 возможны комбинации, коrда одна из
шести частиц слева смещается направо или же частица справа возвращается
в левую половину. Так как первая комбинация может реализоваться пятью
различными способами, вероятность данноrо события Р(п = 4,t = 2) = 5/6,
395

j

l!..и-:'!....п-.!?.'!!е!!!.I!!!. Mo!!.'!!.."!:.J!.'!!."!'5.:I1.P!!..l/..:"O!'!.!'!'!..fl:!1:!!::i... . Ш
11
Вторая комбинация реализуется единственным способом, поэтому вероят
ность данноrо события Р(п = 6, t = 2) = ]/6. Следовательно, при t = 2 cpeд
нее число частиц в левой половине ящика составляет
2
(п) = 4Р(п = 4,1 = 2)+ 6Р(п = 6,1 = 2) = 4.
6
На следующем шаrе по времени имеем Р (п = 3, t = 3) = (4/6)
Р (п = 4, t = 2) = 20/36, что отвечает перемещению одной из четырех OCTaB
шихся частиц вправо. Рассуждая аналоrично, найдем
Р(п = 5,1 = 3) = (l)P(n = 6,1 = 2) + (2/6)Р(п = 4,1 = 2) = ]6/36.
Следовательно, при 1 = 3 среднее число частиц в правой половине ящика
составляет
! 1
11
8
(п) = 5Р(п = 5,1 = 3)+ 3Р(п = 3,1 = 3)= 3.
9
Так как полное число частиц мало, перебор удается продолжить еще He
сколько временных шarов. Однако, как леrко видеть, количество комбина
ций быстро увеличивается с ростом 1. При достаточно больших N и 1 число
возможных комбинаций становится столь велико, что не хватит мощности
даже современных компьютеров.
В этих условиях, как и в задаче о случайных блужданиях, весьма эффек
тивным оказывается метод МонтеКарло. Напомним, что в методе MOHTe
Карло rенерируется репрезентативная выборка случайных перемещений,
являющаяся подмножеством множества всех возможных перемещений. При
этом, чем больше окажется объем выборки, тем более высокая точность бу
дет у получаемых результатов.
Для реализации метода МонтеКарло необходимо задать вероятность
перехода частицы из левой половины ящика в правую. Так как любая час
тица с равной вероятностью может пройти через отверстие, вероятность пе
ремещения в единицу времени частицы из левой половины ящика в правую
пропорциональна числу частиц в левой половине в данный момент времени,
деленному на полное число частиц п1N. Используя данный факт, можно MO
делировать временную эволюцию модели в соответствии со следующим ал
rоритмом:
] . Задание числа шаrов Т.
2, Инициализация счетчикаj=О.
3, rенерация случайноrо числа РroЬ в интервале от О до 1.
4. Сравнение РroЬ с текущим значением п/N в левой половине сосуда.
I
I I
396

..! !.!.й-е.ЛJр"й.:!.(J!I!J!'!!.(J.п:..'!::'!'.'!.?.!!с!!'!'!..
5. Перемещение частицы слева направо, если Prob:::;; п/N; в противном
направлении перемещаем частицу при РroЬ ;:::: п/N.
6. Повторение пунктов 3  5, покаj :::;; Т.
Для реализации описанноrо алrоритма в пакете МА ТLAВ необходимо
создать два файла: 1) файл ParticleAtTheLeft.m, содержащий описание
функции, возвращающей единичную реализацию зависимости числа частиц
в левой половине ящика п = п(О; 2) файл EnsembIe.m, содержащий описа
ние функции, возвращающей ансамбль реализаций зависимостей п = п(1).
% листинr файла ParticleAtTheLeft.m
function z=ParticleA tTheLeft(NParticle,NStep)
% функция, возвращающая единичную реализацию зависимости п = п(1)
% NParticle  число частиц в левой половине ящика в момент времени t = О
% NStep  длина единичной реализации
LeftN(I)=NParticle;
for i=2:NStep
Prob=LeftN (i-l )INParticle;
if rand(1)<=Prob
LeftN (i)=LeftN (i-l )-1;
else
LeftN(i)=LeftN(i-l)+ 1;
end;
end;
z=LeftN;
% листинr файла Ensemble.m
function z = EnsembIe(NTrial,NParticle,NStep)
% NTrial  объем ансамбля реализаций
% NParticle  число частиц в левой половине ящика в момент времени t = О
% NStep  длина единичной реализации
for i=I:NTrial
Z=ParticleAtTheLeft(NParticle,NStep );
if i==l
z=Z;
else
z=cat(3,z,Z);
end;
end;
397

'1
I!"
1,1
.'!..п-.!!!!!!.9!!!с:!!.с:..е!!'.!р,!J,!l..'!.!U=-.1!.'!!.II=-.'.Р/JУ=-.с..'!...!..'.'e.'!!!'!:!:!.f!.......... ............ ,.ш ...... .....
11
!i '1
1':, .
, I
! '1
Далее необходимо выполнить следующую последовательность команд:
» NParticle=lOO; % число частиц системы
» NStep=lOOO; % длина единичной реализации
»NTrial=lOO; % объем ансамбля реализаций
»E=EnsembIe(lOO,NParticle,NStep); % вычисление ансамбля реализаций
% визуализация выбранных из ансамбля реализаций зависимостей п = п(t)
» figure(l);plot(i,E(l,:,l),'k')
» figure(2);plot(i,E(1,:,50),'k')
» figure(3);plot(i,E(1,:,lOO),'k')
% вычисление средней по ансамблю реализаций зависимости п = п(t)
» for i=l:NStep
for j=l:NTrial
sG)=E(l,iJ);
end;
Em(i)=mean(s);
end;
% визуализация средней по ансамблю реализаций зависимости п = п(t)
» i=l:NStep;
» figure(4);plot(i,Em);
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 13.2IЗ.5.
11
1
1
I
I
11'
:,,1
: !
I
I
100 --
90\
\
\
70 \
. l' Iл/NI
· \i \I()\VNjV', '"
40
300 .100.'. 500
, .L..............
600 700 600 900 100с
1 I
11
,
Рис, 13,2, Зависимость числа частиц в левой половине ящика от времени N! 1
398

ш ..и... м-. /Jд.ef}UрО'!.!1 ..'!.!."-,-и-.с:!'!и-.'!.еС'5../J.с:....",---
]Ш , ..',Ш.Ш
1\
во! 1
1 \
1 \
" '
\ \
''I /1 '1"',
\\ i  IV,/ I I 1
''11 1\1 ,Ic' '1 ' l' \\
r \ ,1,. l' 'l,.,ial.l
( ,. \ '\ IH l' \;\ *'Ч.
\! ,-} ,i' '\-,\, ,nl
\' :', I 
 'I,!'
.
5<>
"1
..l
J
о
Рис. 13,3, Зависимость
числа частиц в левой
половине ящика
от времени N! 50
700
ш . J
&00 900 1000
.
'00
2ОС
300
400
"'"
600
Рис, 13.4, Зависимость числа
частиц в левой половине
ящика от вреАlени N!! 100
100( l
J
1\
'\
60 '1
, I
1 v
701 \.л
1 ',
,!O\,
'01 !'  I f
i \ .J\ ,w,yl\fi ,,\ I i " 1,
50" \ji\'Y, ,/   d\,\}''I', (/ '1liJ'II\
! . '!'I \/11 \. \ 1\ ...  I
I ' ," '''''. (I
, \f
,J , ,, '.ШШ ШШ. .
О 100 m _ m     m 1
100 .
\
I
90 '
I
601
I
sof
J
с 1ОС
 . ' ',.............
Рис. 13,5, Усредненная
110 ансамблю реализаций
зависимость числа
частиц в левой половине
ящика от времени
400
, ............I.._., 
500 ВО{) 700 800 900 1000
200
000
399

ii?':"!.Ь!'!."!.:[J!.'!!е..J:!.f!.l!!!.'!Р..!!.!!..f!!!..'!:.Р.'!-з!!!.ч!'!.е.:!!.I!..!.'!.'!.:тeMA!!::4.l!.._
Анализ зависимости п = п(О, представленной на рис. 13.5, показывает,
что с течением времени рассматриваемая система стремится к состоянию,
в котором в обеих половинах ящика находится примерно одинаковое число
частиц. Если пренебречь малыми случайными флуктуациями, то с MaKpo
скопической точки зрения (коrда нас интересует не номера частиц, находя
щихся в левой половине системы, но их количество) можно считать, что,
начиная с HeKoToporo момента, параметры системы перестают зависеть от
времени. Данное состояние системы называется равновесным. Время, необ
ходимое системе для достижения paBHoBecHoro состояния, называют BpeMe
нем релаксации Trel' Для оценки irel аппроксимируем зависимость п = п(t)
u Ф u ь,
аналитическои ункциеи вида се + с, дополнив описываемый документ
блоком, позволяющим оценивать неизвестные коэффициенты функции, ис
пользуя метод наименьших квадратов.
для аппроксимации нахождения коэффициентов аппроксимирующей
функции в пакете МА ТLAВ необходимо выполнить следующую последова
тельность команд:
1'1
1
i
» NParticle=100; % число частиц системы
» NStep=1000; % длина единичной реализации
» NTrial=100; % объем ансамбля реализаций
»E=EnsembIe(NTrial,NParticle,NStep); % вычисление ансамбля
% реализаций
% вычисление средней по ансамблю реализаций зависимости п = п(t)
» for i=I:NStep
for j=I:NTrial
s(j)=E(I,iJ);
end;
Em(i)=mean(s );
end;
% нахождение функции, аппроксимирующей зависимость п = п(t)
»FI0=inline('exp(u(I)+u(2).*z)+u(3)','u','z') % задание
% аппроксимирующей функции
FI0=
Inline function:
FI0(u,z) = exp(u(1)+u(2).*z)+u(3)
.» i=I:NStepj
»x(i)=ij
» beta=nlinfit(x,Em,FI0,[5 -0.1 1]) % функция, возвращаюшая решение
% системы уравнений метода

I
400
r
....._. ...J}:_А!.'!..'!:'!.UЕй---'!..'Iи-:.. :"!.и-:'!!.,!e?!!'!.'!!...e.!:.'ы
% наименьших квадратов
% [5 -0.1 1]  начальные значения
% искомых коэффициентов
Ьеtз=
3.9297
-0.0198
49.9048
% визуализация зависимости п = п(t), усредненной по ансамблю
% реализаций, и аппроксимирующей ее функции
» plot(x,Em,'k' ,x,FIO(beta,x), 'k')
Результат выполнения описанной последовательности команд представ
лен на рис. 13,6.
100r""""'.'
l
i
i
1

i
1
I
i
1
\
00\
w \
\
: \

...."'-- 
1
I
I t I I I 
40 О 1 200'" зоо 400 500 600 700 800 900 1000
Рис. 13.6. Зависимость п = п(t) и аппроксимирующая ее функция
50
"-
Время релаксации изучаемой системы к состоянию равновесия может
быть определено из очевидноrо равенства
Ь; 1
N 'ae re +с
left . ,
(13.1 )
откуда
1 (!ANI)
irel := b1n  '
(13.2)
rде AN = I-  cl\ ' N  число точек зависимости п = п(О.
12
401
............

.:'!.п!'.,?п e.P"I?.!!Oe1!.P'?в'!.,lи .1.)I:.:'С_КIР.и-ч..I?,,'!в-.в-.п(/I?"!I?!о!...1:'ZL1l!.___
в обозначениях, выбранных в документе МА TLAB, формула (13,2) при
нимает следующий вид:
] - l1N )
'reZ := beta(2) '1П( el;eta(1) ,
(13,3)
rде
l1N := Ipa;ticle  Ьеtа(з)l. (13.4)
Таким образом, для вычисления оценки времени релаксации необходимо
дополнить описываемый документ следующими командами:
» dN=abs(NParticle/2-Ьеta(3»;
» tau=floor(I/beta(2)*log( dN/beta(I»)
tau=
187
.._..... .-.-.,
Задача 13.1
Дополните, описанную выше последовательность команд, блоком KO
.манд, позволяющим для заданною набора числа частиц рассматривае
мой систeJI.tы проводить автолштические вычисления врeJI.tени релакса
ции, Отобразите зависимость 'reZ = 'reZ(N  Particle) zрафически, Ka
кой функцией можно аппроксимировать данную зависимость?
Объясните полученный результат с физической точки зрения,
Мерой равновесных флуктуаций служит дисперсия (J N числа частиц в
левой половине ящика, определяемая равенством
(Y"p = (NZe/)(NZefJ,
(13.5)
здесь ( ) означают усреднение по времени, про водимое после достижения
системой состояния равновесия. Для автоматизации вычислений величины
относительной флуктуации ((J N,,p ) /( NZef/) при различном числе частиц сис
темы необходимо создать файл Fluct.m, описание функции, возвращающей
значения относительных флуктуаций числа частиц, находящихся в левой
половине ящика, для заданных значений числа частиц системы.
% листинr файла F1uct,m
function Z = Fluct(VecCParticle,NTrial,NStep)
% функция, возвращающая значения относительных флуктуаций числа
% частиц, находящихся в левой половине Ящика, для заданных в векторе
% VectPartic1e значений числа частиц системы VecCPartic1e  вектор,
% содержащий заданные значения числа частиц системы
% NTria1 . число испытаний
I i
i 11
1',
402

,
......_1.!. .t:!?д-.eJll!.?в-.{l!'!.:с.'!!CI.'':'!..,,'!!..'!.'!().!!...с./rlь..l.
% NStep  длина единичной реализации
M=length(V ecCParticle);
FI0=inline('exp(u(1)+u(2).*z)+u(3)','u','z'); % задание вида функ:щи,
% аппроксимирующеи
% зависимость п = п(О
n=I:NStep;
х(п)=п;
for m=I:М
E=EnsembIe(NTrial,V ecCParticle(m),NStep); % вычисление MrHoBeHHbIx
% значений зависимости п = п(t)
% для системы, состоящей из
% VecCParticle(m) частиц
% вычисление MrHoBeHHbIx значениЙ зависимости 11 = 11(t),
% усредненной по ансамблю реализаций
for i=l:NStep
for j=I:VecCParticle(m)
s(j)=E(I,iJ);
end;
Em(i)=mean(s);
; 
% оценка времени релаксации системы, состоящеи
% из Vect particle(m) частиц
beta=nlh.fit(x,Em,FI0,[5 -0.11]);
dN=abs(V ecCParticle(m)/2-Ьеta(3»;
tau=floor(I/beta(2)*log( dN/beta(I»);
% вычисление MrHoBeHHbIx значений числа частиц, находящихся
% в левой половине ящика в равновесном состоянии
k=l;
for j=tau:NStep
z(k)=Em(j)- VecCParticle(m)/2;
zl(k)=Em(j);
k=k+l;
end;
Z(m)=std(z)/mean(zl); % относительная флукация .-шсла, частиц
% находящихся в лево и половине ящика,
% в равновесном состоянии от времени
eod; манд'
Далее необходимо выполнить следующую последовательность ко '
> i=I:13;
» V(i)=10+З*(i-l);
» NTrial=lOO; % число испытаний
403

!!:(),:"!.'!..!()'!!9!.!'oe :1I?е.рй-'!.'.I.и1!.'!..::х. !!Рй-.II..:.:с...й- . !.Iil.e'!!:A!..AJL! l! ...
» NStep=1000; % длина единичной последовательности вычисление
% и визуализация зависимости величины относительных флуктуаций
% от числа частиц статистической системы
» A=Fluct(V,NTrial,NStep);
» plot(V,A,'kx'); axis([9 49 О 0.1])
i I
o.11'--"""".""""""_' --'T,.,.. -
ОМ!
OO8r
0.07 [
008
I
::f
003
O.02f.
0.01 
1
01
10
'I
i
I
,
15
_........L....
30
,
35
40

45
20
25
Рис, 13,7, Зависимость величины относительных флуктуации
от числа частиц системы
Результат выполнения описанной последовательности команд представ
лен на рис. 13.7. Анализ зависимости, представленной на рис. 13.7, позволя
ет предположить, что величина относительных флуктуаций числа частиц,
находящихся в левой половине ящика, зависит от числа частиц системы как
1/  N . Для про верки rипотезы аппроксимируем данную зависимость функ
цией вида aj-Ib: + .
Для нахождения коэффициентов аппроксимирующей функции необхо
димо выполнить следующую последовательность команд:
» i=I:IЗ;
» V(i)=10+3*(i-l);
» NTrial=100; % число испытаний
»NStep=1000; % длина единичной последовательности
% вычисление и визуализация зависимости величины относительных
% флуктуаций от числа частиц статистической системы
» A=Fluct(V,NTrial,NStep);
» plot(V,A,'kx'); axis([9 49 О 0.1])
% вычисление коэффициентов функции, аппроксимирующей
I
i:
, '
, i I
I
I
404

. ..._!...J:!,!!".f!}!Р...й-!.il.I:,!!,!!,!:,!!:.:й-:':'(",!:
% зависимость относительной величины флуктуаций
% от числа частиц системы
» Fl1=inline('u(I)J(u(2). *z+u(3)). ЛО.5', 'и' ,'z');
» beta=nlinfit(V,A,Fll,[1 3 1]);
% визуализация аппроксимирующей функции
» Nx=500;
» j=I:Nx;
» s(j)=miп(V)+(maх(V)-miп(V))lNх*j;
»plot(V,A,'kx',s,Fll(beta,s),'k');axis([9 49 О 0.1])
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 13.8.
O.1r'""""'

0.09 \
\ '
0.08 \
\
\
\
\
'\
',,-- х
"----,
"'-",-
')('......... х
'---------;:------.,..
l
0.07
0.06
0.05
004
0.03
0.02
001 
О '
10
,
20 25
35

40 45
,
30
,
15
Рис. 13.8. Зависимость величины относительных флуктуации
от числа частиц системы
Задача 13.2
Аппроксимируите зависимость (а N'<ft) /(Nteft) функциями дРУ2020 вида.
Для каждой функции вычислите сумму квадратов отклонении между
точными значениями зависимости (а N'.ft ) /(Ntefl) и значениями aппpOK
симирующей функции в соответствующих точках9!авните данные
значения и проверьте, что для функции вида а/ J ь 'х + с данная величи-
на оказывается наименьшеи,
405

.l<:.",/J/О".!fl..II(J(J:l!.':'fJl!l!!.I!!1':'.::!..:К-'!..!.'!!й-lf::.!п...к-=-,!!!!.:!:!!::AВ-.....
13.3. Энтропия
Результаты, полученные в вычислительных экспериментах, описанных в
предыдущем разделе, демонстрируют фундаментальное свойство систем,
состоящих из большоrо числа частиц, Оказывается, что любая изолирован
ная статистическая система независимо от начальноrо состояния стремится
с течением времени прийти в состояние равновесия. В этом состоянии все
макроскопические величины, характеризующие термодинамическое paBHO
вес ное состояние системы, в пренебрежении малыми флуктуациями
не зависят от времени.
Для изучения основных свойств статистических систем мы использова
ли модель, состоящую из относительно небольшоrо числа частиц, движение
которых подчинялось вероятностным законам. Для выбранной модели OKa
зывается возможным подсчитать для каждоrо макросостояния число воз
можных микросостояний, так как, вопервых, каждая частица может пребы
вать только в одном из двух состояний (в левой или правой половине ящи
ка), BOBTOpЫX, местонахождение каждой частицы не зависит от положения
остальных частиц. Данные условия означают, что распределение чаСТИll
подчиняется биномиальному закону, Следовательно, число возможных
микросостояний Q/l дЛЯ макросостояния, в котором слева находится п,
справа  п' (n+II'=N), равно NVn!n'!. Число микросостояний Qn для
N = 16 приводятся в табл. 13.1.
I
j i
Таблица 13.1.
Число Jllикросостояний Q/l и энтропия S/l = 1nQ/l для N = 16 частиц в ящике
n Qn ln(Qn) n Qn ln(Qn)
О 1 О 9 11440 9.34
1 16 2.77 10 8008 8.99
2 120 4.79 11 4368 8.38
3 560 6.33 12 1820 7.51
4 1820 7.51 13 560 6.33
5 4368 8.38 14 120 4.79
6 8008 8.99 15 16 2,77
7 11440 9.34 16 1 О
8 12870 9.46
Анализ данных, представленных в табл. 13,1, показывает, что макси
мальное число микросостояний соответствует значению п = 8, т, е, paBHO
весному СОСТОЯНИI9, Так как число микросостояний является показателем
I
! ,
I i
I
1,
i,
406

.. .... J.:.(J:J'!..fJ.?Bl!.'!!!e:'!!".'.'.!..:'!!.'!..e...c.:',!:'Ile. I
«степени беспорядка» системы, можно утверждать, что равновесное состоя
ние отвечает «состоянию максималЬНОI'О беспорядкю), В отличие от этоrо
макросостояние с n = О отвечает состоянию нулевor'о беспорядка, так как
систему можно обнаружить в единственном микросостоянии, В качестве
количественной характеристики степени беспорядка используют энтропию
S, введенную в физику Л, Больцманом,
Sll = kв1пQ/l' (13,6)
[де Q/l  полное число всех возможных микросостояний, соответствующих
n; k в  постоянная Больцмана.
Данная величина определяется так, чтобы при существовании только
одноrо микросостояния ее значение равнял ось нулю и возрастало при YBe
личении числа микросостояний. Присутствующая в (13.6) постоянная обес
печивает соответствие между термодинамическим и статистическим опре
делением энтропии S. ДЛЯ целей наших исследований значение постоянной
Больцмана не имеет принципиальноrо значения, поэтому в дальнейшем мы
будем полаrать k в равным единице, что эквивалентно измерению энтропии
в единицах k в .
Для вычисления энтропии требуется перебор всех возможных микросо
стояний, что В общем случае оказывается неразрешимой задачей, потому
для измерения энтропии применяют метод, в котором используются Ha
блюдаемые характеристики статистической системы. В данном методе ис
пользован тот факт, что всякая система, состоящая из большоrо числа час
тиц, в течение времени t  00 обязательно повторит любое микросостояние
(или близкое к нему микросостояние). При этом, чем меньше времени IIрО
ходит до совпадения двух некоррелированных микросостояний, тем меньше
имеется различных микросостояний и, следовательно, меньше энтропия
системы. Наблюдаемая характеристика системы, которая может быть изме
рена,  это отношение числа совпавших пар к полному числу проведенных
сравнений микросостояний R/l (частота совпадений микросостояний), Эн
троп ия связана с частотой совпадений микросостояний выражением
Sll = lnRll' (13.7)
Формула (13.7) позволяет построить алrоритм вычисления энтропии,
реализующийся следующей последовательностью действий,
1, Создать систему, находящуюся в состоянии равновесия,
2. Наблюдать состояние системы в течение длительноrо времени, ocy
ществляя на каждом шаrе по времени обмен двумя частицами, номера KOTO
407

l' ,
К-й-b!a "!:'Р.й-=:'!.й-е.Л'!Рй-.ц--':!.:.4:!!.:'!:!=К-и-!...'!l!.й-,lf.=-=:? .l!.._e.'!!:.A!....A..L:!l!.... .. .._шш.,._. .
рых выбираются случайным образом независимо друr от друrа и микросо
стояния В соответствующие моменты времени.
3. Вычислить число совпадающих микросостояний.
4. Вычислить значение энтропии в соответствии с (13.7).
Отметим, что формула (13.7) применима только к равновесным систе
мам, поэтому для реализации описанноrо алrоритма требуется обеспечить
постоянство частиц в левой и правой половинах ящика. Следовательно, BЫ
числительный алrоритм, использованный нами в разделе 13.2, в котором
число частиц в каждой половине ящика флуктуировало за счет случайных
перемещений частиц, 1ребует определенной модификации. Удовлетворить
требованию нахождения системы в состоянии равновесия удается, если ис
пользовать модель, в которой система эволюционирует путем обмена одной
частицы справа на одну частицу слева. При этом возникает необходимость в
маркировке каждоrо микросостояния для их последующеrо сравнения и
подсчета числа совпадающих микросостояний. Один из известных методов,
который мы будем использовать в дальнейшем, состоит в описании каждоrо
микросостояния числом М
N',ft
М = L21 ,
1=1
( 13.8)
{'де l  номер частицы, а суммирование проводится по всем частицам,
находящимся в левой половине ящика,
для реализации описанноro выше aлrоритма в пакете МА 1LAВ необходи
мо создать два файла: файл Exchange.m, содержащий описание функции, воз
вращающей вектор, содержащий мrnoBeHHыe значения числа; файл Entropy.m,
содержащий описание функции, возвращающей значение энтропии.
% листинr файла Exchange.m
Cunction z = Exchange(NParticle,NExchange)
% функция, возвращающая мrновенные значения числа М
% NParticle  полное число частиц системы
% NExchange  число обменов
% задание начальной конфиrypации
NL=NParticle/2;
s=O;
Cor i=I:NL
L(i,I)=i;
Цi,2)=i+NL;
s=s+2AJ(i,I);
I
11
1; !i
1,1
, 11
'1'
i'
408

. _Ш   _  _   и.:....Nfel}'!Р.ва!!.'!:.. :'!.'.l!ш,!!!,сm.!!.'5.? :."!.=м..l
end'
% ВIчисление MrнoBeHHЫx значений числа М
M(I)=s;
for m=I:NExchange
Ri=floor(NL*rand(I)+ 1);
Li=floor(NL*rand(I)+ 1);
Rp=L(Ri);
Lp=L(Li,I);
L(Li,I)=Rp;
L(Ri,2)=Lp;
М(m+ 1)=М(m)+2. л Rp-2. л Lp;
end;
z=M;
% листинr файла Entropy.m
function z = Entropy(M)
% функция, возвращающая значение энтропии
% вектор, возвращенный функцией Exchange
к=о;
Nc=O;
N=length(M);
for i=I:N
Cor j=i:N
к=к+l;
if M(i)==M(j)
Nc=Nc+ 1;
end;
end;
z=-lоg(NdК);
end;
Далее необходимо выполнить следующую последовательность команд:
»N=10; % число частиц системы
» Ne=4000; % число обменов 
» A=Exchange(N,Ne); % маркировка мrновенных МИКР-:lСОСТОЯНИИ
» Entropy(A) % вычисление энтропии
ans=
5.3867
» lоg(fасtоriаl(N)/fасtоriаl(N/2).Л2) % вычисление точноrо
% значения энтропии
аns=
5.5294
409

I(ОII1ь.l?111{:р"IУ_: ..11!..е:.1.!!.?Й-'1111:'-!..з.и- ч _cк-и-x.'1P?H_e.cco 11й-к-е_fI1:.:..А._ т!::!.!!.ш_ш_, ш.. .
Задача 13.3
Модифицируйте функцию Епиору так, чтобы она возвращала частоту
совпадений Rn и энтропию 5п для кажд020 JltUкросостояния частиц
в ящике. Сравните полученные результаты для Rn> 5п с точными, Oцe
ните п02реИlНости значений R/J> 5п, найденных методом МонтешКарло.
Исследуйте завИСUАtoсть точности вычисляемых значений Rn, 5п для за-
даНН020 числа частиц от числа перестановок, Рассмотрите случаи
систем, содержащих различное число частиц N. Какое наибольшее знаш
чеllие N JltoЖНО использовать при выбранном способе маркировки мик
росостояний? Объясните полученные результаты,
''- .. .....'H'HH'HH"''HH ..H"'H'H.H'HH'H'_H''HH.HHH
11.
Задача 13.4
Модифицируйте функцию Exchaпge так, чтобы она возвращала массив,
содержащий номера частиц даНН020 .микросостоянuя, находящихся в
левой и правой половинах ящика в заданные MO-'Wенmbl времени. Задайте
функцию, вычисляющую по заданному массиву временной интервал, co
ответствующий появлению микросостояния, в котором нет ни одной
Частицы, из присутствующих в начальном микросостоянии (в момент
вре.нени t = О). Данное событие Jl1ОЖНО трактовать как появление пep
в020 состояния некоррелироваНН020 с начальным микросостоянием,
а соответствующий временной интервал как время корреляции Те'
Оцените значение Те для задаНН020 числа частиц по результатам не-
скольких испытаний. Вычислите значение энтропии системы, анализи-
руя _никросостояния, достИ2аемые системой в моменты времени t > Те '
Оцените точность вычисления значений Rn, Sn в данном случае. Рас-
СJlютрите случаи систе.м, содержащих различное число частиц N.
Определение энтропии (13.8), использованное нами выше, приrодно
только для равновесных статистических систем, т. е. систем, находящихся в
оnеделенном макросостоянии, В то же время результаты исследования пош
ведения системы невзаимодействующих частиц в ящике, проведенноrо Ha
ми в разделе 13.2, показывают, что даже в положении равновесия количест
во частиц п, п' в левой и правой половинах ящика меняются во времени,
Существование флуктуаций (т. е, фактическое отсутствие фиксированноrо
макросостояния) определяет необходимость обобщения (13.8). Для ПОЛуче
ния обобщенной формулы заметим, что вероятность появления paBHOBeCHO
[о макросостояния, характеризующеI'ОСЯ числом частиц п в левой половине
ящика, равна Р", а энтропия, соответственно, равна SII' Совокупность всех
возможных 'шачений 5" для данной статистической системы можно расш
i.
I i
11
410

. _ J!:f?f!!IР?.Й-U!..:fI1:.й-"!.'!..с.'!.'ши-ч-::к-?__с_и-:fI1:.':.1
сматривать как реализацию некоторой случайной последовательности, а co
ответствующие значения Р" как частоты их появления. Следовательно, эн
тропИЯ 5 рассматриваемой системы может быть определена, как взвешенная
сумма, вычисляемая по всем возможным реализациям:
5 = L Р',5" . (13.9)
"
Для модели частиц в ящике вероятность появления макросостояния с п
частицами слева Р" может быть вычислена путем подсчета микросостоя
N!
ний, отвечающих данному макросостоянию, n!(N .:.:)! и делением на пол
N N'
ное число возможных микросостояний L '(N  )' = 2N .
,,=0 п. п .
.
Задача 13.5
Вычислите аналитически Р" (п = О, N) для N=lO, 20.
Значение вероятности Р" можно также вычислить по последовательно
сти состояний, подсчитав количество появлений каждоrо маросостояния и
разделив соответствующие суммы на полное число событии. Для повыше
ния точности следует проводить вычисление данной величины по ансамблю
независимых реализаций. Напомним, что в 13.2, был писан ДOKYMeH, ПОш
зволяющий rенерировать ансамбль независимых случаиных реализации при
релаксации статистической системы к равновесию, вычислять усредненные
значения параметров, характеризующих макроскопическое состояние сис
темы, и оценивать время релаксации, Для нахоения значения вероятности
Рп следует создать файл Prob.m, содержащии описание функции, возвра
щающеЙ значение вероятности обнаружить данное микросостояние, однош
значно описываемое числом частиц в левой половине ящика.
% листинr файла Prob.m
fuoctioo z = Prob(B,NParticle,TauRel)
% функция, возвращающая вероятность появления paBHoBecHoro
% макросостояния
Nс=sizе(В,З);
Nr=size(B);
for k=O:NParticle
0=0;
for j=l:Nc
411

.!!:?!I1?_rrlfJ../?е..i?Il!..?_в.,: '!!:'Р.'!.З--l!.:'К-'::"I1fJ.?е.?_в_.  К-:.!!l_е..J.:f.1:... 1.l!..__._.
for i=TauRel:Nr
if В(1,iJ)==k
п=п+l;
end;
end;
end;
N(k+l)=n;
end;
Nf=sum(N);
z=N/Nf;
Далее необходимо выполнить следующую последовательность команд:
» NTrial=100; % число испытаний
»NParticle=100; % число частиц системы
» NStep=200; % длина единичной реализации
»E=EnsembIe(NTrial,NParticle,NStep); % rенерация ансамбля реализаций
» tau=150; % момент времени, начиная с KOToporo про водится
% подсчет числа макросостояний системы
» A=Prob(E,NParticle,tau); % вычисление вероятности появления
% данноrо макросостояния
% вычисление теоретическоrо значения вероятности
» for i=O:NParticle
PTheory( п+ 1 )=factorial(NParticle )/. . .
(factoriaI(n) *factorial(NParticle-п) )/2 л NParticle;
end;
% визуализация экспериментальной и теоретической зависимостей
% вероятности появления данноrо макросостояния от числа,
% частиц, находящихся в левой половине ящика
» рlоt(п,А,'k',п,РТhеjry,'--k')
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 13.9.
...... '"''''И'М"М''..
Задача 13.6
Сравните для заданных значений N (например, 10, 20) вычисленные
и точные значения вероятности Р", Как зависит точность численных
значений Р', от числа частиц системы и объема ансамбля реализаций?
412

.}:..!v!.'!.':!.fJ.'!./_U:'.rrll!"'!.':!':'rrI':!.:'=К'!..Й.С':!.=rrI
Задача 13.7
Вычислите для заданных значений N равновесную энтропию, в cooт
ветствии с соотношением (13,9), При этом используйте значения
вероятностей l, найденные в задаче 13,6, и соответствующие
значения энтропии, вычисленные с пОАЮЩЬЮ документа, описаННО20
в данном разделе, Сравните точное и расчетные значения равновеС1ЮЙ
энтропии, Оцените тОЧl-lOсть расчетНО20 значения,
o.09
I
::1
I
0061L
005
i
0.04:
о.озl
I
0021
0.011
1
о'
о 20
'l
fv'
1 \
//\ \
1/ \ \
I1 \
, '
!; \'\
,1 ,
" \
;/ :
:;' \\
: :\
f 1:\
11' \\
, '\
!/ \\
1, \\
; I \\
/} ;\
 ",
40 60
80
100
120
Рис. 13.9, Зависимость вероятности появления даННО20 макросостояния от числа
частиц, находящихся в левой половине ящика (сплошная кривая  эксперимент,
пунктиРllая кривая  теория)
Задача 13.8
В функции, возвращающей значения вероятности появления равlювесно
со макросостояния, характеризующесося числом частиц п в левой поло
вине ящика (рис. 13.6), использован не самый эффективный с вычисли
тельной точки зрения алсоритм, так как проводится проверка на нали
чие всех возможных макросостояний (цикл по пеу,?Менной k), Можно
существенно сократить время вычислений, если предварительно oпpe
делять Аtuнимальное и максимальные отклонения числа частиц от paв
новеСНО20 значения и затем рассматривать только данный диапазон
возможных макросостояний, Дополните текст функции Р( ) cooтвeт
ствующu...., Фра2Ментом. Убедитесь в том, что внесенные вами uзме
нения в пp02pa.tМy действительно привели к уменьшению времени вы
числениu.
413

..li?.л:':..!?. п.::J1.?!?i}"е!!'.!.fJ.й-6!'.!.: .1!.'.!.!'.!.:к-пp?.:==o .6 . а.К-:'!'!..!:!Т/lJ!.....
Задача 13.9
Используя усредненную по ансамблю реализаций завиСlL'wость п = (n(I)) ,
вычислите по точной формуле значения энтропии в соответствующие
моменты времени. Изобразите 2рафически зависимость энтропии от
времени. Исследуйте, как зависит величина флуктуаций энтропии от
числа частиц системы. Объясните полученный результат.
ЛИТЕРАТУРА
1, Райф ф, Статистическая физика. М,: Наука, 1986.
2, Матвеев А. Н. Молекулярная физика, М.: Высшая школа, 1981,
3. Климонтович Ю, Л. Статистическая физика. М.: Наука, 1982,
4, Методы Монте-Карло в статистической физике/Под ред. К. Биндера, М,: Мир, ] 982,
5, [мурман В. Е, Теория вероятностей и математическая статистика, М,: Высшая школа,
1998.
6, rулд Х" Тобочник Я, Компьютерное моделирование в физике, М,: Мир, ] 990.
11
I
414
I
1\
I
rлава 14
МОДЕЛИРОВАНИЕ
МИКРОКАНОНИЧЕскоrо АНСАМБЛЯ
МЕТОДОМ МОНТЕ-КАРЛО
14.1. Микроканонический ансамбль
Введем, следуя общепринятому в статистической физике подходу, поня
тие <<микроканонический ансамблы}. Рассмотрим для этоrо замкнутую сис
тему, состоящую из N частиц. Выберем в качестве макроскопических xapaK
теристик системы объем V и полную энерrию системы Е, которые будем
считать постоянными. Кроме Toro, предположим, что система является изо
лированной, т. е. можно пренебречь влиянием на нее внешних факторов.
Замкнутые макроскопические системы, как было показано в rл, 10 и 13,
стремятся перейти в стационарное равновесное состояние, обладающее
максимальной энтропией. Отметим, что если на макроскопическом уровне
система характеризуется тремя величинами N, V, Е, то на микроскопиче
ском уровне существует OI'Ромное число конфиrураций, реализующих за
данное макросостояние (N, V, Е) .
Таким образом, на возможные микросостояния накладывается единст
венное оrpаничение, они должны быть таковыми, чтобы обеспечить задан
ные физические характеристики системы: число частиц, объем, полную
энерrию. Так как причины, по которым следует предпочесть одно состояние
дpyrOMY, отсутствуют, можно постулировать, что система в любой момент
времени может оказаться с равной вероятностью в одном из возможных
микросостояний (постулат о равенстве априорных вероятностей). Это озна
чает, что для системы с n достижимыми состояниями вероятность обнару
жить систему в микросостоянии s равна
! 1
Р  , если s  достижимо
s = n .
О, в противном случае
Как очевидно, сумма Ps по всем n равна единице.
Для определения средних значений физических величин, характеризую
щих макроскопическую систему, можно использовать два способа, В пер
вом способе измеряют физические величины в течение достаточно большо
ro промежутка времени, в течение KOToporo система успевает побывать в
большом числе достижимых микросостояний, и про водят последующее yc
(14.1 )


!!..?!..f!.!Й-,!IС:J!.Il!!!!..!'!=l!.Р'й-.'!'."!:"1!.':!з--':!. :'5..'!!.!!.Р.Й--IJ:::п.l!К-'!!!!:'.!:!:.Т:!:.I!..ш.. Ш .. Ш"' ..
реднение, Данный подход был уже использован нами в rл. 1 О, коrда Meтo
дом молекулярной динамики рассчитывались средние значения температу'
ры и давления неидеальноrо rаза, С точки зрения проведенноrо усреднения
во времени, вероятность Ps есть доля времени, коrда система за время на-
блюдений находится в данном микроскопическом состоянии S.
Несмотря на очевидный физический смысл средних по времени, в стати.
стической физике вводят понятие статистических средних в данный момеН1
времени, которые вычисляются по ансамблю микросостояний, соответст-
вующих заданному макросостоянию. (rипотеза о совпадении средних зна.
чений величин, вычисляемых усреднением по времени и усреднением по
ансамблю реализаций, называется эрrодической rипотезой.) Полное число
систем в ансамбле равно числу возможных микросостояний. Вероятность
обнаружить в ансамбле тождественных систем s-ую реализацию, определя-
ется выражением (14.1). Ансамбль систем, характеризуемый величинами Е,
Т, V, и описываемый распределением вероятностей вида (14.1), называется
микроканоническим ансамблем.
Будем считать, что система характеризуется некоторой величиной А,
значение которой в S-M состоянии равно As. Тоrда среднее значение А по
ансамблю определяется как взвешенное среднее
(А) = LAsPs . (14.2)
s
Из (14.2) видно, что для нахождения среднеrо по ансамблю значения ве-
личины необходимо знать значения вероятностей Ps. При небольшом числе
частиц значения вероятностей можно определить методом перебора, анало.
rично тому, как это сделано в rл. 12 при моделировании случайных блужда-
ний. Однако при увеличении числа частиц данный метод становится непри
емлемым из-за большоrо объема вычислений. В этих условиях приходится
использовать приближенные методы, среди которых одним из самых эф
фективных является метод Монте-Карло.
14.2. Моделирование
микроканоническоrо ансамбля
Общая идея метода Монте. Карло для микроканоническоrо ансамбля cocтo
ит в получении репрезентаrnвной выборки из полноro числа микросостояний и
оценке с ее использованием значения верОЯ'ПIости Ps. для этоro можно исполь-
зовать достаточно очевидную процедуру: зафиксировать полное число чаСТИIl
N и объем системы V, изменять случайным образом координаты и скорости от-
дельных чаCl1Щ, принимать конфиrypации микросостояний, имеющих задан-
ную полную энерrnю, К сожалению, данная процедура оказывается весьма не.
1,
l'
I
416
ш..ш....ш.ш!...':!'!.1!.!Я!,Й-!!Il:'!'!':!.У!.К-l!.'.!'.':!:::..к-':!::..й-..l!.'!!!!!..l!..'!!..одомш.!,!!!:.:f!c!.!!.l!!!..
эффекrnвной, так как большинство конфиrypаций вообще не будут иметь тре-
буемую полную энерrnю и должны быть отверrnуrы.
Эффективная вычислительная процедура метода Монте-Карло для мик
роканоническоrо ансамбля была предложена в [1]. Она состоит в разделе
нии исходной макроскопической системы на две подсистемы: исходную,
называемою далее системой, и подсистемы, состоящей из одноrо элемента,
которую авторы назвали демоном (по аналоrnи с демоном Максвелла). Роль
демона аналоrична роли члена кинетической энерrии в методе молекуляр
ной динамики, обсуждавшеrося в rл. 10. Обходя элементы системы и пере
давая энерrnю, он обеспечивает изменение конфиrypации системы. Если
энерrии, запасенной в манrnи демона, оказывается достаточно, он cдaeт
энерrию тому элементу системы, которому требуется энерrия, для осущест
вления изменения конфиrypации. И наоборот, если для изменения конфиry
рации требуется уменьшить энерrию системы, энерrия передается частицей
демону. Единственное оrpаничение состоит в том, что энерrnя демона
должна быть положительной. Описанная процедура алrоритмически выrля-
дит следующим образом.
1. Сrенерировать начальную конфиrypацию системы с заданным значе.
нием полной энерrии.
2. Выбрать случайным образом частицу и произвести пробное изменение
ее координат.
3. Вычислить полную энерrию системы в новом состоянии.
4. Если в новом состоянии энерrия системы оказывается меньше, то
система отдает энерrию демону, и новая конфиrypация принимается.
5. Если в новом состоянии энерrия системы оказывается больше, то HO
вая конфиrypация принимается, если энерrии демона достаточно, чтобы пе
редать ее системе. В противном случае новая конфиrypация не принимает
ся, и частица сохраняет свои старые координаты.
6. Если пробное изменение не меняет энерrию системы, то новая
конфиrypация принимается.
Перечисленные выше действия повторяются до получения репрезента
rnвной выборки микросостояний. Можно ожидать, что через некоторый
промежуток времени система достиrнет paBHoBecHoro состояния, в котором
у системы и демона будут некоторые средние (для каждоrо) значения энер-
rии, При этом значение полной энерrии системы остается постоянной. Так
как демон представляет собой только одну степень свободы, в отличие от
рассматриваемой статистической системы можно ожидать, что флуктуации
системы будут невелики,
Применим описанный aлrориrм к классическому одномерному идеальному
raзу, скорости частиц KOToporo непрерывны и неоrpаниченны, а энерrия частиц
не зависит от положения чаCl1Щ, поэтому полная энерпlЯ частиц есть сумма
14---,1576
417

 I
1 I
I I
.l!.?А1.'2ъ.!?'!!l!I?А1.й-l!.l!()l!.'.I.Р.!III'Сll!:l!Оlf.?в- в..!!.,:е.'!!...J.1.А.Т!!13.
........ ......... .:J.1.<!.=-Л!:!f..?в.!!.I!Il!"Л:!:!'5?CI..l!.()!.!.l!..:'5!!.:().l!..,.,:б!!!!.!1е..'!!.й-?:!A1..J.1.()!.'!!.:l!!!P..l!.CI..
кинетических энерrий отдельных частиц, для изменения конфш-урации будем
случайным образом изменять скорость случайно выбранной частицы.
Для реализации описанноrо алrоритма в пакете МА ТLAB создадим два
mфайла: 1) файл InitD.m, содержащий описание функции, возвращающей
абсолютные значения скоростей в момент времени t = о; 2) файл Demon.m,
содержащий описание функции, возвращающей усредненные по ансамблю
реализаций значения: энерrии демона (Edave), средней энерrии системы на
одну частицу (Esysave), средней скорости на одну частицу системы (Уауе),
среднеrо числа принятия (Accept).
% листинr файла InitD.m
function z = Init(N,Esystem)
% функция, возвращающая абсолютные значения скоростей в момент t = О
% N  число частиц системы
% Esystem  энерrия системы
V =(EsystemJN). ЛО.5j
for i=I:N
z(i)=Vj
endj
% листинr файла Demon.m
function [Edave,Esysave, V ave,Accept] =
Demon(N,Esystem,NTriaI, V el,dV)
% функция, возвращающая усредненные по ансамблю реализаций
% значения: энерrии демона (Edave), средней энерrии системы на одну
% частицу (Esysave), средней скорости на одну частицу системы (Уауе),
% среднеrо числа принятия (Accept).
Edemon=Oj
Vtot=sum(Vel)j
V соm=О;
Escum=Oj
Edcum=Oj
Accept=Oj
for j=I:NTrial
for i=I:N
dv=(2*rапd(I)-I)*dVj % случайное изменение скорости
Iр=Пооr(N*rапd(I)+I)j % случайный выбор частицы
VTrial=Vel(Ip)+dVj % пробное изменение скорости
dе=0.5*(VТriаl.Л2-Vеl(Iр)Л2)j % пробное изменение энерrии
if de<=Edemon % если энерrия уменьшается изменение принимается
Vel(Ip)=VTrialj
Vtot=Vtot+dvj
Accept=Accept+ 1 j
Еdеmоп=Еdеmоп-dеj
Esystem=Esystem+dej
endj
Edcum=Edcum+Edemonj
Escum=Escum+Esystemj
Vcum=Vcum+Vtotj
endj
endj
Edave=Edcum/(NTrial*N)j
Accept=Acceptl(NTrial*N)j
Esysave=I/N*Escum/(NTrial*N)j
V ave=I/N*V cum/(NTrial*N)j
Далее необходимо выполнить следующую последовательность команд:
» Esystem=40j % энерrия системы
» N=40j % число частиц системы
»NTrial=4000j % число испытаний
»dV=2*2ЛО.5j % максимальное значение изменения скорости
» Vel=InitD(N,Esystem)j % задание начальных скоростей
% вычисление характеристик состояния идеальноrо rаза
»[Edave Esysave Vave Accept]=Demon(N,Esystem,NTrial,Vel,dV)
Edave =
0.9566
Esysave =
0.9761
Vave =
1.5695е-004
Accept =
0.5119
Задача 14.1
Проведите численные расчеты для заданных значений числа частиц
(N = 10,20,40,80), и различных значений отношения dV / {E;y:em,
Изобразите 2рафически зависимости коэффициента принят ия (Accept)
11 Esystem
от dV IJ  при заданном числе частиц. Используя метод Haи
меньших квадратов, подберите аналитическое выражение, описываю-
/ I Esystem
щее зависи-lюсть коэффициента прuнятия (Accept) от dV/  N ,
418
419

1!.й-:'!.п..?'!!Р!.::'!.й-:Л-'!.Ей-а.'!.: rf!'!..!и-Ч-,='.<.I'.х.п.Fй-не:?l!..!!а..."!.:..-!:..!1:..
При каком отношении
/' /' Es)'stem
dV '\ . . значение коэффициента приня
\ N
тия оказывается zO.5?
, i
i
Задача 14.2
Модифицируйте описанную выше функцию петоп( ) так, чтобы номера
частиц, скорость которых подлежит изменению (переменная lр), выби
рались последовательно, Приводит ли иЗАlенение способа выбора НОАlера
частицы к изменению средней энерzии систеА1Ы на частицу и средней
энеР2Uи демона?
1 I
I
Задача 14.3
Можно ввести кинетическое определение тедтературы, в cooтвeтcт
вии с которым температура определяется из соотношения
 т( v2) = l Tkill ' (14.3)
zде m(v2) средняя кинетическая энеРZltЯ на частицу, Tkill тeмпepa
тура zаза, измеряемая в единицах kB. Модифицируйте описанную выше
функцию петоп(), представленную на рис, ]4,2, так, чтобы
в npozpaммe дополнительно вычислялось и дополнительно выводuлось
в векторе, возвращаемом данной функцией, значение средней киilетиче
ской энерzии на одну частицу. Используя соотношение (14,3), получите
Tkill . Как связаны значения температуры и энерzии де)l1Она?
Один из наиболее важных результатов, полученных в задаче 14.3, COCTO
ит в демонстрации возможности введения кинетическоrо определения TeM
пературы, как средней на одну частицу кинетической энерrии частицы мик
роканоническоrо ансамбля. При этом значение температуры снекоторой
поrpешностью оказывается равной энерrии демона. В то же время микрока
нонический ансамбль нельзя считать абсолютно адекватной моделью pe
альных статистических систем, так данные системы не являются термоди
намически изолированными, но находятся в тепловом контакте с окружаю
шей средой. Это приводит к возникновению потока тепла между изучаемой
системой и окружаюшей средой. Так как размер исследуемой системы
обычно MHOI'O меньше размера окружаюшей среды, первую будем называ1Ь
микросистемой, а последнюю  тепловым резервуаром (термостатом), При
этом закон сохранения полной энерrии относится к составной системе, co
стоящей из микросистемы и тепловоrо резервуара,
420

... ... ,..... .. !:.!v!с:.:.л.!!I!..й---а.'!.и-:!!.l!..f!.C}'.<.:z..'.'.().!.1'!.Ч-.::'2й-. и--II,с.б.:.!!:'!!..й-_д!!,.,:!й-!I,!,,::1!.а.Р..й-..
Рассмотрим большое число воображаемых копий микросистемы и теп
ловоrо резервуара. Рассматриваемые как единое целое микросистема и теп
ловой резервуар являются изолированной термодинамической системой
и Moryт быть описаны с помощью микроканоническоrо ансамбля. Так как
в данном случае наибольший интерес представляют равновесные значения
физических величин, описывающих микросистему, необходимо знать Bepo
ятность Ps, с которой микросистема обнаруживается в состоянии s с энерrи
ей Es, Ансамбль, который описывает распределение вероятностей состоя
ний микросистемы, находящейся в термодинамическом равновесии с :,пло
вым резервуаром, называется каноническим.
В общем случае в качестве микросистемы может выступать любая MaK
роскопическая система, размер которой меньше тепловоrо резервуара, в том
числе и отдельная частица, выделенная среди друrих частиц тепловоrо pe
зервуара. Примером такой микросистемы служит демон, KOToporo можно
считать микросистемой, микроканоническое состояние которой определяет
ся только ее энерrией. Таким образом, метод отыскания распределения Be
роятностей в каноническом ансамбле заключается в том, чтобы выполнить
численное моделирование демона, который обменивается энерrией с иде
альным rазом, состоящим из N частиц. Идеальный rаз в данном случае иr
рает роль термостата и задача состоит в определении плотности вероятно
сти P(Ed) Toro, что демон имеет энерrию Ed' Вычислительный алrоритм,
позволяющий решить данную задачу, достаточно очевиден.
1. Провести моделирование каноническоrо ансамбля методом MOHTe
Карло, сохраняя на каждом шаrе МонтеКарло значение энерrии демона.
2. Для найденной реализации значений энерrии демона вычислить pac
пределение вероятностей P(Ed)M.
3. Определить функциональную зависимость P(Ed)M от температуры.
Для реализации данноrо алrоритма в пакете МА ТLAB создадим mфайл
DemonE.m, содержащий описание функции, возвращающей MrнoBeHHыe
(на каждом шаrе МонтеКарло) значения энерrии демона.
% листинr файла DemonE.m
function z = DemonE(N,Esystem,NTrial,Vel,dV)
% функция, возвращающая мrновенные значения энерrии демона
% N  число частиц системы
% Esystem  энерI'ИЯ системы
% NTria\  числО испытаний
% Уе]  вектор, возвращенный функцией InitD
421

.f!..f!Il}:.?п-:!/!.!?.:..l!.?.!:!...fJl!!.I!!:..1!'!.!I.:.=UХI}!!.?lI.:.=С..?l!.'5..:!!!!.111.!?:1.!!........
% dV  максимальное изменение скорости
Edemon=O;
z(I)=Edemon;
k=l;
for j=I:NTrial
for i=I:N
dv=(2*rапd(I)-I)*dV; % случайное изменение скорости
Ip=f1oor(N*rand(I)+ 1); % случайный выбор номера частицы
Vtrial=Vel(Ip)+dv;
de=0.5*(V trial. л 2- V el(Ip). л 2); % пробное изменение энерrии
if de<=Edemon % если энерrия уменьшается, то пробное
% изменение принимается
Vel(Ip)=Vtrial;
Еdеmоп=Еdеmоп-dе;
end;
k=k+l;
z(k)=Edemon;
end;
end;
Далее необходимо выполнить следующую последовательность команд:
» Esystem=40; % энерrия системы
» N=40; % число частиц системы
» NTrial=500; % число испытаний
»dV=2*2ЛО.5; % максимальное изменение скорости
» V el=InitD(N,Esystem); % вычисление начальных скоростей частиц
»Ed=DemonE(N,Esystem,NTrial,Vel,dV); % вычисление мrновенных
% значений энерrии демона
% визуализация зависимости мrновенных значений энерrии
% демона от времени
» i=I:length(Ed);
» figure(I);plot(i,Ed,'k');axis([O 20000 О 8])
% вычисление и визуализация распределения вероятностей P(Ed)M
» xl=min(Ed);
» x2=max(Ed);
» Nint=50;
» i=1 :Nint;
» х(О=хl +(х2-х 1)/(Nint-l)*(i-l);
» h=hist(E,x);
I
1:
422

 .  ..........:..f!:.fl}-!l!..?l!.l!.:":!.!I.fJ?..аllо.'ll/.:.=-'5..0о...'!=?l!.":!.:.п-:.??!!I>!..1!..о..'п-:::!il!.f!.l!?..
»figure(2);bar(x,h); colormap white
% вычисление и визуализация функции, аппроксимирующей
% распределение P(Ed)M
» FI0=iпliпе('u(I)*ехр(-u(2)*z)','u','z') % задание аппроксимирующей
% функции
FI0=
Inline function:
FI0(u,z) = u(I)*exp(-u(2)*z)
»Ьеta=пliпfit(х,h,FI0,[ЗООО 1]); % вычисление коэффициентов
% аппроксимирующей функции
% визуализация rистоrpаммы последовательности MrнoBeHHЫx
% значений энерrии демона и аппроксимирующей функции
» Ni=500;
» i=I:Ni;
» X(i)=xl+(x2-хl)/(NИ)*(i-l);
» figurе(З);Ьаr(х,h); colormap white
» hold оп
» plot(X(i),FI0(beta,X(i»,'k')
» hold off
Результаты выполнения описанной последовательности команд пред-
ставлены на рис. 14.114,3.
02 04 06 06
12 14 1.6 16 2
J: 10J
Рис. 14.1. Зависимость McHoвeHHыx значений энеРi?ии демона от времени
(номера шаi?а Монте-Карло)
423

OM п ЬЮ!!!!J!!.'.?!..:!с:!.':!Р.!!l!..а//и'!...1!.':!з-!!:!..:с.l5..'!!..!'-J?.:!.'i::l!.!!.!!. пal!!!!,e '!}!'!::I!...
4000 ,'__4."""""""'""",,.,
r
.500 '
3000
2500
2000
1500
1000
Рис, 14.2,
Распределение по
энеР2ии демона
N. P(Ed)M
500
llinllitrtтr
2 3 4
00
4000
3500
3000
2500 \
\
2000 \
1500 
,
Рис, 14.3. Функция, 1000
аппроксимирующая 500
распределение по энеР2ии
демона N. P(Ed)M 00
Таким образом, результаты моделирования идеальноrо rаза методами
микроканоническоrо и каноническоrо ансамблей позволяют сделать сле
дующие выводы.
1. Распределение вероятностей энерrии демона описывается функцией
вида
.!JL
P(Ed ) = Ае 1ieпп,
{'де А  постоянный коэффициент, I;erm:::o 0.9901 З.
(14.4 )
424
...............
...Ос:!.'!.fJ.й-.':!.е..!!..и.'РУ..с:..I!!!!.'.':!.е.?z...f!...l!.!/:!!!!!!!!..!.I!!..f!...д-:!"!...O!,I!!'!.:l}.I!.:?
2. Температура идеальноrо rаза, определяемая как средняя кинетическая
энерrия, приходящаяся на одну частицу, Tkiп совпадает в пределах точности
модели с температурой термостата T/erm. Это позволяет сделать вывод о
том, что демон находится в термодинамическом равновесии с термостатом.
Распределение вероятности (14.4) называется распределением Больцма
на или каноническим распределением. Данное распределение принято запи
сывать в следующем виде:
Е
Р(Е) = e  kbT ,
( 14.5)
rде Z  нормировочный множитель, выбираемый из условия равенства еди
нице суммы по всем состояниям демона, kB =1.38.1016 ЭР2'2рад1 посто
янная Больцмана. Параметр Т называется абсолютной температурой. TeM
пература может измеряться в единицах kB, тоrда распределение Больцмана
принимает вид
Е
Р(Е) = eT . (14.6)
Формулы (14.5), (14.6) обеспечивают простой способ вычисления темпе
ратуры по средней энерrии демона (Ed), которая по определению равняется
Е
J Ее T dE
(Ed) =  E = Т . (14.7)
JeTdE
Таким образом, средняя энерrия демона равняется температуре TepMO
стата. Данный результат справедлив, только при условии, что значения
энерrии принимают непрерывные значения.
Отметим, что формулы (14.5), (14.6) применимы для любой микросисте
мы, находящейся в тепловом равновесии с термостатом,  каноническоrо
ансамбля  при этом всякое макросостояние задается температурой Т, чис
лом частиц системы N и объемом V. В отличие от каноническоrо ансамбля
микроканонический ансамбль характеризуется энерrией Е, числом частиц
системы N и объемом V.
.........H.
Задача 14.4
Исследуйте зависимость точности определения температуры, oпpeдe
ляемой с помощью }.1икроканоническоzо и каноничеСКО20 аНС(J)l1блей от
числа частиц CUCme..'.tbl N и числа шаzoв метода МонтеКарло.
425

. к ?Л:I.l!"о!'!е.Р.'..l!.':.:!'::'I.I!Р:!Cl!.'!:.':_1!.l!.З---l!..':...СР'?":<:!!...f!.':!!!.:!:T1.!!.._.. .
14.3. Модель Изинrа
Одной из простейших моделей, используемых в статистической физике
для моделирования фазовых переходов в маrнитных веществах или бинар
ных составах, является модель Изинrа. Данная модель относится к ши-
рокому классу решеточных моделей, в которых рассматриваются локальные
взаимодействия, т. е. взаимодействия между ближайшими узлами решетки.
В маrнитных системах локальные взаимодействия обусловлены спинами,
расположенными в узлах решетки. Спины MOryт представлять собой, Ha
пример, маrнитные моменты атомов в твердом теле, взаимодействующие
дрyr с друrом и внешним маrнитным полем,
Рассмотрим решетку, состоящую из N узлов. Свяжем с каждым i-M уз-
лом решетки число s; = 11, характеризующее направление маrнитноrо мо-
мента системы, rде s; = +1, если спин ориентирован в положительном Ha
правлении оси oZ , и s; = ] , если спин ориентирован в отрицательном на-
правлении оси oZ. (Данная картина характерна для частиц с полуцелым
спином, хотя далее мы рассматриваем спины как классические степени CBO
боды и не вводим для них используемые в квантовой механике правила
коммутации уrловоrо момента). Любое микросостояние решетки задается
набором переменных {S)' S2'" ., S N }. Так как макроскопические свойства
системы определяются свойствами ее достижимых МИКрОСОСТОЯНИЙ" необ-
ходимо вычислить зависимость энерrии Е от конфиrурации спинов. Полная
энерrия при наличии маrнитноrо поля h в модели Изинrа равняется
N N
Е = ] '" s.s.  h'" s , (14.8)
L.JI) L.Jl
и.л ;=1
rде (i, Л означает, что сумма берется по всем ближайшим соседним парам
СiIИНОВ, константа обменной связи J характеризует силу взаимодействия co
седних спинов (рис. 14.4).
11I
i!
11 11
11 11
E=-J
E=+J
Рис, Z 4.4. Энерzия взаимодействия между ближайшиА1U соседНlL'I1И спинами
в отсутствие маснитносо 1/ОЛЯ
Если J > О , то в состоянии tt и ,j,,j,, т, е, при одинаковой ориентации
спинов ближайших соседей, энерrетически выrоднее состояний t,j, и ,j, t ,
426

Ш_.. .!...:.!!?f!!!..Р..?в--r:..'!.l!!...!!!!?У.!.r:..'!!!!!.l!.'!!!I5!!:..?...'!..'::!:':!._f!!'!!.!!..:'!!..?...:!-':!А!....О!.I!!!!._____l!..'!.P..ll!!
у которых соседние спины ориентированы в противоположные стороны.
Следовательно, можно ожидать, что для J > О состояние с наименьшей
полной энерrией является ферромаrнитным, т. е. в среднее число спинов
сориентированных в одном направлении не равно нулю. Если J < О, то
с энерrетической точки зрения более предпочтительными оказываются co
стояния t,j" ,j, t , ДЛЯ которых соседние спины антипараллельны. Следова
тельно, среднее число спинов, сориентированных в одном направлении,
равно нулю, т. е. спины упорядочены через один (антиферромarнитное co
стояние). При наложении внешнеrо маrнитноrо поля, направленноrо парал-
лельно оси oZ, спины t и ,j, приобретают дополнительную внутреннюю
энерrию, равную h и +h, соответственно.
Выделим основные упрощающие предположения, положенные в основу
модели Изинrа.
1. Кинетическая энерrия узлов решетки принимается равной нулю.
2. В выражении, описывающем энерrию взаимодействия, учитывается
только вклад от ближайших соседей и предусматривается только два
дискретных состояния для спинов.
Так как в дальнейшем нас будут интересовать термодинамические xa
рактеристики данной системы, оказывается удобным измерять энерrии свя
зей J и h в единицах температуры, Тоrда нarpевание системы будет приво
дить к ослаблению этих связей. Возможные конфиrypации системы опреде-
ляются заданием значений всех спиновых переменных, число которых
составляет 2N, а вклад любой из 2N спиновых конфиrураций s определяется
функцией распределения для каноническоrо ансамбля
eE(s)
w(s) = ш.. Z . (14.9)
rде
N
Z(J,h) = Le E(').
(14.10)
Предваряя применение алrоритма демона к исследованию модели Изин
ra методом микроканоническоrо ансамбля, необходимо получить выраже-
ние, связывающее энерrию демона и температуру термостата. Напомним,
что в непрерывном случае распределение энерrии демона подчинялось
формуле Больцмана (14,6), Предположим, что данное распределение веро-
ятностей справедливо для любой макроскопической системы, находящейся
в состоянии термодинамическоrо равновесия, Тоrда
427

l! С:!.!!!!!!Й-:.!!."!.Е.'!..!,!!еrJ:."!.!.и-.:"!.f!.l!.()Zi::С!!..'!..'5.!!!!..!:.f!:..!:!:.!!. ..
Е"
. LEde'T
(Ed)=E ,
d
LeT
(14,]1)
rде суммы вычисляются по всем возможным значениям Ed' Минимальная
ненулевая потеря энерrии системы в нулевом мarнитном поле составляет,
как видно из рис, 14.5, 2sJ, rде s  суммарный спин ближайших соседей,
опрокидывающеrося спина,
, I
i
) )) ) 1 )
ДО поrлr
Рис, 14,5, Изменение энерzии, обусловленное изменением ориентации
центральноzо спина
В одномерном случаем суммарный спин ближайших соседей равен О, или
2, т. е. минимальная ненулевая потеря энерrии равняется У. Следовательно,
энерrия демона, может равняться О, У, 4J, ... . Если ввести обозначение х =
2JП", то выражение (14.11) для бесконечной решетки принимает вид
'"
L(x.п)elI'x
( i ) = 11=0 '"
LeII'x
,,=0
Бесконечные суммы, стоящие в числителе и знаменателе, MOryт быть
вычислены аналитически. Так как обсуждение методов их вычисления BЫ
ходит за рамки нашей книrи, мы используем для ее вычисления встроенный
в пакет MAТLAB символьный процессор.:
(14.12)
СУмма беСКОllеЧIIО20 ряда (J 4, J 3) lIаходuтся вЫnОЛllеlluем следующей nоследователыlO
сти комаllд:
»expr=syт('x"n"exp(-x*n)') % задаlll/е выражеllllЯ, стОЯще20 под Зllаком су.ммы
ехрт =
х"n"ехр(-х"n)
»syтsuт( ехрт, 'n ',O,inf) % вЫЧl/слеlluе суммы ряда
aпs =
х*о.р(-х)/( 1 exp(-x)Y 2
А l/аЛО;'иЧIIО Ilаходится Cy.M-"1а беСКОllеЧl1020 ряда (J 4.4).
428
...............
. . .ш ':!!!..еЛI!.l!..()'!..и-/"!.:л."!..!!()'!!!!!и-..Ч,ес КО20 аl':.Л!!.е..'!!.()!!.!'.!'!'!.:!.!!!!'
'"
L(x'll)elI'x X. xp(..x) :2'
11=0 (1 exp(x))
 II'X 1 (14.14)
L.J е  1  exp( .;) .
/1=0
Разделив (14.13) на (14.14) и выполнив очевидное преобразование, по
лучаем
(i)=e/::"]' (14.15)
Подставив в (14.15) вместо х выражение 2JП"и решив получившее ypaB
нение оmосительно Т, получаем
т = 2] (14.16)
lп(1 + 2] /(Ed))
(14.13)
Задача 14.5
Получите аналитические выражения для средней энеР2ИИ демона для
системы, состоящей из конеЧНО20 числа Спинов, Может ли быть найде
но аналитическое выражение для зависимости температуры от энер
2ИИ демона в данном случае? Сравните значения средней энеР2ИИ демона
для системы, состоящей из N спинов (Ed)N' получаемые по точной
формуле с соответствующими З1-Iачениями (Ed)"" получаемыми по
формуле (14.15). Постройте зависимости !(Ed)N (Ed)",1 при различных
температурах. Оцените п02решность определения значения тeмпepa
туры, получаем020 по формуле (14.16), для системы, состоящей из N
спинов, Как зависит данная п02решность от N и Т?
Отметим, что в одномерной модели Изинrа демон должен выбирать
спины случайно, что позволит избежать подсчета периодически повторяю
щихся конфиrypаций. Так как нашей целью является оценка термодинами
ческих характеристик бесконечной термодинамической системы, следует
учесть краевые условия. В качестве таковых в описываемом ниже ДOKyмeH
те нами выбраны периодические (тороидальные) краевые условия: решетка
считается кольцом, в котором спины Sj, находящиеся в узлах i = 1 и i = 1,
взаимодействуют друr с друrом. Это обеспечивает равное число взаимодей
ствий для всех спинов в изучаемой системе.
 моделирования одномерной модели Изинra методом микроканониче
cKoro ансамбля в пакете МА П..АВ необходимо создать файл Ising.m, содержа
щий описание функции, возвращающей значения полной энерrии системы,
энерrии демона, намаrниченности и среднее число принятия решений,
429

.!!:.?!'!:!?!!!!J?!?I!.:Л-'!!!..?'!..I!!.I'!.:.1!..l!.!l!.'!!.Е?е.::.!!'!..!!..I5..:'!!.:!.!:i!!:1.!!..
1:
% листинr файла Ising.m
function [Es,Ed,SpM,Accept]=Ising(NspinJ ,h,Esi,NTrial)
% функция, возвращающая MrнoBeHHыe значения полной энерrии
% системы (Es), энерrии демона (Ed), намаrниченность (SpM)
% и среднее число принятия (Accept)
% Nspin  число спинов системы
% J  константа обменноrо взаимодействия
% h  внешнее маrнитное поле
% Esi  конечная энерrия системы
% NTrial  число испытаний
% задание конфиrурации спинов в момент времени t = О
for i=I:Nspin
s(i)=lj
endj
M=Nspinj
Esystem=-(J +h)*Nspin j
Edemon=2* J*ceil(Esi-Еsуstеm)/(2* J»j
Es(I)=Esystemj % энерrия системы в момент времени t = О
Ed(I)=Edemonj % энерrия демона в момент времени t = О
SpM(I)=Mj % маrнитный момент системы в момент времени t = О
Accept=Oj
k=lj
% реализация метода микроканоническоrо ансамбля
for i=1 :NTrial
for j=I:Nspin
Ispin=floor(Nspin*rand(I)+I)j % случайный выбор номера
% спина периодические rpаничные условия
if Ispin==1
Left=s(Nspin) j
else
Lеft=s(Isрiп-l)j
endj
if Ispin==Nspin
Right=s(l)j
else
Right=s(Ispin+l)j
endj
dе=2*s(Isрiп)*(-h+J*(Lеft+Right»j % пробное изменение энерr"ии спина
if de<=Edemon % принятие пробноrо изменения
430

..........__ш.:!!.?,f!J!..Р...?'!..и..:II!.fJ.?,r:..о!!z:..:.к:!!..? .?.':_Л-!! 1>!.'!.'.??.?}I'!.'.:"!!.!:.f!..1!!!
s(Isрiп)=-s(IsрiП)j
Accept=Accept+lj
Еdеmоп=Еdеmоп-dеj
Esystem=Esystem+dej
endj
k=k+lj
Es(k)=Esystem;
Ed(k)=Edemonj
SpM(k)=sum(s );
end;
end;
Accept=Accept/(NTrial*Nspin)j
Далее необходимо выполнить следующую последовательность команд:
» Nspin=200; % число спинов системы
»J=I; % константа обменноrо взаимодействия
» ь=о; % внешнее поле
»Esi=-10j % задание конечноrо значения энерrии системы
» NTrial=100j % число испытаний
% вычисление мrновенных значений полной энерrии системы (Es),
% энерrии демона (Ed), мrновенной намаrниченности (SpM),
% числа принятия решений
»[Es Ed SpM Accept]=Ising(NspinJ,h,Esi,NTrial)j
% визуализация зависимостей мrновенных значений полной
% энерrии системы и энерrии демона от времени
» i=I:1200j
» tigure(l)jplot(i,Es(i), 'k')j
» tigure(2)jplot(i,Ed(i), 'k')j
% вычисление распределения вероятностей мrHoBeHHЫx значений
% энерrии демона
» Nint=50;
» i=I:Nint;
» xl=min(Ed)j
» x2=max(Ed)j
» x(i)=xl +(x2-xl)/Nint*ij
» h=hist(z2,x);
% нахождение и визуализация функции, описывающей
% распределение вероятности
» FI0=inline('u(1)*exp( -u(2)*z)' ,'о' ,'z')
FI0=
431

, I
.!!. ()!!...n!:!!!"!:l!.():..'!..дел'!Е().l!..I!!.:'Р'!..з-!!:.!.:'С!5....!l'?'й-.:: :!!!!.!.!:4..T!::'.!.!!............ .. .. ...
. . . 4.:!!.I}!.'!3!!.!!..I!.I!.I'!!!.:'P....0l!..'!.()I':'.::():(). а.!:"!..(;:!l.е.."!.й-(),-';!й-!.I1!!!!.!!арл-..()
IoHoe fuoctioo:
FI0(u,z) = u(I)*exp(-u(2)*z)
» beta=0Iiofit(x,h,FI0,[10000 0.05]);
» bar(x,h);colormap white
» hold 00
» Ni=500;j=I:Ni;
» XG)=xl+(x2-хl)lNi*j;
» plot(X,FIO(beta,x),'k')
» hold ot'f
»meao(Es)lNspio % средняя энерrия системы на один спин
aos=
-0.0941
» meao(z3) % средняя намаrниченность системы
aos=
1.4352
» meao(z3)lNspio % средняя намаrниченность на один спин
aos =
0.0072
» 2Лоg(1 +2Jmeao(z2»
aos=
9.7904
С[' 
-2О! IRfI/'Ч"I1''(f'П'II\ r'l\j.fv'if'Vlt\NIiV liYNYV''1
... 11\ ( \. ! 1
. I
 I 1
-во I
I
.''''' 
I
i
.'20 I
.,,,, I
I
.,..!
i
-180 r
Рис. 14,6. Зависимость
М2новенных значений полной
энер2ии системы
от времени
-200.
......J.......,.
200 400 600 еоо 1000 120':
: !
m i
'20 \
\ I
:\ 1
'" \ j
! Д I I 
20r '\ \ j J. Л . 1 r, 1\ 1
.Ll\kif,,l. (#1JVflI\!l,i
о m    1 1
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 14.614.8.
Задача 14.6
Так как изначально неизвестны конфиzурации спинов, обеспечивающие
искомое значение энерzuи, в качестве начальной конфиzурации мы выби
раем конфuzурацию с минимальной энерzией, поэтому для достижения
равновесносо состояния с заданной полной энерzией системе требуется
некоторое конечное время (время релаксации). Это хорошо видно из рис,
/4,//, /4,/2. Аппроксимируйте зависимости E,fystem(t), EdemOl,(t), иc
пользуя метод наименьших квадратов. Оцените время релаксации пол
ной энерzии системы ",fysteт и время релаксации энерzии демона "deтOIl'
Как зависят "systeт' "dem01. от числа спинов Nspiп, образующих систему?
Сравните полученные результаты, с резулыпатами, полученными при
моделировании случайных блужданий,
Рис. 14,7, Зависимость
М2новенных значений энер2ии
демона от времени
зF
'5
I
I
'1
I
'5 \
!
I
.\.
,11'\:
.\
!\
\
05 :\
iA
ol';
0204060
I
, .J
ей 100 120 1'-0 180 180 20V
Рис, 14,8, Функция
распределения энер2uи
демона
432
433

l!..()!'.tJ?!!!.J1..()е?l?J!':!Р.l!.в--()!..I!!:.rJ:!!:!!_'!.l!ких I1poцe={;.? _I!.l!..I!.I:'!!..!:!: в... ...__ .......
Задача 14. 7
Создайте собственные функции, позволяющие исключать переходный
период и вычислять равновесные значения средней полной энерzии cиc
темы (E"y"teт), среднюю энерzию демона (EdeтO/l)' среднюю HaмaCHи
/ 2
ченность системы (М), средний квадрат намаzниченности \М ),
Сравните значения равновесной температуры системы с cooтвeтcт
вующим значением температуры, полученным без учета процесса pe
лаксации системы к равновесному состоянию.
Задача 14.8
После достижения равновесносо состояния значения полной энеР2ии
системы и энеР2ии демона, как видно из рис, 14,11, 14.12, испытывают
случайные флуктуации около средних значений. Исследуйте, как зави
сит величина флуктуаций средней полной энеР2ии системы (Е systeт) ,
средней энеР2ии демона (EdeтO/l)' средней намаzниченности системы
(М), среднесо квадрата нама2ниченности (м2) от Nspin. Сравните
полученные результаты с результатами, полученными при моделирова
нии случайных блужданий.
.
Задача 14.9
Вычислите (E"y"teт) для систем, состоящих из разлиЧНО20 числа спинов
N. Сравните полученные результаты с точным ответом для бесконеч
ной одномерной решетки
!s;eт) = th(f). (14.17)
Как полученные результаты зависят от числа спинов N и количества
Ша20в метода МонтеКарло?
....
Задача 14.10
Про ведите вычисления и постройте зависимость (м2) от me'dnepa
туры т для системы, состоящей из N спинов (N = 200), AппpOKCими
руйте данную зависимость методом наименьших квадратов, Зависит
ли вид аппроксимирующей от числа спинов?
434

,
... ..._ Ш.. ....'!!!l..l?J!!!!!.!!.и--!f}!'5!!..?.'?!.tо!.и--'!.:.()(){/:I{;<1!!:"!!..!!.:''!!.?.()()!..II!!!.!!.!!!!.l!.?._
Задача 14.11
Введите ненулевое маснитное поле h и вычислите (EdellWl1), (М), (М 2),
как функции от h для заданной полной энерzии. Определите связь
(Edeтol1) С температурой для h:f. О. Сравните значения равновесных
температур для случаев h = О, h:f. О при одинаковых значениях средней
полной энер2ии,
Обобщим использованный BЫ
ше метод микроканоническоrо aH
самбля, применяемый нами для
одномерной системы спинов, на
случай двумерной системы
(рис. 14.9).
Как и в одномерном случае,
выбираем периодические (торои
дальные) краевые условия, т, е.
будем представлять решетку коль
ЦОМ, в котором спины sij' Haxo
!
 i i !
! i t !
! i r !
t !
дящиеся в узлах (i = 1, j = 1,. . " N )
взаимодействуют со спинами Ha
ходящимися в узлах (i = 1,
j = 1".., N). А спины, располо
женные в узлах (i =l,...,N ,
j = 1), взаимодействуют со спи
нами, расположенными в узлах
(i =l,...,N , j = N )(рис. 14.10),
Рис. 14,9, Квадратная двумерная решетка,
состоящая из N = 16 спинов
 i i !
! i i 
 i t 
 i i 
[ i t !  i i !  i i 
TTTTTT
1T TT!TT
11TT!1T
 i i 
 i i 
 i t !
 i i !
Рис. 14.1 О, Задание zраничных условий
в двумерном случае
Это обеспечивает равное число взаимодействий для всех спинов
в изучаемой системе. Взаимодействие выбранноrо спина с соседями можно
рассматривать, как взаимодействие с одним спином, величина KOToporo
равна алrебраической сумме величин четырех соседних спинов, которая,
как очевидно, может принимать три значения: О, 2, 4, Следовательно, ми
нимально возможное значение изменения энерrии при опрокидывании oд
Horo спина составляет 21  (21) = 41 , в отличие от одномерноrо случая в
котором квант изменения энерrии равнялся 21. Отмеченное обстоятельство
определяет необходимость замены в (14,16) 21  41 :
435

l!..'?l>1..'!./(!'!!.e.P"Ic:.:':,:!?..!!.IIPO'!.f!.II':' Р.1!з-.'е..I':р'(),ц-е:.:.?в.'!. '!.1!.k-.е.'!!..е..,!.!...А-!:.l!  . .
41
Т = .. .. (14,18)
In(1 + 41/(Е,,))
Алrоритм моделирования двумерной системы, состоящей из N спинов, Me
тодом МонтеКарло реализуется следующей последовательностью действий,
), Задание числа спинов решетки Nspiп .
2. Задание числа шаrов метода МонтеКарло на спин,
3. Задание ориентации спинов в узлах квадратной решетки в момент Bpe
мени t = О (начальной конфиrypации системы),
4. Выбор случайным образом одноrо из спинов системы.
5. Вычисление пробноrо изменения энерrии,
6. Если пробное изменение приводит к уменьшению энерrии системы, то
система отдает энерrию демону и новая конфиrypация принимается.
7. Если пробное изменение увеличивает энерrию системы, то новая KOH
фиrypация принимается в том случае, если демон имеет достаточную энер
rию для передачи ее системе.
8. Если пробное изменение не меняет энерrию системы, то принимается
новая конфиrypация.
9. Повторение пп. 8 (число повторений равно числу спинов в системе).
) О. Повторение пп. 9 (число повторений равно числу шаrов метода
МонтеКарло на спин).
Для реализации описанноrо алrоритма моделирования двумерной сис
темы спинов методом МонтеКарло в пакете MAТLAB создадим файл
Ising2.m, содержащий описание функции, возвращающей MrHoBeHHbIe зна
чения: энерrии системы, энерrии демона, намаrниченности, числа принятия
решений, а также MrHoBeHHbIe конфиrурации спинов.
% листинr файла Ising2.m
function [Es,Ed,SpM,A,S] = Ising2(NspinJ,h,Esi,NTrial)
% функция, возвращающая MrнoBeHHыe значения: энерrии,
% системы энерrии демона, намаrниченности, числа принятия
% решений, а также MrHoBeHHbIe конфиryрации спинов
% Nspin  число спинов решетки
% J  константа обменноrо взаимодействия
% h  напряженность внешнеrо маrнитноrо поля
% ?si  конечная энерrия системы
% NTrial  число испытаний
Ns=Nsрiп.ЛО.5; % число спинов вдоль одной стороны
s=ones(Ns,Ns); % начальная конфиrypация спинов
I j
436

J 4:..!:!.?'!!!!.1?()!!!!..I!..и-:...'.!.'!.Р..?.к-r:..,!!'!.,!'!..е:.:с:...'!.I:.l!!!..f:?f!!..'!!с:...дО\1?!''!!.::1!..'!.рл.
Esystem=-(J+h)*Nsрiп; % начальная энерrия системы
Еdеmоп=4*J*flооr«Еsi-Еsуstеm)/(4*J»; % начальная энерrия демона
Es(I)=Esystem;
Ed(I)=Edemon;
8=s;
k=l;
for i=l:NTrial
Accept=O;
for j=l:Nspin
% случайный выбор узла сетки
Ix=floor(Ns*rand(I)+ 1);
Iy=floor(Ns*rand(l)+ 1);
% rpаничные условия
if Ix==l
Left=Ns;
else
Left=Ix-l;
end;
if Ix==Ns
Right=l;
else;
Right=Ix+l;
епд;
if Iy==l
Down=Ns;
else;
Dоwп=Iу-l;
end;
if Iy==Ns
Up=l;
else
Up=Iy+l;
end;
% пробное изменение энерrии
de=2*s(Iy ,Ix)*( -h+J*(s(Iу ,Left)+s(Iy ,Right)+s(Down,Ix)+s(Up,Ix»);
if de<=Edemon % принятие пробноrо изменения энерrии
s(Iy,Ix)=-s(Iу,Ix);
Accept=Accept+l;
Едеmоп=Едеmоп-де;
437

Ii(}]'!..п._Ь!(}'!!.J1..'.'.!!..I(}':!.'!Р.!!.!!..I!!..'.':!РUШЧ':.':!:п.J!..(}':.':::'()_в.!!.r:.:."!!!.":!...!!:A__...._...
I
I
I
l'
1:1
1.
11
i
Esystem=Esystem+de;
end;
k=k+l;
Es(k)=Esystem;
Ed(k)=Edemon;
A(k-l)=Ассерt;
sl=sum(s);
SpM(k)=sum(sl);
S=cat(3,S,s) ;
end;
end;
A=A/NTrial;
Далее необходимо выполнить следующую последовательность команд:
»Nspin=81; % число спинов системы
»J=I; % константа обменноrо взаимодействия
» ь=о; % напряженность внешнеrо маrнитноrо поля
»Esi=-10; % конечная энерrия системы
» NTrial=50; % число испытаний
> > [Es,Ed,SpM,A,S ]=Ising2(N spin,J ,h,Esi,NTrial);
% визуализация зависимости мrновенных значений полной
% энерrии системы и энерrии демона от времени
» i=I:2000;
» figure(I);plot(i,Es(i»
» figure(2);plot(i,Ed(i»
% визуализация мrновенных конфиrураций системы в виде BeIcropHoro поля
» i=I:9;
» j=I:9;
» V(iJ)=O;
» U(iJ)=O;
» Z(iJ)=O;
» figure(3);quiver3(Z,U,V,S(:,:,I»; colormap white
»figure(4);quiver3(Z,U,V,S(:,:,100»; colormap white
»figure(5); quiver3(Z,U,V,S(:,:,1000»; colormap white
» figure(6); quiver3(Z,U,V,S(:,:,2000»; colormap white
% визуализация МI"новенных конфиrураций системы в виде
% прямоуrольных параллелепипедов
» figure(7);bar3(z5(:,:,I»;axis([0 10 О 10 -1.5 1.5]);colormap white
»figure(8);bar3(z5(:,:,100»;axis([0 10 010 -1.5 1.5]);
» colormap white
438

ш.. ......., _.!: /t.!..(}<?!!.':!I!..()!_а./!..и-':.-":!.и-l!.(}'.'.(}/Iи-,!е:.:() '!./t.с!!--":!.ля-":!.'.(}(},_/t.!..()'.lrtl_еl!.а.р!!.()_
»figure(9);bar3(z5(:,:,1000»;axis([0 10 О 10 -1.5 1.5]);
» colonnap white
» figure(10);bar3(z5(:,:,2000»;axis([0 10 О 10 .1.5 1.5]);
» colonnap white
» mean(Es); % средняя энерrия системы
ans =
-14.1790
» mean(zl)/Nspin; % средняя энерrия системы на один спин
ans =
-0.1750
» mean(z3)/Nspin % средняя намаrниченность на один спин
ans=
0.6627
» mеап(А) % среднее значение коэффициента принятия на один шar
ans=
0.1463
»4/1og(I+4/mean(z2» % равновесная температура системы
ans=
2.7028
Результаты выполнения приведенной выше последовательности команд
представлены на рис. 14.1 1  14.20.
01
: rlrlrrr'W""
-зо
-40
.50 I
.60
.70
. .]
1000 1200 1.00 1600 1800 200с
.80
.90
О
_I
200 400
600

800
Рис. 14.11, ЗавИСUJIlОсть М2/ювенных значений энер2ИИ систеА1Ы от времени
439

Компьютерное моделирование физических процессов в пакете МА тин
00
,О
00
50
'"
)о
20
Рис. 14.12, Зависимость
М2новенных значении энерzuи
демона от времени
15
О"
.....
.,
.,..
1.
Рис, 14.1 З. Конфuzyрацuя
системы спинов в момент
времени ( '= о
i
t t
rt-l,'ф t1'lt
" 1Фt ,!tJ1фt 1'1'1'111'
01 l' l' \ l' !t1' 11' \ -tt.1tt t 11' t 1'1' \ l' l'
., j l' l' Jt  i Т,!, f I t 1'1' T t1' Т' /'---'0
,о ''-----, l' t It l' # 1'/1  '
8> 1'1'1 6'
6 .............  5
 4
4 '................... '3
2>---........../ 2
,
Рис. /4, I4. КонфuzyрацWl
системы спинов в момент
времени (  1 00
440

J 4, Моделирование миКРОКalюническоzо ансамБJ/Jl методам МонтеКарло
l' i 1'ф:,
'1 ' i i i .t i i
О )iljl'1"Hjt,j'jiij'1' '
., i," I l' " l' I I i i l' N II l' I N t.. j ..
,О . t i 1.1' t 1 ,1 t Н11 Н, i
8 "1'111'1 
, е I i I : ...----""O
tt 8
.. t /..".... ·
3 / 4
СУ 2
,
Рис. 14.15. КонфиzyрацWl
системы спинов в момент
времени ( '= 1000
. l' t i' : '. '
'l' i I t ,i ,
О i' i j1'.t tttt ,tttФ.t"trl 1'11" 1':'! '
., t . l' 'tф I i t I .!
. i " tt I i i t t . t t t t. t
,о . t, t t j t . i t t : t t
· ' t t t t r
1 . i t Nt. t i /'''IO
5 ,1 <",. 8
4.
, 2
Рис, 14.1 б. Конфиzyрацuя
системы спинов в
момент времени ('=2000
1.5
0.5
-0.5
.1
.1.5
2 3
4А ....
5 6>-""'" -<,</, 8
7 //: 5 6
6 9"-, ..<'....<2 3
.... ,
441
Рис, /4.17, КонфиzyрацWl
системы спинов в момент
времени (  о

.l!..?".!()"!9?'.()_.:.\1()?"l!.l!.()'!f!!..'!!rf!.l!..З-z.!_чеСКUх:'l!()Ц.С(), ....f!е!!'.':.!!...!!:.l!...ш
,,--<,;.Jt5::J -'
< -?f1:;:lJ:"';'
.r "у;;; ":,,:,,,.,-z i'"-l. '----"-... <-"'Z
05,: J-'(5:}--Ч-( :":1
°1 "-А T'""'''' 'oi'Ч:----;;(-'S,1i' ---."-<'ril
:1 :rfll,11'f];пт\)J)[I>1
1 ---->, .- 1 ""'1::'-::'>'11. ],. (IJ 1---- /1
2 "- , .
3 4""'" .' : .....' - ...:.-
5 '',.. . i 7 8
...:>....  ....." ", 6
8 9......'........-<...->:;з 4
15"
1 ;
15,
1!
05J
I
о.,
1
.05 J
,1 J
l'
, 1':
! iil
I I
111
.1.5 -!.
>---->-.
2 з "-,
4
Рис. 14,20, Конфиzурацuя
системы спинов в момент
времени t  1000
1.5,
,,
'" \frn111' .
з 4'>'----.- l ,_/
5 "-,
6 F".,-"-.
7' ,
0.5
-о 51
-1'1
.15 I
----
в '__"
<--<..9
<:/.---<7 6
-< 6
.//'4 5
. 2 3
442
Рис, 14.18. Конфиzурацuя
системы спинов в момент
времени t  100

6 "
'-
Рис. 14.20. Конфиzурация
системы спинов в момент
времени t  2000

ш_шш..!1:..()!..f!!I.!.!l!..()'!!!..'!..U:' :.\1!!'2!..?!.f!..'()'!.l!..'!!...'5'!..l!...'.!:!!!!..!!ето:!!ш1:!...()'.I!!!.:!!.!!Р..l!!!...
Задача 14012
Проверьте, что распределение энерzии демона описывается функцией
распределения Больцмана. Сравните значение средней температуры
системы, вычисленной по формуле (14_18), и значение температуры, по-
лученное из распределения Больцмана.
Задача 14013
Решите задачи 14,614,11. для рассмотренной выше двумерной систе-
мы спинов. Сравните полученные результаты с аналО2ИЧНЫМИ резуль
татами, полученными для одномерной системы спинов,
ЛИТЕРАТУРА
1. rулд Х_, ТобочннкЯ, Компьютерное моделирование в физике. М,: Мир, 1990, Т, 2,
2, Кунин С, Вычислительная физика, М,: Мир, 1992.
3. Ландау Л, Д" Лифшиц Е,М, Статистическая физика. М,: Наука, 2000,
4, Методы Монте-Карло в статистической физикетод ред. К. Биндера, М.: Мир, 1982,
5, Дайсон ф" Монторолл Э,. Кац М,. Фишер М. Устойчивость и фазовые переходы, М,:
Мир, 1973,
6. Хеерман д, В. Методы компьютерноrо эксперимента в теоретической физике, М,:
Наука, 1990,
443

rлава 15
МОДЕЛИРОВАНИЕКАНОНИЧЕскоrо
АНСАМБЛЯ МЕТОДОМ МОНТЕ-КАРЛО
15.1. Введение
в предыдущей rлаве мы использовали метод микроканоническоrо aH
самбля для моделирования поведения статистических систем. Одним из He
сомненных достоинств данноrо метода является очевидная простота исход
Horo постулата о равенстве априорных вероятностей появления возможных
микросостояний, Необходимо также отметить, что при проведении числен
ных экспериментов с использованием микроканоническоrо ансамбля демон
не предъявляет никаких требований к качеству rенерируемой последова
тельности случайных чисел. Данное обстоятельство определило известную
популярность метода микроканоническоrо распределения и ero модифика
ций. Например, в [1, 2] описаны быстрые вычислительные алrоритмы, ис
ПОльзующие один бит памяти на спин и большое число демонов.
В то же время алrоритму демона присущ целый ряд недостатков, пожа
п:уй, rлавный из которых состоит в трудности получения системы с заранее
заданной внутренней энерrией. Необходимо также отметить, что с физиче
ской точки зрения более естественно изучать зависимости термодинамиче
ских величин, характеризующих макроскопическую систему, от температу
ры, но не от полной внутренней энерrии. Так как в натурных экспериментах
измеряется именно температура системы, но не ее внутренняя энерrия.
В rлаве рассматривается метод каноническOI'О ансамбля, позволяющий
моделировать поведение системы, находящейся при постоянной температу
ре. Данный метод используется для моделирования идеальноrо классиче
cKoro rаза и модели Изинrа,
15.2. Канонический ансамбль
Подавляющее большинство физических систем не являются изолиро
ванными. Это означает, что они обмениваются энерrией с окружающей cpe
дой, Так как размеры изучаемых физических систем, как правило, малы по
сравнению с размерами окружающей среды, можно считать, что любое из
менение энерrии малой системы на влияет заметным образом на температу
ру большой системы. (Например, включение в сеть утюrа (малая система)
I
I 1

...:/,:!..?:qI!Е?в?'_I':!.. .?I!.О.':!.<:О!,_?,,:!.I::.?:,!б..Jl!!._-':'..'tl.?()/:!J:!.()II'tl.е:l!.!!.ЕJl.()
не оказывает заметноrо влияния на температуру воздуха в комнате (боль
шая система», Следовательно, большую систему можно рассматривать как
тепловой резервуар с заданной абсолютной температурой Т (термостат),
При приведении макроскопической системы в контакт с термостатом сис
тема стремится перейти в равновесное состояние путем обмена энерrией с
термостатом. Процесс обмена энерrией продолжается до тех пор, пока TeM
пература системы и температура термостата не станут равными.
В rл, 14 мы показали, что в качестве малой системы может выступать
система, состоящая из одной частицы (демон). Вероятность Ps Toro, что
демон находится в микросостоянии s С энерrией Es описывается формулой
ES
1 ..
PS = e т , (15.1)
Z
[де Т  температура, измеряемая в энерrетических единицах, Z  нормиро
вочный множитель, выбирающийся из условия
м
LPs = 1. (15.2)
S=1
Подставив (15.1) в (15.2), найдем
м ES
Z = Le T (15,3)
S=l
Суммы в (15.2), (15.3) вычисляются по всем М микросостояниям системы.
Знание вероятности Ps позволяет вычислить средние по ансамблю MaK
роскопические характеристики (А) в соответствии с общим правилом
м
(А) = LAsPs . (15.4)
S=l
Например, средняя по ансамблю микросостояний энерrия
ES
1 
(Е)= LEsPs =. LEse т (15,5)
s Z s
Отметим, что из'за большоrо числа слaraемых прямое вычисление сумм в
(15,5) невозможно. Действительно, даже для достаточно малой решетки разме
ром 16х16 имеется 2256::::: 1077 конфиrypаций, В этих условиях для оцеНЮI cpeд
них значений макроскопических характеристик системы приходится использо
445

?1.!!..!:!!!!еl!?!...?.е..l!.".'.l!'?в-.'!.".'.'!...Р.'!..".'.'!.'!..'5..'-!!l!'?.lf..::'?в-..в-.,!Keт!.l!._... ..
вать верояпюстные методы, одним из вариантов которых является aлrоритм
Метрополиса, рассматриваемый нами в следующем разделе.
15.3. Алrоритм Метрополиса
для каноническоrо ансамбля
Рассмотрим систему, состоящую из N частиц, находящихся в объеме V
при постоянной температуре Т. Сrенерируем некоторое оrpаниченное чис
ло конфиryраций т из полноrо числа возможных конфиrypаций М, Тоrда
оценка среднеrо значения (А) может быть получена из следующеrо Bыpa
жения
т ES
" А е T
т L,.s
(А)  LAsPs = S=1 Е
т S
S=1 LeT
S=1
rде Е s' As  полная энерrия системы Е и значение физической величины
А в конфиryрации s.
для вычисления (А) в соответствии с (15.6) можно предложить ДOCTa
точно очевидную процедуру, которая состоит в rенерации случайной KOH

фиrypации, вычислении Es, As и произведения Ase т и подсчете COOT
ветствующеrо вклада каждой конфиrypации в суммы (15.6). Однако появ
ление каждой конкретной конфиrypации достаточно маловероятно,
следовательно, большое число конфиrураций будет давать малый вклад в
суммы (15.6), поэтому, вообще rоворя, такой вычислительный алrоритм
также будет недостаточно эффективным.
Для устранения отмеченноrо недостатка можно воспользоваться Meтo
дом существенной выборки, который применялся нами ранее в rл, 11 для
вычисления определенных интеrpалов методом MOHTe Карло, Идея данноrо
метода состоит в rенерации конфиrурации в соответствии с функцией pac
пределения вероятностей 1L s ' Так как дальнейшее усреднение проводится
по т конфиrурациям смещенной выборки, то для исключения данноrо CMC
щения при вычислении суммы в (15,6) каждая конфиrурация должна брать
ся с весовым множителем 1/ 1L S :
(15.6)
446

ш!J'!.,.'?'!..l!.l!'?в-.,!I!".'.'!...а.'lй- 11_J'!.ec..'??"''!!{:.?113:..Ie..,,!,?o_,?!I'!..I1!..'!.l!l!.o..
т ES
L As 2. е T
(А)  5=1ш,
т ES
,,1 
L,.e т
S=1 1L S
Наиболее целесообразно выбрать 1L s в виде [3]
Es
(15,7)
е
т
7[s
(15.8)
Es
т
Le
s=1
В этом случае, как леrко убедиться прямой подстановкой (15.8) в (15,7)
т т Es т
LAs Le шт LAs
(А)  s=!ш=! . __ . т=1
т т ES т
LLeT
S=1 s=!
т
(15.9)
rде при преобразовании знаменателя учтено условие нормировки
т Es
LеШТ- =1,
S=1
Формула (15.9) позволяет дать общую формулировку алrоритма Meтpo
полиса:
1. Сформировать начальную конфиrypацию системы,
2. Произвести случайное пробное изменение начальной конфиrурации.
3. Вычислить изменение энерrии системы М, обусловленное произве
денным пробным изменением конфиrypации.
4, Если М  О, то принять новую конфиrypацию системы и осущест
вить переход к п, 8.
/l,.Е
5. Если М> О, то вычислить «вероятность перехода» W = е т .
6. Сr"енсрировать случайное число r с равномерным законом распреде-
ления в интервале [0,1].
447

.!!.?!,пь-!.?".!l!.'!!I!.!!.'!!!.<!вР.:!.':...!!.Р..о..'!..е:?!'.,!!,,",!!!LAl! .. , .
7. Если r $ W , принять новую конфиrypацию, в противном случае co
хранить предыдущую конфиryрацию.
8. Определить значения требуемых физических величин,
9. Повторить п. 28 для получения достаточноrо числа конфиrypаций,
10. Вычислить среДНИе по статистически независимым дрyr от дрyrа
конфиrypациям.
Описанный алrоритм можно трактовать как случайные блуждания. Дей
ствительно, про нумеруем различные конфиrypации порядковыми номерами
i = 1,2,3,.. ,. Тоrда каждую конфиrypацию можно считать некоторой (crоч
кой», а вычислительный процесс в соответствии с алrоритмом Метрополиса
случайным блужданием по данным точкам. Действия, выполняемые в COOT
ветствии с пп. 37, позволяют определить условную вероятность Toro, что в
«момент временю) t + 1 прохожий будет находиться в точке i при условии,
что в момент времени t он находился в точке j, т, е. найти отношение
Ри)/ РСЛ. Отметим, что поскольку вычисляется отношение вероятностей,
нет необходимости про водить их нормировку. Так как конфиrypации [eHe
рируются с вероятностью, пропорциональной требуемой вероятности, для
вычисления средних следует использовать формулу (15.9). Отметим, что
данным способом оказывается возможным оценить средние значения Maк
роскопических величин, но не нормировочный коэффициент Z.
Существует cтporoe математическое доказательство Toro факта, что по
сле достаточно большоrо числа шаrов алrоритм Метрополиса rенерирует
состояния, энерrия которых распределена по Больцману. Однако, следуя
выбранному подходу (физическому по своей сути), мы сознательно отказы
ваемся от математически cтpororo доказательства в пользу эмпирическоrо
подхода, т. е. подтверждения данноrо вывода на при мере модели идеально
[о rаза и одномерной системы спинов,
Отметим, что выбор в качестве ;rs распределения Больцмана не являет
ся единственно возможным. Оказывается, что к распределению Больцмана в
асимптотическом пределе приводят и друrие распределения вероятности.
Можно по казать, что существует единственное необходимое условие, за
ключающееся в том, чтобы
i  Е2
W(12)e т =W(21)e т . (15.10)
Равенство (15.10) называется принципом детальноrо равновесия.
Нокажем на примере классическоrо идеальноrо rаза, что алrоритм MeT
рополиса приводит для отдельных микросостояний к распределению
Больцмана, Любое микросостояние rаза полностью описывается заданием
448

....!J.?!!/!'!!.и---ка,I.,!!I(и'!:.::о..I!'(С?....ш:.'!!..е!!!.?с>!!:!..':!...о..(те:!!.'!J!!!..?..
скорости частиц, так как энерrия идеальноrо I'аза зависит только от CKOpO
сти частиц. При этом скорость классическоЙ частицы является величиной
непрерывной, в то время как для количественноrо описания системы необ
ходимо иметь счетное число микросостояний. Следовательно, необходимо
провести разбиение интервала возможных значений скоростей на конечное
число достаточно малых дискретных интервалов, Например, для 20 частиц
и разделении интервала возможных скоростей на 1 О интервалов полное
число возможных микросостояний составляет 1020, Совершенно очевидно,
что весьма проблематично не только пронумеровать данные состояния, но и
вычислить за приемлемое время точные оценки вероятностей и средних Be
личин. Полученная оценка подтверждает правомерность использования MO
дели идеальноrо rаза для демонстрации асимптотических характеристик ал
rоритма Метрополиса.
Для реализации алrоритма Метрополиса в модели идеальноrо rаза, co
стоящеrо из одной частицы, в пакете МА ТLAB необходимо создать файл
IdeaIGas.m, содержащий описание функции, возвращающей мrHoBeHHыe
значения скорости, энерrии, число среднее число принятия.
% листинr файла IdealGas.m
function [V,Es,Accept] = IdeaIGas(Vel,T,dVmax,NTrial)
% функция, возвращающая мrновенные значения скорости, энерrии, число
% среднее число принятия
% V еl  начальная скорость
% Т  температура rаза
% dVmax  максимальное изменение скорости
% NTria!  число испытаний
beta=lfI';
Е=Vеl.Л2/2; % начальная энерrия
Accept=Oj
Сос i=l:NTrial
dV =(2*rand( l)-l)*dVmах;
Vtrial=Vel+dV; % случайное изменение скорости
dе=О.5*(Vtriаl.Л2.Vеl.Л2)j % пробное изменение энерrии
if de>O
(С exp(-beta*de»=rand(1)
* шаr принимается
Vel=Vtrialj
Accept=Accept + 1 j
E=E+dej
end;
15!57!i
449

М1ыoтeplloe 'c:.el!upoBallue ф!lзuческuх I1роцессов l!.I1'!.Ke!e,vA ТLAB
else
% шаr принимается
Vel=Vtrialj
Accept=Accept+ 1 j
E=E+dej
endj
Es(i)=Ej
V(i)=Velj
endj
Accept=AcceptJNTrialj
Далее необходимо выполнить следующую последовательность команд:
» Vel=Oj % начальная скорость частицы
» Т=О.5; % температура rаза
» dVmax=4j % максимальное изменение скорости
» NТriаl=10Л4; % число испытаний
» [V Es Accept]=IdelGas(Vel,T,dVmax,NTrial)j
» mean(V) % средняя скорость частицы
ans =
0.0036
» mean(Es) % средняя энерrия частицы
ans =
0.2604
» Accept % число принятия
Accept =
0.2779
» i=l:NTrialj
% визуализация зависимости мrновенных значений энерrии от времени
» figure(l)jplot(i,Es,'k')j
% вычисление и визуализация функции распределения
% P(Ed)M по энерrии идеальноrо rаза, состоящеrо из одной частицы
» xl=min(Es)j
» x2=max(Es)j
» Nint=lOOj % число интервалов rистоrpаммы
» i=l:Nintj
» x(i)=xl +(x2xl )/Nint*ij
» h=hist(Es,x);
» figure(2);bar(x,h)jcolormap \vhite
450
...........
...'  .. C" .шшш. шш!s.:О?'!.l!.Оl!.,!I"ш'!.ш'5'!.."ОI!'!.:.к-'}z.?'!!.!..с!!!!...б-:'I!!.!.'..'!..'!!..?..?..!!..ш"!...Й--I'!!..е.:!!...-Й-!!'f}?"
Результаты выполнения описанной последовательности команд пред
ставлены на рис, 15,1 и 1 5,2,
25
15
1 i
I
I
Рис, 15,1, Зависимость
М2новенных значений
энеР2Uи идеалЬНО20 2аза,
состояще20 из одной
частицы, от времени
0.5
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
зооо
2500
2000
1500
Рис. 15,2, Функция
распределения 110 энеР2ии
идеалЬНО20 2аза,
состояще20 из одной
частицы
1000
1.5
,
25
J
0.5
Задача 15.1
1. Постройте зависимость ln(P(E))om Е. (Указание. Создайте функцию,
формирующую из массивов х, 11 матрицу, не содержащую значений
hi = О, и используйте ее для дальнейшею решения задачи.)
2, АппРОКСUJнируйте данную завИСИJность функцией вида а' х + Ь .
Сравните значение коэффициеюnа а с точным 'Значением  1fT, ПОш
 Ф Ф a'x+h Ф
строите zpa ик ')-'нкции е' и сравните е.!о с zpa иком распределеш
ния плотности вероятности. С какой точностью распределение zаза,
451

15.(,!I,I!'!..п!P'!'()..::': ().e:'lp"()111Ierj)I.(!li.:,:,CK:,:.."p...():(5:.()II111 ':'.!! Т!:.1.!!. .
получеююе в результате моделирования, аппроксимируется больц.J\1а
новским распределением?
Задача 15.2
Проведите вычисления для различных значений те.7lтерат;ры u по
стройте завuсилtOсть JIlер2UИ 2аза от т е.7ltnературы , MOJ/CI/O Лll aп
пРОКСИJнировать данную зависимость функциеЙ вида а' х -+ h ? Ч\tу pa
вен коэффициент а в данном случае? Какой Физический смысл имеет
коэффициеюп а? Объясните полученный результат с точки зрения
теоре.мы о равнораспределении (см, разд, 10.5),
Задача 15.3
Проведuте вычисления для различных значений температуры и пo
стройте зависимости дисперсии и среднеквадратиЧН020 отклонения
скорости от температуры. Выберите подходящие функции и aппpOK
симируйте данные зависимости методом наимеllыuих квадратов, Объ
ясните получеllllые результаты.
Для моделирования одномерноrо классическоrо идеальноrо rаза, со--
стоящеrо из N частиц, следует использовать модифицированную функ
цию IdealGas2, сохраненную в файле IdeaIGas2.m, Функция IdealGas2 отли
чается от функции Idea1Gas, описанной выше тем, что: 1) полная энерrия ra
за вычисляется как сумма кинетических энерrий всех частиц, 2) помимо
случайноrо выбора величины изменения скорости производится случайный
выбор номера той частицы, для которой производится пробное изменение
скорости. Все остальные действия проводятся в соответствии с алrоритм()м
Метрополиса.
% листинr файла Idea1Gas2.m
fuoctioo [V,Es,Accept] = IdeaIGas(Vel,T,dVmax,NTrial,Np)
9(, функция, возвращающая MrHoBeHHbIe значения средней,
% скорости энерrии, числа принятия
beta=lfI';
i=I:Np;
v(i)=Vel;
Eold=dot(v,v)/2;
V(I)=meao(v);
Es=Eold;
Accept=O;
k=2;
foc i=I:NTriaI
for j=I:Np
452

:A1..0':'j1p"'OI!':' а.Il?lli.Ч,!:К'!.2й-.. tl.!l:tl.:"!..б.:'!.я-!!!..'!!.()?:"!....л.!. ()1l.т..е:}(аf.Л,.О
N=t1oor(Np*raod(I)+ 1);
dV =(2*raod(1 )-1 )*дУmах;
V temp=v(j);
v(j)=v(j)+dV;
Eoew=O.5*dot( v, v);
de=Eoew-Еоld;
if де>О
if ехр( -beta*de»raod(l)
Accept=Accept+ 1;
Eold=Eoew;
else
v(j)=Vtemp;
еод;
else
Accept=Accept+ 1;
Eold=Eoew;
еод;
V(k)=meao(v);
Es(k)=EoldlNp;
k=k+l;
еод;
еод;
Accept=AcceptJ(NTriaI*Np );
Рассмотрим получаемые результаты для случая Т = 2, Vel = О ,
ilvmax := 0.5, NTrial:= 200, Np = 80, опустив промежуточные вычисления,
которые аналоrичны уже описанным выше для классическоrо идеальноrо
rаза, состоящеrо из одной частицы.
Анализ зависимости, представленной на рис, 15.3, показывает, что суще
ствует некоторый переходный период конечной длительности, в течение
KOToporo система приходит в «тепловое равновесие» с термостатом, После
достижения равновесия температура системы ИСПЫТЫJ3ает флуктуации от-
носитеЛьноrо среднеrо значения, соответСтвующеrо заданной температуре,
Анализ rистоrpаммы распределения MrHoBeHHbIx значений энерrии
и теоретической кривой позволяет сделать вывод о близости распределения
вероятности MrHoBeHHbIx значений энерrии к нормальному закону (кривая
[аусса), Таким образом, можно сделать важный вывод о том, что если мик
росостояния системы распределены в соответствии с распределением
Больцмана, то распределения макроскопических величин (например, полная
энерrия) описываются нормальным законом, при этом максимум функции
453

KOMпbIoтeplloe моделuров'!.'..'!!=-1!.'!.'!.':"'!..!1J!I!:.?!!..!!.'!..е'!':.!!....1!!:. ...
.............
распределения соответствует среднему значению величины, вычисленной в
соответствие с (15.9).
14
i i
,А "J, Л\
/.! ft/' ti\JJ 
,. .1 '
о. i
.)
021!
ol
о
2.5
"о'
, 2
l'
,
1.5
Рис, 15.3, Зависимость
мzновеннои энерzии
классическоzо идешtЬНО20
zаза от времени
0.5
1200r ''
I
'I
8001
r
i
600 С
1
.ool
I
/I
/
/
I
I
i
/
/
I
I
/
ji
Рис. 15.4, rucmozpaмMa
распределения мzновенных
значении энерzии
классическоzо идешtЬНОZО
zаза и теоретическая кривая
соответствующеzо
НОРМшtьноzо распределения
200
7
11
Задача 15.4
Проведите численные эксперименты и найдите зависимость числа пpи
нятия на один ша2 mean(A(2))tNp от vmax. Для значения Vmax'
обеспечивающе20 значение коэффициента принятия близкою к 0.5, вы
числите среднюю кинетическую энеР2ию одной частицы и среднюю CKO
рость частиц, Как связаны значение температуры и средllЯЯ кинетиче
ская энеР2ия одной частицы? Сравните полученный результат r pe
зультатами задачи 15,2.
454
..........
'.. ... ...Ш !...:!!...о..е..l!l!...о..ш':!..!.'!..'!.!1!!.!:.О.?':'{!!!IЛ!!.:''':'.?шд.??'1I,,:,,:l!..'!.1!.,7?
Задача 15.5
Выберите критерий достижения системой тепловою равновесия, Oцe
ните число шаюв МонтешКарло на частицу, необходимых для достижеш
ния системой теплов020 равновесия, Исследуйте зависимость времени
достижения равновесия от начальных скоростей системы, Vmax' чисш
ла частиц 2аза, Какими надо выбирать начальные скорости при задан
но.м числе частиц и Vmax для т020, чтобы система дости2ала paвHoвe
сия за наименьшее время?
Задача 15.6
Исключите временной интервал, соответствующий неравновесному СОш
стоянию системы, Для даНН020 случая вычислите средние значения CKO
рости, энеР2ии системы и числа принятия, Сравните вычисленные знаш
чения с анаЛ02ичными значениями, полученными по последовательности
снеисключенным процессом релаксации, Как зависит разность между
этими значениями от числа частиц N и числа ша20в МонтеКарло
(NTrial)?
.
Задача 15.7
Вычислите среднюю энерcuю на частицу для Т = 0.5, 1,5, 10,20,30,40,
50, 70, 90, 100, исключив временной интервал, соответствующий Hepaв
новесному состоянию 2аза, Оцените теплоемкость 2аза cv' равную по
определению (дЕ) , Сравните полученный результат с результа
дТ V =COllst
том, полученным в задаче 15,2.
Задача 15.8
Вычислите средний квадрат флуктуаций энер2ии (м2) = (E2)(E)2 для
Т = 10, 50, 100, Сравните величину отношения (М2)/Т2 с теплоем
костью, вычисленной в задаче 15,8,
Задача 15.9
Используя функцию /singM, сохраненную в файле /siпgM,m, листиН2 кош
торою приведен ниже, промоделируйте одномерную систему спинов в
соответствии с ал20ритмом Метрополиса,
% листинr файла IsingM,m
function [Es,SpM,Accept,S]=Ising(NspinJ ,h,NTrial, Т)
% Nspin  число спинов
% ]  константа обменноrо взаимодействия
% h  напряженность внешнеrо маrнитноrо поля
455

!!.."!!!..!!!тel!.I!!.:" МОl?!!.'!Р..!!.!1..'!!..I!!1!.'!.'!.'.!.Си-!..':.Р!l..IJ'!..:!!!':.'!..!!'..:.fl!.!:!J!__ _ .. __.
% NTrial  число испытаний
% т  температура системы
beta=lff;
s=ones(Nspin);
S(I)=s;
M=Nspin;
Esystem=-(J +h)*Nspin;
Edemon=2* J*ceil( (Esi- Esystem)/(2* J));
Es(I)=Esystem;
SpM(I)=M;
Accept=O;
k=l;
for i=I:NTrial
for j=I:Nspin
Ispin=floor(Nspin*rand(I)+ 1);
if Ispin==1
Left=s(Nspin);
else
Left=s(Ispin -1);
end;
if Ispin==Nspin
Right=s(I);
else
Right=s(Ispin+ 1);
end;
de=2*s(Ispin)*( -h+J*(Lеft+Right));
if (de<=O) I (exp(-beta*de»rand(I))
s(Isрiп)=-s(Isрiп);
Accept=Accept+l;
Esystem=Esystem+de;
end;
k=k+l;
S=саt(З,S,s);
Es(k)=EsystemINspin;
SpM(k)=sum(s)/Nspin;
end;
end;
Accept=AcceptJ(NTrial *Nspin);
], Проведите вычисления для следующих значений переменных Nspin = ]00,
J=], h=O, NTrial=]OOO, T], 2, 5, ]0, 20, 30, 40, 50. Постройте zрафи:
завиСUJI10сти полной энерzии cucmeAIbl на один спин от температуры,
456

............ ....ш..J..?..:....О3..I!Р..о..!!!!!!...К-'!..t.()t.'!.'!_'!..'!..?..?.. а!.I'!!.!.l!!!..!..'!!..?д-:!"!.?!..,--"!..'!..:l!!!!!.l!()ш
:d
i
.
I
;';'
.
-r
Используя метод наименьших квадратов аппрокcuмиР)IЙте данную завиcu
мость функцией вида а' х + Ь, Чему равен УZJlовой коэффициент прямой?
2. Используя найденный коэффициент пропорциональности между энерzи
ей системы и температурой, постройте зависимость температуры
системы от времени, Чему равна начальная юпемпература системы»?
Оцените время, необходимое системе для достижения равновесия,
3. Измените функцию ]singM так, чтобы все спины системы были opиeH
тированы в момент времени t = О хаотично. Чему равна начальная
температура системы в данном случае? Оцените время, необходимое
системе для достижения равновесия,
4. Определите зависимость средней энерzии на один спин (Е) и средней Ha
маzниченности на один спин (М) от температуры в интервалах тем-
ператур [0.1,5] и [5,50]. Представьте данные зависимости zрафически
и проанализируйте их качественные особенности, Зависят ли получен
ные результаты от начальной конфиzурации системы?
5. Сравните результаты вычислений с точным ответом для нулевою мас-
нитносо поля
(Е) = Nspiп. th( f). (15.11)
6. Постройте зависимость коэффициента принят ия решений в интервалах
температур [0.1,5] и [5,50]. Как зависит эффективность алюритма
Метрополиса от температуры?
7. Вычислите плотности вероятностей для различною числа спинов Nspiп
и различных температур Т.
''::;,
;::
t
Задача 15.10
Решите задачи ] 5, ] ] 5,] О, используя вариант вероятности перехода,
следующий из принципа детальною равновесия (15,] О),
ш5..
е т
W'(1  2) = s. _.
е т +е т
Для реализации сUМJt,tетричной фор_мы вероятности
вычислять величину
(15.12)
перехода следует
м.
е т
W'(1  2)= - м. '
1 + е т
(15,13)
rде I'>;.Е  Е2  Е] .
457

..f(?!:/I?'!!(!I!.'.?.'!..й.l!r:Рй.l!..Cl!.I.l.rjJr:.r:.:!'F..'!..:О!.ш'3..Cl..'!.'!!_"!....:!..в... .._.._
15.4. Моделирование двумерной модели Изинrа
методом каноническоrо ансамбля
Целый ряд чистых материалов (например, железо, никель) и различных
сплавов в отсутствие внешнеrо маrнитноrо поля имеют спонтанную HaMar
ниченность. Данные свойства проявляются только при температуре ниже
определенной температуры Те, называемой критической температурой или
температурой Кюри. При температурах Т> Те спонтанная намаrничен
ность исчезает, т. е, происходит переход из упорядоченноrо режима, в KOTO
ром спины расположены упорядочено, в хаотический режим, в котором
ориентация спинов является случайной.
В соответствии с современными представлениями механизм ферромar
нетизма имеет квантовомеханическую природу, поэтому для построения
адекватной модели изучаемоrо явления необходимо использовать MaTeMa
тический аппарат квантовой механики. Однако оказывается, что даже изу
чение классических двумерных и трехмерных моделей Изинrа дает возмож
ность выявить общие закономерности поведения маrнитных систем в близи
фазовоrо Перехода. В то же время важно понимать, что классические Moдe
ли Изинrа, которым присущи известные оrpаничения, не MOryт дать полно
ro aдeKBaTHoro описания ферромаrнетизма, что особенно заметно проявля
ется при температурах, близких к абсолютному нулю.
Приступая к исследованию модели Изинrа, необходимо определить Maкpo
скопические характеристики системы, представляющие интерес с физической
точки зрения. К таковым характеристикам обычно относят среднюю энерrию
Системы (Е), среднюю намаrниченность (М), удельную теплоемкость сис
темы при постоянном объеме Cv и мarнИ11Iую восприимчивость. Отметим, что
наиболее часто исследователей интересуют равновесные значения указанных
величин. Способ определения одной из макроскопических характеристик сис
темы  удельной теплоемкостьи Cv ' равной по определению
В(Е)
С =,
v ВТ'
подробно обсуждался в предыдущем разделе,
Альтернативный метод измерения теплоемкости Cv основан на исполь
зовании связи теплоемкости флуктуациями полной энерrии в каноническом
ансамбле, Для нахождения соотношения, связывающеrо удельную тепло
(15.14)
458
..........
  _  ш ш__ш    ш ш !.!.:..!!.!!3..f!!!!!.I!й.'!!!!I!'.'5.Cl.'!.'!.r:.:"!!.й.ш,!!6j:!!..!!..'!!.I:!...д-'!..А:!!:!..'!..l/т::!!.!:!!!.l!-o.
емкость Cv с флуктуациями энерrии системы в каноническом ансамбле,
подставим в (15.14) выражение для средней энерrии ансамбля (15.5):
Е
В 1 м 
С =  LEse т (15.15)
v ВТ Z S=1
м ES
rде Z = LeT
S=1
Выполняя дифференцирование в (15.15), получаем
Е м ES
1 BZ м .2.. 1 1 2 T
С = '" Е е т . '" Ese
v Z2 ВТ  S Z т2 
S=1 S=1
(15.16)
у читывая, что
м ES
BZ = '" Е eT
ВТ т2  S
S=1
из (15.16) окончательно найдем
Cv = ;2 ((Е? (E2)).
(15.17)
Изотермическая мarнитная восприимчивость Х, характеризующ чувст
вительность системы к воздействию внешнеrо поля при постояннои темпе
ратуре, по определению равна
х = Нт д(М) .
hO Bh
Данную величину, точно так же, как удельную теплоемкость Cv' можно
связать с флуктуациями намаrниченности системы. Запишем энерrию сис
темы в виде
(15.18)
Es = Eo,s hMs,
(15.19)
rде Е  энерrия sro состояния в отсутствие мarнитноrо поля, Н  напря
o,s
женность наложенноrо внешнеrо мarнитноrо поля, Ms  намarниченность
в SM состоянии. Средняя намаrниченность (М) по определению равна
м ES
1 -
(М) =  LMse т (15.20)
Z 5=1
459

. f('?frlе.Р."е.?е.-'!.'.!!!.?Cl'ljе.rjJз.'.!:.к-zхр?.lI..(!с:.?".'!.ClК--:'frl:f.:'!.  _.
:1
Продифференцировав (15,19), по h получаем
aEs
.==M
ah s.
(15,21)
Используя (15.21), имеем
м ES
aZ ,,1  -
==L.JMse т
ah S=1 Т
(15,22)
Следовательно,
Е
М Е S М .....l.
(Мl==дZLМsеТ  1 LaEsMse т
ah Z2 ah S=1 Z Т S=1 ah
Подставив в (15.23) выражения (15,21), (15.22), получим
ai) == V\M2\(M)2).
ah Т /
Подставив (15,24) в (15.18), окончательно найдем
Х ==  ((M2)(M)2),
(15.23)
(15.24)
(15.25)
11
I
rде (М), (м2) отвечают нулевому внешнему полю.
Отметим, что соотношения (15.17), (15,25) являются общими соотноше
ниями между функциями отклика и равновесными флуктуациями.
Следующий шаr после выбора интересующих равновесных характери
стик системы и задания способа их определения состоит в реализации алrо
ритма Метрополиса, который в общем вИде приведен в разделе 15.2. При
меняя алrоритм Метрополиса, можно сrенерировать спиновые конфиrypа
ции S с вероятностью w(S), а затем усреднить искомые величины по всем
конфиrурациям. Для rенерации спиновых конфиrypаций можно, например,
выбр:пь такой пробный шаr от S к Sz, при котором все спины одновременно
меняются случайным образом, Однако такой пробный шаr при водит к по
лучению конфиrурации, значительно отличающейся от исходной конфиry
рации S, и, следовательно, вероятность отбросить данную конфиrурацию
была бы велика, поэтому оказывается более предпочтительным использо
вать более мелкие шаrи, Для этоrо будем рассматривать конфиrурации, OT
личающиеся переворотом одноrо спина. При этом переворачиваемый
спин Sij выбирается случайным образом. Принятие данноrо пробноrо шаrа
зависит от отношения весовых фУНКllИЙ
, 
I
460
';

J ..А!од-еJ/.и-Р"?вl1'.'U: 1C(j" 0/1 U Ч ec:.к--o< .Cl'.' СClЛ:_ЛJlл:,:п-1 Cl.?л:А!Cl!.'frl'!:l!.Cll!.J/.?..
н\. Е
\V(S ) _.,
r==t'==e ТеТ
w(S)
Если r > 1 или если r < 1 , но больше, чем равномерно распределенное
на отрезке [0,1] случайное число, то спин Si} переворачивается и принима
(15,26)
ется новая конфиrypация, в противном случае спин остается неизменным,
На одном шаrе МонтеКарло предпринимается N попыток переворота спина
(N = Nspiп) ,
Для реализации описанноrо алrоритма в пакете МА TLAB необходимо
создать три файла: 1) файл Espin.m, содержащий описание функции, воз
вращающей энерrию заданной конфиrурации спинов; 2) файл InitSp,m, co
держащий описание функции, возвращающей энерrию системы, значение
полноrо маrнитноrо момента, матрицу, содержащую информацию о конфи
ryрации системы, в момент времени t == о; 3) файл IsingКA.m, содержащий
описание функции, возвращающей мrновенные значения энерrии системы,
число принятия, мrновенный маrнитный момент системы, мrновенные KOH
фиrypации спинов системы,
% листинr файла Espin.m
function z = Espin(Nspin,s,hJ)
% функция, возвращающая энерrию заданной конфиrypации
% спинов
% Nspin  число спинов системы
% s  матрица, содержащая информацию о положении спинов
% h  напряженность внешнеrо маrнитноrо поля
% J  константа обменноrо взаимодействия
Ns=Nspin. ЛО.5;
Е=О;
for i=l:Ns
for j=l:Ns
% проверка периодических rpаничных условий
if j==l
Left=Ns;
else
Left==jl;
end;
if j==Ns
461

li?..А!'!...ь!!!п-:!Р../<!.,:!!:!l!.l!.Рй-tI.'!..': Р!l..и.,!':..,'-!!..rlр'й-Ц-й-I!.'!..!.'!''!....1..Т---!.l!_. .,
li
1
!
Right=l;
else
Right=j+l;
end;
if i==Ns
Up=l;
else
Up=i+l;
end;
if i==1
Down=Ns;
else
Down=i-l;
end;
% энерrия системы
E=E-s(iJ)* (Ь+ J *(s(i,Left )+s(i,Right )+s(DownJ)+s(UpJ»);
end;
end;
z=E;
% листинr файла InitSp.m
funetion [E,s,M] = InitSp(NspinJ,h)
% функция, возвращающая энерrию системы, значение полноrо маrнитноrо
% момента, матрицу, содержащую информацию о конфиrypации системы,
% в момент времени t == О
% Nspin  число Спинов системы
% J  константа обменноrо взаимодействия
% h  напряженность внешнеrо маrнитноrо поля
Ns=Nspin. ЛО.5;
M=;
for i=I:Ns
for j=I:Ns
s(iJ)=I;
M=M+s(iJ);
end;
end;
E=Espin(Nspin,s,hJ);
% листиНI' файла IsingКA,m
! I
i !
i.
462
...
.1 ...МОЛ-lР.()l>.II'!.ш'!..IIй-'!llческ-.()20а!'лз:-"..:п-:,й-() .1:.Iп-:::li'!.Рло
funetion [E,Aeeept,M,S] = IsingКA(NspinJ ,h,NTrial, Т ,Sst.art,Mstart,Estart)
% функция, возвращающая MI'HoBeHHbIe значения энерrии
% системы, число принятия, мпювенный маrнитный момент
% системы, MrHoBeHHbIe конфиryрации спинов системы
% Nspin . число спинов системы
% J  константа обменноrо взаимодействия
% h  напряженность внешнеI'О маrнитноrо поля
% NTrial  число испытаний
% т  температура системы
% Sstart  матрица, содержащая информацию об ориентации
% спинов в момент времени t == О
% Mstart  значение маrнитноrо момента системы в момент времени t == О
% Estart  энерrия системы в момент времени t == О
Ns=Nspin. ЛО.5;
M(I)=Mstart;
S=Sstart;
E(I)=Estart;
s=Sstart;
Aeeept=O;
k=2;
for i=I:NTrial
for j=I:Nspin
% случайный выбор номера узла для опрокидывания спина
Ix=floor(Ns*rand(I)+ 1);
Iy=floor(Ns*rand(I)+ 1);
% про верка периодических rpаничных условий
if Ix==1
Left=Ns;
else
Left=Ix-l;
end;
if Ix=;::Ns
Right=l;
else
Right=Ix+l;
end;
if Iy==Ns
463

!.<.с:..л-!.'!.!:!!!!.f!.Й-:'л.!.:!.'!Р.!!!!..'!.'.!!!:1!.':'..кux процессов в пакете MAТLAB
"'"""'"''"'.<..- .
Up=lj
else
Up=Iy+ l;
endj
if Iy==l
Down=Nsj
else
Dоwп=Iу-lj
endj
% пробный переворот спина
Temp=s(Iy,Ix)j
s(Iy ,Ix)=-s(Iу ,Ix)j
de=2 *s(Iy ,Ix)*(h+J*(s(Iy ,Left)+s(Iy ,Right)+...
s(Down,Ix)+s(Up,Ix» );
if or(de<=O,rand(I)<=exp( -dеЛ))
% пробный переворот спина принимается
Accept=Accept+ 1 j
E(k)=E(k-l)-dеj
M(k)=M(k-l)+2*s(Iу,Iх)j
else
% пробный переворот спина не принимается
s(Iy,Ix)=Tempj
E(k)=E(k-l)j
M(k)=M(k-l)j
endj
S=cat(3,S,s)j
k=k+lj
endj
endj
Accept=AcceptJ(NTrial*Nspin)j % среднее число принятия решений
Далее необходимо выполнить следующую последовательность команд:
» Nspin=64j % число спинов системы
»J=lj % константа обменноrо взаимодействия
» ь=о; % напряженность внешнеrо маrнитноrо поля
» Т=1.5; % температура системы
»NTrial=100j 9( число испытаний
i:
11
I!
l'
'I!
il
':1
1,
1,
1:
,1
i
I
464

, /5 'одел' б д .{ V'
,,' ,... .. ...... ш  ..:'!:.J!!.Р.'!..I!'.::,К'!!.!!!!I':!.'!!.:'Й-'!.'!!!:"!../!!!.л.!...е.й-..'!!!,!::.Й-I,!,':=--,,-!!р":,!!!ш
»[Estart,Sstar,Mstart]=InitSp(NspinJ,h)j % вычисление параметров
% начальной конфиryрации
»[E,Accept,M,S]=IsingКA(NspinJ ,h,NTrial, Т ,Sstart,Mstart,Estart);
% визуализация зависимости мrновенных значений энерrии
% и мarнитноrо момента системы от времени
» i=I:length(E);
» tigure(I);plot(i,E,'k');axis([O length(E) -300 10])
» tigure(2);plot(i,M,'k')
% визуализация MrHoBeHHbIx конфиrypаций системы
» tigure(3);bar3(S(:,:,I»jcolormap white;axis([O 9 О 9 -11])
»tigure(4)jbar3(S(:,:,10»;colormap white;axis([O 9 09-11])
»tigure(5);bar3(S(:,:,100»;colonnap white;axis([O 9 09-11])
»tigure(6);bar3(S(:,:,500»;colormap white;axis([O 9 О 9 -11])
» tigure(7);bar3(S(:,:,2000»;colormap whitejaxis([O 9 О 9 -11])
% выделение MrHoBeHHbIx значений энерI'ИИ и мarнитноrо момента,
% соответствующих равновесному состоянию системы
» j=I:1епgth(Е)-2000j
» Еlу)=Еу+2000);
» Мlу)=Му+2000);
% вычисление теплоемкости в соответствии с (15,17)
» Е2=Еl.Л2j
» c=(lff. Л2)*(mеап(Е2)-mеап(Еl). Л2)lNsрiп
с=
0.2708
% вычисление маrнИ1'НОЙ восприимчивости в соответствии с (15.25)
» хi=(ltr)*(mеап(М2)-mеап(Мl). Л2)
xi =
1.1377
» mеап(Мl) % средний маrнитный момент
ans=
0.2204
Результаты выполнения описанной последовательности команд пред-
ставлены на рис. 15,5 15.11.
465

!!.:."!.,!!:!,,!.е!!'I!?:!.'?д-...ш.!.'!Р.!!.в--I!.!1!:'..: .Р'II!I..ч.:с..К.. пр'?'ljес.с.(!вв-- '!.11e,,! ! TL: l!...
'1
!
I
l 1.1 ;' 1" ,J! ". . [, 1 111,' ';" I
Wi" I
1
I
.............J
о 1000 2000 зооо 4000 5000 БООО
r  r
! Чlт (I
,rr1; . Ir
. /'-ut
i (\-"
.100....
!
Рис. 15.5. ЗавиСUАюсть
мсновенных значений энерzии
системы от времени
60
70"-r '''T ,.-.,.
50
'0
'"
20
Рис, 15,6, Зависимость
мсновенных значений
маснитносо момента
системы от времени
10,
:II, '! 1,,,..l":':'&'1
о 1000 2000 зооо 4000 5000 6000
----
'-
",,'  //
/,' .?--С::::.
/'«5J).Y; '" .:'Sxi-:
K   }, 
1.
1
05
о 
-'>,5,:
'1,
"'>
1 '),
2 ''>-.
з "
4 ",
5
",
s -."
..,
5
.<
4
''>,
....., /"2 3
466
/
S
Рис. 15,7, Конфuzурацuя
системы в момент
времени t  О

,
. .. . .l},,:,,!!.!>!l.l!...Й-.в--'!.'.!.!I!..!5.I!.!!..?-,--п!..ч.::''5..?:'?'!!.!!!!л:!..Л:!..'!'.!>:!!!...й-'..I1!!!.:f!c!!!.l!.?
1.
Рис, 15,8, Конфuzурацuя
системы в момент
времени t  1 О
0.5
-'>5
.,
-<,'
'- ":"" 8
5"""' ...---<,,<'6 7
6 ,>, ,4 5
1  ..</; 3
8 ......... 1
0.5
-0.5
.1
Рис. 15,9, Конфuzурацuя
системы в момент времени
t = 100
"-
2 ;>'--:.. ...<"
4 о,:" .<"''/'<7 8
5  ,"",""""" 5 6
1 "---"" _// 4
8 ,,,,,...---'" 1 2
Рис, 15, 10, Конфuzурацuя
системы в момент
времени t 500
467

l<?!J ,:!'?п-..'еl!..::?:..М'?!.'l!.Jl...в--l!:'U '!.r/J.'!..!:',!".C.'?'X ,:роц,,:сй-в-- ,6 п-..а..К!'rrI:...!!../1.!.LА.
 ",
(", -;:
i
i i ii 1
i t
I I
i M3)
. i> 5s:<lf::;'6::1 .
, .1 {">1 <>1 /\,11 j,. " 1 >:: '1: <";:'1
....J.. j.l -,, I k "->.!' ,il.--
<.  I ' '. 11 :,.->. I!U :1:" "(--:r: <, .:." ,/ "
05! '111;111И::.11! :.,'JS1f:1iir.lS
i  ' IlfAJ' У l--/lf ::'il!1 .
о j r'rn fl I l(} :1.,'.J;:r"11 1 i.r] 
I I / I n i 11 I I', 11 I 111 ",
.0.5 I I .. ,J) '1 11 ! 11 (! 1'x:."'I'?
I ' cr f' I F 1"-,, )Iii 1
, "" ч Ill'f .. O\lJrl{ i l i I
1 2"}"J)i I 'llrCjr 111111 ! U I !! 1 J>/
4 "'", '--,j/? ! r I I I '1 "< 8
5---.'>__ : 1 'L '!-.J/<<, 6 '
6 ")., .....,L..-' / /' 4 5
7 '>---.__ __<,,; 3
' 1
1
i i 1i 11
i i
1 1
i i 1r 11
1 1
1 1
lrl111
1 1
I:1E-8 J
r r
r i lr 1
i i
М-4)
Рис, 15,11, Конфи2урация системы в )Iюмент
времени t 2000
MO
., ...............
Задача 15.11
Из выражения для полной энер2UU cиc.
темы (14,8) видно, что вклад в значе
ние переменной r, вычисляемой в cooт
ветствии с (15,26), дают только сла
2аемые, содержащие Sij:
r = е 2!l.f;PS+II) , (15,27)
2де !llij  изменение Sij спина, обуслов
ленное е20 переворотом, S  сумма че
тырех спинов, соседних с переворачи
ваемы-м спином, Так как S может пpи
НИJ.1ать только 5 различных значений О,
:t2,:t4, при h = О имеется все20 5 раз
личных значений энеР2ии (рис, 15,12):
0,:t2J ,Н] ,:t8J ,
Следовательно, чтобы не вычислять каждый раз значение экспоненты,
для уменьшения времени счета можно один раз вычислить и запомнить
таблицу значений r, Внесите в функцию 1siпg2, необходимые изменения
и попробуйте оценить, на сколько сократилось время вычислений,
I:1E 4 J
Рис, 15,12, Возможные измененlIЯ
энеР2ии в двумерной ,иодели
ИзиН2а при перевороте
одНО20 спина
468

I
!!."!.?::l!.Р.ов--а.."l''!...К/11 о!,и чекооcz.','б.l!.Я.л-!.'!.".!..?Й-!"! й--,т::: J.e...й.РЛ-О
i<
Задача 15.12
Исследуйте зависимость времени релаксации системы к равновеснOJ'ЛУ
состоянию 're/ от температуры систеЛfЫ Т" и числа спинов системы
Nspiп. Отобразите зависимости 're/ =T,'e/(TJ, Tlt/ = ','e/(Nspiп) , Aп
проксимируйте данные зависимости JиетодОJW наименыuих квадратов.
Задача 15.13
В описанном выше документе мы оценивали равновесные значения энер
2ии, удельной теплоеЛfкости, ма2нитН020 молtента и нама2ниченности,
как средние значения, вычисляе.мые по соответствующим М2новеннылt
значениям после достижения системой состояния равновесия, В данном
подходе априори пола2ается, что каждое из М2новенных значений явля
ется статистически независимым от остальных значений, т, е, «врелtЯ
корреляцию> между выборками равно нулю, При более правuльном пoд
ходе следует вычислить автокорреляционные функции
С (T) (E(t)E(t+r))(E[/
Е,  (E2)(E)2 '
С (Т)= (M(t)M(t+r))(M)2
м (M2)(M)2
2де ( ) усреднение по всем возможным значениям (, оценить число ша
20в метода МонтеКарло, за которое значение автокорреляционной
функции уменьшается в е раз, и вычислять среднее значения энер2uи,
vдельную теплоемкость, средний мazнитный МОо11ент, удельную Haмa2
иченность, проводя выборку значений, отстоящих дРУ2 от дРУ2а не
менее, чем на r('orr' Дополните описанный выше документ, собственной
функциеu, возвращающей значения автокорреляционной функции, Bы
числите значения автокорреляционных функций системы, состоящей из
N  64 спинов, при температурах т, меняющихся в интервале [1,5,3,5] с
шazом I1Т = 0,1 , Как зависит время Корреляции от 'пемпературы? Дo
полните описанный выше документ функцией, возвращающей среднее
значение энеР2ии системы, удельную теплоемкость, средний ма2нитный
момент, удельную нама2ниченность, вычисляемые по значениям, oт
стоящим дРУ2 от друю по времени не Лtенее, че;,.t на T('or.(T), Сравните
полученные термодинамические характеристики системы с анал02ич
ными характеристикш>tU, найденными усреднением по всей реализации,
469

.!i':.:"!.'._ь.'?!!!.(!.Р!.е..5!.<!...'!!!.!!.!:'!..I!:р'!..!'!..,:_с!!,,!!пр"5!.'!.е..?.!!!!'!.:!!'!..._1T!._.. ..
Задача 15.14
Для более реалистИЧН020 описания процесса релаксации системы к paв
новесию следует проводить выбор спинов, подлежащих опрокидыванию,
случайным образом, Однако. если мы интересуемся равновесными cвoй
ствами системы. то можно сэкономить машинное время, выбирая спи
ны последовательно, Как влияет на время корреляции способ выбора
спинов, подлежащих опрокидыванию, Почему нежелателен последова
тельный выбор спинов в одномерной модели Изинzа?
В пределе бесконечно большой решетки (Nspiп  00) модель Изинrа
имеет точное решение [13]. В предельном случае при h = О энерrия систе
мы Е дается выражением
 = ] .coth(2xJl+K" к,(к)], (15.28)
Nspт t 1r
sinh(2x) 2
к=2- ; K'=2tanh (2x)I;
cosh2(2x)
eXeX eXeX
sinh(x)=; tanh(x)= ; coth(x)  rиперболический apKKOTaH
2 eX+eX '
reHC; к,(к)  полный эллиптический интеrpал первоro рода:
rде х = tanh();
еХ + eX
cosh(x) = 2 ;
'1
;1
!!...
2 d
K,(K)=J rp,
о 1 K2 sin2 rp
у дельная намаrниченность при Т < Те равна
, ,
=+ 6+Z2F66z2 +z1..
 "
Nspiп 6  z2)2
(15.29)
rдe
2tanh( У..)
z =е т.
Задача 15.15
Для бесконечной решетки вычислите и отобразите 2рафически зависи-
мости энер2ИИ, удельной теплоемкости и нама2ниченности на один
спин при h = О от температуры в диапазоне температур [0.1;3.5].
470

.. ..шш ..! 5А! О:'Л!IР'ов'!.II!lеК'!.II(?'Iи-чес..,??_'!.!IС(1:'lУ!I:.:''''-?..':.r/:!Y,,;l:: f!'!.P'j'?..
Задача 15.16
Решив задачу 15.16, вы обнаружили, что в двУ,tерной модели ИзиН2а
возникает фазовый переход: нама2ниченность системы в точке фазо
в020 перехода становится равной нулю, а теплоемкость системы и ее
ма2нитная восприимчивость расходятся, Проведите численные иссле
дования поведения модели Изиll2а вблизи точки фазовО20 перехода и
сравните ваши результаты с точным решением, Каков раз.wер .wa2Hum
ных дОАtенов при т еАт ера туре, близкой к критической? Как влияет KO
нечный раЗА1ер решетки на особенности зависимостей термодИflа.tиче
ских величин от температуры?
Задача 15.17
Используйте описанный выше документ для исследования тepMoдиHa
.wических свойств модели ИзиН2а при h;4J.
ЛИТЕРАТУРА
1, Creutz М" Microcanonical Monte Simulation, Phys, Rev, Letts, 50,1411,1983,
2, Bhanot G" Creutz М., Neuberger Н., Microcanonical simulation of Ising system, Nucl, Phys,
235,417,1984,
3. Metropolis N" Rosenbluth А, W" Rosenbluth М, N" Teller А, Н" Keller Е, Equation of state
calculations for fast computing machines, j, Chem, Phys, 6, 1087, 1953,
4, rулд Х" ТобоЧlШк Я, Компьютерное моделирование в физике, М,: Мир, 1990, Т, 2.
5. Китrель Ч, Введение в физику твердоrо тела М,: Наука, 1978,
6, Кун ин с. Вычислительная физика. М.: Мир, 1992,
7. Ландау Л, Д., Лифшиц Е, М, Статистическая физика, М,: Наука, 2000,
8, Методы МOIпеКарло в статистической физике/Под ред, К Биндера, М,: Мир, 1982.
9, Дайсон ф" Монторолл Э" Кац М" Фишер М, Устойчивость и фазовые переходы, М,:
Мир, 1973,
10, Матвеев А, Н. Молекулярная физика, М,: Высшая школа, 1981,
11, Вильсон К, Koryr Дж, Ренормализационная rpyrтa и Еразложения. М,: Мир, 1975,
12, Хеерман д, В. Методы компьютерноrо эксперимента в теоретической физике, М.:
Наука, 1990.
13, XyaHr К Статистическая механика, М.: Мир, 1966,
471

rлава 16
МОДЕЛИРОВАНИЕ
КВАНТОВЫХ СИСТЕМ
16010 Введение
В квантовой механике любая система полностью описывается заданием
волновой функции 1jf(1',t) (в общем случае комплексной), квадрат модуля
:1jf(F,t)2 которой определяет плотность вероятности обнаружить частицу в
момент времени t в некоторой точке пространства с радиусомвектором F.
Так как частица может находиться в произвольной точке пространства, Be
роятность Toro, что частица находится в элементарном объеме dV = d31' в
точке пространства с радиусомвектором l' в момент времени t равна
Р(1', t )d21' = c211jf(1',t),2 d3r , (16.1)
rде С  нормировочная постоянная, выбираемая из условия
'"
J 1jf0(F,t)IJI(1',t)d31' = 1,
(16.2)
""
здесь 1jf0(1',t)  функция комплеКСlюсопряженная 1jf(1',t) .
Если частица движется в потенциале U(r,t), то временная эволюция
функции Ijf(F,t) описывается нестационарным уравнением Шрединrера
'fo. дljf(r,t) 112 А ( ) u( \ш( )
1ft  дt =  2т lJ.1jf У, t + l' , t IY' 1', t ,
(16.3)
I
. I
rде m  масса частицы, Ii  постоянная Планка, деленная на 2п,
д2 д2 д2
Ll ,-=  , +  ,+ .,  оператор Лапласа,
д X д у2 д Z2
Каждой физической классической характеристике частицы (например,
координате, скорости, импульсу, моменту импульса, энерrии и др.) ставится
в соответствие некоторый оператор, Наблюдаемое значение величины А
есть среднее значение соответствующеrо оператора А
(А) = f f//*(и)A 1jf(1',t)d3p , (16.4)
,
............... ?.:...':!й--<!.=!!Р...?!!.I!!!!!!..!5.ваlt!!!ов
Например, оператор, соответствующий импульсу р, имеет вид
.-t-, д
Р = t"  , а ero среднее
дF
() ,J О( )дljf(r,t) 3
р = /п Ijf 1',t. . d 1'.
д1'
В одномерном случае уравнение Шрединrера принимает вид
ifj дljf(ХД = Ijf(x,t)+U(x,t)Ijf(X,t). (16.5)
дt 2т дх2
Для независящеrо от времени потенциала можно искать решения ypaB
нения (16.3), (16.5) в виде
iEt
Ijf(r,t) = ф(1',t)е h ,
(16.6)
iEt
Ijf(х,t)=ф(х,t)е tl ,
(16.7)
соответственно.
Частица, находящаяся в состоянии, описываемом волновой
(16.6), (16.7), имеет вполне конкретное значение энерrии Е.
(16.7) в (16.5), получаем стационарное уравнение Шрединrера
п2 д2ф(х)
 + U (i)ф(х) = Еф(х).
2т д х2
Отметим, что уравнение можно записать в виде
[ д22 +u(х)]ф(х) = Еф(х) ,
2т дх
функцией
Подставив
(16.8)
(16.9)
п2 д2
из KOTOpOro видно, что  .. .. + U(х) является оператором энерrии
2т дх2
fl (оператор rамильтона), ф(х)  собственная функция rамильтониана,
Еп  собственное значение оператора fl , т. е.
flф(х) = Еф(х) , (16.10)
Вообще rоворя, оператор fl может иметь п собственных функций фп И
п соответствующих им собственных значений энерrии EIl, которые в ряде
случаев Moryт совпадать (вырожденные состояния) ПЛИ принимать конти
нуум непрерывных значений (непрерывный спектр), Основным СОСТClянием
называется состояние с наименьшей энерrией EI'
473
.

J(, ?ЛI/ЫО./11=р'JIО:...1 од'!..l!I!.J1.й.f!.а!..l.и. .чшзи ч ecкl!.x IlpOЦ"CCO в.'I.'!к.еfl!еМ-АТ'!.е.. ,
Общее решение (16,9) можно представить в виде суперпозиции собст
венных функций оператора, отвечающеrо выбранной физической величине.
Например, если Й не зависит от времени, то можно записать
iE"t
ljI(x,t):::: LС"ФIl(х)е t, (16,11)
"
rде ф,,(х)  собственные функции оператора, а суммирование проводится
по всем дискретным Состояниям и интеrpал по непрерывному спектру.
Собственные функции Фll (х), соответствующие различным собственным
значениям, являются ортоrональными, т, е,
+ос:
f ф*,,(х )Ф'z'(Х )dx = д/т' .
(16.12)
'"
Коэффициенты С" в (16.11) определяются по известным значениям
функции IjI(X, t). Например, если известны значения IjI(X,O), то, воспользо
вавшись свойством ортоrональности (16.12), леrко получить
С" = f ф*(Х)IjI(х,О)dх. (16.13)
Коэффициент С" можно интерпретировать, как амплитуду вероятности
обнаружить в измерении значение полной энерrии, равное EIl'
16.2. Стационарное уравнение Шрединrера
Рассмотрим решения одномерноrо стационарноrо уравнения Шрединrе
ра (16.9) частицы, движущейся в одномерном потенциале и(х), форма KO
Toporo представлена на рис. 16.1 (в точках Xmill' Хтах потенциал становится
бесконечно большим), Это означает, что в точках Х" Х Расположены
mш' шах
вертикальные стенки, а между ними находится яма конечной шубины. Для
удобства дальнейшеrо решения запишем уравнение Шрединrера (16,9)
в виде:
d 21j1
d х2 + е (x)ljI(x) = О,
(16.14)
r"де
474
.............
11
I
...J :.?J/!.'.f..?.I!!.и!:!5.'!I!!!!!!:!.."!!:.I!.ec...Cтe.!!
2 2т
k (х) = 2 [Е  U ( Х )] .
1i
(16.15)
с(х)
M
x"uп
хтах
х
Рис, 16.1, К постановке задачи решения стационарноzо уравнения Шрединzера
С математической точки зрения задача состоит в отыскании собствен
d2
ных функций оператора . + k 2 (х) , отвечающих rpаничным условиям
d х2
IjIIl (xmiп) = ljI п (Хтах) = О , (16.16)
и соответствующих собственных значений энерrии Е.
Так как k2(x)0 при XE[X/eft,Xright] И k2(x):5:0 при XE[Xmill'X/eft],
Х Е rx 'h Х ] то можно ожидать, что собственному решению данной за
 пg t' пшх '
дачи соответствует собственная функция, осциллирующая в классически
разрешенной области движения Е  U (х) (х Е [X/eft, X;ght]) И экспоненци
ально затухающим в запрещенных областях, rде Е < и(Х) (х Е [Xmill' X/eft ],
Х Е [Х' Х ]) При Х < Х. х> Х lIf(х) =: О. Так как все состояния
пght' тах '  тт'  mах 'f'
частицы в потенциальной яме оказываются связанными (т, е. локализован
ными в конечной области пространства), спектр энерrий является дискрет
ным, Частица, находящаяся в потенциальной яме конечных размеров
475

f(,?:\tll.IO"!e.P'lt.'?:Af.,??...el}lp',!ltll. rjJ!!.з..l<',!=l':.!lf.Оll,!=с..?. в п'!K!.!11'!!t!./! 1:.!!_
(И(х)::; о при Х Е [xтill,xтaxJ, И(Х) = о при .\  [Xтi/1,xтaxJ), имеет дискрст
ный спектр при Е < О и непрерывный спектр при Е  О ,
Традипионно для решении задачи о нахождении собственных значений
уравнения Шрединrера используется метод пристрелки, Идея метода при.
стрелки состоит в следующем, Допустим, в качестве искомоrо значения
ищется одно из связанных состояний, поэтому в качестве пробноrо началь-
ното значения энерrии выбираем отрицательное собственное значение,
Проинтеrpируем уравнение IlIрединrера какимлибо известным численным
методом на интервале [Xтi/1' ХZФ]' По ходу интеrpирования от XIIliil В CTOpO
ну больших значений Х сначала вычисляется решение Ij/ -t (х) , экспоненци
ально нарастающее в пределах классически запрещенной области. После
перехода через точку поворота XZeft' оrpаничивающую слева область дви
жения, разрешенную классической механикой, решение уравнения CTaHO
вится осциллирующим. Если продолжить интеrpирование далее за правую
точку поворота Xr(llI' то решение становится численно неустойчивым. Это
обусловлено тем, что даже при точном выборе собственноrо значения, для
КОТОрOI"О выполняется условие Ij/ -t (ХlI1ах) = о , решение в области
Х Е [X"(llI' ХIl1Ю] всетда может содержать некоторую примесь экспоненпи
ально растущеrо решения, не имеющеrо физическоrо содержания. OTMe
ченное обстоятельство является общим правилам: интеrpирование по на-
правлению вовнутрь области, запрещенной классической механикой, будет
неточным. Следовательно, для каждоrо значения энерrии более разумно
вычислить еще одно решение Ij/  (х) , интеrpируя уравнение (16.9) от Х/1ШХ В
сторону уменьшения х. Критерием совпадения данното значения энерrии
является совпадение значений функций Ij/ + (х) и Ij/  (х) в некоторой про
межуточной точке Хт. Обычно в качестве данной точки выбирают левую
точку поворота ХZф' Так как функции Ij/ t (х), Ij/ -t (х) являются решениями
однородното уравнения (16.9), их всетда можно отнормировать так, чтобы в
точке Х/ll ВЫПО-тIlIЯЛОСЬ условие If/-t (.\/11):= If/ (хm) , Помимо совпадения зна
чений функций в точке Х/11 дЛЯ обеспечения I'Ладкости сшивки решений по
требуем совпадения значений их производных If/; (Х/11) = Ij/: (хт) :
d\l/J
= I
dx . XX/11
.J !t'i[
dx : \X/11
(16, j 7)
476

l'
- --'
t
16. М'?():Л-l<f!,?!,ll!=«r:.!II'l()в!::с.l<=''!:-''!.
Используя f\ (16,17) простейшие левую и правую конечноразНОСТНblе
анпроксимации прuизводных фУНКIlИЙ Ij/+(X), Ij/j(X) В точке '\111' находим
эквивалентное условие rладкости СШИВI-:И решений:
Ij/ , (Хт ) + If/  (Х т )  [Ij/ + (Хт  11) + Ij/  (х /11 +11)J
f =,  -.. _.H -= (), (16,18)
" шах I/i
Число max!lf/: является масштабирующим множителем, который выби
рается из условия f  1. Если 10Ч1(И поворота отсутствуюr, т, е, Е> (), то в
качестве Х//1 можно выбрать любую точку отрезка [Xтiп,xтaxJ, Для потен
циалов, имеющих более двух точек поворота и, соответственно, три или бо
лее однородных решений, общее решение получается сшивкой отдельных
кусков,
В описанном ниже документе, для интеrpирования дифферснциаль
НОТ'О уравнения второто порядка мы используем 'fСТОД Нумерова, Для полу
чения вычислительной схемы аппроксимируе-м вторую производную Tpex
точечной разностной формулой:
" h 2 "" (, 4)
= )'1/ + 12 )'/1 +- O\h .
X!:I J . 21'I!. + !-,-,-1
/12
Из уравнения (16.9) имеем
нн d2 "2) (k2)')I-tJ2(е)1+(k2}11
у = ::;  к (х) у   -:::-- Ш .
11 d х" х=х" /1"
Подставив (16.19) в (16,20) и переrpуппировав члены, получаем
( !/ 2 '\ (5h 21 r h 2 J
1 +  k 1 j V 1  2 1  2ш k I у + 11 + ш k 1., \' J = О .
. 12 11+ .' 111- \ 12 1/ J' 11 L 12 1/ ,1/
(16.19)
(16.20)
(16.21)
Разрешив (16.21) относительна )'11 + 1 или YIll' найдем рекуррентные
формулы для ИНТСI-рпрования уравнения (16,9) вперед или назад по х с ло
кальной поrpсшностью О(hб). Отмстим, что ПОl--решность ДaIШОП) метода
оказывается на порядок выше, чем lIоrpешность метода PYHTeKyтra чет
вертото порядка Kpo\fC этоrо данныЙ алrоритм более эффективен, потому
2.
что 'шачение функции k (х) вычисляется только в узлах сетки,
Для НRхождения числеННОI"О решения оказывается удобным провести
обезразмеривание уравнения (16,9), используя в качестве единиц измерения
расстояния а  ширину потенциапыlйй ямы, в качестве единиц измерения
энеРПIlf  -модуль минималЫ10rо значения потенциала и о. В выбранных
еДИНI1цал Ю;\1еретlИЯ уравнение (16,Q) инеет ви;,:(
477

Fi?!!'!..?!!!:I!!.If!=-А!.r:..,!!!IР..?в--l!.III-!.ер''!.?ие..с..КUX/Р.?'-!..е..:ов в пa'!.rrle..!1 ПА В
d2
 + у2(Е a(X))rp = о,
dx
(16.22)
,де
!I
i i
X= E= а(Х)=Щ у2=2та2ио. (16.23)
а ' ио ' ио ' 112
Таким образом, вычислительный алrоритм для нахождения собственных
функций и собственных значений уравнения Illрединrера реализуется сле
дующей последовательностью действий.
1. Задать выражение, описывающее безразмерный потенциал а (х) .
2. Задать значение у2 ,
3. Задать пространственную сетку, на которой проводится интеrpирова-
ние уравнения (16.9),
4. Задать Xmil/ ' Хтах.
5. Задать начальное значение энерrии Estart.
6. Задать конечное значение энерr'Ии Е fil/ '
7. Задать шar изменения энерrии АЕ .
8. Проинтеrpировать уравнение (16.9) для значения энерrии Е; слева
направо на отрезке [Xmi//' Хт] ,
9. Проинтеrpировать уравнение (16.9) для значения энерrии Е; справа
налево на отрезке [х//шх,Хт].
10. Вычислить значения переменной fi для значения энерrии Ei.
11. Увеличить текущее значение энерrии на АЕ: Ei+1 = Е; + АЕ .
12. Проинтеrpировать уравнение (16,9) для значения энерrии Ei-+I слева
направо на отрезке [Xmi//' Хт] .
13, Проинтеrpировать уравнение (16,9) для значения энерrии Ei+1 справа
налево на отрезке [х//шх,Хт].
14. Вычислить значения переменной fi-+ 1 для значения энерrии Е, t 1 .
] 5. Сравнить знаки fi, J 11
] 6. Если fi' fr + 1 > О И Ei' 1  Ета.\. увеличить текущее значение энерrии
на I'1E и повторить действия, описанные 11 пп, 8 15,
17, Если f,' f,+ j < О. уточнить собственное значение энерrии :eTOДOl\l
линеЙноЙ интеРПОЛЯIlИИ.
.1
.'
I
478

16 .Moдe...:иP..?в--'!.иe..'!.в--a..//l oebJ:l!c.I11e..
18, Если E'tl  Ета\' повторить деЙСJВИЯ, описанные в пп, 817,
19, Если Е, t 1 > Етах ' закончить вычисления,
Для реализации описанноrо вычислительноr'о алrоритма в пакете
МА TLAB необходимо создать три mфайла: 1) файл Num.m, содержащий
описание функции, возвращающей для заданной энерf'ИИ величину f, BЫ
числяемую в соответствии с (16,18), и значения волновой функции в узлах
координатной сетки; 2) файл U.m, содержащий описание фУНКIlИИ, возвра
щающей значение потенциала; 3) файл Elevel.m, содержащий описание
функции, возвращающей собственные значения и собственные функции
уравнения Шрединrера,
% листинr файла Nuш,m
function [f,psi]=Num(gamma,E, V,Xmin,Xmax,Ngreed)
% функция, возвращающая для заданной энерr'ии величину f,
% вычисляемую в соответствии с (16.18), и значения волновой
% функции в узлах координатной сетки
% gamma  коэффициент, входящий в обезразмеренное уравнение
% Шрединrера (16.22)
% Е  заданное значение энерrии
% V  вектор, содержащий значения потенциала в узлах координатной сетки
% Хmiп  левая rpаница координатной сетки
% Хтах  правая rpаница координатной сетки
% Ngreed  число узлов координатной сетки
dx=(Xmax Xmin)INgreed;
с=dх.Л2*gаmmаЛ2/12;
Imatch=l;
psi(I)=O;
psi(2)=9.99999* 10Л 10;
% интеrpирование уравнения Шрединrера справа налево
Кiml=c*(E- У(1»;
Кi=c*(E- У(2»;
for i=2:Ngreed-l
Кipl=c*(EyH+l»;
if and(Кi*Кipl<=O,Кi>O)
Imatch=i;
i=Ngreed;
end;
if k=N greed-l
psi(i+ 1)=(psi(i)*(2-10*Кi)-psi(i-l )*(1 +Кiтl ))/( 1 +Кipl);
479

l!.'?:"'!.l}:lоп!Е.Ilй-е!...1й-i}=qlР'й-й-иu:..1!..l!.?l!.. ек-.u::.l!й-Iс:о.в: Zй-.к-..:'!.l!: .!ATl!.. ..
if abs(psi(i+l)>=10AJO
for k=l:i+l
psi(k)=psi(k)*9.99999* 10Л 6;
end;
end;
Кiml=Кi;
Кi=Кipl;
end;
end;
if Imatch==1
Imatch=Ngreed-l0;
end;
% интеI-рирование уравнения Шрединrера слева направо
psCLeft=psi(Imatch) ;
psi(Ngreed)=O;
psi(Ngreed-l)=9 .99999* 10Л-l о;
Кipl=c*(E- V(Ngreed));
Ki=c*(E-V(Ngrееd-l));
for i=Ngreed-l:-l:Imаtсh+l
Кiml=c*(E- V(i-l»;
psi(i-l)=(psi(i)*(2-10*Кi)-psi(i+ 1)*(1 +Кipl»/(1 +Кiml);
if abs(psi(i»>10AJO
for k=Ngreed:-l:i
psi(k)=psi(k)*9 .99999* 1 ОЛ-6;
end;
end;
Кipl=Кi:
Кi=Кiml;
end;
if рsil-,еft<О
for i=Imatch:Ngreed
psi(i)=-psi(i);
el1d;
cnd;
psiJ =abs(psi);
PsinIax=max(psi1):
C,i( вычисление разности между ВОIIНОьЫ!\Ш функция, I10;тученными
(1(' !1нrет-рировarшсм ур;шнения Иlрединrl'ра CJleBa направо !j CjTp'lB1
(71- налево. R У'Ч с номером Iтatcl1
480

... ..!..:юА!.й-i}::!ZP.'!!.I!!.еК-:I!!'1r!.овы:.l!."!.
f=(psiLeft +psi (lmatch )-(psi( Imatch -1 )+psi(lmatch + 1» )lPsimax;
% листиНI' файла U.m
function z = U(x,Xmin,Xmax)
% функция, возвращающая значения потенциала в узлах
% координатной сетки
% х  вектор, содержащий координаты узлов
% Хmiп  левая rpаница потенциала
% Хтах  правая rpаница потенциала
if and(Xmin<=x,x<=Xmax)
z=-I;
else
z=10Л309;
end;
% листинr файла Elevel.m
function [EL,Psi]=Elevel(gamma,dE, V,Emax,Xmin,Xmax,Ngreed)
% функция, возвращающая собственные значения и собственные
% функции уравнения Шрединrера
% gamma  коэффициент, входящий в обезразмеренное уравнение
% Шрединreра (16.22)
% dE  при ращение энерrии
% V  вектор, содержащий значения потенциала в узлах координатой сетки
% Етах  максимальное значение энерrии
% Хmiп  левая rpаница координатной сетки
% Хтах  правая l-раница координатной сетки
% Ngreed  число узлов координатной сетки
Тоlf=10Л-6;
Emin=-1 ;
E=Emin+dE;
m=1;
Start=O;
while Е<Етах
if Start==O
Еl=Е;
[f,psi]=Num(gamma,E, V ,Xmin,Xmax,Ngreed);
Е=Е+дЕ;
Fl=f;
Start=l;
end;
16-1576
48]

l!..о..I!IЫ?,lер'llо'!...л:.?:'Р.о!:а.!/:t.I!!I,!еI';(,,!ljJ?цес06 6I1a/((?: A-'!.1.T:!!! .....
Е2=Е;
[f,psi]=Num(gamma,E, V ,Xmin,Xmax,N greed);
F2=f;
if Fl *F2>0
Еl=Е;
Fl=F2;
E=E+dEj
end;
if Fl *F2<0
% уточнение собственноrо значения энерrии и вычисл:ние
% значений собственной функции в узлах координатнои сетки
a=(E2-Еl)/(F2-Fl)j
E=El-а*Fl;
[f,psi]=Num(gamma,E, V ,Xmin,Xmax,Ngreed);
Fl=F2;
Еl=Е2;
EL(m,I)=m;
EL(m,2)=E;
ifm==1
PsiO=psi';
else
PsiO=cat(2,PsiO,psi ');
endj
m=m+ 1;
E=E+dE;
end;
end;
dx=(Xmax-Xmiп)/(Ngrееd-l);
Nl=size(PsiO,2);
% нормировка собственных волновых функций
for i=I:Nl
8=PsiO(:,i);
81=8. Л2;
Norm=O;
for j=1:Ngreed-1
Norm=N orm+0.5*(8 1 О)+81О+ 1) )*dx;
end;
8=8.1(NоrmЛО.5);
if i==1
482

! А!?деI!.l!.?'!.'.I'!.:/(в-.'!.I!rI1?в-.':!..х. =-,-,-п:.л:..
Psi=8;
else
Psi=cat(2,Psi,8) ;
end;
end;
Далее необходимо выполнить следующую последовательность команд:
» Xmin=-0.5; % левая I"Раница координатной сетки
» Хmах=0.5; % правая rpаница координатной сетки
» gamma=20;
»Ngreed=500; % число узлов координатной сетки
% вычисление координат узлов сетки
» i=I:Ngreed;
» x(i)=Xmin+(Xmax- Xmin)/(N greed-l)*(i-l);
»dЕ=10Л-3; % приращение энерrии
» Еmах=-О; % максимальное значение энерrии
» V(i)=U(x(i),Xmin,Xmax); % вычисление значения потенциала
% в узлах координатной сетки
% вычисление собственных значений и собственных функций
% уравнения Шрединrера
» [EL,Psi]=Elevel(gamma,dE, V ,Emax,Xmin,Xmax,N greed);
»EL
EL=
1.0000 -0.9751
2.0000 -0.9005
3.0000 -0.7761
4.0000 -0.6020
5.0000 -0.3782
6.0000 -0.1046
% визуализация собственных функций
» plot(x(i),Psi(:,1), 'k' ,x(i),Psi( :,2),' --k' ,x(i),Psi(: 93)" -.k');
» plot(x(i),Psi(:,4),'k' ,x(i),Psi(:,5),' --k' ,x(i),Psi(:96), '-.k')j
Результат выполнения описанной последовательности команд представ
лен на рис, 16.2 и 16,3.
483

I
I I
, I
I
1
?,'':.?"'!..(!р'.,?еf,?д:'!Р..?в--и--f.I(..4),!з,! t(:II[JОII.с.=:?в--в-- !!и--п! e!:!..!..!!!! ..
, I
15
'.....'
,.
/.' //
/
05.. 1: /
. /
{, //
" /
(/
0(./
.0.5,
Рис. 16.2, ВОЛlювые
функции,
соответствующие
перво,,,,у, второ_ну
и третьему
собственным
значениям энеР2ии
.1',
, ,
1
J
О.. 0.5
-1.'s
L _
02
.  L
-о., О
...L.....
01
.... ...J.
,О, -0.3 .02
03
1.5 
'/\'\ !'-\
::'( ': \ \ \, '
1 /// \ \ \ ;/
/:/ \, \ I Л
'( '.  \ : / \.
'!; '\ I
о 5 ;, I \ \ ' /
! '\ "; I
\ \J \ 1.
\ I \ :
\ 1\ \ /1
/ ; .,:\, j/
\: {\ ('
\\ ; / '\:' !' \ " /j:
\: I " ' '"
'\ ./ \. \.j
.1..ъs -:03 -0:2 '-о:, Q2 . t4 05
. ,
\,
\.
;\
; \
, '
, \
\
,
Рис, 16,3, Волновые
функции,
соответствующие
четвертому, пятому и
шесто,uу собственным
значениям энеР2ии
-05
.,
Задача 16.1
Проверьте условие ортО20нальности собственных функций уравнения
ШредИН2ера (16,12). Оцените точность выполнения даННО20 условия.
Исследуйте завИСUAюсть точности ортО20нальности собственных
функций уравнения ШредИН2ера от ша2а изменения энеР2ии I'1E и числа
шу"зл о f!..!}РЕ.,!!р_q'!.С!!!1:f!..f!...fl_'!!!...qшq"fl'!!JцJ'!.жr..t!..t!..tl:: .ШМ__Ш_ ШШ_Ш_ ш 
Задача 16.2
Для бесконечной прЯАЮУШЛЬНОЙ ЯА1Ы шириной а удается найти ана.1И
тические выра:ж:ения д.7Я собственных функций уравнения и собствен-
ных щачений 11lредИllzера {1. юдача 18].'
484
.........
1
п = 1, Еl = 11 'V/l =(T2 COs( x).
1
V/ 2 = (  J '2 Sin( 2 ) ,
1
V/з =( %Т2 COse: х).
1
V/ 4 = ( % Т2 Sin( 4: х) ,
1
V/ 5 = (% )  i COse: х ).
1
п = 6, Е6 = 36 112л-: =9E1, V/6 = ()Ш2 Siп(6Л- х)
2та 2 а
Используя безразмерные переменные, определяемые в соответствии
с (16.23), получите выражения для безразмерных значений энеР2ИИ и
собственных функций. Сравните численные значения энеР2ИЙ и волновых
функций с соответствующими щачениями, вычисляемыми по анали
тическим выражениям. Оцените точность численных значений энеР2ИИ
и волновых функций, Почему точность зависит от номера собст-
веННО20 значения энер2ИИ?
112л-2
п = 2, Е2 = 4  -:2 = 4Еl '
2та
112л-2
п = 3, Ез =92 =9E1,
2та
112л-2
п=4,Е4 =16=9El'
2та
. 112л-2
п=5 ,Е5 =25=9El'
2та
...... Jб-:??.I!UР...й-!.с:!'!..'5.в---r:.!t!!l.'?в---ь!:с:'!:.п.!.:
Задача 16.3
Для различных собственных значении энер2ИИ.
1. Постройте зависимость плотности вероятности Р(х) от х.
2. Вычислите (х), (х2) в соответствии с (16,4),
3. Вычислите (р), (р2) в соответствии с (16,5),
4. Постройте зависимость разности между соседними уровuями энеР2ИИ
от номера уровня,
...................................
Задача 16.4
1. Определите влияние малО20 возмущения на собственные значения и
собственные волновые функции частицы в бесконечной пРЯМОУ20ЛЬНОЙ
яме, в которой находится небольшой прямоуzольный 20рб высотой и/?
и шириной Ь. СИЛlлtетрично относите.7ЬНО точки х = О, Выберите
485

I i
I
1
!!..'!!'!.':'...?!!':_Р.!t.?:''!.r:J:о.в--Й-/:.rJ!.l!..'!.::'/(,lJ':IЕо.е..СО._!!/("e.!!,:e..T_1.!!.....,_.._
U ь «и о, Ь« а и определите, как зависит энерzия основносо состоя-
ния и соответствующие собственные функции от U Ь ' Ь,
2. Пусть If/o  собственная функция, отвечающая наименьшему собствен-
ному значению энерzии, If/b  собственная функция основноzo состояния
при U Ь '# О , Вычислите 31lачение выражение
{I
J If/b (х )If/(x) dx
.Q..,..
(l
J 1f/2(x)dx
о
при различных значениях Ь, Как связана данная величина с изменением
относительных значений энерzии?
(Указание. Предваряя решение задачи, запишите ее условие в безразмер-
ных единицах.)
...........
Задача 16.5
Так как при х = !I2Лубина ямы конечна, функция If/(X) не равна нулю в
12
запрещенной классической механикой области, в которой Е < U о и
х > 1%1, Используя рис, 16,1, измените функцию, описывающую зависи
мость потенциала от координаты, и рассмотрите движение частицы
в nрямоуzoльной потенциальной яме конечной zлубины.
1. Вычислите собственные функции и собственные значения энерzии, начав
с уровней, близких ко дну ямы, Как me/-fЯются волновые функции по мере
удаления от дна ямы?
2. Определите «2Лубину nроникания под барьер» как расстояние от х = а/2 до
точки, в которой 31lачение функции составляет l/e:::: 0.37 от ее MaKcи
МШlЬНОZO 31lачения, Как зависит 2Лубина nроникания от величины ио?
.     
     и..и И  . 
Задача 16.6
1. Получите несколько первых собственных 31lачений энерzии и собствен
ные функции zармоническоzо осциллятора, оnисываемосо потенциалом
1 ,
и(х) = - k x, Сравните полученные 31lачения с известными аналитиче
2
скими результатами.
486

. .........!. б.:.'??f!!!_и-Е.'?..в--й-!!l!..е._Кв--Cl..I'!!о.в--х:С.lJ::.'!!е.Jo1.
2, Постройте зависимость плотности вероятности Р(х) от х,
], Вычислите (х), (х2) в соответствии с (16.4),
4, Вычислите (р), (р2) в соответствии с (/6,5),
Задача 16. 7
Получите несколько первых собственных значений энерzии и собствен
ные функции анzармоническоzо осциллятора, оnисываемосо noтeHциa
() 1 2 3
лом U Х =  k х + Ь х . Вычислите энерzию основносо состояния для
2
k = 1, Ь = 0,1,0.2.0.5, Как зависят энерzия основносо состояния и форма
волн?вых функций от Ь?
Задача 16.8
Получите численное решение для основносо состояния линейноzо noтeH
циала
u(x)=lxJ .
(Данный потенциал может быть использован при моделировании свя
занной системы кварк  антикварк.)
16.3. Моделирование колебаний двухатомной
молекулы в квазиклассическом приближении
в данном разделе мы рассматриваем задачу об описании колебаний
двухатомной молекулы, методы аналитическоrо решения которой под
робно рассматриваются в работах [24], Следуя выбранному подходу, обсу
дим постановку задачи и основное внимание сосредоточим на вычисли
тельных проблемах, возникающих при использовании для. ее решения в па
кете МА TLAB.
Двухатомная молекула состоит из двух ядер, связанных электронами,
Поскольку масса ядер на три порядка больше массь. электронов, можно
считать, что распределение электронов MrHoBeHHo подстраивается к изме
нению положения тяжелых ядер (приближение Бора4)ппенrеймера), Это
позволяет свести рассматриваемую задачу к задаче о движении двух ядер в
потенциальном поле, зависящем от расстояния между ними. Причем на
больших расстояниях потенциал должен быть притяrивающим (силы BaH
дерВальса), а на близких расстояниях  отталкивающим (кулоновские си
лы и обменное взаимодействие), Таким свойством обладает потенциал Ле
нардаДжонсона
487

.l!..?л.!!?.'!!.l!!l!!!:.!!?...<!....е:!'!Р..?.!!..l!!.I!:!f!...Р''!..'.'.'!.:'!.'!.п.!!о.1j!.о.l!.в----'!.с:..'!.:.''!!!!..,}:!'.!.!!.. . _._______ _
V(r)==4Vo[()12 ()6}
(16.24 )
rде Vo, а  параметры потенциала (рис, 16.4), который рассматривался нами
при моделировании неидеальноrо rаза методом молекулярной динамики в
rлаве 10. Из (16,6) очевидно', что потенциал достиrает cBoero минимума,
paBHoro Vo, в точке rmin==21/6o:
V
Рис, 16.4, Потенциал
r J7ейнарда)1онсона
Принимая во внимание большую массу ядер, можно провести дальней
шее упрощение задачи, считая движение молекулы суммой двух независи
мых друr от друrа движений: медленноrо вращения молекулы как единоrо
целоrо и более быстроrо колебательноrо движения ядер атомов относитель
но центра масс. Первое движение хорошо описывается как KBaHTOBO
механическое вращение жесткой системы типа «rантель». Колебательное
движение ядер описывается уравнением Шрединrера (16.8), в котором
и(х)  потенциал ЛейнардаДжонсона,
Наша задача состоит в нахождении собственных значений энерrии
(энерrетическоrо спектра) колебательноrо движения. Принимая во внима
ние большую массу ядер, можно считать, что их движение близко к класси
ческому. Поэтому приближенные значения энерrии колебаний можно най
ти, решив классическую задачу о движении частицы в потенциальном поле,
а затем для определения энерrетическоrо спектра использовать правила
квантования БораЗоммерфельда [5],
Классическое финитное движение в потенциале V(r) возможно в диапа
зоне энерrий Vo < Е <О, При этом изменение межъядерноrо расстояния
имеет характер периодическоrо движения между точками поворота, KOTO
рые мы будем в дальнейшем обозначать r/ejt, rrig/Jt. Для частицы, двиrающей
ся в потенциальном поле, выполняется закон сохранения энерrии
2
E==+V(r), (16.25)
488
............
..............1?:.fl:!??e.:'!'!.P..?r:!!'!..'!._'!.'!.1!!!!.?..!:..!!.'!!.:!!
rде р  импульс относительноrо движения ядер, Поэтому в фазовом
пространстве движение представляет собой некоторую замкнутую кривую,
в каждой точке которой выполняется условие (16,25), В явной форме
уравнение траектории в фазовом пространстве получается решением
уравнения (16.25) относительно р:
р == х[2т(Е  V(r ))]1/2 . (16.26)
В классическом случае движение частицы возможно при любом значе
нии энерrии в диапазоне [Vo;O], Для нахождения дискретноrо энерrетиче
cKoro спектра Еп уравнения Шрединrера вводится переменная величина 
действие, зависящая от знерrии системы [5]:
S(E) == fk( r )dr, (16.27)
rде k(r) == Iilp(r)  волновое число волны де Бройля, а интеrpирование Be
дется по одному полному периоду колебания, По своему физическому
смыслу переменная действия соответствует площади, охваченной тpaeKTO
рией в фазовом пространстве и измеряемой в единицах п. в соответствии с
правилом квазиклассическоrо квантования разрешены лишь те значения
энерrии Еп, которым соответствует действие, равное 2к(n+ 1/2), rде n
=0,1,2... Таким образом, используя (16.25) и замечая, что траектория сим
метрична относительно прямой х==О, получаем
1/2 rright
S(E,.) == 2[7] J [Еп  V( r )]1/2 dr == 21l'( n + 1), (16.28)
'ieft
В rpаничных точках интервала интеrpирования подынтеrpальное Bыpa
жени е в (16.28) равно нулю,
Для удобства решения данной задачи введем следующие безразмерные
переменные
G == _!i х ==  r ==[2ma2Vo]
V. ' , 2'
О СУ 1;
(16.29)
используя которые, выражение (16.28) можно записать в следующем виде:
Х right
S(c,,) == r J [&"  у(х )]1/2 dx == 21l'( п + i), (16.30)
x[efi
rде
Y(X)=4[ ],
х12 .\'6
489

.Е<. й-.А' '.ICJ.,!,.ерl'.CJ..:.:I!.(}<!.:...r:P.f!...а.'.'.'!.:...rJ!,:!к-.,!::рCJ.е.:.=-(}.!! l!К--.:.'!'.:.А..!.1:.в-...
Из (16,30) видно, что величина r является мерой KBaHToBoro характера
движения в данной задаче, так как в классическом пределе Ii  О, т  00 r
становится большим, Для молекул Н2, HD, 02 величина r составляет 21,7,
24,8, 150 соответственно,
Сравнив (16,30) и (16.27), видим, что выражение k(X)=r...J;=l>(X)
является обезразмеренным волновым числом волны де Бройля,
В соответствии с вышеизложенным решение рассматриваемой задачи
разбивается на следующие этапы.
1. Нахождение зависимости S( &) И спектра &/1 колебаний двухатомной
молекулы в соответствии с (16.30),
2. Построение спектра совместно с зависимостью V( Х ),
3. Решение уравнений rамильтона и построение траектории на фазовой
плоскости.
Будем находить разрешенные значения энерrетическоrо спектра &11 в COOT
ветствии со следующим алrоритмом.
1. Найти по таблице значений функции S(&) дЛЯ заданноrо KBaHToBoro
числа n интервала, на котором выполняется условие S jl :;; 21l"( n + ) :;; S j .
2. Если S jl = 21l"( n +) , принять в качестве значения nro энерrетиче
CKoro спектра Ejl .
3. Если S j = 21l"( n + ), принять в качестве значения nro энерrетиче
CKoro спектра Е j .
4. Если S j 1 :;; 21l"( n + ) :;; S j' принять в качестве n [о значения энерrе
тическоrо спектра значение, получаемое с помощью линейной интерполя
ции зависимости S(&) на отрезке [Ejl,Ej]:
Е/I
( n + )Л"  Ь
а
[де
 SjSi]
а  
EjEj.1
I
I
490
..........
ш:1о:..CJ.3.!!/!'?.!!!!.':'К-l!.а!!,!,CJ.I!..."!!....=-=---"!.
ь = j1 EJ.= S /!i=1
Ej Ejl
5, Увеличить квантовое число на единицу n = n + 1:
. Если 21l"( n + l):;; max(S(E)), повторение пп. l,
. Если 21l"( n + ) > max(S(E)), завершение работы,
rеометрическая интерпретация описанноrо алrоритма представлена на
рис. 16.5,
Для реализации описанноrо выше алrоритма вычисления спектра коле
баний двухатомной молекулы необходимо создать два mфайла: 1) файл Ас-
tion.m, содержащий описание функции, возвращающей значения функции
S(E) дЛЯ заданных значений энерrии; 2) файл Spectr.m, содержащий опи
сание функции, возвращающей собственные значения энерrетическоrо
спектра колебаний двухатомной молекулы.
SiE'
27f(п+)
.
.
.
S,
Sjl .
.
.
.
. . Е
Ejl Е. Е,
Рис, 16,5, rеометрическая интерпретация алzоритма вычисления
энерzетическоzо спектра
% листинr файла Action.m
function z = Action(Emin,Emax,Xmin,gamma)
% функция, возвращающая значения функции S(E) дшl заданных
% значений энерrии;
% Emin  минимальное значение энерrии
% Етах  максимальное значение энерrии
% Xmin  координата минимума потенциальной энерrии
% gamma  коэффициент, входящий в обезразмеренное уравнение
% 1llрединrера (16,22)
% нахождение корней уравнения U(x)=Emax
491

E<.?A.':I? ,!1e.f1.II0e. .!.?iJ.e.I!P.?.I!!.. р!I?и..че:.КI9:: l1.E..o."..:o.в '!к-e.'!: -!.!. '.l!..,. .
sl='4*(I.1r. л 12-1.1r. Л6)';
s2=num2str(Emax);
s=strcat(sl,'-' ,s2);
хО=О.I;
Xleft=fzero(inline(s,'r'),[O.1 Xmin]); % левая точка поворота
xO=10*Xmin;
Xrihgt=fzero(inline(s,'r'),[Xmin хО]); % правая точка остановки
Emin=Emin+ 10Л-3;
Ne=100; % число значений зависимости S(E)
De=(Emax- Emin)/(Ne-l);
Np=1000; % число узлов сетки, используемых для вычисления интеrpала
j=I:Np;
for i=I:Ne
Е=Еmiп+Dе*(i-l);
хО=О.I;
s2=num2str(E);
s=";
s=strcat(sl, '-' ,s2);
Xleft=fzero(inline(s,'r'),[xO Xmin]); % левая точка остановки,
% соответствующая энерrии Е
xO=10*Xmin;
Xright=fzero(inline(s,'r'),[Xmin хО]); % правая точка остановки,
% соответствующая энерrии Е
1, '
1,
z(i,I)=E;
x(j)=Xleft+(Xright-Хlеft)/(Nр-l)*(j-l);
s=strcat('(' ,s2,'-' ,sl, ')','. ЛО.5');
F=inline(s, 'r');
S (j)=gamma *real(F(x(j)));
I=trapz(x,S); % вычисление интеrpала (16.28)
z(i,2)=I;
end;
(Обращаем внимание читателя на строчку проrpаммы S(j)=gamma*
*real(F(x(j))); в файле Action.m, в которой в вектор S заносится значение дей
ствительной части подынтеrpальной функции в (16.28), Необходимость данной
операции обусловлена тем, что для нахождения координат точек остановки мы
используем встроенную в пакет МА ПАВ функцию fzero, возвращающую
приближенное значения корня нелинейноrо уравнения. Так как любое числен-
ное решение имеет поrpешность, может оказаться, что значение соответствую-
щеrо корня окажется левее истинноrо значения левой точки поворота wили
492

1:. '.!де.ЛJр.ова!I'--lе /(в.(]II1!?в':Iх.:'!.",е..
правее правой точки поворота, а потому значения подынтеrpальной функции и,
соответственно, интеrpала (16.28) становятся мнимыми,)
% листинr проrpаммы Spectr,m
function [Xleft,Xright,EL] = Spectr(z,Xmin)
% функции, возвращающая собственные значения энерI'етическоrо
% спектра колебаний двухатомной молекулы, и соответствующие
% данным значениям координаты точек поворота
% z  матрица, возвращенная функцией Action
% Хшiп  координата минимума потенциальной энерrии
п=О;
Ml=max(z(: ,2));
j=l;
sl='4*(I.1r. л 12-1.1r. Л6)';
while and(n+0.5)*pi<Ml,j+ 1 <Iength(z))
while z(j,2)«n+0.5)*pi
j=j+l;
end;
if j+ 1 <Iength(z);
x=[z(j-l,l) z(j,I)];
y=[z(j-l,2) z(j,2)];
а=(у(2)-у( 1) )/(х(2)-х(I));
Ь=у(I)-а*х(I);
EL(n+ 1 )=( (n+0.5)*pi-b )/а;
хО=О.I;
s2=num2str(EL(n+ 1));
s=";
s=strcat(sl,'-' ,s2);
Xleft(n+ 1)=fzero(inline(s,'r'),[xO Xmin]);
xO=10*Xmin;
Xright(n+ 1)=fzero(inline(s,'r'),[Xmin хО]);
п=п+l;
end;
end;
Далее необходимо выполнить следующую последовательность команд:
»Хmiп=2Л(I/6); % координата минимума потенциала
»gamma=80; % коэффициент, входящий в обезразмеренное
о/с уравнение Шрединrера (16,22)
» Emin=-l; o/r минимальное значение энерrии
493

к...?ь.f!р"'/?:.!!.?..е'lI.Р..()'С:!..'!:,р''!!..'!.'!..:,1!. '!.!!?ч..:.:о '!.C:I<!:'.A. т-.E!. .. ...
» Еmaх=-10Л-4; % максимальное значение энерrии
» z = Action(Emin,Emax,Xmin,gamma); % вычисление зависимости S(EI
» tigure(1);plot(z(:,1),z(:,2» % визуализация зависимости S(E)
» [Xleft,Xright,EL] = Spectr(z,Xmin) % вычисление энерrетическоrо
% спектра колебаний двухатомной
% молекулы
» EL % вывод значений энерrетическоrо спектра
EL=
Columns 1 through 7
-0.9346 -0.8120 -0.7002 -0.5987 -0.5071 -0.4249 -0.3519
Columns 8 through 14
-0.2875 -0.2312 -0.1825 -0.1411 -0.1064 -0.0778 -0.0548
Columns 15 through 16
-0.0368 -0.0233
Результат выполнения описанной последовательности команд представ
лен на рис. 16.6.
70 ... , T   ---Т I 
60,
I

}I
;j
/1
, I
/ 1
/ !
//// i
/'
/./
//
.-'......-'/"..-../',.....
------...------...--
50
40
30
20
J
1
I
J
I
J
.о.2 -0.1
10 
/'
--
о ...........L...
-1 .о.9 0.8 -0.7 .о.б
,
.о.5
,
.о.4
,
.о.З
II
l'
Рис, 16,6, Зависимость действия от энеР2ии
Рассмотрим задачу отображения потенциала ЛейнардаДжонсона и
энерrетическоrо спектра колебаний двухатомной молекулы на одном чер
теже, Данный чертеж представляет собой rpафик функции V(x) и набор от-
резков прямых у = Е", параллельных оси абсцисс, координаты левых и
правых концов которых есть решения уравнения V(r) = Е , К сожалению,
l'
I
494

..... .. ! 6.f!д-.eJlи-l!..?вl!!/Uе.. .fl.c:./!'!'?fl.b!:"::''!."!.
rpафические средства МА T1JAB не позволяют автоматически отобразить на
одном чертеже зависимость V(x) и энерrетический спектр колебаний ДBYX
атомной молекулы, поскольку при построении функций, зависящих от од-
ной переменной, линиями соединяется последовательно каждая пара точек,
Основная идея данноrо подхода основана на формировании матрицы, в
одном столбце которой в определенном порядке расположены значения по
тенциала v(x) и энерrетическоrо спектра &", в друrом  соответствующие
значения переменной х и координаты точек остановки, Причем каждое зна-
чение спектра в первый столбец матрицы заносится три раза подряд, при
этом в соответствующие строки нулевоrо столбца матрицы последователь-
но заносятся значения Xfe!/, Xrigh/, Xfef1' Очевидно, что при последовательном
соединении точек линия через данные точки будет про водиться дважды: от
точки с координатами (Хfef/,Ел) к точке с координатами (Хriglil,Ел) И наоборот.
Так как происходит возвращение в начальную точку, то дальнейшее по-
строение rpафика начнется с той же самой точки и искажений не возникнет
(рис, 16.7).
ix- Е'1.\
' 2" 2
) , Е
\ х I<iI..Е;' .\ , ., Х "кп,.' .'
.,xi+l,Ei+11
Xi Vi:XiJ
Х 1'11171 Е 71
Х right71 Е 71
Х 1'11171 Е 71
Х i+l V!:x i+l)
Рис, 16,7, К объяснению метода формирования .натрицы для построения на одном
чертеже энеР2етичеСК020 спектра колебаний двухатомной молекулы и
зависимости V(x)
Друrая проблема, связанная с формированием указанной матрицы, co
стоит в необходимости упорядоченноrо размещения в массиве значений за-
висимости (x) и энерrетическоrо спектра &", Для автоматизации процеду-
ры упорядочивания можно использовать тот факт, что при Х < Xтi" функ-
ция V(x) является монотонно убывающей, Следовательно, нужно создать
495

!5.?!!п-!'.l!!!!У!!.О:..'!.=JlllР'!.l!!.Iи-:..Р..и-llf!.=К-lп-l!..'!.<:?!!.п-l!.е.'!::!!....!.:!.l!....... __.__.
матрицу, которая содержит в нулевом столбце значения apI'YMeHTa на ин
тервале [a,xmiп], в первом  значения функции V(x). Дополнить ее коорди
, I
натами точек остановки и значениями энерrетическоrо спектра & п в COOT
ветствии с описанной выше процедурой, затем провести упорядочивание
матрицы в порядке убывания значений энерrии. После Э1'Оrо дополнить
упорядоченную матрицу значениями координат х из отрезка [xmiп, Ь] и co
ответствующими значениями функции V(x), затем отобразить зависимость,
сохраненную в описанной матрице на rpафике. (Здесь [а,Ь]  выбранный
интервал для построения rpафика функции V(x).)
Для реализации описанноrо алrоритма создадим mфайл Potentialand
Spectr.m, содержащий описание функции, возвращающей искомую MaT
рицу.
% листинr файла PotentiaIandSpectr.m
function z = PotentialandSpectr(EL,Xleft,Xright,xl,x2)
% функция, возвращающая матрицу, используемую для построения на
% одном чертеже rpафика потенциала и значений энерrетическоrо спектра
% EL  вектор, содержащий значения энерrетическоrо спектра
% Xleft  вектор, содержащий координаты левых точек поворота
% Xright  вектор, содержащий координаты правых точек поворота
% Хl  левая rpаница интервала построения rpафика
% Х2  правая rpаница интервала построения rpафика
NO=100;
Tmp=EL;
Dx=(x2-xl)/(NO-l);
i=I:NO;
xO(i)=xl +Dx*(i-l);
yO(i)= V (xO(i));
Ymin=min(yO);
N=I;
for i=I:NO
if Ymin==yO(i)
N=N+i;
end;
end;
for i=I:N
XO(i)=xO(i);
YO(i)=yO(i);
I
i
I
[1,
I i
I
: I
496

J6'!.e,I!!!'!.aI!.lJ..:''5.II,!!'!..bl:cll:пeA1
end;
K=length(Tmp );
т=1;
for i=N:N+K-l
XO(i+m)=Xleft(i-N+ 1);
YO(i+m)=EL(i-N+l);
т=m+l;
XO(i+m)=Xright(i-N+ 1);
YO(i+m)=EL(i-N+l);
m=m+ 1;
XO(i+m)=Xleft(i-N+ 1);
YO(i+m)=EL(i-N+l);
end;
Nl=length(YO);
for i=I:Nl
Sу=-10Л309;
for j=I:Nl
if Sy<YO(j)
Sy=YO(j);
N2=j;
end;
end;
z(i,I)=XO(N2);
z(i,2)= YO(N2);
УО(N2)=-10Л 309;
end;
Xmax=max(XO);
i=l;
Xt=xO(N);
while Xt<Xmax
z(i+Nl,I)=Xt;
z(i+Nl,2)=V(Xt);
i=i+l;
Xt=Xt+Dx;
end;
function z = V(x)
% функция, возвращающая значение потенциала ЛейнардаДжонсона
z=4*(lJx. Л12-1 Jx. Л6);
497

l!. ?'II"-b'.o.",plloe ?е.л.I]Jоа.'III:rfIIЗ.Ч ее KиX.'lp0Y:==O. пr:..к--е/еl А 7!1 В ..
Далее необходимо выполнить следующую последовательность команд:
»Хmiп=2Л(1/6); % координата минимума потенциала
» gamma=80; % коэффициент, входящий в обезразмеренное
% уравнение Шрединrера (16,22)
» Emin=-I; % минимальное значение энерrии
»Еmaх=-10Л-4; % максимальное значение энерrии
» z = Action(Emin,Emax,Xmin,gamma); % вычисление зависимости S(E)
» [Xleft,Xright,EL] = Spectr(z,Xmin) % вычисление энерrетическоrо
% спектра колебаний
% двухатомной молекулы
% формирование матрицы, используемой для построения на одном
% чертеже rpафика потенциала и значений энерrетическоro спектра
» Z=PotentialandSpectr(EL,Xleft,Xright,xl,x2)
» plot(Z(:,I),Z(:,2),'k')
Результат выполнения описанной последовательности команд представ
лен на рис, 16,8.
2-----Т\ """'''l
1 5.
I
\
\
\
'1
\
, /'
.0.5 - r===-=-':--:::::7/ 
.1  Y7_ ..._. _J
08 1 1.2 1.4 1 6 18 2 2,2 2.4 2.6
l'
0.5:
О:
-
1 i
1
,
Рис. 16,8, Зависимость потенциала взаимодействия ядер от расстояния между
ними u энер2етuческий спектр колебаний двухатомной молекулы
При построении фазовой траектории колебаний двухатомной молекулы,
задаваемой (16,26), необходимо учитывать, что данная траектория является
двузначной функцией, поэтому ее построение  выполнение предваритель
ных действий, которые достаточно очевидны, Для построения траектории
,
l'
1
! i
i
498

........ J?: ;"f():'!.jJ_()а.!I:_к--в---а.1!,!!()Ь!.Х,ш='!.е"!
движения на фазовой плоскости сначала необходимо сформировать матри
цу, в верхней половине которой находятся строки, содержащие значения
переменной Х Е [X/efl' Xri)(hl] И соответствующие им значения импульса р(х),
в нижней половине матрицы содержатся значения координаты Х, изменяю
щиеся от X,'ig/II до Xlejl, И соответствующие им значения импульса p(X), а за
тем отобразить искомую зависимость,
Отметим, что поведение рассматриваемой нами модели определяется
единственным параметром у, являющимся комбинацией физических пара
метров системы: xapaKTepHoro размера системы а, массы системы т и rлу
бины потенциала Vo, величину KOToporo мы задавали при нахождении энер
rетическоrо спектра колебаний двухатомной молекулы. Поэтому для описа
ния особенностей движения молекулы в фазовом пространстве удобнее
использовать не импульс, l1РОПОРЦИОНальный массе (значение которой мы
не задавали), но безразмерный волновой вектор волны де Бройля, который
с одной стороны прямо пропорционален импульсу и зависит только от у
с дрyrой.
Для реализации данноrо алrоритма создадим mфайл PТr.m, содержа
щий описание функции, возвращающей координаты точек фазовой тpaeKТO
рии для каждоrо собственноrо значения энерrии.
% листнИl' файла PTr.m
function z = PTr(EL,Xleft,Xright,gamma,Np)
% функция, возвращающая координаты точек фазовой траектории
% для каждоrо собственноrо значения энерrии
N=length(EL);
k=I:Np;
for i=I:N
dx=(Xright(i)-Хlеft(i) )/(Np-l);
x(k)=Xleft(i)+dx*(k-l);
for j=I:Np
Z(j,I)=x(j);
Z(j,2 )=real(p(x(j),EL(i),gamma));
end;
for j=Np+l:2*Np
Z(j,I)=x(2*Np-j+ 1);
Z(j,2)=-Z(2*Nр-j+ 1,2);
end;
Z(2*Np+l,I)=x(I);
Z(2*Np+l,2)=Z(1,2);
499

к ОЛf!1!о'!.ер!/{)_:",-од:л,:роваJl,:е4)иЗll_ЧСК- пРО1/ессов в пaKeп1: A ТLAl!.__
if i==l
Z=z;
else
z=саt(З,z,Z) ;
end;
end;
function z=p(x,E,gamma)
% функция, возвращающая значения импульса
z=gamma*(E V(x)). ЛО.5;
functiOll z=V(x)
% функция, возвращающая значения потенциала
% ЛейнардаДжонсона
z=4*(1./x. л 12-1./x. Л6);
Далее необходимо выполнить следующую последовательность команд:
» Хmiп=2Л(1/6); % координата минимума потенциала
» gamma=80; % коэффициент, входящий в обезразмеренное
% уравнение ШреДИНI-ера (16.22)
»Emin=-l; % минимальное значение энерrии
» Еmах=lОЛ-4; % максимальное значение энерrии
» z = Action(Emin,Emax,Xmin,gamma); % вычисление зависимости S(E)
» [Xleft,Xright,EL] = Spectr(z,Xmin) % вычисление энерrетическоrо
% спектра колебаний
% двухатомной молекулы
» Np=2000; % число точек одной фазовой траектории
» Ph=PTr(EL,Xleft,Xright,gamma,Np); % вычисление координат точек
% фазовых траекторий для каждоrо
% значения энерrетическоrо спектра
% визуализация фазовых траекторий
» plot(Ph(:,1,1),Ph(:,2,1),'k')
» hold оп
» for k=2:length(EL)
plot(Ph(: ,1,k),Ph( :,2,k), 'k');
end;
» hold off
Результат выполнения описанной последовательности команд представ
лен на рис, 16,9,
500

ш!.6 олuров.аl!lJ.ек-в.L!I/_п!'?вых l!пlеи
80. 
60
40
20
.20
_40l
-60,
1
. ш1'5-ш ш--j5
-80',
1
Рис, 16.9. Фазовые траектории колебаний двухатОJl1НОЙ молекулы,
соответствующие первЫJll шестнадцати уровням энер2етuчеСКО20 спектра
Друrой метод построения фазовой траектории основан на использовании
зависимостей r = r(t) , р = p(t), которые являются решением системы
уравнений [амильтона:
, p(r)
r ==
т
, aV(r)'
р ==
ar
Продифференцировав по времени первое уравнение и подставив в Hero
второе уравнение, для переменой r получаем уравнение BToporo порядка
r" =   д\,'.са , (16.32)
т ar
Для выбора начальных условий уравнения (16.32) будем считать, что в
момент времени t=O частица находится в одной из точек остановки, для оп
ределенности  в левой, т, е, r(O) == X/ejt, r'(O) == О. ДЛЯ 11роведения числен
Horo решения уравнения (16.32) целесообразно предварительно записать
r  t Е Е
систему в безразмерных переменных х == , ,t ==  , == V. ' [де а  параметр
а т О
ero ширину (см, (16,24)), Т  характерное
(16,31)
потенциала, характеризующий
. время движения.
501

11'"
'1
i 11
I
I
1I
.l!...О!tllь.,(/,!!еР..::(/:..А!.е::?r:.Р.'!.Й-'l!I_еР.II.II.е..СК-UХ/l!(/!!.:с.:.(/.!..!!..К-:"!..:..'!!/I..!...:!.!!
Потенциал ЛейнардаДжонсона и уравнение движения в выбранных без
размерных переменных имеют следующий вид:
\7(1') = 4('.  ), (16,33а)
1'12 1'6
1" = :;2 (1'З  х\) (16,33б)
Для выбора переменной Т найдем разложение потенциала в ряд Тэйлора
вблизи минимума потенциала (r min=21/6a)
2
18,23 2
V(!o.r):::; Vo + """"""2 Vo!o.r (16.34)
а
Сравнив (16.34) с выражением для потенциальной энерrии линейноrо
rармоническоrо осциллятора
,
\ I
1
U( х)=  Х х2,
2
(16.35)
приходим К выводу О том, что вблизи минимума потенциал Ленарда
Джонсона ведет себя подобно потенциалу rармоническоrо осциллятора, у
2
2.18.23
KOToporo Х = 2 Vo. Следовательно, в качестве характерноrо времени
а
т можно выбрать период колебаний rармоническоrо осциллятора, в данном
случае равный
r;; 2 * r,;;;?
т = 21l"x = 21l"6V; .
Подставляя (16.36) в (16.33б), окончательно получаем
7
. 23'1l"2( 2 1)
l' =  .     --
3 1'13 1'7 '
Для нахождения численных решений (16.37) необходимо создать m
файл Асс2.т, содержащий описание функции, возвращающей значения
первых производных.
% листинr файла Асс2.m
function z = Acc2(t,x);
% функция, возвращающая значения первых производных ОДУ (16.37)
z=zeros(2,1);
(16.36)
(16,37)
502

.
.. 6:J.!..(!!!II.l!О/:lJ..:К-I!.:''!!.(/в-Ь:Х.'::llс'!!.е
z(1)=x(2);
z(2)=2Л(7/3)*рiЛ 2/3*(2.!х(1). л 13-1.!x(1). Л7);
Далее необходимо выполнить следующую последовательность команд:
» Хmiп=2Л(1/6); % координата минимума потенциала
»gamma=80; % коэффициент, входящий в обезразмеренное
% уравнение Шрединrера (16,22)
»Emin=-l; % минимальное значение энерrии
» Еmах=-10Л-4; % максимальное значение энерrии
» z = Action(Emin,Emax,Xmin,gamma); % вычисление зависимости S(E)
» [Xleft,Xright,EL] = Spectr(z,Xmin) % вычисление энерrетическоrо
% спектра колебаний
% двухатомной молекулы
»RO=[Xleft(5) О]; % вектор начальных условий
» Np=5000; % число узлов временной сетки
» Tfin=1.8; % правая rpаница BpeMeHHoro интервала
»[T,M]=ode45('Acc2',[0:Tfin/Np:Tfin],RO); % нахождение численноrо
% решения ОДУ (16.37)
% визуализация зависимостей х = x(t), v = v(t) и
% фазовой траектории
»figure(l); plot(T,M(:,l), 'k')
»figure(2); plot(T,M(:,2), 'k')
»figure(3); plot(M(:,1),M(:,2), 'k')
Результаты выполнения описанной последовательности команд пред
ставлены на рис, 16.1016.12.
Задача 16.9.
ВычиСЛИте энерzетический спектр колебаний двухатомной молекулы,
используя метод, описанный в разделе 16,2, Сравните результаты, пo
лученные в квазиклассическом приближении, с результатами, получен
ными численным интеёрированием уравнения Шрединzера, Постройте
зависимость расстояния между значениями энерzетическоzо спектра
от номера квантовОёО числа,
Задача 16.10
Используя квазиклассическое приближение, определите собственные
значения энерzии частицы, находящейся в пРЯМОУ20ЛЬНОЙ яме с беско
нечно высокими пРЯМОУ20льными стенками, Сравните полученные зна-
чения энеР2ии с соответствующими значениями, найденными аналити
чески/ии А1етодамu. Зависит ли точность квазиклассичеСКО20 прибли-
жения для раССАштриваеМО20 потенциала от номера квантовО20 числа?
503

l!..?.Al1 ЬН?'.1!:.Р!.I?lI!..?r:P.о.l!.I}!.Р".и-.!..и-..:.1!.и-.:..!':.Р.?..l!.:.О!...,!:.l!.15meJ:!.!:.!!::!J!..... ......
"
135"
13:'"
, 25
\2.
j
I
I
,
1 '5
11'
I
,05:/
1........L...........l......... . J
о 02 04 0.6 08 1 12 t4 "'1'61.8
i I
Рис, 16,11, Зависимость
скорости движения ядер
двухатомной молекулы,
находящейся на пятом
энерzетическом уровне,
от времени
1 
..
...
. .
.2
".2
::1
I
.оа!
,l. 
1
..L....  о.. .l
' 11
11!
'1
OOr /',,-
0.1. ! '"
0.:/ '
02V .,
o '..".
I
"'r
'O'
.о,в(
"Or
)
о
Рис, 110,Зависимость
расстояния ,между ядрами
двухатомной молекулы,
находящейся на пятом
энерzетическом уровне,
от времени
'
"
"-
''-о
/1
;
;
I
I
I
;
I
;
i
i
I
i
.1
,j
'",
'"
О.,
..l......."""""""'..............L.....L........
04 06 0.8 1 12 1.. 18
,
'--
,...............
,
\
\
I
/
/
12
'125'' 
I
j
135
"
504
Рис, 16,12, Фазовая
траектория колебаний
двухатомной молеклы,
находящейся на пятО}.1
энерzетическо.« уровне
1.0

... ..... .... . ......ш..... '.. "  .:.!-!!!..':!!!!Е..Оl!!!!!..:..I!..а:.I!!,ь.i!.. r:.:.".!..:'1
Задача 16.11
Используя квазиклассическое приближение, найдите собственные зна
ченuя энерzии для потенциалов, рассмотренных в задачах 16,516.7.
Сравните соответствующие значения энерzий, полученные прямым чис
леннЫМ интеёрированием стационарною уравнения Шрединzера, с
результатами, полученными в квазиклассическом приближении.
Зависит ли разность между значениями энерzии, полученными
численным интеёрированием (16.4), и соответствующими значениями
энерzии, полученными в квазиклассическом приближении от номера
квантовОёО числа? Объясните полученный результат,
им
Е(О)
11
,,"
Рис. 16,13
Задача 16.12
Поле U(х) представляет собой две одинаковые потенциальные ямы,
разделенные барьеро.« (рис. 16.13). При непроницаемом барьере
существуют уровни энерzии, отвечающие движению частицы только в
одной из ям, В данном случае вследствие симметрии ям будут
существовать одинаковые значения энерzии, соответствующие двум
различным состояниЯJIl (КОёда частица находится в правой или левой
ямах), которые называются вырожденными, Возможность прохож
дения частицы через потенциальный барьер при водит к снятию
вырождения и расщеплению каждою из уровня на два близких уровня,
соответствующих состоянию, КОёда частица мпжет одновременно
находиться в обеих ямах, Выберите для описания потенциала
подходящую функцию и определите величину расщепления уровней,
используя квазиклассическое приближение и метод численно?о
интеzрирования уравнения Шрединzера, описанный в разделе 16,2,
505

i!..О:lпЬ:О::'l!!:?:'/?е:!.':'р'<!..ваu:!_е...rp':'?':'Ч(!СКlа:lр?е:с?в .....:'!'!.:'.Л!...Т!:.1J!...... ._......... 
16.4. Нестационарное уравнение Шрединrера
В общем случае для описания эволюции квантовой системы во времени
требуется найти решение '1/(1',1) нестационарноrо уравнения Шрединrера
(16,3). С математической точки зрения данная задача относится к краевым
задачам дифференциальных уравнений в частных производных, в которых
требуется найти решение уравнения '1/(1',1), если известны значения данной
функции в момент времени 1 = О '1/(1',0). РассмО1РИМ численные методы
решения нестационарноrо уравнения Шрединrера на примере одномерноrо
уравнения (16,5).
Введем в рассмотрение пространственную сетку с числом узлов N и ша
1
[ом по пространству h =  , на которой вместо непрерывной производной
N
используем ее конечноразностную аппроксимацию
2 I /1 2 /1 11
 If!  '1/ j+1  '1/ j + '1/ j1
д х? 1=1"  , h2.... ... . (16.38)
Производную по времени аппроксимируем простейшей разностной
формулой первш'о порядка точности, считая дискретный шar изменения
времени равным М:
Ixx = 1f!1H1f!1' .
 /1
Подставляя (16.38), (16,39) в (16.5), получаем
11+1 /1 2 11 2 11 11
i1i 'l/j 'l/j = !!... 'l/j+1  'l/j +'l/j1 +и,
М 2т h2 ) ,
(16.39)
( 16.40)
I i
здесь i  комплексная единица,
При i = 1 и i = N в уравнении (16.40) используют значения функции на
rpанице области, в которой ищется решение уравнения, '1/0 и '1/ N' ИЗ
(16.40) можно выразить 'l/j+l:
[ 1I 2 /1 11 ]
11+1 1/' '1/;+1  'l/j +'l/j!
'1/ j = '1/ j + t '" --'--,.. 2h 2 .. + U j М,
(16.41)
здесь и далее в данном разделе мы полаrаем 11 == 1 , m == 1 .
Для более компактной записи (16.41) введем следующие обозначения
506

.........!: Л!..'!.(!:'!':'.l!й-.с:.'!':'!.!5.'!.'!.'!!й-!>:..:':'.:'!!.1
11 2 1/ 11
 'l/j+1 'l/l +'l/j..1 +и. = (D'I/'!)' (16.42)
2h2 ))
Используя (16.42), запишем (16.41) в виде
'l/T 1 = (1  iMD)yj . (16.43)
Разностная схема (16.43) называется явной, так как она позволяет по из
вестным значенияМ функции '1/(1) в момент времени 1/1 вычислить значе
ния '1/(1) в момент времени 1/111" Однако данная схема, в которой эволюция
решения во времени определяется оператором (1  iMD), оказывается Heyc
тойчивой при любом шаrе /),,1, так все собственные значения даннш"о опе
ратора
li&AM,
равные по абсолютной величине
1
[1 + (&"м)2 р
оказываются больше едиНИЦЫ,
Один из способов, позволяющий сделать схему устойчивой, состоит
в использовании пространственной производной в момент времени 11/+1:
11+1  11 IнI  2111.11+1 + 111./1+1
i ,'!..L = '1/ )+1 !:.....L " (16.44)
М h2
В выбранных обозначениях данная схема имеет следующий вид:
1/+1 /1
'l/j,!j =if)'I/"+1, (16.45)
М )
Так как неизвестные значения 'I/'j+1 входят в обе части уравнения, дaH
ная вычислительная схема называется неявной, Уравнение (16.45) можно
111 1
разрешить относительно '1/ j
'I/'!+I = .... 1 ....'1/11 , (16.46)
) 1 + iMD )
Так как абсолютная величина собственных значений оператора перехо
да, стоящеrо в правой части (16.46)
,
Q+&i/),,12) ,
507

1!.Й-Iп.IOl:Р..Il'!..:-Л--I'!..:,:!р'_ова.'lli:cjJII..Зl!.че,::'х процессов в пакеmе M4ТLAB
.......... . . .................... ..... ........... ......... ............ ш... .... ....
I!
всееда меньше единицы, вычислительная схема оказывается устойчивой
при любых значениях М,
Однако данная схема, так же, как и явная, не может быть использована
для решения уравнения ШреДИН1'ера (16.4), так как получаемое численное
решение не является унитарным  модуль волновой функции оказывается
монотонно убывающим во времени. Свободной от указанных недостатков
оказывается следующая модификация неявной разностной схемы:
If/}+l =lllbjtj/},
1 + i  мЬ
2
Оператор, стоящий в правой части (16.47), оказывается эрмитовым уни
тарным оператором, собственные значения KOTopo1'o равны еДИнице, поэто
му модуль волновой функции остается постоянным при переходе от ОДНО1'о
момента времени к следующему, Кроме 1'01'0, можно ноказать, что COOTHO
шение (16.47) аппроксимирует точный оператор перехода e.itJ.tD с точно
стью до членов O12).
ДЛЯ проведения практических расчетов оказывается более удобным пе
реписать (16.47) в следующем эквивалентном виде
IItl [ 2 1] 11 11 11
If/j  l--  If/j == Х}  If/j ,
1 + i мЬ
2
(16.47)
(16.48)
который устраняет один проход по узлам сетки, необходимый для вычисле
ния числителя,
Для нахождения на каждом ша1'е по времени значений промежуточной
функции Х, определяемой уравнением
(l+ilMD )х) =21f/}, (16.49)
перепишем данное уравнение в явном виде
it..t 11 [ it..t it..t] it..t
 2/12 Xjtl + 1 +,;2 +.:2 и j Х}+I  2h2 X}l = 2(jJ}
it..t
и, разделив обе части (16,70) на ...., окончательно получим
2h2
(] 6,50)
508
...
J6 МодеЛIl..Рос:..'!Il:.к-_аl/lп.()вы СI:'СIп.it
Xj'l+[2+1i2 /12иjJХj+ХjI=-2If/i' (16,51)
Таким образом, на каждом шш'е по времени для нахождения значений
xj'l приходится решать систему линейных уравнений Nro порядка, кото-
рая оказывается 1рехдиаrональной (в каждое уравнение системы входят
только три рядом расположенных неизвестных: переменная, соответствую
щая диаrональному коэффициенту, и переменные, стоящие слева и справа
от диаrональноrо элемента), Для систем линейных уравнений с трехдиа1'О-
нальной матрицей известен эффективный вычислительный алrоритм, назы-
ваемый методом проrонки.
Проведем обсуждение данноrо алrоритма на самом общем случае систе-
мы линейных уравнений
Ах=Ь,
(16.52)
I'де А  трехдиarональная матрица, х  вектор-столбец неизвеC11-IЫХ, Ь  век-
тор-столбец свободных членов. Запишем данную систему в виде, аналоrич
ном (16.51):
AjXj1 +AJxj + A;xj1 = bj,
(16,53)
здесь А j ,А J, А; обозначены отличные от нуля элементы матрицы А.
В частности, для системы линейных уравнений (16.51) А j = А j = 1 ,
АО =2+ 2ih2h2u.,
J t..t J
Для решения системы уравнений (16.53) предположим, что искомое ре-
шение удовлетворяет рекуррентному соотношению, связывающему значе
ния Х} в соседних узлахj иj+l:
Xj+1 =ajxj+fJj'
(16.54)
1'де а j' fJ j  неизвестные коэффициенты, которые необходимо определить.
Подставляя (16.54) в (16.53) получаем
А} Xj_l + AJXj + А; (ajxj + fJj)= bj. (16.55)
Разрешив (16.55) относительно Х j' получаем
Х; = YjAjXJ1 + у;(А} fЗ; bJ, (16,56)
509

1!..():()".!!.Р.():.!!с.>.::'.u?оваll_U:. Фuзuч.ескuх nрйцессов I1Cl.:.".!.:...!A ТLAB
[де
]
у . , -, (16,57)
j лО+АО+а'
} } }
Сравнивая (16,54) и (16.56), видим, что они тождественны, если коэффи
циенты а j' Р} удовлетворяют следующим рекуррентным соотношениям:
ajl =YjAj,
Р. 1 =у'А+Р. b)
J } \; J } J'
(16.58 )
( 16.59)
I
Таким образом, решение трехдиаrональной системы уравнений
осуществляется следующей последовательностью действий:
1. Вычисление коэффициентов Yj' aj, Р} по формулам (16.57)  (16.59),
в KOTOpbIxj=N2, NЗ, "', О" aN] = О, fJN] = XN (обратный ход),
2. Вычисление Х} по формуле (16,54), в которойj = 0,1, .", N  1, [де ХО
известно из начальных условий (прямой ход),
Описанный алrоритм решения системы линейных уравнений, состоящий
из обратноrо и прямоrо ходов, требует 2N арифметических операций, в OT
личие от прямых методов (например, умножение на обратную матрицу),
требующих порядка N2 операций.
Для реализации описанноrо алrоритма в пакете МА ТLAB создадим че
тыре mфайла: ]) файл Barrier.m, содержащий описание функции, возвра
щающей значения потенциальноrо барьера в узлах пространственной сетки;
2) файл Package.m, содержащий описание функции, возвращающей значе
ния действительной и мнимой частей волновоrо пакета; 3) файл Coeff.m,
содержащий описание функции, возвращающей значения коэффициентов,
используемых в методе проrонки; 4) файл Psi.m, содержащий описание
функции, возвращающей значения волновой функции в момент времени
t+M.
% листинr файла Вапiеr.m
function z = Barrier(x,vO,xO,A,Mode);
% функция, возвращающая значения потенциальноrо барьера
% в заданном узле координатной сетки
% х  координата узла
% уО  высота барьера
% хО  координата, определяющая положение максимума оrибающеЙ пакета
% А  ширина барьера
510

16. А1.0:)I1!Р.Й-Cl.ll:"..К-Cl,!.".!й-вh!;r:"с!:!.trI:!!
% Mode  переменная, определяющая тип барьера
if Mode==1
z=Rect(x,vO,xO,A); % прямоyrольный барьер
end;
if Mode==2
z=Gauss(x,vO,xO,A); % барьер, описываемый кривой raycca
end;
if Mode==3
z=StepB(x,vO,xO,A); % ступенчатый барьер
end;
if Mode==4
z=Parabolic(x,vO,xO,A); % параболический барьер
end;
function z = Rect(x,vO,xO,A)
% функция, возвращающая значения прямоуrольноrо барьера
if апd(хО-А/2<=х,х<=хО+Al2)
z=vO;
else
z=O;
end;
function z = Gauss(x,vO,xO,A)
% функция, возвращающая значения потенциальноrо барьера,
% описываемоrо rауссовой кривой
z=vO*exp( -(х-хО). Л2*lоg10(20)/ А. Л2);
function z = StерВ(х,vО,хО,А)
% функция, описывающая ступенчатый барьер
z=(vO*atan«xxO)*2*6.313/ А *21pi)+ 1)/2;
function z = Parabolic(x,vO,xO,A)
% функция, описывающая параболический барьер
if апd(хО-А/2<=х,х<=хО+А/2)
z=vO*(2/ А). Л2*(х-хО). Л2+vO;
else
z=O;
end;
% листинr файла Package,m
function z = Package(x,kO,xO,sigma,Mode)
% функция, возвращающая значения действительной и мнимой
511

!<.():I?''!..'!Р!.I!!!!..!!.'l.:Л<fJ..{).':'II<е.р'и-.!!.' Ч(!.К-I<:fJ()I!,(!О_'-I.':':_fl!..'!..-!i!...._.
% частей волновоrо пакета
Xmin=min(x);
Хmах=mах(х);
if Mode==1
z=exp(j*kO*x)*0.9. *ехр( -(х-хО). Л2*lоglО(2)/sigmа. Л2);
end;
if Mode==2
z=exp(j*kO*x)*sigma. Л2J(sigmа. Л2+(х-хО). Л2);
end;
A=Norm(x,z);
z=zI А. ЛО.5;
function z = Nonn(x,Z)
% фУНКЦИЯ, возвращающая значение нормировочноrо множителя
zl=abs(Z);
zl=zl. Л2;
z=trapz(x,zl);
% листинr Фунющи Coeff.m
function z=Coeff( dt,dx, V)
% фУНКЦИЯ, возвращающая значения коэффициентов в методе проrонки
% dt  шar по времени
% dx  шаr пространственной сетки
% V  вектор, содержащий значения барьера
Npoints=length(V);
for k=I:Npoints
Az(k)=-2+ 2* j*dx Л2/dt-dхЛ2*V (k);
end;
alp ha(N points-l )=0;
gamma(Npoints )=-1/ Az(Npoints);
Ар=l;
k=Npoints;
while k>=2
alpha(k-l)=gamma(k)* Ар;
gamma(k-l)=-l/(Az(k-l )+Ap*alpha(k-l»;
k=k-l;
end;
z=gamma;
'* листинr функuии Psi,m
function z=Psi( Coeff,psi,dx,dt,x)
512
...-....
_ !t:!.(!Лl1fl_й-вс:.l!!.:.с:.'!'!'!.':.Х.3...UlIl.:л.'
% функция, возвращающая значения волновой функции в момент
% времени t + Лt
% Coeff  вектор, возвращенный функцией Coeff
% psi  вектор, содержащий значения волновой функции в момент
% времени t = о;
% dx  шar пространственной сетки
% dt  шаr по времени
% х  вектор, содержащий координаты узлов пространственной сетки
Npoints=length(psi);
% обратный ход
Ар=l;
beta(Npoints )=O+O*j;
k=Nроiпts-l;
while k>=2
beta(k-l )=Coeff(k)* (Ap*beta(k)-4 * j *dхЛ 2/dt*psi(k»;
k=k-l;
end;
% прямой ход
xi(I)=O+O*j;
for k=l:Nроiпts-l
xi(k+ 1 )=CoetТ(k)*xi(k)+beta(k);
psi(k+ 1 )=xi(k+ 1)-psi(k+ 1);
end;
fi=abs(psi). Л2;
B=trapz(x,fi);
z=рsi/ВЛО.5;
Далее необходимо выполнить следующую последовательность команд:
» Xmin=-200; % левая rpаница пространственной сетки
» Хmах=200; % правая rpаница пространственной сетки
»Npoints=500; % число узлов пространственной сетки
» dt=0.5; % шаr по времени
% вычислени координат узлов пространственной координатной сетки
» i=l:Npoints+l;
» dx=(Xmax-Xmiп)/Nроiпts;
» х(i)=Хmiп+dх*(i-l);
% вычисление значений волновой функции в момент времени I = О
» kO=O.5;
» xo=-lоо;
17-J57б
513

.15?:'fll/f)III'!.l!.Ilf)'!.f??'!.:.qиfJf)ClIIи.е1)lfз.llчески:'I?f)II'!.ССовв п.акеll1!! fB .
» sigma=2;
» z = Package(x,kO,xO,sigma,2);
% вычисление значений потенциалЫIOI'О барьера
о/с в узлах координатной сетки
» vO=I.5;
» хО=О;
» А=60;
» Mode=4;
»for i=I:Npoints+l
V (i)=Barrier(x(i), vO,xO,A,Mode);
end;
% вычисление значений волновой функции в последовательные
% моменты времени
» C=Coeff(dt,dx,V);
» for i=I:300
if i==1
Z=Psi( C,z,dx,dt,x);
zl=Z;
else
Z=Psi(C,Z,dx,dt,x);
zl=cat(3,zl,Z);
end;
end;
» figure(l) ;plot(x, V, 'k' ,x,abs(z1(I,: ,1», 'k');
» figure(2);plot(x, V, 'k' ,x,abs(zl(I,:,10»,'k');
» figure(3);plot(x, V, 'k' ,x,abs(z1(I,:,20»,'k');
» figure( 4);plot(x, V, 'k' ,x,abs(zl(I,:,50», 'k');
» figure(5);plot(x, V, 'k' ,x,abs(zl(1,:,75», 'k');
» figure(6);plot(x, V, 'k' ,x,abs(zl(I,:,100»,'k');
» figш"е(7);рlоt(х, V, 'k' ,x,abs(z1(I,:,125», 'k');
» figure(8);plot(x,V, 'k' ,x,abs(zl (1,:,150», 'k');
» 1igure(9);plot(x,V, 'k' ,x,abs(zl(I,:, 175», 'k');
» figure(1 О) ;plot(x, V, 'k' ,x,abs(z1( 1,: ,200», 'k');
» figure(II);plot(x, V, 'k' ,x,abs(zl(I ,:,225», 'k');
» figure(12) ;plot(x, V, 'k' ,x,abs(z 1(1,:,250», 'k');
» figure(13);plot(x, V, 'k' ,x,abs(zl(I,: ,275», 'k');
» figure(14);plot(x, V, 'k' ,x,abs(zl(l,:,300», 'k');
Результат выполнения описанной последовательности команд п-редстав
лен на рис. 16,14 16,27,
514

шшшшшшшш!?,,:,!f)?'!.л-.и.Рf)Cl'Iи.е K-fJ.Cl.III11f)Ы:СlfСII''!.i\1
05
o
.200 1SO
11
1
I!
i\
/ \....
.100 -50
50
100
150
>ос
1 5 T
,',
05
Рис, 16.15, Оzибающая
воЛ/ювоzо nакета в момент
времени ( 1 О
<
/1
; i
I1
/\..
.150 -100 -50
.
1 5  
1
I
o5f
I
I
i '" 1 I
.зё-с""':ОО".1О
515
Рис, 16.14. Оzибающая
волновоzо nакета в
мометn времени (o
1'1
l'
I \
; \
i i
1\
I
I
I
50
100 150
200
Рис. /6.16. Оzибающая
волновО20 пакета
в момент времени 12()

[Ii
iil
.?-':!!!?!!!!Р!i!!!..:!!.?р.!!'!..с:'!!!..Р..z:..з--:.с..пf!.'!..lf..:с..._:.'!I!..fl.!::!.!..L:!!!.__..... __._..
15
05
l'
/P-....
' . \,\
.150 -100 -50
.oo
Рис, 16,18, 02ибающая
волновО20 пакета в момент
времени t75
I
oL ._co.....=C,'
200 .15(1

'00
1\
I 1
i \
, '
i \
I 1
I \
! \
I
I
50
100
150 200
1.'
05L
. ."!
200 '150 .,00 -50
, I
j .. ..-,
о 50 100 15(') мо
..
,50
516
Рис, 16,17, 02ибающая
волновО20 пакета в
момент времени t50
.  7'\ .
J \
I ,
, 1
I
\
\
\
I
I
,
I
i
i
I
i
I
1
I
50
100
150
200
Рис. 16,19. Оzuбающая
волновоzо пакеmа в
.иомент вреЛ1eJ/I! t 100

.....,_Ш.,._....._....___.._Ш_!_?: M-о..:!fJ.'!.l!!!.I!!..._'!...а..I!!!!в---Ь!.ш!!."!
15 . . '.T.',' ''T'T.!
05
/
i
i
i
1
,
i
J
i
I
I
I
i
i
_J
,....  \
l 'чу,!с.
.50 а
--Т'.'ШШ'Ш'
! \
;' \
J I
I I
i \
I I
i \
!
\
\
\
\
\
\

о   
.200 .150 .100
Рис, 16.21, 02ибающая
волновО20 пакета в момент
времени t== 15 О
1.5
(\.
I \
i \
! \
i i
I \
I \
I
\
1
\
!
I
I I
05[ I
I 11
: ,IIU! \
о L"""-v:",,,-=.:-. :.:..:.-----:=:j!,j
200 .150 .100 .50 О 50
,
,
,
I
,
Рис. 16,20, 02ибающая
волновО20 пакета в
Mo/,.feHffl времени t== 125
..
'00
150
200
"r-'I
, 1\ I
i / \
i i \
i i "
: , I
,1 I \
, I I
I ' ,
I i \
I : I
I I :
0..1 , I
i/iili, J
Jgv"... ".
. .1 .100 М О 50 100 1 m
J
150 200
Рис. 16,22. 02ибающая
волновО20 пакета в
момент времени t175
100
517

K-?Аfll'!..п9?11.'!..:!.!ое..l!.Р"?.'!..'fе фии-:есих пp?цe(:c'!.. .,.п.,'!...:'!!.:.N!А.!LАВ
15:
"
Ir\ ;\ 
."N",;=!i:f '\.{J,.
Рис, 16,24, 02ибающая
волновО20 пакета в .'Iюмент
времени (225
1,5 
,Т'\
i
I
i
!
. '' 1:
-ис.
100
150
200
"['
i
05 !
I
I
!
,
./1 '' (', , ,'; r, '1
"v'\:'/\v,-_v '';  1J,V IJ [\
03&i: .150 -100 .50
\
\
I
I
I
,
,
i
I
,
,"
i
..J
, 150 200
50
518
Рис, 16,23, 02ибающая
волновО20 пакета в
момент времени (200
"Т\
i
i \
i \
! I
i
j
i
,
!
I
\
I
I
\
,
i
\
,
i
!
i
..J..-. ",",''''''
50 100
,
150
Рис, 16,25. 02ибающая
волновО20 пакета в
JtOMeHm времени I250
200

. ... 1,6: 1.??е.л!':??а../и.:.'!.а..Il,,:?..::.с':!.(:п.е
"
!
1
I
I
I
1
I
L
50 100 150 ,00
Рис, 16,26, Оzuбающая
волновО20 пакета в
MOJHeHm времени (275
,.
I
I
I
I
,
I
I
i
I
i /у. ' 1\ (1 (\ fi;\ (\ 1\ ('\:
ш",/,у,/}: \/ \J \' ,1/ '", / \J .. 1) 1\
.Зоо 150 -100 -50
".
Рис. 16,27, 02ибающая
волновО20 пакета в момент
времени (300
15,..... ,.............\.,.........,................,............
! \
,
i i
I \
I '\
I \
I \
I I
I I
i \
I \
, ,'. '''-1\1\' I 'L
\f\/>j/'yV\j\/\/\J \: v v\j1...
о ,............... ...,
-200 -150 .100 -50 О 50 100
200
05
,........./"
150
Для рассмотрения эволюции волновоrо пакета в динамике необходимо
создать анимационный КЛИП, выполнив следующую последовательность
команд:
» mov=avifile('example.avi'); % открытие аvjфайла
» for k=1:300 % запись в аviфайл 300 последовательных изображений
h=plot(x, V,'k' ,x,abs(z1(l,:,k)), 'k');
set(h,'EraseMode' ,'xor');
F=getframe;
mov=addframe(mov,F);
end;
» mov=close(mov); % закрытие аviфайла
» movie(mov); о/с воспроизведение анимационноrо клипа
519

l!.'!..п.!!!"!..r!.I.?..: ?е.l!.f!P...й-'!.r:.lllе.cjJlI'!ч.'!...с..'!..х..ll[!.?I!.с..'::.'?!'..п.:!.!!!!.'.'!."!!!J!:.1..l!.....
для чтения ранее созданноro анимационноrо клипа используется команда:
?I!.l0v=--vir('Еар...:':1Ji_ ... Ю __
Задача 16.13
Проверьте точность инте2рирования нестационаРН020 уравнения
ШредиН2ера, используя следующий прием, Проинте2рируйте уравнение
на некотором времеННОАt интервале, затем измените знак ша2а по вpe
мени и проинте2рируйте уравнение ШредиН2ера в обратном направле
нии на временном интервале анаЛ02ичной длины, Сравните начальную
фор\tу волнов020 пакета и волнов020 пакета, получеНН020 иHтe2pиpoвa
ние.м уравнения ШредиН2ера описанным выше способом, Дополните oпи
санный выше документ функцией, возвращающеЙ М2новенные значения
энеР2ии пакета, Проверьте, что точность сохранения энеР2ии не зави
..ит oт ша2!!.иН"!...Р!:!.Р..9..f}...ан,!!!..:..........._...
Задача 16.14
Исследуйте двu:ж:ение квантов020 волнов020 пакета в отсутствие пoтeH
циала, Сравните полученные результаты с результата;о,tи, полученными
при описании двu:ж:ения волнов020 пакета в среде с дисперсией в 207. 9,
'''W",",,,.....
Задача 16.15
Исследуйте рассеивание волновых пакетов с различной формой, шири
ной и энеР2ией на потенциальных ямах и барьерах различной формы и
размера, Объясните особенности наблюдаeJ'.toй эволюции пакетов во
времени. Для пРЯМОУ20ЛЬНОЙ ямы и ступенчат020 потенциала сравните
относительные вероятности прохождения и отражения волнов020 пa
кета с соответствующими аналитическими выражеНUЯA-tll, пpивeдeH
ными в [1, задача 2325]. РаССАютрите резонансный случай при pacceи
вании пакета на потенциальной яме. Пронаблюдайте распад волнов020
пакета на быструю и затухающую компоненты,
Задача 16.16
Опишите эволюцию волнов020 пакета в двойной ЯМе, представленной на
рис, 16,1],
'''""'"H''H... '""'ННЧЧ'Н'Ч"""Н'НH'H''H
Задача 16.17
Замените вычислительную формулу (16,47) на неустойчивый явный Me
тод или на неунитарный неявный метод и исследуйте получаeJ'.tые pe
шения нестационаРН020 уравнения ШредиН2ера,
''"HHH'.H"'H'H 'HH'H''"HHHH'"H'H'H" HH'HH..
Задача 16.18
Замените 2раничное условие Дирuxле \jI = Она одной из 2раниц сетки на
условие Неwлана с нулевой производной на этой же 2ранице, Опишите
эволюцию волновО20 пакета при е20 приближении к данной 2ранице.
520
. . . . .!: '?'!!!.r:.P!l!'.Cl.!!1:'.'!..'5.lJ...a.!!!!.'.?.!x.c':'':f..
16.5. Оценка энерrии OCHoBHoro состояния
квантовой системы методом Монте-Карло
в основу метода нахождения энерrии и волновой функции OCHoBHoro
состояния положена связь уравнения Шрединrера с процессом диффузии в
мнимом времени [2----4], Продемонстрируем основные идеи даннот'о метода
на примере движения частицы в одномерном потенциале, описываемом oд
номерным уравнением Шрединrера (16.5), которое для свободной частицы
имеет вид
i/1 Blf/(x,t) =  If/(x,t). (16.60)
Bt 2т дх2
Выполнив в (16.60) замену переменной t  i, r /1, получим
Blf/(x,t) =  If/(X,t). (16.61)
Bt 2т дх2
Уравнение (16.61) по свой форме совпадает с уравнением диффузии
!'(x,!2  D2!(x,t2 (16,62)
Bt  дх2'
rде p(x,t)  плотность вероятности обнаружить частицу в момент времени
t в точке с координатой х.
Следовательно, можно интерпретировать волновую функцию If/( х, ') как
плотность вероятности диффузионноrо процесса с коэффициентом диффу
/12
зии D = . . Вспомним, что ранее в rл, 12 мы продемонстрировали возмож
2т
ность использования метода случайных блужданий для моделирования реше
ний уравнения диффузии. Таким образом, обнаруженная аналоrия между ypaB
нениями (16.61), (16,62), позволяет вместо непосредственноro решения
уравнения Шрединrера искать решение задачи о случайных блужданиях.
Уравнение Шрединrера (16.5) относится к классу линейных дифферен
циальных уравнений в частных производных, поэтому при решении задачи
можно рассмотреть движение не одноrо, но большоrо количества пешехо
дов, движущихся независимо друr от друrа, Для понимания роли потенци
альной энерrии, перепишем одномерное уравнение Шрединrера (16.5) в
следующем виде:
13/f/(x,r) = /12 a2'f/(r2u(x){l(x.r),
д r 2т д х2
(16,63 )
521

/<'й-:'111ь,?терllое АIO.делuроваl:t.I'!.фюuческих Ilpoцecco. в Ilакете МА ТLAB
При отсутствии члена U(x)lfI(x, т) в правой части уравнения (16,63),
уравнение превращается в обыкновенное уравнение диффузии. С дрyrой
 п282'1/(Х,Т)
стороны, при отсутствии в правои части члена _., уравнение
2т 8 х2
(16,63) можно трактовать как кинетическое уравнение, описывающее Beт
вящиеся процессы, такие как, например, радиоактивный распад или дина
мику численности биолоrической популяции, Следовательно, уравнение
(16.63) можно трактовать как комбинацию диффузионноrо и ветвящеrося
процессов, в которых число пешеходов увеличивается или уменьшается в
зависимости от знака функции и (х). Отметим, что диффузионной интер
претации требуется, чтобы аМплитуда вероятностей была неотрицателыюй
функцией.
Общее решение уравнения (16.5) находится в соответствии с формулой
(16.11), Выполнив в (16,1 1) замену переменной t  i . Т -п , получим общее
решение уравнения (16,63) в виде
'I/(x, т) = LСllфо(х)еЕIlТ. (16.64)
Il
Из (16.64) видно, что для достаточно больших -r основной вклад в сумму
дает член, соответствующий состоянию с минимальной энерrией Ео
(основному состоянию):
'I/(x, ')::::< софо(х)еЕIlТ,
(16.65)
а пространственная зависимость плотности распределения вероятности про
порциональна собственной функции OCHoBHoro состояния Фа(х).
В то же время решение в виде (16.65) имеет существенный недостаток,
заключающийся в том, что
lim 'I/(x, т-) = о
Т-4ОС
для всех х, Для устранения отмеченноrо недостатка можно отсчитывать Ео
от ПРОизвольноrо значения начальной энерrии U ref' которая выбирается из
условия достижения стационарноrо распределения.
Для нахождения формулы при оценке Ео перепишем (16,63) и (16,65) в
явном виде, введя начало от.:;чета энерrии в точке U rej :
Gfll.{r) -п2 02'1/(Х,Т) [ () 1..()
'"   2   и х иl-ef}l/ х,т ,
(! r 2т (J х
(16,66)
522
.. ... ш .1. 6:.Jo,Iй-д'!..ли.р.ов.а.II.и--е.шк.ваllfrlй-,:,хrи..С./I1::':!
\EU )т
'I/(x, т) "'" софо(х)е о ref (16,67)
I1роинтеrрировав (16.66) по х и учтя, что
1im 8'1/ =0,
IXoc д х
получаем
f Jfi:' Т  dx =  f и(х )1fI(x, r)dx + Uref f 'I/(x. т) dx , (16.68)
Продифференцировав (16.67) по т, найдем
lf/i, ') = (и ref Eo),(x, т). (16,69)
8т- .
Падставив (I 6.69) в (16.68), получаем
J (и ref  Ео),(х, Т )dx =  J и (x)'I/(x, Т) dx+ и ref f 'I/(x, Т) dx . (16.70)
Сократив в (16.70) члены, пропорциональные lJref, получаем
Eof'l/(x,r)dx= fи(Х)'I/(х,Т-)dХ, (16.71)
откуда
f и(х){t(х,т)dх
Е  
o f'l/(x, т-) dx .
Так как 'I/(x, т-) равно плотности пешеходов
времени т, дЛЯ случая случайных блужданий
окончательно записать в виде
(16.72)
11(Х, ') в точке х в момент
уравнение (16.72) можно
N
L11(X;,T)U(x;)
Ео = (И) = i...=:lN'''
L11(X;,T)
;=1
(16.73)
[де N  число пешеходов,
Оценка Ео получается, как сrеднее по нескольким значениям т, OTBe
чающим стационарному распределению,
Волновая функция OCHoBHoro состояния Фо(Х) есть функция распреде
ления плотности вероятности пешеходов по узлам сетки п(х;), вычисляе-
523

Й--Ь!.О.'11.Р.ll? !'.(й--i}::'r:.fJ.!!с:.lll!'..Р.'!..з..':!.ч.:К-I:Р?с?._а.К-:.'11..е"!.Ат.!!.___ "....' _ шш_ш
.ш ш ШШ .. л,й-::':!.f!й-,!!Il!!'..!!.'!..CJ..'I'11.?_в---ь!!.':!.'!!...:м....
мая как среднее по нескольким значениям т, отвечающим стационарному
распределению,
Метод случайных блужданий для нахождения энерrии OCHoBHoro co
стояния квантовой частицы и соответствующей волновой функции реализу
ется следующей последовательностью действий,
1, Размещение N о пешеходов случайным образом в начальные точки Х;.
1 N
2, Вычисление опорноrо потенциала U ref =  L U (Х;) .
No .
I
3, Перемещение случайным образом пешехода вправо или влево на за
данный шаr /).S. (Длина шаrа l1s связана с шаrом по времени соотношени
,
ем (/).s) = D" D  коэффициент диффузии, В системе единиц 1i = т = 1,
D=..!. .)
2
4, Вычисление /).и = [и(x)и ref]t.., И случайноrо числа r, равномерно
распределенноrо на отрезке [0.1].
5. Если /).и > О и r < /).и , удалить пешехода.
6, Если /).и ::; О и r::; /),и , добавить пешехода в точку Х.
7. Повторить пп. З дЛЯ каждоrо из N о пешеходов.
8, Заменить опорный потенциал на
1
Uref =(И). (NNo)/)'"
No
rде N  новое число пешеходов, (И)  средняя потенциальная энерпUl N пе-
шеходов, представляющая собой оценку энерrии OCHoBHoro состояния.
9. Повторение пп. З8 дО достижения энерrией стационарноrо значения,
1 О, Повторение пп. 39 для получения нескольких стационарных значе
ний энерrии.
1 1, Получение усредненноrо значения энерrии по нескольким стацио
нарным значениям.
12, Получение усредненной функции распределения плотности вероят
ности по нескольким стационарным значениям,
Для реализации описанноrо алI'оритма создадим файл WalkSh.m, СОш
держащий описание функции, возвращающей среднее значение энерrии oc
HOBHoro состояния и МlЯовенные (на каждом шаrе МонтеКарло) значения
числа пешеходов в заданных интервалах,
% листинr функции WalkSh,m
function [Еm,Ь]= W alkSh(N ,Srange,K,ds,NTrial,Interval)
% функция, возвращающая среднее значение энерrии OCHoBHoro
% состояния и MrнoBeHHыe (на каждом шаrе Монте-Карло) значения
% числа пешеходов в заданных интервалах
% N  число пешеходов
% Srange  размер начальной области размещения пешеходов
% К  доля неиспользуемых нестационарных состояний
% ds  размер шаrа пешехода
% NTrial  число испытаний
% Interval  вектор, содержащий координаты концов отрезка, используемых
% для вычисления плотности распределения пешеходов
Vref=O;
% инициализация начальной конфиryрации пешеходов
for i=l:N
Xsite( i)=Srange*(O.5- rand(l»;
Vref=Vref+ V(Xsite(i»;
end;
Vref=Vref/N;
Ninitial=N; % число пешеходов в начале испытания
Nwalker=N; % число пешеходов в ходе испытания
dt=ds. Л2; % шar по времени
Nequial=K*NTrial; % номер первоrо стационарноrо состояния
m=l;
for i=l:NTrial
Vsum=O; % полная потенциальная энерrия
for j=Niпitiаl:-l:l
if rand(1)<O.5
Xsite(j)=Xsite(j)+ds;
else
Xsite(j )=Xsite(j )-ds;
end;
Potential= V (Xsite(j»;
dv=Potential- Vref;
if dv<O % проверка на добавление пешехода
if rand(])<-dv*dt
Nwalker=Nwalker+ 1;
Xsite(Nwalker)=Xsite(j); о/с новый пешеход
V sum= Vsum+2*Potelltial;
524
525

?А.iы1)пlсрllо.'lо?е.:"lр()в()Illеe физических 11!)Oц(cив в llакеll1ем.АТLJ].щ
... ...!? м.о..?:.1.иf...о.'.IIIк-в-аll,!1()I:tII:'1'е.:н
else
Vsum=Vsum+Potential; % добавляем только знерrию староI'O пешехода
end;
else
if rапd(1)<dv*dt % проверка на удаление пешехода
Xsite(j )=Xsi te(N walker);
Nwalker=Nwalker-1;
else
Vsum=Vsum+Potential;
end;
епd;
end;
Vave=Vsum/Nwalker; % средний потенциал
if i>Nequial
Е(ш)= Vave;
for n=1:Nwalker
X(n)=Xsite(n);
end;
h 1 =hist(X,lnterval);
if ш==1
Ь=Ы';
else
h=cat(2,h,h1');
end;
m=П1+ 1;
end;
Vref=Vave-(Nwаlkеr-N)/(N*dt); % новый опорный потенциал
end;
Еш=шеап(Е);
function z=V(x);
% ф,ункция, описывающая потенциал
z=0.5*х.Л2;
» N=1000; % начальное число пешеходов
»ds=O.l; % длина ша.а пешехода
» NTrial=1000; О/С число испытаний
» Srange=2; % размер начальной области рюмещения пешеходов
» К=0.2; % доля неиспользуемых нсстационарных состояний
» Ni=40; % число интервалов, ИСПО.'1ьзуемых для вычисления
% плотности распределения пешсходов
% вычисление rpаниц интервалов
» i=1:Ni+1;
» Jnterval(i)=-2*Srange+( 4*SrangeINi*(i. 1));
% вычисление усредненной знерI'ИИ OCHoBHoro состояния
% и вычисление MrHoBeHHbIx (на каждом шаrе МонтеКарло)
% волновых функций
»[А h]=WalkSh(N,Srange,K,ds,NTrial,lnterval);
» А % энерrия OCHoBHoro состояния
ans =
0.4978
% вычисление значений усредненной волновой функции
» Nx=size(h,1)
» Ny=size(h,2)
» for i=1:Nx
for j=1:Ny
A(j)=h(iJ);
end;
А1 (i)=sum(A);
end;
% визуализация потенциала и усредненной волновой функции
» Ni=500;
» dх=(mах(lпtеrvаl)-miп(lпtеrvаl))/(Ni-1);
» i=1:Ni;
» х(i)=IПiп(lпtеrvаl)+dх*(i-1);
» plot(x,O.5*x. Л2, 'k' ,lnterval,A1/max(A1),'k')
Результаты выполнения описанной последовательности команд пред
ставлены на рис. 16,28.
Задача 16.19
Сравните найденное значение энеР2UИ ОСlювНО20 состояния с е20 точ
ным значением [1, задача зо}. Исследуйте завUСИJvtoсть точности чис
леЮ-1020 значения энеР2ИИ ОСl1ОвНО20 состояния, найдеННО20 методо,н
МонтеКарло, от числа пешеходов и числа ша20в }vfO/-llпеКарло,
Задача 16.20
Дополните описанный выше документ б.1ОкоAt, позволяющим НОрАtирО
вать волновую ф)'ю'-Цию так, чтобы она удовлетворяла условию (16.2).
СравН1l1пе Чllсленное значение liОр:vtированной волновой функции с cooт
веmсmвУIОЩllми значениялtll извеС1l1НОй анаЛll111ичеС1<:Ой функции Л, зада
ча 30]. (Указание. Для вЫЧllслеНlIЯ 1l1lПlе2рала (/6.2) проведите
lIЮl1ерl10.7яцию усредненноЙ завиСIlAtостu п(х,)),
526
527

.!!.с.!!.'.':!?.'!!.l!!..?е...?..I!'!Р...оаl'':!:..1!.':!!lI.ч.:ки.л.:II]J!!..!f?'!..a:,!! "!'i пr!!!.....
8.-'
7' /1
/1
/ J
i I
/
1\
7 \,
.
5:
I
4
./
\
, /
\ /
\ /
, /
" .-"'.. '" /
,..''-./ ...../
<''''''' />,,: .
.3 .2 .1 О 1
1
I
J
,
2'
':
i
о
.,
Рис, J 6,28, Волновая функция основносо состояния, нормированная
на ее максимальное значение, и zрафик завиСUJofOсти nотенциG.%НОЙ энерzии
ит координаты
j;дча16.2Т' .... .........Ш.........Ш..
Получите числеююе решение для анzaрмоничеСК020 осциллятора с по--
тенциалом
и(Х) = J..x2 +Ьх3.
2
Рассмотрите следующие :;начения пара.,иетра: Ь = 0.1,0,2,0,5, В чем
проявляется увеличение нелинейности потенциала?
>........ ..... .....
Задача 16.22
Внесите необходимые изменения в описанный выше документ и вычис--
лите энеР2ию и волновую функцию ОСlювН020 состояния пРЯМОУ20ЛЬНОЙ
потенциальной ямы, Найдите зависимость Эllер2ИИ основНО20 состоя
1/ия от ио, Сравните полученные резулыпаты с анаЛО2ИЧНЫЛ1U резуль
татaJIЩ полученны/t-1U методтиu, описанными в разделах 16.2, 16.4.
..    .   'H H  ''""'H'>'H'..H.. '"H.'.. .. . . ..
Задача 16.23
ВычиС.ште иНtенения значений энер2и1t 1I волновых функций волновО20
состояНlЩ частицы, находящеiiся в пря.моу?Ольной потенциальноЙ я.ме,
оБУС70вленные люлы,и вОЗJtущением:
! UhПРИ ;xisO,2
и(х)= Опри O,2<X]sl,
ио Ix! > I
528
1
. .!о.:..?деl!О'!.!lI'5.!!.'!!!!..С!.'.'.:,!!
16.6. Оценка энерrии основносо состояния
квантовой системы вариационными методами
Монте-Карло
Альтернативный ПОДХОД к оценке энерrии OCHoBHoro состояния KBaHTO
вых систем состоит в использовании вариаuионноrо метода, позволяющеrо
получить оценки верхних rpаниц значений энерrии OCHoBHoro состояния,
Данный вариационный метод находит мноrочисленные приложения в aTOM
ноЙ физике, молекулярной физике, ядерноЙ физике и физике кuнденсиро
ванных сред. Подробное рассмотрение мноrочисленных примеров, относя
щихся к перечисленным выше разделам физики, выходит за рамки нашей
книrи, поэтому далее мы оrpаничиваемся обсуждением основных идеЙ Ba
риационноrо метода МонтеКарло,
Рассмотрим квантовую систему, описываемую оператором rамильтона
й вида (16.9). Вариационный принцип утверждает, что для произвольноЙ
функции qJ( х) выполняется неравенство
, J qJ*(Х)ЙqJ(Х)dx
(Н) = .. .. .. 2. Ео,
. J qJ*(x)qJ(x)dx
(16.74)
[де Ео  энерrия OCHOBHoro состояния системы.
Неравенство (16.74) превращается в точное равенство только в том слу
чае, коrда фунющя qJ(X) является собственноЙ функцией оператора Й , co
ответствующеЙ собственному значению ЬQ. Величину (Н) можно тpaKTO
вать как математическое ожидание полноЙ энерrии для приближенноЙ вол--
новой функции qJ(X) ,
Нсравенство (16.74) является основоЙ вариационноr'о метода, Механизм
реализации даннOI'О метода состоит в физически обоснованном выборе
проб ноЙ функции, зависящей от нескольких параметров" вычислении (Н) в
соответствии с (16,74), варьировании одноrо или более параметров до тех
пока не будет достиrнуто минимальное значение (Н). Данное значения яв--
ляется верхней I'Рашщей ИСТИННОI"О значения энерrии OCHoBHoro состояния,
Рассмотрим реализацию вариационноrо метода МонтеКарло на при мере
одномерной системы, Введем пространственную временную сетку Х; =if..x,
['де Лх  шаr се1КИ, в УЗJlах которой будем вычислять значения функции,
18! 576
529

?t.I!I?Iп.I!Р'.I?I!.'.оеlll!оа.I'.и-.l!rJ)и-.?и-.'!.l!с_к--и-х..'.![Jй- е.й-в.в./lаК--l!l1:.еfl:!Атr.1:.В-. ..
Алrоритм вариационноrо метода МотнеКарло реалюуется следующей по
следовательностьюдействий:
1, Выбрать физически обоснованных значений пробной функции tp(X) в
точках Х;,
2, Выбрать случайную точку Х; и изменить значение tp; = tp(X;) на слу
чайную величину Atp Е [д-;д-].
З. Вычислить изменение энерrии АЕ дЛЯ (Н),
4. Если АЕ:::;; О , принять выполненное изменения tp; ,
5, Если АВ> О, отклонить выполненное изменение tp; .
6. Повторять пп. 25 до достижения постоянноrо (с заданной точностью)
значения (Н),
Рассмотрим реализацию описанноrо алrоритма в пакете МА TLAB дЛЯ
случая, коrда волновая функция является симметричной, Далее приводится
листинr mфайла Variation.rn, содержащеrо описание функции, возвра
щающей верхнюю r-раницу значения энерrии OCHoBHoro состояния, COOTBeT
ствующую волновую функцию, И мшовенные (на каждом шаrе итсрацион
Horo процесса) значения энерrии.
% листинr файла Variation,m
function [Ern,psi, W] = Variation(Xrnax,delta,N)
% функция, возвращающая верхнюю rpаницу значения энерrии OCHoBHoro
% состояния, соответствующую волновую функцию, и мrновенные
% (на каждом шаrе итерационноrо процесса значения энерrии)
% Хmах  максимальное значение координаты
% delta  максимальное изменение волновой функции
% N  число узлов координатной сетки в каждом направлении
dx=Xrnax!N; % расстояние между узлами координатной сетки
delta=2 *delta;
Nrnove=lOOO*N; % число шаrов итерационноrо процесса
Norrn=O;
k=l;
% вычисление значений начальноrо приближения
for i=1:2*N+l
psi(i)=f( -Xrnax+dx*(i-l»;
епд;
Nоrrn=surn(рsi.Л2); о/с нормировочный множитель
% вычисление начальной энерr'ии
530

...!:..л.!?I!3'Р.?f!!!и-.:К--3.!'.?/::и-.:...'п._
Е=О;
for i=N+2:2*N
x=-Xrnax+(i-l)*dx;
pe=psi(i)*psi(i)*V(x); о/с потенциальная энерrия
ke=O.5*psi(i)*(2*psi(i)-рsi(i+l)-рsi(i-l»/dхЛ2; % кинетическая энерrия
E=E+2*(pe+ke);
епд;
E=E+E*V(O)*psi(N+ l)ЛZ;
E=E+O.5*psi(N+ 1)*(2*psi(N + 1)-рsi(N+2)-рsi(N) )/dхЛ 2;
% варьирование волновой функции
Есиrn=О;
for Irnove=l:Nrnove
i=floor«N-l)*rапd(1»+N+2; % координата точки
dpsi=delta*(rand(1)-O.5); % изменение волновой функции
PsiTrial=psi(i)+dpsi; % пробное значение волновой функции
% в iM узле вычисление изменения энерrии, обусловленное
% изменением волновой функции в iOM узле
dpsi2=PsC Trial *Psi Trial-psi(i)*psi(i);
dV=dpsi2*V(-Xrnах+(i-l)*dх); % изменение потенциальной энерrии
dK=(dpsi2-dрsi*(рsi(i+ l)+psi(i-l»)/dxЛZ; % изменение
% кинетической энерrии
ifi==N+l
Etrial=E+dK+dV;
Norrn Trial=Norrn+dpsi2;
else
Etrial=E+2*(dV +дК);
Norrn Trial=Norrn+2 *dpsi2;
епд;
dE=Etrial/Norrn Trial- E/Norrn;
if дЕ<О % принятие изменения волновой функции
psi(i)=PsC Trial;
psi(2*N+2-i)=Рsi Trial;
Norrn=Norrn Trial;
E=Etrial;
епд;
Ecum=Ecum+E/Norrn;
W(Irnоvе)=Е/Nоnп;
епд;
Em=Ecum/Nmove;
531

'!?,"!п-lопj(!.Р,.1I0е M-?(!:Iрй.6а.llиеljJl/'lчесюlX прО'!:.СС?6.. в .пиксте МА ПАВ.
function z = С(х)
% ФУНКЦИЯ, описывающая начальное приближение
z=exp(-x. Л2);
function z = V(x)
% функция, описывающая потенциал
z=0.5*x. Л2;
Далее необходимо выполнить следующую последовательность команд:
» Хmах=4; % максимальное значение координаты
» N=40; % число узлов в каждом направлении оси оХ
» delta=O.l; % максимальное изменение волновой функции
»[Еm psi W] = Variation(Xmax,delta,N)j
% визуализация волновых функций и зависимости MrHoBeHHoro
% значения энерrии от номера шаrа итерации (рис. 16,29)
» Ni=lOOO;
» i=l:Nij
» dx=Xmax!Ni;
» x(i)=-Xmax+2*dx*i;
» j=l:length(psi);
» X(j)=-Хmах+2*ХmаxJlепgth(рsi)*(j-1)j
» plot(X(j),psi(j), 'k' ,х,ехр« -х. Л2)/2),' -.k' ,х,ехр( -х. Л2),' --k');
» plot(W,'k'); plot(W,'k')jaxis([O length(W) 0.5 0.65])
J
I
О.вl
0.7
06
05 3, ,
0.4 [
О.З .
021
0,1
I " "
o..... ::I
.< -3 -2
'. \
"
::C.,.L.;,..... ......;
2 , 4
Рис. i 6.29. Волновая фую-:цuя основНО20 состоянuя сармоническосо ОСЦ!Н7ятора:
J  начальное прuб.7!I.1/ссние, 2. после 40000 итерациЙ, 3  точное ЗliGчеНtlс
532
...............
. ...ш . ..!!}. Мое:q'2!.й.а.!:'!..'.l'!!о.!:ll:-"!.
065
06
'"
\"
".
055:..
......................
0.5:
о
............J._................
15 2 2.5 3
05
35 4
x101
Рис, 16,30. 'Зависимость М2новеННО20 значения энерzuи основНО20 состояния
сармоничеСКО20 осциллятора от номера шаса итерации
Задача 16.24
Сравните скорость сходимости итерациОННО20 процесса при выборе в
качестве пробной волновой функции ф( х) = cos( х) , ф(Х) = 1 ,
х2
ф(Х) = е 1,5, Исследуйте влияние величины максималЬНО20 изменения
волновой функции на точность вычисления собствеННО20 значения энер
сии и собственной волновой функции основНО20 состояния,
Задача 16.25
Модифицируйте функцию Variatioп( ) так, чтобы изменения волновой
функции проводuлись последовательно для каждО20 узла пpocтpaHcт
венной сетки, Приводит ли данная модификация прО2раммы к YCKope
нию сходимости итерациОННО20 процесса?
Задача 16.26
Вычислите энеР2ию основНО20 состояния нелинеЙНО20 2армоничеСКО20
1
осциллятора с потенциалом и(Х) = x2 +ьх4, Сравните полученные
2
значения собственной энеР2ии и волновой функции основНО20 состояния,
полученные вариационным методом МонтеКарло, с соответствующи
ми значения/ии, полученными в квазиклассическом приближении, Meтo
дшt пристрелки и методом случайных блужданий. Рассмотрите случаи
533

()!!.!II()_"!!!.I!!!?:,:«О=Jl..'!Р...CJ...с:!..I}!!!1!..'!..и-:.'!.'!Р.?lf.=()._.f!.15.!!'!!.'!..!4!!.:....ш ..
Ь > О, Ь < О, Как зависит энер2ИЯ основн02О состояния от коэффици
ента Ь, определяюще20 степень нелинейнасти системы?
Задача 16.27
Используйте, описанный выше докуменщ для расчета энеР2ИИ OCHoвHO
20 состояния пРЯМОУ2ОЛЬНОЙ потенциальной ямы с параметрами
Uo=2,20, а == 1, Положите Хтах:=2, N=40, 11=0.1. PaCCMoт
рите начальные пробные волновые функции Iр(Х) = cos(x), Iр(Х) = 1,
х2
Iр(Х) = е 1.5, Какая из пере численных выше фУНКЦИЙ дает наиболее бы
струю сходимость к искомому результату? Чему равна 2лубина пoд
барьерною проникания волновой функции? Сравните полученные З/-lаче
ния собственной энер2ИИ и волновой функции основною состояния, пo
лученные вариационным методом МонтеКарло, с соответствующими
значениями, полученными в квазиклассическом приближении, методом
пристрелки и .методом случайных блужданий,
Задача 16.28
Вычислите вариационным методом МонтеКарло изменение значений
энерzuи и волновых функций волновою состояния, частицы, находящейся в
пРЯМОУ2ОЛЬНОЙ потенциальной яме, обусловленные малым возмущением:
{ Uь при !xi::;; 0.2
Щх) = О при 0.2 < !х!::;; 1.
И о Ixi > 1
Сравните полученные значения собственной энер2ИИ и волновой функции
основН020 состояния, полученные вариационным методом MOHтe
Карла, с соответствующими значениями, полученными в квазиклассиче
СКОАl приближении, методом пристрелки и методом случайных блуж
даний,
Задача 16.29
Сравните скорость сходшюсти итераЦИОНН02О процесса при выборе в
качестве пробной волновой функции Iр(Х) = cos(x) , Ip(х)=1.
х2
'Р(х) = е 1,5, Исследуйте влияние величины лшксималЬН02О ИЗЛlенения
волновой функции на точность вычисления собствеНН020 значения энер
?ии и собственной волновой функции основн020 состОяния,
534
}'
1\
, '"
"
[1
'1\'
.
l...... А!..()д..=Л-'!.fJ.О'!.(l!!и-:'15.!l!!'!!.'?.'!.:_и-'!!.:':I.
Задача 1 6.30
Модифицируйте функцию Variation( ) так, чтобы изменения волновой
функции проводились последовательно для кажд02О узла пpocтpaHcт
венной сетки, Приводит ли данная модификация пр02раммы к YCKope
ниiO сходимости итераЦИОНН02О процесса?
"'"''"''"'Ш"Н"'Н.Ш.. 'НН'''Н""'ННш
Задача 16.31
Используйте докуменщ описанный в данном разделе, для вычисления
энер2ИИ основн020 состояния нелинеЙН02О zармоничеСКО2О осциллятора
() 12 4
С потенциалом И х =  х + Ьх , Сравните полученные значения собст
2
венноЙ энер2ИИ и волновой функции основНО20 состояния, полученные вa
риационным методом МонтеКарло, с соответствующими значениями,
полученными в кваЗиклассическом приближении, методом пристрелки и
методом случайных блужданий, Рассмотрите случаи Ь> О, Ь < О, Как
зависит энер2ИЯ основН020 состояния от коэффициента Ь. определяю
ще2О степень нелинейности системы?
'>'НШШННШ'ШНН'НН'Н"ШН"НШ'Н'НН'шшНШ'Ш"'Н'ш
Задача 16.32
Используйте, описанный выше докуменщ для расчета энер2ИИ OCHoвHO
20 состояния пРЯМОУ20ЛЬНОЙ потенциальной ямы с параметрами
Uo=2,20, а == 1, Положите Хтах:=2, N=40, А=О.I. PaCCMoт
рите начальные пробные волновые функции Iр(Х) = cos(x) , 'Р(х)=1,
х2
'Р(х) = е 1,5. Какая из перечисленных выше функций дает наиболее бы
струю сходимость к искомому результату? Чему равна 2Лубина пoд
барьерною проникания волновой функции? Сравните полученные значе
ния собственной энер2ии и волновой функции основН020 состояния, пo
лученные вариационным методом МонтеКарло, с соответствующими
значениями, полученными в квазиклассичеСКОЛl приближении, методом
пристрелки и методОЛl случайных блужданий,
''''"'Н"Н'ШНШНН"НН'НШНННШШШН_Ш..Ш..
Задача 16.33
Вычислите вариационным методом МонтеКарло изменения значений
энер2ИИ и волновых функций волнов020 состояния частицы, находящeiiся в
пРЯМОУ20ЛЬНОЙ потенциальной яме, обусловленные малым возмущением:
{И" при lxi::;; 0.2
U(х)= О при 0.2<lxl::;;1,
UО хl > 1
535

.l!.?Al....п-.!.?'!!!3?.'..?е_:'._е!!.II!!...й-r:.'!!_е...rJ!..и-.llчс:..п-.Р.:'.ей-.!!е!'.'.fl!..1.!:!..._._....ш..
Сравните полученные значения собственноЙ энеР2ИИ и волновой функции
основН020 состояния, полученные вариационным методом Аl0нте-Кар-
ло, С соответствующими значениями, полученны,ми в квазиклассическом
приближении методом пристрелки и методом случайных блужданий.
Для вычисления собственноrо значения энерrии OCHoBHoro состояния
можно использовать принцип вариации постоянных коэффициентов
разложения волновой функции по полному набору ортоrональных базисных
функций 1,,:
rp = Lc,J" .
(16,75)
"
Подставив (16.75) в (16.74), получим
JLс:fтЙLс,Jпdх Lc;,cnJ I,;ЙI"dх
(Н) = т ,, = т," > Е
J "" 2  о.
LC:fmLcnf"dx L.,lc,,!
т n п
(16.76)
Неравенство (16.76) превращается в точное равенство только в том слу-
чае, коrда функция ф( х) является собственной функцией оператора Й , со-
ответствующей собственному значению Ео. Для вычисления математиче-
cKoro ожидания (Н) необходимо вычислить матричные элементы
J I,;ЙI"dх. (При необходимости вычисления матричных элементов в про-
странстве больших размерностей можно использовать для вычисления ин
теrpалов метод Монте-Карло.) После вычисления матричных элементов
проводится вариация коэффициентов с;, ст до тех пор, пока не будет дос-
тиrнуто минимальное значение (Н). Данное значения является верхней
rpаницей истинноrо значения энерrии OCHoBHoro состояния.
Рассматриваемый алrоритм вариационноrо метода МонтеКарло реали-
зуется следующей последовательностью действий.
1. Выбрать ортонормированный набор базисных функций.
2, Выбрать числа используемых базисных функций Nb.
З. Вычислить значений матричных коэффициентов J I,;ЙI"dх ,
4, Задать начальные значения коэффициентов Cj,
5. Вычислить начальное значение энерrии Е.
6, Выбрать случайным образом коэффициент с; и изменить ero значение
на случайную величину Ас Е [д;д].
536
...............
.._]?: !1..й-.С?'1I!!..й-'!.1!!.1I:.!5.,!!!..1!'!!!!..в::!!'!:..."!.с:..
7, Вычислить изменение энерrии (Н), обусловленное изменением значе-
ния коэффициента,
8. Если АЕ  О принять новое значение коэффициента.
9. Если АЕ > О отклонить новое значение коэффициента,
10, Повторять пп. 69 до достижения постоянноrо (с заданной точно-
стью) значения (Н),
Задача 16.34
Решите задачу 16,29, используя метод вариации постоянных разложе-
ния собственноЙ функции по ортонормированному базису. В качестве
ортонормироваНН020 базиса выберите собственные волновые функции
частицы, находящейся в бесконечно 2лубокой потенциальной яме,
Задача 16.35
Определите, используя метод вариации постОЯ1l1lЫХ разложения собствен-
ной фУIllЩИИ по ортонормированному базису, собственное значение энеР2ИИ
основН020 состояния частицы, находящейся в потенциале Морза
u(x)=uo2ax 2eax), (16.77)
используя в качестве набора ортонормироваНН020 набора базисных
функций базисные функции линеЙН020 zap.1o-10ничеСК020 осциллятора:
,
X
fn (х) = NnHn (х)е"'2-,
(16.78)
2де Нп(х) полиномы Эрмита, Nn нормировочная постоянная,
) ( )" х2 d" x2
Н п (х =  1 е- - е ,
dx
(16.79)
!I
N =[ !"-]
п I .
1l'22fIn!
J, Создайте функцию, позволяющую для заданных волновых функций вычис-
лять матричные элеАlенты J f;ЙI"dх, вычислите значения элементов
Аштрицы для n,ш=2,3,...,JO.
2. Создайте функцию, реализующую описанный выше ал20рИтм вариации по-
стоянных разложения волновой функции по ортонормированному базису,
3. Проведите вычисления для раЗЛИЧНО20 числа используемых базисных
функций п, выбирая в качестве начальных значений со = 1, сп = О для
п i' О. Как зависят 1l0.1учае.\1ые значения э/-/ер2ИИ от числа используе.мых
( 16.80)
537

i!.:AII1.IOпl. IО..:":I.CJ.':.llРCJ.в{llluс:.1!.I.I.зllч-с:к-uх..':Е5'.С::'О....'.'..{l.к-e.'!!.e!'!.1..!:4:!!.
базисных функций? Как зависят получаемые значения энерzии от MaK
С1L\taльной величины изменения шаzа? Сравните полученные численные
значения с известными точными значениями энерzии {l, задача 70].
ЛИТЕРАТУРА
1, Флюrrе З. Задачи по квантовой механике, Т. 1. М.: Мир, 1974.
2, Anderson J, В. А random walk simulation of Schrodinger equationl/J. Chem, Phys, 63, 1499,
1975.
3. Anderson J, В, Quantum chemistry Ьу random wa1k1/J, Chem. Phys, 65,4121,1976,
4, Anderson J, В, Quantum chemistry Ьу random walk//Higher accuracy, j, Chem, Phys,
73,3897, 1980,
5, Ландау Л. Д., Лифшиц Е, М. КваН10вая механика, Нерелятивистская теория. М.: Нау-
Ka,2001,
6, Давыдов А. С, Квантовая Механика, М.: Наука, 1973,
7, Крайнов А, В" Миrдал А. Б, Качественные методы в квантовой механике. М.: Наука, 1976.
8, Миrдал А, Б, Качественные методы в квантовой теории, М,: Наука, 1975,
9, Методы Монте-Карло в статистической физике. Под ред. К. Биндера, М,: Мир, 1982.
1 О, rулд х., Тобачник Я, Компьютерное моделирование в физике, М,: Мир, 1990, Т, 2.
11. Кунин С, Вычислительная физика, М,: Мир, 1992,
538
...............
Приложение 1
ОСНОВНЫЕ ПРИЕМЫ РАБОТЫ
Пl.l. Введение в пакет MATLAB
I1
МА TLAB является интерактивным, матричноориентированным паке
том, предназначенным для выполнения научных и инженерных расчетов.
Имя па кета МА TLAB является аббревиатурой двух слов МА Trix
LABoratory (МАТричная ЛАБоратория), Цель данноrо раздела  познако
мить читателя с необходимыми сведениями для начала работы с пакетом
MATLAB. Мы рекомендуем совместить изучение данноrо раздела с OДHO
временным выполнеНИ'ем приведенных в разделе примеров,
Отметим, что во время работы с системой можно пользоваться BCTpoeH
ной оперативной помощью, которая содержит сведения, необходимые для
успешной работы с пакетом. После входа в систему команда help выведет
список rpупп, в которые объединены функции:
» help
То get started, select "MATLAB Help" from the Help menu.
HELP topics:
matlab\gelleral  General purpose commands.
matlab\ops  Operators and special characters.
matlab\lang  Programming language constructs.
matlab\elmat  Elementary matrices and matrix manipulation.
matlab\elfun  Elementary math functions.
matlab\<ipecfun  Specialized math functions.
matlab\matfun  Matrix functions . numericallinear algebra.
matlab\datafun  Data analysis and Fourier transforms.
matlab\audio  Audio support.
matlab\polyfun  Interpolation and polynomials.
matlab\funfun  Function functions and ODE solvers.
matlab\<iparfun  Sparse matrices.
matlab\graph2d  Two dimensional graphs.
matlab\graph3d  Three dimensional graphs.
matlab\<ipecgraph  Specialized graphs.
matlab\graphics  Handle Graphics.
matlab\uitools  Graphical user interface tools.
matlab\<itrfun  Character strings.
matlab\iofun  File inpuUoutput.
matlab\timefun  Time and dates.
matlab\datatypes  Data types and structures.
matlab\verctrl  Version control,

5с:п.,!!'!!.ер'I{?од.л-tp?(l!:l!.:1)l!..l!.::с.к;(пр'(),:!:с.с.?вI1'!:!<.'!!f!../>!.1.!...-!!!.
matlab\winfun  Windows Operating System Interface Files (DDE/ActiveX).
matlab\demos  Examples and demonstrations.
toolbox\local  Preferences.
simulink\simulink  Simulink
simulink\blocks  Simulink block library.
simulink\simdemos  Simulink 4 demonstrations and samples,
simdemos\aerospace  Simulink: Aerospace model demonstrations and samples.
simdemos\automotive  Simulink: Automotive model demonstrations and samples.
simdemos\simfeatures  Simulink: Feature demonstrations and samples.
simdemos\simgeneral  Simulink: General model demonstrations and samples.
simdemos\simnew  Simulink: New features model demonstrations and sampls.
simulink\dee  Differential Equation Editor.
stateflow\stateflow  Stateflow.
stateflow\sfdemos  Stateflow demonstrations and samples.
stateflow\coder  Stateflow Coder.
rtw\rtw  Real- Time W orkshop.
rtw\rtwdemos  Real- Time Workshop Demonstrations:
asap2\asap2  (No tabIe оС contents filе).
asap2\user  (No table оС contents flIе).
cdma\cdma  CDMA Reference В1ockset.
cdma\cdmamasks  CDMA Reference В10ckset mask helper functions.
cdma\cdmamex  CDMA Reference В10ckset S-Functions.
cdma\cdmademos  CDMA Reference В10ckset demonstrations and examples.
commblks\commblks  Communications Blockset.
commblks\commmasks  Communications В10ckset mask helper functions.
commbIks\commmex  Communications В10ckset S-functions.
commblks\commblksdemos  Communications В10ckset Demos.
commblks\commblksobsolete  Archived Simulink Files from Communications Tool-
Ьох Version 1.5.
соmm\соmm  Communications Toolbox.
comm\commdemos  Communications Toolbox Demonstrations.
comm\commobsolete  Archived МА TLAB Files from Communications Toolbox
Version 1.5.
control\control  Control System Toolbox.
control\ctrlguis  Control System Toolbox -- GUI support functions.
control\ctrlobsolete  Control System Toolbox -- obsolete commands.
control\ctrlutil  (No table оС contents filе)
control\ctrldemos  Control System Toolbox -- Demos.
dspblks\dspbIks  DSP В1ockset.
dspblks\dspmasks  DSP В10ckset mask helper functions.
dspblks\dspmex  DSP В10ckset S-Function MEX-flIеs.
dspblks\dspdemos  DSP В10ckset demonstrations and examples.
dsprtw\utiCc  (No table оС contents flIе).
daq\daq  Data Acquisition Toolbox.
daq\daqdemos  Data Acquisition Toolbox - Data Acquisition Demos.
database\database  Database Toolbox.
540
ш .ш шшl}Р.'-!3.С::lil!Я
J
database\dbdemos  Database Toolbox Demonstration Fппсtiопs.
database\vqb  Visual Query Builder functions.
datafeed\datafeed  Datafeed Toolbox.
datafeed\dfgui  Datafeed Toolbox Grapblcal User lnterface
toolbox\dials  Dials & Gauges В1ockset.
toolbox\exlink  (No table оС contents flIе).
flIterdesign\filterdesign  Filter Design Toolbox.
flIterdesign\quantization  (No tabIe оС contents filе).
filterdesign\filtdesdemos  Filter Design Toolbox Demonstrations.
finderiv\finderiv  Financial Derivatives Toolbox.
ftseries\ftseries  Financial Time Series Toolbox.
ftseries\ftsdemos  (No table оС contents filе).
ftseries\ftsdata  (No tabIe оС contents filе).
ftseries\ftstutorials  (No table оС contents tilе).
finance\finance  Financial Toolbox.
finance\calendar  Financial Toolbox calendar functions.
finance\findemos  Financial Toolbox demonstratlOn functions.
finance\finsupport  (No table оС contents tilе).
toolbox\fixpoint  Fixed.Point В1ockset.
fixpoint\fxpdemos  Fixed-Point В10ckset Demos.
fixpoint\obsolete  Obsolete Fixed.Point В1ockset.
fuzzy\fuzzy  Fuzzy I.ogic Toolbox.
fuzzy\fuzdemos  Fuzzy Logic Toolbox Demos.
garch\garch  GARCH Toolbox.
garch\garchdemos  (No table оС contents tilе).
images\images  Image Processing Toolbox.
images\imdemos  Image Processing Toolbox ... demos and sample images.
instrument\instrument  Instrument Control Toolbox.
instrument\instrumentdemos  (No tabIe оС contents tilе).
Imi\Imictrl  LMI Control Toolbox: Control Applications.
Imi\lmilab  LMI Control Toolbox.
toolbox\compiler  МА TLAB Compiler.
toolbox\rptgen  МА TLAB Report Generator.
map\map  Mapping Toolbox.
map\mapdisp  Mapping Toolbox Мар Definition and Display.
map\mapproj  Mapping Toolbox Projections.
mpc\mpccmds  Model Predictive Control Toolbox.
mpc\mpcdemos  Model Predictive Control Toolbox.
motdsp\motdsp  Motorola DSP Developer's Кit.
motdsp\motdspmex  Motorola DSP Developers Кit.
mоtйsраsm\Ып  (No table оС contents tilе).
motdsp\motdspbIks  Motorola DSP Developers Кit block libraries.
mоtdsр\mоtdsршаsks  Motorola DSP bIockset mask helper functions.
motdsp\motdspdemos  MOTDSP Toolbox demonstrations and examples:
пшtооls\сошmапds  MuAnalysis and Synthesis Toolbox.
mutools\subs  MuAnalysis and Synthesis Toolbox.
541

1\?!..I?f!fJ.l?:'!<.?:''!..':l.Е.?вII,:!:ф'!'1:'с:...к-fJ..'?Уе..?....1<..:.I11.e.A??:::!в..
nnet\nnet  Neural Network Toolbox.
nnet\nnutils  (No tabIe оС contents Ше).
nnet\nncontrol  Neural Network Toolbox Control System Functions.
nnet\nndemos  Neural Network Demonstrations.
nnet\nnobsolete  (No tabIe оС contents Ше).
toolbox\ncd  Nonlinear Control Design Вlockset.
toolbox\optim  Optimization Toolbox.
toolbox\pde  Partial Differential Equation Toolbox.
powersys\powersys  Power System Вlockset.
powersys\powerdemo  Power System Вlockset Demos.
rtw\ada  Real-Time Workshop Ada Coder.
targets\ecoder  Real- Time Workshop Embedded Coder.
toolbox\reqmgt  Requirements Management Jnterface.
toolbox\robust  Robust Control Toolbox.
toolbox\sb2s1  SB2SL (converts SystemBuiId to Simulink).
signal\signal  Signal Processing Toolbox.
signal\fdatoolgui  Signal Processing Toolbox GUl.
signal\sptoolgui  Signal Processing Toolbox GUI.
signal\sigdemos  Signal Processing Toolbox Demonstrations.
rtw\accel  Simulink Accelerator.
simulink\mdldiff  Model Differencing for Simulink and Stateflow.
simulink\simcoverage  Simulink Model Coverage Tool.
toolbox\rptgenext  Simulink Report Generator.
toolbox\splines  Spline Toolbox.
toolbox\stats  Statistics Toolbox.
toolbox\symbolic  Symbolic Math Toolbox.
ident\ident  System Identification Toolbox.
ident\idobsolete  (No tabIe оС contents Ше).
ident\idguis  (No table оС contents Ше).
ident\idutiIs  (No tabIe оС contents Ше).
ident\iddemos  (No tabIe оС contents Ше).
ident\idhelp  (No table оС contents Ше).
wavelet\wavelet  Wavelet Toolbox.
wavelet\wavedemo  Wavelet Toolbox Demonstrations.
хрс\хрс  хРС Target.
build\xpcblocks  (No table оС contents Ше).
xpc\xpcdemos  хРС Target -- demos and sample script files.
kernel\embedded  хРС Target Embedded Option.
MatIabR12\ork  (No tabIe оС contents Ше).
For more help оп directory/topic, type "help topic".
» help
HELP topics:
matIab\general  General purpose commands.
matlab\ops  Operators and special characters.
542
..I.!P.':l.:I(),!,::IU!!.
,
.
I
шаtlаЬ\Iапg  Рrоgrашmiпg language constructs.
matlab\elmat  Elementary шаtriсеs and шаtriх шапiрulаtiоп.
matlab\elfun  Elementary шаth functions.
matIab\specfun  Specialized шаth functions.
шаtlаЬ\mаtfuп  Matrix functions - numericallinear algebra.
шаtlаЬ\dаtаfuп  Data analysis and Fourier transforms.
matIab\audio  Audio support.
matlab\polyfun  Jnterpolation and polynomials.
шаtlаЬ\fuпfuп  Function functions and ODE solvers.
matlab\sparfun  Sparse matrices.
matlab\graph2d  Two dimensional graphs.
шаtIаЬ\grарh3d  Three dimensional graphs.
matlab\specgraph  Specialized graphs.
matlab\graphics  Handle Graphics.
matlab\uitools  Graphical user interface tools.
matIab\strfun  Character strings.
шаtIаЬ\iоfuп  File inpuUoutput.
matIab\timefun  Time and dates.
matIab\datatypes  Data types and structures.
matlab\verctrl  Version control.
matIab\winfun  Windows Operating System Jnterface Files (DDE/ActiveX).
matIab\demos  Examples and demonstrations.
toolbox\Iocal  Preferences.
simulink\simulink  Simulink
simulink\bIocks  Simulink block library.
simulink\simdemos  Simulink 4 demonstrations and samples.
simdemos\aerospace  Simulink: Aerospace model demonstrations and samples.
simdemos\automotive  Simulink: Automotive model demonstrations and samples.
simdemos\simfeatures  Simulink: Feature demonstrations and samples.
simdеmоs\siшgепеrаl  Simulink: General model demonstrations and samples.
simdemos\simnew  Simulink: New features model demonstrations and sашрlеs.
simulink\dee  Differential Equation Editor.
stateflow\stateflow  Stateflow.
stаtеflоw\sfdешоs  Stateflow demonstrations and samples.
stateflow\coder  Stateflow Coder.
rtw\rtw  Real-Time Workshop.
rtw\rtwdешоs  Real- Time Workshop Demonstrations:
asap2\asap2  (No table оС contents Ше).
asap2\user  (No tabIe оС contents Ше).
cdma\cdma  CDMA Reference Вlockset.
cdma\cdmamasks  CDMA Reference Вlockset mask helper functions.
cdma\cdmamex  CDMA Reference Blockset S-Functions.
cdma\cdmademos  CDMA Reference Вlockset demonstrations and examples.
соmшblks\соmmblks  Communications Вlockset.
соmmЫks\сошmmаsks  Communications Вlockset mask helper functions.
соmшЫks\сошmшех  Communications Blockset S-functions.
543

к А1/jы
ерll''А1()l!.р''?,!'.!!.рu:1.l!е_с,: !!.Р?це,:?в!1(lкс..'!.j ei\.1. /TI:!!!...
_Il!.I':1.?JiCUUJl
commblks\commblksdemos Communications Вlockset I>emos.
commbIks\commblksobsolete  Archived Simulink Files from Communications 1'001.
Ьох Version 1.5.
соmm\соmm  Communications 1'oolbox.
comm\commdemos  Communications 1'oolbox I>emonstrations.
comm\commobsolete  Arcblved МА TLAB Files t'rom Communications Toolbox V el'
sion 1.5.
control\control  Control System 1'oolbox.
control\ctrlguis  Control System Toolbox - GUl suppurt functions.
control\ctrlobsolete  Control System Toolbox  obsolete commands.
control\ctrlutil  (No table of contents Ше).
control\ctrldemos  Control System Toolbox  Demos.
dspblks\dspbIks  DSP Вlockset.
dspblks\dspmasks  DSP Вlockset mask helper functions.
dspblks\dspmex  DSP Вlockset SFunction MEX-files.
dspblks\dspdemos  DSP Вlockset demonstrations and examples.
dsprtw\utiCc  (No table of contents Ше).
daq\daq  Data Acquisition 1'oolbox.
daq\daqdemus  Data Acquisition Toolbox . Data Acquisition Demos.
database\database  Database Toolbox.
database\dbdemos  Database Toolbox Demonstration Functions.
database\vqb  Visual Query Builder functions.
datafeed\datafeed  Datafeed 1'oolbox.
datafeed\dfgui  Datafeed 1'oolbox Graphical Uscr Interface
toolbox\dials  Dials & Gauges Blockset.
toolbox\exlink  (No table of contents Ше).
filterdesign\filterdesign  Filter Design 1'oolbox.
filterdesign\quantization  (No table of contents filе).
filterdesign\filtdesdemos  Filter Design 1'oolbox Demonstrations.
finderiv\finderiv  Financial Derivatives 1'oolbox.
ftseries\ftseries  Financial 1'ime Series 1'oolbox
ftseries\ftsdemos  (No table of contents Ше).
ftseries\ftsdata  (No table of contents filе).
ftseries\ftstutorials  (No table of contents Ше).
finance\finance  FinanciaI Toolbox.
finance\calendar  Financial 1'oolbox calendar functions.
finance\findemos  Financial Toolbox demonstration functions.
finance\finsupport  (No tabIe of contents Ше).
toolbox\fixpoint  FixedPoint Вlockset.
fixpoint\fxpdemos  Fixed-Point Вlockset Demos.
fixpoint\obsolete  Obsolete FixedPoint Вlockset.
fuzzy\fuzzy  Fuzzy Logic 1'oolbox.
fuzzy\fuzdemos  Fuzzy Logic Toolbox Demos.
garch\garcll  GARCH 1'oolbox.
garch\garchdemos  (No table of contents filе).
images\images  Image Processing Toolbox.
images\imdemos  Image Processing Toolbox щ demos and sample images.
instrument\instrument  Instrument Control Toolbux.
instrument\instrumentdemos  (No table of contclits filе)
Imi\lmictrl  IJMI Control 1'oolbox: Control Applications.
Imi\lmilab  I.MI Control 1'oolbox.
toolbox\compiler  MATLAB Compiler.
toolbox\rptgen  МА TLAB Report Generator.
map\map  Mapping 1'oolbox .
map\mapdisp  Mapping Toolbox Мар Definition and Display.
map\mapproj  Mapping Toolbox Projections.
mpc\mpccmds  Model Predictive Control Toolbox.
mpc\mpcdemos  Model Predictive Control Toolbox
motdsp\motdsp  Mutorola DSP Developer's Кit.
motdsp\motdspmex  Motorola DSP Developers Кit.
motdspasm\bin  (No tabIe of contents filе).
motdsp\motdspblks  Motorola DSP Developers Кit bIock Iibraries.
motdsp\motdspmasks  Motorola DSP blockset mask helper functions.
motdsp\motdspdemos  M01'DSP 1'oolbox demonstrations and examples:
mutools\commands  Mu-Analysis and Synthesis Toolbox.
mutools\<iubs  MuAnalysis аnд Synthesis 1'oolbox.
nnet\nnet  Neural Network 1'oolbox.
nnet\nnutils  (No table of contents filе).
nnet\nncontrol  Neural Network 1'oolbox Control System Functions.
nnet\nndemos  Neural Network Demonstrations.
nnet\nnobsolcte  (No table of contents Ше).
toolbox\ncd  Nonlinear Control Design Вlockset.
toolbox\optim  Optimization 1'oolbox.
toolbox\pde  Partial Differential Equation Toolbox.
powersys\powersys  Power System Вlockset.
powersys\powerdemo  Power System Вlockset Demos.
rtw\ada  Real 1'ime W orkshop Ada Coder.
targets\ecoder  Real 1'ime Workshop Embedded Coder.
toolbox\reqmgt  Requirements Мапаgешеnt Interface.
toolbox\robust  Robust Control 1'oolbox.
toolbox\<ib2sl  SB2SI, (converts SystemBuild to Simulink).
signal\<iignal  Signal Processing 1'oolbox.
signal\fdatoolgui  Signal Processing 1'oolbox GUI.
signal\<iptoolgui  Signal Processing 1'oolbux GUI.
signal\<iigdemos  Signal Processing 1'oolbox Demonstrations.
rtw\accel  Simulink Accelerator.
simulink\mdldiff  Model Differencing for Sinшlink and Stateflow
simulink\<iimcoyerage  Simulink Model Coverage 1'001.
toolbox\rptgenext  Simulink Report Generator.
toolbox\<iplines  Spline 1'oolbox.
toolbox\<itats  Statistics Toolbox.
toolbox\<iymbolic  SущЬоliс Math Toolbox.
544
545

l!.?lll.lь,:!'.'!..еfJ.I!?е_.'?t!!!и-Р"?.вl!.'ll'.с?1.!.lIзи-ч.:./(и-lif}О!l.е?... f1ак-.:l:!v.1 !!. 
JI!.'!!!.?:J!:..:'..I!'.}l
ident\ident  System Identification Toolbox.
ident\idobsolete  (No tabIe оС contents filе).
ident\idguis  (No tabIe оС contents filе).
ident\iduti1s  (No tabIe оС contents filе).
ident\iddemos  (No tabIe оС contents filе).
ident\idhelp  (No tabIe оС contents filе). .
wavelet\wavelet  Wavelet Toolbox.
wavelet\wavedemo  Wavelet Toolbox Demonstrations.
хрс\хрс  хРС Target.
build\xpcbIocks  (No tabIe оС contents filе).
xpc\xpcdemos  хРС Target  demos and sample script files.
kernel\embedded  хРС Target Embedded Option.
MatlabR12\work  (No tabIe оС contents filе).
For more help оп directory/topic, type "help topic".
»
dbaux  Daubecllies wavelet filter computation.
dbwavf  Daubechies wavelet filters.
tЪspwavf  Complex Frequency B-Spline wavelet.
gauswavf  Gaussian wavelet,
mexihat  Mexican hat wavelet.
meyer  Meyer wavelet.
meyeraux  Meyer wavelet auxiliary function.
morlet  Morlet wavelet.
rbiowavf  Reverse Вiorthogonal spline wavelet fШеrs.
shanwavf  Complex Shannon wavelet.
symaux  Symlet wavelet filter computation.
symwavf  Symlet wavelet filter.
Continuous Wavelet: One-Dimensional.
cwt  Real or Complex Continuous wavelet coef1icients 1-О.
Discrete Wavelets: OneDimensional.
аррсоеС  Extract 1O approximation coefficients,
detcoef  Extract 1-D detail coef1icients.
dwt  Singlelevel discrete 1O wavelet transform.
dwtmode  Discrete wavelet transform extension mode.
idwt  Singlelevel inverse discrete 1-О wavelet transform.
ирсоеС  Direct reconstruction from 1O wavelet coef1icients.
upwlev  Single-Ievel reconstruction оС 1O wavelet decomposition.
wavedec  MultileveI1-D wavelet decomposition.
waverec  Multi-leveI1-D wavelet reconstruction.
wrcoef  Reconstruct single branch from 1-D wavelet coefficients.
Discrete Wavelets: Two-Dimensional.
appcoef2  Extract 2-О approximation coef1icients,
detcoef2  Extract 2-О detail coef1icients.
dwt2  Single-Ievel discrete 2-О wavelet transform.
dwtmode  Discrete wavelet transform extension mode.
idwt2  Single-Ievel inverse discrete 2-D wavelet transform.
upcoef2  Direct reconstruction from 2-D wavelet coef1icients.
upwlev2  Single-Ievel reconstruction оС 2-D wavelet decomposition.
wavedec2  Multi-IeveI2-D wavelet decomposition.
waverec2  Multi-Ievel 2-D wavelet reconstruction,
wrcoef2  Reconstruct single branch from 2-О wavelet coeffkients.
Wavelets Packets Algorithms.
best1evt  Best level tree (wavelet packet).
besttree  Best tree (wavelet packet).
entrupd  Entropy update (wavelet packet).
wentropy  Entropy(wavelet packet).
wp2wtree  Extract wavelet tree from wavelet packet tree.
wpcoef  Wavelet packet coef1icients.
wpcutree  Cut wavelet packet tree.
Команда bp <имяrруппы> выведет на экран список функций, разме
щенных в этои rpуппе с краткими пояснениями. Например, команда help
wavelet выдаст список функций, реализующих методы вэйвлет анализа:
» help wavelet
Wavelet Toolbox.
Version 2.0 (R12) 16-June-2000
What's new.
Readme  New features, bug fixes, and changes in this version.
То display the Readme filе for Version 2.0, type
"whatsnew wavelet" in the MATLAB command window.
Wavelet Toolbox GUI (Graphical User Interface).
wavemenu  Start graphical user interface tools.
Wavelets: General.
biorfilt  Biorthogonal wavelet filter set.
centfrq  Wavelet center frequency.
dyaddown  Dyadic downsampling.
dyadup  Dyadic upsampling.
intwave  Integrate wavelet function psi.
orthfilt  Orthogonal wavelet filter set.
qmf  Quadrature mirror filter.
scal2frq  Scale to frequency.
wavefun  Wavelet and scaling functions.
wavemngr  Wavelet manager.
wfilters  Wavelet filters.
wmaxlev  Maximum wavelet decomposition level.
Wavelet Families.
biorwavf  Вiorthogonal spline wavelet filters.
cgauwavf  Complex Gaussian wavelet.
cmorwavf  Complex Morlet wavelet.
coifwavf  СоiПеt wavelet filter.
546
547

K-()А!.IЬ!:)IIе.l!.IIО1 ()е.!'.'!Р()в.1!.1 '!:':сри..з-.и..'!.:С!IХ:.1Р:):ССОв. в .IJI!.:I'!e.!,!:.1T 1.f!..
1l!.и..:1й...J/CеIIШI
wpdec  Wavelet packet decomposition lD.
wpdec2  Wavelet packet decomposition 2-D.
wpfun  Wavelet packet functions,
wpjoin  Recompose wavelet packet.
wprcoef  Reconstruct wavelet packet coefficients.
wprec  Wavelet packet reconstruction l-D.
wprec2  Wavelet packet reconstruction 2-D.
\vpsplt  Split (dесошроsе) wavelet packet.
Discrete Stationary Wavelet Transform Algorithms.
iswt  Inverse discrete stationary wavelet transform lD.
iswt2  Inverse discrete stationary wavelet transform 2-D.
swt  Discrete stationary wavelet transform l-D.
swt2  Discrete stationary wavelet transform 2-D.
De-noising and Compression for Signals and Images.
ddencmp  Default values for de-noising or compression.
thselect  Threshold selection for de-noising.
wbmpen  Penalized threshold for wavelet l-D or 2-D denoising.
wdcbm  Thresholds for wavelet l-D using Birge-Massart strategy.
wdcbm2  Thresholds for wavelet 2-D using Birge-Massart strategy.
wden  Automatic l-D de-noising using wavelets.
\vdencmp  De-noising or compression using wavelets.
wnoise  Generate noisy wavelet test data.
wnoisest  Estimate noise of l-D wavelet coefficients.
wpbmpen  Penalized threshold for wavelet packet denoising.
wpdencmp  De-noising or compression using wavelet packets.
wpthcoef  Wavelet packet coefficients thresholding.
wthcoef  Wavelet coefficient thresholding l-D.
wthcoef2  Wavelet coefficient thresholding 2-D.
wthresh  Perform soft or hard thresholding.
wthrmngr  Threshold settings manager.
Tree Management Utilities.
allnodes  Tree nodes.
dep02ind  Node depth-position to node index.
drawtree  Draw wavelet packet decomposition tree (GUI).
dtree  Constructor for the class DTREE.
get  Get tree object field contents.
ind2depo  Node index to node depth-position.
isnode  True for existing node.
istnode  Determine indices of terminal nodes.
leaves  Determine terminal nodes.
nodeasc  Node ascendants.
nodedesc  Node descendants.
nodejoin  Recompose node.
nodepar  Node parent.
nodesplt  Split (decompose) node.
noleaves  Determine nonterminal nodes.
ntnode  Number of terminal nodes.
ntree  Constructor for (Ье class NTREE.
plot  Plot tree object.
read  Read values in tree object fields.
readtree  Read wavelet packet dесошроsitiоп tree from а figure.
set  Set tree object field contents.
tnodes  Determine terminal nodes.
treedpth  Tree depth.
treeord  Tree order.
wptree  Constructor for the class \VPTREE.
wpviewcf  Plot wavelet packets colored coefficients.
write  Write values in tree object fields.
wtbo  Constructor for the class WTBO.
wtreemgr  NTREE object manager.
General Utilities.
wcodemat  Extended pseudocolor matrix scaling.
wextend  Extend а Vector or а Matrix.
wkeep  Кеер part of а vector or а matrix.
wrev  Flip vector.
Other.
instdfft  Inverse non-standard l-D fast Fourier transform.
nstdfft  Non-standard lD fast Fourier transform.
wvarchg  Find variance change points.
Wavelets Information.
waveinfo  Information 011 wavelets.
Demonstrations.
wavedemo  Wavelet Toolbox demos.
See also W А VEDEMO,
»
Команда help <ИМЯфУНКЦИИ> выдаст подробную информацию о функ
ции. Например, команда help waveil1fo выдаст информацию о функции, воз
вращающей справочную информацию о вэйвлете KOHKpeTHoro вида:
»help waveinfo
W А VEINFO Information оп wavelets.
W А VEINFO provides information for аll the wavelets
within the toolbox.
W А VEINFO('wl1ame') provides il1formation for the wavelet
СатНу whose short пате is specified Ьу the string
'wl1ame'.
А vailable family short names are:
'haar' : Haar wavelet.
'дЬ' : Daubechies wavelets.
548
549

15?.л:..!5"rl!!fJ..'.'.'!.<:'.I.?.9f!и-J1...?l!.!'.и-<:.1)и-з-!!.:.и-х: P'?,/j.?.I!'!./(e1l}:'.1T!:!JJ!.
.. !!РUЛОЖСIIUЯ
'sym' : Symlets.
'coif : Coiflets.
'bjor' : Вiorthogonal wavelets.
'rbio' : Reverse biorthogonal wavelets.
'meyr' : Meyer wavelet.
'dmey' : Discrete Meyer wavelet,
'gaus' : Gaussian wavelets.
'mехЬ' : Mexican hat wavelet.
'morl' : Morlet wavelet.
'cgau' : Complex Gaussian wavelets.
'cmor' : Complex Morlet wavelets.
'shan' : Complex Shannon wavelets.
'tЪsp' : Complex Frequency B-spline wavelets.
or user-defined short names for their own ,vavelet
families (see W А VEMNGR).
W А VEINFO('wsys') provides information оп wavelet packets.
See also W А VEMNGR.
ва Windows, используется собственный встроенный редактор текста',
В обоих случаях командное окно пакета МА ТСАВ находится в одном окне,
а редактор текста  в друrом окне,
В командном окне МА ТСАВ помимо собственно команд МАТСАВ
можно использовать системные команды ОС MS DOS, Например, команда
dir выводит на экран содержимое текущет'о каталоrа, команда what выводит
только список mфайлов. текущеrо каталоrа, Команда cd позволяет сменить
текущий каталоr, а команды delete имяфайла и type имя файла стирают и
печатают на экране содержимое файла соответственно,
Пl.2.2. Интерактивный доступ к справочной информации
и документации
Существуют следующие способы получить информацию о функциях па
кета МА TLAB в процессе работы:
. команда help;
. команда lookfor;
. меню Help;
. просмотр и вывод на печать страниц документации;
. обращение к WEBcepBepy фирмы ТЬе MathWorks,
Пl.2.2.1. Команда help
Основной и наиболее быстрый способ выяснить синтаксис и особенно
сти применения mфункции  использовать команду help <ИМЯ т-
функции>. Соответствующая информация появляется непосредственно в
командном окне,
Например, команда help zeros выведет в командное окно следующую
информацию на анrлийском языке:
» help zeros
ZEROS Zeros array.
ZEROS(N) is ап N-by-N matrix оС zeros.
ZEROS(M,N) or ZEROS([M,N]) is ап M-by-N matrix оС zeros.
ZEROS(M,N,P,...) or ZEROS([M N Р ...]) is ап M-by-N-by-P-by-...
array оС zeros.
ZEROS(SIZE(A» is the same size as А and аН zero::.
See also ONES.
»
Вы можете также познакомиться с некоторыми возможностями системы
МА пАВ с помощью команд intro и demo. Для более основательноrо зна
комства с системой желательно ознакомиться с книrой «MATLAB User's
Guide» (Руководство пользователя),
Система MATLAB работает на таких платформах, как Sun/Apollo/
V AXstation/HP workstations, V АХ, Micro V АХ, Gould, РС и А Т совместимые,
компьютеры с с процессором 80386 и выше, Apple Macintosh, и на ряде па
раллельных машин, В настоящем руководстве будут описаны основные
свойства системы, которые одинаково применимы при использовании Bep
сий 5,0" 5.1,5.2. и 6.0. МАпАВ является собственным знаком фирмы Math
Works, Inc., Cochituate Р1асе, 24 Prime Park Way, Natick, МА 01760, (508)653
1415, Fax: (508)6532997, Email: info@mathworks.com,
Пl.2. Работа в командном окне
Пl.2.1. Вход в систему МА TLAB
Войти в пакет МА TLAB в большинстве операционных систем (напри
мер, в системе MS DOS) после входа в саму операционную среду можно,
набрав в ответ на системный запрос команду matlab. При работе в ОС
Windows-9x, Windows-2000, Windows ХР необходимо найти COOTBeTCT
вующую иконку и кликнуть на ней. Выход пакета осуществляется с помо-
щью команды quit, В версии пакета 5,0 и выше, работающих в ОС семейст
· Далее речь будет идти только о версии 5.Х и выше и работе в ОС семейства
WiтiО\'s-95,
. Здесь и далее тфайлом AIbl будеАt называть любой текстовой файл, coдep
жащий набор Ко.lIанд пакета MATLAB. имеющий расширение .т. Подробнее об
этих файлах и их роли в системе MATl,AB см. в 11. 7 данною приложения.
550
551

,!i:й-.А.fl1ь'.й-.п1S!.'.'.й-.. Лlй-.д---е:!IР.й-.!!I!!'.':. ФI!ЗU'lеск I1р(ще.'!. 11.'!.'!!.':.!:.!..:,!!!:,:!!!, Ш
...ШШ. .,!!РИ70'.'.и-.!!
Следует обратить внимание, 'ПО текст интерактивной справки использу
ет верхний реrистр для написания имен функций и переменных, 'lтобы вы.
делить их из основной части тскста, Однако при использовании функций их
имена необходимо вводить с помощью символов нижнеr'о реrистра.
Команда help без apryMeHToB выводит на экран список каталоrов, KOTO
рые имеются в системе с кратким описанием их содерЖИМОI'О. Повторный
набор этой команды с именем каталоrа, например help elmat, выведет спи.
сок функций, предназначенных для создания и работы с матрицами специ.
альноrо вида. Ввод команды с именем определенной функции выдаст на эк'
ран описание этой функции, Следует особо обратить внимание, что в каче.
стве ответа на запрос о помощи выводятся все строки комментариев,
которые написаны в начале каждой функции  как созданной разработчи.
ками системы, так и собственными функциями пользователя,
Пl.2.2.3. Меню Не/р
Это меню командноrо окна системы МА TLAB позволяет активизировать
следующие окна:
. HelpWindow
. Help Tips
. Help Desk (НТМЦ
. Examples and Demos
. AboutMatlab
. S u bscri Ье (НТМЦ
Окно справки HelpWindow позволяет получить в отдельном окне то же
самое, что и команда help, Отличие состоит в том, что в этом окне можно
поrpужаться внутрь ращела с помощью двойноrо щелчка мыщи, а не по'
вторно набирая команду help с новыми арryментами,
В пункте меню Help Tips приведена краткая справка по использованию
помощи, т, е, описаны все пункты этоrо меню,
Вызов пункта меню Help Desk позволяет получить доступ к больщому
объему справочной информации и к документации по системе, размещае,
мой на жестких дисках, либо на диске CD.ROM в формате HTML, При ис
пользовании этоrо пункта меню желательно, чтобы в системе был установ,
лен какой,либо Iпtеmеt,браузер (например, Intemet Explorer или Netscape
Navigator), Все операторы и функции пакета MATLAB описаны подробно и
с больщим числом примеров, Реализована поисковая система, позволяющая
выполнить необходимые запросы,
В пункте меню Examples and Demos приведено больщое число приме-
ров использования пакета MAТLAB дЛЯ рещения задач из разных областей.
Пункт меню AboutMatlab выводит на экран стандартную заставку
МА TLAB, а в пункте меню Subscribe HTML предлar-ается подписаться
(при наличии лицензии на продукт) на доступ через сеть Internet к услуrам
фирмы Math W orks.
Просмотр и распечатка документации. Версии справочной докумен'
тации доступны для просмотра и распечатки в формате PDF с помощью
проrpаммы Adobe Acrobat, Он позволяет просматривать текст в формате пе.
чатной страницы, с полным набором шрифтов, rpафики и изображений, с
полным ощущением чтения книrи, Одновременно это и наилучший способ
получения копий нужных страниц,
Пl.2.3. Редактирование и повторный вызов командной строки
Командная строка MATLAВ леrко редактируется. Курсор можно пере
мещать с помощью стрелок <= => и удалять неправильно набранные сим.
волы с помощью клавиш Backspace или Delete, При работе на IВM РС со'
вместимом компьютере доступны также и друrие редактирующие клавиши:
Ноте, End и Delete. При работе на дрyrих системах необходимо использо'
вать команду edit для ознакомления со списком доступных команд, У доб-
ным свойством системы является возможность использовать клавиши
стрелки ft .u. для доступа к буферу с ранее введенными командами, Это дает
возможность осуществить повторный вызов ранее выполненной команды,
отредактировать ее и выполнить вновь, Для небольших процедур это rораз.
до удобнее, чем писать и отлаживать m,файлы, что требует постоянноrо
перехода из командноrо окна МА TLAB в окно TeKcTOBoro редактора (см, п,
8 и 8,2), Например, если вы хотите сравнить rpафики функций sin(l1lx) и
Пl.2.2.2. Команда lookfor
Эта команда позволяет выполнить поиск m,функции по ключевому сло-
ву; при этом анализируется первая строка комментария, и она же выводится
на экран, если в ней встретилось ключевое слово. Например, в системе МА-
TLAB нет m,функции с именем inverse, и поэтому на команду
» help inverse
ответом будет
inverse.m not found (inverse.m не найден),
Однако команда lookfor il1verse покажет все совпадения, найденные в
справо'lНЫХ файлах пакетов прикладных проrpамм, подключеных к пакету
МATLAB,
Добавление к команде lookfor опции -аН в виде lookfor <слово> -аН
расширяет область поиска  <слово> ищется в первом блоке коммента-
риев, т. е, в блоке комментариев между заrоловком функции и первым
оператором.
552
553

. '!..о.t!1ь.,от_ер"l/ое.:I.'од.,!:IIР...(}l!! luер_:..'!.Кt.IIIр'(}lt(?й-6 .61/ (1 К (?"!.'!.!>!..1TL.:!.!!..
...J!Р...I1!?,?,!:'!.!t!Я
sin(nx) на интервале [О, 2,] для различных значений n и т, то можете BOC
пользоваться командной строкой
»m=2;n=3;x=O:oOl:2*pi;y=sin(m*x);z=sin(n*x); plot(x,y,x,z)
с последуюшим ее вызовом и редактированием, Проделайте все описанное
выше самостоятельно,
с одной строкой или одним столбцом интерпретируются как век':"'ора, В сис
теме MATLAB матрицы MOryт быть созданы разными способами,
. Введены явно с помошью списка элементов;
. Сrенерированы встроенными операторами или функциями;
. Созданы в mфайлах (см, прил, 2);
. Заrpужены из внешнеrо файла данных,
Пl02.40 Формат вывода
Поскольку все вычисления в МА TLAB выполняются с двойной точно
стью, формат вывода может управляться с помощью следующих команд:
Пl.30 Создание матриц
Пl.3010 Явное задание матриц
Например, любой из приведенных далее операторов
» A=[l 2 3; 4 5 6; 7 8 9] <Enter>
или
» A=[l 2 3 <Shift>+<Enter>
4 5 6 <Shift>+<Enter>
7 8 9] <Enter>
создает матрицу 3х3 и присваивает ее значение переменной:
А=
123
456
789
Элементы внутри строки матрицы MOryT отделяться друr от дрyrа н:
только пробелами, но и запятыми. При вводе чисел в экспоненциальнои
форме (например, 2.34e9) не следует иснользовать пробелы, Ввод больших
матриц лучше выполнять с помощью mфайлов, в которых леrко находить и
исправлять ошибки (см, прил. 2), В пакет MAТLAB встроен ряд функции,
позволяющих создавать функции специальноrо вида, например, rand,
magic, zeros и ones позволяют леrко сrенерировать матрицы, 
Функция rand(n) возвращает матрицу размером пхп, случаиных чисел с
. равномерным законом распределением в диапазоне [О 1]. 
Функция rand(m,n) создает матрицу размером тхп, состоящую из случаи
ных чисел, которые распределены по равномерному закону в диапазоне [О 1],
Функция magic(n) создает матрицу размером пхп, которая является Ma
rическим квадратом (суммы элементов по строкам и СТОJ;5цам равны),
Функция zeros(m,n) создает нулевую матрицу размера тхп.
Функция ones(m,n) создает матрицу размера тхп, каждый элемент KO
торой равен единице,
Матрицы MOryт быть сrенерированы также с помощью ЦИКJШ for (см. Пl,5),
Ссылки на отдельные элементы матриц и векторов осуществляются с
помощью индексов в круrлых скобках обычным образом, Например, А(1,3)
означает элемент матрицы, стоящий на 1 й строке и 3M столбце !\штрицы А,
fоmшt short С фиксированной точкой и 4 знаками после точки
(по умолчанию)
fопnаt 10ng С фиксированной точкой и 14 знаками после точки
fопnаt short е Научная нотация с 4 десятичными знаками
fопnаt long е Научная нотация с 15 десятичными знаками
fопnаt short g С фиксированной точкой и 3 знаками после точки
fопnаt long g Научная нотация с 13 десятичными знаками
После вызова одноrо из приведенных выше форматов он сохраняется до
вызова друrоrо формата, Команда format compact подавляет большинство
пустых строк, позволяя большее количество информации вывести на экран
или страницу. Она не зависит от друrих команд формата,
Пl02050 Копия протокола сессии
Леrче Bcero протокол сессии получить с помощью команды diary. Вызов
команды diary <имяфайла> приведет к тому, что все появившееся далее
на- экране (кроме rpафики) будет записано в файл <имяфайла>. Если имя
файла в команде будет опущено, то протокол сессии будет записан в файл с
именем diary, Команда diary off приведет к выключению режима записи
команд в протокол сессии, а команда diary оп к восстановлению режима за
писи. После завершения записи сессии вы можете отредактировать этот
файл как обычный текстовой файл и при необходимости распечатать ero
или использовать для последующеrо написания mфайла,
МА TLAB работает практически с одним видом объектов  с числовыми
прямоуrольными матрицами, элементами которых MorYT быть в общем слу
чае комплексные числа, Все переменные представляют собой матрицы, В
некоторых случаях матрицы 1 х 1 интерпретируются как скаляры, а матрицы
554
555

K--о'tllI?ер'I?_"?:'!.tlР"?,!'!./Iр"l{з.tI .e(:,'!.пpO'leC,:? в. lJ а еl'!.е_.м.::iТ:r1..!!....
шJfJ.l(70Jl<:еllUЯ
а х(3) означает 3й элемент вектора х, В качестве индексов векторов
и матриц MorYT использоваться ТОШ.ко положительные числа. Ссылать
ся на элементы матрицы А можно, используя единственный ИНДекс, A(k).
В этом случае эта матрица рассматривается как один длинный BeKTOp
столбец, сформированный из столбцов исходной матрицы. Например, обра
титься ко второму элементу второй строки матрицы А можно, указав А(2,2)
или А(5).
Пl.3.2. I10дматрицы и использование двоеточия (:)
Для записи алrоритмов сложной обработки данных в компактной форме
в системе МА TLAB используются векторы и подматрицы. Использование
нотации с двоеточием (которая используется и для rенерации векторов и
подматриц) и векторов вместо индексов является ключом к эффективной
манипуляции этими объектами, Эффективное использование этих возмож
ностей позволяет минимизировать число явных циклов, использование KO
торых существенно замедляет работу MATLAB, и делает написанную про
rpaMMY простой и леrко читаемой, (Правда, овладение данной технолоrии
требует от пользователя пакета определенных усилий,) Например, выраже
ние 1:5 фактически является векторстрокой [1 2345], Отметим, элементы
вектора Moryr быть Не только целыми, но и действительными. Например,
команда
» х=0.2:0.2:1.2
создает вектор х = [0,2,0.4, 0,6, 0,8, 1,0, 1.2], а команда
» 5:-1:1
создает в результате вектор [54321].
Для создания и вывода на экран таблицы синусов необходимо выпол
нить следующую последовательность команд:
» х ::: [0.0:0.1:2.0]'; % транспонирование вектора
»У = sin(x); % вычисление вектора, содержащеrо значения sin
»[х У] % вывод таблицы значений
Отметим, что, так как sin является скалярной функцией (т. е. функцией,
действующей поэлементно), результатом ее применения к вектору х будет
вектор у,
Для доступа к подматрицам может быть использовано двоеточие. Ha
пример, A(1:2,3) является векторстолбцом, состоящим из двух первых эле
ментов TpeTbero столбца матрицы А:
» А(2:3,З)
ans :::
6
9
Двоеточие само по себе означает всю строку или весь (.'ТОлбец, например:
» А(:,3)
ans :::
3
6
9
» А(3,:);
ans =
789
В качестве индекса подматрицы может использоваться произвольный
целый вектор:
» А(1,[2 3])
ans=
2 3
Описанные способы индексирования МОТУТ использоваться с обеих CTO
рон знака присваивания, Например, после выполнения команды
» А(:,[2 4 5]) = В(:,1:3)
2,4 и 5й столбцы матрицы А будут за!\lенены на первые три
матрицы В.
столбца
Пl.3.3. Функции построения матриц
Имеются следующие стандартные функции для построения матриц:
еуе(т,п)  создание единичной матрицы размером тхп;
zeros(m,n)  создание нулевой матрицы размером тхп 
ones(m,n)  создание матрицы размером тхп, каждыи элемент которои
равен единице;
diag(x)  создание матрицы, у которой на rлавной диаrонапи стоят эле
менты вектора х;
diag(A)  создание матрицы, у которой на rлавноЙ диаrонали (,тоят диа
rOHaJIbHbIe эле:.rенты матрицы А;
triu(A)  создание верхней треУI ольной маТРИЦI, элемеНIЫ коrорой,
расположенные на I'лавной диат'онали и выше rпавнои диаrонали равны co
ответствующим элементам матрицы А; 
tril(A)  создание нижней треуrольной матрицы, элементы которои, pac
положенные на rлавной диаrонаJIИ и ниже пraвной диаrошiЛИ, равны COOT
ветствующим элементам матрицы А;
556
557

!!.?п...Iй-п:.:'р"I?.А.!5'.д.::!'!.!!!!...а.'.'.!:.Фll!..':'..'!.':'.!;>;.пЕЙ-lf::':'Й-I!...'!.а'5:""ЛI!.lv!.А.:.Т_L...1!......_ ...
.....,_!Р..!q?:т.т.':'..я-.
Пl.4. Операции, выражения и переменные
Пl.4.1. Правила записи операторов
Пакет МА l1...AВ является интерпретирующим языком непосредственных
вычислений, Это означает, что выражения, которые вы вводите, иmерпрети
руются и вычисляются, Операторы пакета МА TLAВ обычно имеют форму:
»имяпеременной = выражение
или просто
» выражение
Выражение, как правило, формируется из операторов, функций и имен
переменных. После выполнения выражения rенерируется матрица, которая
выводится на экран и присваивается соответствующей переменной для по
следующеrо использования. Если имя переменной в левой части и знак =-
отсутствуют, автоматически rенерируется переменная ans (answer  ответ),
которой присваивается результат вычислений.
Обычно оператор завершается клавишей <Enter>, Однако при необхо
димости оператор может быть продолжен на следующей строке. Для этоrо
ero необходимо завершить тремя или более точками, после которых следует
<Enter>, С друrой стороны, в одной строке может быть несколько операто
ров, разделенных запятой или точкой с запятой.
Если последним символом в строке является точка с запятой, то вывод
значений результата не производится, но присвоение значения выражения
переменной выполняется, Это помоrает подавить вывод ненужных проме
жуточных результатов, Важно помнить, что МА TLAB различает строчные и
прописные буквы в именах команд, функций и переменных.
Для получения списка всех переменных, расположенных в рабочем про
странстве, используется команда who. Переменная может быть удалена из
рабочеrо пространства командой clear <имяпеременной>, Команда clear
без aprYMeHToB очищает все непостоянные перемеНIIые, расположенные в
рабочем пространстве, Примером постоянной переменной является пере
менная eps (epsilon), значение которой по умолчанию paBHol06. Данная пе
ременная используется для оценки точности вычислений итеративных про
цессов.
Вывод на дисплей или вычисления MorYT быть прерваны на большинстве
компьютеров, не поющая МА TLAB, с помощью комбинации клавиш
<Ctrl>+<C> «Ctrl>+<Break> на РС).
Пl.4.2. Матричные операции
В пакете МА TLAB доступны следующие матричные ОlIераllИИ:
<+>  сложеНJ!С:
<>  вычитание;
<*>  умножение;
<Л>  возведение в степень;
<'>  транспонирование;
<\>  левое деление
<1>  правое деление
Данные матричные операции применимы, конечно, и к скалярам  MaT
рицам 1хl, Если размерность матриц не соответствует используемой опера
ции, то система rенерирует сообщение об ошибке за исключением случаев,
коrда одним из операндов является скаляр, потому что в этом случае опера
ция выполняется между скаляром и каждым элементом матрицы BToporo
операнда,
Отметим, что операция возведения в степень применима только для
квадратных матриц.
Если А является невырожденной квадратной матрицей, а Ь  BeKTOp
столбец или BeKTopCTpOKa, соответственно, тоrда вектор х = A'JJ является
решением уравнения А х = Ь, а вектор х = Ь/А является решением уравнения
х,л = Ь, Если А  квадратная матрица, то при левом делении для факториза
ции используется метод исключения raycca. Если матрица не квадратная, то
для ее факторизации используется метод ортоrонализации Хаусхольдера с
ведущим столбцом, а приведенная матрица используется для решения He
дили переопределенной системы уравнений в смысле наименьших KBaдpa
тов. Правое деление определяется в терминах левоrо деления по формуле
Ь/А = (А '\b'
Пl.4.3. Операции с массивами
Матричные операции сложения и вычитания действуют поэлементно, а oc
тальные приведенные выше операции  нет, они являются maTPW--IНЫМИ опера
циями. Следует отметить, что приведенные выше операции * ,', \ / MOryr стать
поэлементными, если перед ними поставить точку, Например, команда »
[1,2,3,4].*[1,2,3,4] или »[1,2,3,4].ЛZ дадут один и тот же результат
ans=
[1,4,9,16]
Пl.4.4. Сохранение данных из рабочей области
При выходе из системы МА l1...AB значения всех перемеННIХ, находя
щихся в рабочей области, теряются, Для сохранения их значении на диске в
нетекстовом формате в файле с именем matlab.mat перед выходом из паке
та необходимо выполнить команду save, Для восстановления ранее coxpa
558
559

t'O'111:_)_}_.pJIOt .Hcп:k_I/l{,.:?eallfi(___lt__L jlItlCc 1<";1\ J.lP'Jlf(-С.()В ь' пlK.т,' .1-111 ]L'1.j)
Jr;;;НПЫ" знаЧ":1НIj.i IН:rсмснных исн:ц,/iУ,Т;;Я ':OMi.lHitil lтHi, БОi:с'rанав;шна!<J 
щая ВСС: m:pC\iCf1HbIC ра60чеr о IIр\>странс J на.
п 1.5. Операторы t'or, wltile, Н', case
и операторы отношения
ОпераТОрL: управления М:\ 1[. АН f'or \\,tlile, if, case и онеР;:;ТОjJЧ OTHO
шения (and, or, X01'. поО при ИСПО;П:30Вi.lнтJ f; своеЙ ОСНCilliЮЙ фОРI\Н" pa60
,'Ю{)Т TitK же, кш, и 1< бо.1ЬШИJ!сп\е языков прor--раымирования.
ПI,S.l. ЦИКl for
НаПРИIсr, Д:IЯ riaHHoro п. ош;ратОР
»х::;: [ ]; t'or j :::: 1:5,х=[х,iЛ2], end
х=
1
х=
1 4
х=
1 4 ')
х :
1 4 <; ]6
х=
1 4 9 16 25
»
с:)здает определенный BCKfOp ра1мерностн П, оператор
»х = []; for i:::: 5:1:1,х=[х,iЛ21, end
х=
"
b.
х=
25 !()
х=
2S 16 9
х=
25 16 9 .!
..
х=
b ]() 9 4
со<дает 1Jt';K HJp С 1 С!V1И же !.I\?1tH I.t\fИ H\ ра3ЧС'II[СННhIП] R c)ora1HO\1 JI('rяд
K..:. З.1fеrН\l, Чl() ,larpl!ua 1(1Жf'1 fыIьь ilуТТОЙ (Н(ЧlрlIlеr. в Сl,'Ч:}t: {\I('paTopa
х ::: 11 ) ПОС:1С:Н1В;П"ПЫf(1СТЬ опсr(1Тl'РО:\
» ш=3:
560
llрUЛОЖС!/i/Я
п=3
fOl" i = l:ш
forj=l:n
Н(i, j) = l/(i+j 1);
el1d
end
Н
Н=
1.0000
0.5000
0.3333
0.5000
0.3333
0.2500
0.3333
0.2500
0.2000
создаст и вьшодит на экран матрицу I'ильберта размерности шхп, Точка с
запятой, которая завершает ВНУТРОШИЙ оператор, предотвращает вывод на
экран ненужных ПрОМСiКуточных результатов,
Пl.5.2. ЦИКЛ while
в общем виде цикл while записывается следующим образом:
while <условие>
<операторы>
end
<операторы> будут повторяться до тех пор, пока <условие> будет OCTa
ваться истинным. Например, для заданнOI'О числа а припеденная далее по
следовате:IЬНОСТЬ операторов вычислит и выведет на дисплей наименьшее
неотрицательное число п, такое что пЛ2 < а:
»п = 0;а=100;
»while пЛ2 < а
n = n + 1;
end
n
п=
10
Пl.5.3. Условный оператор if
в общем Виде простой оператор if записывается следующим образом:
if <условие>
<операторыl>
else
<операl0ры2>
епд
19 ,i57б
561

1\():.fIllAUтt!pJfO(: .\.fйdС7l{j.f!вullие I!JU ЗUЧ(!( kOlH Jlff(!l O6" (J IltlkСП/L' ,НА 11.,18
fJРUЛОЖ'О/lIЯ
<операторы] > ВЫlIOЛНЯЮН;Я, если <уt'J1uвие> IIС пшно, <операторы2>  се,
JIИ <условие> ложно, В lraKCTe МЛ TI"AB IЮ3МОЖНО тш:жс множееlвеННОt::
Rствление, например,
if n < О
parity :::: о;
elseif rem(n,2) :::::::: О о/, сели условие п <: О не ВЫП\JJшяется
parity = 2; 0/,-, если число I1 четное
else
parity :::: 1; 0/,' ссли число I1 нечетное
end
При использовании двухвариантноrо условноrо оператора часть, снязан
ная с elseif, не используется,
J-ШЯ (или, друrими словами, лоrические переменные, которые они создак)])
мО1 ут объединяться с помощью следующих :юrичсеких операторов:
&и
I  ИЛИ
.  НЕ
Пl.5.4. Оператор переключения case
При необходимости построить конструкцию ветвления с более чем
двумя лоrическими условиями, удобнее использовать не вложенные опсра
торы if, а оператор переключения switch ... case, Этот оператор имеет сле.
дующую структуру:
switch <выражение> % <выражение> , обязательно скаляр или строка
case <значениеl>
<операторыl> % <операторы!> выполняются, если
% <выражение>  <значение1>
case <значение2>
<операторы2> % <операторы2> выполняются, если
% <выражение>  <значение2>
Операторы отношения, примененные к ска:lярам, также возвращают
ска.ляр, значение KOToporo равняется 1 или О в завиеИ'-10СТИ от Toro, является
jШ результат истиной ини ложью,
Операторы отношения, примененные к матрицам одноrо размера, ВО:З
вращают матрицу Toro же раЗ1сра, у которuй в качестве элементов стоят О
или 1, в зависимости от соотношения между соответствующими элементами
исходных матриц.
Операторы while и if интерпреп!руют отношение меw,ду Ма1рицами как
истинное в том случае, если результирующая матрица не имеет нулевых
элементов,
Например, если необходимо выполнить оператор <операторы>, коrда
матрицы А и В совпадают, следует использовать оператор соотношения
if А == В <операторы> end
Ь:.'Jи необходимо вЫполнить оператор в том случае, коrда матрицы А и
В не равны, можно использовать следующий оператор
if А == В else <операторы> end
Пl.6. Функции MATI.,AB
otherwise
<операторы> % <операторы> выполняются, если <выражение>
% не совпало ни с одним из значений
в системе МА TLAB еушествует большое количество функций, создан
ных разработчиками системы, МНОI'ие из которых предоставлены в виде rn
файлов, содержащих исходные тексты, Можно подойти к классификации
данных функций различными способами, например, по областям их исполь
зования (триrонометрические, спецфункции, Функuии линейной алrебры и
т, д,), Далее мы используем подход, основанный на виде aprYMeHTa функ
ции: скаляр, вектор, матрица,
Пl.5.5. Условия (операторы отношения)
В MATLAB I!СПОЛЬЗУЮТСЯ следующие операторы отношения:
<  меньше чем
>  больше чем
<=  меньше или равно
>=  больше или равно
=:::  равно
.=  не равно
Отметим, что знак = используется в операторах rrрисваивания, R ТО Hpe
IЯ как в операторах ОТН(ЧJIСНИЯ IIСПО:Jиуется знак ='=, Оl1С:Р:ЛОРЫ ОJIЮШ\.?'
Пl.6.1. Скалярные функции
Скалярные функции МА TLAB деЙствуют только на скаляры, Если apr'y
менто:»! данных функций является матрица, то они действуют поэлементно,
К таким функциям, например, относятся
sin asin ехр abs round
cos acos log (натура.lЬНЫЙ лоrар!:фм) sqrt floor
tan atan rem (ост ат ок от де.lеЮIЯ двух чисел) sign ceil
562
563

j<':O.iiilIifUf/1':j)1l0l- .\1\)()t!.71!_:,_)f\ll[//L 1/1!l.-'11.:C'( ки), lIe_;цc, '( II{{ f-) fiUf(!'/Jlt!".l, i 1'1/11:,
lljJlI.7UJIССIIШ{
1]1.6,2. Веюориые функпии
Л р1 ументами векторных ФУНПШЙ ЮJ;JЯЮТ еЯ век r \ \р!'! (СЧ!\)К1I 1I.1И С 10:[6
цы). Если в качестве apr у!еш а ФункtIии указавз шtТрl!Ш1 pajMepa шп
(Ш >= 2), то данная Фушщия ,1еЙст нуст !ТОС! ()лбцово, 1. t реЗУЛh1 атом .1l'и
СIВIIЯ является ReKTOpC10JIf)eL!, каждыЙ :тс\!\Снт КОТОрОТ'О яв:rяется резу.'1[,
Та10"! действия 'Ной функции на соответствуюший столбец. 110ст рочное
действие т'акой функпи!! (еспи необходимо) \ЮЖСI был. ,'IOLТИ!'НУТО
ИС!ТI)Льзованием операпии трRнспонирования,
Некоторые из этих ФУНI\IШЙ приведены далее:
шах suш шеdiаll апу
шiп prod шеаll аll
sort std
Например, максимальный -элемент прямоуrолыIйй матрицы находится с
по!Ошью команды шах(mах(А)), а не с помошью mах(А), так как ре'3УЛk
тат, возвращенный функцией mах(А)  вектор, каждая компонста КОТОр01'0
есть максимальный элемент соответствующеr'о столбца.
торстолбеIl, содержащий собст венные значения МаТРИЦЫ А, в то время КаК
оператор [Н,О] = eig(A) rенерирует матрrщу О, чьи С10лбцы являются соб,
ственны1И векторами А, а диаrональная матрица 1) содержИl на ['лавноli
,1иаrонали собственные -значения rоЙ матрицы,
Приложение 2. МФАЙЛЫ
Пl.6.3, Матричные функции
Наибольшую мощь системе МА TLAB дают матrИЧНЫt функции, наибо
лее употребительные из которых приведены ниже:
eig  собственные значения и собственные вектора;
chol  факторизация Холсцкоrо;
svd  сишулярная дскомпозиция;
inv  обратная матрица;
lu  LUфакторизация;
qr . QRфакторизация;
hess  вычисление формы Хессенберrа;
schur  декомпозиция Шура;
rref  приведенпе к треуrольной форме методом [аусса;
ехрш  матричная экспонента;
sqrtш  матричныЙ корень квадратный;
poly  характеристический полином;
det  определитель;
size  размерность;
norm  норма вектора или матрицы:
cond , число обусловленности:
("ank , раЮ' матрицы;
ФУНК!II!И MATI"AH МOI'ут но-зврашать lчновременно н,с,<о:ты:о lJE'pe
\lCI!I!h!X, НаI!рИfСр, Функrщя у = eig(i\), 11.1\1 l!p<)CTO eig(A) !,нсрирует BeK
МА TLAB может ВЫПОЛНЯIЬ последовательность онсраторов, записанных
в фаЙл на диске, Такие Фай,ты называюrся mфайлами, потому что имена
-этих фаЙлов имеют вид <ИМЯ>.m, Большая часть раБОlЫ в МА TLAB cocтo
ит В создании, редактировании и выполнении таких mФайлов, СущеСТВУСl
два типа П1файлов: файлы-проrраммы (или сценарии) и файлы-функции.
02.1.1. Файлыпроrраммы
ФаЙлыпроr-раммы состоят из последовательности обычных операторов
пакета МА TLAB. Если шфаЙл с таким сценарием имеет имя, например, in
verse.m, то команда inverse, введенная в командной строке, вызовет ВЫПОJI
нение последовательности операторов, находящеЙся в данном файле, Пере
менные в проrpамме являются r-лобальными и изменят значения таких же
переменных (если таковые есть) в рабочей области текущей сессии. Про
IpaMMbI или сценарии часто используются для ввода данных в большие MaT
рицы; в таких фаЙлах леrко исправить ошибки ввода. Если, например, файл
на диске с именем data.m содержит строки
А=[
1234
5678
];
то выполнение команды data приведет к тому, появлению в рабочей облас
ти матрицы А, Внутри mфайлов можно ссылаться на друrие mфайлы, в
том числе и рекурсивно на caMoro себя,
02.1.2. Файлы-функции
Файлыфункции фактически дают возможность расширять MATLAB,
поскольку определенные пользователем новые функции, специфические для
решения конкретных задач, имеют тот же статус, что и друrие ФУНКЦИИ
MATLAB, Переменные в функциях являются по умолчанию локальными,
но начиная с версии 4.0 и выше, разрешено объявлять r-лобальные перемен
ные (global).
РаССМОIРИМ пример фаЙла фУНКШН!, находящейся в файле rапdiпt.ш
fllnction z = ('al1dil1t(m,I1,a,bI
364
565

f!.?flь.'.?п:..:р'I!!!.:!'!!!..?е.!!.'!!!...О!..l!!.'!!!!..!Р_!:::_СК-':!.:'Р.?.lf_:()l!.'!..fl.l!к-.е..'!!.:!!.1J.1:!!. ..... .. . ... .Ш
Il!..l'!!.?:н::.:.и-.я-.
% randint(m,n,a,b)  функция, возвращающая случайную матрицу
% с целыми элементами из диапазона [а,Ь]
% randint(m,n)  функция, возвращающая случайную матрицу с целыми
% элементами из диапазона [0,9]
if nargin < 3, а = о; Ь = 9; end
z = Ooor«b-a+l)*rand(m,n» + а;
Отметим, что совпадение имени функции и имени файла является в па
кете МА ТLAB обязательным условием.
Первая строка функции содержит объявление выходных apryMeHToB,
имени функции и входные арryменты (списка формальных параметров). Без
такой строки весь следующий файл является проrpаммой (или сценарием),
но не функцией. Так, например, оператор z = randint(4,5) приведет к пере
даче чисел 4 и 5 переменным m и п, а выходной результат будет передан
переменной z. Поскольку переменные в файлефункции локальные, их име
на никак не влияют на имена и значения переменных в текущей рабочей об
ласти MATLAВ.
Символ % указывает на то, что вся строка символов после Hero является
комментарием и иrнорируется при исполнении. Тем не менее несколько
первых строккомментариев, которые являются кратким описанием данной
функции, доступны при вводе оператора, т. е. являются той помощью, KOTO
рая вызывается с помощью команды help randint. Как показал опыт работы
с пакетом MAТLAВ версии 6.06.2, при использовании в комментариях
строчной буквы я возникает ошибка периода исполнения. Выход из данной
ситуации состоит в использовании прописной (зarлавной) буквы Я, что по
зволяет избежать указанной ошибки.
Отметим, что здесь мы использовали функцию nargin, возвращающую
длину списка формальных параметров функции. ИСПО}Iьзование функции
nargin в данном примере позволяет установить значение отсутствующих
входных apryMeHToB по умолчанию переменных а и Ь. В общем случае Ha
личие такой функции позволяет использовать функции с переменным чис
лом входных apryMeHToB и в зависимости от их числа направлять вычисле
ния по разным лоrическим веткам функции.
Функция может иметь множественные выходные арryменты, например:
function [теап, stdev] = STAT(x)
* ST А Т  функция, возвращающая для вектора х, среднее значение
% и стандартное отклонение функция ST А Т возвращает для матрицы х
% две строки, первая из которых содержит средние значения,
* вторая  стандартные отклонения, соответствующих столбцов матрицы х
[т п] = size(x);
ifm == 1
m = п; % если входные данные вектор
end
теап = sum(x)/m;
stdev = sqrt(sum(х.Л2)/m - mеап.Л2);
Данный файл следует записать на диск под именем stat.m. Если ввести
команду
» [xm,xd]=stat(x)
то, переменным хт, xd будут присвоены среднее значение и стандартное
отклонение элементов вектора х, Несмотря на наличие нескольких BЫXOД
ных apryMeHToB, можно присвоить значение функции одной переменной.
Например, хт = stat(x) (никаких скобок BOKpyr хт не требуется) присвоит
хт среднее значение х,
Отметим, оператор х. Л2, который является возведением в степень каж
доrо элемента вектора х, оператор с функцией sum, которая является BeK
торной функцией (см. прил. 1), функцию sqrt, которая является скалярной
функцией (см. прил. 1.), и деление в выражении sum(x)/m, которое является
матричноскалярной операцией.
Друrим примером является функция, позволяющая вычислить наиболь
ший общий делитель двух чисел.
function [Ь, steps] = bisect(fun, х, tol)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% функция, возвращающая решение уравнения fun(x}=O методом
% половинноrо деления
% входные переменные:
% fun  строка, содержащая имя вещественной функции, зависящей от
% вещественной переменной
% х  начальное приближение, используемое для поиска корня
% tol  переменная, определяющая точность нахождения корня
% выходные переменные:
% Ь  значение корня
% step  матрица, содержащая значения корня и соответствующие значения
% функции на концах отрезка на каждом шаrе вычислиельноrо процесса
if nargin < 3, tol = eps; end % проверка длины списка формальных
% параметров, если значение переменной
% tol не указано, то точность корня
% определяется встроенной переменой eps
trace = (nargout == 2); % проверка длины списка выходных параметров,
% если список состоит из двух переменных, то trace = 1
% выбор шarа изменения переменной х
if х = О
566
567

,
15!!.п-!?'!!..:Е!!!!!.-::.'?:!...':!.'!F..?l!!.':!!.. rp!':!.l!...ск-'!!.п-I!?1iеС:"?l!зп-.l!..к-:'!!.:.!..'!..1.!..!J!.
.J!.l!..l1!!!!.!':..е.'lия
dx = х/20;
else
dx = 1/20;
end;
а = х - dx; % левый конец отрезка
fa = feval(fun,a); % значение функции в левом конце отрезка
Ь = х + dx; % правый конец отрезка
fЪ = feval(fun,b); % значение функции в правом конце отрезка
% поиск отрезка, на котором функция меняет знак
while (fa > О) == (fЪ > О)
dx = 2.0*dx;
а = х - dx;
fa = feval(fun,a);
if (fa > О) = (fЪ > О)
break
end;
Ь = х + dx;
fЪ = feval(fun,b);
end;
if trace
steps = [а fa; Ь fЪ];
end;
% основной цикл
while abs(b - а) > 2.0*tol*max(abs(b),1.0)
с = а + О.5*(Ь - а);
fc = feval(fun,c);
if trace
steps = [steps; [с fc]];
end;
if(fЪ > О) == (fc > О)
Ь = с; fЪ = fc;
else
а = с; fa = fc;
end;
end;
Здесь для вычисления значения функции, имя которой передается в
функцию bisect через строковою переменную fun, используется функция
feval, арryментами которой являются имя функции и координата точки, в
которой вычисляется значение данной функции,
Отметим, что некоторые функции МА TLAB являются встроенными, в то
время как друrие поставляются в виде тфайлов. Текст реально имеющихся
т-файлов (пакета МА TLAB или ваших собственных) можно просмотреть с
помощью команды type <имя  функции>.
П2.1.3. Текстовые строки, сообщения об ошибках
Текстовые строки вводятся в MATLAB в виде текста в одинарных Ka
вычках. Например, оператор s = 'This is а test' присваивает данный текст
переменной s.
Вывод текстовой строки осуществляется с помощью оператора disp. На-
пример, оператор disp(s) выведет на экран сообщение:
This is а test
Сообщения об ошибках лучше выводить с помощью функции error, так
как после обращения к данной функции выполнение тфайла будет пре
кращено. Например, если в процессе выполнения тфайла будет выполнен
оператор error('Sorry, the matrix must Ье symmetric'), то после вывода co
общения на экран выполнение т-файла будет прекращено.
В тфайле может быть запрос на интерактивный ввод данных, орrанизо
ванный с помощью оператора input. Коrда вводится оператор iter = input
('Введите число итераций: '), на экран выводится запрос на ввод, и выпол
нение проrpаммы приостанавливается до Toro момента, пока пользователь
не введет с клавиатуры требуемые входные данные. После нажатия клави-
ши Enter данные присваиваются переменной iter, и выполнение проrpаммы
будет продолжено.
П2.2. Работа с т-файлами
Во время работы в МА TLAB часто возникает необходимость создавать
или редактировать т-файлы, после чеrо возвращаться в командное окно
пакета MATLAB дЛЯ отладки и/или вычислений, Начиная с версии 5.0
(в ОС Windows95) в пакете имеется специальный редактор/отладчик, в KO
тором можно исправлять текст тфайлов и выполнять пошarовую отладку
проrpаммы. Для работы с редактором/ отладчиком необходимые т-файлы
должны быть доступны. Для этоrо либо текущая директория должна быть
директорией с вашими файлами, либо необходимо I1РОЛОЖИТЬ туда путь
(в смысле MS DOS). Это можно сделать либо с помощью команд MS DOS
непосредственно из командноrо окна (команда cd), либо с помощью пункта
меню FilelSet Path, который позволяет установить путь к соответствующим
папкам.
П2.2.1. Список путей доступа
Для поиска тфайлов система МА TLAB использует механизм путей
доступа, поскольку т-файлы записываются в каталоrи или папки файловой
568
569

КОAlI:ь!отерl!о=",!од,:!Р?,!!lUе ф/lЗUЧ:СКIIХ '!Р?!!:с:..и-вв!jl5.:'!!(?fl1.1т..А в
_._.!fJIи.!??!:..:.'.'.':!f!.
системы, Например, при поиске файла с именем test пакет МА TLAB BЫ
полняет следующие действия:
1) просматривает, не является ли test именем переменной;
2) просматривает, не является ли test встроенной функцией;
3) ищет в текущем каталоrе mфайл с именем test.m;
4) ищет mфайл с именем test.m во всех каталоrах списка путей ДОС1Упа,
Реально применяемые правила поиска являются более сложными изза
оrpаничений, которые связаны с использованием подфункций', личных
(private) функций и объектноориентированных механизмов, Однако Приве
денный выше упрощенный порядок поиска точно отражает механизм поис
ка mфайлов, с которыми обычно работает пользователь.
П2.2.1.1. Работа со списком путей доступа
В процессе сеанса работы можно вывести на терминал или внести
изменения в список путей доступа, используя следующие функции:
. path  выводит на экран список путей доступа;
. path (s)  заменяет существующий список списком s;
. addpath /home/lib и path(path,'/home/lib')  добавляют новый каталоr
текущеrо подкаталоrа в список путей доступа;
. rmpath /homellib  удаляет путь /home/lib из списка.
Список путей доступа, используемый по умолчанию, определен в файле
pathdef.m, который размещен в каталоrе local; этот файл выполняется при
каждом запуске пакета MATLAB.
Кроме работы из командной строки существует средство просмотра пу
тей доступа Path Browser (см. далее), которое поддерживает удобный rpa
фический интерфейс для просмотра и изменения списка путей.
П2.2.1.2. Текущий каталоz
Пакет MATLAВ использует понятие текущеrо каталоrа при работе
с m и mаtфайлами во время сеанса работы,
Начальный текущий каталоr определен в файле запуска, который ac
социирован с ярлыком запуска пакета МА TLAВ, расположенном на рабо
чем столе.
Для вывода текущеrо каталоrа на экран терминала предназначена KO
манда cd. Для изменения текущеrо каталоrа следует использовать команду
cd <новый путь доступа>.
П2.2.1.3. Средство просмотра и редактирования
путей доступа Path Browser
Как было указано выше, при работе в системе Windows95 имеется спе
циальное средство для просмотра и изменения путей доступа Path Browser
(рис, П2,l), Показанное далее окно открывается либо из меню File/Set Path
командноrо окна, либо с помощью кнопки на инструментальной панели.
Curreпt DlrectQf а 13'
amscipts
IIAT:;;; .
[iAcc.m
[iAcc2.m
[i Action. m
[i AF. m
[iAng1e.m
Mflle
Mfile
Mfile
Mfile
Mfi1e
Mfile
fot i
26ИIOН2002 10:57
101<юл2002 06:03
09июл2002 08:49
27мей2002 08:.20
20мей2002 07:08
Рис, П2,], Окно Path Browse
После дополнения списка nyreй доступа необходимо сохранить новый путь
с помощью пункта меню File/Save Path, в противном случае установленный
путь будет известен системе только на время одноrо сеанса работы.
П2.2.2. Использование редактора/отладчика
Редактор/отладчик предоставляет как средства редактирования текста m
файла, так и средства пошаrовой ero отладки. Один из способов вызова pe
дактора  вызов из командной строки МА TLAВ с помощью команды edit.
Например, команда edit test откроет встроенный редактор для редактирова
ния файла test.m, если в меню File в диалоrовом окне Preferences не YCTa
новлен вами друrой редактор.
Можно открыть редактор и друrим способом  с помощью меню
File/New или кнопки New File на панели инструментов (см. далее). ДЛЯ OT
крытия существующеrо mфайла выберите пункт File/Open или щеЛКНИТе
на кнопке Ореп File.
После вызова редактор/отладчик будет иметь вид, показанный на
рис, П2.2,
. Внутри функций допускается определение друzих Функций, при этОА</ следует
lt.llemb в виду, что доступ к таки.Н Функция., волюжен только из функций, внутри
которых они определены,
570
571

.15.'!.ь.,?!.пер"l!о:"!<1:..zp,й-::'!.if!.?'!...:/(,'.':.:пр'Оlf.,,Й-.в п-а./(,:.п::.t:!...1!1J!
.ш.!!!!l!:''!.:'I'.'!,
29

в командное окно) с помощью пункта меню Debug=>Save and Run. При
этом предварительное сохранение текста исправлений не требуется.
Одна из важных особенностей данноrо редактора состоит в том, '1то по
сле проведения ВЫ'lислений можно в редакторе просмотреть зна'lения пс
ременных, которые они имеют в текущий момент в рабочей области
(рис, П2,3.). Для этоrо достаточно установить курсор мыши на этой пере
менной, и появится прямоуrольник с желтым фоном, на котором выводится
текущее значение переменной,
'#orkspace аа
Ema ilxl i8 double ап:ау
\llijanз ,
10xO :0 chaz: az: z: ау
Emn I :8 double
Ilxl az: z: ау
\llijз 11:<4 18 chaz: az: z: ау
Рис, П2.2. Общий вид редактора/отладчика
Редактор, используемый в системе, имеет синтаксическую раскраску,
т. е, слово или символ по мере ввода приобретают тот цвет, который COOT
ветствует их типу.
Редактор различает такие типы вводимых слов:
. комментарии;
. ключевые слова;
. незаконченные строки;
. законченные строки;
. друrой текст.
е помощью пункта меню ToolsIFonts можно настроить такие важные
параметры, как используемый шрифт. Это особенно важно для работы с
русским текстом, поскольку не все шрифты правильно воспроизводят pyc
ский текст. В остальном данный редактор не отличается от обычноrо MHO
rooKoHHoro TeKcToBoro редактора  в нем работают все редактирующие кла
виши (Del, Bspace, Ноте и т. д.). При редактировании файлов вы можете
непосредственно перейти к требуемой строке при помощи пункта меню
EditlGoTo Line и указать номер требуемой строки в появившемся окне. По
сле редактирования файла и повторноrо ero запуска из командноrо окна же
лательно предварительно сохранить новый вариант файла. Но можно запус
кать редактируемый файл на счет, не выходя из редактора (т, е, не переходя
Рис, П2.3. Окно прослtoтра и редактора используелtЫХ переменных
Если переменная представляет собой большую матрицу, то увидеть цe
ликом ее не удастся. Для про смотра (и возможноrо исправления при отлад
ке) всех значений матрицы необходимо перейти в окно Workspace и BЫ
полнить двойной клин по имени строки, содержащей имя выбранной пере
менной.
П2.2.3. Отладка mфайлов
Отладка проrpаммноrо кода  это процесс, в ходе KOToporo MorYT быть
выявлены ошибки двух видов:
1) синтаксические, связанные с неточностью записи имен mфункций
и/или арифметических выражений. Пакет МА TLAB обнаруживает боль
шинство синтаксических ошибок, сопровождая их сообщением об ОIllибке с
указанием номера строки соответствующеrо mфайла;
572
573

:?'"'!:р"I.:?:'А1_?_е:!.Р!!!!'!.:::..Р.и.?IJ. e.к-и..x .IР?':I:..:.?.lj'!.К-:.'!!е./:!..1!..:!.l! ..
..._....._efJ_'!:.::l!f!
2) ошибки периода выполнения, связанные, в первую очередь, с ошиб
ка ми алrоритма и приводящие к непредвиденным результатам.
Как показывает опыт работы, достаточно леrко можно исправить син
таксические ошибки, которые сопровождаются сообщениями о причинах их
возникновения. Ошибки времени выполнения выявить более сложно пото
му что локальная рабочая область mфункции оказывается потерянноЙ, если
ошибка приводит к возврату в рабочую область системы пакета МА TLAB,
ДЛЯ выявления причины данной ошибки, можно использовать один из сле
дующих приемов:
1) реализовать вывод результатов промежуточных вычислений на дис
плей, удалив в соответствующих операторах точки с запятой, которые по
давляют вывод на экран промежуточных результатов;
2) добавить в mфайл команды keyboard, которые останавливают BЫ
полнение mфайла и разрещают проверить и изменить переменные рабочей
области вызываемой mфункции. (В этом командном режиме появляется
специальное приrлашение К)). ДЛЯ просмотра значений доступных пере
менных можно использовать окно Workspace, или ввести имя COOTBeTCT
вующей переменной в командной строке и нажать клавишу <Enter>. Воз
врат к выполнению функции реализуется командой return.);
3) закомментировать заrоловок функции и выполнить mфайл как cцeHa
рий. (Это позволяет проследить результаты промежуточных вычислений
в рабочей области системы.) ;
4) использовать отладчик системы МА TLAB.
Отладчик полезен для исправления ошибок во время выполнения про
rpaMMbl, так как он дает возможность отслеживать рабочие области функ
ции и проверять или изменять значения соответствующих переменных. OT
ладчик позволяет устанавливать и удалять контрольные точки, т. е. специ
альным образом помеченные строки mфайла, в которых выполнение
останавливается. Это дает возможность изменять содержимое рабочей об
ласти, просматривать стек вызова mфункций и выполнять mфайл по
строчно. Отладчик может функционировать как в режиме командной cтpo
ки, так и в режиме rpафическоrо интерфейса пользователя. Далее мы pac
смотрим отладку только в режиме rpафическоrо интерфейса пользователя,
так как он наиболее прост и наrляден.
Рассмотрим возможности отладки, которые нам предоставляет
EditorlDebuger.
Для ero запуска используется команда edit <имя файла> или пункт Me
ню File/Open. Можно открыть окно редактора/от'Jiадчика и с помощью
пункта меню File/Nеw/М-filе. При таком варианте имя отлаживаемоrо фай
ла открывается уже из меню caMoro редактора/отладчика. Общий вид окна
редактора показан на рис, П2,2, а кнопки нанели инструментов, которые
удобнее Bcero использовать при отладке, показаны на рис. П2.4,
N ew M-fi1e Save Са! Рао! Undo Show function Сlем aJ1 breakpoints Run
6 .....  !} .фj....)'" ".T,",) fj  in_21.iist',*,IHH,
'1----.-----t-------I-- -----I----c.1 .! T).-
Ореn file Рrin! Сору Redo Find SetlClear Bteakpoints Exit Debugg Mode
Рис, П2.4, КНОnКН основной nанели редактора/отладчика
.:J
Способ использования этих кнопок понятен из их названия. Часть кно--
пок представляет собой обычные редактирующие кнопки, используемые
при сохранении, копировании, печати и поиске файлов в проrpаммных про
дуктах, работающих под управлением ОС Windows. Друrая часть связана
непосредственно с отладкой. Это кнопки установки и очистки точек OCTa
новки, кнопки пошаrовоrо перемещения по проrpамме (Step) с заходом в
подпроrpаммы (Step in) и без захода в подпроrpаммы (Step out), кнопка Ha
чала вычислений (Run) и кнопка остановки отладки (Exit Debugg Mode).
Приложение 3.
СОЗДАНИЕ ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛЯ
В настоящее время одним из непреложных атрибутов любой прикладной
проrpаммы является интерактивный интерфейс пользователя, который раз
рабатывается для неоднократно решаемых задач с несколькими входными
параметрами. Наличие интерфейса, вопервых, освобождает пользователя
от необходимости вникать в детали проrpаммирования данноrо проrpамм
Horo продукта, во--вторых, позволяет менять исходные данные, не прекра-
щая выполнения текущей проrpаммы, и в реальном времени наблюдать за
изменения решения задачи.
В настоящее время выработаны достаточно общие требования, которым
должны соответствовать проrpаммные интерфейсы, определены основные
элементы управления rpафическим интерфейсом. Например, если речь идет
о решении учебной и/или научной задачи, обязательными элементами ин-
терфейса должны быть:
1. Одно или несколько окон для визуализации результатов расчетов;
2, Редактируемые окна, позволяющие задавать значения входных пара-
метров задачи;
3. Управляющие кнопки, предназначенные для запуска и остановки про
цесса расчета, вывода результатов, завершения работы с проrpаммой;
4. Поясняющие надписи (статический текст).
574
575

.1!.-':!.пIй."!.:I!..й..:.:!...й..::2'!.1!...й..1!..I!,:.Р'':.зи-.:':.у!..й.Zf:()!!i..к-.<?е. rJJ::!
Необходимо отметить, что разработка rpафическоrо интерфейса являет
ся достаточно трудоемкой задачей, которая может быть решена с использо
ванием функций rpафическоrо ввода, а также специальной функцией uicon-
trol, разработанной для интерактивноrо взаимодействия пользователя с ри.
сунком. Однако для упрощения процедуры создания интерфейса поль.
зователя в пакете МА TLAВ, как и во всех современных проrpаммных
средствах, основанных на объектноориентированной парадиrме проrpам
мирования, существует возможность визуальнOI'О проектирования интер.
фейса, называемая технолоrией визуальноrо проrраммирования.
В данном приложении мы познакомимся с основными этапами техно.
лоrии визуальноrо проrpаммирования пакета МА TLAB на примере созда
ния интерфейса задачи моделирования 011ЮСИтельных движений материальной
точки, участвующей в двух круrовых движениях (rл, 1), Напомним, что
в данной задаче приходится задавать значения переменных Rl  радиус первой
окружности; Тl  период обращения по первой окружности; R2  радиус BТO
рой окружности; т2  период обращения по второй окружности; Tfin  правая
rpаница BpeMeHHoro интервала, на котором вычисляются кинематические
характеристики; N  число точек, в которых проводится вычисление значе
ний кинематических характеристик материальных точек.
Перед созданием rpафическоrо интерфейса желательно разработать ero
проект, т. е. изобразить на листе бумаrи примерный вид вашеrо интерфейса,
Для рассматриваемой задачи интерфейс должен содержать пять окон для
ввода значений переменных Rl, Тl, R2, Т2, Tfin, N, и, соответственно, пять
поясняющих надписей к каждому полю ввода значения переменной, три.
кнопки, позволяющие завершить работу с проrpаммой, построить траекто.
рию движения материальной точки и MrHoBeHHbIe значения разности отно-
сительной скорости материальной точки, движущейся по окружности
меньшеrо радиуса.
Для создания rpафическоrо интерфейса (GUI  Graphics User Interface) с
помощью средств визуальноrо проrpаммирования необходимо запустить
соответствующую проrpамму командой guide или через меню: File -..+New
-..+GUI. По истечению HeKoToporo времени, определяемоrо быстродействи.
ем компьютера, на экране появится окно, представленное на рис. П3.1.
576
. ... JIl!..UJи.!.(:"и.Jl.
1
f,
!.
,1..;
i
(
i
J
Рис, ПЗ,]
ДЛЯ ввода названия формы открыть окно Property Inspector, нажав на
кнопку i или сделав двайной клик в любом месте поля формы, затем ус.
тановить новое значение поля Name (рис. П3.2).
: InterruplibIe
i InvertHardcoPY
t---- KeyPressFcn
1.... MenuBar .
i!:J попе
tIJШ!1!]
i!:J add
i!:Jo1f
Bportrail
[0,25 2,5 8 6]
i!:J таnиаl
[8,511}
В usletter
В inches
Barrow
[16х16 doubIe array}
Рис, ПЗ,]
Naтe
f". NextPlot
r'" NumberTille
- PaperOrienlation
:$.. PaperPosition
f-..-- PaperPosilionMode
fi PaperSlZe
.. PaperType
r' PaperUnits
i Polnler
 PointerShapeCData
....
577

}('о.\fJ/}IП1(,Рl.()е .\f/}()l 'ЛlР()f)а}{(.! .(/!и 3UЧСО,/{Х .'l})(JlfCl'C\J6 в паk'тt' А/А 71. ,1 [{
I/plll/J JiCC!ilU/
н левой части окна расположена панс;п, унраВJIСНИЯ, содержащая 'ЭЛС
менты интерфейса. Дпя размещения на пане.ТИ 10РМЫ окна, в котором БУДУI
выводится I'рафики, ИСIIОЛЬ1уется кнопка . Ut::1KHYB ПО данному 'Элс
менту на пане.1И управления 11 пере ведя IЫШЬ на IIанеш, формы, необходи
l\Ю поместить указате-т-rь мыши, ЮlеющиЙ фОрIУ крсс r а, в ту точку, riJe бу-
дет находиться :rевый верхниЙ yroJl окна, Нажав и удерживая левую кнопку
мыши, необходимо вы1нутьь получающийся ПрЯМОУI'ОЛЬНИК до нужных
размеров, При необходююсти размещения неСКО,lЬКИХ окон на панели фор
J\IЫ повторяется описанная выше поспеДОВ31ельность дейсТвиЙ:........
i '
i ТХТ I
Надписи на пане.1И фОрJ\IЫ создаются с помощью кнопки i,,<. , которая
персносится повторенисм описанной выше ПОС.lедовательности деЙствиЙ.
После эrоrо на панели формы появится надпись Static Text, Для изменения
надписи необходимо выбрать надпись, ще:1КНУВ по неЙ левой кнопкоЙ MЫ
ши, открытъ окно Property Inspector, и ввести новый текст надписи в поле
String, Для изменения цвета фона, на котором выводится надпись, следует
установить новые значения поля BackgroundColor<
задап. СДИНИ!{Ы 1Л\1ерения раlмера ВССХ 'Элементов в безразмерных пер,>
МСННЫХ  долях рюмсра окна. Данный рюмер Нa-Jывается поrшаlizеd. ДЛЯ
ЭТШ'О IJсоБХОДII\10 ВЫ.1С,1!ПЬ С помошью У,lерживаемой К.lаВ!!Irш Ctr! 11 :1(-
вой кнопки !\-IЫШИ Бсе объекты, раз!\-r<.СЩСlшые на форме. Затем ОII,РЬПЬ ОКНО
Property Il1spector ;! УСТ;ШОRИТЬ l3 попс L'l1its значение поrшаlizеd. Л.на,lО'
П1ЧНО сле,:,усr за,lать раЗ!\-lер шрифтов н 1Н:iЧС:НШI rЮ:IЯ l'ont L'l1its.
Поел,? р,рабоп:и внешнет'о вида Т1)афИ'IССКШ'О интерфеЙса нсо6х(',:;юю
сохр:шить '.нот файл на диске, вызвав стандартное оню \Vil1dows для coxpa
hel-l!lЯ файла: Fiie  Save< После сохраНСН:1Я на диеке rюявлются ;\ва
файла: АМЕ.ш и NAME.fig (r'де NAME  Быбрат-юе ваШI имя фай;ш)
Первый файл  это текст ПРОТ'f'аммы, РСi1.1ИЗУЮЩИЙ разработанный шпср'
феЙс, второй  набоr данных, необходимых для работы интерфейса. Лля за.
пуска проrраммы на выполнение доста10ЧНО R командной строке МАТlд<\В
ввести имя вашсrо файла
Проскт I1JафиqеСКОI<О интерфейса решения задаqи, раССМО1реН!IОЙ в
ПI, 1, предстаВ.lен на рис, П3,3,
Для создания редактируемых окон ввода используется кнопка KO
торая переносится повторением описанной выше последовательности дей
ствий, Для изменения значения окна установить в окне Property Inspector
новое значение в поле String.
Для создания и размещения кнопок на панели формы используется
;oliJ 
кнопка .:::,,', которая переносится повторением описаннои выше последова
тельности действий. Для изменения надписи на кнопке установить в окне
Property Inspector новое значение в поле String.
Построенные таким образом КНОПКИ, окна вывода и редактирования, OK
на статическOI'О текста, кнопки, а также друrие объекты, размещенные на
панели формы, можно выровнять и установить определенные промежуrки
между НИМИ с помощью панели Аligпшепt Tools, Для включения данной
панели используется кнопка I, ДЛЯ задания ряда объектов, с которыми
будут выполняться каКllелибо действия, необходимо их выделить, щелкая
по каждому из них при нажатой клавише Shift. Выделенные объекты OTMe
чаются черными точка1И BOKpyr соответствующих объектов< При необхс.
ДИМОСПl изменить размер какоrо.lибо объекта, размещеннот'о на панели
формы, необходимо шелкнуть по данному объекту левой кнопкой мыши и
!lЗмеl-l!lТЬ раЗlер, так же, как Iеняется размер ,lюбоrо окна Windows.
Так как по УМО:IчаШIЮ размер окна устанаВ.lивается в пикселях, 'НО MO
же1 принести к тому. что при изменении размеров окна !1 кнопки I-юrут Ha
t:xaтb дрУ!' на lpYJ'a. J.lЯ УС1'f'анения ЭТOIО неже.lа1е:lьноrо яв:rеШIЯ следует

,
; \
;E31 1 Т2>о
.==.L........J Tl':'\!lx'"'
1'J : .
I
[01'
i'07'"
11
[1'ОС.О'
1 0r"''"'""""'
iO:8 i
I
o,sf
::1 I
, ooL....J
пд о) ОА Оа O 10
Тра8:ТОРИil I ОТНCJСИ'eJ1bН8111 СI<.ОРОИЬ! '
8Ыx
Рис. П3.З
Ниже приведен соответствующий проrраммный код, сохраненный на
диске под именем Мооп.ш,
function varargout = шооп(уаrаrgiп)
Ck MOON Applicatiol1 Mfile t'or шооп,fig
с;у ПG = MOON lau!1cl1 П1О0!1 GUI.
578
579

.k'U.1tf1/;fOIll9J!ir)l' ;f(;{Jc {/.{!),){,(!II[{( фllflfЧI;:('к.'/f\ "jJ?Цt'l ( U..t' Н llt.. I Ill(' ,\11'1 Т f, H
! [ри рп{( I:'lillЯ
L/ МООN('саlНшсk паIПе', .,.) invokc 111C паtl]l'(] c,ll1i,:!ck.
c/r !.а5! !\1ndificc1 !)У (Jt:JI)E \2 () !6.Мау oт 2330:06
ifnaI'gin == О ck j,At:NCH (;СI
fig = openfig( rnfilепаше.' '"euse' );
clc Gспстtс :1 slI'uсtше (\{ 11andle ((\ pass (о culll'ack. апd torc i!.
haI1dles = guihalldles(fig);
guidаtа(fig,lшпdlеs);
if ш!rgоut > О
yal"at'gout{ 1} = fig;
еllй
eL<;eifi<;chal"(yarargin{l}) ck 1NYOKE A\1FI) SUBFUNC ПОN OR CAl,LBACK
try
[yarat'gout{1 :nargout}J := fеПll(vаrаrgiп{; }); o/r FI:::V А!. s\\.itchyard
catch
disp(lasterr);
eld
(!r. i t!1i ,ta!C!urc а! Gl'! stш.tuр, ап(1 уои -::аl! Cil(\J12'l' :11-: >.trш:turс
9с 1 dur'ing cal!bucks. Сз11 guidзtа(11, 11апdJc) a!kl' .:!1апgiI1?! УОШ'
Я! сору (О 1'cp1ztC:\ й1С чшсd ()]'igiI1u! so tl1at LJhsсquепt ca]I!Jacks sef'
clr Ithc updates, Туре "!1eip gl!iI1:1пdlcs" апс] "I1c1р guid,\ta' ("1' j]]Шt'
9сI iпfОПllutiоп,
9r1
Ckl V ARARGIN сопtаiпs апу схН'а :1Т gШ11Сl1ts уОLl lHl\c passed I() ([1('
%1 ca11baek. Speci[y the ext1'a ar'lJ1nепr, "у ellitil1g the callhack
c/r 1 pI'Operty iп thc insrcctO!'. Ву ое1'аlllt, (.Il.IDE sets thc rЮрС1'tу [о:
9,1 <MFIL-ЕNАМЕ>('<SUВFl'СТЮNNА]\IЕ>'" gcbo, [j, guidata(pct'1()))
(7сl Add апу cxt1'a a1'gumcnts af'tc1' tl1e IdSl d!gurneI1t, IK'fore thc fiПJl
9с I c]osing ра1'епt!lсsis,
end
%1 ABOUTCALlBACKS:
(;Ы GlJIЛЕ automatiea11y аrрепds SUЫU!1еtiоп рюtоtуреs (О this Лlе, апd
(Jcl sets objects' са]]Ьаск рюре1'tiеs (О са]! t.hcm through й1С FEV Al,
С:{ I switc!lyard ahoye, This соттеп! ..:IescrilJes that mechanism.
'ус I
ckl Each ca11back subfuпеtiОI1 dес1аrаtiоп has :he [o]]owing fОПll:
%1 <SlJВFUNСТIONNАМЕ>Ш, ЕVЕNТПАТА. HANDI"ES, V ARARGlN)
7cl
o/r.l Tlle subf'uпсtiоп пате is coтnposcd llsing the object's Tag and the
9<1 ca]]back (уре separated Ьу '', e,g, 's1ider2Caj]back',
(k! 'figше 1C1oseRequestFcn\ 'ахis1ВuttопdоwпFсп'.
%1
C.iC1 Н is thc callback ohject's handle (obtained usiпg GCBO).
'7r1
}I EVENTDA Т А is ешрtу, btH reseI ved ['о1' future use.
'Ус I
'7<1 HANDlES is з stI'uсtше СОПlаiпiI!g !шпdles 01' сошр,тепts in GlJI usiп
,;;-! tags as riеlдпа!Пеs, e.g. hапd1еs.figшс 1, !1aI1d1es,slicJet-2. Tl1is
C 1 stПJCtur'с is с!сзtеd а! GlT] stш.tuр using CJUIHANDLES апd sto1'ed i!]
 1 !he t'igш-е's app]ication <iata lIsing GUlf)ЛТА. А сору 01' ttle s(!'uсtше
'7r! is po.SSC(j to cacl1 co.lll'o.ck Yr]U сап S!П1'е adcJi!iona! infOlll1atiol1 iп
9с  ---- ---------------------oo----  ________H    -- ---"""---- .,,--,,-"
function varargout = edit1 Callback(ll, eyentd.ata, Jlandles, varargin)
lJ{, Stub for Ca]]baek of the uicontl'Ol hапd1еS.еdit 1.
disp('editl callback not implemented уе! .')
% __________ __,,______ "__H __________ __ ____ ,____OO______
function varargout = edit2 Callback(h, eventdata, handles, vararginl
% Stub [о!' Cal1back of (l1е uiсопtrо! hand1es.edit2"
disp('edit2 caIlback not implemented yet .')
ck оо______ ___ __ _________ ._______ ___._  OO__   _ _  _ н_и__
function varargout = edit3CaIlback(h, eventdata, handles, varargill)
% Stub [О1' Callback of the uicontro111and1es,edit3.
disp('edit3 callback not implemented уе! .')
0/0 ________H __ _  ____.__.___. ___________HH
functioIl vaI"argout = edit4 Callback(h, eventdata, handles, varargin)
% Stub [01' Callhack 01" the uiеопtюllыпcJ1еs,еdit4.
disp('edit4 callback not implemented yet .')
   .        .
function varargout = edit5Callback(ll, cyentdata, handles, varargin)
% Stub for Callback of the uicontrol handles.edit5,
cisp('edit5 caIlback not implemented yet .')
о/с -- H ______ ___.___   _  ____ .. .-.--- -OO H ----- ---.-
function yarargout = edit6Callback(h, eventdata, handles, varargin)
'1; Stuh 1'01' Ca11hack of thc uicontl'o; 11апdlеs,сditб,
disp('edit6 calIback not implemented yet .')
  .  .>..      . .   -, 
fuпсtiоп varaI-gоut = pushbuttonlCallback(h, eventdata, handles, varargin)
lJ{ Sшl1 j"щ Ca]]hack ot' !Ile uicontl'O] IlаIldks.рusl1huttоп 1.
580
581

lif1!..!?.тep! IOe!I'??e.l!.p.?..a.!:e.1),:,.':!. :.L.'I<;:Iх..п-Р''?l}:.С':.f!.. !,акет е м А ТLAB
disp('pushbuttonl callback not implemented yet .')
%                                            
function varargout = pushbutton2Callback(h, eventdata, handles, varargin)
% Stub for Callback of the uicontro! hand1es.pushbutton2,
disp('pushbutton2 callback not implemented yet .')
%                                    
function varargout = pushbutton3Callback(h, eventdata, handles, varargin)
% Stub for Callback of the uicontro! hand!es.pushbutton2.
disp('pushbutton3 callback not implemented yet ,')
Созданный GUI, текст, KOToporo приведен выше, не обладает никакой
функциональностью  он обладает только стандартными функциями Win
dows  менять размеры окна и закрывать окно и выводить сообщения о He
которых событиях (команды disp). Событие с точки зрения интерфейса
происходит при нажатии на левую кнопку мыши. Сообщения, выводимые
командой disp в командное окно пакета MAТLAB, призваны помочь разра
ботчику интерфейса установить взаимно однозначное соответствие между
элементом управления, размещенном на панели формы, и именем COOTBeт
ствующей ему функции.
Основным средством взаимодействия rpафическоrо интерфейса с функ
циями, выполняющими требуемые действия, является задание значений по
лей, определяющих свойства кнопок и редактируемых окон, называемое
Callback. Значение (тип строка), присваемое данному полю, есть имя функ
ции, вызываемой при активации соответствующеrо объекта. Обратите вни
мание на тот факт, что в проrpаммном коде, сrенерированном редактором
GUI, название каждой функции состоит из двух слов: названия Toro элемен
та, который вы разместили на панели формы, и названия средства взаимо
действия Callback.
Дальнейшая доработка интерфейса состоит в редактировании COOTBeтCT
вующих функций в тексте исходноrо файла, осуществляемых в текстовом
редакторе пакета МА ТLAB. Так как перед выполнением каждоrо вычисле
ния проrpамма должна получить значения переменных Rl, Тl, R2, Т2, Тбп,
N, предста!!ляется целесообразным создать специальную функцию, считы
вающую значения соответствующих полей (строковые переменные) и пре
образующую их в числовые значения, текст которой приводится ниже:
function readdata(handles)
global Rl Тl R2 Т2 Тбп N % задание rлобальных переменных
Rl = str2doubIe(get(handles.edit1,'String'»; % преобразование значения
% поля edit 1 в число
Тl= str2doubIe(get(handles.edit2,'String'»; % преобразование значения
% поля edit2 в число
582
... I!p"lli:0:J"..:'!:!!
,
I
i
R2 = str2doubIe(get(handles.edit3,'String'»; % преобразование значения
% поля edit3 в число
Т2 = str2doubIe(get(handles.edit4,'String'»; % преобразование значения
% поля edit4 в число
Тбп = str2doubIe(get(handles.editS,'String'»; % поля преобразование
% значения editS в число
N = str2doubIe(get{handles.edit6,'String'»; % преобразование значения
% поля edit6 в число
Кнопка Выход становится функционирующей после добавления в функ
цию pushbuttonl Callback команды close:
function varargout = pushbuttonCCallback(h, eventdata, handles, varargin)
% Stub for Callback of the uicontro! hand!es.pushbuttonl,
close;
При решении рассматриваемой задачи мы проводили два вида расчетов:
1) вычисление и визуализации траектории, 2) вычисление MrHoBeHHbIx зна
чений скорости движения Луны относительно Солнца. Выполнение первоrо
вида расчетов при проектировании интерфейса мы связали с кнопкой Tpa
ектория (функция pushbuttonCCallback). Следовательно, необходимо дo
полнить функцию pushbuttonlCallback соответствующей последователь
ностью команд, описанных в 1.2:
function varargout = pushbutton2Callback(h, eventdata, handles, varargin)
% Stub for CaIlback of the uicontro! handles.pushbutton2.
global Rl Тl R2 Т2 Тбп N % список rлобальных переменных задается
% в теле каждой функции
readdata(handles); % получение значений переменных Rl, Тl, R2, Т2,
% Tfin, N
% блок вычислений и построения траектории
t=O:Tfin/N:Tfin;
Xz=Rl *cos(2*pi*tffl);
Yz=Rl *sin(2*pi*tffl);
Xm=R2*cos(2*pi*tff2);
У m=R2*sin(2*pi*tff2);
Xotn=Xz+Xm;
Yotn=Yz+Ym;
plot(Xz, У z,Xotn, У otn);
Выполнение BToporo вида расчетов при проектировании интерфейса мы
связали с кнопкой Относительная скорость (функция pushbutton2Callback),
Следовательно, необходимо дополнить функцию pushbutton2 Callback COOT
ветствуюшей последовательностью команд, описанных в },2:
583

! /pи..'lfJ)fCCltll51
А.й.\I.'IЫ()llk'jJiIk' Jf{)(...?I._а/Il..ф.l!l.JчеL''.l) II()l{L;с()в 611(1/\'(;/11(' ЛJА TIAB
fuпсtiоп vю'аrgоut = pushbuttoI13 Callback(h, C\'cl1tdata, 11al1dles, varargi,,)
7с S\llh jш Callback 01' thc uicontro! IшпJlеs,рusl1l)uttопЗ,
glоЬаl Rl 1'1 R2 1'2 Tfin N (lc СПИСОК !'лобальных переменных задается
% !J теле каждой функции
l'eaddata(handles); Clc пuлучение значений псремеННЬLХ R1, Т1. R2, Т2. Tfin, N
с;; Gлок вычислсний И постросния MrHoBeHHbIX значений
с;;, 01носительной скорости
dt=Тfiп/N;
t=O:dt:Tfin;
Xz=R 1 'cos(2*pi*tlТl);
Yz=IH *sin(2*pi*tlТl);
Хш=R2*соs(2*рi *t/Т2);
у ш=R2*siп(2*рi*tlТ2);
Vx=diff(Xz)/dt;
Vу=tjiЩУz)/dt;
vх=diff(Хш)/dt;
vу=diff(Уш)/dt;
V=( Ух. Л2+ Vy. Л2). ЛО.5-(Vх. *vx+ Vy.*vy)J(Vx. Л2+ Vy. Л2). ло.5;
H=O:dt:Tfill-dt;
plot(tl,V);
Состояние интерфейса, после нажатия на кнопки Траектория и OTHO
сительная скорость, показано соответственно на рис. П3.4 и П3.5"
D.J... '1 \-.f..'" .: ....,.! ,< ш; ,. ':?};:;:;Д&':"+:':';:;
Fie Eq, ...-." Inseft Too!f .",, "*
яt.. i i .
Т1.. i ']
А'2.0 ro1
Т2а 1""6;
1"".. r,'
_. rТriT
"r--'--'' .
I
12
, I
, .
,i ,,' j !
; I " '! I! !! I
i I ! I i I i i '11
, I ! t, I [" I :]
! i. ; i I !
,1 t. I \ i!! I iil
, ,: I i t I '! '1
! ,! \:' 'r: 11 :1
I! i \ I . r I i t ')
',1 ; .11\, l' 'J'
l' \, I1 i ',1 I! '
.J!..,.{ 1
O 06 08 1
I
1'"
tl
! I
т-тi
Рис. П3.5. Состояние интерфейса после нажатия на кнопку
Относительная скорость
ПРИJIожение 4. ОЦЕНКА поrРЕШНОСТЕЙ
ЧИСЛЕнноrо ИНТЕrРИРОВАНИЯ
"/;T,.,,
Для нахождения зависимостей I10rpешности вычисления опредепснноrо
интеrpала на отрезке [а,Ь] от числа отрезков разбиения интервала Ilнтеrри
рования разложим I10дынтеrральную функцию в ряд Тейлора:
j(x) = j(x;) + j'(x; )(x Х;) +! j'"(x; ХХ  х;)2 +.". (Н4,1)
2
Тor-да интсrpал от данной функции на отрезке [x;,X;tl] будет равен
\+1
f j(xfJx -= j(x;)& +  j'(XJ(&)2 + J"(x; )(Li.t)3 +... . (П4.2)
Х;
Оценим по!-решность метода левых прямоуrольников, По!-решность пн
те!рирования /'1,; на отрезке [Х;,.\,; t J] равняется раности между точным
значение интеrрала и СТ'О оцснкой j(.\'; )Ах :
Л,  ['f>(X)d-']  Лх, ),,"'  ; Н,, )Iл,)' . (1143)
1]з (П4,3) видно, что ОСВОВНО!! Ч!lСН !ют'решности на каждом отре:н,:с
П1\Iс'ет порядок (/'1,,\)2 И,1!I, В СИМВОЛIIЧССКОЙ З31ШСИ, ол,):') ПОСКО:lhКУ
Рис. П34. Состояние llНl/1ерфейса 110С.7е нажатия на KHOI1KY Траектория
,  Oтнocиre! СМ1ЮCTh 1 в f
584
585

л.-о.НI1I.!rJтеjJJ/i){ \{Ui)L 1UjJU(j.l"!"/( :j'l' JlIЧС( J..:U\" "}-1,)l(:"L (/ф,..: 'j.1f,"cтe AiA 11,AlJ
1 J!J/i ]lu/{еlllfЯ
lIOJШОС ЧИСJЮ отрезков равно N, а Л\ = (1, 'I.I)! N , ТО полная ПOfрсшносrь
MCTO;lJ J1CBhIX ПРЯМОУПJЛЬНИК<JВ rю порядку вешJt\ИНЫ равна
Л'L\ :::: N(;\,\)2.,:; O(Nl). АнаЛlХИЧ!lО )сюжно [/Оказать, что IЮJреШНОС1Ь MC
тода ПРJВЫХ IIРЯМОУJ'OЛЬНИКОВ также rrрОJJОрШlOнальна Nl.
ПOJ'решноС1Ь фор:-.!улы трапеций О!l<еНивае['ся аналOl'ИЧНЫ\1 обраЗО:-'1. Так
как значенис ИJпс[ pa:la на отрсзю: [Х" Х, '11 вычисляется по формуле
lJC\i) i [С\, , 1 )].'\,1)2 , то ПОlрешностъ равна
1'.,;" 1 l].
А, с II JI х l<ix j  2 [Jlx.) 'ЛХ, , , )]i\x. (114.41
3а"IСНИВ в (114.4) первый член выражением (П4.7.), значение функции в
точке Xi" 1 разложением в ряд Тэйлора:
объемов параллелспипедов с площадью основания ""XL\Y 11 НЬ:(\ I mi. равноЙ
значснию функции Лх,у) в одном из уrлов, Для опредеЖ;НIIЯ П''!11Сшности
раз.l0ЖИМ функцию f(x, у) в ряд Тейлора:
f(x, у) = f(xi' У,)+ f;(x"Yi )(х xi)+ f;.(.'i' У; )(У  \',) i . (П4,5)
f' {,  частные Производны по соответствующим перемеНI!ЫМ.
\' J У
'(. ) [() "() 1 ,"( Х ) z
j Лi + 1 == Х,' + j х, Ах +  f Xi ,'\" + . .. ,
2 '. .
раскрыв скобки и приведя подобные, обнаруживаем, что член, пропорцио
Ш1ЛЬНЫЙ первой производной функции, сокращается, и I10I'решностъ на oд
1 "( )( 3 ,; , , \ (. . \ )
ном orрезкс равна '4 fx &) ;:>:; О{дх)' F О !I' ,Следовательно, полная
ПOl-решность Фuрмулы трапеций на отрезке [а,Ъ] по порядку величины paB
на oy2) ,
Так как формула Симпсона основывается на приближении функции
f(x) параболой, можно ожидать, что в данном случае поrpешность по по
рядку величины будет определяться членами, пропорциональными третьей
производной функции, Однако последовательное повторение действий, BЫ
полненных при оценке поrpешности метода трапеций, показывает, <{то эти
члены сокращаются в силу их симметричности, поэтому в разложении в ряд
Тейлора следует удержать член, пропорциональный f""(X)(I1.\:)4, Следова
тельно, поrрешность формулы Симпсона на отрезке [х" х/ + 1 ] пропорцио-
нальна /""(.\;)(&)5; а полная поrрешность на отрезке [a,lJ] по порядку ве-
личины составляет O(N ---4 ) ,
ПО;IСЗНО получить оценку поrрешносIИ вычисления интеIрала от функ-
ШШ, зависящей от двух пере:-'Iенных, котпрый с rеометрической точки зре-
НИЯ предстаюяет собой пбъе:-.! фпrуры ПОД поверхностью, заданной функ-
ШIеii f ( \', .\ ) , в прямоут-ольном ПРl!6'Пlжении данный IIнтеlрал равен сумме
Поrpсшность вычисления интеrpала д; равна
д, = Н f(x. y)dxdy  /(xi' у;)дхду , ([14,6)
Подставив (П4.5) в (П4,6), выполнив интеI-рирование и приведя '!о:J,об
ные, получаем, что член, пропорциональный f(Xi' у;), сокрашасн:я, а {-IНTe
трал от (х  Х; )ах дает (дх)2 /2. Интеrpал от данноrо выражения по (!У дает
еще один множитель ду, Аналоrичный вклад дает интеrpал от члена, про
порциональноrо (у  Yi) , Так как порядок поrpешности ДУ также составля
ет О (А\' ) , то поrрешность интеrpирования по прямоут-ольнику Xi:5: х::; Хн 1 ;
У; :5: у:5: Yi+I равна
д; ""  [1; (Х; , У;) + /;(Xi,)Jlдx)3, (114,7)
Из (П4,7) видно, ПOIрешность интеrpирования по одному параллелепи
педу составляет OAx)'). Так имеется N параллелепипедов, полная по
rpешность по порядку величины равна N(дx)', Однако в двумерном случае
N  7' поэтому полная поrpешность д,  (.ili)  o(rv1/2), Напомним,
(А,)-
что в одномерном случае полная поrpешность метода ПРЯМОУI'ОЛЬНИКОВ
д;  O(NI).
Соответствующие оценки для двумсрных обобщений формулы трапеций
и Симпсона показывают, что они соответственно равны O(Nl) и oGv2).
Вообще можно показать, что если для одномернот'о случая поrpешность со-
ставляет O1 a), то В dMepHoM случае она равна о(п a'i1), Отмстим, что
в отлпчие от данных методов поrрешность ыетода MOHTeKap.l0 не зависит
ОТ размсрности и :\1еняется как O(n\;:'), С;lс;ювате:JЬНО, для .тОСТа10'lНО
бо:JЬШИХ d ПН1СI'рироваНllе по методу MOH1c-Кар:1O будст праводи1Ъ к
меныш!м поrреШНОСТЯ:-'1 при тех же знач<:сниях N,
586
587

()('.'<IU [си[,('
оrJ1АВЛЕНИЕ
5.]. '):н;ктричсское поле СИСIС1Ы НСIlОДВИЖ!lЫХ заР>Ц()[1.. ......... ..... ХУ
5.2. МаПiJl1;ЮС ,JO!Je ВИ1К:l с lIOС10ЯНIIЫ,.\ [ОКОМ .......... .. ...... .... ..... ]О()
5.3. М:НlIIп!!t)с !Ю:Iе co;rCHO!!:!(\ с постоянным 10кОм............... .... .107
5.4 l\1ШI-I1IТНfJС ,IO:IC ll']1О1ЦiiЛЬНOJI 06:-,ютю! с !l()СIОНIIНЫМ ;OKOi\r.. ! 2('
5.':. l{rlc,lcHHOC решение УрЗВНСНI!Й Jlэпласа I! :lyaccolIu ..... ....... ] 28
I .1,jН;] 6, I\ЮДЕ.:lИРОI3АНИЕ ДВ1!ЖЕНИЯ 'ЭЛЕКТРИЧЕСКИХ
ЗАРЯДОВ I3 'ЭЛЕКТРИЧЕСКИХ И МАI'Н1'1ТНЫХ ПОЛЯХ ....... ,146
6.1, 13ве.'\с!ше............................................................... ....,.. ..............'.146
(),2. Рассеиванис частиц в H(,HTpЫ10M ПО,1е, Опыт РсзсрФоrЛ:1. .14.7
6.3. Ноде.1!,!ров;:шие ДВЮКСIIИЯ 'шсктрическ!!х заряJJ.ОВ
п IJOС10ЯННОМ мапlИТНОМ [ЮНС ,.................................................... ]62
6.4, Модслирование движения электрических зарядов
в ПОСТОЯННЫХ электрических и мапIИТНЫХ полях........... ........ 168
]"лзпа 7, ФУРЬЕ.АНАЛИЗ НЕIIРЕРЫВНhIХ И ДИСКРЕТНЫХ
фу НКЦI1Й ............................... ........,................... ............ ......'.... ........ ] 73
7,1. Нведенис.............................................................,.............................] 73
7,2. Разложение периодических сиrналов в rяды фурье.................. j 73
7,3, ЭффеК1 rиббса .......................................................'...................177
7.4. Спектра.пьный анализ непреrывных непериодических
СПП1алов ,.."..,...,...... ...............,....,..,...."..,..............,. ...,."......,..,...... ] 83
7,5, Спектральный анализ дискретных функuий,...............................187
7.6. СнеКТР:ШI>НЫЙ анализ дискретных функций конечноЙ
длитспьности ....,............,............,..'...,.... .....,..........,.,..., ........, ....... ,190
7.7, Быстрое преобразование фурье....................................................193
}"лава 8, МОДЕЛИРОВАНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ ...........200
8,1. Линейный rармонический осциллятор ....................................,... 200
8,2. Математический МаяIНик....,.,..... ..,..,....',............,... ....",. ..,...,...,.." 205
8.3. 'Затухающие колебаНия..,................................................................211
ХА, Вынужденные колебания линеЙноrо rаrмоническоrо
ОСЦИ.1Лятора ............................ ................ ............................... ........ 213
r:Ht133 <). МОДЕЛlIРОI3АНИЕ НОЛНОНЫХ ЯНПЕНИй..............,.......216
9.]. Введение............................... ......... .................................. .. .....216
9.2. Модс.1иrовюшс СR(\бодных КО.'Jебаний JjеПОЧ}(J1 связанных
I'ap:-'!ОНiIческих ОсIщл.1яторов..... ............. ..... ...... ................ . ......'216
ч. '. Модепированис вынужденных колебаний цепочки
СВЯ'3аН!IЫХ r'ЩJ:-'ЮНlJчеСI-.J!Х ОсцилляI.оров.................... ..... .. .....232
9А. МО,1СЛЩJOваш!с ВО.'1НОВЫХ двlIжений......................... ....240
I.laJ:H !. 7\1(хс:шРОВАlшЕ ОТlЮСIПFЛЫ:!ЫХ ДВИЖЕшIi1
13 К.l\СП!ЧF:СКОЙ MEXAl-:IIIКI::,....................................................... 3
] !. Вf.е;!С!П!с............................................................... .......................... 3
j .2. 1l0CJ-РОСНИС орБИlЫ Луны в I'слиоцеIпрической системе
о [счета......... ........ ..... ........... .........,. .. ........ ................ ............. ............ 4
1,3. Построение орбиты Марса в системе отсчета, связанной
с Землей ..............................,.............................................................13
1';raBa 2, l\.10ДЕJ!И ФИЗИЧЕСКИХ ЛРОЦЕССОI3, ИСПОЛЬЗУЮЩИЕ
ДИФФЕРЕIЩИАЛЬНЫI:: УРАВНЕНИЯ Ц"О ПОРЯДКА ..............'22
2,1. 10дс:IИрование остывания наrретых тел ....................................... 22
2,2. Алrоритм Эйлера'..'.'.""'.."'..."".""."..'.."'.".'."".'."..""."'.""'."'...' 23
2.3. I1porpaMMa для rешсния )щфференциапьных урапнений
псрвоrо порядка методом Эйлера........,..............................,.......,.. 24
2.4. Опснка коэффициента остывания по эксперимснтальным
реЗУЛЬ'I 3Таы..,.......,......,.,...,.,....., ..............,...,........... ....,.. ....,............. 30
2,5, Решение дифференциальных уравнений методом
Pyнr cKyттa 4ro порядка....'...'..'....'.....'.. ...."....,....,....,......,..,....... 42
2.6. l\Лоделирование радиоактивноrо распаll<l......................................,45
2,7, Моделирование цепной реакции ядернOI'О взрыва.......................4б
rлава 3, ДIШАМИКА МАТЕРИАЛЬНОЙ ТОчКI1.......................................,49
3.1. Введение ................. ..........., ...................................................... .......... 49
3,2, ДЩ1женис тел в rpавитационном поле Земли без учета трения.., 50
3,3, Движение в rpавитационном ноле Земли с учетом
силы трения ...,.,.,. ..... .....,.. ........,'.,.....' ..... ."..."........ ..,..., ......,'...,.,.", 56
rлава 4. ЗАДАЧА КЕПЛЕРА.. .......................................................................'63
4,]. Введение ,....,... ...",.,.... ......,'..,....,.,.............,... .,."..,...,.."...,'..,."..,... .." 63
4,2. Уравнения движения планет............................................................ 63
-1.3. Численное моделирование орбиты ..........................................."...68
4.4. Провсрка В10роrо закона Кеп.'!ера....................................,............ 72
45, П!ЮСlранство скоростей ..... ....... .................. ........ ........... ......... ......81
4.6. 1o;le.1IIpoBaHIfe Солнечноi-i систеМы..................'............. ............85
1':]а8;1 5. МО.'(Е.rШРОНАНIIЕ СТАТИЧЕСКИХ ЭЛFКТРJ1ЧЕСКIIХ
11 J\.1;\IТ!JПНЫХ ПО.:1Еf1.... ..... ......................... .......:-;9
5S9

J<'o..fJ'llJl()::lep'::!,_).. ,н()де.'j.j/.(1Jlli": )/l_:тчеu..IС\ J_ipufe[l..-oq  n(п'.l!le л!., 7 EB
9.5, Фурьеанализ волновых пакстов, ДВIIЖУliШХСЯ в Срt:ДС
с дисперсией............................. ...................................... ......... --1 с.
9.6. i'lнтсрференция и дифраКI1ИЯ ..,.".............,...".............. ..",.......... 2(н)
9.7, I'еометрическая опТиКа.......... ........ ................................... . ..27 .
9,8, Поляризация..................................'. ,............................. ..........
[':ыва 1 О, МОДЕЛИРОВыАНИЕ сиеп СОСТОЯЩИХ
из Большоrо ЧИСЛА ЧАП ИЦ (МЕТОД МОЛЕКУЛЯРНОЙ
ДИНАМИКИ) ,.. ,.,..."". ,.", ..,,'....'.. ,...". ,..,...". ,."...,..'..",.,."., ,.....,.. '..,.... 2 ('
10.1. ВВе,J:сНие................... ..............',...................... ..............", ........,..., 2S '
10.2. М3Т('/'. ::.rнческая модель стати;;тической системы ...........:......2/<:
10,3, ЧИСJ!СННЫЙ алrОРi1ТМ решения системы уравнений движения '2;-;:
10.4. Моделирование системы, состоящеЙ и'3 большоrо ЧИСflа
частиц, методом молекулярной динамики ......................."... ...291
1 0,5, Оцеш-;а макроскопических характеристик статистической
системы ,.,.. ......',....................... ...,...'.......,.. .........,...'...............,....... 30;;
10,6, Оценка коэффициентов псрсносз в методе МОЛСКу.'Iярноi1
" . . <;
динамикн '" ............................................................................. 1..
10,7, Модспирование фазовых псреходов методом
молекулярноЙ динамики .............................................................. 321
10.8, Заключение ..... ......................,....................................................... 324
rлава 11. МЕТОДЫ J\юВП>КАРЛО..............................................,..............326
11.1, Вr<еденис................................... ......................................, ....,...... ....326
11,2, Численные методы интеr'}Jирования функпий, зависящих
от одной псременной ..,....'......,......' ....,..'...."..,......,..,.. ...,....,......... 326
] 1,3, Основы метода Монте.Карло ......................................................330
11.4, Алrоритм rснерации случайных чисел с равномерным
законом раСl1ределения .......................................... ..,..... ........ .......342
]! ,5, Алrоритм МетрОПОJJиеа......................................................,........ 345
rлава 12, СЛУЧАЙНЫЕ БЛУЖДАНИЯ ..'..................................................352
12.1, Введение."""'..' ,.",.",..""",.""..."""",.""",.".,..,.", " .".,.,.....,.,.,..., 352
12.2, Одномерные случайные блуЖ;.lания.................,.......................352
]2.3, t\-1етод случайных блужданиЙ на ПJ10СКОСТИ '.............................364
12.4, Моделирование движения решеточноrо rаза............................ 385
12,5, Нспрерывная моде:ть СJIУЧnЙНЫХ G:rуждаllий................... .. .....391
[.1ава 13 МО;ЕлИРОВАНиЕ СТАТIIСПiЧЕСКОI1 СllСТЕМЫ
в ПРUl]ЕССЕ РЕЛАКС:ЛЦIIl1 11 (ОСТОЯНlШ J'ЛВНОВН!JЯ...3(.Ч.
13.]. BBcTcIНlc......................... ..................................... ........ .........394
590
Oыв.lcиllc
13.2. Моде;шрованис процесса релаксации статистической
cl!cTc:>lbI.... ...... ........................... ............................ ......... ........'.......'395
13.3. ЭНlрorшя ................................ .............. ......... .... .... ...................406
Т':шва 14, \1ОiЕJ1иРОВАНиЕ МНКРОКАНОНИЧЕскоrо
АНСАМБЛЯ ;-"HTOДOM МОНТЕКАРЛО ........... ....................4]5
14.1. Микrоканонический aIмбль ................................................415
14.2. Моделирование МИКр,.,\аноническоrо анс;щбля .....................'4]6
14.3, \10ДСЛЬ I1зинr'а ............................................ ..............................'426
['.1ава 15 МОДЕЛИРОВАНИЕ КАНОIШЧЕСКОП) ЛНСЛМБJIЯ
МЕТОДОМ МОНТЕКАРЛО .......'.............'............................'.............444
15.1. 8всденис.........................,..........................................................'...444
15.2. Канонический ансамбль ...............................................................444
]5,3. АлrОрИТ:I1l'ЛеТРОПОJIJ!са для KaHOHI!L!eCKOl'o ансамбля ...........446
15.4. Моделирование двумерной модели Изинrа методом
КЭJ!ОническOl'О ансамбля .............................. .............., ................458
Т'шша 16 МОДЕЛИРОВАНИЕ КВАНТОВЫХ сисТЕМ..........................,472
16.1, Введение..............'.............'.........."..'..". ,.."..'......,.. .............'..'....'.472
16,2, Стационарное уравнение IlIрединr'ера .......................................474
16,3, Моделирование колебаний двухатомной молекулы
в квазиклассическом приближении '..','...,..,....................,....'..... .487
16.4. Нестационарное уравнение IlIрединrера ...................................506
16,5, Оцепка энерrии основното состояния квантовой систеыы
методом МонтеКарло...,..... ..........,....."..,. .....,...,.........,....,..,......" 52]
16,6. Оценка энерr'ии OCHOBHoro состояния квантовой системы
вариационными методами МонтеКарло............,......................,529
IIриложснис] ОСНОВНЫЕ ПРИЕМЫ РАБОТЫ........,..............................539
Пl,]. Введение в пакет МАТ СА В ........................................................539
П1,2. Работа в командном окне .................................... .....................550
П1.2,1, Вход в систе,ну MAТLAB.................................................550
П 1.2.2. Иll!l1ераЮl1uвныЙ доступ !( справочноЙ
ш{(fюр.нации и дOl-Т.ЛtеНтации.................., ...... ..... ..............551
111  3. РеааКl!llIр(1вйю/е и повторныЙ Р.ызов
/-.:О.1Ю/{С)НОll строки. ..,'.. .,..... ..'... ..., ....... ...,. ....... ...,..,....... .,. .'.'...553
!l1.2.4. Фор.нат сьишда. ..........................................,....... ........554
111.2.5. А.-0I111Я np0Il10Ko.7a сеСпll1.............................. ........ ........554
11] .3. СОЗДЙНIIе МRТрИl1 ....., ..,.....,....".".............,.... ..", ,,-. ........ "'" ,55-.4
1113.1. Явное -юдйlill(' 1tCl/llf1l1lf ............. .......... ..... ..555
111.3.2 ll(Jf).lIптРUllЫ ц IIСI10.71,'твПНlIС (1востО'lllЯ (.). . 556
591

А"о)ttl'IЬ!.J1117:/IО(}..\fОdе..lщтt)а;IU{' ФlПllЧ(;;.1<:ll '.lpOii.C1 (,-Н. f'; ',,;Ас.'.!!1,---' A!. 1,1 А 8
[[1.3.3. ФУIlК/IIШ nостросния .Нат;пlll..........,..,... ........ .... .1,'
1114 Оr!срщии выражения и пер'-jеННhJс.... ..........." ":'\х
П 1.4.1. l1ратl.ю записи опера/пор'!", .......................... -' ".')
I71.4.2. .i!(l!llрuчньzе ()IlCPцuи.. ..0, "........0. ",,,,,.,,... "." .,,;-5,'
lJ1.4.3 ()ncjJ{llJUU r .нассиЬ'.7.ни. "".",.."....",., 5.5)
II144. Сохранеиие даиных 1iЗ раfiочсЙ 0671.юпu............... ,у
П1,5. ОПСj1атоrь; [or, \vhiie, if. case и олераrnры UJношения ". ., .. :'1'>0
IlI.5.1.l1иКлfпr......,.................................................... ........ ..560
П J. 5,2. [JuК7 H111!e ............ .......... .,... ....... ........ ..... ".. ................... 56 j
П1.5 З. УС'.7С6НЫй операпюр if........................................... ..... .. .'i6!
П1.5,4. Оператор псреЮ1l0чеНllЯ ,ase........................................562
П 1.5.5 }Iс.70GUЯ (операторы отНоше/:шl)................................... 562
П1.6, ФУНКЦИИ MATLAB .............................,,,,.......... ..... .... .......... '\63
П1.6,1. СJ.:а:lярные функции .........,..........................................,.... 563
П1. 62. Векторные фУ/iкции ......................................,.., ....."....... 564
llJ.б.3. Матричные ФУIiIЩliи ....... ...................... ...................... 5М
Приложснис 2, I'ЛФАЙЛЫ ...........................................................................565
П2,1.1. фаiiлы.проzра.11Мbl,..............................................,........, 565
П2,l.2. фаii.'lbl1?)'I//{ции......,.............................................. ..... ..565
П2.1.3, Текстовые строки, сообщения об ошибках ............. ....569
П2,2, Работа с шфайлами ..................................................................569
П2.2,l. Списо" путеЙ дОсl11)'I1(1....................................................569
П2,2.2, l1С110.7Ь306Шluе редuюI10ршотладчиКа............,......,........ 571
/72.2,3. Отладка l1нjНlЮО6 ........................................................... 573
ПРИJ!ожение 3, СОЗДАНИR ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛЯ ....".........575
ПРИЛОЖСНJlе 4. ОЦЕНКА ПОrPЕШНОСТЕЙ ЧИСЛf.ННOl'О
иНТЕrриРОВАНия......,.........,....".. '.,..,.,....' ............."....................... 585
592

s.
ine@
\
I
I
www.softl
n е
r u
BCI ППП АУ И
Научное ПО
ДПЯ исспедований и расчетов
Почему студенты, преподаватепи и научные работники приоб
ретают нужные им проrраммы в компании SоftLiпе?
. Низкие цены  компания работает напрямую с вендорами и явля
ется привилеrированным партнером по образовательным про
rpaMMaM для мноrих производителей ПО
. Возможность получения демоверсий и обновлений для широкоrо
спектра проrрамм.
. Возможность удобноrо выбора проrрамм по каталоry SоftLlпе
direct или на сайте www soft/iпe.ru
. Подцержка сообщества ПОЛЬЗ0вателеи на сайте wwwexpoпeпta.ru
Какое научное проrраммное обеспечение поставляется SоftLiпе?
. Языки проrраммирования математических задач (MathWorksl
. Моделирование электронных схем и устройств (Еlесtroп!(
WоrkЬепсh. РСАО)
. Универсальные математические пакеты, обмен данными
AutoCAD (Wolfram Research, Waterloo Maple, MathSoft)
. ПО дЛЯ химиков (CambridgeSoft)
. Статистические пакеты (MathSoft, StatSoft)
. Редакторы формул (DеSlgп SClепсе, Multi Edlt)
. Пакеты бизнесанализа (Pallsade)
. Математические надстройки к MS Office (Frопtllпе Systems'
SoftLine  зто сво60да вы60ра
119991 r. Москва,
ул. rубкина, Д. 8
тел.: (095) 2З2002З
email: info@softline.ru
The
МАТН

MathSoft
"'1:.+,jf+
 StatSoft
WOLFRAM
RESEARCH
Waterloo Ма .Ie
.. i:iectronics
CambridqeSoft
'"temet ChemlSm' So{tware Leader
ISBN 5935171287
111111111111111111111111
9785935 171285

,
. '.
(
, .....,
1
t
 I
I
&
 J
'
 Iп
.....С)
..... -.L
с:[
С,
1
I ,--
lL!..:ai \ I 
I \I'" 1
[Ъ: ..
lLU... .,
III
-I

::I! 
ctSl:
са
оса
.,'" I
I
I
.. "1
I
 ':::: j
..