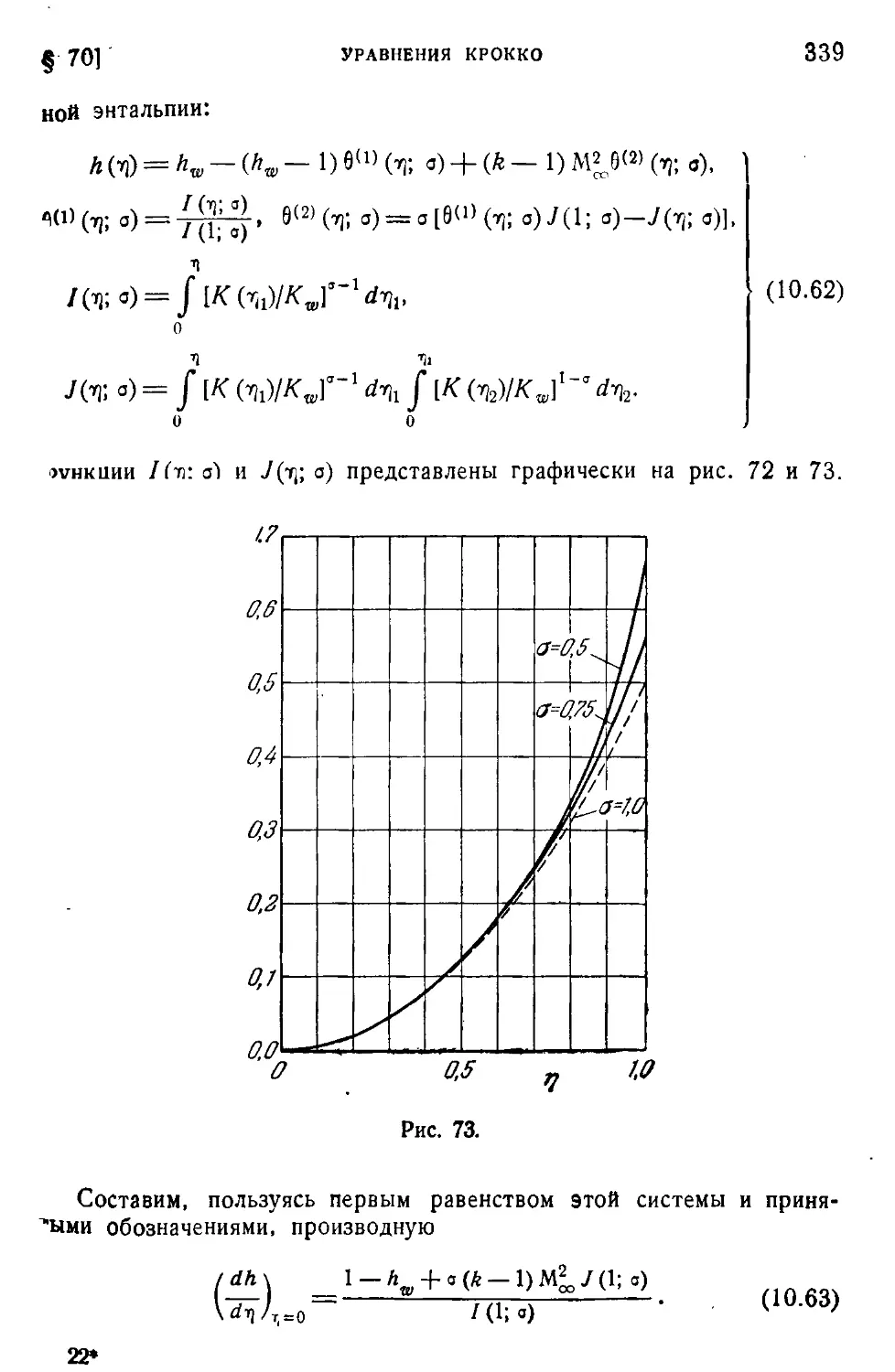
Author: Лойцянский Л.Г.
Tags: физика термодинамика аэродинамика теория пограничного слоя теория ламинарного слоя
Year: 1962
Text
л..г. лойцянский
ЛАМИНАРНЫЙ
ПОГРАНИЧНЫЙ
СЛОЙ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1962
ОНИ? -А
ОГЛАВЛЕНИЕ
Предисловие - .......'..... 7
Введение 9
Глава 1. Уравнения Прандтл» и простейшие случаи точного
их решения 12
§ 1. Пограничный слой и внешний поток . . .' , 12
§ 2. Вывод уравнений Прандтля 16
§ 3. Уравнение Прандтяя — Мизесз 23
, § . 4. Пограничный слой на пластинке (задача Блазиуса) 26
§ 5. Задача о затопленной струе 34
§ 6. Применение уравнения Прандтля — Мизеса к задаче о затоплен-
ной струе . . 39
§ 7. Распространение затопленной струи вдоль твердой плоской
поверхности 42
| 8. Аэродинамический след за телом . 49
§ 9, Отрыв пограничного слоя от поверхности . 54
§ 10. Толщина вытеснения и ее влияние на распределение дав-
ления ...... ...... 58
Глава II. Точные решения уравнений Прандтля для некоторых
классов задач ..... ............... 64
§ 11. Степенное распределение скорости вдоль внешней граница
слоя . .... .~ 64
§ 12. «Односкатный» профиль скоростей ..;....... 74
'§ 13. Многовараметричёский класс задач Блаэиуса — Хоуарта . . . . , 78
§ 14. Классы точных решений Тани и Гертлера т— Виттийга" 84
Глава1 III. Приближенные однояараметрические методы ..... 87
§ 15. Некоторые общие соображения 87
§ 16. Интегральное условие импульсов 88
§, 17. Метод Кармана — Польгаузена 92
§ 18. Применимость метода Кармана — Польгаузена ........... 96
§ 19. Обобщение метода. Кармана — Польгаузена 98
§ 20. Ошределение характеристических функций " 101
§ 21. Линеаризация уравнения однбпараметрического метода 105
§ 22, Обзор других приближенных методов . 107
Глава IV. Плоский нестационарный пограничный слой ..... 114
§ 23. Пограничный слой в начальной стадии движения тела ...... 114
§ 24. Пограничный слои на'теле, внезапно приведенном в поступатель-•
нее равномерное движение .................'... 116
4 ~ -
4 ОГЛАВЛЕНИЕ
§ 25, Равноускоренное движение цилиндра ............... 121
§ 26. Случай скорости, зависящей от времени по степенному закону . . 124
§ 27. Продольное нестационарное обтекание пластинки 128
§ 28. Применение приближенного однопараметрического метода .... 132
§ 29. Применение методов, не связанных с уравнением импульсов. . . 139
Глава V. Неплоские двумерные пограничные слои 141
§ 30. Пограничный слой на продольно обтекаемых удлиненных телах
вращения 141
§ 31. Примеры стационарного и нестационарного пограничных' слоев
на удлиненном теле вращения 143
§ 32. Преобразование Степанова — Манглера 148
§ .33. Однопараметрический метод расчета двумерного стационарного
пограничного слоя , 150
§ 34. Обобщение на случай нестационарного слоя 153
§ 35. Пограничный слой на длинном, тонком теле вращения; продольное
обтекание цилиндра 154
§ 36. Расчет влияния поперечной кривизны по однопараметрическому
методу . 163
§ 37. Круглая струя в затопленном пространстве 167
Глава VI. Трехмерные осесиммехричные пограничные слои . . . 173
§ 38. Равномерное вращение диска в безграничной вязкой жидкости . . 173
§ 39. Равномерное вращение диска, ограниченного кожухом 177
§ 40. Пограничный слой на диске, вращающемся в однородном осевом
потоке ...... 183
§ 41. Пограничный слой на диске, приводимом во вращение из состо-
яния покоя ............... 192
§ 42. Пограничный слой на теле вращения, внезапно приведе'нноМ
в равномерное винтовое движение 196
§ 43. Распространение закрученной струи в затопленном простран-
стве 200
§ 44. Радиально-щелевая закрученная струя в затопленн. м лростран»
стве '......" 206
§ 45. Гидродинамическая модель вихревой форсунки . . .^»^. .... 212
Глава VII. Некоторые задачи теории трехмерного пограничного
слоя ¦. 218
§ 4.6. Пространственный пограничный слой на скользящем крыле . . . 218
§ 47. Пространственный пограничный слой на вращающемся цилинд-
рическом крыле ......................... 226
§ 48. Обратное влияние пространственного пограничного слоя на
внешний поток 232
§ 49. Вращающийся цилиндр в косо набегающем потоке 235
§ 50. Уравнения трехмерного пограничного слоя в любой ортогональ-
ной системе- координат 244
§ 51. Некоторые общие свойства пространственного пограничного
слоя; теорема о вторичных течениях 247
§ 52. Пространственный пограничный слой вблизи линии пересечения
двух плоскостей . . . 249
Глава VIII. Пограничный слой в однородном или неоднородном
газе при больших скоростях ................. 254
§ 53. Некоторые особенности теорий пограничного слоя в газе. .... 254
§ 54. Основные уравнения движения вязкого совершенного газа. . . , 256
§ 55, Две основные формы уравнений пограничного слоя в газе. ,. . . 259
ОГЛАВЛЕНИЕ 5
§ 66. Области применимости уравнений пограничного слоя ...... 266
§ 57, Уравнения пограничного слоя в потоке смеси реагирующих
между собой газов , 272
Глава IX. Температурный и диффузионный пограничные слои
в несжимаемой жидкости ..." . 280
§ 58. Температурный пограничный слой на продольно обтекаемой
пластинке 280
§ 59. Температурный пограничный слой при продольном перепаде
давления 284
§ 60. Температурный пограничный слой при заданном распределении
температуры на поверхности тела 287
§ 61. Температурный пограничный слой на продольно обтекаемом теле
вращения 292
§ 62. Температурный пограничный слой на длинном цилиндре в про-
дольном потоке . ." 295
§ 63. Температурный пограничный слой на вращающемся диске .... 299
§ 64. Распространение нагретой ламинарной струи в затопленном
пространстве 305
§ 65. .Приближенные методы расчета температурного пограничного слоя 308
§ 66. Ламинарная диффузия в изотермическом пограничном слое . . . 314
§ 67. Примеры диффузионных пограничных слоев ........... 316
Глава X. Ламинарный пограничный слой на пластинке в про-
дольном газовом потоке 319
§ 68. Стационарный пограничный слой на пластинке при линейной
зависимости вязкости от температуры 319
§ 69. Продольное обтекание пластинки при числе Прандтля, равном
единице 330
§ 70. Уравнения Крокко 334
§ 71. Применение?,реременных Мизеса—Прандтля 342
§ 72. Ламинарн;.''*' пограничный слой на пластинке при переменной
температу - поверхности 346
§ 73. Взаимод твие пограничного слоя со сверхзвуковым потоком . . 352
§ 74. Нестационарные явления на безграничной пластинке, импульсивно
приведенной в равномерное движение 356
§ 75. Влияние излучения на распределение температуры в пограничном
слое в абсолютно прозрачном газе 362
§ 76. Продольное обтекание пластинки слабо разреженным газом при
учете скольжения 364
Глава XI. Пограничные слои с постоянным давлением 371
§ 77. Ламинарный пограничный слой на конусе в продольном сверх-
звуковом потоке 371
§ 78. Образование пограничного слоя на стенке ударной трубы .... 378
§ 79. Ламинарная струя в газовой среде . 387
§ 80. Ламинарный пограничный слой на быстро вращающемся в газе
диске 390
§ 81. Распространение радиально-щелевой ламинарной газовой струи
вдоль твердой стенки 393
§ 82. Свободная радиально-щелевая закрученная струя 401
§ 83. Пограничный слой при равновесной диссоциации газа 404
§ 84. Пограничный слой в диссоциированном и ионизированном газе
ири наличии магнитного1 поля , 410
6 ' ОГЛАВЛЕНИЙ
Глава XII. Пограничный слой при заданном распределении
давлений на внешней границе 418
§ 85. Пограничный слой на теплоизолированной поверхности при
5 = 1 и небольших Моо ; ¦ 418
§ 86. Пограничный слой при а==1 и произвольном Моо 424
§ 87. Преобразование уравнений пограничного слоя в газе к форме,
полностью соответствующей несжимаемой жидкости ....... 431
§ 88. Применение модифицированного преобразования в случае тепло-
отдающей поверхности" " 440
§ 89. Приближенный метод расчета пограничного слоя в случае произ-
вольного распределения скоростей во внешнем потоке и наличия
теплоотдачи с поверхности тела 448
§ 90. Влияние диссоциации воздуха на теплообмен в носовой части
тела вращения • 457
Именной указатель 474
Предметный указатель 477
ПРЕДИСЛОВИЕ
Быстрое развитие теории пограничного слоя, особенно в связи
с новыми задачами аэродинамики и термодинамики газа при .больших
скоростях и высоких температурах, делает в настоящее время со-
ставление сравнительно краткого руководства в этой области крайне
затруднительным. Вот почему, представляя себе фундаментальное
значение классических методов расчета ламинарного пограничного
слоя для решения новых задач теории пограничного слоя, мы удо-
вольствовались пока изложением теории ламинарного пограничного
слоя и, кроме того, опустили некоторые специальные вопросы этой
теории, как, например, пограничный слой на пористой поверхности
при наличии поддува или отсоса. Что касается вопроса устойчивости
движения жидкости и газа в ламинарном пограничном слое, то он,
будучи тесно связан с теорией перехода ламинарного движения в тур-
булен-тное, естественно, может и должен быть отнесен к теории
турбулентного пограничного слоя, изложению которой автор надеется
посвятить в дальнейшем специальную книгу. Такой выбор содержа-
ния настоящей книги позволил, с одной стороны, глубже и систе-
матичнее остановиться на наиболее фундаментальных вопросах теории
ламинарного пограничного слоя, а с другой — осветить и ряд новых
задач этой теории.
Первые три главы книги содержат изложение теории плоского
стационарного слоя, включая сюда как точные, так и приближенные
методы решения. В главе IV изложены аналогичные решения клас-
сических и некоторых современных плоских задач теории .нестацио»
нарного слоя. В главе V рассмотрены двумерные осесимметричные
стационарные и нестационарные задачи о продольном обтекании удли-
ненных тел вращения, а также задача о незакрученной круглой струе.
В главе VI разобраны аналогичные задачи, усложненные вращатель-
ным движением тела, а также задачи о закрученной круглой струе
и закрученном пограничном слое внутри конического сопла. Глава VII.
посвящена изложению основных методов решения наиболее простых
задач трехмерного пограничного слоя и выяснению некоторых общих
свойств пространственных пограничных слоев.
Перечисленные семь глав книги относятся к теории однородного изо-
термического пограничного слоя в несжимаемой жидкости, В главе VIII
О ПРЕДИСЛОВИЕ
выводятся общие уравнения ламинарного пограничного слоя в газе
при больших скоростях и температурах; там щ& нашли себе место
специальные уравнения пограничного слоя в разреж&нном газе и в смеси
химически реагирующих между собою газов,
В главе IX рассматриваются применения простейших частных слу-
чаев этих уравнений к точному и приближенному решению плоских
и пространственных • задач о теплопередаче и диффузии примесей
в несжимаемой жидкости в условиях малых ларепадов температур
и малых изменений концентраций примесей.
В главе X излагается теория ламинарного, стационарного и не-
стационарного пограничных слоев на пластину в газовом потоке
больших скоростей без учета и при наличии учета влияния луче-
испускания. Рассматривается также случай слабой разреженности газа,
когда граничные условия для скоростей и температур на поверх-
ности обтекаемого тела соответствуют режиму «скольжения» газа.
Примеры изобарических пограничных слоев, относящиеся к дви-
жениям, отличным от продольного обтекания пластины, помещены
в главу XI. Это — задачи о пограничных слоях на поверхности конуса
в сверхзвуковом осевом потоке, на стенке ударной трубы при про-
хождении сквозь нее ударной волны, на поверхности быстро вра-
щающегося в газе диска, в сверхзвуковой струе, а также о погра-
ничном слое на пластине в гиперзвуковом потрке при равновесной
диссоциации газа и при движении ионизированного газа во внешнем
магнитном поле.
Заключительная глава XII содержит изложение методов расчета
пограничного слоя при продольном изменении давления во внешнем
потоке как в условиях тепловой изоляции поверхности тела, так
и при наличии теплоотдачи. Особое внимание зд,щь уделяется методу
сведения задачи о пограничном слое в газе к соответствующей ей
задаче в несжимаемой жидкости (метод Ддродн.ицына и его моди-
фикации), позволяющему в конечном счете ' иадользовать простые
приемы расчета, изложенные в начале книги, шавершающее главу
решение задачи о гиперзвуковом пограничном слое на тупоносом
теле вращения в области за отошедшей головной волной не претен-
дует на полноту, а ставит себе целью лишь поййнить те трудности,
которые возникают перед исследователем, желающим приблизиться
к действительной физической картине явлений в пограничном слое
на носу снаряда, проникающего с гиперзвуковыми скоростями в плот-
ные слои атмосферы.
Л. Г. Лойцяяский
Ленинград
23 июля 1961 г.
ВВЕДЕНИЕ
Пятьдесят лет — небольшой срок для истории развития науки,
и если теория пограничного слоя к своему пятидесятилетию, отпразд-
нованному в 1954 г., пришла как крупная самостоятельная область
современной гидроаэродинамики, то только потому, что развитие
этой, сравнительно молодой области механики жидкости и газа ни-
когда не отрывалось от задач, выдвигаемых такими важнейшими
разделами техники, как самолетостроение, кораблестроение, энерго-
машиностроение, двигателестроение, а в последнее время ракето-
строение.
Теория пограничного слоя, основные уравнения которой для лами-
нарного потока были установлены Л. Прандтлем в 1904 г., вскоре,
после своего возникновения была с успехом использована (Г. Бла-
зиусом в 1907 г.) для первого в истории гидроаэродинамики рацио-
нально обоснованного метода расчета сопротивления трения, а по
прошествии примерно двадцати лет после этого и для теоретиче-
ского расчета теплоотдачи с поверхности тела. Благодаря суще-
ственному вкладу, сделанному Т. Карманом, предложившим в 1921 г.
простой приближенный метод расчета ламинарного и турбулентного
пограничного слоя, идеи теории пограничного слоя быстро распро-
странились в кругах инженеров и заняли заслуженное место в разно-
образных практических применениях.
¦ Разработанные Прандтлем A926 г.) и Карманом A930 г.) про-
стые полуэмпирические законы турбулентных движений позволили
распространить теорию пограничного слоя на случай турбулентных
слоя, струи и следа за телом.
Вскоре после появления основных уравнений теории погранич-
ного слоя, наряду с плоскими стационарными задачами, были раз-
решены простейшие пространственные (двумерные осесимметричные
обтекания длинных тел вращения) стационарные и нестационарные
задачи. Однако строгое решение нестационарных задач было выпол-
нено лишь в последнее время. Точно так же расширение теории
пространственного пограничного слоя на случай тел вращения
небольшого удлинения и общих трехмерных потоков растянулось на
длительный период: от первой работы Леви-Чивита 1929 г. до на-
ших дней,
10 . ВВЕДЕНИЕ
Основное значение для современных приложений имели работы
по теории пограничного слоя в газе при больших скоростях. От-
дельные решения простейших задач появились еще в тридцатых годах
(А. Буземан, Л. Крокко, Т. Карман — Чень Сюэ-сень, Ф. Франкль).
В дальнейшем развитии этого важного раздела современной теории
пограничного слоя большую роль сыграло преобразование уравнений
пограничного слоя в газе К виду, близкому к уравнениям погранич-
ного слоя в несжимаемой жидкости, предложенное в 1942 г.
А. А. Дородницыным и в дальнейшем несколько модифицированное,
многими авторами (Стюартсон, Хоуарт). Другой путь решения, осно-
ванный на использовании в качестве аргумента продольной компо-
ненты скорости, указал в 1939 г. Л. Крокко. •
Параллельно с чисто гидродинамическими вопросами теории по-
граничного слоя (определение поля скоростей, сопротивления трения
и давлений, подъемной силы при внешнем обтекании тел, расчет
входных участков при протекании жидкости сквозь каналы и др.)
получили свое развитие "близкие друг к другу по математическому
содержанию тепловые и диффузионные задачи.
Расцвет теории пограничного слоя относится к последнему пятна-
дцатилетию, в связи с переходом к сверхзвуковым и гиперзвуковым
скоростям полета. Этот современный этап развития авиационной
и ракетной техники поставил перед конструкторами и учеными много
новых комплексных физических задач, относящихся к сопротивлению
движению тел в плотных нижних и разреженных верхних слоях
атмосферы, явлениям разогрева, плавления или сублимации твердого
вещества, покрывающего носовую часть тела, и уноса (абляции)
этого вещества.
Возникающая при прохождении через образующуюся вблизи но-
совой части тела мощную головную ударную волну неоднородность
в химическом составе воздуха, обусловленная происходящей при
высоких температурах диссоциацией молекул газов и последующей
рекомбинацией атомов вблизи лобовой поверхности тела, вызывает
дополнительное выделение тепла, которое вместе с теплом, подве-
денным путем теплопроводности и излучения, создает тот сильный
разогрев носовой части ракеты, который угрожает ей разрушением.
Сложность этих физико-химических процессов, усугубленная ещё
релаксационными явлениями, связанными с неравновесностью распре-
деления температуры по. степеням свободы молекул, сближает совре-
менную теорию пограничного слоя с- кинетической теорией газов, из
которой ей приходится черпать те макроскопические законы связи
между параметрами движущегося газа и основными его термодина-
мическими и физико-химическими характеристиками, без которых
постановка задач теории пограничного слоя становится невозможной.
С математической стороны задачи теории пограничного слоя
с самого своего возникновения потребовали для своего решения при-
ВВЕДЕНИЕ 11
менения приближенных методов численного интегрирования систем
нелинейных дифференциальных уравнений, как обыкновенных, так и
в частных производных. Если в начале еще можно было пользо-
ваться методами разложения решений в ряды, применением последо-
вательных приближений или всевозможными приемами линеаризации,
то постепенное усложнение вопросов, трактуемых теорией погранич-
ного слоя, привело к неизбежности перехода на машинное интегри-
рование, сначала на специальных моделирующих электромагнитных
устройствах, а затем уже и на электронных машинах дискретного
счета, В этом отношении теория пограничного слоя не отклонилась
от общего для всех физических наук пути.
ГЛАВА I
УРАВНЕНИЯ ПРАНДТЛЯ И ПРОСТЕЙШИЕ СЛУЧАИ
ТОЧНОГО ИХ РЕШЕНИЯ
§ 1. Пограничный слой и внешний поток
Интенсивность действия сил внутреннего трения (вязкости)в реаль-
ных жидкостях зависит от степени неоднородности поля скоростей
в потоке. Эта же неоднородность вызывает в жидкости конвектив-
ные ускорения и, следовательно, инерционные эффекты. В зависи-
мости от того, превалирует ли вязкое воздействие или инерционное,
можно, в порядке упрощения, говорить о двух предельных случаях
движения: «медленном», когда пренебрегают конвективными инер-
ционными силами и учитывают лишь действие сил вязкости, перепада
давления и внешних объемных сил, и движений «идеальной» жидкости,
не обладающей вязкостью. Такой подход широко использовался ранее
при решений многих практических задач, но в настоящее время,
в связи с появлением интереса к изучению более тонких характери-
стик движения, таких, как трение, теплоотдача и т. п., гидродинамика
уже не может довольствоваться столь приближенными подходами и
требует более детального изучения происходящих в жидкостях явлений.
Особый интерес для практики представляют движения, в которых
инерционные эффекты в жидкости, если говорить о потоке в целом,
преобладают над влиянием сил трения, в частности, сил вязкости.
Как известно, мерой соотношения этих двух основных классов сил
служит рейнольдсово число потока, так что рассматриваемый случай
представляет движение с большими значениями числа Рейнольдса.
Как мы увидим ниже, при движениях с большими числами Рей-
нольдса весь поток может быть приближенно разбит на две об-
ласти: 1) область весьма малой протяженности, называемая «погра-
ничным слоем», где влияние сил вязкости столь же существенно,
как и влияние всех других сил, и 2) область пренебрежимого влия-
ния вязкости—«внешний поток». В пограничном слое благодаря его
сравнительно малой толщине уравнения движения могут быть упро-
щены и легче поддаются решению, чем общие уравнения Стокса. Во
внешнем потоке жидкость можно рассматривать как «идеальную»
§ 1] ПОГРАНИЧНЫЙ СЛОЙ И ВНЕШНИЙ ПОТОК 13
(лишенную вязкости) и для определения ее движения пол зоваться
сравнительно простыми, классическими методами расчета. Вопрос
сводится к раздельному рассмотрению таким образом упрошенных
уравнений движения жидкости.в этих двух областях и последующему
«сшиванию» полученных решений в одно целое. В зависимости от
соотношения между инерционными и вязкими воздействиями или, что
то же, в зависимости от величины рейнольдсова числа потока, изме-
няется сравнительная протяженность пограничного слоя и внешнего
потока. Чем больше рейнольдсово число, т. е. чем значительнее
относительная величина инерционных сил, тем тоньше область по-
граничного слоя и соответственно больше протяженность области
внешнего потока, и наоборот, с возрастанием роли вязкости утол-
щается пограничный слой и уменьшается «внешняя» часть потока.
В этой определяющей роли рейнольдсова числа, от порядка вели-
чины которого зависит, будет ли та или другая часть потока при-
надлежать области пограничного слоя или внешнего потока, заклю-
чается основная особенность того приближенного подхода к решению
задач динамики реальной жидкости, который носит наименование
теории пограничного слоя.
Движения жидкости в пограничном слое и во внешнем потоке
неразрывно связаны между собой. В первоначальной постановке
Прандтля эта связь рассматривалась как односторонняя; считалось,
что внешний поток существует независимо от пограничного слоя
и задается наперед как известный, движение же в пограничном слое
определяется по заданному внешнему потоку. Последующее развитие
теории пограничного слоя показало, что это не так и что только
в некотором, не всегда удовлетворительном приближении можно
производить расчет по такой схеме. Прежде всего заметим, что
в результате подтормаживания жидкости в пограничном слое трубки
тока расширяются, линии тока смещаются и оттесняют внешний по-
ток. Вызываемое этим оттеснением изменение продольных скоростей
на границах слоя оказывается в большинстве случаев пренебрежимо
малым; существенным обратным влиянием пограничного слоя на внеш-
ний поток является возникновение поперечных скоростей, которые
сохраняются во внешнем потоке и в ряде случаев становятся осно-
вой изучаемого процесса (инжекция жидкости извне внутрь струи,
см. далее, § 5). В некоторых, более редких случаях (отрыв и гфед-
отрывное состояние) имеет значение и обратное влияние погранич-
ного слоя на продольные скорости во внешнем потоке. В этом случае
внешний поток уже нельзя считать наперед известным; его опреде-
ление требует учета движения в пограничном слое, которое в свою
очередь зависит от внешнего потока. Даже весьма приближенное
рассмотрение такого типа задач представляет пока что значительные
трудности. .Некоторые соображения по этому вопросу будут даны
в конце настоящей главы (§ 9).
14
УРАВНЕНИЯ ТИ'АНДТЛЯ
[гл. i
Многообразие движений', поддающихся анализу методами теории
пограничного слоя, далеко не исчерпываетея теми случаями внешнего
обтекания твердых тел, которые рассматривались на1 заре возникно-
вения теории и которые послужили причиной появления терминов
«внешний поток» и «пограничный слой». Перечислим вкратце наи-
более часто встречающиеся классы движений, изучаемые с помощью
теории пограничного слоя. Для всех них характерно наличие обеих
областей: внешнего потока и пограничного слоя:
При набегании жидкости на погруженное в нее неподвижное тело
(рис. 1) переход от нулевой скорости частиц жидкости, «прилипаю-
щих» .к поверхности тела, к скорости порядка скорости набегаю-
щего потока происходит очень резко в области, расположенной
Рис. 1.
в_ непосредственной близости к поверхности тела. В этой области —
пограничнам слое на поверхности тела—.развиваются значительные
силы вязкого трения, сравнимые по своей интенсивности с инер-
ционныМ'И .сдлами. В удаления от тела, где скорости уже в значи-»
тельной степени 'Выровнялись и достигли величин порядка скорости
набегающего потока, силы вязкости становятся ничтожными и ими
можно пренебрегать, рассматривая этот «внешний поток» как область
движения идеальной жидкости. Вниз по потоку за телом на некото-
ром протяжении еще сохраняется область подторможенной телом
жидкости; скорости. в ней стремятся выровняться за счет взаимо-
действия с внешним потоком и достигнуть вновь скорости внешнего
¦потока, имевшей место вдалеке впереди тела. Такого рода область
течения носит наименование «аэродинамического следа» за телом; ее
иногда еще называют «аэродинамической тенью». Аэродинамический
след дает нам другой типичный пример «пограничного слоя». Здесь
мы также имеем ярко выраженное взаимодействие пограничного слоя
с внешним потоком.
Струя жидкости, проникающая в пространство, заполненное не-
подвижной жидкостью с теми же или близкими физическими свой-
ствами, дает нам ещё один пример пограничного слоя (рис. 2),
Вначале, при входе в неподвижную жидкость, эффект вязкости сосре s
§ 1]
ПОГРАНИЧНЫЙ СЛОЙ И ВНЕШНИЙ ПОТОК
15
дотсшйвается в пограничном слое на периферии струи, затем1 в вязкие
торможение струи внешним потоком постепенно вовлекаются частицы
струи, находящиеся в областях, все более близких к оси струи; на»
конец, тормозящее влияние внешнего потока распространится на всю
струю, которая в целом станет пограничным слоем. В этом погра-
ничном слое и будут .развиваться процессы смешения струи с окру-
жающей ее неподвижной жидкостью.
Внешний потом:
Инешнай поток
Рис. 2.
Если струя втекает в движущуюся жидкость, — примером может
служить распространение струи в спутном по отношению к ней по-
токе,— то здесь мы вновь имеем дело с пограничным слоем — самой
струей — и внешним спут-
ным потоком.
Рассмотрим еще «началь-
ный» участок некоторого
сопла, в который втекает
вязкая жидкость (рис. 3). На
внутренних стенках сопла,
как на всяких твердых по-
верхностях, возникает по-
граничный слой,' постепенно
развивающийся вниз по по-
току. Внутри сопла, вне
этого пограничного слоя, существует «внешний поток», который исчез-
нет только тогда, когда сомкнутся пограничные слои, образовавшиеся
на стенках. Вниз йо потоку за этим сечением не будет «внешнего по-
тока», не будет и «пограничного слоя»; в этой области происходит
установившееся движение вязкой жидкости, Для расчета которого
надо применять общие методы динамики вязкой жидкости. Пользо-
ваться методами теории пограничного слоя можно будет, очевидно,
только в области «начального» участка. При этом, как легко видеть.
Рис. 3.
16
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ. I
по мере нарастания пограничного слоя должно изменяться и движе-
ние во внешнем потоке. Таким образом, начальный участок дает нам
простой пример существенного взаимного влияния пограничного слоя
и внешнего потока.
При очень больших значениях числа Рейнольдса потока, с кото-
рыми приходится иметь дело в практических приложениях теории
пограничного слоя, толщина пограничного слоя бывает очень мала
по сравнению с характерным для потока продольным размером. Так,
например, максимальная толщина пограничного слоя, достигаемая на
задней кромке лопатки рабочего колеса паровой турбины, измеряется
в долях миллиметра, а на крыле самолета не превышает сантиметров.
Сравнительно толстые пограничные слои нарастают вдоль судовых
корпусов, имеющих длину до ста и более метров; толщина погра-
ничного слоя вблизи кормы таких корпусов может доходить до пяти
и более десятков сантиметров. Как ранее уже было отмечено, тол-
щина пограничного слоя зависит от рейнольдсова числа; только что
указанные порядки величин приведены как некоторые средние и дают
лишь общее представление об относительной малости толщины по-
граничного слоя.
§ 2. Вывод уравнений Прандтля
Воспользуемся отмеченной в предыдущем параграфе малостью
толщины пограничного слоя по сравнению с характерными для по-
тока продольными размерами и примем еще, что радиусы кривизны
линий тока имеют порядок этих продольных размеров. Такое допу-
щение позволяет значительно упростить выбор системы координат,
в которых должны быть составлены уравнения движения жидкости
внутри пограничного слоя. Выберем какую-нибудь одну линию тока,
целиком расположенную внутри пограничного слоя, за основную
и построим сетку линий, параллельных и перпендикулярных к этой
основной линии тока. На рис. 4 в качестве примера рассмотрен
случай обтекания крылового профиля, и за основную линию тока
§ 2] ВЫВОД УРАВНЕНИЙ ПРАНДТЛЯ 17
принята «нулевая», совпадающая с контуром тела. В этом случае
допускается, что радиусы кривизны в точках контура очень велики
по сравнению с соответствующими этим точкам толщинами слоя. Это
и на самом деде обычно имеет место, так как радиусы кривизны
сравнительно невелики только вблизи носика, но здесь и толщина
слоя особенно мала.
Пользуясь малостью поперечного к направлению потока размера
пограничного слоя, можно изображенную на рис. 4 криволинейную
сетку считать внутри пограничного слоя прямолинейной ортогональ-
ной сеткой декартовых координатных линий (х, у). Такое допущение
не является обязательным и сделано лишь для упрощения изложе-
ния *). В принятых координатах, если пренебречь объемными силами,
уравнения Стокса плоского движения вязкой несжимаемой жидкости
будут иметь вид
да , да , да 1 dp , / д2и , д2и\
dt дх ' ду р дх \ дх2 ' ду2)'
dv , dv . dv 1 dp . I d2v . d2v \
dx "+" dy ~~ U' J
где приняты обычные в гидромеханике плоского движения обозначе-
ния: и, v—продольная и поперечная компоненты скорости, р — да-
вление, р и v = — — соответственно плотность и кинематический
коэффициент вязкости жидкости.
Имея в виду произвести в дальнейшем сравнительную оценку по-
рядка величин отдельных членов, входящих в систему уравнений A.1),
перейдем к безразмерной форме этих уравнений. При этом будем
иметь в виду ранее уже отмеченную «анизотро-пию» пограничного
слоя — малость поперечных размеров этой области движения по срав-
нению с продольными размерами потока и связанную с нею малость
поперечных скоростей по сравнению с продольными. Не имея еще
никаких определенных количественных суждений по этому поводу,
выберем, исходя просто из интуитивных соображений, различные по
величине постоянные масштабы измерения продольных и поперечных
длин, в частности, координат, и различные масштабы для продольных
и поперечных компонент скорости;
') Более общий вид уравнений и оценку входящих в них дополнитель-
ных членов, учитывающих влияние кривизны координатных линий, можно
найти в книге; К о ч и н Н. Е., К и б е л ь И, А. и Розе Н. В., Теорети-
ческая гидромеханика, Гостехиздат, 1948, стр. 435—437, а также в моно-
графии: Ш л и х т и н г Г., Теория пограничного слоя, перев. с нем., ИЛ,
1956, стр. 108—109.
Вопрос этот не является существенным для практических задач теории
пограничного слоя и поэтому нами опускается.
2 Зак. 297. Л, Г, ЛоЙЦяискнй
18:
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ, I
Обозначим через X масштаб продольных координат х, через
У—масштаб поперечных координат у; через ?/и V^ соответственно
масштабы продольных и поперечных компонент скорости.
Примем в качестве масштабов скалярных величин времени и да-
вления некоторые, пока неопределенные, постоянные величины Т и Р.
Условимся отмечать Штрихом соответствующие безразмерные пере-
менные, положив
t—Tt', x = Xx', y-=Yy'
u=Uur, v =
p-=Pp'.
(L2)
Тогда, подставив эти величины в систему уравнений A.1), получим
после простых преобразований:
X ди'
ди,'
UT dt
X dv'
дх'
, XV
-г уи v
P
хГ
1 YU u
PX
, da'
dp'
дх'
, dv'
Z'
д2и'
ду'
ди'
дх'
XV
1 XU dx"
l v d2v
ду'
-+
vX
ду'г
(L3)
Используем имеющийся пока произвол в выборе постоянных мас-
штабов измерения входящих в уравнение переменных величин.
Прежде всего, независимо от того, задаются ли в рассматриваемом
¦случае движения какие-то конкретные длины и скорости (например,
линбйный размер обтекаемого тела, скорость набегающего на него
потока), или их можно лишь условно составить но заданным наперед,
характерным для> потока параметрам другой природы (например, им-
пульс струи в теории затопленной струсь лобовое сопротивление тела
в теории следа за телом), будем считать основными масштабами ве-
личины X и U и составим при их помощи рейнольдсово число потока
XU
A.4)
В общем случае в числителе может стоять любая комбинация
заданных в количественной постановке задачи характерных для потока
величин, лишь.бы только эта комбинация имела ту же размерность,
что и знаменатель. Условимся в дальнейшем под рёйнольдсовьГм числом
потока понимать любую безразмерную комбинацию заданных наперед
параметров потока, содержащую кинематический коэффициент вязко-
сти в минус первой степени.
§ 2] ВЫВОД УРАВНЕНИЙ ПРАНДТЛЯ 1-9
Выбрав таким образом основные, в общем случае условные, мас-
штабы продольных длин и скоростей, выразим через них прежде всего
масштабы времени и давления, положив
T=~r P = ?U2. A.5)
и
В общем случае масштабы Т и Р не имеют простого физического
смысла. В частном случае задачи, о внешнем обтекании тела за мас-
штаб измерения времени принимается время, потребное для прохо-
ждения' частицей жидкости пути, равного характерной длине тела,
с характерной для потока скоростью, например скоростью набегающего
потока; за масштаб давления выбирается удвоенный скоростной напор,
составленный по характерной скорости потока.
Остается распорядиться масштабами поперечных длин и скоро-
стей Y и V. Выберем их из условия, чтобы система уравнений A.3)
содержала в качестве, единственного параметра основной параметр
потока — рейнольдсово число Re, определенное равенством A.4). Для
этого, как легко видеть, следует положить
XV __ -яХ _, .
YU ~~ Г2СТ ' ' '
причем выбор в правой части числовых значений, равных единице,
конечно', произволен и служит лишь упрощению окончательной формы
уравнений. Из равенств A.6) вытекает следующее определение мас-
штабов, поперечных длин и скоростей:
A.7)
При установленном выборе масштабов система уравнений A.3) при-
обретает вид
ди' , , да' , , да'
\- и' \- vr —
dt дх' ду'
' dv' , , dv' , , dv' \
- v 1 =
Re V dt' дх' ду'
' ди' , dv'
dp'
дх'
ду'
+
1
Re
Re2
dhi'
дх'2
дх'2
, д*и'
1 ду"
1 Re
дЧ'
ду'2
дх' [ ду'
A.8)
Полученная система уравнений представляет собой исходную си-
стему A.1) уравнений Стокса, преобразованную к безразмерному виду
Я'Вно содержащему основной параметр —рейнольдсово число потока Re.
Не останавливаясь на рассмотрении безразмерной формы начальных
и граничных условий — они весьма разнообразны для различного типа
задач, — заметим, что система A.8) содержит малый параметр, за ко-
торый естественно принять величину l/]/Re, входящую в равенства
A.7), а следовательно, и в выражения безразмерных поперечных коор-
динат и скоростей. Рассматривая формально разложения решений
20
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ. I
системы A.8) по степеням этого малого параметра
I/Re
/Re
A.9)
где в0
, p'Q, u'v v'v p'v . . . представляют собой функции безраз-
мерных координат и времени, подставим эти разложения в систему A.8)
и сравним коэффициенты при нулевых степенях малого параметра
в обеих частях уравнений этой системы. Результат будет такой же,
как если бы мы просто устремили в уравнениях системы A.8) число
Рейнольдса Re к бесконечности, считая, что при этом неизвестные
функции и', v' и р' будут стремиться к некоторым конечным пре-
дельным функциям а'о, v'o, p'Q. Тем или иным путем получим уравне-
ния этого нулевого приближения:
dt
' i
дх'
дип
ду'
дх'
дх'
дРр
ду'
ду'2
ду'
—0
A.10)
Как это непосредственно следует из равенств A.7), конечным
значениям безразмерных поперечных координат у' при больших зна-
чениях Re соответствуют малые абсолютные значения размерных
координат у. Таким образом, уравнения A.10) описывают движение
жидкости в тонкой области, расположенной вдоль основной (нулевой)
линии тока, причем, согласно тем же равенствам A.7), размеры этой
области должны убывать с ростом рейнольдсова числа, как l/]/Re.
Эту область мы и назовем пограничным слоем, а уравнения A.10)
примем за безразмерную форму уравнений движения вязкой несжи-
маемой жидкости в пограничном слое. Возвращаясь к обычным раз-
мерным величинам и опуская индекс нуль, получим следующую си-
стему уравнений плоского движения вязкой несжимаемой жидкости
в пограничном слое в том виде, как они были опубликованы их
автором Л. Прандтлем в 1904 г.1):
ди
~дТ~
1-й
~дТ~т
ди
дх '
¦ V
|
ди
^у
dv
~ду
1 др
дЧ
ду2
= 0.
A.11)
J
) Prandtl L, Ober FIQssigkeltsbewegung bei sehr kleiner Reibung;
Verhandt. d. Ill Intern. Mathem. Kongress, Heidelberg, 1904 (имеется русский
перевод, см. П р а н д т л ь Л., Теория несущего крыла, ч. I, Движение жидко-
сти с очень малым трением, ГНТИ, 1931).
§ 2] ВЫВОД УРАВНЕНИЙ ПРАНДТЛЯ 21
Второе уравнение системы A.10) опущено, но в дальнейшем всегда
будет приниматься во внимание, что давление р представляет функ-
цию только от координаты х, а в случае нестационарного слоя — и
от времени.
Система A.11) является неопределенной, так как содержит три
неизвестные функции: a, v и р. Для устранения этого недостатка
необходимо использовать дополнительные соображения.
Так, следуя Прандтлю, можно принять, что при больших значе-
ниях рейнольдСова числа, когда пограничный слой очень тонок, можно
пренебречь его влиянием на внешний поток. При этом под внешним
' потоком следует понимать то течение идеальной жидкости, которое
происходило бы в рассматриваемом случае при полном отсутствии
влияния вязкости, т. е. без пограничного слоя. Так при решении
задачи о плоском, безотрывном обтекании крылового контура рас-
пределение давлений рассчитывается заранее путем применения мето-
дов теории плоского обтекания крыла бесконечного размаха безвихре-
вым потоком идеальной жидкости. Точно так же в задачах о следе
на достаточном удалении от тела и о затопленной струе давление при-
нимается одинаковым во всем пространстве, что соответствует усло-
вию отсутствия вязкого влияния этих течений на окружающий поток.
В тех случаях, когда такое пренебрежение обратным влиянием
пограничного слоя на внешний поток недопустимо, приходится либо
вводить теоретические поправки на это идеальное распределение да-
вления, либо определять действительное распределение давлений
опытным путем.
Если сохранить введенное Прандтлем представление о том, что
распределение давления в пограничном слое совпадает с тем, кото-
рое было бы на поверхности тела или просто на нулевой линии тока
при отсутствии пограничного слоя, то, обозначая через U=U(x, t)
величину продольной скорости и замечая, что на поверхности тела,
так же как и в более общем случае на нулевой линии тока, г>=0,
получим из первого уравнения системы A.11):
dt ~" дх У дх ' ^ ' '
Определенная таким образом скорость U носит наименование «ско-
рости на внешней границе пограничного слоя».
Исключая давление из первого равенства системы A.11) и урав-
нения A.12), получим следующую форму уравнений пограничного слоя:
dt ' дх ' ду dt - дх ' v dv2
22 УРАВНЕНИЯ ПРАНДТЯЯ [ГЛ. f
Граничные условия при внешнем обтекании тел имеют обычно вид
и = г! = 0 при у = 0,
U при у-^оо. '
Стоящие во второй строке условия соответствуют асимптотиче-
скому стремлению продольной скорости и к «скорости на внешней
границе пограничного слоя» U, которая считается наперед заданной
и, как уже указывалось, должна быть определена из решения задачи
о движении идеальной жидкости.
При исследовании задач о нестационарном пограничном слое к этим
граничным условиям присоединяются начальные условия, выражающие
распределение скоростей внутри пограничного слоя в некоторый на-
чальный момент времени.
Граничные условия A.14) представляют собой простейший вариант
этих условий, относящихся к задачам внешнего обтекания тел. В дру-
гих случаях можно встретиться с разнообразными типами других гра-
ничных условий, примеры которых мы в дальнейшем укажем.
Так, например, в случае струи с прямолинейной осью вместо A.14)
будем иметь вытекающие из соображения симметрии условия
~=0, х>=0 при у=0, 1
дУ У У } A.15)
и->0 при у-^оз. J
Для получения решения, отличного от очевидного, тривиального
решения a==t/ = 0, в этом случае используется условие сохранения
вдоль струи заданного начального ее импульса.
В некоторых .задачах наряду с граничными условиями, заданными
по координате у, т. е. по поперечному сечению пограничного слоя,
приходится иметь дело с заданием начального профиля скоростей
ио(у) при некотором х = х0 (задача о «продолжении» слоя).
Вопрос об условиях единственности решений уравнений погранич-
ного слоя составил предмет многих математических изысканий, но
остается до сих пор в значительной степени открытым, так же как и
соответствующий вопрос теории движения вязкой жидкости вообще!).
В частном случае стационарного движения уравнения пограничного
слоя упрощаются и будут иметь один из следующих видов:
ди , ди 1 dp , д2и
«fc+ifc о,
дх ' ду
A.16)
') См. Пискунов Н. С, Изв. АН СССР, сер. матем., 7, № 1 A943);
Долидзе Д. Е„ Сообщения АН Груз. ССР, 5, № 9 A944).
§ 3] УРАВНЕНИЕ ПРАНДТДЯ — МИЗЕСА 23
ИЛИ - -
ди, , ди ,-j dU , д2и
ди , dv „
дх * ду
A.17)
Стоящий в правой части символ полной производной объясняется
тем, что в случае стационарного движения давление р или связанная
с ним скорость на внешней границе слоя U зависят только от одной
переменной х.
Приведенный в настоящем параграфе вывод уравнений Прандтля,
как уравнений нулевого приближения в методе представления решений
уравнений Стокса при больших значениях Re разложениями по сте-
пеням малого параметра 1/]/Re, имеет чисто интуитивный характер.
Строгая постановка этого вопроса составила предмет тонких иссле-
дований Го Юн-хуая ')> указавшего способ избежать возникновения
неравномерной точности приближений из-за наличия особенностей
в уравнениях задачи. Им же установлены приемы определения при-
ближенных граничных условий для последовательных приближений.
Дело в том, что с повышением номер'а приближения область «погра-
ничного слоя» расширяется за счет «внешнего потока», так что,, если
в нулевом приближении, скажем, для задачи внешнего обтекания тела,
должно быть выполнено ранее уже указанное условие асимптотиче-
ского стремления продольной скорости к «скорости на внешней гра-
нице слоя»', то в старших приближениях эта скорость должна быть
заменена соответствующим членом в разложении скорости «внешнего
потока» по степеням малого параметра l/]/"Re.
Теория пограничного слоя относится к столь большим значениям
числа Рейнольдса, что довольствуется нулевым приближением, соот-
ветствующим Re—>со; исследование последующих приближений уже,
собственно говоря, выходит за рамки теории пограничного слоя и
относится к общей теории движения вязкой жидкости.
§ 3. Уравнение Прандтля — Мизеса
Чтобы удовлетворить уравнению неразрывности, вводят функцию
тока ф, положив
') См. обзорную статью Чень Сюэ-сеня «Метод Пуанкаре — Лайт-
хилла — Го» в сб. «Проблемы механики», ИЛ, I960, а также оригинальную
работу Го Юн-хуая, помещенную в Journ. Math, and Phys. 32 A953).
24 УРАВНЕНИЯ ПРАНДТЛЯ [ГЛ. I
При этом уравнения Прандтля A.11) или соответственно A.13)
сводятся к уравнению третьего порядка
дЦ , di/ dsi> д'\> дЧ
dt ду ~^~ ду дх ду дх ду2
р дх ' ду3 dt ' дх ' ду3 ч '
В случае задачи внешнего обтекания тремя граничными условиями
для этого уравнения третьего порядка будут
¦ = 0 при у = О,
1 при у-»оо.
A.20)
J
Первые два условия означают, что линия у — 0 совпадает с нулевой
линией тока ф = 0, а продольная скорость а=-~ равна нулю на
поверхности тела; третье выражает асимптотическое стремление про-
дольной скорости к скорости внешнего потока. Условие г»==—- -^- —О
при у — О является следствием равенства ф = 0 на поверхности тела.
Уравнение A.19) в случае стационарного пограничного слоя может
быть преобразовано к более простому виду, если, как это независимо
друг от друга сделали Прандтль и Мизес*), ввести вместо у в ка-
честве новой независимой переменной функцию тока ф.
Обозначим' новые независимые переменные так: \ = х, ч\ = ^\
тогда, согласно A.18), будем иметь следующие формулы преобразо-
вания от старых переменных к новым
д д , д-п д d,.JL. 1
A.21)
Применяя их к первому из уравнений системы A.17), получим
ди ди\ | ди jTd[/ , д I ди
дя О-q / ' д-q di ' d-q \ д-q J ч /
или
ди ,, dU д
') v. Mises R,, Bemerkungen zur Hydrodjrnamik, ZkiAK, 7 A927),
стр. 425. См, также P r a n d 11 L, Zur Berechnung der Qrenzschichteri, ZAMM,
18, № 1 A938). Уравнения Мизеса, опубликованные в 1927 г., были известны
Прандтлю еще в 1914 г.
§ 3] . УРАВНЕНИЕ ПРАНДТЛЯ — МИЗЕСА 25
Это уравнение можно дополнительно упростить, если ввести
в рассмотрение так называемый «дефект-кинетической энергии»
Тогда, замечая, что U является функцией только \ = х, пре-
образуем уравнение A,23) к окончательному виду
дг ™ d*z ' A 9^
m ( }
Это и есть уравнение Прандтля — Мизеса.
Граничные условия в простейших случаях не содержат задания
начального распределения z -при ? — 0, а только условия при tj=O
и т)= оо:
(ад
2=0 при т] = од. J
Нелинейное уравнение A.26) по внешнему виду напоминает линей-
ное уравнение распространения тепла, но существенно отличается.
от него тем, что коэффициент при второй производной не постоянен,
а является функцией z. Можно сказать, что уравнение Прандтля —
Мизеса соответствует уравнению теплопроводности с коэффициентом
температуропроводности, зависящим от температуры. Чтобы конкре-
тизировать эту зависимость, заменим в уравнении A,25) величину и
ее явным выражением через z по A.24):
и = у IP — 2z = У 2 уТ^г; A.27)
тогда уравнение Прандтля — Мизеса примет новую форму
Предположим, что уравнение Прандтля — Мизеса каким-то спо-
собом разрешено, т. е. найдено выражение z(l, t\). Тогда для дове-
дения решения до конца необходимо воспользоваться очевидным
равенством
[^(Л=. - A-29)
2
из которого путем обращения интеграла можно найти искомое выра-
жение функции тока ф в переменных х, у.
26 УРАВНЕНИЯ ПРАНДТЛЯ .[ГЛ. I
Преобразование Прандтла — Мизеса можно несколько обобщит^
задав I неопределенным интегралом от произвольной функций ш (л:)
и сохранив прежний вид для преобразования у г)
х у
fw(x)dx==i, J а{х, y)dy — t\. A.30)
о о
Формулы A.21) переходят при этом в такие:
_д__ ш_д _д_
дх дс, дч\
д д д2 д
ду дт\ ду2 от]
A.31)
после чего окончательная форма уравнения [z определяется тем же
равенством A.24)] будет
Ж^'-vw (L32)
при этом предполагается, что со выражено в функции от %. Возмож-
ность выбора различных видов функций ш позволяет не только
упростить решение задачи ламинарных течений, но окажется полез-
ной и при рассмотрении некоторых плоских турбулентных потоков.
§ 4. Пограничный слой на пластинке (задача Блазиуса)
В качестве первого примера рассмотрим пограничный слой на
пластинке в стационарном однородном (U == const) внешнем потоке.
Обозначим скорость набегающего потока (рис. 5) через ?/ю; напра-
вим ось х по пластинке, ось у—перпендикулярно к ней, а начало
координат поместим в переднюю кромку О пластинки. В рассматри-
ваемом случае будет
dt ^""' дх -""'
и уравнение A.19) сведется к следующему:
ду дхду дх ду* ~~ ду
Граничными условиями будут
ф == 0 ¦ при у = 0 и —oo
|i- = o прш y = Q и 0<
-V—>• и со нри у->со и —сю
д3 ' к '
A.34)
') Лойцянский Л. Г., Труды ЛПИ (Энергомашиностроение, Техни-
ческая гидромеханика), № 176, Машгиз, 1955, стр. 101—103.
§ 4] ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНКЕ (ЗАДАЧА БЛАЗЙУСА)
27
где L — длина пластинки. Кроме того, на оси Ох вне пластинки
должно выполняться условие
ду2
при
= 0, х<0
и
У
В такой полной постановке задача до сих пор не разрешена
из-за непреодолимых трудностей, связанных с выполнением различ-
ных граничных условий на пла-
стинке и вне ее на той же
оси х.
Блазиусом х) была предло-
жена приближенная постановка ц
той же задачи, допускающая
удовлетворительное решение
повсюду, кроме областей вблизи
передней и задней кромок пла- -
стинки, и позволяющая с доста-
точной точностью найти сопро-
тивление пластинки. Вместо Рис. 5.
пластинки заданной длины рас-
сматривается полубесконечная пластинка с передней кромкой в начале
координат. При этом граничные условия A.34) принимаются в сле-
дующем упрощенном виде:
О
V
\
Д
) = 0, ^=0 при
-|i- -> t/o, при
= 0, x > 0,
A.35)
Отсутствие в граничных условиях характерной длины — в данном
случае длины пластинки L — позволяет свести уравнение в частных
производных A.33) к обыкновенному. Следуя ранее изложенной
теории, составим безразмерные координаты задачи в форме:
х' = х/1 и у' = уЦь/УШ) = У YUcoHyL).
Из первого равенства системы A.19) следует, что масштабом
функции тока должна быть величина C/0OZ./")/"l^e = |/VG^Z. Из ра-
венства
и условия независимости ф от L заключаем, что структура ф должна
быть следующей:
В 1 a s I u s Нч Zeitechr. fur Math. u. Phys., 66 A908).
28 УРАВНЕНИЯ ПРАНДТЛЯ [ГЛ. I
Будем искать поэтому решение задачи Блазиуса в форме
^=/v[/coxcp('/]), 7j = у l/ i^2 . л .36)
Вычисляя значения производных (штрих—-производная по rj)
и подставляя их в уравнение A.33) и граничные условия A.35),
получим следующее обыкновенное нелинейное уравнение:
= 0> A.37)
которое должно быть проинтегрировано при граничных условиях
<р = 0, ср'=О при т]= О,
, i A-38)
1 при tj—>оо. ¦
Блазиус представил решение этого уравнения в виде совокуп-
ности степенного ряда при малых т/ и асимптотического выражения
при больших т)J):
. . а , а2 - . Па3 , 375а4 „ .
где а =0,332 при малых т) и
i
<р(т])~ т)—1,73 + 0,231 J-
-7(т,-1.78)»
со со
при больших г) (.— — знак асимптотического равенства).
В дальнейшем уравнение A.37) с большой степенью точности
было решено численным методом Тепфером2), а затем и рядом
других авторов (Хоуарт, Хартри).
В таблице 1 приведены рассчитанные Хоуартом3) значения функ-
ции ср (т|) и первых ее двух производных.
Пользуясь таблицей 1, легко найти местное напряжение трения
на поверхности пластинки тщ и полное ее сопротивление трения W^.
') См. подробное изложение этого пути решения в книге: К о ч и и Н. Е.,
К и б е л ь И. А. и Р о з е Н. В., Теоретическая гидромеханика, ч. И, изд. 3,
Гостехиздат, 1948, стр. 456—459.
2) Toepfer С, Zeitschr. f. Math. u. Phys. 60 A912), 397.
3) H о w a r t h L., Proc. Roy. Soc. London, ser. A, 1938, № 164.
4]
ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНКЕ (ЗАДАЧА БЛАЗИУСА) 29
Таблица 1
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3;4
3,6
3,8
4,0
4,2
4,4
f
0
0,00664
0,02656
0,05974
0,10611
0,16557
0,23795
0,32298
0,42032
0,52952
0,65003
0,78120
0,92230
1,07252
1,23099
1,39682
1,56911
1,74696
1,92954
2,11605
2,30576
2,49806
2,69238
, и
0
0,06641
0,13277
0,19894
0,26471
0,32979
0,39378
0,45627
0,51676
0,57477
0,62977
0,68132
0,72899
0,77246
0,81152
0,84605
0,87609
0,90177
0,92333
¦0,94112
0,95552
0,9.6696
0,97587
0,33206
0,33199
0,33147
0,33008
0,32739
0,32301
0,31659
0,30787
0,29667
0,28293
0,26675
0,24835
0,22809
0,20646
0,18401
. 0,16136
0,13913
0,11788
0,09809
0,08013
0,06424
0,05052
0,03897
4,4
4,6
4,8
5,0
5,2
5,4
5,6
5,8
.6,0
6,2
6,4
6,6
6,8
7,0
7,2
7,4
7,6
7,8
8,0
8,2
8,4
8,6
8,8
2,69238
2,88826
3,08534
3,28329
3,48189
3,68094
3,88031
4,07990
4,27964
4,47948
4,67938
4,87931
5,07928
5,27926
5,47925
5,67924
5,87924
6,07923
6,27923
6,47923
6,67923
6,87923
7,07923
ф' - и
0,97587
0,98269
0,98779
0,99155
0,99425
0,99616
0,99748
0,99838
0,99898
0,99937
0,99961
0,99977
0,99987
0,99992
0,99996
0,99998
0,99999
1,00000
1,00000
1,00000
1,00000
1,00000
1,00000
0,03897
0,02948
0,02187
0,01591
0,01134
0,00793
0,00543
0,00365
0,00240
0,00155
0,00098
0,00061
0,00037
0,00022
0,00013
0,00007
0,00004
0,00002
¦0,00001
0,00001
0,00000
0,00000
0,00000
Замечая, что
-ср"(О);
= 0,332,
юлучим формулу Блазиуса
xw = 0,332 J/
A.39)
огласно которой напряжение трения на поверхности пластинки убы-
:ает вдоль пластинки обратно пропорционально квадратному корню
13 х; кривая этого изменения показана на рис. 5.
Вводя местный коэффициент сопротивления
шйдем следующее его выражение через местное число Рейнольдса'
^„= t/cox/v:
A.40)
80
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ.
Полное сопротивление трения пластинки длины L, смоченной
с обеих сторон, будет
L
= 2 J т„ dx = 1,
328
A.41)
а коэффициент полного, сопротивления трения
Г1'
Ч
(S—смоченная поверхность)
определяется формулой
с = 1>т
f /Re
¦Re=-
A.42)
На рис. 6 в безразмерных координатах
U
ставлен график распределения скоростей в сечениях пограничного
слоя на' пластинке. Это — плавная кривая, близкая к прямой при
малых абсциссах и асимптотиче-
ски переходящая в горизонталь-
ную прямую -^- = 1 при боль-
^ со
ших значениях этих абсцисс. На
том же графике указаны экспери-
ментальные точки по опытам Хан-
зенаJ). Небольшие отклонения
в сечении х = 3 см могут быть
объяснены близостью, передней
кромки пластины, имевшей форму
узкого клина. Теория Блазиуса
была также подтверждена позд-
В нейшими опытами И. Никурадзе2).
На рис. 7 приводится сравнение
результатов опытов Никурадзе
с теоретической кривой Блазиуса
. (на рисунке сплошная кривая).
По-видимому, первой экспериментальной проверкой формулы
сопротивления A.42) явилось исследование Фейджа3), проведенное
в .интервале рейнольдсовых чисел . от 14 000 до 200 000. Не имея
,-аозможност» непосредственно динамометрировать малые силы, Фейдж
определял сопротивление косвенным путем по метод)^ импульсов,
1 П
O.S
-4.
/
+
f
У
/
и
У'
+
ъх-Юсм -
®х=15ем
4 S
Рис.-6.
') Hansen M., Zeitschr. f. Angew. Math, u, Mech. 3, Щ 3 A928).
2) Nikuradse J., Laminare Reibungsschichten an der langsangestromten
Platte. Zentrale i Wiss. Berlchtwesen, Mflncben — Berlin A942),
3) F a g e A., ARC, R & M, 15.80 A934).
ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНКЕ., (ЗАДАЧА БЛАЗИУСА)
-81
основанному на измерении продольных скоростей в следе за пла-
стинкой. По опытам Фейджа величина коэффициента сопротивления
оказалась выше соответствующего значения коэффициента по Блазиусу
примерно на 6%, что скорее всего можно объяснить наличием
v пластинки конечной толщины и неточностью метода измерений,
Более поздние измерения И. Никурадзе, опубликованные в только
то цитированной его монографии, дали значения: С^= 1,315/]/Re
по способу дифференцирования экспериментального профиля ско-
юстей) и С.= l,319/]/]Re (метод импульсов). Отклонения от фор-
(.421 не превосходят 1%,
'.О
0,6
o,4
0,2
О 1,0 2,0 3,0 4,0 50 6,0 7,0
/
/
А
ЗЭНИЗР
+ 1,08-10 s
•Ш -10s
п7,28-105
Рис. 7.
летод непосредственного замера силы сопротивления при помощи
jecoB типа крутильных был разработан Шульцем — Груновым1),
Тот факт, что профили продольных скоростей в различных сече-
шях пограничного слоя, построенные в координатах
.ожатся (рис. 6) на одну и ту же кривую, показывает, что распре-
деления скоростей подобны между собою, отличаясь при различных х
'олько масштабами скорости и поперечной координаты.
Движения в пограничном слое, обладающие свойством подобия
л описываемые в связи с этим такими дифференциальными уравне-
ниями, число аргументов в которых может быть сведено к меньшему
числу (в рассматриваемом сейчас случае плоского движения уравне-
ния в частных производных сводятся к обыкновенному), носят наи-
менование «подобных» или «автомодельных». Задача Блазиуса дает
нам первый пример такого рода «автомодельных» движений. В сле-
l) Schujtz — Qrunow F., Lufifahrt-Forschung, 17, № 8 A940).
32 УЕАВНЕНИЯ ПРАНДТЛЯ [ГЛ. !
дующих параграфах настоящей главы и неоднократно на протяжении
настоящей книги мы будем еще встречать примеры «автомодельных»
движений. Заметим, что понятие «автомодельности» относится к ши-
рокому классу физических явлений и изыскание автомодельных
решений представляет практический путь рассмотрения разнообраз-
ных задач математической физики.
Если выбрать за масштаб поперечных координат «толщину погра-
ничного слоя» 8, понимая под этой толщиной такое значение у, при
котором продольная скорость и отличается от скорости внешнего
потока Um на выбранную наперед малую величину, то распределение
скоростей представится приближенно в выражающей свойство подо-
бия форме
Из третьего столбца таблицы 1 можно, задаваясь, например, значе-
нием скорости и, отличающимся от U^ на 1 %, определить толщину
пограничного слоя (в принятом условном смысле слова) приближен-
ной формулой
8 = 5}/"-^-. A.44)
Определенная таким образом «толщина слоя» растет вниз по потоку
вдоль пластины пропорционально корню квадратному из абсциссы
сечения слоя и представляется графически параболой (рис. 5).
Зависимость толщины слоя 8 от рейнольдсова числа задачи
Г^е = —— получим, переписав последнее равенство в форме
A-45)
Это равенство подтверждает ранее уже высказанное общее свой-
ство ламинарного пограничного слоя: его толщина в любом сечении
обратно пропорциональна корню квадратному из рейнольдсова числа.
В рассмотренной в предыдущих параграфах асимптотической тео-
рии понятие о конечной «толщине» пограничного слоя имеет совер-
шенно условный характер и может способствовать лишь приблизи-
тельной оценке порядка ширины области пограничного слоя. В главе III
будет изложен приближенный метод решения задач теории погра-
ничного слоя, основанный на использовании представления о слое
конечной толщины.
Как уже отмечалось, решение Блазиуса непригодно вблизи перед-
ней и задней кромок пластинки. Можно заметить, что ввиду наличия
резкого продольного изменения скорости и сами уравнения Прандтля
вблизи этих точек становятся несправедливыми, и для анализа тече-
§4]
ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНКЕ (ЗАДАЧА БЛАЗИУСа)
33
ния приходится обращаться либо к непосредственному интегрирова-
нию полных уравнений Стокса, либо к тому методу разложения
решения в ряд по степеням малого параметра, о котором уже шла
речь в § 2. По первому пути для исследования движения вблизи
передней кромки пошел И. Е. Кочин в не доведенном им до конца
исследовании задачи об обтекании вязкой жидкостью полубесконечной
пластинки]). Избегнуть возникновения неравномерных уточнений при
построении первых двух при-
ближений по методу малого ^
параметра удалось Го Юн-
хуаю; его работа по этому
поводу уже была цитиро-
вана ранее.
Если числа Рейнольдса
не слишком велики, напри- д^
мер порядка сотен или даже
тысяч, то пользоваться вы-
ражением коэффициента пол-
ного сопротивления A.42),
вычисленным по теории по-
граничного слоя, т. е. ио
О
¦
и
/
/
/
/
/
, /
/
/
/
/
———
We.
I
s
б
нулевому приближению, уже
нельзя. В этом случае необ-
ходимо учитывать следую-,
щие приближения в разло- рис g
женин решения по отрица-
тельным степеням корня квадратного из рейнольдсова числа. Приво-
дим формулу
1>328
4,18
Re
A.46)
выведенную Го Юн-хуаем и хорошо подтверждаемую опытами, если
число Рейнольдса превосходит значение 10.
В расчетах по теории пограничного слоя основное значение
имеет продольная компонента скорости и, что же касается поперечной
компоненты v, то она в большинстве случаев играет второстепенную
роль, определяя собой так называемые «вторичные течения».
Пользуясь A.36), нетрудно составить выражение поперечной
скорости
и, пользуясь таблицей 1, вычислить ее значения при разных вели-
чинах т]. Результаты вычислений приведены в таблице 2, а .на рис. 8-
') К о ч и н Н. Е., Собрание сочинений, том И, Изд. АН СССР, стр. 493,
3 Зак..297. Л. Г. Лойцянский
34 УРАВНЕНИЯ ПРАНДТЛЯ . [ГЛ. I
представлен график поперечной скорости в форме зависимости
величины v'
безразмерной продольной скорости aj
v ~ТГ от ^' там же для сРаюения приводится и график
Т а б ли ца 2
¦1
0
0,2
0,4
0,6
0,8
1,0
2,0
/ X
¦0
0,00332
0,01328
0,02981
0,05283
0,08211
0,30475
3,0
4,0
5,0
6,0
7,0
8,0
8,4
Tj/ x
°У */<*
0,57066
0,75816
0,83723 .
0,85712
0;86004
0,86038
0,86038
Поперечная компонента скорости сначала слабо возрастает от
своего нулевого значения на поверхности пластины (как rf), затем
начинает расти быстрее, а в бесконечном удалении (вблизи внешней
границы слоя) стремится к некоторой конечной величине, зависящей
от х.
Как видно из последних строк таблицы 2, с возрастанием t\ до
бесконечности величина v
стремится к конечному пределу,
равному примерно 0,8604. Таким образом, пограничный слой, не
искажая в принятом приближении распределения продольных ско-
ростей во внешнем .потоке, создает в нем поперечные токи, легко
объясняемые с физической стороны торможением жидкости о по-
верхность пластины. В этом заключается обратное влияние погранич-
ного слоя на внешний поток.
§¦ 5. Задача о затопленной струе
Второй простой иллюстрацией решения уравнений пограничного
слоя может служить задача q распространении струи жидкости
в безграничном пространстве, заполненном той же, но неподвижной
жидкостью.
Будем считать, что из бесконечно тонкой щели (рис. 9), распо-
ложенной в точке О, в направлении оси Ох бьет струя с бесконеч-
ной скоростью, но с некоторым Конечным по величине секундным
количеством движения или импульсом Jo.
Вспоминая, что секундный импульс получается умножением
секундного расхода на скорость, заключим, что при конечности
§5]
ЗАДАЧА О ЗАТОПЛЕННОЙ СТРУЕ
35
импульса в бесконечно узкой щели расход через нее должен равняться
нулю. Физически это означает, что если щель очень мала, а скорость
истечения велика, то импульс может быть конечен только при очень
малых расходах; заметим, что нечто подобное обычно и наблюдается
в разнообразных струйных аппаратах, например в эжекторах, имею-
щих целью при малом расходе эжектирующей жидкости, но конеч-
ном ее импульсе, получить конечный расход эжектируемой жидкости.
При отсутствии вязкости пограничный слой не образовывался бы
и бесконечно тонкий слой жидкости, выходящий из щели в точке О,
двигался бы с бесконечно большой скоростью вдоль оси Ох, не
взаимодействуя с окружающей его неподвижной жидкостью. При
наличии вязкости этот бесконечно тонкий слой сразу же поале
выхода из щели смешивается
с окружающей жидкостью, во-,
влекает ее в движение и одно-
временно подтормаживается
сам. При больших числах Рей-
нольдса симметрично по обе
стороны от оси Ох, которую
примем за основную, нулевую
линию тока, образуется тонкий
пограничный слой, в этом кон-
кретном случае называемый
«затопленной струей».
По общему свойству погра-
ничных слоев давление поперек
струи не меняется, а так как во внешнем потоке — неподвижной жидко-
сти — давление повсюду одинаково, то и во всех точках струи
давление будет одним и тем же, Отсюда следует, что -j^ = 0, так'
что уравнение A.19) примет следующий вид:
Рис. 9.
ду дх ду
Граничными условиями будут
дЧ
дх ду2
ду3
W
= 0 при у = 0,
—*¦ 0 при у—»-+оо.
A.48)
A.49)
Очевидным тривиальным решением этой задачи является ф = О,'
т. е. отсутствие течения. Это противоречит заданию конечного- им--
" пульса струи JQ на выходе из щели.
Поставим в явной форме это основное условие задачи. Согласно
теореме о сохранении количества движения, имеющей место при
3*
36 УРАВНЕНИЯ ПРАНДТЛЯ [ГЛ. Г
условии отсутствия внешних сил (-т?%=0|, заключим, что секунд-
ное количество движения, протекающее сквозь произвольное сечение
струи, будет одним и тем же, так что
со
J == I ри2 dy = const = Jo. A.50)
Это интегральное условие и послужит условием существования
нетривиального решения.
Уравнение A.50) может быть выведено и из уравнений погранич-
ного слоя. Переписывая первое из уравнений A.16) при -у?- = 0, на
основании второго, в форме
д , 0, , д , . д2и
(«2)+(Р^)
и интегрируя его -поперек струи по у от — go до со, получим
со
/ й2 dy -f- [av] = v
-т- / й2 dy f [av]
dx
в силу принятых граничных условий для и и да/ду, подстановка
пределов дает нулевые значения, откуда и следует равенство A.50).
В рассматриваемом в настоящем параграфе случае нет ни харак-
терной скорости, ни характерной длины, но зато задана определяю-
щая данную конкретную струю величина ее импульса Уо.
Согласно ранее изложенной теории, заключим, что условные
масштабы продольных длин L и продольных скоростей U связаны
с масштабом функции тока ? соотношением
С другой стороны, в силу соотношения A.50), переписанного
в форме
получим в безразмерных переменных i]/, у'
)' = J0. A.53)
— СО
Приняв
/= 1, A.54)
й 5] ЗАДАЧА О ЗАТОПЛЕННОЙ СТРУЕ 37
найдем следующие выражения Ш и L через U:
¦' (L55)
l
Функция тока ф (х, у) должна иметь форму
- Вид функции / подчиним условию независимости ф от U; этого
можно добиться, приняв, что
При таком задании зависимости ф от безразмерных координат
величина U выпадает и функция тока выразится следующим образом:
Подставляя полученное выражение функции тока в' уравнение
в частных производных A.48), составим, после очевидных сокраще-
ний, обыкновенное дифференциальное уравнение третьего порядка
(штрих — производная по rj)
?'" +у (/+ <?<?") = О, A.58)
которое должно быть, проинтегрировано при граничных условиях
Ср=:О, Ср"=О ПрИ 7} = О,
ср'->0 при т\ ^-±оо A.59)
и интегральном условии
со
]У21. A.60)
Интегрирование уравнения A.58) не составляет труда и приводит
к следующему выражению для функции тока:
= 1,651 fT^ th (V275/^ ^=r). A-61)
полученному впервые Г. Шлихтингом 1). Из определения функции
тока следует, что секундный объемный расход Q через сечение
') Schlichting H., Zeitschr. f. Angew. Math. ц. Mech. 13, № 4
88
УРАВНЕНИЯ ПРАНДТЛЯ
[гл. i
струя с абсциссой х будет равен
Q = (j> (со) — ф (— со) = 3,302 ТЛ^Г.
A.62)
Поле скоростей в струе определяется совокупностью равенств
1
и ==0,454
fix ch2 @,275?)) '
A.63)
Соотношение A.62) показывает, что секундный расход жидкости
сквозь сечение струи растет от нулевого значения в щели (х—0)
пропорционально корню кубиче-
скому из расстояния от щели.
Продольная осевая скорость ат
определится из первого равенства
A.63) при 7j=Q и окажется рав-
ной
з
: 0,454'
1,0
0.8
0,6
0,2.
\
\
\
\
\
¦и„
V-,
A,64)
О
0,2
as пв
/
Полученное Г. Шлихтингом
решение, как показали опыты
Андрада 1), хорошо описывает
явление распространения плоской
ламинарной струи в пространстве,
заполненном той же жидкостью.
Однако следует указать, что сама
задача лишена практического т&-
чения, так как ламинарные струи
Рис. 10. устойчивы лишь при очень малых
рейнольдсовых числах. Уже при
рейнолъдсовбм числе, содержащем в качестве характерной длины ши-
рину щели, а характерной скорости-—скорость истечения из щели,
превышающем значение 30, такие плоские щелевые .струи теряют
свой ламинарный характер и становятся турбулентными. Закономер-
ности турбулентного распространения струи устанавливаются в теории
турбулентного пограничного слоя.
Рассмотренное только что движение относится к числу «подоб-
ных» или «автомодельных». Пользуясь первым равенством си-
стемы A.63), определим такое значение у, равное Ь{х), при кото-
') A n d г a d e E. N., Pro?. Phys. Soc. London 51 A939), 784.
§ 6] ПРИМЕНЕНИЕ УРАВНЕНИЯ ПРАНДТЛЯ МИЗЕСА 39
ром продольная скорость и составит лишь один процент от ит.
Будем иметь
Ь(х) = 10,91 (^Y'V/s. A.65)
Величину Ь(х) можно принять приближенно за полуширину
струи. Пользуясь этой мерой ширины струи, а также равенством A.64),
можно выражению продольной скорости в первом из равенств A,63)
придать вид
^ (L66)
наиболее наглядно выражающий свойство подобия профилей ско-
рости. На рис. 10 показан безразмерный профиль продольных
скоростей, общий для всех сечений струи и заданный равен-
ством A.66).
§ 6. Применение уравнения 'Прандтля—'Мизеса к задаче
о затопленной струе
Задача-о затопленной струе.дает пример точного решения урав-
нений пограничного слоя с помощью переменных Прандтля — Ми-
зеса !). Положим в уравнении A.32) ш = vam я перепишем его
в виде ((У — 0)
Пойдя для разнообразия несколько иным путем, чем раньше,
будем искать решение уравнения A.67) в форме
«2 = й*т(р(С). A-68)
где ит— пока неизвестная функция 5, а С — некоторая одночленная
степенная комбинация 5 и т?, заданная формулой
С = ¦»)?". A.69)
Подставляя значение С в A.67), после простых преобразований
получим уравнение (штрих — производная по С)
Для выполнения з^словия автомодельности решения, т. е. незави-
симости ср в явной форме от %, необходимо положить
2«-j-l = 0. A.71)
') Лойцянский Л. Г., Труды ЛПИ (Энергомашиностроение, Техни-
ческая гидромеханика), № 176, Машгиз, 1955, стр. 103—107.
40 УРАВНЕНИЯ ПРАНДТЛЯ ' [ГЛ. I
Отсюда следует, что (с и <у — некоторые константы)
йга=.у7е?. « = -va. A-72)
Постоянные с и q найдем, выполняя интегральное условие
сохранения количества движения A.50), которое в переменных
Прандтля — Мизеса может быть представлено так:
dfi = J0; A.73)
здесь ± а корни уравнения ср(С) —0.
Используя A.73), получим
откуда вновь, по условию автомодельности, найдем
из предыдущего уравнения при этом следует, что
c=L/fp /]/VdCj . A.74)
Выражением ит(?) будет служить равенство
A-75)
после чего решение A.68) примет окончательный вид
«2=-fcpOj/vD- ¦ A76)
Вопрос сводится, таким образом, к интегрированию обыкновен-
ного уравнения второго порядка
^О A.77)
при граничных условиях
<р=1 и (р' = 0 при С = 0, A.78)
вытекающих из A.68), а также условий симметрии и плавности поля
продольных скоростей в струе..
Уравнение A.77) последовательно интегрируется и при граничных
условиях A.78) имеет решение
4)\ . A.79)
§ 6] ПРИМЕНЕНИЕ УРАВНЕНИЯ ПРАНДТЛЯ -^ МИЗЕСА. 41
Корнями многочлена ф(С) будут значения ± 2 и, следовательно,
постоянная с, согласно A.74), окажется равной
A.80)
Окончательное выражение продольной скорости в переменных
Прандтля — Мизеса будет
1Р
A—1\. (L81)
' 8 р / ? 8 р /g \ 4?
Остается вернуться к декартовым координатам х и у, для чего
используем сначала равенство A.29), в настоящем случае имею-
щее вид
11 ^ 1 )- ^_
Р тд- Г ^1 _8ff ln 2/S
а затем найдем из него искомую связь между т] и )>>
_3=r=C=2thf—^Л. A.82)
/S U6 р 6 У
Для установления связи между х и \ вспомним первое из ра-
венств A.30), в данном случае приводящееся к такому:
X
v Г ит (х) dx = |;
J
о
дифференцируя обе части этого равенства по х и заменяя после
этого ат{х) его выражением A.75) в функции от %, получим
dx
откуда интегрированием найдем
"' W"x2/3, (I.83)
Подставляя это значение Ё в A.82), получим выражение для t\,
или, что все равно, для функции тока <Ь
42 УРАВНЕНИЯ ПРАНДТЛЯ
которое, может быть написано в форме
ту
[ГЛ. I
A.84)
полностью совпадающей с ранее полученным другим методом выра-
жением A.61).
§ 7. Распространение затопленной струи вдоль твердой ¦
плоской поверхности
Рассмотрим задачу о распространении плоской струи, бьющей
из щели в полупространство, затопленное той же жидкостью, вдоль
некоторой плоскости, причем щель расположена в той же плоскости
(рис. 11). В этом случае, подобно тому как это имело место в двух
предыдущих задачах, реше-
ние будет автомодельным,
т. е. уравнения движения
жидкости в пограничном
слое сведутся к одному
обыкновенному уравнению.
_х Рассматриваемое движе-
ние представляет в известном
р w- смысле соединение обоих,
ранее разобранных движе- -
ний; продольного обтекания
полубесконечной пластины и распространения струи в безгранич-
ном пространстве. Конечно, при нелинейности уравнений движе-
ния не может быть речи о каком-то наложений потоков друг на
друга; однако, как далее будет показано, некоторое сходство про-
филя продольных скоростей вблизи ограничивающей струю плоскости
с соответствующим профилем вблизи пластинки (задача Влазиуса) и
профиля скоростей вдалеке от плоскости с профилем в струе все же
наблюдается.
Задача о распространений плоской струй вдоль твердой плоской
поверхности была впервые поставлена и разрешена Н. И. Акатно-
выи г). Впоследствии та же задача рассматривалась Глауертом 2).
Уравнение движения остается прежним и имеет вид
О
ду дхду дх ду*
ду3
п 85)
') А к а т н О' в Н. И., Распространение плоской ламинарной струи
жидкости вдоль твердой стенки. Труды ЛПИ (Энергомашиностроение, Тех-
ническая гидромеханика), № 5, Машгиз, 1953, стр. 24—31.
г) О I a u е г i M., Journ. of Fluid Mech., № 1 A956),
& 71 РАСПРОСТРАНЕНИЕ ЗАТОПЛЕННОЙ СТРУЙ ВДОЛЬ ПОВЕРХНОСТИ 43
Граничные условия будут следующими:
-т1—>0 при у—>сю,
<L8jB>
J
Для существования решения, отличного от тривиального и = и,
v=0, необходимо задать некоторую количественную характеристику
явления. Импульс струи уже не является в данном случае харак-
терной постоянной, так как, в отличие от безграничной струи,
имеется подтормаживающее влияние твердой поверхности, уменьшаю-
щей импульс струи с удалением' от ее источника. Установим соот-
ветствующее рассматриваемому составному движению «уравнение
сохранения», которое вместе с тем и явится условием нетривиайь-
ности решения.
Проще всего это уравнение получить следующим образом. Пере-
нисав первое из уравнений Прандтля, согласно второму, в форме
д /,.оч , д ,,.„., ^ дЧ
дх у ' ' ду v ' ду*
и проинтегрировав обе части поперек слоя от у до оо» получим
/¦
, п. , , , ,оо Г ди
(и2) dy -4- [iw] = Ч-д—
у 1 ду
Поменяем в первом интеграле порядок интегрирования и диффе-
ренцирования'; тогда, используя граничные условия. A.86) и асимпто-
тичность последнего из них, найдем.
со
д Г „ . ди
дх J J ду
У
Умножим теперь обе части последнего равенства на и и возьмем
от них почленно определенный интеграл поперек слоя от 0 до оо.
Будем иметь
44 УРАВНЕНИЯ ПРАНДТЛЯ" [ГЛ. f
или, совершая очевидные преобразования в первом интеграле и
вычисляя второй интеграл по частям,
аз /со
[СО -1 СО СО
J J Ол \ <J I
у Jo 0 \у '
Согласно тем же граничным условиям, подстановка пределов дает
нулевое значение, и после сокращений получим •
со , со
•/"
о
откуда и следует искомое условие сохранения
° / °° \
i а и1 dy ay = const = с. A.8/)
J \ J j
О \у У
Левая часть этого равенства только формой отличается от уста-
новленного Н. И.. Акатновым инварианта и легко в него переходит,
если произвести повторное интегрирование по частям; действительно,
имеем
f иП a2dy\dy = f П иЧу\ d П udy\= ¦
о Ь / 'о [у / \о /
р со ¦ г' у
= \ \ tt2dy • I udy
Ly о
что приводит к такой, тождественной с A.87), форме «уравнения
сохранения»:
со / у >
Г я2/ f айГу di» = ?1. A.88)
J [ J
¦ о \о /
Вводя функцию тока ф, можем переписать предыдущие равен-
ства A,87) и A.88) еще в таком виде:
dty\dty=E, A.89)
о U /
A.90)
§ 7] РАСПРОСТРАНЕНИЕ ЗАТОПЛЕННОЙ СТРУИ ВДОЛЬ ПОВЕРХНОСТИ 45
Интегрирование по частям переводит одно из этих равенств
в другое. Последние выражения закона сохранения удобны при
решении задачи в переменных Прандтля — Мизеса.
Величине Е нельзя дать заранее наглядное физическое истолко-
вание; в дальнейшем в связи с анализом полученного решения выяс-
няется, что Е только численным множителем отличается от сохра-
няющегося постоянным произведения секундных объемного расхода
и количества движения.
Обозначим через L и U условные масштабы продольных длин и
скоростей; тогда, согласно общей теории, масштабом поперечных
длин будет служить величина
а масштабом функции тока
Обращаясь к условию нетривиальности решения в форме A.88),
получим (штрихом обозначены соответствующие безразмерные
величины)
со , V ,
v?/2L С и'2 I Г и' dy' dy' = E;
о \о /
считая масштабы выбранными так, что
СО , у' ,
j a'2 J ur dy' dy'= I, ¦ A.91)
о \о /
получим следующее выражение основных масштабов через 17:
Функция тока ф должна была бы при этом представляться в форме
но, имея в виду, что U не входит в число заданных величин и,
следовательно, ф не зависит от U, потребуем наличия следующей
структуры фзгнкции тока:
46 УРАВНЕНИЯ ПРАНДТЯЯ [ГЛ. I
или, окончательно,
'г--г—- (L93>
Подставив это значение ф в уравнение A.85), убедимся в авто-
модельности задачи: уравнение сведется к 'обыкновенному (штрих —
производная по tj)
AF'" + FF" + 2F'2 = 0; A.94)
граничные условия по A,86) примут вид
F=F' = 0 при т) —О,
A.95)
7'—>0 при т]—>оо, J
причем присоединяется еще интегральное условие
A.96)
легко выводимое из A.91).
Уравнение A.94) допускает интегрирующий множитель F. Найдем,
один раз интегрируя и определяя постоянную интегрирования из гра-
ничных условий A.95),
= 0. A.97):
Совершая в этом уравнении замену переменных
F' = <b A.98)
и принимая за независимую переменную F, получим линейное урав-
нение первого порядка
решение которого будет таким:
Ф=:Р' = СУР~ — ^Р*. A.100)
Обозначим через Fa, значение F при т;—со и Ф = 0. Тогда
определим постоянную С как
и уравнение A.100) может быть преобразовано к виду
§ 7] РАСПРОСТРАНЕНИЕ ЗАТОПЛЕННОЙ СТРУИ ВДОЛЬ ПОВЕРХНОСТИ
Постоянную Fa, определим, подставляя значения
4?
в интегральное условие A.96), Получим
Fa= 2,515.
Уравнение A.101) интегрируется и приводит к соотношению
tj= 0,7952 In
A.102)
Сравнивая его с уравнением A.101), переписанным в форме
F' = ~ (У 6 — 62) = 1,054 (VF— б2), AЛ 03)
получим F' в параметрической форме. График функции F' (tj) при-
веден на рис. 12.
Теперь нетрудно определить основные характеристики течения.
Выпишем выражения секундных объемного расхода Q и количества
движения К через данное сечение пограничного слоя;
« 4
= ? и dy= 2,515V v
К^ и»dy = 0.884T/ ^-.
A.104)
48
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ. I
Произведение их, как уже упоминалось, является величиной по-
стоянной и просто связано с константой Е
Приведем еще формулу выражения касательного напряжения трения
на плоской стенке
(да
1 \ду
: 0,221р.
A.105)
На рис. 13 и 14 сравниваются графики распределения скоростей
во внутренней (от стенки до точки максимума скорости) и внешней
Urn'
7,0
0,8
0,6
OA
0,2
J
I
Профиль Влазиуй г
—— Струму етеиии
0 1,0 2,0 3,0
Рис. 13.
(за точкой максимума скорости) областях струи с графиками ско-
ростей на пластинке и в свободной струе. По оси ординат в обоих
случаях отложены отношения и/ит, где ит — максимальная скорость,
а по оси абсцисс: .в первом случае отношение текущей ординаты у
к ординате у „, соответствующей значению скорости ат/2, во вто-
V — V
ром — отношение —-—ljLS—.
Графики оправдывают высказанное ранее соображение о сходстве
между графиками скорости для рассматриваемого случая сложного
движения и для ранее рассмотренных более простых случаев. Прак-
тически полное совпадение наблюдается во внешней области.
АЭРОДИНАМИЧЕСКИЙ СЛЕД ЗА ТЕЛОМ
49
Применение метода Прандтля —Мизеса1) к решению той же
задачи не даст ничего нового, так как легко видеть, что преобра-
зование A.98) и последующий переход к независимой переменной F
¦ИМ
10
0,8
0,6
OJ
0,2
О
O,S
7,0
2,0
Рис. 14.
представляет собой, собственно говоря, не что иное, как исполь-
зование в качестве аргумента функции тока, а в качестве неизвест-
ной функции величины скорости, на чем как раз и основан метод
Прандтля — Мизеса.
8.
след за телом
Задача о движении вязкой жидкости в пограничном слое, сошед-
шем с тела и образовавшем непосредственно за ним аэродинамиче-
ский след, в полной своей постановке представляет пока непреодо-
лимые трудности; известно лишь решение для продольно обтекаемой
пластинки, да и то в незначительной (не превышающей половины
длины пластинки) области за задней кромкой пластинки2). Сравни-
тельно просто решается вопрос о движении жидкости в следе на
большом удалении от тела, когда влияние формы обтекаемого тела
становится пренебрежимым и движение в следе определяется сум-
марной характеристикой подтормаживающего влияния тела—его
!) А к а т н о в Н. И., Применение переменных Мизеса к задаче о рас-
остранений ламинарной струи вдоль стенки, ПММ, 1960, т. XXIV, вып. 1;
м же можно найти "обобщение изложенной в настоящем параграфе задачи
случай наличия вне струи однородного спутного потока.
2) Goldstein S., Proc, of the Cambr. Phil. Soc. 25 A930), 1—25.
4 Зак. 297, Л. Г. Лойцянсвий
50
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ.
сопротивлением. Эта задача1) и будет рассмотрена в настоящем
параграфе.
Обозначим через U^ скорость однородного потока, набегающего
на тело (рис. 15). Направим ось Ох по направлению этого потока,
ось Оу — перпендикулярно к нему. Удовольствуемся рассмотрением
той, достаточно удаленной от обтекаемого тела области погранич-
ного слоя—-следа, где уже можно пренебречь влиянием формы тела
на внешний поток, который принимается однородным и имеющим
скорость Uoa. В этой области давление может считаться постоянным
и уравнения движения в следе совпадут с обычными уравнениями
пограничного слоя
ди , . да д2и
1 ду ду2
дх
дх
'ду
AЛ06)
а граничные условия будут
ди
ду
==0,
¦иа
при
при
A.107)
Такая система уравнений имеет тривиальное решение и = Um,
которое, очевидно, соответствует полному выравниванию потока
в 'бесконечном удалении от тела. Найдем условие существования
нетривиального решения, для чего обычным путем установим сначала
«закон сохранения» для рассматриваемой задачи.
Перепишем, как мы уже это делали ранее! систему A.106) в виде
д (и2) , d{uv) дги^
ду
ди
~дх~
ду
умножим обе части второго уравнения на постоянную величину ?/«,
и вычтем из него почленно обе части первого уравнения. Тогда
получим
д , ,,т N, , д] ... ,. д2и
ж(а (г/» — «)]-f- -^-{v(I/» — «)] — — v -^ .
Проинтегрируем теперь обе части этого равенства поперек следа,
изменяя у от —со до схэ. Замечая, что, согласно граничным усло-
виям» второй член в левой части и вся правая часть пропадут (условие
') Т о 11 ш i e n W., Grenzcschichttheorle, Handbuch der Experlmentalphysik,
4, ч. 1, Leipzig, 1931, стр. 269. "
§ 8] АЭРОДИНАМИЧЕСКИЙ СЛЕД ЗА ТЕЛОМ 51
асимптотического стремления а к Ua,), будем иметь, меняя порядок
дифференцирования и интегрирования,
= О,
откуда следует искомый закон сохранения
О
'«(?/«,—-a) dy = const. A.108)
Чтобы выяснить физический смысл постоянной, применим теорему
количеств движения в форме Эйлера к прямоугольной контрольной
области с границами (± L, ± А), удаленными от тела (на рис. 15
эта область выделена пунктиром). Обозначим через /г поперечный
к направлению потока размер этой области и через W лобовое
сопротивление тела. Теорема количеств движения в проекции на
ось Ох ери достаточно больших L и h дает
л
pf/oo ¦ 2А — I pa2 dy — W = О,
а уравнение постоянства расхода
pUoo • 2/z— f pady = 0,
-h
Умножая обе части второго равенства на {/«> и вычитая из него
почленно обе части первого равенства, получим приближенно
-А
что при А—> со дает окончательное выражение закона сохранения
= W. A.109)
Таким образом, в достаточном удалении от тела вниз по потоку
левая часть равенства A.108) сохраняет не зависящую от расстояния
до тела величину, и эта величина по A.109) представляет собою
лобовое сопротивление тела.
Совокупность граничных условий A.107) и интегрального усло-
вия A.109) полностью определяет решение системы A.106).
4*
52
УРАВНЕНИЯ ПРАШГМЯ
[ГЛ. I
Пользуясь тем, что в достаточном удалении от тела разница
скоростей
и' = U со— а
мала, произведем линеаризацию первого из уравнений системы A.106),
а также граничных и интегрального условий. Для этого подставим
во все эти равенства вместо и его выражение 1/ет— а' и будем
считать и', так же как и v, малыми первого порядка. Тогда, отбра-
сывая квадраты этих величин и их производных, получим
UG
ди'
дх
ду2 '
== 0 ери у = О,
ди'
ду
af —> 0 при у —> ± оо;
W
a' dy = ¦
A.110)
Линеаризированное уравнение рассматриваемой задачи, стоящее
в первой строке системы равенств A.110), аналогично известному
уравнению одномерного распространения тепла. Его простейшее
решение типа «источника» будет
A.111)
Входящую сюда постоянную С легко определить из последнего
равенства системы A,110) (интегрального условия); она равна
W
Окончательно находим
р/ — U га U -
ехр
A.112)
A.113)
На оси следа (у == 0) разность скоростей во внешнем потоке и
в следе максимальна и будет равна
W
A.114)
она убывает по закону обратной пропорциональности корню квад-
ратному из расстояния до тела.
8]
АЭРОДИНАМИЧЕСКИЙ СЛЕД ЗА ТЕЛОМ
53
Для конкретного случая пластинки длины L в продольном потоке
-о скоростью ?/оэ имеем по A,41)
\?= 1,328 VVpZ-f/L.
^ак что, переходя к скорости а, получим вместо A.113) и A.114)
ц 0,664 / х
ит _ __ 0,664 /_?_\
ехР Г
x
A.115)
Профили продольных скоростей в сечениях следа, соответствую-
щих пязличным значениям параметра x/L. приведены на рис. 16.
3,0 \
2,0
7,0
v/L=ff,5~
x/L=$O -
^7
О - 0,2
0.6 0.8
Рис. 16.
Сривые с малыми значениями этого параметра (до x/L = 0,256 вклю-
'ительно) составлены по ранее цитированной теории Голдстейна,
1,0
'00
04
0,8
О
'ривые для x/L = Q,5 и
¦ оиведена зависимость u
Яр
{00-
/
/¦
фвйн,-—
0,5 7,0
Рис, 17.
15
= 40 — но теории Толмина. На рис. 17
o от x[L по материалам тех же работ.
54
УРАВНЕНИЯ ПРАНДТДЯ
[ГЛ. I
Только что рассмотренная задача не имеет большого практиче-
ского значения; ламинарное движение в следе, так же как и в струе,
неустойчиво и сразу же переходит в турбулентное.
§ 9. Отрыв пограничного слоя от поверхности
Во всех рассмотренных в настоящей главе простейших примерах
давление во внешнем потоке было постоянным. При наличии про-
дольного перепада давления в пограничном слое могут возникать
существенные изменения. Особый интерес представляет явление от-
рыва пограничного слоя от поверхности обтекаемого тела. В отяичие
от инерционного отрыва
у у идеальной жидкости, возни-
кающего на острых кромках
тела, в реальной вязкой жид-
кости отрыв может проис-
ходить и на плавных участ-
ках поверхности, как, на-
пример, это ' имеет место
на поверхности круглого
или эллиптического цилин-
дров.
Отрыв вязкой жидкости
с поверхности тела проис-
ходит в результате совмест-
ного влияния двух основных
факторов: подтормаживания
жидкости твердой стенкой и действия перепада давления. Осо-
бенно отчетливо эти влияния проявляются при больших рейнольд-
совых числах в пограничном слое. В этом случае, по основному
свойству пограничного слоя, распределение давления вблизи поверх-
ности мало отличается от того теоретического, которое было бы при
обтекании тела идеальной жидкостью. В лобовой области тела дав-
ление, начиная от максимального своего значения в передней «рити-
Рис. 18.
0) до
ческой точке О (рис. 18) разветвления потока, убывает \—f-
некоторого "минимального значения в точке М, где ~- = 0, а затем
вновь возрастает (-гг-> 0], стремясь в кормовой области восстано-
вить свое прежнее значение в задней критической точке. Из-за наличия
потерь механической энергии при реальных движениях вязкой жид-
кости в пограничном слое такая картина изменения давления соблю-
дается лишь приближенно, но может все же служить для качествен-
ного объяснения явления отрыва.
§ 9] ОТРЫВ ПОГРАНИЧНОГО СЛОЯ ОТ ПОВЕРХНОСТИ 55
В лобовой «конфузорной» области перепад давления имеет благо-
приятный характер для безотрывного обтекания тела, он ускоряет
жидкость, причем продольная скорость на внешней границе слоя
возрастает до своего максимального значения в точке М минимума
давления. В «диффузорной» области за этой точкой вниз по потоку
перепад давления — его называют «обратным перепадом»,—наоборот,
тормозит движение жидкости, скорость на внешней границе убывает.
В результате совпадения тормозящих влияний твердой поверхности
тела и обратного перепада давления скорости частиц жидкости,
движущихся вблизи поверхности тела, быстро убывают, так что в не-
которой точке S не только скорость на стенке, которая на всей по-
верхности тела равна нулю, но и первая ее производная по нормали
к стенке, а следовательно, и напряжение трения iw на стенке, станут
равными нулю,
Щ =0, \=0. A.116)
За этой точкой в непосредственной близости к стенке появятся об-
ратные токи (и < 0), которые оттеснят набегающий поток в погра-
ничном слое от поверхности тела. В точке S—ее называют точкой
отрыва пограничного слоя (на самом деле, как всегда в плоском
движении, вдоль перпендикулярной плоскости чертежа линии от-
рыва)—пограничный слой отделяется от поверхности тела, превра-
щаясь в струю, имеющую в качестве своей границы отошедшую от
поверхности тела нулевую линию тока. В дальнейшем оторвав-
шийся пограничный слой перемешивается с жидкостью, располо-
женной вниз по потоку за кормой тела, и образует аэродинамический
«след» за телом.
Для определения абсциссы х= xs точки отрыва S, которая, по
предыдущему, может быть расположена только в диффузорном
участке слоя, служит уравнение A.116). Если расчет пограничного
слоя произведен и распределение скоростей и(х, у) найдено, .то
разыскание величины xs не составляет труда. Основной трудностью
при решении задачи об оеределении положения точки отрыва яв-
ляется отсутствие в этом случае возможности пользоваться распре-
делением давлений, рассчитанным по теории обтекания тела идеальной
жидкостью. Дело в том, что при приближении к точке отрыва линии
тока настолько значительно оттесняются от поверхности тела, а об-
ласть пограничного слоя настолько утолщается, что уже нельзя пре-
небрегать возмущающим влиянием этого пристеночного движения на
«внешний» поток. Теоретическое распределение давлений во всей
кормовой области тела резко искажается и становится непригодным
для расчета пограничного слоя. На рис. 19 приведены для примера
графики теоретического распределения коэффициента давления
66
УРАВНЕНИЯ ПРАНДТЛЯ
ГЛ. I
P — (P — Pco)l{pUloj2) по поверхности двух симметричных крыловых
профилей Жуковского с относительными толщинами 15% и 40%; Tail
же крестиками и точками показаны замеренные опытные значения
коэффициента давления. На
'•"\ i i ¦ ' i m—i более тонком, 15-процент-
ном профиле имеет место
безотрывное, плавное его
обтекание по всей поверхно-
сти; крестики начинают чуть
заметно отходить от теоре-
тической кривой лишь в не-
посредственной близости от
задней кромки, что является
неизбежным влиянием нара-
стающего пограничного слоя.
Иначе обстоит дело на тол-
стом, плохо обтекаемом 40-
процентном профиле. Здесь
наблюдается резкое расхо-
ждение опытных точек и теоретической кривой, уже начиная с точки,
заметно удаленной от задней кромки профиля; обратное, влияние от-
рыва пограничного слоя на распределение давлений выражено здесь
совершенно отчетливо. Еще от-
четливее это влияние можно на-
блюдать на1 распределениях давле-
ний по поверхности таких плохо
обтекаемых- тел, как круглый
Рис. 19.
1,0
о
-1,0
-з,о,
\
\\
\
Зясп.
Твор,
\
J
/
/
/
Г
V
1,0
Р-Роо
о
-1,0 -
О 30 ВО 90 120
Рис. 20.
180
\
V
V
V
Э,ГВГ7.
х_^"Г'
\Теор. /
У
: /
г
О 30 60 30 120 ISO 130
Рис. 21.
цилиндр или шар. В этих случаях разница между теоретическим и
экспериментальным распределениями давлений обнаруживается не
только в кормовой области, но и в лобовом участке поверхности
тела. Как это видно на рис. 20 и 21, теоретические кривые рас-
§ 9] ОТРЫВ ПОГРАНИЧНОГО СЛОЯ ОТ ПОВЕРХНОСТИ 57
пределения давления по поверхности круглого цилиндра и шара
в случае наличия отрыва ламинарного слоя качественно отличны от
соответствующих экспериментальных кривых. Обращает на себя
внимание факт значительного смещения вверх по потоку точки мини-
мума давления до 8 = 72° вместо обычного значения 0 — 90°,
резкое отличие величины максимального разрежения и общего харак-
тера хода кривых.
При расчетах пограничного слоя на плохо обтекаемых телах при-
ходится пользоваться экспериментальными кривыми распределения
давления по поверхности тела, форма которых может зависеть от
рейнольдсова числа. В этих случаях и положение точки отрыва S
будет зависеть от рейнольдсова числа. Если рейнольдсово число
обтекания тела меньше некоторого критического, для которого по-
граничный слой сохраняет свой ламинарный характер вплоть до
точки отрыва, то распределение давлений не будет зависеть от рей-
нольдсова числа обтекания. Тогда, как легко показать пользуясь
формулой A.116), и абсцисса точки отрыва ламинарного слоя не
будет зависеть от рейнольдсова числа. Действительно, если безраз-
мерное распределение скоростей на внешней границе пограничного
слоя 67?/со = / (xjL) не зависит от рейнольдсова числа, то не будет
от него явно зависеть и безразмерное распределение скоростей
внутри пограничного слоя
= <?(x', у'),
представляющее решение безразмерной системы уравнений A.10).
При составлении условия отрыва A.116) в безразмерной форме
ди'
s
у'=0
уравнение для определения абсциссы x's
y'=0
также не будет содержать рейнольдсова числа. Так, например, при
возрастании скорости набегающего на круглый цилиндр бесконечного
размаха плоского потока точка отрыва будет находиться на 82Э от
лобовой критической точки (об этом подробнее будет сказано
в следующей главе), пока рейнольдсово число цилиндра Re — и^сЦч
не превзойдет свое критическое значение, приблизительно равное
2 ¦ 10°. При дальнейшем возрастании рейнольдсова числа точка от-
рыва начнет перемещаться, но зто уже будет следствием изменения
структуры движения жидкости в' пограничном слое (перехода лами-
нарной формы движения в турбулентную).
58
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ. I
Угол между отделяющейся от тела нулевой линией тока и по-
верхностью тела имеет порядок 1/]/{?ё, т. е. отрыв пограничного
слоя происходит по касательной к поверхности тела. Условие отрыва
ламинарного слоя A.116) не всегда приводит к отрыву жидкости от
поверхности тела и образованию обратного тока за точкой отрыва.
Дело в том, что оторвавшийся ламинарный слой неустойчив и дви-
жение в нем становится турбулентным. При этом область оторвав-
шегося пограничного слоя резко расширяется и пограничный слой,
став турбулентным, сразу же возвращается («прилипает») обратно на
поверхность тела, чтобы в зависимости от характера распределения
давлений в диффузор ном участке сохраниться на теле до задней его
кромки или вновь оторваться от него, но уже значительно ниже по
потоку. В этом случае точка отрыва ламинарного слоя является и
точкой перехода ламинарного пограничного слоя в турбулентный.
§ 10. Толщина вытеснения и ее влияние
на распределение давления
В том случае, когда обратное влияние пограничного слоя на
внешний поток приводит лишь к сравнительно небольшому оттеснению
линий тока от поверхности тела и обтекание тела остается безотрыв-
ным, можно указать простой прием приближения теоретического рас-
пределения давлений по поверхности
обтекаемого тела к действительному.
Сравним между собой (рис. 22)
расположение линий тока при плос-
ком обтекании тела идеальной жидко-
стью с действительным их положе-
нием внутри пограничного слоя. Пусть
в некотором сечении слоя с абсцис-
сой х действительная линия тока (на
рис. 22 показанная сплошной линией)
будет оттеснена от идеальной (на
рис. 22 показанной пунктиром) на не-
которое расстояние М'М = А (л;, у).
Вне пограничного слоя действительные и идеальные линии тока со-
впадают, следовательно, в выбранном' сечении внз'три пограничного
слоя расходы через MQM и М0М' будут одинаковы. Вспоминая, что
скорость на внешней границе слоя 0 (х) является скоростью идеаль-
ного обтекания, в пределах данного сечения слоя постоянной соста-
вим условие равенства расходов
Рис. 22.
= U(y — Д).
A.117)
§ 1GJ ТОЛЩИНА ВЫТЕСНЕНИЯ 59
Пользуясь независимостью U от у, найд&м смещение линии тока
,в действительном движении по отношению, к идеальной линии тока
в форме
у
/(?)у. A.118)
При у = 0 это смещение равно нулю, что и естественно, так как
нулевой линией тока внутри пограничного слоя служит твердая по-
верхность тела- С удалением от поверхности тела смещение А воз-
растает и .на внешней границе слоя y — h приобретает значение о*,
равное
О
/(?)y. . - A.119)
Под о мы понимаем здесь конечную толщину пограничного слоя
в том условном смысле, как об этом ранее уже говорилось. Имея
в виду, что u~>U при у—>оо и, следовательно, подынтегральное
выражение стремится к нулю .при у—>оо, можно предположить
существование интеграла (в дальнейшем это оправдывается конкрет-
ными примерами) .с бесконечным пределом и положить
Величина 8*, выражающая смещение действительной линии тока
по отношению к идеальной, вычисленное на внешней границе слоя,
называется толщиной вытеснения.
Толщина вытеснения представляет некоторую меру толщины по-
граничного слоя и может считаться условной толщиной слоя. Если
распределение скоростей в сечениях слоя известно, то не составляет
труда определить и величину В*. Так, в пограничном слое на про-
дольно обтекаемой пластине из решения Блазиуса (§ 4), предста-
вленного таблицей 1, можно найти, вычисляя интеграл A.120),
Сравнивая с формулой A.44) для толщины пограничного слоя 8,
определенной как ордината, для которой продольная скорость в дан-
ном сечении слоя только на 1% отличается от скорости на внешней
границе, видим, что закон зависимости от х-, Uw и v в обоих слу-
чаях один и тот же. Разница в численных коэффициентах показы-
вает, что толщина вытеснения S* примерно в три раза меньше тол-
щины пограничного слоя, определенной выше. Пользуясь таблицей 1,
60
УРАВНЕНИЯ ПРАНДТЛЯ
[ГЛ. I
можно сказать, что толщине вытеснения соответствует расстояние от
поверхности тела, на котором скорость равна, в грубом приближении,
половине скорости внешнего потока, 1
Толщину вытеснения, как это следует из равенства
= j (U— u)dy,
A.122)
можно еще трактовать как такой отрезок, секундный объемный рас-
ход идеальной жидкости че-
рез который при отсутствии
пограничного слоя равнялся
бы потере расхода через
.сечение пограничного слоя
из-за наличия торможения в
действительном течении. На
рис. 23 потеря секундного
объемного расхода, стоящая
в правой части A.122), и
эквивалентный ей расход в
идеальном течении сквозь
толщину 8* показаны в ви-
ff де различным образом за-
штрихованных площадей.
В дальнейшем часто бу-
дет встречаться еще одна
условная'толщина слоя, обо- ¦
{или 8) и выражаемая интегралом
Рис. 23.
значаемая обычно символом
8:
A.123)
Переписывая это равенство в тождественной форме
A.124)
можем по аналогии с A.122)' сказать, что через отрезок §** при
отсутствий пограничного слоя проходило бы секундное количество
движения идеальной жидкости, равное потере количества движения
в действительном течении сквозь сечение пограничного слоя из-за
торможения жидкости. Величина о** носит наименование толщины
§
ТОЛЩИНА ВЫТЕСНЕНИЯ
61
потери импульса. В случае пластинки по таблице 1 и форму-
ле A,122) можно найти следующее выражение для о**:
8**== 0,664
УХ
A.125)
Толщина потери импульса тесно связана с величиной сопроти-
вления тела. Вспоминая соотношение A,109), заключим, что сопро-
тивление W произвольного по форме цилиндрического тела в плоском
потоке может быть выражено через толщину потери импульса 3**,
вычисленную на бесконечном удалении в следе за телом, по формуле
W = ?Ul
A.126)
Перейдем теперь непосредственно к изложению приближенного
приема, о котором шла речь в начале параграфа.
Для этого наряду с действительным плоским обтеканием тела
вязкой жидкостью рассмотрим в области пограничного слоя и следа
за телом некоторый воображаемый поток идеальной жидкости, кото-
рый вне пограничного слоя совпадал бы с действительным и имел бы
в каждом сечении слоя постоянную по сечению скорость, равную
скорости U на внешней гра-
нице слоя в действительном
течении. Давления в таком во-
ображаемом потоке будут так-
же совпадать с искомыми в дей-
ствительном движении реальной
жидкости. -Следует обратить
внимание на то, что введенный
только что воображаемый по-
ток идеальной жидкости не со-
впадает с ранее рассмотренным
идеальным обтеканием тела.
В то время как последний был
заранее известен во всей обла- Рис 24.
сти течения вне контура тела,
интересующий нас воображаемый поток идеальной жидкости определен
лишь вне пограничного слоя и должен быть продолжен внутрь слоя.
Чтобы это сделать, заметим, что, в отличие от рис. 22, линии
гока рассматриваемого сейчас воображаемого потока, показанные на
рис. 24 пунктиром, расположатся выше, чем действительные линии
тока, изображенные на том же рисунке сплошной кривой, так как
сечение МХМ', через которое жидкость проходит со скоростью U,
должно быть меньше сечения МгМ, где скорость и <С U.
Отсюда следует, что трубка тока воображаемого потока, ограни-
ченная линией тока, проходящей через точку Мх внешней границы
слоя и точку М' сечения слоя, тоньше трубки тока действительного
62 УРАВНЕНИЯ ПРАНДТЛЯ [ГЛ. I
движения, ограниченной линиями тока, проходящими через точки Мг
и М, Воображаемый поток, таким образом, не может заполнить всю
область пограничного слоя.
Составляя условие равенства расходов сквозь отрезки МгМ и
МХМ', отложенные уже, в отличие от предыдущего, от внешней гра-
ницы слоя Mv найдем (ММ' — Aj)
j =U(b — у— Дх),
у
откуда следует
1(±уу. A.127)
у
При совпадении точки М с точкой Мо поверхности тела нижняя
линия тока воображаемого потока не дойдет до поверхности тела
на расстояние
(Д,)у=0 = У(l --?)</у = &\ A.128)
о
т. е. как раз на величину, равную толщине вытеснения 8*, вычислен-
ной, подчеркнем это еще раз, для действительного потока с поправ-
ленной уже на обратное влияние скоростью внешнего потока U (х).
Итак, можно прийти к выводу, что для определения действитель-
ного распределения давлений по поверхности тела в плоском безот-
рывном потоке вязкой жидкости при больших значениях рейнольдсова
Рис. 25.
числа необходимо найти распределение давления при обтекании идеаль-
ной жидкостью полутела (рис. 25), образованного путем наращивания
на поверхность заданного тела и по обе стороны от нулевой линии
тока, сходящей с задней кромки тела вслед за ним, толщины вы-
теснения, вычисленной по действительному, распределению скорости
на внешней границе !),
В предложенном только что приеме, имеется некоторое противо-
речие, заключающееся в том, что для расчета толщины вытеснения
!) Идея такого приема была высказана Л. Прандглем в статье «Меха-
ника вязких жидкостей», помещенной в третьем томе книги: Дюрэнд В.,
Аэродинамика, пер. с англ., Оборонгиз, Москва, 1939, стр. 108.
§ 10J ТОЛЩИНА ВЫТЕСНЕНИЯ , 63
необходимо заранее знать действительное распределение давлений
или скоростей на внешней границе слоя, которое, однако, на самом
деле не может быть разыскано, пока не определена толщина вытес-
нения. Чтобы обойти это противоречие, можно, как это обычно
делается, применить метод последовательных поправок, т. е. сначала
следует определить толщину вытеснения для теоретического распре-
деления давлений без учета влияния пограничного слоя, затем по-
строить полутело, найти распределение давления по его поверхности,
по этому уточненному распределению давлений вновь определить
толщину вытеснения, и т. д. Численные расчеты, проведенные на
кафедре гидроаэродинамики Ленинградского политехнического инсти-
тута и в работах других авторов, показывают, что практически нет
необходимости повторять последовательные поправки. Достаточно
провести одну операцию, чтобы уже получить- главную количествен-
ную часть поправки, учитывающей обратное влияние пограничного
слоя на теоретическое распределение давления. При расчете S* вблизи
задней кромки следует только1 заблаговременно заменить теоретическое
нулевое значение скорости U непосредственно в задней кромке от-
личным от нуля значением, полученным, например, хотя бы простым
сохранением тех значений U, которые имели место до резкого спада
ее к нулю; это позволяет избежать не имеющего физического смысла
бесконечно большого значения подынтегрального выражения при U = 0.
ГЛАВ А II
ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ
ДЛЯ НЕКОТОРЫХ КЛАССОВ ЗАДАЧ
§ 11. Степенное распределение скорости вдоль
внешней границы слоя
Перейдем к рассмотрению более сложных, чем в предыдущей
главе, случаев интегрирования уравнений Прандтля при разнообраз-
ных условиях задания изменения скорости потенциального потока
вдоль внешней границы пограничного слоя. Особый интерес пред-
ставляют классы задания внешнего потока, зависящие от одного или
нескольких параметров. Решения такого рода задач могут быть по-
ложены в основу широко используемых в настоящее время прибли-
женных методов расчета пограничных слоев; о них пойдет речь
в следующей главе.
Наибольшее применение получили однопараметрические решения
и среди них, в первую очередь, решение Фокнера и Скэн1) задачи
о стационарном ламинарном пограничном слое с одночленным степен-
ным распределением скорости U (х) на внешней границе слоя
U(x)=^cxm, B.1)
где с и т — некоторые произвольные положительные постоянные,
причем вторая из них безразмерна2).
Наличие в задании потока только одной размерной постоян-
ной с заранее наводит на мысль, что искомое решение будет авто-
модельным. Чтобы в этом убедиться, введем условно в рассмотрение
масштаб длин L; тогда', «Гласно B.1), роль масштаба скоростей Uo
должна играть величин:"
m 22
О Fa Ik пег V. №., Skan S. W., ARC, R&M, 1314 A930).
2) Некоторые авт jpbi трактуют эту задачу как плоское обтекание клина;
по этому поводу см.- например: Щ лихтинг Г., Теория пограничного слоя,
пер, с нем., ИЛ, IP'S, стр. 130.
§ 11]
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ СКОРОСТИ
65
а следовательно, условное рейнольдсово число представится ком-
плексом
ПГ с ¦ !т+г
р и 0^ ь -° /г) о\
У У >
Масштабы поперечных размеров У и функции тока W по тем же
соображениям, что и в предыдущей главе, определятся как
Выражение функции тока будет таким:
B.4)
B.5)
Для того чтобы масштаб длин L, отсутствующий в условиях задачи,
не входил в выражение B.5), функция тока должна иметь структуру
следовательно, представляться в виде
j = у
схп-
B ..6)
Уравнение A.19) после подстановки в правую часть вместо U (х)
не зависящего от времени выражения B.1) и значений производных
(штрих — производная по vj) • . " ¦
3m-1
т--1 г m I 1
—1
B.7)
легко вычисляемых по B:6), приведется к следующему, подтверждаю-
щему автомодельность решения B.6), обыкновенному дифференциаль-
ному уравнению третьего порядка:
,„' т. +1 „_¦ /
1).
B.8)
Граничные условия имеют вид
ср==О, ¦-ср'= 0 при" i\== О,
ср' —* 1 ¦ при Tj-^cxp,
B.9)
5 Зак. 297. Л. Г. Лойцянский
66 . ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАИДТЛЯ [ГЛ. II
Согласно B.9) на твердой поверхности обтекаемого тела, служа-
щей нулевой линией тока, скорость равна нулю, а на внешней гра-
нице слоя скорость- определена равенством B.1).
Нетрудно убедиться, что -при. т = 0, U = c уравнение B;8) и
граничные условия B.9) совпадут с теми, что фигурировали в задаче
Блазиуса о продольном обтекании полубесконечной пластинки (§ 4).
Интересно отметить специальный случай m=z—], U = c/x, до-
пускающий при с < 0 физическую интерпретацию как движения
жидкости в пограничном слое на
стенке плоского суживающегося ка-
нала—конфузора бесконечной длины
(рис. 26). Действительно, обозначив
через Q > 0 секундный объемный рас-
E ход жидкости сквозь любое сечение ка-
^?х нала- получим (а—угол раствора канала)
— U (х) ¦ ах = —ел = Q;
Рис. 26. О
^ 0
В этом случае следует, согласно B.6), положить (знак минус соот-
ветствует сохранению условия B.9) при т]—>схз для и <С 0)
|. B.10)
Вместо уравнения B.8) будем иметь
ср"'_у2_|-1 =о, B.11)
а граничные условия сохранят вид B.9).
Используя наличие очевидного интегрирующего множителя ср", ¦
получим, умножая обе части B.11) на этот множитель и один раз
интегрируя,
I2I/ = const,
Замечая, что в силу асимптотичности решения можно положить
<р'—>1, ср"—>0 при 7]—з-со, найдем для постоянной значение 2/3,
после чего последнее уравнение приведется к виду
Выражение в круглых скобках раскладывается на множители, так
что уравнение преобразуется к виду
Ц] СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ СКОРОСТИ 6^
Это уравнение ПРИ выполнении граничного условия ср'-*! прн
легко интегрируется и дает решение в замкнутой форме
B.12)
¦которым и определяется искомое распределение скоростей — и/11.
Граница' "пограничного слоя в том приближенном смысле, который
'§ьт 'принят в предыдущей главе, будет в настоящем случае прямо-
линейной и совпадает с линией тока. Действительно, обозначим
'Через | такое значение г\, при котором правая часть B.12) будет
Мало отличаться от единицы; тогда при т] —т получим по B.10)
= const.
Интересно отметить, что, в отличие от всех рассмотренных
в ареаыдущей главе примеров, пограничный слой в настоящем случае
¦щ утолщается, а, наоборот, утончается вниз по течению (направле-
ние движения в сторону убывающих х!¦).
-Другим сравнительно простым решением, входящим в класс задач
($'Л),,. будет случай /и= 1, ?/= сх, с > 0. Таково распределение ско-
ростей в потенциальном потоке вблизи лобовой критической точки на;
цилиндрическом теле при плоском его обтекании. Уравне-
' вне Щ..Щ в этом случае принимает вид ф == ргдр (rf), т\ = у у —
фда + ^"-?'2+1^-0; • B.13)
граничные условия сохраняют ферму B._9).
Уравнение B.13) било численно' проинтегрировано Хименцем в его
диссертация, относящейся к 1911 г. Впоследствии Хоуарт ') дал
¦й'вдроб'Н'Ые та'блИць! значений" функций ср и ср' в чисяе других функ-
ций, входящих в более общий класс рассмотренных им решений,
о которых будет «дти |речь в §¦ 13.
¦ 'Вернёмся теперь к общему случаю произвольного т и будем
в дальнейшем Макать всегда с j> 0. Подстановка
B.14)
') Н о w a r t H L., ARC, R & М, 1632 A935).
Таблицы функций ср и о' кожно найти также в книге: Л о й ц я н-
ский Л. Г., Аэродинамика погранияного слоя, Гостехиздат, 1941, стр. 403
(второй и третий столбцы йблицы I).
S*
ТОЧНЫЕ РЕШЕНИЯ- УРАВНЕНИЙ ПРАНДТЛЯ
[гл. if
с \
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
,. 4,2
4,4
4,6
4,8
5,0
5,2
5,4
',6
5,8
6,0
6,2
6,4
—0,1988
0,0000
0,0010
0,0040
0,0089
0,0158
0,0248
0,0358
0,0487
0,0636
0,0803
0,0991
0,1423
0,1927
0,2498
0,3126
0,3802
0,4509
0,5230
0,5946
0,6635
0,7278
0,8158
0,8364
0,8789
0,9132
0,9399
0,9598
0,9741
0,9839
0,9904 :
0,9945
0,9969
0,9984
0,9992
0,9996
0,9998
0,9999
1,0000
—0,19
.0,0000
0,0095
0,0209
0,0343
0,0495
0,0665
0,0855
0,1063
0,1289
0,1533
0,1794
0,2364
0,2991
0,3665
0,4372
0,5095
0,-5814
0,6509.
0,7162
0,7754
0,8273
0,8713
0,9071
0,9352
0,9563
0,9716
0,9822
0,9893
0,9938
0,9965
0,9981
0,9-990
0,9995
0,9997
0,9999
0,9999
—0,18
0,0000
0,0137
0,0293
,0,0467
0,0659
0,0868
0,1094
0,1338
0,1598
0,1874
0,2166
0,2791
0,3463
0,4170
0,4896
0,5621
0;6327
0,6995
0,7605
0,8146
0,8607:
0,8986
0,9286
0,9515
0,9681
0,9798
0,9876
0,9927
0,9959
0,9978
0,9988
0,9994
0,9997
0,9999
0,9999
!
—0,16
0,0000
0,0198
0,0413
0,0643
0,0889
0,1151
0,1427
0,1719
0,2023
0,2-341
0,2671
0,3362
0,4083
0,4820
0,5555
0,6269
0,6944
0,7561
0,8107
0,8574
0,8959
0,9265
0,9499
0,9669
0,9789
0,9871
0,9924
0,9957
0,9977
0,9988-
0,9994
0,9997
0,9999
0,9999
—0.14
0,0000
0,0246
0,0507
0,0781
-0,1069
0,1370
0,1684
0,2010
0,2347
0,2694
0,3050
0,3784
0,4534
0,5284
0,6016
0,6712
0,7354
0,7927
0,8422
0,8836
0,9168
0,9425
0,9616
0,9752
0,9845
0,9907
0,9946
0,9970
0,9984
0,9992
0,9996
0,9998
0,9999
—0,10
0,0000
0,0324
0,0659
0,1003
0,1356
0,1718
0,2088
0,2466
0,2849
0,3237
0,3628
0,4415
0,5194
0,5948
0,6660
0,7314
0,7896
0,8398
0,8817
0,9153
0,9413
0,9607,
0,9746
0,9841
0,9904
0,9944
0,9969
0,9983
0,9991
0,9996
0,9998
0,9999
0
0,0000
0,0469
0,0939
0,1408
0,1876
0,2342
0,2806
0,3266
0,3720
0,4167
0,4606
0,5453
0,6244
0,6967
0,7610
0,8167
0,8633
0,9011
0,9306
0,9529
0,9691
0,9804
0,9880
0,9929
0,9959
0,9978
0,9988
0,9994
0,9997
0,9999
0,9999
1 .
0,1
0,0000
0,0582
0,1154
0,1715
0,2265
0,2803
0,3328
0,3839
0,4335
0,4815
0,5274
0,6135
0,6907
0,7583
0,8160
0,8637
0,9019
0,9315
0,9537
0,9697"
0,9808
0,9883
0,9931
0,9961
0,9978
0,9988
0,9994
0,9997
0,9998
0,9999
0,2
0,0000
0,0677
ОД 334
0,1970
0,2584
0,3177
0,3747
0,4294
0,4816
0,5312
0,5782
0,6640
0,7383
0,8011
0,8528
0,8940
0,9260
0,9500
0,9612
0,9792
0,9873
0,9924
0,9957
0,9976
0,9987
0,9993
0,9996
0,9998
0,9999
0,3
0,0000
0,0760
0,1490
0,2189
0,2858
0,3495-
0,4100
0,4672
0,5212
0,5718
0,6190'
0,7033
0,7743
0,8326
0,8791
0,9151
0,9421
0,9617
0,9754
0,9847
0,9908
0,9946
0,9970
0,9984
0,9991
0,9995
0,9997
0,9999
0,9999'
§ us
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ' СКОРОСТИ
69
Т а-б л и-ц а 3
0,4
O.GQGO
0,0834
0,1628
„ 0,2382
: о,зо97
0,3771
'. 0,4403
0,499.4
0,5545
0;6055
ё',6526
0,7351
: Q.8027
> 0,856.8
0,8988
0,9305
0,9537
а,97ое
¦0;9812
¦0,9886
0,9933
0;9962
0,9979
0,9989
0j9994
0,9997
0,9999
0,9999
-
0,5
. 0,0000
0,0903
0,1756
0,2558
0,3311
0,4015
0,4670
0,5276
0,5834
0,6344
0,6811-
0,7615
' 0,8258
0,8860
0,9141
0*9421
0,9621
0,9760
0,9852
0,9913
0,9952
в;9974
0,9986
0,9993
0,9994
0,9999
0,6
0,0000
0,0966
0,1872
0,2719
0,3506
0,4235
0,4907
0,5524
0,6086
0,6596
0,7056
¦0,7837
0,8449
0,-8917
0,9264
0,9.514
0,9689
0,9807
0,98.84
0,9933
0,9962
0,9979
0,9989
0,9995
0,9997
0,9999
¦0,8
0,0000
0,1080
0,2081
0,3003
0,3848
0,4619
0,5317
0,5947
.0,6512
0,7015
0,7460
0,8194
0,8748
0,9154
0,9443
0,9644
0,9779
0,9867
0,9922
0,9956
0,9976
0,9987
0,9993
0,9997
0;9998
0,9999
1,0
0,0000
0,1183
0,2266
0,3252
0,4144
0,4946
0,5662
0,6298
0,6859
0,7350
0,7778
0,8467
0,8968
0,9324
0,9569
0,9732
0,9841
0,9905
0,9946
0,9971
0,9985
0,9992
0,9996
0,9998
0,9999
1;2
0,0000
0,1276
0,2433
0,3475
0,4405
0,5231
0,5959
0,6596
0,7150
0,7629
0,8037
0,8682
0,9137
0,9450
0,9658
0,9793
0,9879
0,9931
0,9962
0,9980
0,9989
0,9995
0,9997
0,9999
1
1,6-
0,0000
0,1441
0,2726
0,3859
0,4849
0,5708
0,6446
0,7076
0,7610
0,8058
0,8432
0,8997
0,9375
0,9620
0,9775
0,9871
0,9928
0,9961
0,9980
0,9990
0,9995
0,9998
0,9999
2,0
0,0000
0,1588
0,2980
0,4186
0,5219
0,6096
0,6834
0,7449
0,7858
0,8376
0,8717
0,9214
0,9530
0,9726
0,9845
0,9914
0,9954
0,9976
0,9989
0,9994
0,9997
0,9999
2,4
0,0000
0,1720
. 0,3206
0,4472
0,5537
0,6424
0,7155
0,7752
0,8235
0,8624
0,8934
0,9373
0,9640
0,9799
0,9892
0,9944
0,9970
0,9985
0,9993
0,9996
0,9998
0,9939
'/
I.
0,0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1;2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
A fi
4,0
4,8
5,0
5,2
5,4
5,6
5,8
6,0
6,2
6,4
70 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ [ГЛ. IJ
преобразует уравнение B.8) к более удобному для численного инте-
грирования виду
где введено дополнительное обозначение
Ы = » /Л 1 ?\
U :—т~ s [ Л| 1 О!
граничные условия в новых переменных сохраняют ту же форму B.9)
Ф = 0, -"ТйТ —° ПРИ 5 = 0; -^т-->1 при 5->°о. B.17)
Выражения функции тока ф и составляющих (а, о) скорости через
функцию Ф (?; Р) представятся совокупностью равенств (штрих далее
означает производную по ?)
/--— m+l
B.18)
Численное интегрирование уравнения B.15) при граничных усло-
виях B.17) было проведено Фокнером и Скэн, а затем на специаль-
ной интегрирующей машине — Хартри1). Результаты этого интегри-
рования (значения йФ/di-) приведены в таблице 3 для значений 5
с интервалом 0,1 и для девятнадцати значений ' р. Как заметил
Хартри, при р < 0 последнее условие в системе B.17) не определяет
однозначно величину Ф"@), входящую в выражение напряжения тре-
ния на стенке
Выяснилось, что существует целый интервал значений Ф"@; р),
при которых удовлетворяются граничные условия B.17). Хартри
выбрал такое наибольшее возможное значение Ф" @; Щ, при кото-
ром Ф'(?; Р) при стремлении Е к бесконечности подходит к единице
со стороны меньших значений, что соответствует монотонности воз-
растания скорости в сечениях пограничного слоя.
Величины Ф"@; р) при различных значениях параметра р при-
ведены в таблице 4. Полученный Фокнером и Скэн класс решений
уравнений пограничного слоя относится к числу «однопараметриче-
ских», так как многообразие решений характеризуется изменением
лишь одного параметра т или р. Так, профили скоростей в сече-
') Наг tree D. R., Proc, of the Qambr. Phil, Soc, 1937, стр. 33.
§ 11]
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ СКОРОСТИ
71
ниях слоя образуют однопараметрическое семейство; основные харак-
теристики слоя (условные толщины, напряжение трения) являются
функциями того же параметра.
Таблица 4
р
^-0,1988
—0,19
—0,18
—0,16
—0,14
—0,10.
0,00
одо
0,20
Аф)
2,359
2,007
1,871
1,708
1,597
1,444
1,217
1,080
0,984
0,585
0,577
0,568
0,552
0,539 ¦
0,515
0,470
0,435
0,408
Ф" @)
0,0000
0,086
0,1285
0,1905
0,2395
0,3191
0,4696
0,5870
0,6869
Р
0,30
0,40
0,50
0,60
0,80
1,00
1,20
1,60
2,00
Л(Р)
0,911
0,853
0,804
0,764
0,699
0,648
0,607
0,544
0,498
В(р)
0,386
0,367
0,350
0,336 .
0,312
0,292
0,276
0,250
0,231
Ф" @)
0,7748
0,8542
0,9277
0,996
1,120
1,2326
1,336
1,521
1,687
Рассматривая таблицу 3, можно заметить целый ряд особенностей
исследуемого класса решений. Прежде всего напомним, что> еще
» предыдущей главе мы условились отличать «конфузорные» участки
пограничного слоя с возрастающей вниз по потоку скоростью на
внешней границе слоя от «диффузорных» с убывающей скоростью
внешнего потока. Значения т > 0 соответствуют «конфузорному»
участку, значения т < 0 —«диффузорному». При т > — 1, а только
такие значения в дальнейшем и рассматриваются, знак J3 совпадает
со знаком т.
Введем, подобно тому как это уже делалось в предыдущей главе,
понятие об условной толщине пограничного слоя; заданной, например,
отличием tijU от единицы на внешней границе слоя на величину
порядка i%. Обозначим через ?8 значение ?, удовлетворяющее этому
условию. Тогда, рассматривая таблицу 3, можно заметить сравни-
тельно 'большую толщину пограничного слоя в области замедленного
движения (р < 0) — диффузорной области — по сравнению с областью
ускоренного движения — конфузорной областью. Так, наибольшее
значение ?s = 4,8 имеет место при р == — 0,1988; далее, Е8 = 3,5
при р === 0; Ig === 1,8 при р = 2,4. Вспоминая выражение для ? по
B.14) и B.6), заключаем, что размерные толщины слоя 8 (в том
приближенном смысле, о котором только что была речь) будут опре-
деляться в функции от х по формуле (?8 — постоянная, зависящая
только от т или C)
I—
B-20)
Из этой формулы сразу видно, что значение т=\ (C=1) отделяет
Движение с возрастающей вниз по течению толщиной пограничного
72
ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ
[гл. и
слоя от движения с убывающей толщиной. При т < 1, т. е. во всей
диффузорной области и в части умеренно конфузорных областей,
толщина пограничного слоя растет вниз по потоку; при т > 1 (резко
конфузорная область) толщина пограничного слоя убывает. При /я= 1,
а это, как мы уже упоминали, соответствует пограничному слою
вблизи лобовой критической точки на цилиндрическом теле, толщина
пограничного слоя постоянна во всех сечениях слоя и в принятом
приближении равна
Из приведенных формул нетрудно усмотреть, что, в полном
согласии с общей теорией, толщины пограничного слоя при всех т
обратно пропорциональны корню квадратному из рейнольдсова числа;
так, из B.20) следует
/
схт+'
=; л/
/и + 1
Ux
Для дальнейшего полезно еще привести зависимость от параметра
других условных толщин слоя, таких, как 8* и S**, физический смысл
и прикладное значение которых были выяснены в § 10.
По определению этих величин имеем
о
~~ У тех"
B.21)
Интегралы в правых частях этих формул представляют собой функ-
ции параметра C, обозначаемые как
п. B.22)
после чего предыдущие равенства можно переписать в одном из сле-
дующих видов (точка обозначает дифференцирование по х):
8- =
B.23)
§ 111
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ СКОРОСТИ
73
Так же, как и ранее определенная величина й, условные толщины 8
и о** при гр = 1 (т=1) сохраняют постоянное (не зависящее от х
значение. При т> 1 эти толщины убывают с х, при /к< 1—воз-
растают.
Функции А ({3) и В ф) приводятся в таблице 4. Сравнивая между
собою составленные по B.6), B.14) и B.16) выражения
//
у =
?
= Ф'[я (Р) ¦?;?]==/(-?¦;
5** В (?) V 3
заключаем, что I = В ф) (у/о**), и следовательно, по второму из
равенств B.18) будет
B.24)
Отсюда следует, что профили скоростей в сечениях слоя образуют
при различных р однопараметрическое семейство с параметром р
(рис. 27).
В заключение рассмотрим У
выражение для напряжения тре- и
ния B.19). Можно заметить,
что т. = Уз ф = V2) соответ-
ствует течению с постоянным
вдоль поверхности напряже-
нием трения. При т < :/3 на"
пряжение трения с увеличе-
нием х убывает, при т > 1/z, О
наоборот, возрастает. Вспом-
ним, что на пластинке (т = 0,
0,6
и"
/7*
//у
?^
/^
us ty
//
/ у
У74 /
-am
2
Рис. 27.
задача Блазиуса) напряжение убывало, как l/Yx. При движении
вблизи критической точки т — 1 напряжение трения растет пропор-
ционально х, начиная от нулевого значения в самой критической
точке.
Особо следует выделить случай т = — 0,0904 ф = — 0,1988),
при котором напряжение трения обращается в нуль во всех точках
поверхности тела. Вспоминая определение точки отрыва, данное
в § 8, можно утверждать, что рассматриваемые значения параметра т.
(или р) определяют собой границу начала отрывного течения в том
смысле, что при т > — 0,0904 в данном классе течений отрыва не
может быть ни при каком значении х. При т < — 0,0904 решение
теряет смысл, так как заотрывная область уже не описывается урав-
нениями Прандтля.
74 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ [ГЛ. II
Изученный класс точных решений будет использован нами в сле-
дующей главе для установления приближенного метода расчета
пограничного слоя с произвольным распределением скоростей на
внешней его границе.
§ 12. «Односкатный» профиль скоростей
Предыдущий однопараметрический класс задач пограничного слоя
заключал в себе как конфузорный, так и диффузорный участки слоя.
Сейчас будет рассмотрен другой, также представляющий интерес,
однопараметрический- класс решений, описывающий только диффу-
зорный участок слоя и соответствующий линейному уменьшению ско-
рости внешнего потока на этом участке
согласно формуле
где Ьо и Ьх — две константы. Вынося
первую из них за скобку, можем пе-
реписать предыдущее равенство в виде
^_^ */($) = t/ffl A — 5). 5 = -!г-*. B.26)
О ' Ь„/Ь, К
рис 28 где П°Д Um понимается значение U (?)
при ? = 0.
Показанный на рис. 28 профиль скорости «внешнего» потока
носит наименование «односкатного». Пологость ската характеризуется
величиной bv В этом случае имеются две размерные константы, из
которых можно составить как масштаб длин L = -^-, так и масштаб
скоростей Uт = Ьо; движение не автомодельно, и уравнение для
функции тока ф не сводится к обыкновенному.
Следуя Хоуарту1), представим функцию тока степенным разложе-
нием по \
ф = Уь~^с [/0 (т,) - 86/, ft) + №2/2 (Ч) -•••]. B.27)
где по аналогии с задачей Блазиуса, являющейся частным случаем B.26)
при Ч, = 0, положено (сохраняем в правой части множитель i/г. как
это принято Хоуартом)
4/1? B-28>
Разложение B.27) составлено формально в предположении, что
при некоторых ограниченных значениях \ ряд в правой части сходится.
l) H о w a r t h L., Proceed. Roy. Soc, Ser. A, 164 A938), 919.
§ 12]
«ОДНОСКАТНЫЙ» ПРОФИЛЬ СКОРОСТЕЙ
75
Подставим значение ф из B.27) в уравнение A.19) и сравним
коэффициенты при одинаковых степенях ?. Тогда (штрих означает
производную по т;) получим следующую систему обыкновенных урав-
нений для функций /,(т)):
B.29)
/г+/о/; -
/Г
+5/072=—g-+2/;2 - з/, /»,
+7/073=е/;/; - ъ/j; - bf"j2,
В оригинале работы Хоуарта выписана система уравнений до
индекса «8» у функций ft включительно').
Граничные условия приняты такими:
= 0 при 7j =
2
n-i' /;=/;=
¦О при 7j—>oo.
B.30)
Первое уравнение системы B.29) отличается от соответствующего
задаче Блазиуса уравнения A.37) только коэффициентом при третьей
производной; объясняется это наличием коэффициента 1/2 в выраже-
нии т) по формуле B.28).
Остальные уравнения линейны и содержат каждое последовательно
только одну неизвестную функцию, выражаемую через другие ранее
вычисленные функции. Функции /;(tj) и их производные до / = 7
включительно были вычислены Хоуартом и приводятся в ранее цити-
рованной его работе. Те же таблицы, но до /=6 можно найти
в конце только что цитированной нашей монографии 1941 г.
Удовольствуемся приведением таблицы 5 зависимости безразмерной
скорости иЦЬ^2) от 5 и 7),
« = T-[/iD)-85/I'D) + (8SJ/JGj)- ...]• B.31)
Толщины вытеснения и потери импульса будут соответственно
равны ос
') См. также Лойцянский Л. Г., Аэродинамика пограничного слоя,
Гостехиздат, 1941, стр. 159.
76
ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
0,0125
0,000
0,125
0,251
0,377
0,498
0,611
0,711
0,796
0,864
0,914
0,949
0,972
0,985
0,993
0,997
0,998
0,999
1,000
—
0,025
0,000
0,117
0,237
0,358
0,477
0,590
0,692
0,779
0,850
0,904
0,942
0,967
0,983
0,991
0,996
0,998
0,999
1,000
—.
—
0,0375
0,000
0,108
0,222
0,338
0,455
0,567
0,670
0,760
0,834
0,891
0,934
0,962
0,979
0,990
0,995
0,998
0,999
1,000
—
—
0,050
0,000
0,099
0,205
0,317
0,430
0,541
0,645
0,738
0,815
0,877
0,923
0,954
0,975
0,987
0,994
0,997
0,999
1,000
—
—
0,0625
0,000
0.089
0,188
0,293
0,403
0,513
0,617
0,712
0,794
0,860
0,910
0,946
0,969
0,984
0,992
0,996
0,999
1,000
—
¦—
0,075
0,000
0,078
0,168
0,267
0,372
0,480
0,585
0,682
0,769
0,839
0,894
0,934
0,961
0,979
0,989
0,995
0,998
0,999
1,000
—
—
0,0875
0,000
0,066
0,146
0,237
0,337
0,442
0,546
0,646
0,736
0,812
0,872
0,918
0,951
0.972
0,985
0,992
0,997
0,999
1,000
—
—
—
0,100
0,000
0,052
0,120
0,202
0,294
0,394
0,498
0,598
0,692
0,776
0,844
0,897
0,936
0,962
0,978
0,989
0,994
0,998
0,999
1,000
—
Г а б л i
0,1125
0,000
0,034
0,085
0,152
0,234
0,325
0,426
0,527
0,625
0,716
0,794
0,858
0,908
0,943
0,967
0,982
0,991
0,995
0,998
0,999
1,000
—
1ца 1
0,120
0,000
0,010
0,038
0,085
0,149
0,227
0,318
0,416
0,517
0,616
0,708
0,787
0,853
0,903
0,940
0,965
0,981
0,990
0,995
0,998
0,999
1,000
где положено
-^/I A) +
1 —
2A-6)
Ha рис. 29 приведен график функции рE). Таблица 6 содержи-
значения fJ(;) и ^2(?)' полезные для дальнейшего.
Таблица г
6
0,0000
0,0125
0,0250
0,0375
0,0500
0,0625
0,000
0,076
0,110
0,137
0,162
0,186
0,0000
0,0058
0,0121
0,0188
0,0262
0,0346 '
0,0750
0,0875
0,1000
0,1125
0,1200
?F)
0,209
0,231
0,254
0,276
0,290
Э2E)
0,0437
0,0437
0,0645
0,0762
0,0841
——
121 «односкатный» профиль скоростей
Замечая, что, согласно B.28),
77
2 ' чх 2
южем переписать B.31) в форме
V
2A-6)
_ / У \
Это — однопараметрическое семейство профилей скорости с пара-
летпом Е. Обший характер профилей тот же, что и у приведенных
1,3
0,2
0,1
О
/
/
/
отрь/В
\
0,05
Рис. 29.
ojo 41
юльзуясь равенством B.31), найдем напряжение трения на стенке
Х" = «* (SL. = Т ^о VI [П @) - «У Г @) +...]. B.32)
78 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ t™. II
Коэффициенты в этом уравнении, согласно вычислениям Хоуарта,
соответственно равны
/;' @) = 1,32824, /1 @) = 1,02054, f\ @) = — 0,06926,
/1@) = 0,0560, /^@) = —0.0372, /д@) = 0,0272,
/^@) = —0,0212. /?@) = 0,0174. /,@) = —0.0147.
Чтобы определить значение $., соответствующее точке отрыва, при-
равняем выражение, стоящее в B.32) в квадратной скобке, нулю.
Получим следующее уравнение для определения безразмерной абс-
циссы \s точки отрыва
/; @) - 85,/; @) + (8у2/2" @) + ... = 0. B.33)
Как показал Хоуарт, искомое значение безразмерной абсциссы точки
отрыва !-, будет приблизительно равно
^ = 0,12, B.34)
или в размерной форме
*, —0.1^. B.65)
Можно заметить, что чем положе скат профиля скоростей (рис. 28),
тем позже возникнет отрыв и, наоборот, чем круче спад этого про-
филя, тем ранее произойдет отрыв. Это общее свойство всех диф-
фузорных участков пограничного слоя.
§ 13. Многопараметрический класс задач Блазиуса — Хоуарта
Основной задачей является расчет пограничного слоя, образую-
щегося на поверхности обтекаемого жидкостью тела при произволь-
ном распределении скорости во внешнем потоке. Задачи, рассмотрен-
ные в предыдущих двух параграфах, были весьма частными, хотя и
содержали параметры, позволяющие варьировать форму кривой (§ 11)
или уклон прямой (§ 12).
В первые годы после появления теории пограничного слоя Бла-
зиус ') дал численное решение уравнений Прандтля для случая рас-
пределения скорости на внешней границе пограничного слоя в виде
степенного ряда
где И], и3- us> •••—заданные константы, зависящие от формы тела.
Такой ряд определяет U (х) как нечетную функцию абсциссы х,
что соответствует обтеканию произвольного симметричного крылового
профиля под нулевым углом атаки (начало координат — в передней
>) В 1 a s 1 и s H., Zeitschr. f. Mathem. u. Phys., 56 A908).
§13) МНОГОПАРАМЕТРИЧЕСКИЙ КЛАСС ЗАДАЧ БЛАЗИУСА — ХОУАРТА 79
критической точке; абсциссы на нижней поверхности отрицательны).
При этом предполагается, что рассчитанная по теории обтекания
крылового профиля идеальной жидкостью или пересчитанная с экспери-
ментально замеренного распределения давления функция U (х) может
быть с достаточной точностью представлена таким степенным рядом
с не слишком большим числом членов. Опыт расчетов показывает,
что это не всегда так.
Для первых двух функций <|>j и фз вычисления были проведены
Блазиусом; дальнейшие расчеты с большей точностью и в расширен-
ном объеме сделаны Хоуартом *); полученные им результаты и будут
сейчас изложены.
Представим функцию тока ty(x, у) в виде ряда по степеням х,
аналогичного B.36),
ф = ф1* + Фз*3+Ф5*5+ .... B.37)
где ф4— функции у.
Подставив формально это разложение в уравнение для функции
тока A.19) и сравнивая коэффициенты при одинаковых степенях х,
придем к системе обыкновенных уравнений (штрих означает диф-
ференцирование по у)
«К2 -4vK" =
- 3Мз ~ Мз = 4м1 "з
-3 (tf-фзФз) +
B 33)
которые должны быть проинтегрированы при граничных условиях
ПРИ
B 39)
Принимая во внимание необходимость применения численных
методов интегрирования, постараемся привести систему уравнений
B.38) и граничных условий B.39) к чисто численному, т. е. не содер-
жащему характерных параметров их, и3, м5, ... отдельной задачи,
') Howarth L, ARC, R « М, 1632 A935).
80
ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ
[ГЛ. I
виду. Это позволит раз навсегда произвести численное интегрировь
ние системы уравнений для всего весьма широкого класса задач
определенного распределением скорости B.36).
С этой целью перейдем от у к новому, линейно с ним связан
ному аргументу т;, равному
/"? B.40
кроме того, заменим функции фг новыми, линейно с ними связаннымр
функциями /,; /3; g5, /z5; g7, h7, k7 и т. д., положив
v Фз=4К ^«з/з-
«в (ft+ ^в
. I
им-, и?
3 5 3
и т-
B.41.
Тогда будем иметь следующую, не содержащую параметров систем1
обыкновенных дифференциальных уравнений:
^ - 5/>5 - /,А* = I + АГ -
8/; л; -7/; h7-/^=
= 1 + А- - 3
8/;а; - 7f;k7 - /] а; = ц' - з
1Л9 — 9/ГАа — /, Л9 =
B.42
§ 13] МНОГОПАРАМЕТРИЧЕСКИЙ КЛАСС ЗАДАЧ БЛАЗИУСА—ХОУАРТА 81
1
Jl = Л' A0/л;
-7/зЛ)-1
,
B.42)
и граничные условия к ней
—- fl§ — fl§ — *l-j —• Лу = Kj — ftj —- Лд —¦ ftg —¦ . . . —¦ U
при 7)= 0, B.43)
/l=I> /з=Т' #5= "б"' ^7 — "§"' ^9=10'
Ag= Л? :^ k'7-= k'g = j'§ — qlj = 0 при т)= со.
Значения функций /,. /;. /;'; Д. Д. Д'; ^ ^, #*; Л5> Ag. A*;
й?, k'v k'7 приведены в таблице I, помещенной в конце нашей моно-
графии 1941 г. (см. сноску на стр. 75).
Дадим еще выражения компонент скорости и, v и напряжения
трения xw, сохраняя в разложениях только те члены, которые заклю-
чают протабулированные функции
2 + 30 (a5g5 4- ^
«7^+-^л7+4^Ь6 .
«, /Г @) х + 4«3/;' @) ^3 4- б [ «^ @)+
% К @)] ^5 + «[ «:?" @) + ^-5 h] @) +
B.44)
6 Зак. 297. Л. Г. ЛойцянскиЛ
82 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ [ГЛ. II
Блазиус применил полученные им разложения для расчета погра-
ничного слоя на круглом цилиндре при поперечном его обтекании,
причем в качестве распределения скоростей на внешней границе слоя
принял известную теоретическую синусоидальную зависимость. Точка
отрыва получилась примерно на 110°, считая от лобовой критической
точки, т. е. вниз по потоку за миделевой плоскостью цилиндра.
Опыты Хименца J) показали, что на самом деле точка отрыва лами-
нарного слоя с поверхности цилиндра определяется приблизительно
углом 81°, отсчитанным от передней критической точки цилиндра.
На первый взгляд можно было подумать, что точка отрыва опере-
дила точку минимума давлений в теоретическом распределении давле-
ний, расположенную в миделевом сечении, и попала в область уско-
ренного потока (конфузорную область), а это противоречит механизму
возникновения отрыва (§ 9).
Хименц разъяснил это противоречие между теорией и опытом,
сравнив действительное распределение давления с синусоидальным и
показав, что максимум скорости (минимум давления) в действительном
обтекании оказывается расположенным вблизи 70° и, следовательно,
в полном соответствии с теорией, точка отрыва находится в области
замедляющего потока (диффузорной области). Случай поперечного
обтекания круглого цилиндра дал первый яркий пример обратного
влияния пограничного слоя на внешний поток. В этом случае, так же
как и в других случаях отрыва пограничного слоя, получить удовле-
творительное распределение давления по поверхности тела не удается
ни с помощью расчетов по теории идеальной жидкости, ни с помощью
поправок в духе изложенного § 10 приема, и до сих пор нет сколько-
нибудь рационального решения этого вопроса. Хименц положил
в основу расчета пограничного слоя на круглом цилиндре экспери-
ментальное распределение скорости
U (х) = 7,151* — 0.04497л;3 — 0,0003300л;5,
соответствующее условиям опытов, проведенных им в водяном лотке:
радиус цилиндра 4,87 см, скорость набегающего потока 19,2 см/сек,
рейнольдсово число — около 18 500. График этой функции показан
на рис. 30. Там же пунктиром приведено расположение теоретической,
синусоидальной кривой. Не будем останавливаться на деталях этого,
представляющего в настоящее время скорее исторический интерес
вопроса 2).
Хоуарт 3) привел решение и для случая несимметричного крыло-
вого профиля (или для симметричного, но расположенного к напра-
') Hiemenz К., Dingl. Polytechn. Journal, 32a A911), 321.
2) См. ранее уже цитированную нашу монографию «Аэродинамика погра-
ничного слоя», стр. 155, 1515, а также Шлихтинг Г., Теория пограничного
слоя, пер. с нем., ИЛ, 1956, стр. 142—150.
3) Н о w a r t h L., ARC, R & M, 1632 A935).
§ 13] МНОГОПАРАМЕТРИЧЕСКИЙ КЛАСС ЗАДАЧ БЛАЗИУСА ХОУАРТА
83
влению потока под углом атаки) с распределением скорости на внеш-
ней границе ц = ^ + ^ + ^ + ... B.45)
И в этом случае ему удалось свести расчет к использованию
заранее составленных таблиц ').
Задача Блазиуса — Хоуарта относится к числу многопараметриче-
ских, так как в зависимости от наличия достаточно подробных таб-
лиц по ним можно рассчитывать пограничные слои с полиномиаль-
ными распределениями ско-
рости на внешней границе,
содержащими большое число
параметров.
Следует отметить основ-
ную трудность, заключаю-
щуюся в невозможности по-
линомиального представле-
ния сколько-нибудь слож-
ного распределения скорости
внешнего потока при помощи
небольшого числа парамет-
ров. Даже для представле-
ния такой «гладкой» кривой,
как синусоида в интервале
0—180°, необходимо исполь-
зовать не менее четырех па-
раметров. Практика показала,
что полиномиальное пред-
ставление скорости в сколько-нибудь сложных случаях становится
почти совершенно невозможным; это еще раз говорит о необходи-
мости разыскания принципиально других, более простых и пригод-
ных для массовых расчетов приближенных методов. Этому вопросу
будет посвящена следующая глава.
А. А. Дородницын 2) использовал решение Хоуарта в случае
U (х) = ихх + и3*3 + и5х5
для получения одно- и двупараметрических семейств профилей ско-
рости. В этом случае первое из соотношений B.44) может быть пред-
ставлено так:
и = игх (/; + 4T/^+ 6fmg'5
и
40
35
30
25
20
15
10
5
/
//
/
/ft
w
' >
У
\
4
оыв
3 4 5
Рис. 30.
') См. оригинал только что цитированной работы Хоуарта или нашу
монографию «Аэродинамика пограничного слоя», где соответствующие таблицы
помещены в конце в качестве приложения (таблица II, стр. 405 и 406).
2) Дородницын А. А., Ламинарный пограничный слой в сжимаемом
газе, Сборник теоретических работ по аэродинамике, ЦАГИ, Оборонгиз,
1957, стр. 150.
84 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ [ГЛ. II
где положено
^ B.46)
"i «з
При этом будет
Чтобы найти искомые наборы профилей скорости в сечениях по-
граничного слоя, составим выражение
» _ /i (*l) + 4у/з (ч) + 6mY2^5 М + 6?2/г5 М
77— 1 -f- -f + mf С^-4')
и заменим в нем аргумент -ц на у/8**. Имеем, согласно B.40),
5** =
о
где положено
о
Таким образом, можно в равенстве B.47) произвести замену
__ 1 _у_
71~ Х(-Г. т) ' Ь**
и получить двупараметрическое семейство
1Г = Р{-$г'. Т. «)• B-48)
Задаваясь отдельными значениями не зависящего от х параметра т,
будем получать различные однопараметрические семейства. А. А. Дород-
ницыным были построены семейства для значения т = — 0,2; 0;
— 0,4. О применении этих семейств профилей скорости к прибли-
женному расчету пограничного слоя при произвольном задании ско-
рости внешнего потока будет сказано в следующей главе.
§ 14. Классы точных решений Тани
и Гертлера — Виттинга
Разложения скорости внешнего потока U (х) в степенной ряд,
использованные Хоуартом, не содержали свободного члена. Более
общие классы решений были исследованы Тани '), который рассмо-
трел случай
?/=и0+«„*«. и0Ф0, «>0. B.49)
') Т а п 1 J., J. Phys. Soc. Japan, 4 A949), 149—154.
§ 14] КЛАССЫ ТОЧНЫХ РЕШЕНИЙ ТАНИ И ГЕРТЛЕРА— ВИТТИНГА
85
и Гертлером — Виттингом'), разобравшими случай задания U (х)
в форме
..]. B.50)
Остановимся на рассмотрении второго класса решений.
Гертлер и Виттинг используют, так же как и все другие авторы,
уравнение пограничного слоя A.19), составленное для функции тока
ф(х, у), но совершают преобразование аргументов х, у и неизвестной
функции ty(x, у) к новым переменным ?, ч\ и функции F (?, у]),
полагая
4
/г
(?. 71) = Ф(*. У)/ 2v J
B.51)
Тогда уравнение A.19) переходит в следующее нелинейное урав-
нение в частных производных:
<2-52)
а граничные условия сохраняют обычный вид:
/="=0. ^=0прит] = 0, ^->1 при
B.53)
При этом заданное распределение скорости U (х) на внешней
границе слоя входит в уравнение B.52) только через величину Р(|),
равную
B.54)
причем предполагается, что правая часть выражена в функции от ?
при помощи первого равенства системы B.51); в граничные условия
функция U (х) явно не входит.
Зададимся функцией C(?) в форме степенного ряда
!+ ... B.55)
') G or tier H., Witting H., Osterr. Ing.-Archlv.il, № 2 A957),
86 ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПРАНДТЛЯ [ГЛ. II
и, пользуясь связью B.51) между л; и с, а также равенствами B.50)
и B.54), найдем, что показатель степени от связан с ро соотношением
_ ftp „ _ 2т
а числа и0, щ, ... могут быть последовательно выражены через
Ро, Pj, ... Гертлер и Виттинг исследовали случай от = 0, Р0 = 0.
Решение уравнения B.52) разыскивается в виде ряда
Тогда F0(-f]) совпадет с решением Блазиуса, а остальные функции
Fn(ri) могут быть выражены так:
Л От) = Pi/i ft). ^2 (т) = Pi/п (i) 4- Р2Л A).
'J). и т. д.,
причем функции fv /п, /2, /12, ... определяются из дифферен-
циальных уравнений и граничных условий, не содержащих никаких
характерных для данной задачи величин.
Большое число этих функций было авторами затабулировано и
таблицы приведены в статье Гертлера и Виттинга. Там же можно
найти формулы для безразмерного напряжения трения, толщин выте-
снения и потери инпульса, абсциссы точки отрыва и др.
ГЛАВА III
ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
§ 15. Некоторые общие соображения
Решение практических задач теории ламинарного пограничного
слоя путем непосредственного интегрирования уравнений Прандтля
при произвольном распределении скорости во внешнем потоке пред-
ставляет значительные трудности. Представить заданное распределе-
ние скоростей достаточно точно при помощи одного из тех распре-
делений, которые были использованы в классах решений, рассмотренных
в предыдущей главе, удается только в самых редких случаях. На
помощь приходят хорошо разработанные приближенные методы,
начало которых относится к ставшим уже классическими работам
Кармана и Польгаузена 1921 г. !). Основная идея этих методов за-
ключается в использовании вместо точных распределений скоростей
в сечениях пограничного слоя некоторых наборов профилей, пред-
ставленных семейством кривых с одним параметром. Изменение па-
раметра создает то разнообразие форм профилей, которое необхо-
димо для приближенного описания движения жидкости во всем
пограничном слое, включая как конфузорную, так и дйффузорную
части. Параметр — его обычно называют «формпараметром» — пред-
ставляет собой функцию продольной координаты в пограничном слое,
указывающую, к какому сечению слоя следует отнести данный про-
филь семейства.
В качестве такого рода набора профилей скорости Польгаузен
выбрал семейство полиномов четвертой степени, коэффициенты ко-
торых были определены из граничных условий на твердой поверх-
ности и на внешней границе слоя. Выполнение этих условий при-
ближало выбранные профили скорости к действительным.
Для определения зависимости параметра семейства от продольной
координаты Карман использовал выведенное им интегральное усло-
вие, являющееся результатом применения теоремы импульсов к эле-
ментарному объему пограничного слоя и называемое поэтому урав-
нением импульсов.
') Karma n v. Th., Zeitschr. f. Angew. Math. u. Mech. 1 A921), 233;
Pohlhausen К., там же. стр. 235.
88 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
За протекшие после появления работ Кармана и Польгаузена
почти сорок лет метод получил дальнейшее развитие. Многие совет-
ские и зарубежные исследователи занимались уточнением и упроще-
нием этого метода. В качестве набора профилей использовались
различные семейства кривых. Делались попытки повышения степени
многочлена, использовались тригонометрические и показательные
функции, трехчлены с нецелыми степенями и др. Применение впер-
вые введенного в работах Кармана и Польгаузена приближенного
представления о пограничном слое конечной толщины не является
принципиальной особенностью метода; впоследствии толщина слоя
была заменена толщиной потери импульса, представляющей точный
образ в теории асимптотического слоя.
Постепенно стало ясным, что метод, использующий только один
параметр, а следовательно, и только одно уравнение для его опре-
деления, может быть удовлетворительным лишь при достаточно
удачном выборе профилей скорости в сечениях слоя. В связи с этим
стали применять однопараметрические семейства профилей, состав-
ленные при помощи классов точных решений, соответствующих не-
которым распределениям скорости во внешнем потоке. Это сразу же
значительно повысило точность однопараметрических методов. Пре-
терпело также изменение и выражение формпараметра Польгаузена,
в котором условная конечная толщина слоя была заменена
более определенной величиной — толщиной потери импульса. Значи-
тельно упростилось и уравнение, служащее для определения измене-
ния формпараметра вдоль пограничного слоя. Попытки применения
двупараметрических методов потерпели неудачу по причине их чрез-
мерной вычислительной громоздкости.
Однопараметрические методы близки по идее к прямым методам
вариационного исчисления Ритца и Галеркина. Так же как и в этих
методах, в теории пограничного слоя используются для профилей
скорости в сечениях слоя «конкурирующие» функции, с той или
другой степенью приближения выражающие некоторые свойства не-
известных решений задачи. Использование при этом уравнения им-
пульсов вместо некоторого вариационного принципа не существенно;
аналогичный метод может быть основан и на применении вариационного
принципа 1).
§ 16. Интегральное условие импульсов
На основании уравнения неразрывности перепишем первое из
уравнений теории плоского пограничного слоя A.17) в виде
, d(uv) ,, dU . д*и
И= U + v
дх ^ ду ~ " dx ^ ду
Л о й ц я н с к и й Л. Г., ПММ, т. V, в. 3, 1944.
§ 16] ИНТЕГРАЛЬНОЕ УСЛОВИЕ ИМПУЛЬСОВ 89
Умножив обе части уравнения неразрывности на U (х), найдем
д (Ци) д (С/у) __ dU
дх ' ду dx
Вычитая почленно обе части предыдущего уравнения из только что
полученного, придем к выражению
д , .,, ... д . ,,, .. . ,,, . dU дги
_[„(?/_„)] + _[*,(?/_«)] + (?/_„) _==-^,
формальное интегрирование которого поперек слоя по у от нуля до
бесконечности дает
^J {U-u)dy = ,(<?)¦ C.1)
о о у
здесь использовано обращение в нуль величины [v(U — и)]у1"> сле-
дующее из граничных условий, а также асимптотическое стремление
к нулю производной ди/ду при' у—>со.
Предполагая существование интегралов
СО ОО
/ (U-u)dy=U f' (l - -g.) dy = Ub\
о о
и допуская возможность замены порядка интегрирования и дифферен-
цирования в первом интеграле в левой части C.1), получим, вводя
напряжение трения на стенке т^, —jxl-r-1
JL(U4**)-\-u4?-?>* = 1sl . C.2)
dx y ' ' dx p v '
или, записав в развернутом виде производную в первом слагаемом,
Уравнение C.3) в несколько иной форме было впервые выведено
Карманом в ранее цитированной его работе, относящейся к 1921 г.,
и получило название «интегрального условия Кармана». В настоящее
время его принято именовать «уравнением импульсов»; происхожде-
ние последнего наименования вскоре будет объяснено. В дальнейшем
будет принято обычное в литературе обозначение
Ът/Ъ** = Н, C.4)
90 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
после чего уравнение импульсов C.3) перепишется в форме (здесь
и далее штрих —производная по х)
(П' + -^-B + //) = -^-. C.5)
Во многих приближенных методах используется понятие о тол-
щине пограничного слоя 8 как о некоторой конечной величине,
представляющей собой неизвестную функцию продольной коорди-
наты х. При этом толщина слоя 8 определяется не как значение
ординаты у, в которой продольная скорость и на заданный малый
процент отличается от скорости внешнего потока U. В отличие от
сказанного по этому поводу в главе I, принимается, что на внешней
границе (у = 8) выполняются одновременно два условия
u = U{x), Щ- = 0 при у = Ь(х). C.6)
Эти два равенства выражают основные допущения приближенной
теории пограничного «слоя конечной толщины», которую мы будем
в дальнейшем отличать от более точной теории «асимптотического
слоя».
Заметим, что при пользовании понятием слоя конечной толщины
уравнение импульсов сохранит свой вид C.3) или C.5). В этом слу-
чае следует только величины 8* и 8** определять как интегралы
в конечных пределах
о о
Благодаря наличию определяющих пограничный слой конечной
толщины граничных условий C.6) весь вывод уравнения импульсов
C.3) может быть буквально повторен с той лишь разницей, что пер-
вый интеграл в левой части C.1) должен быть преобразован так:
f ^-[u{U-u)\dy = -^ f
Пользуясь понятием пограничного слоя конечной толщины, пояс-
ним происхождение наименования «уравнение импульсов». С этой
целью дадим другой, более близкий к приведенному в ранее цити-
рованной работе Кармана вывод этого уравнения.
Применим теорему об изменении количества движения в форме
Эйлера или, как ее принято именовать в зарубежной литературе.
§ 16]
ИНТЕГРАЛЬНОЕ УСЛОВИЕ ИМПУЛЬСОВ
91
теорему импульсов, к объему жидкости ABCD (рис. 31), заключен-
ному между двумя бесконечно близкими сечениями пограничного
слоя АВ и CD с абсциссами х и х-\-йх, твердой стенкой AD и внеш-
ней границей слоя ВС. Обозначим через М и У соответственно секундную
массу и проекцию на ось Ох секундного количества движения
жидкости, протекающей через рассматриваемое сечение слоя АВ,
М = jpudy, У= fpu2dy.
dx
Тогда из условия сохранения массы будет следовать, что секундная
масса, протекающая через отрезок границы слоя ВС, равна -^- • dx.
Принимая во внимание, что
на всем отрезке ВС внешней
границы слоя можно с ошиб-
кой высшего порядка малости
принять скорость равной U,
найдем, что проекция на ось Ох
секундного количества движе-
ния, переносимого жидкостью
сквозь сечение ВС, равна
Проекции на ось Ох внеш- рис 3j
них сил, приложенных к грани-
цам АВ, ВС, CD и AD, выбранного элемента объема будут соот-
ветственно равны
Применяя к контрольной поверхности ABCD теорему количеств дви-
жения в проекции на ось Ох, получим
'-('+?<*)+«'?
или, откидывая малые величины второго порядка малости и деля
после этого обе части на dx,
dJ_,udM_ dp _
dx^ dx ~ ~dx"-
92 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. II!
Подставляя сюда значения У и Ж и заменяя -j- на —p(J -z—,
получим
откуда уже нетрудно найти уравнение импульсов в форме C.3). Та-
ким образом, мы убедились, что уравнение C.3) действительно вы-
ражает теорему импульсов в проекции на продольную ось движения
жидкости в пограничном слое.
Уравнение импульсов содержит три неизвестные величины: о*, 8**,
xw или, что все равно, 8**, Н и xw. Задаваясь формой профиля ско-
ростей в сечениях пограничного слоя, мы получаем возможность
свести эти три неизвестные к одной — параметру, определяющему
вариации форм профилей скорости.
§ 17. Метод Кармана — Польгаузена
Зададимся, следуя ранее цитированной работе К. Польгаузена,
набором профилей скорости в сечениях слоя в виде многочлена
четвертой степени G1 = 8
? = 77 :== ao 4- ^i7] 4" ^T 4~ азТ 4" °47Г*
Чтобы приблизить это выражение к действительному профилю
скоростей, подчиним выбор пяти коэффициентов аг во-первых, трем
очевидным граничным условиям [см. C.6)]
tp=O при т] = 0, ip=l, -~ =.О при т]=1 C.7)
и затем еще двум дополнительным условиям
1ГЪ* _
C.8)
при -г; = 1 -
Первое из этих дополнительных условий непосредственно следует
из первого уравнения A.17) Прандтля, второе выражает условие
§ 17] МЕТОД КАРМАНА ПОЛЬГАУЗЕНА 93
того, что сопряжение профиля скоростей и(х, у) со скоростью U (х)
на внешней границе имеет второй порядок, т. е. удовлетворяет
условию равенства нулю кривизны профиля скоростей в точке со-
пряжения его с горизонтальной прямой u—U{x).
Из принятых пяти условий легко определяются коэффициенты at.
Если ввести в рассмотрение формпараметр Польгаузена
Х=-№) =i^, ^ C.9)
то искомый профиль скоростей будет иметь вид
X „ , 4-Х ч . 6 —X
f22r (ЗЛ0)
или, выделяя явно условия сопряжения при т)=1,
\ (З.п)
Определим границы возможного изменения формпараметра X. Как
сразу видно из C.10), условию отрыва слоя A.116)
d9\ __ 12 +
= 0
\ari/ri=o °
соответствует
Х = Х5=— 12. C.12)
С другой стороны, составляя по C.11)
= A—1
заключим, что условие монотонности роста скорости в сечениях по-
граничного слоя соответствует требованию о том, чтобы корень
уравнения
т. е. величина
2Х/3 — 4 '
был больше или равен единице. Отсюда найдем Х^ 12. Итак, допу-
стимая область изменения а оценивается неравенствами
— 12<Х<12. C.13)
Семейство кривых, ограниченное этими значениями параметра,
приведено на рис. 32 сплошными линиями. Пунктиром показаны при-
меры немонотонных кривых с параметром X, не удовлетворяющим C.13)t
94
ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
Перейдем к составлению уравнения для определения формпаря
метра Х(л:). Имея в виду дальнейшие обобщения, приведем вывоа
этого уравнения, несколько отличный от изложенного в работе Поль
гаузена1). Отвлекаясь от частной формы профилей скорости C.11,
принятой Польгаузеном, предположим, что u/U представляет общук
U.
и
as
0,6
ол
0,2
/
/
и
1 1 ^
1 ^ 1
Ул=/2^
fFja4c
/
7
--~
¦~~~
>—
^ Й41 #?
Рис. 32.
0,8
функцию <p(tj; X), и введем в рассмотрение следующие, завися1щи
только от \ величины:
Переписывая уравнение импульсов C.3) в виде
(ЯП)' + -^ B/Г + Щ -
и замечая, что по определению C.9) параметра X будем иметь
') Л о й ц я н с к и й Л. Г., ДАН СССР, 35, № 8 A942).
§17] МЕТОД КАРМАНА ПОЛЬГАУЗЕНА
перепишем предыдущее равенство в виде
95
Выполняя дифференцирование в левой части и сокращая обе части
-щ-, получим
где положено
Ь(Х) — Х BЯ ** + И*)
к ^ —
C.16)
Уравнение C.15) представляет общий вид преобразованного уравне-
ния импульсов в том случае, когда используется произвольный одно-
параметрический набор профилей с параметром X
Возвращаясь теперь, в частности, к однопараметрическому семей-
ству Польгаузена C.10) или C.11), вычислим по C.14)
w*m_ 3 х
37 X X2
//-(X)
315
945
"9072"'
А.
C.17)
Подставляя найденные значения Н*(\), Н**(Х), Ь(к) в выражения
функций g(k) и к (к), будем иметь
" 213,12 —5.76Х — Х2 '
_ 213.12Х — 1.92Л2 — 0.2Х*
213,12 — 5/76Х —X2 '
Функции эти затабулированы ¦).
Интегрирование обыкновенного дифференциального уравнения
C.15) первого порядка представляет значительные вычислительные
') См. таблицу V нашей монографин «Аэродинамика пограничного слоя»,
Гостехиздат, 1941.
96 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
трудности, так как это уравнение имеет особые точки в начале коор-
динат х — О, где U (х) = 0, и в точке минимума давления х = хт,
где U' (х) = 0. Польгаузен интегрировал эквивалентное C.15) урав-
/ 82 * \
нение (* = _ =
)
Г / UU" \ /, , UU"\ I
0,8 —9072 -f 1670.4Х — 47,4 + 4,8 -7772" IX2 — П + "ТТЛ") *3
_/ L \ U I \ U I \ ,~ 1 о\
?/(—213,12 + 5.76Х + X2) .(о.ю)
Для интегрирования применялся графоаналитический метод изоклин-
Вычисления начинались с лобовой критической точки х =¦ 0, где
U(x) = 0. Для определения начального значения Х = ХО использова-
лось то, что точка лг = О, z — z0 является особой точкой уравнения
(«седлом»). Приравнивая нулю числитель в правой части уравнения
Польгаузена C.18) при ?/ = 0, получим кубическое уравнение, корни
которого будут: (—70), 7,052 и 17,75. По условию C.13), смысл
имеет лишь корень
Aq = 7 ,\)о2ш
который принимался за начальное значение X.
Как показали многочисленные расчеты, метод Польгаузена ока-
зался и сложным, и недостаточно точным. Было сделано много по-
пыток уточнить метод путем использования многочленов других сте-
пеней, а также и других функций1). В настоящее время сохранилась
лишь общая идея этого метода, а созданные на его основе другие
однопараметрические методы с вычислительной стороны гораздо более
точны и просты.
§ 18. Применимость метода Кармана — Польгаузена
Чтобы составить себе представление о возможности применения
метода Польгаузена для практических расчетов, остановимся прежде
всего на простейшем случае продольного обтекания пластинки (за-
дача Блазиуса). В этом случае U = const = U^, U' — 0, следова-
тельно, \ повсюду равно нулю. Согласно C.17), имеем
Н* = 0,3; Н** = 0,1175, Ь = 2.
Уравнение импульсов непосредственно сводится к такому:
O,11755/ = 2v/(t/co8),
откуда при начальном условии 5 = 0 при х = 0 получим
') Подробнее см. ранее цитированную нашу монографию «Аэродинамика
пограничного слоя», стр. 171.
§ 18]
ПРИМЕНИМОСТЬ МЕТОДА КАРМАНА — ПОЛЬГАУЗЕНА
97
и, следовательно, будем иметь
о* = 0,33 = 1.751/"-^.
0,11750 = 0,685
ис
'
Сравнивая эти результаты с ранее полученными точными реше-
ниями задачи Блазиуса, убеждаемся в пригодности метода Польгау-
зена для случая отсутствия продольного изменения давления. Весьма
удовлетворительные результаты получаются и в конфузорных обла-
стях пограничного слоя с ускоренным движением во внешнем по-
токе. В оригинальной работе Польгаузена можно найти расчет плос-
кого конфузора с распределением
скоростей U = — А/х. Аналогич-
ная задача в точной постановке
была уже решена в § 11. Как
показывает сравнение этих двух
решений, разница между ними
очень невелика. 0,8
Иной результат получается при
применении метода Польгаузена
к расчету диффузорных участков
пограничного слоя, где внешний
поток замедляется, а давление вос-
станавливается. Расчеты показы-
вают, что профили скоростей, оп-
ределенные по методу Польгау-
зена, отстают в своем развитии от
точных и дольше сохраняют свою
О
Рис. 33.
«полноту». Это отставание сказывается особенно резко при прибли-
жении к точке отрыва; точка отрыва, определенная по Полыаузену,
как правило, располагается ниже по потоку, чем в действительности!
а иногда и вообще не обнаруживается. Так, например, в случае по-
перечного обтекания круглого цилиндра точка отрыва по Полыау-
зену лишь незначительно смещается по сравнению с результатом
расчета по более точной теории. В случае же поперечного обтека-
ния эллиптического цилиндра, экспериментально изученного Г Шу-
бауером*) (отношение осей а :Ь = 2,96:1), теория Польгаузена не
предсказывает отрыва, между тем как опыты обнаруживают отчетли-
вый отрыв в точке, отстоящей от передней критической точки на
расстоянии, примерно равном длине Ь меньшей оси эллипса. На
рис. 33 приводятся для сравнения несколько профилей скорости в
сечениях пограничного слоя на эллиптическом цилиндре, рассчитанных
') S с h u Ъ a u e r G. В.. NACA, Rep. 527, 1935.
7 Зак 297 Л. Г Лойиянский
98 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. lit
по методу Польгаузена, и экспериментальные точки по Шубауеру.
Бросается в глаза отмеченное выше отставание в развитии польгау-
зеновского профиля скорости по сравнению с экспериментальным
(пунктирным), который при х/Ь= 1,946 уже имеет типичный пред-
отрывный вид с отчетливо заметным перегибом, в то время как
у польгаузеновского профиля (сплошная кривая) точка перегиба еще
только еле заметна. Интересно заметить, что в случае обтекания
эллиптического цилиндра минимальное экспериментальное значение
параметра Польгаузена X оказывается равным Х = -—5,37, т. е. еще
очень далеким от Ху = —12.
Конечно, причина такого неудовлетворительного состояния тео-
рии Польгаузена заключается главным образом в неудачном выборе
основного полинома C.10). Попытки перехода к полиномам пятой
и шестой степени, учитывающим более широкую совокупность гра-
ничных условий, чем C.7) и C.8), и, в первую очередь, непосред-
ственно следующее из уравнений Прандтля условие
показали возможность уточнения метода Польгаузена, но в настоя-
щее время в связи с развитием других, гораздо более простых и
точных методов, о которых будет речь впереди, вряд ли такие
уточнения представляют интерес.
§ 19. Обобщение метода Кармана — Польгаузена
Изложенный в предыдущих параграфах однопараметрический метод
может быть легко обобщен и на случай произвольного семейства
профилей скорости и асимптотического или конечного по толщине
пограничного слоя. Такое обобщение приводит к значительному упро-
щению и уточнению метода.
Примем в качестве характерной толщины пограничного слоя
вместо условной толщины 8 строго определенную величину — тол-
щину потери импульса 8**. Зададим однопараметрическое семейство
профилей скорости в сечениях слоя в виде
/). C.19)
где формпараметр /, аналогично C.9), определим как взятую с обрат-
ным знаком безразмерную вторую производную скорости по нормаль-
ной к стенке координате, вычисленную непосредственно на стенке,
т. е. положим
UU'\ U'b**1
C.20)
§ 19] ОБОБЩЕНИЕ МЕТОДА КАРМАНА ПОЛЬГАУЗЕНА 99
Этот новый параметр отличается от старого параметра Польгау-
зена X C.9) тем, что в нем толщина 8 заменена 6**; оба параметра
связаны очевидным 'соотношением .
= кп . C,21)
Нет необходимости вновь выводить уравнение для определения пара-
метра /. Достаточно вернуться к уравнению C.15) и заметить, что
входящие в него функции g(k) и А(Х) при помощи C.21) могут быть
выражены через /(X) и функцию
. C.22)
Так,
после чего уравнение C.15) перейдет в искомое уравнение для опре-
деления формпараметра
f' = ?rF<J) + %rf- C-23)
В этом уравнении предполагается, что Р выражено в функции
от / путем исключения X из совокупности уравнений C.21) и C.22).
Чтобы произвести это исключение, введем, подобно тому как это
делалось для определения величины Ь(к), безразмерную первую произ-
водную от скорости при задании семейства профилей скорости C.19)
Заметим еще. что
№Н~ = №*. Н = /Н. C.25)
Тогда, раскрывая скобки в C.22), получим новое выражение для
функции /=•(/)
F{f) = 2 [С -B + Я)/], C.26)
где величины
C.28)
<Р О —
уже являются функциями параметра /. Таким образом, исключение X
произведено.
7*
100 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
Изложенный только что вывод1) основного уравнения C.23) пока-
зывает непосредственную связь нового однопараметрического метода
со старым методом Кармана — Польгаузена. По Тсоду вывода стано-
вится ясным существенное преимущество уравнения C.23) по срав-
нению с уравнением Польгаузена C.15). Переход от параметра X
к параметру / свел две, содержащиеся в уравнении C.15) характе-
ристические функции g(k) и k(k) к одной F (/), причем, как далее
будет показано и что очень существенно, новая характеристическая
функция F(f), в отличие от двух предыдущих, допускает в первом
приближении замену ее линейной функцией, что позволит свести
уравнение C.23) к простому линейному дифференциальному уравнению.
Можно дать другой вывод уравнения C.23), не связанный с урав-
нением Польгаузена C.15), а непосредственно использующий урав-
нение импульсов в общем его виде C.5).
Будем исходить из того, что профили скоростей в сечениях слоя
заданы однопараметрическим семейством C.19) с некоторым, пока
неизвестным формпараметром /. Тогда будет
y=o Ub*
Jw_ _ _J__ Г dju/U) ] _
pi/s Ub** L d (y/5**) Jy=0 ~~
cx
„ r /
/
о
и уравнение импульсов C.5) перепишется в форме
Умножая обе части этого уравнения на 2 , преобразуем его
к виду
и (^т-)' +2 -^т-12+н W =2С (^-
t/'B**2
Неопределенный пока формпараметр положим равным
ч
тогда предыдущее уравнение приобретает однопараметрический вид
U(-?.)' = Г,(/)-2/[2+H(f)] = F(J); C.29»
') Лойцянскнй Л. Г., ДАН СССР 35, № 8 A942).
Л 20] ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИЧЕСКИХ ФУНКЦИЙ 101
выполняя дифференцирование слева, вновь получим уравнение C.23).
Если после преобразования уравнения C.23) к виду C.29) ввести
в качестве размерного параметра величину
*" = V = 7F- (з.зо)
„ Ь2
представляющую собой аналог параметра Польгаузена z ——, то
можно получить уравнение
00' = -^-. C-31)
не содержащее второй производной U", т. е. не требующее двух-
кратного дифференцирования задаваемой обычно приближенно вели-
чины U (х). Уравнение C.31) удобно для интегрирования числен-
ными и графическими приемами.
Переход от параметра X к / и вместе с тем к уравнениям вида
C.23) или C.31) был предложен независимо друг от друга рядом
исследователей в период 1940—1942 гг. По-видимому, впервые по
времени уравнение C.31) было предложено Г. Хольштейном и
Т. Боленом'). Можно, однако, заметить что на два года раньше
Хоуарт2) уже пользовался, по существу, аналогичным параметром
X = Yf и уравнением типа C.23), применяя класс точных реше-
ний, соответствующих «односкатному» профилю скоростей внешнего
потока, для расчета пограничного слоя с произвольным распределе-
нием скоростей на внешней границе3). Тот же параметр, что и
предложенный Хольштейном — Боленом, был, независимо от этих
авторов, введен у нас одновременно А. П. Мельниковым4) и авто-
ром настоящей книги5). Уравнения типа C.23) и C.31) были исполь-
зованы и другими авторами6).
§ 20. Определение характеристических функций
Для определения входящей в уравнения C.23) и C.31) функции
F(f), а .вместе с тем и функций С(/) и #(/), остается задаться
тем или другим однопараметрическим набором профилей скорости
.в сечениях пограничного слоя.
') Н о I s t e I n Н., В о h i е п Т., Liliental — Berlcht, S—10, № 5, 1940
2) Н о w а г t h L., Proceed. Roy. Soc, Ser. A, 164, № 919 A938).
3) Подробнее см. Л о й ц я н с к и й Л. Г., Аэродинамика пограничного
слоя, Гостехиздат, 1941.
4) Мельников А. П., Труды Ленингр. военно-воздушной академии,
В 11 У4^
5) Лойцянский Л. Г., ДАН СССР 35, № 8 A942).
e) Y о u n g A., W i n t е г b о 11 о га N.. ARC, Rep. 4697, 1940; W a 1 z A.,
Liliental — Bericht, 141, 1941; Tani J., Aero. Res. Inst. Tokyo Univ., 199, 1941;
H u d 1 m о t о В., Journ. Soc. Aero. Sci. Japan, № 8, 1941.
102
ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
[ГЛ. III
В ранее цитированной нашей работе 1942 г. использовалось
семейство профилей (С= 1—у/8)
-?- = ? (С) =
C.32)
с переменным вдоль слоя показателем степени п, характеризующим
очевидно, степень плавности перехода профилей скорости C.32)
к значению u/U= 1 на границе слоя (С = 0). Коэффициенты ах, а2, а3
определялись из условий на стенке
представляющих условия Польгаузена, дополненные последним усло-
вием, непосредственно следующим из первого уравнения Прандтля,
если обе его части продифференцировать по у, воспользоваться
уравнением неразрывности и положить у = 0. Было получено
C.34)
п — 1
и после этого вычислены характерные для слоя величины
— _ ~'fn — -
Jy = O П +
»*¦*
Г Г** ___. LJ*
2л + 3 п + '.
В точке отрыва слоя (%w = 0, 6 = 0) будет
C.35)
). C.36)
Границы значений X, в которых указанные профили обладают
свойством монотэнности, будут
C.37)
Предложенное семейство профилей C.32) является двупара-
метрическим. Его можно сделать однопараметрическим, если за-
даться связью между параметрами л и X.
§20]
Определение характеристических функций
103
Заметив, что в конфузорной области слоя профили скоростей
1Олее заполнены, чем в диффузорной области, где благодаря нали-
¦ию перегиба профили имеют урезанный вид, можно предположить,
то степень плавности смыкания внутреннего и внешнего потоков
должна непрерывно уменьшаться при переходе из конфузорной
власти в диффузорную. Сообразно с этим п должно уменьшаться
юи убывании X. В цитированной работе был принят линейный закон
той связи
\ = Щ-(п — 4), « = 0,15I + 4. C.38)
оответствующий использованию многочлена четвертой степени в точке
шнимума давления (к = 0) и многочлена третьей степени в точке
•трыва (Х = А, = — 20/3).
Равенство C.38) позволяет выразить характерные для Слоя вели-
ины Н*, Н**, b в функции одного параметра п, а затем составить и
^личины /, С, Н, F в функции от я. после чего окончательно
'Пределить функции С(/), H{f) и F(f). Таблица 7 содержит зна-
ения этих функций в интервале изменения / от отрывного
t=—0,089, где С = 0, до критического в лобовой точке
= 0,084 ч-0,085, где должно быть U = 0 и, следовательно,
огласно C.31), F = 0.
Таблица 7
/
—0,089
-0,085
—0,08
—0,07
—0,06
-0,05
-0,04
—0,03
—0,02
—0,01
0,00
у
0,000
0,019
0,039
0,071
• 0,097
0,120
0,142
0,162
0,181
0,2000
0,219
Н
3,85
3,66
3,50
3,28
3,12
3,00
2,90
2,82
2,74
2,67
2,61
F
1,04
1,00
0,96
0,88
0,81
0,74
0,68
0,615
0,55
0,495
0,44
/
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,084
0,085
г
0,236
0,253
0,270
0,286
0,302
0,318
0,335
0,350
0,357
Н
2,55
2,50
2,46
2,41
2,36
2,32
2,28
2,24
2,22
F
0,38
0,33
0,275
0,22
0,17
0,12
0,07
0,02
0,003
—0,002
Класс точных решений Фокнера и Скэн (§ 11) приводит к одно-
1араметрическому семейству B.24) с параметром р. Пользуясь вы-
ражениями B.19), B.23) и таблицей 4, легко найдем выражения
1ля /, С, Н и F в функции от параметра р, а затем и С(/), H{f)
-J f(/)- Значения этих функций приведены в таблице 8')•
') Кочин Н. Е. и Лойцянский Л. Г., ДАН СССР 36, № 9
104
ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Таблица I
f
—0,0681
—0,06
—0,05
—0,04
—0,03
—0,02
—0,01
0,00
0,01
0,0000
0,064
0,098
0,130
0,155
0,178
0,200
0,221
0,240
И
4,03
3,35
3,12
2,96
2,84
2,74
2,66
2,59
2,53
F
0,821
0,772
0,715
0,658
0,602
0,548
0,495
0,441
0,388
/
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,257
0,274
0,291
0,307
0,323
0,338
0,352
0,366
0,380
Н
2,48
2,43
2,38
2,34
2,30
2,26
2,23
2,20
2,18
F
0,336
0,283
0,232
0,180
0,130
0,078
0,028
—0,023
—0,074
Аналогично можно было бы использовать и однопараметрически^
семейства профилей скорости, получаемые из класса точных реше-
ний для «односкатного» профиля Хоуарта (§ 12) или класса точны:
решений А. А. Дородницына (§ 13) при нескольких значениях т
можно было бы использовать однопараметрическое семейство А. М. Ба-
сина 1)
-i
удовлетворяющее тем же условиям, что и профили Польгаузена, i
также условию (д3й/ду3)у_0 = 0 в точке отрыва.
На рис. 34 сплошными линиями приведены сравнительные дан
ные для С, Н и F, рассчитанных по степенной зависимости C.32
при связи C.38) (на рисунке обозначены буквой Л.), по семейств1
точных решений Фокнера—Скэн (на рисунке К.—Л.) и для С, кром^
того, по данным А. А. Дородницына (§ 13) для трехчленного про
филя скоростей при т = 0,2 (на рисунке Д.). Кроме того, пункта
ром обозначены соответствующие кривые, рассчитанные по семейств*
многочленов четвертой степени Польгаузена (§ 17).
Анализируя эти кривые, можно заметить, что выбор типа одно-
параметрического семейства профилей скорости меньше всего ска-
зывается на форме кривой F (/). Даже пунктирная кривая, рассчи
тайная по польгаузеновскому приближению, наименее, как уже ране^
указывалось, пригодному для расчетов, и то мало отличается о"
других; это говорит об «устойчивости» определения функции F (f.
Относительно более значительны различия в кривых С(/) и //(/,
Кривые ? дают заметный разброс при приближении к точке отрыв;.
(С=0). Совершенно непригодной является пунктирная кривая, про
веденная по данным Польгаузена. Она дает слишком запоздалы?
отрыв, о чем уже и было сказано ранее, в § 18. Кривая, рассчи
') Б а с и н А. М., ДАН СССР 40, № 1 A943).
, 21) ЛИНЕАРИЗАЦИЯ УРАВНЕНИЯ ОДНОПАРАМЕТРИЧЕСКОГО МЕТОДА
-энная по Дородницыну, при всех использованных им значениях т
je точна вблизи точки минимума давления (/ = 0), но при т = 0,2
ложится между кривыми Л. и К.—Л. При м = 0 и т = — 0,4
ривые ?(/) вблизи отрыва располагаются влево от кривой Л. Кри-
вая С (О- рассчитанная по «односкатному» профилю Хоуарта, прак-
"ическй совпадает с соответствующей кривой Л. и поэтому не при-
снится: не показанная на рисунке кривая С(/). по Басину, вблизи
-W -О,К -0,70 -0,06 -0,06 -0,0/' -0,02 О 0,02 0,04 0,06 006 0,70
Рис. 34 /
•трыва располагается между кривыми Л. и К.—Л. ближе к кри-
юй Л. (по Басину fs= — 0,077), а далее все менее отличается от
юеих этих кривых. В следующем параграфе будут приведены резуль-
аты некоторых расчетов, которые покажут, как отражаются разли-
ия в этих общих крирых, построенных для разных наборов профи-
.ей скорости, на конкретных расчетах пограничных слоев.
§ 21. Линеаризация уравнения однопараметрического метода
Существенным преимуществом излагаемых в настоящей главе
таиближенных методов расчета ламинарного пограничного слоя
вляется простая возможность линеаризации основного уравнения C.23).
Сак видно из графиков функции F (f) на рис. 34, кривые, пред-
Ц)б ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
ставляющие эту функцию, мало отличаются от прямой, что позво-
ляет положить
a-bf. C.39)
Уравнение C.23) приводится к линейному уравнению
интегралом которого является
Если, как это имеет место при обтекании тел, U = 0 при х = О
то из условия конечности / при х = 0 следует С = 0, и решение
уравнения C.40) принимает окончательную форму
Приближенное значение формпараметра / в начальной точке (л; = 0)
будет равно
Как показали многочисленные расчеты, введение в полученное
решение поправки, учитывающей отклонение функции от линейности,
не существенно, так как она очень мала и ее влияние лежит в пре-
делах допущенного приближения.
Определив по C.41) f(x), найдем толщину потери импульса
5" (*) = ^Р$>' C'43)
а затем по таблицам //(/) и С(/) определим 8*(х) и
4 = 1*-ртС (А ¦ C-44)
Расчеты показали, что выбор приближенных значений постоян-
ных а и b мало влияет на окончательную величину параметров слоя.
Наибольший интерес в этом смысле представляет изменение вели-
чины *w/pUlo. На рис. 35 приведены результаты расчетов величины
Vil)
w/ip) в функции от безразмерной абсциссы х% по верхним
поверхностям двух крыловых профилей. Расчеты проводились при
« 22)
ОБЗОР 1РУГИХ ПРИБЛИЖЕННЫХ МЕТОДОВ
107
шачениях а и Ь, характерных для кривых F(f), Л. и К. — Л.
а = 0,44; 6 = 5,75 (Л.);
а = 0,45; ? = 5,35 {К. -Л.)
i по таблицам 7 и 8 для '-.{/). Римская цифра / на рис. 35 озна-
'ает, что расчет сделан по К.—Л. и таблице 8, цифра // — по Л.
i таблице 7. Различие, как видно, невелико и сказывается лишь
о
1
\
1
\
/А
\
>
//
0,1 0,2
0,3 0,4
Рис. 35.
0.5 0,6
непосредственно вблизи точки отрыва. Сравнения с точными реше-
ниями показывают, что расчет по таблице 7 ближе к действитель-
ности. Так, положение точки отрыва, рассчитанное по таблице 7
для «односкатного» профиля Хоуарта (§ 12), определяется величи-
ной ^ = 0,125 вместо точного значения ^ = 0,12. Расчет по таблице 8
дает заниженное значение абсциссы ^ = 0,106.
§ 22. Обзор других приближенных методов
Уравнение импульсов C.3) не является единственным уравнением,
которое может быть использовано в приближенных и, в частности,
однопараметрических методах.
Как показал впервые Л. С. Лейбензон!), а затем в более общей
форме В. В. Голубев2), удается составить бесчисленное множество
') Лейбензон Л. С. Труды ЦАГИ, в. 240, 1935.
!) Г о л у б е в В. В., Первая публикация в курсе: К о ч и н Н. Е.,
Кибель И. А., Розе Н. В. Теоретическая гидромеханика, ч. II, ОНТИ,
1937; доложено в Институте механики Московского университета в 1936 г.
108 ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. III
разнообразных интегральных условий путем умножения обеих частей
первого из уравнений пограничного слоя на степени продольной
скорости и последующего интегрирования обеих частей таким обра-
зом полученных равенств поперек слоя.
Несколько видоизменяя вывод В. В. Голубева с целью полу-
чения уравнений, справедливых не только при пользовании понятием
слоя конечной толщины, но и более строгим представлением об
асимптотическом слое, поступим аналогично тому, как мы уже де-
лали в § 16 при выводе уравнения импульсов1).
Введем для краткости обозначение разности скоростей q— U — и
и, пользуясь уравнением неразрывности, перепишем первое уравне-
ние системы A.17) в виде
J-(ai\ t(av) — 2U'a — U dq — v d*q
dx {q > dy Wv) ZU q U dx ~ dy*'
Умножая обе части этого уравнения на qlt(k = O, 1, 2, . ..) и
интегрируя поперек слоя от у = 0 до у = 8 либо оо, получим после
простых преобразований уравнение
оо, 5
где введены обозначения
оо, <
О
со, 5
C.46)
Уравнение C.45) по форме напоминает C.3), но отличается от него
правой частью. При к = 0 получим вновь уравнение импульсов C.3),
при k = 1 придем к преобразованной форме уравнения Л. С. Лей-
бензона, которую можно было бы рассматривать как уравнение
изменения энергии в пограничном слое; при k ^>2 получаются урав-
нения, не имеющие простого физического смысла.
Другую систему интегральных условий можно получить, умно-
жая обе части уравнения пограничного слоя на последовательные
степени ординаты yk(k — 0, 1, 2, ...) и интегрируя поперек слоя.
>)Лойця некий Л. Г., ПММ, т. V, в. 3, 1941.
s 22] обзор других приближенных методов 109
Таким путем нами была найдена система уравнений1)
f ^f ^- при ft =
о
оо,б
iL f yu(U — u)dy — f v{U — u)dy-\-
cot 3
/ y(U — u)dy=vU при /? = 1,
• о о
со, 3
, dU
r dx
о
оо» 5
Их
6 О
СО, й СО , S
-\-—г- yk(U — u)dy = k(k—l)v / yk~2(U—u)dy при
dx J J
о о
C.47)
Система C.47) представляет совокупность последовательных
«моментов», взятых от обеих частей уравнения Прандтля. Первое
из этих уравнений — уравнение «нулевого момента» — дает не что
иное, как известное уже уравнение импульсов, второе представляет
уравнение «первого момента» и т. д. Поперечная компонента ско-
рости v может быть исключена из системы C.47) при помощи ура-
внения неразрывности.
Если бы с вычислительной стороны оказалось выполнимым исполь-
зование многопараметрических наборов профилей скорости, то для
определения этих параметров в функции от продольной координаты
можно было бы применять системы дифференциальных уравнений
вида C.45) или C.47). При этом, по аналогии с известным методом
Галеркина, следовало бы, по-видимому, пользоваться «полной» систе-
мой уравнений, начиная с ? = 0, потом k = l и т. д. Строить,
например, однопараметрический метод на уравнении Лейбензона,
как это делали некоторые авторы, или на более простом, втором
уравнении системы C.47) с методической стороны не оправдано и
допустимо только потому, что такое приближение никогда не рас-
сматривается как первое в некоторой цепи сходящихся последова-
тельных приближений, а скорее просто как проверенный на прак-
тике вычислений прием. В этом смысле гораздо более оправданными
являются изложенные в предыдущих параграфах однопараметрические
методы, использующие одно и, кстати говоря, самое простое из
') Лойцянский Л. Г., ПММ, т. XIII, в. 5, 1949.
ПО ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ [ГЛ. Ill
возможных, уравнение импульсов, но зато применяющие в качестве
«конкурирующих» наборов профилей скорости в сечениях погранич-
ного слоя такие, пригодность которых проверена на точных реше-
ниях классов задач, близких к заданным.
Что касается применения многопараметрических наборов скоро-
стей и многих интегральных условий, то нам известна лишь одна
работа]), где семейство профилей скорости с двумя параметрами и
два интегральных условия — уравнение импульсов и уравнение энер-
гии — были применены к простейшей задаче об обтекании пластинки.
Методы такого рода с вычислительной стороны оказываются слиш-
ком громоздкими.
Простые и близкие по идее приближенные методы расчета лами-
нарного пограничного слоя разработали С. М. Тарг2) и М. Е. Швец3).
Оба автора пользуются понятием слоя конечной толщины и, исклю-
чая при помощи уравнения неразрывности поперечную скорость v,
представляют уравнение Прандтля в форме
у
дги да да Г да , ,, dU
дуг дх ду J дх ¦" dx
о
Правая часть этого уравнения заменяется ее приближенным зна-
чением, получаемым в результате подстановки вместо скорости и
ее полиномиального представления, после чего обе части уравнения
дважды интегрируются по у при выполнении обычных граничных
условий. На этом этапе разница в методах М. Е. Швеца и
С. М. Тарга заключается в том, что первый сначала вычисляет
нулевое приближение, подставляя в правую часть и = 0, а уже затем
повторным двойным интегрированием получает (tq = у/Ь, штрих —
производная по л;)
C.48)
а второй исходит из начального профиля скоростей
— — — C — 3)
и после интегрирования получает
^-i4 C.49,
') S u 11 о n W., Phil. Mag. 7 A937), 23.
2) T a p г С. М., Основные задачи теории ламинарных течений, Гостех-
издат, 1951, стр. 178—186.
3) Ш в е ц М. Е., ПММ, т. XIII, в. 3, 1949.
с 221 ОБЗОР ДРУГИХ ПРИБЛИЖЕННЫХ МЕТОДОВ 1 1 1
Оба выражения принципиально одинаковы, но относятся к раз-
ным начальным профилям скоростей в сечениях слоя.
Остается составить обыкновенное дифференциальное уравнение
для определения единственного неизвестного параметра задачи —
толщины слоя 8 (л;). М. Е. Швец с этой целью требует, чтобы про-
филь скоростей C.48) удовлетворял граничному условию
(ди/ду)у«5 = 0 на внешней границе слоя, и это приводит его
к уравнению
4^
в то время как С. М. Тарг подчиняет свой профиль скоростей
C.49) условию и = U на внешней границе слоя и получает
5,64 -^1 +2 ^- = 23,27. C.51)
Уравнения разнятся коэффициентами при основных комплексах
?/'82/v и ШЬ'/v, легко интегрируются и дают
[U{x)\
о
C.52)
где постоянные а и Ь равны
а = 16, 6 = 6 (по М. Е. Швецу),
а = 23,27, 6 = 5,64 (по С. М. Таргу).
Равенство C.52) для 82(л;) аналогично по типу полученному
в предыдущем параграфе выражению C.41) для /. Если обе части
C.41) сократить на U'(х), то получится соответствующее C.52)
равенство для 8**2. После определения величины 82/v, а вместе с тем
и Х== в функции от л:, дальнейший расчет характеристик
пограничного слоя уже не составляет труда.
Преобразуя основные для этих методов уравнения, например,
уравнение C.50) к виду, явно содержащему А = , получим
Сравнивая это линейное относительно X уравнение с нелинейным
уравнением Польгаузена C.15), видим, что оно соответствует случаю,
когда, согласно C.16),
=16 — 6Х,
112
ПРИВЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
[ГЛ. III
Если перейти от X к /, то легко убедиться, что F(/) будет
линейной функцией от /. Таким образом, методы М. Е. Швеца и
С. М. Тарга совпадают по результатам с линеаризированным одно-
параметрическим методом, изложенным в предыдущем параграфе;
повторные применения тех же приемов слишком громоздки и не
всегда оправданы.
Среди приближенных методов, позволяющих быстро и с доста-
точной точностью решать задачи ламинарного пограничного слоя,
не прибегая к решению уравнения импульсов, отметим метод Смита!).
Идея метода заключается в выборе такого степенного распределения
скорости внешнего потока (UM — скорость набегающего потока,
с — хорда крылового профиля или другая характерная длина)
U . ( X Хо \т
к() C-53)
которое в некотором интервале (—-, ——J приближенно совпа-
дало бы с заданным (рис. 36). В распоряжении расчетчика имеются
Хд/С О
для этой цели три параметра: k, — и ш= 0 й , где В — извест-
ный параметр в решении Фокнера — Скэн (§ 11). Выбор частных
значений этих параметров для данного интервала (—-, —-J подчи-
ним условиям прохождения кривой скоростей U/U^ через заданные
значения UJUco и ?/2/?/со в точках xjc и х2/с и, кроме того,
потребуем, чтобы безразмерная толщина потери импульса в точке /
ц
, имела бы заданное наперед значение.
где Rc —
Smith A., Journ. Aeron. Sci. 23, № 10 A956).
§ 22] ОБЗОР ДРУГИХ ПРИБЛИЖЕННЫХ МЕТОДОВ 113
Пользуясь приведенными в цитированной статье Смита номограм-
мами, можно сразу, почти без вычислений, определить значения
параметров k, xojc и C для данного интервала, а также разыскать
величину 82 yWjc в точке 2. Таким путем шаг за шагом опреде-
ляются значения толщины потери импульса по всей поверхности
тела, а затем уже по таблицам, приведенным также в § 11 настоя-
щей книги, находятся значения коэффициента местного трения и
толщины вытеснения. В работе даются указания по простому приему
начала расчета вблизи передней кромки крылового профиля. Про-
веденные нами испытания метода показали, что он действительно
очень прост, но уступает в точности ранее изложенному однопара-
метрическому методу.
Зак 297 Л Г Лойцянский
ГЛАВА IV
ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
§ 23. Пограничный слой в начальной стадии движения тела
При приведении тела, погруженного в вязкую жидкость, в дви-
жение из состояния покоя можно наблюдать следующее характерное
для такого рода нестационарных процессов явление. Пограничный
слой образуется не мгновенно, а требует на свое развитие конеч-
ного промежутка времени, сравнимого по величине с характерным
для данного движения временем, например, потребным для прохож-
дения телом пути, равного размеру тела. Достаточно внимательно
рассмотреть известные фотографии Титьенса'), описывающие начало
движения круглого цилиндра в водяном лотке, чтобы убедиться
в справедливости этого утверждения. На этих фотографиях отчет-
ливо наблюдается, как вначале отсутствующий пограничный слой
постепенно утолщается до тех пор, пока при некоторой максималь-
ной толщине вблизи кормовой критической точки цилиндра не воз-
никнет отрыв слоя. В дальнейшем этот отрыв развивается и
распространяется, стремясь занять свое предельное положение,
соответствующее установившемуся обтеканию цилиндра. Результаты
экспериментов по измерению распределений давления по повгрх-
ности круглого цилиндра на разных стадиях его движения из со-
стояния покоя, выполненных М. Швабе2), подтверждают, что
в начале движения распределение давлений очень близко к теорети-
ческому, соответствующему безвихревому обтеканию цилиндра
идеальной жидкостью. Это также говорит о том, что в начале дви-
жения пограничный слой даже на таком плохо обтекаемом в устано-
вившемся движении теле, как круглый цилиндр, весьма тонок,
полностью охватывает поверхность тела и поэтому не оказывает
заметного обратного влияния на внешний поток. Только после
зарождения отрыва и перемещения его от задней кромки цилиндра
') См., например, Шлихтинг Г. Теория пограничного слоя, пер.
с нем., ИЛ, 1956, стр. 201 или Голдстейн С, Современное состояние
гидроаэродинамики вязкой жидкости, т. 1, пер. с англ., ИЛ, 1948,
фото 7 — 8.
2) S с h w a b.e M., Ing.-Archiv 6 A935).
§23] ПОГРАНИЧНЫЙ СЛОЙ В НАЧАЛЬНОЙ СТАДИИ ДВИЖЕНИЯ ТЕЛА 115
вверх по потоку появляется резкая деформация кривой распределе-
ния давления, заканчивающаяся переходом к тому обычному рас-
пределению, которое наблюдается при реальном установившемся
обтекании цилиндра.
Аналогично, если тело совершает установившееся движение и
в некоторый момент времени это движение нарушается, например
внезапно меняется угол атаки крыла, то переход к новому устано-
вившемуся движению, соответствующему новому положению крыла
в потоке, не происходит столь же быстро, как изменение угла
атаки, а запаздывает. На реконструкцию обтекания, в связи с дей-
ствием в пограничном слое вязких сил, необходима некоторое ко-
нечное время. За счет такого рода затягивания плавного обтекания
крыла на закритические углы атаки можно на короткое время
получить заметное увеличение коэффициента максимальной подъем-
ной силы крыла (динамический коэффициент подъемной силы).
Теория нестационарного пограничного слоя, начавшая развиваться
почти одновременно с теорией стационарного слоя, значительно
отстает от последней по степени разработки методов расчета. При-
чина сравнительной сложности решения задач нестационарного по-
граничного слоя заключается в наличии в его уравнениях наряду
с членами, выражающими конвективное ускорение, еще дополнитель-
ного члена — локального ускорения.
. Известно, что соотношение между величинами локального и кон-
вективного ускорений характеризуется порядком величины числа
Струхала, равного частному от деления характерной для данного
движения длины на произведение характерных скорости и времени.
Существенные особенности нестационарных движений проявляются
'C достаточной отчетливостью только при сравнительно больших
- значениях числа Струхала. При малых значениях этого параметра
достаточно пользоваться квазистационарными приемами, т. е.
-рассматривать нестационарное явление в каждый момент так, как
будто оно стационарно, но имеет в качестве определяющих па-
раметров их мгновенные значения. Возможность такого упрощен-
ного подхода для вязких явлений зависит еще, конечно, и от вели-
чины рейнольдсова числа.
Первые исследования в области теории нестационарного погра-
ничного слоя были выполнены вскоре после появления теории
Прандтля его сотрудником Блазиусом'), который рассмотрел вопрос
О внезапном приведении покоящегося цилиндрического тела в равно-
Мерное движение, а также равномерно ускоренное движение. Голд-
'стейн и Розенхед2) дополнили решение Блазиуса расчетом следую-
-, ' ') Blasius Н., Zeltschr. f. Math. u. Phys. 56 A908), 1—37.
v_ *) Golds tein S., Rosenhead L., Proc. of the Cambr. Phil. Soc. 32
?.0936), 392—401.
if
t- 8»
116 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [гЛ. IV
щего приближения. Гёртлер') дал решение задачи о пограничном слое
на цилиндрическом теле при степенном законе возрастания скорости
движения со временем. Ватсон2) обобщил решение Гёртлера на
случай любого не целого показателя степени и экспоненциального
закона возрастания скорости. Представляющую особую сложность
задачу о приведении в движение пластинки в своей плоскости рас-
смотрели В. В. Струминский3) и Л. А. Розин4). Последний довел
приближенное (для малых времен) решение этой задачи до числен-
ных результатов, причем ему благодаря использованию уравнений
Стокса удалось изучить течение во всей области, включая поток
перед пластинкой.
Ряд советских исследователей (С. М. Тарг5), Е. М, Добрыш-
ман6)) пользовались для решения задач теории нестационарного слоя
приближенным методом, аналогичным изложенному в конце главы III
методу теории стационарного пограничного слоя.
Другое, более пригодное для практических расчетов направление,
связанное с применением однопараметрических методов, аналогичных
изложенным в предыдущей главе, было указано в работах
В. В. Струминского 7) и Л. А. Розина8), причем в работе послед-
него решение было доведено до простых вычислительных приемов.
Первое применение уравнения импульсов для расчета нестацио-
нарного пограничного слоя изложено в диссертации В. Толмина,
упоминание о которой можно найти в разных статьях и моно-
графиях 9). К сожалению, содержание этой работы не получило
широкого опубликования и осталось нам неизвестным.
§ 24. Пограничный слой на теле, внезапно приведенном
в поступательное равномерное движение
В случае равномерного движения цилиндра распределение ско-
рости U на внешней границе пограничного слоя будет функцией
только продольной координаты х. При этом в первом из уравнений
') Oortler H., Ing.-Archiv 14 A944), 286—305.
2) Watson E., Proceed. Roy. Soc, ser. A, 231 A955), 1184.
3) Струминский В. В., Сборник теоретических работ по аэродина-
мике, ЦАГИ, Оборонгиз, 1957, стр. 247—250.
*) Розин Л. А., ПММ, т. XXII, в. 3, 1958.
5) Т а р г С. М., Основные задачи теории ламинарных течений, Гостех-
издат, 1951, стр. 210—224.
6) Д о б р ы ш м а н Е. М., ПММ, т. XX, в. 3, 1956.
7) С т р у м и и с к и й В. В., Цит. сборник, стр. 232—247.
8) Розин Л. А., ПММ, т. XXI, в. 5, 1957.
9) Toll mien \V., Die zeitliche Entwicklung der laminaren Orenzschicht
am rotierenden Zylindern. Dissertation, Gottingen, 1924 (цитируем по его
статье о пограничном слое, помещенной в Handbuch der Experimentalphysik,
т. 4, ч. 1, Leipzig, 1931).
& 24] ТЕЛО, ВНЕЗАПНО ПРИВЕДЕННОЕ В ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ 117
A.13) главы I будет отсутствовать член dUjdt, так что решению
подлежит упрощенная система уравнений
ди , ди . ди ,, dU , д*и
L^L
дх ' ду
, при
граничных
и =
и -=
и начальных
:U(X). V =
0, v =
¦U(x)
условиях
0 при у =
0 при у —
при у-*
0 и
0 и
оо.
г">0,
D.2)
Как уже указывалось в предыдущем параграфе, в начальный
момент t = 0 пограничный слой бесконечно тонок и жидкость сколь-
зит по поверхности тела, что и выражено в первой строке усло-
вий D.2). При малых значениях t слой очень тонок, скорости и
близки к значению U (x), a v мало отличается от нуля, так что
первое из уравнений D.1) приводится к линейному уравнению теории
распространения тепла
Полагая в нем
получим для /j (т)) обыкновенное дифференциальное уравнение вто-
рого порядка (штрих — производная по rj)
/7 + 24/! = О, D.5)
которое при принятых граничных условиях D.2) имеет решение
в форме гауссовой функции ошибок
2 ?
fx = Eri^ = y^ j e-*'da. D.6)
о
Для продольной скорости и, получим значение
«1 = {/(*) Erf 7j. D.7)
Соответствующее этому первому приближению значение попе-
речной скорости vi легко выводится из уравнения неразрывности и
имеет вид
=- 2 V^4t hErf t,-
& ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
Во втором приближении положим
причем поправку и2 определим из неоднородного теплового уравнения
д2и2 диг ,. dU , дщ
= U — [Erf2 7) == tie-12 Erf t| — 1 -+-1 (e-V + e-2i2)l. D.8)
d* |_ ' У п л J
Разыскивая и2 в форме
u, — tU^-f,(tii, D.9)
получим для определения функции /2(т|) неоднородное уравнение
2 —1-^г)_1_|_ 2 (.e_T]J_e_2T]!), D 10)
решение которого, удовлетворяющее граничному условию /2 = 0
при т) = 0 и т| = оо, будет
-v]. D.11)
Входящие сюда постоянные i и р определяются из принятых
граничных условий обращения /2 (т;) в нуль при tj = 0 и т| = оо;
найдем
/ ^ ^ f " .12)
Пользуясь вновь уравнением неразрывности, определим поперечную
скорость v во втором приближении
4
а = —/l +—^ = —1,212; В = -^= fl +—"\ =0,804. D.
=- (l+
-i BтK - Зт!) Erf2 7) + ^1=-[4 - Dtj2 - 11) е-Я Erf t) - 7j -
§ 24] ТЕЛО, ВНЕЗАПНО ПРИВЕДЕННОЕ В ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ 119
Поступая аналогичным образом и дальше, можно было бы разыскать
и третье приближение. Для этого следовало бы решить неоднород-
ное уравнение
д2и3 ди, ди2 . ди, , ди2 , ди.
Функция и3 должна содержать в качестве множителя t2 и будет
иметь вид
где функции /3 и Fa удовлетворяют следующим неоднородным
уравнениям:
/з 4-271/3-8/3 = 49G,),
Fl + 2tjF; - 8/>8 = 49 (tj) + 4Ф (tj).
Выписывать в развернутом виде правые части не будем, отсылая
интересующихся к ранее цитированной работе Голдстейна и Розен-
хеда; в этой статье авторы не пожалели труда, чтобы вычислить
величину поправки иъ в замкнутом виде •)• К сожалению, вопрос об
области сходимости получаемых таким образом рядов функций
остается открытым.
Для разыскания связи между абсциссой точки отрыва лс^ и со-
ответствующим ей временем ts определим корень уравнения
(дн/ду)у^о —0 или, что то же, (ди/д-ф^о — О. Тогда получим во
втором принижении
Отрыв может произойти только в области отрицательного значе-
ния продольной производной от скорости на внешней границе слоя
1-з— < О J и начнется ранее всего в точке с максимальным по абсо-
лютной величине значением этой производной. Промежуток вре-
мени /, от начала движения до момента возникновения отрыва оп-
ределится формулой
,_! 0.702 r41Ev
') Авторы допустили в расчетах ряд ошибок, которые были впослед-
ствии указаны Вундтом (W u n d t H., Ing.-Archiv 23, № 3 A955), 218) и при-
няты няии рп рнчиянчр
120 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
В случае обтекания круглого цилиндра радиуса а будем иметь
= 2 t/ro sin (лг/я), ^-=2-^-cos (л/в),
где х — длина дуги по обводу цилиндра. Максимальное по абсо-
лютной величине значение этой производной найдем при х = ¦ка,
т. е. в кормовой критической точке. По прошествии времени
2A + -^-
= 0,351 т^-, D.16)
отсчитанного от начала движения, в кормовой критической точке
поверхности цилиндра возникнет отрыв. Путь о, который пройдет
цилиндр от начала движения до момента возникновения отрыва,
равен
о =?/„*, = 0.351 с D.17)
т. е. примерно трети радиуса цилиндра. Отметим, что этот путь не
зависит ни от плотности, ни от вязкости жидкости.
Третье приближение по Голдстейну и Розенхеду дает для мо-
мента начала отрыва ts в задней критической точке круглого ци-
линдра значение
t^ U,OZ ~Tr— »
со
а для пути а — величину
о = 0.32а,
т. е. примерно на 9% меньше, чем во втором приближении D.17).
Аналогичный анализ, проведенный для эллиптического цилиндра,
обнаруживает некоторую особенность. Обозначим через k отношение
полуосей эллипса b: а; представим себе, что движение будет про-
исходить вдоль полуоси а. Как показали вычисления Толмина1),
в зависимости от величины k отрыв может начаться не только
в задней критической точке, но и в точках на поверхности эллипти-
ческого цилиндра, расположенных выше по потоку. Ординаты точек
отрыва определяются так:
0 при &<
гЧ *>2^ ' <4'8)
') Toll mien W., цитир. на стр. 116, а также О or tier H., Arch. d.
Mathem., 1948, 1.
§25]
РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ ЦИЛИНДРА
121
Промежуток времени ts от момента начала движения до момента
возникновения отрыва определяется следующей системой формул:
а
при
при
.2/3
2/3
D.19)
Безразмерный путь о, проходимый эллиптическим цилиндром на без-
отрывном этапе движения, представлен графиком на рис. 37.
Легко видеть, что при k=l вновь получаем D.17). При воз-
растании k до бесконечности время ts стремится к нулю, а орди-
ната точки отрыва — к +Ь.
На пластинке, поставленной 0,5
перпендикулярно к направле- j
нию потока, отрыв возникает
на кромках пластинки сразу же
при начале движения; напом-
ним, что скорости, рассчитан-
ные по теории безвихревого
обтекания идеальной жидко-
стью, в этих точках равня-
лись бы бесконечности.
Предельный переход А—>0,
соответствующий случаю про-
дольного обтекания пластинки,
приводит к появлению особен-
ности и требует специального
рассмотрения.
Случай несимметричного об-
текания, возникающего при
импульсивном приведении в равномерное движение эллиптического
цилиндра с большой осью, наклоненной к направлению потока под
углом в 7°, был рассмотрен Хоуартом:).
§ 25. Равноускоренное движение цилиндра
Случай равноускоренного движения цилиндрического тела из со-
стояния покоя также был рассмотрен Блазиусом в ранее уже ци-
тированной его работе 1908 г. Полагая
U(x. t) = tV{x), D.20)
0,4
0,3
0,2
0,1
>
/
Л
1\
1
К
\
\
\
О,/ 0,2 0,30,50,7/
Рис. 37.
2 3 5 7 /О к
') Howarth L, Proc. of the Cambr. Phil. Soc. 31 A935).
122 плоский нестационарный пограничный слой [гл. iv
приведем первое из уравнений A.13) главы I к виду
Граничные и начальные условия будут сводиться к таким:
и = 0, V — 0 при v = 0, />0, \
\ (А 22^
u->U(x, t) = tV(x) при у->оо. J *• ;
Пользуясь соображениями размерности, составим функцию тока
, у, t) в форме
[ ^ ...]. D.23)
где Cj. C3. ... суть неизвестные функции той же переменной ч\, что
и в предыдущем параграфе. Вычисляя (штрих — производная по ¦*))
D.24)
подставляя эти выражения в уравнение D.21) и приравнивая в обеих
частях коэффициенты при одинаковых степенях времени t, получим
следующую систему обыкновенных дифференциальных уравнений
третьего порядка:
D.25)
граничные условия будут аналогичны указанным в предыдущем па-
раграфе, а именно:
^ = ^' = 0, С3 = Сз = 0 при tj = O,
При 7|=СО.
D.26)
Решения уравнений D.25) могут быть представлены в замкнутом
виде при помощи той же функции ошибок и экспоненциальной
функции, как и в случае внезапно возникающего движения.
Выражение для первой производной от функции Cj будет
;B)An2_27i2. D.27)
-A-7i<.n_27i.
Выражения для следующих функций более сложны и поэтому не
приводятся. На рис. 38 даются графики двух первых функций: Ci и'3
¦ 25]
РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ ЦИЛИНДРА
123
Момент начала отрыва ts с поверхности цилиндра определим,
як и ранее, из условия обращения в нуль производной от про-
дольной скорости по координате у или, что то же, по безразмерной
временной г). Блазиус составил уравнение для определения ts с точ-
юстыо до членов с t\\ приводим это уравнение
1+0,427/? 4? _[О,О2бD?
0.0101/
^O. D.28)
) случае круглого цилиндра отрыв начинается вблизи задней критической
-пики, где второй член в квадратных скобках в уравнении D.28)
с
as
/
/
/
*
с;
^—
¦—¦—
Рис. 38.
фопадает. Решая остающееся биквадратное уравнение, получим
D.29)
*(•?).—»¦«¦
Если сохранить только первые два члена в левой части D.28).
*о решение будет
2(dV
Замечая, что для круглого цилиндра
<айдем, соответственно тому или другому приближению.
=A.04-н1.17)-
D.30)
124 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
Пройденный за это время в ускоренном движении путь будет,
по тем же приближениям, равен
o = -iV04 = @,52-4-0,59)a. D.31)
Сравнивая с формулой D.17), убедимся, что при равноускорен-
ном движении путь, пройденный цилиндром до возникновения от-
рыва, больше соответственного пути при скачкообразном переходе
к равномерному движению. Блазиус подсчитал полное сопротивле-
ние W равноускоренно движущегося цилиндра, складывающееся из
сопротивления давлений Wp и сопротивления трения Wf. Состав-
ляющие эти
ТС ТЕ
W. = 2ab /*/>coscpflfcp, Wf=2ab I ?(—) sincpflfcp.
где b — длина цилиндра, ср — полярный угол элемента площади на
поверхности цилиндра, по Блазиусу равны
Wp = 2краЧ ¦ Vo, Wf= AY^tab ¦ Vo. D.32)
§ 26. Случай скорости, зависящей от времени
по степенному закону
Замеченный в конце предыдущего параграфа факт увеличения
времени и пути безотрывного этапа движения при переходе от слу-
чая внезапного приведения в равномерное движение к случаю рав-
ноускоренного движения не лишен интереса. Возникает вопрос, как
будут изменяться эти характерные для нестационарного движения
величины с увеличением быстроты изменения ускорения во времени.
Для решения этого вопроса зададимся степенным законом возраста-
ния скорости на внешней границе пограничного слоя во времени
U(x, t) = AfV(x) = y(t)V(x). D.33)
Полагая здесь <х = 0, придем к случаю внезапного перехода к рав-
номерному движению (§ 24), при а=1 получим равноускоренное
движение (§ 25). Гёртлер') рассмотрел случаи целых а. от нуля до
четырех. Ватсон2) провел общее исследование при любых а. Изложим
некоторые из наиболее интересных его результатов.
¦) G о г 11 e r H., Ing.-Archlv 14 A944).
2) Wai son E., Proceed. Roy. Soc, ser. A, 231, № 1184 A955).
§ 26] СКОРОСТЬ, ЗАВИСЯЩАЯ ОТ ВРЕМЕНИ ПО СТЕПЕННОМУ ЗАКОНУ 125
Обращаясь вновь к первому из уравнений A.13) главы I и при-
меняя его к рассматриваемому сейчас распределению D.33), будем
иметь
ди , да . да ,...,,, . . ,,„., rfK д2и . „..
Откидывая, как и ранее, нелинейные конвективные члены, при-
дем в первом приближении к интегрированию уравнения
^ 4-^, D.35)
которое может быть представлено в форме
д(СГ— и)
—й" 6у^' D-36)
граничные условия для разности U — и будут
U — и = ср (t) V (х) при у = 0,
Сохраняя тот же аргумент Г1 = у/{2У^), будем искать решение D.36)
в виде
D.38)
Тогда для определения функции т) получим уравнение (штрих да-
лее— производная по -ц)
/" + 2т)/' — 4а/= 0, D.39)
интеграл которого, удовлетворяющий граничным условиям /@)=1,
/(оо)=0, может быть представлен в форме
/(*!) = 22Т (а+1)?а(г,). D.40)
где, кроме обычного символа гамма-функции, введено еще обозна-
чение для Bа)-кратного интеграла от гауссовой функции ошибок
D-4П
Таким образом, определим скорость в первом приближении:
u1 = At'V(x)\l—2*T(<i+ l)g.(-n)\. D.42;
126
ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
[ГЛ. IV
Для получения второго приближения введем в рассмотрение функ-
цию тока ф(*. у, t). Полагая
ф = 2 У* ¦ AfV (х) 47 (х, т), t),
dii dl>
D.43)
и подставляя эти выражения в D.34), придем к уравнению в част-
ных производных
D.44)
Представим функцию W в виде ряда по возрастающим степеням t:
= Wo
At
a+1
(tj) + .. .
D.45)
Используя этот ряд для решения уравнения D.44), получим сле-
дующую систему обыкновенных дифференциальных уравнений для
последовательного определения функций Wo, Wv ... (штрих — произ-
водная по т^)
4« A — ф?) = 0.
- 4 Bа+ 1)ЧГ; = - 4 A -
с граничными условиями
qr @) = »Ро @) = 0, Фо(оо)==1,
D.46)
D.47)
Первое из уравнений системы D.46), аналогичное уравнению D.39),
имеет решение
^о (Ч) = 1 — 22Т (а + 1) ga (Ч).
откуда, по определению функций ^а (tj), следует
) ==,! - г^Г(а + 1)g(Ti) -1 Г(a
D-48)
D.49)
эти решения соответствуют граничным условиям D.47).
26] СКОРОСТЬ, ЗАВИСЯЩАЯ ОТ ВРЕМЕНИ ПО СТЕПЕННОМУ ЗАКОНУ 127
Второе уравнение системы D.46) приводится к виду
-7
g __
2
D.50)
и может быть решено в замкнутом виде; решение его, удовлетво-
ряющее граничным условиям D.47), представляется в форме
ГBа + 2)^ Ч
Используя выражение
и приравнивая его нулю, найдем с указанной точностью уравнение
для определения промежутка времени ts от начала движения до мо-
мента возникновения отрыва
Л =4^- D.52)
dX)s ч-;'@)
Путь о, пройденный цилиндром за это время, равен
D,з,
128 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ IV
Вычисляя входящие сюда производные при tj = О, окончательно
получим
dx I r>- -L A ~r~ ' Q ч ~~^~ °~ ' A
X
. D.54)
Для круглого цилиндра радиуса а в задней его критической точке
будет (—-г-) — 2/а, и последняя формула позволяет рассчитать
значения о для любых а. Так, при <х = 0 вновь получаем о = 0,35а.
При стремлении а к бесконечности выражение для пути о стре-
мится к своему предельному значению
о = 0,85а. D.55)
Отсюда можно заключить, что, как бы быстро ни возрастала со
временем скорость, продолжительность этапа безотрывного движения
будет все же меньше того времени, которое затрачивается на про-
хождение пути, равного радиусу цилиндра.
Рассмотренный Ватсоном случай экспоненциального роста со
временем скорости цилиндра приводит к значениям времени и пути
безотрывного этапа, соответствующим предыдущему случаю при
а—>оо. Таким образом, и при этом, казалось бы, более резком
росте скорости со временем получить сколько-нибудь затянутый
режим безотрывного обтекания не удается. Заметим, что рассчитан-
ное в этом случае второе приближение приводит к несколько мень-
шему значению коэффициента в правой части D.55), а именно 0,74
вместо 0,85.
Нестационарный пограничный слой на круглом цилиндре, совер-
шающем гармонические колебания малой амплитуды, был исследован
Г. Шлихтингом]), который теоретически подтвердил наличие подте-
кания окружающей жидкости к цилиндру в направлении, перпенди-
кулярном к прямолинейной траектории центра цилиндра.
§ 27. Продольное нестационарное обтекание пластинки
Изложенный в предыдущих параграфах метод расчета нестацио-
нарного обтекания цилиндрических тел неприменим к случаю обте-
кания пластинки. Легко убедиться, что все поправки к первому при-
') Schlichting H., Phys. Zeitschr.33 A932); см. также монографию
того же автора «Теория пограничного слоя», ИЛ, 1956, стр. 202—207.
§ 27) ПРОДОЛЬНОЕ НЕСТАЦИОНАРНОЕ ОБТЕКАНИЕ ПЛАСТИНКИ 129
ближению как в случае внезапного приведения тела в движение D.9),
так и в случае ускоренного движения D.24) и D.45), при t/= const
или соответственно V= const, обращаются в нуль. Что же касается
остающегося первого приближения, то оно в этом случае при при-
нятых начальных и граничных условиях становится полностью неза-
висимым от х, т. е. совпадает с решением задачи о нестационарном
обтекании вязкой жидкостью безграничной пластинки, приходящей в
движение в своей плоскости. Решение этой простой задачи при
любом степенном законе роста ускорения дается изложенным в пре-
дыдущем параграфе первым приближением D.42), в котором надо
положить V (x) = Voa. Как мы только что пояснили, построение сле-
дующих приближений но методу, изложенному в предыдущих пара-
графах, невозможно.
Точное решение задачи о нестационарном пограничном слое на
пластинке, даже в постановке Блазиуса, заменяющей пластинку дан-
ной конечной длины полубесконечной вниз по потоку пластинкой,
представляет большие математические трудности. Причина этих
трудностей заключена в наличии особенности в точке х=0, т. е.
на передней кромке пластинки. В теории стационарного слоя можно
было пренебречь этим «краевым эффектом», быстро убывающим при
удалении от передней кромки и ничтожно влияющим на суммарное
сопротивление длинной пластинки; при нестационарном движении
это не так.
Остановимся на рассмотрении случая внезапного возникновения
равномерного поступательного движения полубесконечной пластинки
в своей плоскости и отметим две основные тенденции в картине
развития пограничного слоя в пространстве и во времени. Заметим,
что в той части поверхности полубесконечной пластинки, которая
удалена от передней кромки, пограничный слой будет развиваться
так же, как и на безграничной в обе стороны пластинке, т. е. в со-
ответствии с профилем скоростей D.42) при U (x)= Um иа = 0:
? D-56)
Что касается облкти в непосредственной близости от передней
кромки, то чем ближе к передней кромке, тем скорее установится
режим стационарного погршичного слоя с не зависящим от времени
распределением скоростей по Блазиусу. Области эти непрерывно
переходят одна в другую, прич;м прикромочная область расширяется
вниз по течению, постепенно захватывая все большую часть поверх-
ности пластинки. В пределе установится известное уже нам по
главе I стационарное течение в пограничном слое.
Количественное описание процесса образования пограничного слоя
на внезапно приведенной в движение полубесконечной пластинке
было произведено рядом авторов (С. М. Тарг, Е, М. Добрышман,
9 Зак 297 Л Г. Лойцянскнй
130 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
Л. А. Розин), ссылки на работы которых были уже даны в § 23.
Первые два из них получили приближенные решения, основанные
на использовании понятия слоя конечной толщины. Это привело их
к установлению решения с резкой границей между областями ста-
ционарного и нестационарного режимов, где первые производные от
толщины слоя по времени и координате терпят разрывы; при этом,
конечно, и профили скоростей не будут гладкими. Л. А. Розину1)
удалось избавиться от этого недостатка и получить непрерывное
и гладкое решение. Имея в виду наличие особенности в уравнениях
пограничного слоя в области переднего края пластинки, Л. А. Розин
обращается к полным уравнениям Стокса относительно функции тока,
переписанным в форме
w^ —?*¦ = #? W> - ш ? (*¦>• <4-57>
Как и в предыдущих работах, в качестве нулевого приближения
рассматривается обтекание пластинки идеальным потоком с функ-
цией тока iJiQ^t/ooy. Добавка их к продольной скорости будет вы-
ражаться через добавку <3/1 к функции тока по формуле их = -Р-.
Для построения первого приближения надо решить уравнение, полу-
чающееся из D.57), если положить правую часть равной нулю. Та-
ким образом, задача может быть сведена к решению уравнения
в частных производных по переменным х, у и t
D.58)
при граничных и начальных условиях
«1 = 0 при * = 0, «! = — Uа, при у = 0, х > 0,
«j->0 при | у | —>¦ со. лг>0 D.59)
и при |*| или |у|->со, * < 0.
Автор довольствуется этим приближением, соответствующим на-
чальному этапу движения и первым двум членам в разложении
функции тока
ty(x, у, t) = i
(>% H)Mh Hi - D-60)
Если положить
Ф1 =* «/» l^rf Ti (S. ¦»»). 5 = -^, П = ^~' D.61)
У vt У' «
то потребуется решить уравнение в частных производных от двух
') Розин Л. А., ПММ, т. XXII, в. 3, 1958.
§ 27] ПРОДОЛЬНОЕ НЕСТАЦИОНАРНОЕ ОБТЕКАНИЕ ПЛАСТИНКИ
переменных S и ¦») вида
при граничных условиях
и,=—1 при 7j =
В1==0 ПрИ ?->
при |т)|-
при h|,
-оо,
> О,
131
D.62)
D.63)
Для решения используется математическая аналогия с задачей
стационарного пространственного пограничного слоя на боковой
кромке пластинки, решенной Хоуартом'). Искомое поле продольной
скорости и определяется одним из следующих двух выражений через
ряды или интегралы специальных функций:
X
=\—
при jf<0.
D.64)
/
m = 0 или 1,
где применены общепринятые обозначения для специальных функций.
Первое из них удобно для расчетов при малых R, когда ряд
быстро сходится, второе — при больших R. Из второго выражения
для скорости и сразу видно, что при заданном / и больших х, т. е.
больших ?, а следовательно, и больших R, поле скоростей прибли-
жается к виду
l fa D-65>
соответствующему нестационарному полю скоростей в пограничном
') Н о w a r t h L., Proc. Cambr. Phil. Soc. 46, № 4 A950).
132
ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
[ГЛ. I'
слое на безграничной в обе стороны пластинке, приведенной вш-
запно в равномерное движение со скоростью ?/„,.
На рис. 39 приведены графики зависимости u/U^ от S при ра.-
личных значениях tj, рассчитанные по формулам D.64). Прежде
всего непосредственно замечается асимптотическое стремление ско
рости при ?^оо к значениям, определенным по D.65). Обрашак"
на себя внимание кривые скоростей при отрицательных ?, выражу
щие, очевидно, подтормаживающие влияния пластинки на обля
течения вверх по потоку относительно переднего коая плас
~2,0
Как видно, это распространяющееся вверх по потоку возмущена
ограничено областью примерно ?>—2—. 3.
Исследование более сложного нестационарного движения пл*
стинки принадлежит Ротту!). Им рассмотрено плоское движен^
вязкой несжимаемой жидкости на пластинке, совершающей гармони
ческие колебания в своей плоскости и находящейся во внешне\
продольном потоке со скоростью, пропорциональной расстоянию дс
среднего положения передней кромки пластинки. Решение полу-
чается путем использования уравнений Стокса, которые разрешаются
при помощи рядов, расположенных по положительным степеням чэ
стоты колебания пластинки (случай малых частот) или по отрица-
тельным степеням той же величины (случай больших частот).
§ 28. Применение приближенного однопараметрического методе
Лежащее в основе приближенных однопараметрических методо!
расчета нестационарного пограничного слоя уравнение импульсоь
может быть выведено совершенно аналогично тому, как это делалосс
в теории стационарного движения.
" ') Rott N., Quart. Appl. Math. 13, № 4 A956), 444—451,
§ 28] ПРИМЕНЕНИЕ ПРИБЛИЖЕННОГО ОДНОПАРАМЕТРИЧЕСКОГО МЕТОДА 133
Переписывая первое из уравнений Прандтля при помощи урав-
нения неразрывности в виде
и вычитая обе его части почленно из обеих частей преобразованного
уравнения неразрывности
d(Uu) . d(Lfv)_ д_Ц_
дх ' ду ~~ и дх '
получим
Интегрируя обе части этого равенства по у поперек слоя и сохра-
няя те же обозначения для толщин вытеснения и потери импульса,
что и раньше, придем к следующей форме уравнения импульсов
в случае нестационарного пограничного слоя:
иж + жь*+и2ш + иш^**+^ = т- D-66>
Отличительной особенностью этого уравнения является то, что
входящие в него величины §*, 8** и ~w, так же как и U, предста-
вляют собой функции двух переменных х и t. Легко видеть, что
при отсутствии зависимости от t уравнение D.66) переходит в из-
вестное уже нам уравнение импульсов теории стационарного погра-
ничного слоя.
Обобщим на случай нестационарного пограничного слоя изло-
женный в предыдущей главе однопараметрический метод. С этой
целью допустим, что в качесте семейств профилей скорости в сече-
ниях нестационарного слоя могут быть использованы стационарные
«наборы» профилей
?=»(*¦• /) «•")
с формпараметром /, зависящим не только от х, но и от t, и с не-
которой пока произвольной условной толщиной h слоя, которая
также является функцией переменных х и t. Принятое только
что допущение соответствует в известном смысле «квазистацио-
нарному» приему рассмотрения явлений в нестационарном погра-
ничном слое.
Выразим через Ли/ входящие в уравнение импульсов D.66)
неизвестные 5*, <Г* и "„,- Прибегая к тем же обозначениям, что
134 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
и ранее, и полагая т) = у/Л, найдем
где, подчеркнем это, Я*, Я** и С являются функциями только фор it-
параметра /.
Для определения структуры формпараметра / используем то >Kt
его определение, как и в случае стационарного слоя. Примем за
взятое с обратным знаком безразмерное выражение второй прои?
водной скорости и по у при у = 0. Используя первое из уравненш
нестационарного пограничного слоя A.13), согласно которому буде-
(д*и\ \ (dU dU\
+u)
получим
Таким образом, вводя для краткости обозначение
Q_ I dU dU и7П
найдем для формпараметра выражение
/-!?. D.71
соответствующее использованному нами квазистационарному подход1
и представляющее очевидное обобщение формпараметра стационар-
ного слоя.
Составляя по D.68) входящие в уравнение импульсов D.66
производные
^!_ H*dfl-L- hdH*df
dt —" dt ~T~n~~dflty
db** _ „„ dh . . dH** df
dt ~n dt~T~ df dt
df
и подставляя эти их значения в уравнение D.66), получим поел;
простых преобразований следующее нелинейное уравнение в частны;-
§ 28] ПРИМЕНЕНИЕ ПРИБЛИЖЕННОГО ОДНОПАРАМЕТРИЧЕСКОГО МЕТОДА 135
производных первого порядка, служащее для определения заданного
равенством D.71) формпараметра /:
Уравнение это служит обобщением уравнения C.23) предыдущей
главы на случай нестационарного слоя.
Если перейти в этом уравнении к случаю стационарного слоя,
положив (штрих — производная по л;)
?-•• ?=»¦ %-* *-"•• /=™.
но сохранить произвол в выборе условной толщины слоя h, то
уравнение D.72) преобразуется к виду
«+Я*)/1 +-^Я*7- D.73)
Из определения величин Я* и Я** по D.68) сразу видно, что
для упрощения вида уравнения D.73) следует положить А = 5**,
так как при этом будет
и уравнение D.73) придет к известной форме C.23). Таким образом,
в случае стационарного слоя выбор в выражении формпараметра
в качестве характерной условной толщины А величины В** вполне
оправдан. Иначе обстоит дело в случае нестационарного погранич-
ного слоя. Полагая в уравнении D.72)
А =
придем к уравнению
136 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
В. В. Струминский ]), введя для краткости обозначения (штрих —
производная по х, точка — по /)
D75)
uu' + u
U(UU' + U)
и сохраняя то же обозначение F(f) для характеристической функ-
ции, что и в стационарном случае, свел предыдущее уравнение
к такому окончательному виду:
, t)H(f) + M(x. t)]f ( ^)
D.76)
В только что цитированной статье В. В. Струминского можно
найти график функций Ф(/), рассчитанный путем использования
класса решений Фокнера и Скэн. Эта функция при приближении
к точке отрыва возрастает более резко, чем известная уже нам
функция //(/), что не позволяет так просто линеаризировать задачу,
как это было сделано в случае стационарного слоя.
Если принять в качестве характерной величины h толщину вы-
теснения 8*, то будем иметь
D.77)
и основное уравнение D.72) приобретет вид
D.78)
Уравнения D.74) и D.78) одинаково сложны, однако, как пока-
зал Л. А. Розин2), уравнение D.78) имеет то преимущество, что
входящие в него функции K(f*) и С*(/*) допускают замену на
линейные, а функция К(/*), кроме того, настолько слабо зависит
от /*, что без большой погрешности просто может быть принята за
постоянную величину.
') Струминский В. В., Теория нестационарного пограничного слоя,
Сборник теоретических работ по аэродинамике, ЦАГИ, Оборонгиз, 1957,
стр. 230.
2) Роз и и Л. А., ПММ, т. XXI, в. 5, 1957.
-> 28] ПРИМЕНЕНИЕ ПРИБЛИЖЕННОГО ОДНОПАРАМЕТРИЧЕСКОГО МЕТОДА 137
Для определения зависимостей K(f*) и (,*(/*) достаточно вспом-
нить, что
де /, С и Н могут быть взяты из таблиц 7 или 8, помещенных
i конце § 20. Используя для этой цели таблицу 7 как дающую
юлее близкие к действительности результаты и рассматривая / как
r,
0.5
включающийся параметр, составим новую таблицу зависимости С* и К
от /*. По полученным таким образом числовым значениям на рис. 40
построены графики С(/*) и K(f*). Из рассмотрения этих графиков
следует, что уклон кривой K(f*) сравнительно мал, так что в пер-
вом приближении можно считать /((/*)= const, а кривая С*(/*) не-
значительно, особенно в наиболее важной области отрицательных /*,
отличается от линейной функции, так что можно положить
D.79)
138 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
В этом приближении уравнение D.78) становится линейным и при-
обретает вид
Г + «I*//*' ~ [¦§" ~ 22 + a,U (°J- - 4 -?)+ 2«3q] /•=2o22. D.80)
Интегрирование его может быть выполнено обычными методами
интегрирования линейных уравнений в частных производных первого
порядка.
Соответствующая этому уравнению система обыкновенных диф-
ференциальных уравнений (характеристик) может быть легко соста-
влена. В ряде простейших случаев решение приводится к квадратурам,
в других случаях требует применения приближенных методов.
Значение формпараметра /* в точке отрыва, где С* = 0, согласно
D.79), будет равно
/.=—*¦• <4-81>
Проиллюстрируем применение уравнения D.80) на следующем про-
стейшем примере. Определим, как это уже делалось в предыдущих
параграфах настоящей главы, время ts от начала движения до мо-
мента возникновения отрыва в кормовой критической точке круглого
цилиндра, где скорость внешнего потока равна нулю, если распре-
деление скоростей на внешней границе слоя задано уравнением
U (х. t) = 2Um sin (-J-), D.82)
т. е. когда цилиндр внезапно приводится в равномерное движение
со скоростью Uoo. В этом случае имеем
U
' = 2 — cos (—), 0 = 0. 2 = 0,
а \ а )
В = f/'=2-^= cos D
а \ а
Применяя уравнение D.80) в задней критической точке, где х = ira
и, следовательно, ?/ = 0, ?/' = — 2 —, 2__2 —, 2' = 0.
а а
придем к обыкновенному дифференциальному уравнению
41= 4-^A +2a1-a3)r-4a2i?L, D.83)
которое легко решается и при начальном условии /* — 0 при t = 0
дает
^{[ i1]} D-84)
§ 291 ПРИМЕНЕНИЕ МЕТОДОВ, НЕ СВЯЗАННЫХ С УРАВНЕНИЕМ ИМПУЛЬСОВ 139
В момент отрыва t = ts, Ua>ts = a и, согласно D.81), будет
D.85)
Определяя уклон прямой D.79), найдем а3 = 0,4. Если принять
для лг в точке отрыва значение К, то получим (см. график К на рис. 40)
aj = 0,26; тогда путь, пройденный цилиндром до момента начала отры-
ва у задней кромки, будет характеризоваться значением о = 0,30а,
мало отличающимся от значения о = 0,32а, рассчитанного Голдстей-
ном и Розенхедом по третьему приближению к кстрогому решению.
§ 29. Применение методов, не связанных с уравнением
импульсов
Как уже ранее указывалось, применение уравнения импульсов не
является единственным путем приближенного решения задач однопара-
метрическими приемами. С. М. Тарг !) применил к расчету нестацио-
нарного слоя метод, предложенный им первоначально для стационарного
слоя; понятие об основах этого метода дано нами в § 22.
Переписав основное уравнение нестационарного пограничного слоя
Ifi ^U ... dU\
в форме Ш = -тг, U' = -g—\
у
дги , .-. , ..... ди . ди ди Г ди ... ,. __ч
о
подставляя в правую его часть приближенный профиль скоростей
e=l*/Cij —ч»). т)= у/8, D.87)
где U и 8 рассматриваются как функции двух переменных х и t,
и совершая повторное двойное интегрирование обеих частей урав-
нения D.86) по у, получим следующее выражение для продольной
скорости в сечениях пограничного слоя (z = 82/v):
Используя условие u — U при tj= 1, СМ. Тарг приходит к линей-
ному дифференциальному уравнению в частных производных первого
') Тарг С. М., Основные задачи теории ламинарных течений. Гостех-
¦ЗДат, 1951, стр. 210.
140 ПЛОСКИЙ НЕСТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ [ГЛ. IV
порядка
где постоянные т, п и b имеют значения
m = 2,33, n = 5,64, Z» = 23,27. D.90)
Условие отрыва получим, полагая
= 0.
Произведя дифференцирование D.88) и полагая затем т; = 0,
найдем условие отрыва в форме
\ = U'zs = — 6,21— 0,0976 (-^) — 0,8162 ^j-zs, D.91)
где j- уже исключено при помощи основного уравнения D.89),
играющего ту же роль, что и уравнение D.80) в однопараметрическом ме-
тоде, изложенном в предыдущем параграфе. Уравнение D.89) несколько
проще уравнения D.80), так же как уравнение C.31) для z** в слу-
чае стационарного пограничного слоя проще уравнения C.23) для /.
Не останавливаясь на полном исследовании уравнения D.89),
сравним результат применения его для решения простейшей задачи
об определении момента возникновения отрыва на задней кромке
круглого цилиндра, приведенного внезапно в равномерное движение
со скоростью Um. В этом случае уравнение D.89) приведется к виду
~, az 9я * h (A Q9\
III — ,, ^~^ ^ilt — ¦?> —— U • \ <3?*)
Интегрирование при начальном условии г = 0 при ^ = 0 дает
Чтобы найти значение ts для момента отрыва, необходимо под-
ставить значение zs из D.93) и \—п-\ из D.92) в обе части уравне-
\ «' Is
ния D.91) и определить после этого ts или величину о=и^5.
Расчеты показывают, что при этом получается значение о = 0,25а,
заниженное по сравнению с полученным ранее значением о = 0,30а,
более близким к третьему приближению Голдстейна и Розенхеда.
Применение к нестационарному слою метода М. Е. Швеца (см.
§ 22 настоящей книги) произвел Е. М. Добрышман').
') Добрышман Е. М., ПММ, т. XX, в. 3, 1956.
ГЛАВА V
НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ
§ 30. Пограничный слой на продольно обтекаемых удлиненных
телах вращения
В настоящей главе рассматриваются пограничные -.пи, образую-
щиеся при неплоских двумерных движениях вязкой жидкости. Под
двумерными подразумеваются движения, определяемые двумя компо-
нентами скорости, каждая из которых зависит от двух координат. При-
мерами такого рода могут служить: пограничный слой и аэродинамиче-
ский след, образующиеся при про-
дольном обтекании тел вращения,
а также осесимметричные струи.
Начнем с рассмотрения задачи
о пограничном слое на теле вра-
щения большого удлинения в ус-
ловиях его обтекания однородным
потоком, параллельным оси тела;
при этом линии тока располагаются
в меридиональных сечениях, что
и делает поток двумерным.
Выберем в плоскости мери-
аионального сечения поверхности
тела (рис. 41) координаты х, у
и составляющие скорости и, v
так же, как при плоском обтекании профиля. Вместе с тем отметим
и обычные цилиндрические координаты точки М (г, г) и соответ-
ствующие им компоненты скорости Vг и Vz; угловая координата,
так же как и трансверсальная компонента скорости, в уравнениях
движения будет отсутствовать. Уравнения Стокса представятся в виде
Рис. 41.
dt
дг
г~дТ
т дг
'г~~дг
р дг
_
дг
E.1)
142 неплоские двумерные пограничные слои (гл. v
В предположении, что тело вращения имеет достаточно большое
удлинение, примем за малую величину угол а, образованный каса-
тельной к меридиональному контуру тела с осью тела. Это предпо-
ложение не оправдывается вблизи передней критической точки, если
тело тупоносое, т. е. если угол а близок или равен я/2, и вблизи
кормовой критической точки, где а также бывает заметно отличаю-
щимся от нуля. Как обычно в теории пограничного слоя, неточность
решения в области начала появления слоя слабо сказывается на
дальнейшем его развитии вниз по потоку. Что касается задней кри-
тической точки, то в непосредственной близости к ней поток обычно
отрывается или находится в предотрывном состоянии и методы теории
пограничного слоя все равно оказываются либо очень неточными,
либо вообще неприменимыми. Если же по какой-нибудь причине
представляет особый интерес изучение течения вблизи критических
точек, то это также может быть выполнено дополнительным анали-
зом, о чем пойдет речь далее.
Приняв предположение о малости а, произведем в уравнениях E.1)
приближенную замену Vz на и, V на v, а производных т- на т-,
02 ОХ
д д
-а— на -J—; тогда получим следующую приближенную систему урав-
нений:
ди . ди . ди 1 др , / д2и . дги , 1 ди
dv^, dv , dv_ \.ЦР.\ /d2f . d2v . I dv
dt ' dx ' dy p dy ' \dx2 ' dy2' r dy
E.2)
Рассуждая аналогично тому, как это уже делалось в теории пло-
ского пограничного слоя, сможем во всей области слоя, где г ~^. г0 > О,
пренебречь в круглой скобке в правой части первого уравнения E.2)
д2и 1 ди
членами -з-j и —-с— по сравнению со старшим по порядку членом
д2и/ду2. Второе уравнение сведется к известному условию постоянства
давления в поперечном сечении слоя. Тогда, вводя еще в рассмо-
трение скорость U(x, f) на внешней границе пограничного слоя,
придем к такой системе уравнений осесимметричного пограничного
слоя н» теле вращения:
du du . du__dU_ , .. dU d4
~дТ~т~" f)^" dy — dt ~rU~d7~i~*dy2'
d(ru) . d(rv) ^Q
E.3)
§ 311 ПРИМЕРЫ СТАЦИОНАРНОГО И НЕСТАЦИОНАРНОГО СЛОЕВ ИЗ
Заметим, что при наличии (рис. 41) очевидного равенства
г = го(х)-\- у cos a E.4)
можно повсюду в пограничном слое, кроме области, близкой к кор-
мовой критической точке, где пограничный слой сравнительно толст,
а радиус поперечной кривизны поверхности тела г0, наоборот, стре-
мится к нулю, положить во втором уравнении E.3) приближенно
г===го(х). Это приводит к следующему окончательному виду уравне-
ний неплоского двумерного пограничного слоя:
ди . ди . да dU . ,, dU . д*и
д(гои) [ d(rov) ^^ E>5)
справедливому, конечно, лишь при тех ограничительных условиях,
о которых шла речь в начале параграфа.
В случае стационарного пограничного слоя будем иметь более
простую систему уравнений
ди ди _ц dU дЧ
д(гаи) d(rov) ^0 E)
дх ' ду )
Граничные условия как в случае нестационарного, так и стацио-
нарного слоя ничем не отличаются от соответствующих условий для
плоского пограничного слоя.
Отбрасывание второго члена в правой части равенства E.4) допу-
стимо только в таких областях пограничного слоя, где его толщина
значительно меньше радиуса поперечной кривизны ф<^г0). На длин-
ных и очень тонких телах вращения пограничный слой может вы-
расти настолько значительно, что это условие окажется не выпол-
ненным даже в области, еще сравнительно далекой от кормы. В этом
случае необходимо применять более точные уравнения (см. § 35).
§ 31. Примеры стационарного и нестационарного пограничных
слоев на удлиненном теле вращения
Примером стационарного двумерного слоя на теле вращения может
служить случай задания уравнений поверхности го — го(х) и распре-
деления скорости на внешней границе U = U (х) в виде степенных
рядов
Г"Х~аХ а~Х ¦¦'¦ E.7)
144 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Такого рода класс задач, представляющий обобщение на случай
неплоского двумерного слоя задачи Блазиуса — Хоуарта (§ 13), был
ртссмотрен Н. Фрёсслингом; решение в дальнейшем было уточнено
Ф. Шолькемейером ').
Если ввести в рассмотрение функцию тока 6(л\ у), положив
. г0 ду гп дх
то уравнения E.6) заменятся одним уравнением третьего порядка
E.
ду дх ду \ дх ' r0 dx 7 ду2 dx ' V ду3
с граничными условиями
** ,п\ EЛ0)
-^¦-+U(x) при у-*оо.
Решение уравнения E.9) при граничных условиях E.10) прово-
дится методом, аналогичным изложенному в § 13 методу Блазиуса —
Хоуарта.
Вводя вместо у координату
!-. E-11)
представим функцию тока в виде ряда
u3x%W+ ••¦]• E-12)
где следует также положить
§зО?) E-13)
и принять аналогичные дополнительные разложения для последующих
функций.
Подставляя значение ф в виде ряда E.12) в уравнение E.9) и
приравнивая нулю последовательные коэффициенты при различных сте-
пенях х, получим для определения неизвестных функций /,, g^- А3, ...
систему обыкновенных дифференциальных уравнений третьего по-
рядка, которые, благодаря дополнительному разложению E.13), не
будут зависеть от частных значений параметров at, ut, а смогут быть
проинтегрированы раз и навсегда.
') F г 0 s s 11 n g N., Lunds. Univ. Arsskr. N. F., Adv. 2, 35 A940);
Scholkemeyer F., Archiv d. Mathem. 1 A949). Цитируем по монографии
Шлихтинга Г., «Теория пограничного слоя», ИЛ, 1956, стр. 176—179.
§ 31] ПРИМЕРЫ СТАЦИОНАРНОГО И HFCTAUHOHAPHOrO СЛОЕВ 145
Выпишем соответствующие дифференциальные уравнения и гранич-
ные условия лишь для первых двух функций /j и /3 в разложении E.12);
в ранее цитированной работе Шолькемейера вычисления доведены
до функции /7, стоящей коэффициентом при х7, включительно, при-
чем эта функция должна быть подвергнута дополнительному разло-
жению типа E.13) на десять слагаемых.
Уравнения для функций fv gs и hz имеют вид (штрих—произ-
водная по ч\)
;с?1)
E.14)
к+/л* - у?г + 2/л = -
причем им соответствуют граничные условия
^Т1 лз = 0 ПРИ
E.15)
Первое из уравнений E.14) совпадает с уравнением Фокнера и
Скэн B.15) при Р = -о- или, что все равно, т = 1/3. Значения функ-
ции /, могут быть взяты из таблицы 3. Заметим, что полученное
таким образом решение отвечает частной задаче о течении в погра-
ничном слое вблизи лобовой критической точки на тупоносом теле
вращения (а^-^-), когда можно положить
ro(x) = x. U=ulx; Ci=l. a3 = a5=z ... =0,
и3 = и5= ... =0.
Значения характерных параметров пограничного слоя для этого
простейшего случая можно найти в таблице 4.
Второе и третье уравнения системы E.14) являются линейными
дифференциальными уравнениями с переменными коэффициентами и
допускают лишь численное интегрирование. Соответствующие вычи-
сления для этих и последующих уравнений выполнены Фрёсслингом
и Шолькемеиером. Результаты интегрирования были сведены в таб-
лицы, которые можно найти в оригиналах цитированных статей;
кроме того, таблицы f[, g'3, h'v g'5, h'5, k'., j'5 и q'. и численные зна-
чения вторых их производных при т) = 0, необходимые для вычисле-
ния сопротивления трения, приведены в цитированной выше моно-
графии Г. Шлихтинга.
10 Зак ОТ л г n«n,,.u^^is
146 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Примером нестационарной задачи того же рода может служить
задача Больце ') о развитии пограничного слоя при внезапном при-
ведении тела вращения в движение вдоль его оси со скоростью U (х).
Введем функцию тока t|> при помощи отличных от E.8) равенств
«= з1-, v = г- E.16)
и разложим функцию тока в ряд по степеням времени
где принято, как и в случае плоского слоя (§ 24),
r, = y/BVVt). E.18)
Подставляя значение ф в E.16), а затем в первое из уравне-
ний E.5) при —- = 0 и приравнивая коэффициенты при одинако-
вых степенях t в обеих частях равенства, придем к системе обыкно-
венных дифференциальных уравнений третьего порядка
-/1/;'-1).
E.19)
Первое из этих уравнений совпадает с уравнением D.5) соответ-
ствующей плоской задачи и имеет решение D.6). Второе совпадает
с уравнением D.10) плоского случая и имеет решение D.11). Отли-
чие от плоского случая, заключающееся во влиянии поперечной кри-
визны, отражено вторым членом в квадратной скобке E.17) и соот-
ветственно функцией /щС^)' удовлетворяющей третьему уравнению
системы E.19).
Значения функций f'2l и f'n приведены в таблице 9.
Для установления связи между моментом отрыва tt и абсциссой
точки отрыва xs необходимо решить уравнение
(ди\ „ (дЧ\ п
(-3—1 =0. т. е. (-д-т) =0,
которое, согласно E.17), приводится к виду
Гг @) + ', [Dг1 Гп @) + U, (± Q)a fn @)] = 0. E.20)
>) В о 11 z е Е., Orenzschichten an Rotationskdrpern In Flussigkeiten mit
er Reibung. Dissertation, Outtingen, 1908.
ЛЦИОНАРНОГО И НЕСТАЦИОНАРНОГО СЛОЕВ 147
Таблица 9
/я
0
0,142
0,246
0,318
0,362
0,382
0,382
0,367
0,340
0,307
0,269
f'n
0
0,017
0,034
0,051
0,066
0,080
0,091
0,099
0,103
0,102
0,099
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
/я
0,231
0,191
0,158
0,126
0,099
0,075
0,056
0,041
0,029
0,021
0
/и
0,092
0,083
0,072
0,061
0,050
0,040
0,031
0,023
0,016
0,011
0
. численными значениями /" @), f"n @) и /^ @), согласно
и таблицы 9, получим уравнение
шара радиуса а имеем
двляя в уравнение E.21), придем к приближенному равен-
..^це провел разложение в фигурной скобке E.17) до t3 вклю-
чительно и получил в результате более точное уравнение
+ 2,360-^р- cos 4~ ("Т1-) (o.662cos2y— O.18o)-f
+ (—|-*-) (o.OlO cos3^ — 0,017 cos 4) = °- E-22)
огласно этому уравнению, момент ts начала возникновения отрыва
* задней критической точке шара (cos — = —l) и пройденный
* этому моменту шаром путь а определяются величинами
ts = 0,392 ~, о = /,?/«, = 0,392а.
E.23)
Можно заметить, что эти значения несколько больше изученных
§ 24 величин для круглого цилиндра, что объясняется фактом
10*
148 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
более медленного развития пограничного слоя на поверхности шара
по сравнению с цилиндром.
Если пренебречь обратным влиянием отрыва пограничного слоя
с поверхности шара на распределение скоростей U (х) на внешней
его границе, то можно, пользуясь уравнением E.22), подсчитать по-
следовательные моменты ts прохождения отрыва через различные
точки xja поверхности шара. Приводим хотя и имеющие скорее
качественное значение, но все же представляющие интерес резуль-
таты такого расчета:
(xs/a)°= 180°; 160°; 120°; 110°;
-"^- = 0.392; 0,521; 0,853; 1,505.
Обращает на себя внимание любопытный факт резкого возраста-
ния времени продвижения точки отрыва при удалении ее от кормо-
вой критической точки.
§ 32. Преобразование Степанова — Манглера
При рассмотрении предыдущих примеров можно было заметить
наличие некоторой связи между решениями соответствующих двумер-
ных неплоской и плоской задач. Различие между этими задачами, по
крайней мере в той приближенной постановке, которая могла быть
принята в случае удлиненных тел вращения, сводилось к наличию
влияния поперечной кривизны поверхности тела вращения. На самом
деле в случае стационарных движений нет необходимости специально
заниматься решением задач о неплоском двумерном слое на удли-
ненных телах вращения, так как эти задачи могут быть сведены
к некоторым своим плоским аналогам.
Как показал Е. И. Степанов 1), а затем несколько позднее за
рубежом В. Манглер 2), уравнения E.6) неплоского стационарного
слоя могут быть сведены к уравнениям плоского слоя путем сле-
дующего преобразования координат х, у и проекций скорости
и, v, U к новым переменным, отмеченным черточкой сверху:
X
r-2 (=) dl, y = r0 (x) y,
0
.5.24)
') С т е п а н о в Е. И., ПММ, т. XI, в. 1, 1947.
2) М a n g I е г W., Zeitschr. f. Angew. Math. u. Mech. 28 A948), 97.
§32] ПРЕОБРАЗОВАНИЕ СТЕПАНОВА—МАНГЛЕРА 149
Будем иметь формулы преобразования производных
_д_ _2 J_ , _д_ д _г д
и после простых вычислений получим вместо E.6)
— ди . — ди ,-т d.U. . д2и ди . dv „
дх ду dx ду2 дх ду
т. е. действительно уравнения плоского стационарного слоя.
Граничные условия сохранят при таком преобразовании свой обыч-
ный вид, одинаковый как для неплоского, так и для плоского слоя.
В качестве простейшего случая применения преобразования Сте-
панова рассмотрим осесимметричное течение жидкости в пограничном
слое вблизи передней критической точки тупоносого тела вращения.
Вблизи этой точки распределение скорости на внешней границе слоя
задается линейной функцией U = сх; кроме того, можно прибли-
жено считать, что го(х) = х. Преобразование E.24) в этом случае
примет вид
х = ^ х3, у = ху.
Как это следует из последнего равенства системы E.25), дело
свелось к решению задачи о плоском слое с распределением скоро-
сти на внешней границе по закону
Это частный случай класса точных решений Фокнера и Скэн (§ 11)
при т = 11ъ. Нет необходимости повторять ход этого решения. Поль-
зуясь таблицами 3 и 4 при C = —тл~~"' определим все харак-
терные величины плоского слоя, а затем, совершив обратный пере-
ход к переменным осесимметричного слоя, найдем искомые значения
этих величин и для неплоского слоя.
Так, местное напряжение трения tw в пограничном слое на теле
вращения можно выразить через соответствующее ему напряжение iw
в плоской задаче по формуле
0=^- E-26)
Точно так же найдем связи для условных толщин слоев
o' = f . 8-=f. E.27)
'о 'о
150 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ, V
Преобразование E.24), интересное с принципиальной стороны,
может принести пользу лишь в случаях наиболее простых зависимо-
стей го(х) и U(х). Чтобы по заданному закону U' (х) найти U (х),
необходимо сначала разыскать зависимость х от л;, а для этого со-
ставить обращение интеграла, заключающегося в первом преобразо-
вании системы E.24). Подставляя таким образом определенное зна-
чение х в U (х), приходим в большинстве случаев к очень сложным
аналитическим выражениям для V (х), которые не подходят ни под
один из известных, далеко не многочисленных классов точных реше-
ний, большинство которых изложено в главе II. Это обстоятельство
умаляет значение преобразования E.24) для разыскания точных реше-
ний задач о двумерных пограничных слоях на удлиненных телах
вращения и заставляет обратиться к другим путям решения такого
рода задач.
§ 33. Однопараметрический метод расчета двумерного
стационарного пограничного слоя
Обобщим на случай двумерного неплоского пограничного слоя
однопараметрический метод, изложенный в предыдущих двух главах
для плоского слоя. Начнем со стационарного слоя.
Выведем прежде всего соответствующее уравнение импульсов.
Для этого поступим так же, как и в случае плоского слоя. Поль-
зуясь вторым уравнением системы E.6), перепишем первое уравнение
этой системы в форме
| д (rouv) ,. dU дЧ
дх "*" ду — r°u dx "Г" v/<> ду* •
Умножая обе части второго уравнения той же системы на U (лг)>
преобразуем его к виду
д {ruuU) , д (rovU) dU
дх I ду~ — Г°и ~1х~ •
после чего вычтем почленно из обеих частей этого уравнения обе
части предыдущего. Тогда получим
Проинтегрируем теперь обе части этого уравнения поперек слоя по
у от 0 до со (или 8 — при пользовании понятием слоя конечной
толщины). Тогда в полной аналогии с выводом, помещенным в § 16,
придем к равенству
§ 33] ОДНОПАРАМЕТРИЧЕСКИЙ МЕТОД РАСЧЕТА ДВУМЕРНОГО СЛОЯ 151
в котором 8* и 8** обозначают, как и в случае плоского слоя,
толщины вытеснения и потери импульсов, причем выражаются теми
же самыми интегралами.
Выполняя в первом члене слева дифференцирование и деля обе
части на r0U2, получим окончательное выражение уравнения импуль-
сов в рассматриваемом случае двумерного неплоского слоя на удли-
ненном теле вращения (штрих — производная по х)
/
^ -^-5м = ^7Т. E-28)
где
От известного уравнения импульсов в случае плоского слоя ура-
внение E.28) отличается наличием последнего члена в левой части,
выражающего влияние переменной поперечной кривизны поверхности
тела вращения. Заметим, что в принятой приближенной постановке
(8 <^ г0) при r0 = const, т. е. на поверхности круглого цилиндра,
уравнение E.28) ничем не отличается от случая плоского слоя.
Следует отметить, что с помощью преобразования E.24) уравне-
ние E.28) можно вывести и непосредственно из уравнения импульсов
плоского пограничного слоя
Ш1 ^ E.29)
dx
В силу E.24), E.26) и E.27) имеем
Я~ = 1 d ( n== I <">** - 1 dra 8„
dx r\ dx r0 dx r\ dx
Подставляя эти выражения в E.29), вновь получим E.28).
Введем, как и в плоском случае, формпараметр / и величины
H(J) и С(/), положив
Тогда уравнение E.28) после умножения обеих его частей на
¦^— сможет быть переписано в виде
152 НЕПЛОСКГЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ Ггл. V
После преобразования левой части
v ~~ U \ v ) ~~ 2 \ U' ) ~~ 2U' J 2(J'2
придем к искомому выражению основного уравнения однопараме-
трического метода в случае двумерного неплоского слоя на удлинен-
ном теле вращения 1)
E.30)
где функция F (f) та же, что и в случае плоского слоя.
Уравнение E.30) отличается от соответствующего уравнения для
плоского пограничного слоя вторым членом в круглой скобке в пра-
вой части, выражающим влияние изменения поперечной кривизны.
Можно вновь заметить, что в принятом приближении (8<С!/"о) ПРИ
постоянном г0 уравнение E.30) ничем не будет отличаться от уравне-
ния для плоского слоя.
Используя, как и в случае плоского слоя, близость функции F (/)
к линейной зависимости
приведем решение уравнения E.30) к простой квадратуре
Постоянные а и Ь имеют те же значения, что и в плоском слу-
чае; они зависят от выбора семейства профилей скорости в сечениях
с л л. Дальнейший порядок расчета ничем не отличается от изложен-
ного в § 21.
Полиномы четвертой степени, использованные Польгаузеном
в плоском пограничном слое, были применены Томотика 2) для рас-
чета пограничного слоя на шаре, причем в качестве распределений
давления на внешней границе были приняты как теоретическое по-
тенциальное, так и экспериментальное, полученное в систематических
опытах Фейджа 3). Профиль скоростей в сечениях слоя в форме пара-
болы второй степени принял К. Милликен 4). При таком приближении
уже нельзя определять положение линии отрыва пограничного слоя
с поверхности тела вращения; метод Милликена пригоден лишь для
хорошо обтекаемых тел.
') Л о й ц я н с к и й Л. Г., ДАН СССР 36, № б A942).
2) Tomotika S., ARC, R4M, 1678 A935), а также Proc. Phys. Math.
Soc. Japan 20 A938).
3) F a g e A., ARC, R&M, 1766 A936).
*) M 111 i k a n C-, Trans. Amer. Soc. Mech. Eng. 54, № 2 A932).
§ 34] ОБОБЩЕНИЕ НА СЛУЧАЙ НЕСТАЦИОНАРНОГО СЛОЯ 153
§ 34. Обобщение на случай нестационарного слоя
Обратимся теперь к уравнениям нестационарного слоя E.5).
Умножим обе части первого из уравнений E.5) на г0 и, используя
уравнение неразрывности, перепишем первое уравнение в форме
да , д . „. . д , . ' (dU . ,,dU\ . дги
Умножив обе части второго уравнения на U, преобразуем его к виду
д (rouU) , д (rov(J) _ . dU
^TJc ! Ту -r»?"'
Вычтем последовательно из обеих частей полученного уравнения
обе части предыдущего. Будем иметь
dU,,, . д2и
= -ro-g7(^-«)-^o-g^
или
dU (. и\ д2и
Проинтегрируем обе части этого уравнения поперек слоя по у
от 0 до со, либо В — при пользовании понятием слоя конечной тол-
щины. Тогда получим следующий вид уравнения импульсов:
J* (?/5*) + — 4~(r0U4~)-f U^-8* = ^.
dt v ' ' г0 дх v ° ' г дх р
Его можно привести к форме, аналогичной уравнению D.66) пло-
ского нестационарного слоя
Обращаясь теперь к применению однопараметрических методов,
выберем, как и в случае плоского нестационарного слоя (§ 28),
в качестве формпараметра величину
/= —. 2 = -^- + -^ E.33^
и введем вновь характерные параметры
^- E.34)
154 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Переписывая уравнение E.32) после умножения обеих его частей
на 8*/v в виде
и выполняя очевидные преобразования, направленные на выделение
по E.33) параметра /*, найдем окончательную форму искомого ос-
новного уравнения однопараметрического метода для нестационарного
двумерного неплоского слоя:
Уравнение это служит обобщением уравнения D.78) нестационар-
ного плоского слоя на случай неплоского слоя и вместе с тем об-
общением уравнения E.30) на случай нестационарного слоя; не сле-
дует забывать, что формпараметр /* в уравнении E.35) отличается
от формпараметра / тем, что в качестве характерной толщины при-
нята величина 8*, а не 8**.
Функции К(/*) и С*(/*) в случае двумерного неплоского слоя
берутся теми же, что и в случае плоского слоя. Следовательно, при
интегрировании уравнения E.35) можно использовать в качестве пер-
вого приближения равенства D.79), согласно которым /((/*) = const,
а С*(/*) — линейная функция /*. Это позволяет значительно упростить
решение; на примерах останавливаться не будем !).
Изложенные только что методы приближенного расчета двумер-
ного неплоского слоя, основанные на использовании уравнения им-
пульсов, не являются единственными. Для той же цели могут быть
использованы и методы Швеца и Тарга 2).
§ 35. Пограничный слой на длинном, тонком теле вращения;
продольное обтекание цилиндра
При продольном обтекании длинного, тонкого тела вращения на
его поверхности, на достаточно большом расстоянии от носовой кри-
тической точки образуется пограничный слой с толщиной, не только
сравнимой, но даже и превосходящей по величине радиус попереч-
ного сечения тела (8 > г0). В этом случае сделанное ранее упрощение
правой части формулы E.4), заключающееся в откидывании второго
') См. ранее цитированную статью Л. А. Розина (стр. 136).
2) См. ранее цитированную монографию С. М. Тарга (стр. 139) и статью
Е. М. Добрышмана (стр. 140).
§ 35] ПОГРАНИЧНЫЙ СЛОЙ НА ДЛИННОМ, ТОНКОМ ТЕЛЕ ВРАЩЕНИЯ 155
члена по сравнению с первым, уже неприменимо. Продолжая считать
угол а малым, можно заменить E.4) приближенным равенством
г=.го-\-у. E.36)
Уточненные уравнения стационарного пограничного слоя могут быть
выведены из E.1), если опустить второе уравнение, сводящееся
к условию др/дг = О, и член d^VJdz2 в круглых скобках в правой
части первого из уравнений, как малый по сравнению с другими
членами. Произведя замену: Vz = u, Vr — v,-jp = -^, -gp = -^- и
вводя скорость на внешней границе слоя U (х), получим следующую,
более точную, чем E.3), систему уравнений пограничного слоя:
ди . ди ,, dU , / дЧ , 1 диN
яг
+¦&<">=
E.37)
¦оо.
E.38)
с граничными условиями
и = 0, •и = 0 при у
и-* U (х) при у
В уравнениях E.37) можно, когда это потребуется, заменить у
на г, а в граничных условиях E.38) — у = 0 на r = rQ(x), y->co
на г-*-со.
Уравнения E.37) перепишем еще в виде
ди
ди
ди , ди ..
~Ш "Т" V ~ду~ — U
.dU
~ду~
1
ди
dv
17
го(дс) и
Го + У
= 0.
E.39>
Интегрирование этой системы уравнений при граничных условиях
E.38) представляет большие трудности даже в наиболее простом
случае продольного набегания однородного потока со скоростью ?/«,
на полубесконечный круглый цилиндр радиуса а. В этом случае
г* —а и равенство E.36) выполняется точно; так как при этом
¦^-? = 0, -^- = 0. то уравнения E.39) переходят в следующие:
ди . ди I д2и .
U -ч hV -з— = V 1-т-г-г-
дх ' ду \ ду1 '
1
ди ,
при граничных условиях
« = 0,
dv
ду
у + а ду,
= 0
v = i
при
при
' = 0, \
E.40)
E.41)
156 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Основная сложность в решении этой простейшей из возможных
задач такого рода заключается в наличии, кроме заданной скоро-
сти Uco< еще заданной длины а (радиуса цилиндра). При существо-
вании двух таких определяющих движение величин з'равнения E.40)
уже не могут быть сведены к одному обыкновенному уравнению,
как это было в предыдущих случаях. Приходится искать решение
уравнения в частных производных, разлагая его по положительным
или отрицательным степеням какой-нибудь характерной для задачи
малой или соответственно большой величины. В данном случае та-
кого рода характерной величиной может служить отношение местной
толщины пограничного слоя к радиусу цилиндра, т. е. величина,
пропорциональная отношению 1/ jj— : а, или какая-нибудь функция
этого отношения.
В лобовой части поверхности цилиндра, где толщина слоя еще
достаточно мала по сравнению с радиусом цилиндра, можно прене-
бречь влиянием поперечной кривизны. Тогда развитие пограничного
слоя на цилиндре ничем не будет отличаться от соответствующего
развития на плоской пластине (задача Блазиуса). Действительно, при
а-+оо уравнения E.40) переходят в обычные уравнения плоского
пограничного слоя при отсутствии продольного перепада давления,
что при граничных условиях E.41) приводит к задаче Блазиуса
о пограничном слое на пластине. Первые поправки на влияние по-
перечной кривизны в рассматриваемой задаче были даны Севаном и
Бондом1) в 1951 г. и в несколько уточненном виде Кэлли2) в 1954 г.
Было показано, что в формуле напряжения трения по Блазиусу
тю = 0,332р.?7 УиЦух) появляется поправочный член OJOpU/a, кото-
рый при vx/(?/ooa2) = 0,001 дает поправку в 7%.
Глауэрт и Лайтхилл 3) дали приближенное решение этой задачи,
справедливое при любых значениях параметра vx/(?/ooa2) и, кроме
того, асимптотическое решение, соответствующее большим значениям
того же параметра. Взамен уравнений E.40), составленных в пере-
менных х, у и содержащих явно величину а, и граничных условий
E.41), от нее не зависящих, авторы предпочли пользоваться не со-
держащими а уравнениями в переменных х, г
ди . ди I д2и , 1 ди
дх ' дг
') Seban R. A., Bond R., Journ. Aeron. Sci. 18 A951), 671.
2) Kelly H. R., Journ. Aeron. Sci. 21 A954), 634.
3) Olauert M. В., Light hill M. J., Proc. Roy. Soc, ser. A. 230,
1181 A955), 188—203.
§ 35) ПОГРАНИЧНЫЙ СЛОЙ НА ДЛИННОМ, ТОНКОМ ТЕЛЕ ВРАЩЕНИЯ 157
с граничными условиями
и = г» = 0 при r = a, \
U = t/oo при Г = СО, J ' ' '
зависящими явно от а.
Если ввести обычным путем функцию тока ty(x, г), удовлетво-
ряющую равенствам
-т?- —±& <»¦«>
и воспользоваться вместо г в качестве основного переменного без-
размерным комплексом
^=-^г- E-45)
то можно попытаться разыскать решение уравнений E.42) в форме
асимптотического ряда
Ф ~ v* [/о (Ч) + у /i A) + ^ /2 (Ч) + • ¦ • ] = vx/ (к|. *), E.46)
расположенного по отрицательным степеням большой величины
Вычисляем (штрих — производная по г[)
, E.48)
тогда первое из уравнений E.42) сведется к такому:
V"/ + /" + YV'4-Y^^/"-|^^// = 0, E.49)
причем, согласно E.47) и E.46), будет
Пользуясь этими соотношениями, подставим разложение f (у\, х)
по E.46) в E.49) и приравняем коэффициенты при одинаковых от-
рицательных степенях параметра р. Получим следующую систему
158 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ
обыкновенных дифференциальных уравнений:
<+/;-+у л/;
2 -TJ2
2 ' l-'o 2
f
1'
fn-m ~
я-1
-42
E.51
Обратимся к рассмотрению граничных условий. При использовг
нии введенной по E.45) переменной -ц будем иметь следующие гра-
ничные условия на поверхности цилиндра (/¦ = а) для функции /(rj, х)
/ = /' = 0 при г) = е-Р,\
/'-*•2 при т)-»-оо. J
При малых rj в уравнениях E.49) можно откинуть нелинейньи
члены и из полученного таким образом уравнения
Г = 0
при граничных условиях E.52) получить асимптотическое решени*
f _ А -}- Б 1п т),
выражающее поведение функции /(tj, л:) вблизи т) = 0. Использу»
граничные условия E.52) и замечая, что при больших (J можно счи
тать г] = 0 с ошибкой, меньшей, чем любая отрицательная степень \.
получим
/ = 0 при 17 = 0.
и, следовательно.
/л = 0 при т) = 0 и при всех я. E.53
Кроме того, замечая что f'n, так же как и /', вблизи т\ = t
ведет себя, как
E-54
§ 35] ПОГРАНИЧНЫЙ СЛОЙ НА ДЛИННОМ, ТОНКОМ ТЕЛЕ ВРАЩЕНИЯ 159
получим, подставляя это значение f'n в условие /' = 0 при т] = е~?,
со
л=0
откуда будут следовать условия для коэффициентов ап и Ь„'.
#о = О, *i==a0. &2 = ei *« = e«-i- E-55)
Наконец, граничное условие на бесконечности /'->2 при т]->со
даст
/о"*2- /л^°(«>°) ПРИ 1-»>«>- E.56)
При этих условиях первое из уравнений системы E.51) при
/'¦—а0 удовлетворяется линейной функцией
/о^ВД- E-57)
причем, в силу последнего условия E.52), должно быть а0 —2; это
нулевое приближение соответствует однородному потоку со ско-
ростью ию.
Второе уравнение системы E.51) при этом приобретает форму
Ч/Г+ 0+1)/; = 0 E.58)
и должно удовлетворять условиям
/. -> 0, /' —' а. + 2bnri при •») -> 0, \
*> л E-59)
/[^•0 при 1)->оо. J v '
Решением его будет
ч
f^L. E.60)
Замечая, что при rj->0 можно принять Ei(—-rj) --— 1 п rj —(— -f
(? = 0,5772 — известная постоянная Эйлера), получим
С = 2, ai = 2T,
так что окончательно
/; = 2Ei(-ii). /, = 2r,El(-7j)+2*-4-2. E.61)
Таким образом, по E.52) получим уравнение следующего при-
ближения:
E.62)
160 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
с граничными условиями
/2-*0, /2~а2 + 2т1П71 при tj-*O, \
/2->0 при 7j —> оо. J
Решением его будет служить выражение
/; = 2<TT'Ei (- п) - 4Ei (- 2r,) - Ei»(— kj) +
-h 4Ei (— 7]) In т)— 6EI(—T))-fCEi(-ij). E.64)
где введено обозначение
El (--п) = f^=^.dt. E.65)
оо
При малых 7j имеет место асимптотическое выражение
Е1(_?,)~±Aт;+ТJ + -1-*2,
так что
/2~(С — 2 — 4Т) In 7J -|- (СТ — i тег — 4 1п 2 — 2Т — 4f); E.66)
согласно граничным условиям E.63), получим
С = 2+6Т, a2 = 2f — I,;2_4in2. E.67)
Напряжение трения Тц, на поверхности цилиндра, равное
представляется асимптотическим равенством
(ОО //
л=0
которое в силу соотношения E.54) примет вид
- E-68)
Принимая во внимание полученные значения для коэффициентов Ьп
Ьо = 0, *, = о0 = 2, *2 = а, = 2^.
< 35] ПОГРАНИЧНЫЙ СЛОЙ НА ДЛИННОМ ТОНКОМ ТЕЛЕ ВРАЩЕНИЯ 161
[айдем окончательно следующее асимптотическое выражение для на-
фяжения трения:
¦а»'
Q9 I
оШ-
E.69)
Результаты расчета по этой формуле величины силы F сопроти-
1ления на единицу длины цилиндра
2 -^
F =
¦4- •••
форме зависимости \g [FK^U^)] or lg [чхЦи^а1)] показаны на
inc. 42 штрих-пунктиром в правой части рисунка. Аналогичная
Рис. 42.
слева соответствует результату расчета по формуле Себана —
">онда — Кэлли. Длинным пунктиром показана интерполяция, соеди-
няющая обе эти кривые при значениях десятичного логарифма от
1араметра, не превышающих по абсолютной величине единицы.
Более общий случай пограничного слоя на длинном тонком кру-
"овом цилиндре г = а, когда скорость внешнего потока задается
тепенной функцией U = схт, был изучен Стюартсоном :).
') Stewartson К., Quart. Appl. Mathem. 13, № 1 A955), 113—122.
11 Зак. 297. Л. Г Лойцянский
162 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ V
Вводя переменные
?7j = -^- E.70)
и выбирая функцию тока в форме vx/(?, tj), автор приходит к диф-
ференциальному уравнению в частных производных третьего порядка
E.71)
с граничными условиями
(i_m)?^. = 0 при fc,= l.
-Д—>1 при т|—>-в для всех 5,
при ?-*¦ + 0 при ?т!>1.
Простейшим случаем является случай т — 1, когда ф предста-
вляет собой функцию одного переменного tj, а пограничный слой
имеет постоянную толщину. Случай т > 1 неинтересен, так как при
этом пограничный слой утончается и теряется необходимость введе-
ния уточненной поправки на поперечную кривизну. Подробно иссле-
дуется случай т — 0, соответствующий только что разобранной
задаче Глауэрта и Лайтхилла. Для этого случая устанавливается
асимптотическое разложение для больших %, т. е. больших расстоя-
ний от переднего края цилиндра
Ф~7! + Е|Ш!
.5=1
где f — постоянная Эйлера, а функции Р5{у\) определяются из системы
обыкновенных уравнений третьего порядка. Не останавливаясь на
деталях, приведем данное Стюартсоном асимптотическое выражение
для трения
(it/со 'w ^[А-'хКчаЩю)) {In [4'
Это выражение отличается от формулы E.69) Глауэрта и Лайт-
хилла.
Как показывают расчеты, наличие поперечной кривизны вызывает
некоторое уменьшение падения напряжения трения по сравнению
с решением Блазиуса для пластины. Этот эффект сказывается и на
явлении отрыва пограничного слоя, как об этом можно судить, рас-
§ 36] РАСЧЕТ ВЛИЯНИЯ ПОПЕРЕЧНОЙ КРИВИЗНЫ 163
сматривая случай т < 0. Можно констатировать, что в области,
где толщина слоя сравнима с радиусом поперечной кривизны ци-
линдра, наличие этой кривизны приводит к затягиванию безотрыв-
ного обтекания.
§ 36. Расчет влияния поперечной кривизны
по однопараметрическому методу
Положив в основу уточненные уравнения E.37) и граничные
условия E.38), выведем основное уравнение импульсов в общем слу-
чае произвольной формы тела вращения и распределения скорости
на внешней границе слоя.
Умножая обе части первого из уравнений E.37) на г и используя
второе уравнение той же системы, получим
дх ' ду dx ' ду \ ду
Умножим обе части второго уравнения системы E.37) на U (х)
и преобразуем его к виду
djruU) , d(rvU) _ dU
дх ' ду dx
Вычитая почленно из обеих частей полученного уравнения соот-
ветственно обе части предыдущего, найдем
Проинтегрируем обе части этого уравнения поперек слоя от
у = 0 до у = оо, 8, подобно тому как это неоднократно делалось
ранее при выводе уравнения импульсов. В результате интегрирования
получим
или, выполняя дифференцирование в первом члене левой части и
умножая обе части на 2тг,
E-72)
где уже принято во внимание, что r = rQ(x) при у = 0 и введены
для краткости следующие обозначения:
ОО, ', ОО, S
1»
-Т/НУ- E.73)
о
164 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Величины Д* и Д** имеют размерности площадей и могут быть
по аналогии с 5* и 3** названы соответственно «площадью вытесне-
ния» и «площадью потери импульса». Заслуживает внимания тот
факт, что при пользовании такого рода обобщенными понятиями
левая часть уравнения импульсов E.72) ничем формально не будет
отличаться от левой части уравнения импульсов в плоском погранич-
ном слое C.3). Вместе с тем уравнение E.72) содержит в себе как
частный случай упрощенное уравнение импульсов E.28), соответ-
ствующее сделанному в § 30 приближенному допущению г = го(х).
Действительно, при этом допущении 2w0 может быть вынесено за
знак интегралов E.73), после чего величины Д* и Д** с точностью
до множителя 2w0 перейдут в 8' и о**, а уравнение E.72) легко
преобразуется в E.28).
Удовольствуемся простейшей иллюстрацией применения уравне-
ния E.72) на примере круглого цилиндра радиуса а в продольном
однородном потоке со скоростью 1!ш ]).
Исходя из уравнений E.40) и граничных условий E.41), найдем
следующие условия, которым должны быть подчинены профили ско-
ростей в сечениях пограничного слоя. Прежде всего непосредственно
из первого уравнения системы E.40) следует
Далее, взяв от обеих частей первого уравнения системы E.40)
производную по у и используя второе уравнение той же системы,
получим
д2и (д2и 1 ди\_ Г д3и , 1 д2и 1 ди
\_
дх ду ~ \ ду'' у + а ду j L ду3 ' у -\- а ду2 (
Полагая в этом уравнении и = г> = 0 при у = 0, найдем второе
условие, связывающее производные от скорости в сечениях слоя
/ дъи \ . 1 / д2и \ 1 / ди \ „
Введем в рассмотрение формпараметр <*(х) семейства профилей
скорости, связав его с безразмерной первой производной от ско-
рости соотношением
iriW^L] E.76)
0 (у/a)
>y=U
') См. ранее цитированную статью Глауэрта и Лайтхилла.
§ 36] РАСЧЕТ ВЛИЯНИЯ ПОПЕРЕЧНОЙ КРИВИЗНЫ 165
Тогда, согласно уравнениям E.74), E.75) и E.76), первые три про-
изводные от скорости на стенке могут быть выражены через пара-
метр а равенствами
Разлагая и (у; а) в ряд вблизи у—0, получим
или, пользуясь предыдущими равенствами,
" _ 1 Г У Уг | У3 | п / У4 \1
f/oo "" a L а 2а2 ^ За3 ^~ U4 /J '
Замечая, что первые три члена в квадратной скобке совпадают
с разложением функции In И -(-—J, можем с той же точностью на-
писать
Довольствуясь этим приближением, выберем толщину погранич-
ного слоя 8 из обычного условия и = t/oo при у =: 5; тогда по
E.77) будет
8 = а(««—1). E.78)
В разбираемом случае (г = a, U = Um) уравнение импульсов E.72)
упрощается и принимает вид
причем Д** и -zw определяются равенствами
о
Т~и1 = ^- E.81)
Полагая для вычисления интеграла E.80)
166 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
получим
а
(<i-l)e*+\(a+ 1)].
0 E.82)
Подставляя это значение, а также значение т<^ по E.81) в урав-
нение импульсов E.79), придем к обыкновенному дифференциальному
уравнению для определения формпараметра а(дг),
Bаг — За + 2) е** — (а + 2) di __ 4v
а2 dx ~ U
интегрирование которого (f — постоянная Эйлера) дает
gL = е2, + з _ 1^~ >> + Ei ,2а) - In Bа) - т.
Разлагая правую часть при малых а в ряд, получим
или, совершая обращение,
1 __ дтц, __ / \2чх \-'/д 2 13 / 12vx \Ч' __
а ~~ Ff/oo ~ \ /Уооа2 j +3 60 \ f/ооа2 J "Г • • • —
+ ••• E83)
Пользуясь этим разложением для а, можно определить зависи-
мость от параметра чх^и^а2) наиболее характерных для погранич-
ного слоя величин: F=2t:aTw по (.5.83), Д** по E.82) и, наконец,
Д*. равной по E.73)
/
о
',1а
~\~ 2а , E.84)
о
причем при малых а будет
|1 ) E.85)
§ 37] КРУГЛАЯ СТРУЯ В ЗАТОПЛЕННОМ ПРОСТРАНСТВЕ 167
Результаты расчетов по только что приведенным приближенным
формулам показаны сплошными кривыми на рис. 42. Сравнение
с пунктирными кривыми, рассчитанными по асимптотической теории,
изложенной в предыдущем параграфе, показывает систематическое,
но не слишком большое отличие.
§ 37. Круглая струя в затопленном пространстве
Уравнения E.42) могут быть использованы для рассмотрения
задачи о круглой струе, представляющей пример неплоского «сво-
бодного» пограничного слоя при отсутствии продольного перепада
давления. Аналогично тому, как это было в случае плоской струи (§ 6).
уравнения E.42) обладают интегралом
Г ru2dr = const,
о
который связан с законом сохранения секундного количества дви-
жения (импульса) вдоль струи
ПО
J рм2 • 2w dr = Jo, E.86)
представляющим собой следствие постоянства давления во всей
струе.
Рассмотрим сначала простейшую задачу о струе, бьющей из бес-
конечно тонкого отверстия 1). В этом случае граничные условия
¦^• = 0, г> = 0 при /- = 0, |
дг E.87)
и—у0 при г—>оо, j
так же как и уравнения E.42), не содержат характерной длины.
Это позволяет получить автомодельное решение задачи путем состав-
ления функции тока в форме
ф = vjca"(rj), 7j=—^—-. E.88)
л] v
') Schlichting Н„ Zeitschr. f. Angew. Math. u. Mech. 13, № 4 A933),
168 НЕПЛОСКИП ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ V
Определяя входящие в уравнения E.42) величины (штрих—произ-
водная ПО 7])
— J-Z. v — J^T
X г, ' X
\ т) / dr2 ~~ vx3 \ tj /
и подставляя их значения в E.42), убедимся, что вопрос сведется
к интегрированию обыкновенного дифференциального уравнения
-0
при граничных условиях
а = 0, а' = 0 при ti = 0,
E.90)
а конечно при т] = оо. j
Второе условие следует из конечности продольной скорости на
оси струи, третье — из конечности расхода сквозь сечение струи.
Кроме граничных условий E.90), необходимо удовлетворить условию
нетривиальности решения уравнений E.86), которое сводится к та-
кому соотношению:
о
Уравнение E.89) интегрируется один раз непосредственно и вслед-
ствие конечности а" при т\ = 0 его интеграл имеет форму
щ" — ~а' -\- аа' — 0.
Интегрируя еще раз, получим
щ' — 2а -f- -g- а2 = 0,
после чего уже нетрудно найти
а(п) = Т^77' E-92)
Использование условия E.91) позволяет определить постоянную
интегрирования
§ 371 КРУГЛАЯ СТРУЯ В ЗАТОПЛЕННОМ ПРОСТРАНСТВЕ
Решение имеет вид
169
U =
2а2
V -
E.94)
Из второго равенства системы E.94) найдем максимальную ско-
рость ит на оси струи
Точечность источника приводит к особенности в точке х = 0.
Секундный массовый расход сквозь сечение пограничного слоя,
расположенное на расстоянии х от источника, определим по фор-
муле
М
оо со
= f ?и ¦ 2tir dr = 2irp j
о о
= 2тгрф (со) =
E.96)
Этот расход равен нулю при х = 0 и растет пропорционально
расстоянию от источника.
Тот факт, что при нулевом расходе в точке х = 0 импульс ко-
нечен и равен Уо, объясняется бесконечной малостью диаметра трубки,
из которой происходит истечение жидкости. Естественно, что при
конечности импульса, имеющего порядок квадрата скорости, расход,
зависящий от первой степени скорости, должен быть равен нулю.
Задача о струе, вытекающей из точечного источника, в общей
постановке при любых числах Рейнольдса, а не только при больших
их значениях, как это принято в теории пограничного слоя, была
решена Л. Д. Ландау ¦)•
Можно наперед задать конечную величину секундной массы Л10,
вытекающей из источника. В этом случае, кроме Уо, появляется еще
характерное отношение JJM0, имеющее размерность длины, и задача
перестает быть автомодельной. Для решения этой задачи2) представим
') Ландау Л. Д. и Лифшиц Е. М., Механика сплошных сред, Гос-
техиздат, 1953, стр. 108—110.
*) Р у м е р Ю. Б., ПММ, т. XVI, в. 2, 1952. а также Л о й ц я н с к и й Л. Г.,
ПММ, т. XVII, в. 1, 1953.
170
НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[гл. v
функцию тока в виде асимптотического ряда, годного при боль-
ших х,
X '
E.97)
где а, а0, ... суть функции того же комплекса ч\, что и ранее.
Будем иметь следующие асимптотические выражения для скоро-
стей и и v:
1 oi a I aQ I dj 1
и~Т~дг ^" ' Т ~^~ "Т ' ^" ^~ Т" ^~
1 di* Y' v Г~, а /1
г с)х х *п 0 х
E.98)
Подставляя эти разложения и составленные при их помощи про-
изводные в первое из уравнений E.42) и приравнивая коэффициенты
при одинаковых степенях х, придем к следующей системе обыкно-
венных уравнений:
т) +1т^(т)
Зя'
— = 0.
1
/2
ао
E.99)
с граничными условиями
.. =0,
При 7j =
E.100)
/ —^ri = -o—• / ^т)=0, /
а, а0, а! ... ограничены при 7] = оо;
кроме того, та же операция сравнения коэффициентов при одинако-
вых степенях х приводит к условиям нетривиальности решения
% + 2аа[
— -й-ц = О. E.101)
о о о
Первое уравнение системы E.99) с соответствующими ему гра-
ничными условиями и условием нетривиальности решения было уже
рассмотрено в задаче о точечном источнике с Мо = 0. Остается
найти поправку за счет наличия Мо, отличного от нуля. Обратимся
ко второму уравнению системы E.99). Полагая в нем
<N=A E.102)
КРУГЛАЯ СТРУЯ В ЗАТОПЛЕННОМ ПРОСТРАНСТВЕ
171
и переходя от аргумента ?) к новому аргументу
с г, по E.92) соотношением
= -j- а, связанному
E.103)
придем к гипергеометрическому уравнению
с (С— п -*4 - -dA - 6А = о.
E.104)
регулярным решением которого, удовлетворяющим граничным усло-
виям и условию нетривиальности, будет
СA — СJA — 4С). E.105)
Возвращаясь к уравнению E.102) и выполняя новое интегриро-
вание, получим
4
1)=
E.106)
где р—постоянная интегрирования. Исправленное на конечность
расхода уИ0 решение имеет вид
•X —
1 +1 «V
з
2а*
¦ — 4-Ra2.
x2
X
у + 4 a'rt
v?+-
15.107)
Постоянная (З выражается через заданный секундный массовый
расход Жо при х —0. Имеем, аналогично E.96;, общую формулу
массового расхода
¦+27tfoi. E.108)
E.109)
Отсюда при х = 0 и М = Мп следует
172 НЕПЛОСКИЕ ДВУМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ Ггл V
Максимальная скорость на оси струи (¦*) = 0) по второму равен-
ству системы E.107) будет равна
Следующее приближение, включающее определение функции ai(t]),
было найдено В. С. Дубовым ').
Радиальная щелевая струя, бьющая из тарельчатого клапана (ее
иногда называют «кольцевой» струей), была рассмотрена автором
настоящей книги 2), Задача эта при отсутствии закрутки не пред-
ставляет никакой сложности. Л. А. Вулис и В. П. Кашкаров3)
обобщили плоскую задачу о струе, ограниченной с одной стороны
стенкой (§ 7), на случай струи, распространяющейся на поверхности
конуса. Ряд работ выполнен по распространению струй в спутных
потоках4). Обзор точных решений по ламинарным струям можно
найти в статье В. П. Кашкарова 5). Следует заметить, что в настоя-
щее время теория струй уже отделилась от теории пограничного
слоя и превратилась в самостоятельную область, имеющую свою
специальную литературу 6). В дальнейшем мы еще вернемся к неко-
торым вопросам теории струй. Как показали опыты, ламинарные
струи мало устойчивы и сразу же по выходе из источника переходят
в турбулентное состояние. То же относится и к аэродинамическому
следу за телами.
') Д у б о в В. С, Труды ЛПИ (Энергомашиностроение, Техническая
гидромеханика) № 176, Машгиз, 1955, стр. 138 —145.
2) Л о й ц я н с к и й Л. Г., Труды ЛПИ (Энергомашиностроение, Техни-
ческая гидромеханика) № 5, 1953.
3) Вулис Л. А., Кашкаров В. П., ЖТФ, № 2, 1956.
«) S q u i г е Н., Т г о и п с е г J., ARC R&M, 1974, 1944; БушмаринО. Н„
Труды ЛПИ (Энергомашиностроение, Техническая гидромеханика) № 176,
1955.
5) Кашкаров В. П., Некоторые точные решения в теории струй не-
сжимаемой жидкости, Сб. «Исследование физических основ рабочего про-
цесса топок и печей», АН Казах. ССР, Алма-Ата, 1957.
6) Б а й Ш и - и, Теория струй, пер. с англ., Физматгиз, 1960.
ГЛАВА VI
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
§ 38. Равномерное вращение диска в безграничной вязкой
жидкости
В отличие от рассмотренных в предыдущей главе неплоских двумер-
ных течений с двумя компонентами скорости, зависящими от двух коор-
динат, в настоящей главе будут разобраны осесимметричные простран-
ственные движения с тремя компонентами скорости, в силу симметрии
зависящими только от двух координат.
Начнем с рассмотрения погранич-
ного слоя, образующегося на диске,
равномерно вращающемся в безгранич-
ной жидкости вокруг оси, перпендику-
лярной к его плоскости. Задача эта
была впервые решена Карманом '). Бо-
лее точные вычисления впоследствии
выполнил Кокрен 2). Обозначим (рис. 43)
через и, v, w соответственно радиаль-
ную, окружную (азимутальную) и нор-
мальную к плоскости диска компоненты
скорости в системе цилиндрических
координат г, z (азимутальная коорди-
ната при наличии осевой симметрии
течения в уравнения не входит).
Рис. 43.
Полные уравнения движения (уравнения Стокса) будут имгть вид
да
ди
Or V~t~ w Hz
dv . uv , dv
P дг "Г" L
d2u
дг2
и
ди
dw
dw
'~dT
dw
d2v
1 dp
p dz
d2v
d2w
1 dw
F.1)
') v. К arm an Th., Zeltschr. f. Angew. Math. u. Mech. 1 A921).
г) Cochr an W. O., Proc. of the Cambr. Phil. Soc. 30 A934).
См. также монографию: Д о р ф м а н Л. А., Гидродинамическое сопро-
тивление и теплоотдача вращающихся тел, Физматгиз, 1960.
174
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ \г.П VI
Граничные условия при равномерном вращении диска вокруг
оси Oz с угловой скоростью ш будут такими:
= 0; \
F.2)
и = 0, v = го), ад = 0 при ? = '
и=О, г> —О при
Если отвлечься от влияния конечности радиуса диска, т. е. пре-
небречь периферийным эффектом и заменить диск безграничной пло-
скостью, то задача будет автомодельной. Следуя Карману, положим
и = /чо/(?), v — nog (С), w = |/"vu)A (С), |
где за аргумент принято выражение
F.3)
-. F.4)
Задача сведется к интегрированию совокупности обыкновенных
дифференциальных уравнений (штрих—производная по С)
F.5)
P'-\-hh' —
при граничных условиях
/=0. g=\, А = 0, Р
/ = 0, ^
при
при
F.6)
Карман проинтегрировал эту систему уравнений приближенно,
используя понятие о пограничном слое конечной толщины 8, которая
в этом случае не может зависеть от г, т. е. будет постоянной ').
Из второго и третьего уравнений системы F.5), пользуясь пер-
вым, легко вывести следующие два, содержащие только две неиз-
вестные функции fug, интегральные соотношения,
F.7)
') Указанные Кокреном [см. сноску на предыдущей странице,
Collected Works of Th.v. Karman, 2 A956), London, стр. 89J неточное
исправлены.
а также
неточности здесь
§ 38] РАВНОМЕРНОЕ ВРАЩЕНИЕ ДИСКА В ВЯЗКОЙ ЖИДКОСТИ 175
где Со = о 1/ — характеризует толщину пограничного слоя в безраз-
мерной форме.
Используя обычные для метода Кармана — Польгаузена граничные
условия
% 8
зададим функции / и g в виде полиномов
F.8)
-о2.
где X — пока неизвестный формпараметр, а ^ = С/С0. Для определения
двух неизвестных X и Со имеем два уравнения F.7). Составляя вхо-
дящие в эти уравнения интегралы
Г/2 Л = @,030IX2 — 0.00675Х +0,000397) ?;>,
F.9)
= 0,2357С0, J fg<K. = @.0607X — 0.00564)Cg,
о о
а также необходимое для дальнейшего выражение
с
F.10)
получим вместо F.7) два алгебраических уравнения, корни которых
равны
Х = 0.1945. Со = 2,794. F.11)
Отсюда следует, что толщина пограничного слоя равна
= 2,794l/ —.
Г о>
F.12)
Увлекаемые вращением диска частицы жидкости в пограничном слое
двигаются от оси вращения к периферии по спиральным траекториям.
На их место сквозь внешнюю границу пограничного слоя со скоро-
стью (w)z=b поступают новые частицы. Определим эту скорость; она
равна
= w (Cq) = У^Н (Ср) = V^Wt.i = - 0,545 Y^.
176
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[гл v
Найдем момент сопротивления жидкости вращению диска рь
диуса а (диск смочен с обеих сторон):
' @)
По второму из равенств F.11) получим
= Way @) = - ^ ?а* ¦ -1.
3.38
F.13
Кокрен, как уже упоминалось, непосредственно разрешил си
стему уравнений F.5) численным методом, пользуясь понятие:,
асимптотического слоя. Значения вычисленных им функций поиво
дятся в таблице 10.
Таблица 1<
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,4
1,6
1,8
2,0
2,5
3,0
4,0
со
/
0
0,046
0,084
0,114
0,136
0,154
0,166
0,174
0,179
0,181
0,180
0,173
0,162
0,148
0,133
0,118
0,084
0,058
0,026
0
g
1,0
0,939
0,878
0,819
0,762
0,708
0,656
0,607
0,561
0,517
0,468
0,404
0,341
0,288
0,242
0,203
0,131
0,083
0,035
0
— Л
0
0,005
0,018
0,038
0,063
0,092
0,124
0.158
0,193
0,230
0,266
0,336
0,404
0,466
0,522
0,572
0,674
0,746
0,826
0,886
Г
0,510
0,416
0,334
0,262
0,200
0,147
0,102
0,063
0,032
0,006
-«,016
—0,046
—0,064
—«,073
—0,076
—0,074
—0,061
—0,046
—0,022
0
Пользуясь данными таблицы 10, можно определить величину коэа-
фициента момента ст. Точное значение этой величины оказывается
равным
ст =
3,87
/Re'
F.14
§ 39] РАВНОМЕРНОЕ ВРАЩЕНИЕ ДИСКА. ОГРАНИЧЕННОГО КОЖУХОМ 177
т. е. значительно превосходит приближенное, подсчитанное по методу
Кармана значение и близко подходит к опытным данным.
Пользуясь таблицей 10, можно подсчитать секундный объем
жидкости, подтекающей в осевом направлении к вращающемуся диску
сквозь внешнюю границу слоя, или, что то же, отбрасываемой одной
стороной диска в радиальном направлении. Этот расход Q опреде-
лим по формуле
СО СО
Q = 2-ка I и dz = 2тга2со у ^ I / (С) Л.
о о
Но по первому из уравнений системы F.5) находим
•о
2 J / (С) Л = — [Л (со) — h @)] = - А (оо)
о
и, следовательно, пользуясь таблицей 10, получим
Q = 0,88&^V^ = ^^. F.15)
У Re
Хоуарт1) рассмотрел задачу о вращении сферы вокруг одного из
своих диаметров в безграничной жидкости и показал, что вблизи
полюсов имеет место движение, аналогичное движению на вращаю-
щемся диске вблизи его оси. Образующиеся в пограничном слое
сферы течения от полюсов к экватору в некоторой мере соответ-
ствуют полярным пассатам, наблюдаемым в земной атмосфере2).
§ 39. Равномерное вращение диска, ограниченного кожухом
При равномерном вращении диска в ограниченном пространстве,
в частности в соосном с диском цилиндрическом кожухе (рис. 44),
возникают новые явления, расмотрение которых представляет инте-
рес. Отмеченное в предыдущем параграфе подтекание жидкости
к вращающемуся диску и последующее ее отбрасывание к периферии
диска вызывает перетекания, образующие циркуляцию жидкости по
стенкам кожуха. При этом на основаниях кожуха движение жидкости
происходит от периферии к оси.
Если зазор между плоскостью диска и основаниями кожуха очень
мал, в частности меньше, чем сумма толщин пограничных слоев,
возникающих на диске и основаниях кожуха, то получается движе-
ние, аналогичное тому, которое имеет место под обильно смазанной
пятой и описывается в гидродинамической теории трения. В задачу
') How art h L.. Philos. Mag. 7, № 42 A951), 1308—1315.
!) Ahlborn F., Beitriige zur Physlk der freien Atmosphere 11, № 4.
12 Зак 247 Л Г ЛпИи.иров
178
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
теории пограничного слоя входит изучение более сложного, промежу-
точного случая, когда на рассматриваемых поверхностях образуются по-
граничные слои, не перекрывающие друг друга и взаимодействующие
между собой через разделяющую их область «внешнего» потока.
Этот случай был разобран впервые Шульц-Груновым'), использо-
вавшим приближенный метод, аналогичный изложенному в преды-
дущем параграфе методу Кармана.
Как показали опыты Шульц-Грунова, между пограничными слоями
образуется объем жидкости с распределением азимутальных скоростей
как в твердом теле, вращающемся
с некоторой угловой скоростью ш,
средней между нулевой угловой
скоростью кожуха и угловой ско-
ростью о> вращения диска.
Рассмотрим в связи с этим две
самостоятельные задачи: 1) о по-
граничном слое на основании ко-
жуха — неподвижном диске ра-
диуса Ь > а — при наличии внеш-
него потока с азимутальной ско-
ростью
V=Zr F.16)
С
~)
С
J
с
С
V///77/7/////////////,
Рис. 44.
и 2) о пограничном слое на диске, вращающемся с угловой ско-
ростью о> при наличии внешнего спутного квазитвердого вращения
жидкости с тем же распределением азимутальных скоростей F.16).
Величина ш может быть затем определена из условия равенства
моментов сил трения жидкости о поверхность диска и основания
кожуха.
В отличие от вращения диска в безграничном пространстве,
в рассматриваемом случае внешний поток обладает азимутальными
скоростями F.16), благодаря чему во внешнем потоке образуется
изменение давления в радиальном направлении, характеризуемое про-
изводной
dp V1 ~2 ,
—г- = р—= ршгг. F.17)
В связи с этим при рассмотрении системы уравнений F.1) уже
нельзя пренебрегать радиальными производными, как это делалось
ранее, в главе V. Воспользовавшись уравнением неразрывности (чет-
вертое уравнение системы), перепишем левую часть первого из
') S с h u 11 z-0 r u n o w F., Zeitschr. f. Angew. Math. u. Mech. 15, № 4
A935), 191.
§ 39] РАВНОМЕРНОЕ ВРАЩЕНИЕ ДИСКА, ОГРАНИЧЕННОГО КОЖУХОМ 179
уравнений F.1) в виде
ди v2 . д (uw) dw д (и2) .и2 v2 ,
после чего умножим обе части уравнения на г dz и проинтегрируем
по z от нуля до толщины слоя на неподвижном диске, которую,
в отличие от толщины 8 слоя на вращающемся диске, обозначим
через 80. Замечая, что
f Г А (И2) dZ = f-± (ГU*) dZ - f
Я2 dZ
и что, по условию, радиального потока на внешней границе слоя нет
(й = 0 при z = oQ), я и и да=0 при 2 = 0, придем окончательно
к следующему первому интегральному соотношению импульсов:
/
о
Аналогично перепишем левую часть второго уравнения системы
F.1) в виде
и, умножив обе части уравнения на r2dz, проинтегрируем по z от
нуля до 80. Используя уравнение неразрывности и интегрируя по
частям, получим второе интегральное соотношение
-J— [г2 / uv dz — cor2 -г- г \ и dz 1 = — vr2 (-^- \ , F.19)
dr \ ,1 1 dr \ J I \dz)z-0 \™-1^;
выражающее теорему об изменении момента количеств движения.
В качестве приближенных профилей скорости примем следующие:
в= - я0Г1 — B у Л'] и v = rm\l — (l —fJ|, F.20)
где и0—неизвестная максимальная радиальная скорость, а знак
минус при ней взят в связи с тем, что на основании кожуха ради-
альная составляющая скорости направлена от периферии к оси.
Вычисляя интегралы, входящие в левые части уравнений F.18)
и F.19), и производные, стоящие справа, и принимая еще вместо г
новую безразмерную независимую переменную ф — радиус кожуха)
180
ТРЕХМЕРНЫЕ ОСЁСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. Vt
перепишем уравнения F.18) и F.19) в виде (штрих—производ-
ная по х)
A — х)ФЧ'о— 2A — х)ФФ'80+ф280-|-
3A — х)Ф'80+11Ф0§0 = 3(М>A —х),
где введено обозначение Ф = и0Ь0.
Шульц-Грунов получает решение этих уравнений в виде степен-
ных рядов
ф = Ь Vwx'' [3,04 — 4,64х + 2,839x2 —
— 2,855х3— I,814x4-f ...],
= \f ~ хи [4,385 — 5,845х-(- 4,015х2 —
F.22)
— 4,46х3 — 1,29лг4Н- ...].
Расчеты показывают, что момент сил трения жидкости о непо-
движное основание равен
Ж=3,39AО)*4|/ —.
F.23)
Переходя ко второй задаче — расчету пограничного слоя на вра-
щающемся с угловой скоростью о) диске при наличии спутного
квазитвердого вращения внешней жидкости с угловой скоростью
о) < ш, заметим, что интегральные соотношения F.18) и F.19) оста-
нутся по форме теми же (следует только заменить 80 на 3), а по-
линомиальные представления скоростей в сечениях слоя будут несколько
иными, а именно:
-(l -?-)'].
где и*0—новая неизвестная максимальная радиальная скорость.
Опуская детали вычислений, которые почти дословно повторяют
только что изложенные для случая неподвижного основания кожуха ]),
придем к системе уравнений, имеющей в качестве решений
И
0
7з
F.24)
F.25)
') См. цитированную статью Шульц-Грунова или подробное ее изложе-
ние в нашей монографии «Аэродинамика пограничного слоя», Гостехиздат,
1941, стр. 224.
§ 39] РАВНОМЕРНОЕ ВРАЩЕНИЕ ЛИСКА. ОГРАНИЧЕННОГО КОЖУХОМ 181
Момент трения, приложенный к вращающемуся диску радиуса а,
будет равен
М— 1,79[ха4(ш — ш) V^/2+Зи)/ш у llt^h_7!i. F.26)
Положив здесь ш =: 0, получим
что соответствует задаче Кармана; сравнивая с формулой F.13),
видим, что в связи с использованным в расчете полиномиальным
приближением, отличным от принятого Карманом, коэффициент по-
лучится несколько большим (примерно на 15%), чем в теории Кар-
мана.
Остается определить оставшуюся до сих пор неизвестной величину
угловой скорости со квазитвердого вращения жидкости между погра-
ничными слоями. С этой целью приравняем между собою выражения
моментов F.23) и F.26), которые должны быть равны, так как
внешнее ядро вращается равномерно. Графическое решение соот-
ветствующего уравнения дает
ш/ш = 0,54, F.27)
т. е. квазитвердое ядро между пограничными слоями вращается при-
мерно с половинной угловой скоростью по сравнению с диском.
Окончательная формула момента сопротивления диска в кожухе
F.26) принимает после этого вид
/с^. F.28)
Если ввести опять коэффициент момента ст, равный
то получим
На основании проведенного расчета можно сделать следующие за-
ключения: 1) момент сопротивления диска, вращающегося в кожухе,
не зависит от зазора между плоскостью диска и основанием кожуха
(если, конечно, зазор превышает сумму толщин пограничных слоев
на диске и основании кожуха) и 2) этот момент значительно меньше,
чем при отсутствии кожуха, т. е. при вращении диска в безгранич-
ной жидкости. Оба эти заключения тесно связаны со сделанным до-
пущением о существовании между пограничными слоями области
квазитвердого вращения жидкости с постоянной угловой скоростью.
При увеличении зазора, начиная с некоторой, достаточно большой
182 TPFXMEPHblE ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ (ГЛ. V!
его толщины, принятое допущение потеряет свою силу, так как
квазитвердое вращение, обусловленное замкнутостью циркуляции
жидкости, прекратится. Причина уменьшения значения момента по
сравнению со случаем безграничной жидкости заключается в том,
что при наличии кожуха азимутальная скорость убывает на протя-
жении толщицы слоя примерно до половины своего первоначального
значения, а при отсутствии кожуха — до нулевого значения. Эта
разница сказывается на величине производной скорости по нормали
к поверхности диска, т. е. на интенсивности трения о поверхность
диска, а тем самым и на величине момента.
Как при вращении диска в безграничной жидкости, так и при
вращении его в цилиндрическом кожухе внутри пограничных слоев
образуются радиальные течения, отсутствующие во внешнем потоке.
Такие течения, вызываемые в подторможенной в пограничном слое
жидкости перепадами давлений, носят наименование «вторичных
течений».
Вопрос о характере вторичных течений при различных соотноше-
ниях между угловыми скоростями двух соосно вращающихся дисков
изучался многими авторами. Так, Батчелор]) рассмотрел спутное
квазитвердое вращение жидкости с угловой скоростью как меньшей,
чем у вращающегося диска (аналог задачи Шульц-Грунова), так и
большей. Во втором случае вторичные течения в пограничном слое
диска будут иметь направление, противоположное указанному на
рис. 43; жидкость будет подтекать от периферии диска к его оси
и уходить сквозь внешнюю границу пограничного слоя наружу.
Стюартсон2), основываясь на работах Кармана и Батчелора, получил
в замкнутом виде приближенное решение (по методу Озеена — Релея)
задачи о движении вязкой жидкости между двумя соосными дисками,
вращающимися с разными угловыми скоростями, и дал подробный
анализ образующихся при этом вблизи поверхностей дисков вторичных
течений. В дальнейшем3) Стюартсон получил более точную оценку
толщин областей вторичных течений, образующихся за счет пере-
текания жидкости из пограничного слоя более быстро вращающегося
диска в пограничный слой диска с меньшей угловой скоростью4) и
изучил поведение жидкости между дисками вне пограничных слоев.
') Batch el or О. К., Quart. Journ. of Mech. and Appl. Math. 4 A951),
29—41.
2) Stewartson K., Proc. Cambr. Phil. Soc. 49, № 2 A953), 333—341.
3) Stewartson K., Journ. of Fluid Mech. 3, № 1 A957), 17—26.
*) Критическую оценку существующих работ во вопросу о вторичных
течениях в пограничных слоях на соосно вращающихся дисках можно найти
в обзоре: Ф. М у р, Теория трехмерного пограничного слоя Проблемы меха-
ники, в. 2, ИЛ, 1959, стр. 245—249.
В ьедавно появившейся статье С. Розенблата освещен вопрос о потоке
вязкой несжимаемой жидкости между двумя крутильно-колеблющимися
дисками (см. R о s e n Ы a t S.( J. Fluid Mech. 8, № 3 (I960), 388—399).
§ 40] ДИСК, ВРАЩАЮЩИЙСЯ В ОДНОРОДНОМ ОСЕВОМ ПОТОКЕ 183
Близкой к рассмотренному кругу вопросов является группа осе-
симметричных задач о вращательном движении вязкой жидкости вблизи
неподвижной поверхности. К этой группе относятся, например, дви-
жения в вихревых форсунках и циклонах, вторичные движения внутри
смерча и др. Часть этих вопросов будет освещена в конце настоя-
щей главы (§ 45).
§ 40. Пограничный слой на диске, вращающемся
в однородном осевом потоке
Как обобщение двух ранее рассмотренных задач о пограничных
слоях, образующихся вблизи лобовой критической точки тела вра-
щения и на вращающемся диске, можно поставить задачу о погра-
ничном слое на равномерно вращающемся диске, помещенном в одно-
родный поток, направленный перпендикулярно к его плоскости.
Задача эта допускает решение в строгой постановке теории асимпто-
тического слоя, но требует при этом применения численных методов
интегрирования'). Изложим простое наглядное решение той же задачи
методом слоя конечной толщины, принадлежащее Шлихтингу и Тру-
кенбродту2),3).
Сохраним прежние обозначения. Уравнения движения при любой
форме носовой части вращающегося с угловой скоростью <о тела
будут представлены системой F.1), а граничные условия F.2) перей-
дут в следующие:
и = 0, г> = шг, •да=0 при г = 0, )
,, ,, w, 6.30)
u=.U, v = V, w = W при z = oo, J '
где
U = *r, V=0, W = — 2yiz F.31)
являются компонентами скорости внешнего потенциального потока,
а постоянная х зависит от формы носовой части тела вращения.
Для определения постоянной ¦/. следует сравнить скорости, задан-
ные равенством F.31), со скоростями вблизи критической точки при
') В a t с h е 1 о г О. К., Quart. Journ. of Mech. and Appl. Math. 4 A951),
2)Schllchting H., Truckenbrodt E., Zeitschr. f. Angew. Math.
u. Mech. 32, N° 4/5 A952).
Tifford A. N.. Sheng To-chu, Journ. Aeron. Sci. 19, №4 A952),
284, 285.
3) Впервые вопрос о пограничном слое на тела*, вращающихся в набе-
гающих на них вдоль их оси однородных потоках, был поставлен И. М. Бюр-
герсом: Burgers J. M., Коп. Acad. v. Weltenschappen, Amsterdam, 45,
№ 1-5 A941)
184
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЙ СЛОИ [ГЛ. V!
поперечном обтекании диска радиуса а1) однородным потоком со
скоростью Woo- Тогда получим
F.32)
В дальнейшем в качестве основного параметра будет фигуриро-
вать отношение
- = - —=--^, F.33)
которое с точностью до множителя 2/тс равно отношению скорости
набегающего потока к периферийной окружности скорости диска
Пользуясь соотношениями, аналогичными F.3), но не выделяю-
щими явно ш (в данном случае наряду с ш имеется еще другая харак-
терная величина х той же размерности), можно положить
u = rf(z), v — rg(z), w =
Тогда система уравнений F.1) преобразуется в систему
F.34)
dz* '
dz
h dh = 1 dp,
dz p dz
F.35)
dz* •
аналогичную F.5), но с несколько иными граничными условиями:
/ = 0, g = u>, A = 0 при z = 0,
/—>х, g—> 0, h —> — 2кг при z—>оо.
F.36>
При х = 0, т. е. ^„ = 0, вернемся к задаче Кармана.
Интегрируя обе части второго уравнения системы F.1) поперек
слоя от 2 = 0 до z = оо, либо 8 (толщина слоя) при граничных
условиях F.30) и, как обычно, используя последнее уравнение (не-
разрывности) той же системы, получим интегральное соотношение
') См., например, К о ч и н Н. Е., К и бе ль И. А., Розе Н. В., Теоре-
тическая гидромеханика, Гостехиздат, 1948, стр. 359.
§ 40] ДИСК, ВРАЩАЮЩИЙСЯ В ОДНОРОДНОМ ОСЕВОМ ПОТОКЕ
185
импульсов в радиальном направлении
со, f
•¦%- I (U-u)dz +
о
со, 5
¦¦ = "(¦?) =г*+. F.37)
г- СО, О
^ \rf u(U-u)dz
Тем же путем получим из третьего уравнения системы интеграль-
ное соотношение моментов количеств движения
= -*(?).-<> = "'¦f. F.38)
Заменяя здесь скорости их выражениями F.34), перепишем уравне-
ния F.37) и F.38) в форме
f (*2 + 2х/ - 3/2 + g2) dz = v (^)г_о.
F.39)
т. е. примем пограничный слой конечным по толщине. Обозначим
эту толщину через 8 и введем вместо z новую переменную Л рав-
ную отношению z/b. Тогда уравнения F.39) заменятся следующими:
Л**-
mi,-
F.40)
Перейдем к заданию формы профилей скорости в сечениях по-
граничного слоя или, что то же, к подбору функций f (t) и g(l)
в виде некоторых полиномов. Коэффициенты этих полиномов опре-
деляются путем выполнения граничных условий при t = 0 и t = 1.
В качестве «первого приближения» выбираются полиномы
— 2t-\-t2),
= 1@B-3/-И3).
К6.41;
186 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОЙ [ГЛ. VI
удовлетворяющие граничным условиям
/ — ¦к, /' = 0, g-^=0, #' = 0 при f=l, ]
причем второе условие для /" при t = 0 следует непосредственно
из первых двух уравнений системы F.35) при z = 0, т. е. / = 0,
и условия h = 0 при / = 0.
«Вторым приближением» служат полиномы
F.43)
— 3/ + 3/2—
построенные по тем же условиям F.42), но с добавлением еще двух
/" = 0, /' = 0 при t=\. F.44)
Оговоримся, что не следует придавать сколько-нибудь строгий смысл
терминам «первое» и «второе» приближения, так как никакого опре-
деленного алгоритма приближений не дается.
Постоянная сх = /' @) представляет собой первый неизвестный
формпараметр задачи, а с2 — второй, выражаемый через неизвестную
толщину слоя по формуле
с2 = у/ @) = ^ -. F.45)
Используя указанные полиномы, получим из F.40) уравнения для
определения формпараметров сг и с2. Уравнения эти будут иметь вид
¦p-Cl —<*!*'+в**!"
Cl
F.46)
где а( и ^ — числа в таблице 11.
Величина с, легко исключается и задача приводится к решению
одного уравнения четвертой степени относительно квадрата неизвест-
ной толщины пограничного слоя.
Если ввести еще следующие дополнительные обозначения:
v. «в2 .
Р = —. а = т?Г" ПРИ ш^>*
lO] ДИСК, ВРАШАЮШИЙСЯ В ОДНОРОДНОМ ОСЕВОМ ПОТОКЕ 187
Таблица 11
а2
19/210
52/1155
а7
33/140
23/126
а3
1/210
1/770
6,
105/17
630/47
а4
5/140
3/770
Ь2
19/102
13/94
1/210
9/1540
Ьъ
27/34
54/47
-равнение четвертой степени может быть пред-
¦оом:
- р*) а3 + (С -f Dp2) а2 4- Ера. = 1,
если ш ^ х,
Г6 481
если и) ^ х.
;в Л, Б, .... ? приведены в таблице 12.
Таблица 12
жение
389
361
798
540
573
2-е приближение
—0,01147
0,08214
0,60435
3,29461
1,20404
толщины пограничного слоя по второму
чсны в таблицу 13.
кобках приведены цифры по первому прибли-
. метить, что разница в значениях толщины слоя по
<му приближению получается сравнительно большой,
•ялее станет ясно, слабо отражается на величинах на-
188 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. V
Таблица 1;
При ш ;> у.
<л/х
• Г Ш 3!
0
схэ
3,615
B,793)
7,
4
3,061
'/а
2
2,546
'/«
4/з
2,189
1
1 ,
1,931
A,526)
ПрИ У. > (О
1
1
1,931
7з
3/,
1,957
2
V2
1,974
4
7«
1,987
со
оо
1,992
A,575)
пряжений трения и суммарного момента трения, что лишний ра:
подтверждает несущественность точной оценки этой, совершенж
условной величины.
Компоненты напряжения трения
F.49
могут быть также легко вычислены по F.41), F.46) и известног
уже величине 8. В таблице 14 приводим значения величин т? и .
при разных значениях характерного параметра х/ш или обратной
его значения ш/х, сосчитанных по второму приближению. В скобка:
помещены те же величины по первому приближению, а в последнее
строке для сравнения приведены точные значения ir по данным ТисЬ
форда и Ченг То-шу').
') См. выше цитированную их работу.
ИСК, ВРАШАЮШИЙСЯ В ОДНОРОДНОМ ОСЕВОМ ПОТОКЕ 189
Таблица 14
9
»/*
;]/ —
xe, точное
чначение
0
со
—0,553
(—0,537)
0,534
@,544)
0,512
'Л
4
-0,653
0,597
0,588
V,
2
—0,785
0,806
0,771
3/,
7з
—0,914
1,120
—
1
1
— 1,033
(—0,981)
1,531
A,500)
1,294
1
1
—1,036
1,531
1,294
4/з
3/,
—0,766
1,412
—
2
Vs
—0,503
1,312
1,302
4
V.
-0,252
1,277
1,299
оо
0
0
@)
1,255
A,222)
1,310
Вычислим еще коэффициент ст в формуле момента сопротивле-
жидкости вращению диска. Имеем по второму равенству F.49)
а а
М = — 2
"ак что будет
F.50)
190
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[гл v
Значения функции F(y./m) приводятся в таблице 15; там же в по
следней строке даны результаты точного расчета по Тиффорду t
Ченг То-шу.
Таблица 1"
То же, точное
значение
х/ш
То же, точное
значение
0
1,74
1,94
1
3,25
3,21
2,05
2,24
7з
3,69
—
Vo
2,46
2,65
2
4,49
4,82
ги
2,47
—
4
6,35
6,67
Из приведенных таблиц можно сделать некоторые качественныь
выводы. Из таблицы 13 следует, что при фиксированном х, но пере
менном ш толщина 8 почти не меняется; наоборот, при фиксироваь
ном оо и переменном х изменение толщины пограничного слоя знaч^
тельно. При возрастании х/ш от нуля до единицы 8 в этом случае
меняется почти в два раза. Аналогично, как это следует из таблицы К
тг при фиксированном к и переменном <о изменяется всего лиш.
на 30%, в то время как при фиксированном ш и переменном х
почти в три раза. Для т^ можно отметить противоположный фак"
несколько более слабого изменения при фиксированном ш, чем пр\
фиксированном х.
Поле скоростей в пограничном слое представлено в виде вектор
ной диаграммы на рис. 45. Числа, стоящие около концов стрелок
характеризуют расстояние z плоскости измерения от поверхност!
диска, выраженное в частях длин: j/v/ш при ю>хи Wx при х > а.
Как станет ясным в дальнейшем, такие диаграммы очень полезны npi
рассмотрении течений в пространственном пограничном слое.
Первые систематические опыты по изучению пограничных слоеь
на телах, вращающихся вокруг своей оси симметрии в однородно.1
потоке, набегающем параллельно их оси, и в том числе на диске \
; 40]
ДИСК, ВРАЩАЮЩИЙСЯ В ОДНОРОДНОМ ОСЕВОМ ПОТОКЕ
191
ia сфере, были произведены Визельсбергером *). Эти опыты показали,
то с возрастанием отношения окружной скорости вращения к ско-
юсти набегающего потока сопротивление тела возрастает, причем
"го возрастание, незначительное для диска, становится существенным
;ля тел вращения, в частности для шара. Причиной этого возраста-
1ия служит возникновение в области задней (кормовой) критической
^очки обратного по отношению к набегающей на тело жидкости
давления и противотока, о которых была речь в настоящей
д_ 0,5 и/шг I n 0,5 и/ыг /
Рис. 45.
•лаве. Наличие этих факторов приводит к ускорению отрыва погра-
(ичного слоя и к увеличению размера кормовых застойных зон, что
;лечет за собой ухудшение обтекания тел и увеличение их сопро-
тивления. Как станет ясно из дальнейшего, тот же фактор должен
гоиводить к ускорению перехода ламинарного пограничного слоя
¦ турбулентное состояние.
Заметим, что вращение потока, набегающего на неподвижное тело
винтовой поток), должно, наоборот, улучшать обтекание тела,
меньшать его сопротивление.
Рассмотренный в настоящем параграфе пример имеет, кроме фи-
зического, еще большое методическое значение, так как отчетливо
')Wieselsberger С, Phys. Zeitschr. 28 A927), 84.
192 ТРЕХМЕРНЫЕ ОСЁСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [|'Л VI
поктзывает, какие большие возможности до настоящего времени про-
должает сохранять ставший уже классическим метод Кармана — Поль-
гаузена. Вместе с тем необходимо отметить одно, важное для даль-
нейшего обстоятельство. При применении в пространственных задачах
метода, основанного на понятии пограничного слоя конечной толщины,
не следует думать, что толщина пограничного слоя для продольной
компоненты скорости должна обязательно совпадать с толщиной для
азимутальной компоненты. В изложенной работе Шлихтинга и Трукен-
бродта, так же как и в работах Кармана и Шульц-Грунова, было
сделано в скрытой форме допущение, что эти толщины одинаковы.
Однако в ряде случаев такое допущение становится неудовлетвори-
тельным. С одним из таких случаев мы встретимся в § 45.
§ 41. Пограничный слой на диске, приводимом
во вращение из состояния покоя
Задача Кармана о вращении диска в безграничной вязкой жидкости
вокруг оси, перпендикулярной к плоскости диска, была обобщена
на случай приведения диска во вращение из состояния покоя по
заданному наперед закону изменения угловой скорости со временем.
Этой нестационарной задачей теории пограничного слоя занимались
многие ученые у нас в Союзе и за границей. Д. Е. Долидзе :) указал
строгий путь решения задачи при произвольном законе изменения ш (t)
угловой скорости диска. Однако предложенный им для решения си-
стемы интегродифференциальных уравнений метод последовательных
приближений оказался связанным с весьма сложными вычислениями
и не позволил автору довести его решение до количественно обо-
зримых результатов. Работы Нигама2) и Тирио3) были посвящены
простейшему случаю ш (t) — const при t > 0, соответствующему мгно-
венному приведению в равномерное движение или внезапной оста-
новке диска. Этот случай был подробно разобран и доведен до на-
глядных количественных результатов. Л. А. Розин4) опубликовал
решение, относящееся к любому степенному закону изменения угло-
вой скорости диска.
Уравнения настоящей, нестационарной задачи отличаются от урап-
„,„.., ди dv dw
нений F.1) добавлением в левых частях членов -j-, -т-, ~~j7~'
выражающих компоненты локального ускорения в цилиндрических
координатах.
') Долидзе Д. Е., ПММ, т. VIII, в. 3, 1954.
2) Nig am S. D., Quart. Journ. of Mech. and Appl. Math. IV, 9, 1 A951),
88—91.
3) T h 1 r i о t K. H., Zeitschr. f. Angew. Math. u. Mech. 20, 1 A940).
4) Розин Л. А., Изв. АН СССР (ОТН), № 4, серия механики и машино-
строения A.960).
§ 41] ДИСК, ПРИВОДИМЫЙ ВО ВРАЩЕНИЕ ИЗ СОСТОЯНИЯ ПОКОЯ
193
Граничные условия аналогичны F.2), с той лишь разницей, что <о
в данном случае зависит от времени. Кроме того, присоединяется
начальное условие, которое при приведении диска во вращение из
состояния покоя будет иметь вид
u=v = w = 0 при ^ = 0. F.51)
Будем искать решение в форме
u=:rF(z, t), •и = гФ(г, t), w = 2W(z, t), p = P(z,t)\ F.52)
тогда задача сведется к интегрированию системы уравнений в част-
ных производных
dt
дг
дг
1 dp
¦ 2? дг
дг
6.53)
при граничных и начальных условиях
F = Q, Ф==ш@, 47 = 0 при 2 = 0, t> 0,
/=" = 0, Ф = 0 при z = oo, t>0, F.54)
/=" = 0, Ф = 0, 4^ = 0 при ^ = 0.
В задаче об импульсивном приведении диска в равномерное вра-
щение с угловой скоростью <о0 можно положить
F(z, *) = u#/(t]), Ф{г, 0 =
W(z, t) = —
где введена новая независимая переменная
г
F.55)
F.56)
Тогда система уравнений F.53) сведется к следующей системе
Обыкновенных дифференциальных уравнений второго порядка
(штрих — производная по ~q):
F.57)
13 Зак. 297. Л. Г. Лойдянский
194
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[ГЛ. V
которую надо разрешить при граничных условиях
/ = 0, ср = 1, ф = 0 при т)= О,
/ = 0, ср = 0 при т)=оо.
F.58
Система F.57) может быть проинтегрирована в замкнутом вид^-
подобно тому, как это было уже сделано в задаче о приведение
в поступательное, прямолинейное и равномерное движение цилиндра
ческого тела (§ 24). Действительно, второе уравнение системы F.57
полностью совпадает с уравнением D.5), а первое отличается от D.10
только свободным членом. Результаты интегрирования показань
в форме графиков на рис. 46; аналитические выражения приведем
О
J.0 1,5
Рис. 46.
2,0
ниже для более общего случая. Интересен факт наличия конечной
значения ф, а следовательно, и нормальной к диску скорости npi
больших 7j и t > 0. Это соответствует известному уже нам по ста-
ционарному движению осевому подтеканию жидкости к диску и рас
теканию ее в направлении от оси диска к периферии.
Случай степенной зависимости угловой скорости вращения диск;,
от времени, ш —ш^", также приводится к квадратурам. Полагая npi
том же выражении F.56) для у\
F{z, *) = ' „
F.59
? (z, t) = — 4
Р (z, 0 = g
получим по F.53) следующую систему уравнений:
/" ¦+¦ 2т}/' _ 4 Bа + 1) / = — 4ср2,
ср" -j- 2т]ср' — 4аср = 0,
F.60
§ 41] ДИСК, ПРИВОДИМЫЙ ВО ВРАЩЕНИЕ ИЗ СОСТОЯНИЯ ПОКОЯ 195
с теми же граничными условиями F.58), что и в случае а = 0. Не-
трудно убедиться, что уравнения F.60) при <х = 0 переходят в F.57).
Обращаясь прежде всего к решению второго уравнения системы
F.60), совпадающего с D.39), найдем
ср (<q) = 22<T (a-f l)ga(yd> F.61)
где принято обозначение D.41) для 2а-кратного интеграла функ-
ции вероятности.
¦ Решение первого из уравнений F.60) после этого запишется
в форме
f XI /О I О\ -
rib+iW-tf. .1A) • F-62)
Из третьего уравнения системы F.60) найдем ф простой квадра-
турой, а затем по четвертому уравнению той же системы и распре-
деление давлений.
Столь же просто решается задача о развитии пограничного слоя
на начинающем вращаться из покоя шаре при степенном законе
возрастания его угловой скорости !). Случай внезапно приведенного
в равномерное вращение шара был ранее изучен Нигамом2).
По-видимому, впервые Ф. Мур 3) указал на принципиально иной
метод подхода к решению задач о пограничном слое на диске,
совершающем произвольное неравномерное вращение. В общем
случае вращения диска в безграничной области, заполненной несжи-
маемой вязкой жидкостью, решение уравнений Стокса может быть
представлено в форме разложений
и = га) [F (т,) + р^, (уд + hF2 (Уд +...].
w = по
р = р> [Р (гд + р,/>, ^ + №2 (Ч) +•••]•
где у; —2/(u)/v) \ а коэффициенты (Зг, равные последовательно (точка —
символ дифференцирования по времени)
') Р о з и н Л. А., цитированная выше статья.
2) Nlgam S. D., Zeitschr. f. Angew. Math. u. Phys. 4, № 3 A953),
стр. 221—223.
3) Цитируем по статье: Sparrow E. M., О г e g g J. L., Journ. Aero/Space
Sciences 27, № 4 A960), 252—256.
1.4*
196 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
представляют заданные функции от времени, определяющие характер
изменения угловой скорости ш диска со временем.
Подставляя предыдущие разложения в уравнения Стокса и при-
равнивая коэффициенты при (Зг, получим систему обыкновенных
уравнений относительно функций F, Fv F2 G, Gv G2 и т. д.,
причем функции F, G, Й, Р совпадают с ранее упомянутыми функ-
циями задачи Кармана—Кокрена. Последующие функции были вычи-
слены при помощи машин и приведены в форме графиков в цити-
рованной статье Спарроу и Грегга. Там же поставлен и разрешен
вопрос об условии, при выполнении которого нестационарное вра-
щение диска может рассматриваться как «квазистационарное», т. е.
в каждый данный момент времени как равномерное, но со своей
угловой скоростью <о(/), где t играет роль параметра. Это условие
с достаточным приближением может быть выражено в виде
ш/ш2< 0,0834.
§ 42. Пограничный слой на теле вращения, внезапно
приведенном в равномерное винтовое движение1)
Зададим уравнение поверхности тела вращения так, как это уже
делалось в § 30, при помощи уравнения меридионального контура
г о = г о (х)
и примем те же обозначения для координат и компонент скорости —
продольной и нормальной к поверхности тела. В данном случае име-
ется дополнительно азимутальная компонента скорости w. Уравнения
пограничного слоя будут иметь вид
dw . dw , dw . uw dr0 d2w
W^'u'dI~f'vW±W~d7~s)'W
d(rBu) , d(rov) _n
~~d~x ! W~~
F.63)
Член -5T- в правой части первого уравнения этой системы от-
сутствует, так как предполагается, что тело мгновенно приведено
в равномерное винтовое движение вдоль оси тела с постоянными
скоростью поступательного движения ?/<» и угловой скоростью вра-
щения (о0.
0 IJJingworth С, Phil. Mag. 45 A954), 360.
§ 42] ТЕЛО ВРАЩЕНИЯ, ВНЕЗАПНО ПРИВЕДЕННОЕ В ВИНТОВОЕ ДВИЖЕНИЕ 197
Пренебрегая в первом приближении конвективными членами,
придем к системе уравнений
ди,
IF
~дТ
ду* '
~dy*~'
F.64)
которую надо решить при граничных условиях
их = U (x), «^ = 0 при у = оо.
Решение это хорошо известно; оно представится в виде
и,= U (x) Erf ri,
F.65)
_ 1 и Г
V! = -2 Vvt-{--?-(r0U) /
Erf т dx.
<wx = шл0 erf 7j,
F.66)
где положено
} = -?=¦ fe-^'d-z, erf-n=-^ fe-t'dt.
Компоненты скорости во втором приближении положим равными
Wj-r-Mj, v1-\-v2, w1-\-w2. Тогда добавки и2, v2, w2 будут удовле-
творять системе уравнений
d2«o ди* ди.
ду2
дщ Щ dro dU
ду* dt ~~Ul дх
ду
F.67)
Интегрирование этой неоднородной системы при нулевых гранич-
ных условиях не представляет принципиальных трудностей, но гро-
моздко с вычислительной стороны. Приводим результаты
4.
w2 = t
dU
rQ -?¦ g3lH-
dro
dr0
g22)
F.68)
198 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
где введены следующие обозначения (<х= l/]Ar):
Лз = - A - 2«2) У + B - 2а2) А -
4 ,. /1 4 ,\ , ,
?21 = — -Ja2J— [-J — Т а )k+n>
у = 1 -J- 2т,2, к = A + 2тJ) Erf т) + т, (Erf т,)',
4- \ [(Erf 7,)']2+2Erf 7,-1,
» = (f + ^)ErF^ +1^)Erf 7) (Erf 7,)'4-4a (Erf 7,)'.
Мы не приводим выражения для v2, так как оно очень громоздко
и имеет значение лишь для получения третьего приближения, кото-
рое мы здесь не помещаем, отсылая интересующихся к цитированной
в начале параграфа статье, где это третье приближение вычислено.
Для продольной ix и поперечной хг компонент напряжения тре-
ния по поверхности тела вращения будем иметь с точностью до чле-
нов с t2 следующие выражения:
4-0,72676u>o/-o4§-]' — [0,05975?/2-^4- 0,219871/ (^-
4- 0,02876t/2 ?"L _L i?o _j_ 0,02005t/3 — -^f —
' dx r0 dx ' r0 dx2
-0.03154^^(^4-0,102869.^,^4-
4- 0,007592u)? Ur0 ^ 4- 0.220731 cejj tf (-^J-V] ^24- . .. 1,
t, == 0,56419 (^)'A {шого4- [0,1512«v0 ^ + 0,6977^-g-] / +
4- [0,040\%U -|^ r0 + 0,0716Шо(-^Jло+ 1,9568^-^g -
- О,О879шо<Я -04-1.6404^2.
4-0,01826^-g 4-0,16698u,^r0 (-^J]^24-...}.
42] ТЕЛО ВРАЩЕНИЯ. ВНЕЗАПНО ПРИВЕДЕННОЕ В ВИНТОВОЕ ДВИЖЕНИЕ 199
В частном случае сферы радиуса а получим
_3
2
U = -й- U«, sin ~, г0 — a sin ~,
: предыдущие формулы, если ввести еще для краткости обозначения
Uoot =? *У _-
перейдут в такие:
•,. = 0,84628 ("т^-O2 ^оо sin ji\ + [B,3634 + 0,48451^)cos-^J? —
— Г— @,17955 + 0.007592P) sin2 -^ +
. = 0,56419 ^Y/!uHasin-^|l + 1,2732 cos~
+ [@,1077 — 0,01826^) sin2 -^
В силу симметрии можно считать, что отрыв пограничного слоя
поверхности сферы происходит по окружности, на которой хх = 0.
Лтрыв в задней критической точке начнется в момент времени t = ts,
'довлетворяющий уравнению
^ = B,3634-|-0>48451р)
ч первом приближении и квадратному уравнению
@,48844 + 0,323601^) & + B,3634 + 0,484513)
;о втооом приближении.
Та б л и ц а 16
— 1 = 0
р
0
0,1
1,0
10
0,423
0,415
0,351
0,139
0,391
0,383
0,322
0,130
Из таблицы 16 можно заключить, что чем больше угловая ско-
чость вращения, тем ранее возникнет отрыв в задней критической
очке. Этот любопытный факт объясняется теми же причинами,
гто noni. n i/nutm
200 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
§ 43. Распространение закрученной струи в затопленном
пространстве *)
К области вопросов, затрагиваемых в настоящей главе, относятся
и движения жидкости в закрученных струях, бьющих из некоторого
источника в пространство, затопленное той же жидкостью.
Выбирая в системе цилиндрических координат ось струи за ось х
и обозначая через и, v, w соответственно осевую, радиальную и
азимутальную компоненты скоростей, получим уравнения распростра-
нения закрученной струи в виде
ди ди _ I др (д2и , j_ ди\ '
" дх ~T~V дг ~" дх +vUr2" г дг)'
др pw2
дг г '
\ F 69)
dw dw , vw / d2w 1 dw w\ v ' '
1 dw w\
r dr~r*)'
d
(ru) , d(rv) _
dx I W~~
В отличие от незакрученной струи (§ 37) в этих уравнениях по-
является еще азимутальная скорость w и сохранены величины
-rj— и -J--, так как благодаря центробежному эффекту внутри струи
образуется поперечный перепад давлений, а он в свою очередь вы-
зывает и продольный перепад. К граничным условиям незакрученной
струи E.87) присоединяются еще условия для азимутальной компо-
ненты w— мы будем в дальнейшем называть ее скоростью закрутки —
w — 0 при г —0, w = Q при г = со. F.70)
Условие наличия нетривиального решения этой задачи с нулевыми
граничными условиями можно получить, задавая импульс и момент
количества движения струи.
Выведем следующие два интегральные условия сохранения им-
пульса и момента.
Пользуясь уравнением неразрывности (последнее уравнение си-
стемы F.69)), перепишем первое уравнение той же системы в виде
Проинтегрировав его поперек струи от г = 0 до г=±оо, найдем
со
Lfr(p + г и*) dr -+- [г (puv-1» |?)]'" J = 0.
') Лойцинский Л. Г., ПММ, т. XVII, в. 1, 1953.
§ 43] РАСПРОСТРАНЕНИЕ ЗАКРУЧЕННОЙ СТРУИ 201
Примем, что
lim гиг> = 0, lim г-т- = 0 при х > О,
причем заметим, что правильность этих допущений может быть про-
верена впоследствии. Тогда из предыдущего равенства сразу следует
закон сохранения импульса, который запишем по аналогии со случаем
незакрученной струи так:
F.71)
Под величиной р в данном случае подразумевается разность да-
влений в данной точке струи и вне струи. При х->оо давление
в струе выравнивается и становится одинаковым с давлением в окру-
жающей струе жидкости; тогда JQ совпадает с константой незакру-
ченной струи.
Для вывода второго интегрального условия используем вновь
уравнение неразрывности и, умножая еще обе части третьего урав-
нения на г, перепишем его в форме
д (ruw) , д (rvw) , д Г 1 д
дх ' дг ~т~ дг L г дг
или, после повторного умножения на г, еще так:
-Jj {r4w) + -^ (r2vw) = w-^^r~(rw)j — 2v-^ (rw).
Тогда, интегрируя обе части этого равенства от г — 0 до г = со
и делая вновь предположения о достаточной быстроте убывания ком?
понент скорости и и w при бесконечном удалении от оси струи
(оправдать их можно по найденному решению), получим
dx
о
I r2uw dr = О,
откуда следует второе интегральное условие
2лр J r2uw dr = const = Lo, F.72j
202
ТРЕХМЕРНЫЕ ОСЕСИММЕТРНЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
где через LQ обозначается постоянный вдоль всей струи секундный
перенос сквозь сечение струи главного момента количества движений
жидкости относительно оси струи.
Итак, для получения нетривиального решения задачи о закручен-
ной струе необходимо задать по крайней мере две характерные кон-
станты струи: ее импульс и момент количества движения. Задача не
будет автомодельной, так как наличие двух констант Lo и Уо с отно-
шением, имеющим размерность длины, уже служит препятствием этому.
Следуя тому же приему, что и в случае незакрученной струи,
введем функцию тока ф(х, г) для движения в меридиональной пло-
скости и будем искать ее в виде асимптотического разложения при
больших значениях х,
F.73)
где а, а0, av .. . — неизвестные функции той же самой коорди-
наты т), что и в § 37. Скорость закрутки w и давление р, отсчи-
тываемое от давления вдалеке от струи, зададим также асимптоти-
ческими разложениями
w~-^- + A- + .... F.74)
р
F.75)
где bv b2, .... cv c2, ... суть неизвестные функции tj.
Вычисляя компоненты скорости течения в меридиональной пло-
скости (штрих —• производная по г\)
— г дг— 1) " л: 1 1) ¦
1 д<\> /7 Г- а
F.76)
и подставляя принятые разложения в систему уравнений F.69), путем
приравнивания коэффициентов при одинаковых степенях х получим
уравнения для определения искомых функций.
Так, из первого уравнения системы F.69) будем иметь
Cl+TiC; = o. 1
(а'Л" 1 + а ( а0У За' ао , Ч/
-+- "пс, = О,
F.77)
§ 43] РАСПРОСТРАНЕНИЕ ЗАКРУЧЕННОЙ СТРУИ
Точно так же из второго получим
203
s, F.78)
а из третьего —
1 +а ., 1— а
F.79)
Наконец, интегральные условия F.71) и F.72) приведут к системе
равенств
7
J
F.80)
¦ца bx dt\ = О,
о о
Считая ось струи нулевой линией тока и используя условие ко-
нечности скоростей на оси струи и ограниченности расхода сквозь
сечение струи, получим следующие граничные условия для функций
а, а0, ...:
а = а0 = flj = ... = 0, )
_ \ при т] = О,
а, а0, й]
ограничены при
F.81)
По определению скорости закрутки придем к соответствующим
граничным условиям
Ьх = Ь2 = ... =0 при т) = О,
&j = ?2= ... =0 при т; = со,
и, наконец, по принятому отсчету давлений
Сх = С2 = С3 = . . . = 0 при 7J = ОО.
F.82)
F.83)
204 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
Из пятого условия системы F.80) и первого уравнения си-
стемы F.79) можно заключить, что ^ = 0 удовлетворяет условиям
задачи. Но тогда по F.78) и F.83) следует
<?i = с2 = с3 == 0.
При этом функции а (¦/;) и ао(т)) будут удовлетворять тем же
уравнениям E.99) и граничным условиям E.100), что и в случае
незакрученной струи, и соответственно определятся равенствами E.92)
и E.106). Довольствуясь в разложениях для скоростей членами,
содержащими 1/х2, приходим к необходимости определить лишь еще
одну функцию b2(fj), характеризующую первый член в разложении
скорости закрутки w. Представив с этой целью второе уравнение
системы F.79) в виде
получим, используя граничные условия F.82),
¦ф'2 = {\ — а)Ь2,
откуда следует
ад = Тт г-^г
Напомним, что здесь постоянная а имеет то же значение, что
и в случае незакрученной струи (§ 37), а постоянная f должна быть
определена из шестого интегрального условия системы F.80), пере-
писываемого в виде
/
F.85)
Выполнив указанное здесь интегрирование, найдем
_Ш.ЬП^. F.86)
Давление определится асимптотическим равенством F.75) с пер-
вым, не равным нулю коэффициентом
§43]
РАСПРОСТРАНЕНИЕ ЗАКРУЧЕННОЙ СТРУИ
205
Собирая полученные результаты, придем к следующему оконча-
тельному решению поставленной задачи:
2аа
л , i 2
V ^ 4
= 7
. (i+j«vJ *
1
2_
3
1
У ~ZT > "max
_ 2а* 1
6.88)
В принятом приближении движение в меридиональных плоскостях
с компонентами скоростей и, v оказывается независимым от наличия
закрутки, влияние которой на продольное и поперечное течение
сказывается только начиная с третьего приближения (члены с 1/х3).
Третье приближение в рассматриваемой задаче было изучено В. С. Дубо-
вым х). Задачу о закрученной струе в общей постановке (для любых
рейнольдсовых чисел) рассмотрел М. С. Цуккер 2).
Отметим важный с качественной стороны результат: продольная
и поперечная скорости в закрученной струе убывают по законам,
в которых первые члены имеют порядок 1/х, скорость же закрутки
по закону Ijx2. Это означает, что в достаточном удалении от источ-
ника струи, где только, собственно говоря, и верно предлагаемое
асимптотическое решение, скорость закрутки убывает значительно
быстрее, чем продольная скорость. Рассмотренное решение пред-
полагает, что начальная закрутка струи достаточно мала, чтобы
в центре струи не образовывалось попятного движения. Такого рода
явление аналогично отрыву пограничного слоя с поверхности тела
в области положительной производной dp/dx. В сильно закрученных
струях отрицательное (при отсчете от внешнего) давление возрастает
') Дубов В. С, Труды ЛПИ, № 176 (Энергомашиностроение), 1955.
*) Цуккер М. С, ПММ, т. XIX, в 4, 1955.
206
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[ГЛ. VI
вниз по потоку, т. е. в этом случае также имеет место положи-
тельность dp/dx, что вызывает подтормаживание жидкости вблизи
оси струи и может привести к образованию обратного тока. Начало
области попятного движения будет характеризоваться условием и = О
при т] = 0. Для решения задач о сильно закрученных струях с по-
пятным движением необходимо определить поля скоростей при ма-
лых, а нечпри больших л:, как это сделано в вышеизложенном асимп-
тотическом решении.
Распространение закрученной струи в однородном спутном по-
токе было исследовано О. Н. Бушмариным 1), который выявил отли-
чия такого рода течения от закрученной струи в покоящейся жидкости.
§ 44. Радиально-щелевая закрученная струя
в затопленном пространстве
Рассмотрим пространственную осесимметричную струю, вытекаю-
щую из круговой щели во внешнее пространство; физические свойства
жидкости в пространстве и в
струе предполагаются одинако-
выми. Такого рода струя может,
например, образоваться при вы-
ходе жидкости из тарельчатого
клапана (рис. 47), если ее пред-
варительно закрутить вокруг оси
симметрии клапана.
Вводя радиальную, попереч-
ную и азимутальную компоненты
скорости и, v, w и пользуясь
в качестве цилиндрических ко-
ординат величинами х = ОМ = г,
у и ср (последняя координата в
силу симметрии нигде не фигу-
рирует), запишем сначала урав-
нения стационарного движения
виде:
/ д2и ,J_du и_. д2и\
Рис. 47.
жидкости в струе в общем
ди ди да' 1 др
дх ду х о дх
dv
dy
ix*
T~дх + dp/'
dw , dw . uw I дгур . _1_ dw w _. d2w\
U!te^Vl)y^~~W\lb?~f'TlJ7~~xT^~l)yT)'
д(хи)
дх
d(xv)
ду
= 0.
F.89)
') БушыаринО. Н., Труды ЛПИ, № 176 (Энергомашиностроение), 1955.
§ 44] РАДИАЛЬНО-ЩЕЛЕВАЯ ЗАКРУЧЕННАЯ СТРУЯ 207
При больших значениях рейнольдсова числа пограничный слой
струи будет тонок в направлении оси у, скорости v будут малы по
сравнению с и и w, и, наоборот, производные по у будут велики
по сравнению с радиальными производными. Из второго уравнения
следует, что др/ду имеет тот же порядок малости, что v; это
позволяет пренебречь изменением давления поперек слоя, а следова-
тельно, поскольку вне слоя давление всюду одинаково, и радиаль-
ной производной давления в первом уравнении системы. Выполняя
все указанные пренебрежения, приведем общую систему F.89) к сле-
дующим уравнениям пограничного слоя струи:
ди . ди w2 д2и
U —I— V -г = V
/?*¦ I Аи у
дх ^ " ду х — ду* '
dw . dw . uw d2w
д (xu) , д (xv)
F.90)
Полученная нелинейная система дифференциальных уравнений
в частных производных должна быть разрешена при граничных
условиях
ди п „ dw n n \
^— = 0, г> = 0, -г— = 0 при у = 0,
дУ дУ \ F.91)
й = 0, |К»=:0 При у—±ОО. J
Что касается начальных условий выхода струи из радиальной
щели, то они для упрощения анализа заменяются более простым
требованием удовлетворения некоторым интегральным условиям,
выражающим индивидуальные особенности рассматриваемой струи.
Чтобы получить такого рода интегральные условия, установим две
«формулы сохранения». С этой целью, пользуясь последним уравне-
нием системы F.90), перепишем первое уравнение той же системы
после умножения обеих его частей на л: в виде
д , ,, , д . . ,
Интегрируя обе части этого уравнения поперек пограничного
слоя от у = — оо до у —со и предполагая, что при выполнении
принятых граничных условий F.91) на внешней границе слоя обра-
щается в нуль и первая производная ди/ду, получим, допуская суще-
ствование нижестоящих интегралов, следующее интегральное условие:
оо оо
-jj f' xu*dy= f w2 dy. F.92)
208 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
Это равенство выражает собой теорему об изменении количества
движения в проекции на радиальное направление, примененную к эле-
ментарному объему струи в цилиндрических координатах.
Аналогичным образом, умножая обе части второго уравнения
системы F.90) на х2, получим, в силу последнего уравнения,
д / 9 \ i d / 9 \ д2 (x2w)
-з— (xzuw) -4- -д— (xlvw) — v —\ , ',
дх х ' ' ду v ' ду2
отсюда после интегрирования поперек слоя и учета граничных усло-
вий будет следовать, что
СО
-г- I x2uw dy = 0.
— со
Из полученного равенства вытекает независимость интеграла
от х, что приводит к формуле сохранения момента количества дви-
жения L в радиально-щелевой струе
со
Г uwdy — const == Lo. F.93)
— оо
Введем опять функцию тока меридионального течения (в пло-
скости, проходящей через ось Оу симметрии струи) <j>(je, у), кото-
рая по последнему уравнению системы F.90) связана со скоро-
стями и, v соотношениями
e = i~*fc., v = i-Д. F.94)
х ду х дх
Будем искать ф в виде ряда
^ ) F.95)
где а, а0, ах ... — неизвестные функции переменной
т) = —L F.96)
х\ ч
Проекции скорости и и v представятся асимптотическими рядами
(штрих — производная по rj)
—/
a
— a
F.97)
§44]
РАДИАЛЬНО-ЩЕЛЕВАЯ ЗАКРУЧЕННАЯ СТРУЯ
209
Азимутальную скорость (скорость закрутки) зададим асимптоти-
ческим разложением
Подстановка в F.90) и приравнивание коэффициентов при одина-
ковых степенях х приводит к следующей системе уравнений:
F.99)
b\ -\- ~ab\ — Q,
которую надо проинтегрировать при граничных условиях
а = ео = с" = ао = О, Ь[ = Ь'2 = О при tj = 0,
а' = ац = 0, dj = й2 = 0 при tj = co,
F.100)
к которым еще присоединяются интегральные условия F.92) и F.93).
Из этих условий путем приравнивания коэффициентов при одина-
ковых степенях х получим
— со
со
2rcp/v '
F.101)
Введем еще обозначение для постоянной
a' a-nz=.
п?f v '
F.102)
величина Уо имеет смысл радиального импульса на бесконечном
удалении от источника струи
:= Hm 2r,px Г и2 dy.
Х-Ь со "
А. Ълк 9Q7 Л Г Лпйттянгкий
210 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
Из первого интегрального условия системы F.101) следует, что
Довольствуясь первыми членами разложений и и w, придем
к необходимости решить однородную систему уравнений
a'" + aa" + «'2 = 0, ]
} F. ЮЗ)
при нулевых граничных условиях F.100), но при следующих двух
интегральных условия^, делающих задачу не тривиальной,
Решение системы F.103) не составляет труда. Интегрируя один раз
первое уравнение, найдем
или, в силу граничных условий F.100),
Повторное интегрирование дает
Замечая, что с = 0 при т] = 0и что (а'I=0 = (лиO)=0 > 0-, поло-
жим С2 = (а') с0 = у а<2'> тогда предыдущее уравнение примет вид
a'=y(a2 — с2) F.105)
и будет иметь интеграл
(V F.106)
Для определения постоянной интегрирования а применим первое
из интегральных условий F.104). Получим
^Ц ^ ^, F.107)
откуда найдем
a = лГ ^° . F.108)
' 4 у v
§44]
раДиаЛьно-щелевая закрученная струя
211
Обращаясь ко второму уравнению системы F.103), непосред-
ственным интегрированием получим
Но в силу граничных условий а = 0 и Ь2 = 0 при т) = 0; следова-
тельно, С3 —0. Повторное интегрирование дает
I л I
Ь2 = С4 ехр — | a dr\ I.
Вычисляя интеграл, согласно F.106) получим
&,=¦
ch2 4
Постоянную интегрирования С4 определим из второго интеграль-
ного условия F.104). Вычисления, аналогичные предыдущим, дают
так что окончательно получим
F.109)
В рассматриваемом приближении поле скоростей радиально-щеле-
вой ламинарной струи будет определяться системой равенств
и =
1
2x
а/ч ат) — sh
~2x
ch2U-ai
W=-rr
ch2 4-
F.110)
Радиальная и и азимутальная w скорости достигают своих макси-
мальных значений в плоскости симметрии струи, причем первая
убывает с удалением от источника обратно пропорционально рас-
стоянию, а вторая — обратно пропорционально квадрату расстояния.
14*
212 ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. VI
Секундный расход жидкости сквозь полное сечение струи опреде-
ляется по формуле
со со
Q — 2кх С udy = 2кх }/~^ С а' d-ц =
— с —со
= 2тг -\П,Х [а (оо) — ~а (— оо)] = х ^48u2vi0/p.
Рассмотренное решение соответствует нулевому расходу жидкости
из источника. Пользуясь следующими приближениями, можно было бы
получить радиально-щелевую струю с заданным конечным расходом
из щели.
При L0 = 0, <а>==0 получим решение частной задачи о незакру-
ченной радиально-щелевой струе. В этом случае интегральное усло-
вие F.92) сводится к условию сохранения радиального импульса Уо.
§ 45. Гидродинамическая модель вихревой форсунки
Как показал Тэйлор '), принципиальная схема движения жидкости
в вихревой форсунке заключается в образовании вторичных течений
в пограничном слое внутри конуса, по оси которого расположена
Рис. 48.
вихревая нить, создающая вне пограничного слоя вращательное дви-
жение с заданной циркуляцией.
Представим себе внутренность конуса с углом раствора 2а (рис. 48),
по оси которого расположен вихрь с циркуляцией Г, так что ази-
мутальная скорость вне пограничного слоя будет равна
') Taylor О. J., Quart. Journ. of Mech. and Appl. Math. 3 A950), 129—139.
§ 45] ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ ВИХРЕВОЙ ФОРСУНКИ 213
а продольная и нормальная к поверхности составляющие скорости
отсутствуют: U = Q, V = 0. Давление вне, а следовательно, и внутри
слоя будет определяться равенством
oW2 рГ2 рГ2
р = const —V = const —fe» = const - 8д2^2 s.n2 6 , F.112)
sin2 6
т. е. будет возрастать от вершины конуса в сторону его раскрытия.
Наличие такого перепада давления, тем более значительного, чем
больше циркуляция Г, вызовет внутри пограничного слоя, где ази-
мутальные скорости резко уменьшаются при приближении к поверх-
ности конуса, спиралевидное вторичное течение, направленное к вер-
шине конуса. Если в вершине конуса сделать отверстие, то этот
поток и будет тем потоком, который осуществляет выбрасывание и
распыление топлива в вихревой форсунке.
Используя сферические координаты, составим приближенные урав-
нения пограничного слоя внутри конуса в форме 1)
да . v да w2 1 dp . v д2и \
11 dR ' ~R~~dl R~ ~ ~~ У dR ' Ж ^§2 •
dw . v dw , wu v
U dR ~i~R ~dT'~R~ ~~Ri
da , 2a 1 dv -
dR "+" "^~ "+" ~R Ж
Первое из этих уравнений благодаря наличию F.112) может
быть переписано еще так:
п да v да Г2 в>» v ^a f6H4
dR ^ R дЬ ^ 4тг2/?з sin2 e R — -цг дЬ2 ¦ @-1IV
С целью дальнейшего применения метода Кармана — Польгаузена
установим граничные условия, характеризующие выбор приближен-
ных семейств профилей скоростей и и w в сечениях слоя. На поверх-
ности конуса @ = а) эти условия будут иметь вид
причем поясним, что последние два условия вытекают из уравне-
ний F.114) и второго уравнения системы F.113).
Пусть граница пограничного слоя для распределения скоростей и
будет отлична от соответствующей границы для распределения w.
') Со оке J. С, Journ. Aeron. Sci. 19, № 7 A952), 486—490.
214
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЁ ПОГРАНИЧНЫЕ СЛОИ
[ГЛ. V!
Толщину пограничного слоя для продольной компоненты обозначим
через 8, а для азимутальной компоненты — через Д. Тогда будем
иметь следующие условия на внешних границах пограничных слоев:
.-0. ^ =
Г
w
dw
при б = а — b/R,
Д
F.116)
Профили скоростей в сечениях пограничного слоя, удовлетворяю-
щие условиям F.115) и F.116), зададим в приближенной полино-
миальной форме
Г25'
Г252
" ~ 2*R sin a
где приняты обозначения для безразмерных аргументов
Введем вместо S и Д две новые неизвестные функции
F.117)
F.118)
а вместо аргумента R — безразмерную величину
где под L подразумевается длина образующей конуса.
Будем предполагать, что Д < 8, т. е. К < 1, и что величина g
в интервале 1 > т\ > К равна единице. Тогда, интегрируя уравне-
ния F.114) и второе уравнение системы F.113) поперек слоя по ¦»)
от т| = 0 до т)=1, получим следующие аналоги уравнений импуль-
сов (штрих — производная по С):
к
L
F.120)
§ 45] ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ ВИХРЕВОЙ ФОРСУНКИ 215
В этих уравнениях приняты сокращенные обозначения
а =1/1680, b =1/3360, с= 18АГ/35,
<* = -, = 1/48. b = -i(-w-w
причем, согласно F.117),
Уравнения F.120) могут быть упрощены, если ввести еще допол-
нительное преобразование, положив
Тогда система F.120) сведется окончательно к такой:
У' = (<х — p/Q/C; а = 336, р = 691,2;
_ ю 080 —
К' = -
120UB
F.121)
А = (9К2 — 35/С + 42) К3, В = A1К2 — Ъ5К + 28) К2,
причем начальные значения У и К при С=1 равны
/0 = 0, Ко = 0,87933, Ко = — 0,06824,
как это показывает обычное для теории Кармана — Польгаузена
исследование поведения интегральных кривых вблизи особой точки.
Уравнения F.121) были решены численным методом Куком в ци-
тированной ранее его работе. Результаты приведены в таблице 17.
Кроме выше введенных функций J и К, в таблицу включены: харак-
теризующая толщину пограничного слоя 8 ве'личина §j, равная
и угол х между силой трения на поверхности конуса и его обра-
зующей.
Анализ полученного решения раскрывает ряд интересных как
с физической, стороны, так и с точки зрения общих положений тео-
рии пограничного слоя фактов.
Прежде всего из F.117) следует вывод об образовании весьма
интенсивного вторичного течения в пограничном слое вдоль обра-
зующей конуса, направленного к его вершине. Максимальная ско-
рость этого потока, имеющая место при ti = 43, пропорциональна
квадрату циркуляции и обратно пропорциональна кубу расстояния
сечения от вершины конуса. Азимутальная составляющая при этом
216
ТРЕХМЕРНЫЕ ОСЕСИММЕТРИЧНЫЕ ПОГРАНИЧНЫЕ СЛОИ
[ГЛ V
пропорциональна первой степени циркуляции и обратно пропорцио-
нальна первой степени расстояния до вершины.
Таблица Г
Y
J
К
»i
1
г
J
К
»|
1
1,0
0
0,879
0
90°
0,50
199
0,924
1,88
24°,8
0,95
14,44
0,883
1,85
60°,8
0,40
267
0,940
1,62
2Г,3
0,90
28,9
0,886
2,09
5Г,6
0,35
309
0,949
1,47
19°,8
0,80
62,7
0,893
2,25
40°,5
0,30
359
0,962
1,31
18°,2
0,70
100
0,902
2,22
34°,1
0,25
421
0,975
1,13
16°,7
0,60
144
0,912
2,08
28°,7
0,20
497
0,994
0,94
15°,2
Вторым интересным фактом является поведение толщины погра-
ничного слоя о и связанной с нею при помощи множителя К тол-
щины Д. Как видно из таблицы, толщина слоя сначала возрастав"
от нулевого значения на входе (при С= 1) до некоторого максимума
примерно при /? = 0,8Z,, а затем убывает. При таком убывании тол
щины пограничного слоя, характерного для сильно конфузорных те
чений (см. § 11, формулы B.23) при т > 1), жидкость, вместо топ
чтобы поступать в пограничный слой сквозь его внешнюю границ}
начинает, наоборот, выходить из него во внешнюю область. Такое
явление иногда называют «прорывом» пограничного слоя.
Чтобы рассмотреть детальнее поведение толщины пограничной
слоя вблизи входа в коническое сопло, т. е. вблизи точки /?=== х = *.
или С=Ь заметим, что фукция J хорошо аппроксимируется равен
ством
У =2,722A — С'/1A)С'/8.
Вспомним, что, согласно определению J и первому из равенст!
F.119), будет (^ — знак пропорциональности)
§ 45] ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ ВИХРЕВОЙ ФОРСУНКИ 217
Тогда, вводя вместо С дополняющую ее до единицы величину ; = 1 - С,
найдем при малых \
8 « iu.
Закон этот резко отличается от закона Ъ-^\'\ характерного для
продольного ламинарного обтекания пластинки или полого цилиндра.
Как заметил в своем, ранее уже нами цитированном обзоре Ф. Мур,
закон «одной четверти» приближает разбираемое сейчас явление
к свободной тепловой конвекции на нагретой вертикальной пластинке,
помещенной в неподвижную жидкость. В случае вихревой форсунки
продольный перепад давления образуется за счет центробежных сил,
а в случае нагретой пластинки — за счет архимедовой силы. И в том
и другом случае поток образуется только внутри пограничного слоя.
Что касается поведения пограничного слоя вблизи вершины конуса
(при малых С), то этот вопрос остается'открытым. Вопрос о харак-
тере особенности в точке С = 0 пока еще неясен.
Задача о вихревой форсунке при образовании в ней как лами-
нарного, так и турбулентного слоя, была позднее вновь рассмотрена
Вебером '). Для решения этих задач Вебер, так же как и Кук, поль-
зовался методом слоя конечной толщины. Составив уравнения коли-
честв движения и моментов количеств движения, автор использовал
двухпараметрические семейства профилей скорости: многочленные
для ламинарного и степенные для турбулентного пограничных слрев.
В качестве формпараметров им использовались безразмерная толщина
пограничного слоя и отношение касательных напряжений на поверх-
ности конуса. Решение полученной системы обыкновенных нелиней-
ных дифференциальных уравнений пришлось искать также численным
методом. Полученное решение сравнивалось с опытными материалами,
и была обнаружена хорошая сходимость.
При 8 = у задача о форсунке переходит в задачу о погранич-
ном слое на поверхности земли вблизи оси «смерча», перпендику-
лярного к этой оси.
') Weber H. E., Paper Amer. Soc. Mech. Engrs, APM-31, 1956, стр. !— 6.
ГЛАВА VII
НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО
ПОГРАНИЧНОГО СЛОЯ
§ 46. Пространственный пограничный слой
на скользящем крыле
Задача о стационарном пограничном слое на цилиндрическом теле
бесконечного размаха в косо набегающем на него однородном потоке
представляет самую простую из задач теории пространственного по-
граничного слоя. Легко видеть, что ее решение сводится к некото-
рому дополнению известного уже по первым главам решения плоской
задачи для того же цилиндра в перпендикулярном к его оси потоке.
Пренебрегая, как и ранее, ролью кривизны поверхности цилин-
дрического те-ла (крыла) и выбирая оси координат согласно рис. 49,
придем к следующей общей системе уравнений трехмерного стацио-,
нарного пограничного слоя:
да . du . да 1 dp . d2a
d2w G-1)
dw . dw . dw 1 dp . dH
dx ' dy dz ~~~ p dz ~* dy-
du , dv , dw „
с граничными условиями
u = v = w = 0 при у = 0,
u->U, w^>W при з>->эс (
Ё первых двух уравнениях системы G.1) предполагается, что давле-
ние может быть исключено при помощи уравнения Бернулли для
внешнего потока
p + ip(t/2-(-r2) = const. G.3)
Задача о косом обтекании цилиндрического крыла бесконечного
размаха облегчается тем, что в этом случае движение перестает за-
§ 46] ПРОСТРАНСТВЕННЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА СКОЛЬЗЯЩЕМ КРЫЛЕ 219
висеть от трансверсальной (направленной по размаху крыла) коорди-
наты z. Тогда уравнения движения будут иметь вид
да
U дх +'
dw ,
da
ду
dw
~ду-
dv_
ду
dU
"by-'
д2и
G.4)
— -4-—— О
л- ^~ ду ~
при граничных условиях
и
и
U(х),
w
при у = 0,
- W&, = const
при у—>оо.
G.5)
Здесь U(х) определяется обтеканием крыла в плоскости, перпенди-
кулярной к его оси, a Woo представляет собой трансверсальную ком-
поненту скорости набегающего
потока.
Система G.4) с граничными
условиями G.5) в этом случае
распадается на две автономные
системы: первое и третье уравне-
ния соответствуют известной пло-
ской задаче обтекания крыла,
а второе уравнение служит для
последующего определения рас-
пределения трансверсальных ско-
ростей w в пограничном слое.
Задача в такой постановке
была разрешена у нас в Союзе
В. В. Струминским '), а затем за
рубежом Сирсом 2). Следует заме-
тить, что при наличии указанной автономности рассматриваемая за-
дача с математической стороны ничем не отличается от задачи об
определении температуры в плоском неизотермическом пограничном
слое при числе Прандтля, равном единице, и при условии пренебре-
Рис. 49.
') С т р у м и н с к и й В. В., ДАН СССР 54, № 7 A946), 57S—578; см.
также «Сборник теоретических работ по аэродинамике», ЦАГИ, Госизобпром,
1957, стр. 175-188.
2) S e a r s W. R., Journ. Aeron. Scl. 15, № 1 A948), 49; в неоднократно
цитированной нами монографии Г. Шлихтинга «Теория пограничного слоя»
имеется указание на относящуюся к 1945 г. неопубликованную рукопись
Г. Шубарта, в которой та же задача была решена по Блазиусу при заданном
разложении в степенной ряд функции U (х).
220 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [гл. VII
жения тепловой диссипацией механической энергии. Эта задача была
поставлена и решена значительно раньше, чем в цитированных выше
работах (для пластинки — Э. Польгаузеном в 1921 г., для цилиндри-
ческого тела — Н. Фрёсслингом в 1940 г.); к этому вопросу мы вер-
немся в дальнейшем. Точное решение задачи о косом обтекании
цилиндра при степенном задании продольной скорости внешнего по-
тока (случай Фокнера — Скэн, см. § 11) было дано Куком1).
В. В. Струминский привел во второй из выше цитированных ра-
бот приближенное решение задачи о пограничном слое на косо обте-
каемом цилиндрическом крыле, основанное на использовании для
плоского течения однопараметрического метода, изложенного в §§ 19
и 20. Аналогичная с математической стороны, но несколько более
общая тепловая задача была тем же методом решена М. Б. Скопец 2).
Многие авторы применяли обычный метод Польгаузена (В. В. Стру-
минский, Уайльд 3) и др.).
Укажем вначале, что поставленная задача в случае косого обте-
кания пластинки (U = const = U,x, W = const = Wm) имеет очевидное
решение
где и (х, у) — решение плоской задачи, например известное решение
Блазиуса. Таково продольное, косое обтекание пластинки потоком,
направленным под углом (90° — fco) к ее передней кромке. Равен-
ство G.6) означает, что в этом частном случае в любой точке по-
граничного слоя результирующая скорость.в плоскости, параллельной
поверхности пластинки, совпадает по направлению с результирующей
во внешнем потоке и, следовательно, «вторичные течения» отсут-
ствуют. Косое обтекание пластинки потоком, параллельным ее пло-
скости, не влияет на развитие пограничного слоя.
В случае косого обтекания симметричного цилиндрического теля
[U — U(x), W = const = "/со] положим
G.7)
') Cooke J. С, Proc. Cambr. Phil. Soc. 46 A950), 645—648.
2) Скопец М. Б., ЖТФ 23, в. 1 A953), 76—92.
3) W i 1 d J. M., Journ. Aeron. Sci. 16, 1 A949), 41—45.
46] ПРОСТРАНСТВЕННЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА СКОЛЬЗЯЩЕМ КРЫЛЕ 221
Тогда функции /((т)) будут определяться так, как это сделано
§ 13. Для определения функций g^-q) будем иметь уравнения
G.9)
фи граничных условиях
«o = ft= ••• =° ПРИ "П = 0'
go-+l, g2~>0 при т)->оо
Первое из уравнений G.8) непосредственно интегрируется и дает
Ti /^ \ / °° / *i \
go(rj) = I exp I — I /j^t; I drjl I exp I — I f^dt\ I й?т;. G.10)
о »o / / о » о /
Значения функций ?„(¦»)) и ^q(t)) приводятся в таблице 18 J).
Таблица 18
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
<7о (ri)
0
0,0570
0,1140
0,1709
0,2275
0,2836
0,3389
0,3932
0,4461
0,4975
0,5469
0,5941
0,6388
0,6808
0,7200
0,7561
0,7892
0,8192
0,5705
0,5703
0,5695
0,5675
0,5636
0,5574
0,5486
0,5369
0,5221
0,5042
0,4835
0,4600
0,4340
0,4061
0,3767
0,3463
0,3154
0,2847
•1
1,8
1,9
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3.8
4,0
4,2
4,4
4,6
4,8
5,0
goft)
0,8461
0,8702
0,8913
0,9257
0,9508
0,9686
0,9807
0,9885
0,9934
0,9963
0,9980
0,9990
0,9995
0,9997
0,9999
0,9999
0,9999
1,0000
0,2544
. 0,2253
0,1975
0,1475
0,1059
0,0731
0,0485
0,0309
0,0190
0,0111
0,0063
0,0034
0,0018
0,0009
0,0005
0,0002
0,0001
0,0000
Направление линий тока внутри пограничного слоя можно опре-
делить углом т между касательными к линии тока и криволинейной
кью Ох, равным
т = arctg —-
G.11)
') Шлихтинг Г., Теория пограничного слоя, ИЛ, 1956, стр. 186.
222 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
и представляющим собой функцию координат л: и у. Согласно G.7),
этот угол будет равен
— arctg
G.12)
Значение -J на стенке (i\=0 = Tf0 дает возможность построить
«предельную» линию тока на поверхности крыла. Сравнивая распо-
ложение «предельных» линий тока с линиями тока внешнего потока,
можем судить о наличии «вторичных течений» в пограничном слое.
Так, полагая в предыдущих формулах и1 > 0, и$ — и5— .. . =0,
получим течение вблизи критической линии, для которого будет
Используя значения g'Q @) = 0,5705 по таблице 18 и /1@)= 1,2326
по таблице 4 при /и=1, получим
То - arctg@.463 |^arcctgB,160 ??),
в то время как угол, образованный «внешней» линией тока -\е, будет
равен
Сравнивая эти выражения, видим, что угол «предельной» линии
тока с осью Ох уменьшается быстрее, чем угол внешней линии тока
с той же осью.
Уравнение «предельной» линии тока будет
4?°. = tg-ro = 0,463 — ,
dx lu U{X
в то время как для «внешней» линии тока имеем
dx 6 •*"" щх
Лобовая критическая точка (х = 0) является особой точкой. Инте-
гральные кривые ведут себя, как логарифмические:
z0 = 0,463 ~- \nx-\- const,
Woo .
ze = In jc -f- const.
§ 46] ПРОСТРАНСТВЕННЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА СКОЛЬЗЯЩЕМ КРЫЛЕ 223
Более общий случай, соответствующий заданию U (х) в форме B.50)
§ 14 был изучен Гёртлером'). Далее (§ 56) в связи с рассмотрением
эквивалентной с математической стороны задачи о температурном
пограничном слое при числе Прандтля, равном единице, мы еще вер-
немся к этому случаю.
Обратимся к приближенным методам, основанным на использова-
нии интегральных условий импульсов.
В силу автономности продольного движения в пограничном слое
на крыле [первое и третье уравнения в системе G.4)] будем иметь,
как и в случае плоского движения,
)И?)и <7ЛЗ)
здесь 8* и 8** — обычные толщины вытеснения и потери импульса
для продольного плоского движения.
Преобразуя аналогичным путем второе уравнение той же системы,
в общем случае W — W (х) получим
откуда, интегрируя поперек слоя по у от у = 0 до у = оо, ow,
где bw — толщина пограничного слоя при изменении w от нуля
до W (х), получим
bw Jr~JfL = -rjw[-^-\ n, G.14)
где положено
о
Примем, согласно общей идее одно- или двухпараметрического
метода,
/)¦ -j?- = <Ky/C; /Л
Вводя формпараметры / и fw, как взятые с обратным знаком
величины вторых производных от безразмерных скоростей по без-
размерным координатам на поверхности крыла
. Г дЦи/U) I _ Г 0» (w/W) I
7 Ld<y/»")*W Iw~~ H(y/CJJy=0'
и пользуясь дифференциальными уравнениями G.4), получим
у^?Т1 f _0
') О a 111 е г Н., Journ. of Math. Mech. 6, № 1 A957), 1—66.
224 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ (ГЛ. VII
Замечая, что при U' — O, т. е. при / = 0, будет выполняться
равенство
или
олучим для первых производных
y=o
y-o
G.16)
Таким образом, задача может решаться однопараметрическим
методом с тем же формпараметром /, что и в случае плоского дви-
жения.
Преобразуя уравнения G.13) и G.14), получим систему двух
уравнений
U
U
G.17)
где F {/) и С@) имеют те же значения, что и в главе III,
a zw = ow /v.
Вопрос об интегрировании первого из уравнений системы G.17)
уже был во всех подробностях разобран в главе III. Второе урав-
нение этой системы интегрируется непосредственно и дает
G.18)
Остальное зависит от выбора семейств профилей скорости в сече-
ниях пограничного слоя в соответствующей плоской задаче.
Системе G.17) можно было бы придать более симметричный вид,
вводя вместо zw величину, аналогичную по структуре параметру /:
— и'ъ**2
fw=U'zw = —^-. G,19)
Тогда получим
где положено
Г —MLp (Тлл-ML 7
= 2[;tO) —/j.
G.20)
G.21)
§ 46] ПРОСТРАНСТВЕННЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА СКОЛЬЗЯЩЕМ КРЫЛЕ 225
Решением второго уравнения системы G.20) служит выражение
- 2Ц0)Ц'(х) f U(i)(P G22)
Близким к предыдущему является метод Ротта и Крабтри'). При-
нимая для плоского поперечного обтекания круглого цилиндра экспе-
риментальное распределение давления по Хименцу (см. § 13), эти
авторы определили взаимное расположение предельных и «внешних»
линий тока в случае косого обтекания цилиндра под углом 45°; это
расположение показано на рис. 50.
Авторы привели фотографию «пре-
дельных» линий тока, сделанных
видимыми при помощи покрытия
поверхности цилиндра раствором
сажи в керосине. Совпадение тео-
ретических и экспериментальных
линий можно признать вполне
удовлетворительным. Непосред-
ственно за линией отрыва отчет-
ливо вырисовывается область чи-
сто трансверсального потока, а
несколько ниже по потоку — по-
пятное продольное течение, увле-
каемое трансверсальным.
Укажем на ряд других изучен- Рис. 50.
ных случаев движений в трехмер-
ном пограничном слое, допускающих выделение автономного двумер-
ного движения с компонентами и, v. Так, Лус2) исследовал движение
в пограничном слое на полубесконечной пластине с распределением
скоростей во внешнем потоке
U = const,
и с «внешними» линиями тока в форме парабол. Им получено точ-
ное решение этой задачи и подробно исследованы «вторичные дви-
жения» в пограничном слое. Обнаружено и объяснено специфическое
свойство пространственных пограничных слоев, заключающееся в том,
что полное давление внутри пограничного слоя может превосходить
полное давление во внешнем потоке. Отмечено также, что при до-
стижении продольным (автономным) потоком отрывного состояния
отрыв может не осуществляться за счет кинетической энергии «вто-
ричных течений».
') Rott N., Crabtree L., Journ. Aeron. Scl. 19,
*) Loos H. O., Journ. Aeron. Sci. 22, № 1 A955).
15 Зак 297. Л. Г. Лойцянский
8 A952), 556—560.
226 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ (ГЛ. VII
Более сложное движение
при т = 0 переходящее в случай Луса, было исследовано В. В. Бог-
дановой ¦), которой удалось дать точное решение для этого более
общего класса течений и использовать этот класс для построения
приближенного параметрического метода решения задач с произволь-
ной функцией U {х).
§ 47. Пространственный пограничный слой на вращающемся
цилиндрическом крыле
При рассмотрении движений вязкой жидкости вблизи поверх-
ностей вращающихся тел особый интерес представляет изучение трех-
мерных пограничных слоев на лопастях винтов и рабочих колес
турбомашин. Схематически можно
представить себе цилиндрическое
крыло (рис. 51), вращающееся во-
круг оси OY, перпендикулярной к его
образующим. Соединим с крылом
вращающуюся вместе с ним с по-
стоянной угловой скоростью ш си-
стему координат OXYZ. Внутри по-
граничного слоя будем пользоваться,
как и ранее, системой координат
х, у, z, пренебрегая ее криволиней-
ностью.
Прежде всего обратимся к опре-
делению внешнего потока2). Обо-
значим через Ф(Х, Y) потенциал
скоростей плоского обтекания крыла
с единичной скоростью на бесконеч-
ности. Тогда легко проверить, что обтекание крыла в относительном
движении будет определяться формулами
Рис. 51.
дФ
дФ
= a>Z^. V = <oZ~, Г = ю(Ф-2*).
G.23)
Действительно, будем иметь
dU , dV , dW7
¦+¦
дХ1 ^ дУг
dU_
dZ
dW
дХ
дФ
)=.о.
') Богданова В. В., Изв. АН СССР, ОТН, серия механики и машино-
строения, № 1, 1960.
s) Sears W. R., Journ. Aeron. Sci. 17, № 3 A950), 183.
§ 47] ПОГРАНИЧНЫЙ СЛОЙ НА ВРАЩАЮЩЕМСЯ ЦИЛИНДРИЧЕСКОМ КРЫЛЕ 227
кроме того, очевидно, выполняются граничные условия на поверх-
ности цилиндра и на бесконечности; вдалеке от цилиндра
Ф(*. Y)-+X, U->o>Z, V->0, W-> — u>X,
как это и должно быть в относительном движении покоящейся
жидкости в системе координат, равномерно вращающейся с угловой
скоростью ш.
Зададим') распределение на внешней границе пограничного слоя
степенной функцией по Фокнеру — Скэн (§ 11)
u=*zDT- G-24)
так что единичный потенциал скоростей вблизи внешней границы
слоя будет равен
т+1 G.25)
При этом, согласно последнему равенству G.23), трансверсальная
скорость на внешней границе слоя будет равна
W = (о {[с/(т -+- 1)] (х/с)т+1 — 2х cos a} + С. G.26)
где положено
X = xcosa,
а а в случае симметрии формы носа крыла относительно плоскости
XOZ — угол того клина, обтеканию которого идеальной несжимае-
мой жидкостью соответствует степенной закон изменения скоро-
стей G.24); при отсутствии симметрии угол а имеет некоторый
обобщенный смысл. В случае пластины, наклоненной к плоскости XOZ
под некоторым углом (угол атаки), а равно этому углу.
Относительно аддитивной постоянной С заметим, что если считать
трансверсальный внешний поток образующимся только над крылом
(х > 0) и равным нулю при х ^ 0, то, согласно G.26), можно по-
ложить С = 0, что соответственно упростит формулы G.25) и G.26).
Уравнения пограничного слоя во вращающейся системе координат
будут отличаться от уравнений G.4) невращающегося косо обтекае-
мого крыла тем, что во втором уравнении появятся члены, выражаю-
щие влияние кориолисовой силы и зависимости U от г; кроме того,
в некотором удалении от оси вращения можно пренебречь членами
с w по сравнению с и (в дальнейшем эта ошибка будет оценена)
') Rott N.. Smith W., Journ. Aeron. Sci. 23, № 11 A956), 991—996.
15*
228 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
и упростить систему, приведя ее к виду
ди ди .. dU
u^vu
dw
dw
dU
д2и
d2w
ди
dv „
~ду~ ~
G-27)
граничные условия при этом таковы:
u = v = w = 0 при у —О,
u=U, w — W при у = оо.
'
Случай пластины, расположенной в плоскости XOZ(a — 0), был
исследован ФогартИ'). В этом случае (-;—= 0) первое и третье
уравнения системы G.27) с соответствующими граничными усло-
виями G.28) автономны, так что и и v представляются известными
решениями плоской задачи Фокнера — Скэн (§ 11). То же имеет
место и в общем случае неплоской лопасти, но z будет входить при
этом как параметр в выражение для U. Профили скоростей в сече-
ниях пограничных слоев, относящихся к различным нормальным сече-
ниям крыла, образуют подобные семейства с множителем подобия wz
[как это следует из G.24)]
? = у /(»+l)t7Bv*). G.30)
где Ф'(?) — та же функция, что и в § 11. При этом толщины слоев
в различных плоскостях будут меняться, как (ш)''1', а напряжения
трения — как (wz)'1'.
Трансверсальная скорость w может быть после этого определена
из линейного однородного уравнения [второе уравнение системы
G.27)]. Будем искать решение этого уравнения в виде суммы
w = wl-\- w2,
G.31)
w2 = — 2(од;А @ cos a,
где неизвестные функции §¦(!¦) и h(\) удовлетворяют обыкновенным
дифференциальным уравнениям (штрих — производная по \)
h" 4- ФА' — B —
= —2,
= — B — р)Ф'.
Л
') Fogarty L. E., Journ. Aeron. Sci. 18, № 4 A951), 247—252.
> 47J ПОГРАНИЧНЫЙ СЛОЙ НА ВРАЩАЮЩЕМСЯ ЦИЛИНДРИЧЕСКОМ КРЫЛЕ 229
ч р — константа Фокнера — Скэн, равная
р /я + 1
Зторое уравнение системы G.32) можно сделать однородным, по-
южив
А— 1 =Л.
юсле чего получим
?"_Ф6'_B — р)ф'Л = О. G.33)
При этом граничные условия таковы:
g- = 0. А = 0 (или А = — 1) при | =
g = l, А=1 (или А = 0) при
1 = 0, |
;=ОО. J
G.34)
Первое из уравнений системы G.32) и второе из уравнений той же
истемы, приведенное к виду G.33), были решены численным ме-
-одом пои граничных условиях G.34). Кривые, соответствующие
7,/Ж
W
'\
=0,2 \
j8*-O,&
Р=2А
/3=0^
J3=-OJ4-
w
У
^¦/3=0,5
0,5 1,0
О 0,5 /,0 1,5 2,0 О
Рис. 52.
оункциям g{\) и А('), приведены на рис. 52; угловые коэффициенты
;тих кривых на поверхности крыла g' @) и А'@) даны в та-
¦лице 19.
Чтобы отчетливее выделить образующиеся на поверхности вра-
цающейся лопасти «вторичные течения», т. е. те течения, которые
•тличают поток внутри пограничного слоя от внешнего потока,
230 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VI
Т аблица И
р
—0,1988
—0,14
0
0,2
0,5
1,0
1,6
2,0
т
—0,0904
—0,0654
0
0,11
0,33
1,0
4,0
?'@)
2,70
2,22
2,02
1,91
1,83
1,76
1,74
1,69
А'@)
0,48
0,66
0,76
0,82
0,84
0,81
0,70
0,60
*"@)
2,70
1,98
1,55
1,22
0,90
0,53
0,22
0,00
Л*' @)
0,48
0,42
0,29
0,13
—0,09
—0,42
-0,82
—1,09
введем наряду с и и w компоненты и* и w*, соответствующие
проекциям скорости на направление результирующего внешнего по
тока (U, W) и перпендикулярное к нему направление. Вводя с этог
целью угол S линии тока на внешней границе с осью ОХ, удовле
творяющий равенству
получим
и* = и cos 0 + w sin 0,
w* = — и sin 6 -f- w cos 0.
Считая, по условию, отношение wju, а следовательно, и угол 0 ма-
лыми, положим
W
и* = и, -ш* =^== -а; — и -—¦.
Тогда будем иметь
или, вводя еще обозначения
_ ф') _ 2шх (Л — Ф') cos a.
получим следующие безразмерные соотношения для w*:
' = {(xjcflim + 1)] g* - Ж cos a,
w*
G.35
G.36
Функции g* ($) и h*{\) показаны на рис. 53, а соответствующие
им угловые коэффициенты на поверхности крыла — в последни:
двух столбцах таблицы 19.
Из формул G.29) и G.31) можно сделать заключение, что npi
одинаковых \ и х/с отношение wfu имеет внутри пограничного слог
значение порядка c/z, т. ё. обратно пропорционально расстояния
¦ 47] ПОГРАНИЧНЫЙ СЛОЙ НА RPA'UWUF.MCfl ЦИЛИНДРИЧЕСКОМ КРЫЛЕ 231
_ечения крыла от оси вращения. Это заключение обобщает на слу-
чи движения вязкой жидкости при больших рейнольдсовых числах
:звестную «гипотезу цилиндрических сечении», согласно которой
фи достаточно большом относительном удалении z/c от оси вра-
дения обтекание сечения крыла идеальной жидкостью может рас-
матриваться как плоское. Приведенное решение дает количествен-
юе уточнение этого общего качественного заключения.
Будить о деталях вторичных течений непосредственно по при-
графикам нельзя, так как необходимо еще учитывать роль
;оэффициентов, стоящих при функциях §¦*(!•) и /?*($)• Важно обра-
:пъ внимание на рис. 53, из которого видно, что слагаемое в ра-
;енствах G.35) или G.36), содержащее g*, всегда дает компоненту,
оправленную наружу по отношению к линии тока внешнего потока,
1 то время как слагаемое, содержащее множителем /г*, может быть
направленным в разные стороны в зависимости от величины коэф-
эициента р, характеризующего ускоренность (р > 0) или замедлен-
юсть (Р < 0) внешнего потока.
Если подсчитать при разных р, а следовательно, и т максималь-
нее значения безразмерной величины w*/u>c при cosa=l, то соот-
ветствующие кривые будут иметь вид, указанный на рис. 54. Можно
заметить, что вторичные течения заключают в себе трансверсальное
лВижение наружу, подобно имеющему место при вращении диска
} покоящейся жидкости. При этом, как видно из графика на рис. 54,
232 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VI!
наибольшая величина компоненты скорости w* наблюдается при
замедленном движении, т. е. в диффузорном участке слоя, наимень-
шая — при ускоренном движении, т. е. в конфузорном участке, при
значениях р около 0,2 ч- 0,5.
Исключая параметр р, можно приемом, аналогичным изложенному
в § 20, составить решение, справедливое при любом задании рас-
пределения давлений по сече-
нию вращающейся лопасти; это
было сделано Сирсом ').
Задача о пространственном
пограничном слое на вращаю-
щейся лопасти была рассмот-
рена Таном 2), искавшим ре-
шение в форме рядов, распо-
ложенных по степеням вели-
чины x/z, которую он прини-
мал за малую, тем самым огра-
ничивая область решения бли-
зостью к передней кромке или
удаленностью от оси вращения.
Применяя свой метод к плоской
лопасти, вращающейся в своей
плоскости (задача, которая ра-
нее была решена, как указы-
as
Рис. 54.
О 0,2 0,4 O,S 0,3 .
валось, Фогарти), Тан показал,
что система обыкновенных диф-
ференциальных уравнений, к
которой сводятся в этом случае
последовательные приближения, совпадает с системой, знакомой нам
по решению задачи о плоском пограничном слое с «односкатным»
профилем скоростей во внешнем потоке (§ 12).
§ 48. Обратное влияние пространственного пограничного слоя
на внешний поток
При рассмотрении плоского пограничного слоя было показано
(§ 10), как можно учесть обратное влияние подтормаживания жидко-
сти в пограничном слое на оттеснение линий тока внешнего (потен-
циального) потока. Для получения действительного, т. е. исправлен-
ного на влияние вязкости, распределения давления по поверхности
обтекаемого тела достаточно было рассмотреть обтекание идеальной
жидкостью «полутела», образованного из данного тела путем нара-
') Sears W. R., Appl. Mech. Rev. 7, № 7 A954), 281—285.
2) Tan H. S., Journ. Aeron. Sci. 20, № 11 A953).
§ 48] ОБРАТНОЕ ВЛИЯНИЕ ПОГРАНИЧНОГО СЛОЯ НА ВНЕШНИЙ ПОТОК 233
У \
щивания вдоль нормалей к его поверхности величин «толщин вытес-
нения», вычисленных по искомому действительному распределению
давлений. Это возможно выполнить при помощи последовательных
поправок к получаемым распределениям давлений по указанным обра-
зом деформированным поверхностям.
Аналогичный вопрос встает и при изучении пространственных
пограничных слоев. Можно предположить, что и в этом общем слу-
чае существует «толщина вытеснения» Ь*, являющаяся уже функцией
координат х, z на поверхности обтекаемого тела (в этом параграфе,
как и ранее, будем пренебрегать кривизной координатных линий,
считая радиусы их кривизны большими по сравнению с толщиной
пограничного слоя) и обладаю-
щая тем же свойством, что и
аналогичная величина в пло-
ском случае.
Для- определения величины
Ь*(х, z) повторим рассуждение,
близкое к приведенному в пло-
ском случае, но обобщенное на
пространственный пограничный
слой.
На элементарном коорди-
натном прямоугольнике со сто-
ронами dx. dz и вершиной в не-
которой точке Мо (рис. 55)
поверхности у=О рассматри-
ваемого тела построим ортого- Рис. 55.
нальную к поверхности тела
призму, которую пересечем поверхностью у = 8(лг, г), представляю-
щей собой границу пограничного слоя, и искомой поверхностью
у = Ь'{х,г).
Как и в плоском случае, сравним между собой два потока:
1) действительный, вязкий поток с компонентами скорости (и, v, w),
простирающийся от поверхности тела у = 0, где все три компоненты
равны нулю, до границы пограничного слоя у —8(лг, z), где значе-
ния этих компонент будут и = U, v — V, w = W, и 2) фиктивный,
идеальный поток с компонентами скорости (U, V, W), зависящими
только от х и z, т. е. принимающими вдоль нормали МаМ к по-
верхности в данной точке Мо одни и те же значения, причем область
изменения у ограничена интервалом М*М [0 < g*(x, z) ^ у ^ Ь (х, z)\.
Фиктивный поток, у которого скорости в этом интервале больше,
чем у действительного, а секундный объемный расход, в силу
совпадения трубок тока вдалеке от тела, должен быть тем же самым,
что и у действительного, не может, естественно, заполнить все
сечение слоя и не доходит до поверхности тела на расстояние
234 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
М0М* = Ь*(х, z). Определим эту величину. Для этого воспользуемся
тем очевидным фактом, что секундные объемные расходы рассма-
триваемых потоков сквозь верхнее основание ММ1М'М2, располо-
женное на границе пограничного слоя, где оба потока совпадают,
одинаковы и могут быть определены как разности расходов сквозь
задние и передние площади боковых граней призмы, ограниченные
поверхностями у = О и у = 8 (х. z) для действительного потока и
у = Ь*(х, z) и у = Ъ(х, z) для фиктивного потока.
Таким образом, будем иметь
иdy dz —
+ lfwdy) dx-i Ifwdyj dx + -?r \lj wdy
dx \dz \ =
J I
dz
или, после очевидных сокращений.
(8_8*)U7 — fwdy =0. G.37)
Введем в рассмотрение следующие две вспомогательные «толщины
вытеснения»:
о о
у. G.38)
Тогда предыдущее равенство может быть переписано в окончатель-
ной форме так:
Как видно, в отличие от плоского случая движения, искомая
толщина вытеснения Ь*(х, z) не получается в конечной форме,
а должна определяться путем интегрирования уравнения в частных
производных G.39), в котором U и W — заданные наперед функ-
ции х и z, а Ьх. ог вычисляются по формулам G.38) после того,
как расчет пограничного слоя произведен и поле скоростей стало
известным.
§49]
ВРАЩАЮЩИЙСЯ ЦИЛИНДР В КОСО НАБЕГАЮЩЕМ ПОТОКЕ
235
Уравнение G.39) было впервые выведено Ф. Муром '). В част-
ном случае плоского пограничного слоя B = 0) уравнение G.39)
непосредственно интегрируется и дает 8 =8*. т. е. приводит к обыч-
ному определению «толщины вытеснения».
Приведенное рассуждение могло бы быть распространено и на
более общий случай, когда нельзя уже пренебрегать кривизной
координатных линий на поверхности тела. Такого рода необходи-
мость может возникнуть при рассмотрении пограничных слоев на
очень длинных осесимметричных телах при наличии косого их об-
текания или, более общо, на длинных не осесимметричных телах.
В наиболее общем виде этот вопрос был рассмотрен в статье
Сэдни 2).
§ 49. Вращающийся цилиндр в косо набегающем потоке
Отмеченное в предыдущем параграфе обратное влияние погра-
ничного слоя на внешний потенциальный поток проиллюстрируем
расчетом силы Магнуса 3), приложенной к вращающемуся вокруг
своей оси артиллерийскому снаряду в косо набегающем на него
Сечете поМ0удг
&
Рис. 56.
однородном потоке. Приводимый далее расчет представляет хороший
пример практического применения теории пространственного погра-
ничного слоя.
Примем следующие, упрощающие расчет допущения. Считая сна-
ряд достаточно длинным, пренебрежем влиянием оживальности носа
и представим себе поверхность снаряда как полый сквозной ци-
линдр, учтя тормозящее влияние носа соответствующей длиной
начального участка цилиндра 4). Обозначим (рис. 56) радиус цилиндра
') Moore F. К., NACA Rep. 1124, 1953.
s) S e d п е у R., Quart. Appl. Math. 15, № 2 A957).
») М а г t i n J. С, Journ. Aeron. Sci. 24, № 6, A957), 421—429.
4) Пространственный пограничный слой на вращающемся вокруг своей
оси сквозном цилиндре при продольном его обтекании был рассмотрен
Хоуартом (Howarth L, Phil. Mag. 42 A951), 1308—1345).
236 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
через а, окружную скорость его вращения через с = ша, где ш —
угловая скорость вращения снаряда вокруг его оси. Скорость набе-
гающего потока равна U^ и образует с осью снаряда угол атаки
(или скольжения) а, который примем за малую величину первого
порядка. Столь же малой величиной будем считать отношение
т.— = -^— окружной скорости снаряда к скорости набегающего по-
U СО U СО
тока, так что величины a2, (c/UmJ, ac/U^ будут в дальнейшем
рассматриваться как имеющие одинаковый, второй порядок малости.
Оси координат выберем, как обычно, направив ось х вдоль
образующей цилиндра, ось у— по нормали к его поверхности,
а ось z—по окружности в сечении поверхности цилиндра перпен-
дикулярной к его оси плоскостью. При составлении уравнений по-
граничного слоя пренебрежем кривизной координатной линии z,
т. е. будем считать Ь<^а. Уравнения движения в пограничном слое
будем составлять в неподвижной системе координат х, у, z, учиты-
вая вращение цилиндра в граничном условии для трансверсальной
скорости w на его поверхности.
Эти уравнения будут иметь вид
dw 1 dp . d2u
ди
dw
UTx
-\-v
-\-v
ди
dx
du
dy
dw
~д~У
У '
*
^ ш dz — р дх ^ ду
, dw 1 dp . d2w , ,, ...
\-w-^— = -^- + v^-2-> } G-40)
' dz p dz ' dy2 ' v '
dv . dw
~dy i~ Hz ~
С целью определения производных др/дх и dp/dz составим прежде
всего выражения для скоростей U и W на внешней границе погра-
ничного слоя. В принятом приближении будем иметь (рис. 56)
\ 2 / \ G.41)
W = 2t/co sin a sin (z/a) = 2U^a. sin (z/a), J
где i/ooCOsa и U^sina соответствуют продольной и поперечной
составляющим скорости на бесконечности U^. Применяя теорему
Бернулли, найдем
р = const — у р (U2 + W2) =
= const—jpt/?o[(l — j*2)! + 4a2 sin2(z/a)],
откуда следует
•37 = °' Tz~ = - 4? №) ^sin B/fl)cos ^"
ВРАЩАЮЩИЙСЯ ЦИЛИНДР В КОСО НАБЕГАЮЩЕМ ПОТОКЕ
237
Таким образом, задача сводится к интегрированию системы
уравнений
ди , ди , dw д2и
dw . dw
дх ду
ди
dv
dw
dw
G.42)
при граничных условиях, составленных с той же точностью,
ц/Ь^ = 0, v/UiX = 0, wlUm=cjUco=(aalUm при у = 0,
«/?7^= l_±a2, w/t/0O=2asin(z/a) при у = оо.
Будем искать решение в виде суммы решений
G-44)
где совокупность компонент (и0, v0) соответствует приближению
нулевого порядка, которое основано на пренебрежении вращением
цилиндра и влиянием угла атаки (ш = 0, a = 0). Компоненты (и1ш vv w^
и (и2, v2, w2) определяют собой члены первого и второго порядка
относительно а или c/t/«j.
Подставляя разложения G.44) в систему G.42), получим:
1) уравнения и граничные условия для нулевого приближения:
¦ = 0;
дх ^ dy
uo = vo = O при у = 0, «0=1 ПРИ У = °°> ,
2) то же для первого приближения:
G.45)
dwx
1 ду UM dy2 '
dw i v d^w i
d.ut
, w^c/Uix, при у —0,
= 2a sin (z/a) при у = са;
G.46)
238 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ ГгЛ. VI
3) то же для второго приближения:
ди, . ди, , ди0 , ди2 , ди, .
#^.
= 4 (а'/а) sin (zld) cos (г/а) + ¦$- Sfi-, <7'47
ди2 , di>2 . d
11
к2 = г>2 = да2 = 0 при у = О,
и2 = — -g-a2« «'г —° ПРИ У==°°-
Уравнения нулевого приближения G.45) ничем не отличаются о~
уравнений задачи Блазиуса для пластинки (§ 4). Решения этих ypat
нений представим в форме (штрих — производная по tj)
о; ), G.48
причем функция /0(т|) тождественна с ср (i^) в § 4; величины этог
функции и первых ее двух производных приведены в таблице 1.
Обращаясь к уравнениям и граничным условиям G.46) первой.
приближения и сравнивая второе уравнение этой системы с первыи
уравнением системы G.45), заключим, что решение для wt имеет вил
f G.49
где функции A (z) и В (г) должны быть определены из граничны:
условий, входящих в G.46). Найдем
wi = С1и<*> + [2а sin <*/<*) - CIUA /о W- G.50
Компоненты и, и vi будем искать в форме
). I
v, = (а/а) у vx/Um g0 (rj) cos (z/a).
Это приводит к системе обыкновенных дифференциальных ураь
нений
,° ' . ' ° 1' \ G 52
с граничными условиями
/i = gb=° при tj = O,
/1 = 0 При 7)=ОО.
§ 49] ВРАЩАЮЩИЙСЯ ЦИЛИНДР В КОСО НАБЕГАЮЩЕМ ПОТОКЕ
239
Аналогично уравнения G.47) для определения второго приближе-
ния дают
w2 =
o) (х/а) Ао (rj) cos (г/а) +
+ а2 (х/а) Л: (i|) sin (z/a) cos (z/a). G.54')
причем функции /zo(tj) и Н1(-ф удовлетворяют следующим уравнениям
и граничным условиям:
1 ,
G.54")
/Л - Т foK + B^о - 2Ч/,) /о + B/;J - 4 = h\,
Ао=Л1=:0 при 7/ = 0,
Ao = Ai = O при 7/ = оо.
Наконец, компоненты скорости во втором приближении, и2 и v2,
определятся как
и2 = a (c/Uao) (х/аJ /2 (vj) sin (z/а) -f-
:^/aJ [/a A) + Л A) cos Bz/a)] - (a2/2) /^ (т,),
) gift) sin (z/a) +
G))cosBz/aI} —
-(a2/4)f7
G.55)
: G,) - /5 (tj)],
причем вновь введенные неизвестные функции удовлетворяют системе
обыкновенных дифференциальных уравнений
2/а—
;-*„= °-
- Т /о/; + Щ ~ I/,/! - т
G.56)
240 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
с граничными условиями
fo — g. = Л = go = /a = gi — /е = /с = 0 ПРИ Tj == 0, )
1 3 2 4 3 5 5 .... G-57)
Все эти неизвестные функции и их производные были определены
численным путем и включены в таблицы, помещенные в подробном
1) Продольные с пор ост и (х/а=2О)
а=О, ¦
0,2 O.ff 1,0 " 0,2 O,S 10 0,2 Об 1,0
u/Uvo u/l/oo и/О„
2) Трансверсальные скорости (х/а =20)
°
0,2 о,е
и/1/ао
0
Рис. 57.
отчете Мартина'). Приводим общий вид профилей продольных и
трансверсальных скоростей внутри пограничного слоя для нескольких
значений z/a и параметров а и c/Um (рис. 57).
Пользуясь полученными значениями компонент скорости
/о (^ -+¦2 («/«) /»A) cos (z/o) +
-+¦а (c/Um) (х/ср /2 (tj) sin (г/в) +
[/3(т,) + /4 (tj) cosBг/в)] -
). G.58)
') М а г 11 n J. С, Ballistic Research Laboratory Rep. № 870, Aberdeen
Proving Ground, 1955.
§ 49] ВРАЩАЮЩИЙСЯ ЦИЛИНДР В КОСО НАБЕГАЮЩЕМ ПОТОКЕ 241
+ a (c/Um) (x/af gl (Tj) sin (z/a) -f-
-f- (ax/aJ [g2 (tj) + g3 (Ti) cos Bz/a)] - ~ [^ (rt) - Д Щ},
?- = с/и*, + f2a sin (z/fl) - c/f/J /; (t,) +
o) (ajf/a) Ло (т]) cos (z/a) +
-f- a2 (x/a) Aj (t\) sin (г/a) cos
G.58)
и выражениями U и U/ из G.41), можно подсчитать значения вспо-
могательных толщин вытеснения:
&;= / {1 — «
-a2/2
a2/2)]} rfy = / [1 — u/U0, — o?u/BUoa)] dy,
8
§; = J {1 —
sin (z/a)]} dy.
После проведения численного интегрирования по упомянутым выше
таблицам функций (верхний предел интегрирования повсюду прини-
мался бесконечным) получим
8^ ={1,721 — 1,721 (ах/а) cos (z/a) —
— 1,526 (асIUсо) (xjaf sin (z/a) —
—a2(x/aJ[— 0,1434-1- l,667cosBz/a)]-r-0,4240a2}
5* = {1,721 [ 1 — c/Bat/oo sin (z/a)] -f-
+ 1,380 (c/U^) (x/a) ctg (z/a) -
— 4.943 (ax/a) cos (z/a)}
G.59)
Уравнение G.39). служащее для определения толщины вытесне-
ния 8*. в настоящем случае будет выглядеть так:
А
C* - Ъ*х) + 2a A [sin (z/a) (8* _ 8;)] = о.
Разлагая искомое решение на три слагаемых: нулевого, первого
и второго порядка малости:
6 Зак. 297. Л. Г. Лойцянскнй
242 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
и используя G.59), получим уравнения
^-[81+1,721 (ax/a)
-?rj§2+l. 526 (oc/t/oc
, cos (z/a)] +
*¦[($- 1J21
+ 2a ^- [(83 — 1,721 У vjc/t/oo) sin (z/a)] = 0.
'?/«,) (x/aJ yvx/t/a, sin (г/а) +
+ (ax/aJ yvx/t/a, [—0,1434+1,667cosB2/a)]—0,4240a2 У vx/t/co)-f-
+ 2a^-{[8t—1,380(^/^00) (x/a)
+ 4,943 (ax/a) У^
c/t/oo ctg (г/а)+
, cos (z/a)] sin (г/а)} = 0
интегралы которых будут иметь вид
83—1.721 V vx/t/oo,
SJ = — 1,721 (ах/а) Vvx/^ cos (г/а),
8J = {— 2,630a (c/t/oo) (x/af sin (г/а) —
— (ax/aJ [— 0,1434 + 4,245 cos Bг/а)] + 0.4240a2}
Окончательно найдем
8*= {1,721 — 1,721 (ax/a) cos (г/a) — 2,630 (ac/t/«,) (x/aJ sin (z/a) —
— (ax/aJ [—0,1434 + 4,245 cos Bг/а)] + 0,4240a2} V^xZT^
. G.60)
Выделим асимметричную часть этого выражения, содержащую
в качестве множителя sin (г/а).
8* = — 2,630 (ac/t/oo) (x/aJ Vvx/t/a, sin (г/а).
G-61)
Тол;ко благодаря асимметрии в распределении давления, вызван-
ной асимметрией толщины вытеснения, может возникнуть поперечная
сила Магнуса. Для вычисления этой силы составим потенциал воз-
мущений скорости ср в плоскости нулевого угла атаки (или скольже-
ния) 6 = те/2; по теории тонких тел этот потенциал в полярных коор-
динатах (г, 9 — z/a) будет равен
= — 6,575ac (x/a)(
/a) (а2/л) sin (г/а).
§ 49] ВРАЩАЮЩИЙСЯ ЦИЛИНДР В КОСО НАБЕГАЮЩЕМ ПОТОКЕ 243
Коэффициент давления р, равный
1
(ду/дх) + (ду/дх?
ul
с точностью до членов, имеющих множителем dcjll,^, предста-
вится так:
~р = 19,725 (ос/г/») (Y^fUZ/a) (a/r) sin (г/с),
а на поверхности тела л=с будет равен
~р = 19,725 (а/с) (с/?/ет) Y^x/UZ sin (z/а).
Интегрирование по углу 6 = z/a дает сначала силу Магнуса, от-
несенную к единице длины цилиндра,
/= 2 • -J-pt/L //msin9rf0= 19,725u ¦ -J-pt/L(«/?/„) V^x/ZT^, G.62)
о
а затем и полную силу на длине L цилиндра,
L
F= f fdx= l3,2Y^UZ
о
= 7,64171 ¦±-PUi(aclUa,)L ¦ b*0L, G.63)
где
Si= 1,721 VvZyZTT G.64)
представляет собой толщину вытеснения на корме цилиндра при от-
сутствии вращения и угла атаки или скольжения. Сила F лежит в пло-
скости нулевого угла атаки или скольжения @ = те/2) и перпендику-
лярна к оси цилиндра.
Вводя еще коэффициент силы Магнуса (d — диаметр цилиндра)
найдем
КР = 6,001 (L/d)(b*0L/d) G.65)
или, исключая 8Ji по G.64),
'', G.66)
244 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
где положено
В заключение можно определить координату центра приложения
параллельных сил Магнуса
L I L
х= f xfdx f fdx = jL. G.67)
о / о
Предложенный метод справедлив, конечно, только для не очень
длинных цилиндров, когда можно быть уверенным в допустимости
пренебрежения влиянием поперечной кривизны цилиндра, т. е. счи-
тать малой величину Ь/а. Применяя более точную теорию и пользуясь
обобщенным понятием «площади вытеснения» (§ 36), можно решить
и более сложную задачу.
Следует отметить, что рассмотренное только что решение имеет
скорее чисто методическое значение, так как относится к ламинар-
ному пограничному слою и к случаю малых скоростей '). Можно при-
нять, что закономерности G.65) и G.67) справедливы и для турбу-
лентного пограничного слоя, если ввести поправки в численные
коэффициенты. Сравнение с опытами показало допустимость такого
подхода. В частности, для точки приложении силы Магнуса в фор-
муле, аналогичной G.67), был получен коэффициент 9/14, мало отли-
чающийся от 3/5.
§ 50. Уравнения трехмерного пограничного слоя
в любой ортогональной системе координат
Н шболее общие уравнения теории пространственного пограничного
слоя, образующегося при обтекании тела с произвольной гладкой
поверхностью, были впервые выведены в классической работе Леви-
Чивита, относящейся к 1929 г.2), который использовал для этой
цели систему общих косоугольных криволинейных координат.
Хотя в настоящее время некоторые авторы предпочитают при
рассмотрении трехмерных пограничных слоев на данной поверхности
пользоваться косоугольными криволинейными координатными систе-
мами3), все же наибольший интерес представляет применение орто-
гональных криволинейных координатных систем, как более простых.
') Эффект Магнуса на конусе в сверхзвуковом потоке см. S e d n e у R.,
Journ. Aeron. Sci. 24, № 6 A957), 430—436.
2) L e v i - С i v i t а Т., Allgemeine Folgerungen aus der Prandtlschen Greaz-
schichttheorie. Vortrage aus dem Gebiete der Aerodynamik. Aachen, 1929.
3) S q u i r e L. C, ARC, R & M, 3006, 1957.
§ 50] УРАВНЕНИЯ В ЛЮБОЙ ОРТОГОНАЛЬНОЙ СИСТЕМЕ КООРДИНАТ 245
п'
Условимся в следующем выборе системы ортогональных криво-
линейных координат. Поверхность обтекаемого жидкостью тела вы-
берем за координатную поверхность q2 — 0 (рис. 58), так что коор-
динатные линии <72 будут представлять собой кривые, ортогональные
к поверхности тела. На самой поверхности обтекаемого тела выберем
ортогональную сетку координат-
ных линий (д{) и (д3). Примем для
перпой криволинейной оси обозна-
чение х, второй — у, третьей—z,
а соответствующие этим коорди-
натам коэффициенты Ляме и ком-
поненты скорости обозначим че-
рез Нх, Н2, Н3 и и, v, w.
Сохраним в уравнениях Стокса,
составленных в ортогональной си-
стеме криволинейных координат *),
лишь те члены, которые при
тонкости пограничного слоя имеют
старший порядок. Кроме того, не
нарушая общности, можем поло-
жить Н2=\, тем самым рассма- рис 58.
тривая координату у как рас-
стояние точки до поверхности тела. Тогда получим следующую си-
стему уравнений пространственного пограничного слоя:
п'
ди
dw
1
ди
ди
1
ди
дН3
Я, " дх
дх 1
dw , 1 dw
<?у ~* Н3 дг
Я, йл "+"V ду' '
др
ду2 '
G.68)
Давление р в этой системе рассматривается как функция времени
и координат х и z на поверхности; поперек слоя давление прини-
мается неизменяющимся.
Можно различным образом выбирать направление координатных
линий на поверхности тела и тем самым по-разному определять коэф-
') Выписывать их из-за громоздкости не будем; см., например, К о -
чин Н. Е., К и бе ль И. А., Розе Н. В., Теоретическая гидромеханика,
ч. II, Гостехиздат, 1948, стр. 288—289.
246 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
фициенты в уравнениях G.68). Так, например, Хоуарт1), В. В. Стру-
минский2), Саниаль3) использовали в качестве координатных линий
линии кривизны поверхности тела. Наиболее, по-видимому, интересную
с прикладной стороны систему координат выбрал Хейз4), приняв
в качестве координатных линий на поверхности тела линии тока внеш-
него потока и ортогональные к ним траектории. При таком выборе
трансверсальная компонента скорости внешнего потока W равна нулю,
а следовательно, продольная скорость внешнего потока на границе
пограничного слоя U будет связана с производными от давления
соотношениями
дЦ . 1 6U _ 1 1 др
dt "т" Я, дх ~ р Я, дх '
U
,/2_ 1 1 др
U — Я дг '
HtH3 дг р Я3 дг
Аналогичную, но более простую систему криволинейных коорди-
нат, не учитывающую кривизну поверхности тела, а только кривизну
линий х, предложил Мэйджер5). Если обозначить кривизну коорди-
натных линий х, лежащих в плоскости xz (касательной к поверх-
ности тела у = 0), через я, то коэффициенты Ляме приобретают зна-
чения
//] = 1 —\- kz, Н2 z== 1, Н% = 1.
Уравнения пограничного слоя при этом будут иметь форму более
простую, чем G.68):
ди . ди . ди , ди , , 1 др , д2и
____ 1 it _____ I (TI „. —I— Iff) , _L_ ff.ii*fff\ ^__г —\— V ~^^"^~
dt ' дх ' ду г^ йг '^ р йд; т dy2
dw , dw | dw , dw . , \ dp , d2w
dt ' дх ' ду ' dz p дг ' dy2
G.70)
Ж + 17"
В случае системы координат, равномерно вращающейся с угловой
скоростью w (со^., соу, ш2), в правые части первых двух уравнений
добавляются члены, соответствующие центробежной и кориолисовой
силам
о. dh n ,, dh 1 „
') Howarth L., Phil. Mag. 42, 326 A951) (русск. пер. в сб. «Механика»,
ИЛ, в. 3, 1952).
2) С т р у м и н с к и й В. В., ДАН СССР 114, № 2 A957).
3) S a n у а 1 U Zeitschr. f. Angew. Math. u. Mech. 37, № 5/6 A957).
») Hayes W. D., Nav. Ord. Rep. 1313, 1951.
6) M a g e r A., NACA, Rep. 1067, 1952.
§ 51] ОБЩИЕ СВОЙСТВА ПРОСТРАНСТВЕННОГО ПОГРАНИЧНОГО СЛОЯ 247
где h — кратчайшее расстояние от точки потока до оси вращения.
Кроме того, при этом уже нельзя пренебрегать изменением давления
в нормальном к поверхности тела направлении.
§ 51. Некоторые общие свойства пространственного
пограничного слоя; теорема о вторичных течениях
Пользуясь вторым уравнением системы G.69), можно выяснить,
какому условию должен удовлетворять внешний поток, для того
чтобы во всех точках пограничного слоя отсутствовал трансверсаль-
ный перепад давления, т. е. dp/dz равнялось нулю. С этой целью
напомним предварительно некоторые простые соотношения из теории
поверхностей.
Пусть на поверхность у = 0 нанесена кривая М0М (рис. 58) и
вдоль этой кривой, начиная от точки Мо, отсчитываете я длина ее
дуги 5. Построим в точке М на кривой триэдр осей с единичными
векторами т, га', га", ориентированными по касательной к кривой,
по нормали к поверхности (и кривой) и по лежащей в касательной
плоскости к поверхности второй нормали к кривой. Кривая на по-
верхности, обладающая тем свойством, что нормаль к поверхности
во всех точках кривой совпадает с главной нормалью к кривой,
называется геодезической кривой рассматриваемой поверхности.
В этом случае единичный вектор второй нормали га" может отличаться
только знаком от единичного вектора бинормали к кривой Ь. Поль-
зуясь обычными свойствами единичных векторов, образующих триэдр,
можно получить соотношения
il = x'«'-xra". 4f = _x'x+ *"«", -^1 =„-*"/*'.
as ds ds
Здесь коэффициенты х, х' носят соответственно наименования гео-
дезической и нормальной кривизны, а х" — геодезического круче-
ния кривой на поверхности. Из предыдущих равенств непосредственно
вытекает выражение этих величин как скалярных произведений еди-
ничных векторов триэдра на их производные по длине дуги:
ds ds ' ds ds '
«" = „". *«. = -*<?.. G.71)
Замечая, что (га — единичный вектор главной нормали к кривой,
направленный к центру ее кривизны, а К—кривизна кривой)
получим по G.71)
¦*. — — Кпп". %'~Кпп'. G.72)
248 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
Если рассматриваемая кривая является геодезической для данной
поверхности, то п • п' — ± 1 и нормальная кривизна х' может только
знаком отличаться от обычной кривизны К; геодезическая кривизна х
будет при этом равна нулю.
По определению производной по направлению и по известным
формулам векторного анализа найдем (х • х = 1)
-^1 =z (х • V) х = grad ~ — xXrot x = rot х X* =
НгНх ~~ЫГП ~ НХЩ ~ду~ п J* х ~
_i____a//L , 1 днх „ __
1 ая, „ 1 днх ,
НХЩ ду
и из первого равенства системы G.71) следует, что
дНх
G-73)
Таким образом, второе равенство системы G.69) переходит
в следующее:
¦g- = //3x.pt/». G.74)
Отсюда можно заключить, что для того, чтобы в пограничном
слое было повсюду dp/dz = 0, должно быть х = 0, т. е. линии тока
внешнего потока должны быть геодезическими линиями поверхности
обтекаемого тела.
При х = 0, в случае стационарного обтекания, второе уравнение
системы G.68) приобретает вид
1 dw . dw . 1 dw . 1 дН3 d2w
Ж и ТГ"+" "a + MW v
т" 777 "aF"+" 7Щ~ ~aX MW ~v ~W'
и при граничных условиях
¦да = 0 при у = 0, w->-0 при у->оо,
соответствующих пограничному слою на неподвижном твердом теле,
будет иметь очевидное решение
Таким образом, если линии тока внешнего потока представляют
собой геодезические кривые поверхности обтекаемого неподвижного
тела, то вторичные течения в пограничном слое отсутствуют. Эта
теорема принадлежит Сэдни :).
») S e d n е у R., Quart. Appl. Math. 15, № 2 A957).
§ 52] СЛОЙ ВБЛИЗИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
249
Для иллюстрации теоремы укажем, что из всех косых обтеканий
цилиндрических тел бесконечного размаха только в случае пластины
в потоке, параллельном ее плоскости, не будет вторичных течений.
Не будет вторичных течений и при продольном обтекании полу-
бесконечной пластины с передним краем, имеющим вид произвольной
кривой. Все это, конечно, верно лишь в предположении отсутствия
обратного влияния пограничного слоя на внешний поток, т. е. в пре-
небрежении деформацией прямолинейных линий тока внешнего потока
за счет подтормаживающего влияния вязкости жидкости.
§ 52. Пространственный пограничный слой вблизи
линии пересечения двух плоскостей
Своеобразным примером пространственного пограничного слоя
на поверхности с изломом может служить случай обтекания внутрен-
ности двугранного прямого угла однородным потоком, параллельным
линии пересечения граней (рис. 59).
Вдалеке от линии пересечения пло-
скостей будет иметь место обыч-
ный плоский пограничный слой на
пластинке. Целью исследования яв-
ляется определение взаимодействия
этих плоских пограничных слоев
в области, близкой к линии пересе-
чения плоскостей. Задача эта в упро-
щенной постановке была рассмо-
трена автором '), 2), 3) в 1936—
1937 гг. В дальнейшем та же за-
дача исследовалась Карьером4) в 1946 г., а в более общей по-
становке Соуэрби5) и Соуэрби и Куком6).
Система уравнений пограничного слоя в этом случае при обозна-
чениях, указанных на рис. 59, будет состоять из двух уравнений
Рис. 59.
ди
дх
ди
ди
д2и
ди . dv . dw
дх ' ду ' дг ~~~
G.75)
') Лойцянский Л. Г., Труды ЦАГИ, в. 249, 1936.
2) Лойцянский Л. Г., Большаков В. П., Труды ЦАГИ, в. 279.
3) Лойцянский Л. Г., Труды Ленингр. индустриального института,
разд. физ.-матем. наук, № 1, 1937.
*) Carrier G. F., Quart. Journ. of Mech. and Appl. Math. 4 A946),
367—370.
5) Sower by L., Phil. Mag. 7 A951), 42.
6) Sowerby L., CookeJ., Quart. Journ. of Mech. and Appl. Mathem. 6,
№ I A953), 50—70.
250 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ (ГЛ Vlt
так как остальные уравнения сведутся к условию постоянства давле-
ния в пограничном слое. Попытка Карьера замкнуть систему G.75)
дополнительным уравнением диффузии продольной составляющей
вихря вызывает возражения'), так же как и предложенная им картина
образования пары вихрей с осями, тянущимися вниз по потоку внутри
угла.
Для приближенного описания явления применим следующий прием,
позволяющий оценить поле продольных скоростей и(х, у, z) в области
взаимодействия пограничных слоев; поперечные компоненты скорости
при этом остаются неопределенными.
Перепишем уравнение G.76) в форме
,г ди I дги , дги\ ., . ди ди ди ._ _„.
Заменим в правой нелинейной части коэффициенты при производных
вначале нулями, т. е. положим u=Ux, v = 0, w = 0, и соответ-
ствующее решение обозначим индексом «1». После этого заменим
те же коэффициенты значениями Ux, 0, 0, положив и, v, w вне
знаков производной равными нулю, а в остающееся справа выраже-
ние t/oo-г— подставим вместо и полученное перед этим значение и'1';
соответствующее решение обозначим через иB).
Таким образом, будем иметь сначала уравнение
С7.П,
с граничными условиями
«(') = 0 при у = 0 или z —0,
иA) = ?/оо при у = z — оо. /
Из обычных соображений следует, что решение уравнения G.77)
при граничных условиях G.78), не содержащих характерную длину,
должно иметь вид
G.79)
«(О = ?/«„/, (т). С),
С =
При этом уравнение G.77) переходит в следующее:
') См. подстрочное примечание редактора и переводчика к статье
Ф. Мура в сб. «Проблемы механики», ИЛ, в. 2, стр. 284.
§ 52J СЛОЙ ВБЛИЗИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ 251
с граничными условиями
/, = 0 при 71 = 0 или С = 0, )
fx—\ при *] = !. = со. J
Уравнение G.80) решается методом разделения переменных и
дает следующее окончательное выражение для и'1':
G.82)
где введено обозначение для функции Гаусса
Решение G.82) при стремлении одного из аргументов к беско-
нечности асимптотически переходит в соответствующее принятому
приближению распределение продольных скоростей в плоском по-
граничном слое на пластинке.
Напряжение трения на грани z~0 будет равно
G.83)
При у->оо получим формулу, определяющую напряжение трения для
плоского пограничного слоя с численным коэффициентом, значительно
превышающим точное значение напряжения трения по Блазиусу (коэф-
фициент 0,564 больше точного 0,332 почти в 1,7 раза).
Выполняя оценку правой части уравнения G.76) другим образом,
придем к линейному неоднородному уравнению
которое заменой, аналогичной G.79), приведется к виду
, 1 i&i Ir dft _ 1 dfi , 1 , dfi _
"•" 2 4 ft) "•" 2 ^ dC —YriT^^Y^~dC~
G.85)
Решение однородного уравнения будет тем же, что и в предыду-
щем случае. Частным решением неоднородного уравнения будет слу-
жить выражение
252 НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ТРЕХМЕРНОГО ПОГРАНИЧНОГО СЛОЯ [ГЛ. VII
Искомое решение уравнения G.84), удовлетворяющее тем же
граничным условиям G.78). что и в предыдущей оценке, будет иметь
вид
Ачх
> /?exp(_i^\Erf(l/^). G.86)
2/я * чх *\ 4чх ) \2 У чх ) Ч '
Соответствующее выражение для напряжения трения по грани
= 0 приобретает форму
1 Z I Z2Uc
РС/2-ехр
G.87)
Если положим в правой части z=oo, то получим напряжение
трения на пластинке в плоском движении:
с коэффициентом, примерно на 15% меньшим, чем его точное зна-
чение.
Можно определить поправку ^w = ('^w)Zs.co — zw> которую надо
вносить в выражение местного напряжения трения на пластинке при
плоском ее обтекании, чтобы учесть взаимодействие со слоем на
перпендикулярной плоскости. Эта поправка равна
где
У я J
для первой оценки и
bxw = 0,282
для второй.
§ 52] СЛОЙ ВБЛИЗИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ 253
Можно подсчитать поправку AW на полное сопротивление одной
стороны пластинки продольной длины L. Эта поправка определяется
интегралом
о о
и просто вычисляется. Она равна
по первой оценке и
по второй.
Поправка эта невелика, так как ширина области взаимодействия
слоев имеет тот же порядок, что и толщина слоя, т. е. 1/^Re.
В цитированных выше наших работах дается, наряду с только
что изложенным, метод решения, основанный на использовании по-
нятия слоя конечной толщины для течения внутри прямого и острого
двугранных углов.
В настоящее время рассмотрены задачи продольного течения
вязкой жидкости вдоль ребра двугранного угла {3 при любых р
в интервале @, 2тс).
В вышеуказанных работах Соуэрби и Кука решена задача о по-
граничном слое, образующемся на внешней стороне прямого дву-
гранного угла C = Зтг/2, образованного двумя квадрантами координат-
ных плоскостей.
Особый интерес представляет вопрос о развитии пространствен-
ного слоя вблизи боковой кромки пластины ф = 2-). Эта задача
приближенным, аналогичным изложенному в настоящем параграфе
приемом была впервые рассмотрена автором1) еще в 1938 г. В столь
же приближенной постановке этот вопрос был рассмотрен позднее
(в 1950 г.) Хоуартом2), а в 1957 г. Соуэрби3). В текущей литературе
продолжают появляться работы, уточняющие математическую сторону
вопроса4).
Изложенные в настоящей и предшествующих главах задачи теории
пространственного пограничного слоя далеко не исчерпывают все
многообразие решенных к настоящему времени задач такого рода.
') Л о й ц я и с к и й Л. Г., ПММ, т. II, в. 2, 1938.
2) Но wart h L, Proc. Cambr. Phil. Soc. 46 A950), 4.
3) Sower by L, Quart. Journ. of Mech. and Appl. Math. U A958), 3.
4) S t e w a r t s о n K, HowarlhL, Journ. of Fluid Mech. 7, № 1 A960),
1-21.
ГЛАВА VIII
ПОГРАНИЧНЫЙ СЛОЙ В ОДНОРОДНОМ ИЛИ НЕОДНОРОДНОМ
ГАЗЕ ПРИ БОЛЬШИХ СКОРОСТЯХ
§ 53. Некоторые особенности теории пограничного слоя в газе
При скоростях движения реального (вязкого) газа, сравнимых по
величине или превосходящих скорость распространения в нем малых
возмущений (скорость звука), возникают специфические для этих ре-
жимов движения явления, теоретический анализ которых до сих пор
представляет значительные, часто непреодолимые трудности. Необ-
ходимость учета переменности таких входящих в уравнение погра-
ничного слоя величин, как температура, плотность, вязкость и тепло-
проводность газа, приводит к затруднениям чисто вычислительного
характера, которые в настоящее время можно считать в значитель-
ной степени преодоленными. Методы интегрирования уравнений по-
граничного слоя в этих случаях уже установлены и могут быть
отнесены к «классической» теории. Более серьезные трудности
возникают при рассмотрении движений газа в пограничных слоях при
гиперзвуковых скоростях. Сопровождающие такого рода движения
физико-химические явления очень сложны и до сих пор еще недо-
статочно изучены.
Основное значение приобретает явление прохождения газа через
ударную волну, где, как известно, происходит переход механической
энергии упорядоченного движения газа в беспорядочное тепловое
движение молекул; газ разогревается, и температура его может достичь
высоких значений. Так, например, газ, обтекающий тело с тупым
носом, прежде чем попасть в область пограничного слоя на поверх-
ности тела, проходит через «головную волну», образующуюся впереди
тела на некотором, небольшом расстоянии от него. При этом разо-
грев газа происходит в области, толщина которой имеет порядок
длины свободного пробега молекулы. Газ не успевает прийти в термо-
динамически равновесное состояние, при котором сообщенная моле-
кулам газа энергия распределится по всем степеням свободы моле-
кулы (поступательной, вращательной и колебательной), причем
известно, что наибольшая задержка в передаче энергии происходит
§ 53] НЕКОТОРЫЕ ОСОБЕННОСТИ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 255
с последней, колебательной частью. Пройдя сквозь головную волну,
молекулы газа в течение некоторого времени (так называемого «вре-
мени релаксации») сохраняют неравновесное значение колебательной
части энергии, пока под действием повторных соударений молекул
газ не достигнет равновесного состояния. В пограничном слое в области
лобовой критической точки тела происходит течение релаксирующего
газа, свойства которого должны быть учтены при расчетах тепло-
передачи.
При достаточно высоких температурах газа (начиная примерно
с 3000—4000° К) в нем возникают явления диссоциации молекул,
сопровождаемые обратным процессом рекомбинации. Газ перестает
быть однородным, превращаясь, по существу, в смесь газов с раз-
личными физико-химическими свойствами.
Концентрации отдельных компонент, входящих в такого рода
газовую смесь, в условиях отсутствия равновесия переменны и зависят
от быстроты протекания процессов диссоциации, ионизации и ре-
комбинации. Явления определяются не только основными термодина-
мическими факторами, но и такими чисто химическими причинами,
как, например, каталитические свойства обтекаемой поверхности.
Движение ионизированных газов представляет для изучения особые
трудности в связи с необходимостью учета возникающих при движе-
ниях такого рода электромагнитных явлений, образования объемных
сил взаимодействия заряженных частиц с внешними и внутренними
магнитными полями и др.
Для описания всех этих явлений приходится не только вводить
дополнительное дифференциальное уравнение диффузии возникающих
в процессе движения компонент, но и значительно усложнять основ-
ное уравнение баланса тепла, принимая во внимание приток к газу
«скрытой» теплоты образования компонент, перенос тепла при диф-
фузии этих компонент и др. Вопрос усложняется еще и за счет того,
что при высоких температурах возникают фазовые превращения по-
верхности обтекаемого тела (плавление, испарение) и, кроме того,
возможны химические реакции, например горение.
Особого типа трудности возникают при рассмотрении погранич-
ных слоев в разреженных газах. Известно, что если при сравнительно
небольших разрежениях газ может еще рассматриваться как непре-
рывная среда и отличие его от неразреженных газов заключается
лишь в том, что в этих условиях газ перестает быть «ньютоновской»
жидкостью, т. е. движение его не описывается уравнениями Навье —
Стокса и обычными граничными условиями прилипания к твердой
границе (явление «скольжения»), то при значительных разрежениях,
в условиях, когда длина свободного пробега молекул становится сравни-
мой или даже превосходящей размеры обтекаемого тела, уже нельзя
пользоваться методами механики сплошных сред и на смену им при-
ходят статистические методы кинетической теории газов.
256 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VIII
Появление этих новых, трудных для теоретического анализа во-
просов, естественно возникших в эпоху ракетных самолетов и
космонавтики, не привело к «кризису» аэродинамики. Новые вопросы
оказались тесно связанными с классическими вопросами газовой ди-
намики и методы решения этих вопросов остались прежними, «макро-
скопическими» методами механики сплошных сред. Уравнения движе-
ния вязкого (реального) газа частично сохраняются теми же, что и
лля обычного, однородного газа, но содержат также и дополнитель-
ные члены, выражающие особенности новых процессов. Повысилась,
естественно, роль физики и химии и, в частности, современной кине-
тической теории материи и электродинамики. Закономерность про-
цесса продолжающегося сближения механики жидкостей и газов
с физикой и химией оправдывается сложностью тех физико-хими-
ческих явлений, которые развиваются в газах при очень больших
скоростях их движения.
Не потеряли до сих пор своего значения и «классические» во-
просы теории пограничного слоя. Многочисленные исследования
показывают, что для большинства встречающихся на практике дви-
жений тел сохраняет свое значение классическая постановка задачи
о пограничном слое в недиссоциированном и неионизированном газе.
Во всяком случае тепловые расчеты дают в этих условиях вполне
удовлетворительные результаты ').
§ 54. Основные уравнения движения вязкого совершенного газа
При выводе уравнений движения вязкого совершенного газа
примем следующие обычные допущения2):
1) давление р, плотность р и абсолютная температура Т газа
связаны уравнением Клапейрона
? А=±Л, (8.1)
где h = JcpT 3) — энтальпия (тепловая функция) газа, k = cp/cv — отно-
шение коэффициентов теплоемкостей газа при постоянном давле-
нии ср и постоянном объеме cv, J—механический эквивалент тепла,
') Подтверждение этого факта было дано в систематическом обзоре,
составившем предмет доклада А. Ферри (США) на X Международном кон-
грессе по прикладной механике в Стрезе (Италия) 31 августа — 7 сен-
тября 1960 г.
2) См., например, Лойцянский Л. Г., Механика жидкости и газа,
Гостехиздат, 1957, гл. X.
т
3) В общем случае ft = / Г cp(T)dT, откуда при условии ср = const
о
следует равенство h = JcpT.
; 54] ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОГО СОВЕРШЕННОГО ГАЗА 257
i — газовая постоянная, связанная с предыдущими величинами про-
тым соотношением
R = J(cp-cv).
"акого рода газы называют совершенными. Часто употребляемый
ермин «идеальный газ» лучше сохранить для обозначения газа,
.пшенного внутреннего трения — вязкости;
2) газ представляет «ньютоновскую» жидкость, т. е. удовлетво-
>яет обобщенному закону Ньютона о линейном характере связи
?ежду тензорами напряжений Р и скоростей деформаций 5. Принимая
;ля второго коэффициента вязкости [*' условие [i/ = — 2/3[а, получим
:ли в матричной форме
Рхх> Рух- Ргх
1 / dw , ди \ 1 / dw _, dv \ dw
/1. 0. 0\
— (р + I- У-div У)\ 0. 1, 0 I;
\0. 0, 1/
(8.3)
3) динамический коэффициент вязкости р. является функцией
олько абсолютной температуры Т. В дальнейшем используются раз-
:ичные законы этой зависимости. Прежде всего отметим выводимую
1 кинетической теории газов формулу Саттерлэнда
(8.4)
т+т.
-де Ts — постоянная Саттерлэнда, имеющая для воздуха значение,
•лизкое к 102°С, а То и jx0 — абсолютная температура и коэффи-
1иент вязкости, соответствующие некоторому начальному состоянию
-аза. Широко применяется также степенная формула
(8.5)
п = %
п =: 3/4
де я = 72 для сравнительно высоких температур и л=1 для
юлее низких. По Карману в среднем л = 0,76. Иногда считают
= % при 90° < 7 < 300° К.
при 250° < Т < 600° К.
17 Зак 297. Л Г Лойияиский
258 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VII
Чепмен и Рубезин') предложили для пользования в теории погрь
ничного слоя простой линейный закон связи fi и Т:
-?^ = C-r- = C-F- (8.6
Г^СО 00 СО
с постоянной С, равной (Гш — температура на стенке, Т^ — темпе-
ратура на внешней границе слоя)
, j. . i/j ¦p | -р
С = I -у— I -= , _ ; (8.7
4) коэффициенты теплоемкости ср и cv, а следовательно, и и:
отношение k не зависят от абсолютной температуры газа и являются
физическими константами газа;
5) коэффициент теплопроводности газа X пропорционален дина
мическому коэффициенту вязкости, так что число Прандтлг
Pr = (icp/X, в дальнейшем для простоты письма обозначаемое через с
рассматривается как физическая постоянная газа
р.ср/Х = о = const. (8.8
Пользуясь принятыми допущениями и основными законами дина
мики и термодинамики, можно вывести систему основных уравнени?
движения жидкости. Не будем этого делать, а лишь напомним2
главные этапы вывода.
Закон сохранения массы приводит к уравнению неразрывности
(t — время, V—вектор скорости)
|f+div(PVO = 0. (8.9
Закон сохранения импульса при отсутствии объемных (массовых
сил дает основные динамические уравнения движения газа
du dp . о д I ди \ . д Г (ди , dv
д Г
ди
д Г
,(du |
0 «^ (
-4- д Г
<)» \
1 dz )
2
3 (
/ dv
2
, I 1—
2
3 с
d
I ( djvV
)z ^ -*¦
dv p , 0 ( \
. д г (dv . dwU 2 д ...... (-бли
dw dp
') Chapman D. R., Rubesin M. W., Journ. Aeron. Sci. 16, №'
A949), 547—565; русск. пер. см. сб. «Механика», ИЛ, 1950, в. 4, стр. 50.
2) См. наш ранее цитированный курс «Механика жидкости и газа..
Гостехиздат, 1957, гл. X.
§ 55] ДВЕ ОСНОВНЫЕ ФОРМЫ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 259
Наконец, из общего закона сохранения энергии совершенного
газа следует уравнение баланса энергии в одной из следующих
двух форм:
rih dn 2
или
Величину
h + ~=h0 (8.13)
будем в дальнейшем называть «полной энтальпией» газа; входящая
в правые части уравнений (8.11) и (8.12) величина q представляет
отнесенное к единице массы секундное количество тепла, подводи-
мого к данной точке потока. Если подвод тепла происходит при
помощи теплопроводности, то при принятых допущениях будем иметь
Jpq = div (— grad h) = — div (p.grad h). (8.14)
Случай притока тепла путем излучения будет в дальнейшем рас-
смотрен особо.
Индивидуальные производные, входящие в левые части уравне-
ний (8.10), (8.11), (8.12), могут быть обычным путем разложены
на локальную и конвективную части по формуле -тт = -*г-\- V • V.
Не будем выписывать в координатной форме таким образом пре-
образованные уравнения (8.11) и (8.12), в которых еще надо заме-
нить последний член, выражающий приток тепла, его представлением
по (8.14).
Приведенная в настоящем параграфе система уравнений является
замкнутой и может служить для определения неизвестных величин:
компонент скорости и, v, w, давления р, плотности р и темпера-
туры Т газа. Для получения конкретного решения должны быть
заданы известные из общего курса аэродинамики граничные,
а в случае нестационарного движения и начальные условия.
§ 55. Две основные формы уравнений пограничного
слоя в газе
Вывод уравнений ламинарного движения газа в пограничном слое
при больших скоростях содержит по сравнению с выводом, приве-
денным в главе I, некоторые существенные особенности. Остано-
вимся, чтобы подчеркнуть основную идею вывода, на наиболее про-
стом случае стационарного плоского пограничного слоя при отсутствии
17»
260
ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ
[ГЛ. VII
объемных сил. Обобщение выведенных уравнений на другие случае
не составит труда.
Как и в главе I, будем считать, что толщина слоя мала по срав
нению с кривизной поверхности тела, так что вблизи поверхносп-
криволинейные координаты, отсчитываемые вдоль и поперек слог,
можно рассматривать как обычные ортогональные декартовы коор-
динаты. В этих предположениях система уравнений Навье — Стоке;
при пользовании уравнением баланса тепла (8.12) может быть пое^
ставлена в форме
ди
dv
ди \ др
ди
2 d
dv
d ( ди\, d
ду Vх dy)^"dy~
dv
dv
dp
ди
dv
3 dy
dy ) 3 dy V4 dx )'
Ox
v
d I h . 4 u2 v2\
-53^7+3-2- +TV
ди
dv
Приведем систему (8.15) к безразмерному виду, причем, имег
в виду уже отмеченное в главе I основное свойство пограничной
слоя—малость поперечных размеров и скоростей по сравнении
с продольными, выберем различные постоянные по величине мас-
штабы: X и U — для продольных размеров и скоростей, Y v
V — для поперечных. Положим для определенности X равным харак
терному продольному размеру тела L (например, хорде крыла,
a U — скорости Um набегающего на тело потока. Масштабы Y и *
пока оставим произвольными.
В качестве масштабов плотности, вязкости и теплопроводное™
используем их значения в какой-нибудь фиксированной точке потоки
для определенности в набегающем потоке (т. е. р^, ц,^, \\. Остается
еще выбрать масштабы для давления и температуры (или энтальпии'.
В этом направлении имеет место некоторый произвол. В первыг
двух (динамических) уравнениях системы (8.15) сохраним для давле-
§ 55] ДВЕ ОСНОВНЫЕ ФОРМЫ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 261
ния тот же масштаб — удвоенный скоростной напор pJU2^, что и
в случае несжимаемой жидкости. Масштаб абсолютных давлений р
связан с предыдущим масштабом очевидным соотношением
(8.16)
Примем за масштаб энтальпии или температуры их значения A^
или Гсо в набегающем потоке. С точки зрения размерности с той же
целью можно было использовать, соответственно, величины Ua,
U2m
или -т—• Отношение этих различных по природе, но одинаковых
по размерности масштабов, так же как и в случае давления, выра-
жается через основные определяющие движение газа величины k
и Ma, по формуле
(8Л7)
Обозначая штрихом безразмерные значения входящих в уравнения
величин, т. е.
x' = x/L, y' = y/Y, и'= и/U и, v' =
после простых приведений получим следующую безразмерную форму
уравнений Навье — Стокса:
f f ди' VL / ди' др' 4 v^ д I ди'
2 V VL д ( ,dv'
/_^ч» д ( ,ди'\
3 UJL ' UJT дх' yj
¦ ^ VL
^ U^L UJT dy
dv' VL dv' U^L dp' v U L
udv'\
' V1 dx' I'
dv'
2 ^ UmL д I t ди' \
~ "з" 77\Г ' ~W W V" IFJ'
dy'
д(/и') VL d (p V) __ _
dx' + V^F dy' —U>
262 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VIII
д [ U'L. / и.'2 V2 v'2 \
V —• \h' + —— ( 1 r —— ) +
дх'[ АД2Т^ 2 ]\^
VL д Г (У2 /и'2
dx'V-V ду'П 3 A^Z.
I
2
2 V-^ д
^3 Ul 2
dv'\ 2 vjf д i du'
h
ду' V дх' I ' 3
- °° a' t.' —
— .л " • Г
Распорядимся пока еще произвольными поперечными масшта-
бами К и V, так же как и в случае несжимаемой жидкости (глава I),
положив
¦=1. ~ L
вводя рейнольдсово число Reco=—— , будем иметь равенства
,. (8.19)
Эти равенства выражают важный факт, что в пограничном слое
в сжимаемой жидкости, так же как в несжимаемой, поперечный
размер слоя и поперечная скорость убывают с ростом рейнольдсова
числа по закону (8.19).
Пользуясь соотношениями (8.18) или (8.19), а также (8.16) и
(8.17), получим безразмерные уравнения движения газа в следующем,
.содержащем явно рейнольдсово число Reo5 число Маха М», число
§ 55] ДВЕ ОСНОВНЫЕ ФОРМЫ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 263
Прандтля о и показатель адиабаты k, виде:
да' , , , да' др' д
Г 4 д I , ди'\ 2 _д_ ( , dv^\ J_( , дх^ЛЛ
U l^V" ~dF)—-3 дх' V1 ду')^~ду'\^ дх')Г
— — 1 ' <*L\—.?--!*—( 'ifil
3 dy' V dy'l 3 dy' V dx'
eL^ dx
' V dx' 1'
dx'
(k -1) M'
Reco
Reo
дх'
4 и'
"
Reo
(8.20)
7 =
Предполагая, что при больших значениях Re^ решения этой
системы уравнений можно искать в виде разложений по степеням
малого параметра 1/ У Reoo, удовольствуемся нулевым приближением,
которое легко составить, полагая просто в (8.20) Reoa=oo при конеч-
ности остальных величин. Это нулевое приближение и представляет
то, что мы называем уравнениями пограничного слоя. Заметим
прежде всего, что при таком предельном переходе второе уравнение
системы (8.20) приводится к условию др'/ду' = 0, выражающему
известный уже из теории пограничного слоя в несжимаемой жидкости
факт постоянства давления в данном сечении слоя. Это позволяет,
опустив второе уравнение системы (8.20), заменить в первом урав-
нении др'/дх' на dp'jdx'.
Совершая в системе (8.20) указанный предельный переход, полу-
чим первую основную форму уравнений плоского стационарного
264 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ
пограничного слоя в газе в безразмерном виде:
[ГЛ. VII
Р
и'— -1-oV — — dp
U дх' ~t~p v ду' ~ dx'
дх'
—
ду'
д(9'и')
дх'
dx'
U' ди'\
ду' \Р ду')'
"•"
— 1
,2\ , / , д (,. . k — 1 „2 ,2\
(8.21
Возвращаясь к размерным величинам и используя обозначение я,
для полной энтальпии (8.13), получим первую основную
уравнений пограничного слоя в обычном, размерном виде:
ди
dp
дх
ди
(f) +
f822
Дл-я дальнейшего представит интерес еще вторая форма ура>.
нений пограничного слоя, отличающаяся от первой видом уравнени.
баланса тепла. Эту вторую форму можно получить, обращаясь к урар
нению баланса (8.11). Проще, однако, чтобы не повторять кропо!
ливые вычисления, обратиться к первой форме уравнений погр<-
ничного слоя в безразмерном виде (8.21). Переписав третье уравнениь
этой системы в виде
, , dh' . , , dh'
1 д
, dh'
./ ди' \
используем первое уравнение той же системы; это упростит полу
ченное только что равенство и позволит установить следующук
вторую основную форму уравнений плоского стационарноп
55] ДВЕ ОСНОВНЫЕ ФОРМЫ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 265
пограничного слоя в безразмерном виде:
ди' , ./-./^1 = _^1, д
ду' dx' ' ду'
д(9'и') d(?'v'
дх' "+" ду'
, , dh'
Р" дх7
(8.23)
Возвращаясь к обычным, размерным величинам, найдем вторую
основную форму уравнений плоского стационарного пограничного
слоя в размерном виде:
ди . ди dp , д / ди \
Р ^jc ~" " dy dje "' dy v ду j'
дх
+ ^TTL = (
ду
dh
dh
dp
ди \г
й—1
(8.24)
Третье уравнение в системе (8.24) имеет простой физический
смысл: оно выражает в явной форме очевидный факт баланса кон-
пективного изменения энтальпии (левая часть уравнения) с суммой
мощности сил давления (первый член справа), тепла, возникшего
8а счет диссипации механической энергии (второй член справа), и
тепла, подведенного путем теплопроводности (третий член справа).
В некоторых случаях представляется необходимым иметь дело
не с энтальпией h, а непосредственно с абсолютной температурой Т.
Первые два уравнения системы (8.24) остаются прежними, а осталь-
ные, очевидно, должны быть переписаны так:
дТ
дт
p=RPT,
(8.25)
Аналогично могли бы быть преобразованы и уравнения (8.22).
Для простоты рассуждения нами был рассмотрен выше лишь
случай плоского стационарного пограничного слоя. Заметим, что
в случае пограничного слоя при осесимметричном обтекании тела
вращения можно приближенно пользоваться теми же уравнениями,
266 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VIII
что и в плоском движении, заменив лишь второе уравнение (уравне-
ние неразрывности) следующим:
где го = го(х) представляет собой радиус поперечного сечения тела
вращения. Такая замена достаточна, конечно, лишь в предположе-
нии о допустимости пренебрежения толщиной слоя по сравнению
с радиусом сечения тела. Как было показано в § 35, в случае длин-
ных тел такое допущение может привести к неудовлетворительным
результатам.
Если плоский пограничный слой нестационарен, то в уравнениях
должны быть учтены дополнительные локальные изменения входя-
ди
щих в них величин: р—зт- в левой части первого (динамического) урав-
нения, -^—в левой части второго (уравнения неразрывности), р-^
в левой части третьего уравнения (8.24) и ~ — в правой части
того же уравнения. Кроме того, конечно, как и в случае несжимае-
мой жидкости, производная dp/dx должна быть заменена на др/дх,
так как в нестационарном движении давление зависит еще от вре-
мени t.
Граничные и начальные условия для уравнений пограничного слоя
в случае газа, движущегося с большими скоростями, в своей дина-
мической части остаются теми же, что и в случае несжимаемой
жидкости. Это — условия прилипания газа к поверхности твердого
тела, задание скорости газа вдалеке от тела, а также начального
распределения скоростей в случае нестационарного движения. Новыми
являются граничные и начальные условия для температуры (энталь-
пии) газа. Может быть задано распределение температуры или тепло-
отдачи (производной от температуры по нормали к поверхности)
по поверхности тела, в частном случае температура тела, одинаковая
по всей поверхности, и температура набегающего потока. В неста-
ционарном случае задается начальное распределение температуры
в потоке.
§ 56. Области применимости уравнений пограничного слоя
Приведенный в предыдущем параграфе вывод нуждается в неко-
торых оговорках. Предельный переход Re,»—>-oo, совершенный в си-
стеме (8.20), относился к безразмерным уравнениям, в которых по-
перечные координата и скорости выражены в частях величин, зависящих
в свою очередь от рейнольдсова числа Re^ и стремящихся в пределе
к нулю. Понимать это можно только так, что уравнения погранич-
ного слоя приближенно справедливы при достаточно больших зна-
§ 56] ОБЛАСТИ ПРИМЕНИМОСТИ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ 267
чениях Reoo. Само собою разумеется, что при не слишком боль-
ших Ret» уравнения пограничного слоя, так же как и само пред-
ставление о пограничном слое, теряют свой смысл. Нельзя указать
границу значений Re,», начиная с которой можно пользоваться урав-
нениями пограничного слоя (8.21) и их видоизменениями. Некоторые
представления об этой границе были даны в главе I, когда говори-
лось о приближениях высшего порядка в разложениях решений по
степеням малого параметра и, в частности, о формуле A.46) сопро-
тивления, предложенной Го Юн-хуаем для пластинки и справедливой
при Ret» !> Ю. При меньших значениях Reco необходимо обращаться
к следующим приближениям или, быть может, правильнее пользо-
ваться непосредственно общими уравнениями Навье — Стокса.
Обращаясь к уравнениям (8.20), заметим, что кроме членов,
содержащих в качестве множителей нулевые и отрицательные сте-
пени числа Re^, имеются еще такие члены, как последний член
в четвертом уравнении баланса тепла системы (8.20). Порядок
этого члена оценивается величиной mL/R^co. При сравнительно боль-
ших значениях числа М^, (порядка 10) и не слишком больших Re,»
(порядка сотен) отбрасывание соответствующего члена в уравнении
баланса не оправдано.
Оценим в связи с этим порядок величины отношения M^/Reao.
Для этого, наряду _ с ранее введенными характерными размерами
тела L и пограничного слоя 8, рассмотрим еще основной молекуляр-
ный размер'—длину / свободного пробега молекул газа между двумя
последующими столкновениями их. Из известной формулы для дина-
мического коэффициента вязкости
jj. = 0,499рг>/,
где © — средняя скорость свободного пробега молекул, выражаю-
щаяся через давление и плотность или скорость звука согласно
соотношению (k — cp/cv)
р
получим
/=1.255 1/"*-.
'а
Составим1) характерное для рассматриваемого явления — движе-
ния газа в пограничном слое — отношение
') TsJen H. S., Journ. Aeron. Scl. 13, № 12 A946); русс*, пер. в сб.
«Газовая динамика», ИЛ, 1950, стр. 310—357.
268 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VII!
При больших значениях числа Рейнольдса Re,» — —^—, со-
гласно (8.19), 8/Z,= 1/y Reco, так что
— = 1.255 V~k-
8
Отсюда следует, что интересующая нас величина Moc/yReco имеет
порядок отношения длины свободного пробега молекул газа к тол-
щине пограничного слоя.
Таким образом, можно прийти к заключению, что уравнения
пограничного слоя, выведенные в предыдущем параграфе, спра-
ведливы, во-первых, при достаточно больших рейнольдсовых чис-
лах и, во-вторых, при условии сравнительной малости длины сво-
бодного пробега молекулы по отношению к толщине пограничного
слоя. Последнее условие означает, что газ не должен быть разре-
женным.
Если движение газа происходит при малых значениях рейнольд-
сова числа ¦), то, как уже указывалось, теряется само представление
о пограничном слое. Можно сказать, что пограничный слой стано-
вится сравнимым по толщине с потоком в целом (Ь-zaL), и тогда,
в отличие от только что составленной формулы для отношения //8
при больших рейнольдсовых числах, при малых значениях Reco будет
Мсо
ReM '
Пользуясь отношением //8 как основным критерием применимости
уравнений пограничного слоя (или, более общо, уравнений Навье—
Стокса), можно весьма приближенно наметить области соотношения
чисел Рейнольдса Reco и Маха Мш, при которых при данном k.
сравнительно мало меняющемся от газа к газу, должны применяться
те или другие методы расчета течений вязкого газа. На заимство-
ванной нами из цитированной статьи Ченя диаграмме, показанной
на рис. 60, нанесены в полулогарифмическом масштабе линии связи
между Мсо и Reco при трех заданных значениях параметра //8: 0,01;
1; 10. Эти линии, конечно, весьма условно и грубо разграничивают
области применимости различных методов исследования газовых
потоков.
') ? статье, помещенной в «Abhandl. aus dera Aerod. Inst. Aachen», № 4,
1925, Карман заметил, что рейнольдсово число, как это сразу следует из
тех же кинетических соображений, что и при выводе предыдущих формул,
может быть представлено в виде Reco = (f/m/tT) (Ljl). Мал?сть этой величины
может иметь место в следующих Случаях: 1) L яй /, Uaa <^C v (броуновское дви-
жение мелких частиц, взвешенных в жидкости или газе), 2) L ~^>> I, ?/<» <^1J
(обычные условия «медленного» движения тела в вязкой жидкости);
3) L <^ /, t/oo^f (движение тел в сильно разреженных газах).
§ 56] ОБЛАСТИ ПРИМЕНИМОСТИ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ 269
Правая крайняя область характеризует совокупность значений Re»
и Моо, для которой справедливы уравнения обычной газовой дина-
лики, т. е. при принятых ранее допущениях уравнений Навье — Стокса.
При больших рейнольдсовых числах в этой области можно пользо-
ваться уравнениями пограничного слоя в газе при больших скоро-
стях, если числа Моо значительно отличаются от нуля, и уравнениями
пограничного слоя в несжимаемой жидкости, если числа Моо мало
отличаются от нуля. Асимптотический ход ограничивающей рассматри-
ваемую область кривой при очень малых рейнольдсовых числах
показывает, что в этих условиях только при совершенно незначи-
тельных величинах Моо. т. е. при очень малых абсолютных скоро-
стях движения, допустимо приме-
нение уравнений гидродинамики;
это соответствует классической
области «медленных движений»,
задаче Стокса о шаре и т. п.
Левая крайняя область значе-
ний Моо И Re,» ОТНОСИТСЯ К СИЛЬНО
разреженным газам, когда" уже
вообще нельзя говорить о газе
как о непрерывной среде. Это —
область свободного молекулярного
движения газа, описываемого ста-
тистическими методами кинетиче-
ской теории газов. В настоящее
время эти методы заняли свое
место в расчетах силовых и теп-
ловых воздействий разреженной атмосферы на летящее в ней тело
при очень больших высотах полета (супераэродинамика)J).
Наибольшие трудности представляет, как всегда, промежуточная
область. До сих пор нельзя еще говорить об установившихся мето-
дах расчета движений, и в частности, движений в пограничных
слоях в этой области значений Re,» и Моо. хотя вопросами этого
рода во второй половине XIX века занимался еще Максвелл,
а в начале нашего века Кнудсен, Милликен и др. Если говорить
о той части рассматриваемой промежуточной области, которая гра-
ничит с крайней правой областью применимости уравнений Навье —
Стокса, то здесь, по-видимому, можно удовольствоваться введением
некоторых поправок в обычные методы механики жидкости и газов.
Поправки эти идут в двух направлениях. Во-первых, становится
-2 -/ О /
2 3 4 5 ff 7 в
Iff Я»
Рис. 60.
') Некоторое представление о задачах и методах этого раздела аэро»
динамики можно получить, ознакомившись с содержанием гл. X моногра-
фии Hayes W., Р г о b s t e i n R., Hypersonic flow theory, Acad. Press.
N. Y.-London, 1959.
270 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VIII
необходимым введение дополнительных членов в уравнения Навье—
Стокса, появляющихся за счет невозможности пользоваться в этих
условиях обычными линейными законами Ньютона и Фурье для вязких
напряжений и потока тепла. Как показал Барнетт 1), из кинетических
соображений следует, что в рассматриваемой части переходной области
наряду с обычными линейными членами в выражения компонент
тензора вязких напряжений и вектора потока тепла должны входить
нелинейные комбинации производных скоростей по координатам,
абсолютной температуры и ее производных по координатам. Не
выписывая этих сложных выражений, укажем лишь на основной
принципиальный факт: отношение этих дополнительных членов
к основным, соответствующим законам Ньютона и Фурье, имеет
тот же порядок M^/Reoo. что и последний член в четвертом урав-
нении (баланса энергии) системы (8.20). Таким образом, в рассма-
триваемой сейчас промежуточной области не имеет смысла брать
старшие приближения в разложениях решений по малому пара-
метру ll^Reoo, если не учтены добавочные члены в самих уравнениях
Навье — Стокса.
Во-вторых, и это, быть может, имеет наиболее принципиальное
значение, изменению подлежат граничные условия на поверхности
твердого тела как для скоростей, так и для температур, Еще
в 1875 г. Кундт и Варбург 2) при проведении опытов с затуханием
колебаний диска в газе обратили внимание на факт уменьшения зату-
хания диска при снижении давления в газе. Этот факт, никак не
укладывающийся в законы механики ньютонианской вязкой жидкости,
смог быть объяснен лишь отказом от свойства прилипания вязкой
жидкости к поверхности движущегося в ней тела. Было сделано
предположение о наличии скольжения газа по поверхности диска,
причем скорость uw этого скольжения для изотермического движе-
ния была принята пропорциональной величине нормальной к поверх-
ности диска производной от скорости движения газа вблизи диска:
«w = -r|H (8-26)
коэффициент f получил наименование коэффициента «скольжения».
Кундт и Варбург на основании своих опытов показали, что коэф-
фициент скольжения, имеющий, очевидно, размерность длины, про-
порционален длине свободного пробега молекул и близок к ней по
своей численной величине; коэффициент этот должен быть обратно
пропорционален абсолютному давлению в газе. Теория «скольже-
') Burnett D., Ргос. of Lond. Math. Soc. 40 A935), 382—435.
2)Kundt, Warburg, Ann. d. Physik, 155 A875).
§ 56] ОБЛАСТИ ПРИМЕНИМОСТИ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ 271
ния» была дана в 1879 г. Максвеллом '), предложившим формулу
7 = 0,998-^=^-/; (8.27)
величина / выражает долю касательного к поверхности тела коли-
чества движения молекул, теряющегося при ударе молекул о поверх-
ность тела. Эта доля также близка к единице.
Физически явление происходит так. Молекулы газа при встрече
с твердым телом попадают на сложную по молекулярной структуре
«шероховатую» поверхность тела. При этом только небольшая часть
молекул непосредственно отражается от поверхности тела, а пода-
вляющее число молекул «застревает», абсорбируется поверхностью
и лишь затем уже как-то диффузно, т. е. независимо от направле-
ния падения молекул на поверхность, испускается, реэмитируется.
Как показывают опыты, коэффициент / имеет близкие к единице
значения при течении воздуха над металлической поверхностью или над
ртутью и несколько отличается от единицы при течении над стек-
лом или маслом.
При неизотермическом движении разреженного газа граничные
условия для скорости усложняются и принимают вид
Кроме того, возникает необходимость выполнения еще гранич-
ного условия для температуры на стенке. Подобно скорости, тем-
пература Т вблизи поверхности тела также претерпевает скачок,
пропорциональный длине I пути свободного пробега молекулы,
а именно
^.-^.^/lf; (8.29)
здесь: а — коэффициент аккомодации, введенный Кнудсеном и выра-
жающий долю той части молекул, которые после соприкосновения
с поверхностью при реэмиссии их приобретают среднюю энергию,
«аккомодированную» (приспособленную) к энергии молекул, имеющих
температуру поверхности тела Тр\ k = cpjcv, X — коэффициент тепло-
проводности. Таблицу значений коэффициентов аккомодации а,
так же как и коэффициентов скольжения ~[, можно найти в цитиро-
ванной статье Ченя и в специальных руководствах по кинети-
ческой теории газов.
Применение уравнений движения разреженных газов (уравнений
Барнетта) к расчету конкретных потоков, в частности к погранич-
ному слою, представляет пока еще непреодолимые трудности. В пер-
') Maxwell С, Philos. Trans, of the Roy. Soc. of London, 170 A879),
231-256.
272 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VII!
вых работах, относящихся к этой области, довольствуются лишь
изменением граничных условий, т. е. решают обычные уравнения
пограничного слоя, но с принятием во внимание скачков скорости
и температуры на поверхности обтекаемого тела ').
§ 67. Уравнения пограничного слоя в потоке смеси
реагирующих между собой газов
Уравнения пограничного слоя, выведенные в § 55 для случая
однородного газа, могут быть обобщены и на случай движения смеси
разнородных и химически реагирующих друг с другом газов, как
это имеет место, например, в случае диссоциации или ионизации
газа при высоких температурах и обратной рекомбинации, при
явлениях горения и др.
Сохраним обозначения плотности р, давления р, скорости V(u, v),
энтальпии h (или абсолютной температуры Т) и других величин для
смеси газов и условимся обозначать индексом / соответствующие
значения этих величин для отдельных компонент, входящих в смесь
газов.
Обозначим через tnl отнесенную к единице объема секундную
массовую скорость образования i-й компоненты в данной точке
потока. Тогда уравнение неразрывности для этой компоненты в слу-
чае плоского стационарного движения запишется в форме
Закон сохранения массы смеси требует выполнения условий баланса
секундных масс отдельных компонент
2«( = 0. (8.31)
Определяя плотность и вектор скорости смеси условиями
рн=2р<«/' Р«=2рЛ» (8-32)
/ t
получим, суммируя обе части уравнения (8.30) по всем компонентам
и используя (8.31) и (8.32),
-^(Р«) + ^г(Р*) = О. (8.33)
Это — уравнение неразрывности для смеси газов, ничем не отли-
чающееся от уравнения неразрывности для однородного газа.
') Простые примеры такого рода решений см. в гл. X, § 76.
§ 57] СЛОЙ В ПОТОКЕ СМЕСИ РЕАГИРУЮЩИХ МЕЖДУ СОБОЙ ГАЗОВ 273
Динамическое уравнение для смеси газов будет тем же, что и
для однородного газа с плотностью и коэффициентом вязкости, соот-
ветствующими смеси газов, т. е.
ди , ди dp , д
Пусть уравнение состояния для 1-й компоненты смеси имеет
вид (Rt — газовая постоянная /-й компоненты)
где pi — парциальное давление J-й компоненты смеси.
Принимая температуру всех компонент равной общей равновесной
температуре Г смеси и вспоминая закон Дальтона, согласно кото-
рому давление смеси равно сумме парциальных давлений компонент,
будем иметь
Обозначая через с, массовую (весовую) концентрацию 1-й компо-
ненты, равную
с, = Р,/р. (8.35)
преобразуем предыдущее равенство к виду
p=RpT, (8.36)
где величину
/? = 2Sc,/?, (8.37)
можно принять за газовую постоянную смеси газов. Уравнение со-
стояния (8.36) для смеси газов сохраняет при этом ту же форму,
что и в случае однородного газа.
Для вывода уравнения баланса тепла можно воспользоваться
соответствующим однородному газу третьим уравнением системы (8.24),
но принять во внимание следующие дополнительные соображения.
Конвективный подвод тепла определяется так же, как и в случае
однородного газа, с той лишь разницей, что энтальпия смеси опре-
деляется по простому правилу смешения, как сумма энтальпий ком-
понент смеси, умноженных на соответствующие им концентрации,
т. е. суммой 2 еА-
i
Наряду с членами, стоящими в правой части третьего уравне-
ния системы (8.24) и выражающими, как уже упоминалось, мощность
сил давления, секундное количество тепла, возникшего за счет дис-
сипации механической энергии и подведенного путем теплопровод-
ности, необходимо еще принять во внимание два новых источника
тепла, характерных для рассматриваемого движения смеси газов.
18 Зак. 297. Л. Г. Лойцянский
274 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VUI
Во первых, при образовании /-и компоненты с массовой ско-
ростью mi выделяется секундное количество тепла /И;Л,-, где под hi
понимается постоянная, характерная для данной компоненты смеси
энтальпия или «скрытая» теплота образования компоненты. Это при-
водит к необходимости присоединения к правой части третьего урав-
нения системы (8.24) члена
%mth*, (8.38)
i
равного, согласно уравнению неразрывности (8.30) и соотноше-
нию (8.35), величине
<) + (С
Диффузия частиц компонент газа в смеси является также дополни-
тельной причиной переноса тепла. Замечая, что скорость диффу-
зии 1-й компоненты определяется скоростью движения этой компо-
ненты по отношению к газовой смеси, т. е. векторной разностью
абсолютных скоростей компоненты и смеси, получим соответствую-
щий поток тепла в форме вектора с проекциями
—и)А,. ?i{vi — v)hi
или, согласно (8.35), с проекциями
p(ul~u)cih[, p(vt — v)c,hl. (8.40)
Дополнительный член в правой части третьего уравнения си-
стемы (8.24), соответствующий этому источнику переноса тепла,
определится взятой с обратным знаком дивергенцией суммы векто-
ров потоков тепла (8.40), вызываемых отдельными компонентами,
т. е. величиной
Таким образом, уравнение баланса энергии для движущейся смеси
газов приведется к виду (Л/ = const)
]--^-[2р^-^с'а'1- (8-42)
§ 57] СЛОЙ В ПОТОКЕ СМЕСИ РЕАГИРУЮЩИХ МЕЖДУ СОБОЙ ГАЗОВ 27?
Проведя тождественное преобразование
\ %
перенося последние два члена в левую часть равенства и принимая
во внимание уравнение неразрывности для смеси газов (8.33), пере-
пишем уравнение баланса (8.42) в несколько более простой форме,
содержащей в качестве основной неизвестной разность энталь-
пий hi — hi,
-gj Г^ ci (hi — Л*I -Н P^^jfr ("S Ci
dp . / ди\2 . д /s dT
Al;l.
] ^
Предпоследним членом справа можно, как всегда в пограничном
слое, пренебречь по сравнению со вторым и переписать уравнение
баланса в виде
Oh . dh dp . I ди \2 .
здесь для краткости введено обозначение
А = 5С'(*'~ **)• (8-44)
Вспомним основной закон диффузии, согласно которому скорость
диффузии /-Й компоненты определяется через градиенты концентра-
ции, температуры и давления по формуле
D, D\ DP
V/-V = --^gradc/--y-gradr —gradp. (8.45)
Слагаемые в правой части выражают последовательно скорости
массодиффузаи, тпермодиффузии и бародиффузии, т. е. те ско-
рости распространения /-й компоненты относительно смеси, которые
возникают за счет неоднородности полей концентраций компоненты
смеси, а также температуры и давления, общих для всех компонент
276 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VIII
в смеси. Соответственно этому и коэффициенты Dit Dit Df носят
наименование коэффициентов массодиффузии (или просто диффузии),
термодиффузии и бародиффузии.
Подставляя значение проекций скорости диффузии на ось, пер-
пендикулярную к направлению скорости движения в пограничном
слое, получим
D, дс, DT дТ D? dp
v,— v = ~^г- --^ —Lt- • (8 46)
' Ci ду Т ду р ду v '
Последнее слагаемое в правой части этой формулы, согласно
известному свойству пограничного слоя, может быть опущено. Роль
бародиффузии в пограничном слое ничтожна.
Используя (8.46) для преобразования выражения, стоящего
в квадратной скобке в правой части уравнения (8.43), получим сле-
дующую форму этого уравнения:
и ^--4- vd~b —и dp • -(даУ \ д (\ дТ
д
"+• ду
[VI/ »ч / дс.
Наконец, составим уравнение баланса концентраций или уравне-
ние переноса г-й компоненты смеси газов. Так же как и преды-
дущее уравнение баланса энергии, оно должно содержать в левой
части характеристику конвекции i-Я компоненты движущейся смеси
газов, а в правой — члены, определяющие диффузию и возникно-
вение этой компоненты из других компонент, как это имеет место,
например, в процессе диссоциации или ионизации газа и рекомби-
нации его. Искомое уравнение баланса получим в форме
дс{ дс1 д Г / dct Dj ^T\~\
Заметим, что по определению энтальпии h будет
и аналогично
y
где величины
, dh.
§ 57] слой в потоке смеси реагирующих между собой газов 277
представляют собой коэффициенты теплоемкости при постоянном
давлении для /-й компоненты смеси. Введем в рассмотрение услов-
ный коэффициент теплоемкости при постоянном давлении для смеси
газов _
ср = ^с,ср1. (8.49)
определенный по простому правилу смешения, справедливому, со-
гласно (8.44), только при -—; — 0, т. е., как иногда говорят, для
„ dh dh
«замороженного» газа. Тогда производные -т— и -т— представятся
так:
dh
Р dv ***v ч ду
(8.50)
Пользуясь этими выражениями производных, перепишем уравне-
ние баланса (8.47) в другом виде, а именно
В последнем члене правой части можно произвести замену выра-
жения в круглой скобке по (8.48). Тогда, раскрывая еще произ-
водную в предпоследнем выражении, найдем
дх
ду
ду \ ду
SI дс,
JW\D4it-
дс,
dT
дТ \ дТ
l
278 ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ [ГЛ. VII!
Произведя сокращение, окончательно получим ') уравнение ба-
ланса энергии в виде, явно содержащем абсолютную температуру,
дТ дТ\ dp , (ди\2 . д
Подобно тому как это делалось в § 55, уравнение баланса
энергии можно представить еще в виде, содержащем полную
энтальпию,
*„ = * + -?. (8.53)
Используя вновь выражения для производных (8.50) и динами-
ческое уравнение (8.34), непосредственно из (8.47) получим следую-
щую форму уравнения баланса:
( +
ду ду\ср дуГдуУУ с„) ду
Если ввести общепринятые обозначения для чисел Прандтля,
Шмидта и Льюиса
g (8.55)
связанных между собою соотношением
Sc/Ci/ = Pr, (8.56)
причем, подчеркнем это, числа Льюиса и Прандтля заключают в себе
ранее введенную условную величину коэффициента теплоемкости ср
при постоянном давлении, то уравнения (8.48) и (8.54) приобре-
тут вид
дс, . дс/ д ( ц дсЛ . д /„г рс; дТ\ , /о __ч
') Fay J. A., Rid dell F. R., Journ. Aeron. Sci. 25, № 2 A958),
73—77.
§ 57] слой в потоке смеси реагирующих между собой газов 279
Полученные уравнения упрощаются, если принять числа Рг и Sc^,
а следовательно и Ьег, равными единице и, кроме того, пренебречь
термодиффузией, т. е. положить D,- = 0. В этом случае уравне-
ния (8.57) и (8.58) перепишутся так:
(8-б0>
В случае нереагирующих газов изменение концентрации компо-
нент в смеси определяется только конвекцией и диффузией; ско-
рость массообразования т1 будет при этом равна нулю, и уравне-
ния баланса вещества (8.59) и баланса тепла (8.60) по "форме
совпадут.
ГЛАВА IX
ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ
В НЕСЖИМАЕМОЙ ЖИДКОСТИ
§ 58. Температурный пограничный слой на продольно
обтекаемой пластинке
Настоящая глава посвящена вопросу о тепло- и массопереносе
в стационарном ламинарном пограничном слое при малых скоростях.
Как будет показано в конце главы, с математической стороны ре-
шения задач о теплопереносе и массопереносе полностью совпадают.
Поэтому в настоящем и последующих семи параграфах будут рас-
смотрены сначала тепловые задачи. Использование полученных ре-
зультатов для расчета диффузии вещества в пограничном слое
составит предмет последних двух параграфов. В этой главе мы огра-
ничимся лишь случаем настолько малого перепада температуры
в потоке, что можно пренебречь влиянием этого перепада на плот-
ность, вязкость и теплопроводность жидкости. Более общие допу-
щения будут приняты в следующих главах, где рассматривается
газовый поток больших скоростей.
В случае малых скоростей (М^^О) в безразмерном уравнении
баланса энергии [третье уравнение системы (8.23)] член с квадратной
скобкой в правой части исчезает; возвращаясь к размерным величи-
нам, получим следующее уравнение баланса тепла:
дТ , .. дТ ч д2Т
Величину
называют обычно «коэффициентом температуропроводности».
Та же форма (9.1) сохраняется и в случае продольного обтека-
ния тел вращения, если толщина пограничного слоя может рассма-
триваться как величина малая по сравнению с радиусом поперечной
кривизны тела. Отличие от плоского пограничного слоя скажется
§ 58] ТЕМПЕРАТУРНЫЙ СЛОЙ НА ПРОДОЛЬНО ОБТЕКАЕМОЙ ПЛАСТИНКЕ 281
лишь в структуре уравнения неразрывности. Если же, подобно тому
как это имело место при движении, рассмотренном в § 35, нельзя
пренебречь толщиной слоя по сравнению с радиусом поперечной
кривизны тела, то приходится пользоваться более общим уравнением
баланса тепла в цилиндрических координатах
дх ' дг а г дг \ дг } v '
Это же уравнение применяется и при решении задач о свободном
осесимметричном пограничном слое в струях и следе за телом.
Наряду с гидродинамическим пограничным слоем, определяемым
как область, где продольная скорость изменяется от нулевого зна-
чения на поверхности тела до значения, соответствующего внешнему
потенциальному потоку, возникает понятие о температурном (его
иногда называют тепловым) пограничном слое, в котором темпера-
тура изменяется от температуры поверхности тела, одинаковой или
переменной вдоль поверхности тела, до температуры внешнего
потока.
Начнем с простейшего примера тепловой задачи Польгаузена 2)
о поле температур и теплоотдаче пластинки в продольном потоке
вязкой теплопроводной жидкости.
Обозначим через Tw температуру пластинки и будем считать ее
одинаковой вдоль всей поверхности пластинки, а через Тт — темпе-
ратуру набегающего потока.
В рассматриваемом случае dp/dx = 0, и дело сводится к инте-
грированию системы уравнений
ди . ди д2и
идт v дт — v дп
дх ' ду и ду2
<»¦»
v
дх ' ду и ду
с граничными условиями
u = v=Q, T=TW при у = ,
г г т т I (9-4)
u—Uoo, T^T^ при у — со. ]
Первые два уравнения системы (9.3) при граничных условиях (9.4)
автономны и соответствуют гидродинамической задаче Блазиуса о по-
граничном слое в изотермическом потоке (§ 4).
') Р о h I h a u s e n E., Zeitschr. f. Angew. Math. u. Mech. 1 A921).
282
ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ IX
Представим поле скоростей в гидродинамическом пограничном
слое в виде (аргумент отличается множителем 7г от аргумента,
принятого в § 4)
(9.5)
где функция ср(т]) удовлетворяет уравнению и граничным условиям
(9.6)
1 = 0, ср' = 0 при т] = О,
ср' —> 2 при т]—>сс
Приведенная в § 4 таблица ср, ср', ср" может быть легко пересчи-
тана на новый аргумент и функцию.
Введем безразмерную разность температур
т т
iw I
8 = 0 при т] = 0, fl=l при tj^co. (9.7)
Переходя в последнем из уравнений (9.3) от переменных (х, у)
к переменным (х, г\), получим после простых преобразований обык-
новенное дифференциальное уравнение
= О, (9.8)
интегралом которого при граничных условиях (9.7) будет
d-ц ].
Замечая, что по (9.6)
О — Г? ^
ч" @) J '
перепишем предыдущее выражение в окончательной форме
(9-9)
§ 58] ТЕМПЕРАТУРНЫЙ СЛОЙ НА ПРОДОЛЬНО ОБТЕКАЕМОЙ ПЛАСТИНКЕ 283
При числе Прандтля о = 1 из последнего равенства следует
С/с
(9.10)
Ч
100
что выражает условие подобия при а = 1 распределений разности
между температурой на стенке и в данной точке сечения погранич-
ного слоя и скорости потока в том же сечении.
В общем случае (о ф 1) распределение 6G]) в температурном
пограничном слое отличается от распределения u(f}) в гидродинами-
ческом слое. Для обычных газов о сравнительно мало отличается
от единицы и разница между кривыми 6(tj) и и(г}) невелика. Для
жидкостей о изменяется в широких пределах (о^> 1 для вязких
масел, глицерина; о <С! 1 Ддя жидких металлов) и разница становится
весьма заметной. На рис. 61 приве-
дены кривые распределения 8 (tj) для
нескольких знамений о, подтверждаю-
щие сказанное; кривая а = 1 пред-
ставляет одновременно и распределе-
ние безразмерной скорости u/Uco.
Обратим внимание на один отчет-
ливо выраженный на графике факт.
Толщина температурного погранично-
го слоя (в том условном смысле, как
это было принято ранее) возрастает с уменьшением числа Прандтля о,
совпадая с толщиной гидродинамического слоя только при о=1.
При о > 1 температурный слой тоньше гидродинамического; при
о< 1, наоборот, гидродинамический слой толще температурного.
Определим местный коэффициент теплоотдачи а(х), равный
Рис. til.
Tw — Та
где <7W — секундное количество тепла, переносимого через единицу
площади стенки,
со
/ (с) = (|L) _о = [ср" (О)]3: f [f (т))]' drt; Rx = ^, (9.12)
а также местное число Нуссельта
(9.13)
Функция /(о) была вычислена Э. Польгаузеном в ранее цитирован-
ной его работе и в интервале 0,6^ а ^15 оказалась приближенно
284 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
представимой равенством
/(а) = 0,664 fa, (9.14)
так что в указанном интервале о можно положить приближенно
Ях = 0,332 V
Интегрирование теплоотдачи по длине L пластинки приводит
к суммарной характеристике теплоотдачи пластинки в форме числа
Нуссельта
L
о
или, согласно (9.14),
Nu = 0,664 f 7 ]/Т^; R00 = i^. (9.16)
Для газов такое приближение вполне допустимо, так как в ин-
тервале 0,6О<[1 разница между точным (9.12) и приближен-
ным (9.14) значениями /(о) не превосходит 1,5%.
§ 59. Температурный пограничный слой при продольном
перепаде давления
Только что рассмотренное решение задачи о температурном по-
граничном слое на пластинке при ее продольном обтекании (U ¦= const)
легко обобщается и на случай заданного распределения скорости U (х)
на внешней границе. Основные уравнения имеют в этом случае вид
ди , ди .. dU , д2и
W+dy~U> " дх ~^~V ~ду— а ду2 '
причем для безразмерной разности температур б сохранено то же
обозначение (9.7), что и в предыдущем параграфе.
Граничные условия примем в форме
u = v = 0. 8== 0 при у = 0, \
a = U(x), 6 = 1 при у = оо. } (9Л8)
Можно заметить, что при о = 1 величина S играет в точности ту же
роль, что трансверсальная скорость w в задаче о пограничном слое
на косо обтекаемом цилиндре (§ 46). Действительно, в этом случае
8 59] ТЕМПЕРАТУРНЫЙ СЛОЙ ПРИ ПРОДОЛЬНОМ ПЕРЕПАДЕ ДАВЛЕНИЯ 285
система уравнений (9.17) и граничных условий (9.18) полностью
совпадает с системой уравнений G.4) и граничными условиями G.5).
Интегрирование уравнений (9.17) при граничных условиях (9.18)
для частных видов функций U (х) и разных о рассматривалось многими
авторами (Фрёсслинг, Голанд, Эккерт и Древиц, Тиффорд и др.) !).
Для случая Фокнера — Скэн, U — cxm, имеем (§11; штрих — про-
изводная по ?)
и = схтФ (с).
(9.19)
и подстановка в третье уравнение системы (9.17) приводит к обык-
новенному дифференциальному уравнению
(&) = 0, (9.20)
которое при граничных условиях (9.18) имеет решение
6 E; р. о) = J ехр I -в J* Ф
J* ехр [ —о J* Ф Д
Значения Ф($; C) можно получить путем численного интегрирова-
ния величин Ф^(Е; fi), представленных в таблице 3.
. Не приводя кривых распределения б($; C, 1), заметим, что анализ
их показывает следующее интересное соотношение между толщинами
скоростного и температурного пограничных слоев при а=1. Если
Р > 0, что соответствует конфузорному участку слоя, где dp/dx < 0,
температурный слой толще скоростного; наоборот, если р < 0, т. е.
в диффузорной части слоя, где dp/dx > 0, температурный слой
тоньше скоростного. Этот важный факт будет в дальнейшем (см.
конец § 88) подтвержден и в более общем случае пограничного слоя
в газе при любом значении температурного фактора.
Определяя местное число Нуссельта N^., найдем
ц,=х-=;
Тш—Тю X Wy/y=0
- х =
_
m + l Ux_ __
') См. Шлихтинг Г., Теория пограничного слоя, ИЛ, 1956.
стр. 282—286.
286
ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. I..
Пользуясь распределением 8(?), выраженным формулой (9.21,
получим окончательно
ГЪ = К(о; m)R'l', (9.2-2
где положено
К (о; т) =
Г
—
ехр — о У Ф (?) d6 rf« . (9.23
о L о J J
В частном случае плоского температурного пограничного слог
вблизи лобовой критической точки цилиндрического тела1) (т=1,
получим следующую формулу для местного числа Нуссельта:
дг. (9.24
где коэффициент А" (о; 1) может определяться из таблицы 20.
Таблица 2(
3
К (а; 1)
0,6
0,466
0,7
0,495
0,8
0,521
0,9
0,546
1,0
0,570
1.1
0,592
7,0
1,18
10
1,34
15
1,54
Для круглого цилиндра диаметра d вблизи лобовой критическо?
точки (т = 1) будет
U = 21/ао sin ~ ^ W
U ooX ja = сх,
так что c = 4UC!Jd и формула (9.24) приводится к виду
Пх=2К(а; :
(9.25
Более общий случай характеризуется заданием скорости внешнеп
потока функцией
U (х) = хт [«„-)- и,лгт+! + u2x2im+» + ...],
и с гидродинамической стороны рассмотрен Гертлером и Виттиь-
гом (§ 14).
Выполняя над уравнением теплового баланса преобразование B.51,
придем к уравнению в новых переменных %, у\
••^-] = 0. (9.26
26 *П-?--2;
о« / д
') См. Современное состояние гидроаэродинамики вязкой жидкости по;
ред. С. Голдстейна, ИЛ, т. 2, 1948.
§ 60] ЗАДАННОЕ РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ПОВЕРХНОСТИ 287
где 0 — то же, что и ранее, а граничные условия будут
6(с, 0) = 0. 6E, оо) = 1. (9.27)
Для случая т— 1 и о= 1, вводя, так же как и в § 14, функцию
х
р E) = 2U' (х) f U (х)
о
и пользуясь разложением
можно получить следующее выражение для числа Nv'):
(N,/R,) B;I/з = 0,5705 + 0,06212^ + (— 0,02105^ + 0,06345^) $2 +
+ @.00826$ - 0,03880ЭД2 + 0,06273р3) I3 +
+ (—0.00364р{ + 0,02222р2р2 —0,03632PiP3 — 0,01769^ -f-
-f-0,06150p4)S4-h@,00175pf — 0,01299p3p2_j_o,02050p2p3_j_
,01994^2 _ o,O3437p,p4 — 0,03300^ + 0,06016p5)$5. (9.28)
В частном случае лобовой критической точки мы получим ро=1,
=: р2 = ... =0, % = -ту R^, и предыдущее равенство сводится
к соотношению
в полном соответствии с (9.22) и таблицей 20.
§ 60. Температурный пограничный слой при заданном
распределении температуры на поверхности тела
Предыдущая задача значительно усложняется, если температура
на поверхности тела Тт не постоянна, а задана как функция про-
дольной координаты х. Впервые такого рода задача была прибли-
женно рассмотрена Фэйджем и Фокнером в 1931 г.2). Уравнение
баланса тепла при тех же обозначениях, что и ранее, приводится
к виду
«jL + B.'-l ±bL + v*2-™. (9.29)
дх ' Tw — Tm dx ' ду з ду2 у
Если распределение скоростей на внешней границе U(х) и тем-
пературы на стенке Tw(x) представляются степенными функциями
') Sparrow E. M., Journ. Aeron. Sci. 25, № 1 A95S).
') Fage A., F a 1 k n e r V., ARC, R & M, 1408, 1931; см. также «Совре-
менное состояние гидроаэродинамики вязкой жидкости», т. II, ИЛ, 1948, § 271.
288 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
то по аналогии с (9.19), вводя в качестве аргумента величину
и выражая компоненты скорости в форме
и = Uf' ft), v = - у (v{//*)Vf [(« -f 1) / ft) + (и - 1) V ft)l-
можно преобразовать (9.29) в обыкновенное дифференциальное урав-
нение (штрих — производная по rj)
' — Т/'-F-1I = 0. (9.30)
Вместо того чтобы воспользоваться известным к тому времени
табличным выражением функции /ft) no Фокнеру и Скэн [подробное
решение в широком диапазоне т было дано Хартри только в 1937 г.
(см. § 11)], авторы предпочли принять приближенное выражение
/ft)=="o °2> гДе я = /"(())• после чего уравнение (9.30) смогло быть
численно проинтегрировано. Следует заметить, что уже это прибли-
женное решение дало удовлетворительное совпадение с опытными
материалами.
Точное решение рассматриваемой задачи было выполнено двадцать
лет спустя Леви'). При тех же степенных заданиях скорости внеш-
него потока и температуры на поверхности тела заменим в уравне-
нии (9.30) неизвестную температурную функцию б на 1 —б и примем
в качестве аргумента вместо t\ переменную Хартри (§ 11)
=уу
U
При этом уравнение (9.30) переходит в следующее (штрих —
производная по \):
б"-f оФб'— оB — р)тФ'6 = 0, (9.31)
где Ф (?) представляет собой функцию Хартри (§ 11), а р = 2/яДот -j- 1).
При у = 0 уравнение (9.31) сводито: к уравнению (9.20) преды-
дущего параграфа.
Уравнение (9.31) было проинтегрировано на электронной счетной
машине при различных значениях параметров у, о и т (или D). С этой
целью был применен метод конечных разностей. Замена производных
конечными разностями переводит уравнение (9.31) в разностное урав-
нение вида (Д? — интервал разбивки значений S)
') L e v у S., Journ. Aeron. Scl. 19, № 5 A952).
; 60) ЗАДАННОЕ РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ПОВЕРХНОСТИ 289
пкуда следует рекуррентное соотношение
де
1
Фя_, Д=
"--I— 14-аФя_,Д= •
Коэффициенты а„, Ьп при заданных о, -[ и fi легко вычисляются
ю таблице 3 производной функции Ф(?). Подробности вычислений
i обсуждение точности вычислительного метода можно найти в до-
юлнении к только что цитированной статье Леви.
В таблице 21 приводим значения производной (dQ/cft\=0, характе-
шзующей теплопередачу на поверхности тела, при различных f и о.
Таблица 21
из
II
СП.
II
га.
8
г>
1
Н
00.
т ^\^
-2,5
-1,5
—0,5
0
0,5
1.0
2,0
4,0
—1,0
—0,75
—0,25
0
0,25
0,5
1,0
2,0
—1/2, 801
—0,25
0
0,25
0,50
1,0
2,0
4,0
0,7
0,0000
—0,2687
—0,4413
—0,5062
—0,5626
—0,6120
—0,6975
—0,8315
0,0000
—0,1755
—0,4093
—0,4879
—0,5535
—0,6094
—0,7033
—0,8461
0,0000
—0,1955
—0,2930
—0,3476
—0,3861
—0,4412
—0,5134
—0,6041
1
0,0000
—0,3101
—0,5085
—0,5828
—0,6468
-0,7031
—0,7995
—0,9512
0,0000
—0,2001
—0,4708
—0,5603
—0,6345
—0,6979
—0,8116
—0,9647
0,0000
—0,2168
-0,3227
—0,3820
—0,4237
—0,4835
—0,5622
—0,6608
5
0,0000
—0,5587
-0,9303
-1,064
-1,176
—1,275
—1,442
-1,701
0,0000
—1,011
—1,141
-1,251
-1,432
0,0000
—0,3290
—0,4884
—0,5760
-0,6375
-0,7257
—0,8424
—0,9890
10
0,0000
-0,7005
-1,186
-1,357
-1,501
—1,626
—1,836
—2,159
0,0000
—0.4062
—1,081
—1,286
— 1,451
-1,590
—1,818
-2,159
0,0000
—0,3894
—0,5806
—0,6848
-0,7581
—0,8629
—1,002
—1,176
19 Зак 297 Л. Г. ЛоАцянский
290
ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. I"
для значений ^=1,6; 1,0; —0,199. В таблице 22 даны значена
той же производной для пластинки (J3 = 0).
Таблица 2L
о
li
СП.
—0,50
—0,25
0,00
0,25
0,50
1,00
2,00
3,00
4,00
0,7
0
—0,4065
—0,4989
-0,5690
-0,6746
—0.8218
—0,9296
— 1,017
2
0
—0,3789
—0,5822
- 0,7130
-0.8112
-0,9593
— 1,165
—1,316
—1,437
10
0
—0,6257
—0,9863
-1,210
—1,377
-1,625
-1.985
—2,211
—2,406
20
0
—0,7668
-1,230
—1,513
—1,721
—2,024
—2,445
-2,741
—2,974
В первой строке таблиц помещены нулевые значения, соотве--
ствующие при любых о и [3 значению f — 1/ф — 2), при которок
уравнение (9.31) преобразуется к виду
интегрируемому в конечном виде и имеющему интеграл
6 = ,
= ехр — о f
Ф @ d'A
Легко видеть, что при этом действительно (dQjdl\-0 = 0.
Возвращаясь к общему случаю любого -р введем местное числе
Нуссельта Nx на поверхности тела, равное
ах Х(дГ/ду)у = 0 х 1 / rfO \ _ /"ОТ
Аналитическая зависимость числа N^ от параметров а, р, -[¦ може1-
быть представлена приближенной формулой
I ь Иг
N, = .8(8, -г) У R,-o *, Р=—, (9.33
причем функция 5C, 7) с достаточной степенью точности (отклоне
ние не превышает ±5%, если f в области отрицательных значений
не слишком велико по абсолютной величине) равна
= 0,57(B-f-0,205H'104[7B — 9)-)-
(9.34
§ 60) ЗАДАННОЕ РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ПОВЕРХНОСТИ 291
а показатель степени k при числе Прандтля в формуле (9.33) близок
в среднем к 0,355 и изменяется в зависимости от р в пределах, ука-
занных в табличке:
р
k
1,6
0,367
1,0
0,355
0
0,327
—0,199
0,254
Отметим, что при [3 = 0 показатели степеней при R^. и а практи-
чески те же, что и в формуле Польгаузена (9.15).
В цитированной работе Леви можно найти графики распреде-
ления температуры по сечениям пограничного слоя при различных
значениях параметров о, [3 и
f, а также зависимости (rf6/df)^=0
и N*R*'/z = Вф, т)о* от т при
заданных о и р.
График последней зависи-
мости приводится на рис. 62.
Основной вывод, который мож-
но сделать, изучая ход кривых
на рис. 62, заключается в су-
щественности влияния харак-
тера изменения температуры
вдоль поверхности на развитие
температурного слоя. Так, на-
пример, видно, что при возра-
1.2
1,0
0.8
0,4
0,2
1
/
/
/
1,
1
/
/
У
/Л
^-—¦
-
-0,
!99_
-2 -/
2 3
Г
Рис. 62.
стании показателя степени f
в заданном распределении тем-
пературы по поверхности тела
от отрицательных значений к
положительным местная тепло-
отдача при данной величине [3 резко возрастает. Резкость этого воз-
растания ослабевает при переходе от положительных [3 к отрицатель-
ным, т. е. от конфузорных участков пограничного слоя к диффузор-
ным. Каково бы ни было [3, всегда существует такое отрицательное
значение f, при котором местная теплоотдача на всей поверхности
будет равна нулю. При малых отрицательных [3, вплоть до предель-
ного случая полностью отрывного обтекания, это значение f близко
к y — '/
к- 7 — /2-
Анализ температурных кривых показывает, что при данных з и [3
толщина температурного слоя возрастает с убыванием параметра у,
причем это возрастание тем заметнее, чем больше о при данном р
и чем меньше р при данном о.
10»
292 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
§ 61. Температурный пограничный слой на продольно
обтекаемом теле вращения
Преобразование Степанова [E.24), § 32] позволяет свести задачу
о температурном слое на теле вращения к плоской задаче, рассмо-
тренной в предыдущем параграфе.
Выбирая оси координат обычным образом, т. е. направив оси х
и у вдоль контура меридионального сечения и по нормали к нему,
учитывая роль поперечной кривизны (радиус поперечной кривизны
обозначим через г0) в уравнении неразрывности, получим систему
уравнений
ди , ди ., dU . дги
дх ' ду dx ' ду2
дТ дТ _ v д*Т
дх ' ду а дуг
~~дх ' ду~ —U>
(9.35)
причем под Т будем понимать избыток температуры в данной точке
пограничного слоя над температурой набегающего потока. Тогда гра-
ничные условия приведутся к виду
в = 0. * = 0. T=Tw(x) при У = 0
u = U. Т=0 при у = оо.
Преобразование Степанова выполним в безразмерной форме, обозна-
чая черточкой сверху величины в воображаемом плоском потоке,
соответствующие величинам действительного неплоского пограничного
слоя; положим (L — характерная длина тела, Сх — произвольная по-
стоянная)
*= / -tf-dx. y=-^y. (9.36)
Вводя функцию тока ф меридионального течения, связанную со
скоростями и, v формулами
и полагая
(9.36")
получим уравнение соответствующего «плоского» пограничного слоя
df дЦ df d'J ^-ndU сРф 9
дх ду дх ду* dx^~ ду* К ' }
ду дх ду дх ду* dx^ ду*
§ 61] ТЕМПЕРАТУРНЫЙ СЛОЙ НА ПРОДОЛЬНО ОБТЕК. ТЕЛЕ ВРАЩЕНИЯ 293
Ограничиваясь случаем степенного задания скорости внешнего
потока __
. U = C3xm, (9.37')
введем переменные Хартри [[3 = 2tnj{m-\- 1)]
с /2 — J V ™ (9 38)
'х Ф(Т).
Тогда функция Ф будет удовлетворять уравнению (штрих—произ-
водная по О
Ф'" (Т) +- Ф (Т) Ф" (Г) + Р [ 1 — Ф'2 (I)J = 0. (9.39)
Рассматривая настоящую задачу как аналог задачи Фокнера —
Скэн об обтекании клина, возьмем конус с углом раствора 2а и рас-
пределением скоростей U = С3хт, причем для такого конуса будет
ro = xsina; тогда по (9.36) найдем
_ С] sin2 а
х3,
л~ L* 3
1С.
U = Сгхт = С2у-±-
Сравнивая, получим
Кроме того, из равенств
будет следовать
р = р/C-р). р =
Совершая преобразование (9.36) над вторым уравнением системы
(9.35), получим
с%дТд1дГд*Т (9>40)
ду дх дх ду а дуг
Решение этого уравнения будем искать в виде произведения
T=fwu)g<?);
294 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
Тогда уравнение (9.40) сведется к обыкновенному дифференциаль-
ному уравнению второго порядка (штрих — производная по ?)
которое при задании степенного профиля температур по поверхности
тела
х . л ~Zt л v-T
совпадает с уравнением (9.31). Таким образом, результаты предыду-
щего параграфа легко пересчитываются на случай тела вращения').
Пограничный слой на теле вращения вблизи лобовой критической
точки при малых скоростях обтекания и при Tw = const может быть
исследован достаточно просто и без применения преобразования
Степанова.
Действительно, при т = 1 будет U = сх, а радиус поперечной
кривизны вблизи критической точки может быть принят приближенно
равным го=^=х. Система уравнений (9.35), если положить
х ду х дх
(с VI,
сведется к системе двух уравнений (штрих — производная по г[)
f2 — 2 ff"= I -\- f",
g"-2afg' = 0.
\ (9.42)
Решение первого из них было выполнено численным методом Хома-
ном2), второго (при граничных условиях ? = 0 при т)=^0, ^=1
при т] = со) — Сибулкиным3). Введя обозначение
[СО , Г) . -.-1
Jexpf —2eJ/d4 dij , (9.43)
о \ о / J
получим
оо , ^ \
= С (о) J exp - 2o J/ dr, rfT,. (9.44)
о V о /
') D r a k e R., Journ. Aeron. Sci. 20, № 5 A953).
2) Нот an n F., Zeitschr. f. Angew. Math. u. Mech. 16, № 3 A936).
s) S i b u 1 к i n M., Journ. Aeron. Sci. 19, № 8 A952) (русск. пер. в сб.
«Механикам ИЛ, в. 3, 1953, стр. 45—47).
• 62]
ТЕМПЕРАТУРНЫЙ СЛОЙ НА ДЛИННОМ ЦИЛИНДРЕ
295
Определим местный коэффициент теплоотдачи а(х) вблизи лобовой
;ритической точки, вводя, как всегда, местное число Нуссельта
= C(e)R* R, = ^. (9.45)
Вычисление интеграла (9.43) показало, что в интервале чисел
1рандтля 0,6 < о < 10 можно приближенно положить
С(о) = 0,763б°.4, (9.46)
:ак это следует из таблицы 23, в которой сравниваются точные и
фиближенные значения С (о).
Таблица 23
о
С (а)
0,763а0'4
0,6
0,625
0,622
0,8
0,700
0,698
1,0
0,763
0,763
2,0
0,988
1,01
10
1,76
1,92
Окончательное выражение для местного числа Нуссельта в функ-
ши от местного числа Рейнольдса и числа Прандтля будет
N, = 0,763R°'56°'4. (9.47)
1ля случая шара, вводя вместо х диаметр шара d и замечая, что
! этом случае
U = j Ur<» sin -j~ = 2> U^x/d, с = 3 U^jd,
юлучим
Nd = 4~= 1.32 Re°'5o°.4; Re — —-—. (9 47')
§ 62. Температурный пограничный слой на длинном
цилиндре в продольном потоке
Как уже указывалось в § 35, при продольном обтекании длин-
юго цилиндра кругового сечения пограничный слой успевает нарасти
настолько, что становится сравнимым по толщине с радиусом цилиндра.
В этом случае уравнения движения несжимаемой вязкой жидкости
•пограничном слое образуют вместе с уравнением баланса тепла
*>лее сложную систему уравнений, чем (9.35), так как уже нельзя
296 температурный и диффузионный пограничные слои [гл. ix
больше принимать расстояние г точки в пограничном слое от оси
вращения тела равным радиусу rQ поперечной кривизны тела.
В рассматриваемом сейчас случае продольного обтекания цилиндра
(У = U^ = const) будем иметь следующую систему уравнений:
ди . ди 1 д I ди \
иТх-+*-д7 = -Ш\г-дт)'
дТ , дТ ч 1 д 1 дТ\
д(ги) , d(rv)
(9.48)
Совокупность первого и третьего уравнений представляет собой
автономную систему гидродинамических уравнений, интегрирование
которой было выполнено в § 35 и может рассматриваться как извест-
ное. Зададимся следующим асимптотическим выражением для функ-
ции тока ф на больших расстояниях х от передней части цилиндра
(а — радиус цилиндра):
где функции /0, /1? .... как было показано в § 35, выражаются
при помощи различных комбинаций интегральной показательной функ-
ции Ei и ее интеграла EI [см. § 35, формулы E.57), E.61), E.64)].
Переходя к исследованию температурного слоя'), положим ана-
логично первой строчке (9.48')
?^ А|Э>.Ч_М!1+ ... (9.49)
Пользуясь принятым выражением для функции тока (9.48') и со-
ответствующими выражениями продольной и поперечной скорости
придем к следующей форме уравнения баланса тепла:
()-1Г«^17 = 0. (9.50)
Подставляя сюда асимптотические разложения f(i\\ x) по (9.48')
и 6(tj; х) по (9.49), приравняем коэффициенты при членах с оди-
наковыми отрицательными показателями степени при р. Тогда полу-
чим следующую систему обыкновенных линейных дифференциальных
') Bourne D. E., D a v i e s D. R., Quart. Journ. of Mech. and Appl.
Math. 11 A958), 1.
fi 62] ТЕМПЕРАТУРНЫЙ СЛОЙ НА ДЛИННОМ ЦИЛИНДРЕ 297
уравнений второго порядка для определения неизвестных функций бя
(штрих обозначает производную по tj):
(9.51)
Граничные условия для функций бя должны быть выведены из
общих граничных условий для 6
6 = 0 при т .-=«-? (или г = с), )
(9.52)
8 = 1 при fi= эо. J
Желая избежать зависимости функций 6Л(irj) от параметра [3, вхо-
дящего в первое граничное условие (9.52), заменим это точное усло-
вие на приближенное: 0 = 0 при ttj = 0. При этом уравнение (9.50)
вблизи У1 — 0 (/ = 0, -р- = 0, -^- = 0) сведется к уравнению
и будет иметь решение
6 = C + D In yj,
так что все функции бя в асимптотическом разложении (9.49) будут
иметь общий вид
где сп, dn—константы. Чтобы их определить, подставим только
что полученные выражения для 6„ в первое граничное условие (9.52);
тогда получим
л=0
откуда следует, что
rfo = 0, dl = co, d2~cv .... dn = cn_l. (9.53")
Совокупность равенств (9.53') и (9.53") определяет собой гранич-
ны, условия при Y|->0. При i]->oo будем, очевидно, иметь
90—>1, 6я->0 (при л > 0), если т]-*зо. (9.54)
Первое из уравнений системы (9.51), если вспомнить [E.57),
§ 35], что /0 = 2т), приведется к виду
¦»j0J-t-O-r-<"l)fl') = O
298 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
с очевидным решением 6 = const = c0= 1, удовлетворяющим гранич-
ным условиям (9.53') и (9.53").
Физический смысл этого решения заключается в однородности
поля температур 0О, находящейся в соответствии с однородностью
поля скоростей: fQ=2~r\, f'Q=z2, U — U&,.
Второе уравнение системы (9.51) приведется к тому же виду,
что и предыдущее, а именно
и при принятых граничных условиях будет иметь решение
8j — A Ei (— от)), А = const. (9.55)
Замечая, что (f — постоянная Эйлера)
Ei (—о7])~ In ч] + (? + 1п о) при 7J—>0,
найдем по (9.52) и (9.54)
/1=1, сг = d2 — f -\- In о,
и, следовательно,
6i (Ч) = Ei (— оЧ). (9.56)
Аналогичными рассуждениями — не будем их воспроизводить —
можно показать, что
62 (т,) ~ ехр (- от,) Ei (- г)) - A + a) Ei [- A + о),,] +
~a j e~3tEi(—t)t ' dt, (9.57)
oo
где постоянная интегрирования В равна
При этом попутно выясняется, что
(9.58)
"о \2 22 ' З2
Ряд 5„ сходится при о^1; при а> 1 ряд расходится, но ока-
зывается суммируемым в смысле Эйлера. Для значений 0^о<!5 ряд
этот затабулирован').
') Powell Е. О., Phil. Mag. 34 A943), 600,
в 63) ТЕМПЕРАТУРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ВРАЩАЮЩЕМСЯ ДИСКЕ 299
Секундное количество тепла Q, отнесенное к единице длины
цилиндра, можно определить как
Q г,
= 2
так что, согласно (9.49), будет иметь место асимптотическое равенство
Используя полученные только что значения dv d2 и dz, придем
к приближенному равенству
XG'tt,-7>co)
f + (а + 2Т) In с 4- (l — j а) 1П2 а - A + а) In A + а) — ^ A + о) + aS,!
(9.59)
в котором отброшенные члены имеют порядок f)~ .
Полученное решение описывает температурный пограничный слой
в области, значительно удаленной от носа тела [¦vx/{Uooai)'^> \0].
При малых значениях того же параметра [vx/(f/cofl2) < 0,04] можно
пользоваться степенным разложением1)
Для промежуточных значений параметра Бурн, Дэйвис и другие
авторы предложили различные приближенные формулы, вывод кото-
рых основан на использовании понятия слоя конечной толщины.
§ 63. Температурный пограничный слой на вращающемся диске
Как уже упоминалось в § 38, точное решение гидродинамической
части задачи о вращающемся в покоящейся вязкой жидкости диске
было дано Кокреном в 1934 г. Задача о температурном пограничном
слое на вращающемся диске в столь же точной постановке была
разрешена И. А. Кибелем в 1947 г.2), который провел расчеты для
числа Пранд?ля, равного единице, и в более общем случае Милл-
сапсом и Польгаузеном в 1952 г.3).
') Seban R. A., Bond R., Journ. Aeron. Scl. 18 A951), 671.
*) Кибель И. А., ПММ, т. XI, в. 6, 1947, стр. 611—614.
') М 111 s a p s К., Р о h I h a u s e n К., Journ. Aeron. Sci. 19, № 2 A952),
120—126.
300 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ IX
К уравнениям F.1), приведенным в § 38, присоединим уравнение
баланса тепла, причем в отличие от предыдущих примеров сохраним
вначале, следуя изложению авторов, диссипативные члены, которые
до сих пор откидывались как малые.
Принимая те же обозначения, что и в § 38, будем считать тем-
пературу поверхности диска постоянной и равной Tw, а температуру
жидкости вдалеке от диска обозначим через Т^. Уравнение баланса
тепла и соответствующие ему граничные условия (У—механический
эквивалент тепла, с — коэффициент теплоемкости несжимаемой
жидкости) записываются в виде
дТ , дТ v I дЧ , 1 дТ , дгТ\ ,
дг ~T~W~te—^\dr* +7~5F~t~ dz*
dv v \2 , / dv \2 , / du ,
W~7) ~^\d7) +11Г"
T=TW При 2 = 0, T= ^ При Z = ОО.
(9.61)
Напомним, что здесь, так же как и в гидродинамической части
задачи, диск заменяется бесконечной плоскостью, вращающейся
с угловой скоростью со вокруг оси Oz. Конечность радиуса диска
принимается во внимание лишь после того, как решение уже полу-
чено и остается только разыскать суммарный момент сопротивления
или, в случае тепловой задачи, общее количество тепла, снимаемого
жидкостью с подогретого диска или передаваемого диску нагретой
жидкостью. Именно такой приближенной постановке соответствуют
граничные условия, помещенные в последнюю строчку системы (9.61).
Используя обозначения F.3) и F.4) и присоединяя к ним допол-
нительное выражение для температуры
получим вновь систему обыкновенных дифференциальных уравне-
ний F.5), к которой присоединятся еще два уравнения для s(C)
и /(С)
t" — aht' = — Ds -j- 12o/2;
со следующими из (9.62) граничными условиями:
\ (9.64)
(=0, / — 0 при С=оо. I
§ 63) ТЕМПЕРАТУРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ВРАЩАЮЩЕМСЯ ДИСКЕ 301
Если разбить функцию /(С) дополнительно на две функции /,(С)
и /2(С), положив
t (С) = —- G"_, — Тт) tx (С) A-12 (С), (9.65)
то граничные условия для /, и t2 уже не будут зависеть от харак-
терного перепада температур (Tw— T^).
Искомое решение в явной форме представится так:
(9.66)
Согласно выражению (9.66), распределение температуры характе-
ризуется двумя группами членов. Первые два слагаемых зависят от
температуры жидкости 7^ и температуры поверхности диска Tw;
вторые два слагаемых от этих характерных параметров задачи не за-
висят. Совокупность этих двух, по происхождению чисто динами-
ческих слагаемых, представляет собой, очевидно, ту добавку темпе-
ратуры, которая получается за счет вязкой диссипации механической
энергии в тепло. Как уже упоминалось ранее, при малых значе-
ниях числа Мсо диссипативные члены уравнения баланса тепла могут
быть опущены по сравнению с членами, характеризующими процесс
теплопроводности. Рассчитанные Миллсапсом и Польгаузеном при-
меры лишний раз подтвердили правильность этого положения.
Если последние члены в равенстве (9.66) откинуть, то оно при-
ведется к форме
Интересно отметить, что в рассматриваемом случае одинаковости
температуры Tw по всей поверхности диска безразмерная темпера-
тура в не зависит от расстояния г до оси диска, а только от рас-
стояния г от поверхности диска. Заметим, что откинутые малые
добавки температуры, соответствующие диссипации механической
энергии, зависели бы не только от-я, но и от г, как это непосред-
ственно видно из равенства (9.66).
Секундное количество тепла Q, отдаваемого жидкости одной сто-
роной нагретого диска радиуса а, может быть получено интегриро-
ванием (диссипативные члены опущены, <р — азимут):
2» а
/* / AT \
-'/»/(@). (9.68)
Обратимся к определению функции ^(С). удовлетворяющей диф-
ференциальному уравнению
(9.69)
302
ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
как это следует из второго уравнения системы (9.63) при условии
пренебрежения диссипативными членами, содержащими s и /2. Тогда,
интегрируя, найдем
f
6
( \1
о V 6 /
При граничных условиях
tx = 1 при С = 0 и /j = 0 при С — со
отсюда получается
С) = 1 — fexplafhdU dC If ехр [о f kdUdL (9.70)
График функции ^(С)
приведен на рис. 63.
Из (9.70) находим
[
o / о \o '
для ряда значений о в интервале 0,5 <] а
4@) = - /ехр (о J Add Л .
(9.71)
Числовые значения t\ @) в функции от числа Прандтля а при-
ведены в виде графика на рис. 64. При пользовании этим графиком
1,0
О,в
О.2
о
а=/о\
1 2
Рис. 63.
вычисление теплоотдачи вращающегося диска по формуле (9.68) не
составляет труда.
Как видно из графиков распределения температуры на рис. 63,
при больших значениях чисел Прандтля а толщина температурного
пограничного слоя мала по сравнению с толщиной гидродинамиче-
ского слоя (о толщине последнего можно судить по кривой темпе-
, 63] ТЕМПЕРАТУРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ВРАЩАЮЩЕМСЯ ДИСКЕ 303
(атуры при а=1). В этом случае функция /(',), входящая в опре-
деление радиальной скорости (вспомнить § 38), может быть заменена
-воим приближенным линейным или степенным выражением, справед-
ливым при тех малых изменениях С, которые соответствуют области
"емпературного слоя при больших а.
-и, 5
(
—¦—¦
—-—
о
д 4 5 6
Рис. 64.
7 в 9 70
1ренебрегая в правой части уравнения баланса тепла (9.61) про-
1зводными по г по сравнению со второй производной по z, играю-
дей в пограничном слое главную роль, и опуская диссипативные
яены, будем иметь упрощенное уравнение баланса тепла в форме
- дт ¦ - дт =JLi!J.. (9.72)
Переходя от координат (г, z) к переменным Мизеса (г, ф) (§ 3),
1ерепишем уравнение (9.72) в форме
1ри больших о, согласно только что сказанному, в этом уравнении
южно положить
д<\> _ __
лкуда (ф = 0 при z = 0) следует
, 1 1
i +4-« -4- «
2
a)
'равнение (9.73) после этого переходит в следующее:
дТ _ д / 9 дГ\
(9.74)
304 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. I.
где положено
= Г2 (8+
- а).
(9.75
Интегрирование уравнения (9.74) приводит к формуле секундной
количества тепла, аналогичной (9.68), со следующим замкнутым вы
ражением ') для величины /] @):
где для краткости введено обозначение
Приводим таблицу 24 относительного отклонения Д% приближен
ного значения t\ @) по формуле (9.76) от точного, рассчитанного m
теории Миллсапса и Полыаузена.
Таблица 2-.
при
a = 0,67
при
0=1,0
0
Д %
Д %
1
27
55
2
21
48
6
5
23
10
3
19
25
1
12
50
0
8
100
1
6
200
4
4
500
6
2
1000
8
1
Линейное (а== 1) приближение для /(С) дает удовлетворительньи
результаты при о > 100, степенное (а = 0,67) — при 6 < о < 500.
В статье Л. А. Дорфмана2) рассмотрен частный случай задач1
о теплоотдаче вращающегося диска с переменной температурой по-
верхности, зависящей от расстояния г точки от оси вращения диск-
а именно
Tv-T^cf*. (9.77
Введем вместо Г функцию 6 (С) согласно равенству
') D а v I e s D. R., Quart. Journ. of Mech. and Appl. Mathem. 12 A959),
в том же журнале см. также статью D a v i e s D. R. and Bourne D. E. v
A956), 457.
2) Дорфман Л, А., Инженерно-физический журнал 1, № 6 A958).
64]
РАСПРОСТРАНЕНИЕ НАГРЕТОЙ ЛАМИНАРНОЙ СТРУИ
305
Тогда уравнение баланса тепла сводится к обыкновенному диф-
т.впрнниальному уравнению
6" — а (Л6' -(- 2/6) = 0 (9.78)
условиями
|=1 при С = 0, 9 = 0 при С = со.
ксг)
18
~ ¦—
0,7 1 1,4 18 2 3
Рис. 65.
5 6 7 в 10
интегрирование приводит к следующему выражению
,ля местного числа Нуссельта:
N, = x = Tw4lToo'T = 0,616#'-<р(о); Rr=~. (9.79)
Функция ср (а) представлена графиком на рис. 65. Для сравнения
(унктиром показан график функции (р(а) = а'/« для пластинки.
§ 64. Распространение нагретой ламинарной струи
в затопленном пространстве
Примерами простых автомодельных задач температурного «сво-
бодного» пограничного слоя могут служить задачи о распространении
огретых плоской и осесимметричной круглой струй, бьющих из бес-
:онечно тонких трубок в пространство, заполненное той же
жидкостью'). При этом предполагается, что, начиная с некоторого
деленного от источника сечения струи, разность между максималь-
'Ой температурой жидкости на оси струи и температурой окружаю-
щей струю жидкости настолько мала, что можно пренебречь влиянием
'емпературы на физические константы жидкости: плотность и тепло-
роводность.
Чтобы упростить постановку задачи, заметим, что наряду с из-
устным законом сохранения вдоль оси струи потока количества
'Внжения сквозь сечение струи (§ 5), имеет также место аналогичный
') Chia Shun-Yih, Journ. of Appl. Mech. 17, № 4 A9.50), 381, 382.
3) Зак. ?97. Л. Г- ЛойцянскиЯ
306 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
закон сохранения потока тепла. Поэтому для задания струи можно
использовать две ее константы: поток количества движения Уо и поток
тепла Но. Искомыми величинами в задаче являются распределения
скоростей и температур в сечениях струи.
Начнем с рассмотрения плоской струи. Пусть 7^ — температура
жидкости, в которой распространяется струя, Т—температура в лю-
бой точке струи. Введем безразмерную разность температур
6= ГТГо° , (9.80)
1 ОО
удовлетворяющую уравнению баланса тепла
Ц ! ЯШ __ __ /Q 81)
дх ' ду а ду3 '
с нулевыми граничными условиями
-|^ = 0 при у = 0, 9=0 при у = со (9.82)
и интегральным условием
ОО
J и {Т— Гсо) йу = const = Яо. (9.83)
— ОО
которое является условием нетривиальности решения.
Гидродинамическая часть задачи уже была рассмотрена в § 5;
приведенное там решение A.63) может быть представлено так:
ЗУI У'' I v/0 \V>
У 2 U)
1 = const.
(9.84)
Искомая безразмерная разность температур 9 должна представлять
собой комбинацию безразмерных величин
Обычные соображения размерности дают
Как легко убедиться, совершая подстановку значения 9 из (9.85)
в (9.81) и вводя наряду с х переменную tj, неизвестная функция т(т()
удовлетворяет обыкновенному дифференциальному уравнению (штрих —
производная по rt)
] = 0. (9.86)
§641
РАСПРОСТРАНЕНИЕ НАГРЕТОЙ ЛАМИНАРНОЙ СТРУИ
307
Непосредственное интегрирование при граничном условии т'@)= 0
дает
T'GJ)=— 20XGj)thTJ.
а повторное приводит к окончательному результату
т (т;) = С seen2" т).
(9.87)
причем постоянная интегрирования С определяется из условия нетри-
виальности (9.83) и оказывается равной,
Г sech2+2* 7j
J
о
C=0,455 при о=1, С = 0,421
Таким образом, окончательно имеем
f
при о = 0,733.
(9.88)
(9.89)
Сравнивая с (9.84), заключаем, что при о = 1 распределения
избытка температуры 9 и скорости и в соответствующих сечениях
струи подобны между собою.
Аналогично решается задача о распространении круглой струи.
.В этом случае уравнение баланса тепла приходится составлять
в цилиндрических координатах (х, г), причем угловая координата
(азимут) в уравнение не входит. При том же выборе безразмерной
разности температур 9 получим уравнение
(9.90)
которое надо рассматривать, считая, что гидродинамическая часть
вадачи уже разрешена. Имеем (здесь ч\ соответствует ат) в форму-
лах § 37)
и =
1
3/0
V. r
х
1
4
Уо =
тер
г и2 dr.
(9.91)
Решение уравнения (9.90) по соображениям размерности должно
иметь вид
Нл Сч). (9.92)
20»
SOS ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. ГХ
где заданная характерная постоянная Но в случае круглой струи
равна
fu(T—TM)dr. (9.93)
Согласно уравнению (9.90) и выбору аргумента ч\ (отличающегося
от аргумента в плоском случае!), новая неизвестная функция х(г\)
должна удовлетворять обыкновенному дифференциальному уравнению
^'-Ь-' + оГ—^ h , 2Г гг1=0. (9.94)
Однократное интегрирование при выполнении условия ограничен-
ности хит' дает
, i^ ij2^ г.
повторное приводит к искомому результату
.-2»
который после использования условия нетривиальности решения (9.93)
окончательно дает
1 Ч 2°. (9.95)
При о=1 вновь обнаруживается подобие в распределении 9 и и.
Как это непосредственно следует из формул (9.89) и (9.95), тем-
пература жидкости в источнике струи (х = 0) равна бесконечности.
Между тем предположение о постоянстве р и \х справедливо лишь
при малой разности температуры струи и окружающей жидкости.
Таким образом, полученные решения пригодны лишь в достаточном
удалении от источника струи, где разности температур сравнительно
невелики.
§ 65. Приближенные методы расчета температурного
пограничного слоя
В предыдущих параграфах температурный пограничный слой рас-
сматривался как бесконечный по толщине и суждение о сравнитель-
ной толщине (§ 58) слоев в зависимости от величины о делалось на
основании характера асимптотического поведения температуры на
бесконечности (см. рис. 58). Так же, как при изучении гидродина-
мического пограничного слоя, можно и в случае температурного слоя
§65]
ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА ТЕМПЕРАТУРНОГО СЛОЯ 309
пользоваться понятием слоя конечной толщины. Это позволяет при-
менять для расчета температурных слоев приближенные методы, ана-
ло ичные методу Польгаузена или другим однопараметрическим мето-
дам, являющимся его обобщением.
Первым шагом в этом направлении явилось относящееся к 1936 г.
исследование Г. Н. Кружилина1), в котором рассматривалось про-
дольное обтекание пластинки жидкостью, имеющей температуру 7^,
отличную от температуры Tw пластинки. При этом использовались
два интегральных условия: 1) уравнение импульсов и 2) уравнение
суммарного баланса тепла. Первое из них уже было выведено
в главе III, второе легко может быть получено из совокупности урав-
нения баланса тепла и уравнения неразрывности:
ОТ дТ _ v д2Т
U дх 4rV~df— а дУ> •
дх ' ду
Перепишем первое из этих уравнений при помощи второго в форме
Интегрируя обе части этого уравнения поперек температурного
слоя от у=:0 до у = оо или у = 8г (толщина температурного слоя)
и принимая во внимание, что по определению температурного слоя
-g- = 0 при у = со или у = 8Г, получим
= - "?- =~r- (9-96)
Если ввести в рассмотрение «смешанную» толщину й", характе-
ризующую как распределение скоростей, так и температур,
о о
то при Тт = const уравнение (9.96) может быть переписано в форме
db7 4w
-.Этому уравнению можно было бы дать наименование «уравнения
местного баланса тепла».
') К р у ж и л и н Г. Н., ЖТФ, 6, в. 3 A936).
310 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
Следуя общей идее метода Кармана — Польгаузена, зададим про-
фили скоростей и температур в виде двух многочленов четвертой
степени:
T—Tu
/ оо — 11
(9.99)
Первый из них, выражающий распределение скоростей, выбран из
условия удовлетворения граничным условиям
„ дг(и/[/оо) _
° ^ °
при „=
Второй многочлен в системе (9.99), служащий для задания профиля
температур, удовлетворяет тем же граничным условиям для безраз-
Т т
мерного перепада температур -=—=?-. Многочлены совпадают по
форме, но отличаются аргументом. Как уже указывалось ранее (§ 58),
если число Прандтля равно единице, то толщины гидродинамического
и температурного слоев совпадают. При Ьт = 8 многочлены станут
тождественными, что будет говорить о подобии распределения ско-
ростей и температур в сечениях слоя при а=1.
Заменим в интегральном соотношении (9.98) и и (Т— Т^) соот-
ветствующими им выражениями по (9.99). Вводя обозначение е(а)
для функции, выражающей зависимость от а отношения толщин 8J./81),
и замечая, что в выбранном приближении (§ 18)
получим уравнение для определения е(а)
еЮ(г) = ~^, (9.100)
где положено
2 3 , , 1 . ^ ,
тт? —тш ~^~ 1Ш если ? < ' •
3 31 91 31 11
"lcr^TcrT + Ts^" WT^ + W?1 если ?>1>
Уравнение (9.100) имеет приближенное решение
(9.101)
/а
') Ш л и х т и н г Г., Теория пограничного слоя, пер. с нем., ИЛ, 1956,
стр. 281.
§65] ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА ТЕМПЕРАТУРНОГО СЛОЯ 311
Коэффициент теплоотдачи а (х) будет равен
t \ - Ч*> — }(дТ\ 1 _ 2?.
aW— Tw— Too ~ \dy)y=0'Tw-Tco «В •
Подставляя сюда значения е и 8 и переходя к местному числу
Нуссельта N^, получим
N, =-^- = 0,343R?a'/|; R =-^-, (9.102)
что отличается от (9.15) лишь значендал численного коэффи-
циента 0,343, близким к точному 0,332.
Аналогичное приближенное решение более общей задачи о темпе-
ратурном слое на продольно обтекаемой пластинке с заданным рас-
пределением температуры t(i) по ее поверхности (? — безразмерная
координата, равная отношению абсциссы „с
х к длине пластинки) было дано Лоу1). ' г
Решение Лоу позволяет представить отно-
шение толщин температурного и скорост-
ного слоев в замкнутом виде
2.0
(9.103)
Для случая пластинки с постоянной
температурой вдоль поверхности формула
Лоу дает
8г/2 = 0,958/а1/.
1.5
10
0.5
О
—
/
•
-формула
- Теория Л
1
'У.Щ)
а=2О
3 4
Г
Рис 66
рместо вышеприведенной формулы (9.101).
В случае степенного задания распределения температуры по
поверхности пластинки (§ 60) равенство (9.103) дает следующую
формулу для местного числа Нуссельта:
И» = 0.358RK42f-И)'А.
(9.104)
На рис. 66 приводится сравнение формулы (9.104) с точным
решением Леви [§ 60, формулы (9.33) и (9.34) при Р —0].
Выбирая более высокие степени многочленов, выражающих при-
ближенное распределение скоростей и температур, например шестую
степень2), можно получить более точное выражение для N
') Lowe О., Journ. Aeron. Scl. 24, № 12 A957).
) Лойцянский Л. Г., Аэродинамика погран
, стр. 86,
()
пограничного слоя, Гостехиздат,
312 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
Для приближенного исследования температурного пограничного
слоя при произвольном задании скорости U (х) на внешней границе
слоя нет необходимости пользоваться понятиями скоростного и тем-
пературного слоев конечной толщины. Сохраняя для скоростного слоя
характерные для него асимптотические толщины 8* и 8**, введем,
обобщая (9.97) на случай произвольной функции U (х) и Tw = const,
смешанную асимптотическую толщину слоя
со оо
С и Т—Тоо, С и (.
3.105)
Следуя основной идее однопараметрического метода, заключаю-
щейся в использовании классов точных решений, положим в основу
расчета автомодельное решение Фокнера — Скэн (§ 11) для скоро-
стей и соответствующее ему решение для температурного погранич-
ного слоя, изложенное в § 59J).
Пользуясь формулами § 11 и полученным в § 59 распределением
температур (9.21), можно найти отношение Ьт/Ь**, равное
о о
(9.106)
Кроме того, вводя тепловую величину ?г = —.—дг-1 , ана-
Ld(y/8r)J,=o
логичную известной гидродинамической величине С = [ д . L*l 1
выразим через нее местное число Нуссельта:
ах^ gwx х I дТ\
— X — X(TU-Tm) ~ Tw-Tm\dy)y=0 —
— х Г dli I —JLr Г9 1071
ьг L д{У1ът) Jy=o ьт
Величина Сг, так же как и отношение толщин х = Ът/& , может
быть вычислена раз навсегда как функция только от 8 и а. Действи-
тельно, по (9.21) имеем
= х(?; о) В (?) /ехр(-а/ф^Ц =Сг(В;о). (9.108)
') Скопец М. Б., ЖТФ 23, в. 1 A953).
651
ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА ТЕМПЕРАТУРНОГО СЛОЯ
313
Пользуясь таблицами функций Ф и Ф', а также формулой (9.21),
южно найти ^
; функции от параметра р, а затем, вспомнив таблицу связи между
I и /. и в функции от формпараметра /. В таблице 25, заимство-
анной из только что цитированной статьи М. Б. Скопец, присогятся
(начения /r = t/'Sr А и Cr = [«?9/«?(y/Sr)]y=o B Функции от / =
= t/'8**2/v для значений числа Прандтля: о = 0,73 и а=1. При
жданном U(х) разыскание f(x) однопараметрическим методом
глава III) и последующее определение по таблице 25 величин Сг, /т
je составляет труда.
Таблица 25
f
—0,068
—0,06
—0,05
-0,04
-0,03
—0,02
-0,01
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,085
О = (
/г
—0,033
—0,039
—0,040
—0,037
-0,031
—0,023
-0,013
0,000
0,016
0,039
0,067
0,100
0,145
0,205
0.278
0,391
0,470
),73
Сг
0,122
0,152
0,176
0,193
0,206
0,219
0,231
0,242
0,253
0,264
0,275
0^86
0,298
0,310
0,324
0,338
0,346
а =
/г
—0,022
—0,025
—0,026
—0,024
—0,021
—0,015
—0,008
0,000
0,011
0,026
0,045
0,068
0,099
0,138
0,193
0,271
0,325
1,0
0,109
0,135
0,156
0,173
0,187
0,199
0,211
0,221
0,232
0,242
0,253
0,264
0,276
0,288
0,302
0,317
0,325
.удя по ссылке, приведенной в статье Дрэйка, цитированной на
стр. 294, аналогичный приближенный метод, распространенный и на
случай переменной температуры поверхности тела, был опубликован
ранее Себаном (Seban R. A., Univ. of California, Inst. of Engin.
Research Rep. 2—12, iWay, 1950). Температурный пограничный слой
на продольно обтекаемом теле вращения был рассмотрен в цитирован-
ной работе Дрэйка аналогичным приближенным методом.
314 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
§ 66. Ламинарная диффузия в изотермическом
пограничном слое
Рассмотрим явление ламинарной (молекулярной) диффузии неко-
торого вещества (примеси) в плоском ламинарном пограничном слое.
При этом будем предполагать, что поток стационарен и изотерми-
чен, а внутри потока вещество не возникает и не исчезает, как это
могло бы быть при наличии химических реакций. Примешивание или,
наоборот, удаление вещества происходит лишь на поверхности обте-
каемого тела (например, растворение тела в потоке, удаление при-
меси твердым катализатором и т. п.).
Уравнение диффузии при принятых ограничениях получим как
частный случай общего уравнения диффузии (8.57). Опуская в этом
уравнении последние два члена справа, выражающие эффект термо-
диффузии и возникновения вещества, будем иметь при постоянных р,
jx, D и числе Шмидта Sc = v/D
uto+dc=D»c_ = _JL |f?.. (9.109)
дх ' ду ду* Sc ду2 ч '
В этом уравнении величина с обозначает переменную весовую
или массовую концентрацию примеси. Уравнение (9.109) по своему
внешнему виду ничем не отличается от уравнения (9.1) стационарного
распространения тепла в плоском пограничном слое в несжимаемой
жидкости с постоянными физическими константами.
Соответствие между концентрацией примеси с и температурой Т
определяется соотношением между коэффициентом диффузии D, стоя-
щим в качестве множителя при второй производной справа в уравне-
нии (9.109), и коэффициентом температуропроводности а = Х/(рср) =
= v/a, занимающим аналогичное положение в уравнении (9.1); отно-
шение D/a эквивалентно отношению чисел Рг и Sc. Аналогия в зна-
чении этих чисел для процессов тепло- и массопередачи очевидна и
позволяет, сохраняя за первым из них термин «числа Прандтля»,
называть второе, т. е. число Шмидта Sc, «диффузионным» числом
Прандтля. Для упрощения письма условимся в дальнейшем обозначать
собственно число Прандтля Рг = цср/А буквой а, а диффузионное
число Прандтля — символом <sd.
Чтобы проанализировать связь между решениями уравнений (9.109)
и (9.1), необходимо еще сопоставить граничные условия, используе-
мые в задачах тепло- и массопереноса. Для рассмотренных в настоя-
щей главе тепловых задач всегда применялись граничные условия
одного типа:
T=TV при у = 0. Т=ТХ при у = со, (9.110)
с gg] ЛАМИНАРНАЯ ДИФФУЗИЯ В ИЗОТЕРМИЧЕСКОМ ПОГРАНИЧНОМ СЛОЕ 315
так как встречающееся в дальнейшем условие отсутствия теплоотдачи
на твердой стенке: дТ/ду = О при у = О, в случае несжимаемой
жидкости приводит к изотермическому движению.
Очевидно, что и при исследовании процесса диффузии вещества
применимы аналогичные граничные условия, выражаемые заданием
концентрации cw на поверхности тела и ?„, в набегающем потоке:
c = cw при у = 0, с = Соо при у = оо. (9.111)
При процессе растворения тела в движущейся жидкости величина
с =снас представляет собой концентрацию насыщенного раствора
примеси на поверхности растворяющегося тела, Соо = 0—-нулевую
концентрацию примеси на границе пограничного слоя в набегающей
на тело чистой, не содержащей примеси жидкости.
Если на поверхности тела происходит процесс поглощения при-
меси, содержащейся в набегающем потоке, то в предельном случае,
когда скорость поглощения примеси велика по сравнению со ско-
ростью диффузии примеси к поверхности, будет с = cw = 0 при у — О
и с = Соо при у = оо, где с^ представляет собой концентрацию при-
меси в набегающем потоке. При скорости поглощения примеси, очень
малой по сравнению со скоростью диффузии, поверхность тела будет
как бы непроницаемой для потока примеси, и концентрация в этом
втором предельном случае сохранит постоянное значение с = сот во
всем потоке.
Кроме этих двух простейших предельных случаев, может иметь
место более сложный промежуточный случай, когда скорости погло-
щения и диффузии вблизи поверхности сравнимы между собою.
В этом случае граничное условие на поверхности тела должно выра-
вить баланс между скоростью поглощения, которую можно принять
пропорциональной некоторой, в частности первой степени концентра-
ции вещества вблизи поверхности, и скоростью диффузионного под-
вода вещества, пропорциональной градиенту концентрации. Это
граничное условие обычно записывается в форме равенства
где х — некоторый постоянный коэффициент, характеризующий про-
исходящую реакцию и не зависящий от концентрации, а показатель
степени п определяет «порядок» реакции. При я=1 граничное
Условие (9.112) имеет линейный характер.
7 Уравнение диффузии в плоском ламинарном пограничном слое
«ожет быть обобщено и на случай пространственного пограничного
«ГОя. Не будем давать систематическое изложение этих вопросов,
!# Становимся на нескольких простых примерах.
ч
316 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ Тгл. IX
§ 67. Примеры диффузионных пограничных слоев
Как это следует из содержания предыдущего параграфа, все
решения задач о температурном слое, изложенные в настоящей главе,
могут быть текстуально повторены и в случаях диффузионного слоя,
лишь бы имела место аналогия в постановке граничных условий
Начнем с задачи о диффузионном слое на продольно обтекаемой
пластинке. Используя для решения этой задачи соответствующее
решение для температурного слоя (§ 58), введем в качестве аналога
безразмерной температурной функции б безразмерную концентрацион-
ную функцию
С = 1Г=Г' (9-113)
которая будет удовлетворять тем же граничным условиям,
С = 0 при у = 0 и С—\ при у = оо, (9.114)
что и функция 6 [сравнить (9.113) и (9.114) с (9.7)]. Тогда искомое
решение для С совпадет с (9.9), с той лишь разницей, что число
Прандтля а теперь должно быть заменено на диффузионное число
Прандтля <sd. При ad = 1 будет иметь место подобие между распре-
делением безразмерной концентрационной функции С и безразмерным
распределением скоростей; рис. 61 одновременно представляет как
графики распределения 6A7) при разных о, так и С(у\) при разных ad.
В полной аналогии со случаем температурного слоя можно утвер-
ждать, что, согласно рис. 61, диффузионный слой, в известном
условном смысле слова, толще скоростного, если orf<l, и, наобо-
рот, скоростной слой толще диффузионного, если ad > 1. При ad — 1
оба слоя совпадают по толщине.
Введем в рассмотрение местный коэффициент массопереноса ad
(аналог местного коэффициента теплоотдачи а), положив, подобно (9.11).
*j ^4j|A| —-UaI It-... boo I L^ _i. /!•-..¦ С jo I
dy
^/-> / л/ о
где функция / — та же (9.12), что и в случае температурного слоя.
Диффузионный аналог местного числа Нуссельта N^ будет равен
у =0/
~ R, = ^. (9-115)
^4 (9-116)
а диффузионный аналог суммарного числа Нуссельта Nd для всей
, * g7] ПРИМЕРЫ ДИФФУЗИОННЫХ ПОГРАНИЧНЫХ СЛОЕВ 317
поверхности пластинки определится равенством (L — длина пластинки)
$ их
Принимая приближенное выражение для функции f (ad), предло-
женное Э. Польгаузеном,
/(orf)= 0.664]'^. 0,6<ad<15,
безотносительно к тому, рассматривается ли тепло- или массоперенос,
получим з _
N^ = 0,3321 о. ^Rr> |
, _ * (9.118)
Nd = 0,664 V a, VRM. j
Местный, рассчитанный на единицу длины пластинки поток веще-
ства qd или суммарный поток вещества Qd для всей поверхности
пластинки могут быть найдены отсюда обычным путем.
. Приведенные только что формулы одинаково справедливы как
в случае растворения поверхности пластинки (cw — снас, см = 0), так
и в предельном случае поглощения вещества (с = cw = 0 при у = 0,
с = с,» при у = сю).
Совершенно так же используется решение плоской задачи о темпе-
ратурном слое на теле при переменной скорости U (х) на внешней
границе пограничного слоя, изложенное в § 59. Укажем просто, что
при степенном задании скорости, U =схт, безразмерное распреде-
ление концентрации будет определяться формулой (9.21), в которой
следует только 6($; р, о) заменить на С(?; C, <sd), а в правой частив
заменить на ad. Местное диффузионное число Нуссельта Nxd будет
определяться формулой, аналогичной (9.22),
N,d = K(ad; m)VWx\ R*=V' <9Л19>
где коэффициент K(ad; m) задается в точности тем же интегральным
представлением (9.23), что и в случае тепловой задачи, лишь при
аамене в правой части о на <за. Конечно, в случае произвольного
падания распределения скоростей лучше пользоваться приближенным
однопараметрическим методом, изложенным в конце § 65. И здесь
все, включая рассчитанную М. Б. Скопец таблицу 25, можно сохранить,
ваыенив лишь 9 на С и введя ad вместо о, Cd вместо Сг, 87 вместо о~
¦ ¦ fd вместо /г. К сожалению, в вопросах диффузии уже нельзя удо-
влетвориться значениями od = 0,73 и 1,0, приведенными в таблице 25,
;* необходимо существенно расширить диапазон этих значений.
* Если скорость внешнего потока и концентрация на поверхности
не постоянны, а определяются некото ыми степенными Лункци ми
318 ТЕМПЕРАТУРНЫЙ И ДИФФУЗИОННЫЙ ПОГРАНИЧНЫЕ СЛОИ [ГЛ. IX
продольной координаты, то для решения диффузионной задачи
можно применить совершенно тот же метод, что и изложенный в § 60.
Данные таблиц 21 и 22 для (db/dl)iir0 пригодны также для опреде-
ления (dCjd\)^0, т. е. для местного диффузионного числа Нуссельта,
согласно следующему аналогу формулы (9.33):
N,d = S(p. т)°*/С- (9.120)
причем В (р, f) определяется по (9.34), а показатель степени k при od
задается следующей за формулой (9.34) табличкой.
Наконец, остановимся еще вкратце на диффузионной задаче для
диска, вращающегося вокруг своей оси в жидкости. Соответствующая
тепловая задача была рассмотрена в § 63. Задача эта имеет большое
практическое значение для теории массопереноса, так как на лабора-
торной установке с вращающимся диском удобно изучать процессы
химической кинетики ').
Опуская в тепловом решении (9.66) последние два члена, выра-
жающие диссипацию механической энергии в тепло, получим решение
диффузионной задачи
из которого видно, что распределение концентрации вокруг вращаю-
щегося диска не зависит от расстояния до оси диска, а только от расстоя-
ния z от плоскости диска. Функция tx\z l/ —) определяется равен-
ством (9.70), в правой части которого а должно быть заменено на ad,
и представлена графически на рис. 63 для ряда значений ad в интер-
вале 0,5 ^ Qd^C 10. Для диффузионных задач этот интервал совер-
шенно недостаточен, так как часто ad достигает величин порядка 103.
Для этих значений ad можно пользоваться упрощенными асимптоти-
ческими формулами, как это делается в § 63.
Секундный поток вещества, приходящийся на одну сторону диска
радиуса а, определится аналогом формулы (9.68)
Qd — _ M*Dv>'h-llH[ @), (9.122)
где <j@) задается формулой (9.71), в которой о заменяется на od,
и графиками на рис. 64. При больших <sd (порядка сотен и тысяч)
с успехом применяется асимптотическое выражение для ^@) со-
гласно (9.76).
') См. Л е в и ч В. Г., Физико-химическая гидродинамика, Физматгиз, 1959.
ГЛАВА X
ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНКЕ
В ПРОДОЛЬНОМ ГАЗОВОМ ПОТОКЕ
§ 68. Стационарный пограничный слой на пластинке
при линейной зависимости вязкости от температуры
Настоящая глава посвящена вопросу о продольном обтекании пла-
стинки плоским потоком вязкого газа при больших рейнольдсовых
числах и любых числах М,». не превосходящих значений, при кото-
рых газ уже нельзя считать однородным, а коэффициенты тепло-
емкости постоянными.
При продольном обтекании пластинки давление во внешнем потоке
повсюду одинаково (р = const = р^,, -?=0\; при этом вторая
основная форма уравнений пограничного слоя в безразмерном виде
(8.23) приведется к виду
, ди' , ,д'и'
A0.1)
р'А'=1,
Предпоследнее равенство системы выражает в безразмерной форме
условие
/ _ Р =ш. />оо 1
а последнее соответствует степенной зависимости коэффициента вяз-
кости от абсолютной температуры или энтальпии.
Граничные условия для рассматриваемой стационарной задачи
состоят из динамических условий
н' = 0, v' = 0 при у' = 0; и'в=1 при у' = оо A0.2)
и температурных условий, которые могут быть двух родов:
320 ЛАМИНАРНЫЙ СЛОЙ НА ПЛЛСТИНКЕ В ПРОДОЛЬНОМ nOTOKF [ГЛ. v
а) задание энтальпии (или температуры) на поверхности пластинки
h' = h'w при / = 0; h'=\ при / = со; A0.3)
б) условие отсутствия теплоотдачи с поверхности пластинки (пла-
стинчатый термометр)
dh'/dy' = 0 при у' = 0, h' = \ при у' = оо. A0.4)
А. А. Дородницын ') указал общее преобразование координат,
сообщающее уравнениям пограничного слоя в газе форму, близкую
к форме уравнений пограничного слоя в несжимаемой жидкости. Это
преобразование имеет вид
где р0 и р0 — постоянные величины, выражающие давление и плот-
ность в адиабатически и изэнтропически заторможенном внешнем
потоке.
Используя в случае продольно обтекаемой пластинки вместо р0
и р0 величины рсо и р^, примем преобразование Дородницына в форме
у'
9'dy'. A0.5)
С целью упрощения записи откинем в дальнейшем штрихи в обо-
значении безразмерных величин.
Формулы перехода от дифференцирования по х, у к дифферен-
цированию по S, •») записываются как
+ A06)
Первое равенство системы A0.1) преобразуется к виду
ди , dri ди . ди д I ди\
P^ + P^ + P^PPIW)
после сокращения на р и принятия в расчет последних двух равенств
системы (ЮЛ) получим
ди . / д-п , \ди д / .п-\ди\
цу A07)
Из второго равенства системы A0.1) найдем
') Дородницын А. А., ПММ, т. VI. 1942.
§ 68] ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ 321
так что
—й- •fi+f—3- <10-8>
Если ввести обозначение
fj o. (Ю.9)
то уравнение A0.7) приведется к виду
ди , ~ ди д I ,п-\
причем
dli dl>
A0.11)
Подвергнем преобразованию A0.6) уравнение баланса тепла [третье
уравнение системы A0.1)]; получим
или, после сокращения обеих частей на р и принятия в расчет A0.9),
а также последних двух равенств в системе A0.1),
dh ~ dh 1 д ( .n-\dh\ ... ,. М2 ,п-\ (ди\2 п(л . оч
+ ^Д* j + CADMA ^) A0.12)
Используя, как и в задаче Блазиуса для пластинки в потоке не-
сжимаемой жидкости, наличие автомодельного решения, получаемого
вследствие независимости граничных условий от продольной коор-
динаты х, будем искать выражения для продольной скорости и ($, т;)
и энтальпии А(?, 7j) как функций от одного аргумента d равного
ф 00.13)
Тогда, согласно первому равенству системы A0.11), будем иметь
//
Вводя обозначение
21 Зак, 297. Л. Г. Лойцянский
322 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ (ГЛ. X
получим (штрих — производная по С)
(С). a p(Q, ^=(c<p
dt* 1_ г „ ди_ 1 „ <Э% \_
д\~ 45^' д(. ~~4fl ^2 8;
— —— — rh' dh = X - ti
дя 2? ~* ' dTj 2 ^ 5
Подставляя эти выражения в уравнения A0.10) и A0.12), получим
систему двух обыкновенных уравнений третьего и второго порядка,
служащих для определения неизвестных функций ср и к:
A0.14)
Граничные условия для ср будут
<р = 0, <р' = 0 при С = 0,
ср' = 2 ириС-оо.
Граничные условия для энтальпии h, согласно A0.3) и A0.4),
выразятся в одной из следующих форм:
а) задание температуры на поверхности пластинки
h — hw при С = 0, \
и , г A0.16)
А = 1 при С = со; J v '
б) случай отсутствия теплоотдачи
ЗГ=° ПРИ С = °- 1 A0.17)
й= 1 при С = оо. J
Интегрирование системы уравнений A0.14) в общем случае тре-
бует применения численных методов.
Рассмотрим сначала простейший случай, когда связь между коэф-
фициентом вязкости и температурой линейна (я=1). В этом случае
первое уравнение системы A0.14) становится автономным; имеем
Первое из этих уравнений при граничных условиях A0.15) отли-
чается от соответствующего уравнения и граничных условий задачи
§ 68] ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ 323
о пограничном слое на пластинке в несжимаемой жидкости только
тем, что аргумент С в настоящем случае по сравнению с аргументом tf,
определенным по A.36), содержит множитель 1/2. Следовательно, для
определения функции ср(С) и ее производных с указанной поправкой
можно пользоваться приведенной ранее таблицей 1. Тогда, интегрируя
второе уравнение системы A0.18) подобно тому, как это было сде-
лано в § 58 предыдущей главы, найдем значение /г (С) в фэрме
| f A0.19)
оо
где введено обозначение
оо С
0(С) = 2о J [f (С)]' dl f [f (С*)]2"Л*. A0.20)
с о
а постоянные интегрирования С и С, должны быть определены из
граничных условий A0.16) или A0.17). Полагая С —оо, найдем зна-
чение постоянной С1=\; полагая С —0, получим
C = f . A0.21)
-о- / W (ОГ dl
0
Обозначим через ht и Tt значения энтальпии и температуры пла-
стинки в условиях A0.17) отсутствия теплоотдачи, что соответствует
использованию пластинки в качестве измерителя температуры потока —-
пластинчатого термометра. В этом случае, дифференцируя A0.19) и
учитывая, что 0'@) = 0, найдем С = 0, т. е. по A0.21) при hw = ht
получим
А, = 1-|- j(k— 1)М^& @). A0.22)
Перейдем в этой формуле к размерным температурам; найдем
Tt = Го, Г1 -f- -g- 9 @) (k — 1) ML I = ^ Г1 -f- r (o) • -g- (A — 1) Мм ] •
A0.23)
Множитель г (сз) =-j f) @), характеризующий отличие величины Tt от
температуры адиабатически и изэнтропически заторможенного газа
То= Tool 1 -)--^-9—Мсо). носит наименование коэффициента восстано-
21»
324 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
вления (recovery factor — в американской и английской литературе),
а величина 9@), согласно A0.20), равна
оо С
Ь @) = 2с f [f (С)Г Л / I?" (С*)]2"' Л*. A0.24)
о о
Возвращаясь теперь к общему случаю наличия теплоотдачи
с поверхности пластинки и пользуясь выражением A0.22), можно
представить постоянную С, определенную соотношением A0.21), в виде
Исключая постоянную С из A0.19) при помощи A0.25), получим
искомое распределение энтальпии (или температуры) в окончательной
форме
*(О = -§-(*—l)ML&@ + (Ae —А,)с— hi- (Ю.26)
/ W (ОГ «
о
Остановимся на некоторых частных случаях. При отсутствии тепло-
отдачи с поверхности пластинки hw = ht, т. е. для пластинчатого
термометра будем иметь безразмерное распределение энтальпии
А @=1 + j(ft—1)ML»C:). A0.27)
или, переходя к размерным температурам,
] A0.28)
Если, кроме того, в=1. то. согласно A0.20), будет (а — раз-
мерная скорость)
0 @ = 2 / ср" (С) 9' (О Л = [?'2 (Of = 4 [ 1 - (^
с
и, следовательно, равенство A0.28) переходит в такое, тождественное
со случаем изэнтропического движения идеального (невязкого) газа
равенство:
Г}Ц^I A0.29)
68] ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ 325
В частности, на поверхности пластинки (и = 0) будет
Ти = Tt = Г- [l + ^ (* - О MLJ = ^о. (Ю.ЗО)
где То — температура адиабатически и изэнтропически заторможенного
газа или, короче, «температура торможения». Таким образом, при
а = 1 и ранее принятом допущении о линейности связи между коэф-
фициентом вязкости и абсолютной температурой газа показание пла-
стинчатого термометра, расположенного параллельно потоку, совпа-
дает с температурой торможения газа.
В случае с ф 1 формула A0.23) отличается от A0.30) наличием
коэффициента восстановления г (о), характеризующего неадиабатич-
ность движения в пограничном слое. Как показывают расчеты по
A0.24), этот коэффициент для газов меньше единицы (/¦ = 0,770;
0,895; 1 соответственно при о = 0,6; 0,8; 1). Можно с достаточным
приближением считать
г(о) = 10@)^=У~^ A0.31)
Только для воображаемого газа со значением о = 1 возникновение
тепла за счет диссипации механической энергии уравновешивается
теплоотводом путем теплопроводности, что уподобляет движение
адиабатическому. Коэффициент восстановления г служит мерой этого
теплового дисбаланса в реальном вязком газе. Если в общей фор-
муле A0.26) устремить Моо к нулю, т. е. перейти к движению
с малыми (точнее, далекими от скорости звука) скоростями, то после
перехода к размерным температурам и простых преобразований
получим
с
/ [?" (ОГ <К
Тю—Т о
о
Это соотношение, правая часть которого представляет собой функ-
цию от аргумента С, выраженного, согласно A0.13), через перемен-
ные Дородницына, справедливо как для случая р = const, p. = const,
рассмотренного в начале предыдущей главы [§ 58, формула (9.9)],
так и для переменных р и ;х, связанных соотношением |хр = const
или п = 1.
Определим местный коэффициент теплоотдачи пластинки с темпе-
ратурой поверхности Tw. Вычислим размерную производную от
температуры по нормали к пластинке, dTjdy, на поверхности
326 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ Г™. X
пластинки. Имеем, переходя в правой части к размерным величинам,
dh __ J2_ , rj дТ _ __ /^? р
d*, ~ Too V *дц — То, V [/„ ' р ду '
откуда следует
(¦,—. T r-j-f— , ...
01 \ /оо л/ Uoo Ра, 1ап\
ду)у=о~~~~2~ * wp^A5cVc=l0*
Но по A0.19)
dh\ С . i,
кроме того, в случае пластинки (р = р ) по формуле Клапейрона
будет
Рху Too
poo Tw '
Используя выражение A0.25) для С, в размерных обозначениях
принимающее форму
Tol«
{ / W (ОГ
0
получим
где, как и в § 58 [формулы (9.12) и (9.14)], положено
0.664^ A0.33)
о
Вводя число Нуссельта Nu, получим, подобно § 58.
Q __ 1 Л /^
ТТ / w\~A
у 7\ х 7- /~77— /* //»•
Принимая во внимание, что коэффициентн теплопроводности на-
ходятся в том же соотношении, что и динамические коэффициенты
§ 68] ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ 327
вязкости, т. е. при я— 1
lw = Tw
Лоо * оо
и выполняя интегрирование, окончательно получим
11 /(o)/R^; A0.34)
' w — ' со
входящая сюда величина Tt определяется по A0.23) и характеризует
влияние числа Маха Mqo-
Если наряду с Nu ввести еще условное • число Нуссельта
l^t = Q/[Xoo(Tw—Tt)\, то получим не зависящее явно от М^ соотно-
шение
> ,t r,/()/R^fy^ A0.35)
Аоо A w — If)
аналогичное соотношению (9.16), установленному ранее для несжи-
маемой ЖИДКОСТИ, Моо = 0.
При отсутствии теплоотдачи Tw=Tt и Nu = 0. При наличии
теплоотдачи, но малых М^,, т. е. при малых скоростях, когда влия-
ние сжимаемости несущественно, Tt = Тх и, следовательно,
Это — уже рассмотренный ранее в § 58 случай (9.16).
Наконец, при с= 1 получаем
Nu = 0,664 1W~I° VRZ- A0.36)
Обращаясь к вопросу о сопротивлении пластинки, найдем сначала
напряжение трения тш. Имеем, переходя к размерным величинам,
/oo Uco р ду
откуда следует
2 гоо^оо
причем ср"(О) имеет то же значение <р"@)= 1,328, что и в несжи-
маемой жидкости. Итак, если при п=^\ величины ;л и р в формуле
коэффициента местного трения отнесены к значению температуры
в набегающем потоке, то коэффициент местного трения остается
тем же, что и в случае несжимаемой жидкости [см. A.39) и A.40I;
__ 0,664 __ ^оо*
328 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ X
Uoo
Как можно заключить из проведенных выкладок, для вычисления
коэффициентов сопротивления и теплоотдачи нет необходимости
иметь явные формулы связи
' ' ' ^^ i между новым переменным С
и обычным у/Yх, так как
в окончательные выражения
иходят лишь значения этих
величин при у = 0 или
у = оо. Сложнее решается
вопрос о распределении ско-
ростей и температур в се-
чениях пограничного слоя,
так как полученные распре-
деления скоростей u/Uoo =
==72<р'(О и температур
A0.31) выражены через
0,5
О
/
Tw=Tm
п=/
0=0,7
к=1,4
2,0
о
аргумент С, связанный с
обычными размерными ко-
ординатами по формуле
1 Л— Гт
=== ~о V / ~т~ "У*
конкретный вид которой зависит от распределения температур. Диф-
ференцируя по у, получим
А (оо)
- ! лГ
¦-2V -
Связь между С и у/У х определится интегральным соотношением
с ¦
2
Voo
A0.38)
Приведем несколько результатов расчетов по выведенным только
что формулам, соответствующим рассмотренному пока случаю линей-
ной зависимости (я=1) коэффициента вязкости от абсолютной тем-
пературы. На рис. 67 приводятся профили скоростей при о = 0,7 и
двух условиях охлаждения поверхности пластинки: 1) когда темпе-
ратура пластинки поддерживается равной температуре набегающего
потока (Tw = Г,») и 2) когда охлаждение настолько сильно, что тем-
пература стенки составляет четверть температуры набегающего по-
тока \Tw = -? Гоо]. Можно заметить, что с ростом числа Моо без-
размерные профили скоростей становятся более пологими или, как
68]
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ
329
:ногда говорят, более урезанными. Это означает вместе с тем, что
ростом Моо возрастает и толщина пограничного слоя. Если при
ггсутствии теплоотдачи в выра- - _
;сение безразмерного расстояния
)Г поверхности пластинки вместо ju_
«ачений физических констант Uoo
\ набегающем потоке [Хк,, р^ вве-
ти их значения \>.w и pw на стенке
рис. 68), то можно заметить, что
|рофили скоростей с ростом
До. делаются более крутыми (за-
юлненными) и приближаются при
•том к прямолинейной форме.
0,5
//
/
—
<J=0,7
к=7,4
6,0
Для тех же условий охлажде-
шя поверхности пластинки при-
ведем графики распределения тем-
Соис. 69) в форме зависимостей (Г—Гоо)/(Г0—7со) и
0.2 т
70,!}
7,0
0,5
Моо-5^.
/
//
If/
V
¦
' ^2
—- ¦
""-—
.
^=
—-—,
п =
¦ 0=0
к=7,
•
г
7
4
10 2,0 3,0 4.0 5,0 6,0
и<ю от оезразмерной координаты уУ UoopooKv-ozX). Обращает на
ебя внимание немонотонность температурных кривых. Так, например,
330 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
при интенсивном охлаждении поверхности пластинки ( Tw = -j 7^, J
внутри температурного пограничного слоя имеет место максимум
температуры, который растет с возрастанием числа Моо- Такое
явление объясняется диссипацией механической энергии газа в погра-
ничном слое за счет вязкости. Подтверждение этого факта можно
видеть в графике для случая Tw = Г^,, где по оси ординат отло-
жено выражение, содержащее в знаменателе температуру адиаба-
тического и изэнтропического торможения TQ. При такой интерпре-
тации распределения температур величины максимумов не зависят от
роста числа М^, а положение максимумов с ростом Мю несколько
оттесняется от поверхности пластинки.
§ 69. Продольное обтекание пластинки при числе Прандтля,
равном единице
Если принять б=1 и сохранить произвольным значение показа-
теля п в законе зависимости коэффициента вязкости от температуры,
то из уравнений пограничного слоя можно сделать общий вывод
о связи между температурой и скоростью. Обратимся с этой целью
к первой форме уравнений пограничного слоя, представленной си-
стемой (8.22). Полагая в третьем уравнении системы о=1, получим
линейное относительно h0 уравнение
которое в случае dp/dx = 0, в силу первого уравнения системы
(8.22), имеет очевидный частный интеграл (а и b — постоянные)
ho — au-\-b. A0.39)
Вспоминая (8.13), можем этот интеграл, носящий имя итальян-
ского аэродинамика Л. Крокко'), переписать в виде (а', Ь' — новые
постоянные)
Используя граничные условия
T=TW при в = 0.
Т=Тоо при И = (/оо,
определим а' и Ь', после чего найдем следующую квадратичную
связь между распределениями температур и скоростей в погранич-
') С г о с с о L., L'Aerotecnlca 12 A932).
§ 69]' ОБТЕКАНИЕ ПЛАСТИНКИ ПРИ ЧИСЛЕ ПРАНДТЛЯ, РАВНОМ ЕДИНИЦЕ 331
ном слое при б=1:
A0.41)
Обозначим, как и ранее, значком нуль температуру, соответствую-
щую адиабатически и изэнтропически заторможенному газу; тогда
для любой точки пограничного слоя
^ 2 Т U*
и, следовательно, согласно A0.41), будет существовать линейная
связь между температурой торможения и скоростью:
-^ + -^. A0.42)
Uao I oo
На внешней границе слоя («= U^) и на поверхности пластинки
(и = 0) будет
== * оо ( 1 I 2 ^оо 1 > / щ,о ==
*¦oi *
Из A0.42) и последних формул непосредственно следует равенство
¦р f u
служащее обобщением на случай движения сжимаемого газа при
больших скоростях известного уже нам по § 58 соотношения подо-
бия (9.10). Согласно A0.43), можно утверждать, что в любом сече-
нии слоя при о = 1 и произвольном показателе степени п в законе
зависимости вязкости от температуры поле перепадов температур
торможения газа подобно полю скоростей.
Определение профиля скоростей по сечению пограничного слоя
Для случая ?5=1, а вместе с тем по A0.41) и профиля температур,
представляет значительные трудности, так как приводит к необходи-
мости интегрирования сложного нелинейного уравнения второго по-
рядка. Для составления этого уравнения исключим ср из совокупности
первого уравнения системы A0.14) и результата дифференцирования
того же уравнения по С.
332 ламинарный слой на пластинке в продольном потоке [гл. X
Умножим с этой целью первое уравнение на <р"\ второе — на <р"
и вычтем почленно одно из другого. Получим
(А»-ут <р"+?У2 — (А«-Y)' f = о.
Примем во внимание, что безразмерная энтальпия h является,
согласно интегралу A0.41), известной функцией безразмерной ско-
рости и; кроме того, вспомним, что функция <р(С) была выбрана из
условия и =-к-ср'С")- Полагая
ср' — 2и, hn~lu' = s,
перепишем предыдущее уравнение в форме
йЧ 2« ... ...
S <1044)
причем предполагается, что h(u) заменено его выражением согласно
A0.41). Исследование случая о=1, связанное с интегрированием
уравнения A0.44), по существу уже не использует преобразование
Дородницына, так как координата у не входит в число аргументов.
Из первого уравнения системы A0.14), переписанного в преобра-
зованной форме
1
следует граничное условие (<р"=?0, ср = 0 при и = 0)
^- = 0 при и = 0. A0.45)
Имеем, кроме того, по определению s
s = 0 при и = 1. A0.45')
Эта точка является особой для нелинейного уравнения второго
Порядка A0.44). Полагая в правой части уравнения s=l и замечая,
что при Этом по A0.41) будет А=1, составим приближенное урав-
нение
интегральные кривые которого совпадают с искомыми интегральными
кривыми точного уравнения A0.44) вблизи особой точки и= 1, s — Q.
Определение интегральных кривых приближенного уравнения не со-
ставляет труда. Имеем (а—постоянная интегрирования)
ds d*s __2_ds_ /rf?
~Ш~Ш— s da' \du
. 69] ОБТЕКАНИЕ ПЛАСТИНКИ ПРИ ЧИСЛЕ ПРАНДТЛЯ, РАВНОМ ЕДИНИЦЕ 333
•ткуда при помощи подстановки
— In (as) = z1
j использования граничного условия A0.45') легко получить
«=l-^-erf[/-ln(<w)J.
Задаваясь различными значениями произвольной постоянной инте-
оирования а, выберем такую интегральную кривую, чтобы, выйдя
1ри ее помощи из особой точки и продолжая затем численным ме-
тодом интегрирование точного уравнения A0.44), прийти в точку
ds
i = 0 с нулевым значением производной — = 0 в соответствии
граничным условием A0.45).
Таким образом определяется функция s(u), зависящая также от
(араметров Мт, TJTm, k и я, а затем и функция и (С). На рис. 70
1,0
ч 0,8
16
/А
1
и
II
//
/,
is*
/
-4 ,
/
/
/
4
/
к
/-
/
¦в
У
по
14
» 16
12
8
Л
¦ i и.
— -
d
6
— —
!
"X
-—
Iff
-8
Ч
24
~ма
ч
по
ч
32
ч
ч
4Ъ
ч^
в
Рис. 70.
«оказаны распределения безразмерных скоростей и температур, соот-
ветствующие условию отсутствия теплоотдачи с поверхности пла-
танки [пластинчатый термометр, \-g—) = 0 ПРИ показателе
334 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДбЛЬНОМ ПОТОКЕ [ГЛ. X
степени п в законе зависимости коэффициента вязкости от температуры,
равном 0,76. Как видно из графиков, в этом случае отчетливо виден
факт резкого выполаживания и спрямления профилей скорости,
а также рост толщины пограничного слоя с возрастанием числа Мсо.
Вместе с тем обращает на себя внимание сильный рост температуры
пластинки, естественный при отсутствии теплоотдачи (охлаждения).
Как будет показано в § 75, в действительности столь резкое возра-
стание температуры поверхности пластинки не наблюдается, так как
при высоких температурах уже нельзя пренебрегать лучеиспусканием,
заметно снижающим температуру поверхности.
На рис. 71 для сравнения со случаем отсутствия теплоотдачи
приведены данные по распределению скоростей и температур в погра-
ничном слое пластинки при охлаждении ее поверхности ( Tw = -j- Tm\.
Наблюдается резкое ослабление
только что перечисленных для
случая отсутствия охлаждения
фактов. Кривые скорости стано-
вятся менее пологими и более
искривленными; толщины погра-
ничного слоя при соответствую-
щих Моо существенно умень-
шаются. Наконец, максимальные
температуры, значительно мень-
шие по величине по сравнению
1,0
_u_0,8
Uoo 0,6
0,b
0,2
t,
\°
\l
r
/
/
fo
/
f
/>
-5
s
^M00=10
\
-to
\
fоо=10
4
4
со случаем отсутствия охлажде-
ния, достигаются уже не на по-
верхности пластинки, а в толще
пограничного слоя.
Как уже отмечалось, рас-
q ^ 8 12 16 смотренный только что метод
интегрирования уравнений A0.14)
при ?5=1 уже не связан, соб-
Рис. 71. ственно говоря, с преобразова-
нием Дородницына, а прибли-
жается к методу, основанному на использовании в качестве аргу-
мента вместо у продольной скорости и (метод Крокко), о котором
пойдет речь в следующем параграфе.
§ 70. Уравнения Крокко
Наличие при ?5=1 простой квадратичной связи A0.41) между
энтальпией h и продольной компонентой скорости и наводит на
мысль попытаться и в общем случае использовать в качестве одного
из аргументов скорость. Переход в уравнениях пограничного слоя
? 70] УРАВНЕНИЯ КРОККО 335
от аргументов х, у к новым аргументам $, ч\ по формулам
Ъ = х, ц = и(х, у) A0.46)
был предложен итальянским гидродинамиком Л. Крокко ')•
Дифференцируя предварительно обе части второго равенства си-
стемы A0.46) по ? и т), получим
„ да дх . ди ду ди . ди ду
Ж'Ж^~~дуг'~дТ~~~дх~^~~ду~'~д1~'
. ди дх . ди ду ди ду
дх ' дт) * ду ' д-ц ду ' д-ц '
откуда следует (т — напряжение трения)
dri ди т 1 ду f- )
~т ¦ -. — — ' -, ... ИЛИ .. —¦— | I
^У ду [х ду/дц д-ц 1 I ЛП/17ч
йд: с*х ду ' dS (a di J
Пользуясь этими выражениями производных d~q/dx и d-q/dy, составим
основные формулы перехода от дифференцирования по старым пере-
менным к дифференцированию по новым переменным:
д _ di д дц д _ д т ду д
дх~ дх д$~^ дх <Ь ~ di a d't dv '
At Л А А Л \ (Ю.48)
_d di д , dt) _д_ т д ч '
ду ~~ ду di ду дг) ;х дт\
Совершим указанный переход к новым переменным в системе
уравнений пограничного слоя (8.24). Если принять во внимание, что
в новых переменных
ди dri ди . др _
то после сокращений обеих частей на одинаковый множитель т/р
первое уравнение исходной системы приведется к виду
_p7,i^ + Pf = -4r--^ + -^==-^- + -!L- A0.49)
v ' дЪ ' r di di) ' д-rj d$ х ' дц ч '
Уравнение неразрывности [второе уравнение системы (8.24)] пе-
репишется так:
д(П) х ду д (рг)) х д _ -
di ~ ii~dT~~&r~*'Tdn(9)~
или, согласно A0.47),
') Crocco L, Atti di Qidonia 17, № 7 A939), 118; Rendiconti Circ. Ma-
them. di Palermo, M» 63, 1941, стр. 121; Monographie scientifiche di aeronau-
Иса, № 3, 1946.
336 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Продифференцируем обе части A0.49) по "Ц- получим
J)_ I dy \ ду д (^-ц) \ д . . dp д I \х. \ . дгх
Вычитая почленно обе части этого равенства из A0.50) и исполь-
зуя равенство ду/дт\ = [а/т, исключим v и найдем
Аналогичному преобразованию подвергнем и третье уравнение
системы (8.24) — уравнение баланса энергии. Переписывая его сна-
чала в новых переменных в форме
ду
1Г
д
и исключая затем выражение, стоящее в круглых скобках в левой
части, при помощи A0.49), получим после простых приведений
1
дх2 dh
d2h
dp
A0.52)
Два уравнения второго порядка A0.51) и A0.52), содержащие
две неизвестные величины т и h, дают в совокупности общие урав-
нения ламинарного пограничного слоя в независимых переменных
Крокко 1-х и у\ = и.
В случае продольного обтекания пластинки dp/d% = 0 и уравне-
ния примут более простой вид:
A0.53)
Аналогичные по типу уравнения для случая пластинки получили
Хантцше и Вендт'), положившие с самого начала
т = ,»*!. = О
A0.54)
и принявшие степенной закон связи (i и Т с показателем л.
') Hantzsche W., Wendt H., Jahrbuch 1940 der deutschen Luftfahrt-
orschung, S. I, 517; Jahrbuch 1942 der deutsqhen Luftfahrtforschung, S. 1, 40.
§ 70] УРАВНЕНИЯ КРОККО 337
При этом переменная х исключается, и решение задачи приво-
дится к системе двух обыкновенных уравнений (штрих — производ-
ная по у)):
~~ A0.55)
ijj)x~n = b. 1
:/" -н о) = о J
с граничными условиями
g' = Q при >j = 0, ? = 0 при -rj = 1,
/ = 0 или ] — jw — const при г) = О, у = Joe при 7i=l.
A0.56)
Уравнения A0.55), таким образом, представляют собой частный слу-
чай уравнений A0.53), соответствующий задаче типа Блазиуса—Поль-
гаузена, т. е. задаче о полубесконечной пластинке с постоянной тем-
пературой поверхности. Из уравнений A0.55), так же как из
уравнений A0.14), сразу видно, каких упрощений можно достигнуть,
полагая п=1 или о=1.
Возвращаясь к поставленной задаче, используем систему уравне-
ний A0.53), но перейдем предварительно в ней к безразмерным ве-
личинам. Заменим с этой целью аргументы (L — некоторая длина,
Ua, и hoo = JcpT0O — соответственно скорость и энтальпия набегаю-
щего потока)
?—на Ц, ч\ — на и^-ц, Л—на JcpTm-h;
кроме того, введем вместо напряжения трения т новую безразмер-
ную величину AT(-yj), равную
ip^l). A0.57)
Тогда, замечая, что в рассматриваемой задаче dhjd% si 0, после
выполнения дифференцирования по \ и простых приведений получим
следующую основную систему обыкновенных уравнений (штрих —
производная по tj):
Начнем с простейшего предположения р.р = 1, что соответствует
принятому в предыдущем параграфе условию я = 1. В этом случае
первое уравнение приводится к автономной от второго уравненил
форме
KK" + 2ri = 0. A0.59)
Зак. 297. Л. Г. Лойцянский
338 ЛАМИНАГНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. Г
Это — обыкновенноедифференциальное уравнение второго порядка
которое, конечно, эквивалентно уравнению Блазиуса A.37) и могло Оь
быть непосредственно из него получено заменой переменной <р" на Л
Отсутствие в уравнении третьего порядка A.37) первой произвол
ной <?' (fj) и в явной форме аргумента ч\ позволяет обшепоинятык
'6,7
0,6
05
0,4
0,3
02
MF
/
/
щ
/
/
¦ч
у
\
/
\
\
/
о ц
\
f
х
1
1/
у
7,0
\
\
\
W
0,8
0,6
0,5
1,0
Рис. 72.
способом снизить порядок уравнения; это и приводит к уравнении
второго порядка A0.59). Функция /С(т]) определяется численным иь-
тегрированием; для ее вычисления можно воспользоваться уже roTi-
выми таблицами для задачи Блазиуса, например таблицей 1. hu
рис. 72 приведен график К (-q). который допускает приближена
в виде четверти эллипса.
A0.60
где, как это следует из определения AT (tj) по A0.57),
= 0,664.
A0.61
Считая К (г,) известным, найдем из второго равенства системь
A0.58) (Лц, — TJToo — температурный фактор) выражение безразмер-
* 70]
ной энтальпии:
уравнения крокко
339
°> = "ПгНг 9<2>(ri; a) =
; o)-7(tj; о)].
о
A0-62)
jvhkuhh /fn: oi и У(т); о) представлены графически на рис. 72 и 73.
0,6
0,5
0,4
0,3
0,2
0,1
•
у
/
/
/
/
/
/
i
j
I
' <
НО
О
0,5
Рис. 73.
Составим, пользуясь первым равенством этой системы и приня-
тыми обозначениями, производную
/dh\ _
Ut)/T|=0
A0.63)
22»
340 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [гл. X
Имея в виду независимость /A; а) и УA; о) от Моо. применим
эту формулу к случаю несжимаемой жидкости (М^ = 0). Получим
Ч=о
Сравнивая это выражение f-т—) с результатом расчета той же
величины по A0.32) и A0.33), получим
/A; o) = o-V». A0.64)
Из A0.63) в условиях отсутствия теплоотдачи (пластинчатый тер-
мометр) получается
hw = ht= 1 +о(А— 1)М200УA; о);
с другой стороны, по A0.23)
* 1+()(А
Сравнивая с предыдущим выражением, найдем
УA; о) =^4 б-1/..
Возвращаясь к равенству A0.63), перепишем его в виде
; о) =^4 б-1/.. A0.65)
Имея это выражение, найдем отношение количества тепла Q, от-
даваемого пластинкой, к ее полному сопротивлению F:
х
0 ™
Замечая, что
и вводя число Нуссельта N* как
Q
получим
t 70] уравнения крокко 341
Отсюда можно перейти и к обычному числу Нуссельта [Tt опре-
деляется по A0.23) и A0.31)]
Nu = N* • I» "г' =» т C/R~a'/3 • г" ~г' <10-66>
/„, — У» ^ ' 'а;—'оо
И вновь, таким образом, прийти к A0.34).
В случае о=1и при любом п в первом уравнении системы A0.58)
можно положить прей"". Тогда получим уравнение
А7Г + 2А'?-17)=0, A0.67)
в котором А представляет собой квадратичную функцию от i\,
согласно A0.41) равную
h = - ?^! Mttf + A - hw + -^=± М*,) ч + A.. A0.68)
Можно составить приближенную формулу сопротивления, если
уравнение A0.67) переписать в виде
й затем в знаменателе произвести приближенную замену A0.60), но
не задавать при этом Kw по A0.61), а считать его зависящим от
переменных параметров задачи п, Moo. hw — Tw/Too, k. Полагая еще
в нижнем пределе первого интеграла в предыдущем равенстве т\ =¦ О,
Получим
С другой стороны, по самому определению A0.57) величины К
Имеем
к*=2^ VkZ VTKfaUl)=c,Vr^ VI-
Сопоставление последних двух равенств приводит к искомой при-
ближенной формуле для местного коэффициента сопротивления cf,
в при желании и для коэффициента полного сопротивления Cf. По-
правку на влияние числа Прандтля можно дополнительно ввести при
помощи коэффициента восстановления /-(o) = V^<T при ( Т М
* выражении А по A0.68).
342 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Следуя таким путем, А. Янг1) предложил приближенные аналити-
ческие выражения для коэффициента сопротивления:
1-я
'.= 0,664 Го,45 + О,55-^ + О,О9(А—l)M?o/^j 2 A0.69)
для общего случая и
1-я
= 0,664 [Г+0,365 (ft—1)ML/о] 2
A0.70)
в случае отсутствия теплоотдачи. Соответствующие выражения
для CfVRZ, которые бу-
дут отличаться от преды-
дущих лишь множителем
1,328 перед квадратными
скобками вместо 0,664,
могут быть подставлены
в A0.66) для получения
коэффициентов теплоот-
дачи.
Ю На рис. 74 приведены
расчетные графики измене-
ния величины c,YRxb за-
висимости от числа Моо-
при отсутствии теплоотдачи. Сплошными линиями показаны резуль-
таты строгих расчетов, пунктирными — по формуле A0.70).
§ 71. Применение переменных Мизеса — Прандтля
Обобщим уравнения пограничного слоя в форме Мизеса —
Прандтля (§ 3) на случай газового потока больших скоростей. Введем
функцию тока |(лг, у) в безразмерных переменных, принятых в § 55,
положив (штрихи опускаем)
д&> д&> /in 7i\
Ри = ~л • PV= -г1. AU.71)
Примем вместо х и у в качестве новых аргументов величины
\ = х. ч = <К*. у). A0.72)
') Цитируем по его статье в сборнике «Современное состояние аэроди-
намики больших скоростей», под ред. Л. Хоуарта, ИЛ, 1955, т. I, стр. 433.
§711
ПРИМЕНЕНИЕ ПЕРЕМЕННЫХ МИЗЕСА — ПРАНДТЛЯ
343
Формулы дифференцирования по новым переменным будут связаны
со старыми так:
дх ~~ д~ ¦+" дх д-ц ~ di pV
дх
д~
дх д-ц
di
д д-п д
-г— = ! — = 0U -
ду ду 01] г
A0.73)
Первое и третье уравнения системы (8.23) в безразмерных коор-
динатах в случае продольного обтекания пластинки [-—- = 0) пре-
образуются при этом следующим образом:
,.(ди „*• ди\ ¦ — --- ди - д I--- ди
* \di v о
dh
dh
dh
dh
и после очевидных сокращений приобретут вид
ди д I ^ ди
dh
д
A0.74)
Если поставить вопрос о решении задачи типа Блазиуса, т. е.
автомодельной задачи о продольном обтекании полубесконечной
пластинки с постоянной температурой поверхности, то уравнения A0.74)
с помощью введения новой переменной
могут быть сведены к системе двух обыкновенных уравнений
1 r du d I du
1 . dh
d?u
1 d
dh
A0.75)
Первый вариант применения переменных Мизеса в задаче о лами-
.нарном пограничном слое на пластинке в продольном газовом по-
'.токе был опубликован Карманом и Ченем х). Считая число Прандтля о
равным единице, эти авторы пользовались вместо второго уравнения
системы A0.75) его интегралом, аналогичным A0.41). Первое урав-
') Kdrraan Th., Tslen H. S., Journ. Aeron. Scl. 5, Ш 6 A938).
344 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
нение системы интегрировалось путем последовательных приближе-
ний. В первом приближении в круглой скобке в правой части этого
уравнения выражение рри заменялось по решению Блазиуса и по-
следним двум уравнениям системы A0.1), в которых безразмерная
энтальпия определялась по A0.41). Таким образом составлялось
уравнение первого приближения
Отсюда можно получить
с ехр
где постоянная С может быть найдена из граничного условия
иA)—>1 при С->-оо.
Подставляя значение мA) в A0.41), находим AA), затем [*A) и р(*'
и /j = jj-^y'V1'; после этого получим уравнение второго приближе-
ния
и т. д. Как показано в статье Кармана и Ченя, третьего или чет-
вертого приближения оказывается совершенно достаточно для до-
стижения требуемой точности. Возврат от переменной С к комплексу
размерных координат у Л/ —— Не составляет труда и определяется
формулой
,/7сГ Г Л
У -^c=J -pir-
Результаты вычислений по методу Кармана — Ченя при и = 0,76
и отсутствии теплоотдачи показаны на рис. 70.
Анализируя системы уравнений A0.10) и A0.12), а также A0.53)
и A0.74), можно заметить, что основную трудность для интегриро-
вания представляет наличие в них комплекса |лр = А", связывающего
динамическую часть систем с тепловой. Эта трудность исчезала в слу-
чае п=1, что соответствовало линейному закону связи коэффи-
циента вязкости и энтальпии [i = h. К сожалению, этот простой
закон справедлив лишь при сравнительно малых температурах, а при
более высоких уступает место степенному закону [i. = А", где п
С возрастанием температуры приближается к '/«• В § 54 уже упа-
& 71] ПРИМЕНЕНИЕ ПЕРЕМЕННЫХ МИЗЕСА — ПРАНДТЛЯ 345
миналось о том, что Чепмен и Рубезин предложили столь же про-
стой линейный закон (8.6), содержащий множитель С, выбором
которого в форме (8.7) можно приблизить результаты расчетов по-
граничного слоя к более строгому закону Саттерлэнда.
Примем в выбранных безразмерных величинах
i?, A0.76)
где hw обозначает среднее значение энтальпии hw на поверхности
пластинки, если hw переменна, и hw = hw в случае постоянной
энтальпии на поверхности пластинки; Л. = ^-, причем постоянная
1 со
Саттерлэнда 7^=102° С.
Формула A0.76) представляет те же вычислительные выгоды, что
и ранее рассмотренный случай п=\, а вместе с тем удовлетвори-
тельно описывает связь между коэффициентом вязкости и темпера-
турой в широком диапазоне температур.
Из предыдущих решений было видно, что наиболее высокие
температуры имеют место или на поверхности пластинки (при от-
сутствии теплоотдачи) или вблизи ее (при охлаждении поверхности
пластинки). Таким образом, используя степенную зависимость, сле-
довало бы брать различные п на разных расстояниях от поверхности
пластинки. Предложенное Чепменом и Рубезиным введение постоян-
ного множителя С в значительной мере сглаживает связанный с этим
недостаток линейного закона. Произведенные этими авторами расчеты
показали, что даже при числах Маха порядка 5 использование фор-
мулы A0.76) сохраняет точность 5—6% в конечных результатах как
для условий сверхзвуковой аэродинамической трубы (Т^ = — 233° С),
так и для условий свободного полета на высоте порядка 50 км
(Г» «86° С).
Пользуясь формулой A0.76) и тем, что в пограничном слое на
пластинке в безразмерных величинах будет р=1/А, получим
К> = С. A0.77)
Сохраним те же формулы перехода к переменным \ и ч\ A0.72),
но примем в качестве масштаба размерной функции тока вместо
величины V^ooUoaL, как это было раньше, величину Y^oaUmLC,
содержащую тот коэффициент С, который входит в выражение A0.76).
Тогда вместо A0.74) будем иметь следующую систему уравнений
ламинарного пограничного слоя на пластинке в переменных Мизеса:
ди д / ди
J^__/a_ .ч «2 „{ди\2 , 1 д i лл\ ' (Ю-78)
д\ ^
346 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ X
с граничными условиями
.-О. * = *.« при , = 0. ,
и=1, Л—1 при 7j = oo. J
В частном случае hw = const, Аш = /гш возвращаемся к задаче,
аналогичной рассмотренной в § 68 (га=1, а =? 1), но при новом,
справедливом в более широком диапазоне температур законе связи
вязкости с температурой. В этом случае при обтекании полубеско-
нечной пластинки задача будет автомодельной и переход к перемен-
ной fj/Y^ позволит свести систему A0.78) к системе обыкновенных
уравнений A0.75).
Как легко заключить из вида уравнений A0.78) и граничных
условий A0.79), первое из уравнений системы A0.78) автономно и
может быть разрешено независимо от второго.
§ 72. Ламинарный пограничный слой на пластинке
при переменной температуре поверхности
Задача о ламинарном пограничном слое на пластинке в потоке
несжимаемой жидкости при заданном распределении температуры 7w(x)
по поверхности пластинки была уже ранее рассмотрена в § 60.
Основная трудность этой задачи заключается в том, что при пере-
менной температуре поверхности пластинки теряется свойство авто-
модельности решения. Распределение температуры (энтальпии) в по-
токе определяется в этом случае в результате решения дифферен-
циального уравнения в частных производных.
Для газового потока с большими скоростями задача была решена
Чепменом и Рубезиным!), которые использовали для этой цели
сначала уравнения A0.78), но затем при решении основной, тепловой
части задачи вновь вернулись от переменных Мизеса — Прандтля
к обычным координатам. Проще, как сейчас будет показано, исхо-
дить непосредственно из уравнений A0.10) — A0.12), преобразован-
ных в связи с принятием нового закона изменения вязкости A0.76).
Система уравнений A0.10) — A0.12), если принять для изменения
вязкости закон A0.76), перейдет в следующую:
') Chapman D., Rubesin M., Journ. Aeron. Sci. 16, №9 A949),
547—565; русск. пер. сб. «Механика», ИЛ, 1950, в. 4, стр. 50.
72] ПЕРЕМЕННАЯ ТЕМПЕРАТУРА ПОВЕРХНОСТИ 347
Сохраним в этой системе без изменения координату $ и заменим ч\
V
на tj/JAC, а ф на ^/VC. Тогда, как легко заметить, система A0.80)
может быть сведена к двум, не содержащим постоянную С урав-
нениям:
д^ dh «Эф dh_\ d*h
следует помнить, однако, что в настоящем случае масштабы функ-
ции тока и поперечной координаты отличаются от старых множи-
телем ус.
Введем, как и ранее, новый аргумент и новую функцию
С = 4 7)/^", <р(С) = ф/уХ A0.82)
причем подчеркнем, что в рассматриваемом сейчас случае переменной
температуры поверхности пластинки энтальпия h будет функцией
как С, так и t
Повторив в точности те же расчеты, что и в § 68, придем,
очевидно, к такой системе уравнений (штрих — производная по С):
d*h . dh o , , dh I ,, ....2 „г \ A0.83)
Граничные условия для ср сохраняются прежними A0.15). Что
касается граничных условий для А($, С), то их можно представить
в следующей форме:
A = *w(9 A/tx(9 ПРИ ^ = 0' h=l ПРИ С = оо, A0.84)
где ht определяет постоянную, равновесную, безразмерную энтальпию,
соответствующую энтальпии поверхности пластинки в тех же усло-
виях обтекания, но при отсутствии теплоотдачи; функция ^(^) — за-
данная функция безразмерной абсциссы ?, определяющая отличие
энтальпии hw{t) на поверхности пластинки от равновесной энталь-
пии ht.
Первое из уравнений системы A0.83) с соответствующими гра-
ничными условиями A0.15) уже было решено ранее. Как указывалось
в § 68, его решение совпадет с решением задачи Блазиуса для не-
сжимаемой жидкости и значения функции ср(С) и ее первых двух
производных могут быть получены из таблицы 1, если только при-
нять во внимание, что в настоящем случае, в отличие от § 4, в вы-
ражении A0.82) для аргумента С стоит множитель '/г; соответствую-
щий пересчет не составляет труда.
348 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Для решения второго уравнения системы A0.83), представляю-
щего собой линейное неоднородное дифференциальное уравнение
в частных производных второго порядка параболического типа, при-
меним метод разделения переменных. Будем сначала искать частное
решение А(Е, (.) неоднородного уравнения в виде суммы
А E, 0 = ^@ + 2@.
Подставляя это значение h во второе уравнение системы A0.83),
получим
-TS—г I Z" ~\- amZ' -\--г a (k — 1)ML"! =$—7j- = const = К.
zatp L ' ' 4 ' J a;
Тогда для Х (?) получим значение
имеющее логарифмическую особенность при ? = 0. Требование огра-
ниченности энтальпии при $ = 0 приводит к значению ^ = 0 и,
следовательно, X (?) = 0. Для определения функции Z ((.) получим
уравнение
Z" + oTZ' = - i a (k — 1) MLf*.
которое имеет частное решение
Z* (С) = 1 + ! о (* - О ML /[/ (^)Г Л / [/ (С*)]2 Л*.
с о
равное, согласно A0.20),
Z*(C)=l-r--|-(ft—1)М2о»(С). A0.85)
Вспоминая определение A0.31) коэффициента восстановления г (а),
заключим, что
2*@)=1+/-(о)-Ц^-м2,= А,. A0.86)
где, согласно A0.22), величина Л, представляет собой равновесную
энтальпию. Функция Z*(C) удовлетворяет граничным условиям
Z*@) = A,. Z*'@) = 0. Z*(oo)=l. A0.87)
Решение однородного уравнения
(?2Л . 6А п . , dh
¦3F-И? If-2*?'-35- = 0
§ 72] ПЕРЕМЕННАЯ ТЕМПЕРАТУРА ПОВЕРХНОСТИ 349
ищется в форме произведения двух функций от каждого переменного
в отдельности,
Подставляя это в предыдущее уравнение и разделяя переменные,
получим
Приравнивая обе части постоянной величине, выберем эту по-
стоянную в форме 2ап (я = 0, 1, ...)¦ Тогда
а для определения Zrt(C) будем иметь линейное однородное уравне-
ние второго порядка
Z^ + acpZn — 2on<p'Ze = 0 A0.88)
с граничными условиями
Zn@)=l. Zn(oo) = 0. A0.89)
Решение однородной части второго из уравнений A0.83) пред-
ставим как сумму
2в„
а полное решение рассматриваемого второго уравнения системы A0.83)
выразится в форме
h(l C) = Z'(C) + 2 an?Zn(Q. A0.90)
л = 0
Из граничных условий A0.87), A0.89) и из возможности пред-
ставления решения в виде A0.84) сразу следует результат
со со
h (?. 0) = Г @) + 2 aninZn @) = ht + 2 ап\п = ht + x (?).
л=0 л=0
так что получим
Вспоминая, что /_($) есть заданная функция, характеризующая
распределение по поверхности пластинки величины hw — ht, т. е.
разности между действительной энтальпией и равновесной, заключим,
что неизвестные величины ап определяются как коэффициенты раз-
ложения функции х(?) в степенной ряд.
350 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Перейдем к определению теплоотдачи с поверхности пластинки.
Секундное количество тепла, снимаемого с единицы площади, qw
в размерных величинах будет равно
«. = " К (?)_ = - КТ- (§¦) ? аГг'п @).
По A0.37), в случае масштаба поперечных координат, увеличен-
ного в У~С раз, имеем в размерных величинах
и, следовательно,
л=0
Введем в рассмотрение функцию
которая служит естественным обобщением постоянной Чепмена и
Рубезина С на случай переменной температуры стенки. Тогда по
формуле Саттерлэнда (8.4) получим уже в размерных величинах
^w VW /> / у.\ *w
Лоо (Лею ' сх>
Подставляя в A0.92), придем к результату
со
@). A0.94)
л=0
Отсюда уже нетрудно найти полное секундное количество тепла Q,
снимаемого потоком с пластинки длиной L и рассчитанного на еди-
ницу ширины пластинки,
anbnZ'n{% (Ю.95)
л=0
где положено
Значения Z'n@) при первых шести значениях п приведены в таб-
лице 26.
ПЕРЕМЕННАЯ ТЕМПЕРАТУРА ПОВЕРХНОСТИ 351
Таблица 26
я
•>)
0
— 0,5915
1
— 0,9775
2
—1,1949
3
—1,3680
4
—1,4886
5
—1,5975
Легко подсчитывается также и напряжение трения
Сх
.куда интегрированием по х от 0 до L можно найти полный
юэффициент трения
С — !'328 Гг ,n dl
UacL
Voo
A0.96)
1 частном случае пластинки с постоянной температурой поверхно-
сти (CW = C) найдем
п _ 1.328, г^
1,4
На рис. 75 приведены кривые
зависимости коэффициента полного
сопротивления теплоизолированной
пластинки Сf от чисел R^ и М^
при двух значениях температуры д
внешнего потока: ТОО = 86°С (атмо- ; ~
сфера, высота 50 км) и Т^ =
= — 233° С (аэродинамическая труба .,
больших скоростей). Пунктирные '
прямые соответствуют линейному ;д
закону D/A.00 = Т/Та,, а сплошные
кривые — соответственно закону f g
|х/Dсо = С777'00 Чепмена и Рубезина
(на рисунке Ч.—Р.) и точным рас-
четам Крокко J) по формуле Сат-
терлэнда (на рисунке Саш.). Пре-
имущество метода Чемпена — Ру-
безина достаточно убедительно.
Численные методы решения уравнений пограничного слоя на
пластинке были разработаны Эммонсом и Брайнердом2).
') С г о с с о L, Lo strato iimite laminare nei gas. Monogr. Scientif. di Aeronau-
Hca. Assoc. Cult. Aeron., Rome, 3 A946).
2)EmmonsH., Brainerd G., Journ. of Appl. Mech. 8 A941), A-105;
в том же журнале и тех же авторов 9 A942), А-1.
ч.-р.
Cam.
— ¦«.
О
Мао
Рис. 75.
352 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЧНОМ ПОТОКЕ [ГЛ. X
Не будем останавливаться на приближенных способах расчета
ламинарного пограничного слоя на пластинке, аналогичных методу
Польгаузена (слой конечной толщины); литература по этому раз-
делу очень обширна, укажем лишь некоторые важнейшие исследо-
вания ').
§ 73. Взаимодействие пограничного слоя со сверхзвуковым
потоком
Изложенные в предыдущих параграфах решения задачи о про-
дольном обтекании полубесконечной пластинки газом при больших
скоростях основываются на предположении, что давление на поверх-
ности пластинки постоянно и равно давлению в набегающем пото-
ке. Предположение это, пригодное в случае малых скоростей,
когда обратное влияние пограничного слоя на внешний поток не
слишком существенно, перестает быть таковым, если скорости
велики и набегающий поток является сверхзвуковым. В этом случае
подтормаживающее влияние трения в пограничном слое и вызывае-
мое этим подтормаживанием оттеснение линий тока от поверхности
пластинки становится причиной существенного изменения обтекания
пластинки, особенно в области ее передней кромки.
С качественной стороны явление развивается подобно тому, как
это было описано в § 10. Обратное влияние пограничного слоя
на внешний поток можно себе представить так, как будто газ во
внешнем потоке идеален, но обтекается не пластинка, а некоторое
новое тело, форму которого можно определить, наращивая по обе
стороны от поверхности пластинки плоское «полутело» с ордина-
тами, равными толщине вытеснения, рассчитанной по действитель-
ному течению. Под толщиной вытеснения S* здесь следует уже
понимать некоторую обобщенную на случай газового потока вели-
чину, а именно
Существенная особенность сверхзвукового газового потока заклю-
чается в том, что между обтеканием пластинки и указанного «полу-
тела», представляющего собой вблизи передней кромки нечто вроде
тонкого клина, имеется большая, принципиальная разница. На перед-
ней кромке этого клина, эквивалентного по распределению давле-
ний пластинке в вязком газе, образуется присоединенная головная
') Дородницын А. А., ПММ, т. VI, в. 6, 1942; К а л и х м а н Л. Е.,
ПММ, т. IX, в. 3, 1945; Morris D., Smith J., Journ. Aeron. Sci. 20,
№ 12 A953).
§ 73] ВЗАИМОДЕЙСТВИЕ СЛОЯ СО СВЕРХЗВУКОВЫМ ПОТОКОМ 353
волна в виде косого скачка, интенсивность которого при больших
числах -М.с оказывается достаточно большой. Перепад давления
в таком косом скачке достигает значительной величины. При дви-
жении газа в пограничном слое вдоль пластинки давления по-
немногу выравниваются, и на большом удалении от передней
кромки давление становится постоянным и равным давлению вда-
леке от пластинки. Отсюда следует, что давление в погранич-
ном слое и на повержости пластинки не сохраняется постоян-
ным, как это ранее предполагалось при решении задачи об обтекании
пластинки.
Количественная сторона рассматриваемого вопроса составила
предмет исследования Го Юн-Хуая1). Применяя метод последова-
тельных приближений, автор сращивал решения двух систем урав-
нений, описывающих движение вязкого газа в пограничном слое и
движение идеального газа во внешнем потоке. При этом внешний
поток в первом приближении строился по распределению попереч-
ных скоростей на границе пограничного слоя, рассчитанного по нуле-
вому приближению при постоянном давлении во внешнем потоке.
Полученное таким путем распределение давления во внешнем
потоке в первом приближении служило основой для нового рас-
чета пограничного слоя, и т. д.
Вводя такого рода последовательные поправки и исключив
возникающие при этом на передней кромке пластинки «особенности»,
Го Юн-хуай получил искомое решение в приближенной, но зато
замкнутой форме.
Отсылая интересующихся деталями анализа к оригиналу только
что цитированной работы, изложить которую ввиду большой ее
вычислительной сложности здесь не представляется возможным,
остановимся на некоторых окончательных выводах этого исследо-
вания.
Рассматривая случай теплоизолированной пластинки, принимая
для зависимости коэффициента вязкости от температуры формулу
Чепмена и Рубезина A0.76) и полагая число Прандтля равным еди-
нице, Го Юн-хуай вводит в качестве основного малого параметра
задачи величину (С — коэффициент в только что упомянутой фор-
муле Чепмена и Рубезина, R = р U Liu. )
J J со Гсо со ' too'
? —rr
По степеням этого малого параметра и ведется разложение
искомых функций (функции тока, давления, температура).
') Kuo Y. Н., Journ. Aeron. Sci. 23, № 2 A956), 125-136; русск. пер.
см. в сб. «Механика», ИЛ, 1956, № 6.
23 Зак. 297. Л. Г, Лойцянский
354 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ б ПРОДОЛЬНОМ ПОТОКЕ [гл X
Распределение безразмерного давления р (равного р/р^) опреде-
ляется в функции безразмерных координат х (равной xjL) и у (рав-
ной yjL) формулой
р=1-\ ^ \~О(е.3),
где vQ и р — постоянные, определяемые равенствами
г>0 = 0,860-1-0,596 (ft— 1)ЛС, р^
а величина ?. являющаяся функцией л;, у, определяется как корень
уравнения
l B — А) М2
На поверхности пластинки (у = 0) имеем
±i^_2) /, + ^(i±i
и распределение давлений принимает окончательный вид
где введены для краткости обозначения
На рис. 76 сплошная кривая представляет собой график рас-
пределения величины (р—\)jK в зависимости от х по формуле
A0.97). На том же рисунке приведены для сравнения результаты
опытов Коулза, Нагаматцу и Кендалла, Бертрама, Богдонова и Хам-
мита, причем для всех опытных точек принято одно и то же обо-
значение. Можно заключить, что теория Го Юн-хуая находится
в хорошем соответствии с опытом.
На рис. 77 показаны линии Маха и присоединенный косой
скачок на передней кромке пластинки, рассчитанные теоретически
при Мое =10 и е=10. При удалении от передней кромки напра-
вление косого скачка стремится к направлению линий Маха. Косой
скачок имеет значительную интенсивность; так, по расчетам
Го Юн-хуая при М^^б давление за скачком в пять раз превы-
шает давление перед скачком. Вдоль поверхности пластинки при
этом имеет место убывание давления от сильно повышенного сразу
731
ВЗАИМОДЕЙСТВИЕ СЛОЯ СО СВЕРХЗВУКОВЫМ ПОТОКОМ
355
л скачком до давления, равного давлению в набегающем потоке,
щалеке от передней кромки.
Напряжение трения на пластинке вдалеке от передней кромки
jdh учете пеоеменности давления и наличия скачка оказывается
1
'.О
ю
0,6
ом
6,3
0,2
0,1
O.Od
ОМ
6,0,3
0,02
0,01)
/
f
/
•
/
•
•
m
•
(
•
t
f
•b
7
/i
I
«
*
i
0,010,020,03Щ'0,1 0.2 ОА
Рис. 76.
тесколько оольшим, чем при постоянном давлении. При приближе-
1ии к передней кромке напряжение трения достигает максимума и
Рис. 77.
;атем падает до нуля, в то время как при постоянном давлении
'но, как известно, стремится к бесконечности; однако, по-видимому,
близи передней кромки решение Го Юн-хуая недостаточно точно.
23*
356 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. Г
§ 74. Нестационарные явления на безграничной пластинке,
импульсивно приведенной в равномерное движение
Расчет нестационарного пограничного слоя, образующегося npi
приведении пластинки в движение в своей плоскости из состояни;
покоя, связан с очень сложными математическими выкладками. Вс:-
существующие методы подхода к решению этой задачи являются
весьма приближенными и основаны либо на линеаризации, либс
на разложениях по степеням числа .Маха, которое при этом, естест
венно, предполагается не слишком большим 1).
Основные физические особенности явления можно отчетливс
изучить, если рассмотреть следующую упрощенную постанови
задачи2). Бесконечная пластинка приводится импульсивно из сост<-
яния покоя в равномерное движение в своей плоскости с постояь
ной скоростью U. Пластинка предполагается теплоизолированной
число Прандтля равным единице, коэффициент вязкости пропорции
нальным энтальпии. Безграничность пластинки позволяет считать, чт(
все характерные для задачи переменные величины (и, v, p, р, h
зависят только от у (координата, нормальная к плоскости пла
стинки) и /. Полная система уравнений движения вязкого газа, со-
гласно (8.1), (8.9), (8.11) и (8.14), имеет вид
/ди . ди\ д I ди\
= 0,
ду
dv\ dp , 4 д Iim dv^
A0.98
_д_( dh
"Г ду
здесь и далее индекс 0 относится к покоящемуся газу. Граничные
') Howarth L, Quart. Journ. of Mech. and Appl. Math. 4, № 2 A951,
157—169. II ling worth С R, Proc. Cambr. Phil. Soc. 46 A950), 003—61o
Stewarts on K., Quart. Journ. of Mech. and Appl. Math. 4, № 2 A951,
182-198.
2)v-Dyke M., Zeitschr. f. Angew. Math. u. Phys. 3, № 5 A952), 343—35;.
74] НЕСТАЦИОНАРНЫЕ ЯВЛЕНИЯ НА БЕЗГРАНИЧНОЙ ПЛАСТИНКЕ 357
и начальные условия представятся так:
и (у, 0 = 0, v(y,t) = O при *=0.
u(y,t)=U при у = 0 и ^>0,
О = Ро< рО'-0 = Ро ПРИ ' = 0.
dh
ду
= 0 при у =
A0.99)
Переходя от у к переменной Дородницына т] и вводя тождест-
венное преобразование времени
Ро
A0.100)
получим
д . дг) j)^ д р д
так что оператор, фигурирующий в левых частях второго, треть-
его и четвертого уравнений системы A0.98), будет равен
д , д с)./дг).р \ о
~dt~T~v ~ду~ ~ Ж"+" \дГ + "^ vj ~д^•
Но в силу первого уравнения той же системы
dt — 9о J dt ау — ~^J
ду
так что предыдущее равенство переходит в такое:
^ "*" v ду ~ дв '
Кроме того, в соответствии с последними двумя равенствами си-
стемы A0.98) получим
A0.101)
АоРо Ро
A0.102)
Таким образом, после проведения указанных преобразований
придем к системе уравнений (v0 = р-0/р0)
ди д / р ди\
Ро
— — (JL
3 ^ drt \Ро
дЪ
д (р dh
A0.103)
358 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. ..
Имея в виду дальнейший путь расчета последовательными при
ближениями, преобразуем систему A0.103) тождественно к следую
щему виду:
_1_ др_ А_ д lp_ dv_\ __ dv_
ди д2и д I р — р0 ди
dh I ди
М
р0
д (Р—Ро dh
¦)•
A0.104
т); ^ р <эе ^ 'о дг, \ Ро
Остановимся на решении типа пограничного слоя, справедливок
лишь при больших значениях числа Рейнольдса Re = , практи
чески — при больших /. При этом правые части уравнений A0.104
становятся малыми и могут быть в первом приближении откинуты
тогда в первом приближении получим решения
р = р0, и = ?/егК. h = ho + Uu — \ и2. A0.105
где введен новый аргумент
С= ?— . A0.106
су •%/ о ч
В этом приближении имеем [М = U/a0; a\ = (k—1)А0]
2±- = ?- = 4-=\ + {k— l)M2erfC- (l — ierfcV A0.107
Связь между координатой у и переменной Дородницына ч\ полу-
чим, замечая, что ,,
f р
о
и, следовательно, по A0.107) придем к результату
— l)M2[erfC(l— -g-i
A0.108
Здесь приняты обычные обозначения
X ОС
е
U ' " X
§ 74] НЕСТАЦИОНАРНЫЕ ЯВЛЕНИЯ НА БЕЗГРАНИЧНОЙ ПЛАСТИНКЕ 359
Чтобы определить поперечную скорость v, применим оператор
A0.101) к аргументу у; тогда по A0.108) найдем
Во внешнем потоке (С = оо) получим
A0.110)
а соответствующее значение толщины вытеснения b*(t) определим,
как
t
Лу. A0.111)
Скорость v по A0.111) можно рассматривать как скорость
поршня, расположенного в точке у —&*@ и вытесняющего газ при
движении пластинки.
Чтобы исследовать создаваемое этим поршнем поле давлений,
перепишем систему A0.98) в виде
dp . dv . dv dp
dt ^^ ° dy "" " dy dy
ди ди . д / ди'
dt " ду dy у д.
dy . dp_ . . jh>_ dv _. 4 d I dv'
dt ~^ dy "" dt " dy ~^ 3 dy
^*_^Р_/Л _^dh .. dh . „. dp
ди ,
Ро Ж = (Ро -
i Г/ du \2 , 4
+ M (-3—1 -4--T
L\ dy / з
d
dh
A0.112)
Откидывая в первом приближении правые части, получим для v
обычное уравнение распространения малых возмущений в идеальном
газе
d'v ! д2%> 0. A0.113)
dy2
< dtz
которое при начальном и граничном условиях
v(y. 0) = -
v@. /) =
A0.114)
360 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ (ГЛ. X
(второе условие, как всегда в задачах такого рода, выполняется
при у = 0 вместо у = 8*) будет иметь решение
при
¦ " "' A0.115)
i = 0 при
Аналогично выразится и разность давлений р—pQ; получим
A0.116)
При малых значениях величины у/(а,/) можем представить это
решение в форме ряда
или, переходя к переменным Сив,
+ yifM2Povoj+--. A0ЛШ
Получив в первом приближении поле давлений во внешнем по-
токе, перейдем к вычислению второго приближения для распределе-
ния давления в пограничном слое. Для этого, исходя из первого
приближения A0.105) для р, т. е. используя равенство р = р0 и
значения v по A0.100\ подспвим эти значения в правую часть пер-
вого равенства системы A0.104) и проинтегрируем обе части по ч\;
найдем
Р =
^С Erf (/2 С)] + С@), A0.118)
где С@)—произвольная функция времени, которая должна быть
определена из условия сращивания этого решения с решением A0.117)
для внешнего потока.
При больших С будем иметь вместо A0.118) асимптотическое
равенство
р^~^-MVo| + C(Q). A0.119)
Сравнивая с A0.117), убедимся, что с точностью до R'"'" сле-
дует положить внутри пограничного слоя
r-. A0.120)
§ 74]
НЕСТАЦИОНАРНЫЕ ЯВЛЕНИЯ НА ВЕЗГРАЧИЧНОЙ ПЛАСТИНКЕ
361
Вводя малую поправку и' к продольной скорости и, рассчитанной
по первому приближению A0.105), сможем найти эту поправку, под-
ставляя в правую часть второго равенства системы A0.104) вместо и
его значение в первом приближении и вместо р его выражение по
A0.120). Тогда придем к неоднородному уравнению
k[k~X) М31Л~ГЧ<ГСЗ A0.121)
дт?
с нулевыми начальными и граничными условиями
имеющему решение
1)М3
A0.122)
A0.123)
убывающее до нуля на бесконечном удалении от пластинки.
Далее, можно найти и распределение энтальпии во втором при-
ближении. Соответствующая поправка h' к первому приближению
A0.107) будет равна
A0.124)
Подсчитав по исправленному значению h новые значения р и
найдем поправку v' к поперечной скорости в виде
— --L Се-'2 Erf С]}. A0.125)
Применяя вновь ту же схему «поршня», что и при выводе урав-
нений A0.115) и A0.116), найдем выражения для v и р во внешнем
потоке во втором приближении:
2т. а0 t-y/at
У/gQ \
t — yla0)'
Р =
t-yla0)
A0.126)
362 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ X
Аналогичным путем вычисляется и третье приближение. Приведем
в заключение выражение для местного коэффициента трения Ср рас-
считанного в третьем приближении
^^ A0Л27)
Полученное решение пригодно только при условии, когда, как
это имеет место в пограничном слое, поперечная скорость v мала
по сравнению с (У и, кроме того, применение линеаризированных
уравнений распространения волн возмущений допустимо лишь при
условии, что скорость движения «поршня» v мала по сравнению
с а0. Эти условия накладывают следующие ограничения на основные
параметры явления М и Re:
/Re ^ /Re ^"
Рассмотренная задача является интересным примером взаимодей-
ствия пограничного слоя с внешним потоком. Так же как и в § 73,
это взаимодействие благодаря проявлению сжимаемости газа приво-
дит к возникновению волн возмущений, при наложении которых
друг на друга образуются ударные волны. В только что рассмотрен-
ном случае импульсивного приведения в равномерное движение пла-
стинки по обе стороны от нее будут распространяться ударные
волны, параллельные поверхности пластинки. Как следует из фор-
мулы A0.127), наличие обратного влияния пограничного слоя на
внешний поток приводит к уменьшению коэффициента трения, кото-
рый при отсутствии этого взаимодействия равнялся бы величине,
стоящей множителем перед фигурной скобкой в правой части ра-
венства A0.127). Это уменьшение невелико, так как, по предыду-
щему, изложенная только что теория справедлива лишь при малых
значениях параметра M2/V^Re, т. е. при больших значениях t.
§ 75. Влияние излучения на распределение температуры
в пограничном слое в абсолютно прозрачном газе
При высоких температурах, возникающих на поверхности пла-
стинки в газовом потоке большой скорости, уже нельзя пренебрегать
лучеиспусканием, наличие которого резко снижает температуру ее
поверхности. Если считать воздух абсолютно прозрачным, то учет
влияния лучеиспускания потребует лишь изменения теплового гра-
ничного условия на поверхности пластинки. Это условие должно
выражать баланс секундных количеств тепла, подводимого к пла-
стинке за счет теплопроводности газа и отводимого от нее путем
лучеиспускания. Будем считать лучеиспускание подчиняющимся закону
§ 75] ВЛИЯНИЕ ИЗЛУЧЕНИЯ НА РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ 363
Стефана — Больцмана. Если материал пластинки абсолютно тепло-
проводен, то суммарный баланс по всей поверхности пластинки
длины L приведет к граничному условию (о — постоянная Стефана —
Больцмана для абсолютно черного тела)
L L
{i* — T$dx. A0.128)
Если же материал пластинки абсолютно нетеплопроводен, то гра-
ничное условие будет иметь локальный характер
В промежуточном случае не абсолютно теплопроводной пластинки
(коэффициент теплопроводности k имеет конечное значение) необхо-
димо в последнем равенстве дополнительно принять во внимание
отвод тепла вдоль поверхности пластинки, что выразится дополни-
„тельным членом —k . ™ в правой части этого равенства. Остано-
вимся на . первом случае абсолютно теплопроводной пластинки
(Тю =const), причем примем для простоты линейный закон зависи-
мости коэффициентов вязкости и теплопроводности от температуры.
Тогда, воспользовавшись готовым решением § 68, а именно форму-
лой A0.32), получим
Замечая, что (не смешивать число Прандтля о с постоянной Сте-
фана — Больцмана о)
Т
и используя равенство A0.23), придем к следующему алгебраическому
уравнению четвертой степени для определения искомой температуры:
Ш-
где под К понимается величина
12Т6 L
= VK, A0.130)
A0.131)
Сложнее решается задача об учете влияния лучеиспускания в слу-
чае абсолютно нетеплопроводной пластинки. В этом случае Tv пред-
364 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
ставляет собой функцию х и определяется из обыкновенного диф-
ференциального уравнения'), которое составляется приближенным
способом из основного уравнения баланса энергии в пограничном
слое, в случае Tw Ф const представляющем собой уравнение в част-
ных производных. В только что цитированной работе И. Н. Соко-
ловой можно найти анализ промежуточного случая конечной тепло-
проводности пластинки. Там же приводится пример расчета темпе-
ратуры поверхности пластинки длиной L=b м, которая движется
на высоте 10 км (Г0О = 233°) со скоростями (/со = 336 м/сек
(Mra=l,12) и ?/со=1342 м/сек (МСО = 4,47). В первом случае
температура поверхности пластинки Tw = 263° (при абсолютно тепло-
проводной пластинке) и Tw = 260° (при абсолютно нетеплопроводной
пластинке), в то время как при отсутствии лучеиспускания было бы
Tw — 279н- 271°. Уменьшение температуры за счет лучеиспускания
в этом случае невелико. Иначе будет во втором случае, когда
Моо = 4,47. Вместо температуры Tt= 1028-^- 1115° при отсутствии
лучеиспускания имеют место температуры порядка Tw = 663-r-618°,
т. е. абсолютная температура пластинки за счет лучеиспускания
в этом случае снижается почти вдвое. Следует оговориться, что
принятое значение я=1 в законе связи коэффициента вязкости
с температурой при высоких температурах недостаточно точно. Пер-
вое теоретическое исследование влияния лучеиспускания на темпера-
туру пластинки, расположенной в продольном газовом потоке больших
скоростей, принадлежало И. А. Кибелю2). Случай произвольного п
при о = 1 был разобран Хантцше и Вендтом3), приведшими решение
вопроса к рассмотрению уравнения
VI g @) УШ, (l - TJTco +
где К определяется по A0.131), а ^@) представляет собой решение
системы A0.54) при о=1 и т; = 0.
§ 76. Продольное обтекание пластинки слабо разреженным
газом при учете скольжения
Строгое рассмотрение задачи о движении газа в пограничном
слое в области значений чисел Рейнольдса и Маха, где уже нельзя
пренебрегать влиянием скольжения газа вдоль поверхности тела,
') Соколова И. Н., Температура пластинки в сверхзвуковом потоке
с учетом излучения, Сб. теоретических работ по аэродинамике, Оборонгиз,
1957, стр. 206.
2) К и б е л ь И. А., ДАН СССР 25, № 4 A939).
3)Hantzsche W., Wendt H., Jahrbuch 1942 der deutschen Luft-
fahrtforschung, стр. 1—40.
§ 7-6]' OBTF.KAHIIF РАЗРЕЖЕННЫМ ГАЗОМ ПРИ V4F.TF. СКОЛЬЖЕНИЯ 365
представляет значительные и по сие время непреодоленные трудности.
Сложность этого вопроса связана, как уже было ранее (§ 56) выяс-
нено, с необходимостью отказа не только от уравнений пограничного
слоя, но, собственно говоря, даже и от тех, более общих уравнений
Навье—Стокса, первым приближением к которым являются уравне-
ния пограничного слоя. Что касается уравнений Барнета, предста-
вляющих собой более точное приближение к общим кшичичг к им
уравнениям движения газа, чем уравнения Навье —Стокса, и стокши >.
непосредственно на пути исследователя, который пожелал бы достич.
существенного прогресса в задаче о движении разреженного газа, то
на их интегрирование вряд ли можно рассчитывать в ближайшее
время.
Ряд исследователей (В. П. Шидловский, М. Ф. Широков, А. И. Бу-
нимович, В. П. Мясников у нас в Союзе, Шааф и Шерман, Белл,
Нонвейлер, Лиз и Пробштейн за рубежом), желая отдельно выяснить
влияние специфических для этой области граничных условий — сколь-
жения газа по поверхности тела и разрыва в изменении температуры
при приближении к поверхности, —рассмотрели приближенные ре-
шения задач о продольном обтекании пластинки, находящейся в сла'ю
разреженном газе, основанные на использовании обычных уравнений
теории пограничного слоя, но с новыми, только что упомянутыми
граничными условиями'). Последний из только что цитированных
советских авторов, В. П. Мясников, вместо обычных уравнений по-
граничного слоя использовал уравнения следующего приближения
Го Юн-хуая, о которых шла речь в § 73.
Остановимся на рассмотрении случая продольного обтекания
полубесконечной пластинки 1-^ — = 0) слабо разреженным газом, при-
чем для простоты положим а=1 и п=\.
Следуя выше цитированному решению В. П. Шидловского, будем
исходить из обычной системы уравнений пограничного слоя (8.22),
приобретающей в данном случае вид
ди . ди д / ди \ д (рд
. дх ' ' ду ду V ду )' дх _,
dho ^ Л , ЛЬ i „2 (Ю.133)
г дх ' ' ду ду у ду ) ° р ' 2
1) Шидловский В. П., Изв. АН СССР, ОТН.ЛаЭ, 19.58, стр. 83—93;
Широков М. Ф., Физические основы газодинамики, Физматгиз, 1958,
стр. 325—331; Бунимович А. И., Изв. АН СССР, ОТН, Механика и ма-
шиностроение № 5, 1959; Мясников В. П.. там же, стр. 127—130;
Schaaf S. A., Sherman F. S., Journ. Aeron. Sci. 21, № 2 A953),
стр. 85—90 (русск. пер. см. сб. «Механика», ИЛ, 1955. № 1); Bell S., Univ. of
California Instit. of Engin. Res., Techn. Rep. 20—106, 1955.
366 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
граничные условия выразим в соответствии с формулами (8.26) и
(8.29) (Тр — температура поверхности пластинки)
ди . , ди _ „ 2k дТ . 2k , дТ п \
и = "Г -з— = / -з—. Т—Т„ — т-г-7 т -s- =^= , , Л-т- при у = О, I
1 ду ду »" * +1 ' ду k-\-\ ду v * I
и = t/oo, Г= Too при у = со, )
A0.134)
где, как упоминалось в § 56, коэффициент скольжения f близок
к длине I свободного пробега молекул при данной температуре и
может быть приближенно ею заменен. Поясним, что температура
пластинки Тр в общем случае не равна температуре газа у поверх-
ности пластинки Тю, которая определяется условием A0.134). При
дТ\ Т ~Т
отсутствии теплоотдачи
Переходя, как это уже делалось в § 68, к переменным Дород-
ницына
о
получим вместо системы A0.133) следующую систему уравнений:
ди , ~ ди д2и
A0.135)
Замечая, что из известных соотношений (яй — знак пропорциональ-
ности, v — средняя скорость пробега молекулы)
следует, что
и, таким образом.
Исходя из предположения об отсутствии теплоотдачи, получим
§ 76] ОБТЕКАНИЕ РАЗРЕЖЕННЫМ ГАЗОМ ПРИ УЧЕТЕ СКОЛЬЖЕНИЯ 367
следующие граничные условия в переменных Дородницына:
A0.136)
U = Um, Г= Та, При fj = ОО.
Введем новые независимые переменные
• t = rjl/"^ A0.137)
A0.138)
и новые безразмерные зависимые переменные
Тогда, определяя функцию тока равенствами
A0.139)
перепишем первое и третье уравнения системы A0.135) в виде
A0.140)
Граничными условиями для этой системы будут
=1 при С = со.
<=*¦
A0.141)
Отметим основную особенность рассматриваемого решения. На-
личие заданного наперед масштаба длин /ra делает задачу не авто-
модельной, несмотря на то, что в данном случае, как и во всех
задачах типа Блазиуса (§§ 4, 58, 68, 69), пластинка рассматривается
как полубесконечная. Этим и объясняется тот факт, что после вве-
дения второго из комплексов переменных A0.137) уравнения A0.135)
не свелись к обыкновенным дифференциальным уравнениям, содер-
жащим в качестве единственного аргумента С. Устремив е к нулю,
что можно рассматривать как пренебрежение длиной пути свободного
пробега молекулы по сравнению с размером пластинки, вернемся
к обычной задаче Блазиуса.
368 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Будем в связи со сказанным искать решение системы A0.140)
при граничных условиях A0.141) в виде рядов
A0.142)
входящая в первое из граничных условий A0.141) величина
также может быть представлена рядом
Поскольку порядок величины s равен (Z. — характерный размер
пластинки, о — толщина пограничного слоя)
r = 0 (W§) =
а в самих уравнениях пограничного слоя сохранены члены только
до этого порядка включительно, тогда как члены более высокого
порядка откинуты, то, собственно говоря, при применении разложе-
ний A0.142) может идти речь лишь об учете влияния членов по-
рядка г в первой степени, выражающих собой связанную с влия-
нием разреженности газа поправку к решениям сро(?) и 0о(С).
Подставим разложения A0.142) в систему уравнений A0.140) и
граничные условия A0.141), сохраняя лишь члены нулевого и пер-
вого порядков относительно е. Путем обычного приравнивания коэф-
фициентов при одинаковых степенях s получим следующую систему
обыкновенных дифференциальных уравнений и граничных условий
к ним (штрих—производная по С)
A0.143)
2?'Г + ?o?i' -t- ?o?'i = °; ?i @) = о- ?; @)
?;(oo)=0;
К + T ?«si + i ?oei = - 2 (ft - 1) .M
@),
e; @; = о,
A0.144)
§ 76]
ОБТЕКАНИЕ РАЗРЕЖЕННЫМ ГАЗОМ ПРИ УЧЕТЕ СКОЛЬЖЕНИЯ
369
В системе A0.143) нетрудно узнать обычную постановку задачи
Блазиуса для газа при з= 1, п= 1 и при условии отсутствия тепло-
отдачи с поверхности пластинки. Отличие от уравнений A0.18) и
граничных условий A0.15) и A0.17) заключается только в числовых
коэффициентах и объясняется разницей в определении аргумента С;
в равенстве A0.13), в отличие от второго из равенств A0.137),
введен множитель 1/2.
Значения функции сро(Ч> и ее производных приводятся в таблице 1.
Эта функция тождественна функции ср(т)), определенной в § 4. Функ-
ция бо(С) легко определяется из второго уравнения A0.143) и, так
же как и в § 68 [см. A0.29)], равна
причем
k — 1
A0.145)
A0.146)
Обратимся к рассмотрению системы уравнений A0.144). Легко
видеть, что первое из уравнений этой системы имеет решение
9iQ=VK,f'o(^ A0.147)
удовлетворяющее соответствующим этой функции граничным усло-
виям. Второе уравнение системы A0.144) почленным интегрированием
сводится к уравнению первого порядка, после чего легко получить
искомое решение
A0.143)
Аналогично решается вопрос об обтекании пластинки с заданной
постоянной температурой поверхности Ьр. В этом случае надо раз-
личать величины hp и в@) = 8то, так как, согласно A0.134),
2k /дТ\
1\ду /у=о'
а при наличии теплоотдачи правая часть уже не равна нулю. Реше-
ние имеет вид [<ро(С) то же, что и в предыдущем случае]
Тр k
= - (ft - 1) .М
?' (О ?"
A0.149)
24 Зак. 297. Л. Г. Лойцянск
ий
370 ЛАМИНАРНЫЙ СЛОЙ НА ПЛАСТИНКЕ В ПРОДОЛЬНОМ ПОТОКЕ [ГЛ. X
Оно удовлетворяет граничным условиям
«,_,, .,<»-.,?->т,Чт.1 A0.150)
90(оо)=1, 9j(oo) = 0. )
Приводим в заключение сводку результатов расчета основных,
наиболее интересных величин для двух режимов: 1) отсутствия тепло-
отдачи с поверхности пластинки и 2) задания ее температуры.
Сохраняя члены только сев первой степени, т. е., как ранее
уже упоминалось, пренебрегая в решении членами, порядок которых
одинаков с опущенными при составлении уравнений, получим:
1) при отсутствии теплоотдачи с поверхности пластинки
[?0" @) = 0,332]
uJUoa= 0,332
т =0,332A. U ,.
2) при заданной температуре пластинки Тр
= 0,332 У%г = 0,332 1 / i e.
ь i ь .1 т \ f т
?,
Анализ полученных выражений показывает, что в принятом при-
"ближении в случае отсутствия теплоотдачи только наличие скольже-
ния (тем более сильного, чем больше М^,) отличает разреженный газ
от неразреженного. Температура на поверхности пластинки и напря-
жение трения остаются при этом неизменными. Во втором случае,
когда задана температура пластинки, проявляется влияние разрежен-
ности газа на его температуру у поверхности пластинки. Вычисленная
поправка зависит не только от Моо. но и от отношения Тр/Т^.
Сделанное предположение о линейности связи между |а и Т по-
зволяет применять полученные результаты только в случае сравни-
тельно низких температур. При высоких температурах, как мы знаем,
следует пользоваться значениями показателя я, меньшими единицы1).
[) См. цитированную выше статью А. И. Бунимовича.
ГЛАВА XI
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
§ 77. Ламинарный пограничный слой на конусе
в продольном сверхзвуковом потоке
Настоящая глава по своему содержанию служит прямым про-
должением предыдущей: в ней рассматриваются примеры пограничных
слоев также с постоянным давлением на внешней границе, но отлич-
ные от продольного обтекания пластинки. Таковы примеры продоль-
ного обтекания кругового конуса, образования пограничного слоя
на стенке ударной трубы, плоской струи в затопленном тем же газом
пространстве, пограничного слоя на вращающемся в газе диске,
радиально-щелевой газовой струи, распространяющейся вдоль твердой
стенки и свободной закрученной радиально-щелевой струи. В заключе-
ние главы мы возвращаемся вновь к случаю продольного обтекания
пластинки, но рассматриваем его в предположении, что газ в силу
тех или других причин приведен в равновесное диссоциированное и
ионизированное состояние. В последнем случае учитывается наличие
электропроводности газа, в связи с чем движение в пограничном
слое изучается при взаимодействии газа с внешним магнитным полем.
м
///////////////////////
Рис. 78.
Начнем с рассмотрения пограничного слоя на поверхности круго-
вого конуса, симметрично расположенного в однородном сверхзвуко-
вом потоке, параллельном оси конуса. Будем предполагать, что угол
раствора конуса 0О (рис. 78, а) соответствует при заданном числе
Маха Ме набегающего потока случаю наличия присоединенной к вер-
шине конуса ударной волны, на рис. 78, с не показанной. За этой
24*
372
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
[ГЛ. X!
волной движение идеального (невязкого) газа будет потенциальным
и «коническим», т. е. все параметры газа должны сохранять постоян-
ные значения вдоль любой конической поверхности, соосной с обте-
каемым конусом, имеющей общую с ним вершину и расположенной
между ним и ударной волной. В частности, давление в этом движе-
нии идеального газа должно сохранять постоянное значение на по-
верхности обтекаемого конуса, а следовательно, по известному свой-
ству пограничного слоя, давление будет постоянным и во всем
пограничном слое в вязком газе. Этот факт сближает движение в
пограничном слое на конусе со случаем продольно обтекаемой пла-
стинки. Можно показать, что между этими двумя движениями суще-
ствует простое соответствие').
С этой целью сопоставим уравнения пограничного слоя на конусе
в сферических координатах (рис. 78, а)
ди
v ди
d(9v)
~W~
1 д
ди
дг
2ра _
r —и>
/ dh . v dh \ _ 1 1 д I dh \ . р. I ди \2
A1.1)
и соответствующие им граничные условия F^ > Go — условный угол,
представляющий границу слоя)
A1.2)
и = 0, v = 0, h = hw(m\i -^- == 0j при 6 =
u->ue, h-> he при 0 -> бда
с уравнениями пограничного слоя и граничными условиями на пла-
стинке (рис. 78, б) в том же газе
- ди . - ди
п-д1+"-ду
д(?и) , д(ру) _
~оЧ~^~~дУ~ —
(- dh . - dh
ди
dh
дп\2
или
dh
dy
= 0)
при
u^ue,
при у—> oo.
(П.З)
')Hantzsche W., Wendt H., Jahrbuch 1941 der deutschen Luft-
fahrtforschung, стр. 1-76, 77.
§ 77) ЛАМИНАРНЫЙ СЛОЙ НА КОНУСЕ В СВЕРХЗВУКОВОМ ПОТОКЕ 373
Замечая, что обе задачи автомодельны (образующие конуса, так же
как и линия пересечения пластинки с плоскостью чертежа — полу-
бесконечные прямые, и нет характерного масштаба длины), будем
искать решение задачи о продольном обтекании пластинки в обычном
виде:
У
А =
а для пограничного слоя на конусе — в аналогичной форме
(П.4)
= Л (С),
A1.5)
Тогда система уравнений A1.1) переходит в систему обыкновен-
ных дифференциальных уравнений
2 +f
С d(?u)
2 dt,
~\ du
du
d
A1.6)
а система A1.3) — в следующую:
1 -. , л\ tin d
1 r rf (p«) d 7 _
-ГГ Y AL7)
и = 0, 1^=0, й = Ада(или -ff-= О) при С = (
u-*ue, h-+he при С->оо.
Если в системе A1.6) совершить дополнительное преобразование
A1.8)
374 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
то она переходит в систему уравнений
(ГЛ. XI
С d (9и) , d (p W) _^
2 rfC ~^~ dC
\ 2
dl
A1.9)
и граничных условий
и = 0. W = О, Л = hw (^ = 0\ при С"= 0,
и—*-ие, h—>he при С—> оо,
A1.10)
ничем не отличающихся от уравнений и граничных условий A1.7)
для пластинки.
Отсюда можно заключить, что если функции аргумента С
У х
A1.11)
представляют собой решение для пластинки, то те же функции от
аргумента С
^[> ] А = /г*(Г) A1.12)
дадут искомое решение для конуса.
Сопоставляя эти решения, можно прийти к следующим выводам.
Условные толщины слоя на конусе 8*. 8** при тех же значениях
абсциссы г = х в ]/~Ъ раз тоньше, чем на пластинке (8*. 8**). Действи-
тельно, имеем, например,
так
что 8* = 8~7]/~3. и т. п.
§ 77] ЛАМИНАРНЫЙ СЛОЙ НА К0НУСЕ В СВЕРХЗВУКОВОМ ПОТОКЕ 375
Сравним напряжения трения: tw — на конусе и тго — на пластинке.
Имеем
([л ди \ /p. du* rfC \
C=0 v иУ'у = О
т. е. при одном и том же значении абсциссы г = х напряжение тре-
ния на конусе в У раз больше, чем напряжение трения на пластинке.
Точно так же убедимся, что коэффициент полного сопротивления
п
трения на конусе при прочих равных условиях в -j уЗ раз больше
соответствующего коэффициента на пластинке. Действительно, пер-
в'ый из этих коэффициентов равен
/- 1
,,dr [2nrY^wdr
о D/VD с
где постоянная с = т^ у г, а второй —
mdx
2с
4 m?.i 4 ?#* '
что при равенстве величин ие и йе приводит к высказанному заключе-
нию. Точно в таких же отношениях У~3 и -jV% находятся мест-
ные и средние коэффициенты теплоотдачи.
К тем же результатам можно прийти проще и с гораздо более
общей точки зрения, применяя к уравнениям пограничного слоя на
продольно обтекаемом конусе преобразование Е. И. Степанова, обоб-
щенное, как уже упоминалось в § 32, на случай пограничного слоя
в газе Манглером. Преобразование это заключается в переходе от
координат х, у, отсчитываемых вдоль меридионального сечения по-
верхности тела вращения и по нормали к нему, к координатам х,
У в соответствующем плоском пограничном слое по формулам
376 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
(/•0—радиус поперечной кривизны тела вращения)
[гл.
A1.13)
и сохранении всех остальных параметров потока:
A1.14)
кроме поперечной скорости v, которая преобразуется согласно ра-
венству
-_ v г'0(х)
A1.15)
Составим уравнения пограничного слоя на теле вращения при
продольном его обтекании газом [сравнить с E.6) § 30] в коорди-
натах хну, причем используем то приближение, о котором шла
речь в § 30 при выводе системы уравнений E.6); тогда получим
A1.16)
ди\*
)
Введем функцию тока ф(х, у) согласно равенствам
_J_ дф _. 1 дф
о — р
A1.17)
удовлетворяющим второму уравнению системы A1.16). Применяя
преобразование A1.13), согласно которому
д
дх
д
д
дх
д
д
ду
A1.18)
к системе равенств A1.17), получим
_J_ д^ 1_
Р ду р
1 д'Ь
дх
77) ЛАМИНАРНЫЙ СЛОЙ НА КОНУСЕ В СВЕРХЗВУКОВОМ ПОТОКЕ
377
откуда следует
1 дЬ
? ду
р дх
Применяя к первому и третьему уравнениям системы A1.16) пре-
образования A1.18) и используя для второго уравнения той же си-
стемы равенства A1.19), получим по A1.14) следующую систему
уравнений в новых переменных:
р
(— ди . — ди \
\ дх ду ]
- ди^
д~у
д(?п)
дх
-- йи„
е dx
д'у
1 д I-
д (-
ду
- диЛ
ду I
A1.20)
дТГ \ 2
совпадающую с уравнениями пограничного слоя в плоском 1азовом
потоке; совпадут и преобразованные граничные условия.
Пользуясь этим общим преобразованием в рассмотренном в начале
параграфа частном случае конуса, будем иметь по первому равен-
ству системы A1.13)
г0 (х) = ах, х = -=- а2х3,
у = аху,
A1.21)
где а = sin а (а — половина угла раствора конуса). Сравним между
собою, например, напряжения трения для конуса, xw, и для пла-
стинки, тго. По второму равенству системы A1.13) получим в соот-
ветствующих точках (х, у) и (х, у) общее соотношение
У /у=о
Вспомним, что Хантцше и Вендт провели сравнение х^ и хда при
одинаковых значениях абсциссы на образующей конуса и вдоль пла-
стинки; по A1.21) это означает, что надо положить
1 , ,
= -тг а2хл
о
или
ах =
Возвращаясь после этого к равенству A1.22), получим
в полном соответствии с предыдущим результатом Хантцше и Вендта.
Аналогичным образом можно получить и остальные их результаты.
378
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
. [ГЛ. XI
е
§ 78. Образование пограничного слоя на стенке
ударной трубы
Рассмотрим пограничный слой на плоской стенке ударной трубы
постоянного сечения, образующийся за проходящей ударной волной.
Обозначим через б скорость распространения ударной волны и
через V скорость спутного потока газа за ударной волной. Считая
стенку трубы плоской и безграничной, обратим движение так, чтобы
ударная волна стала неподвижной. При этом поставленная задача
сведется к следующей стацио-
нарной задаче: бесконечная
плоскость (рис. 79) движется
слева направо со скоростью б.
В точке О системы координат
Оху вдоль оси Оу располо-
жен неподвижный скачок уплот-
нения. Слева от скачка газ дви-
жется вместе с плоскостью,
как твердое тело, со сверх-
звуковой скоростью 9, справа
от него скорость скачкообразно
уменьшилась до постоянного
дозвукового значения ?7^ — 0— V, а стенка продолжает дви-
гаться с той же скоростью б. Область перехода от скорости и=9
при у = 0 до и= Uqo при у = со образует пограничный слой,
расчет которого приводится ниже ¦).
В связи с отсутствием продольного изменения давления за скачком
уллотнения (сопротивлением самой трубы пренебрегаем) основные
дифференциальные уравнения движения вязкого газа в пограничном
слое, развивающемся за ударной волной, будут теми же, что и на
пластинке в однородном продольном потоке газа. Отличие будет
заключаться в граничных условиях.
Примем за масштаб длин произвольную величину L, а за масштаб
скоростей величину ?/^=0— V. Символом go будем обозначать
в дальнейшем величины на внешней границе пограничного слоя.
Прим-ем линейный закон связи между динамическим коэффициентом
вязкости и температурой и ограничимся исследованием случая постоян-
ства температуры вдоль стенки трубч. Тогда задача сведется к инте-
грированию системы дифференциальных уравнений A0.18) с авто-
номным динамическим уравнением, но с измененными граничными
в
Рис. 79.
') Ф о р с о в а Т. Я., Некоторые вопросы аэродинамики ударных труб.
Дипломная работа, кафедра гидроаэродинамики Ленинградского политехи,
ин-та, 1957.
78] ОБРАЗОВАНИЕ ПОГРАНИЧНОГО СЛОЯ НА СТЕНКЕ УДАРНОЙ ТРУБЫ 379
условиями, а именно
<р = 0. ?'= 2и„ = 28/F — V) при С = 0,
ср' = 2 при
С = 0, I
- (П.23>
С = оо, J
где по элементарной теории прямого скачка будет
(А4-1)е + А —1
uw—
w~ в— V (А —1)е + А + 1 '
а величина в обозначает отношение давления за скачком к давлению
перед скачком. При этом, как известно,
1<S<OO, 1<И_.<-г г!
для воздуха (ft =1,4) имеем 1^яв,<6. Можно еще заметить,
что uw равно отношению плотности газа за скачком к плотности
газа до скачка.
Совершив переход к новому аргументу z и новой функции Ф
A1.24)
убедимся, что рассматриваемое дифференциальное уравнение в новых
переменных сохранит свою форму (штрих означает производную по z)
= 0, A1.25)
а граничные условия A1.23) преобразуются к виду
ф = 0, Ф' = 2 при г = 0, |
*/ 2 A1.26)
Ф' = -— ПрИ 2 = ОО.
Решение уравнения A1.25) при граничных условиях A1.26) можно
представить в форме ряда
= 2! *"*„(*) (П.27)
л = 0
ПО степеням малого параметра
Подставляя выражение A1.27) в уравнение A1.25) и приравнивая
коэффициенты при одинаковых степенях а, получим систему уравнений
Ф«+ 2 ФтФл-ш = 0 (й = 0. 1, 2 ...) A1.28)
380 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
с граничными условиями
[ГЛ. X
A1.29
Фл = 0, Фо = 2, Фл = 0 (ге>0) при z = 0,
Фо = 2, Ф| = 2, Фл = 0 (я > 1) при z = co. ]
Функция Ф0(г) определяется из уравнения и граничных условий
Фо = 0, Фо = 2 при 2 = 0; Фо = 2 при z = oo;
при этих граничных условиях уравнение обладает очевидным решением
Для функции Ф1 (z) получим уравнение
ф'" Ч- 2гФх = 0,
которое при граничных условиях A1.29) имеет решение
Ф
г
= 2 f
Таблица 2*
N. tl
г ^ч.
0
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
1
0
0,2250
0,4457
0,6572
0,8568
1,2078
1,4842
1,6854
1,8206
1,9046
1,9526
1,9782
1,9906
1,9962
1,9986
1,9996
1,9998
2
0
0,0409
0,0805
0,1179
0,1508
0,1981
0,2144
0,2003
0,1648
0,1209
0,0800
0,0476
0,0257
0,0126
0,0056
0,0023
0,0009
3
0
—0,0046
—0,0091
—0,0139
—0,0192
—0,0316
—0,0469
—0,0618
—0,0715
—0,0719
—0,0630
—0,0484
—0,0325
—0,0191
—0,0097
—0,0040
—0,0008
4
0
0,0009
0,0018
0,0027
0,0035
0,0054
0,0080
0,0124
0,0188
0,0257
0,0305
0,0306
0,0261
0,0190
0,0116
0,0056
0,0013
5
0
—0,0002
—0,0005
—0,0007
—0,0009
—0,0013
—0,0016
—0,0022
—0,0032
—0,0057
—0,0092
—0,0126
—0,0138
—0,0129
—0,0097
—0,0056
—0,0029
< 78] ОБРАЗОВАНИЕ ПОГРАНИЧНОГО СЛОЯ НА СТЕНКЕ УДАРНОЙ ТРУБЫ 381
аналогично находим функцию Ф2Сг)
= (l ——)Erf z-(Erf zf
j последовательно Ф3(.г) и т. д. Для дальнейшего особенно суще-
твенно знание первых производных Ф^(г); в таблице 27 приво-
]ятся значения этих производных для л=1, 2, 3, 4 и 5.
/25
/.20
I.W
/Мб
О
Ц05
пт
¦
^7
1
I
1
=
/
——
/*
_——
N
;,
\
ф;
0
\
\
Ф'г
\
\
+~-
¦— ¦—
Ф'
*^
\
— —
5-=
Рис. 80.
ia рис. 80 приводятся кривые Фп(г) для значений й = 2, 3, 4, 5
дл-! п~\ это — хорошо известная кривая функции Гаусса).
Обращает на себя внимание факт резкого спадания максимального
качения производных с ростом п, обеспечивающий быстроту сходи-
юсти ряда, полученного дифференцированием обеих частей A1.27).
Тользуясь этим рядом, найдем значения функции Ф' (z). Эти значения
юи различных величинах параметра uw, а следовательно, и а при-
водятся в таблице 28.
382
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X
Таблица 2;
г ^ч
0
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
"to
2
1,9636
1,9279
1,8938
1,8615
1,8043
1,7588
1,7249
1,7014
1,6862
1,6770
1,6717
1,6691
1,6677
1,6670
1,6668
1,6666
1,5
2
1,9297
1,8607
1,7946
1,7318
1,6207
1,5309
1,4629
1,4143
1,3816
1,3608
1,3482
1,3409
1,3370
1,3350
1,3340
1,3336
2,0
2
1,8983
1,7985
1,7028
1,6119
1,4501
1,3178
1,2160
1,1411
1,0886
1,0537
1,0311
1,0171
1,0090
1,0043
1,0018
1,0006
3,0
2
1,8697
1,7419
1,6190
1,5022
1,2934
1,1214
0,9863
0,8845
0,8109
0,7594
0,7241
0,7007
0,6857
0,6765
0,6709
0,6680
4,0
2
1,8565
1,7155
1,5802
1,4515
1,2208
1,0300
0,8790
0,7640
0,6792
0,6188
0,5758
0,5466
0,5272
0,5144
0,5064
0,5021
5,0
2
1,8490
1,7004
1,5579
1,4225
1,1792
0,9774
0,8172
0,6941
0,6027
0,5366
0,4891
0,4555
0,4328
0,4176
0,4079
0,4026
Чтобы получить основную зависимость безразмерной скорости i
от комплекса у/Bух), где х и у— безразмерные геометрически
координаты, необходимо еще вернуться от z к С = т)/B ]А) и с
у
переменных Дородницына ? — х и т}= I pdy к координатам л: и у
о
Для этого в случае о= 1 следует использовать интеграл Крокко A0.41
и равенство р=1/Л.
Остановимся на простейшем случае /1=1 и примем постояннук
Чепмена — Рубезина С равной единице; кроме того, положим о == .
Для этого случая Т. Я. Форсовой даны окончательные результать
в форме таблиц и графиков. Пересчет на более общий случай С Ф
не представляет труда.
Опуская переход от одних переменных к другим, дадим окончи
тельный вид параметрической зависимости безразмерной продольно?
скорости и от геометрического комплекса у/B У~х) через параметр z
u = j ujb' (z),
У_ _
2 Yx
^= \ h{z)dz;
A1.30
> 781 ОБРАЗОВАНИЕ ПОГРАНИЧНОГО СЛОЯ НА СТЕНКЕ УДАРНОЙ ТРУБЫ 383
[апоминаем, что величина h (z) определяется путем подстановки ско-
юсти и в интеграл Крокко A0.41). В таблице 29 искомая зависи-
юсть дана для ряда значений параметра uw. Кривые распределения
кпоостей поиводятся на рис. 81.
1
1,
\
~~~п—
ч. X
^?
=5
— --
— 1—
О Q2 Q4 Q6 О,в 7,0 J,2 /А
$)
Рис. 81.
.яая начальные значения (значок 0) физических констант в непо-
движном газе, можно определить напряжение трения на поверхности
¦дарной трубы в спутном потоке
"*,,, толщины вытеснения 5* и по-
¦ери импульса 8**; эти величины
сражаются по формулам (а0 —
скорость звука в неподвижном
азе до прихода ударной волны)
2,0
»•* ** -| / ^о*
A1.31)
о
\
\
ч
S*
ч
—,
—' -
- 1
ч
/
1——
'¦ щ
I
_
2,0
1,0
О
1
Рис. 82.
Входящие в уравнения A1.31)
1вличины тш> 5*. о** представлены
j таблице 30 в функции от uw
! изображены на рис. 82.
Разобранная стационарная задача просто связана с поставленной
1 начале параграфа нестационарной задачей о пограничном слое,
•бразующемся за ударной волной, распространяющейся по трубе.
хли обозначить через X, Y абсолютные координаты в плоскости,
3*4 ПОГРАНИЧНЫЕ СЛОН С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X
Таблица 2^
г
0
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
z
0
од
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
y/i2r.v)
0
0,0919
0,1839
0,2759
0,3678
0,5515
0,7349
0,9182
1,1013
1,2844
1,4672
1,6500
1,8328
2,0156
2,1985
2,3814
2,5643
uw =
ylB\rx)
0
0,0712
0,1421
0,2127
0,2825
0,4194
0,5407
0,6695
0,7951
0,9173
1,0374
1,1558
1,2730
1,3896
1,5055
1.6213
1,7368
= 1,2
I a
1,2000
1,1782
1,1568
1,1363
1,1170
1,0826
1,0553
1,0349
1,0208
1,0117
1,0062
1,0030
1,0015
1,0006
1,0002
1,0001
1,0000
= 3,0
и
3,0000
2,8044
2,6130
2,4285
2,2533
1,9401
1,6821
1,4766
1,3266
1,2162
1,1391
1,0860
1,0512
1,0284
1,0146
1,0062
1,0020
I
ll-v -
УД2-П-)
0
0,0842
0,1683
0,2523
0,3362
0,5033
0,6696
0,8352
0,9999
1,1642
1,3279
1,4915
1,6550
1,8183
1,9816
2,1449
2,3083
aw =
y/B\rx)
0
0,0696
0,1337
0,2072
0,2748
0,4062
0,5320
0,6520
0,7668
0,8776
0,9850
l.o;-99
1,1932
1,2951
1,3962
1,4969
1,5972
= 1,5
и
1,5000
1,4472
1,3956
1,3460
1,2988
1,2156
1,1481
1,0971
1,0608
1,0362
1,0206
1,0112
1,0056
1,0028
1,0012
1,0005
1,0002
= 4,0
и
4,0000
3,7128
3,4312
3,1604
2,9032
2,4416
2,0600
1,7580
1,5280
1,3584
1,2376
1,1516
1,0932
1,0544
1,0288
1,0128
1,0040
0
0.0771
0,1542
0,2316
0,3074
0,4587
0,6080
0,5734
0,9010
1,0450
1,1881
1,3305
1,4726
1,6144
1,7559
1,8974
2,0389
y/B Vx)
0
0,0693
0,1382
0,2062
0,2732
0,4024
0,5246
0,6396
0,7484
0,8519
0,9511
1,0472
1,1409
1.2330
1,3240
1,4141
1,5039
= 2,0
и
2,0000
1,8984
1,7984
1,7028
1,6120
1,4500
1,3178
1,2160
1,1412
1,0886
1,0536
1,0312
1,0172
1,0090
1,0038
1,0018
1,0006
= 5,0
и
5,0000
4,6225
4,2510
3,8950
3,5560
2,9480
2,4435
2,0430
1,7355
1,5090
1,3415
1,2230
1,1390
1,0820
1,0440
1,0200
1,0065
. 78] ОБРАЗОВАНИЕ ПОГРАНИЧНОГО СЛОЯ НА СТЕНКЕ УДАРНОЙ ТРУБЫ 385
'О они будут связаны с использованными ранее относительными коор-
динатами лг, у соотношением
Х = х-\-Ы, Y = y.
Произведя в выражениях A1.31) замену л: на X— 6/, получим
пормулы зависимости iw, Ь* и 8** от координат и времени, что и
соответствовать поставленной нестационарной задаче.
Таблица 30
1,2
1,122
0,427
0,239
1,5
0,925
0,386
0,254
2,0
0,785
0,331
0,283
3,0
0,618
0,262
0,413
* 4,0
0,526
0,220
0,745
5,0
0,444
0,190
2,760
о'
ельная простота решения этой задачи определялась
о стенка ударной трубы считалась безграничной, а газ за вол-
однородным. Только благодаря этим допущениям удалось
ввести обращение движения, которое привело к постановке про-
стационарной задачи. Не-
одолимые трудности предста-
яет решение существенно не- [/т [ $
аационарных задач, возникающих
фи более строгом рассмотрении ^/
действия ударной волны на огра- N
шченную по размерам стенку. —
Представим себе, например,
юлубесконечную пластинку Ох, У'
юмещенную параллельно стенкам Рис. 83.
'дарной трубы. Пренебрегая влия-
шем стенок, попробуем изучить явление взаимодействия пластинки Ох
проходящей вдоль нее ударной волной // (рис. 83). Примененный
* предыдущем параграфе квазистационарный подход к решению
;адачи в данном случае уже, очевидно, непригоден. Как показано
схематически на рисунке, в этом более общем случае из простых
Физических соображений ясно, что область пограничного слоя
1=±5(лг) должна быть ограничена по оси абсцисс точками:
= 0) и О' (х = 6/), в которых толщина пограничного слоя
нулю.
25 Зак. 297. Л. Г Лойцянский
386
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
[ГЛ XI
Применяя при решении рассматриваемой сейчас задачи уравнения
нестационарного пограничного слоя в газе для пластинки (-^- = О,
-^г= СМ, которые, согласно заключительным замечаниям § 55,
должны иметь вид
(ди
ди
ди
д
ди
dp |
dh0
dt
¦-(- и
дх
dh0
дх
ду
ду
следует, строго говоря,
так и по х:
A1.32)
учитывать граничные условия как по у,
ди
«=о. i* =о
при у = 0, л: < О,
U =
А = ATO при у = 0, л: > О,
А = Лоо при у — со, х < 6/,
h = h0 при у = оо, х > б/.
A1.33)
Следуя известному приему Блазиуса (§ 4), можно отказаться
от строгого выполнения первой строчки условий A1.33). Как изве-
стно, при этом точка (х = 0, у = 0) становится особой, в ней
продольная скорость и скачкообразно меняется от значения и = U&,
при х — — 0 до м = 0 при x = -j-0, а напряжение трения при-
обретает бесконечное значение. Такое упрощение решения допустимо,
если пластинка не слишком коротка, и его можно принять при
исследовании данной задачи.
Основные граничные условия, представленные двумя последними
строчками системы A1.33), никак не могут быть заменены одним,
не учитывающим коренное отличие носовой части поверхности пла-
стинки (х < bt), по которой ударная волна уже прошла, от осталь-
ной части (х > 6/), где газ еще покоится. Такое упрощение при-
вело бы к решению элементарной задачи о стационарном обтекании
пластинки по Блазиусу ¦).
Строгое решение системы уравнений A1.32) при граничных усло-
виях, учитывающих различие внешних потоков до волны и за ней
представляет значительные затруднения. В качестве некоторого при-
ближения можно пользоваться решением, состоящим из двух частей;
') См., например, Демьянов Ю. А,, ПММ, т. XXI, в. 3, 1957.
стр. 368—374.
§ 79] ЛАМИНАРНАЯ СТРУЯ В ГАЗОВОЙ СРЕДЕ 387
для стационарного течения в носовой части пластинки — по одному
из методов, изложенных в главе X, и для квазистационарного течения
в области, непосредственно следующей за распространяющейся по
пластинке ударной волной, — согласно решению, приведенному в на-
стоящем параграфе.
§ 79. Ламинарная струя в газовой среде
Простейшей задачей о «свободном» пограничном слое в газе
может служить задача о распространении плоской ламинарной струи
в пространстве, заполненном тем же газом'). Чтобы иметь дело
с автомодельной задачей, будем считать, как и ранее в § 5, что
струя бьет из бесконечно тонкой щели с бесконечно малым расхо-
дом, но конечным импульсом. Кроме того, аналогично тому, как
это имело место в рассмотренной в § 64 тепловой задаче, будем
считать, что струя переносит некоторое конечное количество тепла.
Зададим, таким образом, струю двумя характерными константами,
соответствующими двум «законам сохранения»
со
Г рм2 dy = const = Jo,
A1.34)
/I и2 \
рм I h + -~ Ac» I dy = const = Ho,
-co
которые легко выводятся обычным путем из уравнений в размерных
величинах (8.22), если использовать граничные условия (индекс со
относится к покоящемуся газу, окружающему струю)
A1.35)
Полагая в дальнейшем число Прандтля равным единице, вос-
пользуемся наличием при такой постановке задачи интеграла
Крокко A0.39), который в размерных координатах можно пред-
ставить в форме
ду
и
= 0, ',
= 0, /
v = 0,
l== floa
dh
ду
= 0
при
при
У
У
= 0,
= со
Для определения двух констант используем, во-первых, граничное
условие для энтальпии A1.35), согласно которому будет C2 = hoa,
') Т о о s s e D. О., Quart. Journ. of Mech. and. Appl. Math. 5, part 2
A952). РезниченкоЮ. Т., Труды ЛПИ, № 5 A953), стр. 32.
25*
388 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X'
и, во-вторых, второй закон сохранения A1.34), приводящий к ра-
венству
J ри • Схи dy = Ио,
так что С, = HqJJq. Окончательно, интеграл Крокко примет вид
(в размерных величинах)
А = —-^- + -^-и + Асо. A1.36)
Примем еще для упрощения задачи линейную связь (ге = 1) между
коэффициентом вязкости и энтальпией. Тогда уравнения в перемен-
ных Дородницына A0.10) и A0.11) совпадут с соответствующими
уравнениями плоской струи в несжимаемой жидкости (§ 5). соста-
вленными в безразмерных скоростях и координатах. Используя
соображения о масштабах, приведенные в начале § 5, перепишем
решение A.63) в форме
и = 0.454л:-1/. sech2 @,275у/л:г/0.
v = 0,550х-'1> [0,550 (у/х'/>) sech2@,275y/x!/>) — th @,275yjx'i>)).
Заменяя здесь х и у на переменные Дородницына
у
и вводя новый аргумент C = '»i/E/\ получим следующие выражения
для безразмерных продольной и поперечной компонент скорости:
и = 0,454rv>sech2 @,2750.
v = 0,550rJ/'[0,550C seen2 @,2750 — th @,2750]-
Сохранив в первом из равенств A1.37) безразмерную перемен-
ную С. вернемся к размерным и н х, для чего вспомним, что
масштабы U и L связаны равенством A.55). Найдем
/A0 Х\~'/г
и = 0,454 ( з ) sech2@,275C). A1.38)
Чтобы перейти от С к обычным размерным координатам х и у,
представим связь переменной tj с размерной координатой у в форме
§ 79] ЛАМИНАРНАЯ СТРУЯ В ГАЗОВОЙ СРЕДЕ 389
откуда будет следовать
i\V'^/^C. A1.39)
Подставим значение скорости и по A1.38) в равенство A1.36);
получим
/и. а х\-2<*
h — — 0,1031 ( °°2°° ) sech4@,275O +
+ 0.454 H±{iX™9~x\ 'sech2 @.2750 +Лоо. A1.40)
Уо \ Уо /
Заменяя после этого в правой части A1.39) величину h только
что указанным ее значением, найдем искомую связь между лг,
y/jc!/» и С в форме
^'\/ХЧ' = _ 0.3745/ii1 (^^\ ''("th @.2750-
— — th* @,27501+1.651 -^-(^w-) 'th@.275O + C. A1.41)
Рассматривая С как параметр, найдем из системы уравнений A1.38).
A1.40) и A1.41) размерные продольную скорость и и энтальпию h
как функции размерных координат лг, у.
Полагая в A1.38) и A1.40) С = 0, получим выражения для ско-
рости и энтальпии на оси струи:
A1.42)
Не будем останавливаться на дальнейших деталях, так как по
соображениям, приведенным еще в §§ 5 и 64, рассмотренная задача
имеет чисто методическое значение.
Задачи теории ламинарных струй подробно изложены в моногра-
фии Бай Ши-и!), к которой мы и отсылаем интересующихся этой
специальной областью теории пограничного слоя. Автор упомянутой
•) Бай Ши-и, Теория струй, Физматгиз, 1960.
390 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X
монографии применил для решения задачи о смешении двух одно
родных потоков различных газов переменные Мизеса — Прандтля1,
Те же переменные можно было бы с успехом применить и длг
решения задачи о плоской ламинарной струе, подобно тому как этг
было сделано для несжимаемой жидкости в § 6.
К тому же классу задач относятся и задачи о следе за тело!п
о струях, граничащих с твердыми поверхностями, и др. Все они пp^
упрощающих предположениях о законе изменения вязкости сводятсг
к соответствующим задачам о течении несжимаемой жидкости.
§ 80. Ламинарный пограничный слой
на быстро вращающемся в газе диске
Приемами, аналогичными изложенным в предыдущих параграфа,,
можно решить и осесимметричную задачу о диске, быстро вращаю-
щемся в газе вокруг оси, перпендикулярной к его плоскость
Задача эта в своей постановке и методах решения является обобше
нием изложенных ранее, в § 38 изотермической и в § 63 неизотер
мической задач о диске, вращающемся с малыми скоростями.
Чтобы сохранить автомодельность, будем, как и раньше, рас-
сматривать диск как безграничную плоскость, вращающуюся вокру
перпендикулярной к ней прямой. Координаты и соответствующие
им компоненты скорости выберем согласно рис. 41, помещенном'
в начале главы VI.
Дифференциальные уравнения пограничного слоя в газе в pat
сматриваемом осесимметричном случае приведутся к виду (малыми
изменениями давления в дальнейшем пренебрегаем)
ди . ди v2\ д I ди
dv , . dv , uv \ д f dv
A1.43
1 д (rpu) . d (i>w)
r dr ' dz
дТ . дГ\ Id
с граничными условиями (ш — угловая скорость диска)
и = 0, v=wr, w = 0, T=T при z=i
ц==0 v = 0 Г=Г пи Д=~ ^ A144
') Pai S. I., Journ. Aeron. Sci. 16, № 8 A949).
§ 80] ЛАМИНАРНЫЙ СЛОЙ НА БЫСТРО ВРАЩАЮЩЕМСЯ В ГАЗЕ ДИСКЕ 391
Следуя в дальнейшем изложении В. П. Шидловскому '), сохраним
для перехода к безразмерным скоростям и нормальной к поверхности
диска координате те же масштабы, что и в § 38, для радиальной
координаты примем в качестве масштаба линейную величину У/ioo/ui,
а за масштабы коэффициента вязкости, абсолютной температуры и
плотности — их значения во внешнем потоке; кроме того, удоволь-
ствуемся принятием линейного закона зависимости вязкости от
температуры. Положим, таким образом (со — угловая скорость вра-
щения диска, штрихами обозначаются безразмерные координаты),
и = шг/(г', z'), v = wrg(r',z'), w= Yvxuih(r', z'),
T=TJi(r', z'), p = PooD(/•'.*')• (i = (ioor/roo = li006(r/, z').
A1.45)
Кроме того, совершим переход к переменным Дородницына
z' г'
r[ = rl = -j=r. • С= f -Z-dz1 =f D(r', z')dz'. A1.46)
V °° о Рос о
Тогда, если ввести, как обычно, преобразованную поперечную ком-
поненту скорости w, положив
jr. (П-47)
то совокупность первых трех динамических уравнений пограничного
слоя A1.43), автономная от теплового, сведется к следующей си-
стеме обыкновенных дифференциальных уравнений [штрих — произ-
водная по С; принято: f{r', z') = /(С), аналогично для g и А]:
2/-f-A' = 0. y — hf'—p = g*, g"—hg' — 2/? = 0A1.48)
с граничными условиями
/@) = 0, /(оо) = 0. ?@)=1. ?(оо) = 0, А@) = 0.A1.49)
Легко видеть, что система эта ничем не отличается от первых
трех уравнений системы F.5) с граничными условиями F.6), состав-
ленных для несжимаемой жидкости. Значения функций /, g, A
могут быть определены, таким образом, по таблице 10, причем
столбец этой таблицы (—А) соответствует значениям (—А).
') Шидловский В. П., ПММ, т. XXIV, в. 1, I960, стр. 161—164.
392 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ Ггл XT
Переходя к тепловой части задачи, обратимся к четвертому
уравнению системы A1.43), которое при принятых обозначениях
A1.45) принимает вид
+ 7!^'+*'); (П.50)
граничные условия для 6 (tj, С) будут
в(Ч. 0) = е„. 9G,, со) =1. A1.51)
Для решения уравнения в частных производных A1.50) положим,
следуя Миллсапсу и Польгаузену, работа которых была процитиро-
вана в начале § 63,
. (П.52)
что полностью соответствует сделанному в § 63 представлению
решения в форме (9.62). Для функций /(С) и s(C) получается при
этом два обыкновенных дифференциальных уравнения (9.63), реше-
ние которых было дано Миллсапсом и Польгаузеном в выше цити-
рованной их работе (см. также § 63).
Составляя коэффициент момента для диска, смоченного с двух
сторон, по формуле
а
2 [2пгг% dr
ал J w
Р М о
_
а» — Роо («Ai*/2) a*
и замечая, что
Aй)т Ь Vt= Po° V^5^ @).
получим [g/@) = 0.616]
с= 3'87 =
т. е. ту же формулу F.14), что и в случае несжимаемой жидкости.
Переходя к тепловой части задачи, составим число Нуссельта
Г
J
2nrq dr
где qw определится как
A1.54)
§ 81) РАСПРОСТРАНЕНИЕ РАДИАЛЬНО-ЩЕЛЕВОЙ ГАЗОВОЙ СТРУИ 393
Используя вычисленные В. П. Шидловским значения /'@) и s'@)
при 6 = 0,72 (воздух), получим
(о,329 — 0,108-т^-- . Т<хт ), A1.55)
> \ JCp' jo ' w~ ' оо I
или, вводя еще число Маха М для точек на периферии диска
Nu =
0,329—0,043М2-
7\
Т — 7V
A1.56)
§ 81. Распространение раднально-щелевой ламинарной
газовой струи вдоль твердой стенки
Изотермическая задача о распространении плоской струи несжи-
маемой жидкости вдоль твердой стенки, разобранная в § 7, легко
обобщается на случай радиальной газовой струи :).
Выбирая оси координат так же, как в § 44 (рис. 47), и имея
в виду, что в данном случае трансверсального потока нет (w = 0),
будем иметь уравнения распространения газовой струи в форме
(ср = const)
ди . ди д I ди\
д ....... , д , „ A1.57)
дТ . дТ 1 . д I дТ\ , а / ди\2
-г- 4- PV -г- — s— M. -з— М- -т— Нгг I •
Предполагая, что твердая стенка, вдоль которой распростра-
няется радиальная струя, совпадает с плоскостью у — 0 (л: отсчи-
тывается от оси симметрии радиальной струи), установим гранич-
ные условия
и = 0, v = 0. T=TW (или Jj^-=o\ при у —0,
Удовольствуемся рассмотрением случая радиального щелевого источ-
ника струи с бесконечно малой толщиной щели; тогда можно будет
построить сравнительно простое автомодельное решение задачи.
Для этого, подобно тому как это было сделано в § 7, предвари-
тельно установим основную формулу сохранения, представляющую
собой интегральное условие нетривиальности решения. С этой целью
•) R11 е у N., Journ. of Fluid Mech. 4, № 6 A958), 615—628.
394 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. XI
поступим так же, как в § 7. Умножим обе части первого из уравне-
ний A1.57) на л: и проинтегрируем по у от у до оо. Используя
граничное условие и->0 при у->оо и замечая, что
СО со
pxv jjdy==
со
= — pxuv + j u-^ (pxu) dy,
У
получим
оо
~ I pxu2dy — pxuv = — [j-x —¦. A1.59)
У
Умножая обе части этого уравнения на рхи и интегрируя по у от О
до оо, получим
оо
d
dx
ОО # CU 1 tX> й (Х> \
J pxul j pxu2dy)dy— j ~j (pxu) j pxu2dy\ dy —
0\y / 0 \ у /
CO ^JJ
— I p2x2u2vdy+ I wx2u~dy = 0. A1.60)
6 6
В силу второго уравнения системы A1.57)
ОО
/ \
^хи) 1 рхи2 dyJdy==if\ Ipx dy) Ту
0\v /
too со
= рхг> / рхи2 dy\ -\- p2x2u2v dy,
L у Jo о
так что уравнение A1.60) приводится к виду
) У j\? ^y = 0. A1.61)
В простейшем случае (хр = const (в частности, jj, = const,
р = const) второй член в левой части A1.61) обратится в нуль,
§ 81] РАСПРОСТРАНЕНИЕ РАЦИАЛЬНО-ЩЕЛЕВОЙ ГАЗОВОЙ СТРУИ 395
после чего сразу можно будет установить искомый закон сохранения
Г Г \
/ рхи / pxu2dy ]dy = const = F,
J It/ /
0 \y '
A1.62)
представляющий собой обобщение интегрального соотношения A.87)
на случай радиальной (множитель х) струи переменной плотности
(множитель р).
Введем функцию тока ф, положив
— -T1-, DXV =
ду г
дх
A1.63)
и перейдем от переменных х, у к переменным Мизеса — Прандтля
$ = лг, 7] = ф. Аналогично § 71 получим следующие формулы пере-
хода к новым переменным:
дх — д- ' pXV д-п ~ д;
ду
д _ д
д
A1.64)
Система трех уравнений A1.57) переходит при этом в такую
совокупность двух уравнений:
ди
д
дТ _?2 д ( дТ\
Jcp
c U / "
/
A1.65)
Введем безразмерные величины (U — произвольная скорость)
U
u = u/U. \ = — Ч_, ¦»)=¦
A1.66)
и полагая (лр = 1, перепишем A1.65) в виде
ди Тп д I — ди \
?2 f ц J
д- drt \ drt I
д;
JcpT ,
,-jTT \ 2
A1.67)
Первое из уравнений A1.67) автономно и совпадает с соответ-
ствующим уравнением распространения вдоль плоскости радиальной
396 ПОГРАНИЧНЫ? СЛОИ С ПОСТОЯННЫМ ДАВЛРНИЕМ [ГЛ XI
струи несжимаемой жидкости'). Решение этого динамического урав-
нения может быть представлено в виде
{ A1.68)
где в качестве параметра принята величина С, равная
С = |х-"у 1=*=^. у = ^. A1.69)
Функция /(С) удовлетворяет обыкновенному дифференциальному
уравнению третьего порядка (штрих — производная по С)
/'" + //" +Я/'2 = О A1.70)
при граничных условиях
/@) = /'@) = 0. /(оо) = 1. A1.71)
Решение может быть представлено в параметрической форме
-. A1.72)
Подставляя полученное решение в интегральное условие A1.62),
найдем связь между произвольно введенной величиной U и харак-
терной константой задачи F:
р = 10-С^- 01-73)
Как это сразу следует из A1.68), источник струи A = 0) яв-
ляется особой точкой, в которой скорость обращается в беско-
нечность. Можно избежать этого недостатка, если вместо A1.68)
использовать более общее решение2)
A1-74)
произвольный параметр / = — также может быть выражен через
константу струи F. Представляя себе источник струи как щель
высоты 8 между плоскостью у — 0 и параллельным ей диском
радиуса а и полагая поток сквозь щель однородным, имеющим
') Olaueri М. В., Journ. of Fluid Mech. 1 A956).
') Olauert M. В., Symposium iiber Orenzschichtforschung, herausgeb.
H. QOrtler. Springer-Verlag, 1957.
§ R1] РАСПРОСТРАНЕНИЕ РАДИАЛЬНО-ЩЕЛЕВОЙ ГАЗОВОЙ СТРУИ 397
скорость Uа и температуру Та, найдем
При этом величина / определится из условия, чтобы максималь-
ная скорость при х = а, вычисленная по A1.74), была равна Uа.
Напряжение трения zw определится как
(ди \ 9 Г v х* п1'4
^U—wV-A-vW+Wl Г@) A1J6)
и при принятом законе линейной связи между вязкостью и темпера-
турой ничем не будет отличаться от величины напряжения в случае
несжимаемой жидкости.
Для обратного перехода к обычным координатам лг, у будет
служить формула
требующая знания распределения температуры Т. Обратимся к реше-
нию этой, второй части задачи. Если число Прандтля принять рав-
ным единице, то решением второго из уравнений системы A1.67)
будет служить интеграл Крокко
причем, согласно граничному условию и->0, Г-> 7^, при у-хэо
получим А = Too. Если стенка, вдоль которой распространяется
струя, теплоизолирована, то 5 = 0 и, следовательно, поле темпера-
тур будет определяться равенством
причем температура на стенке Tw будет совпадать с темпера-
турой Та, окружающей среды.
Если, как уже это ранее было сделано, предположить, что струя,
вытекающая из радиальной щели радиуса а, однородна, то, полагая
в A1.78) А = 7*00, u — Ua, t=Ta, получим
(П.80)
где Ма — число Маха на выходе струи.
Если отказаться от упрощающего предположения о=1, но со-
хранить закон линейности связи между ц и Т, то уравнение баланса
398 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. XI
тепла примет форму
a
16 Ус
которую легко вывести из второго уравнения системы A1.67) путем
перехода к переменным ; и С, определенным по A1.69). Уравнение
A1.81) имеет частный интеграл
%С). (П.82)
а однородная его часть — совокупность решений
Гвл(<:). (и.83)
причем функции 6Л(С) (га = 0, 1 ...; я=1 при га = 0) удовлетво-
ряют уравнению
„) = 0. A1.84)
Рассмотрим несколько частных задач. Полагая п = 0, я = 1 и выби-
рая постоянную Со равной
9 U2
Со==~1в7ГГ' A1.85)
р ijO
придем к уравнению
о) = а/, (п.8б)
которое надо решать при граничных условиях: б0 @) = 0, если
температура стенки постоянна и равна температуре внешнего
потока 7^, или 9^@) = 0, если стенка теплоизолирована; кроме
того, 60(со) = 0. Этот частный случай соответствует нагреванию
струи только за счет диссипации. В случае теплоизолированной
стенки имеем
(Ц.87)
Уравнение A1.86) может быть численно проинтегрировано и
дает при a = 0,72 (воздух) 80@) = 0,0060.
Если температура стенки поддерживается постоянной, равной
температуре внешнего потока Т^, то секундное количество тепла,
которое необходимо для этого отводить через единицу площади
стенки, будет равно
где 9ц@) = 0,0036.
§ 81]
РАСПРОСТРАНЕНИЕ РАДИАЛЬНО-ЩЕЛЕВОЙ ГАЗОВОЙ СТРУИ
399
Для того чтобы получить решение задачи о чистом подогреве
или охлаждении струи стенкой (Tw Ф Т^), используем функцию Qv
причем положим а = 0. Будем иметь
= G^—1)9, (С), 6,@)= 1. в, (оо) = 0;
A1.89)
при этом, согласно A1.84), при п=\ и а = 0 получим, проводя
интегрирование,
» / С \ / со / С \
6,(С) = Jexp — oJ/dCU: / /exp aJ/Л Л. A1.90)
с \ о I I о *o /
Возвращаясь к A1.72), заметим, что
так что
= /A -,
dg
e
или, если ввести подстановку
то
; 7з).
A1.91)
где приняты следующие обозначения для неполной и полной функ-
ции «бэта»:
в (о; Va) =
A1.92)
Секундное количество тепла, снимаемого с единицы площади
стенки, равно
^ (т Г) [ У* ]и е; со), (П.93)
где в; @) = 0,2861.
В качестве третьего решения рассмотрим случай заданного подо-
грева струи при выходе ее из круговой щели (х == а). В этом
400 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. XI
случае используем функцию 92(С), положив при произвольном а
Г2 = С2(^_|-7зГа92(!;). A1.94)
Функция б2 удовлетворяет, согласно A1.84), уравнению
2) = o. (п.95)
которое путем почленного интегрирования может быть приведено
к виду
2 + ° А + (**-1)//'8аЛ =
о
Останавливаясь на случае теплоизолированной стенки (92 = 0
при С = 0), убедимся, что в этом случае константа справа равна
нулю. Применяя предыдущее равенство при С = оо и замечая, что
б2 (со) = 0, получим
Da- 1]
о
замечая, далее, что из физических соображений интеграл в левой
части не может быть равен нулю, заключим, что a = 1/i. Таким
образом, уравнение A1.95) упрощается; решение его представится
в виде
A1.96)
так что дополнительная температура будет равна
^71/'A -g*f. A1.97)
Если температура стенки поддерживается постоянной, то постоян-
ная а. и функция 92(С) должны определяться согласно равенствам
В этом случае секундное количество тепла, снимаемого с единицы
площади стенки, равно
v(lle+3)A2o) ^ |'
) ^] м). (п.99)
причем 62 @) = уз.
Входящая в равенства A1.97) и A1.99) постоянная интегрирова-
ния С2 может быть определена заданием величины максимальной
температуры в радиально-щелевом источнике.
§ 82]
СВОБОДНАЯ РАДИАЛЬНО-ЩЕЛЕВАЯ ЗАКРУЧЕННАЯ СТРУЯ
401
Имея решения для разобранных частных случаев тепловых задач,
можно, пользуясь линейностью основного уравнения A1.81), составить
решения более общих задач путем наложения решений и подходящего
подбора постоянных.
§ 82. Свободная радиально-щелевая закрученная струя
Рассмотренный в § 44 случай распространения радиально-щелевой
закрученной струи в несжимаемой жидкости легко обобщается на
случай соответствующей газовой струи '). При обозначениях § 44
имеем следующие уравнения движения газа и теплопереноса в нем:
ди
dw
ди
w2
dw , dw , guw д
ди
dw
dh0
1 \ д
J
A1.100)
где положено
A1.101)
В число уравнений входят еще, как обычно, уравнение состояния
и уравнение зависимости вязкости от температуры. Граничные усло-
вия будут иметь вид
ду
и = 0,
°" -ду- = 0' ду-^0 ПРИ
. = 0, 7=7^ при у=±
1
J
A1.102)
К этим граничным условиям должны быть присоединены еще три
интегральных условия сохранения потоков: количества движения,
момента количества движения и избыточной энтальпии, которые
вместе с тем являются условиями наличия нетривиального решения.
Перейдем к безразмерным величинам
= х/Х, y~y/Y, u = a/U, v — v/V,
= w/U,
p = pfpQO,
') Бейлина А. 3., К а ш к ар о в В. И., Тр. Казахского университета,
Сб. «Исследование процессов переноса», Алма-Ата, 1959, стр. 137—152.
Зак. 297. Л. Г. Лойцянский
402 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X
где X— масштаб радиальной координаты, at/ — радиальной и окрум-
ной скоростей; масштабы Y координаты у, нормальной к плоскост*
симметрии струи, и V — соответствующей компоненты скорости-
определяются, как всегда, по формулам
Re=: —.
Voo '
В этих безразмерных координатах, над которыми черточки в даль-
нейшем опущены, уравнения A1.100) сохранят свой вид, с той лишг
разницей, что безразмерная полная энтальпия будет равна
Ь^2). A1.103
где под числом М,» понимается величина
Moq=-f=^ A1.104
У (A— \)JcpTo=
Уравнения состояния газа и связи между вязкостью и темпера
турой приводятся к виду
РЛ=-= 1, р = Тп. A1.105
Условия нетривиальности решения задачи выводятся путем, совер
шенно аналогичным принятому в §§ 44, 64 и в предыдущем параграфе
в принятых безразмерных величинах эти условия имеют виг.
оо оо
-г- \ рхи2 dy= / рты2 dy,
—оо — из
оо
2пх2 jpuwdy = L, A1.106
— со
оо
2ъх fpu(ho—l)dy = H.
— оо
Полагая во втором равенстве A1.105) я=1 и используя пере-
менные Дородницына
у
^ = х, т] = Г р dy.
§ 82]
СВОБОДНАЯ РАДИАЛЬНО-ЩЕЛЕВАЯ ЗАКРУЧЕННАЯ СТРУЯ
403
приведем уравнения A1.100) к виду
ди . ~ ди w2 дги
dw , ~ dw . uw d2w
и -±г + v з^ = srS- — A г) ^-5
A1.107)
Граничные и интегральные условия при этом перепишутся в форме
ди п ~ п dw n dh n Л
¦т— — О, %} — \)t —-— =^ \)у з— — и При VI — U
дх d^i дч]
оо оо
-p. I %u2dri= I w2 dri.
A1.108)
Первые три из этих уравнений совпадают с уравнениями F.90)§ 44
для струи в несжимаемой жидкости, так что можно непосредственно
написать решение в переменных ?, tj:
_а2 1_
Xu* di\, ^ =
A1.109)
26*
404 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. XI
Прежде чем вернуться к физическим переменным х, у, необхо-
димо определить поле температур.
Представим безразмерную энтальпию в форме асимптотического
ряда
A=l+|i+... A1.110)
и ограничимся рассмотрением первых двух членов этого разложения.
Подставим выражение A1.110) вместе с выражениями и, v, w no
A1.109) в четвертое уравнение системы A1.107) и приравняем коэф-
фициенты при одинаковых отрицательных степенях ?. Тогда, после
простых вычислений, найдем
л /2
и, следовательно, будет
^IД A1.112)
Формулой перехода от ч\ к у служит равенство
у= fhd7l = 7l+N Г f
о ch
Если N=0, то переменная ч\ совпадает с у; это позволяет считать
величину N параметром сжимаемости.
Изложенное здесь решение имеет скорее качественное, чем количе-
ственное значение, как первое, сравнительно грубое приближение,
справедливое лишь в достаточно большом удалении от щелевого
источника. Сохранение в разложениях скоростей и энтальпии сле-
дующих членов со старшими отрицательными степенями радиального
расстояния от щели привело бы к уточнению задачи. Удовольствуемся
поэтому лишь следующими общими замечаниями. Толщина струи
увеличивается с возрастанием параметра сжимаемости N. Возрастание
числа Прандтля резко влияет на распределение избыточной энтальпии
в струе и слабо влияет на распределение радиальных и окружных
скоростей.
§ 83. Пограничный слой при равновесной
диссоциации газа
Вернемся к рассмотрению ламинарного пограничного слоя на про-
дольно обтекаемой газом пластинке, причем примем во внимание
возможную диссоциацию молекул газа, возникающую при тех высоких
ЯЗ] ПОГРАНИЧНЫЙ СЛОЙ ПРИ РАВНОВЕСНОЙ ДИССОЦИАЦИИ ГАЗА 405
температурах, которые имеют место в пограничном слое при больших
сверхзвуковых скоростях. Для упрощения задачи будем предполагать
диссоциацию «равновесной», т. е. считать, что степень диссоциации
в каждой точке пограничного слоя соответствует той температуре,
которая установилась в этой точке. Такой квазистатический подход
значительно облегчает решение задачи. На самом деле явление, конечно,
гораздо более сложно. Неравновесность температур (о явлении релак-
сации колебательной степени свободы молекул уже упоминалось
в § 53) и неравновесность диссоциации газа обусловлены тем, что
при больших скоростях движения газа и резких неоднородностях
поля температур время, потребное для достижения равновесного со-
стояния газа, оказывается велико по сравнению с характерным для
рассматриваемого движения временем (так получается, например, при
прохождении газа сквозь область за головной ударной волной в носо-
вой области тела). Для разбираемого далее примера продольного
обтекания пластинки допущение
о равновесности вполне пригодно,
если отвлечься от области, непо-
средственно примыкающей к перед-
ней кромке.
Основное отличие от предыду-
щего заключается в том, что в слу-
чае очень высоких температур и
наличия диссоциации уже нельзя
довольствоваться теми упрощаю-
щими допущениями: up = const,
ср = const, Рг = const, которые при-
нимались ранее, а необходимо вы-
бирать более близкие к действи-
тельности соотношения. Не оста-
навливаясь на изложении термоди-
намических основ выбора этих
соотношений, приведем графики зависимостей абсолютной темпера-
туры, числа Прандтля и произведения up от энтальпии для равновесного
диссоциированного газа. Условимся пользоваться безразмерными вели-
чинами энтальпии /г, динамического коэффициента вязкости [а и плот-
ности р, относя размерные их значения h, \x, p к соответствующим
значениям hb, u4, р4 при 7^ = 220° К.
На рис. 84 приведена связь между безразмерной энтальпией h и
абсолютной температурой Т. Если при отсутствии диссоциации произ-
водная (в размерных величинах)
Рис. 84.
dh
dT
A1.114)
406
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
[гл. xt
Рг
2
слабо зависит от температуры и при сравнительно малых температу-
рах может приниматься постоянной, то, как это отчетливо видно из
рис. 84, при больших температурах величина ср резко меняется
с температурой и зависит также от абсолютного давления р.
При наличии диссоциации уже нельзя считать, что входящее
в выражение числа Прандтля Рг = \icpfk отношение jx/X не зависит от
температуры и давления. Равновесно диссоциированный газ предста-
вляет собой смесь диссоциированных и недиссоциированных молекул;
так что, несмотря на общность механизма молекулярного переноса
количества движения (вязкость) и кинетической энергии (теплопро-
водность), отношение соот-
ветствующих коэффициентов
переноса при наличии смеси
газов уже не сохраняет
постоянной величины, как
в однородном газе. Как по-
казали расчеты по кинети-
ческой теории газов J). влия-
ние энтальпии смеси газов
на ее число Прандтля сравни-
тельно невелико, а влияние
давления совсем мало. Как
п\ i i [ i i i i i видно из рис. 85 (сплошная
О 80 40 SO вО JOO i20 J4O Ш кривая с точками на ней),
h число Прандтля колеблется
рис. 85. около некоторого среднего
значения, которое можно
принять приблизительно равным 0,7. Сплошной кривой без точек пока-
зана та же зависимость, основанная на допущении о сохранении
постоянства отношения jx/X, ошибочно принятом Муром2). Как видно из
рисунка, при этом получаются резко завышенные значения числа Рг.
Приведенная сплошная кривая может представить некоторый интерес,
так как при |*./Х == const она иллюстрирует характер зависимости ср (ft).
Пунктиром на том же рисунке показана кривая в недиссоциирован-
ном потоке. На рис. 86 приведен график зависимости от h безраз-
мерного отношения (fip)/([xftpft) = a(/F), входящего в основные уравне-
ния задачи.
Следуя в дальнейшем решению, изложенному в только что цити-
рованной работе Мура, применим уравнения Хантцше и Вендта (§ 70).
Останавливаясь на автомодельной задаче типа Блазиуса и считая, что
все основные параметры газа представляют собой функции от ком-
/
-^
\
\
\
P=0,JamM
—1 —=
V
\
Д
') Hansen С. F., Journ. Aeron. Scl. 20, № 11 A953), 789
*) Moore L., Journ. Aeron. Sci. 19, № 8 A952), 508-511.
-i 83] ПОГРАНИЧНЫЙ СЛОЙ ПРИ РАВНОВЕСНОЙ ДИССОЦИАЦИИ ГАЗА 407
1лекса z = y/Yx> придем к системе уравнений ш=;\>.-^, как и
§ 70)
du* 2 ' A1.115)
dG dh^ d_ IG_ dh\ . _
du du du \Pr duj* '
юторая после перехода к безразмерным величинам
A1.116)
финимает следующий', аналогичный A0.54) вид (штрих — производ-
ная по 7j):
gg" = — а (А) т), ]
A1.117)
]
1
V этой системе величины Рг и а являются заданными функциями h-
"•ешение системы уравнений A1.117) требует применения численных
1
1
V
— —
— —
1—
'/
— 1 —
0,80
0,60
O/fO
0,20
о
О 20 40 60 80 /00 120 МО /60
h
Рис. 86.
•етодов интегрирования и использования современной машинной
"ехники.
Замечая, что для машины наличие граничного условия 1/g-—>со
ча внешней границе слоя непригодно, Мур предложил ввести новые
переменные t и w, положив
g = dri/dt, a. (h) т) = dw/eft.
(П.118)
408
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
[ГЛ XI
Решение задачи сводится после этого к интегрированию следующей
системы обыкновенных дифференциальных уравнений первого порядка:
¦q— Г g dt, w = Г ост; dt,
g=-j wdn. h =
A1.119)
с пятью граничными условиями, необходимыми для решения системы
пяти обыкновенных дифференциальных уравнений первого порядка
A1.119); такими условиями будут
) = 0, w=^ — dg/dfj = 0, h =
dh_(dh\
dt—\dt )w
или -гг = 0 для изолированной
A1.120)
пластинки при ^ = 0.
Эта система вполне пригодна для машинного счета. Возврат к физи-
ческим координатам х, у должен производиться по формуле
t^f f Eat.
A1.121)
Граничные условия A1.120) даны при ? —0 или у = 0, т. е. на
поверхности пластинки, что соответствует постановке задачи Коши,
а не краевой задачи. Этот искусственный прием необходим при пользо-
вании счетными машинами. Величины hw, gw и (dh/dt)w на самом
деле неизвестны и задаются произвольно, чтобы затем быть опре-
деленными из условия прохождения интегральных кривых через задан-
ные значения т] = т]0О, h — fio, на внешней границе слоя. В расчетах
Мура предполагалось, что температура во внешнем потоке равна
Ть = 222° К; таким образом, было принято, что йоо—1.
Допущенная автором существенная ошибка в определении зависи-
мости числа Рг от h обесценила числовые результаты; приведенное
изложение самого метода Мура необходимо, так как является осно-
вой содержания следующего параграфа !).
Как показали расчеты, равновесная диссоциация мало сказывается
на величине местного коэффициента трения Ср определяемого как
1 Исправленные вычисления были проведены Ромигом и Дором (М. R о-
m i g, F. D о г е), работа которых осталась для нас недоступной (Convair
Rep. № ZA-7-012, San Diego, 1954).
-; 83] пограничный слой при равновесной диссоциации газа 409
-де величины слева построены по значениям, характерным для внеш-
sero потока. Сплошная кривая зависимости Cj Y^-x 0T числа Маха
внешнего потока Мсо до Моо?^20 (рис. 87) почти не отличается от
данных Янга и Янсена ') (на рисунке точки), полученных без учета
диссоциации, но с использованием близких к действительности соот-
юшений между физическими параметрами газа и абсолютной темпе-
1атурой. Пунктиром показана кривая, рассчитанная без принятия
1 расчет диссоциации, при Рг = 0,75. Существенным оказывается влия-
ше диссоциации на величины, характеризующие тепловые процессы:
•емпературу Tt поверхности теплоизолированной пластины и местный
~чсЬ(Ьициент теплоотдачи (число Нуссельта Nx) в случае теплоот-
"Ч
к.
М
Рг
- —
2 4 ff в 70 72 14 IS /8 20
Мао
Рис. 87.
;м же методом В. Я. Нейланд решил аналогичную задачу о
юграничном слое в равновесно диссоциированном потоке газа при
(родольном (без угла атаки) обтекании кругового конуса. Матема-
лческая эквивалентность задачи о круговом конусе задаче о пла-
тине была показана уже в § 77. В. Я. Нейланд учел ошибку
*ура и использовал для числа Прандтля кривую Ханзена.
Вычисления подтвердили, что, так же как и в случае пластины,
чет наличия равновесной диссоциации мало отражается на сопроти-
.лении и теплоотдаче даже при таких значительных числах Маха
вбегающего потока, как Моо=10-т-18 (при температуре поверх-
юсти конуса Tw = 2000 — 3000е К). Как уже указывалось ранее, на
линных телах (в некотором удалении от передней кромки пластины
1ли вершины конуса) влияние релаксации невелико и процесс диссо-
.шации может рассматриваться как равновесный. Иначе обстоит дело
') Young О., J a n s s e n E., Journ. Aeron, Sci. 19, № 4 A952), 229.
410 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. XI
на затупленном носике тела в гиперзвуковом потоке, когда газ попа-
дает в пограничный слой сразу же после прохождения ударной волны.
В этом случае учет неравновесности процесса диссоциации очень
существен. В следующей главе этот вопрос будет подвергнут рас-
смотрению.
§ 84. Пограничный слой в диссоциированном
и ионизированном газе при наличии магнитного поля
При высоких температурах, характерных для области пограничного
слоя при сверхзвуковых скоростях, наряду с диссоциацией газа возни-
кает также и ионизация, благодаря которой газ становится электро-
проводным. Если такой ионизированный газ г) движется в электри-
ческом или магнитном полях, то в нем возникает электрический ток,
который, взаимодействуя с приложенным магнитным полем (сам газ
предполагается не магнитным), приводит к появлению объемной
силы F (ее иногда называют электрической объемной силой, лорен-
цевой или пондеромоторной силой), равной векторному произведению
плотности тока / на напряженность магнитного поля В
F=jXB. A1.122)
Плотность тока выражается суммой двух слагаемых
B. A1.123)
из которых первое представляет собой плотность тока, возникающего
благодаря наличию электрического поля с напряженностью ?, а вто-
рое— за счет взаимодействия с магнитным полем; а обозначает элек-
тропроводность газа, т. е. величину, обратную его удельному сопро-
тивлению, V — вектор скорости частиц газа.
При прохождении сквозь газ электрического тока выделяется
джоулево тепло в количестве, равном произведению квадрата плот-
ности тока на удельное сопротивление, т. е. р/а. Эти два обстоя-
тельства— возникновение электрической объемной силы и выделение
тепла — приводят к появлению в динамическом и тепловом уравне-
ниях дополнительных членов: лоренцевой силы в первом и удельного
джоулева тепла — во втором. В дальнейшем предполагается, что
внешнее электрическое поле отсутствует (? = 0); тогда электрическая
объемная сила сведется к вектору о(УХв)Хв. а удельное джоу-
лево тепло — к <j| VX^|2- Заметим, что сила пропорциональна пер-
') В дальнейшем основы магнитной гидродинамики предполагаются изве-
стными. Рекомендуем простое и краткое изложение этих основ, приведенное
в статье Реслера и Сирса «Перспективы магнитной аэродинамики», помещен-
ной в сб. «Механика», ИЛ, 1958, № 6, стр. 3—22; см. также исправление и
добавление к этой статье в № 6 того же сборника за 1959 г., стр. 47.
« 84] ИОНИЗИРОВАННЫЙ ГАЗ ПРИ НАЛИЧИИ МАГНИТНОГО ПОЛЯ 411
вой степени скорости движения газа, а джоулево тепло — квадрату этой
скорости; обе величины пропорциональны, кроме того, квадрату напря-
женности магнитного поля и коэффициенту электропроводности газа.
Пользуясь условием малости толщины пограничного слоя, можно
пренебречь изменением напряженности магнитного поля по сечению
слоя и считать, что обе компоненты напряженности Вх и Ву являются
функциями только продольной координаты х. Учитывая обычным
образом порядки величин внутри пограничного слоя, получим следую-
щие уравнения пограничного слоя на продольно обтекаемой пластинке:
ди , ди д I ди \ „» 1
¦"¦ = — (и.—) — оН'и I
ду v ду I I
I
A1.124)
dh . dh д ( <х dh\ (ди \2
где Н(х) обозначает нормальную к поверхности пластинки компо-
ненту напряженности магнитного поля. Во избежание путаницы число
Прандтля в дальнейшем обозначается символом Рг, а о сохранено
для общепринятого обозначения электропроводности.
Уравнения A1.124) отличаются от второй основной формы урав-
нений пограничного слоя в размерных переменных (8.24) (для рас-
сматриваемого случая продольного обтекания пластинки ~ = 0)
лишь дополнительными членами: — оН2« в динамическом уравнении
и аН2и2—в тепловом. Кроме того, число Прандтля, так же как и
в случае диссоциированного газа, переменно и не вынесено за знак
дифференцирования.
Для упрощения задачи будем искать автомодельное ее решение.
С этой целью, считая пластинку полубесконечной, потребуем, чтобы
продольная скорость и и энтальпия h зависели от комбинации
= г, а не от координат х и у по отдельности, т. е. u = u(z),
h = h(z). При обычном предположении о зависимости плотности,
вязкости и коэффициента теплоемкости ср от энтальпии будем иметь
также
Р = р(г). {i = i* (г), ср = ср{г). Рг = Рг(г), T=T(z), о = о(г);
при этом принято, что электропроводность • газа з является также
функцией только температуры (энтальпии). Можно заметить, что
введенные дополнительные магнитные члены, содержащие заданную
наперед функцию общего вида Н(х), нарушают автомодельность
задачи. Если произвести в первом и третьем уравнениях системы A1.124)
412 ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X!
переход от переменных х, у к новым переменным х, z== у/Ух,
то легко убедиться, что в правых частях этих уравнений появятся
нарушающие автомодельность члены, содержащие произведение хН2(х).
Для возможности приведения уравнений в частных производных
к обыкновенным дифференциальным уравнениям с аргументом z,
необходимо положить
^ = -^. (П.125)
у х
Такое распределение напряженности магнитного поля имеет осо-
бенность на передней кромке пластины (х = 0), что не представляет
дополнительной трудности, так как ту же особенность имеют напря-
жение трения на поверхности пластинки и нормальная к поверхности
пластинки скорость.
Тот факт, что дополнительные магнитные члены содержат явно
скорость и, естественно, наводит на мысль принять вместо z в ка-
честве аргумента и, т. е. перейти к уравнениям пограничного слоя
в форме Крокко или Хантцше и Вендта (§ 70). Следуя Бушу1), будем
рассматривать настоящую задачу как обобщение задачи о пограничном
слое на пластинке в потоке равновесно диссоциированного газа, рас-
смотренной в предыдущем параграфе.
Основная система уравнений будет иметь вид
du2 2 ^^ du \ G /
dh dG d I G dh\ A2 I dh
du
A1.126)
представляя собой очевидное обобщение системы A1.115) на случай
пограничного слоя на пластинке в продольном потоке ионизирован-
ного газа при наличии магнитного поля.
Приведем систему A1.126) к безразмерному виду, приняв обо-
значения A1.116) и положив дополнительно
Как и в предыдущем параграфе, индексом b обозначены завися-
щие от температуры (энтальпии) величины при Ть =222° К, индек-
сом 0 отмечены постоянные, выбранные произвольно, в том числе а0,
которое принято равным 100 ом/м.
') Bush W. В., Journ. Aerospace Sci. 27, № 1 A960), 49—58; русск. пер.
в сб. «Механика», ИЛ, 1960, № 6, стр. 89—109.
§ 84J ИОНИЗИРОВАННЫЙ ГАЗ ПРИ НАЛИЧИИ МАГНИТНОГО ПОЛЯ 413
После указанного приведения получим систему уравнений (штрих —
производная по -ц)
A1.128)
V Pr / g
отличающуюся от системы A1.117) последними слагаемыми в правой
части.
Система A1.128) подлежит интегрированию на машине. В связи
с этим, так же как и в предыдущем параграфе, следует выполнить
переход к новым переменным / и и, положив
— dr. dw ,.
Тогда придем к необходимости интегрирования следующей системы
обыкновенных уравнений первого порядка:
d-ц — dw ds - i л ЛН
dt s ' <« "~ '' dt
A1.130)
dt ' Pr dh
с граничными условиями типа задачи Коши
к) = 0, <а» = 0, g = gw, h = Hw, C = CW при /=0, A1.131)
где, как и в предыдущем параграфе, предполагается, что вели-
чины gw, hw и Сд, подбираются из условия, чтобы интегральные
кривые 7j и А при подходе к внешней границе слоя (t—>oo) стреми-
лись, к заданным в основной граничной задаче величинам i70O = u^JYhb,
hao=ha>lhb; величина g1 при этом, очевидно, должна стремиться
к нулю. Возврат к обычным координатам х, у должен производиться
по той же формуле A1.121), что и в случае, рассмотренном в преды-
дущем параграфе.
В результате обработки разнообразных литературных источников
Буш предложил следующие таблицы для функций а (Л), р (Л), а также
T(h) при двух значениях абсолютного давления: р= 10~3 атм и
/?=1 атм (см. табл. 31).
Из рассмотрения этих таблиц видно, что а (Л) сравнительно слабо
зависит от давления. Для современного машинного счета необхо-
димо иметь аналитическое представление входящих в интегрируемое
414
ПОГРАНИЧНИК СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ [ГЛ. X
Таблица 3
г к
200
300
400
500
1000
1500
2000
3000
4000
5000
6000
7000
8000
h
0,88
1,35
1,79
2,22
4,65
—
10,6
31,4
42,4
106,0
168,0
185,0
221,0
= 10 3 атм
а
1,03
0,944
0,881
0,821
0,642
—
0,505
0,360
0,282
0,193
0,142
0,137
0,142
_
—
—
—.
—
—
0,0174
0,910
6,14
36,4
122
207
h
0,88
1,35
1,79
2,22
4,65
7,29
10,2
18,2
34,4
45,9
67,0
117,0
170,0
р = 1 атл
а
1,03
0,946
0,881
0,821
0,639
0,539
0,500
0,422
0,332
0,290
0,256
0,214
0,189
i
Р
.—
.
—
0,00185
0,174
2,14
10,7
35,4
114
уравнение функций. Для функции а (Л) таким приближенным прел
ставлением во всем диапазоне давлений может служить формула
а = А'35. A1.132
График на рис. 88 аналогичен ранее приведенному на рис. 8с
но сделан в логарифмическом масштабе. По этому графику можн^
судить о точности формулы A1.132): при р=10~3 атм точное^
несколько лучше, чем при р=\ атм.
Сложнее обстоит дело с функцией C(А). Для р= 10
предложил аналитическое представление
-з
1 = 1,20
I = 0 при
10-V'79
при
А < 4,65.
А > 4,65 (Т > 1000° К),
атм Буш
A1.133
График этого представления в логарифмическом масштабе (рис. 89
показывает, что функция C (А) заметно зависит от давления р, причек
зависимость эта сказывается главным образом на коэффициент^
а не на показателе степени. Так, при р= 1 атм для этого коэффи
циента следовало бы вместо 1,20 • 10~9 принять 5,68 • 10 8. Как ви^-
но из таблицы 31, до Г=2000°К значениями р можно вообш^
пренебрегать. Заметное влияние электропроводности газа начинае-
сказываться лишь при сравнительно высоких температурах, т. t
в пределах пограничного слоя.
: 84] ионизированный газ при наличии магнитного поля 415
Отметим наиболее интересные с физической стороны выводы,
; которым приводит интегрирование системы A1.130). Проанализи-
руем влияние магнитного поля на две основные характеристики
юграничного слоя: напряжение трения на поверхности пластины xw
; секундный удельный поток тепла qw, равные по предыдущему
ди
d7"
A1.134)
; этой целью рассмотрим отношения *J(im\t=0 " Qj(qw)b=0 в функ-
ши от магнитного параметра f0 при заданных значениях числа Маха
или yjJ hw, h^ и р. Приведем для
тимера один из графиков (рис. 90), со-
(тветствующий давлению р= 10 с/яж л
j значениям: Аоо= 1, Лто= 10, Моо = 25.
Отчетливо видна следующая особен-
юсть рассматриваемых кривых. Пред-
тавляемая ими зависимость не одно-
11
Ж
ГО
-Д 1 атм
• 0,01'атм
° О.ОО/атм
+ Q000/атм
)о
0.1
W T"mo 0>0Ji
h
Рис.
^начна. В двух точках этих кривых. А к. В (рис. 91), имеются вер-
¦икальные касательные. Влево от точки С простирается область
;есьма слабого влияния ионизации на трение и теплоотдачу, что
оответствует малым значениям температуры (энтальпии) газа. Вправо
it точки В, наоборот, простирается область высоких температур и
ильного влияния ионизации: и трение, и теплопередача с поверхности
[ластинки резко уменьшились по сравнению со своими значениями
|ри малых ?о- Между вертикальными касательными в точках С и В
416
ПОГРАНИЧНЫЕ СЛОИ С ПОСТОЯННЫМ ДАВЛЕНИЕМ
[ГЛ. XI
располагается область неоднозначной зависимости трения и теплопе-
редачи от fQ. Как обычно бывает в таких случаях, эта область
1А
1,2
1,0
0,8
0,6
0,4
о,г
—-^
У
( у
)
/
1 1 1 I 1 11
10
100 1000
Рис. 90.
Рис 91.
соответствует неустойчивому течению. Действительное развитие про-
цесса происходит так, как это показано стрелками на рис. 91. При
возрастании ^0 от нулевого значения
явление развивается согласно верхней
ветви АВ, затем скачкообразно пере-
ходит на нижнюю ветвь в точке D и
далее протекает по этой ветви. Наобо-
рот, при убывании т0 от больших его
значений явление следует нижней ветви
DC до точки С, затем происходит ска-
чок из точки С в точку А и непре-
рывное перемещение влево. Замеча-
тельной особенностью рассматривае-
мого процесса служит, таким образом,
явление гистерезиса с петлей ABDCA.
Это явление было отмечено ранее Бле-
виссом') для случая куэтовского дви-
жения.
Приводим сводный график зависи-
мости границ этих областей от числа
^=1, Л„,=
103
Г,
1Ог
W
10°
ю-'
1
ОЗлаа
I
\
\
\
\ \ Область
\\
7!i> \
\
\
\
Ш
\
\
\
\
\
20
Ясс
60
Рис. 92.
при
1-3
и при
/7=10 атм (рис. 92). Из графика сле-
дует, что в этих условиях при 7о<ЮО и М0О<21,4 эффект
ионизации не будет существен. Заметим, что при Ло,—7(^=10 и
') Bleviss Z., Journ. Aerospace Sci. 25, № 10 A958), 601—615.
§ 84] ИОНИЗИРОВАННЫЙ ГАЗ ПРИ НАЛИЧИИ МАГНИТНОГО ПОЛЯ 417
том же пределе для f0 верхний предел для Моо. при котором отсут-
ствует влияние ионизации, снизился бы до 6,4.
При выбранном значении Tfe = 2223K и о0=100 ом/м имеем по
определению величины ^0 [формула A1.127)]
fo/Л2 = 2,66 • 102 м ¦ сек/ом ¦ кг.
Вспоминая A1.125), получим при у0 = 100
А2 = В\ х — 0,376 ом • кг/м • сек,
откуда при х — 1 м следует
fiy = tf = 6,15- 103 гаусс.
В тех же условиях при у0 = 1 было бы
Ву = Н = 6,15- 102 гаусс.
Таковы порядки напряжений магнитного поля, при которых влия-
ние ионизации мало.
ГЛАВА XII
ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ
ДАВЛЕНИЙ НА ВНЕШНЕЙ ГРАНИЦЕ
§ 85. Пограничный слой на теплоизолированной поверхности
при о = 1 и небольших М^
Расчет пограничного слоя с переменной скоростью на внешней
границе, или, что то же, при наличии продольного изменения давле-
ния во внешнем потоке газа, представляет значительно большие труд-
ности, чем аналогичный расчет в несжимаемой жидкости. Так же как
и в предыдущих двух главах, основу этих расчетов составляет пре-
образование Дородницына и некоторые его модификации (Стюартсон).
В дальнейшем не следует смешивать скорость на внешней границе
пограничного слоя ие со скоростью набегающего потока ?/«,. Усло-
вимся обозначать индексом е величины на внешней границе слоя,
а индексом со — соответствующие величины в набегающем потоке.
Начнем с рассмотрения простейшего, имеющего практическое
значение для расчета обтекания газом крыловых профилей случая
теплоизолированной поверхности в потоке сравнительно небольших
скоростей (Me ^ 2), в предположении, что число Прандтля о может
быть принято приближенно равным единице').
Составим основные уравнения плоского стационарного погранич-
ного слоя в переменных Дородницына % и tj, определенных ра-
венствами 2)
х у
6= [-Zz-dx, <n=[j-dy, A2.1)
./ Рео ' J ?ео У
О О
где хну представляют собой размерные координаты в погранич-
ном слое, ре — давление на внешней границе слоя, а ре0 и peQ — зна-
чения давления и плотности в адиабатически и изэнтропически затор-
моженном (индекс 0) внешнем (индекс е) потоке.
') Д о р о д н и ц ы и А. А., Л о й ц я н с к и й Л. Г., ПММ, т. IX, в. 4, 1945.
2) Д о р о д н и ц ы н А. А., ПММ, т. VI, в. 6, 1942.
§ 85]
ПОГРАНИЧНЫЙ СЛОЙ ПРИ 5=1 И НЕБОЛЬШИХ Мо
419
Обращаясь к первой форме уравнений пограничного слоя (8.22),
убедимся, что в рассматриваемом случае имеет место упрощенный
интеграл
2 ]
Из A2.2) находим
A2.2)
A2.3)
Замечая, что вне пограничного слоя поток потенциален, а давле-
ние поперек пограничного слоя не меняется (р — ре), получим для
всех точек пограничного слоя
*
..2 ( „_,
A2.4)
По закону Клапейрона найдем соответствующее соотношение для
плотности
ft i
„2 \ угт , „2
Будем пользоваться степенной связью между динамическим коэф-
фициентом вязкости и абсолютной температурой; получим
(Т \П / „2 \Л
Приняв во внимание, что интеграл уравнения баланса энергии A2.2)
уже найден, остановимся на первых двух уравнениях пограничного
слоя в размерных величинах
ди , ди\ dp , д I дм'
A2.7)
дх ^ ду '
и, введя для краткости обозначения
A2.8)
совершим над уравнениями A2.7) преобразование A2.1), в настоящем
случае имеющее вид
A2.9)
= /(l-a;)*-i Ae.
27*
420 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XII
Заметим, что
Т^— V aJ di ^ дх дц '
д _.0-4)
ду -
k
2\*-1
1—а2
[12.10)
кроме того, по первой из этих формул и соотношению A2.4) будет
(штрих означает дифференцирование по %)
к+\
«x.
Применяя формулы преобразования A2.10) и используя только
что полученное выражение A2.11), приведем первое из равенств A2.7)
к виду (ve0 = [Vp<;o)
где положено для краткости
~ v
v =
1-а2
дх
A2.13)
Из уравнения неразрывности [второго равенства системы A2.7I
следует
ои =-J-=-!—-г1-,
dy р0 dij
dA: — I e) di dx dn
или
1
?е0
v 1 д<\)
9 ' -1-
дх
Вводя опять скорость v по A2.13), перепишем последние два
равенства в виде
1 д-Ь 1 д'Ь
Рео д-ц ' ре0 di
откуда сразу получим уравнение неразрывности в переменных Дород-
ницына
§ 85] ПОГРАНИЧНЫЙ СЛОЙ ПРИ 0=1 И НЕБОЛЬШИХ Me 421
Пользуясь равенствами A2.12) и A2.14), путем, аналогичным
ранее примененному в § 16, выведем уравнение импульсов в новых
переменных \, т\
A2.15)
где под 8^ понимается конечная толщина пограничного слоя, опре-
деленная как значение tj, при котором и — ие. Заметим, что в урав-
нении импульсов A2.15) показатель степени п в законе зависимости
коэффициента вязкости от абсолютной температуры исчез, так как
а = 0 при 7j = 0.
Введем условные толщины пограничного слоя
о
Тогда, используя тождество
1—а2
{ие — И)].
преобразуем уравнение A2.15) к виду
Устремляя ae->0, %->x, r)-*y, v^-^-v, т. е. переходя к малым
скоростям, получим известное уже нам по § 16 уравнение импульсов
для несжимаемой жидкости.
Предположим теперь, что профили скоростей в сечениях погра-
ничного слоя могут быть заданы однопараметрическим семейством
«/«e = cpGj/5**; /), A2.18)
не зависящим явно от числа Моо. т. е. таким же, как и в случае
несжимаемой жидкости (Моо = 0). При этом, конечно, сохраняется
неявное влияние числа Моо через величины ие, Ьп , ч\ и /.
Принятое допущение справедливо при не слишком больших зна-
чениях Моо- Так, например, для пластины (/ = 0) величина
^ __ Г д (и/ие) I = Г д (и/ие) I = , 0. 0
L^(y/s**)Jy=0 [ а (ч/в;*) Lo
422 пограничный слой при заданном распределении Давлений [гл. xii
должна быть при этом независимой от числа Мсо и равной 0,221.
Точные расчеты показывают, что на самом деле эта величина возра-
стает с числом Моо. достигая значений: С = 0,222 при Моо = 0,65,
С = 0,227 при Моо =1,59 и С = 0,234 при Моо = 3,05. Изложенное
ниже решение, привлекающее к себе своей простотой, может быть,
таким образом, использовано лишь при сравнительно небольших
числах Моо ё=2.
Используя A2.18), будем иметь, как в § 19,
A2.19)
После подстановки этих выражений в A2.17) получим
Умножим обе части этого уравнения на 1 —а?е и приведем к виду
Теперь можно заметить, что роль формпараметра играет величина
/ «*2
/= ",'* 2ч. A2.20)
так как при этом выражение, стоящее внутри фигурных скобок,
будет являться функцией только формпараметра /. Предыдущее
уравнение приводится к виду
и
е
или после выполнения дифференцирования в левой части
df d и d и.
— = /=•(/) —In , е +/ —'g ? ¦ A2.21)
d- d\ V\-4 dl A-4)
Таково основное уравнение однопараметрической теории, пред-
ставляющее собой обобщение уравнения C.23) на разбираемый частный
§ 85] ПОГРАНИЧНЫЙ СЛОЙ ПРИ 3=1 И НЕБОЛЬШИХ Мл 423
случай движения газа с большими скоростями. Входящая сюда
функция
F = 2 JC (/)- [2 -+- Н(/)]/} A2.22)
по внешней форме ничем не отличается от соответствующей функции
для несжимаемой жидкости.
Вернемся теперь к основной переменной х; будем иметь
— in—тйдаг A2>23)
dx dx У1 — а2е dx A —
Так же как и в случае несжимаемой жидкости, заменим функ-
цию F (/) ее линейным приближением
и после простого интегрирования A2.23) получим
где положено
«^^S + Tzry-T- A2-25>
Для воздуха k =1,4; принимая ? = 5,75 (см. конец § 21) и
несколько округляя числа, найдем от = 2,5. Выражение A2.24)
можно окончательно переписать в виде
A2-26)
более удобном для расчетов. Для пересчета заданного распределения
коэффициента* давления на поверхности крылового профиля в несжи-
маемой ЖИДКОСТИ (Моо — 0)
р~р°
на распределение ае(х) при различных Мщ < Мкр служит предлагае-
мая на рис. 93 сетка кривых.
Сделанное ранее допущение A2.18) заставляет считать отрывное
значение fs при больших скоростях не зависящим от Моо- Но воз-
растание числа Мсо в докритической области вызывает увеличение
разрежения, а следовательно, и градиента | dujdx | за точкой минимума
424 пограничный слой при заданном распределении давлений [гл. xi
давления. Это повлечет за собой возрастание / по абсолютной вели
чине, т. е. перемещение точки отрыва вверх по потоку. Отсюда
следует, что сжимаемость жидкости при докритических скоростя;
ускоряет отрыв ламинарного пограничного слоя, т. е. ухудшает обте-
кание крыла. Расчеты подтверждают это соображение. Так, напри
мер, точка отрыва ламинарного слоя с верхней поверхности крыл<-
вого профиля NACA-4412 при су = 0,146 и М^^О лежи-
примерно на 11% хорды от передней кромки, а при Моо^О.^
Рис. 93.
Перемещается в точку, лежащую на 5% хорды от носика. В дало
нейшем отмеченный только что факт будет подтвержден и боле^
строгими методами расчета.
§ 86. Пограничный слой при яФ\ и произвольном Мда
Перейдем к более общему случаю, когда аф\, а числа Мго н*
столько велики, что уже нет оснований пренебрегать их вл шниек
на форму профилей скорости в сечениях слоя'). Как уже ране^
неоднократно указывалось, в этом случае интеграл A2.2) отсутствует
и необходимо решать полную систему уравнений (8.22), котораг
') Дородницын А. А., Ламинарный пограничный слой в сжимаемс»
газе, Сб. теорет. раб. по аэродинамике ЦАГИ, Оборонгиз. 1957, стр. 140—17;..
§ 86]
ПОГРАНИЧНЫЙ СЛОЙ ПРИ Я ф \ W ПРОИЗВОЛЬНОМ
425
может быть переписана в форме
dpe , д
dx ~Т~ ду
<?(рц)
ди . ди
дх ' ду
¦ ov-
1 д
ду
dh
ди
к—\
где положено
a Ao представляет собой переменную полную энтальпию
A2.27)
A2.28)
A2.29)
причем в рассматриваемом сейчас общем случае к^Фк^.
Правая часть третьего уравнения системы A2.27) получена
тождественным преобразованием соответствующей части третьего
уравнения системы (8.22) при помощи A2.28). Последнее равенство
системы A2.27) выражает некоторый общий закон зависимости коэф-
фициента вязкости от температуры (энтальпии).
По определению параметров адиабатически и изэнтропически
заторможенного газа будем иметь
A2.30)
Применим к первым трем уравнениям системы A2.27) общее
преобразование Дородницына A2.1). Аналогично тому, как это имело
место в предыдущем параграфе, найдем
A2.31)
кроме
или по
того
d
(штрих —
Ре Ре
dx peo
A2
30)
д
дх =
д
ду ~
_ Ре
Рео
~ PfO
d
di
производная
dpe
di
1
k
+
по
1
di] д
дх д-q '
Ре *//,
ft+1
dx
A2.32)
426 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. ХП
Применяя преобразование A2.31) к первому равенству системы
A2.27) и используя формулу A2.32), получим
ди
ди
ft+1
откуда, деля обе части на величину
2ft
придем к следующему выражению для первого (динамического)
уравнения:
.. ди , ~ди 7 .. , ,
д Г"-Л-?-1. A2.33)
причем положено
Рео
A2.34)
Вводя функцию тока ф при помощи системы равенств
получим
так что будет
и =
?ео
дх
. v=-
ре0 di
di
д-п
A2.35)
A2.36)
Наконец, преобразуем аналогичным образом третье уравнение
системы A2.27), а именно, уравнение энергии. Введем вместо полной
Энтальпии Ао ее безразмерную величину
2Л„
— v -4- а* — ft
A2.37)
§ 86] пограничный слой при з Ф 1 и произвольном М^ 427
Применяя к вышеупомянутому уравнению системы A2.27) преобра-
зование A2.31), получаем
Р д \аМ Р <*»] /1 Л У-ео д Г р
после чего, разделив обе части на ppJPgQ, окончательно установим
следующий вид уравнения энергии в переменных Дородницына:
Совокупность уравнений A2.33), A2.36), A2.38) и граничных
условий
и = г; = 0 при т^ == 0,
и = ие(?) при т) = со,
-з— = 0 при 7j = 0, если поверхность тела теплоизолирована,
8 = bw (?) при т) = 0, если поверхность тела поддерживается при
заданной температуре, и
О = 1 при т) = со во всех случаях представляет собой искомую
систему уравнений и граничных условий для рассматриваемой задачи
о плоском ламинарном пограничном слое на крыловом профиле в газо-
вом потоке больших скоростей при заданном распределении давления
на внешней границе пограничного слоя.
Рассматривая полученные уравнения, убедимся, что (как и в более
простом случае, изложенном в предыдущем параграфе) преобразо-
вание Дородницына приводит левые части первого и третьего урав-
нений системы A2.27) к такому же виду, как и в случае несжи-
маемой жидкости, а в правых частях уравнений влияние температуры
на изменение физических констант газа сохраняется и выражается
наличием величин х/Хе и ^(х) в первом, динамическом уравнении и
величины Ь(у) ве втором, энергетическом. При использовании зави-
симости коэффициента вязкости от температуры (энтальпии) в форме
Чепмена — Рубезина (8.6) будем иметь Ь{у)=\. Действительно.
по (8.6)
так что
Р/Лю = а ОС) = 1Ь (X) = h/keo = X • "
В выше цитированной работе Дородницына принимается, наряду
с этим простейшим, более близкий к формуле Саттерлэнда линейный
закон
*(*)= 1 + 0.3A-х).
428 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XI
Соответствующая этому закону пунктирная прямая (рис. 94
располагается между кривыми Саттерлэнда для Те = 330° и Г( = 660'
показанными сплошными линиями.
При наличии такого рода связи между ц и 71, для значения
14
о = -уд-, справедливого для двухатомных газов, и в предположена
об отсутствии теплоотдачи А. А. Дородницыным было проведет
численным методом определение не
известных функций и и 8 для тре:
случаев задания ие(?): 1) парабг-
лического распределения ие(?) =
= Cji--)-с3'3- 2) для продольногг
обтекания пластины ие = const \
3) односкатного профиля ие ($) —
= Ьй— #!?. Таблицы соответствую
щих вспомогательных функций, че-
рез которые выражаются искомые
решения, можно найти в цитироваь
ной выше работе. Пользуясь этим1
классами решений последовательш
для конфузорного участка погра-
ничного слоя, для области минимума
давления и диффузорного участк;.
слоя, А. А. Дородницын построй.*
приближенное однопараметрическс
решение рассматриваемой задачи
которое является обобщением решения, изложенного в предыдуще!^
параграфе.
Как и ранее, составим два основных интегральных соотношениг
(штрих — производная по ?)
BJX)
1,6
1,0
0.5
О
г
-Ге=660а
Те=330°
0,5
Рис. 94.
1,0 X
где приняты следующие обозначения:
я =.
A2.40
§ 86] пограничный слой при о Ф 1 и произвольном Vt-a 429
Заметим, что при условии тепловой изоляции поверхности тела
дЪ „ „\
-3—= О при 77 = 01 второе интегральное соотношение сводится
к равенству
(«Х7 = о,
что дает
С = 0, A2.41)
так как в лобовой критической точке (? == 0) либо а = 0, либо
С = о.
Предположим теперь, в отличие от предыдущего параграфа, что
безразмерные профили скоростей и температур в сечениях слоя могут
быть представлены в форме
J-. = ср! (т)/8**; /, Ше, о),\
ие } A2.4
& == ср2 (>)/§**; /, Ме, а), |
где роль параметров играют:
1) формпараметр
имеющий ту же форму A2.20), что и в рассмотренном в предыдущем
параграфе более простом случае,
2) местное число Маха Ме, связанное с ае очевидным соот-
ношением
A2.44)
и 3) число Прандтля о.
Тогда, подставляя выражения A2.42) в интегральные выраже-
ния A2.40) и первое из интегральных соотношений A2.39), придем
для определения формпараметра / к тем же уравнениям A2.21) и
A2.23), что и в предыдущем параграфе. Разница будет лишь в выра-
жении для функции F(f; ae, а), которая в рассматриваемом сейчас
общем случае равна
F(J; a,. o) = 2C-2/B-f-tf-tf9); C = ^-ft (xj(^=q. A2.45)
Как показали расчеты, в интервале изменения Ме от нуля до
2,378 и при а = 14/19 вид функции /="(-/; %е, а) слабо зависит от ае'
что подтверждает сделанное в предыдущем параграфе упрощающее
допущение о независимости F от Ме при не слишком больших зна-
чениях этого параметра. Это позволяет вновь воспользоваться линей-
430 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XI
ным представлением функции F (/) и получить значение f(x
в форме A2.24) при тех же значениях констант а и Ь.
Точно так же и r,(f; ae, а) при а =14/19 слабо зависит от
и может определяться по обычному графику или таблице, как дл:
-0,05 О 0,05 0,7 Г
Рис. 96.
несжимаемой жидкости. Напряжение трения rw, согласно определе
нию ч по A2.45), выразится как
причем 8** вычисляется заранее по известному уже f (х) и фог-
муле A2.43), переписанной для переменной х в виде
A2.47
§ 87] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 431
Таким образом, при числе Мсо, доходящем примерно до значе-
ния 2,4, динамические величины определяются сравнительно просто.
Пользуясь теми же классами решений, можно определить и тепловые
величины. На рис. 95 и 96 приводятся рассчитанные А. А. Дород-
ницыным зависимости Xw=TwITe0 и Я9 от / при различных <хв
в пределах от 0 до 0,6, что соответствует пределам Ме от 0 до 2,4.
Как видно из приводимых графиков, влияние параметра <хе на эти
величины весьма значительно.
§ 87. Преобразование уравнений пограничного слоя
в газе к форме, полностью соответствующей
несжимаемой жидкости
Преобразование Дородницына, как уже указывалось выше, даже
в простейшем случае линейной связи между коэффициентом вязкости
и абсолютной температурой (л=1) не может полностью привести
уравнения пограничного слоя в газовом потоке больших скоростей
к виду, соответствующему случаю несжимаемой жидкости. Это видно
на примере уравнения A2.33); даже при ?(х)= 1> что соответствует
/1=1, множитель х/Хе в пеРвом члене справа делает это уравнение
отличным от уравнения пограничного слоя в несжимаемой жидкости.
Преобразование Дородницына A2.1) в случае отсутствия тепло-
отдачи с поверхности тела и при п=\, а—\ путем простой моди-
фикации может быть усовершенствовано так, что преобразованные
уравнения в точности совпадут с уравнениями пограничного слоя
в несжимаемой жидкости. Такая модификация была выполнена
Стюартсоном 1).
Преобразование Стюартсона имеет вид
у
= 2. f-*-dy.
A2.48)
где а — скорость звука; индекс 1 заменяет индекс еО предыдущих
параграфов и соответствует состоянию адиабатически и изэнтропи-
чески заторможенного газа во внешнем потоке, как это принималось
уже в .предыдущих параграфах; определение v будет дано ниже.
Легко заметить, что преобразование Стюартсона A2.48) отли-
чается от преобразования Дородницына A2.1) дополнительным мно-
жителем aja1 в формулах преобразования координат (л:, у) в новые
') S t e w a r t s о n K., Proc. Roy. Soc. A949), A-200, стр. 84—100,
432 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
координаты ($, т)) и таким же делителем в формулах преобразования
компонент скоростей и и v в новые (U, V).
Для упрощения дальнейших выкладок используем определение
A2.28) величины уе\ зададим ее отношением
Те /аеу , ?_! v-i / k-l 2l
A2.49)
и заметим еще, что по известным изэнтропическим соотношениям
будет
* * i
ггг. A2.50)
Тогда преобразование A2.48) может быть представлено так:
% — J Х« х- V — Xe J "р7 У- A2.51)
Обратимся к рассмотрению динамической системы уравнений по-
граничного слоя
ди , ди dug ,_ д
A2 52)
и имеющего место при принятых ограничительных условиях (я=1,
о=1) и отсутствии теплоотдачи с поверхности тела интеграла
который в принятых обозначениях может быть переписан еще в форме
k-l ul k-l U2
1
2 а2 2 а2 y 2 a2
Формулы преобразования к новым переменным будут
•. A2.53)
дх
di
ft+i
A2.54)
§ R7] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 433
Заметим, что из равенств
Т р р/ ре
' — т » — х ;
'l /?1 Pl'l P\
следует
В силу A2.54) и полученного только что соотношения перепишем
первое равенство системы A2.52) сначала в форме
ТГь—iT OU , 011 . ят*—ГГ Р
3ft-1
а затем, разделив обе части на x|(*~1JP> eu^e TaK:
в *i + v-jL = —я.^-Н-^тт. A2-55)
где под величиной г» понимается выражение
A2.56)
Теперь используем преобразование компонент скорости. Будем
иметь, согласно второй строке A2.51), вместо A2.55)
д2и
Произведя дифференцирование и воспользовавшись A2.53), получим
(штрих — производная по ?)
4--
А —1 f
Пользуясь легко получаемой из A2.49) связью между %'е и U'e
а,
28 Зак 297. Л. Г Лойцянскнй
434 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XII
найдем следующие два представления для выражения, стоящего во
второй круглой скобке в первом члене правой части A2.57):
у U U' -4--y'U2 = y U V —
А< < «Т 2 е е 1-е ее
yU = y U V — -^—!
2 е е 1-е ее 2а2
а\ /I *-1 tf*V_, а\
k — 1
Относя первое из этих представлений к первому слагаемому в пер-
вой скобке правой части A2.57), а второе — ко второму слагаемому
в той же скобке, получим вместо A2.57)
и после очевидных сокращений придем к уравнению
,, дСГ . лгди .. dUe , d2L/
A2>59)
соответствующему уравнению пограничного слоя в несжимаемой
жидкости.
Покажем, наконец, что преобразованные компоненты U и V удо-
влетворяют условию неразрывности. Введем функцию тока tj», положив
P« = Pi|jr' P^-Pi-Ё" A2>60)
Пользуясь вновь преобразованиями A2.51) и дифференциальными
соотношениями A2.54), получим
U = у-'Аи = у-1/, ii yV. -L it = il;
аналогично, по тем же формулам и определению A2.56) величины v
найдем
36-1
#
§ 87] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗВ 435
Итак, имеем
U = ^L V — — ^L-
т. е. приведенные компоненты скорости U, V соответствуют неко-
торому потоку несжимаемой жидкости и функция тока для этого
движения в плоскости (I, rj) является одновременно и функцией тока
рассматриваемого газового потока в плоскости (х, у).
Уравнения пограничного слоя в плоскости (Е, tj) могут быть за-
писаны в форме одного уравнения относительно функции тока
Граничные условия для системы уравнений A2.59) и A2.61) или
для одного уравнения A2.62) совпадают с обычными условиями для
несжимаемой жидкости
U = V = 0 при 71 = 0, U-+Ue{\) при т)->оо
или
(j) = ii- = 0 при т) = 0, -fif->Ue® ПРИ т7->°о-
Напряжение трения на поверхности тела определится по формуле
Основное затруднение, возникающее при практических расчетах
по только что изложенному методу, заключается в том, что при
наличии простой связи действительной скорости внешнего потока ие
с продольной координатой х соответствующая ей связь Ue (?) в вообра-
жаемом потоке несжимаемой жидкости может оказаться достаточно
сложной, не подходящей под известный класс точных решений. В дру-
гих случаях, наоборот, простая зависимость Ue(?) будет связана со
сложным распределением ие(х). Так, например, степенной формуле
соответствует, согласно A2.51), выражение
где Хе п0 A2.53) задается формулой
-1
28*
436 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ Ггл. XII
Вся трудность сводится к определению связи между х и ?, ко-
торая по A2.51) задается следующим дифференциальным соотноше-
нием:
T Р^И 2<*"П
Даже в простейшем случае 2т = 1 имеем (х = 0 при ? = 0)
Аа] Г/ А_1 чE*-3,Л2*-2)
X
Наоборот, простому действительному распределению скорости
вблизи лобовой критической точки
в фиктивном потоке несжимаемой жидкости при ? = 1,4 будет соот-
ветствовать распределение
? = * — 0,267Р2д;3-)-0H48р4л;5— ...,
л: = $ + 0,267^3 +0,165^+ ....
т. е. распределение, отвечающее разобранному в § 13 случаю обте-
кания несжимаемой жидкостью симметричного профиля.
Имея уравнение A2.59), а также последнее из уравнений си-
стемы A2.61), легко построить приближенный однопараметрический
метод решения поставленной задачи'). Условимся обозначать через Д*
и Д** соответственно толщины вытеснения и потери импульса в пре-
образованных переменных, т. е. величины
A2-64)
Тогда интегральное условие импульсов в новых переменных будет
совпадать с соответствующим уравнением импульсов в несжимаемой
R о 11 N.. С г a b t r e e L., Journ. Aeron. Scl. 19, N° 8 A952), 561.
§ 87] ПРЕОВРАЗОВАНИЕ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 437
жидкости, а именно:
Приемом, изложенным в § 19, составим основное уравнение од-
нопараметрической теории
di Ue di г^а>^ dUe\d\ fb' (
где приняты обычные для несжимаемой жидкости обозначения
_ д«2 dUe _гд{щие)-\
'* — ~ Ж~' ^-[IWEnl^o1 A2-67)
а заданная функция Ue(%) определяет распределение преобразованной
скорости на внешней границе слоя.
Составим формулы связи преобразованных величин /А, Сд, Яд
с соответствующими им в действительном движении газа величи-
нами /,С и Н.
Прежде всего заметим, что, в отличие от предыдущего, «тол-
щина вытеснения» 8* в последующем будет определяться по формуле
A2-68)
так как именно эта форма соответствует изложенному в § 10 физи-
ческому представлению об оттеснении линий тока от поверхности
обтекаемого тела за счет вязкого торможения газа и указанному
там же приему определения обратного влияния пограничного слоя
на распределение давлений во внешнем потоке'). Толщина потери
импульса 8** будет задаваться тем же выражением
A2-69>
что и неоднократно использованное ранее.
Пользуясь преобразованием независимых переменных и скоро-
стей A2.51), найдем формулы преобразования условных толщин.
') Л о й ц я н с к и й Л. Г., Механика жидкости и газа, Гостехиздат, 1950,
стр. 641 — 645.
438 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
Для этого перепишем сначала выражение для толщины вытесне-
ния A2.68) в тождественной форме
и используем справедливый в рассматриваемом частном случае (теп-
лоизолированная стенка, число Прандтля равно единице) движения
газа интеграл уравнения энергии
Т k —~-1
Тогда найдем
со
/
M A +М) + A +
Совершая в правой части переход по формулам A2.51) к преоб-
разованным координатам и скоростям, получим
со
Z;-^ J (l —?
о
A2.70)
§ 87] ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ В ГАЗЕ 439
Аналогично найдем
оо
о
Деля почленно обе части равенства A2.70) на соответствующие
части равенства A2.71), составим выражение Н через НА
Определим далее связь между / и /4:
R«s rfu __*+! л**г 3*~2 rf,r
У ~~ v, dx ~~ *•<> v, *„ rfj — Ae
а также между С и Сд (в данном случае Tw = Tj):
Гд(Ц/иеI
L J
C4. A2.74)
Дальнейшие вычисления могут быть выполнены теми же прие-
мами, что и в случае несжимаемой жидкости (§§ 19—21). Произ-
ведя линеаризацию (§ 21), найдем
A2.75)
а затем, переходя по только что выведенным формулам и основной
системе A2.51) от преобразованных величин к физическим, получим
х
я*** ± - k+1 -ь [ 2к~1 L
-— = ау2 »-'«, у*-1 aj"'to. A2.76)
О
Значения постоянных а и Ъ могут быть выбраны теми или другими
в зависимости от использованного класса точных решений (§ 21).
440 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XII
В цитированной выше статье Ротта и Крабтри рекомендуется сле-
дующая приближенная в округленных числах формула для воз-
духа (k =1,4):
A2.77)
§ 88. Применение модифицированного преобразования
в случае теплоотдающей поверхности
Рассмотрим сначала наиболее общий случай наличия теплоотдачи
и числа Прандтля о, не равного единице; для связи между коэф-
фициентом вязкости и абсолютной температурой примем формулу,
аналогичную ранее указанной формуле Чепмена — Рубезина (8.6), заме-
нив 7"оо на температуру адиабатически и изэнтропически заторможен-
ного внешнего потока Ту = Те0.
В этом случае интеграл Крокко несправедлив и необходимо ре-
шать полную систему уравнений
ди .
дх '
ди
д(9и)
дх
due
d(9v)
ду
да
= 0,
A2.78)
Напомним, что здесь символ k0 обозначает переменную энтальпию
адиабатически и изэнтропически заторможенного газа в любой точке
пограничного слоя («полную энтальпию»), а индекс 1 относится
к состоянию адиабатически и изэнтропически заторможенного газа
во внешнем потоке и заменяет двойной индекс еО.
Введем функцию')
при
A2.79)
Тогда, произведя в системе уравнений A2.78) преобразование
A2.51), несколько видоизмененное по сравнению с предыдущим
') Cohen СВ., Res hot ко Е., NACA, Rep. 1293, 1956. Функция S
была Введена Стюартсоиом (см. его статью, цитированную в предыдущем
параграфе).
§ 88] ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОГО ПРЕОБРАЗОПАНИЯ 441
благодаря применению соотношения Чепмена — Рубезина, а именно:
х у
\= Cv2**-1' dx, i7 = v2(*-1) —rfy, A2.80)
о о
придем к следующей системе уравнений пограничного слоя:
,, ди , „ ди _у dUe_
dU , dV
1—а
, 1
3 1 + 1=1м2
с граничными условиями
при 7j =
при 7)->оо
;.!
A2.81)
A2.82)
В качестве приложения рассмотрим задачу, аналогичную задаче
Фокнера — Скэн (,§ 11) для несжимаемой жидкости; положим, следуя
пути, указанному в § 11,
A2.83)
Тогда система уравнений A2.81) приведется к такой системе
двух уравнений в частных производных (штрих обозначает производ-
ную по С; Ме является функцией %)
," = {3(<р'2 — 1—5),
A2.84)
Можно указать ряд случаев, когда поставленная задача станет
автомодельной, т. е. функции у и S станут функциями только С, и
предыдущая система превратится в систему двух обыкновенных диф-
ференциальных уравнений. Это произойдет, например, если будет
442 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
k=\, или Ме=0, или, наконец, а=1; кроме того, условие авто-
модельности, очевидно, приближенно выполняется при любых о и k.
если Ме достаточно велико.
Остановимся на наиболее общем из этих предположений, а —1.
В этом случае задача сведется к интегрированию системы обыкно-
венных дифференциальных уравнений
ср"' _|_ щ" — S (со'2 —1—5),
при граничных условиях
ср = ср' = О, S = SW при С = 0. J б)
<р'->1, 5->0 при С->эо. J
Получаемая таким образом система была численным методом
проинтегрирована Коэном и Решотко'). Применялся следующий прием
последовательных приближений. Вместо т; и ср вводились две новые
безразмерные переменные и и К (переменные Крокко, см. § 70)
ср' = ы, <f" = K.
Тогда, как уже было показано ранее,
f
оо о
и первог из уравнений системы A2.85) перепишется в новых пере-
менных в виде
du J K&) К(п
&) К(п)
о
или, интегрируя еще раз и выполняя очевидные преобразования,
К(п) = О - а) /
V fw / *<«> { <w A2.87)
') См. выше цитированную статью этих авторов.
§ 88] ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОГО ПРЕОБРАЗОВАНИЯ 443
Аналогичному преобразованию подвергается и второе уравнение
системы A2.85). Переписывая его сначала в форме
5" Г
-&- =— ср или In S'— const— 1<р^
и замечая, что, согласно первому из уравнений A2.84), будет
получим по предыдущему
lnS' = \nC-t-J ^-РУ jp-^du.
и, следовательно,
Sf^CK(u)J(u) или ^¦ = СУ(а). A2.88)
где введено обозначение
Интегрируя еще раз обе части A2.88) и принимая во внимание
граничные условия A2.86), найдем
1
У (м) du
A2-89)
J
V
J
J(u)du
о
Уравнения A2.87) и A2.89) служат основными в примененном
методе последовательных приближений. Можно заметить, что инте-
гралы, входящие в эти уравнения, являются несобственными, так как
/С —0 при и=1, что соответствует внешней границе слоя (т] = оо).
Для исследования поведения функций К (и) и S(u) при и->1 сле-
дует возвратиться к уравнениям A2.85) и рассмотреть асимптоти-
ческое поведение tp и S при больших rj. Для этого, прежде всего,
замечая, что
lim (p'Gj)=l. lim 5=0,
заключаем, что искомые асимптотические решения могут быть пред-
ставлены как суммы (k — постоянная)
S = Sl -j- 52 = 52;
444 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XII
таким образом, уравнения A2.85) переходят в следующие асимпто-
тические уравнения:
Второе из них сразу интегрируется и дает (а3 — произвольная
постоянная интегрирования)
Первое уравнение после этого также интегрируется и при боль-
ших т] имеет интеграл (otj, a2 —произвольные постоянные интегри-
рования)
Вспоминая известное асимптотическое разложение
а
erf t — * ( 1 s- + • • Л<
будем иметь следующие окончательные асимптотические выражения
для ср'Оч) и 5(т]):
t^W — «) >
-«зС7! — k)~
Из условия стремления <р'(т])—>1 при т)->оо сразу следует, что
при р >- О должно быть а2 = 0. Приведенное только что исследова-
ние асимптотического поведения решения вблизи и = 1 аналогично
ранее изложенному в конце § 69 для случая обтекания пластинки.
Выполненный только что анализ показывает, что уравнением A2.87)
можно пользоваться непосредственно, а в уравнении A2.89) правую
часть следует понимать как предельное выражение
1-е
lim-
»-»о
§ 881
ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОГО ПРЕОБРАЗОВАНИЯ
445
В цитированной статье Коэна и Решотко приводятся подробные
таблицы и графики величин ср, ср' и <р", а также 5 и 5' в функции rj,
составленные для различных значений параметров fi и Sw; воспроиз-
вести эти таблицы в настоящей книге нет возможности. Остановимся на
некоторых особенностях приведенной методики расчета.
Как легко заключить из первого асимптотического соотношения
системы A2.85), при C < 0, <х2 > 0 и при достаточно больших tj,
т. е. на внешней границе пограничного слоя, безразмерная скорость
<p'Gj) будет стремиться к единице от значений, больших единицы,
нарушая тем самым монотонность роста скорости в сечении погра-
ничного слоя. Расчеты показали, что в этом случае единственность
решения нарушается и из двух
решений следует выбрать то,
которое лишено указанного
недостатка. Напомним, что та
же особенность решения была
отмечена Хартри в цитирован-
ной в § 11 его статье, по-
священной численному методу
расчета пограничного слоя
в несжимаемой жидкости при
степенном распределении ско-
рости во внешнем потоке.
При сравнительно боль-
ших положительных C и Sw,
когда постоянная <х2 в силу
конечности величины скорости Рис. 97.
должна быть равна нулю, от-
мечается также наличие немонотонности роста скорости в сечении
пограничного слоя (рис. 97). Эта особенность течения газа является
естественной и получает простое физическое объяснение. При резком
убывании давления (C = 2 для верхней кривой рис. 97) и значитель-
ном подогреве стенки E^=1) плотность газа в слоях, близких
к стенке, резко падает, и наличие этих двух факторов, даже при
тормозящем влиянии вязкости, приводит к появлению внутри погра-
ничного слоя более высоких скоростей, чем во внешнем потоке.
Еще в § 11 было отмечено, что изучение класса точных решений
уравнений пограничного слоя, соответствующих степенному распреде-
лению скорости на внешней границе слоя, позволяет установить
некоторые основные отличия конфузорного течения (J3 > 0, -~- < 0)
от диффузорного (р < 0, "^v^O)- Точно так же и в рассматриваемом
сейчас случае по кривым зависимости 5 от ср', приведенным в про-
цитированной статье Коэна и Решотко, можно судить об общих
446 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
свойствах движения газа в пограничном слое при-наличии теплоотдачи
с поверхности обтекаемого тела.
В § 69 было выведено важное соотношение A0.43), утверждаю-
щее, что на пластинке ф = 0) при числе Прандтля, равном единице,
имеет место подобие распределений по сечению слоя разности тем-
ператур торможения и продольных скоростей. В принятых в настоя-
щем параграфе обозначениях равенство A0.43) перепишется так:
h{-h
-Sw
Если сетки кривых S(cp'). приведенные в разбираемой работе для
различных значений параметров fj и Sw, перечертить в координа-
тах ( ^-, tp' 1 , то можно убедиться, что независимо от того,
будет ли 5 больше или меньше нуля. т. е. будет ли поверхность
тела подогреваться или охлаж-
даться {Sw = 0 при о=1 со-
ответствует теплоизолированной
поверхности), кривые в этих но-
вых координатах примут форму,
показанную на рис. 98. Биссек-
триса, соединяющая нижний
левый и верхний правый углы
диаграммы, соответствует ?5 = 0;
кривые, расположенные сверху
этой прямой, безотносительно
к тому, будет ли Sw > 0 или
Sw < 0 (при Sw — 0 имеем 5 =
= 0), относятся к значениям
C < 0, а нижние кривые — к зна-
чениям р > о.
рис gg Определим толщину скорост-
ного (динамического) погранич-
ного слоя как значение ординаты у = 8, соответствующее некоторому,
условно принятому значению ср^, например ср^ == 0,95. Аналогичным
образом зададим и толщину температурного (энтальпийного) слоя как
_5 ^
ординату у = Ьт, при которой -—^- = 0,95. При р = 0 по преды-
дущему будет ог — 8, т. е. условно определенные характеристики
толщины динамического и температурного слоев будут одинаковы.
Как это непосредственно следует из диаграммы (рис. 98), при C < О
(кривые, расположенные выше биссектрисы) точкам на границе теп-
лового слоя соответствуют значения <р' < <?'о, т. е. внутри скорост-
0
/
§ 88] ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОГО ПРЕОБРАЗОВАНИЯ 447
ного пограничного слоя, а при [3 > 0 (кривые, расположенные ниже
биссектрисы), наоборот, значения ср' > ср^. Отсюда непосредственно
следует, что при [3 > 0 (конфузорный слой) динамический погранич-
ный слой тоньше теплового, а при [3 < О (диффузорный слой) дина-
мический пограничный слой толще температурного. Подчеркнем еще
раз, что это справедливо при о = 1 и любых, как положительных,
так и отрицательных, значениях температурного параметра Sw.
Аналогичное соотношение имеет место, как уже указывалось в § 59,
и в несжимаемой жидкости.
Имея поле скоростей и температур, можно определить и основные
выходные характеристики пограничного слоя — сопротивление трения
и теплоотдачу на поверхности тела.
Простые вычисления, основанные на использовании формул преоб-
разования к новым переменным A2.51) и A2.83), позволяют прежде
всего найти выражение для напряжения трения в любой точке се-
чения пограничного слоя
da Л ,, ~ъ
7 = С^Л
2А — 1 I
~ъ~~г •¦ / т + 1 Ue „ .».
У —2-^f •? (С)>
а после этого и искомое значение местного коэффициента трения Су,
выражаемое через значение напряжения трения на стенке tw по формуле
/(О). A2.90)
Замечая, что, в отличие от предыдущего, при определении cf
используется значение pw, а не р , введем число Рейнольдса
= ~
A2-91)
также отнесенное к vw. Тогда можно получить следующую формулу
для определения cf\
Для определения местной теплопередачи с поверхности тела вве-
дем местное число Нуссельта, положив, как уже это делалось не-
однократно ранее,
(дТ\
х
N —
1J~
Tt-Tw ¦
В рассматриваемом сейчас случае числа Прандтля, равного единице,
температура теплоизолированной поверхности тела — так называемая
448 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ 1АВЛЕНИЙ Ггл XII
«равновесная» температура Т, — совпадает с температурой адиабати-
чески и изэнтропически заторможенного газа на внешней границе
слоя Те0=Т1. Таким образом, будем иметь
Ц^-. A2.93)
Совершая преобразования к новым переменным, получим (штрих
обозначает дифференцирование по С)
N — — ~ 1/ R
Для вычисления коэффициента теплоотдачи удобнее всего поль-
зоваться получающимся путем почленнного разделения левых и пра-
вых частей равенств A2.92) и A2.94) соотношением
cfRwx 2«>"@)
Nwx —bw/bw
правая часть которого представляет раз навсегда определяемую функ-
цию основных двух параметров задачи C и Sw. Значения этой функ-
ции можно найти в последнем столбце приводимой в следующем
параграфе таблицы 32. Формула A2.95) позволяет вычислять N^,.
по известному значению cf.
§ 89. Приближенный метод расчета пограничного слоя
в случае произвольного распределения скоростей
во внешнем потоке и наличия теплоотдачи с поверхности тела
Пользуясь описанным в предыдущем параграфе классом точных
решений, соответствующим степенному заданию приведенной ско-
рости, можно в полной аналогии с тем, как это было сделано
в главе III (класс точных решений Фокнера — Скэн), предложить
следующий приближенный метод, который по существу задачи уже
не может быть однопараметрическим ').
Обратимся вновь к системе уравнений A2.81), причем, согласно
изложенному в предыдущем параграфе, предположим, что число
Прандтля равно единице. Поступая обычным образом, из первых
двух уравнений этой системы найдем
^^ = 7МтЧ ' <12-96)
Cohen С. В., Res hot ко Е.. NACA, Rep. 1294, 1956.
§ 89]
ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ПОГРАНИЧНОГО СЛОЯ
449
где сохранены те же обозначения, что и в предыдущем параграфе,
за исключением «толщины вытеснения», которую в рассматриваемом
сейчас случае приходится принять равной
A2.97)
Аналогично из совокупности второго и третьего уравнений той же
системы A2.81) получим
S dUe
dS
где введено представление о толщине теплового слоя
ио
A2.98)
A2.99)
причем предполагается, что благодаря граничному условию
U^Ue, 5->0 при т)->со A2.100)
интеграл A2.99) имеет смысл.
Следуя общему пути, изложенному в главе III, введем следую-
щие безразмерные «формпараметры»:
Ue
( дг" \
ue Te
__ A*»2 dUe _ 8**2 due
A2.101)
я __ А**3 / d*U\ __f Tw Г д I T
*~~и7\дг? )„— ~и~т71~ду\ Те
При составлении выражений производных (-т—j , ) ,
/ d3U\ w M ""
I . 3 1 использованы непосредственно следующие из уравнений си-
стемы A2.81) и граничных условий A2.82) равенства
(d*U\ _ Ue
\~WL~ ~ —
dUe
дЧ/
Ue dUe I dS
A2.102)
') Введенную здесь величину С не следует смешивать с аргументом
A2.83) предыдущего параграфа.
29 Зак. 297. Л. Г. Лойцянский
450 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
Кроме того, принято во внимание соотношение A2.71), выражаю-
щее связь между Д** и физической толщиной потери импульса о**.
Легко показать, что в рассматриваемом более общем, чем в преды-
дущем параграфе, случае сохранится и соотношение между 8* и тол-
щинами Д*. А**, представленное равенством A2.70).
Действительно, по принятому ранее определению будет
dy = _±
0 0 0
С другой стороны, из определения величины 5 следует
2 i-7". i_
и] Те ( и \2 Те ( Т k—\ 2 И2
( и \ Те ( Т
^ttW ~1==Т\т'~{
откуда получаем
2
Возвращаясь к выражению й*. перепишем его тождественно так:
l
?еие \ ие
о
после чего, принимая во внимание A2.97) и переходя по A2.51)
к новым переменным, нетрудно получить искомое соотношение
A2.70). Отсюда следует, что и необходимая для дальнейших расче-
тов связь между величинами Яд = Д*/Д" и Н = о*/Ь** сохранит то же
выражение A2.72), что и в случае теплоизолированной поверхности
обтекаемого тела. Таким образом, к системе формпараметров A2.101)
§ 891 ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ПОГРАНИЧНОГО СЛОЯ 451
присоединится еще один
Яд = -^Я+-^ — 1. A2.103)
В рассматриваемом частном случае равенства единице числа
Прандтля приближенное решение задачи расчета пограничного слоя
при произвольном распределении скорости на внешней границе
строится из соображений, представляющих простое обобщение ме-
тода главы 111.
Прежде всего заметим, что при принятом выборе «формпараме-
тров» Сл и /д уравнение A2,96) обычными преобразованиями сво-
дится к такому:
где положено
F{/l, SW) = 2<U — 2/дB + Яд). A2.105)
Совокупность равенств A2.104) и A2.105), как легко убедиться,
в точности соответствует уравнению C.29) однопараметрической тео-
рии для несжимаемой жидкости; разница лишь в том, что в рассма-
триваемом случае потока газа при больших скоростях в число
параметров, кроме /д, входит еще существенный тепловой пара-
метр Sw.
Используя класс точных решений, описанный в предыдущем па-
раграфе, можно сопоставить значения формпараметров и их функ-
ций F при различных р и Sw. Это сделано в таблице 32. При рас-
смотрении таблицы обращает на себя внимание одна особенность,
а именно, отсутствие в некоторых интервалах изменения параметров
однозначной связи между ними. Этот факт наглядно обнаруживается
при рассмотрении графиков на рис. 99—101.
Обратимся к анализу семейства кривых F(fA) с параметром Sw,
приведенных на рис. 101. При Sw = 0 кривая мало отличается от
прямой линии. Это же можно сказать и о случае Sw < 0, если от-
влечься от значений /д, близких к условиям отрыва (Сд = 0), где
функция F(fa) становится двузначной. При Sw > 0 в области поло-
жительных значений /д (конфузорный участок слоя) замечается также
возникновение двузначности функции F(fA).
Близость кривых F(/a) при заданных значениях Sw к прямым
линиям позволяет и в случае наличия теплоотдачи применить метод
линеаризации, аналогичный изложенному в главе III.
Полагая по предыдущему
F = a — bfA, A2.106)
29*
452 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XI
Таблица 3-
sw
—1,0
—0,8
—0,4
0
1,0
Р
—0,326
—0,3657
—0,3884
—0,360
—0,300
—0,140
0
0,5
2,0
—0,3088
—0,325
—0,3285
—0,3285
—0,325
—0,30
—0,14
0
0,50
1,50
2,00
—0,246
—0,2483
—0,24
—0,20
0
0,50
2,00
—0,1988
—0,16
0
0,50
1,00
1,60
2,00
—0,1295
—0,10
0
0,30
0,50
1,00
1,50
2,00
—0,1335
—0,1579
—0,1591
—0,1257
—0,0907
—0,0343
0
0,0897
0,2938
—0,1215
—0,1304
—0,1298
—0,1260
—0,1212
—0,1017
—0,0355
0
0,0837
0,2008
0,2522
—0,0899
—0,0894
—0,0826
—0,0615
0
0,0722
0,1733
—0,0681
—0,0487
0
0,0602
0,0803
0,1002
0,1064
—0,0417
—0,0294
0
0,0334
0,0735
0,0312
0,0186
0,0089
0
0,0329
0,0896
0,1446
0,1749
0,2063
0,220
0,2459
0,2829
0
0,0312
0,0436
0,0681
0,0827
0,1214
0,1935
0,220
0,2678
0,3179
0,3366
0
0,0300
0,0624
0,1210
0,220
0,3019
0,3924
0
0,1051
0,220
0,3220
0,3556
0,3808
0,3892
0
0,0980
0,220
0,3277
0,3384
0,3065
0,2382
0,1663
2,063
1,530
1,013
0,630
0,404
0,134
0
—0,257
—0,538
2,240
1,828
1,708
1,501
1,396
1,138
0,692
0,519
0,199
—0,083
—0,166
3,041
2,679
2,399
2,034
1,556
1,185
0,759
4,032
3,094
2,591
2,298
2,218
2,180
2,152
6,723
5,671
5,187
5,493
6,012
7,850
11,125
17,105
F
1,0845
1,1804
1,1382
0,9504
0,7858
0,5590
0,440
0,1793
—0,2933
1,0305
1,0606
1,0499
1,0185
0,9885
0,882
0,5781
0,44
0,1676
—0,1332
—0,2517
0,9087
0,8968
0,8519
0,7379
0,440
0,1442
—0,1713
0,822
0,7068
0,440
0,1232
0
—0,0748
—0,1040
0,7280
0,6476
0,440
0,1558
0,0755
0
—0,0114
—0,0088
в*
0,0212
0,0307
0,0359
0,0297
0,0212
0,0077
0
—0,0188
—0,0586
0,0172
0,0210
0,0216
0,0220
0,0216
0,0187
0,0064
0
—0,0138
—0,0313
—0,0388
0,00679
0,00730
0,00696
0,00554
0
—0,00573
—0,0118
0
0
0
0
0
0
0
—0,00803
—0,00644
0
0,00607
0,00588
0,00338
0,00133
0,00034
(Cftwx\
\NWJ
0
0,3381
0,7939
1,224
1,493
1,830
2,000
2,347
2,837
0
0,3100
0,4194
0,6245
0,7438
1,058
1,712
2,000
2,599
3,263
3,502
0
0,2941
0.5775
1,074
2,000
3,042
4,628
0
0,9480
2,000
3,436
4,317
5,122
5,565
0
0,8956
2,000
3,602
4,315
5,644
6,662
7,527
§ 89] ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ПОГРАНИЧНОГО СЛОЯ 453
получим в рассматриваемом приближении (штрих — производная по ?)
aUe Г 6_j
Ub J e
A2.107)
или, возвращаясь в правой части к физическим переменным,
xlL
где L—некоторая характерная длина, а введенный для краткости
письма параметр % равен
х = 23^~1п • A2.109)
Определение величин а и Ъ зависит от способа проведения ап-
проксимирующей прямой A2.106). При этом следует в каждом
отдельном случае принимать во внимание интервал изменения /д.
"ак, например, в случае малых продольных перепадов давления,
D0
-4
0.32
0,24
0,78
0,08
О
——«.
\
\
\
" J
\
\
\
V
\
_^
\'
\\
Г
Sm
=
N
\
\
Л
1
и
0,32 0,24 Q7ff 0,08 О -0,08 -0,/S
Рис. 99.
:огда /д олизко к нулю, проще всего аппроксимирующую прямую
фоводить через общую точку (/д = 0, /7 = 0,44) пересечения кри-
вых F(/a; Sw) (см. рис. 101) по касательной к той из этих кривых,
:оторая соответствует выбранному значению параметра Sw. При
454 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XI
будет а = 0,44, a b представится функцией Sw, показанной на рис. 10-
сплошной кривой. Если же рассматривается, например, движение
вблизи лобовой критической точки (ие = 0, Ue = 0), то аппроксимь
рующую прямую естественно проводить через точку, где F = С
Если при этом сохранить и точку (fi, = 0, F = 0,44), то b = 0,44/|/д0,
где /до — значение /д в лобовой точке. Соответствующая крива;
b(Sw) показана на том же рис. 102 простым пунктиром. Наконец
если аппроксимирующую прямую провести по касательной в точке
в
е\\\\\ \~А 1/1 | | | | 1*
5\ I I I U\ П I I I I к
4
3
2
1
zIA
— —-
ч
— —
/
s*=/,o/
\°
\
\
г
S
1\
\
)^
О
0,32 0,24
0,08 О -008 -Ц/8
Рис. 100.
где F = 0, то обе величины а и b станут зависимыми от Sw; в част-
ности, при Sw = — 0,8 будет: а = 0,372, * = 2,53.
В диффузорном участке слоя (/д < 0) из условия лучшего со-
впадения аппроксимирующей прямой A2.106) с действительной кри
вой F(fb) можно принять а = 0,44, a b определять по штрих-пунк-
тирной кривой на рис. 102.
Напомним, что, так же как и в случае несжимаемой жидкость
из структуры формулы A2.107) для /д вытекает слабая зависимое^
этой величины от изменений параметра Ъ.
Предположим, что по формулам A2.107) или A2.108) формпар*
метр /д в функции от х для данной конкретной задачи определен
Обратимся к рассмотрению основных расчетных величин: коэффи
циента трения и коэффициента теплоотдачи. Введем местные значь
ния коэффициента трения, числа Рейнольдса и числа Нуссельта
-,_t р =.»??, к„ = 4№, (I2.no
2 ¦"«) 'ото—'w
с, = -
где ТОа1 — температура адиабатически и изэнтропически заторможен
ного газа на поверхности тела (TOw = Tw, если теплоотдача отсут
89]
ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ПОГРАНИЧНОГО СЛОЯ
455
твует, т. е. (dT/dy)w~Q). Из определения A2.101) величин d и /д
^посредственно следует
(due/dx)
A2.111)
тичем в лобовой критической точке {иет^х, Те=Т{), очевидно,
)удет
{cfV^ZX = ^o/V77o, A2.112)
де Сдо и /до представляют собой значения Сд и /д в лобовой кри-
•ической точке.
.2
.0
/J
/,5
/Л
J.2
-0,4
-К
А
//
4
7
Хтфрзорный
i/vae/non
S,
-0,
О.
у
f
1,0
°'дп-
/
Диффужрный
yvacmo/t
'0,320,24 a/6 0,06 О -,
Рис. 101.
16
14
¦2
.'3
в
5
4
2
/
/
/
/
/
/
/
/
t
' -0,4 О
Рие. 102.
3W
0,8
Пользуясь после этого помещенными в таблице 32 значениями
)езразмерного комплекса CjRwx/Nwx, найдем величину числа Нус-
ельта Nwx по формуле
де выражение, стоящее в скобках в знаменателе правой части, бе-
зется непосредственно из таблицы 32.
Пересчет на число Прандтля о, не равное единице, но близкое к
:тому значению (например, а = 0,/), приводящий к малым поправкам
тля локального трения, но достаточно существенным для локальной
456 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XII
теплоотдачи, можно в грубом приближении совершать, используя
понятие о коэффициенте восстановления, который, так же как и
в случае отсутствия продольного изменения давления, может быть
принят равным У о. Более точно эту поправку можно находить по
формуле
' J^ CfV^a', A2.113)
где показатель а заключен в интервале 1/4^a^1/2i причем нижнее
значение относится к большим положительным градиентам давления
(в диффузорной области), а верхнее — к нулевому и отрицательному
градиенту давления (конфузорная область).
Метод применим и к случаю продольного обтекания удлиненных
тел вращения. Точно так же как в главе V, все отличие сводится
к необходимости учета влияния радиуса поперечной кривизны тела
го(х) путем введения в правой части формулы A2.108) множителя
1/го(х) перед интегралом и ^(т") под знак интеграла. Остальные
формулы в случае удлиненного тела вращения сохраняют тот же
вид, что и в плоском пограничном слое. За деталями расчета отсы-
лаем к цитированной работе Коэна и Решотко, где можно найти
также иллюстративные примеры.
Важность проблемы ламинарного пограничного слоя при сверх-
звуковом обтекании крыловых профилей и тел вращения послужила
причиной появления большого числа приближенных приемов расчета,
в частности непосредственного применения метода Польгаузена с по-
линомиальным представлением распределений скоростей и темпе-
ратур. Сюда прежде всего должна быть отнесена основная для всего
последующего развития теории пограничного слоя в газе работа
А. А. Дородницына, цитированная в главе X 1), где был рассмотрен
простейший случай пограничного слоя при о = 1 и отсутствии тепло-
отдачи с поверхности тела. Расчет теплоотдачи по аналогичному ме-
тоду был выполнен Л. Е. Калихманом2). Целый ряд работ иностран-
ных авторов был также посвящен применению метода Кармана —
Польгаузена3).
Изложенный в настоящем параграфе метод Коэна—Решотко был
в дальнейшем упрощен и модифицирован У. Хайсом4). Пользуясь
') Дородницын А. А., ПММ, т. VI, 1942.
!) К а л и х м а н Л. Е., ПММ, т. IX, 1945.
3) Oinzel J., Zeltschr. f. Angew. Math. u. Mech. 29, H. 11/12A949);
Morris, Dean N.. Smith J., Journ. Aeron. Sci. 20. № 12 A953);
Libby P., Morduchow M., NACA TN 3157, 1954.
") Hayes W., Jet Propulsion 126, № 4 A956); русск. пер. см. сб. «Во-
просы ракетной техники», № 3, 1957, стр. 85—95.
§ 90] ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН 457
преобразованиями координат и скоростей, аналогичными преобра-
зованиям Дородницына — Стюартсона, У. Хайскладет в основу расчета
некоторую приближенную зависимость между плотностью, скоростью
и энтальпией с константами, выбираемыми из условия справед-
ливости ее и получаемой из нее дифференцированием зависимости
на стенке; в невозмущенном потоке эта зависимость является точной.
Такой подход позволяет ему получать более простые, чем у Коэна—
Решотко, основные уравнения, составить автомодельные их решения
и использовать эти решения для расчета пограничного слоя при про-
извольном распределении скоростей на внешней границе. Последнее
выполняется методом интегральных соотношений. Метод Хайса при-
меним не только для совершенных, но и для реальных газов.
Простой практический прием расчета пограничного слоя для
конфузорной области (dp/dx < 0) при любых а был предложен
Э. С. Левинским1).
§ 90. Влияние диссоциации воздуха на теплообмен
в носовой части тела вращения
Среди большого числа проблем, возникающих при исследовании
гиперзвукового обтекания газом носовых частей тел вращения, осо-
бенное значение приобретает изучение теплообмена в ламинарном
пограничном слое вблизи лобовой критической точки. Важность уста-
новления рационального метода расчета температур поверхности но-
совой части снаряда вряд ли нуждается в пояснении.
Чтобы преодолеть серьезные трудности, возникающие при иссле-
довании теплообмена при гиперзвуковых скоростях, приходится де-
лать ряд дополнительных допущений, значительно ограничивающих
постановку задачи. Прежде всего предположим, что рейнольдсово
число обтекания, несмотря на малую плотность газа на больших вы-
сотах, все же настолько велико, что можно пренебречь непосредстт
венным взаимодействием пограничного слоя на затупленном носе тела
с головной ударной волной. Такое упрощение задачи допустимо, так
как при достаточно больших значениях числа Рейнольдса толщина,
пограничного слоя, обратно пропорциональная корню квадратному
из рейнольдсова числа, окажется малой по сравнению с расстоянием
отошедшей ударной волны от носа тела, не зависящим от рейнольд-
сова числа.
Далее будем пренебрегать влиянием головной волны как источ-
ника лучистого нагрева поверхности тела. Как показали специальные
исследования2), только при очень больших скоростях и сравнительно
') Lev in ski E. S., Trend Engln. Univ. Wash. 9, № 2 A957).
2) См., например, Kivel В., Journ. Aerospace Sci. 28, № 2 A961),
96—102; там же приводится подробная библиография по этому вопросу.
458 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
малых высотах лучистый нагрев поверхности от разогретых прохож-
дением сквозь головную волну слоев воздуха превосходит эффект
аэродинамического нагрева, о котором будет речь в настоящем па-
раграфе.
Аэродинамический нагрев носовой части поверхности тела осу-
ществляется, во-первых, путем ламинарной (молекулярной) теплопро-
водности, во-вторых, за счет диффузии диссоциированных частиц
(атомов, электронов) к поверхности тела и сопутствующего переноса
энергии диссоциации, выделяющейся при рекомбинации атомов в мо-
лекулы. Последний эффект особенно существен при наличии катали-
тической способности поверхности тела к рекомбинации. Как пока-
зывают прикидочные расчеты и количественные оценки эффектов,
по-видимому, при учете влияния диффузии можно пренебрегать явле-
ниями термо- и бародиффузии, во всяком случае, в тех пределах
изменения температур и давлений, о которых пойдет речь впереди.
Наиболее легко поддаются расчету два крайних случая движения
диссоциированного газа в пограничном слое. Первый из них соответ-
ствует «равновесному» состоянию газа, т. е. такому, что в каждой
точке пограничного слоя степень диссоциации (концентрация атомов)
определяется только температурой (энтальпией) в этой точке. Такого
рода термохимическое «равновесное» состояние может осущест-
вляться в газе только при очень больших скоростях рекомбинации.
Промежуточный случай, соответствующий конечной скорости ре-
комбинации, требует знания зависимости скорости рекомбинации от
других термодинамических факторов (температуры, концентрации),
а также и от геометрических и кинематических особенностей дви-
жения. К сожалению, до сих пор наши сведения в этой области
еще очень элементарны, а применяемые закономерности основываются
на самых грубых схемах процессов рекомбинации.
Второй предельный случай относится к так называемому «замо-
роженному» состоянию газа, когда скорость рекомбинации, наоборот,
близка к нулю и местная степень диссоциации определяется только
диффузией атомов из внешнего потока к поверхности тела. В этом,
втором предельном случае можно считать распределения температуры
и концентрации атомов не зависящими друг от друга.
Приведенные соображения позволяют судить, хотя бы в общих
чертах, о тех трудностях, которые возникают при попытках созда-
ния сколько-нибудь рациональных методов расчета ламинарного по-
граничного слоя в гиперзвуковом потоке вблизи лобовой критической
точки тела при наличии диссоциации.
Применим в дальнейшем уравнения аэро-термодинамики смеси
реагирующих между собой газов, которые были выведены ранее,
в § 57, с той лишь разницей, что в уравнении неразрывности (8.33)
учтем влияние поперечной кривизны тела вращения путем введения
в круглые скобки в качестве множителя местного радиуса тела
§ 90] ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН 459
вращения го(х); остальные обозначения остаются прежними. Кроме
того, как уже было выше указано, опустим в этих уравнениях члены,
относящиеся к термо- и бародиффузии.
Будем иметь следующую систему уравнений [см. § 57, уравнения
(8.33), (8.34), (8.48), (8.52)]:
^г(Р^) = О, A2.114)
ди , ди dp . д
^^, A2.116)
10+'и<- A2Л17)
В некоторых случаях полезнее вместо уравнения A2.116) использовать
уравнение для полной энтальпии [см. § 57, уравнение (8.54)]
ду ду\с
р
С целью исследования возможности получения автомодельных ре-
шений, т. е. сведения только что перечисленных уравнений в част-
ных производных к системе обыкновенных уравнений, Фэй и Рид-
делл') используют следующие преобразования к новым независимым
и зависимым переменным:
A2.119)
и д/ А+и72 _ Т С[
— =-S—, т = S, -if- = о, • = S,.
ие д-г\ я, ° 1е сг< »
') F а у J., R i d d e 1! F., Journ. Aeron. Sci. 25, № 2 A958), 73—85; русск.
пер. см. в сб. «Проблемы движения головной части ракет дальнего действия»,
ИЛ, 1959, стр. 217—256.
460 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
Совершив эти преобразования, можно после некоторых приведе-
ний получить систему уравнений
+ f
JL + /2*_# *Ll, A2.120)
дх^У д^ дх\
d*f
"J df
^1 L Срю \ a^p^, / <?ttj J Срю di) ^ L 9^e(di/dx) JcDWTe J
¦+ ,- r — tt + Zt Ц —— =
Jcpw' e \ V-wVw I \Щ I i cpw а(*Р О О
d/ [2 j
&ц I 7pw
^-E-i. — --г— . A2.
122)
^ Z' W Lc ^Л , > dst , 2?ffif
e(d?/dx)
_ot(df ds, df dst\ . 2 d/
й / ^ dg) \ fdg \ U2<! д \(\ l
\x.waw д-ц di}2
Здесь А, означает энтальпию торможения в лобовой критической
точке, о = у-Ср/к (число Прандтля), Le; = pD^^X (число Льюиса).
Условия автомодельности последней системы сведутся к тому,
чтобы все величины /, g, 8 и s; были функциями только т). Для
этого в первую очередь необходимо, чтобы термодинамические
параметры во внешнем потоке и вдоль поверхности тела не зависели
от 5. Кроме того, следует еще потребовать, чтобы подчеркнутые
§ 90) ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН 461
в левых частях уравнений A2.122) и A2.123) выражения, содержа-
щие От;, не зависели от к, так как эти величины, характеризующие
процессы рекомбинации атомов, определяются локальными значениями
термодинамических параметров, а эти последние, в свою очередь,
в условиях автомодельности зависят только от t\. Если отвлечься
от частных случаев: т1 — 0 («замороженный» пограничный слой) и
т{ = оо («равновесный» пограничный слой), то наибольший интерес
для поставленной задачи представит требование выполнения условия
удовлетворяемого вблизи лобовой критической точки тела вращения.
Замечая, что при принятых условиях автомодельности правые
части уравнений (i2.121), A2.122), A2.123) и A2.124) обращаются
в нуль, придем к следующей системе четырех обыкновенных диффе-
ренциальных уравнений:
<*i) \cpw о^ря, drj / cpw dt] [ [dx/tl ;\P JcpwTi
d I
d Г М-Р \Л ci\ihi — h*i) ds, 1
di\ I °(*wPw *f h\ ' dri I
+
— (Ье,-^)=О. A2.126)
= 0, A2.127)
A2.128)
При выводе этих уравнений принято, что вблизи критической точки
u2<^hx; индекс 1 соответствует заторможенным значениям величин
во внешнем потоке в лобовой критической точке.
Составим выражение для удельного потока тепла qw на лобовую
часть поверхности тела вращения. Как уже упоминалось ранее, этот
поток образуется не только за счет теплопроводности газа, но и за
счет того подвода к поверхности тела энергии (тепла) рекомбинации,
который осуществляется путем диффузии атомов к поверхности тела
из внешней области. Удельный приток тепла qw, согласно соображе-
ниям, приведенным в § 57 при составлении уравнения баланса
462 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
тепла (8.47), выразится так:
Те [ d6 v h, — h* ds,
L t r ' Aw
или в принятом для лобовой критической точки приближении
1 ж ' ' " 1Ч ' ' , A2.129)
ds: 1
причем вблизи лобовой критической точки можно положить
A2.130)
Тот же тепловой поток можно выразить еще иначе через ком-
бинацию чисел Нуссельта и Рейнольдса в форме
— N^ !,/"„ о (due\ h\
~h
A2.131)
Тогда отношение ^WJV4WX сможет быть представлено одной
из следующих двух форм:
tiwx V~2JcpwTl
Л; k: US,
Для дальнейшего необходимо задаться законами зависимости [а, а,
Le от температуры, плотности и состава газа. Было принято, что
вплоть до 9000° К коэффициент вязкости можно вычислять по фор-
муле Саттерлэнда, а числа а и Le (для атомно-молекулярной смеси)
слабо зависят от температуры. Число Прандтля при расчетах при-
нималось для воздуха равным а = 0,71, числу Льюиса придавались
различные значения в интервале (l^Le^2).
§ 90] ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООВМЕН 463
Входящая в предыдущие уравнения скорость рекомбинации
атомов ГП[ — тА может быть просто рассчитана, если предположить,
что рекомбинация происходит по схеме тройных соударений
Атом -f- Атом -f- Частица -> Молекула -j- Частица.
Обозначим через NA, NM и N соответственно числа молей ато-
мов, молекул и частиц в единице объема; тогда скорость рекомби-
нации атомов задается выражением
* WNT1*. A2.133)
где «[ — некоторая константа.
Для обратной реакции появления атомов принимается формула
dN. , _,5
—^Л. =- _ kiNANT ' -f- k-i (T) NMN,
причем входящая в правую часть функция k2(T) определяется из
условия равновесия (dNA/dt = 0). Тогда окончательно получим
dN. , ,, Г NM I N.„ \П
_^i=_ kiN2ANT'llb I— -fj-У- -jT^-J , A2.134)
где индекс ? соответствует концентрациям при равновесном состоя-
нии газа при данных значениях давления и температуры.
Рассматривая газ как смесь двухатомных молекул с молекуляр-
ным весом М и атомов с атомным весом М/2, составим выражение,
связывающее число молей Af в единице объема с весовыми концен-
трациями
'л= N +A2N • A2.135)
и определим плотность смеси
/ N .\
A2.136)
Тогда, пользуясь формулой A2.134), получим для массовой ско-
рости образования атомов тА следующее выражение:
М dNA 2Aip37"~li5 ГA +сА)(с2А — cAF)'\
тА = - -== 1~ v )У „—— . A2.137)
А 2 dt М2 \ \-с\с
Замечая, что в рассматриваемом процессе рекомбинации массовая
скорость тА образования атомов играет ту же роль, что и вели-
чины mi в уравнениях A2.126) и A2.127), можем, используя фор-
мулу Клапейрона, приближенно получить следующее, входящее в эти
464 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
уравнения выражение:
)J ^ = -^-3'5-fp7f. A2.138)
где коэффициент пропорциональности (R — универсальная газовая
постоянная)
^адаD)Г A2Л39)
носит наименование «параметра скорости рекомбинации».
Величина производной от скорости внешнего потока в лобовой
критической точке при пользовании ньютоновым приближением может
быть представлена в форме
A2Л40)
где SR — радиус кривизны носка тела, /?от — давление в окружающей
среде. Обратная величина этой производной, имеющая размерность
времени, может быть принята за характеристику «времени диффу-
зии» атомов сквозь слой воздуха за головной волной. С другой
стороны, как это следует из равенства A2.133), величина NaiT[1'5
обратно пропорциональна «времени жизни» атомов. Замечая, что по
закону Клапейрона
,т2 -Т.-1.5 ^.2 7,-1,5 27,-2.7.-1,5 2T.-3.5
NMTl ~Pl?l ~ЛГ1 Tl =PlTl •
заключаем, что «параметр скорости рекомбинации» Сх имеет физи-
ческий смысл отношения «времени диффузии» атомов к «времени
жизни» атомов. Согласно определению A2.139) и равенству A2.140),
заключим, кроме того, что параметр скорости рекомбинации про-
порционален радиусу кривизны носовой части тела.
Уравнения A2.125)-A2.128) интегрировались численными мето-
дами на счетно-решающей машине для предельных случаев «равно-
весного» (Сх = оо) и «замороженного» (Cj = 0) движений и,
кроме того, для общего случая конечной скорости рекомбинации
@ < Cj < 00).
Проще всего, конечно, решается вопрос о «равновесном» дви-
жении газа, когда концентрация атомов может рассматриваться как
заданная функция температуры (энтальпии). В этом случае дело сво-
дится к численному решению системы только двух уравнений:
A2.125) и A2.128), причем последнее, если считать Le, = Le = const,
может быть приведено к виду
^l + /? = 0. A2.141)
§ 90] ЧЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН
где положено
465
A2.142)
Входящие в уравнения A2.125) и A2.141) величины: |ip/(|iwpw);
Pj/p, 8 рассчитываются по таблицам для воздуха, находящегося в рав-
новесном состоянии, и могут, таким образом, рассматриваться как
заданные функции g (безразмер-
ной полной энтальпии). Графики
изменения первых двух из этих
функций для воздуха показаны на
рис. 103. Входящая в выражение 8
величина производной от концен-
трации по энтальпии (dcjdfi)p вы-
числяется при постоянном давле-
нии. Для машинного счета, как
известно, необходимо иметь анали-
тические выражения заданных функ-
ций. В качестве таковых принима-
лись следующие:
10
0,8
0,6
0,2
О
1
V
\
/
Pi
/
/
О 0,2 0,4 0,6 QS
Рис. 103.
где постоянные а, р, f подбирались при помощи таблиц для воздуха
в равновесном состоянии.
Граничные условия были обычными:
' = 0, /' = 0, g = gw при
/'=1, g = 0 при
4 = 0. |
7] = 0О. /
A2.143)
Не останавливаясь на деталях расчета — о них вкратце уже упоми-
налось по аналогичному поводу в § 83, — отметим, что особенно
просто рассчитывается случай Le= 1. Для этого случая [8 = 0 в урав-
нении A2.141)] было получено следующее соотношение, приближенно
выражающее расчетный коэффициент теплоотдачи:
A2.144)
Для учета влияния числа Льюиса, отличного от единицы, или,
что то же, влияния величины 3 в уравнении A2.141), была принята
30 Зак. 297. Л. Г. Лойцянскнй
466 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XII
упрощенная схема воздуха как двухатомного газа, состоящего из
молекул и атомов со средней энергией образования атомов
Ад = Sc/iA*/51 сп. A2.145)
i i
причем суммирование здесь распространяется только на атомарный
кислород и азот. Введем среднюю энтальпию диссоциации воздуха,
отнесенную к единице массы внешнего потока,
Ао = 21спА* = Ал21сл- A2.146)
i i
Тогда, как показали проведенные расчеты, влияние среднего числа
Льюиса Le на теплоотдачу в «равновесном» пограничном слое можно
выразить приближенной аналитической формулой
П _f-(Le°.52_l)_V|. A2.147)
Общее выражение для удельного теплового потока в точке
торможения «равновесного» потока при а = 0,71 будет иметь вид
qw = 0.94 (W w)<» (Wl)°'< [ 1 + (Le0^ - 1) -^] (A, - hw)
A2.148)
причем при а Ф 0,71 рекомендуется стоящий впереди коэффи-
циент 0,94 заменять на 0,76а~0'6.
При «равновесном» движении газа концентрация атомов на
стенке будет определяться температурой стенки, а не ее каталити-
ческими свойствами. В случае «неравновесного» пограничного слоя
весовая концентрация атомов сА становится такой же переменной
величиной, как скорость и температура. При этом систему уравне-
ний A2.125) — A2.128) уже нельзя свести к двум уравнениям,
а необходимо решать систему трех уравнений, включая уравнение
концентраций A2.127). При принятом допущении о воздухе как
двухатомном газе, уравнение энергии A2.126) приводилось к упро-
щенному виду
d I см dfi \ db Le up dc. db
(±1)|с/(?lZ^ ^Cx« = 0. A2.149)
(_±1__)_|_с/—(_? Z.^
di\ \ ацдарю di\ 1 ' J di\ ' о (i^pa, d-ц di\
где для краткости введены следующие обозначения (Cv как и
ранее, — коэффициент скорости рекомбинации):
СРА ~~ СРМ . __ СР .. D
¦ > с-—¦= > л — ~~г.
Cpw "W
A2.150)
§ 90] ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН 467
а уравнение A2.127) для концентрации сА приобретает форму
d i Le up dc. \ dc.
-A ——/*-)-\-/—т4-—С1т = 0. A2.151)
d-q \ о |xwPte, d-q I J drt 1 v
d-q
Дело сводится к численному интегрированию системы трех урав-
нений: A2.125), A2.149) и A2.151), причем в случае «неравновес-
ного» пограничного слоя выражения для параметров ^/(^р^), е, с
через температуру и концентрацию значительно более сложны, чем
в случае «равновесного» слоя. Так, например, принимались следую-
щие, выведенные из кинетических соображений или взятые из экспери-
мента выражения F^ = 800°К/Ге):
е7"> V'
__1_ 1 (_J1_ _ 2 J
0Г, + 113 "^ 7 U000O/ ZlOOl, 10000
\4
с = -у- сл + {l +1 exp [-
P
Граничные условия для / и б сохраняются теми же A2.143), а для
концентрации сА берутся следующими:
cA = 0 при v\ = 0 (каталитическая стенка),
dc
—А = о при т] = О (некаталитическая стенка),
A2.152)
СА — СМ При 7] —ОО.
Подчеркнем, что на каталитической стенке газ считается полностью
рекомбинированным.
Случай «замороженного» пограничного слоя (С, = 0) является
особым для уравнения A2.151). При отсутствии рекомбинации атомы,
диффундирующие к стенке, будут иметь ту же концентрацию, что и
во внешнем потоке, если стенка некаталитическая, и «равновесную»,
т. е. соответствующую температуре стенки, если стенка каталити-
ческая. В этом особенность случая Ci= 0 по сравнению с гранич-
ными условиями A2.152) для концентрации при Сх > 0. Расчетами
при Cj = 0, проведенными для теплоотдачи в случае каталитической
стенки, была установлена приближенная формула
= l+(Le°-63_ 1) о A2.153)
где величина (NOJt./yrR^)Le=1 определяется той же формулой A2.144).
что и в случае «равновесного» пограничного слоя. С удалением
30*
468 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ. XI
значения Le от единицы разница в определении теплообмена m
двум предельным случаям возрастает, но она все же сравнительнг
невелика. Увеличение показателя при Le в формуле A2.153) т
сравнению с A2.147) соответствует основной роли диффузии в случае
«замороженного» газа по сравнению с «равновесным» при наличш
каталитической поверхности.
Если же при «замороженном» движении газа стенка тела н^
обладает каталитической способностью, то, как уже упоминалось
концентрация атомов вплоть до стенки будет одинаковой и равно*
концентрации на внешней границе пограничного слоя. Тогда ви-
жение для теплоотдачи к стенке можно получить из «оавновр—
О $4 пв 12
Рис. 104.
1,6 2{
V
формулы A2.148), пренебрегая ролью диффузии, т. е. по.
в этой формуле Le = 0. При этом теплоотдача становится проа.-
циональной разности hx — hD. О влиянии каталитической способное
поверхности головной части тела на теплоотдачу в «замороженном
¦ пограничном слое будет сказано далее.
Распределение весовой концентрации атомов поперек пограни^
ного слоя вблизи лобовой точки тела с некаталитической поверхностьк
при различных конечных значениях параметра скорости рекомби
нации показа'но на рис. 104. Как видно из графиков этого рисунка
при больших значениях Сл («равновесный» пограничный слой) кривые
ничтожно разнятся между собой и свидетельствуют о том, что атомь
рекомбинируются в газе, не доходя до стенки. Наоборот, при очет
малых С{ («замороженный» пограничный слой) рекомбинация почп
не происходит.
Интересно отметить факт резкого уменьшения теплоотдач!
к некаталитической поверхности тела, если параметр скороеп
рекомбинации С1 мал. Этот факт наглядно показан на рис. \0г
(кривая А — каталитическая, В — некаталитическая поверхности) i
может быть просто объяснен тем, что малым значениям Сх cooi
ветствуют малые значения отношения «времени диффузии» атомов и;
§90]
ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН
469
внешнего потока к поверхности тела, ко «времени жизни» атомов.
Уменьшение времени диффузии, пропорционального, как уже ранее
/ due\~l
упоминалось, величине \—^г~\ ¦ может быть достигнуто, согласно
A2.140), уменьшением радиуса кривизны носовой части тела
вращения.
Результаты расчетов по теории Фэя и Ридделла были проверены
экспериментально Роузом и Старком:) на цилиндрическом теле
с полусферическим носком,
помещенном в ударную тру-
бу. Моделировались условия
гиперзвукового полета сна-
ряда на высотах от 6000 м д/,
до 36 000 м в диапазоне
скоростей от обеспечиваю- уз
щих температуру торможе-
ния порядка 3000° К до Ц2
первой космической ско-
рости. Расчеты, проведенные gj
для этих условий по фор-
мулам Фэя и Ридделла, дали
—
/
л
л
Ю
-6
/О'4 Ю
Рис. 105,
-2
/ О,
вполне удовлетворительное
совпадение с эксперимен-
тальными данными Роуза и
Старка.
Более простая, приводящая к результатам в замкнутой форме
теория была ранее выдвинута Л. Лизом2), использовавшим ряд
упрощающих допущений, в частности предположившим, что погра-
ничный слой «заморожен» (mt = 0), а температура поверхности
тела пренебрежимо мала по сравнению с температурой торможения
внешнего потока; кроме того, число Прандтля принималось рав-
ным 0,715, а отношение рр/(\>-ере) равным единице. Как легко видеть,
при этом система уравнении A2.125)—A2.128) сильно упрощается
и допускает в первом приближении проведение интегрирования, ана-
логичного случаю теплового и диффузионного пограничного слоя
в несжимаемой жидкости. Это приводит к решению в замкну-
той форме.
Влияние каталитической способности поверхности носовой части
тела исследовал Р. Гуляр3). Вместо принятого в предыдущих
') Rose P., Stark W., Journ. Aeron. Sci. 25 A958); имеется русск.
пер. в сб. «Проблемы движения головной части ракет дальнего действия»,
ИЛ, 1959, стр. 277—311.
2) Lees L., Jet Propulsion 26, № 4 A956).
3) Goulard R., Jet Propulsion 26, № 11 A958); русск. пер. см. сб.
«Вопросы ракетной техники» № 5, 1959.
470 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИЙ ДАВЛЕНИЙ [ГЛ. XII
теориях в качестве граничного условия на каталитической стенке
равенства концентрации атомов нулю Гуляр записывает это условие
в форме уравнения баланса потока массы атомов на стенку и ката-
литической абсорбции их на стенке со скоростью, пропорциональ-
ной некоторой степени концентрации атомов на стенке,
A2.154)
Предельный случай xw ¦= оо относится к каталитической стенке
с cAw = 0; некаталитической стенке соответствует х№ = 0 и условие
(dcA/dy)w = O. Условие A2.154) аналогично общему уравнению
баланса (9.112), изложенному в конце § 66. Показатель степени п
определяет «порядок» реакции, в данном случае абсорбции атомов
(у Гуляра принято я=1), а коэффициент v.w — каталитическую
способность поверхности тела. В цитированной статье Гуляра дока-
зывается, что полный удельный поток тепла на стенку вблизи носо-
вой части тела в случае «замороженного» пограничного слоя может
быть представлен в замкнутой форме
1A<p-l)-^-]. A2.155)
где величина <р, определяемая равенством Sc = -^- =
L ^е
число Шмидта
0,47Sc-!/^2jx
1P1
A2.156)
является поправочным множителем к приближенной формуле
Лиза — равенству A2.155) при <р=1« что, согласно A2.156), соот-
ветствует х^ = оо, — выражающим влияние каталитической спо-
собности тела @ < хш < оо) при «порядке» абсорбции я=1.
Аналогичный метод может быть применен к описанию тех,
вызывающих в последнее время особый интерес явлений, которые
связаны с химическими реакциями смешивающихся в пограничном
слое газов, с плавлением, испарением (сублимацией) и уносом
(абляцией) частиц твердой поверхности тела в гиперзвуковом потоке.
Детальное изложение этих вопросов, а также заключающего в себе
особые трудности и мало еще разработанного вопроса о гиперзву-
ковых движениях газа в пограничном слое при наличии релаксации
возбуждения степеней свободы молекул выходит за рамки настоящей
книги. Остановимся лишь на кратком описании тех новых обстоя-
тельств, которые возникают, например, при изучении явления
сублимации затупленной носовой части снаряда при гиперзвуковом
§ 90]
ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН
47)
его движении. Явление сублимации (испарения) носовой части
поверхности затупленного тела в гиперзвуковом потоке возникает
в том случае, когда температура поверхности тела вблизи лобовой
критической его точки лежит ниже тройной точки на известной
диаграмме фазовых состояний, а набегающий поток далек от состоя-
ния насыщения парами сублимирующего тела. Для исследования
этого явления можно пользоваться теми же уравнениями многофаз-
ного пограничного слоя, что и изложенные в настоящем параграфе.
Дополнительные сложности возникают в связи с необходимостью
установления граничных условий на фронте сублимации, учитываю-
щих быстроту изменения формы поверхности носовой части испаряю-
щегося тела и те термодинамические процессы, которые происходят
как в самом теле, так и вблизи его поверхности.
Следуя Г. А. Тирскому'), выпишем для случаев стационарного
плоского (я=1) или осесимметричного (га = 2) обтеканий тупоно-
сого тела следующую основную систему уравнений пограничного слоя:
а) динамические уравнения [см. A2.114) при ro = x и A2.115)]
д '-~—л ч ' д (pxn-lv) = 0,
ду
ди
ди
ди
A2.157)
где приняты обычные обозначения (х, у) и (и, v) для продольных и по-
перечных координат и скоростей, а р = (-^-\ _ характеризует распре-
деление скоростей на внешней границе пограничного слоя вблизи но-
„ dp due . п„
совой критической точки тела, так что—-f— = рдаце j — Рс»ргх
(Роо — плотность за головной волной);
б) уравнение переноса тепла
dh . dh\ д
+v)
в котором, напоминаем (суммирование по всем компонентам смеси),
A2.159)
ср = .
Le =
причем с(-—концентрация, D\i — коэффициент диффузии в двух-
фазной смеси (набегающий газ — пар сублимирующего тела).
') Т и р с к н й Г. А., Журнал вычислительной математики и математи-
ческой физики 1, 5 A961).
472 ПОГРАНИЧНЫЙ СЛОЙ ПРИ ЗАДАННОМ РАСПРЕДЕЛЕНИИ ДАВЛЕНИЙ [ГЛ XI
В уравнении A2.158), в связи с малостью скоростей за ударно?
волной вблизи носовой части, опущены члены, содержащие квадрать
скоростей, т. е. положено йо = Л и откинут второй член справь
Кроме того, сделан обычный переход [см. главу VIII, § 57] к сред-
ним числам Прандтля о и Льюиса Le;
в) уравнение переноса вещества [см. A2.117) при ml = Q)
г) уравнение состояния [см. (8.36) и (8.37)]
-> A2.161
где, в отличие от указанных формул главы VIII, введена универсаль-
ная газовая постоянная R* по формуле (Mt — молярная масса /-гс
компонента)
?
Входящие в эти уравнения коэффициенты вязкости, теплопровод
ности и диффузии, а также числа Прандтля и Льюиса определяются т
тех или других дополнительных кинетических соображений. Граничные
условия на внешней границе пограничного слоя обычны; это
и = фх, cl~ciao, h==hao. A2.163
Сложнее обстоит дело с граничными условиями на поверхнот
сублимации, которую, строго говоря, нельзя уже рассматривать ка;_
неподвижную. Вводя понятие о нормальной к поверхности телг.
скорости N перемещения относительно тела фронта сублимацик
получим совокупность равенств (р— средняя плотность газопарово^
смеси, pj и Xj — плотность тела и коэффициент теплопроводности
в твердой его фазе)
p(W —e)
¦Le (h — E С<Л)] = \ ^~ — P^uLe-gJ-.
V
A2.164
выражающих уравнения баланса вещества и тепла, проходящи:
через поверхность сублимации. Здесь индекс / соответствует компо
§ 90) ВЛИЯНИЕ ДИССОЦИАЦИИ ВОЗДУХА НА ТЕПЛООБМЕН 473
нентам смеси образующихся при сублимации тела паров, индекс j —
компонентам набегающего газа; двойной индекс is относится к зна-
чениям концентрации паров на поверхности сублимации при подходе
со стороны испаряющегося тела; индекс 1 соответствует условиям
в твердой фазе, причем температура Г] удовлетворяет стационар-
ному уравнению теплопроводности в твердом теле
0 A2Л65)
с граничными условиями: Т1 = Т0 при у = 0, Т{ = Т-^ при
у= — оо, а коэффициент теплопроводности \ является заданной
функцией температуры 7\. Температура То на поверхности тела,
так же как и скорость перемещения фронта сублимации N, пред-
ставляют в принятой общей постановке неизвестные величины,
которые должны быть определены из системы равенств A2.164).
В последнем уравнении системы A2.164) учитывается скрытая
теплота парообразования l(TQ), являющаяся функцией неизвестной
температуры То поверхности тела. Касательная к поверхности тела
компонента скорости и подчиняется условию равенства нулю на
поверхности сублимации.
В цитированной статье Г. А. Тирского можно найти системати-
ческое и в значительной степени исчерпывающее изложение тех
дополнительных кинетических соображений, которые позволяют
замкнуть систему уравнений процесса сублимации. Там же изла-
гаются пути решения этой задачи при различных значениях чисел
Льюиса, Прандтля и Шмидта.
В более упрощенной постановке несколько ранее та же задача
о сублимации тупой носовой части осесимметричного тела была
рассмотрена С. В. Иорданским и Ю. Д. Шмыглевским *), а впослед-
ствии (одновременно с Г. А. Тирским) также В. В. Щенниковым 2) —
у нас в Союзе и Робертсом3) — за рубежом.
Первые два из перечисленных авторов исследовали сублимацию
тела, состоящего из твердой углекислоты, в сверхзвуковом потоке
воздуха при числе Маха, равном 6,2. Ими показано, что явление
сублимации резко снижает теплоотдачу с поверхности тела.
В. В. Щенников рассматривал сублимацию тела, состоящего из
графита, в потоке кислорода.
') Иорданский С. В., Шмыглевский Ю. Д., Инженерный
сборник 28 A960).
2) Щенников В. В., Журнал вычислительной математики и матема-
тической физики 1, 5 A961).
») Roberts L., NASA, TR, R-9 A959).
ИМЕННОЙ УКАЗАТЕЛЬ
Акатнов Н. И. 42, 49
Альборн Э. (Ahlborn E.) 177
Андраде Э. Н. (Andrade Е. N.) 38
Баи Шн-и (Pai S. I.) 172, 389, 390
Барнетт Д. (Burnett D.) 270
Басин А. М. 104
Батчелор Г. К. (Batchelor G. К.) 182
Бейлина А. 3. 401
Белл С. (Bell S.) 365, 366
Бертран 354
Ьлазиус Г. (Blasius H.) 9, 27 78,
82, 115, 121
Блевисс 3. (Bleviss Z.) 416
Богдонов 354
Богданова В. В. 226
Болен Т. (Bohlen Т.) 101
Большаков В. П. 249
Больце Э. (Boltze E.) 146
Бонд P. (Bond R.) 156
Брайнерд Г. (Brainerd G.) 351
Буземан A. (Busemann A.) 10
Бунимович А. И. 365, 370
Бурн Д. Э. (Bourne D. Е.) 296, 299
Буш У. Б. (Bush W. В.) 412
Бушмарин О. Н. 172, 206
Бюргере И. М. (Burgers J. М.) 183
Вальц A. (Walz A.) 101
Варбург (Warburg) 270
Ватсон Э. (Watson E.) 116, 124
Вебер Г. Э. (Weber H. Е.) 217
Вендт Г. (Wendt H.) 336, 364, 372,
377, 406
Визельсбергер К. (Wieselsberger К.)
191
Виттинг Г. (Witting H.) 85
Вулис Л. А. 172
Вундт Г. (Wundt H.) 119
Гёртлер Г. (Gortler H.) 85, 116, 124, 223
Гиниель И. (Ginzel J.) 456
Глауэрт М. Б. (Glauert M. В.) 42,
156, 164, 396
Голанд Л. (Goland L.) 285
Голдстейн С. (Goldstein S.) 49. 53,
114, 115, 139, 286
Голубев В. В. 108
Го Юн-хуай (Kuo J. H.) 23, 33, 267,
353, 365
Грегг Дж. Л. (Gregg J. L.) 195
Гуляр P. (Goulard R.) 469
Дайк M. (Dyke v. M.) 356
Демьянов Ю. A. 386
Дин Н. (Dean N.) 456
Добрышман Е. M. 116, 129, 140, 154
Долидзе Д. Е. 22, 192
Дор Ф. (Dore F.) 408
Дородницын А. А. 10, 83, 104, 320,
352, 418, 424, 428, 431, 456
Дорфман Л. А. 304
Древиц О. (Drewitz О.) 285
Дрейк Р. (Drake R.) 294, 313
Дубов В. С. 172, 205
Дэйвис Д. P. (Davies D. R.) 296,
299, 304
Дюренд В. Ф. (Durand W. F.) 62
ИллингвортК. (Illingworth С.) 196,356
Иорданский С. В. 473
Калихман Л. Е. 352, 456
Карман Т. (v. Karman Th.) 9, 87,
173, 182, 192, 268, 343
Кашкаров В. П. 172, 401
Кендалл 354
Кибель И. А. 17, 28, 108, 184, 245,
299 364
Кивел'ь Б. (Kivel В.) 457
Кнудсен 269
Кокрен У. Г. (Cochran W. G.) 173,
176, 299
Коулз Д. (Coles D.) 354
Кочин Н. Е. 17 28, 33, 103, 108, 184,245
Коэи К. Б. (Cohen С. В.) 440, 442,
445, 448, 456
Крабтри Л. (Crabtree I,.) 436
Крокко Л. (Crocco L.) 10,330,335,351
ИМЕННОЙ УКАЗАТЕЛЬ
475
Кружилин Г. Н. 309
Кук Дж. (Cooke J.) 213, 215, 217,
220, 249, 253
Кундт (Kundt) 270
Кэлли Г. P. (Kelly H. R.) 156
Кэрьер Г. Ф. (Carrier G. F.) 249
Лайтхилл (Lighthill) 156, 164
Ландау Л. Д. 169
Леви С. (Levy S.) 291
Левинский Э. С. (Levinski E. S.) 457
Левич В. Г. 314
Леви-Чивита Т. (Levi-Civita Т.) 9, 244
Лейбензон Л, С. 107
Либби П. (Libby P.) 456
Лившиц Е. М. 169
Лиз Л. (Lees L.) 365, 469
Лайцянс-кий Л. Г. 26, 39, 75, 88, 94,
100, 101, 103, 108, 109, 152, 172,
200, 249, 253, 256, 311
Лоу Г. (Lowe G.) 311
Лус Г. (Loos H.) 225
Максвелл К. (Maxwell С.) 269, 271
Манглер В. (Mangier W.) 148, 375
Мартин Дж. К. (Martin J. С.) 235,
240
Мельников А. П. 101
Мизес P. (v. Mises R.) 24
Милликен К. (Millikan С.) 152, 269
Миллсапс К (Millsaps К.) 299, 392
Мордухов М. (Morduchow М.) 456'
Моррис Д. (Morris D.) 352, 456
Мур Л. (Moore L.) 406
Мур Ф. К. (Moore F. К.) 182, 195,
217, 235, 250
Мэйджер A. (Mager A.) 246
Мясников В. П. 365, 366
Нейланд В. Я. 409
Нигам С. Д. (Nigam S D.) 192, 195
Никурадзе И. (Nikuradse J.) 30
Нонвейлер 365
Пискунов Н. С. 22
Польгаузен К- (Pohlhausen К.) 87,
92, 299, 392
Польгаузен Э. (Pohlhausen E.) 220,
281, 283
Поуэлл Э. О. (Powell E. О.) 298
Прандтль Л. (Prandtl L.) 9, 20, 24,
62, 115
Пробштейн P. (Probstein R.) 269, 365
Резниченко Ю. Т. 387
Реслер 410
Решотко Е. (Reshotko E.) 440, 442,
445, 448, 450
Риддел Ф. (Riddell F.) 278, 459,
469
Рилей Н. (Riley N.) 393
Роберте Л. (Roberts L.) 473
Розе Н. В. 17, 28, 108, 184, 245
Розеиблат С. (Rosenblat S.) 182
Розенхэд Л. (Rosenhead L.) 115,
139
Розин Л. А. 116, 130, 136, 154, 192,
195
Ромиг М. (Romig M.) 408
Ротт a (Rott N.) 132, 225, 227, 436
Роуз П. (Rose P.) 469
Рубезин М. В. (Rubesin M. W.) 258,
345, 346, 353
Румер Ю. Б. 169
Саниаль Л. (Sanyal L.) 246
Себаи P. A. (Seban R. А.) 156, 299,
313
Сибулкин М. (Sibulkin M.) 294
Сире В. P. (Sears W. R.) 219, 226,
232, 410
Сквайр Г. Б. (Squire H. В.) 172
Сквайр Л. К. (Squire L. С.) 244
Скопец М. Б. 220, 312
Скэн С. В. (Skan S. W.) 64, 70
Смит A. (Smith A.) 112
Смит В. (Smith W.) 227
Смит Дж. (Smith J.) 352, 456
Соколова И. Н. 364
Соуэрби Л. (Sowerby L.) 249, 253
Спарроу Э. М. (Sparrow E. М.) 195,
287
Старк У. (Stark W.) 469
Степанов Е. И. 148, 375
Струминский В. В. 116, 136, 219.
220, 246
Стюартсон К. (Stewartson К) 10,
161, 182, 356, 431
Сэдни P. (Sedney R.) 235, 248
Сэттон У. (Sutton W.) ПО
Тан Г. С. (Tan H. S.) 232
Тани И. (Tani J.) 84
Тарг С. М. ПО, 116, 129, 139, 154
Тейлор Дж. И. (Taylor G. J.) 212
Тёпфер К. (Toepfer С.) 28
Тирио К. Г. (Thiriot К. Н.) 192
Тирский Г. А. 471, 473
Тиффорд А. Н. (Tifford A. N.) 183,
188, 285
Толмин В. (Tollmien W.) 50, 116,
120
476
ИМЕННОЙ УКАЗАТЕЛЬ
Томотика С. (Tomotika S.) 152
Троунсер Дж. (Trouncer J.) 172
Трукенбродт Э. (Truckenbrodt E.)
183, 192
Туес Д. Г. (Toosse D. G.) 387
Уайльд Дж. М. (Wild J. M.) 220
Уиитерботтом Н. (Winterbottom N.)
101
Ферри A. (Ferri A.) 256
Фогарти Л. Е. (Fogarty L. Е.) 228,
232
Фокнер В. М. (Falkner V. M.) 64,
70, 287
Форсова Т. Я. 378, 382
Франкль Ф. И. 10
Фрёсслинг Н. (Frossling N.) 144,
145, 220, 285
Фэй Дж. A. (Fay J. A.) 278, 459,
469
Фэйдж A. (Fage A.) 30, 152, 287
Хаммит 354
Ханзен М. (Hansen M.) 30
Хаицше В. (Hantzsche W.) 336, 364,
372, 377, 406
Хартри Д. P. (Hartree D. R.) 28, 70,
288, 445
Хейз У. Д. (Hayes W. D.) 246, 269,
456
Хименц К. (Hiemenz К.) 67, 82
Хольштейн Г. (Holstein H.) 101
Хоман Ф. (Homann F.) 294
Хоуарт Л. (Howarth L.) 10, 28, 67,
74, 79, 82, 101, 121, 131, 177, 235,
246, 253, 356
Худимото Б (Hudimoto В.) 101
Цуккер М. С. 205
Ченг То-шу 188
Чень Сюэ-сень (Tsien H. S.) 10, 23,
267, 271, 343
Чепмен Д. P. (Chapman D. R.) 258,
345, 346, 353
Чиа Шун-их (Chia Shun-Ich) 305
Шааф С. A. (Schaaf S. А.) 365, 366
Швабе М. (Schwabe M.) 114
ШвецМ. Е. ПО, 140, 154
Шерман Ф. С. (Sherman F. S.) 365,
366
Шидловский В. П. 365, 391, 393
Широков М. Ф. 365
Шлихтинг Г. (Schlichting H.) 17, 37,
64, 82, 114, 128, 144, 167, 183, 192,
219, 221, 285, 310
Шмыглевский Ю. Д. 473
Шолькемейер Ф. (Scholkemeyer F.)
144, 145
Шубарт Г. (Schubart H.) 219
Шубауэр Г. Б. (Schubauer G. В.) 97
Шульц-Грунов Ф. (Schultz-Gru-
now F.) 31, 178, 180, 192
Щенников В. В. 473
Эккерт Э. (Eckert E.) 285
Эммонс Г. (Emmons H.) 351
Янг A. (Young A.) 101, 342
Янг Г. (Young G.) 409
Янсен Е. (Janssen E.) 409
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомодельность 32
Анизотропия пограничного слоя 17
Блазиуса задача 26, 66, 73, 74, 96
Блазиуса—Хоуарта задача 78, 83,
144
Больце задача 146
Влияние взаимное пограничного слоя
и внешнего потока 34, 232, 352
Газ идеальный 257
— совершенный 257
Гипотеза цилиндрических сечений
231
Движение смеси реагирующих ме-
жду собой газов 272
Движения автомодельные 31, 38
— подобные 31, 38
Дефект кинетической энергии 25
Диск вращающийся 173, 177, 183,
192, 299
Диссоциация 255, 404, 410
— равновесная 405
Диффузия 314
Длина свободного пробега 267
Дородницына преобразование 320,
418, 431
Единственность решений уравнений
пограничного слоя 22
Жидкость ньютоновская 257
Жуковского профиль 56
Задача Блазиуса 26, 66, 73, 74, 96
— Блазиуса—Хоуарта 78, 83, 144
— Больце 146
Инжекция жидкости 13
Интеграл Крокко 330
Ионизация 255, 410
Испарение обтекаемого тела 255
Кармана интегральное условие 87,
89
Кармана—Польгаузена метод 92, 96,
98, 213
Клапейрона уравнение 256
Конус в сверхзвуковом потоке 371
Коэффициент аккомодации 271
— бародиффузии 276
— восстановления 323, 325
— массодиффузии 276
— скольжения 270
— температуропроводности 280
— термодиффузии 276
Крокко интеграл 330
— уравнение 334
Крыло скользящее 218
— цилиндрическое вращающееся 226
Линия тока предельная 222, 225
Лучеиспускание 362
Льюиса число 278
Магнуса сила 235
Метод Кармана—Польгаузена 92, 96,
98, 213
Мизеса—Прандтля переменные 342,
390
Навье—Стокса уравнения 258, 260
Отрыв пограничного слоя 54, 114
Оттеснение внешнего потока 13
Параметр скорости рекомбинации
464
Переменные Мизеса — Прандтля 39,
342, 390, 464
Перепад давления 54
Плавление обтекаемого тела 255
Пластинка в газовом потоке 319
— , импульсивно приведенная в дви-
жение 356
— обтекаемая 26, 281
478
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Пластинка, обтекаемая нестационар-
ным потоком 128
—, — при высокой температуре на
поверхности 346
—, — при числе Рг = 1 330
—, — слабо разреженным газом при
учете скольжения 364
Поле магнитное 410
Польгаузена формпараметр 93
Постоянная Саттерлэнда 257
Поток внешний 12, 14, 21
Прандтля—Мизеса переменные 39,
342, 390, 464
уравнение 25, 39
Прандтля число 258, 278, 314
диффузионное 314
Преобразование Дородницына 320,
418, 431
— Степанова—Манглера 148, 292,375
— Стюартсона 431
Прорыв пограничного слоя 216
Профиль Жуковского 56
— скоростей односкатный 74
Рекомбинация 255
Релаксация 470
Саттерлэнда формула 257
Сила Магнуса 235
— пондеромоторная (Лоренцова) 410
Скорость бародиффузии 275
— вдоль внешней границы погранич-
ного слоя, степенное распределе-
ние 64
— массодиффузии 275
— на внешней границе погранич-
ного слоя 21
— термодиффузии 275
След аэродинамический 14, 49, 55
Слой пограничный 12, 14
в абсолютно прозрачном газе
362
— — в газе при больших скоростях
254, 255
в диссоциированном и ионизи-
рованном газе при наличии маг-
нитного поля 410
в начальной стадии движения
тела 114
— — в потоке смеси газов, реаги-
рующих между собой 272
— — в случае произвольного рас-
пределения скоростей во внешнем
потоке и наличие теплоотдачи с
поверхности тела 448
гидродинамический 281
Слой пограничный диффузионный
280, 314, 316
и внешний поток, их взаим-
ное влияние 13, 14, 15, 21, 82,
352
на диске, быстро вращающем-
ся в газе 390
, вращающемся в одно-
родном осевом потоке 183
, приводимом во враще-
ние из состояния покоя 192
— ¦— на конусе в продольном сверх-
звуковом потоке 371
— ¦ при обтекании равновес-
ным диссоциированным газом 409
— — на крыле скользящем 218
— — на пластинке 26
— , импульсивно приведен-
ной в равномерное движение
356
¦ при высокой темпера-
туре поверхности 362
при линейной зависимо-
сти вязкости ог температуры
319
— — с учетом скольжения
364
на стенке суживающегося ка-
нала 66
ударной трубы 378
на сфере вращающейся 177
на теле, внезапно приведен-
ном в равномерное движение 116
— — вращения, внезапно при-
веденном в винтовое движение
196
— длинном 141, 143, 154
— — на теплоизолированной по-
верхности при числе Рг Ф 1 424
при числе Рг = 1 418
неплоский двумерный 141, 148,
150, 153 J
плоский нестационарный 114
при заданном распределении
давления на внешней границе
418
— — при равновесной диссоциации
газа 404
— — пространственный вблизи ли-
нии пересечения двух плоскостей
249
— на вращающейся лопасти
232
— на вращающемся цилин-
дрическом крыле 226
— — с постоянным давлением 371
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
479
Слпй пограничный температурный 280,
281
— — — на диске 299
— — — на пластинке 280
— на теле вращения 292
— — — на цилиндре 295
— — —. приближенные методы рас-
чета 308
— — — при заданной температуре
на поверхности тела 287
— при постоянной темпера-
туре стенки 284
— — тепловой 281
¦ трехмерный 218, 244, 247
¦ осесимметричный 173
Степанова—Манглера преобразова-
ние 148, 292, 375
Струхала число 115
Струя 14
— в газовой среде 387
— закрученная в затопленном про-
странстве 200
— — радиально-щелевая в затоплен-
ном пространстве 206
— затопленная 35, 39, 42, 167
— кольцевая 172
— нагретая 305
— радиально-щелевая- 172
¦ вдоль твердой стенки 393
¦ — свободно закрученная 401
Стюартсона преобразование 431
Сублимация 470
Супераэродинамика 269
Сфера, вращающаяся в жидкости
177
Тело вращения, внезапно приведен-
ное в винтовое движение 19В
• , продольно обтекаемое 141,
143, 154, 292
Температура торможения 325
Тень аэродинамическая 14
Термометр пластинчатый 32?
Течение встречное 228
— вторичное 33, 182, 247
¦— коническое 372
Толщина вытеснения 59
— пограничного слоя 16, 32
— потери импульса 60
Точка отрыва 55
Труба ударная 378
Уравнение баланса энергии 259
— диффузии 314
— импульсов 87, 89
— Клапейрона 256
— Крокко 334
— Прандтля—Мизеса 25, 39
Уравнения Навье—Стокса 258, 260
— пограничного слоя 20, 21, 22
— Прандтля 20
— Стокса 17
Условие интегральное Кармана 87,
89
Участок начальный 15
Формпараметр 87
— Польгаузена 88, 93
Формула Саттерлэнда 257
Форсунка вихревая 212, 217
Функции характеристические 101
Цилиндр в косо набегающем потоке
218, 225
—, вращающийся в косо набегаю-
щем потоке 235
—, обтекаемый в поперечном напра-
влении 82
—, — в продольном направлении
154, 295
—, равноускоренно движущийся 125
Число Льюиса 278
— Прандтля 258, 278, 314
диффузионное 314
— Рейнольдса 18
— Струхала 115
— Шмидта 278, 314
Эжектор 35
Энтальпия полная 259
Эффект краевой 129