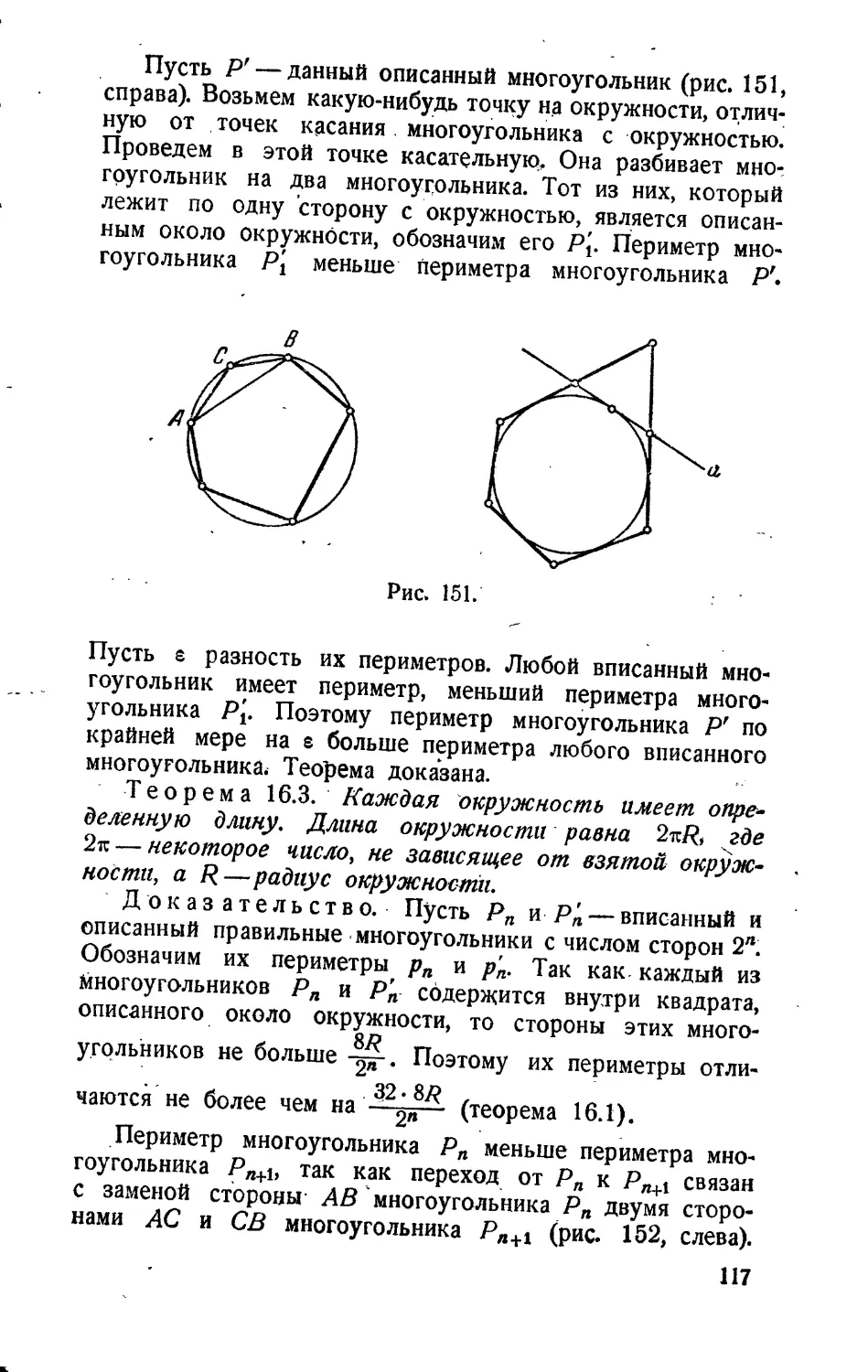
Author: Погорелов А.В.
Tags: математика геометрия планиметрия издательство наука общая геометрия
Year: 1969
Text
А. В. ПОГОРЕЛОВ
ЭЛЕМЕНТАРНАЯ
гвомвтрия
ПЛАНИМЕТРИЯ
\...._...../
ИЗДАТЕЛЬСТВО ‹НАУКА›
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
M 0 C к В А 1 9 6 9
513
П 43
УДК 513.
2-2-2
Ы -Ю
Книга содержит строгое изложение школьного
курса геометрии. Отличительной особенностью
изложения является простая, компактная и eme-
ственная аксиоматика (12 аксиом). Эта аксиома-
тика не обременяет изложения, как это ‘бывает
в серьезных курсах по основаниям геометрии.
Она не нарушает традиционного порядка в nano-
жении школьного курса геометрии и сохраняет
традиционные доказательства теорем. Однако она
делает эти доказательства совершенно безупреч-
ными. Книга будет полезна для студентов вузов
педагогических специальностей и для учителей
средних школ. `
СОДЕРЖАНИЕ
Предисловие для учителей д д . . . . . . . . . . . . . . . 4
§ 1. Основные свойства простейших геометрических фигур 7
§ 2. Аксиомы, теоремы и доказательства . . , . . . . . ь 15
§ 3. Равенство треугольников ‚ . . . . . о . . . . . . . . 20
§ 4. Смежные углы. Прямой угол . ‚ , . . . . . . . . . 25
§ 5. Соотношения между сторонами и глами треуголь-
ника.........‚................о 30
§ 6: Геометрические построения . . . . . . . . . . . . . . 88
§ 7. Параллельные прямые . . . . . . . . . . . . . . . . . 46
§ 8. Четырехугольники. Параллелограмм. Трапеция. ‚ . . 52
§ 9. Движения. Равенство фигур, Симметрия. Параллель-
ныйперенос.......ьь.............о 60
§,10.OKpy>KHocrb...................... 67
°§ 11. Подобие треугольников . . . . . . . . . . . . . . . о 74
§ 12. Преобразование подобия. Г омотетия. Инверсия о о о 83
§ 13. Теорема Пифагора и ее следствия . . . . . . . . . д 90
§ 14. Выпуклые многоугольники . . . . . . . . . . . .« . . 100
ё15.Площадифигур.. . . . . . . 107
§ 16. Длина окружности. Площадь круга . . . . . . . . . 115
§ 17. Некоторые сведения из истории геометрии . . . . . 124
предисловие для учителей
Преподавание геометрии в школе имеет целью не
только сообщать учащимся геометрические результаты, но
также научить их методу, при помощи которого эти ре-
зультаты получаются. Как известно, геометрические резуль-
таты (теоремы) получаются путем логических рассуждений
(доказательств) из некоторых отправных положений (аксиом).
Логические рассуждения являются необходимой частью
всякого познания. Геометрия отличается ясностью и про-
стотой как в формулировке результата, так и в тех исход-
ных положениях, из которых этот результат должен быть
получен. Поэтому геометрия дает нам лучшие возможности
для развития логическогомышления в школе. Посмотрим,
однако, как реализуются эти возможности. '
Знакомство учащихся с геометрией начинается в млад-
ших ~ классах. Здесь вводятся основные геометрические
понятия, формулируются основные свойства простей-
ших фигур; решаются простейшие задачи. Где-то в шестом
классе мы впервые произносим три слова-аксиома, тео-
рема,‘ доказательство,-—и тогда начинается настоящая гео-
метрия. в `
Аксиомы весьма многочисленны, и мы ограничиваемся
формулировкой одной из них, аксиомы о возможности
провести через две данные точки прямую. В действитель-
ности не многочисленность аксиом удерживает нас от
их формулировки. Для этого есть другая, более серьезная
причина. Дело в том, что вслед за аксиомами идут мно-
гочисленные теоремы очевидного содержания, доказатель-
ство которых часто далеко не просто. Поэтому мы
сознательно не формулируем другие аксиомы и при-
ступаем сразу к доказательству весьма содержательных
теорем.
4
Мы формулируем теорему и приводим некоторое pac-
суждение, которое называем доказательством. Мы пишем,
что даны, скажем, какие-то треугольники и надо доказать
их равенство или что-либо другое. Действительно ли даны
только треугольники? Конечно, нет. Есть нечто, данное
нам еще,—это аксиомы, которые составляют основу на-
шего доказательства. Если переставлять всеми способами
слова, содержащиеся в условии теоремы, мы еще не полу-
чим доказательства. Но наше рассуждение настолько про-
сто и аргументы настолько привычны учащемуся, что он
с ними охотно соглашается.
В другой раз мы предлагаем ‘учащемуся доказать ту
же теорему. Представим себе, что учащийся проявляет
некоторую самостоятельность в рассуждении и предлагает
нам столь же убедительные аргументы, опираясь, по суще-
ству, на теорему, которую мы намерены доказывать дальше.
Это ставит нас в затруднительное положение. Проходит
много времени, прежде чем из многочисленных доказа-
тельств теорем учащийся самостоятельно выловит те аргу-
менты, которые составляют’ основу всякого геометриче-
ского доказательства.
В настоящей книге мы делаем попытку дать такое из-
ложение школьного курса геометрии‚‘в котором отмечен-
HHS выше затруднения устранены. Изложение строится на
простой, компактной системе аксиом, которая подготовлена
знакомством с геометрией в младших классах. Всего аксиом
двенадцать. Они вводятся в виде напоминания свойств
простейших фигур, хорошо знакомых учащемуся.
Компактность предлагаемой системы аксиом достигается
за счет подключения к ней аксиом арифметики, которые,
естественно, не формулируются: свойства вещественных
чисел и операции над ними предполагаются хорошо извест-
ными. Подключение арифметики осуществляется через
определение равенства отрезков и углов. Именно, мы на-
зываем отрезки равными, если они имеют одинаковые
длины. Аксиома об аддитивности меры отрезков и углов из-
бавляет нас от необходимости проделать мучительный
путь к обоснованию этого понятия и изучению его основ-
ных свойств в самом начале курса.
Предлагаемая система аксиом хорошо согласуется с
традиционными доказательствами теорем и позволяет не-
сколькими штрихами сделать эти доказательства совер-
шенно безупречными. Отчетливая формулировка исходных
5
положений позволяет дать ясное изложение вопроса 0 геомет-
рическом доказательстве, которое иллюстрируется на про-
стых примерах взаимного расположения точек и прямых.
Содержание предлагаемого псурса-традиционное как
по материалу, так и по его расположению. Известное
усложнение, естественно вызванное строгостью доказач
тельств, нарастает постепенно и не может создать серьез-
ных трудностей для преподавания в школе.
В заключение отметим, что путь, избранный нами для
построения школьного курса геометрии, близок пути,
указанному в свое время Г. Д. Биркгофом, популярному
среди американских авторов школьных учебников. Опыт
американской школы дает основание утверждать разумность
предлагаемого пути.
§ 1. основные СВОЙСТВА простейших
гвомвтричвских фигур
Г еометрия-это наука о свойствах геометрических
фигур. Слово «геометрия» греческое. В переводе на
ADO
Рис. 1.
русский язык обозначает землемерие. Такое название связано
с применением геометрии для измерении на местности.
Примеры геометрических фигур: треугольник, квадрат,
окружность (рис. 1).
Рис. 2.
Геометрические фигуры могут быть весьма разно-
образны. Часть любой геометрической фигуры является
геометрической фигурой. Объединение нескольких геомет-
рических фигур есть снова геометрическая фигура. На
7
„рис. 9 ‚фригура слева составлена из треугольника и трех
квадратов‘, а "фигура справа состоит из окружности и частей
окружности. ‚Всякую геометрическую фигуру мы представ-
ляемсебе составленной из точек, По
Раздел геометрии, в котором изучаются фигуры на
плоскости, называется планиметоией. Мы начнем изучение
геометрии с этого раздела.
Основные геометрические фигуры на плоскости.
Основными геометрическими фигурами на плоскости яв-
ляются точка и_ прямая. На чер-
0,4 д теже точки и прямые наносятся остро
отточенным карандашом. Для того
чтобы изображение точки было от-
четливым, ее обводят малым круж-
ком. Точки принято обозначать про-
рис 3_ ПИСНЫМИ латинскими буквами: А, В,
С, D, . .. Прямые обозначаются строч-
ными латинскими буквами: а, b, c, d, Ha рис. 3 вы ви-
дите точку А и прямую а.
Основные свойства принадлежности точек и прямых
на плоскости. Посмотрите на рис. 4. Вы видите прямые
а, b и точки А, В, С. Точки А и С лежат на прямой а.
Можно сказать также, что точки А и С принадлежат пря-
мой а или что прямая а проходит через точки А и С.
Точка В лежит на прямой b. Она не лежит на пря-
мой а. Точка С лежит и на прямой а и на прямой b.
Прямые а и b пересекаются в точке С. Точка С является mott-
кой пересечения прямых а и b.
РИС. 4. Рис. 5.
Для построения прямых на чертеже пользуются линей-
кой. I;Ia рис. 5 вы видите, как с помощью линейки строится
прямая, проходящая через две заданные точки А и В.
8
Основными свойствами принадлежности точек и прямых
мы будем называть следующие два свойства.
1,. Какова бы на была прямая, существуют точки,
принадлежащие прямой, и точки, не принадлежащие
гирямой.
lg. Каковы бы на были’ две точки, существует и при-
том только одна прямая, проходящая через эти точки.
Прямую можно обозначать двумя точками, лежащими
на ней. Например, прямую а на рис. 4 можно обозначить
АС, а прямую b можно обозначить ВС.
Основные свойства взаимного расположения точек
на прямой и на плоскости. Посмотрите на рис. 6. Вы
видите прямую а и три точки на этой прямой: А, В, С.
б’ X
Рис. 6. Рис. 7.
Точка В лежит между точками А и С. Точки А и С
лежат по разные стороны от точки B. Точки А и С разде-
ляются точкой В. Точки А и В лежат по одну сто-
рону от точки С. Точки В и С лежат по одну сторону
от точки А.
Пусть на прямой а лежат различные точки А и В
(рис. 7). Отрезком АВ называется
часть прямой а, точками которой б’
являются точки А и В и все точки
Х прямой а, лежащие между А и
В. Точки А и Вназываются кон-
цами отрезка.
Посмотрите на рис. 8. Прямая
а разбивает плоскость на две
полуплоскости. Точки А и В
лежат в одной полуплоскости. Рис. '8.
Отрезок АВ не пересекается *
с прямой а. Точки А, и B, лежат в разных полуплоско-
стях. Отрезок А1В1 пересекается с прямой а. По'лупло‹
скости мы будем обозначать греческими буквами а, р, т,
9
Основными свойствами расположения точек на прямои
и плоскости мы будем называть следующие два свойства.
11,. Из трех точек на прямой одна итолько одна
лежтът между двумя другими.
I12. Прямая разбивает плоскость на‘ две полуплоско-
emu. Если концы какого-нибудь отрезка принадлежите
одной полуплоскости, то опгрезок не пересекается с
прямой. Если концы отрезка принадлежат разным полу-
плоскостям, то отрезок пересекается с прямой.
Основные свойства измерения отрезков и углов.
Для измерения отрезков применяются различные измери-
тельные инструменты. Простейшим инструментом является
A 6‘ __‚5
~47, ‚ч ‚и А?” ‘1
Ё0е‘ 7:ге2’ ее?
Л //"‘/"'3
‚Х /:.—-"’;-// ‚ —//Q ж"
Рис. 9. ’
линейка с делениями на ней. На рис. 9 отрезок АВ равен
10 см, отрезок АС равен 6 см, отрезок BC равен 4 см.
Длина отрезка АВ равна сумме длин отрезков АС и ВС.
Основными свойствами измерения отрезков мы будем
называть следующие свойства.
1111. Каждый отрезок имеет определенную длину,
большую нуля. ”
Illa. Если точка С прямой АВ лежит между точ-
ками А и В, то длина отрезка АВ равна сумме длин
отрезков АС и BC. я
line. 10. Рис. 11.
Посмотрите на рис. 10. Вы видите прямую а и точкуА
на ней. Проведем через точку А какую-нибудь прямую b,
10
„отличную ‚от Она разбивает плоскость на две люду-
плоскости. Часть прямой а, лежащая в одной из этих
полуплоскостей, называется полупрямой, или лучом. ‘Tou-
ка А называется начальной точкой полупрямой. Разби-
ение прямой а на полупрямые независит от прямой b.
Оно вполне определяется точкой А. Полупрямые обозна- I
чаются строчными латинскими буквами. Можно обозначать
полупрямую двумя точками: начальной точкой и еще какой-
нибудь точкой, принадлежащей полупрямой. При этом
начальная точка ставится на первом месте. Например, полу-
прямую а на рис. 11 можно обозначить АВ.
Углом называется фигура, которая состоит из двух
полупрямых, не лежащих на одной прямой, с общей на-
чальной точкой. Эта точка называется вершиной угла, а
полупрямые-сторонами угла. На рис. 12 вы видите
угол с вершиной О и сторонами а, b. Угол обозначается
либо указанием его вершины, либо указанием его сторон,
либо указанием трех точек: вершины и двух точек на сто-
ронах. Слово «угол» часто заменяют значком А. Например,
угол на рис. 12 можно обозначить тремя способамиддд,
g_(a, b), 4 АОВ. В третьем способе обозначения угла
вершина ставится посредине.
щ а
а А
/I
д С’
0
д
б’
b
Рис. 12. Рис. 13.
Посмотрите на рис.- 13. Мы будем говорить, что полу-
прямая с проходит между сторонами а, b угла (а, b), если
она пересекает какой-нибудь отрезок АВ с концами на
сторонах угла. ‘
Углы измеряются в градусах при помощи транспортира.
На рис. 14 угол (а, b) равен 12О°. Полупрямая с проходит
между сторонами угла (а, b). Угол (а, с) равен 90°‚ а угол
(b, с) равен 30°. Угол (а, b) равен сумме углов (а, с)
и (b, c).
‚Ц
Основными свойствами измерения углов мы бупемна-
зывать следующие свойства.
III3. Каждый угол имеет определенную градусную
M619)’, большую нуля и меньшую 18О°.
1114. Если луч с исходит из вершины угла (а, д) и
проходит между его сторонами, то угол (а, b) pa-
Рис. 14.
вен сумме углов (а, с)
и (b, c).
Основные свойства
равенства простейших
фигур. Посмотрите на
рис. 15. Здесь показано,
как с помощью линейки
на полупрямой с началь-
ной точкой А можно or-
ЛОЖИТЬ отрезок данной
длины (3 см).
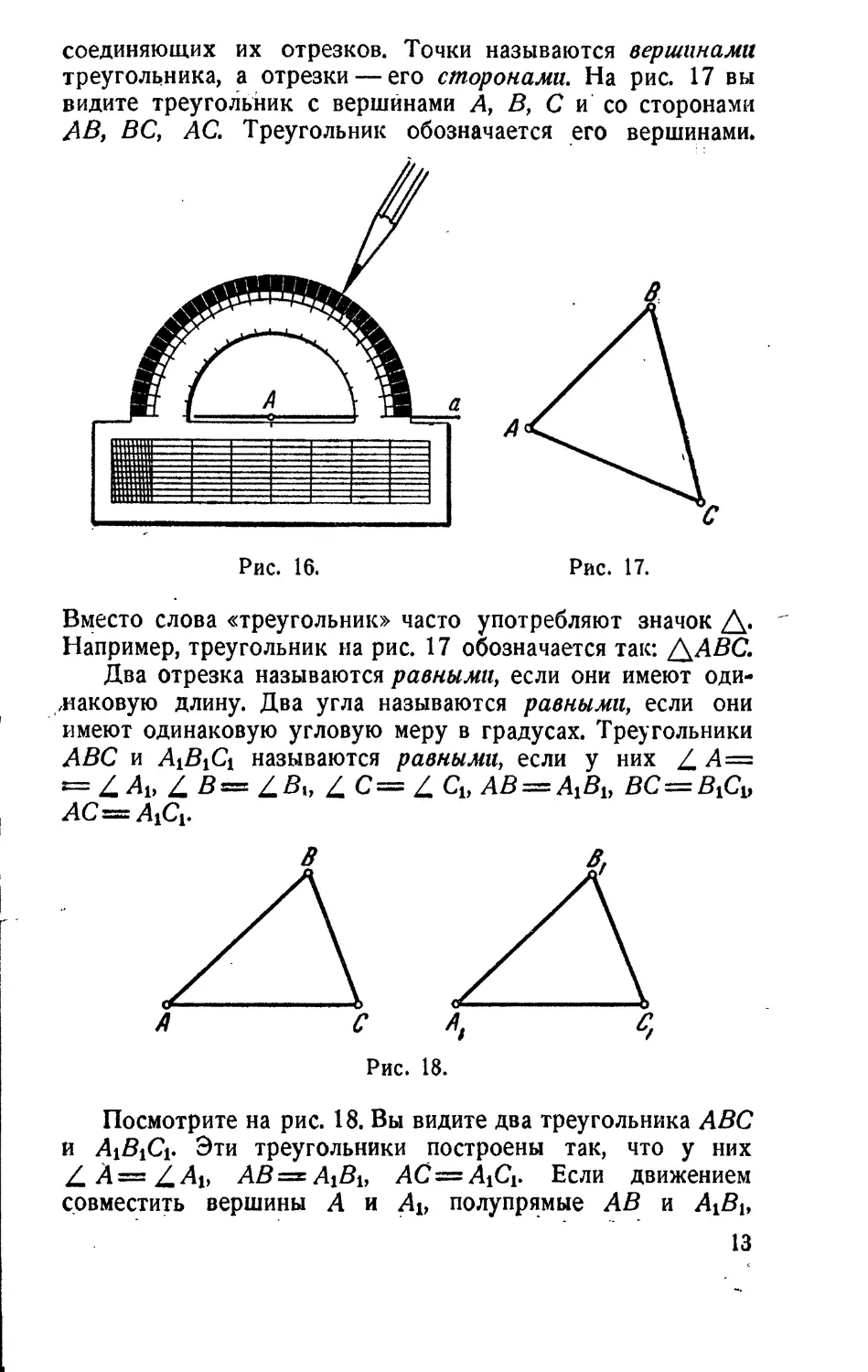
Посмотрите на рис. 16.
Полупрямая а, будучи
продолжена за начальную
точку, разбивает плоскость на две полуплоскости. На ри-
сунке показано, как отложить в верхнюю полуплоскость от
‘E9
Рис. 15.
полупрямой а угол, заданный
транспортира.
в градусах, при помощи
Треугольником называется фигура, которая состоит из
трех точек, не лежащих на одной прямой, и трех попарно
12
соединяющих их отрезков. Точки называются вершинами
треугольника, а отрезки——его сторонами. На рис. 17 вы
видите треугольник с вершинами А, В, С и’ со сторонами
АВ, BC, АС. Треугольник обозначается _его вершинами.
Рис. 16. Рис. 17.
Вместо слова «треугольник» часто употребляют значок А.
Например, треугольник на рис. 17 обозначается так: ААВС.
Два отрезка называются равными, если они имеют оди-
дНЗКОВУЮ ДЛИН)’. Два угла НЗЗЫВЗЮТСЯ равными, ЕСЛИ ОНИ
имеют одинаковую угловую меру в градусах. Треугольники
ABC И А1В‚С1 называются равными, если у них A А=
‘-'-”‘ А A1» А B-"'= LB» L C= Z. C1, AB:-"A131, BC=B1C1:
AC== A;C,.
д 4
Ъ‹
г д,
Рис. 18.
\%‘
Посмотрите на рис. 18. Вы видите два треугольника ABC
и А‚В‚С1. Эти треугольники построены так, что у них
4.5424141, AB:--A131, AC‘--...=A1C,. Если движением
совместить вершины А и Аь полупрямые АВ и А‚В‚,
13
\
АС n~A;C'1, то вершины В и 81, С и C, также сов-
местятся, т. е. треугольники ABC и А1‚т равны.
Следующие три свойства мы будем называть основны-
ми свойствами‘ равенства простейших фигур.
1\7‚. Каково бы ни было положительное число т,
на данной полупрямой из ее начальной точки можно
отложить отрезок, равный т.
Ша. Каково бы ни было положительное число п,
меньшее 180, от данной полупрямой в данную полупло-
скость можно отложить угол, равный п градусов.
IV3. Если у двух треугольников АВС zzA1B1C, LA:
== AA1, AB-==/1181, AC =2 A1C,, mo треугольники равны,
т. д. LB1, L01, BC-"'—""’-B’gC1.
Свойство IV3 называется первым признаком равенства
треугольников.
Основное свойство параллельных прямых. Две пря-
мые на плоскости называются параллельными, если они
.1 не пересекаются, При
о этом прямые считаются не-
ограниченно продолжен-
ными B обоих направле-
ниях. На рис. 19 показано,
как с помощью угольника
и линейки провести через
данную точку В прямую b, “
параллельную прямой а.
Основное свойство па-
раллельных прямых со-
стоит в следующем.
V. Через данную точку В, не лежащую на данной
прямой а, можно провести на плоскости не более одной
прямой, параллельной прямой а. `
к
Ь.
Рис.19.
Вопросы для повторения
1.‘4то такое геометрия?
2. Назовите основные геометрические фигуры на плоскости.
З. Сформулируйте основные свойства принадлежности точек
‘и прямых на плоскости.
4. Сформулируйте основные свойства расположения точек
на прямой и на плоскости.
5. Сформулируйте основные свойства измерения отрезков
и углов.
6. Сформулируйте основные свойства равенства простейших
геометрических фигур.
7, Сформулируйте основное свойство параллельных прямых.
14
§ 2. АКСИОМЫ, ТЕОРЕМЫ И ДОКАЗАТЕЛЬСТВА
Правильность утверждения о свойстве той или иной
геометрической фигуры устанавливается путем рассуждения.
Это рассуждение называется доказательством. pen-
ложение‚ выражающее свойство геометрической фигуры,
называется теоремой. Таким образом, установление свойств
геометрических фигур сводится к доказательству теорем.
Основные свойства I—-—V простейших фигур, сформу;
лированные в предыдущем параграфе, являются ОТПраВНЫМИ
свойствами в доказательствах других свойств. Эти сройо
ства не доказываются и называются аксиомами. Аксиома -
слово греческое, в переводе на русский язык обозначает
«предложение, не вызывающее сомнений», '
Аксиомы выражают собой отношения, в которых на.
"ходятся основные понятия. В нашем изложении такими
понятиями являются понятия, выражаемые словами: «точка»,
«прямая», «принадлежать» (для точек и прямых), «лежать
между» (для точек на прямой), «мера» (длина для отрез-
ков, градусная мера для углов). Эти понятия взаимно
определяются системой аксиом. Другие понятия, относя-ъ
щиеся к геометрическим фигурам, являются производными
и определяются явно через указанные основные. Таковы,
‚‚ например, понятие отрезка, угла, треугольника.
При доказательстве теорем разрешается пользоваться
основными свойствами простейших фигУР› т. e.‘ аксиомами,
а также свойствами уже доказанными, т. е. доказанными
теоремами. Никакими другими свойствами фигур, даже если
они не вызывают сомнений, пользоваться нельзя.
При доказательстве теоремы разрешается пользоваться
чертежом как геометрической записью того, что мы вь1ра‹
“жаем словами. Не разрешается использовать в рассужде—
нии свойства фигуры, видные из чертежа, если мы не
можем обосновать их, опираяс на аксиомы и теоремы,
доказанные ранее.
Формулировка теоремы обычно состоит из двух частей.
В одной части говорится о том, что дано. Эта часть Hasbr-
вается условием теоремы. В другой части говорится
о том, что должно быть доказано. Эта часть называется
утверждением теоремы.
Умение доказывать теоремы приобретается опытом.
Однако есть общее правило, с чего надо начинать дока‹
зательство теоремы. Прежде всего надо уяснить, что дано
1'5
и что требуется доказать. Часто понимание теоремы под-
оказывает путь к ее доказательству. Рассмотрим несколько
примеров. '
Тео р ем а 2.1 *). Если прямая а не проходит ни че-
рез одну из вершин треугольника АБС и пересекает его
сторону BC. mo она пересекает одну и только одну
из двух других сторон.
Условие этой теоремы состоит в том, что прямая а не .
проходит ни через точку А, ни через «точку B, ни через
точку С и пересекает отрезок ВС. Утверждение теоремы
— состоит в том, что прямая пересекает один и только один
из двух других отрезков АВ или АС.
Уясним формулировку теоремы. Что значит: прямая а
пересекает отрезок BC? Это значит, что точки В и С
И
д
‘Ъ‹
\ д 5 / 5’ Q
Рис. 20.
лежат в разных полуплоскостях‚ на которые плоскость у
разбивается прямой а. Такое понимание условия теоремы I
подсказывает доказательство. 5
Действительно, вершины В и Слежат в разных полу-
плоскостях. Вершина А лежит в одной из этих полупло-
скостей. Если она лежит в той же полуплоскости, что и
вершина В, то отрезок АС пересекается с прямой а,
а отрезок АВ не пересекается (рис. 20, слева). Если же 4
вершина А лежит в той полуплоскости в которой лежит 4
вершина С, то отрезокФАВ пересекается с прямой а,
а отрезок АС не пересекается (рис. 20, справа). Таким
образом, в любом случае прямая а пересекает одну и
только одну из двух других сторон треугольника. Вот
и все доказательство.
Теорема 2.2. Если точка С прямой АВ лежит у
между точками А и B, mo AC<AB.
*) B нумерации теорем первое число указывает параграф, I
a второе — порядковый номер предложения (теоремы или задачи)
внутри параграфа. '
16
Показатель ство. Условие теоремы состоит в ‘том,
что точка С лежит на прямой АВ между точками А и В.
Утверждение теоремы в том, что длина отрезка АС меньше
длины отрезка AB.
По свойству измерения отрезков (аксиома III.,) длина
отрезка АВ равна сумме длин отрезков АС и ВС. Ho-
этому АС<АВ. Теорема доказана.
Теорема 2.3. Если точка А на гфямой ВС нв pas-
деляет точки В и С и если АС<АВ, то точка С
лежит между А` и В.
Доказательство. В условии теоремы сказано, что
три точки А, B, C лежат на прямой. Далее сказано, что
точка А не разделяет точек B и С, т.‘ е. не лежит между
ними. Наконец, сказано, что отрезок АС меньше отрезка АВ.
Утверждение теоремы в том, что точка С лежит между
А и В.
По свойству расположения трех точек на прямой
(аксиома 111) одна и только одна из трех точек А, В, С
лежит между двумя другими. По условию теоремы этой
точкой не может быть точка А. Поэтому теорема будет
доказана, если будет доказано, что и В не может лежать
между А и С.
Допустим, однако, что точка В лежит между А и С.
‚Тогда по теореме 2.2 АВ<АС. Но это противоречит
условию теоремы: АС<АВ. Отсюда мы заключаем, что С
лежит между А и В. Теорема доказана.
Способ рассуждений, который мы применили в дока-
зательстве этой теоремы, называется доказательством от
противного. Доказательство от противного применяется
очень часто. Сущность его состоит в том, что делается
‚предположение, противоположное тому, что утверждается
теоремой. А затем путем рассуждений выводится след-
ствие из этого предположения, противоречащее условию
теоремы. .
Поясним сказанное на примере доказательства тео-
ремы 2.3. По условию теоремы точка А не лежит между
В и С. Поэтому остаются две возможности: либо В
между А и С, либо С между А и В. Теоремой утверж-
дается, что точка С лежит между А и В. Противополож-
ное утверждение состоит в тсм, что С не лежит между
А_ и В, т. е. В лежит между А и С. Сделав это предпо-
ложение, мы получили следствие (АВ< АС), противоре-
чашее условию теоремы.
17
Тео ре м а 2.4. Если конец А отрезка АВ лежит на
прямой а, а конец В не лежит на этой прямой, то все
точки отрезка AB,’ кроме точки А, лежат в одной из
полуплоскостей, на которые прямая а разбивает пло-
скость. .
Доказательство. Применим доказательство от
противного. Точка В лежит в одной из полуплоскостей.
Теоремой утверждается, что все точки отрезка АВ, кроме
точки А, лежат в той же полуплоскости. Допустим, что
некоторая точка C отрезка АВ лежит в другой полупло—
скости. Тогда отрезок ВС пересекается с прямой а в ne-
которой точке.
Этой точкой не может быть точка А, так как она не
лежит между В и С. В самом деле, точка С лежит между А
и В, а из трех точек А, В, С только одна лежит между
двумя другими. Таким образом, отрезок ВО пересекается
с прямой а в некоторой точке Ад, отличной от А. Следо—
вательно, прямая а и прямая АВ пересекаются в двух
точках: А и А1.
По свойству принадлежности точек и прямых (аксиома I2)
через точки А и А, проходит одна и только одна прямая.
Поэтому прямая АВ есть не что иное, как прямая а,
а значит, точка В лежит на прямой а, вопреки условию
теоремы. Теорема доказана.
Теорема 2.5. Пусть а--прялсая‚ А——точка на
ней и ад, аандве полупрямые, на которые прямая а
разбивается точкой А. Пусть ь, и сг-две полупрямые
с начальной точкой А, расположенные в одной из
полуплоскостей, на которые прямая а разбивает плач
скость (рис. 21).
“'2 “а Ад /7 ‚ /7, д:
Рис. 21.
Тогда либо полупрямая b, проходит между а, и Cp
a полупрямая с1 проходит между ь, и ад (рис. 21, слева),
18
МЬ ..д.—____
либо с, подходит лгежду а, и Ь„ а Ь, проходит между
с,`и а, (рис. 21, справа). у I
До к а з ате ль ств о. Обозначим‘ через Ь и с‘ прямые,
которые содержат полупрямые Ь, и с,; Отметим на полу-
прямых а„ а, и Ь, точки А„ А, и В,‘(рис. 21). Прямая с
пересекает сторону А,А, треугольника А,А,В,. По теореме 2.1
она пересекает одну из двух других сторон А,В, или А,В,.
Допустим, прямая с пересекает сторону A28, (рис. 21, слева).
По теореме 2.4 отрезок A28, кроме точки А, лежит
в одной полуплоскости относительно прямой а. Поэтому
точка пересечения С, отрезка A28, c прямой с принадле-
жит полупрямой с,. A это значит, что с, проходит между
Ь, и ад. Докажем, что Ь, проходит между а, и с,.
Соединим точки А, и С, отрезком А,С,. Прямая Ь nee
ресекает сторону А,А, треугольника А,А,С,. Поэтому она
пересекает одну из двух других сторон. Прямая Ь пересе-
кает прямую АдС, в точке В„ которая не принадлежит от-
резку A201. Поэтому прямая Ь не может пересекать отрезок
А„С,. B противном случае прямые АдС, и Ь имели бы
две общие точки и три точки А, A2, В, лежали бы на
одной прямой, т. е. на прямой а. Итак, прямая Ь пере-
секает сторону А,С, треугольника А_,А,С,. Так же как и
в предыдущем рассуждении, заключаем, что точка пересе—
чения принадлежит полупрямой Ь,. А это значит, что
полупрямая Ь, проходит между а, и с,.
Итак, если прямая Ь пересекает сторону А,В, тре‹
угольника А,В,А„ то с, проходит между Ь, и ад, а Ь,
проходит между а, и с,. Теперь надо рассмотреть тот
случай, когда прямая Ь пересекает
сторону 44,8, треугольника А,В,А,
(рис. 21, справа). этом случае по- ь
лучается, что полупрямая с, проходит \\
между а, и Ь,‚ а полупрямая Ь, про- д 7
ходит между с, и a.2. Читателю пред-
лагается провести это рассуждение
самостоятельно.
Теорема 2.6. Пусть а, Ь, ” Рис. 22-
с --три полупрямые, исходящие
из точки О. Пусть ‘полупрямые Ь и с расположены‘ в одр
ной из полуплоскостей, определяемых полупрямой а и ее
продолжением (рис. 22). Тогда:
у 1) если полупрямая Ь проходит между а и с, то
угол (а, Ь)‘ меньше угла (а, с);
б’
19
2) если угол (а, Ьуменьше угла (а, с), то полупря-
мая Ь проходит между а и с.
Доказательство. Эта теорема содержит два
утверждения: 1) и 2). Начнем с первого. Согласно свойству
измерения углов (аксиома 1114), если полупрямая b прохо‹
дит между а и с, то угол (а, с) равен сумме углов (а, Ь)
и (b, c). Поэтому угол (а, b) меньше угла (а, с). Утверж-
дение 1) теоремы доказано.
Докажем утверждение 2). Согласно теореме 2.5 либо
полупрямая b проходит между а и с, либо полупрямая с
проходит между а и Ь. Допустим, что с проходит между а
и Ь, Тогда по первой части теоремы, которая уже дока‹
зана, угол (а, с) меньше угла (а, Ь). Но это противоречит"
д условию теоремы, поэтому случай,
I когда с проходит между а и Ь не-
возможен. Следовательно, Ь. прохо-
дит между а и с. Теорема доказана
полностью.
Теорема 2.7. Если полупря-
мая b1 проходит между полупря-
A мыми a1 и c1, то она пересекает
а любой отрезок АС с концами на
полупрямых a1 и с, (руде, 23).
Доказательство. ПустьЬ--
прямая, содержащая полупрямую Ьд.
По условию теоремы полупрямая b1 проходит между a1 и
cl, Это значит, что она пересекает некоторый отрезок A1C1
c концами на полупрямых a1 и c1 B некоторой точке D.
Прямая Ь пересекает этот отрезок в той же точке D. По
теореме 2.1 прямая Ь пересекает сторону C1A треугольника
AC1A1, следовательно, по той же теореме, прямая Ь пере-
секает сторону АС треугольника ACC1 В некоторой точке Е.
Точка Е лежит в той же полуплоскости относительно пря-
мои, содержащей полупрямую a1, что и полупрямая Ь‚.
Поэтому точка пересечения прямой Ь с отрезком АС upm-
надлежит полупрямой b1. Теорема доказана. .
Рис. 23.
§ 3. PABEHCTBO ТРЕУГОЛЬНИКОВ
Теор е M a 3.1. Если у треугольников АВС и A1B1C1
AB --.--= A1B1, _ A А = Z. A1. L B = A B1, mo треугольники
равны (РИС. ИМЁННО, А1С1, B1C1, L C: L C1.
20
Доказательство. Отложим на полупрямой АС
отрезок AC2, равный АдСд. Треугольник ACgB равен тре-
угольнику A1C,B1 no первому признаку равенства тре—
угольников (аксиома IV3). Действительно, ACg=A,C, no
построению, а АВ=А‚В‚ и 4А= AA, по условию Teo-
ремы. Если точка Св совпадает с С, то треугольник ABC,
б’ 4
~35
А- од A". v
Рис. 24.
совпадает с ‘треугольником ABC и, следовательно, тре-
угольники ABC И А1В1Сд равны.
Допустим, точка Св не совпадает с С. Тогда либо
точка С, лежит между А и С, как на рис. 24, либо С
лежит между А и Св. Рассмотрим первый случаи. В этом
случае полупрямая ВС, проходит между полупрямыми ВА
и ВС, так как пересекает отрезок AC. По теореме 2.6
угол ABC2 меньше угла АВС. Но это невозможно, так
" как угол ABC равен углу А‚‚т по условию теоремы,
а угол А‚В‚С1 равен углу АВС„ по доказанному. Итак,
точка С, не может быть между A и C. Аналогично nona-
зывается, что точка С не может быть между А и С,
Теорема доказана. ~
Теорема 3.1 называется вторым д; д
нризнаком равенства треугольников.
' Равнобедренным треугольником на-
зывается такой треугольник, у которого
две стороны равны. Эти равные стороны
называются боковыми сторонами, д
а третья сторона называется основанием 1,3
треугольника. -
Теорема 3.2. B равнобедренном P"°- 25-
треугольнике углы при основанииравны. ’ . "
Именно, если АС == BC в треугольнике АВС, то А А==д В.
Доказательство. Переобозначим вершины тре-
угольника. Именно, вершину А обозначим B1, вершину В
обозначим А„ а вершину С обозначим С, (рис. 25). Тре-
угольник ABC равен треугольнику А‚‚т по первому
21
Д
' ‘I
дризнаку равенства треугольников, ттак как [_C== 4C1,
АС== А1С1, BC=B1C,. Поэтому AA: 4A,, Т. е.. LB:-=
= 424. Теорема доказана.
Треугольник называется равносторонним, если все его
стороны равны. Из теоремы 3.2 следует, что в равносто-
роннем пгреугольнггке все углы равны.
д Теорема 3.3. Если 4А=4Вв
6; треугольнике ABC, mo треугольник
равнобедренный. Именно, АС== BC.
Доказательство. Допустим,ут-
верждение теоремы неверно и BC < AC.
Отложим на полупрямой АС отрезок
‘д д AC1, равный ВС (рис. 26). Точка С1
Рис. 26. лежит между А и С. Треугольники
С‚АВ и СВА равны, так как у них
сторона АВ общая, АС1=СВ по построению, а углы СВА
и С‚АВ равны по условию теоремы. Поэтому углы CAB
И CIBA равны. А значит, равны углы СВА и СдВА. Но
это невозможно, так как полупрямая BC, проходит между
сторонами угла СВА. Мы пришли к противоречию. Тео—
рема доказана.
Теорема 3.3 является обратной теореме 3.2. Утверж‹
пение теоремы 3.2 является условием теоремы 3.3, а усло‹
вие теоремы 3.2 является утверждением теоремы 3.3. Не
всякая теорема имеет обратную. А именно, если данная
теорема верна, то обратная может быть неверна.
Теорема 3.4. Если у треугольников АВС и А‚‚т
АВ=А1ВЬ AC =/-1101 и BC =B,C1, то треугольники
равны, т. е. [_A=-=[_A1, AB-::-=[_B1, АС; AC1.
'9 в
А д‘ д Ад д
д; 52
Рис. 27.
Д о к а з а т е л ь с т в о. Прямая АС разбивает плоскость
на две полуплоскости (рис. 27, слева). Точка В лежит
22
в одной из этих полуплоскостей. Отложим от полупря-
мой АС в другую полуплоскость угол, равный A-A1, и на
его стороне отложим отрезок ’АБ‚, равный А‚Б‚. Тре-
угольники АСВ9 и А‚С‚Б‚ равны по первому признаку
равенства треугольников. Отсюда заключаем, что АБ2=
:A1B1-—-"“'-—‘-AB,
Отрезок ВБ, пересекает прямую АС в некоторой
точке D. Могут представиться два случая: 1) точка D He
совпадает ни с одной из точек А и С, 2) точка D совпа-
дает с одной из этих точек. В первом случае одна из
трех точек А, С, D лежит между двумя другими. Допу-
стим сначала, что точка D лежит между А и С, как
изображено на рис. 27, слева.
Треугольник АББ„ равнобедренный, так как АБ=АБ„.
По теореме 3.2 угол АББд равен углу АБаБ. Треугольник
BCB2 также равнобедренный. У ‘него угол BBgC равен
углу BQBC. Так как полупрямая BD проходит между сто-
ронами угла ABC, то угол ABC равен сумме углов АББд
и Б2БС. Аналогично угол АБдС равен сумме углов АБ„Б
и ББЗС. Поэтому углы АБС и АБдС равны. По первому
признаку равенства треугольников треугольники ABC и
АБдС равны, так как у них АВ==АБ9‚ BC=B2C и
[_ABC=--' AABQC Так как треугольник АБдС равен тре—
‚угольнику A1B,C,, то получается, что треугольники ABC
и А‚Б,С‚ равны. Случай, когда точка С лежит между А
и D, и случай, когда точка А лежит между С и D, рас-
сматриваются аналогично. Предлагается провести это рас-
смотрение самостоятельно.
Допустим теперь, что точка D совпадает с одной из
точек А или С. Пусть для определенности точка D сов-
падает с A (рис. `27, справа). Треугольник BCB2 равно-
бедренный, так как БС==В9С. Отсюда по теореме 3.2
AB: 482. Треугольники ABC и АБдС равны по первому
признаку равенства. У них АБ==АБ‚‚ BC.-:=B2C и 4Б===
== 489. Так как треугольник АБЗС равен треугольнику
А‚Б1С‚, то треугольники АБС и А1В1С‚ равны. Случай,
когда точка D совпадает с точкой С, рассматривается
аналогично. Теорема доказана.
Теорема 3.4 называется пгретьим признаком равенства
треугольников. .
Срединой отрезка АБ называется такая точка С, что
АС===СБ. По свойству измерения отрезков (аксиома 111,)
каждый из отрезков АС и СБ равен половине отрезка-АБ.
23
Медианой, проведенной из вершины, С треугольника ABC,
«называется отрезок, соединяющийвертцину С со срединой
противоположной стороны, т. .е. стороны АВ. В треуголь-
нике имеется три медианы. . -
Любые две медианы треугольника пересекаются.
"Действительно, проведем, медианы в треугольнике ABC
ИЗ двух вершин, например А и В (рис. 28). По теореме 2.1
в применении к треугольнику ACA1 прямая ВВ1 пересе-
кает медиану АА1. По той же причине прямая АА, пере-
секает медиану ВВ1. Таким образом, прямыеААд и BB,
д пересекаются. Так как эти прямые
различны, то они могут иметь толь-
ко одну общую точку. Эта точка
‚ принадлежит медиане AA, И медиа-
не ВВ1. Следовательно, медианы ne-
д „д ресекаются.
= Биссекжприсой угла (а, Ь) назы-
Pm 28. вается полупрямая с, проведенная из
вершины угла между его сторонами,
делящая угол (а, Ь) на равные части: [_(a, с)= 4(с, Ь). По
свойству измерения углов (аксиома 1114) каждый из углов
(а, с) и (с, b) равен половине угла (а, Ь).
По теореме 2.7 биссектриса угла треугольника пере-
секает противолежащую сторону.
Биссентрггсой треугольника АВС, проведенной из
вершины А, называется отрезок биссектрисы угла А
с концами в точке А и точке пересечения с противопоч
ложной стороной, т. е. со стороной ВС. В треугольнике
три биссектрисы. Любые две биссектрисы треугольника
пересекаются.
Теорема 3.5. B равнобедренном треугольнике ме-
‘диана, проведенная к основанию, является одновременно
биссектрисой.
Предлагается доказать эту теорему в качестве упраж‹
нения. ~
Упражнения
1. Привести полное доказательство теоремы 8.4, разобрав
все случаи расположения точки D Ha прямой АС. .
2. Привести доказательство теоремы: любые две биссектрисы
треугольника пересекаются. ‘
' 3. Доказать теорему 3.5.
24
угольнике медианы, ПРОВЕДЕННЫЕ ИЗ УГЛОВ
.4. Доказать, что y_~- равных треугольников соответствующие
медиаъы равны, соответствующие биссектрисы paBHb1._CQom-
ветствующими медианами (биссектрисами)
называются такие, которые проведены из соот-
ветствующих вершин.
5. Доказать, что в равнобедренном тре-
при основании, равны, биссектрисы, про-
веденные из углов при основании, равны.
6. На сторонах а и а, угла с верши-
ной О отложены отрезки ОА==ОА, и
ОВ==ОВ, (рис. 29). Доказать, что отрезки
АВ, и ВА, пересекаются и притом на бис-
сектрисе угла.
6'
„- Д’
§ 4. СМЕЖНЫЕ углы. прямой угол
Пусть а и Ь-—-две пересекающиеся прямые. Точкой
пересечения О прямая а разбивается на полупрямые а, и ад,
а прямая b разбивается на полу-
.5, прямые 17, и д, (рис. 30). Углы
(а,‚ и) и (ад, bl) называются смеж-
fl ными. Углы (а„ bl) и (ад, b2) назы-
аг о, ваются вертикальными.
Те о р е м а- 4.1. Если дваугла
дг равны, то смежные с ними углы
авны.
Рис. 30 р
Доказательство. Пусть
‘Iv
Q'-
%
35. ‹
Q
\% 1
-Q
„Зъ ‹
‘Q
I
Рис. 31.
точки А, В, С. Отложим на полупрямых’ а„ bl, с, отрезки
О,А„ 0,8, и О,С,‚ равные ОА, OB и ОС соответственно.
*- Треугольники ОАСи О,А,С, равны, так как углы АОС
и А,О,С, равны по условию ‚теоремы, а OAK: 0,/11
25
и ОС=О,С‚ по построению. Следовательно, углы C,/110,
“E CAO" равны- и AC-'.:= A101. ‚
По свойству измерения отрезков‘ (аксиома 1119) АВ==
-_=А1В‚. Поэтому треугольники ВАС и В1А‚С‚ равны.
Следовательно, BC=.-..B,C,. Треугольники ВСО и В‚С,О‚
равны по третьему признаку равенства треугольников.
Отсюда заключаем о равенстве углов ВОС и В‚О‚С‚,
т. е. углов (b, с) и (bl, cl). Теорема доказана.
Теорема 4.2. Вертикальные углы равны.
Доказательство (рис. 30). Угол (Ь„ ад) является
смежным для углов (щ, bl) и (a2, bg). По теореме 4.1 от-
сюда следует, что вертикальные углы (щ, Ь‚) и (ад, Ьд)
равны. Теорема доказана. -
Угол называется прямым, если он равен своему смеж-
ному.
Теорема 4.3. Прямой угол равен ‘90°.
Доказательство. Пусть (ад, Ь)-—прямой угол
(рис. 32). Это значит, что он равен углу (ад, b). Обозна-
д чим через т градусную меру
прямого угла (щ, b). Если
т 7: 90, то либо т<90,
либо т>90. Предположим
д gm сначала, что т< 90.
Так как 2т<180, то по
д д д аксиоме Ш, существует угол
г „ I
(щ, с), равный 2т. По теореме
Рис. 32. 2.5 в расположении четырех
- лучей ад, b, c, а, могут быть
дгрлько две возможности: 1) b проходит между щ и с,
а с проходит между ад и b, 2) c проходит между щ и b,
a b проходит между а, и с. По теореме 2.6 второй слу-
чай исключается, так как угол (щ, с)‚_ равный 2т, больше
угла (щ, b), равного т. Итак, Ь проходит между щ и с,
а с проходит между а, и Ь.
По свойству измерения углов (аксиома 1114) угол (щ, с)
равен сумме углов (ад, Ь) и (Ь, с). Поэтому угол (Ь, с) ра-
вен т. Угол (Ь, ад) равен сумме углов (Ь, с) и (с, ад), сле-
довательно, больше т. С другой стороны, угол (Ь, ад)
равен т, как смежный к прямому углу, равному т. Мы
пришли к противоречию. -
Допустим теперь, что т>90. Возьмем число п==
.—=т—-—9О. Оно меньше т. Отложим угол, равный п,
от полупрямой ад (рис. .33). Такжак- n<m, то по-
26
лупрямая с проходит между а, и-Ь. Отсюда по теореме
2.6 заключаем, что Ь проходит между а, и с.,По свой-
ству измерения углов угол (b, с) равен т—-п, так как
угол (Ь, аз) равен т, .а угол (ад, с)
равен п. Угол (а„ с) равен сумме
углов (ад, Ь) и (Ь, с), следовательно,
равент+ (т—--п)=—..т+9О> 180.
Но это невозможно, так как каждый
угол по аксиоме III3 имеет градус-
ную меру, меньшую 18О°. Итак, оба
предположения, т<9О и т>9О,
приводят к противоречию. Следо-
вательно, т==9О. Теорема доказана.
Угол, меньший прямого, называется остыла, угол,
больший прямого, называется тупым.
Теорема 4.4. Сумма смежных углов равна двум
прямым, т. е. 18О°.
Доказательство. Пусть (а‚, Ь) и (ад, Ь)——смеж-
ные углы (рис. 34). Если угол (а‚, Ь) прямой, то смежный
’ угол (аз, Ь) тоже прямой и их сумма
д равна двум прямым. Допустим, что
угол (ад, Ь) не прямой. Отложим от
„ полупрямой а, прямой угол (ад, с)
(рис. 34). По теореме 2.5 в распо-
ложении четырех лучей ад, Ь, с, а,
0* д а могут быть только две возможности:
5’ ’ 1) Ь проходит между а и с а с про-
1 ›
РПС- 34- ходит между аз и Ь; 2) с проходит меж-
ду а, и Ь, а Ь проходит между а, и с.
Рассмотрим первый случай. Пусть угол между лучами Ь
и с равен п. Тогда по свойству измерения углов угол
(ад, с) равен сумме углов (щ, Ь) и (Ь, с). Поэтому угол
(а‚, Ь) равен 90-——n. Далее, угол (аз, Ь) равен сумме
углов (ад, с) и (с, Ь), т. е. равен 9О+п. Поэтому сумма
углов (а1, Ь) и (аз, Ь) равна (9О-—п)-{-(9О+п), т. е.
18О°.
Рис. 33.
6’
Второй случай, когда с проходит между а, и Ь, а Ь
проходит между а, и с, рассматривается аналогично. Пред-
лагается читателю провести это рассмотрение самостоя-
тельно. В этом случае также получается, что сумма углов
(а‚, Ь) и (аз, Ь) равна 180°. Теорема доказана.
Две прямые называются перпендикулярными, если они
пересекаются под прямым углом.
27
Через каждую точку плоскости
одну прямую, nep-
Теорема на
можно провести и притом только
пендикулярную данной.
Доказательство. Пусть А-дданная точка и а--
данная прямая. В расположении точки А и прямой а могут
д д быть две возможности: 1) точка А
’ Ч лежит на прямой а; 2) точка А не
лежит на прямой а. Рассмотрим
сначала случай, когда точка А лежит
на прямой а (рис. 35). Точка А раз-
бивает прямую а на две полупрямые
а, и ад. По аксиоме Ш, от полу-
прямой а, можно отложить угол
(щ, (7), равный 90°, В любую полу-
плоскость, определяемую прямой а.
Прямая, содержащая луч b, проходит через точку А и
пересекает прямую а под прямым углом.
Покажем, что эта прямая единственная. Допустим, су-
шествует другая прямая, также проходящая через точку А
и пересекающая прямую а под прямым углом. Обозначим
через b, полупрямую этой прямой, лежащую в одной полу-
плоскости с b (CM. рис. 35).
По теореме 2.5 либо b проходит между а,
Ь, проходит между а, и b. '1`ак как оба угла (щ,
(щ, 121) прямые, т. е. равны 9О°,
то оба расположения лучей не- А
возможны по теореме 2.6. Та-
ким образом, через точку А
проходит только одна прямая,
перпендикулярная прямой а.
Пусть теперь точка А не
лежит на прямой а (рис. 36).
Отметим на прямой а две д
произвольные точки В и С. 1
Точка А лежит в одной из
полуплоскостей, на которые
прямая а разбивает плоскость. Отложим от полупрямой
ВС в другую полуплоскость угол, равный АВС. На сто-
роне этого угла отложим отрезок ВА1‚ равный ВА. Тре-
угольники ABC И А‚ВС равны, так как у них сторона ВС
общая, а углы ABC, A,BC и стороны АВ, А1В равны по
построению. Отсюда следует, что AC=A,C, и 4 АСВ=
1 А А1СВ.
28
_....____.L__.
“г /1 а!
Рис. 35.
и др либо
b)u
Рис. 36.
' - W ’ - -..~ ‚. - ’ н‘ м ..
„итак-тж „ ,„гппштгнг-ньжтеьгящчдд„щд‚ „в „_ ч”
_ ' ‘— ' ч 1:1.’ “ I _ __?,.~,:.
r ’.'l?."7z-$"§‘z'3’v< и
. д к .
‚ Ёг:дС\Ё„е ;;м;; _:_.;.;‚_,„„.:_„5‚. „ ‚ U
—
Точки А и А, находятся в разных полуплоскостях от-
носительно прямой а. Поэтому отрезок AA, пересекается
с прямой а в некоторой точке D. По крайней мере одна-
из точек В, С отлична от D (на рис. 36 обе точки от-
личны от D). Пусть для определенности В отлична от D.
Треугольники BAD и BA,D равны. Так как углы D этих
треугольников являются смежными,
то они прямые. Таким образом, пря-
мая ААд пересекает прямую а под А
прямым углом.
Докажем единственность прямой,
проходящей через точку А перпенди- д д д
кулярно прямой а. Допустим, что,
кроме построенной прямой ААд, есть
другая прямая, проходящая через д
точку А и пересекающая прямую а д,1_
под прямым углом. Обозначим эту Рис 37
прямую b, a точку ее пересечения ° '
с прямой а обозначим Ц (рис. 37).
Точка Ц отлична от D, так как через две точки (А
и D) можно провести только одну прямую (аксиома 1,).
Треугольники АПЦ и АдПЦ равны, так как у них сто-
рона ПЦ общая, AD.-.=A,D, a углы при вершине D пря-
мые. Поэтому углы АЦП и А1ЦП равны. Но угол АЦП
прямой. Поэтому угол А1ЦП тоже прямой, Полупрямая
ЦП пересекает отрезок АА, с концами на сторонах угла
АЦАд. Следовательно, угол АЦА, равен сумме углов
АЦП и А1ЦП, т. е. равен 180°. А это невозможно по
аксиоме 1113. Итак, не существует другой прямой, прохо-
дящей через точку А, пересекающей прямую а под пря—
мым углом.
Теорема доказана.
Упражнения
1. Доказать, что биссектрисы смежных углов образуют пря-
мой угол.
2. Из точки О исходят три луча ад, ад, a3. Никакие два луча
е лежат на одной прямой. Доказать, что сумма углов (ад, ад),
€02, ад), (аз, ад) не больше 360°.
3. Доказать, что две прямые, перпендикулярные третьей, не
пересекаются. -
4. Доказать, что в треугольнике не может быть двух пря-
мых углов. - I
29
§ 5. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ
И УГЛАМИ ТРЕУГОЛЬНИКА
Внешним углом треугольника АВС при вершине А
называется угол, смежный углу А. _
Теорема 5.1. Внешний угол треугольника АВС npu
вершине А больше угла В и больше угла С. [Сороче го-
воря, внешний угол треугольника больше любого внч
треннего угла треугольника, не смежного с ним.
Доказательство. Пусть АВС——-данныи треуголь-
ник (рис. 38). Обозначим О средину стороны АС. Отлое
жим на полупрямои ВО отрезок
6’ Л BD, равный 2во. Тогда 00: ов,
д точка О лежит между В и D.
Отметим на полупрямой ВА Tou-
ку Е так, чтобы точка A была
между B и Е. Полупрямая АО
проходит между АВ и AD, так
как она пересекает отрезок BD.
Поэтому по теореме 2.5 полу-
прямая AD проходит между AC И АЕ. По свойству
измерения углов угол OAD меньше угла ОАЕ‚ внешнего
угла треугольника ABC при вершине A.
Треугольники ВОС и DOA равны, так как у ни);
АО=СО, БОь-ВО по построению, а углы при вершине
О равны, как вертикальные. Из равенства этих треуголы
ников следует, что угол BCO равен углу DAO. А по до‹
казанному угол DAO меньше внешнего угла треугольника
ABC при вершине А. Итак, угол С треугольника меньше
внешнего угла при вершине А. Аналогично доказывается,
что угол В треугольника также меньше внешнего угла
при вершине A. Теорема доказана.
Теорема 5.2. У каждого треугольника no крайней
мере два угла острых, т. е. меньше прямого.
Доказательство. Допустим угол А треугольника
ABC не меньше прямого. Тогда внешний угол при веро
шине А, как смежный углуА, будет не больше прямого,
По теореме 5.1 углы В и С треугольника меньше внеша
него угла треугольника при вершине А, т. е. острые. T eo-
рема доказана.
Т ео рема 5.3. Если AB>BC в пгреугольнггке ‘ABC,
то А С больше 4 А. И обратно, если A C больше A А,
то AB>BC. Короче говоря, в треугольнике против
30
д A f
Рис. 38.
_-——
большей ‘стороны лежит больший угол, против боль-
шего угла лежит большая сторона. '
Доказательство. Пусть АВ>ВС в треугольнике
ABC (рис. 39). Отложим на ‘полупрямой BA отрезок ВСЬ
равный ВС. Точка C1 лежит между
А и В. Полупрямая CC, проходит 5’
между CA И СВ, так как пересекает
отрезок АВ. Поэтому угол ВСС,
меньше угла ВСА, т. е. угла С тре-
угольника ABC. Углы ВСС1 и ВСдС
равны, как углы при основании д
равнобедренного треугольника СВС‚. д
Угол ВСЮ является внешним углом РИС. 39-
для треугольника АС1С при? вершине
С, и поэтому больше угла А. В итоге угол С треуголь-
ника ABC больше угла А этого треугольника. Первое
утверждение теоремы доказано.
Докажем теперь, что, если A C больше А А, то
AB>BC. Допустим, утверждение неверно. Тогда либо
АВ==ВС‚ либо АВ<БС. В первом случае треугольник
ABC равнобедренный и, следовательно, углы А и С при
его основании равны. Но это противоречит условию: А С
больше 4 А. Если же АВ<ВС, то по доказанному A A
больше Д С, что также противоречит условию. Итак,
если 4 С больше A A, то
19 АВ>ВС. Теорема доказана пол-
ностью.
Теорема 5.4. У каждого
треугольника сумма двух сто-
рон больше третьей стороны.
Доказательство. Пусть
АБС-данный треугольник (рис.
Рис. 40. 40). Докажем, что АВ <AC+ CB.
Отложим на полупрямой АС отре—
зок AD, равный AC + CB. Тогда точка С будет между А
и D, a CD.-=CB. Углы В и D треугольника BCD равны,
как углы при основании равнобедренного треугольника.
Угол ABD больше угла CBD, так как полупрямая ВС
проходит между BA И BD. Таким образом, угол ABD боль—
ше увла ADB. По теореме 5.3 отсюда заключаем, что
AD>AB, T. e. AC+BC>AB. Теорема доказана.
Ломаной называется фигура, которая состоит из
точек’ Ад, Ад, A3, ..., A,, и отрезков, соединяющих
31
~53
последовательные точки: A1A3, A3A3. ..., А‚,.1А‚,. Точки Ад.
A3, A3, называются вершинами ломаной, а отрезки A,Ag,
A3A3, называются звеньями ломаной. Точки А, и А,
называются концами ломаной. Длиной ломаной Hasn-
вается сумма длин ее звеньев. На рис. 41 изображена ло-
маная с вершинами Ад, A3, ..., Ад.
Рис. -41. Рис. 42.
Теорема 5.5. Длина ломаной не меньше длины
отрезка, соединяющего ее концы.
Доказательство. Если некоторые вершины noma-
ной совпадают, то мы Выбросим часть ломаной между
этими вершинами. При этом длина ее только уменьшится.
Так, на рис. 42 изображена ломаная, у которой совпадают
вершины A3 И A7. От этой ломаной мы перейдем к ло-
маной A1A3A3A3A3. Эта ломаная имеет длину меньшую,
чем исходная. Таким путем, не увеличивая длину ломаной,
мы можем прийти к ломаной с теми же концами, у кото-
рой все вершины будут различны. Допустим, исходная
ломаная A1A3...A,, уже обладает этим свойством.
Рассмотрим ломаную А1А3Ад. . . An. Вместо звеньев A,A3
и A3A3 она имеет звено А1Аз. Если точки A1, Ад, A3 не
лежат на одной прямой, то по теореме 5.4 A,A3<A1A3+
+A3A3. Поэтому новая ломаная имеет длину меньшую,
чем исходная. Допустим, точки А1‚ A3, A3 лежат на одной
прямой. Тогда одна из них лежит между двумя другими;
Если это точка Ад, то A1A3=.-A1A3+A3A3. Если точка А;
лежит между A3 и A3, то A,A3<A3A3 И, тем более.
A,A3<A,A3+A3A3. To же заключение в случае, когда
точка А, лежит между А, и A3. Одним словом, переход
к ломаной A3A3...A,, не увеличивает длины ломаной.
Затем мы перейдем к ломаной A,A3...A,,, опуская
вершину A3, И т. д. В конце концов, мы придем к лома-
32
£=-‘msan “-' же
ной А‚А„ с одним звеном; которое представляет собой от-
резок, соединяющий концы исходной ломаной. Так как
каждый раз длина ломаной не увеличивалась, то исходная
ломаная имеет длину, не меньшую длины отрезка, соеди-
няющего ее концы. Теорема доказана.
Пусть а-прямая и А—точка‚ не лежащая на этой
прямой (рис. 43). Отрезок АВ с концом В на прямой а
называется перпендикуляром, опу- A
щенным из точки А на прямую а,
если прямые а и АВ перпенди-
кулярны, т. е. пересекаются под
прямым углом. Точка B называется
основанием перпендикуляра. Со- v 7; д д
гласно теореме 4.5 из точки А на д’
прямую а можно опустить и при- Рис. 43-
том только один перпендикуляр.
Пусть С——точка на прямой а, отличная от точки В. Тогда
отрезок АС называется наклонной, проведенной из точки
А к прямой а. Точка С называется основанием наклон-
ной, а отрезок BC ——-проекцией наклонной на_прямую а.
Теорем а 5.6. Перпендикуляр, опущенный из точки
А на прямую а, короче любой наклонной, проведенной
из точки А к прямой а. Из двух наклонных короче та,
у которой проекция меньше. И обратно, большая на-
' клонная имеет большую проекцию.
Д о к а з а т е л ь с т в о. Сравним перпендикуляр АВ с на-
клонной АС (рис. 43). У треугольника АВС угол В пря-
мой. По теореме 5.2 углы А и
А С этого треугольника острые.
~ ' Отсюда по теореме 5.3 заключаем,
что АВ<АС.
Сравним длины двух наклон-
ных АС и AD. Пусть BC<BD.
д д д д д Будем различать два случая:
’ 1) точка В не разделяет точки
Рис. 44- С и D (рис. 43); 2) точка В раз-
деляет точки С и D (рис. 44).
Рассмотрим первый случай. Так как BC<BD, ТО точка С
лежит между В и D. Угол АСВ является внешним углом
треугольника ACD при вершине С. Так как этот угол
острый, то угол С треугольника ACD тупой. Два других
угла треугольника ACD острые. Отсюда по теореме 5.3
заключаем, что AD>AC.
2 A, B. l'1orope.noa- 33
\
Рассмотрим второй случай. Точка В разделяет точки С
и D (рис. 44). Отложим на полупрямои СВ отрезок СС‚,
равный 2СВ. Точка В лежит между С и С‚. Треугольники
АСВ и АС1В равны. Отсюда АС==АС1. А по доказанному
АС‚<АВ.
Третье утверждение теоремы о_том‚ что большая на-
клонная имеет большую проекцию, доказывается от про-
тивного. Читателю предлагается провести это доказатель-
ство самостоятельно.
Треугольник, у которого один из углов прямой, назы-
вается прямоугольным. Два других угла прямоугольного
треугольника острые. Стороны прямоугольного треуголь-
ника имеют специальные названия. Сторона, противолежа-
щая прямому углу, называется гипотенузой. Две другие
стороны называются катетамиг. Для прямоугольных тре-
угольников, кроме уже известных нам трех признаков
равенства, можно указать другие признаки. Именно, имеет
место следующая теорема.
Теорема 5.7. Два прялюугольных треугольника
АВС и A1810, c np;mbMm углами С и С, равны, если
выполняется одно из следующих условий:
1) A181, I A1C1;
2) /-1C“=== A101, A B = А 81;
3) AB=A,B,, 4 В== 4 B1. ‚
Доказательство. Пусть выполняется условие 1).
Докажем равенство треугольников (рис. 45). Отложим на
С
А д,
б’ д с; 5/
Рис. 45.
полупрямой СВ отрезок CD равный C,B,. Треугольники
АСВ и А1С‚В1 равны по первому признаку равенства тре-
угольников. У них АС= А1С1 по условию, углы С и C,
прямые, а СВз-ЩВ, по построению. Из равенства тре-
угольников заключаем, что АО=А1В‚. Но по условию
AB1=AB. Поэтому AD:/LB. Из теоремы 5.6 следует,
что CD»: СВ, т. е. точка D совпадает с В. Следовательно.
треугольник A1018, равен треугольнику АСВ.
84
«',.»"-,3«;_‘.\'@;,,~,,~,«?.-._:‘., ‘дм; .
Пусть теперь выполняется условие 2). Докажем равен-
ство треугольников АВС и А‚‚т. Снова отложим на
полупрямой CB отрезок CD, равный С,В‚. Утверждаем,
что точка D совпадает с B. Допустим, это неверно. Тогда
из трех точек C,B,D одна лежит между двумя другими.
Этой точкой может быть либо B, либо D. Допустим,
точка D лежит между С и B, как изображено на рис. 45.
Так как треугольник ADC равен треугольнику A1B1C1,T0
угол ADC равенуглу ABC. Но угол ADC является внеш-
ним углом треугольника ADB и, следовательно, больше
угла ABD. МЫ пришли к противоречию. Итак, точка B
совпадает с D. Поэтому треугольник А‚‚т равен тре-
угольнику ABC.
Пусть, наконец, выполняется условие 3). Докажем ра-
венство треугольников ABC И А1‚т. Отложим на полу-
прямой ВС отрезок BD, равный ‚т (рис. 46). Треуголь-
ники ABD И A1B1C, равны, так как АВ==А‚В‚‚ В0===
=.==B,C1, A В: A B1. Поэтому угол ADB прямой, т. е.
A A,
сд д 2; Ё
Рис.46.
АВ-„перпендикуляр к СВ. Но из точки A Ha прямую СВ
можно опустить только один перпендикуляр. Поэтому
точка D совпадает с С и, следовательно, треугольник
А,В‚С1 равен треугольнику АВС. Теорема доказана пол-
ностью. '
Теорема 5.8. Биссвктрггсы треугольника пересе-
каются в одной точке.
‘Доказательство. Пусть АВС——данныи треуголь-
пик (рис. 47,_ слева). Напомним, что биссектрисой угла A
треугольника ABC называется полупрямая, проведенная
из вершины А, проходящая между полупрямыми AB И АС,
делящая угол А пополам. По теореме 2.7 эта полупрямая
пересекает сторону ВС в некоторой точке A1, отрезок AA,
называется бггссектрггсой глреугольнггка, проведенной из
вершины А. `
2- 8.5
Проведем биссектрису BB, треугольника из вершины В.
Полупрямая BB, пересекает отрезок AA,. Аналогично
полупрямая AA, пересекает отрезок BB,. Таким образом,
прямые AA, и BB, пересекаются. Они могут иметь только
одну точку пересечения. Эта точка принадлежит и отрезку
б’
fin
A З; с
Рис. 47.
AA, и отрезку BB,. Следовательно, биссектрисы треуголь-
ника, проведенные из вершин А и В, пересекаются в не-
которой точке З.
Проведем полупрямую
и поэтому проходит между полупрямыми CA и СВ. По-
кажем, что полупрямая СЗ является биссектрисой угла С
треугольника. Опустим из точки З перпендикуляры на
прямые AB, BC и СА (рис. 47, справа). Прямоугольные
` треугольники АЗВ, и ASC, равны, так -как у них сторона
АЗ общая, а углы при вершине А равны. Отсюда следует,
ЧТО SBg:-SCQ. ' i
Аналогично из равенства прямоугольных треугольни-
ков BSA, И ВЗС„ заключаем о равенстве SC,..—.—-.SA,,.
Отсюда следует, что SA,===SB,. ‘ .
Прямоугольные треугольники CSA, И CSB, равны,
так как у них гипотенуза SC общая, а катеты SA, и SB,
равны по доказанному. Из равенства этих треугольников
следует равенство углов SCA, и SCB,,. Следовательно,
полупрямая ЗС является биссектрисой угла С треуголь-
ника. Теорема доказана. _
Высотой треугольника ABC, опущенной из вершины А,
называется перпендикуляр AD, опущенный из точки А
на прямую BC (рис. 48). -
Теорема/ 5.9. Если углы В и С треугольника ABC
оба острые, то основание D высоты, опущенной из
вершины А, лежит на стороне
36
СЗ. Она пересекает отрезок AA, ,
.>'s‘-,:a'5‘><,!“\';’3.“ “Ё ,‘;‘. н
ВС, т. е. между точками е";
*'-‘a?<
- .1 .;;,_
В и С. Если угол В тупой, то вершина В лежит между
точками С и D.
Доказательство. Пусть углы В и С острые. Если
точка D He лежит между точками В и С, то либоСрлежит
между В и D, либо В лежит между С и D. Пусть для
определенности точка С лежит между В и D. Тогда острый
угол АСВ является внешним углом треугольника ADC
с прямым углом D. Но это невозможно, так как внеш-
А А
Ё д“, д’ 17 Ё б‘
Рис. 48.
ний угол больше внутреннего не смежного с ним. Ана-
логично доказывается, что точка В не может быть меж-
fly С и D.
ПУСТЬ теперь угол В тупой. Покажем, что точка В
‚лежит между С и D. Допустим, что точка В не лежит
между С и D. Тогда С и D лежат по одну сторону от
точки В. Поэтому внешний угол при вершине В треуголь-
ника ABC является внешним углом при вершине В тре-
угольника ABD. Но это невозможно, так как угол D прямой,
а внешний угол при вершине В острый.
Теорема доказана.
Упражнения
1. Из точки А, не лежащей на прямой а, проведены три
наклонные: АВ, АС и AD. Точка С лежит между В и D. До-
казать, что наклонная АС меньше по крайней мере одной на-
клонной, AB или AD.
2. У треугольников ABC и А,‚т стороны АВ=А‚В‚‚
АС=А‚С„ AA‘ меньше 4А‚.-Доказать‚ что ВС<‚т.
3. Из вершины А треугольника АВС провеёхена биссектриса
п. AD. Доказать, что если АВ> АС, то BD >D
4. Доказать, что медиана треугольника ABC, проведенная
из вершины A, меньше полусуммы сторон AB И АС.
5. Доказать, что биссектриса треугольника не больше ме-
дианы, проведенной из- той же вершины. .
„З?
§ 6. ГЕОМЕТРИЧЕСКИЕ постровнияч
В задачах на построение речь идет о построении reo-
метрической фигуры с помощью данных чертежных ин-
струментов. Такими инструментами чаще всего являются
линейка и циркуль. Решение задачи состоит не столько
в построении фигуры, сколько в решении вопроса о том,
как это сделать, и соответствующем доказательстве. За-
дача считается решенной, если указан способ построения
фигуры и доказано, что в результате выполнения указанных
построений действительно получается фигура с требуемыми
свойствами.
С помощью линейки как инструмента геометрических
построений можно провести произвольную прямую, про-
извольную прямую, проходящую через данную точку,
прямую, проходящую через две данные точки. Никаких
других операций выполнять линейкой нельзя. В частности,
нельзя откладывать линейкой отрезки, даже если на ней
имеются деления. Нельзя пользоваться обоими краями ли-
нейки и т. п.
Циркуль как инструмент геометрических построений
позволяет описать из данного центра окружность данного
радиуса. В частности, циркулем можно отложить данный
отрезок на данной прямой из данной точки.
Рассмотрим простейшие задачи на построение.
Задача 6.1. Построить треугольник с данными
сторонами а, Ь, с (рис. 49, слева).
:‚— а ~1-
Т
Т
д ф а ‘д,
Рис. 49.
Р е ш е н и е. Линейкой проведем произвольную прямую
и отметим на ней произвольную точкуВ (рис. 49, справа).
Раствором циркуля, равным а, описываем окружность с
*) Замечание для учителей. По методическим со-
ображениям мы переходим к вопросу о геометрических по-
строениях. Так как этот вопрос недостаточно подготовлен ‘upe-
дыдущим ‚изложением, то наши рассмотрения в этом параграфе
будут в ряде случаев неполными и не вполне строгими.
-38
а:
а
».1‘..
‚э‘:
‚г‘
.1‘
ь
центром В и радиусом а. Пусть С’——точка ее пересечения
с прямой. Теперь раствором циркуля, равным с, описываем
окружность из центра B, a раствором циркуля, равным b,
описываем окружность из центра С. Пусть А-точка
пересечения этих окружностей. Треугольник АВС имеет
стороны, равные а, b, с.
Задача 6.1 не всегда имеет решение. Согласно теореме
5.4 отрезки а, b, с должны удовлетворять условиям:
a—}—b>c, b—J,—c>a, c+a>b.
‚ Задача 6.2. ‘Отложить от данной полупрямой в
данную. no/Lyn/zocrcocmb угол, равный данному углу.
Р ешени е. Проведем произвольную окружность с
центром в вершине А данного угла (рис. 50, слева)._Пусть
В и С—-точки пересечения окружности со сторонами угла.
6‘ ‘ 6’
Гд д‘ Тд; ‚ч
Рис. 50.
Радиусом АВ проведем окружность C центром в точке
О---начальной точке данной полупрямой. Точку пересече-
ния этой окружности с данной полупрямой обозначим B,
(рис. 50, справа). Опишем окружность с центром В, и радиу-
сом ВС. Точка С, пересечения описанных окружностей в
указанной полуплоскости лежит на стороне искомого угла.
Для доказательства достаточно заметить, что треуголь-
ники АВС и 0810, равны, как треугольники с соответч
ственно равными сторонами. Углы
А и О являются соответствующи- б’
ми углами этих треугольников.
Задача 6.3. Разделить дан- д X”
ный угол пополам.
Решение. Из вершины А д
данного угла, как из Центра, описы-
ваем окружность произвольного Рис. 51.
радиуса (рис. 51). Пусть B и
С--—-точки ее пересечения со сторонами угла. Из то-
чек В и С тем же радиусом описываем окружности.
39
Пусть D ИХ точка пересечения, отличная от А. Полупрямая
AD делит угол А пополам. Это следует из равенства
треугольников. ABD и ACD, y которых углы DAB и DAC
__ ._..._._._.__ _,.._-—..;..-._..
HBHHIOICH соответствующими.
Задача 6.4. Разделить данный отрезок пополам. г
Решение. Пусть АВ-данный отрезок (рис. 52). а
Из точек А и В радиусом АВ описываем окружности.
Пусть С и С‚—точки пересечения этих
окружностей. Они лежат в разных полу-
‘ плоскостях относительно прямой АВ.
Отрезок CC, пересекает прямую AB B
некоторой точке О. Эта точка и есть
средина отрезка АВ.
Действительно, треугольники САСд
и СВС, равны по третьему признаку
равенства треугольников. Отсюда сле-
дует равенство углов АСО и ВСО.
Теперь треугольники АСО и ВСО рав-
с; ны по первому признаку. Стороны АО з’
Р 52 И ВО этих треугольников являются р
"°° ° с0ответству1ощими‚ апоэтому равны. Та-
ким образом, О-—средина отрезка АВ.
Задач а 6.5. Из данной точки О провести перпен-
дикуляр к данной прямой а.
V'.$;%;§:c3Z%1:9k'7
. к п V
б’
am т: .= д‘-
4
Рис. 53.
Решение. Возможны два случая: 1) точка О лежит
на прямой а; 2) точка О не лежит на прямой а.
Рассмотрим первый случай (рис. 53, слева).
Из точки О проводим произвольным радиусом окруж-
ность. Она пересекает прямую в двух точках А и В. Из
40
точек А и В проводим окружности радиусом АВ. Пусть
С—-их точка пересечения. Искомая прямая проходит через
точки О и С. Перпендикулярность прямых ОС и АВ сле-
дует из равенства углов при вершине О треугольников
АСО и ВСО. Эти треугольники равны по третьему при-
знаку равенства треугольников.
Рассмотрим вторсй случай (рис. 53, справа). Из точки
О произвольным радиусом проводим окружность, пере-
секающую прямую а. Пусть А и В-точки ее пересечения
с прямой а. Из точек А и В тем же радиусом проводим
окружности. Пусть О1°-ИХ точка пересечения, отличная
от О. Искомая прямая проходит через точки О и 0,.
Читателю предлагается обосновать это построение.
Одним из методов решения задач на построение яв-
ляется метод геометрических мест. Г еометрическим местом
точек называется фигура, которая состоит из всех точек
плоскости, обладающих определенным свойством. Напри-
мер, по определению, окружность есть геометрическое
место точек, равноудаленных от данной точки. Эта
точка называется центром окружности, а расстояние точек
окружности от центра называется раджа/сом окружности.
Важное геометрическое место точек дает следующая
теорема. „ ‘
Теорема 6.6. Геометрическое место точек, равно-
удаленных от двух точек А и В, есть прял1ая, перпен-
дикулярная отрезку АВ, проходя-
щая через его средину 0 (рис. 54). д
Доказательство. То, что
каждая точка С указанной прямой
находится на одинаковом расстоянии д
от точек А и В, следует из равен- ‘4 д’
ства треугольников АОС и ВОС.
У этих треугольников углы при 5
вершине О прямые, сторона ОС об- Л
щая, а АО==ОВ, так как О—-сре- РИС- 54-
дина отрезка AB. Покажем теперь,
что каждая точка D плоскости, равноудаленная от точек
А и В, лежит на прямой ОС.
Допустим, что точка D не лежит на прямой ОС. Точки
A и В лежат в разных полуплоскостях относительно
прямой ОС. Пусть для определенности точка D находится
в одной полуплоскости с точкой В, как это изображено
на рис. 54. Тогда отрезок AD пересекается с прямой ОС
41
в некоторой точке Е. По доказанному АЕ=ВЕ. По пред-
положению AD:-=BD. Отсюда следует, что в треуголь-
нике ВОЕ DB.-=BE + ED. А это невозможно, так как
сумма двух сторон больше третьей.
, Расстоянием от точки до прямой называется длина
перпендикуляра, опущенного из точки на прямую.
Теорем а 6.7. Геометрическое место точек, равно-
удаленных от двух пересекающихся прямых, состоит
из биссектрис углов, которые получаются в пересечении
этих прямых.
Доказательство (рис. 55). Пусть а-биссектриса
одного из углов и А -— произвольная точка на ней. Опустим
из точки А перпендикуляры на
,9 стороны угла. Пусть В и С—-
основания этих перпендикуля-
‘I’ ров. Из равенства прямоуголь-
д ных треугольников АОВ и АОС
(теорема 5.7) заключаем, что
АВ=АС, т. е. точка А равно-
удалена от данных прямых.
Пусть теперь В-произ-
вольная точка плоскости, равно-
удаленная от данных прямых.
Покажем, что она лежит на
биссектрисе одного из углов. Опустим из точки D nep-
пендикуляры на данные прямые. Пусть B, и С, -——основания
перпендикуляров. По теореме 5.7 треугольники DOB, и
DOC, равны. Отсюда следует равенство углов 0001 и
DOB,. A это значит, что точка D лежит на биссектрисе
угла С1ОВд.
Сущность метода геометрических мест решения задач
на построение состоит в следующем. Пусть, решая задачу
на построение, нам надо построить некоторую точку Х,
удовлетворяющую двум условиям: некоторому условию 1)
и некоторому условию 2). Геометрическое место точек,
удовлетворяющих условию 1), есть некоторая фигура 131,
а. геометрическое место точек, удовлетворяющих условию
2), есть некоторая фигура F9. Искомая точка Х принад-
лежит F, и F2, T. е. является их точкой пересечения.
Если наши геометрические места простые, состоят из
прямых и окружностей, то мы можем их построить и, таким
образом, найти интересующую нас точку Х. Приведем
пример.
42
Рис. 55.
.___‚_. __---„___ ___...._..._._-‘ 1
\
окружностью, описанной около треугольника, назы-
вается окружность, которая проходит через каждую из
вершин треугольника.
Задача" 6.8. Найти отсружность, описанную около
данного треугольника ABC.
Решение (рис. 56). Центр О искомой окружности
находится на одинаковом расстоянии от всех трех вершин
А, В, С. ‘Вместо этого можно сказать, что центр О удовле-
творяет двум условиям: 1) центр окружности находится
на одинаковом расстоянии от вершин А и С; 2) центр
окружности находится на одинаковом расстоянии от вершин
B и С. Геометрическое место точек, удовлетворяющих
первому условию, есть перпендикуляр к стороне АС, про-
веденный через ее средину. Гео-
метрическое место точек, удов-
летворяющих второму условию,
есть перпендикуляр к отрезку
ВС, проведенный через его сре-
дину. Таким образом, Центр О
описанной окружности лежит на
пересечении этих перпендикулярен.
Из этого решения получается
важное следствие. Так как центр
О описанной окружности нахо-
дится на одинаковом расстоянии
от точек А и В, то по теореме 6.6 он лежит на перпендику-
ляре к отрезку АВ‚ проведенном через его средину. Отсюда
следует, что три прямые, проходящие через средины
сторон треугольника, перпендикулярно этим сторонам,
пересекаются в одной точке -— центре описанной окруж-
нести.
Применение метода геометрических мест не всегда так
просто, как в задаче 6.8. Рассмотрим более сложный пример.
Задача 6.9. Даны прямая а, точка А на ней и
точка В, не лежащая на прямой а (рис. 57). Требуется
найти на прямой а такую точку Х, чтобы АХ +XB
было равно данному отрезку т.
Решение. Условия, которым подчинена точка Х,
можно представить в виде двух условий: 1)точка Х лежит
эна прямой а; 2) AX -f—XB== m. Геометрическое место
точек, удовлетворяющих первому условию, есть сама прямая
а. Однако геометрическое место точек, удовлетворяющих
второму условию, довольно сложно. Оно не сводится к
43
прямым и окружностям. Недостаточно представить условия,
определяющие положение точки Х, в виде двух условий.
Надо еще, чтобы каждое из них определяло простое гео-
метрическое место, состоящее из прямых и-ли окружностей.
Умение найти эти условия и является главным в решении
задачи. -
Покажем, как найти эти условия в данной задаче. До-
пустим, что задача решена. Отложим на полупрямой АХ
отрезок АС, равный т. Тогда ХС==ХВ‚ т. е. точка Х
равноудалена от точек В и С. Теперь мы можем форму-
лировать два условия, определяющих положение точки Х:
1) точка Х лежит на отрезке АС; 2) точка Х равноудалена
б’
Рис. 57.
от точек В и С. Первое геометрическое место есть отрезок
АС, второе геометрическое место есть прямая, перпен-
дикулярная отрезку ВС, проходящая через его средину.
Точка Х находится -на_ пересечении этих геометрических
мест. .
Решение задачи на построение предполагает обычно
исследование вопроса о разрешимости задачи и определении
числа решений. Приведем такое исследование для за-
дачи 6.9.
В расположении точки В относительно точки А могут
быть три случая: 1) АВ>т‚ 2) AB.-=m 3) AB<m.
Покажем, что в первом случае задача не имеет решения,
во втором случае задача имеет единственное решение,
в третьем случае задача имеет ровно два решения.
Рассмотрим первый случай. Допустим, некоторая точка Х,
отличная от A, дает решение задачи. Тогда АХ +ХВ=т.
С другой стороны, по свойству сторон треугольника АХВ
АХ+ХВ>АВ Мы пришли к противоречию.
44'
u
J‘, щ и ;Ш_:,щ,‘:‚ддд ;;"%д i_.‘¢f_“;»vv,/.‘»/,- д. д
„1
Е?
9
Если же точка Х совпадает с А (в этом случае предпо-
лагается АХ == О), будем иметь АХ -{— ХВ=АВ>т, т. е.
снова противоречие. Итак, в первом случае, при АВ>т,
задача не имеет решения.
Во втором случае, при АВ=т, единственная точка Х,
дающая решение задачи, есть точка А. Для любой другой
точки AX—|—XB>AB=m.
Рассмотрим, наконец, третий случаи (АВ<т). Покажем
сначала, что задача не может иметь больше двух решений.
Пусть точка Х прямой а дает решение задачи. Как по-
казано выше, точка Х есть пересечение отрезка АС с
перпендикуляром к отрезку ВС в его средине (рис. 57,
слева). Так как отрезок АС, равный т, можно отложить
только двумя способами из точки А на прямой а, то за-
дача может иметь не более двух решений.
Докажем теперь, что два решения действительно су-
ществуют. Для этого достаточно доказать, что перпен-
дикуляр к отрезку ВС в его средине всегда пересекает
отрезок АС, в какую бы сторону ни откладывать отрезок
АС=т из точки А на прямой а.
Допустим, перпендикуляр не пересекает отрезок АС
(рис. 57, справа). Тогда "по теореме 2.1 он пересекает
сторону АВ треугольника ABC B некоторой точке D.
Так как BD=CD, то AB=AD—|—CD>AC. Но в рас-
сматриваемом случае АВ<АС. Мы пришли к противо-
речию. Итак, перпендикуляр к отрезку ВС в его средине
пересекает отрезок АС. Точка пересечения Х дает решение
задачи. Двум способам откладывать отрезок АС==т из
точки А на прямой а соответствуют два решения. Эти реше-
ния, очевидно, различны.
Упражнения
1. Разделить угол на 4 и 8 равных частей.
2. Построить точку Х, которая равноудалена от точек А и
В и находится на данном расстоянии от точки С.
З. Построить треугольник АБС, если заданы сторона АВ,
угол А и сумма двух других сторон AC+BC-.:.-.m.
4. Построить треугольник ABC, если заданы сторона АВ,
угол А и разность дну‘): других сторон АС--ВС==-п.
5. Даны [прямая а и две точки В и С, не лежащие на этой
прямой. I-Iafim на прямой а точку Х такую, чтобы сумма рас-
стоянии ВХ+ХС была наименьшей. Рассмотреть два случая
расположения точек В и С относительно прямой а: 1) точки В
и С лежат по разные стороны от прямой а; 2) точки В и С
лежат по одну сторону от прямой а.
45
‘ § 7. ПАРАЛЛЕЛЪНЫЕ ‚прямые
Теорема 7.1. Если прямые а и Ь_ параллельны, то
каждая из них лежит в одной из полуплоскостей;
определяемых другой прямой.
Д о к а з а т е л ь с т в о (рис. 58). Пусть В —— какая-нибудь
точка на прямой Ь. Она лежит в одной из полуплоскостей,
- на которые прямая а разбивает пло-
..€ «—4_.fi д скость. Допустим, некоторая точка С
прямой b лежит в другой полуплоскости,
а Тогда отрезок ВС пересекается с пря-
_ мой а. Но тогда прямая Ь пересекает-
Рис. 58. ся с прямой а. А это противоречит
условию теоремы. Теорема доказана.
Теорем а 7.2. Если прямая а пересекает прямую b,
то она пересекает любую прямую с, параллельную Ь.
Доказательство. Если прямая а не пересекает
прямую с, то через точку пересечения прямых а и Ь про-
ходят две прямые, параллельные с: прямая а и прямая Ь.
Но это невозможно по аксиоме параллельных V. Теорема
доказана.
Теорема 7.3. Если прямая а параллельна прямой
Ь, а прямая Ь параллельна прямой с, то прямые а и с
параллельны.
Доказательство. Если прямые а и с не па-
раллельны‚ т. е. пересекаются, то через точку их пере-
сечения проходят две прямые, параллельные Ь‚———прямая а
м прямая с. Но это противоречит аксиоме параллельных
V. Теорема доказана.
- б’ к с
А .5’ 2
N
ЁЖ’ Чё
2’ 12- 3,2, д
>——————-
“Е -—'7*7“""‘
Рис. 59.
Пусть а и Ь--различные прямые (рис. 59). Пусть
прямая с пересекает прямые ‘а и Ь в различных точках
А и В. Прямая с разбивает плоскость на две полуплоскости.
Обозначим их 1 И 71. Пусть для определенности полу-
46
Ё `
_..1...._,..———
—.
плоскость т будет правой полуплоскостью на рис. 59.
Прямая а разбивает плоскость на две полуплоскости:
on и щ. Пусть оъ—-—та полуплоскость, в которой лежит точ-
ка В. Прямая b разбивает плоскость на две полуплоскости:
(З и (3,. ПУСТЬ В——та полуплоскость, в которой лежит
точка А.
Прямые а и с, пересекаясь в точке А, разбиваются
этой точкой на две полупрямые. Взяв по одной полупрямой
на каждой из прямых а и с, мы получим угол. Этот угол
вполне определяется указанием двух полуплоскостей: полу‹
плоскости, определяемой прямой а, в которой лежит полу-
прямая прямой с, и полуплоскости, определяемой прямой с,
в которой лежит полупрямая прямой а. Например,
угол, отмеченный цифрой 1, задается полуплоскостями и
и т. В связи с этим углы при точке А можно обозначать
парой полуплоскостей. Например, угол 1 обозначается (а, т).
Углы, образуемые в пересечении прямых а и b с пря‹
мой с, имеют специальные названия. Углы (т, ос) и (т, В),
отмеченные цифрами 1 и 2’ на рис. 59, называются внутрен-
ними односторонними. Углы (т’, оп) и (т’, В), отмеченные
цифрами 4 и 3’, также внутренние односторонние. Углы
(т, ос’) и (т, В), т. е. 2 и 2’, называются соответствующими.
Соответствующие также углы 1 и 1’, 4 и 4’, 3 и 3’. Углы
1 и 3’, 4 и 2’ называются внутренними накрест/лежащими.
Углы 2 и 4’, 3 и 1’ называются внешними накрест/изжа-
щами.
Теорема 7.4. Если две прямые а и b в пересечении
с третьей прямой с образуют внутренние односторонние
углы, сумма которых равна двум
прямым, то прямые а и b не пере-
секаются, т. е. параллельны. \/7
Доказательство. Сохраним
введенные выше обозначения для
полуплоскостей, определяемых пря-
мыми а, b, с. Допустим, прямые а ‚/
и b пересекаются. Точка их пересе- ч
чения С (рис. 60) принадлежит одной ` рис 60
из полуплоскостей т или т1. Пусть ° ' '
для определенности точка С при- '
надлежит правой полуплоскости, т. е. т. Внутренние одно-
сторонние углы (т, ос) и (т, (З), отмеченные на рисунке
Цифрами 1 и 2’, являются угламитреугольника ABC при
вершинах А и В. Таким образом, сумма углов А и В
47
I
2!
29
треугольника АБС равна, двум прямым. Отсюда по cama-
ству смежных углов заключаем, что внешний угол тре-
угольника при вершине А равен углу B треугольника.
Но это противоречит теореме 5.1, согласно которой внеш-
ний угол треугольника больше любого внутреннего, не
смежного с ним. Теорема доказана.
Из свойств смежных и вертикальных углов следует,
что если два соответствующих угла равны или два на-
крестлежащих угла равны, то сумма внутренних односто-
ронних углов равна двум прямым (рис. 59). Поэтому верна
следующая теорема.
Теорема 7.5. Пусть даны две прямые а и b, R70-
торые пересекаются прямой с. Тогда прялсые а и ь
параллельны, если выполняется одно из следующих
условий:
1) два соответствующих угла равны;
2) два накрестлежахцих угла равны.
Теорема 7.6. Если две параллельные прямые а и b
пересекаются прямой с, то сумма двух внутренних
односторонних углов равна двум прямым, сумма двух
внешних односторонних углов равна двум прямым, лю-
бые два соответствующих угла равны, любые два
накрестлежащхгх угла равны.
Доказательство. Пусть А и В-точки пересе-
чения прямой с с прямыми а и b (рис. 61). `Докажем‚ что
сумма двух внутренних односто-
ронних углов равна двум прямым.
Допустим, что она не равна
двум прямым. Тогда существует
отличная от а прямая ад, прохо-
прямые а, и ь в пересечении
с с образуют внутренние одно-
сторонние углы, сумма которых
равна двум прямым. По теореме
7.4 прямая а, параллельна прямой b. Таким образом, через
точку А проходят две прямые а и ад, параллельные b.
Но это противоречит аксиоме параллельных. Первое ут-
верждение теоремы доказано.
Остальные утверждения теоремы вытекают из дока-
занного свойства внутренних односторонних углов
при параллельных и свойств смежных и вертикальных
углов.
48
Рис. 61.
I
дящая через точку А, такая, что‘
Теорема 7.7. Если прямая с пересекает прялшю а
под прямым углом, то она пересекает любую прямую b,
параллельную а, под прямым углом.
Доказательство. То, что прямая с пересекает
прямую b, следует из теоремы 7.2. То, что прямая с пе-
ресекает прямую b под прямым углом, следует из тео-
ремы 7.6. Теорема доказана. С
Т е о р е M a 7.8. Параллельные прямые -- равноотстоя-
щие. Это значит, что перпендакуляры, опущенные из
любых двух точек одной прямой на другую прямую,
равны.
Доказательство. Пусть а и 12-——данные парал-
лельные прямые (рис. 62). Пусть А и В——-две произволь-
ные точки на прямой а. Опустим из
них перпендикуляры на прямую b. 4 д Л
Пусть A, И [За-основания этих
перпендикуляров. По теореме 7.5
прямые AA, И BB, параллельны. д
Треугольники ABA, и B,A,B ‘ r д д
равны. У них сторона A,B общая. ’ ‘ ’
Углы ABA, и B,A,B равны, как P”°' 62'
внутренние накрестлежащие при па-
раллельных а и b. Углы B,BA, И AA,B равны, как внут-
ренние накрестлежащие при параллельных AA, и B8,. из
равенства треугольников заключаем, что AA,=BB,. Teo-
рема доказана.
Теорема 7.9.- Геометрическое место точек пло-
скости, расположенных по одну сторону от данной
прямой а и равноудаленных от этой прямой, есть пря-
мая, параллельная а.
Доказательство. Пусть В-точка геометриче-
ского места и Ь—-прямая, параллельная прямой а, проход
дящая через точку В. По теореме 7.8 прямая 12 принад-
лежит геометрическому месту. Покажем, что каждая точка
геометрического места принадлежит прямой b.
Пусть Х --- произвольная точка искомого геометриче-
ского места. Проведем через точку Х прямую, перпенди-
кулярную прямой а. Она пересекает прямую а в некото-
рой точке А, а прямую b B некоторой точке B,. Точка Х
лежит на полупрямой AB,. Так как отрезки AB, и AX
равны, то точка Х совпадает с B,. Таким образом, req-
метрическое место состоит из точек прямой b И только
этих точек. Теорема доказана. '
49
Теорема 7.10. Сумма углов треугольника равна
двум прямым. -
Доказательство. Пусть АВС——данный треуголь-
ник (рис. 63). Проведем через вершину С треугольника
прямую а, параллельную прямой АВ. Отметим на прямой а
две точки А, и 81, расположенные в разных полупло-
скостях относительно прямой АС. Пусть для определен-
41 д д; ноститочка B, будет в той же по-
ч? луплоскости, в которой лежит точ-
ка В. Точки А, и В лежат в разных
полуплоскостях относительно пря-
‘мой "АС. Поэтому отрезок А1В пе-
ь - ‚ ресекается с прямой АС. Точка пере-
44 сечения принадлежит полупрямой СА‚
Pnc..63. так как эта полупрямая и отрезок
А1В лежат в одной полуплоскости
относительно прямой а. Отсюда следует, что полупрямая
СА проходит между СА, и CB. Поэтому угол А1СВ ра-
вен сумме углов А1СА и АСВ.
По свойству нракрестлежащих углов при параллельных
угол А1СА равен углу ВАС, угол B1CB равен углу ABC.
Поэтому сумма углов треугольника АБС равна сумме
смежных углов АдСВ и ВЮВ, т. е. двум прямым. Теорема
доказана.
Теорема 7.11. У прямоугольного треугольника
острые углы дополняют друг друга до прямого, ,т. е.
сумма острых углов равна прямому. '
Эта теорема непосредственно вытекает из теоремы 7.10.
Теорема 7.12. Внешний угол треугольника равен
сумме двух внутренних, не смежных с ним.
Доказательство. Пусть АВС——даннь1й треуголь-
а
%1
НИК. Внешний угол при вершине А является смевжным_
углу А треугольника и поэтому дополняет угол А до двух
прямых. Так как сумма всех трех углов треугольника
равна двум прямым, то внешний угол при вершине А
.равен сумме углов В и Стреугольника. Теорема доказана.
Мы будем говорить, что два угла имеют параллельные
стороны, если прямые, на которых лежат эти стороны,
параллельны.
Теорема 7.13. Углы с параллельными сторонами
либо равны, либо дополняют тдругдруга до двух прямых.
Доказательство. Пусть стороны и, и b, первого
угла лежат на прямых а и b, a стороны с, и л, второго
50
угла лежат на прямых с и d. Пусть для определенности
прямая а параллельна с, а прямая b параллельна d (рис. 64).
Прямая с пересекает прямую Ь в некоторой точке С.
По свойству углов, образуемых параллельными прямыми Ь
и d B пересечении с прямой с, углы, образуемые пря-
мыми Ь и с в точке С, и углы, образуемые прямыми с
4’;
б;
‚4 -
/д Ь
‚д с
Рис. 64.
и d B точке В, либо равны, либо дополняют дРУг друга
до двух прямых. То же относится к углам, которые обра-
зуют прямые а и Ь в точке А, и углам, которые образуют
прямые Ь и с в точке С. Отсюда заключаем, что углы
(ад, Ь1) и (с1‚ d1) либо равны, либо дополняют друг друга
до двух прямых. Теорема доказана.
Теорема 7.14. Углы с перпендикулярными CHIOPO1
налил либо равны, либо их сумма равна двум прялшм.
Доказательство. Пусть а и Ь-—-прямые, содер-
жащие стороны первого угла, а с и с1—прямые, содер-
жащие стороны второго угла. Пусть для определенности
прямая а перпендикулярна с, а прямая Ь перпендику-
лярна d. Будем различать два случая: 1) прямые а и Ь
перпендикулярны; 2) прямые а и Ь не перпендикулярны.
Рассмотрим первый случай. Так как прямая а перпен-
дикулярна Ь и перпендикулярна с, то прямые Ь и с либо
параллельны, либо совпадают. Аналогично прямые а и d,
будучи перпендикулярны прямой Ь, либо параллельны, либо
совпадают. Отсюда по теореме 7.12 заключаем, что пря-
мые с и d перпендикулярны.
Рассмотрим второй случай. Пусть прямые а и Ь не
перпендикулярны. Пусть 0-- их точка пересечения (рис. 65)
Возьмем на прямой а точку А и опустим из нее перпен-
дикуляр АВ на прямую Ь. Опустим из точки В перпенди-
куляр BC на прямую а. По теореме 5.9 T0‘lKa C лежит
51
между О и А. Углы АОВ и АВС равны, так как оба они
дополняют угол ОАВ до прямого. Стороны угла ABC
параллельны прямым с и d. Отсюда по теореме 7.13
заключаем, что углы между прямыми
д а а и b, c и d либо равны, либо до-
полняют друг друга до двух прямых.
д Теорема доказана.
д Задача 7.15. Провести через
д д ь точку В прямую, параллельную
данной прямой а.
PW 55- P em е н и е. Проводим через точ-
ку В прямую b, перпендикулярную
прямой а (задача 6.5). Проводим через точку В пря-
мую с, перпендикулярную прямой b. По теореме 7.4 пря-
мая с параллельна прямой а.
Упражнения
1. АвСе-равнобедренный треугольник с основанием АВ и
боковыми сторонами АС и ВС. Доказать, что сумма расстояний
произвольной точки Х, взятой на основании АВ, от прямых AC
и ВС постоянна, т. е. не зависит от точки Х.
2. Найти геометрическое место точек, сумма расстояний
которых от двух пересекающихся прямых постоянна.
З. Найти геометрическое место точек, находящихся на дан-
ном расстоянии от заданной прямой.
4. Найти геометрическое место средин отрезков с концами
на двух данных параллельных прямых.
5. Найти геометрическое место точек, равноотстоящих от
двух данных параллельных прямых.
6. Доказать, что медиана прямоугольного треугольника, про-
веденная из вершины прямого угла, равна половине гипотенузы.
7. Доказать, что если в прямоугольном треугольнике один
из острых углов равен 30°, то противолежащий ему катет равен
половине гипотенузы.
8. Найти геометрическое место средин отрезков данной
длины с концами на двух перпендикулярных прямых.
§ в. чвтьпрвхугольники.
ПАРАЛЛЕЛОГРАММ. трапеция
Четырехугольником ABCD называется фигура, кото-
рая состоит из четырех точек А, В, С, D no три, не ле-
жащих на одной прямой, и четырех отрезков АВ, BC, CD
и AD, соединяющих эти точки (рис. 66). Точки А, В, С,
52
D называются вершинами. четырехугольника, а отрезки
АВ‚ BC, CD, DA называются его сторонами. Вершины А
и С, В и D называются противолежащими вершинами.
Стороны АВ и CD, BC и AD называются противолежа-
щими сторонами. четырехугольник называется выпуклым,
если он расположен в одной полуплоскости относительно
\\5/’
\
\\
//A
c\
A
L‘ //_fi\\
в
Рис. 66. Рис. 67.
прямой, содержащей любую его сторону (рис. 67). От-
резки, соединяющие противолежащие вершины четырех-
угольника, называются диагоналями.
Теорема 8.1. Диагонали выпуклого четырехуголь-
ника пересекаются.
Доказательство. Пусть АВСВ—выпуклый че-
тырехугольник (рис. 67). Полупрямые DA И DB лежат
в одной полуплоскости относительно прямой DC. По тео-
реме 2.5 либо полупрямая DA проходит между полупря-
мыми DB И DC, либо полупрямая DB проходит между
полупрямыми DA и DC. Первая возможность исключается,
так как полупрямая DA не пересекает отрезок ВС. Таким
образом, полупрямая DB проходит между полупрямыми
DA И DC. Отсюда следуеъ что отрезок AC пересекается
с прямой DB. Аналогично доказывается, что отрезок BD
пересекается с прямой АС. Так как прямые АС и BD
могут иметь только одну точку пересечения, то она при-
надлежит отрезкам AC и BD, T. e. диагоналям четырех-
угольника. Теорема доказана.
Углом А выпуклого четырехугольника ABCD назы-
вается угол между полупрямыми АВ и AD. Угол B—~—-are
угол между полупрямыми BA и ВС и т. д.
_ Теорема 8.2. Сумма углов выпуклого чепгырех-
угольника равна четырем прямым.
53
Доказательство (рис. 68). Полупрямая DB про-
ходит между полупрямыми ОА и DC, так как пересекает
отрезок АС (теорема 8.1). Поэтому угол D четырехуголь-
ника равен сумме углов АОВ и СОВ.
д’ Аналогично угол В четырехугольника
д равен сумме углов АВО и СОВ. От-
сюда следует, что сумма углов че-
тырехугольника равна сумме углов
д двух треугольников АВО и СОВ, т. е.
четырем прямым. Теорема доказана.
А Параллелограмм-это четырех-
угольник, у которого противолежа-
Рис‘ 68‘ щие стороны параллельны т. е. ле-
жат на параллельных прямых.
Теорема 8.3. Параллелограмм есть выпуклый rte-
тырехугольник.
Доказательство (рис. 69). Возьмем какую-нибудь
сторону параллелограмма, например AD. По теореме 7.1
прямая BC лежит в одной полуплоскости относительно
прямой AD. По теореме 2.4 отрезки АВ и CD лежат
в той же полуплоскости. Таким образом, весь паралле-
лограмм лежит в одной полуплоскости относительно пря-
мой, содержащей сторону AD. Взяв другую сторону па-
раллелограмма, приходим к такому же выводу. Теорема
доказана.
Теорема 8.4. У параллелограмма противолежащие
стороны равны, протпволежащие углы равны.
Д о к а з а т е л ь с т в о (рис. 69). Проведем диагональ ВО.
Треугольники ВОС и ОВА равны. У них сторона ВО
общая. Углы СВО и АОВ равны,
как внутренние накрестлежащие д- --д
при параллельных прямых ВС и
AD. Углы СОВ и АВО равны,
как внутренние накрестлежащие
при параллельных AB И СО. Из -
равенства треугольников заклю- P140-59.
чаем, что АВ==СО‚ ВС==АО‚
А A-..-..-- А С. Равенство других противолежащих углов
доказывается проведением другой диагонали. Теорема
доказана.
Теорема 8.5. Если у выпуклого четырехугольника
две противолежащие стороны параллельны и равны, то
четырехугольник есть параллелограмм.
54
Если у выпуклого четырехугольника противолежащие
стороны равны, то он есть параллелограмм.
Д о к а з а т е л ь с т в о. Проведем диагональ BD четырех-
угольника ABCD (рис. 69). Оба утверждения теоремы сле-
дуют из равенства треугольников ABD И CDB. B первом
случае эти треугольники равны по первому признаку pa-
венства треугольников. Во втором случае—по третьему
признаку равенства треугольников.
Теорема 8.6. Диагонали параллелограмма делятся
точкой пересечения пополам.
Доказательство (рис. 70). По теореме 8.1 диаго-
нали параллелограмма пересекаются в некоторой точке О.
Треугольники АОВ и COD равны. У этих треугольников
АВ=С[), как противолежащие стороны параллелограмма.
Углы АВО и СОО, ВАО и DCO равны, как внутренние
накрестлежащие при параллельных AB И CD. Из равенства
треугольников следует, что АО===ОС, B0=OD. Теорема
доказана.
4- ч? “у ЁГ
й > 0 < Й
д- —д ~ то
Рис. 70. Рис. 71.
9
Прямоугольник- это четырехугольник, у которого все
углы прямые (рис. 7_1). \
Teo p ем а 8.7. Прямоугольник есть параллелограмм.
Диагонали прямоугольника равны.
Доказательство. Пусть АВСО——данный прямо-
угольник (рис. 71). Прямые AD и ВС‚ будучи перпенди-
кулярны АЬ’, являются параллельными (теорема 7:4). Ана-
логично заключаем о параллельности сторон AB и DC.
Следовательно, прямоугольник есть параллелограмм.
Второе утверждение теоремы следует из равенства
прямоугольных треугольников DAB И СВА. У них углы
А и B прямые, катет АВ общий, а катеты DA И СВ
равны, как противолежащие стороны параллелограмма.
из равенства треугольников следует, что AC=BD. Teo-
рема доказана.
Ромб —это параллелограмм, у которого все стороны
равны (рис. 72).
55
Теорема 8.8. Диагонали ромба пересекаются под
прямиым углом. Диагонали ромба являются биссектри-
сами его углов.
. Доказательство. Пусть АВСВ-данный ромб
(рис. 72). Треугольники АОВ и СОВ равны‚'так как
д АВ==ВС по определению ромба,
АО===ОС по теореме 8.6, сторона OB
общая. Так как углы АОВ и СОВ смеж-
ные, то они, будучи равны, прямые.
д Из равенства треугольников АОВ
и СОВ следует также, что углы АВО
и СВО равны, т. е. диагональ BD яв-
ляется биссектрисой угла В ромба.
Теорема доказана.
Квадрат —— это прямоугольник, у ко-
торого все стороны равны. Квадрат
является ромбом, поэтому обладает
. свойствами прямоугольника и ромба.
Теорема 8.9. Пусть три параллельные прямые а,
ь, с пересекаются прямыми d и а, в точках А, В, С и
А1‚ В1, С, соответственно (рис. 73).
Тогда, если точка В лежит между А и С, то
точка В, лежат между “A1 и Сд. Если АВ=ВС‚ то
A18,-:—=B1C1.
Л
Рис.’ 72.
0'
а [А фи ` А \4’ —^Д
д I5 И ‘ в д;
° с [С д} (‘Г .]\6}
I \ Г Е \
Рис. 73. Рис. 74.
Доказательство. По теореме 7.1 прямая ь лежит
в одной из полуплоскостей относительно прямой а. Обо-
значим эту полуплоскость а. Ту полуплоскость, опреде-
ляемую прямой с, B которой лежит прямая b, обозначим_
через т. Таким образом, прямая b лежит в каждой из
полуплоскостей а и т. Часть прямой щ, которая лежит
в полуплоскостях а и т, состоит из точек отрезка А1Сд
и только этих точек. Поэтому точка B1, B которой пере-
56
Ёьцььдд
секаются прямые b и 41, принадлежит отрезку А1С1.' Пер-
вое утверждение теоремы доказано.
Докажем второе утверждение (рис. 74). Проведем через
точку B, прямую ED, параллельную прямой d. Треуголь-
ники В1А1В и В1С1Е равны. У них В1В==В1Е, так как
В1В=АВ, а В1Е=БС. Углы А1БВ1 и С1ЕВ1 равны, как
внутренние накрестлежащие при параллельных AD И СЕ.
Углы А1В1!) и С1В1Е равны, как вертикальные. Из равен-
ства треугольников следует, что
А1В1=В1С1. Теорема доказана в д
полностью.
Транецией называется выпук-
лый четырехугольник, у которого д‘ д
только две противоположные сто- Рис. 75.
роны параллельны. Эти стороны
называются основаниями трапеции. Две другие стороны
называются боковыми сторонами (рис. 75). Трапеция,
у которой боковые стороны равны, называется равнобокой.
Отрезок, соединяющий средины боковых сторон, называется
средней линией трапеции.
Т е о р е м а 8.10. Средняя линия пфанеции параллельна
основаниям и равна полусумме оснований.
Доказательство. Пусть АВВ1А1—-данная трапе-
ция, АА1 и ВВ1 ее основания и СС1--средняя линия
' (рис. 76). Проведем через точ-
ку С прямую, параллельную
‚61 ё? 17}
` основаниям. По теореме 8.9
/ она пересекает отрезок А1В1
д 5}
‘Ё 4
/ посредине. Следовательно, сред-
" няя линия трапеции параллель-
д" на основаниям.
Проведем через точку С1
прямую Е1В1, параллельную
стороне АВ. Точки A и В ле-
жат по одну сторону прямой Е1О1. Точки В1 и А1 лежат
по разные стороны этой прямой. Пусть для определенно-
сти точка B, лежит с той же стороны, что и точки А, B.
Точки B, и ID, лежат по одну сторону от АВ. Поэтому
В не лежит между В1 и 01. Следовательно, В1 лежит
между В и 01.
Из равенства треугольников С1В101 и С1А1Е1 следует,
что В1О1=Е1А1. По свойству ‚параллелограмма СС1=
3 BD1-'7-3 BB1+B1D1,CC1 1 AE1 1" AA} """"‘ А1В1. СКЛЗДЫВЗЯ
57
Рис. 76.
P
эти равенства почленно, получим 2CC1-_:.—AA1+BB1.
Теорема доказана.
Средней линией пгреугольнагка называется отрезок,
соединяющий средины двух сторон.
Теорема 8.11. Средняя линия A181 треугольника
АВС (рис. 77) параллельна стороне АВ и равна nono-
вине этой стороны.
Доказательство этой теоремы аналогично доказательству
предыдущей теоремы и предлагается читателю в качестве
упражнения.
Рис. 77.
Рис. 78.
T еорем а 8.12. Все три медианы птреугольнтгка пере-
секаются в одной точке. Эта точка делит каждуют
медиану в отношении 2: 1, считая от вершины.
Доказательство. Пусть АБС-данный треуголь-
ник, AA1 и BB1-—-mse его медианы (рис. 78). Полупрямая
AA1 пересекает отрезок ВС, поэтому пересекает медиану
BB1. Аналогично заключаем, что полупрямая BB1 nepece-
кает отрезок AA1. Прямые BB1 и AA1MoryT иметь только
одну точку пересечения. Она принадлежит каждой из ме-
диан, т. е. медианы пересекаются. Пусть О-—точка пере-
сечения медиан AA1 И BB1.
Проведем среднюю линию A1B1 треугольника ABC
и среднюю линию A1B1 треугольника AOB. Обе они па-
раллельны стороне АВ и равны половине этой стороны.
Отсюда следует, что четырехугольник A1B1A1B1 есть парал-
лелограмм. По свойству параллелограмма B10-—-—-OB1,
a OBg=BgB по построению. Таким образом, медиана AA1
делит медиану BB1 B отношении 2: 1. Медиана, прове-
денная из точки С, делит медиану BB1 B том же отно-
шении. Поэтому и она проходит через точку О. Теорема
доказана.
58
.4
‚Теорема 8.13. Три прямые, перпендикулярные сто-
ронам треугольника, проходящие через средины сторон,
пересекаются в одной точке.
Доказательство. Пусть АВС—данный треуголь-
ник и а, Ь, с——прямые‚ перпендикулярные его сторонам,
проходящие через средины сторон (рис. 79). Прежде
всего покажем, что прямые а и Ь
пересекаются. Действительно, если
они не пересекаются, т. е. параллель-
ны, то прямые АС и ВС, будучи им
перпендикулярны, тоже параллельны.
Но прямые АС и BC пересекаются
в точке C. Итак, прямые а и Ь пе-
ресекаются’ в некоторой точке О.
По теореме 6.6 точка О одинаково
удалена от точек А и С и от точек РИС- 79-
B и C. Следовательно, она одинаково
удалена от точек А и В. По теореме 6.6 она принадле-
жит прямой с. Теорема доказана. "
Теорема 8.14. Три прямые, проведенные через вер-
шины треугольники: перпендикулярно его сторонам, nape-
секаются в одной точке.
Доказательство. Пусть АБС-данный треуголь-
ник и а, Ь, с——прямые‚ проходящие через его вершины
перпендикулярно противополож-
4 ным сторонам (рис. 80). Про-
" ведем через вершины треуголь-
д ника прямые, параллельные про-
д тивоположным сторонам. Они
А д пересекаются в точках А1, B1, C1.
д По свойству параллелограмма
AC=BA,, AC-=C1B. Отсюда
C1B=BA,. Аналогично заклю-
25; чаем, что С1А=АВ1, В1С=СА1.
Из теоремы 8.13 следует, что
прямые а, Ь, с, проходящие че-
рез средины сторон треуголь-
ника А,В1С‚ перпендикулярно этим сторонам, пересекаются
в одной точке. Теорема доказана, ‚
Задача 8.15. Разделить данный отрезок АВ на п
равных частей.
Решение. Проведем из точки А произвольную полу-
прямую а, не лежащую на прямой АВ. Отложим на
59
Ч
ъй
Щи
Рис. 80.
полупрямой а равные отрезки AA” A,A9, . . . , A,,_,A,,. Прове-
дем через точки Ад и В прямую b. Прямые, параллель-
ные b, проходящие через точки Аь Ад, A3, . . ., А‚,_„ пересекают
отрезок АВ в точках B1, Bg, ..., B,,__,, которые делят
отрезок АВ на п равных отрезков (теорема 8.9).
Упражнения
1. Доказать, что сумма диагоналей выпуклого четырехуголь-
ника меньше периметра четырехугольника (суммы его сторон),
но больше полупериметра.
2. Доказать, что если диагонали четырехугольника пересе-
каются, то он выпуклый.
З. четырехугольник деформируется, оставаясь выпуклым,
так что его стороны не изменяются по длине. Доказать, что если
одна диагональ увеличивается, то вторая уменьшается.
4. Доказать, что средины сторон выпуклого четырехугольника
являются вершинами параллелограмма.
5. Доказать, что если диагонали выпуклого четырехугольника
точкой пересечения делятся пополам, то этот четырехугольник
“ЕСТЬ napannenorpamm.
6. Доказать, что параллелограмм, у которого диагонали равны,
есть прямоугольник.
7. Доказать, что если диагонали параллелограмма являются
биссёектрисами соответствующих углов, то параллелограмм есть
ром .
° 8. Доказать, что выпуклый четырехугольник, у которого
противоположные углы равны, есть параллелограмм.
9. Пусть а-—прямая‚ не пересекающая сторон треугольника.
Доказать, что сумма расстояний вершин треугольника от пря-›
мой а равна утроенному расстоянию точки пересечения медиан
треугольника от этой прямой.
9. ДВИЖЕНИЯ. РАВЕНСТВО ФИГУР. СИММЕТРИЯ.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС '
Пусть даны две фигуры F И F’. Мы будем говорить,
что между точками фигур установлено взаимно однознач-
ное соответствие, если точки фигур объединены в пары
(Х, Х’) так, что каждая точка Х фигуры F и каждая
точка Х’ фигуры F’ принадлежит одной и только одной
паре. Точки Х и Х’ фигур будем называть соответст-
вующими точками. Таким образом, каждая точка Х фи-
гуры F имеет вполне определенную соответствующую
точку Х’ фигуры F’ и наоборот. Вместо взаимно однознач-
ного соответствия между точками фигур F и Р’ можно
говорить о взаимно однозначном отображении фигуры Р
60
на фигуру F’. Взаимно однозначное отображение называется
так же одно-однозначным. Приведем пример.
Пусть фигура F есть прямая а, а фигура F’ есть пря-
мая а’. Пусть, далее, Ь—произвольная прямая, пересекаю-
щая а и а’ (рис. 81). Произвольная прямая, параллельная b,
пересекает прямую а в некоторой точ- ‚
кеХ,апрямуюа’внекоторойточкеХ’. 0/ \€ д
Объединим каждые такие Цветочки
в пару (Х, Х’). Это объединение то- у/ ‚у
чек в пары есть одно-однозначное 7 \
соответствие между прямыми а и а’. -
Взаимно однозначное отображе- Рис. 81.
ние плоскости на себя называется
движением, если оно сохраняет расстояния. Это значит,
что если Хи У-две произвольные точки и Х’, Y’-——co-
ответствующие им точки, то Х Y.=X’Y’.
Teop ем а 9.1. Если при движении mpzz точки А, В, С,
лежащие на прялюй, переходят в точки А’, В’, С’, то
эти точки также лежат на одной прямой. Если точка В
лежит между А и С, то точка В’ лежит между А’ и С’.
Доказательство. Если точки А’, В’, С’ не лежат
на одной прямой, то они являются вершинами треуголь-
ника. Поэтому A’C'<A’B’+B'C’. По свойству движения
отсюда следует, что AC<AB—{,—BC. Однако по свойству
I
"измерения отрезков АС==АВ+ВС. Мы приходим к про-
тиворечию. Итак, точки А’, В’, С’ лежат на одной прямой.
Покажем, что точка B’ ЛЕЖИТ между А’ и С’. Допустим,
что А’ лежит между В’ и С’. Тогда А’В’—{—А’С’=В’С’ и,
следовательно, АВ+АС=ВС. Но это противоречит
равенству, полученному выше: АВ+ВС=АС. Аналогично
доказывается, что точка С’ не может лежать между А’ и В’.
Теорема доказана.
Пусть задано некоторое движение, т. е. взаимно одно-
значнсе отображение плоскости на себя, сохраняющее рас-
стояния. Пусть F —произвольная фигура в этой плоско-
‘cm. Когда точка Х описывает фигуру F, соответствующая
ей пртдвижении точка Х’ описывает некоторую фигуру F’.
Эта фигура называется равной F. _
Тео р е м а 9.2. Фигура, равная отрезку, есть равный
ему отрезок. Фигура, равная треугольнику, есть равный
ему пгреугольник.
Читателя не должна смущать формулировка этой Teo-
ремы. Дело в том, что понятие равенства отрезков и
61
треугольников нами введено раньше, до понятия‘ равенства
фигур вообще, которое введено только что. Отрезки мы
называли равными, если они имели одинаковые длины.
Треугольники мы называли равными, если они имели рав-
ные углы и соответствующие стороны. Теоремой утверж-
дается, что понятие равенства фигур в применении к от-
резкам и треугольникам имеет прежнее значение.
Доказательство теоремы 9.2. Пусть Р-дан-
ный отрезок и Р’——равная ему фигура. Пусть А и B--
КОНЦЫ отрезка F, a A’ и Н-соответствующие им точки
фигуры F’. Возьмем произвольную точку Х на!‘ отрезке F.
По теореме 9.1 соответствующая точка Х’ фигуры F’ при-
надлежит отрезку А’В’. Таким образом, все точки фигуры F’
принадлежат отрезку А’В’.
Покажем теперь, что каждая точка отрезка А’В’ при-
надлежит фигуре F’. Пусть Х’-—произвольная точка от-
резка А’В’. Три точки А’, X’, B’ лежат на одной прямой,
причем точка Х’ лежит между А’ и В’. По свойству дви-
жения (теорема 9.1) точка Х, соответствующая X’, лежит
на прямой АВ между точками А и В, т. е. принадлежит
отрезку АВ. Следовательно, точка Х’ является точкой
фигуры F’. Итак, точки отрезка А’В’ и только они являются
точками фигуры F’. Следовательно, фигура F’ есть отре-
зок А'В’. Этот отрезок имеет ту же длину АВ=А’В’.
Первое утверждение доказано.
Пусть теперь F есть треугольник ABC. Обозначим
А’, B’, С’-—точки фигуры F’, соответствующие точкам
A, B, C. Точкие А’, B’, C’ не лежат на одной прямой, так
как в противном случае точки А, В, С лежали бы на
одной прямой (теорема 9.1). По первой части теоремы,
которая доказана, фигура F’ состоит из трех отрезков
А’В’, В’С’ и С’А’‚ т. е. является треугольником. Этот тре-
угольник равен треугольнику ABC, так как AB---—-A’B’,
АС =А’С’‚ BC.-=B’C’. Теорема доказана. '
Точка X плоскости называется неподвижной точкой
при данном движении, если соответствующая ей точка Х’
плоскости совпадает с Х.
Теорема 9.3. Если при движении три точки IMO-
скости, не лежащие на одной прямой, неподвижны, то
все точки плоскости неподвижны.
Доказательство. Пусть А и В—-—две неподвиж-
ные точки плоскости. Покажем‘, что все точки прямой АВ
являются неподвижными. Пусть Х ---произвольная точка
62 ’
прямой АВ, отличная от точек А и В. Из трех точек А,
B и Х одна лежит между двумя другими. Пусть для опре-
деленности это ‘будет точка X. По теореме 9.1 соответст-
вующая точке Х точка Х’ лежит на прямой AB между
А и В. Таким образом, обе точки, Х и Х’, лежат на по-
лупрямой АВ. Так как АХ = АХ’, то Х’ совпадает с Х.
В других случаях взаимного расположения точек А, В
и Х доказательство аналогично.
Пусть теперь А, В, С-—три неподвижные точки, не
лежащие на одной прямой. Пусть Х —произвольная точка
плоскости. Проведем через точку Х какую-нибудь прямую,
которая имеет с прямыми АВ, АС и ВС две общие точки Р
и Q. По доказанному точки Р и Q являются неподвижными.
Поэтому все точки прямой PQ являются неподвижными.
В частности, неподвижной будет точ-
ка Х. Теорема доказана. 4
Пусть а-некоторая прямая и Х --
произвольная точка плоскости. Прове- ‚
дем через точку Х прямую b, перпенди- __f
кулярную а. Она пересечет прямую а д
в некоторой точке А. Построим теперь
точку Х’ по следующему правилу. Если
точка Х лежит на прямой а, то-Х’ сов-
падает с Х, если Х не лежит на а, то P14032-
Х’ лежит в другой полуплоскости отно-
сительно прямой а на прямой b, причем расстояния АХ и
АХ’ равны (рис. 82). Точка Х’ называется симметричной
точке Х относительно прямой а. Точка Х является симмет-
ричной точке Х’ относительно прямой а. Отображение пло-
скостигна себя, при котором точке Х сопоставляется точ-
ка“ ’‚ симметричная относительно прямой а, называется
преобразованием симметрии или зеркальным опграженагем.
Теорем а 9.4. Зеркальное отражение относительно
прямой есть движение.
‚Доказательство. Пусть Х и Y—-11Be произволь-
ные точки и Х’, У’--соответствующие им симметричные
относительно прямой а точки. Утверждение теоремы со-
стоит в том, что Х Y =X’Y’. Рассмотрим сначала случай‚
когда точки Х и Y не лежат на прямой а и не лежат
на прямой, перпендикулярной а (рис. 83). Прямоугольные
“треугольники АВХ и АВХ’ равны, так как у них катет
-АВ обьций, а катеты ХА и Х’А равны по определению
‘зсимметрии. Отсюда следует, что ХВ== Х’В, A XBA=
63
=4Х’ВА. Теперь треугольники X YB и X’Y'B равны.
У них ХВ=Х’В‚ YB-= YB, A YBX=4 Y’BX’. Из
равенства этих треугольников. следует, что Х Y-..:X’ Y’.
B других случаях расположения точек Х и Y, когда
одна или обе они лежат на прямой а или лежат на пря-
мой, перпендикулярной а, устанавли-
X, вается то же равенство Х У== X’Y'.
««- Читателю предлагается проверить
это в качестве упражнения. Теорема
доказана.
Если при зеркальном отражении
у 5 y’ относительно прямой а фигура F .
l переходит в себя, то эта фигура .
P1/;c,83, называется симметричной, а пря-
- мая а называется осью симметрии
фигуры. Биссектриса угла при вершине равнобедренного
треугольника является его осью симметрии. Диагонали
ромба являются его осями симметрии. Прямые, проходящие
а
{Г А
Рис. 84.
через точку пересечения диагоналей прямоугольника па-
раллельно его сторонам, являются осями симметрии. Диа-
гонали квадрата и прямые, проходящие через точку nape-
сечения диагоналей параллельно , ‚ ‘
его сторонам, являются осями X
симметрии (рис. 84). Читателю д
предлагается доказать эти утверж-
дения в качестве упражнения. X
Пусть О—-—некоторая точка
плоскости и X -—произвольная Рис. 85.
точка. Построим точку Х’ по сле-
дующему правилу. Если точка Х совпадает с 0. то Х’ есть
точка О. Если точка Х не совпадает с О, то точка Х’ лежит
на прямой ХО, причем точка О лежит между Х и Х’ и рас-
стояния ХО и ОХ’ равны (рис. 85). Построенная так
64
точка Х’ называется стшметричной относительно точки О.
Преобразование плоскости в себя, при котором каждой
точке Х по указанному правилу сопоставляется точка Х’,
называется преобразованием симметрии относительно
точки О.
Тео р е м а 9.5. Преобразование czmmenzpzzu относи-
тельно точки есть движение, ‘
Доказательство. Пусть Х и Y--11136 ПрОИЗВОЛЪ-
ные точки и Х’, Y’ ——соответствующие им точки при сим-
метрии относительно точки О. Теоремой утверждается,
что Х Y= X’Y’. Рассмотрим I
сначала случая, когда точки Х X 7
и Y не совпадают с точкой
О и не лежат на одной пря-
мой, проходящей через точку 0
О (рис. 86). -.
Треугольники XOY и X’O.Y’ V Х’
равны. У них углы при вер- Рис. 86.
шине О равны, как вертикаль-
ные, а ХО=ОХ’‚ YO==OY’ no определению симметрии.
Из равенства треугольников следует, что Х Y =X'Y’. ‘
B других случаях расположения точек Х и Y ornam-
TEJIBHO точки О получается то же заключение X Y :.-...-X’Y’.‘
Читателю предлагается проверить это в качестве упраж-
нения. Теорема доказана.
Если при симметрии относительно точки О фигура F
переходит сама в себя, то она называется цгнпгральносггм-
медициной. Точка О называется центром симлеепдоии.
Параллелограмм является центральносимметричной фигурой.
Егоцентром симметрии является точка пересечения диаго-
налей. Читателю предлагается доказать это утверждение
в качестве упражнения.
Пусть Од и ОГ-две различные точки плоскости. Пусть
X ——произвольная точка плоскости. Построим точку Х’,
симметричную точке Х относительно точки 0,, a затем
построим точку Х”, симметричную точке Х’ относительно
точки O2 (рис. 87). Так как преобразование симметрии
относительно точки сохраняет расстояния, то последователь-
ное выполнение этих преобразовании есть движение. Движе-
ние, которое сопоставляет точке Х точку Х”, построенную
указанным образом, называется параллельным переносом.
Отрезок 0105, является средней линиеи треугольни-
ка XX’_X” (рис. 87). Отсюда следует, что отрезок XX’
3 A, B, Погорелов ' 65
параллелен отрезку 0102 и в два раза больше этого отрезка.
Таким образом, ‚при параллельном переносе точка Х пере-
ходит B точку Х” прямой, параллельной 0109, проходящей
через точку Х. Точка Х” находится на расстоянии 20109
от точки 26
Пусть щ и саг-две различные прямые, пересекающи-
еся в точке 0. Пусть Х -— произвольная точка плоскости.
Построим точку Х’, симметричную точке Х относительно
прямой щ, а затем построим точку Х”, симметричную
точке Х’ относительно прямой ад (рис. 87, справа). Так
как преобразование симметрии относительно прямой со-
храняет расстояния, то последовательное выполнение этих
X II
92
X I
д х
Рис. 87.
преобразований есть движение. Движение, которое сопостав-
ляет точке Х точку Х" указанным образом, называется
поворотом относительно точки 0.
Если прямые щ и ад перпендикулярны, то поворот
сводится к симметрии относительно точки 0. Если прямые щ
и ac; не перпендикулярны, то угол ХОХ” не зависит от
точки Х и равен удвоенному острому углу, под которым
пересекаются прямые щ и ag. Этот угол называется углом
поворота. Наметим доказательство этого утверждения.
Пусть точка Х’ находится внутри острого угла, обра-
зуемого прямыми щ, ад, и оъд, сиг-части этого угла, на
которые он разбивается полупрямой ОХ’ (см. рис. 87,
справа). Тогда по свойству симметрии относительно пря-
мой угол XOX’ равен Ёщ, а угол X'OX” равен 2%. Соот-
ветственно угол ‘ХОХ” равен 2оъ1+2оъ9=2(оъ1+оъ9). Чита-
телю предлагается рассмотреть случай, когда точка Х’
лежит внутри тупого угла, образуемого прямыми ад и ад,
а также случай, когда прямые ад и ад перпендикулярны.
Упражнения
1. Доказать, что треугольник ABC можно совместить с лю-
бым равным ему треугольником А’В'С' не более чем тремя
зеркальными отражениями.
2. Доказать, что любое движение можно получить не более
чем тремя зеркальными отражениями.
3. Доказать, что если две точки А иВ при движении остаются
неподвижными, то либо все точки неподвижны, либо это движе-
ние есть зеркальное отражение относительно прямой АВ.
4. Доказать, что если точки Х и У при параллельном пере-
носе переходят в точки Х’, У’, то либо прямые XY И X’Y’ совпа-
дают, либо они параллельны.
5. Доказать, что два зеркальных отражения, выполненных
последовательно относительно двух параллельных прямых, дают
параллельный перенос.
6. Даны две окружности м, kg И прямая а. Найти на окруж-
ностях k, И kg такие точки Х, и X2, чтобы прямая а была пер-
пендикулярна отрезку X,X9 и пересекала его посредине.
7. Даны две окружности kl, kg И точка О. Найти на окруж-
ностях такие точки Х, и X2, чтобы точка О была среднной
отрезка X ,X2.
§ 10. окружность
Окружное/пью называется геометрическое место точек
плоскости, равноудаленных от некоторой данной точки.
Эта точка называется центром окружности, а расстояние
от центра до точек окружности называется радиусом.
Радиусом называется также отрезок, соединяющий центр
окружности с какой-нибудь ее точкой.
Отрезок, соединяющий две точки ок— L
ружности, называется хордой. Хорда, А \ I
X
а
проходящая через центр окружности, 2’ К
называется диалгепгром.
Т е о р е м а 10.1. Каждый диаляетр д
окружности является осью симмепг-
рии. Центр окружности является
центром силшегприи.
Доказательство. Пусть a--
диаметр окружности и X -—произволь- РИС- 88-
ная точка окружности (рис. 88). Построим
точку Х’, симметричную точке Х относительно диаметра а.
Из равенства прямоугольных треугольников ОХА и ОХ’А
заключаем, что ОХ = OX’. A это значит, что точка Х’‚лежит*
на окружн.ости. Итак, при симметрии относительно диаметра
з» . 67
/Y/I
е‘ .
окружность переходит в себя, т. е. диаметр является осью
симметрии. _
Построим теперь точку X”, симметричную точке Х
относительно центра (рис. 88). По определению симметрии
ОХ ==OX", т. е. точка X” ЛЕЖИТ на окружности. Следо-
вательно, центр окружности является
центром симметрии. Теорема доказана.
.4 д’ Теорема 10.2. Диаметр, перпен-
дикулярный хорде, делит хорду по-
полам.
Доказательство. Пусть АВ--
данная хордаи С--ее средина (рис. 89).
Проведем диаметр через точку С. Тре-
РИС- 89- угольники ОАС и ОВС равны по
третьему признаку равенства. Из равен-
ства этгтх треугольников следует, что их углы при вер-
шине С, будучи равными и смежными, прямые. Таким об-
разом, диаметр ОС перпендикулярен хорде AB и делит
ее пополам. Другого перпендикулярном хорде АВ диаметра
не существует, так как через точку О можно провести
только одну прямую, перпендикулярную прямой AB. 'Гео-
рема доказана.
Теорем а 10.3. Всякая хорда не больше диаметра.
Она равна диаметру пголько тогда, если сама является
дхтамепцэом.
Д о к а з а т е л ь ств о. Допустим, хорда АВ не является
диаметром (рис. 89). Тогда в треугольнике ОАВ имеем
АВ<АО+ВО, а АО+ВО равно
диаметру. Теорема доказана.
Теорема 10.4. Равные хорды
одинаково удалены от центра on:--
руэюноспти. Большая хорда ближе
к центру.
Доказательство. Пусть АВ
и шву-данные хорды, С и C,-—
их средины (рис. 90). Если хорды
равны, то прямоугольные треуголь-
ники ОСВ н ОС1В1 равны. Отсюда - .
следует, что хорды одинаково удалены от центра: ОС= ОС1.
Пусть АВ<А1В1. Покажем, что ОС> OC1. Допустим,
что OCQ OC1. Построим треугольник ВСЕ, равный ОС‚А1.
По свойству наклонных ED,,>.:OE> OB. Но DE и OB равны
радиусу. Мы пришли к противоречию. Теорема доказана.
68
Прямая, проходящая через точку А окружности, назы-
вается касательной, если она перпендикулярна радиусу,
проведенному в точку А. Точка А называется точкой ка-
сания.
Т е о р е м а 10.5. Касательная имеет с окружностью
только одну общую точку.
Дока_зательство. Пусть БМ-любая точка каса-
тельной, отличная от точки касания А (рис. 91). По cacti-
ству перпендикуляра и наклонной ОВ>ОА, т. е. точка В
не может быть точкой окружности. Теорема доказана.
Рис. 91. ‘ Рис. 92.
Пусть А и В-тдве точки окружности (рис. 92). Про-
ведем через них прямую. Она разбивает плоскость на две
полуплоскости. Части окружности, лежащие в этих полу-
плоскостях, мы будем называть дугами окружности. Если
АВ-диаметр, то дуги окружности называются полуок-
ружнослгнмгг.
Если хорда AB не является диаметром, то мы различаем
дуги окружности следующим образом. Одна из полупло-
скостеи, определяемых прямой АВ, содержит центр окруж-
ности. Дугу, которая лежит в этой полуплоскости, будем
называть дугой, большей полуокружность, а другую дугу —-
дугой, меньшей полуокружносгпи. Радиусы, проведенные
в точки дуги, тяеньшеи полуокружности, пересекают отре-
зок АВ, а радиусы, проведенные в точки‘ дуги, большей
полуокружностп, не пересекают отрезок AB. .
Центральным углом, отвечающим данной дуге, мы
будем называть ‘фигуру, которая состоит из лучей, исхо-
дящих из центра окружности и пересекающих эту дугу.
На рис." 92 показаны лучи угла, большего полуокружности.
' Для центральных углов вводим угловую меру по сле-
дующему правилу. Если соответствующая дуга меньше
69
полуокружности, то за меру‘ центрального угла принимаем
обычную меру угла, образуемого полупрямыми ОА и ОВ.
Если дуга равна полуокружности‚ т. е. АВ есть диаметр,
ности)
Угол, вершина которого А ne-
угол‚ соответствующий той из этих дуг, которая не содер-
жит точку А, называется центральным углом, соответ-
случае центральный угол, соответствующий вписанному
л
то угловую меру полагаем равной 180°. Наконец, если
A дуга больше полуокружности, за
- угловую меру принимаем 360°--оъ°,
где оъ°——градусная мера дополни-
тельного угла (меньшего полуокруж-
жит на окружности, а стороны пере-
Aw
секают окружность в точках В и С,
Рис. 93. отличных от А, называется ammun-
ным в окружность (рис. 93). Пря-
мая ВС разбивает окружность на две дуги. Центральный
ствующим данному вписанному углу. .
Т ео ре м а 10.6. Угол, вписанный в окружность, равен
половине соответствующего центрального угла.
Д о к а з ат е л ь с т в о. Рассмотрим сначала случай, когда
одна из сторон угла является диаметром (рис. 94). В этом
Рис. 94. Рис. 95.
углу А, равен углу ВОС. Треугольник АОВ равнобедрен-
ный. Его углы А и В равны. Внешний угол треугольника
при вершине О равен сумме углов А и В. Отсюда следует,
что угол А равен половине соответствующего централь-
ного угла.
Пусть теперь ни одна из сторон вписанного угла не
является диаметром. Проведем диаметр из вершины А
вписанного угла. Будем различать два случая: 1) стороны
угла А разделяются диаметром АО (рис. 95); 2) стороны
70
угла А не разделяются диаметром. Рассмотрим первый
случай. По доказанному дВАВ=-%- ДВОЕ, (CAD:
==== Ё- A COD. Если центральный угол, соответствующий
углу А, меньше полуокружности (рис. 95, слева), то от-
сюда заключаем, что L BAC== -2- BOC. Следовательно, угол
ВАС равен половине соответствующего центрального угла.
Если центральный угол, соответствующий вписанному
углу А, больше полуокружности (рис. 95, справа), то
ABOD= l80°— A/-10B, A_COD==180°— ДАОС. От-
сюда заключаем, что A ВАС ._—-= -%—(360° -— Д, ВОС), т. е.
угол ВАС равен половине соответствующего центрального
угла. Второй случай рассматривается аналогично. Теорема
доказана.
Из теоремы 10.6 непосредственно вытекает следующая
теорема.
Теорема 10.7. Все вписанные углы, стороны кото-
рых проходят через точки А и В окружности, а вер-
шина лежит на одной из дуг, определяемых прямой
АВ, равны (рис. 96). В частности, углы, опщяающиеся
на диаметр, прямые.
Рис. 96. Рис. 97.
Теорема 10.8. Углы между касательной к окруж-
ности и хордой с концом в точке касания измеряются
половиной центральных углов, отвечающих дугам, на
которые хорда делит окружность (рис. 97).
Читателю предлагается доказать эту теорему в качестве
упражнения.
Теорема 10.9. Пусть даны окружность paauyca R
с центром О и прямая а, которая проходит на рас-
cmomum h om центра окружности. Тогда прямая не
71
пересекает окружное
онруоюносгпа, если h ==
в двух точках, если h<R.
ТО каждая точка прямой нахо
та, если h>R, прямая касается
R, прямая пересекает окружность
В одном из пунктов доказательства этой теоремы мы
воспользуемся теоремой 13.1 (теоремой Пифагора). Эта Teo-
рема гласит, что
квадрат гипотенузы равен сумме квад
к доказательству теоремы Пифагора лежит через теоре-
мы 11.5, 11.4, 11.2, 11.1. B этих теоремак и их доказа-
ТСЛЬСТВЗХ даже СЛОВО «ОКРУЖНОСТ
этому теорема Пифа
ремы 10.9 И ссылка на теорему Пифагора в доказательстве
теоремы 10.9 вполне допустима.
у каждого прямоугольного треугольника
ратов катетов. Путь
ь» не произносится. По-
гора доказывается независимо от тео-
Доказательство теорем ы 10.9. Если h>R,
ДИТСЯ на расстоянии, боль-
шем R, от’ центра окружит
сти и, следовательно, не мо-
жет принадлежать окружно-
сти, т. е. прямая и окружность
не пересекаются.
Если h == R, то основание
в птерпендвтсуляра, опущенного
I из центра окружности на
- прямую, лежит на окруж-
17 ности. В этой точке окруж—
Рис. 98. ность касается прямой по
определению касательной.
Рассмотрим случай h<R (рис. 98). Опустим из Центра
окружности перпендикуляр на прямую а. Пусть A-ocuo~
вание этого перпендикуляра. Отложим от точки А на Epst-
мой а отрезки АА1 и ААд, равные
Пифагора h
ОАЁ =_____. he +(1,/R2 _____ на? Z Не,
оА; = не + (1/R9 _- 11%)? =..- т.
Итак, 0A1:-—-OAg=R. Следовательно, точки А, и Ад ле‹
жат на окружности, т. е. являются точками пересечения
прямой а и окружности.
Докажем, что других точек пересечения прямой и
окружности несуществует, Допустим, существует третья
точка пересечения A3. Тогда либо AA3>AA,, либо
A/-13<AA1. По свойству наклонных, проведенных из од-
72
1/R2-- т. По теореме =
‘fj‘:“..', .‘T‘.I . ‚ м... _ .. .. .
' ^ мьдд. - ч. у _ _ _. ~12. ‚г. ;.‹‚_ .- .- „ж. . „А _ .;
~ ~ 21.4 и к к ~ д, д: . - '
гной точки (теорема 5.6), в первом случае OA3> OA1:=_— R,
во втором случае OA3<OA,, Т. е. точка A3 He лежит на
окружности. Теорема доказана.
четырехугольник называется вписанным в окружность,
если его вершины лежат на окружности.
Теорема 10.10. Сумма противолежащих углов
вписанного выпуклого четырехугольника равна двум
прямым.
Доказательство. ПустьАВСВ-- 5
выпуклый четырехугольник, вписан-
mm в окружность (рис. 99). Согласно
теореме 8.1 диагонали выпуклого че- 17
тырехугольника пересекаются. Отсюда
следует, что вершины А и С принад- д
лежат различным лугам, на ‚которые д
прямая BD разбивает окружность. По-
этому центральные углы, соответствую- РИС- 99-
щие этим дугам‚ дополняют друг друга
до 360°. А это значит, что углы А и С четырехугольника
дополняют друг друга до 180°, т.- е. их сумма равна двум
прямым. Аналогично доказывается, что сумма углов B и
D четырехугольника тоже равна
двум прямым. Теорема дока-
зана. `
четырехугольник называется
описанным около окружности,
если его стороны касаются ок-
ружности.
Т е о р е м а 10.11. Суммы про-
тиволежащих сторон описанно-
го четырехугольника равны.
Доказательство. Пусть
Pm 100. АВСВщ-описанный четырехуголь-
ник (рис. 100). Пусть Ад, B1, Си
„ 01*—"ТОЧКИ касания сторон с ок-
ружностью и 0-——центр окружности. Прямоугольные тре-
угольники ОА1В и ОВдВ равны. У них гипотенуза OB об-
щая, а катеты ОА, и OB, равны, как радиусы. Отсюда
следует ВА1=ВВ‚. Аналогично доказываются равенства
AA,==AD,, DC,=DD,, CC,-..=.-CB1. Складывая эти равен-
ства почленно, получим АА‚-{—ВА‚+СС‚+ВС1=ВВ1 -
+CB,+DD1+AD,, T. e. AB+CD=:—-AD+BC. Тео-
рема доказана. ..
73
Задача 10.12. Построить касательную н данной
окружности: с центром О, проходящую через данную А.
Решение (рис. 101). Строим окружность на отрезке
OA, как на диаметре. Пусть B И Вр-точки пересечения
этой окружности с данной. Прямые
АВ и AB, являются касательными
к данной окружности, так как углы
OBA и ОВ1А прямые (теорема 10.7).
Упражнения
1. Найти геометрическое место ос-
нований перпендикулярен, опущенных
рис- 101- из данной точки В на прямые, про-
ходящие через данную точку А.
2. Найти геометрическое место вершин С треугольников
ABC с заданным основанием АВ и углом при вершине С.
3. Найти геометрическое место средин хорд, проходящих
через данную точку.
4. Две окружности пересекаются в двух точках: С и С1.
Через точку С, проводят произвольную прямую а, которая пере-
секает окружности в точках A и В. Доказать, что угол
не зависит от прямой а.
5. Через точку касания двух окружностей проводят произ-
вольную прямую а. Она пересекает окружности в точках А и В.
Доказать, что касательные в точках А и В параллельны.
6. Построить треугольник ABC no стороне АВ, углу С,
высоте или медиане из угла С.
§ п. половин треугольников
Треугольники ABC И А‚В‚С1 называются подобными,
если у них
AA: AA1. AB: 1.81. AC:-= АС:
АВ АС вс
Е??? ‘”‘" ТЮ? “ЕЁ?
Короче говоря, треугольники подобны, если у них соот-
ветствующие углы равны, а соответствующие стороны
пропорциональны. Подобие треугольников обозначается
значком м. В данном случае AABCN AA1B1C1.
Теорема 11.1. Если у двух треугольников ABC u
A1810, LA:-= AA, и [_B-.= 481, то треугольники
подобны. ‘
74
Доказательство. Так как сумма углов треуголь-е
ника равна двум прямым, то из равенства углов А и Ад,
В и В1 следует равенство углов С и С1. Докажем про-
порциональность сторон.
Отложим на полупрямой АВ отрезок ABg, равный 21,3,
(рис. 102). Проведем через точку B2 прямую, параллель‹
ную ВС. Она пересечет полупрямую АС в некоторой
точке Се. По свойству углов при параллельных ВС и ‚ф
д Д
5 д,
3 дд
6’ д д) д
б’
9 б; /L “д?
Рис. 102. Рис. 103.
и секущей ВВ, углы АВС и АввСа равны. Поэтому тре-
угольник АВЕС, равен треугольнику А‚В1С‚, в частности
AC9-"=A1C1.
Возьмем малый o'rpe3o1</AP, на полупрямой AB так,
чтобы два отношения АЗ и -421 не были целыми. По-
АР, АР,
строим на полупрямой AB точки Pg, P3, P4, так, чтобы
АР‚‚=/гАР1. Пусть п-целое от деления ‚ а т——
1
целое от деления AB” . Тогда точка В находится тиежду
АР,
Р„ и P,,+,, a B2—Me>K11y Pm и Рт +1.
Проведем через точки Pk прямые, параллельные ВС.
По теореме 8.9 эти прямые пересекают полупрямую АС
в точках 621, С2е‚ Q3: причем отрезки С21С2ь Q2Q3.
Q3Q4, равны. Точка С лежит между точками Q” и Q,,+,,
а точка С‚—между Qm и Q,,,+, (рис. 103).
Имеем
nAP1< АВ <(п +1)AP1,
тАР1 < 1482 +1)AP1.
Отсюда следует, что
п АВ n + 1
т +1 <"z§;< m о (1)
75
Аналогично получаем
п АС п + 1 `
т + 1 < ‘но; <"7r'- (г)
Из неравенств (1) и (2) следует, что
n n+1 AB AC n+1 n
<AB2 < """
"" "75? т“
т+1 т т m+1’
T. е.
АВ ___ AC <m+n+1
AB; AC2 т (m+1)’
Так как п<т‚ то
m+n+1 1 ‚1 З
т(т+1) < m+1+W<zrz'
Поэтому
\ AB AC
2 p
--—-—---—--—.:- --. 3
‘AB, AL2 < т ( )
Если взять отрезок AP, достаточно малым, то число
т будет сколь угодно велико, а будет сколь угодно
мало. Поэтому неравенство (З), справедливое при любом т,
возможно только тогда, когда
АВ ____ АС
АВ, щ AC2 '
Так Как ABg=A1B,, а Acgix’-11C}, TO
` .5:.§_.... „ее.
A,B, "" A,C, '
Аналогично доказывается, что
АС ___ BC
A,C, "" B,C ‘
Теорема доказана.
‘Г е о р е м а 11.2. Если -y треугольников АВС и А‚В‚С1
AA з: A A1 и АВ AC
...._. „т .......,_ 4
A18, мс, ’ ( )
то треугольники подобны.
Д о к а з а т е л Ь с т в о. Построим треугольник А9‚т‚
у которого А‚в‚=А‚в‚‚ 4A9 т: ДА, A B9: AB. По
76
теореме 11.1 треугольники ABC и A2896, подобны. Следо-
вательно‚
AB AC `
<5’
Так как А9В‚=А,В,‚ то из равенств (4) и (б) следует,
что A269.-.-.--A,C1. Теперь заключаем о равенстве треуголь-
НИКОВ A1B1C1 И АдВддСЗ. у НИХ A131-""-‘JAQBQ, АдСдшАдСд,
4;/1, в 4.42. Так как треугольники АВС и AgBgCg подобны,
а треугольники A.3BgCg И АдвдСд равны, то треугольники
АВС и А‚ВдС‚ подобны. Теорема доказана.
Т е о р е м а 11.3. Если у треугольников АВС и АдвдСд
_d§..._4_§_...££'_. (д,
Адвд — Адб‘, "° 8,6‘, ’
то илреугольнггпи подобны. у
Д о к а з а т е л ь с т в о. Построим треугольник А‚‚т‚
у КОТОРОГО AgBg ""--3'-'“ A181, Ада; 1 A161 Н А Ag Ё А А. ’
По теореме 11.2 треугольники АВС н A,B,C, подобны.
Следовательно,
АС ____ BC
<7’
Так как A902...--=A,C,, то из равенств (б) и (7) следует,
что BgCg=B,C,. Теперь заключаем о равенстве треуголг»
пиков /1985.0, И АдвдСд по третьему признаку равенства.
Так как треугольник АВС подобен треугольнику А‚В9С‚‚
а треугольник A9BgCg равен треугольнику 2113101,’ то
треугольники АВС и A1310, подобны. Теорема доказана.
Теорем а 11.4. Два прямоугольных треугольники
подобны, если выполняется одно из следующих условии’:
1) один из острых углов первого треугольника равен
одному из ослгрых углов второго нгреуголвника;
2) катеты первого треугольника пропорциональны
кометам второго треугольники,-
3) гипотенуза и катет первого теугольнина про-
порциональны гипотенузе и катету второго треуголь-
нива.
Д о к а з а т е л ь ст в о. Подобие треугольников при усло-
вии 1) следует из теоремы 11.1, так как прямые углы тре-
угольников равны. Подобие треугольников при условии
2) следует из теоремы 11.2. так как катеты заключают
равные (прямые) углы.
7?
‚Докажем подобие‘ треугольников при выполнении
третьего условия.
Пусть АБС и А1Б‚С1-—прямоугольные треугольники
с прямыми углами С и С1‚ причем
АВ АС
<8’
Построим прямоугольный треугольник АьвьСд с прямым
углом Cg, скатетом А2Сь‚ равным A1C,, и острым углом Ад,
равным A.
Треугольник АьБаСд подобен треугольнику ABC, так как
выполняется условие 1). Поэтому
АВ АС
<9’
Так как А„С„==А1С„ то из равенств (8) 121(9) следует, что
AgBg=A1B,. По теореме 5.7 о равенстве прямоугольных
треугольников треугольники А2В2Сь и А1Б1С1 равны. Так
как треугольник ABC подобен треугольнику AgB2C2, a тре—
угольник АьвдСд равен треугольнику А‚Б‚С‚‚ то треуголь-
ники ABC и A1B,C1 подобны. Теорема доказана.
Пусть ABC “прямоугольный треугольник с прямым
углом С (рис. 104). Проведем из вершины прямого угла
высоту CD. По теореме 5.9 основание D высоты лежит
между А и Б. Отрезки AD и BD называются проекциями
катетов на гипотенузу. ~
Теорема 11.5. У прямоугольного треугольника au-
сота, проведенная из прямого угла, есть среднее гео-
метрическое ‚между проекциями катетов на гипотенузу.
Каждый катет есть среднее геометрическое „между
гипотенузой и проекцией катета на гипотенузу.
Доказательство (рис. 104).
д Углы CAD и BCD равны, так как
каждый из них дополняет угол АВС до
прямого. По теореме 11.4 треугольни-
ки CAD И BCD подобны. Из подобия
д д 5 треугольников следует
Рис. 104. Q_[_)_ г: fig
BD CD °
Отсюда CD’:-—-—AB-BD, T. e. CD:-=1/AD-BD. Первое
утверждение доказано.
78
‘ ‹_‹;;„с‚:.‘:м„ t . .‚ у 7:2: м. .-. ‚- у 1.
' - А.“ ‘ .- -. 5 '.. . м-‚да *- ( ,.‚
' ~ не‘ у- А _ .,. __. ‚„.. - ,.~:_:.~,:';x ‘ r
Из подобия треугольников ВС0 и ВАС следует, что
ЁЁ__Ё
‘CB""BD’
Отсюда CB’.-== AB - во, т. е. св == V AB . во. Аналогично
доказывается, что AC=..-I/AB-AD. Теорема доказана.
Теорема 11.6. Buccercmpuca AD треугольника ABC
делит противоположную сторону ВС на отрезки, про-
порциональные сторонам АВ и АС, т. е.
5f‘_§._..é§
BD""'CD‘
Доказательство (рис. 105). Если угол А0С Спря-
мои, то утверждение теоремы следует из равенства тре-
угольников А0В и ADC. Если угол
ADC не прямой, то один из углов
ADB или ‘ADC тупой. Пусть для оп-
ределенности А0В-—тупой угол. Опу‹
стим из точки B перпендикуляр ВЕ
на прямую А0. Точка D лежит между
А и Е (теорема 5.9). Построим точку
01, симметричную точке D относитель-
но точки Е. Угол 80,0 равен углу
8001, следовательно, равен углу ADC. «Q4
Треугольники АВ0‚ и АС0 подобны, РИС- 105-
так как А ВА01= А CAD, a А А0‚В==
-== А ADC. Из подобия треугольников следует пропорция
I
£Q_n...fl!.3i.
DC ‘AC’
Но В01=В0. Поэтому %%=%Ё„ т. е.
§_l2......l2§
AB""AC’
Теорема доказана.
Пусть дана окружность с центром О и радиусом R.
Если точка Х плоскости находится на расстоянии, мень-
шем R, от центра О окружности, то мы будем говорить,
что эта точка лежит внутри окружности. Если- точка X
79
находится на расстоянии, большем R,- то ‘M51 будем гово-
рить, что она лежит вне окружности. _ ~
' T e о р е м а 11.7. Если прямая проходит через точку 8,
лежащую внутри окружности, то ama прямая пересе-
кает окружность в двух точках, причем точка 8
лежит между этими точками
Доказательство. То, что прямая пересекает ок-
ружность в двух точках, следует из теоремы 10.9, так как
прямая отстоит от центра на расстоя-
д нии, меньшем радиуса. Докажем, что
точка 8 леэкит между точками пере—
сечения. '
‘Пусть Отцентр окружности и
А, ,В--точки пересечения прямой
с окружностью (рис. 106). Если точ-
ка 8 не лежит между А и В, то
либо точка А лежит между B И S,
либо точка В лежит между А и 8
Пусть для определенности А лежит между В и 8, как
изображено на рисунке. Треугольник АОВ равнобедренный,
ОА=ОВ. Поэтому угол ОАВ острый. Соответственно
смежный ему угол ОА8 тупой. Поэтому в треугольнике
S A д
Рис. 106.
О8А должно быть- 08 > ОА. Но ОА --— радиус окружности, -
а 08 меньше радиуса по условию. Мы пришли к противо-
речию. Теорема доказана.
Теорема 11.8. Пусть через топку 8, лежащую
внутри окружности, npoxoaum произвольная прямая.
Пусть А и В-тонки пересечения д
этой прямой с окружностью. Тогда
произведение отрезков А8'и В8 не
зависит от взятой прялюгг, т; е. д
AS-BS постоянно. ‘
Доказательство. Проведем
любую другую прямую через точку 8.
Она пересечет окружность в точках
С и D (рис. 107). Проведем через
точки В и D прямую. Она раз-
деляет окружность на две дуги. Точки А и С лежат в однои
полуплоскости относительно прямой BD, именно в Ton
полуплоскости, где лежит точках8. Поэтому точки A и С
принадлежат одной дуге. Отсюда по теореме 10.6 заклю-
чаем, что углы DAB и DCB равны. Аналогично доказы-
вается, что углы АВСи ABC равны. Теперь по теореме 11.1
80
д д’
Рис. „107.
.::‘.-.v;!_-' д у . ‚М ‚7
‘ч
заключаем о подобии треугольников ASD и С8В. Из по-
добия треугольников следует пропорция
’ As__os
С? "‘ ЁЁ '
T. e. AS-BS:-CS-DS. Теорема доказана. ‚ ‚
Теорема 11.9. Пусть точка 8 лежит вне окруж-
ности с ценгпром О и а -—прямая‚ проходящая через
точку 8, пересекающая окруж- 0
ность в точках А и В. Тогда точка
8 не разделяет точки А и В, т. е.
не лежит между А и В.
Доказательство. _1_Tpe1mo.r1o-
жим, что точка 8 разделяет точки д - ч д
А и В(рис. 108); Треугольник АОВ A 5
равнобедренный, так как ОА и OB —- Рис. 108-
радиусы. Поэтому углы А -и В ост-
рые. Из двух смежных углов О8А и OSB _ один не
меньше прямого. Допустим, это угол О8А. Тогда в тре-
угольнике О8А должно быть ОА>О8. ‚Но ОА-радиус
окружности, а 08 больше радиуса по условию. Мы при-
шли к противоречию. Теорема доказана. `
Теорема 11.10. Пусть через точку 8, лежащую
вне окружности, проходит произвольная прямая, пере-
.. секгающая окружность в точках А
С Ё и В. Тогда произведение отрезков 8А
и 8В не зависит от взятой пряной
и равно квадрату отрезка касатель-
ной 8С (рис. 109).
Доказательство. Пусть точка
_ B лежит между А и 8, как изображено
А на рисунке. Тогда треугольники 8АС
и 8СВ подобны. У них угол 8 общий,
РИС- 109- a углы CAB и ВС8 равны, так как
измеряются половиной одного и того же
центрального угла. Из подобия треугольников следует про-
порция
CS ____ §§_
XS‘ — СЗ‘
Отсюда А8— Б8=(С8)°. Теорема доказана.
За д а ч а 11.11. Даны три отрезка а, b, с. Поспгроить
.‚ be
четвертая; о/нрезок x==—--3.
81
Решение. Проведем из произвольной точки О две
полупрдмые р и q, не лежащие на одной прямой (рис. 110).
На полУпрямой р отложим отрезки ОА=а и‘ 0B=b. Ha
полупрямой q отложим отрезок ОС = с. Соединим точкиА
и С прямой и проведем прямую, параллельную ‘АС, через
точку В. Она пересекает полупрямую q B точке D. из.
подобия треугольников ОАС и OBD следует, что отрезок
ОП-т-ЁЧ.
Л .
7 ё
Рис. по. Рис. ш.
Задача 11.13 Даны два отрезка а и b. Построить
отрезок x.-=1/ab.
P e ш е н и е. На произвольной прямой р отметим точку С
и отложим от этой точки в разные стороны на прямой р
отрезки CAM СВ, равные а и b соответственно (рис. 111).
Построим на отрезке АВ, как на диаметре, окружность.
Перпендикуляр к АВ, проходящий через точку С, пересе-
кает окружность в двух точках: D, и Щ. Отрезок CD1
1-..-
равен 1/аь, так как СО‚=СВ‚‚ а CD1-CD.3=-...-ab (тео-
рема 11.8).
Упражнения
1. Биссектриса внешних углов при вершине С треуголь-
ника ABC пересекается с прямой АВ в точке D. Доказать, что
AD ___ AC
BD BC‘
2. доказать, что геометрическое место точек плоскости, от-
ношение расстояний которых от двух данных точек постоянно
(не равно единице), есть окружность.
3. Доказать, что геометрическое место точек, отношение pac-
стоянии которых от двух данных пересекающихся прямых по-
стоянно, состоит из двух прямых.
4. Пусть диагонали выпуклого четырехугольника точкой пед
ресечения делятся на отрезки, произведения которых одинаковы.
Доказать, что тогда четырехугольник — вписанный в окружность.
82
5. На прямой даны три точки А, В, С. Точка Влежит между
А и С. Через точки А и В проводим произволь ую окружность,
а из точки С проводим касательную к этой ок ужности. Дока-
зать, что геометрическое место точек касания есть окружность
с центром С.
6. Доказать, что геометрическое место точек, для которых
касательные к двум данным пересекающимся окружностям равны,
есть прямая, проходящая через точки пересечения окружностей.
Эта прямая называется радикальной осью окружностей.
7. Доказать, что радикальные оси трех попарно пересекаю-
щихся окружностей либо параллельны, либо пересекаются в одной
точке.
8. Угол при вершине равнобедренного треугольника равен З6°.
Доказать, что биссектриса треугольника, проведенная из вер-
шины при основании, отсекает треугольник, подобный данному.
§ 12. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ.
Г ОМОТЕТИЯ. ИНВЕРСИЯ
Преобразованием подобия называется взаимно одно-
значное отображение плоскости на себя, при котором для
любых двух точек Х и Y и соответствующих им точек Х’, Y’
XY
отношение -X-77-,7 постоянно, т. е. не зависит от взятых точек
Х и Y. Это отношение называется коэффициентом по-
добил.
Пусть О--произвольная точка плоскости. Поставим
в соответствие каждой точке Х плоскости точку Х’ по
следующему правилу. Если точка Х совпадает с 0, то Х’
есть точка О. Если Х отлична от О, то Х’ лежит на по-
лупрямой ОХ на расстоянии lz-OX от точки О, т. е.
0X’=:=k-OX. Отображение плоскости на себя, при кото-
ром точке Х сопоставляется та- ‚
ким образом точка Х’, называется Х
гомотетиеи’. Точка О называется у
центром гомотетии, а число `
k —- коэффициентом гомотетии.
Теорема 12.1. Гомоте/пия
есть преобразование подобия. д
Доказательство. Пусть У yr
Х и Y -—— две произвольные точки рис, 112,
плоскости, не лежащие на одной .
прямой с точкой О (рис. 112). Треугольники ОХ Y И OX’Y’
подобны, так как у них угол О общий, а
QX ___ OY ____ k ”
отток“ -
83
„КУ.
Из подобия треугольников следует, что отношение -55-}-,—,
постоянно (равно k). К тому же выводу приходим в слу-
чае, когда точки О, Х и Y лежат на одной прямой. Теоэ
рема доказана.
Теорема 12.2. Любое преобразование подобия сво-
дится я: голютетгггг и движению, т. е. получается no-
следовательным применентдем гомотетии и движения.
Д о к а з а т е л ь с т в о. Рассматриваемое преобразование
подобия сопоставляет каясдои точке Х некоторую точку Х’. .
Пусть пщкоэффициент подобия. Рассмотрим гомотетию
относительно произвольного центра О c‘ коэффициентом
гомотетии k. Эта гомотетия переводит точку Х в некото-
рую точку Х”. Преобразование подобия сводится к двум
преобразованиям: первое переводит точку Х в точку Х"-—
это гомотетия‚ второе переводит точку Х” в Х’. Второе
преобразование сохраняет расстояния и, следовательно,
является движением. Теорема доказана.
Из определения гомотетии следует, что каждая прямая-
при гомотетии переходит или в себя, если она проходит
через Центр гомотетии, или в параллельную прямую. Цепь
ствительно, пусть Х Уипроизвольная прямая, не прохо-
дящая через центр гомотетии (рис, 112). Из подобия тре-
угольников ОХ Y и ОХ’ Y’ следует, что прямая X Y переходи-т
в прямую Х’ Y’, T. e. параллельную прямую. Отсюда следует,
что параллельные прямые при гомотетии переходят в па-
раллельные. Прямые пересекающиеся переходят в прямые
пересекающиеся, причем углы между пересекающимися
прямыми сохраняются. Очевидно, что указанные свойства
сохраняются при движении. Поэтому получается следующая
теорема. _ '
Теорема 12.3. Преобразование подобия переводит
прямые в прямые, прямые параллельные переводит в пря-
maze параллельные, прямые пересекающиеся переводит
в прямые пересекающиеся и сохраняет углы между пе-
ресекающимися прямыми.
Пусть Оюпроизвольная точка плоскости. Рассмотрим
следующее преобразование плоскости. Пусть Х -—точка
плоскости, отличная от О. Сопоставим точке Х точку Х’,
2
лежащую на луче ОХ на расстоянии от точки О, равном Ё-Х,
где R-—-Hekoropoe число. Это преобразование называется
инверсией относительно центра О. Число R называется
84
v.
‘Е;
__ . ‚щ ,,,,.';,,.: - „ 2
п радио/сои: инверсии. Преобразование инверсии определено
для всех точек Х, кроме О.
Преобразование инверсии можно наглядно представить
себе следующим образом. Проведем окружность с цент-
ром О и радиусом R (рис. 113). _
Для того чтобы построить точку X
X’, соответствующую точке Х,
надо провести касательную к ок-
ружности и опустить перпенди-
куляр из точки касания на прямую
2
OX. По теореме 11.5 ОХ’ 2681.
Очевидно, при инверсии точке Х’
соответствует точка Х. Поэтому Рис. 113.
ясно, как найти точку X’, co— . -
ответствующую Х, когда Х « лежит внутри окруисности.
‘Теорема 12.4. Два последовательных преобразова-
ния инверсии относительно одного и того же центра О
сводятся к: гомотетии относительно этого центра.
Доказательство. Пусть К’, и Rg——-—pa1mycb1-uep-
вой и второй инверсии. Первая инверсия переводит точку Х
2
1
в точку X’ луча ОХ на расстоянии ОХСтЁХ от центра О.
Вторая инверсия переводит точку Х’ в точку Х” луча ОХ
на расстоянии OX"-=—.---0g§,—;=!-3-3-3'-,e—?—’Z{— от точки О. В итоге,
1
как видим, получается гомотетия с центром О и коэффи- '
2
циентом гомотетии k Теоре-
1 .
Ma „доказана.
А’ ' Т е о р е м а 12.5. При инверсии
окружность, не проходящая tw-
рез центр инверсии, переходит в
у онрушсность.
' Доказательство. Пусть
0 . д г?’ .
О -— центр инверсии, а R -—- радиус
рис, 114, инверсии. Рассмотрим сначала слу-
чаи, когда точка О лежит вне ox-
ружности (рис. 114). Обозначим через t длину отрезка ОА
касательной, проведенной из точки О, к окружности. Дан-
ную инверсию мы можем получить, выполняя последователь-
но сначала инверсию с центром 0 И радиусом инверсии г,
2
a затем гомотетию с коэффициентом гомотетии
85
По теореме 11.10 ОХ -OX’=t“ (рис. 114). Отсюда
следует, что данная окружность в случае радиуса инвер-
сии t переходит в себя, следовательно, в окружность.
Последующая гомотетия переводит ее снова в окружность.
В итоге окружность переходит в ок-
ружность при любой инверсии.
Пусть теперь точка О находится
внутри данной окружности (рис. 115).
Обозначим через s среднее геомет-
рическое отрезков ОХ и ОУ какой-
нибудь хорды окружности, проходя-
щей через точку О. По теореме 11.8
s не зависит от хорды. Данную ин-
версию можно получить, выполняя
последовательно инверсию с радиусом s и гомотетию
Рис. 115.
г
с коэффициентом Инверсия с радиусом s переводит
данную окружность в окружность, симметричную от-
носительно точки О, а гомотетия переводит эту ок-
ружность снова в окружность. Теорема доказана полно-
стью.
. Теорема 12,6. Прямая, проходящая через центр
инверсии, при инверсии переходит в себя. Прямая‚ не про-
ходящая через центр инверсии,
переходит в окружность, про-
ходящую через центр инверсии.
Окружность, проходящая через
центр инверсии, переходит в
прямую.
Доказательство. Первое д
утверждение теоремы очевидно.
Докажем второе утверждение
(рис. 116). Пусть 12--расстояние
до прямой. Данную инверсию с ра-
диусом R можно получить, выполняя последовательно ин-
2
версию с радиусом h и гомотетию с коэффициентом
X’ Х
Рис. 116.
Опустим из точки О-центра инверсии перпендикуляр
на данную прямую. Пусть А—-основание этого перпенди-
куляра. Построим на отрезке ОА, как на диаметре, окруж-
ность. По теореме 11.5 ОА*=ОХ’-ОХ. Отсюда следует,
что инверсия с радиусом h переводит данную прямую
в окружность, проходящую через точку О. Последующая
86
` "“n'§4"' .. .. . .
.„. ;..(-.—щ ъ —-—-- ¢........./._._L _, L., днд-‚ЁШ
у
гомотетия переводит ее снова в окружность, проходящую
через точку О. Второе утверждение доказано.
Докажем третье утверждение. Пусть а-диаметр
окружности. Данную инверсию можно получить, выполняя
сначала инверсию с радиусом d, a затем гомотетию с коэф-
2
фициентом -5д-. Инверсия с радиусом d переводит окруж-
ность в‘прямую——касательную в точке диаметрально про-
тивоположной О. Последующая гомотетия переводит ее
снова в прямую. Теорема доказана полностью.
Мы говорим, что прямая и окружность пересекаются
под таким-то углом, имея в виду угол, под которым пере-
секаются данная прямая и касательная к окружности
в точке пересечения. Углом пересечения двух окружно-
стей мы называем угол, под которым пересекаются их
касательные в общей точке.
Теорема 12.7. Преобразование инверсии сохраняет
касание прямых и окружностей. Преобразование инвер-
сии сохраняет углы пересечения прямых и окружностей.
Доказательство. Прежде всего заметим, что если
прямая и окружность или две окружности касаются, то
они имеют только одну общую
точку. И обратно, если прямая
и окружность или две окруж-
ности имеют только одну об-
щую точку, то они касаются
в этой точке.
Преобразование инверсии
является взаимно однозначным
отображением плоскости, из
которой удалена одна точка -—-
Центр инверсии. Отсюда сле-
дует, что если окружность и
прямая или две окружности
имеют только одну общую
точку, то полученные преобра-
зованием инверсии прямые или окружности также имеют
только одну общую точку. Поэтому преобразование инвер-
сии сохраняет касание. `
Покажем теперь, что углы пересечения при инверсии
сохраняются. Пусть мы имеем две‘ окружности ми kg
пересекающиеся в точке А (рис. 117). Пусть касательные
к этим окружностям в точке А не проходят через центр
87
Рис. 117.
инверсии. Возьмем на отрезке O-A произвольную точку В
и проведем окружности Ь; и kg, касательные к Ь, и Ь,
соответственно в точке А и проходящие через точку В.
Окружности Ь; и Ь; пересекаются в точках А и В под
равными углами, так как фигура, составленная из этих
окружностей, симметрична относительно перпендикуляра,
проведенного к отрезку АВ через его средину.
По теореме 11.10 касательные к окружностям Ь; и Ь;
имеют одинаковую длину t. Инверсия с радиусом t nepe-
водит каждую из окружностей Ь; и Ь; в себя, а точку
пересечения А в точку пересечения B. Таким образом,
эта инверсия действительно сохраняет углы пересечения
окружностей Ь; и kg. .
Так как окружности Ь, и Ь; касаются окружностей
Ь; и kg, a касание сохраняется при инверсии, то угол пере-
сечения окружностей Ь, и Ь, тоже сохраняется. Общая
инверсия получается из инверсии с радиусом t и гомоте-
тии, а гомотетии сохраняет углы. т ›
В случае, если касательная к одной из окружностей
kg, kg B точке—А проходит через точку О, вместо окруж-
ности Ь; или Ь; берем прямую ОА. Читателю предлагается
рассмотреть случаи пересечения прямой и окружности u,
двух прямых. A
Преобразования гомотетии и инверсии являются важным
средством решения задач на построение с помощью unp-
кули и линейки. Приведем пример. .
Задача 12.8. Построить окружность, проходящую
через данную гпочгсу А и касающуюся двух данных пере-
секающихся прялшх.
Рис. 118.
Р еш е ни е. Пусть Ь-—— искомая окружность (рис. 118).
Проведем биссектрису угла, образуемого прямыми а, и ад,
внутри которого лежит точка А. Центр О окружности Ь
88
- 5
*...-,:<'.'- ' .
' ' а‘:
......__.-.... _ __„__
_ ____v_..j—
—
лежит на этой биссектрисе. Возьмем на биссектрисе произ-
вольную точку О’, опустим из нее перпендикуляр ОБ’
на прямую а, и радиусом O’B' из центра О’ опишем
окружность k’. Проведем полупрямую SA и обозначим А’
точку пересечения ее с окружностью /г'.
Преобразование гомотетии с центром S и коэффициен-
SA
TOM гомотетии 371-, переводит окружность la’ в /г._ Отсюда
следует, что для построения центра О искомой окруж-
ности надо провести прямую через точку А параллельно
прямой А’О’. Точка пересечения этой глрямой с биссект-
рнсой и есть Центр окружности k.
Задача 12.9. Uocnzpozzmb oxcpyo/c1toc'mb /2. ягроходя-
идую через данную глочку А и rcaca;ou;y1oc';z двух дан-
ных пересекающихся
окружностей la, u kg
(рис. 119).
Решение. Пусть
S --— ТОЧКЗ пересечения
окружностей kl И до. Под-
вергнем наши окружности
преобразованию инверсии
относительно точки S. При
этом окружности la, нед
перейдут в прямые а, и
(2.2. Точка А перейдет в
ятекоторуто точку А’. Окружность la перейдет в окружность
la’, касающуюся прямых а, и ад и проходящую через точку
А’. Мы знаем, как построить окружность la’ (задача 12.8).
Обратное преобразование, являющееся также инверсией,
переведет окружность la’ B искомую окружность /e.
Рис. 1 19.
Упражнения
1. Даны две пересекающиеся окружности д, и Ед. Окруж-
ность k пересекает под прямым углом каждую из окружностей
Ia, и k,. Доказать, что окружность k __пересекает под прямым
углом любую окружность, проходящую через точки пересечения
окружностей д, и k._..
2. Построить окружность, проходящую через данную точку,
пересекающую под прямым углом две данные пересекающиеся
окружности.
3. Найти геометрическое место центров окружностей, пере-
секающих две данные пересекающиеся окружности под прямым
углом.
89
§ 13. ТЕОРЕМА ПИФАГОРА И ЕЕ СЛЕДСТВИЯ
Теорема 13.1 (теорема Пифагора). В пря-
моугольном треугольнике квадрат гипотенувы равен
сумме квадратов катетов.
Д о к а з а т е л ь с т в о. Пусть ABC -— прямоугольный
треугольник с прямым углом С (рис. 120). Проведем
высоту треугольника из вершины С. Согласно теореме 5.9
основание высоты лежит между точками А и В. По тео—
реме 11.5
AC’ п: AD - AB, BC’ == BD - AB.
Складывая эти равенства почленно и замечай, что AD+
-—|—BD=='-AB, получим
AB2 -"-"--" Асе + ВСЁ.
Теорема доказана.
If" д Б’ Л С д’
Рис. 120. _ Рис. 121.
Теорема 13.2. B любом треугольнике квадрат
стороны, лежащей против тупого угла, равен сумме
квадратов двух других сторон, сложенной с удвоенным
произведением одной из этих спгорон на проекцию дру-
гой стороны.
Доказательство. Пусть Авбтданньпи треуголь‹
ник с тупым углом С (рис. 121). Проведем высоту AD_
из вершины А. По теореме 5.9 точка С лежит между В
и D. Применим теорему Пифагора к прямоугольным тре-
угольникам ADB И ADC, получим
AB’ = Ат + BD’,
AC’ = AD“ + DC’.
Вычитая эти равенства почленно, получим
AB’ -—- AC” г: ВО“ ——- DC“.
Замечая, что BD = BC —]— DC, получим
AB“ = АС“ —}-— BC” —[-— 2BC- DC.
Теорема доказана.
Теорем а 13.3. В любом треугольнике квадрат
стороны, лежащей против острого угла, равен сумме
квадратов двух других сторон без уд-
военного произведения одной из этих А
сторон на проекцию другой стороны.
Доказательство. ПустьАВС—--
данный треугольник с острым углом
С (рис. 122). Проведем высоту AD б, д д
треугольника. По теореме 5.9 точки В
и D лежат по одну сторону от точки РИС- 122-
С на прямой ВС. Поэтому либо точка
D лежит между С и В, либо точка В лежит между С и
D. Пусть для определенности D лежит между С и В,
как изображено на рисунке.
Применяя теорему Пифагора к треугольникам ADC и
ADB, получим
AB’:BD"’+/ID“,
AC2:-CD9+-AD“.
Вычитая эти равенства почленно и замечая, что BD:-.=
==BC—--CD, получим
AB” =..— Ас? + BC? -— 230. CD.
Если точка В лежит между С и D, доказательство ана-
логично. Теорема доказана.
Теорема 13.4. В любом параллелограмме сумма
квадратов диагоналей равна сумме квадратов сторон.
Д о к а з а т е л ь с т в о. Если Параллелограмм являетёя
прямоугольником (рис. 123, слева), то по теореме Пифагора
AC2 m AD“ —|— DC’,
во? = BC’ + DC”.
Складывая эти равенства почленно и замечая, что DC == АВ,
получим
АС“ + во? = AB?‘ + 30* + CD’ + AD”.
Пусть теперь параллелограмм не является прямоуголь-
ником (рис. 123, справа). Опустим перпендикуляры AA,
И ВВ1 из вершин А и В на прямую CD. Из равенства
91
треугольников ADA, и ВСЕ, следует, что ВА‚=СВ,.
Углы ADC И BCD, как внутренние односторонние при
параллельных .AD и ВС, дополняют друг друга до 180°.
Поэтому, если один из углов острый, то другой-тупой.
Л 46‘ A в
§__.._I 4 _l
L -
Л ' С’ Z7 И, Б 1?
Рис. 123.
Пусть для определенности угол ADC острый, а угол BCD
тупой, как изображено на рисунке. -
Применяя теорему 13.2 К треугольнику BCD И теорему
13.3 к треугольнику ADC, получим _ .
BD’ „т: BC’ —,L— CD“ —1,— 2DC- CB1,
AC’ а: AD” -+5 CD? ——- 2DC - DA1.
Складываа эти равенства почлепно и замечая, что СВ1=
=ВА‚‚ С0=АВ‚ получим
AC9 + во‘! .-.-.—. AB‘i + все + ст + AD“.
Теорема доказана.
Согласно теореме 5.4 сумма любых двух сторон тре-
угольника больше третьей стороны. Естественно возникает
вопрос: всякие ли три числа могут быть сторонами неко-
торого треугольника, если сумма любых двух из этих
чисел больше третьего. Утвердительныи ответ на этот
вопрос дает следующая теорема.
ц Теорема 13.5. Karcoabt бы ни были три числа а,
b, c такие, что судами любых двух из этих чисел
больше третьего, существует треугольник со сторо-
нами, равными а, b, c.
Доказательство. Пусть для определенности c,,>.
‚ё b г; а. Обозначим
св + as ____ д:
Число а, > 0, так как с 2 b. Число а, меньше а. В са-
мом деле,
c‘-‘+ a2—-bi _____b*—-(c-—a)’
a_~a‘:a_— 2c 2c
92
ч м‘, ч-ьцд
Так как a-|—b>c, то b>c--a>0. Поэтому b"“’>
>(c--a)”. Следовательно, а>а‚.
Построим треугольник АБС следующим образом. Возь-
мем отрезок АВ, равный с (рис. 124). Из точки А на
полупрямой АВ отложим отрезок AD, равный ад. Из точки
D восстановим перпендикуляр DC, равный a“'--af.
Утверждаем, что треугольник ABC
имеет стороны а, b, с.
Действительно, сторона АВ с
равна с. По теореме Пифагора
AC9...-=AD“+CD9..-=
п =аг+(т/а”‘='-"“аб =;>“=а*› ,4’ 7 в
т. е. АС=...--а. По теореме 13.3
BC%=a2__l__ C2__2ca1:b2, PHC.:l24.
T. e. BC=b. Теорема доказана.
Теорема 13.5 позволяет полностью охарактеризовать
взаимное расположение двух окружностей. Именно, пусть
даны две различные окружности с центрами 01 и 09,
радиусами Н, и R2, Маке, и расстоянием между цент»
рами cl. Тогда:
1. Отсужносигг: не пересекаются, т. е. не синеют
общих точек, если
R1+Rg<d Пли Н9°—-Н1>С1.
2. Отруб/снасти синеют одну общую точку, в Immo-
рой они касаются, т. е. илгеют общую касательную,
если
R1 + Не 3 d или R2 """ R1 Ё 61.
3. Окружности хгересекаются в двух точках, т. е.
синеют две общие точки, если
R1+Rg>d ll
Мы ограничимся доказательством третьего утверждения
и предлагаем читателю рассмотреть первые два.
По теореме 13.5 существует треугольник АдААд со
сторонами А,А..-=Н1, AgA=Rg, A,A2=d. Действительно,
1{’‚+Н„>аЁ, R,—|—d>R2 no условиям (1), a Rg+d>R1
потому, что Rg,>,R1. о
Отложим от полупрямой 0,09, угол, равный углу Ад,
треугольника A,AAg. a стороне этого угла отложим
отрезок 018, равный А‚А_-=Н1. Треугольник 0,802 равен
93
треугольнику А1АА1. Отсюда 01В=А1А=Н1, 018:
=А2А=Ны Следовательно, точка В является точкой
пересечения наших окружностей. Точка В’, симметричная
точке В относительно прямой 0102, будет второй точкой
пересечения окружностей.
Покажем, что окружности не имеют других точек пе-
ресечения, кроме В и В’. Допустим, что В”-—третья точка
пересечения. Пусть для определенности она лежит в той
же полуплоскости относительно прямой 0101, что и точка В.
Треугольники 01801 и 01В”0„ равны по третьему при-
знаку равенства треугольников. Из равенства углов 020,3
и 01018” следует, что полупрямая 018 совпадает с полу-
прямой 01В”. После этого из равенства отрезков 01В=
==01B"='-=R1 следует, ЧТО ТОЧКИ B" и В совпадают,
Утверждение доказано.
Задача 13.6. Дан пгреугольнггк ABC. Выразить
медиану, биссектрису и высоту mpeyeo/zbmma. проведен-
ные из вершины С, через стороны треугольника.
Р еш е н и е. Начнем с медианы треугольника (рис. 125).
Пусть Оиоснование медианы. Построим точку D, сим-
. метричную точке С отно-
сительно точки 0, OD = ОС.
С
А 0 D B
Рис. 125. . Рис. Х26С
Применяя теорему 13.4 к параллелограмму ABCD, получим
AB2 + (20C)* === 2AC9 + 2BC".
Отсюда находим медиану ОС. у
Найдем биссектрису угла С (рис. 126). Согласно тео-
реме 11.6 точка 0--основание биссектрисьь-делит сто-
рону АВ на отрезки, пропорциональные сторонам АС и
ВС. Это позволяет, зная АВ, АС и ВС, найти АО и OB.
Допустим, они уже найдены. Применяя теорему 13.2 или
13.3 к треугольникам ABC и АОС, получим
BC’: AC2 —{— AB’ i 2AB - AD,
0C2 = AC’ + АО? :t 2A0 - AD.
94
уж
Умножая первое равенство на АО, а второе на АВ и
вычитая их почлённо, получим уравнение, содержащее
только одно неизвестное ОС—биссектрису угла С. Из этого
уравнения и находится биссектриса.
Найдем высоту CD (рис. 126). Прежде всего по теоре-
ме 13.2 или 13.3 находим отрезок AD. Затем из прямо-
угольного треугольника ACD находим высоту CD.
Проведем полуокружность с радиусом, равным единице
(рис. 127). Возьмем на полуокружности произвольную точ-
ку А и обозначим через ос угол АОВ. Опустим из точки А
Qt
§<
В
д
Рис. 127.
перпендикуляр AD Ha диаметр ВС. Синусом угла ос назы-
вается длина отрезка АО. Синус угла ос обозначается так:
sin ос. По определению считаем sin 0°=..-0, sin 180°=_.-0.
Определим теперь понятие косинуса угла. Косинус
угла ос обозначается так: cos ос. Если угол ос острый, дто
cos ос равен отрезку OD (рис. 127, слева). Если угол awry-
пой, то созос есть отрицательное число, по абсолютной
величине равное длине отрезка OD (рис. 127, справа). По
определению считаем cos 0° =1, cos 90°: О, cos 180°=—-— 1.
Тангенсом угла ос называется отношение sin ос к cos ос,
т. е.
sin a
tga‘-=cosa'
Тангенс угла ос не определен для ос=9О°.
Теорема 13.7. Если угол ос оспсрьсй, то
sin (90° — ос) = cos ос, соз (9О° - ос)=31п ос, tg (90° ——- on): из“ .
Доказательство (рис. 128). Пусть угол АОВ ра-
вен ос, а угол A108 равен 90°—-ос. Прямоугольные тре‹
угольники ODA И А‚О1О равны, так каку них гипотенузы
равны, как радиусы, а углы AOD и ОА1О1 равны ос. Из
равенства этих треугольников следует, что А1О‚=ОО,
ООг-ъ-АП, т. е. sin(90°-- )==cos ос, соз(90°-—ос)=$1п ос.
95
Третья формула получается почленным делением первой
на вторую. Теорема доказана. - '
Рис. 128. - Рис. 129.
Теорема 13.8. Для любого угла on
sin (180° -- ac) ..--..-. sin oz, cos (180° ——— ос) = —- cos а.
Д о к а з а т е л ь с т в о. Утверждение очевидно, если
oc=90°. Пусть угол АОВ равен ос, а угол АЮВ равен
180°—-on (рис. 129). Из равенства треугольника OAD и
OA1D1 следует; что АВ=А1О‚‚ т. е. sin(180°-—ez)~_—...-sin ac.
Если ос не равно 90°, то один из углов on, 180°--on ост-
рый, а другогЬ-тупой. Поэтому cos об "и cos (180°--a)
имеют противоположные знаки. Так как OD-.-...-OD1, то
cos(180° --—-on):-:———C0s оъ. Теорема доказана.
' Теорема 13.9. Для любого oz-
` з1п9оъ+соз“оъд-_:=1..
Доказател ь ство. При оъ=0°, 90°, 180° утверж-
дение теоремы проверяется подстановкой соответствую
щих значений синуса и косинуса. Если сам-острый угол,_
то утверждение теоремы следует из теоремы Пифагора
в применении ее к ‘треугольнику OAD (рис. 129). Если
угол а тупой, то утверждение теоремы также следует из
теоремы Пифагора в применении ее
к треугольнику ОАдВд (рис. 129). Тео-
рема доказана.
Теорема 13.10. В прямоуголь-
ном треугольнике АБС с прямым
‘4v ‚ углом С
- _ 5; 5 BC .—=..- AB sin A,
Рис. 130. АС == АВ cos A, BC...-2: АС tg А.
‚Показатель ство (рис. 130). Отложим на полупри-
мой АВ отрезок АВ‚‚ равный единице, и опустим перпен-
дикуляр източки B, на прямую —АС. По определениюуси-
96
нуса и косинуса зйпАгЦ-Вюд, с_озА=АС‚. Треугольники
A1310, и ABC подобны, так как у них угол A общий, а
углы С‘ и C1 прямые. Отсюда следует, что
BC „ЕЁ _/_*_§_....,4_£ §iQ...."3»Cn
B,C,'_ 1 ’ AC,” 1 ’ AC— AC,’
Подставляя сюда В1С1=зйп А, АСд==соз А, получим
BC==ABsin A, AC:-=ABcos A, BC== AC н; А.
Теорема доказана.
Теорем а 13.11.
1
. o______
s1n45 ...—1/2.,
'sin3O°=..--L, cos30°..—..=-L/13-, tg30°..—-.=——1-=.
2 2 3
П. ок а з а т е ь с т в о. Построим прямоугольный тре-
угольник АВС с прямым углом С и углом А, равным 45°
(рис. 131). У этого треугольника угол ‘В будет также 45°.
24
/7 с 6’
Рис. 131. Рис. 132.
‘Следовательно, треугольник равнобедренный: АС=ВС.
Применяя ‘к нему теорему Пифагора, получим
AB” = AC’ + BC’ = 23C’ == ЁАС”.
. 1 1
Отсюда s1n2 45° = -5- , cos“ 45° = д- . Следовательно,
sin45°.-.-..--3-.-_ cos45°=—‘—= t 45°_—=1.
V-2 э Э g
Построим теперь равносторонний ътреугольник АБС
(рис. 132). У него все углы равны, следовательно, каждый
из них равен 6О°. Проведем медиану BD треугольника.
Она является биссектрисой.и высотой. Поэтому в тре-
угольнике ABD угол ADB прямой, аугол ABD равен З0°.
4 А, В, Погорелов . v 97
Так как AD=-15 АС, то sin 30°...-=—}—. ‘Ho теореме 13.9
ъ/ЁГ
отсюда находим cos 30°=-5-. После этого tg 30°.-zfi,
Теорема доказана.
Теоремы -13.7 и 13.8 позволяют найти синусы‚ коси-
нусы и тангенсы ряда других углов: 60°‚ 120°, 135°,150°.
Читателю предлагается проделать ' это в качестве упраж-
нения.
Для синусов, косинусов и тангенсов острых углов со-
ставлены специальные таблицы. Эти таблицы позволяют
по данному углу найти соответствующий ему синус, коси-
нусщйили тангенс, а также по заданному синуру, косинусу
илидтангенсу найти соответствующий угол. Теорема 13.10
поёвбляет с помощью таблиц найти все элементы прямо-
угольного треугольника, т. е. его углы и стороны, если
известны два катета, гипотенуза и катет, острый угол и
гипотенуза или острый угол и катет.
Теорема 13.12 (теорема косинусов). Влюбом
треугольнике ABC
AB’ = AC’ + BC’ -—— 2AC . вс . сов с.
Доказательство. Если угол С равен 9О°, то
утверждение теоремы следует из теоремы Пифагора, так
как соз90°=—-.;О. Пусть С-острый угол (см. рис. 122).
Тогда по теореме 13.3 `
AB’ = AC2 + BC’ - 2BC - CD.
По теореме 13.10 B_ применении к треугольнику’ AC D
CD = АС о cos C. Поэтому
AB“ == AC’ -1- BC“ —- 2BC - AC ‘- cos C.
Пусть теперь С — тупой угол (см. рис. 121). По тео-
реме 13.2 ~
AB’ = АС“ + BC’ + 2BC - CD.
По теореме 13.10 в применении к треугольнику ADC
CD=AC cc’>s(4 ACD). Но угол АСВ дополняет угол С
треугольника ABC до 180°. Поэтому, по теореме 13.8,
cosg; ACD)=..-—-—cosC И, следовательно, AC-cosC-_=
=--CD. Таким образом, и в случае тупого угла
AB” == АС“ -|- BC“ - 2BC - AC - cos C.
Теорема доказана.
98 ' „
Теорема 13.13 (теорема синусов). В любом
треугольнике АБС '“
sinA_sinB____sinC
"§‘C”""R—C"""71"B"'
Д о к а з а т е л ь с тв о. Опишем около треугольника ABC
окружность (рис. 133). Пусть 81 и Сг-точки {окружно-
сти, диаметрально противоположные вершинам В и С тре-
угольника. Треугольник BCB, прямо-
угольный, так как вписанный угол
С опирается на диаметр. Поэтому
BC:-_2Rsin B1. Угол 81 равен углу
А треугольника ABC, так как они
опираются на одну и ту же дугу
окружности. Поэтому ВС = 2R sin A.
Рассмотрим треугольник СдСА.
Он тоже прямоугольный. АС ===
‹.==212з1пС‚. Угол С1 и угол В треу- РИС- 133-
гольника АВС опираются на допол-
нительные дуги. Поэтому эти углы дополняют друг друга
до 18О°. По теореме 13.8 sin C1:-=sinB. Таким образом,
2RSi1’l B.
Аналогично доказывается, что AB=2R sin С. Сопо-
ставляя полученные три формулы, заключаем, что
sinA _sinB______sinC__1
. BC ““ АС — АВ ‘"27?’
Теорема доказана.
‚Теоремы 13.12 и 13.13 позволяют найти все элементы
треугольника, т. е. его углы и стороны, если заданы три
элемента, однозначно определяющие треугольник. Такими
тремя элементами являются: три стороны треугольника,
две стороны и угол, заключенный между ними, сторона и
два угла.
Упражнения
1. Пусть а, b, 0--C'l‘0p0HbI треугольника. Доказать, что угол
треугольника, противолежащий стороне с, будет тупым, прямым
или острым в зависимости от ТОГО, будет выражение c9-—a"-—-b9
положительным, равным нулю или отрицательным.
2. Пусть а и В-положительные числа, причем а>В. Дока-
зать, что треугольник со сторонами ‚
a2+s=. as--32. гав
является прямоугольным.
4° 99
Ц
3. Доказать, что геометрическое место точек, сумма квадра—
тов расстояний которых от двух данных точек постоянна, есть
окружность. .
4. Доказать, что геометрическое место точек, разность квад-
ратов расстояний которых от двух данных точек постоянна, есть
прямая.
5. Найти следующее выражение для высоты я, треугольника
со сторонами а, b, с, опущенной на сторону с:
ЁсЁЁЕУРФЁ`°)(Р-'Ь)(Р_С)
a+b—|-c
2 О
где р-полупериметр, т. е. р=
§ 14. Bbll'lyKJIblE' МНОГОУГОЛЬНИКИ
Многоугольником АдАд Ад называется фигура, ‘ко-
торая состоит из точек Ад, A2, . .. , An И соединяющих их
отрезков A1Ag, Аид, ‚ А‚,А‚ (рис. 134). Точки A1, Ag, . . . x
, An называются вершинами многоугольника, а отрезки
в
дг
A.
A A’ ‘A 3
г д!’ 1
Рис. 134. *Рис. 135.
Аида, A3143, , A,,A, называются его сторонами. Две вер-
шины называются соседними, если они соединяются сто-
роной многоугольника. У каждой вершины есть две со-
седние с ней вершины.
Каждая из прямых АдАд, АдАз, . .. , A,,A, разбивает Imo-
скость на две полуплоскости. Многоугольник A1Ag An
называется выпуклым, если он располагается в одной
полуплоскости относительно каждой из этих прямых, при-
чем каждая прямая АрАрд не имеет других общих точек
с многоугольником‚ кроме точек отрезка ApAp+l (рис. 135).
Теорема 14.1. Если концы ломаной B18, 8,,
лежат в разных полуплоскостях относительно пря-
мой b, mo ломаная пересекает прямую b.
100
._
_.'?'~.u«;»;'..».‘- ‘Зет 24721‘ ’»,"':*;" ":éa~r~w:3$r£«.*.-< ‚мы ‹:-« `- - . . . ~ .- .- .. ::- _ и -
A ‹ - -. - v - - . - . .. ..‘ - - 1_._ -:-,-:v~.-,,.;§.-:,‘:..§‘_'.-;a';-:-.__-‘-.--3..--3.: „т? ‚г - „ ‹ ‚ ‚
A . - .- а - '- ‘=1-x-..' n, в-
‚многоугольника. Утверждаем, что
- Показ ательство. Допустим, ломаная дне пересе-
кается с- прямой b.. Тогда, следуя вдоль ломаной от вер-
шины B, к Бр, мы встретим две соседние вершины, ле-
жащие в разных полуплоскостях относительно прямой b.
Звено ломаной, соединяющее эти вершины, пересекается
кг-прямой 12.-Мы „пришли к противоречию. Теорема до-
казана. ~ ' р
Теорем а 14.2. Если прямая имеет три общие
точки с выпуклым многоугольником, то она содержит
одну из его сторон. ‚ ч’
Доказательство. Пусть
А, В, С ——три точки прямой а,
принадлежащие многоугольнику.
Пусть для определенности точка В
лежит между А и С. Точка В
принадлежит одной из сторон
Рис. 136.
эта сторона принадлежит прямой а.
Действительно, в противном случае прямая, содержащая эту
сторону, разделяет точки А и С. А это противоречит усло-
вию выпуклости многоугольника. Теорема доказана.
диагональю многоугольника называется отрезок, соеди-
няющий две несоседние вершины (рис. 136, АВ).
T ео—р‘е м а 14.3. Диагональ А1Ар разбивает выпуклый
многоугольник: Аид . .. Ар Ар на два выпуклых много-
угольника АдАь Ар и АрАр+‚ А‚,А‚. Эти многоуголь-
ники лежат в разных полуплоскодтях относительно
гъиямой А1Ар. Полупрямахё А1Ар проходит между полу-
прямыми АдАь и АдАр.
Доказательство. По теореме 14.2 прямая AIAP
не ‚имеет других общих точек с многоугольником, кроме
точек А1 и Ар. По Ieope'Me__14.1 ломаная АдАд Ар ле-
жит no одну сторону от прямой АдА . Так как исходный
многоугольник лежит по одну сторону от каждой из пря-
Mb1x,A1Ag, АдАз ...., то этим свойством обладает‘ и мно-
гоугольник Аир. А. Аналогично доказывается вы-
пуклость многоугольника А АрАд.
Докажем, _что эти многоугольники лежат в разных
полуплоскостях относительно прямой АдА .
Из трех полупрямых АдАд, АаАр и A,A,,,' лежащих
в одной полуплоскости относительно прямой АдАъ "либо
полупрямая А1Ар, либо полупрямая А‚А‚‚_ проходит между
двумя другими. Это не может быть полупрямая А‚А‚„ так
101
от
как тогда точки Ар и Ад лежат .в разных полуплоскостях
относительно прямой А1А‚„ что противоречит выпуклости
исходного многоугольника. Итак, полупрямая АдАр про-
ходит между полупрямыми А1Асд и А1А‚,. А это значит,
что прямая А1Ар разделяет точки Ад и Ад, следовательно,
разделяет многоугольники AIAQ . .. Ар и Ар . .. А,‚А1. Тео- ‚
рема доказана.
Пусть А—-вершина выпуклого многоугольника и В,
С-соседние с ней вершины. Внутренним углом много-
угольника при вершине А называется угол между полу-
прямыми АВ и АС. Внешним углом многоугольника при
вершине А называется угол, смежный внутреннему.
Теорема 14.4. Сумма внутренних углов выпуклого
многоугольника равна (n—2) 180°, где п-ышслосторон
или вершин многоугольника.
Сумма внешних угловвыпуклого многоугольника не
зависит от п и равна 360°. х
Доказательство. Каждый треугольник является
выпуклым, и для него теорема верна, так как (3 --— 2) 180°.-:-..
=180°. Будем вести доказательство теоремы по индук-
ции. Допустим, теорема верна для всех многоугольников
с числомсторон, меньшим п. Докажем, что она верна для
многоугольников с п сторонами. '
Пусть Р—многоугольник с п сторонами. Соединим
две его несоседние вершины А и В диагональю АВ. По
теореме 14.3 мы получим два многоугольника Р, и, Ре
с числом сторон пд и не, причем п‚<п, п‚<п‚ 121+ пат...
-_-..-—n+2. Так как диагональ АВ проходит между сосед-
ними сторонами с общей вершиной А, то внутренний угол
при вершине А многоугольника Р равен сумме углов мно-
гоугольников P, и Ре, при вершине А. Аналогично угол
при вершине В многоугольника Р равен сумме углов мно-
гоугольников Р1_и Pg. при вершине В. Отсюда следует,
что сумма углов многоугольника Р равна сумме углов
многоугольников Р, и Ре, т. е. (п, —- 2) 180°+(п„——2)1 80°=-..
=(п--2)18О°. Первое утверждение теоремы I’ доказано.
Так к_ак внешний угол многоугольника является смеж-
ным соответствующему внутреннему углу, а сумма смежных
углов равна 180°, то сумма внешних углов много-
угольника равна 180°n-—(n---2)180°, T. e. 360°. Теорема
доказана.
Пусть A,/lg... A,,—’Bb1ny1<J1b1ti многоугольник. Каждая
из прямых A1/-lg, .AgA3,...,.A,,A1 разбивает плоскость-на
102
две полуплоскости. Отметим ту из них, которая содержит
многоугольник. Мы будем говорить, что точка Х лежит
внутри многоугольника, если она принадлежит каждой из
отмеченных полуплоскостей и не при-
надлежит многоуголь_нику. Часто мно-
гоугольником называют фигуру, ко-
торая состоит не только из сторон " »4,
и вершин, но также из точек плоско- да
сти, лежащих внутри многоуголь-
ника. Чтобы различать их, мы будем ‚45 ‚44
называть многоугольник в этом _
смысле пополненным многоугольни- р"°° 137°
ком. .Сам многоугольник образует
границу пополненного многоугольника. На рис. 137 по-
полненный многоугольник заштрихован.
Пусть Р, и Р9—-два выпуклых многоугольника, P,’ и
Р;——соответствующие им пополненные многоугольники.
Мы будем говорить, что многоугольник Рд расположен
внутри многоугольника Ре, если каждая точка многоуголь-
ника P; принадлежит многоугольнику pg. Периметром
многоугольника называется сумма длин его сторон.
Теорема ’14.5. Если выпуклый многоугольник P,
содержится внутри выпуклого многоугольника P9, mo
периметр Р, не больше периметра Pg.
Если многоугольник Р1 не совпа-
дает с P2, то его периметр мень-
ше периметра P2.
Доказательство. Проведем
прямую а, содержащую какую-нибудь
сторону многоугольника P, (рис. 138).
Многоугольник P, расположен по
Рис. 138.
угольник Pg либо расположен по
одну сторону прямой а, либо есть
точки многоугольника Pg, лежащие по разные стороны
от прямой а. Во втором случае прямая а пересекает много-
угольник P2 B двух точках: А и В. Действительно, пусть С
и В--точки многоугольника P2, лежащие по разные сто-
роны от прямой а. Точки С и D разбивают многоуголь-
ник P2 на две ломаные. Каждая из них пересекает пря-
мую а (теорема 14.1). _
Прямая а разбивает. многоугольник Pg Ha два много-
угольника. Пусть Qg---TOT из них, который лежит в одной
103
одну сторону этой прямой. Много-.
полуплоскости с Р, относительно прямой а. Многоуголь-
ник Qg содержит внутри многоугольник Р, и имеет пери-
метр меньший, чем‘ периметр многоугольника Pg. Действи-
тельно, переход от многоугольника Pg К Qg связан с за-
меной ломаной отрезком АВ‚ соединяющим ее концы.
Проделав такое построение с каждой стороной много-
угольника Р„ мы получим, в конце концов, из многоуголь-
ника Pg многоугольник Р,. Отсюда следует, что если мно-
гоугольник Р, не совпадает с Pg, то он имеет периметр
меньше периметра Pg. Теорема доказана.
Ломаная 1: А, Ag... А‚‚ называется выпуклой, если мно-
гоугольник Р со.сторонами А,А,‚ Ag/lg, ..., А‚‚А, является
выпуклым. Ломаная 1': А,А;А; An называется объемлю-
щей для выпуклой ломаной А, Ag А„, если обе лома-
ные проходят в одной полуплоскости относительно пря-
мой А, А‚‚,и ‘ломаная 1' не содержит внутренних точек
многоугольника Р (рис. 139) ;
Рис. 139. ‘ ‘ ‘ — ‘ Рис. 140.
Теорема 14.6. Ломаная 1', объемлющая выпуклую
ломаную 1, имеет длуну не меньшую, чем 1; Если’ ло-
маные не совпадают, то ‘т’ имеет большую длину:
Доказательство (рис. 140). Проведем через звено
ломаной 1 прямую а. Следуя-вдоль ломаной 1' 1x13*ee на-
чальной точки А в конечную точку В, отметим первую
и последнюю точки ломаной 1’, принадлежащие прямой а.
Пусть это будут точки С и D. Заменим участок CD ло-
маной 1’_ прямолинейным отрезком CD. Полученная при
этом ломаная также объемлет ломанусю 1 и имеет длину,
не большую 1’, причем заведомо. меньшую, если’ у лома-
ной 1' есть точки по разные стороны от прямой а. Про-
делав эту операцию столько раз, сколько звеньев у ло-
маной 1, мы получим такую Побъемлющую ломаную 1,,
которая расположена целиком на 1. Утверждаем, что она
совпадает с 1.
Р 104
„Пусть $---вершина ломаной т. Покажем, что она при-
надлежит 11. Возьмем точку S, на отрезке АВ, отличную
от А и В. Точки А и В-концы ломаной т‚—лежат
по разные сторо`ны от прямой 881. Поэтому т, пересекает
прямую“ 881. Точка пересечения должна принадлежать т,
так как 1, лежит на т. Но единственная точка т,’ которая
лежит на прямой 86}, есть точка S. Итак, точка S при-
надлежит т, и, следовательно, ломаные т, и т совпадают.
Исходная ломаная т’ имеет длину, не меньшую 11. Если 1
не совпадает с 1’, то т’ имеет длину большую, чем т.
Теорема доказана. ‘
Выпуклый многоугольник называется вписанным
в окружность, если его вершины лежат на некоторой
окружности (рис. 141, слева). Выпуклый многоугольник
Рис. I41.
\
называется описанным около окружности, если его сторо-
ны касаются некоторой окружности (рис. 141, справа).
_TeopeMa\1.4.7. Пусть точки А‚‚ Ag, ..., А‚‚ разби-
’ ' /‘\
воют, окружность. на дуги A,A9, AgA;.;, . ,,., А‚,А1 так, что
любые две дуги не имеют других общих точек, кроме,
„лижет быть, концов. Тогда, многоугольник А, Ag.../1,,
выпуклый, вписанный в окружность.
Доказ а тель ств о. _ Точки Ар и Ад, разбивают
/'5
окружность на две дуги, одна из них АрАрд. По условию
Z“\
теоремы на дуге АрАрд нет других точек Ад, ..., An,
кроме Ар и Ард. Поэтому многоугольник A,A2...A,,
расположен по одну сторону от прямой АрАр+1 и, следо-
вательно, выпуклый. Теорема доказана.
Выпуклый многоугольник называется тавпльным, если
у него все стороны равны, все углы’ равны.
Теорема 14.8. Правильный выпуклый многоуголь-
ник‘ является вписанным в некоторую окружность
105
и описанным около некоторой окружностщ Эти окруж-
ности кониентричны, т. е. имеют ‚общий центр.
Доказательство. Пусть А1‚ Ад, A3-Tpn после-
довательные вершины правильного многоугольника. Про-
ведем биссектрисы внутренних углов многоугольника
в вершинах А1 и Ад (рис. 142).
ОНИ пересекаются в некоторой
точке О. Треугольник АЮА,
равнобедренный, так как углы
его Ад и Ад равны. Отсюда
следует, что ОА‚=ОА‚. Тре-
угольники OAgA1 и ОАдАз рав-
ны, так как у них 0A,=0Ag,
”“°- 142- A1A2=A2A3, 40A1A2=
= ;_0A2A3. Отсюда следует,
что OAg=-OA3. Аналогично доказываем, что ОА3=ОАд и
т. д. Из равенства всех отрезков ОА‚‚ ОА‹д‚ OA3, следует,
что окружность с центром О и радиусом OA, проходит
через все вершины многоугольника. Окружностьс центром
О и радиусом, равным высоте OB треугольника ОА1А„‚ ка-
сается всех сторон многоугольника. Теорема доказана.
Т еорем а 14.9. Прямые, проходящие через средины
сторон правильного многоугольника перпендикулярно
этим сторонам, и биссектрисы внутренних углов пра-
вильного многоугольника являются осями симметрии.
Если у правильного многоугольника четное число сто-
рон, то он имеет центр симметрии. Центр силгметрии
совпадает с центром вписанной и описанной отгруж-
ностей. A
Te о р ем а 14.10. периметры правильных многоуголь-
ников с одинаковым числом сторон относятся, как
стороны или как радщ/сы вписанных или описанных
окружностей. а
0
Доказательство этих теорем предоставляется читателю
в качестве упражнения.
Найдем стороны некоторых правильных многоуголь-
ников, вписанных в окружность радиуса R. Начнем
с шестиугольника. Сумма его внутренних углов равна
(6——2)180°=4-18О°, поэтому каждый угол равен 12О°.
Углы при вершинах А1 и Ад в треугольнике 0A1'Ag (рис. 142)
равны по 60°. TpeyroJ1bHvu<-——pasnocropouuufi. Поэтому
у правильного шестиугольника, вписанного в окружность
радиуса R, сторона равна радиусу R. ’
106
В случае правильного четырехугольника, вписанного
в окружность, внутренние углы равны 9О°, т. е. четырех-
угольник-квадрат. „В треугольнике ОАдА9 (рис. 142)
углы, прилежащие стороне A1142, равны по 45°. Поэтому
А‚А‚= 20,4, соз 45°=н 1/ 2.
B случае правильного треугольника, вписанного в окруж-
ность, углы, прилежащие к стороне А1Ад, равны ЗО°.
Соответственно получается A1/lg = 20A1 cos 3Q° == R I/5.
Упражнения
1. Доказать теорему 14.9.
2. Выпуклый многоугольник с равными сторонами, вписан-
ный в окружность — правильный.
.' Если у описанного выпуклого многоугольника число cro-
рон нечетное и стороны равны‚‚то он правильный. Если число
сторон ‚четное, то он может не быть правильным, например ромб.
4. Установить связь между радиусом окружности и сторо-
нами правильного вписанного и описанного многоугольников
с одинаковым числом сторон. ~
5. Выразить сторону правильного вписанного 2п-угольника
через сторону правильного вписанного п-угольника.
6. Найти сторону правильного десятиугольника‚ вписанного
в окружность радиуса R. Воспользоваться упражнением 8 к § 11.
§ 15. площАди фигур
Пусть F ———произвольная фигура (рис. 143). Проведем
две перпендикулярные -прямые так, чтобы фигура F pac-
полагалась по одну сторону от
каждой из этих прямых. Tou-
кой пересечения О каждая из
этих прямых разбивается на две
полупрямые. Полупрямые а и b
этих прямых образуют прямой
угол, содержащий фигуру F.
Отложим на полупрямых а
и b от точки О отрезки, рав-
ные'1 см, 2 см, З см, Кон-
Цы этих отрезков обозначим
АЬ A2: АЗ: 0"; B11 B29 Вт 00°
Проведем через точки A1, Ag, Аз, прямые щ, ад, a3, .,.,
параллельные b, a через точки Вд, Вд, B3, проведем пря-
мые 121, I72, b3, ..., параллельные а. Эти прямые разбивают
наш угол на равные квадраты со стороной 1см.
Ь ч
*\~F° Q55 45° ь.
д}
д ,4, /I2 4, А,
Рис. 143.
107
Обозначим через Мр-число тех квадратощкоторые
целиком содержатся в фигуре F, a через М; ——-ч.исло тех
квадратов, которые имеют ‘хотя бы одну точку фигуры Е.
Очевидно, М. <~N},.
~ 'C_l'IOM0u1bIO аналогичного построения разобьем прямой
угол на квадраты со стороной 1мм=0,1 см и опреде-
лим снова два числа М, и N} N1-3\T0 число квадратов,
целиком содержащихся в фигуре F, a 1\/;-—число` квадра-
тов, содержащих хотя бы одну точку фигуры. Затем опре-
деляем два числа М, и N; с помощью разбиения на квад-
раты со стороной 0,01 см и так далее.
Рассмотрим теперь две последовательности чисел:
_ ‘so, S1, S2,
з; 3;, з,
где
5,=м„‚ в,=о‚о1.м,‚ ‚9,__-=о‚0оо1нм,‚_.‚;‚
$;==1\/;, S;=—'-0,01-N;, S;=0,0001-Ng, .„
Вообще ' W - ’
Sk=(0.1)*'*«Nk, $;x<0.1)*’*-N,;. .
Эти последовательности чисел обладают следующими оче-
видными свойствами: —
1) оси,
2) s;,;,s;>s;>
3) ton " '
Мы будем говорить, что фигура F имеет определен-
ную площадь, если разность 8‚‚;—-8‚, сколь угодно мала
при достаточно большом п. Это значит, что, каково бы
ни было задано положительное число е, всегда можно
указать такое число по; что при n>n.,
‘Площадью фигуры F МЫ будем называть число S, не
меньшее любого 8‚‚ и не большее любого Sn. Существо-
вание такого числа обеспечивается следующей теоремой.
Т ео р ем а 15.1. Пусть две последовательности чисел
So, 81, 89, ...; So, S1, S2, обладают следующими
четырьмя свойствами:
1)
2) S;2S;2S,;...,
3) So?/S0; 000’
~108 ”
с
4) разность ‘Sf, ———S,, сколь угодно мала гари доста-
точно большом п. *
Тогда существует и притом только одно число S,
не меньшее любого из чисел S,, и не большее любого
из чисел SI, ' е : -
Эту теорему мы примем без доказательства.
Фигуру F мы будем называть простой, если ее можно
разбить на конечное число треугольников.
Те о р ем а 15.2. Простая фигура имеет определен-
ную площадь. —Площадь простой фигуры равна сумме
площадей треугольников. из которых она составлена.
Доказательство. Будем пользоваться обозначе-
ниями, которые были введены при определении понятия
площади фигуры. Оценим, насколько
отличаются числа М, и М}. Так как
фигура простая, то она составлена
из конечного числа треугольников.
Если некоторый квадрат входит в N},
и не входит в Nk, то он пересекает
сторону одного из треугольников.
Оценим число квадратов со сто-
роной (0,1)"‚ которые пересекают
отрезок АВ длины l. Прямая АВ д
образует с одной из полупрямых а д ‚и
или b угол, не больший 45° (рис. 144).
Пусть для определенности этой по-
лупрямой является ь. Тогда между
двумя горизонтальными прямыми разбиения плоскости на
квадраты со стороной (0‚1)" будет не более двух квадратов,
пересекающих отрезок АВ. Общее число квадратов, пере-
секающих отрезок АВ, будет не больше ‘2 (Z-6-5;-)-5+ 1),
Если фигура F состоит из т треугольников и наи-
большая сторона у этих треугольников равна _[‚, то число
квадратов, на которые отличаются числа N,, И М}, не
больше
Рис. 144.
6m((¢Ll7,5+1).-=-.s¢z(1o*L+1).
Соответственно числа S, и Si, отличаются не более чем
на 6m ((0,1)"L —|--(0,l)”‘), т. е. сколь угодно мало, если
велико la. Отсюда мы заключаем, что простая фигура дей-
ствительно имеет площадь.
109
Покажем теперь, что, площадь простой фигуры F равна
сумме площадей треугольников, из которых она состав-
лена. Пусть AW, A”), ..., AV")-—TpeyronbHm<u, из кото‹
рых составлена фигура F. Обозначим через S площадь
фигуры F, a через S“), S”), ..., S"")—1you1a1m тре-
угольников. Обозначим через N,(;'> число квадратов, содер-
жащихся в треугольнике А“). Если некоторый квадрат
содержится в треугольнике А“), то он содержится и в
фигуре F. Отсюда`следует, что
мр+м;3›+...+м‚;т><м„
Если некоторый квадрат содержится в фигуре F, НО
не содержится ни в одном треугольнике, то он пересе-
кается со стороной одного из треугольников. Отсюда
следует, что ' - “
Nk —- (Аду + м? + . . . + при) < 6т(1О"[. + 1).
Соответственно А и
sk _. (S<k1>+ 3(3) + . . . + зри) 4 6m ((0,1)"L + (0,1)‘2'=),
Правая часть этого неравенства сколь угодно мала, если
достаточно велико k. -
' При достаточно большом la число Sk СКОЛЬ угодно
мало отличается от S, числа S}? сколь угодно мало omn-
чаются от 8“). Так как 8,, сколь угодно мало отличается
от суммы величин Sg), то отсюда следует, что числа S
И $(”+$Ш+...+8(”” отличаются сколь угодно мало.
Но это значит, что они равны. Таким образом, площадь
фигуры F равна сумме площадей S“) треугольников А“),
из которых составлена фигур_а Р. Теорема доказана.
Теорема 15.3. Площадь треугольника равна nono-
вине произведения стороны треугольника на высоту,
опущенную из противоположной вершиньн
Доказательство. Определяя площадь фигуры F,
мы взяли две перпендикулярные прямые, пересекающиеся
в точке О (см. рис. 143). Отправляясь от этих прямых,
мы построили сетку квадратов, с помощью которой опре-
делили числа Зд, S}, и, в конце концов, площадь фигуры.
Естественно возникает вопрос: получим ли мы ту же
площадь, если возьмем другую пару прямых, пересекаю-
щихся в другой точке О? Рассмотрим тот случай, когда
110
.,
новые прямые параллельны старым. Будем называть пря-
мые, с помощью которых строится сетка квадратов, ба-
зисными прямыми, а точку, в которой они пересекаются,
базисной точкой.
Пусть число М, относится к старой сетке, а Мг-к
новой сетке. ‘Гак как квадраты имеют сторону (O,1)”, то
старую сетку можно совместить с новой сдвигом (парады
лельным переносом) на расстояния, не большие (0,1)" no
направлениям базисных прямых. При таком сдвиге сетки
некоторые квадраты из Nk, содержащиеся в фигуре Р,
могут уже не принадлежать фигуре, но заведомо содержат
хотя бы одну ее точку. Число таких квадратов, как мы
знаем, не больше 6т(1О"[. —]— 1), поэтому М, >_М, —
—- 6m (10"L + 1). Аналогично заключаем, что М, >__N,, —-—
-6m(10"L—|—l). Соответственно для чисел Sk и S,,, по-
лучаются неравенства
Е, г. 8,, ——.— 6m (_(O,l)"L +(0,1)‘-”*),
з, ,>.. з‘, —- 6m((0,1)"L +(0,1)9'°).
Из этих неравенств видно, что 3,, и 8,, отличаются сколь
угодно мало при достаточно большом /г. *
Пусть 8-—площадь фигуры F, которая получается,
если исходить из новых базисных np;1Mb1x,nepece1<a1o_-
щихся в точке д Так как 8,, СКОЛЬ угодно мало отли-
чается от S при достаточно большом /2, a S,,_, сколъ угодно
мало отличается от S, то S и S отличаются сколь угодно
мало. Но S И 8-—вполне определенные числа и могут
отличаться сколъ угодно мало только‘ тогда, если они
равны. Итак, площадь фигуры}? не зависит от выбора
базисной точки О при заданном направлении базисных
прямых.
Докажем теперь, что площадь прямоугольника со сто-
ронами р и q, параллельными базисным прямым, равна
произведению р на q. Число квадратов со стороной (О,1)"‚
содержащихся внутри прямоугольника, будет, очевидно,
не меньше
(z<T.’%V“)(<o3>»"‘)-
Число квадратов, содержащих по крайней мере одну
11!
точку прямоугольника, будет не больше
кап-чинные). П —
ПОЭТОМУ 8» 21961 - (P + q) (0.1)" +(0‚1)"‘‚
8:2 épq -HP + q)(0.1)" -I-(0,1)*".
Так как площадь S прямоугольника не меньше любого 1
Sk и‘ не больше любого Sh’, то S может быть равно
только pq. ‘
Найдем теперь площадь треугольника. Прежде всего
заметим, что если фигура F’ получается из F параллель-
ным переносом или симметрией относительно точки, то
они имеют одинаковую площадь. Пусть, например‚_Р и F’
симметричны относительно точки О. Приняв ату точку за
д - базисную‚ мы получим для обеих
д; ‚д фигур одинаковые числа Nk И М;
а следовательно, одинаковые площа-
ди. Если фигура F’ получается сдви-
д ‚д гом фигуры F, то надо взять базис-
_ные точки в соответствующих точ-
как фигур. у
Sb
Пусть АВС —— прямоугольный
треугольник с катетами, параллель-
ными базисным‘ прямым (рис. 145).'IIo
симметрии относительно средины отрезка АВ дополним его
до прямоугольника. Площади треугольников АВС и ABC,
равны ввиду указанной симметрии. Площадь прямоугольника
по доказанному равна АС - ВС. Поэтому площадь треуголь-
ника АВС равна Ё-АС-ВС.
Рис. 145.
д б, Ь д-
6’ .
„ Д д ‘4 5 б;
а
ЛГ д
Рис. 146.
‘A
й
Пусть теперь у треугольника АВС только одна сто-
рона параллельна базисной прямой, например, сторона АВ
112
)
параллельна а. Рассмотрим сначала случат-когда углы
А и В острые (рис. 146, слева). Имеем
5(А АВС)=$(ААСС`1)Ч—5(АВСС1)= .
—’3“%‘AC1°CC1+ '21-BC1-CC1=—‘ Ё‘
т. е. площадь треугольника ABC равна половине произ-
ведения стороны АВ на высоту ССд. `
Допустим, угол В треугольника АБС тупой (рис. 146,
справа). Тогда _ =
8(А АСС‚)=$(А АВС)—|—$(А СВС1),
I —;—Ac,.cc,=s(A A3c)+—§Bc1 . C0,.
Отсюда
S (А ABC).-.—_.—-% АВ- cc,
Пусть, наконец, ни Ъдна сторона треугольника АБС
не параллельна базисным прямым (рис. 147). Проведем
прямую BD, параллельную а, пере- - д
д
секающую сторону АС в точке D.
По доказанному площадь треуголь-
ника ABC равна сумме площадей ll
треугольников ABD и ВВС, т. е. д ‚с ‘
8(А АВС)= `
‚ 1 _ 1 __
_—=—2—BD-’AE—‘{1——§BD-CF...
имеем AE=AD cos ос, CF==CD Рис. 147.
cos ос, AE~[;—CF == АСсоз а, BH='
==BD cos оъ. Поэтому площадь треугольника
6‘
7
S(AABC)==-£-/1C-BI-I."
Итак, мы доказали, что площадь треугольника равна
половине произведения стороны треугольника на высоту,
опущенную на этусторону. Выбор стороны был связан с
расположением треугольника относительно базисных пря-
мых. Покажем, что результат не изменится, если в_зять
113
любую другую сторону и опущенную на нее высоту.
Пусть ABC -данный треугольник. Опустим высоты из
вершин В и С (рис. 148). Из подо-
В бия треугольников ABB, и АСС1 сле-
дует, что ' '
9: .49T__§.C_x
А АВ н‘ BB, '
д Отсюда
с %Ас.вв‚=;„4в.сс‚.
Рис. 148.
Теорема доказана полностью.
‘Г еор ема 15.4. Площадь параллелограмма равна
произведению основания на высоту (рис. 149).
° Доказательство. Треугольники ABD И ADC име-
ют равные стороны АВ и CD и равные соответствующие
им высоты. Поэтому площадь параллелограмма ABDC
равна АВ - СЕ.
Рис. 149. Рис. 150.
‚а _
б ч” fl
\ А Е д Е Л ч ‘
T e о р е м а 15.5. Площадь трапеции равна произве-
дению полусуммы оснований на высоту.
Д о к а з а т е л ь с т в о. Пусть ABCD —- данна_я трапеция
(рис. 150). Ее площадь равна сумме площадей треуголь-
ников ABC и ACD, Т. е. равна
~12-(AD -1: BC)- BE.
Теорема 15.6. Площади равных фигур равны.
Площади подобных фигур относятся, как квадраты
соответствующих линейных размеров.
Д о к а з а т е л ь с т в о. Мы ограничимся случаем простых
фигур. В этом случае утверждение теоремы сводится к
вопросу о соотношении площадей равных или соответст-
венно подобных треугольников. У равных треугольников
соответствующие стороны и высоты равны. Поэтому рав-
114
ны и площади. Если треугольники подобны, то их соответ-
ствующие высоты относятся, как стороны. Поэтому их
площади относятся, как квадраты соответствующих линей-
ных размеров. Теорема доказана.
д
Упражнения -
1. Вывести следующую формулу для площади треугольника
со сторонами а, 12, с:
S=-Vp <p——-a> <p——b)<p—-c>,
где р—-полупериметр треугольника (формула Герона).
2. Доказать, что площадь треугольника равна половине про-
изведения двух сторон треугольника на синус угла, заключенного
между этими сторонами.
З. Доказать, что выпуклый многоугольник является простой
фигурой, т. е. может быть разбит на конечное число треуголь-
ников.
4. Доказать, что площадь выпуклого многоугольника, oun-
санного около окружности, равна полупериметру многоугольника,
умноженному на радиус описанного круга.
§ 16. ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА
Длиной окружности называется число L, обладающее
следующими двумя свойствами:
1. L не меньше периметра любого вписанного в эту
окружность‘ выпуклого многоугольника. '
2. Существуют вписанные выпуклые многоугольники,
периметры которых сколь угодно мало отличаются от L.
Эти свойства числа L выражают словами: L есть
точная верхняя грань периметров выпуклых многоуголь-
ников, вписанных в окружность.
Т е о р е M a 16.1. Периметр любого вписанного в окруж-
ность выпуклого многоугольника меньше периметра
любого описанного выпуклого многоугольника.
Если стороны вписанного и описанного выпуклых
многоугольников не больше а и а< ё, где R-—pa0uyc
окружности, то периметры их отличаются не более
чем на 32а. '
Д о к а з а т е л ь с т в о. Первое утверждение теоремы
очевидно, так как любой вписанный выпуклый многоуголы
ник содержится внутри любого описанного и поэтому имеет
меньший периметр. Докажем второе утверждение.
115
Пусть‘ Р-г-вписанный, а Р’ -—описанный многоуголь-
ники, р и р’——их периметры. ‘Так как стороны многоуголь-
ников не больше а, то многоугольникР лежит вне окруж-
ности радиуса R—-a, а многоугольник Р’ лежит внутри
окружности радиуса R+a. Подвергнем многоугольник Р
преобразованию гомотетии с коэффициентом гомотетии,
а
R
R—-a °
Многоугольник Р’ содержится внутри многоугольника Рд.
Поэтому его периметр меньше, чем периметр многоуголь-
ника Рд, т. е.
' R-l—a
р Р'<7г:-дР-
Отсюда получаем *-
(R-—a)(p’-p)1<2azz
Периметр многоугольника Р меньше периметра квадрата,
равным Тогда он перейдет в многоугольник Рд.
описанного около окружности, т. е. p<8R. По условию _
теоремы а < ё- , следовательно, R -—- a > Поэтому
-R—(p'-——p)<2a-8P, или '
2 ‚
р'—-р<З2а. \
Теорема доказана, ~ .
Т е о р е м а 16.2. Для данного вписанного многоуголь-
ника можно указать такое положительное число е,
что любой описанный многоугольник имеет периметр,
больший периметра данного вписанного многоугольника
по крайней мере на е. ‚„
Для данного описанного многоугольника можно ука-
зать такое положительное число е,_что любой ammun-
ный многоугольник имеет периметр, меньший периметра
данного описанного многоугольника по крайней мере на е.
Доказательство. Пусть Р—-—данный вписанный
многоугольник, А и В -—две его смежные вершины (рис. 151,
слева). Возьмем точку С на дуге АВ и обозначим через Р,
многоугольник, вершинами которого являются вершины
многоугольника Р и точка С. Периметр многоугольника Р;
больше периметра многоугольника Р. Пусть разность их
периметров е. Периметр любого описанного многоуголь-
ника больше периметра многоугольника Р‚, следователь-
но, больше периметра многоугольника Р по крайней
мере. на е. _ ‘
116
‚Пусть Р’--данный описанный многоугольник (рис. 151,
справа). Возьмем какую-нибудь точку на окружности, отлич-
ную от ‚точек касания. многоугольника с окружностью.
Проведем в этой точке касательную, Она разбивает мно:
гоугольник на два многоугольника. Тот из них, который
лежит по одну сторону с окружностью, является описан-
ным около окружности, обозначим его P1’. Периметр мно-
гоугольника Pj меньше‘ периметра многоугольника Р’.
б’
б’
Рис. 151.`
‘I
Пусть е разность их периметров. Любой вписанный мно-
гоугольник имеет периметр, меньший периметра много-
угольника P1’. Поэтому периметр многоугольника Р’ по
крайней мере на е больше периметра любого вписанного
многоугольника. Теорема доказана.
‘ «Теорема 16.3. ' Каждая окружность имеет опре-
деленную длину. Длина окружности ‘равна 21:12’, \где
2п:—- некоторое число, не зависящее от взятой окруж-
ности, а R—-paazzyc окружности.
`Д'оказательство.- Пусть Р„ и›Р‚;—-—вписанный и
описанный правильные многоугольники с числом сторон 2”;
Обозначим их периметры р„ и p,',. Так как. каждый из
многоугольников P,, и P,',~ содержится внутри квадрата,
описанного около окружности, то стороны этих много-
. 8
угольников не больше —2—,,—. Поэтому их периметры omn-
- — . 32 о 8
чаются не более чем на 2,,R (теорема 16.1).
Периметр многоугольника Р„ меньше периметра мно‹
гоугольника P,,+1, так как переход, от Р‚, к Р„+‚ связан
с заменой стороны- АВ многоугольникаРд двумя сторо-
нами АС и СВ многоугольника PM, (рис. 152, слева).
117
A что периметр любого вписанного многоугольника меньше L.
Периметр многоугольника P,', больше периметра много-
угольника P,',+-1, так как переход от P,',1< Р{‚+‚ связан
с заменой ломаной АВС на ломаную ААдСдС, которая
имеет меньшую длину (рис. 152, справа). ‘
Рис. 152.
Таким образом, последовательности чисел р„ и р},
обладают следующими свойствами:
1- P2<Pa<P4<--- 2
2и>и>и>„„
3- pn<P£..
4° РЁ: ""'pn< 32in8R °
По теореме 15.1 существует число L, не меньшее любого
из чисел р„ и не большее любого из чисел р}‚. Докажем,
что число L И есть длина окружности, как мы ее опре-
делили вначале. '
Так как p,',-—p,, сколь угодно мало при достаточно
большом п, а L заключено между р}, и, рт то L--p,,
сколь угодно мало при достаточно большом п. Покажем,
Пусть р-—периметр данного вписанного многоугольника.
По теореме 16.2 существует положительное число е такое,
что периметр любого описанного многоугольника больше р
по крайней мере на е. При достаточно большом п пери-
метр р; сколь угодно мало отличается от L. Поэтому L
больше р. Итак, существование длины окружности дока-
вано. Докажем теперь, что она пропорциональна радиусу.
Подвергнем данную окружность и многоугольники P,,,
P}, преобразованию гомотетии шкоэффициентом гомотетии
1
Ё- относительно центра окружности. При этом данная
окружность перейдет в окружность единичного радиуса.
118 '
_ .. _ ___,__..__.-__- ..
..:—— -—.._._._
Обозначим pa и р}, периметры 2"-угольников, полученных
этим преобразованием из многоугольников Р‚, и P,',.
Имеем
___—}— ___I_____1_ I
pt!“ R рт Pn-— R рт
Обозначим через 27:: длину единичной окружности. Тогда
р‘‚,<2п <р;,. Отсюда р„< 21cR<p,',. По теореме 15.1
существует одно число, не
меньшее любого р‚, и не боль-
шее любого p,',. Поэтому
L==21tR. Теорема доказана. д д
Число п, которое вхо- Рис. 153.
дит в выражение длины ок-
ружности, иррациональное. Приблизительное значение
п: яз 3,1416.
Длиной дуги EB окружности называется точная верхняя
‚грань вписанных выпуклых ломаных в эту дугу (рис. 153).
Теорема 16.4. Любая дуга окружности имеет
определенную длину. Длина дуги окружности
l=7cR
(Z
180 ’
где ос-градусная мера соответствующего цен/таль-
ного угла.
Д о к а з а т ел ь с тв о. Доказательство _ существования
длины дуги проводится так же, как доказательство суще-
ствования длины окружности. При этом роль вписанных
многоугольников играют вписанные ломаные, а роль описана
ных многоугольников играют описанные ломаные. Мы не
будем повторять этих рассуждений. Докажем второе
утверждение теоремы, предполагая первое утверждение
доказанным.
Пусть ‚ТВ—-—дуга окружности и С-—точка этой дуги.
Она разбивает дугу A? на две дуги: АЁ‘ и С/Ё. Докажем
сначала, что длина дуги АЁ равна сумме длин дуг AZ‘ и
ЁЁ. Обозначим через l длину дуги АЁ, через 11—длину
дуги АС и через [др-длину дуги СВ. Требуется доказать,
что 1.-.-.—_. !‚-]—!,. -
H9
/
Возьмем произвольное положительное число е. По
определению длины дуги АЁ существует ломаная т, впи-
санная в дугу A79, длина которой отличается от длины
дуги АТ? меньше чем на е. Точно так же существуют
ломаные 11 н 1;, вписанные в АС и B73, _такие, что их
длины отличаются от ll и [д меньше чем на. е. Пополним
ломаную т вершинами ломаных 11 и та, а ломаные 11 и 12
вершинами ломаной т. Тогда получим ломаные т’, т; и 1;.
Так как пополнение ломаной новыми вершинами не умень-
шает ее длины, то длины ломаных 1’, т; и 1; отличаются
от l, Z, И [а также не более чем на е. Ломаная т’ состав-
лена из ломаных т; и 1;. Поэтому ее длина равна сумме
длин ломаных т; и 1;. Отсюда "следует, что {отличается .
от 1‚+1„ неболее чем на 2е. Так как In l,+lg-—coBep-
шенно определенные числа, а е произвольно, то это может
быть, только если Z:-..l,—}-lg.
Из доказанного свойства длины дуги следует, что если
некоторая дуга окружности является частью ‘другой дуги,
то ‘первая дуга имеет‘ меньшую длину. Очевидно, равные
‘дуги имеют равные длины.
Пусть данная дуга отвечает центральному углу об’.
Разобьем окружность на п равных дуг, взяв точку А дуги
KB за начальную, точку деленияокружности. Пусть т—-
целая часть 3-Q630-. Тогда на дуге A753 будет расположено т
целых дуг деления окружности и одна, может быть, не
п `
целая nyra, ЕСЛИ. 3810, Не ЯВЛЯОТСЯ целым.
Одна дуга при делении окружности на п равных частей
ТЕ
п
будем обозначать ее l, заключена в пределах
имеет длину . Отсюда следует, что д`лина дуги KB,
2:” (m +1).
31:?-m<l<
Так как .
т<-3%%<т+1,
то из предыдущего неравенства получаем
2-:cR па 21cR па
п a('?3—6*()___1)<l<—r'i—(360 +1)’.
ч
а
120
T.€. ' ›
а 2:61? а .21rR
“RT§b""""}T<1<"‘R’ 180 +7‘
Так как п произвольно, то
Теорема доказана.
Радианной мерой центрального угла называется отно-
шение длины дуги окружности, соответствующей этому
углу, к радиусу окружности. Единицей радианной меры
углов является радиан. Это угол, которому соответствует
дуга, равная радиусу. Градусная мера одного радиана
равна приблизительно 57,З°. Радианная мера прямого угла
равна -3-,
дКругом радиуса R с Центром в точке О называется
фигура, точками которой ‚являются точки плоскости, уда-
ленные от точки Она расстояние, не большее R. Окруж-
ность радиуса R c центром О является границей этого
круга. _ r .
Теорема 16.5. Круг имеет определенную площадь.
Площадь S круга радиуса R равна произведению длины
ограничивающей круг окружности на половину радиуса,
т. е. г .
,$=тсН”. ц
радианная мера угла 180° равна 1:.
Д о к а з а т е л ь с т в о. Впишем в окружность круга
ли» опишемоколонее правильныехТ-угольники Р„ и P,',.
Обозначим их- площади через 4,, и А}, соответственно.
Так как P, расположен внутри P,;, то A,,<A,§. Покажем,
что A,, и А}, отличаются сколь- угодно мало, если доста-
точно велико п. Стороны‘ многоугольников Р‚, и P,'_,_ не
8 ‚ -
более чем Если Р‚‚ подвергнуть преобразованию го-
мотетии относительно центра круга с коэффициентом гомо-
тетии . *
8R
R+"27{'
12 Z‘-".———§"R;",
....... „Г:
то, как мы знаем, получится многоугольник, содержащий
L 121
внутри многоугольник Р’. Отсюда следует, что
16R
п
.2]2
An.
‚ 2
А,‚</г9А„=_-А„+————Ё—Ёт
(’*""2"п'>
Так как An меньше площади квадрата, описанного около
окружности, т. е. меньше 4R“, a при 12> 3‘ имеем
8 1
R —— д’; > 5- R, T0 из этого неравенства получаем
/
16R-2R- 16
А:‚<А„+ 2,, .
Итак, А; и An отличаются сколь угодно мало при доста-
точно большом п. `
Определяя площадь произвольной фигуры F, мы ввели
два числа Nk И М; и соответствующие им числа 8„ и Si,
(СМ. начало § 15, стр. 108). N,,——-aTo число квадратов
сетки со стороной (0,1)", которые принадлежат фигуре
целиком, а МЗ-число тех квадратов, которые содержат
хотя бы одну точку этой фигуры. Пусть теперь фигура F
есть наш круг. Обозначим через П}, число квадратов, co-
держащихся в пополненном многоугольнике Р„‚ а через
М; обозначим число тех квадратов, которые содержат
хотя бы одну точку пополненного многоугольника p;,.
Очевидно, 1Т/‚‚<1\/‚,<1\/; ‘<1?/k. Обозначим через Ёд, Sh,
8}, и Зькчисла, которые получаются из соответствующих N
умножением на (0,01)". Тогда
Ёь<$ь<8Ь<ЁЬ.
Как мы знаем, при достаточно большом la число 3},
сколь угодно мало отличается от A-,,, a число Si, сколь
угодно мало отличается от Ag. Отсюда следует, что Sk
сколь угодно мало отличается от Sk, и, следовательно,
круг имеет определенную площадь. Так как 8‚, и S}, при‘
достаточно большом k СКОЛЬ угодно мало отличаются от
площадей многоугольников Р„ и p;,, то и 8 сколь угодно
‚ МЗЛО ОТ НИХ ОТЛИЧЗСТСЯ.
‚ ‚ 1 ‚
Площадь Ад многоугольника P,, равна -2—p,,R. Так как
р}, сколь угодно мало отличается от длины окружности
122
_.:_._--.._ __‚_ ___
"_"" ———“..—-.__._ -_——_._ д... д’ ‚
_r-
21:12, то площадь круга S сколь угодно мало отличается
' от »n:R“. Но это значит, что 8=тп129‚ Теорема доказана.
круговым сектором называется часть круга, лежащая
внутри соответствующего центрального угла (рис. 154).
Круговой сектор имеет, определенную
площадь. Площадь кругового сектора
равна
__ 2 “
.3-——fl¥? 366,
где Н-радиус круга, а оъ-градусная
мера сооддвфетствующего центрального
угла. ‘ Доказательство существования PM 1545
площади сектора аналогично доказа-
тельству существования площади круга. Доказачтдельстро
формулы для площади сектора аналогично доказательству
формулы для длины дуги окружности.
круговым сегментом называется общяя часть круга
и "полуплоскости (рис. 155). Сегмент имеет определенную
‚ _ Рис.155.
площадь. Площадь сегмента, не равного полукругу, опреч
деляется по формуле
а
—‘=WR2‘§-6'6-.'._§._— SA,
где ЗА-площадь треугольника с вершинами в Центре
круга и концах радиусов, ограничивающих соответствую‹
щий сектор. Знак — надо брать в случае, если oc< 180,
а знак -|- в случае, если оъ>18О. Доказательство этого
утверждения аналогично доказательству теоремы 15.2 о
том, что площадь простой фигуры равна сумме площадей
составляющих ее треугольников.
123
517. HEK(3TOPblE СВЕДЕНИЯ из истории
геометрии \ а . с. ‘
Первые геометрические результаты относятся‘ иглу-
бокой древности и имеют опытное происхождение. Они
были отмечены людьми в связи с их практической деятель-
ностью. Геометрия как Эмпирическая наука в ранний период
дости`гла особенно высокого уровня в Египте в связи c
землемерными и ирригационными работами.
В первом тысячелетии до нашей эры геометрические
сведения от египтян перешли к грекам, „в Греции начался
новый этап развития геометрии. ‚За период с VII no Ill век
до нашей эры греческие геометры не только обогатили
геометрию многочисленными новыми результатами, но пред-
‘приняли также серьезные шаги к строгому ее обоснова-
нию. ‚ .
Многовековая работа греческих геометров за этот
период была подытожена и систематизирована Евклидом
‚(3304-275 гг._д0 н. э.) вчего знаменитом трудежНачала».
Это сочинение дает первое дошедшее до нас строгое по-
строение геометрии. В нем изложение настолько безупречно
для своего времени, что в течение двух тысяч лет с мо-
мента появления «Начал» оно было единственным руковод-
ством для изучающих геометрию.
«Начала» Евклида состоят из тринадцати книг. Из них
восемь книг посвящены собственно геометрии, а осталь-
ные ——арифметике. Каждая книга «Начали начинается опре-
делением понятий, которые встречаются. В первой книге
«Начал» за определениями следуют постулаты иаксномы.
Например: ‘ ‚ д -
Постулат 1. Требуется, чтобы от каждой точки
ко всякой другой точке можно было провести прямую.
' Постулат V. Требуется, чтобы всякий раз, когда
прямая при пересечении с двумя другими прямыми образует
с ними внутренние односторонние углы, сумма которых
меньше двух прямых, эти прямые пересекались c той сто-
роны, с которой эта сумма меньше двух прямых.
Аксиома 1. Равные порознь третьему равнымежду
собой. ‘
Аксиома 11. Если к равным прибавить равные, то
получим равные. с d Ш
И постулаты и аксиомы представляют собойутвер-
ждения, принимаемые без доказательства. По какому прин-
124
ципу одни утверждения относятся к постулатам, а другие-
к аксиомам, неизвестно. В современном изложении мы все
такие утверждения называем аксиомами.
Вслед за аксиомами идут теоремы и задачи на по-
строение под общим названием «Предложения». Они рас-
положены в строгой последовательности так, что доказа-
тельство (решение) каждого последующего предложения
опирается на предыдущие.
В связи с таким построением геометрии возникло
естественное желание у геометров свести число постулатов
и аксиом, т. е. утверждении, принимаемых без доказатель-
ства, до минимума. Поэтому сам Евклид и многие геометры
после Евклида пытались вывести некоторые постулаты и
аксиомы из других постулатов и аксиом. В частности,
многие геометры, начиная с Евклида, пытались доказать
пятый постулат. ч
Было предложено много доказательств пятого посту-
лата. Однако во всех этих доказательствах авторы исполь-
зовали то или другое утверждение, не содержащееся в
других постулатах и аксиомах, эквивалентное пятому по-
стулату. Вот некоторые из таких утверждений:
. 1. Все перпендикуляры к одной стороне острого угла
пересекают другую его сторону. =
2. Существуют подобные и не равные треугольники.
З. Существуют треугольники сколь угодно большой
площади.
4. Существуют треугольники с суммой
двум прямым.
5. Параллельные прямые-— равноотстоящие.
В результате неудачных попыток доказательства пятого
постулата у некоторых “геометров, начиная с конца
XVIII века, возникло сомнение относительно самой: воз-
углов, равной
`можности доказательства пятого постулата. Полное реше-
ние этого вопроса принадлежит великому русскому гео-
метру Николаю Ивановичу Лобачевскому (179З--1854).
Один из эквивалентов пятого постулата состоит в
утверждении, что через точку вне данной прямой проходит
не более одной прямой, параллельной данной. Лобачевский
заменил пятый постулат следующим:
Через точку вне прямой на плоскости
прямые, не пересекающие данную.
Подобно предшественникам, Лобачевский имел надежду
обнаружить противоречие в системе следствий, вытекающих
125
проходят две
из этого нового постулата. Однако, развив систему след-
ствий до объема «Начал» Евклида, Лобачевский не обна-
ружил в ней противоречий и на этом основании сделал
правильный вывод о существовании геометрии, отличной
от геометрии Евклида, в которой пятый постулат Евклида
не имеет места. Эта геометрия теперь называется геомет-
рией Лобачевского.
Геометры после Лобачевского строго доказали, что
если в геометрии Евклида_нет противоречий, то их не
может быть и в-геометрии Лобачевского. Таким образом,
в отношении логической непротиворечивости эти две гео-
метрии находятся в равном положении. Вопрос о том,
какая из этих геометрий лучше описывает окружающий
нас мир, может быть решен только опытом. В настоящее
время установлено, что геометрия окружающего нас мира
в больших, космических масштабах имеет более сложное
строение, чем геометрия Евклида и Лобачевского. В от-
носительно небольших масштабах эта геометрия близка
к евклидовой. Поэтому в повседневной жизни мы пользуемся
евклидовой геометрией.
Приведем некоторые теоремы геометрии Лобачевского.
Прежде всего, в геометрии Лобачевского верны все теоремы
евклидовой геометрии, которые мы доказали до параграфа
о параллельных линиях. Таким образом, в геометрии Ло-
бачевского верны теоремы, формулирующие признаки ра-
венства треугольников, теоремы, устанавливающие соот-
ношения между сторонами и углами треугольника, теорема
о существовании и единственности перпендикуляра, опу-
щенного из данной точки на данную прямую, и многие
другие теоремы евклидовой геометрии.
Однако теоремы, в доказательстве которых исполь-
зуетсяаксиома параллельных Лобачевского, звучат совсем
по-другому. Например, используя аксиому V, мы доказали,
что сумма углов треугольника равна двум прямым. Соот-
ветствующаЯ теорема геометрии Лобачевского гласит: сумма
углов треугольника меньше двух прямых. Оказывается,
она зависит от треугольника. В частности, если один тре-
угольник содержится внутри другого, то объемлющий
треугольник имеет сумму углов меньшую.
В геометрии Евклида, как мы знаем, для данного тре-
угольника существует бесконечное множество подобных,
не равных ему треугольников. В геометрии Лобачевского,
если у двух треугольников соответствующие углы равны,
126
. H ‚г _ x _
2:: __ 2 у
‘С _ ‚_ .
_ ~ 1 ‚аз-зад к и
:__.?_____--._.__-_....__
Ir
то треугольники равны, т. е. не существует подобных, не
равных треугольников.
В геометрии Евклида непересекающиеся прямые яв-
ляются равноотстоящими. В геометрии Лобачевского, если
прямые не пересекаются, то они неограниченно расходятся
по крайней мере в одном направлении.
В геометрии Евклида к двум непересекающимся прямым
можно провести сколько угодно общих перпендикуляров.
В геометрии Лобачевского общии перпендикуляр либо
только один, либо вообще не существует общего перпен-
дикуляра. _
Все эти теоремы геометрии Лобачевского можно no-
казать, если принять вместо/нашей аксиомы V о параллель-
ных аксиому Лобачевского, сохранив остальные аксиомы.
Однако доказательства оказываются довольно сложными.
Это объясняет, почему решение вопроса о недоказуемости
пятого постулата заняло более двух тысяч лет.
Алексей Васильевич Погорелов
Элементарная геометрия
Планиметрия
М.‚ 1969 гт, 128 стр. с илл.
Редактор А. Ф. Лапка
Техн. редактор А. А. Благовещенская
Корректоры Л. С. Кугушева, И. Я. Кришгаль
Сдано в набор 28/XI 1968 r. Подписано к пе-
чати 3/III 1969 г. Бумага 84><108‘/д2. Физ. печ.
л. 4. Условн. печ. л. 6,72. VII.-u3,u. Л. 6,03.
Тираж 200000 экз. T-02700. Цена книги 17 коп.
Заказ м 104.
Издательство «Наука»
Главная редакция
физико-математической литературы.
Москва, B-7_l, Ленинекий проспект, 15.
Главполиграфпром Комитета по печати при
Совете Министров СССР. Отпечатано в Ленин-
градской типографии N2 2 им. Евг. Соколовой,
Измайловский пр., 29, c матриц Ордена Тру-
дового Красного Знамени Ленинградской ти-
пографии N9 1 «Печатный Двор» им. А. М. Горь-
кого г. Ленинград, Гатчинская ул.‚ 26.