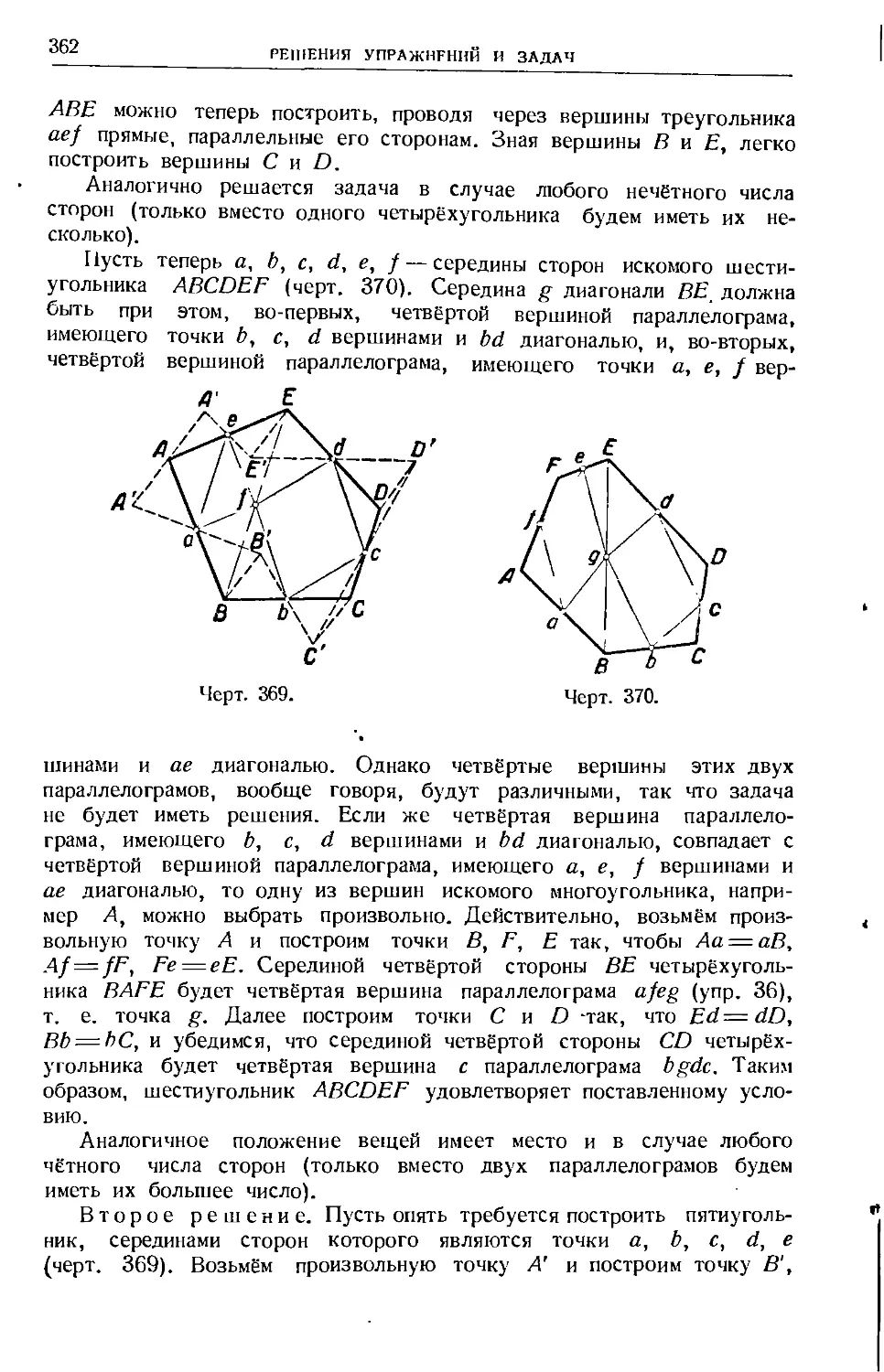
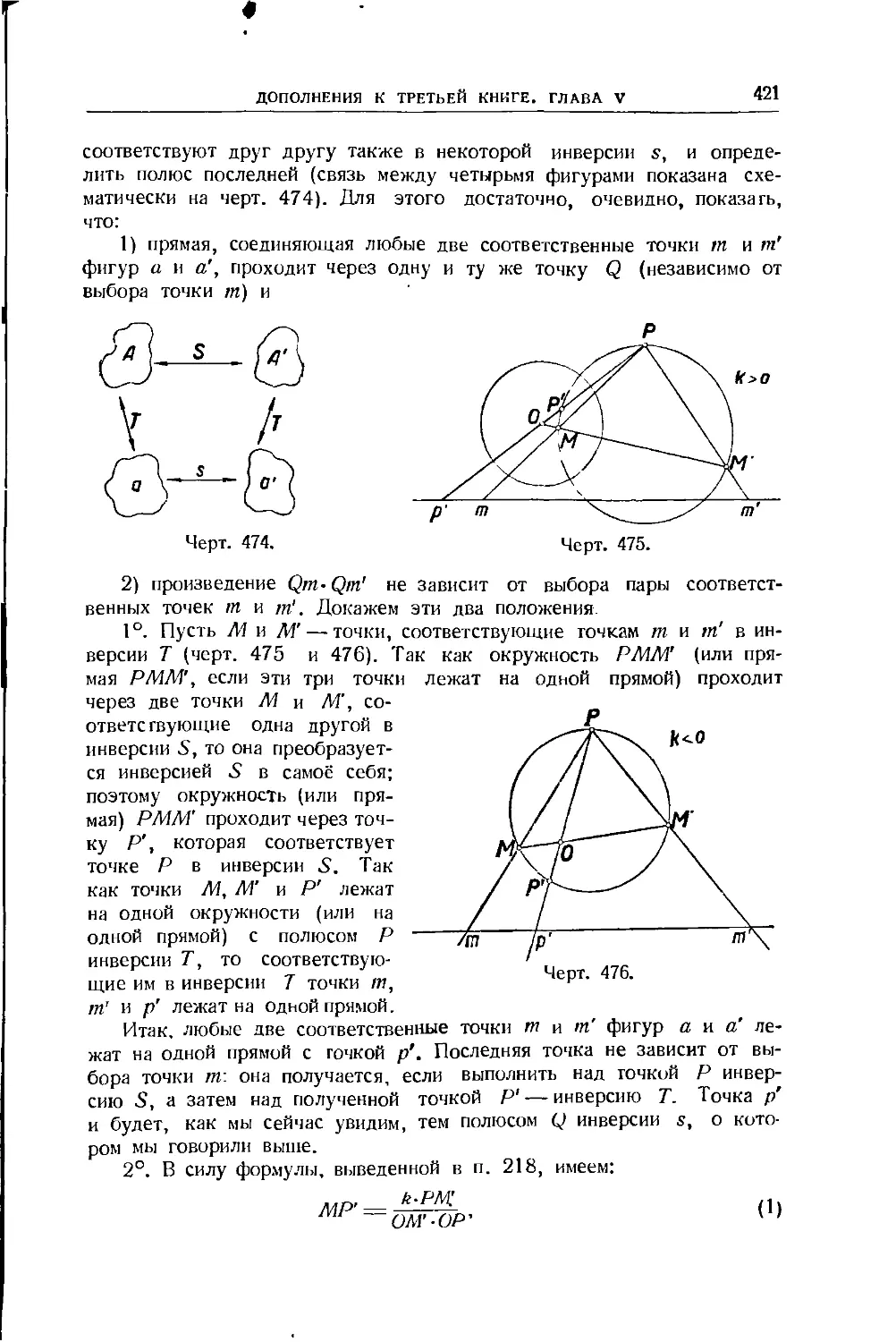
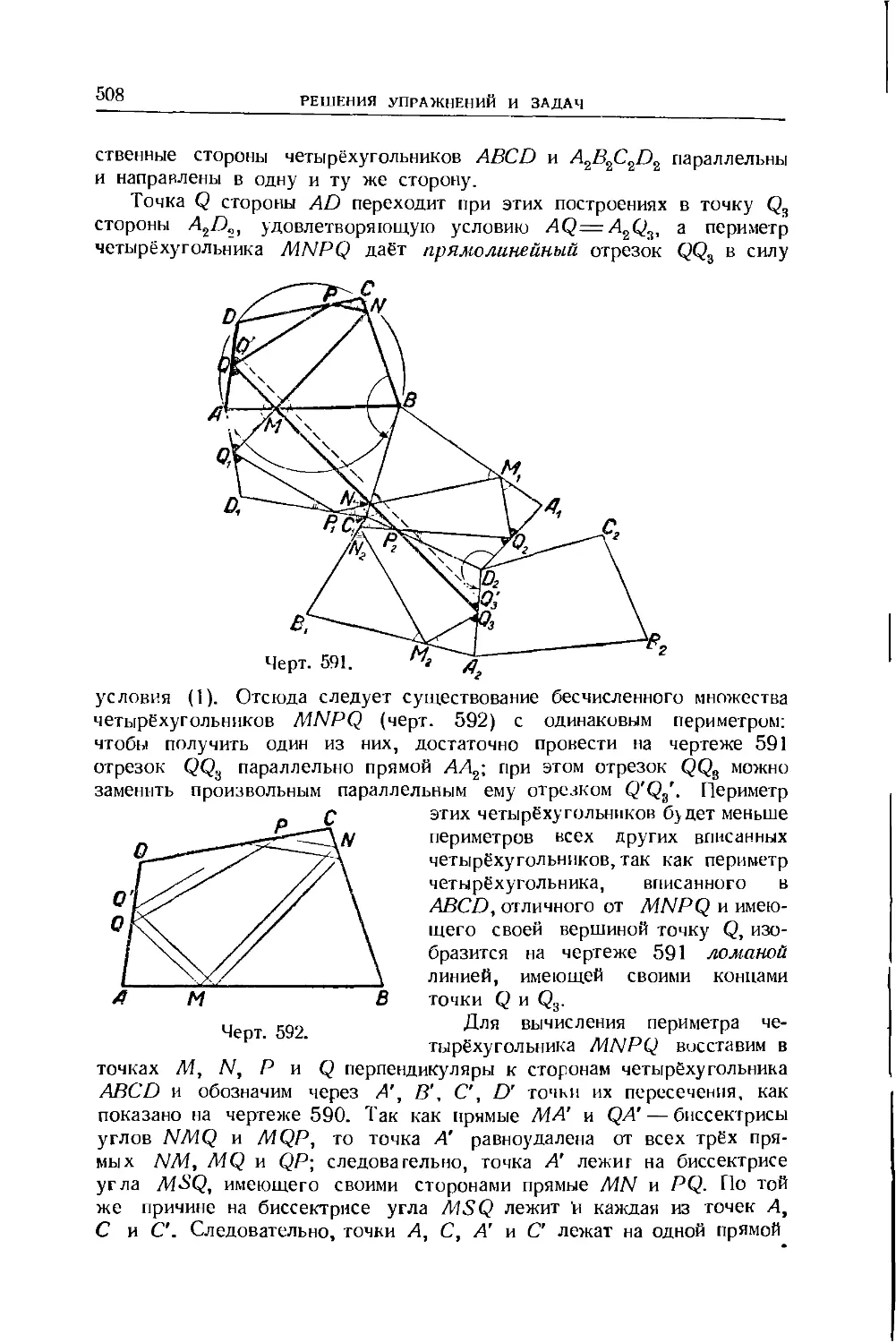
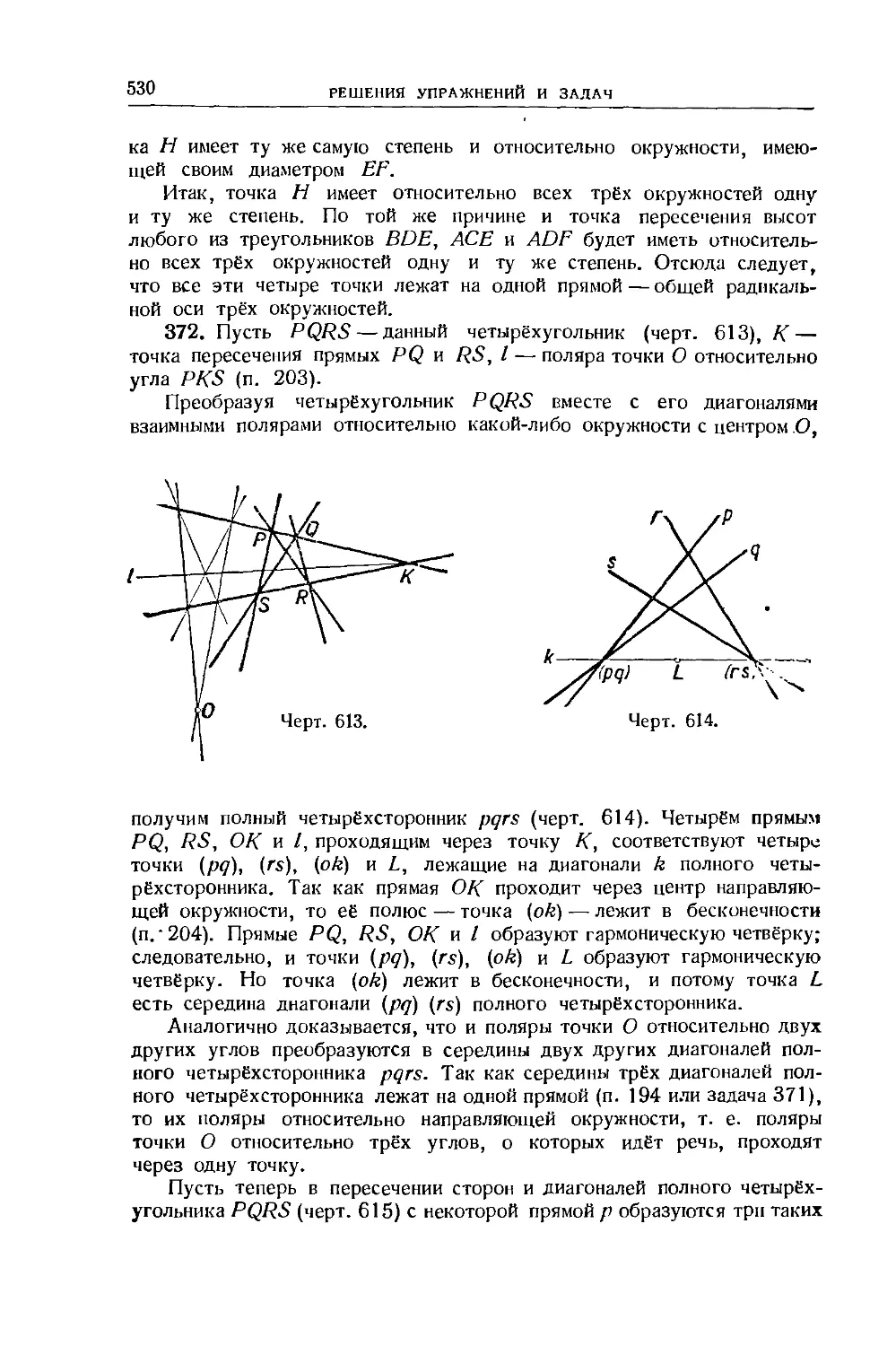
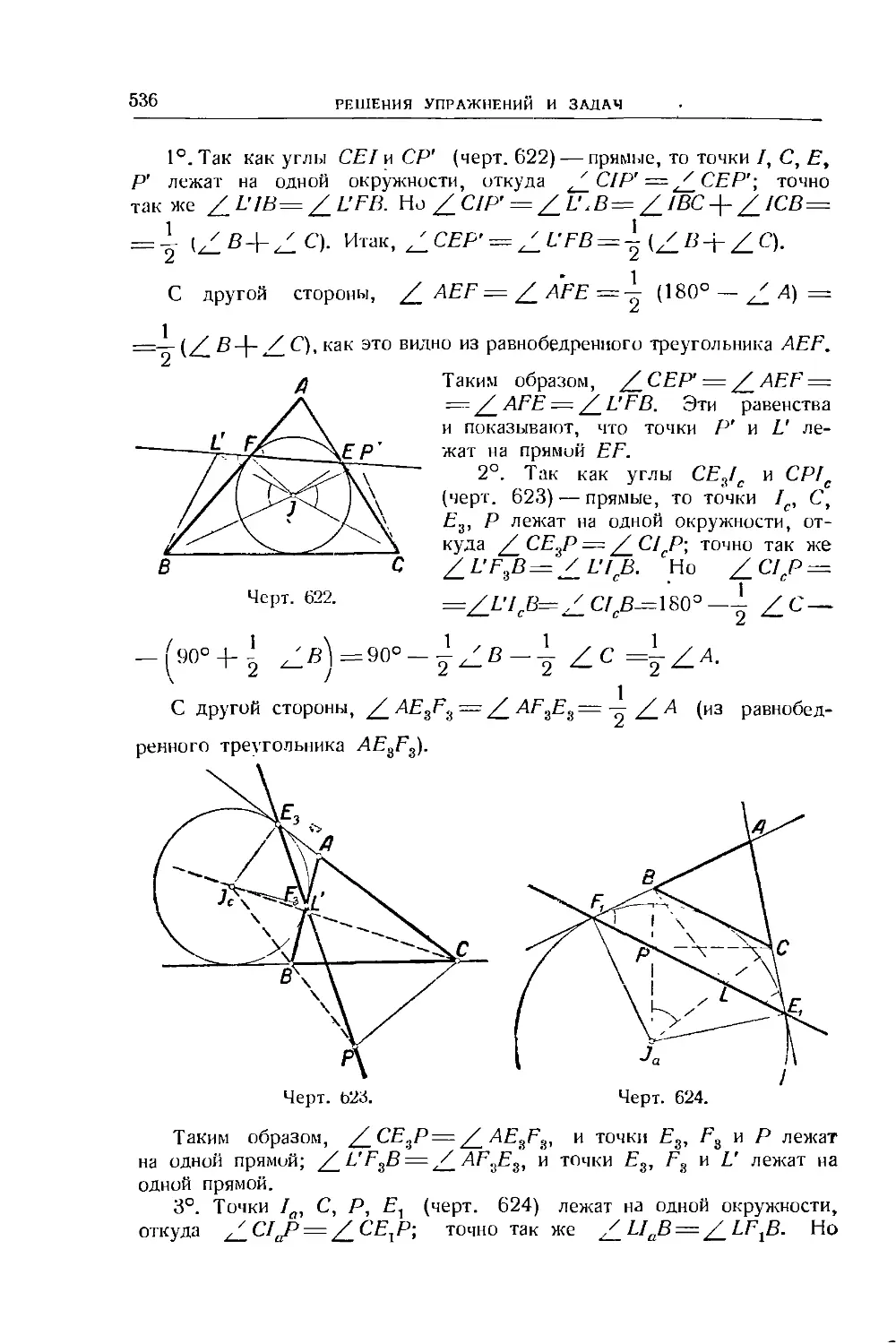
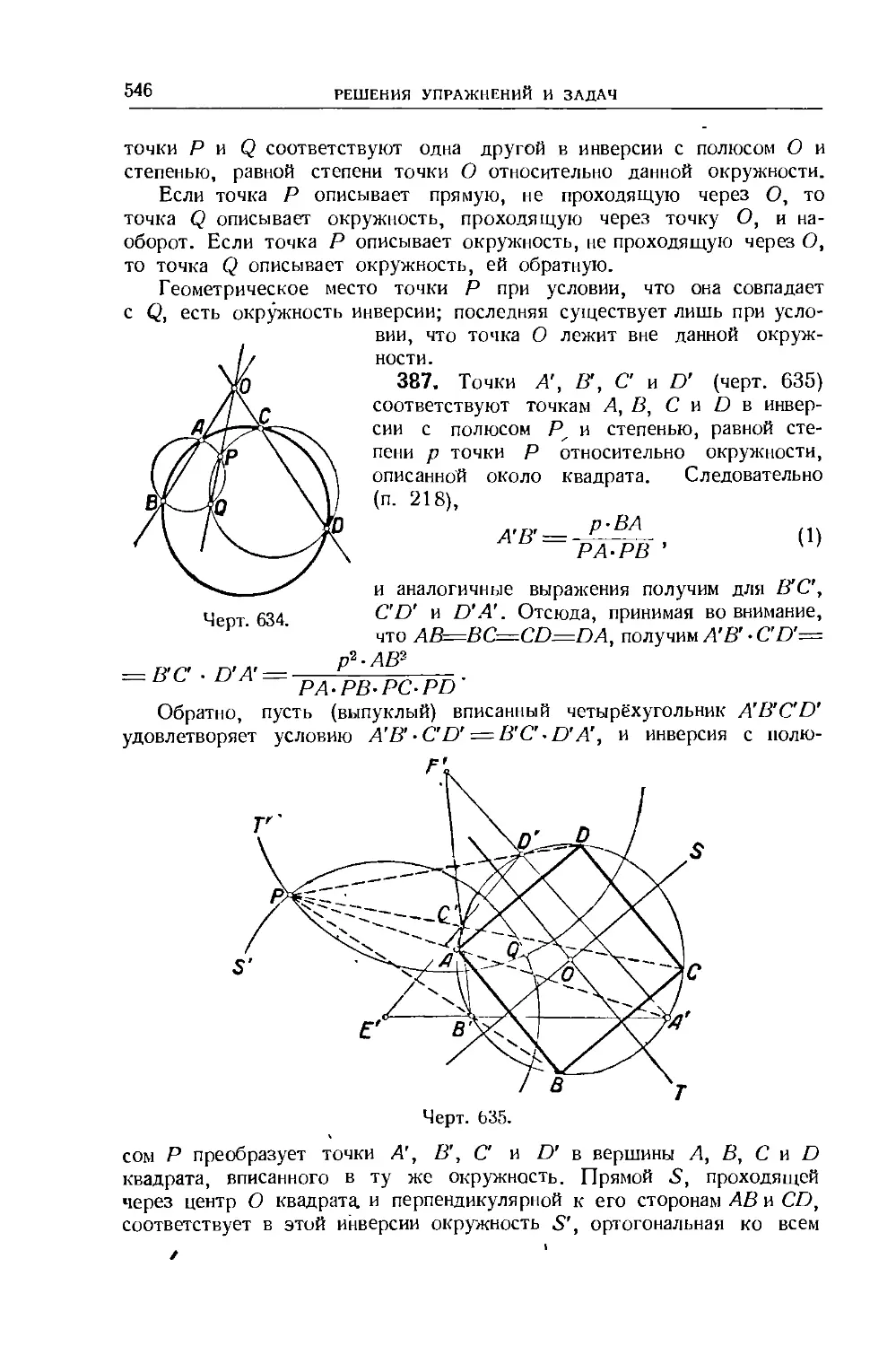
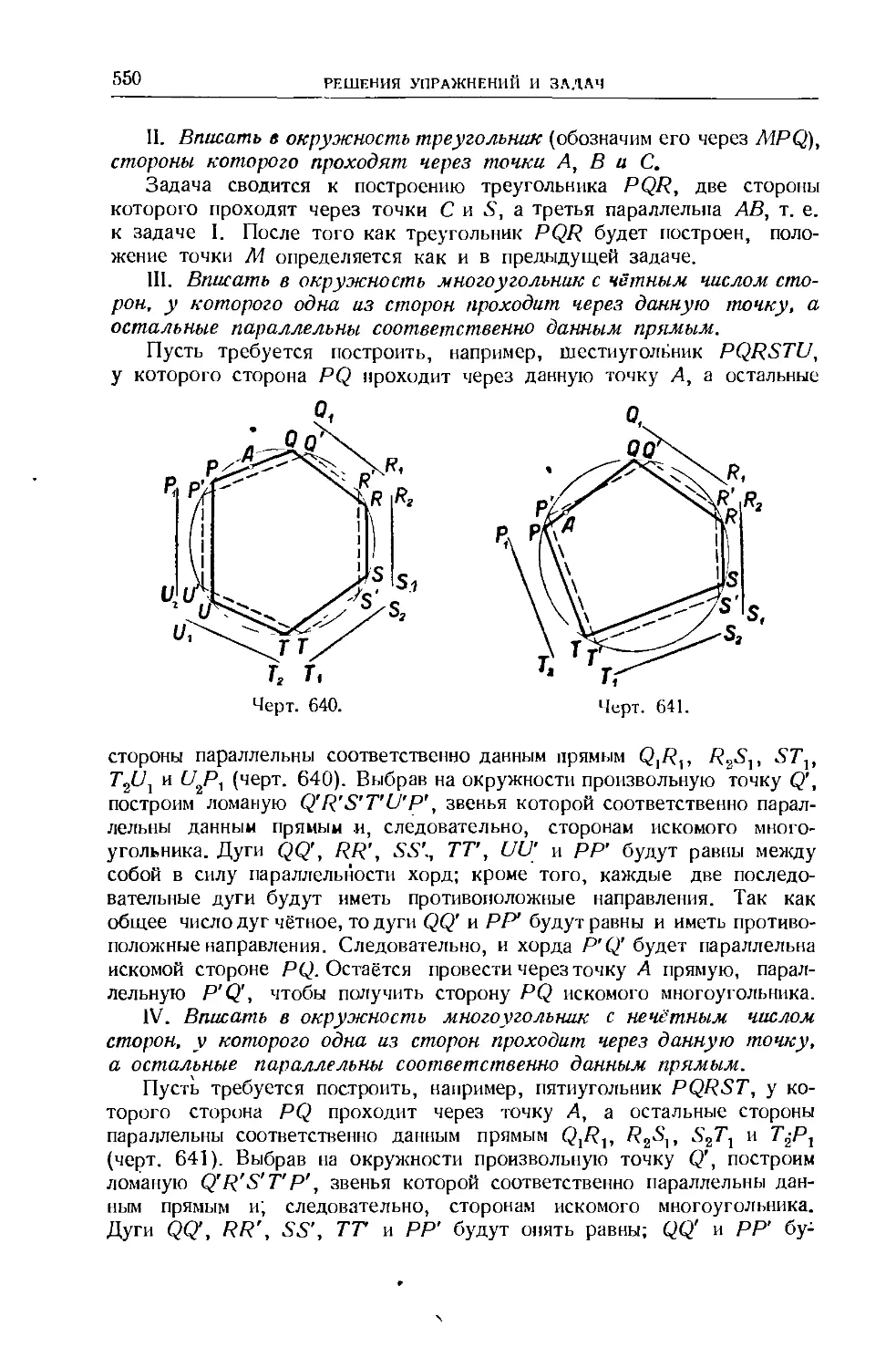
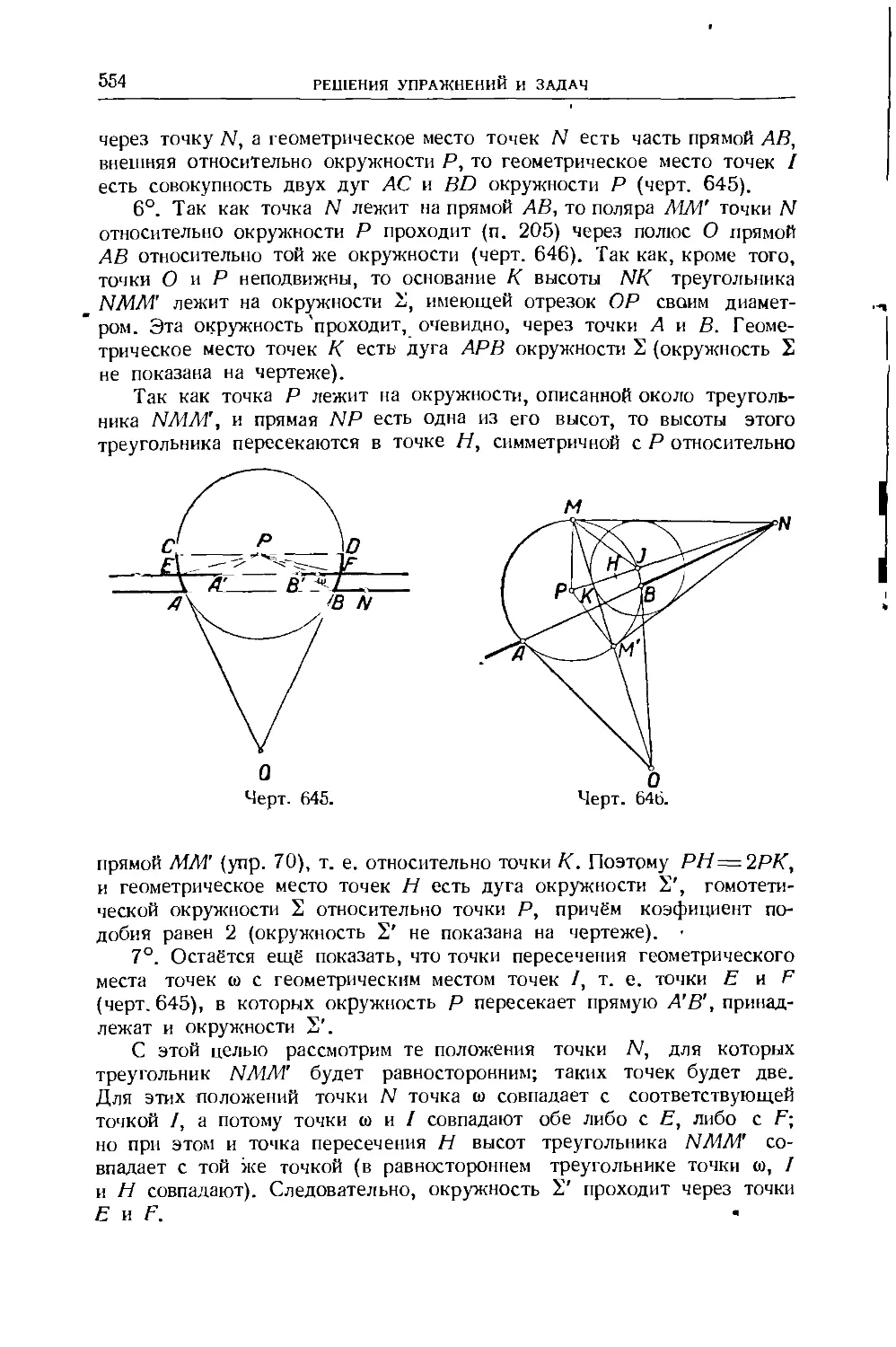
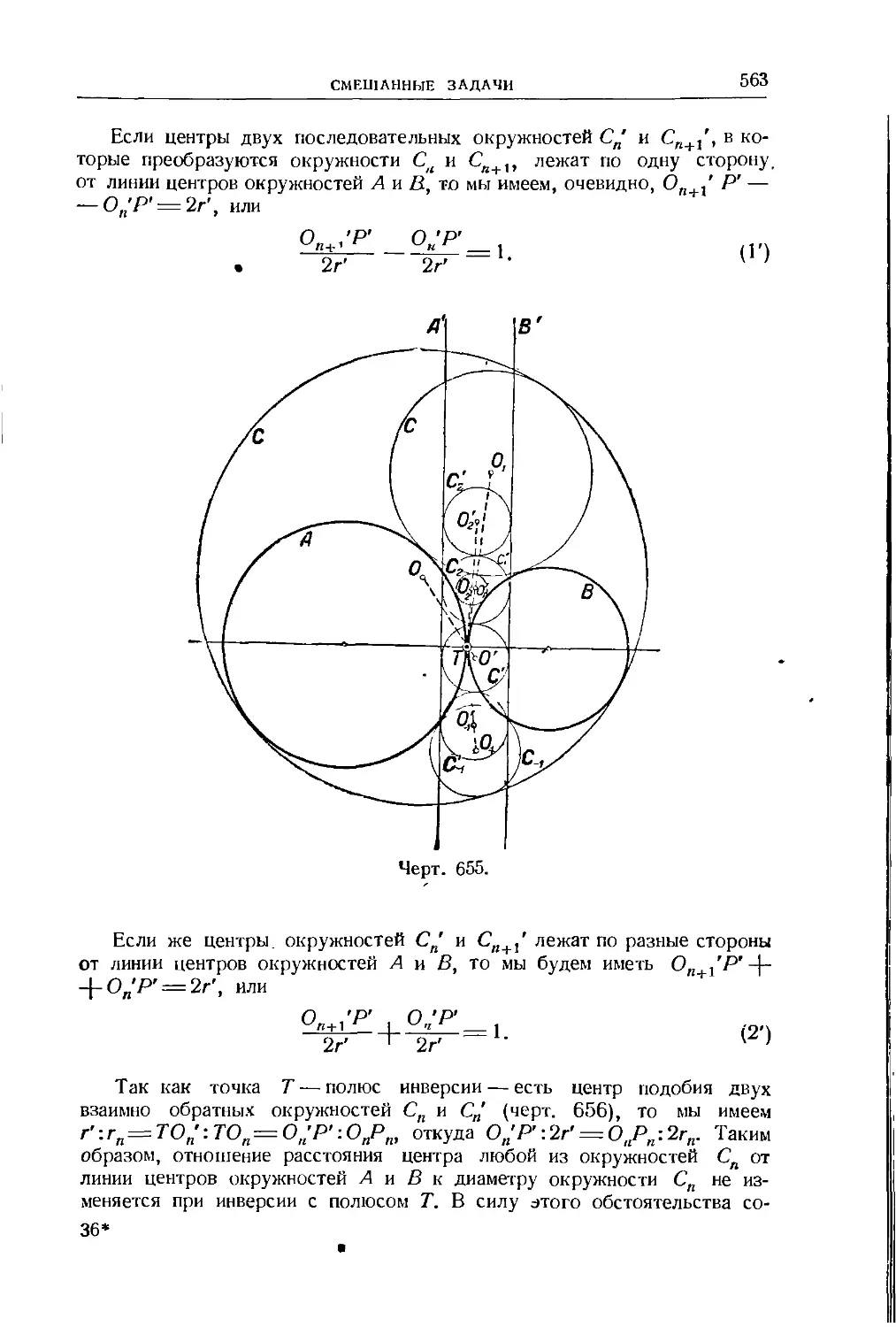
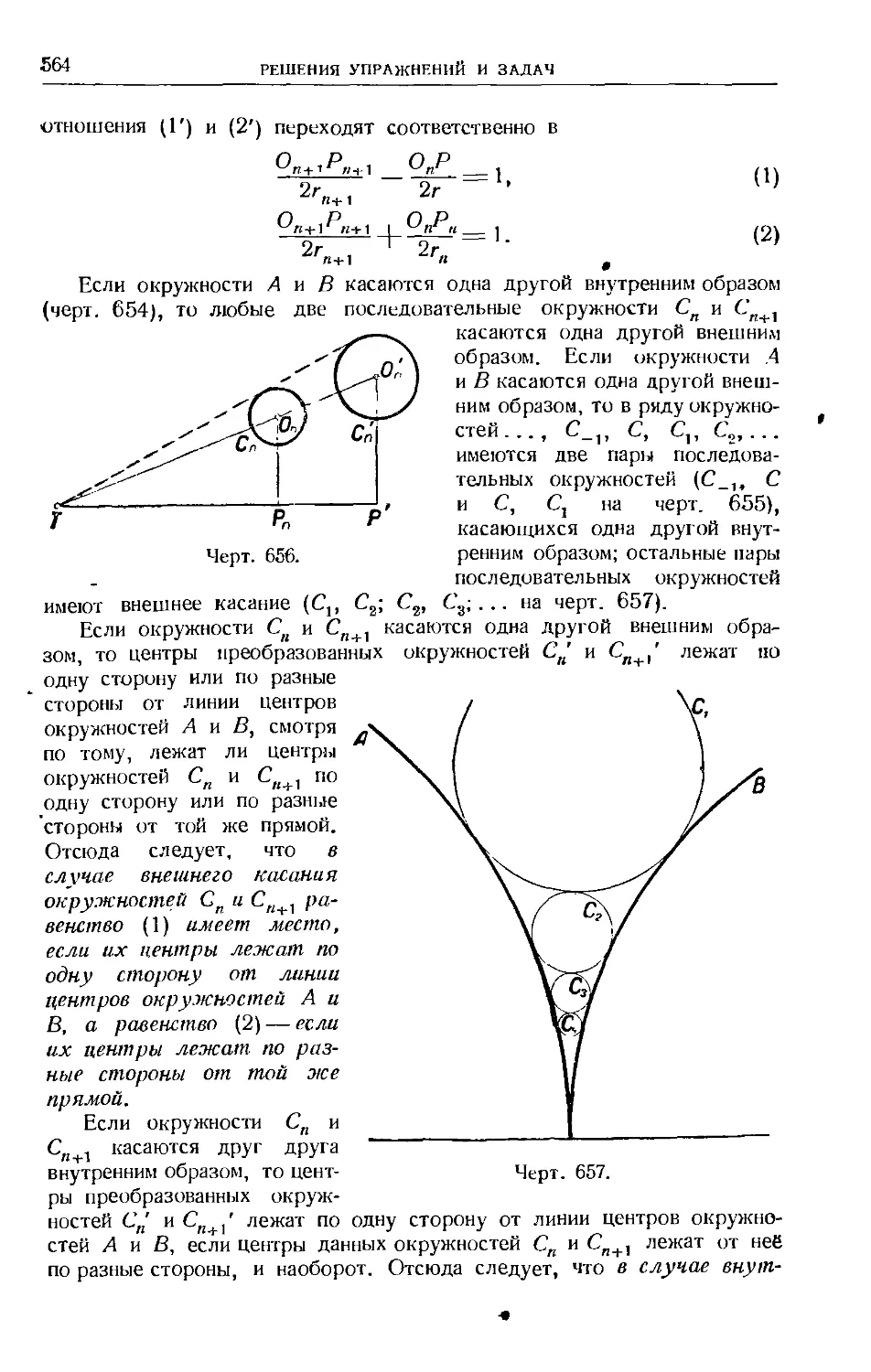
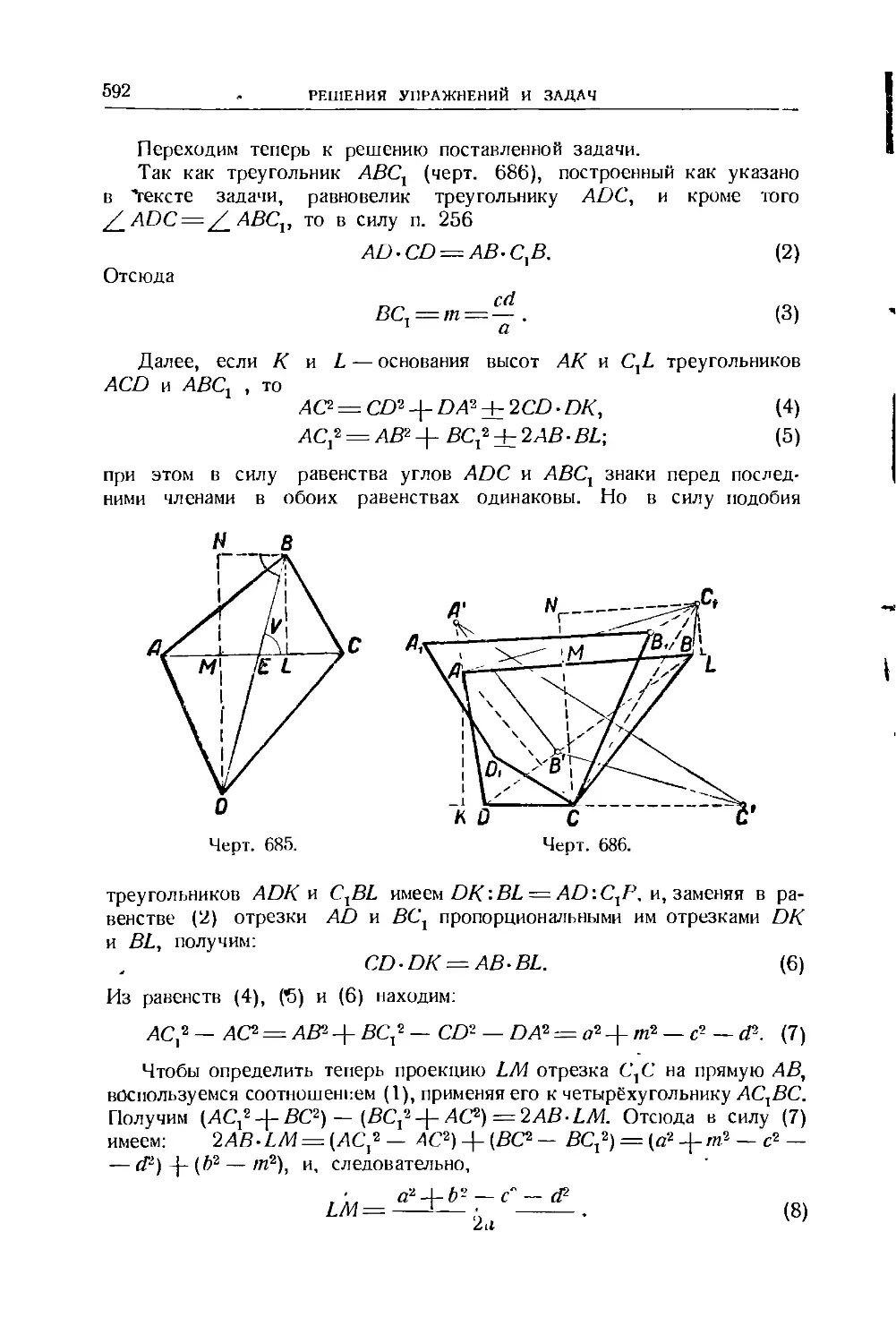
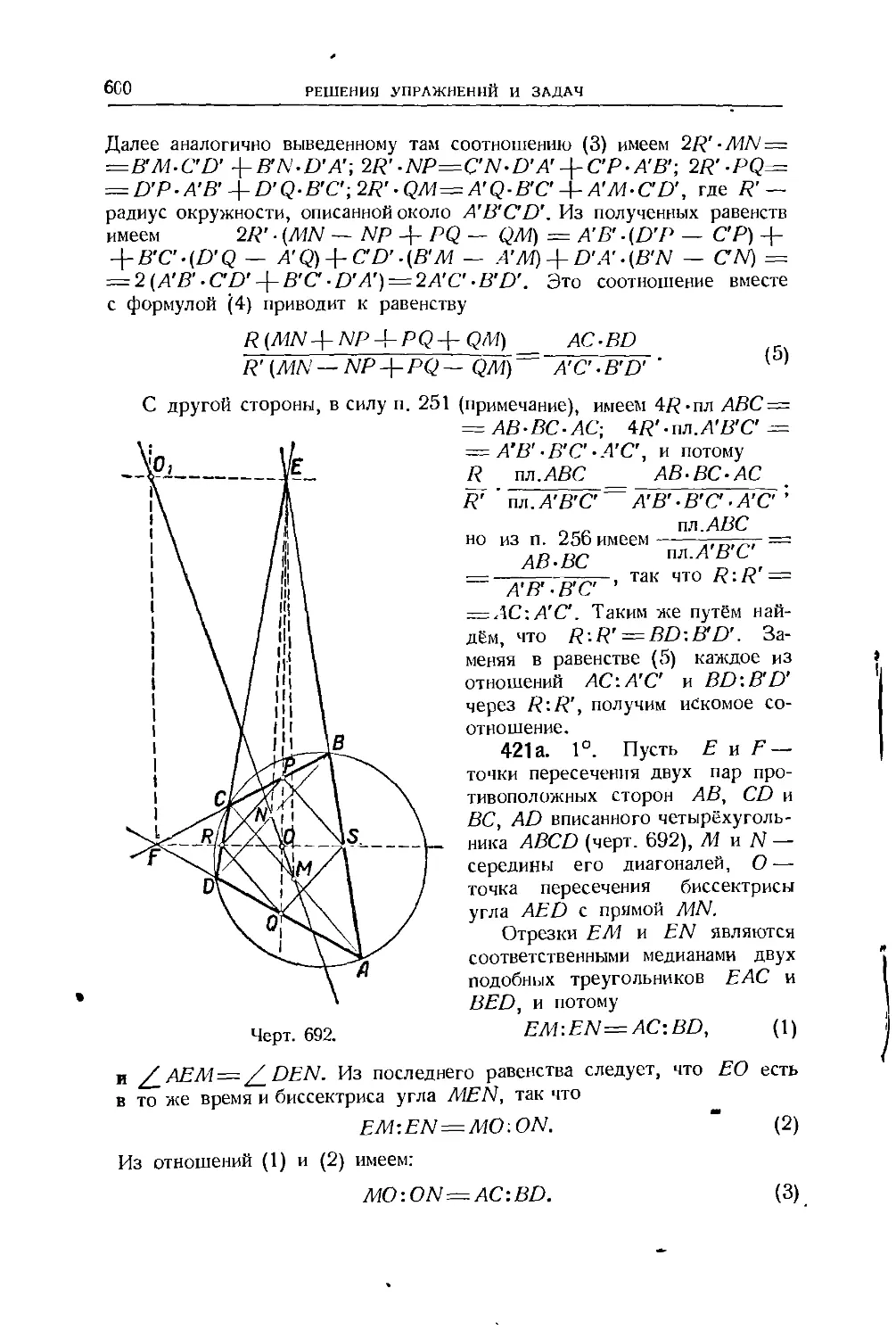
Text
щт=^
Ж. АДАМАР
11: i I /
:i
1
1 , i i's
11
, и
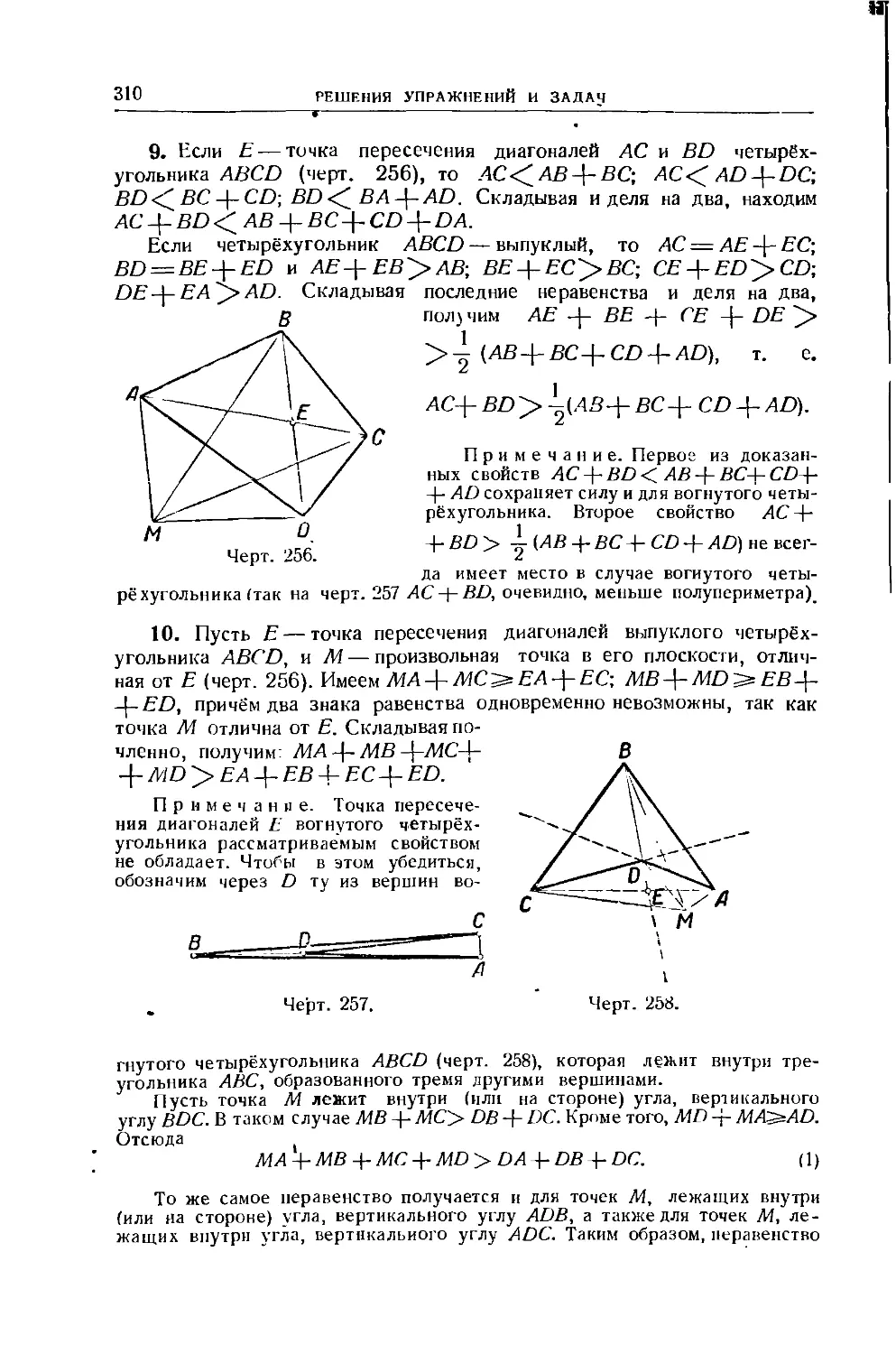
ii.ii
ч !
ЭЛЕМЕНТАРНАЯ
ЧАСТЬ
I
ПЛАНИМЕТРИЯ
УЧПЕДГИЗ
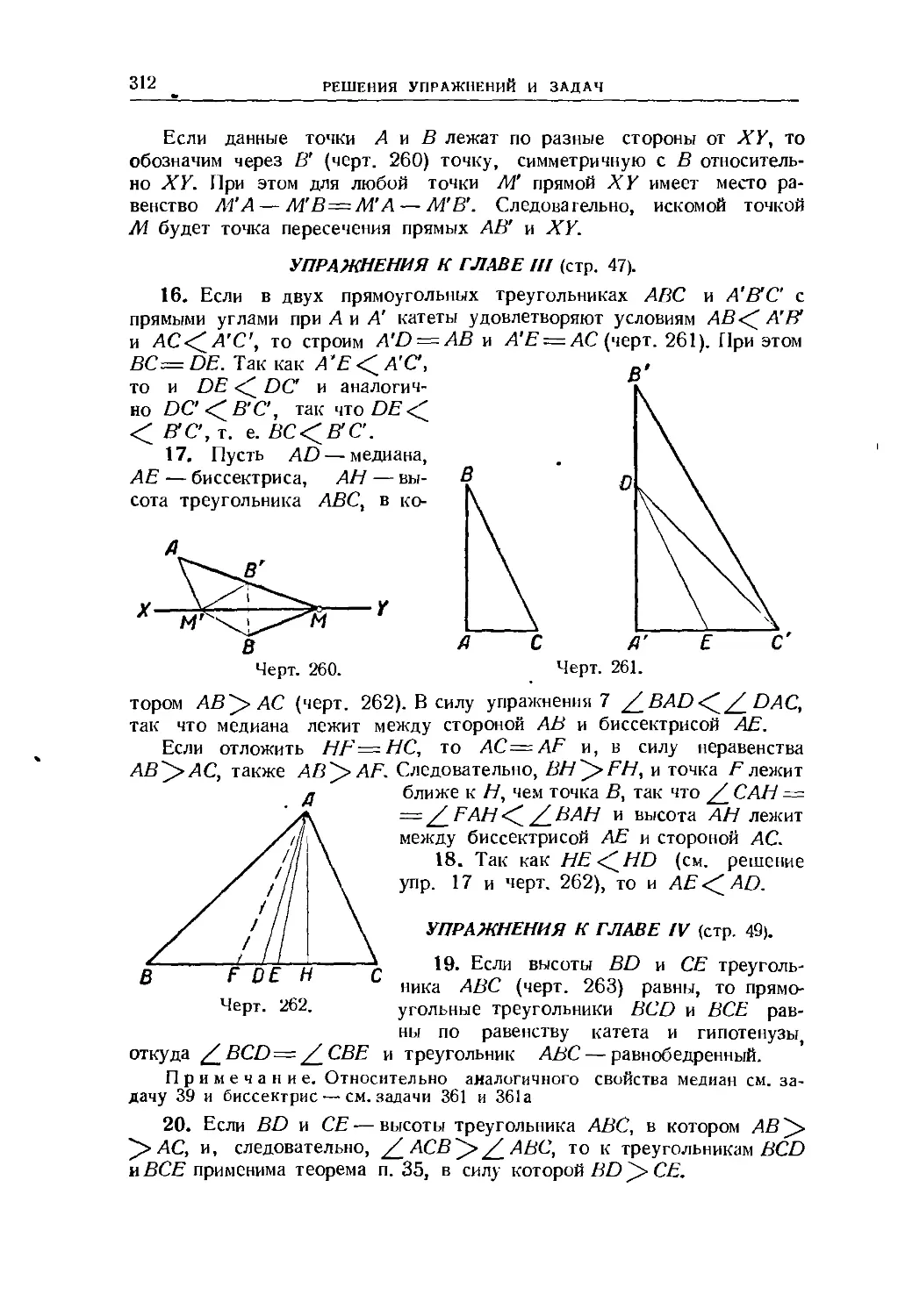
1H8
г*'
i •
л, i
f Mil
ti
J
1'
Акад. Ж. А ДАМ АР
Библиотека
А.А. Кириллова
ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРИЯ
ЧАСТЬ ПЕРВАЯ
ПЛАНИМЕТРИЯ
. ПЕРЕВОД С 11-го ИЗДАНИЯ
\У\ ПОД РЕДАКЦИЕЙ
"^л ПРОФ. Д. И. ПЕРЕПЁЛКИНА
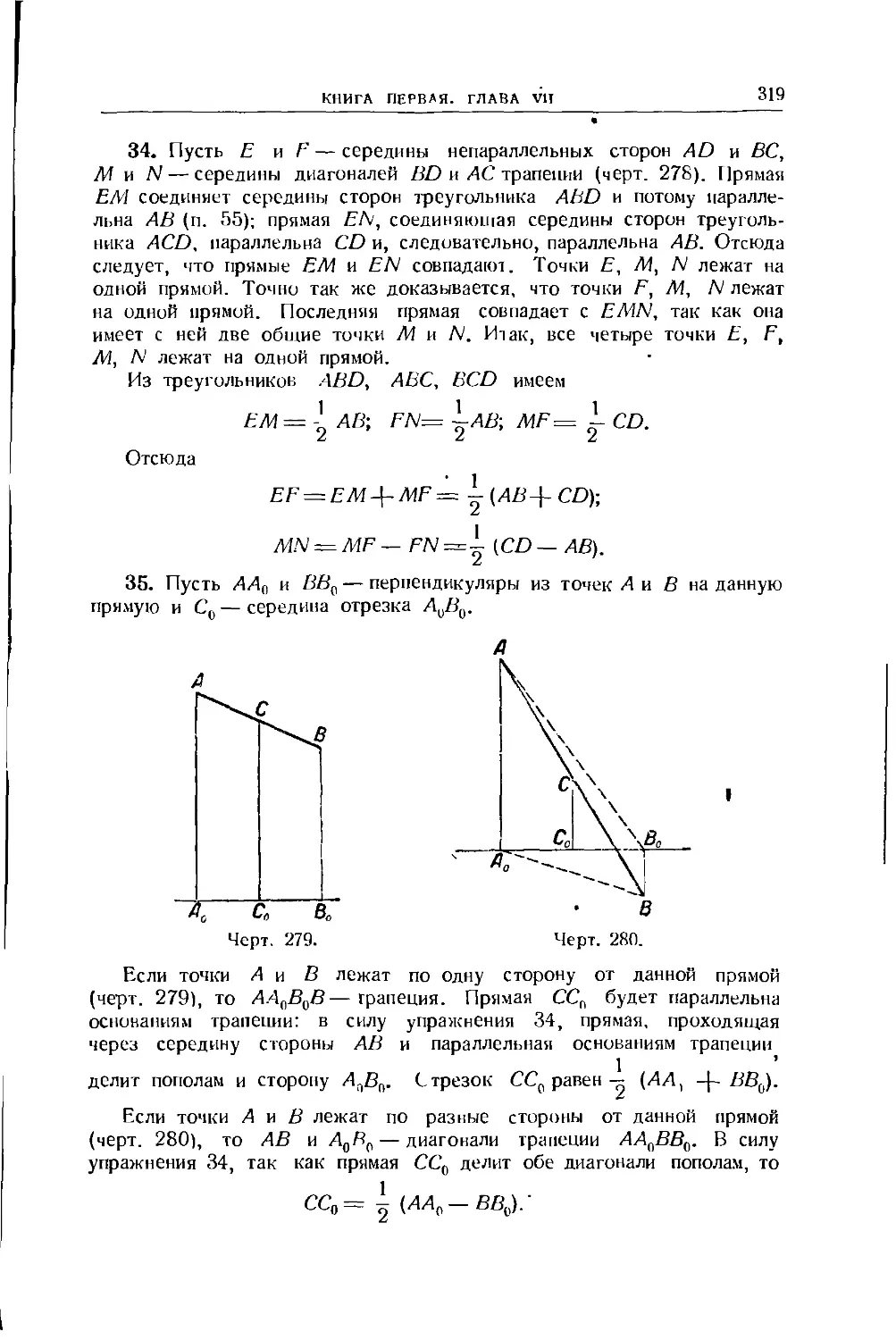
ПОСОБИЕ
ДЛЯ ВЫСШИХ ПЕДАГОГИЧЕСКИХ УЧЕБНЫХ ЗАВЕДЕНИЙ
И ПРЕПОДАВАТЕЛЕЙ СРЕДНЕЙ ШКОЛЫ
Издание третье
С ПРИЛОЖЕНИЕМ СОСТАВЛЕННЫХ
ПРОФ. Д. И. ПЕРЕПЁЛКИНЫМ
РЕШЕНИЙ ВСЕХ ПОМЕЩЁННЫХ В ТЕКСТЕ ЗАДАЧ
БИБЛИОТЕКА НМУ
ШГМЧЧЕСКИЯ
КОЛЛЕДЖ
ГОСУДАРСТВЕННОЕ УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
МОСКВА -Х- 1948
•
r> p > if I Утверждено
' Министром просвещения РСФСР
¦—""""¦""¦ к переизийнию 3 октября 1947 г., протокол № 326
Основой книги служит обыкновенный школьный курс геоме-
геометрии на плоскости: однако сооержание её выходит за рамки
существующих программ. Это энциклопедия элементарной
геометрии, стояшая на уровне современной науки и написанная
выдающимся математиком. Существенным оостоинством книги
является наличие большого числа задач, многие из которых
могут дать материал для творческой работы. В третьем изда-
издании книги помещены полные решения всех этих задач.
Редактор Т. Козьмина. Техн. ред. М. Натапов.
Подпигано к печати 30 'IV 1948 г. А 04704. Прчятных листов 38.
Учётно-издательских листов 44,14. Заказ Лг 7729.
Отпечатано в тип. Н-12 с матриц 1-ой Обрачповой тип. треста
„Полнграфкнига" Огиза при Совете Министров СССР.
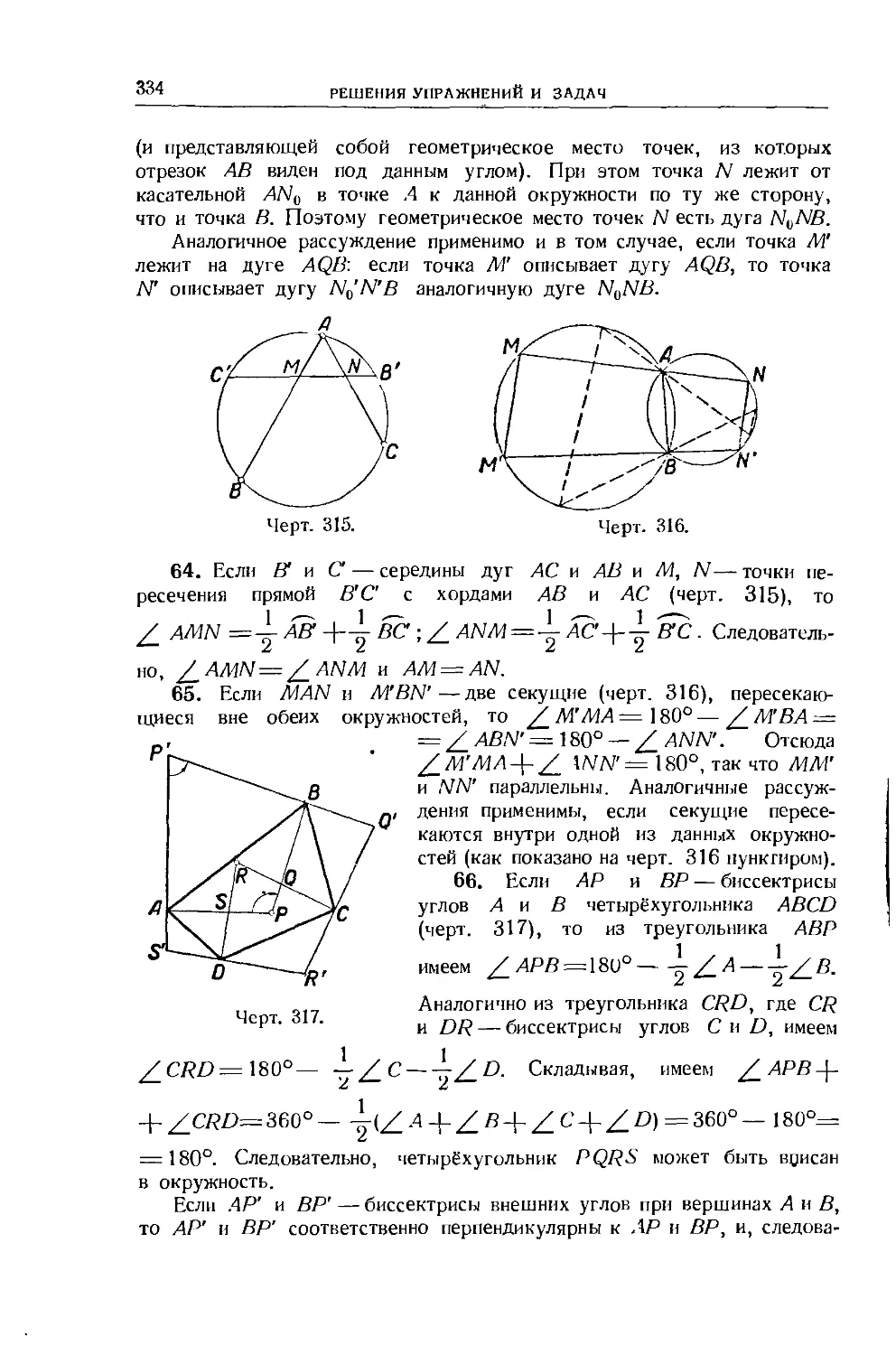
Москва, Валовая, 28.
СОДЕРЖАНИЕ.
Стр
Предисловие к третьему русскому изданию .... 13
Предисловия автора к первому, второму и восьмому изданиям 15
Введение.
1. Тела, поверхности, линии, точки 19
1а. Геометрические места 19
2—2а. Математические предложения . . 19
3. Равные фигуры ..... 20
4. Прямая линия 21
5. Отрезки, их сравнение . . 21
6. Плоскость ... . 22
7. Окружность ... ... 22
8—8а. Дуги . 23
9. Диаметр . . 24
КНИГА ПЕРВАЯ.
ПРЯМАЯ ЛИНИЯ.
Глава I. Углы.
10—11. Сравнение углов . .26
12. Равенство вертикальных углов . .27
13. Дуги и углы 27
14. Перпендикуляры. Через точку, лежащую на прямой, можно
провести к этой прямой перпендикуляр и притом только
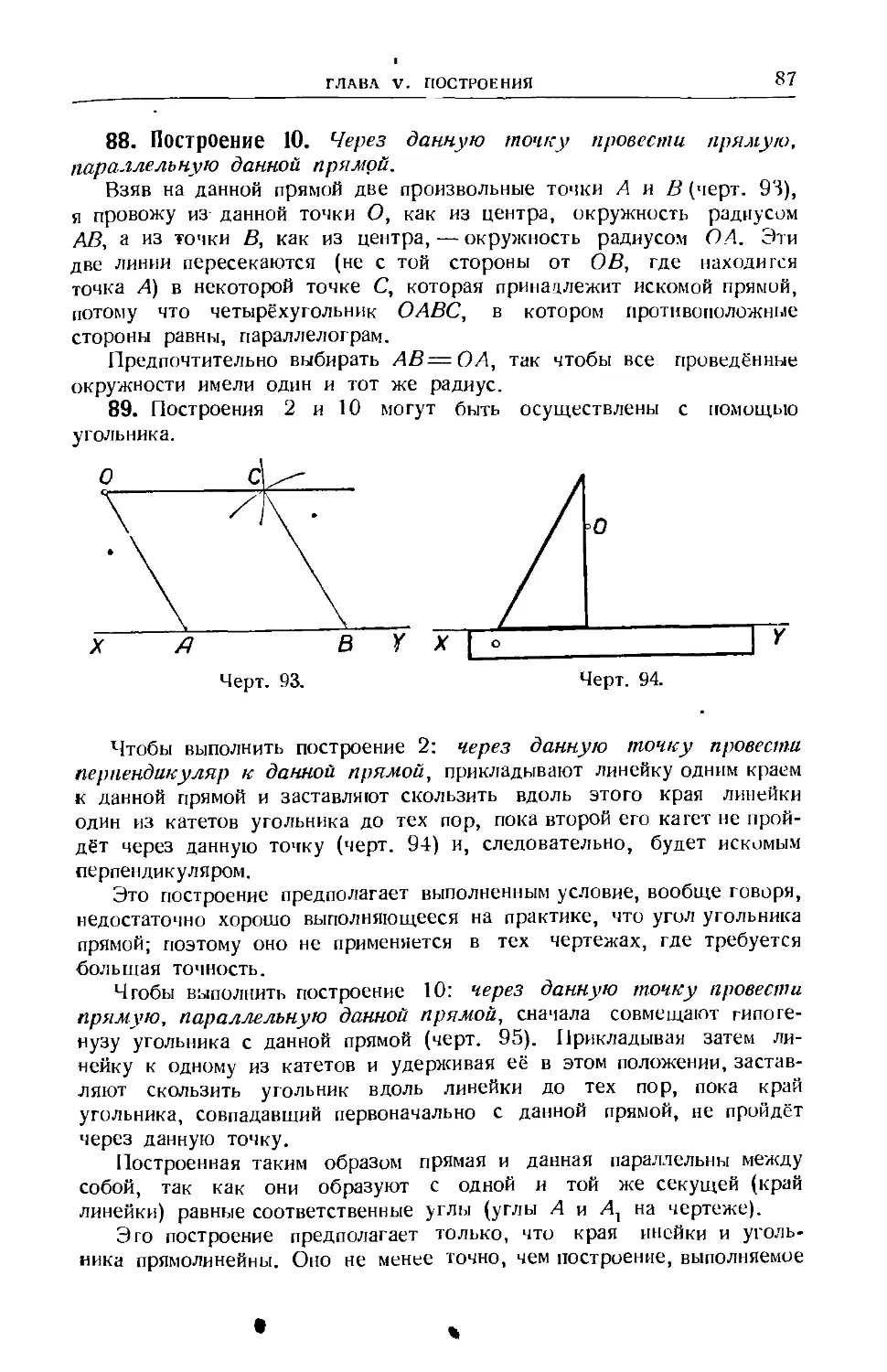
один. Прямой угол .... 28
15. Сумма углов, образованных несколькими полупрямыми, вы-
выходящими из одной точки . 29
15а. Биссектрисы четырёх углов, образованных двумя пересека-
пересекающимися прямыми . . 29
16. Углы острые, тупые, дополнительные и пополнительные . . 30
17—18а. Измерение углов .30
19. Через точку, взятую вне прямой, можно провести перпен-
перпендикуляр к этой прямой и притом только один 33
1*
СОДЕРЖАНИЕ
19а. Симметрия относительно прямой 33
20—20а. Направление вращения 34
Упражнения 1—4 35
Глава II. Треугольники.
21. Многоугольники вообще . 36
22—22а. Треугольники . . .37
23. Свойства равнобедренного треугольника 37
24. Признаки равенства треугольников 38
25. Внешний угол треугольника. Во всяком треугольнике против
большей стороны лежит больший угол, и обратно 39
26. Прямолинейный отрезок короче любой ломаной линии, име-
имеющей с ним общие концы 40
27. Объемлющие и объемлемые ломаные линии 41
28. Если два треугольника имеют по неравному углу, заключён-
заключённому между соответственно равными сторонами, то против
большею угла лежит и большая сторона 42
Упражнения 5—15 . ... 43
Глава III. Перпендикуляры и наклонные.
29—30. Перпендикуляры и наклонные 44
31. Расстояние точки от прямой 45
32—33. Геометрическое место точек, одинаково удалённых от двух
данных точек . . 45
i Упражнения 16—18. . . 47
Глава IV. Признаки равенства прямоугольных треугольников.
Свойство биссектрисы угла.
34—35. Признаки равенства прямоугольных треугольников ..... 47
36. Свойство биссектрисы угла 48
Упражнения 19—20. 49
Глава V. Параллельные прямые.
37. Внутренние накрестлежащие, соответственные и внутренние
односторонние углы 49
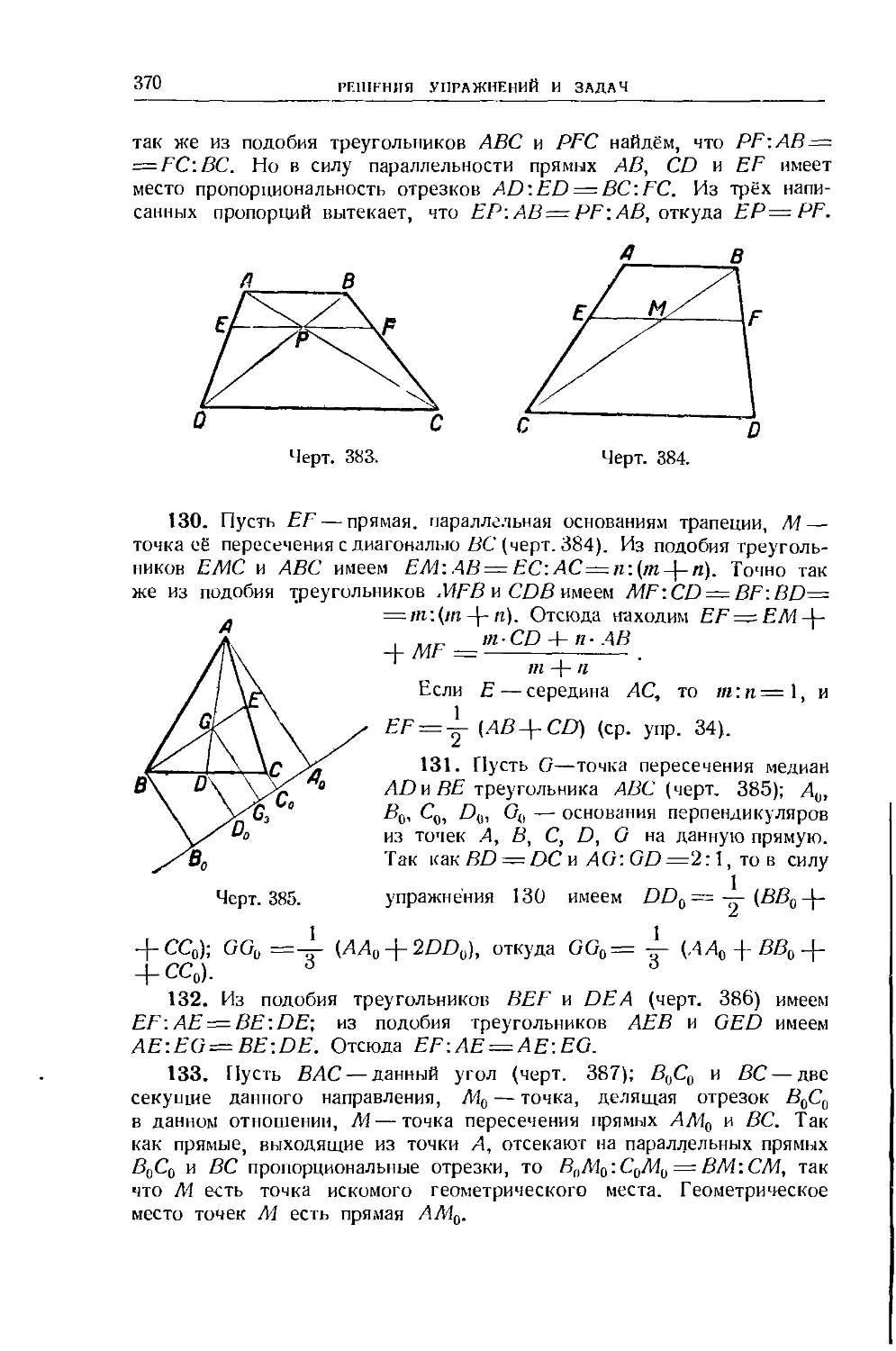
38. Параллельные прямые 50
39. Через точку, взятую вне прямой, можно провести прямую
линию, параллельную этой прямой 51
40. Через точку, взятую вне прямой, можно провести только
одну прямую, параллельную этой прямой 51
41—42. Теоремы, обратные предыдущим 51
43. Углы с соответственно параллельными или перпендикуляр-
перпендикулярными сторонами 52
СОДЕРЖАНИЕ
44. Сумма углов треугольника 53
44а. Сумма углов произвольного многоугольника . ... 54
Упражнения 21—25. 54
Глава VI. Параллелограмм. Поступательные перемещения.
45—47. Параллелограмы 55
48. Ромб, прямоугольник .... 59
49. Квадрат . . . 60
50—51. Поступательные перемещения 60
Упражнения 26—32. 61
Глава VII.. Прямые в треугольнике, проходящие через одну точку.
52. Перпендикуляры, восставленные в серединах сторон .... 62
53. Высоты 62
54. Биссектрисы 63
55—56. Медианц . . 63
Упражнения 33—38. 64
Задачи C9—46) к первой книге 65
КНИГА ВТОРАЯ.
ОКРУЖНОСТЬ.
Глава I. Пересечение прямой с окружностью.
57. Окружность определяется тремя точками 67
58. Пересечение прямой с окружностью; касательная к окруж-
окружности . . 67
59. Общее определение касательной . 68
60. Нормаль - - . . 69
60а. Угол между двумя окружностями . . . 69
Упражнения 47—49 .69
Глава II. Диаметры и хорды.
61. Диаметр есть ось симметрии окружности. ... 69
62. Хорда 70
63—64. Расстояние точки от окружности . . . .70
65—66. Равные и неравные дуги и хорды 71
67. Касательная имеет с окружностью две общие точки, слив-
слившиеся между собой .... 72
Упражнения 50—54 72
Глава III. Пересечение двух окружностей.
68—71. Исследование пересечения двух окружностей 73
72. Две окружности, касающиеся друг друга, имеют две общие
точки, слившиеся между собой .... .... . 75
Упражнения S3—59 76
СОДЕРЖАНИЕ
Глава IV. Свойства впнсанного угла.
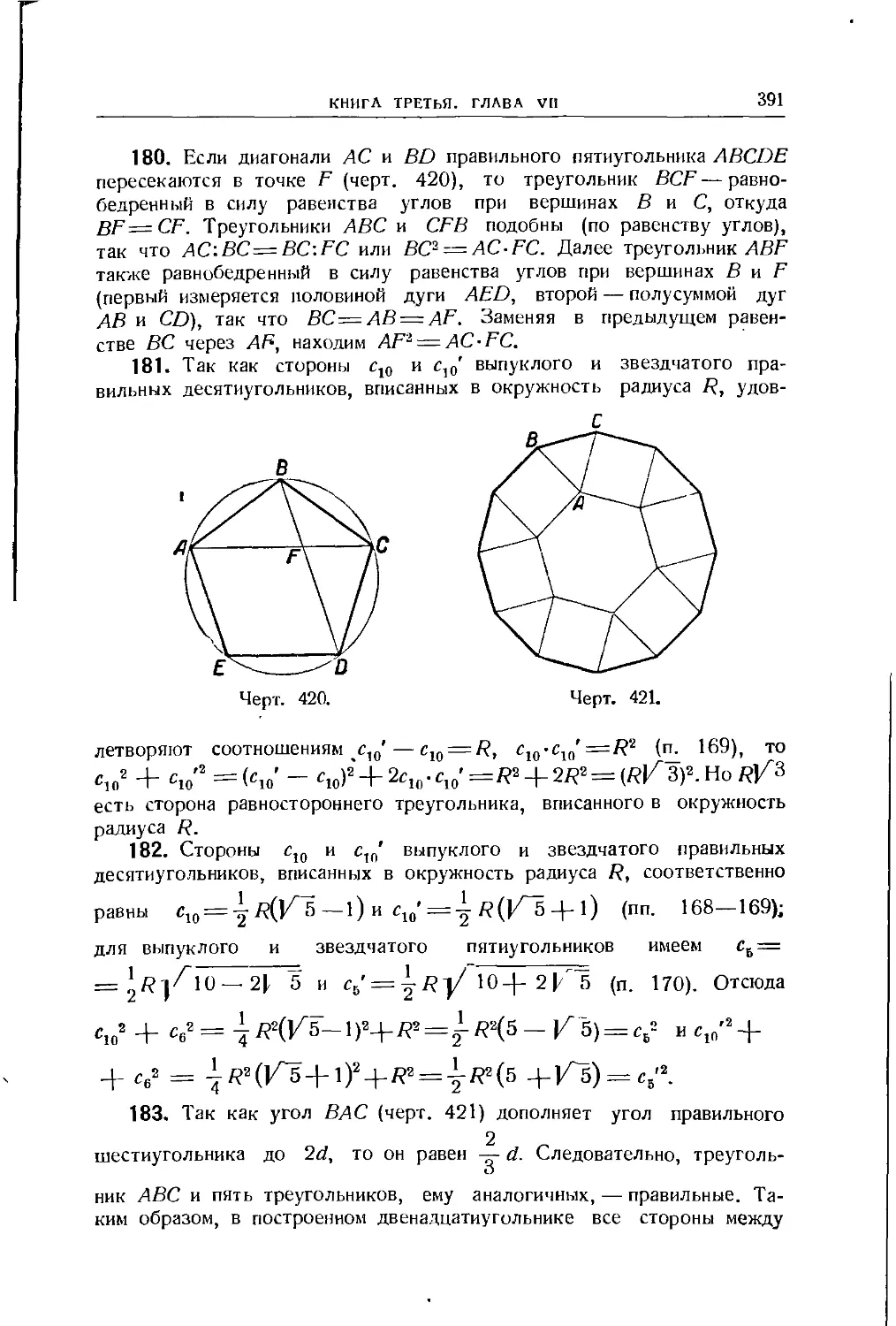
73. Измерение вписанного угла 76
74. Измерение угла, образованного касательной и хордой, выхо-
выходящей из точки касания 77
75—76. Угол, образованный двумя секущими 78
77—78. Геометрическое место точек, из которых данный отрезок
виден под данным углом . 79
79—82. Угловые свойства четырёхугольника, вписанного в круг . . 79
82а. Геометрическое место вершин равных и одинаково направ-
направленных углов, стороны которых проходят через две данные
точки, есть окружность ... 81
Упражнения 60—72. . . . . - . . 81
Глава V. Построения.
83—84 Геометрические построения. Геометрические инструменты . 82
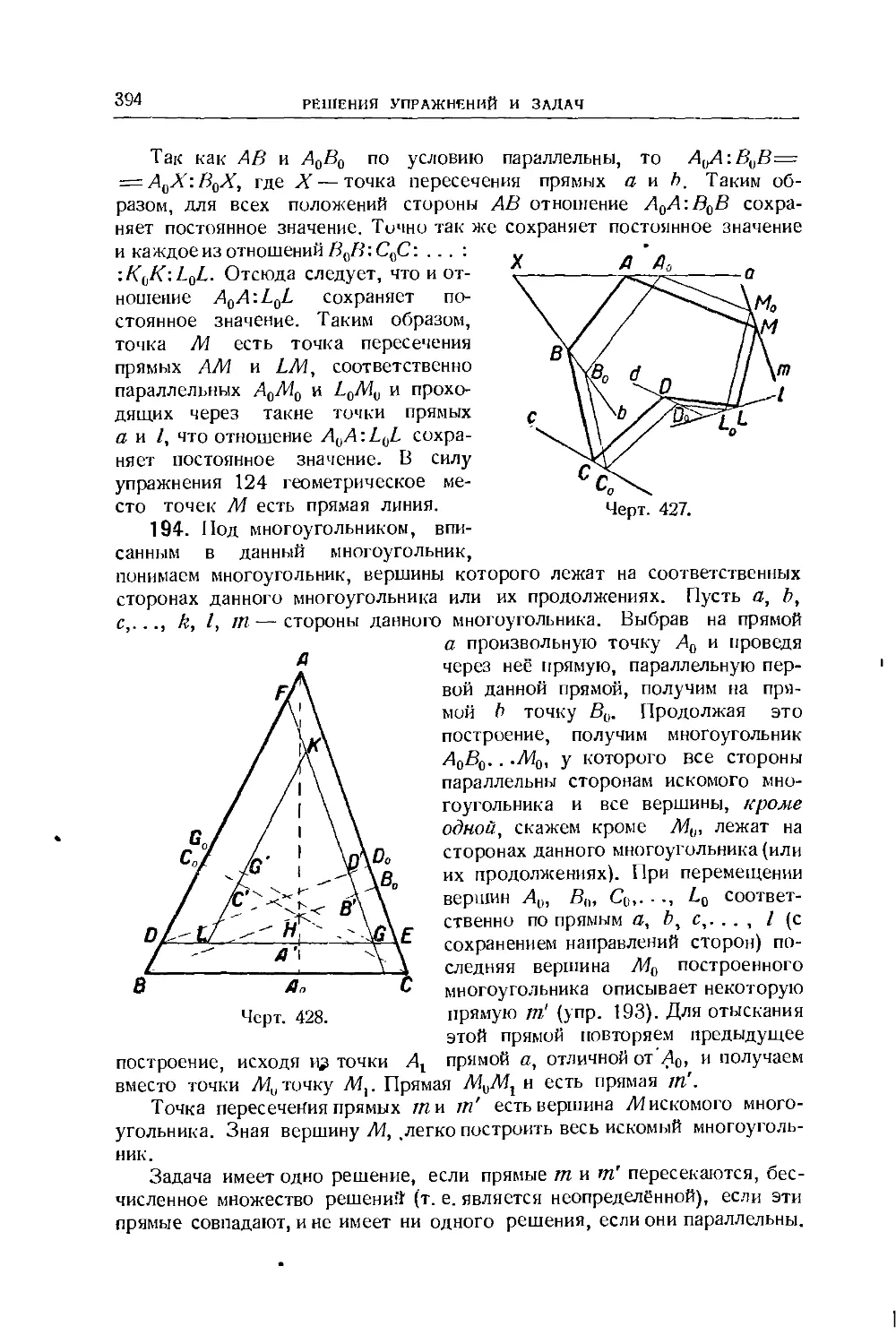
85. Построения 1—3. Перпендикуляры к данной прямой. Биссек-
Биссектрисы 83
86—87а. Построения 4—9. Углы и треугольники 84
88. Построение 10. Прямая, проходящая через данную точку и
параллельная данной прямой . . 87
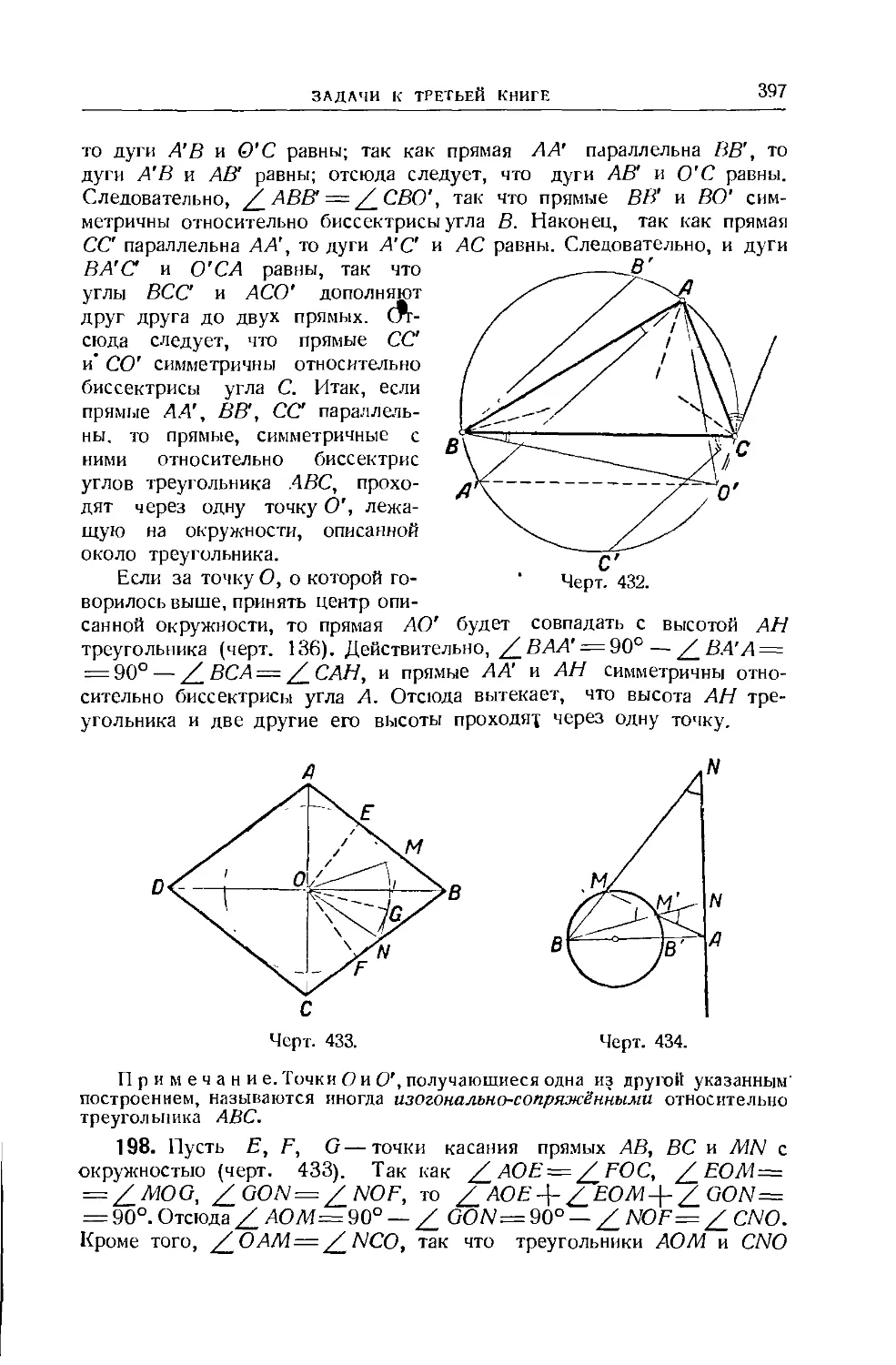
89. Употребление угольника ... . 87
90. Построения 11—14. Окружность . .88
91—92. Построения 15—17. Касательная к окружности . . 89
93. Построение 18. Общие касательные к двум окружностям . 91
94 Построение 19. Окружности, касающиеся трёх данных пря-
прямых . 93
Упражнения 73—91 94
Глава VI. Перемещение фигур.
95. Равные фигуры, имеющие одинаковое направление вращения. 96
96—98. Поступательное перемещение, вращение ... .96
99. Симметрия относительно точки . 98
100—101. Д1 е равные фигуры, имеющие одинаковое направление вра-
вращения, могут быть получены одна из другой с помощью
поступательного перемещения, сопровождаемого вращением.
Угол между двумя фигурами 98
102. Две равные "фигуры, имеющие одинаковое направление вра-
вращения, получаются одна из другой с помощью поступатель-
поступательного перемещения или с помощью вращения 99
102а—103. Другое доказательство (разложение перемещения на симмет-
симметрии) .100
104. Мгновенный центр вращения . . . 102
Умажнения 92—97 ¦ ¦ ¦ ¦ ¦ ¦ ¦ 103
Задачи (98—123) ко второй книге .... . . 104
СОДЕРЖАНИЕ
КНИГА ТРЕТЬЯ.
ПОДОБИЕ.
Глава I. Пропорциональные отрезки.
105—107. О пропорциях вообще 107
108—110. Деление отрезка .... 109
111—112. Гармоническое деление ... 110
113. Основная теорема 111
114. Прямая, параллельная основанию треугольника 113
115. Свойства биссектрисы 114
116. Геометрическое место точек, отношение расстояний которых
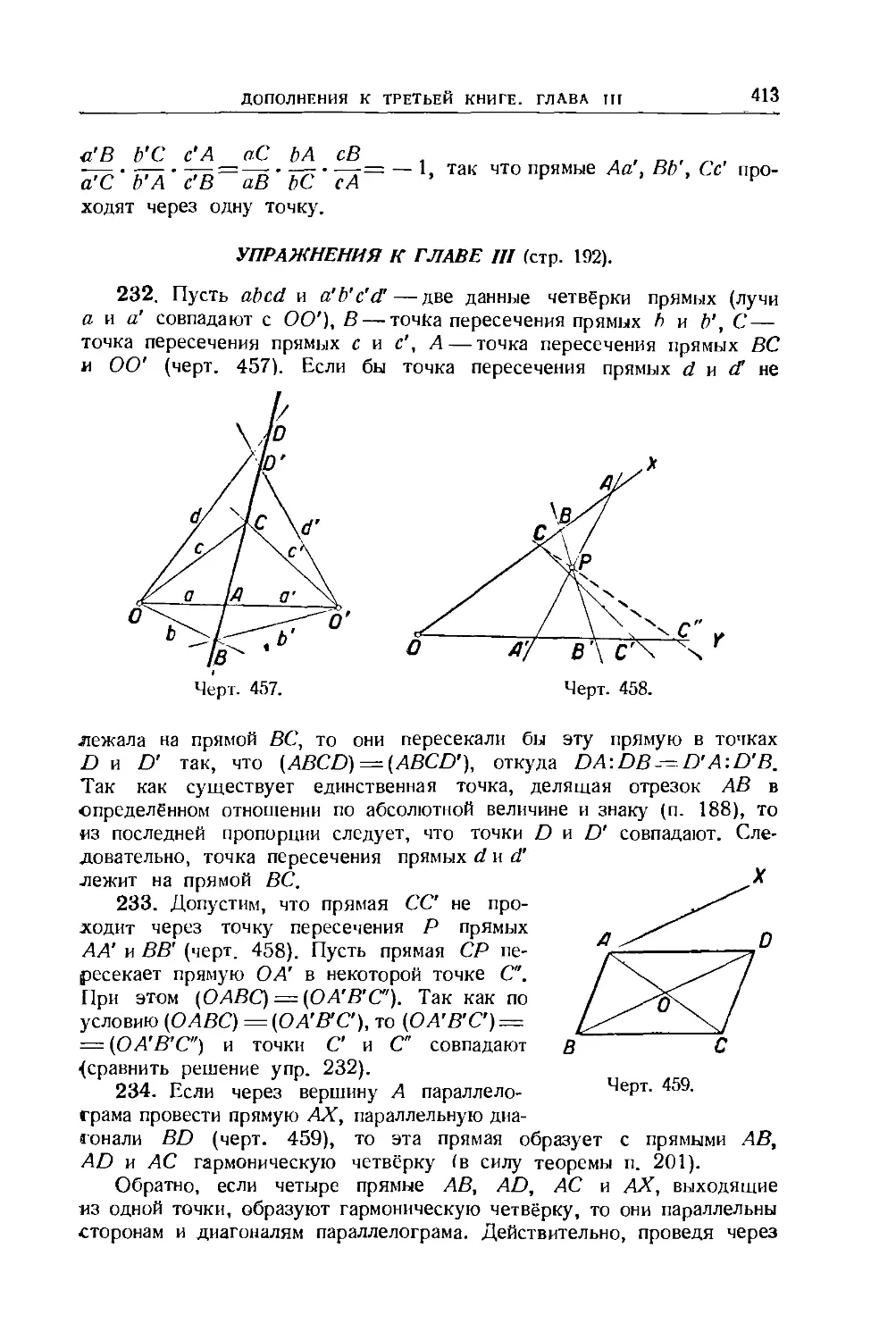
от двух данных точек постоянно . . 115
Упражнения 124—128. 116
Глава II. Подобие треугольников.
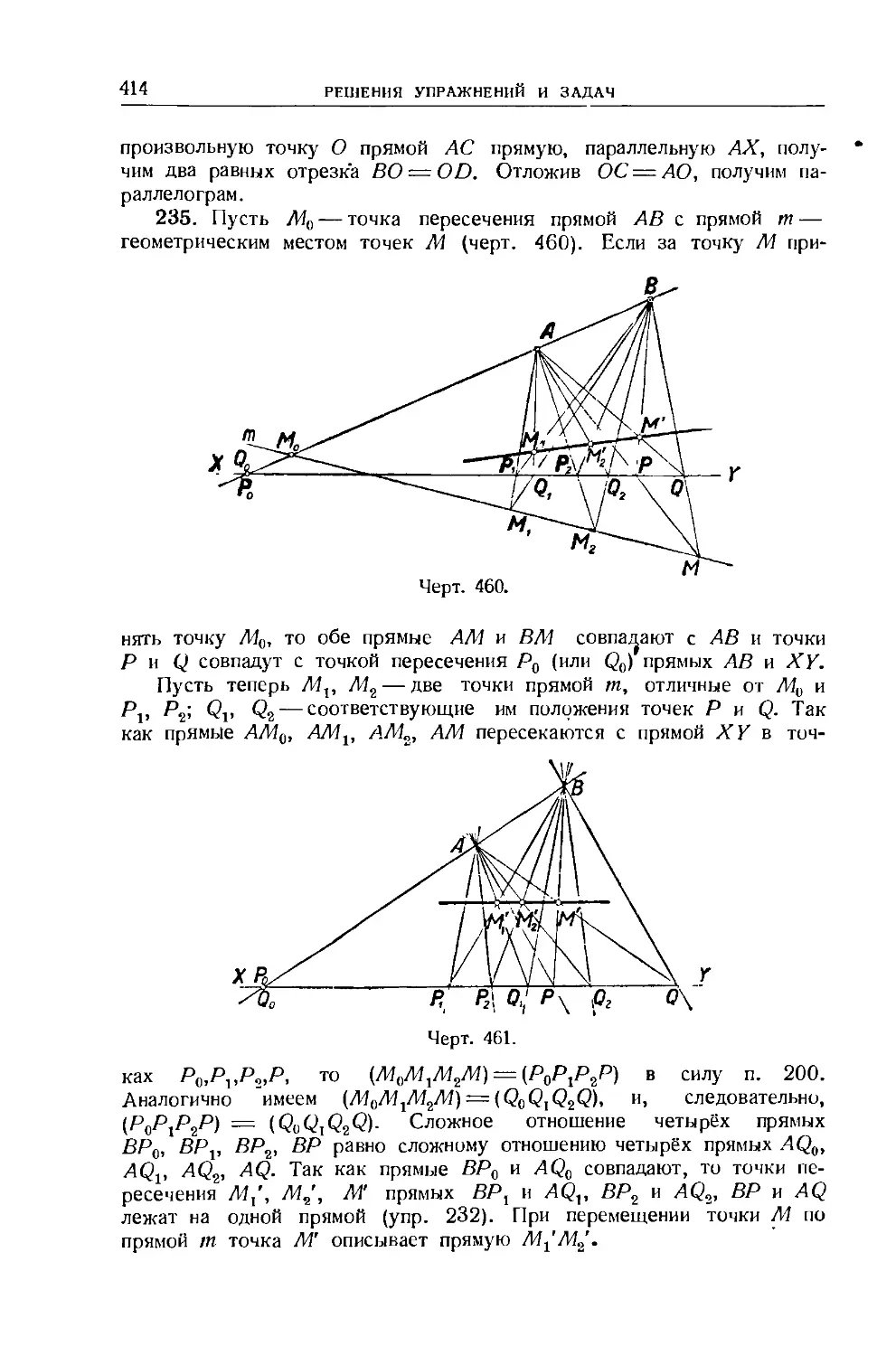
117. Лемма . .116
118—120. Признаки подобия .117
121. Отрезки, отсекаемые на параллельных прямых прямыми
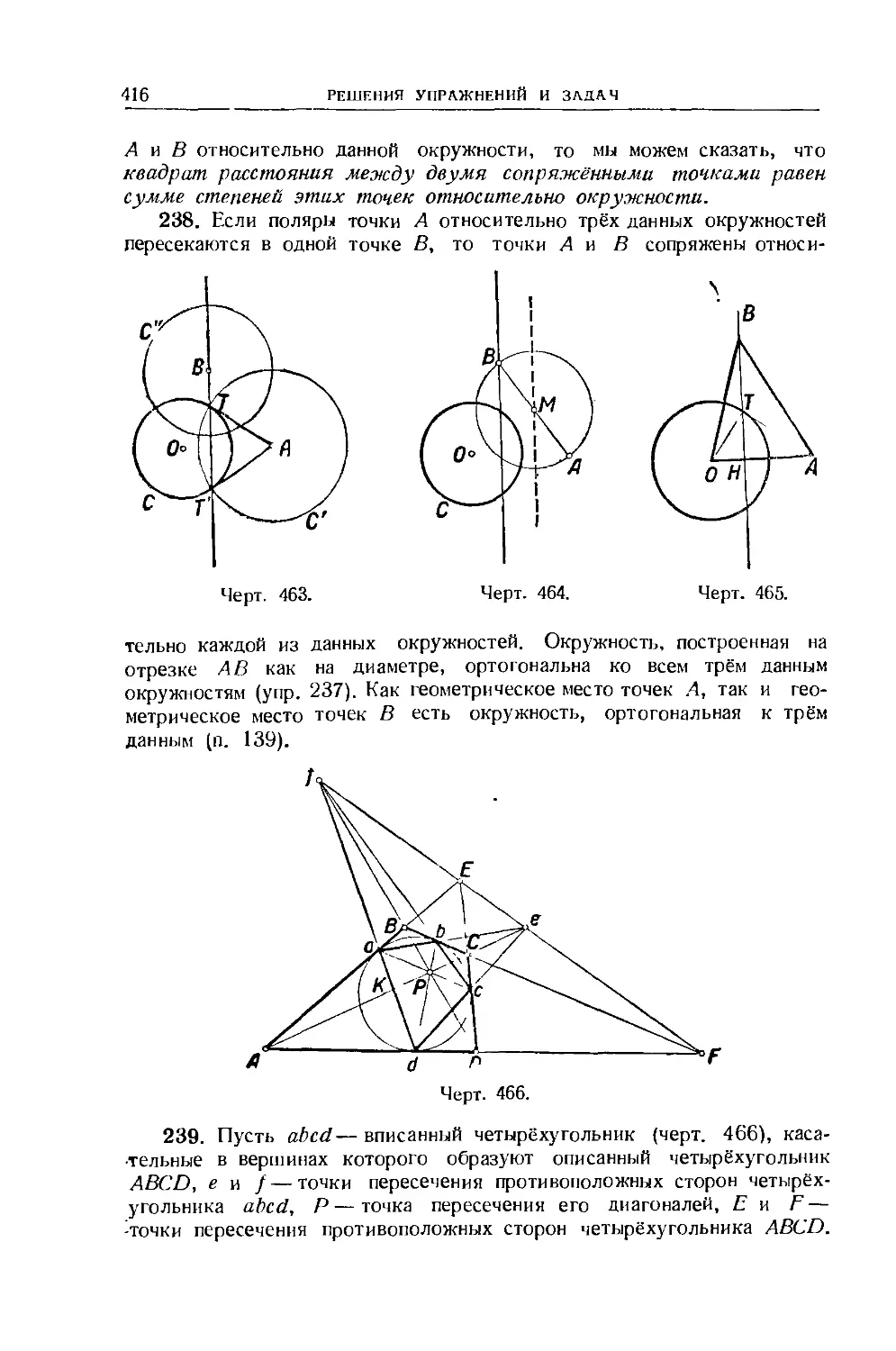
пучка 119
Упражнения 129—134 120
Глава III. Метрические соотношения в треугольнике.
122. Проекция 121
123—125. Прямоугольные треугольники. Теорема Пифагора . . . 121
126—127. Произвольные треугольники. Теорема Стюарта 122
128—130. Вычисление длин замечательных линий треугольника . . .124
130а. Радиус описанной окружности 126
Упражнения 135—147 127
Глава IV. Пропорциональные отрезки в круге.
Радикальная ось.
131- -135. Степень точки относительно окружности . 128
136—138. Радикальная ось 130
139. Радикальный центр . . ... .... 132
Упражнения 148—154 132
Глава V. Гомотетия и подобие.
140. Определение гомотетии ... 133
141—142. Общие свойства . . 133
143. Случай двух окружностей . . 135
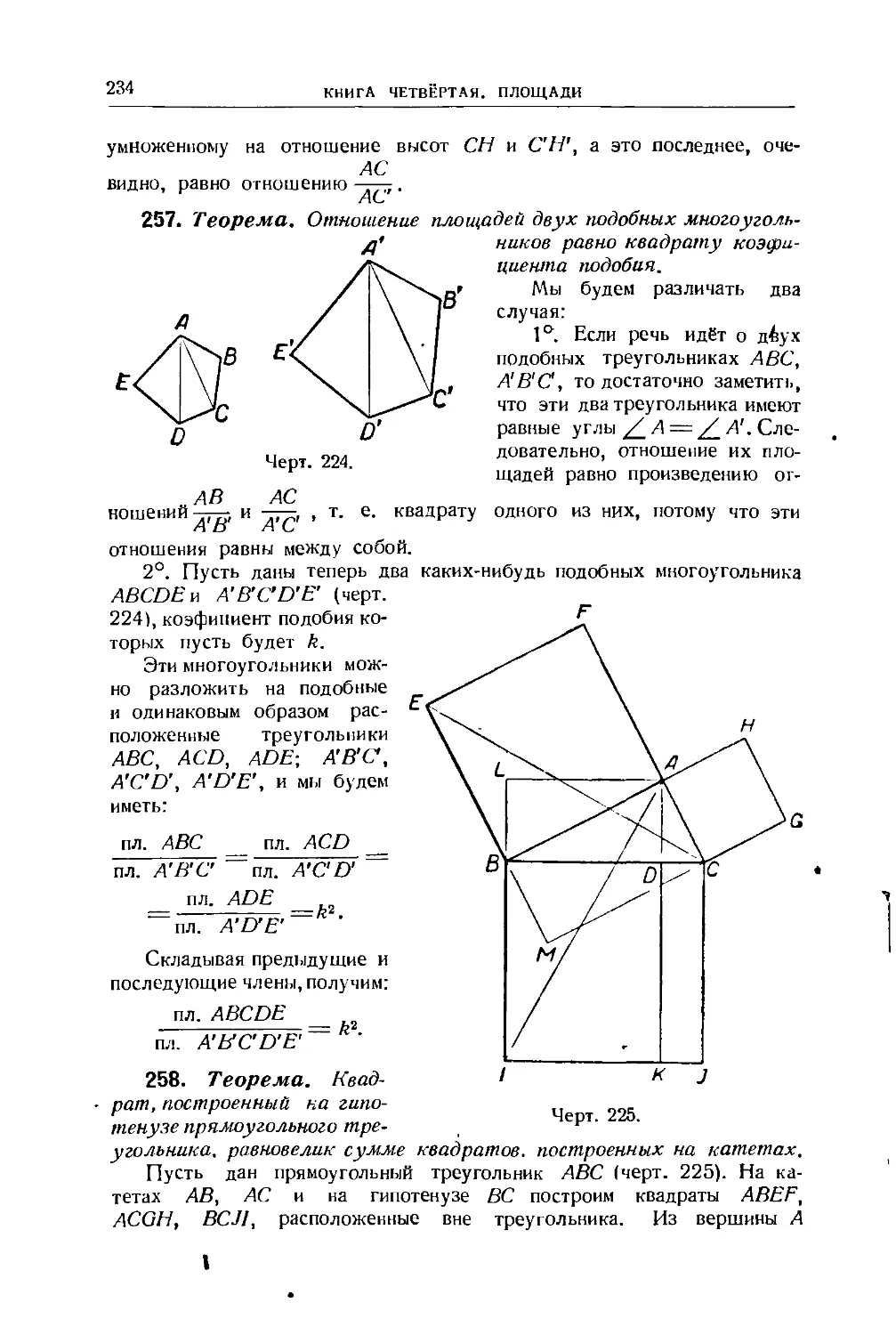
СОДЕРЖАНИЕ
144. Две фигуры, гомотетичные третьей, гомотетичны между
собой 136
145. Оси подобия трёх окружностей . . .137
146—149. Подобие многоугольников 137
150. Точка, сама себе соответствующая 140
150а. Пантограф . . . . .141
Упражнения 155—162. . .142
Глава VI. Построения.
151. Построения 1—2. Пропорциональные отрезки 143
152. Построения 3—За. Подобные многоугольники 144
153—156. Построения 4-—9. Среднее пропорциональное; отрезок
х := 1^в2 ;t fc2; отрезки, определённые их суммой или раз-
разностью и их произведением; деление в среднем и крайнем
отношении 144
157. Построение 10. Точки, расстояния которых от данных прямых
имеют данные отношения . . 149
158. Построения. 11—13. ОСщие касательные; радикальная ось;
ортогональные окружности 150
¦' 159. Построения 14—15. Окружности, касающиеся данной прямой
или данной окружности и проходящие через две данные
точки . 151
Упражнения 163—177 . 152
Глава VII. Правильные многоугольники.
160—163. Определение прагильных многоугольников и их существова-
существование ... 153
164. Звездчатые правильные многоугольники 155
165—170. Построение правильных многоугольников, вписанных в
окружность; квадрат, шестиугольник, треугольник, десяти-
десятиугольники, пятиугольники .... . . 156
171—175. Пятнадцатиугольники 160
176—178. Длина окружности. Отношение длины окружности к диаметру 164
179—179а. Длина дуги окружности . . . 167
180—181. Вычисление я. Метод периметров . . . 169
182—183. Вычисление г.. Метод равных периметров . . 171
184. Результат вычислений ... . 174
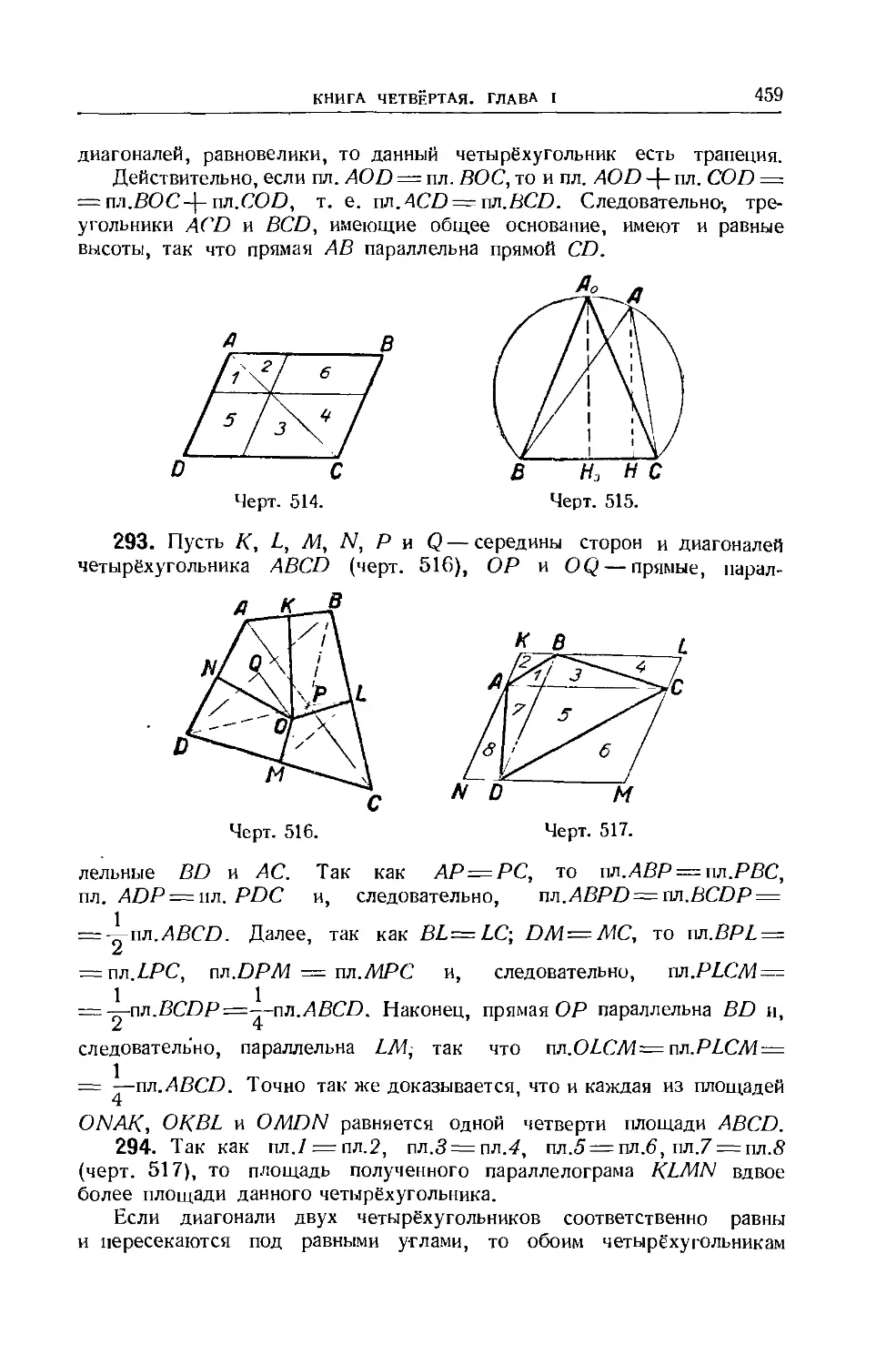
Упражнения 178—189 175
Задачи A90—216) к третьей книге ... . 176
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ.
Глава I. Знаки отрезков.
185- -187. Соглашение о знаках; основное тождество . . 178
188—189. Свойство гармонических точек . . 179
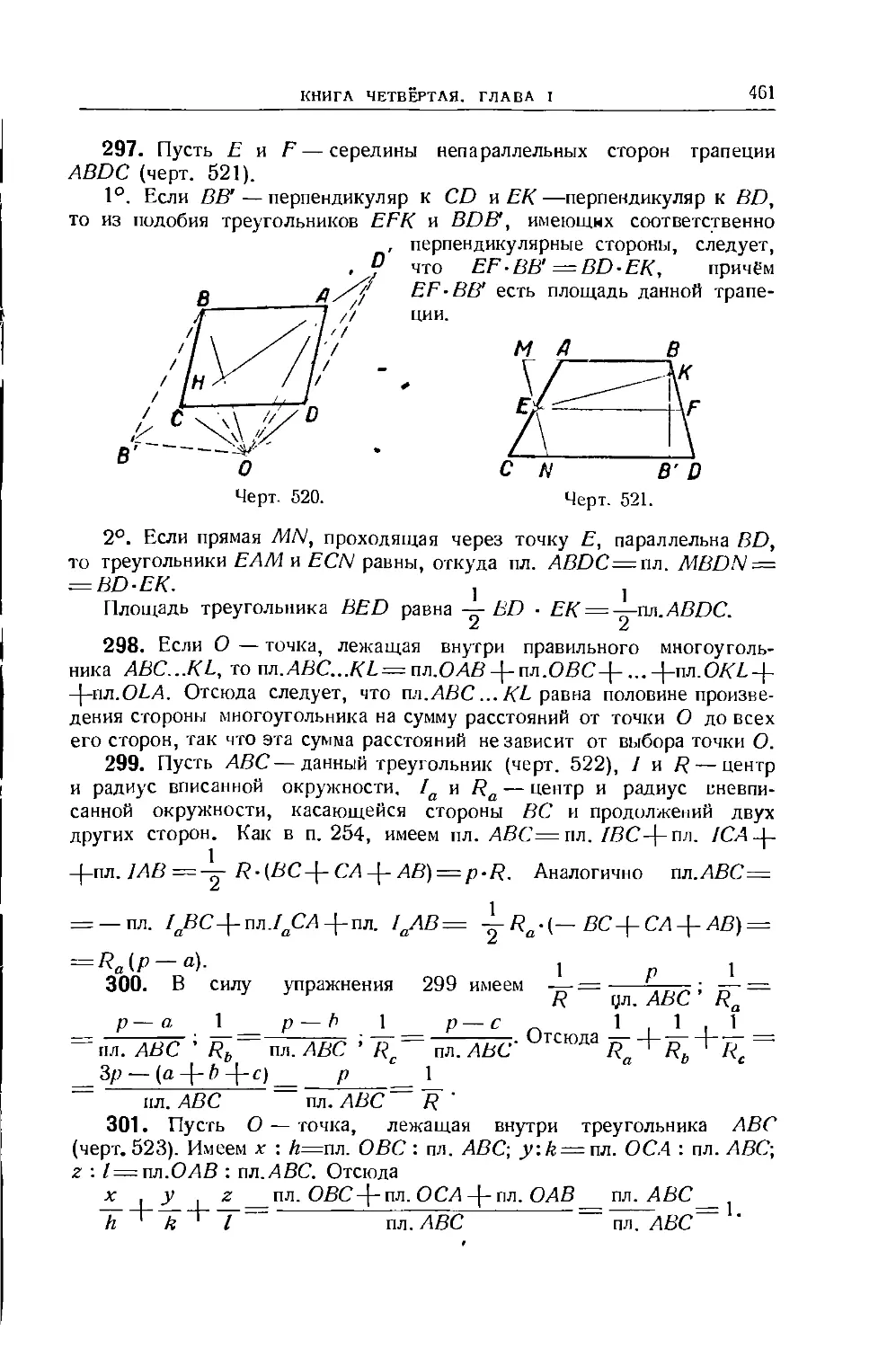
СОПЕРЖ\НИР
191, 191. Приложение к гомотетии и к степени точки относительно
окружности . . 181
Упражнения 217—222. 181
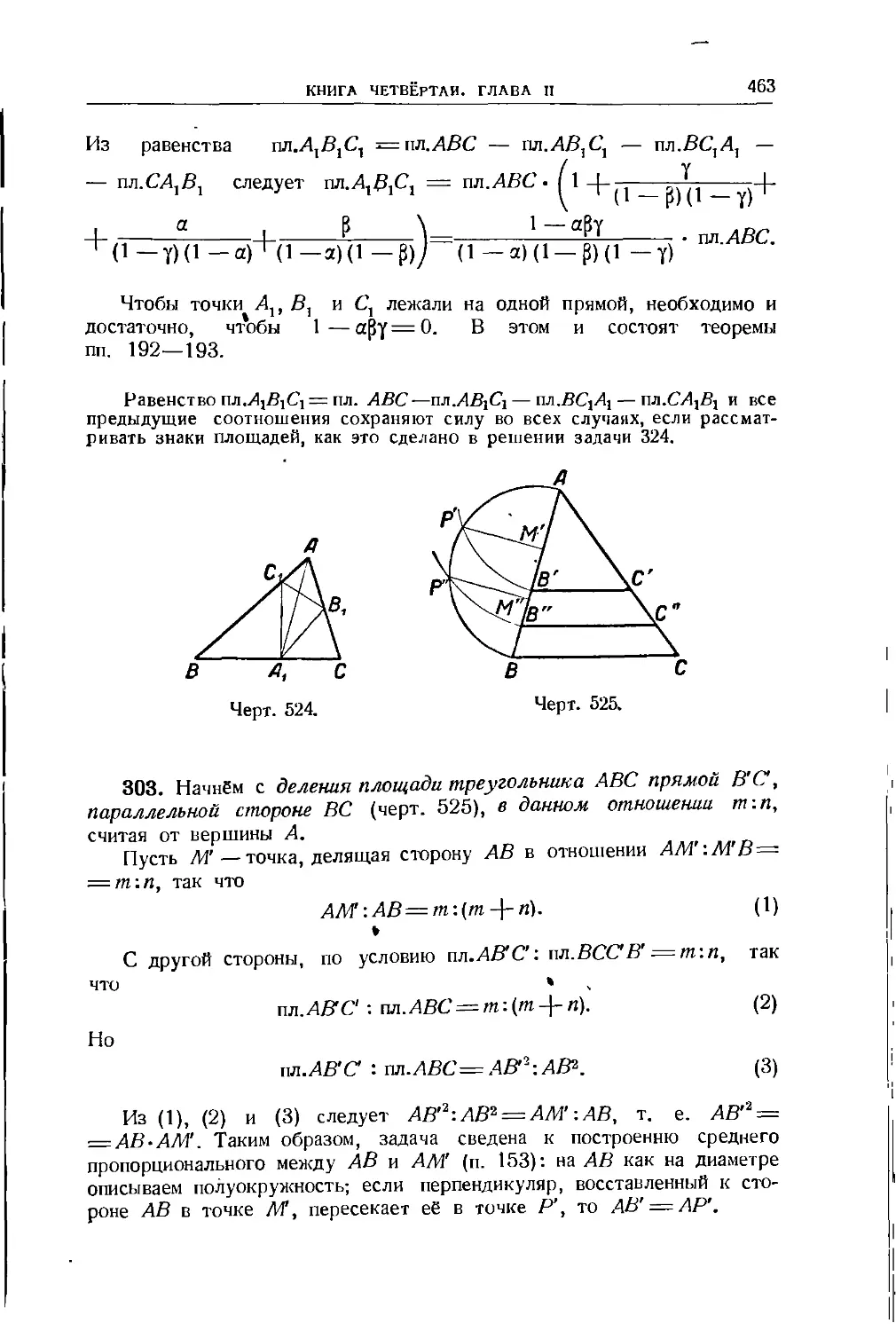
Глава II. Трансверсалн.
192—193. Теорема о трансверсалях. Обратная теорема 182
194—196. Приложения: середины диагоналей полного четырёхсторон-
четырёхсторонника; гомологические треугольники; теорема Паскаля . 184
197—198. Отрезки, отсекаемые на сторонах треугольника прямыми, вы-
выходящими из вершин треугольника и проходящими через
одну точку 187
Упражнения 223—231 • 188
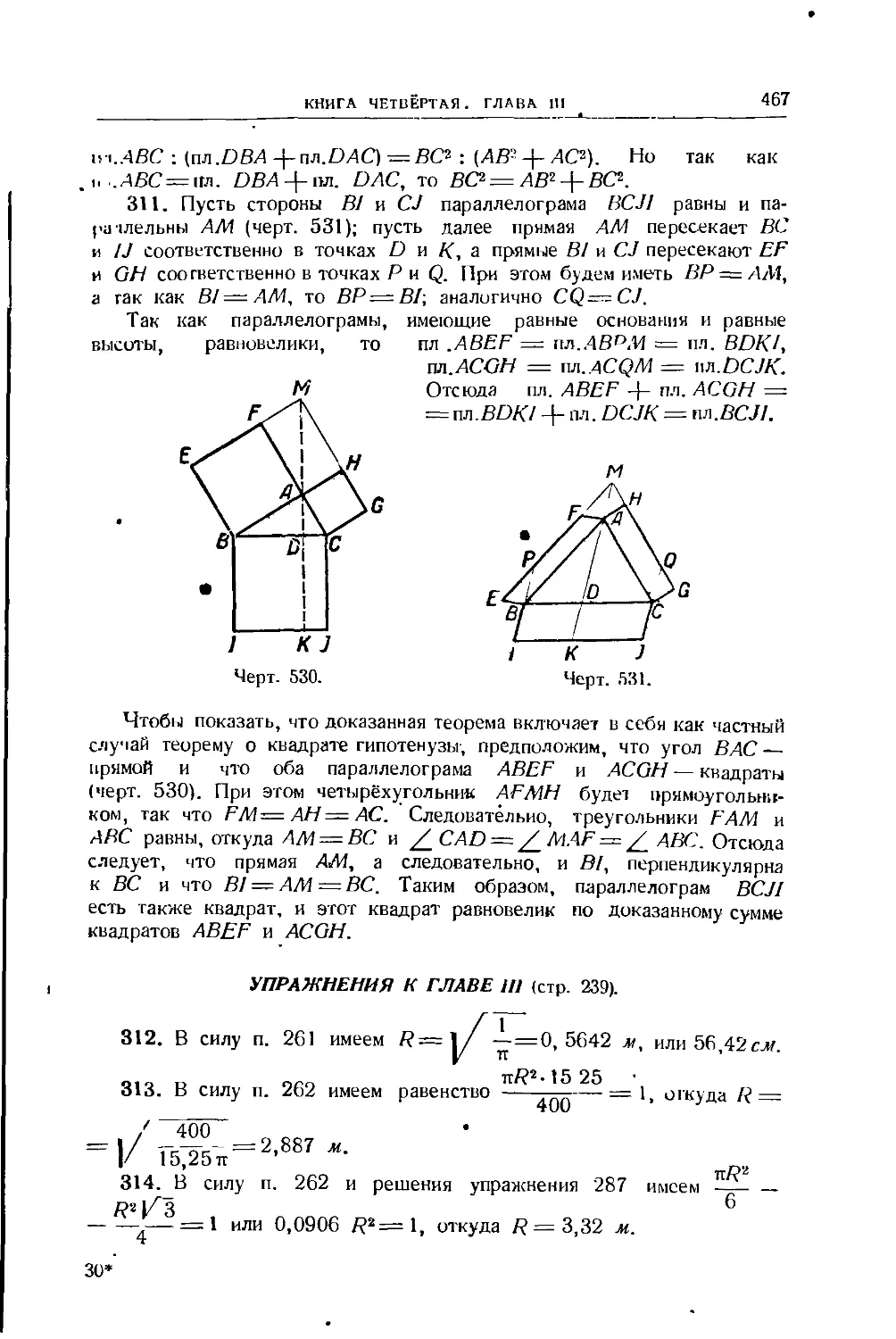
Глава III. Сложное отношение. Гармонические четвёрки
прямых.
199. Сложное отношение . 189
2С0. Основная теорема 189
201. Гармонические четвёрки прямых 190
202. Свойство полного четырёхсторонника 191
203. Поляра точки относительно угла 191
Упражнения 232—236. • ' . . 19?
Глава IV. Полюсы и поляры относительно окружности.
204- Определение поляры и её построение 193
205. Теорема о сопряжённых точках 194
206. Взаимно-полярные фигуры 195
207—208. Приложение к гомологическим треугольникам и к теореме
Брианшона _ . . 195
209—210. Преобразование метрических свойств 196
211. Новое определение поляры и её построение 197
212. Сложное отношение точек, лежащих па окружности .... 198
213. Приложение к сопряжённым хордам 199
Упражнения 237 — 241 199
Глава V. Взаимно обратные фигуры.
214—216. Определения. Окружность инверсии. Симметрия относительно
прямой как предельный случай инверсии . 200
217-—218. Направление и длина отрезка, соединяющего точки, обрат-
обратные двум данным точкам t 201
219. Касательные к взаимно обратным кривым. Угол между кри-
кривыми, обратными данным 202
220. Фигура, обратная прямой линии 203
221. Фигура, обратная произвольной окружности . . . 204
222. Взаимно обратные окружности 204
10
СОДЕРЖАНИЕ
223—226. Антигимологнческие точки и хорды . 205
227—228. Окружности, пересекающие две данные окружности под
одним и тем же углом 206
Упражнения 242—257. 208
Глава VI. Задачи о касании окружностей.
229—231. Первое решение . . 209
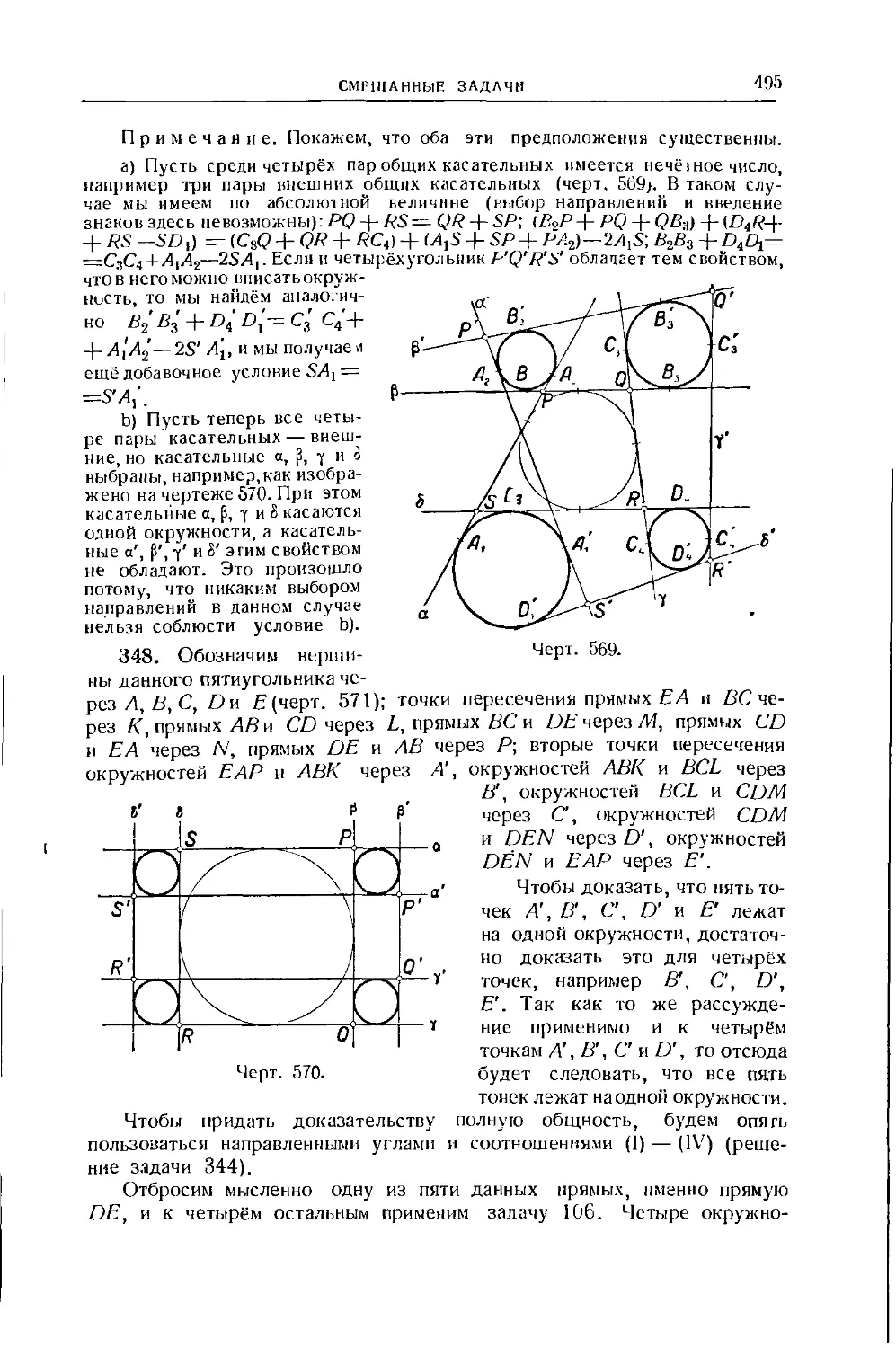
232—236. Решение Жерюнна . . . . 211
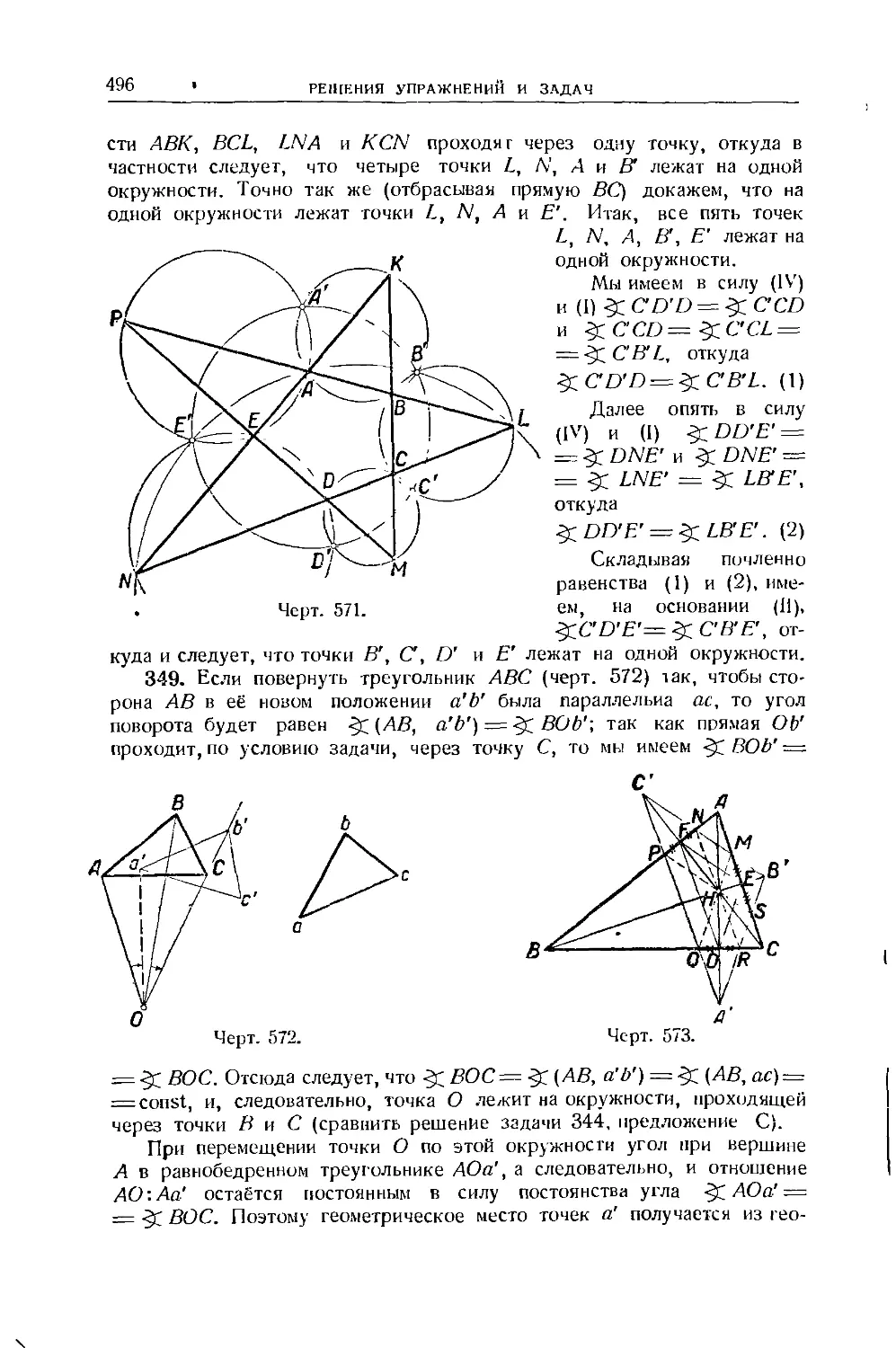
Упражнения 258—268. . 214
Глава VII. Свойства вписанного четырёхугольника.
*"*. Инверсор Поселье.
237—238. Теорема Птоломея. Случаи точек, лежащих на одной прямой 215
239. Вычисление хорды дуги a + b по заданным хордам дуг а и Ь. 217
240—240а.Отношение диагоналей вписанного четырёхугольника; вычи-
вычисление этих диагоналей и радиуса описанной вкружности . . 217
241. Инверсор Поселье 220
241а. Инверсор Гарта ... ... ........ 221
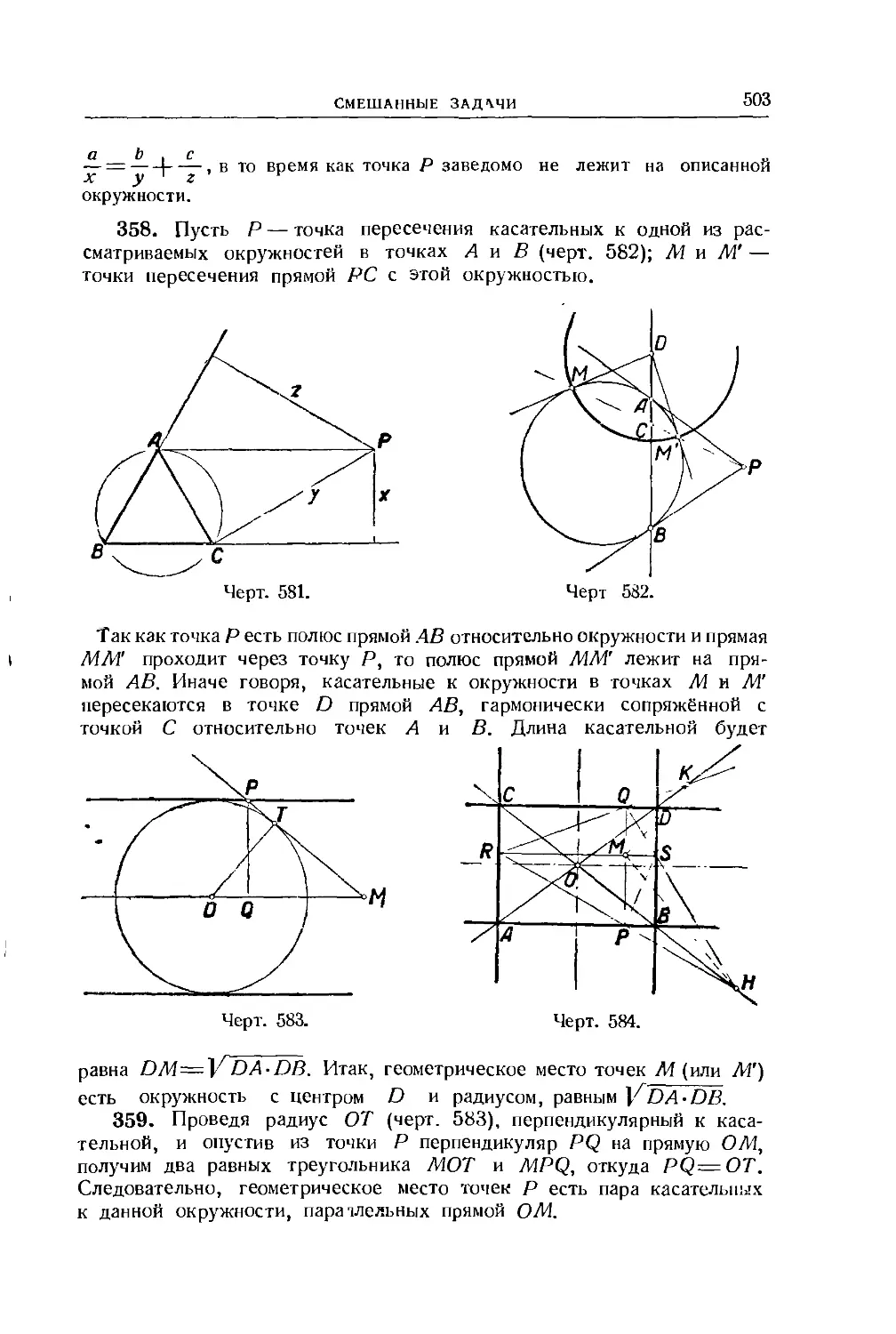
Упражнения 269—271а 222
Задачи B72—286) к дополнениям к третьей книге 223
КНИГА ЧЕТВЁРТАЯ.
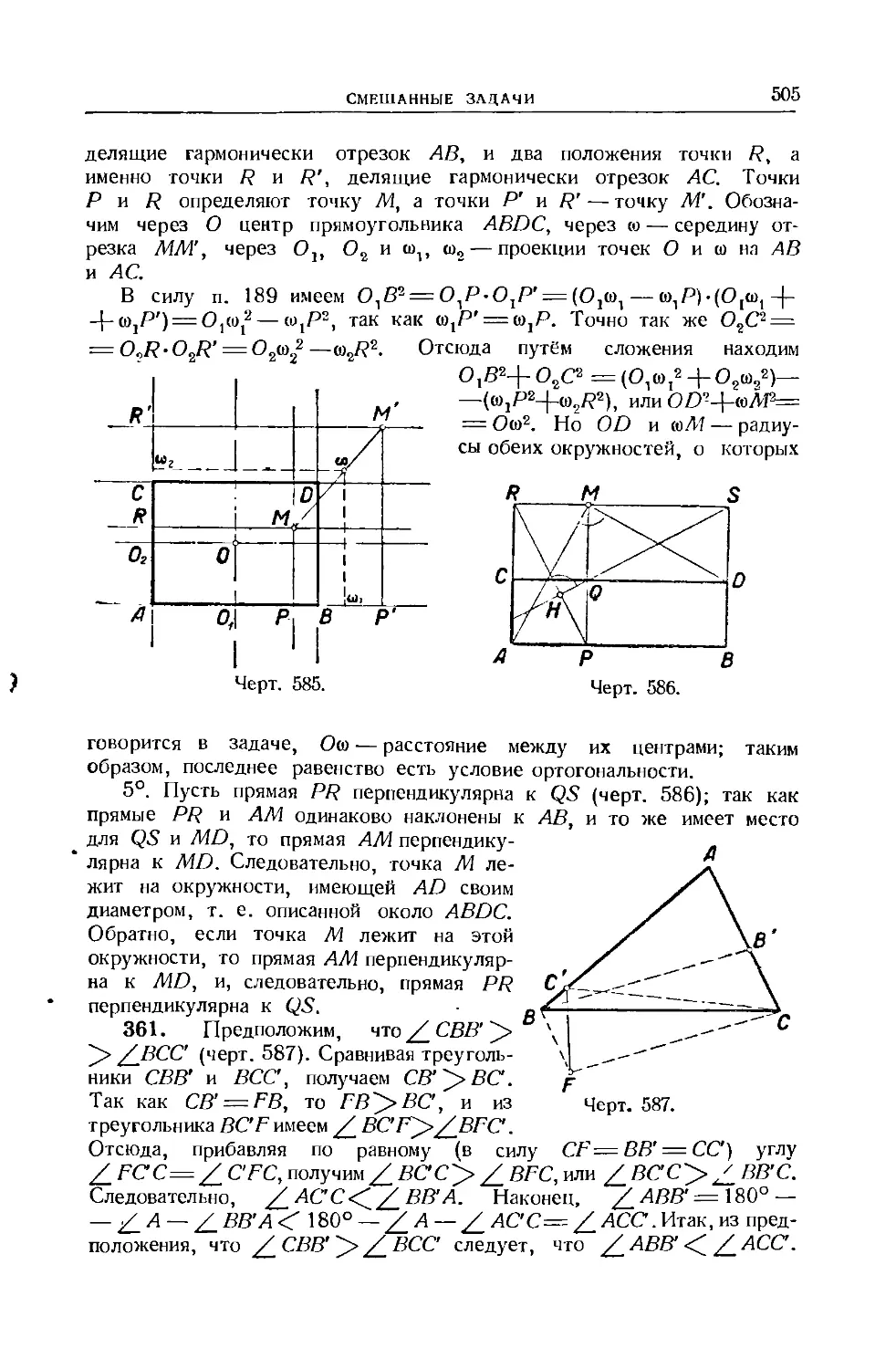
ПЛОЩАДИ.
Глава I. Измерение площадей.
242—246. Определения ... ... ... 225
247. Площадь прямоугольника . 226
248. Площадь параллелограма . . .... 228
249—251. Площадь треугольника . . 229
252—252а. Площадь произвольного многоугольника; плошадь трапеции. 230
253—254. Площадь правильного многоугольника; площадь мноюуголь-
ного сектора; площадь описанного многоугольника 230
255. Площадь вписанного четырёхугольника 231
Упражнения 287—301 232
I
Глава II. Сравнение площадей.
256. Отношение площадей двух треугольников, имеющих по рав-
равному углу . 233
257. Отношение площадей двух подобных многоугольников . . - 234
258. Квадрат гипотенузы ... ... . . 234
Упражнения 302—311 235
СОДЕРЖ\НИЕ И
Глава III. Площадь круга.
259—260. Определение площади круга 236
261—262. Формула для плошали круга. Площачь кругового сектора . 238
263. Площади фшур, ограниченных лугами круга 238
Упражнения 312—318 239
Глава IV. Построения.
264—266. Равновеликие треугольники и многоугольники . .... 239
267. Задача о квадратуре круга не разрешима с помощью цир-
циркуля и линейки 241
Упражнения 319—323. . . ... 241
Задачи C24—342) к четвертой книге. . ... 241
ПРИБАВЛЕНИЯ.
Прибавление А. О методах, применяемых в геометрии . . . 244
a) Теоремы, предлагаемые для доказательства . . . 244
b) Геометрические места. Задачи на построение . . 251
О Методы геометрических преобразований. . . . 254
Прибавление В. О постулате Эвклида. . .... . . 262
Прибавление С. Задача о касании окружностей ... . 272
Прибавление D. О понятии площади . . 278
Прибавление Е. Задача Мальфатти. . . 283
Смешанные задачи и задачи, предлагавшиеся на конкурсных
экзаменах C43—422). . . 292
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ.
Составлены Д. И. Перепёлкиным.
Книга первая. Прямая линия.
Упражнения . . . 307
Задачи . . . . .... 322
Книга вторая. Окружность.
Упражнения . ... 327
Задачи . . . . . ... 351
Книга третья. Подобие.
Упражнения . . 368
Задачи . . 393
12 СОДЕРЖАНИЕ
Дополнения к третьей книге.
Упражнения . 407
Задачи 448
Книга четвёртая4. Площади.
Упражнения . 458
Задачи ^ . . 472
Смешанные задачи и задачи, предлагавшиеся на конкурсных
экзаменах . . . 488
Указатель содержания задач .' . . 608
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ РУССКОМУ ИЗДАНИЮ.
Настоящее—третье — издание перевода первой части „Элементарной гео-
геометрии' Адамара существенно отличается от двух предыдущих тем, что
в нём помещены решения всех имеющихся в первой части задач.
Несомненно, что самостоятельное решение этих, по большей части
трудных, задач потребовало бы от читателя весьма большого количества
времени и весьма значительных усилий. В то же время многие из этих
задач представляют интерес не только как темы для упражнений, но и не-
независимо от этого по самому их содержанию. Эти соображения и заставили
нас приняться за составление решений задач, помешенных в курсе Адамара.
Содержание задач перепечатано здесь в основном без изменений.
Исправлено, однако, несколько ошибок, вкравшихся в русский перевод
(задачи 13, 49, 378, 406), Далее в процессе решения задач выявилась необ-
необходимость исправить отдельные погрешности или уточнить редакцию ряда
задач, данную Адамаром (№№ 9, 10, 41, 88, 191, 222, 223, 256, 260, 270, 276,
284, 339, 34?, 363, 372, 399, 400); в задачах 220, 253а, 265, 308 и 419а мы
позволили себе опустить имевшиеся там указания на путь решения. Само
собой разумеется, что автор этих строк принимает на себя ответственность
за внесенные изменения.
Что касается характера и стиля приведённых нами решений, то, пре-
предоставляя судить о них читателю, ограничимся несколькими замечаниями.
При выборе того или иного пути решения (если в нашем распоряжении
имелось их несколько) мы стремились выбрать тот из них, который наибо-
наиболее подходит к стилю Адамара, руководясь тем местом, где им помещена
данная задача в книге, стилем изложения соответствующих вопросов в курсе,
прямыми указаниями в тексте задачи на метод её решения, содержанием
предшествующих ей и следующих за ней задач, и т. д. Мы помещали
в книге два решения одной и той же задачи лишь в тех случаях, когда
нам не удавалось сделать такого выбора, а также в тех немногих случаях,
когда путь решения, намечаемый автором в самом тексте задачи, не пред-
представлялся нам наилучшим.
При изложении решения мы стремились оттенить наиболее ценные
с нашей точки зрения логические моменты решения: значение тех или иных
предположений, необходимость отдельных условий, доказательство правиль-
правильности приведённого построения и т. п. Более трудные, но существенные
моменты решения выделеКы нами в отдельные абзацы, набранные мелким
шрифтом; они могут быть опущены читателем, не интересующимся этими
более тонкими вопросами. Мы опускали илн излагали весьма коротко те
части решений, которые, по нашему мнению, легко могут быть развиты
читателем: так, во многих задачах на построение опущено исследование
и указано, только (но избежание ошибок у читателя) наибольшее число
решений, которое допускает задача; в доказательствах часто опускаются
мотивы, по которым те или другие треугольники равны или подобны, пря-
прямые параллельны, и т. д. В особенности это относится к решениям более
сложных залач.
Необходимо особо остановиться на задачах на отыскание наибольшего
или наименьшего значения; таких задач в предлагаемой первой части
имеется около 25. Дело в том, что в более трудных задачах такого рода
14 ПРЕДИСЛОВИЕ К TPFTbFMy РУССКОМУ ИЗДАНИЮ
*
(№№ 366, 419а, 420) автор пр^мо рекомендует решать задачу, исходя из
предположения, что существует фигура, для которой имеет место экстре-
экстремум. Такой путь решения, более или менее естественный в ту эпоху, когда
составлялась книга Адамара, мы считаем в настоящее время неприемлемым
и в области элементарной геометрии. Поэтому во всех задачах на наиболь-
наибольшее и наименьшее значение нами даны такие решения, ь которых сущест-
существование экстремума не предполагается, а доказывается (за исключением
задач 419а и 420, где мы ограничились соответствующим примечанием, так
как подробный разбор изопериметрических свойств завёл бы нас слишком
далеко).
Чтобы облегчить читателю ориентировку в содержании задач и помочь
в подборе задач на ту или иную 1ему, мы поместили в конце книги не-
небольшой „Указатель содержания задач". Заметим по этому поводу, что он
далеко не исчерпывает и не может исчерпать всего содержания задач.
Мы отказались совершенно сознательно от помещения в решениях
задач тех или иных библиографических данных ' по нескольким причинам.
Прежде всего известно, что именно к области элементарной геометрии одни
и те же теоремы и задачи встречаются по нескольку раз у различных ав-
авторов в разное время независимо друг от друга, и потому помещение
в книге библиографических данных исторического характера представляло
бы слишком сложную задачу. Далее составителем, естественно, была просмот-
просмотрена и использована большая литература. Однако и в тех случаях, когда
идея решения была заимствована из литературы, приходилось иногда про-
проделывать большую работу, чтобы придать решению вид, подходящий к сти-
стилю настоящей книги в целом. Во многих случаях составитель даже и не
мог бы сказать сейчас с полной уверенностью, было ли данное решение
найдено им самостоятельно или заимствовано из литературы. Наконец,
библиографические указания принесли бы в данном случае небольшую
пользу и читателю, желающему расширить свои познания, так как соответ-
соответствующая литература (за исключением нескольких общеизвестных книг)
разбросана и, как правило, мало доступна.
Рукопись настояшей книги была полностью прочитана доцентом Мос-
Московского государственного педагогического института им. В. И. Ленина
М. А. Ю к и н ы м: составитель обязан ему рядом цепных замечаний, устра-
устраняющих те или иные пробелы в решениях, выделяющих исключительные
случаи, и т. д. Доц. Н. Т. Зерченинов и Е. Д. "Загоскина, также
ознакомившиеся с рукописью, поделились с составителем своими сообра-
соображениями по поводу методической стороны в редакции решений ряда задач,
особенно к первым главам книги. Идея решения задачи 121а была сообщена
составителю И. А. В и л ьп е р о м. Ряд ценных указаний автор получил также
от рецензентов | проф. В. Н.Депутатова) и доц. С. И. Зетеля.
Редактор издательства канд. наук Т. Л. Козьмина своим внимательным отно-
отношением к рукописи способствовала улучшению изложения ряда решений.
Всем перечисленным товарищам составитель выражает здесь свою иск-
искреннюю признательность.
Принимая во внимание, что именно в решениях задач особенно легко
можно осуществить дальнейшее улучшение путём указания более простых
или более изящных решений, составитель обращается ко всем читателям
с просьбой сообщать ему (по адресу: Москва, Чистые пруды, 6, Учпедгиз,
редакция математики) свои замечания и предложения, за которые он будет
весьма благодарен.
Москва, февраль, 1м7. Д. ПерепёЛКЧН.
ПРЕДИСЛОВИЕ АВТОРА К ПЕРВОМУ ИЗДАНИЮ.
При составлении настоящего курса геометрии я всё время имел в виду
то особое место, которое эта наука занимает в элементарной математике.
В самом деле, будучи oihhm из первых математических предметов, с кото-
которым встречается учащийся, геометрия представляет собой наиболее простую
и доступную форму математического рассуждения. Сила её методов и их
плодотворность непосредственно более ощутимы, чем в случае относительно
абстрактных арифметических и алгебраических теорий. Поэтому геометрия
оказывается в состоянии оказывать бесспорное влияние на развитие актив-
активного мышления. Я в первую очередь стремился усилить это влияние, про-
пробуждая инициативу учащегося и всячески ей содействуя.
Вот почему мне казалось необходимым увеличить число упражнений,
насколько это позволяли рамки настоящего труда. Эта необходимость боль-
большого числа упражнений была для меня, так сказать, единственным
принципом, руководившим мною в части подбора задач. Я считал
необходимым поместить задачи различной степени трудности и притон
в порядке возрастания этой трудности: в то время как упражнения,
помещённые в конце каждой главы, в особенности первые из них, очень
просты, упражнения, помещённые в конце каждой книги, уже не решаются
так просто и непосредственно; наконец, я отнёс в конец тома относительно
трудные задачи. Содержание некоторых задач заимствовано из тех или
других важных теорий; отметим в частности задачи, относящиеся к теории
инверсии и систем окружностей, многие из которых заимствованы из ме-
муара Дарбу: „Sur les relations entre Ies groupes cle points, de cercles et de
spheres dans le plan et dans l'espace" lf, другие задачи имеют единственной
целью приучить мысль учащегося к проведению рассуждений. Столь же
разнообразны были и те источники, из которых я заимствовал содержание
упражнений: наряду с классическими задачами, представляющими собой
наиболее непосредственное приложение теории, которые было бы почти
странным не поместить в данной кпше, имеются задачи, заимствованные
у различных авторов и из различных периодических изданий как француз-
французских, так и иностранных, а также довольно большое число оригинальных
задач.
С другой стороны, я поместил в конце тома особое Прибавление, в ко-
котором я имел в виду вкратце изложить основные идеи математических
методов — идеи, которыми учащиеся должны были бы проникнуться с пер-
первого года обучения, но которые очень часто забываются даже учащимися
наших высших учебных заведений. Следует признать, что та догматическая
^орма изложения, которую я здесь избрал, не является наиболее подходя-
шей для данного случая: вопросы такого рода должны изучаться путём
соответствующих бесед, причём каждое правило должно появляться лишь
в тот момент, когда в нём возникает надобность. Я всё же счёл себя обя-
обязанным сделать попытку такого рода изложения, надеясь, что читатель
отнесётся снисходительно к её неизбежному несовершенству. Быть может
') Annales scientifiques de l'Ecole Normale Supgrieure B), 1, 18~2. — Содержание задачи 401
(построение окружностей, касательных к трём далным) сообщено мне преподавателем лицея
имени Ампера Жераром (Gerard).
ПРЕДИСЛОВИЕ АВТОРА К ПЕРВОМУ ИЗДАНИЮ
эта попытка, какова бы она ни была, принесёт некоторую пользу и будет
содействовать внедрению в преподавание тех идей, о важности которых
нет надобности распространяться.
Другие прибавления, помещённые в конце тома, носят более специ-
специальный характер. В Прибавлении В рассмотрен вопрос о постулате Эвк-
лида. Взгляды современных геометров на этот вопрос приняли настолько
ясную и определённую форму, что представляется необходимым и полезным
дать их краткое изложение даже в курсе, носящем элементарный характер.
Прибавление С относится к задаче о касании окружностей. Как было
отмечено Кёнигсом1), известное решение Жергоцна, если даже его допол-
дополнить соответствующим доказательством, отсутствующим у его автора, всё
же обладает некоторым недостатком. Этот пробел я и имел в гзиду воспол-
восполнить.
Наконец, Прибавление D посвящено понятию площади. Обычное учение
о плошадях обладает, как известно, серьёзным логическим недостатком. Оно
a priori предполагает, что эта величина определена и обладает известными
основными свойствами. Теория, которую я излагаю в данном Прибавлении,
обходи гея без этого предположения и потому заслуживает предпочтения,
особенно если учесть, что она переносится без значительных изменений
и на пространство.
В самом тексте книги оказалось возможным внести в классические
рассуждения некоторые изменения, представляющие преимущества либо
с точки зрения строгости, либо с точки зрения простоты; к их числу при-
принадлежит, например, помешенное в самом начале первой книги доказатель-
доказательство существования перпендикуляра, восставленного к прямой линии в ка-
какой-либо из её точек; соображения, основанные на лепрерывности, которыми
здесь обычно пользуются, пришлось оставить, поскольку в другом месте
мы допускаем без доказательства возможность разделить отрезок или угол
пополам. Рассмотрение направления углов позволило мне внести в пред-
предложение второй кни> и, а также в ряд предложений последующих книг
полную чёткость и общность без того, чтобы сделать их менее простыми
или менее элементарными. - '
В дополнениях к третьей книге изложены те вопросы, которые хотя
и не относятся к элементам геометрии в смысле Эвклида, тем не менее
завоевали определённое место в преподавании. Я ограничился изложением
элементов соответствующих теорий и последовательно опускал всё то, чю
не является .рейслвшелыю существенным. Впрочем, курс составлен таким
образом, что эти дополнения, а также те разделы текста, которые напеча-
напечатаны мелким шрифтом, могут быть опущены при первом чтении без нару-
нарушения СВЯЗНОС1И остальной части текста.
Проф. Дарбу, который оказал мне большую честь, поручив состав-
составление настоящего курса, чрезвычайно облегчил мою задачу теми ценными
советами, которые он постоянно давал мне при его составлении. Заканчивая
настоящее предисловие, я хотел бы выразить ему здесь свою почтительную
признательность. v
Ж- Адалшр.
1) „Lemons de l'agrtgation cfassique de Mathematiques-, Paris, 1892, стр. 92.
ПРЕДИСЛОВИЕ АВТОРА КО ВТОРОМУ ИЗДАНИЮ.
За время, истёкшее с момента выхода в свет первого издания, обучение
математике и в частности геометрии претерпело глубокие изменения не
только в отдельных деталях, но и в самом своём характере, изменения,
которых давно ждали и которых все добивались. В основу обучения мате-
математике, в начальной его стадии, стремятся положить соображения прлкти-
ческого и наглядного характера вместо логического метода Эвклида, пользу
которого начинающие не в состоянии оценить.
Напротив, к эвклидовскому методу приходится, конечно, возвращаться,
когда речь идёт о пересмотре и о пополнении первоначальных сведений.
Наш курс и соответствует этой именно второй стадии обучения, и потому
нам не пришлось менять его характера.
Однако даже с точки зрения строгой логики классическое изложение
обладало ненужной ' сложностью и схоластичностью в его первой главе,
посвященной учению об углах. Условие не пользоваться в nepiiofi книге
понятием окружности, остававшееся неприкосновенным до настоящего ире-
мени, чрезвычайно затемняло здесь веши, сами по себе очень простые
и естественные. Изложение этих вопросов оказалось возможным значительно
упростить, вводя с самого начала наряду с понятием об угле и понятие
о дуге окружности. Мы уже раньше отказались здесь от традиционного
использования непрерывности, на которой обычно основывали существова-
существование перпендикуляра; теперь оказался излишним и тот простой искусствен-
искусственный приём, которым мы раньше заменили соображения, основанные на не-
непрерывности.
В то же время измерение центральных углов оказывается при этом
естественным образом сближенным с учением об углах и занимает своё
настоящее логическое место в курсе.
Не меньше выигрывает от этой перестановки и вторая книга. В самом
деле, основное свойство вписанного угла отделяется при этом от вопроса
об измерении углов, а прежнее соединение этих двух вопросов могло дать
самое неправильное представление об этом свойстве вписанного угла и об
его значении.
За исключением этого пункта план курса в целом остался неизменным.
С другой стороны, те дополнения, которые были внесены в программу
1902 г., уже раньше нашли себе место в первом издании курса. Программа
1905 г., которая скорее снизила роль этих дополнений, тем самым не по-
потребовала от нас никаких существенных изменений. Она содержит только
одно добавление—инверсор Поселье. Единственная дополнительная глава,
которая остаётся в программе, по крайней мере в области геометрии на
•плоскости1;, — инверсия и её приложения — соответствует главам V—VII
наших дополнений.
l) Надо ли говорить по этому поводу, что я вовсе не стремился к слиянию геометрии на
плоскости с геометрией в пространстве. Я охотно признаю, что такое слияние заслуживает
предпочтения с точки зр*мия чисто логической. Однако с точки зрения педагогической сле-
Дует стремиться, мне кажется, к разделению встречающихся трудностей. Уменье „видегь
в пространстве" само по себе представляет собою серьёзную трудность, и ч не думаю, чтобы
ЭтУ трудность следовало присоединить к другим трудностям с самого начала обучения.
Элементарная геометрия
18 ПРЕДИСЛОВИЕ АВТОРА КО ВТОРОМУ ИЗДАНИЮ
За последние голы в преподавательской среде наметилась и другая
тенденция, которой нельзя не одобрить. Теперь очень часто говорят об
эвристическом метоле, и я надеюсь, что кое-где его применяют на прак-
практике. Прибавление, которое я поместил в первом издании настоящего курса
(Прибавление А), как раз и имело своей целью показать, как следует по-
понимать этот метод, столь существенный с моей точки зрения, по крайней
мере, как его следует понимать сточки зрения теоретической, так как для
его применения на практике необходимо наличие двух лиц. Мне хотелось
бы, чтсбы это Прибавление могло принести теперь некоторую пользу,
указывая по крайней мере те принципы, которые следует применять
в этом случае.
Я уже указывал (см. предисловие к геометрии в пространстве), что
изложенный в Прибавлении С метод решения задачи о касании окружно-
окружностей в действительности принадлежит Ф у ш е (Fouche) или даже По нее л е
(Pontelet) и что Жерару (Gerard) принадлежит решение вопроса о пло-
площади плоской фигуры, правда отличное от того, которое я дал в Прибавле-
Прибавлении D. Пользуюсь случаем отметить, что Фонте не (Fontene) было выска-
высказано одно возражение, касающееся теории двугранных углов, и им же оно
было устранено.
Ж. Адамар.
ПРЕДИСЛОВИЕ АВТОРА К ВОСЬМОМУ ИЗДАНИЮ.
Настоящее издание не представляет, по сравнению с предыдущими,
существенных изменений. Однако следует отметить, что наши взгляды на
постулат Эвклида существенно изменились в связи с успехами физики:
я должен был изменить конец Прибавления В (пп. 308, 308а), чтобы принять
во внимание эту эволюцию научной мысли.
Некоторые изменения были также внесены в настоящее издание
с целью уделить большее внимание свойствам наиболее» простых шарнир-
пых систем. х
Ж. Аоамар.
ВВЕДЕНИЕ.
1 Телом называется часть пространства, ограниченная со всех
сторон.
Поверхностью называется общая часть двух смежных областей про-
пространства. Лист бумаги может дать нам приблизительное представление
о поверхности. В самом деле, он ограничивает две области простран-
пространства, которые расположены по обе стороны от листа. Но лист бума-
бумаги не будет, строго говоря, поверхностью: эти две области разде-
разделяются целой промежуточной областью, так как лист бумаги имеет
толщину. Мы пришли бы к понятию поверхности, рассматривая лист
бумаги, толщина которого бесконечно уменьшается.
Линией назынается общая часть двух смежных областей поверхно-
поверхности. Это определение, очевидно, эквивалентно такому определению:
линия есть пересечение двух поверхностей.
Линии, которые мы проводим, дают нам представление о геомет-
геометрических линиях и притом неточное представление, так как, как бы
они тонки ни были, они всегда имеют толщину, в то время как
геометрические линии толщины не имеют.
Наконец, тачкой называется то общее, что имеют две смежные
части одной линии, или, иначе, пересечение двух встречающихся ли-
линий. Точка не имеет никакого измерения.
Любая совокупность точек, линий, поверхностей и тел называется
фигурой.
1а. Всякая линия содержит бесчисленное множество точек.
Её можно рассматривать как след перемещающейся по ней точки.
Это имеет место, когда мы проводим линию на бумаге остриём каран-
карандаша или пера (получающиеся при этом точки мы уподобляем геомет-
геометрическим точкам, когда они достаточно тонки). Точно так же поверх-
поверхность может быть образована перемещающейся линией.
Фигура, вообще говоря линия или поверхность, образованная сово-
совокупностью бесчисленного множества положений, которые может зани-
занимать некоторая точка, называется геометрическим местом точек.
Точно так же мы можем рассматривать поверхность как геометри-
геометрическое место линии, которая перемещается.
2. Геометрия изучает свойства фигур и их взаимоотношения. Ре-
Результаты этого изучения формулируются в виде предложений.
Предложение состоит из двух частей: первая, называемая коротко
условием, указывает на совокупность всех имеющихся налицо условий;
2*
20 ВВЕДЕНИЕ
вторая — заключение—выражает тот факт, который в силу этих ус-
условий неизбежно имеет место.
Так, в следующем предложении: „Два количества А и В. равные
одному и тому же третьему С, равны между собой", условием
является следующая часть предложения: количества А и В порознь
равны С; заключением — эти два количества А и В между собою
равны.
Среди предложений имеются такие, которые принимаются как оче-
очевидные без доказательства. Их называют аксиомами. Таким, напри-
например, является предложение, которое было приведено выше: „Две ве-
величины, равные третьей, равны между собой". Все другие предложе-
предложения называются теоремами и должны быть доказаны при помощи
особого рассуждения. Чтобы провести это рассуждение, надо, ос-
основываясь на условии теоремы и предполагая, что это условие вы-
выполнено, вывести из него факты, указанные в заключении.
Согласно с этим мы должны допустить, что некоторое обстоятель-
обстоятельство имеет место:
1) если оно является частью условия;
2) если оно является частью определения одного из элементов, о
которых идёт речь1);
3) если оно вытекает из аксиомы;
4) если оно вытекает из одного из предыдущих доказательств.
В геометрических рассуждениях ни одно положение не должно
считаться верным иначе, как в силу одной из этих четырёх причин.
2а. Предложением, обратным данному предложению, называется
другое предложение, в котором заключение Полностью или частично
совпадает с условием первого предложения, и обратно.
Следствием называется предложение, непосредственно вытекающее
из теоремы.
Леммой называется, напротив, подготовительное преЯложение, вво-
димде для того, чтобы облегчить доказательство последующего пред-
предложения.
3. Всякая фигура может быть перемещена в пространстве бесчис-
бесчисленным множеством способов без изменения своего вила совершенно
так же, как это может быть сделано с обыкновенными твёрдыми те-
телами. Равными фигурами называются такие две фигуры, которые
можно совместить одну с другой так, чтобы они в точности
совпадали во всех своих частях; одним словом, две равные фигуры
представляют собою одну и ту же фигуру, расположенную в двух
различных местах.
Фигура, которая подвергается только перемещениям и при этом
не деформируется, называется неизменяемой фигурой.
!) Часто случается, что в процессе доказательства вводят в фигуру
вспомогательные элементы. Некоторое положение может быть при этом
верным в силу определения этих новых элементов. В таком случае гово-
говорится, что оно верно по построению.
ВВЕДЕНИЕ 21
4. Простейшая из линий — прямая линия; представление о ней
даёт нам натянутая нить. Понятие прямой линии очевидно само по
себе; чтобы иметь возможность пользоваться этим понятием в наших
рассуждениях, будем рассматривать прямую линию, как определяемую
её очевидными свойствами и в частности следующими двумя:
1°. Веяная фигура, равная прямой линии, есть прямая личия;
и обратно, каждая бесконечная прямая линия может быть сов-
совмещена со всякой другой и притом таким образом, что какая-
либо одна точка первой совмещается с любой точкой второй.
2°. Через две точки можно провести прямую линию и притом
только одну.
Таким образом, можно говорить о той прямой линии, которая
проходит через точки А и В (или короче: о ггрямой АВ).
Из .определения непосредственно вытекает, что две различные
прямые могут встретиться только в одной точке, потому что,
если бы они имели две общие точки, они не были бы различными.
Ломаной линией называется линия, состоящая из частей прямых
линий. Другие линии, которые не являются ни прямыми, ни лома'
ными, называются кривыми линиями.
5. Часть прямой линии, заключающаяся между двумя точками А
и В, называется отрезком прямой АВ.
Можно также рассматривать часть прямой, не ограниченную с од-
одной стороны и ограниченную с другой стороны точкой. Такая часть
называется полупрямой. Две произвольные полупрямые являются на
основании предыдущего равными фигурами.
ЛВС Ц С В
Черт. 1. Черт. 2.
Отрезок АВ называется равным отрезку А'В', если первый отре-
отрезок можно наложить на второй отрезок таким образом, чтобы точ-
точка А совпала бы с точкой А' и точка В — с точкой В'.
При этих условиях два отрезка совпадут во всех своих точках
на основании двух предложений, которые служат определением пря-
прямой линии. Следовательно, определение равных отрезков вполне со-
согласуется с данным выше общим определением равных фигур.
Совмещение двух равных отрезков АВ и А'В' может быть осуще-
осуществлено двумя различными способами, а именно: точка А может сов-
совпасть с точкой А' и точка В — с В', или обратно. Это равносильно
тому, что отрезок АВ можно повернуть таким образом, чтобы после
поворота каждая из двух точек А, В заняла бы место другой из
этих точек.
Если два отрезка АВ и ВС расположены на одной и той же пря-
прямой линии и представляют собой продолжение один другого (черт. 1),
то отрезок 1С называется суммой двух первых отрезков. Сумма двух,
22 ВВЕДЕНИЕ
а следовательно, и нескольких отрезков не зависит от порядка сла-
слагаемых частей ').
Чтобы сравнить два отрезка, их переносят на одну и ту же пря-
прямую линию так, чтобы они выходили из одной и той же точки и
были направлены в одну и ту же сторону, например АВ и АС
(черт. 1 и 2). Если при этом точки следуют в порядке А, В, С
(черт. 1), то отрезок АС равен сумме АВ и другого отрезка ВС;
в этом случае он больше, чем АВ, а этот последний меньше, чем АС;
если, напротив, порядок следующий: А, С, В (черт. 2), то отрезок АВ
больше АС. В обоих случаях третий отрезок ВС, который при сло-
сложении с одним из двух данных отрезков даёт второй, называется
разностью этих двух отрезков. Наконец, точки В и С могут сов-
совпасть. В этом случае, как мы знаем, данные отрезки равны.
На каждом отрезке прямой АВ существует точка М — середина АВ,
одинаково удалённая от Л и В; всякая точка прямой, лежащая между
М и .4, очевидно, ближе к А, чем к В, и обратное имеет место
для всякой точки, расположенной между М и В.
¦ Вообще отрезок прямой АВ может быть разделён на какое угодно
число равных между собой частей2).
6. Плоскостью называется такая безграничная поверхность, что
всякая прямая, соединяющая две её точки, лежит на ней целиком.
Мы допускаем, что через всякие три точки пространства прохо-
проходит плоскость. Прямая линия, проведённая на плоскости, делит её
па две области, каждая из которых расположена по одну сторону от
прямой линии и называется полуплоскостью. Нельз,я перейти из од-
одной области в другую по непрерывному пути, не^ зыхо'дя из плос-
плоскости и не пересекая прямой линии. Эти две области можно сов-
совместить одну с другой, заставляя одну из них вращаться около
данной прямой линии, как около оси.
Мы будем заниматься прежде всего фигурами, расположенными
на плоскости; изучение их составляет предмет плоской геометрии
(планиметрии).
7. Окружностью называется геометрическое место точек плоско-
плоскости, расположенных на данном расстоянии от данной точки этой плос-
плоскости 3) (О, черт. 3); эта точка называется центром окружности.
!) Для двух отрезков это следует непосредственно из предыдущего
абзаца. ,
2) Мы понимаем под этим, что на АВ существуют точки, которые де-
делят этот отрезок на равные части. Вопрос о том, можно ли найти эти
точки фактически с помощью имеющихся у нас инструментов, будет рас-
рассмотрен нами позднее (книга III).
3) Геометрическое место точек плоскости, расположенных на данном
расстоянии от данной точки, лежащей вне плоскости, равным образом есть
окружность (если такие ючки вообще существуют); это мы докажем в
геометрии пространства.
Геометрическое место точек пространства, расположенных на данном
расстоянии от данной точки пространства, представляет некоторую по-
поверхность — сферу.
ВВЕДЕНИЕ
23
Отрезок прямой линии, который соединяет центр с какой-нибудь
точкой окружности, называется радиусом. Следовательно, все радиусы
между собою равны. Зто имеет место для спиц колеса, так как оно
имеет форму окружности.
На основании предыдущего определения, чтобы доказать, что точ-
точка плоскости лежит на окружности, расположенной в этой плоскости,
достаточно показать, что ее расстояние до
центра равно радиусу. '
Всякая окружность делит плоскость, в ко-
которой она лежит, на две области: одну внеш-
внешнюю, безграничную, образуемую точками, рас-
расстояния которых до центра больше радиуса;
другую — внутреннюю, ограниченную со всех
сторон, образованную такими точками, рас-
расстояния которых до центра меньше радиуса.
Эта последняя область называется кругом.
Ясно, что окружность вполне определена, когда даны плоскость,
в которой она лежит, её центр и радиус.
Окружность часто обозначают (когда это не может дать повода
к недоразумениям) той же буквой, как её центр, или двумя буквами,
которые обозначают один из её радиусов, причём на первом месте ставят
ту, которая обозначает центр. Таким образом, окружность, представ-
представленная на чертеже 4, обозначается через О или (если приходится
рассматривать несколько окружностей с центром в О) через ОМ.
М ' ~~
Черт. 3.
Черт. 4.
Черт. 5.
Две окружности одного радиуса представляют собою равные
фигуры; ясно, что они совмещаются, коль скоро мы совместим их
центры.
Две равные окружности могут быть наложены друг на друга бес-
бесчисленным множеством способов: их можно наложить одну на дру-
другую так, чтобы некоторая точка М' второй окружности совместилась
бы с данной точкой М первой окружности (черт. 4). Для этого до-
достаточно совместить два радиуса ОМ и О'М', что возможно, так как
эти два прямолинейных отрезка равны.
8. Дугой называется часть окружности {АрВ, черт. 5).
Из того обстоятельства, что две равные окружности moi\t быть
наложены друг на друга бесчисленным множеством способов, следует
24 ВВЕДЕНИЕ
возможность сравнивать душ, принадлежащие одной и той же окруж-
окружности или двум равным окружностям, так же, как мы сравни-
сравниваем отрезки прямой. Для этого перенесём эти две дуги таким обра-
образом, чтобы они имели один и тот же центр, один общий конец и
были расположены по одну сторону от этого общего конца. Пусть
АВ и АС—две дуги, расположенные таким образом; мы скажем, что
первая больше второй, если, перемещаясь из точки А по дуге АВ'),
мы встречаем точку С раньше точки В (черт. 6). Мы скажем, что
первая дуга меньше второй, если порядок будет обратный: А, В, С
(черт. 5).
8а. Точно так же можно определить сумму двух дуг АВ, ВС
(черт. 5), принадлежащих одной и той же окружности (или двум рав-
Черт. 6. Черт. 7.
t
ным окружностям), располагая эти .две -дуги так, чтобы конец одной
совпал с концом другой и дуги были направлены в разные стороны
от их общего конца. ' -
Дуга АВ может быть, так же как отрезок прямой, разделена на
две или несколько равных частей2). Она делится своей средней точ-
точкой1 на две дуги, из которых одна состоит* из точек М, таких, что
дуга AM больше, че\) дуга MB, другая — из таких точек, что дуга AM
меньше, чем дуга MB.
9. Две точки окружности называются диаметрально противопо-
противоположными (А, В, 4epf. 7), если отрезок, который их соединяет, про-
проходит через центр. Этот отрезок называется диаметром. Ясно, что
длина диаметра равна удвоенной длине радиуса.
Окружность, очевидно, определена, коль скоро дан один из её
диаметров. В таком случае её центром будет середина диаметра.
') Здесь очень важно точно определить направление, в котором происхо-
происходят перемещения (что было не нужно в случае прямой), потому что точ-
точки А, В делят окружность на две дуги, и порядок, в котором мы встре-
встретим точки В, С, не будет одним и тем же, если мы будем перемещаться
из точки А по той или другой из этих дуг.
2) То же замечание, которое ранее сделано (стр. 22, сноска 2).для от-
отрезков прямой.
ВВЕДЕНИЕ 25
Диаметр АВ делит окружность на две дуги, которые представляют
собой части окружности, расположенные соответственно в т.вух полу-
полуплоскостях, определяемых прямой АВ.
Эти две части равны между собой: их можно совместить, нало-
наложив полуплоскости, о которых идёт речь, одну на другую (п. 6).
Мы имеем, таким образом, две полуокружности.
Точно так же круг делится диаметром на две равные части, кото-
которые совмещаются друг с другом при совмещении двух полуокружностей.
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ.
„ ГЛАВА I.
УГЛЫ.
10. Углом называется фигура, образованная двумя полупрямыми,
выходящими из одной и той же точки. Эта точка называется верши-
вершиной угла, а две полупрямые — его сторонами.
Угол обозначается той же буквой, что и его вершина, помещён-
помещённой между двумя другими буквами, которые служат для. обозначения
его сторон: перед буквами часто ставится специальный знак. Если,
впрочем, фигура содержит только один угол,
имеющий данную вершину, то буква, обозна-
обозначающая эту вершину, будет вполне достаточна
для обозначения угла. Так, угол, образованный
полупрямыми АВ, АС (черт. 8), будет обозна-
обозначаться: /_ВАС, или проще /А.
Два угла называются равными по определе-
д1 ' g нию равных фигур (п. 3), если их можно приве-
„ сти в совпадение, накладывая один на дру-
Черт- * гой.
Два равных угла ^_ВАС и ^В'А'О могут быть наложены один
на другой двумя различными способами, а именно: или так, что сто-
сторона А'В" совпадает со стороной АВ и А'С со стороной АС, или
наоборот. От одного способа совмещения можно перейти к другому,
перевёртывая один из углов и накладывая его
на самого себя, например, перемещая угол ВАС
так, чтобы сторона' АВ приняла положение,
ранее занимаемое АС, и обратно. ¦
11. Два угла называются прилежащими
друг к другу, если они имеют общую вершину,
одну общую сторону и расположены по раз-
разные стороны от этой общей стороны.
Если два угла /_АОВ и ^_ВОС — приле-
прилежащие (черт. 9), то угол АОС называется сум-
суммою этих двух углов. Сумма нескольких углов не зависит от по-
порядка слагаемых.
Чтобы сравнить два угла, их перемещают таким образом, чтобы
они имели общую вершину, одну общую сторону и чтобы они были
расположены по одну сторону от их общей стороны.
Пусть даны два угла ^/_АОВ и ^_АОС, расположенные таким
образом. Если при вращении вокруг точки О мы встретим стороны
ГЛАВА 1. УГЛЫ 27
в порядке ОА, ОВ, ОС (черт. 9), то угол АОС равен сумме углов
АОВ и ВОС; в этом случае говорят, что он больше угла АОВ, а
этот последний меньше угла АОС\ если, напротив (черт. 10), поря-
порядок таков: О А, ОС, ОВ, то угол АОВ больше угла АОС. Угол ВОС,
от прибавления которого к одному из лвух данных углов получается
другой угол, есть разность этих двух углов.
Наконец, в случае промежуточном, когда ОВ совпадает с ОС, оба
угла равны (см. предыдущий пункт).
Внутри всякого угла ВАС существует полупрямая AM, которая
делит этот угол на две равные части. Она называется биссектрисой
угла. Полупрямые, выходящие из Л и расположенные
внутри угла ВАМ, образуют с АВ угол меньший,
чем с АС; обратное имеет место для полупрямых,
расположенных внутри угла MAC.
Некоторый угол называется удвоенным, утроен-
утроенным и т. д. углом по отношению к данному углу, "
если он представляет собою сумму двух, трёх Черт. 10.
и т. д. углов, равных этому углу. Этот по-
последний Называется при этом половиной, третью и т. д. первого.
Примечание. Очевидно, величина угла не зависит от вели-
величины его сторон, которые мы должны всегда предполагать неогра-
неограниченно продолженными.
12. Если мы имеем угол, образованный двумя
полупрямыми ОАиОВ (черт. 11) и если продол-
продолжить ОА за точку О, проведя ОА', и го же самое
сделать с ОВ, проведя ОВ', то образуется новый
угол А'О В'.
Вертикальными углами называются два угла,
/_АОВ, j/_A'OB', таких, что стороны одного
являются продолжениями сторон другого.
Теорема. Два вертикальных угла равны
между собой.
В самом деле, перевернём угол BOA и наложим его на самого
себя (черт. 11). Сторона ОВ займёт положение ОА', и, с другой сто-
стороны, сторона ОА' займёт первоначальное положение стороны ОВ; полу-
полупрямая ОА, как продолжение ОА', пойдет по ОВ, как по продолже-
продолжению ОВ. Угол \ОВ займёт тогда положение угла А'ОН; следователь-
следовательно, эти два угла равны.
13. Всякая полупрямая, выходящая из центра окружности, пере-
пересекает эту окружность в одной и только в одной точке.
Всякий угол АОВ (черт. 5), имеющий вершину в центре О окруж-
окружности (центральный угол), определяет на этой последней дугу АВ,
ограниченную точками пересечения окружности со сторонами угла. Эта
дуга во всяком случае меньше, чем полуокружность, как в этом можно
убедиться, принимая за концы полуокружности точку А и точку, ей
диаметрально противоположную.
Обратно, всякую лугу, меньшую полуокружности, можно рассматри-
23
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
вать как отсекаемую центральным углом; этот угол образован радиу-
радиусами, проведёнными в концы данной дуги.
Теорема. На одной и той же окружности или на равных
окружностях:
1) равным дугам (меньшим полуокружности) соответствуют
равные центральные углы, и обратно;
2) неравным дугам (меньшим полуокружности) соответствуют
неравные центральные углы, и большей дуге соответствует боль-
больший центральный угол;
3) если некоторая дуга (меньшая полуокружности) есть сум-
сумма двух других дуг, то и соответствующий ей центральный угол
будет суммой центральных углов, соответствующих двум дру-
другим дугам.
1°, 2°. Пусть АВ, АС (черт. 5)—две дуги одной и той же окруж-
окружности, выходящие из одной точки А в одном и том же направлении
/
(п. 8). Два центральных угла /_АОВ,
будут при этом расположены так, как это
было сказано в п. 11. Полупрямые О А, ОВ,
ОС следуют в том же порядке, как%оч-
ки Л, В, С на окружности. Кроме того, если
прямые ОВ и ОС совпадают, то это же имеет
место для точек В и С, и обратно.
3°. Так как для построения суммы двух
дуг (п. 8а) эти дуги располагают так, как
расположены дуги АВ, ВС (черт. 5), то цен-
центральный угол АОС, соответствующий сумме
дуг, будет суммой двух центральных углов
и ^/_ВОС, которые будут прилежащими друг к другу.
На этом основании, чтобы сравнить различные утлы, можно из их
вершин, как из центров, описать окружности одним и тем же раз на-
навсегда выбранным радиусом и сравнить дуги, отсекаемые на этих
окружностях.
Деление угла на две- или больше равные между собой части сво-
сводится к делению на равные части' дуги, отсекаемой сторонами угла
на окружности, имеющей центр в вершине угла.
14. Говорят, что две прямые взаимно перпендикулярны, если из
четырёх углов, которые они образуют, два угла, прилежащих друг
к другу, равны между собой. Например, прямая АО А' (черт. 12) пер-
перпендикулярна к прямой ВОВ', если углы, обозначенные на чертеже
номерами 1 и 2, между чюбой равны. В этом случае все четыре угла
при точке О будут между собою равны, потому что / 3 и / 4
(черт. 12) соответственно равны ^/_ 1 и ^_2 как вертикальные.
Угол, стороны которого перпендикулярны между собой, называется
прямым.
Теорема. В данной плоскости через точку, взятую на пря-
прямой, можно провести к этой прямой перпендикуляр и притом
только один.
ГЛАВА I. УГЛЫ
29
Пусть через точку О требуется провести перпендикуляр к данной
прямой, проходящей через эту точку. Достаточно провести из точки О,
как из центра, окружность, которая пересечёт данную прямую в точ-
точках А и А' (черт. 12), и разделить на две равные части точкой В
полуокружность ABA'. OB будет искомым перпендикуляром; и обратно,
перпендикуляр к АА', проходящий через точку О, должен делить на
две равные части полуокружность ABA'.
Следствие. Мы видим, что прямой угол от-
отсекает на окружности, имеющей центр в
вершине угла, дугу, равную четверти этой
окружности.
Все прямые углы равны между собой, так
как на равных окружностях, имеющих центры в
вершине каждого из них, они отсекают равные дуги.
15. Если через одну точку провести
несколько полупрямых, то сумма всех последовательных углов
{/_АОВ, /_ВОС, /_COD, Z.DOA, черт. 13), образованных таким
образом около этой точки, равна четырем прямым.
Действительно, сумма дуг, отсекаемых этими углами на окружно-
окружности, имеющей своим центром данную точку, равна полной окруж-
окружности.
Если через точку, лежащую на прямой,
провести по одну сторону от этой прямой
несколько полупрямых (черт. 14), то сум-
сумма образованных таким образом углов
равна двум прямым, так как сумма дуг,
отсекаемых этими углами, равна полуокруж-
полуокружности.
О
Черт. 14.
Обратно, если два или несколько углов при одной и той же
вершине, из которых каждый .является прилежащим к предыду-
предыдущему {/_АОС, /_COD, /_DOE, /_ЕОВ, черт. 14), составляют
в сумме два прямых, то крайние стороны этих углов лежат на
одной прямой линии.
В самом деле, эти крайние стороны пересекают окружность, имею-
имеющую центр в общей вершине углов, в двух диаметрально противо-
противоположных точках, так как луга, заключённая между ними, составляет
полуокружность.
15а. Теорема. Биссектрисы четырех углов, образованных
двумя пересекающимися прямыми, образуют две бесконечные пря-
прямые, перпендикулярные между собой.
Пусть АА' и BE? (черт. 15)—две прямые, которые пересекаются
в точке О и образуют углы АОВ, BOA', А'ОВ, BOA, биссектри-
биссектрисами которых служат От, On, От', On'; я утверждаю:
1) что От и От' являются продолжениями одна другой, так же
как On и On';
2) что полученные таким образом две прямые взаимно перпенаи-
кулярны.
30
К НИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Прежде всего От перпендикулярна к On, так как два угла ^/_ АОВ
и ,/ BOA в сумме составляют два прямых, а потому их половины —
/_ тОВ и _/ ВОп,— дают в сумме один прямой. Но, применяя то же са-
самое рассуждение к углам BOA' и А'ОВ', мы видим, что прямая От'
перпендикулярна к On. Следовательно, От' является продолжением
От; и точно так же On' есть продолжение On.
16. Острым углом называется угол, меньший прямого; тупым —
угол, больший прямого.
Два угла называются дополнительными, если их сумма равна пря-
прямому углу, и пополнительными, если их сумма равна двум прямым.
17. Отношением двух величин одного и того же рода называется
число, которое показывает, сколько раз одна величина содержит- дру-
другую величину или какую-либо р-ую часть другой
величины (р — целое), и какую именно.
Например, если, разделив АВ на 5 равных ча-
частей, мы >видим, что одна из этих частей ровно
три раза содержится в отрезке ВС, то мы скажем,
3
что отношение ВС к АВ равно —.
о
Если же, напротив, пятая часть отрезка АВ не
содержится целое числи раз в отрезке ВС, напри-
например, если она в этом отрезке содержится больше
3
чем 3 раза и меньше чем 4 раза, то — будет
ЙС
приближенным значением отношения —— , причём это будет значе-
I АВ
ние, взятое с точностью до — по недостатку (значение с точно-
о
1 4
стью до -=- , взятое по избытку, будет —).
о о
Отношение этих двух величин а и b одного рода равно отноше-
отношению двух других величин а', Ь' одног рода (но не обязательно того
же рода, как первые), если, каково бы ни было п, 'значение первого
1
отношения, взятое с точностью до — , равно значению второго отноше-
1
ния, взятому с точностью до —-.
Мера данной величины по отношению к определённой величине
такого же рода, принятой за единицу, есть отношение данной вели-
величины к этой единице.
Можно доказать следующие свойства:
1°. Две величины, имеющие одну и ту же меру по отношению
к одной и той же единице, равны.
2°. Отношение двух величин одного и тог,о же рода Нравно от-
отношению чисел, служащих их мерой по отношению к одной и той
же единице.
ГЛАВА I. УГЛЫ 31
8°. Отношение двух чисел равно частному этих двух чисел.
Теорема. В одной окружности .или равных окружностях
отношение двух центральных углов равно отношению двух дуг,
которые заключены между их сторонами.
Пусть1) даны (черт. 16) две дуги АВ и CD окружности О. Раз-
Разделим центральный угол АОВ, например, на три равные части и пред-
предположим, что одна из этих частей содержится в угле COD больше
чем 4 раза, но меньше чем 5 раз; тогда с точностью до — величи-
/ COD 4
на отношения ~; есть —..
Но, деля угол АОВ на три равные части, мы в то же время раз-
разделили дугу АВ на три равные части (п. 13). Если бы треть угла АОВ
могла уложиться 4 раза, но не 5 раз в
угле COD, то это показывало бы, что
треть дуги АВ могла бы уложиться в ду-
дуге CD 4 раза, но не 5 раз.
Значения двух отношений, измеренные с
1
точностью до — , равны; совершенно так
о
же равны между собою значения двух от-
1
ношений, взятые с точностью до — для
п
любого значения «; теорема, таким об-
образом, доказана. Черт. 16.
Следствие. Если принять за единицу
угла центральный угол, который заключает между сторонами
дугу, принятую за единицу, то всякий центральный угол имеет
ту же меру, как и дуга, заключённая между его сторонами.
Это предложение сводится к предыдущему, так как мера величины
есть отношение этой величины к своей единице.
Предполагая, как мы это будем делать в последующем, что на
каждой окружности за единицу дуг принимается дуга, заклю-
заключённая между сторонами центрального угла, принятого за еди-
единицу углов, можно предыдущее следствие сформулировать так. цент-
центральный угол измеряется дугой, заключённой между его сторонами.
18. Только что установленные определения позволяют нам ввести
Одно важное соглашение.
1) Теорема становится очевидной, если допустить следующее арифме-
арифметическое предложение (Т а н н е р и, Курс арифметики, 1л. XIII, п° 493):
Две величины пропорциональны, если: 1) оиному и тому же значению
первой соответствует всегда одно и то же значение второй и 2) сумме
двух значений первой величины соответствует сумма двух соответствую-
соответствующих значений второй величины. Эти два условия здесь выполнены (п. 13).
Доказательство в тексте лишь воспроизводит для данного частного
случая доказательство общей арифметической теоремы.
32 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Прежде всего мы можем предположить, что все величины, о кото-
которых мы будем говорить, измерены определённо выбранной единицей
для каждого рода величин; далее, что во всех равенствах, которые
мы будем писать, количества, входящие в ту и другую часть равенства,
представляют собой ие самые величины, а лишь меры этих величин.
Таким образом, мы можем написагь целый ряд равенств, которые
без этих предположений не имели бы никакого смысла. Например,
можно приравнять друг другу две разнородные величины, если имеет-
имеется равенство двух чисел, которые их измеряют; смысл равенства в
этом случае совершенно ясен. Мы сможем точно так же писать произ-
произведение двух каких-либо величии, так как произведение двух чисел
уже определено, и т. д.
Впрочем, когда мы будем писать, как до сих пор, равенство двух
величин одного и того же рода, — это равенство будет иметь точно
такой же смысл, как и раньше, так как равенство двух величин и
равенство их мер сводится одно к другому (п. 17).
На основании этого соглашения возможно написать, если АВ—
некоторая дуга и О—центр окружности:
/_АОВ = дуге АВ.
Во всяком случае йчень важно подчеркнуть, что это равенство
существенно предполагает, что единица угла и единица дуги выбраны
так, что указанное выше условие удовлетворено.
18а. Окружность обычно делится на 360 равных частей, называе-
называемых градусами, каждый из которых содержит 60 минут; каждая
минута в свою очередь делится на 60 секунд. При этом дуги изме-
измеряются в градусах, а следовательно, и углы тоже измеряются в граду-
градусах. Число градусов, минут и секунд, заключающееся в угле, равно
числу градусов, минут и секунд дуги, отсекаемой этим углом на
окружности, имеющей центр в вершине угла; прямой угол соответствует
четверти окружности, или 90 градусам. Отсюда следует, что мера
центрального угла не зависит от радиуса окружности, на которой
отсчитываются дуги, так как выбранная угловая единица (градус) по
величине не зависит от этого радиуса, а именно составляет одну
девяностую часть прямого угла.
Для записи величины углов (или дуг) в градусах, минутах и се-
,кудцах пользуются следующими обозначениями: угол в 87 градусов,
34 минуты и 25 секунд записывается так: 87°34'25".
Введение десятичной системы во всех других видах измерений
.приводит к установлению другого способа подразделения окружности,
,при котором она делится не на 360, а на 400 равных частей, назы-
называемых градами. Град, очевидно, несколько меньше градуса и состав-
составляет сотую часть прямого угла. *
Град подразделяется также по принципу десятичной системы: строго
.говоря, нет необходимости давать этим подразделениям специальные
.названия, они пишутся просто по принципу десятичной нумерации.
ГЛАВА I. УГЛЫ
33
Таким образом, можно говорить об угле 3°,5417 (т. е. 3 града
и 5417 десятитысячных).
Однако сотую часть града часто называют десятичной минутой
<i обозначают её значкомг (вместо значка ', обозначающего шестидеся-
шестидесятиричную минуту, т. е. шестидесятую долю градуса); точно так же со-
сотая часть десятичной минуты (десятитысячная часть града) представ-
представляет собой десятичную секунду, обозначаемую знакомв. Таким обра-
образом, предыдущий угол пи этой системе может быть написан так:
360э 9
Один град составляет -—-, или -— градуса, или 54 . Один гра-
400° ,_ N 1U
дус составляет ——— =1и11 ,1...шли иначе - града).
19. Теорема. Через точку, взятую вне прямой, можно про-
провести перпендикуляр к этой прямой и притом только один.
1°. Возможно провести перпендикуляр. Пусть даны точка О и
прямая XY (черт. 17). Повернём полуплоскость, содержащую точку О,
около прямой XY, как около оси, так, п
чтобы она совместилась с другой полу-
полуплоскостью. Точка О попадёт в О'.
Соединим их прямой 00'.
Эта прямая пересечёт XY, так как
она соединяет две точки, расположен-
ные по разные стороны от прямой XY. X
Пусть /— точка пересечения. Углы О IX
и OIX—прямые, так как угол О'IX
представляет собою то положение,
которое принимает угол О/Х, когда О'
одну из полуплоскостей совмещают с Черт. 17.
другой путём вращения около XY.
Следовательно, две прямые XY и 00' перпендикулярны.
2°. Можно провести только один перпендикуляр. Пусть ОМ —
какой-либо перпендикуляр к XY, проведённый через точку О; продол-
продолжим эту прямую на длину МО'1, равную ОМ. Если мы совместим
снова одну из полуплоскостей с другой, прямая МО пойдет по ЛЮ",
так как углы ОМХ и О"MX равны как прямые, а так как МО" = МО,
то точка О попадёт в точку О"; следовательно, точка О" совпадёт
с точкой О', и прямая 00" совпадет с 00'.
19а. Точка называется симметричной с данной точкой О относи-
относительно прямой XY, если она лежит на продолжении перпендикуляра,
проведённого к прямой XY через точку О, на расстоянии, равном длине
этого перпендикуляра. Из предыдущего следует, что точка, симмет-
симметричная с точкой О, представляет собой то положение, которое зани-
занимает точка О после поворота (п. 19, 1°) около оси XY. Если дана
какая-нибудь фигура, можно построить симметричные точки для каж-
3 ^.|ементарная геометрия
34
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
дой точки этой фигуры. Совокупность симметричных точек образует
новую фигуру, которая называется симметричной с первой фигурой.
Отсюда видно, что для получения фигуры, симметричной с данной
фигурой относительно прямой XY, можно повернуть плоскость,
в которой лежит фигура, вокруг XY так, чтобы каждая полу-
полуплоскость, определяемая этой прямой, совместилась с другой полу-
полуплоскостью, и отметить новое положение, занятое данной фигурой.
Отсюда следует:
Теорема. Лее симметричные плоские фигуры равны.
Следствие. Фигура, симметричная прямой линии,—прямая
линия.
Если какая-либо фигура совпадает со своей симметричной относи-
относительно прямой XY, то говорят, что она симметрична относительно
этой прямой, или, иначе, что она имеет эту прямую осью симметрии.
20. Чтобы совместить фигуру F с фигурой F', ей симметричной,
мы должны выполнить такое движение, при котором фигура выйдет из
своей плоскости. Следует заметить, что1) не-
невозможно достигнуть совмещения без такого
движения; это происходит оттого, что на-
направление вращения обратно в обеих фи-
фигурах. Объясним, что следует понимать иод
этим выражением.
Прежде всего заметим, что плоскость
фигуры делит пространство на две области.
Назовём одну из этих областей для краткости областью, расположен-
расположенной над плоскостью, другую — под плоскостью, к.
Допустим, что на фигуре F имеем угол ВАС, который можно
рассматривать как образованный полупрямой, перемещающейся внутри
угла из положении АВ в положение АС (черт. 18). При взгляде на
плоскость сверху мы б^дем говорить об этом угле, что он имеет
отрицательное или положительное направление, смотря по тому, пред-
представляется ли вращение атой полупрямой происходящим по часовой
стрелке или в обратном направлении").
Положим для определённости, что имеет место последний случай.
Тогда наблюдатель, лежащий на АВ ногами в сторону .4, а головой
по направлению к В и смотрящий под плоскость, увидит сторону АС
слева от себя; следовательно, если, оставаясь расположенным вдоль
по АВ, он посмотрит на сторону АС, то окажется, что часть ' прост-
пространства, находящуюся под плоскостью, он увидит справа от себя.
Ясно, что при взгляде на плоскость снизу можно повторить всё
вышеизложенное, заменяя слово „над" словом „под" и обратно. Так
как наблюдатель, расположенный вдоль по АВ и смотрящий на АС,
]) В общем случае. Прим. ред. перевода.
") Заметим, что для того, чтобы указать направление вращения, следует
принимать во внимание порядок, в котором рассматриваются стороны угла.
Так, угол ВАС имеет противоположное направление по отношению к
углу CAB.
ГЛАВА 1. УГЛЫ 35
будет необходимо иметь верх плоскости слева, если низ плоскости
находится от него справа, и обратно, то направление вращения ме-
меняется в зависимости от того, смотрим ли мы на плоскость
с одной или -с другой стороны плоскости!).
Предположим теперь, что некоторый угол произвольно переме-
перемешается в своей плоскости, не выходя из неё. Наблюдатель, участву-
участвующий в этом движении, не изменит своего положения по отношению
к верху и низу плоскости, так что направление вращения остаётся
неизменным при всяком перемещении, не выводящем фигуры из её
плоскости.
Чтобы показать, что такое движение не может совместить фигуру F
с симметричной ей фигурой F', достаточно поэтому показать, что
направление вращения противоположно в обеих фигурах. Действи-
Действительно, мы видели, что переход от F к F' можно осуществить враще-
вращением плоскости около оси XY так, чтобы она совпала сама с собой
(п. 19а). При этом повороте точки, расположенные над плоскостью,
оказываются под плоскостью, и обратно. Направление какого-либо
угла фигуры F при взгляде снизу будет то же, что и направление
угла с ним симметричного при взгляде сверху. Таким образом, при
взгляде с одной и той же стороны направление углов будет противо-
противоположным.
20а. Примечания: 1°. Ясно, что, точно так же как и угол, дуга
может иметь направление положительное или отрицательное, что за-
зависит, конечно, от порядка, в котором мы рассматриваем концы дуги.
2°. Иногда говорят, что плоскость ориентирована, если на ней
указано положительное направление углов. На основании предыдущего
ориентировать плоскость—значит указать, которую из двух областей
пространства мы будем называть расположенной над плоскостью.
УПРАЖНЕНИЯ.
1. Если точка М—середина отрезка АВ, то расстояние СМ равно
полуразности отрезков СА и СВ, если точка С лежит на самом отрезке,
и mwiycviuMe СА и СВ, если точка С взята на продолжении АВ (доказать).
2/ Если ОМ — биссектриса угла АОВ, то угол СОМ равен полуразности
углов СОА и СОВ, если полупрямая ОС лежит внутри /. АОВ; и дополняет
эту полуразность до двух прямых углов, если полупрямая ОС лежит внутри
угла А'ОВ', вертикального к углу АОВ. Он равен Полусумме углов СОА
и СОВ, ¦ ели эта полупрямая расположена внутри одного из двух других
углов BOA' или АОВ', образованных данными прямыми (доказать).
3. Из точки О выходят четыре полупрямые ОА, ОВ, ОС, OD (следую-
(следующие одна за другой в том порядке, как они перечислены), причём ? АОВ =
= /_COD и /_ ВОС =/_ DOA; доказать, что ОА и ОС суть продолжения
одна другой и точно так же ОВ и OD.
4. Если четыре последовательные полупрямые ОА, ОВ, ОС, OD таковы,
что биссектрисы vrflOB АОВ и COD и точно так же биссектрисы углов ВОС
и AOD образуют одну прямую, то четыре полупрямые представляют по-
попарно продолжения одна другой (доказать).
|) Совершенно так же, как надпись, просвечивающая через лист, ка-
кажется с обратной стороны листа перевёрнутой справа налево.
3*
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
ГЛАВА II.
ТРЕУГОЛЬНИКИ.
21. Многоугольником называется часть плоскости, ограниченная
отрезками прямых линий (черт. 19). Эти последние образуют стороны
многоугольника. Их концы образуют вершины многоугольника.
Однако мы будем, вообще говоря, называть многоугольниками
только части плоскости, ограниченные одним контуром, который можни
/ описать одним росчерком пера. Таким образом, часть плоскости, ко-
которая заштрихована на чертеже 21, не будет являться для нас много-
многоугольником. Многоугольник называется выпуклым, если ни одна из
прямых, полученных неограниченным продолжением каждой его стороны,
не пересекает многоугольника. В противном случае (черт. 20) он
называется вогнутым.
Многоугольники классифицируют по числу ¦ сторон. Простейшими
многоугольниками будут: многоугольник с тремя сторонами, или тре-
треугольник, многоугольник с четырьмя сторонами, или четыргхуголь-
Черт. 19.
Черт. 20.
Черт. 21.
ник, многоугольник с пятью сторонами, или пятиугольник, много-
многоугольник с шестью сторонами, или шестиугольник. Мы будем еще
рассматривать многоугольники с 8, 10, 12, 15 сторонами, называемые
соответственно восьмиугольником, десятиугольником, двенадцати-
двенадцатиугольником., пятнадцатиугольчико.ч.
Диагональю многоугольника называется отрезок, соединяющий две
непоследовательные вершины многоугольника.
Примечание. Иногда, с несколько более общей точки зрения, на-
называют многоугольником любую замкнутую ломаную линию, стороны ко-
которой могут пересекаться между собой (как на черт. 22). В этом последнем
случае, когда/ ломаная линия не ограничивает единственной плошали, можно
назвать эту ломаную несобственным многоугольником. Наоборот, мы ска-
скажем, что имеется многоугольник в собственном смысле, если мы хотим
указать, что мы имеем случай, изображённый на чертежах 19 или 20, а не
случай, изображённый на чертеже 22.
ГЛАВА II. ТРЕУГОЛЬНИКИ 37
22. Среди треугольников в частности различают:
Равнобедренный треугольник. Так называется треугольник с двумя
равными сторонами. Вершину, общую ьтим двум сторонам, назы-
называют просто вершиной треугольника, а сторону, расположенную про-
против нее, — основанием.
Равносторонний треугольник, или треугольник с тремя равными
сторонами.
Прямоугольный треугольник, или треугольник с одним прямым
углом. Сторона, лежащая против прямого угла, называется гипотену-
гипотенузой; стороны, образующие прямой угол, —
катетами ').
22а. Высотой треугольника называется
перпендикуляр, опущенный из вершины на
противоположную сторону; медианой назы-
называется отрезок, соединяющий вершину с се-
серединой противоположной стороны.
23. Теорема. Во всяком равнобедренном
треугольнике углы, лежащие претив еРт"
равных сторон, равны между сооой.
Пусть треугольник ABC— равнобедренный (черт. 23). Перевернём
угол ВАС и наложим его на самого себя (п. 10) так, чтобы сторона
АВ пошла по АС, и обратно.
Так как АВ и АС равны, точка В займёт положение точки С,
и наоборот. Следовательно, угол ABC совместится с углом АСВ, так
что эти два угла равны.
Обратная теорема. Если в треугольнике
два угла равны, то треугольник равнобедренный.
Пусть ABC — треугольник, в котором ^ В^ , С.
Перевернём этот треугольник так, чтобы сторона ВС
наложилась на самоё себя (п. 5), точка В перешла в
точку С, и обратно. Так как угол ABC равен
углу АСВ, то сторона ВА пойдёт по СА, и обрат-
обратно: СА — по ВА. Точка А, как точка пересечения
ВА и СА, сохранит своё прежнее положение, и сторона АВ займёт
положение АС.
Следствие. Равносторонний треугольник будет в то же время
и равноугольный (т. е. все его углы будут равны), и обратно.
Теорема. Во всяком равнобедренном треугольнике биссектриса
угла при вершине перпендикулярна к основанию и проходит через
его середину.
Пусть AD — биссектриса угла .4 в равнобедренном треуголь-
треугольнике ABC (черт. 24).
Если перевернуть угол ВАС и наложить его на самого себя, то
эта биссектриса не изменит своего положения, и то же самое будет
*) Определение катетов добавлено при переводе: во французском языке
соответствующий термин не употребляется, и в оршиниле каждый раз
говорится: „стороны, образующие прямой угол". Прим. реи. перевода.
• 38 книга первая, прямая линия
иметь место для точки D, в которой биссектриса пересекает основа-
основание. Так как DB будет совмещено с DC н угол ADB с углом ADC,
то мм будем иметь DB=DC и /_ ADB =/_ ADC. t
Примечание. Во всяком треугольнике ABC можно рассматривать
четыре прямые:
1) биссектрису угла А;
2) высоту, выходящую из точки А;
3) медиану, выходящую из той же точки;
4) перпендикуляр к стороне ВС в её середине.
Вообще эти четыре прямые будут отличны друг от друга (см. упраж-
упражнение 17). Предыдущая теорема показырает, что в равнобедренном тре-
треугольнике они все сливаются в одну прямую, которая является осью сим-
симметрии треугольника (п. 19а).
Эта теорема может быть также сформулирована иначе, а именно:
высота равнобедренного треугольника является в то же время его бис-
биссектрисой и медианой; или ещё: медиана равнобедренного треугольника
является в то же въемя его высотой и биссектрисой: перпендикуляо
к основанию в его середине проходит через вершину треугольника и яв-
является биссектрисой угла nvu вершине.
Следствие. В равнобедренном треугольнике высоты, выходящие из
концов Основания, между собой равны: то же самое имеет место Оля
меоиан, выходящих пз тех же вершин, и для биссектрис углоз при этих
точках, так как эти прямые попарно симметричны.
24. Следующие предложения, известные под названием признаков
равенства треугольников, дают необходимые и достаточные условия
* для того, чтобы два треугольника были равны.
Первый признак равенства. Два треуголь-
треугольника равны, если они имеют по равной стороне
и прилежащие к этим,сторонам углы того и дру-
другого треугольника соответственно равны друг
другу.
В и С Пусть даны два треугольника ABC и А'В'С
Черт 24 (черт. 25), в которых ВС = ВС; /В=/В\
ic lc
Наложим угол В на равный ему угол В так, чтобы сторона В А'
приняла направление ВА, а сторона ВС — направление ВС. Так как
ВС =ВС, то точка С совпадёт с С, а так как угол С равен углу С, то
сторона С А' примет направление СА. Вследствие этого точка А', как
точка пересечения прямых В А' и С А', обязательно попадёт в точку
пересечения прямых ВА и СА, т. е. в точку А. Совпадение треуголь-
треугольников, таким образом, доказано.
Второй признак равенства. Два треугольника равны, если они
имеют по равному углу и заключающие эти углы стороны того
и другого треугольника соответственно равны друг другу.
Пусть даны два треугольника ABC и А'В С, в которых / А = ^/ А';
АВ=А'В\ ACz=A'C (черт. 25).
Наложим угол А' на равный ему угол А так, чтобы сторона А'В'
приняла направление АВ и сторона А'С — направление АС. Так как
А'В =¦¦ АВ, то точка В попадёт в точку В; точно так же точка С"
ГЛАВА II. ТРЕУГОЛЬНИКИ 39
попадёт в С. ВС совпадёт, таким образом, с ВС, и совмещение тре-
треугольников будет полное.
Третий признак равенства. Два треугольника равны, если они
имеют по три соответственно равные стороны.
Пусть даны два треугольника ABC и А' ВС, стороны которых
соответственно равны между собой. Расположим второй треугольник
таким образом, чтобы сторона ВС совпала с равной ей стороной ВС
и оба треугольника лежали по одну и ту же сторону от ВС. Пусть
ВСАЛ — новое положение треугольника ВС А'. Я утверждаю, что
точка -4, совпадёт с точкой А. Это было бы очевидно, если бы пря-
прямая В'А' приняла направление ВА или прямая С А' приняла направле-
Б С f J. В С
Черт. 25. Черт. 26.
ние СА. Если же это было бы не так, то мы имели бы два равнобед-
равнобедренных треугольника ВААЛ и СААЛ (черт. 26), и перпендикуляр к отрез-
отрезку ААЛ в его середине должен был бы пройти через точки В и С (гг. 23,
мелкий шрифт), иначе говоря, совместиться с прямой ВС. Это невозмож-
невозможно, так как точки Л и Л, лежат по одну сторону от ВС, и пото-
потому ВС не может пройти через середину отрезка AAV Точки Л и Л,
не могут быть, таким образом, различными, и два треугольника совпа-
совпадают между собой.
Примечания: 1°. Для того чтобы доказать, что точка Л, сов-
совпадёт с точкой Л, мы смотрим, что произошло бы, если бы эти две
точки были различны; и приходя в этом случае к явно ошибочному за-
заключению, мы утверждаем, что этого быть не может.
Этот метод рассуждения называется доказательством от против-
противного и часто применяется при доказательствах.
2°. В треугольнике имеется шесть главных элементов: три угла и
три стороны. Мы видим, что достаточно установить равенство трёх
из этих элементов (выбранных надлежащим образом) в двух треуголь-
треугольниках, чтобы иметь возможность утверждать, что треугольники равны,
и в частности, что равны три остальных элемента.
3°. Два равные треугольника (или вообще два многоугольника)
могут отличаться друг от. друга направлением вращения (п. 20).
В этом случае они могут быть наложены друг на друга только с по-
помощью движения, выводящего один из них из плоскости. Напротив,
если направление вращения одинаково, то два многоугольника могут
быть приведены к совмещению простым скольжением в плоскости, как
мы это увидим дальше.
25. Внешним углом выпуклого многоугольника называется угол,
образованный одной стороной и продолжением следующей стороны.
40 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЧ
Теорема. Всякий внешний угол треугольника больше каждого
из внутренних углов, к нему не прилежащих.
Пусть имеется треугольник ABC, в котором построен внешний'
угол В'АС (черт. 27).
Я утверждаю, что этот угол больше, например, внутреннего угла С.
Чтобы это доказать, я провожу медиану BD, которую продолжаю на
длину DE, равную ей самой. Точка Е находится внутри угла В'АС,
который будет больше угла ЕАС.
А этот последний равен углу С,
так как два треугольника DAE
и DCB равны как имеющие по рав-
равному углу, заключённому между
соответственно равными сторонами.
Действительно, углы при точке Г)
равны как вертикальные: AD -= DC
и BD = DE по построению. Сле-
Следовательно, внешний угол В'АС
больше внутреннего угла С, что и
требовалось доказать.
Внешний угол В'АС будет по-
пополнительным для внутреннего
угла А. Угол С, будучи меньше угла В'АС, в сумме с углом А даёт вели-
величину, меньшую двух прямых. Наша теорема может быть сформулиро-
сформулирована так: сумма двух углов треугольника меньше двух прямых.
В частности треугольник не может иметь бо-
более одного прямого или тупого угла.
Теорема. Во всяком треугольнике против
большей стороны лежит и больший угол.
Пусть в треугольнике ABC (черт. 28) АВ~^> А С.
^С^/ Д
у р ) ^
Мы докажем, что ^С^>/_В. Для этого мы от- В С
ложим на АВ отрезок AD = AC. По предположе- Черт. 28.
нию отрезок DC расположен внутри первоначаль-
первоначального угла С, а следовательно, угол ACD меньше угла С. Но в
равнобедренном треугольнике ACD угол ACD равен углу ADC,
который больше угла В, как это следует из предыдущей теоремы,
применённой к треугольнику DCB. Теорема, таким образом, доказана.
Обратно, большему углу соответствует^) и большая сторона.
Это положение, очевидно, равносильно предыдущему.
26. Теорема. Во всяком треугольнике любая сторона меньше
суммы двух других сторон. .
В треугольнике ABC продолжим АВ на длину AD = АС (черт. 29).
Требуется доказать, что BC<^BD2).
!) Стороной, соответствующей данному \тлу треугольника, называется
сторона, ему противолежащая.
2 Теорема очевидна, если ВС— не самая большая из сторон тре-
треугольника.
ГЛАВА II. ТРЕУГОЛЬНИКИ
41
Проведя CD, мы видим, что угол D равен углу ACD (п. 23) и,
следовательно, меньше угла BCD.
Искомое неравенство вытекает, таким образом, из предыдущей тео-
теоремы, применённой к треугольнику BCD.
Следствия: I. Во всяком треугольнике любая сторона больше
разности двух других.
Действительно, неравенство ВС<^ АВ-\- АС даёт после вычитания
АС из обеих частей:
ВС—АС<^АВ.
II. Каковы бы ни были три точки А, В, С, каждое из рассто-
расстояний ВС, С А, АВ равняется самое большее сумме двух других а
самое меньшее их разности, причём
равенство может иметь место толь-
только, если три точки расположены на
одной прямой.
Теорема. Прямолинейный отрезок
короче всякой ломаной лакни, имеющей
с ним общие концы.
Если ломаная линия составлена из двух
отрезков, то теорема сводится к преды-
предыдущей. ЧсРт- 29-
Пусть теперь ломаная линия ABCD
состоит из трёх отрезков (черт. 30). Соединив В с D, получим
и так как BD<^BC-\-CD, то
AD < А В 4- BD < А В 4- ВС-}- CD.
Теорема, таким образом, доказана для линии, состоящей из трёх
отрезков; совершенно так же убедимся последовательно в справедли-
справедливости теоремы для ломаных линий, со-
составленных из 4, 5 и т. д. отрезков. Тео-
Теорема оказывается справедливой при всяком
чисае отрезков, образующих ломаную ли-
линию.
1 .27. Периметром мпогоугольника или ло-
ломаной линии называется сумма всех сторон.
Черт. 30.
Теорема. Периметр выпуклой . ломаной меньше периметра
любой ломаной, объемлющей данную и имеющей с ней общие концы.
Путь ACDB—выпуклая ломаная линия и AC'D'E'F'B—объем-
AC'D'E'F'B—объемлющая её ломаная (черт. 31). Продолжим стороны АС и CD в одном
и том же направлении \CDB, т. е. сторону АС за точку С, а сто-
сторону CD — за точку D. Эти продолжения пересекут объемлющую
линию соответственно в точках G и Н.
Путь ACDB короче пути АСНВ, так как они имеют общую часть
ACD, а остающаяся часть DB первого короче остающейся части DHB
42
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
второго. В свою очередь, путь АСНВ меньше, чем AGD'E'F'B, так
как, отбрасывая общие части АС, ИВ, получим отрезок СН, который
короче ломаной линии CGD'E'F'H.
Наконец, точно так же AGD'E'F'B меньше AC'D'E'F'B, так kjk
AG меньше AC'G.
Таким образом, имеем:
A CD В < А СИВ < A GD'E'F'B < AC'D'E'F'B.
Следствие. Периметр выпуклого многоугольника меньше пери-
периметра замкнутой ломаной линии, которая объемлет его со всех
с порон.
Пусть (черт. 82) имеем выпуклый многоугольник ABCDE и лома-
ломаную линию A'8'C'D'E'F'G'A', которая объемлет его со всех сторон.
D'
Черт. 31.
Продолжим сторону АВ в обоих направлениях до пересечения с объ-
объемлющей линией в точках М, N; мы видим, что линия AEDCB мень-
меньше AMB'A'G'NB (по предыдущей теореме), так что многоугольник
AEDCBA имеет периметр меньший, чем многоугольник NMB'A'G'N.
/Е С
В'
С
ЧертГ 33.
А этот в свою очередь по длине меньше данной объемлющей линии,
так как часть MB'A'G'N у них общая, a MN<^MC'D'E'F'N.
28. Теорема. Если два треугольника имеют по неравному
углу, заключённому между соответственно равными сторонами,
то третьи стороны неравны и против большего угла лежит
и большая сторона.
Пусть ланы треугольники ABC и А'В'С, в которых АВ = А'В",
АС=А'С, /_А^>/_А' (черт. 33^. Я хочу доказать, что ВС больше
НС.
ГЛАВА И. ТРЕУГОЛЬНИКИ 43
Наложим треугольник А'В'С на треугольник ЛВС так, чтобы две
равные их стороны Л'В' и АВ совпали. Так как угол А' меньше угла А,
то сторона А'С займёт положение AD внутри угла ВАС. Проведём
биссектрису АЕ угла DAC; эта прямая точно так же лежит внутри
угла ВАС. Следовательно, точки В и С лежат по разные стороны
от неё, и прямая АЕ должна пересечь сторону ВС в некоторой точке ?,
расположенной между В и С. Если мы проведём DE, то увидим, что
два треугольника АСЕ и ADE равны как имеющие по равному углу
(углы при А), заключённому между двумя соответственно равными
сторонами (АЕ общая, AC=A'C = AD); отсюда следует равенство
сторон DE и ЕС. Далее неравенство BD<^BE-\-ED, вытекающее из
треугольника BDE, даёт нам
или
Обратная теорема. Если две стороны одного треугольника
соответственно равны двум сторонам другого, а третьи стороны
неравны между собой, то углы, противолежащие этим сторонам,
также неравны и против большей стороны лежит и больший угол.
Это положение равносильно предыдущему.
Примечание. Предыдущая теорема ни в какой мере не предпола-
предполагает доказанным третий признак равенства треугольников (п. 24;. Наобо-
Наоборот, она даёт для него новое доказательство.
Если, в самом деле, одновременно с АВ = А'В' и АС = А'С имеем
ВС = В'С', то необходимо, чтобы углы при точках А, А' в двух треуголь-
треугольниках были равны, так как иначе стороны ВС и В'С были бы неравны
между собою, как мы только что видели. Но если ?_А = ^_ А', то два
треугольника равны (второй признак равенства).
УПРАЖНЕНИЯ.
5. Доказать, что треугольник равнобедренный:
1) если его биссектриса является в то же время и высотой;
2) если его медиана является в то же время и высотой;
3) если его биссектриса является в то же время и медианой.
6. На стороне ОХ некоторого угла отложены два OTpejKa ОА и ОВ,
а на другой стороне угла ОХ' два отрезка ОА', ОВ', соответственно рав-
равные первым, и концы отрезков накрест соединены между собой: А с В',
г А' с В. Доказать, что точка /, в которой пересекаются прямые АВ'
и А'В, лежит на биссектрисе данного угла.
7. Если две стороны треугольника "не равны между собой, го ме™<жа
злключённая между ними, образует с меньшей из этих сторон угол боль-
больший, чем с другой стороной (доказать, пользуясь построением, аналогичным
построению п. 25).
8. Если соединить точку, взятую в плоскости треугольника, с тремя
вершинами, то сумма полученных отрезков больше полупериметра треуголь-
треугольника; если точка взята внутри треугольника, то она меньше его периметра
(доказать).
8а. Если соединить точку, взятую в плоскости многоугольника, со
всеми его вершинами, то сумма полученных отрезков больше полупери-
метра многоугольника (доказать).
9. Сумма диагоналей выпуклого четырёхугольника заключается между
его полупериметром и периметром (доказать).
44
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
10. Точка пересечения диагоналей выпуклого четырёхугольника есть
точка плоскости, которая имеет наименьшую возможную сумму расстояний
до его четырёх вершин (доказать).
11. Медиана треугольника меньше полусуммы сторон, её заключающих,
и больше разности л.ежду этой полусуммой и половиной третьей стороны
(доказать).
12. Сук.ма медиан треугольника больше полупериметра и меньше пе-
периметра (доказать).
13. Найти па дгииой прямей точку, сумма расстояний которой до двух
заданных точек наименьшая. Рассмотреть два случая: когда обе точки
находятся по одну и ту же или по разные стороны от прямой.
Свести перььй случай ко ьторому (пользуясь симметрией части фигуры
относительно данной прямой).
14. (Задача о биллиарде.) Даны прямая XY и две точки А, В по одну
н ту же сторону от этой прямой; найти на этой прямой точку М такую,
чтобы угол АМХ был бы равен углу BMY.
Полумается та же точка, что й в предыдущем упражнении.
15. Найти на ланной прямой такую точку, чтобы разность расстояний
её от двух заданных точек была наибольшей. Рассмотреть два случая,
когда обе точки находятся по одну и ту же или по разные стороны от
прямой.
ГЛАВА III.
ПЕРПЕНДИКУЛЯРЫ И НАКЛОННЫЕ.
29. Теорема. Если из одной точки, взятой вне прямой, про-
провести к этой прямой перпендикуляр и несколько наклонных, то:
1) перпендикуляр короче всякой наклонной?
2) две наклонные, основания которых одинаково удалены от
основания перпендикуляра, равны;
3) из двух наклонных длиннее та,
сснование которой дальше отстоит
от основания перпендикуляра.
1°. Пусть даны перпендикуляр ОН
и наклонная ОА, проведённые из точ-
точки О к прямой XV (черт. 34). Продол-
Продолжим отрезок ОН на равную ему длину
НО'; точка О' симметрична с точкой О
относительно прямой XY, так что отре-
отрезок О'А равен отрезку ОА как от-
отрезок, с ним симметричный. Рассматривая
треугольник 00'А, в котором ОО' < ОА-\-О'А, мы видим, что ОО'
можно заменить через 2ОН и ОА-\-О'А — через 20А. Отсюда сле-
следует, что
2О.4>2ОЯ, или ОИ<С_ОА.
2°. Пусть даны две такие наклонные О А и ОБ, что НА = НВ.
Эти две наклонные будут равны как симметричные относительно
прямой ОН.
3°. Пусть даны две такие наклонные О А и ОС, что НС ^> НА
(черт. 34). Предположим сначала, что точки А и С находятся но
ГЛАВА III. ПЕРПЕНДИКУЛЯРЫ И НАКЛОННЫЕ
45
одну сторону от И. Тогда точка А лежит внутри треугольника 00'С.
Следовательно, мы будем иыегь (п. 27):
ОА -f О'А < ОС + О'С.
Но, как мы видели выше, 0.4 равно О'А и ОС равно О'С. Деля
почленно на два, получим, как раньше,
О А < ОС.
Если рассматривать наклонную ОВ менее удалённую, чем ОС, но
лежащую по другую сторону от точки Н, то достаточно отложить
в направлении НС отрезок НА = НВ: наклонная ОА будет равна ОВ
B°) и будет меньше ОС, как мы только что видели.
30. Обратная теорема. Если две наклонные равны, то их
основания одинаково удалены от основания перпендикуляра, так как
иначе они были бы неравны; если две наклон-
наклонные неравны, то та из них, которая длиннее
другой, дальше отстоит от основания пер-
перпендикуляра .
Следствие. Из данной точки О к данной
прямой XV нельзя провести более двух на-
клонных, имеющих одну и ту лее длину. д 0 О' В
Действительно, основания этих наклонных лолж- ,, _г
Черт. So.
ны оыть равноудалены от основания Н перпен-
перпендикуляра на прямую AT; но одно и то же расстояние может быть
отложено на прямой XY от точки Н только двумя способами.
31. Расстоянием точки от прямой называется длина перпенди-
перпендикуляра, опущенного из этой точки на прямую Предыдущая теорема
показывает, что этот перпендикуляр действительно представляет со-
собою кратчайший путь от точки до прямой.
32. Теорема. 1°. Любая точка, лежащая на перпендикуляре
к данному отрезку, проходящем через его середину, одинаково
удалена от обоих концов этого отрезка.
2°. Всякая точка, не расположенная на этом перпендикуляре,
неодинаково удалена от двух концов отрезка.
1°. Пусть М — точка, расположенная на перпендикуляре в сере-
середине О отрезка АВ (черт. 35). Отрезки /И.4, МЬ равны как наклон-
наклонные, одинаково отстоящие от основания перпендикуляра МО.
2°. Пусть М' — точка, не лежащая на перпендикуляре в середине
отрезка АВ, например, расположенная с той же стороны от перпен-
перпендикуляра, где находится точка В. В таком случае и основание пер-
перпендикуляра О', опущенного из точки М' на прямую, будет лежать
от перпендикуляра в середине отрезка с той же стороны, где нахо-
находится точка В (иначе оба перпендикуляра пересеклись бы и через точ-
точку пересечения можно было бы провести два перпендикуляра к АВ).
Следовательно, будем иметь
О'АУО'В, откуда (п. 29) М'А > М'В.
46
книга первая, прямая линия
Примечания: 1°. Можно было бы доказать эту вторую часть
теоремы иначе, доказав предложение, ей равносильное: всякая точка,
одинаково удалённая on А и В, лежит на перпендикуляре к от-
отрезку АВ, восставленном в его середине. Это предложение вытекает
из обратной теоремы п. 3D (основания двух равных наклонных равно-
равноудалены от основания перпендикуляра) или ещё из свойства равнобед-
равнобедренного треугольника (п. 23, примечание). Однако следует заметить,
что наш способ доказательства имеет то преимущество, что он по-
показывает, какое из двух расстояний больше в том случае, когда они
неравны.
2°. Предложение, которое мы только что сформулировали (всякая
точка, одинаково удалённая от А и В, лежит на перпендикуляре
к отрезку АВ, проходящем через его середину), является обратным
по отношению к первой части предыдущей теоремы. Таким образом,
мы имеем здесь два способа доказательства обратной теоремы. Первый
состоит в повторении первоначального рассуждения в обратной по-
последовательности. Это то, что мы сделали в предыдущем, примечании.
В первоначальном рассуждении (доказательство предыдущей теоремы,
1°> мы исходили из предположения, что точка М лежит на перпенди-
перпендикуляре к отрезку АВ, проходящем через его середину, или что МА
и MB были равноудалены от основания перпендикуляра, а отсюда
мы делали вывод, что они равны. Теперь же мы исходили из того,
что точка М одинаково удалена от А и В или что обе наклонные
равны, и делали заключение, что они одинаково удалены от перпен-
перпендикуляра.
Второй способ доказательства обратной теоремы состоит в том,
чтобы доказать то, что называется противоположным предложением.
Так называется предложение, в котором условие противоположно
условию первоначального предложения, а заключение противоположно
первоначальному заключению. Таким образом, вторая часть предыду-
предыдущей теоремы является предложением, противоположным первой её части,
и равносильна обратной ей теореме.
Мы встретим в дальнейшем (см., например, п. 41) третий способ
доказательства обратных теорем.
33. Воспользуемся теперь определением п. 1а. На основании этого
определения предыдущая теорема может быть сформулирована так:
Теорема. Геометрическое место точек, одинаково удаленных
от двух данных точек, есть перпендикуляр, восставленный в се-
середине отрезка, соединяющего эти точки.
Действительно, фигура, образованная точками, одинаково удален-
удаленными от А и В, есть перпендикуляр к отрезку АВ, проходящий че-
через его середину.
Заметим, что для того, чтобы в этом убедиться, необходимо до-
доказать"
1) что любая точка перпендикуляра удовлетворяет данному условию,
ГЛАВА [V. РАВЕНСТВО ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ 47
2) что всякая точка, удовлетворяющая данному условию, лежит
на перпендикуляре, или, что сводится к тому же самому, что всякая
точка, не расположенная на перпендикуляре, не удовлетворяет условию.
Необходимость в таком доказательстве, состоящем из двух час-
частей, представляется во всех задачах, касающихся отыскания геомет-
геометрических мест.
УПРАЖНЕНИЯ.
16. Если два прямоугольных треугольника таковы, что катеты первого
треугольника соответственно меньше катетов второго, то и гипотенуза
первого треугольника меньше гипотенузы второго (доказать).
17. Если углы В и С треугольника ABC—острые и стороны АВ,
АС неравны, то линии, выходящие из вершины Л, следуют в таком порядке:
большая сторона, медиана (см. упражнение 7, гл. II), биссектриса, высота,
меньшая сторона (доказать).
18. В нерлвнобедренном треугольнике отрезок биссектрисы от вершины
до противолежащей стороны меньше, чем медиана, выходящая из той же
ьершнны.
ГЛАВА IV.
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ.
СВОЙСТВО БИССЕКТРИСЫ УГЛА.
34. К прямоугольным треугольникам применимы, само собой разу-
разумеется, признаки равенства произвольных треугольников. Например,
два прямоугольных треугольника равны, если они имеют соответственно
равные катеты (второй признак равенства произвольных треугольников).
Кроме разобранных ранее признаков равенства треугольников, су-
существуют два других, которые приложимы
только к прямоугольным треугольникам.
Первый признак равенства. Два прямо-
прямоугольных треугольника равны, если они
имеют равные гипотенузы и по одному
равному острому углу.
Пусть (черт. 36) даны два прямоуголь-
прямоугольных треугольника ABC и А'Ь'С, в которых
ВС~В'С, /_В=/_В'. Черт. 36.
Наложим второй треугольник на пер-
первый так, чтобы их равные углы В и Ь' совпали. Тогда В'С пойдёт
по направлению ВС, и так как эти два отрезка равны, точка С по-
попадёт в точку С. При этом В'А' пойдёт по направлению ВА, и, сле-
следовательно, С'А' должна пойти но направлению перпендикуляра, опу-
опущенного из точки С на ВА, т. е. по направлению С А.
Второй признак равенства. Два прямоугольных треугольника
равны, если они имеют по равной гипотенузе и по одному равному
катету.
С Л
48
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Пусть даны два прямоугольных треугольника ABC и Х'В'С, в ко-
которых ВС = В'С\ АВ = А'В'. Наложим второй треугольник на пер-
первый так, чтобы совместились равные стороны АВ и А'В'.
Сторона А'С пойдёт по направлению АС. Мы будем иметь теперь
две наклонные из точки Б к прямой АС, а именно ВС и новое поло-
положение стороны В'С, которые по условию будут равны и, следовательно
(п. 30), одинаково удалены от основания перпендикуляра. Таким об-
образом, А'С = АС, откуда и
следует равенство двух тре-
треугольников.
35. Теорема. Если два
прямоугольных треугольника
имеют по равной гипотенузе
и по неравному острому углу,
то стороны, противолежа-
противолежащие неравным углам, неравны, и против большего угла лежит
большая сторона.
Пусть даны треугольники ABC и А'В'С (черт. 37), в которых
ВС=В'С; Z.B>AB>. Я утверждаю, что АС'уА'С.
Чтобы в этим убедиться, отложим на продолжении стороны АС
равный ей отрезок AD и точно так же на продолжении стороны
А'С — равный ей отрезок А'ГУ. Мы будем иметь прежде всего
(п. 29) BD = BC — B'C' = B'D'. Кроме того, в равнобедренном тре-
треугольнике DBC медиана ВА будет также биссектрисой, так что угол
DBC будет в два раза ботьиге первоначального >гла В. Точно так
же угол D'B'C будет в два раза больше первоначального угла Ь',
так что мы будем иметь /_DBC~^>^_D'B'C.
Два треугольника DBC и D'B'C будут иметь тогда но неравному
углу, заключённому между соответственно равными сторонами, откуда
следует, что DC~j> D'C, а следовательно АС~^>А'С.
36. Теорема. Биссектриса угла есть геометрическое место
точек, расположенных внутри угла и одинаково удалённых от
сторон угЛа.
Доказательство, как мы объяснили раньше (п. 33), состоит из
двух частей:
1°. Любая точка, лежащая на биссектрисе угла, одинаково
удалена от сторон угла.
Пусть даны угол ВАС и точка М (черт. 38), лежащая на биссек-
биссектрисе этого угла. Если из точки М опустим на стороны угла перпен-
перпендикуляры MD и ME, то два прямоугольных треугольника AMD,
АМЕ будут равны как имеющие общую гипотенузу и равные острые
углы (при вершине А). Следовательно, перпендикуляры MD и ME
будут равны.
2°. Любая точка, расположенная внутри угла, но не на бис-
биссектрисе, неодинаково удалена от двух сторон угла.
Пусть дана точка М', расположенная, например, между биссек-
биссектрисой и стороной АС.
ГЛАВА V. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
49
При этом угол ВАМ' будет больше угла М'АС. Следовательно,
если мы опустим на АВ и АС перпендикуляры M'D' и М'Е', то два
прямоугольных треугольника AMD' и АМ'Е' будут иметь общую ги-
гипотенузу и неравные углы при вершине А; следовательно, МЧУ будет
(п. 35) больше ME'.
Точно так жеГ* как для теоремы п. 32, мы могли бы доказать
ооратную тео-
вместо противоположного предложения, данного в 2°
рему: Всякая точка, расположенная внут-
внутри угла и одинаково удал- лная от его
сторон, лежит на биссектрисе.
Для ^того пришлось бы, повторяя в обрат-
обратной последовательности первоначальные рас-
рассуждения, рассмотреть точку М Depf. 38),
которая но предположению одинаково удалена
от АВ и АС, и применить к двум прямо-
прямоугольным треугольникам AMD, AME, в кото-
которых гипотенуза — общая и MD = ME, вто-
второй признак равенства (п. 34). Таким обра-
образом, мы доказали бы равенство углов при А,
откуда и следовало бы, что AM есть биссек-
биссектриса.
Но таким путём мы не смогли бы узнать,
которое из двух расстояний больше в том случае, когда они неравны.
Следствие. Геометрическое место точек, одинаково удаленных
от двух прямых, состоит из двух биссектрис (п. 15а) углов, обра-
образованных этими прямыми.
УПРАЖНЕНИЯ.
19. Доказать, что если две высоты треугольника равны, то треуголь-
треугольник — равнобедренный.
20. Доказать более общее предложение, что во всяком треугольнике
большей стороне соответствует меньшая высота 1).
ГЛАВА V.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
37. Если две прямые линии пересечены одной и той же секущей
(черт. 39), то эта секущая образует с данными прямыми восемь углов,
перенумерованных на чертеже, взаимное расположение которых харак-
характеризуется следующими названиями:
') Высотой (медианой, биссектрисой), соответствуют ей данной
стороне, называется высота (медиана, биссектриса), проведённая из проти-
противолежащей вершины. Прим. ред. перевода.
4 Элементарная геометрия
50 КНИГА ПЕРВАЯ1. ПРЯМАЯ ЛИНИЯ
Два угла, такие как ^3 и /^5, находящиеся между двумя дан-
данными прямыми и по разные стороны от секущей, называются внутрен-
внутренними накрестлежащими.
Два угла, такие как ^/3 и ^/6, расположенные между двумя
данными прямыми, но по одну сторону от секущей, называются вну-
внутренними односторонними.
Два угла, такие как ^/6 и ^/2, расположенные по одну сторону
от секущей и обращенные — один к части плоскости, заключённой
между двумя прямыми, другой к части плоскости, внешней по отно-
отношению к данным прямым, на-
зываются соответственны-
соответственными.
38. Параллельными прямы-
прямыми называются две1 прямые,
лежащие в одной и той же пло-
плоскости, которые, сколько бы их
ни продолжать в обе стороны,
не пересекаются между со-
У бой.
Теорема. Две прямые ли-
линии, пересеченные одной и
Черт. 39. той же третьей, парал-
параллельны:
1) если внутренние односторонние углы являются пополни-
пополнительными углами '); или
2) если внутренние накрестлежащие углы, равны; или
3) если соответственные углы равны. ¦
' 1°. Если две прямые пересекались бы с той или другой стороны
от секущей, то они образовали бы треугольник, в котором (п. 25)
сумма двух внутренних односторонних углов должна была бы быть
меньше, чем два прямых.
Два других случая сводятся к первому:
2°. Если внутренние накрестлежащие углы /_3 и /_5 равны, то
это сводится к тому, что ^/3 является пополнительным для /6,
иначе говоря, к тому, что внутренние односторонне углы являются
пополнительными.
3°. Если соответственные углы /_6 и/2 равны, то /_3\\ /_6
снова будут пополнительные, так как /_ 3 будет пополнительным
для /_2. I
Этой теоремой приходится пользоваться для доказательства парал-
параллельности двух прямых.
Следствие. В частности, две прямые, перпендикулярные к одной
и той же третьей и лежащие в одной плоскости, параллельны.
!) Если /_3 и /. 6 (черт. 39) пополнительные, то и ?_ 4 и ?_5 пополни-
пополнительные, так как сумма этих четырёх углов равна четырем прямым.
ГЛАВА V. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
39. Теорема. Через точку, взятую вне прямой, можно про-
провести прямую линию, параллельную этой прямой.
Пусть даны точка О и прямая XY (черт. 39). Соединим точку О
с произвольной точкой А прямой XY и проведём прямую 00', кото-
которая с О А образует такой угол, что /_АОО' -\- /_OAY =2dx)\ она
и будет параллельна XY.
40. Предыдущее построение может быть выполнено бесчисленным
числим способов, потому что точка А может быть взята i роизвольно
• на прямой XY. Может показаться, что оно даёт бесчисленное множе-
множество различных параллельных линий.
Однако это не так в силу следующей аксиомы.
Аксиома2). Через точку, взятую вне прямой, можно провести
только одну прямую, параллельпу.о этой прямой.
Следствия: I. Две различные прямые, параллельные одной и той
же третьей, параллельны между собой, так как, если бы они
имели общую точку, то через эту
точку можно было бы провести две /
прямые, параллельные третьей. r/ g
П. Если две прямые параллель- ?-.
ны, то всякая третья прямая,
которая пересекает первую, пересе-
пересечет и вторую; иначе две прямые,
параллельные второй прямой, пересе-
пересекались бы между собой8). р
41. Теорема п. 38 допускает У-—
обратную теорему, которую мы сейчас
докажем.
Обратная теорема. Если
две параллельные прямые пересе-
пересечены одной и той же секущей, то:
1) внутренние односторонние углы являются углами пополни-
пополнительными;
2) внутренние накрестлежащие углы равны;
3) соответственные углы равны.
Доказательство- будет одним и тем же для всех трёх случаев.
Пусть даны две параллельные прямые АВ, CD, пересечённые се-
секущей EFX (черт. 40). Я утверждаю, например, что соответственные
углы—^_ХЕВи /^XFD—равны. В самом деле, прямая ЕЛ', образую-
образующая при точке Е с прямой EF угол ХЕВ', равный углу. XFD, будет
параллельна CD и потому совпадёт с ЕВ.
!) Буква d — начальная буква французского слона droit (прямой) — слу-
служит для обозначения прямого угла.
2) Эта аксиома известна пол именем постулата Эвхлидл. В действи-
действительности её следует рассматривать как часть определения основных по-
понятий геометрии (см. Прибавление В и конце тома).
3) Здесь мы имеем новый пример доказательства от противного (см.
п. 24, примечание 1°J.
4*
52 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Следствия I. Если две прямые линии образуют с одной и той
же секущей два внутренних односторонних угла, сумма которых
отлична от двух прямых, то они непараллельны и пересекаются
с той стороны от секущей, где сумма углов меньше двух прямых.
II. Если две прямые линии параллельны, то всякий перпенди-
перпендикуляр к одной ил них является перпендикуляром и к другой.
Действительно, он непременно пересечёт вторую прямую (п. 40,
следствие II) и образует с ней прямой , угол на основании теоремы,
которую мы только что доказали.
Примечания: 1°. Равные соответственные углы ХЕВ н XFD
имеют одно и то же направление вращения.
О двух параллельных полупрямых ЕВ и FD, расположенных по одну
и ту же сторону от секушей, говорят, что они параллельны и на-
направлены в одну и ту лее сторону.
2°. Мы применили здесь новый способ доказательства обратных
теорем, отличный от тех, которыми мы пользовались в п. ,12, и кото-
который состоит в доказательстве обратной теоремы с помощью соответ-
соответствующей прямой теоремы. Заметим, что в данном случае это дока-
доказательство существенно основывается на том обстоятельстве, что прямая,
проходящая через точку Е и параллельная CD, — единственная.
42. На основании теоремы п. 38 и ей обратной данное выше опре-
определение параллельных прямых в точности сволится к следующему.
Лее прямые параллельны, если они образуют с какой-нибудь
секушей равные соответственные углы (или равные внутренние
накрестлежащие углы или пополнительные внутренние односторон-
односторонние углы).
Это последнее определение следует, вообще говори, предпочитать
первоначально данному определению, которому оно равносильно.
Выражение параллельные прямые часто заменяют выражением
прямые, имеющие одно и то же направление, смысл которою ясен
из пречыдущих предложений.
Примечание. С этой точки зрения две совпа 1ающие между
собой прямые должн^ы рассматриваться как частный случай двух па-
параллельных прямых.'
43. Теорема. Ива угла, стороны которых соответственно
параллельны, или равны, или являются пополнительными углами:
они равны, если обе пары их соответственных сторон направлены
в одну и ту же сторону или обе пары их соответственных сто-
сторон направлены в противоположные стороны; они пополнительны,
если ^одна пара сторон направлена в одну и ту же сторону, а дру-
другая пара сторон — в противоположные стороны.
Прежде всего два угла, у которых одна сторона общая, а две
другие параллельны и направлены .в одну и ту же сторону (черт 41),
равны как соответственные. Следовательно, два угла, стороны которых
параллельны и направлены в одну и ту же сторону, равны м-ежду
собою, так как сторона одного из них образует в пересечении со
стороной другого третий угол, равный каждому из данных углов.
ГЛАВА V. ПАРАЛЛЯЛЬНЫЕ ПРЯМЫЕ
53
Если два угла имеют пару параллельных сторон, направленных
в одну и ту же сторону, и пару параллельных сторон, направленных
в противоположные стороны, то, продолжая одну из сторон второй
пары, мы получим угол, пополнительный первому и равный второму.
Если обе пары сторон направлены в противоположные стороны, то,
продолжив обе стороны первою угла, мы получим угол, равный пер-
первому как вертикальный, а с другой сто-
стороны, равный и второму.
Примечание. Два соответствен-
соответственных угла, а, следовательно, также и два
учла, обе пары сторон которых парал-
параллельны и направлены в одну сторону,
имеют одинаковое направление. Поэто-
Поэтому можно сказать еще так:
Два угла, имеющие соответственно
параллельные стороны, равны или по- J Г\
полните льны, смотря по тому, имеют
ли оба угла {динаксвое направле- Черт. 41.
hue или различные направления.
Теорема. Ива угла, стороны которых соответственно пер-
перпендикулярны друг другу, ровны или являются углами пополни-
пополнительными, в зависимости от того, имеют ли оба угла оОинаковое
направление или различные направления.
Пусть углы ВАС, В'А'С (черт. 42) таковы, что А'Б' и А'С со-
соответственно перпендикулярны к АВ и АС. Проведя перпендикуляр Ав,
к прямой АВ, перевернем угол
В,АС и наложим его на самого
себя так, чтобы сторона ABf пош-
пошла по АС; прямая АВ, перпенди-
перпендикулярная к АВЛ, займет положение
ЛС,, перпендикулярное к АС.
Таким образом, мы имеем угол
ВгАС{, равный данному углу ВАС
и одною с ним направления (так
как он представляет собой пере-
перевёрнутый угол CAB, который имеет
направление, противоположное углу ВАС); стороны угла fir4C, соответ-
соответственно перпендикулярны сторонам угла ВАС, а, следовательно, парал-
параллельны сторонам учла В" А' С. Так как утлы Z?r-AC,, В'А'С будут равными
или пополнительными, смотря по тому, имеют ли они одинаковое на-
направление или различные направления, то то же будет иметь место
и для данных углов.
44. Теорема. Сумма углов треугольника равна двум прямым.
В треугольнике ABC (черт. 43) продолжим ВС по направлению СХ
и проведём СЕ параллельно АВ. Мы образуем при точке С три угла
(на чертеже они обозначены: /. 2. 3), сумма которых равна двум пря-
прямым. Но эти три угла соответственно равны трём углам треугольника,
54
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
в
с
Черт. 43.
в силу того, что /_1 является углом С треугольника; ^_2 равен
углу А (как углы внутренние накрестлежащие, образованные секущей АС
с шраллельными прямыми АБ, СЕ); ^_ 3 равен В (как углы соответ-
соответственные, образованные секущей ВС с теми же параллельными прямыми).
Следствия: I. Внешний угол треугольника равен сумме внут-
внутренних углов, к нему не прилежащих.
II. Острые углы прямоугольного треугольника суть углы до-
дополнительные.
III. Если два треугольника имеют
по два соответегпвенно равных угла, то
и третьи их углы равны.
44а. Теорема. Сумма внутренних
—т: углов выпуклого многоугольника*) равна
двум прямым, умноженным на число
сторон многоугольника, уменьшенное на
два.
Пусть дан многоугольник ABCDE (черт. .44). Соединяя точку А
с другими вершинами диагоналями, мы разобьём этот многоугольник
на треугольники. Треугольников будет на два меньше числа сторон,
потому что точка .4 взята за общую верши-
вершину всех этих треугольников, так что все
стороны многоугольника являются основа-
основаниями треугольников, кроме тех двух, кото-
которые примыкают к А. Сумма углов всех ьтих
треугольников даёт сумму углов многоуголь-
многоугольника. Теорема, таким образом, доказана.
Если п—число сторон ,мн,)гоу1ильника,
то сумма его углов будет 2d {n — 2) или
Bn — 4)d.
Следствие. Сумма внешних углов вы-
выпуклого многоугольника, образ ванных про-
продолжением всех сторон в еднэм и том же направлении, равна
четырём прямым.
Сумма каждого внешнего угла с соответствующим ему внутренним
углом равна 2 прямым. Складывая углы, расположенные при п вер-
вершинах, получим 2я прямых; из них 2я—4 прямых дают сумму внут-
внутренних углов.
Сумма внешних углон составляет, следовательно, 4 недостающих
прямых угла.
УПРАЖНЕНИЯ.
Параллельные прямые.
21. Если в треугольнике ABC через точку пересечения биссектрис уг-
лон В к С провести прямую MN, параллельную ВС, до пересечения в гоч-
li Точно так же, только несколько сложнее, доказывается та же тео-
теорема и для вогнутого многоугольника с помощью надлежащего определе-
определения уишв такого многоугольника.
ГЛАВА VI. ПАРАЛЛЯЛОГРАМЫ. ПОСТУПАТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ 55
ках М и N со сторонами АВ и АС, то отрезок MN равен сумме отрезков
ВМ и CN (доказать).
Как изменится это предложение, если провести прямую,' параллель-
параллельную ВС, через точку пересечения биссектрис внешних углов при В и С;
через точку пересечения биссектрисы угла при В с биссектрисой внеш-
внешнего угла при С?
Сумма углов многоугольника.
22. Доказать теорему п. 44а, разбивая многоугольник на треугольники
прямыми, выходящими из одной и той же внутренней точки много-
многоугольника.
23. В произвольном данном треугольнике ABC проведены из точки А
к стороне ВС две прямые AD и АЕ, из которых первая образует с АВ
угол, равный углу С, в то время как вторая образует с АС угол, рав-
равный углу В. Доказать, что треугольник ADE равнобедренный.
24 Во всяком треугольнике ABC:
1) биссектриса угла А образует с высотой, выходящей из вершины А,
угол, равный полуразности углов В и С,
2) биссектрисы углов В к С образуют между собой тупой угол, рав-
ный прямому, сложенному с углом -^;
3) биссектрисы внешних углов В к С образуют между собой острый
А
угол, дополнительный к углу — (доказать).
25. В выпуклом четырёхугольнике:
1) биссектрисы двух последовательных углов образуют между собою
угол, равный полусумме двух других углов; i
2) биссектрисы двух противоположных углов образуют между собою
угол, пополнительный к полуразности двух других углов (доказать).
Ч
ГЛАВА VI.
ПАРАЛЛЕЛОГРАММ. ПОСТУПАТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ.
45. Частными случаями четырёхугольников являются трапеции и
параллелограмы.
Трапецией называется (черт. 45) четырёхугольник; у которого две
стороны параллельны. Эти параллельные стороны
называются основаниями трапеции.
Параллелограмом назы-
называется (черт. 46) четырёхуголь-
четырёхугольник, стороны которого попарно
параллельны. _
Теорема. В параллело- Черт. 45. Черт. 46.
граме противоположные углы
равны, а углы, прилежащие к одной и той же стороне, пополнительны.
В самом деле, в параллелограме ABCD (черт. 46) углы А и В,
прилежащие к одной и той же стороне АВ, являются углами вну-
внутренними односторонними при параллельных прямых AD и ВС, пересе-
пересечённых секущей Ab; следовательно, они пополнительные. Что касается
56 • КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
углов А и С, то они равны как углы с параллельными сторонами, на-
направленными в противоположные стороны.
Примечание. Очевидно, что если известен один угол паралле-
лограма, то известны и все остальные.
Обратная теорема. Если в четырёхугольнике противополож-
противоположные углы равны, то четырёхугольник — параллелограм.
В самом деле, сумма углов любого четырёхугольника равна четы-
четырём прямым (п. 44а).
Но если ^_А = /_С и ^_В-= /^_D, то сумма четырёх углов:
?А--\~?В^-Z- С~{~/1 D может быть написана в виде 2 / А-|-2 / В.
Отсюда следует, что /_ А-\~/_ B=2d и прямые AD, ВС будут па-
параллельны, так как они образуют с АВ пополнительные внутренние
односторонние углы. Точно так же докажем, что АВ параллельна CD.
46. Теорема. Во всяком параллелограме противоположные
стороны равны.
В параллелограме ABCD (черт. 47) провед&м диагональ АС. ,
Она разбивает параллелограм на два треугольника ABC, CDA,
которые равны, так как имеют общую сторону АС, заключённую между
двумя соответственно равными углами:
^/-4,=^/С'[ (как углы внутренние накрест-
лежащие при параллельных АВ и CD);
^_ Аг -= ^/ С8 (как углы внутренние накрест-
лежащие при параллельных AD и ВС).
Из равенства треугольников следует ра-
венство сторон:
AB=CD; AD=BC.
В этой теореме условие состоит из двух частей: 1) две противо-
противоположные стороны параллельны; '2) две другие стороны также парал-
параллельны. Заключение состоит точно так же из двух частей: 1) две про-
противоположные стороны равны; 2) две другие также равны.
Так как заключение обратного предложения можно получить, беря
либо часть условия, либо полностью всё условие данного предложения,
н обратно, то доказанная теорема имеет две обратные теоремы.
Обратные теоремы. Четырёхугольник будет параллелограмом:
1) если противоположные стороны равны;
2) если две противоположные стороны равны и параллельны.
1°. Предположим, что в четырёхугольнике ABCD (черт. 47)
AB=CD и AD — BC. Проведём диагональ АС. Треугольники ABC и
CDA будут равны как имеющие соответственно равные стороны.
Углы А, и С, будут также равны, и так как эти углы занимают по
отношению к секущей АС положение внутренних накрестлежащьх, то
пряные АВ и CD, которые их образуют, параллельны.
Точно так же из равенства углов Л2 и С„ следует параллельность
прямых AD и ВС.
2°. Предположим теперь, что AB—CD и одновременно АВ па-
параллельна CD. Оба треугольника ABC и CDA будут равны, так как
ГЛАВ* VI. ПАРАЛЛЕЛОГРАММ. ПОСТУПАТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ
57
они будут иметь по одному равному углу (,/^, = ^_СХ как внутрен-
внутренние накрестлежащие), заключённому между соответственно равными
сторонами: АС—общая сторона и AB=CD. Из равенства треуголь
ников следует равенство углов А„ и С2 и параллельность сторон AD
и ВС.
46а. Примечания: 1°. Четырёхуюльник может иметь две рав-
равные стороны АВ, CD, а две другие ВС, AD параллельные между
собою и в то же время не быть параллелограмом (в атом случае он
называется равнобочной трапецией).
Выбрав произвольно сторону АВ, достаточно принять за DC от-
отрезок DXC (черт. 48), симметричный с АВ относительно некоторой
прямой XY плоскости, лишь бы только эта прямая не была парал-
параллельна АВ и пересекала бы её в точке /,
расположенной на продолжении АВ (а не
на самом отрезке АВ). Четырёхугольник
ABCD, будет иметь две параллельные сто-
стороны (та и другая перпендикулярны к XY)
и две другие стороны, равные между со-
собою (как симметричные одна с другой от-
относительно XY); причём эти последние не
будут параллельны, так как они имеют
общую точку /. Обратно, всякий четырех-
четырехугольник, у которого две стороны ВС и AD
параллельны, а две другие равны между
собой, будет параллелограмом или будет А
иметь (случай равнобочной трапеции) ось
симметрии. Действительно, пусть XY будет
перпендикуляром, восставленным в середи-
середине ВС. Мы уже имеем две наклонные к прямой AD, проходящие
через Си равные АВ: 1) СОЛ, симметричную с АВ относительно XY,
и 2) CD2, образующую параллелограм вместе с точками А, В, С; кон-
концы этих наклонных лежат на AD, так как последняя параллельна СВ.
Следовательно, точка D должна совпадать либо с D,, либо с D2, так
как через С можно провести к AD только две наклонные, равные АВ.
Кажется, что это рассуждение теряет силу, если D, совпадает
с D2, т. е. если CDX параллельна АВ. Но в этом случае АВ парал-
параллельна XY, т. е. перпендикулярна к AD; тогда между точкой С и
прямой AD действительно нельзя провести другого отрезка, равного
перпендикуляру АВ.
2°. Первое обратное предложение п. 46 существенно предпола-
предполагает, что мы имеем дело с четырёхугольниками в собственном смысле
этого слова (п. 21, примечание); только в том случае, когда оба тре-
треугольника ABC и ADC (черт. 47) расположены по разные стороны от
общей стороны АС, углы Ах и С\ этой фигуры будут внутренними
накрестлежащими.
Нетрудно построить четырёхугольник в несобственном смысле (на-
(называемый антипараллелограмом), противоположные стороны которого
58 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ i
. \
будут равны. Для этого достаточно в параллелограме ABCD (черт. 49)
заменить точку D точкой Е, ей симметричной относительно диаго-
диагонали АС.
Можно получить также антипараллелограм АВСЕ^, выбирая точку Ел,
симметричную с В относительно перпендикуляра, восставленного в сере-
середине АС таким образом, чтобы четырёхугольник АВЕХСбыл равнобочной
трапецией. Но эта точка Zf, не может быть отличной от Е, так как
(п. 24, греши признак) по определённую сторону от АС существует
только одна точка, которая будет одновременно находиться на рассто-
расстоянии АЕ = ВС от Л и на расстоянии СЕ = АВ от С. Следовательно,
всякий несобственный четырёхугольник, проти-
противоположные стороны которого равны, будет
(С образован двумя непараллельными сторонами и
диагоналями равнобочной трапеции.
3°.. Два четырёхугольника, имеющие все че-
четыре стороны соответственно равные, не обя-
обязательно равны между собою. Другими слова-
словами, можно деформировать данный четырёх-
четырёхугольник ABCD (в собственном смысле или
нет), не изменяя длин его сторон.
Пусть неизменные длины сторон будут АВ=а, BC=b, CD:=c,
DA^=d. Можно построить треугольник ABC со сторонами а и b и
произвольным углом, заключённым между ними. Этот треугольник даёт
длину АС (диагонали четырёхугольника). Каждому значению АС будет
соответствовать (при условиях возможности п. 86, книга II) треуголь-
треугольник ACD, построенный на этом отрезке как на основании и с двумя
другими сторонами CD, DA, соответственно равными с, d. Следова-
Следовательно, угол В будет иметь произвольную величину (по крайней мере,
в известных пределах). Четырёхугольник, изменяющийся при соблюде-
соблюдении этих условий, называется шарнирным четырёхугольником. Это
понятие имеет большое значение в приложениях геометрии.
Согласно предыдущему параллелограм останется параллелограмом,
а антипараллелограм — антипараллелограмом, если сделать каждый из них
шарнирным г).
47. Теорема. Диагонали параллелограма делят друг друга в
точке пересечения пополам.
В параллелограме ABCD (черт. 50) проводим диагонали АС и BD,
которые пересекаются в точке О. Два треугольника АВО и CDO
равны как имеющие соответственно равные углы и равные стороны
!) Это заключение теряет силу только в том случае, если параллело-
параллелограм преобразуется в антипараллелограм или наоборот (так как паралле-
параллелограм и антипараллелограм будут единстпенными четырёхугольниками,
противоположные стороны которых соответственно равны). Если преобра-
преобразование происходит непрерывно, то для преобразования параллелограма
в антипараллелограм необходимо, чтобы параллелограм вытягивался в пря-
прямую, т. е. чтобы две его соседние стороны, а также и две остальные
становились продолжением одна другой.
ГЛАВА VI. ПАРАЛЛЕЛОГРАМЫ. ПОСТУПАТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ
59
(по предыдущей теореме). Следовательно, АО = СО,
B0
Обратная теорема. Если диагонали четырёхугольника делятся
е точке пересечения пополам, то четырёхугольник — параллелограм.
Допустим, что в четырёхугольнике ABCD (черт. 50) АО = СО,
дО = Е>О. Два треугольника АВО и CDO будут равны как имеющие
по равному углу (углы при точке О равны как вертикальные), заклю-
заключённому между соответственно равными сторонами.
Поэтому углы при вершинах А и С в этих треуголь- А_ В
никах будут равны и, следовательно, АВ будет па-
параллельна CD. Равенство треугольников ADO и ВСО
доказывает таким же образом, что AD параллель- ,
на ВС. j
Примечание. Мы доказали обратные теоремы „ ,•„
в пп. 46 и 47, повторяя в обратной последовательности черг. ои.
первоначальные рассуждения, как это было объяснено в п. 32, примечание 2°.
48. Прямоугольником называется четырёхугольник, у которого
все углы между собой равны, и, следовательно, — все углы прямые.
Прямоугольник — параллелограм, так как его противоположные углы
равны между собой.
Ромбом называется четырёхугольник, у которого все четыре сто-
стороны равны. Ромб является параллелограмом, так как противополож-
противоположные его стороны равны. Следовательно, в пря-
прямоугольнике, как и в ромбе, диагонали делятся в
точке пересечения пополам.
Теорема. Диагонали прямоугольника равны
между собой.
В прямоугольнике ABCD (черт. 51) диагонали АС
и BD равны; действительно, треугольники ADC и
BCD равны, так как /_ADC = /_BCD как прямые
углы, сторона DC — общая и AD = ВС как проти-
противоположные стороны параллелограма.
Следствие. В прямоугольном треугольнике медиана, выходящая
из вершины прямого угла, равна половине гипотенузы, потому что,
проведя через концы гипотенузы прямые, параллельные катетам, полу-
получим прямоугольник, в котором рассматриваемая медиана является полови-
половиной диагонали.
Обратная теорема. Всякий параллелограм, в котором диа-
диагонали равны. — прямоугольник.
Пусть дан параллелограм ABCD (черт. 51), у которого диагонали
равны. Из того, что AD = ВС, следует, что треугольники ADC и BCD
Равны по трём сторонам. Углы ADC и BCD также равны, и так как
они пополнительны, то каждый из них прямой, откуда и следует, что
пара члелограм — прямоугольник.
Следствие. Треугольник, в котором медиана равна половине со-
соответствующей стороны, — прямоугольный.
60
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Теорема. Диагонали ромба взаимно перпендикулярны и делят
его углы пополам.
Если четырёхугольник ABCD (черт. 52) — ромб, то треугольник
ABD — равнобедренный. Диагональ АС, являясь медианой этого тре-
треугольника, является в то же время его высотой и биссектрисой.
Обратная теорема. Всякий параллелограм, диагонали кото-
которого перпендикулярны, есть ромб.
В самом деле, каждая вершина будет одинаково отстоять от двух
смежных вершин, так как она лежит на прямой, проходящей через
середину соединяющей их диагонали и перпенди-
перпендикулярной к последней.
49. Квадратом называется четырёхугольник,
у которого все стороны равны и все углы прямые.
Таким образом, квадрат одновременно является
ромбом и прямоугольником, так что его диагона-
диагонали равны между собой, перпендикулярны и делятся
пополам.
Обратно, всякий четырёхугольник, в котором
диагонали равны, перпендикулярны и делятся попо-
пополам, есть квадрат.
Дв*а квадрата, имеющие по равной стороне,
равны между собой.
50. Лемма. Две фигуры F и F' равны между собою и имеют
одно и то же направление вращения, если точки обеих фигур со-
соответствуют друг другу таким образом, что треугольники ABC
и А'В'С, образованные соответственными точками обеих фигур,
будут равны между собой и их соответственные углы будут иметь
одно и то же направление, как бы ни были выбрана точка С.
В самом деле, пусть А, В — две точки фигуры F, и А', В'—.точки,
им соответственные. Отрезок АВ, очевидно, должен быть равен А'В'.
Перенесём вторую фигуру и наложим её на первую так, чтобы эти
два равных отрезка совместились. Я утверждаю, что при этом обе
фигуры целиком совместятся. Пусть С будет какая-либо третья точка
первой фигуры, и С—точка, ей соответственная. Так как два тре-
треугольника ABC, А'В'С будут равны, то и углы В'А'С и ВАС будут
равны и одинаково направлены. Следовательно, при совмещении А'В'
с АВ прямая А'С должна пойти по направлению АС. Так как, кроме
того, А'С = АС, то точка С" совпадает с С.
Так как это доказательство приложимо ко всем точкам обеих фи-
фигур, то обе фигуры совпадают целиком.
Примечания: 1°. Мы нашли достаточное условие равенства двух
фигур; это же условие является, очевидно, и необходимым.
2°. Из предыдущего рассуждения следует:
Чтобы совместить две равные фигуры, соответственные углы
которых имеют одно и то же направление, достаточно совместить
две точки одной фигуры с двумя соответствующими им точками
другой
ГЛАВ<\ VI. ПАРАЛЛЕЛОГРАММ. тСТУПАТЕ ЛЬНЫЕ ПЕРЕМЕЩЕНИЯ 61
• •
51. Теорема. Если из всех точек данной фигуры провести рав-
нЫе отрезки, параллельные между собой и направленные в одну
mv же сторону, то концы этих отрезков образуют фигуру,
равн\'Ю данной.
Пусть прежде всего 4, В—две точки первой фигуры, которым со-
соответствуют точки 4', В' второй фигуры. Так как отрезки .4-4' и ВВ'
наралчельни и равны, то четырёхугольник ABB'А'— параллелограм.
Следовательно, отрезки АВ и А'В' равны и параллельны между собой
и направлены в одну и ту же сторону. Таким образом, отрезки, соеди-
соединяющие между собой соответственные точки в каждой фигуре, равны,
параллельны и направлены в одну и ту же сторону.
Далее, трём каким-либо точкам первой фигуры, образующим тре-
треугольник, соответствуют три точки,- образующие треугольник, равный
первому, и так как стороны соответственных углов этих треугольников
параллельны и направлены в одну и ту же сторону, то направления
соответственных углов одинаковы. Следовательно, обе фигуры равны.
Операция, при помощи которой мы переходим от первой фигуры
ко второй, называется поступательным перемещением. Очевидно, что
поступательное перемещение вполне определено, если даны величина
и направление какого-нибудь отрезка ЛА', соединяющего одну из то-
точек первой фигуры с соответствующей ей точкой второй. Пост) патель-
ное перемещение обозначают поэтому такими же буквами, как и этот
отрезок, например, говорят: „перемещение АА'".
Следствия. I. Если из всех точек прямой провести равные, па-
параллельные и направленные в одну и ту же сторону отрезки, то
геометрическое место концов этих отрезков есть прямая, парал-
параллельная первой прямой.
В частности, геометрическое место точек, расположенных по
одну а ту же сторону от некоторой прямой и на данном от неё
расстоянии, есть прямая, параллельная этой прямой.
II. Лее параллельные прямые на всём cboJm протяжении одина-
одинаково отстоят др \>г от друга.
Следовательно, можно говорить о расстоянии между двумя парал-
параллельными прямыми.
III.- Геометрическое место точек, одинаково отстоящих от двух
параллельных прямых, есть третья прямая, параллельная нервы н.
УПРАЖНЕНИЯ.
Параллелограм ы.
26 Биссектрисы углов пяраллелограма образуют прямоугольник; бис-
биссектрисы его внешних углов также образуют прямоугольник (доказать).
27 Отрезок любой прямой, проходящей через точку пересечения диа-
диагоналей параллелогрлма, заключённый между его противоположными сто-
сторонами, делится в этой точке пополам (доказагм
В силу этого обстоятельства точка пересечения диагоналей иараллело-
грама называется его центром.
62 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
28. Два параллелограма, вписанных один в другой, иначе говоря, таких,
у которых четыре вершины первого соответственно лежат на четырёх
сторонах второго, имеют общий центр (доказать).
29. Угол треугольника будет острым, прямым или тупым, смотря по
тому, будет ли противоположная сторона меньше, равна или больше уд-
удвоенной" соответствующей медианы (доказать).
30 Если в прямоугольном треугольнике один из его острых углов вдвое
больше другого, го один из катетов равен половине гипотенузы (доказать;.
Поступательные перемещения.
31. Нлйти геометрическое место точек, для которых сумма или раз-
разность их расстояний до двух данных прямых равна данной длине.
32. Даны две параллельные прямые и две точки А и В, находящиеся
вне этих параллельных и расположенные по обе стороны от них. Найти
ломаную линию наименьшей длины,'соединяющую точки А и В, если вер-
вершины этой ломаной лежат на данных прямых, и отрезок ломаной между
обеими прямыми имеет данное направление.
ГЛАВА VII.
ПРЯМЫЕ В ТРЕУГОЛЬНИКЕ, ПРОХОДЯЩИЕ ЧЕРЕЗ ОДНУ
ТОЧКУ.
52. Теорема. Во всяком треугольнике перпендикуляры, вос-
восставленные в серединах сторон, пересекаются в одной тсНке.
Пусть дан треугольник ABC (черт. 53). Прямые, перпендикулярные
к сторонам АВ и АС треугольника и проходящие через их серединь1,
не могут быть параллельными (иначе АВ и АС лежали бы на одной
прямой) и пересекаются в некоторой точ-
точке О. Требуется доказать, что эта точка
лежит также и на перпендикуляре к сти-
роне ВС, прохогящем через её середину.
Точка О, лежащая на прямой, пер-
перпендикулярной к стороне АВ и проходп-
, щей через её середину, одинаково отстоит
" I от точек А и В; кроме того, она од,,-
Черт. 53. наново отстоит от точек А и С как точ-
точка, лежащая на перпендикуляре, восстав-
восставленном в середине стороны АС. Следовательно, она одинаково от-
отстоит от точек Вч С и потому лежит на перпендикуляре, восставлен-
восставленном в середине стороны ВС.
53. Теорем ~. Во всяком треугольнике три высоты пересе-
пересекаются в одной точке.
Пусть дан треугольник ABC (черт. 54). Проведём через точку А
прямую, параллельную ВС, через точку В—прямую, параллельную
АС, и через С—прямую, параллельную АВ.
Мы получим, таким образом, новый треугольник А'В'С. Мы дока-
докажем, что высоты треугольника ABC являются перпендикулярами, вое-
ГЛАВА VII. nPHMblF В ТРЕУГОЛЬНИК. ПРОХОДЯЩИЕ ЧЕРЕЗ ОДНУ ТОЧКУ
63
ставленными в серединах сторон нового треугольника, откуда будет
следовать, что они проходят через одну точку.
Параллелог рам АВСВ' даёт нам ВС=АВ'; точно так же парал-
лелограм АСВС даёт ВС^АС, так что точка А является середи-
серединой В'С.
Высота AD треугольника ABC пройдёт через середину В'С и, кроме
того, будет перпендикулярна к В'С, так как она перпендикулярна
к параллельной ей прямой ВС.
Так как то же самое рассуждение
может быть повторено для двух других
высот, то теорема доказана.
54. Теорема. Во всяком тре-
треугольнике:
1) биссектрисы трёх углов пере-
пересекаются в одной точке;
2) биссектриса одного из углов и
биссектрисы двух внешних углов, к не-
Черт. 54.
му не прилежащих, пересекаются в одной точке.
1°. Проведём в треугольнике ABC (черт. 55) биссектрисы углов
В и С: они пересекаются в точке О, лежащей внутри треуголг ника.
Эта точка, как принадлежащая биссектрисе угла В, щинаков» отстоит
от прямых АВи ВС. При-
Принадлежа также биссектри-
биссектрисе угла С, эта точка оди-
одинаково отстоит от АС
и ВС. Таким образом, она
одинаково отстоит от АВ
и АС, и так как она ле-
лежит внутри угла А, то
она находится на биссек-
биссектрисе этого угла.
2° Так как сумма двух
внешних углов СВХ, BCY
меньше четырёх прямых,
то сумма их половин мень-
меньше, чем два прямых. Сле-
Следовательно, биссектрисы
ьтих двух углов пересе-
пересекаются (п. 41, следствие)
в точке О', лежащей внут-
внутри угла А. Эта точка О'
будет, как и точка О, одинаково отстоять от трёх сторон треуголь-
треугольника. Она будет принадлежать, таким образом, биссектрисе угла А.
55. Теорема. Отрезок, соединяющий середины двух сторон
треугольника, параллелен третьей стороне и равен ее половине.
Пусть в треугольнике ABC (черт. 56) D — середина АВ, Е— се-
середина АС. Отложим на продолжении DE отрезок EF, равный DE.
64
КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Черт. 56.
Четырёхугольник ADCF будет параллелограмом (п. 47), и, следовательно,
CF будет равна и параллельна DA или, что то же самое, BD. В та-
таком случае четырёхугольник DBCF будет в свою очередь параллело-
параллелограмом, а потому DE параллельна ВС и, как половина DF, равна по-
половине ВС.
56. Теорема. Три медианы тре-
треугольника пересекаются в одной точ-
точке, лежащей на одной трети длины
каждой из них, считая от соответ-
соответствующего основания.
Пусть в треугольнике ABC про-
проведены сначала две медианы BE и CF
(черт. 57); я утверждаю, что их точка
пересечения О находится на одной
трети каждой из них. Чтобы это показать, обозначим через М и N
середины BG и CG. Отрезок MN, соединяющий серелины двух
сторон в треугольнике BCG, параллелен ВС и равен её половине.
Но EF также параллелен ВС и равен её по-
половине. В таком случае EFMN — параллелограм,
в котором диагонали делятся в точке пере-
пересечения пополам. Таким образом, имеем EG=
= GM—MB и FG=GN=KC.
Следовательно, медиана BE проходит че-
через точку, лежащую на трети расстояния CF.
Но таким же рассуждением можно показать, что
третья медиана AD также пройдёт через эту точку.
Примечание. Точка пересечения медиан называется также цент-
центром тяжести треугольника. Обоснование этого названия даётся
в механике.
УПРАЖНЕНИЯ.
33. Соединить ланную точку с точкой пересечения двух данных прямых,
если эта последняя лежит за пределами чертежа (п. 53).
34. Во всякой трапеции середины непараллельных сторон и середины
диагоналей лежат на одной и той же прямой, параллельной основаниям
трапеции; расстояние между серединами непараллельных сторон равно по-
полусумме оснований; расстояние между серединами диагоналей равно полу-
полуразности оснований (доказать).
35. Если из точек А, В и из середины С отрезка АВ опустить перпен-
перпендикуляры на произвольную прямую, то перпендикуляр, опушенный из точки
С, равен полусумме или полуразности перпендикуляров, опушенных из А
и В, смотря по тему, имеют ли эти два перпендикуляра одинаковое направ-
направление или противоположные направления (доказать).
36. Середины сторон произвольного четырёхугольника являются вер-
вершинами параллелограма; стороны этого параллелограма соответственно па-
параллельны диагоналям данного четырёхугольника и равны половинам этих
диагоналей; его центр лежит на середине отрезка, который соединяет се-
середины диагоналей данного четырёхугольника (доказать).
37. Доказать, что медианы треугольника ABC проводят через одну точку,
продолжая медиану CF (черт. 5/) "за точку F на длину, равную FU.
ЗАДАЧИ К ПЕРВОЙ КНИГЕ 65
38. Даны три (различные) прямые, проходящие через одну точку О
и точка А на одной из них. Доказать, что существует:
1) треугольник с вершиной в точке А, высотами которого служат дан-
данные прямые (есть одно исключение;;
2) треугольник с вершиной в точке А, медианами которого служат дан-
данные прямые;
3) треугольник с вершиной в точке А, для которого данные прямые
служат биссектрисами внутренних или внешних углов (есть одно исключение);
4) треугольник, имеющий середину одной из сторон в точке А, для
которого данные прямые служат перпендикулярами, восставленными в се-
серединах сторон (привести к случаю 1).
ЗАДАЧИ К ПЕРВОЙ КНИГЕ.
39 Во всяком треугольнике наибольшей стороне соответствует наимень-
наименьшая медиана (доказать).
.Треугольник, имеющий две равные медианы, — равнобедренный 1).
40. Допустим, что билл^ардный шар отражается от прямолинейного борта
таким образом, что две прямые, по которым" он движется до и после удара,
одинаково наклонены к борту. Пусть теперь Db D2,..., Dn — п прямых,
лежащих в одной плоскости; А и В— две точки, расположенные с одной
и той же стороны от каждой из этих прямых. В каком направлении должен
быть пущен шар из точки А, чтобы он прошёл через точку В, после того
как он отразится последовательно от всех данных прямых?
Доказать, что путь, по которому пройдёт шар, есть кратчайшая лома-
ломаная линия, идущая из точки А в точку В и имеющая вершины последова-
последовательно на данных прямых2).
Частный случай. Данные прямые являются четырьмя сторонами прямо-
прямоугольника, взятыми по порядку, и точка В совпадает с точкой А, которая
взята внутри прямоугольника. Показать, что в этом случае путь, пройден-
пройденный шаром, равен сумме диагоналей прямоугольника.
41. Диагонали обоих прямоугольников, рассмотренных в упражнении
26, расположены на одних и тех же двух прямых, параллельных сторонам
данного параллелограма [обстоятельство, аналогичное3) рассмотренному
в п. 54]; одна из этих диагоналей равна разности, а другая — сумме сторон
параллелограма (доказать).
42. В равнобедренном треугольнике сумма расстояний от точки, лежа-
лежащей на основании, до двух других сторон есть величина постоянная (до-
(доказать).
Как изменится это предложение, если рассматриваемая точка взята на
продолжении основания?
В равностороннем треугольнике сумма расстоянии внутренней точки
от трёх его сторон есть величина постоянная (доказать).
2) Относительно аналогичного свойства высот см. упражнения 19—20
и биссектрис — упражнения 361—361а (в конце тома).
2) Если имеется только одна прямая, задача сводится к той, которая
была рассмотрена в упражнениях 13—14.
После того как решена эта первая задача, надо найти способ, который
позволял бы из найденного уже решения для случая одной прямой полу-
получить решение для случая двух прямых, перейти затем к случаю трёх пря-
прямых и т. д.
8) Аналогия, на которую указывает автор, состоит в том, что в п. 54
изучается расположение биссектрис в треугольнике, а здесь — расположе-
расположение биссектрис в параллелограме. Прим. ред. перевода.
5 Элементарная геомстпня
66 КНИГА ПЕРВАЯ. ПРЯМАЯ ЛИНИЯ
Как изменится это предложение, если рассматриваемая точка стано-
становится внешней?
43. Если в треугольнике ABC через середину стороны ВС провести
перпендикуляр к биссектрисе угла А, то эта прямая образует на каждой
.„ .„ АВ + АС АВ — АС
из сторон АВ и АС два отрезка, соответственно равные j и
(доказать).
44. Пусть ABCD и DEFG — два квадрата, помещённые рядом таким
образом, что стороны DC, DE имеют одно и то же направление и стороны'
AD, DG являются продолжением одна другой. На AD и на продолжении
DC отложены два отрезка АН и СК, равные DG. Доказать, что четырёх-
четырёхугольник HBKF— также квадрат.
45. На сторонах А ч, АС треугольника вне этого треугольника постро-
построены квадраты ABDE, ACFG (D и F— противоположные вершины по отно-
отношению к А).
Доказать:
1) что отрезок EG перпендикулярен к медиане, выходящей из А, и вдвое
длиннее этой медианы;
2) что четвёртая вершина / параллелограма, у которого три другие
вершины будут Е, A, G (Е и G — противоположные вершины), лежит на
высоте данного треугольника, выходящей из А;
3) что CD, BF соответственно равны и перпендикулярны В/, С/ и пе-
пересекаются также на высоте, выходящей из А.
46. Даны прямой угол АОВ и две взаимно перпендикулярные прямые,
выходящие из точки Р. Первая прямая пересекает стороны данного угла
в точках А и В; вторая пересекает те же стороны в точках С и D. До-
Доказать, что перпендикуляры, проведённые из точек D, О, С к прямой ОР,
отсекают на АВ два отрезка, равные соответственно АР и РВ, но распо-
расположенные в обратной последовательности.
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
ГЛАВА I.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ.
57. Теорема. Через три точки, не лежащие на одной прямой,
можно провести окружность и притом только одну.
Иначе говоря, окружность определяется тремя точками, не
лежащими на одной прямой.
Пусть, в самом деле, А, В, С (черт. 58)—три точки, не лежа-
лежащие на одной прямой линии. Мы уже доказали (п. 52), что перпен-
перпендикуляры, восставленные в серединах отрез-
отрезков ВС, СА и АВ, проходят через одну
и ту же точку О, равноудалённую от то-
точек А, В и С. Окружность, описанная из
точки О, как из центра, радиусом ОА, прохо-
проходит через три данные точки. Эта окруж-
окружность — единственная окружность, удовле- q J ~q
творяющая поставленному условию, так как Черт 58
центр окружности, которая пройдёт через
точки А, В и С, должен "обязательно принадлежать трём перпенди-
перпендикулярам, о которых мы говорили.
Следствие. Мы видим, что окружность не может иметь двух
различных центров, а следовательно, не может иметь и двух нерав-
неравных радиусов.
58. Теорема. Прямая не может пересекать окружность
более чем в двух точках.
Если расстояние от центра до прямой больше радиуса, прямая
не пересекает окружности. Если это расстояние меньше радиуса,
р , прямая пересекает окружность в
—^J|—? D двухточках. Наконец, если расстоя-
расстояние равно радиусу, прямая имеет
с окружностью одну общую точку.
В последнем случае прямая назы-
q вается касательной к окружности.
Черт 59 ¦ Пусть дана окружность с цент-
центром О и прямая D. Из центра О
(черт. 59) опустим на прямую D перпендикуляр ОН.
1°. Окружность не может иметь более двух общих точек с пря-
прямой D. Это сводится к тому, что из точки О нельзя провести к
прямой D более двух наклонных, равных радиусу R (п. 30, след-
следствие).
5*
6S
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Черт. 60.
2°. Если расстояние ОН больше радиуса, то расстояние от центра
любой точки прямой и подавно (п. 29) будет больше радиуса;
следовательно, все точки прямой являются внешними по отношению
к кругу.
3°. Если, напротив, ОН меньше радиуса, точка Н находится вну-
внутри окружности, но по обе стороны от Н есть точки, расположенные
вне окружности. Чтобы в этом убедиться, отложим на прямой D от
точки Н два отрезка HP и ИР', равные радиусу; расстояния ОР
и ОР' будут непременно больше радиуса. Сле-
Следовательно, будем иметь две точки пересечения
с окружностью: одну между Н и Р и другую—
между Н и Р'; это будут единственные точки
пересечения A°).
4°. Если, наконец, ОН равно радиусу
(черт. 60), то точка Н будет общей точкой
прямой и окружности, но, так же как в 2°,
убедимся, что всякая другая точка прямой на-
находится вне окружности.
Следствие. Через тонну, взятую на
окружности, можно провести к ней касатель-
касательную и только одну, причём эта касательная перпендикулярна к
радиусу, проведённому в эт\> точку.
59. Предыдущее определение касательной не годится в качестве
определения касательной к произвольной кривой.
Касательной к какой-либо кривой в точке М этой кривой (черт. 61)
называется предельное положение, к которому стремится прямая ММ',
когда точка /И', описывая кривую, без-
гранично приближается к М. Иначе
говоря:
, Прямая МТ называется касательной
в точке М, если для всякого данного
угла е можно выбрать по обе стороны
от точки М две дуги ММ, и ММг та- Черт. 61.
кие, чтобы для всякого положения точ-
точки М', взятой на одной из этих дуг, прямая ММ' образовала бы с
прямой МТ или с её продолжением угол, меньший е ').
Покажем, что для случая окружности это определение сводится
к тому, которое мы дали выше.
Проведём в точке М окружности О перпендикуляр МТ к радиусу
ОМ и на хорду ММ' (черт. 62) опустим из центра перпендикуляр ОН.
Эта прямая является высотой равнобедренного треугольника ОММ'
и в то же время биссектрисой угла при О Угол ТММ' равен углу
МОН (как углы с перпендикулярными сторонами) и, следовательно,—
половине угла MOM'. Но этот последний можно сделать меньше вся-
М
х) Можно доказать, как это вообще доказывается в теории пределов,
что если такая прямая существует, го она единственная.
ГЛАВА II. ДИАМЕТРЫ И ХОРДЫ
69
кого данного угла,- если выбрать точку М' достаточно близко к точ.
ке М.
60. Нормалью к кривой в данной точке называется перпендику-
перпендикуляр к: касательной в этой точке. Следовательно, нормаль к окружности
j в данной 'точке есть не что иное
как радиус, проведённый в эту
,М точку.
Черт. 62.
Черт. 63.
На любой данной окружности имеются две (и только две) такие
точки, что нормали в этих точках проходят через данную точку Р
плоскости (отличную от центра): этими точками будут концы диаметра,
проходящего через точку Р.
60а. Углом между двумя кривыми в точке их пересечения
называется угол, образованный их касательными в этой точке (черт. 63).
Следовательно, угол между двумя пересекающимися окружностями
равен углу между радиусами, проведёнными в их общую точку, или
углу, ему пополнительному.
УПРАЖНЕНИЯ.
47. Из всех точек окружности проведены отрезки, равные и парал-
параллельные одному и тому же данному отрезку.
Найти геометрическое место концов этих отрезков.
48. Найти геометрическое место середин отрезков, соединяющих дан-
данную точку с различными точками окружности.
49. АВ— диаметр окружности О, С—точка, взятая на продолжении
этого диаметра за точку В, CDE— секущая из точки С, которая пересе-
пересекает окружность в точках D и Е. Если внешняя часть CD равна радиусу,
то утл ЕОА в три раза больше угла DOB (доказать;.
ГЛАВА II.
ДИАМЕТРЫ И ХОРДЫ.
61. На основании определения, данного в п. 19а, сказанное в п. 9
может быть сформулировано так:
Теорема. Всякий диаметр служит огью симметрии для
окружности и для круга.
Отсюда видно, что окружность имеет бесчисленное множество
осей симметрии.
70
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
62. Хордой называется отрезок, соединяющий концы дуги окруж-
окружности. Эта дуга, как говорят, стягивается хордой. Следует заметить,
что всякая хорда стягивает две различные дуги — одну меньшую, а
другую большую полуокружности (или обе равные полуокружности, если
хорда есть диаметр).
63. Теорема. Диаметр, перпендикулярный хорде, делит эту
хорду и каждую из стягиваемых ею дуг на две равные части.
В самом деле, диаметр окружности О, перпендикулярный к хорде АВ,
служит осью симметрии, с одной стороны, окружности, а с другой
стороны, — равнобедренного треугольника ОАВ; следовательно, он
является осью симметрии и для образованной ими фигуры в целом.
Следствие. Каждые два из пяти следующих условий:
1) быть перпендикулярным хорде,
2) проходить через центр,
3) проходить через середину хорды,
4), 5) проходить через середину одной из двух стягиваемых дуг,—
определяют прямую.
Все определённые таким образом прямые сливаются в одну.
Геометрическое место середин ряда параллельных xopd есть
диаметр, перпендикулярный к этим хордам.
Черт. 64.
Черт. 65.
Черт. 66.
Касательная параллельна тем хордам, которые делятся диа-
диаметром, проведённым в точку касания, на две равные части.
Теорема. Две дуги окружности, заключённые между двумя
параллельными прямыми, равны (черт. 64).
Действительно, эти дуги симметричны друг с другом относительно
диаметра, перпендикулярного к обеим параллельным прямым.
64. Теорема. Если в плоскости окружности дана некоторая
точка Р, то из всех точек, лежащих на окружности, точка, наибо-
наиболее близкая к Р. и точка, наиболее удалённая от Р, представляют
собой основания нормалей к окружности (п. 60), проходящих
через точку Р.
Если А — та из двух точек, которая расположена на полупря-
полупрямой OP, a В — та точка, которая лежит на противоположной полу-
полупрямой (черт. 65 и 66), то расстояние РА равно разности ОР и
радиуса, а расстояние РВ — сумме тех же длин. Следовательно, любая
t ГЛАВА И. ДИАМЕТРЫ И ХОРДЫ
71
точка М окружности находится от точки Р на расстоянии, большем РА
и меньшем РВ, как третья сторона треугольника ОРМ.
Расстояние РМ постоянно увеличивается, когда точка М опи-
описывает окружность, перемещаясь из А в В, потому что сторона РМ
треугольника ОРМ лежит против угла, который всё время увеличи-
увеличивается и заключён между двумя сторонами постоянной длины.
Следствие. Диаметр есть наибольшая хорда окружности.
Если, в самом деле, совместить точку Р с точкой А, то хорда РМ
будет, очевидно, меньше диаметра РВ.
65. Теорема. В одном круге или в двух равных кругах:
1) равным дугам соответствуют равные хорды, и обратно;
2) из двух неравных дуг, меньших полуокружности, большая
дуга соответствует большей хорде.
Черт. 67.
Черт. 63.
Черт. 69.
1°. Если мы совместим две равные дуги, совмещая их концы, то
совместятся и хорды.
Обратно, если хорды равны, то центральные углы равны по
третьему признаку равенства треугольников, и, следовательно, дуги
также равны.
2°. Если дуга АВ меньше дуги А'В' (черт. 67) и, следовательно,
угол АОВ меньше угла А'ОВ', то хорда АВ будет меньше А'В', как
это показывает теорема п. 28, примененная к треугольникам ОАВ
и О А'В'.
66. Теорема. В одном и том же круге или в двух равных
кругах:
1) две равные хорды одинаково удалены от центра, и обратно;
2) из двух неравных хорд большая менее удалена от центра.
1°. Две равные хорды в одном и том же круге соответствуют
двум равным дугам; достаточно наложить друг на друга эти две дуги,
чтобы убедиться, что середины обеих хорд находятся на одинаковом
расстоянии от центра.
Обратно, если две хорды АВ и А'В' круга О (черт. 68) одинаково
отстоят от центра, прямоугольные треугольники ОНА и ОН'А' имеют
равные гипотенузы и равные катеты ОН = ОН'; следовательно, НА =
— Н'А' и АВ — А'В'.
72 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ •
2°. Предположим, что хорда АВ больше хорды А'В' (черт. 69).
Отсюда следует, что угол АОВ больше угла А'ОВ', и если опустить
перпендикуляры ОН и ОН', то угол АОН больше угла А'ОН'.
Но в таком случае угол ОАН. являющийся дополнением первого
угла, меньше угла О А'И', представляющего собой дополнение второго.
Два прямоугольных треугольника ОНА и ОН'А' имеют, таким образом,
равные гипотенузы и неравные острые у1лы, откуда следует (п. 35),
что ОН<СОН'.
67. Представим себе хорду ММ' (черт. 70), которая перемещается
таким образом, что расстояние её от центра, вначале меньшее ради-
радиуса, увеличивается и становится равным
этому радиусу. Предположим для опреде-
лённости, что эта хорда перемещается,
оставаясь перпендикулярной к определён-
определённому диаметру О А.
Длина ММ' уменьшается по мере то-
того, как хорда приближается к касатель-
касательной в точке А, на основании предыдущей
теоремы, и точку М можно взять настоль-
настолько близко к точке А (иначе говоря хор-
q 70 ду, настолько близко к касательной), что
эта длина будет сколь шодно малой, так
как ММ'<2МА "^
Мы видим, что точки М и Л/ безгранично приближаются одна
к другой и стремятся слиться с точкой А;. мы выражаем это обстоя-
обстоятельство следующими словами: касательная имеет с окружностью
две общие точки, сливающиеся в А. Мы увидим, что такой способ
выражения позволяет проще сформулировать некоторые теоремы.
УПРАЖНЕНИЯ.
50. Окружность проходит через две данные точки А и В. Пусть С —
одна из точек, в которой эта окружность встречает данную прямую, пер-
перпендикулярную к прямой АВ. Найти геометрическое место точек/диамет-
точек/диаметрально-противоположных точке С, если окружность, изменяясь, всё
время проходит через точки А к В (использовать упражнение 34).
51. Если разделить хорду на три равные части и соединить с центром
точки деления, то соответствующий центральный угол не разделится на
три равные части (доказать).
Какая из трёх частей угла будет наибольшей (использовать упражне-
упражнение 7)? Обобщить на случай большего числа частей.
52. Если две хорды одной окружности равны между собой, то расстоя-
расстояния от точки пересечения этих хорд или их продолжений до концов той и
другой хорды соответственно равны между собой (доказать).
53. Найти геометрическое место середин хорд данной окружности,
имеющих данную длину.
54. Найти наименьшую хорду окружности, которую можно провести
через данную точку, находящуюся внутри этой окружности.
ГЛ<ША ПГ. ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ 73
ГЛАВА III.
ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ.
68. Две окружности не могут иметь более двух общих точек
по теореме п. 57.
Теорема. Если две окружности пересекаются, то прямая,
соединяющая их центры, перпендикулярна к общей хорде и делит
ее на две равные части. Если они имеют только одну общую
точку, то эта точка лежит на линии центров, и обратно.
В самом деле, линия центров обеих окружностей является их
общей осью симметрии. Если две окружности пересекаются в некото-
некоторой точке, не лежащей на линии центров, то второй их общей точкой
будет точка, симметричная с первой относительно линии центров.
Если общая точка — единственная, то она необходимо должна
лежать на линии центров.
Черт. 71. Черт. 72.
Обратно, если имеется общая точка, лежащая на линии центров,
то эта точка будет единственной общей точкой. Действительно, вто-
вторая общая точка окружностей лежача бы либо на линии центров, либо
вне её: в первом случае обе окружности имели бы общий диаметр, во
втором случае существовала бы и третья точка пересечения. В обоих
случаях окружности совпадали бы между собой.
69. Говорят, что две кривые касаются друг друга, если они
имеют общую касательную в их общей точке.
На основании предыдущей теоремы это определение в случае двух
окружностей сводится к следующему:
Две окружности касаются друг друга, если они имеют только
одну общую точку, потому что общая точка, через которую прохо-
проходит общая касательная к окружностям, необходимо является точкой
линии центров, и обратно (п. 58, следствие).
70. Пусть О, О' — центры двух окружностей, радиусы которых
/?, /?'; предположим для определённости, что R' S R.
При этом могут иметь место следующие пять случаев:
1°. 00' >/? + /?' (черт. 71).
Предположим, что М — точка, лежащая на окружности О' или
внутри её, так что O'M^==R'. Тогда (на основании п. 26, следствие)
будем иметь: ОМ ^00'— O'Af>/?-f#' — O'M >/?.
74
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Таким образом, всякая точка, взятая внутри или на второй окруж-
окружности, является внешней по отношению к первой, а всякая точка вну-
внутри или на первой окружности — внешней по отношению ко второй.
Две окружности, как говорят, расположены одна вне другой.
2°. 00' ^R-\- R'. В таком случае 00' можно рассматривать как
сумму двух отрезков ОА и О'А (черт. 72), соответственно равных R
и R'. Точка А — общая; кроме того, ко всякой другой точке можно
применить предыдущие рассуждения. Следовательно, окружности ка-
касаются друг друга внешним образом.
Черт. 73.
Черт. 74.
3°. /?-|-/?'^>ОО'^>/?—R'. В этом случае R заключается между
суммой и разностью двух отрезков 00' и R'.
Таким образом, из двух точек А и В, в которых окружность О
пересекает линию центров, одна внешняя, а другая — внутренняя отно-
относительно окружности О' (черт. 73); отсюда следует, что окружность О,
представляющая собою линию, идущую из точки А в точку В, встре-
встретит вторую окружность в точке, отличной от Л и В, т. е. в точке,
не лежащей на линии центров. Следовательно, обе окружности имеют
две общие точки. Окружности называются пересекающимися.
4°. 00'= R — R'. В этом случае 00' можно рассматривать как
разность двух отрезков ОА и О'А (черт. 74), соответственно равных
R и /?'. Точка А их линии центров — общая, так что окружности
касаются.
Пусть М—точка, лежащая на окружности О' или внутри этой
окружности. Мы будем иметь
-^ОО' + R'',
т. е. O/Wf§/?.
Круг О' целиком, за исключением только точки А, находится
в этом случае внутри круга О. Окружности касаются друг друга
внутренним образом.
5°. 00' </? — /?' (черт. 75). Пусть снова М — точка, находя-
находящаяся внутри или на окружности О'.
ГЛАВА I». ПЕРЕСЕЧЕНИЕ ДВУХ ОКРУЖНОСТЕЙ 75
Тогда пол)чим:
ОМ § 00' + О'М <i 00' 4- R' < R-
Следовательно, круг О' полностью находится внутри круга О.
Две окружности лежат одна внутри другой.
71. Перечисленные выше случаи охватывают все возможности.
Отсюда следует, что предложения, обратные предыдущим заключениям,
также справедливы. Например, если две окружности пересекаются, то
расстояние их центров заключается между суммой радиусов и их раз-
разностью; действительно, если бы это расстояние было больше суммы
радиусов, то окружности лежали бы одна вне
другой; если бы это расстояние было равно той
же сумме, то обе окружности касались бы друг
друга внешним образом и т. д.
Впрочем, каждое из этих положений можно
доказывать и непосредственно. Так, в случае пе-
пересекающихся окружностей точка пересечения
образует с двумя центрами треугольник, и те-
теоремы п. 26 приводят к предыдущему заключению.
Итак, мы можем сформулировать следующую
теорему: Черт 75.
Теорема. 1°. Если две окружности рас-
расположены одна вне другой, то расстояние
между их центрами больше суммы радиусов, и обратно.
2°. Если они касаются друг друга внешним образом, то рас-
расстояние между их центрами равно сумме радиусов, и обратно.
3°. Если они пересекаются, то расстояние между их центрами
заключается между суммой радиусов и их разностью, и обратно.
4°. Если они касаются друг друга внутренним образом, то
расстояние между их центрами равно разности радиусов, и об-
обратно.
5°. Если одна окружность лежит внутри другой, то расстоя-
расстояние между их центрами меньше разности радиусов, и обратно.
Можно сказать ещё и так: две окружности находятся одна вне
другой, одна внутри другой, пересекаются или касаются друг
друга, смотря по тому, отсекают ли они на линии центров
отрезки, из которых один лежит вне другого, внутри другого
или один частично перекрывает другой, или, наконец, оба отрезка
имеют общий конец.
72. Если две окружности, вначале пересекающиеся, изменяются
таким образом, что становятся касательными в точке А, то их точки
пересечения неограниченно приближаются одна к другой и к точке А
(см. упр. 55).
Поэтому, как и выше (п. 67), говорят, что две окружности, ка-
касающиеся друг друга, имеют две общие точки, слившиеся между
собой.
76 Книга вторая, окружность
УПРАЖНЕНИЯ.
55. Пусть О—центр окружности радиуса /?; О' — центр другой окруж-
окружности радиуса /?', которая пересекает'первую окружность; А— одна
из точек, в которых прямая 00' пересекает "окружность О; В — произ-
произвольная точка, взятая на этой же самой окружности, и в частном случае
сколь угодно близко от А
Показать, что:
1) в том случае, когда точка О' лежит на продолжении отрезка ОА за
точку А, одна из точек пересечения обеих окружностей лежит на мень-
меньшей'дуге АВ, если разность /?+/?' — ОО' меньше ОВ-\-О'В — 00';
2) в том случае, когда точка О' лежит на самом отрезке ОА, то же
обстоятельство имеет место, если разность ОО' — (/?—/?') меньше разно-
разности О.О' — (ОВ—О'В);
3) в том случае, когда точка О' лежит на продолжении отрезка ОА за
точку О, то же" обстоятельство имеет место, если разность ОО' — (/?' — 7?)
меньше разности ОО',— Ю'В — ОВ).
56. Найти наименьший и наибольший отрезки, которые можно прове-
провести между двумя окружностями.
57. Найти геометрическое место центров окружностей данного ради-
радиуса, касающихся данной окружности.
58. Если через точку прикосновения двух касающихся окружностей
провести произвольную прямую, то она пересечёт обе окружности в двух
других точках, таких, что радиусы, проьелённые в эти точки, параллельны
между собой (доказать).
59. Две окружности, касающиеся друг друга внутренним образом,
остаются касающимися друг друга, если, не изменяя положения центров,
увеличить или уменьшить оба радикса на одну и ту же величину (доказать,.
Две окружности, касающиеся друг друга внешним образом, остаются
касающимися друг друга, если, не изменяя положения центров, уменьшить
один из радиусов и увеличить другой на ту же самую величину (доказать;.
ГЛАВА IV.
СВОЙСТВА ВПИСАННОГО УГЛА.
73. Углом, вписанным в окружность, называется угол, образован-
образованный двумя хордами, имеющими общий конец; таким образом, вписан-
вписанный угол есть угол, вершина которого находится на окружности.
Теорема. Всякий вписанный в окружность угол измеряется
половиной дуги, заключённой между его сторонами.
Он равен половине центрального угла, заключающего ту же
дугу.
Заметим, что первая часть этой теоремы предполагает соглашение,
установленное в п. 17 (следствиеI).
Мы будем различать три случая:
') Вторая часть имеет пока смысл только тогда, когда дуга, заключён-
заключённая между сторонами угла, меньше полуокружности (п. 13), следовательно,
когда вписанный угол меньше 90°, т. е. прямого угла.
Однако в тригонометрии приходится рассматривать (см. учебники три-
тригонометрии) центральные углы, превосходящие 180°; это позволяет выска-
высказать теорему, приведённую в тексте, для всех случаев.
глава iv. свойства вписанного угла 77
*
Первый случай. Одна из сторон вписанного угла проходит
через центр.
Пусть /_ВАС — вписанный угол (черт. 76), сторона которого АС
проходит через центр. Соединим В с О. Мы образуем, таким образом,
равнобедренный треугольник ОАВ, в котором углы А и В равны.
Внешний угол ВОС этого треугольника равен сумме
следовательно, равен удвоенному углу А.
Так как угол ВОС измеряется дугой ВС,
то угол ВАС измеряется половиной той же
дуги.
Второй случай. Центр находится
внутри вписанного угла.
Пусть j/_BAD—вписанный угол (черт.
76). Прлведя прямую АО, которая пере-
пересечёт окружность в точке С, мы разби-
разбиваем вписанный угол на две части:
j/_BAC, j/_CADs для каждой из которнх
наша теорема уже доказана j 1-й случай).
Таким образом (в соответствии с п. 18),
имеем:
= у дуги ВС, ^_CAD=±- дуги CD;
складывая, получим:
= y дуги BD.
Третий случай. Центр находится вне вписанного угла.
Пусть j/_ ЕАВ — вписанный угол (черт. 76). Проводя опять
диаметр АС, мы сможем написать:
= ^ дуги ВС, ^/ЕАС = ^ ДУГИ ЕС>
откуда, вычитая,
/^ЕАВ=~ дуги ЕВ.
Следствия: 1. Все углы, вписанные в одну и ту же дугу окруж-
окружности, равны как имеющие одну и ту же меру.
II. Угол, вписанный в полуокружность, — прямой как измеряю-
измеряющийся четвертью окружности.
74. Теорема. Угол, образованный касательной и хордой, вы-
выходящей из точки касания, измеряется половиной дуги, отсекаемой
этой хордой.
Угол ВАТ, образованный касательной AT и хордой АВ (черт. 77),
можно рассматривать как предельное положение угла, образованного
хордой АВ с хордой АА', когда точка А' безгранично приближается
к точке А.
78
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Впрочем, доказательство, данное для третьего случая предыдущей
теоремы, применимо и в данном случае; равенство /_ЕАС^ — дуги ЕС
должно быть просто заменено равенством /_ ТАС= — дуги АС,
Черт. 78.
которое вытекает из того, что угол ТАС — прямой, а дуга АС равна
полуокружности.
75. Теорема. Угол, образованный двумя секущими, пересекаю-
пересекающимися внутри окружности, измеряется полусуммою дуг, заклю-
заключающихся одна — между его сторонами,
другая — между их продолжениями.
Пусть продолжения сторон угла ВАС
(черт. 78) пересекают окружность в точ-
точках В' и С". Соединим В с С'. Углы С и В
измеряются соответственно дугами ВС и В'С
Но эти два угла в сумме составляют угол А,
внешний для треугольника ABC.
76. Теорема. Угол, образованный двумя
секущими, пересекающимися вне окружно-
окружности, измеряется полуразностью дуг, за-
заключённых между его сторонами.
Пусть угол ВАС (черт. 79) образован
секущими АВ'В, АС'С. Проведём опять ВС'.
Угол ВС'С — внешний по отношению к тре-
треугольнику ABC,— равен сумме / А -\~ / В.
Следовательно, угол А можно вычислить как
разность ^/ ВСС — ^/ В; это доказывает
теорему, так как угол ВС'С заключает дугу
ВС, а угол В — дугу ВС.
Примечание. Если одну из секущих, например АВ'В, заменить
касательной AT (черт. 80), то теорема и её доказательство имеют
место без всяких изменений, при условии, что точка Т одновременно
играет роль точки В и точки В1, одним словом, при допущении, что
В
Черт. 79.
ГЛАВА IV. СВОЙСТВА ВПИСАННОГО УГЛА
касательная имеет с окружностью две общие точки, сливигиеся в
точке Т, в согласии с условием п. 67.
77. Теорема. Геометрическое место точек, расположенных по
одну сторону от прямой, из которых данный отрезок этой пря-
прямой виден под данным углом, есть дуга окружности, имеющая
своими концами концы данного отрезка.
Пусть АВ— данный Отрезок прямой; М—точка искомого геомет-
геометрического места'), иначе говоря, такая точка, что угол АМВ равен
данному углу (черт. 81). Если через точки А, М
и В провести дугу окружности, ограниченную
точками А и В, то всякая точка этой дуги
принадлежит искомому геометрическому месту,
так как угол АМ'В равен углу АМВ (п. 73).
Напротив, всякая другая точка /V-плоскости (рас-
(расположенная с той же стороны от прямой АВ)
лежит или внутри или вне окружности, кото-
которую мы только что провели. В первом случае
угол ANB больше данного угла (п. 75); во
втором случае меньше его (п. 76), и, следо-
следовательно, точка N не будет точкой искомого гео-
геометрического места, что и требовалось доказать.
Построенная таким образом дуга называется
дугой, вмещающей данный угол и опирающейся
на отрезок АВ.
Если бы мы отказались от условия, чтобы
точки искомого геометрического места находи-
находились с определённой стороны от АВ, то ясно, что геометрическое
место точек состояло бы из двух дуг, сим-
симметричных друг с другом относительно АВ.
78. Если данный угол — прямой, преды-
предыдущая формулировка, в соединении со след-
следствием II п. 73,показывает нам, что геометриче-
геометрическое место точек, из которых данный
отрезок виден под прямым углом, есть
окружность, для которой этот отрезок
служит диаметром.
Это вытекает также из двух следствий
п. 48.
Ъ
Черт. 81.
79. Четыре произвольно взятые точки вообще не будут лежать
на одной окружности, потому что три из них определяют окружность,
которая, в общем случае, не пройдет через четвёртую точку. Усло-
Условие, при котором четыре точки лежат на одной окружности, даёт нам
следующая теорема: #
') Такие точки несомненно существуют. Мы получим одну из них,
проведя через точки А и В прямые, параллельные сторонам некоторого
угла, равного данному углу, и выбирая ту или другую из двух новых вер-
Шин построенного таким образом параллелограма.
80
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Теорема. Во всяком выпуклом четырёхугольнике, вписанном в
окружность, противоположные углы — пополнительные.
Во вписанном четырёхугольнике ABCD (черт. 82) угол А изме-
измеряется половиной дуги BCD; угол С измеряется половиной дуги BAD.
Дуги BCD и BAD составляют в сумме полную окружность; поэтому
сумма ?А-\-? С равна центральному углу, который соответствует
полуокружности, т. е. равна двум прямым.
80. Обратная теорема. Если в выпуклом четырёхугольнике
противоположные углы пополнительные, то четырехугольник
может быть вписан в окружность.
Пусть в четырёхугольнике ABCD (черт. 82)
углы А и С — пополнительные. Дуга BD
окружности BAD, не содержащая точки А,
является геометрическим местом точек, из
которых отрезок BD виден под постоянным
углом (п. 77), пополнительным к углу А
(п. 79). Эта дуга проходит, следовательно,
через точку С.
Черт. 82. 81. Приме ч а ни е. Во всяком четырёх-
четырёхугольнике можно рассматривать четыре угла
/_А, /_В, /_С, /_D, и далее, проведя диагонали АС и BD, ещё
восемь углов, которые обозначены цифрами с / по 8 на чертеже 83.
Если четырёхугольник вписанный, то:
1) ^/Л и ^_С — пополнительные;
2) ^_ В и ^_ D — пополнительные;
3) ^_1 и ^_4 равны (как вписанные в одну и ту же дугу);
точно так же:
4) /5 и ^/_8 равны;
5) 2 2 и /__ 7 равны;
6) /_S v\ /_6 равны.
Обратно, если какое-либо одно из этих условий имеет место, то
четырёхугольник — вписанный (пп. 77, 80).
Таким образом, каждое из условий 1, 2, 3, 4, 5, 6 влечёт за
собою все остальные.
82. Условия 1 и 2; указанные в предыдущем примечании, могут
быть представлены в форме, которая их сближает с условиями 3—6.
Заметим прежде всего, что точки А и В (черт. 83) находятся
с одной и той же стороны от CD; следовательно, треугольники CDA
и CDB имеют одно и то же направление вращения, так что равные
углы DAC и DBC имеют одинаковое направление. То же самое имеет
место для углов АСВ, ADB и т. д. Напротив, углы DAB и DCB
имеют противоположное направление, так как А и С находятся по
разные стороны от BD. Продолжим DA за точку А по направлению
АХ; таким образом получается угол ХАВ одного направления с уг-
углом DCB. Мы видим, что эти два одинаково направленных угла
равны, если углы DAB и DCB — пополнительные, и мы приходим к
следующему заключению
ГЛАВА IV. СВОЙСТВА ВПИСАННОГО УГЛА 81
Если четыре точка А, В, С, D лежат на одной окружности,
дао углы одного направления, образованные, с одной стороны, пря-
прямыми АС и AD и, с другой стороны, прямыми ВС и BD, равны
между собою; кроме того, при этом выполняются все те усло-
условия, которые получаются из этого последнего условия любой
перестановкой букв А, В, С и D.
Обратно, любое из шести получаемых, таким образом, условий
влечёт за собою возможность вписать данный
четырёхугольник в окружность и, следовательно,
выполнение пяти остальных условий.
82а. Формулировка п. 77 может быть точно
так же заменена следующей: геометрическое
место вершин равных и одинаково направлен-
направленных углов, стороны которых (или их продолже-
продолжения) проходят через две данные точки, есть
окружность, проходящая через эти две точки.
Так как всякая окружность может быть по-
получена таким путём, то эту формулировку можно е^т'
рассматривать как новое определение окружности, которое равно-
равносильно первоначальному и может в случае надобности его заменить.
УПРАЖНЕНИЯ.
60. Найти геометрическое место середин хорд окружности, которые
проходят через заданную точку.
61. На каждом из радиусов окружности откладывают от центра отре-
отрезок, равный расстоянию конца этого радиуса до одного определённого
диаметра. Найти геометрическое место концов построенных таким образом
отрезков.
62. Дана окружность и её хорда АВ. Пусть CD—подвижная хорда той
же окружности, имеющая постоянную длину. Найти:
1) геометрическое место точек пересечения / прямых АС и BD;
2) геометрическое место точек пересечения К прямых AD и ВС;
3) геометрическое место центров окружностей, описанных около
.треугольников /CD и KCD. Показать, что эти два геометрических места
соответственно равны двум предыдущим.
63. Пусть А и В — заданные "точки некоторой окружности и М —
переменная точка той же окружности. На продолжении отрезка AM от-
откладывают отрезок MN=MB. Найти геометрическое место точек N.
64. Показать, что прямая, соединяющая середины дуг АВ и АС, где
А, В и С—три точки одной окружности, отсекает на хордах АВ и АС
равные отрезки, считая от точки А.
65. Если через точки пересечения А и В двух окружностей провести
две произвольные секущие, то хорды, соединяющие между собою новые
точки пересечения этих прямых с двумя окружностями, параллельны
(доказать).
66. Биссектрисы углов любого четырёхугольника образуют четырёх-
четырёхугольник, который может быть вписан в окружность. То же" имеет место
для биссектрис внешних углов (доказать).
67. Через середину С дуги АВ проводят две произвольные прямые,
которые пересекают окружность в точках D, Е и хорду АВ в точках F, G.
Доказать, что четырёхугольнлк DEGF может быть вписан в круг.
о Элементарная геометрия
82 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
68. Дана окружность и на ней определённая точка Р, далее дана пря-
прямая и на этой прямоч определённая точка Q. Через точки Р и Q проводят
произвольную окружность, которая второй раз пересекает данную окруж-
окружность в точке R, а чанную прямую — в Лчке 5. Доказать, что прямая RS
пересечёт данную окружность в одной и той же точке, как бы ни была
выбрана вторая окружность.
69. Две окружности пересекаются в точках А и В. Через точку А
проведена произвольная секущая, которая второй раз пересекает окруж-
окружности в точках С и С. Показать, что хорда СО видна из то «и В под
одним и тем же углом, как бы ни была выбрана секущая, и что этот угол
равен углу и.ежду радиусами, проведёнными в точки С и С'.
Через точку А проведена вторая секущая, пересекающая окружности
в точках D и D'. Показать, что угол между хордами CD, CD' равен тому
же углу или углу, ему пополнительному.
Как изменится эта формулировка, когда обе секущие сольются?
70. Во всяком треугольнике точки, симметричные с точкой пересечения
высот относительно трёх сторон треугольника, лежат на описанной
окружности (доказать).
71. Доказать, что высоты треугольника являются биссектрисами углов
треугольника, образованного их основаниями.
Применить метод п. 82 к четырёхугольникам, образованным двумя
сторонами и двумя высотами, доказав, что эти четырёхугольники вписан-
вписанные, и используя вытекающие отсюда угловые свойства.
Тот же путь доказательства применим в ряде других вопросов, и в
частности в следующем 1):
72. Основания перпендикуляров, опущенных из любой точки окруж-
окружности на три стороны вписанного треугольника, лежат на одной прямой
(прямая Симеона).
Обратно, если основания перпендикуляров, опущенных из какой-либо
точки плоскости треугольника на три его стороны, лежат на прямой ли-
линии, то эта точка лежит на описанной окружности (доказать).
ГЛАВА V. f
ПОСТРОЕНИЯ.
83. Под геометрическими построениями понимают построения,
производимые при помощи линейки и циркуля.
Эти построения теоретически абсолютно точны. Практически эти
построения действительно очень точны, но тем не менее и они, как
и все другие построения, дают поводы к ошибкам (например, вслед-
вследствие того, что линии, проводимые карандашом, имеют толщину).
Линейка есть инструмент, служащий для того, чтобы проводить
прямые линии. Для того чтобы линейка была правильной, необходимо,
чтобы оба её края были прямолинейны. Чтобы убедиться, выполнено
ли это условие, пользуются самим определением прямой линии. Про-
Проводят сначала линию вдоль по краю линейки (черт. 84); затем повёр-
повёртывают линейку и прикладывают её тем же краем с другой стороны
к проведённой линии. Если линейка достаточно верна, то вторая
!) То же самое рассуждение применимо и в нескольких задачах,
помещённых далее — На стр. 104—106.
ГЛАВА V. ПОСТРОЕНИЯ
83
V
\
линия, проведённая вдоль края линейки в её новом положении, должна
совпадать с первоначальной.
Циркуль состоит из двух заострённых стержней, соединённых
между собой шарниром. Растворение циркуля есть расстояние между
^___ остриями; инструмент позволяет пе-
1 ° ~~\ реносить отрезки или описывать из
i •_• ,_ , произвольного центра окружность,
1 " ' имеющую радиусом это расстояние.
Черт. 84. 84. Кроме двух инструментов, о
которых мы говорили, на практике
употребляются ещё угольник и транспортир.
Угольник — это прямоугольный треугольник, сделанный из дерева
или другого материала. Хороший угольник должен удовлетворять
двум условиям: 1) стороны его долж-
должны быть прямолинейны; 2) угол уголь-
угольника должен быть прямой.
Первое из этих условий прове-
проверяется так же, как для линейки;
угольники, которыми приходится поль-
пользоваться на практике, обычно удов-
удовлетворяют ему с достаточной сте- | ° |
пенью точности. Чтобы проверить,
выполняется ли второе, прикладывают Черт. 85.
угольник к краю лицейки (черт. 85)
и проводят прямую вдоль того края, который должен быть пер-
перпендикулярен к линейке. Прикладывая затем угольник в обратном
направлении, как показано на чертеже, проводят снова прямую,
которая должна совпадать с первой. Это второе усло-
условие часто выполняется только приближённо; поэтому
второе условие и не предполагается в точных геомет-
геометрических построениях.
Транспортир служит для измерения углов в гра-
градусах. Он обыкновенно состоит из рогового или мед-
медного полукруга, разделённого на 180 частей. При
~g этом деления могут быть нанесены только прибли-
приближённо; транспортир, будучи полезен на практике, не
является геометрическим инструментом.
85. Построение 1. (Первое основное построе-
построение.) Построить прямую, перпендикулярную к
отрезку АВ и проходящую через его середину
(черт. 86).
Черт. 86. Эта прямая есть геометрическое место точек, оди-
одинаково удалённых от точек А и В (п. 33). Поэтому,
если из точек А и В, как из центров, описать равные окружности
радиусом, достаточно большим для того, чтобы они пересекались,
то точки пересечения будут принадлежать искомому перпендикуляру;
остаётся только соединить эти две точки.
6* '
84
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
К этому построению приводятся следующие два:
Построение 2. Через данную точку провести перпендикуляр
к данной прямой.
Из данной точки О (черт. 87 или 88), как из центра, описывают
окружность, которая пересекает данную прямую в двух точках А и В.
Перпендикуляр, восставленный в середине АВ, проходит через точку О,
\
о ]в
Черт. 87.
\
X
Д
\
\
/
0
k
в/
/ У
Черт. 88.
так как О А = ОБ; следовательно, этот перпендикуляр и есть искомая
прямая
Если точка О находится вне прямой, то можно принять расстояние
ОА за общий радиус тех окружностей, которые мы проводим
(построение \), чтобы построить перпендикуляр, в середине АВ: нам
не придётся, таким образом, менять растворение цир-
циркуля. Две окружности пересекаются в точке О и в
точке О', симметричной с первой относительно прямой
АВ (черт. 88). Это упрощение неприменимо, когда
точка О находится на прямой, так как в этом
случае она совпала бы с О'; оно нецелесообразно,
если точка О расположена очень близко от прямой,
потому что обе точки О и О', будучи очень близкими
одна к другой, не определяют достаточно точно
прямой, которая их соединяет.
Построение 3. Построить биссектрису данного
угла АОВ (черт. 89).
Отложим на сторонах угла два равных отрез-
отрезка О А и ОБ так, чтобы образовался равнобедренный
треугольник. Биссектриса данного угла является не
чем иным, как перпендикуляром в середине АВ (п. 23).
В отношении проведения дуг возможно то же самое упрощение,
как и выше.
86. Построение 4. (Второе основное построение.) Построить
треугольник по трем сторонам.
Взяв отрезок ВС, равный первой стороне (черт. 90), описываем
из точек В а С, как из центров, две окружности, которые имеют своими
радиусами соответственно две другие стороны; точка их пересечения А
Черт. 89.
ГЛАВА V. ПОСТРОЕНИЯ 85
даёт третью вершину треугольника. Таким образом, эта вершина
имеет два возможных положения, так как окружности пересекаются
в двух точках, но соответствующие треугольники, будучи симметрич-
симметричными друг другу относительно ВС, между собою равны.
Условия возможности построения. Чтобы две окруж-
окружности пересекались, необходимо и достаточно (пп. 70, 71), чтобы
одна сторона была заключена между суммой двух других и их раз-
разностью или (п. 26) чтобы
каждая сторона была меньше
суммы двух других сторон.
Когда известны длины
сторон, достаточно убедить-
убедиться, что наибольшая сторона
меньше суммы двух других. ^ ^ 01 '
Построение 5. Через Черт. 90.
точку, взятую на прямой,
провести другую прямую, образующую с данной угол, равный
данному углу.
На сторонах данного угла О берём две произвольные точки А и В
и строим треугольник, равный ОАВ, откладывая сторону, соответст-
соответствующую ОА, на данной прямой от данной точки. На практике
треугольник ОАВ берут равнобедренным, чтобы иметь только два
различных растворения циркуля.
Построение 6. Зная два угла треугольника, найти третий.
Строим два прилежащих друг к другу угла, равных соответственно
двум данным углам, и продолжаем одну из необщих сторон; получаем
третий угол, пополнительный для суммы двух первых, иначе говоря,
равный искомому третьему углу треугольника.
Условие возможности. Сумма двух данных углов должна
быть меньше двух прямых.
Построение 7. Построить треугольник по двум сторонам
и углу между ними.
На сторонах угла, равного данному углу, откладываем данные
стороны.
Построение 8. Построить треугольник по стороне и двум
углам1).
Прежде всего, зная два угла, мы знаем и третий (построение 6)
и в частности — оба угла, прилежащие к данной стороне; их мы
и строим при концах этой стороны (построение 5).
Условие возможности то же, что и для построения 6.
87. Построение 9. Построить треугольник по двум сторонам
и углу, противолежащему одной из них.
Пусть в треугольнике ABC даны угол А и стороны а и Ь, про-
противолежащие соответственно углам А и В.
') При этом предполагается, что для каждого из двух данных углов
указано, прилежит ли он к данной стороне или нет. Прим. ред. перевода.
86
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Построив угол, равный углу А (черт. 91), отложим на одной из
его сторон отрезок АС, равный Ь. Точка С, таким образом, опреде-
определена; точка В должна находиться на окружности, имеющей точку С
своим центром и отрезок а — радиусом. Пересечение этой окружности
со второй стороной угла А и даст искомую вершину В, положение
которой окончательно определяет треугольник.
Исследование. Задача будет иметь решение во всех случаях,
когда окружность, о которой мы говорим, пересечёт полупрямую АХ
(черт. 91) — вторую сторону угла А.
Из точки С опустим перпендикуляр
СИ на АХ.
1 °. Если СИ ^> а, окружность. не пе-
пересекает прямой, и задача невозможна.
2°. Если СИ <^ а, окружность пере-
пересекает бесконечную прямую АХ в двух
точках В', В". Необходимо узнать,
находятся ли эти точки на полупрямой
АХ или но другую сторону от точки А.
Мы будем различать два случая:
1) Угол А — острый. В этом случае точка И, середина В'В'',
расположена на полупрямой АХ. Следовательно, то же самое имеет
место, по крайней мере, для одной из двух точек В" и В', так что
всегда имеется, по крайней мере, одно решение. Имеется и второе
решение, если вторая из этих точек лежит между точками А и И,
а это будет в том и только в том
случае, когда а<^Ь.
2) Угол А — тупой (черт. 92). При
этом точка И не будет находиться
на полупрямой АХ; следовательно, по
крайней мере одна из точек В", В'
не будет отвечать поставленному усло-
условию: имеется самое большее одно ре-
решение. Это решение существует, если
вторая точка более удалена от И, чем точка А, а это будет в том
и только в том случае, когда а^> Ь.
87а. Наконец, если угол А — прямой, задача формулируется так:
Построить прямоугольный треугольник по гипотенузе и ка-
катету. Решение — единственное, если данная гипотенуза больше дан-
данного катета.
Примечание. Из всего предыдущего следует такая теорема:
Теорема. Если две стороны оиного треугольника соответственно
равны двум сторонам другого треугольника, и угол первого треугольника,
лежащий против одной из этих сторон, равен углу второго треугольника.
Лежащему против соответственной стороны, то углы, противолежащие
вторым равным сторонам, или равны или пополнительны. Первый слу-
случай (который влечёт за собой равенство треугольников) имеет место
всегда, если углы, равенство которых дано, прямые или тупые.
ГЛАВА V. ПОСТРОЕНИЯ 87
88. Построение 10. Через данную точку провести прямую,
параллельную данной прямой.
Взяв на данной прямой две произвольные точки А и В (черт. 93),
я провожу из данной точки О, как из центра, окружность радиусом
АВ, а из точки В, как из центра, — окружность радиусом О А. Эти
две линии пересекаются (не с той стороны от О В, где находится
точка А) в некоторой точке С, которая принадлежит искомой прямой,
потому что четырёхугольник ОАВС, в котором противоположные
стороны равны, параллелограм.
Предпочтительно выбирать АВ=ОА, так чтобы все проведённые
окружности имели один и тот же радиус.
89. Построения 2 и 10 могут быть осуществлены с помощью
угольника.
Черт. 93. Черт. 94.
Чтобы выполнить построение 2: через данную точку провести
перпендикуляр к данной прямой, прикладывают линейку одним краем
к данной прямой и заставляют скользить вдоль этого края линейки
один из катетов угольника до тех пор, пока второй его кагет не прой-
пройдёт через данную точку (черт. 94) и, следовательно, будет искомым
перпендикуляром.
Это построение предполагает выполненным условие, вообще говоря,
недостаточно хорошо выполняющееся на практике, что угол угольника
прямой; поэтому оно не применяется в тех чертежах, где требуется
большая точность.
Чтобы выполнить построение 10: через данную точку провести
прямую, параллельную данной прямой, сначала совмещают гипоте-
гипотенузу угольника с данной прямой (черт. 95). Прикладывая затем ли-
линейку к одному из катетов и удерживая её в этом положении, застав-
заставляют скользить угольник вдоль линейки до тех пор, пока край
угольника, совпадавший первоначально с данной прямой, не пройдёт
через данную точку.
Построенная таким образом прямая и данная параллельны между
собой, так как они образуют с одной и той же секущей (край
линейки) равные соответственные углы (углы А и АЛ на чертеже).
Эго построение предполагает только, что края инсйки и уголь-
угольника прямолинейны. Оно не менее точно, чем построение, выполняемое
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
при помощи циркуля, но проще его и потому часто употребляется
вместо него на практике.
90. Построение 11. Разделить дугу окружности на две рав-
равные части. .
Проводим через середину хорды, стягивающей эту дугу, прямую,
к ней перпендикулярную (построение 1).
Построение 12. Построить окружность, проходящую через три
данные точки, А, В, С, не лежащие на одной прямой.
Строим перпендикуляры в серединах отрезков, попарно соединяю-
соединяющих данные три точки; точка их пересечения даёт центр искомой ок-
окружности О, О А — её радиус.
Полученная таким образом
окружность называется описан-
описанной около треугольника, обра-
образованного тремя точками.
Вообще, многоугольник (или
ломаная линия) называется впи-
вписанным в некоторую линию, а
эта последняя — описанной
около него, если все вершины
многоугольника находятся на
этой линии.
Примечание. Если бы
три точки А, В и С лежали
на одной прямой, то окруж-
ерт- ность не существовала бы; но
мы должны были бы считать, что она Заменяется прямой линией ABC.
В самом деле, прямую линию можно рассматривать как пре-
предельный случай окружности, центр которой безгранично удаляется.
Действительно, прямая АВ есть геометрическое
место точек, из которых отрезок АВ виден
под постоянным углом, равным нулю или двум
прямым. Возможно, кроме того, и непосредствен-
непосредственно доказать, что окружность, проходящая через
две точки А и В, центр которой безгранично
удаляется, имеет своим пределом прямую линию
АВ (определив предварительно надлежащим
образом, как следует понимать это выраже-
выражение).
Построение 13. Построить окружность,
зная две точки А и В и касательную AT в одной из них.
Центр О будет точкой пересечения перпендикуляра к отрезку АВ,
проходящего через его середину, и перпендикуляра к AT в точке А.
Действительно, окружность с центром О и радиусом ОА будет ка-
касаться AT в точке А и пройдёт через точку В (черт. 96).
Примечание. Это построение представляет собою предельный
случай предыдущего на основании общего определения касательной (п. 59).
ГЛАВА V. nOCTPOFHHH
89
Построение 14. Построить дугу, имеющую своей хордой данный
отрезок и вмещающую данный угол.
Пусть АВ— данный отрезок. Строим одну из точек М искомого
геометрического места (см. сноску п. 77) и проводим окружность АМВ'').
Иначе: заметим, что касательная в точке А к искомой окружности об-
образует с отрезком АВ данный угол (пп. 73 и 74); это позволяет по-
построить касательную в точке А (построение 5) и свести построение
к предыдущему.
91. Построение 15. Провести касательную в данной точке ок-
окружности.
Строим перпендикуляр к радиусу в точке касания.
Построение 16. Построить касательную к окружности, парал-
параллельную данному направлению.
Диаметр, проходящий через точку касания, должен быть перпен-
перпендикулярен к данному направлению; так как этот диаметр пересекает
окружность в двух точ-
точках, то задача имеЛ два
решения.
Построение 17. Про-
Провести касательную к
окружности из какой-ли-
какой-либо точки, лежащей в её
плоскости.
Первый способ.
Пусть требуется из точки
А провести касательную
к окружности О (черт. 97).
Допустим прежде все-
всего, что задача решена,
и пусть Т— точка каса-
касания. Так как угол АТО—прямой, то точка Т
сти, имеющей своим диаметром отрезок О А.
Обратно, если точка Т данной окружности принадлежит окружно-
окружности, построенной на ОА как на диаметре, то касательная в точке Т
пройдёт через тСчку А, так как угол ОТ А — прямой.
Следовательно, точки 7", которые отвечают условию зацачи, будут
общими точками данной окружности и окружности, построенной на
отрезке ОА как на диаметре.
Второй способ. Пусть Т—снова искомая точка касания.
Построим на продолжении отрезка ОТ за точку Т отрезок ТО',
равный ОТ (черт. 98). Так как отрезок ТА перпендикулярен ОТ, то
точка О' симметрична с точкой О относительно AT, в силу чего
АО' = АО. Точка О' принадлежит, таким образом, окружности с цен-
центром А и радиусом ОА.
Черт. 97.
принадлежит окружно-
1) Так обозначается окружность, проходящая через точки А, М и В.
Прим. fed. перевода.
90
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Так как она принадлежит, кр.ше того, окружности, имеющей об-
общий центр с данной окружностью и удвоенный радиус, то она опре-
определится пересечением этих двух окружностей.
Обратно, если точка О' такова, что АО' = АО, то точка Т, се-
середина 00', есть точка прикосновения касательной, проведенной че-
через А к окружности с центром О и радиусом ОТ, в силу свойств
равнобедренного треугольника.
Исследование. Будем исходить, например, из второго способа
построения. Для существования реления необходимо, чтобы две ок-
окружности, определяющие точку
О', пересекались, иначе говоря
(п. 71), чтобы расстояние их
центров заключалось' между
суммой и разностью их радиу-
радиусов. Это даёт, если обозначить
через R радиус данной окруж-
ности:
A)
и, кроме того,
АО ^ АО — 2R,
или
~ АО
B)
C)
(смотря по тому, будет ли АО
больше или меньше 2R).
-Неравенства A) и B), оче-
очевидно, выполняются сами со-
собой. Неравенство C) может
быть записано в виде 2 АО 5? 2R
или АО ^R-
Черт. 98. Таким образом, задача не-
невозможна, если точка А нахо-
находится внутри окружности. Если точка А лежит вне окружности,
имеются два решения, так как окружности пересекаются.в двух точках.
Наконец, если точка А находится на окружности, то окружности,
которые определяют точку О', касаются друг друга, и имеется только
одно решение, касательная в точке А, или, скорее, два слившихся
в одно решения. Действительно, на основании сказанного ранее (п. 72),
если точка А неограниченно приближается к окружности, то обе точки
касания, а следовательно, и обе касательные, стремятся совпасть.
92. Теорема. Две касательные, проведенные к окружности из
одной точки, равны и образуют равные углы с диаметром, про-
проходящим через эту точку (черт. 99). Этот диаметр перпендику-
перпендикулярен к хорде, соединяющей точки касания.
Действительно, обе точки касания симметричны друг с другом от-
относительно ОА (черт. 99), так как они определяются пересечением
двух окружностей, имеющих центры на этой прямой (п. 68).
ГЛАВА V. ПОСТРОЕНИЯ
91
Черт. 99.
93. Построение 18. Построить общие касательные к двум дан-
данным окружностям. »
Пусть требуется построить общтш касательные к двум данным ок-
окружностям О и О', имеющим радиусы R и Я?'. Эти общие касательные
могут быть двоякого рода: они могут быть внешними (черт. 100), т. е.
такими, что обе окруж-
окружности лежат по одну сто-
сторону от касательной, тши
внутренними (черт. 101),
когда обе окружности
лежат по обе стороны от
касательной.
1°. Общие внеш-
внешние касательные.
Предположим, что задача
решена, и пусть АЛ' —
искомая касательная (черт.
100), А и А' —точки ка-
сантш, так что О А и О'А'
перпендт!кулярны к АА'.
Пусть через точку О' проведена прямая О'С, параллельная АА', до
пересечентщ с ОА в точке С. Эту точку С мы и собираемся найти.
С этой целью заметим, что четырёхугольник С АЛ'О' есть прямо-
прямоугольник, так что AC = Rr ti, следовательно, OC = R— R''1). Таким
образом, точка С принадле-
принадлежит окружности, которую мы
можем построить, так как
мы знаем её центр О и ра-
радиус, равный разности данных
радиусов.
Далее прямая СО' касает-
касается этой окружности, так как
угол ОСО' — прямой. Мы
приходим, таким образом, к
построению 17.
Поскольку точка С опре-
определена, продолжение радиу-
радиуса ОС даст точку А. Ка-
Касательная в точке А к окружности О является действительно общей
касательной, так как, опуская из точки О' на эту прямую перпенди-
перпендикуляр О'A' ti пользуясь равенством OC^R — R'. получим О'А' =
Черт. 100.
!) Мы предполагаем для определённости, что за окружность О принята
большая из двух окружностей Но это предположение, которое мы всегда
вправе сделать, в данном случае несущественно: если бы оно не было вы-
выполнено, то мы имели бы OC=R' — R.
92
КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Задача возможна только (п. 91), если OO'^R— R', иначе говоря
(п. 70), если окруусности лежат одна вне другой, касаются друг
друга внешним образом, пересекаются между собой или касаются
друг друга внутренним образом. В первых 'трёх случаях задача
имеет два решения, так как из точки О' можно провести две каса-
касательные к окружности ОС, в четвёртом случае — только одно реше-
решение, которое можно рассматривать как два слившихся решения, так
как обе касательные, проведённые из точки О' к окружности ОС, сли-
сливаются в одну.
2°. Общие внутренние касательные. Пусть В В' — общая
внутренняя касательная (черт. 101), В и В'—точки касания. Через
точку О' проведём
прямую O'D, параллель-
параллельную касательной, до
пересечения в точке D
с радиусом ОВ. Четы-
Четырёхугольник DBB'O' —
прямоугольник, так что
BD = R', и точка D
лежит на окружности с
центром О и радиусом
R-\-R'. Мы построим
эту окружность и через
точку О' проведём к ней
касательную. Когда
точка D таким образом
определена, пересече-
ние радиуса OD с дан-
данной окружностью О
определит точку В. Касательная в В есть общая касательная, как в
этом можно убедиться, повторяя первоначальное рассуждение в обрат-
обратной последовательности.
Задача возможна только, если 00' ^R-{-R', иначе говоря,.
если окружности расположены одна вне другой или касаются
друг друга внешним образом. В первом случае задача имеет два ре-
решения, во втором случае — одно решение (иначе говоря, два слив-
слившихся решения).
Итак:
Две окружности, лежащие одна вне другой, имеют две внешние
общие касательные и две внутренние.
Две окружности, касающиеся друг друга внешним образом, имеют
две общие внешние касательные и одну внутреннюю (касательную-
в точке их прикосновения).
Две пересекающиеся окружностинмеютдве общие внешние касательные.
Две окружности, касающиеся друг друга внутренним образом,
имеют одну общую внешнюю касательную (касательную в точке их
прикосновения).
Черт. 101.
ГЛАВА V. ПОСТРОЕНИЯ
93
лежащие одна внутри другой, не имеют общих
tnpj'x
Две окружности,
касательных.
94. Построение 19. Построить окружности, касающиеся
данных прямых.
Задача сводится к следующей: найти точки, одинаково отстоящие
от трёх прямых. Окружность, имеющая одну .из таких точек своим
центром и расстояние этой точки до каждой из трёх прямых — своим
радиусом, отвечает условиям задачи. Но геометрическое место точек,
одинаково отстоящих от двух пересекающихся прямых, состоит из
двух биссектрис углов, которые эти прямые образуют между собой.
Черт. 102.
Предположим сначала, что данные прямые попарно пересекаются и
не проходят через одну и ту же точку, так что они образуют тре-
треугольник (черт. 102); в этом треугольнике мы должны построить бис-
биссектрисы внутренних и внешних углов. Нам известно из предыдущего,
что: 1) биссектрисы внутренних углов пересекаются в одной точке,
2) биссектриса всякого внутреннего угла пересекается с биссектри-
биссектрисами внешних углов, к нему не прилежащих, в одной точке. Четыре
определённые таким образом точки (точка пересечения внутренних
биссектрис и три вершины треугольника, образованного биссектрисами
внешних углов) будут, следовательно, искомыми точками, и притом
единственными.
94 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Первая из окружностей, которые имеют центры в этих четырёх
точках, расположена внутри треугольника. Она называется вписанной
окружностью; вообще, кривая называется вписанной в многоугольник,
когда она касается всех его сторон. Три другие окружности, точно
так же касающиеся всех сторон треугольника, но лежащие вне тре-
треугольника, называются вневписаннылш; каждая из них расположена
внутри одного из углов треуголь-
треугольника, но отделена от вершины это-
— го угла противоположной сторо-
стороной, как это видно на чертеже.
Если три прямые пересекают-
пересекаются в одной точке, то в этом слу-
случае задача, собственно говоря, не
имеет решения, так как из одной
точки можно провести к окружно-
Черт. 103. сти только две касательные. Пре-
Предыдущее построение даёт круг,
обращающийся в точку — точку пересечения данных прямых.
Если две из прямых параллельны, а третья их пересекает (черт. 103),
то биссектрисы углов, образованных этой последней линией с двумя
первыми, попарно параллельны. В этом случае получаются только две
окружности, расположенные по обе стороны от секущей.
Наконец, если три данные прямые параллельны, решения вовсе не
существует, потому что к окружности можно провести только две ка-
касательные, параллельные данному направлению.
УПРАЖНЕНИЯ.
73. Пострсигь окружность данного радиуса:
1) проходящую через две данные точки;
2) проходящую через данную точку и касающуюся данной прямой;
3) касающуюся двух данных прямых;
4) касающуюся данной прямой и данной окружности.
74. Построить окружность, касающуюся данной прямой в данной точке
и в то же время касающуюся данной окружности.
75. Провести между двумя данными прямыми (или окружностями) отре-
отрезок данной длины и данного направления.
76. Провести к данной окружности касательную, на которой данная
прямая отсекает отрезок данной длины.
11. Построить треугольник, зная сторону, противолежащий угол и вы-
высоту (рассмотреть два' случая: когда данная высота опущена на данную сто-
сторону и ксгда данная высота опущена на другую сторону).
78. РаздеЛить отрезок на три равные части, пользуясь теоремой п. 56
о медгаиах треугольника.
79. Построить треугольник, зная:
1) две стороны и медиану (рассмотреть два случая, когда данная ме-
медиана выходит из середины одной из данных сторон и когда она выходит
из общей вершины этих сторон);
2) сторону и две медианы (два случая);
3) три медианы.
80. Построить треугольник, зная его сторону, высоту и медиану (пять
случаев).
глава v. построения 95
81. Построить треугольник, зная его угол, высоту и медиану (пять
случаев).
82. Построить треугольник по стороне, противолежащему углу и сумме
или разности двух других сторон.
83. Та же задача для случая, когда дай угол, прилежащий к данной стороне.
84. Построить треугольник по углу, высоте и периметру (два случая).
85. Построить треугольник по стороне, разности прилежащих углов и
по сумме или разности двух других сторон.
86. Построить биссектрису угла между двумя прямыми, считая, что
эти прямые невозможно продолжить до точки их пересечения (в пределах
чертежа).
Теоремы о касательных к окружности (п. 92).
87. В четырёхугольнике, описанном около окружности (и таком, что
окружность заключена внутри его), сумма двух противоположных сторон
равна сумме двух других сторон. Обратно, всякий выпуклый четырёхуголь-
четырёхугольник, в котором суммы противоположных сторон равны, может быть опи-
описан около окружности (доказать).
Если неизвестно, лежит ли окружность внутри данного описанного
четырёхугольника или нет, то всегда можно утверждать, что сумма двух
надлежащим образом выбранных сторон равна сумме двух других (доказать).
Рассмотреть обратную теорему.
88. Окружность, касающаяся трёх сторон выпуклого четырёхугольника
и расположенная с той же стороны от каждой из этих сторон, что и внут-
внутренняя область четырёхугольника, пересекает или не пересекает четвёр-
четвёртую сторону, в зависимости от того, будет ли сумма этой стороны и сто-
стороны, противоположной ей, больше или меньше суммы двух других сторон
(доказать).
88а. Если две точки лежат вне окружности, то прямая, их соединяю-
соединяющая, будет лежать вне окружности или её пересекать, смотря по тому,
будет ли расстояние между двумя точками заключено между суммой и
разностью касательных, проведённых к окружности из этих точек, или
нет (доказать).
89. Отрезок, отсекаемый двумя неподвижными касательными к окруж-
окружности на подвижной касательной, виден из центра под постоянным углом
(доказать).
Рассмотреть случай, когда обе неподвижные касательные параллельны
между собой.
90. Если две неподвижные касательные к окружности пересечены под-
подвижной касательной, точка касания которой находится на меньшей из двух
дуг, определяемых точками касания неподвижных касательных, то тре-
треугольник, образованный этими тремя касательными, имеет постоянный пери-
периметр (доказать).
Как изменится эта формулировка, когда подвижная касательная будет
иметь точку прикосновения на большей из двух дуг, образуемых непод-
неподвижными касательными?
90а. Если а, Ь, с — три стороны треугольника ЛВС (черт. 102); р—по-
р—полупериметр Bр = а-{-b-\~ с); D, Е, F—точки прикосновения вписанной
окружности; Оъ Еъ F^ D2, Е2, F2; Ьз, Е$, F%—точки прикосновения вне-
вписанных окружностей, лежащих соответственно внутри углов А, В, С,
то отрезки, отсекаемые этим точками прикосновения на сторонах, имеют
следующие величины:
АЕ= AF= CD2 = CE2 = BD3 = ВЕъ=р — а;
BF=BD= АЕ\ = AF% = СЕЛ = CDi—p — b;
CD=CE=BF1 = BD1 = AF2 = AEi=p —с;
АЕ} = AF) = BF2 = BDo = CD3 = СЕЬ = p.
91. Описать из вершин данного треугольника, как из центров, три
кружности, попарно касающиеся друг друга.
96 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
ГЛАВА VI.
ПЕРЕМЕЩЕНИЕ ФИГУР.
95. Мы определили выше (п. 20), какие две фигуры называются
равными и имеющими одинаковое направление вращения. Мы знаем
(п. 50), что если две точки одной из таких фигур совпадают с со-
соответственными им точками другой фигуры, то обе фигуры совпадают
между собой. Иначе говоря, нельзя поместить фигуру F, равную
данной фигуре F и имеющую с ней одинаковое направление враще-
вращения1), двумя различными способами так, чтобы две точки А' и В'
этой фигуры (соответственные двум данным точкам А и В фи-
фигуры F) имели наперёд заданное положение.
Мы можем также по этим данным (т. е. зная положение точек А'
и В', соответственных точкам А к В) определить точку С, соот-
соответствующую любой третьей данной точке С фи-
фигуры F.
В самом деле, для этого достаточно построить
треугольник А'В'С, равный треугольнику ABC (по-
(построение 4), выбирая то из двух возможных положе-
положений третьей вершины, которое соответствует двум
треугольникам, имеющим одинаковое направление вра-
Я ** щения.
Черт. 104. Так как такое построение можно выполнить для
каждой точки первой фигуры, то мы имеем, очевидно,
возможность решить следующую задачу (по крайней мере для фи-
фигур, состоящих из конечного числа точек и прямых).
Задача. Построить плоскую фигуру F\ равную данной фигу-
фигуре F (и имеющую с ней одинаковое направление вращения), зная
точки, соответственные двум ее данным точкам.
Следует заметить, что ничто не обязывает нас строить каждую
следующую искомую точку, исходя всё время непосредственно из дан-
данных точек А' и В'.
Напротив, можно получить точку, соответствующую произвольной
точке фигуры F, пользуясь тем треугольником, который эта точка обра-
образует не с данными точками, а с двумя другими уже построенными точ-
точками 2).
Таким образом, можно построить фигуру, равную ABCDE (черт. 104),
строя последовательно три треугольника, равные треугольникам ABC,
BCD, CDE.
96. Операция, которую мы назвали поступательным перемеще-
перемещением, преобразует любую, фигуру в фигуру, ей равную и имеющую
1) Ясно, что без последней оговорки ничего не помешало бы нам, на-
напротив, заменить фигуру F' фигурой, ей симметричной относительно пря-
прямой, соединяющей эти две точки. •
•) Мы узнаем впоследствии, что совершенно так же приходится посту-
поступать при съёмке планов (см. Геометрия в пространстве, книга X, п. 590).
ГЛАВА VI. ПЕРЕМЕЩЕНИЕ ФИГУР 97
с ней одинаковое направление вращения. Это перемещение можно рас-
рассматривать, как получающееся непрерывным скольжением фигуры в её
плоскости. Для этого достаточно выполнять поступательное перемеще-
перемещение непрерывно, начиная с перемещения, равного нулю (при котором
преобразованная фигура совпадает с первоначальной), и кончая тем
перемещением, которое фактически должно быть выполнено над данной
фигурой.
При этом непрерывном перемещении все точки описывают пря-
прямые линии, параллельные между собой и направленные в одну и ту
же сторону.
97. Вращением (поворотом) называется перемещение, при котором
каждая точка перемещаемой фигуры повёртывается около некоторой
неподвижной точки, называемой центром
вращения, в определённом направлении на
один и тот же угол, который характеризует
величину вращения "и называется углом по-
поворота. Иначе говоря, если дана произволь-
произвольная точка .4 первоначальной фигуры F, то мы
получим соответствующую ей точку А' пере-
перемещённой фигуры F, соединяя точку А с цент-
центром вращения, строя (в направлении враще-
вращения) угол АО А', равный углу поворота, и от-
откладывая на второй стороне этого угла отре-
отрезок О А', равный отрезку О А (черт. 105).
Мы видим, что вращение вполне определяется своим центром, углом
поворота и направлением.
Фигура F', которая получается из фигуры F с помощью лю-
любого вращения, равна фигуре F. Чтобы это доказать, возьмём какие-
нибудь две точки А к В (черт. 105) фигуры F, и пусть А' к В' —
точки, им соответственные. Угол А'ОВ' равен углу АОВ (и имеет с ним
одинаковое направление). Действительно, предположим для определён-
определённости, что угол АОВ имеет направление, совпадающее с направлением
вращения ') (черт. 105). Заменяя сторону ОБ стороной ОВ', мы уве-
увеличиваем этот угол АОВ на угол, равный углу поворота, но мы его
уменьшаем на ту же величину, заменяя сторону О А стороной О А'.
Следовательно, треугольники АОВ и А'ОВ' равны и имеют одина-
одинаковое направление вращения, как имеющие по равному углу, заклю-
заключённому между соответственно равными сторонами (ОА = ОА'; ОВ^=
= ОВ'). Так как это имеет место для любой точки В, то равенство
двух фигур доказано.
Вращение можно осуществить непрерывным скольжением фигуры
в её плоскости, так как можно предполагать, что угол поворота изме-
!) Напомним, что мы рассматриваем угол АОВ как описываемый пря-
прямой, вращающейся от UA к UB (п. 20). Поэтому всегда можно считать, что
имеет место сделанное предположение, обозначая через ОА ту сторону
угла, которая будет первой, если считать по направлению рассматриваемого
вращения.
' Элементарная геометрия
S>8 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
ыяется непрерывно от значения, равного нулю, до того значения, кото-
которое он должен окончательно иметь. При этом движении каждая точка
описывает дугу, имеющую своим центром центр вращения. Все эти
дуги соответствуют равным центральным углам.
98. Теорема. В двух равных фигурах, которые получаются
одна из другой с помощью вращения около точки О (черт. 106),
1^ соответствующие друг другу направления на двух соответ-
соответственных прямых образуют между собой угол, равный углу по-
поворота и одного с ним направления;
" 2) центр вращения, любые две соответ-
соответственные точки А и А' и точка пересечения
I каких-либо двух соответственных прямых,
проходящих через точки А и А', представляют
. л собой четыре точки, лежащие на одной окруж-
окружности.
Черт. 106. \о Первая часть теоре'мы справедлива, по
определению, для двух соответственных прямых,
проходящих через центр вращения; следовательно, она будет справед-
справедлива и для любых соответственных прямых, потому что каждую из
них можно заменить параллельной ей прямой, направленной в ту же сто-
сторону и проходящей через центр вращения.
2°. Каждая из точек О, I служит вершиной угла, который равен
углу поворота и стороны которого проходят через точки А и А'.
Следовательно, все четыре точки принадле-
принадлежат геометрическому месту вершин углов,
обладающих этими свойствами, а это геоме-
геометрическое место есть окружность1).
99. Частным случаем вращения является
тот, при котором угол поворота равен двум
прямым, или 180°. В этом случае точку А',
соответствующую точке А, можно получить,
соединяя точку А с точкой О (центром вра-
вращения) и откладывая на продолжении отрез-
отрезка АО отточки О отрезок ОД', равный О А. Точка Л', определяемая этим
построением, называется симметричной с точкой А относительно
точка О. Таким образом, в геометрии на плоскости симметрия отно-
относительно точки и вращение на 180° около этой точки представляют
тождественные между собой операции.
100. Если в двух равных фигурах, имеющих одинаковое направ-
направление вращения, два соответственных отрезка АВ и А'В" (черт. 107)
параллельны между собой и направлены в одну и ту же сторону,
то эти две фигуры можно совместить между собой с помощью
поступательного перемещения.
В самом деле, так как четырёхугольник ABB'А' — параллелограм,
то отрезки АА' и ВВ' будут параллельны и равны между собой и на-
В силу п. 82а. Прим. ред. перевода.
ГЛАВА VI. ПЕРЕМЕЩЕНИЕ ФИГУР 99
правлены в одну и ту же сторону; следовательно, поступательное пе-
перемещение АА' совмещает точки А и В с их соответственными точ-
точками, что влечёт за собой полное совмещение обеих фигур.
Если в двух равных фигурах, имеющих одинаковое направление
вращения, точка О совпадает со своей соответственной точкой, то
обе фигуры можно совместить между собой с помощью вращения
около этой точки.
Действительно, если А и А' — две произвольные соответственные
точки, то вращение на угол АО А' около точки О совмещает точку А
с точкой А', в то время как точка О попрежнему совпадает со своей
соответственной точкой.
101. Мы видели (п. 20), что две равные фигуры, имеющие проти-
противоположные направления вращения, не могут быть совмещены без того,
чтобы одна из них не вышла из своей плоскости. Напротив, две рав-
равные фигуры, имеющие одинаковое направление вращения, всегда могут
быть совмещены между собой с помощью перемещения в их плоскости,
а именно с помощью поступательного перемещения, сопровождаемого
вращением. Действительно, если А и А' — две соответственные точки
обеих фигур, то поступательное перемещение АА', выполненное над
первой фигурой, совместит между собой эти две то'чки, после чего
достаточно будет вращения около точки А' (см. предыдущий пункт),
чтобы совместить обе фигуры.
Замечая, что поступательное перемещение не изменяет направления
прямой, мы заключаем отсюда, что любые две соответственные пря-
прямые двух равных фигур, имеющих одинаковое направление враще-
вращения, образуют между собой постоянный угол; таким образом, можно
говорить об угле между двумя фигурами. Ф
102. Можно доказать, что из двух только что указанных операций
(поступательного перемещения и вращения) необходимой является только
одна. Это вытекает из следующей теоремы.
Теорема. Две равные фигуры, имеющие одинаковое направле-
направление вращения, могут быть всегда совмещены между собой либо
с помощью одного поступательного перемещения, либо с помощью
одного вращения около надлежащим образом выбранной точки.
Эта точка называется центром вращения (обеих фигур).
Пусть А и В — две точки первой фигуры, А' и В' — соответст-
соответственные им точки второй фигуры. Мы достигнем совмещения обеих
фигур, если нам удастся совместить отрезки АВ и А'В'.
1°. Если прямые АВ и А'В' параллельны между собой и направ-
направлены в одну и ту же сторону (черт. 107), то фигуры получаются
одна из другой с помощью поступательного перемещения.
2°. Предположим теперь, что этого не будет. Посмотрим, можно
ли одну из двух фигур получить из другой с помощью вращения.
Угол поворота нам известен: он равен углу между двумя фигурами,
например углу между прямыми АВ и А'В' (черт. 108). Мы должны,
следовательно, найти такую точку О, чтобы поворот около неё на
этот угол совместил бы точку А с точкой А'. Эта задача сводится
100 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
к отысканию дуги, имеющей своей хордой отрезок АА' и вмещающей
угол, равный половине угла поворота и одного с ним направления (так
как центральный угол в два раза больше вписанного угла, опирающе-
опирающегося на ту же дугу).
Следовательно, точка О будет лежать, с одной стороны, на пер-
перпендикуляре, восставленном в середине отрезка АА', с другой сторо-
стороны,— на перпендикуляре к касательной1) к дуге окружности, постро-
построенной как было указано в п. 90 (построение
14).
Обратно, если точка О определена таким
образом, то вращение, имеющее своим цент-
центром эту точку и углом поворота — угол
между двумя фигурами, совместит точк> А
с точкой А'; это вращение преобразует от-
отрезок АВ в некоторый отрезок, параллель-
параллельный А'В' и направленный с ним в одну сто-
сторону, т. е. в отрезок, совпадающий с А'В',
так как оба отрезка имеют общий конец А'.
Следовательно, обе фигуры совпадут.
Примечание. Можно было бы доказать то же самое предло-
предложение, определяя точку О или как точку пересечения перпендикуля-
перпендикуляров, восставленных в серединах отрезков АА' и ВВ или (п. 98) как точку
пересечения окружностей, описанных около треугольников /АА', IBB',
где /¦—точка пересечения прямых ЛВ и А'В'. «
В том и другом случае можно было бы дока- ?
зать, что треугольники ОАВ и ОЛ'В' равны.
П. Нг
1С2а. Предыдущая теорема вытекает Тежже
из разложения любого поступательно) о переме-
перемещения или вращения на две симметрии.
J/емл.а. Две последовательные симметрии '
относительно прямых D\ и ZJ равносильны: Г)) ";1
1) если две прямые Dx и Ог параллель- ~~|
ны. — поступательному перемещению по на- Мб
правлению, перпендикулярному :с этим пттмым Черт. 109.
и по величине равному усвоенному поступа-
поступательному перемещению, которое переводит первую прямую во вторую:
2) если эти бее прямые Dx и Ьг пересекаются. — вращению около
точки их пересечения с углом поворота, равным удвоенному углу пово-
поворота, переводящего первую прямую во вторую.
Пусть F—некоторая фигура, f — фигура, ей симметричная относи-
относительно прямой Ог, F"— фигура, симметричная F' относительно прямой D?.
1°. Предположим, что прямые [\ и D2 параллельны между собой
(черт. 109). Если М—пекоторая точка фигуры F, то построим симметрич-
симметричную ей точку ЛГ относительно прямой Dit откладывая иа продолжении
перпендикуляра МН\, опущенного ил точки М на /)ь отрезок Н\М!', рав-
равный ЛШ(; далее построим точку М", симметричную ЛГ относительно пря-
прямой D2, откладывая на продолжении перпендикуляра М'Н2, опущенного из
точки М' на /Л, отрезок И2М", равный М'Н2. Непосредственно очевидно,
В точке А. Прим. ред. перевода.
ГЛАВА V). ПЕРЕМЕЩЕНИЕ ФИГУР Ю1
что три точки М, М', М" лежат на одном и том же общем перпендикуляре
к прямым Di и Z>2. Кроме того, если предположить для определённости,
что точка М' находится между прямыми Д и ZJ, то отрезок ММ", равный
сумме отрезков ММ' и М'М" (черт. 109;, в два раз.) больше отрезка Н-^Н,,
который представляет собою сумму отрезков М'Н-^ и М'Н-±
Это заключение будет иметь силу и в том случае, если точк<1 М' нахо-
находится вне двух параллельных прямых Z>j и ZJ: отрезок MAY' будет при этом
разностью отрезков ММ' и М'М", а отрезок Нф2 — разностью отрезков
Af'#i и М'Н2- Следовательно, поступательное перемещение, представляемое
отрезком, перпендикулярным к двум данным прямым н вдвое большим,
чем H-Jiz, совмещает произвольную точку фигуры /•' с соответствующей ей
точкой фигуры F".
2°. Предположим, что две оси симметрии пересекаются в точке О
(черт. ПО), и пусть М, М', М" — снова три соответственные точки трёх
фигур F, F", F", причём точки М и М' сим-
симметричны относительно прямой Dlt а точки М'
и М" — относительно прямой Dz. Очевидно, что
три точки М, М', М" лежат на одной окружно-
окружности с центром О. Кроме того, угол MOM", рав-
равный сумме или разности углов MOM' и М'ОМ", в
два раза больше угла между прямыми D\ и /Э2,
который можно рассматривать как сумму или
разность углов, образованных прямой ОМ' с пря-
прямыми Z5j и Dr,. Вращение, указанное в условии
теоремы, совмещает, таким образом, каждую точ-
точку Л? с соотве1Ствующей ей точкой М".
Примечание. Две последовательные сим-
симметрии относительно одной и той же прямой вза-
взаимно уничтожаются, так как при этом каждая точ-
точка возвращается в её первоначальное положение.
Следствие. Обратно, всякое постуттельное перемещение можно за-
заменить двумя последовательными симметриями относительно двух пря-
прямых, перпендикуляъных к направлению перемещения, причём одну из этих
прямых можно выбрать произвольно.
Всякое вращение можно заменить двумя последовательными сим-
симметриями относительно двух прямых, пиоходящих через центр враще-
вращения, причём одну из этих пюямых молено выбрать произвольно.
В самом деле, выбрав произвольно первую ось симмегрии, достаточно
взять за вторую ось симмегрии в случае поступательного перемещения ¦—
прямую, параллельную первой оси и отстоящую от неё на расстоянии, рав-
равном половине иеличины данного поступательного перемещения, а в случае
вращения — прямую, проходящую через центр вращ ння и образующую
с первой осью симметрии угол, равный половине угла поворота.
103. Теорема. Последовательные поступательные перемещения или
вращения, выполненные в любом числе, можно заменить либо одним по-
поступательным перемещением, либо одни.ч вращением.
Эта замена называется сложением данных перемещений; полученное
окончательное перемещение называется результирующим перемещением.
Достаточно уметь сложить два перемещения: действительно, если бы
их было три, то мы сложили бы сначала два первых, а затем сложили бы
полученное перемещение с третьим: так же следовало бы продолжать и
далее, если бы число данных перемещений было больше трёх.
Два последовательных поступательных перемещения преобразуют про-
произвольный отрезок в отрезок, ему параллельный и направленный в ту же
сторону, и потому эквивалентны одному поступательному перемещению
(п. 100;. Следовательно, нам достаточно рассмотреть только случай сложе-
сложения поступательного перемещения и вращения (причём поступательное пе-
перемещение может или предшествовать вращению, или следовать за ним; и
случай сложения чвух вращений.
102 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
Возьмём, например, первый случаи, предполагая для определённости,
что поступательное перемещение выполнено первым.. Данное иоступатель-
ное перемещение можно разложить на две симметрии относительно двух
прямых Dx и D2 и точно так же данное вращение— на две симметрии
относительно прямых D{ и D2, так что нам придётся выполнить последо-
последовательно всего четыре симметрии относительно прямых ?>ь D2, Д', D2. Но
так как D2—произвольная прямая, перпендикулярная к направлению по-
поступательного перемещения, a D{ — произвольная прямая, проходящая
через центр вращения, то мы можем совместить обе эти прямые с перпен-
перпендикуляром к направлению поступательного перемещения, проведённым
через центр вращения.
При этом две симметрии относительно зтих двух прямых уничтожатся,
и останутся только две симметрии относительно прямых Ил и D2, кото-
которые (на основании предыдущей леммы) равносильны одному вращению
или одному поступательному перемещению.
Если бы требовалось сложить два вращения, то мы взяли бы как за
прямую D2, так и за прямую D\ прямую, соединяющую оба данные
центра вращения. Таким образом, теорема доказана для всех случаев.
Теорему п. 102 можно рассматривать как следствие теоремы, которую
мы только что доказали, гак как любое перемещение плоской фигуры можно
получить с помощью одного поступательного
\ перемещения, сопровождаемого вращением, а
N именно (если через А и А' обозначить какие-
\р либо две соответственные точки первоначальной
\ \г и перемещённой фигуры) поступательного ш-
\ ремещения АА', сопровождаемого вращением
^ N4 хч около точки А', на угол, равный углу между
"~"-\ \ двумя фигурами (черт. 111). Прямые D2 и /у
G\- ч совпадают в этом случае с перпендикуляром к
ч -, -\ • прямой АА' в точке А'; следовательно, прямая L»,
\ ^у^ t будет перпендикуляром в середине отрезка АА',
4 -"' ч^"-~ /J а прямую D2 мы получим из Dit повёртывай
\ """ её на угол, равный половине угла поворота. Точ-
у ч ка пересечения прямых Dl и D2 определяет
Д \ центр вращения, и мы видим, что это построение
NN вполне согласуется с тем, которое было дано
\Д выше; действительно, проводя касательную ')
4 к дуге, построенной иа отрезке АА' как на хор-
i]epT in де и вмещающей угол, равный половине угла
н ' ' поворота, мы получим перпендикуляр к пря-
прямой D'-2.
104. Теорема. Если неизменяемая фигура перемещается в своей пло-
плоскости, то в каждый момент времени нормали к траекториям всех
точек прохооят через одну точку (если они все не параллельны между
собой), которая называется мгновенным центром вращения.
Не рассматривая случая, когда все нормали к траекториям различных
точек М, N, Р,... подвижной фигуры параллельны, мы предположим, что
две из них, например нормали в точках М и N. пересекаются в точке О
(черт. 112).
Рассмотрим второ? положение подвижной фигуры, близкое к первому;
новые положения точек М, N, Р, ¦ - пусть будут М', Л/', Р',... . Перпен-
Перпендикуляры, восставленные в серединах отрезков MM', NN', РР' при-
приходят через общую точку Оь центр юго вращения, которое совместило
бы первое положение фигуры со вторым. Если теперь предположить, что
второе положение неограниченно приближается к первому, то середина
1) В точке А'. Прим. ред< перевода.
ГЛАВА V). ПЕРЕМЕЩЕНИЕ ФИГУР
103
отрезка ММ' будет иметь своим пределом точку М, а прямая ММ' — каса-
касательную в точке М к траектории этой точки; перпендикуляр, восставлен-
восставленный в середине ММ', будет стремиться при этом к нормали к этой траек-
траектории. Точно так же перпендикуляр, восставленный в середине AW, будет
стремиться к нормали в точке N. Точка О\ имеет, следовательно, своим
предельным положением точку О, так что нормали к траекториям то-
точек Я,... , представляющие собою предельные положения перпендикуля-
перпендикуляров, восставленных в серединах от-
отрезков РР',..., проходят через эту
точку О1).
Следствие. Если мы умеем най-
найти касательные к траекториям
двух точек движущейся неизменяе-
неизменяемой фигуры, то мы сможем найти
касательную и к траектории лю-
любой точки фигуры.
Действительно, перпендикуляры
к двум известным касательным к
траекториям определяют мгновен-
мгновенный центр вращения и, следователь-
следовательно, позволяют провести нормаль к
траектории любой точки.
м
Черт. 112.
УПРАЖНЕНИЯ.
92. Если неизменяемая фигура
перемешается таким образом, что две
из её прямых проходят каждая че-
через неподвижную точку, то существует бесчисленное множество прямых
этой фигуры, каждая из которых при её перемещении также вращается
около неподвижной точки.
Всякая другая прямая подвижной фигуры остаётся касательной к не-
неподвижной окружности. Центр вращения двух любых положений фигуры
лежит всё время на некоторой неподвижной окружности (доказать).
93. Если даны три равные фигуры F\, Fit F3, имеющие одинаковое на-
направление вращения, и если определить три центра вращения этих фигур,
взятых попарно, то требуется доказать, что углы треугольника, имеющего
своими вершинами эти три точки, равны половинам углов между этими
фигурами, взятыми попарно, или пополнительным углам этих половин.
94. Сложить два вращения около двух различных центров, имеющих
один и тот же угол поворота, но противоположные направления.
95 Две равные фигуры, имеющие противоположные направления вра-
вращения, всегда могут быть совмещены между собой:
J) Мы допускали здесь в качестве аксиом такого рода предложения:
если переменная точка AJt имеет своим предельным положением опреде-
определённую точку М и если переменное направление ОЛ имеет своим предель-
предельным положением направление D, то прямая, проведённая через точку Мх
по направлению ?>г, имеет своим предельным положением прямую, прове-
проведённую через точку М и параллельную D. Если две прямые Du D\ имеют
предельными положениями D, D', то точка пересечения -D^ и D[ стре-
стремится к точке пересечения D и D' и т. д. В действительности эти пред-
предложения представляют собою теоремы, которые должны быть доказаны,
но мы не приводим их доказательств, так как они не могут быть изло-
изложены с достаточной простотой, не опираясь на такие сведения о пределах,
которые излагаются в курсах исчисления бесконечно малых.
104 КНИГА ВТОРАЯ ОКРУЖНОСТЬ
1) бесчисленным множеством способов с помощью трёх симметрии;
2) бесчисленным множеством способов с помощью поступательного пе-
перемещения, сопровождаемого одной симметрией, или с помощью одной сим-
симметрии, сопровождаемой поступательным перемещением;
3; одним и только одним способом с помощью поступательного пере-
перемещении, сопровождаемого одной симметрией, или с помощью одной сим-
симметрии, сопровождаемой поступательным перемещением, если ось симмет-
симметрии параллельна направлению перемещения.
9Ь. Построить равносторонний треугольник, вершины которого лежат
соответственно на трёх данных параллельных прямых или на трёх данных
концентрических окружностях.
97. Найти на данной окружности дугу, равную данной дуге и такую,
чтобы прямые, соединяющие её концы соответственно с двумя данными
точками, были бы параллельны между собой.
Найти на данной окружности дугу, равную данной дуге и такую, чтобы
прямые, соединяющие её концы соответственно с двумя данными точкам.i,
ооразовали между собой данный угол.
ЗАДАЧИ КО ВТОРОЙ КНИГЕ.
98. Если соединить какую-либо точку окружности М с точками при-
прикосновения А к В касательных, проведённых через определённую точку Р
плоскости, и через точку Р провести прямую, параллельную касательной
в точке М, то доказать, что прямы MA, MB отсекают на этой прямой
отрезок, длина которого не зависит от положения точки М, и что этот
отрезок делится в точке Р пополам.
99. Пусть ABC—равносторонний треугольник, вписанный в круг, и М —
точка дуги ВС. Доказать, что отрезок МА равен MB-j-MC.
100. Через три вершины равностороннего треугольника проведены три
прямые так, что биссектрисы углов, которые каждая из них образует
с высотой, выходящей из той же вершины, параллельны. Доказать, что эти
три прямые пересекаются в одной точке, лежащей на круге, описанном
около треугольника.
101. Середины сторон треугольника, основания высот и середины отрез-
отрезков высот, заключённых между каждой из вершин и точкой пересечения
высот, представляют собой девять точек, лежащих на одной окружное!и
(круг девяти точек). Центром этой окружности служит середина отрезка,
который соединяет точку пересечения высот данного треугольника с цент-
центром описанного круга; её радиус равен половине радиуса описанного круга
(доказать). Вывести отсюда предложение, данное выше, в упражнении 70.
101а. Во всяком треугольнике центр окружности, проходящей через
центры трёх вневписанных кругов, лежит в точке пересечения радиусов
каждого из этих кругов, проведённых в точку его касания с соответствую-
соответствующей стороной, или, иначе, центр этой окружности симметричен с центром
вписанного круга относительно центра описанного круга. Её радиус вине
больше радиуса описанного круга (доказать).
102. Если в каком-либо треугольнике из основания каждой высоты
опустить перпендикуляры на две стороны треугольника, выходящие с дан-
данной высотой из одной вершины, то основания этих перпендикуляров пред-
представляют собой шесть точек, лежащих на одной окружности (доказать).
103. В треугольнике ABC перпендикуляр, восставленный в середине
стороны ВС, и биссектриса угла А пересекаются на описанном круге. Их
точка пересечения равноудалена от точек В и С, от цешра вписанного
круга и от це.чтра пневписаннаго круга, расположенного внутри угла А
(доказать^.
Доказать аналогичную теорему для биссектрисы внешнего угла при А.
Вывести отсюда, что сумма радиусов вневписанных кругов равна радиусу
вписанного круга, сложенному с учетверённым радиусом описанного круга.
ЗА ЧАЧИ КО ВТОРОЙ КНИГЕ '05
103а. Построить треугольник, зная длины высоты, медианы и биссект-
биссектрисы, выходящих из одной вершины, считая от этой вершины до точек пе-
пересечения с противоположной стороной.
104. Две касательные к окружности и хорда, соединяющая точки их
касания, отсекают равные отрезки на перпендикуляре, проведённом через
произвольную точку этой хорды, к прямой, соединяющей эту точку с цент-
центром (доказать).
105. На трёх сторонах треугольника ABC построены вне треугольника
равносторонние треугольники ВСА', CAB', ABC' и проведены отрезки АА',
ВВ1, СС. Доказать:"
1) что эти отрезки равны между собой;
2) что эти отрезки пересекаются в такой точке, из которой три стороны
треугольника видны под одним и тем же углом;
3) что если эта точка находится внутри треугольника, то сумма её рас-
расстояний до трёх вершин треугольника равна длине каждого из отрезков
АА', ВВ', СС (см. задачу 99).
106. Круги, описанные около четырёх треугольников, образованных че-
четырьмя попарно пересекающимися прямыми, проходят через одну точку
[доказать эгу теорему: 1) непосредственно, 2) пользуясь упражнением 72J.
Центры этих кругов лежат на одной окружности, также проходящей через
ту же точку (доказать).
107. Если продолжить стороны вписанного четырёхугольника до их пе-
пересечения, то биссектрисы углов, образованных продолжениями этих сюрон,
взаимно перпендикулярны. Они соответовенно параллельны биссектрисам
углов, образованных диагоналями того же четырёхугольника (доказать).
С рормулировать и доказать обратную теорему.
107а. Две произвольно взятые окружности пересечены двумя произ-
произвольными прямыми; хорды, соединяющие попарно точки пересечения обеих.
прямых с первой окружностью, пересекают хорды, соединяющие попарно
точки пересечения тех же прямых со второй окружностью, в четырёх точ-
точках одной окружности (доказать).
108. Дан треугольник ABC; найти геометрическое место таких точек М,
чтобы перпендикуляры к прямым AM, BM, СМ, проведённые соответственно
через вершины А, В, С, пересекались в одной точке.
109. Найти геометрическое место вершин прямоугольников, рассматри-
рассматриваемых в упражнении 26 и задаче 41, если данный параллелоурам рассмат-
рассматривать как шарнирный (п. 46а).
110 На двух взятых. последовательно отрезках АВ, ВС одной прямой
линии описываются две произвольные, но равные между собой окружности
Эти окружности пересекаются в точке Вив некоторой второй точке, гео-
геометрическое место которой и требуется найти.
111. Пусть О А и ОВ — два произвольных взаимно перпендикулярных
радиуса круга О. Через точки А и В проводят прямые, соответственно
параллельные двум данным взаимно перпендикулярным прямым. Найти
геометрическое место точек пересечения этих двух прямых, если прямой
угол АОВ вращается около центра круга.
112. Две окружности, каждая из которых касается данной прямой в опре-
определённой течке, изменяются, оставаясь всё время касательными между со-
собой. Найти геометрическое место нх точек касания.
113. Найти геометрическое место вершин прямого угла неизменяемого
прямоуюльного треугольника, если две другие его вершины скользят по
двум взаимно перпендикулярным прямым.
114. Построить прямую, ты которой две данные окружности отсекают
хорды данной длины.
115. Вписать в данную окружность треугольник, стороны которого были
бы параллельны данным прямым или две стороны которого были бы парал-
параллельны данным прямым, а третья сторона проходила бы через данную точку.
116. Даны прямая XY и две точки А и В; найти на прямой такую точ-
точку /И, чтобы угол АМХ был вдвое больше угла BMY.
106 КНИГА ВТОРАЯ. ОКРУЖНОСТЬ
117. Построить пятиугольник (или вообще многоугольник с нечётным
числом сторон), зная середины его сторон.
Что будет в случае многоугольника с чётным числом сторон?
118. Построить трапецию по четырём её сторонам.
Общее, построить четырёхугольник по четырём сторонам и углу между
продолжениями двух его противоположных сторон *).
119. Пересечь стороны АВ и АС треугольника ABC прямой данного
направления, которая отсекла бы на этих сторонах равные отрезки, считая
соответственно от вершин В и С.
120. Построить общий перпендикуляр к двум данным параллельным
прямым, который был бы виден из данной точки под данным углом.
121. Даны окружность, две точки Р и Q этой окружности и прямая.
Найти на окружности такую точку М, чтобы прямые МР и MQ отсекали
на данной прямой отрезок 1К данной длины.
121а. Решить ту же задачу, если вместо длины отрезка 1К дана сере-
середин & этого отрезка.
122. Построить квадрат, стороны которого проходят через четыре дан-
данные точки. Может ли эта задача допускать бесчисленное множество решений?
Найти в этом случае геометрическое место центров квадратов, удов-
удовлетворяющих поставленному условию.
123. Каким условиям должны удовлетворять длины сторон шарнирного
четырёхугольника ABCD (п. 46а, примечание 3°), для того чтобы опреде-
определённая его вершина В представляла собой шарнир, обладающий полной
свободой вращения, т. е. чтобы величина угла при этой вершине четырёх-
четырёхугольника была совершенно произвольной? Показать, что угол при проти-
противолежащей вершине D не будет'в этом случае, вообще говоря, вполне про-
произвольным. В каком случае последнее предложение допускает исключение?
!) Относительно этого и следующих упражнений см. Прибавление А,
п. 284.
КНИГА ТРЕТЬЯ. ПОДОБИЕ.
ГЛАВА I.
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ.
105. Известно, что пропорцией называется равенство двух отно-
отношении и что две величины называются пропорциональными, если их
значения соответствуют друг другу таким образом, что отношение
двух каких-либо значений первой равно отношению соответствую-
соответствующих значений второй. Так, два отрезка АВ, CD называются пропор-
пропорциональными отрезкам А'В', CD', если имеет место равенство
АВ А'В'
CD~'CD"
106. В предыдущем равенстве -^ обозначает отношение двух
отрезков АВ и CD; однако мы будем применять здесь и в дальнейшем
соглашение, установленное в п. 18, и, выбрав произвольно, но раз на-
навсегда единицу длины, заменим самые отрезки числами, которые
, АВ мера АВ ,,
их измеряют: таким образом, ^= означает —г . Мы имеем право
так поступить, так как такой заменой мы отнюдь не изменили вели-
величины отношения, что следует из приведённой уже теоремы (п. 17, 2°).
Мы можем применять вследствие этого к отношению отрезков
свойства, доказываемые в курсах арифметики для отношения чисел,
как, например, следующие:
Отношение не изменяется, если умножить или разделить оба
его члена на одно и то же число.
Чтобы перемножить два отношения, перемножают их предыду-
предыдущие и их последующие члены.
В ряде равных отношений сумма предыдущих членов так от-
относится к сумме последующих, как один из предыдущих относится
к своему последующему.
Точно так же к пропорциям, составленным из отрезков, мы сможем
применять свойства пропорций, составленных из чисел, как, например,
следующие:
В каждой пропорции:
\) произведение крайних членов равно произведению средних;
2) можно переставить крайние или средние члены:
Ъ) сумма (или разность) членов первого отношения относится
к одному из них как сумма (или разность) членов второго отно-
отношения к соответствующему члену второго отношения.
108
КНИГА ТРЕТЬЯ.
Обратни, каждое из равенств, полученных таким образом,
влечёт за собою первоначальную пропорцию.
-г п с
1ак, равенство -г = -г эквивалентно следующим:
. , п b аЛ-b г Л-d а —Ь с — d
ad = ос, — = -j ; —— = —^— ; —— = —-— ,
(• d ' b d ' b d
т. е. каждое из этих равенств влечёт за собою все остальные.
В частности, если известно, что три точки прямой Л, В, С
(черт. 113) следуют одна за другой в том же порядке, как три
Д В q точки прямой А', В', С", то
1 1 г-—- пропорции
АВ A't? AB_A'B'
А' В' С' ВС Ь'С" АС~~ А'С"
, t ^ АС_А'С
Черт. 113. BC — VC
эквивалентны друг другу.
Напомним также, что, зная три члена пропорции, можно
пс..
найти неизвестный член: пропорция — = — дает, если предполо-
предположить, что известны a, b и с:
> Этот член d называется четвёртым пропориисналъным к коли-
количествам а, Ь. с.
Очевидно, что в двух пропорциях, у которых три соответст-
соответствующих члена общие, четвёртые члены равны между собой.
107. Говорят, что число Ь есть среднее пропорциональное (или
среднее геометрическое) между двумя другими числами а и с, если
можно написать пропорцию, у которой крайние члены равны а и с, а
оба средних члена равны Ь:
и_ Ь_
b 7"
Это равенство эквивалентно следующему:
так что для того, чтобы найти среднее пропорциональное между
двумя числами а и с, нужно извлечь квадратный корень из произ-
произведения этих двух чисел. Число с называется иногда третьим про-
пропорциональным к числам а и Ь.
Разумеется, согласно предыдущим условиям мы скажем, что
отрезок b есть среднее пропорциональное или среднее геометри-
геометрическое между двумя другими отрезками а и с, если число, измеряю-
измеряющее Ь, есть среднее пропорциональное между числами, измеряющими
отрезки аи с, т. е. если из трёх чисел (или, что го же самое, из
ГЛАВА I. ПРОИОРЦИОНАЛЬННР ОТРЕЗКИ
104
трёх отрезков) можно составить пропорцию:
F 7'
108. Существует точка, и притом только одна, которая де-
делит данный отрезок в данном отношении.
Черт. 114.
В самом деле, пусть даны: отрезок ЛВ (черт. 114Л и отношение г.
до найти такую точк]
сать в виде пропорции:
найти такую точку М, что -тгг\ = г\ это равенство можно напи-
напиAM ?
MB 1 '
а эта пропорция эквивалентна пропорции:
AM г
которая верна для одного и только одного значения AM:
Определённый, .таким образом, отрезок меньше ЛВ. Откладывая
его на АВ.of toikh А, получим точку М, удовлетворяющую данному
условию.
109. Рассмотрим точку М, которая перемещается по отрезку ЛВ
от точки А к точке В. Отношение -гг^ всё время возрастает, так
как возрастает числитель, в то время как знаменатель убывает. Это
отношение согласно предыдущему предложению может принять вообще
любое данное значение, в частности сколь угодно малое (если точка
/И достаточно близка к А) и сколь угодно большое (если точка М
достаточно близка к В). Короче говоря, это отношение, начиная от 0,
всё время возрастает и притом неограниченно, если точка М пере-
перемещается из' А в В.
AM'
110. Изучим теперь отношение ^тл , когда точка ЛГ (черт. 114)-
находится на продолжении отрезка АВ. Отношение ——-, называется
при этом отношением, в котором точка М' делит отрезок АВ внеш-
внешним образом.
Существует точка, и притом только одна, которая делит
внешним образом данный отрезок в данном отношении, при усло-
условии, что это отношение отлично от 1.
по
КНИГА ТРЕТЬЯ. ПОДОБИЕ
В самом деле, пусть требуется найти на продолжении АВ такую
точку М, для которой отношение тгтт- было бы равно какому-либо
данному числу г. Предположим для определённости, что г~^>\; в дан-
данном случае мы должны искать точку М на продолжении отрезка \В
AM' r
за точку В. Пропорция ^т« = —,— эквивалентна пропорции
AM' _ г
АВ г^А '¦
которой удовлетворяет одно и только одно значение AM':
г— I
Этот отрезок больше Л/я так как-——г больше 11. Откладывая его
от точки А в направлении АВ, мы получим точку М', которая отве-
отвечает условию вопроса. Если /5ы отношение г было меньше 1, то ана-
аналогичное рассуждение дало бы
АМ = АВ-г;
1 —г
отрезок, который, будучи отложен от точки А в направлении, проти-
противоположном направлению отрезка АВ, даёт точку М'. Предложение,
таким образом, доказано.
Рассмотрим точку М, которая, выходя из точки В, беспредельно
¦ AM'
удаляется в направлении ВХ (черт. 114). Отношение ^,,, больше 1.
Если точка, удаляясь, переходит из положения М' в положение /И/,
то это отношение приближается к 1, так как мы переходим от от-
АМ' AM'
ношения -~гг, к отношению н—, прибавляя одну и ту же величину
D/Vl dJVIy
ММ\ к обоим членам. К тому же это отношение может принимать все
значения (большие 1), в частности сколь угодно большие значения
(если точка М' достаточно близка к В) и значения, сколь угодно
близкие к 1 (если точка М' достаточно удалена).
.. AM'
Короче говоря, отношение -j^tt; , начиная с бесконечности, всё
время уменьшается и стремится к 1, если точка М' двигается
от точки В и неограниченно удаляется в направлении ВХ.
Точно так же мы убедимся, что если точка М' двигается
от А и неограниченно удаляется в направлении АХ' (черт. 114),
AM'
то отношение - , начиная от нуля, все время возрастает и
стремится к 1.
111. Определение. Две точки С и D (черт. 115), которые делят,
одна внутренним образом, другая внешним образом, один и тот же
отрезок АВ в одном и том же отношении, называются гармони-
ГЛАВА I. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ
чески сопряжёнными, относительно концов этого отрезка (говорят
ё, чт0 они делят гармонически этот отрезок).
Если отрезок CD делит гармонически отрезок АВ, то и об-
обратно, последний отрезок делит гармонически первый, так как
СА DA
из пропорции —-= = -j—j, перестановкой средних членов получается:
СВ DB
СА=СВ
DA DB'
Любая точка, взятая на данном отрезке АВ или на одном из его
продолжений, имеет гармонически сопряжённую точку относительно
концов данного отрезка, за исключением середины / отрезка АВ
(так как отношение — равно II).
Два отрезка, которые делят друг друга гармонически, час-
частично заходят друг на друга (это значит, что ни один из двух
отрезков не лежит целиком ни внутри, ни вне другого).
J
~* ' с'с В D "^
Черт. 115.
112. Напротив, два отрезка CD, CD', которые делят гармо-
гармонически один и тот же третий отрезок АВ, лежат целиком
либо один вне другого, либо один внутри другого.
_ , СА С А '
В самом деле, если отношения —> и , г> таковы, что одно из
СВ С Ь
них больше 1, другое меньше 1, то отрезки CD, CD' являются
внешними один относительно другого: они расположены по разные
стороны от середины / отрезка АВ. Если это не так (черт. 115) и если,
например, оба отношения, о которых мы только что говорили,
больше 1, то оба отрезка CD и CD' лежат по одну сторону от
точки / и оба содержат точку В. Но рассуждения пп. 109—110 до-
АМ
казывают, что отношение -—- приближается к 1, если удаляться от
NIB
точки В в том или ином направлении (по крайней мере не переходя
через точку /). Следовательно, тот из двух отрезков, который соот-
соответствует отношению, более близкому к 1, содержит второй отре-
отрезок внутри себя.
113. Основная теорема. Любые две секущие рассекаются
параллельными прямыми на пропорциональные части.
1) Точку, гармонически сопряжённую с точкой /, следует рассматривать
как удалившуюся в бесконечность. Под этими словами мы понимаем, что
AM , AI
отношение jrj-, стремится к 1, т. е. к значению у^, если точка М нео-
неограниченно удаляется.
112 КНИ1 \ ТРЕТЬЯ. ПОДОБИР
Пусть ABCD и A'BCD'—две секущие, пересечённые параллель-
параллельными прямыми АА', ВВ, СС, DD'. Точки А', В', С, П следуют
друг за другом в том же порядке, как и точки А, В, С, D (в про-
противном случае две из прямых АА', ВВ', СС, DD' пересекались бы).
CD CD'
Я утверждаю, что имеет место равенство —- = —— .
Мы будем различать два случая:
1°. Если отрезки АВ и CD равны между собой (черт. 11G),
то отрезки А'В' и CD' также равны между собой.
Действительно, проведём через точку В прямую ВЬ, параллельную
А'В', до её пересечения с АА' в точке Ь, а через точку D — пря-
. ч мую Dd, параллельную той
/ \п' же прямой, до её пересе-
пересек чения с СС в точке й.
Если AB = CD, то два тре-
С/- ^ \с угольника АВЪ и CDd равны
р/_ \о' между собой, так как сто-
\ роны АВ и CD равны между
собой и углы того и дру-
Д/- ^ \Д гого треугольника, примы-
/ \ кающие к этим сторонам,
Черт 116. также равны друг другу как
соответственные; следова-
следовательно, имеем: Bb = Dd. Но ВЬ и Dd соответственно равны А'В"
и CD', как ито видно из параллелограмов BbA'B' и DdC'D'.
2°. Общий случай1). Пусть А, В, С, D — произвольные точки;
CD CD'
докажем, что значения обоих отношений -—- и ——, взятые с точ-
Лй A D
ностыо до —, равны, каково бы ни было п.
Пусть, например, п=5; разделим АВ на пять равных частей точ-
точками 1, 2, 3, 4 (черт. 117) и предположим, что пятая часть отрез-
отрезка АВ содержится в отрезке D больше, чем 2 раза, но меньше, чем 3
раза; пусть /, //, 111 — конечные точки трёх отрезков, равных пятой
части АВ и последовательно отложенных на прямой CD от точки С,
так что точки / и // лежат между С и D (точка // может совпасть
также с D), точка ///—по ту сторону точки D.
!) Доказательство может считаться законченным, если опираться па
следующую теорему, которую мы уже приводили: две величины пропорци-
пропорциональны, если: 1; одному и тому же значению первой соответствует всегда
одно и то же значение второй и 2) сумме двух значений первой величины
соответствует сумма двух соответствующих значений второй.
Первое условие в данном случае выполняется, как это доказано в
тексге A°), второе условие, очевидно, также выполняется в силу того,
что соответственные точки следуют на прямых ABCD и А'В'СЧУ в одном
и том же порядке. В тексте мы воспроизводим доказательство общей
теоремы, применяя это доказательство к данному случаю.
ГЛАВА I. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ
113
Через все эти точки /, 2, 3, 4, I, II, ///проводим прямые, парал-
параллельные прямым А А'', ВВ', СС, DD', до пересечения в точках /', 2',
3', 4', /', //', ///' с прямой А'В'CD'. Мы разделили, таким образом,
отрезок А'В' на пять равных частей и отложили три раза одну из
этих частей отточки С в направлении CD' A°). Точки /', //' нахо-
находятся в интервале CD', а точка ///' — по ту сторону точки D'
В'
А1
3*
Черт. 117.
В С
Черт. 118.
В
(в силу замечания, сделанного в самом начале доказательства). Тео-
Теорема доказана.
114. Теорема. Прямая DE, параллельная одной из сторон
треугольника ABC, делит две другие стороны АВ и АС
на пропорциональные части (черт. 118).
Действительно, если мы проведём через
вершину А прямую XY, параллельную ВС, то
согласно предыдущей теореме параллельные
ВС, DE, XY делят секущие АВ, АС на
пропорциональные части.
Примечание. Прямая, о которой идёт
речь, может делить каждую из сторон тре-
треугольника внутренним образом или внеш-
внешним образом; однако она делит обе сторо-
стороны треугольника одинаковым образом.
Обратная теорема. Если прямая делит две стороны тре-
треугольника на пропорциональные части, то она параллельна третьей
стороне.
Пусть DE — прямая, которая делит стороны АВ и АС на пропор-
пропорциональные части (черт. 119).
Проведём через точку D прямую, параллельную ВС, и пусть Е' ¦—
АЕ'
точка, где эта параллельная пересекает АС. Отношение -р^ равно
AD .
отношению ¦— (по предыдущей теореме) и, следовательно, отноше-
L)t>
8 Элементарная геометрия
Черт. 119.
114
КНИГА ТРЕТЬЯ. ПОДОБИЕ
АЕ
нию ¦== (по условию). Следовательно, точки Е и Е' совпадают
(п. 108), и прямая DE параллельна ЕС.
115. Теорема. Во всяком треугольнике:
1) биссектриса любого угла делит противоположную сторону
на части, пропорциональные прилежащим сторонам;
2) биссектриса внешнего угла делит противоположную сторону
внешним образом на две части, также пропорциональные при-
прилежащим сторонам.
1°. Пусть AD — биссектриса угла
А треугольника АЬС (черт. 120).
BD АВ
Я хочу доказать, что тг~,= —^.
С этой целью проведём прямую
СЕ, параллельную AD, до пересе-
пересечения в точке Е с АВ. Тогда в
треугольнике BAD, пересечённом
прямой СЕ, параллельной AD, бу-
BD ВА
дем иметь:— = —.
Но треугольник АСЕ имеет при вершинах Е и С равные углы,
как равные соответственно двум половинам — /_ 1 и /_2 угла А
(/_Е = /_1 как соответственные, /_С = /_2 как внутренние
накрест лежащие); следовательно, этот треугольник — равнобедренный,
и в предыдущей про-
пропорции можно заменить
АЕ через АС, откуда
и следует теорема.
2°. Биссектриса AF
внешнего угла А (черт.
121) треугольника ABC
пересекает продолже-
ние стороны ВС в точ-
точке F (если треуголь-
С
Черт. 121.
ник — не равнобедренный). Мы хотим доказать, что —,= - .
Сг АС
Доказательство вполне аналогично предыдущему. Проведём через
точку С прямую CG, параллельную \F, и заметим, что: 1) параллель-
ГГ лг BF BA m
ные прямые СО и Аг дают пропорцию —=..= - и 2) треугольник
ACG — равнобедренный (как имеющий в точках С и G углы, соот-
соответственно равные двум половинам внешнего угла при вершине А и,
следовательно, равные между собой), что позволяет заменить AG
через АС.
Примечание. Мы видим, что биссектриса угла треугольника
и биссектриса прилежащего внешнего угла делят гармонически
противоположную сторону.
I
ГЛАВА I. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ 115
Обратная теорема. 1°. Если прямая, выходящая из вершины
треугольника, делит внутренним образом противоположную сто-
сторону на Части, пропорциональные двум прилежащим сторонам,
то она является биссектрисой угла при вершине.
2°. Если прямая, выходящая из вершины треугольника, делит
внешним образом противоположную сторону на части, пропорци-
пропорциональные прилежащим сторонам, то она является биссектрисой
соответствующего внешнего угла.
Так как имеется только одна точка (п. 108), которая делит
внутренним образом сторону ВС (черт. 120) на части, пропорциональ-
пропорциональные прилежащим сторонам, то эта точка и есть основание биссектрисы
угла А. Точно так же имеет-
имеется лишь одна точка (п. ПО),
которая делит внешним образом
сторону ВС (черт. 121) на ча-
части, пропорциональные приле-
прилежащим сторонам; эта точка и
есть основание биссектрисы
внешнего угла А.
116. Теорема. Геометри-
Геометрическое место точек, расстоя-
расстояния которых от двух дан- Черт 122.
ных точек находятся между
собой в данном отношении (отличном от \), есть окружность.
Пусть А и В (черт. 122)—данные две точки; требуется найти
геометрическое место таких точен Л{, чтобы отношение
MA ^
-— было равно данному числу т.
Существуют две точки этого геометрического места, одна С на
отрезке АВ, другая D на его продолжении. Это те точки, о сущест-
существовании которых мы знаем из пп. 108—110. Пусть затем М есть
какая-либо точка искомого геометрического места точек. Прямая МС,
которая делит отрезок АВ на части СА и СВ, пропорциональные
отрезкам МА и MB, есть биссектриса угла при М треугольника
АМВ. Прямая MD, которая делит внешним образом сторону АВ этого
треугольника на части, пропорциональные прилежащим сторонам, есть
биссектриса внешнего угла при точке М. Эти две прямые взаимно
перпендикулярны (п. 15а), и точка М, следовательно, принадлежит
окружности О, описанной на CDt как на диаметре (п. 78).
Обратно, предположим, что точка М лежит на окружности О.
Проведём через точку М прямую МА', симметричную с MB относи-
относительно МС, и пусть А' — точка, в которой она пересекает прямую АВ.
Так как прямые МС и MD — биссектрисы угла A'MB и его пополни-
пополнительного угла, то точка А' гармонически сопряжена с точкой В отно-
относительно концов отрезка CD (п. 115, примечание); поэтому она со-
совпадаете точкой А. Так как прямые МС и MD — биссектрисы угла
6*
КНИГА ТРЕТЬЯ. ПОДОБИЕ
АМВ и его пополнительного угла, то имеет место зависимость
МА__СА_
мв~св~ т'
Следствие. Если разделить гармонически диаметр окружности точ-
точками А и В, то отношение расстояний любой точки окружности до
двух точек А и В постоянно.
УПРАЖНЕНИЯ.
124. На двух определённых прямых откладывают от двух определен-
определенных точек А и В, соответственно лежащих на этих прямых, два отрезка
AM и BN, которые изменяются пропорционально друг другу, и через
точки М и N проводят прямые, соответственно параллельные двум дру-
другим данным прямым. Найти геометрическое место точек пересечения
построенных таким образом прямых.
125. Две секущие, выходяшие из одной точки окружности, делят гар-
гармонически диаметр, перпендикулярный к прямой, соединяющей их необ-
шие концы (доказать).
126. В какой области плоскости расположены такие точки, отношение
расстояний которых до двух данных точек А и В больше заданного числ.а
(пп. 112, 71)?
127. Найти точку, расстояния которой от вершин треугольника про-
пропорциональны заданным числам.
Эта задача, если она возможна, имеет вообще два решения. Доказать,
что дЕе точки, отвечающие условию, лежат на одном и том же диаметре
круга, описанного около данного треугольника, и делят гармонически
этот диаметр.
128. Через общую точку А двух окружностей проводят произвольную
секущую, которая вторично пересекает окружности в точках М и М'.
Найти геометрическое место точек, делящих отрезок ММ' в данном отно-
отношении (упр. 65).
ГЛАВА II.
ПОДОБИЕ ТРЕУГОЛЬНИКОВ.
117. Определение. Два треугольника называются подобными,
когда они имеют равные углы и их соответственные стороны пропор-
пропорциональны.
Примечание. Два равных треугольника тем самым подобны.
Два треугольника, подобные одному и тому же третьему, подобны
между собой; в частности, если два треугольника подобны, то любой
треугольник, равный первому, подобен второму.
Лемма. Всякая прямая, параллельная одной из сторон тре-
треугольника, образует с двумя другими его сторонами треугольник,
подобный первому.
Пусть DE — прямая, параллельная стороне ВС треугольника ABC
(черт. 123). Я утверждаю, что новый треугольник ADE подобен тре-
треугольнику ABC.
ГЛАВА II. ПОДОБИЕ ТРЕУГОЛЬНИКОВ 117
Прежде всего углы обоих треугольников попарно равны, так как
угол при вершине А — общий, и углы D и В, Е и С равны как
соответственные.
AD AE
Во-вторых, мы имеем (п. 114): —==—- и нам остаётся только
Ad AC
доказать, что общее значение этих двух отношений равно значению
DE
отношения ——-.
ЬС
Для этого проводим через точку D прямую DF, параллельную
АС, так, чтобы получить параллелограм DECF.
Прямая DF делит стороны ВА и ВС на пропорциональные части;
следовательно, имеем:
D?_FC_AD
ВС~ ВС~~ АВ'
Примечание. Прямая DE может быть внутренней по отноше-
отношению к треугольнику (черт. 123) или внешней (черт. 124 и 12о), что
не изменяет доказательства.
Д
А
л—ч xz
в f со
Черт. 123. Черт. 124.
Однако в случае, данном на чертеже 125, необщие углы обоих
треугольников, лежащие против соответственных сторон, равны между
собой не как соответственные, а как внутренние накрестлежащие.
118. Следующие предложения, известные под названием признаков
подобия треугольников, дают необходимые и достаточные условия
для того, чтобы два треугольника были подобны.
Первый признак подобия. Два треугольника подобны, если
они имеют по два угла, соответственно равных друг другу.
Пусть ABC и А'В'С—треугольники, в которых /_А = /_А' и
^_В = ^_Б (черт. 12G). Я откладываю на АВ отрезок AD^A'B' и
провожу через точку D параллель DE к стороне ВС. Треугольник
ADE подобен ABC (по предыдущей лемме); кроме того, он равен
А'В'С, как имеющий с ним соответственно равные углы и равную
сторону.
Второй признак подобия. Два треугольника подобны, если
они имеют по равному углу, заключённому между пропорциональ-
пропорциональными сторонами.
118
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Пусть ABC и А'В'С—треугольники, у которых /А — /_А' и
-г~=-тг~; (черт. 126). Отложим на стороне АВ отрезок AD = А'В'
и проведём параллель DE к стороне ВС. Треугольник ADE подибен
треугольнику ABC. Он равен треугольнику А'В'С, как имеющий с
ним равный угол (^_А = ^_А'), заключённый между соответственно
равными сторонами. Действительно, AD равна А'В' но построению, и
„ АВ А'В' . , АВ АО
из двух пропорций -д-с=1~п7у (условие) и ^ = т^. имеющих по
три общих члена, следует., что А'С' = АЕ.
Третий признак подобия. Два треугольника подобны, если три
стороны одного пропорциональны сторонам другого.
3
С В'
Черт. 126.
AS AC ВС
Пусть ABC и А'В'С' — треугольники, в которых •тгб!' = ~лП^ ~srrf •
Отложим на АВ отрезок AD = A'BI и проведём параллель DE к сто-
стороне ВС. Треугольник ADE, подобный треугольнику ABC, равен тре-
треугольнику А'В'С, так как их стороны соответственно равны; действи-
действительно, AD=A'BI по построению, а из пропорций ~аТ>== ~аР и
АВ ВС .
jtt^^TTf (предыдущий пункт), имеющих потри равных члена соответ-
АВ
АС
А'С
ственно с пропорциями, данными в условии теоремы: тгн7=ттт^
Ш1==Ш~" следУет> что АЕ=А'С и DE = B'C.
Примечание. Определение подобных треугольников содержит
пять условий: три выражаются равенством соответственных углов,
два — пропорциональностью сторон.
Следствие III п. 44 показывает, что можно опустить одно из трёх
первых условий, что сводит общее число условий к четырём.
Но признаки подобия, которые мы рассматривали, позволяют заклю-
заключить, что Достаточно двух (надлежащим образом выбранных) условий
из числа пяти первоначальных.
119. Теорема. Два треугольника, стороны которых соответ-
соответственно параллельны или перпендикулярны, подобны.
Действительно, в данном случае углы обоих треугольников соответ-
соответственно или равны или пополнительны (п. 43), так что (если ABC и
ГЛАВА II. ПОДОБИЕ ТРЕУГОЛЬНИКОВ
119
А'ВС— данные треугольники) имеем:
В=В
или
или
или
B-\-B =
треугольники
S
Три равенства второго столбца не могут быть одновременно верны,
иначе общая сумма углов в двух треугольниках была бы равна шести
прямым, а не четырём. Два из тех же равенств также не могут суще-
существовать одновременно; например, нельзя иметь в одно и то же время
А -4- А' = 2d и В -\- В' = 2d, так как в таком случае общая сумма углов
равнялась бы 4-d-\-С-\-С. Следует поэтому взять по крайней мере
два равенства из первого столбца, и таким образом
имеют по два соответственно равных угла
(первый признак подобия).
120. Теорема. Два прямоугольных
треугольника подобны, если отношение
одного из катетов к гипотенузе одно и
то же в обоих треугольниках.
Действительно, мы можем поступить
как в п. 118 и построить третий треуголь-
треугольник, подобный первому и имеющий ту же
гипотенузу, что и второй. Второй и тре
тий треугольники имеют, таким образом,
ещё и по равному катету и будут равны
по второму признаку равенства прямоугольных треугольников.
Примечание. Кроме этого признака подобия можно, конечно,
применять к прямоугольным треугольникам признаки подобия произ-
произвольных треугольников. Например, два прямоугольных треугольника
подобны, если они имеют по равному острому углу (первый признак
подобия произвольных треугольников) или если их катеты пропорцио-
пропорциональны (второй признак подобия треугольников).
121. Теорема. Пучок прямых, проходящих через одну точку,
отсекает на двух параллельных прямых пропорциональные отрезки.
Пусть, например, SAA', SBB, SCC (черт. 127) — три прямые,
проходящие через одну точку, которые пересекают обе параллельные
прямые ABC и А'ВС.
Из подобии треугольников SAB и SA'B (п. 117} имеем:
А'В-
SB'
''SB '
и из подобных треугольников SBC и SBC:
В'С
ВС
SB'
~~SB
откуза следует пропорциональность отрезков А'В и ВС отрез-
отрезкам АВ и ВС.
!20
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Примечание. Каждые два отрезка, соответствующие друг
другу, направлены либо в одну и ту же сторону, либо в противо-
противоположные стороны, в зависимости от того, лежит ли точка 5 вне
обеих параллельных прямых или между ними.
Обратная теорема. Если три прямые отсекают на двух
параллельных прямых пропорциональные отрезки (причём каждые
два соответственных отрезка направлены в одну и ту же сторону
или каждые два соответственных отрезка направлены в противо-
противоположные стороны), то эти три прямые либо проходят через одну
точку, либо параллельны между собой.
Если отрезки соответственно равны и направлены в одну сторону,
то прямые параллельны (п. 4G, вторая обратная теорема).
Итак, пусть АА', ВВ', СС — прямые, которые отсекают на парал-
параллельных ABC и А'В'С пропорциональные отрезки, так что имеют
место равенства
А'В' _В'С _А'С
АВ ВС АС '
причём если отрезки обеих прямых направлены в одну сторону, то
общее значение трёх отношений отлично от 1. Это ограничение делает
невозможным (п. 4G) параллельность прямых АА' и ВВ'; следовательно,
они пересекаются в некоторой точке S.
Соединив-" затем S с С, мы видим, что эта прямая пересечёт пря-
прямую А'В'С в точке С\ , которая обязательно совпадает с С, так
как имеем:
А'СГ' АС , „ . А'С .
„, , = р-^ (по предыдущей теореме) =—7—7 (по условию).
УПРАЖНЕНИЯ.
129. Через точку пересечения диагоналей трапеции проводят прямую,
параллельную основаниям. Доказать, что непараллельные стороны и точка
пересечения диагоналей определяют на этой прямой дл-а равных отрезка.
130. Пусть а — АВ, b = CD — основания трапеции ABDC. Одну из её непа-
ЕА т
раллельиых сторон делят в отношении -рг-.= —• и проводят через точку Е
прямую, параллельную основаниям. Доказать, что отрезок этой параллели,
m-CDA-n-AB г)
заключенный внутри трапеции, равен -±- . Рассмотреть случай,
когда Е—середина стороны АС.
131. Если из вершин треугольника и точки пересечения меднан
опустить перпендикуляры на прямую, лежащую вне треугольника, то по-
последний из этих перпендикуляров есть среднее арифметическое трёх пер-
первых (см. предыдущее упражнение).
132. Через вершину А параллелограма ABCD проводят произвольную
секущую, которая пересекает диагональ BD в точке Е и прямые ВС и
CD — в точках F и О. Доказать, что АЕ есть среднее пропорциональное
между EF и EG.
ГЛАВА III. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ
121
133. Найти геометрическое место точек, которые делят в данном отно-
отношении отрезки, отсекаемые сторонами данного угла на параллельных прямых
данного направления.
134. Найти геометрическое место точек, из которых две данные окруж-
окружности видны под равными углами х).
ГЛАВА III.
МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ.
122. Определение. Ортогональной проекцией (или ради сокра-
сокращения просто проекцией) точки на прямую называется основание пер-
перпендикуляра, опущенного из точки на прямую.
Проекцией отрезка на прямую называется отрезок, концами кото-
которого служат проекции концов данного отрезка.
123. Пусть ABC (черт. 128)—прямоугольный треугольник с прямым
углом при А. Из этой вершины опустим на гипотенузу высоту AD.
' д Между различными элементами фигуры, та-
таким образом полученной, существуют неко-
некоторые соотношения, с которыми мы теперь и
i познакомимся.
Л Теорема. В прямоугольном треуголь-
С нике каждый из катетов есть среднее про-
пропорциональное между гипотенузой и его
проекцией на гипотенузу.
Так, АВ есть среднее пропорциональное между BD и ВС. Действи-
Действительно, прямоугольные треугольники ABD и ABC подобны как имеющие
общий угол при В (п. 120, примечание). Сторонам АВ и BD первого
треугольника соответствуют стороны ВС
и АВ второго, так что имеем равенство:
АВ
'ВС
В
D
Черт. 128.
^ = ~ или
Следствие. Всякая хорда круга есть
среднее пропорциональное между диа-
диаметром и её проекцией на диаметр,
проходящий через один из её копире
(черт. 129).
Действительно, этот диаметр и данная
хорда являются гипотенузой и катетом
Черт. 129.
одного и того же прямоугольного треугольника (п. 73, следствие II).
Примечание. Подобные треугольники ABD и ABC (черт. 128,
129) дают ещё:
Ц = ^, откуда AB.AC = BC-AD.
*) угол, под которым окружность видна из определённой точки, есть
угол, образованный касательными, проведёнными к этой кривой из данной
точки. i
•22 КНИГА ТРЕТЬЯ. ПОДОБИЕ
Таким образом, произведение катетов прямоугольного треуголь-
треугольника равно произведению гипотенузы на соответствующую высоту,
124. Теорема Пифагора. В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов.
Мы видели, что имеет место равенство ABi^=BC-BDr
Та же теорема, применённая к катету АС, даёт АС2 = ВС-CD.
Складывая почленно, имеем:
А В2 + АС* -= ВС (BD -f- CD) = ВС*.
Примечание. Эта теорема служит для вычисления какой-либо
стороны прямоугольного треугольника, если заданы две другие.
Так-, например, пусть требуется вычислить гипотенузу прямоуголь-
прямоугольного треугольника, катеты которого равны 3 м и 4 м. Единицей
длины взят метр; квадрат числа, измеряюще-
измеряющего гипотенузу, равен сумме квадратов чисел 3
и 4, измеряющих катеты. Эта сумма равна
числу 32-j- 42 = 25, квадратный корень из
которого 5; гипотенуза будет равна 5 м.
Пусть ещё требуется вычислить один из
катетов прямоугольного треугольника, если
гипотенуза равна Юли другой катет' ра-
равен 7 м. Квадрат искомой стороны, сложенный с
49( = 72), должен датьЮСН = 102); этот квадрат, таким образом, будет
равен 100 — 49 = 51. Квадратный корень из 5] (т. е. 7,14 — с точ-
точностью до одной сотой) даёт длину искомой стороны в метрах.
125. Теорема. В прямоугольном треугольнике перпендикуляр,
опущенный из вершины прямого угла на гипотенузу, есть среднее
пропорциональное между двумя отрезками, на которые он рассе-
рассекает гипотенузу.
Действительно, треугольники ABDu ACD (черт. 128) подобны,
как имеющие взаимно перпендикулярные стороны. Отрезки BD, AD,
таким образом, пропорциональны отрезкам AD, CD.
Следствие. В круге перпендикуляр, опущенный из какой-либо
точки окружности на диаметр, есть среднее пропорциональное
между отрезками, на которые он рассекает диаметр.
126. Теорема. Разность квадратов двух сторон треугольника
равна разность квадратов их проекций на третью сторону.
В треугольнике ABC (черт. 130) спроектируем вершину В в точку
И прямой АС.
Равенства
АВ2 = AN* -f- ВН\
ВС* = СН* -f ВНг
дают после почленного вычитания:
АВ' — ВС? — АН* — СИ*.
ГЛАВ\ III. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В TPEYrOibHHKF
123
Теорема. Во всяком треугольнике:
1) квадрат стороны, лежащей против острого угла, равен
сумме квадратов двух других сторон без удвоенного произведения
одной из этих сторон и проекции на неё другой стороны;
2) квадрат стороны, лежащей против тупого угла, равен сумме
квадратов двух других сторон, сложенной с удвоенный произведе-
произведением одной из этих сторон и проекции на неё другой стороны.
1°. Пусть в треугольнике ABC (черт. 130) ВС—сторона, лежащая
против острого угла А. Опустим из точки В перпендикуляр ВН на
прямую АС. Имеем (по предыдущей теореме)
ВС2 = АВ2 -(- СИ"- — АН2.
Но так как СИ есть разность между АС и АИ, то можно за-
заменить1) Ш2 через АС1 — ЧАС-АН-\-АН*.
Таким образом, получаем:
ВС2 = АВ2 -\- АС2 — 2 АС ¦ АН.
2°. Пусть в треугольнике ABC (черт. 131) ВС — сторона, лежащая
против тупого угла А. Опустим из точки В
перпендикуляр ВН на прямую АС. Имеем снова: В
Так как СИ — сумма отрезков АС и АН, то
можно заменить') СИ2через АСЦ-2АС- АН-\- АН"-.
При этом получим:
В&-—А& + АС?-1Г2АС-АН. Черт. 131.
Следствие. Угол треугольника будет острым, прямым или
тупым, смотря по тому, будет ли квадрат стороны, лежащей
против этого угла, меньше, равен ила больше
суммы квадратов двух других сторон.
127. Теорема Стюарта. Если даны тре-
треугольник ABC и на его основании точка D, ле-
лежащая между точками В а С, то имеем равен-
равенство:
В D Н с
Черт. 132.
АВ- ¦ DC -f АС2 ¦ BD — AD2 ¦ ВС = ВС ¦ DC • BD.
Опустим из точки А (черт. 132) на ВС перпен-
перпендикуляр АН и предположим для определённости,
что точка Н лежит с той же стороны от точки D, как и вершина С.
Применив обе теоремы предыдущего пункта: одну — к треугольнику
ACD, другую — к треугольнику ABD, получим:
АС2 = AD" -\- DC2 — 2DC- DH,
АВ2 = AD2 -\- BD2 + 2BD - DH.
1) Мы предполагаем здесь известными формулы, дающие квадрат суммы
или разности двух чисел: (a -f-bfl = a* -J-2ab -J-№, (а — bp = a?—2ab-\-№.
124 КНИГА ТРЕТЬЯ. ПОДОВИЕ
Умножим эти два равенства: первое на BD, второе на DC и сло-
сложим их почленно.
Член 2-BD'DC-DM, который встречается один раз со знаком —,
другой раз со знаком -|-, исчезает, и мы получим:
AC2-BD-)-ABi-DC = ADi- (BD -J- DC) -f- DC- ¦ BD -f- BD- ¦ DC =
128. Вычисление длин замечательных л.иний треугольника.
Пусть ABC—произвольный треугольник, стороны которого ВС,
СА, АВ соответственно измеряются числами (по предположению данными)
д а, Ь, с. Поставим себе задачей вычислить ме-
медианы, биссектрисы и высоты треугольника.
1°. Медианы. Пусть AD—медиана, выходя-
выходящая из вершины А (черт. 133). В равенстве, по-
полученном при помощи предыдущей теоремы, следует
заменить ВС, СА, АВ соответственно через а,
В ОН С а , ¦
и „ Ь, с; CD и BD — через —-. Можно все члены ра-
Чбрт. loo. 2, *
венства разделить на а, и мы получим:
откуда
Итак, полусумма квадратов двух сторон треугольника равна
квадрату половины третьей стороны, сложенному с квадратом
соответствующей медианы.
128а. С другой стороны, если в равенствах (п. 127)
АО- = AD* + DC — 2DC- DH, АВ* = AD* -\- BD* -{-2BD-DH
заменить снова ВС, СА, АВ через а, Ъ, с; DC и BD — через — и если
вычесть почленно первое равенства из второго, то получим:
с2 — bv- = 2
Итак, разность квадратов двух сторон треугольника равна
удвоенному произведению третьей стороны и проекции на эту сто-
сторону соответствующей медианы.
Следствие, Геометрическое место точек А, разность квадратов
расстояний которых до двух определённых точек В и С постоянна,
есть перпендикуляр к прямой ВС.
Действительно, если разность АВ2 — АС2 постоянна, то проек-
проекция И точки А на прямую ВС есть определённая точка.
129. 2°. Биссектрисы. Обозначим теперь через AD биссектрису
угла А (черт. 134). Точка D разделит ВС пропорционально сторо-
ГЛАВА 411. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ
125
нам АВ и АС, так что будем иметь:
С?_ ВС а
b b-\-c b-\-c
или BD =
ас
и CD =
ab
b-\-c'
Заменим в соотношении, полученном на основании теоремы п. 127,
BD и CD их выражениями и одновременно ВС, СА, АВ — их значе-
значениями; мы получим, разделив на а,
ab ас
b-{-c ' b-\-c '
откуда
be1 -4- b-c
b-\-c
a2 be
(b-\*cY
Пусть теперь АЕ—биссектриса внешнего угла при А (черт. 134);
предположим для определённости, что АВ больше АС, так что точка Е,
которая делит внешним образом сторону ВС пропорционально сторо-
сторонам АВ и АС, лежит на продолжении стороны ВС за точку С.
В
И С
Черт. 135,
Имеем:
I
BE CE
с
ВС
или
ВЕ =
Т~~ с — Ь
ас
с—Ь
и СЕ =
с — Ь
ab
с — Ь'
Мы применим теорему п. 127 к треугольнику ABE и к точке С,
взятой на основании BE. Заменив ВС, СА, АВ, BE и СЕ их значе-
значениями и разделив на а, имеем:
откуда
с—Ъ '
a" be
ЪЧ
с — b с
Ъсп- — ЪЧ
ас
ab
-Ь с — Ь '
а?-(с- b?
(c~bf
130. 3°. Высоты. Опустим из вершины А высоту АН (черт. 135).
Из двух углов В и С по крайней мере один острый. Предположим для
определённости, что острым будет угол В. Можно применить теорему
126
КНИГА ТРЕТЬЯ. ПОДОБИЕ
п. 126 к стороне АС^Ь, лежащей против этого углл, и записать:
?2 = й2 -f- с2 — 2а ¦ ВН
или
Й? + С2 — Л2
2а '
Но из прямоугольного треугольника АНВ имеем:
Это равенство, правая часть которого есть разность двух квадратов,
может быть записано в виде:
АН*=
(-¦
2а
Bас — а* —с
2а
а2 4- с2 — Л2
)=
_ [й= — (д — сK1 \(а 4- с)° —
Но каждый из множителей в числителе правой части представляет
собою разность квадратов. Предыдущая формула может быть, таким
образом, ещё записана в виде:
АН* = -
— h)(a-{-h
Если обозначить через р половину периметра треугольника, так
o а-\- Ь-\~с = 2р, то величины Л-f-c — а, с-\-а — Ь, а-\-Ъ — с
_ будут соответственно равны 2р — 2а, 2р — 2Ь,
2р — 2с и .
_ 4р (р — а)(р — Ь)(Р — с)
Если, с другой стороны, выполнить умножение
[(a-\-cj2—№] [б2—(а — с)г], то можно записать;
~ 1402^2 _ (Й2 + f2 __ №J] = _L (
Черт. 136. 130а. Теорема. Произведение двух сто-
сторон треугольника равно произведению высоты,
опущенной на третью сторону, и диаметра описанного круга.
В треугольнике ABC (черт. 136) пусть АН—высота, опущенная
из вершины А, АА'—диаметр описанного круга. Треугольники АНС
и ABA' — прямоугольные, один с прямым углом при вершине Н, другой
с прямым углом при вершине В; они имеют по равному острому углу
(/ А' = ^/_С, как опирающиеся на одну и ту же дугу АВ)\ следова-
ГЛАВА III. METPHMECKW СООТНОШЕНИЯ В ТРЕУГОПЬНИКЕ 127
I
тельно, эти треугольники подобны и лают:
— = \- и™ АВ-АС=АН-АА'.
АС АА
Пользуясь найденным выше значением отрезка АН, можно получить
из этой теоремы следующее выражение для радиуса описанной окруж-
окружности R:
А А' be abc
К = ~2~ = 2~АН =
УПРАЖНЕНИЯ.
135. Произведение отрезков, отсекаемых подвижной касательной к кругу
на двух параллельных касательных к тому же кругу, есть величина постоян-
постоянная (доказать)
136. Обратная величина квадрата высоты прямоугольного треугольника
равна сумме обратных величин квадратов катетов (доказать).
137. Найти отношение суммы квадратов медиан треугольника к сумме
квадратов его сторон.
138. Разность между суммой квадратов расстояний произвольной точки
плоскости до двух противоположных вершин параллелограма и суммой
квадратов расстояний той же точки до двух других его вершин есть вели-
величина постоянная (доказать). Рассмотреть случай прямоугольника.
139. Сумма квадратов четырёх сторон четырёхугольника равна сумме
квадратов его Лиагоналей, сложенной с учетверённым квадратом отрезка,
соединяющего середины диагоналей (доказать).
140. Если А, В, С—вершины треугольника, (у —точка пересечения
медиан, М— произвольная точка плоскости, то имеем:
МА* + MB* + МО = GA* -\- GB* +- GO -+- 3jWG*
Сдоказать).
141. Найти геометрическое место точек, квадраты расстояний'которых
до двух постоянных точек, соответственно умноженные на данные числа,
имеют данную сумму или разность. Доказать этим путём теорему п. 116.
142. Найти геометрическое место точек, квадраты расстояний которых
до трёх данных точек, соответственно умноженные на три данных числа,
имеют постоянную сумму. Рассмотреть ту же задачу для случая, когда
вместо трёх точек дано произвольное число точек.
143. Квадрат биссектрисы угла треугольника равен произведению сто-
сторон, её заключающих, уменьшенному на произведение отрезков, на которые
она рассекает третью сторону (доказать).
Сформулировать и доказать аналогичную теорему для биссектрисы
внешнего угла.
144. Из формул для медианы и для биссектрисы (пп. 128, 129) вывести
неравенства, указанные в упражнениях 11 и 18.
L45. Если медиана треугольника есть среднее пропорциональное между
сторонами Ъ и с, которые её заключают, то квадрат, построенный на раз-
разности этих сторон, имеет своей диагональю третью сторону треугольника.
146. Через внутреннюю точку круга проведены под прямым углом две
хорды. Доказать, что сумма квадратов двух противоположных сторон четы-
четырёхугольника, вершинами которого служат концы этих хорд, равна квадрату
диаметра.
128
КНИГА ТРЕТЬЯ. ПОДОБИЕ
147. Произведение расстояний любой точки окружности до двух противо-
противоположных сторон четырёхугольника, вписанного в эту окружность, равно
произведению расстояний этой же точки до двух других сторон или до
двух диагоналей (доказать).
Как изменится формулировка этой теоремы, если две противоположные
стороны обратятся в касательные?
ГЛАВА IV.
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В КРУГЕ.
РАДИКАЛЬНАЯ ОСЬ.
131. Теорема. Если через точку А, взятую в плоскости дан-
данной окружности, провести к этой окружности секущие, то произ-
произведение расстояний от точки А до двух точек пересечения каждой
секущей с окружностью есть величина постоянная.
Будем различать два случая:
1°. Точка А лежит внутри окружности (черт. 137). Пусть
через эту точку проведены секущие ВАВ' и САС. Соединим точку В
с точкой С и точку С с точкой В'. Треугольники ABC и АСВ'
подобны, как- имеющие равные
углы. В самом деле, у них углы А д
равны как вертикальные и / В' —
^ так как оба измеряются
в
Черт. 137.
половиной дуги ВС. Пропорциональность сторон даёт
откуда, приравняв произведение крайних
АВ АС
АС А В"
произведению средних,
имеем:
АВ-АВ'=АС-АС.
2°. Точка А лежит вне окружности (черт. 138). Пусть ABB'
и АСС — две секущие, проходящие через эту точку. Соединим снова
точки С и В', В и С. Треугольники ABC и АСВ' опять подобны,
как имеющие равные углы. В самом деле, у них угол А — общий и
/fi'=/C, так как оба измеряются половиной дуги ВС. Пропор-
' АВ АС
циональность сторон даёт, как и выше: Tri==:2c7i откуда следует до-
доказываемое предложение.
ГЛАВА rV. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В КРУГЕ
129
131а. Обратная теорема. Если на двух прямых ВАВ и
САС, проходящих через точку А (черт. 139), взять такие четыре
точки В, В', С, С, что произведение АВ-АВ' равно произведению
АС'АС (причём точка А либо лежит на продолжении обоих от-
отрезков ВВ а СС, либо лежит на самих отрезках), то эти
четыре точки лежат на одной окружно-
окружности.
В самом деле, три тички В, С, С", не ле-
лежащие на одной прямой, определяют окруж-
окружность,, и эта окружность пересекает прямую
ВАВ' в некоторой точке Bx', так что
AS-ABj' —/4С-/4С. Сравнение этого равен-
равенства с условием теоремы АС• АС = АВ-АВ'
показывает, что АВ^'=АВ'. Следовательно,
точка В' совпадает с точкой В".
132. Теорема. Если через точку, ле-
лежащую вне окружности, провести каса-
касательную и секущую, то касательная есть средняя пропорциональная
между всей секущей и ei внешней частью.
В самом деле, пусть ABB' — секущая, AT— касательная (черт. 140).
Следует повторить без всякого изменения доказательство теоремы
п. 131 B°), заменив лишь
две буквы С и С буквой. Т.
Мы имеем в данном слу-
случае также пример того что
касательная (п. 67) должна
рассматриваться как прямая,
имеющая с окружностью две
общие точки, слившиеся в
точке касания.
Обратная теорема.
Черт. 139.
Черт. 140.
Если отложить на пря-
прямой ABB' от точки А в
и АВ1 и на другой прямой,
отрезок AT, представляющий
одном направлении отрезки АВ
выходящей из той же точки А,
сабою среднее пропорциональное между АВ и АВ, то три точ-
точки В, В', Т лежат на окружности, касающейся прямой AT в точке Т.
В самом деле, окружность ВВТ имеет с прямой АТ общую точку 7";
если бы она имела ещё однуоэщую точку Т' (черт. 141), то имело бы
место (п. 131) равенство:
АВ-АВ = AT-AT.
Это равенство при сравнении с условием АВ-АВ'= AT2 показы-
показывает, что точка Т необходимо совпадёт с точкой Т.
133. Определение. Степенью точки А относительно окружно-
окружности называется произведение отрезков какой-либо секущей, выходя-
выходящей из этой точки, считая отрезки от точки А до точек пересечения
9 Элементарная геометрия
130
КНИГА ТРЕТЬЯ. ПОДОБИЕ
с окружностью (произведение это согласно п. 131 не зависит от
направления секущей); это произведение берётся со знаком -|-, если
точка А лежит вне окружности, и со знаком—, если она лежит вну гри
/окружности.
Если точка лежит вне окружности, то степень точки равна квад-
квадрату касательной, проведённой через эту точку.
134. Степень точки А относительно окружности с центром О
равна разности квадратов расстояния О А и радиуса.
В самом деле, примем за секущую ABB' прямую ОА. Отрезки АВ
и АВ представляют собою: один сумму, другой — разность отрезка О А
и радиуса; их произведение,
следовательно, равно разности
квадратов этих двух вели-
величин.
Если принять во внимание
знак степени, то степень всег-
всегда равна d2 — R2 (где d — рас-
расстояние О A, R — радиус).
135. Если две окружности
пересекаются под прямым
углом, то квадрат радиуса
каждой из них равен сте-
степени её центра относительно другой окружности, и обратно.
Если окружности О и О' (черт. 142) пересекаются в'точке А под
прямым углом, то касательная к окружности О' в этой точке есть О А
и степень точки О относительно окружности О' равна ОА2.
Обратно, если степень точки О относительно окружности О' равна
О А2, то О А — касательная к окружно-
окружности и обе окружности ортогональны.
136. Геометрическое место то-
точек, имеюьицх одну и ту же степень
относительно двух данных окруж-
окружностей, есть прямая, перпендикуляр-
перпендикулярная к линиа центров.
Эта прямая называется радикальной
осью двух окружностей.
Пусть даны две окружности с центра-
центрами О и О' (черт. 143) и радиусами R и R'.
Если точка М имеет одну и ту же степень относительно этих двух
окружностей, то мы имеем: ОМ2— R2 = О'М2 — /?'2; это равенство
можно переписать в виде ОМ2 — O'M2 = R2 — R'2, откуда и следует
(п. 128а) заключение теоремы.
Согласно п. 128а расстояние между точкой пересечения И ради-
радикальной оси с линией центров и серединой D расстояния между цен-
центрами даётся формулой: 2DH-00'= R2—R'2.
Примечания: 1°. Предыдущее доказательство справедливо, если
одна из окружностей имеет радиус, равный нулю, и, следовательно,
Черт. 142.
ГЛАВА IV. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В КРУГЕ
131
обращается в свой центр. Таким образом, геометрическое место
точек, степень которых относительно данной окружности равна
квадрату их расстояния до данной точки, есть прямая, перпендику-
перпендикулярная к прямой, соединяющей данную точку с центром окруж-
М
\
Н
Черт. 143.
нести.
Эту прямую можно
назвать радикальной осью
окружности и точки.
2°. Две концентриче-
концентрические окружности не
имеют радикальней оси1).
3°." Разность степе-
степеней какой-либо точки
относительно двух ок-
окружностей равна удвоен-
удвоенному произведению рас-
расстояния этой точки до
радикальной оси и рас-
143).
— её проекция на 00'.
стояния между центрами (черт.
В самом деле, пусть N— заданная точка, п
Разность степеней этой точки относительно обеих окружностей будет:
ОДР — R2 — (O'N2 — R'2) = ON2 —
— ON'2—(R- — R'2).
Но мы имеем:
ON- — O'N- = 2Dn ¦ 00'
и R'~R'3 = 2DH.OO',
откуда, вычитая, получаем:
ON2 — O'N2 — (R2 ~ R'2) =
= 2Нп-ОО'.
137. Если две окружности пе-
пересекаются, то радикальной осью
служит прямая, соединяющая точ-
точки пересечения.
В самом деле, понятно, что лю-
любая точка прямой АВ (черт. 144)
принадлежит геометрическому месту точек, имеющих одну и ту же
степень относительно обеих окружностей. Обратно, из предыдущего
вытекает, что любая точка М этого геометрического места при-
принадлежит прямой АВ. Это можно усмотреть и непосредственно,
если соединить точку М с точкой Л: если бы эта прямая пересекла
Черт. 144.
[) Радикальную ось двух концентрических окружностей можно рас-
рассматривать как лежащую в бесконечности. Действительно, если при гюсто-
янной разности R2 — К'- точки О и О' неограниченно приближаются друг,
к другу, то длина отрезка DH обращается в бесконечность.
9*
132
КНИГА ТРЕТЬЯ. ПОДОКНЕ
обе окружности в двух новых, различных между собою точках В' и
Вх', то обе степени MA MB' и МА-МВХ' были бы различны.
Точно так же, если две окружности касаются друг друга, то
радикальная ось есть их общая касательная.
138. Радикальная ось двух окружностей (по крайней мере,
часть этой оси, внешняя относительно обеих окружностей) есть
геометрическое место центров окружностей, которые пересекают
две данные окружности под прямым углом.
Действительно, центр одной из таких окружностей имеет одну и
ту же степень относительно двух данных окружностей, -9 именно ква-
квадрат радиуса окружности.
Рада/<альная ось делит общую касательную на две равные
части.
139. Теорема. Радикальные оси трех окружностей, взятых
попарно, пересекаются в одной и той же точке или параллельны.
Действительно, точка пересечения двух из трёх радикальных осей
имеет одну и ту же степень относительно трёх окружностей, следова-
следовательно, она принадлежит и третьей радикальной оси. Эта точка назы-
называется радикальным центром трёх окружностей. Если это — внешняя
точка, то она служит центром окружности, которая пересекает все
три окружности под прямым углом.
Примечание. Если две радикальные оси совпадают, то преды-
предыдущее рассуждение доказывает, что третья совпадает с первыми. Три
окружности имеют одну и ту же радикальную ось. Каждая окруж-
окружность, ортогональная к двум из трёх данных окружностей, ортого-
ортогональна и к третьей.
УПРАЖНЕНИЯ.
148. В плоскости даны: окружность и две точки А и В\ через точку А
проводят различные текущие ANM, которые пересекают окружность
в точках М и N.
Доказать, что окружность, проходящая через точки М и N и точку В,
проходит через другую неподвижную точку.
149. Геометрическое место точек, отношение степеней которых отно-
относительно данных двух окружностей равно данному числу, есть окружность,
которая с двумя первыми окружностями имеет одну и ту же радикальную
ось (доказать). Вывести отсюда геометрическое место точек упражне-
упражнения 128.
150. Параллельно стороне ВС треугольника проведена секущая DE,
которая пересекает сторону АВ в точке D и сторону АС—в " точке Е.
Показать, что радикальной осью двух окружностей, диаметрами которых
служат соответственно BE и CD, всегда является высота треугольника ABC,
проведённая через точку А.
151. Пусть D и D' — две точки па стороне ВС треугольника, Е и Е' —
две точки на стороне CA,Fh F'-^ две точки на стороне АВ. Если известно,
что существуют окружность, Проходящая через точки D, D', Е, Е',
окружность, проходящая через точки Е, Е1, F, F', и окружность, прохо-
проходящая через точки F, F', D, D', то отсюда следует, что шесть точек
D,U,E, ?', F, F1 лежат на одной окружности (доказать).
152. В каком случае различные окружности, ортогональные к двум
данным окружностям О и О', пересекают линию центров 00'? Показать,
что все они пересекают её в этом случае в одних и тех же двух точках
ГЛАВА V. ГОМОТЕТИЯ И ПОТОБИР 133
(предельных точках Понселе), а именно в тех точках, которые имеют
с данными окружностями одну и ту же радикальную ось.
153. Через точки А и В проведена какая-либо окружность и через
точки Cut), лежащие па одной прямой с первыми, — другая окружность,
также произвольная. Доказать, что общая хорда этих двух окружностей
прохочит через одну неподвижную точку.
154. Если радикальный центр трёх окружностей лежит внутри этих
окружностей, то он служит центром окружности, которая каждой из дап-
•аых окружностей делится на две равные части (доказать/.
ГЛАВА V.
ГОМОТЕТИЯ И ПОДОБИЕ.
140. Определение. Пусть выбрана точка S, которая называется
центром подобия (или центром гомотетии), и число k, кото-
которое называется коэсрициентом подобия; точкой, гомотетичной какой-
либо точке /И, называется точка /И', которая получается, если соединить
точку М с точкой 5 прямой линией и отложить на этой прямой от
точки 5 в направлении SM (черт. 145) 1,ли в противоположном направ-
направлении (черт. 145а) такой отрезок SM',
SM'
что имеет место равенство -^щ- = k.
Гомотетия называется прямой, если
отрезок SM откладывается в ту же
сторону, как и SM (черт. 145), и обрат-
обратной, если оба эти отрезка направлены в
противоположные стороны (черт. 145а).
Фигура, гомотетичная (или пер- ЧеРт-
спективно-подобная, или подобная и по-
подобно расположенная) какой-либо фигуре F, есть фигура, обра-
образованная совокупностью точек М\ гомотетичных точкам, образующим
фигуру F.
Примечания: 1°. Центр гомотетии есть точка, сама себе
гомотетичная; это — единственная точка, которая обладает дан-
данным свойством (за исключением, конечно, случая, когда гомотетпя
прямая и коэфициент подобия равен 1; в этом случае любая точка
совпадает со своей гомотетичной).
2°. Симметрия относительно точки (п. 99) есть частный случай
обратной гомотетии.
141. Теорема, В двух гомотетичных системах точек отрезок,
соединяющий две какие-либо точки одной аз систем, и отрезок,
соединяющий соответственные им точки другой, всегда парал-
параллельны, и их отношение равно коэфипиенту 'подобия; они направ-
направлены в одну гг ту же сторону или в противоположные стороны,
смотря по тому, будет ли гомотетия прямой или обратной.
Действительно, пусть Аи В— две точки первой фигуры, А'и В' —
точки, им гомотетичные (черт. 146), 5 — центр гомотетии, k — коэфнци-
134
КНИГА ТРЕТЬЯ. ПОДОБИЕ
SA1 SS1
ент подобия. Пропорция -j~a~ = -v~d — ^ показывает (п. 114, обрат-
ная теорема), что отрезки А'В1 и АВ параллельны, а подобие тре-
треугольников SA'B' и SAB — что отношение этих отрезков равно
отношению SA' к SA.
Следствия: I. Фигура, гомотетичная прямой линии, есть пря-
прямая линия. '
Действительно, если точка В перемещается по прямой АВ, причём
последняя остаётся неподвижной, то точка В' описывает прямую, про-
проходящую через А' и параллельную АВ.
II. Фигура, гомотетичная окружности,
есть окружность, прич-м их центры — го-
гомотетичные точки.
Действительно, если точка В перемещается
гак, что её расстояние от определённой точки А
остаётся постоянным, то точка В' опишет
окружность с центром в А' и радиусом А'В' =:
Черт. 146.
данному
111. Фигура, гомотетичная
треугольнику, есть треугольник, подобный первому.
142. Обратная теорема. Если на плоскости, в которой лежат
две системы точек, существуют две такие точки О и О', что
отрезок, соединяющий точку О с какой-либо точкой М первой
системы, и отрезок, соединяющий точку О' с соответственной
точкой М' второй системы, всегда параллельны и имеют данное
отношение (причём оба отрезка f
всегда направлены либо в одну s^, ??
и ту же сторону, либо всегда
направлены в противоположные
стороны), то эти две системы
гомотетичны.
Для того чтобы эта теорема бы- Черт. 147.
ла верна во всех случаях, необхо-
необходимо считать прямо-гомотетичными и такие две системы, в ко-
которых отрезки ОМ и О'М' равны и направлены в одну и ту же
сторону, т. е. две системы, которые равны между собой и полу-
получаются одна из другой с помощью поступательного переме-
перемещения.
Пусть М и М — две какие-либо соответственные точки (черт. 147).
Соединим М с М'. Если эта прямая параллельна 00', то четырёх-
четырёхугольник ОММ'О' — параллелограм и ОМ = О'М'\ обе системы полу-
получаются одна из другой с помощью поступательного перемещения.
В противном случае прямая ММ' пересекает 00' в точке S, которая
неподвижна, т. е. не зависит от выбора пары точек М, М'\ действи-
действительно, эта точка делит отрезок 00' в данном отношении k (внеш-
(внешним образом, если отрезки ОМ и О'М' направлены в одну и ту же
сторону, и внутренним образом, если они направлены в протнвополож-
ГЛАВА V. ГОМОТЕТИЯ И ПОДОБИЕ . 135
ные стороны) нследствие подобия треугольников SOM и SO'M'.
Далее, вследствие подобия тех же треугольников имеем:
SM1 О'М' _,
SM ~~ ОМ
ш
143. Следствие. Две любые окру ясности можно рассматривать
как гомотетичные и притом двумя различными способами.
Действительно, если О и О' -— центры этих окружностей, то концы
М и М' двух соответственно параллельных радиусов, направленных
в одну и ту же сторону, удовлетворяют условию предыдущей теоремы
и описывают две прямо-гомотетичные фигуры (черт. 148); точно также
концы М1 и М двух параллельных радиусов, направленных в противо-
М,
Черт. 148.
положные стороны, служат соответственными точками двух обратно-
гомотетичных фигур: в обоих случаях коэфициент подобия равен
отношению радиусов.
Следовательно, две окружности имеют два центра подобия'1) —
S, 5t; один, соответствующий прямой гомотетии, называется внешним,
другой, соответствующий обратной гомотетии, — внутренним. Центры
подобия делят гармонически отрезок, соединяющий центры окружно-
окружностей, так как каждый из центров подобия делит его в отношении,
равном отношению радиусов.
Точки касания внешней общей касательной прямо-гомотетичны,
так как радиусы, проведённые в эти точки, параллельны и направлены
в одну и ту же сторону. Точно так же точки касания внутренней
общей касательной обратно-гомотетичны.
Далее, общие внешние касательные (если они существуют) пере-
пересекаются во внешнем иентре подобия; внутренние общие касатель-
касательные (если они существуют) — во внутреннем центре подобия.
Если окружности касаются друг друга, то точка касания есть
один из центров подобия.
1) Впрочем, две равные окружности не имеют внешнего центра подо-
подобия; их можно рассматривать как прямо-гомотетичные только благодаря
тому обобщению этого понятия, которое было дано в предыдущем пункте.
136 КНИГА ТРЕТЬЯ. ПОДОБИЕ
Примечание. Две окружности не могут быть гомотетич-
гомотетичными более чем двумя различными способами.
Действительно, если имеет место гомотетия, то центры окружно-
окружностей соответствуют друг другу (п. 141, следствие II) и соответственные
радиусы параллельны.
В зависимости от того, будут ли они направлены в одну и ту же
сторону или в противоположные стороны, мы будем икеть ту или
иную из двух гомотетий, установленных выше.
144. Теорема. Две фигуры, гомотетичные третьей, гомоте-
гомотетичны между собой, и три центра подобия лежат на одной прямой.
Пусть фигуры F2 и Fs (черт. 149) гомотетичны одной и той же
фигуре Fj-, пусть О2 и Os — точки, соответствующие в фигурах /%,
и Fa некоторой определённой точке О1 фигуры F^ M2 и /И3 —
Черт. 149. с
точки, соответствующие произвольной точке Мг фигуры Ft. Отрезки
О2М2 и OSM3 параллельны, так как они оба параллельны Oj^M^, они
либо всегда направлены в одну и ту же сторону (если они оба иаправ-.
лены в ту же сторону, как и OtMu и."и сба — в сторону, противо-
противоположную О1М1, т. е. если гомотетии {Fv F2) и (F,, Fs) одного и
того же рода), либо всегда накрав; ены в противоположные стороны
(если две исходные гомотетии различного рода); наконец, их отно-
отношение постоянно, так как из равенств рртт^"" и п м СЛе"
дует, что ——-3 = —. Итак, две фигуры F., и Fs действительно
гомотетичны между собой, причём гомотетия будет прямой, если дЕе
исходные гомотетии одьою рода, и обратной, если эти гомотетии
различного рода.
ГЛАВА V. ГОМОТЕТИЯ И ПОДОБИЕ
137
Пусть теперь Sos — центр гомотетии фигур F2 и /%,, Ssl— центр
гомотетии фигур FY и Fs, SK—центр гомотетии фигур F{ и F.,; я
утверждаю, что эти точки лежат н а одной прямой. Действительно,
точка 5?3, рассматриваемая как принадлежащая фигуре F4, сака себе
соответствует в фигуре Fa; она имеет в качестве соот ветственгюй
в фигуре Fx некоторую точку s. Прямая sS2g пройдёт через точку
S3l (как соединяющая соответственные точки фигур Z7, и /%) и через
точку S^n (как соединяющая соответственные точки фигур Z7, и F2).
Примечание. Мы видим, что если три фигуры попарно гомоте-
гомотетичны, то из трёх гомотетий прямыми будут или одна или все три1).
145. Три окружности С,, С2, Са можно рассматривать как фшуры
попарно гомотетичные и притом четырьмя различными способами;
действительно (п. 143), можно выбрать произвольно прямую или обрат-
обратную гомотетию между окружностями С, и С2 и между окружностями
С, и Cs (что составляет четыре возможных , сочетания); гомотетия
между окружностями С, и Са определяется двумя первыми гомотетиями.
мы видим, что три внешние центра
Е /г
Применяя предыдущую теорему,
подобия лежат на одной пря-
прямой; точно так же лежат
на одной прямой каждый внеш-
внешний центр подобия с двумя
внутренними центрами подо-
подобия, ему не соответствен-
соответственными. Четыре прямые, таким
образом определённые, назы-
называются осями подобия: одна
из них — внешняя ось подо-
подобия, три другие —внутренние;
они попарно пересекаются
в шести центрах подобия.
Определения: Полным че-
четырёхсторонником называется (черт. 150) фигура, которая получится,
если продолжить противоположные стороны обыкновенного четырёх-
четырёхугольника до их пересечения. Полный четырёхсторонник имеет 6 вер-
вершин: А, В, С, D, E, F (черт. 150), попарно противоположных. Диа-
Диагональю полного четырёхсторонника называется всякая прямая, соеди-
соединяющая две противоположные вершины, так что полный четырёхсторон-
четырёхсторонник ABCDEF имеет три диагонали — АВ, CD и EF.
Согласно этим определениям оси подобия трех окружностей
образуют полный четырёхсторонник, имеющий своими диагоналями
три линии центров.
146. Определение. Две фигуры называются подобными между
собой, если их можно расположить таким образом, чтобы они были
гомотетичными.
!) Так как либо из трёх соответственных отрезков OvMb O.M^ и OSMS
два направлепы в одну сторону, а третий — в противоположную, либо
все три отрезка направлены в одну сторону. Прим. ред. переведа.
138
КНИГА ТРЕТЬЯ. ПОДОБИИ
Две дуги круга, которым соответствуют равные центральные углы,
будут, например, подобными фигурами.
Теорема. Два подобных многоугольника имеют равные углы
и их соответственные стороны пропорциональны.
Действительно, рассмотрим эти два многоугольника в том положении,
в котором они гомотетичны; при этом их углы будут соответственно
равны, так как их соответственные стороны параллельны и направлены
в одну и ту же сторону или параллельны и направлены в противопо-
противоположные стороны (в зависимости от того, будет ли гомотетия прямой
или обратной); отношение любых двух соответственных сторон равно
коэфициенту подобия.
Следствие. Отношение периметров двух подобных многоуголь-
многоугольников равно коэфициенту подобия.
Это вытекает из пропорциональности сторон на основании следую-
следующей арифметической теоремы: в последовательности равных отноше-
отношений сумма предыдущих членов относится к сумме последующих,
как один из предыдущих к своему последующему.
147. Обратная теорема. Если углы двух многоугольников,
взятые в последовательном порядке в обоих многоугольниках, соот-
соответственно равны между собой и каждые два соответственных
угла имеют одинаковое направление или каждые два угла имеют
противоположное направление, а соответственные стороны много-
многоугольников пропорциональны, то эти много угольники подобны.
Пусть два многоугольника P(ABCDE) и Р (A'b'C'D'E') удовле-
удовлетворяют условиям теоремы, так что мы имеем
А'В' В'С CD' D'E' E'A'
АВ ВС CD DE ЕА '
Построим многоугольник РЛ, гомотетичный многоугольнику Р отно-
относительно произвольной точки, выбрав коэфицнент подобия равным общему
„ А'В' ВС .,
значению отношении , —— и т. д. Мы получим, таким обра-
зом, новый многоугольник Р1 (A^B^C^D^^), углы которого соответ-
соответственно равны углам многоугольника Р (и имеют либо все то же
самое направление, либо противоположное направление) и стороны
которого равны сторонам многоугольника Р'. Я утверждаю, что мно-
многоугольник Рх равен многоугольнику Р.
Прежде всего можно предположить, что равенство )глов имеет
место с сохранением направления (иначе мы заменили бы многоуголь-
многоугольник Р' многоугольником, симметричным ему относительно некоторой
прямой). При этих условиях наложим многоугольник Р (не изменяя его
направления вращения) на Pt так, чтобы сторона А'В совпала с рав-
равной ей стороной AjBr Равенство углов В1 и В по величине и по
направлению показывает, что сторона В'С пойдёт по направлению 5,С,,
и гак как эти два отрезка равны, то они совпадут. Далее мы точно
ГЛАВА V. FOMOTFTHH И ПОДОБИЕ 139
так же докажем, что сторона CD' совпадает с С,/), и т. д. Таким образом,
оба многоугольника совпадают.
Примечание. Два четырёхугольника могут иметь соответ-
соответственно равные углы, не будучи подобными, например: квадрат и прямо-
прямоугольник. Равным образом для подобия двух четырёхугольников недо-
недостаточно пропорциональнее™ их сторон, также как для равенства
четырёхугольников недостаточно (п. 46а,примечание 3°) равенства их сто-
гон (см. ниже Прибавление А, п. 281, а также том II, Прибавление F).
148. Всякий многоугольник можно разбить на треугольники
и притом бесчисленным множеством способов. Действительно:
1°. Если многоугольник выпуклый, то можно соединить одну из
его вершин со всеми остальными (черт. 151)
или какую-либо внутреннюю его точку со
всеми вершинами.
2°. Если многоугольник невыпуклый
(черт. 152), то его можно разбить на
выпуклые многоугольники (которые в свою
огередь могут быть разбиты на тре- Черт. 151.
угольники, как уже было указано).
С этой целью продолжаем неограниченно все стороны многоуголь-
многоугольника и тем самым разбиваем плоскость на некоторое число областей
(например на черт. 152 области перенумерованы от / до 16) таких,
что нельзя пересечь какую-либо сторону или её продолжение, не
Черт. 152.
перейдя из одной области в другую, и обратно. Каждая из этих
областей лежит целиком внутри или целиком вне многоугольника (так
как от какой-либо одной точки этой области можно перейти к какой-
либо другой её точке, не пересекая ни самих сторон ни их продол-
продолжений). Таким образом, многоугольник состоит из совокупности тех
областей, которые буд}т по отношению к нему внутренними (на
НО КНИГА ТРЕТЬЯ. ПОДОБИЕ
чертеже 152 эти области перенумерованы от / до 3). Эти области по
определению будут выжклыми многоугольниками.
149. Теорема. Два подобных многоугольника могут быть разби-
разбиты на подобные треугольники, расположенные одинаковым образом.
Действительно, достаточно, расположив оба многоугольника так,
чтобы они были гомотетичны, и разбив один из них на треугольники,
разбить другой на треугольники, гомотетичные первым.
Обратная теорема. Два многоугольника, которые могут
быть разбиты на подобные треугольники, одинаковым образом
расположенные, подобны.
Прежде всего два многоугольника, составленные из соответственно
равных треугольников, расположенных одинаковым образбм, равны между
собою. Действительно, пусть ABC, BCD, CDE и т. д. (черт. 153) —
треугольники, составляющие первый многоуголь-
многоугольник Р; А'В'С, B'C'D', C'D'E' и т. д. — треуголь-
треугольники, соответственно равные первым и расположен-
расположенные одинаковым образом, которые составляют
второй многоугольник Р'. Если мы построим на А'В\
как на основании, многоугольник, равный Р (п. 95),
пользуясь треугольниками ABC, BCD, CDE, то
мы получим как раз многоугольник Р'.
Теперь, если два многоугольника образованы
из подобных треугольников, расположенных оди-
одинаковым образом, с коэфиииентом подобия1) k,
то, построив многоугольник, гомотетичный перво-
А' В' му многоугольнику, с тем же коэфиииентом подобия
u ,co k, мы получим многоугольник, равный (в силу того,
еР ' " что было сказано выше) второму многоугольнику.
150. Теорема. Если на отрезках, соединяющих некоторую точку О
с каждой точкой М фигуры F, построить подобные между собой тре-
треугольники, имеющие одинаковое направление вращения, то третьи вер-
вершины М' этих треугольников образуют фигуру F', подобную F.
Действительно, если повернуть фигуру F около точки О на угол, рав-
равный углу MOM', то получится фигура,"равная фигуре F и гомотетичная
фигуре /•" относительно центра О.
Обратная теорема. Если, даны две подобные фигуры, имеющие оди-
одинаковое направление вращения, то всегда существует такая точка, что
треугольники, имеющие вегшинами эту точку и две какие-либо соответ-
соответственные точки, все подобны между собою.
Если повернуть одну из фигур около этой точки на надлежащий
угол, то она будет гомотетична другой фигуре относительно той же
точки.
Пусть F II F' — две подобные фигуры, имеющие одинаковое направ-
направление' врашения, так что F' гомотетична некоторой фигуре Flt равной фи-
фигуре F и имеющей с нею одинаковое направление вращения. Отсюда
1) Коэфициент подобия k будет необходимо одпмм и тем же для двух
смежных треугольников, так как два смежных треугольника имеют в той
и другой фигуре по обшей стороне; следовательно, он будет одним и тем
же Д.-1Я всех треугольников.
ГЛАВА V. ГОМОТЕТИЯ И ПОДОБИЕ
141
Черт. 154.
прежде всего следует, что два соответственных отрезка АВ и А'В' (черт.154)
ооеих фигур образуют между собою постоянный угол (который можно
назвать углом между двумя фигурами), так как эпш свойством обладают
две равные фигуры F и Fy, и все прямые линии фигуры F' параллельны
соотвтствующим прямым фигуры Fy. Так как эти отрезки, кроме того,
пропорциональны, то, проведя через точку А отрезок АВ0, равный и парал-
параллельный А'В' и направленный с ним в одну сторону, мы получим тре-
треугольник АВВ0, подобный
некоторому определённому
треугольнику Т п имеющий
с ним одинаковое направ-
направление вращения, незаг.и-
симо от положения точек
А и В.
Теперь найдём точку,
которая сама себе соот- л
ветствует, если её рас- ^'~ X
сматривать один раз как t<—--'"'*
принадлежащую фигуре F,
другой раз как принадле-
принадлежащую фигуре F'. Пусть
такой точкой будет точ-
точка О. Если мы повторим
предыдущее построение и
примем за точку А точку О,
то точка Вп совпадёт с точкой В', так что треугольник ОВВ' будет подо-
подобен треугольнику Т и иметь с ним одинаковое направление вращения; су-
существует одна и только одна точка, удовлетворяющая этому условию *).
Обратно, если, выбрав точку О, как только чго было указано, рассма-
рассматривать её как принадлежащую фигуре F, то соответственная ей точка
в фигуре /¦" будет лежать на примой, со-
соответственной ВО, а эта последняя оудет
как раз прямая В'О (так как она обра-
образует с ВО угол, равный углу между
двумя фигурами), и притом от точки В' на
расстоянии, равном В'О (так как отно-
В'О
шение ^рг- равно коэфицненту почобия
ви
обеих фигур). Точка О совпадёт, таким
образом, со своей соответственной.
Вследствие этого все треугольники,
такие как треугольник ОВВ', подобны
треугольнику Т; если теперь повернуть
фигуру F около точки О на угол, равный углу между обеими фигурами,
то она будет гомотетичной фигуре /•"', при этом точка О будет центром
гомотетии.
Примечание. Оба угла АОА' и ВОВ' должны быть равны yi лу
ыгжду прямыми АВ и А'В'', следовательно, если продолжить эти последние
до точки их пересечения /, то можно найти точку О, как точку пересече-
пересечения окружностей, описанных около треугольников А/А' и BIB'.
150а. Теорема. Пусть PRMQ — параллелогра.и, О и N — две точки,
взятые соответственно на продолжениях соседних сторон FQ и PR и
лежащие на одной прямой с вершиной М, противоположной Р,'черт. 155;.
Если параллелогра.и PRMQ изменяется так, что длины его сторон
Q
- М
Черт. 155.
Построение этой точки указано далее (п. 152).
142 КНИГА ТРЕТЬЯ. ПОДОБИЕ
остаются постоянными (шарнирный параллелограм), причём отрезки
РО и PN также остаются постоянными, и одна из трёх точек О, М, N
остаётся неподвижной, то две другие описывают фигуры, гомотетичные
оруг другу.
Прежде всего четырёхугольник PRMQ останется параллелограмом,
если длины его сторон остаются постоянными, так как всегда имеем
PQ = RM и PR = QM. Кроме того, точки О, М, N останутся на одной
прямой. Действительно, так как эти точки в первоначальном положении
фигуры лежат на одной прямой, то имеем г-тз~=="л/р- ^то Равенство ос"
таётся справедливым при деформации, так как длины, входящие в эту про-
пропорцию, постоянны. Следовательно, обратно, треугольники MRN и OPN
постоянно подобны (как имеющие равные углы при R к Р, заключённые
между пропорциональными сторонами), и потому углы PNO и RNM всегда
равны между собою. *
ОМ PR
Наконец, отношение j-r-, постоянно, оно равно — . Таким образом
теорема доказана.
На этой теореме основано устройство пантографа — прибора, предна-
значеиного для воспроизведения фигуры с увеличением или без увеличе-
увеличения её размеров; при этом OQP, PRN, MQ и MR — твёрдые стержни, со-
соединённые один с другим шарнирами в точках М, Р, Q и R. Закрепляют
одну из трёх точек О, М, N; в одной из двух других точек находится ка-
карандаш; третья ючка описывает контур фигуры, которую требуется
воспроизвести.
УПРАЖНЕНИЯ.
155. Вписать в треугольник квадрат.
156. Данную точку А соединяют с произвольной точкой В окружности
с центром О. Найти геометрическое место точки пересечения прямой АВ
с биссектрисой угла АОВ.
157. На стороне ОХ данного угла XOY взята произвольная точка М,
и на отрезке СМ, как на диаметре, построена окружность; затем построена
окружность, касающаяся первой окружности и сторон ОХ и ОУ. Найти
геометрическое место точки касания обеих окружностей.
158. Точка пересечения G медиан треугольника лежит на прямой,
которая соединяет центр описанного круга с точкой пересечения высот и
делит отрезок между этими точками внутренним образом в отношении 1:2
(доказать). (Показать, что эта точка G — центр гомотетии двух треугольни-
треугольников ABC и А'В'С, которые встречаются в доказательстве и. 53.)
159. Даны коэфициенты подобия трёх гомотетичных фи1 ур, взятых
попарно. Найти отношение, в котором один из центров гомотети делит
отрезок, соединяющий два других.
160. Даны две параллельные прямые и точка О, лежащая в их плоско-
плоскости. Через эту точку проводят произвольную секущую, которая пересекает
параллельные прямые в точках А и А'. Найти геометрическое место конца
А" перпендикуляра к секущей, проведённого через точку А' и имеющего
длину, равную ОА.
161. Пусть F и F' — две подобные (но не равные) фигуры, имеющие
противоположные направления вращения. Доказать, что можно найти две
различные фигуры F', каждая из которых симметрична с F относительно
некоторой прямой и одновременно гомотетична F' относительно некоторой
точки, лежащей на этой прямой; в обоих случаях центр подобия будет
один и тот же, но из двух соответствующих гомотетий одна будет п рямой,
другая — обратной.
ГЛАВА VI. ПОСТРОЕНИЯ
ИЗ
162. На каждом из отрезков, соединяющих две соответственные точки
двух подобных фигур, имеющих одинаковое направление вращения, строят
треугольник, подобный данному треугольнику Т и 'имеющий с ним одина-
одинаковое направление вращения; или делят отрезок, соединяющий эти две
точки, в постоянном отношении. Третьи вершины построенных таким об-
образом треугольников или точки деления образуют фигуру, подобную двум
первым (доказать).
ГЛАВА VI. „
ПОСТРОЕНИЯ.
151. Построение 1. Разделить отрезок на части, пропорцио-
пропорциональные данным отрезкам, или на равные части.
Способ первый (черт. 156). Пусть требуется разделить отре-
отрезок АВ, положим, на три равные части. Проводим через точку А про-
произвольную прямую и откладываем на ней от точки .4 три равных
Черт. 156.
Черт. 157.
отрезка AC, CD, DE. Достаточно затем соединить точки В и Е
прямой линией и провести через точки С и D прямые, параллельные
атой прямой.
Эти параллельные прямые разделят отрезок АВ на три равные
части (и. 113).
Если требуется разделить отрезок АВ на части, пропорциональ-
пропорциональные трём данным отрезкам, откладываем отрезки AC, CD, DE, со-
соответственно равные заданным отрезкам
(черт. 157).
Способ второй (черт. 158) Пусть
требуется разделить отрезок АВ на три рав-
равные части. На произвольной прямой at), парал-
параллельной АВ, откладываем равные отрезки ас,
cd, db и соединяем точки Лис, В и b пря-
прямыми, которые пусть пересекутся в точке О;
прямые Ос и Od делят отрезок АВ на три
равные части (п. 121).
Если требуется разделить отрезок АВ па
части, пропорциональные трём данным отрезкам, то выбираем отрезки
ас, cd, db, соответственно равные этим отрезкам.
Построение 2. Найти отрезок, четвёртый пропорциональный
к данным трем отрезкам.
Построение вполне аналогично предыдущему.
В
Черт. -151?.
144
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Способ первый (чгрт. 159). Пусть даны три отрезка — a, b
а с
и с, и пусть требуется найти такой отрезок х.
а
ЧТО -7-:
о
Черт. 159.
Откладываем на обеих сторонах ОА и ОВ произвольного угла от
вершины О отрезки а и Ь; затем откладываем отрезок с, безразлично
где именно, на стороне ОА (на чертеже СС). Прямые, параллельные
АВ, проведённые чергз конечные точки отрезка с, определят на сто-
стороне ОВ искомый четвёртый пропорцио-
пропорциональный отрезок.
Чтобы проводить только одну парал-
параллельную, следует совместить один из кон-
концов отрезка с с точкой О или с точкой А.
Предоставляем читателю применить и
к данной задаче способ второй, указанный
для предыдущего построения.
152. Построение 3. Построить на
данном отрезке треугольник, подобный
данному треугольнику.
Пусть даны треугольник ABC и отре-
отрезок А'В'. Откладываем отрезок AD, рав-
равный А'В' на стороне АВ; проведя через точку D прямую DE, парал-
параллельную ВС (черт. 160), до пересечения в точке Е со стороной АС,
строим на отрезке А'В', как на основании, треугольник, равный
треугольнику ADE (п. 86, построе-
построение 4).
Это построение даёт, очевидно, реше-
решение следующей задачи.
Задача. Даны две точки А и В фи-
фигуры F и соответственные им точки А'
и В подобной фигуры F'; найти точку,
соответствующую какой-либо третьей точке фигуры F.
В частности повторное применение данного построения позволяет
выполнить следующее построение.
Построение За. Построить на данном отрезке многоугольник,
подобный данному многоугольнику.
153. Построение 4. Построить отрезок,
средний пропорциональный между двумя дан-
данными отрезками.
Мы указали три теоремы, приводящие к
среднему пропорциональному (пп. 123, 125, 132).
Каждая из этих трёх теорем даёт способ ре-
решения поставленной задачи.
Способ первый (черт. 161). Отклады-
Откладываем на какой-либо прямой от одной и той же
точки в одном и том же направлении два отрезка BD и ВС, равные
данным отрезкам а и b (обозначая через BD меньший из построен-
построенных отрезков), и будем рассматривать отрезок ВС ц»к гипотенузу пря-
о в
Черт. 160.
ГЛАВА VI. ПОСТРОЕНИЯ
145
моугольного треугольника, а отрезок BD — как проекцию одного из ка-
катетов на гипотенузу. Для этого достаточно поместить вершину А
прямого угла в точке пересечения перпендикуляра к BD, проведён-
проведённого через точку D, с окружностью, построенной на ВС как на диа-
диаметре. Если точка А, таким образом, определена, то АВ—средний
пропорциональный отрезок (п. 123).
Способ второй (черт. 162). Откладываем на какой-либо пря-
прямой от одной и той же точки D в противоположных направлениях два
отрезка DB и DC, равные данным отрезкам а
и й, и будем рассматривать их как проекции
катетов на гипотенузу. Для этого достаточно
поместить точку А, вершину прямого угла, в
точке пересечения перпендикуляра к BD,
проведённого через точку D, с окружно-
окружностью, построенной на ВС как на диаметре.
Если точка А, таким образом, определена,
то AD — искомый средний пропорциональный
отрезок (п. 125).
Способ третий (черт. 163). Пусть требуется найти отрезок,
средний пропорциональный между двумя отрезками а и Ь. Отклады-
Откладываем на какой-либо прямой от одной и той же точки О в одном и
том же направлении два отрезка ОА и ОВ, равные отрезкам а и Ь.
Через точки А и В проводим произволь- ^
ную окружность, к которой в свою очередь
проводим из точки О касательную ОТ;
длина этой касательной и будет искомым
средним пропорциональным (п. 132).
154. Построение 5. Построить отре-
отрезок, квадрат которого был бы равен
сумме квадратов двух данных отрезков.
Откладываем два данных отрезка на
сторонах прямого угла; искомый отрезок
будет гипотенузой построенного таким
образом прямоугольного треугольника.
Чем. 162.
Черт. 163.
Построение 6. Построить отрезок, квадрат которого был бы
равен разности квадратов двух данных отрезков.
Строим (п. 87а) прямоугольный треугольник, у которого больший
отрезок служит гипотенузой, а другой отрезок — катетом; второй его
катет будет искомым отрезком.
155. Построение 7. Построить два отрезка, зная их сумму
и их произведение.
Пусть требуется найти два отрезка, сумма которых равна данному
отрезку а = ВС и произведение которых равно произведению двух
данных отрезков b и с.
Предположим, что на перпендикулярах, проведённых в концах
отрезка ВС, отложены в одном и том же направлении два отрезка
ВВ' и СС, соответственно равные Ъ и с (черт. 164). Искомые два
10 Элементарная геометрия
146
КНИГА ТРЕТЬЯ. ПОДОБИЕ
отрезка, сумма которых равна ВС, могут быть представлены отрезками
ВМ и СМ, где М — определённая точка отрезка ВС. Но, с другой
стороны, произведение ВМ-СМ должно быть равно произведению
ВЬ'• СС; это равенство может быть записано в виде пропорции
ВВ' СМ
г-,*, — rw и показывает, что прямоугольные треугольники В'ВМ и
ВМ L.C
МСС — подобны. Следовательно, угол ВМВ', равный соответственно-
соответственному углу МСС, будет углом дополнительным к углу CMC, а потому
f угол В'МС — прямой. Таким образом, точка М
В лежит на окружности, имеющей своим диаметром
отрезок В'С.
Обратно, если окружность, имеющая своим
диаметром В'С, пересекает ВС в точке М, то
треугольники В'ВМ и МСС подобны, так как
стороны их взаимно перпендикулярны; таким
образом, получается равенство произведений
ВМ-СМи ВВ'-СС.
Условия возможности построения. Мы взяли произ-
произвольные отрезки b и с, но мы можем считать их равными: действи-
действительно, не изменяя произведения, можно заменить оба отрезка их
средним пропорциональным. Итак, предположим, что ВВ = СС; тоi да
четырёхугольник ВВСС будет прямоугольником. Середина отрезка
В'С отстоит при этом от отрезка ВС на расстоянии, равном ВВ',
и рат.иус окружности будет равен половине В'С, или, что то же
самое, половине ВС. Следовательно, окружность будет пересекать ВС,
если отрезок ВВ1 равен самое большее половине ВС, другими словами,
если данное произведение равно самое большее квадрату половины
отрезка ВС.
Если точка М — точка, отвечающая условиям вопроса, то, построив
фигуру, симметричную с данной относительно середины отрезка ВС,
или, что одно и то же, повернув отрезок ВС так, чтобы точка В
совпала с точкой С и точка С—с точкой В, мы получим точку М',
обладающую тем же свойством, что и первая, так как ВМ' = СМ и
ВМ^СМ'. Мы видим, что обе точки пересечения М и М' окруж-
окружности, имеющей своим диаметром В'С, с прямой ВС симметричны
относительно середины ВС, в чём можно убедиться непосредственно
с помощью п. 63.
Если данное произведение равно квадрату половины ВС (в силу
предыдущего это наибольшее из возможных значений произведения),
то окружность с диаметром В'С касается ВС. Следовательно, точки
М и М' совпадают с серединой ВС, так что ВМ=СМ. Отсюда
заключаем, что произведение двух отрезков, сумма которых посто-
постоянна, будет наибольшим, если эти отрезки равны.
Примечание. Пусть х — отрезок ВМ. Имеем СМ = а — х. и
равенство ВМ-СМ = ВВ'-СС напишется так:
х(а — х) = Ьс
ГЛАВА VI. ПОСТРОЕНИЯ
147
ИЛИ
х2 — ах-\~Ьс =
Предыдущее построение позволяет, таким образом, найти отрезок
х, удовлетворяющий уравнению
х2 — ах -f- q = О,
где а — данный отрезок и q — произведение двух данных отрезков.
Построение 8. Построить два отрезка, зная их разность и произ-
произведение.
Пусть требуется найти два отрезка, разность которых равна дан-
данному отрезку а = ВС и произведение которых равно произведению
данных отрезков Ъ и с. Предположим, что на перпендикулярах, про-
проведённых в концах отрезка ВС, отложены в противоположных направ-
направлениях отрезки ВВ1 и СО, соответственно равные b и с (черт. 165).
Так как разность искомых отрезков равна ВС, то искомые отрезки
могут быть представлены отрезками ВМ и СМ, где М — точка, взя-
Черт. 165.
4epi. i66.
тая на продолжении ВС, и мы должны иметь: ВМ-СМ = ВВ'-СС.
Как и в предыдущем построении, можно доказать, что точка М
должна лежать на окружности, описанной на В'С как на диаметре,
и что, обратно, точка пересечения этой окружности с продолжением
отрезка ВС отвечает условию вопроса.
Так как точки В' и С расположены по разные стороны отрезка
ВС, то окружность всегда пересечёт отрезок, а потому задача всегда
возможна.
Примечание. Пусть х — меньший из двух найденных отрезков;
тогда другой отрезок равен у = а-\-х, равенство же ху=^Ьс может
быть записано либо в виде:
либо в виде:
10*
х (а -\- х) = be или х2-\-ах — be = 0,
(у—а)у=Ьс или у2 — ау—Ьс = О.
148
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Таким образом, мы имеем возможность найти отрезок, удовлетво-
удовлетворяющий одному из двух уравнений:
где а — данный отрезок и q — произведение двух данных отрезков.
156. Говорят, что отрезок разделён в среднем и крайнем отно-
отношении, если большая часть отрезка есть среднее пропорциональное
между всем отрезком и другой его частью.
Построение 9. Разделить отрезок в среднем и крайнем отно-
отношении.
Пусть дан отрезок ВС (черт. 166), на котором требуется найти
Л ВС BD _,
такую точку D, чтобы -=-= = -^-т- . Взяв отношение суммы числите-
BJL) CD
ВС BC-\-BD
леи к сумме знаменателей, получим -^= = — .
BLJ НС
Мы видим, что отрезки BD и BC-\-BD, разность которых равна
ВС, дают в произведении ВС2. Таким образом, мы пришли к преды-
предыдущему построению. Необходимо из двух конечных точек отрезка
ВС провести в противоположных направлениях перпендикуляры ВВ' и
СС, равные ВС, и построить затем на отрезке В'С, как на диаметре,
окружность, которая пересечёт продолжение отрезка ВС за точкой С
в некоторой точке М, так что BD = CM будет искомым отрезком.
Отложим от точки В в направлении, противоположном ВС, отрезок
BD', равный ВМ. Точка ГУ, полученная таким построением, обладает
свойством, вполне аналогичным свойству точки D, а именно отрезок
BD' есть среднее пропорциональное между отрезками ВС и D'C.
I
В самом деле BD' = BC-\-BD, так что пропорция —— = ^-
Ни ВС
ВС В ГУ CD'
может быть представлена в виде -—=¦ = -=— = -=-— .
BD aC oD
Говорят, что точка D' делит внешним образом отрезок ВС в
среднем и крайнем отношении1).
Обратно, чтобы точка D' обладала этим свойством, она должна
BD'
быть выбрана так, как было указано, потому что из пропорции -^-^ =
ВС
CD'
= —— получается обратно (составляя отношение разности числителей
BD
к разности знаменателей) —^ = ttf^ бп. так что BD' служит од-
ВС BD — оС
ним из отрезков, разность которых равна ВС, а произведение — ВС2.
Пусть ВС=а; предположим, что требуется вычислить BD и BD'.
Прежде всего заметим, что в силу равенства отрезков ^ВВ1 и СС
!) Точки D и D' не будут, конечно, гармонически сопряжёнными от-
относительно точек В к С (см. упр. 173).
ГЛАВА VI. ПОСТРОЕНИЯ
149
окружность, построенная на В'С, как на диаметре, имеет центром
точку О, середину отрезка ВС, так что ОС= —. Теорема о квадрате
гипотенузы, применённая к прямоугольному треугольнику ОСС, даёт:
Таким образом, имеем:
CM=BD = a^5~^ и
aVb
157. Задача. Найти геометрическое место точек, отношение
расстояний которых от двух данных прямых равно данному от-
отношению.
Пусть даны две прямые D и ГУ, которые пересекаются, положим,
в точке О (черт. 167); мы ищем геометрическое место точек, расстоя-
расстояния которых от этих двух пря-
прямых относятся как данные два
отрезка d и d'. Если точка
М, — одна из точек искомого
геометрического места, то лю-
любая точка М' прямой ОМХ так-
также принадлежит этому геомет-
геометрическому месту. Действитель-
Действительно, перпендикуляры, опущен-
опущенные из точки М1 на прямые D
и D', и перпендикуляры, опущен-
опущенные из точки М на те же пря-
прямые, образуют, очевидно, две
фигуры, гомотетичные относи-
относительно центра гомотетии О.
Отсюда следует, что искомое
геометрическое место состоит
из прямых, проходящих через
точку О. Мы можем построить
точки этого геометрического
места, отыскивая точки, рас-
расстояния которых от прямых D
и D' соответственно равны d
и d'. Мы знаем, что геометри-
геометрическое место точек, расположен-
расположенных на расстоянии d от прямой D, состоит из двух прямых D, и ?>2, па-
параллельных D; точно так же геометрическое место точек, расстояния
которых от прямой D' равны d', состоит из двух прямых D[ и D'v па-
параллельных П. Пусть точки Ж, и М% — точки пересечения прямых
Dj и D2 с прямой D'v Прямые ОМ, и ОМ2 принадлежат искомому
черт.
167.
150 КНИГА ТРЕТЬЯ. ПОДОБИЕ
геометрическому месту точек. Вместе с тем этими прямыми исчерпы-
исчерпывается это геометрическое место; действительно, если точка М' при-
принадлежит геометрическому месту, то прямая ОМ' пересекает D^ в не-
некоторой точке М[, которая, находясь на расстоянии d' от D', должна
находиться на расстоянии d от D и, следовательно, должна совладать
с точкой М1 или с точкой М2.
Если прямые D и D' параллельны, то две точки искомого геомет-
геометрического места будут лежать на каком-либо общем перпендикуляре к
этим прямым!); это будут две гармонически сопряжённые точки, ко-
которые делят этот перпендикуляр в данном отношении. Искомое гео-
геометрическое место состоит из двух прямых, проведённых через эти
точки параллельно данным прямым.
Построение 10. Построить точки, расстояния которых от
трёх данных прямых имеют данные отношения.
Сначала строим две прямые, представляющие геометрическое место
точек, отношение расстояний которых от двух первых данных прямых
равно первому из данных отношений, затем поступаем так же относи-
относительно двух других из данных прямых. Таким образом, получаем ещё
две новые прямые, которые пересекают построенные ранее в четырёх
точках, отвечающих условию задачи.
158. Построение 11. Построить общие касательные к двум
окружностям.
Мы решили эту задачу в п. 93. Предыдущие теоремы позволяют
нам дать решение, совершенно отличное от данного выше. В самом
деле, достаточно провести два параллельных радиуса так, чтобы опре-
определить центры подобия (п. 143), и провести через один из центров
подобия касательную к одной из окружностей: она будет касательной
и к другой окружности в силу гомотетии обеих окружностей.
Построение 12. Построить радикальную ось двух окружностей.
Если две окружности пересекаются или касаются, то достаточно
провести только общую секущую или общую касательную.
Если они не пересекаются и не касаются, то строим какую-либо
третью окружность, пересекающую две данные. Точка пересечения
обеих общих секущих принадлежит (п. 139) искомой радикальной оси.
Через эту точку проводим перпендикуляр к линии центров данных
окружностей или же повторяем первоначальное построение, чтобы
определить вторую точку искомой радикальной оси.
Примечание. Применение предыдущего построения к данной
окружности и данной прямой приводит к необходимости допустить,
что радикальная ось окружности и прямой есть сама прямая.
Это построение применимо также и в том случае, если одна из
окружностей обращается в точку, при этом необходимо, чтобы вспомо-
вспомогательная окружность проходила через эту точку.
!) Случай, когда данное отношение равно единице, представляет исклю-
исключение. В этом случае имеется только одна точка деления, середина общего
перпендикуляра; другая точка удаляется в бесконечность. '
ГЛАВА VI. ПОСТРОЕНИЯ . 151
Из предыдущего построения непосредственно вытекает способ
построения радикального центра трёх данных окружностей, а следо-
следовательно (п. 139), и следующее построение.
Построение 13. Построить окружность, ортогональную к трём
данным окружностям.
Частными случаями этой задачи являются следующие:
Провести:
1) через данную точку окружность, ортогональную к двум дан-
данным окружностям;
2) через данные две точки окружность, ортогональную к данной
окружности.
159. Построение 14. Построить окружность, проходящую через
две данные точки и касающуюся данной прямой.
Даны две точки А и В (черт. 168) и прямая XY; пусть Т — точка
касания искомой окружности с прямой XY. Продолжим отрезок АВ до
пересечения в точке /
с прямой XY. Извест-
Известно, что отрезок IT пред-
представляет собой среднее
пропорциональное меж-
между отрезками /А и IB.
Обратно, если точ-
точка Т удовлетворяет это-
этому условию, то суще-
существует (п. 132) окруж- X ™ 7" Г ^*~Т*^ Y
ность, проходящая че- т
рез А и В и касающая-
ся в точке Т прямой XY: она определяется построением 13 п. 90.
Так как среднее пропорциональное между /А и IB можно отложить
на прямой XY от точки / в двух различных направлениях, то суще-
существуют две окружности, удовлетворяющие условию.
Задача, очевидно, возможна только, если точки А и В лежат по
одну сторону от XY.
Примечания. 1°. Предыдущий метод неприменим, если прямая
А В параллельна прямой XY. Задача имеет в этом случае только одно
решение: точка касания есть точка пересечения прямой XY с прямой,
перпендикулярной к отрезку АВ и проходящей через его середину.
2°. Напротив, этот метод применим и в том случае, когда точки
А и В сливаются в одну на данной прямой IA (пересекающей XY в F)t
другими словами, когда речь идёт об отыскании окружности, ка-
касающейся прямой /Л в точке А и прямой XY. Точка касания Т с
прямой XY получается, если отложить в том или другом направлении
отрезок /Г = /Л.
Построение 15. Построить окружность, проходящую через две
данные точки и касающуюся данной окружности.
Пусть даны две точки А и В (черт. 169) и окружность С. Оты-
Отыскиваем снова точку касания Т искомой окружности.
152
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Пусть точка / есть точка пересечения прямой АВ с касательной
в точке Т. Проводим через точки А и В произвольную окружность,
которая пересечёт окружность С в точках Р и Q. Точка / лежит на
прямой PQ (п. 139).
Пересечение прямой АВ с прямой PQ определяет точку /; доста-
достаточно провести через эту точку касательные к окружности С. Задача
имеет, следовательно, два реше-
решения.
Условие возможности
построения. Необходимо, что-
бы точка/лежала вне окружности
С. Для этого необходимо и доста-
достаточно, чтобы эта точка лежала на
продолжении отрезка PQ, другими
словами, лежала бы вне вспомо-
вспомогательной окружности. Это будет
иметь место, когда точки А и В
будут находиться обе на идной из
двух дуг, определяемых точка-
точками Я и Q на этой окружности,
т. е. когда точки А и В будут обе внутренними или обе внешни-
внешними относительно данной окружности.
Здесь можно сделать то же замечание, что и в предыдущем построе-
построении, относительно того случая, когда А и В сливаются в одну точку,
лежащую на данной прямой.
Черт. 169.
УПРАЖНЕНИЯ.
163. Построить отрезок, отношение которого к данному отрезку равно
отношению квадратов двух данных отрезков.
164. Найти отрезок, отношение квадрата которого к квадрату данного
отрезка равно отношению двух данных отрезков.
165. Через данную точку провести прямую таким образом, чтобы отрезок
этой прямой, заключённый между двумя данными прямыми (или между дву-
двумя данными окружностями), делился в этой точке в данном отношении.
166. Через точку, лежащую вне окружности, провести секущую, кото-
которая делится этой окружностью в среднем и крайнем отношении.
167. Найти точку, из которой видны под равными углами три после-
последовательных отрезка АВ, ВС, CD одной и той же прямой.
168. Через две точки, лежащие на одном диаметре окружности, про-
провести две равные хорды так, чтобы они имели общий конец.
169. Построить треугольник, зная две его стороны и биссектрису
угла, заключённого между ними.
170. Построить треугольник, зная одну его сторону, соответствующую
ей высоту и произведение двух других сторон.
171. Построить треугольник, зная его углы и периметр; или его углы
и сумму его медиан; или его углы и сумму его высот, и т. д.
172. Построить квадрат, зная разность диагонали и стороны.
173. Чтобы получить точку, гармонически сопряжённую с точкой В от-
относительно концов отрезка ЛГУ (черт. 166, п. 156), достаточно отложить на
продолжении отрезка ВС за точку С равный ему отрезок (доказать;.
ГЛАВА VII. ПРАВИЛЬНЫ? МНОГОУГОЛЬНИКИ 153
Точка, гармонически сопряжённая с точкой D относительно концов
отрезка ВС, есть точка, симметричная с точкой D относительно середины
отрезка ВС (доказать).
Доказать, что окружность, построенная на DD', как на диаметре, про-
проходит через вершины (отличные от В и С) квадрата, диагональю которого
служит ВС.
174. Даны прямая и две точки А и В; найти на этой прямой точку, из
которой отрезок АВ виден под наибольшим углом.
Эта задача решается косвенным путём, который заключается в том, что
сначала отыскивают на прямой точку, из которой АВ виден под данным
углом, и исследуют, какова наибольшая величина данного угла, для кото-
которой эта задача возможна.
Так же поступают при решении упражнений 175 и 176.
175. Даны две параллельные прямые. Построить перпендикулярную к
ним прямую так, чтобы отрезок этой прямой, заключённый между данными
прямыми, был виден из данной точки под наибольшим углом.
176. Провести через две точки окружность, которая отсекает на дан-
данной прямой хорду данной длины.
Найти наименьшую возможную длину этой хорды, если точки лежат по
одну и по другую стороны от прямой.
177. Провести через данную точку окружность, имеющую одну и ту
же радикальную ось с двумя данными окружностями.
ГЛАВА VII.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ.
160. Определения: Правильным многоугольником называется вы-
выпуклый многоугольник, у которого все стороны равны и все углы равны.
Правильной ломаной линией называется ломаная, у которой все сто-
стороны равны и все углы равны и имеют одинаковое направление.
161. Теорема. Если разделить окружность на некоторое чис-
число п равных частей, то:
1) точки деления служат вершинами правильного многоуголь-
многоугольника;
2) касательные к окружности в этих точках служат сторо-
сторонами второго правильного многоугольника.
1°. Две последовательные стороны многоугольника, имеющего сво-
своими вершинами точки деления, очевидно, симметричны относительно
радиуса, проведённого в их общую точку; два последовательных угла
этого же многоугольника симметричны относительно радиуса, перпен-
перпендикулярного к их общей стороне.
2°. Два последовательных угла многоугольника, образованного ка-
касательными в точках деления, очевидно, симметричны относительно
радиуса, перпендикулярного к их общей стороне; две последовательные
стороны этого же многоугольника симметричны относительно радиуса,
перпендикулярного к хорде, соединяющей их точки касания.
162. Обратная теорема. Всякий правильный многоугольник,
или, общее, всякую правильную ломаную, можно вписать в одну
окружность и описать около другой окружности.
154 КНИГА ТРЕТЬЯ. ПОДОБИЕ
Пусть, например, ABCDEF (черт. 170)—правильная ломаная. Опи-
Опишем около треугольника ABC окружность; центр О этой окружности
лежит на прямой, перпендикулярной к отрезку ВС и проходящей через
его середину. Я утверждаю, что эта окружность пройдёт также через
точку D. Чтобы это доказать, достаточно заметить, что стороны АВ
и CD симметричны одна с другой относительно прямой, перпендику-
перпендикулярной к отрезку ВС и проходящей через его середину, потому что
отрезок, симметричный с ВА, совпадает с CD по направлению (в силу
равенства углов при В и С) и по величине (так как BA^CD). Сле-
Следовательно, будем иметь OA=^OD. Точно так же убедимся, что та
же самая окружность, описанная около треугольника BCD, проходит
через точку Е, и так далее.
Кроме того, стороны АВ, ВС и т. д., • как равные хорды по-
построенной окружности, равно отстоят от её центра; следовательно,
данную ломаную можно описать
около второй окружности с
центром О.
Радиус этой второй окруж-
окружности, или расстояние какой-
либо стороны до центра, назы-
называется апофемой правильной
ломаной (или правильного мно-
многоугольника.)
Примечание. - Всякий
правильный многоугольник с п
сторонами может быть наложен на самого себя с помощью враще-
вращений (а именно таких, угол которых измеряется целым числом п-х частей
окружности) и симметрии (симметрии относительно прямых, перпенди-
перпендикулярных к сторонам многоугольника и проходящих через их середи-
середины, и относительно биссектрис его углов).
163. Мы доказали существование бесчисленного множества пра-
правильных многоугольников с каким-либо данным числом сторон п. До-
Докажем, что все эти многоугольники между собою подобны.
Теорема. Два правильных многоугольника с одинаковым чис-
числом сторон подобны; коэфициент подобия равен отношению их ра-
радиусов и отношению их апофем.
Действительно, два правильных многоугольника с одинаковым чис-
числом сторон, вписанных в две равные окружности, очевидно, равны; они сов-
совмещаются, если совместить обе описанные окружности и одну из вершин.
Итак, пусть даны два правильных многоугольника Р и Р', вписан-
вписанных в окружности С и С Пересекая радиусы окружности С, прове-
проведённые в вершины многоугольника Р, окружностью, концентричной с С
и равной С, мы получим правильный многоугольник, гомотетичный
многоугольнику Р относительно центра окружности С и равный мно-
многоугольнику Р'.
Примечание. В частности, углы всех правильных многоуголь-
многоугольников с одинаковым числом (п) сторон имеют одну и ту же величину.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 155
Легко вычислить эти углы. Так как сумма углов любого из этих мно- _
гиугольников равна 2nd — 4J, то каждый из них составит л-ю часть
D \
2 j d.
164. Разделив окружность на л равных частей, соединим одну из
делящих точек с точкой, отстоящей от неё на р делений, эту послед-
последнюю точку — с точкой, отстоящей от неё также на р делений, и т. д.
до тех пор, пока мы снова не придём в одну из уже пройденных
делящих точек. Если точка Р будет первой из тех точек, в которую
мы придём во второй раз, то эта точка не может быть отличной от
той точки, с которой мы начали; действи-
действительно, если бы точка Р была концом сто-
стороны NP, однажды уже пройденной, то
мы пришли бы в точку N во второй раз
раньше, чем в точку Р.
Фигура, таким образом построенная,
представляет собой несобственныйх) много-
многоугольник (п. 21, примечание) и называется
звездчатым правильным многоугольни-
многоугольником. Например, чертёж 171 изображает
звездчатый правильный пятиугольник, полу-
полученный делением окружности в точках А,
В, С, D, Е на пять равных частей и соединением этих точек через два
деления в порядке ACEBDA (л =5; /7 = 2).
Можно предположить числа пир взаимно-простыми. В самом деле,
если бы эти числа имели общий наибольший делитель d, то всё про-
происходило бы так, как будто бы мы разделили окружность на -г рав-
равных частей и соединили делящие точки через каждые — делений.
Если пир — взаимно-простые числа, то звездчатый многоугольник
будет иметь точно п сторон. Действительно, так как каждая сторона
содержит р делений, то, построив k сторон, мы пройдём kp делений.
Мы вернёмся в исходную точку, когда мы пройдём целое число
окружностей, т. е. когда kp—число, кратное п. В арифметике дока-
доказывается, что это обстоятельство наступает для некоторых значений /г,
меньших п, если число р — не взаимно-простое с числом п; если, на-
наоборот, число р — взаимно-простое с числом п, то это обстоятельство
впервые наступает для /г, равного п.
Итак, звездчатый многоугольник с п сторонами образуется, если
разделить окружность на п равных частей и соединить делящие точки
через каждые р делений, где р — любое целое число, взаимно-простое
ели меньшее, нежели л. Однако каждый звездчатый многоугольник
получается, таким образом, двумя различными способами. Действитель-
Действительно, если его сторона служит хордой дуги, содержащей р делений, то она
1) Если р не является делителем числа и; в противном случае много-
многоугольник—выпуклый. Прим. ред. перевода.
156
КНИГА ТРЕТЬЯ. ПОДОБИЕ
данную окружность.
В
же будет и хордой дуги, содержащей п — р делений. Так, например,
звездчатый многоугольник, изображённый на чертеже 171, получается
соединением делящих точек через каждые два деления или соедине-
соединением их через каждые три деления. В силу этого следует отбросить
половину значений р, если мы хотим получить каждый многоугольник
только один раз. Значение р=1 (и, следовательно, также значение
р = л—1) соответствует многоугольнику в собственном смысле слова.
Пример. Пусть я=15. Числами меньшими 15 и взаимно-просты-
взаимно-простыми с 15 будут, кроме 1 и 14, числа 2, 4, 7, 8, 11 и 13. При этом
нет надобности рассматривать значения р = 8, 11, 13, которые соот-
соответствуют тем же многоугольникам, которые получаются при значе-
значениях р=7, 4, 2.
Таким образом, существует один правильный пятнадцатиугольник
в собственном смысле слова и три звездчатых пятнадцатиугольника.
165. Построение правильных многоугольников, вписанных в
Если мы умеем вписать в окружность пра-
правильный многоугольник, то мы умеем
и описать около той же окружности
правильный многоугольник с тем же
числом сторон.
Этот последний образуется касатель-
касательными к окружности в вершинах вписанного
многоугольника.
Если мы умеем вписать в окруж-
окружность правильный многоугольник, то мы
умеем вписать и правильный многоуголь-
многоугольник с удвоенным числом сторон.
Для этого достаточно разделить на
две равные части дугу, стягиваемую сто-
стороной первого многоугольника.
166. 1 °. Квадрат. Чтобы вписать в окружность О (черт. 172) квад-
квадрат, достаточно провести два взаимно перпендикулярных диаметра АС
и BD: окружность разделится, таким образом, на четыре равные
части.
Предыдущее построение позволяет далее построить правильный
вписанный восьмиугольник, далее правильный многоугольник с 16,
32,... и вообще с 2" сторонами.
Сторона квадрата, вписанного в круг радиуса R, равна с4 =
= R]^2, так как из прямоугольного треугольника АОВ (черт. 172)
имеем:
АВ2 = АО2 + ВО2 = 2R2.
Апофема правильного многоугольника, сторона которого известна,
вычисляется по следующему правилу: квадрат апофемы равен квад-
квадрату радиуса описанного круга без квадрата половины стороны.
Это вытекает из того, что апофема, половина стороны и радиус опи-
описанного круга образуют прямоугольный треугольник.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
157
Итак, апофема а правильного многоугольника со стороною с, впи-
вписанного в круг радиуса R, равна
Для квадрата эта апофема равна
Она равна половине стороны, что очевидно й priori.
167.2°. Шестиугольник. Теорема. Сторона правильного вписанно-
вписанного шестиугольника равна радиусу окружности. Пусть АВ
(черт. 173) — сторона правильного ше-
шестиугольника, вписанного в окружность
с центром О. Я утверждаю, что тре-
треугольник ОАВ равносторонний.
Прежде всего этот треугольник —
равнобедренный. С другой стороны,
угол при точке О, заключающий между
своими сторонами шестую часть окруж-
4 2
ности, равен — d, или — d. Остаётся
о о
следовательно,
2 4
Id d=--d для
и о
суммы углов при А и В. Так как эти два угла равны между собою,
2
то каждый из них равен — d. Рассматриваемый треугольник равно-
о
угольный и, следовательно, равносторонний.
Апофема правильного вписанного шестиугольника равна
3°. Равносторонний треугольник. Соединяя через одну вершины
шестиугольника, получим вписанный равносторонний треугольник АСЕ
(черт. 173).
Сторона АС этого треугольника, будучи перпендикулярной к ра-
радиусу ОВ, равна удвоенной высоте треугольника АОВ, т. е. (так как
три высоты равностороннего треугольника равны) удвоенной апофеме
шестиугольника, а потому с^^кУ^З.
В этом можно ещё убедиться, замечая, что точки В и Е диамет-
рально противоположны (как заключающие между собою—части окруж-
окружности). Следовательно, треугольник ABE — прямоугольный с прямым
углом при А, и сторона АЕ равна удвоенному перпендикуляру, опу-
опущенному из середины О отрезка BE на сторону АВ.
158
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Апофема вписанного равностороннего треугольника равна а„ =
R
Умен строить вписанный шестиугольник, можно построить вписан-
вписанные многоугольники с 12, 24,... и вообще 3-2" сторонами.
168.4°. Десятиугольник. Теорема. Сторона правильного вписан-
вписанного десятиугольника равна большему отрезку радиуса, разделен-
разделенного в среднем и крайнем отношении.
Пусть АВ (черт. 174) — сторона пра-
правильного десятиугольника, вписанного в
окружность с центром О. Угол при О ра-
4 2
вен — d, или — d. Сумма углов А и В
1U о
треугольника АВО равна, следовательно,
2d —¦ -=-d = — d, и каждый из них равен
о 5
4
-=- d. Проведём теперь биссектрису AI
угла А (/ — точка пересечения этой биссек-
биссектрисы с ОБ), которая образует с О А и
2
АВ углы в -=- d. Угол AIB—внешний угол треугольника АЮ, рав-
о
ный сумме двух внутренних не прилежащих к нему углов, равен в дан-
4
ном случае -=- d. Отсюда следует, что два треугольника AJB и А/0 —
о
равнобедренные и что AB = AJ = O/. На основании свойства биссект-
биссектрисы (п. 115) имеем:
01 _ОВ
или 1В~О1 '
Черт. 174.
01 ОА
что и доказывает теорему.
Следовательно, сторона правильного вписанного десятиугольника
определяется построением 9 (п. 156).
Ьта сторона равна
а апофема десятиугольника:
169. Кроме правильного выпуклого десятиугольника, существует
правильный звездчатый десятиугольник, который получается, если
соединить вершины первого через каждые две его вершины.
Стороны выпуклого десятиугольника и звездчатого десятиугольни-
десятиугольника можно получить при помощи следующего предложения:
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 159
Теорема. Разность сторон обоих правильных вписанных деся-
десятиугольников равна радиусу, а их произведение равно квадрату
радиуса.
Пусть снова АВ (черт. 174)—сторона правильного выпуклого
десятиугольника, так что половина окружности AF разделена на пять
равных частей точками В, С, D, E. AD — сторона звездчатого де-
десятиугольника; кроме того, прямая AD совпадает с биссектрисой А/
угла ОАВ, так как вписанные углы FAD и DAB отсекают на окруж-
окружности равные дуги. Радиус OD параллелен АВ, так как каждый из внут-
внутренних накрестлежащих углов — /_ODAvl /_DAB—равен углу О AD;
следовательно, треугольники Alb и DIO подобны, и потому треуголь-
треугольник DIO, как и треугольник AIB,—равнобедренный (сравнить п. 168).
Отсюда имеем прежде всего:
AD—AB = AD — AI = ID = OD.
Что касается соотношения
АВ- AD = AI- AD = ОА\
то оно вытекает из подобия треугольников А/О и AOD, имеющих
соответственно равные углы.
Итак, стороны двух правильных десятиугольников соответствуют
двум способам деления (внутреннему и внешнему) радиуса в среднем
и крайнем отношении (п. 156, построение 9).
Сторона звездчатого десятиугольника равна
а его апофема:
170. 5°. Пятиугольник. Соединяя через одну вершины правиль-
правильного выпуклого десятиугольника, мы получаем правильный выпуклый
пятиугольник. Соединяя далее через одну вершины этого правильного
пятиугольника, или, что то же, соединяя вершины правильного выпук-
выпуклого десятиугольника через три, мы получаем звездчатый правильный
пятиугольник.
Сторона АС правильного выпуклого пятиугольника равна удвоенной
высоте треугольника АОВ (черт. 174), выходящей из точки А. Таким
образом, её можно вычислить, зная сторону десятиугольника, так как
можно вычислить высоты треугольника, три стороны которого из-
известны. Однако проще заметить, что сторона выпуклого пятиуголь-
пятиугольника равна удвоенной апофеме звездчатого десятиугольника] Дей-
Действительно, в этом можно убедиться либо из равнобедренного тре-
треугольника АЮ, две высоты которого (т. е. половина стороны выпуклого
пятиугольника и апофема звездчатого десятиугольника) равны, либо из
прямоугольного треугольника ADF, сторона DF которого равна сто-
160
КНИГА ТРЕТЬЯ. ПОДОБИЕ
роне пятиугольника, а параллель к стороне пятиугольника, проведённая
через точку О, — апофеме звездчатого десятиугольника. Следователь-
Следовательно, сторона и апофема правильного выпуклого пятиугольника соответ-
соответственно равны:
c6 = 2aw' = -^y 10-21 5 и аъ = -^
Точно так же убедимся из рассмотрения прямоугольного треуголь-
треугольника ABF, что сторона звездчатого пятиугольника равна удвоенной
апофеме выпуклого десятиугольника, т. е.
с --2-Х
2^5, а его апофема: а6'=— (|/б— 1).
Примечание. Аналогичное рассуждение доказывает вообще, что
вычисление стороны и апофемы многоугольника (выпуклого или звездчато-
звездчатого), полученного делением окружности на 2л -(- 1
й (^ В равных частей-и последовательным соединением
"?—-^^г ^^Ч~^ делящих точек через каждые р делений, приво-
приводится к вычислению апофемы и стороны мно-
многоугольника, полученного делением окружности
на Ап-\-2 равных частей и последовательным
соединением делящих точек через каждые q де-
делений, если число q связано с числом р равен-
равенством !)
171. 6°. Пятнадцатиугольник. Пусть
требуется вписать правильный выпуклый пят-
пятнадцатиугольник. Мы сумеем вписать этот
многоугольник, если построены шестиугольник
и десятиугольник, с помощью следующей теоремы.
Теорема. Дуга, стягиваемая стороной правильного вписанного
пятнадцатиугольника, есть разность дуг, стягиваемых сторонами
шестиугольника и десятиугольника.
Действительно, эта дуга равна одной пятнадцатой части окружно-
« Х 11
сти, а дробь т-= равна разности -х — •
1 о и 10
Итак, строим в данной окружности с помощью циркуля от одной
и той же точки А (черт. 175) хорды АВ и АС, равные соответствен-
•) Это же замечание позволяет, и обратно, свести вычисления, относя-
относящиеся к многоугольнику с 4л-|-2 сторонами, к вычислениям, относящимся
к многоугольнику с 2п-\- 1 сторонами. Действительно, многоугольник, име-
имеющий An + 2 сторон, соответствует нечётному значению q (п. 164); поэто-
поэтому число 2и-(-1 — q будет чётным и соотношение 2р = 2п-\-\ —q опреде-
определяет целое число р, взаимно-простое с 2п-\- 1, которому в свою очередь
соответствует многоугольник с 2л +1 сторонами; достаточно вычислить
сторону и апофему этого последнего многоугольника. Так, выполнение вы-
вычислений для пятнадцатиугольников (пп. 174 и 175) даст также и результа-
результаты, относящиеся к тридцатиугольникам.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 161
но стороне шестиугольника и стороне десятиугольника. ВС будет
искомой стороной.
Кроме правильного выпуклого пятнадцатиугольника, существуют
три звездчатых пятнадцатиугольника (п. 164), стороны которых стя-
2 4 7
гивают соответственно дуги в—, —и — окружности. Эти дуги,
15 15 15
которые, очевидно, можно получить из первого пятнадцатиугольника,
получаются, впрочем, построениями, совершенно аналогичными построе-
построению выпуклого пятнадцатиугольника.
Дуга, стягиваемая стороной первого звездчатого пятнадцати-
пятнадцатиугольника, равна разности дуг, стягиваемых стороной звездчатого
десятиугольника и стороной шестиугольника.
Дуга, стягиваемая стороной второго звездчатого пятнадцати-
пятнадцатиугольника, равна сумме дуг, стягиваемых стороной выпуклою де-
десятиугольника а стороной шестиугольника.
Дуга, стягиваемая стороной третьего звездчатого пятнадца-
пятнадцатиугольника, равна сммме дуг, стягиваемых стороной звездчатого
десятиугольника и стороной шестиугольника.
В самом деле, имеем:
15» 10 6' 15~ТЬ+ 6 ' 15~10+6~"
172. Вообще, если мы умеем вписать правильные многоугольники с
тип сторонами, где числа тип — взаимно-простые, то мы умеем впи-
вписать и правильный многоугольник с тп сторонами.
Действительно, стороны двух известных многоугольников стягивают
дуги, соответственно равные одной tn-й и одной п-й части окружности.
Откладывая х раз подряд первую дугу и отнимая у раз вторую, получаем
дугу, стягиваемую стороной искомого многоугольника, если целые числа х
и у удовлетворяют равенству
? __v _1_
т п тп'
или
пх — ту = 1.
Как известно, это равенство невозможно, если т и п имеют общий
делитель, но если т и п — числа взаимно-простые, то всегда можно най]и
два нелых числа х и у, которые ему удовлетворяют.
Например, правильные двенадцатиугольники вписываются непосред-
1 1 1
ственио с помощью квадрата и треугольника, так как — = — -;
А —1 — 1
12 — 3 4 "
В примечании к п. 170 рассматривается частный случай этого положе-
положения, когда из двух чисел /пи// одно равно двум, а другое — число не-
нечётное.
173. Гаусс доказал, что с помощью линейки и циркуля можно вписать в
окружность любой правильный многоугольник, число сторон которого есть
простое Мисло вида 2" + 1. Таким образом, мы сможем вписать правиль-
11 Элементарная геометрия
162 КНИГА ТРЕТЬЯ. ПОДОБИЕ
ные треугольник B+1 = 3) и пятиугольник Bг+ 1 = 5), далее идут мною-
угольники с 17( = 24-f- 1), 257 (= 28 -f- 1) и т д. сторонами1).
Это предложение в соединении с теми, которые мы ранее доказали,
показывает, что можно вписать с помощью линейки и циркуля правильный
многоугольник с N сторонами, если число Л', разложенное на простые мно-
множители, содержит только: 1) простые множители вида 2"+1, различные
между собой, и 2) множитель 2 в какой-либо степени. Доказывается, обрат-
обратно, что нельзя вписать многоугольник с помощью линейки и циркуля, если
число N не принадлежит к той категории, которую мы определили.
Таким образом, правильный многоугольник с 170( = 2-5-17) сторонами
может быть вписан, но не может быть вписан многоугольник с 9 сторо-
сторонами, так как число 9 хотя и paiHO степени 2, увеличенной на 1, но оно
не есть число простое, с щ угон стороны, хотя простые его множители, из
которых оно составлено (9 = 3-3), имеют вид 2" + 1, но они равны меж-
между собою.
1 74. Чтобы вычислить сторону правильного выпуклого пягнадцати-
угольника, вписанного в окружность радиуса R, положим, что АВ и АС
(черт. 175) — соответственно стороны вписанного шестиугольника и де-
десятиугольника, так что ВС— искомая сторона. Из точки А опустим
на прямую ВС перпендикуляр АИ; имеем ВС = ВН— СИ.
Но угол АВИ, как вписанный угол, опирающийся на дугу АС,
равен половине центрального угла, соответствующего стороне десяти-
десятиугольника, так что отрезок ВН равен апофеме выпуклого десятиуголь-
десятиугольника, вписанного в окружность радиуса АВ; отсюда, так как AB = R,
5= ^
Точно так же угол АСИ, равный вписанному углу, спирающемуся
на дугу АСВ (так как оба эти угла — пополнительные углу АСВ),
равен половине центрального угла; соответствующего стороне правиль-
правильного шестиугольника, так что СИ есть апофема правильного шести-
шестиугольника, вписанного в окружность радиуса АС, т. е.
CH-ACV* -
и, следовательно,
BC=— j/ 10-1-2» 5 — J 3A/5 — 1)
4
Ясно, что последний метод применяется каждый раз, когда тре-
требуется решить следующую задачу: даны хорды двух дуг окружно-
окружности данного радиуса; найти хорду дуги, равной их разности.
В частности, чтобы вычислить сторону первого звездчатого пятна-
дцатиугольника, мы повторяем то же самое рассуждение, заменяя сто-
сторону и апофему выпуклого десятиугольника стороной и апофемой
!) Пользуясь тем, что сумма одинаковых нечётных степеней делится
без остатка на сумму оснований, легко доказать, что для того, чтобы
2"-(-1 было простым числом, необходимо, чтсбыябыло степенью двух (од-
(однако это условие недостаточно).
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
163
звездчатого десятиугольника. Следовательно, искомая сторона будет
равна:
Пусть теперь требуется вычислить сторону второго звездчатого
пятнадцатиугольника.
Пусть АВ и АС — стороны шестиугольника и выпуклого десяти-
десятиугольника, но отложены в данном случае на окружности в противо-
противоположных направлениях, так что ВС есть иско-
искомая сторона (черт. 176).
Из точки А опустим снова перпендикуляр
АН' на ВС. Отрезки ВН' и СИ' равны —
один апофеме выпуклого десятиугольника,
вписанного в окружность радиуса АВ, дру-
другой — апофеме шестиугольника, вписанного в
окружность радиуса АС. Их сумма ВС
будет, таким образом, равна:
fic = |[/^T^+K3(ir5_,J.
Ясно, что так следует поступать каждый раз, если требуется,
зная хорды двух дуг окружности данного радиуса, найти хорду
дуги, равной их сулеме.
В частности, мы найдём для стороны третьего звездчатого пят-
пятнадцатиугольника значение
~{A/5+1I/3+ ]Ло-
175. Можно вычислить апофему пятнадцатиугольника, зная его
сторону, но при этом потребуется извлечение нового квадратного кор-
корня вместо этого можно получить апофему (без такого извлечения
корня) приёмом, аналогичным приёму, использованному для вычисле-
вычисления стороны.
На чертеже 175 мы проводим диаметр CD через точку С. Прямо-
Прямоугольный треугольник BCD показывает нам, как и прежде, что BD
равна удвоенной искомой апофеме. Из точки А опускаем перпендику-
перпендикуляр АК на BD. Так как угол ADB равен (как вписанный угол) по-
половине центрального угла, соответствующего стороне шестиугольника,
то отрезок DK равен апофеме шестиугольника, вписанного в круг ра
диуса AD; следовательно,
или DK=
так как AD равна удвоенной апофеме правильного десятиугольни-
десятиугольника, вписанного в данную окружность.
11*
КНИГА ТРЕТЬЯ. ПОДОБИЕ
С другой стороны, угол ABD равен углу ACD, т. е. дополнению
половины центрального угла, соответствующего стороне правильного
десятиугольника, а следовательно, угол КАВ равен половине этого
центрального угла; поэтому отрезок ВК равен половине стороны деся-
десятиугольника, вписанного в круг радиуса АВ, т. е.
Таким образом, искомая апофема будет:
BD
Аналогичное рассуждение даёт для апофемы первого звездчатого
пятнадцатиугольника значение:
для апофемы второго звездчатого пятнадцатиугольника—значение:
для апофемы третьего звездчатого пятнадцатиугольника—значение:
176. Теорема. Пусть Р — периметр правильного описанного
около окружности многоугольника, р — периметр правильного
вписанного в ту же окружность многоугольника с тем же числом
сторон. Если безгранично удваивать число сторон, то Pup стре-
стремятся к одному и тому же пределу L.
Пусть abed... (черт. 177)—вписанный в окружность многоуголь-
многоугольник и ABCD ... — описанный многоугольник, стороны которого имеют
своими точками касания вершины первого многоугольника. Удвоим число
сторон этих многоугольников, деля на две равные части каждую из
дуг ab, be, ей,. .. так, чтобы образовался новый правильный вписан-
вписанный многоугольник aebfcg... и соответствующий новый описанный
правильный многоугольник EFGHKL... (черт. 177). Поступим с но-
новыми многоугольниками так же, как с первоначальными, и так далее
до бесконечности.
Я утверждаю, что периметры р вписанных многоугольников и пери-
периметры Р описанных многоугольников стремятся к общему пределу.
Мы докажем это, основываясь на следующих соображениях.
1°. Периметры р возрастают; например, многоугольник aebfcg...
имеет больший периметр, чем многоугольник abed.... так как послед-
последний многоугольник лежит внутри первого.
ГЛАВА VTI. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 165
2°. Периметры Р убывают; например, многоугольник EFGHKL. ..
имеет меньший периметр, чем многоугольник ABC..., так как первый
многоугольник лежит внутри второго.
3°. Любой периметр р меньше любого периметра Р, так как всякий
вписанный многоугольник лежит внутри любого описанного многоугольника.
Величина /; постоянно возрастает, оставаясь всё время меньше неко-
некоторого постоянного значения (именно меньше какого-либо из значе-
значений Р), и, следовательно, стремится к пределу.
В Н КС
Черт. 177.
Точно так же величина Р постоянно убывает, оставаясь всё время
больше определённого значения (именно больше какого-либо из значе-
значений р), и, следовательно, также стремится к пределу *)-
Оба эти предела равны. Действительно, два правильных много-
многоугольника, вписанный и описанный, с одинаковым числом сторон —
подобны, и их периметры относятся, как их апофемы. Апофема опи-
описанного многоугольника равна радиусу R данной окружности, так что
где а обозначает апофему вписанного многоугольника.
Но при неограниченном удвоении числа сторон апофема а стремится
р
к R. Таким образом, предел отношения — , т. е. отношение обоих
предыдущих пределов, равен 1 2).
1) Автор предполагает известными следующие предложения теории
пределов:
Если переменная- величина возрастает, оставаясь всё время меньше не-
некоторого постоянного числа, то эта величина стремится к некоторому
пределу.
Если переменная величина убывает, оставаясь всё время больше неко-
некоторого постоянного числа, то эта величина стремится к некоторому пре-
пределу. Прим. реО. перевода.
*) Автор точно так же предполагает известным следующее предложе-
предложение: Предел отношения двух переменных величин равен отношению пре-
пределов этих величии, если предел второй из них неравен нулю. Прим.рео.
перевооа.
166
КНИГА ТРЕТЬЯ. ПОДОБИЕ
177. Я утверждаю теперь, что периметр всякого выпуклого мно-
многоугольника, вписанного или описанного1), все стороны которого
неограниченно убывают, также стремится к пределу L, рассмот-
рассмотренному в предыдущей теореме.
В частности, этот предел не зависит от выбора исходного правиль-
правильного многоугольника abed...
Действительно, пусть а'Ь'с'... (черт. 178) — какой-либо вписанный
многоугольник, А'В'... — выпуклый описанный многоугольник, образо-
образованный касательными в точках а', Л',
с',. ¦.; и пусть р' и Р' — периметры этих
двух многоугольников.
Рассмотренный в предыдущем пункте
предел L заключён между // и Р', так
как р', например, меньше какого-либо
из периметров Р, рассмотренных в пре-
предыдущем пункте и имеющих своим пре-
пределом L, так что мы имеем: р' !5S L;
точно так же находим, что Р' > L.
С другой стороны, прямая О А' пересекает сторону а'Ь' в её сере-
середине Н, и из прямоугольных треугольников Оа'Н и Оа'А', которые
подобны как имеющие общий острый угол, мы имеем:
Точно так же
а'А
' + А'Ь'
а'Ь'
Ь'В' +
b'c
В
а'А'
а'Н
'с'
R
ОК
R
ой-
где К обозначает середину стороны b'c') и т. д.
Рассмотрим левые части всех этих равенств и возьмём сумму чисчи-
телей и сумму знаменателей: мы получим, таким образом, отношение,
заключённое между наибольшим и наименьшим из первоначальных отно-
отношений, так что
п
п
где / заключено между наибольшим и наименьшим из значений ttjj ,
ОК'
Если теперь многоугольник изменяется так, что все его стороны
неограниченно уменьшаются, то все расстояния, аналогичные ОН, стре-
п ОЛ ОК , т-
мятся к А? и все отношения —pr-, -g к 1. 1о же самое относится
R Н
!) При этом, однако, предполагается, что окружность расположена
внутри описанного многоугольника.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 167
Р' L Р'
к -г и, следовательно, также к отношениям -7 или -=- , каждое из
Р'
которых заключено между 1 и —, .
Таким образом, Р' и р' стремятся к L.
Определение. Длина L, общий предел периметров вписанных в
окружность и описанных около неё многоугольников, стороны которых
неограниченно уменьшаются (существование этого предела нами дока-
доказано), называется длиной окружности.
178. Теорема. Длины двух любых окружностей относятся
между собою как их радиусы.
Пусть С, Cj — длины окружностей радиусов R, Rv Впишем в эти
окружности два правильных многоугольника с одинаковым числом сто-
роа. Эти многоугольники подобны; следовательно (п. 146, следствие),
их периметры Р и Р1 относятся между собой как радиусы окружностей.
Но когда число сторон неограниченно возрастает, отношение р- стре-
Q
мится к отношению -^ длин двух окружностей. Итак, теорема доказана.
Следствие. Отношение длины окружности к диаметру есть число
постоянное.
С R
В самом деле, пропорцию -гг = п можно записать в виде
L-1
С Q С Ci
ЛИ
Отношение длины окружности к диаметру будет, таким образом
одно и то же для двух любых окружностей.
Это постоянное число, выражающее отношение длины окружности
к диаметру, обозначается греческой буквой тт.
Следствие. Длина окружности радиуса R равна 2-nR.
179. Определение. Длина дуги окружности есть предел, к ко-
которому стремится длина выпуклой ломаной, вписанной или описанной,
концами которой служат конечные точки дуги и длины всех сторон
которой неограниченно уменьшаются.
Существование такого предела доказывается с помощью тех же
рассуждений, которые были применены для длины всей окружности.
Рассматривают сначала правильную ломаную, вписанную или описанную,
число сторон которой неограниченно удваивается-, после этого рас-
рассматривают произвольную ломаную').
ij Этот способ доказательства можно распространить на любую выпук-
выпуклую дугу А, т. е. такую дугу, что никакая её часть не пересекается с со-
соответствующей ей хордой. Для этого достаточно, чтобы любому числу т
(сколь-угодно близкому к 1; можно было поставить в соответствие такую
длину е, что для любой части дуги А, концы которой находятся друг от
друга на расстоянии, меньшем е, отношение хорды аЪ к сумме отрезков
касательных ас -\-Ъс (черт. 179) заключалось между т и 1: это условие (как
доказывается в курсах анализа бесконечно-малых) всегда выполняется в
силу известных предположений относительно тех кривых, которые прихо-
163
КНИГА ТРЕТЬЯ. ПОДОБИЕ
Любая дуга окружности длиннее соответствующей ей хорды,
так как она служит пределом ломаных, которые все длиннее этой
хорды и периметры которых возрастают. По аналогичной причине эта
дуга короче всякой объемлющей её ломаной, имеющей с ней общие
концы1).
Отношение дуги окружности к соответствующей хорде стре-
стремится к единице, когда дуга стремится к нулю (если окружность
остаётся постоянной). Действительно, длина дуги а'Ь' (черт. 178) зак-
заключена между длиной соответствующей хорды и периметром ломаной
а'А'Ь', образованной касательными в её концах; отношение этих двух
величин стремится, как мы видели (п. 177), к еди-
>/"ч. нице, когда дуга а'Ь' неограниченно убывает.
С>^ ^^-Р 179а. Две равные дуги имеют одинаковую дли-
^ч ну, так как ломаные, служащие для определения
их длин, могут быть выбраны соответственно рав-
Чепт 17Q
v ' ныыи друг другу. Сумма двух дуг имеет своей
длиной сумму длин этих дуг, так как ломаные, вписанные в каждую
из этих дуг, образуют вместе ломаную, вписанную во всю дугу.
Итак, согласно основному положению, на которое мы уже несколько
раз ссылались, отношение длин двух дуг одной и той же окружности
равно отношению самих дуг (п. 17). В частности эти длины относятся
между собой как числа, измеряющие эти дуги в градах (п. 18а) или
в градусах.
Так как длина окружности радиуса R равна 2nR и эта окружность
2-nR -nR
содержит 360 градусов, то длина дуги в один градус равна -— = —— .
Дуга в одну минуту имеет длину в 60 раз меньшую, а именно
¦nR
С
f
18СЬ6О ! ДУГЗ В °ДНУ СеКУВДУ ~ 180.60-60
дится рассматривать. При этом (как и в п. 177) отношение периметра впи-
вписанной ломаной к периметру соответствующей описанной ломаной необ-
необходимо стремится к 1, когда число сторон неограниченно возрастает таким
образом, что каждая из них стремится к нулю.
Существование предела доказывается сначала для такой последователь-
последовательности ломаных, что вершины каждой ломаной принадлежат к числу вершин
последующей ломаной (рассуждение, применённое в п. 176); далее перехо-
переходят к общему случаю, как в п. 177.
Невыпуклую дугу можно разбить на несколько выпуклых дуг.
1) Это рассуждение, очевидно, распространяется на длины дуг произ-
произвольных кривых, определяемые с помощью рассуждений) приведённых в
предыдущей сноске. В частности, прямая линия представляет собой крат-
кратчайшее" расстояние между двумя точками. Выпуклая дуга (см. предыду-
предыдущую сноску) короче любой (ломаной или кривой) линии, объемлющей эту
дугу и имеющей с ней общие концы.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
169
Следовательно, длина дуги окружности радиуса R, содержащая
т градусов, п минут, р секунд, равна
¦nR / , я ¦ Р
Ш \'И + 6О+6(М
Длина дуги в п градов равна
в
200 '
180. Таким образом, мы видим, что можно вычислить длину дуги
какой-либо данной окружности, если известно число п.
Вычисление тт. Метод периметров. Чтобы вычислить это число,
или, что то же самое, чтобы вычислить длину окружности данного
радиуса R, мы должны по определению вычислить периметры правиль-
правильных 'вписанных многоугольников, число сторон ко-
которых неограниченно удваивается. Периметр каж-
каждого из этих многоугольников даёт приближённое
значение с недостатком искомой длины, причём это
значение даёт тем большее приближение, чем боль-
больше число сторон. Если однонременно с вычисле-
вычислением периметра вписанного многоугольника мы умеем
вычислить периметр соответствующего описанного
многоугольника, то мы можем получить, таким обра-
образом, приближённое значение с избытком, и разность
приближённых значений с избытком и с недостат-
недостатком даст верхнюю границу ошибки, которую мы
допустим, принимая за длину окружности значение одного из двух пе-
периметров. Но мы умеем вычислять стороны некоторых правильных впи-
вписанных многоугольников, в частности сторону квадрата. Чтобы полу-
получить из неё стороны многоугольника с 4-2, 4-2",..., 4.2",... сто-
сторонами, достаточно решить следующую задачу.
Задача. Зная сторону правильного многоугольника, вписанного
в окружность данного радиуса, вычислить сторону правильного
многоугольника, вписанного в ту же окружность и имеющего вдвое
большее число сторон.
Пусть АВ=с (черт. 180)—сторона данного многоугольника, впи-
вписанного в круг радиуса OA = R.
Деля дугу АВ на две равные части радиусом ОС, перпендикуляр-
перпендикулярным к хорде АВ в её середине И, получаем сторону АС правильного
вписанного многоугольника с удвоенным числом сторон.
Теперь имеем из тре} гольника О АС:
АС2 = О А2 -)- ОСг — 1ОС ¦ ОН = 2R2— 2R-OH = 2/? (R — ОН)'
/ с1
но ОН равно |/ R2——. Таким образом, искомая сторона с, будет.
/ с2\
170 КНИГА ТРЕТЬЯ. ПОДОБИЕ
Отсюда, так как сторона квадрата равна
R \ 2, а его периметр 4R У2,
то сторона правильного вписанного восьмиугольника равна
R у 2 — У2, а его периметр ER у 2 — У2 ,
сторона правильного вписанного шестнадцатиугольника равна
Ry 2— /2-J-1/2, а его периметр 16/?у 2— /2-|- |/2,
и т. д.
180а. Чтобы получить приближённое значение с избытком длины
окружности, достаточно вычислить периметр правильного описанного
многоугольника и, следовательно, решить следующую задачу.
Задача. Зная сторону правильного многоугольника, вписанного
е окружность данного радиуса R, вычислить сторону правильного
описанного около той же окружности многоугольника с тем же
числом сторон.
Искомую сторону с' находим непосредственно, замечая, что оба
многоугольника подобны и, следовательно, их стороны относятся между
собою как их апофемы, Так как апофема описанного многоугольника
R2 — — , то искома» сторона полу-
получается из пропорции
CL- R
с ~
Мы показали, как вычислить сторону с правильных вписанных мно-
многоугольников с всё большим и большим числом сторон; предыдущая
пропорция позволяет вычислять стороны соответствующих описанных
многоугольников.
181. Можно также, зная сторону с правильного многоугольника, впи-
вписанного в окружность радиуса /?, получить сразу сторону^ и апофемуа1
правильного многоугольника с удвоенным числом сторон, вписанного в ту
же окружность (что даёт сторону соответствующего описанного много-
многоугольника без нового квадратного корня), с помощью следующего приёма.
Пусть С —точка, в которой продолженный радиус ОС пересекает
окружность (черт. 180); треугольник АСО— прямоугольный и даёт (п. 123,
примечание)
AC-АО = CC'-AH=2R.-2=Rc
и, с другой стороны,
/1 С2 -|- И С'2 = СС'2 = 4#2.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
171
Умножим первое равенство на 2 и прибавим его ко второму; получим:
И С2 + АС2 + 2АС-АС = (АС+ АСJ = 4#2 + 2Rc.
Таким образом,
АС + АС = YW1 + 2Rc = 2 |' r
Если после умножения первого равенства на 2 мы вычтем его из второго
то получим:
АС + АС'2 — 2АС- АС = (АС — АС)* = AR2 — 2/?-.
Таким образом:
ЛС — AC = Y4R-* — 2Rc = 2 |/ W #_?-).
Складывая и вычитая почленно эти два равенства, получим:
ас= //?1/? + ^)-|
7"
J7* (*-¦?),
что даёт ответ на поставленный вопрос, так как отрезок АС равен иско-
искомой стороне Cj и ЛС — удвоенной апофеме ах.
Итак, мы знаем теперь, как вычислить хорду половины каждой изовух
дуг, которые стягивает данная хорда в Окружности данного радиуса.
182. Вычисление тт. Метод равных периметров. Предыдущий
метод можно представить в несколько иной форме.
Действительно, задача состоит в вычислении отношения периметра
р правильного многоугольника к радиусу R описанного круга и к апо-
апофеме а, или, что то же, к ради\су вписанного круга, причём это
вычисление должно быть выполнено для многоугольников, число сто-
сторон которых неограниченно возрастает. Но совершенно безразлично,
будут ли многоугольники, которые мы последовательно рассматриваем,
вписанными в одну и ту же окружность или нет, так как отношения
— и — зависят только от числа сторон многоугольника (п. 163).
Метод равных периметров заключается в рассмотрении правиль-
правильных многоугольников, число сторон которых неограниченно удваивается
И которые имеют один и тот же периметр. Таким образом, мы должны
сперва решить следующую задачу.
Задача. Зная радиус R и апофему а правильного многоугольни-
многоугольника1), вычислить радиус R' и апофему а' правильного многоугольника
с удвоенным числом сторон, имеющего с первым равный периметр.
Пусть АВ (черт. 181)—сторона правильного многоугольника с п
сторонами, вписанного в окружность радиуса О A = R. Опустим на АВ
перпендикуляр ОИ^а и продолжим его до встречи с окружностью
в точке С, середине дуги АВ. Соединим точки А и В с точкой С и
') Под „радиусом" правильного многоугольника здесь и далее понимается
радиус описанной около него окружности. Прим. реО. перевода.
172
КНИГА ТРЕТЬЯ. ПОДОБИЕ
пусть А и В будут середины этих двух отрезков, а отрезок А'В1
пусть пересекает ОС в точке Н'.
Отрезок А'В' есть сторона правильного многоугольника с 2л
сторонами, вписанного в окружность радиуса О А'.
Действительно, так как угол АОВ отсекает на окружности ради-
радиуса ОА дугу, равную одной я-й части окружности, то угол А'ОВ',
который равен его половине (так как
угол Л'ОС равен половине угла АОС
и угол В'ОС — половине угла ВОС),
отсекает на окружности радиуса ОА'
дугу, равную одной 2/г-й части этой
окружности.
Этот многоугольник имеет тот
же периметр, кто и данный.
Действительно, сторона А'В' этого
многоугольника, соединяющая середины
АС и ВС, равна половине первоначальной стороны АВ, в то время как
число сторон многоугольника удвоено.
Искомые длины R' и а' суть, таким образом, ОА' и ОН'.
t Точка Н' есть середина СИ, так что имеем:
ОН'—
Зто можно переписать в виде
20Н'==0С-\-ОН или OH' =
т. е. ОН' есть среднее арифметическое между ОС и ОН.
С другой стороны, прямоугольный треугольник ОА'С даёт
О А' = \fOC-OH',
т. е. ОА' есть среднее геометрическое между ОС и ОН.
Таким образом, а' вычисляется по формуле
«•=*+-'.
затем R' по формуле
Повторяя эти две операции, получаем значения а и R для много-
многоугольников с числом сторон всё большим и большим. Отношения зна-
значений этих двух величин к общему полупериметру многоугольников
1
дают примерные значения —, — первые с недостатком, вторые с из-
тг
бытком, — и при этом всё с большим и большим приближением.
Предположим для упрощения, что общий периметр многоугольни-
многоугольников равен удвоенной единице длины, и примем за первый из них квад-
квадрат. Апофема этого многоугольника будет равна половине стороны
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 173
т. е. —, а радиус — стороне, делённой на \^2, т. е. —-*=.. Приняв
я=^ —, a R= ,._ , получим из предыдущих формул значения а'
и /?', соответствующие правильному восьмиугольнику, и т. д.
Но, если принять я=;0 и /? = — 1), то эти формулы дадут
о' = — ; /?' = ,— . Таким образом, мы приходим к следующему
предложению (теорема Шваб а).
Теорема. Если составить ряд чисел, первые два числа кото-
1
рого О и — и каждый член которого попеременно является сред-
средним арифметическим и средним геометрическим двух предыдущих,
то члены составленного таким образом ряда стремятся к —.
тт
183. Так как числа а и R, последовательные члены предыдущего
ряда, представляют собою приближённые значения числа — , — первые
с недостатком, вторые с избытком, — то ошибка, которую мы полу-
получим, если примем одно из них за приближённое значение —, будет
меньше, нежели R — а.
Но мы имеем:
Чтобы это доказать, возьмём снова чертёж 181 и отложим на ОС
длин> 0C = OA' = R'. Отрезок СН' даёт R'—a'. Но углы САН'
и С А'С равны, так как они измеряются половиною равных дуг С В'
и А'С окружности ОА' (один как вписанный угол, другой как угол,
образованный касательной и секущей). Теорема о биссектрисе (п. 115)
показывает, что отрезки Н'С и СС относятся между собою, как
А'И' и А'С. Следовательно, Н'С меньше половины отрезка Н'С,
равной четверти СН или .
') Эти два числа соответствуют делению окружности на две равные
части. Если обозначить точки деления через А и В, то диаметр АВ можно
рассматривать как сторону правильного многоугольника, имеющего две
стороны, периметр которого равен 2АВ. Если принять этот периметр за 2,
то радиус R выразится числом -=¦ , а апофема (расстояние стороны от
центра)—числом 0.
174 КНИГА ТРЕТЬЯ. ПОДОБИЕ
Но первые два члена последовательности Шваба дают R — а^=— .
Таким образом, допущенная ошибка, если принять за приближённое
1
значение — член, который занимает в этой последовательности 2я-е
тт
место, меньше
1 1
2.4"—' 22"~' '
184. Греческий геометр Архимед, который первый определил и
вычислил длину окружности, нашёл методом периметров приближённое
значение тт с избытком с точностью до одной сотой-
22
Можно получить, впрочем, только приближённые значения тт и ни-
никогда нельзя получить его точного значения, потому что доказано,
что это число несоизмеримо, т. е. оно не равно никакому целому
числу и никакому дробному числу.
Первые десятичные знаки числа тт таковы '):
тт = 3,1415926535.
1
и числа — :
тг
— =0,3183098...
тт
Часто пользуются для тт приближённым значением 3,1416 (с из-
избытком).
Знаменитая задача о квадратуре круга приводит (как мы это уви-
увидим позже) к построению отрезка, равного длине окружности, радиус
которой дан. Эту задачу нельзя решить, пользуясь только линейкой
1) Это значение я было получено не теми методами, которые мы ука-
указали, а методами, значительно более совершенными, заимствованными из
анализа бесконечно-малых. Эти десятичные знаки легко запомнить с по-
помощью следующего стиха, в котором числа букв в отдельных словах дают
последовательные цифры числа я:
Que j'aime a faire apprendre un nombre utile aux sages.
31415 9 2 6 53 5
355
Приближённое значение -рг^ , дающее число я с точностью до одной
миллионной с избытком, было дано Адрианом Мецием.
ГЛАВА VII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ 175
и циркулем. Эта невозможность, которая ещё не вытекает из несоиз-
несоизмеримости тт'), также доказана2).
УПРАЖНЕНИЯ.
Правильные многоугольники.
178. Вымостить (т. е. заполнить без пробелов и перекрытий) плоскость
правильными многоугольниками, равными между собою. Показать, что
эта задача возможна только для трёх видов правильных многоугольников.
179. Построить правильный пятиугольник, зная его сторону.
180. В правильном пятиугольнике две диаюнали, не проходящие через
одну и ту же вершину, взаимно делятся в среднем и крайнем отношении
(доказать).
181. Прямоугольный треугольник, катеты которого равны сторонам
двух правильных десятиугольников, вписанных в одну и ту же окружность,
имеет своей гипотенузой сторону равностороннего треугольника, вписан-
вписанного в ту же окружность (доказать).
182. Доказать то же предложение для выпуклого десятиугольника,
шестиугольника и выпуклого пятиугольника; для звездчатого десятиуголь-
десятиугольника, шестиугольника и звездчатого пятиугольника.
183. Если на сторонах правильного шестиугольника построить вне
шестиугольника 6 квадратов, то 12 внешних вершин этих квадратов суть
вершины правильного двенадцатиугольника (доказать).
184. Проверить, что два выражения для стороны съ приведённые в
пи. 180 и 181, равны между собою.
Длина окружности.
185. Найти радиус окружности, дуга которой в 18С15' равна 2 м.
186. На радиусе GA окружности, как на диаметре, построена вторая
окружность. Пусть В и С—точки, в которых обе окружности пересе-
пересекаются с одним и тем же радиусом, выходящим из центра О первой окруж- '
ности. Доказать, что дуги АВ и АС имеют одну и ту же длину.
187. Если две окружности внутренним образом- касаются одной и той
же третьей окружности и сумма их радиусов равна радиусу третьей ок-
окружности, то дуга последней, заключённая между точками касания, равна
сумме дуг внутренних окружностей, заключённых между их точкой пе-
пересечения, ближайшей к большей окружности, и теми же точками касания
(доказать).
188. Сумма сторон вписанных квадрата и равностороннего треуголь-
треугольника даёт приближённое значение длины половины окружности (предел
ошибки: одна сотая радиуса) (доказать).
189. Периметр прямоугольного треугольника, катеты которого равны
ОС ¦
-=- и — диаметра, даёт приближённо значение длины окружности (предел
о о
ошибки: одна десятитысячная радиуса) (доказать).
') Например, диагональ квадрата несоизмерима с его стороной, и тем
не менее очень легко, зная один из этих отрезков, построить другой.
а) Теорема о несоизмеримости т. принадлежит Ламберту A770). Что
касается невозможности квадратуры круга, то её доказал Лиидеман в
1882 г., обобщая теоремы, принадлежащие французскому математику
Э р м и т у.
КНИГА ТРЕТЬЯ. ПОДОБИЕ
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ.
190. Даны две концентрические окружности; провести прямую, на
хоторой эти окружности отсекают две хорды, из которых одна вдвое
длиннее другой.
191. На стороне АВ треугольника от точки В отложен отрезок BD,
а на продолжении стороны АС за точку С—равный ему отрезок СЕ.
Отрезок DE делится стороной ВС внутренним образим в отношении, об-
обратном отношению сторон АВ и АС (доказать).
192. Пусть А и А' — точки касания общей касательной к двум окруж-
окружностям; М и М' — дв> точки пересечения этих окружностей соответствен-
соответственно с некоторой прямой, параллельной АА'. Найти геометрическое место
точек пересечения прямых AM и А'М'.
193. Стороны многоугольника остаются соответственно параллельными
определённым направлениям, в то время как все вершины, кроме одной,
скользят по заданным прямым. Найти геометрическое место последней
вершины (упр. 124).
194. Вписать в данный многоугольник другой многоугольник, стороны
которого параллельны данным прямым. Может ли эта задача быть не-
неопределённой?
195. Высоты треугольника разделены в данных отношениях и через
каждую точку деления проведена прямая, параллельная соответствующей
стороне. Найти коэфцциент подобия треугольника, построенного таким
образом, и первоначального треугольника.
196. Пусть а, Ь, с —точки, симметричные с какой-либо одной и той
же точкой О плоскости относительно середин сторон ВС, СА и АВ тре-
треугольника ABC. Прямые Аа, ВЬ и Сс пересекаются в одной точке Р. Когда
точка О перемещается, описывая какую-либо фигуру, точка Я описывает
фигуру, гомотетичную первой (доказать).
197. Через три вершины треугольника проведены три прямые, прохо-
проходящие через одну точку О\ затем построены прямые, симметричные с каж-
каждой из них относительно биссектрисы того угла треугольника, из вершины
которого данная прямая выходит. Доказать, что эти три новые прямые
также проходят через некоторую точку С.
Доказать, что теорема сохраняет силу, если первоначальные прямые,
вместо того чтобы проходить через одну точку, будут параллельны и что
в этом случае точка О' лежит на окружности, описанной около треуголь-
треугольника.
Вывести из этой теоремы, что три высоты треугольника пересекают-
пересекаются в одной точке.
198. ABCD — ромб, описанный около окружности; доказать, что произ-
произвольная касательная MN отсекает на смежных сторонах АВ и ВС отрез-
отрезки AM и CN, произведение которых постоянно.
199. Если через точку А, взятую в плоскости круга, провести к кругу
произвольную секущую AM'М, то прямые, соединяющие точки М и М'
с одним из концов диаметра, проходящего через А, отсекают на прямой,
перпендикулярной к этому диаметру и проходящей через точку А, два
отрезка, произведение которых постоянно (доказать).
200. Внутренняя общая касательная двух окружностей делит внешнюю
общую касательную (а последняя делит внешним образом первую) на два
отрезка, произведение которых равно произведению радиусов (доказать).
Отрезок, отсечённый общими внутренними касательными на общей
внешней касательной, имеет ту же середину, что и эта обшая внешняя
касательная, и ту же длину, что и общая внутренняя касательная (дока-
(доказать).
201. Прямоугольный треугольник имеет вершиной прямого угла опре-
определённую точку А, в то время как две другие вершины В и С остаются
постоянно на определённой окружности О. Найти: 1) геометрическое мес-
ЗАДАЧИ К TPETbFfi КНИГЕ 177
то середин сторон ВС; 2) геометрические место проекций точки А на сто-
сторону ВС.
202. Построить треугольник, зная одну сторону, соответствующую ей
высоту и произведение двух других сторон.
203. Построить треугольник, зная две его медианы и высоту (два
случая).
204. Вписать в данную окружность равнобедренный треугольник, зная
сумму или разность основания и высоты.
205. Вычислить диагонали трапеции, зная четыре её стороны.
206. Даны окружность и две точки А и В; провести хорду, парал-
параллельную АВ, так, чтобы прямые, соединяющие её конпы соответственно
с точками А и В, пересеклись на окружности.
207. Через концы А и В диаметра" круга проведены две хорды АС и
BD, которые пересекаются в точке Р внутри круга. Доказать, что:
АВ1 = ACAP-\-BD- BP.
208. Через две данные точки А и В проведена -произвольная окруж-
окружность и через данную точку С, лежащую на одной прямой с точками А
и В, — касательные к этой окружности. Найти геометрическое место середин
отрезков, соединяющих точки касания.
209. Построить три попарно ортогональные окружности, имеющие свои-
своими центрами три данные точки.
210. Даны: окружность и на ней две точки А и В; далее дана произ-
произвольная прямая и на ней точка С. Найти на окружности точку М, обла-
обладающую тем свойством, лто расстояние между точками пересечения пря-
прямых МА и MB с данной прямой делится точкой С в заданном отношении.
211. На сторонах АВ, АС и ВС треугольника ABC, как на основаниях,
построены три равнобедренных подобных треугольника АВР, ACQ и BCR;
два первых расположены вне данного треугольника, третий, напротив, по
ту же сторону от ВС, как и данный треугольник (или обратно). Доказать,
что APRQ — параллелограм
212. Фигура, оставаясь сама себе подобной, изменяется так, что три
прямые, принадлежащие этой фигуре и не проходящие через одну точку,
проходят каждая через неподвижную точку. Доказать: 1) что всякая
другая прямая той же фигуры точно так же проходит через
некоторую неподвижную точку; 2) что любая точка фигуры описывает
окружность.
213. Построить четырёхугольник, подобный данному четырёхугольни-
четырёхугольнику, так, чтобы его стороны проходили через четыре данные точки.
Может ли задача быть неопределённой? Найти в этом случае геомет-
геометрическое место точек пересечения диагоналей различных четырёхугольни-
четырёхугольников, отвечающих условию задачи.
214. Фигура, оставаясь постоянно себе подобной, изменяется так, что
три точки этой фигуры описывают каждая прямую линию. Доказать, что
некоторая точка этой фигуры остаётся неподвижной. Вывести отсюда,
что любая другая точка описывает прямую.
215. Даны две подобные фигуры, имеющие одинаковое направление
вращения; найти геометрическое место таких точек, чтобы, если их рас-
рассматривать как принадлежащие первой фигуре, то прямая, которая сое-
соединяет их с гомотетичными им точками второй фигуры, проходила чергз
данную точку.
216. Провести через данную точку О секущую M0N, которая отсе-
отсекает на двух данных прямых, считая от двух данных точек А и В этих
прямых, два отрезка AM и BN, имеющих данное отношение.
12 Элементарная геометпия
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ.
ГЛАВА Г.
ЗНАКИ ОТРЕЗКОВ.
185. До сих пор |<ы измеряли прямолинейные отрезки существен^
но положительными числами. Однако если приходится сравнивать от-
отрезки, лежащие на одной и той же прямой, то оказывается предпоч-
предпочтительным поставить^ соответствие этим отрезкам как положительные,
так и отрицательные числа, пользуясь некоторым соглашением, кото-
которое мы сейчас установим.
Выберем на рассматриваемой прямой Х'Х (черт. 182) раз навсег-
навсегда определённое направление, которое назовём положительным на-
направлением, например направление Х'Х, показанное на чертеже стрел-
У О А В С X
Черт. 182.
кой. Произвольному отрезку АВ мы ставим в соответствие чис-
число, измеряющее его длину, взятое со знаком -}-, если этот от-
отрезок имеет положительное направление, и со знаком —, если он
имеет противоположное направление.
Следует заметить, что знак отрезка существенно зависит от по-
порядка, в котором заданы две его конечные точки, а именно
АВ = — В А.
186. Предыдущее соглашение позволяет писать некоторые соот-
соотношения в форме, не зависящей от расположения рассматриваемых то-
точек.
Пусть, например, А, В, С — три точки на одной прямой; отре-
отрезок ВС равен сумме или разности отрезков АВ и АС, смотря по тому,
в каком порядке следуют друг за другом три точки. Если отрезки
задаются по величине и по знаку, то оба эти соотношения заме-
заменяются одним соотношением
АВ-\~ВС-{-СА = 0, A)
которое имеет место независимо от расположения данных точек.
Действительно, если, двигаясь по прямой ABC в положительном
направлении, мы встречаем эти точки в порядке А, В, С (как на
черт. 182), то отрезки АВ, АС и ВС положительны и мы имеем
ЛС= АВ-\-ВС, что равносильно соотношению A).
ГЛАВА I. ЗНАКИ ОТРЕЗКОВ
179
Но это соотношение не изменится, если переставить две из вхо-
входящих в него точек; например, переставив В и С, имеем равенство
АС-\-СВ-\-ВА = 0,
эквивалентное предыдущему; следовательно, предыдущее равенство
верно, если порядок точек таков: А, С, В.
Далее известно, что с помощью последовательных перестановок
двух элементов можно изменить порядок элементов произвольным об-
образом. Следовательно, равенство A) верно во всех случаях.
Это равенство непосредственно распространяется на любое число
точек, лежащих на одной прямой. Например, пять точек А, В, С, D, Е
на одной прямой Х'Х дают равенство
АВ -\- ВС 4- CD -\- DE + ЕА — 0.
Чтобы его доказать, заметим, что искомое равенство доказано
для случая трёх точек. Следовательно, достаточно установить, что
если это равенство справедливо для некоторого числа точек, то оно
справедливо и для числа точек, на единицу большего. Мы можем по-
поэтому предположить, что оно уже доказано для случая четырёх то-
точек, и написать:
АВ + ВС 4- CD + DA = 0.
С другой стороны, три точки A, D, Е дают:
AD 4- DE 4- ЕА = 0.
При почленном сложении обоих равенств два члена DA и AD
уничтожаются, и получается искомое равенство.
187. Возьмём на прямой Х'Х некоторую неподвижную точку О
(черт. 182) и будем определять положение какоИ-либо точки с по-
помощью отрезка ОА, данного по величине и по знаку. Этот отрезок
называется абсциссой точки А относительно начала О. Очевидно,
что абсолютная величина и знак абсциссы вполне определяют поло-
положение точки А.
Если две точки А и В даны своими абсциссами относительно од-
одного и того же начала О, то расстояние АВ определяется равенст-
равенством
АВ=ОВ — ОА,
которое эквивалентно равенству A) предыдущего пункта.
188. Если точка С взята на прямой АВ, то отношение —отри-
цательно, если точка С лежит между точками А и В, и положитель-
положительно, если точка С лежит вне отрезка АВ.
Поэтому существует только одна точка, которая делит данный от-
отрезок в определённом отношении, заданном по величине и по знаку.
Если точки Си О гармонически сопряжены относительно концов от-
12*
180 дополнения к третьей книге
СА DA
резка АВ, то отношения -^р- и -=г-=- равны по абсолютной величине
СВ UB
и имеют противоположные знаки.
189. Пусть О — середина отрезка CD (черт. 183), концы которо-
которого гармонически сопряжены относительно концов отрезка АВ. При
этом мы будем иметь:
= 0А-0В.
Действительно, определим точки А, В, С и D с помощью их
абсцисс относительно начала О. Равенство ——- = — —— даёт:
LB UB
СА DA ОС —О A OA — OD
СВ DB ОВ—ОС OB—OD '
Составим одно отношение, взяв сумму предыдущих членов двух
последних отношений и сумму их последующих членов, и другое от-
отношение, взяв разности тех же членов. Замечая, что OD^—ОС,
мы получим таким образом:
CA__DA _2ОС_2О,4
~ СВ ~"DB ~ 2OB~2OC'
Итак, мы имеем следующую теорему.
Теорема. Половина прямолинейного отрезка есть среднее про-
пропорциональное между расстояниями середины отрезка до двух
точек, делящих его гармонически.
О А
Мы видим, кроме того, что общее значение отношений ——•
ОС СА DA
и -г-— равно общему значению отношении ———¦ и——.
О В СВ DB
Обратная теорема. Если от середины О отрезка CD от-
отложить в одном и том же направлении dez отрезка ОА и ОВ,
имеющие своим средним пропорциональным половину данного отрезка,
то точки А и В делят гармонически данный отрезок CD.
„ ОС ОА
Действительно, из равных отношении -—— = —— получаются с
ОВ ОС
помощью сложения и вычитания предыдущих и последующих членов
отношения, им равные:
О А ~ ОС _ ОА-{-ОС #
ОС—ОВ ~~ ОВ-\-ОС '
отсюда, принимая во внимание равенство OD = —ОС, имеем:
С A DA
Следствие. Если два отрезка гармонически сопряжены, то
окружность, описанная на одном из них, как на диаметре, Пересе-
ГЛАВА I. ЗНАКИ ОТРЕЗКОВ 181
кает под прямым углом любую окружность, проходящую через
кониы второго отрезка (черт. 183).
Действительно, квадрат радиуса первой окружности равен степени
её центра относительно второй окружности.
Обратно, если две окружности пересекаются под прямым уг-
углом, то любой диаметр одной окружности делится гармонически
другой окружностью.
190. Если две прямые параллельны, то мы выбираем, вообще го-
говоря, одно и то же положительное направление на обеих прямых.
Благодаря этому соглашению мы можем сказать, что отношение
отрезков ВС и DE, отсекаемых сторонами некоторого угла на
двух параллельных секущих,
равно по величине и по знаку
отношению отрезков АВ и AD,
которые эти параллельные
отсекают на одной из сторон
угла (черт. 123, 124 и 125,
п. 117).
Это равенство было доказа-
доказано в п. 117 для абсолютных
величин отрезков. Кроме того, Черт. 183.
оба отношения имеют один и
тот же знак: отрезки ВС и DE будут иметь одно и то же направле-
направление (черт. 123 и 124) или противоположные направления (черт. 125)
одновременно с отрезками АВ и AD. ,
Пусть в частности даны две гомотетичные фигуры; очевидно, воз-
возможно считать их коэфициент подобия положительным или отрица-
отрицательным, смотря по тому, будет ли гомотетия прямой или обратной.
При этом коэфициепт подобия равен по величине, и по знаку отно-
отношению двух каких-либо соответственных отрезков.
191. Соглашение относительно знаков, установленное в п. 13'3
для степени точки относительно окружности, есть не что иное, как
частный случай того условия, которое мы теперь установили.
Действительно, на секушей ЛЕВ' (черт. 137 и 138, п. 131), про-
проведённой через точку А, выберем какое-либо направление за положи-
положительное; тогда отрезки АВ и АВ' будут иметь одинаковое направле-
направление или противоположные направления, смотря по тому, будет ли
точка А лежать вне или внутри окружности; их произведение будет,
таким образом, положительно в первом случае и отрицательно во вто-
втором.
УПРАЖНЕНИЯ.
217. Если первые две из четырёх точек А, В, С, D делят гармонически
две другие, то имеет место (по величине и по знаку) равенство:
* JL__L i J_
АВ AC^AD '
182 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
218. Как можно изменить формулировку теоремы Стюарта (п. 127),
чтобы она сделалась независимой от порядка точек В, С, D (обозначения
те же, что и в п. 127) на прямой, на которой они лежат.
Доказать непосредственно теорему в этой новой формулировке для
случая, когда точка А лежит на прямой BCD. Вывести отсюда формули-
формулировку, пригодную для всех случаев.
219. Если в теореме п. lib изменять величину данного отношения,
оставляя точки А и В (обозначения те же, что и в п. 116) неподвижными,
то различные окружности, получающиеся таким образом, имеют одну и
ту же радикальную ось. Их предельными точками будут точки А и В (дока-
(доказать;.
Вывести отсюда решение следующей задачи: найти на данной
прямой или на данной окружности положение, которое должна занять точка
М, для того чтобы отношение сё расстояний до двух данных точек было
бы наибольшим или наименьшим из возможных (построение, вполне анало-
1ичное построениям п. 159).
219а. Найти две точки, которые делят гармонически два данных от-
отрезка. Всегда ли задача возможна?
220. Окружность, построенная на отрезке, соединяющем центры по-
подобия двух данных окружностей, как на диаметре, имеет оОщую радикаль-
радикальную ось с двумя данными окружностями.
221. Как изменится формулировка упражнения 130, если точка Е вы-
выбрана на продолжении отрезка АС?
Решить тот же вопрос для упражнения 131, если данная прямая пе-
пересекает стороны треугольника.
222. Через вершины А, В, С, D данного квадрата (предполагается, что
вершины кьадрата перечислены в их последовательном порядке) проведены
перпендикуляры Аа, Bb, Cc, Dd к некоторой прямой, лежащей в плоско-
плоскости квадрата, но не пересекающей его сторон. Показать, что при этих ус-
условиях величина
* 2 -ЧВЪ-Dd
не зависит от положения прямой.
(Преобразовать данное выражение так, чтобы в него входили суммы
Аа -(- Сс и Bb-\-Dd и разности Аа — Сс и ВЪ — Dd, и принять во внима-
внимание, что первые две из этих величин равны между собой в силу упр. 130.)
Как следует видоизменить формулировку этого предложения для слу-
случая, когда прямая пересекает квадрат?
ГЛАВА II.
ТРАНСВЕРСАЛИ.
192, Теорема. Если стороны ВС, СА, АВ треугольника ABC
(черт. 184) пересекаются с одной и той же прямой в точках а,
Ь, с, то между отрезками, определёнными таким образом на
сторонах, имеем соотношение:
аВ_Ъ?_с_А_=х B)
аС ЬА'сВ ' V '
Чтобы это доказать, проведём через вершины треугольника до пере-
пересечения с трансверсалью') три прямые, параллельные какому-нибудь
х) Трачсверсалью называется любая прямая, пересекающая стороны
треугольника. Прим. ред. перевода.
ГЛАВА II. ТРАНСВЕРСАЛИ 183
одному и тому же направлению, на которых установим одно и то же
положительное направление.
Пусть а, р, Y — расстояния вершин от трансверсали, считая пи
проведённым параллельным прямым; имеем:
аВ р ЪС j_ сА а
НС~~Т' ЬА~"а'г ~cB~~J'
откуда, перемножая, получим:
аВ_ ЪС сА__^а_
аС 'ЪА ' сВ Y«fi
193. Обратная теорема (теорема Мене лая). Если на сто-
сторонах ВС, СА, АВ треугольна- д
ка ABC взяты три точки а,
Ъ, с, удовлетворяющие соотно-
шению
аВ ЪС сА
7с'ьХ'Ш = *' B)
то эти три точки лежат на "
одной прямой.
Действительно, прямая ab пе-
пересекает сторону АВ в некоторой точке с' так, что имеет место равенство:
аВ ЬС_ с'А
~аС"ЪА'~сТВ~Х'
Это равенство, при сравнении его с предыдущим, показывает,
что
сА с'А
сВ с'В
и что, следовательно, точки сие' совпадают.
Примечание. Эта теорема в сущности сводится к геореме, до-
доказанной в п. 144. Действительно, можно найти такие три отрезка
a, ft и у (заданные по величине и по знаку), что имеют место равен-
1) Если бы трансверсаль была параллельна стороне ВС, то точку а
следовало бы рассматривать как лежащую в бесконечности, а отноше-
отношение ^-уг как равное 1. Искомое соотношение обратилось бы при этом
в тгг=—б~> т. е. в теорему п. 114. Если бы две стороны АВ и АС тре-
угольника сделались параллельными, то точка А лежала бы в бесконеч-
аВ ЬС сА аВ ЪС сА
ности; написав выражение—-^г-——¦—— в виде —-~ ^-- ту, мы замени-
сА
ли бы -г-г через 1 и получили бы теорему п. 117.
и А
184
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
ства:
ЪС
аС
откуда в силу соотношения B) следует
сА а
Вследствие этого три попарно гомотетичные фигуры, в которых
точки А, В, С будут тремя соответственными точками и а, р, Y — тре-
тремя соответственными отрезками,
будут иметь точки а, Ь, с цент-
центрами подобия.
194. Этой теоремой пользуют-
пользуются, когда требуется доказать, что
три точки лежат на одной прямой.
Пример I. Середины трёх ди-
диагоналей полного четырёхсторон-
четырёхсторонника лежат на одной прямой.
Пусть ABCDEF (черт. 185) —
полный четырёхсторонник, диаго-
диагонали которого АВ, CD, EF имеют
своими серединами точки L, М, N.
Рассмотрим треугольник АСЕ,
Черт. 185. образованный тремя сторонами
четырёхсторонника, и пусть а, с,
е — середины сторон СЕ, ЕА, АС. Прямая се параллельна СЕ и про-
проходит через точку L; прямая еа параллельна АЕ и проходит через
точку М; прямая ас параллельна АС и проходит через точку N. Чтобы
доказать, что точки L,M, N лежат на одной прямой, нам достаточно
доказать соотношение:
Lc Me Na
Но
и точно
Le
параллельные прямые
так же имеем:
Me
Ma
DA
DE
Ma
Lee и
Lc
Те'
И
Nc ~
ВСЕ
BE
~BC '
Na
Nc ~
-1.
дают
.FC
~~FA
Но произведение трёх правых частей
BE DA FC
b~c"de"Fa
ГЛАВА II. ТРАНСВЕРСАЛИ
185
равно 1, поскольку точки В, D, F, взятые на сторонах треугольника
АСЕ, лежат на одной прямой.
195. Пример П. Если вершины двух треугольников a be, a'b'c'
соответствуют друг другу таким образом, что прямые аа', ЬЬ', ее',
которые соединяют соответствующие вершины, пересекаются в одной
точке о, то точки пересечения соответствующих сторон лежат на
одной прямой.
Пусть / (черт. 186).— точка пересечения прямых Ьс и Ъ'с';
т—точка пересечения са и cf-а'; п — точка пересечения ab и а'Ь'.
Требуется доказать, что
точки/, т, п лежат на од- с
ной прямой, другими сло-
словами, что имеет место ра-
равенство:
1Ъ тс па .
1с та nb
Действительно, тре-
треугольник obc, пересечённый
трансверсалью Ib'c', даёт
lb с[с_ Ь[о
te'c'o" ?b '
Точно так же тре-
треугольники оса и oab,
пересечённые соответст-
соответственно трансверсалями тс'а'
и па'Ъ', дают
Черт. 186.
тс
та
па
nb
a'a
" a'o
b'b
'Wo"
с
с
a'
a7
0
V
0
a
1.
— i,
= 1.
При почленном перемножении трёх последних равенств и сокраще-
сокращении на множителей a'a, b'b, e'e, a'o, b'o, c'o получается требуемое
соотношение.
Два треугольника таких, что прямые, соединяющие их соответствен-
соответственные вершины, проходят через одну точку, называются гомологическими.
196. Пример III (теорема Паскаля). Во всяком шести-
шестиугольнике, вписанном в окружность, точки пересечения противопо-
противоположных сторон лежат на одной прямой.
Пусть ABCDEF (черт. 187) — шестиугольник, противоположные
стороны которого АВ и DE пересекаются в точке L, стороны ВС и
EF — в М, стороны CD и FA — в N. Рассмотрим треуч ольник IJК,
образованный сторонами АВ, CD, EF, другими словами, сторонами
данного шестиугольника, взятыми через одну.
Точки L, М, N расположены соответственно на сторонах JK. KI,
IJ этого треугольника. Эти точки лежат на одной прямой, если имеет
186
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
место соотношение:
LK' MI ' NJ
C)
Но, если мы пересечём последовательно треугольник IJK каждой
из оставшихся сторон DE, ВС, FA шестиугольника, мы получим со-
соотношения:
L? EK
LK' El
MK CI
DJ '
BJ
mi ' cj"bk~~ '
Л7 A/ FK_,
NJ' AK' FI
Перемножив почленно эти три равенства, мы можем написать, груп-
группируя надлежащим образом ,множители числителя и знаменателя:
L? MK NI CI-DI AJBJ EK-FK
LK' MI ' NJ' EIFI ' CJ DJ ' AK-BK
Черт. 187.
Но каждая из трёх последних дробей, которые входят в левую
часть, равна 1. Например, произведения. CI-DI и EI-FI равны как
произведения отрезков, отсечённых окружностью на секущих, выходящих
из точки /. Таким образом, получается соотношение C), и теорема дока-
доказана.
Примечание. Предыдущее доказательство остаётся в силе, если
точки А ч В, С и D, Е и F попарно совпадают и стороны треуголь-
треугольника UK являются касательными к кругу.
При этом теорема принимает следующую форму: Касательные,
проведенные через вершины треугольника, вписанного в круг, пере-
1ЛАВА II. Т;-АНСВЕРСАЛН
187
секают соответствующие стороны в трёх точках, лежащих на
одной прямой.
197. Теорема. Если через вершины треугольника ABC (черт. 188)
провести прямые Аа, ВЬ, Сс, пересекающиеся в одной и той же
точке О, /но эти прямые пересекают стороны ВС, СА. АВ
соответственно в трех точках а, Ь, с таких,
что имеет место соотношение:
аС ЪА сВ к '
Действительно, треугольник АаС, пересечён-
пересечённый трансверсалью ВЬ, даёт1):
ВС ЪА Оа
о С
Черт, 188.
ОА
—
Оа
Треугольник АаВ, пересечённый трансверсалью Сс, даёт:
Са_ сВ 0А_
СВ ' сА' 0а~~ '
При почленном делении двух последних равенств и сокращении на
мы получаем:
аВ ЬС сА С В
aC"bA" сВ'~ВС~~ '
это равенство равносильно равенству D), так как
СВ = — ВС.
198. Обратная теорема (теорема Чевы). Если на сторонах
треугольника ABC взяты три точки а, Ь, с так, что имеет место
равенство
аВ ЬС_ сА___
аС" ЬА"сВ^~ '
то прямые Аа, ВЬ, Сс проходят через одну точку.
Действительно, пусть О — точка пересечения прямых Аа и ВЬ.
Прямая СО пересекает сторону АВ в некоторой точке с' так, что
аВ ЬС с'А_
~аС"Ш'сГВ~~~ '
!) Рассуждение сохраняет силу, если точка О удаляется в бесконечность,
т. е. если прямые Аа, ВЬ и Сс параллельны. В самом деле, мы видели, что
теорема п. 192 сохраняет силу для трансверсали, параллельной одной из
сторон треугольника.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
Это равенство при сравнении его с тем, которое дано в условии
теоремы, даёт:
с А с'А
сВ^ТВ'
Следовательно, точки сие' совпадают, и теорема 'доказана.
Если бы прямые Аа и ВЬ были параллельны, то прямая Сс была
бы параллельна этим двум прямым, и три прямые следовало бы рас-
рассматривать как пересекающиеся в одной и той же точке в бесконеч-
бесконечности.
Этой теоремой пользуются, когда требуется доказать, что три пря-
прямые проходят через одну точку.
Пример. Медианы треугольника проходят через одну точку.
Так как а, Ь, с — середины сторон треугольника, то каждое из отно-
аВ ЬС сА
шении ^' Га' Тв р3™0-1-
Аналогичным образом можно доказать, что биссектрисы углов тре-
треугольника проходят через одну точку; и т. д.
УПРАЖНЕНИЯ.
223. Вывести теорему Менелая для случая, когда все точки деления
являются внешними, пользуясь тремя окружностями, аналогичными тем,
которыми приходится пользоваться в упражнении 127, и ограничиваясь слу-
случаем, когда эти окружности пересекаются.
224. Прямая пересекает стороны треугольника ABC в трёх точках а,
Ь, с. Для каждой из трёх этих точек строим точку, ей симметричную от-
относительно Середины стороны, на которой она лежит. Доказать, что но-
новые точки а', Ъ', с', полученные таким образом, лежат на одной прямой.
Если точки а, Ъ, с служат проекциями на стороны треугольника не-
некоторой точки, лежащей на описанной окружности (упр. 72), то то же
самое имеет место и для точек а', Ъ', с'.
225. Сторона ОАВ некоторого угла неподвижна, как и точки А и В,
взятые на этой стороне, в то время как сторона ОАВ' вращается вокруг
вершины О вместе с точками А' и В', взятыми на этой стороне на посто-
постоянном расстоянии от О. Найти геометрическое место точек пересечения
прямых АА' и ВВ'.
226. Даны угол и три точки А, В, С, лежащие на одной прямой. Про-
Произвольная прямая, проведённая через А, пересекает стороны угла в точ-
точках М и N. Найти геометрическое место точек пересечения прямых ВМ
и CN.
227. Три прямые, выходящие из вершин треугольника ABC и прохо-
проходящие через одну точку, пересекают противоположные Стороны в точках
а, Ь, с. Строим точки а', V, с', симметричные с этими точками относи-
относительно середин сторон, на которых они лежат. Доказать, что прямые Аа\
ВЬ', Сс' также проходят через одну точку.
228. Прямые, соединяющие вершины треугольника с точками касания
противоположных сторон со вписанной окружностью, проходят через одну
точку (доказать).
229. Пусть А'В'С — треугольник, полученный из треугольника ABC
путём проведения (как в п. 53) через каждую его вершину прямой, парал-
параллельной противоположной стороне; а, Ъ, с—точки, взятые соответственно
на сторонах ВС, СА, АВ.
ГЛАВА III. СЛОЖНОЕ ОТНОШЕНИЕ 189
Если прямые Аа, ВЬ, Сс проходят через одну точку, то прямые А'а,
В'Ь, Сс также проходят через одну точку (доказать).
230. Если прямые Аа, ВЬ, Сс проходят через одну точку и на сторо-
сторонах ВС, СА, АВ треугольника ABC взяты точки, гармонически сопряжённые
с точками а, Ъ, с относительно вершин треугольника, то эти гармонически
сопряжённые точки лежат на одной прямой (доказать).
Применить к биссектрисам Аа, ВЬ, Сс треугольника.
231. Если прямые Аа, ВЬ, Сс, где точки а, Ъ, с лежат соответственно
на сторонах ВС, СА, АВ треугольника ABC, проходят через одну точку и
окружность аЪс пересекает стороны второй раз в точках а', V, с', то пря-
прямые Аа', ВЬ', Сс' также проходят через одну точку (доказать;.
ГЛАВА III.
СЛОЖНОЕ ОТНОШЕНИЕ. ГАРМОНИЧЕСКИЕ ЧЕТВЁРКИ
ПРЯМЫХ.
199. Определение. Пусть А, В, С, D — четыре точки, лежащие
на одной прямой. Сложным (или ангармоническим) отношением этих
четырёх точек, которое обозначается символом (ABCD), называется
частное от деления отношения расстояний точки С до точек А и В
на отношение расстояний точки D до тех же точек, а именно:
САш РА
с~в''Ш'
CA-DB
Это выражение может быть также записано в виде: - —; сле-
CB'UA
довательно, это есть частное двух из тех произведений, которые можно
составить из отрезков, соединяющих попарно данные точки и не имею-
имеющих общих концов.
Сложное отношение зависит от того порядка, в котором мы рас-
расположим четыре точки; однако без труда можно убедиться, что оно
не меняется, если переставить между собою две из точек, лишь
бы только одновременно были переставлены и две другие.
DA
Если точка D удаляется в бесконечность, то отношение стре-
DB
мится к 1. Следовательно, сложное отношение точек А В, С и со1)
СА
равно -^Ъ •
СА DA
Если данные четыре точки гармонические, то отношения — и
СВ DB
равны по абсолютной величине, но имеют противоположные знаки и
сложное отношение равно — 1. Очевидно, что и, обратно, последнее
условие влечёт за собой первое.
200. Основная теорема. Четыре прямые, проходящие через од-
одну точку, пересекают любую секущую в четырёх точках, сложное
отношение которых не зависит от положения секущей.
1) Знак оо обозначает, как и в алгебре, бесконечность.
190
ДОПОЛНРНИЯ К ТРЕТЬЕЙ КНИГЕ
Пусть О А А', ОВВ', ОСС, ODD' (черт. 189) — четыре прямые.
Если эти четыре прямые пересечены двумя секущими ABCD и A'B'C'D',
то я утверждаю, что
СА DA_CA_ шР'А'
~св : Ъ~в~~св :Тув' "
Чтобы это доказать, проводим через точки В и В' прямые Bed и
В'с'а", параллельные О А; при этом пусть первая прямая пересечёт ОС
в точке с и OD в точке d, а вторая пересечёт ОС в точке с' и OD
в точке d'.
Имеем:
DA ОА
СВ сВ DB dB '
откуда почленным делением получаем
СА _ DA__dB
СВ' DB~~cB'
Также получаем
С А' ПА' __ d" В
D LJ D С ID
Искомое соотношение, таким обра-
образом, доказано, 'так как отноше-
dB d'B'
ния — и ——- , очевидно, равны, потому что секущие Bed и В с d
параллельны.
Постоянное сложное отошение, определяемое точками пересечения
четырёх лучей с произвольной секущей, называется сложным отноше-
отношением четырёх лучей.
Операция, которая состоит в переходе от точек А, В, С, D к точ-
точкам А', В', С, П, принадлежит к категории операций, называемых
перспективой, или центральной проекцией1).
Длина отрезка, например отрезка АВ, изменяется при этой опера-
операции; отношения отрезков также изменяются, но мы видим, что слож-
сложное отношение не изменяется при произвольном проектировании; это
свойство выражают в следующих словах: сложное отношение проек-
тивно.
201. В частности, если точки С и D гармонически делят отрезок
АВ, то, соединив четыре точки А, В, С, D с какой-либо одной и той
же точкой О, мы получим четвёрку лучей, которая в пересечении
С любой прямой даёт четыре гармонические точки
Такая четвёрка называется гармонической четвёркой; два луча ОС
и OD называются гармонически сопряжёнными относительно лучей
ОА и ОВ, и обратно.
1) Эти операции будут нами определены в геометрии пространства.
ГЛАВА III. СЛОЖНОЕ ОТНОШЕНИЕ 191
Теорема. Чтобы четвёрка лучей была гармонической, необхо-
необходимо а достаточно, чтобы на какой-либо прямой, параллельной
одному из лучей четвгрки, три других её луча отсекали два рав-
равных отрезка.
Действительно, из чертежа 189 мы видим, что сложное отношение
СА DA dD ,
—-:—- равно отношению — , которое может быть равно — 1 в том
СВ DB со
и только в том случае, если точка В есть середина отрезка ей.
Следствия: 1. Две прямые ОМХ и ОМЧ (черт. 167, п. 157), ко-
которые служат геометрическим местом точек, отношение рассто-
расстояний которых до двух прямых D и D' имеет данное значение,
образуют вместе с последними гармоническую четверку.
Действительно, на чертеже 167 отрезок М^Мп разделён на две рав-
равные части прямою D.
Обратно, если два луча ОС и OD гармонически сопряжены отно-
относительно двух других ОА и ОВ, то отношение расстояний какой-либо
точки прямой ОС до прямых ОА и ОВ равно отношению расстояний
какой-либо точки прямой OD до тех же прнмых1).
11. Биссектрисы углов, образованных двумя прямыми, опреде-
определяют вместе с ними гармонический пучок (п. 115).
Обратно, если в гармонической четвёрке лучей два сопряжён-
сопряжённых луча образуют прямой угол, то они являются биссектрисами
углов между двумя другими лучами.
Действительно, если прямые ОА, ОВ, ОС и OD образуют гармо-
гармоническую четвёрку, то отрезок Bed, параллельный лучу ОА, делится
на две равные части в точке В. Следовательно, если ОА и ОВ взаим-
взаимно перпендикулярны, то луч ОВ есть перпендикуляр в середине от-
отрезка ей и делит угол cOd пополам.
202. Теорема. Каждая диагональ полного четырёхсторонника
делится гармонически двумя другими его диагоналями.
В полном четырёхстороннике ABCDEF (черт. 190) диагонали CD
и EF пересекаются в точке Н; пусть К — точка, гармонически сопряжён-
сопряжённая с точкой И относительно отрезка EF. Прямые АЕ, AF, АИ, АК
образуют гармоническую четвер^', а следовательно, точка L, в которой
прямая АК пересекает диагональ CD, гармонически сопряжена с точ-
точкой Н относительно отрезка CD. Но прямые BE, BF, ВН, ВК также
образуют гармоническую четвёрку, и точка L', в которой ВК пересе-
пересекает CD, также гармонически сопряжена с точкой Н относительно
отрезка CD; следовательно, она совпадает с точкой L, а прямая KL —
с прямой АВ.
203. Если через некоторую точку, лежащую в плоскости данного
угла, провести произвольную секущую, то геометрическим местом то-
точек, гармонически сопряжённых с этой точкой относительно точек
1) Это заключение должно быть видоизменено, если принять во вни-
внимание знаки отрезков (выбрав положительные направления на прямых,
перпендикулярных к ОА, и на прямых, перпендикулярных к ОВ): при этом'
оба отношения будут иметь различные знаки.
192 дополнения к третьей книге
пересечения секущей со сторонами угла, будет, очевидно, прямая ли-
линия: а именно, этим геометрическим местом булет служить прямая,
гармонически сопряжённая относительно сторон данного угла с пря-
прямой, соединяющей вершину угла с данной точкой.
Ута прямая называется полярой точки относительно угла.
Черт. 190.
Теорема. Если через точку А, взятую в плоскости угла CBD
(черт. 190), провести секущие ADE и AFC и соединить попарно
точки пересечения С и D. Е и F этих секущих со сторонами угла,
то геометрическое место точек Н, в которых пересекаются пря-
прямые CD и EF, есть поляра точки А относительно угла.
Действительно, прямые ВС; BD, ВА, ВИ образуют гармоническую
четвёрку, так как они делят гармонически отрезок EF.
Эта теорема даёт весьма простой способ построения поляры точки
относительно угла.
УПРАЖНЕНИЯ.
232. Если две четвёрки прямых, преходящих соответственно через
точки О и О', имеют одно и то же сложное отношение и соответственно
общий луч (прямую 00'), то точки пересечения других соответственных
луч^й лежат на одной прямой (доказать).
233. Если на двух прямых ОХ и OY, пересекающихся в точке О, взять
на одной три точки А, В, С и на другой три точки А', В', С так, чтобы
сложные отношения (OABCj и (ОА'В'С) были равны, то прямые АА', ВВ', СС
приходят через одну и ту же точку (доказать).
234. Найти необходимое и достаточное условие возможности постро-
построения параллелограма, стороны и диагонали которого были бы соответст-
соответственно параллельны четырём данным прямым.
235. Даны: прямая AT и две точки А и В вне этой прямой. Соединим
произвольную точку М плоскости с точками А и В. Пусть Р и Q— точки
пересечения прямых МА и MB с прямой XY. Найти геометрическое место
точки пересечения М' прямых РВ и QA, если точка М описывает данную
прямую.
Рассмотреть случай, когда прямые АР и BQ, вместо того чтобы пере-
пересечься в какой-либо точке М, лгжащей на данной прямой, параллельны.
ГЛАВА IV. ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ
193
236. Если через две точки, делящие гармонически диаметр окружно-
окружности, провести перпендикуляры к этому диаметру, то эти прямые пересе-
пересекаются с любой касательной в двух точках, отношение расстояний кото-
которых до центра есть величина постоянная (доказать).
ГЛАВА IV.
ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ.
204. Теорема. Если через точку а, взятую в плоскости круга,
провести произвольную секущую, пересекающую окружность
в точках М и N, то геометрическое место точек Р. гармонически
сопряжённых с точкой а от-
относительно точек М и N, есть
прямая линия (черт. 191).
Действительно, середина /
отрезка аР удовлетворяет
(п. 189) равенству
Эта точка / принадлежит,
таким образом, определённой
прямой — радикальной оси дан-
данной окружности и точки а
(п. 136, примечание 1°). Черт. 191.
Точка Р опишет прямую,
гомотетичную этой прямой относительно точки а, причём коэфициент
подобия равен 2.
Обратно, какая-либо точка Р прямой, таким образом определён-
определённой, принадлежит рассматриваемому геометрическому месту, если луч
аР пересекает окружность (что всегда имеет место, если точка а ле-
лежит внутри окружности).
Эта прямая — геометрическое место точек Р — Называется полярой
точки а относительно окружности, а точка а — полюсом этой
прямой.
Следствие. Поляра точки а перпендикулярна к прямой, соеди-
соединяющей эту точку с центром О окружности, и пересекает эту
прямую в некоторой точке Н, которая лежит по ту же сторону от
центра, как и точка а, и определяется равенством
Oa-OH = R2, E)
где R — радиус окружности.
Действительно, это равенство показывает, что точки а и //делят
гармонически диаметр, лежащий на прямой Оа.
Из отрезков Оа и ОН один больше, а другой меньше радиуса,
так как радиус является их средним пропорциональным; следовательно,
поляра пересекает окружность или не пересекает её, смотря по
тому, лежит ли полюс вне или внутри окружности.
13 Элементарная геометрия
194 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ KHHrF
Если точка а лежит вне окружности, то полярой этой точки
служит хорда, соединяющая точки прикосновения касательных,
проходящих через эту точку.
Действительно, рассуждения, которыми мы пользовались для обо-
обоснования существования поляры, остаются верными, если секущая
aMN на чертеже 191 обращается в касательную, причём обе точки
М и N совпадут с точкой прикосновения Т этой касательной. Точка
Р будет в этом случае совпадать с точкой Т, и поляра должна про-
проходить через эту точку.
Если точка а лежит на окружности, то определение поляры
как геометрического места точек, собственно говоря, теряет свой
смысл '); но мы можем найти эту прямую с помощью доказанного выше
следствия: точка Н в данном случае совпадает с точкой а, и полярой
является касательная в этой точке.
Отрезок ОН, определённый равенством E), бесконечно велик
только в том случае, когда точка а совпадает с точкой О; только
в этом случае соответствующее построение невозможно. Впрочем, й
priori очевидно, что поляра удаляется при этом в бесконечность, так
как- точка О есть середина всех хорд, проходящих через эту точку.
То же самое равенство позволяет, обратно, найти полюс, если
известна поляра. Проводим из центра перпендикуляр ОН к данной
поляре и откладываем на прямой ОН отрезок Оа, определяемый ра-
равенством E). Это невозложно сделать, только если ОН равно нулю,
т. е. если данная прямая есть один из диаметров окружности:
при этом полюс удаляется в бесконечность в направлении, перпен-
перпендикулярном к диаметру.
205. Наиболее важным является следующее свойство поляры.
Теорема. Если точка а лежит на поляре точки Ь, то, об-
обратно, последняя лежит на поляре точки а.
Точки а и b называются в этом случае сопряжёнными относи-
относительно окружности. Их поляры, т. е. две прямые, каждая из которых
проходит через полюс другой, точно также называются сопряжён-
сопряжёнными.
Так как точка а (черт. 192) лежит на поляре точки Л, то её
проекция на Oh есть такая точка К, что OK -Ob = R2. Пусть точка
Н — проекция точки b на Оа\ тогда четырёхугольник аНЬК можно
вписать в окружность (а именно в окружность, построенную на от-
отрезке ab как на диаметре), и мы имеем:
ОН • Оа = ОК ¦ ОЬ = /?2.
Следовательно, прямая НЬ — поляра точки а.
') Одна из точек пересечения М » N всё время совпадает с точкой а,
и, следовательно, точка Р также, вообще говоря, совпадает с точкой а;
однако, если секущая обращается в касательную, то обе точки М п N сов-
совпадают с точкой а, и положение точки Р на этой касательной неопре-
неопределе но.
ГЛАВА IV. ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ
195
Примечание. Теорема очевидна, если прямая ab пересекает
окружность, так как в этом случае условие и заключение выражают
одно и то же, а именно, что ^окружность делит отрезок ab гармо-
гармонически.
206. Предыдущая теорема позволяет переходить от свойств неко-
некоторой фигуры (F) к свойствам другой фигуры \F'), которую мы сейчас
определим и которая называется 4игУР°й взаимно-поля рной (или кор-
коррелятивной) данной
Пусть F—фигура, состоящая из любого числа точек и прямых1).
Каждой точке а этой фигуры поставим в соответствие пряф'Ю А, а
именно—поляру точки а относительно некоторой окружности, выбран-
выбранной раз навсегда и называемой на-
направляющей окружностью. Каж-
Каждой прямой В фигуры (F) поставим
в соответствие точку Ь, а именно —
полюс этой прямой относительно на-
направляющей окружности. Прямые
А и точки b образуют фигуру (F1),
взаимно-полярную фигуре (F).
В силу предыдущей теоремы бу-
будем иметь следующее предложе-
предложение:
Если прямая В фигуры (F) про-
проходит через точку а, то соответст-
соответствующая точка b фигуры (F') лежит на
прямой А, соответствующей точке а.
Следовательно, если прямая фигуры (F) вращается около не-
неподвижной точки, то соответствующая точка фигуры {F1) опи-
описывает прямую линию, и обратно,
Или иначе, если три прямые линии фигуры (F) проходят через
одну точку, то соответствующие им точки фигуры (F1) лежат
на одной прямой, и обратно.
207. Предположим, например, что фигура (F) есть фигура п. 195
(черт. 186), образованная такими двумя треугольниками abc и а'Ь'с',
что прямые аа', bb', ее' проходят через одну точку о. Поляры .4, В,
С, А', В', С точек а, Ь, с, а', Ь', с' образуют два новых треуголь-
треугольника. Прямым аа', bb', cc' соответствуют точки пересечения сто-
сторон А, А'; В, В1; С, С; так как первые три прямые проходят через
одну точку, то последние три точки лежат на одной прямой.
Обратно, каждую пару треугольников, стороны которых соответ-
соответствуют друг другу так, что точки пересечения соответственных сто-
сторон лежат на одной прямой, можно рассматривать как фигуру, вза-
взаимно-полярную паре треугольников, аналогичных треугольникам
abc и а'Ь'с'.
Черт. 192.
') Определение взаимно-полярных фигур распространяется с помощью,
соображений, которые мы будем рассматривать в |еиметрии пространства
и на фигуры, содержащие кривые линии.
13*
196 дополнения к третьей книге
Мы доказали (п. 195), что точки пересечения соответственных
сторон треугольников abc, a'b'c лежат на одной прямой; следова-
следовательно, прямые, которые соответствуют этим точкам, т. е. прямые,
которые соединяют соответственные вершины треугольников, образо-
образованных прямыми А,В,С; А',В',С', пересекаются в одной точке. Дру-
Другими словами, теорема, обратная теореме, доказанной в п. 195,
верна.
208. Предположим теперь, что фигура (F) — шестиугольник, впи-
вписанный в окружность; пусть Л, В, С, D, Е, F (черт. 193) — стороны
этого шестиугольника.
Примем окружность, описанную около шестиугольника, за напра-
направляющую окружность; поляры вершин шестиугольника будут каса-
касательными в этих точках и будут попарно пе-
пересекаться в точках а,Ь, с, d, et f—полю-
f—полюсах сторон А, В, С, D, Е, F. Эти последние
точки будут вершинами шестиугольника, опи-
описанного около окружности. Обратно, всякий
шестиугольник, описанный около окружности,
можно рассматривать как взаимно-полярный
некоторому вписанному шестиугольнику.
Но мы доказали, что во вписанном шести-
шестиугольнике точки пересечения A, D; В, Е;
С, F лежат на одной прямой (п. 196). Таким
образом, мы имеем теорему Брианшона:
Во всяком шестиугольнике abodef, описанном около окружности,
диагонали, соединяющие противоположные вершины, пересекаются в
одной точке.
Точно так же предельный случай, относящийся к вписанному тре-
треугольнику (п. 196, примечание), даёт:
Во всяком треугольнике, описанном около окружности, прямые,
соединяющие каждую вершину с точкой касания противоположной
стороны, пересекаются в одной точке.
209. Мы знаем, что соответствует в фигуре (F1) трём лежащим
на одной прямой точкам или трём пересекающимся в одной точке
прямым фигуры (F); эти свойства (т. е. свойство трёх точек лежать
на одной прямой и свойство трёх прямых проходить через одну точку)
называются дескриптивными в отличие от тех, в которых фигури-
фигурируют значения тех или других величин и которые называются метри-
метрическими. Мы рассмотрим теперь законы преобразования некоторых из
последних.
Прежде всего, если две прямые линии фигуры F параллельны,
то их полюсы лежат на одной прямой с центром О направляю-
направляющей окружности (на диаметре, перпендикулярном к направлению па-
параллельных прямых), и обратно.
Например, мы могли бы, так,им образом, легко доказать теорему
п. 195, рассмотрев фигуру, взаимно-полярную данной относительно
направляющей окружности с центром в точке о (черт. 186).
ГЛАВА IV. ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ 197
Точкам а, а'; Ь, Ь'\ с, с' соответствовали бы прямые, попарно
параллельные,' и, следовательно, образующие два гомотетичных тре-
треугольника, так что прямые, соединяющие соответственные вершины
двух последних треугольников, пересекались бы в одной точке; от-
отсюда, возвращаясь к первоначальной фигуре, мы получили бы требу-
требуемое заключение.
Вообще угол между двумя прямыми равен углу, под которым
отрезок, соединяющий их полюсы, виден изе центра- О направляю-
направляющей окружности (или углу, ему пополнительному), так как эти
два угла имеют соответственно перпендикулярные стороны (черт. 192).
Преобразуем, например, теорему о высотах треугольника (п. 53).
Вершинам а, Ь, с какого-либо треугольника соответствуют стороны
А, В, С нового треугольника. Высота' опущенная из точки а, даёт
в новой фигуре точку, лежащую, с одной стороны, на прямой А и,
с другой стороны, на прямой, проходящей через центр направляющей
окружности О и перпендикулярной к прямой, которая проходит через
точку О и соответствующую вершину (точку пересечения сторон В и С)
нового треугольника.
Так как три высоты треугольника abc пересекаются в одной и
той же точке, мы имеем1) следующее предложение:
Если через какую-либо точку О, лежащую в плоскости тре-
треугольника, провести прямые, перпендикулярные к прямым, кото-
которые соединяют эту. точку с тремя вершинами, то проведённые
прямые пересекают соответствующие стороны в трёх точках,
лежащих на одной прямой.
210. Сложное отношение четырёх прямых Dv D2, D3, D4, пе-
пересекающихся в точке а, равно сложному отношению их полюсов
dv rf2, d&, dit так как четвёрки прямых (Odx, Od2, Od.6, Od^) и (Dx,
D2, D3, D4), где О — центр направляющей окружности, равны: они
получаются одна из другой, если переместить первую параллельно са-
самой себе из точки О в точку а и повернуть её затем на прямой
угол около этой точки. Следовательно, обе четвёрки имеют одно и то
же сложное отношение.
В частности, эта теорема позволяет преобразовать отношение рас-
расстояний точки d.d до точек dx и d%. В самом деле, достаточно пред-
предположить, что точка di находится в бесконечности. Прямая D4 про-
ходит при этом через точку О; итак, отношение -~—i равно сложному
отношению прямых D,, Dv D3, aO.
211. Теорема. Если, через точку а, взятую в плоскости дан-
данной окружности, провести к окружности две секущие aMN и
aM'N' (черт. 194) и соединить попарно точки пересечения М, N,
М, N' этих секущих с окружностью, то полученные прямые пе-
') Как и в предыдущих примерах, доказательство не будет полным, если
мы не убедимся, что надлежищим выбором точек а, Ь, с можно достичь
произвольного расположения точки О и прямых А. В, С.
198
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
ресекаются в двух точках Н и К, геометрическое место которых
есть поляра точки а, если секущие вращаются около этой точки.
Действительно, пусть И — точка пересечения прямых ММ и NN',
К— точка пересечения прямых MN' и NM'.
Прямая НК пересекает хорды MN и M'N' в точках Р и Р', гар-
гармонически сопряжённых с точкой а относительно концов этих хорд
(п. 202). Следовательно, она будет полярой точки а.
Эта теорема даёт простой способ построения поляры точки отно-
относительно окружности. Если точка лежит вне окружности, то она поз-
позволяет, следовательно, пост-
построить с помощью одной линей-
линейки касательные к окружности,
выходящие из этой точки.
Если обе секущие сливают-
сливаются в одну, то предыдущее ге-
геометрическое место обращается
в геометрическое место точек
пересечения касательных к ок-
окружности в концах хорды MN.
Но это геометрическое место
мы уже знаем (п. 205), так как
точка пересечения двух каса-
касательных есть полюс прямой MN.
212. Теорема. Если А,
В, С, D — четыре точки одной
окружности, то сложное отношение четырёх прямых, полученных
соединением этих точек с какой-либо точкой М окружности, не
зависит от положения точки М на кривой.
Действительно, если М и М' — две точки окружности, то две
четвёрки (MA, MB, MC, MD) и (М'А, М'В, М'С, M'D) равны, так как
прямые, их составляющие, можно всегда рассматривать (п. 82) как
образующие между собою одни и те же углы с одним и тем же на-
направлением вращения.
Примечание. Ничто не мешает принять за точку М одну из
данных точек, например А. Прямая МА заменяется при этом касатель-
касательной в точке А и предыдущее рассуждение остаётся в силе.
Постоянное сложное отношение, о котором была речь, называется
сложным отношением четырёх точек А, В, С, D, лежащих на
окружности. Если оно равно—1, то говорят, что четыре соответ-
соответствующие точки, лежащие на окружности,—гармонические.
Следствие. Четыре данные касательные к одной окружности
определяют на подвижной касательной к той же окружности че-
четыре точки, имеющие постоянное сложное отношение.
Действительно, фигура, образованная четырьмя точками пересече-
пересечения неподвижных касательных с перемещающейся касательной, имеет
в качестве взаимно-полярной фигуры относительно данной окружности
четвёрку лучей (MA, MB, MC, MD) предыдущей теоремы.
Черт. 194.
ГЛАВА IV. ПОЛЮСЫ И ПОЛЯРЫ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ 199
Сложным отношением четырёх касательных к одной окруж-
окружности называется сложное отношение четырёх точек пересечения этих
касательных с какой-либо подвижной касательной. Из нашего рассуж-
рассуждения следует, что сложное отношение четырёх касательных равно
сложному отношению их точек касания.
213. Теорема. Две хорды, сопряжённые
относительно окружности, делят эту окруж-
окружность гармонически.
Пусть АВ и CD (черт. 195)—две такие
хорды, что CD проходит через полюс Р хорды АВ.
Прямые АР, АВ, AC, AD образуют гармони-
гармонический пучок, так как они делят гармонически
секущую PCD.
Но сложное отношение этих прямых равно слож-
сложному отношению точек А, В, С, D окружности,
так как прямая АР касается окружности в точке Л. Черт. 195.
Следствие. Четыре касательные, проведён-
проведённые к окружности через две сопряжённые точки, делят любую
касательную гармонически.
Теоремы, обратные двум последним теоремам, также справедливы.
Их доказательство мы предоставляем читателю.
УПРАЖНЕНИЯ.
237. Две точки А и В сопряжены относительно окружности О. Дока-
Доказать, что:
1) окружности, имеющие своими центрами точки А и В и ортогональ-
ортогональные к окружности О, ортогональны между собою;
2) окружность, построенная на отрезке АВ как на диаметре, пересе-
пересекает ортогонально окружность О.
Найти зависимость, существующую между тремя сторонами треугольника
ОАВ и радиусом R окружности.
238. Найти, пользуясь предыдущим упражнением, геометрическое место
точек, поляры которых относительно трёх данных окружностей пересекаю-
пересекаются в одной точке, и геометрическое место точек пересечения этих поляр.
239. Если провести в вершинах вписанного в окружность четырёх-
четырёхугольника касательные к этой окружности так, чтобы получился описанный
четырёхугольник, то
1) диагонали обоих четырёхугольников проходят через одну и ту же
точку и образуют гармоническую четвёрку;
2) третьи диагонали соответствующих полных четырёхсторонников ле-
лежат на одной и той же прямой и делят друг друга гармонически.
240. Через две точки прямой D проведены к окружности касательные.
Таким образом, получается полный четырёхсторонник, одной из диагоналей
которого служит сама прямая D. Доказать, что две другие диагонали про-
проходят через полюс прямой D.
241. Даны две окружности О и О' и их предельные точки (упр. 152) Р
и Q; доказать, что
1) полярой каждой из предельных точек относительно той и другой
окружности будет одна и та же прямая, проходящая чергз другую пре-
предельную точку;
2) не существует других точек (на конечном расстоянии), которые имели
бы одну и ту же поляру относительно обеих окружностей;
200 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
3) перпендикуляр к линии центров, проведённый через точку пересе-
пересечения внутренней общей касательной и внешней общей касательной, про-
проходит через одну из точек Р или Q (доказать, что этот перпендикуляр
имеет один и тот же полюс относительно обеих окружностей);
4) прямая, которая соединяет между собой точки касания одной из
окружностей с внешней общей касательной и с внутренней общей касатель-
касательной, проходит через одну из точек Р или Q.
ГЛАВА V.
ВЗАИМНО ОБРАТНЫЕ ФИГУРЫ.
214. Определение. Если выбраны точка О — полюс инверсии (черт
196 и 196а) и число k — степень инверсии, то точка М прямой ОМ
называется обратной (или преобразованной обратными радиусами-
векторами) точке М при условии, что
0M-0M' =
Черт. 196.
Отрезок !) ОМ должен быть отложен в направлении ОМ (черт. 196)
или в противоположном направлении (черт. 196а), в зависимости от
того, будет ли число k положительным или отрицательным.
Непосредственно ясно, что:
1) любая точка плоскости имеет обратную точку, исключая полюс
инверсии: точка, обратная полюсу, лежит в бесконечности;
2) если М' — точка, обратная точке М, то, обратно, последняя
есть точка, обратная первой.
Фигура F называется фигурой, обратной фигуре F, если она об-
образована точками, обратными всем точкам фигуры F.
215. Теорема. Две фигуры, обратные одной и той же третьей
фигуре F относительно одного и того же полюса О, гомотетичны.
Действительно, пусть М — точка фигуры F, М' н /И,' — точки,
соответствующие ей в двух инверсиях с общим полюсом О и степе-
Отрезки ОМ и ОМ' называются радиусами-векторами точеи
ГЛАВА V. ВЗАИМНО ОБРАТНЫЕ ФИГУРЫ 201
нями инверсии, соответственно равными k и kx. Из равенств ОМ-ОМ1' =
= &, ОМ-ОМ^ = ky, разделив одно на другое, получим:
ОЩ _ kx
ОМ k '
что и доказывает теорему.
Мы видим, что выбор степени инверсии не влияет на форму полу-
полученных фигур. Эта форма изменяется только при изменении полюса
инверсии.
216. Если степень инверсии k положительна, то можно описать
окружность с центром в полюсе и радиусом, равным |/7Г (черт. 196).
Эта окружность, задание которой, очевидно, достаточно для опреде-
определения преобразования, называется окружностью
инверсии (или кругом инверсии); она представ- О
ляет собою геометрическое место точек, кото-
которые совпадают с точками, им обратными.
Две взаимно обратные точки сопряжены отно-
относительно окружности инверсии и лежат на пря-
прямой, проходящей через центр этой окружно-
окружности.
Всякая окружность, проходящая через
две взаимно обратные точки, пересекает ок-
окружность инверсии под прямым углом (п. 135).
Обратно, если две точки М и М таковы,
что всякая окружность, проходящхя через
эти две точки, пересекает под прямым углом
данную окружность, то эти точки взаимно обратны относительно
последней.
Если две точки симметричны относительно прямой, то всякая
окружность, проходящая через эти две точки, пересекает эту прямую
под прямым углом, так как она является диаметром. Это позволяет
нам рассматривать симметрию относительно прямой, как пре-
предельный случай инверсии, если окружность инверсии — прямая линия
и полюс, следовательно, лежит в бесконечности').
217. Две какие-либо точки А и В (черт. 197) и точки А' и В',
им обратные, лежат всегда на одной и той же окружности
(п. 131а).
Отсюда следует (п. 82), что угол, образуемый хордой АВ с ра-
радиусом-вектором ОАА', равен углу, образуемому хордой А'И с ра-
радиусом-вектором ОВВ' (черт. 197), но имеет противоположное
направление.
1) Обратно, так как симметрия относительно прямой называется также
отражением от этой прямой, то в более общем смысле и инверсия отно-
относительно окружности часто также называется отражением; взаимно об-
обратные точки М и М' называются симметричными относительно окруж-
окружности.
202
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
Это свойство позволяет найти направление хорды А 'В", если из-
известны направления хорды АВ и радиусов-векторов.
Это направление А'В' называется антипараллельным направлению
АВ относительно угла АОВ; оно параллельно направлению, симметрич-
симметричному с АВ относительно биссектрисы угла АОВ, так как в этой сим-
симметрии прямой ОА соответствует прямая ОВ и угол АОВ преобра-
преобразуется в равный ему угол, имеющий противоположное направление.
218. Задача. Зная расстояние между двумя точками А иВи
их радиусы-векторы, найти расстояние между обратными им
точками А' и В'.
Подобные треугольники ОАВ и О В'А' (черт. 197) дают:
А'В'
ОА' :
ВА
'ов-
k
Определив отсюда А'В' и заменив ОА' через , получим:
k
~~ А' ОА-ОВ'
Примечание. Предыдущее рассуждение не применимо в том
случае, если точки А и В лежат на одной прямой с полюсом, но ре-
результат сохраняет силу и будет верным не толь-
только по величине, но и по знаку (если на их общем
радиусе-векторе выбрано положительное направле-
направление). В этом можно убедиться, заменяя А'В'
и ВА соответственно через ОБ" — ОА' =
219. Теорема. Касательные в соответ-
соответственных точках двух взаимно обратных
кривых образуют с общим радиусом-вектором
точек касания углы, равные между собою,
но имеющие противоположные направления.
Пусть А (черт. 198) — точка кривой С, А' —
соответственная точка обратной кривой С. Пусть
М — точка кривой С, близкая к точке А, М' —
точка, ей обратная. Проводим к окружности,
проходящей через точки А, А', М, М' (п. 217),
касательные АХ и А'Х'. Если точка М неогра-
неограниченно приближается к точке А (и, следовательно, точка М' к точ-
точке А'), то углы АА'М и A'AM' стремятся к нулю, и то же самое
будет с равными им углами МАХ и М'А'Х'.
Поэтому, если прямая AM стремится занять предельное поло-
положение AT, то и АХ стремится к тому же предельному положению.
Вследствие этого прямая А'Х' займёт предельное положечие AT',
образующее с радиусом-вектором ОАА' угол такой же величины, как
и прямая AT, но противоположного направления; наконец, так как
ГЛАВА V. ВЗАИМНО ОБРАТНЫЕ ФИГУРЫ 203
угол М'А'Х' стремится к нулю, то и прямая А'М' тоже стремится
к AT.
Следствие. Касательные в соответственных точках двух вза-
взаимно обратных кривых симметричны относительно прямой, пер-
перпендикулярной к отрезку, соединяющему точки касания, и про-
проходящей через его середину.
Примечание. Всё предыдущее, очевидно, остаётся справедли-
справедливым, если инверсия обращается в симметрию относительно прямой.
Теорема. Две кривые пересекаются под тем же углом, как
и обратные (или симметричные) им кривые, если не учитывать
направления углов.
Действительно, угол, образованный касательными к двум кривым
в их общей точке А, и угол, образованный касательными к обратным
кривым в соответствующей точке А',
симметричны относительно перпенди-
перпендикуляра, восставленного в середине
отрезка АА'.
Следствие. Если две кривые ка-
касаются, то то же самое имеет
место для кривых, им обратных.
220. Теорема. Фигура, обрат-
обратная прямой линии, есть окруж-
окружность, проходящая через полюс
инверсии.
Пусть XY (черт. 199)—данная
прямая, для которой мы ищем обрат-
обратную фигуру, и точка О — полюс инверсии. Возьмём какую-либо
определённую точку А, обратная которой — точка А'. Пусть теперь
М — произвольная точка прямой XYy и точка М — точка, ей обрат-
обратная. Угол между прямыми М'А' и ОМ равен углу между AM и ОА,
но противоположного направления; следовательно, этот угол остаётся
постоянным, если точка М перемещается по прямой, и геометрическое
место точек М есть окружность, проходящая через точки О и А\
что и требовалось доказать.
В частности, мы можем принять за точку А точку И, проекцию
точки О на прямую XY; обозначим через Н' точку, ей обратную.
Угол ОМ'Н' будет в этом случае прямой, и мы видим, что касатель-
касательная в точке О к окружности, обратной данной прямой, парал-
k
лельна этой прямой, причём диаметр окружности равен -^, где
k — степень инверсии и 8—расстояние ОН.полюса инверсии до пря-
прямой.
Примечание. Предыдущее рассуждение предполагает, что пря-
прямая не проходит через полюс инверсии: в противном случае она сама
себе соответствует.
Следствие. Фигура, обратная окружности, проходящей через
полюс инверсии, есть прямая. Эта прямая перпендикулярна к диа-
204
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
метру, проходящему через полюс инверсии, и проходит через точку,
обратную той точке окружности, которая диаметрально противопо-
противоположна полюсу.
221. Теорема. Фигура, обратная окружности, не проходящей
через полюс инверсии, есть также окружность.
1°. Если степень инверсии k равна степени р полюса инверсии от-
относительно данной окружности, то последняя сама себе соответ-
соответствует, и точки пересечения её с какой-либо секущей, выходящей из
полюса, будут, очевидно, попарно взаимно обратны.
Черт. 200.
2°. Если степень инверсии k произвольна (черт. 200), то обрат-
обратной фигурой будет окружность, гомотетичная дайной (п. 215); цент-
центром подобия будет полюс инверсии, а коэфициентом подобия — вели-
k
чина — .
Р
222. Обратно, две произвольные окружности С и С (черт. 200)
можно рассматривать как взаимно обратные друг другу и при-
притом двумя различными способами, поскольку их можно рассматри-
рассматривать как гомотетичные двумя различными способами. Полюс
инверсии будет при этом центром подобия, а степень инверсии, равна
степени полюса относительно одной из данных окружностей, умножен-
умноженной на соответственный коэфициент подобия.
Эти две инверсии — единственные, которые преобразуют данные
две окружности одна в другую. Действительно, если эти окружности
взаимно обратны относительно некоторого полюса S, то они гомонг-
тичны относительно точки S, так как одна из них обратна самой
себе относительно этого полюса.
ГЛАВА V. ВЗАИМНО ОБРАТНЫЕ ФИГУРЫ
205
223. Пусть некоторая секущая, выходящая из центра подобия S,
пересекает окружность С в точках М и N и окружность С — в точ-
точках М' и N' (черт. 200), так что точка М' есть точка, соответственная
точке М, и точка N' — точке /V, если рассматривать окружности как
гомотетичные фигуры. При этом в силу предыдущего рассуждения
взаимно обратными точками будут, с одной стороны, М и /V', с дру-
другой, — М' и N. Эти точки называются также антигомологичными
точками.
Единственными точками, одновременно соответственными и антиго-
антигомологичными, являются точки прикосновения общих касательных, вы-
выходящих из точки S.
Общие точки двух окружностей, если такие точки существуют,
сами себе антигомологичны.
Хорда, антигомологичная хорде одной окружности, есть хорда
другой окружности, соединяющая точки, соответственно антигомоло-
антигомологичные концам первой хорды.
224. Лее пары антигомологичных точек лежат на одной ок-
окружности (п. 217) и, следовательно, две антигомологичные хорды
пересекаются на радикальной оси (п. 139).
Кроме того, две антигомологичные хорды двух окружностей
пересекают поляры центра подобия относительно обеих окружно-
окружностей в двух соответственных точках. Действительно, хорда N'P',
антигомологичная хорде MQ (черт. 200), будет соответственной хорде
NP, которая пересекает хорду MQ в некоторой точке /, лежащей
на поляре точки 5 относительно окружности С (п. 211), и соответ-
соответственная ей точка /' есть точка пересечения хорды N Р' с полярой
точки S относительно окружности С
Эти два свойства позволяют построить хорду, антигомологичную
данной хорде, не строя концов этих хорд.
Эти два свойства применимы, конечно, к касательным в антигомо-
антигомологичных точках, так как эти касательные представляют собою пре-
предельный случай указанных хорд.
Примечание. Если обе окружности сливаются в одну (случай
1°, п. 221), то хорды MQ и NP, соединяющие—одна какие-либо
две точки, другая — точки, им обратные, пересекаются на поляре по-
полюса инверсии S. Следовательно, с этой точки зрения поляра точки S
играет роль радикальной оси двух слившихся окружностей, если
их рассматривать как взаимно обратные относительно полюса S.
225. Если две окружности равны, то внешний центр подобия ле-
лежит в бесконечности и соответствующая гомотетия обращается в по-
поступательное перемещение, а соответствующая инверсия — в симметрию;
однако свойства антигомологичных точек остаются при этом теми же,
что и в общем случае.
226. Прямую и окружность можно рассматривать как две вза-
взаимно обратные фигуры и притом двумя различными способами.
Полюсами инверсии (п. 220) будут концы диаметра, перпендику-
перпендикулярного к этой прямой. Свойства антигомологичных точек позволяют,
206
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
следовательно, рассматривать концы этого диаметра как центры подо-
подобия окружности и прямой. Одной из двух антигомологичных хорд бу-
будет данная прямая; следовательно, и в этом случае можно сказать, что
эти две хорды пересекаются на радикальной оси в силу п. 158 (по-
(построение 12, примечание).
Наконец, две прямые симметричны друг с другом двумя раз-
различными способами, причём осями симметрии служат биссектрисы уг-
углов, образованных этими прямыми. Антигомологичными хордами будут
тогда эти самые прямые и они пересекаются в одной и той же точке.
227. Если даны две взаимно обратные окружности, то всякая
окружность ?, проходящая через две антигомологичные точки,
обратно самой себе, так как степень полюса инверсии относительно
атип окружности ряинч степени инверсии.
Эта окружность пересекает, следовательно, две данные окр \>ж-
ности под одним и тем же углом, и если она касается одной
окружности, то она касается и другой.
Обратно, всякая окружность 2, которая пересекает две
окружности С и С (черт. 201) под одним и тем же углом, пересе-
пересекает их в четырех попарно антигомологичных точках.
Действительно, пусть 4 и Z?, А' к В' — четыре точки пересечения,
выбранные таким образом, что равные (по условию) углы, образуемые
окружностями С и 2 в точке А, с одной стороны, и окружностями
С и S в точке А', с другой стороны, имеют противоположное на-
направление; то же самое относительно точек В и В'. Если точка 5 —
точка пересечения .4.4' и ВВ' и k — Степень этой точки относительно
окружности 2, то инверсия с полюсом 5 и степенью k не изменяет
2; она преобразует .4 в А', В в В'; следовательно, она преобразует
окружность С в некоторую окружность, которая проходит через точки
А' и В' и касается окружности С в точке А' (по условию и в силу
п. 219), т. е. в окружность, совпадающую с окружностью С (п. 90,
построение 13).
Это заключение остается в силе, когда окружность ^ касает-
касается окружностей С и С Чтобы убедиться в этом, достаточно по-
повторить предыдущее рассуждение, принимая за точку Л — точку Пересе-
ГЛАВА V. ВЗАИМНО ОБРАТНЫЕ ФИГУРЫ 207
чения прямых \А' и ВВ', где точки А и А' — точки касания, В и
В' — соответственно вторые точки пересечения окружностей С и С
с какой-либо окружностью, проходящей через точки А и А' (черт. 201).
В последнем случае, впрочем, предыдущее положение вытекает из
теоремы п. 144; действительно, точки касания служат центрами подо-
подобия: одна для окружностей 2 и С, другая для окружностей 2 и С;
• следовательно, они лежат на одной прямой с центром подобия S
окружностей С и С. Таким образом, мы убеждаемся, кроме того, что
S будет внешним центром подобия, если окружность 2 касается
обеих окружностей одинаковым образом'), и внутренним в про-
противном случае.
Конечно, приведённые выше рассуждения остаются в силе, если
одна из окружностей С или С, или они обе, или окружность 2 за-
заменяются прямыми линиями.
227а. Если бы окружность 2 пересекала окружности С и С под »
прямым углом, то можно было бы произвольно рассматривать точки
пересечения как попарно антигомологичные друг другу, так как пря-
прямые углы можно всегда рассматривать как равные и имеющие проти-
противоположное направление (если в случае надобности заменить одну из
сторон её продолжением). Итак, окружность, которая пересекает
окружности С и С под прямым углом, соответствует сама себе как в од-
одной, так и в другой инверсии, преобразующей окружность С в
окружность С.
228. Если инверсия, которая имеет полюсом точку 5 и преобра-
преобразует окружности С и С одну в другую, имеет окружность инверсии,
то эта окружность инверсии Г пересекает окружность 2 под прямым
углом, так как степень точки 5 относительно 2 равна степени ин-
инверсии.
Это свойство соответствует свойству биссектрис углов между двумя
прямыми. Действительно, эти последние образуют геометрическое место
центров окружностей, касающихся двух прямых; это сводится к тому,
что какая-либо одна из этих окружностей пересекает ту или другую из
биссектрис под прямым углом. Здесь мы убеждаемся, что любая
окружность 2, касательная к окружности С и к окружности С, или,
общее, любая окружность 2, которая пересекает окружности С и С
под одним и тем же углом, пересекает под прямым углом окружность
Г или аналогичную окружность, имеющую своим центром второй центр
подобия (?сли эти окружности существуют).
Окружность Г существует всегда, если окружности С и С пере-
пересекаются: в этом случае она проходит через точки их пересечения.
В общем случае, если она существует, она имеет с окружностями
С и С одну и ту же .радикальную ось, так как эти три окружности
имеют (см. предыдущий пункт) один и тот же ряд ортогональных ок-
окружностей.
1) Т. е. обеих окружностей внутренним опраЗом или обеих внешним
образом.
208 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ KHHrF
УПРАЖНЕНИЯ.
242. Если две точки взаимно обратны относительно окружности, то их
расстояния до какой-либо точки этой окружности находятся в постоянном
отношении (доказать).
243. Показать, что в том случае, когда данная окружность пересе-
пересекает данную прямую в некоторой точке /, можно привести упражнение 68
к упражнению 65, пользуясь инверсией с полюсом в точке /.
244. Через общую точку Л двух окружностей проведены две секущие
АММ' и ANN', которые пересекают первую окружность в точках М и N
и вторую — в точках М и N'. Окружности AMN' и ANM' пересекаются
в точке Лив некоторой второй точке; найти геометрическое место этой
второй точки при условии, что обе секущие принимают независимо друг
от друга всевозможные положения, вращаясь около точки А,
245. Окружности, обратные окружностям, имеющим общую радикаль-
радикальную ось, имеют также общую радикальную ось (доказать).
246 Преобразовать путём инверсии определение окружности (п. 7).
Таким образом, получается теорема п. 116.
247. Построена окружность, обратная данной окружности относительно
данного полюса инверсии. Найти точку, обратную центру новой окруж-
окружности.
248. Преобразовать две данные окружности (не имеющие общей точки)
в две концентрические окружности путём одной и той же инверсии.
249. Даны три точки на одной прямой; найти на той же прямой чет-
четвёртую точку — такую, что инверсия относительно этой точки преобразует
три данные точки в три точки, одна из которых делит пополам отрезок,
образованный двумя другими.
250. Две фигуры преобразованы одна в другую с помощью инверсии S.
Обе эти фигуры подвергают одной и той же инверсии Т. Показать, что
новые фигуры, таким образом полученные, — также фигуры взаимно об-
обратные, и найти новый полюс инверсии. В частности, исследовать случай,
когда степень инверсии S положительна (в этом случае новая окружность
инверсии получается из окружности инверсии 6" с помощью инверсии Т).
. 251. К данной фигуре А применяют инверсию S, которая преобразует
её в фигуру В, затем применяют к последней инверсию У, которая преоб-
преобразует её в фигуру А'. Ограничимся случаем, когда степени инверсий S
и S' положительны.
1°. Показать, что можно с помощью инверсии Т, надлежащим образом
выбранной, преобразовать фигуры А и А' или в дье гомотетичные, или в две
равные; при этом эти две возможности взаимно исключают друг друга1).
2°. Показать, что можно найти бесчисленным числом способов пару
инверсий S1 и 6\', равносильных паре S и S', т. е. таких, что инверсии Ь\
и S{, выполненные одна после другой над'фигурой А (подобно тому как
раньше были выполнены инверсии S и S'), приводят к той же окончатель-
окончательной фигуре А'. В частности, всегда можно заменить две данные инверсии
инверсией, которой предшествует или за которой следует симметрия, за
исключением только одного случая (а именно, когда фигуры А и А' по-
подобны).
3°. Выяснить, в каком случае фигуры, полученные из Л и Л' с помощью
инверсии 7", определённой в 1°, получаются одна из другой путём посту-
поступательного перемещения.
4°. Выяснить, что произойдёт, если выполнить несколько раз подряд
последовательно операции S и S' (т. е. если преобразовать фигуру А' с
•) За исключением случая, указанного в 3°, который можно рассмат-
рассматривать как предельный случай для обеих возможностей, так как поступа-
поступательное перемещение можно рассматривать как предельный случай гомо-
гомотетии.
ГЛАВА VI. ЗАДАЧИ О КАСАНИИ ОКРУЖНОСТЕЙ 209
помошью инверсии S в фигуру В', последнюю с помощью инверсии S' в фи-
фигуру А", эту с помощью инверсии S в фигуру В'', затем преобразовать по-
последнюю с помощью S' в А"' и т. д.). Может ли случиться, что в конечном
счёте получится снова первоначальная фигура Л?
252. Выполнены последовательно (как в предыдущем упражнении) не-
некоторые инверсии Sj, S2, S3 и т- Д- Показать (ограничиваясь случаем, когда
степени инверсий положительны), что эту последовательность операций
можно заменить одной инверсией, которой предшествует или за которой
следует одна, две или три симметрии, если только первоначальная и окон-
окончательная фигуры пе будут подобными (упр. 251, 2° и упр. 95).
253. Предположим, что число инверсий Slt S2, S3,... (предыдущее упраж-
упражнение)— число нечётное. Найти точку, которая возвращается в первона-
первоначальное положение с помощью этих операций, выполненных в последователь-
последовательном порядке.
253а. Вписать в круг многоугольник, стороны которого проходят со-
соответственно через данные точки или параллельны данным прямым.
254. На данной касательной к некоторой окружности откладывают от
точки касания Т два переменных отрезка ТМ и 77V, произведение которых,
однако, постоянно. Пусть V — точка данной окружности, диаметрально про-
противоположная точке Т.
1°. Показать, что если соединить между собой точки пересечения пря-
прямых Т'М и T'N с данной окружностью, то полученная, таким образом,
прямая проходит через определённую неподвижную точку.
2°. Решить ту же задачу для прямой, которая соединяет между собой
точки прикосновения вторых касательных, проведённых к данной окруж-
окружности через точки М и N (приводится к предыдущему).
3°. Найти геометрическое место точек пересечения этих вторых каса-
касательных.
255. Через точку О, взятую в плоскости некоторой окружности, про-
проведена секущая, которая пересекает окружность в точках М и N. Окруж-
Окружности, диаметрами которых служат соответственно отрезки ОМ и ON, пере-
пересекают второй раз данную окружность в точках М' и N'. Найти геометрическое
место точек переселения прямых MN и M'N', если секущая вращается около
точки О.
256. Все окружности, пересекающие две данные окружности А и В под
данными углами, образуют два таких семейства, что какая-либо окружность
С, имеющая с А и В общую радикальную ось, пересекает все окружности
одного и того же семейства под одним и тем же углом (доказать).
257. На данных двух отрезках АВ и CD одной и той же прямой по-
построены дуги, вмещающие один и тот же угол. Если изменяется этот угол,
найти:
1) геометрическое место середин общих хоря тех окружностей, к ко-
которым принадлежат эти дуги;
2) геометрическое место точек пересечения тех же окружностей, иначе
говоря, геометрическое место точек, из которых отрезки прямой АВ и CD
видны под равными углами или под пополнительными углами.
ГЛАВА VI.
ЗАДАЧИ О КАСАНИИ ОКРУЖНОСТЕЙ.
229. Задача. Построишь окружность, проходящую через две
данные точка и касающуюся данной прямой или данной окруж-
окружности.
Мы уже решили эту задачу (п. 159). Однако инверсия позволяет
дать другое решение. Действительно, если мы преобразуем фигуру
14 Элементарная геометрия
210
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
с помощью обратных радиусов-векторов, приняв за полюс одну из
данных точек, то искомая окружность преобразуется в прямую, которая
должна пройти через известную точку (обратную второй из данных
точек) и касаться известной окружности (обратной данной окружности).
230. Задача. Построить окружность, которая проходит через
данную точку и касается двух данных прямых (или окружностей).
Способ первый. Искомая окружность сама себе соответствует
в одной из двух инверсий (или симметрии), которые преобразуют дан-
данные линии одну в другую. Таким образом, известна, кроме данной
точки, вторая точка искомой окружности, а именно та, в которую
преобразуется данная точка с помощью рассматриваемой инверсии или
симметрии, и задача сводится к предыдущей. Здесь возможны четыре
решения, так как предыдущая задача имеет два решения.
Черт. 202.
Способ второй. Возьмём фигуру, обратную рассматриваемой
фигуре, принимая за полюс данную точку. Мы приходим тогда к задаче
об общих касательных к двум окружностям.
231. Задача. Построить окружность, касающуюся трёх данных
окружностей.
Эта задача сводится к предыдущей. Действительно, пусть С, С,
С" (черт. 202) — данные окружности, радиусы которых соответственно
равны г, г', г", и О — искомая окружность радиуса /?, которая ка-
касается всех трёх данных окружностей, предположим, внешним образом.
Окружность радиуса R-\-r" с центром в точке О пройдёт через центр
окружности С" и будет касательной к окружностям, которые концен-
тричны окружностям С и С, причём радиусы этих новых окружностей
соответственно равны разностям радиусов г и г", г и г".
Совершенно так же можно рассмотреть случай, когда не все дан-
данные окружности имеют внешнее касание с окружностью О; при этом
ГЛАВА VI. ЗАДАЧИ О КАСАНИИ ОКРУЖНОСТЕЙ
211
придётся только заменить некоторые из разностей радиусов суммами
тех же радиусов, и обратно.
232. Рассмотрим решение той же задачи способом, совершенно
отличным от предыдущего (метод Жергонна).
Пусть. .4, В, С — данные окружности. Найдём сперва окружность
2 (черт. 203), которая касается в точках а, Ь, с данных окружностей
Черт. 203.
одинаковым образом, т. е. либо всех трёх внешним образом, либо
всех трёх внутренним образом.
Если такая окружность существует, то необходимо существует ещё
вторая такая же окружность 2'. Действительно, радикальный центр /
данных трёх окружностей имеет одну и ту же степень относительно
этих трёх окружностей: если принять эту степень за степень инверсии
и точку / за полюс инверсии, то инверсия не изменит данные окруж-
окружности и преобразует окружность 2 в некоторую окружность 2', кото-
14*
212 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
рая будет касаться окружностей А, В, С в точках а', Ь', с', обрат-
обратных точкам а, Ь, с. Окружность 2'' будет касаться всех окружностей
одинаковым образом; при этом характер касания окружностей S и Г
с данными окружностями будет одним и тем же, если точка / служит
внешним центром подобия окружностей 2 и 2', и не будет одним
и тем же, если точка / служит внутренним центром подобия окруж-
окружностей 2 и 2'.
Докажем, что радикальная ось XY двух искомых окружностей яв-
является внешнею осью подобия (п. 145) трёх данных окружностей. Для
этого проведём прямые ab и а'Ь'; пусть они пересекутся в точке Л\
Точка 5 лежит на радикальной оси окружностей 2 и 2', так как точки
а и а', Ь и Ь' попарно взаимно обратны относительно точки / (п. 224).
Но точка 5 есть внешний центр подобия данных окружностей А и В
(п. 227). Так же убеждаемся, что радикальная ось XY проходит через
другие два внешних центра подобия данных окружностей.
Доказав это, проводим общие касательные в точках касания а и а'
окружности А с окружностями 2 и 2'. Точка а, в которой пересека-
пересекаются эти касательные, лежит на прямой XY, так как точки а и а'
взаимно обратны относительно точки /. Эта точка а служит полюсом
аа' относительно окружности А.
Следовательно, хорда аа проходит через точку р, которая слу-
служит полюсом относительно окружности А внешней оси подобия XY.
Таким образом, мы пришли к следующему построению: Находим
радикальный центр I и внешнюю ось подобия XY данных окруж-
окружностей. Соединяем .точку I с полюсами p. q, r прямой XY отно-
относительно данных окружностей. Прямые, построенные таким обра-
образом, соответственно пересекают данные окружности в искомых
точках касания а и а', Ь и Ь', с и с'.
233. Остаётся показать, что это построение действительно даёт
окружности, удовлетворяющие требуемым условиям.
Для этого мы покажем, что точки а, Ь, с, а', Ь', с', полученные
указанным построением, являются попарно антигомологичными точками
данных окружностей. Действительно, найдём хорду окружности В,
антигомологичную хорде аа' окружности А. Эта хорда определяется
(п. 224) следующими двумя условиями: 1) обе хорды пересекаются
на радикальной оси двух окружностей А и В; 2) обе хорды пересе-
пересекают поляры точки 5 относительно соответствующих окружностей
в двух соответственных точках. С другой стороны: 1) точка пересече-
пересечения / прямых аа' и ЬЬ' принадлежит радикальной оси окружностей 4
и В, 2) точки pug, полюсы прямой XY относительно окружностей
Л и В, лежат на полярах точки 5 относительно этих окружностей,
и эти точки — соответственные точки, так как в гомотетии, имеющей
своим центром точку 5 и преобразующей окружность А в окружность
В, прямая XY сама себе соответствует, и, следовательно, её полюсы
соответствуют друг другу. Следовательно, хордой, антигомологичной
хорде аа', является хорда ЬЬ'. Так же будут антигомологичными хорды
ее' и аа' в окружностях С и Л и хорды ее' и ЬЬ' в окружностях С и В.
vi. задачи о касании окружнострй 213
Мы обозначим через b и с две точки, антигомологичные точке а
(этим самым ещё не доказано, что эти две точки антигомологичны
друг другу); при этом точки Ь' и с' будут точками, антигомологичными
точке а'. Через точки а, Ь, с проводим окружность 2, и через точки
а', Ь', с'—окружность 2'.
Эти две окружности взаимно обратны относительно точки /,
так как точки a, a'; b, b'\ с, с' попарно взаимно обратны относительно
точки /; таким образом, окружностью, обратной окружности abc, будет
окружность а'Ь'с'.
Радикальной осью этих окружностей является прямая XY, так
как эта радикальная ось, с одной стороны, должна пройти через точки
пересечения прямых ab и а'Ь', с другой стороны, через точки пересе-
пересечения прямых ас и а'с'.
Пусть теперь ах — точка пересечения касательных в точках а и а'
к окружности А. Эта точка лежит на прямой XY, так как прямая аа'
проходит через точку р; она также лежит на перпендикуляре, прове-
проведенном через середину отрезка аа'.
Но точка а, в которой пересекаются касательные, проведённые
в точках а и а' соответственно к окружностям Ji н У, также лежит
на прямой XY, так как эга прямая является радикальной осью окруж-
окружностей 2 и 2'; следовательно, она лежит также на перпендикуляре
в середине отрезка аа', так как касательные аа и аа', проведённые
соответственно к окружностям 2 и 2', равны. Итак, точки а и а1
совпадают, а окружности 2 и 2' касаются окружности А в точках
а и а'. Следовательно, они касаются также окружностей В и С в точ-
точках b и V, с и с' (п. 227).
234. Мы отыскивали окружность 2, касающуюся окружностей А, В
и С одинаковым образом. Окружности, которые касаются окружностей
А, В и С не одинаковым образом, можно найти, заменяя в предыду-
предыдущих рассуждениях внешнюю ось подобия последовательно каждой из
внутренних осей подобия.
Так как существуют четыре оси подобия, то задача о касании
окружностей может иметь восемь решений. Однако все или часть этих
решений могут не существовать: это имеет место, если, например,
прямая 1р не пересекает окружности А. Мы видим, что если степень
точки / относительно трёх данных окружностей отрицательна и точка
/, следовательно, лежит внутри всех окружностей, то существуют все
восемь решений. Все восемь решений существуют также, если данные
окружности являются внешними относительно друг друга, как в этом
легко убедиться, исследуя решение задачи методом, указанным в п. 231.
235. Решение Жергонна применимо также, если одну или две из
данных окружностей заменить точками или прямыми, как в этом можно
убедиться, повторяя при этих новых условиях рассуждения п. 232.
Однако построение применимо только к отысканию точек касания ис-
искомых окружностей с окружностями. В частности, это построение не
приводит ни к какому результату, если заменить все данные окруж-
окружности точками или прямыми.
214 дополнрния к третьей книге
236. Метод, предложенный Жергонном, неприменим в отдельных
частных случаях. Действительно, если центры данных окружностей ле-
лежат на одной прямой, то радикальный центр и три полюса каждой оси
подобия лежат в бесконечности в направлении, перпендикулярном к
данной прямой. Можно избежать этого частного расположения, под-
подвергнув фигуру инверсии.
Обратно, три окружности вообще могут быть преобразованы одноЧ
и той же инверсией в три окружности, центры которых лежат на одной
прямой. Для этого достаточно, чтобы общая степень радикального
центра относительно данных окружностей была положительна и чтобы,
следовательно, существовала окружность, которая пересекала бы все
три окружности под прямым углом. Если принять за полюс инверсии
какую-либо точку этой окружности, то данные окружности преобра-
преобразуются в три другие окружности, которые пересекаются с одной и той
же прямой под прямым углом, т. е. центры которых лежат на этой
прямой.
Следовательно, затруднение, которое мы отметили, исчезло бы,
если бы мы сумели сделать так, чтобы в предыдущее решение вхо-
входили только свойства, не изменяющиеся при инверсии, как-то: каса-
касание двух окружностей, угол между двумя окружностями и т. д. Реше-
Решение Жергонна, действительно, можно видоизменить в этом направлении1).
УПРАЖНЕНИЯ.
258. Провести через две точки окружность, которая пересекает данную
оьружность под данным углом.
259. Построить окружность, ортогональную к двум данным окружностям
и касающуюся третьей данной окружности.
Более общая задача: построить окружность, ортогональную к двум дан-
данным окружностям и пересекающую третью данную окружность под данным
углом.
260. Через точки А и В проведены две окружности, касающиеся одной
и той же окружности С, и третья окружность, которая пересекает С под
прямым углом." Показать, что эта последняя окружность делит на две рав-
равные части угол между двумя первыми и что её центр есть одни из центров
подобия.
261. Через точку А проведены две окружности, касающиеся (одинако-
(одинаковым образом) двух данных окружностей, и'третья, которая пересекает эги
окружности ортогонально. Показать, что эта последняя окружность прохо-
проходит через вторую точку В, общую двум первым окружностям, и обладает
свойствами, указанными в предыдущем упражнении.
2Ь2. Через точку А проведены две окружности, касающиеся двух дан-
данных окружностей (как в предыдущем упражнении^. Пусть Р и Q — точки
их касания с первой данной окружностью, точки Р' и у' — их точки каса-
касания со второй.
1°. Окружности APQ и APQ' касаются друг друга; они пересекают
третью окружность, о которой говорится в предыдущем упражнении, орто-
ортогонально (доказать).
2°. Окружности APQ и BPQ (где В, как и в предыдущем упражнении,—
вторая общая точка окружностей АРР1 и AQQ') взаимно обратны относи.
1) См. Прибавление С в конце книги.
ГЛАВА VII. СВОЙСТВА ВПИСАННОГО ЧЕТЫРЁХУГОЛЬНИКА 215
тельно первой данной окружности; окружности AP'Q' и BP'Q' взаимно об-
ратны относительно второй окружности (доказать).
3°. Как изменятся эти предложения, если заменить данные окружности
прямыми линиями? Показать, что в этом случае четыре окружности APQ,
AP'Q', BPQ и BP'Q' равны между собою.
263. Построить окружность, проходящую через данную точку и касаю-
касающуюся двух данных прямых; для этого построить произвольную окружность
С, касающуюся обеих прямых, и принять во внимание, что искомая окруж-
окружность должна быть гомотетична окружности С относительно точки пересе-
пересечения Р данных прямых.
264. Построить аналогичным способом (упр. 263) окружность, касаю-
касающуюся двух прямых и данной окружности. (Прямая, которая соединяет
точку Р с точкой касания, пересекает окружность С н данную окружность
под одним и тем же углом.)
265. Решить ту же задачу при условии, что прямые заменены двумя
концентрическими окружностями.
266. Две окружности, касающиеся Друг друга, касаются каждая двух
данных окружностей. Найти 1еометрическое место точек, в которых они
касаются др'уг друга (первый способ п. 230 даёт условие, при котором об-
общие точки двух окружностей, касающихся каждая двух данных окружностей,
могут сливаться в одну).
267. Центры восьми окружностей, касающихся трёх данных окружностей,
лежат попарно ИЛ перпендикулярах, проведённых из радикального центра
к четырём осям подобия (доказать).
268. Через точку, лежащую внутри угла, провести секущую, образующую
со сторонами этого угла (не продолженными за вершину) треугольник,
имеющий наименьший периметр. (Использовать косвенный метод упр, 174
и упр. 90.)
ГЛАВА VII.
СВОЙСТВА ВПИСАННОГО ЧЕТЫРЁХУГОЛЬНИКА.
ИНВЕРСОР ПОСЕЛЬЕ.
237. Теорема Птоломея. Произведение диагоналей вписанного
в круг четырёхугольника равно сумме произведений его противо-
противоположных сторон.
Пусть ABCD (черт. 204) — вписанный в круг четырёхугольник.
Преобразуем его путём инверсии, приняв точку А за полюс. Окружность
ABCD преобразуется в прямую, которая проходит через точки В', С,
D', обратные точкам В, С, D. Если точка С—вершина данного че-
четырёхугольника, противоположная вершине Л, то точки В и D, а, сле-
следовательно, и точки Б' и D' лежат по разные стороны прямой АС;
таким образом, точка С лежит между точками В' и D', а потому (по
абсолютной величине)
B'D' = B'C'-\-CD'.
Но если k — степень инверсии, то имеем (п. 218):
ABAC
216
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
Подставляя эти значения в предыдущее равенство, умножая на
AB-AC-AD и деля на k, получим:
АС ¦ BD = AD ¦ ВС 4- AB-CD.
237а. Предыдущее свойство характерно для вписанного четырёх-
четырёхугольника. Это вытекает из следующей теоремы.
Теорема. В четырёхугольнике, который не может быть вписан
в круг, произведение диагоналей меньше суммы произведений про-
противоположных его сторон {и больше их разности).
Черт. 204.
Черт. 205.
Пусть ABCD (черт. 205) — четырёхугольник, который не может
быть вписан в круг. Если мы повторим для этого четырёхугольника
предыдущее построение, то точки Ь', С, D' не будут лежать на
одной прямой и образуют треугольник.
Но найденные в предыдущем пункте значения для B'D'. B'C, CD'
пропорциональны произведениям BD-AC, BC-AD, CD-AB; таким об-
образом, каждое из этих произведений меньше суммы двух остальных-
В CD
D' С'
В'
Черт. 206.
238. Равенство, выражаемое теоремой Птоломея, также справедливо
и доказывается таким же образом, если четыре точки А, В, С, D,
вместо того чтобы лежать на одной окружности, лежат на одной прямой
и следуют друг за другом в порядке: Л, В, С, D (черт. 206). Итак,
если четыре точки лежат на одной прямой, то произведение от-
отрезков, которые частично заходят друг на друга, равно сумме
произведений отрезков, которые расположены один вне другого и
один внутри другого.
ГЛАВА VII. СВОЙСТВА ВПИСАННОГО ЧЕТЫРЁХУГОЛЬНИКА
217
Принимая во внимание знаки, имеем, каков бы ни был порядок
четырёх точек на одной прямой, соотношение:
AB-CD-\-AC-DB-\-AD-BC = O.
Это можно доказать, повторяя рассуждения п. 237; в самом деле
соотношения, которыми мы пользовались при доказательстве, верны,
как по абсолютной величине, так и по знаку (п. 218, примечание).
239. Задача. Зная хорды двух дуг круга радиуса R, найти
хорду дуги, равной сумме этих дуг или их разности.
Эту задачу нам пришлось решать в п. 174, чтобы вычислить сто-
стороны различных правильных пятнадцатиугольников.
Черт. 207.
1°. Пусть дуги АВ и АС отложены в противоположных направле-
направлениях, так что дуга ВАС служит их суммой (черт. 207). Проводим
диаметр АА'; получим:
AA' = 2R; A'B = \ 4R2 — AB~\ A'C = \ 4R2 — AC2 .
Но вписанный четырёхугольник АВА'С даёт:
ВС ¦ АА' = АВ- А'С + АС- А'В;
в этом равенстве всё известно, кроме ВС, а потому
^ AB-V4R2 — -4С2 + AC-V^R- — АВ2
2R '
2°. Пусть дуги АВ и АСХ отложены в одном и том же направле-
направлении, так что дуга ВС) является их разностью (черт. 207). В данном
случае вписанный четырёхугольник АВС^А' даёт:
А'В-АС1 = АВ-А'С1 -\-'АА' • ВСХ,
откуда получаем:
'_А'В-АС1 —АВ-А'С1_ AC) V4R* — АВ2 — АВ \ r4R- — ACf
BLv— АА' ~~ 2R
240. Теорема. Диагонали вписанного в круг четырёхугольника
относятся между собою как суммы произведений сторон, сходя-
сходящихся в концах диагоналей.
218 дополнения к третьей книге
Пусть ABCD (черт. 208) — вписанный четырёхугольник, диагонали
которого пересекаются в точке О.
Треугольники OAD и О ВС подобны (п. 131) и дают:
OA_AD _OD
ОВ~ВС~~'Ь~С'
что можно записать так
ОА ОВ ОС OD
AB-AD АВ-ВС ' ВС-CD AD-CD'
Точно так же подобные треугольники ОАВ и ODC дают:
ОА АВ ОА OD
или
OD CD AB-AD AD-CD'
Это показывает, что четыре отношения:
ОА ОВ ОС OD
AB-AD' АВ-ВС ВС-CD' AD-CD
равны.
Составляя отношение суммы предыдущих членов первого и треть-
третьего отношений к сумме их последующих и поступая так же со вторым
и четвёртым отношениями, получаем:
AC BD
AB-AD-\- ВС-CD АВ-ВС-{-AD-CD'
Другое доказательство. Пусть АВ=а, ВС=Ь. CD = c,
DA=d—четыре стороны четырёхугольника. Если изменять всевоз-
всевозможными способами порядок сторон, то получим ещё четырёхугольники,
вписанные в тот же круг, так как сумма дуг, которым соответствуют
хорды а, Ь, с, d, каждый раз составляет полную окружность.
Ясно, что за первую сторону можно всегда принять сторону а, так
что имеем следующие перестановки:
abed, adeb,
aedb, abdc,
adbc, acbd.
Но две перестановки, стоящие в одной строке, дают тот же четырёх-
четырёхугольник: например, в четырёхугольнике ABCD (черт. 209) порядок
сторон будет а, Ь, с, d, если читать их в порядке, указанном стрел-
стрелкой, и a, d, с, Ь, если читать в обратном направлении. Таким образом,
остаются три сочетания: abed, aedb, adbc, которым соответствуют
три четырёхугольника ABCD, ABEF, ABGH. Дуги BF и АС равны
как суммы равных дуг; точно так же равны дуги ВН и АЕ, дуги BD
и АО; три четырёхугольника имеют только три различные диагонали:
AC=BF=_x, BD = AG = y, AE=BH=z; применяя теорему Птоло-
мея к четырёхугольникам ABEF и ABGH, имеем xz = ad-\- be;
ГЛАВА VII. СВОЙСТВА ВПИСАННОГО ЧЕТЫРЁХУГОЛЬНИКА
219
yz=^ab -\- cd; отсюда, разделив одно равенство на другое, получаем
искомое отношение.
240а. Задача. Вычислить диагонали х и у вписанного четырех-
четырехугольника, стороны которого равны а, Ь, с, d.
Известно произведение диагоналей:
ху = ас -\- bd
и их отношение:
л- ad-\-bc
у ab-\-cd'
Перемножая почленно эти два равенства, имеем:
(ac-\-bd)(ad-\-bc)
ab-\-cd
и аналогично получаем у-.
Черт. 209.
Задача. Зная стороны а, Ь, с, d вписанного четырёхугольника, вычислить
радиус описанного круга.
В треугольнике ABD (черт. 209, первый) радиус R описанною круга
определяется (пп. 130, 130а) по формуле
\(a +¦ ap — №!| \BD->— (a — ap\ '
Заменяя BD найденным значением, получим:
la | j,, nD. = (g + rfJ W + fcf) - 'og + bOAab + rrf) =
y ~r ' ad-{-be
_ ori [(g + rf,2 — (fc — f)"] _ ad (a + ri + b — c) (a + rf -f- с — ») _
ad + Sr ad -\-bc '
BD* — (a—df =
Таким образом,
ad -{-be
(ac -f- ftrf)(gfr + cd) (ad + be)
a — c)(b + a + c — d)'
это выражение не зависит от порядка сторон в соответствии с замеча-
замечаниями, сделанными выше (п. 240).
220
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
Обозначая через р полупериметр Bр = а -\- Ъ -f- с -\- d), можно зависать
это выражение ещё так:
_ (ас + bd) (ab + cd) (ad + be)
Н
Q
Черт. 210.
241. Инверсор Поселье. Теорема. Пусть MPAi'Q — ромб: О—
точка, для которой OP = OQ (черт. 210). Предположим, что ромб
шарнирный (п. 46а) и что (равные) длины ОР и OQ постоянны, а
точка О остается неподвижной. Если соблюдаются эти условия,
то точки М и М' описывают две взаимно обратные фигуры. }
Действительно, точки М, М', О, находящиеся на равных расстоя-
расстояниях от точек Р и Q, лежат прежде всего на одной прямой — на пер-
перпендикуляре к отрезку PQ, прохо-
проходящем через его середину. Опишем
теперь, приняв точку Р за центр,
окружность, которая пройдёт через
точки Ми М. Произведение ОМ-ОМ'
будет равно степени точки О отно-
относительно этой окружности, т. е. рав-
равно OPi — РМ'1; следовательно, оно
постоянно. Таким образом теорема
доказана.
^та теорема позволяет решить
вопрос, который представляет собой
некоторый теоретический, если не практический, интерес.
Из самого определения инструмента, служащего для проведения
окружностей — циркуля, следует, что этот прибор будет точным, если
оба острия остаются на постоянном расстоянии друг от друга, т. е.
если имеется достаточное трение в его головке.
В противоположность этому линейка будет точной только в том
случае, если её край — прямая линия: это осуществляется только при-
приближённо с большей или меньшей точностью, в зависимости от тща-
тщательности её изготовления.
Возможно ли построить прямую линию, не имея в своём распоря-
распоряжении такой линейки и опираясь лишь на свойства неизменяемых Ц
фигур? Это-то построение и позволяет осуществить следующий прибор,
принадлежащий Поселье. В самом деле, предположим, что OP, OQ,
РМ, РМ', QM, QM'—шесть твёрдых стержней2), соединённых друг
с другом с помощью шарниров, и что точка О неподвижна. При этом
точки М и М' необходимо будут взаимно обратны относительно точки О.
Заставим точку М описывать окружность, соединив её седьмым твёр-
твёрдым стержнем с неподвижной точкой 5 (черт. 210). Если эта окруж-
!) Причём неизменяемыми фигурами (в смысле, указанном в п. 3) будут
отдельные части описываемого далее инструмента. Прим. ред. перевода.
2) Мы изобразили на чертеже 210 стержни OP, OQ и т.д. прямыми ли-
линиями; однако вовсе не обязательно, чтобы они были прямолинейными.
Требуется только, чтобы, например, точки Р и Q так или иначе оставались
на постоянном расстоянии одна от другой.
ГЛАВА VII. СВОЙСТВА ВПИСАННОГО ЧЕТЫРЁХУГОЛЬНИКА
221
ность проходит через точку О (т.е. если SM^SO), то точка М
описывает прямую линию (и. 220).
241а. Инверсор Гарта. Теорема. Пусть ABCD (черт. 211) —
антипараллелограм (п. 46а, примечание 2°), образованный непарал-
непараллельными сторонами и диагоналями равнобедренной тралении; О,
М, М — точки, в которых стороны АВ, AD, ВС пересекаются с
одной и той лее прямой, параллельной основаниям трапеции. Если
этот ашпипараллело- д ~
грам — шарнирный, при-
чём общая длина а сто-
сторон АВ и CD и также
общая длина Ь сторон ВС
и AD остаются постоян-
постоянными, и точки О, М, М
неизменно связаны с эти-
этими сторонами (т. е. дли-
длины АО, AM, BM также
остаются постоянными по
величине и по знаку);
если, наконец, точка О
неподвижна, то точки М
Черт. 211.
и М описывают фигуры, взаимно обратные относительно точки О.
Мы знаем (п. 46а), что данный четырёхугольник останется антипарал-
лелограмом.
С другой стороны, прямые ОМ и ОМ', параллельные по условию
основаниям трапеции в первоначальном положении фигуры, будут всё
время оставаться им параллельными. Действительно, параллельность
этих прямых выражается соответственно следующими пропорциями:
AM
АО ВМ'
~~АВ И ~ВС
ВО
эти пропорции останутся неизменными по условию.
В частности, мы видим, что точки О, М, М' остаются на одной
прямой.
Доказав это, предположим предварительно, что не только точка О,
но и вся сторона АВ неподвижна. Точки М и М опишут окружности
соответственно с центрами А и В и радиусами AM и ВМ' = MD.
Так как отношение этих радиусов равно отношению ОА к ОВ, то
точка О будет центром подобия обеих окружностей. Поскольку радиусы
обеих окружностей, проведённые в точки М и М, не параллельны между
собой, эти две точки (п. 223) антигомологичны и, следовательно, взаимно
обратны. Таким образом, произведение ОМ-ОМ' остаётся постоянным,
если деформировать антипараллелограм, сохраняя неподвижными точки
А и В.
Так как это произведение не изменяется также при вращении всей
фигуры около точки U, то теорема доказана.
222 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
Следствие. Если соединить точку М с некоторой неподвижной
точкой S твёрдым стержнем, длина которого равна SO, то точка
М' опишет прямую линию.
Примечание. Произведение оснований АС и BD трапеции
остаётся постоянным при деформации в cavioM деле, основание BD
1 АВ
сохраняет постоянное отношение -г = -ттт к отрезку ОМ, а основание
п Аи
1 ВА >
АС — постоянное отношение — = т^г к отрезку ОМ'.
h ВО
УПРАЖНЕНИЯ.
369. Доказать теорему, обратную теореме, приведённой в упражнении 99:
если в плоскости равностороннего треугольника ABC выбрана такая точка М,
что МА = МВ-\-МС, то эта точка лежит на описанном круге. В противном
случае имеем: МА<С МВ-\- МС.
270. Если повторить доказательство пп. 237 и 237а, начав не с верши-
вершины А четырёхугольника ABCD, а с другой вершины, то получится другой
треугольник, аналогичный треугольнику B'C'D'.
1°. Доказать, что все такие треугольники подобны.
2°. Вычислить углы какого-либо одного из этих треугольников, если
известны углы, которые образуют между собою стороны и диагонали дан-
данного четырёхугольника.
3°. Доказать, что можно получить треугольники, подобные предыдущим,
опуская из одной из вершин А, В, С, D перпендикуляры на стороны тре-
треугольника, образованною тремя другими, или иначе, соединяя точки В и D
между собою и с третьей вершиной Е треуюльника AED, подобного тре-
треугольнику ABC и имеющего с ним одинаковое направление вращения,
в котором стороной, соответствующей стороне АС, будет отрезок AD.
4°. Доказать, что форма предыдущих треугольников не изменяется, за
исключением направления вращения, если подвергнуть четыре точки А, В,
С, D одной и той же произвольной инверсии, другими словами, доказать,
что если повторить для преобразованных точек то же построение, как и
для точек А, В, С, D, то получились бы треугольники, подобные перво-
первоначальным.
5°. Обратно, если два четырёхугольника ABCD и A|fi,CiA таковы, что
треугольники, образованные в каждом из них с помощью построений, указан-
указанных выше, между собою подобны, то существует (за исключением того
случая, когда четырёхугольники ABCD и /Ij/^QDj подобны) инверсия, кото-
которая преобразует точки А, В, С, D в другие четыре точки, образующие
четырёхугольник, равный четырёхугольнику Аф^С^п^ {доказать). Определить
эту инверсию.
270а. Найти инверсию, которая преобразует три данные точки в другие
три точки, которые образуют треугольник, равный данному треугольнику.
271. Прибор Поселье также достигал бы своей цели, если бы шарнир-
шарнирный четырёхугольник MPM'Q не был ромбом и имел бы попарно равные
между собою стороны МР = М'Р и MQ = M'Q и если, кроме того,
Oin^CQi — MP^ — MQ1 (доказать).
271а. В инверсоре Гарта вычислить степень получаемой инверсии, зная
стороны а и Ъ антипараллелограма, а также отношения h и Л' ^= 1—Л. Вы-
Вычислить произведение оснований трапеции, зная а и Ъ.
ЗАДАЧИ К ДОПОЛНЕНИЯМ К ТРЕТЬЕЙ КНИ1 Е 223
ЗАДАЧИ К ДОПОЛНЕНИЯМ К ТРЕТЬЕЙ КНИГЕ.
272. Радикальная ось и центр подобия делят отрезок, соединяющий лпе
какие-либо антиюмологические точки, в постоянном сложном отношении
(доказать).
273. Сложное отношение четырёх точек окружности равно сложному
отношению точек, им обратных, лежащих на окружности (или прямей),
обратной первой (показать).
274. Сложное отношение четырёх точек окружности можно получить,
разделив яруг на друга произведения противоположных сторон четырёхуголь-
четырёхугольника, образованного этими точками, или одно из этих произведений на
произведение диагоналей (доказать).
275. Найти иннерсии, преобразующие две данные окружности в две
равные окружности.
Преобразовать три данные окружности в три равные окружности с по-
помощью одной и той же инверсии.
276. Лапы три окружности. Если провести для данных окружностей,
взятых попарно, три окружности Г (п. 228), т. е. три окружности, инверсии
относительно которых преобразуют данные окружности, взятые попарно,
одну в другую, выбрав эти три окружности так, чтобы их центры лежали
на одной прямой, то эти три окружности имеют одну и ту же радикальную
ось (доказать).
277. Найти геометрическое место полюсов инверсий, с помощью кото-
которых можно преобразовать две данные окружности в две другие так, что
первая разделит вторую на две равные части, или обшёе так, что первая
из преобразованных окружностей отсекает на второй окружности дугу,
соответствующую центральному углу данной величины.
278. Показать, что отрезки, образованные двумя окружностями на не-
некоторой прямой, видны из одной из их предельных точек (упр. 152) под
углами, имеющими одну и ту же биссектрису (или взаимно перпендикуляр-
перпендикулярные биссектрисы). Рассмотреть случай, когда прямая касается одной из
окружностей.
279. Доказать теорему Паскаля (п. 196), построив три окружности, ко-
которые, взятые попарно, имеют своими центрами подобия точки пересечения
противоположных сторон шестиугольника (каждая из этих окружностей
проходит через две противолежащие вершины).
280. Построить окружности, касающиеся трёх данных окружностей,
используя упражнение 253.
281. Вокруг точки, лежащей в плоскости круга, вращается прямой угол;
в точках, в которых стороны этого угла пересекают окружность, проведены
к окружности касательные. Найти геометрическое место вершин образован-
образованного, таким образом, четырёхугольника (линия, обратная геометрическому
месту, полученному в задаче 201).
282. Четырёхугольник ABCD описан около окружности о и вписан в
окружность О. Пусть a, b, c,d — точки касания его четырёх сторон с окруж-
окружностью о. Доказать, что:
1°. Точка Р, в которой пересекаются диагонали четырёхугольника ABCD
и в то же время (упр. 239) четырёхугольника abed, является предельной
точкой окружностей о и О (упр. 241, 2°).
2°. Диагонали четырёхугольника abed служат биссектрисами углов, обра-
образованных диагоналями четырёхугольника ABCD (задача 278).
3°. Окружность О совпадает с окружностью, которую мы получили бы
в предыдущей задаче (задача 281), если бы мы исходили из окружности о
и точки Р.
4°. Заключить отсюда, что если даны две окружности, то в общем слу-
случае нельзя вписать в одну из них четырёхугольник, описанный около дру-
другой. Чтобы эта задача была возможна, необходимо, чтобы имело место
определённое соотношение между расстояниями центров данных окруж-
224 ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ
иостей и их радиусами. Но если это соотношение выполнено, то сущест-
существует бесконечное множество четырёхугольников, удовлетворяющих усло-
условию задачи.
283. Если треугольник тупоугольный, то существует окружность (и
только одна), относительно которой каждая вершина этого треугольника
является полюсом противолежащей стороны; центром этой окружности
служит точка пересечения высот треугольника (доказать). Эта окружность
и треугольник называются сопряжёнными друг с другом.
284. Чтобы существовал треугольник, вписанный в данную окружность
и сопряжённый с другой данной окружностью, необходимо, чтобы квадрат
радиуса второй окружности был равен половине степени её центра отно-
относительно первой окружности. Если это условие выполнено для двух
пересекающихся окружностей, то существует не один, а бесконечное мно-
множество треугольников, обладающих одновременно обоими требуемыми
свойствами (доказать, использовав упр. 70).
285. Даны три окружности,которые попарно пересекаются; рассмотреть
криволинейный треугольник, сторонами которого служат соответственно три
дуги этих трёх окружностей, а вершинами — точки пересечения этих окруж-
окружностей, взятых попарно, причём этот треугольник выбран так, что на его
контуре не имеется других точек пересечения. Доказать, что сумма внутрен-
внутренних углов этого треугольника меньше или больше двух прямых Brf), в за-
зависимости от того, существует или не существует окружность, пересекаю-
пересекающая данные три окружности под прямым углом 1).
286. Чтобы какой-либо четырёхугольник был вписанным, необходимо и
достаточно, чтобы точки В', С, D' (п. 237), обратные трём вершинам В, С,
D относительно четвёртой вершины А, лежали на одной прямой; из этого
последнего условия можно вывести все свойства вписанного четырёхуголь-
четырёхугольника. Вывести, в частности, теорему об отношении диа1 оналей (примене-
(применение теоремы Стюарта, п. 127).
1) См. Прибавление А, п. 290.
КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ.
ГЛА В А I.
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ.
242. Два многоугольника называются смежными, если они име-
имеют одну или несколько общчх сторон (черт. 212) или частей сто-
сторон (черт. 213), но не имеют на одной общей внутренней точки.
Если в двух данных смежных многоугольниках Р, Р' не рассмат-
рассматривать их общих сторон, то образуется1) третий многоугольник Р",
Черт. 212.
Черт. 213.
который называется суммой первых двух. Внутренняя область этого
многоугольника содержит все точки, расположенные внутри того или
другого из дв>х первоначальных многоугольников, и только эти
точки.
243. Определить площадь плоского многоугольника—значит по-
поставить в соответствие каждому плоскому многоугольнику величину
(её-то и называют поверхностью или площадью многоугольника),
обладающую следующими свойствами:
1. Два. равных многоугольника имеют одну и ту же площадь
независимо от занимаемого ими положения в пространстве.
1) Мы отказываемся в четвёртой книге от ограничения, установленного
в п. 21 (книга первая) относительно смысла слова „многоугольник", так
что часть плоскости, заштрихованная на чертеже 21,будет рассматриваться
в этой книге как многоугольник. Впрочем, такой многоугольник можно
получить как сумму двух смежных обыкновенных многоугольников, как
это показано на чертеже 213.
Однако в этой главе рассматриваются лишь многоугольники в собст-
собственном смысле (п. 21).
15 Элементарная геометрия
226 КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
11. Многоугольник Р", представляющий собою сумму двух смеж-
смежных многоугольников Р и Р', имеет своею площадью сумму пло-
площадей многоугольников Р и Р'.
Мы допускаем, что возможно установить подобное соответствие').
244. Площадь может быть определена бесчисленным множеством
различных способов, потому что, если каждому плоскому многоуголь-
многоугольнику поставлена в соответствие величина, обладающая свойствами I и
II, то величина, ей пропорциональная, также будет обладать зтими
свойствами.
Для измерения площадей, которым мы будем сейчас заниматься,
сначала нужно выбрать некоторый многоугольник, площадь которого
будет принята за единицу площади; мерой какой-либо площади бу-
будет отношение этой площади к единице площади.
Мы условимся здесь и во всам дальнейшем считать за единицу
площади площадь квадрата, имеющего своей стороной выбранную
единицу длины. В дальнейших теоремах мы всегда будем предпола-
предполагать это условие, не считая нужным включать его в формулировку
каждой теоремы.
245. О двух многоугольниках, имеющих одну и ту же площадь,
говорят, что они равновелики. Следовательно, два равных много-
многоугольника равновелики. Конечно, обратное утверждение будет неверно;
два многоугольника не будут обязательно равными, если они равнове-
равновелики. Например, мы покажем, что можно построить квадрат, равнове-
равновеликий любому заданному многоугольнику.
246. Основанием прямоугольника называется одна из его сторон.
Длина стороны, 'Перпендикулярной к первой, называется при этом вы-
высотой прямоугольника. Основание и высота прямоугольника называются
его измерениями.
Основанием параллелограма. называют какую-либо его'сторону;
вчеотой будет при этом расстояние от этой стороны до противопо-
противоположной стороны (измеренное, разумеется-, по общему перпендикуляру
к обеим сторонам).
Основаниями трапеции будут её параллельные стороны, а высотой
трапеции — расстояние между параллельными сторонами.
Наконец, основанием треугольника называют какую-либо из его
сторон; высотой — перпендикуляр, опущенный на эту Сторону (или на
, её продолжение) из противолежащей вершины.
247. Теорема. Площади двух прямоугольников, имеющих рав-
равные основания, относятся между собою как их высоты.
В самом деле:
1°. Два прямоугольника, имеющие равные основания и равные вы-
высоты, равны между собою и, следовательно, равновелики на основании
свойства I.
!) Это допущение в действительности излишне, так как возможность уста-
установить такое соответствие можно доказать (см. Прибавление D в конце
книги).
глава i. измерение площадей
227
2°. Если три прямоугольника ABDC, A'B'D'C, A"B"D"C" (черт. 214)
имеют равные основания, а высота третьего составляет сумму высот
первых двух, то площадь третьего будет суммой площадей первых
двух (свойство И). Действительно, третий прямоугольник можно рас-
рассматривать как сумму двух прямоугольников A"B"FE и CDTE, рав-
равных соответственно двум первым.
Поэтому можно доказать, так же как и в п. 113 (книга третья)
или в п. 17 (книга первая), что значение отношения двух площадей,
вычисленное с точностью до — , будет равно значению отношения днух
1
высот, вычисленному с точностью до — ; это и доказывает теорему.
Черт. 214.
Следствие. Так как каждая сторона прямоугольника может быть
принята либо за основание, либо за высоту, мы могли бы об основа-
основаниях высказать то, что мы говорили о высотах, и обратно; одним сло-
словим, площади двух прямоугольников, имеющих по равной стороне, от-
относятся между собою, как их неравные стороны.
Теорема. Отношение площадей двух прямоугольников равно
произведению отношений их соответствующих измерений.
Действительно, мы только что видели, что площадь всякого пря-
прямоугольника пропорциональна его основанию или его высоте, если
изменяется только высота или только основание. Отсюда уже следует,
что площадь прямоугольника пропорциональна их произведению.
Впрочем, здесь можно повторить то рассуждение, которое приме-
применяется для этого случая в арифметике. Действительно, пусть А и А' —
площади двух данных прямоугольников; а и Ъ — измерения одного из
них, а' и Ь' — измерения другого. Рассмотрим прямоугольник, у кото-
которого измерениями будут а' и Ь. Если А" будет площадью этого пря-
прямоугольника, то будем иметь:
А"
Ъ
В этих равенствах мы можем полагать, что -4, А', А" обозначают
не площади, как таковые, а числа, которые измеряют эти площади
в одних и тех же единицах, например в выбранных нами единицах пло-
15*
228 КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
щади (квадрат, сторона которого равна единице длины). При этих
условиях, если мы перемножим почленно предыдущие равенства, то
А А" „ . АА" А
произведение —- -—; можно оудет записать в виде „ , = —- . Это
А А Л л л
А „ а Ь
отношение — действительно равно произведению отношении — и —,.
/л ^ О, Р
Теорема. Площадь прямоугольнику равна произведению двух
его измерений.
В самом деле, эта теорема представляет собою не что иное, как
предыдущую теорему, применённую к данному прямоугольнику и квад-
квадрату, имеющему стороной единицу длины. Площадь А' этого послед-
последнего является единицей площади, и каждое его измерение а' и Ь'
А
равно единице длины; таким ооразом, отношение —, есть не что иное>
А
a b
как мера площади А, и отношения , , — суть меры длин а, п.
Примечания: 1°. Эта формулировка имеет смысл только бла-
благодаря соглашению, установленному в п. 18 (книга первая) и повто-
о д ренному в п. 106 (книга третья). Смысл сказан-
сказанного таков: число, которое измеряет площадь
прямоугольника, равно произведению чисел,
измеряющих соответственно его основание
и его высоту.
2°. Эта формулировка верна только благо-
благодаря соглашению, установленному в п. 244, ко-
которое в данном случае весьма существенно.
Очевидно, a priori, что доказанное равенство не будет иметь места,
если единица длины и единица площади будут выбраны как-нибудь,
независимо друг от друга.
Из этого видно, что единица длины может быть выбрана произ-
произвольно; но если этот выбор сделан, то тем самым из него необходимо
вытекает выбор единицы площади.
Поэтому говорят, что единица площади — единица производная.
248. Теорема. Площадь параллелограма измеряется произведе-
произведением его основания на высоту.
Пусть имеем параллелограм ABDC (черт. 215). Проведём перпен-
перпендикуляры к стороне АВ через точки Л и В до пересечения н точках
с и d со стороной CD так, чтобы образовался прямоугольник ABdc.
Этот прямоугольник равновелик параллелограму, потому что, прибав-
прибавляя к этим дзум многоугольникам соответственно два прямоугольных
треугольника BdD, AcC, которые равны как имеющие по равному
острому углу и по одной равной стороне, мы получаем одну и ту же
сумму (п. 242) — трапецию AcDB. Теорема доказана, так как пря-
прямоугольник имеет своими измерениями основание параллелограма и его
высоту.
ГЛАВА I. ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
229
249. Теорема. Площадь треугольника измеряется половиной
произведения основания на высоту.
Пусть дан треугольник ABC (черт. 216). Через точку А проведём
прямую AD, параллельную ВС, и через точку С — прямую CD, па-
параллельную АВ. Таким образом, получается параллелограм ABCD,
имеющий то же основание и ту же высоту, что и данный треуголь-
треугольник. Но этот параллелограм делится диагональю АС (п. 46) на два
равных треугольника ABC и CD А. Поэтому rpej гольник ABC состав-
составляет половину параллелогра.ма.
250, Следствие. Геометрическое место вершин С треугольников,
имеющих одно и то же основание АВ (черт. 217) и одну и туже
площадь, составляют две прямые, параллельные АВ.
Черт. 216.
Черт. 217.
Действительно, вершины этих треугольников будут расположены
на постоянном расстоянии от прямой АВ.
251. Задача. Вычислить площадь треугольника, если даны три
его стороны.
Мы видели (п. 130), что если a, ft, с — стороны треугольника и
р — его полупериметр, то нысота АН, опущенная на сторону а, бу-
будет равна
АН =
-V
4р(р-а)(р-Ь)(р-с) 2
— a)(p — b)(p — с).
Следовательно, площадь треугольника 5 будет ранна
S = п-^1 = Vp(p-a) (p-b)[p-c) =
-j- 2c2c- -f- 2aW — а* — ft* — с*.
Примечание. Произведение трех сторон треугольника равно
учетверённому произведению площади на радиус описанного круга.
Если в треугольнике ABC АИ—высота, опу[ценная из вершины Л,
и R — радиус описанной окружности, то имеем (п. 13Ua):
AB-AC=2R-AH;
230
КНИГА ЧЕТВЕРТАЯ. ПЛОЩАДИ
умножая обе части этого равенства на ВС, получим
AB-AC-BC=2R.AH-BC=^R-S.
252. Площадь какого-либо многоугольника находят, разлагая его
на треугольники, площади которых складывают между собою. Следую-
Следующие две теоремы являются только приложением этого способа.
Теорема. Площадь трапеции измеряется произведением полу-
полусуммы её оснований на высоту.
Пусть имеем трапецию ABDC (черт. 218). Диагональю AD мы де-
делим эту трапецию на два треугольника ABD и ACD, за основания ко-
которых мы принимаем стороны АВ и CD. Высоты DD' и .4.4' треуголь-
треугольников будут равны между собою и равны высоте трапеции h.
Поэтому будем иметь:
~™ ^fi , CD h(AB4-CD)
площадь ABDC =h-~-\-h.— = -^ ^ '- .
252а. Следствие. Площадь трапеции измеряется произведением
её высоты на отрезок, соединяющий середины её непараллельных
сторон.
Действительно, середины Е, F сторон
АС и BD (черт. 218) и середина / диаго-
диагонали AD лежат на одной и той же пря-
прямой, параллельной основаниям; следователь-
следовательно, отрезок EF равен полусумме этих осно-
оснований, потому что две его части EI и IF
Черт. 218. CD AB
соответственно равны -— и —?— .
253. Теорема. Площадь правильного многоугольника изме-
измеряется произведением его периметра на половину апофемы.
В самом деле, правильный многоугольник ABCDEF (черт. 219)
разбивается радиусами, проведёнными в его вершины, на треугольни-
треугольники ОАВ, ОВС, ..., равные между собою и имеющие, следовательно,
одну и ту же высоту, равную апофеме ОН многоугольника; поэтому
имеем:
АВ
площадь ОАВ = ОН—— ,
FIC
площадь О ВС = ОН- — ,
FA
площадь OFA = OH'•——- .
Складывая, получим:
.„,.„..,, OH(AB-\-BC-\-...-\-FA)
площадь ARfithh ¦— : ! ! _J l
ГЛАВА I. ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
231
Примечание. Если число сторон многоугольника четно, то
его площадь равна половине радиуса описанной окружности, умно-
умноженного на периметр многоугольника, полученного от соединения
вершин данного через одну.
Действительно, площадь треугольника ОАВ (черт. 219) равна поло-
половине произведения ОВ на опущенную из точки А высоту А1, равную
половине отрезка АС.
Черт. 219.
Черт. 220.
253а. Многоугольным, сектором (черт. 220) называется многоуголь-
многоугольник, ограниченный ломаной линией, вписанной в окружность, и радиу-
радиусами этой окружности, проведенными в концы ломаной.
Многоугольный сектор называется правильным, если ломаная ли-
линия, которая служит его основанием, будет правильной.
Теорема. Площадь правильного многоугольного сектора изме-
измеряется произведением периметра ломаной линии, которая служит
его основанием, на половину апофемы.
Доказательство этой теоремы точно та-
такое же, как и предыдущей (п. 253).
254. Теорема. Площадь выпуклого
многоугольника, описанного около круга
(и заключающего этот круг внутри себя)
(черт. 221) равна произведению его пери-
периметра на половину радиуса этого круга.
Действительно, многоугольник можно раз-
разложить на треугольники, соединяя вершины
многоугольника с центром круга. Эти тре-
треугольники имеют своими основаниями стороны многоугольника, вы-
высоты их все одинаковы — радиусы круга.
255. Задача. Найти площадь вписанного четырёхугольника, зная,
четыре его стороны.
Пусть ABCD — вписанный четырёхугольник, у которого АВ = а,
BC=b, CD—с, DA = d Если R будет радиусом описанного кр>га, ю
(п. 251, примечание)
а-Ъ-АС— 4А> X площадь ABC,
c-d-AC=4RX площадь ACD.
Черт. 221.
232 КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
Сумма площадей ABC и ACD равна искомой плошали S. Складывая,
получим (в силу п. 240а):
4RS —. AC-(ab + rd) = 1 (ас -f fcrf) (ad + be) (ab -f cd)
и, заменяя /? ею значением (п. 240а), найдём:
S - У(р —а)(р — Ь) [р — с) (р — d)-
Примечание. Результат не зависит от последорателыюсти сторон,
что было ясно и a priori, потому что четырёхугольники ABCD, ABEF,
ABGH (и. 240) равновелики, как составленные из попарно равных треуголь-
треугольников.
УПРАЖНЕНИЯ.
287. Найти площадь равностороннего треугольника со стороною а.
288. Найти длину стороны равностороннего треугольника, площадь
которого равна 1 ж2.
289. Каждая вершина данного квадрата соединяется с серединой сто-
стороны, предшествующей противоположной вершине при обходе периметра
квадрата в определённом направлении. Полученные таким образом прямые
образуют стороны нового квадрата, составляющего пятую часть данного
(доказать).
290. Через точку, взятую на диаюнали АС параллелограма ABCD
проведены прямые, параллельные его сторонам. Данный параллелограм
делится, таким образом, на четыре параллелограма, из которых два имеют
своими диагоналями части диагонали АС. Доказато, что два других парал-
параллелограма равновелики.
291. Какой из треугольников, имеющих равные основания и равные
углы при вершине, будет иметь наибольшую площадь?
292. Во всякой трапеции два треугольника, образованные каждой из
двух непараллельных сторон и отрезками двух диапл.алей, равновелики
(доказать). Сформулировать и доказать обратную теорему.
293. Через середину каждой диагонали четырёхугольника проведена
прямая, параллельная другой диагонали; точка пересечения этих прямых
соединена с серединами сторон четырёхугольника. Показать, что четырёх-
четырёхугольник разбирается таким образом на четыре равновеликие части.
294. Через каждую вершину четырёхугольника проведены прямые,
параллельные диагонали, не проходящей через эту вершину. Показать,
что полученный таким Образом параллелограм вдвое больше четырёх-
четырёхугольника. . •
Если диагонали двух четырёхугольников соответственно равны и пе-
пересекаются под равными углами, то четырёхугольники равновелики (до-
(доказать).
295. Внутри треугольника найти такую точку, которая, будучи соеди-
лена с тремя его вершинами, разделила бы треугольник на три равнове-
никие части или, общее, на три части, площади которых пропорциональны
трём данным отрезкам или трём данным числам.
295а. Исходя из рассмотрения площадей (см. предыдущее упражнение),
доказать, что произведение отношений, в которых прямые, соединяющие
какую-либо точку плоскости с тремя вершинами треугольника, делят его
противоположны г стороны, равно единице (теорема, доказанная в п. 197).
296. Некоторая точка О плоскости соединена с вершинами параллело-
параллелограма ABCD (AC, У3?> —его диагонали;; доказать, что:
1°. Если "точка О находится внутри нараллелеррама, то сумма площа-
площадей противолежащих треугольников ОАВ и OCD равна сумме площадей
треугольников ОВС и ODA.
2°. Где бы ни лежала точка О, треугольник О АС равновелик сумме
или разности треугольников ОАВ и OAD.
ГЛАВА II. СРАВНЕНИЕ ПЛОЩАДЕЙ
233
297. Плошаль трапеции измеряется произведением одной из непарал-
непараллельных её сторон на перпендикуляр, опушенный из середины другой из
непараллельных сторон на первую. Доказать это предложение двумя спо-
способами: 1) преобразуя в другую <{орму выражение, данное в п. 252а;
2) показав непосредственно, что трапеция равновелика параллелограму,
имеющему указанное выше основание и высоту.
Если соединить середину одной из непараллельных сторон трапеции
с концами противоположной стороны, то получится треугольник, равнове-
равновеликий половине трапеции (доказать).
298. Сумма расстояний какой-либо точки, взятой внутри правильного
многоугольника, от всех его сторон есть величина постоянная (доказать).
299. Площадь треугольника равна произведению полуиериметра на ра-
радиус вписанного круга (доказать).
Площадь треугольника равна произведению радиуса вневписанного
круга на разность между полупериметром и соответствующей стороной
(или на полуразность между суммой двух других сторон и этой стороной).
300. Обратная величина радиуса круга, вписанного в треугольник,
равняется сумме обратных величин радиусов вневписанных кругов (до-
(доказать).
301. Если х, у, z обозначают соответственно расстояния точки, лежа-
лежащей внутри треугольника от трёх его сторон, и h, k, I — соответствую-
х . у , г , ,
щие высоты треугольника, то имеет место равенство: ——\-~--^- -—=z \ (до-
(доказать).
Как изменится это предложение, если точка будет лежать вне
треугольника?
ГЛАВА II.
СРАВНЕНИЕ ПЛОЩАДЕЙ.
256. Теорема. Если угол одного треугольника равен углу дру-
другого (или является углом ему пополнительным), то площади
обоих треугольников относятся между собой, как произведения
сторон, заключающих эти углы.
С
Й Н ВН' В'
Черт, 222.
В А НИ1 В'
Черт. 223.
Мы мо».ем совместить друг с другом равные углы или сделать
прилежащими друг к другу пополнительные углы; тогда в треуголь-
треугольниках ABC, АН С совпадут по направлению стороны АС и АС; сто-
стороны АВ и АВ1 либо также совпадут по направлению (черт. 222), либо
будут служить продолжением одна другой (черг. 223). Отношение
площадей двух треугол! ннков равно отношению оснований АВ и АВ',
234
КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
умноженному на отношение высот СИ и СИ', а это последнее, оче-
АС
видно, равно отношению
АС
257. Теорема. Отношение площадей двух подобных многоуголь-
многоугольЧерт. 224.
равно квадрату коэсри-
циента подобия.
Мы будем различать два
случая:
1°. Если речь идёт о дАух
подобных треугольниках ABC,
А'В'С, то достаточно заметит!.,
что эти два треугольника имеют
равные углы / А = / А'. Сле-
довательно, отношение их пло-
площадей равно произведению от-
И
АВ АС
ношений-гттг, и ——-, , т. е. квадрату одного из них, потому что эти
отношения равны между собой.
2°. Пусть даны теперь два каких-нибудь подобных многоугольника
ABCDEh A'B'C'D'E' (черт.
224), коэфиииент подобия ко-
которых пусть будет k.
Эти многоугольники мож-
можно разложить на подобные
и одинаковым образом рас-
расположенные треугольники
ABC, ACD, ADE; А'В'С,
A'C'D', A'D'E', и мы будем
иметь:
пл. ABC _ пл. ACD __
пл. А'В'С' ~пл. A'C'D' ~~
пл. АРЕ
~пл. А1 НЕ' '
Складывая предыдущие и
последующие члены, получим:
пл. ABCDE __
пл. А'ИСПЕ'~
258. Теорема. Квад-
Квадрат, построенный на гипо-
гипотенузе прямоугольного тре-
треугольника, равновелик сумме квадратов, построенных на катетах.
Пусть дан прямоугольный треугольник ABC (черт. 225). На ка-
катетах АВ, АС и на гипотенузе ВС построим квадраты ABEF,
ACGH, BCJI, расположенные вне треугольника. Из вершины А
Черт. 225.
I
ГЛАВА II. СРАВНЕНИЕ ПЛОЩАДЕЙ 235
опустим на гипотенузу ВС перпендикуляр AD, продолжение которого
пусть пересечёт IJ в точке К. Я утверждаю, что прямоугольник BDKI
равновелик квадрату ABEF.
Чтобы это доказать, проведём А/ и СЕ. Треугольник ABI и пря
моугольник BDKI имеют общее основание В/ и общую высоту AL =
— BD; следовательно, площадь треугольника равна половине птощади
прямоугольника. Точно так же треугольник ЕВС имеет то же основа-
основание BE и ту же высоту СМ = АВ, что и квадрат ABEF; следова
тельно, площадь этого треугольника равна половине площади квад-
квадрата.
Но два треугольника ABI и ЕВС фавны, так как имеют равные
углы при вершине В (к углу В треугольника ABC прибавляется пря-
прямой угол), заключённые между равными сторонами (АВ^=ВЕ и В/=
= ?С). Поэтому прямоугольник BDKI равновелик квадрату ABEF.
Можно точно так же доказать, что прямоугольник CDKJ равнове-
равновелик квадрату ACGH. Квадрат ВСЛ, представляющий сумму двух пря-
прямоугольников, тем самым равновелик сумме квадратов ABEF и ACGH.
Примечание. Эта теорема по существу сводится к той, кото-
которую мы доказали в п. 124, потому что квадраты ABEF, ACGH,
ВСЛ измеряются соответственно квадратами чисел, измеряющих длины
их сторон. Даже и доказательство идёт по тому же пути, потому что
равновеликость прямоугольника BDKI и квадрата ABEF выражает
то же самое, что и равенство Л/32 = ВС- BD, которым мы пользова-
пользовались в указанном п. 124.
УПРАЖНЕНИЯ.
302. Каждая сторона треугольника разделена в данном отношении.
Требуется найти отношение площади треугольника, вершины которого
лежат в точках деления, к площади данного треугольника. Рассмотреть
случай, когда одна или более сторон разделены внешним образом. Вывести
отсюда теоремы пп. 192—193.
303 Разделить треугольник прямыми, параллельными основанию1, на
данное число равновеликих частей.
304. Разделить трапецию прямыми, параллельными основанию, на дан-
данное число равновеликих частей.
305. Радиусы окружности, проведённые в вершины вписанного в неё
равностороннего треугольника, продолжены до пересечения с окруж-
окружностью, которая проходит через вершины квадрата, описанного около дан-
данной окружности Полученные три точки пересечения определяют треуголь-
треугольник, равновеликий вписанному в эту окружность правильному шестиуголь-
шестиугольнику (доказать).
306. Через каждую вершину четырёхугольника проведена прямая, па-
параллельная заданному направлению, до её пересечения с диагональю, ко-
которая не проходит через эту вершину; доказать, что:
1) четырёхугольник, вершины которого находятся в этих точках пере-
пересечения, равновелик данному;
2) он будет трапецией или параллелограмом, если первый будет трапе-
трапецией или параллелограмом;
3) в общем случае отношения, в которых противолежащие стороны
делят друг друга в точке пересечения, будут одни и те же для обоих че-
четырёхугольников.
236
КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
307. На плоскости даны несколько многоугольников; через все их вер-
вершины проведены прямые, параллельные данному направлению, и на этих
прямых отложены отрезки, пропорциональные расстояниям соответствую-
соответствующих вершин от заданной прямой (так что все эти отрезки направлены от
вершин либо в сторону заданной прямой, либо в противоположную сто-
сторону).
Доказать, что площади многоугольников, вершинами которых служат
концы построенных таким образом отрезков, пропорциональны площадям
данных многоугольников* (упр. 297). —
В каком случае новые многоугольники будут равновелики первым?
308. Показать, что предыдущее упражнение содержит как частный
случай упражнение 306.
Другие доказательства теоремы о квадрате гипотенузы.
309. В задаче 44 (киша первая) доказать, что третий квадрат HBK.F
равновелик сумме двух данных квадратов. Вывести отсюда теорему и. 258.
310. Доказать теорему о квадрате гипотенузы с помощью теоремы
п. 257, замечая, что прямоугольный треугольник представляет сумму двух
треугольников, на которые он делится своею высотой.
311. На сторонах АВ и АС некоторого треугольника ABC, как на соот-
соответствующих основаниях, построены два каких-либо параллелограма ABEF,
ACGH, расположенные вне треугольника, а в остальном совершенно про-
произвольные; стороны EF u ОН продолжены до взаимного пересечения в
точке М. Показать, что нараллелограм, построенный на стороне ВС и
имеющий другую сторону, равную и параллельную AM, равновелик сум-
сумме первых двух.
Показать, что эта теорема включает в себя как частный случай теорему
о квадрате гипотенузы.
ГЛАВА III.
ПЛОЩАДЬ КРУГА.
259. Площадью круга называется предел, к которому стремится
площадь вписанного или описанного многоугольника, если длины всех
его сторон стремятся к нулю.
Чтобы доказать, что такой предел существует и не зависит от за-
закона, но которому длины сторон стремятся к нулю, надо провести
рассуждения, аналогичные тем, которые мы проводили, определяя
длину окружности.
Сначала рассматривают правильные вписанные мнигоугольники, число
сторон которых неограниченно удваивается,- и соответствующие опи-
описанные многоугольники (черт. 177). При этих условиях:
Площади вписанных многоугольников будут возрастать, потому
что каждый из них заключает предыдущий внутри себя. При этом
каждая из этих площадей будет меньше площади какого-либо опи-
описанного многоугольника. Поэтому эти площади етремятс я к пределу.
Точно так же площади описанных многоугольников будут убы-
убывать, потому что каждый из них находится внутри предыдущего. При
этом каждая из этих площадей будет больше площади какого-либо
вписанного многоугольника.
ГЛАВА III. ПЛОЩАДЬ КРУГА 237
Поэтому площади описанных многоугольников также стремятся
к пределу.
Эти два предела равны между собою, пото»чу что отношение
площадей вписанного многоугольника и соответствующего описанного
равно квадрату коэфициента подобия, который стремится к единице
(п. 176).
260. Пусть 5 — значение общего предела, которое получается,
например, -если исходить из квадрата и рассмаг'ривать последовательно
правильные многоугольники с 4, 8, 16, 32, ..., 2я, ... сторонами.
Возьмём теперь какие-нибудь вписанные многоугольники а'Ь'с'.. .
(черт. 178) и соответствующие описанные многоугольники А'В'С ...,
налагая единственное условие, чтобы число сторон этих многоугольни-
многоугольников увеличивалось безгранично так, чтобы длины всех сторон стреми-
стремились к нулю.
Площадь вписанного многоугольника а'Ь'с'.. . меньше, чем S, по-
потому что 5 является пределом для площадей описанных многоуголь-
многоугольников, каждая из которых больше, чем площадь многоугольника а'Ь'с'. ..
Величина 5, будучи заключена между площадями многоугольников,
вписанного и описанного, отличается от каждого из них на величину,
меньшую разности между площадями обоих многоугольников.
Но эта разность стремится к нулю. В самом деле, она состоит из
суммы площадей треугольников a'b'A', b'c'В',..."; следовательно, она
измеряется величиной
1 {a'b'.A'H+b'c'.B'K-L-...Х: -I {a'b' + b'c1 + ...)•/,
где А'Н, В"К, ... — высоты треугольников a'b'A', З'с'В', ... и /
представляет наибольшую из этих высот.
Множитель a'b' -\- b'c' ~\~. .. стремится, как мы знаем, к длине
окружности. Что касается высот АИ, ВК, . .. , то они стремятся
к нулю. Действительно, например, длины отрезков ОН и О А' стремятся
к радиусу круга, и, следовательно, их разность А'Н имеет своим пре-
пределом нуль.
Поэтому площади вписанных и описанных многоугольников стре-
стремятся к одному и тому же пределу S, который есть площадь
круга ''.
1) Это рассуждение распространяется на любые выпуклые кривые при
условии, что высота, опушенная из вершины с треугольника аЪс (сноска 1
к п. 179), стремится к нулю вместе с расстоянием аЪ независимо от по-
положения дуги аЪ на данной кривой. Это условие выполняется одновременно
с аналогичным условием, указанным в сноске п. 179. При этом разность
между площадью вписанного многоугольника и площадью соответствую-
соответствующего описанного необходимо стремится к нулю вместе с длинами сторон
этих многоугольников. Как было отмечено в сноске, о которой идёт речь,
цоказательство разделяется на две части, соответствующие содержанию
пп. 259 и 260. Что касается площадей невыпуклых фигур, то их вычисляют
как сумму или разность площадей выпуклых фигур.
КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
261. Теорема. Площадь круга измеряется длиной окружности,
умноженной на половину радиуса.
Действительно, площадь правильного многоугольника измеряется
произведением его периметра на половину апофемы. Когда число сто-
сторон его неограниченно увеличивается, периметр стремится к длине
окружности, апофема — к длине радиуса.
Примечание. Можно получить тот же результат, применяя тео-
теорему п. 254 об описанном многоугольнике. В самом деле, периметр
такого многоугольника стремится к длине окружности, когда число
сторон его неограниченно возрастает.
Следствие. Площадь круга радиуса R есть
Действительно:
262. Круговым сектором называется часть плоскости, ограничен-
ограниченная дугой окружности и радиусами, проведёнными в концы этой дуги.
Черт. 227.
Черт. 228.
Площадь сектора есть предел, к которому стремится площадь впи-
вписанного многоугольного сектора, когда все стороны соответствующей
ломаной линии неограниченно уменьшаются. Существование этого пре-
предела устанавливается так же, как и для площади круга.
Теорема. Площадь кругового сектора равна длине дуги, кото-
которая служит его основанием, умноженной на половину радиуса.
Действительно, периметр вписанной правильной ломаной линии,
когда число сторон её неограниченно возрастает, стремится к длине
дуги, а апофема её стремится к радиусу.
Длина дуги окружности радиуса R, содержащей п градов, равна
—- , а площадь кругового сектора равна .
Аналогично этому площадь кругового сектора радиуса R, имею-
имеющего центральный угол в т°п'р", равна
тг/?у , п . р \
360 у ' 60 "Т" 3600 у
263. Круговым сегментом (черт. 226 и 227) называется часть
плоскости, заключённая между дугой и её хордой. Ясно, что для по-
ГЛАВА IV. ПОСТРОЕНИЯ 239
лучения площади сегмента надо из площади сектора вычесть площадь
треугольника, имеющего основанием хорду, а вершиной — центр круга,
если соответствующая дуга меньше половины окружности (черт. 226),
и надо прибавить площадь того же треугольника в противоположном
случае (черт. 227). ¦
Измерение площади фигуры, ограниченной дугами окружности,
сводится к вычислению площади многоугольника с последующим при-
прибавлением или вычитанием из нее площадей секторов или сегментов.
Например, площадь криволинейной фигуры AbCD (черт. 228)
равна площади четырёхугольника ABCD, уменьшенной на сумму пло-
площадей сегментов АН и ВС и увеличенной на сумму площадей сегмен-
сегментов CD и DA.
Резюмируя, скажем, что мы можем найти площадь всякой части
плоскости, ограниченной прямыми ими дугами окружности.
УПРАЖНЕНИЯ.
312. Найти длину радиуса круга, площадь которого равна 1 лА
313. Найти длину радиуса круга, в котором площадь сектора с углом
в 15G2&* составляет 1 м2.
314. Найти длину радиуса круга, в котором площадь сегмента, огра-
ограниченного дугой в 60° и её хордой, равна 1 л2.
315. Площадь кругового кольца, заключённого между двумя концентри-
концентрическими окружностями, равна площади круга, который имеет своим диамет-
диаметром хорду большей окружности, касающуюся меньшей окружности (дока-
(доказать).
316. В и D — две точки, лежащие на дуге ABC, представляющей собой
четверть некоторой окруи ности, и находящиеся на о^инчкивом расстоянии
от её концов; если из этих двух точек опустить перпендикуляры BE и
DF на радиус ОС, то полученная криволинейная трапеция BEFD, ограни-
ограниченная прямыми линиями и дугой окружности, равновел\1ка сектору OBD
(доказать).
317. На катетах и гипотенузе прямоугольного треугольника, как на
диаметрах, построены полуокружности — две первые вне треугольника,
третья, наоборот, расположена по ту же сторону от гипотенузы, где ле-
лежит треугольник. Показать, что сумма площадей двух луночек, заключён-
заключённых между каждой из меньших окружностей и большой окружностью,
равна площади треугольника.
318. На стороне АВ квадрата, вписанного в окружность с центром О,
как на диаметре, описана полуокружность, расположенная вне квадрата.
Радиус 0MN пересекает эту полуокружность, в точке N, а первоначаль-
первоначальную окружность — в точке М. Показать, что криволинейный треугольник,
заключённый между отрезком прямой MN и дугами А1А, NA, кваирируем,
т. е. что можно найти 1/ сторону равновеликого ему квадрата.
ГЛАВА IV.
ПОСТРОЕНИЯ.
264. Задача. На данном основании построить треугольник,
равновеликий данному треугольнику.
Высота искомого треугольника, очевидно, будет четвёртой пропор-
пропорциональной к данному основанию и к основанию и высоте данного треуголь-
1) Пользуясь только циркулем и линейкой. Прим. рео. перевооа.
240 КНИГА ЧЕТВЁРТАЯ. ПЛО1ЦЛТ.И
t
ника, так как четыре таких числа, что произведение двух из них равно
произведению двух других, составляют пропорцию. Когда высота най-
найдена, мы отложим её на каком-либо перпендикуляре к данному осно-
основанию и, таким образом, получим вершину одного из бесчисленного
множества треугольников, который удовлетворяет условиям.
Ясно, что точно так же можно построить треугольник, имеющий
данную высоту и равновеликий данному треугольнику.
265. Задача. Построить треугольник, равновеликий данному
многоугольнику. *
Разложим многоугольник на треугольники и превратим их в тре-
треугольники с общим основанием с помощью предыдущего построения.
Треугольник, имеющий то же основание и высоту, равную сумме вы-
высот всех составляющих треугольников,
будет равновелик сумме этих треугольни-
треугольников, т. е. данному многоугольнику.
Это построение может быть значительно
сокращено; мы это сейчас покажем, пред-
предполагая для простоты, что многоугольник
выпуклый.
Пусть дан многоугольник ABCDE
г— (черт. 229). Проведём диагональ СЕ, ко-
D Е О торая соединяет две вершины, смежные с
Черт. 229. одной и той же вершиной D, и через эту
вершину D проведём параллельно СЕ пря-
прямую DD' до пересечения с продолжением стороны АЕ в точке D'.
Треугольник CED' равновелик треугольнику CED (п. 250), а много-
многоугольник АВСБ)' — соответственно многоугольнику ABCDE; таким
образом, мы заменим данный многоугольник равновеликим ему много-
многоугольником, имеющим на одну сторону меньше, чем первоначальный. Мы
продолжаем это построение до тех пор, пока не придём к треугольнику.
Задача. Построить квадрат, равновеликий данному много-
многоугольнику.
Сторона искомого квадрата будет средним пропорциональным между
основанием и половиной высоты треугольника, полученного предыду-
предыдущим построением.
266. Задача. Построить многоугольник, равновеликий данному
многоугольнику и подобный другому данному многоугольнику.
Пусть требуется построить многоугольник Р, подобный данному
многоугольнику Р' и равновеликий другому данному многоугольнику
Р.. Пусть а'—сторона квадрата, равновеликого многоугольнику Р',
а—сторона квадрата^ равновеликого многоугольнику Рг; эти стороны
можно определить тем же путём, как это было указано выше. Отно-
Отношение плошадей многоугольников Р' и Pv т. е. отношение площадей
многоугольника Р' и искомого многоугольника, будет
я'2 / а1
а
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ 241
Следовательно, если А'В' — какая-нибудь сторона многоуголь-
многоугольника Р', то соответствующая сторона АВ искомого многоугольника
определяется из пропорции
а' __АгВ
~а~~~АВ;
поэтому её можно найти построением четвёртой пропорциональной
(п. 151), и задача приведена к построению За, п. 152.
267. Знаменитая задача о квадратуре круга состоит в построе-
построении стороны квадрата, равновеликого данному кругу.
Эта сторона, как видно из выражения для площади круга, есть
средняя пропорциональная между радиусом и длиной полуокружности,
и задача была бы разрешена, если бы была известна последняя.
Обратно, если бы была построена сторона квадрата, равновели-
равновеликого данному кругу, то длина полуокружности получилась бы как третья
пропорциональная к радиусу и стороне квадрата. Задача о квадратуре
круга сводится к той задаче, о которой мы говорили в п. 184: По-
Построить отрезок, равный длине окружности данного радиуса. Как
мы уже говорили, эта задача, а следовательно, и задача о квадра-
квадратуре" круга не могут быть решены с помощью линейки и циркуля.
УПРАЖНЕНИЯ.
319. Построить прямоугольник, зная его периметр и площадь.
Какой из прямоугольников, имеющих данный периметр, будет иметь
наибольшую площадь?
320. Вписать в круг прямоугольник данной площади.
Какой из прямоугольников, вписанных в данный круг, будет иметь на-
наибольшую площадь?
321. Разделить треугольник на равновеликие части прямыми данного
направления.
Та же задача для произвольного многоугольника.
322. Разделить четырёхугольник прямыми, выходящими из одной его
вершины, на данное число равновеликих частей. Показать, что для по-
построения точек пересечения искомых прямых со сторонами четырёхуголь-
четырёхугольника достаточно разделить на равные части диагональ, которая не прохо-
проходит через данную вершину, и через точки деления провести прямые, па-
параллельные другой диагонали, до пересечения со сторонами четырёхуголь-
четырёхугольника.
323. Разделить произвольный многоугольник на равновеликие части
прямыми, выходящими из одной и той же вершины.
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ.
324. Показать, что формулировку предложений упражнения 296 можно
видоизменить так, что они будут верны, каково бы ни было положение
точки О на плоскости, условившись перед числом, выражающим площадь
треугольника, ставить знак -\- или — в зависимости от направления вра-
вращения.
325. Если два многоугольника нрямо-гомотетичны и меньший располо-
расположен внутри большего, то площадь любого многоугольника, описанного
около одного из них и вписанного в другой, будет средней пропорциональ-
пропорциональной между площадями данных многоугольников.
16 Элементарная геометрия
242 КНИГА ЧЕТВЁРТАЯ. ПЛОЩАДИ
326. Найти отношение площади данного треугольника к площади тре-
треугольника, имеющего своими сторонами медианы данного треугольника.
327. Через две вершины треугольника проведены прямые, делящие
противоположные стороны в данных отношениях. Найти отношения площа-
площадей тех частей, на которые эти прямые делят площадь треугольника.
328. Через три вершины треугольника проведены прямые, делящие
противоположные стороны в данных отношениях. Найти отношение пло-
площади треугольника, оСразОванного ^тими прямыми,, к площади данного
треугольника. Вывести отсюда теоремы пп. 197 и 198, которые дают усло-
условие, при котором все три прямые проходят через одну и ту же точку.
329. Через точку внутри угла провести секущую так, чтобы она обра-
образовала со сторонами угла треугольник данной площади. (Прежде всего
строим параллелограм, имеющий заданную площадь, один из углов кото-
которого совпадает с данным углом и одна из сторон которою проходит через
данную точку. Искомая секущая должна отсекать от этого параллепо-
грама треугольник, площадь которого равнялась бы сумме площадей двух
цругих треугольников, лежащих вне построенного параллелограма и
образованных этой секущей, сторонами параллелограма и сторонами дан-
ного угла.)
330. Среди всех прямых, которые проходят через точку, заданную
внутри угла, и пересекают его стороны (но не их продолжения), найти ту,
которая образует со сторонами угла треугольник, имеющий наименьшую
площадь.
331. Среди всех многоугольников с одним и тем же числом сторон и
вписанных в один и тот же круг наибольшую площадь будет иметь пра-
правильный многоугольник 1) (доказать).
332. Построить треугольник, зная его сторону, соответствующую вы-
высоту и радиус вписанной окружности.
333. В данный круг вписать трапецию, зная один из её углов и пло-
площадь.
334. Треугольник и параллелограм имеют одно и то же основание,
по равному углу при основании и одну и ту же площачь. Разрезать одну
из этих фигур на такие две части, чтобы они, будучи сложены иначе, да-
давали бы другую фигуру.
335. Два треугольника имеют одно и то же основание и одну и ту же
высоту. Разрезать один из них на части так, чтобы сложенные иначе' они
дали бы другой. (Свести эту задачу к подобному же вопросу о параллело-
грамах, пользуясь результатом предыдущей задачи.)
336. Та же задача для каких-либо двух равновеликих треугольников.
337. Та же задача для каких-либо двух равновеликих многоугольников.
338. Пусть даны четыре точки А, В, С, D; произведение площади тре-
треугольника BCD на степень точки А относительно круга, описанного около
этого треугольника, равно каждому из произведений, образованных таким
же образом точкой В и треугольником CAD, или точкой С и треугольни-
треугольником АЬО, или точкой D и треугольником АСВ (доказать).
1) Если в круг вписан многоугольник, отличный от правильного, то,
по крайней мере, одна из его сторон больше стороны правильного много-
многоугольника с тем же числом сторон и, по крайней мере, одна из его сто-
сторон меньше стороны того же правильного многоугольника; всегда можно,
не изменяя ни площади многоугольника, ни описанного круга, сделать так,
чтобы чти две стороны АВ и ВС были смежными. Переметая теперь вер-
вершину В так, чтобы слелать ВС ранной стороне правильного вписанного
многоугольника, мы площадь многоугольники увеличим; выполняя эту опе-
операцию столько раз, сколько будет необходимо для того, чтобы заменить
ванный многоугольник правильным мноюугольником, получим искомое
предложение.
ЗАДАЧИ К ЧЕТВЁРТОЙ KHHTF 243
Показать, кроме того, что эти равенства можно считать верными как
по величине, так и по знаку, если использовать соглашение, установлен-
установленное в задаче 324.
339, Каждое из произведений, рассмотренных в предыдущей задаче,
равно площади треугольника, стороны которого выражаются теми же чис-
числами, что и произведения AB-CD, AC-DB, ADBC (доказать; см. п. 218,
упр. 270а). '
340. Разрезать треугольник на равнобедренные треугольники. Та же
задача для произвольного многоугольника.
341 Вычислить площадь треугольника, образованного тремя дугами окру-
окружности одного и того же радиуса R. попарно пересекающимися под прямым
углом.
342. Если два треугольника симметричны друг с другом относительно
центра их общей вписанной окружности, то площади восьми треугольни-
треугольников, которые образуются их сторонами, дают в произведении шестнадца-
шестнадцатую степень радиуса этой окружности.
16*
ПРИБАВЛЕНИЯ
ПРИБАВЛЕНИЕ А.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ.
268. Под этим названием мы хотели бы собрать некоторые указа-
указания, которые, по нашему мнению, полезны как для понимания мате-
математики вообще, так в частности для решения задач.
Действительно, учащийся должен твёрдо Знать, что для того,
чтобы изучение математики принесло ему пользу, не требовало от него
чрезмерных усилий и привело бы его к правильному представлению
о геометрии, мало понимать предлагаемые ему рассуждения; он дол-
должен в той или иной мере научиться самостоятельно строить на осно-
основании изученного новые умозаключения, находить доказательства тео-
теорем и решать задачи.
Вопреки укоренившемуся предубеждению этого результата могут
достичь все или, по крайней мере, все те, кто" будет заставлять себя
размышлять и следовать в своих рассуждениях определённому методу.
Указания, которые мы хотим здесь сделать, вытекают просто из здра-
здравого смысла (le bon sens le plus vulgaire). Среди них нег ни одного,
которое не могло бы показаться читателю совершенно тривиальным.
Однако опыт показывает, что несоблюдение того или другого из этих
очевидных правил является почти единственной причиной тех затруд-
затруднений, которые возникают при решении элементарных задач; то же
самое имеет место чаще, чем это можно было бы думать, при занятиях
более или менее высокими областями математических наук.
а) Теоремы, предлагаемые для доказательства.
269. Доказать теорему — значит перейти с помощью рассуждения
от условия теоремы к её заключению.
Пример. В теореме:
Любая точка, лежащая на биссектрисе угла, одинаково удалена от
сторон угла In. 36, черт. 38),
условием и заключением будут:
Условие: Если точка М лежит на биссектрисе угла ВАС,
Заключение: то она будет одинаково удалена от его сторон АВ и АС.
Мы должны вывести второе из первого, т. е. представить свой-
свойства, выраженные в условии теоремы, в такой форме, чтобы из них
получить свойства, составляющие её заключение.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ
245
Очевидно, необходимо прежде всего точно знать, в чем состоит
условие и в чём—заключение теоремы; следовательно, учащийся
должен прежде всего учиться их уверенно формулировать.
270. Но этого ещё мало, и мы можем теперь же сделать первое
важное замечание. Всякое доказательство имеет своей целью показать,
что заключение теоремы верно, если предположить, что условие тео-
теоремы выполнено. Если бы условие теоремы не рассматривать как вы-
выполненное, не было бы никаких оснований утверждать, что выполнено
её заключение. Так, если бы в примере, приведённом в предыдущем
пункте, точка М не лежала на биссектрисе, то она не была бы, как
мы знаем (п. 36), равноудалена от сторон угла.
Очевидно, что не имеет смысла делать какие-либо предположения,
если не пользоваться ими в своих рассуждениях, иначе говоря, если
сделанное предположение не входит где-либо в доказательство. Мы
видим, таким образом, что в рассуждениях необходимо использовать
условие теоремы и даже использовать его, вообще говоря, полностью.
271. Несколько ниже мы ещё вернёмся к только что изложенному
правилу. Но раньше мы должны дать ещё одно правило, вполне ана-
аналогичное предыдущему. На него надо обратить особое внимание, так
как о нём чаще всего забывают, несмотря на то, что оно является
совершенно необходимым. Это правило относится к определениям тех
понятий, которыми мы пользуемся. *
С одной стороны, очевидно, что мы не можем пользоваться в на-
наших рассуждениях такими понятиями, которые не были нами опреде-
определены; с другой стороны, понятно, что не пользоваться каким-либо
определением при доказательстве — всё равно, что не знать этого
определения.
Мы видим, таким образом, что прежде всего необходимо использо-
использовать определение каждого из тех понятий, которые нам встречаются.
Пример. Возьмём снова ту же теорему:
Любая точка, лежащая на биссектрисе угла, одинаково удалена от
сторон угла.
Мы должны прежде всего задать себе следующие вопросы:
Что значит, что прямая AM (черт. 38) есть биссектриса угла?
Ответ. Это значит, что она делит угол ВАС на две равные части.
Что называется расстоянием точки М от прямой АВ?
Ответ. Длина перпендикуляра, опущенного из точки М на прямую АВ.
После этого формулировка теоремы принимает следующий вид:
/_ MAD = /_ МАЕ;
1 /_ MALI = ?_ МЛИ\
Условие: < MD перпендикулярно к AD;
У ME перпендикулярно к АЕ.
Заключение: MD —ME.
Мы надеемся, что этот пример достаточно уясняет смысл следую-
следующего правила, которое Паскаль даже считал основой всей логики:
Необходимо заменять определяемые понятия их определениями').
1) В тех случаях, когда определение состоит из нескольких частей,
вообще говоря, бывает необходимо использовать все части определения;
по этому поводу можно было бы повторить сказанное ниже (в п. 275) отно-
относительно условия теоремы.
246 ПРИБАВЛЕНИЕ А
272. Определение одного и того же понятия часто может быть
дано в различных формах; в этом случае следует выбрать форму
определения, наиболее подходящую для той цели, которая имеется
в виду. Так, например, можно было бы ещё определить биссектрису АЛ1
угла, как прямую, которая образует с одной из сторон данного угла
угол, равный его половине и имеющий надлежащее направление.
Эта форма определении не подходит для доказательства приведён-
приведённой выше теоремы; напротив, именно этой формой определения мы
пользовались при доказательстве теоремы п. 15а.
Некоторые теоремы точно так же позволяют заменить одно опреде-
определение известного понятия другим определением, равносильным первому.
Так, например, первоначальное определение параллельных прямых
(п. 38) мы вовсе не употребляли, начиная с п. 39, где мы заменили
еги следующим определением, вполне ему равносильным: Параллель-
Параллельные прямые — это две прямые, которые с одной и той же секу-
секущей образуют равные внутренние накрестлежащие углы (или
равные соответственные углы, или пополнительные внутренние
односторонние углы).
273. Только что высказанное правило является, быть может, самым
важным из всех, которые нам придётся здесь рассматривать. Его зна-
значение становится особенно ясным, если учесть, что многие вспомога-
вспомогательные построения, которые иногда представляются на первый взгляд
совершенно произвольными, являются простым приложением зтого правила.
Приведём только один пример. В начале второй книги мы при всех
рассуждениях, относящихся к точке, лежащей на окружности, начи-
начинали с того, что соединили эту точку с центром окружности. Чита-
Читатель, который продумал предшествующие замечания, поймёт, что
в этом построении нет ничего искусственного и что онр является не-
непосредственно необходимым. Действительно, оно выте'кает из самого
определения окружности. Согласно определению, для того чтобы по-
показать, что точка М лежит на окружности, надо показать, что рас-
расстояние ОМ равно радиусу окружности.
Начиная с главы IV (пп. 73 и ел.), положение меняется. Здесь уже
не всегда приходится соединять с центром те точки окружности, ко-
которые мы рассматриваем. Это происходит потому, что здесь мы уже
знаем, что первоначальное определение окружности можно заменить
другим, данным в п. 82а. Согласно этому определению, для того чтобы
показать, что точка М лежит на окружности, можно соединить её
с тремя точками А, В к С этой окружности и показать, что четырёх-
четырёхугольник АВСМ обладает одним из свойств вписанного четырёхуголь-
четырёхугольника, указанных в п. 81. В дальнейшем во всех рассуждениях, отно-
относящихся к окружности, мы можем выбирать между этими двумя
определениями: в зависимости от обстоятельств мы пользуемся тем
или другим определением ').
!) В дальнейшем, например в п. 131, встречаются и другие определе-
определения окружности, равносильные двум предыдущим.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ
247
274. После того как выполнено то, о чём мы говорили (т. е. опре-
определяемые понятия заменены их определениями), необходимо преобразо-
преобразовать, как было указано, условие теоремы так, чтобы обнаружить спра-
справедливость её заключения.
В наиболее простых случаях непосредственно видна та теорема,
с помощью которой можно выполнить такое преобразование.
Пример. Условие, приведённое в п. 2П (нр.шер;, непосредственно
длёт соответствующее заключение, если воспользоваться одним из при-
признаков равенства прямоугольных треугольников.
В противоположность этому, в других случаях приходится прохо-
проходить через несколько промежуточных этапов. При этом можно, напри-
например, попытаться придать условию теоремы другую форму, кото-
которая возможно ближе подходит к её заключению.
Пример. Пусть требуется доказать тео-
теорему (п. 25):
Во всяком треугольнике против большей сто-
стороны лежит и больший угол.
Мы должны выр.тигь, что АВ больше, чем АС
(черт. 28). Для этого мы откладываем на АВ отре-
отрезок AD^= АС, так что точка D лежит между А и В.
Условие и заключение теоремы будут поэтому
таковы:
(U Уппвие- •! DA еСТЬ Г!Р0Л0лжение DB\
(I) Условие. у DA = AC. Черт. 230.
Заключение: /_ АСВ > /_ ABC.
Равнобедренный треугольник ADC, в котором углы при основании
равны, позволяет прцдат теперь условию теоремы новую форму:
DA есть продолжение DB;
/ADC /ACD.
(II) Условие:
р
= /_
/_ АСВ = /_ ADC + Z DCB > /_ ABC,
Заключение:
или проще:
(III) Условие: DX есть продолжение DB (черт. 230).
Заключение: /_ XDC+ /_ DCB > / ХВС.
Последнее заключение очевидно в силу теоремы о внешнем угле тре-
треугольника (в том же п. 25).
Как видно из разбора доказательства, мы достигли цели с помощью
ряда последовательных преобразований условия теоремы.
275. При каждом из таких преобразований следует, в частности,
не забивать нашего первого правила (п. 270) и каждый раз следить,
не осталась ли неиспользованной какая-либо часть условия, в чём
можно убедиться, исследуя, сводится ли новое условна в точности
к предыдущему, будет ли оно ему вполне равносильна.
Пример. В прет.ыдущем примере формулировка (II) условия теоремы
вполне эквивалентна формулировке (I): это значит, что если условие (I)
выполнено, то выполняется и условие (II), и обратно. В самом деле, раз-
разница между ними заключается только в том, что равенство DA^AC за-
заменено через /_ADC=?ACD. Но мы знаем, что люэог из этих двух
условий влечёт за собой другое. Услозие (II) поэтому можег быть безого-
безоговорочно поставлено на место условия (I): безразлично, дано ли условие
теоремы в той или в другой форме.
248
ПРИБАВЛЕНИЕ А
Иногда может случиться, что какая-либо часть условия теоремы
может быть отброшена без всякого ущерба'); однако этого в общем
случае не будет2), и если мы встретим затруднение при доказатель-
доказательстве какой-либо теоремы, то мы должны всегда выяснить, не воз-
возникло ли это затруднение потому, что в процессе рассуждений мы
опустили какую-либо часть данного условия.
Пример. Пусть требуется доказать следующую теорему:
В плоскости треугольника ABC выбрана точка М; если построить
/_ВАР ==/. MAC (черт. 231) и отложить АР=АМ, если далее постро-
построить /_ CBQ = /_ MB A: BQ=BM и /_ ACR=
= /_МСВ, CR—CM, то точки М, Р, Q,
R лежат на одной окружности.
В этой теореме условие и заключение
будут:
( / ВАР— / MAC; AP= AM
(I) Условие: \ ?_ CBQ = /_ MBA; BQ = ВМ;
\ ? ACR— /_MCB; CR=CM.
Заключение: Точки М, Р, Q, R лежат
на одной окружности.
Пусть dj — биссектриса угла А. Сто-
Стороны АВ и АС симметричны относитель-
относительно этой прямой, а в силу равенства углов
ВАР и MAC будут симметричны и отрез-
В
Черт. 261.
уду р р
ки AM и АР. Следовательно, точка Р симметрична с точкой М относи-
относительно прямой di; точно так же точка Q симметрична с точкой М отно-
относительно биссектрисы d2 Угла В, а точка R симметрична с точкой М от-
относительно биссектрисы ds угла С. Поэтому мы могли бы попытаться
преобразовать условие следующим образом:
(II) Условие:
Точка Р симметрична с М относительно прямой d,;
Q М d
м
м
Заключение: Точки М, Р, Q, R лежат на одной окружности.
Однако, исходя из этой формы условия, невозможно доказать теорему:
действительно, сформулированное таким образом предложение неверно.
Неверно, что произвольная точка М и точки Р, Q, R, симметричные с ней
относительно трёх произвольных прямых, лежат на одной окружности.
1) Это имеет место в том же примере при переходе от условия (П)
к условию (III). Условие fll), в самом деле, равносильно следующему:
DX есть продолжение DB;
,„ I на полупрямой DX существует такая точка, что треуголь-
I ' \ ник, имеющий эту точку своей вершиной, а отвезок DC —
* своим основанием, имеет равные углы при основании.
Действительно, последнюю точку можно, .очевидно, обозначить через А.
Но эта точка может и не существовать, даже если выполнено условие (III):
DX есть продолжение 'DB.
Для того чтобы она существовала, необходимо, в силу теоремы о
внешнем угле треугольника, чтобы /_ XDC был острым.
Следовательно, условие (III) может иметь место и без того, чтобы вы-
выполнялось условие (II).
2) Следует стремиться к тому, чтобы давать такие формулировки
теорем, в которых условие не содержало бы ни одного лишнего элемента.
В более тонких вопросах, и особенно в приложениях математики, наиболь-
наибольшая трудность часто заключается именно в том, чтобы выяснить, какими
из имеющихся данных следует воспользоваться для решения вопроса.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ
249
Черт. 232.
В этом можно убедиться при одном взгляде на чертёж 232, или ещё, при-
принимая во внимание, что люГые три точки Р, Q, R можно рассматривать
как симметричные с некоторой точкой М относительно прякых dit d2, d3—
перпендикуляров в серединах отрезков МР, MQ, MR.
Таким образом, мы сделали ошибку, заменив формулировку (I) теоремы
формулировкой (II). Ошибка заключается в том, что прямые db d2, ds не
произвольны." они служат биссектрисами углов данного треугольника и по-
потому проходят через одву точку. Следовательно, правильной формулиров-
формулировкой преобразованного условия теоремы будет следующая 1).
( Точка Р симметрична с точкой М относительно прямой А;
AГ) Условие: j " Ъ " м " и-
[ прямые dx, rf2, d3 проходят через одну точку О;
эта форма условия непосредственно приводит к результату, так как непо-
непосредственно очевидно, что четыре точки М, Р,
Q, R лежат на одном круге с центром в точке О.
276. Вместо топ> чтобы преобразовывать,
условие теоремы так, чтобы сблизить его с
заключением теоремы, часто оказывается пред-
предпочтительнее сначала обратить внимание на
заключение и постараться заменить первона-
первоначальное заключение другим, из которого
вытекает первое и которое легче было бы
вывести из условия теоремы.
Пример. Рассмотрим теорему (упр. 72):
Если из /почки М, лежащей на окружности, описанной около тре-
треугольника ABC, опустить перпендикуляры МР, MQ, MR на его стороны,
то основания этих перпендикуляров
лежат на одной прямой.
Мы докажем, что точки Р, Q, R
(черт. 233) лежат на одной прямой,
если докажем, что углы BPR и CPQ,
получающиеся при соединении точ-
точки Р с точками Q и R, будут равны
между собой. Следовательно, в то вре-
время как условие теоремы будет:
Точки А, В, С, М лежат на одном,
круге; МР, MQ, MR соответствен-
соответственно перпендикулярны к ВС, СА, АВ,
заключению теоремы мы можем при-
придать следующую форму:
Z_BPR=/_CPQ.
Но так как углы BRM и ВРМ—
прямые, то четырёхугольник BRPM мо-
может быть вписан в круг (п. 81), и по-
потому /_BPR= /_BMR; точно так же четырёхугольник CQMP может быть
описан в круги потому /_CPQ = /_CMQ. Следовательно, нам достаточ-
достаточно (при том же условии) доказать следующее заключение:
/_ В MR — ?_ CMQ.
!) Эта новая формулировка условия теоремы может заменить первона-
первоначальную: три прямые, проходящие через одну точку, можно, вообще го-
говоря, рассматривать как биссектрисы углов некоторого треугольника (см.
упр. 38).
250 прибавление А
Первоначальное заключение, таким образом, заменено другим, более
простым для доказательства; читатель легко докажет это последнее за-
заключение 1).
Пользуясь при доказательстве теоремы этим новым способом, мы
должны, конечно, подобно тому, как мы это делали выше, убедиться
в гом, что, изменив заключение, мы не стремимся доказать больше
того, что сояержится в первоначальном заключении, за исключением
тех случаев, когда у нас есть основание думать, что и новое заклю-
заключение, более общее, чем первоначальное, также будет справедливо.
277. Теперь следует сделать ещё одно нажное замечание, на ко-
котором мы не имели возможности остановиться в самом начале наших
указаний. Его следует использовать непосредственно по ознакомлении
с формулировкой той теоремы, которую требуется доказать.
Замечание это заключается в том, что многие теоремы могут быть
сформулированы несколькими различными способами. Мы приводили
соответствующие примеры в тексте книги.
Пример I. Мы отметили в п. 32, что предложение:
Вся.сая точка, одинаково удалённая от А и В, лежит на перпенди-
к\ляпе, восставленном в середине огпрезка АВ,
можно сформулировать так:
Всякая точка, которая не лежит на перпендикуляре, восставлен-
восставленном в середине отрезка АВ, не одинаково уоплена от двух концов от-
отрезка.
Мы видели2), что здесь имеется общее положение: предложение,
противоположное какому-либо предложению, и предложение, обратное
тому же предложению, равносильны.
К тому же порядку идей относится и метод доказательства, на-
называемый' доказательством от противного. Этот метод состоит
в том, чтобы показать, что получается противоречие, если предполо-
предположить условие теоремы выполненным, а её заключение неверным.
Пример II. Предложение (п. 23):
Во всяком равнобедренном треугольнике биссектриса угла при вер-
вершине перпендикулярна к основанию и делит его пополам,
сводится, как мы видели3), к любому ш следующих:
Высота равнобедренного треугольника, проведённая из его вершины,
проходит через середину основания и делит угол при вершине пополам.
1) В своём рассуждении мы допускали, что точки фигуры расположены
так, как это показано ва чертеже (черт. 233). Следовало бы видоизменить
доказательство так, чтобы оно не зависело от этого расположения; это
легко выполнить, пользуясь замечаниями, сделанными в п. 82. Однако в дан-
данном случае можно всегда предполагать, что имеет место случай, к кото-
которому отностсл наше рассуждение: для этого достаточно изменить в слу-
случае надобности расположение букв А, В, С.
2) См. п. 32, примечание 2°. Поим. ptd. перевода.
3) Напомним (ср. ещё п. 41), что равносильность обеих формулировок
проистекаег из того, что существует только одна биссектриса угла при
вершине, -только одна высота, только один перпендикуляр в середине ос-
основания, и т. д.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ 251
Перпендикуляр к основанию, восставленный в его сереоине, проходит
через вершину равнобедренного треугольника и является биссектрисой
угла при вершине.
И т. д.
Ясно, что этот пример носит, как и предыдущий, общий харак-
характер, мы встречались с тем же обстоятельством, например, в п. 63.
Впрочем, с ним приходится встречаться с самою начала геометрии.
Доказательство теоремы, обратной теореме п. 38, проведённое в п. 41,
представляет cojokj пример доказательства такого рода. .
Эти два случая, в которых данная формулировка может быть за-
заменена другой форуулировкой, ей эквивалентной, не являются един-
единственными. В каждом отдельном случае следует всегда подумать о
различных возможных формулировках одной и той же теоремы. Оче-
Очевидно, существенно иметь их в виду, чтобы выбрать из них ту, ко-
которая наиболее подходит для доказательства; короче говоря, следует
ставить перед собой вопрос таким образом, чтобы его решение
становилось возможно легче'1).
278. Этим последним замечанием мы заканчиваем изложение тех
основных правил, на которые мы хотели здесь указать. Очень полезно
изучить с точки зрения этих принципов те доказательства, которые
были даны в тексте книги, ставя перед собой, например, вопросы,
аналошчные следующим.
При доказательстве теоремы о медианах треугольника (п. об) мы рас-
рассматривали середины отрезков ВО к СО (черт. 57). Можно ли было логи-
логическим путём прийти к таьиму построению? Можно ли заменить его дру-
другими построениями? 2).
Можно ли заменить формулировку теоремы п. 55 (прямая, соединяю-
соединяющая середины сторон треугольника) другой, ей равносильной? Можно ли «
доказать теорему в этой последней формулировке непосредственно?
Обе ли части заключении упражнения 8 предполагают, что данная
точка лежит внутри треугольника? Не указывает ли ответ на этот вопрос
на ту теорему, которой "следует роспользоваться для доказательства каж-
каждой из двух частей этого заключения?
В кодом месте доказательств, данных в п. 27, мы воспользовались
предположением, что объемлемый многоугольник — выпуклый?
И 1. д.
Ь) Геометрические места. Задачи на построение.
279. Сказанное только что о доказательствах предлагаемых теорем
избавляет нас от необходимости подробно останавливаться на других
возможных формах геометрических задач; решение последних следует
искать, руководствуясь теми же принципами, что и выше, как мы это
сейчас увидим при рассмотрении вопроса о геометрических местах и о
задачах на построение.
Геометрические места. Некоторые геометрические места
были нами рассмотрены в самом тексте книги4, например, геометриче-
!) „Каждой задаче следует придать такую форму, чтобы её можно
было решить" (А бе л ь).
2) Одно из таких построений дано в упражнении ЗГ.
252 ПРИБАВЛЕНИЕ А
ское место точек, одинаково удалённых от двух данных точек или от
двух данных прямых, геометрическое место точек, находящихся на
данном расстоянии от данной прямой, и т. д.
Другие геометрические места очевидны сами по себе; например,
точка, обладающая тем свойством, что прямая, соединяющая её с дан*
ной точкой А, параллельна данной прямой XY, имеет своим геометри-
геометрическим местом прямую, проходящую через точку А и параллельную XY.
Таким образом, если дано какое-либо свойство точки М или об-
общее — какие-либо свойства изменяемой фигуры, в состав которой вхо-
входит точка /И, то для отыскания геометрического места точки М сле-
следует преобразовать данные условия в другие, дающие для точки М
уже известное геометрическое место.
Мы имеем здесь, следовательно, перед собой вопрос, аналогичный
тому, который стоял перед нами, когда требовалось доказать теорему.
В самом деле, там требовалось из совокупности данных свойств (уело*
вие) вывести другие свойства, так же заданные (заключение). В дан-
данном случае требуется точно так же преобразовать данное условие.
Единственное различие состоит в том, что в данном случае известна
отправная точка — условие, но не известен конечный результат — за-
заключение: мы знаем только, что этот результат должен нам дать искомое
геометрическое место. (Ясно, что при этом следует прежде всего искать
общие свойства различных положений подвижной фигуры, и, в частно-
частности, свойства, не изменяющиеся при её перемещении.) Следовательно,
здесь приходится итти тем же путём, как и выше, и, нам ничего не
оставалось бы, как только повторить те указания, которые мы только
что сделали.
Одно из этих указаний следует соблюдать здесь даже с большей
строгостью, чем при доказательстве теорем. Мы уже видели, что
в вопросах, относящихся к доказательству теорем, иногда случается,
что при последовательных преобразованиях условия некоторые части
его могут оставаться неиспользованными. Подобное обстоятельство
никогда не может встретиться при отыскании геометрического места,
так как искомое геометрическое место должно состоять из точек,
удовлетворяющих данному условию, и только из них. Следовательно,
мы должны каждый раз проследить за тем, чтобы наше заключение
было вполне равносильно условию.
Мы делали это для большинства геометрических мест, которые мы
искали (см. пп. 33, 36, 77 и др.); мы опускали эту вторую часть
рассуждения только в некоторых случаях, где она представлялась на-
настолько лёгкой, что на ней не было надобности останавливаться.
280. Задачи на построение. Предположим далее, что тре-
требуется построить геометрическую фигуру, удовлетворяющую данным
условиям. Результат рещения такого рода задачи может быть весьма
различным, в зависимости от того, будет ли число данных условий
как раз достаточным для определения неизвестной фигуры или нет.
Пример I. Пусть требуется построить прямую, касательную
к данной окружности.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ 253
Касательная в любой точке данной окружности будет отвечать усло-
условиям задачи. Имеется бесчисленное множество решений; следовательно,
данных условий недостаточно для определения искомой фигуры. Такая
задача называется неопределённой.
Пример II. Пусть требуется построить общую касательную
к двум данным окружностям.
Очевидно, что по сравнению с предыдущим примерим мы имеем одним
условием больше.
Теперь задача—определённая: она имеет (самое большее) четыре ре-
решения (п. 93).
Пример III. Пусть требуется построить общую касательную
к трём данным окружностям.
В общем случае не существует ни одной прямой, удовлетворяющей
поставленным условиям. Действительно, tiepBbie две окружности имеют
(самое большее) четыре общие касательные, так что искомой прямой мо-
может быть только одна из этих четырёх прямых, но третья окружность,
заданная произвольно, в общем случае, не будет касаться ни одной из
этих прямых. Следовательно, задача будет, за исключением некоторых
частных случаев, невозможной. На искомую фигуру наложено слишком
много .условий.
Задачи, предлагаемые учащимся, являются, как общее правило,
¦определёнными.
281. Задача на построение часто сводится к построению некото-
некоторой точки.
Пример 1.' Провести окружность через три данные точки (п. 90).
Достаточно определить её центр.
Пример II. Построить треугольник, зная одну из сторон, проти-
противолежащий угол и соответствующую высоту.
После того как выбрано положение данной стороны (где именно —
безразлично), остаётся только построить противолежащую вершину.
В этом случае обычно применяемым способом построения является
Метод геометрических мест, который заключается в том, чтобы вы-
вывести из условий задачи два геометрических места, на которых должна
лежать искомая точка: пересечение обеих линий и определит положе-
положение с)ТОЙ ТОЧКИ.
Решение примера 1. Чтобы найти центр окоужности, прохо-
проходящей через три данные точки А, В, С, достаточно заметить, что требо-
требование, чтобы искомая точка была равноудалена от точек А и R, даёт одно
геометрическое место, а требование, чтобы искомая точка оыла равноуда-
равноудалена от точек А и С,— другое геометрическое место.
Решение примера 11. Пусть требуется построить треугольник
ABC, зная сторону ВС, противолежащий угол А и соответствующую
высоту. Если выбрано положение стороны ВС, мы имеем два геометриче-
геометрических места для точки А: 1) дуга, вмещающая данный угол и построенная
на ВС, как на хорде; 2) прямая, параллельная ВС и отстоящая от нее на
расстоянии, равном высоте.
Условие, налагаемое на положение точки, называется простым
условием, если существует некоторая линия — геометрическое место
Точек, удовлетворяющих этому условию. При ытом точка определяется
двумя простыми условиями, и если известны два соответствующих гео-
254 riPHKABlEHHF A
метрических места'), то искомая точка найдётся как точка их пере-
пересечения.
Вообще, всякая фигура определяется некоторым числом простых
условий (мы вернёмся к этому вопросу во II томе, кн. X и Прибав-
Прибавление F). Многоугольник, имеющий п сторон, определяется по вели-
величине и положению 2л простыми условиями, так как при этом требуется
определить положение п точек. Чтобы определить его только по ве-
величине и по форме, достаточно 2п — 3 простых условий, так как
можно задать произвольно одну вершину и направление одной из вы-
выходящих из этой вершины сторон. Это число 2и—3 равняется «для
треугольника, но не равняется п, если п превосходит 3; отсюда и
вытекают те замечания, которые были нами сделаны в п. 46а (приме-
(примечание 3°) и п. 147 (примечание).
282. В силу этого, когда мы встречаемся с какой-либо задачей на
построение, мы должны постараться преобразовать условие задачи та-
таким образом, чтобы свести её к одной из тех задач, которые мы
умеем решать; например, преобразовать условие так, чтобы вывести
из него два геометрических места для одной из точек, связанных с ис-
искомой фигурой.
Для этого мы рассматриваем фигуру, которая по предположению
удовлетворяет поставленным условиям2), и эти условия служат нам
как бы условием теоремы; однако, как и в случае задач на геометри-
геометрические места, заключение мы должны найти сами.
И в этом случае следует соблюдать те же общие правила, как и
при доказательстве теорем. Как и в случае задач на геометрические
места, полученное заключение должно быть вполне равносильно усло-
условию. Действительно, если, с одной стороны, из условий задачи должно
следовать найденное построение, то, с другой стороны, мы должны
убедиться в том, что любая фигура, построенная найденным нами спо-
способом, необходимо удовлетворяет всем условиям задачи.
Мы не будем подробнее останавливаться- на тех особенностях,
которые представляют различные задачи на построение. Ограничимся
в этом направлении ссылкой на книгу Петерсена „Методы и теории
решения геометрических задач на построение" в), книгу во всех отно-
отношениях превосходную, из которой мы многое позаимствовали.
с) Методы геометрических преобразований.
283. Если учащийся привыкнет применять на практике предыдущие
указания; если он будет подставлять, в известном смысле механически,
определения на место определяемых понятий; если он будет уметь
i> В элементарной геометр.и.и мы ставим своей целью решение задач
при помощи циркуля и линейки, т. е. рассматриваем только 1еометриче-
ские места, представляющие прямые или окружности.
-) Мы говорили выше в таких случаях, например в п. 93- „Предполо-
„Предположим, что задача решена".
3) Имеется русский перевод — Харьков, 1883. Прим. реО. перевода.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ 255
быстро находить различные формы, которые можно придать той задаче,
которую он намерен решить, то он очень скоро научится решать мно-
многие задачи элементарной геометрии. Тем не менее некоторые из этих
задач могут показаться ему очень трудными или даже неразрешимыми,
в то время как в действительности они решаются иногда весьма про-
просто; однако решение этих задач не получается непосредственно теми
рассуждениями, которыми мы пользовались до сих пор. Они требуют
для своего решения других способов, служащих для упрощения задачи,
о которых нам и осталось рассказать. Эти способы упрощения пред-
представляют собой методы геометрических 'преобразований.
Собственно говоря, после того что было сказано выше, мы в праве
были бы назвать все геометрические методы „методами преобразова-
преобразований". Однако мы относим это название исключительно к тем методам,
которые состоят в переходе от некоторых свойств одной фигуры к
соответствующим свойствам другой фигуры.
Определить какое-либо геометрическое преобразование — значит
поставить любой данной фигуре в соответствие некоторую другою
фигуру по определённому закону так, чтобы вторая фигура была
вполне определена, как только дана первая фигура, и обратно. На
основании каждого свойства одной фигуры можно сделать заключение
о некотором свойстве второй фигуры, которое можно в известном
смысле рассматривать как перевод данного свойства первой фигуры.
Пример ы. Мы определили выше фигуру F', гомотетичную F отно-
относительно данного центра при данном коэфициенте подобия. Если фигура/-"
дана, то можно построить фигуру /•". Мы видели, что прямой линии фи-
фигуры F соответствует в F' -также прямая, что любому треугольнику
фигуры F соответствует в /•" подобный ему треугольник, любой окружно-
окружности фигуры F— окружность в фигуре F1, и т. д.
Точно так же, если дана фигура F, то можно построить фигуру F',
которая получается из неё с помощью данного вращения, поступательного
перемещения или симметрии; или обшёе — фигуру/7', подобную фигуре F,
так, чго двум данным точкам А и В фигуры F будут соответствовать две
данные точки Л' и б' в фигуре /•". Свойства фигуры F' непосредственно
вытекают из свойств фигуры F.
284. Однако не всегда следует применять преобразование ко всей
рассматриваемой фигуре. Напротив, во , многих случаях оказывается
удобнее преобразовывать только часть фигуры.
Последнее имеет, в частности, место в случае тех простых преоб-
преобразований, о которых мы только что говорили: перемещения, симмет-
симметрии, гомотетии и общего случая подобия. В большинстве случаев нет
никакого смысла применять эти преобразования ко всей фигуре, по-
поскольку свойства преобразованной фигуры не проще и не сложнее свойств
первоначальной фигуры: обе 4ИГУРЬ! обладают одними и теми же
свойствами1). Напротив, во многих задачах бывает необходимо подвер-
подвергнуть одному из этих преобразований определённую часть фигуры.
1) Геометрия как раз изучает re свойстьа фигур, которые не изме-
изменяются при их перемещении.
256 прибавлена А
Пример 1. Рассмотрим следующую задачу (упр. 32): Даны dee парал-
параллельные прямые и две точки А и В, находящиеся вне этих параллельных
и расположенные по обе стороны от них; найти ломаную линию наи-
наименьшей длины, соединяющую точки А а В, если вершины этой ломаной
лежат на данных прямых и отрезах ломаной между обеими параллель-
параллельными имеет данное направление.
Пусть AMNB—искомая ломаная (черт. 234); точка N получается из
точки М с помощью поступательного перемещения, которое можно, оче-
очевидно, считать известным, так как отрезки, отсекаемые двумя данными
параллельными прямыми на любой прямой данного направления, имеют
одну и ту же длину. Мы можем выполнить это поступательное перемеще-
перемещение над отрезком AM; точка А преобразуется в точку С, положение кото-
которой известно, а отрезок AM — в отрезок CN той же длины. Отсюда
легко вывести, что точки В, N, С
должны лежать на одной- прямой.
Аналогичные соображении при-
применимы к задачам 118—121 (книга
вторая).
П р и м е р II. В упражнении 14
отрезок, симметричный с отрезком
AM относительно данной прямой,
будет лежать на одной прямой с
отрезком ВМ.
Черт. 234. 285. Однако есть некоторые за-
задачи на построение, для которых
следует подвергнуть перемещению, симметрии или преобразованию
подобия всю рассматриваемую фигуру. Преимущество, которое может
дать это преобразование, состоит в замене неизвестных элементов
епрвоначальной фигуры известными элементами преобразованной
фигуры.
Пример. Пусть требуется в данный четырёхугольник ABCD впи-
вписать другой четырёхугольник, подобный некоторому данному четырёх-
четырёхугольнику mnpq.
Существует фигура, которая подобна искомой и в которой искомому
четырёхугольнику MNPQ соответствует четырёхугольник mnpq. Четырёх-
Четырёхугольнику ABCD будет соответствовать четырёхугольник abed, описанный
около mnpq, и который, следовательно, можно построить, пользуясь реше-
решением упражнения 213.
286. Остальные преобразования, которые мы рассматривали, изме-
изменяют в отличие от преобразований, перечисленных в п. 284, свой-
свойства преобразуемых фигур более или менее заметным образом.
Такова, например, инверсия, преобразующая каждую прямую перво-
первоначальной фигуры в окружность, или преобразование с помощью вза-
взаимных поляр. С помощью этих преобразований мы упростили в до-
дополнениях к третьей книге доказательства нескольких теорем.
Другим преобразованием, о котором мы только упомянули и которое
следует здесь отметить, является перспектива. В том виде, в котором
мы имели возможность её определить "в геометрии на плоскости, она
применима только к фигурам, состоящим из точек, лежащих на одной
прямой. Преобразованная фигура получается путём соединения каждой
\\ъ точек первоначальной фигуры с определённой точкой, лежащей вне
данной прямой, пересекая полученные таким образом прямые неко-
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ
257
торой секущей и выполняя над полученными точками произвольное
перемещение, мы и получаем преобразованную фигуру.
287. Следует отметить существенное различие, которое существует
между преобразованием с помощью взаимных поляр и другими пере-
перечисленными преобразованиями, как-то: подобием, инверсией и перспек-
перспективой. Последние представляют собой точечные преобразования, т. е.
такие, в которых каждой точке первоначальной фигуры соответствует
определённая точка преобразованной фигуры. Этим свойством не обла-
обладает преобразование с помощью взаимных поляр, в котором каждой
точке одной из фигур соответствует в другой фигуре прямая.
Другое преобразование, которым мы в нескольких местах пользо-
пользовались в настоящей книге, обладает, как и предыдущее, тем свойством,
что оно не является точечным преобразованием. Это преобразование,
которое можно назвать расширением (dilatation), мы применяли к
фигурам, образованным окружностями и прямыми. При этом преобразова-
преобразовании мы увеличиваем или уменьшаем (в зависимости от обстоятельств) ра-
радиус каждой окружности на одну и ту же данную величину а. Конечно,
при этом может случиться, что радиус какой-либо окружности обра-
обратится в нуль: соответствующая окружность обратится в точку. Обратно,
точку следует рассматривать при этом преобразовании как окружность
с радиусом, равным нулю, и она преобразуется поэтому в окружность
радиуса а. Что касается до прямых, входящих в состав преобразуе-
преобразуемой фигуры, то каждая из них переносится перпендикулярно к её
направлению в ту или другую сторону на то же самое расстоя-
расстояние а').
Существенное свойство расширения состоит в том, что две линии,
касающиеся друг друга, остаются касательными и после выполнения
расширения при надлежащем выборе его направления (см. упр. 59) 2).
отим именно свойством расширения мы и пользовались в пп. 93
и 231.
к.88. Приведённые формы. Поскольку целью геометрического
преобразования является упрощение преобразуемой фигуры, следует
стремиться в каждом отдельном случае к наибольшему упрощению.
С этой целью заметим, что перечисленные выше различные геомет-
геометрические преобразования содержат в себе произвольные элементы.
Так, например, в случае гомотетии необходимо выбрать центр подобия
и коэфициент подобия; в случае инверсии—полюс инверсии и её
') Мы видим, что расширение окружности или прямой можно выпол-
выполнить всегда в двух противоположных направлениях; в каждом отдельном
случае приходится выбирать одно из этих двух направлений.
-) Понятие расширения обобщается (с помощью соображений, которые
иыходят из рамок данной книги) и на фигуры, в состав которых входят
произвольные кривые, можно доказать, что и в таком обобщённом виде это
преобразование сохраняет свойство преобразовывать две линии, касающиеся
друг друга, в две линии, которые также касаются друг друга. Этим свой-
свойством обладает и преобразование с помощью взаимных поляр, если его
cooTBeiciBviomiiM образом обобщить (см. том II, п. 819).
17 Э-лемешарнаи геометрия
258 ПРИБАВЛЕНИЕ А
степень1); в случае расширения — величину а, о которой говорилось
в предыдущем пункте, и т. д.
Следовательно, к каждому из перечисленных видов геометрических
преобразований принадлежит бесчисленное множество различных пре-
преобразований.
Из этих преобразований надо выбрать одно так, чтобы преобра-
преобразованная фигура удовлетворяла одному или нескольким вполне опре-
определённым условиям. Принимая во внимание то, что было сказано в
п. 280, следует брать возможно большее число таких условий. Пре-
Преобразованная фигура называется в этом случае приведённой формой
первоначальной фигуры.
Пример I. Окружность всегда можно подвергнуть такому расшире-
расширению, которое преобразовывало бы её в точку: для этого достаточно выбрать
величину а, равной её радиусу.
Приведённой фоюмой фигуры, содержащей некоторую окружность С,
относительно расширения будет та фигура, в которой эта окружность
обращается в точку. Этой приведённой формой мы пользовались в пп. 93
и 231.
Пример II. Две окружности, имеющие общую точку, можно преоб-
преобразовать с помощью одной и той же инверсии в две прямые (выбирая за
полюс инверсии их общую точку,; две окружности, не имеющие общих
точек, — в две концентрические окружности (см. упр. 248). Иначе говоря,
приведённой формой фигуры, состоящгй из двух окружностей, будет сово-
совокупность двух прямых или двух концентрических окружностей, смотря по
тому, имеют ли две данные окружности общиг точки или нет.
Пример III. В приведённом выше, в п. 285, примере мы воспользо-
воспользовались в качестве приведённой формы данной фигуры относительно подо-
подобия той формой преобразованной фигуры, которая определяется требова-
требованием, чтобы искомый четырёхугольник преобразовался в. данный четырёх-
четырёхугольник mnpq.
289. Инварианты. Преимущества геометрического преобразования
могли бы быть лишь кажущимися, если бы оказалось, что при упро-
упрощении известных свойств данной фигуры усложнились "другие её
свойства. Следовательно, мы должны выполнять это преобразование
только в том случае, если различные свойства фигуры, упоминаемые
в условии задачи, изменяются при данном преобразовании достаточно
простым образом.
Оказывается, что почти во всех типах преобразований, обзор ко-
которых мы только что дали, известные свойства фигуры не испытывают
никакого изменения; эти свойства, как говорят, инвариантны.
Пример I. Мы видели, что в случае гомотетии углы преобразованной
Лигуры равны углам первоначальной фигуры, что рамыми остаются отно-
отношения отрезков, и т. д.
Пример П. Мы видели, что расширение преобразует две окружности,
касающиеся друг друга, в две другие окружности, также касающиеся
друг друга. Касание есть свойство, инвариантное по отношению к преоб-
преобразованию расширения.
1) Мы видели (п. 215), что наибольшее значение имеет, вообще говоря,
выбор полюса инверсии.
О МЕТОДАХ, ПРИМЕНЯЕМЫХ В ГЕОМЕТРИИ 259
Пример III. Угол между двумя линиями представляет собой свой-
свойство, инвариантное по отношению к инверсии (п. 219).
И т. д.
290. Выполнение преобразования не может вызвать никаких затруд-
затруднений, если в условии задачи упоминаются только инвариантные свой-
свойства фигуры. В этом случае возможно, в частности, всегда предпола-
предполагать, что заданная фигура уже преобразована в её приведённую
форму.
Примеры. Касание есть свойство, сохраняющееся при расширении;
поэтому при отыскании общих касательных к двум окружностям можно
предполагать, что одна из них обращается в точку. Мы следовали этому
пути в п. 93.
То же самое относится и -к отысканию окружности, касательной к трём
данным окружностям (п. 231).
Касание есть свойство инвариантное также и по отношению к инвер-
инверсии. Следовательно, при отыскании окружности, касательной к трём дан-
данным окружностям, можно предполагать, что две из них обращаются в пря-
прямые линии или что две из них концентричны (упр. 264 и 265).
То же самое относится и к доказательс!ву теорем, аналогичных сле-
следующей: все окружности, пересекающие ове дтнные окружности not
постоянными углами, касаются двух определённых окружностей; или
теоремы, составляющей содержание задачи 285, и т. д.
291 .Группы преобразований1). Рассмотренное свойство тех
преобразований, о которых мы говорили — существование инвариантов,
является следствием другого их основного свойства, о котором мы
также скажем несколько слов.
Произведением двух или нескольких преобразований называется
преобразование, равносильное этим преобразованиям, выполненным в
том порядке, в каком они перечислены2). Иначе говоря, если преоб-
преобразование 5 преобразует фигуру F в фигуру /"', а преобразование Т,
применённое к фигуре F, преобразует её в фигуру F", то произведе-
произведением обоих преобразований будет то преобразование, с помощью кото-
которого происходит переход от F к F'.
Пример. Результат, доказанный в п. 102а, может быть сформулиро-
сформулирован .следующим оиразом: произведение двух симметрии представляет
собою либо вращение, либо поступательное перемещение.
Установив определение произведения преобразований, мы будем
говорить, что некоторая совокупность преобразований представляет
') Конец этого прибавления рассчитан главным образом на тех чита-
читателей, которые знакомы с содержанием „Дополнений к третьей книге'.
2) Произведение двух преобразований изменяется, вообще говоря,
с изменением порядка сомножителей. Так, произведение двух симметрии
относительно двух различных осей будет либо вращением, либо поступа-
поступательным перемещением. В первом случае соответствующий угол поворота
будет иметь то же направление, как и угол поворота, совмещающего
первую ось симметрии со второй, и вдвое большую величину. Вп втором
случае соответствующее поступательное перемещение будет иметь то же
самое направление, как и поступательное перемещение, совмещающее первую
ось симметрии со второй, и вдвое большую величину.
*17
260 ПРИБАВЛЕНИЕ А
собой группу, если произведение любых двух из этих преобразований
есть преобразование той же совокупности.
Так, совокупность всех гомотетий есть группа: это предложе-
предложение равносильно утверждению, что две фигуры, гомотетичные третьей,
гомотетичны между собой. Совокупность всех гомотетий, центры ко-
которых лежат на одной прямой, есть также группа, так как мы знаем,
что центр гомотетии, являющейся произведением двух других гомоте-
гомотетий, лежит на одной прямой с центрами этих двух гомотетий.
Все перемещения образуют группу, так как две плоские фигуры,
равные одной и той же третьей фигуре и имеющие с ней одинаковое
направление вращения, равны между собой и имеют одинаковое на-
направление вращения.
292. Совокупность всех инверсий не образует группы. Произведе-
Произведение двух инверсий не есть инверсия. Однако можно получить резуль-
результат, аналогичный предыдущему, рассматривая преобразования, состоящие
из нескольких последовательных инверсий.
Назовём для краткости преобразованием 5 всякое произведение
каких-либо инверсий (или симметрии)^ взятых в любом числе. Преоб-
Преобразования этого типа содержат как частный случай все перемещения,
так как перемещение можно разложить на две симметрии, все гомоте-
гомотетии, так как гомотетия получается как произведение двух инверсий
с общим полюсом, но с различными степенями, а следовательно, и все
преобразования подобия, так как подобие получается как гомотетия,
сопровождаемая или не сопровождаемая перемещением и симметрией.
Может показаться, судя по определению преобразований S, что для
того, чтобы их все исчерпать, необходимо рассматривать преобразо-
преобразования, состоящие из п инверсий, где п последовательно пробегает
все целые числа, и что, останавливаясь на каком-либо значении я, мы
получим лишь часть рассматриваемых преобразований.
Однако это не так: любое преобразование 5 может быть сведено
к инверсии и одной, двум или трём симметриям, предшествующим
этой инверсии или следующим за ней, за исключением того случая,
когда данное преобразование является простым подобием (упр. 252).
Следовательно, достаточно четырёх простых операций (инверсий или
симметрии), чтобы получить любое из преобразований S.
Так как каждая из любых двух операций 5 равносильна некоторой
последовательности инверсий, то же самое имеет место и для их про-
произведения: операции S образуют группу, которую можно было бы
для краткости назвать группой инверсий.
293. Две фигуры F, F', которые преобразуются друг в друга
одним из преобразований данной группы, называются эквивалентными
(homologues) относительно этой группы. Например, две фигуры, рав-
равные между собой и имеющие одинаковое направление вращения, экви-
эквивалентны относительно группы, образованной всеми перемещениями.
В силу определения группы, две фигуры F, F\ эквивалентные
третьей фигуре /¦*, эквивалентны между собой, так как преобразова-
преобразование, с помощью которого происходит переход от f к F", есть произ-
О МЕТОДАХ, ПРИМЯНЯЕМЫХ В ГЕОМЕТРИИ 261
ведение тех преобразований, которые преобразуют, с одной стороны,
F в Р, с другой стороны, Р в F".
Приведённая форма Fo фигуры F относительно данной группы есть
та из фигур, эквивалентных F относительно этой группы, которая
удовлетворяет некоторым заданным условиям. Если этих условий будет
достаточное число и они выбраны надлежащим образом, то их доста-
достаточно для полного определения фигуры Fo, являющейся приведённой
формой фигуры F.
Предположим, что это так и есть: если мы применим к фигуре F
какое-либо из преобразований данной группы, то полученная при этом
новая фигура Р будет иметь своей приведённой формой также Fo,
так как фигуры, эквивалентные фигуре F, будут в то же время экви-
эквивалентными фигуре Р, и обратно.
Гак как приведённая форма некоторой фигуры F будет та же
самая, как и приведённая форма любой фигуры, получаемой из F с
помощью преобразований группы, то всякое свойство приведённой
фигуры есть инвариантное свойство фигуры F.
294. Поясним сказанное на примере.
Пусть дана фигура, образованная четырьмя произвольными точками
А, В, С, D; поставим себе задачей найги инварианты этой фигуры
относительно группы инверсий. С этой целью рассмотрим фигуру,
обратную данной фигуре, принимая за полюс инверсии / точку А.
Если точки В, С, D имеют своими обратными точками точки Ь, с, d,
то мы имеем фигуру, эквивалентную первой (её приведённую форму),
в которой одна из четырёх точек (га, которая соответствует точке .4)
удалена в бесконечность. Повторяя для этого частного случая то
общее рассуждение, на которое мы только что указывали, мы убе-
убедимся, что углы треугольника bed являются инвариантами фигуры ABCD
(это как раз то предложение, непосредственное доказательство кото-
которого требуется найти в упр. 270).
Пусть А', В', С, D' — точки,, получающиеся из точек А, В, С, D
с помощью некоторой инверсии Т. Поступим с точками А', В\ С, П
так, как мы выше поступали с А, В, С, D; пусть Ь', с', d' — фигура,
которая получается нз B'C'D' с помощью инверсии /', имеющей своим
полюсом точку А'. Фигура, состоящая из точек Ь', с', d' и точки, лежащей
в бесконечности, получается из фигуры, состоящей из точек Ь, с, d и
точки, лежащей в бесконечности, с помощью одного из преобразований
нашей группы, а именно с помощью произведения трёх инверсий /, Т, /'.
Это преобразование сводится, как мы знаем, либо к одной инверсии,
сопровождаемой симметриями, либо к подобию. Но первое предположе-
предположение в данном случае невозможно, по крайней мере, в том случае,
когда инверсия, о которой идёт речь, есть инверсия в собственном
смысле слова; действительно, инверсия необходимо преобразовывала
бы точку, лежащую в бесконечности, в точку, лежащую в конечной
части плоскости (а именно — в полюс инверсии). Следовательно, тре-
треугольники bed и b'e'd' подобны между собою, что и требовалось
доказать.
262 ПРИБАВЛЕНИЕ В
Следовательно, углы и отношения сторон треугольника bed дей-
действительно являются инвариантами фигуры ABCD относительно данной
группы. Из этих инвариантов независимыми будут только два, т. е.
достаточно задать два из них, чтобы знать все остальные: действи-
действительно, знания двух углов треугольника bed достаточно, чтобы по-
построить треугольник, ему подобный.
295. Мы только что видели, что существование инвариантов выте-
вытекает из существования группы; обратно, совокупность всех преобразований,
обладающих одними и теми же инвариантами, образует группу: в
самом деле, если какое-либо свойство фигуры не изменяется при двух
данных преобразованиях, то то же свойство фигуры не изменяется и
при преобразовании, представляющем собой произведение этих двух
преобразований.
Пример I. Гомотетия преобразует все отрезки в отрезки, параллель-
параллельные первоначальным и им пропорциональные. Обратно, любое точечное
преобразование, обладающее этими двумя свойствами, есть гомотетия
(п. 142),. Следовательно, совокупность всех гомотетий образует группу.
Рассужд'ение, приведённое в п. 144, представляет собою лишь видоизме-
видоизменённую форму того рассуждения, которое мы только что провели.
Пример II. Перспективное преобразование сохраняет сложное отно-
отношение четырёх точек; и обратно, любое преобразование, выполняемое над
точками одной прямой, которое не изменяет сложного отношения, будет
перспективным преоСразеванием J).
Следовательно, все перспективные преобразования образуют группу.
Мы ограничимся здесь этими общими указаниями относительно гео-
геометрических преобразований, а за подробностями, касающимися их
применения, отошлем читателя к цитированной уже книге Петерсена.
ПРИБАВЛЕНИЕ В.
О ПОСТУЛАТЕ ЭВКЛИДА.
I.
296. Мы допустили в качестве аксиомы (в п. 40), что через дан-
данную точку нельзя провести более одной прямой, параллельной
данной прямой.
Это предложение или, точнее говоря, следующее равносильное ему
предложение (п. 41, следствие I):
Если две прямые линии образуют с одной и той же секущей
два внутренних односторонних угла, сумма которых отлична от
двух прямых, то они не параллельны и пересекаются с той сто-
стороны от секущей, где сумма углов меньше двух прямых,
ij Это можно доказать, перемещая преобразованную фигуру так, чтобы
одиа из её точек совпала со своей соответственной и обе прямые были
бы отличны друг от друга; при этом вопрос сводится к разобранному в
упражнении 233.
О ПОСТУЛАТЕ ЭВКЛИДА 263
фигурирует также среди предложений, принимаемых за очевидные
в „Началах" греческого геометра Эвклида1), где в первый раз
и с замечательным совершенством были полностью изложены основы
геометрии, а также и во всех последующих сочинениях (для которых
это фундаментальное сочинение Эвклида всегда служило основой).
Однако продолжателей Эвклида, как в древности, так и в средние
века и в новое время, постоянно удивляло место, отводимое этому
предложению, которое в действительности далеко не носит того оче-
очевидного характера, которым обладают другие предложения, принимае-
принимаемые без доказательства, и вовсе не представляется a priori более
очевидным, чем многие из тех предложений, которые обычно доказы-
доказываются. В частности, им казалось странным, что Эвклид принимает
как самоочевидное такое свойство прямых, которое вовсе не является
общим свойством всех линий2) (значение этого замечания будет видно
из дальнейшего).
297. Поэтому делались многочисленные попытки доказать постулат
Эвклида. Все эти попытки оказались неудачными. В частности, с целью
доказать этот постулат от противного были выведены всевозможные
следствия из предположения, что постулат Эвклида неверен; получился
ряд заключений, сильно отличающихся от тех, которые получаются
к обычной теории параллельных. Однако, как бы далеко ни развива-
развивались эти следствия, в них нельзя было заметить (по крайней мере,
поскольку рассуждения были правильны) ни между собой, ни с дока-
доказанными ранее предложениями никакого противоречия, которое дока-
доказывало бы невозможность сделанного предположения.
298. Гениальный математик Гаусс3) задался вопросом, суще-
существует ли такое противоречие и не является ли предположение, что
постулат Эвклида не имеет места, совместимым с другими аксиомами
геометрии и вытекающими из них следствиями; другими словами, не
окажется ли невозможным доказать рассматриваемое предложение.
Около того же времени Лобачевский4) и Болиаи (Bolyai)8)
высказали, независимо друг от друга, ту же гипотезу и построили
геометрию, в которой все предложения, предшествующие постулату
Звклида или от него независимые, остаются теми же, как и в обычной
геометрии, в то время как все остальные предложения видоизменяются.
Результаты, к которым мы приходим в такой геометрии (называемой
неэвклидовой геометрией), во многих случаях носят совершенно пара-
парадоксальный характер н противоречат нашим обычным взглядам на вещи;
¦однако, какими бы удивительными ни казались они на первый взгляд, среди
1) Около 300 г. до н. э.
2) Вал-лис (Wallis), 1663.— См. Stackel ц. Engel, Die Theorie der
Parallellinien, von Euklid bis Gauss, Leipzig, 1895.
3) 1777-^1855 гг.
*) 1793—1856 гг.
6) 1802—1860 гг. — Существование неэвклидовой геометрии более или
¦мевее чётко предвиделось с различных точек зрения (ср. цитированную
работу S t а с k e I und Engel).
264
ПРИБАВЛЕНИЕ В
них нет ни одного, нелепость которого могла бы быть установлена. Приво-
Приводим некоторые из наиболее простых предложений.
В неэвклидовой геометрии:
Через точку А, лежащую вне прямой D, можно Провести бесчисленное
множество прямых, лежащих с этой прямой в одной плоскости, но не
пересекающих этой прямой!). Все эти непересекающие прямые располо-
расположены внутри некоторого угла с вершиной в точке А (и угла, ему верти-
вертикального). Этот угол, называемый углом параллелизма 2), увеличивается
с увеличением расстояния точки А от прямой (черт. 235).
Черт.- 236.
Любая прямая D', лежащая внутри угла параллелизма, имеет с пря-
прямой D один (и только один; оощий перпендикуляр, который даёг кратчай-
кратчайшее расстояние между двумя прямыми, так что если точка М описывает
прямую D', неограниченно удаляясь от этого общего перпендикуляра в ту
или другую сторону, то её расстояние от прямой D всё время возрастает
и притом возрастает неограниченно. Иначе обстоит дело для прямых D{,
D2', служащих сторонами угла параллелизма: каждая из этих двух прямых
неограниченно приближается к прямой D, не пере-
пересекая её, если продолжать её в том направлении, ко-
которое образует острый угол с перпендикуляром, опу-
опущенным из точки А на прямую ?); если точка М
удаляется в бесконечность по одной из этих прямых
в выбранном таким образом направлении, то её рас-
расстояние от прямой D стремится к нулю. Геометри-
Геометрическое место точек, равноудалённых от данной пря-
прямой, есть кривая линия.
Сумма углов треугольника меньше двух прямых,
причём разность между двумя прямыми и суммой
углов пропорциональна площади треугольника. Отсюда следует, что пло-
площадь любого треугольника мепьн.е определённой величины, как бы вели-
велики ни были его стороны (когда стороны треугольника увеличиваются, то
углы уменьшаются и стороны треугольника в известном смысле „вдавли-
„вдавливаются" подобно тому, как это изображено на черт. 2Ь6). Точно так же
сумма углов л-угольника меньше Bч — 4)d, причём разность пропорцио-
пропорциональна площади многоугольника. Следовательно, не существует прямо-
прямоугольников: если четырёхуюльник имеет три прямых угла, то четвёртый
угол — острый.
Не существует подобных3) фигур (за исключением, конечно, равных
фигур). Два треугольника равны между собою, если они имеют соот-
!) Можно доказать, что постулат Эвклида будет либо всегда вереи,
либо всегда неверен: нельзя допустить, что существует вне данной прямой
одна точка, через которую проходит только одна прямая, параллельная
данной прямой, не допустив того же самого для всех точек и всех прямых.
2) В русской литературе углом параллелизма обычно называют /_OAD%
(черт. 23b;. Прим. реО. перевода.
3) Под этим термином мы понимаем здесь (в отличие от определения,
принятего в тексте книги) фигуры, у которых каждые два соответственных
угла равны и соответственные" стороны пропорциональны.
о постулате эвклидл 265
вегственно равные углы. Допустить существование подобных фигур — зна-
значит допустить постулат Эвклида.
И. т. д.
Существует бесчисленное множество неэвклидовых геометрий. В са-
самом деле, в соотношения, связывающие между собой различные эле-
элементы одной и той же фигуры, входит, если принять гипотезу Лоба-
Лобачевского, некоторое число /г2, раз навсегда определённое, которое
может иметь, однако, произвольное значение: например, отношение
площади треугольника к разности между Id и суммой его углов (как
мы только что говорили, это отношение постоянно). Эвклидову гео-
геометрию можно рассматривать как предельный случай неэвклидо-
неэвклидовых геометрий: она соответствует k = oo.
299. Неэвклидова геометрия представляется нам, таким образом,
как лишённая противоречий, как логически возможная. Является ли
она и в действительности непротиворечивой, как это думали её осно-
основатели? Быть может, она только кажется нам такой в силу того,
что ещё недостаточно развита цепь её следствий? Не придём ли мы
к противоречию, которое не встретилось ни Гауссу, ни Болиаи, ни
Лобачевскому, с помощью более тщательных и более глубоких иссле-
исследований?
Можно утверждать, что этого не будет. Не развивая здесь де-
детально тех соображений, которые обосновывают непротиворечивость
неэвклидовой геометрии1), мы заимствуем у Пуанкарэ2) следующий
поразительно простой способ их изложения:
„Вообразим сферу 5 и внутри этой сферы—среду с переменным
показателем преломления и переменной температурой. Пусть в этой
среде перемещаются некоторые подвижные предметы; перемещения этих
предметов пусть происходят настолько медленно и пусть их теплоём-
теплоёмкости настолько малы, что они постоянно находятся в температурном
равновесии с окружающей средой; кроме того, пусть все эти пред-
предметы имеют один и тот же коэфициент расширения, так что можно опре-
определять температуру по величине любого из них. Пусть R — радиус шара
!) Можно заметить, что между изложенными выше фактами неэвклидо-
неэвклидовой геометрии и некоторыми фактами сферической геометрии имеется изве-
известная аналогия, причём эти факты в известном смысле слова противопо-
противоположны друг другу: так, сумма углов сферического треугольника больше
двух прямых и разность между суммой углов и двумя прямыми пропорци-
пропорциональна площади треугольника; два сферических треугольника, имеющих
соответственно равные углы, либо равны, либо симметричны, и т. д. Дей-
Действительно, геометрия на некоторых поверхностях (называемых псевдисфг-
рическими) оказывается тождественной с геометрией Лобачевского. Этим пу-
путём была даже впервые доказана логическая возможность последней; однако
это доказательство ещё несовершенно, так как: I) псевдосферические по-
поверхности нельзя рассматривать как неограниченно простирающиеся во всех
направлениях подобно плоскости; 2) оно приложимо лишь к плоской неэвк-
неэвклидовой геометрии и не исключает предположения о возможности доказать
постулат Эвклида с помощью соображений, относящихся к геометрии в про-
пространстве.
2) Foincare, Revue generaie des sciences pures et appliquees, r. Ill,
1892, стр. 75.
266 ПРИБАВЛЕНИЕ В
II р — расстояние некоторой точки рассматриваемой среды от его
центра; я предполагаю, что абсолютная температура в этой точке1)
равна /?2 — р2, а показатель преломления равен -^ —.
Что думали бы при этом разумные существа, которые никогда не
имели бы возможности выйти за пределы такого мира?
1°. Так как размеры двух маленьких предметов, перемещающихся
из одной точки в другую, изменялись бы в одном и том же отноше-
отношении в силу того, что оба предмета имеют один и тот же коэфициент
расширения, то эти существа считали бы, что размеры предметов не
изменяются. Эти существа не имели бы никакого представления о том,
что мы называем разностью температур. Никаким термометром они не
могли бы эту разность температур обнаружить, так как .расширение
оболочки термометра было бы одинаково с расширением термометри-
термометрической жидкости.
2°. Они считали бы, что сфера 5 бесконечна; действительно, они
никогда не смогли бы достичь её поверхности, потому что по мере
приближения к поверхности они попадали бы всё в более и более хо-
холодные области; они становились бы всё меньше и меньше, не дога-
догадываясь об этом, и потому делали бы всё более и более мелкие
шаги 2).
3°. То, что они назвали бы прямыми линиями, были бы окружности,
ортогональные к шару S, в силу следующих трёх причин:
a) это были бы траектории световых лучей;
b) измеряя с помощью масштаба различные кривые, наши вообра-
воображаемые существа обнаружили бы, что эти окружности представляют
собой кратчайшие расстояния между двумя точками: действительно, их
масштаб сокращался бы или растягивался при переходе из одной обла-
области в другую, а они не подозревали бы этого обстоятельства;
• с) если бы твёрдое тело вращалось таким образом, чтобы одна из
линий, проведённых внутри этого тела, оставалась неподвижной, то
такой линией могла бы быть только одна из этих окружностей; так
же как, если бы цилиндр медленно вращался около двух опор и при
этом нагревался бы с одной стороны, то геометрическим местом его
неподвижных точек была бы кривая линия, обращенная выпуклостью
к нагретой стороне, а не прямая линия.
') Абсолютной температурой называется в физике температура, отсчи-
отсчитываемая от нуля, выбранного таким образом, что температура оказывается
пропорциональной объёму термометрического вещества (в физике опреде-
определённо предполагается, что этим веществом служит газ, далёкий от его точки
сжижения; в данном случае речь идёт о любом теле, так как все предметы
имеют по предположению один и тот же закон расширения и абсолютную
температуру можно принять пропорциональной не объёму, а линейным раз-
размерам тела).
2) Можно добавить, что в силу тех свойств, которые приписаны пока-
показателю преломления, они не могли бы видеть того, что происходит вне
данного шара.
О ПОСТУЛАТЕ ЭВКЛИ1А 267
Отсюда следует, что эти существа приняли бы геометрию Лоба-
Лобачевского" :).
Теперь мы видим, что доказать постулат Эвклида с помощью пред-
предшествующих ему предложений невозможно; действительно, если би
такое доказательство существовало, то оно было бы признано верным
и теми фиктивными существами, о которых шла речь (так как все пред-
предложения, предшествующие постулату Эвклида, были бы с их точки
зрения верными); однако оно приводило бы их к неверному резуль-
результату, так как для этих существ постулат Эвклида не имеет места2).
11.
300. Какую же роль следует приписать этому предложению, кото-
которое не столь очевидно, как аксиомы, и которое нельзя доказать, как
доказываются теоремы?
Роль этого предложения та же, что и определения. Чтобы понять,
что под этими словами следует подразумевать, мы должны сослаться
на сказанное в предыдущем прибавлении (Прибавление А, п. 271).
Как там было указано, необходимо иметь определение каждого по-
понятия, встречающегося в наших высказываниях, — определение, кото-
которое приходится употреблять в рассуждениях, подставляя его каждый
раз на место определяемого.
Однако существуют понятия, которые нами не были определены и
вообще не могут быть определены.
Действительно, ни одно понятие нельзя определить иначе, как
с помощью предшествующих ему понятий3), но это невозможно для
первых из вводимых нами понятий.
Но так как эти первые понятия ясны сами по себе и, следовательно,
обладают некоторым числом очевидных свойств, то роль определения
1) Произвольное постоянное, которое встречается в иеэвклидовой гео-
геометрии, будет здесь радиусом R шара.
2) Этим фантастическим примером Пуанкарэ наглядно иллюстрирует ту
воображаемую обстановку, в которой правильной была бы именно геомет-
геометрия Лобачевского. Смысл рассуждения Пуанкарэ при этом сводится к сле-
следующему. Поскольку это один из логически возможных („мыслимых") ми-
миров, то логически возможна („мыслима"), следовательно, и геометрия Лоба-
Лобачевского, т. е. постулат Эвклида не может быть логическим следствием
остальных аксиом эвклидовой геометрии, справедливых, как было указано,
и в геометрии Лобачевского. Подлинного доказательства непротиворечи-
непротиворечивости геометрии Лобаческого этот пример, однако, не содержит, поскольку
не доказана самая „мыслимость" воображаемого мира Пуанкарэ. Непроти-
Непротиворечивость этой геометрии доказывается построением не воображаемых
миров, а такой модели („интерпретации") для геометрии Лобачевского, ко-
которая осуществима в обыкновенном эвклидовом пространстве. О различных
эвклидовых интерпретациях неэвклидовой геометрии см. во втором томе,
упр. 1295 и 1296. Прим. ред. перевода.
s) Например, мы не могли бы определить окружность, как „геометри-
„геометрическое место точек плоскости, расположенных на данном расстоянии от
данной точки в этой плоскости", не определив предварительно понятий
расстояния, плоскости и геометрического места.
268 припивление В
(которое, как мы только что пояснили, необходимо и в этом случае)
выполняют здесь именно те свойства, которые мы принимаем без до-
доказательства. Так именно мы поступили с прямой линией, которая вовсе
не была нами определена в собственном смысле этого слова; однако мы
дали то, что можно было бы назвать её косвенным определением,
допустив, что она обладает некоторыми основными свойствами.
301. При этом, однако, существенно, чтобы число допускаемых,
таким образом, свойств было достаточным, чтобы охарактеризовать
определяемое ими понятие. Например, мы не вполне определили бы пря-
прямую линию, если бы, вместо того чтобы допустить, как мы это делали
выше:
1) что любая фигура, равная прямой линии, есть прямая линия и
что обратно, любые ;.ве прямые можно наложить одну на другую бес-
бесчисленным множеством способов;
2) что через две точки проходит прямая линия и притом только одна,
— мы допустили бы только первое свойство, не допуская второго.
Действительно, это первое свойство не явпяется исключительным свой-
свойством прямых линий: им обладают, например, также окружности, имею-
имеющие радиус, равный 1 м. Следовательно, мы не имели бы возможности
доказать, исходя из этого неполного определения, ни одного свойства
прямых линий, которое не принадлежало бы также и этим окружностям,
например, мы не могли бы доказать, что сумма двух углов треуголь-
треугольника меньше двух прямых, так как это свойство не всегда имеет место
для криволинейных треугольников, образованных дугами равных окруж-
окружностей.
302. Вся геометрия основана на фундаментальном понятии переме-
перемещения, которое мы ввели в п. 3. Мы рассматривали там, как очевид-
очевидное само по себе, понятие фигуры, которая перемещается без измене-
изменения её формы и размеров, другими словами, понятие неизменяемой
фигуры. Попытаемся исследовать, -каким образом это понятие опреде-
определяется своими свойствами.
Если дана фигура, которая испытывает некоторое перемещение, и
произвольная точка М, то мы можем вообразить, что эта точка неиз-
неизменным образом связана с данной фигурой и движется вместе с послед-
последней при её перемещении, так что она занимает некоторое положение М'.
Следовательно, можно сказать, что каждой точке пространства М со-
соответствует при данном перемещении некоторая точка М'', а именно то
новое положение, в которое переносится точка М. Перемещение пред-
представляет собой поэтому точечное преобразование1) пространства.
Далее, очевидное свойстно интересующего нас понятия состоит
в том, что два перемещения, выполненные одно за другим, равносильны
одному перемещению.
Другими словами, эти преобразования образуют группу2).
Мы могли бы, следовательно, сказать:
1! См. Прибавление А. п. 287.
-j См. Прибавление А, п. 291 и следующие.
О ПОСТУЛАТЕ ЭВК/1ИЛА 269
(I)
Неизменяемая фигура есть фигура, которая подвергается
только преобразованиям некоторой группы (называемой группой
перемещений), обладающей следующими свойствами 1):
Существует бесчисленное множество преобразований группы,
переводящих какую-либо точку А в ка-<-ую-либо точку А'.
Не существует, вообще говоря, преобразования группы, кото-
которое преобразовывало бы одновременно две данные точки А и В
соответственно в А' и В'; чтобы преобразование существовало,
необходимо, чтобы некоторая величина, зависящая от то-
точек А и В, равнялась бы аналогичной величине, образованн й
с помощью точек А' и В'.
Если существует одно преобразование группы, переводящее
две определ. нные точки А и В соответственно в две опреде-
определенные точки А' и В", то существует бесчисленное множество
таких преобразований. В частности, существует бесчисленное
множество преобразований, оставляющих на месте две опре-
определённые точки А и В, причем существует бесчисленное мно-
множество других точек, которые остаются на месте при всех
этих преобразованиях. Эти точки образуют безграничную
линию (называемую прямой линией). Через две точки проходит
прямая линия и притом только одна.
Существуют такие поверхности (называемые плоскостями),
что всякая прямая, имеющая с одной из них две общие точки,
целиком лежит на поверхности; через три точки простран-
пространства проходит одна плоскость.
303. Во всяком случае существенно отметить, что предыдущее опре-
определение, как и все другие косвенные определения, заключает в себе
аксиому; очевидно, что это определение предполагает следующую аксиому:
Аксиома (А): Существует группа, обладающая свойствами (I).
Отметим также, что понятия прямой и плоскости вытекают из
понятия перемещения, без которого они не могут быть определены.
304. Как в эвклидовой, так и в неэвклидовой геометрии мы при-
приписываем группе перемещений свойства (I) и, следовательно, допускаем
аксиому (А). Эти две геометрии разделяет вопрос о том, будет ли
верно суждение:
.. | Через точку, лежащую вне прямой, можно провести
' | только одну прямую, параллельную данной прямой.
Согласно предыдущему, это суждение выражает свойство группы
перемещений, так как прямая линия и плоскост'ь определены с помощью
этой группы; вопрос принимает теперь следующую форму:
Обладает ли группа перемещений, определенная свойствами (I),
также и свойством (II)?
1) Мы не стремимся перечислить здесь все те свойства, которые слу-
служат определением понятия перемещения. Под „свойствами (I)" следует по-
понимать все те свойства, которые мы принимали без доказательства в пер-
первой книге, до введения постулата Эвклида.
270 прибавление В
Но если мы установили, что невозможно решить этот вопрос, то
значит вопрос просто неправильно поставлен и не имеет точного смысла.
Действительно, группа перемещений не определяется вполне свой-
свойствами A). Если (в согласии с аксиомой (А), которую мы принимаем)
существует группа, обладающая этими свойствами, то их существует
бесчисленное множество. Воображаемые существа, существование ко-
которых предполагает Пуанкарэ,, понимали бы под „неизменяемыми фигу-
фигурами" нечто совсем другое, чем мы, так как предметы, которые они
перемещали бы, расширялись бы или сокращались бы без их ведома;
тем не менее, группа перемещений,-как они её понимали бы, удовлет-
удовлетворяла бы условиям (I) во всякой внутренней области шара 5 (т. е. во
всём бесконечном, с их точки зрения, пространстве, к которому отно-
относились бы их рассуждения).
Теперь полностью дан ответ на вопрос. Положение (L) будет вер-
верным, если из всех групп, обладающих свойствами (I), сохранить назва-
название группы перемещений только за группой, удовлетворяющей усло-
условию, выражаемому этим положением; другими словами, если определить
группу перемещений уже не свойствами (I), а свойствами (I) и (II).
305. Во всяком случае остаётся устранить одно возражение. По-
Подобно тому как первоначальное определение содержало в себе аксио-
аксиому (А), так и предлагаемое нами сейчас определение возможно лишь
после решения следующего вопроса:
Существует ли группа, удовлетворяющая условиям (I) и (II)?
Ответ на этот вопрос утвердительный. Можно доказать [принимая,
конечно, аксиому (А)], что среди бесчисленного множества групп, удов-
удовлетворяющих первоначальным условиям, существуют группы как не-
неэвклидовы (для которых постулат Эвклида неверен), так и эвклидовы
(для которых он верен).
Таким образом, устранены все затруднения. Постулат Эвклида
входит в состав определения тех основных понятий, на которых
основывается геометрия.
306. Можем ли мы вследствие этого сказать, что не может возни-
возникать вопроса о том, верен или неверен постулат Эвклида, что такой
вопрос совершенно лишён смысла?
Мы имели бы на это право, если бы мы имели возможность опре-
определять геометрические понятия совершенно произвольно. Однако это
не так; эти понятия даны нам из опыта. Понятие о неизменяемой фи-
фигуре возникает у нас из рассмотрения тех неизменяемых фигур (твёр-
(твёрдых тел), примеры которых мы находим в природе. Неизменяемое
фигуры в геометрии и их перемещения должны быть определены по
образцу этих тел и их перемещений, если мы хотим, чтобы геометрия
была приложима к реальным, обьектам.
307. Мы видим, таким образом, что действительно существует
вопрос о постулате Эвклида: вопрос заключается в том, чтобы узнать,
согласуется ли данное вмше определение с опытом, будут ли свойства
существующих в природе перемещений, тех перемещений, которые мы
наблюдаем, аналогичны свойствам эвклидовой группы или нет.
О ПОСТУЛАТЕ ЭВКЛИДА 271
Однако эта проблема не является уже проблемой чисто математи- •
ческой; решение такого рода вопроса требует не рассуждений, а на-
наблюдений.
И если нам пришлось развивать концепцию Эвклида, а не Лоба-
Лобачевского, то это происходит именно благодаря тому, что наши чувства
показывают нам, что постулат Эвклида верен, по крайней мере, в тех
пределах, которые доступны этим чувствам. Мы видим, что две прямые,
параллельные третьей, параллельны между собой, что существуют по-
подобные фигуры с любыми коэфициентами подобия, что существуют
прямоугольники и т. д.
308. Однако это лишь первая грубая проверка. Желая подвергнуть
вопрос более глубокому исследованию, пробовали прежде всего изме-
измерять со всей возможной точностью углы некоторого треугольника, чтобы
выяснить, равна ли их сумма двум прямым; треугольник выбирали на-
насколько возможно большим, так как при этих условиях разница между
эвклидовой и неэвклидовой геометрией сказывается всего заметнее.
С помощью таких измерений было установлено (насколько это позво-
позволяли экспериментальные трудности), что равенство суммы углов тре-
треугольника двум прямым вполне под i верждается (или по крайней мере,
что отклонение меньше, чем ошибка наблюдения).
Поэтому до некоторого времени считали возможным утверждать,
что геометрией, наиболее верно представляющей действительность,
является эвклидова геометрия или геометрия, очень мало от неё отли-
отличающаяся (т. е. такая, что соответствующая постоянная k очень велика;
другими словами, что если геометрию, о которой идёт речь, можно
сравнивать с геометрией фиктивных существ Пуанкарэ, которые дви-
движутся внутри сферы радиуса R, то радиус сферы R весьма велик по
сравнению со всеми обычными размерами): короче говоря, что эвкли-
эвклидова геометрия физически верна.
308а. Положение изменилось в связи с той эволюцией, которую
претерпели в последнее время наши взгляды в области физики (тео-
(теория относительности).
Новая теория, прежде всего, глубоко изменила науку о движении,
или кинематику (являющуюся непосредственным приложением геомет-
геометрии). Построения, выполняемые над скоростями, били основаны в старой
кинематике на эвклидовой геометрии (главным, образом на свойствах
параллелограма). Мы и теперь допускаем, что эти построения практи-
практически сохраняют свою силу для скоростей „очень малых", т. е. изме-
измеряемых очень малыми числами, если за единицу принята скорость
света V (равная в круглых числах 300 000 км в секунду) и, следова-
следовательно, для всех обычных скоростей1), но не приложимы к скоростям
того же порядка, что и V. Для этих последних скоростей согласной
с физической реальностью 2) является неэвклидова геометрия. Роль
величины R играет V.
х) Так как V имеет большое значение, то "даже скорости артиллерий-
артиллерийских снарялов будут с этой точки зрения очень „малыми".
2) С точки зрения теории относительности. Прим. ред. перевоОа.
272 прибавление С
В этой теории неэвклидова геометрия и даже ещё более общие
геометрии находят и другие применения (общая теория относшпель-
нссти).
Однако все эти изменения не оказывают, как это видно из преды-
предыдущего, никакого влияния на текущую жизнь (например, на инженер-
инженерное дело). Эвклидова геометрия сохраняет силу для всех фигур, кото-
которые мы можем окинуть взором или непосредственно измерить.
ПРИБАВЛЕНИЕ С.
ЗАДАЧА О КАСАНИИ ОКРУЖНОСТЕЙ.
309. Как было указано в п. 236, метод Жергонна построения окруж-
окружности, касательной к трём данным окружностям, применим не во всех
случаях: он не приводит ни к какому результату в том случае, когда
центры трёх окружностей лежат на одной прямой. Мы добавили при
этом, что это затруднение можно было бы устранить, представив ре-
решение в такой форме, чтобы в него входили только свойства, не изме-
изменяющиеся при любой инверсии. Это мы и собираемся сейчас сделать.
Пусть, как и ранее, А, В и С—три данные окружности. Возьмём
точку Ь, антигомологичную какой-либо точке а окружности А относи-
относительно одного из центров подобия 5„ окружностей А и В; а также
точку с, антигомологичную точке Ь относительно одного из центров
подобия 528 окружностей В и С. Окружность о, проходящая через
точки а, Ь и с, пересекает три данные окружности в трёх новых
точках а', Ь\ с' и притом под одним и тем же углом (п. 227), так
что точки а! и Ь' антигомологичны относительно центра S}2, а точки
Ъ' и с' — относительно центра S,,s; кроме того, точки а и с', а так-
также а' и с будут попарно антигомологичны1) относительно одного из
центров подобия Su окружностей А и С.
Заменяя точку а другой точкой ах окружности А, мы получим дру-
другую окружность Oj, аналогичную о. Точка Sl2 имеет одну и ту же
степень относительно окружностей о и о, (равную степени той инвер-
инверсии, которая преобразует окружность А в окружность В); то же са-
самое относится и к точке S2S. Следовательно, радикальная ось XV
окружностей о и о, будет осью подобия данных окружностей; отсюда
ясно, что центр подобия 5,3, о котором мы только что упоминали,
будет тем из центров подобия окружностей А и С, который лежит
с центрами подобия Sn, S23 на одной оси подобия2).
li Что точка а антигомологична точке с\ а не точке с, легко доказать,
заметив, что fn. 227) углы, которые окружность о образует с окружиоС1Я-
ми А и С соответственно в точках ь и с, будут иметь одно и то же на-
направление 'в то время как в двух антиюмологических точках эти у!лы
должны име!ь противоположные направления)
2) Это рассуждение, правда, предполагает, что точка S\% будет одна и
та же для обеих окружностей о и oj. Но н противном случае, по крайней
мере одна из точек Svi, которые com BeiciByioi окружностям о и оь напри-
ЗАДАЧА О КАСАНИИ ОКРУЖНОСТЕЙ
273
310. Мы видим, таким образом, что существуют четыре семейства
окружностей з (соответственно четырём осям подобия) и что окруж-
окружности каждого из этих семейств имеют общую радикальную ось.
Обратно, любая окружность, имеющая общую радикальную ось с двумя
окружностями з одного семейства, сама принадлежит к этому семейству
(так как она сама себе соответствует в двух инверсиях с полюсами Sl2
и 513); таким образом, это семейство определяется заданием двух его
окружностей или оси XY и одной из его окружностей. За эту окруж-
окружность можно, вообще говоря, принять окружность о0, ортогональную
к трём данным окружностям,
которая принадлежит ко
всем четырём семействам
(п. 227а).
Геометрическим местом
центров окружностей каж-
каждого из этих семейств слу-
служит перпендикуляр, опущен-
опущенный из радикального центра
трёх окружностей А, В а С
на одну из их осей подобия.
311. Окружности, каса-
касательные к данным окружно-
окружностям, принадлежат, очевид-
очевидно, к тем семействам, о ко-
которых мы говорили; и об-
обратно, любая окружность о,
касательная к одной из дан-
данных окружностей, будет Черт. 237.
касаться и двух других.
Задача о касании окружностей сведена, таким образом, к следующей:
Найти окружность, имеющую с двумя данными окружностями
а и з, общую радикальную ось и касающуюся данной окружности А
(черт. 237).
Решение этой последней задачи не представляет трудности: если
а — точка касания искомой окружности с окружностью А, то окруж-
окружность, проходящая через эту точку и пересекающая окружности а и з,
под прямым углом, будет ортогональна и к искомой окружности, а сле-
следовательно, и к окружности А; эти условия её определяют (п. 158,
построение 13). Иначе говоря, достаточно из радикального центра а.
окружностей о, о, и А провести касательные к окружности Л, чтобы
мер та, которая соответствует о,, лежала бы на одной прямой с точками
S12 и S2s, она имела бы, следовательно, относительно окружности oj ту же
степень, как и относительно о, т. е. степень, равную степени инверсии,
преобразующей окруж-ность А в окружность С. Следовательно, окруж-
окружность Oj пересекала бы и окружности А и С в точках, попарно соответ-
соответствующих друг другу в этой инверсии.
18 Элементарная геометрия
274 прибавлена С
получить искомые точки касания. Можно убедиться и обратно, что по-
полученные таким образом точки дают решения поставленной задачи.
Как мы уже отмечали, одну из окружностей о и о, можно заменить
их радикальной осью XY, так что решение задачи о касании окруж-
окружностей принимает следующий вид:
Через одну из точек окружности А и две точки, ей антигомо-
логичные, проводим окружнссть а. Общая хорда этой окружности
и окружности А пересекает ось подобия XY в точке а, через ко-
которую достаточно провести касательные к окружности А, чтобы
получить точки касания этой окружности с искомыми окруж-
окружностями.
311а. Если за окружность о принять окружность оп, имеющую своим
центром радикальный центр / трёх данных окружностей и пересекаю-
пересекающую их под прямым углом, то мы вернёмся к решению Жергонна.
Действительно, общие точки окружностей А и о0 будут точками при-
прикосновения касательных, проведённых из точки / к окружности А, так
что общая хорда обеих окружностей будет полярой точки / относи-
относительно окружности А. Следовательно, точка а пересечения этой пря-
прямой с прямой XY будет, действительно, иметь своей полярой прямую,
соединяющую точку / с полюсом прямой XY.
Отсюда становится понятным, почему это решение неприменимо,
когда центр.л трёх данных окружностей лежат на одной прямой. Дело
в том, что в этом случае и окружность а0 и прямая XY обращаются
в линию центров. Чтобы избежать затруднения, достаточно, как мы
сказали, воспользоваться окружностью з, отличной от о,.
Рассматриваемое решение имеет, по сравнению с решением Жер-
гоппа, ещё и то преимущество, что оно применимо и в тех случаях,
когда одна или несколько из данных окружностей заменяются точками
или прямыми, и непосредственно даёт точки касания искомой окруж-
окружности с каждой из данных прямых; эти точки лежат на окружности,
имеющей своим центром точку пересечения данной прямой с осью по-
подобия XY и пересекающей под прямым углом OKpya<HjCTh з{. это
построение, очевидно, обобщает построение 14 (п. 159). Оно прп-
ложимо и тогда, когда в числе данных нет ни одной окружности,
что не имеет места для решения Жергонна. Оно теряет силу только
в том случае, когда все три данные окружности обращаются в точки.
312. Из сказанного в п. 309 следует, что общая хорда окружно-
окружностей о и А представляет собой не что иное, как ту прямую, которая
в п. 309 была обозначена через аа', где а' — точка, антигомологичная
точке с.
В силу этого можно сказать, что указанное выше построение со-
состоит:
в определении точки Ь, антигомологичной точке а (т. е. произволь-
произвольной точке окружности А) относительно центра подобия 6'12, затем
точки с, антигомологичной точке b относительно центра подобия 52„,
и точки а', антигомологичной точке с относительно центра подобия 513;
ЗАДАЧА О КАСАНИИ ОКРУЖНОСТЕЙ 275
в повторении того же построения с заменой точки а другой точкой
а, окружности А.
Точка пересечения обеих хорд аа' и ага^, построенных таким обра-
образом, будет той точкой а, из которой надо провести касательные
к окружности А, чтобы получить точки касания искомых окружностей
с окружностью А.
Исследование. Та форма, которую мы сейчас придали нашему
решению, позволяет (в противоположность первоначальному решению
Жергонна) очень просто исследовать число действительных окружно-
окружностей, отвечающих условию задачи.
Заметим прежде всего, что предыдущее построение оказывается
возможным или невозможным, смотря по тому, лежит ли точка а вне
окружности А или внутри её.
Примем за произвольную точку ал точку, близкую к а. Очевидно,
что точка а будет лежать внутри окружности А, если малые дуги да,
и а'ах' будут иметь одно и то же направтение, и вне её, если эти
дуги будут иметь противоположное направление.
Мы должны, таким образом, исследовать, перемещается ли точка а'
при перемещении точки а в одном с ней направлении или в противо-
противоположном.
Чтобы ответить на этот вопрос, рассмотрим сначала, в каком на-
направлении перемещается при этом точка Ь.
Так как точка, гомотетичная точке а относительно центра подо-
подобия 512, движется по окружности В, очевидно, в том же направлении,
как точка а по окружности А, то непосредственно очевидно (п. 223),
что точка b движется в том же направлении, как и точка а, если
центр подобия Sl2 лежит внутри окружности вив противоположном
направлении, если он лежит вне окружности В.
Условимся называть центр подобия Sl2 двух окружностей А и В
положительным, если он лежит вне этих окружностей, и отрицатель-
отрицательным, если он лежит внутри их; другими словами, центр подобия счи-
считается положительным или отрицательным, смотря по тому, проходят ли
через него действительные общие касательные или нет.
Если две окружности расположены одна вне другой, то их оба
центра подобия положительны. Если они пересекаются, то внешний
центр подобия будет положительным, а внутренний — отрицательным.
Если одна окружность лежит внутри другой, то оба центра подобия
отрицательны.
При этом условии относительно знаков, направления движения то-
точек а и b будут одинаковы или противоположны, в зависимости от
того, будет ли центр подобия Sl2 отрицательным или положительным.
Точно так же точка с перемещается по окружности С в том же
направлении, как точка b no окружности В, или в противоположном,
смотря по тому, будет ли центр подобия S2a отрицательным или поло-
житечьным; точка а' перемещается в том же направлении, как с, или
в противоположном, смотря по тому, .будет ли центр подобия Sl3 отри-
отрицательным или положительным.
18*
276 ПРИБАВЛЕНИЕ С
Сопоставляя эти замечания с тем, что было сказано выше, мы ви-
видим, что точка а лежит вне окружности .4, другими словами, что имеют-
имеются две действительные точки касания, если среди центров подобия,
расположенных на рассматриваемой оси подобия XY, положительных
будет один или три.
Чтобы получить общее число действительных окружностей, доста-
достаточно применить это рассуждение последовательно к каждой из четы-
четырёх групп центров подобия, лежащих на одной прямой.
Мы будем в дальнейшем обозначать цифрой 0 группу трёх внешних
центров подобия, цифрой 1 — групп), состоящую из внешнего центра
подобия окружностей Б и С и внутренних центров подобия окружно-
окружностей А и В и окружностей А и С; цифрами 2 и 3 — аналогичные
группы центров подобия, получаемые заменой окружности А через В
или через С.
312а. Принимая теперь во внимание взаимное расположение данных
окружностей, мы замечаем, что (если исключить из рассмотрения случай,
когда две изданных окружностей касаются друг друга)') имеется один-
одиннадцать различных возможностей"); эти возможные случаи обозначены
на чертеже 239 цифрами от I до XI.
В каждом из этих случаев предыдущие рассуждения непосредст-
непосредственно приводят к результату. Например, в случае I все центры подо-
подобия юложительны, так что имеется восемь решений, в то время как
в случае V имеется только четыре решения, так как оба центра подо-
подобия окружностей А и В, а также оба центра подобия окружностей А и
С отрицательны, и потому приходится пользоваться положительным цент-
центром подобия окружностей Б и С, т. е. их внешним центром подобия.
Таким образом, мы без затруднения приходим к следующей таблице,
в которой для каждого из одиннадцати случаев указаны положитель-
положительные и отрицательные центры подобия (буквы 5 обозначают внешние,
1) Случаи касания должны рассматриваться как предельные для тех слу-
случаев пересечения или непересечения окружностей, по отношению к кото-
которым данный случай касания является промежуточным. Если две из данных
окружностей касаются одна другой, то два из ре-
решений задачи сливаются в одно.
2) В каждом из одиннадцати случаев, изобра-
изображённых на чертеже 239, можно переставить меж-
между собой буквы А, В и С. Так как различные рас-
расположения, получаемые в каждом случае такого ро-
рода перестановками, соответствуют одному и тому
же числу решений, то мы сохранили на чертеже
лишь по одной перестановке букв для каждого из
¦ ¦ ооо одиннадцати случаев.
Черт. ля$. в случае XI возможны и другие расположения
окружностей (черт. 238): точки пересечения окруж-
окружностей А и В могут лежать обе внутри или обе вне окружности С (в то
время как на чертеже 239 одна точка лежит вне окружности, другая внут-
внутри её) Однако это ничего не меняет в наших рассуждениях по поводу
исследуемой задачи. Если рассматривать другие задачи, например задачу
об окружности, ортогональной к окружностям А, В и С, то это различие
может оказаться существенным.
278
ПРИБАВ1ЕНИЕ D
буквы S' — внутренние центры подобия), число решений и те группи
центров подобия (обозначенные цифрами 0, 1, 2, 3 в п. 312), которые
дают эти решения.
I
11
III
IV
V
VI
VII
VIII
IX
X
XI
Положительные центры
подобия
Все
SM- S23
3» -^13' ^23. ^3
Нет
SiS
S,2. 5,2, S23
S,3
•5i2,Sj2, Sjg.Stj.S.s
¦^12» "^13' -^23» ^*23
S* Sl3> 5m
Отрицательные центры
подобия
Нет
S,2, 512, S]3. 5,з
^12. -5,2
Все
523, S,2, 512, SI3> 5,3
523. ^13, 5,з
5,3, ST2. 5^, S,3, 513
S23"
12* 14* 231 94
512- 513
<? ' С ' <? '
Oin. J.-i. Onn
li* lO* iO
Число
решений
8
8
Нет
„
4
4
4
4
4
4
8
Группы
центров по-
подобия
@,1)
B,3)
@,1)
@,1)
B,3,
@,1)
Заметим, что число подлежащих исследованию возможностей легко
было бы значительно уменьшить, приняв во внимание, что случаи I
и II приводятся один к другому с помощью инверсии; то же самое
относится к случаям III и IV, к случаям V, VI, VII, VIII и к случаям
IX и X.
ПРИБАВЛЕНИЕ D.
О ПОНЯТИИ ПЛОЩАДИ.
313. В книге четвёртой настоящего сочинения мы следовали обще-
общепринятому пути, при котором a priori допускается (п. 243), что можно
определять площади многоугольников, т. е. что каждому плоскому
многоугольнику можно поставить в соответствие некоторое число
(называемое площадью), обладающее следующими свойствами:
I. Два равных многоугольника имеют одну и ту же площадь,
как бы эти многоугольники ни были расположены в простран-
пространстве.
II. Многоугольник Р", представляющий собой сумму двух
смежных многоугольников Р и Р', имеет своей площадью сумму
площадей многоугольников Р и Р'.
В изложенной выше теории возможность такого рода соответствия
представляет собой постулат. Однако в этом постулате нет надоб-
надобности: возможность, о которой идёт речь, отнюдь не предполагается
о понятии площади 279
заранее, а строго доказывается при следующем методе из южения.
который в силу этого заслуживает предпочтения перед изложением,
данным выше.
314. Теорема. Во всяком треугольнике произведение одной из
сторон на соответствующую ей высоту имеет одно и то же зна-
значение независимо от выбора стороны.
Пусть дан треугольник ABC (черт. 240), в котором сторонам ВС,
АС соответствуют вчеоты АН, ВК. Прямоугольные треугольники АСН,
ВСК имеют общий yroi при С; следовательно,
эти треугольники подобны, откуда
^=^. или ВС-АН = АС-ВК.
АС ВС
Мы будем называть площадью треугольника
это произведение, умноженное на некоторое раз В НС
навсегда выбранное число k, к вопросу о выбо- Черт. 240.
ре числа k мы вскоре вернёмся. Площадь будет
равна нулю, если треугольник в собственном смысле не сущест-
существует, т. е. если три вершины лежат на одной прямой, и только в этом
случае.
Площади двух треугочьников с общей высотой пропорциональны
их основаниям.
Очевидно, что равные треугольники имеют равные площади.
315. Рассмотрим теперь, с другой стороны, какую-либо точку О
в плоскости треуюльника; соединяя эту точку с тремя вершинами,
мы получим три треугольника, имеющих своими основаниями различ-
различные стороны данного треугольника и общей вершиной точку О. Какой-
либо из этих треугольников мы будем называть положительным (па-
гример треугольник ОВС, черт. 244), если он с данным треуголь-
треугольником лежит по одну и ту же сторону от общего основания; и отри-
отрицательным (например треугольник ОВС, черт. 245) — в противном
случае1).
Теорема. Если выбрать в плоскости треугольника какую-
либо точку О и соединить её с тремя вершинами данного тре-
треугольника, то разность между суммой площадей положительных
и суммой площадей отрицательных треугольников (или первая
из этих сумм, если отрицательных треугольников не будет) равняется
площади исходного треугольника.
Стороны треуго1ьника делят плоскость на семь областей (черт. 24 1):
одну внутреннюю (/), три области B—4), отделённые от внутренней
1) Если перечислить вершины данного треугольника в каком-либо опре-
определённом порядке, а вершины треугольника с вершиной О в таком порядке,
что общие вершины двух треугольников будут оба раза следовать в одном
и том же порядке, то можно сказать, что треуго иъник с вершиной О буоет
положительным или отрицательным, смотря по тому, бубет ли он
иметь с банным треугольником одинаковое направление вращения или
противоположное.
280
ПРИБАВЛЕНИЕ D
области соответственно тремя сторонами, и, наконец, три области
E—7), лежащие внутри каждого из углов, вертикальных углам тре-
треугольника.
Мы будем различать далее пять случаев:
1°. Точка О лежит на одной из сторон. Если точку О взять на
стороне ВС треугольника ABC (черт. 242), то треугольника ОВС не
будет. Что касается двух треугольников ОАВ и О АС, то они действи-
действительно будут иметь своей суммой
треугольник ABC: в самом деле, три
треугольника имеют одну и ту же
высоту (перпендикуляр, опущенный
из вершины А на ВС) и основание
ВС третьего равно сумме основа-
оснований ОВ, ОС двух первых.
2°. Точка О лежит на продол-
продолжении одной из сторон. Если точ-
точку О взять на продолжении сторо-
стороны ВС треугольника ABC (черт. 243),
то треугольника ОВС не будет. Что
касается двух треугольников ОАС
и ОАВ, то они действительно будут
иметь своей разностью треугольник ABC: в самом деле, три тре-
треугольника имеют одну и ту же высоту и основание ВС третьего равно-
разности оснований ОС, ОВ двух первых.
3°. Точка О лежит внутри треугольника (черт. 244). Продол-
Продолжим отрезок О А до пересечения в точке / со стороной ВС. Треуголь-
Д
V
Черт. 241.
О С
Черт. 242.
бв с
Черт. 243.
ник ABC равен сумме треугольников ABI, АС/, которые могут быть
разложены на AOB-\-BOl\ АОС-\-СО1. Треугольники АОВ и АОС
будут положительными треугольниками, а треугольники ВО1 и СО/
дают в сумме положительный треугольник ВОС.
4°. Точка О лежит вне данного треугольника ABC, но внутри
одного из его углов, например А (черт. 245). Если прямая О А пере-
пересекает сторону ВС в точке /, то сумма треугольников ОАВ и ОАС
может быть заменена суммой треугольников А/В, А/С, О/В, О/С. Но
сумма двух первых из этих четырёх треугольников равна ABC, а сумма
двух последних — ОВС; следовательно, будем иметь соотношение
ОАВ-\-ОАС= АВС+ ОВС или ОАВ -f ОАС — ОВС — ABC,
О ПОНЯТИИ ПЛОЩАДИ
281
т. е. искомое соотношение, так как треугольник О ВС—отрицате-
ВС—отрицателен.
5°. Точка О лежит внутри угла, вертикального одному из
углов треугольника ABC, например углу А (черт. 246). При этом
точка А лежит- внутри треугольника ОВС, и мы имеем C°):
ОВС—ABC-\-ОАВ-\-О АС или ОВС— ОАВ— ОАС= ABC;
это и есть искомое соотношение, так как треугольник ОВС положи-
положителен, а два других—отрицательны.
Д О
Черт. 246.
316. Пусть теперь ABCDE—произвольный многоугольник (черт. 247),
и О — какая-либо точка в плоскости этого многоугольника. Соединяя
эту точку со всеми вершинами, мы опять получим ряд треугольников,
имеющих общей вершиной точку О, а основаниями — стороны данного
многоугольника; каждый из этих треугольников мы будем считать
положительным или отрицательным, смотря
по тому, лежит ли он с данным многоуголь-
многоугольником !) по одну сторону или по разные
стороны от их общего основания.
Теорема. Пусть даны: многоуголь-
многоугольник, разложенный каким-либо способом
на п треугольников, и какая-либо точ-
точка О в его плоскости, которую мы сое-
соединим со всеми вершинами многоуголь-
многоугольника. Разность S между суммой пло-
площадей положительных треугольников с
вершиной в точке О и суммой площадей
отрицательных треугольников с той
же вершиной (или первая из этих сумм,
если отрицательных треугольников не будет) равняется сумме У
площадей п треугольников, на которые разложен многоугольник.
Если теорема верна для двух смежных многоугольников Р и Р',
разложенных на треугольники, то она верна и для их суммы Р". Дей-
1) Говоря и расположении многоугольника относительно очной из его
сторон, мы подразумеваем при этом ту область, которая непосредственно
примыкает к этой стороне. Например, треугольник ОАВ (черт. 247) будет
положительным, так как он лежит по ту же сторону от АВ, что и за-
заштрихованная часть многоугольника.
282 прибавление D
ствительно, в контурах многоугольников Р и Р' следует различать две
части: стороны или отрезки сторон1), не являющиеся общими, которые
вместе с соответствующими им положительными или отрицательными
треугольниками входят в состав многоугольника Р", и стороны или
отрезки сторон, общие обоим многоугольникам. Этим- сторонам или
отрезкам сторон соответствуют треугольники, которые будут положи-
положительными для одного из двух многоугольников Р и Р' и отрицатель-
отрицательными для другого (потому что многоугольники Р, Р' расположены по
обе стороны от их общей стороны) и которые, следовательно, взаимно
уничтожатся, если составить сумму величин S, соответствующих двум
многоугольникам. Следовательно, эта сумма будет действительно равна
величине 5 для многоугольника Р". Так как, с другой стороны, вели-
величина 2 для Р" будет, очевидно, равна сумме аналогичных величин для
многоугольников Р и Р', то равенство этих двух величин будет дей-
действительно иметь место для третьего многоугольника Р", если оио
имеет место для двух первых.
Теперь доказательство можно считать законченным, так как, с одной
сторон:.1, теорема доказана для я = 1 (она совпадает в этом случае
с предыдущей теоремой), а с другой, если она верна для одного зна-
значения я, то она верна и для следующего (так как многоугольник,
составленный из п -\- 1 треугольников, представляет собой сумму
одного треугольника и многоугольника, составленного из п треуголь-
треугольников).
Следствия: Величина S не зависит от выбора точки О, так
как величина 2 от этого выбора не зависит.
Точно так же величина 2 не зависит от способа разложения
многоугольника на треугольники.
317. Назовём площадью многоугольника общее значение двух вели-
величин S и ?.
Два равных многоугольника имеют одну и ту же площадь,
так как их можно разложить на попарно равные треугольники; с дру-
другой стороны, предыдущее доказательство показывает, что если два
многоугольника смежны между собой, то площадь составленного
из них многоугольника равна сумме площадей обеих частей.
Короче говоря, определённые таким образом площади обладают
свойствами I и II.
318. Отсюда следует, что многоугольник невозможно разложить
на такие части, которые, будучи расположены иначе (но так,
чтобы они были смежными друг с другом), образовывали бы мно-
многоугольник, лежащий внутри первого многоугольника, так как
!) Может оказаться необходимым разделить какую-либо сторону много-
многоугольника Р на итрезки (из которых одни будут общими с периметром
многоугольника Р, другие нет) и заменить треугольник, имеющий О своей
вершиной и данную сторону основанием, несколькими треугольниками,
имеющими эти отрезки своими основаниями. Величина S при атом не изме-
изменится, так как (предыдущая теорема) эти треугольники имеют своей сум-
суммой исходный треугольник. Точно так же поступим и с Р н Р".
ЗАДАЧА МАЛЬФАТТИ
233
второй многоугольник должен иметь необходимо ту же площадь, что
и первый.
Это предложение оставалось вовсе не доказанным в теории, данной
в тексте книги, так как там существование площадей представляло
собой постулат.
319. До сих пор мы ничего не говорили о выборе числа k. Оче-
Очевидно, что изменение этого числа вводится к замене всех площадей
пропорциональными им площадями. Мы уже указывали (п. 244), что
эта замена не нарушает обоих основных свойств площади.
Мы определим теперь k так, чтобы квадрат, построенный на еди-
единице длины, имел площадь, равную единице. Этот квадрат состоит из
двух треугольников, каждый из которых имеет как основанием, так
и высотой единицу длины. Следовательно, его площадь равна 2k, так
что мы выберем & = —-; всякий треугольник будет при этом иметь
своей площадью половину произведения основания на высоту. Опреде-
Определённые этим путём площади совпадают при таком выборе k с темп,
которые мы рассматривали в четвёртой книге1).
ПРИБАВЛЕНИЕ Е.
ЗАДАЧА МАЛЬФАТТИ.
320. Пользуясь основными свойствами окружностей, касательных
к двум данным окружностям или к ним изогональных (т. е. пересекаю-
пересекающих их под равными углами), изложенными как в дополнениях к третьей
книге (пп. 227—236), так и в Прибавлении С, мы имеем возможность
решить известную задачу Мальфатти, которая формулируется следую-
следующим образом.
Пусть даны три прямые (aj, (a2), (as), лежащие на одной пло-
плоскости2); требуется найти три окружности (л:,), (хч), (л:3), из
которых первая касается прямых (а2) и (as), вторая — прямых
(а3) и (а,), а третья — прямых (с,) и (а2), которые попарно ка-
касаются друг друга3).
1) Рассуждения, приведённые выше, показывают, что данное нами
определение площадей является единственным, которое обладает указан-
указанными выше двумя свойствами и удовлетворяет тому условию, что квадрат,
построенный на единице длины, имеет своей плошадью единицу.
2) Мы будем формулировать решение задачи в общем предположении,
что прямые образуют треугольник (вершины которого мы обозначим черед
/4j, A2l Дк); в частном предположении, что две из зтих прямых параллельны,
можно было бы применить те же рассуждения.
3; Мы предполагаем, что девять точек касания (искомых окужностей
с данными прямыми и между собой) отличны друг от друга; иначе говоря,
мы не рассматриваем того случая, когда прямая (ах), например, будет обшей
касательной к окружностям (х2) и (лг3) в точке их прикосновения друг
к другу (впрочем, пользуясь теми же самыми методами, можно было бы
рассмотреть и этот случай).
284 прибавление Е
321. Решение, полученное впервые Штейнером, которое мы
изложим, следуя Шрётеру, использует прежде всего свойство, дока-
доказанное в п. 228.
Мы видели там, что окружности i!, касательные к двум определённым
окружностям С и С, или, общее, окружности, изогональные к этим
окружностям, т. е. пересекающие их под равными углами, можно рас-
распределить в два семейства; каждое из этих двух семейств можно
охарактеризовать (в случае, когда обе инверсии, преобразующие С
в С, имеют положительную степень) тем свойством, что окружности
одного семейства пересекают под прямым углом некоторую окружность Г,
а окружности второго семейства — другую окружность Г1#
Так как окружности Г и Г, аналогичны, как мы указывали, бис-
биссектрисам углов между двумя прямыми, то мы будем называть их в даль-
дальнейшем б иссек тральными окружностями (cercles bissecteurs) окруж-
окружностей С и С.
Одна из двух биссектральных окружностей обращается в прямую
линию в том и только в том случае, когда окружности С и С равны
между собою (п. 225).
Если окружности С а С касаются друг друга, то одно из двух
семейств изогональных окружностей состоит, очевидно, из окружностей,
проходящих через точку касания. Соответствующая биссектральная
окружность обращается в ту же точку касания. При этом не сущест-
существует соответствующей инверсии, которая преобразовывала бы окруж-
окружность С в С, так как степень этой инверсии равнялась бы нулю.
В дальнейшем, когда мы будем говорить об окружностях ?, изогональ-
изогональных к окружностям С и С, касающимся друг друга, мы будем иметь
в виду не эти окружности, проходящие через точку касания, а семейство
окружностей 2 в собственном смысле, т. е. то семейство, окружности
которого не проходят через одну и ту же точку и преобразуются
сами в себя с помощью некоторой инверсии (со степенью, неравной нулю).
Если преобразовать окружности С и С с помощью одной и той же
инверсии в окружности С, и Сг', то та же самая инверсия преобразует
и биссектральные окружности окружностей С и С в биссектральные
окружности окружностей Cj и С,'. В самом деле, определение бис-
сектральной окружности основано исключительно на понятии угла
между двумя окружностями, а этот- угол не изменяется при инверсии.
322. Пусть, с другой стороны, C,), (?2), (?3)— три окружности
с центрами в точках ?,, ?2, ~3, попарно касающиеся друг друга (для
определённости — внешним образом) в точках TCj, тс2, тс3 (черт. 248).
Соединим точки тс2 и тс3 прямой линией, и пусть ji, и v, — вторые точки
пересечения этой прямой соответственно с окружностями (у и ($3).
Через точки jji, и v, проходит новая окружность (оц), касающаяся
в этих точках соответственно окружностей A>) и B3), центр которой а,
лежит в точке пересечения прямых ц^., и v,?3. Радиус этой окруж-
окружности равен сумме радиусов трёх данных окружностей.
Это видно из того, что прямые ц,;» и 3,3:1 параллельны, так как
точка тсд есть центр подобия окружностей (E,j и ^2); по аналогичной
ЗАДАЧА МАЛЬФАТТИ
285
причине прямые v,3g и SjS2 также параллельны. Равенство противопо-
противоположных сторон параллелограма а,3оч,5я показывает, что каждое из
расстояний сцц, и a,v, равно сумме трёх радиусов.
Если мы теперь соединим точно так же прямой линией точки тг, и тт8
и обозначим через ).„ и v2 точки пересечения этой прямой соответ-
соответственно с окружностями (?,) и (?3), 'то окружность (а2), касающаяся
в этих точках соответственно окружностей (;,) и (?3), равна
окружности (а,), потому что
к этой новой окружности при-
ложимо предыдущее рассужде-
рассуждение.
Легко далее убедиться, что
равенство окружностей (а,)
и (а2) сохранило бы силу и в
том случае, если бы не все
окружности C,), (Ss), (S3) по-
попарно касались друг друга внеш-
внешним образом').
Из равенства этих окружно-
окружностей легко выводится следую-
следующая лемма, на которой основа-
основаны наши дальнейшие рассуж-
рассуждения.
Лемма. Пусть три
окружности (х,), (л:,), (хв) по-
попарно касаются друг друга2)
в точках Р,, Р2, Ps; обо-
обозначим через (с,) окружность, Черт. 248.
касательную к (х„) и (х3) в
точках тг и и,; через (с2)—окружность, касательную к (л:,)
и (х3) в точках L, и п„, так что точки mv nv Pn, Ps лежат
(пп. 227, 224K) на одной окружности (ft,) и точки /,, п2, Ри
Ps — на одной окружности (ft2).
Точка пересечения N:i (отличная от Р3) окружностей (kx) и (ft2)
лежит на биссектральной окружности*) (ga) окружностей (с,)
и (й2).
!) В этом случае две из окружностей (I) необходимо касались бы друг
друга внешним образом, а третьей окружности — внутренним образом.
Радиус каждой из окружностей (а) был бы при этом равен разности между
радиусом большей окружности и суммой радиусов двух меньших.
2) Каждая из точек Р есть точка касания двух окружностей (х), индексы
которых отличны от индекса данной точки Р.
3) Чтобы иметь право пользоваться теоремой п. 224, необходимо в об-
шем случае убедиться, что окружности <а{) и (х^) принадлежат к одному
и тому же семейству окружностей, касательных к (д:2) и (х3); однако в дан-
данном случае существует лишь одно семейство (в собственном смысле).
4) Это будет биссектральная окружность, соответствующая тому семей-
семейству окружностей, касательных к (а^) и (я2), к коториму принадлежит
окружность (.*г3).
2S6 ПРИБАВЛЕНИЕ Е
В самом деле, преобраз>ем с помощью обратных радиусов рассмат-
рассматриваемую фигуру, выбрав за полюс точку 7V3. Окружности (хх), (х2)
и (ха) преобразуются в новые окружности (?,), ($2) и (?3); окружности
(а,) и (й2) — в окружности (aj и (а2), окружности (?,) и (k2)— в две
прямые1). Таким образом, мы получаем только что рассмотренную
фигуру, и окружности (а,) и (а.,) будут, как мы доказали, равны между
собой. Их биссектральная окружность будет прямой линией, откуда
и следует, что биссектральная окружность окружностей (а,) и (а„)
проходит через точку Na, что и требовалось доказать.
Далее, окружность, проходящая через точки «,, п2, N3, ортого-
ортогональна к окружностям (ха), (аг), (а2), (ga).
Окружность (?,) пересекает окружности (с,) и (о-,,) /год одним
и тем же ^глом; moino также окружность (k2)— окружности
(а.г) и (g3). Угол, который окружность (&,) образует с окружностью (ga)
в точке N5, имеет направление, противоположное углу, который та же
окружность образует в точке л, с окружностью (cj.
Все эти свойства непосредственно очевидны на фигуре (черт. 248),
преобразованной с помощью инверсии, имеющей полюс в точке Ns,
где точки v, и V., — диаметрально противоположные точки окружности
E,).
323. Доказав эти свойства, мы можем приступить к решению по-
ставчеиной задачи.
I. Обозначим, как и выше, через Рл, Р2, Р3 точки касания иско-
искомых окружностей (Xj), (x2), (х3), взятых попарно (черт. 249). К этим
трём окружностям мы можем применить только что доказанную лемм),
принимая за окружности (at) и (а2) соответственно прямые (аг) и (а2).
Мы видим, таким образом:
1) что через точки Р„, Р3 и через точки касания т1 и пх окруж-
окружностей (х2) и (х3) со стороной (й,) проходит окружность (kx); через
тичкн Р3, Рх и точки касания п2 и /2 окружностей (л:3) и (хх) со сто-
11 Пряные hjv, и ).2v2 на чертеже 248. Прим. рео. перевода.
ЗАДАЧА МАЛЬФАТТИ 287
роной (а2)—окружность (k2); через точки Я,, Я2 и через точки каса-
касания окружностей (л:,) и (хп) со стороной (ад)—окружность (ks);
2) что, например, окружности (fej) и (&2) пересекаются, кроме
точки Я3, в некоторой точке /V3I лежащей на биссектрисе {gs) угла
между прямыми (о,) и (&,), которая играет в данном случае роль
биссектральной окружности (если, как мы пока будем предполагать,
искомые окружности лежат внутри треугольника, то это будет бис-
биссектриса внутреннего угла); окружности (k2) и {ks) точно так же
пересекаются в некоторой точке 1чх, лежащей на биссектрисе (gr)
угла между прямыми (а2) и (й3), а окружности (k.d) и (/г,) — в некото-
некоторой точке yV2, лежащей на биссектрисе {g2) угла между прямыми
К) и К);
3) что окружность (А:,) пересекает прямые (о,) и (g\,) под одним
и тем же углом.
Можно сейчас же заметить, что по вполне аналогичной причине угол,
образованный окружностью (kr) с (g2), равен углу, который окружность
(&,) образует с (ах) или с (gs).
Он равен также углу, который окружность (kr) образует с окруж-
окружностью (л:2) в точке /и, (где последняя касается стороны ах) или, что
одно и то же, с точностью до направления ') в точке Я3.
II. Обозначим через (.<,), (t2), (ts) общие касательные к искомым
окружностям соответственно в точках касания Я,, Яа, Я3. Мы видим,
что прямая (/3) пересекает окружность (k^) под тем жг углом, как и
прямая (ga), причём в точке Р3 этот угол имеет, как в этом легко
убедиться с помощью сказанного выше '), направление, противополож-
противоположное направлению аналогичного угла между (kr) и (gg) в точке Л^.
Точка Р3, очевидно, симметрична с точкой Л^3 относительно линии
центров окружностей (kr) и (k2); поэтому прямая (/3) будет симмет-
симметричной с (g3) относительно той же прямой, так как обе прямые обра-
образуют с окружностью (fej) равные углы, имеющие противоположные
направления.
Наконец, по той же причине и прямая (/3) пересекает окружность
(&j) под тем же углом: она симметрична с прямой (g4) относительно
линии центров окружностей (k3) и (&j).
Но прямые, пересекающие данную окружность под одним и тем же
углом, будут, очевидно, касательными к одной и той же окружности,
концентричной с данной окружностью.
Следовательно, пять прямых (й,), (g), (g3), (<2), (>3) касаются од-
одной а той же окружности-) (k v), концентричной с окружностью (&,).
1) Чтобы определить направления рассматриваемых углов, приходится
воспользоваться тем обстоятельством, что две окружности (или окружность
и прямая), пересекающиеся в двух точках, образуют при этих точках углы,
имеющие противоположные направления (это очевидно, так как эти угли
симметричны друг с другом относительно некоторой прямой).
2) На чертеже 249 не показаны окружности (A'), (k') и (k'), чтобы не ус-
усложнять чертежа.
288 ПРИБАВЛЕНИЕ Е
Это г результат равносилен решению поставленной задачи. Дей-
Действительно, окружность (&j') можно считать известной, так как три из
пяти её касательных, а именно (ал), (g2), (gs) известны, коль скоро
задан треугольник.
Так как те же самые рассуждения применимы и к окружностям (k^)
и (&д), аналогичным окружности (k't) и соответственно концентричным
с окружностями (k2) и (ks), то мы приходим к следующему постро-
построению:
Пусть О — центр одной из окружностей, касательных к тре'м
данным прямым; {gx), (g2), (g5) — прямые, соединяющие точку О
с вершинами треугольника, образованного данными прямыми.
Строим окружность (k{), касательную к прямым (а^, (gz),
(g3I), окружность (k^), касательную к прямым (а2), (gs), (#,), и
окружность (k?), касательную к прямым (as), (,§",), (gj.
Пусть (^,) — вторая общая касательная окружностей (k^) и
(k^), симметричная с (?",) относительно линии центров этих окруж-
окружностей; (/5) — общая касательная окружностей (k^) и (k^), симмет-
симметричная с (g2) относительно линии центров этих окружностей; (t3)—
общая касательная окружностей (k^) и (k!2), симметричная с (gs)
относительно линии центров этих окружностей.
Одна из искомых окружностей (л:,) касается2) прямых (а„),
(as), (t2). (t3); точно так же окружность (х2) касается прямых (а3),
(aj), (<3), (^,), а окружность (х3) — прямых (с,), (а2), (tx), D).
Прямые (^,), (g2), (gs) могут быть при этом биссектрисами любых
трёх углов, образованных данными прямыми, взятыми попарно, лишь бы
они проходили через одну точку3).
) Существуют четыре окружности, касательные к прямым toi), (^2),
^3). Если мы хотим, чтобы искомые окружности (х^), (х2), (х3) лежали
внутри данного треугольника, то необходимо, очевидно, чтобы окружность (k{)
была вписанной в треугольник, образованный этими прямыми. В противном
случае за окружность (k^t можно принять любую из этих четырёх окруж-
окружностей; но в таком случае две другие аналогичные окружности будут вполне
определены; действительно (возвращаясь с помощью инверсии с'полюсом
в Ni к фигуре, рассмотренной вначале при доказательстве леммы;, можно
убе1иться, что хорды Мз^ь N%n2 должны быть симметричны друг с другом
относительно прямой (g3), так что тем же самым свойством должны обла-
обладать и биссектрисы углов между прямыми (aj) и (g3) и между прямыми (я2) и
(Ss)> проходящие соответственно через центры окружностей (k^\ и (k2).
2) Центр этой окружности лежит на прямой (gx), а не на перпендику-
перпендикулярной к (.^,) биссектрисе угла треугольника; выбирая определённые направ-
направления на прямых (g) и (t), можно также доказать, что он лежит иа той из
биссектрис углов между прямыми (?3) и (*я), которая проходит через центр
окружности (k\).
3) Это следует из того, что искомые окружности необходимо должны
касаться друг друга внешним образом, а прям"ые(я) должны быть внешними
общими касательными [см. ниже аналогичное замечание для случая, когда
(их), (a.j), (a3)— окружности].
ЗАДАЧА МА1ЬФАТТИ 289
Осталось ещё доказать, что приведённое построение действительно
даёт окружности, отвечающие условиям задачи. Мы не будем приво-
приводить здесь соответствующего доказательства, принадлежащего Петер-
сену !).
324. Замечательно, что предыдущее решение непосредственно
распространяется на тот случай, когда вместо трёх прямых даны три
произвольные окружности (Cj), (й2), (й3) 2).
В этом случае (g",), (^2), (Р3) будут биссектральными. окружностями
соответственно для окружностей (я5), (й3); (а3), (aj); (a,), (й2) 8). При
этом все предыдущие рассуждения, относящиеся к (Cj), (й9), (а3), (g,),
(?Г2)> (?з)> (^i)> (^г)> (^з) (ТРИ последние окружности определяются как
!) Journal de Crelle, т. 89, стр. 130—135. Прежде всего, очевидно, необ-
необходимо доказать, что четыре прямые (я2), (а3), (?2), (ts) касаются одной и
той же окружности. Читатель, который решит упражнение 422, убедится,
что это действительно так и будет, даже в том случае, когда О — произволь-
произвольная точка (а не центр вписанной окружности), и что при тех же условиях
прямые (tj)t (f3), (t3) проходят через одну точку.
Напротив,"то обстоятельство, что три построенные таким образом
окружности попарно касаются друг друга, существенно зависит от выбора
точки О (см. цитированный мемуар Петерсена). Ограничиваясь случаем,
когда окружности (х) лежат внутри данною треугольника, заметим, что
существование решения очевидно из соображений непрерывности. Пусть
построена какая-либо окружность (х{), касательная к прямым (а2) и (о3) и
лежащая внутри треугольника; существует окружность (х2), также лежащая
внутри треугольника и касательная к (а,), (ал) и (хх), й точно так же —
окружность (х3), лежащая внутри треугольника и касательная к (ях), (о2)
и (Xi).
Очевидно, что обе окружности (х2) и (лг3) пересекаются, если окруж-
окружность (Xi) имеет очень малый радиус, и лежат одна вне другой, если (дГ])
совпадает с вписанной окружностью треугольника. Следовательно, при
некотором значении радиуса окружности (хх) окружности (х2) и (х3) будут
касаться друг друга.
2) Эта новая задача непосредственно приводилась бы к предыдущей,
если бы окружности (oj), (я2), (<?з) имели общую точку S (а именно: с по-
помощью инверсии, имеющей точку S своим полюсом). Однако задачу при-
приходится решать заново, если это условие не выполняется.
8) Среди шести биссектральных окружностей данных окружностей (аЦ, (я2),
(ая), взятых попарно, окружности (gj), (g,), («3) должны бьпь выбраны таким
образом, чтобы они имели (задача 2/6) общую радикальную ось. В самом
деле, предположим для определённости, что'искомые окружности касаются
друг друга внешним образом. Окружность (а{) будет при этом иметь с окруж-
окружностями (х2) и (xs) касание того же рода, что и окружность (х{), так как
существует лишь одно семейство, в собственном смысле, окружностей,
касательных к (х2) и (х3); точно так же (а2) будет иметь с окружностями (д:3)
и (Xj) касание одного и того же рода, а окружность (я3) — касание одного
и того же рода с окружностями (х^ и (х3). Рассматривая все возможные
предположения относительно характера касания этих окружностей, легко
убедимся в том, что окружности (g) удовлетворяют указанному в тексте
условию.
Случай, когда две из трёх окружностей касаются друг друга внутрен-
внутренним образом, сводится к предыдущему с помощью надлежащим образом
выбранной инверсии (инверсия даёт также возможность упростить иссле-
исследование первого случая).
19 Элементарная геометрия
290 ПРИБАВЛЕНИЕ Е
и выше), т. е. все предыдущие рассуждения до части II п. 323, со-
сохраняются без изменения').
Чтобы распространить на настоящий случай и вторую часть реше-
решения предыдущей задачи, надо определить, что мы будем теперь пони-
понимать под (*,), (/,), (/3).
С этой целью обозначим через (С) окружность, ортогональную
к окружностям (с,), (а2), (ав) (предполагая для определённости, что
такая окружность существуетJ).
Мы будем обозначать через (•',) окружность, касательную к окруж-
окружностям (х2) и (х3) в их точке касанья Рл и в то же время ортогональную
к (С). Точно так же (/„) и (t3) будут окружностями, каждая из которых
касается двух из искомых окружностей в их точке касания и в то же
время ортогональна к окружности (С).
Проведённые выше рассуждения показывают, что окружность (/?])
пересекает под равными углами3), с одной стороны, окружности (х2)
и (х3), а с другой стороны,— окружности (aj, (g2), (g3).
Три последние окружности ортогональны к (С).
Отсюда следует (см. Прибавление С, в частности п. 310), что
любая окружность (&/), имеющая общую радикальную ось4) с окруж-
окружностями (&,) и (С), также будет изогональна к окружностям (й,), (g),
(g3), и что если выбрать эту окружность так, чтобы она касалась
одной из них (построение п. 311), то она будет касаться также и двух
других.
Окружность (t3) получается из (g&) с помощью инверсии6), которая
преобразует самих в себя окружности (С), (kx) и (fe2); эта инверсия
останется тою же самой, если заменить (kr) и (k2) через (kx') и (k2).
Таким образом, получается следующее построение: пусть (аг),
(д2), (as) — данные окружности и (g^, (g2), (g3) — бассектральные
окружности соответственно окружностей (а?) и (а3), (ая) и (ах),
(аг) и (й2), причём эти биссектральные окружности выбраны так,
чтобы они имели общую радикальную ось; пусть далее (Q —
окружность, ортогональная к трём данным.
1) Отсюда следует, что рассматриваемые биссектральиые окружности
необходимо существуют всякьй раз, когда задача имеет решение, так как,
вапример, окружность (&) должна иметь своим центром один из центров
подобия окружностей (п2) и (с3) и проходить через точку Ns.
*) Эта окружность обращается в точку в случае, отмеченном в сноске2)
ва стр. 289.
s; Относительно направления этих равных углов можно сделать те же
замечания, что и выше.
*; Понятно, что в отличие от того, что мы имели при решении первой
вадачи, окружность (k^) не будет, вообще говоря, концентричной с (&i).
*) Это вытекает, как и выше, из того, что окружность, которая полу-
получается из (?з) путём указанной инверсии, удовлетворяет, — в отношении её
ючки пересечения с (gj), а также в отношении величины и ваправления
угла, который она образует с (gx), — тем же условиям, как и окружность (t3i,
и, кроме того, она должна быть ортогональна (С)\ этв условия вполне
определяют окружность {t3). Инверсия, о которой идёт речь, имеет своим
Сим общий радикальный центр трёх названных окружностей.
ЗАДАЧА МАЛЬФАТТИ 291
Определяем окружность (А,'), касательную к (a,), {g.,) и (gs);
окружность {k2'), касательную к (а.,), (g3) и (g,), и окружность
(ks'), касательную к (а3), (#-,) и (goI); ила общее2): определяем
окружность (&,"), изогональную к (a,), (g2) и (о^); окружность (kj),
изогональную к (а2), (gs) и (gj), и окружность (&/), изогональную
к (а3). (&) и (g.,).
П\>сть (g^) преобразуется инверсией, преобразующей самих в
себя окружности (С), (k2"), (k3"), в окружность (/,); точно так
же (?г) — инверсией, преобразующей самих в себя окружности (С),
(ks"), (k{"), в окружность (fo); наконец (gs) — инверсией, преобра-
преобразующей самих в себя окружности (С), (&,"), №%'). в окруж-
окружность (/.,).
Первая из искомых окружностей будет касательной к окруж-
окружностям (я2), (а3), (<2), (/3), вторая — к окружностям (а&), (а,), (^3),
(tx) и третья — к окружностям (я,),, (а9\, (tx), (t2).
Нетрудно убедиться, что всё сказанное сохраняет силу и в том
случае, когда радикальный центр / трёх окружностей (а,), («2), (аа)
лежит врутри этих окружностей, так что окружность (С) не сущест-
существует. В этом случае надо только заменить слова ,.окружность, орто-
ортогональная к (Г)"> словами „окружность, относительно которой точка /
имеет ту же степень, как и относительно окружностей (а,), (#2), (#3)",
и условиться говорить, что „некоторая окружность (А,') имеет общую
радикальную ось с окружностями (/г,) и (С)", если любая окружность,
ортогональная к (&,) и относительно которой точка / имеет ту же
степень, как и относительно (aj, будет в то же время ортопжальна
и к (&,').
') Как и выше, мы убедимся, что за (k^) можно принять любую из
окружностей, касательных к (а^), [g,) и (g3); но, что после того, как эта
окружность выбрана, с необходимостью определяется то семейство окруж-
окружностей, изогональных к окружностям (а2), (^3) и (&',, к которому должна
принадлежать окружность (k4) или (&2").
2) Знать это обобщение весьма существенно; в самом деле, может слу-
'читься, что окружность (&/) не существует (т. е. построение п. 311 ока-
окажется невозможным) даже и в том случае, когда рассматриваемая задача
имеет решение.
19*
СМЕШАННЫЕ ЗАДАЧИ И ЗАДАЧИ, ПРЕДЛАГАВШИЕСЯ
НА КОНКУРСНЫХ ЭКЗАМЕНАХ 1).
343. Пусть А, В, С, D — четыре точки, лежащие иа одной окружности
<следующие друг за другом в том порядке, как они перечислены); возьмём
середины а, Ь, с, d дуг АВ, ВС, CD, DA. Показать, что прямые ас и bd
перпендикулярны.
344. На сторонах ВС, СА, АВ треугольника взяты три произвольные
точки D, Е, F и проведены окружности AEF, BFD, CDE. Доказать:
1) что эти три окружности проходят через одну точку (У,
2) что если соединить какую-нибудь точку Р плоскости треугольника
с его вершииам-и А, В, С, то вторые точки а, Ъ, с, в которых эти прямые
РА, РВ, PC пересекают соответствующие окружности, лежат на одной
окружности, проходящей через точки О и Р.
345. Построим на каждой стороне вписанного четырёхугольника как на
хорде какую-пибуть окружность. Четыре новые точки, в которых каждая
из построенных таким образом окружностей пересекает следующую за ней,
будут также вершинами вписанного четырёхугольника (доказать).
346. Пусть А и А' — точки пересечения окружности Sj с окружностью
S2; В и Е> —точки пересечения окружности S2 с окружностью S3; С и С —
точки пересечения окружности S3 с окружностью 6; D и D' — точки пере-
пересечения окружности S4 с окружностью Sy, условие, при котором четырёх-
четырёхугольник ABCD (а, следовательно, в силу предыдущего и четырёхугольник
А'В'CD') может быть вписан в окружность, заключается в том, чтобы
сумма углов между S, и 55 и между S3 и $4 [ПРИ условии, что эти углы
берутся в надлежащем направлении2)] равнялась сумме углов между S2
и Ss и между St и S, (доказать).
347. Если четыре окружности Slt S2,S3, S4таковы, что, построив „пару"
общих касательных (т. е. две внешних или ^две внутренних общих каса-
касательных) о и о' к S, « S2, пару общих касательных р и f к S8 и S3> пару
общих касательных р / к 53 и S, и пару общих касательных Ъ и Ь'
к S4 и S{ и выбрав „надлежащим образом" по одной касательной из каж-
каждой пары, мы получим четыре прямые а, р, -у ц &t касательные к одной
окружности, то и четыре прямые а', $', -f и 8' будут касательными к одной
окружности.
h Задачи 349, 350, 353, 354, 384, 386, 387, 393, 394, 400, 404, 413 заим-
заимствованы из тем, предлагавшихся на .Concours general des lycees el col-
colleges"; задачи 365, 374, 397, 406, 409, 412, 421 — из тем, предлагавшихся на
.Concours de I'Agregation des sciences mathematiques". Впрочем, мы не счи-
гали необходимым воспроизводить в точности предлагавшиеся там формули-
формулировки; в частности, мы должны были внести в них некоторые изменения,
чтобы привести их в согласие с упражнениями, предложенными в тексте
настоящей книги.
2) Следует стремиться, рассматривая направленные углы и используя
в случае надобности указания, имеющиеся в курсах тригонометрии, к
получению доказательств, пригодных при любом расположении элементов
фигуры.
СМЕШАННЫЕ ЗАДАЧИ 293
Выбрав на каждой из четырёх окружностей определённое направление
и рассматривая отрезки общих касательных как имеющие знак, выяснить,
как именно следует выбирать четыре касательные а, р, f и &, чтобы это
предложение имело место.
Это будет иметь место при условии, что сумма длин двух из общих
касательных (считая от одной точки касания до другой) равняется сумме
длин двух других общих касательных.
348. Около каждого треугольника, образованного тремя последователь-
последовательными сторонами (или их продолжениями; произвольною пятиугольник.!,
описана окружность. Доказать, что пять точек (отличных от вершин пяти-
пятиугольника), в каждой из которых одна из окружностей пересекает следую-
следующую за ней, лежат на одной окружности (задача 106).
349. Даны два равных треугольника ABC и abc. Найти геометрическое
место точек О таких, что если повернуть 1реугольник ABC около точки О
так, чтобы сторона АВ заняла положение а'Ь'\ параллельное ас, то новое
положение Ь' вершины В будет находиться на прямой ОС. Найти также
при этих услоьиях геометрические места, описываемые точками а',
ft', с'.
350. Пусть А', В', О—точки, симметричные с точкой пересечения высот
треугольника ABC относительно трёх его сторон ВС, СА, АВ. Пусть да-
лее М и N — точки, в которых прямая В'С пересекает соответственно
стороны АС и АВ; Р и Q — точки, в которых прямая С А' пересекает ВА
и ВС; К и S — точки, в которых прямая А'В' пересекает СВ и С А. Пока-
Показать, что прямые MQ, NR, PS пересекаются в одной точке (эта точка будет
точкой пересечения ьысот треугольника ABC).
351. Вписать в данную окружность тралению, зная её высоту и сумму
или разность оснований.
352. Пусть АВ~- диаметр некоторой окружности, CMD — другая окруж-
окружность с центром в точке А, пересекающая первую окружность в точках
С и D; точка М — произвольная точка второй окружности; N, Р, Q —
точки, в которых прямые ВМ, CM, DM пересекают соответственно первую
окружность.
1°. Доказать, что MPBQ — параллелограм.
2°. Доказать, что MN — среднее пропорциональное между NC и ND.
353. Дан равнобедренный треугольник ОАВ (ОА = ОВ). Опишем из
вершины О, как из центра, окружность с переменные радиусом, к которой
проведём соответственно из точек А к В две касательныг, не пересекаю-
пересекающиеся на высоте треугольника.
1°. Найти геометрическое место точек М пересечения этих двух
прямых.
2°. Показать, что произведение МА-МВ равно разности квадратов
отрезков ОМ и ОА.
3°. Найти геометрическое место точек / — концов отрезков, равных МА,
отложенных на прямой MB от точки М.
354. Возьмём на основании ВС какого-либо треугольника ABC произ-
произвольную точку D и опишем около треугольников ABD и ACD две окруж-
окружности, центрами этих окружностей пусть будут О и О1.
1°. Показать, что отношение радиусов этих окружностей есть величина
постоянная.
2°. Найти положение точки D, для которого эти рачиусы будут иметь
наименьшую длину.
3°. Показать, что треугольник АОО' подобен треугольнику ABC.
4°. Найги геометрическое место точек М, делящих отрезок 00' в дан-
данном отношении; исследовать случай, когда соответствующая точка будет
проекцией вершины А на прямую 00".
355. Вокруг одной из точек пересечения двух окружностей вращается
угол постоянной величины, стороны которого пересекают окружности
соответственно в точках М и М'. Найти геометрическое место точек, де-
294 СМЕШАННЫЕ ЗАДАЧИ
ляшнх отрезок ММ' в данном отношении. Найти геометрическое место
вершин треугольников, построенных на ММ' как на основании и подобных
данному треугольнику.
356. Если пять прямых А, В, С, D, Е таковы, что на двух из них,
например на А и В, три другие прямые отсекают пропорциональные от-
отрезки, то и на двух любых из них три другие прямые будут отсекать
пропорциональные отрезки (доказать).
(При доказательстве следует различать два случая, смотря по тому,
принадлежи г ли к числу тех двух прямых, для которых доказывается тео-
теорема, одна из двух первых прямых или нет.)
357. Пусть а, Ь, с — стороны треугольника; х, у, г —расстояния какой-
нибудь точки плоскости от его сторон. Доказать, что если эта точка лежит
иа окружности, описанной около треугольника, то одно из отношений
а- Ъ с , ,,
— , —, —будет равно сумме двух других. Рассмотреть ооратную теорему.
358. Пусть С—некоторая точка отрезка АВ; найти геометрическое
место точек пересечения переменной окружности, прохо 1ящей через точки
А и В, с прямой, соединяющей точку С с точкой пересечения касательных
к этой окружности в точках А и В.
359. Из переменной точки М, взятой на провдлжении определённого
диаметра окружности О, проведена касательная к этой окружности. Найти
I еометричеекое место таких точек Р на этих касательных, что РМ — МО
(п. 92).
360. Из точки М, лежащей в плоскости прямоугольника, опущены пер-
перпендикуляры на его стороны, причём один из перпендикуляров пересекает
дье протиноположные стороны («ли их нроло 1жения) в точках Р и Q, а
вюрой пересекает две другие стороны (или их продолжения) в точках/? hS.
1°. Какова бы ни была точка М, точка пересечения Н прямых PfinQS
лежит всегда на одной и той же прямой; точка пересечения К. прямых
PS и QR также лежит всегда на одной и той же прямой, отличной от пер-
первой (доказать,.
2°. Биссектриса угла НМК параллельна одной из сторон прямоуголь-
прямоугольника (доказать).
3°. Найти точку /И, зная точки Н и К.
4°. Последняя задача имее1 два решения. Показать, что окружность,
имеющая своими диаметрально противоположными точками точки М и М',
удовлетворяющие условиям задачи, пересекает ортогонально окружность,
описанную около прямоугольника.
5°. Найти геомефическое место таких точек М, чтобы прямая Р/?была
перпендикулярна к QS.
361. Если в треугольнике ABC через вершины В к С провести две
прямые ВВ' и СО, пересекающие треугольник так, чтобы отрезки этих
прямых, считая от точек В и С соответственно до точек пересечения В' и
С со сторонами АС и АВ, были равны между собою, то два угла — /_СВВ'
и /_В'ВА, на которые прямая ВВ' делит угол В, не могут быть оба оольше
или оба меньше аналогичных углов ВСС и ОСА, на которые прямая
СО делит угол С (т. е. что не может быть одновременно: /_СВВ' >
> ?ВСС'\ /_В'ВА> /_С'СА) (доказать).
(Дополнить треугольник ВВ'С до параллелограма BB'CF, принимая
В и С за его противоположные вершины, и, соединив точки С и F, срав-
сравнить углы при точках О и F.)
Треуюльник, имеющий две равные биссектрисы,—равнобедренный
доказать).
361а. Во всяком треугольнике большей стороне соответствует меньшая
биссектриса (доказать).
(С помощью формулы п. 129 найти разность квадратов двух биссектрис
и выделить в полученном выражении множитель, равный разности соответ-
соответствующих сторон.)
СМЕШАННЫЕ ЗАДАЧИ 295
362. Среди всех треугольников, вписанных в данный треугольник,
найти тот, который имел бы наименьший периметр.
362а. Вписать в данный четырёхугольник ABCD четырёхугольник MNPQ
с наименьшим периметром. Показать, что задача не имеет решений в соб-
собственном смысле этого слова (т. е. таких, чтобы получались настоящие
чвтырёхугольники) в том случае, если данный четырёхугольник нельзя
вписать в круг.
Но если ABCD будет вписанным четырёхугольником, то существует
бесчисленное множество четырёхугольников MNPQ с одинаковым перимет-
периметром, меньшим периметров всех других четырёхугольников, вписанных в
ABCD. Этот общий периметр будет четвёртым пропорциональным к радиусу
окружности ABCD и диагоналям АС и BD.
Каким условиям должен, кроме того, удовлетворять четырёхугольник
ABCD для того, чтобы найденные таким образом различные четырёхуголь-
четырёхугольники MNPQ сами были вписанными?
Найти в этом случае геометрическое место центров описанных около
них окружностей.
363. Показать, что если точка, найденная в задаче 105, лежит внутри
треугольника, то оиа обладает тем свойством, что сумма её расстояний от
трёх вершин будет наименьшей (упр. 269). Вычислить эту сумму (её квад-
квадрат равен полусумме квадратов трёх сторон, сложенной с произведением
площади треугольника на 2|^3).
Что случится, если эта точка будет лежать вне треугольника? (Это
-будет в том случае, если один из углов, например угол А, будет больше
120°. Теорема Птоломея дает отношение суммы АВ-\-АС к отрезку А/,
отсекаемому описанной окружностью на биссектрисе угла А. Применяя
теорему п. 237а к четырёхугольнику ВМС1, увидим, что сумма МА -{- МВ-\-
-f- МС будет наименьшей, когда точка М совпадает с А.)
364. Найти такую точку, чтобы сумма её расстоянии от трёх вершин
данного треугольника ABC, соответственно умноженных на 1ри данных
положительных числа /, т, я, была наименьшей. Предполагается, что на
трёх отрезках, пропорциональных данным числам, можно построить тре-
треугольник.
(Пусть Т — такой треугольник: a, (S, -у—его углы. Построим при точке А
два угла ВАС, CAB1, равные а; при точке В — два угла СВА', ABC, рав-
равные (S; при точке С—два угла АСВ', ВС А', равные -j, так. чтобы все углы
были расположены вне треугольника ABC. Прямые АА', ВВ1, СС пересе-
пересекутся в одной точке, которая и будет искомой точкой, если оиа лежи!
внутри данного треугольника. В противном случае, а также в случае, если
данные числа не пропорциональны сторонам треугольника, минимум будет
иметь место в вершине треугольника ABC.
В первом случае, когда минимум имеет место не для вершины тре-
треугольника, квадрат этого минимума может быть выражен через величину
/2 ф1 _(- c-i _ Я2) _|- щЪ (С2 + Й2 _ fc2j _|_ П1 (а _|_ ?2 _ с^
и через произведение площадей треугольника ABC и треугольника Т.)
365. Разделим каждую сторону треугольника на части, пропорциональ-
пропорциональные квадратам прилежащих сторон, и соединим точки деления с противо-
противоположными вершинами. Доказать, что:
1) полученные таким образом прямые пересекаются в одной точке О*;
2) эга точка совпадёт с точкой, которая получается в задаче 197, если
принять за точку О центр тяжести треугольника;
3) эта точка будет центром тяжести треугольника PQR, образованного
её проекциями на стороны данного треугольника.
366. Вписать в данный треугольник другой треугольник так, чтобы
сумма квадратов его сторон была наименьшей. (Допустить, что ыинныук
существует, и показать, что он будет иметь место только в случае тре-
треугольника PQR предыдущей задачи.;
296
СМЕШАННЫЕ ЗАДАЧИ
Вывести отсюда, что точка О', найденная в предыдущей задаче, обла-
обладает тем свойством, что сумма квадратов её расстояний от трёх сторон
Судет наименьшей (упр. 137, 140).
Более общая задача: вписать в данный треугольник другой треуголь-
треугольник так, чтобы сумма квадратов его сторон, умноженных соответственно
иа данные числа, была наименьшей.
367. Вписать в данную окружность такой треугольник, чтобы сумма
квадратов его сторон, умноженных соответственно на данные числа, была
наибольшей.
368. Для того чтобы задача, поставленная в упражнении 127 (найти
точку, расстояния которой от трёх вершин треугольника ABC были бы
пропорциональны трём данным числам т, п, р), имела решение, необходимо
и достаточно, чтобы можно было построить треугольник, длины сторон
которого были бы соответственно равны т-ВС, п-СА, р-АВ.
369. Пусть через вершины А, В, С треугольника проведены три пря-
прямые таким образом, что отрезки AD, BE, CF этих прямых от вершин до
противоположных сторон раины между собою. Если провести через любую
точку О внутри треугольника прямые, параллельные этим прямым, до пе-
пересечения с соответствующими сторонами, то сумма отрезков, полученных
таким образом из этих прямых, считая от точки О, будет постоянной, где
бы ни была расположена эта точка.
370. Если три прямые проходят через одну точку, то всегда сущест-
существуют такие два числа, что расстояние любой точки плоскости от одной из
прямых будет равно сумме или разности расстояний той же точки от двух
других прямых, умноженных на эти часла (доказать). Сформулировать ре-
результат так, чтооы он совершенно не зависел от положения точки (с по-
помощью соответствующего условия относительно знаков).
Обратно, сумма или разность расстояний любой точки М плоскости от
двух данных прямых, умноженных, соответственно на данные числа, будет
пропорциональна расстоянию точки М от некоторой прямой, проходящей
через^точку пересече шя двух первых прямых (доказать).
3?1. Найти геометрическое место таких точек, что сумма их расстояний
от п данных прямых, взятых с надлежащими знаками и умноженных на
какие-либо данные числа, будет постоянна; другими словами, найти геомет-
геометрическое место таких точек, чтобы алгебраическая сумма площадей тре-
треугольников, имеющих вершинами каждую из них и основаниями п данных
отрезков, была постоянной. (Предыдущее упражнение даёт возможность
решить задачу для некоторого значения п, если она уже решена для пре-
предыдущего значения.)
Вывести отсюда, что середины трёх диагоналей полного четырёхсто-
четырёхсторонника лежат на одной прямой.
371а. Три окружности, имеющие своими диаметрами диагонали полного
четырёхсторонника, имеют общую радикальную ось. Эта радикальная ось
проходит через точки пересечения высот четырёх треугольников, образо-
образованных сторонами четырёхсторонника, взятыми по три (доказать).
3/2. Противоположные стороны и диагонали любого четырёхугольника
образуют три таких угла, что поляры любой точки О плоскости относи-
относительно каждого из этих углов пересекаются в одной точке (доказать).
(Преобразовать взаимными полярами, принимая точку О за центр на-
направляющей окружности.)
Те же прямые отсекают иа любой прямой три таких отрезка, что отре-
отрезок, делящий гармонически два из них (если такой отрезок существует),
делит гармонически и третий (доказать).
Три отрезка, обладающие этим свойством, называются отрезками, нахо-
находящимися в инволюции.
373. Прямая Симеона (упр. 72), соединяющая основания перпендикуля-
перпендикуляров, опущенных на три стороны треугольника из точки Р описанной
окружности, делит на две равные части отрезок, соединяющий эту точку
с точкой пересечения Н высот треугольника. (Для доказательства показать,
СМЕШАННЫЕ ЗАДАЧИ 297
используя упражнение 70, что точки, симметричные с точкой Р относи-
относительно трёх сторон, лежат на одной прямой, проходящей через точку Н.
Вывести из этой теоремы и из результата, полученного в задаче 106,
что точки пересечения высот четырёх треугольников, образованных че-
четырьмя прямыми, взятыми по три, лежат на одной прямой.
374. Точка пересечения М двух прямых Симеона относительно треуголь-
треугольника ABC, вписанного в данную окружность S, соответствующих двум
точкам Р и Р' этой окружности, списывает окружность S', если точка С
описывает окружность S (г точки Л, В, Р, Р' — неподвижны) (доказать).
Найти геометрическое место центров окружностей У, если точки А
и В остаются неподвижными, а точки Р и Р1 перемещаются по окружно-
окружности S, оставаясь на постоянном расстоянии одна от другой.
Найти также геометрическое место, описываемое точкой М, если (при
неподвижных точках А, В и С) точки Р и Р' перемещаются, оставаясь
диаметрально противоположными друг другу.
375. Найти геометрическое место середин сторон треугольников, впи-
вписанных в данную окружность и имеющих одну и ту же точку пересечения
высот.
376. Окружность девяти точек (задача 101) какого-нибудь треугольника
преобразована с помощью инверсии, имеющей полюс в середине одной из
сторон треугольника и степень, равную степени полюса инверсии относи-
относительно вписанной окружности, или, что сводится к тому же (упр. 90а),—
относительно вневписанной окружности, соответствующей выбранной сто-
стороне. Показать, что прямая, в которую преобразуется окружность девяти
точек, будет опщей касательной к двум последним окружностям (отличной
от стороны треугольника).
Отсюда следует, что окружность девяти точек касается вписанной и
вневписанных окружностей треугольника.
377. Между радиусами Инг описанной и вписанной окружностей
треугольника и расстоянием d между их центрами существует соотношение
(доказать, пользуясь задачей 103 и п. 125)').
Обратно, если между радиусами двух окружностей и расстоянием
между их центрами существует предыдущее соотношение, то можно вписать
в первую из них бесчисленное множество треугольников, описанных около
второй (доказать).
Получить аналогичный результат, заменив вписанную окружность
вневписанной.
378. Во всяком треугольнике ABC:
1) прямая, соединяющая проекцию вершины В на биссектрису угла С
с проекцией вершины С на биссектрису угла В, совпадает с хордой, сое-
соединяющей точки касания Е и F (черт. 102 и упр. 90а) вписанной окружно-
окружности с прямыми АС и АВ\
2) прямая, соединяющая проекцию вершины В на биссектрису угла С
с проекцией вершины С на биссектрису внешнего угла при точке В, сов-
совпадает с хордой, соединяющей точки касания Е3 и Fg вневписанной окруж-
окружности, лежащей внутри угла С, с теми же прямыми;
3) прямая, соединяющая проекцию вершины В на биссектрису внешнего
угла при точке С с проекцией вершины С на биссектрису внешнего угла
при точке В, совпадает с хордой, соединяющей точки касания Е1 и Fx
вневписанной окружности, лежащей внутри угла А, с теми же прямыми;
4) проекции точки А на биссектрисы внутреннего и внешнего углов
с вершиной в точке В и. на биссектрисы внутреннего и внешнего углов
с вершиной в точке С лежат на одной прямой, параллельной ВС, на рас-
расстояниях, последовательно равных р— с, р — а, р — b друг от друга;
См. другое решение той же задачи в упражнении 411.
298
СМЕШАННЫЕ ЗАДАЧИ
5) проектируя вершины каждого из углов А, В, С треугольника иа
биссектрисы внешних углов, к ним не прилежащих, получим шесть
точек, лежащих на одной окружности (сводится к задаче 102); эта окруж-
окружность ортогональна к вневписанным окружностям данного треугольника;
её центр будет центром окружности, вписанной в треугольник А'В'С,
имеющий своими вершинами середины сторон треугольника ABC; её радиус
равен гипотенузе прямоугольного треугольника с катетами, равными полу-
полупериметру треугольника А'В'С и радиусу вписанной в него окружности;
существуют ещё три аналогичные окружности, каждая из которых прохо-
проходит через две проекции вершин на внешние биссектрисы и через четыре
проекции вершин иа внутренние биссектрисы (доказать).
379. Соединим между собою точки касания каждой из вневписанных
окружностей треуюльника с продолжениями его сторон. Показать, что
построенные прямые образуют треугольник, вершины которого лежат иа
соответствующих высотах первого треугольника, и что центр описанной
около второго треугольника окружности лежит в точке пересечения высот
первого треугольника.
380. Пусть дана точка О, соответствующая самой себе (п. 150) в двух
подобных и имеющих одинаковое направление вращения фигурах F и Р',
а также треугольник Т, подобный треугольнику, образованному этой точкой
и двумя какими-нибудь их соответственными точками (п. 150); далее, пусть
даны точка О', сама себе соответствующая в двух подобных и имеющих
одинаковое направление вращения фигурах F' и F", а также треугольник V,
подобный треугольнику, образованному точкой О' и двумя какими-нибудь
соответственными точками этих двух фигур. Построить точку, соответст-
соответствующую самой себе в двух фигурах F и F', и треугольник, подобный тре-
треугольнику, который образован этой точкой и двумя любыми соответствен-
соответственными точками фигур F и F".
3S1. Построить многоугольник, зная вершины треугольников, имеющих
своими основаниями стороны многоугольника и соответственно подобных
данным треугольникам (предыдущее упражнение позволяет свести задачу,
относящуюся к многоугольнику с определённым числом сторон, к задаче,
относящейся к многоугольнику, число сторон которого иа единицу меньше
предыдущего; таким же образом можно поступать до тех пор, пока не
сведём задачу к определению двух вершин мноюугольника). *
В каких случаих задача будет невозможна или неопределённа?
382. Пусть дан треугольник ABC и четыре произвольные точки О,
а, Ь и с. Построим на ВС, как иа основании, треугольник ВСА', подобный
треугольнику ЪсО и имеющий с ним одинаковое направление вращения
(причём точки В и С соответствуют точкам b и су, точно так же — на СА,
как на основании, треугольник CAB', подобный саО, и па АН, как на ос-
основании, треугольник ABC, подобный треутльнику аЬО. Доказать, что
феугольник А'В'С будет подобен треуюльнику, имеющему вершинами
точки, обратные точкам а, Ь, с в инверсии с полюсом в точке О, причём
эти треугольники будут иметь противоположные направления вра-
вращения.
383. Опишем на двух данных отрезках две дуги окружности, вмещаю-
вмещающие каждая один и тот же угол V. Показать, что если угол К изменяется,
то радикальная ось двух окружностей, построенных таким образом, будет
вращаться около некоторой определённой точки (положение этой точки
определяется тем, что треугольники, которые мы получим, соединяя эту
точку с концами каждого отрезка, будут равновелики и имеют равные
углы при их общей вершине).
384. Дан четырёхугольник ABCD (ромбоид), у которого две прилежа-
прилежащие стороны AD, AB равны между собою, так же как и другие две сто-
стороны СИ и CD. Доказать, что стороны этого четырёхугольника касаются
двух окружностей. Найти геометрические места центров этих окружностей
при условии, что данный четырёхугольник— шарнирный и одна из сторон
остаётся неподвижной.
СМЕШАННЫЕ ЗАДАЧИ 299
385. Дан шарнирный четырёхуюльник ABCD, списанный около окруж-
окружности, причём его сторона АВ остаётся неподвижной; при этих условиях
он продолжает оставаться описанным (упр. 87). Найти геометрическое
место центров О вписанных окружностей.
(Предполагая для определённости, что эта окружность лежит внутри
четырёхуюльника, отложить на АВ отрезки АЕ= AD,BF= ВС; тогда, при-
принимая но внимание упражнение 89, мы придём к упражнению 257.)
Показать, что отношение расстояний от точки О до двух противопо-
противоположных вер-шин А и С (или Ь и D) остаётся постоянным при деформации
четырёхугольника.
386. Пусть даны четыре точки А, В, С, D, лежащие на одной окруж-
окружности; возьмём какую-нииудь точку Р в плоскости *той окружности и
построим онр.жности РАВ, PCD, гкресекающиеся во второй раз в точке Q.
Найти 1еоме1рическое место точки Q, если точка Р описывает прямую
или окружность. Найти также геометрическое место точки Р при условии,
что она совпадает с точкой Q.
387. Соединим вершины квадрата А, В, С, D с какой-нибудь точкой Р
его плоскости; полученные прямые пересекут окружность, описанную
около квадрата, в четырёх новых точках А', В', С, D'. Доказать, что в
четырёхугольнике A'B'CD' произведения противоположных сторон будут
равны между собой:
A'B'-CD'=A'D'B'C.
Обратно, пусть имеем вписанный четырёхугольник A'B'CD, произве-
произведения противоположных сторон которого равны между собою; найти такую
точку Р, что прямые PA', PB', PC',PD' пересекают описанную окружность
в вершинах квадрата. (Этот вопрос является частным случаем упр. 270,5°.
Однако задача допускает здесь два решения, в то время как в общем слу-
случае она имеет только одно. Выяснить причину этого различия.)
388. Найти такую инверсию, чтобы вершины данного вписанного че-
четырёхугольника A'B'CD' преобразовались в вершины прямоугольника
(обобщение задачи 387). Покааать, что полюсы инверсии будут предель-
предельными точками (упр. 152) описанной окружности и третьей диагонали четырёх-
четырёхсторонника, порученного продолжением сторон четырёхугольника A'B'CD'.
389. Преобразовать с помощью инверсии четыре данные точки в че-
четыре вершины параллелограма (дальнейшее обобщение задач 387 и 388).
390. Даны две окружности и точка А; найти такую инверсию, чтобы
точка, соответственная точке А, совпала с одним из центров подобия
окружностей, в которые преобразуются данные окружности.
391. Соединим переменную точку М данной окружности с двумя опре-
определёнными точками А и В; пусть Р и Q— вторые точки пересечения полу-
полученных прямых с данной окружностью, /? — вторая точка пересечения той
же окружности с прямой, параллельной АВ и нроходяшей через точку Р.
Показать, что прямая QR пересекает АВ в неподвижной точке.
Вывести отсюда способ вписать в данную окружность треугольник,
две стороны которого проходят через данные точки, а третья параллельна
данному направлению; или треугольник, все три стороны которого прохо-
проходят через данные точки (эти оба вопроса сводятся один к другому и к эа-
даче 115). Решить аналогичную задачу для многоугольника с любым числом
сторон (другой способ был предложен в упр. 253а).
392. Описать около окружности треугольник, вершины которого лежат
на данных прямых.
393. Построим две перемен-ные окружности, касательные к одной
прямой в двух её определённых точках А и В и в то же время касатель-
касательные между собой. Эти две окружности имеют ещё одну общую касатель-
касательную А'В'. Доказать, что окружности, имеющие своими диаметрами отрезки
А'В', касаются одной и той же окружности, и найти геометрическое место
середин отрезков А'В'.
300 СМЕШАННЫЕ ЗАДАЧИ
. 394. Две переменные окружности С и С\ касаются данной окружно-
окружности в двух данных её точках А и В и, кроме того, касаются друг друга
в точке М.
1°. Найти геометрическое место этой точки.
2°. Найти геометрическое место вторых центров подобия N окружно-
окружностей С и С,.
3°. Каждой точке N предыдущего геометрического места соответст-
соответствуют две пары окружностей С и С,, С и С,', удовлетворяющих указанным
условиям, и, следовательно, две точки прикосновения М и М' (доказать).
4°. Найти геометрическое место центров окружностей, описанных
около треугольников NMM'.
5°. Найти 1еометрическое место центров окружностей, вписанных в
эти треугольники.
6°. Найти 1еометрическое место точек пересечения их высот.
7°. Доказать, что всякая точка, общая двум нз этих геометрических
мест, будет принадлежать и третьему из них.
395. Пусть даны две пересекающиеся окружности С и С. Опишем
окружность около треугольника, образованного одной из их точек пере-
пересечения А и точками прикосновения Р и Р одной из их общих касатель-
касательных. Показать, что угол, иод которым оiрезок РР виден из центра этой
окружности, равен углу между окружностями С и С и что радиус атой
окружности есть среднее пропорциональное между радиусами данных
окружностей (откуда следует предложение, указанное в упр." 262, 3°).
АР
Доказать, что -rg? есть корень квадратный из отношения тех же радиусов.
Аг
396. Найти необходимые и достаточные условия, которым должны
удовлетворять четыре окружности А, В, С, D, для того чтобы можно было
преобразовать с помощью инверсии фигуру, образованную первыми двумя
окружностнми, в фигуру, равную той, которую образуют две последние
(или, употребляя выражения, введённые в прибавлении А, пп. 289, 294,
найти инварианты фигуры, образованной двумя окружностями, относительно
группы инверсий).
1°. Если окружности А и В имеют общую точку, то необходимо и
достаточно, чтооы угол между этими двумя окружностями был равен углу
между окружностями С и D, или, что сводится к тому же (предыдущая
задача), чю отношение отрезка общей касательной к среднему пропорцио-
пропорциональному их радиусов имеет одинаковую величину в обоих случаях.
2°. Если окружности А и В не имеют общих точек, то необходимо
и достаточно, чтооы отношение радиусов концентрических окружностей,
в которые их можно преобразовать одной и той же инверсией (упр. 248),
было равно отношению радиусов концентрических окружностей, в кото-
которые можно преобразовать окружности С н D также одной и той же инвер-
инверсией (вообще говоря, отличной от первой).
(Пользуясь терминологией, введённой в Прибавлении А, можно сказать:
необходимо и достаточно, чтобы фигуры (А, В) и (С, D) имели одну и ту
же приведённую форму относительно инверсии.;
Этот результат может быть выражен иначе. Сложное отношение (п. 212)
точек пересечения двух окружностей А и В с любой из окружностей, им
ортогональных, есть величина постоянная, и то же самое имеет место для
сложного отношения двух из этих точек и двух предельных точек. Искомое
условие состоит в том, чтобы это сложное отношение имело одинаковое
значение как для окружностей С и D, так и для окружностей А и В
(доказать).
Наконец, если г, г' — радиусы окружностей А и В, d — расстояние
dP — г2 — г'2
между их центрами, то величина ; должна иметь то же число-
числовое значение, как и аналогичная величина, вычисленная для окружностей CkD
(доказать).
СМЕШАННЫЕ ЗАДАЧИ
301
Можно ещё сказать, что если две окружности А и В имеют общую
касательную (например внешнюю) длины t, и то же имеет место для окруж-
окружностей С и D, то отношение г— должно иметь одно и то же значение в
У гг'
обоих случаях.
397. Пусть даны две точки А, А' и две прямые D, ГУ, параллельные
прямой АА' и находящиеся от неё на одинаковом расстоянии.
1°. Доказать, что каждой точке Я, взятой на прямой D, соответствует
точка Я', лежащая на D' и обладающая тем свойством, что прямая РР
будет общей касательной к окружностям РАА' и Р'АА'. '
2°. Доказать, что произведение расстояний от точек А, А' до пря-
прямой РР есть величина постоянная.
3°. Найти геометрическое место проекций точки А иа прямые РР'.
4°. Найти такую точку Я, чтобы прямая РР проходила через данную
точку Q.
5°. Доказать, что угол между окружностями РАА' и РАА', а также
угол РАР постоянны.
398. Пусть АВ—диаметр окружности С; D — перпендикуляр к этому
диаметру, по предположению пересекающий С; с к с'—окружности, имею-
имеющие своими лиаметрами соответственно отрезки, на которые D делит АВ.
Строим окружность, касательную к С, с, D, и окружность, касательную к
С, с', D. Показать, что эти две последние окружности равны между собою:
их общий радиус будет четвёртым пропорциональным к радиусам окруж-
окружностей С, с, с'.
399. [Арбелос1) греческой геометрии.) Пусть А и В—две окружности,
касающиеся друг друга; С — окружность, касающаяся их обеих; Q — окру-
окружность, касающаяся А, В, С; С2—окружность, касающаяся А, В, Q; С8 —
окружность, касающаяся А, В, С2; и т. д.; С„ — окружность, касающаяся
А, В, Cn_j. Рассмотрим расстояние центра одной какой-нибудь из окруж-
окружностей С, Си С%, ...,С„ от линии центров окружностей 4 и ? и отношение
этого расстояния к диаметру соответствующей окружности. Доказать, что
это отношение изменяется на единицу, если перейти к одной из окруж-
окружностей Сп к окружности, непосредственно за ней следующей, по крайней
мере, в случае, если эти окружности будут касаться внешним образом (что
всегда будет иметь место, если окружности А и В касаются друг друга
внутренним образом), и их центры будут лежать по одну сторону от линии
центров окружностей А и В. Показать, как следует изменить эту формули-
формулировку в остальных случаях.
400. Пусть Л, В, С — три окружности с центрами соответственно в
вершинах треугольника и попарно касаюшиеся друг друга внешним обра-
образом (упр. 91).
Зная стороны а, Ь и с данного треугольника, вычислить радиусы окруж-
окружностей, касающихся этих трёх окружностей (предыдущая задача и упр. 301).
401. Даны три окружности с центрами Л, В, С и радиусами а, Ь, с; пусть
Л — радикальный центр трёх других окружностей, концентрических первым
и имеющих радиусы, равные n-\-h, b-\-ti, c-\-h\ иа АН возьмём такую
AN a
точку N что -ггг = . Показать, что с изменением Л точки Н и N
J ' An a -\-h
описывают прямые, первая из которых проходит через центры окружностей,
касающихся данных окружностей (одинаковым образом), а вторая — через
точки прикосновения этих окружностей к окружности А.
Найти аналогичную теорему для случая окружностей, имеющих с
окружностями Л, В, С разноимённые касания.
402. Найти окружность, пересекающую четыре данные окружности под
равными углами.
1) Арбелос — греческое слово, обозначающее серп.
302
CMFUIAHHhIF ЗАДАЧИ
403. Найти окружность, пересекающую три данные окружности под
данными углами.
(В силу упр. 256 известен угол, под которым искомая окружность
пересекает какую-либо и» окружностей, имеющих с данными
окружностями общий радикальный цецтр. Среди этих окружностей надо,
пользуясь п. 311, найти три окружности, для которых этот угол равен нулю, и,
таким образом, свести задачу к задаче о касании окружностей; или иначе1):
найти среди тех же окружностей две окружности, для которых этот угол
будет прямой, и тогда задача будет снелена к упражнению 259.)
403а. Даны три окружности; построить такую четвёртую окружность,
чтобы отре.шн общих касательных к этой окружности и к каждой из трёх
данных окружностей имели данные длины.
(Эта задача может быть сведена к предыдущей, если провести через
точку касания каждой искомой общей касательной окружность, концентри-
концентрическую соответствующей данной окружности.)
404. Даны; окружность, две точки А, А' иа этой окружности и прямая D.
Показать, что на прямой D существуют две такие точки /, /', что если
через Р, Р" обозначить точки пересечения прямой D с прямыми, соединя-
соединяющими точки А, А' с произвольной точкой М окружности, то произведе-
произведение /P-fP1 постоянно, т. е. не зависит от положения точки М.
405. При тех же обозначениях, что и в предыдущей задаче, показать,
что если прямая D не пересекает окружности, то существуют с той и с
другой стороны от прямой по такой точке, что из каждой из них отре.юк РР'
видеи под постоянным упом 'задача 278).
406. Дйиы две непересекающиеся окружности Sh Sc центрами О и ш и
радиусами, соответственно равными /? и р, рассмотрим окружности С, ка-
касающиеся окружности 5 и ортогональные к окружности S.
1°. Док<пать, что все эти окружности касаются одной и той же окруж-
окружности, отличной от S.
2°. Пусть М и М'— точки пересечения окружностей С и 2; проведём
через определённую точку А, лежащую на прямой Ош, прямые, параллель-
параллельные биссектрисам углов Оь>М, Оъ>М', до пересечения их в точках Р, Р' с
данной прямой D, перпендикулярной к прямой О«. Доказать, что суще-
существуют-две такие точки, что прямые, соединяющие каждую из инх соответ-
соответственно с точками Р, Я', будут взаимно перпендикулярны.
3°. Доказать, что существуют две такие точки, что из каждой из них
отрезок РР' видеи пол постоянным углом (предыдущая задача).
4°. Пусть С\ — то положение окружности С, при котором она пересе-
пересекает окружность S в точках М, М'; С*—второе положение той же окруж-
окружности, при котором она пересекает S в точке М' и третьей точке М"; С3 —
положение той же окружности, при котором она пересекает ? в точках М" и
М"'; и т. д. Найти условие, при котором окружность Сп±х совпадае1 с С\.
(Обозначим расстояние Ои> через d\ тогда прямоугольный треугольник,
гипотенуза которого равна d3—№ — рг (или №-\-р*— rf2), а один из катетов
равен 2/?р, должен иметь один из острых углов, равный половине централь-
центрального угла, соответствующего стороне правильного выпуклого или звездча-
звездчатого мноюугольннка, число сторон которого равно п или одному из дели-
делителей числа п.)
Если окружности S и S пересекаются, то точки М, М', М", М"', ...
будут иметь своим предельным положением одну из их точек пересечения.
407. На прямой, проведённой через точку пересечения диаюналей впи-
вписанного чегырёхуюльника и перпендикулярной к радиусу, проходящему
!) Задача, рассмо1ренная в п. 311, не всегда имеет решение, так как
упомянутая там тпчка а может лежать внутри данных окружностей; это
может иметь место даже в том случае, когда рассматриваемая сейчас
задача имеет решение; показать, что этого затруднения всегда можно из-
Сежать, комбинируя надлежащим обр.иом оба указанных нами метода.
СМЕШАННЫ? ЗАДАЧИ 303
через эту точку, две противоположные стороны четырёхугольника отсекают
равные отрезки (доказать).
408. Даны две окружности С, С и две пересекающие их прямые.
Доказать, что окружность, проходящая (задача 107а) через точки пересечения
хорд, стягивающих дуги, отсечённые иа окружности С, с хордами,
стягивающими дуги, огсечённьге на окружности С, будет иметь общую
радикальную ось с окружностями С и С' (воспользоваться упр. 149).
409. Даны две концентрические, окружности S и С и третья окруж-
окружность С\. Геометрическое место центров таких окружностей, ортогональных
к С, что радикальная ось какой-либо из них и окружности С\ касается S,
есть окружность 5'ь концентрическая с Q (доказать;.
Обратно, геометрическое место центров таких окружностей, ортогональ-
ортогональных к окружности С\, что радикальная ось каждой такой окружности и
окружности С касается окружности S,, есть окружность S (доказать).
410. Примем каждую точку данной окружности С за центр новой окруж-
окружности, радиус которой находится в данном отношении к расстоянию от
этой точки до данной точки А плоскости Гили, общее, к отрезку касатель-
касательной, проьедённой из этой точки к некоторой второй окружности). Показать,
что существует точка Р, имеющая одну и ту же степень относительно всех
построенных таким образом окружностей.
Радикальная ссь каждой из этих окружностей и окружности С будет
касательной к определённой окружности с центром в точке Р (доказать).
411. Проводим через какую-нибудь точку окружности С касательные к
окружности С. Показать, что прямая, соединяющая между собой вторые
точки пересечения этих касательных с окружностью С, будет в сною оче-
очередь касательной к некоторой определённой окружности (сводится к пре-
дычущей задаче). Эта окружность имеет общую радикальную ось с окруж-
окружностями С и С.
Вычислить радиус этой новой окружности и расстояние от её центра
ло центра окружности С, зная радиусы данных окружностей и расстояние
между их центрами.
Вывести отсюда решение задачи 377.
412. Даны угол АОВ и точка Р.
1°. Найти иа стороне О А такую точку М, чтобы две окружности С и
С, касательные к ОБ и проходящие через точки М и Р, пересекались под
данным углом.
2°. Изучить изменение угла между окружностями С и С* при переме-
перемещении точки М по ОА.
3°. Пусть Q и Q' будут точками (отличными от М), в которых эти
окружности пересекают сторону ОА. Показать, что окружность, проходя-
проходящая через точки Р, Q, Q\ остаётся, касательно 4 к некоторой определённой
прямой при перемещении точки М по ОА (сводится к предыдущей задаче).
413. Отложим на двух данных параллельных прямых от точек их пересе-
пересечения А и В с их общим перпендикуляром два таких отрезка АС и BD, чтобы
площадь трапеции ABDC была равна площади данного квадрата. Найти
геометрическое место точек Н — проекций серечипы отрезка АВ на пря-
прямую CD (надо рассмотреть два случая, в зависимости от того, будут ли
отрезки АС и BD отложены в одном направлении или в противоположных
направлениях).
414. Дать другое решение вопроса, предложенного в зацаче 329
(провести через точку, данную внутри угла, секущую так, чтобы она об-
образовала со сторонами угла треугольник данной площади). Построить
сначала параллелограм с вершиной в данной точке, одни из углов которого
совпадает со сторонами данного угла. Этот параллелограм выделяет'из иско-
искомого треугольника две треугольные части, сумма площадей которых известна.
Таким образом, вопрос можно свести к задаче 216.
415. Построить треугольник по углу, периметру и площади (упр. 90а, 299).
Из всех треугольников с одинаковым углом и с одинаковым перимет-
периметром определить тот, который имеет наибольшую площадь.
304
смешанные задачи
416. Построить треугольник по стороне, периметру и плошали (можно
построить фигуру, образованную вписанной и вневписанпой окружностями).
Среди всех треугольников с обшей стороной и одинаковой площадью
найти тот, который имеет наименьший периметр. Из всех треугольников
с общей стороной и одинаковым периметром определить тот, который
имеет наибольшую площадь.
417. Иэ всех треугольников с одинаковым периметром определить тот,
который имеет наибольшую площадь.
418. Построить четырёхугольник по четырём его сторонам и площади
(пусть ABCD будет искомым четырёхугольником, так что АВ — а, ВС = Ь,
CD = c, DA — d. Пусть АВС\ — треугольник, внешний по отношению кэтому
четырёхугольнику, раьнивеликий треугольнику ADC и имеющий
/_ ClBA^= /_ ADC. Надо доказать последовательно, что известны следующие
величины: 1) сторона ВС\, 2) разность квадратов АС и АСг; 3) проекция
CQ иа АВ\ 4) наконец, при помощи данной площади можно узнать проекцию
СС\ на перпендикуляр к АВ, что позволит, отложив где-нибудь отрезок
АВ — а, построить отрезок, равный и параллельный ССЪ и, следовательно,
закончить требуемое построение).
Если задача возможна, то оиа имеет в общем случае два решения. Для
обоих получающихся четырёхугольников треугольник, рассмотренный в
упражнении 270, имеет одну и ту же форму, и, следовательно (упр. 270, 5°),
оба четырёхугольника можно рассматривать как взаимно обратные
(доказать).
Дан некоторый четырёхугольник; построить второй четырёхугольник,
не равный данному, но имеющий те же стороны и ту же площадь.
Доказать, что среди всех четырёхуюльников с данными четырьмя
сторонами наибольшую площадь будет иметь вписанный четырёхугольник.
418а. Доказать, что произведение диагоналей ей/ четырёхугольника
выражается в функции его сторон а, Ь, с и d и его площади S формулой
' — fc2 — d2p + \6S\
а угол между диагоналями — формулой
4S
Вывести отсюда новое решение предыдущей задачи (задавшись положе-
положением одной из сторон, мы определим каждую из остальных вершин как
точку пересечения двух окружностей).
419. Построить вписанный четырёхугольник по четырём сторонам.
419а. ' Доказать, что из всех многоугольников с одинаковым числом
сторон и одинаковым периметром наибольшую площадь будет иметь правиль-
правильный многоугольник.
(Допустить, что существует многоугольник с наибольшей площадью;
тогда можно доказать при помощи задачи 418, что этим многоугольником
может быть только правильный многоугольник).
Предыдущий результат можег быть иначе сформулирован так: если
обозначить площадь многоугольника через S, а его периметр через р, то
отношение -^- будет для правильного многоугольника больше, чем для
неправильного многоугольника с тем же числом сторон.
420. Среди всех замкнутых линий одинаковой длины окружность огра-
ограничивает наибольшую площадь (доказать).
(Рассмотреть отношение — для правильного многоугольника, вписан-
вписанного в окружность, и для многоугольника, вписанного в кривую выпуклую
замкнутую линию той же длины, при условии, что число сторон одинаково
в тим и в другом случае и безгранично возрастает.)
СМЕШАННЫЕ ЗАДАЧИ 305
420а. Если О — точка пересечения диаюиалей четырёхугольника ABCD,
то центры О,, O-i, Од, О4 окружностей, описанных около треугольников ОАВ,
ОВС, OCD, ODA, образуют параллелограм Р.
1°. Если этот .параллелограм дан, то площадь четырёхугольника, а так-
также длины его диагоналей тем самым определяются (доказать).
2°. Если точки Оь О2, Оз, О4 даиы и точка О описывает прямую А, то
вершины четырёхугольника описывают стороны параллелограма Р' (дока-
(доказать). Рассмотреть изменение этого параллелограма в связи с переме-
перемещением А. Найти такое положение прямой Д, для которого его площадь
будет наибольшей.
3°. Построить четырёхугольник ABCD, зная два угла этого четырёх-
угольника и параллелограм Р или зная Я и отношения , (исследо-
вать).
421. Радиусы кругов, описанных (упр. 66) около четырёхугольников,
образованных один биссектрисами внутренних углов, а другой биссектри-
биссектрисами внешних углов данного четырёхугольника, относятся, как
а А-с — b — d
— (а, Ь, с, d — стороны данного четырёхугольника, взятые
й -J- С -у- О -\~ и
в последовательном порядке).
421а. Продолжим до их пересечения в точках Е и F противоположные
стороны вписанного четырёхугольника и проведём биссектрисы полученных
таким образом углов. Показать:
1) что эти прямые пересекаются иа прямой, соединяющей середины диаго-
диагоналей данного четырёхугольника, и делят отрезок этой прямой между
серединами диагоналей в отношении, равном отношению диагоналей;
2) что они будут также биссектрисами углов, под которыми этот отре-
отрезок виден из точек Е и F;
3) что они пересекают стороны данного четырёхугольника в четырёх
точках ютличиых от Е и F), которые будут вершинами ромба. Стороны
этого ромба параллельны диагоналям данного четырёхугольника; их длина
есть четвёртая пропорциональная к этим диагоналям и нх сумме;
4) сформулировать аналогичные предложения для биссектрис углов,
образованных двумя противоположными сторонами, одна из которых про-
продолжена до точки их пересечения, а другая — за точку их пересечения;
5) показать, что отрезок EF относится к отрезку, соединяющему сере-
середины диагоналей, как удвоенное произведение этих последних к разности
их квадратов. Вычислить длину отрезка EF, зная стороны четырёхуголь-
четырёхугольника.
422. Пусть О—внутренняя точка треугольника AxA«As; (ft/), (k2')
{ks') — окружности, вписанные в треугольники /Ц/13О, A^Afi, A^Afi. Дока-
Доказать, что:
1°. Если (kx)—какая-нибудь окружность, концентрическая с (к{), то
можно присоединить к ней окружность (&2), концентрическую с (Л2'), и
окружность [ks), концентрическую с (Л8'), так что (Л2), [k3) будут пересе-
пересекаться в точке Л^1, расположенной на Aft; Ш3), (kx) — в точке Л^2, располо-
расположенной иа А2О\ (&i), (fe2)— в точке Л'д, расположенной иа ASO.
2°. Окружность (&j) пересекает сторону" A%AS в двух точках т^ и nlt
таких, что Ач/Пх = Л2Л/2 и A^nl = A.iNs.
Точно так же окружность (?2) пересекает Л8Д в двух точках /2 и л2,
таких, что Л^з— A^Vi и Л8гс2= А$Мз, окружность (Лд) пе ресекает AiA2 в двух
точках ls и 1Л3, таких, что Л1/8=Л|Л'1 и Л31л3 = А%М2.
3°. Если радиус окружности (к{) изменяется и одновременно с ним
изменяются радиусы окружностей (&2) и (&д) гак, что сохраняются указан-
указанные и 1° соотношения между ними, то точки Ръ Р2, Я8, отличные от УУЬ
Л'г, А^з, в которых попарно пересекаются три окружности, описывают пря-
20 Элементарная геометрия
306 . СМЕШАННЫЕ ЗАДАЧИ
мые (tt), (t2 , (fg)—общие касательные соответственно к парам окружно-
окружностей (А2') и (Л8'), iks') и {ki), (к{) и ik%). Эти три прямые пересекаются в
одной точке, которая получается из О построением, указанным в задаче 197;
при этом треугольник, о котором там говорится, в данном случае будет
образован центрами окружностей {k{), (k.2') и (k$).
4°. Четыре точки Рь Я3, /,, /3 лежат "(применить задачу 345) на одной
и той же окружности 1х{), которая пересекает стороны А^, AXAS и пря-
прямые (f2), (*g) под одинаковым углом; точно так же P:i, Ръ т-6 т1 лежат на
одной окружности (л:,'), пересекающей под одинаковым углом А2А%, А^АЪ
(ts). (tj); Pj, Ръ щ, п2 лежат на одной окружности (дг3'), пересекающей под
одинаковым углом А$АЬ А%А.2, {t{\, (t2).
Центр окружности (х}') остаётся неподвижным, если радиусы окружно-
окружностей (Л,), (k2), lks) изменяются, как было указано в 3°; прямая, соединяю-
соединяющая его с центром окружности [k\), проходит через точку пересечении
прямых ft[), (?2), Us)- ^о же йля центров окружностей (.г,') и (дг3').
Существуют: окружность {х^, касательная к АЛАЪ АхА-6, (t2), ft3);
окружность (х2\ касательная к А2А3, А2АЪ (t3), (tt); окружность (дг8), каса-
касательная к И3ЛЬ И8И2 (^), ft3).
5°. Точка пересечения прямых тхр.6 и пхР2 лежит на радикальной оси
окружностей (дг2'), (xs'y, она описывает |если радиусы окружностей (Ajj,
(*2Л '*sf изменяются! прямую, соединяющую точку пересечения прямых
(*i). (*2>г Уз1 с точкой прикосновения окружности (*!*) к прямой А„АВ.
Условие, при котором окружности {х2), (х.6) будут касаться друг друга,
сосюиг в том, что указанная прямая совпадает с прямой (^).
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ.
КНИГА ПЕРВАЯ.
ПРЯМАЯ ЛИНИЯ.
УПРАЖНЕНИЯ К ГЛАВЕ I (стр. 35).
1. Если точка С лежит между М и В (черт. 250«), то из ра-
равенства АМ=МВ следует, что АС — МС=МС-\-СВ, откуда МС=
= — (АС—СВ), и аналогично, если точка С лежит между А и М.
Если точка С лежит на продолжении отрезка АВ за точку В
(черт. 2506), то АС— МС=МС— ВС, откуда ЛС = -|г- (АС-\-ВС),
и аналогично, если точка С ле-
лежит на продолжении отрезка АВ а-,
за точку 4.
2. Если полупрямая ОСХ про- ь)
ходит внутри угла MOB (черт.
251), то /_АОСХ— /_МОСл =
= /_ М0С1 -\- /_ СгОВ, откуда
1
М
В
в с
л м
Черт. 250.
, = -^- KZ- AOCY — /_ СХОВ), и аналогично, если полупрямая
АСХ проходит внутри угла АОМ.
В'
В
Черт. 251.
Если полупрямая ОС2 проходит внутри угла А'ОВ', то её про-
продолжение OCj проходит внутри угла АОВ, и /_ МОС^ — 180° — /_MOCV
20*
308
РЕЮТНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если полупрямая ОС3 проходит внутри угла BOA', то /_АОСЬ —
- /. МОСЬ = /_ МОС, - /_ ВОС3, откуда Z МОСЬ = у (Z А0Сь +
-\-/_ВОС^\, и аналогично, если OCS проходит внутри угла АОВ'.
3. Из условия следует, что /_АОВ^-/_ВОС= /_COD+/_DOA
(черт. 252); но, очевидно, /_ А0В 4" Z вос + Z C0D + Z DCM = 4d~>
следовательно, ^/ 40fi -f- /_ ВОС= /_ COD -\- /_ DO A = 2d. Из по-
последних равенств следует (на основании обратной теоремы п. 15)(
В
Черт. 252.
Черт. 253.
что ОА и ОС образуют продолжения одна другой. Таким же обра-
образом доказывается, что BOD есть прямая линия.
4. По условию имеем (черт. 253): -^/_AOB-\-/_BOC^-—/_COD —
d' 4" Z C0D +Z D04 + i-/4OB=2
Аналогично покажем, что /_АОВ = /_COD. В силу упражнения 3
четыре полупрямые попарно представляют продолжения одна другой.
УПРАЖНЕНИЯ К ГЛАВЕ II (стр. 43).
5. 1°. Если в треугольнике ABC имеем /^BAD^^CAD и
/_BDA = /_CDA = d (черт. 254), то треугольники ABD и ACD,
имеющие общую сторону AD и соответственно равные углы при А и
D, равны. Из равгнетва этих треугольников и следует, что АВ=АС.
. 2°. Если имеем /_ BD А = /_ CD A = d и BD = CD, то треуголь-
треугольники ABD и ACD равны по равенству двух сторон и заключённого
между ними угла, и АВ= АС.
3°. Пусть /_BAD=^/_ CAD a BD=CD. Откладываем DE = AD
(черт. 254). Треугольники ABD и ECD равны (п. 24, второй признак),
откуда АВ=ЕС и /_BAD = /_CED. В силу равенств /_BAD =
= /_CAD и /_BAD = /_CLD имеем /_CAD= /_CED, так что
треугольник Al С—равнобедренный (п. 23, обратная теорема), и
АС=ЕС. Так как АВ—ЕС и АС—ЕС, то АВ=АС.
КНИГА ПЕРВАЯ. ГЛАВА II
309
6. Треугольники ОАВ и О А' В, имеющие общий угол О и соот-
соответственно равные стороны ОА и ОА\ ОВ и ОБ, равны; следова-
следовательно, /_ОВА = /_ОВА' и /^ О АВ' = ^_ О А' В {черт. 255). Так как
углы ОАВ' и ОА'В равны, то равны и смежные с ними углы:
2_ВА'В=?ВАВ. Треугольники 1АВ и 1А'В равны (лЗ=А'В;
?_1АВ=/_1А'В; /_1ВА = /_1ВА') и потому 1А = 1А'. Наконец тре-
треугольники 01А и О/А' равны (по равенству трёх сторон), откуда
/_АО1= /_А'О1.
7. Пусть BD — медиана данного треугольника ABC и BD—DE
(черт. 27). При этом треугольники DAE и DCB равны (п. 25), откуда
АЕ = ВС; /_DEA = /_DBC. Если ?С>
^> ВА, то в треугольнике АБЕ имеем
АЕ~^>АВ, откуда по известной теореме
(п. 25) /_ ABE > /_ ЛЕВ, т. е. /_ ABD >
> /_ DBC.
8. Для любой точки М плоскости
треугольника ABC имеем: МВ-\-МС^ВС;
МС -\- МА 5= С A; MA -\- MB 3= АВ, причём три знака равенства
одновременно невозможны, так как точка М не может лежать одновре-
одновременно на всех трёх' прямых ВС, СА и АВ. Отсюда МА-\-МВ-\-
y (ВС + С А + АВ).
Так как периметр выпуклой ломаной меньше периметра объем-
объемлющей её ломаной, то для точки М, лежащей внутри треугольника,
имеем поп. 27 неравенства МБ-\-МС < АВ-{-AC; MC-{- MA <SC +
~\-ВА; МА-\-МВ<^АС-\-ВС. Складывая и деля на два, получим
МА + МБ -\- МС < ВС + СА + АВ.
8а. Если ABC...KL — произвольный многоугольник, и М — взя-
взятая точка, то МА -\-МВ 3* АВ; MB-\-МС^ ВС; МС-\-MD ^ CD; ...;
ML-\-MA~^zLA, причём невозможно, чтобы имели место все знаки
равенства одновременно. Складывая и деля на два, получим
-\- MB -\-...-\-ML~>]-{AB-\- ВС +...+ LA)-
HI
310
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
9. Если Е — точка пересечения диагоналей АС и BD четырёх-
четырёхугольника ABCD (черт. 256), то ЛС<^АВ-\-ВС; AC<AD-\-DC;
BD<^BC -\-CD\ BD<^ BA-\-AD. Складывая и деля на два, находим
АС 4- BD < АВ 4- ВС + CD 4- DA.
Если четырёхугольник ABCD — выпуклый, то АС = АЕ -f- EC;
BD = BE-\-ED и АЕ-\- ?5> АВ; ВЕ + ЕС~>ВС; CE + ED^CD;
DE-\-EAj^>AD. Складывая последние неравенства и деля на два,
В пол) чим АЕ 4- BE -{- СЕ +?)?¦>
y]r(AB-\-BC-\-CD-\-AD), т. е.
Примечание. Первое из доказан-
доказанных свойств АС + BD < АВ + ВС+ CD+
-\- AD сохраняет силу и для вогнутого четы-
четырёхугольника. Второе свойство АС-\-
0
Черт. 256.
да имеет место в случае вогнутого четы-
четырёхугольника (так на черт. 257 AC -\- BD, очевидно, меньше полупериметра)_
+ BD> i- {АВ + ВС + CD + AD) не всег-
10. Пусть Е — точка пересечения диагоналей выпуклого четырёх-
четырёхугольника ABCD, и М — произвольная точка в его плоскости, отлич-
отличная от Е (черт. 256). Имеем МА-\-МС^ЕА-\-ЕС; MB-\-MD^zЕВ-\-
-\-ED, причём два знака равенства одновременно невозможны, так как
точка М отлична от Е. Складывая по-
почленно, получим: MA -\- MB -\-MC-\- В
-f MD > ЕА -f- ЕВ 4- EC-\-ED.
Примечание. Точка пересече-
пересечения диагоналей Е вогнутого четырёх-
четырёхугольника рассматриваемым свойством
не обладает. Чтобы в этом убедиться,
обозначим через D ту из вершин во-
Д
Черт. 257.
Черт. 258.
гнутого четырёхугольника ABCD (черт. 258), которая делит внутри тре-
треугольника ABC, образованного тремя другими вершинами.
Пусть точка М лежит внутри (или на стороне) угла, вертикального
углу BDC. В таком случае MB + MC> DB + DC. Крпме того, MD -f MA^AD.
Отсюда
MA + MB + МС + MD > DA + DB + DC.
A)
To же самое неравенство получается и для точек М, лежащих внутри
(или на стороне) угла, вертикального углу ADB, а также для точек М, ле-
лежащих внутри угла, вертикального углу ADC. Таким образом, неравенство
КНИГА ПЕРВАЯ. ГЛАВА II ф 311
A) имеет место для всякой точки М, отличной от D (в том числе и для
точки пересечения диагоналей Е).
Итак, точка D (а не точка Е) есть точка плоскости, которая имеет на-
наименьшую возможную сумму расстояний до четырёх вершин.
11. На чертеже 27 в треугольнике ABE имеем 2BD<^AB-\-AE,
1
т. е. ЯО<
В треугольниках ABD и BCD имеем BD > АВ — AD; Д?>> ВС —DC.
Складывая и деля на два, получаем BD~^> — (АВ-\- ВС—АС).
12. Если АА', ВВ'; СС — медианы треугольника ABC, то в силу
упражнения И имеем — (АВ -\- АС — ВС) < АА' < — (АВ-\-АС);
—ЛС)< fifi'< -^ (АВ-Ь ВС); U
<-2 (ДС-f-SC). Складывая, найдём: — (Д? + ЛС-j-fiC) < ДД' +
-f fifi' -(- СС< АВ+ АС-\- ВС.
Примечание. Пользуясь теоремой п. 56, можно доказать нерав н-
3
ство -j{AB-\- ВС-\- АС)< АА'-\-ВВ' + СС, дающее более узкие границы
для суммы медиан. Если G—точка пересечения медиан, то ВС <^GB-\- GC,
т.е. ВС < -5- (ВВ'+ СС) Аналогично АС < ~{АА'+ СС) и АВ <
о о
2 • 3
< -5- (АА' -\- ВВ'). Складывая, легко получаем-v- (АВ + ВС-\- АС) < АА' +
-\-ВВ' + СС.
13. Если данные точки А и В лежат по разные стороны от дан-
данной прямой XY, то искомой точкой будет точка пересечения М пря-
прямых ХУ и АВ, так как если М — про-
произвольная точка прямой XV, отллчная Д
от М, то МА-{-МВ=АВ<^М'А-{- \\. R
Если данные точки А и В лежат по
одну сторону or XY, то для любой тлч- X j-p
ки М прямой XY имеет место ра-
равенство мл + мв = ма 4- мв. черт- ¦!!5J-
где В — точка, симметричная с В относительно XY. Искомой точ-
точкой будет точка пересечения М прямых АВ' и XY.
14., Если В' — точка, симметричная с В относительно XY, то
^/ BMY = ^_B'MY, и, следовательно, точки А, М, В'лежат на одной
прямой в силу равенства _/_ АМХ = /_ В'MY. Искомая точка есть точ-
точка пересечения прямых АВ' и XY.
15. Если данные точки А и В лежат по одну сторону от данной
прямой XY (черт. 259), то искомой точкой будет точка пересечения М
прямых XY и АВ, так как если М —¦ произвольная точка прямой XY,
отличная от М. то \МА — МВ\ = АВ~>\МА — МВ\.
312
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если данные точки А и В лежат по разные стороны от ХУ, то
обозначим через В' (черт. 260) точку, симметричную с В относитель-
относительно ХУ. При этом для любой точки М прямой ХУ имеет место ра-
равенство М'А— М'В=М'А— MB'. Следовательно, искомой точкой
М будет точка пересечения прямых АВ' и ХУ.
УПРАЖНЕНИЯ К ГЛАВЕ III (стр. 47).
16. Если в двух прямоугольных треугольниках ABC и А'В С с
прямыми углами при Л и Л' катеты удовлетворяют условиям АВ<^АВ
и АС<^А'С, то строим A'D = AB и А'Е = АС (черт. 261). При этом
BC==DE. Так как А'Е < А'С,
то и DE <^ DC и аналогич-
аналогично DC'<^B'C, так что?>?<
< ВС, т. е. ВС<ВС.
17. Пусть AD — медиана,
АЕ — биссектриса, АН — вы-
высота треугольника ABC, в ко-
Вг
В Л С Л' Е
Черт. 260. Черт. 261.
тором АВу> АС (черт. 262). В силу упражнения 7 /_BAD<^/_DAC,
так что медиана лежит между стороной АВ и биссектрисой АЕ.
Если отложить HF=HC, то AC=^AF и, в силу неравенства
АВ^>АС, также АВ~^> AF. Следовательно, BH~^>FH, и точка Улежит
ближе к Н, чем точка В, так что /^ САН =
= /_ FAH <^ /_ ВАН и высота АН лежит
между биссектрисой АЕ и стороной АС.
18. Так как НЕ<^HD (см. решение
упр. 17 и черт. 262), то и AE<^AD.
УПРАЖНЕНИЯ К ГЛАВЕ IV (стр. 49).
19. Если высоты BD и СЕ треуголь-
треугольника ABC (черт. 263) равны, то прямо-
прямоугольные треугольники BCD и ВСЕ рав-
равны по равенству катета и гипотенузы,
откуда ?BCD = /^_СВЕ и треугольник ABC — равнобедренный.
Примечание. Относительно аналогичного свойства медиан см. за-
задачу 39 и биссектрис — см.задачи 361 и 361а
20. Если BD и СЕ—высоты треугольника ABC, в котором АВ~^>
~^> АС, и, следовательно, ^АСВ~^>/_АВС, то к треугольникам BCD
и ВСЕ применима теорема п. 35, в силу которой BD ^> СЕ.
КНИГА ПЕРВАЯ. ГЛАВА V
313
УПРАЖНЕНИЯ К ГЛАВЕ V (стр. 54).
21. Пусть /—точка пересечения биссектрис углов В и С (черт. 264).
Имеем /_NCl= ^_ICB = /_NIC (как внутренние накрестлежащие);
треугольник NIC—равнобедренный и JN^CN. Аналогично 1М = ВМ,
откуда MN = BM-\-CN.
С
Черт. 265.
? С
Черт. 266.
Если /' — точка пересечения внешних биссектрис углов при В и С
и M'1'N' — прямая, параллельная ВС, то треугольники М ВГ и N СГ
оба равнобедренные и М N' = ВМ -\- CN".
Наконец, если /" — точка пересечения биссектрисы угла при В с
внешней биссектрисой угла С и M"I"N" — прямая, параллельная ВС,
то треугольники М"В1" и N"СГ — равнобедренные и M"N' = M" —
22. Пусть дан многоугольник ABCDE (черт. 265). Соединяя
точку О, лежащую внутри многоугольника, с его вершинами, мы ра-
разобьём его на треугольники, которых будет столько же, сколько сто-
сторон. Сумма всех углов этих треугольников будет 2dn (n—число сто-
314
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
рон многоугольника). Чтобы получить сумму углов многоугольника,
надо из этой суммы вычесть сумму углов при точке О, т. е. 4d.
23. Если угол при А острый, то сумма /_&-\-/_С больше угла
А (черт. 266). Из треугольника ABD имеем: /_ADE = 2d — /_B —
— /_С— /_А\ точно так же из треугольника АСЕ имеем /_AED —
= 1d — ^_B — /_C^=Z_A, откуда /_ ADE = /_ AED.
Если угол при А тупой, то /_Н-\- Z.C<^/^A (черт- 267). Из
треугольников ABD и АСЕ имеем: /_ADE= /_B-\-Z.c> /_AED =
= /.B + Z.c> откуда /_ADE =
= /_AED. о
Если угол при А прямой, точки D
и Е совпадают, так как угол А ра-
вен сумме / В -\- / С.
А\
24. 1°. Пусть АЕ — биссектриса, АН— высота и АВ^> АС. так что
угол В острый (черт. 262). При этом /_ЕАН =/_ВАН —/_ВАЕ =
= (90°— /_ В) — ^-/_А=90° — /_В— 1A8UQ— / В— /_С) =
2°. Если /—точка пересечения биссектрис углов В и С (черт. 264),
то ^?/С=180°— /1^/?4-1 /с\ = 180'— 1A80'— /А)=
V I ^ '
= 90° О- тг Z. А.
' 2 ^~
3°. Если /' — точка пересечения биссектрис внешних углов при В
и С, то ^?/'С=180°—1A80°— /_В)~~ A80° — ^_ Q =
= A80Z^)=90Z-4- %
25. 1°. Если АЕ и fif — биссектрисы углов -4 и В (черт. 268), то
из треугольника ABE имеем: /_ Л??=180э—?т^^— «- jl.B =
+/.?>)¦
КНИГА ПЕРВАЯ. ГЛАВА VI
315
2°. Если AF и CF — биссектрисы углов А и С, то из четырёх-
четырёхугольника ADCF (мы предполагаем, что из двух четырёхугольников
ABCF и ADCF выпуклым является ADCF, как на черт. 268) имеем:
/_AFC=360° — _??> — }- /_А— 1 /_С = 360°~^D —1C60°—
J, Z Z
ZD) 18O° (ZDZB)
УПРАЖНЕНИЯ К ГЛАВЕ VI (стр. 61).
26. Если AN и BN—биссектрисы углов А и В параллелограма
ABCD (черт. 269), то /_ ANB= 180° —L/_A—1 /_ B= 180° —
Z Z
—90° = 90°, так как сумма двух
смежных углов параллелограма
равна 180°; если АР и ВР — бис-
биссектрисы внешних углов при Aw В,
то ^Д°?=180о— 1/_ХАВ— 1^КеЛ=90°. Аналогично пока-
Z Z,
жем, что и остальные углы четырёхугольников KLMN и PQRS — прямые.
27. Если О — точка пересечения диагоналей параллелограма
(черт. 270) и MN—произвольная прямая, проходящая через О, то
треугольники АОМ и CON равны (АО = ОС; /_МА0 = ?NCO;
^_А0М= Z.CON), откуда 0M=0N.
28. Пусть О—середина диагонали МР параллелограма MNPQ,
списанного в данный параллелограм /45С?)ч(черт. 271). Треугольники
AMQ и CPN равны, так как MQ = PN и /_AMQ~/_CPN,
/_AQM^/_CNP, как углы с параллельными сторонами, имеющими
противоположные направления. Следовательно, AM = СР. Далее тре-
треугольники АОМ и СОР равны, так как АМ = СР\ ОМ=0Р;/_АМ0 =
= /_СРО. Отсюда следует, что /_АОМ = /_СОР и 0.4 = ОС, так
что АОС — прямая линия (упражнение 3), а О — середина диагонали АС
параллелограма ABCD.
29. Если ВО — медиана треугольника ABC и BO = OD (черт. 50),
то к треугольникам ABC и ABD применима теорема (п. 28) о двух
316
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
треугольниках, имеющих две пары соответственно равных сторон, но
неравные углы, заключённые между ними. В зависимости от того,
б>дет ли ДС<20?, АС=2ОВ, ЛС>2ОД будем иметь ДС<5?>,
AC = BD, ACy>BD, и, следовательно, /_ABC<^/_BAD, /_ABC =
= /_BAD, /_ABCy>/_BAD. Так как /_ABC-\-/_BAD = 2d, то
будем иметь соответственно /_ABC<^d, /_ABC = d, /_ABC~^>d.
BAD
Черт. 272.
30. Пусть в треугольнике ABC (черт. 272) угол В вдвое более
угла С. Если на продолжении стороны АВ отложить отрезок AD —
= ВА, то все углы треугольника BCD будут равны между собой;
откуда BC=BD = 2BA
31. Пусть даны две пересекающиеся прямые ОХ и OY (черт. 273).
Обозначим через А' и А" точки пересечения прямой ОХ с прямыми
A'Y' и A"Y", параллель-
параллельными OY и отстоящими
от нее" на расстоянии, рав-
равном /.
Пусть М — произволь-
ная точка плоскости, и
МР и MQ—её расстоя-
расстояния от прямых ОХ и О У.
С помощью двух посту-
поступательных перемещений,
определяемых по величине
и по направлению отрез-
отрезками О А' и О А", мы по-
получим из точки М две
новые точки М и УИ",
расстояния которых от прямой ОХ буд^т равны МР, а расстояния от
прямой OY будут равны MQ-\-l и I — MQ или MQ-\-l и MQ—1,
смотря по тому, лежит ли точка М между прямыми A'Y' и A"Y"
или нет (оба случая показаны на черт. 273).
Пусть теперь для некоторой точки плоскости М выполняется одно
из условий MP-\-MQ=l, MP — MQ = l, MQ—MP = l, т. е. одно
из условий MP — l — MQ; MP = MQ-{-l; MP—MQ—l. В таком
Черт. 273.
КНИГА ПЕРВАЯ. ГЛАВА VI
317
Черт. 274.
случае одна из точек М' или М", получающаяся из точки М с помо-
помощью указанных выше поступательных перемещений, будет равноудалена
от прямых ОХ и OF. Отсюда следует, что и обратно, точки М, удов-
удовлетворяющие условию задачи, получаются из точек, равноудалённых
от данных прямых, с помощью поступательных перемещений ОА'ч ОА".
Так как геометрическое место точек, равноудаленных от данных
прямых ОХ и О К, есть пара прямых р, q, делящих пополам углы
между данными прямыми, то гео-
геометрическое место точек М,
для которых сумма или разность
их расстояний от данных пря-
прямых ОХ и О Y равна /, пред-
представляет собой две пары пря-
прямых р', д' и р", q", получае-
получаемых из р, q с помощью тех
же поступательных перемеще-
перемещений (черт. 274).
Остаётся ещё решить во-
вопрос, для каких точек этих че-
четырёх прямых отрезок / будет
равен сумме и для каких —
разности расстояний от данных
прямых. Ограничимся решением вопроса для точек прямой q'. Из черте-
чертежа легко усмотреть, что для точек отрезка А'В (черт. 274) сумма
расстояний будет равна /, а для точек, лежащих на продолжении
отрезка А'В, разность расстояний будет равна I.
Таким образом, геометрическое место точек, для которых сумма
их расстояний от двух данных прямых равна /, есть совокупность че-
четырёх сторон прямоугольника А'ВА"В'', а геометрическое место точек,
для которых разность расстояний равна /, — совокупность продолжений
всех сторон того же прямоугольника за его вершины.
Пусть теперь данные прямые XX' и YY1 параллельны и ZZ' —
прямая, равноудалённая от них. Обозначим через МР, MQ и MN рас-
расстояния от точки М соответственно до прямых XX', YY' и ZZ'.
Если расстояние между данными прямыми меньше /, то геометри-
геометрическое место точек М, для которых МР -\-MQ= l, есть пара прямых,
отстоящих от прямой ZZ' на —- /, так как в силу упражнения 1 имеем
(черт. 275) MP-\-MQ=2MM. В этом случае не существует, оче-
очевидно, точек, для которых МР — MQ = -\-l.
Если расстояние между данными прямыми больше /, то не суще-
существует, очевидно, точек М, для которых MP-\-MQ = l. В этом слу-
случае геометрическое место точек, для которых МР — MQ^A-l,
состоит из двух прямых, отстоящих от ZZ' на — /,
так как в силу
упражнения 1 имеем МР—MQ=^ +
(черт. 276).
318
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
j—: _
Наконец, если расстояние между данными прямыми равно /, то для
любой точки М, лежащей между двумя данными прямыми или на
одной из них, имеем MP-\-MQ=l. Для любой точки, лежащей вне
полосы, образованной двумя данными прямыми, или на одной из них,
имеем МР — MQ = ^l. 4
32. Из сказанного в п. 284, пример I, вытекает следующий спо-
способ построения точки N:
У'
Z'
х'
\
1
1
I
\
\
\
м
0
N
Р
V
Т
л
У'
7'
У'
i
1
2
t
Q
I
/
т
t
И
N
P
Черт. 275.
Черт. 276.
Через точку А проводим прямую, имеющую данное направление, и
на этой прямой откладываем отрезок АС, равный искомому отрезку
MN (определение длины последнего не представляет затруднений).
Соединив точки В и С, получим в пересечении с одной из данных
прямых точку N.
УПРАЖНЕНИЯ К ГЛАВЕ VII (стр. 64).
33. Пусть требуется соединить точку О с точкой пересечения пря-
прямых АА' и ВВ' (черт. 277). Проводим через О прямые AD и Ы:,
соответственно перпендикулярные к ВВ1 и АА'. Прямая OF, перпендику-
А Е
/7'
Черт. 277.
Черт. 278.
лярная к АВ, проходит через точку пересечения прямых АА' и ВВ',
так как OF есть третья высота треугольника, образованного прямыми
АА', ВВ' и АВ.
Это построение пригодно лишь в предположении, что точки А и В
и отрезок АВ лежат в пределах чертежа.
КНИГА ПЕРВАЯ. ГЛАВА VII
319
34. Пусть Е и F — середины непараллельных сторон AD и ВС,
М и N — середины диагоналей BD и АС трапеции (черт. 278). Прямая
ЕМ соединяет середины сторон треугольника ABD и потому паралле-
параллельна АВ (п. 55); прямая Efo, соединяющая середины сторон треуголь-
треугольника ACD, параллельна CD и, следовательно, параллельна АВ. Отсюда
следует, что прямые ЕМ и EN совпадают. Точки Е, М, N лежат на
одной прямой. Точно так же доказывается, что точки F, М, /V лежат
на одной прямой. Последняя прямая совпадает с EMN, так как она
имеет с ней две общие точки М и N. Итак, все четыре точки Е, F,
М, N лежат на одной прямой.
Из треугольников ABD, ABC, BCD имеем
Отсюда
ЕМ = - АВ; /7V= ~АВ; MF= I CD.
z z z
=: -(AB-{-CD);
MN = MF— FN=
— AB).
35. Пусть ААп и Шо — перпендикуляры из точек А и В на данную
прямую и Со—середина отрезка AUBO.
С„ ft,
Черт. 279.
Черт. 280.
Если точки А и В лежат по одну сторону от данной прямой
(черт. 279), то АА^В0В—трапеция. Прямая ССп будет параллельна
основаниям трапеции: в силу упражнения 34, прямая, проходящая
через середину стороны АВ и параллельная основаниям трапеции
1
делит пополам и сторону АпВа. Стрезок СС0 равен — (<4Л, -J- ВВЬ).
Если точки А и В лежат по разные стороны от данной прямой
(черт. 280), то АВ и A0R0 — диагонали трапеции АА()ВВ0. В силу
упражнения 34, так как прямая СС0 делит обе диагонали пополам, то
СС0= 1 (АА.-ВВ,).-
320
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
36. Пусть М, N, Р, Q, К, L — соответственно середины сторон АВ,
ВС, CD, DA и диагоналей AC, BD четырёхугольника ABCD (черт. 281).
Отрезок MN, соединяющий середины двух сторон треугольника ABC,
параллелен АС и равен -хАС. По той же причине отрезок PQ па-
раллелен АС и равен -~АС. Четырёхугольник MNPQ есть паралле-
лограм.
Прямые МР и NQ делятся в точке пересечения О пополам, как
диагонали параллелограма MNPQ. Отрезок KN, соединяющий сере-
середины сторон треугольника ABC, параллелен АВ и равен -ргАВ; анало-
гично отрезок LQ параллелен АВ и равен -~-АВ. Следовательно,
KNLQ есть параллелограм, и отрезок KL проходит через середину О
отрезка NQ, как диагональ нового параллелограма, и делится в ней
пополам.
N
В
Черт. 281.
D
Черт. 282.
37. Пусть О — точка пересечения медиан BE и CF треугольника
ABC (черт. 282), а точки К и L выбраны так, что EK = EG; FL =
= FG. Отрезок EF, соединяющий середины сторон в каждом из тре-
треугольников ABC и GKL, параллелен как ВС, так и KL и равен как ~-ВС,
так и -fr KL. Отсюда следует, что отрезки ВС и KL параллель-
ны и равны. Четырёхугольник BCKL есть параллелограм, так что
BG=GK=2GE и CG=GL = 2GF. Следовательно, медиана BE
проходит через точку О, отсекающую одну треть отрезка CF.
Точно таким же путём можно показать, что и третья медиана AD
1 _„
отсекает -г- от отрезка CF и, следовательно, проходит через ту же
о
точку.
КНИГА ПЕРВАЯ. ГЛАВА VII
321
38. Пусть а, Ь, с — данные прямые, проходящие через О, и Л —
точка на прямой а.
1°. Стороны АВ и АС треугольника с вершиной А, имеющего дан-
данные прямые своими высотами, должны быть соответственно перпенди-
Черт. 283.
Черт. 284.
кулярны к с и b (черт. 283). Этим определяется положение вершин
В и С на прямых b и с. Если прямые b и с перпендикулярны, то
прямые, проходящие че-
через А и перпендикуляр-
перпендикулярные к прямым b и с,
будут, очевидно, парал-
параллельны соответственно
прямым с и Ь, и преды-
предыдущее построение невы-
невыполнимо. В этом случае
не существует треуголь-
треугольника, имеющего данные
прямые своими высотами
и точку А — своей вер-
вершиной.
2°. Строим CM j =
= -^ОА (черт. 284); точ-
точка /4, есть середина ВС.
Если А1М=А10,то О ВМС
есть параллелограм. Точки Черт. 285.
В и С лежат на прямых,
проходящих через М и параллельных с и Ь. При этом точка О
будет точкой пересечения медиан треугольника ABC (так как
АХО= ^-\А), а, следовательно, прямые ОВ и ОС будут действи-
о
тельно медианами треугольника ABC.
21 Элементарная геометрия
322 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
.—.—. j
3°. Если прямые a, b и с — биссектрисы углов искомого треуголь-
треугольника ABC, то прямые АВ и ВС симметричны относительно прямой Ь,
а прямые АС и ВС—относительно с (черт. 285). Следовательно, точ-
точки, симметричные с данной точкой А относительно прямых b и с,
лежат на прямой /, проходящей через точки В и С. Это даёт возмож-
возможность построить прямую /, а затем и вершины В и С.
Если прямые Ь и с перпендикулярны между собой, то построенная
прямая / проходит, как легко видеть, через точку О, и задача не
имеет решения. Если прямая а перпендикулярна к одной из прямых
Ь и с, то прямая / будет параллельна другой из них, и задача опять
не имеет решения. В остальных случаях, т. е. когда никакие две из
данных прямых не перпендикулярны друг другу, задача имеет един-
единственное решение.
4°. Рассматриваем треугольник ABC, имеющий прямые а, Ь, с
своими высотами (см. 1°), и через его вершины проводим прямые,
параллельные его противоположным сторонам (сравнить известное до-
доказательство теоремы о высотах треугольника, п. 53).
ЗАДАЧИ К ПЕРВОЙ КНИГЕ (стр. 65).
39. Пусть AD, BE, CF — медианы треугольника ABC (черт. 286)
и О—точка их пересечения. Если АВ~^> АС, то из треугольников ABD
и ACD, имеющих две нары соответственно равных сторон, но нерав-
неравные третьи стороны, имеем /_ ADB ^> ^/_ ADC (п. 28, обратная
теорема). Из треугольников GBD и GCD следует, что BG^> GC (п. 28),
т. е. ^BE>jCF, BE>CF.
Точно так же, если АС~^>АВ, то CF~^>BE. Следовательно, из
BE = CF следует АВ = АС.
40. Пусть для определённости даны четыре прямые Dx, D2, Dg,
D4; обозначим через AXYZUB искомую ломаную (черт. 287). Пред-
Предполагая, что точки X, Y, Z уже построены, мы получим точку U,
соединяя точку Z с точкой В', симметричной с точкой В относитель-
относительно прямой Д, (упр. 14). Таким образом, мы приходим к построению
ломаной AXYZB для случая трёх прямых Dx, D2, D%. Аналогично
для построения точки Z мы должны соединить точку Y с точкой В",
симметричной с В относительно D3, и т. д.
Окончательно приходим к следующему построению: строим точку В1,
симметричную с В относительно ZL, затем точку В", симметричную
с Ь' относительно D%, затем точку В", симметричную с В' относи-
относительно D2, и, наконец, точку Blv, симметричную с В'" относительно
Z),. Прямая ABlv определяет точку X, прямая ХВ" — точку Y, пря-
прямая YB" — точку Z, прямая ZB — точку U. Метод решения не зави-
зависит от числа данных прямых.
Длина ломаной AXYZUB равна AXYZUB = AXYZB = AXYB'=
= АХВ" = ABIV- Длина любой другой ломаной с концами А и В и
ЗАДАЧИ К ПЕРВОЙ КНИГЕ
323
вершинами на прямых Dx, D2, Ds, ZL равна длине некоторой ломаной,
соединяющей А и /?v, и потому больше ABlv.
Частный случай, когда Z),, Ь2, ZK, Di — стороны прямоугольника
и точки А и В совпадают, представлен на чертеже 288. При зтом
В D С
Черт. 286.
Черт. 287.
Черт. 289.
XYZU — нараллелограм и MX=PZ = MX'. Отсюда XU-\-UZ =
= X'Z = МР, так как MPZX' — параллелограм. Таким образом ЛТ-|-
-(- YZ -(-ZU-\- UX = 2МР (обозначения точек понятны из чертежа).
41. Точка К (черт. 269), лежащая на биссектрисах углов DAB и
ADC, равноудалена от прямых АВ и CD (п. 36), и тем же свойством
обладают точки /VI, Q, S. Поэтому точки К, М, Q, S лежат на
прямой — геометрическом месте точек, равноудалённых от прямых АВ
и CD. Точно так же точки L, N, P, R лежат на прямой — геоме-
геометрическом месте точек, равноудалённых от прямых ВС и AD.
324
РЕШЕНИЯ УПРАЖНЕНИИ И 3\ДЛЧ
Далее SM=AB, так как ABMS—параллелограм, и SK—MQ —
= ВС, так как AKDS и BQCM—прямоугольники. Отсюда SQ —
= SM-\-MQ —AB-\-BC и KM=SM—SK = AB—BC.
42. Пусть точка М лежит на основании ВС равнобедренного тре-
треугольника ABC (черт. 289), и МК, ML, MN—перпендикуляры из
точки М на стороны АВ, АС и на высоту CF треугольника. При этом
?CMN' = /_СВА = /JBCL, и прямоугольные треугольники CMN и MCL
равны. Следовательно, ML = CN. Кроме того, MK = NF. Отсю-
Отсюда ML-\-MK=CN-\-NF=CF.
Итак, сумма расстояний точки М
от сторон АВ и АС равна высоте
CF треугольника.
Черт. 291.
Если точка М лежит на продотжении ВС, например, за точку, С,
то аналогично М'К' — M'L'=M'K' — MN' = N'K' = CF.
Пусть теперь точка М лежит внутри равностороннего треуголь-
треугольника ABC (черт. 290) и МР, MQ, MR — перпендикуляры из этой
точки на ВС, АС, АВ. Проводим через точку М прямую BlCv па-
параллельную ВС, и из точки Вх опускаем перпендикуляры ВХК и /?,1
на стороны АС и ВС. Применяем теперь доказанное свойство равнобед-
равнобедренного треугольника дважды: один раз к треугольнику ABXCV другой раз
к треугольнику ABC. Получаем ' MQ-\~MR = BtK; MP-{-MQ-{-
JrMR^=^BlL-\-B^K^= AD, где AD — высота треугольника ABC.
Если точка М лежит вне треугольника, например, в области, внут-
внутренней по отношению к углу ВАС, то —М'Р'-\-М Q'-\-M'R' =
= — Bj'V -\-Bx'K'=AD. Во всех случаях будем иметь 4=MPzhMQ 4;
+ MR = AD.
43. Пусть прямая KL, проходящая через середину D стороны ВС
треугольника ABC и перпендикулярная к биссектрисе АЕ, пересекает
прямые АВ и АС в точках К и L (черт. 291). Так как в треуголь-
треугольнике AKL биссектриса совпадает с высотой, то (упр. 5) AK=AL и
/_ AKL = ^/ ALK-- Треугольники BDK и CDF, где CF параллельно
АВ, равны, откуда BK=CF. Далее /_CF'L = /_AKL = /_ALF', и потому
CF = CL, так что BK = CL. Итак, АВ = АК-\-ВК, AC=AL — CL =
= АК — ВК, откуда АК = AL = \(AB-\-AC);BK=CL=\-(AB— AC).
ЗАДАЧИ К ПЕРВОЙ КНИГЕ
325
44. Имеем ряд равных треугольников АВИ, СВК, EKF, GHF
(черт. 292), откуда НВ = НК = KF=FH. Угол BKF— прямой, так как он
равен сумме острых углов треугольника ВКС. Отсюда уже следует,
что HBKF—квадрат.
45. При решении предложенной задачи мы воспользуемся следую-
следующим замечанием.
Если в двух равных треугольниках, имеющих одинаковое на-
направление вращения, какая-либо сторона одного перпендикулярна
Н D
Черт. 292.
к соответственной стороне другого, то и каждая сторона одного
из этих треугольников перпендикулярна к соответственной сто-
стороне другого.
В самом деле, пусть сторона ВС треугольника ABC (черт. 293)
перпендикулярна к соответствующей ей стороне ВС' треугольника
А'В'С, равного ABC и имеющего
то же направление вращения. Отло-
Отложим от точки В отрезки ВА" и ЕС",
соответственно равные и параллель-
параллельные В'А' и В'С и направленные в
ту же сторону. Углы А"ВС" и А'В'С
будут при этом равны и одинаково
направлены. Так как углы ABC и
А'В'С по предположению равны и
имеют одинаковое направление, то и
углы А"ВС" и ABC равны и имеют
одинаковое направление. Отсюда сле-
следует', что углы С'ВС и А'ВА рав-
равны, как получающиеся путём прибав-
прибавления к двум равным углам А"ВС"
и ABC одного и того же угла С'ВА. Но угол С'ВС — прямой, так
как ВС параллельно В'С, а ВС перпендикулярно к ВС. Следова-
Следовательно, и угол А'ВА, равный углу С'ВС, также прямой, а потому
и ВА", а значит и А'В' перпендикулярны к АВ. Таким же путём
доказывается, что и А'С перпендикулярно к АС.
326
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Переходим к решению предложенной задачи:
1°. Продолжим медиану AM треугольника ABC (черт. 294) на рав-
равный ей отрезок МК- При этом АВ = АЕ, ВК-=-AC =AG и /_АВК =
= ^_EAG, как углы с соответственно перпендикулярными сторонами,
имеющие одинаковое направление, так что треугольники АВК и EAG
равны и имеют одинаковое направление вращения. Отсюда следует,
что EG = AK = 2AM. В силу сделанного вначале замечания из ра-
равенства этих треугольников следует, кроме того, что EG перпендику-
перпендикулярно к АК (так как АВ перпендикулярно к ЕА).
2°. Параллелограм AEIG равен параллелограму BACK в силу ра-
равенства треугольников AEG и ВАК. Следовательно, равны и треуголь-
треугольники EAI и ABC. Кроме того,
эти треугольники имеют одина-
одинаковое направление вращения,
и ЕА перпендикулярно к АВ,
так что и AI перпендикулярно
к ВС (опять-таки в силу сделан-
сделанного вначале замечания). Дру-
Другими словами, точка / лежит на
высоте треугольника ABC.
3°. Отрезки CD и BI равны
и перпендикулярны, так как тре-
треугольники BCD и AIB равны и
имеют одинаковое направление
вращения и, кроме того, их со-
соответственные стороны BD и
АВ перпендикулярны. Таким же
путём доказывается, что отрезки BF и С1 равны и перпендикулярны.
Наконец, прямые CD, BF и AI проходят через одну точку как
высоты треугольника ВС/.
46. Пусть А"—середина AD (черт. 295); при этом КА = КР =
= KO — KD, так как в каждом из прямоугольных треугольников APD
и AOD медианы КР и КО равны половине гипотенузы (п. 48). Если
из точек А, К, D опустить перпендикуляры AAV KKV DDX на прямую
OP, то ОКХ=КХР (в силу КО = КР) и D1Kx=K1Al (ср. решение
упр. 35), откуда D1O = PAy
Если • X — точка пересечения прямых АВ и DDX и прямая OY
перпендикулярна к OP, a YU перпендикулярна к DX, то треугольники
АТС/И.4А4, равны (UY = Dfi=PA1\ ZXYU=Z.APA,)> и ХУ=РА.
Пусть теперь прямая CZ перпендикулярна к ОР. Повторяя рассуж-
рассуждения, вполне аналогичные предыдущим, в которых вместо А берём В,
вместо С—D, вместо X— Z, а точки Р и Y сохраняют своё значе-
значение, можно доказать, что YZ — BP. "т
Черт. 295.
КНИГА ВТОРАЯ. ГЛАВА II 327
КНИГА ВТОРАЯ.
ОКРУЖНОСТЬ.
УПРАЖНЕНИЯ К ГЛАВЕ I (стр. 69).
47. Если из центра О и из произвольной точки А данной окруж-
окружности провести (в одну и ту же сторону) равные и параллельные от-
отрезки 00' и АА', то фигура 00'А'А будет параллелограмом, так
что О'А' = 0.4, и геометрическим местом точек А' будет окружность,
равная данной и имеющая своим центром точку О'.
То же следует и из общей теоремы п. 51.
Черт. 296. Черт. 297.
48. Пусть А' — середина отрезка РА, соединяющего данную точку Р
(которая может лежать вне окружности, на окружности или внутри
ее) с произвольной точкой А окружности О, и О' — середина отрезка
РО (черт. 296). В силу того, что отрезок О'А' соединяет середины
двух сторон треугольника РОА, имеем (п. 55) О'А'=— О А, так что
геометрическое место точек А' есть окружность с 'центром О'.
49. Так как 0D = DC (черт. 297), то/_D0B= /_DC0 и/_ED0 =
= /_D0B-\- /^DC0==2 /_D0B, как внешний угол треугольника
DOC (п. 44, следствие I); далее, так как 0D = 0E, то /_ED0 =
= Z. DE0= 1/_D0B и /_EOA = /_DCO-\-/_CEO =/_D0B-\-
~\- 2 /_ D0B=3 /_ DOB.
УПРАЖНЕНИЯ К ГЛАВЕ II (стр. 72).
50. Пусть D — точка рассматриваемой окружности, диаметрально-
противоположная точке С (черт. 298), Сх—точка пересечения данной
прямой с АВ; D, — основание перпендикуляра из точки D на прямую
АВ и Ох—середина отрезка C^Dr Прямая, соединяющая центр О
Окружности с точкой О,, параллельна данной прямой, так как она про-
проходит' через середины диагоналей трапеции CCyDDx (упр. 34) и,
следовательно, перпендикулярна к АВ. Отсюда следует, что точка Ох
есть середина отрезка АВ. ^
328
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Таким образом, положение точки Ох на прямой АВ не зависит от
выбора той или иной окружности, проходящей через А и В. В силу
равенства OlCl=OlDl и положение
точки Z^ на прямой АВ не зависит от
выбора окружности. Следовательно, гео-
геометрическое место точек D есть перпен-
перпендикуляр к прямой АВ в точке Dv
В приведённом решении неявно пред-
предполагалось, что данная прямая ССг пе-
пересекает самый отрезок АВ, а не его
продолжение. Аналогичные рассуждения
применимы и в том случае, когда она
пересекает продолжение отрезка АВ.
Однако в этом случае точки О и О1
будут•серединами непараллельных сто-
сторон (а не серединами диагоналей) соот-
соответствующей трапеции.
51. Пусть AD = DE = EB (черт.
299). Опустив из центра О окружно-
окружности перпендикуляр ОН на данную хорду, мы видим, что ОЕ =
= OD<^OA (по теореме о длине наклонных, п. 29). Прямая OD
есть медиана треугольника ОАЕ, и из неравенства ОЕ <^ О А сле-
следует (упр. 7), что /_DOE^>/_DOA. По ' гой же причине и
2d /
В
Черт. 298.
Черт. 299.
Черт. 300.
Аналогично, если хорда АВ разделена на п равных частей, то наи-
наибольшим из углов при центре будет угол, внутри которого проходит
перпендикуляр ОН (при нечётном и) или каждый из двух углов,
имеющих ОН своей стороной (при чётном «). Действительно
(черт. 300, для я = 7), OA>OD>OE>OF (п. 29,3°), и при-
применение упражнения 7 к треугольникам ОАЕ, ODF, OEG даёт
/_AOD<^/_DOE<C/_EOF<^/_FOG, так что угол FOG будет
наибольшим.
52. Опустим из центра О перпендикуляры ОН и ОН' (черт. 301)
на равные хорды АВ и А'В', продолжения которых пересекаются в
КНИГА ВТОРАЯ. ГЛАВА III
329
точке Р; при этом НА=НВ = Н'А' =-Н'В (п. 63) и ОН = ОН' (п. 66).
Прямоугольные треугольники ОНР и ОН'Р равны (общая гипотенуза,
ОН = ОН'), откуда РН=РН'.
Следовательно, РА = РН -\- НА =
=РН' -\- Н'А' = РА' и РВ=
= РН— НВ—РН'— Н'В'=РВ.
Те же рассуждения приложи-
мы и к равным хордам, пересекаю-
пересекающимся внутри окружности.
53. Так как середина хорды
есть основание перпендикуляра,
опущенного из центра на хорду, и
равные хорды равноудалены от
центра, то геометрическое место се-
середин равных хорд есть окружность,
концентрическая с данной. Радиус этой последней окружности равен
расстоянию от центра данной окружности до каждой из данных хорд.
54. Наименьшая хорда, которая проходит через данную точку А,
лежащую внутри данной окружности, наиболее удалена от центра О
этой окружности из всех хорд, проходящих через А. Но из хорд,
проходящих через А, наиболее удалённой от центра является хорда
MN (черт. 302), перпендикулярная
к ОА. Действительно, расстояние
Черт. 301.
Черт. 302.
Черт. 303.
О А' от точки О до какой-либо другой хорды Лf/V', проходящей
через А, есть перпендикуляр к хорде Ж'Л', а этот перпендикуляр
короче наклонной (О А' <^ О А).
УПРАЖНЕНИЯ К ГЛАВЕ III (стр. 76).
55. 1°. Если точка О' лежит на продолжении отрезка О А за точ-
точку А и окружности пересекаются (черт. 303), то точка А лежит вну-
внутри окружности О'. Одна из точек пересечения обеих окружностей
будет лежать на дуге АВ, если точка В будет лежать вне окружности
О', т. е. если О'#>/?', откуда /?-f R' — ОО' < ОВ-{-О'В— ОО'.
2°. Если точка О' лежит на самом отрезке ОА и окружности пе-
пересекаются (черт. 304), то точка А лежит внутри окружности О'.
330
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Одна из точек пересечения будет лежать на дуге АВ. если точка В
будет лежать вне окружности О', т.е. если O'B^>R', или 00' —
— (/? - R'XOO' — (OB— О'В).
3°. Если точка О' лежит на про-
продолжении отрезка О А за точку О
и окружности пересекаются, то точ-
точка А лежит вне окружности О'.
Одна из точек пересечения обеих
окружностей будет лежать на дуге
АВ, если точка В будет лежать
внутри окружности О', т. е. если
О'В</?', откуда 00' _(/?' — /?)<
<ОО' —(О'В—ОВ).
56. Пусть линия центров 00' данных окружностей пересекает
окружность О в точках А и А', окружность О' — в точках В к В1.
Выберем обозначения так, чтобы ОА было направлено в сторону,
противоположную 00' и О'В—в сторону, противоположную О'О.
Обозначим далее через С и D две произвольные точки, лежащие
соответственно на окружностях О и О' так, что хотя бы одна из них
не лежит на прямой 00'.
Черт. 304.
Черт. 305.
Черт. 306.
При этом CD < COO'D = СО-\- ОО1 -f O'D = АО -f 00' -f O'B=
= AB, и каждый из отрезков А'В', А'В, АВ' также меньше АВ, так
что АВ есть наибольшее расстояние между точками обеих окружно-
окружностей. Это рассуждение сохраняет силу независимо от того, будут ли
данные окружности располагаться одна вне другой (черт. 305), одна
внутри другой (черт. 306), пересекаться (черт. 307) или касаться
одна другой.
Переходим к отысканию наименьшего расстояния.
Если окружности лежат одна вне другой, то ОО' <^ OCDO' =
— OC-\-CD-\-DO', откуда CD^>00' — О А' — О'В' = А'В', и каж-
каждый из отрезков АВ, АВ', А'В также больше А'В' (черт. 305), так
что А'В' есть наименьшее расстояние.
Если окружность О' лежит внутри окружности О, то ОС <^ ОО' -\-
_|- O'D -}- DC, так что CD ^> ОС ~ОО' — O'D = О А' — ОО' — О'В=
= А'В, и А'В меньше каждого из отрезков АВ, АВ', А'В' (черт. 306),
так что отрезок А'В есть наименьшее расстояние. В случае двух кон-
КНИГА ВТОРАЯ. ГЛАВА IV
331
центрических окружностей за А'В можно принять соответствующий
отрезок любого из радиусов.
Если окружности пересекаются или касаются, вопрос о наименьшем
расстоянии отпадает.
57. Центр О' окружности радиуса /?', касающейся данной окруж-
окружности О радиуса R, удовлетворяет условию 00' = R -|- R' , если ка-
А'
Черт. 307.
Черт. 308.
сание внешнее, и условию 00' — |/? — /?'|, если касание внутреннее.
Отсюда следует, что геометрическое место точек О' есть пара ок-
окружностей, концентрических с данной.
58. Если прямая АА' проходит через точку касания М окружностей
О и О' (черт. 308 и 309), то /_ О AM = /_ ОМА = /_О'МА' =
= /_О{'А''М, откуда и следует, что О А параллельно О'А'.
Черт. 309.
Черт. 310.
59. Окружности остаются касающимися друг друга, так как условия
00'= \R — R'\ в случае внутреннего касания и 00' = R-\-R' в слу-
случае внешнего касания остаются в силе при указанных в тексте задачи
изменениях радиусов.
УПРАЖНЕНИЯ К ГЛАВЕ IV (стр. 81).
60. Если О — центр данной окружности и Л — данная точка, то из
середины М любой хорды, проходящей через А, отрезок ОА виден
под прямым углом. Искомое геометрическое место есть окружность,
построенная на ОА как на диаметре, если А лежит внутри данной
окружности (черт. 310) или на данной окружности, и дуга аналогичной
окружности, если А лежит вне окружности (черт. 311).
332
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
61. Пусть АА'—данный диаметр окружности О (черт. 312),
ВВ'—диаметр, к нему перпендикулярный. На каждом радиусе ОС
откладываем отрезок ОМ, равный расстоянию СР точки С от АА'. Тре-
Треугольники ОСР и ВОМ равны (так как ОС = ВО, СР=ОМ,
Черт. 311.
В'
Черт. 312.
), откуда следует, что угол ОМВ—прямой. Гео-
Геометрическое место точек М состоит из двух окружностей, построен-
построенных на отрезках ОБ и ОБ1 как на диаметрах.
62. Пусть АРВ — меньшая, AQB—большая из дуг, на которые
точки А и В делят окружность (черт. 313). Обозначим / АОВ = а;
1 °. Если точки С и D лежат на дуге АРВ,
то
— а — $I)', то же самое выражение для
угла AIB получается в том случае, если
только одна из точек С и D лежит на
дуге АРВ. Если точки С и D' обе ле-
лежат на дуге AQB, то /_ Л/'?=—АРВ-\-
-\—¦ CD' = — (ас -\- $). Следовательно,
геометрическое место точек / и /' есть
вполне определённая окружность, про-
проходящая через точки Аи В (на чертеже не показана), так как отрезок
АВ виден из точек I под постоянным углом — C60° — а — р), а из
точек V —под постоянным углом -^ (а -\-$), и эти два угла составляют
в сумме 180°.
2°. Если точки С и D лежат на дуге АРВ, то /_АКВ =
= — ~AQB-\—CD = —C60°—сг
2 2 ?
Если точки С и Н обе лежат
J) Знаком у—-- обозначается дуга; по поводу равенства числовых значе-
значений дуг и углов см. пп. 17, 18.
КНИГА ВТОРАЯ. ГЛАВА IV
333
самое выражение для угла АК'В получается и в том случае, если
только одна из точек С и D' лежит на дуге AQB. Геометрическое
место точек К и К' есть также окружность (по той же причине, что
и для точек / и /').
3°. Пусть М—центр окружности, описанной около треугольника
/CD, и IX—касательная к этой окружности в точке I. Так как
вписанный угол равен половине центрального, опирающегося на ту же
дугу, то /_ CMD = 2 /_ CID = 360° — а—р. Следовательно, углы
равнобедренного треугольника CMD не из-
изменяются при перемещении хорды CD. Так
как сторона CD также имеет постоянную
длину, то и отрезки МС = MD = Ml со-
сохраняют постоянную длину. Далее, /_XID =
= ^/ /CD =180°—/_ACD = ^_ABD (так
как четырёхугольник ABCD—вписанный),
так что прямая IX параллельна АВ, а зна-
значит прямая Ml перпендикулярна к АВ. Ана-
Аналогичные рассуждения применимы и к тому
случаю, когда точки С и D занимают поло-
положение С и D' на дуге AQB, а точка / — по-
положение ['.
Так как геометрическое место точек /
(и Г) есть окружность, а отрезок IM сохра-
сохраняет постоянную величину и направление, то
геометрическое место точек М получается из геометрического места точек
/ посредством поступательного перемещения (п. 51), определяемого
отрезком IM. Следовательно, геометрическое место точек М есть
окружность, равная той, которую описывают точки / и /' (упр. 47).
Тем же путём доказывается, что геометрическое место центров
окружностей, описанных около треугольников KCD (и K'C'D') есть
окружность, равная той, которую описывают точки К и К.'¦
Примечание. Из того, что стороны и углы треугольников COD
и CMD не изменяются при перемещении хорды CD, следует, что и рас-
расстояние ОМ при этом не изменяется.
Поэтому центр окружности, являющейся геометрическим местом точек
М, совпадает с центром данной окружности. То же справедливо и для гео-
геометрического места центров окружностей, описанных около треугольни-
треугольников KCD.
63. Если точка М лежит на дуге АРВ (черт. 314), то /_ANB =
= ^/ MBN' = — /_ АМВ. Так как при перемещении точки М по дуге
АРВ угол АМВ сохраняет постоянную величину, то и угол AN В со-
сохраняет постоянную величину. Следовательно, точка N лежит на вполне
определённой дуге окружности, имеющей своими концами точки А и В
Черт. 314.
334
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
(и представляющей собой геометрическое место точек, из которых
отрезок АВ виден под данным углом). При этом точка N лежит от
касательной AN0 в точке А к данной окружности по ту же сторону,
что и точка В. Поэтому геометрическое место точек N есть дуга NVNB.
Аналогичное рассуждение применимо и в том случае, если точка М
лежит на дуге AQB: если точка М описывает дугу AQB, то точка
N' описывает дугу N0'N'B аналогичную дуге N0NB.
Черт. 315.
Черт. 316.
В
64. Если В1 и С — середины дуг АС и АВ и М, /V— точки пе-
пересечения прямой В"С с хордами АВ и АС (черт. 315), то
/_ AMN =-i Ш -\-^ ВС ; Z. ЛЛШ = -1 АС-\-^ ЯС . Следователь-
Следовательно, /_AMN = /_ANM и AM=AN.
65. Если MAN и MBN'—две секущие (черт. 316), пересекаю-
пересекающиеся вне обеих окружностей, то /_ М'МА = 180° — /_ М'ВА =
= /_ ABN' = 180° — Z ANN'. Отсюда
/_М'МА-\~/_ XNN'=\80°, так что ММ'
и NN' параллельны. Аналогичные рассуж-
рассуждения применимы, если секущие пересе-
пересекаются внутри одной из данных окружно-
окружностей (как показано на черт. 316 пунктиром).
66. Если АР и ВР — биссектрисы
углов А и В четырёхугольника ABCD
(черт. 317), то из треугольника АВР
имеем /_ АРВ = 18U° - 4" Z А — 4"Z B-
Аналогично из треугольника CRD, где CR
и DR — биссектрисы углов С и D, имеем
/D С /_АРВ-\-
/_CRD=\80°— —/.C — ~/_D. Складывая,
имеем
= 180°. Следовательно, четырёхугольник PQRS может быть вдисан
в окружность.
Если АР' и ВР'—биссектрисы внешних углов при вершинах А и В,
то АР' и ВР' соответственно перпендикулярны к АР и ВР, и, следова-
КНИГА ВТОРАЯ. ГЛАВА IV
335
тельно, /_АР'В= 180°—/_АРВ. Точно так же, если CR' и DR' -бис-
-биссектрисы внешних углов при вершинах С и D, то /_ CR'D = 180° —
— /_CRD. Отсюда /_AP'B-\-/_CR'D='S№° — (/_APB-\-/_CRD) =
= 180°, и четырёхугольник P'Q'R'S' также можно вписать в окружность.
67. Имеем
отсюда /_CED-{-/_BFD =~(АС-\-СВ-)-веЬ-\-AD) = 180°.
68. Обозначим данную окружность буквой С, данную прямую —
буквой D (черт. 319). Имеем /_PRS = /_PQS. Но угол PQS не
зависит от выбора произвольной ок-
окружности, так как точки Р и Q
и прямая D даны. Следовательно,
и угол PRS сохраняет постоянное
/_ CED = ~ CAD = -^ АС + 4"
2 2 ?
U
Черт. 319.
Черт. 318.
значение. Так как вписанный
в окружность С угол PRS,
или, что то же, угол PRU,
сохраняет постоянную вели-
величину, то положение точки
U не зависит от выбора
окружности PQR (так обо-
обозначается окружность, про-
проходящая через точки Р, Q
и R).
69. Проведём через точку
А секущую ЕЕ' (черт. 320),
перпендикулярную к АВ, и
обозначим через Е и Е' вторые точки её пересечения с окружностями
О и О'. Прямые BE и BE' будут диаметрами окружностей. Из тре-
треугольников ВСС и BEE' имеем /_ СВС = 180° — J_ ССВ—^_ССВ =
= \т° — /_ЕгЕВ—/_ЕЕ'В = 2-ЕВЕ'=^.0Ш- Таким
угол СВС сохраняет постоянную величину.
336
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Из равенства углов СВС и ОБО' следует, что /_ СВО = /_С'ВО'.
Таким образом, имеем /_ВСО = /_СВО = /_СВО' = /_ ВС О''. Если
М—точка пересечения прямых СО и СО', N — точка пересечения
прямых СМ и ВС, то в треугольниках fiC.V и MCN мы имеем по два
равных угла. Следовательно, равны и третьи углы: / СВС = / CMC.
Итак, угол СВС равен углу между прямыми ОС и О'С.
Угол CPD' между хордами CD и CD'
равен 180° — /_PDA — /_ AD'C = 180° —
— /_ СВА — /_ ABC = 180° — ^/ СВС.
Если отрезок СС будет неподвижным, а
прямая DD' будет совпадать с СС, то прямые
С?> и С'?>' обратятся в касательные в точках
Си С, и мы получаем такой результат: угол
между касательными в точках С и С равен
углу СВС или углу, ему пополнительному.
70. Пусть AD,BE, CF—высоты тре-
Черт. 321. угольника ЛВС (черт. 321 и 322); И— точка
их пересечения; К— точка прямой AD, симмет-
симметричная с Н относительно прямой ВС. Прямоугольные треугольники CDH
и CDK равны (по равенству катетов), и потому /_CKD =/_CHD.
Но ^/ CHD = ^/ ABC как углы с соответственно перпендикулярными
Черт. 322.
Черт. 323.
Черт. 324.
сторонами. Следовательно, /_CKD = /_СВА, и четыре точки А, В,
С, К лежат на одной окружности.
Таким же путём доказывается, что и точки, симметричные с И
относительно АВ и АС, также лежат на описанной окружности.
71. Пусть AD, BE и CF — высоты треугольника ABC, и Н—точка
их пересечения (черт. 323 и 324). Четырёхугольник BDHF можно
вписать в окружность, так как /_BDH = ^/_BFH = 90°. Отсюда
следует, что /_ BDF = /_ BHF. Аналогично докажем, пользуясь четы-
четырёхугольником CDHE, что /_CDE = /^CHE. Так как /^BHF =
= /_СНЕ, то и /_BDF = /_CDE. Прямые DE и DF, равно накло-
КНИГА ВТОРАЯ. ГЛАВА V 337
нённые к ВС, равно наклонены и к высоте AD. Высота AD треуголь-
треугольника ABC есть (внутренняя или внешняя) биссектриса угла EDF
треугольника DEF.
Примечание. Так как углы BHF и CAB имеют соответственно
перпендикулярные стороны и одинаковое направление вращения, то
?BHF= ?А. Мы доказали выше, что /_BDF= /.CDE= ?BHF. Следо-
Следовательно, /_ BDF— ?_ CDE= ? А. Итак, отрезки, соединяющие основания
высот треугольника, образуют с каждой его стороной углы, равные тому
углу треугольника, который лежит против этой стороны.
72. Пусть Р — точка окружности, описанной около треугольника
ABC, и X, Y, Z— основания перпендикуляров, опущенных из этой
точки на стороны ВС, АС, АВ треуголь-
треугольника. Предположим для определённости,
что точка Р лежит на дуге ВС (черт.
325). Так как точки Р, X, С, Y лежат на
одной окружности, то /_ Р УХ = /_ PCX;
ана логи чно /_PYZ =/_ PAZ. Но /_ РСХ=
==^ PAZ, так как точки Р, А, В, С ле-
лежат на одной окружности. Следовательно,
/_PYX = /_PYZt и прямая XY совпа-
совпадает с ZY. Точки X, Y, Z лежат на одной
прямой.
Аналогично доказывается и обратное
предложение: так как точки Р, X, Y, С
лежат на одной окружности, то /_PYX — /_PCX, и аналогично
/_PYZ = /_PAZ. Так как. точки X, Y, Z лежат на одной прямой,
то углы PYX и PYZ совпадают, так что /_ PCX = /_ PAZ. От-
Отсюда следует, что точки Р, А, В, С лежат на одной окружности.
УПРАЖНЕНИЯ К ГЛАВЕ V (стр. 94).
73. 1°. Строим окружности данного радиуса с центрами в данных
точках. Если эти две окружности пересекаются (касаются), то их
общие точки служат центрами искомых окружностей; если они не
имеют общих точек, то задача не имеет решений.
2°. Строим прямую, параллельную данной прямой, расположенную от
неё с той же стороны, что и данная точка, и отстоящую от неё на
расстоянии, равном радиусу. Строим окружность с центром в данной
точке и радиусом, равным данному радиусу. Общие точки построенной
прямой и построенной окружности будут центрами искомых окружностей.
Задача может иметь два, одно или ни одного решения.
Если данная точка лежит на данной прямой, построение упрощается.
3°. Если данные прямые пересекаются, то строим две пары прямых,
параллельных данным прямым и отстоящих от них на расстоянии, рав-
равном радиусу. Точки их пересечения между собой будут центрами
искомых окружностей. Задача имеет четыре решения.
22 Элементарная геометрия
338
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если данные прямые параллельны, то задача невозможна, за исклю-
исключением того случая, когда расстояние между ними вдвое более данного
радиуса; в последнем случае задача имеет бесчисленное множество
решений.
4°. Строим пару окружностей — геометрическое место центров
окружностей данного радиуса, касающихся данной окружности (упр. 57),
и пару прямых, параллельных данной прямой и отстоящих от неё на
расстоянии, равном данному
радиусу. Каждая из точек
пересечения одной из по-
построенных окружностей с
одной из построенных пря-
прямых есть центр одной из
искомых окружностей. На-
Наибольшее возможное число
решений — восемь.
74. Пусть О—данная
-D окружность,/) — данная пря-
прямая и А — данная точка
(черт. 326). Центр О' иско-
д' мой окружности лежит на
Черт. 326. перпендикуляре, восставлен-
восставленном к D в точке А. Если
отложить на этом перпендикуляре отрезок АА', равный радиусу дан-
данной окружности, то О'А'=^О'О. Отсюда такое построение. На пер-
перпендикуляре к прямой D в точке А откладываем в обе стороны
радиус данной окружности АА' = АА". Прямые, проходящие через
середины отрезков О А' и ОА" и к ним перпендикулярные, определяют
положение точек О' и О" — центров искомых окружностей — на
прямой АА'.
Задача имеет два решения. Однако, если данная прямая касается
данной окружности и точка А не лежит на окружности, то только
одно; если же точка А лежит на самой окружности, то бесчисленное
множество решений (если данная прямая касается данной окружности)
или вовсе не имеет решения (если данная прямая пересекает данную
окружность).
75. Если через все точки одной из данных прямых (или окружно-
окружностей) С провести отрезки данной длины и данного направления,
то геометрическим местом их концов будет прямая линия С" на ос-
основании п. 51 (или окружность С", равная С, на основании упр. 47).
Точка пересечения прямой (окружности) С" с другой данной пря-
прямой (или окружностью) С определяет положение концов искомого
отрезка.
Так как прямая (окружность) С" может занимать два различных
положения на плоскости, то в случае, когда даны прямые линии, за-
задача может вовсе не иметь решений, иметь два решения или бесчис-
бесчисленное множество решений; если даны две окружности, то задача
КНИГА ВТОРАЯ. ГЛАВА V
339
Черт. 327.
может вовсе не иметь решения, иметь 1, 2, 3, 4 или бесчисленное
множество решений.
76. Есчи на каждой касательной к данной окружности С отложить
отрезок AM, равный данному отрезку а, то геометрическим местом
концов М этих отрезков будет окружность С, концентрическая
с данной (черт. 327). Действительно, если АМ=^а, то ОМ = const.
Искомые касательные выходят из точек
пересечения Ж, и М2 данной прямой D
с этой окружностью С. Наибольшее
возможное число решений — четыре.
77. Пусть даны сторона ВС = а,
угол А и высота ha, выходящая из вер-
вершины А. Строим произвольно основа-
основание ВС, затем геометрическое место
точек, из которых отрезок ВС виден
под данным углом А (п. 77). Точка А
определяется как точка пересечения
этого геометрического места с прямой,
параллельной ВС и отстоящей от неё
на расстоянии ha.
Пусть теперь даны сторона ВС=а,
угол А и высота hb, выходящая из вер-
вершины В. Строим прямоугольный треугольник ВСЕ (черт. 328)
по гипотенузе fiC=a и катету BE=hb. Затем строим угол
ЕВА, равный 90° — /_А (или /_ А—90°). Пересечение второй сто-
стороны этого угла с прямой СЕ определяет положение вершины А.
78. Через конец В данного отрезка АВ проводим произвольную
прямую и откладываем на ней в обе стороны равные отрезки fiM = BN.
Прямая, соединяющая точку М с серединой от-
отрезка AN, отсекает от отрезка АВ одну треть,
так как она является медианой треугольни-
треугольника AMN.
79. 1°. Пусть даны стороны АВ и ВС и ме-
медиана AD, выходящая из вершины А; в таком
случае можно построить треугольник ABD по
трём сторонам и отложить DC —BD (черт. 286).
Пусть теперь даны стороны АВ и ВС и ме-
медиана BD, выходящая из их общей вершины;
если DE^BD (черт. 27), то можно построить треугольник ABE по
трём сторонам, разделить BE пополам в точке D и отложить DC = AD.
'2°. Пусть даны сторона АВ и медианы AD и BE, выходящие из
концов данной стороны. Если G—точка пересечения медиан (черт. 286),
то можно построить треугольник ABG по трём сторонам АВ, — AD,
В а С
Черт. 328.
3
— BE и отложить на лучах AG и ВО соответственно отрезки AD и BE.
о
Пересечение АЕ и BD даёт С.
22*
л
340 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Пусть теперь ¦ даны сторона АВ, медиана AD, выходящая из её
конца, и медиана CF, проходящая через её середину (черт. 286).
Можно построить треугольник AFO, где О — точка пересечения ме-
1 2 1
диан, по трём сторонам AF = -^r AB, AG=—AD и FG = —CF , a
2/ о о
затем построить точки В я С.
3°. Пусть даны три медианы AD, BE, CF. На чертеже 282 (упр. 37)
треугольники AEG и СЕК равны, откуда АО=СК. Можно по-
2 2
строить треугольник СОК по трём сторонам C/f = —AD, GK = — BE,
о о
2
CG = — CF. Далее, откладывая GB=GK, получаем точку В, а деля
о
пополам GK и откладывая ЕА = ЕС, — точку А.
80. Обозначая через а, Ь, с стороны ВС, АС, АВ искомого тре-
треугольника (черт. 329), через ha и та — высоту и медиану, выходящие
из вершины А, и аналогич-
аналогично — через ть и тс две дру-
другие медианы, получим,принимая
за данную высоту АИ = ha, сле-
следующие пять различных слу-
случаев: 1) a, ha, ma; 2) a, ha,
ть; 3) с, ha, mc; 4) с, ha, ma;
5) с, ha, ть. Все остальные
и ?—'— возможности но существу не от-
., _ „ личаются от какой-либо одной
Черт. 329. >
v из пяти, перечисленных.
1°. Строим прямоугольный треугольник AHD по катету AH = ha
и гипотенузе AD = ma, и на прямой DH откладываем в обе стороны
от точки D отрезок DB = DC = —a.
2°. Строим ВС=а, проводим прямую, параллельную ВС на рас-
расстоянии ha от неё, и радиусом 2ть делаем из точки В засечку на этой
прямой. Если К — полученная точка, то середина Е отрезка ВК будет
и серединой стороны АС.
3°. Строим прямоугольный треугольник АН В по катету AH = ha
и гипотенузе АВ = с. Вершина С есть точка пересечения прямой ВН
с окружностью радиуса тс с центром в середине F стороны АВ.
4°. Строим тот же прямоугольный треугольник ЛНВ. Середина D
стороны ВС есть точка пересечения прямой ВН с окружностью ради-
радиуса та с центром в точке А.
5°. Строим тот же прямоугольный треугольник АНВ. Проводим
через А прямую, параллельную ВН, и из точки В, как из центра,
описываем окружность радиуса 2ш6. Их пересечение даёт некоторую
точку К. Середина Е отрезка ВК есть середина стороны АС.
Наиболее возможное число решений — одно в первом из рассмот-
рассмотренных случаев и два — в каждом из остальных.
КНИГА ВТОРАЯ. ГЛАВА V
341
81. Сохраняя обозначения упражнения 80 и считая данной медиану
ВЕ = ть (черт. 330), достаточно рассмотреть следующие пять слу-
случаев: 1) Z.B, hb, mb; 2) /_ A, ha, mb; 3) /_В, ha, mb; 4) /_А, hb, mb;
5)ZC V "V
1°. Строим прямоугольный треугольник BIE по катету В/= hb и
гипотенузе BE = ть и на продолжении отрезка BE за точку Е от-
откладываем ЕК = BE. На прямой El строим точку А такую, чтобы
^/ ВАК = 180° — /_ В
(пользуясь геометрическим L
местом точек, из которых
отрезок ВК виден под дан-
данным углом), и откладываем
ЕС = АЕ. Треугольник
ABC будет искомым.
2°. Строим прямоуголь-
прямоугольный треугольник BKL по
катету BL = ha и гипо-
гипотенузе ВК = 2ть. Пусть Е — середина отрезка ВК. На прямой
KL строим точку А такую, чтобы ^_ВАЕ = ^_А. Откладываем
ЕС=АЕ.
3°. Строим прямоугольный треугольник АВН по катету AH=ha
и углу В. Через ¦ точку А проводим прямую, параллельную ВН, и из
точки В, как из центра, — окружность радиуса 2ть\ пусть К — точ-
точка их пересечения. Середина Е отрезка ВК есть середина стороны
АС. Поэтому С есть точка пересечения прямых ВН и АЕ.
* 4°. Строим прямоугольный треугольник ABI по катету BJ = hb и
углу А. Из точки В, как из центра, описываем окружность радиуса
ть. В пересечении с прямой AI получаем середину Е стороны АС.
5°. Строим прямоугольный треугольник АСН по катету АН = ha и
углу С. Из середины Е стороны АС, как из центра, описываем
окружность радиуса ть. Точка её пересечения с прямой СН и будет
вершиной В.
Наибольшее возможное число решений в первом случае равно еди-
единице (так как обе дуги, из которых отрезок ВК виден под углом
180° — /_ В, приводят к одному и тому же треугольнику), во втором
случае — четырём (так как геометрическое место точек, из которых
отрезок BE виден под данным углом А, есть совокупность двух дуг
окружности, и может случиться, что каждая из этих дуг пересекает
прямую KL в двух точках), в третьем случае — единице, в четвёртом —
двум и в пятом — единице.
82. Пусть ABC—искомый треугольник (черт. 331), в котором
даны ВС = а, угол А и АВ-\-АС (или АВ — АС; для определённости
обозначаем вершины В и С треугольника так, чтобы было АВ^>АС).
Откладываем на прямой АВ отрезки AD = AE = AC. Так как
треугольник DAC равнобедренный, то / ВАС^ / АРС-\- / АСР =
— 2 /_ ADC, откуда /_ ADC= -~ /_ А. Аналогично найдём, что
342 PFUIEHHH УПРАЖНЕНИЙ И ЗАДАЧ
Таким образом, треугольник BCD (или ВСЕ) можно построить по
сторонам BC,BD (или ВС, BE) и углу BDC (или ВЕС), противолежа-
противолежащему одной из них (п. 87).
После того как треугольник BCD (или ВСЕ) построен, точка А
определяется как точка пересечения прямой BD (или BE) с перпенди-
перпендикуляром, восставленным в середине стороны CD (или СЕ).
п 83. Пусть ABC — искомый треуголь-
треугольник (черт. 331), в котором даны ВС,
угол В и АВ-\- АС (или АВ — АС, или
АС—АВ).
Задача решается так же, как и упраж-
упражнение 82;' только треугольник BCD
? ? (или ВСЕ) строится по двум сторонам
ВС и BD (или ВС и BE) и заключённому
Черт. 331. между'ними углу В (или 180° — /_В,
если АС>АВ).
84. Пусть даны угол А, высота ha, выходящая из вершины А,
и периметр треугольника. Если на продолжениях стороны ВС за точ-
точки Ви С отложить отрезки ВВ' = В А и СС = С А, то отрезок В'С
будет равен периметру треугольника, а углы ВВ А и СС А — соответ-
соответственно равны -7J- /_В и — /_ С, откуда следует, что /_ Б АС = 180° —
— ~ч{/-В~\~Z *-•)= 90еЧ~ "о" Z ^- Таким образом, треугольник
АВ'С можно построить по основанию В'С, равному периметру
искомого треугольника, углу при вершине А и высоте (упр. 77).
Точки В и С лежат на перпендикулярах, восставленных в серединах
сторон А В' и АС.
Пусть теперь даны угол А, высота hb, выходящая из вершины,
отличной от А, и периметр треугольника. Строим прямоугольный
треугольник АВН с углом А (или 180° — /_А) и катетом BH = hb.
Гипотенуза АВ будет одной из сторон искомого треугольника.
Последний можно построить, зная сторону АВ, прилежащий угол А
и сумму двух других сторон, равную разности между данным пери-
периметром и стороной АВ (упр. 83).
85. В обозначениях упражнения 82 (черт. 331) имеем:/_ADC —
^ откуда Z BCD ZC\
A80°ZSZC) 90o+y (Z C-
= \ A80°—Z^)=90°— —
— J_B). Если даны ВС и АВ-\-АС (или АВ — АС), то можно по-
КНИГА ВТОРАЯ. ГЛАВА V
343
строить треугольник BDC (или ВЕС) по сторонам ВС, BD
(или ВС, BE) и углу BCD (или ВСЕ), противолежащему одной из
них (п. 87). Построение заканчивается, как в упражнении 82.
86. Проводим прямые, соответственно параллельные данным пря-
прямым и отстоящие от них на одном и том же расстоянии а; точка
пересечения построенных прямых лежит на искомой биссектрисе.
Повторяя построение для расстояния а', отличного от с, находим
вторую точку биссектрисы.
87. Существует ява вида описанных четырёхугольников, у кото-
которых окружность заключена внутри его: выпуклый четырёхугольник
(черт. 332), у которого окружность касается всех сторин, и невы-
невыпуклый четырёхугольник (черт.
333), у которого окружность
касается двух сторон и продол-
продолжений двух других сторон. Если
В М
N
/V
Черт. 333.
М, N, P, Q — точки касания, то в первом случае AB-\-CD-=AM-\-
-\-MB-}-CP-\-PD = AQ4-NB-}-CN-{- QD=BC-\-AD, во втором
случае АВ-\-CD = AM -f MB-f CP — DP = AQ-\-NB -f CN —
— DQ= ВС -\- AD, так как касательные к окружности, проведённые
из одной точки, равны.
М
Черт. 334.
Черт. 335.
Существует три типа описанных четырёхугольников, у которых
окружность расположена вне четырёхугольника: выпуклый, у кото-
которого окружность касается продолжений всех четырёх сторон (черт. 334),
невыпуклый, у которого окружность касается двух смежных
сторон и продолжений двух других сторон (черт. 335), и несобст-
34$
PFLPFHHH УПРАЖНЕНИЙ И ЗАДАЧ
венный (п. 21), у которого окружность касается двух противопо-
противоположных сторон и продолжений двух других сторон (черт. 336).
В первом случае (черт. 334) имеем: AB-\-AD = BM—AM-\-AQ—
~DQ=BM — DQ = BN — DP=BN— CN-f CP— DP = BC-\-CD;
во втором случае (черт. 335) AB-\-AD = BM— AM-\-AQ-{-DQ=
= BM -f- DQ = BN -\-DP= BN—CN-{-CP-\- DP — ВС -\-CD;
в третьем (черт. 336) AB-\- AD=BM — AM-\-AQ-\-DQ = BM-\-
-\-DQ=BN-\- DP =BN-\-CN—CP-\-
-j- DP = ВС -f- CD, так как касательные
к окружности из одной точки равны.
Обратно, пусть, например, в выпуклом
четырёхугольнике ABCD (черт. 337 и 338)
суммы противоположных сторон равны;
АВ -\- CD = BC-\- AD. Построим окруж-
окружность, касающуюся сторон АВ, ВС, CD
четырёхугольника и расположенную с той
же стороны от каждой из этих сторон,
что и внутренняя область четырёхугольника.
Черт. 336.
Предположим, что эта окружность не касается стороны AD. Проведя
из точки А касательную AD' к построенной окружности, будем иметь
АВ-\- CD' = ВС -(- AD'. Из этого и из предыдущего равенств нахо-
находим AD — AD'=CD—CD'~DD', если CD^>CD', и AD'—AD =
=CD'—CD=DD', если CD'~j>CD. В обоих случаях разность
Черт. 337.
двух сторон треугольника ADD' оказывается равной третьей сторо-
стороне, что невозможно. Следовательно, точки D и D' совпадают.
Итак, если в выпуклом четырёхугольнике суммы противополож-
противоположных ' сторон равны, то существует окружность, заключенная
внутри четырёхугольника и касающаяся его сторон.
Аналогичные обратные теоремы имеют место и в остальных слу-
случаях. Доказываются они совершенно так же, как только что дока-
доказанная.
88. Пусть окружность касается сторон АВ, ВС, CD четырёх-
четырёхугольника ABCD, И AD' — касательная из точки А к этой окруж-
окружности, так что AB-{-CD' = BC-{-AD' (упр. 87). Если сторона AD
КНИГА ВТОРАЯ. ГЛАВА V
345
не пересекает окружности (черт. 337), то AB-\-CD' -\-D'D = BC-\-
-\-AD'-\-D'D. Но CD'-f D'D==CD, AD'-\-D'D> AD, откуда АВ-\-
_L CD^> PC-\- AD. Если AD пересекает окружность (черт. 338),
TO.4?-f CD' — D'D = BC-\-AD' — D'D. WoCD'—D'D = CD, AD' —
— D'D<CAD, откуда АВ-\- CD < BC-\- AD.
Итак, если AD касается окружности, то АВ-\-CD = ВС-\-AD;
если AD не пересекает окружности, то АВ-\- CD^>BC-\-AD,
Черт. 339.
Черт. 340.
и если AD пересекает окружность, то АВ-\~ CD <^ ВС-\-AD. Так
как перечисленные случаи охватывают все возможности, то спра-
справедливы и обратные предложения.
88а. Если АВ не пересекает окружности (черт. 339), AM и
BN — касательные к окружности и Р — точка их пересечения,
то AB<iAP-\-BP<CAM-\-.BN; AB>AP — BP =
—(РМ-\-ВР) = АМ— BN. Если АВ
пересекает окружность и точки А
и В лежат по разные стороны от
окружности (черт. 340), AM и BN —
касательные, Р — точка их пересече-
пересечения, то АВ^>АР — ВР=(АМ-\-
-+- МР) — (PN — BN) =zAM-\- BN;
если же точки А и В лежат по
одну сторону от окружности (черт.
341'), то AB<CAPJrBP=(AM—PM)-\-(PN—B\) = AM—BN.
89. Угол, под которым отрезок АВ подвижной касательной,- за-
заключённый между двумя неподвижными касательными РМ и PN
(черт. 342), виден из центра О окружности, сохраняет постоянную
величину, пока окружность остаётся вневписанной в треугольник, обра-
образованный тремя касательными (подвижная касательная занимает поло-
положение АВ или A'ff), и заменяется пополнительным утлом, если
окружность становится вписанной (подвижная касательная занимает
положение А"В"). Действительно, /_ АОВ = /_АОТ-\-/_ ТОВ~
Черт. 341.
346
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
; точно так же /_А'ОВ =
= "Г Z МОИ;
2
? А'ОВ" = Z А"ОГ -f /. Т"ОВ' = у Z М0Т" + y
=. 180°— ^- /_M0N {Т, Т, Т" — точки касания).
Если данные касательные в точках М и N параллельны, то отре-
отрезок подвижной касательной, заключённый между ними, виден из центра
под прямым углом.
Черт. 342.
90. Пусть РМ и PN (черт. 342) — неподвижные касательные к
окружности, АВ—отрезок подвижной касательной, точка прикосновения
которого Т лежит на меньшей дуге MTN; тогда РА + РВ-\- АВ =
= PA^-PB-\-AT-\-BT = PA-\-PB-\-AM-\-BN = PM-\-PN. Но
РМ и PN имеют постоянную длину.
Если точка прикосновения Т (или Т") подвижной касательной ле-
лежит на большей дуге MT'N, то возможны несколько случаев.
1°. Подвижная касательная пересекает прямую РМ в точке А\
лежащей за точкой М, и прямую PN в точке В', лежащей за точ-
точкой Р- В этом случае постоянную величину имеет РА'-\-А'В' —
_ РВ' =РМ -h MA' -f А'В' — (B'N — PN) =РМ-\- ТА' -f А'В —
_B'N-\-PN=PM-\- T'B — BN-\-PN=PM-\-PN.
2°. Подвижная касательная пересекает прямую РМ в точке, лежа-
лежащей за точкой Р, и прямую PN—в точке, лежащей за точкой N.
Этот случай вполне аналогичен предыдущему.
3°. Подвижная касательная пересекает прямую РМ в точке А",
лежащей за точкой М, и прямую PN в точке В', лежащей за точ-
точкой N. При этом постоянную величину имеет РА"-\-РВ'—А"В' =
— ра" -\- рв1 — А"Т" — ТВ' = PA" -f РВ" — А"М — B'N = РМ -\-
+ PN.
КНИГА ВТОРАЯ. ГЛАВА VI
347
Итак, во всех трёх случаях можно сказать: если точка прикосно-
прикосновения лежит на большей из двух дуг, то постоянную величину сохра-
сохраняет разность между суммой двух сторон треугольника, образованного
тремя касательными, и его третьей сториной (причём роль этой третьей
стороны играет отрезок одной из неподвижных или подвижной каса-
касательной в зависимости от расположения последней).
90а. Так как касательные к окружности из одной точки равны
между собой, то (черт. 102) AE = AF; BF = BD; CD = CE. Далее
в силу этих равенств имеем AF-\-BF = AE-\-BF = c, BD-\- CD =
= BF-\-CD = a, CE + AE=CD-\-AE = b. Отсюда AE-\-BF-\-
-\-СЬ = р и AE = p — a, BF = p — b, CD = p — c. Далее АВ-\-
-4- BDX -f CDX + А С = 2p, откуда, в силу BDX = BFX, CDX = CEX,
AFX = AEV получим AEX = AFX = p; далее имеем BDX = BFX = AFi—
— AB = p—с; аналогично CDx=CEx=p— b, и т. д.
91. Если три окружности с центрами в вершинах А, В, С тре-
треугольника ABC попарно касаются одна другой, то точки касания лежат
на сторонах треугольника (или их продолжениях). Если окружности
касаются одна другой внешним образом в точках D, ?, F на сторонах
ВС, АС, АВ, то AE=AF, BF = BD, CD = CE и AE-\-CD=b,
BFA-AE = c, CD-\-BF=.a; откуда следует (упр. 90а), что точки
D, E, F совпадают с точками касания впи-
вписанной окружности. Если окружность с цент»
ром А касается внутренним образом окруж-
окружностей с центрами В и С, то аналогично най-
найдем, что точки касания совпадают с точками
касания Dx, ?,, Fx вневписанной окружно-
окружности со стороной ВС и продолжениями двух
других сторон и т. д.
УПРАЖНЕНИЯ К ГЛАВЕ VI Гетр. 103).
92. Пусть прямые а и b неизменяемой
фигуры проходят при перемещении послед-
ней соответственно через данные неподвиж-
неподвижные точки Аи В (черт. 343). При этом угол,
образованный этими прямыми, сохраняет по- Черт. 343.
стояяную величину и, следовательно, точка их
пересечения М описывает окружность, проходящую через точки А
и В. Любая прямая с неизменяемой фигуры, проходящая через точку
пересечения М, образует с а и b постоянные углы и потому прохо-
проходит через некоторую неподвижную точку С той же окружности.
Всякая другая прямая с' подвижной фигуры параллельна некоторой
прямой с той же фигуры и остаётся от этой прямой на постоянном
расстоянии. Отсюда следует, что прямая с' касается некоторой непод-
неподвижной окружности с центром в точке С.
Центр вращения лежит на нормалях к траекториям всех точек фи-
фигуры (п. 104). Найдём касательную и нормаль к траектории точки Л
348
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
в самой точке А. С этой целью рассмотрим некоторые другие поло-
положения А' и М' точек А и М на плоскости. Прямая А'М будет про-
проходить через точку А (так как прямая AM по условию вращается
около точки Л). Следовательно, прямая АА' совпадает с AM', а пре-
предельным положением прямой АА' будет AM. Итак, траектория точки А
имеет своей касательной в точке А прямую AM, а нормалью — пер-
перпендикуляр к этой прямой в точке А. Траектория точки М (окруж-
(окружность) имеет своей нормалью в точке М диаметр, проходящий через М.
Отсюда следует, что центр вращения О есть точка окружности ABC,
диаметрально противоположная М.
93. Пусть О' (черт. 344) — центр вращения фигур F, и F2, О" —
центр вращения фигур F2 и Fa. Разложим первое из этих вращений
О'
/О'
Черт. 344.
на две симметрии относительно прямых D' и D (п. 102 а), выбрав за
втирую ось симметрии D прямую О'О". При этом один из углов
между прямыми D' и D будет равен половине угла между фигурами
F, и F2. Аналогично, разложим и второе из этих вращений на две
симметрии относительно прямых D и D', приняв за первую ось сим-
симметрии D ту же прямую О'О", Как и в первом случае, один из углов
между прямыми D и D" будет равен половине угла между фигурами
F2 и Fr
Вращение, совмещающее фигуру /^ с г3, можно получить как ре-
результирующее двух вращений, из которых первое совмещает F, с F2,
а второе F2 с F3. Разложив каждое из этих двух вращений на две
симметрии, как указано выше, мы убедимся, что вращение, совмещаю-
совмещающее Fx с Fs, будет результирующим двух симметрии относительно
прямых D' и D" (п. 103). Отсюда следует, что точка пересечения О
прямых D' и D" есть центр этого последнего вращения, и один из
углов между прямыми D' и D" равен половине угла между фигурами
/=", и Fs.
Итак, углы треугольника О'О"О соответственно равны половинам
углов между данными фигурами, взятыми попарно, или дополняют эти
половины до 180°.
94. Вращение около центра О, можно заменить последователь-
последовательностью двух симметрии (п. 102а) относительно прямых Z), и D2, про-
проходящих через Oj (черт. 345). Вращение около центра О2 можно за-
КНИГА ВТОРАЯ. ГЛАВА VT
349
менить последовательностью двух симметрии относительно прямых
D,' и D2', проходящих через О2. Можно предположить, не нарушая
общности, что прямые D2 и ?),' совпадают. Остаётся последователь-
последовательность симметрии относительно прямых Dx и D2', которые параллельны
друг другу, так как образуют с D2 углы, равные половине данного
угла поворота и имеющие противоположные направления. Последова-
Последовательность симметрии относительно Dx и D2' даёт поступательное пере-
перемещение.
95. Пусть А и В— две точки первой фигуры F (черт. 346),
А' и В — соответственные им точки второй фигуры F\ имеющей про-
противоположное направление вращения.
/7
А.
В' ,fl
в
Черт. 346.
1°. Выбрав произвольно прямую Dx, строим фигуру F', симметрич-
симметричную с первой относительно этой прямой, и пусть Л", В' — точки этой
фигуры, соответствующие точкам А, В. Фигуры F" и F', как имеющие
одинаковое направление вращения, можно получить одну из другой
бесчисленным множеством способов с помощью двух симметрии (п. 102).
В общей сложности получаем три симметрии.
2°. Чтобы последние две симметрии были равносильны поступа-
поступательному перемещению, необходимо и достаточно, чтобы отрезок А"В'
был параллелен отрезку А'В' и был направлен с ним в одну сторону,
а для этого прямая Dx должна быть параллельна одной (вполне
определённой) из биссектрис Do углов между прямыми АВ и А'В'
(черт. 347).
3°. Наконец, чтобы направление поступательного перемещения А"А'
было параллельно прямой Dv необходимо и достаточно, чтобы пря-
прямая Dj была выбрана на середине расстояния между прямыми, парал-
параллельными Do и проходящими через точки А и А'. Другими словами,
прямая Dj должна быть параллельна Du и проходить через середину
отрезка АА'.
Аналогично можно получить фигуру F" из F с помощью поступа-
поступательного перемещения, сопровождаемого одной симметрией, и в част-
частности сделать так, чтобы направление перемещения было параллельно
оси симметрии: для этого надо только начать с построения фигуры F*,
симметричной с F (а не с F) относительно прямой Dv
96. Пусть ABC — искомый треугольник (черт. 348). Вершину А
можно, очевидно, выбрать произвольно на одной из данных прямых,
350
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗА1АЧ
например на прямой 2. Построим прямую /', которая получается из
прямой / поворотом около точки А на 60° хотя бы по часовой стрелке.
Для этого опустим из точки А перпендикуляр АР на прямую /, по-
построим угол РАР', равный 60°, отложим АР' = АР и, наконец, про-
С
Черт. 348.
ведём через точку Р' прямую /', перпендикулярную к АР'. Так как
при повороте около точки А на 60° точка В совмещается с точкой С,
то точка С есть точка пересечения прямых /' и 3. Зная положение
точек А и С, можно построить и точку В.
Второе решение (треугольник АВ'С), очевидно, симметрично с пер-
первым относительно перпендикуляра к
трём данным прямым.
Аналогичные рассуждения приме-
применимы и к трём данным окружностям.
97. Пусть О — центр данной
окружности, Я и Q — данные точки,
,, АВ—искомая дуга, равная, данной
дуге MN и расположенная так, что
АР параллельно BQ (черт. 349).
Повернём треугольник ОАР около
точки О на угол а = ^/_AOti:=
^= ^/ ЛЮ/V, определяемый данной
дугой; получим треугольник ОВР'.
Точку Р' можно построить, откла-
откладывая угол POP', равный а, и отрезок ОР' = ОР. При этом и угол
QBP1, равный углу между стороной АР треугольника ОАР и новым
положением ВР' этой стороны, также будет равен а. Следовательно,
точка В будет лежать на дуге, имеющей своими концами точки Р' и Q
и вмещающей угол а. Построив с*ту дугу, мы и получим в пересече-
пересечении с данной окружностью точку В. Соответственно двум возможным
точкам пересечения В и Ь' мы можем получить таким путём самое
большее два решения—дуги АВ и А'В'.
В
Черт. 349.
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
351
До сих пор ыи неявно предполагали, что искомая дута АВ имеет
на окружности то же направление, что и данная дута MN. Можно,
очевидно, получить дальнейшие реления АХВХ и АХ'ВХ, в которых
искомая дута имеет направление, противоположное данной, рассматри-
рассматривая вторые точки пересечения прямых PA. QB, PA', QB' с данной
окружностью.
Если бы требовалось, чтобы прямые, соединяющие концы искомой
дуги с данными точками Р и Q, пересекались под данным углом ji,
то точка В определялась бы как точка пересечения данной окружности
с дугой, из точек которой отрезок P'Q был бы виден под утлом
ЗАДАЧИ КО ВТОРОЙ КНИГЕ (стр. 104).
98. Пусть А'РВ' — отрезок, параллельный касательной в точке М
и заключённый между прямыми МА и MB (черт. 350), и X — точка
пересечения касатечьных в точках Л и М. Так как ХА—ХМ,
то /_ ХМА = /i ХАМ =/_ А'АР, с другой стороны, /_ ХМА = ^_ АА'Р,
Д
Черт. 350.
так как MX параллельно РА'. Отсюда /_ААР = /_АА'Р и РА'=
= РА. Точно так же РВ' = РВ. Так как отрезки РА и РВ равны
между собой и не зависят от положения точки М, то точка Р есть
середина отрезка А'В', и длина этого отрезка не зависит от положе-
положения точки М на окружности.
99. Отложив на МА (черт. 351) отрезок MN=MC, получим рав-
равносторонний треугольник CMN (так как /_ CMN = ^_ CBA = 60°).
Далее, /_ ACN = /_ ACM — 60° = Z. ВСМ, треугольники АСА/ и ВСМ
равны, откуда BM = AN. Итак, MA — MN-\-NA = MB-\-MC.
100. Пусть AD, BE, CF—высоты равностороннего треугольника
ABC (черт. 352) и прямые AD', BE', CF проведены так, что биссек-
биссектрисы АА', ВВ', СС углов DAD', ЕВЕ', FCF' параллельны между
собой. Обозначим через Р точку пересечения прямых BE' и CF' и через
XY — прямую, симметричную с CF относительно ВВ'. Прямая XY
параллельна CF', так как XY получается из CF' с помощью двух
симметрии относительно параллельных прямых СС и ВВ. Прямые BE'
и XV пересекаются под теми же углами, как BE и CF (в силу сим-
симметрии относительно ВВ'у, кроме того, прямые BE' и XY пересека-
352
PELUFHHH УПРАЖНЕНИЙ И ЗАДАЧ
ются под теми же углами, что и прямые BE' и CF1 (в силу парал-
параллельности XY и CF'). Следовательно, прямые BE' и CF' пересекаются
под теми же углами, что и прямые BE и CF. Итак, ^ВРС=\20°,
и потому точка Р, в которой пересекаются прямые BE' и CF1, лежит
на описанной окружности.
Таким же путём докажем, что точка пересечения прямых AD' и BE'
лежит на описанной окружности и, следовательно, совпадает с точкой Р
(так как прямая BE' пересекает описанную окружность, кроме точ-
точки В, только в одной точке). Итак, доказано, что через точку Р про-
проходят все три прямые AD', BE' и CF'. д
Черт. 352.
Черт. 353.
101. Пусть Ах, Bv С,—середины сторон треугольника. ABC
(черт. 353); А2, В2, С2 — основания его высот; Аъ, Bs, Cg — сере-
середины отрезков, заключённых между вершинами и точкой пересечения
высот Н. Отрезок AlBv соединяющий середины сторон треуголь-
треугольника ABC, параллелен стороне АВ и равен её половине; точно так
же отрезок AgBa, соединяющий середины сторон треугольника АВН,
параллелен стороне АВ и равен её половине. Аналогично от-
отрезки A^Bg и A3BV соединяющие соответственно середины сторон
треугольников ВСН и АСН, параллельны отрезку СН и равны
каждый его половине. Так как прямая СН перпендикулярна к АВ,
то отсюда следует, что AlBlA3Bs есть прямоугольник, так что
отрезки AxAg и BXBS равны и делятся в точке их пересечения О,
пополам. Точно так же докажем, что отрезки А^А3 и ClCg равны
и делятся в точке их пересечения пополам. Отсюда следует, что от-
отрезки AyAg, Bjflji С\Сз слУжат диаметрами одной окружности. Эта
окружность проходит через точки А2, В2, С2, так как, например, от-
отрезок AxAg виден из точки Л2 под прямым углом.
Центр О, окружности, о которой идёт речь, лежит на пересечении
перпендикуляров, восставленных к хордам AXAV, ВХВЧ, С^С2 в их сере-
серединах. Но каждый из этих перпендикуляров проходит (сравнить реше-
решение упражнения 35) через середину отрезка ОН, где О — центр
окружности, описанной около треугольника ABC. Следовательно, точка
О, есть середина отрезка ОН.
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
353
Треугольники О]ОА1 и О1ИА3 равны (OjO = O,//; О^^
ОО~А^ =/_НО^А.^. Отсюда следует, что отрезок ОАХ
параллелен отрезку НА3, а следовательно, и отрезку АА3. Так как
в четырёхугольнике ОА}А3А стороны ОАХ и АА& равны и параллельны,
то этот четырёхугольник — параллелограм, и потому О А = Л, Л3. Итак,
диаметр AjA3 окружности Ох равен радиусу описанной окружности.
Если К — точка, симметричная с Н относительно стороны АС, то
отрезок О,В2' есть средняя линия треугольника ОНК, так что ОК =
=2О1В2 = ОВ, и точка К есть точка описанной окружности. Мы полу-
получили предложение, приведённое в упражнении 70.
101а. Пусть / — центр вписанной окружности; 1п, 1Ь, 1С — центры
вневписанных окружностей, касающихся соответственно сторон ВС, АС,
АВ и продолжений двух других сто-
сторон (черт. 102). Так как прямая /А
есть биссектриса угла А треуголь-
треугольника ABC, а прямая 1Ь1С — биссек-
биссектриса внешнего угла при вершине А,
то прямая /А перпендикулярна к lblc.
Точно так же прямая 1В перпендику-
перпендикулярна к IJC, и 1С — к 1а1ь. Следо-
ва гель'но, прямые [A, IB, 1С — вы-
высоты треугольника IJf,lc, и потому
окружность ABC есть окружность
девяти точек треугольника IJtJc
(упр. 101). Центр О окружности
ARC есть середина отрезка, соеди-
соединяющего точку пересечения / высот треугольника IJЬ1С с центром
окружности, описанной около этого треугольника, а радиус окружно-
окружности ABC равен половине радиуса окружности 1а1ь1с.
102. Пусть AD, BE, CF—высоты треугольника ABC (черт. 354),
А' и А", В и В', С и С — основания перпендикуляров, опущенных
из точек D, Е, F на стороны треугольника.
Покажем, что прямая А'Л' образует со сторонами АВ и АС углы,
соответственно равные углам Си В треугольника: / АА' А' =: / С.
/_АА"A =j/_B. В самом деле, четырёхугольник AA'DA" может быть
вписан в окружность (так как углы при А' и А" прямые) и, следова-
следовательно, Z_AA"A'^Z.^DA' = 90D — Z.BDA'=Z.B. Аналогично
/_АА'А" — /_С. Таким же путём доказывается, что прямая В1 В" об-
образует со сторонами ВС и ВА углы, равные /_ВИВ" = /_А и
/_ВВ"В'=/_ С, а прямая С С — со сторонами С А и СВ углы /_ ссС" =
= /_В и ?ССС=/_А.
Далее покажем, что прямая В'С параллельна ВС, т. е.
^АВ"С = /_В и /_АСВ'' = /_С. Действительно, на основании при-
примечания к решению упражнения 71 отрезок EF образует со сторонами
треугольника ABC углы /_AEF = /_В и /_AFE = /_С. Далее, по
той же причине прямая В'С, соединяющая основания В" и С высот
ЕВ' и FC треугольника AEF, образует с его сторонами AF и АЕ
23 Элементарная геометрия
354
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
углы /_АВ" С = /_AEF = /^ В и /_ АС В1 = /_ AFE = /_ С, и сле-
следовательно, параллельна ЕС. Точно так же докажем, что прямая
С А' параллельна С А, так что /_ВС'А' =/_ С; /_ВА'С' = /_А, и что
прямая А" В' параллельна АВ, так что ^/ С А" Б' = ^_ А, / С Б'А" = / В.
Из доказанных равенств вытекает, что четьрёхугольшк А'А'СВ'
можно вписать в окружность, так как /_ А'В'С = 180°—/ АВ"С —
— 180° — Z.B= 180е — /_АА"А', или /_ А'В'С \ /_ А1 АС = 180°.
Далее, четырёхугольник А'В'С'С" можно вписать в окружность, так
как /_ А'В'С = 180° — /_ В= 180° — /_ А'С"С (Z А'С"С =180° —
] — /_ А'С'В =180° — /_А~ /_С =/_ В). Наконец, четы-
четырёхугольник А"С'В'В' можно впи-
вписать в окружность, так как
= 180°— ^/С = 180°—
= ' 80° — Z А —
С
Все три только что названные
окружности совпадают между со-
собой, так как они имеют по три
общие точки.
Доказательство сохраняет силу
(с небольшими видоизменениями)
и для тупоугольного треугольника.
103. Пусть К — точка пересе-
пересечения биссектрисы угла А тре-
треугольника ABC (черт. 355) с опп-
окружностью. Так как /_ ВАК'= ^_КАС, то дуги ВК и КС
Следовательно, КВ = КС, так что точка К лежит на перпен-
перпендикуляре, восставленном в середине .4, отрезка ВС.
Если L — точка пересечения биссектрисы внешнего угла при А с
описанной окружностью, то /_KAL — прямой. Следовательно, KL есть
диаметр описанной окружности, и потому LB = LC.
Так как окружность ABC есть окружность девяти точек треуголь-
треугольника IJhlc (ср. решение упр. 101а), то она проходит через середины
каждого из отрезков IIа (/ — центр окружности, вписанной в треуголь-
треугольник ABC, и в то же время точка пересечения высот треугольника
и lhlc. Следовательно, KI = К1а и LIh = Llc. В каждом из пря-
прясанной
равны.
lalblc
c
1ЬС1С
медиана, проходя-
проходямоугольных треугольников 1В1а, 1С/а, 1ЬВ1С,
щая через вершину прямого угла, равна половине гипотенузы. Отсюда
KI^KI =КВ = КС и Llh^Llc^LB^LC. Итак, биссектриса внеш-
внешнего угла при А пересекает описанную окружность в точке, равно-
равноудалённой от точек lh, lc, В, С.
Если D, Dv D2,
окружностей с прямой ВС,
(согласно решению упр. 35)
-\-D3I), откуда Dxl0-\rD2lf
Оя — точки
касания
то
вписанной и вневписаннь'х
= К1а и Z./6=Z./c имеем
в силу /</=/<
'=^Olla-DI), AXL =
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
355
103а. Пусть дана высота АН, медиана AD, биссектриса АЕ
искомого треугольника ABC (черт. 356). Строим треугольник AHD
по катету АН и гипотенузе AD. Затем из точки Ау как из центра,
описываем окружность радиусом, равным данной биссектрисе, и в
пересечении с прямой DH получаем точку Е. Точка пересечения К
прямой АЕ с прямой, проходящей через точку D и перпендикуляр-
перпендикулярной к DH, лежит на описанной окружности (упр. 103). Центр О
описанной окружности есть точка пересечения прямой DK с перпен-
перпендикуляром, восставленным к отрезку АК в его середине. Построив
эту окружность (её радиус равен 0.4), получим на прямой DH вер-
вершины В и С треугольника.
Черт. 357.
104. Пусть РА и РВ — две касательные к окружности, С—одна
из точек хорды, соединяющей точки касания А и В, и KL — пер-
перпендикуляр к ОС (черт. 357).
Окружность, построенная на ОК как на диаметре, проходит- че-
через точки В и С, из которых отрезок ОК виден под прямым углом.
Следовательно, /_OKL = ^/_ОВС, и таким же путём докажем, что
/_OLK = /_ОАС. Но /_ОВС=/_ОАС, так как треугольник
ОАВ — равнобедренный. Следовательно, /_ OKL = ^/ OLK и OK = OL.
В равнобедренном треугольнике OKL высота ОС есть в то же время
и медиана, т. е. KC—CL.
105. 1°. Треугольники АА'С и ВВС (черт. 358) равны, так как
А'С=ВС; АС=ВС и /_ АСА1 = /_ В'СВ = /_ С + 60°. Отсюда
АА' = ВВ1 и аналогично ВВ' = СС.
¦2°. Если О — точка пересечения прямых АА' и БВ1, то / ОВС =
= ^ОА'С (в силу равенства треугольников АА'С и ВВС), так что
точки О, В, А', С лежат на одной окружности. Следовательно,
/_ВОС= 120°. Таким же путём покажем, что ^4ОС=120°. Сле-
Следовательно, ^/ЛОв=1200, точки О, А, С", В лежат на одной
окружности, и /_ А ОС =/_ ABC = 60°. Отсюда, так как
^/Л'ОС= 60°, вытекает, что точки С, О, С лежат на одной прсмой,
т. е. прямая СС проходит через точку О.
23*
356
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
3°. Если точка О лежит внутри треугольника, то АА'=АО-\-
-f О А'. Но ОА' = ОВА- ОС (задача 99) и АА'= ОА^ОВ + ОС.
Примечание. Дальнейшие свойства этой фигуры рассмотрены
в задаче 363.
106. 1°. Непосредственное доказательство. Пусть
данные прямые я, Ь, с, й пересекаются попарно в точках А, В, С,
D, Е, F (черт. 359) и М — отличная от А точка пересечения окруж-
окружностей ACF и ADE. Имеем /_ВСМ=/_FCM = ^_FAM; /_ВЕМ=^
=z/_DEM = /_DAM = /_FAM. Отсюда /_ ВСМ =/_ ВЕМ, и
окружность, описанная около треугольника ВСЕ, проходит через М.
Так же доказывается, что и окружность, описанная около треуголь-
треугольника BDF, проходит через М.
Черт. 359.
2°. Доказательство, основанное на упражнении 72.
Пусть а, Ь, с, d — данные прямые и М — точка пересечения окруж-
окружностей, описанных около треугольников аЪс и abd. Основания пер-
перпендикуляров, опущенных из точки М на прямые а, Ъ, с, лежат на
одной прямой /, и основания перпендикуляров, опущенных из М на
прямые a, ft, d, также лежат на одной прямой, необходимо совпадаю-
совпадающей с /. Так как основания перпендикуляров, опущенных из М на
а, с, d, лежат на одной прямой, то М лежит на окружности, описан-
описанной около треугольника acd, и то же имеет место для треугольника
bed.
Центры Р, Q, R, S окружностей, описанных соответственно около
треугольников ACF, ADE, BDF, ВСЕ, можно получить, восставляя
перпендикуляры в серединах отрезков МС, MD, ME, MF. Угол
RPS измеряется половиной дуги FMC и потому равен 2l РАС; угол
RQS измеряется половиной дуги DME и потому равен тлвму же
углу DAE. Четыре точки Р, Q, R, S лежат на одной окружности.
Далее, /_MPS= ^_MAC (вписанный угол равен половине централь-
центрального, опирающегося на ту же дугу) и t/_MAE = ^_MQ&. Следова-
Следовательно, /^MPS = ^MQS. Четыре точки М, Р, Q и S также ле-
лежат на одной окружности, и эта окружность совпадает с той, на ко-
, ЗАДАЧИ КО ВТОРОЙ КНИГЕ 357
торой лежат точки Р, Q, R и S. Иначе говоря, последняя окруж-
окружность проходит и через точку М.
107. Пусть ABCD— произвольный четырёхугольник (черт. 360);
? — точка пересечения продолжений сторон AD и ВС; F — точка
пересечения продолжений сторон АВ и CD; ЕМ и ЕМ — биссектрисы
углов при Е и Е; G, Н, К, L — точки их пересечения со сторонами
четырёхугольника. Рассматривая треугольники ЕАМ и ЕМС, можем
написать: /_ AEG = /_DAM — /_ AMG; /_BEG = /^CMH —/_ МСВ.
Так как EG — биссектриса угла при Е, то /_AEG = /_BEG,
т. е. /_DAM— ^_AMG = /_CMh —Z.MCB< 0ТКУДа __
A)
Точно так же из треугольников FAM и ЕМС найдём / ВЕК =
=/_ AML — /_ МАВ; /_ СЕК =/_НСМ — /_ СМК, откуда /_ AML—
— /_МАВ = //_НСМ — /_СМК, или
^МАВ-\- /_HCM = Z.AML-\- /_CMK. B)
Складывая почленно A) и B), получим
C)
Черт. 360. Черт. 361.
До сих пор мы предполагали, что четырёхугольник ABCD — про-
произвольный. Если теперь четырехугольник ABCD — вписанный, то
j/_BAD-\-^/BCD = 180°, так что из равенства C) следует, что
/_ GML = 90°.
Пусть далее Р — точка пересечения диагоналей АС и BD произ-
произвольного четырёхугольника ABCD (черт. 361), Q-a R—точки пересе-
пересечения биссектрисы угла при Е с диагоналями АС и BD (мы предпо-
предполагаем для определённости, что точки Q и R лежат на отрезках
АР и DP; те же рассуждения можно было бы применить и к тому
случаю, когда эти точки лежат на отрезках ВР и СР). Из треуголь-
треугольников AEQ и BER найдём /_ AEQ = /_DAC — /_ AQE = Z.DAC ~
— Z.PQR; /_BEQ = /_DBC—/_PRQ. Так как EQ — биссектриса
угла Е, то /_AEQ= /_BEQ, или /_DAC — /_PQR= /_DBC —
— /_PRQ, откуда
Z.DAC— Z.DBC=/_PQR — /_PRQ. D)
358
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если четырёхугольник ABCD—вписанный, то /_DAC= /_DBC,
так что из равенства D) следует /_PQR — /_PRQ. Это равенство
показывает, что треугольник PQR — равнобедренный. Поэтому бис-
биссектриса угла QPR перпендикулярна к QR, а значит биссектриса
угла CPD параллельна QR, т. е. биссектрисе угла при Е.
Так как доказанная теорема содержит два утверждения, то она
допускает две обратные теоремы:
1°. Если биссектрисы углов, образованных продолжениями
сторон некоторого четырёхугольника, взаимно перпендикулярны,
то этот четырёхугольник можно впи-
вписать в окружность.
Справедливость этой теоремы выте-
вытекает, из равенства C): если / GML = 90°,
то /_BAD-{-/_BCD=\ZUo.
2°. Если биссектриса одного из углов,
образованных продолжениями сторон не-
некоторого четырёхугольника, параллель-
параллельна биссектрисе одного из углов, обра-
зованных его диагоналями, то этот че-
четырёхугольник можно вписать в окруж-
окружность.
В самом деле, если прямая QR па-
параллельна биссектрисе угла CPD, то она
перпендикулярна биссектрисе угла QPR.
Следовательно, треугольник PQR—рав-
PQR—равнобедренный, так что /_PQR = /_PRQ.
Из равенства D) следует, что / РАС=^
=//#?С) и потому точки а, В, С, D
лежат на одной окружности.
107а. Пусть одна из данных прямых АВ пересекает первую
окружность в точках А и В, вторую — в точках А' и В'; другая
данная прямая CD — соответственно в точках С и D, С и D'
(черт. 362). В первой окружности мы можем рассматривать либо пару
хорд (AC, BD) ... (а), либо пару хорд (AD, ВС) ... ('$); точно
так же во второй окружности — пару хорд (А'С, B'D') ... (а'), либо
пару хорд (А'?У, В'С) ... (р'). Выбирая пару хорд первой окруж-
окружности и пару хорд второй окружности, получим четыре комбинации:
(а, а'); (а, ?'); (р, а')- (р, р').
Рассмотрим, например, первую комбинацию хорд (а, а'), т. е.
(AC, BD), (А'С, B'D1), и пусть Р, Q, R, 5—точки Пересечения
хорд первой пары с хордами второй пары. Треугольники РАА' и
SDD' имеют по два равных угла (/_ РАА'= 180° — /_ ВАС =
— /_SDD'\ /J'A'A^/JfAC^^SD'D). Следовательно, их третьи
углы равны: /_RPQ = /_RSQ, и точки Р, Q, R, S лежат на одной
окружности.
Аналогично получим ещё три четвёрки точек таких, что точки
каждой четвёрки лежат на одной окружности (на черт. 362 точ-
Черт. 362.
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
359
= AD+ Dl =AD-\-
ки каждой из трёх четвёрок выделены одинаковым обра-
образом).
108. Пусть перпендикуляры к прямым MA, MB, MC, проведён-
проведённые соответственно через точки А, В, С, пересекаются в одной
точке М. Отрезок ММ виден из каждой точки А, В, С под пря-
прямым углом и потому есть диаметр описанной окружности. Геометри-
Геометрическое место точек М есть описанная окружность.
109. Пусть сторона АВ параллелограма остаётся неподвижной
(черт. 269). В таком случае остаётся неподвижной и точка О — сере-
середина стороны АВ. Точки Е, L, N, Р и R описывают окружности с
центром в точке О, так как отрезки ОЕ--^ AD, OL = O/ — ZV =
= AD — О A, ON=OP = OA,
-f- О А сохраняют постоянную ве-
величину. Точки К, М, Q и 5 опи-
описывают окружности, равные той,
которую описывает точка Е, так
как отрезки КЕ = ЕМ и QE = ES
сохраняют постоянную величину и
направление (упр. 47).
НО. Пусть О и О' — центры
обеих окружностей (черт. 363);
D — вторая точка их пересечения;
М — точка пересечения 00' и BD;
Е, F, N, Р — основания перпенди-
перпендикуляров из точек О, О', М, D на
прямую АВ. При этом положение точек Е и F — середин отрезков АВ и
ВС — на прямой АВ не зависит от выбора окружностей. Точка М
есть, в силу равенства окружностей, середина отрезка 00', и, сле-
следовательно (упр. 35), точка N— середина отрезка EF. Поэтому положение
точки N на прямой АВ также не зависит от выбора окружностей.
Наконец, точка М — середина отрезка BD, и, следовательно, N —
середина отрезка ВР. Отсюда вытекает, что и положение точки Р
на прямой АВ не зависит от радиуса окружностей, и геометрическое
место точек D есть прямая, проходящая через эту точку Р и пер-
перпендикулярная к АВ.
111. Пусть XX', YY'—данные взаимно перпендикулярные пря-
прямые (черт. 364), AM и ВМ соответственно параллельны XX' и YY',
С—середина отрезка АВ. Точки О, А, В и М лежат на окруж-
окружности с центром С, откуда /_ АМО =/_ АВО = 45°. Следова-
Следовательно, так как прямая AM остаётся параллельной XX', то точка М
лежит на прямой, параллельной биссектрисе утла между XX' и YY' и
проходящей через О. Так как ОМ^АВ (ОМ— хорда, АВ — диаметр
одной и той же окружности), то геометрическое место точек М есть
отрезок этой прямой, длиной 2АВ, имеющий О своей срединой.
112. Пусть А и В — данные точки (черт. 365), С—точка каса-
касания окружностей, М — точка пересечения касательной в точке С с
Черт. 363.
360
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
прямой АВ. Из равенств МА = МС; МВ—МС следует, что МС =
= const и геометрическое место точек С есть окружность, имеющая
АВ своим диаметром.
113. Пусть OX, OY — данные прямые (черт. 366), ABC—неиз-
ABC—неизменяемый прямоугольный треугольник. Точки О, А, В и С лежат на
окружности с центром М в середине отрезка АВ. Следовательно,
X'
ж
г
Черт. 364.
Черт.
/_СОХ = /_САВ и OCs^AB. Геометрическое место точек Сесть
отрезок прямой, равный 2АВ, образующий с ОХ угол, равный
/_ CAB, и имеющий точку О своей серединой.
114. Прямые, на которых первая данная окружность отсекает
хорды санной длины, касаются одной и той же окружности, концен-
концентрической с первой данной окружностью. То же и для второй данной
окружности. Задача сводится к по-
построению общей касательной к этим
двум новым окружностям.
115. 1°. Стороны искомого тре-
треугольника ABC, вписанного в дан-
данную окружность с центром О, долж-
должны быть соответственно параллельны
сторонам некоторого данного тре-
треугольника А0В0С0. В таком случае
и углы треугольника ABC будут
соответственно равны углам треуголь-
треугольника АцВцСъ. Следовательно, цен-
Черт. 366.
тральные углы ВОС, СО А и АОВ будут равны удвоенным углам
того же треугольника. Радиус О А данной окружности, перпендикуляр-
перпендикулярный к стороне ВС, будет перпендикулярен и к В0С0.
Отсюда вытекает такое построение. Строим радиус О А, перпен-
перпендикулярный к В0С0, и углы /_АОВ = /_А'ОС, равные углу ВиА0С0.
Тем самым определяются вершины В и С искомого треугольника.
Построение вершины А не представляет затруднений.
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
361
Так как радиус ОА', перпендикулярный к ВОСС, может иметь два
противоположных направления, то задача имеет два решения.
2°. Если стороны АЬ и АС искомого треугольника ABC (черт. 367)
параллельны соответственно двум данным прямым, то сторона ВС
стягивает дуги, вмещающие углы, соответственно равные углам
между двумя данными прямыми. Так как равным (или пополнительным)
вписанным углам соответствуют равные хорды, то, проведя через про-
произвольную точку Ао окружности хорды А0В0 и А0С0, параллельные
данным прямым, мы получим хорду В0С0, равную искомой стороне ВС.
Таким образом, через данную точку Р остаётся провести хорду,
равную Ь0С0, Для этого строим окружность, концентрическую дан-
данной окружности и касающуюся прямой ВЬСО, и из точки Р проводим
к этой окружности касательные. Задача имеет самое большее два
решения (треугольники ABC и „
А'Ь'С на черт. 367). ^ " ,N
Черт. 368.
116. Пусть точки А и В лежат по разные стороны от данной
прямой и М—искомая точка (черт. 368). Так как /_АМХ —
:= 2 /_ BMY, то прямая MB есть биссектриса угла между прямыми
XY и AM. Следовательно, существует окр>жность с центром В, ка-
касающаяся обеих прямых XY и AM. Построив эту окружность (её
радиус равен расстоянию точки В от данной прямой) и проведя к
ней касательную из точки А, получим искомую точку М. Вторая ка-
касательная из точки А к той же окружности определяет точку М,
для которой /_AM'Y=/_ AM'N~\-/_ NM'Y= 2 /_ ВМ'Х.
Если бы данные точки А и В' лежали по одну сторону от пря-
прямой XY, то мы заменили бы точку В' симметричной ей точкой В и
выполнили бы то же самое построение.
117. Первое решение. Пусть ABCDE — искомый пятиуголь-
пятиугольник (черт. 369) и а, Ь, с, d, e — середины его сторон. Проводя диагональ
BE, разложим искомый пятиугольник на треугольник ABE и четырёх-
четырёхугольник BCDE. Середину / диагонали BE можно построить как
четвёртую вершину параллелограма (упр. 36), имеющего своими
вершинами точки с, d, b и диагональю отрезок db. Треугольник
362
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
ABE можно теперь построить, проводя через вершины треугольника
aef прямые, параллельные его сторонам. Зная вершины В и Е, легко
построить вершины С и D.
Аналогично решается задача в случае любого нечётного числа
сторон (только вместо одного четырёхугольника будем иметь их не-
несколько).
Пусть теперь а, Ь, с, d, е, / — середины сторон искомого шести-
шестиугольника ABCDEF (черт. 370). Середина g диагонали BE. должна
быть при этом, во-первых, четвёртой вершиной параллелограма,
имеющего точки Ь, с, й вершинами и bd диагональю, и, во-вторых,
четвёртой вершиной параллелограма, имеющего точки а, е, / вер-
В
Черт. 369.
шинами и ае диагональю. Однако четвёртые вершины этих двух
параллелограмов, вообще говоря, будут различными, так что задача
не будет иметь решения. Если же четвёртая вершина параллело-
параллелограма, имеющего Ь, с, d вершинами и bd диагональю, совпадает с
четвёртой вершиной параллелограма, имеющего а, е, / вершинами и
ае диагональю, то одну из вершин искомого многоугольника, напри-
например А, можно выбрать произвольно. Действительно, возьмём произ-
произвольную точку А и построим точки В, F, Е так, чтобы Ла = я#,
Af=fF, Fe = eE. Серединой четвёртой стороны BE четырёхуголь-
четырёхугольника BAFE будет четвёртая вершина параллелограма afeg (упр. 36),
т. е. точка g. Далее построим точки С и D -так, что Ed=dD,
Bb = bC, и убедимся, что серединой четвёртой стороны CD четырёх-
четырёхугольника будет четвёртая вершина с параллелограма bgdc. Таким
образом, шестиугольник ABCDEF удовлетворяет поставленному усло-
условию.
Аналогичное положение вещей имеет место и в случае любого
чётного числа сторон (только вместо двух параллелограмов будем
иметь их большее число).
Второе решение. Пусть опять требуется построить пятиуголь-
пятиугольник, серединами сторон которого являются точки а, Ь, с, d, e
(черт. 369). Возьмём произвольную точку А' и построим точку В',
ЗАДАЧИ КО ВТОРОЙ КНИГЕ 363
симметричную с А' относительно а, точку С, симметричную с В'
относительно Ь, точку D', симметричную с С относительно с, точку ?",
симметричную с D' относительно d, и, наконец, точку А", симметрич-
симметричную с Е' относительно е. Так как в ряду АА', ВВ, СС, DD', ЕЕ',
АА" каждые два последовательных отрезка равны, параллельны и на-
направлены в противоположные стороны, то отрезки АА' и АА" равны
и направлены по одной прямой в противоположные стороны. Поэтому
точка А есть середина отрезка А'А". Зная вершину А, можно постро-
построить и остальные вершины.
Точно так же решается задача и в случае любого нечётного
числа сторон.
Пусть теперь существует некоторый шестиугольник ABCDEF
(черт. 370), имеющий серединами сторон точки а, Ь, с, d, e, /. По-
Повторяя предыдущее построение, мы получим ряд отрезков АА', ВВ, СС,
DD', ЕЁ', FF, АА', в котором каж-
дые два последовательных отрезка
равны, параллельны и направлены в
противоположные стороны. Отсюда
следует, что отрезки АА' и АА"
равны и направлены по одной пря-
прямой в одну и ту же сторону, так что
точка А' совпадает с точкой А" и
шестиугольник A'B'CD'E'F' также
удовлетворяет поставленному усло-
условию. Итак, если существует хотя Черт. 371.
бы один шестиугольник, удовлетво-
удовлетворяющий условиям задачи, то каждая точка плоскости А' может
быть принята за вершину искомого шестиугольника, и задача имеет
бесчисленное множество решений (которые получаются непосредственно).
Следовательно, если при некотором выборе точки А' точка А'',
построенная как указано выше, не совпадает с А', то задача вообще
не имеет решения.
Аналогичное положение имеет место и в случае любого чётного
числа сторон.
118. Выполним над одной из непараллельных сторон АВ искомой
трапеции ABCDX (черт. 48) поступательное перемещение, определяемое
по величине и по направлению отрезком ВС; сторона АВ
займёт положение D2C. При этом получим треугольник CD^D2, кото-
который легко построить по трём сторонам. Построенный треугольник
легко дополнить до искомой трапеции.
Пусть теперь даны стороны искомого четырёхугольника ABCD и
угол между продолжениями его сторон АВ и CD. В этом случае надо
, между окружностями с центрами в концах А и В данной стороны АВ
и радиусами, равными AD и ВС (черт. 371), поместить отрезок CD,
имеющий данную величину и данное направление, определяемое уг-
углом а между АВ и DC (упр. 75). Задача имеет самое большее два
решения (ABCD и ABCD' на черт. 371).
364
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
119. Пусть DE—искомая прямая (черт. 372), так что BD = CE.
Выполним над отрезком DE поступательное перемещение, определяе-
определяемое по величине и по направлению отрезком ЕС. Отрезок DE зай-
займёт при этом положение КС. Тогда ?Ю = СЕ = /СО. Прямая ВК
образует равные углы с прямыми АВ и DK или, что то же, с АС. От-
Отсюда легко вывести, что прямая ВК параллельна одной из биссектрис
угла при А. Приходим к такому построению:
Через точку С проводим прямую СХ, имеющую заданное направле-
направление. Проведя через точку В прямые, параллельные биссектрисам углов
при А, получим точки К и К'; проведя
прямые DK и D'K', параллельные
АС, найдём точки D и D'. Через D и
D' проводим прямые, параллельные СХ.
120. Пусть XX' и КГ—данные
прямые, А — данная точка (черт. 373).
Обозначим через M0N0 какой-либо
общий перпендикуляр к данным прямым
и рассмотрим пару дуг — геометриче-
геометрическое место точек, из которых отрезок
M0N0 виден под данным углом. Иско-
Искомый общий перпендикуляр можно
получить из M0Nq с помощью некото-
некоторого параллельного перенесения по направлению данных прямых. При
этом и точка А получается с помощью того же параллельного перенесения
из некоторой точки рассмотренного только что геометрического места.
Чтобы определить эту точку (их может оказаться и несколько), достаточно
через точку А провести прямую, параллельную данным прямым.
Черт. 372.
X
Y \
\/
Mo
No
I
I
1
I
\
Mt
N,
Ms,
i
t
t
\
1
/
M2
\
I
1
\ X
M,
N..
Черт. 373.
Отсюда вытекает такое построение. Строим произвольный перпен-
перпендикуляр M0N0 к данным прямым и две дуги A40A2AvN0 и MOASA4NV,
имеющие своими концами точки Мо и Л/о и вмещающие данный угол.
Через точку А проводим прямую параллельно данным прямым. Иско-
Искомые общие перпендикуляры MVNV M2N», M3N3, MiNi отстоят от
M0N0 на расстояниях, соответственно равных АА,, АА„, АА3, AAt.
Наибольшее возможное число решений — четыре.
121. Пусть D — данная прямая (черт. 374). Выполняем над точкой
Q поступательное перемещение, определяемое отрезком /К (длина и
ЗАДАЧИ КО ВТОРОЙ КНИГЕ
365
направление которого известны); получаем точку R. Так как при этом
прямая /Q параллельна KR, то /_PKR — /_PMQ, и точка К лежит на
дуге, имеющей своими концами точки Р и R и вмещающей угол,
равный тому углу, который вмещает данная дуга PMQ. Построив эту
дугу (дугу PKR), мы получим точку К, как точку её пересечения с
У
Черт. 374.
Черт. 375.
прямой D. От точки К откладываем на данной прямой отрезок, рав-
равный данному. Задача имеет самое большее два решения.
121а. Пусть Р и Q—данные точки (черт. 375), D — данная пря-
прямая, L — данная середина искомого отрезка /К, М — искомая точка
окружности. Строим на продолжении отрезка PL точку R так, что
PL = LR. Так как треугольники PLK и RLI равны, то /_PKL =
= /_ R/L, так что прямая R/ па-
параллельна РК. Следовательно, угол
QIR дополняет угол PMQ до 180°
и имеет то же направление. Точка /
лежит на дуге, имеющей своими
концами точки Q и R и вмещаю-
вмещающей угол, пополнительный тому
углу, который вмещает данная
дуга PMQ1). Вторая точка пере-
пересечения /' окружности Q/R с пря-
прямой D определяет второе реше-
решение— точку М.
122. Пусть последовательные
стороны искомого квадрата PQRS
(или их продолжения) проходят
через данные точки А, В, С, D
(черт. 376). Вершина Р, в которой пересекаются стороны, проходя-
проходящие через точки А и В, лежит на окружности, имеющей АВ своим
диаметром. Точно так же вершина R, в которой пересекаются сто-
1) Так как углы PMQ и QIR имеют одно и то же направление, то из
двух дуг, имеюших своими концами точки Q и R и вмещающих данный
угол, приходится выбрать только одну.
366
PEIIIFHHH УПРАЖНЕНИЙ И ЗАДАЧ
роны, проходящие через С и D, лежит на окружности, имеющей CD
своим диаметром. Диагональ PR делит пополам углы при Р и Rt а
потому делит пополам одну из дуг АВ и одну из дуг CD. Если эта
диагональ пересекает первую окружность в точке М, • а вторую
окружность — в точке N, то дуги ANI и CN составляют каждая четверть
окружности; эти дуги имеют, как видно из чертежа, одинаковое на-
направление. Таким образом опре-
определяется положение точек М и N,
а следовательно, и вершин Р и R,
и 'квадрат - можно построить. Мы
получим второе решение, заменяя
точки М и N точками М и N',
им диаметрально противоположны-
противоположными (квадрат PQ'R'S' на черт. 376).
Мы предполагали до сих пор,
что одна пара противоположных
сторон квадрата проходит через
точки А и С, другая — через
точки В и D. Мы получим ещё два
решения, предполагая, что одна
Черт. 377. пара противоположных сторон про-
проходит через А и D, вторая — че-
через точки В и С. Можно показать, что диагонали этих квадратов мы
получим, соединяя точки М и /V' или М' и N (на чертеже эти два
квадрата не показаны). Наконец, третью пару решений мы получим,
если предположим, что две противоположные стороны квадрата про-
проходят через А и В, две другие — через С и D. Для построения
этих двух квадратов пришлось бы воспользовать-
воспользоваться уже другими вспомогательными окружностями.
Если в нашем первоначальном построении точ-
точка М совпадает с точкой N (черт. 377), то за
диагональ можно принять любую прямую, проходя-
проходящую через точку /И, совпавшую с Л/, и мы будем
иметь бесчисленное множество решений. Так как
точки А и С при этом лежат на противоположных
сторонах искомого квадрата и то же имеет место
для точек В и О, то центр искомого квадрата
(безразлично, какого именно) лежит в точке пере-
пересечения прямых, проходящих через середины от-
отрезков АС и BD и параллельных сторонам квадрата. Отсюда сле-
следует, что геометрическим местом центров квадратов является
окружность, имеющая середины отрезков АС и BD диаметрально проти-
противоположными точками.
123. Пусть АВ=а; ВС= b; CD = c; DA — d — данные стороны
четырёхугольника; АС = е—одна из его диагоналей (черт. 378f. Если
величина угла при вершине В совершенно произвольна, то диагональ е
принимает при изменении угла В все значения, удовлетворяющие
ЗАДАЧИ КО ВТОРОЙ КНИГЕ 367
ус.ювию
е,^е^е2, A)
где
е, = ! а — Ь\; еп = а-\- Ь.
Чтобы четырёхугольник существовал при всевозможных значениях
угла В, необходимо, чтобы треугольник ACD со сторонами с, d, e
существовал при всех значениях е. удовлетворяющих неравенствам A);
это же условие и достаточно.
Для существования же треугольника ACD необходимо и достаточно,
чтобы
1) с-\-й~^е при всех рассматриваемых значениях е, а для этого
необходимо и достаточно, чтобы с -\- d ^ е2, т. е.
za-\-b; B)
2) \с — d|^e при всех рассматриваемых значениях е, а для этого
необходимо и достаточно, чтобы \с—й^гс:^, т. е.
|с—tf|<|a —ft|. C)
Итак, стороны четырёхугольника должны удовлетворять условиям
B) и C).
Чтобы и угол D был вполне произвольным, должны, кроме того,
выполняться аналогичные условия а-\-b ^ с-\-d\ \а—?>|г^|с—d\.
Выполнение тех и других неравенств одновременно приводит к соотно-
соотношениям а-\-b = с-\-d; \а — Ь\ = \с — d\, т. е. либокй = с; b = d,
либо к a = d; b = c. В первом случае четырёхугольник будет парал-
лелограмом, во втором — так называемым ромбоидом (ср. задачу 384).
368
РЕШЕНИЕ УПРАЖНЕНИЙ И ЗАДАЧ
КНИГА ТРЕТЬЯ.
ПОДОБИЕ.
УПРАЖНЕНИЯ К ГЛАВЕ I (стр. 116).
124. Пусть Х'Х1 и Y'Y'— прямые, на которых откладываются
отрезки AM и BN (черт. 379); Мл и /Vx — некоторые определённые по-
положения точек М и N. Проводим через точки А к В прямые, соот-
соответственно параллельные двум данным прямым; пусть О — точка их
пересечения. Проводим прямые
OXhOY, соответственно парал-
параллельные Х'Х" и Y'Y". Полу-
Получим четыре параллелограма
АОРМ, AOPXMV BOQN и
fiOQ,/V,. Тогда АМ^=:ОРЛ,
ОР B^ OQBN
= 0Q. Пусть Сх—точка пе-
пересечения прямых Л^Р, и /V,Q,.
Если С — точка пересечения
прямой МР с прямой ОС{,
то ОС-.ОС^ = ОР:ОР^ =
= OQ:OQ1. Следовательно,
прямая QC параллельна Q,^
и ОВ, и потому С есть точка искомого геометрического места. Таким
образом, искомое геометрическое место есть прямая OCV
125. Пусть АВ и АС — секущие (черт. 380), PQ — диаметр, пер-
перпендикулярный к ВС, X и Y—точки пересечения прямых АВ и АС
с PQ. При этом BQ = CQ, и потому /_BAQ =
= /_CAQ. Таким образом, прямая AQ есть бис-
биссектриса внешнего угла при вершине А треуголь-
треугольника AXY. Следовательно, прямая АР, перпенди-
перпендикулярная к AQ, есть биссектриса угла А того же
треугольника, и потому точки Р и Q делят гар-
гармонически отрезок XY (п. 115, примечание).
126. Рассмотрим точки М', для которых
AM': М'В = т' > т. Если /«> 1, то точки С и D'
прямой АВ, делящие отрезок АВ в отношении т',
лежат внутри отрезка CD, где С и D — точки, де-
делящие отрезок АВ в отношении т (пп. 109, 110), а следовательно,
и геометрическое место точек М' — окружность, имеющая CD' сво-
своим диаметром, лежит внутри окружности, построенной на CD, как на
диаметре. Таким образом, все точки М', для которых AM':Ж'?? ^>/и ^> 1,
лежат внутри последней окружности.
Аналогично, если /и<М, все такие точки М' лежат вне той же
окружности.
Черт. 380.
КНИГА ТРЕТЬЯ. ГЛАВА II
369
127. Пусть требуется найти точку, расстояния которой от вершин
А, В и С треугольника ABC (черт. 381) пропорциональны числам /,
тип. Геометрическое место точек, расстояния которых от точек А
и В относятся как 1:т, есть окружность с центром на прямой АВ.
Точно так же геометрическое место точек, расстояния которых от
вершин В к С относятся как /и:я, есть окружность с центром на
прямой ВС. Искомыми точками бу-
дут общие точки обеих окружно-
окружностей.
N'
М
Черт. 381.
Черт. 382.
В зависимости от того, пересекаются ли обе окружности, или ка-
касаются одна другой, или вовсе не имеют общих точек, задача имеет
два решения, или одно решение, или вовсе не имеет решений (срав-
(сравнить ещё задачу 368).
Пусть задача имеет два решения, и U — одна из искомых точек.
Рассмотрим точку V, которая вместе с точкой U делит гармонически
диаметр QP описанной окружности треугольника, проходящий через
точку U. В силу п. 116, следствие, имеем AU: AV = BU:BV = CU:CV,
так что V есть вторая искомая точка.
. 128. Пусть МР:РМ'^т (черт. 382). Через вторую точку пере-
пересечения В окружностей проводим некоторую определённую секущую
NN' и определяем на ней точку Q, для которой NQ: QN' = т. При
этом прямая MN параллельна Ж'/V' (упр. 65), и потому PQ параллельна MN.
Четырёхугольник ABQP можно вписать в окружность, гак как
он имеет те же углы, что и ABNM. Следовательно, точка Р при
любом положении секущей ММ лежит на одной окружности с тремя
неподвижными точками А, В и Q. Так как секущая AM может иметь
любое направление, то геометрическим местом точек Р будет вся окруж-
окружность ABQ.
УПРАЖНЕНИЯ К ГЛАВЕ II (стр. 120).
129. Пусть ABCD—трапеция, Р—точка пересечения диагоналей,
EF—прямая, проходящая через Р и параллельная основаниям
(черт. 383). Так как прямая ЕР параллельна АВ, то треугольники
ABD и EPD подобны, и, следовательно, EP:AB—ED:AD. Точно
24 Элементарная геометрия
370
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
так же из подобия треугольников ABC и PFC найдём, что PF:AB =
= FC:BC. Но в силу параллельности прямых АВ, CD и EF имеет
место пропорциональность отрезков AD:ED^BC:FC. Из трёх напи-
написанных пропорций вытекает, что ЕР: АВ = PF:AB, откуда EP=PF.
Черт. 383.
Черт. 384.
130. Пусть EF — прямая, параллельная основаниям трапеции, М —
точка её пересечения с диагональю ВС (черт. 384). Из подобия треуголь-
треугольников ЕМС и ABC имеем ЕМ:АВ=ЕС:АС=п:(т-\-п). Точно так
же из подобия треугольников MFB и CDB имеем MF:CD — BF:BD=
= т: (т -\- п). Отсюда находим
-\- MF =¦
т + и
Если Е — середина
= y [AB+CD) (ср.
АС, то /в:ге=1, и
упр. 34).
131. Пусть G—точка пересечения медиан
AD и BE треугольника ABC (черт. 385); Ло,
Во, Со, Do, Go — основания перпендикуляров
из точек А, В, С, D, G на данную прямую.
Так как BD = DC и AG: GD =2:1, то в силу
упражнения 130 имеем DD0 = — (ВВй -\-
'„), откуда GG0= — (-4Л0 -\- ВВ0 ~\-
Черт. 385.
); GG0 =—
+ СС0).
132. Из подобия треугольников BEF и D?/4 (черт. 386) имеем
EF:AE^=BE:DE; из подобия треугольников ЛЕВ и GED имеем
AE:EG= BE-.DE. Отсюда EF:AE = AE:EG.
133. Пусть ВАС — данный угол (черт. 387); В(}СЬ и fiC —две
секунше данного направления, Мо — точка, делящая отрезок В0С0
в данном отношении, М — точка пересечения прямых АМ0 и ВС. Так
как прямые, выходящие из точки А, отсекают на параллельных прямых
В0С0 и ВС пропорциональные отрезки, то ВпМ0:С0М0 = ВМ:СМ, так
что М есть точка искомого геометрического места. Геометрическое
место точек М есть прямая АМ0.
КНИГА ТРЕТЬЯ. ГЛАВА II
371
134. Пусть М — одна из точек, из которых окружности О и О'
(черт. 388) видны под равными углами АМВ и А'МВ'. Так как каса-
касательные, проведенные к окружности из одной точки, образуют равные
углы с прямой, соединяющей эту точку с центром окружности (п. 92),
то углы АМО и А1 МО' равны и, следовательно, прямоугольные тре-
треугольники АМО и А'МО' подобны. Из подобия этих треугольников
следует, что МО:МО' = АО:А'О'. Следовательно, точка М принад-
принадлежит окружности С, представляю-
представляющей геометрическое место точек.
отношение расстояний которых от о
точек О и О' равно отношению *
Черт. 387.
радиусов данных окружностей (п. 116). Обратно, всякая точка окруж-
окружности С удовлетворяет поставленному условию, если только она ле>-
жит вне обеих данных окружностей. В этом легко убедиться, по-
повторяя те же рассуждения в обратной последовательности.
Пусть две данные окружности радиусов R и /?'(/?"> R') расположены
одна вне другой. Для точек окружности С отношение их расстояний от точек
О и О' равно R:R' ^> 1. Так как для
точек окружности О то же отношение
меньше R:R', а для точек окруж-
окружности О' больше R:R', то (в силу
сказанного в решении упр. 126) все
точки большей из данных окружно-
окружностей лежат вне окружности С, а все
точки меньшей из данных окружно-
окружностей— внутри окружности С. Так как
данные окружности лежат одна вне
другой, то отсюда вытекает, что
окружность С лежит вне обеих дан-
данных окружностей. Поэтому в этом
случае геометрическое место точек М
есть окружность С.
Если две данные окружности
пересекаются (или касаются одна
другой внешним образом), то окружность С проходит, по самому
своему определению, через точки пересечения данных окружностей
(или касается их в общей точке), и геометрическим местом точек М
будет часть окружности С, расположенная вне данных окружностей.
24*
Черт. 388.
372
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Наконец, если данные окружности расположены одна внутри дру-
другой (или касаются одна другой внутренним образом), то точек /И,
очевидно, не существует.
Если данные окружности равны между собой, то окружность С
заменяется прямой линией, равноудалённой от точек О и О'.
УПРАЖНЕНИЯ К ГЛАВЕ III (стр. 127).
135. Пусть AM и BN — параллельные касательные к окружности О
(черт. 389), MN— подвижная касательная. Так как прямая ОМ перпен-
перпендикулярна к ON (упр. 89), то треугольники ОАМ и N80 подобны,
откуда AM:OA = OB:BN и AM¦ BN=OAK
Л
136. Из подобия треугольников ABD и СВА (черт. 128) имеем
ЛГУ ЛГЛ ПГ ЛП СЛ ] В(У АВ2-\-АС2 1
AB:AD=BC:AL. Отсюда — = ——j = ^__ = _ +
1
"• АС2'
137. Если AD, BE, CF — медианы треугольника ABC, то (п. 128)
c2)
(fl+?) C2 = 3.
138. Пусть ABCD—параллелограм (черт. 390), О — точка пере-
пересечения его диагоналей, АЛ — произвольная точка плоскости. В силу
п. 128 имеем: MA*-\-MC2=2OAi -\- 2OM2;MB2 -\- MD2 = 2ОВ2 + 20АР.
Отсюда (МА2 -\- МС2) — (MB2 + MD2) = 2 (ОА2 — ОЩ.
Если ABCD — прямоугольник, то AC=BD, и, следовательно,
О А = ОВ. Предыдущее равенство принимает вид МА- -\- МС2 = MB2 -\-
-\-MD2.
139. Пусть Е и F—середины диагоналей АС и BD четырёхуголь-
четырёхугольника ABCD (черт. 391). Из треугольника BDE имеем ЬЕ2 -\- DE2 =
= 2BFi-\-2EF2; из треугольников Л?С и ИС.О имеем АВ2-\-ВС~
= 2АЕ*-\-2ВЕ2; CD2+AD2 = 2AE2-\-2DE2. Складывая и заменяя
BE2 -\- DE2 найденным выше значением, получаем АВ' -\- ВС2 -\- CD2-\-,
КНИГА ТРЕТЬЯ. ГЛАВА III
373
•E2) 4-4№= 4AE2-\-4BF*+4EF2 = AC24-
+ BD* + 4EF*.
140. Пусть AD—одна из медиан треугольника ABC (черт. 392).
Применяя к треугольнику AMD и точке О теорему Стюарта (п. 127),
найдём MA2-DG + MD2.AG — MGZ-AD — AD-DG-AG. Заменяя
1 2
здесь DG и AG соответственно через — AD и —- AD и сокращая на
о 3
AD, будем иметь:
1
2_
Черт. 391.
В D
Черт. 392.
Применяя теорему п. 128 к треугольникам МВС и GBC, найдём
MD* = 4- (ЛШ2 + МО) ~ i- fiC2; GD2 = i- (G52 -f- GC2)~ i- fiC2,
откуда AID2 = -i- (/ИБ2 + /ИС2) — -i- (Gfi2 + GC2) -f- GD2. Подставляя
в A), получим ЗМО2 = Л1Л24-ЖВ24-УИС2— (Gfi24-GC2L-2GD2—
2 13
— -^-AD2. Заменяя здесь GD = — GA; AD=^ — GA, получаем тре-
o 2, 2*
буемое соотношение.
141. Пусть сумма умноженных на данные положительные числа т
и п квадратов расстояний некоторой точки АЛ от данных точек А и В
(черт. 393) равняется квадрату данного отрезка k:
k2. A)
Если точка О делит отрезок АВ в отношении, обратном отноше-
отношению данных коэфициентов, то мы имеем 0В:А0:АВ—т:п:{т-{-п).
Применяя теорему Стюарта (п. 127) к треугольнику МАВ, найдём
МА2-ОВ-\-Л1В2-АО — МО2-АВ=АВ-ОВ-АО, или в силу предыду-
предыдущего равенства
т
' т-\-п
¦МА2-\-
т-\-п
.MB2 —
inn
(т + пJ
¦АВ2.
B)
374
PEUIFHHfl УПРАЖНЕНИЙ И ЗА1АЧ
Так как точка М удовлетворяет условию A), то отсюда следует, что
ОМ = -X '^—--АВ2 = const.
in -\- n (m -\- nJ
Геометрическое место точек Мсуществует, если
тп
АВ2,
гп-\-п
и представляет собой окружность с центром О.
Пусть теперь при тех же обозначениях, что и выше, т-МА-—
— n-MB2 = ^=k2, причём /л]>н>0 (случай т=п, очевидно, при-
приводится к п. 128а, следствие). Если точка О' (черт. 394) делит отре-
Черт. 393.
Черт. 394.
зок АВ внешним образом в отношении, обратном отношению коэфи-
циентов т и п, то О'А:О'В:АВ=п:т: (т — п). Применяя теперь
теорему Стюарта к треугольнику МО'В, найдем: МО'*-АВ-\-
-\-МВ2-О'А—МА2-О'В=О'В-О'А-АВ, или в силу предыдущего
равенства
т
т — п
тп
т — п
(т
пJ
(m—nf
•АВ2-\--
т-
¦^ const.
Геометрическое место существует, если
тп
C)
и пред-
т — и ~
ставляет собой окружность с центром О'.
При k=:0 получаем геометрическое место точек, дня которых
т-МА2— П'МВ2^=0, т. е. МА:МВ^\ п : у т.. Таким образом по-
получается геометрическое место, рассмотренное в п. 116.
142. Пусть т-МА*-\-п-МВ2-\-р-МС' = №, где А, В, С—дан-
С—данные точки, in, n, p — данные положительные или отрицательные числа,
k — данный отрезок, М—точка искомого геометрического места. Пусть
обозначения точек А, В, С выбраны так, что т-\-п^=0. В силу ра-
равенств B) и C) решения упражнения 141 имеем иг • МА2 -\- п • MB1 =
тп
^¦(т~\-п) ¦ DM2-\ АВ2, где D — точка, делящая отрезок АВ
т -\- п
(внутренним или внешним образом в зависимости от знаков т и п)
КНИГА ТРЕТЬЯ. ГЛАВА III 375
в отношении |л|:|;л|. Предыдущее равенство принимает вид
(т -\- п) ¦ MD2 -\-p. МС2 = k2 — ' • АВ2 = const. В силу упражне-
упражнения 141 геометрическое место точек М (если оно существует) при
т -\- п ~\-р =? О есть окружность; в силу п. 128а, следствие, искомое
геометрическое место есть прямая при т~\-п-\-р^0.
Аналогичные рассуждения применимы в случае любого числа дан-
данных точек.
143. Выражение для квадрата длины биссектрисы AD2 =
Ift I с\2 а2
z=bc- — . а— , приведённое в п. 129, можно представить так: AD2=
= Ьс— -—i— ¦-.—;—= be— BD-CD. Аналогично для биссектрисы
b-f-c b~\-c
внешнего угла имеем теорему: Квадрат биссектрисы внешнего угла
треугольника равен произведению отрезков противолежащей сто-
стороны, считая от её концов до точки пересечения с биссектрисой,
уменьшенному на произведение сторон, образующих этот угол.
а2 1С М2
Действительно, выражение АЕ2^Ьс , приведённое в п. 129,
[с — Р)-
можно представить так: АЕ2 = • — Ьс = ВЕ-СЕ—be.
с — be — b
144. Преобразуем выражение для квадрата медианы, данное в
п. 128, следующим образом: Л?>2 = — (№-\-с2) — -—а" =—{b-\-cf-\-
^. (Ь-с + а) (Ь-с-а). Так
как а-\~Ь—с^>0 и Ъ — с — а<^0, то полученное значение AD-
меньше (—^—I и медиана меньше —-=—. С другой стороны, Ь2-\-
-\-с2^>'2Ьс, и выражение для квадрата медианы можно преобразовать
так: ADn~= ~ ф2-\-с2)— ^-а2> —{Ь^-\-с^)-\-~-2Ьс — ~
2 ^{bJ\)(b4-a), или
^^ . Так как /Ш<—^— <—!— , то
из полученного неравенства следует, что AD^> — (b-\-c — а).
Чтобы доказать, что биссектриса меньше медианы, если
заметим, что из только что данного выражения — (Ь -]- сJ -[-
-] (Ь — сJ — а2 для квадрата медианы видно, что при Ь=/=с квадрат
376
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
медианы больше, чем —-(Ь~\-сJ а2. Далее, так как при b=f=c
be I
имеет место неравенство 4fec<^(b-f-сJ или . <^ — , то из вы-
выражения, данного в п. 129, следует, что квадрат биссектрисы меньше,
чем —- (Ь -|- сJ — о2. Отсюда и следует, что при Ь=^=с биссектриса
меньше, чем медиана.
145. Если медиана AD треугольника ABC есть среднее пропорци-
пропорциональное между сторонами b и с, то AD2 = be, или — (Ь2 -\- с2) —
— —а?=Ьс, откуда 2 (Ь — с)- = о2, так что a =|fe—с\-уг2. Таким
образом, сторона а треугольника равна диагонали квадрата со сторо-
стороной \Ь — с\, так как диаго-
диагональ квадрата равна его сто-
стороне, умноженной на у 2.
Черт. 396.
146. Пусть через точку М проведены две взаимно перпендикуляр-
перпендикулярные хорды АВ и CD и Е — точка, диаметрально противоположная
точке А (черт. 395). Так как (AC-f- BD) = 90° (п. 75) и АС-\-
4-С?'=180°,"то BD=CE и, следовательно, BD=CE. Отсюда
AC -\- BD2 = АС1 Л- СЕ2 == АЕ"-. Аналогично найдём, что AD"- -f ВС2 =
2\DEZ AE2
147. Пусть Е, F, G, И, К, L — основания перпендикуляров, опу-
опущенных из точки М окружности радиуса R на стороны и диагонали
вписанного четырёхугольника ABCD (черт. 396). Применяя теорему
п. 130а о радиусе описанной окружности к треугольникам МАВ,
MCD, МВС, MDA, MAC, MBD, получим: МА-МВ= 2R-ME;
МС ¦ MD = 2R ¦ MG; MB- MC=2R ¦ MF; MD-MA = 2R ¦ МИ;
MA-MC=2R-MK; MB-MD= 2R-ML, откуда MA-MB-MC-MD =
=z4R?-ME-MG=4R2-MF-MH=4R2-MK-ML, так что ME-MG —
КНИГА ТРЕТЬЯ. ГЛАВА IV
377
Если стороны AD и ВС обращаются в касательные, то мы полу-
получаем такую теорему: Расстояние от точка окружности до хорды
есть среднее пропорциональное между расстояниями той же точки
от касательных в концах хорды (черт. 397J. Действительно, че-
четырёхугольник ABCD обращается в дважды взятую хорду АВ, точки
Е и G совпадают и предыдущие равенства дают: ME2 =
УПРАЖНЕНИЯ К ГЛАВЕ IV (стр. 132).
148. Пусть О — данная окружность (черт. 398), С—вторая точка
пересечения прямой АВ с окружностью BMN. При этом АВ-АС=
:=AM-AN есть степень точки А относительно О, так что положе-
положение точки С не зависит от выбора окружности BMN.
Черт. 397.
149. Пусть требуется найти геометрическое место точек М, отно-
отношение степеней которых относительно двух данных окружностей
O^Rj) и O2(R2) равно т. В силу п. 134 мы должны иметь
Ж),2 — /?,2
мо-! — Ri
0)
или MOj2 — m-MO22 = Rl2 — mR^. На основании упражнения 141 гео-
геометрическое место точек М (если такие точки вообще существуют)
есть окружность. Центр О этой окружности лежит на прямой Ofi2
и делит отрезок OjO2 в отношении /те, т. е.
0,0
B)
Так как степень точки М относительно окружности О равна нулю,
то расстояние точки М от радикальной оси окружностей О, и О
Mf) a g 2
равно (п. 136, примечание 3°) —^-— х ; расстояние точки М от
¦)ЛО '
радикальной оси окружностей О2 и О равно
2 О 2
- . Так как оба
378
РППЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
эти расстояния любой точки М окружности О от обеих радикальных
осей равны между собою в силу соотношений A) и B), то все три
окружности имеют общую радикальную ось.
Если в условии упражнения 128 точка Р делит отрезок ММ' в
постоянном отношении РМ:РМ'^т, то отношение степеней точки
РМ-РА
Р относительно обеих окружностей равно
- = т, и геометри-
РМ'-РА
ческое место точек Р есть окружность.
150. Линия центров обеих окружностей соединяет середины диа-
диагоналей трапеции BCED (черт. 399) и потому параллельна ВС (упр. 34).
Следовательно, радикальная ось этих окружностей перпендикулярна к
Р>
Черт. 399.
Черт. 400.
ВС. С другой стороны, окружности, имеющие BE и CD своими диа-
диаметрами, проходят соответственно через основания М и N высот ВМ
и CN треугольника. Далее, точки В, С, М и N лежат на одной
окружности, имеющей ВС своим диаметром. Радикальные оси всех
трёх окружностей, взятых попарно, проходят через одну точку; но
две из радикальных осей — высоты ?М и CN треугольника (п. 137).
Следовательно, третья радикальная ось проходит через точку пересе-
пересечения И высот треугольника. Так как она перпендикулярна к ВС,
то она совпадает с высотой треугольника.
151. Если бы окружности DD'EE', EE'FF1, FF'DD' были различны,
то прямые АВ, АС, ВС были бы их радикальными осями, что невоз-
невозможно, так как (п. 139) радикальные оси трёх окружностей, взятых
попарно, не могут образовать треугольника. Следовательно, по край-
крайней мере две из трёх окружностей совпадают, но в таком случае все
шесть данных точек лежат на одной окружности.
152. Пусть окружность О, радиуса О, Г, ортогональная к окруж-
окружностям О и О' (черт. 400), пересекает прямую ОО' в точках Р ь Q.
Тогда О1Р2=О,Г2 есть степень точки О, относительно каждой из
окружностей О и О'. Следовательно, радикальная ось ОХН (п. 138)
данных окружностей есть в то же время радикальная ось точки Р и
каждой из данных окружностей (п. 136, примечание 1°). Таким обра-
КНИГА ТРЕТЬЯ. ГЛАВА IV
379
зом, точка Р обладает тем свойством, что HP2 есть степень точки Н
относительно О или О': Отсюда следует, что положение точки Р не
зависит от выбора окружности Ог (и то же относится к точке Q) и
что степень точки Н относительно О или О' есть положительное
число, так что данные окружности не пересекаются.
153. Пусть через точки А и В проведена произвольная окружность
(черт. 401) и через точки С и D—какая-либо окружность, пересе-
пересекающая первую. Точка пересечения Ж радикальной оси этих окружностей
с - прямой АВ удовлетворяет условию
MA -MB= MC -MD,
О)
Черт. 401.
и так как геометрическое место точек,
имеющих равные степени относительно
обеих окружностей, есть прямая линия,
то на прямой АВ существует единствен-
единственная точка М, удовлетворяющая соотно-
соотношению A).
Если теперь провести через данные
точки другую пару окружностей, то их
радикальная ось пересечёт прямую АВ в некоторой точке, удовлетво-
удовлетворяющей тому же самому соотношению A) и, следовательно, совпадаю-
совпадающей с М.
Итак, положение точки М не зависит от выбора окружности, про-
проходящей через точки А и В, и окружности, проходящей через точки
С и D, и прямая, соединяющая
общие точки каждой такой пары
окружностей, проходит через М.
154. Степень точки /, внут-
внутренней относительно окружности О
радиуса г, относительно этой
окружности равна 01- — г2 =
— — (г*—ОР) = — — А&, где
АВ—хорда окружности О, про-
проходящая через точку / и перпен-
перпендикулярная к диаметру 01.
Так как радикальный центр /
трёх данных окружностей О, О', О"
(черт. 402) имеет одну и ту же
степень относительно этих окруж-
окружностей, то хорды АВ, А'В, А"В"
трёх окружностей, проходящие через / и соответственно перпендику-
перпендикулярные к 01, 04, О'Ч, равны между собой и служат диаметрами
одной окружности с центром / (так как в точке / все три хорды
делятся пополам).
Черт. 402.
380
PFllIEHHil УПРАЖНЕНИЙ И ЗАДАЧ
i
/
7 k
^<
L
N'
\
К
L
\
M'
В п'
т
М п N
Черт. 403.
УПРАЖНЕНИЯ К ГЛАВЕ V (стр. 142).
155. Пусть две вершины /Си/, искомого квадрата KLNM (черт. 403)
лежат соответственно на сторонах АВ и АС данного треугольника
ABC (или их продолжениях), а две другие—на стороне ВС (или её
продолжении). Рассмотрим квадрат, гомотетичный искомому, принимая
за центр подобия вершину В
и за точку, гомотетичную
точке К, произвольную точ-
точку k прямой АВ. Этот квад-
квадрат имеет своей стороной
перпендикуляр km из точки k
на сторону ВС и потому за-
занимает одно из двух воз-
возможных положений /г/ишили
kl'n'm. Вершины L и /.'
искомых квадратов KLNM
и K'L'N'M лежат в пересе-
пересечении прямых В1 и В1' с
прямой АС.
Из сказанного вытекает такое построение. Из произвольной точки k
стороны АВ опускаем перпендикуляр km на основание ЬС треуголь-
треугольника и строим квадраты kmnl и kmn't. Точки пересечения прямых В1
и ВГ с прямой АС определяют вершины L и L' искомых квадратов.
Если ни одна из двух прямых Ы и ВГ не параллельна АС, то
задача будет иметь два решеш.я, если же одна из них параллельна АС,
то только одно. При этом мы
допускаем (как это часто де-
делается для общности рас-
суждений) „вписанные" квад-
раты, вершины которых мо-
могут лежать не только на са-
самих сторонах треугольника,
но и на их продолжениях.
Если же рассматривать толь-
только квадраты, вершины ко-
которых лежат на самих сто- Черт. 404.
ронах треугольника (а не на
их продолжениях), то задача будет иметь одно решение, если ни один из
углов Ви Сне тупой, и не будет иметь решения, если один из них тупой.
Аналогично можно построить квадраты, у которых две вершины
лежат на прямой АВ или на прямой АС и по одной вершине — на
двух других сторонах.
156. Так как ОМ есть биссектриса угла О треугольника ОАВ
(черт. 404), то AM:AiB=OA :OB, и, следовательно, АМ:АВ=^
= ОЛ:(ОЛ -f- OB) ^covst. Геометрическое место точек М есть окруж-
окружность, гомотетичная данной относительно точки А.
КНИГА ТРЕТЬЯ. ГЛАВА V
381
157. При изменении положения точки М вся фигура (черт. 405)
остаётся подобной самой себе (относительно центра подобия О), и,
следовательно, точка касания перемещается по прямой, проходящей
через О.
158. Пусть ABC— данный треугольник (черт. 406), G — точка
пересечения медиан, И—точка пересечения высот, О—центр описан-
Черт. 405.
ной окружности, А'В'С—треугольник, стороны которого ПС, А'С,
А В' проходят соответственно через .4, В, С и параллельны сторонам
ВС, АС, АВ данного треугольника. Треугольники ABC и А'В'С го-
гомотетичны, так как отрезки А'В и АС соответственно параллельны
отрезкам АВ и АС, направлены в противоположную сторону и вдвое
больше каждого из них (п. 142).
Прямые АА', ВВ\ СС — медианы
треугольника ABC, так как четырёх-
четырёхугольники АВА'С, ВСВ'А и САСВ —
параллелограмы и, следовательно,
центром подобия служит точка G.
Центр О окружности, описанной око-
около треугольника ABC, и центр окруж-
окружности, описанной около треугольника д(
А'В'С (т. е. точка пересечения Н
в"ысот данного треугольника ABC),
представляют собой две гомотетичные
точки. Следовательно, прямая ОН про-
проходит через точку G и отрезок ОН делится в точке G в отношении 1:2.
159. Пусть О,—произвольная точка первой фигуры (черт. 407), О2
и Os — соответствующие ей точки второй и третьей фигур; 5,3, 5зр
512 — центры подобия трёх фигур, взятых попарно. Обозначим через
k — коэфициент подобия первой и второй фигуры: & = 5|2О( :512О2,
и аналогично положим k' = 53|О1:5з,О3. Проведём через О, прямую,
параллельную 512523, и пусть М — точка её пересечения с прямой
0, И
Черт. 407.
382 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
О5О3. Из подобия двух пар треугольников О353531 и O3MOv O2SngSn
и'СЛЮ, имеем- 5„3581:МО, = SnOa:OlOs = SslO3:(S3lO.i — 531"О,);
S23Sxi:MOl = SKO~2:6fi2 = S12O2:(S]2O2 — SKO,). Отсюда
S2SSK 513Оя-EЯ]О, - ЗД) 1 - *' •
Примечание. Доказательство принимает вполне общий характер,
если рассматривать знаки отрезков (пп. 185—191) и в соответствии с этим
приписать коэфициентам подобия определённые знаки. При этом проще всего
применить к треугольнику C^SjoSgi и прямой 0-J03 теорему п. 192.
160. Пусть Р и Р—основания перпендикуляров из точки О на
данные параллельные прямые (черт. 408). Из равенств СМ': СМ —
= 0Р':ОР и О А = А'А" следует, что О А': А'А" = 0Р':0Р. Треуг ль-
ник О А'А" имеет прямой угол при
вершине А' и постоянное отноше-
отношение катетов; следовательно, он остаёт-
остаётся подобным самому себе. Таким
образом, угол А'ОА" и отношение
О А": О А' остаются постоянными и
точка 4" описывает фигуру (п. 150,
первая теорема), подобную той, кото-
которую описывает точка А', т. е. пря-
прямую линию.
Эгу прямую линию можно проще
всего найти, построив два каких-
либо положения точки А" (на чер-
чертеже построена ещё точка Р", соответств} ющая тому случаю, когда
точка А' совпадает с Р').
Так как отрезок А'А", равный ОА, можно отложить на прямой,
проходящей через А' и перпендикулярной к ОА', в обе стороны, то
искомое геометрическое место состоит из двух прямых линий (вторая
прямая на чертеже не показана).
161. Пусть АВ и А'В' — два соответственных отрезка фигур F
и F' (черт. 409) и А"В" — соответствующий им отрезок искомой фи-
фигуры F", прямо-гомотетичной фигуре F'. Направление оси симметрии
фигур F и F" совпадает с направлением биссектрисы угла, стороны
которого параллельны отрезкам АВ и А'В' и направлены в ту же сто-
сторону (угол ВАЬ' на чертеже). Центр гомотетии S фигур F' и F" ле-
лежит, по условию, на оси симметрии SX. Если Ао, Ао'—проекции то-
точек А, А' на ось симметрии, то мы должны иметь: A0A":A'QA' =
^SA":SA' = A'B№:A'B' = AB:A'B' и, кроме того, АА0 = А,А", так
что ЛЛ0:А'0А' = АВ:А'В'. Заменяя AA0:A'QA' равным ему отношением
АХ:ХА' (где X—точка пересечения оси симметрии с прямой АА'), мы
видим, что искомая ось симметрии, параллельная биссектрисе угла
между направлениями каких-либо двух соответственных отрезков фи-
фигур F и F', должна делить расстояние между какими-либо двумя со-
КНИГА ТРЕТЬЯ. ГЛАВА VI
383
ответственными точками обеих фигур внутренним образом в отношении,
равном отношению соответственных отрезков. Эти условия вполне
определяют искомую ось симметрии.
Вторая искомая фигура F," симметрична фигуре F" относительно
точки 5. Соответствующая ось симметрии SY параллельна другой бис-
биссектрисе угла между АВ и А'В' и делит отрезок АА' внешним обра-
образом в том же отношении, что и ось SX; центром подобия фигур F'
и F" будет опять точка б1.
Рассуждения теряют силу, если фигуры Fn F' равны (сравнить упр. 95).
162. Пусть А, В, С, ... — точки фигуры F; А', В', С,... — соот-
соответственные им точки фигуры F'; О— точка фигуры F, совпадающая
с соответственной точкой фигу-
фигуры F' (п. 150). При этом /I АОА'=
О А: ОА'=ОВ: ОВ'=ОС: ОС=....
СлсдовательнодреугольникиЛСМ',
ВОВ', СОС,... подобны (сравнить
п. 150). Если на отрезках АА', ВВ',
СС,... построить треугольники
АА'А", ВВ'В', ССС",..., подоб-
подобные треугольнику Т и имеющие с
иим одинаковое направление вра-
вращения (причём стороны АА', ВВ',
СС,. . . соответствуют одной и
той же стороне треугольника Т),
ТО', четырёхугольники ОАА"А',
ОВВ"В, ОСС"С\.. . будут по-
подобны (п. 149). Поэтому и тре-
треугольники ОАА', ОВВ", ОСС",. ..
будут подобны. Отсюда следует,
что точки А", В', С", ... образуют
фигуру, подобную двум дан-
данным (п. 150, первая теорема).
• Аналогичное рассуждение применимо и к случаю, когда точки А",
В', С,... делят отрезки АА', ВВ', СС,... в одном и том же отно-
отношении. Только вместо подобных четырёхугольников ОАА А', ОВВ'В,
ОСС'С,.. . будем иметь ряд подобных треугольников ОАА', ОВВ',
ОСС,... и соответственные точки А', В", С',... иа их сторонах.
УПРАЖНЕНИЯ К ГЛАВЕ VI (стр. 152).
163. Пусть требуется построить отрезок х, отношение которого
к данному отрезку а равняется отношению квадратов двух данных
отрезков тип (пусть для определённости т^>я).
Первое построение. Примем отрезки и и я за катеты пря-
прямоугольного треугольника. Проекции т1 и п1 катетов т и я на гипо-
гипотенузу удовлетворяют условиям тхс = т"\ п1с = п2, где с — гипотенуза
Черт. -409.
384
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
треугольника. Отсюда тл\пх=^т2:п2. Отрезок х есть четвёртый про-
пропорциональный к трём данным отрезкам: д;:а = /я1:л1 (п. 151, по-
построение 2).
Второе построение. Примем отрезок т за гипотенузу, а от-
отрезок п за катет прямоугольного треугольника. Проекция- и, катета
я на гипотенузу удовлетворяет условию тп1^=п2, или т:пх=т2:п2.
Отрезок х есть четвёртый пропорциональный к трём данным отрезкам;
х:а^т:пл (п. 151, построение 2).
Примечание. Второе построение имеет то преимущество, что оио
легко обобщается на случай, когда требуется построить несколько отрез-
отрезков, пропорциональных квадратам данных отрезков. Пусть даиы хотя бы
Черт. 410.
Черт. 411.
четыре отрезка т, л, р, q и требуется построить отрезки, пропорциональ-
пропорциональные их квадратам (для определённости примем т за наибольший из данных
отрезков).
На отрезке т как на диаметре строим полуокружность (черт. 410). Из
одного конца этого отрезка засекгем дуги радиусами, соответственно рав-
равными п, р и д, и из точек пересечения этих дуг с полуокружностью опу-
опускаем перпендикуляры на диаметр. Полученные отрезки "удовлетворяют
сотноошениям ял| = д2; пгрх=ръ, та^ = #3, откуда m:ni:p1:g1=^m2:n2:p2:g'K
164. Пусть требуется построить отрезок лг, отношение квадрата
которого к квадрату данного отрезка а равняется отношению двух
данных отрезков т и и, так что х2:а2 = т2:я2, или х:а = Ут:\ п
(пусть для определённости т ^> я).
Первое построение. Примем отрезки т и я за проекции
катетов прямоугольного треугольника на гипотенузу. Для построения
вершины прямого угла строим на сумме данных отрезков как на диа-
диаметре полуокружность. Катеты т1 и пх удовлетворяют условиям
ml2 = mc, п2 — пс, где с— гипотенуза треугольника. Отсюда тх:пх =
¦=у т:уп. Отрезок х есть четвёртый пропорциональный к трём
данным отрезкам: х:а = т1:пл (п. 151, построение 2).
Второе построение. Примем отрезок т за гипотенузу,
а отрезок п за проекцию катета на гипотенузу. Вершина прямого
угла лежит на полуокружности, построенной на отрезке т как на диа-
диаметре. Катет «j, имеющий и своей проекцией, удовлетворяет условию
КНИГА ТРЕТЬЯ. ГЛАВА VI 385
/яя^я,2, или т:пл^\т: \ я. Отрезок х есть четвёртый пропор-
пропорциональный к трём данным отрезкам: х'.а^т'.п^
Пр имечание. Второе построение имеет то преимущество, что оно
легко обобщается на случай, когда требуется построить несколько отрез-
отрезков, квадраты которых пропорциональны данным отрезкам. Построение
выполняется в порядке, обратном по отношению к тому, который описан
в примечании к решению упражнения 163 (черт. 410). При этом т, пър1г
Щ\ — данные отрезки, а п, р, q — искомые.
165. Пусть через точку О (черт. 411) требуется провести прямую
ОАВ так, чтобы отрезок АВ этой прямой, заключённый между двумя
данными прямыми (или окружностями) а и Ь, делился в точке О внеш-
внешним или внутренним образом в данном от-
отношении.
Строим прямую (окружность) а', гомо-
гомотетичную прямой (окружности) а, принимая
за центр подобия точку О и за коэфици-
ент подобия данное отношение. Гомотетия
должна быть прямой или обратной, смотря
по тому, делит ли точка О отрезок АВ
внешним или внутренним образом. Искомая
прямая проходит, очевидно, через точку пе-
пересечения В прямых (окружностей) а' и Ь.
Если даны две пересекающиеся пря- Черт. 412.
мне линии в и ft, то получается одно реше-
решение для того случая, когда точка О делит отрезок АВ внешним обра-
образом, и одно решение для случая, когда точка О делит отрезок внут-
внутренним образом. Если даны две параллельные прямые, то задача либо
вовсе не имеет решений, либо имеет их бесчисленное множество.
Если даны две окружности а и Ь, то наибольшее возможное число
решений для каждого из двух случае^в (деление внешним образом и де-
деление внутренним образом) равно двум.
166. При решении задачи следует различать два случая.
Первый случай. Пусть хорда СС (черт. 412) есть средняя
пропорциональная между всей секущей АС и её внешней частью АС,
так что СС'2 = АС-АО. Проводя из точки А касательную AT, будем
иметь AT2 = АС-АС. Из этих двух равенств получаем СС' = АТ.
Так как все хорды данной окружности, равные данному отрезку AT
(точнее говоря, отрезку AT, который мы умеем построить), касаются
одной и той же окружности, концентрической с данной, то задача
сводится к проведению из точки А касательной к этой концентрической
окружности.
Задача не имеет решений, если AT больше диаметра, имеет одно
решение, если AT равно диаметру, и два решения, если AT меньше
диаметра. Если О — центр дайной окружности, R — её радиус, то
условие возможности задачи AT s? 2R даёт AT2— АО2 — 2
или АО sS R )/1Г.
25 Элементарная геометрия
386
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Второй случай. Пусть внешняя часть секущей АС (черт. 412)
есть средняя пропорциональная между всей секущей ACw хордой СС\
так что АС1 = АС-СС. Отсюда АС:АС = АС:(АС — АС). Умножая
каждый член ьтой пропорции на АС и заменяя АС-АС через квад-
квадрат касательной AT, получим:
AT*: АС* = AC3: (AT* — АС'г). A)
Если мы разделим касательную AT в среднем и крайнем отноше-
отношении в точке М (так что AM будет- большим отрезком) и построим
прямоугольный треугольник АТР, имеющий AT своей гипотенузой
и AM—-проекцией катета на гипоте^зу, то
AT: AM = AM: (AT—AM), B)
и (упр. 163, второе построение) AT:AM = AT*:АР2. Заменяя в ра-
равенстве B) отрезки AT и AM пропорциональными нм величи-
величинами AT2 и АР2, получим АТ2:АР*- =
= АР2:(АТ2 — АРг). Сравнивая это равен-
равенство с A), находим, что АС = АР. Чтобы
найти теперь точку С, достаточно из
точки А как центра описать окружность
радиуса АР.
Чтобы задача имела решение, необ-
необходимо и достаточно, чтобы отрезок АС =
= АР был меньше касательной AT и
в то же время чтобы этот отрезок АС = АР
был не меньше наименьшего расстояния АК
от точки А до окружности. Первое усло-
условие всегда выполнено, второе даёт
или АР2 5э (О А — Rf. Но (в силу п. 156)
Черт.
АР*- —AT2-
Отсюда (ОА2 — R2)X
¦¦(О А — RJ, или, после сокращения иа О А — R и алге-
алгебраических преобразований, О A ^R{2-\~ \^5).
167. Пусть М—искомая точка. Так как MB есть биссектриса
треугольника АМС, то МА:МС= АВ:ВС. Аналогично MB:MD =
= ВС: CD. Искомая точка определяется как точка пересечения двух
окружностей — геометрического места точек, расстояния которых от
точек .4 и С относятся как АВ: ВС, и геометрического места точек,
расстояния которых от точек В и D относятся как BC:CD (п. 116).
168. Пусть А и В—данные точки (черт. 413), МА' и MB' —
искомые равные хорды, проходящие соответственно через точки А и В.
Так как равные хорды равноудалены от центра О окружности, то ра-
радиус ОМ есть биссектриса угла AM В, и потому М А: МБ = О А: О В.
Искомая точка М принадлежит кроме данной окружности ещё од-
одной окружности — геометрическому месту точек, отношение расстояний
которых от точек А и В равно О.4:ОВ. *
КНИГА ТРЕТЬЯ. ГЛАВА VI 387
169. Пусть ABC — искомый треугольник (черт. 120), в котором
известны стороны АВ, АС и биссектриса AD, и Е — точка пересече-
пересечения прямой АВ с прямой, параллельной AD и проходящей через С.
Так как АС=АЕ, то отрезок СЕ можно построить как четвёртый
пропорциональный к трём данным, пользуясь пропорцией CE:AD =
= (АВ-\- АС):АВ. Далее можно построить равнобедренный треуголь-
треугольник АСЕ по его сторонам и на продолжении стороны АЕ отложить
данную сторону АВ.
170. Пусть произведение двух сторон треугольника равно произ-
произведению двух данных отрезков. Частное от деления произведения этих
двух сторон на удвоенную высоту, опущенную на третью сторону,
равно радиусу описанной окружности. Следовательно, этот радиус
можно построить как четвёртый пропорциональный к трем данным
отрезкам. Построив окружность, имеющую найденный радиус, и про-
проведя в ней хорду, равную данной стороне, мы определим положение
третьей вершины, проводя прямые, параллельные ьтой стороне и от-
отстоящие от неё на расстоянии, равном высоте.
171. Пусть даны углы треугольника и ею периметр. Построим
BcnoMoi ательный треугольник, имеющий данные у1лы, выбрав произ-
произвольно одну из его сторон. Так
как построенный треугольник
подобен искомому, то их пери-
периметры Чфопорциональны соот- /^7
О <
D С
ветственным сторонам. Сторону "
искомого треугольника можно ft
построить как отрезок, четвёр- qepT ^
тый пропорциональный к соот-
соответствующей ей стороне вспомогательного треугольника и к периметрам
обоих треугольников.
Так как в подобных треугольниках суммы медиан, суммы высот
"и т. д. пропорциональны соответственным сторонам, то описанный спо-
способ построения применим и тогда, когда даны углы и сумма медиан
или у1лы и сумма высот и т. д.
172. Так как стороны двух квадратов пропорциональны их диаго-
диагоналям, а следовательно, и разностям между диагоналями и сторонами,
то сторона искомого квадрата есть отрезок, четвёртый пропорциональ-
пропорциональный к разности между его диагональю и стороной, к стороне произ-
произвольного квадрата и разности между диагональю и стороной последнего.
173. Если точка D делит отрезок ВС (черт. 166) в среднем
и крайнем отношении, то BC:BD^= BD:CD. С другой стороны, если
точка D' делит отрезок ВС внешним образом в среднем и крайнем
отношении, то BD' — BC-\-BD (п. 156). Из этих двух соотношений
вытекает (п. 156), что BC:BD = BD:CD= BD' :BC= CD' :BD'.
Из пропорции BD:CD=BD':BC мы найдём, что BD':BD =
= BC:CD=CD':BC. Отсюда BD' :BD= (CD' -\- BC):(BC+ CD).
Если на продолжении отрезка ВС за точку С отложить отрезок СЕ
(черт. 414), равный ВС, то CD' -f BC=ED', ВС-{-DC—ED, и ripe-
26*
388
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
дыдущая пропорция принимает вид: BD' :BD^ED':ED. Таким обра-
образом, Е есть точка, гармонически сопряжённая с точкой В отно-
относительно концов отрезка DD'.
Далее из равенства CD':BD' = BD:CD, которое мы имели выше,
следует, что CD': BD' = CF': BF', если F—точка, симметричная с точ-
точкой D относительно середины О отрезка ВС (так как BD^CF;
CD=BF). Таким образом, F есть точка, гармонически сопряжен-
сопряженная с точкой D' относительно концов отрезка ВС.
Наконец, так как точки F и D' гармонически сопряжены относи-
относительно концов отрезка ВС, т. е. CD':BD' ~CF:BF, то для сере-
середины О отрезка ВС имеем
(ОС+ 0D'): {0D' — ОВ) =
= @С-\- OF):(OB — OF),
откуда в силу 0В= ОС нахо-
находим OB2=0Cz = OF ¦ OD' =
=OD-OD' (сравнить п. 189).
Так как отрезок ОВ^ ОС
есть среднее пропорциональ-
пропорциональное между 0D и 0D', то
окружность, построенная на
DD' как иа диаметре (на
чертеже не показана), отсе-
Черт 415 кает на перпендикуляре к
прямой DD', восставленном
в точке О, отрезки OM = ON=OB (п. 125, следствие). Отсюда и
следует, что эта окружность проходит через вершины М и N
квадрата, имеющего ВС своей диагональю.
174. Сначала найдём на данной прямой D точку, из которой дан-
данный отрезок АВ виден под данным углом. Геометрическое место то-
точек, из которых отрезок АВ виден под данным углом, есть совокуп-
совокупность двух дуг окружности, имеющих своими концами точки А и В.
Точки пересечения этих дуг с данной прямой D и будут искомыми
точками.
Задача имеет решения, если построенные дуги имеют общие точки
с прямой D, и ке имеет решений, если таких точек не будет. Пре-
Предельным случаем будет окружность, касающаяся прямой D. Если дан-
данные точки А и В лежат по одну сторону от прямой D, то сущест-
существуют две такие окружности. Пусть АМВ — одна из них (черт. 415).
Легко убедиться, что если точка М прямой D лежит по ту же сто-
сторону от прямой АВ, что и точка М, то угол АМВ больше угла AM'В.
В самом деле, угол АМВ—вписанный, а угол AM'В имеет вершину
вне окружности. Точно так же вторая точка касания /V будет давать
наибольшее значение угла ANB по сравнению со всеми точками, ле-
лежащими с ней по одну сторону от АВ. Следовательно, наибольшее
значение угла будет соответствовать точке М или точке N в за-
зависимости от того, будет ли угол АМВ больше или меньше
угла ANB.
КНИГА ТРЕТЬЯ. ГЛАВА VI
389
Если бы точки А и В лежали по разные стороны от D, то наи-
наибольшее значение угла A80°) соответствовало бы точке пересечения
прямой АВ с прямой D.
175. Построение общего перпендикуляра к двум данным парал-
параллельным прямым, который был бы виден из данной точки .4 под
данным углом, приведено в решении задачи 120. Так как длина этого
общего перпендикуляра MN постоян- д
на, то угол, под которым он виден
из данной точки, будет тем больше,
чем меньше радиус окружности AMN,
если этот угол острый.
Если точка А не лежит между
двумя данными параллельными пря-
прямыми (черт. 416), то наименьший
возможный радиус окружности AMN
есть перпендикуляр из точки А на -
прямую, равноудалённую от двух
данных параллельных прямых. Строя окружность, проходящую через
точку А и имеющую этот перпендикуляр своим радиусом, получаем
решение задачи. В этом случае задача имеет два решения.
Если точка А лежит между двумя данными параллельными прямыми,
то наибольший угол A80°) соответствует перпендикуляру MN, про-
проходящему через точку .4.
Черт. 416.
Черт, 417.
В
Черт. 418.
' 176. Пусть данные точки А и В лежат по одну сторону от дан-
данной прямой (черт. 417). Обозначая через т длину данной хорды
и через С—точку пересечения прямой АВ с данной прямой, прихо-
приходим к задаче: найти два отрезка х и у (х— секущая, у — её внеш-
внешняя часть), зная их разность т и произведение СА-СВ. Согласно
п. 155, построение 8, задача всегда возможна и имеет одно решение.
Если данные точки А к В лежат по разные стороны от данной
прямой (черт. 418), то задача сводится к построению двух отрезков
х и у по их сумме т и произведению СА-СВ (п. 155, построение 7).
Задача возможна, если СА-СВ^[—
Если
то за-
дача имеет два решения, так как каждый из отрезков х и у можно
390
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗЛД\Ч
отложить в ту или другую сторону от точки пересечения прямой ЛВ
с данной прямой.
Наименьшая возможная длина хорды есть т = 2 ]^СА ¦ СВ.
177. Пусть через точку А требуется провести окружность, имею-
имеющую с окружностями Cj и С2 общую радикальную ось — прямую D
(черт. 419). '
Проводим через А произвольную окружность С, пересекающую
одну из данных окружностей, например С,, в двух точках М и N.
Точка пересечения Р прямых D
и ММ есть радикальный центр
окружностей С,, С и искомой
окружности С. Отсюда следует,
что прямая АР есть радикальная
ось окружностей С и -С, и,
следовательно, искомая окруж-
окружность С проходит через вторую
точку пересечения В прямой АР
с окружностью С. Центр иско-
искомой окружности лежит в пере-
пересечении перпендикуляра к от-
отрезку АВ, восставленного в его
середине, с линией центров дан-
данных окружностей.
Построение упрощается, если окружности С, и С2 пересекаются
или касаются. В этом случае искомая окружность проходит через их
точки пересечения или касается их в их общей точке.
УПРАЖНЕНИЯ К ГЛАВЕ VII (стр. 175).
178. Чтобы равными между собой правильными многоугольниками
можно было вымостить плоскость, необходимо, чтобы угол этих мно-
многоугольников содержался целое число раз в Ad (для того, чтобы
около вершины поместилось несколько многоугольников без перекры-
перекрытий). Это условие выполнено для правильных треугольника, четырёх-
четырёхугольника и шестиугольника, не выполнено для правильного пятиуголь-
I 6 Л
ника ( его угол равен — d) и для правильных многоугольников с числом
/ 4 \
сторон, ббльшим шести ( их углы больше „ d и меньше Id . Не-
V 6 I
посредственно очевидно, что правильными треугольниками, квадратами
и правильными шестиугольниками вымостить плоскость можно.
ГУ
179. Угол правильного (выпуклого) пятиугольника равен — d, т. е.
о
прямому углу, сложенному с половиной центрального угла, соответст-
соответствующего стороне правильного (выпуклого) десятиугольника. Это заме-
замечание даёт возможность построить угол правильного пятиугольника,
а значит и самый пятиугольник.
КНИГА ТРЕТЬЯ. ГЛАВА Vtl
391
180. Если диагонали АС и BD правильного пятиугольника ABCDE
пересекаются в точке F (черт. 420), то треугольник BCF—равно-
BCF—равнобедренный в силу равенства углов при вершинах В и С, откуда
BF=CF. Треугольники ABC и CFB подобны (по равенству углов),
так что AC:BC=BC:FC или BC2 = AC-FC. Далее треугольник ABF
также равнобедренный в силу равенства углов при вершинах В и F
(первый измеряется половиной дуги AED, второй — полусуммой дуг
АВ и CD), так что BC=AB = AF. Заменяя в предыдущем равен-
равенстве ВС через АР, находим AF2 = AC-FC.
181. Так как стороны с10 и cl0' выпуклого и звездчатого пра-
правильных десятиугольников, вписанных в окружность радиуса R, удов-
А
Черт. 421.
летворяют соотношениям с10'— cl0 = R, cl0-cw' =R2 (п. 169), то
+ с10" = (с10' - cj + 2с10.с10' = Я« + 2Я* =
. Но
есть сторона равностороннего треугольника, вписанного в окружность
радиуса R.
182. Стороны с10 и с1П' выпуклого и звездчатого правильных
десятиугольников, вписанных в окружность радиуса R, соответственно
^~ 1)и с,/= 1 tf (j/~5 _j_ J) (пп. 168—169);
равны cw = ^R{V5~ 1)и с,/= 1
для выпуклого и звездчатого пятиугольников имеем съ =
(п. 170). Отсюда
- К 5) = ^ и cl0'2 +
— 2], 5 и сь' = 1
183. Так как угол ВАС (черт. 421) дополняет угол правильного
2
шестиугольника до 2rf, то он равен — d. Следовательно, треуголь-
о
ник ABC и пять треугольников, ему аналогичных, — правильные. Та-
Таким образом, в построенном двенадцатиугольнике все стороны между
392
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
собой равны и все углы между собой равны (каждый равен сумме
прямого угла и угла равностороннего треугольника). Следовательно,
построенный двенадцатиугольник —правильный.
184. В силу п. 180 имеем с,2 = 2/?2 ~2R \ #2 _ — с2. Точно
так же в силу п. 181 имеем с,2 = /?(/? -\- —с)+/?(/? — — с) —
\ 1 I V *• )
— 2R у R2 -г с2- Так как оба выражения для с^ совпадают, то
совпадают и значения сх, получающиеся тем и другим путём.
П 1 СП
185. По формуле п. 179а (т= 18,25) имеем /? = ——— м —
18,2отг
= 6,279 м. ¦
186. Если Oj — центр второй окружности, то /_АО^С = 2/_АОС
(черт. 422). Дуге АВ соответствует вдвое больший радиус, чем ду-
дуге АС, но вдвое меньший центральный угол. Длины обеих дуг равны
в силу формулы п. 179 а.
б
Черт. 422.
Черт. 423.
187. Пусть окружности Ot и Ог касаются внутренним образом
окружности Os в точках А и В (черт. 423), и пусть С—точка пе-
пересечения окружностей О1 и О2, ближайшая к окружности О3'). Так
как по условию O2C-\-OtA = OaA и ()?-{-O2B = OSB, то О2С=
OOO ф
у 2t ?{2 S 2
= О3О^; OjC=OsO2 и фигУРа О^СО2ОЙ есть параллелограм. Всем
трём дугам АС, ВС, АВ соответствуют центральные углы, имеющие
одну и ту же величину, и из условия, что сумма двух радиусов рав-
равна третьему, следует, что сумма дуг АС и ВС равна дуге АВ.
188. По формулам пп. 166—167 имеем с' -\-cz=RV2-\rRV~?> —
= 1,414. ..R-\- 1,732... /?=3,14б.. .R, в то время как длина пи-
луокружности равна тг/?=3,1414. . .R.
]) Пользуясь условием, что сумма радиусов окружностей Oj и С2 рав-
равна радиусу окружности О3, можно показать, что окружности О1 и О2 не-
необходимо имеют общую точку.
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
393
189. Если катеты прямоугольного треугольника равны 1,2R и
2,4/?, то его гипотенуза равна 1, 2 -R У 5 = 2,68328 . . .R, а его пе-
периметр— 6,28328.../?, в то время как длина окружности равна
2nR=^ 6,28318.../?.
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ (стр. 176).
190. Пусть АВ— искомая прямая (черт. 424), так что АВ=2А1В1.
Если ОР — перпендикуляр к АВ, то РАХ = АХА. Проведя прямую
А{М, параллельную ОР, получим на радиусе О А точку М, для кото-
которой 0М = МА. Так как угол МАЛА— прямой, то получаем такое
построение. Произвольный радиус ОА делим в точке М пополам, и
Черт. 424.
Черт. 425.
Черт. 426.
на отрезке AM, как на диаметре, строим окружность. Точка её пере-
пересечения с меньшей из данных окружностей и будет точкой At. Усло-
Условие возможности задачи ОА^2ОАу
191. Проведя прямую DK, парал-
параллельную ВС (черт. 425), найдем,
пользуясь теоремой п. 113 и равен-
равенством CE^BD, что DF:FE =
— КС: СЕ = КС: BD = АС:АВ.
192. Если R и R' — радиусы
данных окружностей, h — расстоя-
расстояние между прямыми АА' и ММ'
(черт.426), то Л/И2 = 2/?Л; Л7И'2 =
= 2R'h, откуда AM: А'М' = V~R : V~K. Если Р — точка пересече-
пересечения прямых AM и А'М', то AP:A'P=AM:A'M' = \rR\:V~R'. Отно-
Отношение расстояний точки Р от двух данных точек А и А' сохраняет
постоянное значение, и потому геометрическое место точек Р есть
окружность (п. 116).
193. Пусть в многоугольнике ABCDLM (черт. 427) вершина А
перемещается по прямой о, вершина В—по прямой ft,..., вершина L —
но прямой /, и требуется определить геометрическое место вершины
М\ пусть далее ¦Л0??0С„?H/.оУИ0 — одно из положений рассматриваемого
многоугольника, которое мы будем считать неизменным.
394
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Черт. 427.
Так как АВ и А0В0 по условию параллельны, то АиА:ВиВ=
= А0Х:В0Х, где X — точка пересечения прямых а и Л. Таким об-
образом, для всех положений стороны АВ отношение А0А:В0В сохра-
сохраняет постоянное значение. Тично так же сохраняет постоянное значение
и каждое из отношений ВйВ:СйС: .. . :
:KUK:LOL. Отсюда следует, что и от-
отношение A0A:L0L сохраняет по-
постоянное значение. Таким образом,
точка М есть точка пересечения
прямых AM и LM, соответственно
параллельных А0М0 и LQMV и прохо-
проходящих через такие точки прямых
аи/, что отношение AUA:LOL сохра-
сохраняет постоянное значение. В силу
упражнения 124 геометрическое ме-
место точек М есть прямая линия.
194. Под многоугольником, впи-
вписанным в данный многоугольник,
понимаем многоугольник, вершины которого лежат на соответственных
сторонах данного многоугольника или их продолжениях. Пусть а, ft,
с,..., k, /, in—стороны данного многоугольника. Выбрав на прямой
а произвольную точку Ао и проведя
через неё прямую, параллельную пер-
первой данной прямой, получим на пря-
прямой Ь точку Ви. Продолжая это
построение, получим многоугольник
А0В0.. .Мо, у которого все стороны
параллельны сторонам искомого мно-
многоугольника и все вершины, кроме
одной, скажем кроме Ми, лежат на
сторонах данного многоугольника (или
их продолжениях). При перемещении
вершин Ао, В„, С(),. ¦., Z-o соответ-
соответственно по прямым a, ft, с,. . . , / (с
сохранением направлений сторон) по-
последняя вершина Мо построенного
многоугольника описывает некоторую
прямую т' (упр. 193). Для отыскания
этой прямой повторяем предыдущее
построение, исходя и^ точки Ах прямой а, отличной от'Л0, и получаем
вместо точки Миточку Ж,. Прямая МУ)М1 н есть прямая in'.
Точка пересечения прямых /ли т' есть вершина М искомого много-
многоугольника. Зная вершину М, .легко построить весь искомый многоуголь-
многоугольник.
Задача имеет одно решение, если прямые т и т' пересекаются, бес-
бесчисленное множество решений (т. е. является неопределённой), если эти
прямые совпадают, и не имеет ни одного решения, если они параллельны.
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
395
195. Пусть через точку А' высоты ААй треугольника ABC (черт. 428)
проведена прямая DE, параллельная ВС, через точку В' высоты ВВ0—
прямая FG, параллельная АС, через точку С высоты СС0 — прямая
KL, параллельная А В. Получим ряд подобных треугольников ABC,
ADE, FDG, KLG. Обозначим через Do и D' основания высот тре-
треугольников ADE и FDG, выходящих из точки D, через Go и G' —-
основания высот треугольников FDG и KLG, выходящих из точки G.
Коэфициент подобия треугольников ABC и ADE будет равен
DP, ^AA'
BBU AA0
и FDG
A'An
A'A0
А4„
Коэфициеит подобия треугольников ABC
= 1 —¦
будет
B'BD
АА0
ABC и KLG
GG0 _ DD' ___ DD0 — D'D0 _ DD0
Наконец,
Bq BBq BBq BBo
коэфициент подобия треугольников
GG'
будет равен ——- =
GG0 - G'G0 GG0 C'C0
А'А0 В'В0 С'С0
СС0
AA0 BB0 cc0
Примечание. При решении задачи мы неявно предполагали, что
треугольник ABC—остроугольный и что точки А', В', С' лежат (как на
черт. 428) между точкой пересечения Н его высот и соответственно точ-
точками Ап, jB0) Со. Если бы эти условия не были соблюдены, предыдущие
выкладки потребовали бы некоторых видоизменений. Однако все вычисле-
вычисления и полученные результаты приобретают вполне общий характер, ес-
если отношениям отрезков и коэфициентам подобия приписать определён-
определённые знаки в соответствии с п. 190.
196. Пусть Av Вл, Cj — середины сторон данного треугольника
ABC (черт. 429). Треугольники ABC и АЛВХСХ гомотетичны и имеют
своим центром подобия точку пересечения
медиан Сданного треугольника (упр. 158).
Треугольник abc по построению гомоте-
гомотетичен треугольнику A1BiС,, так как Оа =
= 2ОА„ ОЬ=2ОВ1 и Ос = 2ОС1. Сле-
Следовательно (п. 144), и треугольники ABC
и abc гомотетичны, а потому прямые Аа,
ВЬ, Сс проходят через одну точку Р.
Центры подобия О, О, Р треугольников
ABC, А^В{СЛ и abc, взятых попарно, ле-
лежат на одной, прямой.
Прямая АА1 есть медиана треугольни-
треугольника АаО (так как аА1 = А1О), точка G — точка пересечения его медиан
(так как AG=2GA,). Отсюда следует, что OG=2GP. Итак, отре-
отрезок ОР проходит через точку G и делится в этой точке в отно-
отношении OG:GP= 2:1. где бы ни лежала точка О. Следовательно,
точки О и Р описывают гомотетические фигуры, имеющие G своим
центром подобия.
В
V> A,
а
Черт. 429.
396
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
197. Заметим прежде всего, что:
Если прямые AM и AN симметричны относительно биссектри-
биссектрисы AD угла ВАС (черт. 430), то расстояния от сторон угла лю-
любых двух точек М и N, взятых соответственно на этих прямых,
обратно пропорциональны друг другу. В самом деле, строя на пря-
прямой AN точку М\ симметричную с М относительно AD, и опус-
опуская из точек М, М' и N перпендикуляры на стороны угла, будем
иметь MP = M'Q'; MQ=MP'; М'Р':NR = AM':AN=M'Q':NS.
Отсюда MP:MQ=NS:NR.
Имеет место и следующее обратное предложение:
А
В
Р Р'
Черт. 431.
Если расстояния точек М и N от сторон угла ВАС обратно
пропорциональны друг другу и прямые AM и AN проходят обе внутри
или обе вне угла ВАС, то обе прямые симметричны относительно бис-
биссектрисы угла. Это следует из того, что геометрическое место точек N,
отношение расстояний которых от прямых- АС и АВ равно MP:MQ,
есть пара прямых, из которых одна проходит внутри угла ВАС и
одна—вне этого угла (п. 157).
Переходим к решению поставленной задачи. Пусть прямые АО
и АО' симметричны относительно биссектрисы угла А треугольни-
треугольника ABC (черт. 431), прямые ВО и ВО' — относительно биссектрисы
угла В. В таком случае имеем: OQ:OR=O'R':O'Q; OR:OP =
= O'P':O'R'. Перемножая почленно, получим OQ:OP = O'P':O'Q'.
Так как прямые СО и СО' лежат обе внутри или обе вне
угла АСВ (где бы ни лежала точка О), то эти прямые симмет-
симметричны относительно биссектрисы угла С. Итак, прямые, симметричные
с прямыми АО, ВО, СО относительно биссектрис соответствующих
углов треугольника, проходят через одну точку (если только какие-
либо две из этих прямых пересекаются).
Пусть теперь через вершины треугольника ABC проведены парал-
параллельные прямые, пересекающие описанную окружность вторично в точ-
точках А', В", С (черт. 432). Проведём прямую АО', симметричную с
АА' относительно биссектрисы угла А, и пусть она вторично пере-
пересекает окружность в точке О'. Так как при этом /_ВАА' = /_САО',
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
397
то дуги А'В и О'С равны; так как прямая А А' параллельна ВВ', то
дуги А'В и АВ' равны; отсюда следует, что дуги АВ и О'С равны.
Следовательно, /_ ABB = ^/ СВО', так что прямые ВВ' и ВО' сим-
симметричны относительно биссектрисы угла В. Наконец, так как прямая
СС параллельна АА', то дуги А'С и АС равны. Следовательно, и дуги
В А'С и О'С А равны, так что
углы ВСС и АСО' дополняют
друг друга до двух прямых. От-
Отсюда следует, что прямые СС
и" СО' симметричны относительно
биссектрисы угла С. Итак, если
прямые АА', ВВ, СС параллель-
параллельны, то прямые, симметричные с
ними относительно биссектрис
углов треугольника ABC, прохо-
проходят через одну точку О, лежа-
лежащую на окружности, описанной
около треугольника.
Если за точку О, о которой го-
говорилось выше, принять центр опи-
описанной окружности, то прямая АО' будет совпадать с высотой АН
треугольника (черт. 136). Действительно, /_ВАА'= 90° ~/_ВА'А =
= 90° — /_ ВСА= /_САН, и прямые А А' и АН симметричны отно-
относительно биссектрисы угла А. Отсюда вытекает, что высота АН тре-
треугольника и две другие его высоты проходя^ через одну точку.
С
Черт. 432.
Черт. 434.
Примечание. Точки О и О', получающиеся одна из другой указанным'
построением, называются иногда изогонально-сопряжёнными относительно
треугольника ABC.
198. Пусть Е, F, G—точки касания прямых АВ, ВС и MN с
окружностью (черт. 433). Так как /_AOE=/FOC, /_Е0М =
= /_M0G, /_GON=/_NOF, то /_ АОЕ-\-/_ Е0М+/_ GON=
= 90°. Отсюда /_ А0М= 90° — /_ GON= 90° — /_ NOF= /_ CNO.
Кроме того, /_OAM = /_NCO, так что треугольники АОМ и CNO
39S
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
подобны. Из подобия этих треугольников находим AM: CO = AO:CN
и AM-CN = AO-CO.
199. Пусть ВВ' — диаметр икружности, проходящий через А
(черт. 434; точка А могла бы лежать и внутри окружности и на дан-
данной окружности), /V и N' — точки пересечения прямых ВМ и ВМ с
прямой, проходящей через А и перпендикулярной к АВ. Имеем
= 90° — /_АВМ =
— /_MNA. Следовательно, треугольники AMN и AN'M подобны,
откуда AN • AN'= AM • AM' есть степень точки А относительно данной
окружности.
200. Пусть О и О' — центры данных окружностей (черт. 435),
АА' и ВВ' — их внешние общие касательные, СС и DD' — их внут-
внутренние общие касательные, Р, Q, R, S — точки пересечения внутрен-
внутренних общих касательных с внешними.
При этом углы АОС и А'РС равны, так как их стороны соот-
соответственно перпендикулярны, а потому их половины ^/_АОР и/ А'РО'
также равны. Подобные прямоугольные треугольники АОР и А'РО'
дают РА-РА' = ОА-О'А'. Аналогично найдём, что и SA-SA' =
= ОА-ОЛ'.
Из равенств РА ¦ РА' = SA• SA' и РА-\- РА'= SA + SA' следует,
что либо PA=SA, либо PA = SA'. Но так как очевидно РАфЗА,
то PA=SA', откуда в свою очередь следует, что PS и АА' имеют
общую середину. Наконец PS = РА' — SA' = РА' — РА = PC —
— РС= СС.
201. 1°. Пусть М—середина стороны ВС (черт. 436). Так как
МА = МС и прямая ОМ перпендикулярна к ВС, то МА2 -\- МО2 =
= МС2-\~МО~ = ОС2, и из треугольника ОМА находим, обозначая
через Ог середину стороны О А, что О,УИ2 = — I МАъ-\-М0°) —
ОАг = —ОС2—OOj2 (п. 128). Следовательно, геометрическое
место точек М есть окружность с центром Ot; радиус О,УИ этой
окружности определяется только что написанным равенством. *
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ 399
2°. Так как точка О, есть середина отрезка О А, то проекция
М точки О на- сторону ВС и проекция D точки А на ту же сторо-
сторону ВС равноудалены от точки Oj, а потому iеометрическое место
точек D есть та же самая окружность.
202. Задача тождественна по содержанию с упражнением 170.
203. Пусть BE и CF—медианы искомого треугольника ABC,
G — точка их пересечения (черт. 437).
Возможны два случая:
1°. Даны медианы BE и CF и вы-
высота, выходящая из вершины А. Вы-
Высота GK треугольника BGC, выходящая
из вершины О, равна, как легко ви-
видеть, одной трети данной высоты. Этот
треугольник легко построить по дв>м „' тг
сторонам BG и CG и высоте, выходя- Че 437
щей из их общей вершины. Построив
треугольник BGC, откладываем G?=— BG, GF=— CG и проводим
СЕ и BF.
Примечание. Прямые BF и СЕ не могут оказаться параллельными.
Действительно, проведя через точку С прямую, параллельную BF, и обо-
обозначив через М точку её пересечения с BE, будем иметь GM:GB=GC:GF
или GM = 2BG, но GE=— BG; следовательно, точка ? необходимо лежит
между G и М, прямые BF и СЕ пересекаются и притом ,с той Стороны
от ВС, где лежит точка G. Таким оОразом, для возможности построения
треугольника ABC достаточно, чтобы было возможно построить треуголь-
треугольник BGC.
2°. Даны медианы BE н CF и высота ВН, выходящая из верши-
вершины В. Строим прямоугольный треугольник ВЕН по катету и гипоте-
гипотенузе и из точки G, делящей BE в отношении 2:1, как из центра,
2
описываем окружность радиусом — CF. Пересечение её с прямой
О
ЕЙ определяет вершину С. Третья вершина А искомого треуголь-
треугольника получится, если отложить отрезок ЕА, равный ЕС.
Наибольшее возможное число решений в каждом из обоих случа-
чаев равно двум.
204. Пусть ABC — искомый треугольник (черт. 438) и AD—его
высота. Отложим DE=BC и соединим точку Е с вершиной С. Пусть
F — точка пересечения прямой СЕ с касательной к данной окружно-
окружности в точке .4. Из подобия треугольников EDC и EAF следует, что
AF=±-AE.
Отсюда вытекает такое построение. На диаметре окружности от-
откладываем отрезок \Е, равный данной сумме т основания и высоты,
и на касательной в точке А—отрезок AF=-~- AE. Точки пересе-
400
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
чения прямой EF с окружностью определяют возможные положения
вершины С.
Аналогичное построение применимо и в том случае, когда дана
разность высоты и основания m=AD — ВС (строим ЛЯ' = /л; AF' =
Условие возможности задачи состоит в том, чтобы расстояние ОР
от центра до прямой EF не превосходило радиуса. Но ОР:ОЕ =
= AF:EF= 1 -.У 5, и условие OP^R принимает вид ОЕ«S
^/?V^~5, или m = AE^R(V~5-\-l). Если 2tf<> <tf(l-|-/~5),
то обе точки пересечения прямой f/7 с окружностью дают треуголь-
• Черт. 439.
ники, для которых отрезок АЕ = гп есть сумма основания и высоты.
Если же 0<^m<^2R, точка Е займёт положение Е', точка F —
положение F'. При этом одна из точек пересечения прямой E'F' с
данной окружностью даёт треугольник ABC, в котором разность
AD — ВС равна АЕ'^т; другая точка пересечения даёт треуголь-
треугольник АВ'С, в котором сумма AD'-\-BC равна АЕ' = т.
Наконец, если дана разность основания и высоты, т. е. п = ВС— AD,
то на продолжении высоты AD треугольника за его вершину откла-
откладываем отрезок АЕ = п (черт. 439) и на касательной в точке А —
отрезок AF=— AE. Условие возможности задачи OP^R приводит
в этом случае к неравенству п = АЕ =< R {У 5 — 1).
205. Пусть а ^> Ь — основания, с и d — боковые стороны, ей/ —
диагонали трапеции ABCD (черт. 440), хну — проекции боковых
сторон AD и ВС на основание. Из треугольников АСВ и ADB имеем
е* = a -f- d2 ~ 2ay и
A)
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
401
Складывая эти равенства, получим е2 -\- р = 2о2 -\- с2 -\- <Р — 2ах —
—lay, откуда, замечая, что х\-у = а—Ъ, имеем: •
е2 _f- Р = с2
B)
Далее из треугольника ACD находим е2= Ь2-\-с2 -\-2bx. Умножая
это равенство почленно на а, а равенство A) — на b и складывая,
получим:
ae2-\-bp = ab2-\-a2b-\-ac2-\-bc2. C)
Уравнения B) и C) определяют е2 и /2. ер
Ь
Черт. 440.
Черт. 441.
206. Пусть CD — искомая хорда (черт. 441) и Е — точка окруж-
окружности, в которой пересекаются хорды АС и BD. Построим в точке
D касательную к окружности, и пусть она пересекает прямую АВ
в точке Р. При этом /_BDP= /_ACD — /_CAB. Треугольники
ВОР и ВАЕ подобны, и BP-BA = BE-BD есть степень точки В относи-
относительно окружности. Тем самым определяется положение точки Р на
прямой АВ. Проведя из Р касательную
к окружности, найдём точку D.
Наибольшее возможное число реше-
решений — два.
207. Пусть Е — основание перпен-
перпендикуляра из точки Р на АВ (черт. 442).
Из подобия треугольников ABC и АРЕ
имеем АВ• АЕ ^ АР • АС; из подобия
треугольников ADB и РЕВ находим
АВ • BE = ВР ¦ BD. Складывая, получим
АВ (AE-\-BE)=AB2=AP.AC-\-BP-BD.
Черт. 442.
208. Пусть О — центр какой-либо окружности, проходящей через
точки А и В, Т и Т' — точки прикосновения касательных, проведён-
проведённых из точки С, И — середина отрезка АВ, М — середина отрезка
ТТ',Р — точка пересечения АВ и ТТ (черт. 443). Из прямоугольного
треугольника ОСТ имеем СМ-СО = СТ2. Но СМ-СО = СН-СР в си-
силу подобия треугольников СОН и СРМ, а СТ2 = СА-СВ. Следова-
Следовательно, СР-СН=СА-СВ. Отсюда вытекает, что положение точки Р
на прямой АВ не зависит от выбора окружности. Так как угол СМР —
26 Элементарная геометрия
402
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
прямой, то геометрическое место точек М есть окружность, имеющая
отрезок СР своим диаметром.
209. Пусть О1,О2,Оа— центры искомых окружностей; /?,, /?2,
Rs— их радиусы. Если окружности ортогональны, то /?22 -f- /?32 =
ОО + 2W *\R* = Ofi2*. Отсюда /?, =
и аналогичные выражения полу-
получаются для /?2 и Rs.
Задача возможна, если треугольник OjO2O3 — остроугольный, так
как для действительности всех трёх радиусов необходимо и достаточ-
достаточно, чтобы сумма квадратов любых двух его сторон была больше ¦
квадрата третьей стороны (п. 126, следствие).
М'
Черт. 444.
210. Настоящая задача представляет собой обобщение задачи 121а,
и предлагаемое решение есть непосредственное обобщение решения,
данного для этой последней задачи.
Пусть А и В — данные точки (черт. 444), D — данная прямая,
С — данная точка, делящая искомый отрезок /К в данном отношении,
1У[ — искомая точка. Строим на продолжении отрезка АС за точку С
«такую точку /?, чтобы отрезок RA делился точкой С в данном отно-
отношении. Так как треугольники АСК и RCI подобны (в силу равенства
углов при С и пропорциональности сторон AC:RC= CK: CI), то прямая
JR параллельна АК. Следовательно, угол BIR дополняет угол АМВ
до 180° и имеет, очевидно, то же направление. Точка / лежит на
дуге, имеющей своими концами точки В и R и вмещающей угол, по-
пополнительный тому углу, который вмещает данная дуга АМВ1).
Нторая точка пересечения Г окружности BJR с примой D опре-
определяет второе решение — точку М.
!; Так .как углы АМВ и B1R имеют одно и то же направление, то из
двух дуг, имеющих своими концами точки В и R и вмещающих данный
угол, приходится выбрать только одну.
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
403
и в четырёхугольнике
А
Черт. 445.
211. В силу подобия треугольников АВР и CBR (черт. 445)
имеем /_ABP=/_CBR, или /_ABC=Z.PBR, и BP:BR = BA:BC.
Отсюда следует, что треугольники ABC и PBR подобны. Точно так
же докажем, что треугольники ABC и QRC подобны. Следовательно,
и треугольники PBR и QRC подобны. Но их соответствен-
соответственные стороны BR и RC равны, так что и треугольники равны.
Отсюда PA=BP=RQ; AQ=QC=PR,
APRQ противоположные стороны равны.
212. Пусть три прямые АВ, ВС, CD (черт.
446) фигуры ABCD, которая изменяется,
оставаясь подобной самой себе, проходят
соответственно через неподвижные точки М,
N, Р.
1°. Докажем, что и произвольная четвёр-
четвёртая прямая AD той же фигуры проходит через
неподвижную точку Q.
Пусть ABCD и AjBjC,/), — два положе-
положения изменяемой фигуры. Найдём точку О фигуры ABCD, которая
совпадает с соответственной ей точкой фигуры AxB1C1Dl (п. 150).
Так как угол АВО должен равняться углу \В^О (как соответ-
соответственные углы двух подобных фигур), то точка О должна лежать на
окружности МВВЛ. Далее /_ АВС= /_ А^В^СХ и значит точки M,B,BX,N
лежат на одной окружности. Следователь-
Следовательно, точка О лежит на окружности MBN.
Таким же образом докажем,^ что точка О
лежит и на окружности NCP. Итак, отлич-
отличная от N точка пересечения О окружностей
MBN и NCP есть точка фигуры ABCD,
совпадающая с соответственной ей точкой
фигуры A,BJC1D1 (п. 150, примечание),
какое бы положение эта последняя ни зани-
занимала, и потому точка О остаётся на месте
при изменении фигуры ABCD.
Далее, в силу равенства углов CDO
и C^D^O четыре точки О, Р, D, D1 ле-
лежат на одной окружности, а в силу ра-
равенства углов CDA и CiD1A1 та же окруж-
В
Черт. 446.
у i11
ность проходит и через точку пересечения Q прямых AD и ,,
Следовательно, точка Q определяется как вторая точка пересечения
окружности OPD с прямой AD. Таким образом, точка Q не зависит
от положения фигуры AJifi.xDx, так что прямая AD действительно
проходит при изменении фигуры ABCD через неподвижную точку.
2°. Пусть теперь Е — произвольная точка фигуры ABCD. При изме-
изменении последней отношения отрезков BF-.FC и OF:FE, где F—точка
пересечения прямых ВС и ОЕ, не изменяются. Так как прямая ВС
проходит при изменении фигуры ABCDE через общую точку N двух
окружностей 0MN и ONP и точка F делит отрезок ВС этой прямой
26*
404
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗА ^А Ч
С'
в постоянном отношении, то точка F описывает при изменении фи-
фигуры ABCDE окружность, также проходящую через точки О и N
(упр. 128). Так как отрезок ОЕ делится точкой F в постоянном от-
отношении, то точка Е описывает фигуру, гомотетичную той, которую
описывает точка F (центром гомотетии служит точка О). Итак, точка Е
(т. е. произвольная точка изменяемой фигуры) описывает окружность
(проходящую через О).
213. Пусть требуется построить четырёхугольник ABCD, подоб-
подобный данному четырёхугольнику abed, так, чтобы его стороны АВ, ВС,
CD, DA проходили соответствен-
соответственно через данные точки М, N,
Р, Q.
Первое решение. По-
Построим четырёхугольник AXBXCXDX,
подобный abed, так, чтобы три
его стороны A1BV B1CV CXDX про-
проходили через данные точки Л1,
N, Р. Четвёртая сторона D1Al
не будет, вообще говоря, про-
проходить через точку Q. Если че-
четырёхугольник A1BJCiD1 будет
изменяться подобно самому себе,
причём три его стороны АХВХ,
BXCV CXD, будут всё время про-
проходить через точки М, N, Р,
то четвёртая его сторона DXAX будет вращаться около некоторой
точки Q', которую мы умеем построить (задача 212). Прямая QQ
определяет положение стороны DA и позволяет закончить построение.
Задача будет неопределённой, если точки Q и Q' совпадают.
В этом случае обе диагонали изменяемого четырёхугольника (как и
любая прямая изменяемой фигуры) будут вращаться около неподвиж-
неподвижных точек. Так как угол между диагоналями остаётся постоянным, то
точка их пересечения описывает окружность.
Второе решение. Задачу можно также решить аналогично
задаче 122. Вершина А лежит на дуге, имеющей своими концами
точки Q и М и вмещающей угол, равный углу dab (черт. 447), и
аналогичное имеет место для вершины С. Диагональ АС пересекает вто-
вторично окружность MAQ в такой точке Е, что j/_EAQ^=/^cud. Для
построения точки Е достаточно выбрать на дуге QAM произвольную
точку А' и построить угол QA'E, равный углу dac. Аналогично стро-
строится точка пересечения F прямой АС с окружностью NCP. Прямая EF
определяет положение вершин А и С.
Задача будет неопределённой, если точка F совпадает с Е. При
этом направление диагонали АС будет произвольным. Повторяя в этом
случае те же рассуждения для диагонали BD, убедимся, что и она
будет проходить через некоторую определённую точку. Обе диагонали
будут, таким образом, вращаться около неподвижных точек. Так как
Черт. 447.
ЗАДАЧИ К ТРЕТЬЕЙ КНИГЕ
405
угол между диагоналями имеет постоянную величину, то геометри-
геометрическое место точек пересечения диагоналей есть окружность.
214. Пусть фигура ABC, оставаясь подобной самой себе, изме-
изменяется так, что точки А, В, С описывают соответственно прямые
QR, RP, PQ (черт. 448),
Пусть ABC и А'В'С—два положения изменяемой фигуры. Найдём
точку О фигуры ABC, которая совпадает с соответственной ей точ-
точкой фигуры А'В С (п. 150, примечание). При этом треугольники ОАВ
и О А'В' должны быть подобными, откуда //_АОВ=/_А'ОВ', и,
следовательно, /_АОА''= /_ВОВ и, кроме того, ОА:ОА' —ОВ:ОВ'.
Из двух последних равенств сле-
следует, что точку О можно также
рассматривать как точку, соответ-
соответствующую самой себе в двух по-
подобных фигурах, имеющих одина-
одинаковое направление вращения, в
которых точке А соответствует точ-
точка Б и точке А' — точка В'. Сле-
Черт. 448.
довательно, /_ОАА'' =/_ ОВВ',
и точка О должна лежать на ок-
окружности, описанной около тре-
треугольника ABR (А, В — соответ-
соответственные точки, /? — точка пересе-
пересечения соответственных прямых АА'
и ВВ').
Точно так же докажем, что
точка О должна лежать на каж-
каждой из окружностей ВСР и CAQ *). Отсюда следует, что положение
• точки О на плоскости не зависит от выбора треугольника А'В'С.
Точка О сохраняет своё положение на плоскости при изменении данного
треугольника.
Пусть теперь М — какая-либо точка фигуры ABC, и М — соответ-
соответственная точка фигуры А'В'С. Так как О — точка первой фигуры, сов-
совпадающая со своей соответственной, то /_ ОАА'^/_ОММ'. При
изменении фигуры А'ВС'М' угол О А А' не изменяется (точка А' пе-
перемещается по прямой QR). Поэтому и угол ОММ' не изменяется,
т. е. точка М описывает прямую.
215. Пусть А и А'—две какие-либо соответственные точки дан-
данных фигур, Р — точка, совпадающая со своей соответственной
(черт. 449). Пусть точка -М первой фигуры обладает тем свойством,
что прямая, соединяющая её с соответственной точкой М' второй
фигуры, проходит через данную точку О. Так как в силу равенств
РА:РА'=РМ:РМ' и /_АРА' =/_МРМ треугольники РА А' и
РММ' подобны (п. 150), то угол РММ' равен углу РАА', и отре-
1) Легко видеть, что окружности ABR, ВСР и CAQ проходят через
одну точку (см. решение раздела 1 задачи 344).
406
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
зок РО виден из точки М под углом, равным углу РАА' или углу,
ему пополнительному. Геометрическое место точек М есть окружность,
проходящая через точки Р и О.
При этом мы получаем одну такую окружность (а не две симмет-
симметричных относительно прямой РО), если примем во внимание, что
утлы РАА' и РММ должны быть не только равны, но и одинаково
направлены.
216. Пусть АХ и BY— данные прямые (черт. 450). Примем
точки А и В за соответственные точки, АХ и BY — за направления
М
Y'
Черт. 449.
Черт. 450.
соответственных прямых двух подобных фигур, имеющих одинаковое
направление вращения, и данное отношение т:п — за их коэфициент
подобия. Точка Р одной из двух фигур, совпадающая со своей соот-
соответственной в другой фигуре, вполне определяется следующими усло-
условиями: угол АРВ должен равняться углу между АХ и BY и иметь
то же направление, а отношение расстояний от точки Р до точек А
и В должно равняться данному отношению: РА:РВ=т:п. Искомые
точки М и N также будут соответственными точками обеих фигур
в силу равенства AM:BN = m:n. Следовательно (см. решение
задачи 215), углы РАВ и PMN равны и одинаково направлены. Так
как прямая MN проходит, по условию, через данную точку О, то
отсюда следует, что точка М лежит на дуге, имеющей своими кон-
концами точки Р и О и вмещающей угол, равный углу РАВ и одина-
одинаково с ним направленный (или же на тОй дуге, которая дополняет её
до полной окружности).
Мы получим дальнейшие решения, предполагая, что направлению АХ
в первой фигуре соответствует во второй фигуре направление BY',
противоположное BY.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА II. 407
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ.
УПРАЖНЕНИЯ К ГЛАВЕ I (стр. 181).
217. Если точки А и В делят гармонически точки С и Д то
(п. 189) AC: AD = — BC:BD. В силу п. 187 имеем: ВС=АС—АВ;
BD = AD— АВ, так что АС : AD = — (АС — АВ): (AD— АВ). Разре-
2AC-AD
шая это уравнение относительно АВ, найдём АВ = . — , откуда и
получается искомое соотношение.
218. Для того случая, когда точка D лежит между В и С, можно
написать, выбирая за положительное направление на прямой ВС на-
направление от Б к С, равенство (п. 127) АВ1 ¦ DC-\-АО - BD —
— AD2-BC^BC-DC-BD, или в более симметричной форме:
ABZ-CD-^AC-DB-^ADV-BC-^BC-CD-DB^O. A)
Если бы точка С лежала между В и D (или точка В между С и D),
то в полученном равенстве пришлось бы переставить буквы С и D
(или В и D). Легко проверить, что от такой перестановки равен-
равенство A) не изменяется.
Если точка А лежит с точками В, С, D на одной прямой, то ра-
равенство A) принимает вид: AB^-iAD— АС) -\-АО-(АВ~ AD) -f-
-+-AD2-(AC—AB)-\-(AD—AC)(AB—AD){AC—AB)=0 и выпол-
выполняется тождественно. Общая формулировка такова: если В, С, D —
три точки одной прямой и А — произвольная точка, то имеет
место по величине и по знаку соотношение A).
219. Пусть Р — середина отрезка АВ (обозначения п. 116)
и С, D — точки пересечения прямой АВ с одной из рассматриваемых
окружностей. Так как точки С и D делит, по самому своему опре-
определению, отрезок АВ гармонически, то (в силу теоремы п. 189)
PC-PD = PA'1. Следовательно, точка Р имеет одну и ту же степень РД2
относительно всех рассматриваемых окружностей. Поэтому радикаль-
радикальной осью всех этих окружностей будет перпендикуляр, восставленный
в середине отрезка АВ. Из равенств PC-PD=^PA2^PB2 следует,
что А и В—предельные точки (упр. 152).
Наибольшее и наименьшее значение отношения расстояний точки М
от точек А и В получается для точек касания одной из рассматрива-
рассматриваемых окружностей с данной прямой или окружностью.
219а. Пусть АВ и А'В' —два данных отрезка (лежащих по смыслу
задачи на одной прямой), Р и Q — искомые точки (черт. 451).
Окружности, имеющие своими диаметрами отрезки АВ и А'В", обе орто-
ортогональны к любой окружности, проходящей через точки Р и Q
{п. 189). Следовательно, окружности, имеющие отрезки АВ и А'В'
.своими диаметрами, не имеют общих точек (см. решение упр. 152),
и потому отрезки АВ и А'В1 расположены так, что либо один из них
целиком лежит внутри другого, либо каждый из них целиком лежит
вне другого. Только для таких двух отрезков задача возможна.
408
РЕШРНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Обратно, если даны два отрезка АВ и А'В1, расположенные на
одной прямой, как только что было указано, го окружности, имею-
имеющие эти отрезки своими диаметра-
диаметрами, не имеют общих точек. Любая
окружность, ортогональная к ним
обеим, определяет на данной прямой
одну и ту же пару точек Р и Q,
дающих единственное решение поста-
поставленной задачи.
Примечание. Найдём отноше-
отношение, в котором точки Р и Q делят
один из данных отрезков, скажем АВ.
С этой целью рассмотрим точку пере-
пересечения Н прямой АВ с радикальной
осью окружностей, имеющих отрезки
Черт. 451. АВ и А'В' своими диаметрами Мы
имеем НА-НВ = НА'-НВ', откуда
НА:НА' = НВ':НВ = (НВ' — НА):ШВ — НА') = АВ':А'В и НА':НВ —
= НА-.НВ1— (HA'-HA)UHB — ИВ') = АА':В'В. Следовательно,
= (НА:НА')-(НА':НВ) = (АА'-АВ'у.(А'ВВ'В).
0)
С другой стороны, точки А и В делят отрезок PQ гармонически, и точка Н
есть середина отрезка PQ. Следовательно (ср. п. 189), РА:РВ=:
= — QA:QB = PQ:(PB+QB) = 2PH:2HB и РА:РВ = — QA:QB = (PA +
-\-QAy.PQ = 2HA:2PH, откуда (PA:PBf- = HA:HB. Подставляя сюда значе-
значение A) отношения НА:НВ, получим окончательно (РА:РВJ = (QA:QBp =
= (АА'-АВ'у.(ВА'-ВВ').
220. Пусть О и О' — центры данных окружностей, .S и S' — их
центры подобия. Так как точки S и S' делят отрезок 00' внутрен-
внутренним и внешним образом в отношении /?:/?' радиусов данных окруж-
окружностей, то окружность имеющая отрезок SS' своим диаметром, есть (со-
(согласно п. 116) геометрическое место точек Му для которых МО:МО' =
= R:R', откуда (МО2 — /?2): (МО'2 — /?'2) = #2:/?'2. Следовательно, та
же окружность есть геометрическое место точек, для которых отно-
отношение степеней относительно окружностей О к О' равно R^'.R'", и
потому имеет, в силу упражнения 149, с окружностями О и О' общую
радикальную ось.
221. Теоремам, предложенным в упражнениях 130 и 131, можно
придать следующие, более общие формулировки:
Если АВ и CD — два параллельных отрезка и через точку Е,
селящую отрезок АС в отношении АЕ:ЕС=т:п (по величине и
знаку), провести прямую, параллельную АВ, то отрезок EF этой
прямой, заключённый между прямыми АС и BD, будет опреде-
- гг m-CD-\-n-AB
ляться (по величине и знаку) формулой tr = .
lit —I— ft
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА |[
409
Если из вершин треугольника и точки пересечения медиан
опустить перпендикуляры на произвольную прямую, лежащую
в плоскости треугольника, то последний из этих перпендикуляров
равен (по величине и знаку) среднему арифметическому трёх первых.
(При этом в отношении знаков следует придерживаться указаний
пп. 18» и 190.)
Доказательства, приведённые в решениях упражнений 130 и 131,
полностью сохраняют силу, если рассматривать все упоминаемые там
отрезки по величине и знаку.
222. Имеем Аа2-1ГСс2=~ (Aa-\-Ccf -\- ^{Aa — Ccf; 2Bb-Dd=
= L(Bb -f- DdJ —~ (Bb — DdJ. Ho Aa -f Cc = Bb -f Dd= 2Ee,
где Е — точка пересечения диагоналей АС и
BD (черт. 452), e—основание перпендикуля-
перпендикуляра из точки Е на данную прямую (упр. 130).
Если из точек С и В опустить перпендикуля-
перпендикуляры СК и BL соответственно на прямые
Аа и Dd, то треугольники АСК и BDL
будут равны, откуда CK = DL. Следо-
Следовательно, имеем: Аа" -|- Cc2 —2Bb-Dd =
2 *
-f ^DL2 =
= \7AC2 = AB2.
о bed
Черт. 452.
Предложение сохраняет силу вместе с
приведённым доказательством, как бы ни
была расположена данная прямая на плоскости, если рассматривать рас-
расстояния Аа, Bb, Cc, Dd по абсолютной величине и знаку и исполь-
использовать упр. 221.
УПРАЖНЕНИЯ 1С ГЛАВЕ II (стр. 188).
223. Пусть точки а, Ь, с лежат соответственно на продолжениях
сторон ВС. СА, АВ треугольника ABC (черт. 453) так, что выпол-
выполняется условие
liC"bA"cB~ ' * '
Построим окружности (a), (h), (с), имеющие своими центрами точки
а, Ь, с и ортогональные к описанной окружности (это возможно, так
как точки а, Ь, с — внешние). Точки пересечения а' и а" окружности
(а) с прямой ВС делят отрезок ВС гармонически (п. 189, следствие),
а'В а" В ас'—аВ
так что имеет место соотношение v>~~"^ > или
аС-
¦ аи'
аВ — аа"
. Отсюда, принимая во внимание, что аа'= — аа", полу-
— аС—иа"'
чим (сравнить преобразования в начале п. 189), беря один раз отно-
410
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
шение сумм, другой раз — отношение разностей членов двух последних
отношений, —а'В:а'С=а"В:а"С = аа':аС=аВ:аа'. Отсюда путём
возведения в квадрат и перемножения находим a'B1:a'C1=a"Bi:a"C2 =
= аВ:аС. Из последнего уравнения следует, что окружность
(а) есть геометрическое место точек, расстояния которых от точек
В и С относятся как j/ аВ: |/ аС. Точно так же окружность (Ь)
есть геометрнческое ме-
место точек расстояния
которых от точек С
и А относятся как
YbC: }/bA, окруж-
окружность (с) — геометри-
геометрическое место точек, рас-
расстояния которых от то-
точек .4 и ^относятся как
V сА: V сВ. Если две из
трёх окружностей, ска-
скажем (а) и (Ь), пересека-
пересекаются в точках UhV, to
UB-.UC = УаВ: /аС;
UC:UA =Y~bC:VbA,
Черт. 453.
откуда в силу A) UA:UB — \'cA :V сВ, и те же соотношения имеют
место и для точки V. Следовательно, окружность (с) проходит через
точки пересечения окружностей (а) и (Ь), и центры трёх окружностей
лежат на одной прямой.
224. Так как трн точки а, Ь и с лежат на одной прямой, то
аВ ЬС сА
—. • т^г • —р;~ •• 1ак как точка а симметрична относительно середины
аС ЪА сВ
стороны ВС с точкой а, то аВ= — а'С, аС= — а'В, откуда
а'В:а'С^аС:аВ, н аналогично для точек Ъ' и с'. Отсюда следует, что
а'В Ъ'С с'А , , „
——•-—•-—=1, и точки а, о , с лежат на одной прямой.
Если точки а, Ь, с служат проекциями на стороны треугольника
некоторой точки Р описанной окружности, то точки а', Ь', с' слу-
служат проекциями точки Р', диаметрально противоположной точке Р.
Действительно, проекции центра описанной окружности совпадают с
сергдинами сторон, и потому проекции точек Р и Р' симметричны от-
относительно середин сторон.
225. Пусть С—точка пересечения прямых АА' и ВВ' (черт. 454).
Применяя к треугольнику О А А' и секущей ВСВ' теорему п. 192,
имеем —— • —— • — = 1. При вращении прямой О А'В' отношения
О/Ч 1> Су D/л
В1 А'-.В"О и ВО:ВА по условию не изменяются. Следовательно, не
изменяется и отношение АС:А'С, а значит и отношение АС:АА'. Так
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА [1
411
как точка А' описывает окружность, то и точка С описывает окруж-
окружность, гомотетичную первой относительно точки А.
226. Пусть XOY — данный угол, Р — точка пересечения прямых
ВМ и CN (черт. 455). Проведём через точку А некоторую прямую,
отличную от AMN, и обозначим через М и N' точки её пересече-
пересечения соответственно с прямыми ОХ и OY и черэз Р' — точку пересе-
пересечения прямых ВМ' и CN'. Рассмотрим два треугольника ММ'В н
NN'C. Прямые MN, MN1 и ВС, соединяющие попарно их соответст-
соответственные вершины, проходят через одну точку А. Следовательно, в си-
силу теоремы п. 195, точки пересечения их соответственных сторон
/Г
Черт. 454.
должны лежать на одной прямой. Но стороны MB и N'C пересе-
пересекаются в точке Р', стороны МБ и NC—в точке Р, стороны ММ' и
NN' — в точке О. Итак, точки О, Р и Р лежат на одной прямой.
Пусть теперь прямая AMN вращается около точки А, а прямая
AMN' сохраняет своё положение на плоскости. При этом и точка
Р будет сохранять своё положение на плоскости. Так как при лю-
любом положении секущей AMN точка Р лежит на прямой ОР' и так
как прямая MB может пересекать ОР' в любой её точке, то геомет-
геометрическим местом точек Р и будет прямая ОР'.
227. Так как прямые Аа, ВЬ, Сс проходят чергз одну точку, то
аВ ЬС сА
—-=—1. Так как точка а симметрична с а относительно
аС ЪА сВ
середины стороны ВС треугольника, то а'В: а''С = аС: аВ, и анало-
., , _ а'В Ь'С с'А
гичное имеем для точек рис. Отсюда следует, что -77, ¦ ттт ¦ ~гъ'— — '•
а С- о А с В
так что прямые Аа', ВЬ', Сс' проходят через одну точку.
412
PFIUEHUH УПРАЖНЕНИЙ И ЗАДАЧ
ооо о ™ DB ЕС FA
22о. В силу упражнения 90а имеем равенство -=-= • -^— ¦ -=г=г =
JlJLj lZA id
ip — b\ ( p — c\ I p — a\ , ^
= • • 1 == — 1, так что прямые AD,
\ P — cj \ p — a) \ p — b) v
BE и CF проходят через одну точку.
229. Так как прямые Аа, ВЬ и Сс проходят через одну точку
(черт. 456), то —-• — •—= — 1. В силу п. 121 имеем а'В':а'С' =
аС ЬА сВ
= аС:аВ, и аналогично для точек Ь' и с'. Отсюда следует, что
а'В' Ь'С с'А'
—— • тт-г, • —гб, = ~~ ^ так что прямые А'а', В'Ь', С с' проходят
Л L О А С tj
через одну точку.
230. Так как прямые Аа, ВЬ, Сс проходят через одну точку, то
аВ ЬС сА
— • J-Z • — = — 1. если точка а гармонически сопряжена с точкой а
относительно вершин В и С треугольника, то а'В: а'С =
~— аВ:аС, и аналогичное имеем для точек Ь' и с'. Отсюда следует, что
а'В Ь'С с'А , ^
-77; • ггл ' ~гв='> так что точки ai v I c лежат на одной прямой.
Если прямые Аа, ВЬ, Сс — биссектрисы углов треугольника, то
точки а', Ь', с' будут точками пересечения биссектрис внешних уг-
углов треугольника с противолежащи-
ь» ми сторонами (п. 115, примечание),
и мы получаем следующую теорему:
Точки пересечения биссектрис внеш-
внешних углов треугольника с проти-
противолежащими сторонами лежат на
одной прямой.
Мы могли бы принять за прямую
Аа биссектрису угла А треугольника,
а за прямые ВЬ и Сс — биссектри-
биссектрисы его внешних углов (сравнить п. 54)
и получили бы следующий результат:
Точки пересечения двух биссектрис
треугольника и биссектрисы внешнего угла при третьей вершине с
противолежащими сторонами лежат на одной прямой.
231. Так как прямые Аа, ВЬ, Сс проходят через одну точку, то
аВ ЬС сА ,
¦ -—¦-—= — 1. Так как точки а, Ь, с, а , b и с лежат на
аС ЪА сВ
одной окружности, то в силу п. 131 будем иметь Ab-Ab' — Ac-Ac',
и аналогично Вс¦ Вс' — Ва• Ва''; Са-Са' — Cb-Cb'. Отсюда имеем
С
-2
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА III
413
а'В Ъ'С с'А аС ЬА сВ
^с' Fa ¦ 7в=^в ¦ Теа
ходят через одну точку.
ЪС сА аС ЬА сВ ,
Fa ¦ 7в=^в ¦ Теа = ~*• так что прямые Ла' т • Сс
УПРАЖНЕНИЯ К ГЛАВЕ III (стр. 192).
232. Пусть abed и a'b'c'd'—две данные четвёрки прямых (лучи
а и а' совпадают с 00'), В — точка пересечения прямых Ь и Ъ', С—
точка пересечения прямых с и с', А — точка пересечения прямых ВС
и 00' (черт. 457). Если бы точка пересечения прямых d и d не
Черт. 457.
л1/ вш\ С\ N
Черт. 458.
лежала на прямой ВС, то они пересекали бы эту прямую в точках
D и П так, что (ABCD)=^(ABCD"), откуда DA:DB--=D'A:D'B.
Так как существует единственная точка, делящая отрезок АВ в
определённом отношении по абсолютной величине и знаку (п. 188), то
из последней пропорции следует, что точки D и D' совпадают. Сле-
Следовательно, точка пересечения прямых d и d'
лежит на прямой ВС.
233. Допустим, что прямая СС не про-
проходит через точку пересечения Р прямых
АА' и ВВ' (черт. 458). Пусть прямая СР пе-
пересекает прямую О А' в некоторой точке С".
При этом (ОABC) = (ОА'В'С). Так как по
условию (О ABC) = (О А'И С), то (О А'В'С) = ,
= (ОА'В'С") и точки С и С" совпадают в С
{сравнить решение упр. 232).
234. Если через вершину А параллело- Черт. 459.
грама провести прямую АХ, параллельную диа-
диагонали BD (черт. 459), то эта прямая образует с прямыми АВ,
AD и АС гармоническую четвёрку (в силу теоремы п. 201).
Обратно, если четыре прямые АВ, AD, АС и АХ, выходящие
из одной точки, образуют гармоническую четвёрку, то они параллельны
сторонам и диагоналям параллелограма. Действительно, проведя через
414
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
произвольную точку О прямой АС прямую, параллельную АХ, полу-
получим два равных отрезка ВО— OD. Отложив ОС = АО, получим па-
раллелограм.
235. Пусть Мо — точка пересечения прямой АВ с прямой т —
геометрическим местом точек М (черт. 460). Если за точку М при-
т
Черт. 460.
нять точку Мо, то обе прямые AM и ВМ совпадают с АВ и точки
Р и Q совпадут с точкой пересечения Ро (или Qo) прямых АВ и XY.
Пусть теперь /И,, /И2 — две точки прямой т, отличные от Ми и
Рг, Р2; Qv Q2 — соответствующие им положения точек Р и Q. Так
как прямые A/Wo, AMV АМ„, AM пересекаются с прямой XY в точ-
Черт. 461.
ках Р0,Рг,Р2,Р, то (М0МгМ2М) = (РоР^Р) в силу п. 200.
Аналогично имеем (M0MlM2M) = {Q0QJQ2Q), и, следовательно,
(P0PtP2P) = (QuQiQ^Q)- Сложное отношение четырёх прямых
ВР0, BPV BPV ВР равно сложному отношению четырёх прямых ,4Q0,
AQV AQ2, AQ. Так как прямые ВР0 и AQ0 совпадают, то точки пе-
пересечения /И/, /И,', М прямых ВР1 и AQV BP2 и AQ2, BP и AQ
лежат на одной прямой (упр. 232). При перемещении точки М по
прямой т точка М' описывает прямую М^М2.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА IV
415
Если прямые АР и BQ, вместо того чтобы пересекаться в неко-
некоторой точке М, остаются параллельными друг другу (черт. 461), то
сложное отношение четырёх прямых ВР0, ВРг, ВР„, ВР равно слож-
сложному отношению прямых AQlt, AQ,, AQ2, AQ, и предыдущее заклю-
заключение сохраняет силу. ,
236. Пусть точки С и D делят гармонически диаметр АВ окруж-
окружности О (черт. 462) и перпендикуляры к АВ в точках А, В, С, D
пересекают касательную в произвольной
точке Т окружности соответственно в
точках Е, F, G, Н.
Прямые АЕ, BF, CG, DH отсекают
на прямых АВ и EF пропорциональные
отрезки; вследствие этого точки G \\Н
делят гармонически отрезок EF и, сле-
следовательно, прямые OG и ОН делят
гармонически прямые ОЕ и OF. Но
прямые ОЕ и OF перпендикулярны
между собой (упр. 89); в силу п. 201,
следствие II, прямая OF есть биссек-
триса угла GOH; отсюда OG:OH = Черт. 462.
= GF: FH = CB-.BD. Итак, отноше-
отношение OG-.OH сохраняет постоянное значение CB.BD независимо от
выбора касательной.
УПРАЖНЕНИЯ К ГЛАВЕ IV (стр. 199).
237. 1°. Точка В лежит на поляре точки А (черт. 463); эта по-
поляра проходит через точки прикосновения Т и Т касательных из
точки А к данной окружности С. Окружность С, ортогональная к
окружности С и имеющая точку А своим центром, также проходит через
точки Г и Т. Следовательно, точка В лежит на радикальной оси
окружностей С и С", а потому окружность С" с центром В, ортого-
ортогональная к С, в то же время ортогональна и к С.
2°. Точка М—середина отрезка АВ (черт. 464) — лежит в силу
сказанного в п. 204 на радикальной оси точки А и данной окружности
С. Отсюда следует, что /ИЛ2 равняется степени точки М относительно
данной окружности, т. е. квадрату касательной из точки М к данной
окружности. Это и показывает, что окружность, имеющая МА своим
радиусом, ортогональна к данной окружности.
В том случае, когда одна из точек А и В лежит внутри данной
окружности, ортогональность этой окружности к окружности, имеющей
АВ своим диаметром, непосредственно следует из п. 189, следствие.
Из треугольника ОАВ (черт. 465) имеем АВ2 = О А2 + ОН2 —
— 20 А- ОН, где Н — точка пересечения прямой О А с полярой ВТ точки
А. Но OH-OA = R2, и, следовательно, О А2 -\-ОВ* —AB*=2R2, или
АВ2 = (ОА2 — R2) -\- (Ofi2 — R2).
Так как О А2—R2 и OB* — R2 представляют собой степени точек
416
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
А и В относительно данной окружности, то мы можем сказать, что
квадрат расстояния между двумя сопряжёнными точками равен
сумме степеней этих точек относительно окружности.
238. Если поляры точки А относительно трёх данных окружностей
пересекаются в одной точке В, то точки А и В сопряжены относи-
С'"
Черт. 463.
Черт. 464.
Черт. 465.
тельно каждой из данных окружностей. Окружность, построенная на
отрезке А В как на диаметре, ортогональна ко всем трём данным
окружностям (упр. 237). Как геометрическое место точек А, так и гео-
геометрическое место точек В есть окружность, ортогональная к трём
данным (п. 139).
239. Пусть abed—вписанный четырёхугольник (черт. 466), каса-
касательные в вершинах которого образуют описанный четырёхугольник
ABCD, е и /—точки пересечения противоположных сторон четырёх-
четырёхугольника abed, Р—точка пересечения его диагоналей, Е и F —
-точки пересечения противоположных сторон четырёхугольника ABCD.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛЛВА IV
417
В силу п. 211 полярами точек ей/ служат соответственно пря-
прямые Pf и Ре, а следовательно, в силу п. 205 точка пересечения Р
этих прямых имеет своей полярой прямую ef.
1°. Так как прямые ad, he, ef, Pf проходят через одну точку /,
то их полюсы А, С, Р, е лежат на одной прямой. Так как прямые аЬ,
cd, ef, Ре проходят через одну точку е, то их полюсы В, D, P, f
лежат на одной прямой. Таким образом, диагонали АС и BD четы-
четырёхугольника ABCD проходят через точку Р.
Так как прямая Ре есть поляра точки /, то точка пересечения К
прямых ad и Ре и точка / делит гармонически отрезок ad. Следова-
Следовательно, прямые ас, bd, AC, BD,
проходящие соответственно через
точки a, d. К, /, образуют гармони-
гармоническую четвёрку.
2°. Так как прямые ас, bd, AC,
BD проходят через одну точку Р, то
их полюсы Е, F, /, е лежат на одной
прямой. Точки ей/ делят гармо-
гармонически отрезок EF, так как пря-
прямые EF, AC, BD представляют собой
диагонали полного четырёхсторонни-
четырёхсторонника ABCDEF, а каждая диагональ
Ч &D т 4о/
полного четырёхсторонника делит- F "
ся гармонически двумя другими его диагоналями (п. 202).
240. Пусть a,b,c,d—точки прикосновения касательных из точек/3 и Q
(черт. 467), К, L, М, N—вершины четырёхугольника, образованного
этими касательными. Прямые ас, bd, KM, LN проходят через одну
точку R (упр. 239, 1°). Так как прямые bd и ас—поляры точек Р
и Q, то PQ есть поляра точки R.
241. 1°. Так как любая окружность, проходящая через точки Р
и Q (черт. 468), ортогональна к обеим данным окружностям (упр. 152),
то точки Р \\ Q делят (п. 189, следствие) гармонически диаметры АВ
и CD обеих окружностей (обозначения те же, что и Tia черт. 400).
Поляра точки Р относительно любой из данных окружностей проходит
через точку Q и перпендикулярна к линии центров.
2°. Пусть R — какая-либо точка, имеющая относительно обеих
данных окружностей О, и О2 одну и ту же поляру. Так как прямые
ЯО^ и RO2 обе перпендикулярны к этой поляре, то они совпадают,
и, следовательно, точка R лежит на линии центров. Если поляра
точки R пересекает линию центров в точке R', то точки R и R' де-
делят гармонически как АВ, так и CD и, следовательно, совпадают
в силу упражнения 219а с точками Р и Q.
3°. Пусть /И,, Л/,, М„, N2 — точки пересечения внешних и внут-
внутренних общих касательных (черт. 468). Касательные к окружности О2,
проведённые из точек Ж, и Nr, образуют описанный четырёхсторонник.
Точка пересечения диагоналей этого четырёхсторонника, т. е. точка
пересечения прямой M2N2 с линией центров, есть полюс прямой M^NY
27 Элементарная геометрия
418
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
относительно окружности О2 (упр. 240). По той же причине точка
пересечения прямой /И,TV, с линией центров есть полюс прямой MtN9
относительно О1. Отсюда следует, что точки пересечения прямых
vWj/V, и M^NZ с линией центров делят гармонически как диаметр АВ,
так и CD и потому также совпадают с предельными точками Р и Q.
4°. Так как точка Ж, лежит по только что доказанному на поляре
точки Q, то поляра точки М1 относительно любой из данных окруж-
окружностей, т. е. прямая, соединяющая
точки прикосновения касательных
из точки /И, к этой окружности,
проходит через точку Q.
УПРАЖНЕНИЯ К ГЛАВЕ V (стр.208).
242. Пусть точки А и В взаим-
взаимно обратны относительно окруж-
окружности О (черт. 469) и М — про-
произвольная точка этой окружно-
окружности. Из равенства ОА-ОВ — ОМ2
Черт. 468. вытекает подобие треугольников
О AM и ОМВ, откуда в свою оче-
очередь следует, что АМ:ВМ^0А:0М, так что отношение АМ:ВМ не
зависит от выбора точки М.
243. Пусть в упражнении 68 прямая D пересекает окружность С
в точке / (черт. 319). Инверсия с полюсом / преобразует данную
прямую D в самоё себя (так как прямая D проходит через полюс
с к
Черт. 469.
Черт. 470.
инверсии), данную окружность С—в некоторую прямую С (так как
окружность С проходит через полюс инверсии), данные точки Р и Q —
в некоторые точки Р' и Q, лежащие соответственно на прямых С
и D (черт. 470). Произвольная окружность, проходящая через данные
точки Р и Q и пересекающая вторично окружность С и прямую D
в некоторых точках R w S, преобразуется в окружность, проходящую
через точки Р и Q' (обратные точкам Р и Q) и пересекающую ьто-
рично прямые С и D в точках R' и S' (обратных точкам R и S).
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V
419
Наконец, прямая RS преобразуется в окружность /R'S', проходящую
через полюс инверсии /.
Утверждение упражнения 68, что все прямые RS пересекают
окружность С в одной и той же точке U, преобразуется в утверждение,
что все окружности /R'S' пересекают прямую С в одной и той же
точке U' (обратной точке U). Но это прямо вытекает из упражнения 65,
так как в силу последнего прямая IU' параллельна P'Q.
244. Пусть С и С — данные окружности, А и В—точки их пере-
пересечения (черт. 471). Выполним инверсию с полюсом в точке А. Дан-
Данные окружности С и С преобразуются в две прямые линии Ct и С/
(черт. 472), пересекающиеся в точке Bv обратной точке В. Прямые
Черт. 471.
Черт. 472.
ММ и NN', проходящие через полюс инверсии А, преобразуются
каждая в самоё себя; окружности AMN' и AM'N преобразуются в пря-
прямые M^Nt' и /Wj/Vj'. Таким образом, приходим к следующему постро-
построению: через точку А проводим две произвольные прямые МХМ^ и N^N^,
которые пересекают две данные прямые С, и С,' в точках Ж,, M^,N,,
Л/,'. Геометрическое место точек пересечения Рг прямых Л^Л^' и /И/ZV,
есть (согласно п. 203) прямая, проходящая через точку В,, а именно
поляра точки А относительно угла со сторонами Сг и СД
Этой прямой соответствует в нашей инверсии некоторая окружность,
проходящая через точки А и В. Эта окружность и будет геометриче-
геометрическим местом точек Р, обратных точкам Pv т. е. точек пересечения Р
окружностей AMN' и AM'N.
245. Окружности С, имеющие общую радикальную ось, можно
охарактеризовать как окружности, ортогональные к двум данным
окружностям С и С" с центрами на этой радикальной оси. Следова-
Следовательно, окружности С,, обратные окружностям С, будут ортогональны
к окружностям Cj' и С/', обратным окружностям С и С" (так как угол
между двумя окружностями сохраняется при инверсии). Поэтому
окружности С, будут иметь общую радикальную ось—линию центров
окружностей Cj' и С,".
27*
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
ш
246. Пусть А — произвольная точка данной окружности, О — её
центр, А' и О' — точки, обратные точкам Аи О, Р—полюс инверсии
и k — её степень (черт. 473). В силу п. 218 имеем ОА= ?'?!? Из
условия ЮА = Я = const следует, что А'О':A'P=(R-PO'):k = const,
так что преобразованная окружность есть геометрическое место точек А',
отношение расстояний которых от точек О' и Р постоянно.
247. Центр М новой окружности есть точка пересечения прямых,
пересекающих эту окружность под прямым углом. Следовательно,
точка М, обратная центру но-
новой окружности, есть точка пе-
пересечения окружностей, ортого-
ортогональных к данной окружности и
проходящих через полюс инвер-
инверсии. Другими словами, М есть
точка, обратная полюсу инвер-
инверсии относительно данной окруж-
окружности (п. 216).
Черт. 473. 248. Две концентрические
окружности характеризуются
тем, что существует бесчисленное множество прямых, ортогональных
одновременно к обеим окружностям (прямые, проходящие через общий
центр), но не существует окружностей, ортогональных одновременно
к ним обеим (так как две концентрические окружности не имеют
радикальной оси).
Следовательно, чтобы -преобразовать с помощью инверсии две дан-
данные окружности в две концентрические окружности, надо преобразо-
преобразовать окружности, ортогональные к двум данным, в прямые линии.
А для этого надо принять за полюс инверсии одну из общих точек Р
или Q (упр. 152) окружностей, ортогональных к" двум данным, т. е.
одну из предельных точек данных окружностей.
249. Пусть Д, В, С — данные точки, и А', В, С — точки, им об-
обратные, О — искомый полюс инверсии. Если точка С есть середина
отрезка А'В', то окружность, построенная на А'В как на диаметре,
имеет С своим центром; следовательно (сравнить упр. 247), С есть
точка, обратная точке О относительно окружности, имеющей АВ своим
диаметром. Иначе говоря, точки О и С гармонически сопряжены относи-
относительно А и В. Итак, искомым полюсом инверсии является точка, гар-
гармонически сопряжённая с одной из трёх данных точек относительно
двух других.
250. Пусть фигуры Л и Л' преобразуются одна в другую с по-
помощью инверсии 51) с полюсом О и степенью k. Пусть далее ин-
инверсия Т с полюсом Р и степенью kx преобразует фигуры А и А'
в две новые фигуры а и а'. Мы должны показать, что фигуры а и а'
1) Обращаем внимание читателя на то обстоятельство, что здесь одной
буквой S (или Л обозначена не геометрическая фигура (точка, прямая,
окружность и т. п.), а инверсия.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V
421
соответствуют друг другу также в некоторой инверсии s, и опреде-
определить полюс последней (связь между четырьмя фигурами показана схе-
схематически на черт. 474). Для этого достаточно, очевидно, показать,
что:
1) прямая, соединяющая любые две соответственные точки т и т'
фигур а и а', проходит через одну и ту же точку Q (независимо от
выбора точки т) и
к>о
т
т
Черт. 474.
Черт. 475.
2) произведение Qm- Qm' не зависит от выбора пары соответст-
соответственных точек т и т'. Докажем эти два положения.
1°. Пусть М и М — точки, соответствующие точкам т и т' в ин-
инверсии Т (черт. 475 и 476). Так как окружность РММ' (или пря-
прямая РММ', если эти три точки лежат на одной прямой) проходит
через две точки М и М', со-
соответствующие одна другой в
инверсии 5, то она преобразует-
преобразуется инверсией .S в самоё себя;
поэтому окружность (или пря-
прямая) РММ' проходит через точ-
точку Р', которая соответствует
точке Р в инверсии .S. Так
как точки М, М и Р' лежат
на одной окружности (или на
одной прямой) с полюсом Р
инверсии Т, то соответствую-
соответствующие им в инверсии 7 точки in,
m' и р' лежат на одной прямой.
Итак, любые две соответственные точки m и >п' фигур а и а' ле-
лежат на одной прямой с точкой р'. Последняя точка не зависит от вы-
выбора точки т: она получается, если выполнить над точкой Р инвер-
инверсию 5, а затем над полученной точкой Р' — инверсию Т. Точка /?'
и будет, как мы сейчас увидим, тем полюсом Q инверсии s, о кото-
котором мы говорили выше.
2°. В силу формулы, выведенной в п. 218, имеем:
A)
/77
\
Черт. 476.
ОМ'-ОР1
422 РЕШЕНИЯ УПРАЖНЕНИЙ II ЗАДАЧ
Р' =
ОМ-ОР' - К)
Рт=РМГрГР'- D)
Заменяя в равенствах C) и D) отрезки МР' и МР' их выраже-
k к PAY
ниями A) и B), находим Р'т = 0М! .0Р\рм.рр и р'т'=
k-k-\- РМ
== ОМ OP PM' РР' ' Перемножая два последние равенства, получим
?2 ¦ к-Р
р'т-р'т'= ОМ-ОМ'-ОРЪ-РР1'2' Наконец> заменяя здесь ОМ-ОМ че-
через k, получаем:
Р'т-р'т'= 6^pli=zonst. E)
В этом выводе отрезки р'т и р'т' рассматриваются лишь по аб-
абсолютной величине. Но в зависимости от того, будет ли &^>0 или
k <^ 0, точка О будет лежать вне окружности РР'ММ или же внутри
её, и точки М и М будут при k~^>0 лежать на одной и той же из
двух дуг, на которые точки Р и Р' делят эту окружность (черт. 475),
а при &<^0 — на двух различных дугах (черт. 476). Следовательно,
точки т и т' будут при &^>0 лежать по одну сторону от точки р\
а при &<^0 — по разные стороны от р'. Таким образом, равенство E)
имеет место и по знаку.
Итак, точки т и т', соответствующие в инверсии Т произвольной
паре точек М и М', взаимно обратных в инверсии S, не только лежат
на одной прямой с точкой р', но и удовлетворяют условию
р'т • р'т' = const. Другими словами, точки т и т' соответствуют друг
другу в некоторой инверсии s; полюс р' 'этой инверсии мы определили
выше, её степень равна правой части равенства E).
Пусть теперь степень инверсии 5 — положительна: &^>0. В таком
случае существует бесчисленное множество точек М, каждая из кото-
которых совпадает с точкой AV, соответствующей М в инверсии 5. Эти
точки М (или М') преобразуются инверсией Т в точки т, каждая из
которых совпадает с соответствующей ей в инверсии 5 точкой /га'. Эти
точки т и образуют окружность инверсии 5.
Примечания: 1°. Приведённое доказательство теряет силу, если
точка Р совпадает с О или с Р', как это видно из соотношений A) — (А).
Если полюс О инверсии S совпадает с полюсом Р инверсии Т, то все
четыре точки М, AV, m, т', очевидно, лежат на одной прямой с точкой О
(или, что то же, с Р), и мы имеем Рт = -L = ^JL ; Рт- = -А. = ^-L., от.
куда Рт-Рт' = 0т-0т' = ^ ^ =z— . Таким образом, теорема сохра-
сохраняет силу и в этом случае.
Если точка Р совпадает с Р, то полюс Р инверсии Т лежит на окруж-
окружности инверсии S; эта окружность преобразуется инверсией /' в прямую
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V 423
линию. Точки М и М', взаимно обратные относительно окружности инвер-
инверсии S, преобразуются в точки т и т\ симметричные относительно этой
прямой линии (сравнить п. 216). Инверсия 5 обращается в симметрию
относительно прямой.
2°. Другое решение, более короткое, но не столь непосредственное,
как только что приведённое, имеется во второй части курса Адамапа
(пп. 700, 914).
251. 1°. Если окружности инверсий 5 и S' не имеют общих то-
точек, то примем за полюс Р инверсии Т одну из их предельных точек.
Инверсия Т преобразует окружности инверсий 5 и S' в две концен-
концентрические окружности (упр. 248) s и s', фигуры А и В, взаимно об-
обратные относительно S, — в фигуры а и Ь, взаимно обратные относи-
относительно s (упр. 250), фигуры В и А', взаимно обратные относительно S',—
в фигуры b и а', взаимно обратные относительно s' (связь между
всеми этими фигурами показана схематически на черт. 477). Так как
окружности s и s' — концентрические,
то фигуры а и а' — гомотетические,
как две фигуры, обратные одной и той
же фигуре b относительно одного и
того же полюса (общего центра окруж-
окружностей s и s'; сравнить п. 215).
Если окружности инверсий 5 и S1
имеют общую точку, то примем эту
общую точку (или одну из их общих ц 477
точек) Р за полюс инверсии Т. Инвер-
Инверсия Т преобразует окружности инверсий 5 и S' в две прямые линии
5 и s', фигуры А и В—в две фигуры а и Ь, симметричные относи-
относительно s, фигуры В и А' — в две фигуры b и а', симметричные от-
относительно s'. Так как фигуры я и я' получаются одна из другой с
помощью двух симметрии, то они равны.
2°. Если окружности инверсий 5 и S' ие имеют общих точек, то,
не изменяя фигур а и а', можно заменить пару инверсий относительно
концентрических окружностей 5 и s' равносильной ей парой инверсий
относительно окружностей s± и s^. Окружности s2 и s^ имеют с
окружностями s и s' общий центр и то же отношение радиусов (следует
из того, что коэфициент подобия фигур а и а' равен, согласно п. 215,
отношению степеней инверсий относительно окружностей s и s'). Сле-
Следовательно, пара инверсий S и S' равносильна паре инверсий 5, и 5,'
относительно окружностей, обратных окружностям s, и 5,' в инверсии Т.
Эта пара инверсий 5, и 5/, как и пара инверсий относительно 5г и s^,
может быть выбрана бесчисленным множеством способов. В частности
можно выбрать инверсию 5, (или s,') так, чтобы окружность этой ин-
инверсии проходила через полюс Р инверсии Т. При этом инверсия 5,
(или S,') обращается в симметрию относительно прямой. Такой выбор
инверсии Sj (или s,') невозможен только в том случае, когда точка Р
совпадает с общим центром окружностей инверсий s и s'. При этом
424 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
окружности инверсий 5 и 5' также будут концентрическими, а фигу-
фигуры А и А' — подобными.
Если окружности инверсий 5 и 5' имеют общие точки, то те же
самые рассуждения относятся к возможности замены прямых s и s'
другой парой прямых s} и s^ в согласии с п. 102а. В частности можно
выбрать прямую s, (или s,f) так, чтобы она проходила через полюс Р
инверсии Т. При этом инверсия 5t (или 5,') обращается в симметрию
относительно прямой.
3°. Равные фигуры а и а', полученные из Л и Л' с помощью ин-
инверсии Т, получаются одна из другой путём поступательного переме-
перемещения, если оси симметрии s и s' параллельны, т. е. если окружности
инверсий 5 и 5' касаются одна другой.
4°. Если окружности инверсий 5 и 5' не имеют общих точек, то,
выполняя несколько раз подряд последовательно операции 5 и 5',
мы будем получать всё новые и новые фигуры А, А', А",..., так как,
выполняя несколько раз подряд последовательно операции s и s', мы
будем получать всё новые и новые фигуры а, а', а",.. . , имеющие
обилий центр подобия.
То же самое относится и к случаю, когда окружности инверсий 5
и 5' касаются одна другой.
Если же окружности 5 и 5' пересекаются в двух точках, то фи-
фигуры а и а', а' и а",... получаются одна из другой путём поворота
на один и тот же угот около одной и той же точки. Следовательно,
если угол поворота соизмерим с полной окружностью, то одна из фи-
фигур а', а",..., скажем а1"), совпадает с а; при этом фигура ,4(л>, обрат-
обратная а*-") в инверсии Т, совпадает с А. Так как инверсия Т сохраняет
углы между линиями (п. 219), то это будет в том случае, когда угол
между окружностями инверсий 5 и 5' будет соизмерим с полной окруж-
окружностью.
252. Пусть выполнены последовательно инверсии 5,, 6*„,.. . , S-,
имеющие положительные степени1). Последовательность инверсий 5,5,
можно заменить, если полюсы инверсий 5: и Sv не совпадают, сим-
симметрией /, относительно некоторой прямой и некоторой инверсией 52'
(упр. 251, 2°). Таким образом данная последовательность инверсий за-
заменится через /г52'53... Sk. Далее заменяем пару инверсий 5О'53
симметрией /2 и инверсией 53' и получаем последовательность
/,/,53'... Sk. Продолжая таким образом, последовательность инверсий
5,52.. . Sk можно, вообще говоря, заменить последовательностью
IJV. . .lk_lSk', состоящей из нескольких симметрии и одной инверсии.
Это рассуждение требует видоизменения, если инверсии 5г и 52
имеют общий полюс. В этом случае можно сначала заменить пару ин-
инверсий 5253 (опять-таки на основании упр. 251,2°) другой парой ин-
инверсий 5g*5g*, а-.затем уже заменить пару S^^* через /,52' и полу-
получить последовательность ^S^Sg*. .. Sk. Такое же видоизменение при-
1) Возможно, что среди зтих инверсий имеются и симметрии относи-
относительно прямой (п. 216).
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V 425
дётся внести во всех случаях, когда в процессе замены две после-
последовательные инверсии будут иметь общий полюс, если только эти две
инверсии не будут последними.
Итак, данную последовательность инверсий можно заменить последова-
последовательностью /,^2... /fe_,5t' или последовательностью 1Л1Ъ. . -lk_aSk'_lSk,
где инверсии 5Л'_, и Sb имеют общий полюс. Но в последнем случае
первоначальная и преобразованная фигуры подобны между собой, так
как последовательность Sk'_lSk даёт гомотетию (п. 215). Следова-
Следовательно, последовательность инверсий SlS^...Sk можно заменить
через /,/2.. -lk—xS^, если только первоначальная и преобразованная
фигуры не будут подобными.
Заметим теперь, что последовательность симметрии llln...lk_l
можно заменить последовательностью самое большее трёх симметрии.
Действительно, если выполнено чётное число симметрии, то данная
фигура преобразуется в равную ей фигуру, имеющую то же направ-
направление вращения. Следовательно, эта последовательность симметрии
равносильна (п. 102) вращению или поступательному перемещению,
т. е. последовательности двух симметрии (п. 102а). Если же выпол-
выполнено нечётное число симметрии, то данная фигура превращается в рав-
равную ей фигуру, имеющую противоположное направление вращения,
и потому данная последовательность симметрии равносильна (упр. 95)
трём, а в частных случаях — одной симметрии. Таким образом, мы до-
доказали, что данную последовательность инверсий можно заменить
одной инверсией, которой предшествует одна, две или три сим-
симметрии, если только первоначальная и окончательная фигуры не
будут подобны ни между собой.
Если бы мы пожелали, чтобы симметрии не предшествовали един-
единственной инверсии, а следовали за ней, то мы начали бы с замены
Sk_lSk через Sk'_ ,/д,, где lk — симметрия, заменили бы далее Sk_oSk'^1
через Sft'_„/„,_,, и т. д.
Примечание. Указанные выше замены S2S3 через S2*S3* и S^,*
через liSo также оказались бы невыполнимыми, если бы не только две,
но все три инверсии S1? Sb Ss имели общий полюс. Но в этом случае по-
последовательность 6',S2 даёт гомотетию И с центром подобия в полюсе ин-
инверсий, а последовательность гомотетии Н и инверсии S3— инверсию с тем
же самым полюсом и другой степенью. Итак, последовательность трёх
инверсий с общим полюсом равносильна одной инверсии с тем же полюсом.
253. Пусть данная последовательность инверсий содержит инверсии
как с положительной, так и с отрицательной степенью. Инверсию S
с полюсом О и отрицательной степенью — k можно, очевидно, за-
заменить последовательностью симметрии относительно полюса О
и инверсии S' с полюсом О и положительной степенью k.
В свою очередь симметрию относительно О можно заменить последо-
последовательностью симметрии /' и /" относительно каких-либо двух взаимно
перпендикулярных прямых, проходящих через О. Таким образом ин-
инверсию 51 с отрицательной степенью можно заменить последовательно-
426
PELUFHHH УПРАЖНЕНИЙ И ЗАДАЧ
стью трёх инверсий с положительной степенью (в числе которых две
симметрии).
В силу этого замечания можно считать, что данная последователь-
последовательность состоит из нечётного числа инверсий с положительной степенью,
в числе которых могут быть и симметрии.
Эту последовательность нечётного числа инверсий 5,5,... Sk
можно заменить (если первоначальная и преобразованная фигуры не по-
подобны между собой) одной инверсией, за которой следуют две сим-
симметрии. В самом деле, при выполнении нечётного числа инверсий на-
направление вращения изменяется на обратное, а потому число симмет-
симметрии, о которых говорится в
I"
Черт. 478.
упражнении 252, будет в
точности равно двум. Итак,
рассматриваемое преобразо-
2 вание сводится к инверсии 5,
сопровождаемой двумя сим-
метриями относительно пря-
прямых /' и /".
Если прямые /' и /" парал-
параллельны, то задача сводится
к нахождению двух точек А
и А', обратных в инвер-
инверсии S, и притом таких, что-
чтобы отрезок А'А был равен
по величине удвоенному рас-
расстоянию между осями /' и /"
и в то же время перпенди-
перпендикулярен к этим осям. Если обозначить через О полюс инверсии S,
то известными будут разность отрезков О А' и О А, равная удвоенному
расстоянию между прямыми / и /', и произведение тех же отрезков, рав-
равное степени инверсии. Задача сводится к рассмотренной в п. 155, по-
построение 8. Получаются два решения.
Если оси /' и /" пересекаются в точке М (черт. 478), то задача
сводится к нахождению двух точек А и А', обратных в инверсии S,
и притом таких, что точка А получается из А' .путём поворота около
точки М на угол, равный удвоенному углу между осями /' и /" и име-
имеющий то же самое направление. Точки А и А' лежат на окружности 2
с центром М; эта окружность ортогональна к окружности инверсии S,
так как она проходит через две взаимно обратные точки. Угол, под
которым хорда АА' видна из центра М окружности 2, известен, а по-
потому можно считать известной длину этой хорды. Таким образом, прямая
АА' может быть построена (сравнить решение задачи 114) как про-
проходящая через точку О касательная к определённой окружности 2', кон-
концентрической с 1. Задача имеет два решения (точкиЛиВна черт. 478)'),
!) Обращаем внимание читателя на то обстоятельство, что вторые
точки пересечения А' и В' прямых ОА и ОВ с окружностью I условию
задачи не удовлетворяют.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V 427
если точка М лежит вне окружности инверсии 5, одно решение
(а именно самоё точку /И), если М лежит на окружности инверсии S,
и не имеет решений, если М лежит внутри окружности инверсии S.
253а. Пусть в данную окружность 2 требуется вписать много-
многоугольник .4Л, ... Ak _г, стороны которого А4,, А^А2,. .., Ak_xA про-
проходят соответственно через данные точки О„ О2,.. ., Ok или парал-
параллельны данным прямым. Рассмотрим последовательность инверсий Su
S2,..., Sk, имеющих своими полюсами точки Ov О.,, ..., Ок, а своими
степенями — степени этих точек относительно окружности S. Если
какая-либо сторона многоугольника вместо того, чтобы проходить че-
через данную точку, должна быть параллельна данной прямой /, то под
соответствующей инверсией будем понимать симметрию относительно
диаметра окружности 2, перпендикулярного к прямой /.
Инверсия S, преобразует точку А в точку/4,, инверсия S2— точку
/4, в А,, ..., инверсия 5ft —точку Ak_x снова в точку А. Последо-
Последовательность инверсий SXS2... Sk преобразует точку А в самоё себя.
Если все стороны многоугольника должны быть параллельны дан-
данным прямым, то решение задачи значительно упрощается.
Действительно, в этом случае произведение симметрии относительно
* диаметров окружности ? даёт либо симметрию относительно одного из её
диаметров, либо поворот около центра окружности, либо тождество. В
первом случае искомыми точками будут точки пересечения оси симметрии
с окружностью S, во втором — задача не имеет решений, в третьем—за
А можно принять любую точку окружности Т..
Поэтому мы будем предполагать, что сторона ЛА, проходит через
данную точку О, (а не параллельна данной прямой). Таким образом
задача сводится к следующей.
Некоторая окружность 2 преобразуется сама в себя данной
последовательностью инверсий Slt 5О,..., Skl); построить на этой
окружности точку, которая преобразуется этой последователь-
последовательностью инверсий самог в себя. При этом степени инверсий могут быть
как положительными, так и отрицательными; некоторые инверсии могут
обращаться в симметрии. Однако первая инверсия 5, не есть симмет-
симметрия. Число инверсий может быть как чётным, так и нечётным; начнём
с рассмотрения чётного числа инверсий.
Пусть Q'—точка, соответствующая полюсу Ог первой инверсии Sl
в последовательности остальных инверсий S2SS ... Sk (иначе говоря,
точка, соответствующая точке, лежащей в бесконечности, в данной
последовательности инверсий SlS2. .. Sk).
Чтобы охватить все возможные случаи, будем предполагать, что
инверсия 5, не обращается в симметрию, а все последующие инверсии
«S/+P "S'+2> • • • 1 Sk будут симметриями; возможно, конечно, что Sk от-
отлична от симметрии;* в этом случае будем полагать l = k. Обозначим
') В первоначально поставленной задаче о вписанном многоугольнике
каждая инверсия Su S2,. .., Sft в отдельности преобразует окружность S
в самоё себя; однако для дальнейшего достаточно этого более общего пред-
предположения.
428 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
теперь через Р ту точку, которой в последовательности инверсий
S}S2...S^.l соответствует полюс О, инверсии 5, (иначе говоря, ту
точку, которой в данной последовательности инверсий 5,52. ..S^ соот-
соответствует точка, лежащая в бесконечности). Точку Р можно получить,
выполняя над точкой О, последовательно инверсии S,_,, i>,_2,. .., S..
Какая-либо прямая а, проходящая через точку Р, преобразуется
последовательностью инверсий 5,5Q...5'(_1 в окружность или прямую,
проходящую через точку О,, а данной последовательностью инвер-
инверсий — в некоторую прямую линию а'.
Так как инверсия 5, преобразует прямую а в окружность или пря-
прямую, проходящую через точку Ог, а последовательность инверсий
SnS5...Sk — точку О, в точку Q', то прямая а' проходит через точ-
точку Q. Итак, данная последовательность инверсий преобразует каждую
прямую а, проходящую через точку Р, в некоторую прямую а', про-
проходящую через точку Q.
Если теперь А — искомая точка, то последовательность инверсий
5,52.-.5ft до тана преобразовывать прямую РА в прямую QA. При
этом угол между прямой РА и окружностью 2 должен быть равен по
величине углу между прямой QA и окружностью 2 в силу п. 219.
Более того, из соображений, развитых в том же п. 219, следует, что
при каждой инверсии углы, образованные окружностями и прямыми,
сохраняют свою величину, но меняют своё направление на обратное.
Так как число инверсий 5,, 52, ..., Sk, по предположению, четно, то
углы, образованные прямыми РА и Q'A с окружностью ~, должны
быть не только равны, но и одинаково направлены. Отсюда следует,
что прямые РА и QA совпадают.
Итак, для определения искомых точек А достаточно- построить, как
было указано выше, точки Р и Q'\ прямая, соединяющая эти точки,
пересекает окружность X в искомых точках. Задача может иметь два
решения, одно решение или не иметь ни одного решения.
Описанное построение нуждается в видоизменениях при / = 1 (точка Р
не существует), а также при совпадении точек Р и Q'. На рассмотрении
этих частных случаев мы останавливаться не будем.
Для решения задачи в случае нечётного числа инверсий можно
присоединить к последовательности данных инверсий ещё инверсию 5П
относительно самой окружности 2 и решить ту же задачу для последо-
последовательности уже чётного числа инверсий SXSO ... SbSn. Действительно,
точки, которые будут преобразовываться в себя данной последова-
последовательностью инверсий, будут совпадать с теми, которые преобразуются
в себя новой последовательностью инверсий.
Примечание. Другое решение этого упражнения см. в задаче 391.
254. 1 °. Пусть О — центр данной окружности, /И' и N' — точки
пересечения прямых ТМ и Г N с окружностью (черт. 479). Выполним
инверсию с полюсом 7" и степенью, равной квадрату отрезка ТТ'.
При этом окружность, имеющая отрезок ТТ своим диаметром,
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V
429
преобразуется в касательную к окружности в точке Т, а эта
касательная — в указанную окружность. Прямая М N' преобра-
преобразуется в окружность TMN. Вторая точка пересечения Р окружности
T'MN с прямой ТТ удовлетворяет условию ТТ -TP—TM-TN =
= const и потому не зависит от выбора пары точек /И и Л/, удовле-
удовлетворяющих данному со-
соотношению TM-TN= _ —fr^ —q
= const. Следова-
Следовательно, все окружно-
окружности T'MN проходят че-
через общую точку Р,
а все обратные им пря-
прямые МN' — через одну
и ту же точку Р',
. обратную точке Р в
рассматриваемой инвер-
инверсии.
2°. ¦ Пусть вторые
касательные к окруж-
окружности, проведённые из
точек М и N, касают-
касаются её в точках R' и S',
а прямые TR' и TS' пересекают в точках RhS касательную к окружности в
точке Т. Треугольники ОМТ1) и RTT подобны (в силу перпендикулярно-
20 Т2
сти сторон), откуда T'R:OT= ТТ :МТ, т. е. T'R = . Точно так же
Черт. 479.
T'S =
2ОТ2
Отсюда TR-TS =
4 ОТ4
мт
= const. Точки
R' и
NT "" * "" TM-TN'
получаются из точек R и 5 также инверсией, как и точки М и N'
из точек М и N, если только принять за полюс инверсии точку Т и
изменить значение степени инверсии. Следовательно, прямые R'S' пе-
пересекают прямую ТТ в одной и той же точке Q.
3°. Так как прямые R'S' проходят через одну и ту же точку Q,
то точки пересечения X касательных к окружности в точках R' и S'
(т. е. вторых касательных из точек М и N) лежат на одной прямой q —
поляре точки Q' относительно данной окружности.
255. Пусть Р—точка пересечения прямых MN и MN' (черт. 480).
Рассмотрим инверсию с полюсом Р и степенью, равной степени точ-
точки Р относительно данной окружности, т. е. k = PM-PN = PM' -PN'.
В этой инверсии точкам М и М' соответствуют точки N и N"; да-
далее, окружности ОММ' с центром на прямой ОМ, проходящей через
точки М и М', соответствует окружность с центром на той же пря-
прямой, проходящая через точки N и N', другими словами, окружность
0NN'. Следовательно, единственная общая точка О этих окружностей
соответствует сама себе, и потому PM-PN—PM'-PN'=PO2.
1) Отрезок ОМ не изображён, чтобы не затемнять чертежа.
430
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАЦАЧ
Последнее равенство показывает, что точка Р лежит на радикаль-
радикальной оси точки О и данной окружности. Если точка О лежит вне
данной окружности, то геометрическим местом точек Р будет отре-
отрезок Р'Р" этой радикальной оси, заключённый между касательными
ОТ и ОТ' из точки О к данной окружности. Если точка О лежит
внутри данной окружности, то геометрическим местом точек Р будет
вся эта радикальная ось.
256. Под углом между двумя окружностями можно понимать лю-
любой из двух пополнительных углов между касательными в их общей
точке—-другими словами, угол между радиусами, проведёнными в их
общую точку, или угол, ему пополнительный. В тех случаях, когда
придётся делать различие между этими двумя углами, мы будем гово-
говорить, что „угол между двумя ок-
окружностями строго равен а", пони-
понимая под этим, что а есть в точ-
точности угол между радиусами, про-
проведенными в одну из точек пере-
пересечения (а не угол, ему пополни-
пополнительный).
Две окружности, касающиеся
одна другой, образуют угол, стро-
строго равный 2d, в случае внешнего
касания, и угол, строго равный
О, — при внутреннем касании.
Если речь идёт о пересече-
пересечении прямой и окружности, то.
можно произвольно назвать „внутренней" по отношению к прямой одну
из двух полуплоскостей, на которые прямая делит плоскость, и рассмат-
рассматривать угол между радиусом, проведённым в одну из точек пересече-
пересечения, и перпендикуляром к прямой, проведённым во .внутреннюю"
область.
Доказанное в п. 227 предложение: „всякая окружность 2, кото-
которая' пересекает окружности С и С под одним и тем же углом, пере-
пересекает их в четырёх попарно антигомологических точках, и обратно"—
можно теперь высказать в следующей более точной форме.
Всякая окружность (или прямая) 2, которая пересекает окруж-
окружности С и С под строго равными углами, пересекает их в четырёх
точках, попарно антигомологичных относительно внешнего центра
подобия; всякая окружность (или прямая) 2, которая пересекает
окружности С и С под строго пополнительными углами, пересекает
их в четырёх точках, попарно антигомологичных относительно внут-
внутреннего центра подобия.
Действительно, пусть О, О' и Q—центры окружностей С, С и 2
(черт. 481 и 482), А и А'—две антигомологические (согласно п. 227)
точки пересечения окружности 2 с окружностями С и С, А" — вто-
вторая точка пересечения прямой АА' с окружностью С. Если углы
&АО и О.А'0' равны, то точки О и О' лежат по одну сторону от
Черт. 480.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V
431
прямой АА' (черт. 481) и, следовательно, параллельные радиусы О А
и О'А" направлены в одну и ту же сторону, так что прямая АА' про-
проходит через внешний центр подобия 51. Аналогичное рассуждение
применимо и к тому случаю, когда углы QAO и ЙЛ'О' пополнитель-
пополнительные (черт. 482). Вместо внешнего центра подобия получится внут-
внутренний.
С
Черт. 481.
Переходим теперь к решению поставленной задачи. Совокупность
окружностей, пересекающих окружности А и В под углами, соответ-
соответственно равными а и р, можно распределить в четыре группы. А
именно, отнесём к одной группе все окружности, пересекающие А и В
под углами, строго равными
A) а и р для первой группы
B) 2d — а и 2d — ф „ второй
C) а к 2d — р „ третьей
D) Id—а и р „ четвёртой „
Рассмотрим окружности групп G) и B) параллельно, указывая каж-
каждый раз на первом месте (без скобок) то, что относится к окружно-
окружностям группы A) и далее в
скобках то, что относится к
окружностям группы B).
Пусть Г — некоторая
окружность первой группы,
т. е. окружность, пересекаю-
пересекающая окружности А и В (черт.
483) под углами, строго рав-
равными аи р; пусть далее
некоторая другая ' окруж-
окружность Г' принадлежит к пер-
первой (ко второй) группе, т. е. Черт. 482.
пересекает окружности А я В
под углами, строго равными аир (под углами, строго равными
2tf— аи 2d—р). Так как окружность А пересекает окружности
Г и Г' под строго равными (под строго пополнительными) углами, то она
432
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАТ.АЧ
Л
пересекает их в четырёх точках, попарно антигомилогичных относительно
внешнего (внутреннего) центра подобия 6' окружностей Г и Г', и то же
имеет место для окружности В. Отсюда следует, что точка 51 имеет отно-
относительно окружностей А и В одну и ту же степень, а именно степень,
равную степени той инверсии / с полюсом 51, которая преобразует
Г в Г' (и окружности А и В в самих себя). Относительно любой
окружности С, имеющей с А и В общую радикальную ось, точка 5
имеет ту же самую степень. Следовательно, окружность С преобра-
преобразуется инверсией / сама в себя и потому она пересекает окружности
Г и Г' под строго равными (по-
(пополнительными) углами. Итак, все
окружности Г', пересекающие ок-
окружности А и В под углами, стро-
го равными а и '$ (строго равными
2йГ— а и 2cf— j5), пересекают
окружность С под углом, строго
равным (строго пополнительным)
тому, под которым его пересекает
Черт. 483. окружность Г. Если не делать раз-
различия между двумя углами, кото-
которые окружность Г образует с окружностью С, то можно будет сказать,
что все окружности Г', принадлежащие к группам {!) и B), пересе-
пересекают окружность С под одними и теми же углами. В этом смысле они
принадлежат к одному семейству. Теорема сохраняет силу, если одна
из окружностей Г или Г' обра-
обращается в прямую.
Тем же свойством обладают
окружности Г", отнесённые к
группам C) и D); действитель-
действительно, группы окружностей C) и
D) получаются из групп (/) и B)
путём замены значения ?j данно-
данного угла на 2d — ji. Эти окружно-
окружности образуют второе семейство.
Примечание. Распреде-
Распределение окружностей, пересекаю-
пересекающих две данные окружности А
и В под углами, соответственно равными а и ?, в два семейства суще-
существенно, так как окружности различных семейств могут пересекать окруж-
окружность С, имеющую с А и В общую радикальную ось, под углами, не равны-
равными между собой и не дополняющими один другой ао двух прямых.
В этом можно убедиться хотя бы на следующем простом примере.
Пусть окружности А и В (черт. 484) взаимно обратны относительно окруж-
окружности С; все три окружности имеют общую радикальную ось в силу п. 228.
Оба утла аир выбраны равными нулю". Обе изображённые на чертеже
окружности Г и Г (образующая с А ий углы, строго равные нулю, и образу-
образующая с Лий углы, строго равные 2rf) ортогональны к С (п. 228). В то
же время обе окружности Г" (образующие с одной из окружностей А и В
угол, строго равный нулю, с другой — угол, строго равный 2d) заведомо
Черт. 484.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА V
433
не ортогональны к С В случае, изображённом на чертеже, окружности Г'
принадлежат к группам C) и D) и пересекают С под строго пополнитель-
пополнительными углами..
257. Пусть О и О' — центры двух пересекающихся окружностей,
проходящих — первая через точки А к В, вторая — через точки Си D
и обладающих тем свойством, что из их точек отрезки АВ и CD видны
под равными или пополнительными углами. Пусть далее М и /V — точки
пересечения обеих окружностей, К — середина хорды MN, Р и Q —
точки пересечения прямых MN и 00' с прямой АВ.
Черт. 485.
Предположим сначала, что отрезки АВ и CD расположены один
вне другого и что точки А, В, С и D следуют на прямой в том
порядке, в каком они перечислены (черт. 485). В этом случае
углы АМВ и CMD не могут быть пополнительными, так как их сумма
заведомо меньше 180°, и могут быть только равными и притом ост-
острыми. Дуги АМВ и CMD будут каждая больше полуокружности, и
потому центры О и О' необходимо лежат по одну сторону от данной
прямой. Углы АОВ и CO'D также будут равны. Следовательно, ради-
радиусы ОА и О'С параллельны (а также ОБ и O'D), и точка Q есть
внешний центр подобия обеих окружностей. Поэтому точка Q делит
отрезок АС внешним образом в отношении AQ:CQ-=AO:CU'=^
= AB-.CD и не зависит от Выбора окружностей О и О'. Инверсия
с полюсом Q и степенью, равной QA-QD^QB-QC, преобразует
окружности О и О' одну в другую, а каждую из точек М и N в самоё
себя. Следовательно, точки М и N лежат на окружности инверсии.
Другими словами, геометрическое место точек пересечения Ж и ./V
обеих окружностей есть окружность с центром Q и радиусом, равным
V~QD=\ QB-QC.
Точка пересечения Р прямой MN с прямой АВ также не зависит
от выбора окружностей АМВ и CMD (см. решение упр. 153). Так
как отрезок PQ виден из точки К под прямым углом, то геометри-
28 Элементарная геометрия
434
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
ческое место точек К есть окружность, имеющая отрезок PQ своим
диаметром (на чертеже не показана)
Предположим теперь, что один из двух отрезков АВ и CD, ска-
скажем CD, лежит внутри другого и что точки Л, В, С, D следуют в
порядке A, D, С, В (черт. 486). В этом случае углы АМВ и CMD
не могут быть равными и потому
могут быть только пополнительны-
пополнительными. Следовательно, дуга АМВ бу-
будет меньше полуокружности, ду-
дуга CMD больше полуокружности,
и центры О и О' лежат по раз-
разные стороны от АВ. Точка Q
будет опять центром подобия двух
окружностей, на этот раз внутрен-
внутренним. В остальном будут иметь
место те же результаты, что и в
первом случае.
Рассмотрим, наконец, тот слу-
случай, когда отрезки АВ и CD ча-
Черт. 486. стично налегают один на другой
(черт. 487 и 488); пусть данные точ-
точки следуют при этом в порядке А, С, В, D. Центры рассматриваемых
окружностей могут лежать при этом и по одну сторону (как О и О' на
черт. 487) и по разные стороны (как О и О" на черт. 488) от дан-
данной прямой В первом случае отрезки АВ и CD будут видны из точ.
Черт. 487.
ки пересечения М обеих окружностей под равными углами, во втором —
будут видны из точки М" под пополнительными. Точка Q может занимать
на прямой АВ два положения Q и Q", точка Р, как уже было выяснено,
одно. По тем же соображениям, что и выше, геометрическим местом
точек М будет окружность с центром Q' и радиусом yQA-QD^
— \QB-QC, геометрическим местом точек М" — окружность с ценг-
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VI 435
ром Q" и радиусом ]/q»A-Q"C=V~Q"B- Q'D. Геометрическим местом
середин хорд будут соответственно окружности, имеющие своими
диаметрами отрезки PQ и PQ".
УПРАЖНЕНИЯ К ГЛАВЕ VI (стр. 214).
258. Пусть А и В— данные точки, О — данная окружность. При-
Примем одну из данных точек, например В, не лежащую на окружности О,
за полюс инверсии; за степень последней проще всего принять степень
точки В относительно данной окружности.
Задача сводится к следующей. Провести через точку А', обратную
точке Л, прямую, пересекающую данную окружность под данным уг-
углом. Но все прямые, пересекающие данную окружность под данным
углом, в том числе и искомая прямая, касаются определён чой окруж-
окружности, концентрической с данной.
Ггр имечание. Решение задачи упрощается, если искомая окруж-
окружность должна пересекать данную под прямым углом В этом случае иско-
искомая окружность должна проходить через точку, обратную одной из данных
точек относительно данной окружности (п. 216); таким образом, задача сво-
сводится к проведению окружности через три точки.
259. Пусть требуется построить окружность, ортогональную к
окружностям О, и О2 и касающуюся окружности О или пересекающую'
окружность О под данным углом. Рассмотрим отдельно три возможных
случая.
1°. Если О, и О2 пересекаются, то принимаем за полюс инверсии
одну из точек их пересечения и приходим к задаче: построить
окружность, ортогональную к двум данным пересекающимся прямым,
т. е. имеющую своим центром данную точку (точку пересечения
обеих прямых) и касающуюся данной окружности (данной прямой)
или пересекающую её под данным углом.
Решение последней задачи очевидно в случае касания, в случае же
пересечения под данным углом точка пересечения данной окружности
и искомой принадлежит геометрическому месту точек, из которых от-
отрезок, соединяющий центры обеих окружностей, виден под данным углом.
Решив эту новую задачу, мы найдём и решение первоначальной
задачи, подвергнув построенную окружность той инверсии, о которой
говорилось выше.
Наибольшее возможное число решений в этом случае равно двум.
2°. Если О, и О.г касаются друг друга, то окружность, ортого-
ортогональная к ним обеим, очевидно, пройдет через их точку касания.
Принимаем за полюс инверсии точку касания и приходим к задаче:
построить прямую, перпендикулярную к двум данным параллель-
параллельным прямым и касающуюся данной окружности или пересекаю-
пересекающую её под данным углом. Способ решения этой новой задачи оче-
очевиден. Задача имеет два решения.
3°. Если О, и О2 не имеют общих точек, то принимаем за почюс
инверсии одну из их предельных точек Р или Q (упр. 152) и прихо-
28*
436
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
С,
дим к задаче; построить прямую, ортогональную к двум концентри-
концентрическим (упр. 248) окружностям, т. е. проходящую через данную
точку (их общий центр) и касающуюся данной окружности или
пересекающую её под данным углом. Способ решения этой новой
задачи очевиден. Наибольшее возможное число решений два.
Примечание. В том случае, когда искомая окружность должна
касаться третьей данной окружности, задача непосредственно сводится
также к задаче, решённой в п. 311, так как
окружности, ортогональные к двум данным
окружностям С*! и О2, имеют прямую 0^0^
своей радика'льной осью (в силу п. 138).
260. Пусть С, и Сг — окружности,
касающиеся окружности С и проходящие
через точки А и В (черт. 489), Г —
окружность, ортогональная к С и проходя-
проходящая также через А и В.
Инверсия относительно окружности Г
преобразует окружность С в самоё себя,
а окружность С, — в новую окружность, также проходящую через
точки А и В и касающуюся окружности С, т. е. в окружность С2. Отсю-
Отсюда следует, что обе окружности С, и С2 пересекают Г под равными
углами и что центр окружности Г есть центр подобия окружностей
С1 •и С2. .
Й
Черт. 489.
Черт. 490.
261. Пусть через точку А проведена окружность С,, которая ка-
касается одинаковым 'образом данных окружностей С и С (черт. 490),
и окружность Г, пересекающая их под прямым углом. Инверсия отно-
относительно окружности Г преобразует точку А и каждую из окруж-
окружностей С и С, ортогональных к Г, в самоё себя. Окружность С,,
проходящая через точку А и касающаяся окружностей Си С одина-
одинаковым образом, преобразуется той же инверсией в некоторую окруж-
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VI 437
ность С2. Последняя также проходит через А и касается окружностей
С и С, и притом (как можно видеть хотя бы из чертежа) также оди-
одинаковым образом.
В том, что окружность С2 касается окружностей С и О одинаковым
образом, можно с полной строгостью убедиться так: Если Р и Р' — точки
касания окружности Сх с окружностями С и С, Q и Q' — точки касания
окружности to с теми же окружностями, то прямые РО и P'Q' проходят
через полюс инверсии, т. е. через центр И окружности Г. Но точка 2 ле-
лежит на радикальной оси окружностей С и С как центр окружности, к ним
ортогональной (п. 138). Так как окружность С\ касается окружностей
С и С одинаковым образом, то точки касания Р и Р' — антигомологичны
относительно внешнего центра подобия S этих окружностей. Так как пря-
прямые PQ и P'Q, проходящие через две антигомологические точки Р и Рt
пересекаются на радикальной оси окружностей С и С, то они являются
антигомологическими хордами (п. 224). Следовательно, точки Q и Q1 также
антигомологичны относительно внешнего центра подобия S, и потому
окружность Съ касается С и С одинаковым образом.
Итак, инверсия относительно окружности Г преобразует проходя-
проходящие через точку А окружности С, и С2, каждая из которых касается
окружностей С и С одинаковым образом, одну в другую. Отсюда
следует, что вторая точка пересечения В окружностей С, и С2 лежит
на окружности Г, что окружность Г делит угол между окружностями
С, и С2 пополам и что центр ?2 окружности Г есть центр подобия
окружностей Cj и С2.
При меча ние. Таким же образом можно доказать, что проходящие че-
через точку А окружности, каждая из которых касается окружностей С к С
неодинаковым образом, обладают по отношению к окружности Г аналогич-
аналогичными свойствами.
262. Обозначения те же, что и в решении упражнения 261
(черт. 490).
1°. Инверсия относительно окружности Г преобразует каждую из
окружностей APQ и Л P'Q' в самоё себя, так как первая из них про-
проходит через взаимно обратные точки Р и Q, вторая — через взаимно
обратные точки Р' и Q'. Следовательно, обе эти окружности ортого-
ортогональны к окружности Г и потому касаются одна другой в точке А.
Точно так же окружности BPQ и BP'Q1) ортогональны к Г и потому
касаются одна другой в точке В.
2°. Окружности APQ и BPQ пересекают окружность Г в точках
А и В под прямым углом и потому пересекают в этих точках окруж^
ность С, под одним и тем же углом (дополнительным к углу между Г
и С,). Следовательно, окружности APQ и BPQ пересекают в точке Р
под одним и тем же углом окружность С,, а значит и касательную
к ней окружность С. Итак, окружности APQ и BPQ образуют в точ-
точке Р равные углы с окружностью С.
Инверсия относительно окружности С преобразует окружность APQ
в новую окружность, проходящую через точки Р и Q и образующую
!) Окружность BP'Q' на чертеже не показана, чтобы не загромождать
чертежа.
438
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Черт. 491.
с С угол, равный углу между окружностями APQ и С, т. е. в окруж-
окружность BPQ (две точки и касательная в одной из них вполне опреде-
определяют окружность). Итак, окружности APQ и BPQ обратны относи-
относительно С.
Таким же путём докажем, что окружности AP'Q и BP'Q' обратны
относительно С.
3°. Если заменить данные окружности прямыми линиями С и С
(черт. 491), то свойство 1° сохраняет силу, так как инверсия отно-
относительно Г преобразует,
очевидно, каждую из
прямых С и С — в са-
самоё себя, а окружно-
окружности С, и С2 — одну в
другую.
Свойство 2° чи-
читается при этом так:
окружности APQ и
BPQ симметричны от-
относительно прямой С,
окружности AP'Q и
BP'Q — относительно
прямой С. Доказатель-
Доказательство, данное выше, со-
сохраняет силу: окружно-
окружности APQ и BPQ будут симметричны относительно прямой С, так kjk
они пересекают её под равными углами.
Окружности APQ и BP'Q также будут равны, так как они сим-
симметричны относительно биссектрисы угла между прямыми С и С. Сле-
Следовательно, все четыре окружности APQ, AP'Q', BPQ, BP'Q' равны.
263. Пусть требуется построить окружность Со, проходящую через
данную точку Ао и касающуюся двух данных прямых, пересекающихся
в точке Р.
Построим произвольную окружность С, касающуюся двух данных
прямых и расположенную внутри того из углов, образованных данными
прямыми, в котором лежит точка Ао, или внутри угла, ему вертикаль-
вертикального. Так как точка Р есть точка пересечения общих внешних или
внутренних касательных к окружностям С и Со, то точка Р есть
центр подобия обеих окружностей. Точка А, соответственная точке Ло,
есть одна из точек пересечения окружности С с прямой ОД,. Зная
центр подобия Р и пару соответственных точек А и Ао, можно по-
построить окружность Со, гомотетичную окружности С.
Примечание. Если данные прямые параллельны, то гомотетия
относИ|ельно центра подобия Р заменяется поступательным перемещением
(сравнить сказанное в п. 142 о постулательном перемещении как предель-
предельном случае гомотетии).
264. Пусть требуется построить окружность, касающуюся двух
данных прямых, пересекающихся в точке Р, и данной окружности Г
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VI
4">9
(черт. 492). Если С-— какая-либо окружность, касающаяся данных
прямых и имеющая центр на той же биссектрисе угла между данными
прямыми, что и искомая окружность Со, то точка Р есть центр подо-
подобия окружностей С и Со. Прямая, соединяющая точку Р с точкой
касания Т окружностей Со и Г, пересекает окружности Г и Со под
равными углами; окружности Со и С она также пересекает под рав-
равными углами, так как она ггроходит через их центр подобия Р. Сле-
Следовательно, прямая РТ пересекает окружности С и Г под равными
углами и потому проходит через один из их центров подобия 5 (то
же следует и из теоремы п. 145 об осях полоЗия; точка Т есть
центр подобия окружностей Со и Г, точка Р — центр подобия окружно-
окружностей Со и С; поэтому прямая
РТ проходит через один из
центров подобия 5 окружно-
окружностей С и Г).
Итак, строим окружность С,
как было указано, и соединяем
точку Р с одним из центров
подобия 5 окружностей Си Г.
Точки пересечения полученной
прямой с окружностью Г бу-
будут искомыми точками касания.
Наибольшее возможное чи-
число решений равно 8. Дей-
Действительно, центр вспомогательной окружности С можно выбрать на той
или другой из биссектрис углов между данными прямыми, а за центр
подобия 5 принять тот или другой из центров подобия окружно-
окружностей С и Г.
Примечание. Если данные прямые параллельны, то решение упро-
упрощается. В этом случае радиус г искомой окружности равен половине рас-
расстояния между данными прямыми. Центр искомой окружности равноудалён
от данных прямых и лежит от центра данной окружности Г на расстоянии,
равном R-\-r или \R — г\, где R — радиус окружности Г.
265. Пусть О—общий центр двух данных концентрических окруж-
окружностей, гх и г2 (г, ^> г2) — их радиусы, О' — центр третьей данной
окружности, г3 — её радиус, М — центр искомой окружности.
Если искомая окружность касается обеих концентрических окруж-
окружностей внутренним образом, то её радиус равен — (г,-j-r?), а рассгоя-
Чсрг. 492.
1
ние ОМ равно g-(ri — гъ>- При этом О'М =
1
Если искомая окружность касается одной из концентрических
окружностей внутренним, а другой — внешним образом, то её радиус
равен -^-(/"i — г2). При этом будем иметь ОМ = — (гх -\~ г„);
О'М =
440 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
В том и другом случае положение точки М определяется пересе-
пересечением двух окружностей с центрами в точках О и О'; радиусы их
определяются указанными выше выражениями для ОМ и О'М.
Наибольшее возможное число решений равно 8.
266. Пусть две окружности Г и Г', касающиеся друг друга, касаются
каждая двух данных окружностей С, и С2. При этом возможны три
различных случая: 1) каждая из окружностей Г и Г' касается окруж-
окружностей Cj и С2 одинаковым образом; 2) каждая из окружностей Г
и Г' касается окружностей Сл и С2 неодинаковым образом; 3) одна
из окружностей Г и Г', скажем Г, касается окружностей С, и С2 не-
неодинаковым образом, другая Г' — одинаковым образом. В этом послед-
последнем случае можно, не нарушая общности, предположить, что касание
окружностей Сл и Г—внешнее, а касание окружностей С2 и Г-г-внутрен-
Г-г-внутреннее (так как в противном случае мож-
можно изменить обозначение окружно-
окружностей С, и С2).
Рассмотрим все три случая по по-
рядку:
1°. Пусть каждая из окружно-
окружностей Г и Г' касается обеих окруж-
окружностей Cj и С2 одинаковым образом
(черт. 493) J). При этом окружность Г
касается окружностей Сл и С2 в двух
точках, антигомологических относи-
относительно их внешнего центра подобия
Черт. 493. .S, и, следовательно, преобразуется
сама в себя той инверсией с полю-
полюсом S, которая преобразует окружности С, и С2 одну в другую.
То же имеет место и для окружности Г'. Следовательно, точка ка-
касания окружностей Г и Г' лежит на окружности инверсии 2, так как
если бы окружности Г и Г' имели общую точку, не лежащую на
окружности 2!, то они имели бы и вторую общую точку, обратную
первой относительно 2.
Обратно, каждая точка М окружности инверсии 2 принадлежит
искомому геометрическому месту. Действительно, всегда можно по-
построить две окружности Г и Г', которые касались бы в данной
точке М окружности 2 радиуса этой окружности и, кроме того,
касались бы одной из данных окружностей Сх (ср. решение упр. 74).
Каждая из окружностей Г и Г', ортогональных к 2, преобразуется инвер-
инверсией относительно 2 в самоё себя, а потому касается и окружности С2.
Следовательно, геометрическим местом точек М будет вся окруж-
окружность 2.
1) В этом случае безразлично, касается ли окружность Г или Г' данных
окружностей внешним или внутренним образом: может случиться, что все
четыре касания будут внутренними, что все четыре касания будут внеш-
внешними и, наконец, что одна из окружностей Г или Г' касается данных окруж-
окружностей внешним образом, другая — вну!ренним.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ KHHTF. ГЛАВА VI
441
2°. Пусть каждая из окружностей Г и Г' касается окружностей
Cj и С2 неодинаковым образом (черт. 494). Таким же образом, как
и в первом случае, убедимся, что точка их касания М лежит на той
окружности 2' с центром во внутреннем центре подобия данных
окружностей, относительно которой эти окружности обратны друг
другу, и что за точку М можно принять любую точку окружности 2'.
Черт. 495
3°. Если теперь окружность Г касается окружностей С, и С2
неодинаковым образом, а окружность I'—одинаковым образом, то
представляется более или менее очевидным (сравнить хотя бы случай,
изображённый на черт. 495), что касание окружностей Г и Г' может
иметь место только на одной из данных окружностей Сх или С2.
Черт. 496.
Черт. 497.
Чтобы строго доказать это положение, начнём со следующего предва-
предварительного замечания:
Если три окружности касаются одна другой в трёх различных
точках, то из трех касаний либо только одно (черт. 496), либо все три
(черт. 497) будут внешними.
Действительно, если касание окружностей С\ и С-,— внутреннее
(черт. 496), то окружность С%, касающаяся окружностей Cj и С, в различ-
различных точках, необходимо располагается в заштрихованной части плоскости
и потому касается очной из окружностей С\ и С-> внутренним образом,
другой — внешним. Иначе говоря, если имеется одно внутреннее касание,
то" имеется и второе.
Пусть теперь окружность Г касается окружности С, внешним обра-
образом, а окружности С2 — внутренним (черт. 495), и окружность Г касается
окружностей С"} и Cv одинаковым образом. Сделаем предположение, что
точки попарного касания окружностей С\, Г и Г' различны, и точно
так же, что точки касания окружностей С2, Г и Г' различны.
442 PELUFHHH УПРАЖНЕНИЙ И ЗАДАЧ
Если оба одинаковые касания (Г, Сх) и (Г, С2) — внешние (внутренние),
то мы имеем следующее положение вешей. Так как касание (Г, Cj) — внеш-
внешнее и касание (Г, Сх) — также внешнее (внутреннее), то в силу сде-
сделанного замечания касание (Г, Г') должно быть внешним (внутренним).
Но в то же время касание (Г, С2) внутреннее, касание (Г', С2> внешнее
(внутреннее;, и потому касание (Г, Г') должно быть внутренним (внешним).
Итак, окружности Г и I" должны касаться друг друга одновременно и
внешним и внутренним образом.
Полученное противоречие показывает, что либо три точки попарного
касания окружностей Сь Г и Г' совпадают между собой, либо три точки
попарного касания окружностей С?> Г и Г совпадают между собой. Иначе
говоря, точка касания окружностей Г и Г' лежит либо на окружности Съ
либо на окружности С2.
Как и в первом случае, покажем, что через любую точку М одной
из окружностей С^ (или С2) проходят две окружности, касающиеся
в точке М окружности Сл (или С2) и в то же время касающиеся
другой данной окружности. Следовательно, в этом третьем случае
геометрическим местом точек М будет совокупность данных окруж-
окружностей.
Итак, геометрическое место точек М состоит всегда из данных
Окружностей Cj и С2 и, кроме того, включает в себя: а) окружность 2,
если окружности С, и С2 расположены одна вне другой или касаются
одна другой внешним образом (окружность 2' при этом не существует);
b) окружности 2 и 2', если окружности Сл и С2 пересекаются;
c) окружность 2', если окружности С, и С2 касаются одна другой
внутренним образом или расположены одна внутри другой (окруж-
(окружность ^1 при Vtom не существует).
267. В п. 232 было показано, что окружности Ни 2', каждая из
которых касается трёх данных окружностей одинаковым образом, пре-
преобразуются одна в другую инверсией с полюсом в радикальном цент-
центре / данных окружностей. Следовательно, линия центров окружностей
U и Г проходит через /. Далее там же было показано, что окруж-
окружности i! и М1 имеют своей радикальной осью внешнюю ось подобия
данных окружностей, и потому линия центров окружностей 2 и 1'
перпендикулярна к этой оси подобия.
Аналогично, если некоторая окружность 2, касается трёх данных
окружностей неодинаковым образом (скажем, окружностей В и С оди-
одинаковым образом, но неодинаковым образом окружностей А и В), то
та же инверсия с полюсом / преобразует 2!1 в некоторую окруж-
окружность 3^', также касающуюся трёх данных. Следовательно, линия
центров окружностей 2} и 2j' проходит через /. Далее, окружности
2, и 2j имеют своей радикальной осью, как указано в п. 234, одну
из внутренних осей подобия данных окружностей (в указанном выше
случае ту ось подобия, на которэй лежит внешний центр подобия
окружностей В и С, внутренний центр подобия окружностей А и В
и внутренний же центр подобия окружностей А и С). Поэтому линия
центров окружностей 2j и 2j' будет перпендикулярна к этой оси
подобия.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VH 443
268. Чтобы применить к решению предложенной задачи косвенный
метод, рассмотренный в упражнении 174, начинаем с решения следую-
следующей задачи:
A) Через точку М, лежащую внутри данного угла ВАС
(черт. 498), провести секущую ВС, образующую со сторонами
угла (не продолженными за вершину) треугольник АИС, имеющий
данный периметр 2р.
Рассмотрим вневписанную окружность этого треугольника, касаю-
касающуюся стороны ВС и продолжений сторон АВ' и АС соответственно
в точках Р и Q; так как периметр треугольника АВ'С равен 2р, то
мы будем иметь (сравнить ре-
решение упр. 90) АР= AQ = p.
Отсюда вытекает такое реше-
решение задачи А: строим окруж-
окружность, касающуюся прямых АВ
и АС в точках Р и Q, и через
данную точку М проводим к
этой окружности касательные.
Если точка /И будет лежать
вне построенной окружности
и притом в части" плоскости,
ограниченной отрезками АР и Черт. 498.
AQ и меньшей дугой PQ, то
зэдача будет иметь два решения (треугольники АВ'С и АВ"С" на
черт. 498). Если точка М будет лежать на меньшей дуге PQ, задача
будет иметь одно решение. При другом положении точки М задача
не имеет решений.
Чтобы решить теперь предложенную задачу:
B) Провести через точку М прямую В0С0, для которой пери-
периметр треугольника АВ0Си имеет наименьшее возможное значение, —
мы должны отыскать наименьшее значение р, для которого предыду-
предыдущая задача А ещё возможна. Это наименьшее значение р определяется
окружностью, проходящей через М и касающейся прямых АВ. и АС,
точнее говоря — большей из двух окружностей, удовлетворяющих
этим условиям. Построив эту окружность, как указано в решении
упражнения 263, и проведя к ней в точке М касательную ВиСи, мы
и получим искомый треугольник АВиСь.
УПРАЖНЕНИЯ К ГЛАВЕ VII (стр. 222).
269. Пусть точка М, лежащая в плоскости равностороннего тре-
треугольника ABC, удовлетворяет условию М$ = MB -\- MC. Так как
ВС=СА = АВ, то отсюда вытекает, что МА ¦ ВС= MB- С А -\- МС- АВ;
следовательно, четырёхугольник АВМС можно вписать в окружность,
и потому точка М лежит на описанной окружности.
В противном случае МА-ВС<^МВ- СА-\-МС- АВ (п. 237а;, и,
следовательно, MA <^ MB -J- MC.
444
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
270. 1°. Так как точки В, С и П получаются из точек В, С
k-CB
и D инверсией с полюсом Л, то мы имеем (п. 218) ВС = ¦
CD' =
k-DC
D'B' =
k-BD
, где k
AB-AC
степень инверсии. Отсюда
AC-AD ' AB-AD
ВС:CD':D'В = (BC- AD): (CD- AB):(DB- AC).
A)
Так как в правой части этого равенства точки А, В, С и D вхо-
входят вполне симметрично, то мы получим те же отношения сторон,
строя треугольник, аналогичный BCD', исходя не из вершины А,
а из какой-либо другой вершины четырёхугольника 1).
2°. Так как точки В, С, В' и С (черт. 499) лежат на одной
окружности, то углы ВВС и ВС А равны; точно так же равны углы
ВВП и BDA. Отсюда
Z.CBD' = /_BBD' —
— /_ ВВС = /_BDA —
— _/ ВСА. Аналогично и
для других углов треуголь-
треугольника.
3°. Пусть X, Y и
Z — основания перпенди-
перпендикуляров из точки А на
стороны CD, DB и ВС
треугольника BCD. Так
как точки A, D, X и У
лежат на одной окруж-
окружности, то / YXA =
= /_ YD А; так как точ-
точки Л, С, ЛТ и Z лежат
на одной окружности, то ^_ZXA^= ^_ZCA. Следовательно, ^/ YXZ =
= /_YXA — /_ZXA = /_YDA — /_ZCA = /_BDA — /_BCA. Но в
силу 2° имеем /_BDA — /_BCA =/_CВ'D', и значит угол при вер-
вершине X треугольника XYZ равен углу при вершине В' треугольника
BCD'. Таким же путём доказывается и равенство остальных углов
этих треугольников. Итак, треугольники XYZ и BCD' подобны
друг другу.
Далее, если треугольники AED и ABC подобны, то ED:BC=
= AD:AC, откуда ED:BD={AD-BC):{AC-BD) = B'C:B'D' в силу
формулы A). Кроме того, /_BDE=/_BDA — /_EDA = /_BDA —
— j/_BCA =/_CBD'. Следовательно, треугольники BDE и D'B'C
подобны. '
Черт. 499.
i) Если данный четырёхугольник ABCD вписанный, то вместо тре-
треугольника B'C'D' получаются три точки, лежащие на одной прямой; пре-
предоставляем читателю проследить, как видоизменяются в этом случае рас-
рассматриваемые свойства фигуры.
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VII
445
4°. Выполним теперь над точками Л, В, С и D инверсию с про-
произвольным полюсом О и произвольной степенью k; пусть точкам А, В,
С и D соответствуют в этой инверсии некоторые точки .4,, Вх, С1
k-CB
и Dv При этом имеем согласно п. 218: В1С) = ; А,/^ =
A-DA „„ „ &-BC-AD
= 7Гл-77^К' откУда
OA-OB-OCOD
&-CD-AB
. Аналогично най-
&-DB-AC
и, следовательно,
(ВС • AD): (CZ> ¦ АВ): (DZJ ¦ АС) =
B)
Последнее соотношение и показывает, что треугольник В'СD', о
котором говорилось выше, и аналогичный треугольник By'CA'D^',
который получится из четырёхугольника A^B^C-j)^ подобны между
собой. В салом деле, отношения сторон этих треугольников определяются
равенствами A) и аналогичными им равенствами B/C/rC,'/),' :D,'B,'=
= (Б,С,-Л,Д,):(С1?I-А,В1):(Д]В1-Л,С]). В силу соотношений B)
мы имеем, очевидно, B'C':C'D':D'B' =Б,'С,':С1'?>,':?,'?,'.
5°. Пусть четырёхугольники ABCD и A^B^D, обладают тем свой-
свойством, что треугольники BCD' и
указанных выше построений, подо-
подобны. Выбирая надлежащим образом
степень инверсии с полюсом Л,
преобразующей точки В, С и D
в точки В', С и D', а также
степень инверсии с полюсом Л,,
преобразующей В1? С',, D, в В/,
С,', ZJ/, можно сделать так, что
треугольники К CD' и BX'C^'D^'
будут не только подобными, но
и равными.
Далее, перемещая четырёх-
угольник -'IjBjC^.D], можно сделать
так, что треугольник BX'CA'D^' будет совпадать с B'C'D' (черт. 500).
При этом точки А,, Вл, С,, D, получаются из точек А, В, С и D с по-
помощью последовательности двух инверсий. Действительно, инверсия
с полюсом Л преобразует точки В, С, D и А соответственно в точки
В', С, D' и в точку, лежащую в бесконечности, а вторая инверсия с
полюсом Л, преобразует эти последние точки в точки В,, Cj,D, и Л^
Если четырёхугольники ABCD и A^CjD, не подобны между
собой, то эту последовательность инверсий можно заменить (упр. 251, 2°)
одной инверсией / и одной симметрией относительно прямой. Следова-
Следовательно, инверсия / преобразует точки Л, В, С и D в вершины четы-
Черт. 500.
446 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
рёхугольника, симметричного с A^BXC^D^ относительно некоторой
прямой и потому равного A^BXCAD^.
Полюс О и степень k инверсии / можно найти следующим обра-
образом. Так как точки, обратные точкам А, В, С и D в искомой инвер-
инверсии, образуют четырёхугольник, равный данному четырёхугольнику
k ¦ СВ k • DC
AXBXCADU то мы должны иметь В,С7 = 0B,Q?' ciD\= OC-OD '
°л- Отсюда
^^^ О)
и положение полюса инверсии О по отношению к точкам В, С и D
определяется, как указано в решении упражнения 127. Зная полюс
OB-OD-B.D,
инверсии, можем определить и её степень /г= ———! =
__ ОС-ОВ-С^В,
= ЬС ~" CD "
Примечания: 1°. Если четырёхугольники ABCD и Л1б1С1?>] подобны,
то соответствующие им треугольники B'C'D' и B\C{D\ также подобны,
как это следует из соотношения A). Однако в этом случае не всегда суще-
существует инверсия, обладающая требуемым свойством. В самом деле, если
такая инверсии с полюсом О существует, то мы имеем Л1^31 = „ . q^\
k-CA
АХС\ = ~—-7ТТ,- С другой стороны, в силу подобия четырёхугольников*
\J/\ • С/С
AlB\:AB = AiCl:AC. Отсюда непосредственно следует ОВ^ОС. По той
же причине OA~OB = OC = OD, так что четырёхугольник ABCD можно
впигать в окружность, и точка О есть центр этой окружности.
2°. Мы доказали существование 'при определённом условии) инверсии /,
преобразующей точки А, В, С и D в точки, образующие четырёхугольник,
равный данному четырёхугольнику A^B\C\D\. Можно показать, что такого
рода инверсия будет, вооби{е говоря, единственной (с точностью до знака
её степени). В самом деле, пусть инверсия /' с полюсом О' и инверсия /' с по-
полюсом О" преобразуют точки A,B,CnD соответственно в точки А', В', С и D'
и в точки А", В", С и О" такие, что четырёхугольники A'B'C'D' и A"B'C"D'
равны. В таком случае последовательность/'/" инверсий/' и /" преобразует
точки А1, В', С и О' в А", В", С" и D". Если полюсы О'и О'различны,'то
последовательность инверсий /7" можно -опять заменить одной инверси-
инверсией /0 и одной симметрией. Следовательно, инверсия /0 преобразует четыре
точки А', В', С и О' в новые четыре точки, образующие четырёхугольник,
равный А"В"CD". Так как четырёхугольники А'В1 CD' и A'B'C'D" равны,
то, в силу сказанного в предыдущем примечании, это не может иметь
места для произвольного четырёхугольника A'B'C'D', т. е. для произволь-
произвольного четырёхугольника ABCD. Если же полюсы инверсий /' и /" совпадают,
то в силу равенства четырёхугольников A'B'C'D' и A"B"C"D" степени
этих двух инверсий отличаются только знаком.
Один из случаев, когда полюс инверсии / не является единственным,
разобран в решении задачи 387.
3°. Задача, поставленная в упражнении 127, может, вообще говоря,
иметь два решения, одно решение или вовсе не иметь решений. В дан-
ДОПОЛНЕНИЯ К ТРЕТЬЕЙ КНИГЕ. ГЛАВА VII 447
ном случае аналогичная задача отыскания точки О заведомо будет иметь
решение, так как существование инверсии / нами доказано. Однако, как
это следует из предыдущего примечания, из двух точек О, удовлетворяю-
удовлетворяющих условиям C), только одна будет, в общем случае, полюсом искомой
инверсии.
270а. Пусть инверсия с полюсом О и степенью k преобразует
три данные точки А, В и С в три другие точки А', В' и С", которые
образуют треугольник А'В'С, равный данному треугольнику A.B.C..
k-CB
При этом мы должны иметь В'С =- == В^С^ и аналогичные
равенства для двух других сторон. Отсюда
OB.OC = k~r; A)
влсл
из этого равенства и из двух других ему аналогичных имеем
ВС С А АИ
ОА:ОВ:ОС= ¦ ' ' : ' ' : ' ' . Таким образом, положение точки О
ВС С А АВ
определяется, как указано в решении упражнения 127 (сравнить решение
упр. 270, 5°). Зная полюс инверсии О, можно определить из равен-
равенства A) и её степень.
Примечание. В то время как задача, рассмотренная в упражне-
упражнении 127, может иметь, а может и не иметь решений, данная задача все1ла
имеет решения. В самом деле, инвер-
инверсия с полюсом Р на окружности, опи-
описанной около треугольника ABC, преоб-
преобразует точки А б и С в лежащие на
одной прямой точки а, Ь и с (черт. 501>.
Выбрав полюс Р надлежащим образом,
можно достичь того, что будем, напри-
например, иметь аЬ^ас (для этого достаточно,
чтобы РВ:РС=АВ:АС). Точно так же
точки -4^ В\ и С] можно с помощью
аналогичной инверсии преобразовать в
три точки а\, Ь\ и С], лежащие на одной
примой и удовлетворяющие условиям ojfcj =o1'-1 = ofc = яе. Отсюда сле-
следует (как и в решении упр. 270, 5°), что вершины треугольника ABC
можно преобразовать в вершины треугольника, равною АХВ\С\, с помощью
последовательности двух инверсий.
Если треугольник ABC не подобен АХВХС], то эту последовательность
двух инверсий можно заменить одной инверсией / и одной симметрией. Инвер-
Инверсия /, очевидно, преобразует точки А, В и С в вершимы треугольника, рав-
равного AiBtCi.
Если треугольники ABC и АхВ^С^ подобны, то полюсом О искомой ин-
инверсии будет, очевидно, центр окружности, описанной около треугольника
ABC.
271. При указанных в тексте задачи условиях мы имели бы ОР2—OQ2=
==МР* — MQi^MP2 — М'СГ-. В силу п. 128а, следствие, точки О,
М, М лежали бы на одной прямой, и, как и в п. 241, мы имели бы
ОМ -ОМ' = ОР" — PNT- = const.
448
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
271а. Пусть AB=CD = a; BC= AD— b; AO:AB=h; BO:BA =
= h' (черт. 211). В силу подобия треугольников AOMwABD, BOM,
и ВАС имеем OM=BD-—r,=BD-h; ОМ' = АС- — = AC-h''. От-
АВ ВА
сюда ОМ-ОМ'' = AC-BD-h-H'. Но четырёхугольник ABDC—вписан-
ABDC—вписанный, откуда AC-BD'=AD-BC— AB-CD = b* — а2, и ОМ-ОМ =
= hh'(b2 — a-).
ЗАДАЧИ К ДОПОЛНЕНИЯМ К ТРЕТЬЕЙ КНИГЕ (стр. 223).
272. Пусть 5 — один из центров подобия окружностей С и С,
(черт. 502); М и N', а также Q и Р'—две пары антигомологических
точек; К и L — точки пересечения прямых AW и QP' с радикальной
осью. Так как прямые MQ и N'P' пересекаются (как антигомологи-
антигомологические хорды, см. п. 224) на
радикальной оси, то мы имеем
(п. 200) равенство сложных от-
отношений (SKMN')=(SLQP').
Изменяя положение секущей QP'
и оставляя на месте секущую
MN', видим, что (SLQP') =
= const.
273. Пусть Р, А, В, С
и D — пять точек одной окруж-
окружности; Р', А', В', С и D' —
точки, им обратные. Так как
пары прямых РА и Р'А', РВ и Р'В', PC и Р'С, PD и Р'П пере-
пересекаются в точках Ао, Во, Со и Do, лежащих на радикальной оси
обеих окружностей (п. 224), то, обозначая через (РА, РВ, PC, PD)
сложное отношение четырёх прямых, будем иметь (РА, РВ, PC, PD) =
= (A0B0C0D0)=(P'Ar, Р'В', Р'С, P'D'). Но (РА, РВ, PC, PD)
является сложным отношением точек А, В, С и D согласно п. 212,
и то же имеет место для точек А', В', С и D'.
Если окружность, на которой лежат точки А, В, С к D, совпа-
совпадает со своей обратной, то точки Ао, Во, Со и Do лежат на поляре
полюса инверсии (п. 224, примечание), и то же рассуждение сохра-
сохраняет силу.
Если окружность, на которой лежат точки А, В, Си D, прохо-
проходит через полюс инверсии О, то точки А', В1, С и D' лежат на пря-
прямых О А, ОБ, ОС и OD, и равенство (О А, ОБ, ОС, О D) = (А'В'С D')
становится очевидным.
Примечание. Другое доказательство приведено во втором гоме
книги Адамара, п. 719.
274. Пусть А, В, С и D — четыре точки одной окружности, Р—
произвольная точка той же окружности; А', В', С и D' — точки, об-
обратные точкам Л, В, С и В в инверсии с полюсом Р и произвольной
степенью. По определению (п. 212), сложное отношение точек А, В, С и D
Черт. 50Z
ЗАДАЧИ К ДОПОЛНЕНИЯМ К IIГ КНИГЕ 449
равно (PA,PB,PC,PD). Но (PA,PB,PC,PD) = (A'B'C'D') --
Мы имеем А'С = ??L. VC=±^; (п. 218), откуда ^
OB AC . A'D' OB AD _
= ОА'ВС А#налогично "айДём, что giy = (JA'BD' Отсюда полУча-
AC AD
ем (PA, PB, PC, PD)= —: — . Это равенство определяет сложное
отношение точек А, В, С и D только по абсолютной величине; сложное от-
отношение этих точек будет, как легко видеть, положительным, если точки
С и D лежат на одной и той же из двух дуг, имеющих своими концами
точки А и В, и отрицательным, если они лежат на различных дугах.
275. Пусть данные окружности С, и С2 преобразуются в две равные
окружности С7 и С2 с помощью инверсии /. Так как окружности
С, и С'2 симметричны относительно их радикальной оси С, то (упр.
250) окружности Сл и С2 обратны относительно той окружности С,
которая преобразуется инверсией / в прямую С. Следовательно, по-
полюсом инверсии / может быть произвольная точка окружности инвер-
инверсии, преобразующей С, в С2 (а степень инверсии произвлльна).
Чтобы преобразовать три данные окружности в три равные окруж-
окружности, необходимо принять за полюс инверсии одну из точек пересе-
пересечения, двух окружностей, инверсии относительно которых преобразуют
одну из данных окружностей в две другие.
276. Пусть Cj, С2 и С3— данные окружности; Г28, Г31 и Г13 —
окружности инверсий, преобразующих соответственно С2 в Са, С8 в
Q и С, в С2. Центрами окружностей Г будут (в силу п. 222) центры
подобия данных окружностей, взятых попарно. При этом окружности
Г23, Г31 и Г12 выбраны так, что их центры лежат на одной прямой,
т. е. на одной и той же оси подобия данных окружностей.
Окружности С2, С3 и T2S имеют общую радикальную ось (п. 228);
эта радикальная ось проходит через радикальный центр трёх данных
окружностей. Следовательно, радикальный центр данных окружностей
С,, С'2 и С3 имеет относительно Г<,3 ту же степень, что и относительно
каждой из данных окружностей. То же имеет место и для окружно-
окружностей Г31 и Г12. Следовательно, радикальной осью окружностей Г23,
Г31 и Г12 служит перпендикуляр из радикального центра данных окруж-
окружностей на ось подобия, на которой лежат центры трёх окружностей Г.
277. Если инверсия с полюсом О преобразует две данные окруж-
окружности С, и Сг в две окружности С,' и С2', из которых первая (С/)
делит вторую (С'2Г) в точках А' и В' на две равные части, то окруж-
окружности С, и С2 также пересекаются. При этом окружность 2, прохо-
проходящая через точки пересечения окружностей С, и С2 и ортогональная к
окружности С2, преобразуется рассматриваемой инверсией в прямую ли-
линию А'В. Следовательно, полюс О есть произвольная точка окружности ?.
Аналогично, в более общем случае, получаем две окружности 2'
и S", проходящие через точки пересечения данных окружностей и
2У Эпемен! арная геометрия
450
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
пересекающие окружность С2 под углом, равным половине данного
центрального, одна из которых должна преобразовываться искомой ин-
инверсией в прямую линию. Следовательно, полюсом инверсии может
быть любая точка той или другой из окружностей 2' и 2".
278. Пусть некоторая прямая L пересекает две окружности С и С
(или С и С"), имеющие своими предельными точками точки Р и Q
(черт. 503), в точках А, В и А', В' (или А, В и А", В"). Требуется
доказать, что биссектрисы углов АРВ и А'РВ' совпадают (или что
биссектрисы углов АРВ и А"РВ" взаимно перпендикулярны).
D
Черт. 50S.
Обозначим через М точку пересечения прямой L с радикальной
осью D данных окружностей. Мы имеем (в силу упр. 152) МА-МВ —
— МР*, или МА: МР = МР: MB. Отсюда следует, что треугольники
MAP и МРВ подобны, так что
/_МАР = /_МРВ. ^ A)
Таким же образом докажем:
/_МА'Р=МРВ',
/_ МА"Р = /_МРВ".
B)
C)
Из равенств A) и B) следует, что /_АРА' = ^_МА'Р — ^_МАР' =
= /_МРВ'' — /_МРВ= /_ВРВ'. Отсюда вытекает, что углы АРВ и
А'РВ' имеют общую биссектрису.
Аналогично из равенств A) и C) следует, что /_ АРА" =180° —
— /_ МАР—/_МА"Р = 180°— /_МРВ—/_МРВ" = 180° — /_ВРВ"=.
= /_ВРХ, где РХ — продолжение РВ". Отсюда следует, что углы
АРВ и А'РХ имеют общую биссектрису, а углы АРВ и А"РВ" —
взаимно перпендикулярные биссектрисы.
Если, в частности, принять за окружность С окружность Со, каса-
касательную к прямой L, то точки А' и В' обе совпадают с точкой каса-
касания Ло, так что прямая РА0 будет биссектрисой угла АРВ.
279. Пусть ABCDEF—шестиугольник, вписанный в данную
окружность Г; L, М, N— точки пересечения противоположных сторон
(черт. 504).
ЗАДАЧИ К ДОПОЛНЕНИЯМ К III КНИГЕ
451
Проведём через точки А и D произвольную окружность Г,. Постро-
Построим окружность Г2, 'соответствующую Г\ в инверсии с полюсом L и
степенью, равной степени точки L относительно Г. Окружность Г2
пройдёт через точки В и Е; точки А и В, D и Е будут антигомоло-
антигомологическими точками окружностей Г, и Г2 относительно центра подобия L.
Построим далее окружность Г3, соответствующую Г, в инверсии
с полюсом N и степенью, равной степени точки N относительно
окружности Г. Окружность I'g пройдёт через точки С и F; точки Ли/7,
D и С будут антигомологическими точками окружностей 1\ и Г3 отно-
относительно центра подобия N.
Данная окружность Г пересекает окружности Г,, Г2 и Г3 под рав-
равными углами (п. 227); поэтому четыре точки пересечения В, С, Е и
F окружности Г с окружностя-
окружностями Г2 и Г3 будут попарно
антигомологичны относительно
одного из центров подобия
этих двух окружностей; при
этом точка В будет антигомо-
логична именно точке С, а не
точке F, так как угол между
Г и Г2 в точке В и угол меж-
между Г и Г3 в точке F будут иметь
оба одинаковое направление
(противоположное направлению
угла между Г и Гг в точке Л),
в то время как в антигомоло-
антигомологических точках соответствую-
соответствующие углы должны иметь проти-
противоположные направления. Итак,
точки В и С, Е и F будут
попарно антигомологичны относительно одного из центров подобия
окружностей Г2 и Г3, откуда следует, что N будет одним из центров
подобия окружностей Г2 и Г3.
Остаётся ещё показать, что три центра подобия L, Ми N окруж-
окружностей Г}, Г2 и Г8, взятых попарно, лежат на одной оси подобия. Это
вытекает из следующих соображений. Если окружность Г пересекает
все окружности 1\, Г, и Fg под строго равными углами, то все
три центра подобия будут внешними (см. решение упр. 256). Если
же Г пересекает окружности 1\, Т2 и Г3 не под строго равными
углами, то она пересекает две из них под строго равными углами, а
третью—под пополнительным. Имеем один внешний и два внутренних
центра подобия (опять в силу сказанного в решении упр. 256). Как в
том, так и в другом случае три центра подобия Ly M и N действи-
действительно лежат на одной прямой — оси подобия.
280. Пусть для определённости требуется найти окружность, каса-
касающуюся данных окружностей Ох, О2 и О3 одинаковым образом. Обо-
Обозначим через a, b и с точки касания искомой окружности с тремя
29*
Черт. 504.
452
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
и Sls — внешние центры подобия данных
S2S и
данными и через 512, 523 и Sls
окружностей.
Рассмотрим три инверсии соответственно с полюсами 12, 2S 81,
преобразующие последовательно Ох в О,, О2 в Оа, Os в О,. Точка a
преобразуется этими тремя инверсиями (в силу п. 227) последовательно
в точку Ь, в точку с и, наконец, в точку а. Обратно, если а — точка
первой окружности, преобразующаяся последовательностью трёх ука-
указанных инверсий в самоё себя, и b и с — соответствующие ей точки
окружностей О2 и О3, то окружность, проходящая через точки a, b
и с, касается трёх данных, так как иначе точкой, антигомологической
точке с относительно 53], была бы не точка а, а вторая точка пере-
пересечения окружности abc с окружностью Ог (ср. решение задачи 279).
А
В
В
Черт. 505.
Черт. 506.
Таким образом, определение положения точки а сведено к упражне-
упражнению 253; точки b и с можно получить с помощью указанных выше
инверсий.
Аналогичные рассуждения применимы и к окружностям, касающимся
данных неодинаковым образом.
281. Пусть ВАС—прямой угол, о котором идёт речь (черт. 505).
Точка N, в которой пересекаются касательные к окружности в точках
В и С, обратна относительно данной окружности точке М — середине
хорды ВС, так как произведение ОМ-ON равно квадрату радиуса
окружности (п. 216). Так как геометрическое место точек М есть
окружность, то геометрическое место точек N есть также окружность
(хорда ВС не может совпадать с диаметром, следовательно, точка М
не может совпадать с центром О, и геометрическое место точек N
не вырождается в прямую линию; исключение будет только в том
случае, когда точка А лежит на окружности — при этом точка М всё
время совпадает с О, а точки N все лежат в бесконечности).
282. Пусть для определённости окружность о расположена внутри
четырёхугольника ABCD, так что последний принадлежит к тому тину
описанных четырёхугольников, который изображён на чертеже 332.
1°. Прямые ас, bd, AC и BD пересекаются в силу упражнения 239
в одной точке Р (черт. 466 и 506). Эта точка Р имеет своей полнро.1
относительно окружности о ту прямую, на которой лежит точка пере-
ЗАДАЧИ К ДОПОЛНЕНИЯМ К III КНИГЕ
453
сечения е прямых ab и cd, а также точка / пересечения прямых ad
и be (п. 211). Та же точка Р имеет своей полярой относительно
окружности О ту прямую, на которой лежит точка пересечения Е пря-
прямых АВ и CD, а также точка пересеченуя F прямых AD и ВС (опять
в силу п. 211). Так как точки е, /, Е и F лежат, в силу упражне-
упражнения 239, на одной прямой, то точка Р имеет относительно окружностей
о и О одну и ту же поляру и, следовательно, является (упр. 241.2°)
одной из их предельных точек.
2°. Так как прямая АВ касается окружности о в точке а, то пря-
прямая Ра есть биссектриса угла АРВ в силу задачи 278. Точно так же
РЬ есть биссектриса угла ВРС.
3°. Так как прямые Ра и РЬ являются биссектрисами углов АпВ
и ВРС, то эти прямые взаимно перпендикулярны. Поэтому окружность,
которая получилась бы в задаче 281, исходя
из точки Р и окружности о, проходит че-
через точки А, В, С a D и, следовательно,
совпадает с О.
4°. Если существует один четырёх-
четырёхугольник ABCD, вписанный в окружность _|
О и описанный около окружности о, то "
при вращении пары перпендикулярных
прямых ас и bd около точки Р точки пере-
пересечения касательных в точках а, Ь, с
и d будут перемещаться по окружности
(задача 281), и эта окружность будет сов-
совпадать с окружностью О, так как на ней
должны лежать точки А, В, С и D.
Итак, если существует один четырёхугольник, вписанный в окруж-
окружность О и описанный около окружности о, то существует бесчислен-
бесчисленное множество таких'четырёхугольников.
Среди этих четырёхугольников можно найти такой, для которого
одна из диагоналей, например BD, будет совпадать с диаметром
окружности О. Для этого достаточно выбрать такое положение точки а,
при котором касательная аВ пересекала бы окружность О в конце
диаметра, проходящего через Р. Так как точка о лежит на прямой
ОР, то четырёхугольник^ этот будет симметричен относительно прямой
ОР (черт. 507). При этом треугольник ABD будет прямоугольным.
Восставим в точке о перпендикуляр оК к прямой BD. Получим два
равных треугольника оаВ и ойК- Применяя к треугольнику DoK тео-
рему упражнения 136, получим — = — + — = -^ + — или
Черт. 507.
) _ 8J .
A)
где R и г—радиусы окружностей О и о, а с—расстояние между их
центрами.
454
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Чтобы в окружность О можно было вписать четырехугольник,
описанный около окружности о, необходимо, чтобы их радиусы
и расстояние между их центрами удовлетворяли соотношению A).
Обратно, если это соотношение выполнено и R ^> 8 (в выведенное
соотношение R и 8 входят симметрично, и потому возможно как R~^> 8,
так и R <^ 8), то можно построить прямоугольный треугольник ABD,
имеющий своей гипотенузой диаметр DB окружности О, проходящий
через точку о, и основанием биссектрисы — эту же точку о. Окруж-
Окружность, имеющая своим центром точку о и касающаяся сторон AD и
АВ, будет иметь радиус, определяемый соотношением A), и потому
будет совпадать с данной окружностью о. Строя точку С, симметрич-
симметричную с А относительно BD, получим один из искомых четырёхуголь-
четырёхугольников.
Примечание. Мы предполагали, что окружность о располагается
внутри четырёхугольника ABCD.
Если четырёхугольник ABCD—выпуклый, но окружность о касается
продолжений всех его сторон, как на чертеже 334, то гее предыдущие рас-
рассуждения сохраняют силу с единствен-
единственным изменением, состоящим в том,
что в соотношении A) А?<8.
Пусть'теперь описанный четырёх-
четырёхугольник ABCD — несобственный, как
на черт. 336 и 508. Если четырёхуголь-
четырёхугольник ABCD можно вписать в окруж-
окружность, то углы ABC и ADC равны, так
что треугольники ABE и CDE, где Е —
точка пересечения прямых AD и ВС,
подобны. Из подобия этих треугольни-
треугольников имеем AB = k-CD; BE=k-DE;
АЕ= k-CE, где k — коэфициент подо-
подобия. Условие АВ + AD = ВС + CD, при
котором четырёхугольник ABCD—описанный (сравнить решение упр.87), при-
принимает вид k-CD + (k-CE+ED) = (k-DE + EQ + CD или (k— 1) (CD +
+ EC — ED) = 0. Так как CD + EC > ED, то k= I, и, следовательно,
AB—CD; AD = EC. Итак, четырёхугольник ABCD есть антипараллело-
грам (п. 46а), т. е. образован диагоналями AD и ВС и боковыми сторонами
АВ и CD равнобедренной трапеции ABDC.
Обратно, всякий антипараллелограм можно, очевидно, вписать в окруж-
окружность. При этом середины око' дуг АС и BD равноудалены от всех сто-
сторон антипараллелограма, так как прямые Во и Ао' — биссектрисы углов
ABC и BAD. Каждая из точек око' есть центр окружности, касающейся
всех сторон антипараллелограма. Соотношение A) заменяется условием
R = & (причём r<2R).
283. Пусть О-—центр окружности, по отношению к которой каж-
каждая вершина данного треугольника ABC является полюсом противо-
противолежащей стороны. Так как прямая ОА перпендикулярна к поляре ВС
точки А, то точка О должна лежать на высоте AD треугольника,
проходящей через А. По той же причине точка О должна лежать чна
двух других высотах треугольника. Таким образом, О есть точка пе-
пересечения высот треугольника. Радиус искомой окружности должен удов-
удовлетворять соотношениям R*=OA-OD=OB-OE=OC-OF (черт. 509).
Черт. 503.
ЗАДАЧИ К ДОПОЛНЕНИЯМ К III КНИГЕ
455
При этом три последние произведения равны в силу подобия треуголь-
треугольников ОАЕ и OBD, OAF и OCD. Треугольник ABC должен быть тупо-
тупоугольным для того, чтобы точки А и D (а также В и Е, С и F)
лежали по одну сторону от точки пересечения О его высот.
284. Пусть существует треугольник ABC, вписанный в окружность
О, и сопряжённый (задача 283) с окружностью О2 (черт. 51.0). В силу
сказанного в решении задачи 283 точка О2 есть точка пересечения
высот этого треугольника. Так как прямая ВС есть поляра точки А
относительно окружности О2, то радиус /?2 окружности О2 удовлетво-
В
D
Черт. 509.
Черт. 510.
ряет условию R2 =O2A-O2D. Если К—вторая точка пересечения
прямой AD с окружностью Ох, то O2D = —O2K (упр. 70), так что
?
(i)
т. е. квадрат радиуса второй окружности равен половине степени еб
центра относительно первой окружности.
Кроме того, одна из вершин треугольника ABC необходимо лежит
внутри окружности О2, а 'две другие — вне её. В самом деле, если пря.
мая ВС не пересекает окружности О2, то полюс А прямой ВС лежит
внутри этой окружности, а точки В и С — вне её. Если же прямая
ВС пересекает окружность О2, то одна из точек В и С лежит внутри
окружности (так, как одна из точек В и С лежит на поляре другой)
и, следовательно, две другие вершины треугольника — вне её. Так
как на окружности Ох лежат как точки, внутренние по отношению к
окружности О2, так и точки, внешние относительно О2, то окружно-
окружности С\ и О^ пересекаются.
Обратно, пусть Ох и О2 — две пересекающиеся окружности, удов-
удовлетворяющие условию A). Пусть А—одна из точек окружности Ov
456
РЕШЕНИЯ УПРАЖНЕН ИЙ И ЗАДАЧ
лежащая внутри окружности О2,К—вторая точка пересечения прямой
О2/4 с окружностью Ог и D — середина отрезка О2Д\ Так как
и #2~> О2А (так как точка 4 лежит внутри окружности О2), то R2<T>ZD.
Следовательно, О2А <^ O2D <^ ОоЛ". Точка D лежит между точками Л
и Л", т. е. внутри окружности Ov Прямая, перпендикулярная к O2D
в точке D, пересекает окруж-
окружность О, в двух точках В и С.
Точка А есть полюс прямой ВС
относительно окружности О2 в
силу равенства B). Отсюда сле-
следует, что поляры точек В и С
проходят через А. Так как точ-
точки А, В, С и К лежат на одной
окружности и OvD^DK, то
Черт. 511.
р
BD-DC = AD- DK = AD ¦ O2D.
Следовательно, треугольники
BO2D и ACD (а также CO2D
и ABD) подобны друг другу,
и потому прямая АС перпенди-
перпендикулярна к ВО., (а прямая АВ —
к СО2). Таким образом, пря-
прямые АС и АВ являются соответственно полярами точек В и С. Тре-
Треугольник ABC сопряжён с окружностью О2. Таких тре> гольников суще-
существует бесконечное множество ввиду произвола выбора вершины А.
285. Пусть ABC — данный треугольник (черт. 511). Выполним ин-
инверсию относительно окружности ?, проходящей через точку А и име-
имеющей своим центром точку пересечения О
(отличную от А) окружностей, дугами ко-
которых служат стороны АВ и АС данного
треугольника. Дуги АВ и АС преобра-
преобразуются в прямолинейные отрезки АВ' и АС,
дуга ВС — в некоторую дугу В'С. Углы
криволинейного треугольника ЛЕС равны
соответственным углам треугольника АВ'С,
имеющего стороной В'С дугу окружности.
Так как на сторонах данного треугольника ABC не лежит, по усло-
пию, точек пересечения данных окружностей, то на отрезках АВ' и
АС не лежит вторых точек пересечения прямых АВ' и АС С той
окружностью, дугой которой служит В'С. *
Если существует окружность, ортогональная к трём данным, то она
преобразуется рассматриваемой инверсией в окружность с центром А
(т. е. ортогональную к прямым АВ' и АС), ортогональную к окруж-
окружности, дугой которой служит В'С. Точка А будет, следовательно,
внешней по отношению к этой последней окружности (черт. 512), а
ЗАДАЧИ К ДОПОЛНЕНИЯМ К III КНИГЕ 457
сумма углов криволинейного треугольника АВ'С будет меньше суммы
углов прямолинейного треугольника АВ'С
Если не существует окружности, ортогональной к трём данным, то,
выполнив ту же инверсию, мы снова получим два прямолинейных от-
отрезка АВ' и АС. При этом уже не будет существовать окружности
с центром А, ортогональной к той окружности, дугой которой служит
В'С. Следовательно, точка А будет внутренней по отношению к этой
последней окружности (черт. 511), а сумма углов криволинейного тре-
треугольника АВ'С будет больше суммы углов прямолинейного треуголь-
треугольника АВ'С.
286. Так как точки В', С и D' лежат на одной прямой, то мы мо-
можем предполагать, что и точка С лежит между точками В' и D'\ при
этом (п. 127) АВ'2-О'С + АО'~-В'С — AC'-B'D'= B'C-CD'¦B'D'.
Если k — степень инверсии, преобразующей точки В, С и D в точки
в; с и d; to ав =JL ? ± ?gL
L, ас = ?. ad = ;
AC-AD' AB-AD'
Подставляя эти значения в предыдущее соотношение, получим:
ks-CD . ks-BC ks-BD ks-BC-CD-BD
CAD*'
AD*-AB-AC~AC?-AB-AD~ AB?¦ AC*¦ AD>- '
Сокращая на ka и умножая почленно на АВ1•• АС2 - AD2, найдём
CD-AC-AD-{-BC-AB-AC — BD-AB.AD=BC-CD-BD. Отсюда, груп-
группируя члены, будем иметь AC-{AD-CD-\-АВ• ВС) = BD• (АВ• AD-\-
+ ВС-CD), или A %
+ BC.CD=AB.BC +
ношение, выведенное в п. 240.
458
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
КНИГА ЧЕТВЁРТАЯ.
ПЛОЩАДИ.
УПРАЖНЕНИЯ К ГЛАВЕ I Гетр. 232).
287. Так как высота равностороннего треугольника со стороной а
равна -jr- аУз (сравнить п. 167), то его площадь равна —-а • -=- аУ 3 =
•р
288. В силу упражнения 287 имеем равенство — а-УТ = 1 м?,
откуда а =1,52 м. *
289. Пусть ABCD — данный квадрат (черт. 513); Е, F, G и Н —
середины его сторон. Прямые АЕ, BF, CG и DH рассекают площадь
данного квадрата на девять частей, одна из
которых (обозначенная на чертеже цифрой 9)
есть квадрат.
Опустив из точки А перпендикуляр АК на
прямую CG, получим треугольник /', равный
треугольнику /. Следовательно, сумма пло-
площадей частей / и 2 равна сумме площадей ча-
частей /' и 2, т. е. площади квадрата 9.
Итак, пл./ -(-пл. 2 = пл.З + пл.4 = пл.5-[-
-\-nn.6 — пл.7-|-пл.<5 = пл.9. Отсюда и сле-
следует, что площадь нового квадрата в пять раз
меньше площади данного.
290. Так как пл./=пл.2; пл. 3 = пл.4:
пл. / -\- пл. 5 -j- пл.З = пл.2 -\- пл. б-(-пл. 4
(черт. 514), то пл. 5 = пл. 6.
291. Так как из двух треугольников с общим основанием ббль-
шую площадь имеет тот, который имеет большую высоту, то из всех
треугольников с общим основанием и равными углами при вершине
мы должны выбрать тот, который имеет наибольшую высоту.
Геометрическое место вершин А равных углов этих треугольников
есть дуга ВАС (черт. 515); точнее говоря, дуга ВАС и дуга, ей
симметричная относительно ВС; но вторая дуга не приводит к новым
треугольникам. Если Ай — точка пересечения этой дуги с перпендику-
перпендикуляром, восставленным в середине /Уо стороны ВС, А—произволь-
А—произвольная точка этой дуги и АН — высота, треугольника ABC, то мы имеем,
очевидно, АН <^ А0Н0, и, следовательно, наибольшей высотой будет Д//о.
Итак, наибольшую площадь имеет равнобедренный треугольник А0ВС.
292. Если О — точка пересечения диагоналей АС и BD трапе-
трапеции ABCD (черт. 278), то nn.ACD = nn.BCD. Отнимая от равных
площадей площадь треугольника COD, получим nn.AOD = nj\.BOC.
Обратно, если в некотором четырёхугольнике два треугольника,
образованные двумя его противоположными сторонами и отрезками
КНИГА ЧЕТВЁРТАЯ. ГЛАВА
459
диагоналей, равновелики, то данный четырёхугольник есть трапеция.
Действительно, если пл. AOD = пл. ВОС, то и пл. AOD -\- пл. COD =
= пл.ВОС-|-пл.ШД, т. е. nn.ACD — m.BCD. Следовательно', тре-
треугольники ACD и BCD, имеющие общее основание, имеют и равные
высоты, так что прямая АВ параллельна прямой CD.
В
Черт. 514.
В
Нз Н С
Черт. 515.
293. Пусть К, L, M, N, Р и Q — середины сторон и диагоналей
четырёхугольника ABCD (черт. 516), ОР и OQ — прямые, иарал-
д
i
/
'1
к
7
в
L
V
/
N D
Черт. 516.
М
Черт. 517.
лельные BD и ЛС. Так как АР = РС, то пл.ЛВР = пл.РВС,
пл. /4ДР = ил. PDC и, следовательно, nn.ABPD = nn.BCDP =
— —nn.ABCD. Далее, так как BL=LC; DM=MC, то un.BPL =
= nn.LPC, nn.DPM = nn.AlPC и, следовательно, roi.PZ.CM =
= — nn.BCDP=— пл.ABCD. Наконец, прямая ОР параллельна BD и,
следовательно, параллельна /.Ж, так что nn.OLCM=un.PLCM =
= —пл.ЛбС/). Точно так же доказывается, что и каждая из площадей
4
ONAK, OKBL и OMDN равняется одной четверти площади ABCD.
294. Так как пл.У = пл.2, пл.3 = пл.4, пл.5 = пл.б, пл.7 = пл.5
(черт. 517), то площадь полученного параллелограма KLMN вдвое
более площади данного четырёхугольника.
Если диагонали двух четырёхугольников соответственно равны
и пересекаются под равными углами, то обоим четырёхугольникам
460 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
соответствуют равные параллелограмы, аналогичные KLMN, а потому
четырёхугольники равновелики.
• 295. Пусть О — такая точка, лежащая внутри треугольника, что
пл. ОВС: пл. ОСА : пл. OAB=p:q:r (черт. 188). Треугольники ОСА
и ОАВ имеют общее основание О А, и потому их площади относятся
как соответствующие высоты или, что то же, как отрезки аС и аЬ.
' ' В Л
С с D
Черт. 518.
Таким образом имеем aC:aB:=q:r; bA:bC=r:p; cB:cA = p:q.
Следовательно, для построения точки О достаточно разделить две
стороны треугольника в данных отношениях и соединить точки деле-
деления с противолежащими вершинами.
Если треугольники ОВС, ОСА, ОАВ равновелики, то точка О
есть центр тяжести треугольника (п. 56).
295а. Если прямые .4а, ВЬ, Сс (черт. 188) проходят через одну
точку О, то (упр. 295) аВ : аС= пл.ОАВ : пл.ОАС; ЬС:ЬА =
= пл.О ВС :пл.О В А; с А : сВ=пл.ОСА : пл. ОСВ. Перемножая эти три
аВ ЬС сА
равенства, получим — - — • — = 1 (все отрезки рассматриваю ich
лишь по абсолютной величине).
296. 1°. Проводим через точку О прямые, параллельные сторонам
параллелограма ABCD (черт. 518), и обозначим через а, Ь, с и d
точки пересечения этих прямых со сторонами АВ, ВС, CD и DA.
Имеем пл. ОАа = пл. OdA; пл. ОаВ= пл. ОВЬ; пл. ОСс= пл. ОЬС,
пл. OcD = roi. ODd. Отсюда путём почленного сложения и получаем
искомое соотношение.
2°. Проводим через точки В и D прямые ВВ" и DD', параллель-
параллельные АО (черт. 519 и 520), и пусть Б' и D' — точки пересечения этих
прямых с АС. Треугольники ADD' и СВВ' равны, откуда AD' = В'С.
Так как прямая ВВ' параллельна прямой АО, то пл. СМВ=пл. ОАВ1
и аналогично пл. О/Ш = пл. OAD'. Но треугольники OAD' и ОВ'С
равновелики, как имеющие равные основания AD' = B'C и общую
высоту ОН, и потому пл. СМ1)=пл. ОВ'С. Так как АС=АВ'-\-В'С
(черт. 519) или АС=АВ'— В'С (черт. 520), то пл. ОАС=
= ^-АС- ОН = (АВ' ± В'С) • ОН = ~АВ' ¦ ОН ±_~ ВС ¦ ОН =
— xui.OAB1 А-пп.ОВ'С=пл.ОАВ±пл. OAD.
КНИГА ЧЕТВЁРТАЯ. ГЛАВА I 461
297. Пусть Е и F—середины непараллельных сторон трапеции
ABDC (черт. 521).
1°. Если ВВ1—перпендикуляр к CD и ЕК—перпендикуляр к BD,
то из подобия треугольников EFK и BDB, имеющих соответственно
перпендикулярные стороны, следует,
что EF-BB' =BD-EK, причём
EF-BB' есть площадь данной трапе-
трапеции.
С N В' D
Черт. 520. Черт. 521.
2°. Если прямая MN, проходящая через точку Е, параллельна BD,
то треугольники ЕАМ и ECN равны, откуда пл. ABDC= пл. MBDN =
Г) J~\ С" J>*
. /-)/ / ¦ /_, /\ . I -
Площадь треугольника B?D равна — BD ¦ ?7^ = —пл. ЛВ?>С.
298. Если О — точка, лежащая внутри правильного многоуголь-
многоугольника ABC...KL, tonn.ABC...KL=nn.OAB-{-nn.OBC-\-...-\-nn.OKL-\-
-\-пл.OLA. Отсюда следует, что пл.ABC... KL равна половине произве-
произведения стороны многоугольника на сумму расстояний от точки О до всех
его сторон, так что эта сумма расстояний не зависит от выбора точки О.
299. Пусть ЛВС—данный треугольник (черт. 522), / и R — центр
и радиус вписанной окружности, 1а и Ra — центр и радиус иневпи-
санной окружности, касающейся стороны ВС и продолжений двух
других сторон. Как в п. 254, имеем пл. АВС= пл. /ВС-]- пл. 1СА-\-
-f-пл. 1АВ= -у R-(ВС-\-CA-\-AB) = p-R. Аналогично пл.ЛВС=
= —пл. /аВС+пл./аСЛ+пл. IaAB= l-Ra.(—BC-\-CA-{-AB) =
= RJp-a).
300. В
р— а
пл. ABC '
3/; — (а 4-
силу
1
Rb
b+c
упражнения
р — h 1
пл. ABC '
) Р
299
Р
пл.
имеем
ABC
1
R
ул.
1
К
р
ABC
1
1
Ra
1
= _^
нл. ABC пл. ABC R
301. Пусть О — точка, лежащая внутри треугольника ABC
(черт. 523). Имеем х : /г=пл. ОВС: пл. ABC; у:1г = пл. ОСА : пл. ABC;
z : / = пл.СМВ : пл.ABC. Отсюда
х у z _пл. ОВС +пл. ОСА -f-пл. ОЛВ_ пл. ABC_
I"f"i"T~ пл. ABC ~~ пл. АВС~~ "
462
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если точка О' лежит вне треугольника, например в области, при-
прилежащей к стороне ВС и к продолжениям двух других сторон, и х', у' и
Черт. 522.
х' у'
z' — расстояния точки (У от сторон треугольника, то — -\- —— -\-
z' — пл. О'?С+пл.О'С4-1-пл. О'А8 , .
-\ = ¦ =——¦ = 1. Аналогично мы имеем
1 / пл. ABC
х у z
во всех случаях равенство zh-т-Ч—гН г1^1*
п~к I
Примечание. Будем считать расстояние х точки О, лежащей
в плоскости треугольника, от его стороны ВС положительным, если точка О
лежит по ту же сторону от прямой ВС, как и вершина А, и отрицатель-
отрицательным — в противном случае. Аналогичные условия примем для расстояний у
и г. При этом для любой точки О плоскости имеем по абсолютной вели-
величине и по знаку -т- + -4- + -т = 1, или, принимая во внимание, что —=:
ft я I Л
==2плДС— ИТ' Д-ЯС-л-4-СЛ.у + ЛЯ.* = 2пл.ЛЯС.
УПРАЖНЕНИЯ К ГЛАВЕ И (стр. 235).
302. Пусть точки Ди Вл и Сь делят (внутренним или внешним
образом) стороны треугольника ABC (черт. 524) в отношениях
А^.А^С^х, 3^:3^=$; С1А;С1В = у по абсолютной величине и
по знаку. При этом пл.АВ}С} : пл.ABC — ——¦ ¦ ' Но ^ =
AL*
АВ
. Но
АС
\~ВХС:ВХА 1— $
ТЬ- Отсюда пл
АСЛ
~А~В~
АС,
1
/4C,-f-C,S \—СлВ:С,А
= l п
КНИГА ЧЕТВЁРТАИ. ГЛАВА II 463
Из равенства пл.-Д^С, *=пл.АВС — пл.АВгС^ — \\л.ВСхАх —
(у
1 -f- _ 3.' _ .-f-
4 1 V . п
^A — Y)(l — «) 41 —я)<1 — Р)/ A — я)A —Р)A — Y)
Чтобы точки Л,, Вл и С, лежали на одной прямой, необходимо и
достаточно, чтобы 1 — ару ^ 0. В этом и состоят теоремы
пп. 192—193.
Равенство пл.А\В\С\ = пл. ABC-—пл./ЩС]— ълЛС\А\— nn.CAiBi и все
предыдущие соотношения сохраняют силу во всех случаях, если рассмат-
рассматривать знаки площадей, как это сделано в решении задачи 324.
303. Начнём с деления площади треугольника ABC прямой В'С,
параллельной стороне ВС (черт. 525), в данном отношении т:п,
считая от вершины А.
Пусть М—точка, делящая сторону АВ в отношении АМ':М'В =
= т:п, так что
AM :AB = m:(m-\-n). A)
¦
С другой стороны, по условию пл.АВ'С: пл.ВССВ' =т;п, так
что »
пл.АВ'С : пл.АВС = т:(т-]-п). B)
Но
пл.АВ'С : m.ABC=AB''i:AB2. C)
Из A), B) и C) следует АВ>2:АВ2 = АМ:АВ, т. е. АВ'г —
= АВ-АМ'. Таким образом, задача сведена к построению среднего
пропорционального между АВ и AM' (п. 153): на АВ как на диаметре
описываем полуокружность; если перпендикуляр, восставленный к сто-
стороне АВ в точке М, пересекает её в точке Р', то AB'=zAP'.
464
РЕШЕНИЯ УПРАЖНРНИЙ И ЗАДАЧ
Чтобы разделить площадь треугольника ABC прямыми, парал-
параллельными ВС, на данное число равновеликих частей, делим на то
же число равных частей сторону АВ точками М, М",..., и для
каждой из этих точек повторяем предыдущее построение (на черт.
525 показано деление площади треугольника на три равновеликие
части).
Действительно, чтобы разделить площадь треугольника прямыми,
параллельными основанию, например, на пять равны$ частей, доста-
достаточно разделить её (считая каждый раз от вершины) в отношениях
1:4; 2:3; 3:2; 4:1. ,
304. Начнём с деления площади трапеции ВСС'В' (черт. 525) пряхой
В"С", параллельной основаниям ВС и В'С, е данном отношении т:п,
считая от меньшего основания В'С Решение
упражнения 303 приводит к следующем} по-
построению. Пусть А — точка пересечения не-
непараллельных сторон. На отрезке АВ, как на
диаметре, строим полуокружность и засекаем
отрезок АР' = АВ'. Перпендикуляр, опущен-
опущенный из точки Р' на АВ, определяет точку М'.
Делим отрезок MB в точке М" в отношении
т:п. Восставляя в точке М" перпендикуляр
к АВ, получим на полуокружности точку Р".
При этом АВ = АР".
Действительно, хт.АВ'С: пл.АВ'С: пл. ABC
= АВ'2 : АВ" : АВ1 = АР'1 : АР'1.: АВ- =
= (AM ¦ АВ) : (AM' ¦ АВ) : АВ* = АМ : AM" : АВ. Следовательно,
пл .ВС'С'В: пл.Я'С"СВ=(пл. АВ"С"—пл.АВ'С): (пл. ABC— nn.AB'C") =
=(АМ" — AM):(AB~ AM") — MM':М'В = m:n.
Чтобы теперь разделить площадь трапеции на данное число
равновеликих частей, строим, как указано, точку М, делим отре-
отрезок М'В на данное число равных частей точками М", М",..., и для
каждой из точек деления повторяем данное выше построение (сравнить
конец решения упр. 303).
305. Отношение радиусов обеих окружностей равно у~2; следо-
следовательно, отношение сторон треугольников также равно 12, а отно-
отношение их площадей равно 2. Но из чертежа 526 очевидно, что
площадь правильного вписанного шестиугольника равна удв^нной
площади правильного треугольника, вписанного в ту же окружность.
Следовательно, площадь большего равностороннего треугольника дей-
действительно равна площади шестиугольника.
306. Пусть ABCD—данный четырёхугольник (черт. 527), О —
точка пересечения его диагоналей; пусть далее примые А А' и СО,
параллельные данной прямой MN, пересекают диагональ BD в точ-
точках А' и С, а прямые ВВ и DD', параллельные той же прямой MN,
пересекают диагональ АС в точках В' и D'. При этом в силу парал-
параллельности'прямых АА', ВВ', СС и DD', пересекающих прямые ОА и
Черт. 526.
КНИГА ЧЕТВЁРТАЯ. ГЛАВА II
465
ОА',
имеем:
ОА
ОА'
ОВ'
ОВ
ОС
~~0С
0D'
0D
АС
А'С
B'D
ВО
О)
1°. Так как' треугольники ОАВ и О А'В' имеют общий угол, то
пл.ОАВ: пп.ОА'В' = (ОА-ОВ):{ОА'-ОВ'). В силу A) последнее
отношение равно единице, и пл. ОАВ^пл. ОА'Ь'. Точно так же дока-
докажем, что пл.
= пл. ОВ'С и т. д.
Таким образом, четы-
четырёхугольники равнове-
равновелики.
2Э. Если стороны
АВ и CD данного че-
четырёхугольника парал-
параллельны, то ОА:ОВ =
= bC:OD или
OA-OD=OB-OC. B)
НовсилуA)СМ-О?=
=OA'-OD';OB-OC=
= OB"-OC, и равен-
равенство B) переходит в
равенство О A' -OD' =
А'В' и CD'.
То же относится ко второй паре сторон AD и ВС.
3°. Если стороны АВ и CD пересекаются в точке Е, то приме-
применение теоремы п. 192 к треугольнику ОАВ и секущей CD приводит
DO ЕВ СА
к соотношению ^„ • -^-т- ¦ тт= = 1 (в котором все отрезки можно
527.
¦ОС, выражающее параллельность прямых
DB ЕА СО
рассматривать как положительные). Отсюда ЕА:ЕВ=^
DO-CA
Если
стороны А'В' и CD' пересекаются в точке Е',
CO-DB'
то точно так же
Е'А' : ЕВ =
D'0-С'А
-. НовсилуA) DO-CA = D'0-С'А'; CO-DB =
С'0-D'B'
= C'O-D'B\ так что ЕА:ЕВ= Е'А':Е'В'.
307. Пусть через концы некоторого отрезка АВ проведены пря-
прямые АА0 и ВВС (черт. 528), параллельные данному направлению KL
и пересекающие данную прямую XX' в точках Ас и Вс. Отложим на
этих прямых отрезки А А' и ВВ', пропорциональные расстояниям то-
точек А и В от прямой XX', т. е. пропорциональные ААи и ВВи, так
что АА':А40 = ВВ'-.ВВ0. Отсюда будем иметь (ААи — АА'):АА0 =
= (ВВ0 - ВВ'):ВВ0, или А'А0:ААь = В'В{):ВВи = h = const, и
далее (А'А0 -{-В'В0):{АА0 -j- ВВС) = А'А0: ААС = В'В^ВВ^.
Если обозначить теперь через М, М и Мо середины отрезков АВ, А'В1 и
А0В0, то А'А0-{-В'В0=2М'М0 и АА0 -f ВВ0 = 2ММ0, так что
30 Элементарная геометрия
466
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
f. А'АЬ ИВ0 , _ ..... ....
= . " = -=~- = Л. Так как отрезки ММ0 и ЛШ0, очевидно,
0 AAD BB0
пропорциональны расстояниям точек М и М от прямой AqBOj to
в силу упражнения 297 будем иметь пл. А'А^В^В' : nn.AA0B0B=h.
Это соотношение будет иметь место для каждой стороны АВ, ВС,...
данного многоугольника, например данного четырёхугольника ABCD
(черт. 529). Итак, имеем пл.А'А^В1 : пл.А40В0В=пл.В'В0С0С:
:пл.ВВ0С0С— пл.С'С0Д,?>':пл. CCQDoD = nn.D'D0A0A' : nn.DD0A0A —
= А. Так как пл. ABCD = nn. АА0В0В-\-пп. ВВ0С0С — пл. CC0D0D —
—пл. DD0AqA и аналогичное выражение имеем и для nn.A'B'C'D', то
отсюда и следует, что пл. A'B'C'D':nn. ABCD=^h. Доказательство,
очевидно, сохраняет силу для произвольного многоугольника.
К,
н, в0
Черт. 528.
Новые многоугольники будут равновелики исходным, не совпадая
с ними, если А= А'Аи:АА) = В'В0:ВЛ0 = ...= 1 (по абсолютной
величине). При этом будем, очевидно, иметь АА': АА0 = ВВ':ВВ0^
=... = 2 (По абсолютной величине и знаку), так как точки Л0,В0,...
будут серединами отрезков А4', ВВ\ ... .
308. В упражнении 306 прямая XX' (черт. 527), проходящая через
точку О и через середину Ао отрезка АА',. делит- также пополам
отрезки ВВ', СС и DD'. Отсюда следует, что четырёхугольник A'B'C'D'
получается из ABCD построением упражнения 307, причём
АА':АА0=:2.
309. Площадь квадрата HBKF(черт. 292) равна nn.HBCEF-\-nn.BCK-\~
-f xu\.EFK= nn.HBCEF -\-nn.ABH -\-nn.FGH = ш.ABCD-\-пл.DEFG.
Так как квадрат HBKF имеет своей стороной гипотенузу НВ треуголь-
треугольника АВН, а квадраты ABCD и DEFG - катеты В и AH = DE того
же треугольника, то отсюда и вытекает теорема п. 258.
310. Из подобия треугольников ABC, DBA и DAC
(черт. 530) имеем пл.АВС : tm.DBA : ni\.DAC=BO- : АВ2 : АС2, откуда
КНИГА ЧЕТВЕРТАЯ. ГЛАВА III
467
n-\.ABC : (пп.ОВА-\-пп.ОАС)—ВО> : (АВ?-\-АО>). Но так как
„ ...4ВС=1Гл. DBA-\-nn. DAC, то В& = АЕ1 -\-ВС2.
311. Пусть стороны В/ и CJ параллелограма BCJ/ равны и па-
пара члельны AM (черт. 531); пусть далее прямая AM пересекает ВС
и IJ соответственно в точках D и К, а прямые В/ и CJ пересекают EF
и G/V соответственно в точках Р и Q. При этом будем иметь ВР = АЛ1,
а гак как В/=АМ, то ВР=В1; аналогично CQ=CJ.
Так как параллелограмы, имеющие равные основания и равные
то пл .ABEF = пл..4Вр<И = пл. BDK/,
т. ACGH = w.ACQM = nn.DCJK.
Отсюда пл. ABEF -\- пл. ACGH =
= un.BDKI + пл. ОСЖ = nn.BCJI.
высоты, равновелики,
Черт. S31.
Чтобы показать, что доказанная теорема включает в себя как частный
случай теорему о квадрате гипотенузы, предположим, что угол ВАС —
прямой и что оба параллелограма ABEF и ACGH — квадраты
(черт. 530). При этом четырёхугольник AFMH будет прямоугольнк-
ком, так что FM= АН= АС. Следовательно, треугольники FAM и
ЛЯС равны, откуда AM = ВС и /_ CAD = /_ MAF = /_ ABC. Отсюда
следует, что прямая AM, а следовательно, и BI, перпендикулярна
к ВС и что В/ — AM = ВС. Таким образом, параллелограм ВСЛ
есть также квадрат, и этот квадрат равновелик по доказанному сумме
квадратов ABEF и ACGH.
УПРАЖНЕНИЯ К ГЛАВЕ Ш (стр. 239).
312. В силу п. 261 имеем /?=l/ —=0,5642 л, или 56,42см.
313. В силу п. 262 имеем равенство j^—= 1, откуда R —
400
400
тт/?2
314. В силу п. 262 и решения упражнения 287 имеем —
— = 1 или 0,0906 /?2=1, откуда /?=3,32 м.
30*
463
PESUFUHfl УПРАЖНЕНИЙ И ЗАДА'
315. Площадь кольца, заключённого между двумя концентриче-
концентрическими окружностями радиусов ОА и ОВ (черт. 532), главна разности
площадей этих окружностей, т. е. л-О Л2 —тг-О/?2 = тг- (ОА'2 — ОВ2) —
= п-АВ'г (на основании теоремы п. 258). Но п-АВ2 есть площадь
круга, радиус которого равен АВ.
316. Так как отрезки АВ и CD равны, то и дуги АВ и CD равны,
и ^/_АОВ = ^_COD (черт. 533). Следовательно, треугольники ВОЕ
Черт. 532.
Черт. 533.
и DOF равны, и пл.BDFE^nn.OBDF — ил.ПВЕ =*л. OBDF —
— nn.ODF=nn. сектора OBD.
317. Сумму площадей двух луночек, заштрихованных на чертеже
534, можно найти, прибавляя к площади треугольника ABC сумму
площадей двух полуокружностей, построенных на катетах, т. е.
п-АВ*-
Черт. 534.
п-АСг п-(АВ-
Черт. 535.
AC2)
полуокружности, построенной на гишменузе, т. е. также
и вычитая затем площадь
п-ВС
——— .
8
318. Пусть О, — середина стороны АВ и Р— точка пересечения
прямых ОМ и АВ (черк 535). В силу соотнощений / АРМ —
= у /_AOyN и АО = AOt ¦ 1^2 имеем: пл. сектора ОАМ= пл. сек-
сектора 0,.4/Vhjih пл. ОАР-\-пл. АРМ-=пл. O^PN-f-пл.АРМ-\- пл. Л/ИЛ/.
Отсюда пл. Л.ИЛ/=пл. О АР — пл. О,РЛУ. С помощью циркуля
и линейки можно, очевидно, построить некоторый треугольник,
КНИГА ЧЕТВЁРТАЯ. ГЛАВА IV 469
площадь которою равнялась бы разности площадей двух треугольни-
треугольников ОАР и 0}NP, а следовательно, и кьалрат, равновеликий этой
"разности площадей |п. 265). Этот кьадра! и будет равновелик криво-
криволинейному треугольнику AMN.
УПРАЖНЕНИЯ К ГЛАВЕ IV (стр 241).
319. Чтобы построить прямоугольник, зная его периметр и пло-
площадь, надо построить два отрезка — стороны искомого прямоуголь-
прямоугольника. При этом известны-сумма этих отрезков, равная половине дан-
данного периметра, и их произведение — пло-
площадь искомого прямоугольника. Таким обра-
зом задача непосредственно сводится к
рассмотренной в п. 155, построение 7.
Таь как произведение двух отрезков,
сумма которых постоянна, будет наиболь-
наибольшим, если эти отрезки равны (см и. 155),
то из всех прямоугольников, имеющих
данный периметр, наибольшую площадь
имеет квадрат.
320. Пусть ABCD — искомый прямо-
прямоугольник (черт. 536) и ВН — перпенди-
перпендикуляр из вершины В на АС. При этом площадь прямоугольника
ABCD, очевидно, равна АС~ВН. Так как АС есть диаметр окруж-
окружности, то, зная площадь прямоугольника, можно построить отрезок
ВН. (Если площадь искомого прямоугольника задана условием, что он
должен быть равновелик некоторому данному прямоугольнику, то отрезок
ВН определится как четвёртый пропорциональный к АС и к сторонам
этого данного прямоугольника.)
Определив длину отрезка ВН, проводим произвольно диаметр АС.
Далее проводим прямую, параллельную АС и отстоящую от неё на
расстоянии ВН. Эта прямая определяет положение вершины В.
Площадь прямоугольника ABCD будет наибольшей, если ВН
будет иметь наибольшее возможное значение. Но это наибольшее
значение ВН будет равно радиусу окр>жности. Следовательно, наи-
наибольшую площадь имеет вписанный квадрат.
321. Начнём с деления площади данного треугольника ABC
(мер г. 537) в данном отношении т:п прямой EF, параллельной
данной прямой PQ. Если прямая PQ параллельна- одной из сторон
данного треугольника, то задача сводится к упражнению 303. По-
Поэтому предположим, что прямая PQ не параллельна ни одной из сто-
сторон данного треугольника.
Проводим через вершины данного треугольника прямые АА\ ВВ
и СС, параллельные PQ. Одна из этих прямых будет проходить через
внутреннюю область треугольника; пусть это будет 4/V (две другие
прямые будут лежать вне треуюльника). Если обозначить через D
470
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
точку пересечения прямой АА' со стороной ВС, то мы будем иметь:
m.ABD : \m.ADC=BD:DC, A)
пл.АВО : nn.ABC=BD:BC. (Г)
Построим точку М, делящую отрезок ВС в отношении
ВМ:МС = т:п. B)
Пусть эта точка лежит между В и D (иначе мы должны были бы
всём последующем - - - — - - -- " ™ .-.
во всём последующем поменять ролями точки В и С). В та-
к-ом случае BD:DC^>m:n, и из сравнения с A) следует, что
\m.ABD:nn.ADC~^> т:п. Поэтому искомая прямая EF, делящая площадь
треугольника ABC в отношении
пл.BEF:nn.AEFC=^m:n, ' C)
должна проходить внутри треугольника ABD (а не внутри ADC).
Из равенств C) и B) имеем nn.BEF : пя.АВС=т:(т-\-п) =
= ВМ:ВС. Отсюда и из равенства (Г) находим, что nn.BEF : ил.ABD =
= BM.BD Таким образом, задача
сводится к делению площади тре-
Черт. 537.
М У Z
Черт. 538.
и v
угольника APD в отношении BM:MD прямой EF, параллельной стороне
AD (см. решение упр. 303).
Умея разделить площадь треугольника прямой, параллельной PQ,
в отношении т\п, мы без труда разделим её и на данное число равно-
равновеликих частей. Деление на три равные части показано на чертеже 537
(при этом ВМ='ММ' = М'С).
Пусть теперь требуется разделить площадь данного многоуголь-
многоугольника, например пятиугольника ABCDE (черт. 538), е данном отно-
отношении т:п прямой, параллельной FQ. Проведём через все вершины
пятиугольника прямые, параллельные PQ. Пятиугольник разделится
при этом на четыре части—-два треугольника ABB' н CDC и две
трапеции ВВ'ЕЕ' и ЕЕ'СС. Построим на некоторой прямой четыре
отрезка, пропорциональные апощадям этих частей:
пл. ABB': пл. ВВ'ЕЕ' : ил. ЕЕ'СС : пл. CC'D = XY : YZ : ZU:UV. D)
КНИГА ЧЕТВЁРТАЯ. ГЛАВА IV • 471
Делим отрезок XV точкой М в данном отношении XM:MV=:
= т:п. Если точка М лежит между Л' и К, то остаётся только раз-
разделить площадь треугольника ABB' в отношении ХМ: MY прямой,
параллельной ВВ. Действительно,если пл.AKL:nn. KLEDCB=m:n~
= XM:MV, то nn.AKL : nn.LKBB" = XM:MY в силу D). Если бы
точка М лежала между Y и Z, то площадь трапеции ВВ'ЕЕ' приш-
пришлось бы делить прямой, параллельной ВВ, в отношении YM':MZ, и
т. д. Таким образом мы приходим к задачам, рассмотренным в реше-
решениях упражнений 303 и 304.
Умея разделить площадь многоугольника прямой, параллельной PQ,
в данном отношении, мы без труда разделим её и на данное число рав-
равновеликих частей. Так, деление на пять, например, равновеликих частей
сводится к делению в отношениях 1:4; 2:3; 3:2; 4:1. Следовательно,отре-
Следовательно,отрезок XV придётся делить на п равных частей.
322. Начнём с деления площади дан-
ного четырехугольника ABCD (черт. 539)
в данном отношении т:п прямой, вы-
ходящей из вершины А, ^уУ!^ЧМ\
Построим треуюльник ABDV равнове- Q J( L С М, D,
ликий данному четырёхугольнику. Для этого
проведём прямую DD,, параллельную АС, до Черт. 539.
пересечения с ВС-в точке /^(сравнить п.265).
Разделим теперь площадь треугольника ABD^ в данном отноше-
отношении т:п прямой АМЛ, выходящей из вершины А. Для этого доста-
достаточно разделить в данном отношении BMy:MxDl = m:n сторону В1)л
и соединить делящую точку Л4, с точкой .4. Проведя теперь прямую
Ai^M, параллельную АС, до пересечения в точке М со стороной
CD, будем иметь пп.АСМ^ — пп.АСМ. Следовательно, пл.А/WjD, =
= пл. ACDX — пл. АСМХ = пл. ACD — пл. АСМ= пл. AMD, и потому
пп.АВСМ : пл.AMD = пл.АВМХ:пл.AMXD^ = m:n.
Вместо того чтобы делить в данном отношении отрезок BDV до-
достаточно (не строя треугольника ABD^) разделить в данном отноше-
отношении BM':M'D = m:n диагональ BD данного четырёхугольника и про-
провести прямую ММ, параллельную АС.
Умея разделить площадь четырёхугольника прямой, выходящей
из А, в данном отношении, мы без труда разделим её и на данное
число равновеликих частей. Так, чтобы разделить её на четыре
равновеликие части, делим на четыре равные части BK'=K'L' =
— L'M = M'D диагональ BD и проводим прямые К'К, L'L и ММ,
параллельные АС, до пересечения в точках К, L и М со сторонами
данного четырёхугольника. Прямые АК, AL и AM делят площадь
четырёхугольника на четыре равные части.
323. Начнём с деления площади данного многоугольника, напри-
например данного семиугольника ABCDEFQ (черт. 540), в данном отно-
отношении т:п прямой, выходящей из вершины А.
Построим четырёхугольник AB'DO', равновеликий данному много-
многоугольнику, и разобьем этот четырёхугольник прямыми, выходящими
472
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
из вершины А, на части, соответственно равновеликие треугольникам
ABC, ACD, ADE, AEF и AFG. Для этого достаточно провести пря-
прямую ВВ', параллельную АС, до пересечения с прямой CD в точке В,
затем прямую GG^, параллельную AF, до пересечения с EF в точке
О,, и, наконец, прямые FF' и G^G', параллельные АЕ, до пересече-
пересечения с DE в точках F' и G'. Действительно, при этом будем иметь
(сравнить п. 265) пл.АВС=пл.АВ'С; nn.AEF=nn,AEF'; пл.AFG ==
= пл. AFG^ = пл.АРО, — nn.AEF = nn.AEG' — пл. AEF' =nn.AF'G' и
nn.ABCDEFG= nn.ABDG1.
Разделим теперь площадь четырёхугольника АВ1DG' в данном от-
отношении т:п прямой, выходящей из вершины А. Для этого доста-
достаточно (см. решение упр. 322) разделить в данном отношении т:п
диагональ B'G' и провести через точку деления М' прямую М'МХ,
параллельную другой его диагонали AD до пересечения в точке М^
со стороной четырёхугольника.
К D
Черт. 540.
Предположим для определённости, что точка Мл лежит между
точками Е и Г. Проведя через точку Л4, прямую /И,/И, параллель-
параллельную АЕ, до пересечения с EF в точке М, будем иметь пл. АЕМХ =
= пп.АЕМ, и, следовательно, nn.AM^F'= nn.AEF' — пл. АЕМХ =
= nn.AEF—пп.АЕМ = nn.AMF. Отсюда и из выведенных выше ра-
равенств найдём, что пл. ABCDEM : nn.AMFG—- nn.AB'DM^ :nn.AM^G'=
= т:п. Прямая AM делит, таким образом, площадь данного много-
многоугольника в данном отношении.
Умея разделить площадь многоугольника в данном отношении
прямой, выходящей из А, мы без труда разделим её и на данное
число равновеликих частей. Деление на четыре равновеликие части
АВСК, AKDL, ALEM и AMFG показано на чертеже 540 (при этом
ВК' =K'L' = L'M' = MG').
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ (стр. 241).
324. Будем считать площадь какого-либо треугольника ABC по-
положительной, если последовательность вершин А, В, С соответствует
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ 473
обходу данного треугольника против часовой стрелки, и отрицатель-
отрицательной в противном случае. При этом условии знак площади треуголь-
треугольника зависит от порядка, в котором перечисляются ею вершины
(подобно тому как знак отрезка зависит от последовательности, в ко-
которой заданы две его конечные точки; сравнить п. 185), а именно:
площадь треугольника изменяет свой знак на обратный при переста-
перестановке двух вершин и сохраняет свой знак при „круювой пере-
перестановке" вершин. Таким образом, имеем пл.АВС^пл.ВСА =
= пл.С4В=—пл.АСВ^—пл.СВА= — пл.ВАС. Площади двух тре-
треугольников будут иметь одинаковый знак, если они имеют одинаковое
направление вращения, и противоположные знаки — в противном
случае.
Заметим, что при введённом условии относительно знака площади
треугольника для любых трех точек А, В и С одной примой и про-
произвольной точки О плоскости имеет место равенство
пл.О АВ-\~ тт.ОВС-\~ пл.ОСА = О, A)
аналогичное равенству A) п. 186. В самом деле, если точка В лежит
между А и С, то имеет место равенство
пп.ОАВ-\-пп.ОВС=пп.ОАС, B)
равносильное равенству A), так как в этом случае площади ОАВ,
ОВС и О АС имеют одинаковые знаки и AB-±-BC=AC. Но каждое
1
В.
V а 1Д
из равенств A) и B) сохраняет своё значение при перестановке двух
из трёх букв А, В н С; следовательно, оно верно при всяком распо-
расположении точек (сравнить аналогичное доказательство в п. 186).
Предложения, приведенные в упражнении 296, принимают те-
теперь следующую форму:
1°. Где бы ни лежала в плоскости параллелограма ABCD
точка О. имеет место по величине и знаку равенство:
пл. ОАВА-пп. OCD =пл. О ВС-\-an. ODA. C)
При этом точка О может лежать внутри параллелограма (черт. 518)
или в части плоскости, ограниченной одной стороной и продолжениями
двух других (черт. 541), или в части плоскости, ограниченной
продолжениями двух смежных сторон (черт. 542), или, наконец, на од-
одной из сторон параллелограма или её продолжении.
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
-Для доказательства проводим через точку О прямые, параллельные
сторонам параллелограма, и обозначаем через а, Ь, с и d точки пере-
пересечения этих прямых соответственно с прямыми АВ, ВС, CD и DA.
В силу равенства B) имеем по величине и по знаку пл.ОАВ =
= пл.ОАг + пл.ОаВ; пл.ОВС= пл.ОВЬ-\- пл.ОЬС и т. д., откуда
пл. ОАВ-\-пп. OCD = пл. ОАа-4- пл. ОаВ-{-пл. ОСс-f пл. OcD, D)
ил. ОВС-г пл. ODA = пл. ОВЬ-\-пл. ОЬС+ пл. ODrf-f-"-1- ОА4.D')
Так как четырёхугольник OdAa есть параллелограм, то треуголь-
треугольники ОйА и ОАа равны и имеют одинаковое направление вращения.
Следовательно, мы будем иметь по абсолютной величине и знаку
O i. ОАа. Аналогично пл.ОаВ= пл.ОВЬ; пл.О6С = пл.ОСс;
= nn.(JDd. Таким образом, каждый из членов правой части
равенства D) равен одному нз членов правой части равенства D').
Следовательно, левые части этих равенств равны друг другу, и мы
получаем соотношение C).
2°. Где оы ни лежала в плоскости параллелограма ABCD
точка О, имеет место по величине и знаку равенство
пл.ОАС=пл.ОАВ-\-пл.ОАО. E)
Для доказательства проведём через точки В и D прямые, парал-
параллельные прямой ОА, и обозначим через И и П точки пересечения
этих прямых с АС (черт. 519 и 520).
Так как при перемещении вершины
треугольника по прямой, параллель-
параллельной основанию, сохраняется не только
абсолютная величина, но н знак пло-
площади треугольника, то пл.ОАВ=
= пл. ОАВ'; пл.ОАО=пл.ОАП'. Так
как отрезки AD' и В'С не только
равны, но и направлены в одну и ту
M С ~\ же сторону, то треугольники OAD1
и О В" С имеют одинаковое направле-
Черт. 543. Ние вращения, и потому пл.ОАО'=
= пл. ОВ'С. Пользуясь соотношением
B) и тремя последними равенствами, имеем пл.ОАС = пл.ОАВ' -\-
-л пл.ОВ'С = пл.ОАВ' -f ш.ОАО' = пл.ОАВ-\- пл.ОАО. Равенство E)
д. казано.
Если точка О лежит на прямой АС, то приведённое построение
невыполнимо. Но при этом, очевидно, пл. ОАС^пл. ОАВ-\~\\л. 0AD =
= 0, так что равенство E) сохраняет силу.
Примечание. В решениях последующих задач мы будем, если
не оговорено противное, рассматривать площади фигур в обычном смысле,
т. е. брать их лишь по абсолютной величине независимо от знака.
325. Пусть ABCD и A'B'C'D' (черт. 543) — два гомотетических
четырёх) гольнька, и О — их центр подобия (доказательство не'зави-
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ
475
сит от числа сторон), KLMN ¦—четырёхугольник, вписанный в четы-
четырёхугольник ABCD и описанный около A'B'C'D'. Обозначим через к
коэфициент подобия обоих многоугольников k^OA'OA' ^OB:OB' =
= OC:OC' = OD:OD' = AB:A'B' = ... и через К', L\ M и
Л/' — точки пересечения прямых OK, OL, ОМ и ON со сторонами
многоугольника A'B'C'D'. Имеем пл.ОА'К-.пл.ОА'К' — ОК:ОК' = k;
пл.ОВ'К : пп.ОВ'К' = k; и т. д. Складывая, получим nn.KLMN:
:nn.A'B'C'D' = k.
Точно так же пл.ОАК-пл.ОА'К= OA:OA'=k; nn.OKB:nn.OKB'=zk;
.. . , откуда nn.ABCD : nn.KLMN = k.
Йтаь, im.ABCD : i\n.KLMN = n
В С
Черт. 545.
326. Пусть D, Е и F — середины сторон треугольника ABC
(черт. 544) и G—-точка пересечения его медиан. Отложив на про-
продолжении отрезка FE равный ему отрезок ЕК, получим AK=CF;
DK = BE. Обозначим через L точку пересечения прямых АС
и DK. Прибавляя к площади треугольника ADL соответственно
равные площади, получим nn.ADK = nn.ADL-\-nn.ELK-\-m.AEK =
= nn.ADL-\-nn.DLC-\-nn.AEF=\v\.ADC-\-nn.AEF=\- ал.ABC -\-
4- - пл АВС = -пп.АВС.
327. Пусть Р — точка пересечения трансверсалей ВЬ и Сс, деля-
делящих (внутренним образом) стороны треугольника АВС в отношениях
bC:bA = q и сА:сВ=г (черт. 545). Мы будем в дальнейшем рас-
рассматривать отношения направленных отрезков, так что д<^0 и г<^0.
Требуется определить отношения площадей треугольников РВС, РсВ,
РСЬ и четырёхугольника АсРЬ.
Найдём предварительно отношение, в котором точка Р делит от-
отрезок Сс. Для этого применим теорему п. 192 к треугольнику АСс
и секущей ВРЬ. Будем иметь
PC
Рс'
Вс
ВА.'
ЬА
ЪС
— 1
откуда
PC
Рс''
ЬС ВА ЬС
сА
A)
476 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Далее, так как треугольники сВС, АсС и АВС имеют общую вы-
высоту, то пл.сВС : пл. АсС : мл.АВС= Вс:сА:ВА = Ьс:сА:(Вс-\- сА) =
, сА I сА\ ,_
= 1: —: 1 -4-— = 1 :(— г):A — г). Отсюда
Ьс \ ос/
т.ВСс=т^—-пп.АВС B)
и
пл.АсС = -—-• пп.АВС. * C)
1 — г
Так как треугольники СРВ, РсВ и СсВ имеют общую высо-
высоту, то ип.СРВ : \\л.РсВ : пл СсВ= РС:сР:сС= РС:сР:[сР-\-PC) =
PC ( РС\
= —: 1: ( 1 -f- — I ^ — ^(l — г): 1: A — q -\- qr) в сил} равенства A).
Сг^ \ СгI
Отсюда на основании B) имеем:
пл.РВС= ~7Я^~ Г)-пл.ВСс = Ч— пл.АВС, D)
1—q-\-qr 1—q-\-Qr
m.PcB = - пл.^Сс = -г-, j -¦пп.АВС. E)
1 — q -j- qr A — r) A — q -f- qr)
Площадь треугольника РСЬ можно, очевидно, получить из тшо-
щади треугольника РсВ, поменяв в выражении последней ролями
bC:bA = q и сВ:сА = —, т. е. заменив в выражении E) q через
г
— и г через —. Таким образом, получаем:
пп.РСЬ = г-г-т ; г-г • пл. АВС =
р;jТТ *
= ZZ^L— пл. ABC. F)
(\—q)(l—q-\~qr)
•Наконец, площадь четырёхугольника АсРЬ можно получить как
разность площадей треугольников АсС и РСЬ. В силу равенств C)
и F) будем иметь:
пл.АсРЬ
= \— ——
L l—r
^
— г)A— q + qr)
„л. ЛВС G)
Равенства D), E), F) и G) дают решение поставленной задачи.
328. Пусть прямые Аа, ВЬ и Сс, делящие стороны треугольника
АВС (внутренним образом) в отношениях аВ:аС = р, bC:bA = q и
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ
477
cA:cB = r (p<^0, <7<^0, г<^0), пересекаются попарно в точках Р,
Q и R (черт. 546). Требуется определить площааь треугольника PQR.
Прн решении задачи 327 мы нашли, что пл. РсВ =
= — : ; -пл.ABC. В силу п. 256 имеем:
A — r)(\ —q-L-qr) J
1
PQ PR
-Ш1..
A)
A—Г)A —q-\-qr)
и остаётся только найти PQ:Pc и PR-.PB.
Для вычисления отношения PQ:Pc применим теорему п. 192 к тре-
треугольнику ВСс и секущей AQa. Получим
QC Ас аВ Q?__a? АВ /)
Qc \B iiC ' Qc пВ
аС Ас-^-сВ
~~ аВ
Ас
с А
р \ г I
QC
Сс
QC
В
— QC:Qc
г—\
Черт. 546.
1 —
B)
Далее в силу соотношения A) из решения задачи 327 имеем:
C)
Рс~
PC
Сс'~
PC Cc q{\—r)
Pc 'Pc 1 — q-f-qr '
D)
PQ PC QC 9A—r)
Из равенств B) и D) находим — = -?. —=—L =
Сс Сс Сс 1 — q -\- qr
Наконец, пользуясь ра-
E)
_ '"-' = [\-г)(рдг-\-\)
\-r-\-rp A — q -\- qr) A — г -^ гр)
венством C), из последнего равенства получим:
PQ^PQ Сс__(\ —г)(рдг-\-
Рс Сс' Рс I — г 4- гр
PR
Для вычислении отношения —- применим, ту же теорему п. 192
к треугольнику ВСЬ и секущей ARa. Получим — • — - —тз= 1,
RB аВ АС аВ АЬА-ЪС аВ I, ЬС
откуда Ш = ^-аЬ = ^с-аь- = ^сЛ1
478
РПНЕИИЯ УПРАЖНЕНИЙ И ЗАДАЧ
RB
ВЬ~
RB
RB:Rb
F)
СРс.
\—RB:Rb \—p-\-pq'
Далее применяем ту же теорему к треугольнику АВЬ и секущей
РВ _сВ С А
~РЬ~~сА"сЬ
РВ
Получим —
СЬ сА
откуда = . =
cB
сА
СЬА-ЬА
СЬ~~
РВ
сВ
'Та
рв
ЬА
~ЬС
q
РВ:РЬ
q—\
BP-\-Pb \—PB:Pb
G)
Из равенств F> и
pA —q) =
1
G) находим -—- = — бг =^ тi—
Bb Bb Bb 1 — q -j- qr
(q— \)(pgr-\-l)
и
=
— Р-\-рч (i— p
PR
-PR
Bb
Bb
i —
(8)
Подставляя теперь в равенство A) значения PQ:Pc и PR-.PB,
определяемые равенствами E) и (8), получим окончательно:
(pqr 4- 1 )*
пл. PQ/? =
p-\-pq)(\ —
¦•пл. ABC. (9)
Условие, при котором прямые Аа, ВЬ и Сс проходят через одну
точку, состоит в том, что nn.PQR = 0. В силу равенства (9) отсюда
вытекает, что p(jr=— 1. Таким
образом, получаются теоремы
пп. 197 и 198.
329. Пусть ABDC (черт.
547) — параллелограм, имеющий
заданную площадь, один из углов
которого совпадает с данным углом
ДЛСиодна из сторон которого BD
проходит через данную точку Р.
Черт. 547.
Искомая секущая MN (или
M'N') должна пересекать сторону
такой точке Q (или .Q), чтобы
CD (или её продолжение) в
nn.PQD=nn.BPM -\- nn.CNQ (или
— nn.N'CQ, т. е. nn.PQ'D=nn.BM'P-\-nn.CN'Q'). Отсюда сле-
пл. ВРМ , пл CNQ , / _ пл. ВРМ' пл. CN'Q'
пл. PQ'D'wi. PQ'D~
и nn.CNQ : nn.PQD —
чт0
пл. PQDn пл. PQD
Но пл. ВРМ : п
= (BP:PDJ
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ
479
(CQ:QDf, так что (BP:PDJ-\- (CQ:QD)"- = 1, и
— bp* ( го,п,пУрр2-врА
PD
Для построения точек Q и Q' достаточно разделить отрезок CD
Г* К
внутренним и внешним образом в отношении .
Задача имеет два решения при PD^> BP, одно решение при
PD = BP и не имеет решений при PD<^BP.
330. Первое решение. Из решения задачи 329 (черт. 547)
вытекает, что наименьшее возможное значение площади треугольника
AMN соответствует наименьшему значению площади параллелограма
ABDC, т. е. наименьшему зна-
значению отрезка BD, для кото-
которого задача построения тре-
треугольника AMN имеет реше-
решение. Далее из решения того
же упражнения следует, что fix*"' /Р
это наименьшее значение от-
отрезка BD определяется усло-
условием PD=BP и что при этом
CQ=CQ'=0. Из равенства
PD=BP следует, что АС —
Отсюда вытекает такое по- Черт. 548.
строение: через Р проводим
прямую РВ, параллельную стороне АС данного угла, и откладываем
отрезок ДС=2ВР Прямая PC определяет искомый треугольник.
Второе решение. Пусть /ИЛ/-— произвольная секущая, про-
проходящая через точку Р (черт. 548), РВ н РК — прямые, проходящие
через ту же точку и параллельные сторонам данного угла. Проводим
через В прямую BN', параллельную MN.
Есди прямая BN1 пересекает сторону АК параллелограма АКРВ
в точке N' и продолжение стороны РК того же параллелограма
в точке АГ, то пл. /ШЛ/=пл. АКРВ-\- пл. KNP-\-пл. ВРМ =
— пл.АКРВ + пл. AN'B 4- пл. BMP = 2 пл.АКРВ -\- nn.KM'N'.
Аналогичное равенство будет иметь место и в том случае, если пря-
прямая BN' пересекает сторону РК параллелограма АКРВ и продолже-
продолжение его стороны АК. Отсюда следует, что площадь треугольника AMN
будет иметь наименьшее значение, если прямая М!М будет параллельна
ВК, так как при этом пл. KM'N'=0 и пл. АММ—2пл.АКРВ.
331. Пусть в окружность вписан многоугольник, имеющий данное
число сторон п и отличный от правильного. Вершины этого много-
многоугольника делят окружность на п дуг, наименьшая из которых меньше
—ой части окружности. Соединяющая концы этой дуги сторона
480
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
многоугольника меньше стороны сп плавильного выпуклого п-уголь-
ника. вписанного в т\> же окружность.
Рассмотрим теперь наибольшую из дуг, на которые вершины п-
1
угольника делят окружность: эта дуга больше —ой части окружно-
п
сти. Если эта дуга окажется больше
1
всей окружности, то со-
соединяющая её концы сторона многоугольника будет опять-таки меньше
стороны правильного вписанного и-угольника (черт. 549, при п = 4).
Но при этом вписанный многоугольник ABCD целиком расположен
внутри сегмента, отсекаемого от круга стороной MN правильного п-
МД
В
Черт. 549.
угольника, и его площадь заведомо будет меньше площади правиль-
правильного «-угольника, #как это видно хотя бы из построения, выполнен-
выполненного для четырёхугольника ABCD на чертеже 549.
Поэтом} мы можем предположить, что наибольшая из дуг, на ко-
которые вершины вписанного многоугольника делят окружность, меньше
всей окружности, и, следовательно, соединяющая её концы
п
стпрон'1 п-угольника больше стороны правильного п-угольника.
Соединив вершины данного вписанного многоугольника с центром
О окружности, мы разобьём его на треугольники ОАВ, ОВС, ....
Перемещая эти треугольники, мы можем, очевидно, располагать сто-
стороны данного вписанного многоугольника в любом порядке, причём
многоугольник будет оставаться вписанным в данную окружность и бу-
будет сохранять свою площадь. Основываясь на этом, можно заменить
данный вписанный многоугольник, не изменяя длин его сторон и его
площади другим многоугольником (черт. 550), в котором сторона,
меньшая стороны правильного п-угольника, и сторона, бблыиая её,
будут смежными.
Пусть теперь сторона АВ больше сп, а сторона ВС меньше сп
(черт. 551), и прямая ВВ0 параллельна АС. Если мы построим хорду
АВ' = сп, то точка В' будет лежать между Во и В, н потому высота
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ
481
н' и
Черт. 551.
В'Н' треугольника ABC будет больше высоты ВН треугольника ABC,
а следовательно, и пп. АВ'С ^>пл. ABC. Итак, заменяя вершину В
вершиной В' и не изменяя положения остальных вершин, мы сделаем
сторону АВ' равной сл и в то же время увеличим площадь дан-
данного многоугольника.
Повторяя конечное число раз две последние операции (перемена
порядка сторон, замена .стороны, не равной сп, стороной, которая
равна сп), мы заменим д.
данный многоугольник Д> ^^
правильным л-угольни-
ком, вписанным в ту же
окружность и имеющим
ббльшую площадь, чем
данный. Следовательно,
нз всех и-угольников,
вписанных в данную окружность, наибольшую площадь имеет правиль-
правильный и-угольник.
332. Пусть ABC — искомый треугольник, в котором известны сто-
сторона 8С=а, высота AH = h и радиус R вписанной окружности.
Строим полуггермметр р искомого треугольника как четвёртый пропор-
пропорциональный, пользуясь равенством pR = —ah (см. упр. 299). Далее
строим отрезок /; — а, равный (в силу упр. 90а)
расстоянию АЕ = AF от вершины А до точки
касания вписанной окружности со стороной АС
или АВ (черт. 102). Если построить Прямо-
Прямоугольный треугольник по двум катетам R и
/; — а, то угол, противолежащий первому из
.4
этих катетов, будет равен— , а следовательно,
мы получаем угол А искомого треугольника.
Черт. 552. Задача сводится теперь к упражнению 77 (пер-
(первый случай).
333. Пусть ABDC — искомая трапеция (черт. 552). Задание угла D
определяет длину диагонали ВС, а следовательно, и диагонали AD,
так как трапеция, вписанная в окружность, необходило равнобедрен-
равнобедренная и потому имеет равные диагонали. Опустив из точек В и С пер-
перпендикуляры ВР if CQ на диагональ AD, имкем пл.ABDC =
= — AD-(BP-\-CQ). Знание площади позволяет, таким образом, по-
построить сумму BP-\-CQ. Опустив из точки В перпендикуляр ВК на
прямую CQ, будем, очевидно, иметь CK^CQ-\-BP. Прямоугольный
треугольник ВСК, в котором известны гипотенуза ВС и катет СК,
можно построить.
Итак, приходим к следующему построению. Строим хорду ВС гак,
чтобы опирающийся на неё угол BDC имел данную величину. Далее,
31 Элементарная геометрия
482
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Черт. 553.
строим прямоугольный треугольник ВСК по гипотенузе ВС и кате-
катету СК. Наконец, проводим в окружности хорду AD (или A'D'), па-
параллельную ВК и равную ВС. (С этой целью строим вспомогатель-
вспомогательную окружность, концентрическую с данной и касающуюся пря-
прямой ВС.)
Если задача возможна, то она имеет, вообще говоря, два реше-
решения (грапеции ABDC и A'BD'C на черт. 552).
334. Совместим основание данного параллелограма BCFD с осно-
основанием ВС данного треугольника ВСА так, чтобы совпали их рав-
равные углы В (черт. 56). Так
М' как пл.?С.4 = пл. BCFD, то
nn.DEА =пл. CFE, и так как
углы обоих треугольников рав-
равны, то и треугольники равны.
Итак, в треугольнике до-
достаточно провести среднюю
линию DE, а в параллелогра-
ме — соединить вершину С с
серединой Е стороны FD.
335. Совместим основание
одного из дачных треугольни-
треугольников с основанием АВ другого,
располагая оба треугольника так, чтобы их вершины М и М лежа-
лежали по одну сторону от прямой АВ (черт. 553). Выполним в каждом
из треугольников АВМ и АВМ построение, указанное в решении
задачи 334. Получим два параллелограма ABCD и ABC ГУ с общим
основанием и общей высотой. Они состоят из общей части ABCD
и соответственно из треугольни-
треугольников ADD' и ВСС, равных между О J К С О' К'У С'
собой. Мы видим нз чертежа, на
какие пять частей следует разре- "*
зать треугольник АВМ, чтобы
можно было, расположив их ина-
иначе, получить из тех же частей и
треугольник АВМ'. Эти части обоз-
обозначены на чертеже цифрами 1,
2, 3, 4, 5 и 1, 2", 3', 4', 5'.
На чертеже 553 стороны CD
и CD' параллелограмов имели об-
общую часть CD'. Может, однако,
случиться, что эти стороны не бу-
будут иметь общих точек (черт. 554). В таком случае через точку пересече-
пересечения Е сторон ВС и AD' параллелограмов проводим прямую FF', па-
параллельную АВ, далее строим прямые FG и F'G', соответственно
параллельные АЕ и BE, прямую HGG'H', параллельную АВ, и т. д.
Процесс закончится, когда прямые HI и Н'Г, соответственно параллель-
параллельные АЕ и BE, пересекут стороны CD и CD' данных параллелогра-
-ЗАДАЧИ К ЧЕТВЕРТОЙ КИНГЕ 433
мов. При этом оба параллелограма будут разрезаны на'- соответственно
равные части.
Примечание. Построения, которыми мы пользовались при решении
этой задачи, можно рассматривать с более оэщей точки зрения, которая
лучше уясняет их сущность, а также оказывается полезной и при реше-
решении последующих задач.
Будем называть два многоугольника равносоставленными, если один из
них можно разрезать на такие части, которые, будучи сложены иначе, да-
давали бы другой. Решая задачу 334, мы показали, "что треугольник и парал-
лелограм, о которых там говорится, равносоставлены. В настоящей задаче
мы доказали равносоставленность двух треугольников (а также и двух па-
раллелограмов), имеющих одно и то же основание п одну и ту же вы-
высоту. В задачах 336 и 337 мы встретимся с более общими случаями равно-
равносоставленности многоугольников.
Одно из основных свойств равносоставленных многоугольников нахо-
находит своё выражение в следующей теореме: Два многоугольника, равно-
составленные с одним и тем же мноюугольником, равносоставлены
друг с другом. Иначе говоря, если многоугольник Р можно разлить на
части (будем называть их „частями первого рода"; так, чтобы, сложгнные
иначе, они давали многоугольник Q, и если, кроме того, тот же многоуголь-
многоугольник можно разбить на части („части второго рода") так, чтобы, сложен-
сложенные иначе, они давали многоугольник /с1, то и многоугольник Q можно
разбить на части так, чтобы, сложенные иначе, они давали многоугольник R.
Для доказательства проведём в многоугольнике Я и те линии, кото-
которые разбивают его на „части первого рода", и те линии, которые разби-
разбивают его на „части второго рода". Совокупность тех и других прямых
даст разбиение многоугольника Р на новые „мелкие" части (при этом все
или некоторые из „частей первого рода" окажутся в свою очередь подраз-
подразделёнными на части, и то же будет иметь место для „частеуй второго рода').
Из этих „мелких" частей можно составить „части первого рода", а значит,
складывая их иначе, многоугольник Q. Из тех же „мелких" частей можно
составить и „част второго рода", а значит, складывая их иначе, и много-
многоугольник R. Таким образом, теорема доказана.
В приведённом только что решении устанавливалась равносоставленность
треугольника АВМ и параллелофама ABCD, затем параллелограмов ABCD
и ABCD' и, наконец, параллелограма ABCD' и треугольника АВМ'.
Если разрезать параллелограм ABCD на трапецию ABK.D и треуголь-
треугольник ВСК (черт. 553), то из них можно сложить треугольник АВМ, если
разрезать его на трапецию ABCD' и треугольник AD'D, то из них можно
составить параллелограм ABCD'. Если провести в ABCD отрезки ВК и
AD', то получим три части АВКР', ВС/\ и AD'D, из которых можно сло-
сложить как треугольник АВМ, так и параллелограм ABCD' и т. д. Мы ви-
видим, что предлагаемое решение задачи 335 есть лишь применение того
метода, с помощью которого мы доказывали общую теорему о равносо-
равносоставленности.
336. При решении этой задачи мы будем существенно опираться
на сказанное выше в решении задачи 335 и, в частности, на те све-
сведения, которые даны в примечании к этому решению.
Мы должны доказать, что один из двух равновеликих треуголь-
треугольников всегда можно разрезать на такие части, которые, будучи сло-
сложены иначе, давали бы другой. Короче говоря, мы должны доказать,
что всякие два равновеликих треугольника равносоставлены.
Не нарушая общности, можно предположить, что сторона ВС есть
наибольшей из сторон данных треугольников ABC и А'В'С. Отсюда
31*
484
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАЯАЧ
следует, что Соответствующая ей высота АН треугольника есть на-
наименьшая из высот обоих треугольников. На основании этого можно
заключить, что АН меньше сторон второго треугольника.
Пользуясь этим, можно построить треугольник А"ВС (черт. 555),
имеющий то же основание и ту же высоту, что и треугольник ABC,
и притом такой, что А"С=А'С. Треугольник А"ВС равносоставлен
с ABC в силу задачи 335. Далее треугольники А"ВС и А'В'С имеют
равные основания А"С = А'С и равновелики между собой, так как
каждый из них равновелик ARC. Следовательно, эти два треугольника
имеют и одну и ту же высоту, а потому равносоставлены (задача 335).
А В
Итак, треугольники ABC и А'В'С' равносоставлены оба с треуголь-
треугольником А"ВС. По основному свойству равносоставленных многоуголь-
многоугольников (решение задачи 335, примечание) они равносоставлены между собой.
337. При решении этой задачи мы будем опираться на решения
задач 335 и 336 и, в частности, на те сведения, которые даны в при-
примечании к решению задачи 335.
Мы должны доказать, что всякие два равновеликих многоуголь-
многоугольника равносоставлены.
Пусть дан некоторый многоугольник, хотя бы пятиугольник
ABCDE (черт. 229). Строя равновеликий ему четырёхугольник ABCD'',
как указано в п. 265, мы видим, что треугольники CED и CED' не
только равновелики, но и равносоставлены (задача 335). Следовательно,
многоугольники ABCDE и ABCD' также равносоставлены. Продолжая
эти построения и рассуждения, мы можем прийти к треугольнику,
равносоставленному с данным многоугольником.' Действительно, каж-
каждый вновь получаемый многоугольник (имеющий на одну сторону
меньше, чем предыдущий) будет равносоставлен с предыдущим, а по-
потому и все вновь получаемые многоугольники равносоставлены с дан-
данным. Итак, всякий многоугольник равносоставлен с некоторым тре-
треугольником.
Если теперь даны два равновеликих многоугольника Р и Р', то
мы можем найти два треугольника Л и Л', равносоставленных соответ-
соответственно с многоугольниками Р и Р. Эти два треугольника Л и Л' бу-
будут также равновелики, так как площадь каждого из них равна пло-
площади многоугольников Р и Р. Следовательно, треугольники Л и Д'
будут и равносоставлены (задача 336).
ЗА ДАЧИ К ЧЕТВЁРТОЙ КНИГЕ
485
Итак, многоугольник Р равносоставлен с треугольником Д, тре-
треугольник Д—с треугольником Д', треугольник Д'—с многоугольни-
многоугольником Р'. В силу основного свойства равносоставленны.х многоугольни-
многоугольников данные многоугольники Р и Р равносоставлены.
338. Пусть (А) есть степень точки А относительно окружности
BCD (черт. 556), и аналогичное значение имеют (В), (С) и (D); да-
далее пусть О есть центр окружности, описанной около треугольника
BCD, и т. д.
Обозначим через ЛА0 и DD0 перпендикуляры, опущенные из то-
точек А и D на прямую ВС. В силу п. 136, примечание 3°, разность
степеней какой-либо точки относительно двух
окружностей равна удвоенному произведению
расстояния той же точки от их радикальной
оси на расстояние между центрами. При-
Применим это предложение к точке А и окруж-
окружностям BCD и ABC. Так как в данном слу-
случае прямая ВС есть радикальная ось и сте-
степень точки А относительно окружности ABC
равна нулю, то (A) = 2OaOd-AuA. Анало-
Аналогично (D)=2OdOri-D0D = — 20a0d-DuD.
Отсюда (A):(D)=— AnA:DuD.
С другой стороны, имеем пл.ABC:
:пл.DBC= AqA-.D^D. Таким образом получаем
пл.ЛВС:пл. DBC- — (A):(D), т. е. — (А). nn.BCD = {D)-vn.ABC,
или (A)-m.BCD = {D)-nj\.ACB. Аналогично и для других точек.
Все написанные равенства верны как по абсолютной величине, так
и по знаку.
339. Обозначим, как и в решении задачи 338, через (А) степень
точки А относительно окружности BCD. Инверсия с полюсом А и
степенью (А) преобразует окружность BCD в самоё себя, так как
степень точки А относительно этой окружности равна степени инвер-
инверсии, а точки й, С и D—в некоторые точки В', С и D', лежащие
на той же окружности.
В силу п. 218 стороны треугольника В'CD' соответственно равны
В
Черт. 556.
и т.д., откуда
_ (А)-СВ
~~ АВ-АС'
CD'
D'B'
Б'С
ВС-AD ~CD-AB~~DB-AC ~~ АВ-АС-AD'
(А)
0)
Последние
равенства показывают, что треугольник B'C'D' подобен треугольнику
со сторонами ВС-AD, CD-AB, DB-AC и что коэфициент подобия
(А)
равен
AB-ACAD
. Следовательно,
пл. B'CD' =
АВ2¦• АС? ¦ AD"-
B)
486
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
где !—площадь треугольника со сторонами EC-AD, CD-АН и
DB-AC.
С другой стороны, треугольники ECD и В'CD' вписаны в одну и
ту же окружность, и из п. 251, примечание, вытекает, что
пл. Ь'СП: пл. BCD = B ^'SJ^'^fr -Заменяя здесь В'С, CD1 и
(ЛK
; • ПЛ. BCD.
Черт. 557.
BCCD-DB
D'B' их выражениями A), получим пл. В'CD' =
Сравнивая последнее выражение для nn.B'C'D' с её выражением B),
мы и получим (Д)-пл. BCD ^2.
340. Задача неопределённая. Одно кз решений получается так:
Соединяя центр вписанной окружности с вершинами треугольника и
опуская из той же точки перпенди-
перпендикуляры на стороны, разложим дан-
данный треугольник на шесть прямо-
прямоугольных треугольников. Каждый из
них разлагается на два равнобедрен-
равнобедренных медианой, выходящей из вер-
вершины прямого угла.
Другие решения получим, заме-
заменяя центр вписанной окружности
какой-либо внутренней точкой, вы-
выбранной так, чтобы основания пер-
перпендикуляров из этой точки на сто-
стороны лежали на самих сторонах, а не на их продолжениях.
В случае остроугольного треугольника достаточно соединить центр
описанной окружности с вершинами.
Многоугольник разрезаем сначала на треугольники.
341. Пусть три равные окружности О,, О„ и Os радиуса./? пере-
пересекаются попарно под прямым углом в точках А, В и С (черт. 557).
Требуется вычислить площадь 5 криволинейного треугольника ABC.
В силу симметрии фигуры имеем АВ= ВС^СА, и / ОЛАС=
= /_ О2АВ= у (90° — 60с)= 15°. Следовательно, /_BAOl=Z.ABOi=
_ 60°-)-15° =75°, и потому /^.4О,?=30о. Отсюда выте-
вытекает, что АВ есть сторона с,ч правильного выпуклого двенадцати-
двенадцатиугольника, вписанного в данную окружность. Для площади S получим
следующее выражение: S^— ск2\ 3 —j— 3 f —— •n~ci2fli2
апофема' правильного выпуклого двенадцатиугольника.
Согласно формуле п. 181 имеем: с1Ъ=
-^-я) = 2 я(К6 -
задачи к четвёртой книге 487
т. е. а12 =—R (} 6-\~у2). Подставляя эти
значения с12 и а12 в приведённое выше выражение для 5 и выполняя
выкладки, найдём 5 = R2 {-к\ 3 4-- — ] = 0,1514 ... R2.
342. Обозначим через а, 1>, с, р, S и R стороны, полупериметр,
площадь и радиус вписанной окружности данного треугольника ABC,
через Л — его высоту, опущенную на *
сторону а, и через S^ — площадь тре- г уч f
угольника AKL, прилежащего к верши- С К/ \^- §
не А (черт. 558).
Требуется найти произведение пло-
площадей восьми треугольников, а именно
данного треугольника ABC, треуголь-
треугольника А'Б'С, симметричного с данным
относительно центра вписанной окруж-
ности, и шести треугольников, анало- "
гичных AKL и прилегающих соответ- Черт. 558.
ственно к вершинам А, В, С, А', В' и С
В силу подобия треугольников ABC и AKL имеем S1:S=?
= (h—2RJ:h2. Из равенств S=pR=-^ah (см. упр. 299) находим
2R:h = a:p, и, следовательно, ?,:?= (р — аJ:р2. Отсюда 5, =
= 5 • ^ а' = -i^ . Обозначая через 52 и S3 площади тре-
треугольников, аналогичных AKL, но прилежащих соответственно к вер-
вершинам В и С, будем иметь Sv = — ; S» = . От-
2 р > ii р
сюда находим SS^S, = R*. Ь>-*)Чр-ЪПр-Ф Но
(р - аJ {р—Ь)Цр- cf _?(p — a)*(p — h)*{p — c)*_S*_ m
окончательно 55,5253 = /?8.
Так как треугольники, о которых идёт речь, попарно симметричны
относительно центра окружности, вписанной в треугольник ABC, то,
возводя последнее равенство в квадрат, мы и получаем искомый ре-
результат.
СМЕШАННЫЕ ЗАДАЧИ И ЗАДАЧИ, ПРЕДЛАГАВШИЕСЯ
НА КОНКУРСНЫХ ЭКЗАМЕНАХ
343. Дуга аВ по условию рапна половине дуги АВ, т. е. аВ=
= -у АВ; точно так же Bb=—BC; cD = -jCD ; Dd = - DA. От-
Отсюда имеем ab -\-c~d= — (AB-\-BC-\-Cb-\-DA) = 180°. Угол между
прямыми ас и bd измеряется полусуммой дуг ab и ей и потому прямой.
344. При решении этой и некоторых из последующих задач мы
будем рассматривать направленные углы, чтобы получить доказатель-
доказательства, пригодные при любом расположении
элементов фигуры (сравнить подстрочное-
примечание к тексту задачи 346).
Под алгебраической величиной угла
АОВ мы будем понимать абсолютную ве-
величину того из углов между полупрямыми
ОА и ОВ, который не превосходит по-
полуокружности, взятую со знаком-(-или —
в зависимости от того, вращается ли полу-
полупрямая, описывающая этот угол, начиная
• or О А к О В, в положительном или
в отрицательном направлении. Алгебраическую величину угла АОВ
будем обозначать через -§С АОВ. Алгебраическая величина угла за-
зависит от порядка, в котором заданы его стороны: -gC АОВ^ — -З^ВОА
(сравнить п. 185).
При рассмотрении направленных углов оказывается целесообразным
считать равными между собой те углы, алгебраические величины
которых или равны, или отличаются друг от друга на целое
число полуокружностей. При этом условии можно говорить об ал-
алгебраической величине угла между двумя прямыми; этот угол зависит
от порядка, в котором заданы обе прямые, но не зависит от выбора
на этих прямых того или иного направления. Так, если прямые а
(или АА') и b (или ВВ') пересекаются в точке О (черт. 559), то
Черт. 559.
(а, Ь) =
= ЗС А'ОВ=. ? АОЬ' = ? А'ОВ' = — & (Ь, а). A)
При пользовании направленными углами имеют место следующие
предложения, на которые мы будем ссылаться в дальнейшем.
А) Каковы бы ни были лучи ОА, ОВ и ОС, выходящие из
точки О, всегда имеем:
АОВ-\- ЗС ВОС-{- §; СО А = 0.
(II)
СМЕШАННЫЕ ЗАДАЧИ 489
Действительно, если луч ОВ лежит внутри (не превосходящего
полуокружности) угла между ОА и ОС, то углы АОВ, BUC и АОС
имеют один и тот же знак, и их абсолютные величины удовлетворяют
условию /_АОВ^- /_ ВО С ~/_ А ОС, откуда и следует (II). То же
рассуждение применимо и в том случае, когда луч ОА лежит внутри
угла ВОС или луч ОС внутри угла АОВ.
Если же ни один из трёх лучей не лежит внутри угла, образо-
образованного двумя другими, то все три угла АОВ, ЬОС и СОА имеют
один и тот же знак, и сумма их абсолютных величин равна целой
окружности, откуда опять следует (II).
В) Для любых трёх точек плоскости имеем:
Действительно, если последовательность вершин А, В, С соответ-
соответствует обходу треугольника ABC в положительном (отрицательном)
направлении, то все три угла ВАС, СВА, АСВ имеют положительный
(отрицательный) знак, и сумма их абсолютных величин равна полу-
полуокружности, откуда в силу введённого выше условия и следует A11).
Если же точки А, В к С лежат на одной прямой, то каждое из сла-
слагаемых в левой части равенства (III) равно нулю.
С) Если точки А, В, Си D лежат на одной окружности (или
на одной прямой), то имеем (срашшть п. 82а):
ЗС АСВ= <? ADB, (IV)
и обратно, из соотношения (IV) следует, что точки А% В, С и D
лежат на одной окружности (или на одной прямой).
Действительно, если точки А, В, С и D лежат на одной окруж-
окружности и точки С и D лежат по одну сторону от АВ, то углы АСВ
и ADB имеют один и тот же знак и одну и ту же абсолютную ве-
величину: если точки А, В, С и D лежат на одной окружности
и точки С и D лежат по разные стороны от АВ, то углы АСВ
и ADB имеют различные знаки, а сумма их абсолютных величин равна
полуокружности, откуда и получается соотношение
Если точки Л, В и С лежат на одной окружности и точка Т лежит на
касательной к окружности в точке Ь, то раьенство (W) заменяется сле-
следующим:
(IV)
Действительно, первый из этих углов есть вписанный угол, опираю-
опирающийся на дугу АВ, второй—у юл между хордой АВ и касательной в её
конце В. Если точки С и Г лежат по разные стороны от АВ, то углы АСВ
и АВТ имеют один и тот же знак и одну и ту же абсолютную величину;
если же точки С и Т лежат по одну сторону от АВ, то углы АСВ и АВТ
имеют противоположные знаки и сумма их аосолютных величин равна по-
полуокружности. В обоих случаях будем иметь соотношение (IV).
490
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Переходим теперь к решению задачи 344.
1°. Обозначим через U точку пересечения окружностей AEF и
BFD (черт. 560). Так как точка D лежит на одной прямой с точ-
точками В и С, то, согласно (I), <? BDO = <?CDO, и аналогично
3tCEO = <?AEO; 2rAF0=3:BFO. Далее точки А, О, Е и F (а
также В, О, F и D) лежат ка одной окружности, откуда на основа-
основании (IV) ^AEO=^AFO; ^.BDO = ^BFO. Из выписанных ра-
равенств имеем:
§; CDO = §; BDO = §; BFO = -gC AFO = ^AEO=z^_ CEO. A)
Так как точки С, D и Е не лежат на одной прямой и -gC CDO =
= -gc CEO, то точка О лежит на окружности CDE. Наши рассужде-
рассуждения благодаря их полной общности сохраняют силу и в том случае,
когда все или часть точек Z), Е и F лежат не на самых сторонах
треугольника, а на их продолжениях. (Без помощи направленных уг-
углов пришлось бы рассматривать отдельно несколько частных случаев.)
2°. Так как точки Р, а и А лежат на одной прямой, то
ЗС РаО = <? АаО. Из равенства (III) следует. §; АаО = -gC AOa-\-
Черт. 560.
Черт. 561.
-\-<?аАО, так что -gr PaO= §; ДОа-|--gC аЛО. Так как точки Л, я,
О и Г лежат на одной окружности, то <? АО а = 2? AFa; <?aAO =
=$: aFO и, следовательно, -gC РаО = -gC 4Fa-j-gr aFO = -gr ДРО. Итак,
•gC РаО имеет ту же алгебраическую величину, что и каждый hj уг-
углов A). Те же рассуждения можно повторить и для углов РЬО и РсО.
Итак, -gCPaO^-gC РЬО^^-^ РсО и точки Р, О, a, b w с лежат на
одной окружности.
345. Чтобы придать решению полную общность, будем пользоваться
направленныуи углами, как указано в решении задачи 344, и в част-
частности выведенными там соотношениями A) — (IV).
Пусть ABCD — вписанный четырёхугольник (черт. 561), A1BsClD^ —
четырёхугольник, образованный вторыми точками пересечения постро-
построенных окружностей. Мы имеем -gC D^A^ = <? D{At 4-f--gC AAXBA в
силу (II). Далее на основании (IV) -gr DxAxA=^i DVDA; 2? AAlBl =
Смешанные задачи 491
= -gC АВВЛ, и, следовательно, -gC DlAlBA =-§С ДВ?, -f <?D,?>4. Заменяя
здесь точки Д и /4j точками С и С,, получим: -gC DlC\BA = -gc Cfi^ -|-
-|--§C D,DC. Из двух последних равенств имеем- •§? ДД5,—-grплСлВ, =
силу (II). Но на основании (IV) §; Д5С -4- <? CD A = -gC /ШС —
— <Х ADC= 0, и потому <? Dj^fi, = ^ДС,^. Следовательно, точки
Л,, fi,, C( и D1 лежат на одной окружности.
Примечание. Прньедённая теорема сохраняет силу, если четы-
четырёхугольник ABCD заменить треугольником ABC (черт. 562)," а произволь-
произвольную окружность, проходящую через точки С и D, — какой-.-ийо окруж-
окружностью, касающейся в точке С окружнист, описанной около треуголь-
треугольника ABC.
Данное выше доказательство нуждается np:i этом в небольшом видоиз-
видоизменении: углы DiDA, DXDC и CDA заменяются соответственно через
DiCA, DXCT и ТС А, где 7—произвольная точка касательной в точке С. При
этом приходится пользоваться кроме раьенства {IV) tine и раненстьем (IV )
нз решения засади 344.
Черт. 562. Черт. 563.
346. Чтобы придать решению полную общность, будем опять поль-
пользоваться направленными углами, как указано в решении задачи 344,
и в частности выведенными там соотношениями (I)—(IV).
Алгебраическая величина угла между окружностями 5, и 52 в
точке А есть алгебраическая величина угла между касательными в
точке их пересечения А. Угол между двумя окружностями зависит при
этом как от последовательности, в которой даны эти окружности, так
и от выбора одной из двух точек их пересечения А или А' (черт. 563),
но не зависит при сделанных в начале решения задачи 344 условиях
от выбора направления на касательных в силу (I). Если обозначить
через /7 и to касательные к обеим окружностям в точке А и через
•§C5j/45?-—алгебраическую величину угла межлу окружностями в точ-
точке А, то ^С(/„ /,) = ^51AS2 = —^5^5, = —¦§С5,Л'52 =
= -|—§С S^'Sj. Если Мл и УН, — две произвольные ючкь, лежащие соот-
соответственно на окружностях 5, и ?3, то
,A; A)
492
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
действительно, обозначая через Тх и Т„ какие-либо точки на касатель-
касательных 1Л и /„, будем иметь на основании (II) и (IV): -grS AS'2 =
= §: т1 АА' 4- зс л'лг^ = -gr дуи,и' 4- -gc л'/и2а
Переходя к решению поставленной задачи, имеем (черт. 564)
¦gr DA.B=- -gr D.4D' -j- $-D'AA- -f- ^CA'AB" -f- -gr fi'/lfi; §; ABC =
= -gC -4B/A' 4- -gr ,4'/JB' -1- -gr fi'fiC 4- -gOC'BC; -gr BCD = -grfiCfi'+
4- $; fi'cc 4- -gr с CD14- -gc d-cd; -gr cd.4 = $: cdc 4- -gc cdd' +
4- -gr D'D^' 4- -gr 4'Ш. Усло-
Условие, при котором точки А, В,
С и D лежат на одной окруж-
окружности, можно на основании (IV)
представить в виде -gC DAB-\-
4- $:fiCD=:$: Авс 4- 3: cd4,
или, в силупредыдущихравенств,
в виде gC DAD' -j- -gC D'АА' -\-
Ц С CD
= §; /A&4'
—r~ ^C
—I— -^[ ,
+ $:
+ &
= ЗС ,4'fifi';
4- gc ялй -[-
Черт. 5G4.
$; FfiC == -gr B'CC;
и предыдущее соотношение
4- -gc d'cd = -gc
-]- <?A'DA. На основании формулы A) имеем
4- ^C A'BA, -gr 5ofi53 = -gr ЙЛБ' 4- -gr fi'C
4- ? CDC; ^ 54D5, = ^C DCD' +
4 -gr D'AD, откуда -gr 52/«3+ -gr S4DSl=
4- -gC CDD' 4- -gr D'DA' 4-
4" gC A'DA. Но в силу равен-
равенства (IV) имеем -gr-4MB'=
C'CD' = -gCCDD'; -gr D'D^'=
принимает вид: gC DAD' -\-
' + 3CCBC + 3CCDC-I-
, = ^C /1D4' 4-
Черт- 565.
347. Чтобы получить решение, при-
пригодное во всех многочисленных возможных
здесь частных случаях, и в то же время
указать, каким образом следует выбирать
касательные а, ^, у и ^. зададим на каж-
каждой из данных окружностей определённое
направление обхода.
Если на некоторой окружности 6" вы-
выбрано определённое направление обхода,
то тем самым устанавливается определённое положительное направ-
направление на каждой касательной к 6"; это направление определяется
требованием, чтобы вблизи точки касания направление на касатель-
касательной совпадало с выбранным направлением на окружности (черт.
565). Отрезки, отложенные на касательных, мы будем, как обычно,
рассматривать, как имеющие знак 4- или —. В дальнейшем направ-
направленную прямую мы будем считать касательной к направленной окруж-
СМЕШАННЫЕ ЗАДАЧИ 493
ности только в том случае, когда положительное направление на этой
прямой совпадает вблизи точки касания с направлением на окружности.
Если из точки Р проведены к направленной окружности две каса-
касательные, точки прикосновения которых обозначены через Л и В, то
мы имеем по абсолютной величине и знаку (черт. 565):
АР — РВ. A)
Если стороны четырёхугольника PQRS касаются некоторой на-
направленной окружности и А, В, С и D — точки касания прямых SP,
PQ, QR и RS, то мы имеем, в силу A), по абсолютной величине и
по знаку:
PQ + RS = (РВ + BQ) + (RD + DS) = АР + QC+ CR + SA =
= QR + SP. B)
Равенство B) имеет место независимо от того, к какому из рас-
рассмотренных в решении упражнения 87 пяти типов принадлежит данный
описанный четырёхугольник (черт. 332 — 336).
А' В'
Черт. 566. Черт. 567.
Если даны две направленные окружности 5, и 52, то они имеют
самое большее две направленные общие касательные: этими общими
касательными будут внешние или внутренние общие касательные, смот-
смотря по тому, приписано ли обеим данным окружностям одно и то же
направление (обеим — по часовой стрелке или обеим — против часовой
стрелки) или противоположные направления (одной — по часовой стрел-
стрелке, другой — против часовой стрелки) (черт. 566 и 567).
Если одна из двух общих касательных касается первой окружности
в точке А, второй окружности — в точке В, а вторая общая касатель-
касательная— соответственно в точках А' и В", то мы имеем по абсолютной
величине и по знаку:
АВ = В'А'. C)
Обращаясь к решению предложенной задачи, мы будем предпола-
предполагать, что на каждой из четырёх данных окружностей выбрано опре-
определённое направление и что под а,а',... понимаются направлен-
направленные общие касательные. Отсюда легко вывести, что среди четырёх
пар а,2', р,р', у,у', й,5' общих касательных имеется чётное число
пар внутренних общих касательных и, следовательно, также чёт-
494
РЕШЕНИЯ УПРАЖНЕНИЙ II ЗАДАЧ
ное число пар внешних общих касательных. Действительно, выписав на-
направленные окружности в порядке 5,, S2, Ss, Sit 5p мы видим, что каждой
паре внутренних общих касательных к двум последовательным
окружностям соответствуют противоположные направления на этих окруж-
окружностях. Так.как и первой и последней окружностью является S,, то
направление меняется на противоположное при переходе от одной
окружности к следующей чётное число раз, а потому и внутренние ка-
касательные будут встречаться чётное число раз.
Далее выберем касательные a, [S, у и § так, чтобы они, рассмат-
рассматриваемые как направленные общие касательные к данным окружно-
окружностям, касались одной и
Р'
Черт. 568.
той же направленной
окружности (черт. 568).
Обозначим через Р,
Q, R, S соответственно
точки пересечения выбран-
выбранных общих касательных
а и jj, $ и у, у и й, 3
и^: аналогично обозна-
обозначим через Р', Q', R', S'
точки пересечения а' и ^',
f и у', у' и о', с' и а1.
Далее обозначим через АЛ
и А'х точки прикосновения
касательных а и а' к
окружности 5,, через А2 и
A.J — точки прикоснове-
а' к окружности 52, и т. д. При этих
A), PQ-\-RS^ QR-\- SP;
/? откуда (Л,5 +
QBS) -+-
так что
равняется сумме длин двух
ния тех же касательных а
условиях будем иметь, в силу B) и
A,S=SD,: PA2 = BnP; CaQ=QBs; /?
+ SP 4- PA,) + (CSQ + 0/? 4- #Q)
4- (D4/?4-/?5 4-5D,), или /t1A,4-CgC4
сумма длин двух из общих касательных
других общих касательных.
Из последнего равенства с помощью C) получаем: A^'A.J-\-С3'С^'=
= В2'Е>2 -\- D^D^'. Отсюда с помощью соотношений S'At' =Df'S' и
т. Д. находим P'Q'-\-R'S' = Q'R' 4~ S'P', так что и стороны четы-
четырёхугольника P'Q'R'S' касаются одной окружности (в силу обратной
теоремы упр. 87).
Итак, при выборе общих касательных а, р, у и о мы соблюдали
следующие два условия:
a) среди четырёх общих касательных имеется чётное число
(О, 2 или 4) внешних общих касательных;
b) общие касательные а, jj, у и 5, рассматриваемые как на-
направленные касательное к направленным окружностям 51, 52, 5, и
Siy касаются одной и той же направленной окружности.
СМРШАННЫЕ ЗАДАЧИ
495
Примечание. Покажем, что оба эти предположения существенны.
a) Пусть среди четырёх пар общих касательных имеется нечёшое число,
например три пары внешних общих касательных (черт. 569>. В таком слу-
случае мы имеем по абсолютной величине (выбор направлений и введение
знаковздесь невозможны): PQ + RS= QR + SP; (В2Р-\- PQ + QB-d -f-(?>4/?_|_
+ RS —SDt) = (CSQ + QR+ RCi) -f (A^S -f SP -f- PA2)—2Л,5; В2В3 + /?4Di=
=СзС4 + Л|Й2—2S/4i- Если и четырёхугольник P'Q'R'S' облапает тем свойством,
чтов него можно вписать окруж-
окружность, то мы найдём аналогич-
аналогично В% В% -\- /L Л>1 = С3 С4 +
-f- Л|'Л2'— 2S' Л|, и мы получае и
ещё добавочное условие SA{ =
b) Пусть теперь все четы-
четыре пары касательных — внеш-
внешние, но касательные а, р, f и о
выбраны, например,как изобра-
изображено на чертеже 570. При этом
касательные а, р, f и о касаются
одной окружности, а касатель-
касательные а', р', Y и о' этим свойством
не обладают. Это произошло
потому, что никаким выбором
направлений в данном случае
нельзя соблюсти условие Ь).
348. Обозначим верши- Черт. 569.
ны данного пятиугольника че-
через А, В, С, Du ?(черт. 571); точки пересечения прямых ЕА и ВС че-
через К, прямых АВ и CD через L, прямых ВС и DE через М, прямых CD
и ЕА через /V, прямых DE и АВ через Р; вторые точки пересечения
окружностей ЕАР и АВК
ь' ь
As
5'
через А', окружностей АВК и BCL через
Б', окружностей #CL и С DM
через С, окружностей CDM
и D?W через D', окружностей
DEN и ?А» через Е'.
, „ Чтобы доказать, что пять то-
Р чек А', В', С, D' и Е' лежат
на одной окружности, достаточ-
п' но доказать это для четырёх
точек, например В', С, D',
Е'. Так как то же рассужде-
рассуждение применимо и к четырём
точкам А', В', С иО', то отсюда
Черт. 570. будет следовать, что все пять
тонек лежат на одной окружности.
Чтобы придать доказательству полную общность, будем опять
пользоваться направленными углами и соотношениями A) — (IV) (реше-
(решение зядачи 344).
Отбросим мысленно одну из пяти данных прямых, именно прямую
DE, и к четырём остальным применим задачу 106. Четыре окружно-
-Л
\
Т
о]
496
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
сти АВК, BCL, LNA и KCN проходят через одну точку, откуда в
частности следует, что четыре точки L, N, А и В" лежат на одной
окружности. Точно так же (отбрасывая прямую ВС) докажем, что на
одной окружности лежат точки L, N, А и Е'. Итак, все пять точек
Z., N, А, В', ?" лежат на
одной окружности.
Мы имеем в силу (IV)
и (I)
и $:3C
^CB'L откуда
= $:CB'L. A)
Далее опять в силу
(IV) и (I) Z?DD'E' =
= §С DNE' и §С DNE' =
= ЗС LNE' = -gC LffE',
откуда
^DD'E' = ^.LB'E'. B)
Складывая почленно
равенства A) и B), име-
Черт. 571. ем, на основании A1),
¦gC6"D'?'=§:C'fl'?", от-
откуда и следует, что точки В', С, D' и Е' лежат на одной окружности.
349. Если повернуть треугольник ABC (черт. 572) 1ак, чтобы сто-
сторона АВ в её новом положении а'Ь' была параллельна ас, то угол
поворота будет равен ¦§; (АВ, а'Ь') = ¦§; ВОЬ'; так как прямая Ofr'
проходит, по условию задачи, через точку С, то мы имеем ¦§? 60^»' =
М
Черт. 572.
Черт. 573.
= -5С SOC. Отсюда следует, что ¦§; ВОС= §С (ЛЯ, а1/»') = -§С (ЛД ас) =
= const, и, следовательно, точка О лежит на окружности, проходящей
через точки В и С (сравнить решение задачи 344, предложение С).
При перемещении точки О по этой окружности угол при вершине
А в равнобедренном треугольнике АОа', а следовательно, и отношение
АО:Аа' остаётся постоянным в силу постоянства угла ¦§? АОа' =
= §С SOC. Поэтому геолштрическое место точек а' получается из гео-
СМЕШАННЫЕ ЗАДАЧИ
497
метрического места точек О путём гомотетии с центром А и поворота
на угол ОАа', а потому есть окружность. Аналогичное имеет место
и для точек Ь' и с'.
350. Обозначим через D, Е и F основания высот треугольника ABC
(черт. 573), через Н—точку пересечения этих высот. Так как по
условию задачи HD=DA', HE = EB' nHF=FC, to прямые В'С,
С А' и А'В" будут соответственно параллельны EF, FD и DE. В силу
упражнения 71 прямые DH, ЕН и FH будут биссектрисами углов
треугольника DEF; следовательно, те же прямые будут и биссектри-
биссектрисами углов треугольника А'В1 С. Треугольники A'QR, B'SM и CNP
будут равнобедренными (в каждом из них высота совпадает с биссек-
биссектрисой), и потому QD — DR; SE = EM; NF = FP. Четырёхугольники
A'QHR, BSHM и CNHP будут ромбами, так как в каждом из них
С О
Черт. 574.
Черт. 575.
диагонали перпгндикулярны и делятся пополам. Отсюда следует, что
прямые QH и МН параллельны А'В', и потому точки М, Н и Q лежат
на одной прямой. Аналогично доказывается, что точки /V, Н и R, а
также точки Р, Н к S лежат на одной прямой.
351. Пусть ABDC— искомая трапеция (черт. 574). Проведём вы-
высоту АН. Так как трапеция равнобедренная, то отрезок HD будет
равен полусумме (отрезок НС—полуразности) оснований.
Для построения искомой трапеции, если известна сумма (разность)
оснований, строим прямоугольный треугольник AHD (или АНС) по двум
катетам, восставляем перпендикуляр к гипотенузе в её середине М
(или соответственно Л^ и из точки А, как из центра, радиусом данной
окружности делаем на этом перпендикуляре засечку, определяя тем
самым положение точки О и оси симметрии трапеции.
Для возможности задачи, когда дана сумма (или разность) осно-
оснований, необходимо и достаточно, чтобы радиус окружности был боль-
больше AM и меньше AQ, где Q—точка пересечения перпендикуляра
МО с прямой АН (или соответственно больше АР, где Р — точка
пересечения перпендикуляра N0 с АН). Отрезки AM, AQ и АР легко
выразить через данные.
32 Элементарная геометрия
498
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
352. 1°. Так как угол ADB (черт. 575) — прямой, то прямая BD
касается окружности CMD, откуда следует, что /jCDB= 180° —
— /_CMD = /_CMQ. С другой стороны, /_CDB= /_СРВ как впи-
вписанные. Следовательно, /_ CMQ = </_СРВ, и потому прямая MQ парал-
параллельна РВ.
Далее /_DQB = /_СРВ, так как дуги ВС и BD равны. Но
/_СРВ^ /_CMQ в силу параллельности прямых MQ и РВ. Следо-
Следовательно, /_DQB= /J2MQ, и потому прямая BQ параллельна РМ.
Итак, четырёхугольник MPBQ есть параллелограм.
2°. /_CMN=/_QBN=/_QDN; /_CNB=/_DNB, и, следова-
следовательно, треугольники CMN и MDN подобны. Из подобия этих тре-
треугольников следует MN2 =
= NC- ND.
353. Пусть Р и Q (или Р'
и Q') — точки прикосновения ка-
касательных, проведённых из точек
А и В к окружности с центром О
(черт. 576), Ж (или М) — точка
пересечения этих касательных.-.
1°. Так как ОА=ОВи ОР =
=OQ{wnw OP'=OQ), io/_OAM=
= ^/ ОВМ (или /_ О AM' -\-
4-^ОЯМ'= 180°), и точка М
(или М) лежит на окружности
ОАВ.
Обратно, если точка М лежит
на дуге АОВ (или точка М — на
дуге АСВ) окружности ОАВ, то
расстояния ОР и OQ (или ОР'
Черт. 576.
и OQ') точки О от прямых /Ш и ВАЛ (или /Ш' и fi/W') равны между
собой, так как углы О AM и ОВМ равны (углы ОАМ' и Ofi/W' — по-
пополнительные). Поэтому прямые AM и ВМ (или ДМ' и ВМ') касаются
одной окружности с центром О.
Следовательно, геометрическое место точек М и М' есть окруж-
окружность ОАВ.
2°. Имеем МА-МВ=(РА — РМ) (Qfi+ QM) = A42 — РЖ2, так
как Р/4 = Qfi в силу равенства треугольников О АР и OBQ, а РЖ =
= ЖС? как касательные к окружности из одной точки. Отсюда
МА • МВ= (ОД2 — ОР2) _ (СЩ2 _ ОР2) = О А* — OJVP.
Аналогично найдём, что МА- М'В = ОМ'° — О А1.
3°. Отложим на прямой MB (или М'В) от точки М (или Ж') в обе
стороны отрезки Ml и ЖЛГ, равные 4Ж (или отрезки М'Г и М'К',
равные AM').
Если точка Ж лежит на дуге АОВ, то ^/_ AIВ = ^/_ МА/ —
= - /_АМВ= —
(сравнить решение упр. 63) и
СМЕШАННЫЕ ЗАДАЧИ
499
= Z_ AMB-\- /_ МАК = /_ АМВ + -^ A80° — ^_ АМВ) = 90° 4-
4- jZ.АМВ = 90° + 4 Z АОВ-
Следовательно, геометрическое место точек / и геометрическое
место точек К представляют собой дуги окружностей, имеющие своими
концами точки А и В и вмещающие углы, соответственно равные
~ /_ АОВ и 90° + -' Z АОВ-
Если точка М займёт положение М на дуге АСВ, то аналогично
найдём, что^/ Д/'5=90° + ^/_АМ'В= 90° -|--i A80° — /_ АМВ)=
= 180° —
= 180°--.
АОВ и
= ¦1 A80° — ^/ ДЖв) = 90° — ^
Следовательно, геометрическое место точек /' и геометрическое
место точек К' представляют собой дуги окружностей, имеющие
своими концами точки А к В
и вмещающие углы, соответствен-
соответственно равные 180°—— /_ АОВ и
1
90° — ~ /_ АОВ.
Так как /_ А/В -f Z АГВ =
180°-
— Y Z А0В )= 180°- то
Черт. 577.
являющиеся геометрическими местами точек / и /', образуют одну окруж-
окружность. Так как /_АКВ-\-/_АК'в=Ы°Л-\ Z.AOB) + (90° ~
¦ ^/_ АОВ I = 180°, то то же имеет место для геометрических
мест точек К и К' (эти две окружности не показаны на чертеже).
354. 1°. Радиусы АО и АО' окружностей, описанных около тре-
треугольников ABD и ACD (черт. 577), соответственно равны (п. 130а):
АО= и АО'=-^—т-гт- , где АН ~ высота треугольника
2- АН 2-АН
ABC. Отсюда АО:АО'= АВ:АС.
2°. Радиусы АО и АО' будут иметь наименьшую длину при наи-
наименьшем возможном значении AD, т. е. при AD = АН. Точка D сов-
совпадает при этом с основанием высоты //.
32*
500
РКШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
3°. Имеем (по 1 °) АО: АО'= АВ: АС, так что равнобедренные треуголь-
треугольники АВО и АСО' подобны. Отсюда /_OAB=^JD'AC и, следовательно,
/ОАО'=/_ВАС. Так как /ОАО'=/_ВАС и АО:АО' = АЯ:АС, то
треугольник ОАО' подобен треугольнику ВАС.
4°. Если точка М делит отрезок 00' в данном отношении, то
наряду с треугольником A0W сохраняет постоянную форму и тре-
треугольник АОМ, так как угол АОМ и отношение АО:ОМ сохраняют
постоянные значения. Следовательно, отрезок AM образует постоян-
постоянный угол с АО, и отношение AM:АО постоянно. Поэтому точка М
описывает фигуру, подобную той, которую описывает точка О (срав-
(сравнить п. 150 и решение упр. 160).
Так как точка О описывает прямую линию — перпендикуляр, вос-
восставленный в середине стороны АВ, то и геометрическое место точек М
есть прямая линия. "•
Так как основание Р высоты АР треугольника АОО' есть (в силу
равенств AO^OD, АО' ^O'D) середина отрезка AD, то точка Р
описывает прямую, параллель-
параллельную ВС и проходящую через
середины сторон АВ и АС.
355. Пусть А — одна из то-
точек пересечения данных окруж-
окружностей О и О' (черт. 578),
МАМ' — данный угол. Строим
угол МАМ", равный углу ОАО'
и имеющий то же направление.
Точка М" получается из точки М
преобразованием подобия, со-
Н
Черт. 578.
стоящим из поворота на угол
МАМ" => const и гомотетии, так как AM": AM = АО': АО. Точка М
получается из М" поворотом на /_ М'О'М = 2 /_ М"AM' = const.
Итак, точки Ми М" а также М" и УИ' можно рассматривать как
соответственные в двух парах подобных фигур, имеющих одинаковое
направление вращения. Следовательно, и точки М и М можно рас-
рассматривать как соответственные в двух подобных фигурах, имеющих
одинаковое направление вращения. В силу упражнения 162 геометри-
геометрическое место точек, делящих отрезок ММ' в данном отношении, или
геометрическое место вершин треугольников, построенных на ММ' как
на основании и подобных данному треугольнику, есть фигура, подоб-
подобная геометрическому месту точек М, т. е. окружность.
356. Пусть Рхг — точка пересечения прямых А и В, Рп — точка пе-
пересечения прямых А и С, и т. д. (черт. 579). Применяя теорему
п. 192 к треугольнику, образованному прямыми А, С и D, и к секу-
Р Р Р Р Р Р
щей Е, получим —6 J3. 'У'-3—=1. Применяя ту же теорему
к треугольнику, образованному прямыми В, С и D и к секущей Е,
Р Р Р Р Р Р
получим:—?^~~3.-тг^Б^—^-^=1. Приравнивая левые части двух на-
СМЕШАННЫЕ ЗАДАЧИ
501
писанных равенств и производя очевидные сокращения, получим
?^^Л=§ф . ^1. Если прямые С, D и Е отсекают на
14
р р Р Р
прямых Диспропорциональные отрезки, то 15 13= 25 21. Из двух
Р Р Р Р
последних равенств следует —^—— =
35М3
Р Р
, или —3^-12 —
Р Р
т е
прямые Д, В и ? отсекают- на прямых С и D пропорциональные от-
отрезки.
Итак, мы доказали, что если на паре прямых (А, В) три другие
прямые отсекают пропорциональные отрезки, то то же имеет место
и для пары прямых (С, D), в которую не входит ни А, ни В
Следовательно, в этом случае и пары прямых (С, Е) и (D, Е) обла-
обладают тем же свойством.
В
Черт. 579.
Черт. 580.
Чтобы доказать далее, что и пара прямых (А, С), в которую вхо-
входит прямая А, принадлежащая к нашей первоначальной паре (Д, В),
обладает тем же свойством, мы должны дважды применить проведён-
проведённое рассуждение: если рассматриваемое свойство верно для пары
(А, В), то оно верно и дли (D, Е), а если оно верно для (D, Е), то
оно верно и для {А, С).
357. Пусть точка М лежит, для определенности, на не содержа
щей точки А дуге ВС окружности ABC (черт. 580), MD=x, ME=y
MF = z — расстояния этой точки от сторон треугольника ?С= а
СА—Ь, АВ=^с. В силу п. 237 имеем:
МА.а = МВ-Ь-\-МС-с. A)
Если D, Е и F — основания перпендикуляров из точки М на сто-
стороны треугольника, то треугольники MBF и МСЕ подобны (так как
/_АВМ=180° — /_АСМ=/_ЕСМ), откуда МВ:МС= z:y. Анало-
Аналогично из подобия треугольников MBD и МАЕ имеем МА:МВ=у.х.
502 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Следовательно, МА:МВ:МС= —:—: — . Заменяя теперь в равен-
равенстве A) отрезки MA, MB и МС пропорциональными им величинами,
a b с
мы получим — = -| . Аналогично для точек М, лежащих на ду-
дуге АС, мы найдём — = 1 , а для точек, лежащих на дуге АВ,
у х ' z
найдём — = 1 .Теорема доказана.
Z X ' V
Если расстояниям точки М от сторон треугольника ARC приписать
соответствующие знаки (сравнить решение упр. 301, примечание), то для
любой точки М, лежащей на описанной окружности, будем иметь по
абсолютной величине и по знаку
_в + *. + ?= 0. B)
х ' у '. z
Обратная теорема может быть сформулирована так: Если для не-
некоторой точки М плоскости имеет место по величине и по знаку
равенство B), то точка М лежит на описанной окружности.
Для доказательства рассмотрим точку М, не лежащую на описан-
описанной окружности, и обозначим через х', у' и z' её расстояния от сто-
сторон треугольника (взятые с надлежащими знаками). Далее, обозначим
через М точку пересечения прямой AM с описанной окружностью,
через х, у и z — её расстояния от сторон треугольника и через Р —
точку пересечения прямой AM со стороной ВС. Так как точки А, М',
М и Р лежат на одной прямой, то мы имеем по величине и по знаку
y:y' = z:z' = AM:AM; х:х' = РМ:РМ и х: х' = РМ: РМ =
= (PA -\- AM):(PA-\- AM')ф. AM: AM (известно, что при афЬк
сфО имеем , ф—|. Отсюда, так как точка М лежит на опи-
^ b-\-c~ b )
;r a b . с а / b c\ AM a
санной окружности, то —--\~ = —-(-[ ).——== — —¦
" ' х'~ у'* z' х'~\у ' zj AM x'
a AM а / х AM . ,
~" х" ~АМ^~х\~х'~~А~М')^ ' 0ТКУда и следУет обратная теорема.
Доказательство нуждается в видоизменениях (которые представляем
читателю), если прямая AM касается описанной окружности или если
она параллельна прямой ВС.
Примечание. По поводу обратной теоремы заметим, что утвержде-
а Ъ- с
ние: „если одно из отношении —, —, •— равно сумме двух других,
то точка лежит на описанной окружности", неверно, если не учитывать
знаков расстояний, как показывает следующий пример. На внешней бис-
с.ктрисе угла при в ршине; А равностороннего треугольника ABC возьмём
точку Р, для которой прямая PC перпендикулярна к АС (черт. 581). Для
точки Р имеем (по абсолютной величине; 2.t:=j/ = .z, и, следовательно,
смешанные задачи
503
— = 1 , в то время как точка Р заведомо не лежит на описанной
х у ' г F
окружности.
358. Пусть Р — точка пересечения касательных к одной из рас-
рассматриваемых окружностей в точках А и В (черт. 582); М и М —
точки пересечения прямой PC с этой окружностью.
В
Черт. 581.
Черт 532.
Так как точка Р есть полюс прямой АВ относительно окружности и прямая
ММ' проходит через точку Р, то полюс прямой ММ' лежит на пря-
прямой АВ. Иначе говоря, касательные к окружности в точках М и М
пересекаются в точке D прямой АВ, гармонически сопряжённой с
точкой С относительно точек А и В. Длина касательной будет
Черт. 583.
Черт. 584.
равна DM= у DA ¦ DB. Итак, геометрическое место точек М (или М')
есть окружность с центром D и радиусом, равным \^DA-DB.
359. Проведя радиус ОТ (черт. 583), перпендикулярный к каса-
касательной, и опустив из точки Р перпендикуляр PQ на прямую ОМ,
получим два равных треугольника МОТ и MPQ, откуда PQ^=OT.
Следовательно, геометрическое место точек Р есть пара касательных
к данной окружности, параллельных прямой ОМ.
"*" РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
360. Пусть ABDC — данный прямоугольник, О — точка пересече-
пересечения его диагоналей (черт. 584).
1°. Применяя к треугольнику ABC и секущей PR теорему п. 192,
получим для точки пересечения Н прямых ВС и PR следующее
НВ RC РА
равенство: тг^' тГя "db == • 1очно так же> обозначая через И
t* RA гd
точку пересечения прямых ВС и QS, получим из треугольника BCD,
что 2^.5?.^=1. Так как RC:RA = SD:SB, PA:PB =
= QC: QD (по абсолютной величине и по знаку), то И В: НС = И'В: Н'С
(также по величине и по знаку), так что точки И и Н' совпадают.
Итак, прямые PR и QS пересекаются на прямой ВС.
Точно так же доказывается, что прямые PS и QR пересекаются
на прямой AD.
2°. В полном четырёхстороннике, образованном прямыми RQ, QS,
PS и PR, диагональ НК делится гармонически диагоналями PQ и
RS (п. 202); следовательно, прямые MQ, MS, МН, МК образуют
гармонический пучок. Так как прямая MQ перпендикулярна к MS, то
прямые MQ и MS делят пополам углы между прямыми МН и МК
п. 201, следствие II).
3°. Применяя теорему п. 192 к треугольнику ABC и секущей
НВ RC РА л л
PR, мы нашли, что -yj- • - • — = 1. Применяя ту же теорему к
НС RA Pt>
треугольнику ADC и секущей QR, найдём, что —— • —, • — = 1. Так
как QD:QC=PB:PA, то из двух последних равенств получим по-
НВ КА /RC\2
членным перемножением и почленным делением ттт^" 7тц\ ' ТГ~л =: *?
/7С ?\ D у/\/1 '
НВ KD /Р,4\2 . РА /НСУКА RC
КА-{РВ) =1' °ТСЮДа РВ = ±]/
fHC-KD _
= -4-l/ . Знаки надо выбирать так, чтобы произведение
I НВ • К А
PA RC
-— • — имело одинаковый знак с НВ:НС. Эти равенства определяют
РВ RA
положение точек Р и R соответственно на прямых АВ и АС и тем
самым положение точки М на плоскости.
Для возможности построения точки М необходимо, чтобы отноше-
отношения -ТТ- и —- имели одинаковый знак (так как иначе подкоренное
НВ KL)
выражение отрицательно).
4°. Из предыдущего следует, что данным точкам Н и К соответ-
соответствуют два положения точки Р, а именно точки Р и Р' (черт. 585)^
СМЕШАННЫЕ ЗАДАЧИ
505
делящие гармонически отрезок АВ, и два положения точки /?, а
именно точки /? и /?', делящие гармонически отрезок АС. Точки
Р и R определяют точку М, а точки Р' и R'—точку М'. Обозна-
Обозначим через О центр прямоугольника ABDC, через м — середину от-
отрезка ММ', через Ог, О2 и ш.,, ш„— проекции точек О и со нл АВ
и АС.
В силу п. 189 имеем Oie2 = 01P-01P' = @,co1 — io,P)-(Olwl -\-
4-co,P') = 01w12— w,P2, так как со1Р' = со,Р. Точно так же 02О> =
' = О20J—со2/?2. Отсюда путём сложения находим
R'
С
R
ог
д
J
м
i
0
0.
p
D/
V
/ 1
В P'
B/?2), или OD2-\-wAP=
= Oco2. Ho OZ) и гоЛТ — радиу-
радиусы обеих окружностей, о которых
М
D
Черт. 585.
P В
Черт. 586.
говорится в задаче, Осо — расстояние между их центрами; таким
образом, последнее равенство есть условие ортогональности.
5°. Пусть прямая PR перпендикулярна к QS (черт. 586); так как
прямые PR и AM одинаково наклонены к АВ, и то же имеет место
для QS и MD, то прямая AM перпендику-
перпендикулярна к MD. Следовательно, точка М ле-
лежит на окружности, имеющей AD своим
диаметром, т. е. описанной около ABDC.
Обратно, если точка М лежит на этой
окружности, то прямая AM перпендикуляр-
перпендикулярна к MD, и, следовательно, прямая PR
перпендикулярна к QS. ¦
361. Предположим, что/_СВ^
~^> ^/_ВСС (черт. 587). Сравнивая треуголь-
треугольники CBff и ВСС, получаем СВ'^ВС.
Так как CB' = FB, то FB~>ВС, и из
треугольника ВСF имеем /_ BCF^/_BFC.
Отсюда, прибавляя по равному (в силу CF=BB'^CC) углу
/_FCC= /_ C'FC,получим/_ВСС>/_ BFC, или /_ВСС>^ ВВ'С.
Следовательно, /_ АСС<^/_ ВВ'А. Наконец, /_АВВ'^=180° —
— ?_ А — /_ ВВ'А <:\%0° — Z.A—Z. АС'С= /_ АСС. Итак, из пред-
предположения, что /_СВВ'^>/_ВСС следует, что /_ ABB' < /_ АСС.
„<
Черт. 587.
506
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Поменяв ролями точки В и С, мы видим, что из предположения
/_ ВСС > /_СВИ следует, что /_АСС < /_АВВ.
Если равные отрезки ВВ' = СС служат биссектрисами углов В и
С, то предположение ^/_АВС~^> /_АСВ приводит, очевидно, к проти-
противоречию, так как при этом мы имеем одновременно и ^/ СВВ ^>^/ ВСС
и /_ ABB ^> /_ АСС. К такому же противоречию приводит и допу-
допущение ^_АСВ^> /_АВС. Следовательно, / АВС= / АСВ, и треуголь-
ник ABC— равнобедренный.
361а. В силу формул п. 129 имеем для биссектрис 1а и 1Ь углов
a2 be 2
А и В треугольника ABC выражения: la2—bc . 1Ъ =ас —
(о -\-с)
Если
362.
ABC,
то очевидно и
¦ так что 'д>'ь-
Треугольник
если точки D, Е
й
О С
Черт. 588.
будем называть вписанным в треугольник
F лежат соответственно на сторонах ВС,
АС и АВ треугольника или их
продолжениях.
Найдем сначала треугольник,
имеющий наименьший периметр
среди всех треугольников, вписан-
вписанных в данный треугольник и имею-
имеющих своей вершиной заданную
точку D прямой ВС. Построим
точки Dl и D2 (черт. 588), сим-
симметричные с точкой D относитель-
относительно прямых АВ и АС. Периметр
DE'F', вписанного в данный треуголь-
D,E'F'DO. Треугольник наименьшего пе-
D,
произвольного треугольника
ник, будет равен ломаной
риметра DEF получится в том случае, когда линия DtEFD2 окажется
прямой. Таким образом, для построения треугольника DEF наимень-
наименьшего периметра с заданной вершиной D достаточно провести прямую D^Dn.
Чтобы решить теперь предложенную задачу, надо выбрать точку
D так, чтобы отрезок D1D2 был наименьшим. С этой целью заметим,
что /Ш, = AD2 = AD, так как точки D, и О„ симметричны с D
соответственно относительно АС и АВ, и ^/ Z)vlZJ = 2 ^/Л по той
же причине. Следовательно, угол при вершине А равнобедренного
треугольника AD{D2 не зависит от выбора точки D на прямой ВС, а
потому сторона DXD2 этого треугольника будет наименьшей, если
длина равных отрезков AD1 = AD2 = AD будет наименьшей, т. е.
если AD есть высота ADb треугольника ABC (черт. 589).
Докажем, что если Z)n есть основание высоты AD0 треугольника
ABC, то точки Dj и Д, лежат на прямой E(,F0, соединяющей основа-
основания Ео и Fo высот ВЕ0 и CF0 треугольника. В самом деле, если Do, Eo
и Fo — основания высот, то ^/_AEUFQ = ^/_CE0D0 (сравнить упр. 71).
СМЕШАННЫЕ ЗАДАЧИ
507
С другой стороны, ^/_CE0D0 = ^/_ CEODX, так как точки Do и D, сим-
симметричны относительно АС. Следовательно, ^_AE0FB = /_CEUDX, и по-
потому точка О, лежит на прямой E0F0. Аналогично докажем, что и
точка D2 лежит на прямой E0F0.
Итак, искомый треугольник имеет своими вершинами основания
высот данного треугольника.
362 а. 1°. Пусть в данный четырёхугольник ABCD вписан че-
четырёхугольник (в собственном смысле) MNPQ с наименьшим перимет-
периметром (черт. 590). Если бы угол
AMQ не равнялся углу BMN,
то мы могли бы уменьшить
длину ломаной QMN, а следо-
следовательно, и периметр четырёх-
четырёхугольника MNPQ, оставляя на
месте точки N, Р и Q и пере-
перемещая точку М по стороне АВ
(сравнить решение упр. 13, при-
примечание). Итак, для четырёх-
четырёхугольника с наименьшим пери-
периметром имеем:
Черт. 589.
/_CPN=/_DPQ =
Отсюда
A)
= /_B-\-/_D, так что четы-
четырехугольник ABCD можно
вписать в окружность.
2°. Пусть теперь ABCD —
вписанный четырёхугольник, и
MNPQ — четырёхугольник,
удовлетворяющий условиям A).
Построим последовательно че-
четырёхугольник ABClD1 (черт.
591), симметричный с ABCD
относительно стороны АВ, за-
затем четырёхугольник A^BC1D2,
симметричный с ABCXD^ отно- Черт. 590
снтельно ВСХ, четырёхугольник
/42SjCjZJ, симметричный с AXBC1D2 относительно C2D2, и, наконец,
четырёхугольник A,,B2C2D2, симметричный с A2BxCyD2 относительно
D2Ar В силу п. 102а четырёхугольник Л,ВС^D,, получается из ABCD
поворотом около точки В на угол, равный 2 ^/ В, а четырёхугольник
A2B2C^DV из AXBC^D2 поворотом около точки D2 в том же направ-
направлении на угол 2^/D. Так как 2 /_ ??-}-2 ^/ ?) = 360э, то соогвет-
508
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
ственные стороны четырёхугольников ABCD и Л252С2.О2 параллельны
и направлены в одну и ту же сторону.
Точка Q стороны AD переходит при этих построениях в точку Q3
стороны А2О„, удовлетворяющую условию AQ=A2QX, а периметр
четырёхугольника MNPQ даёт прямолинейный отрезок QQ3 в силу
О
N
условия A). Отсюда следует существование бесчисленного множества
четырёхугольников MNPQ (черт. 592) с одинаковым периметром:
чтобы получить один из них, достаточно провести на чертеже 591
отрезок QQ3 параллельно прямой АА2; при этом отрезок QQa можно
заменить произвольным параллельным ему отрезком Q'Qa'. Периметр
этих четырёхугольников б>дет меньше
периметров всех других вписанных
четырёхугольников, так как периметр
четырёхугольника, вписанного в
ABCD, отличного от MNPQ и имею-
имеющего своей вершиной точку Q, изо-
изобразится на чертеже 591 ломаной
линией, имеющей своими концами
точки Q и Qs.
Для вычисления периметра че-
четырёхугольника MNPQ висставим в
М
В
Черт. 592.
точках М, N, Р и Q перпендикуляры к сторонам четырёхугольника
ABCD и обозначим через А', В', С, D' точьн их пересечения, как
показано на чертеже 590. Так как прямые МА' и QA' — биссектрисы
углов NMQ и MQP, то точка А' равноудалена от всех трёх пря-
прямых NM, MQ и QP; следовательно, точка А' лежит на биссектрисе
угла MSQ, имеющего своими сторонами прямые MN и PQ. По той
же причине на биссектрисе угла MSQ лежит 'и каждая из точек А,
С и С. Следовательно, точки А, С, А' и С" лежат на одной прямой
СМЕШАННЫЕ ЗАДАЧИ
509
Совершенно таким же образом докажем, что и точки В, D, В и D'
лежат на одной прямой.
Применяя к четырёхугольнику BMBN теорему Птоломея (п. 237),
находим:
BB'-MN=BM-B'N-\-BN-B'M. B)
Если R — радиус окружности ABC и Е — точка этой окружности,
диаметрально противоположная точке D (черт. 593), то из подобия
двух пар треугольников, а именно BB'N и EDC, а также ВВ'М и
EDA, имеем: ВВ' :B'N:B'M = 2R:CD:DA. Заменяя теперь в равен-
равенстве B) отрезки ВВ', B"N, B'M пропорциональными им отрезками
2R, DC, AD, получаем:
2R-MN = BM-CD-\-BN-DA. C)
Лналогично имеем 2R-NP=CN-DA-\-CP-AB; 2R-PQ=DP-AB-\-
-\-DQ-BC; 2R-QM = AQ.BC+AM-CD. Складывая четыре послед-
последних равенства почленно, получим: 2R-(MN-\-
--NP + PQ + QM) = АВ-{СР-^ PD)\-
-- ВС ¦ {DQ -\- QA) -f CD-{AM -f MB) -f
- - DA ¦ (BN-\-NC) = 2 (AB ¦ CD -\- ВС • DA) =
= 2AC-BD. Итак,
D
H.
D)
* с-—-ы B
Черт. 593.
3°. Чтобы четырёхугольник MNPQ был
вписанным, надо, чтобы ¦/_ NPQ-\- /_ QMN=
= 18U°, т. е. чтобы /_ BMN -\- /_ CPN = 90°
(черт. 590). Ho /_ BMN =/_ BB'N; /_CPN=/_CCN. Следова-
Следовательно, мы должны иметь /_BB'N \/CC'N =/JiB'C-\-/_В"С'А =
= 90°, откуда вытекает, что прямая АС должна быть перпендику-
перпендикулярной к прямой BD.
4°. Если четырёхугольник MNPQ может быть вписан в окруж-
окружность, то центр со последней лежит на пересечении перпендикуляров,
восставленных в серединах К. и L сторон MN и NP. При перемеще-
перемещении точки М по прямой АВ стороны четырёхугольника KNLio сохра-
сохраняют своё направление. Точка К перемещается при этом по медиане
треугольника BMbN0 (где M0NQ P0Q0— какой-либо один из четырёхуголь-
четырёхугольников MNPQ), -точка L — по медиане треугольника CN0P0, точка N —
но прямой ВС. В силу решения задачи 193 четвёртая вершина со че-
четырёхугольника KNLo) перемещается при этом по прямой. i
363. Пусть точка О, найденная в задаче 105, лежит внутри дан-
данного треугольника ABC (черт. 358) и М—произвольная точка плос-
плоскости. В таком случае АА' ^МА-^-МА', причём равенство имеет
место только для точек отрезка АА'. Далее в силу упражнения 269
мы имеем МА' *=; MB + МС, причём равенство имеет место только
для точек дуги ВОС. Отсюда следует, что A A' s? MA -\- MB -f- MC,
причём равенство имеет место только в том случае, когда точка М
совпадает с точкой пересечения О отрезка АА' и дуги ВОС.
510
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Таким образом, для любой точки М, отличной от О, имеем
АА' = О А + ОВ -\- ОС < MA -\- MB -\- МС.
Для вычисления наименьшей суммы расстояний ОА-\-ОВ-\-ОС =
= АА' обозначим через Л" точку, симметричную с А' относительно
прямой ВС, и через D — точку пересечения прямых ВС и А'А"
(черт. 594). Так как AD есть медиана каждого из треугольников
АА'А" и ABC, то' мы имеем (п. 128) А'Аг-\- А"А2= 2AD1-\-2A'Dl и
AC2 -\~AB2 = 2AD2-\ ВС2. Так как из равностороннего треуголь-
треугольника А'ВС имеем A'D = -^BC-Vz, то
следует, что А'А*-\-А" А2 = ВС2-{-AC2-\- A&. Далее, если Н — осно-
основание перпендикуляра из точки
А на прямую А'А", то на осно-
основании п. 128а имеем равенства
А'А* —А'А2 = 2A'A".DH =
из предыдущих равенств
= 2\гд> BC-DH= 4]/з -пл. ABC. Из двух последних уравнений
получаем Л'Л2 = — {ВС2 -\- AC2 -f- АВ2) -\- 2 УЪ ¦ пл.ABC.
Пусть теперь точка О лежит вне треугольника, например на про-
продолжении отрезка А'А за точку А (черт. 595); в таком случае
/_ВАСУ>/_ВОС, т. е. /_ВАС~> 120°. Пусть биссектриса угла 1
пересекает окружность ABC в точке /. При этом 1В=/С и (в силу
неравенства ^/_ВАС^>\20°) 1В^>ВС. Применяя теорему Птоломея
(п. 237) к четырёхугольнику ABIC, найдём
(АВ -\- АС) -В1 =
A)
СМЕШАННЫЕ ЗАДАЧИ
511
Пусть теперь М—произвольная точка плоскости, отличная от точки А.
По теореме п. 237а, применённой к четырёхугольнику ВМС/, имеем
BC-MI ^{МВ^\- МС)-Ш (причём равенство имеет место только для
точек М, лежащих на дуге ВАС окружности ABC), откуда
Далее
B)
C)
причём равенство имеет место только для точек М, принадлежащих
отрезку AI. Из B) и C) находим, что
ВС¦ /А === (МА -Х- МВ-\-МС) • В/, D)
причём равенство имеет место только в том случае, когда точка М
совпадает с А. Сравнение A) и D) показывает, что для любой точки
М, отличной от А, имеем АВ -\- АС < МА -j- MB -\- МС.
Следовательно, сумма МА -\-MB-\-MC будет наименьшей, когда
точка М совпадает с А.
364. Пусть точки А', В" и С' построены как указано в тексте, и
О—точка пересечения окружностей ВА'С и СВ'А (черт. 596). Будем
иметь по величине и по знаку (срав-
(сравнить решение задачи 344)<? ВОС=
= $С ВА'С, $С СО А = $ССВ'А,
откуда ЗС АОВ = $С ЛОС -f
=z а -\- [3 = 180° — у = Y =
= -gC AC'В. Следовательно, точка
О лежит и на окружности АС'В.
Так как точки А', В, С и О
лежат на одной окружности, то
^С Л'ОС^-§С А'ВС, и аналогично
Зс сов' = §: cab' и §: в'оа =
=г- -§С В'СА. Отсюда •§? .4'ОС -}-
\
-\ §: САВ -г ЗС ЦСА =а + ^+
—j— у. и потому АО А'—прямая линия. Так же докажем, что ВОВ' и
СОС' — пр°мые линии.
Пусть теперь точка О лежит внутри треугольника ABC. На ос-
основании пп. 237 и 237а мы имеем для произвольной точки М пло-
плоскости МА' -ВС^МВ-А'С -\~ МС-А'В, причём равенство имеет место
только для точек дуги ВОС Но по построению треугольника А'ВС
имеют место равенства
ВС:СА':А'В = 1:т:п, A)
и предыдущее соотношение принимает вид: / • МА' ^ т • MB -}- п ¦ МС.
Далее/- АА' ^1-(МА -\-МА'), причем равенство имеет место только дли
точек М, лежащих на отрезке АА'. Следовательно, /• АЛ' s^l-MA -\-
-\-m-MB-\-п-МС, причём знак равенства имеет место только в том
случае, когда точка М совпадает с точкой пересечении О отрезка
512
РРШЕНИЯ УПРАЖНРНИЙ И ЗАДАЧ
АА' и дуги ВОС. Таким образом, для любой точки Ж,-отличной от
О, имеем l-0A-\-m-0B-\-n-0C = l-AA'<Ц-МА-\-т-МВ^\-п-МС.
Для вычисления минимума /-.4.4'= /-0.4 4- т-0В-\- п-ОС выра-
выражения / • MA 4- rn¦ МБ-\- п ¦ МС обозначим через А" точку, симметрич-
симметричную с А' относительно прямой ВС, и через D — точку пересечения
прямых ВС и А'А" (черт. 597). Так как AD есть медиана треуголь-
треугольника АА'А", то мы имеем (п. 128) .4'Л24-Л".42 = 2AD2-\-2A'D2.
Применяя теперь к треугольнику ABC и отрезку
AD теорему Стюарта (п. 127), получим AD2 =
юг) Г)С
ACi\ AB''BDDC Подставляя
равным ему
DC ?>C
это выражение для AD2 в предыдущее равен-
равенство и заменяя в последнем A'D1
выражением А'В2 — BD1, найдём:
А'А2 4- А-А2 =
\ВС
BD
—BD-DC)Jr2(A'B2 — BD*)=2 ~. AC* 4-
ВС
B)
Черт. 597.
Далее, так как A'D есть высота треуголь-
треугольника А'ВС, будем иметь (п. 126)
А'В*-\- ВС" — А'С* _ _ А'С24- ВС* — А'В*
BD = ^т^ ; DC = —
2ВС
2ВС
C)
Из
4- /я2
BD
равенств A) и C) получаем: -вт^ =
2/2
DC
ВС'
А'В
НС
-~ 2/2 ' ВС I
и умножая на /2, получим:
АВ п „ /О.
= — . Подставляя эти значения в равенство B)
НС I
„2 4- /2 — /?г2) • ЛС2 4-
D)
С другой стороны, разность квадратов двух сторон треугольника
АА'А" равна (согласно п. 128а) произведению третьей стороны и
проекции на неё соответствующей медианы. Иначе говоря, обозначая
через Н проекцию точки А на прямую А'А'', будем иметь А'А1—
16-пл ЛВС-пл.А'ВС
—A"AZ=2A'A"-DH=AA'D-DH = ~В~C ' откуда в
силу равенства пл. А'ВС: пп.Т = ВС2 :Р (сравнить п. 257) находим
/2.^4'Л'— А"Аг)=^ 16'-пп. ABC-пп.Т.
{
СМЕШАННЫЕ ЗАДАЧИ
513
— JI
Из этого равенства и равенства D) получаем окончательно:
/з. А'Аг = — [I2 (С А2 -\--AB2 — ВС2) -J- in2 (AB2 -J- ВС* — С А2) -\-
-\-п2 (ВС2-{-СА2 — АВ2)]-\-8 ил.АВС-ил.Т. E)
Пусть теперь точка О лежит вне треугольника, например на про-
продолжении АА' за точку А (сравнить черт. 595); в таком случае
/_ ВАС-\-/_ CAB'=/_ Л-)-а^> 180°. Найдём на окружности ABC
такую точку /, что BJ:/C=n:/n, причём из двух точек, удовлетво-
удовлетворяющих этому условию, обозначим через / ту, которая не лежит на
дуге ВАС (черт. 598). Отложим /В" = п, /С' = т. При этом прямая
В"С" параллельна ВС. Обозначим ещё длину отрезка В"С" через /'.
Из подобия треугольников /ВС и 1В"С"
находим:
BC:CI:BI=l':m:n. F)
Далее /_ А -\~/_ В/С= 180°, /_А +
-\-а^> 180°; следовательно, /_ В/С <^а, и
из сравнения треугольников 1В"С" и Т на-
находим:
/'</. G)
Применяя к четырёхугольнику ABIC тео-
теорему Птоломея, найдём АВ-/С-\-АС-В1 =
= ВС:А/, откуда в силу F):
m-AB-\-n-AC = l'-AI. (8) Черт. 598.
Пусть теперь М—произвольная точка плоскости, отличная от точки А.
Применяя к четырёхугольнику BMCI теоремы пп. 237 и 237а,
имеем: Mf-BCs^MB-IC-\-MC-/B, или в силу F) l'-MI^ m-MB-{-
-\-n-MC, причём равенство имеет место только для точек М, лежа-
лежащих на дуге ВАС окружности ABC. Отсюда в силу G) имеем:
l'-MI-{-r-MAzszl-MA-{-m-MB-]-n-MC, (9)
причём равенство имеет место только при МА = 0, т. е. при условии'
что точча М совпадает с А. Далее
/А^М/-{-МА, A0)
причём равенство имеет место только для точек М, принадлежащих
отрезку /А. Из (9) и A0) находим:
1 V -1А<1-МА-\-т-МВ-\-п-МС, A1)
причём равенство имеет место только при условии, что М совпадает
с А. Наконец, сравнение (8) и A1) показывает, что для любой точки
М плоскости, отличной от точки А, имеем: m-AB-\-n-AC<^l'MA-\-
-\-m-MB-\-n-MC. Следовательно, 1-МА -\-m-MB -\- п-МС будет
иметь наименьшее значение, когда точка М совпадает с А.
Рассмотрим, наконец, случай, когда не существует треугольника,
стороны которого были бы пропорциональны числам /, m и п. Пред-
33 Элементарная геометрия
514
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
положим для определённости, что / есть наибольшее из чисел /, т и
п. В таком случае 1^т-\-п, и для любой точки М, отличной от А,
имеем: 1-МА-\-т-МВ^-п-МС^(т-\-п)-МА-\-т-МВ-^п-МС=
=т • (МА-{-МВ) -\- п ¦ (МА -\- МС) ^> т • АВ-f- n • АС, так что наименьшее
значение будет опять получаться, когда точка М совпадает с А.
Примечание. Формулу E) можно получить несколько более корот-
коротким путём,, если воспользоваться основными формулами триюиометрии. А
именно из треугольника САА' (черт. 596) имеем 1--А'А2 = РАС'-\-Р-А'С'1—
— 2Р-АС-А'С-cos (С-{-*(). Заменим, пользуясь подобием треугольников
А'ВС и Т, величину 1-А'С через тп-ВС и раскроем косинус суммы: Р А'А2=
= РАС*-\-т-В(У— 21т-ВС-AC (cos С cos f — sinCsinY). Подставляя сюда
2lm cos т = Р + т* — л2; 2ВС-АС cos С = ВС2 + АС* — А&\ lm sin у = 2 пл. Г,
ВС-AC- sinC=2 пл. ABC, мы и получим формулу E).
365. 1°. Если точки D, Е и F делят стороны треугольника ABC
(черт. 599) на части, пропорциональные квадратам прилежащих сторон,
то мы имеем DB:DC= — c2:b2;
ЕС:ЕА = —а?:с2; FA:FB=—b2:a2,
и прямые AD, BE и CF проходят
через одну точку в силу теоремы
Чевы (п. 198).
2°. Для точки пересечения ме-
медиан О расстояния до сторон тре-
треугольника обратно пропорциональны
длинам этих сторон в силу равно-
великости площадей ОВС, ОСА и ОАВ (см. решение упр. 295). Для
любой точки О' прямой AD имеем ил.ВОА: пл., О'АВ= AD:AO' =
—nn.CDA :пл.О'АС, или xrn.BDA: nn.CDA = nn.O'AB: пл. О'АС. Но,
с другой стороны, i\n.BDA:nn.CDA = BD:DC—c2:b2, откуда
пл. О'АВ:пп.О'АС=с2:Ь2. Обозначая через О'Р, O'Q и O'R рас-
расстояния точки О' от сторон треугольника ABC, будем иметь
ип.О'АВ: пл. O'AC=(O'R-c):(O'Q-b). Из двух последних равенств
находим O'QiO'R = b:c.
Для точки О' пересечения прямых AD, BE и CF находим поэтому:
O>P:O'Q:O'R = a:b:c. A)
В силу сказанного в решении задачи 197 точка О' получается
из точки пересечения О медиан треугольника указанным там построе-
построением, так как расстояния точки О' от сторон треугольника обратно
пропорциональны расстояниям точки О от тех же сторон.
3°. Если Р, Q и R, как и выше, основания перпендикуляров, ,
опущенных из точки О' на стороны треугольника, то / RO'Q-\-
-\- /_RAQ=\%Q°, и, следовательно (п. 256), nn.QO'R:nn.ABC =
= (O'Q-O'R):bc. Точно так же илМО'Р:пл.ABC = (O'R-О'Р):ас;
i\n.PO'Q:i\n.ABC=(O'P-O'Q):ab. В силу равенств A) отсюда
следует, что nn.QO'R = пл.RO'P = nn. PO'Q, так что (сравнить ре-
решение упр. 295) точка О' есть центр тяжести треугольника PQR.
366. Первое решение. Предположим, что среди всех тре-
треугольников, вписанных в данный треугольник, есть треугольник DEF
СМЕШАННЫЕ ЗАДАЧИ
515
(черт. 600), для которого величина s = EF2-\-FD2-\-DE2 имеет наи-
наименьшее значение. Если D,—середина стороны EF, то в силу п. 128
имеем FD2
= yEF* + 2D,D2. Из
этой формулы видно, что если бы медиана /3D, не была перпендику-
перпендикулярной к стороне ВС, то мы могли бы уменьшить s, оставив на месте
точки Е и F и заменив точку D основанием перпендикуляра из точки D,
на сторону ВС. Следовательно, медиана /3D, перпендикулярна к сто-
стороне ВС. Таким же образом докажем, что все медианы треугольника
DEF перпендикулярны к соответствующим сторонам треугольника
ABC. i
Пусть теперь О — точка пересечения медиан треугольника DEF.
В силу упражнения 295 имеем
пл. GEF^=:uji. QFD = i\n. GDE. A)
С другой стороны, /_EGFА-/_ВАС = 180°, и, следовательно (ц. 256),
w\.GEF:nn.ABC — (GE-GF):(AB-AC); аналогично nn.GFD: пл.АВС=
В D
Черт. 600.
во с
Черт. 601.
= (GF ¦ GD): (ВС- АВ); пл. GDE: пл. ABC = (GD . GE): (AC ¦ ВС).
,,. GE-GF GF-GD GD-GE
Отсюда, в силу A), -—=— == _ & =—^rRr, , и следовательно,
GD:GE:GF=BC:CA:AB. Итак, расстояния точки G — центра тя-
тяжести искомого треугольника DEF — от сторон данного треугольника
пропорциональны длинам этих сторон, и точка G совпадает с точкой
О', рассмотренной в задаче 365 (сравнить п. 157, построение 10), а
искомый треугольник DEF — с треугольником PQR из той же задачи.
Пусть теперь М — произвольная точка плоскости (черт. 601), D,
Е и F — основания перпендикуляров из точки М на стороны треуголь-
треугольника ABC и G — точка пересечения медиан треугольника. DEF. В
силу упражнения 140 имеем М D2 -f- ME2 -\- MF2 = GD2 -f- GE2 -J- GF2J\-
-|- 3MG2. Так как точка пересечения медиан треугольника отсекает
от каждой из них одну треть, считая от соответствующего основания
/п. 56), то из решения упражнения 137 следует:
GD" -\- GE2 -j- OF2 = -I (EF2 -\~ FD2 -\- DE2). B)
33*
516
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Отсюда М D2 4- ME2 -f MF2 = -lr(EF* -f FD2 -\- D&) +
о
Из этого равенства видно, что сумма квадратов расстояний точки М
от сторон треугольника, т. е. MD2-\-ME2-\-MF2, будет наименьшей,
когда точка М будет совпадать с точкой О' из задачи 365, так как
при этом, как только что было доказано, сумма EF2 -\- FD2 -j- DE2
будет наименьшей, a MG обра-
обращается в нуль. i
Переходим теперь к отыска-
отысканию треугольника DEF, для ко-
которого величина s=l-EF2-±-
-\-m-FD2-\rn-DE2, где /, т и
п—данные числа, имеет наимень-
наименьшее значение, опять в предполо-
предположении, что такой треугольник cj-
ществует. При этом мы рассмотрим
случай, когда числа /, т и п по-
В
D
Черт. 602.
ложительны.
Если точка Dx (черт. 602)
делит сторону EF искомого тре-
треугольника в отношении ED^:D^F=m:n, то в силу п. 127 (сравнить,
например, решение упр. 141) имеем:
inn
т ¦ DF2 -f п ¦ DE2 = (m-V-n)-D.D2-\ -г— -EF2
1 ' * т-\-п
C)
C')
Если бы прямая DDX не была перпендикулярна к стороне ВС, то
мы могли бы уменьшить s, оставив на месте точки Е и F и заменив
точку D основанием перпендикуляра из точки D, на сторону ВС.
Следовательно, прямая DDV делящая сторону EF в отношении
LD^.DyF = m:n, должна быть перпендикулярна к стороне ВС.
Точно так же докажем, что прямая ЕЕг, делящая сторону FD в
отношении FEl:ExD = n:l, должна быть перпендикулярна к сто-
стороне АС, а прямая FFX, делящая сторону DE в отношении
DFx:F}E^l:m,— перпендикулярна к стороне АВ. Так как при этом
D E E F F D
¦ ' • —1 • J— = — 1, то перпендикуляры к сторонам треугольника
ABC в вершинах D, Е и F искомого треугольника проходят (в силу
п. 198) через одну точку О и делят стороны EF, FD и DE треуголь-
треугольника DEF соответственно в отношениях т:п, п:1 и 1:т.
Так как прямые DDX, EEX и FFV, проходящие через одну точку О,
делят Стороны треугольника DEF в отношениях EDx:DyF =^ т:п;
fEl:ElD = n:I; DFJ:FlE=:l:m, то мы имеем (см. решение упр. 295)
СМЕШАННЫЕ ЗАДАЧИ 517
nn.OFD:i\n.ODE—FD.:D.E~—: — ,и аналогичноnn.ODE:nn.OEF=
11 11
= — '•—г ; nn.OEF:i\n.OFD = —:—,откуда/-пл. ОЕF=m..пл.ОFD=
til I fti
=r.-nn.ODE. С другой стороны, найдём, как и выше, пл. OEF:nn. ABC=
= (ОЕ ¦ OF): (АВ • АС); пл. OFD : пл. ABC = (OF • OD) : (АВ . ВС);
nn.ODE:nn.ABC=(OD-OE):(BC-AC). Отсюда
OE OF_ OF OD _ OD OE
т. e.
OD OE OF
l-ВС т.АС п-АВ'
D)
Итак, расстояния точки О от сторон данного треугольника пропорцио-
пропорциональны произведениям l-ВС, т-АС и п-АВ. Тем самым определяется
(п. 157, построение 10) положение точки О, а следовательно, и по-
положение точек D, Е и F — оснований перпендикуляров из точки О на
стороны треугольника.
Рассмотрим теперь вкратце случай, когда коэфициенты /, т и п имеют
произвольные знаки, причём разберём отдельно следующие предположения:
1)т + я>0, л-|-/>0, 1-\-т>®, 2) m-f-n<0, n-f/<0, l + m<\f,
3) среди сумм т -\- л, п -f- /, 1-\-т имеются как положительные, так и отри-
отрицательные, но ни одна из них не равна нулю; 4) одна из сумм т -\~ п,
п-\-1 и I-\~ m равна нулю.
1°. Пусть коэфициенты /, т и п имеют произвольные знаки, по
m-j-/2>0, n-\-l у- 0, / -\~т > 0. Разделим стороны искомого треугольника
DEF ^черт. 602) так, "чтобы имели место по величине и по знаку равен-
равенства ED}:DiF—m:n; FEx:EyD = n:l; DFl:F-lE=l:m. В силу упражнения 218
будем иметь, как и выш , пользуясь равенством C'):
s = I ¦ EF* + т ¦ DF* + л-DE2 = (l-\--?ZL-\ . EF^ + (m -f- n)
^ f E)
Так как гл-(-л>0, я -f- / > 0 н /-{-/га>0, то сохраняют силу преды-
предыдущие рассуждения, если только площадям треугольников и расстояниям
точки от сторон треугольника приписывать определенные знаки, как
указано в решениях упражнения 301 и задачи 324. Наименьшее значение
* получается для точки О, определяемой опять равенствами D).
2°. Если /га-)-л<0, л-|-/<0 и 1-\-т<0, то рассуждения, вполне
аналогичные предыдущим, показывают, что для точки О, определяемой
равенствами D), величина s достигает не наименьшего, а наибольшею
значения, так как из равенств E) следует, что в этом случае величина л
возрастает, если при неизменных точках Е и F величина D^D уменьшается
(в силу т -f- п < 0), и т. д.
3°. Если среди величин т^-п, п-{-1 и 1-\-т имеются как положитель-
положительные, так и отрицательные, то ветичина s не имеет ни для какого тре-
треугольника DEF ни наибольшего, ни наименьшего значения. В самом деле,
пусть для определённости m-\-n>G и я-[-/<0- В таком случае из фор-
РРШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
мул E) следует, что можно увеличить s, оставляя на месте точки Е и F,
удаляя точку D от основания перпендикуляра, опущенного из точки Di
на сторону ВС. С другой стороны, можно и уменьшить s, оставляя на
месте точки D и F и перемещая точку Е.
4° Остаётся ещё рассмотреть случай, когда среди сумм т -\-п, п-\-1
и / -(- т есть равные нулю. Пусть для определённости т -j-// = 0. Обозна-
Обозначив через DH высоту треугольника ДЁУ^черт. 602), будем иметь s = l-FF2j-
+ m-(DF2 — DE2) = l-FF2 + rn-(EF2±2EF-EH). Отсюда видно, что, не изме-
изменяя положения точек Е и F, можно придать величине s любые значения,
выбирая соответствующим образом точку Н. т. е. точку D. Итак, в этом
последнем случае величина s не достигает ни наибольшего, ни наименьшего
значения ни для какого треугольника DF.F.
Резюмируя всё сказанное, приходим к следующему окончательному
выводу: ^
Если все три суммы т-\-п. п-\-1 и 1-\-т положительны (отрица-
(отрицательны), то вершины треугольника DEF, для которого величина s = l-ВС2-\-
-\-т-АС2-\- п-АВ2 имеет наименьшее (наибольшее) значение, получаются
следующим построением: определяем точку О, расстояния которой от
сторон треугольника пропорциональны произведениям 1-ВС, т-АС и
п-АВ. и из точки О опускаем перпендикуляры на стороны треугольника.
Если среди сумм т-\-п, п-\-1 и I -\-т есть суммы, равные нулю или
имеющие противоположные знаки, то величина s не достигает ни для
какого вписанного треугольника ни наибольшею, ни наименьшего значе-
значения.
Примечание. Приведённое только что решение в случае, когда
т-\-п, п-\-1 и 1-\-т имеют одинаковые знаки, существенно основано на
предположении, что среди всех вписанных треугольников имеется тре-
треугольник, для которою величина s имеет наименьшее (или наибольшее)
значение. Если даже считать очевидным, что для вписанного треугольника
величина s не может принимать сколь угодно малых значений, а остаётся
большей некоторого числа, то и тогда мы ещё не можем быть уверены
в существовании вписанного треугольника, для которого s имеет наимень-
наименьшее значение. В самом деле, логически мыслимо такое положение вещей,
что среди вписанных треугольников имеются треугольники, для которых
величина * имеет значения, большие некоторого числа s0 и сколь угодно
близкие к sn, но не существует треугольников, для которых s равно или
меньше %
Приводим поэтому второе решение, в котором существование тре-
треугольника с наименьшим значением s не предполагается. При этом мы
ограничимся случаем положительных коэфициентов /, т и п.
Второе решение. Будем исходить из тождества
(а2 _|_ Ьг _j_ С2). {Х2 _|_ys _j_ Z2) = (ax -\-by-\- czf -\- (bz — суJ +
+ {ex - azY + (ay - bxJ, F)
имеющего ^есто для любых шести чисел а, Ь, с, х, у и z. Если
под а, Ь и с понимать длины сторон данного треугольника, под х,
у и z—расстояния произвольной точки О плоскости от его сторон,
то мы будем иметь (сравнить решение упр. 301) ах -j- by -\- cz = 25, где
S—площадь данного треугольника. Предыдущее равенство принимает вид:
Отсюда непосредственно следует, что сумма квадратов расстояний
некоторой точки О от сторон данного треугольника имеет наимень-
СМЕШАННЫЕ ЗАДАЧИ 519
шее значение при условии, что каждая из скобок в правой части
равна нулю, т.* е. при x:y:z = a:b:c; следовательно, точка О
совпадает с определённой в задаче 365 точкой О'.
Пусть теперь DEF (черт. 603) — произвольный треугольник, впи-
вписанный в данный треугольник, и G — центр его тяжести. Мы имеем,
как и выше в равенстве B),
= 3 (GD2 -\- GE2 -\- GF2). G)
Если обозначить через Do, Ео и Fv основания перпендику-
перпендикуляров из точки G на стороны данного треугольника, то GD2 =
= GD0t-{-D0D2, и т. д. Следо- „
вательно, s = EF1 -f- FD* -\- DE2 =
@40+Y)+@H
-\-EQE2-\-F0F2). Отсюда непосред-
непосредственно видно, что s имеет наимень-
наименьшее значение, когда точка G со-
совпадает с точкой О', а треугольник
DEF — с треугольником PQR из за-
задачи 365, так как в этом случае
сумма GD02 + GE02 -\- GF02 имеет,
по доказанному, наименьшее воз- ? ~п л~
можное значение, a D0D = E0E=^ °
= F0F=0 (в силу упр. 365, 3°). Черт. 603.
Переходя к отысканию наименьшего значения выражения s =
= l-EF2 -\-m-FD2 -\-n-DE2, где /, т и п — данные положительные
числа, мы рассмотрим следующее обобщение тождества F):
I (mbz — псуJ 4" т (псх —lazJ -\- n (lay — /пЬх)ъ
+ шп • (8)
Это тождество можно получить из F) путём замены а, Ь, с, х, у
и z соответственно через ayl , by in, суп, —т=, -^f= и ——.
yl у т V п
С помощью тождества (8), подобно тому, как и выше, убеждаемся
х" i У2 , z2 а
что величина—-+--— достигает наименьшего значения при
/ ' т ' л v
условии, что каждая из скобок во втором слагаемом правой части
равенства (8) равна нулю, т. е. при условии:
x:y:z = la:mb:nc. (9)
Опуская теперь из найденной точки О, удовлетворяющей усло-
условиям (9), перпендикуляры OD0, OE0 и OF0 на стороны треугольника
ABC (черт. 604), мы и получим, как будет видно из дальнейшего, искомый
треугольник D0E0F0. Обозначим через D', Е и F' точки пересечения
этих перпендикуляров со сторонами ^о/7,,, F0D0 и D^g треугольника
520
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
D^Eff,. В силу п. 256 имеем пл. OE0F0: пл. АВС=(ОЕ0 • OF0): (
=yz : be; nn.OF0D0 : xm.ABC=zx : ca; пл.О?>0?0:пл. АВС= xy.ab.
Отсюда пл. OEf.F-.nn. OF0D0:nn. OD0E0=-: —:—=j:—: — . Следова-
X у Z I TTi tl
тельно, E0D':D'F0 = nn. OD0Ee:nn. OF0Dn = m:n, где?>' — точка пе-
пересечения прямых E0F0 и OD0 (см. решение упр. 295). Аналогично
F0E':E'D0=:n:l; DuF:F'E0=^l:m. Итак, если из точки О, удо-
удовлетворяющей условиям (9), опустить перпендикуляры OD0, OE0
и OF0 на стороны треугольника ABC, то эти перпендикуляры
разделяют стороны треугольника D0E0F0 соответственно в отно-
отношениях т:п, п'Л и 1;т.
Впишем теперь в данный треугольник ABC произвольный треуголь-
треугольник DEF (черт. 605) и разделим стороны последнего прямыми DDt,
Д
В
В
Черт. 604.
D Do
Черт. 605.
ЕЕЛ и FFl в отношениях EDl:DlF=m:n; . FE1:E1D = n:l;
DF,:FX = l:m. Прямые ?>?>,, ЕЕ. и FF. пройдут через одну
D.E E.F F.D
точку О (п. 198). При этом мы будем иметь —'— ¦ -~— ¦ ——; ±= — 1,
?>?, D.E F.D _ „_._ .
или р~э=7Гр" pf- ак как СТОР°НЫ треугольника EDDX (или
их продолжения) пересекаются с прямой FFX в точках О, F и F,,
то мы будем иметь (согласно п. 192) ' ~pf "F^D ~ '
DXE F,D
здесь последний член равной ему величиной ' получим-
DO
DE,
V
m
tnn
откуда
Заменяя
A0)
Отсюда
mn
¦DO;
.^0+0D.=^T^°-<">
СМЕШАННЫЕ ЗАДАЧИ 521
Применим теперь, как' и при первом способе решения настоящей
задачи (сравнить равенство C)), теорему Стюарта (п. 127) к треуголь-
треугольнику DEF и отрезку DDV Мы получим:
J"" EF2. A2)
Применяя ту же теорему к треугольнику OEF и отрезку ODU найдём
аналогично:
EF^ A3)
Заменяя в равенствах A2) и A3) DD1 и ODr их значениями A1),
будем иметь:
[0D = mDF + nDE^
l2(m-\-ri) ' т-\-п
A4)
„ЛТ x-OD = m-OF + n-OE '~-EF2. A5)
12(т-\-п) m-\-n '
и nc, mn-\-nlA-lm
Наконец, умножая все члены равенства A5) на и вы-
вычитая из полученного равенства почленно равенство A4), получим
после алгебраических преобразований равенство
ОП2 OF OF\
\{ ). A6)
OF2 OF2\
Равенство A6) является обобщением равенства G); последнее полу-
получается из равенства A6) при 1==т = п=1.
Опустим из точки О перпендикуляры OD0, OEQ и OF0 на стороны
треугольника ABC и заменим в равенстве A6) OD2 через OD02-\-
-\-D0D2, и т. д. Окончательно будем иметь s = l-EF2-\-m-FD2-\-
j(°a ^!^) (
ЕЕ2 F Fi\~\
-|— 1—-—I . Из этого авенства непосредственно видно, что
величина s имеет наименьшее значение, если точка О удовлетво-
удовлетворяет условиям (9), так как при этом, по доказанному, величина
OD г ОЕ 2 OF2
—-Л--\ —-| — имеет наименьшее значение и D0D = E0E =
= F0F=0 в силу того, что прямые OD, ОЕ и OF совпадают с
перпендикулярами к сторонам треугольника ABC.
367. Первое решение. Предположим, что среди всех тре-
треугольников, вписанных в данную окружность, есть треугольник ABC
черт. 606), для которого сумма s = l-BC2-i-m-AC2-\-n-AB2, где
(/, т и п — данные положительные числа, имеет наибольшее значение.
522 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗЛДЛЧ
Будем для определенности предполагать, что
,п. A)
Если точка D делит сторону ВС (внутренним образом) в отноше-
отношении BD:DC=m:n, то мы имеем (п. 127) в силу теоремы Стюарта
(как и в решении задачи 366, формула C)): т ¦ AC2 -f п ¦ АВ1 =
= (m-\-n)-AD24 ^—-ВС2. Отсюда
и »i \
B)
Величина s имеет при данных точках В и С (и, следовательно,
при определённом положении точки D) наибольшее значение, если
. расстояние AD будет наибольшим из возмож-
возможных. Но наибольшим расстоянием от данной
точки D до точки окружности служит (п. 64)
больший отрезок диаметра, проходящего че-
через точку D. Итак, диаметр окружно-
окружности, проходящий через точку А, делит
сторону ВС в отношении т:п. Аналогич-
Аналогичным свойством должны обладать и диаметры,
проходящие через точки В и С: диаметр, про-
проходящий через В, делит сторону СА в отно-
отношении СЕ:ЕА = п:1; диаметр, проходящий
через С, делит АВ в отношении AF:FB= l: т.
Повторяя теперь для треугольника ABC и прямых AD, BE и CF,
проходящих через одну точку, в точности те же выкладки, которые
привели нас в решении задачи 366 к формуле A0), получим вполне
аналогичное соотношение
AO_AF AE_l I _1(т + а)
т ' п тп
Отсюда
+ П1.+1т.АО==т'1 + П^т R, D)
Цт-\-п) l(m-\-n) v '
где R — радиус данной окружности. Равенства C) или D) определяют
положение точки D на прямой АО.
Далее через точку D требуется провести хорду ВС, которая
делилась бы в точке D в отношении BD:DC^m:n. Это последнее
построение можно выполнить аналогично решению упражнения 165;
надо только предположить, что обе данные там окружности совпадают
между собой. Таким образом строится искомый треугольник ABC.
Чтобы построение было возможно, необходимо и достаточно, чтобы
определяемая условием C) точка D лежала внутри окружности и
чтобы через эту точку можно было провести хорду ВС, которая де-
делилась бы в точке D в отношении да:п. Точка D будет, как это
СМЕШАННЫЕ ЗАДАЧИ 523
видно из равенства C), лежать внутри окружности, если 1 ^> 1,
т. е. если
Через точку D можно провести хорду, которая делится в этой
DA' •m.AD
точке в отношении т:п, если -гтт <. ~ <С гГТ^ ^так как 0ТРезки А^
и A'D представляют собой наибольшее и наименьшее расстояния от
точки D до точек окружности), где А' — точка, диаметрально проти-
2R—AD.m, AD
воположная точке А, т. е. если -— <Г - <^~ ——. Заменяя
AD ^ n 2R — AD
, ^ ,., — тп-\-п1Л-1т - т ^
здесь Аи его выражением D), получим ! ; < <^
тп -\-nl-\-lm ^ п ^
тп -\- nl 4- 1т
< !—; ; — . I теобразуя эти неравенства, будем иметь
^ — тп-\-п1 -\- 1т
— <Ст~~1 • ~ ^ Т^ ' ^ти неРавенства будут выполняться сами
собой, если обозначения коэфиииентов /, т и п выбрать так, чтобы
выполнялись условия A).
Итак, если обозначения коэфициентов /, т и п выбрать так, чтобы
выполнялись условия A), то единственное необходимое и достаточное
условие возможности построения треугольника ABC выражается не-
неравенством E).
Истолковывая неравенство E) геометрически, приходим к следую-
следующему 'окончательному результату: треугольник ABC, для которого
величина s имеет наибольшее значение, существует только при усло-
условии, что можно построить треугольник, стороны которого пропор-
1 1 1
циональны —, — и — , т.е. высоты которого пропорциональны I, тип.
Примечание. В приведённом решении мы предполагали, что тре-
треугольник, для которого s имеет наибольшее значение, существует. По
поводу этого допущения можно было бы повторить сказанное в примечании
к первому решению задачи 366.
И действительно, в процессе решения выяснилось, что искомый тре-
треугольник существует не при всех значениях /, т и п. Проводим поэтому
второе решение, в котором существование искомого треугольника уже не
предполагается.
Второе решение. Предположим опять, что /, т и п —
положительные числа и
Пусть ABC — произвольный треугольник, вписанный в данную
окружность (черт. 607). Разделим его сторону ВС точкой D в отноше-
отношении BD:DC=m:n. Как и в первом решении, будем иметь формулу
B). Проведя через точку D диаметр MN (пусть при этом для опре-
524
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
делённое™ MD^DN), будем иметь BD-DC=MD- BR — MD).
С другой стороны, BD = j ВС и DC=—,— • ВС, откуда
т\п т\п ' у
BD-DC=
т-\-п
-ВС* и ВС* =
ставляя это значение в формулу B), будем иметь
s= P(m + nJ-|-(m + «) | • MB -BR — MD)-\-
т-\-п
MD-BR- MD). Под-
ПодЭто выражение для s можно представить в виде s^
\l
^ —
I
J
. AD2.
тп
/re/2
1
-(- (m-\-n) • AD2 — (m-\-n)'MD2 или, после за-
•/(w-l-яJ . - . .
|-(т-|-я) равным ему выра-
мены
(т 4- л) (/ге/г -I- nl 4- /т)
'жением ¦ и группиров-
тп
ки членов, в виде s = —4—
тп
[2 (/м 4-
-\- nl -f- lm) R ¦ MD — / (т-
Черт. 607. -\-{т -|- л) • (AD2 — ,
Из этого выражения видно, что 5 достигает наибольшего значе-
значения, если выполнены следующие условия:
1) точка А совпадает с М (так как в противном случае
2) функция
y = 2(mn-\-nl-\-lm)-R-MD — Цт-\- n)-MD2 F)
достигает наибольшего значения. ¦
Но функция _у, определяемая равенством F), достигает (как это
следует из свойств функции у=Ах2-\- Вх -\- С при Л<?0) наиболь-
наибольшего значения при
l(m-\-n) v
возрастает при значениях AID, меньших этого значения, и убывает
при значениях MD, больших того же значения. Получили то же по-
положение точки D, что и в первом решении [см. формулу D)].
Если точка D, определяемая условием G), окажется внутри данной
окружности, а это будет иметь место при
т. е. при
СМЕШАННЫЕ ЗАДАЧИ 525
то s достигает в этой точке своего наибольшего значения. Возмож-
Возможность провести через эту точку D хорду ВС, которая делилась бы
точкой D в отношении т:п, требует, чтобы имели место неравенства
DN .m .MD „
< <^ Как и при первом решении задачи, эти неравенства
будут выполнены в силу предположения A). Мы получим при этом
тот треугольник ABC, о котором шла речь в первом решении.
Если же точка D, соответствующая максимуму функции у и опре-
определяемая равенством G), будет лежать на окружности или вне её, то
наибольшее значение s будет получаться при наибольшем допустимом
значении MD, т. е. при MD = 2R. Итак, величина s принимает наи-
наибольшее значение при условии, что треугольник вырождается в дважды
взятый диаметр окружности.
До сих пор мы рассматривали случай, когда /, т ил—положительные
числа. Случай, когда некоторые из коэфициентов /, т и п отрицательны,
сводится к случаю положительных коэфициентов.
В самом деле, пусть два из коэфициентов, скажем т и п, отрицательны.
В таком случае, обозначая через А' точку, диаметрально противоположную
точке А (черт. 607), будем иметь s = l-BC* -f- m-AO-^- п-АВ^~1-ВС +
+ т D/?2 — А'О) + n.DR* — А'В2) — I -ВО- — т¦ А'С* — п¦ А'В" + Цт + п) R\
и дело сводится к отыскалию треугольника А'ВС, которому соответствуют
положительные коэфициенты /, — т, — п, так как постоянный член Mjn-\-n) Ft*
рол+i не играет.
Если среди коэфициентов /, т и п отрицательных окажется один или
три, то мы рассмотрим вместо s величину s" = — s = — I-ВС2 — т-АС2 —
— п-АВг. При этом наибольшему значению s' будет соответствовать уже
наименьшее значение .?. Наибольшее же значение величины s1 найдётся,
как указано выше, так как среди коэфициентов — /, — т и — п отрица-
отрицательных будет либо два, либо ни одного.
368. Пусть существует .точка D, расстояния которой от вершин
данного треугольника пропорциональны трём данным числам. Примем
точку D за полюс инверсии и выберем произвольно степень последней.
Точки А, В и С преобразуются при эшм в точки А', В" и С,
npmuMB'C:CA':A'B' = (DA-BC):(DB-CA):(DC-AB)(n.2l8, сравнить
решение упр. 270, 1°), т. е. В1 С: С А': А'В1 = (т-ВС):(п-СА):(р-АВ).
Таким образом, указанное в тексте условие необходимо.
Обратно, пусть существует треугольник А'В'С, стороны которого
пропорциональны т-ВС, п-СА, р-АВ. Пусть D—полюс инверсии,
преобразующей точки А', В' и (У в вершины данного (по своей фор-
форме и величине) треугольника ABC (существование такой инверсии
следует из упражнения 270а). Расстояния DA, DB и DC удовлетво-
удовлетворяют условиям B'C:CA':A'B' = (DA.BC):(DB-CA):(DC-AB). Так
как по предположению имеем В'С:С'А':А'В' = (т-ВС):(п-СА):(р¦ АВ),
то DA:DB:DC = m:n:p. Приведённое условие является и достаточ-
достаточным.
369. Пусть AD = BE=CF, прямая О А' параллельна AD, О В1
параллельна BE и ОС параллельна CF (черт. 608). Если х, v и z —
расстояния точки О от сторон ВС, СА и АВ треугольника, h, k
526
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
и / — высоты, опущенные из вершин А, В, С треугольника, то в силу
JC \) Z
упражнения 301 будем иметь у-\~—-\~ -=1.
С другой стороны, очевидно, x:h = OA':AD; y:k=OB':ВЕ\
О А' , OR ОС
? ^ О А ,
. Отсюда —— -\-
_[_
—
= 1. В
силу равенств
AD = BE— CF отсюда следует, что О А' -\- ОИ 4- ОС = AD.
370. Пусть a, b и с — три прямые, проходящие через одну
точку О (черт. 609), и х, у, z — расстояния произвольной точки М
от этих прямых. Проведём через М прямую с', параллельную с, и
Л' С
Черт. 60S.
0а
Черт. 60Э.
обозначим через А и В точки её пересечения с прямыми а и Ь.
1 AB(± AM±MB) ±
Имеем
2
ш.ОАВ = 1 AB-z=j(± AM±MB)-z = ±~ AM . z ±
пл. 0MB= ± ^
2
От-
сюда г = ± ^nv x ± Tr. • V-
Л/5 Ad
Коэфициенты ОД МБ и ОВ:АВ в этом
равенстве не зависят, очевидно, от положения точки М на плоскости.
Чтобы сформулировать результат так, чтобы он совершенно не
зависел от положения точки М, будем считать площадь произволь-
произвольного треугольника положительной или отрицательной в зависимости
от направления вращения (как указано в решении задачи 324). Далее
выберем на каждой из прямых а, Ъ и с положительное направление
и будем приписывать отрезкам, лежащим на этих прямых, определён-
определённые знаки. На прямой АВ, параллельной с, выбираем то же положи-
положительное направление, что и на с. Чтобы площадь треугольника MPQ
с вершиной в произвольной точке М плоскости и основанием PQ на
прямой а выражалась по величине и по знаку равенством u
CMFUIAHHblE ЗАДАЧИ
527
= — x-PQ, мы должны приписать определенный знак не только от-
резку PQ, но и расстоянию х точки М от прямой а. А именно, рас-
расстояние х мы должны считать положительным, если для наблюдателя,
находящегося в точке М, положительное направление прямой а ка-
кажется идущим справа налево, и отрицательным — в противном случае.
Аналогично определим знаки расстояний у и z (например, на черт. 609
имеем х~^>0, _у<^0, г<^0).
При этом будем иметь по абсолютной величине и по знаку:
пп.ОАВ= 1 AB-z=^(AM-\-MB)-z = l~AM-z -\- ^ MB ¦ z =
Z Z Z Z
— xm.OAM -|- nn.OMB = —OA-x—— OB-y. При перемещении
точки М по плоскости отношения АВ:ОА:ОВ будут сохранять пос-
постоянные абсолютные величины и постоянные знаки.
Обратно, если мы имеем выражение тх-\~пу, где т и п—данные
положительные или отрицательные коэфиниенты, а х и у — расстояния
от некоторой точки до данных прямых, то отложим отрезки О А и ОВ
так, чтобы имело место по величине и по знаку равенство О А : (—ОВ)=
z=m:n, и проведём через точку О прямую с параллельно АВ. В силу
прямой теоремы будем иметь AB-z = OA-x — ОВ-у, так что выра-
выражение тх-\-пу будет пропорционально расстоянию точки М от пря-
прямой с.
371. Пусть av а2,...—данные прямые, на каждой из которых
выбрано определённое направление; хр х2,... — расстояния произволь-
произвольной точки от этих прямых, взятые с надлежащими знаками, как
указано в решении задачи 370; а0, av а2,... — данные положитель-
положительные или отрицательные числа.
Пусть требуется найти геометрическое место точек, расстояния
которых от двух данных пересекающихся прямых удовлетворяют
условию
На основании обратной теоремы задачи 370 имеем аххх -\-а2х2= р_у,
где р — некоторый коэфициент, у — расстояние точки от некоторой
прямой. В силу этого равенства условие A) принимает вид _у =
а0
= -^= const, и искомое геометрическое место есть прямая линия.
Р
Найдём теперь геометрическое место точек, расстояния которых
от двух данных параллельных и одинаково направленных прямых аЛ
и а2 удовлетворяют тому же условию a1x1-\-aix2 = a0. Если через
х обозначить расстояние от произвольной точки первой прямой до
второй прямой, то мы будем иметь для любой точки плоскости
(черт. 610) дгг == х,-J-дг, откуда для точек, удовлетворяющих уело-
вию A), имеем (а: -\-а2) х1 = av — z2x, т. е. хх = ° -'. — const
528
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
(при а, -\- а2 ф 0). Итак, искомое геометрическое место точек (если
такие точки существуют) есть прямая линия. Искомых точек не суще-
существует, если а, 4- а2 = 0; а0 — а^х ф 0. Условие а,х, -$- а2х2 = а0
будет удовлетворяться для любой точки плоскости, если aj-|-a!2 =
0
Если данные параллельные прямые имеют противоположные направ-
направления, то можно притти к только что рассмотренному случаю, изменяя
направление на одной из данных прямых, хотя бы на прямой а2, на об-
обратное (и одновременно изменяя знак коэфициента а2 на обратный).
При этом изменится и знак расстояния х2 от точки до второй пря-
прямой.
Итак, мы доказали, что в случае двух данных прямых геометри-
геометрическое место точек, удовлетворяющих условию A), есть, вообще
Черт. 610.
говоря, прямая линия; как исключение возможно, что таких точек не
существует вовсе или что условие A) выполняется для любой точки
плоскости.
Предположим, что мы доказали аналогичное предложение для слу-
случая, когда даны п — 1 прямых, и докажем его для п прямых. Пусть
требуется найти геометрическое место точек, для которых
a,*i + ct2x2 + -.. + «„-,*„_, + апха=а0. B)
Выберем обозначения так, чтобы о„_, -\- ап ф 0 (это всегда воз-
возможно). На основании предыдущего имеем ап_лхп_1 -f-алдги = [5_у, и
дело сводится к отысканию геометрического места точек, для которых
а,х, -\-а2х2-\-.. .-\-ап_2хп_2~\- $у = а0, т. е. к случаю, когда дано
п— 1 прямых. Таким образом, задача разрешена для случая любого
числа прямых.
Если на каждой из данных прямых выбрать отрезки А1В1, \В^,...,
удовлетворяющие по величине и по знаку условиям А1В1;а1^А2В2:а2=
==... = р, то равенство B) принимает вид:
пл.А^Х 4- пл.А2В2Х 4-. .. = ра0, B')
где X — любая точка искомого геометрического места.
Пусть теперь ABCDEF — полный четырёхсторонник (черт. 611),
диагонали АВ, CD и EF которого имеют своими серединами точки L,
СМЕШАННЫЕ ЗАДАЧИ 529
М и N (сравнить п. 194). Так как L — середина отрезка АВ, то мы
имеем (по абсолютной величине и знаку) ил. CAL-\- пл. CBL = i). Точно
так же пл. DAL-\-пл. DBL = O. Отсюда
пл. ACL^- пл. BCL-\-n^. ADL-\-nn. BDL = 0. C)
Таким же путём найдём, что пл. АСМ -(-пл. ADM = 0; пл. ВСМ-\-
4-чл. BDM = 0 и
пл. АСМ-{-пл. ВСМ-\~пл. ADM-\-nn. BDM=0. D)
Далее имеем wn.AEN -\- nn.AFN=0; nn.BEN-\-rw. BFN=0; nn.CEN~\-
-{-пл. CFN=0; пл. DEN-\-пл. DFN=0. Отсюда, складывая по-
почленно первые два из этих равенств и вычитая два последних, получим
(пл. AFN ~пл. CFN) -{- (пл. BEN — пл. CEN)-\-(nn. AEN— пл. DEN)-{-
-|-(пл. BFN — m.DFN) = 0. Но пл. 4F/V — пл. CFA/=rui./inV-f-
-j-пл. FCN=nn. ACN и т. д., и предыдущее равенство принимает
вид:
пл. ACN~\-nn. BCN + пл. 4Z3N-f пл. BDN=0. E)
Равенства C), D) и E) показывают, что точки L, М и N принад-
принадлежат геометрическому месту точек X, для которых имеет место
равенство
пл. АСХ-\-т. ВСХ-\-пл. ADX + пл. BDX = 0. F)
Но это геометрическое место есть по предыдущему прямая линия
[сравнить равенство B')].
Примечание. Чтобы последнее заключение было вполне обосно-
обосновано, надо ещё показать, что равенство F) не выполняется для всех Точек
плоскости. Но если это равенство выпол-
выполняется для точек А и С, то мы имеем F^ ^г
пл.ВСА-\-пл.ВОА=0; пл.АОС+пл.ВОС—О.
Отсюда легко вывести, что четырёхуголь-
четырёхугольник ACBD есть параллелограм, и вопрос
теряег смысл. Итак, равенство FJ опреде-
определяет прямую линию.
371а. Пусть АВ, CD и EF (черт.
612)—диагонали полного четырёхсто-
четырёхсторонника, И — точка пересечения высот
ВК, CL'h FM треугольника BCF,
образованного тремя из четырёх сто-
сторон данного полного четырёхсторонника.
Так как прямая ВК перпендикулярна
к FC, а CL — к BF, то точки В, С, К
и L лежат на одной окружности, откуда HB-HK=HC-HL. Так как
по той же причине точка К лежит на окружности, имеющей АВ
своим диаметром, а точка L — на окружности, имеющей CD своим
диаметром, то равенство НВ-НК. = HC-HL показывает, что точка Н
имеет относительно обеих окружностей одну и ту же степень. Таким же
образом получим НВ-ИК = HF-ИМ, откуда будет следовать, что точ-
34 Элементарная геометрия
530 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
ка И имеет ту же самую степень и относительно окружности, имею-
имеющей своим диаметром EF.
Итак, точка И имеет относительно всех трёх окружностей одну
и ту же степень. По той же причине и точка пересечения высот
любого из треугольников BDE, АСЕ и ADF будет иметь относитель-
относительно всех трёх окружностей одну и ту же степень. Отсюда следует,
что все эти четыре точки лежат на одной прямой — общей радикаль-
радикальной оси трёх окружностей.
372. Пусть PQRS— данный четырёхугольник (черт. 613), К —
точка пересечения прямых PQ и RS, I — поляра точки О относительно
угла PKS (п. 203).
Преобразуя четырёхугольник PQRS вместе с его диагоналями
взаимными полярами относительно какой-либо окружности с центром О,
Черт. 613.
получим полный четырёхсторонник pqrs (черт. 614). Четырём прямым
PQ, RS, OK и /, проходящим через точку К, соответствуют четыре
точки (pq), (rs), (ok) и L, лежащие на диагонали k полного четы-
четырёхсторонника. Так как прямая ОК. проходит через центр направляю-
направляющей окружности, то её полюс — точка (ok) — лежит в бесконечности
(п.-204). Прямые PQ, RS, OK и / образуют гармоническую четвёрку;
следовательно, и точки (pq), (rs), (ok) и L образуют гармоническую
четвёрку. Но точка (ok) лежит в бесконечности, и потому точка L
есть середина диагонали (pq) (rs) полного четырёхсторонника.
Аналогично доказывается, что и поляры точки О относительно двух
других углов преобразуются в середины двух других диагоналей пол-
полного четырёхсторонника pqrs. Так как середины трёх диагоналей пол-
полного четырёхсторонника лежат на одной прямой (п. 194 или задача 371),
то их поляры относительно направляющей окружности, т. е. поляры
точки О относительно трёх углов, о которых идёт речь, проходят
через одну точку.
Пусть теперь в пересечении сторон и диагоналей полного четырёх-
четырёхугольника PQRS (черт. 615) с некоторой прямой р образуются три таких
СМЕШАННЫЕ ЗАДАЧИ
531
отрезка АА', ВВ' и СС\ что существует (сравнить решение упр. 219а)
отрезок UV, делящий гармонически как АА', так и ВВ'. При этом
в силу определения поляры точки относительно угла (п.203) поляра точки U
относительно пары прямых PQ и RS проходит через точку V, и то
же имеет место для поляры точки U относительно пары прямых PS
и QR; в силу предыдущего и поляра точки U относительно третьей
пары прямых PR и QS проходит через V. Поэтому отрезок UV делит
гармонически и отрезок СС.
373. Пусть ABC—данный треугольник (черт. 616), И — точка
пересечения его высот, X, Y и Z — основания перпендикуляров, опу-
опущенных из точки Р описанной окружности на его стороны. Точки X,
Черт. 615.
Черт. 616.
Y и Z лежат на одной прямой в силу упражнения 72. Обозначим че-
через А' точку, симметричную с точкой И относительно ВС; точка А'
будет лежать в силу упражнения 70 на описанной окружности. Далее
обозначим через Q точку, симметричную с точкой Р относительно ВС,
через К и L — точки пересечения прямой XY с прямыми АА' и РИ.
Так как точки Н и Q симметричны с А' и Р относительно ВС, то
/_PA'H=/_QHA'.
О)
Точки Р, С, X и Y лежат на одной окружности (потому что пря-
прямая РХ перпендикулярна к ХС, a PY—к КС), и потому ^/СРК=
= j/_CXY. Следовательно,
/_ РАН = /_ PC А = 90° — /_ СР Y= 90° — /_ CXY=/_ A'KX. B)
В силу равенств A) и B) углы A'HQ и А'КХ равны, так что
прямая HQ параллельна XY. Итак, точка Q, симметричная с точкой Р
относительно стороны ВС данного треугольника, лежит на прямой,
параллельной XY и проходящей через точку И; очевидно, что то же
имеет место и для точек, симметричных с Р относительно прямых СА
и АВ.
Так как в треугольнике PQH точка X есть середина стороны PQ
и прямая XL параллельна HQ, то PL = LH.
34*
532
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Пусть теперь а, Ь, с, d—четыре произвольные прямые; Р— точка
пересечения четырёх окружностей, описанных около треугольников bed,
acd, ubd и abc (задача 106). Основания перпендикуляров, опущенных
из точки Р на четыре данные прямые, лежат на одной примой / (сравнить
решение задачи'106, второе доказательство) — общей прямой Симеона
четырёх треугольников. Следовательно, в силу только что доказанного,
точки пересечения высот четырёх треугольников лежат на одной пря-
прямой, параллельной / и отстоящей от точки Р на расстоянии вдвое
большем, чем /.
374. Пусть Q и Q—точки, симметричные с Р и Р' относительно
стороны ВС (черт. 617). Точки Q и Q' и точка пересечения Н высот
треугольника лежат на окружности, симметричной с описанной окруж-
окружностью S относительно ВС (упр. 70).
Прямая Симеона XZ, соответствующая точке Р. параллельна пря-
прямой QH как средняя линия треугольника PQH (задача 373). Точно
так же прямая X'Z', соответствующая точке Р', параллельна Q'H.
Отсюда следует, что угол /_ ZMZ' = /_ QHQ' измеряется половиной
дуги QQ' или, что то же, половиной дуги РР'.
Если точка С описывает окружность S, а точки А, Б, Р и Р' не-
неподвижны, то точки Z и Z' остаются на месте, и угол ZMZ' сохра-
сохраняет постоянное значение. Следовательно, точка М описывает некото-
некоторую окружность S', проходящую через точки Z и Z'.
Пусть теперь О и О' — центры окружностей S v\ S' (черт. 617
и 618). Так как угол ZMZ' измеряется половиной дуги РР', то
/_ZO''Z'' = /_РОР'. Если / и АГ —середины отрмков РР' и ZZ', то
t)l:O'K=PP':ZZ' в силу подобия треугольников ОРР' и О'ZZ'.
С другой стороны, если N — основание перпендикуляра из точки О на
прямую IK, то, как легко показать, OI-.IN = PP':ZZ' ( рямая 01
перпендикулярна к РР', a IN к ZZ'). Итак, имеем IN=0'K, так что
Ю' =^KN=C1O, где С, — середина АВ, и, следовательно, OI=Cfi'.
СМЕШАННЫЕ ЗАДЛЧИ
533
Так как при перемещении точек Р и Р', остающихся на постоян-
постоянном расстоянии друг от друга, по окружности S (и неподвижных точ-
точках А и В) отрезок 01 сохраняет постоянное значение, то и О'Су
сохраняет постоянное значение. Геометрическое место центров О'
окружностей S' есть окружность с центром С, и радиусом, равным 01.
Пусть, наконец, Р и Р' — две диаметрально противоположные точки
окружности S, описанной около треугольника ABC (черт. 619). Обоз-
Обозначим через L и L' середины отрезков HP и HP'. Так как отрезок LL'
равен половине диаметра описанной окружности и делится пополам в
точке О, — середине отрезка ОН, то LL' представляет собой (на ос-
основании задачи 101) один из диаметров окружности девяти точек тре-
треугольника ABC. Прямые Симеона, соответствующие точкам Р и Р',
проходят (в силу задачи 373) через о>
точки L и И и перпендикулярны "
между собой, так как угол между
ними измеряется, по доказанному,
половиной дуги РР'. Следовательно,
геометрическое место точек их пере-
пересечения есть окружность девяти то-
точек треугочьника ABC
375. Пусть О — центр данной
окружности, Н — данная точка пе-
пересечения высот вписанного тре-
треугольника ABC. Точка пересечения
медиан G любого треугольника де-
делит отрезок ОН, имеющий своими
концами центр описанной окружно-
окружности и точку пересечения высот, в
отношении OG:GH = 1:2 (упр. 158). Следовательно, все треугольни-
треугольники, о которых идёт речь, имеют общую точку пересечения медиан G.
¦ Так как медианы ААг, ВВ^ и ССЛ проходят через точку G и де-
делятся в ней в отношении AG: G.4, =BG: GBX = CG: GC^ = 2:1, то то-
точки Av Bl и Cj лежат на окружности, гомотетичной данной относи-
относительно точки G (коэфициент подобия равен GA1:GA = — 1:2).
376. Пусть ABC—данный треугольник; -4,, В, и С,— середины
его сторон; / и 1с — центры вписанной и вневписанной окружностей,
лежащие на биссектрисе угла С; F и Z7, — точки касания этих окруж-
окружностей со стороной АВ; D и Dl — точки их касания со стороной ВС;
СС2 — высота треугольника; М — точка пересечения внутренних общих
касательных к окружностям / и 1С (черт. 620).
Так как в силу упражнения 90а С^^С,/7,, то точка Сх имеет
одну и ту же степень относительно окружностей 1 и Iс. Её мы и
примем за степень инверсии с полюсом С1.
Так как прямые В/ и В1С служат биссектрисами внутреннего и
внешнего углов при вершине В треугольника ВСМ, то точки / и 1С
делят гармонически отрезок СМ (п. 115), а следовательно, и точки F
и Fx делят гармонически отрезок A4CV. Поэтому на основании п. 189
Черт. 619.
534
РЕШЕНИЯ УПРАЖНЕНИЙ II ЗЛДАЧ
имеем С,/72= CXF\ = СгМ- СгС2. Это равенство показывает, что точка С,
преобразуется рассматриваемой инверсией в точку М, а окружность
девяти точек — в прямую PQ, проходящую через точку М и парал-
параллельную касательной к окружности девяти точек в точке С,..
Покажем теперь, что касательная к окружности девяти точек в
точке Са параллельна касательной к описанной окружности в точке С.
В самом деле, так как отрезок OrCs (черт. 353) есть средняя линия
треугольника НОС, то диаметр СуСя окружности девяти точек парал-
параллелен ОС, а касательная к окружности девяти точек в точке С*: па-
параллельна касательной к окружности ABC в точке С.
су
D, В
Q D Л,
Черт. 620.
Отсюда следует, что касательная к окружности девяти точек в точ-
точке С, образует со стороной ВС угол, равный углу А треугольника.
Итак, окружность девяти точек преобразуется рассматриваемой
инверсией в прямую линию PQ (черт. 620), проходящую через точку М
и образующую со стороной ВС угол MQC, равный углу А данного
треугольника. Иначе говоря, прямые АВ и PQ образуют с биссектри-
биссектрисой угла С, т. е. с линией центров окружностей / и 1С, равные углы.
Так как прямая АВ есть внутренняя общая касательная этих окружно-
окружностей, то PQ есть их вторая внутренняя общая касательная.
Как указано в тексте задачи, отсюда непосредственно вытекает,
что окружность девяти точек, в которую рассматриваемая инверсия
преобразует прямую PQ, касается вписанной окружности и вневписан-
ной окружности 1С\ по той же причине она касается и остальных вне-
вписанных окружностей.
377. Пусть О и / — центры окружностей, описанной около тре-
треугольника ABC и вписанной в него (черт. 621), К—точка пересече-
пересечения перпендикуляра, восставленного к стороне ВС в её середине Av
с биссектрисой угла А (эта точка лежит на описанной окружности в
силу задачи 103), L — основание перпендикуляра из точки / на пря-
прямую ОК.
СМЕШАННЫЕ ЗАДАЧИ
535
Из треугольника OIK на основании п. 126 имеем d2 = OI2=OKi-\~
-}-!№ —2OK-KL. Но в силу задачи 103 /К=ВК, а в силу п. 123,
следствие, /К2= B№ = 2R-AfK. Следовательно, d2 = R2 -\- 2R ¦ (АХК—
Переходим к доказательству обратной теоремы. Пусть даны две
окружности О и /, удовлетворяющие условию d2 = R2— 2/?л(черт. 621).
Отсюда следует, что R~^>r v\d'2<^(R— гJ, т. е. d<^R— г. Окруж-
Окружности Owl расположены одна внутри другой.
Выберем на окружности.О произвольную точку А, проведём пря-
прямую А/ и обозначим через К вторую точку её пересечения с окруж-
окружностью О. Строим касательную ВС к окружности /, перпендикулярную
к ОК и проходящую между точками / и К. Пусть Ах — точка пересе-
пересечения этой касательной с ОК, и L — основание перпендикуляра из
точки /на ОК. Из треугольника О/К имеем di = Ri-\-IK2— 2R-KL.
Но по условию d2 ^R- — 2Rr. Из этих двух
равенств находим l№= 2R (KL — r) = 2R- KAr=
^КЕР (последнее равенство на основании п. 123,
следствие), так что 1К=КВ.
Если мы соединим теперь точку А с точ-
точками В и С, то в силу равенства дуг ВК и КС
прямая АК будет биссектрисой треугольника
ABC. Так как ВК = /К, то точка / будет в
силу задачи 103 центром вписанной окружности
этого треугольника. Так как данная окружность
с центром / касается стороны ВС, то эта
окружность и будет вписанной в треугольник ABC.
Итак, любая точка А данной окружности О служит вершиной тре-
треугольника, вписанного в окружность О и в тоже время описанного
около окружности /.
Заменяя вписанную окружность / вневписанной окружностью 1а(га),
касающейся стороны ВС и продолжений двух других сторон, мы по-
получим с помищью рассуждений, вполне аналогичных предыдущим,
соотношение OIa2 = R2 -\- 2Rra.
Примечание. Относительно аналогичного вопроса для четырёх-
четырёхугольника см. задачу 282.
378. Обозначим через / центр окружности, вписанной в треуголь-
треугольник ABC, через 1п, 1Ь и /. — центры вневписанных окружностей (при-
(причём через 1а обозначаем центр окружности, лежащей на внутренней
биссектрисе угла А, и т. д.), через G и К (G' и К') — основания
перпендикуляров, опущенных из точки А на биссектрисы внешних
(внутренних) углов при точках В и С, через L и М (L' и М) — ос-
основания перпендикуляров, опущенных из точки В на биссектрисы внеш-
внешних (внутренних) углов при точках С и Л, через N и Р (N' и Р') —
основания перпендикуляров,, опущенных из точки С на биссектрисы
внешних (внутренних) углов, при точках А и В. Остальные обозначе-
обозначения те же, что и в упражнении 90а (черт. 102).
536
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
1°.Так как углы CEIuCP' (черт. 622) — прямые, то точки /, С, Е,
Р' лежат на одной окружности, откуда ^_С1Р' = ^_СЕР'\ точно
также Z.L4B=/_L'FB. Но /_С1Р=
4 ^S+ZO- Итак,
4 l^S+ZO- Итак, ^CEP ^UFB (
С другой стороны, /_ AEF=/_ A'FF =-^ A80° — /_ А) =
— (^/ В-\- /_ С), как это видно из равнобедренного треугольника AEF.
Таким образом, /_СЕР" =/_AEF =
= ^/ Л/^Ё = Z L'FB. Эти равенства
и показывают, что точки Р' и L' ле-
лежат на прнмий EF.
2°. Так как углы CEJC и CPI'с
(черт. 623) — прямые, то точки /с, С,
Е3, Р лежат на одной окружности, от-
откуда /_ СЕ3Р = ^/_ CIcP\ точно так же
/_L'F-fi = Z- L>lcB- Но Z- ClcP =
^\ 80° —1 /. С —
В
с
— С 90
Черт. 622.
1
2 *—
С другой стороны,
ренного треугольника /
(из равнобед-
равнобедЧерт. Ь26.
Черт. 624.
Таким образом, /_ СЕ.ЛР=^^_ AEgFg, и точки Es, F3 v\ P лежат
на одной прямой; /_ L'F&B^^_ AFJis, и точки Es, Fs и U лежат на
одной прямой.
3°. Точки /й, С, Р, Ел (черт. 624) лежат на одной окружности,
откуда ^_С1СР = /_СЕХР; точно так же /_LIaB = ^LF1B. Но
СМЕШАННЫЕ ЗАДАЧИ
537
Z CIaP=/_LlaB= 180°- (90° -i
= — {/_ 6 + /С), как это видно из тре> гольника 1аВС. Итак,
С другой стороны,
) (из равнобедренного треугольника AE^Fy). Таким
образом, /_СЕ^Р= /_AE^Fj, и точки Е,, F, и Р лежат на одной
прямой; точно так же ^LF.,B=
= ^.AF^E^, и точки /:,, F, и
L лежат на одной прямой.
4°. Фигура AGBG' (черт.
625) есть прямоугольник; отсюда G / К' 1С\i>5_
1 ~
y-lC'==fiC' = C'G= -с и
так что прямая GG' параллель-
на ДС Таким образом, точки ., „о^
^ г,, „ „,„, Черт. 62о.
С и С лежат на прямой ВС, •
соединяющей середины сторон АС и АВ треугольника ABC. Точно
так -же покажем, что точки К и К' лежат на той же прямой.
Расстояние GK= GC + С В' -f В'К — -^ с -\- \~ a -f -^ Ь = р. Да-
Далее GK'=GK — K'K=GK—AC = p~b; G'K = GK — GG' =
= GK—AB = p — c; G'K'=GG'-\-K'K— GK=c± b — p=(a-\-
-\-b-\-c) — p — a = p — a. '
5°. Точки А, В а С (черт. 626) служат основаниями высот тре-
треугольника 1а 1Ь Iс (так как прямая А1 а перпендикулярна к 1Ь1 с и
т. д.); поэтому точки G, К, L, M, N, Р лежат на одной окружности
в силу задачи 102.
Из прямоугольного треугольника falhB имеем laL-lJb-= 1JP.
Точно так же из прямоугольного треугольника lJbA имеем 1аК- 1а1ь =
= 1аА2. Отсюда laK-IaL = [I^A' a У. Но треугольники IaBDy и
V 'а'ь I "
lJbA подобны (так как /_IaBD^ = 90° — /_ CBI = 90° — 1 /_ В, а
Z. VH = 90° - yZ В. в силу упр. 24, и потому /_ IaBDi = /_ IJbA) t
откуда 1аА: IaD1 = IJb: IaB; IaD1 = ¦" " . Таким образом находим
'Jb
538
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
lJ<.-\aL=InD\. Степень точки 1а относительно окружности GKLMNP
равна квадрату радиуса /OD, вневписанной окружности /о. Это значит,
что обе окружности ортогональны.
Одним из диаметров окружности GKLA1NP служит перпендикуляр
к отрезку MN в его середине. Этот перпендикуляр проходит через
середину отрезка ВС (как это видно из трапеции MNCB) и параллелен
биссектрисе А1а угла А. Иначе говоря, этот перпендикуляр есть бис-
биссектриса угла В'А'С, где А', В' и С — середины сторон треугольни-
треугольника ABC. Таким же образом покажем, что центр окружности GKLMNP
лежит на биссектрисах углов
СВ'А' и А'С'В', т. е. совпа-
совпадает с центром окружности,
вписанной в треугольник А'В'С.
Опуская из центра О окруж-
окружности GKLMNP перпендикуляр
OQ на прямую GK, найдём, что
квадрат радиуса окружности О
равен OG2^OQ"-\~ GQ~. Но
OQ, как радиус окружности,
вписанной в треугольник А'В'С,
1
равняется — г, где г — радиус
окружности, вписанной в тре-
треугольник ABC, так как тре-
треугольники ABC и А'В'С подоб-
подобны и имеют коэфициент по-
подобия, равный —. Далее GQ —
= -GK=- р(см. 4°). Отсюда
t Черт. 626. 2ч 2
Окружности, аналогичные GKLMNP, мы получим, замечая, что точ-
¦ ки \, В и С служат основаниями высот каждого из треугольников
^Vc HJa< flJb (чеРт- 102), и опуская из точек А, В и С перпенди-
перпендикуляры на стороны любого из этих треугольников. Беря треугольник IIhIc,
получим окружность G'K'L'MNP и т. д.
< 379. Пусть ЛВС —данный треугольник (черт. 627); а, Ь, с, р —
'его стороны и полупериметр. Обозначим через Еу, Fx, F2, D2, Ds и Е3
(как в упр. 90а, черт. 102) точки касания вневписанных окружностей
с продолжениями сторон, через Н и К — точку пересечения высот и
основание высоты АН треугольника.
Мы докажем, что прямые D2FO и D3ES пересекаются на высоте АК
треугольника, если докажем, что обе прямые делят (внешним образом)
отрезок АК в одном и том же отношении.
Пусть А' — точка пересечения прямых АК и DOF2. Чтобы найти
отношение АА':КА\ применим теорему п. 192 к треугольнику АВК
СМЕШАННЫЕ ЗАДАЧИ
539
и секущей D2F2A'. Получим ~^ • -—¦ • -—- = 1. Но AF2 = p — <
, = BD2=p (упр. 90а); далее ВК =
4- с2 —
(п. 126), от-
BD,BK = ^ = .
Подставляя эти выражения отрезков AF2, BF2i BD2 и KD2 в преды-
предыдущее соотношение, получим после преобразований К.А' : АА' =
^(^_[_с):а. Применяя ту же теорему п. 192 к треугольнику АСК и се-
секущей D3ES, мы найдём, что прямая ?>3Е3 делит отрезок АК в том
Черт. 627.
же самом отношении и потому пересекает прямую АК в той же самой
точке А' (это видно уже из того, что в найденное значение отношения
КА':АА' стороны b и с входят равноправно). Таким образом, прямые
D2F2 и DaEs пересекаются на высоте АК треугольника ABC.
Точно так же докажем, что и остальные две точки пересечения
В' и С прямых fj/7], E2D2 и DgEs лежат на высотах данного тре-
треугольника.
Далее имеем /_ НА1 В =90° — /_ ESD3C= 90° — /_ ?»3^3С =
= /_НВ'А', откуда НА'=НВ'. Таким же путём докажем, что НВ1^
= НС. Точка Я есть центр окружности А'В'С.
380. Пусть А — произвольная точка фигуры F (черт. 628). Строя
треугольник ОАА'', подобный треугольнику Г, получим точку Л' фи-
фигуры F', соответствующую точке А фигуры/7. Далее, строя Tpeyi олfa-
ник О'А'А", подобный треугольнику Т', найдём точку А" фигуры F",
соответствующую точке А фигуры F.
Построим теперь треугольник ОА'К, подобный треугольнику О'А'А'
и имеющий то же направление вращения. Так как угол АОА' есть
угол между фигурами FuF' (п. 150), а угол А'ОК, равный углу А'О'А",—
угол между фигурами F' и F", то угол АОК есть угол между фи-
540
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
OA OA О A' OA O'A'
гурами F»F. Имеем _=—-_ = _
есть
О' А'
отношение соответственных отрезков
так как
фигур F и
ОА
О А'
Г, а
Оп-г
А
ргтп — такое же отношение для фигур F' и F", то ОА:ОК есть
отношение длин соответственных отрезков фигур F и F". Отсюда сле-
следует, что треугольник OAK подобен треугольнику, образованному
искомой точкой О" и соответственными точками фигур F и F".
Построим, наконец, на отрезке АА" треугольник О"АА", подобный
треугольнику OAK. Его третья вершина О" и будет искомой точкой,
т. е. точкой Лигуры F, совпадающей с соответственной точкой фигу-
фигуры F". Это следует из того, что
угол АО"А' есть угол между фигу-
фигурами F и F", отношение О"А":О"А -^
коэфициент подобия тех же фигур,
а А и А" — пара их соответственных
точек.
Из сказанного следует, что по-
поставленная задача имеет, вообще
говоря, одно решение.
Приведённое построение нуждает-
нуждается в небольшом видоизменении в том
случае, если точки О, А и К ока-
окажутся на одной прямой. F-сли при
этом точки А и К различны, то фигуры F и F" будут гомотети-
ческими. Для построения точки О" придётся отрезок АА" разделить
в отношении О"А:О"А"^ОА:ОК (по величине и по знаку). Если же точ-
точки А и К будут совпадать, то соответственные отрезки фигур F и F'
будут равны, параллельны .и направлены в одну и ту же сторону: фи-
фигуры F и F" получаются одна из другой поступательным перемещением,
величина и направление которого определяются отрезком АА" (точка О"
не существует). В том случае, когда и точки А и А" совпадают, каж-
каждая точка фигуры F совпадает с соответственной точкой фигуры F"
(любая точка плоскости есть точка О").
381. Пусть АЛА2 .. . Ап_хАп — искомый многоугольник (черт. 629);
О,, О2,. . ., Оп_х,Оп —вершины треугольников ОХАХА2, О2А2А3,..., со-
соответственно подобных данным треугольникам Tlt Tv,... .
Будем рассматривать Оп_г как точку, соответствующую самой себе
в двух подобных фигурах Fn_l и Fn, имеющих одинаковое направле-
направление вращения; точно так же Оп — как точку, соответствующую самой
себе в фигурах Fn и Fv Точки Ап_х, Ап и Л, будем считать соот-
соответственными точками фигур /?„_1, Fn и Fx. Пользуясь задачей 38U,
можно построить точку Оп_л', соответствующую самой себе в фигурах
Fn_.l и Z7,, а также треугольник 7V,—ъ подобный треугольнику, об-
образованному этой точкой и любыми двумя соответственными точками
фигур Fn_1 и Z7,.
СМЕШАННЫЕ ЗАДАЧИ
541
Мы пришли к задаче построения многоугольника АХА^ . .. Ап_х по
точкам О1 ,О2,..., О„_2, О„_1 и треугольникам 7„ Т2,.. ., Тн_2, 7„_,'.
Повторяя этот процесс, придём к задаче: построить отрезок Л,А>,
зная, что две данные точки О: и О2' служат вершинами треугольни-
треугольников О1А1А2 аС^А^А^ соответственно подобных данным треугольникам
Tj и Т2'. Примем точку О^ за двойную точку фигур F1 и F2, имею-
имеющих соответственными точками А1 и А2; точку О-2—за двойную точку
Фигур F2 и F3, имеющих своими соответственными точками А, и Л,.
Точка Аг может быть построена как двойная точка фигур Fx и F3 по
данным точкам О, и О2 и треугольникам 7~: и 7г, опять-таки как ука-
указано в задаче 380.
Черт. 630.
После того как точка А1 построена, точка А, найдётся как третья
вершина треугольника O^AtA2, подобного данному треугольнику 7^.
Далее аналогичным образом строятся точки Л3, А,,..., Ап.
Задача будет неввзможной или неопределённой, если в процессе
решения мы встретимся с одним из случаев, оговорённых в решении
задачи 380.
382. Будем рассматривать точки А, В и С (черт. 630) как соот-
соответственные точки трёх попарно подобных фигур Fa, Fb и Fc, имею-
имеющих одинаковое направление вращения. Точку А' будем рассматривать
как точку, соответствующую самой себе в фигурах Fb и F?, точку В' —
как точку, соответствующую самой себе в фигурах Fс и Fa. При этом
угол между соответственными отрезками фигур Fb и Fс будет равен
(по величине и направлению) ^_ВА'С= ^/_ЬОс\ угол между соответ-
соответственными отрезками фигур Fc и Fa — ^/_СВ'А^/^сОа. Следова-
Следовательно, угол между соответственными отрезками фигур Fa и Fh будет
равен /_аОЬ = /_АС'В. Отношение соответственных отрезков для
фигур Fb и Fc равно А'В:А'С^ОЬ:Ос, для фигур Fc и Fa соответ-
соответственно В'С:В'А = Ос:Оа. Следовательно, отношение соответственных
отрезков для фигур Fa и Fb будет равно Оа : Ob = С'А : СВ. Отсюда
следует, что С' будет точкой, соответствующей самой себе в фигу-
фигурах F и Fb.
542
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Построим точку А", соответствующую точке А в фигуре Fa. При
этом треугольник С А'А' будет подобен треугольнику С'АВ и иметь
с ним одинаковое направление вращения, так что /_ С А А' = /_ С'ВА =
= /_ОЪа (по величине и направлению). Точно так же треугольник
В'А'А" будет подобен треугольнику В'СА и иметь с ним одинаковое
направление вращения, так что /_ В'А'А = /_ В'СА — /_ Оса. Отсюда
следует, что /_ В'А С = /_ В'А А" + /_ А" АС = /_ Оса -\- /_ аЬО =
= 2_с'а'О-\-/_Оа'Ь' = /_с'а'Ь', где а', Ь' и с'—точки, обратные
точкам а, Ъ и с в инверсии с полюсом О (п. 217).
К
Черт. 631.
Итак, имеем по величине и направлению ^/_В'А'С'=^/_с'а'Ь', и
аналогично для двух других углов треугольника А'В'С. Треугольники
А'В'С и а'Ъ'с' подобны, но имеют противоположные направления вра-
вращения.
383. Пусть АВ и CD—данные отрезки (черт. 631), Р — точка
пересечения прямых АВ и CD.
Построим точку О, обладающую следующими свойствами: а) тре-
треугольники ОАВ и OCD равновелики; Ь) углы АОВ и COD имеют
одинаковое направление; с) углы АОВ и COD равны по величине.
Так как пл. ОАВ^=пп. OCD, то точка О принадлежит геометри-
геометрическому месту точек, отношение расстояний которых от прямых АВ
и CD обратно отношению отрезков АВ и CD. Согласно п. 157, это
геометрическое место состоит из двух прямых РХ и PY, проходящих
через точку пересечения прямых АВ и CD. При этом, как видно из
чертежа, для любой точки X одной из этих прямых углы АХВ и CXD
смешанный задачи 543
имеют одинаковое направление, для любой точки Y другой из них
углы AYB и CYD имеют противоположные направления.
Так как углы АОВ и COD имеют, по предположению, одинаковое
направление, то искомая точка О лежит на прямой РХ (а не на пря-
прямой PY).
Далее
АВ> = ОА2-\-ОВ2±2ОВ-ОЕ, A)
CD2 = OC2-{-OD2±2OD-OF, B)
где Е и F — основания перпендикуляров из точек Аи С на прямые
ОВ и OD. При этом знаки перед последними членами в правых частях
равенств A) и B) одинаковы в силу равенства углов АОВ и COD.
В силу равенства этих углов треугольники ОАЕ и OCF подобны,
откуда OA:OE = OC:OF. С другой стороны, в силу равновеликости
треугольников ОАВ и OCD и равенства углов АОВ и COD мы имеем
(п. 256):
OA-OB = OC-OD. Cj
Деля это равенство почленно на предыдущее, получим:
OB-OE — OD-OF. ¦ D)
Вычитая теперь почленно равенства A) и B) и принимая во вни-
внимание D), найдём:
АВ2 — CD* = О А2 -\- ОВ2 — ОС2 — OD2. E)
Обозначив, наконец, через М и N середины отрезков АВ и CD,
будем иметь (п. 128) ОА2-\-ОВ* = 2ОМ2-\-~ АВ2 и OC2-f-OD2 =
= 2ON2 -\- —- CD2. С помощью этих соотношений равенство E) при-
водится к виду
ОМ- — ON2 = — {АВ2 — CD2). F)
Итак, существует единственная точка О, удовлетворяющая
условиям а), Ь) и с), указанным в начале решения; эта точка опре-
определяется как точка пересечения прямой РХ с прямой линией UU' —
геометрическим местом точек, разность квадратов расстояний которых
от точек Ж и N равна — (АВ2 — CD2) (сравнить п. 128а, следствие).
Построим теперь дуги АКБ и CLD, из точек которых отрезки АВ
и CD видны под равными и одинаково направленными углами / АКВ^
= /_CLD=V, и обозначим через В' и D' вторые точки пересече-
пересечения прямых ОВ и OD с соответствующими дугами.
544 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Мы имеем /_ АОВ = /_ АВ'В-\-Z_OAB или ?_ АОВ = /_ ABB —
— /_ ОАВ в зависимости от того, лежит ли точка О внутри или вне
окружности АКВ, и аналогично /_ COD = /_ CD'D + /_ OCD'. Так как
/_АОВ= /_COD и /_АВВ = /_CD'D= V, то отсюда следует,
что </_OAB'=/_OCD'. Следовательно, треугольники ОАВ' и OCD'
подобны, откуда
OA:OB = OC:OD'. G)
Деля равенство C) почленно на G), получим OB-OB = OD-OD',
так что точка О имеет относительно окружностей АКВ и CLD одну
и ту же степень и потому лежит на их радикальной оси.
Итак, радикальная ось окружностей АКВ и CLD, удовлетворяю-
удовлетворяющих условию /_АКВ= /_CLD= V, проходит через точку О, не зави-
зависящую по самому её определению от выбора этих окружностей.
Примечание. Мы предполагали, что углы АОВ и COD не только
равны, но и имеют одинаковое направление вращения, и что то же имеет
место для углов АКВ и CLD. Случай, когда эти углы имеют противополож-
противоположные направления, сводится к рассмотренному, если поменять рилями точки
С и D.
При этом роль точки О будет играть точка, в которой прямая PY пере-
пересекается с прямой UU' — геометрическим местом точек, удовлетворяющих
условию F;.
384. Так как треугольники ABC и ADC (черт. 632) равны (по трём
сторонам), то биссектрисы внутренних углов при В и D пересекают
Черт. 632.
прямую АС в одной и той же точке О, удовлетворяющей условию
АО:ОС= АВ:ВС. То же относится и к внешним углам при верши-
вершинах В и D, биссектрисы которых пересекают АС в точке О', для
которой АО':СО'=АВ:ВС. Точки О и О' равноудалены от всех че-
четырёх прямых АВ, ВС, CD и DA и потому служат центрами тех
окружностей, о которых идёт речь в тексте.
Если данный четырёхугольник — шарнирный и сторона АВ ос-
остаётся неподвижной, то точка С описывает окружность с центром В (или
дугу такой окружности), а точки О и О'—фигуры, гомотетичные
относительно точки А той фигуре, которую описывает точка С, т. е.
также окружности. Действительно, расстояние ВС и отношения АО:ОС
и АО':СО' сохраняют при этом постоянную величину.
СМЕШАННЫЕ ЗАДАЧИ ,545
385. Если четырёхугольник ABCD (черт. 633) описан около окруж-
окружности и эта окружность лежит внутри четырёхугольника, то ЛВ-|-
-\- CD = AD -\- ВС (упр. 87). Последнее соотношение сохраняет силу
при деформации четырёхугольника, так что он остаётся описанным.
Отложим на прямой АВ от точки А в сторону точки В отрезок
АЕ, равный AD, а от точки В в сторону точки А — отрезок BF, рав-
равный ВС (точки Е и F могут обе лежать на.самом отрезке АВ, как на
чертеже 633, или одна из точек Е и F мо-
может лежать на самом отрезке АВ, дру-
другая — на его продолжении; наконец, обе
точки Е и F могуг лежать на продол-
продолжениях отрезка АВ; однако во всех случаях
АЕ-\- BF=AD-\-BC>AB, так что от-
отрезки АЕ и BF налегают.один на другой). д с с о
Треугольники АОЕ и AOD будут равны,
так как /_OAD = /_OAE, откуда OD= Черт. 633.
= ОЕ. Аналогично OC = OF. Наконец в
силу' равенства АВ-\-CD = AD-\-ВС имеем CD = AD-\-ВС — АВ —
= АЕ-\-BF—AB^EF. Треугольники OCD и OFE равны, и потому
^/_COD^= ^/_EOF. Но в силу сказанного в решении упражнения 8У
имеем /_ АО В -\-/_ COD =180°, так что
^_ АО В-\-/_ EOF =\80°. A)
Обратно, пусть некоторая точка О удовлетворяет условию A).
Построим треугольники AOD и ВОС, соответственно равные АОЕ
и BOF. Будем иметь /_ AOD-\-/_ BOC =/_AOE-\-/_BOF =
=/_АОВ -(- /_EOF = 180°; следовательно,^.ЛОВ 4- /_C°D = 360°—
—(^_AOD-\-/_BOC)= 180°, и потому/_COD = /_EOF. Кроме того,
OC=OF, OD = OE, и треугольники COD и EOF равны, так что
CD = EF. Поэтому AD~\-BC = AE-\-BF= AB-\-EF=AB-\-CD,
и четырёхугольник ABCD — описанный.
Отсюда следует, что геометрическое место центров О вписанных
окружностей совпадает с геометрическим местом точек, из которых
отрезки АВ и EF видны под пополнительными углами, и потому пред-
представляет собой окружность .S с центром на прямой АВ (упр. 257).
Из сказанного в решении упражнения 257 следует, что концы
одного из отрезков АВ и EF обрагны относительно окружности Окон-
Оконцам другого. В данном случае точка А обратна точке F, точка В —
точке Е. Из упражнения 242 следует, что отношение расстояний про-
произвольной точки О окружности 5 от двух взаимно обратных точек
А и F есть постоянная величина, так что в силу OF=OC имеем
OA:OC^const. Аналогично OB:OD = const.
386. Прямые АВ, CD и PQ проходят через одну точку О — ра-
радикальный центр данной окружности и окружностей РАВ и PCD
(черт. 634). Точка О остаётся неподвижной при перемещении точ-
точки Р как точка пересечения прямых АВ и CD. Произведение OP-OQ
равно степени точки О относительно данной окружности. Следовательно,
35 Элементарная геометрия
546
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
точки Р и Q соответствуют одна другой в инверсии с полюсом О и
степенью, равной степени точки О относительно данной окружности.
Если точка Р описывает прямую, не проходящую через О, то
точка Q описывает окружность, проходящую через точку О, и на-
наоборот. Если точка Р описывает окружность, не проходящую через О,
то точка Q описывает окружность, ей обратную.
Геометрическое место точки Р при условии, что она совпадает
с Q, есть окружность инверсии; последняя существует лишь при усло-
условии, что точка О лежит вне данной окруж-
окружности.
387. Точки А', В, С и D' (черт. 635)
соответствуют точкам А, В, С и D в инвер-
сии с полюсом Я_ и степенью, равной сте-
степени р точки Р относительно окружности,
описанной около квадрата. Следовательно
(п. 218),
р-ВА
А'В' =
РА-РВ '
A)
Черт. 634.
и аналогичные выражения получим для ВС,
CD' и D'A'. Отсюда, принимая во внимание,
что AB=BC=CD=DA, получим А'В • СП=
-ВС С А' р
— ВС ' UA— PA-PB-PC-PD-
Обратно, пусть (выпуклый) вписанный четырёхугольник A'B'CD'
удовлетворяет условию А'В-CD'= В'С •D'A', и инверсия с полю-
Черт. 635.
сом Р преобразует точки А', В', С и D' в вершины А, В, С и D
квадрата, вписанного в ту же окружность. Прямой S, проходящей
через центр О квадрата и перпендикулярной к его сторонам АВ и CD,
соответствует в этой инверсии окружность S', ортогональная ко всем
СМЕШАННЫЕ ЗАДАЧИ
547
окружностям, проходящим через точки А и В' (в том числе и к пря-
прямой А'В'), и ко всем окружностям, проходящим через точки С и D'
(в том числе и к прямой CD'). Окружность 5" имеет своим центром
точку пересечения Е' прямых А'В' и CD' и ортогональна к окруж-
окружности A'B'CD'. Такая окружность S' существует, так как точка Е'
лежит вне окружности A'B'CD' в силу выпуклости четырёхуголь-
четырёхугольника A'B'CD'. Точно так же прямая Т, проходящая через точку О
и перпендикулярная к AD и ВС, преобразуется в окружность Т, имею-
имеющую своим центром точку пересечения F' прямых A'D' и ВС и орто-
ортогональную к окружности A'B'CD'.
Так как окружности S' и Т преобразуются в прямые линии, то
искомым полюсом инверсии может быть только одна из точек их пере-
пересечения Р или Q (окружности S' и
Т наверное пересекутся, так как одна
из них пересекает дуги А'В' и CD',
другая — дуги A'D'. и ВС окруж-
окружности A'B'CD'). Рассмотрим'хотя бы
точку Р. Покажем, что инверсия с
полюсом Р преобразует вершины дан-
данного четырёхугольника действительно
в вершины квадрата ABCD. Так как
все окружности, проходящие через Л'
и В', ортогональны к окружности S',
то прямая АВ, соответствующая
окружности РА'В', перпендикулярна
к той прямой S, которая соответ-
соответствует окружности S'. По той же при-
причине прямая CD перпендикулярна
к прямой S, а прямые AD и ВС —
к той прямой Т, которая соответствует окружности Т. Следовательно,
четырёхугольник ABCD—параллелограм. Так как точки А', В, С и
ГУ лежат на одной окружности, то и обратные им точки А, В, С и D
также лежат на одной окружности, а следовательно, ABCD есть пря-
прямоугольник. Наконец, соотношение А В-СП = A'D'-ВС преобра-
преобразуется с помощью формул, аналогичных A), в соотношение AB-CD =
= AD ¦ ВС. Из последнего следует, что прямоугольник ABCD — квад-
квадрат. Те же соображения применимы и к инверсии с полюсом Q.
Задача преобразования данного четырёхугольника в квадрат имеет
два решения: полюсом инверсии может быть любая из точек пересече-
пересечения Р и Q окружностей S' и Т. Это объясняется тем, что четырёх-
четырёхугольник A'B'CD'—вписанный (сравнить решение упр. 270 5°, примеча-
примечание 2°).
388. Пусть инверсия с полюсом Р преобразует вершины данного
вписанного четырёхугольника ABCD' в вершины прямоугольника ABCD
(черт. 636). Не нарушая общности, можно предположить, что прямо-
прямоугольник ABCD вписан в ту же окружность, что и четырёхуголь-
четырёхугольник A'B'CD'.
35*
Черт. 636.
548
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Прямая S, соединяющая середины сторон АВ и CD, пересекает под
прямым углом как все окружности, проходящие через точки .4 и В,
так и все окружности, проходящие через С и D. Следовательно, обрат-
обратная ей окружность S' пересекает под прямым углом прямые А'В и CD'
и окружность А'В CD'. Ценгр этой окружности S' есть точка пере-
пересечения Е' прямых А'В и CD', её радиус — касательная из точки Е'
к окружности ABCD'. Точно так же получаем вторую окружность Т'
с центром в точке пересечения F' прямых A'D' и В'С, обратную пря-
прямой Т, которая соединяет середины
сторон AD и ВС.
Так как окружности S' и Т
преобразуются искомой инверсией
в прямые линии S а Т, то полюс
инверсии есть одна из точек пере-
пересечения Р или Q этих окружностей.
Окружности S' и Т обе ортогональ-
ортогональны как к прямой E'F', так и к окруж-
окружности VBCD'; следовательно, Р и
Q — предельные точки этой прямой и
этой окружности (упр. 152). Степень
инверсии, преобразующей точки А',
Ь', С и D' в вершины прямоуголь-
прямоугольника, остаётся, очевидно, произвольной.
389. Пусть точки А', В', С и D' преобразуются с помощью неко-
некоторой инверсии в вершины параллелограма ABCD (черт. 637, 638).
Если точки А', В, С и D' лежат на одной окружности, то ABCD —
прямоугольник, и мы приходим к задаче 388. Поэтому мы предполо-
предположим, что точки А', В', С и D' не лежат на одной
окружности.
Так как треугольники ABC и ADC равны, то и
окружности ABC и ADC должны быть равны между
собой, и прямая АС образует с обеими окружностя-
окружностями равные углы. Следовательно, полюс инверсии дол-
должен лежать на окружности, проходящей через точки
А' и С и делящей пополам угол между окружно-
окружностями А'В'С и A'D'C, точнее угол между дугами
А'В'С и A'D'C (так как точки В и D лежат по
Черт. 637.
Черт 638.
разные стороны от АС, то точки В' и D' лежат по разные стороны
от окружности) (сравнить задачу 275). Точно так же, полюс инверсии
лежит на определённой окружности, делящей пополам угол между
окружностями В A'D' и BCD'.
Так как эти окружности, на которых должен лежать полюс инвер-
инверсии, пересекаются в двух точках, то получаем два возможных положе-
положения полюса инверсии; степень инверсии остаётся произвольной.
390. Прямая, пересекающая две данные окружности под равными
углами, необходимо проходит через один из их центров подобия (так
как радиусы, проведённые в точки пересечения, попарно параллельны
СМЕШАННЫЕ ЗАДАЧИ
549
(сравнитьп. 227), и обратно. Таким образом, центр подобия можно охарак-
охарактеризовать как точку, через которую проходит бесчисленное множество
прямых, пересекающих обе данные окружности под равными углами.
Если точка А', соответствующая точке А в искомой инверсии /,
есть центр подобия для двух окружностей, в которые преобразуются
данные окружности, то бесчисленное множество окружностей, проходя-
проходящих через точку А и пересекающих обе данные окружности под одним
и тем же углом, должны преобразовываться в прямые линии, проходя-
проходящие через точку А'.
Окружность, проходящая через точку А и пересекающая две дан-
данные под одним и тем же углом, преобразуется сама в себя с помощью
одной из двух инверсий J' или J",
преобразующих данные окруж-
окружности одну в другую (п. 227).
Отсюда следует, что вс*якая
окружность, проходящая через
точку А и изогональная к двум
данным, проходит либо через
точку Р', обратную точке А в
инверсии У, либо через точку Р",
обратную точке Л в инверсии У".
Чтобы эти окружности преоб-
преобразовались в прямые линии, у , ,,
за полюс инверсии / надо ., „п
,- п. ,- г>/ Черт. 639.
принять либо Р, либо Р .
Итак, полюсом искомой инверсии / служит точка, обратная точке А
в одной из двух инверсий, преобразующих две данные окружности
одну в другую. Степень инверсии остаётся произвольной.
391. Пусть S — точка пересечения прямых QR и АВ (черт. 639).
Так как /_ RQM=/_ RPM —/_ ВАМ, то треугольники BQS и ВАМ
подобны, откуда BS = — . Произведение BM-BQ (степень точ-
АИ
ки В относительно окружности) не изменяется при перемещении точки М
по окружности, а следовательно, точка 5 будет при этом неподвижной.
Если окружность и точки А и В даны, то легко построить точку S,
выбирая точку М произвольно.
Переходим к решению задач на построение.
I. Вписать в окружность треугольник (обозначим его через MPQ),
две стороны которого проходят через точки А а В, а третья
параллельна прямой KL.
Задача сводится к построению треугольника PQR, две стороны
которого соответственно параллельны прямым АВ и KL, а третья про-
проходит через S (см. задачу 115). После того как треугольник PQR
будет построен, достаточно соединить вершину Р с точкой А, чтобы
получить на окружности точку М. При этом точка пересечения" пря-
прямой MB с окружностью будет лежать в силу доказанной теоремы на
прямой RS и, следовательно, будет совпадать с Q.
550
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
II. Вписать в окружность треугольник (обозначим его через MPQ),
стороны которого проходят через точки А, В и С.
Задача сводится к построению треугольника PQR, две стороны
которого проходят через точки С и S, а третья параллельна АВ, т. е.
к задаче I. После того как треугольник PQR будет построен, поло-
положение точки М определяется как и в предыдущей задаче.
III. Вписать в окружность многоугольник с чётным числом сто-
сторон, у которого одна из сторон проходит через данную точку, а
остальные параллельны соответственно данным прямым.
Пусть требуется построить, например, шестиугольник PQRSTU,
у которого сторона PQ проходит через данную точку А, а остальные
Pi
стороны параллельны соответственно данным прямым Q,/?,, R^S^, ST^,
TOU^ и U2P^ (черт. 640). Выбрав на окружности произвольную точку Q',
построим ломаную QR'S'T'U'P', звенья которой соответственно парал-
параллельны данным прямым и, следовательно, сторонам искомого много-
многоугольника. Дуги QQ', RR\ SS'., ТТ, UU' и РР' будут равны между
собой в силу параллельности хорд; кроме того, каждые две последо-
последовательные дуги будут иметь противоположные направления. Так как
общее число дуг чётное, то дуги QQ' и РР' будут равны и иметь противо-
противоположные направления. Следовательно, и хорда P'Q' будет параллельна
искомой стороне PQ. Остаётся провести через точку А прямую, парал-
параллельную P'Q', чтобы получить сторону PQ искомого многоугольника.
IV. Вписать в окружность многоугольник с нечетным числом
сторон, у которого одна из сторон проходит через данную точку,
а остальные параллельны соответственно данным прямым.
Пусть требуется построить, например, пятиугольник PQRST, у ко-
которого сторона PQ проходит через точку А, а остальные стороны
параллельны соответственно данным прямым Q,/?,, R2^> ^гЛ и Т$Р1
(черт. 641). Выбрав на окружности произвольную точку Q', построим
ломаную Q'R'S'T'P', звенья которой соответственно параллельны дан-
данным прямым и; следовательно, сторонам искомого многоугольника.
Дуги QQ', RR', SS', ТТ и РР' будут опять равны; QQ' и РР' бу-
СМЕШАННЫЕ ЗАДАЧИ 551
дут иметь в данном случае (в силу нечётности числа вершин) одинако-
одинаковое направление.
Следовательно, будут равны и дуги PQ и P'Q', а значит и хор-
хорды PQ и P'Q'. Остаётся провести через точку А хорду, равную
хорде P'Q', чтобы получить сторону PQ искомого многоугольника.
V. Вписать в окружность многоугольник с данным числом
сторон, у которого некоторое число последовательных сторон {в ча-
частности все стороны) проходят через данные точки, а остальные
параллельны соответственно данным прямым.
В том случае, когда только одна сторона должна проходить через
данную точку, задача уже решена (см. выше III и IV). Пусть тре-
требуется построить, например, ше-
шестиугольник' PMQUVW (черт.
639), у которого стороны РМ
и MQ проходят соответственно
через данные точки Л и В, а на
каждую из остальных сторон
наложено определённое усло-
условие — проходить через данную
точку или быть параллельной
данной прямой. Поступая таким
же образом, как при решении
задачи I, сводим нашу задачу к
следующей: вписать шестиуголь-
шестиугольник PRQUVW, у которого сто-
сторона PR параллельна АВ, сто-
сторона RQ проходит через данную точку S, а остальные стороны под-
подчинены первоначально данным условиям. Таким образом, требование,
чтобы две последовательные стороны искомого многоугольника прохо-
проходили через данные точки, заменяется требованием, чтобы одна из
сторон некоторого вспомогательного многоугольника (с тем же числом
сторон) была параллельна данной прямой, а другая проходила через
данную точку. При этом требования, наложенные на остальные сто-
стороны, не изменяются.
Так как условие проходить через данную точку наложено на пот
следователъные стороны искомого многоугольника, то, повторяя эту
замену несколько раз, сведём задачу V к задаче III или IV.
VI. Переходим, наконец, к наиболее общей задаче рассматривае-
рассматриваемого типа:
Вписать в окружность многоугольник с данным числом сторон,
на каждую из сторон которого наложено определённое условие —
проходить через динную точку или быть параллельной данной
прямой. (Обобщение по сравнению с задачей V состоит в том,, что
стороны, на которые наложены условия проходить через данные точки,
не являются обязательно последовательными.)
Пусть требуется построить, например, шестиугольник PJQRSTU
(черт. 642), у которого сторона PQ должна быть параллельна данной
552
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
прямой KL, а сторона QR — проходить через данную точку А. Про-
Проведём через точку R хорду /?Q,, параллельную KL, и обозначим
через Ал точку пересечения прямой PQr с прямой, проходящей через
точку А и параллельной KL. Так как четырёхугольник PQRQU а сле-
следовательно, и ARQ^Ar является равнобедренной трапецией, то точки
Л и Л, равноудалены от центра О данной окружности. Это даёт воз-
возможность построить точку Аи не зная многоугольника PQRSTU (пря-
(прямая АА^ параллельна KL и ОА^ОАг). Для построения многоуголь-
многоугольника PQRSTU, у которого сторона PQ параллельна АХ, а сторона QR
проходит через данную точку А, достаточно построить многоуголь-
многоугольник PQ^RSTU, у которого сторона PQ{ проходит через данную точку Av
а сторона QXR параллельна KL.
Повторяя это рассуждение несколько раз, сведём задачу VI к за-
задаче V.
Примечание. Как искомый многоугольник так и вспомогательные
многоугольники, о которых илёт речь в настоящей задаче, могут оказаться
и несобственными, т. е. их стороны могут иметь точки пересечения, отлич-
отличные от вершин (ср. п. 21). Так, например, вспомогательный многоугольник
PQRSTU на чертеже 642 — несобственный (его стороны QXR и UP пересе-
пересекаются).
392. Применим к решению этой задачи метод взаимных поляр
(пп. 206 и след.). Если вершины искомого треугольника лежат на дан-
данных прямых а, Ь и с, то поляры
этих вершин образуют вписанный
треугольник, стороны которого
проходят через полюсы А, В а С
этих прямых. Таким образом зада-
задача сводится к уже решённой' за-
задаче 391.
393. Пусть Т — точка касания
рассматриваемых окружностей меж-
между собой (черт. 643), I и К —
точки пересечения общей касатель-
касательной в точке Т с касательными АВ и А'В'. Очевидно, IA^IT = IB и
К А' = КТ = КВ'. Кроме того, 1Т = КТ, так как линия центров есть
ось симметрии фигуры.
Отсюда следует, что IK= AB= const. Геометрическое место то-
точек К есть окружность с центром / и радиусом АВ. Окружности,
построенные на отрезках А'В' как на диаметрах, имеют постоянный
радиус К А' = KB' ^/A = IB=;— АВ; их центры* лежат на окруж-
окружности с центром / и радиусом 1К=АВ. Следовательно, все эти окруж-
окружности касаются определённой окружности и даже двух окружностей —
с центром в точке / и радиусами, соответственно равными — АВ
Смешанные задачи
553
394. 1°. Пусть Р — точка пересечения касательных в точках А
и В к данной окружности О (черт. 644). Так как прямая РА есть
радикальная ось данной окружности О и окружности С, а прямая
РБ—радикальная ось окружностей О и С,, то точка Р есть ради-
радикальный центр окружностей О, С и С,. Поэтому прямая РМ касается
в точке М окружностей С и С, и РА=^РВ = РМ. Геометрическое
место точек М есть окружность' с центром Р и радиусом РА.
2°. Так как данная окружность О касается в точках А и В окруж-
окружностей Си С,, то центр подобия N окружностей С и С, лежит на
прямой АВ. Кроме того, линия центров окружностей С и С, касается
в точке М окружности Р, и потому точка N лежит вне окружности Р7
а следовательно, и вне данной окружности О.
Таким образом, геометрическое место точек N есть часть пря-
прямой АВ, внешняя относительно данной окружности (сравнить ещё 3°).
3°. Обратно, каждой точке N прямой АВ, которая лежит вне дан-
данной окружности, соответствуют две точки М и М — точки прикосно-
прикосновения касательных, проведённых из точки Л' к окружности Р, и две
пары окружностей С, С, и С, С,'. Центры последних лежат на пере-
пересечении прямых MN и MN с О А и ОВ.
4°. Окружность, описанная около треугольника NMM', имеет отре-
отрезок NP своим диаметром (так как углы NMP и NM'P — прямые);
её центром ы служит середина отрезка NP. Но геометрическое место
точек N есть часть прямой АВ, состоящая из обоих продолжений
отрезка АВ, а точка Р неподвижна. Следовательно, геометрическое
место точек ш есть совокупность обоих продолжений отрезка А'В',
где А' и В' — середины отрезков РА и РВ (черт. 645).
5°. Центр / окружности, вписанной в треугольник NMM' (черт. 646),
лежит на биссектрисе NP угла MNM и на биссектрисе угла NMM1'
При этом /_ РМ/ = 90° ~ /_NMI=90° — ?IMM = /_PIM, u,
следовательно, РМ = Р1. Таким образом, все точки / лежат на окруж-
окружности 'Р. Но так как продолжение отрезка PI за точку / проходит
554
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
через точку N, а геометрическое место точек N есть часть прямой АВ,
внешняя относительно окружности Р, то геометрическое место точек /
есть совокупность двух дуг АС и BD окружности Р (черт. 645).
6°. Так как точка N лежит на прямой АВ, то поляра ММ' точки N
относительно окружности Р проходит (п. 205) через полюс О прямой
АВ относительно той же окружности (черт. 646). Так как, кроме того,
точки О и Р неподвижны, то основание К высоты NK треугольника
NMM лежит на окружности 2, имеющей отрезок ОР своим диамет-
диаметром. Эта окружность 'проходит, очевидно, через точки А к В. Геоме-
Геометрическое место точек К есть дуга АРВ окружности 2 (окружность 2
не показана на чертеже).
Так как точка Р лежит на окружности, описанной около треуголь-
треугольника NMM', и прямая NP есть одна из его высот, то высоты этого
треугольника пересекаются в точке Н, симметричной с Р относительно
о
Черт. 646.
прямой ММ' (упр. 70), т. е. относительно точки К. Поэтому РН=2РК,
и геометрическое место точек И есть дуга окружности 2', гомотети-
ческой окружности 2 относительно точки Р, причём коэфициент по-
подобия равен 2 (окружность 2' не показана на чертеже). •
7°. Остаётся ещё показать, что точки пересечения геометрического
места точек ш с геометрическим местом точек /, т. е. точки Е и F
(черт. 645), в которых окружность Р пересекает прямую А'В', принад-
принадлежат и окружности 2'.
С этой целью рассмотрим те положения точки N, для которых
треугольник NMM' будет равносторонним; таких точек будет две.
Для этих положений точки N точка ш совпадает с соответствующей
точкой /, а потому точки ш и / совпадают обе либо с Е, либо с F;
но при этом и точка пересечения И высот треугольника NMM со-
совпадает с той же точкой (в равностороннем треугольнике точки ш, /
и Н совпадают). Следовательно, окружность 2' проходит через точки
Е и F.
СМЕШАННЫЕ ЗАДАЧИ
555
395. Пусть 5 — внешний центр подобия окружностей С и С
{черт. 647) и А', А' — вторые точки пересечения прямой SA с окруж-
окружностями С и С. Треугольники А"РА и АР'А' гомотетичны относительно
центра подобия S. Далее, '^_РА"А = /^АРР\ так как оба эти угла
измеряются половиной дуги АР окружности С. Аналогично / Р'АА =
= /^_АР'Р. Следовательно, треугольники А"РА, РАР' и АР'А' по-
подобны. Центры О, О' и Ё окружностей С, С и АРР' будут соответ-
соответственными точками фигур А"РА, РАР' и АР'А', и потому четырёх-
четырёхугольники А"РАО, PAP'Q и АР'А'О' также будут подобными.
Из подобия этих четырёхугольников имеем: у ОАР= / пР'А
/О'А' /0 ;Q % /А
откуда/;PQP' = 360° — /_%РА — /_РАР'—
/_О'АР'—/_РАР' — /_ОАР = /_ОАО', т. е.
угол, под которым отрезок РР' виден из точки Q, равен углу между
окружностями С и С, точнее говоря, между радиусами этих окруж-
окружностей, проведёнными в точку их пересечения.
Черт. 647.
Обозначая через г, г' и р радиусы окружностей С, С и РАР',
мы получим из подобия тех же фигур г:р = АР: АР' и $:г' = АР:АР',
откуда г:р = р:г' и г:г' = АР°-:АР'2. Таким образом, р есть' среднее
пропорциональное между г и г', и АР:АР' = у г: у г'.
Если В—вторая точка пересечения окружностей Си С, a Q и
Q' — точки прикосновения второй общей касательной, то из предыду-
предыдущего следует, что радиус каждой из' окружностей АРР', ВРР', AQQ'
и BQQ' есть среднее пропорциональное между г и г'. Таким образом,
получается предложение, указанное в упражнении 262, 3°.
396. 1°. Пусть окружности А и В пересекаются в двух точках.
Чтобы с помощью инверсии их _можно было преобразовать в окруж-
окружности А' и B't образующие фигуру, равную той, которую образуют
окружности С и D, необходимо, чтобы окружности С и D также пе-
пересекались в двух точках и чтобы угол между окружностями А а В
равнялся углу между С и D.
556
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Покажем теперь, что эти условия и достаточны. Инверсия 6" с по-
полюсом в одной из точек пересечения Р окружностей И и В и произ-
произвольной степенью преобразует их в некоторые две прямые а и Ь
(черт. 648), угол между которыми равен углу между окружностями
А и В. Точно так же инверсия Т сч полюсом в одной из точек пере-
пересечения Q окружностей С и В и произвольной степенью преобразует
их в некоторые две прямые cud, угол между которыми равен углу
между С и D, т. е. углу между окружностями А а В ила между
прямыми а и Ь. Перемещая фигуру, состоящую из окружностей С
и D, можно достичь того, что прямые с и d будут совпадать с а и Ь,
как на чертеже 648. При этом окружности С a D будут получаться
Черт. М8.
из И и В с помощью последовательности двух инверсий: первая ин-
инверсия S с полюсом Р преобразует окружности А и В в прямые а
и Ь, вторая Т с полюсом Q преобразует прямые а и Ь в окружности
С и D. На степени инверсий S и Т (остававшиеся до сих пор совер-
совершенно произвольными) мы наложим теперь только одно ограничение:
точки Р и Q не должны совпадать между собой.
Так как полюсы Р и Q инверсий S и Г не совпадают, то после-
последовательность этих двух инверсий можно заменить (упр. 251, 2°)
одной инверсией S' и одной симметрией относительно прямой. Следо-
Следовательно, инверсия S' преобразует пару окружностей А и В в пару
окружностей, симметричных с С и D относительно некоторой прямой
и потом} образующих фигуру, равную фигуре (С, D). Равенство углов
между окружностями Л и Б и между окружностями С и D оказывается,
таким образом, и достаточным.
Итак, можно сказать, что угол между двумя пересекающимися окруж-
окружностями есть единственный независимый инвариант пары окружностей
относительно группы инверсии (ср. пп. 292 и 294).
Так как угол между пересекающимися окружностями С и С равен
(в обозначениях задачи 395 и черт. 647) углу РпР', то этот угол
определяется отношением отрезка РР' общей касательной к отрезку
РО.—среднему пропорциональному их радиусов (см. решение задачи 395).
CMFIIlAUHhIE ЗМАЧИ
557
Если бы окружности А и В не пересекались, а касались одна дру-
другой, то мы могли бы повторить предыдущие рассуждения. При этом
две пары пересекающихся прямых (а, Ь) и (с, d) заменились бы двумя
парами параллельных прямых. Выбрав произвольно степень инверсии ?,
преобразующей окружности А и В в прямые а и Ь, мы можем подо-
подобрать степень инверсии Т, преобразующей окружности С и D в пря-
прямые cud, так, чтобы расстояние между cud было равно расстоя-
расстоянию между а и Ь, и затем совместить обе пары прямых. Этот случай
можно рассматривать как частный случай предыдущего, когда угол
между окружностями равен нулю (или 180°).
2°. Пусть теперь окружности А и В, не имеющие общих точек,
можно преобразовать с помощью некоторой инверсии S в две окруж-
окружности А' и В' (также без общих точек), образующие фигур), равную
той, которую образуют окружности С и D. Перемещая окружности
С и D, можно совместить их с окружностями А' и В'. Итак, пусть
инверсия S преобразует пару окружностей (А, В) в пару окружностей
(С, D).
Преобразуем окружности С и D с помощью инверсии Т с полюсом
в одной из их предельных точек в две концентрические окружности
с и d (см. решение упр. 248). Так как окружности С и D имеют две
предельные точки, то можно выбрать полюс инверсии Т отличным ог
полюса инверсии S. Последовательность инверсий S и Т преобразует
окружности А а В в две концентрические окружности cud. Но эту
последовательность инверсий можно заменить одной инверсией 6V и сим-
симметрией относительно некоторой прямой. Следовательно, инверсия $'
преобразует окружности А и В в две концентрические окружности,
равные окружностям с и d, а инверсия Т — окружности С и D в кон-
концентрические окружности с и d. Таким образом, указанное в тексте
условие необходимо для возможности преобразования пары окружно-
окружностей А, В в фигуру, равную той, которую образуют С и D.
Покажем теперь, что то же условие и достаточно. Если это усло-
условие выполнено, то окружности А и В преобразуются с помощью не-
некоторой инверсии в концентрические окружности а и Ь, а окружности
С и D в концентрические окружности с и d, причём радиусы окруж-
окружностей cud будут пропорциональны радиусам окружностей а и Ь.
Выбрав произвольно степень инверсии, преобразующей окружности
A vl В в окружности а и Ь, мы можем (в силу пропорциональности
радиусов окружностей а а Ь, с и d) подобрать степень инверсии,
преобразующей окружности С и D в окружности cud, так, что фи-
фигура, состоящая из окружностей cud, будет равна фигуре, состоя-
состоящей из окружностей а и Ь. Перемещая фигуру, состоящую из окруж-
окружностей С и D, можно достичь того, что пара окружностей (а, Ь)
будет совпадать с парой окружностей (с, d). Далее можно рассуждать,
как и в случае пересекающихся окружностей. Окружности С и D
получаются из Л и В с помощью последовательности двух инверсий
Путём поворота фигуры (С, D) около общего центра окружностей
а и Ь можно избежать совпадения полюсов обеих инверсий. Эту по-
558
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
следовательность двух инверсий можно заменить одной инверсией S'
и одной симметрией. Инверсия S' преобразует фигуру (А, В) в фи-
фигуру, равную (С, D).
Итак, можно сказать, что единственным независимым инвариантом
двух непересекающихся окружностей относительно группы инверсий яв-
является отношение радиусов тех концентрических окружностей, в которые
данные окружности можно преобразовать одной и той же инверсией.
Переходим далее к рассмотрению сложного отношения А четырёх
точек пересечения двух данных окружностей (или прямых) с ортого-
ортогональной к ним окружностью (или прямой). В силу задачи 273 это
сложное отношение сохраняет свою величину при инверсии.
Черт. 649.
Черт. 650.
Если даны две окружности и выбрана окружность, к ним ортогональ-
ортогональная, то значение X зависит от порядка, в котором рассматриваются точки
пересечения. Мы можем для определённости принять за первые две точки
точки пересечения ортогональной окружности с одной из данных окруж-
окружностей, за вторые — две точки её пересечения с другой данной окружностью.
Пользуясь результатом задачи 274, легко убедиться, что сложное отноше-
отношение \ будет иметь при этом (в зависимости от выбранного порядка точек>
два значения, произведение которых равно единице. Мы можем поэтому
ограничиться тем значением, которое не превосходит единицы по абсолют-
абсолютной величине (| A =S 1).
Начнём со случая двух пересекающихся прямых KL и MN (черт. 649)
и ортогональной к ним окружности KNLM. На основании задачи 274
сложное отношение (KLMN), где точки К и L лежат на различных дугах
MN, будет равно (по абсолютной величине и знаку) а =—T~M'TW~
== — (ттг) • Отсюда следует, что а не зависит от выбора окружности,
ортогональной к двум данным прямым, и определяется лишь углом между
ними.
Так как любые две пересекающиеся окружности можно с помощью
инверсии преобразовать в две пересекающиеся прямые и сложное отно-
отношение i, не изменяется при инверсии, то и в случае двух пересекающихся
окружностей величина а не зависит от выбора окружности, ортого-
ортогональной к двум данным, и определяется углом между ними.
В случае двух концентрических окружностей (черт. 650) радиусов /?
и г (R^>r) сложное отношение равно (по величине и по знаку) а =
СМЕШАННЫЕ ЗАДАЧИ " 559
KM KN /R — г\ г
= jj-z : YJJ~ I ui ) и П0Т0МУ зависит лишь от отношения радиусов
ное отношение jj. четырёх т
обеих окружностей. Отсюда следует, что в случае двух непересе-
непересекающихся окружностей величина X не зависит от выбора окружности,
ортогональной к двум данным, и выражается через отношение радиусов
тех концентрических окружностей, в которые их можно преобразовать
с помощью диверсии.
Из всего сказанного до сих пор вытекает, что условие возмож-
возможности преобразования фигуры (А, В) в фигуру, равную (С, D),
состоит в равенстве значений X для обеих пар окружностей.
Далее в случае двух концентрических окружностей имеем (черт. 650)
KO:MO^r:R. Так как мы видели выше, что ( п , ) ^Х, то от-
отсюда следует, что К0:М0 = {\—У X): A-^]/ЛХ). Но отношение
КО:МО можно рассматривать как сложное отношение |л четырёх то-
точек К, М, О и ос (п. 199). Точ-
Точки О и оо преобразуются, если
подвергнуть концентрические окруж-
окружности какой-либо инверсии в общие
точки всех окружностей, ортого-
ортогональных к обеим преобразованным
окружностям, т. е. в предельные точ- Черт 651
ки преобразованных окружностей.
Итак, если две окружности не имеют общих точек, то1 сложное отно-
отношение ji двух из точек их пересечения с какой-либо окружностью
(или прямой), к ним ортогональной, и двух их предельных точек не
зависит от выбора ортогональной окружности. Со сложным отноше-
отношением X оно связано соотношением |л=A—\Г X): A -\-\г X).
Переходим теперь к рассмотрению величин v= и
гг'
t
.— Рассматривая вместо окружности, ортогональной к двум данным
У гг' •
их линию центров (черт. 651), получим (независимо от того, имеют ли
данные окружности общие точки или нет): \=(KLMN) = : =
= d-\~r— r\d+r + f d2 — {r — r'J d? — r? — rri-\-2rrl
~ d—r—f d—r-\~r'~ dl — (r-\-r'J~ d2 — r2 — r'2-- 2rr' ~
Наконец, если две данные окружности имеют общую касательную,
скажем внешнюю, длины t, то t2=d2 — (г — r'J= d2 ¦— г2 —rri-\- 2rr'\
откуда t: У~гг' = |А< -|-'2.
Таким образом, величины ji, v и t-.У гг' выражаются определён-
определённым образом через X, и потому в предыдущем условии возможности
560
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
преобразования фигуры (А, В) в фигуру (С, D) вместо I можно
рассматривать любую из этих величин.
397. 1°. Выбрав на прямой D произвольную точку Р (черт. 652),
строим окружность РАА' и в точке Р — касательную к этой окружности.
Обозначим через Р' и М точки пересечения этой касательной с пря-
прямыми ГУ и АА'. Имеем:
МА-МА' = МР2, A)
и МР = МР' (так как прямые D и D' равноудалены от ЛИ'), откуда
МА-МА' = МР'\ Последнее равенство показывает, что прямая МР'
(т. е. РР') касается и окружности Р'АА'.
2°. Пусть Н и Н' — основания перпендикуляров, опущенных из
точек А и А' на прямую РР', М—основание перпендикуляра из
точки М на прямую D. В силу подобия треугольников МАН, МА' Н'
и РММ' имеем МА:АН=МА':А'Н' = РМ:ММ'. Заменяя в равен-
равенстве A) отрезки МА,
МА' и МР пропорцио-
пропорциональными им отрезками
АН, А'Н' и ММ, най-
найдём, что произведение
АН-А'Н' равно постоян-
постоянной величине ММ2.
3°. Пусть N — проек-
проекция точки А' на прямую
АН. Из треугольника
АА'Н имеем АА'2= АН2-\-
-\-А'Н2— 2 АН-NH (в си-
силу п. 126). UoNH=A'H',
так что АН2-\- А'Н2 =
= АА'1 -\- 2АН • А'Н'.
Отсюда видно, что
АН2 4- А'Н2 равняется постоянной (в силу 2°) величине АА''14-
-\- 2АН- А'Н' = АА'2 ~\- 2ММ2. Геометрическое место точек Н есть
иа основании упражнения 141 окружность с центром в середине отрезка
АА'. Квадрат радиуса этой окружности равен (сравнить решение упр. 141)
)-(АН2 + А'Н2)— Х- ААЛ^~АА'-^ММ] = АК2, где К — точка
2 4 4
прямой D, равноудалённая от И и А'.
Из рассмотрения треугольника АА'Н' следует, что геометрическое
место точек Н' есть та же окружность.
4°. Чтобы прямая РР' проходила через данную точку Q, соответ-
соответствующая точка Н должна лежать на окружности, построенной на от-
отрезке AQ как на диаметре, так как прямая АН перпендикулярна к РР'.
Кроме того, точка Н лежит на окружности, рассмотренной в 3°. Если
обе окружности пересекутся, то точки их пересечения определят два
возможные положения точки Н, соответствующие данной точке Q,
а следовательно, и два положения точки Р.
СМЕШАННЫЕ ЗАДАЧИ
561
в тре-
тре5°. Пусть О и О' — центры окружностей РАА' и Р'АА', К и К' —
точки пересечения их линии центров с прямыми D и D'. Отложим на
линии центров отрезок КО", равный О'К'. Треугольники АКО" и АК'О'
будут, очевидно, равны, откуда
/_КАО" =-/_К'АО'. B)
Из подобия треугольников ОРКи О'Р'К' имеем ОР:О'Р' = ОК:О'К'.
Заменяя здесь ОР равным ему отрезком О А, О'Р' — отрезком О'А или
О"А и О'К' ~ отрезком КО", получим ОА:О°А = ОК:КО". Это ра-
равенство показывает, что прямая АК есть биссектриса угла А
угольнике ОАО". Принимая во внимание равен-
равенство B), находим / OAK = / KAJ" =
= /_О'АК\ откуда /_ ОАО' = /_КАК'.
Таким чобразом, угол между двумя окружно-
окружностями, равный углу ОАО', сохраняет по-
постоянную величину, он равен углу КАК'.
Так как угол ОАО' при вершине А тре-
треугольника ОАО' сохраняет постоянную вели-
величину, то не изменяется и сумма двух других
углов того же треугольника: ^_ АОО' -f-
4- Z А0'° = 180°— /_ОА0' = 180° —
— ^/_КАК'. Рассмотрим теперь равнобедрен-
равнобедренные треугольники О АР и О' АР': сумма углов
при вершинах О и О' в этих треугольниках
постоянна, так как Z АОР -j- Z АО'Р' =
= (/_О'0Р — /_ О'ОА) 4- (Z 00'Р' —
— i_ 00'А) = (Z О'ОР + /_ОО'Р') —(/_ ЛОО'-\-^/АО'О) =
= 180° —A80°- /_КАК') = /_КАК'. Сумма углов при верши-
вершине А в тех же треугольниках также не изменяется: /_ОАР-\-
'АР'=
— /_АО'Р')=\%0° —
\
— \-{/_ АОР + /_ АО'Р') = 180° — L /_ КАК'. Наконец, в силу посто-
Z Z
янства угла ОАО' и суммы углов ,/_ ОАР-\-/_ О'АР' и четвёртый угол при
точке А будет постоянным: /_ РАР' = 360° — /_ ОАО' — (/_ О АР \-
Л-^Р'АР')=360°—/КАК1— A80°—^ /_КАК')= 180°— ~^_КАК'.
Итак, угол РАР' остаётся постоянным.
398. Пусть М — точка пересечения прямых АВ и D (черт. 653);
с и с' — окружности, имеющие своими диаметрами отрезки AM и MB;
S — окружность, касательная к С, с и D; S' — окружность, касатель-
касательная к С, с' и D.
Инверсия с полюсом А и степенью, равной АМ~АВ, преобразует
окружность С и прямую D друг в друга, а окружность с' — в самоё
себя. Отсюда следует, что та же инверсия преобразует и окружность
36 Элементарная геометрия
562
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
S' в самоё себя. Поэтому общая касательная к окружностям с* и S'
в точке их касания Т проходит через полюс инверсии А.
Пусть о' и Р'—центры окружностей с' и S'; N — основание пер-
перпендикуляра из точки Р' на диаметр АВ; R, г, г' и р' — радиусы
окружностей С, с, с' и S'. Из подобия треугольников AT о' и P'No'
2
имеем Ао':Р'о'= To':No\ т. е.
r
= - ;.. Упрощая это ра-
' г' — р'
p + р
венство, находим р'/? = (/?— г')г'. Так как f} = r-\-r', то p'R = rr'.
Таким образом, радиус окружности S' есть четвёртый пропорциональ-
пропорциональный к ради\сад\1 окружностей С, с и с'.
Черт. 654.
Так как в полученное выражение для р1 радиусы г и г' входят
вполне равноправно, то мы придём к тому же выражению, вычисляя
радиус р окружности S. Это и показывает, что окружности S и S'
равны между собой.
399. Выполним инверсию с полюсом в точке касания Т окружностей
А и В (черт. 654 и 655) и произвольной степенью. Окружности А и В
преобразуются в две параллельные прямые А' и В'; окружности
. .. ,С_,, С, Cj, С2,... — в равные окружности..., С_1', С, С/, С2',...,
касающиеся этих прямых.
Пусть..., r_j, r, /-j, /v,... — радиусы окружностей..., С_,, С,
С1? С2,. .. ; г'—радиус каждой из окружностей.. . , С_/, С, С/, С2', ...;
.... О_,Р_У, OP, O,PV О2Р2,... и . . . ., О_'Р\О'Р\ О'Р\
О2'Р',... — расстояния центров тех же окружностей от линии цент-
центров окружностей А и В.
СМЕШАННЫЕ ЗАДАЧИ
563
Если центры двух последовательных окружностей Сп' и Сп+1', в ко-
которые преобразуются окружности Сл и Ся+1, лежат по одну сторону,
от линии центров окружностей А и В, то мы имеем, очевидно, On+l' P' —
или
-Оп'Р' =
О 'Р'
2г' — •
Черт. 655.
Если же центры, окружностей Сп' и Сп+1' лежат по разные стороны
от линии центров окружностей А и В, то мы будем иметь On+l'P" -f-
+ О'Р' = 2г', или
Г)
п+\
2г'
' П 'Р'
' 2л'
B')
Так как точка Т — полюс инверсии — есть центр подобия двух
взаимно обратных окружностей Сп и С„' (черт. 656), то мы имеем
г':гп = ТОп':ТОп=Оп'Р':О„Рп, откуда О„'Я':2л' = ОпРп:2л„. Таким
образом, отношение расстояния центра любой из окружностей Сп от
линии центров окружностей А и В к диаметру окружности Сп не из-
изменяется при инверсии с полюсом Т. В силу зтого обстоятельства со-
36*
564
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
отношения (Г) и B') переходят соответственно в
^ п л
2л - '
о„
n+l
¦"•" 2л„
A)
B)
Если окружности А и В касаются одна другой внутренним образом
(черт. 654), то любые две последовательные окружности Сп и Сп+1
касаются одна другой внешним
образом. Если окружности А
и В касаются одна другой внеш-
внешним образом, то в ряду окружно-
стей..., С_„ С, С„ С,,...
имеются две пары последова-
последовательных окружностей (С_,, С
и С, С, на черт. 655),
касающихся одна другой внут-
внутренним образом; остальные пары
последовательных окружностей
имеют внешнее касание (Clt C2; CgI Cs; ... на черт. 657).
Если окружности Сд и Сп+] касаются одна другой внешним обра-
образом, то центры преобразованных окружностей Сп' и Св+|' лежат по
одну сторону или по разные
стороны от линии центров
окружностей А и В, смотря
по тому, лежат ли центры
окружностей Сп и Сд+1 по
одну сторону или по разные
стороны от той же прямой.
Отсюда следует, что в
случае внешнего касания
окружностей Сп и Си+1 ра-
равенство A) имеет место,
если их центры лежат по
одну сторону от линии
центров окружностей А и
В, а равенство B) — если
их центры лежат по раз-
разные стороны от той же
прямой.
Если окружности Сп и
Сп+1 касаются друг друга
внутренним образом, то цент- Черт. 657.
ры преобразованных окруж-
окружностей Сп' и Св+]' лежат по одну сторону от линии центров окружно-
окружностей А и В, если центры данных окружностей Сп и Сп+] лежат от неб
по разные стороны, и наоборот. Отсюда следует, что в случае внут-
СМЕШАННЫЕ ЗАДАЧИ
565
реннего касания окружностей Спи Сп+1 равенство A) имеет место,
если их центры лежат по разные стороны от линии центров
окружностей А и В, а равенство B) — если их центры лежат по
одну сторонv от той же прямой.
Чтобы придать выведенным соотношениям большую общность, заметим,
что в случае внешнего касания двух окружностей Сп и Сп + 1, центры ко-
которых лежат по одну сторону от линии центров окружностей А и В, «по-
«последующей» окружностью С„"+1 будет га, которая лежит «ближе» к точке
касания Т. Для расстояний х и X' центров двух окружностей от прямой
X1 X
РТ и их радиусов гиг' будем иметь -^—, гр = 1, причём х' и г' соот-
соответствуют «последующей» окружности. То же равенство имеет место и для
окружностей, центры которых лежат по разные стороны от РТ, если счи-
считать х' положительным, а х — отрицательным.
Черт. 658.
В случае внутреннею касания двух окружностей, центры которых лежат
по одну сторону от линии центров окружностей А и В, будем иметь
jr' х
¦i__i__=l. To же равенство будет иметь место и для окружностей, цен-
центры которых лежат по разные стороны от прямой РТ, если считать «по-
«последующей» внутреннюю окружность и расстояние х' считать положитель-
положительным," а X — отрицательным.
400. Если а, Ь, с и р — стороны и полупериметр треугольника ABC,
то радиусы попарно касающихся окружностей с центрами А, В и С
соответственно равны р—-а, р — Ь и р—с (упр. 91).
Существуют две окружности, касающиеся этих трёх попарно касаю-
касающихся друг друга окружностей и притом одинаковым образом (черт. 658
566
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
и 659). Пусть О — центр и f — радиус окружности, касающейся трёх
данных и лежащей внутри криволинейного треугольника, ограниченного
дугами данных окружностей. Обозначим через х, у и z расстояния
точки О от сторон треугольника, через h, k и / — его высоты.
Применяя формулу A) решения задачи 399 к двум окружностям
А и О, каждая из которых касается окружностей. В и С и которые
касаются друг друга внешним образом (сравнить черт. 657), будем иметь
х
у
= 1; и аналогично -^
) 2Р
= 1; и аналогично ^=
2р 2(р — а) 2Р 2{р
= 1. Отсюда-
х р 2р у р 2р z p 2р
h v — a h ' k p — Ь k ' I р — с /"
z I
) 2р 2{р
2р
Складывая и применяя результат упражнения 301, находим р
О' 1 1
/ i \ о
Черт. 659.
вы-
ражение для р можно преоб-
преобразовать следующим образом:
если Д — площадь треуголь-
треугольника, ra, rb wrc — радиусы
вневписанных окружностей,
то^-=^ит. д. (упр.
299); |-=|- и т. д. Пре- .
дыдущее уравнение даёт для
р следующее выражение: р^
Га\ьЛ с
Пусть теперь О'и р'—центр и радиус второй окружности, касаю-
касающейся трёх данных. Эта окружность может касаться трёх данных как
внутренним (черт. 658), так и внешним (черт. 659) образом; в первом
из этих случаев центр её может лежать как внутри, так и вне данного
треугольника. ¦ i
Для радиуса р' окружности О' получим аналогично
Если X', у', z' — расстояния точки О' от сторон треугольника, взятые
¦ с определёнными знаками, как указано в решении упражнения 301, то
в случае внутреннего касания (черт. 658) мы будем иметь систему уравне-
ний 2^~+57 = 1; 2Г~Г"^;==1: 2г + 2сг = 1> аВ случае внешнего ка"
сания (черт. 659) — систему п ^-, ^1,
2гь
у' .
— ^-, = 1,
' -il = l.lto
2/-,. 2р'
СМЕШАННЫЕ ЗАДАЧИ
567
этих двух систем получим, как и выше, в первом случае р' = ,-
Л
во втором случае р'з=— —
— . Если
+гс) '
р, то
окружность О' обращается в прямую линию.
401. Для достижения полной общности решения будем рассматри-
рассматривать как положительные, так и отрицательные значения h и обозначим
через Ah, Bh и Ch три. окружности с центрами А, В и С и радиусами
|ai-/z|, \b-\-h\ и |/-|-Л| (черт. 660). В соответствии с этим дан-
данные окружности обозначим через Ао, Во и Со.
/
/
/
А
Черт. 660.
Пусть D — середина отрезка АВ и' К—проекция точки Я на пря-
прямую АВ. Так как прямая НК есть радикальная ось окружностей
Ah и Bh, то мы имеем (согласно п. 136) DK=
Применим эту формулу к случаю, когда Л=0; при этом точка Н
будет совпадать с радикальным центром Но данных окружностей, а
точка К—с его проекцией Кь на прямую АВ, и мы найдём DKD =
2АВ
. Из двух последних равенств имеем:
A)
568
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Обозначая через I и i, проекции точек Н и Не на прямую АС,
найдём совершенно таким же путем, что L0L= ———, откуда
а—.Ь АС
LJL
а — с ' АВ'
Итак, точки Н можно получить следующим построением (черт. 661):
на прямых АВ и АС откладываем от точек Ко и Lo отрезки К0К и L0L,
которые изменяются пропорционально друг другу, и через точки К и
L проводим прямые, перпендикулярные соответственно к АВ и АС.
В силу упражнения 124 геометрическое место точек Н есть пря-
прямая линия.
Рассмотрим теперь наряду с точкой И, соответствующей произ-
произвольному значению Л, точку Н', соответствующую некоторому фикси-
рованному значению ff (черт. 661) величины Л, и обозначим через 1С
проекцию точки Н' на прямую- АВ'. Мы будем иметь наряду с соот-
соотношением A) аналогичное соотношение
'ч°'4 — АВ
Из соотношений A) и (Г) следует:
H^1:H<>H'^KuK:K0K'=h:h'.
B)
Пусть теперь точки N и N' (черт. 662) делят отрезки АН и АН'
соответственно в отношениях AN: АН= a: (a -J- Л) и AN':AH'=:
= а:(а-\- Л'). При этом
AN:NH = a:h, C)
и
AN':N'H' = a:h'. C')
Из соотношений B), C) и C') вытекает, что ггтт, • -т„ . • ryvj = 1
Таким образом, точки //0, N и /V' лежат на одной прямой, как это
следует из применения теоремы Менелая (п, 193) к этим трём точ-
точкам и к треугольнику АНН'.
СМЕШАННЫЕ ЭАЧАЧИ *569
Другими словами, геометрическим местом точек N при перемен-
переменном h является прямая линия, а именно прямая HQN' (где точка N'
соответствует некоторому определённому значению Л).
Выберем теперь h равным радиусу г окружности S, касающейся
внешним образом трёх данных окружностей 40) BQ и Се (черт. 660).
При этом окружности ,4Г, Вг и Сг пройдут, очевидно, через
центр О окружности ^!, и точка О будет радикальным центром зтих
трёх окружностей. Отсюда следует, что прямая линия, которая слу-
служит геометрическим местом точек Н, проходит через О. Итак, пря-
прямая линия, являющаяся геометрическим местом точек Н, прохо-
проходит через центр окружности, касающейся внешним образом тр х
данных окружностей. Соответствующая значению п=±г точка N
делит линию центров АО окружностей Ао и ^ в отношении
AN:АО^а:(а-\-г) и потому совпадает с их точкой касания. Итак,
прямая линия, являющаяся геометрическим местом точек N, про-
проходит через точку касания окружности Ао с окружностью, ка-
касающейся внешним образом трёх данных окружностей.
Таким же образом покажем, что те же прямые линии проходят
соответственно через центр О' окружности 1', касающейся внутрен-
внутренним образом трёх данных окружностей, и через, точк^ касания окруж-
окружностей 2' и Ло.
В случае окружностей, имеющих с данными окружностями разно-
разноимённые касания, например в случае окружностей, касающихся внеш-
внешним образом окружности Ио и внутренним образом окружностей Во
и Св, или наоборот, можно получить вполне аналогичный результат.
Вместо окружностей радиусов \a-\-h\, \b-\-h\, \c-\-h\ надо только
рассматривать окружности радиусов \а — h\, \b-\-h\, \c-\-h\.
Примечание. Доказанные теоремы дают новое построение окруж-
окружностей S и ?', касательных к трём данным (ср. ни. 231—236 и 309—312а).
Строим радикальный центр //0 данных окружностей и радикалышй центр
Н окружностей Ah, Дй и Q, (при произвольном h). Далее строим точку N,
как указано в тексте. Точки пересечения прямой H^N с окружностью ,40
определяют точки касания искомых окружностей с Аи. Соединяя =>ти точки
касания с центром А окружности Ао, получим в пересечении с прямой
tiH центры искомых окружностей.
\
402. Пусть С,, Сз, Са и С4 — данные окружности, з—искомая
окружность, пересекающая их под равными углами.
В пп. S09—310 было показано, что все окружности, пересекаю-
пересекающие три данные окружности Сх, Со и Са под равными углами, обра-
образуют четыре различных семейства: каждой из четырёх осей подобия
данных окружностей соответствует одно из этих четырёх семейств в
том смысле, что все окружности семейства имеют общей радикальной
осью эту ось подобия, а линией центров — перпендикуляр из радикачь-
ного центра данных окружностей на эту ось подобия. Точки пересе-
пересечения какой-либо из окружностей одного из этих семейств с двумя
из данных окружностей, скажем с Сг и С2, попарно ангигомологичны
570 * РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
относительно того из центров подобия окружностей С, и С„, который
лежит на рассматриваемой оси подобия.
Отсюда следует, что центр искомой окружности з лежит на пер-
перпендикуляре, опущенном из радикального центра /4 окружностей С,,
С2 и С3 на одну из их осей подобия s4, и в то же время на перпен-
перпендикуляре, опущенном из радикального центра /3 окружностей С,, С2
и С, на одну из их осей подобия ss. При этом, если точки пересече-
пересечения окружности а с окружностями С, и С9 попарно антигомологичны
относительно их центра подобия S12, то точка Sin лежит как на пря-
прямой sv так и на прямой s4.
Таким образом, получается следующее построение центров иско-
искомых окружностей: выбираем произвольно одну из четырёх осей по-
подобия 54 окружностей С,, С2 и С3 и одну из тех двух осей подобия
s3 окружностей С,, С2 и С4, которые проходят через центр подобия
¦S12 окружностей Сх и С2, лежащий на оси s4. На прямые s4 и s3
опускаем перпендикуляры соответственно из точек /4 и /3; точка пе-
пересечения этих двух перпендикуляров и будет искомой точкой.
Каждой из четырёх осей подобия окружностей С,, С2 и С3 соот-
соответствует два возможных положения центра искомой окружности, а
г.сего получаем 8 искомых точек. i
Рассмотрим одну из этих восьми точек — точку О — и построим
окружность а с центром О. Для этого построим какую-либо окруж-
окружность з4, пересекающую под равными углами окружности Сх, С„ и С3
и соответствующую выбранной оси подобия s4. Окружности з и з4
должны иметь своей радикальной осью прямую s4. Остаётся построить
окружность а с центром О так, чтобы прямая si была радикальной
осью окружностей j и j4 (прямая, соединяющая точку О с центром
окружности а4, заведомо перпендикулярна к s4). Для этого строим
произвольную окружность с с центром на s4, ортогональную к о4, а
затем окружность а с центром О, ортогональную к с. Задача будет
или не будет иметь решение в зависимости от того, будет ли точка
О лежать вне или внутри окружности с.
Построенная таким образом окружность с будет, по самому способу
её определения, пересекать под равными углами окружности Сь С2 и Cs.
Однако мы должны ещё показать, что она пересекает пол равными углами
все четыре данные окружности. С этой целью рассмотрим какую-либо
окружность с3, пересекающую окружности Съ С2 и С4 под равными углами
и' соответствующую оси подобия s3. Линия центров окружностей о и з3
есть перпендикуляр из точки /3 на прямую ss. Точка nepi сеч ния S12ocefi
подобия ss и s4 име т относительно обеих окружностей s и с3 одну и ту
же степень, равную степени той инверсии с полюсом S12, которая преоб-
преобразует окружности С, и С2 одну в другую; это следует из того, что каж-
каждая из окружностей с и с3 пересекает С1 и С2 в точках, попарно антиги-
мологичных относительно Si2- Из того факта, что линия центров окружностей
о и с3 перпендикулярна к 53 и что точка S12 прямойs3 имеет относительно
обеих окружностей одну и ту же степень, следует, что ss есть радикаль-
радикальная ось этих двух окружностей. Следовательно, окружность о пересекает
окружности С], С2 и 64, а значит и все четыре данные окружности, под
равными углами.
СМЕШАННЫЕ ЗАДАЧИ
571
В
Наибольшее возможное число решений задачи равно восьми.
403. Чтобы не прерывать дальнейшего изложения, решим предва-
предварительно следующие две задачи:
А) Построить окружность, пересекающую две данные окруж-
окружности А и В соответственно под данными углами а и $ и притом
первую из них, т. е. окружность А, в данной точке М.
Пусть О, и О2 — центры данных окружностей А и В, О — центр
искомой окружности, N—одна из точек пересечения искомой окруж-
окружности с окружностью В (черт. 663).
Рассмотрим треугольник ОМК, равный треугольнику ONO2 и
имеющий с ним (для определённости) одинаковое направление враще-
вращения. Прямая ОМ образует с
радиусом ОХМ угол а, пря-
прямая МК образует с ОМ
угол р, и отрезок МК pa- Y'__^ "'
вен NO%. Наконец, точка О
равноудалена от точек К и
О2, и мы приходим к такому
построению.
Строим прямую MX, об-
образующую с ОгМ угол а;
далее строим прямую MY,
образующую с MX угол р,
¦откладываем на ней отре-
отрезок МК, равный радиусу
окружности В, и восставляем
Перпендикуляр в середине
отрезка КО2. Точка пересечения этого перпендикуляра с прямой MX
и будет искомой точкой О.
Задача имеет, вообще говоря, четыре решения. В самом деле, за
прямую MX можно принять любую из двух прямых, пересекающих
О,Л4 под углом а, и отрезок МК можно отложить от точки М на
прямой MY в двух противоположных направлениях.
Замена прямой MY другой прямой MY', образующей с MX угол р, не
приводит к новым решениям. Действительно, точка К заменяется при
этом точкой fC, симметричной с f( относительно прямой ОМ. Но 002 =
= O/Sf=OA", и перпендикуляр, восставленный в середине отрезка О»/С,
пересекает прямую MX в той же точке О, что и перпендикуляр, восстав-
восставленный в середине отрезка О2^-
Если, как это сделано в решении упражнения 256, принимать во
внимание угол между радиусами двух окружностей, проведёнными в
точку их пересечения, то искомые окружности распределятся в два
семейства. К первому будут относиться окружности, пересекающие
¦окружности А и В под углами, строго равными аир или 2d— а и
Id—Р; ко второму — пересекающие их под углами, строго равными
Id—а и р или а и 2d—р.
\
Черт. 663.
572 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если построить полупрямую MX так, чтобы угол О}МХ в точ-
точности равнялся а, и отложить отрезок МК так. чтобы угол ХМК в
точности равнялся fj, то мы получим окружность первого семейства.
Действительно, если точка О будет лежать на полупрямой MX, то
построенная окружность будет, очевидно, пересекать данные под уг-
углами, строго равными аир. Если же точка О будет лежать на про-
продолжении полупрямой MX за точку М, то построенная окружноегь
будет пересекать данные под углами 2d— а и 2d— р.
B) Построить окружность, имеющую с двумя данными окруж-
окружностями А и В общую радикальную ось и ортогональную к третьей
данной окружности Г.
Пользуясь п. 138, легко построить какие-либо две окружности Г'
и Г", ортогональные одновременно к Л и к В. В силу п. 139, приме-
примечание, каждая из окружностей Г' и Г" должна быть ортогональна и
к искомой окружности. Поэтому искомую окружность (если она су-
существует) можно построить, с помощью п. 139, как окружность, ор-
ортогональную к окружностям Г, Г' и Г"; центром искомой окружности
будет радикальный центр этих трёх окружностей, её ради) сом — ка-
касательная из радикального центра к одной из тех же трёх окружно-
окружностей.
Переходим теперь к решению самой поставленной задачи.
C) П>сть требуется построить окружность, пересекающую три
данные окружности А, В и С под углами, соответственно равными
a, fi и Y-
Если опять принимать во внимание угол между радиусами двух
окружностей, проведёнными в точку их пересечения, то искомые
окружности будет естественно распределить в 4 семейства в зависимости
от того, пересекает ли искомая окружность три данные под углами,
строго равными:
t) a, ?, Y или 2d — a. 2fi?—p, 2d-y;
2) 2d—a, [5,у или а, 2d—\, 2d~\\
3) a, 2d—$, у или 2d~ а, fi, 2d — у;
4) a, fi, 2d— Y или 2d — a, 2d—$, Y-
Для определённости начнём с отыскания окружностей, принадле-
принадлежащих к первому из этих семейств, и даже предположим, что искомая
окружность с пересекает данные под углами, строго равными а,
Р и г
Построим, как было указано выше (задача А), какую-либо окруж-
окружность а, (черт. 664), пересекающую -окружности Л и В под углами,
строго равными аир (или же какую-либо окружность о,', пересекаю-
пересекающую их под углами, строго равными 2d — аи 2d—р). При этом
исходная окружность з и окружность з, (или з/) будут принадлежать
к одному и тому же семейству (в смысле упр. 256) окружностей, пе-
пересекающих А и В под углами аир. Следовательно, любая окруж-
окружность, имеющая с Л и В общую радикальную ось, пересекает окруж-
окружности j и Cj, на основании решения упражнения 256, под строго
равными (а окружности з и з/ — под строго пополнительными) углами.
СМЕШАННЫЕ ЗАДАЧИ 573
Найдём далее среди окружностей, имеющих с Л и В общую ра-
радикальную ось, две окружности А' и В', касающиеся окружности з,
(или з,'), пользуясь способом, указанным в п. 311. Мы предположим
пока, что такие окружности существуют. Эти две окружности А' и В"
будут касаться в силу только что сказанного и искомой окружности о
(так как касание есть пересечение под углом 0 или 2d). При атом
окружность А' будет касаться окружностей з из, одинаковым образом
(а окружностей а и о,' — неодинаковым образом), так как она должна
пересекать их пол строго равными (под строго пополнительными) уг-
углами. То же относится и к окружности В'.
Итак, искомая окружность а должна касаться, и притом вполне
определённый образом (либо внутренним, либо внешним), каждой
из окружностей А' и В1 и
пересекать окружность С под S N. g
углом, строго равным у-
Построим теперь какую-
либо окружность оа, пересекаю-
пересекающую окружность С под углом,
строго равным у, касающуюся
окружности А' таким же обра-
образом, как её касается окруж-
окружность з (или же какую-либо
окружность о2', пересекающую
окружность С под углом, стро-
строго равным 2d—у> и имеющую
с окружностью А' касание про- Ч
тивоположного характера, чем еРт'
касание окружности а с А'). В силу упражнения 256 любая окруж-
окружность, имеющая с окружностями 'А' и С общую радикальную ось,
пересекает окружности а и о? под строго равными углами (а окруж-
окружности аи з2' — под строго пополнительными углами).
Так как среди окружностей, имеющих с А' и С общую радикаль-
радикальную ось, есть окружность (а именно Л'), касающаяся окружности з2
(или а2'), то среди тех же окружностей найдётся (п. 311), вообще
говоря, и вторая окружность С", касающаяся окружности а2 (или з„').
При этом окружности з и з2 касаются окружности С одинаковым
образом (а окружности з и о2' касаются её различным образом).
Следовательно, искомая окружность а должна касаться трёх
окружностей А', В' и С, которые мы. можем построить, и притом
каждой и? них вполне определённым (либо внешним, либо внут-
внутренним) образом.
Мы отыскивали окружность з, пересекающую данные окружности
под углами, строго равными а, р и {. Легко видеть, повторяя анало-
аналогичные рассуждения, что окружность о', пересекающая три данные
окружности под углами, строго равными Id—a. Id—$ и Id—Yi
должна касаться тех же окружностей А', В' и С", что и окружность з.
Однако с каждой из трёх окружностей А', В' и С" две окружности а
574 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
И
а' имеют разноимённые касания. Это вытекает из того, что при по-
строении окружности а' можно воспользоваться той же самой вспомо-
вспомогательной окружностью Jj или а/, что и выше, и той же самой
Вспомогательной окружностью а3 или а2', что и выше. Однако окружности
ох и а/, а также а2 и а2' меняются теперь ролями.
Можно показать и обратно, что всякая окружность, касающаяся
окружностей А', В' и С указанным образом (в смысле внешнего или
внутреннего касания), пересекает данные окружности под углами, строго
равными а, р и у или 2d—a, Id— JS и 2d— у-
В самом деле, пусть некоторая окружность и касается каждой из ок-
окружностей А' и В' таким же образом, каким той же самой окружности
касается окружность яъ а окружности С — таким же образом, каким её
касается окружность с2.
Окружности а и oj касаются окружности А' одинаковым образом, т. е.
пересекают её под строго равными углами (равными 0 или 2d). Те же
окружности а и oj пересекают под строго равными углами и окружность В'.
Следовательно, любая окружность, имеющая с А' н В' общую радикальную
ось, и в частности окружность А, пересекает и и зг под строго равными
углами. Но окружность ^ пересекает, по построению, окружность А под
углом, строго равным а. Следовательно, и окружность а пересекает А
под углом, строго равным а. По той же причине и пересекает В под углом,
строго равным р.
Далее окружности а и о2 касаются окружности А' одинаковым образом,
так как окружности а и о, касаются А' одинаковым образом (по определе-
определению окружности о); кроме того, окружности oj и о2 также касаются окруж-
окружности А' одинаковым образом (по определению окружности о2). Те же
окружности а и о2 касаются (по определению окружности о) одинаковым об-
образом окружности С Следовательно, всякая окружность, имеющая с
окружностями А' и С общую радикальную ось, и в частности окружность С,
пересекает окружности а и о2 под строго равными углами. Но окружность
о2 пересекает, по построению, окружность С под углом, строго равным ^.
Следовательно, и окружность я пересекает С под углом, строго равным 7.
Совершенно таким же образом покажем, что всякая окружность о',
которая касается каждой из окружностей А' и В' иначе, чем её касается
окружность Qh а окружности С —иначе, чем её касается о2, пересекает
окружности А, В и С под углами, строго равными 2d — a, 2rf — р и 'Ы — f.
К тем же заключениям мы пришли бы, если в качестве вспомогатель-
вспомогательной окружности взяли oj' вместо oj, или о2' вместо о2, или, наконец, <з{ и о2'
вместо oj и с2.
Итак, искомые окружности, принадлежащие к первому из четырёх
семейств, перечисленных в начале решенил настоящей задачи, т. е.
пересекающие данные окружности под углами, строго равными а,
[S, у или 2d — a, 2d—р, Id—у. касаются трёх окружностей А',
В' и С. При этом они образуют одну из четырёх пар окружностей,
касающихся А', В' и С, в смысле решения упражнения 267. Дейст-"
вительно, из сказанного выше следует, что если одна из искомых
окружностей первого семейства касается двух из трёх окружностей,
скажем А' и В', одинаковым образом, то и всякая окружность первого
семейства касается их одинаковым образом.
Мы предположили выше, что среди окружностей, имеющих с А
и В общую радикальную ось, найдутся две окружности А' и В', каса-
СМЕШАННЫЕ ЗАДАЧИ
575
ющиеся вспомогательной окружности аг (или з;'). Это всегда будет
иметь место, если окружности А и В не имеют общих точек. Дейст-
Действительно, отыскивая окружности А' и В', как указано в п. 311, мы
получим в этом случае два решения, потому что радикальный центр а
окружностей А, В и з1 (или А, Вив/), которым мы там пользовались,
будет лежать вне каждой из этих трёх окружностей. Однако окруж-
окружности А' и В' могут существовать и в том случае, когда окружности
А и В пересекаются (сра'внить черт. 664).
В том случае, когда среди окружностей, имеющих с Аи В общую
радикальную ось, не существует окружностей, касающихся искомой
окружности, и то же обстоятельство имеет место для каждой из пар
окружностей В и С, А и С, описанный способ оказывается непримени-
неприменимым. Это может случиться лишь в том случае, когда все три данные
окружности имеют попарно общие точки. Примером может служить
расположение данных и искомой окруж- .
ностей, приведенное на чертеже 665.
Чтобы дать решение поставленной за-
задачи, пригодное и в этом случае, поступим
следующим образом. Построив вспомога-
вспомогательную окружность з, (или 3]'), как ука-
указано выше, найдём среди окружностей,
имеющих с А и В общую радикальную ось,
окружность В{1, ортогональную к з, (илиз/).
Способ построения был указан выше (зада-
(задача В). Искомая окружность о (или з') долж-
должна быть также ортогональна к Во, так как
окружности з и 3j (или о и з,') пересе-
пересекают Во под равными углами. Аналогичным образом, построив далее
новую вспомогательную окружность з2, пересекающую Л и С под угла-
углами, соответственно равными 2 и у, можно найти окружность Сс, имею-
имеющую с .4 и С общую радикальную ось и ортогональную к окружности и2.
Окружность Сс будет ортогональна и к искомой окружности з.
Итак, искомая окружность о (или з') должна пересекать окруж-
окружность А под углом, строго равным а (или 2й— а), и быть ортогональ-
ортогональной к окружностям Во и Сс. Можно показать и обратно, что всякая
окружность, удовлетворяющая этим последним условиям, будет удов-
удовлетворять и условиям первоначальной задачи. Таким образом мы при-
приходим к упражнению 259.
Заметим, что этот второй путь решения будет заведомо пригоден
в тех случаях, когда первый способ может оказаться неприменимым,
т. е. когда три данные окружности попарно пересекаются. В самом
деле, через всякие две точки, например через точки пересечения
окружностей А и В, можно провести окружность, ортогональную к дан-
данной окружности з, (сравнить решение упр. 258, примечание).
Однако этот второй путь может оказаться непригодным в тех слу-
случаях, когда первый способ заведомо применим. В самом деле, если две
окружности (скажем А и В) не пересекаются, то среди окружностей,
576
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
имеющих с ними общую радикальную ось, может не существовать
окружности, ортогональной к данной окружности (скажем к а,).
До сих пор мы искали окружности, принадлежащие к первому из
четырёх семейств, о которых говорилось в начале решения. Таким же
путём можно найти окружности, принадлежащие к каждому из осталь-
остальных трёх семейств. Надо топько заменить один из углов a, fi и у углом,
ему пополнительным. Существенно, что при этом каждый раз придётся
пользоваться некоторыми вспомогательными окружностями, аналогич-
аналогичными А', В' и С" или Во и Сс., но, вообще говоря, отличными от
последних.
Каждое из четырёх семейств окружностей содержит самое большее
две искомые окружности, и потому наибольшее возможное число реше-
решений задачи — восемь.
403а. Отложим на касательной в произвольной точке а данной
окружности А с центром в точке О некоторый отрезок асС (черт. 666)
В'
¦ Черт. 666.
и проведём через точку а' окружность .4', концентрическую с .4. Оче-
Очевидно, что все окружности 2, имеющие с окружностью А общую ка-
касательную длиной аа', пересекают окружность А' под углом, равным
углу аОа'. При этом, если аа' является внешней общей касательной,
то окружность 2 пересекает А' под углом, строго равным углу аОа',
а если аа' является внутренней общей касательной, то 2 и А' пере-
пересекаются под углом, строго равным 2d—, аОа'.
Итак, если отрезок общей касательной к данной окружности А
и к искомой окружности 2 имеет данную длину аа', то искомая
окружность должна пересекать определённую окружность А', концен-
концентрическую с А, под углом, равным углу между окружностью А' и
произвольной касательной к окружности .4. Точно так же определяем
углы между искомой окружностью и вполне определёнными окруж'но-
стями В' и С, концентрическими соответственно с окружностями В и С.
Таким путём рассматриваемая задача непосредственно сводится
к задаче 403.
404. Через точки .4 и А' проводим хорды АВ и А'В' (черт. 667),
параллельные прямой D, и обозначим через / и /' точки пересечения
прямых АВ' и А'В с прямой D.
СМЕШАННЫЕ ЗАДАЧИ
577
Углы AIP и А'/'Р' равны, так как они равны соответственно углам
ABA' и ВА'В' равнобедренной трапеции ABA'В'. Далее ^/_1АР =
= ^/_В'А'М = ^_А'Р'Г. Следовательно, треуготьники AIP и РТА'
подобны. Из подобия этих треугольников имеем 1Р:1А = ГА':ГР'
или IP-ГР'=1А-ГA' — const.
405. Обозначения те же, что в задаче 404 (черт. 667). Пусть
прямая D не пересекает данной окружности. Обозначим через U
одну из предельных точек данной окружности и прямой D (упр. 152).
Будем иметь, как в решении упражнения 152:JU2 = I'U2 = JA-IB',
или, в силу задачи 404, 1U2 = I'U2= IP-I'P'. Последние равенства
вместе с равенством углов UIP и UI'P' показывают, что треуголь-
треугольники UIP и P'1'U подобны. Из подобия этих треугольников следует,
что /_1UP = /_I>P'U, откуда /_PUP' = 2d — /_IPU — /_I'P'U =
— 2d — /_ /PU — Z.IUP = Z. UIP = const-
Черт. 668.
Тем же свойством обладает и вторая предельная точка панной
окружности и прямой D.
406. 1°. Инверсия относительно окружности 2 преобразует окруж-
окружности С в самих себя, а окружность S — в некоторую окружность S'
(черт. 668), также касающуюся всех окружностей С. ,
2°. Предположим сначала, что за точку А, о которой говорится
в тексте задачи, принята одна из точек пересечения прямой Ою и
окружности 2 (черт. 668). При этом прямые, проведённые через точку А
параллельно биссектрисам углов Оа>М и 0<лМ, пройдут соответственно
37 Элементарная геометрия
578 ' РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
через точки М и М', так как /_ ОАМ= — /_ОтМ и / ОАМ =
Выполним теперь инверсию с полюсом А, преобразующую окруж-
окружность 2 в данную прямую D. Эта инверсия преобразует точки Л1
и М в точки Р и Р', а окружность С, ортогональную к 2,— в
окружность с, имеющую отрезок РЯ' своим диаметром. Обозначим через
s окружность, обратную окружности S. Так как окружность С касается
окружности S, то окружность с касается s в некоторой точке Т. Точ-
Точка Т есть центр подобия окружностей с и s, и потому прямые РТ
и Р'Т пересекают вторично окружность 5 в концах диаметра QQ',
параллельного прямой D. Точки Q и Q', не зависящие, очевидно, от
положения окружности С, обладают тем свойством, что прямые PQ
и P'Q' взаимно перпендикулярны.
Итак, мы доказали существование точек Q и Q', обладающих ис-
искомым свойством, для того случая, когда данная точка А совпадает
с одной из точек пересечения прямой Ош и окружности 2 (а прямая D,
перпендикулярная к Ош, задана произвольно). Если теперь выполнить
над этой точкой .4, данной прямой D и найденными точками Q и Q'
одно и то же поступательное перемещение в направлении прямой О<л,
то свойство точек Q и Q' сохранится: прямые PQ и P'Q' и в новом
своём положении останутся взаимно перпендикулярными.
Отсюда и вытекает существование точек Q и Q', обладающих ис-
искомым свойством, для всякой точки прямой Оа>. Чтобы их найти, можно
поступить так. Выполним над данной точкой и над данной прямой по-
поступательное' перемещение, которое совместило бы данную точку с той
точкой, которая обозначена через л на чертеже 668. После этого
построим точки Q и Q', как указано выше, а затем выполним над ними
обратное поступательное перемещение.
3°. Точки Р и Р' получаются из точек Q и Q' с помощью по-
построения, указанного в тексте задачи 404. Действительно, точки Р и
и Р' являются точками пересечения прямой D с прямыми, соединяю-
соединяющими две данные точки Q и Q' окружности ¦? с произвольной точкой
Т окружности. j
Так как окружности S и 2 по условию задачи не пересекаются,
то окружность 5 не пересекает прямой D. Следовательно, отрезок РР'
виден (в силу задачи 405) под постоянным углом из каждой из пре-
предельных точек окружности 5 и прямой D.
4°. Пусть окружность Ся+1 совпадает с С,. Так как окружности S
и 2 не пересекаются, то их можно преобразовать с помощью одной
инверсии (упр. 248) в две концентрические окружности б1 и 2
(черт. 669). При этом окружность 6", обратная окружности S относи-
относительно 2, преобразуется в окружность 6", также обратную (в силу
упр. 250) окружности 5 относительно 2 и потому концентрическую
с б1 и 2. Окружности С,, С2, ... , С„ преобразуются в равные
СМЕШАННЫЕ ЗАДАЧИ
579
окружности С,, С2,...,Сп, касающиеся окружностей S и S' и по-
попарно касающиеся друг друга.
Обозначим через О общий центр окружностей S, 2 и S', через
М и М — точки пересечения окружности С1 с окружностью 2 и
через т — центр окружности Сг При этом произведение угла MOM
на п. будет равно (в силу совпадения окружности Сп , с С,) целому
числу окружностей. Отсюда следует, что центральный угол MOM соот-
соответствует стороне ММ одного из тех правильных многоугольников,
о которых говорится в тексте
задачи. Угол МОт есть поло-
половина этого центрального угла.
Черт. 669.
Черт. 670.
Если R — радиус окружности S, р — радиус окружности 2, то ра-
радиус окружности S', обратной S относительно 2, равен р2:/?, и
1 / — о2\ 1 / —
От = -7j( R-\- = ). Треугольник О Mm с гипотенузой От = —1/?-|-
-\-^= j и катетом ОМ=р подобен треугольнику с гипотенузой
/?2 Ц-р2 и катетом 2Rp.
Так как в силу задачи 396 имеет место равенство —^^- =
2А-р
то тот же самый острый угол МОт будет иметь и
_i_
прямоугольный треугольник с гипотенузой ±(d* — /?2—р2) и катетом
2#
р
Таким образом, мы получили то условие совпадения окружности Сп+1
с окружностью Cv которое указано в тексте задачи.
До сих пор мы рассматривали случай, когда окружности S и 2
не пересекаются Пусть теперь эти окружности пересекаются в точках
X и Y (черт. 670) Окружность S', которой касаются окружности С,
также пройдёт через точки .Л' и Y. Построим опять окружности Cv Cv .. ,
как указано в условии 4°.
37*
580
РЕШЕНИЯ УПРАЖНЕНИИ И ЗАДАЧ
Выполним инверсию с полюсом в точке Y и произвольной степенью.
Окружности 5, 2 и S' преобразуются при этом в три прямые S, - и
S' (черт. 671), пересекающиеся в точке X, обратной точке X, а
окружности С,, С2,. . . —в окружности С\, С2,... с центрами на пря-
прямой 2, касающиеся прямых 5 и S' и попарно касающиеся друг друга
в точках М', М",.. . , обратных точкам М', М",. .. ¦
Рассматривая гомотетию с центром X, в которой точке М соот-
соответствует точка М, мы убедимся, что имеют место равенства
ХМ:ХЛГ==ХМ:ХЛГ==ХМ':ХМ"' = ... Отсюда видно, что точки
/W, М, М",... имеют своим предельным положением точку X, а точки
М, М, М",... — точку X.
407. Пусть ABCD — четырёхугольник, вписанный в окружность О
(черт. 672), Е — точка пересечения его диагоналей, F—точка пере-
Черт. 671.
Черт. 672.
сечения прямых AD и ВС, KL — хорда, проходящая через Е и перпен-
перпендикулярная к ОЕ (так что EK=EL), M и N — точки пересечения
этой хорды со сторонами AD и ВС.
Применяя к треугольнику FMN и каждой из секущих ЛЕС и BED
mo к х ЕМ CN AF . ЕМ RN DF . п
теорему п. 192, найдём _._._=1; шг ^,._л=1. Пере-
EN CF АМ
множая почленно эти два равенства и сокращая на произведение
AF • DF^=BF-CF, равное степени точки F относительно окружности О,
получим.
?Ж2 BN-CN
EN2 AM-DM
= 1.
A)
Преобразуем теперь произведение BN-CN, равное степени точки N
.относительно окружности О, пользуясь равенством EK = EL, следую-
СМЕШАННЫЕ ЗАДАЧИ
581
щим образом:
Таким же путём найдём:
AM • DM = ЕК2 — ME2.
B)
C)
С помощью равенств B) и C) соотношение A) можно привести
к виду
ду
= _ FN2 или, составляя производную пропорцию, к ви-
^ = ЕК2'-ЕК2=\. Отсюда и следует, что EM = EN.
408. Применим к треугольнику PQU, где U—точка пересечения
прямых PR и QS, и секущим АВ и CD (черт. 362) теорему п. 192;
АР B'Q A'U . СР D'Q CU . „
— '• = 1. Перемножая по-
получим -0-ЁГ
\'Р ' СО D'U
членно эти два равенства и при-
принимая во внимание, что A'U-C'U =
= B'U ¦ D'U, получим:
PA PC QAQC
PA' PC QB'-QD'- t1'
Точно так же, применяя тео-
теорему п. 192 к треугольнику RSU
и секущим АВ и CD, получим:
RBRD SB-SD
RA'RC~~SB'-SD- ¦
СР
B)
Черт. 673.
Наконец, из подобия треуголь-
треугольников РАА' и SDD' (см. ре-
решение задачи 107а), а также тре-
треугольников РССиSBB' имеем РА:РА'= SD;SD'\ PC:PC^
Перемножая эти два равенства, получим:
PA-PC SB,- SD .„v
PA' PC SB'-SD1' { '
Равенства A), B) и (З) показывают, что отношения степеней каж-
каждой из точек Р, Q, R и S относительно окружностей ABCD и A'B'C'D'
имеют одно и то же значение. В силу упражнения 149 точки Р, Q,
R и S лежат на одной окружности, имеющей с двумя данными окруж-
окружностями общую радикальную ось.
Примечание. Рассматривая предельный случай, когда данные пря-
прямые, пересекающие обе окружности, сливаются в одну (черт. 673), можно
аналогично, но более просто доказать следующую теорему:
Даны две окружности С и С и пересекающая их прямая: точки пе-
пересечения касательных к окружности С в точках её пересечения с оан-
ной прямой с касательными к окружности С в точках её пересечения
с той же прямой лежат на одной окружности, имеющей с окружностями
С и С общую радикальную ось.
Действительно, обозначим через V точку пересечения прямых PS и QR
(черт. 673^ Применяя к треугольнику PQV и секущей АА' теорему п. 192,
582
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
АР A'Q B'V
АР* A'Q1 ff'V*
= \. Ho
A'V B'P — AQ*~ ' A'V* ' B'P*-
^ prjTi • Итак, отношение степеней каждой из точек Р
будем иметь: ^- • ^г^ • ^-^ = 1 или
= В' V\ и потому
и О относительно окружностей С и С имеет одно и то же значение. Анало-
Аналогично покажем, что то же имеет место и для любых двух из точек Р, Q, R и Л'.
В силу упражнения 149 точки Р, Q, R к S лежат "на одной окружности,
имеющей с данными общую радикальную ось.
409. Обозначим через О общий центр окружностей С и S, через г
и R — их радиусы, через О, и г, — центр и радиус окружности С\
(черт. 674). Пусть ш — центр одной из окружностей 2, ортогональных
к С и обладающих тем свойством, что радикальная ось D окружно-
окружностей 2 и С, касается 6".
Черт. 674.
В силу п. 136 (примечание 3°) разность степеней точки О отно-
относительно окружностей 2 и С, (равных соответственно г2 и 00* — г,2)
равняется удвоенному произведению расстояния между центрами ыО1
этих окружностей на расстояние R точки О от радикальной оси D, т. е.
г2 — (ООг* — г,2) = 2R ¦ 0.0,
или
2^.(o01=r2+r12—OO,2. A)
Отсюда видно, что расстояние шО, есть величина постоянная. Обратно,
если центр ш окружности, ортогональной к С, выбрать так, чтобы
удовлетворялось соотношение A), то расстояние от точки О до ради-
радикальной оси D будет равно R. Следовательно, геометрическое место
точек ш есть окружность S^ с центром в точке Ох.
Вторая половина доказываемого предложения вытекает из того, что
соотношение A) симметрично как относительно г и rt, так и относи-
относительно R и О,ш.
410. Пусть каждая точка М окружности С с центром О слу-
служит центром окружности радиуса k-MA, где k — данный коэфициент
(черт. 675). В силу симметрии фигуры относительно прямой ОА
искомая точка Р должна лежать на этой прямой. На основании реше-
Смешанные задачи
583
ния упражнения 218 имеем для любой точки Р прямой О А равенство
РА ОР
МР2 — МО2-—я-Л-МА2-—~ — ОР-РА. Степень точки Р относи-
ОА ' пл
тельно окружности
равна
ОА
с центром М и радиусом k-MA будет при этом
РА, ...„(ОР ... ор.рЛЭта
— kA—
степень не будет зависеть от положения точки М на окружно-
окружности С, если в правую часть не будет входить МА, т. е. если выбрать
точку Р так, чтобы удовлетворялось условие OP = k2-OA.
При этом расстояние точки Р от радикальной оси обеих окруж-
окружностей определится (на основании п. 136, примечание 3°) как частное
от деления разности степе-
степеней точки Р относительно
обеих окружностей на удво-
удвоенное расстояние между их
центрами. Отсюда непесред-
ственно следует, что и это
расстояние точки Р от ради-
радикальной оси не зависит от
положения точки М на
окружности С.
Приведённые рассужде-
рассуждения сохраняют полностью
свою силу (видоизменяются
несколько лишь приводимые
выше формулы), если вме-
вместо k-MA радиус окружно-
окружности с центром М взять равным •
ky МАг — а2, где Л и а — центр и радиус второй данной окружно-
окружности. В частности при этом сохраняется соотношение OP = k2-OA.
411. Пусть О и О' —центры данных окружностей (черт. 676), г и
/ — их радиусы. Далее пусть касательные из точки L окружности С
к окружности С пересекают второй раз окружность С в точках М
и N. Прямая LO' пересекает вторично окружность С в некоторой
точке Р, равноудалённой от точек Ж и N в силу равенства углов
MLP и NLP. Опустим из О перпендикуляр OQ на прямую NP. Если
п -^ точка касания прямой LM с окружностью С, то треугольники
POQ и O'Ln подобны, так как Z.MLP- — /_PON= /_POQ. Из
N
Черт. 676.
подобия этих треугольников имеем
Отсюда
— NP:r = r':LO'\ NP =
2rr'
Id7
NP
PO'
2rr'
' LO'-PO'
2rr'
r2 — 00'
¦ = k,
(i)
584
РППЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
так как LO'-PO' есть (по абсолютной величине) степень-точки О'
относительно окружности С.
Окружность а с центром Р и радиусом PM^PN удовлетворяет
условию задачи 410 (так как k = PN-.PO' не зависит от выбора точ-
точки L); следовательно, радикальная ось окружностей С и о, т. е. пря-
прямая MN касается (при любом положении точки L) определённой
окружности С" с центром О" на прямой 00'.
Рассмотрим теперь две произвольные точки L и L' окружности С
(внешние по отношению к окружности С*) и построим соответствующие
L'
N
• Черт. 677.
треугольники LMN и L'M'N' (черт. 677). Пусть т, п, т' и п' —
точки касания прямых LN, LM, L'1\' и L'М с окружностью С.
Пусть прямая пп' пересекает прямые LU и ММ в точках р и q;
при этом /_pLn=j/_qM'n'; /_pnL = /_qn M и, следовательно,
/_Lpn= /_Mqn . Поэтому существует окружность Г, касающаяся
прямых LL' и ММ в точках их пересечения р и q с прямой пп'.
Применим теперь сказанное в примечании к решению задачи 408
к окружностям С и Г и секущей пп'. Касательные к С в точках п
и п' и касательные к Г в точках р и q имеют своими точками пере-
пересечения точки L, L', М и М' окружности С. Следовательно, окруж-
окружности С, С и Г имеют общую радикальную ось.
Итак, мы доказали, что существует окружность Г, имеющая
с С и С общую радикальную ось и касающаяся прямых LL' и
СМЕШАННЫЕ ЗАДАЧИ 585
ММ в точках р и q пересечения этих прямых с прямой пп'. Та-
Таким же образом можно доказать, что существует окружность Г' (на
чертеже не показана), имеющая с Си С общую радикальную ось и
касающаяся прямых LU и NN' в точках их пересечения с прямой
mm'.
Применим теперь к четырёхугольнику mm'пп' второе предложение
упражнения 239. Из этого предложения следует, что прямые mm' и пп' пе-
пересекаются в точке р прямой LL'. Окружности Г и Г' совпадают,
так как они обе касаются прямой LL' в точке р, а их центры лежат
на прямой 00'.
Итак, окружность Г, имеющая с окружностями С и С общую
радикальную ось, касается прямых LL', MM' и NN' в точках р,
q и s, где эти прямые пересекают прямые mm' и пп'.
Прямая qs образует с прямыми ММ' и NN' равные углы. Кроме
того, будут равны углы MM'N' и MNh'. Следовательно, в треуголь-
треугольниках M'l'q и Ms, где / и /'—точки пересечения прямой qs с MN
и М!N', будут равны и третьи углы — ^M'l'q и /_ Ms. Поэтому
существует окружность С, касающаяся прямых MN и M'N' в точках
/ и I' (окружность С не показана на чертеже). Совершенно таким же
образом, как это было сделано выше для окружностей С, С и Г,
покажем, что эта новая окружность С имеет с окружностями С и Г
общую радикальную ось. *
Обе окружности С и С" касаются прямых MN и M'N', а их цен-
центры лежат на прямой 00'. Кроме того, центры обеих окружностей лежат,
как в этом можно убедиться хотя бы из рассмотрения чертежа 677, на
одной и той же биссектрисе углов между прямыми MN и M'N'. От-
Отсюда вытекает, что С совпадает с С".
«В том, что окружность С совпадает с С", можно более строгим обра-
образом убедиться так. Окружность С имеет с окружностями С и Г общую ра-
радикальную ось и касается прямой MN. Так как существуют (п. 31 lj лишь
две окружности, удовлетворяющие этим обоим условиям, то окружность
С необходимо совпадает с одной из них. Далее, при непрерывном переме-
перемещении точки /.', а следовательно, и точек М" и Л" по окружности С, окруж-
окружность С, касающаяся также и M'N', могла бы изменяться лишь непрерыв-
непрерывным образом; но непрерывное изменение в данном случае невозможно (су-
(существует всего-навсего два возможных положения окружности С). Следова-
Следовательно, окружность С не изменяется при перемещении прямой M'N'\ иначе
говоря, окружность С касается прямой M'N' в любом её положении, и по-
потому совпадает с С".
Итак, окружности С и Г имеют общую радикальную ось как с
окружностью С, так и с окружностью С, т. е. с окружностью С".
Следовательно, окружности С, С и С" имеют общую радикальную
ось.
Пусть теперь, как и выше, гиг' — радиусы окружностей С и С
(черт 676) и d^OO'. Расстояние центра О" окружности С" от цен-
586
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
тра О окружности С равняется (согласно решению задачи 410) ОО" =
NP 2 г г'
= k2-OO', где, в силу A), к=~,= r2_d2 ¦ Отсюда
ОО" = -
B)
Для вычисления радиуса г" окружности С" рассмотрим точку
пересечения La окружности С с линией центров окружностей С и
С, отстоящую от О' на рас-
расстоянии ^-1-4 (черт. 678).
Так как окружность С по смыс-
смыслу задачи не может лежать
внутри окружности С, то Lo
лежит вне окружности С. Пусть
Мо и /Vo —• вторые точки пере-
пересечения с окружностью С ка-
касательных, проведённых из точ-
точки Lo к окружности С, /п —
точка касания окружности С" С
прямой MoN0, /z0 — точка каса-
касания окружности С с прямой
L0M0 и Ро — точка окруж-
„,„ ности С, диаметрально проти-
678' воположная 10.
Из подобия треугольников L0O'n0 и L0P0M0 имеем Ж0Р0:10Р0 =
2/т'
= О'n0:L0O', откуда М0Р0 = ,.. Далее, из прямоугольного тре-
• 2гг'2
угольника 10Ж0Р0 находим /0Р0 = Ж0Р02:10Р0 — . 8. Отсюда
2 2/т'а
( )
Окружность С" будет совпадать с окружностью С, т. е. окружность С
будет вписанной или вневписанной окружностью треугольника LMN,
если точка О" будет совпадать с О', т. е. если мы будем иметь
00" =d. Это будет иметь место, как видно из B), при сР — г2 =
=-\-2rr'. Таким образом получаем результат задачи 377. •
412. Применим к рассматриваемой фигуре (черт. 679) инверсию
с полюсом Р и степенью, равной (для определённости) ОР2. Прямые
ОА и ОВ преобразуются в две окружности ОА^Р и ОВХР (черт.
680).
1°. Две окружности С и С, касающиеся прямой ОБ и проходящие
через точки Р и М, преобразуются в две прямые^ и С,', касающиеся
окружности ОВХР и проходящие через точку Мл окружности ОАЛР.
При этом угол между окружностями С и С', обращенный к части
СМЕШАННЫЕ ЗАДАЧИ 587
плоскости, внешней по отношению к обеим окружностям (т. е. к части
плоскости, содержащей прямую ОВ), будет равен углу между прямыми
С, и С,', в котором лежит окружность ОВ^Р. Мы приходим к задаче:
найти на окружности ОАЛР точку, из которой окружность ОВХР видна
под данным углом.
Геометрическое место точек, из которых данная окружность видна
под данным углом, есть окружность, концентрическая с данной. Сле-
Следовательно, точка Мл есть точка пересечения окружности ОАХР с
вполне определённой окружностью S^, концентрической с окружностью
ОВ^Р, а М есть точка пересечения прямой ОА с окружностью S,
обратной по Отношению к окружности 5р
Черт. 679. Черт. 680.
2°. При перемещении точки Мх по дуге ОАЛР от О к Р, т. е.
при перемещении точки М по стороне ОА угла АОВ, угол, о кото-
котором идёт речь, убывает от 2rf до некоторого определённого значения
(соответствующего наибольшему расстоянию точки Мх от центра
окружности ОВХР), а затем снова возрастает до 2d.
3°. Окружность PQQ' преобразуется в прямую QxQt', соединяю-
соединяющую вторые точки пересечения касательных С, и Су с окружностью
ОАЛР. Но прямая Q,Q/ остаётся касательной к некоторой окружности
(задача 411), имеющей с окружностями ОАХР и ОВХР общую ради-
радикальную ось и потому проходящей через точки О и Р. Следовательно,
окружность PQQ', обратная прямой Q,Q,', остаётся касательной к
некоторой прямой, проходящей через точку О.
413. Так-как площадь трапеции и её высота АВ сохраняют по-
постоянные значения, то и сумма оснований AC-\-BD сохраняет посто-
постоянное значение.
Если отрезки АС и BD отложены в одну сторону (черт. 681), то
середина F отрезка CD остается неподвижной. Основание Н перпен-
перпендикуляра, опущенного из середины Е отрезка АВ на прямую CD, ле-
лежит на окружности, имеющей EF своим диаметром. Геометрическое
место точек Н есть часть этой окружности, внешняя по отношению
к треугольнику AFB.
533
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Если отрезки АС и BD отложены в противоположные стороны
(черт. 682), то проекции CbD диагонали CD на прямую BD, равная
AC-\-BD, сохраняет постоянную величину. Следовательно, угол CDB
сохраняет постоянное значение, и прямая CD перемещается парал-
I N/
Черт. 681.
В
Черт. 682.
лельно самой себе. Геометрическое место точек И есть отрезок
прямой ЕК, перпендикулярной к CD и проходящей через Е. Этот
отрезок имеет своими концами точки пересечения М и N прямой ЕК
с прямыми, параллельными CD и проходящими через точки А и В
(так"как точка А есть крайнее по-
положение точки С, а точка В— "
точки D).
414. Через точку О, лежащую
внутри угла XSY, пусть требуется
М,
S В О N В' X
Черт. 683.
провести секущую MON так, чтобы площадь треугольника MNS рав-
равнялась данной величине Д. Строим параллелограм SAOB (черт. 683).
Тогда, проводя прямые ОР и OQ, перпендикулярные соответственно
к SY и к SX, будем иметь AM-OP-\-BN-OQ= 2 (Д — пл. SAOB).
Строим отрезок ВВ' так, чтобы Д — пл. SAOB=nn. BOB'. Тогда
AM-OP-\-BN-OQ=BB' -OQ, или AM-OP=NB"-OQ. Задача сво-
сводится к построению по данным точкам Л и Б' секущей MON, для
которой AM:B'N=OQ:OP (упр. 216).
415. Зная угол А и периметр 2р искомого треугольника ABC,
можно построить точки касания Е1 и Е{ (черт. 684) вневписанной
СМЕШАННЫЕ ЗАДАЧИ
589
окружности, касающейся стороны ВС, с продолжениями сторон АС и АВ,
так как АЕЛ^ Д/7,=/? (упр. 90а). Следовательно, можно построить
и самую вневписанную окружность.
Зная площадь 6" и периметр, можно построить радиус R вписан-
ной окружности, равный — (упр. 299), а следовательно, и самую впи-
вписанную окружность. Сторона ВС искомого треугольника будет внутрен-
внутренней общей касательной к обеим построенным окружностям.
В силу соотношения S = pR наибольшая возможная площадь по-
получится при данных значениях угла А и полупериметра р, если R
будет иметь наибольшее возможное значение, т. е. если обе построен-
построенные окружности будут внешним образом касаться друг друга. При этом
треугольник -ABC будет равнобедренным.
416. Пусть ВС^а, 2р, S — данные сторона, периметр и площадь
треугольника, / и 1Х — центры вписанной окружности и вневписанной
окружности, касающейся стороны ВС и продолжений двух других сто-
сторон, R и Rl —радиусы тех же окружностей, Е и Ел —точки их ка-
касания со стороной АС (черт. 684).
В силу упражнения 90а имеем: ЕЕХ = АЕХ — АЕ = р — (р —а] = а.
В силу упражнения 299 имеем:
Таким образом, можно построить отрезок ЕЕг = а: и окружности
/ и /,; строя общие касательные к обеим окружностям, получаем ис-
искомый треугольник.
Для возможности задачи необходимо и достаточно, чтобы окруж-
окружности / и /, были расположены одна вне другой или касались одна
другой внешним образом, т. е. чтобы Z,/2 = a2 -f- (#, — RJ ^ (/?, -J- RJt
откуда после упрощений находим: a2^4RR1.
При данных ои 5 радиусы R и Rt оба возрастают с уменьшением
р в силу формул A). Наименьшее значение р соответствует по-
поэтому равенству a2:=4RRl, т. е. I/l = R-\-Rl. При этом треуголь-
треугольник ABC будет равнобедренным. Итак, из всех треугольников с дан-
данными стороной а и площадью ? наименьший периметр имеет равно-
равнобедренный треугольник.
Точно так же при данных а и р радиусы R и /?, возрастают с
увеличением 5 в силу формул A). Наибольшее значение S соответ-
соответствует опять равенству а2 = 4/?/?,, т. е. //, = /?-(-/?,. Итак, из% всех
треугольников с данными стороной а и периметром 2р наибольшую
площадь имеет равнобедренный треугольник.
Примечания: 1°. Выбрать среди всех треугольников с данным
периметром 2р и данной стороной а тот, который имеет наибольшую
площадь, можно также, исходя из выражения площади треугольника че-
через его стороны, приведённого в п. 251. Представив выведенную там фор-
формулу в виде S3 = —т р (р—а) [а2 — (Ь—с)Ц, мы видим, что при данных р
590 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
и а площадь S будет тем больше, чем меньше будет \Ь — с\, и будет наи-
наибольшей при Ь = с.
2° Выбрать среди всех треугольников с данной площадью S и данной сто-
стороной о тот, который имеет наименьший периметр, можно ещё так. Пусть
Д — равнобедренный треугольник, имеющий площадь S, периметр 2р и ос-
основание о, У — произвольный неравнобедренный треугольник с площадью
S, периметром 1р' и основанием а. Требуется показать, что р<р'.
Построим равнобедренный треугольник \ с основанием а и перимет-
периметром 2/7' и обозначим через S] его площадь. Тогда, сравнивая треугольни-
ники Д' и Aj, имеющие одно и то же основание и один и тот же пери-
периметр 2р', получим в силу предыдущего Sj >¦ S. Отсюда следует, обозначая
через h высоту каждого из треугольников Л и А', опущенную на сторону
а, и через ht — соответствующую высоту треугольника Aj, что hx > h, a
следовательно, из сравнения равнобедренных треугольников А и Alf что и
ff >¦/? (так как большей проекции соответствует большая наклонная, то
в равнобедренных треугольниках с равными основаниями большей высоте
соответствует и большая боковая сторона).
417. Первое решение. Допустим, что среди всех треуголь-
треугольников с одинаковым периметром 2р есть треугольник ABC, имеющий
наибольшую площадь. Если бы две из сторон, например АВ и АС,
были не равны между собой, то мы могли бы увеличить площадь тре-
треугольника, заменив его равнобедренным треугольником А'ВС с тем же
основанием ВС и с тем же периметром (задача 416). Отсюда следует,
что АВ=АС. Точно таким же путём докажем, что АВ=ВС. Итак,
среди всех треугольников с данным периметром наибольшую площадь
имеет равносторонний треугольник.
Примечание. Приведённое только что решение основано на пред-
предположении, что среди всех треугольников с данным периметром сущест-
существует треугольник, имеющий наибольшую площадь. Однако существова-
существование такого треугольника не может считаться очевидным (ср. примечание
к первому решению задачи 366). Приводим поэтому второе решение, в
котором существование треугольника с наибольшей площадью заранее не
предполагается.
Второе решение. Пусть Д — равносторонний треугольник с пе-
периметром 2р, и Л' —какой-либо другой треугольник с тем же пери-
периметром. Среди сторон а',Ь' и с' треугольника Л' должна найтись сторона,
2 * 2 2 2
меньшая — р, и сторона, ббльшая — р. 11усть а' <^ — р и irP<Zc' •
о о о о
2
Рассмотрим сначала случай, когда Ь' ^> — р; в этом случае име-
о
2 2
, ем - р — а'^>с' — -г- р. Построим треугольник Д" со сторонами
3 о
а"=~р; b'=b'; <Г = а'+с'-1р.
Легко проверить, что а" +с" > b"; a"-\-b" >c"; b"-\-c">a". Дей-
Действительно,
1) а" + -с" = a' + c>>b'= b";
СМЕШАННЫЕ ЗАДАЧИ 591
2 2 2
2) а" 4- Ь" = -з-Р 4- Ь'. н0 -о-/° + *'> а -Ь с' Т/7- так как в Данном
со о
2 4
случае *' > —р; а1 4- С <— р;
3, *" + с"= 1/0>а".
Сравним площади S" и 5" треугольников Л" и Л'. Имеем Ь"' =Ь'
и а'<^с"<^а"<^с', откуда | а" — с \ <^| а'—с'\. В силу примечания 1°
к решению задачи 416, найдём, что S"^>S'. Сравнивая далее та-
таким же образом площади S и 5" треугольников Д и Л", находим 6" ^> S".
Итак, .S >?">?', и потому 5>5'.
2
Рассмотрим далее случай, когда Ь'<^ — р; в этом случае имеем
о
2 2
-—р—а'<^с' р. Построим треугольник Л" со сторонами с"^ =
3 3
4
Легко проверить, что а" + с" = а' -\- с' > V = й"; о" 4- Ъ" = -^- р~> с";
jp-\-b'>a' + c' — jP = a", так как V > ~р и a'4-f'—b'<JP-
Сравним площади S" и S' треугольников Д" и Д'. Имеем Ь" = Ь'
и а' <^с"<^а"<^с', откуда \а" — с"\<^\с' — а'\ ив силу задачи 416
опять S"^>S'. Далее, как и в первом случае, S^>S" и потому S^S'
2
2
Если, наконец, Ь'= — р, то мы имеем S~^>S' в силу последнего
о
предложения задачи 416.
Таким образом показано, ч'то площадь S треугольника А больше
площади S' любого другого треугольника с тем же периметром.
418. Чтобы не прерывать дальнейшего изложения, докажем пред-
предварительно следующую теорему:
Во всяком четырёхугольнике разность между суммами квад-
квадратов двух пар противоположных 'сторон равна удвоенному про-
произведению одной из его диагоналей на проекцию на неё другой
диагонали. (При этом из суммы квадратов сторон АВ и CD, черт. 685,
которым соответствует тупой угол^/ АЕВ = ^_ CED между диагоналями,
вычитается сумма квадратов сторон, соответствующих острому углу
/_BEC='/_AED.)
Пусть L и М — проекции вершин В и D четырёхугольника ABCD
иа диагональ АС. Мы должны доказать, что
И. A)
Имеем АВ? = АЕ* + ВЕг + ЧАЕ-EL; ВС2 = BE*-\-СЕ* — 2EC-EL;
CD* = СЕ* -|- DE"' + 2 ЕС • ME; AD* = АЕ* -\- DE* — ЧАЕ • ME.
Отсюда (АВ* + CD2) — (ВС* -j- AD?) = ЧАЕ ¦ tL -\- 2EC ¦ ME -\-
~\-2EC-EL-\-2AE-ME = 2(AE^EQ(ME~\-EL) = 2AC-ML. Таким
образом, соотношение A) доказано.
592
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Переходим теперь к решению поставленной задачи.
Так как треугольник АВСХ (черт. 686), построенный как указано
в "тексте задачи, равновелик треугольнику ADC, и кроме того
/_ADC = /_ABCV то в силу п. 256
AD-CD = AB-C^B. B)
Отсюда
ВС1 = т = —. C)
Далее, если К и L — основания высот АК и CXL треугольников
ACD и АВСХ , то
AC2=CD2-\-DA2±2CD-DK, D)
AC? = AB2 + ВС* ± 2AB-BL; E)
при этом в силу равенства углов ADC и АВС1 знаки перед послед-
последними членами в обоих равенствах одинаковы. Но в силу подобия
В
К О
Черт. 686.
треугольников ADK и CXBL имеем DK:BL = AD:ClP. и, заменяя в ра-
равенстве B) отрезки AD и ВСХ пропорциональными им отрезками DK
и BL, получим:
CD-DK = AB-BL. F)
Из равенств D), C) и F) находим:
АС* — АС? = АЕГ- -f ВС* — CD"- — DA* = о2 -f '«2 — с2 — rf2. G)
Чтобы определить теперь проекцию LM отрезка СЛС на прямую АВ,
воспользуемся соотношением A), применяя его к четырёхугольнику АСХВС.
Получим (АС^-\-ВС2) — (ВС12-\-А<У) = 2АВ-ЬМ. Отсюда в силу G)
имеем: 2AB-LM = (АС* — АС2) -\- (ВС* — ВСХ2) = (а*-\-т? — с* —
b2 — т*), и, следовательно.
! 1
сР
(8)
СМЕШАННЫЕ ЗАДАЧИ 593
Наконец, проекцию CN отрезка СС1 на прямую СМ, перпендику-
перпендикулярную к АВ, можно найти из соотношения пл. ABCD = пл.ABC-\-
-f-пл. АСО = пл. АВС-\- пл. АВС1 =~ АВ-(СМ-\- С/) = 1 AB-CN.
1
2,
Отсюда
(9)
Итак, мы приходим к следующему построению. Строим отрезки
CXN = LM и CN по формулам (8) и (9) и отрезок СС1 как гипоте-
гипотенузу прямоугольного треугольника CCjN. Построив отрезок ВС1 = т
по формуле C), можно построить по трём сторонам треугольник ВССу
Вершину А можно теперь найти, проводя прямую ВА, параллельную
Cj/V, и откладывая отрезок ВА, равный а. Наконец, положение вер-
вершины D определяется её расстояниями CD = c и AD = d от точек
С я А.
Если задача возможна, то она имеет, вообще говоря, два решения.
Действительно, при построении треугольника ВСС1 по трём сторонам
мы получим два возможных положения точки В (точки В и В1
на черт. 686), симметричных относительно прямой СС1. Получаем че-
четырёхугольники ABCD и i4jBjCDj.
Если построить точки А', В' и С, соответствующие точкам А, В
и С в инверсии с полюсом D и произвольной степенью, то мы будем
иметь /_АВВ=/_ВАА' и /_ВВ'С= /_ВСС', откуда
/_ А'В'С = /_ А" В'В -\-/_ВВС~ 360° — /_ BAD — /_ BCD =
= /_ ADC -\- /_ ABC = /_ ciBA + Z ABC = Z CiBC- A0)
Далее мы имеем, согласно решению упражнения 270,1°,
A'B':B'C^=(AB-CD):(BC-AD) = oc:bd. A1)
Если построить аналогично точки А^, Вх' и С,' (для упрощения не
показанные на чертеже), исходя из четырёхугольника A1B1CD1, то
мы получим:
Z.A'B'C'=Z.C1B,O, A0')
A^B^-.BiCi — ac-.bd. A1')
Полученные соотношения A0), (П), A0') и AГ) показывают, что тре-
треугольник, рассмотренный -в упражнении 270, имеет для четырёхуголь-
четырёхугольников ABCD и A1BlCD1 одну и ту же форму.
Пусть теперь дан четырёхугольник ABCD, и требуется построить
четырёхугольник, ему не равный, но имеющий те же стороны и ту же
площадь.
Мы могли бы построить искомый четырёхугольник, строя точку Ср
как указано в тексте задачи, затем точку Bv симметричную с В от-
относительно прямой ССг, и закончить построение четырёхугольника
A^BxCDlt как было указано выше. Однако можно указать и более
простое построение.
38 Элементарная г&ометрия
594 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Чтобы прийти к этому новому построению, примем во внимание, что
вершины Ао, Во, Со и Z)o искомого четырёхугольника {в некотором опреде-
определённом положении его на плоскости) можно рассматривать как точки, об-
обратные вершинам данного в некоторой инверсии. Если О—полюс этой
к-ВА
инверсии и /г-—ее степень, то мы должны иметь АпВг, = _ = АВ
О Л -UB
и аналогичные равенства для остальных сторон. Из этих равенств непосред-
непосредственно следует, чток=ОА-ОВ=ОВ-ОС—ОС-OD=OD-ОА, так что ОА=ОС
к О А • ОВ
и ОВ = OD. Далее ОА0 = -~пт = —тут— = ^' и таким же образом ОА0 =
— OC0=OB = OD и Ofi0^OZH:= ОА = ОС. Мы приходим к следующему
построению:
Строим точку О, удовлетворяющую условиям ОА = ОС и ОВ=
= OD, т. е. точку пересечения перпендикуляров, восставленных
в серединах диагоналей четырёхугольника. На полупрямых ОА и ОС
откладываем отрезки ОАй и ОС0, оба равные ОВ, а на полупрямых
ОВ и OD — отрезки ОВ0 и OD0, оба равные О А (черт. 687). Спра-
Справедливость построения непосредственно вы-
Ji текает из равенства четырёх пар треуголь-
треугольников ОАВ и ОД,Д0, ОВС и ОСъВй, и т. д.
Площадь четырёхугольника ABCD
(черт. 686) будет в си чу соотношения (9)
равна — a-C/V. Наибольшее возможное зна-
значение площади четырёхугольника, имею-
имеющего данные стороны, отвечает поэтому
наибольшему возможному значению отрез-
ка CN. В свою очередь это значение
"о CN соответствует наибольшему значению
Черт 687 отрезка CCV так как отрезок CXN = LM
определяется по формуле (8) данными сто-
сторонами. А отрезок CCj будет иметь наибольшее значение, если точ-
точки С, В и С, будут лежать на одной прямой.
Итак, площадь четырёхугольника с данными сторонами будет на-
наибольшей, если точки С, В и С, лежат на одной прямой, т. е. если
/_ СВСХ =/_В-\-/_D= 180°. Последнее равенство и показывает, что
четырёхугольник ABCD, имеющий наибольшую площадь, — вписанный.
418а. Пусть в четырёхугольнике ABCD (черт. 685) АВ= а;
BC=b; CD=c\ DA = d; AC = e; BD=f. Обозначим через Е
точку пересечения диагоналей, через L и М—проекции вершин В
и D на прямую АС, через Л' — проекцию вершины В на пря-
прямую DM.
Из прямоугольного треугольника BDN имеем /2 = BN2-(-DN2 =
= ML2\-DN'i, откуда, умножая почленно на 4е2 = 4/1С2, получим
? = BAC. MLf -f- BACDNJ.
Преобразуем каждый из членов правой части этого равенства от-
отдельно. На основании соотношения A), выведенного^ решении задачи 418,
находим 2АС¦ ML = АВ2 -f- CD2 — ВС2 — AD2 = a2 -)- с2 — № — сР.
СМЕШАННЫЕ ЗАДАЧИ 595
Далее имеем 2AC-DN = 2AC-DM-\-2AC-BL = b пл. ACD-\-
-j-4 пл. ABC=^S. Подставляя эти выражения для 2AC-ML и
2AC-DN в предыдущее равенство, мы и получим первое из приве-
приведённых в тексте задачи соотношений.
Чтобы получить второе соотношение, заметим, что
DN DN lAC-DN
и знаменатель нх полученными выше зна-
значениями, мы и придём к данному в тек-
тексте задачи выражению для tgl/.
Переходим теперь к построению че-
четырёхугольника ABCD (черт. 688) по его
сторонам и площади. Пусть Р — такая
точка плоскости, что треугольник АВР
подобен ADC. Из подобия этих двух
ас
треугольников находим, что ВР=—г- и
что AC:AP = AD:AB = d:a. Кроме Черт. 688.
того, /_ САР = /_ DAB, так что тре- е *
угольники АСР и ADB подобны, откуда СР = —.
Задавшись теперь положением стороны ВС на плоскости, можно
ас ef
построить точку Р по её расстояниям ВР = —-т- и СЛ = —т- от то-
точек В и С. При этом отрезок СР можно построить, пользуясь пер-
первым из доказанных выше соотношений, из которого следует, что
е/у__1/я2 cs b2 Y\{2SY
d j $\d d d } x \ d j '
Далее можно определить положение вершины А, пользуясь двумя
окружностями: 1) геометрическим местом точек А, удовлетворяющих
выведенному выше соотношению AC:AP = d:a (п. 116) и 2) окруж-
окружностью с центром В и радиусом а.
Наконец, вершина D определяется её расстояниями CD = c и
AD = d от точек С я А.
419. Пусть ABCD — искомый вписанный четырёхугольник (черт. 689)
и Р — такая точка плоскости, что треугольник АВР подобен ADC.
Точки Р, В и С лежат на одной прямой, так .как /_ АВР-\- /_ АВС=
= /_ ADC-\-/_ ABC= 180°. Кроме того, из подобия треугольников
АВР и ADC следует, что ВР = — , так что, задавшись положе-
/\LJ
нием стороны ВС, можно построить точку Р. Далее из подобия треуголь-
треугольников АСР и ADB следует, что AC: AP = AD: AB. Таким образом, по-
положение вершины А можно определить, пользуясь двумя окружностями:
1) геометрическим местом точек, расстояния которых от точек С и Р
относятся как AD-.AB (п. 116), и 2) окружностью с центром В и дан-
данным радиусом А.В.
38*
596
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Наконец, вершина D определяется её расстояниями CD и AD от
точек С я А.
419а. Пусть ABCDE ... — многоугольник с данным числом сторон
и данным периметром, имеющий наибольшую площадь (существование
такого многоугольника мы предполагаем). Так как соответствующая
задача для треугольника разрешена нами полностью (задача 417), то
мы можем предполагать, что данное число сторон равно по крайней
мере четырём.
Рассмотрим четыре последовательные вершины А, В, С и D иско-
искомого многоугольника. Если бы эти вершины не лежали на одной окруж-
окружности, то мы могли бы увеличить площадь
данного многоугольника, не изменяя его пе-
периметра: для этого достаточно заменить
четырёхугольник ABCD вписанным четы-
четырёхугольником AB"CD с теми же сторонами
(задача 418, последнее предложение). Сле-
Следовательно, точки А, В, С и D лежат на
окружности. Так как это рассуждение
можно повторить для любых четырёх по-
последовательных вершин, то все вершины
многоугольника ABCDE ... лежат на одной
окружности. Итак, если среди всех мно-
многоугольников с данным числом сторон и
данным периметром существует много-
многоугольник, имеющий наибольшую площадь,
то этот многоугольник может быть
вписан в окружность.
Предположим теперь, что две смежные
стороны многоугольника, хотя бы АВ и
ВС, не равны между собой. В таком случае мы можем заменить тре-
треугольник ABC равнобедренным треугольником с тем же периметром,
но с большей площадью (задача 416). Отсюда следует, что все сто-
стороны искомого многоугольника, имеющего наибольшую площадь,
должны быть равны между собой, а так как этот многоугольник, кроме
того, можно вписать в окружность, то он правильный.
Если мы имеем правильный и неправильный многоугольники с одним
н тем же числом сторон и одним и тем же периметром, то отношение
— для правильного многоугольника будет больше, чем для неправильного,
так как площадь первого больше площади второго. Но отношение —
для правильного многоугольника не зависит от его размеров при за-
заданном числе сторон, так как два правильных многоугольника с одним
и тем же числом сторон подобны между собой.
Примечание. При решении этой задачи мы предполагали существо-
существование многоугольника, имеющего наибольшую площадь среди ьсех много-
СМЕШАННЫЕ ЗАДАЧИ
597
угольников с данным числом сторон и данным периметром (ср. примечание
к первому решению задачи 366). Доказательство, свободное от этого пред-
предположения, читатель найдёт, например, в книге Д. А. Крыжановского:
«Изопериметры», М.-Л., 1938.
420. Рассмотрим окружность, имеющую длину С и некоторую замк-
замкнутую линию, имеющую ту же длину. Впишем в окружность правиль-
правильный многоугольник с п сторонами и обозначим через Sn и Рп его
площадь и периметр. В замкнутую линию впишем какой-либо много-
многоугольник с п сторонами и обозначим через sn и рп его площадь и
периметр. В силу задачи 419а будем иметь при любом п неравенство
P2," pi ¦
Если мы будем неограниченно увеличивать число сторон и, выбирая
вершины и-угольника, вписанного в отличную от окружности замкнутую
линию, так, чтобь^ каждая его
сторона стремилась к нулю, то
мы будем иметь: Рп—»- С, рп—>-С,
n n
и ь- обозначены площади, ограни-
ограниченные окружностью и выбран-
выбранной кривой, и из предыдущего
S
неравенства следует, что — Зз
— , откуда
. Итак, ере-
ди всех замкнутых линий, имею- /,-
щих заданную длину, нет ни Д
одной, которая ограничивала бы
площадь большую, чем окруж-
окружность, имеющая данную длину.
Черт. 690.
Примечание. Осталось ещё не доказанным, что окружность есть
единственная кривая, ограничивающая наибольшую площадь среди вех
кривых, имеющих заданную длину. В самом деле, ввиду соотношения S^s
мыслимо, что кроме окружности существуют среди замкнутых линий дан-
данной длины С и другие кривые, ограничивающие ту же площадь S (это будет,
если S = S). Свинство окружности ограничивать наибольшую площадь при
заданной длине (так называемое изопериметрическое свойство) весьма
подробно рассмотрено в книге Крыжа::овского (см. ссылку в решении за-
задачи 419а). В частности, там доказана единственность кривой наибольшей
площади.
420а. Прямые О^О4 и OnOs (черт. 690) параллельны друг другу,
так как они представляют собой перпендикуляры, восставленные в се-
серединах отрезков ОА и ОС. По такой же причине прямая OjO2 парал-
параллельна OSO4. Следовательно, точки О1, О2, О3 и О4 образуют парал-
лелограм Р.
1°. Длины диагоналей четырёхугольника равны удвоенным высотам
параллелограма, так как точки А и С симметричны с О относительно
598 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
двух противоположных сторон параллелограма, и то же относится к
точкам В и D. Если прямая ВЦ перпендикулярна к AC, a DH парал-
параллельна АС, то nn.ABCD^-?-АС-ВН (сравнить решение задачи 418а).
Пусть О^К— высота параллелограма, опущенная из Oi на OjO2. Прямо-
Прямоугольные треугольники BDH и OfixK подобны, так как нх
острые углы DBH и ОХО±К имеют соответственно параллель-
OKB
dlj OAK-BD „ .
ные стороны, откуда ВН= . 1аким образом, задание парал-
Ojt>4
лелограма Р определяет АС и ВН, а потому и площадь четырёхугольника
ABCD, равную -^-АС-ВН.
2°. Так как точки А я О симметричны относительно стброны OlOi
параллелограма Р, то при перемещении точки О по прямой А точка А
описывает прямую а, симметричную с А относительно OjO4. Точно так
же точки В, С и D описывают при этом прямые Ь, с, d. Прямая с
получается из прямой а с помощью двух последовательных симметрии —
относительно OjO4 и относительно O2OS; так как прямые OlOi и O2Ot
параллельны, то последовательность этих двух симметрии даёт поступа-
поступательное перемещение, и прямые а к с параллельны. Точно так же
покажем, что прямые Ь и d параллельны. Таким образом, прямые а,
Ь, с и d образуют параллелограм Р'.
Если прямая А перемещается параллельно самой себе, то прямые а,
Ь, с и dt очевидно, сохраняют своё направление. Так как прямые а и с
получаются одна из другой с помощью поступательного перемещения,
перпендикулярного к прямым OjO4 и О2О3 и по величине равного
удвоенному расстоянию между ними, то расстояние между прямыми а и
с не изменяется при параллельном перемещении прямой Д. Не изменяется
при этом по аналогичным соображениям и расстояние между прямыми
bud. Отсюда непосредственно следует, что при перемещении прямой А
параллельно самой себе параллелограм Р' испытывает лишь поступа-
поступательное перемещение.
При вращении прямой Д углы параллелограма Р' не изменяются, так
как при повороте прямой Д на некоторый угол около произвольной
точки прямые а и Ь обе повёртываются на тот же самый угол в одном
и том же направлении, а потому угол между ними не изменяется.
Так как при перемещении прямой Д параллельно самой себе площадь
параллелограма Р' не изменяется, то для отыскания наибольшей площади
параллелограма достаточно рассмотреть вращение прямой А около не-
некоторой неподвижной точки, например около центра М параллелограма
Р (черт. 691, на котором параллелограм Р не показан). При этом
прямые а, Ь, с, d будут вращаться соответственно около точек а, |5,
у, 5, симметричных с М относительно сторон параллелограма Р. Так
как точки сг, р, у и й сами образуют параллелограм, то мы приходим
к следующей задаче: описать около параллелограма afly^ параллело-
параллелограм UVWT, углы которого имеют заданную величину (напомним, что
СМЕШАННЫЕ ЗАДАЧИ
599
углы этого параллелограма не изменяются при вращении прямой А), и
притом так, чтобы его площадь была наибольшей. Вершина (J пере-
перемещается при этом по окружности, проходящей через точки а и р.
Очевидно, что пл. UVWT = 2 пл.ау VLJ или (в силу упр. 297)
пл. LJVWT = 2.ау-5Х, где SL—перпендикуляр, опущенный из середины
5 стороны UV на прямую ау. Но 2SL = UN, где UN— перпендикуляр
из точки U напрямую ау. Итак, wi.UVWT = ay-UN. Но отрезок UN
будет иметь наибольшее значение, когда точка U выбрана так, чтобы
отрезок UN совпадал с диаметром окружности z$U', по которой пере-
перемещается точка U (как изображено на чертеже).
Определив, таким образом, то положение точки U, для которого
площадь параллелограма Р' будет наибольшей, легко построить и
соответствующее положение прямой А. Дей-
Действительно, как было указано выше, прямая А
симметрична с прямой а (т. е. с прямой Ua) от-
относительно Oj О4.
3°. Пусть дан параллелограм Р и углы А
и С (черт. 690). Диагонали АС и BD опре-
определены при этом по величине н направле-
направлению. Геометрическое место каждой из вер-
вершин А и С при произвольно расположенной
на плоскости диагонали BD состоит из дуг
окружностей. Определение положения диа-
диагонали АС непосредственно сводится к упраж-
упражнению 75.
Пусть теперь даны параллелограм Р и
углы А и В. Диагонали АС и BD опять опре-
определены по величине и направлению; следова-
следовательно, можно построить параллелограм (см. упр. 36 и черт. 281), имеющий
своими вершинами середины сторон искомого четырёхугольника: сто-
стороны этого параллелограма параллельны диагоналям четырёхугольника
и равны их половинам. Геометрическое место каждой из вершин А и В
будет дугой окружности. Через вершину построенного параллелограма
остаётся провести прямую так, чтобы отрезок её АВ, заключённый
между двумя построенными окружностями, делился в этой вершине
пополам. Эта задача решается, как указано в решении упражнения 165.
Если даны параллелограм Р и отношения АВ:AD и CB:CD,
(черт. 690), то, выбрав произвольно положение диагонали BD, получим
в качестве геометрического места каждой из точек А к С окружность
(п. 116), и задача снова сводится к упражнению 75.
4-21. Данный четырёхугольник MNPQ и четырёхугольники ABCD
и А'В1 CD', образованные соответственно биссектрисами его внешних
и внутренних углов, образуют ту же фигуру, которая нам встречалась
при решении задачи 362а (черт. 590). Мы имели там соотношение
Черт. 691.
R.{MN-\-NP-\-PQ-\-QM) = AC-BD, D)
где R — радиус окружности, описанной около четырёхугольника ABCD.
6C0
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Далее аналогично выведенному там соотношению C) имеем 2R'-MN =
—BM-C'D' -\-B"N-D'A'; 2R' -NP=C N • D' А' Л-С'Р • А' В; 2R'-PQ=
= D'P-A'B'4-D'Q-BC';2R'.QM= A'Q-BC-+-A''M-CD', где R' —
радиус окружности, описанной около A'B'C'D'. Из полученных равенств
имеем 2R' ¦ (MN — NP -{- PQ — QM) = A'B'-(D'P — C'P) -\-
-\-BC-(D'Q — A'Q)±C'D'.(B'M — А' М) + D'А'. (ВN — CN) =
= 2(A'B'-C'P'-\-B'C'-D'A') = 2A'C'-B'D'. Это соотношение вместе
с формулой D) приводит к равенству
AC-BD
A'CB'D' '
E)
С другой стороны, в силу п. 251 (примечание), имеем 4R-nn ABC =
= АВ-ВС-АС; 4R'-пл.А'В'С =
= А'В'-В'С'-А'С, и потому
/^ пл.ЛВС _ АВ-ВС-АС
W
пл.А'В'С
но из п. 256 имеем
АВ-ВС
Черт. 692.
А'В'-В'С-А'С '
пл.АВС
пл.А'В'С ~
=zAC:AC. Таким же путём най-
найдём, что R:R' = BD:B'D'. За-
Заменяя в равенстве E) каждое из
отношений АС:А'С и BD:BD'
через R:R', получим искомое со-
соотношение.
421а. 1°. Пусть Е и F —
точки пересечения двух пар про-
противоположных сторон АВ, CD и
ВС, AD вписанного четырёхуголь-
четырёхугольника ABCD (черт. 692), Ж и N —
середины его диагоналей, О —-
точка пересечения биссектрисы
угла AED с прямой MN.
Отрезки ЕМ и EN являются
соответственными медианами двух
подобных треугольников ЕАС и
BED, и потому
EM:EN=AC:BD, A)
и /_AEM = /_DEN. Из последнего равенства следует, что ЕО есть
в то же время и биссектриса угла MEN, так что
EM:EN = MO:ON. " B)
Из отношений A) и B) имеем:
MO:ON=AC:BD. C)
СМЕШАННЫЕ ЗАДАЧИ 601
Итак, биссектриса угла AED делит отрезок MN на части, пропорцио-
пропорциональные диагоналям четырёхугольника.
Таким же образом докажем, что и биссектриса угла AFB делит
отрезок MN в том же отношении. Отсюда следует, что биссектрисы
углов AED и AFB пересекаются в точке О прямой MN.
2°. В 1° мы уже доказали, что биссектриса угла AED есть и
биссектриса угла MEN. To же имеет, очевидно, место и для биссект-
биссектрисы угла AFB.
3°. Если прямая ЕО пересекает стороны ВС и AD в точках Р и
Q, а прямая FO — стороны CD и АВ в точках R и S, то мы имеем
{ЕР— биссектриса треугольника ЕВС) СР:РВ=ЕС:ЕВ. Но ЕС:ЕВ=
— AC-.BD в силу подобия треугольников ЕАС и EDB, так что
CP-.PB—AC-.BD. Аналогично найдём, что AS:SB= AC-.BD.
Отсюда следует, что прямая PS параллельна АС, так что
PS ВР BD тл пс> AC-BD
^' PS= AC + BD- Т° Ж
ние мы получим и для каждого из отрезков SQ, QR и RP. Таким
образом четырёхугольник PRQS есть ромб, сторона которого имеет
указанную в тексте задачи величину.
4°. Назовём для краткости «внешними углами при точках Е и F»
углы, смежные с углами AED и AFB. В таком случае мы будем иметь
следующие предложения:
a) Биссектрисы внешних углов при точках Е и F пересекаются на
прямой, соединяющей середины диагоналей данного четырёхугольника,
и делят внешним образом отрезок этой прямой между серединами
диагоналей в отношении, равном отношению диагоналей.
Если биссектрисы внешних углов при точках Е и F пересекаются
в точке О1( то мы имеем, следовательно,
МО l:NOl = AC-.BD. D)
b) Биссектрисы внешних углов при точках Е и F будут в то же время
и биссектрисами углов, смежных с теми углами, под которыми отрезок,
соединяющий середины диагоналей, виден из точек Е и F.
c) Биссектрисы внешних углов при точках Е и F пересекают про-
продолжения сторон данного четырёхугольника в четырёх точках, которые
будут вершинами ромба. Стороны этого ромба параллельны диагоналям
четырёхугольника; их длина есть четвёртая пропорциональная к этим
диагоналям и к их разности (ромб этот не показан на чертеже).
Доказательства предложений а), Ь) и с) вполне аналогичны приведён-
приведённым выше в 1°, 2° и 3°.
5°. Прямые ЕО и FO пересекаются в точке О под прямым углом
как диагонали ромба PRQS. Следовательно, EOFOX — прямоугольник,
и потому EF = OOy Мм имели выше равенства C) и D), из которых
ON BD NO, BD EF
следует, что Ш = AC+BD »Ш= AC-BD' ™К ЧТ° ЛШ =
602 РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
BD 2AC-BD
TaK>
~ Ш ~AC-\~BD + AC—BD
отрезок EF относится к отрезку M/V, соединяющему середины диагона-
диагоналей, как удвоенное произведение последних к разности их квадратов.
Равенство tj—,= -тт^ д™ могло бы служить для вычисления отрез-
ка EF по сторонам четырёхугольника. Действительно, диагонали АС и BD
можно найти, пользуясь п. 240а, а отрезок MN—пользуясь упражнением 139.
Однако мы значительно быстрее придём к цели следующим образом:
Для вычисления длины отрезка EF заметим прежде всего, что
точки Е и F сопряжены относительно окружности, так как поляра
точки Е проходит через F согласно п. 211. Следовательно, квадрат
отрезка EF равняется сумме степеней точек Е и F относительно окруж-
окружности (см. решение упр. 237), т. е.
EF2 = EA-EB-\-FA-FD. E)
Для сокращения выкладок положим АВ = а; BC=b; CD = c;
DA = d. Из подобия треугольников EAD и ЕСВ найдём: ЕА:ЕС =
DEBb ЕА ЕВ ED ЕС Решая
DA = d. Из подобия треугольников EAD и ЕСВ надём: ЕА:Е
= ED:EB=d:b; кроме того, ЕА — ЕВ = а; ED — ЕС = с. Р
d(ad+bc) • b(ab-\~cd)
эти уравнения, мы найдём tA = —— ——; ЕВ=-————г^—, и,
v, ™ bd(ab-\-cd){ad-\-bc) .
довательно, ЕА~ЕВ = ^ зт^ • Аналогичным путем наи-
(ft- — d-y
с- я с-^ ac(ab-\~cd)(adA-bc)
дём, что FA ¦ FD = —5 ¦ —vr-! - Подставляя найденные зна-
(а2 — с2У
чения ЕА-ЕВ и FA-FD в равенство E), получим окончательно
422. 1°. Пусть произвольная окружность (&,), концентрическая
с (А/), пересекает прямые ОА2 и OAS соответственно в точках Л/а и
Ns (черт. 693). Если обозначить через а2 и а3 точки касания окруж-
окружности (&,') с прямыми ОА2 и OAS, то отрезки Оа2 и Оа3 будут равны
как касательные к окружности из одноЧ точки. Далее из равенства
прямоугольных треугольников Oxa2N^ и Oja3Ng, где Ог — общий
центр окружностей (&,') и (&,), имеем а2Л/а = яг%. Отсюда OjV2 = O-V3,
так как Оа2 = Оа3.
Строим теперь окружность (&2), концентрическую с (A2f) и про-
проходящую через точку Л/3. Для одной из точек пересечения Л/х окружности
(й2) с прямой ОАХ будем иметь аналогично ONb = ONx. Таким образом,
имеем ONj==O/V2, и потому окружность (&3), концентрическая с [k/)
и проходящая через точку Л/а, проходит и через точку Л/х.
2°. Если а и а2 — точки касания окружности (k^) с прямыми Aj/4S
и ОА2, то am1 = a2N2 и А^а = А^а2, откуда А.гт1 = \N2. Точно так
же А2т3 — A2iV2 и т.д.
СМЕШАННЫЕ ЗАДАЧИ
603
604 PFUIFHHH УПРАЖНЕНИЙ И ЗАДАЧ
3°. Точки jVj и Pj пересечения окружностей (k2) и (&3) симметричны
относительно линии центров O2OS. Так как точка jV, лежит на внутрен-
внутренней общей касательной окружностей (k2') и (/г./), то и точка Pv с ней
симметричная, лежит на внутренней общей касательной tx окружностей
(&2') и (k3'), симметричной с ОА1 относительно прямой О2О3. Аналогично
точки Р2 и Ps лежат соответственно на прямых t2 и t.^.
Пусть теперь О' — точка пересечения прямых t2 и ts (черт. 694)
и /j'—касательная из точки О' к окружности (&„'). Далее пусть 5,—
точка пересечения прямых ONt и tx, S2 — точка пересечения прямых
ON2 и t2, Ss—точка пересечения прямых O/V3 и /8. Четырёхугольник
OS.fi'Ss описан около окружности (&/); в силу решения упражнения 87
имеем OS2-\-O'S2 = OSs-\-U'Sa. Четырёхугольник OSfi'S^ описан
около окружности (k2r), и следовательно, OSs-\-O'Ss^=OSlJr0'5,.
Из двух полученных равенств . имеем OSx-\-O'S1^=OS2-\-O'S2, так
что четырёхугольник OSXO'S2 — описанный. Так как три его стороны —
OSV O'S2 и (XSO — касаются окружности (k3'), то и четвёртая его
сторона O'vSj, т. е. tx, касается той же окружности. Отсюда следует,
что прямая /j' совпадает с tlt так что прямые tv t2 и ^8 проходят
через одну точку О'.
Отрезки OSS и O'S4 видны из центра Ох окружности (k^) под
равными углами как отрезки касательных к этой окружности, заклю-
заключённые между касательными ON2 и ts (упр. 89). Иначе говоря, прямые
Oft и ОХО' образуют равные углы О2ОХО и Ofift' соответственно
со сторонами ОХО2 и ОгОа треугольника 0х0„0.6; следовательно, пря-
прямые 0^0 и OjO' образуют равные углы и с биссектрисой угла О2ОгО-3.
Точно так же докажем, что прямые О2О и О2О' одинаково наклонены
СМЕШАННЫЕ ЗАДАЧИ 605
к биссектрисе угла O.SO2OV а прямые О3О и OSO' — к биссектрисе
угла ОХОЪО2. Отсю*да и следует, что точки О и О' получаются одна
из другой с помощью построения задачи 197, применённого к треуголь-
треугольнику Ofi2O^.
4°. Пусть (/j) — окружность с центром /Ц, проходящая через точки
/2, /3 и Nu равноудалённые от А1 в силу 2° (черт. 693). Так как
ON1^ON2 = ON3 в силу 1° и точка N^ лежит на прямой АХО, то
окружность (^j) касается окружности, описанной около треугольника
yVjxV2N3. Поэтому можно применить задачу 345 (сравнить примечание к
решению этой задачи) к треугольнику Л'1Л'2Л'3 и окружностям (&,),
(k2), (k3) и (Аг). Вторые точки пересечения этих окружностей Я2,
Р3, /2 и /3 также будут лежать на одной окружности, которую мы и
обозначим через (х^).
Эта окружность пересекает прямые АгА2 и AVA3 под равными уг-
углами, так как внешние отрезки секущих АХ12 и Ах1г равны, а следо-
следовательно, равны и хорды, отсекаемые окружностью (хг') на прямых
АХА2 и AXAS.
Если р и р' — точки касания окружности (&,') с прямыми А1А3 и
ts, то Д"р=Д"р', где /Г — точка пересечения прямых AvAa и Ц. Кроме
того, р/2 = p'Pg как отрезки касательных к окружности (k2'), ограниченные
концентрической с ней окружностью (k0) (треугольники О2р/2 и О,р'Я3
равны). Отсюда следует, что Kl2z=f(P3 и, следовательно, окружность
(a'j') пересекает под равными углами прямые АХА^ и tg. По той же
причине окружность (х^) пересекает под равными углами прямые АгА2
и tv
Итак, окружность (xt'), проходящая через точки Р2, Р3, 19 и ls,
пересекает под равными углами прямые А^А2 и AXAS, далее прямые
А^А3 и ta и, наконец, прямые АХА2 и t2. Следовательно, окружность (хг')
пересекает под равными углами все эти четыре прямые.
Следовательно, центр wt окружности (jcj1) равноудалён от прямых
А^А2, АгАп, (8 и (, и потому лежит на пересечении биссектрисы угла
A2AV\ с биссектрисой угла между прямыми t^ и ts, т. е. с прямой О'Оу
Так как прямые t2 и ts не зависят от выбора радиусов окружностей
(^i)i (^2) и (^з)> то отсюда и следует, что точка wl не зависит от
выбора радиусов окружностей (&Д (k2) и (ks) и что прямая О1ы1
проходит через О'.
Аналогично определяются окружности (х2') и (л:3') и их центры
си2и w8.
Так как прямые АХА2, A^A.it t2 и ts равноудалены от центра к>г
окружности (ATj'), to существует окружность (jtj), концентрическая с (*,')
и касающаяся всех четырёх прямых. Таким же образом получаются и
окружности (х2) и (х3).
5°. Прямая hi^Pq есть радикальная ось окужностей (kj и (х2),
прямая «jP2 — окружностей (&,) и (лг3г). Следовательно, точка пересече-
пересечения М этих прямых (черт. 695) есть радикальный центр окружностей
(^i). (хг) и {х3') (п. 139) и потому лежит на радикальной оси окруж-
окружностей (х2) и (л:3').
606
РЕШЕНИЯ УПРАЖНЕНИЙ И ЗАДАЧ
Пусть теперь а — точка касания окружности (k^) с прямой
7 и 7 — точки пересечения прямых t^ и t3 с той же самой прямой
А2А3, М — точка пересечения прямых пхР2 и О'а. Покажем, что
точка М совпадает с М.
Применим теорему п. 192 к треугольнику аО'Т2 и секущей пгР2.
п Р2О' п{Г2 М'а . „ „ D _
Получим —=- • ——- ¦ = 1. по Т.2Р% = Т2п1 как секущие окруж-
окружности (л:3'), равноудалённые от её центра, так что М'а:М'О' = п^а:Р2О'.
Применяя ту же теорему п. 192 к треугольнику аО'Т3 и секущей aWjP3,
Черт. 695.
найдём аналогично, что прямая /w,Pg делит отрезок аО' внешним обра-
образом в отношении от,а:Я3О'. Но mla = nla (так как О,а — перпендикуляр
к Wjfij) и О'Р2 = О'Р3, так как прямые О'Р2 и O'PS (т.е. ?, и ?,)
касаются окружности (й/) и потому равноудалены от центра Ох окруж-
окружности кх (сравнить упр. 52). Таким образом, прямые т^Р^ и пхР^ делят от-
отрезок аО' в одном и том же отношении и, следовательно, пересекаются
в точке М прямой аО'. Следовательно, точка М совпадает с М.
Итак, точка пересечения М прямых tn^Ps и пхР% лежит на прямой,
соединяющей точку касания а окружности (&,') и прямой A2AS с точкой
пересечения О' прямых гг,Лъ и t3, как бы ни были выбраны радиусы
окружностей (kx), (&s) и (k3).
Пусть теперь окружности (х2), (xs) касаются друг друга; при этом
прямая tl будет общей касательной в их точке касания. Так как одна
из точек пересечения Р% окружностей (х„г) и (х3'), концентрических
с (х2) и (л:3), лежит на прямой tv то в этом случае и вторая точка их
СМЕШАННЫЕ ЗАДАЧИ 607
пересечения будет лежать на прямой tv Прямая tx как радикальная
ось окружностей (х2') и (л:д') будет проходить через точку пересечения
М радикальной оси т^Рг окружностей (&т) и (х2) с радикальной осью
rtjP2 окружностей (&j) и (х3'). Таким образом прямая tx будет совпа-
совпадать с О'М, так как она проходит через точку О'.
Обратно, если прямая tx совпадает с О'М, то она проходит через
радикальный центр М окружностей (kx), (х2г) и (хя'). Так как она про-
проходит через одну из точек пересечения Р, окружностей (х2') и (х3г),
то она будет их радикальной осью и потому пройдёт через вторую
точку их пересечения. Окружности (х2) и (х3) касаются при этом
прямой гл на линии центров окружностей (х2') и (xsr) и, следовательно,
касаются друг друга.
УКАЗАТЕЛЬ СОДЕРЖАНИЯ ЗАДАЧ.
(Числа обозначают номера задач.)
Биссектрисы (угла, треугольника, четырёхугольника)- 2, 4 17 18 24
26, 38, 66, «6, 107, 143, 144, 230, 361, 361а, 3/8, 421. См. ещё Окружность
вневписанная, вписанная, описанная треугольника.
Высоты треугольника: 17, 19, 20, 38, 70, 71, 101, 102, 136, 158, 197, 350.
Гармонизм:~125, 217, 219а, 239.
Геометрическое место: 31, 48, 53, 57, 60, 124, 133, 134, 141, 142, 149,
193, 238, 246, 257.
Деление отрезка: 1, 78, 173.
Деление площадей: 293, 295, 303, 304, 321—323, 327, 328.
Длина окружности (приближённые построения;: 188, 189.
Знаки отрезков, площадей, углов: 324, 344, 347.
Инверсия: 245, 247—253, 270, 270а, 273, 275, 387, 338, 389, 390, 396.
Инверсор: 271, 271а.
Касание окружностей: 58, 59, 91, 112, 187, 266, 267, 393, 394, 398—400.
См.. ещё Построение окружности.
Касательные к окружности: 89, 90, 93, 104, 135; — общие к двум окруж-
окружностям: 200, 347.
Медианы треугольника: 7, 11, 12, 17, 18, 29, 33, 39, 137, 144, 145, 326.
См. еще Центр тяжести треугольника.
Менелая теорема: 223.
Многоугольник вообще: 8а, 22, 117, 194;— вписанный (в том числе и тре-
треугольник вписанный): 115, 253а, 367,391;—правильный: 178—184, 298, 331,
419а. См. ещё Четырёхугольник.
Наибольшее и наименьшее: 13, 15, 32, 40, 54, 56, 174—176, 219 268, 291
319, 320, 331, 362—364, 366, 367, 415—418, 419а, 420.
Окружность — вневписаиная, вписанная и описанная треугольника: 70
72, 90а, 101а, 103, 108, 158, 228, 299, 300, 357, 377, 379, 411; —девяти точек: .
101, 374, 376;—сопряжённая с треугольником: 2S3, 284. См. ещё Касание,
Касательные, Пересечение, Построение.
Ось радикальная: 154, 177, 220, 245, 256, 272, 408.
Параллелограм: 26—28, 41, 109, 132, 138, 234, 290, 296.
Паскаля теорема: 279.
Перемещения: 92, 93, 94.
Пересечение окружностей: 65, 69, ПО, 128, 256, 346, 355, 395.
Построение окружностей: 73, 74, 176, 177, 209, 258, 259, 263—265, 280,
401—403а;—треугольника: 77—85, 103а, 169—171,203,204, 332, 415, 416;
— четырёхугольника: 118, 122, 213, 319, 320, 333, 351, 418—419.
Равносоставленность: 334—337.
Симеона прямая: 72, 373, 374.
Стюарта теорема: 218.
Точка наименьшего расстояния: 10, 105, 363, 364.
Точки предельные двух окружностей: 152, 219, 241, 278.
Точки изогонально-сопряжённые: 197, 365.
Трапеция: 34, 129, 130, 205, 221, 292, 297. См. ещё Построение четырёх-
четырёхугольника.
Треугольники — равнобедренный: 5, 19, 39, 42,361; — прямоугольный:
16, 30, 136, 309, 310; —равносторонний: 42, 99, 100, 269, 287. См. ещё Бис-
Биссектрисы, Высоты, Медианы, Многоугольник вписанный, Окружность, По-
Построение, Центр тяжести.
Фигуры —гомотетичные: 159;—подобные: 161, 162, 212, 214, 215, 380;—
построенные на сторонах многоугольника или треугольника: 45, 105, 211,
309—311, 363, 381;—равные: 92, 93, 95.
Центр подобия: 220, 272;—тяжести треугольника-. 37, 131, 140, 158,
221, 295, 365.
Четырёхсторонник полный: 106, 240, 371, 371а, 373.
Четырёхугольник вообще: 9, 10, 25, 36, 66, 123, 139, 270, 293, 294, 372,
418а, 421;—вписанный: 107, 147, 239, 282, 286, 345, 362а, 387, 407,421а;
— описанный: 87, 198,239,282,384,385. См. еще Параллелограм, Построение,
Трапеция.
4»