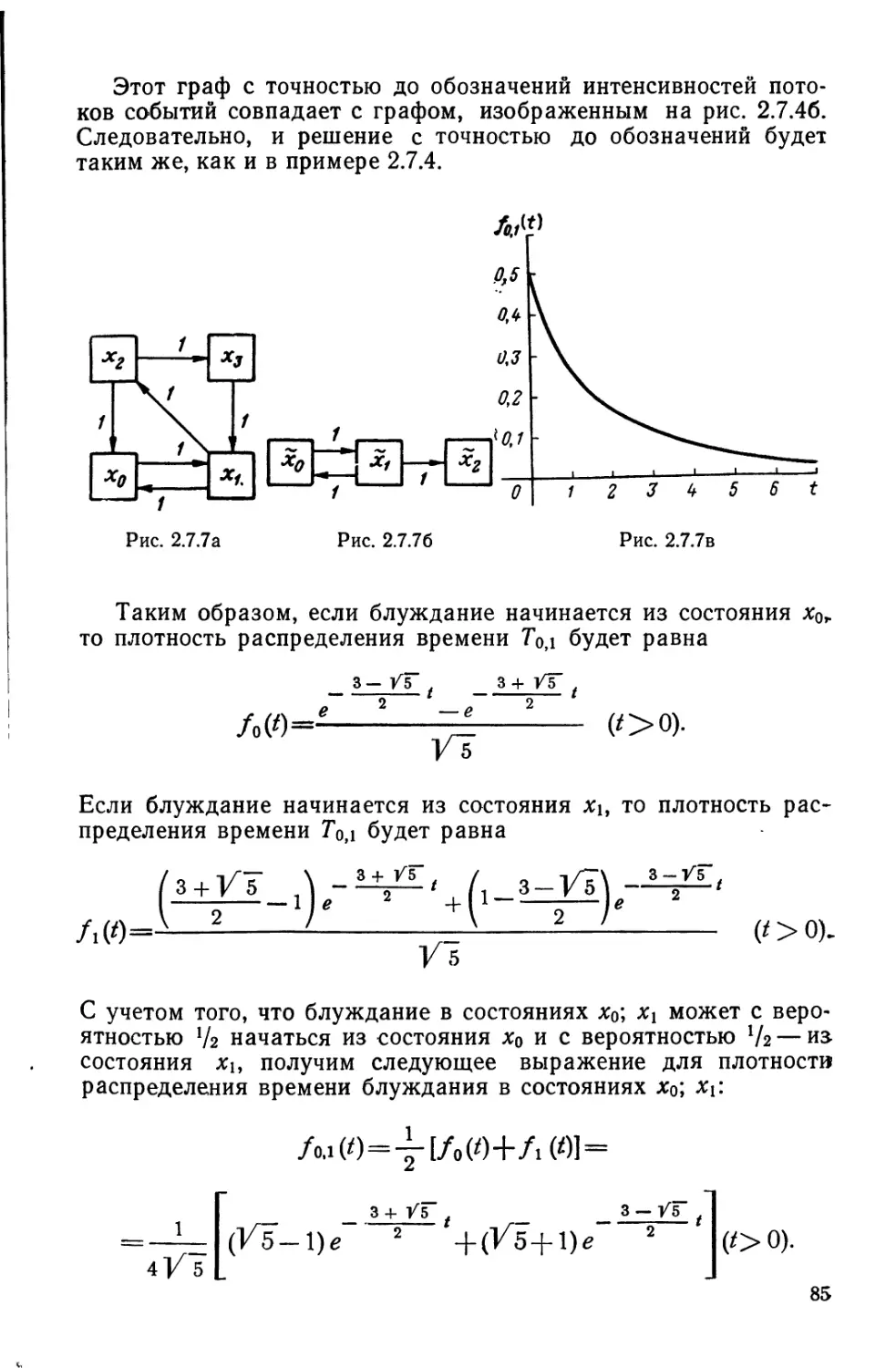
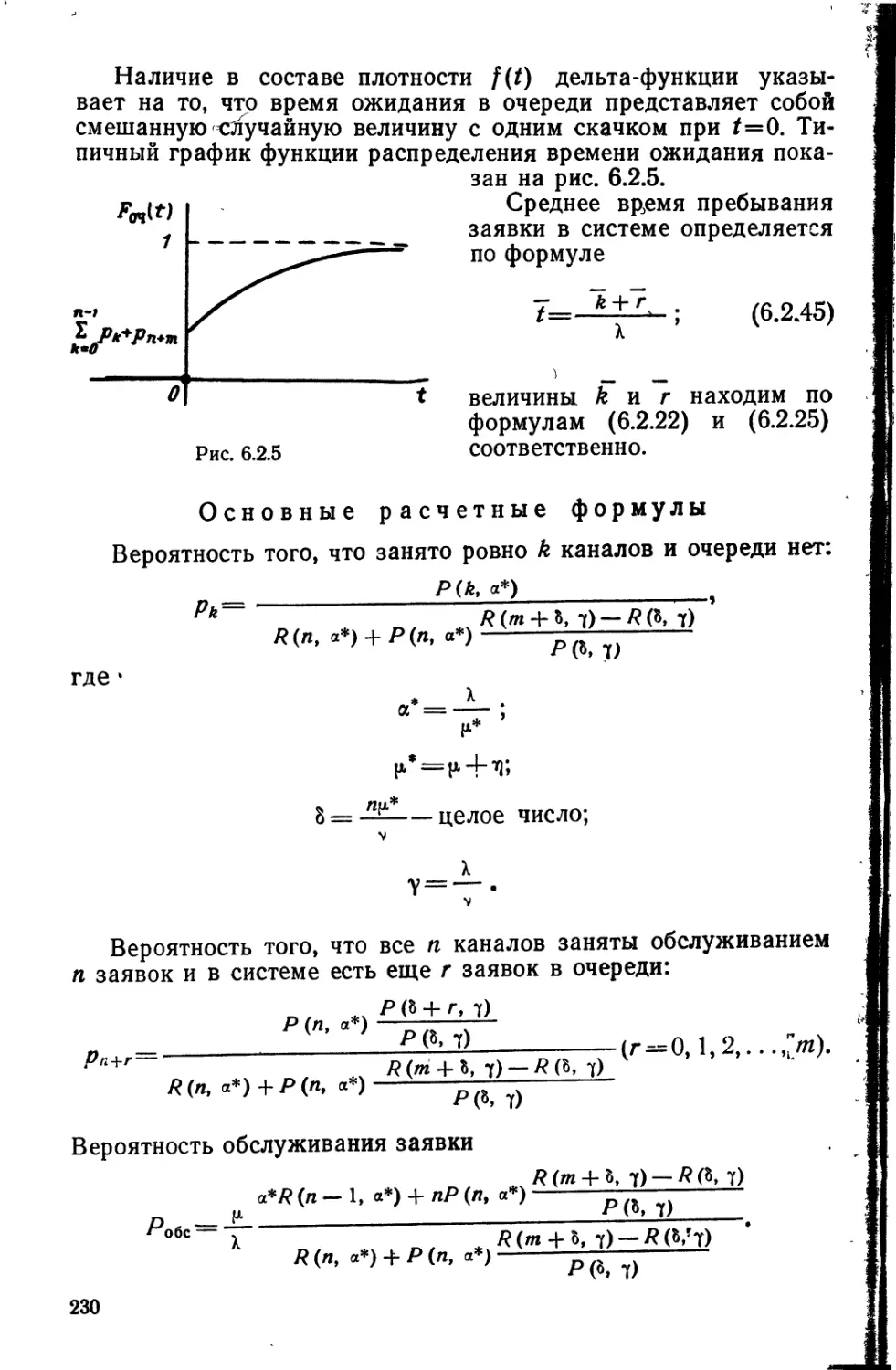
Author: Овчаров Л.А.
Tags: теория вероятностей и математическая статистика экономика менеджмент массовое обслуживание
Year: 1969
Text
Прикладные
задачи
теории
массового
обслуживания
Л. А. ОВЧАРОВ
ПРИКЛАДНЫЕ ЗАДАЧИ
ТЕОРИИ МАССОВОГО
ОБСЛУЖИВАНИЯ
ИЗДАТЕЛЬСТВО
«МАШИНОСТРОЕНИЕ»
Москва 1969
УДК 519.2(01)
В книге изложена прикладная теория массового обслужи-
вания и ее применение в различных областях инженерной
практики. Задача обслуживания решается при условии, что
структура потока заявок носит случайный характер (заявки
поступают в случайные моменты времени) и обслуживание
длится случайное время. Основное внимание в книге уделено
вопросам обслуживания пуассоновских стационарных потоков
заявок. Предполагается, что время обслуживания заявок в ка-
нале распределено по показательному закону.
Подробно проанализированы стационарные режимы работы
различных систем массового обслуживания. Приводятся фор-
мулы, по которым можно рассчитывать характеристики, описы-
вающие пропускную способность систем массового обслужива-
ния, а также временные характеристики работы каналов и про-
хождение заявок на различных этапах обслуживания. При
этом все расчеты конкретных характеристик систем массового
обслуживания по формулам проводятся с помощью функций
распределения Пуассона. В книге большое количество гипоте-
тических примеров с числовыми расчетами. Она может слу-
жить руководством для решения различных инженерных и
экономических прикладных задач типа задач теории массового
обслуживания.
Книга рассчитана на широкий круг специалистов, занимаю-
щихся решением задач исследования операций, она представ-
ляет также интерес для преподавателей и студентов втузов.
Табл. 1. Иллюстр. 130. Библ. 24 назв.
Рецензент д-р техн, наук проф. Л. Т. Кузин
Науч. ред. д-р техн, наук проф. Е. С. Вентцель
2-2-4
371-68
ПРЕДИСЛОВИЕ
Теория массового обслуживания является до некоторой сте-
пени частью теории вероятностей и, опираясь на ее аппарат, в по-
следнее время становится самостоятельной наукой. Это объ-
ясняется теми важными практическими задачами, которые она
может решать.
Примерами таких задач могут служить задачи анализа рабо-
ты аэродрома, телефонного узла связи, морского порта, магазина,
системы противовоздушной обороны (ПВО), многостаночного
цеха и т. п. Общим для всех этих задач является необходимость
количественного анализа процесса «обслуживания» различных
заявок, например, самолетов, взлетающих с аэродрома и произ-
водящих на нем посадку; абонентов, обращающихся на автома-
тическую телефонную станцию (АТС) для соединения с другими
абонентами; судов, прибывающих в порт для разгрузки и погруз-
ки; покупателей, обращающихся в магазин за покупками; само-
летов, обстреливаемых системой ПВО, и т. д. Заявки поступают
на обслуживание в различные, вообще случайные моменты вре-
мени, образуя так называемый «поток заявок». Потоки заявок
могут иметь различную структуру и интенсивность (частоту по-
ступления заявок). Следовательно, для решения задач теории
массового обслуживания нужно прежде всего уметь анализиро-
вать потоки заявок. В первой главе книги рассматриваются раз-
личные потоки и проводится исследование основных характери-
стик этих потоков. Так как заявки следуют друг за другом в
случайные моменты времени, то для анализа потоков заявок
широко привлекается аппарат теории вероятностей.
Исследование работы любой системы массового обслужива-
ния приводит к необходимости анализировать своеобразный слу--
чайный процесс, связанный с переходами этой системы из одного
3
состояния в другое. Например, при работе автоматической теле-
фонной станции она может быть некоторое время занята, а в
другое время — свободна. Если АТС занята, а в этот момент
абонент обращается с вызовом, то он получает отказ (в трубке
частые гудки — «занято»). При анализе таких случайных процес-
сов в книге широко применяется новый методический прием,
в основу которого положено составление «размеченного графа
состояний» (гл. 2). Применение размеченных графов состояний
облегчает математическое исследование случайных процессов и
делает его более наглядным.
Многочисленные расчеты, проведенные при решении различ-
ных задач теории массового обслуживания, показывают, что в
большинстве случаев удовлетворительное по точности решение
можно получить, приняв допущение о том, что все потоки, воз-
действующие на систему, являются пуассоновскими, т. е. что про-
цесс функционирования системы представляет собой марковский
случайный процесс с непрерывным временем. Поэтому в книге
рассматриваются только так называемые пуассоновские системы
массового обслуживания. Основное внимание уделено стацио-
нарным режимам работы.
Сама система массового обслуживания можег состоять из од-
ного или нескольких каналов обслуживания. Например, если рас-
сматривать работу аэродрома с одной взлетно-посадочной поло-
сой (ВПП), то можно считать, что мы имеем дело с одноканаль-
ной системой массового обслуживания. Если рассматривается
работа морского порта с п причалами, где производится разгруз-
ка и погрузка судов, то можно считать, что мы имеем дело с
n-канальной системой массового обслуживания.
Работа каждого канала обслуживания носит, как правило,
случайный характер. Например, при анализе работы морского
порта время разгрузки и погрузки судна зависит от различных
причин: вида груза, его количества, квалификации портовых ра-
бочих и т. п. Поэтому время обслуживания каждой заявки будет
случайным.
Таким образом, работа системы массового обслуживания за-
висит от вида и внутренней структуры потока заявок, поступаю-
щих на обслуживание, числа каналов обслуживания п и закона
распределения времени обслуживания заявки каждым каналом.
Помимо этого, на работу системы значительное влияние оказы-
вают правила (алгоритм) обслуживания. Правила обслуживания
4
предусматривают все особенности поведения заявки, поступив-
шей в систему. К таким правилам прежде всего относятся прави-
ла образования очереди из заявок, нуждающихся в обслужива-
нии. Могут рассматриваться такие правила, когда очередь вооб-
ще не допускается (гл. 4). В других системах массового обслу-
живания допускается образование ограниченной (или неограни-
ченной) очереди (гл. 5). Особое место занимают системы массо-
вого обслуживания с «нетерпеливыми» заявками, когда заявка
может покинуть очередь (или вообще систему), не дождавшись
конца обслуживания (гл. 6). Наиболее типичным примером си-
стемы массового обслуживания с «нетерпеливыми» заявками
является система ПВО: самолет (заявка) стремится вылететь из
зоны обстрела ПВО, «не дождавшись своего обслуживания»
(поражения). Рассматриваются такие системы массового обслу-
живания, в которых допускается «взаимопомощь» между кана-
лами при обслуживании заявок.
Существуют и такие правила, когда заявки определенного ви-
да должны обслуживаться без очереди (иметь приоритет в об-
служивании). Примером такой системы может служить аэро-
дром с одной взлетно-посадочной полосой (ВПП): самолетам,
идущим на посадку, ВПП предоставляется в первую очередь.
При рассмотрении вопросов обслуживания (эксплуатации)
технических устройств (ТУ) мы сталкиваемся с такими условия-
ми, когда определенное количество ТУ должно обслуживаться
несколькими каналами обслуживания. Например, при рассмотре-
нии работы автохозяйства, в котором имеется т машин, возника-
ет вопрос о том, сколько нужно иметь мест для их обслуживания.
Если этих мест будет мало, то машины, нуждающиеся в ремон-
те, будут длительное время простаивать. Если мест ремонта бу-
дет очень много, то машины не будут простаивать, но ремонтные
бригады будут слабо загружены. Такие системы массового об-
служивания рассмотрены в гл. 7.
Перечисленные выше примеры свидетельствуют о разнообра-
зии инженерных задач, которые можно решать методами теории
массового обслуживания. Общим для всех этих задач являются
два следующие положения:
— наличие потока заявок, нуждающихся в обслуживании;
— наличие каналов, где производится обслуживание посту-
пивших заявок.
При написании данной книги автор не ставил себе цель под-
5
робно изложить современную теорию массового обслуживания.
Поэтому применяемый в книге математический аппарат не
выходит за рамки обычного втузовского курса высшей матема-
тики. В основу книги положены лекции, прочитанные автором в
Московском физико-техническом институте и в других высших
учебных заведениях и организациях.
Автор считает своим приятным долгом выразить искреннюю
благодарность своему учителю и товарищу по работе профессору
Елене Сергеевне Вентцель за ту помощь, которую она постоянно
оказывала при работе над этой книгой, начиная от первоначаль-
ного замысла написания этой книги и кончая ее редактирова-
нием.
Автор также приносит глубокую благодарность академику
АН УССР Б. В. Гнеденко, любезно согласившемуся просмотреть
рукопись и сделавшему ряд ценных замечаний, и профессору
Л. Т. Кузину, советы и предложения которого оказали автору
существенную помощь.
Март 1968 г.
Глава 1
ПОТОКИ СОБЫТИЙ
§ 1.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Потоком событий называется последовательность событий,
происходящих одно за другим в какие-то случайные моменты
времени. Примерами могут служить: поток вызовов, поступаю-
щих на АТС; поток изготовленных деталей, поступающих в ОТК
завода; поток машин, нуждающихся в заправке горючим; поток
самолетов, приземляющихся в данном аэропорту; поток заби-
тых в ворота шайб при игре в хоккей и т. п. Различают потоки
однородных и неоднородных событий. Например, по-
ток самолетов, приземляющихся на аэродроме, будет однород-
ным, если не различать самолеты по типам. Если же мы будем
различать типы самолетов (ТУ-104, ИЛ-18 и т. д.), тот же поток
будет уже неоднородным. В
главным образом потоки од-
нородных событий. События
в однородном потоке разли-
чаются только моментами
появления.
Поток событий можно
графически представить как
последовательность точек ti,
вующих моментам появления событий (рис. 1.1.1).
Потоки событий различаются по своей внутренней структуре.
Самым простым потоком с точки зрения его построения является
«регулярный поток». Регулярным потоком называется поток, в
котором события следуют одно за другим через строго опреде-
ленные промежутки времени. Строго регулярных потоков в при-
роде не существует, так как моменты появления событий всегда
содержат элемент случайности. Однако даже как идеализирован-
ная схема, регулярный поток не имеет преимуществ, так как
уступает по простоте расчетов, как мы увидим в дальнейшем,
Другим типам потоков.
Рассмотрим поток, в котором события разделены интервала-
ми времени Тх, Т2,... (рис. 1.1.2.).Эти интервалы вообще являются
7
дальнейшем будем рассматривать
Рис. 1.1.1
t2, ... на числовой оси Ot, соответст-
случайными величинами. Пусть интервалы 7\, Т2, ... независимы
между собой. В этом случае поток событий называется потоком
с ограниченным последействием или потоком Пальма. Примером
потока Пальма может служить поток деталей, обтачиваемых то-
карем на станке, если время изготовления каждой очередной де-
тали не зависит от времени изготовления всех предыдущих де-
талей.
Поток событий называется ординарным, если вероятность
того, что на малый участок Д/ (рис. 1.1.3), примыкающий к мо-
Рис. 1.1.2
Рис. 1.1.3
менту времени t, попадет больше одного события (Р>1(/, ДО)г
пренебрежимо мала по сравнению с вероятностью того, что на
этот же интервал времени попадет ровно одно событие
(Р>4, АО):
Д/). (1.1.1)
Так как для любого интервала Д/
P^i, ДО + Л(Л A0 + /W, д0=1 (1-1-2)
как сумма вероятностей событий, образующих полную группу и
несовместных, то для ординарного потока событий
P0(f, д0 + Л(^ д0~1, (1.1.3)
/>>!(/, ДО=О (Д/), (1.1.4)
где О (ДО—величина, порядок малости которой выше, чем
ДО т. е.
11m -^=0. (1.1.5)
Д/->0 Дг
Примерами ординарных потоков являются поток машин,
пересекающих заданную линию на шоссе (даже с многорядным
движением); поток самолетов, приземляющихся на аэродром;
поток выстрелов, осуществляемых из нескольких орудий и т. п.
Неординарные потоки событий встречаются на практике
реже, чем ординарные потоки событий. Примером неординар-
ного потока событий может быть поток пассажиров, прибываю-
щих в лифте на данный этаж. В этой книге будут рассматри-
ваться только ординарные потоки событий.
Стационарным потоком событий называется поток, для кото-
рого вероятность появления того или другого числа событий на
8
участке времени т зависит лишь от длины этого участка и не
зависит от того, где на оси времени взят этот участок. Очевидно,
регулярный поток с одинаковыми интервалами между события-
ми, а также поток Пальма с одинаково распределенными интер-
валами времени Ть Т2, ... представляют собой стационарные по-
токи.
Рассмотрим на оси (М ординарный поток событий и найдем
среднее число событий, наступающих на интервале времени А/,
примыкающем к моменту времени t (рис. 1.1.3). В соответствии
с приближенным равенством (1.1.3) оно будет
О-Ро(/, Д*)-Н-Л(Л Д*) = Л(Л д0-
Среднее число событий, наступающих на участке времени А/
в единицу времени, составит
-1(t (1.1.6)
Рассмотрим предел выражения (1.1.6) при А/—>0. Если этот
предел существует, то он называется интенсивностью (плотно-
стью, параметром) ординарного потока:
lim P1 (<’Л/) =а (/). (1.1.7)
Д/-.0 Д/
Интенсивность потока может быть любой неотрицательной
функцией времени. Она имеет размерность, обратную размерно-
сти времени Для стационарного потока его интенсив-
ность не зависит от времени и представляет собой постоянную
величину, равную среднему числу событий, наступающих в еди-
ницу времени:
k(/) = k = const
§ 1.2. ЗАКОН РАСПРЕДЕЛЕНИЯ УЧАСТКА ВРЕМЕНИ,
НА КОТОРЫЙ ПАДАЕТ ТОЧКА
В этом параграфе будет рассмотрена внутренняя структура
одного частного вида стационарного потока Пальма, у которого
все интервалы между соседними событиями взаимно независи-
мы и распределены одинаково с функцией распределения F(t) *.
Пусть имеется стационарный поток Пальма (рис. 1.2.1), изо-
браженный на оси 0Л Допустим, что на эту ось падает случайным
образом точка S, отмеченная на рис. 1.2.2 крестом, причем поло-
жение точки S никакие связано с моментами появления событий.
* Такие потоки иногда называют рекуррентными.
9
Требуется определить закон распределения того участка Т*, на
который упала точка S.
Такая ситуация возникает в различных прикладных задачах.
Например, пассажир появляется на автобусной остановке в
какой-то случайный момент времени, не связанный с расписа-
нием движения. Требуется найти закон распределения интервала
времени между уходом предыдущего автобуса и приходом сле-
дующего при условии, что пассажир уже стоит на остановке, а
поток автобусов является стационарным потоком Пальма. Закон
Рис. 1.2.1 Рис. 1.2.2
распределения интервала времени Т* между появлением двух
автобусов, на котором появился пассажир (на который упала
точка S), в общем случае не совпадает с законом F(f). Этот на
первый взгляд парадоксальный факт можно пояснить на следу-
ющем простом примере.
Допустим, что интервал времени Т (в часах) между появле-
нием двух соседних по времени автобусов может принимать
только два значения: /1=0,8 с
вероятностью 0,5 и /2=0,2 с веро-
ятностью 0,5. Тогда на оси 0/ бу-
дем иметь поток, в котором с оди-
наковой частотой будут встре-
чаться длинные (0,8) и короткие
(0,2) участки (рис. 1.2.3).
Предположим, что пассажир
появился на остановке в какой-
Рис. 1.2.3
4—»
О
нибудь момент времени. Что вероятнее — что он попадет на уча-
сток длины 0,8 или на участок длины 0,2? Очевидно, первое более
вероятно: отрезков 0,8 и 0,2 на оси 0/ в среднем одинаковое коли-
чество, но отрезок 0,8 длиннее в 4 раза, значит, отрезки 0,8 зани-
мают на оси в среднем в 4 раза большую протяженность, чем
отрезки 0,2; следовательно, вероятность попадания точки S на
отрезок 0,8 равна уже не 0,5, а 0,8, а вероятность попадания на
отрезок 0,2 равна 0,2. На этом простом примере можно убедиться
в том, что закон распределения того промежутка, на который
попала точка S, в общем случае не совпадает с его априорным
законом распределения.
Решим эту же задачу в общем виде. Пусть априорная функ-
ция распределения случайной величины Т-интервала между
двумя соседними событиями есть F(/), а плотность распределе-
ния f (/) (если случайная величина Т является дискретной слу-
чайной величиной, то плотность распределения может быть вы-
10
ражена через дельта-функцию, о которой подробнее будет сказа-
но ниже). Найдем плотность распределения f*(t) того интервала
Т*, на который случайным образом упала точка S.
Для этого найдем /* (/) dt — вероятность того, что точка S
попадает на промежуток, длина которого заключена в интервале
(t, t+dt). Эта вероятность приближенно равна отношению сум-
марной длины таких промежутков на очень большом интервале
времени к полной длине интервала. Пусть на очень большом ин-
тервале уложилось большое число N промежутков. Среднее
число промежутков, длина которых лежит в пределах (t, t+dt),
равно Nf(t)dt\ средняя суммарная длина всех таких промежут-
ков будет tNf(t)dt. Средняя общая продолжительность всех N
промежутков равна mtN, где
т—М[Т] = ^ tdF (t)=\tf(t)dt (1.2.1)
О 6
— математическое ожидание случайной величины Т.
Следовательно:
/* (/) dt « - = — f (t) dt. (1.2.2)
Nmt mt
Это равенство выполняется тем точнее, чем более длитель-
ный промежуток времени рассматривается (чем больше N).
В пределе при N—><х> закон распределения случайной величи-
ны Т* будет иметь вид
f (f) при / ~> 0;
(1.2.3)*
0 при /<Д. .
Можно убедиться в том, что функция f* (t) обладает всеми свой-
ствами плотности распределения.
Определим числовые характеристики (математическое ожи-
дание и дисперсию) случайной величины Т*. Для решения этой
задачи (и ряда задач в дальнейшем) воспользуемся аппаратом
характеристических функций. Напомним, что характеристической
функцией случайной величины Т называется функция g(x), опре-
деляемая из выражения
оо
£(л)=7И[^П= f e“'/(t)dt, (1.2.4)
— ОО
где f(t)—плотность распределения случайной величины Г.
Характеристическая функция безразмерна, а ее аргумент х име-
ет размерность, обратную размерности случайной величины Т.
Тот же результат можно получить, применяя формулу Бейеса.
11
Напомним следующие основные свойства характеристической
функции:
1. Характеристическая функция суммы п независимых слу-
чайных величин
= (1.2.5)
1=1
равна произведению характеристических функций этих величин:
£(«)(*)= (1.2.6)
/=1
где gi(x) — характеристическая функция случайной величины Л*.
Если складывается п независимых одинаково распределенных
случайных величин с характеристической функцией g(x), то
^)W = (g(x))". (1.2.7)
2. Характеристическая функция по модулю не превышает
единицы
|g(x)|<l (1.2.8)
для любого X.
3. Для определения числовых характеристик случайной вели-
чины Т пользуются равенствами
g(0)=i;
ПО)=(-£г(х))„о=Ш1П (1М)
г»(°) = (£г(^ =-Л1Р|;
следовательно:
ЛЦГ]=-/£'(0);
(1.2.10)
- g"(0)+(g'(0))2.
4. Плотность распределения случайной величины Т выра-
жается через ее характеристическую функцию преобразованием
Фурьё:
/(/)=J- e-itxg(x)dx. (1.2.11)
—— оо
5. Если случайная величина Т имеет характеристическую
функцию gt(x), то случайная величина Y=aT имеет характери-
стическую функцию gy(x) =gt(ax).
12
Вернемся к решаемой задаче. Найдем характеристическую
функцию случайной величины Т* — интервала, на который слу-
чайным образом упала точка S:
g*(x)= ? eUxf*(t)dt= ( e,tx-^-dt.
J J mt
—• oo — oo
Заметим, что
teitx^ — i — eitx.
dx
В этом случае
g*(x)=-i — e!tx-^-di=-^-^ , (1.2.12)
dx J mt mt
— oo
где g(x.)—характеристическая функция случайной величи-
ны Т — интервала между любыми двумя событиями
в исходном потоке Пальма;
mt — математическое ожидание случайной величины Т.
В соответствии с формулой (1.2.10) окончательно получим
(1.2.13)
По формулам (1.2.9), (1.2.10) найдем числовые характеристи-
ки случайной величины Т*:
mtt.=-.M[r] = Sl^ = ^L^L = mt+— • (1.2.14)
i ig' (0) mt
Анализируя формулу (1.2.14), видим, что математическое
ожидание интервала Т*, на который случайным образом падает
точка S, в общем случае всегда больше, чем математическое
ожидание произвольно взятого участка Т. Лишь в случае регу-
лярного потока событий, когда случайные интервалы Т вырожда-
ются в неслучайные интервалы длительностью mt и Dt — 0,
математическое ожидание mt* будет равно mt. Таким образом,
указание на то, что случайная точка S попала на какой-то интер-
вал, как бы увеличивает его среднюю длину по сравнению с тем,
как мы оценивали бы ее без этого указания.
Найдем дисперсию случайной величины Т*, для чего перво-
начально определим g"*(0):
(0)- -- 8"'(0) [Л]ш[ГЗ]- А|[ГЗ]
1 g' (0) g\(0) IM IT] M [TJ ’
откуда
- g* (0) -I- (g '* (0))2= M t (1.2.15)
mt mi
13
' где M[T3J, Л4[Т1 2] — третий и второй начальные моменты случай-
ной величины Т.
Дисперсия D{T*] может быть как больше, так и меньше дис-
персии Dt,
§ 1.3. ЗАКОН РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ДО НАСТУПЛЕНИЯ
ОЧЕРЕДНОГО СОБЫТИЯ
Рассмотрим на оси О/ стационарный поток Пальма и возьмем
произвольную точку S, которая случайным образом занимает на
этой оси любое положение (рис. 1.3.1). Как было показано
в § 1.2, интервал Г* распределен не так, как любой интервал
между событиями. Если интервал Т имел плотность распределе-
ния /(/), то интервал Т* имеет плотность распределения /*(/) =
= —/(/)• В этом параграфе нас будет интересовать закон рас-
mt
пределения остатка времени 0 от
точки S до момента наступле-
ния очередного события при
условии, что плотность рас-
пределения f(t) интервала Т
нам известна.
Для решения этой задачи
введем в рассмотрение гипо-
Рис- 131 тезу, состоящую в том, что
интервал Т*, на который
упала точка S, принял значение, лежащее на элементарном уча-
стке (/*,
Вероятность этой гипотезы будет f* (f)dt*—----------dt*.
В предположении, что эта гипотеза имела место, найдем услов-
ную плотность распределения случайной величины О-ирфр*).
Так как положение точки S на числовой оси 0/ не зависит от
распределения событий в потоке, то нет никаких оснований счи-
тать какой-либо участок интервала t*, на который упала точка S,
более вероятным для положения этой точки, чем другой. Поэто-
му точка S на интервале времени t* будет распределена с рав-
номерной плотностью:
1
t*
о
при ft cz (0, t*\
при ОфО, /*).
(1.3.1)
Плотность распределения системы случайных величин 0 и Г*
будет
/(Г,
14
откуда, учитывая (1.3J), найдем
ео оо
<?(»)= /(/*, &)Л*= J /•(Г)Т(Я|Г)Л*,
— оо — ео
Так как согласно формуле (1.3.1) подынтегральная функция
отлична от нуля только при /*>&, получим
оо со
J Uli J /71/ t ITlf
—-оо Я
где F(t)—функция распределения случайной величины Т:
F(t) = ^f(t)dt.
О
Таким образом, плотность распределения остатка времени 0
от случайного момента S до момента наступления очередного
события будет иметь вид
. ?(&)=
при 0>О;
при & < 0,.
(1.3.2)
О
где fnt — M[T] — математическое ожидание случайной величи-
ны Г — интервала между любыми двумя собы-
тиями.
Найдем числовые характеристики случайной величины 6, Для
этого определим характеристическую функцию gt (х) случайной
величины 0:
•о оо
go (x)= С 6'^(0) \ 6'^(1 -F(0))d0.
J mt J
— co 0
Применим интегрирование по частям:
1-F(O) = «; -/(&)</»;
J»x
v =----.
ix
Тогда
g»(x)=^~ 0-FW)-77-+
nti \ IX J IX
L о 0
15
где g(x) — характеристическая функция случайной величины Т.
Учитывая равенства (1.2.9) и (1.2.10), окончательно получим
<1ЛЗ)
Теперь найдет числовые характеристики случайной величины 0:
М[0] и D[0]- В соответствии с формулами (1.2.10) и (1.3.3) будем
иметь
/ПП = Л1 [61 = -J—(-g- М fg,U)x-g(x)+1| .
mti^ ( dx \ x /)x=o mt ( Jx=o
(1.3.4)
При подстановке в (1.3.4) величины х = 0 получается неопреде-
0 ГТ
ленность вида —. Для раскрытия этой неопределенности вос-
пользуемся правилом Лопиталя:
, ----L Um + (х) = g"(0)
mt д-->о 2х 2mt
Но в соответствии с (1.2.10)
- g" (0)=а2 Г]=М [Г] =-- Dt+ml
£l'
mt .
(1.3.5)
откуда окончательно получим
mt Df 1
=------1----= —
0 2 1 2mt 2
[см. (1.2.14)].
Следовательно, математическое ожидание остатка времени 0
всегда не меньше, чем половина математического ожидания лю-
бого интервала между событиями в стационарном потоке
Пальма.
Для нахождения дисперсии интервала времени 0 до наступ-
ления очередного события нужно найти вторую производную
характеристической функции ge (х):
- = 1 Z"X<1 — 2хё' + 2^~ 2
Раскрывая неопределенность, которая получается при х^0,
получим
ХЗ
(1.3.6)
г;(0)=<Э_Щ
S0V ' 3mzi 3mt
откуда (см. (1.2.10)] дисперсия случайной величины 0 будет
D [0]= -ge'(0)+(gi(0))2=^— • (1.3.7)
6mt 4m;
16
Нами рассматривалась случайная величина 0 — интервал
между точкой S и первым наступившим после точки S событи-
ем. Аналогичные рассуждения можно провести относительно
случайной величины Н — интервала между последним наступив-
шим событием в прошлом и точкой S (см. рис. 1.3.1.) Закон
распределения случайной величины Н будет таким же, как и слу-
чайной величины 0. Случайные величины 0 и Н в общем случае
будут зависимыми. При этом всегда будет выполняться условие
§ 1.4. ПУАССОНОВСКИЙ ПОТОК СОБЫТИЙ
Среди потоков событий особое место занимает так называе-
мый «пуассоновский поток», обладающий, по сравнению с дру-
гими, рядом замечательных свойств, существенно облегчающих
решение прикладных задач теории массового обслуживания.
. Ъ г|
1 • • ♦ —«I I » I—•— ч
/7 Х1 Х2 to
Рис. 1.4.2
Рис. 1.4.1
Пуассоновским потоком событий называется поток, обладаю-
щий двумя свойствами — ординарностью и отсутствием после-
действия. Понятие ординарности было рассмотрено в § 1.1. Здесь
поясним смысл термина «отсутствие последействия».
Поток называется потоком без последействия, если для лю-
бых двух неперекрывающихся участков Ti и т2 (рис. 1.4.1) число
событий, попадающих на один из них, не зависит от того, сколь-
ко событий попало на другой.
Обозначим случайное число событий, наступивших на ин-
тервале времени ть через Xi и на интервале времени т2— че-
рез Х2. Для потока без последействия случайные величины Xi
и Х2 независимы, т. е. вероятность того, что на участке т2 насту-
пит определенное число событий т2, не зависит от того, сколько
событий пгх наступило на участке времени тг.
Р(Х2_m2| X х=тпх)== Р — m2) (т^О, 1,2,...;
дг2 = 0, 1,2...). (1.4.1)
В курсах теории вероятностей доказывается, что для пуассонов-
ского потока число событий X, попадающих на любой интервал
длины т, примыкающий к точке t (рис. 1.4.2), распределено по
закону Пуассона:
Pt- (Х=т)=(а (^,Т))- (1-4.2)
17
где
a(t, т)—среднее число событий, наступающих на интервал,
ле времени т, примыкающем к моменту времени t.
Поэтому поток и называется «пуассоновским».
Среднее число событий, наступающих в единицу времени,
для любого ординарного потока равно интенсивности потока
Х(0- Следовательно, среднее число событий, наступающих на
интервале времени т, примыкающем к моменту времени /, будет
равно
a(t, т)= [ (1.4.3)
7
Если пуассоновский поток событий является стационарным
[Х(0 = Х=const], то величина а не будет зависеть от /:
а (/, т) = а(т)= \dt=Хт. (1-4.4)
7
В этом случае вероятность того, что на произвольно выбранном
участке времени продолжительностью т наступит т событий, оп-
ределяется по формуле
/< (Х = т)=^-^- е-'\ (1.4.5)
Стационарный пуассоновский поток событий часто называют
простейшим потоком. Так он назван потому, что применение
простейших потоков событий
при анализе различных систем
_ массового обслуживания при-
* водит к наиболее простым ре-
шениям.
Рис- 1-4.3 Найдем закон распределе-
ния интервала времени Т меж-
ду двумя любыми соседними событиями в простейшем потоке
(рис. 1.4.3). Вероятность того, что на участке времени t, следую-
щем за одним из событий, не появится ни одного события [см.
(1.4.5)], будет
pt(X=0) = e~u <‘>.
Но эта вероятность равна вероятности того, что случайная вели-
чина Т будет больше величины t. Следовательно:
Р(Г>0=е-и,
(*> Вследствие отсутствия последействия наличие события в начале участка
не оказывает влияния на вероятность появления того или другого числа собы-
тий на самом участке.
18
откуда
F(t) = P(T<f)=l-P(T>t)=l-e-u (/>0), (1.4.6)
где F(t)—функция распределения случайной величины Т.
Дифференцируя (1.4.6), получим плотность распределения слу-
чайной величины Т:
= (/>0). (1.4.7)
Таким образом, в простейшем потоке интервал времени меж-
ду любыми двумя соседними событиями распределен по показа-
тельному закону с параметром X. Вследствие отсутствия после-
действия все интервалы между соседними событиями представ-
ляют собой независимые случайные величины. Поэтому простей-
ший поток представляет собой стационарный поток Пальма. Он
отличается тем, что интервалы времени между соседними собы-
тиями распределены по по- ,
казательному закону. -------*
Рассмотрим на оси 0t t ж | <r г t
простейший поток и точку S, 0 е *
случайным образом падаю-
щую на эту ось. Найдем за- Рис- 14,4
кон распределения того
участка Г*, на который упала точка S (рис. 1.4.4). Воспользуем-
ся результатами, полученными в § 1.2. В соответствии с (1.2.3)
плотность распределения случайной величины 7* будет
/* (/)=J— f (/)=\Че~и (/ > 0). (1.4.8)
mt
Такой закон называется законом Эрланга 1-го порядка. Число-
вые характеристики интервала времени Т* будут (см. (1.2.14) и
(1.2.15)]
; D[Г*] =
/И/ /И/
(Л1[Г2])2
Математическое ожидание и дисперсия случайной величины Т —
интервала между любыми двумя событиями в простейшем пото-
ке, равны
ОО
mt= t\e~udt= —;
о
(1.4.9)
о
\e~udt= —
Х2
(1.4.10)
19
Таким образом:
М [Г] ;
1 1 Х2
(1.4.11)
(1.4.12)
Сравнивая величины Л1[Т*] и mt, а также D[T*] и Dt, видим,
что наличие случайной точки S на интервале как бы «раздвига-
ет» его, увеличивая математическое ожидание и дисперсию
вдвое.
Найдем закон распределения интервала времени 0 между
точкой S и первым наступившим после точки S событием (см.
рис. 1.4.4). В соответствии с формулой (1.3.2) имеем
1—F (ft) 1___/1__
?(»)=------V1-./ -2 (&>о). (1.4.13)
/И/ 1/Л
Сравнивая выражение (1.4.13) с выражением для плотности
распределения интервала Т между любыми двумя событиями
(1.4.7), убеждаемся в том, что случайная величина 0 распреде-
лена так же, как и случайная величина Т.
Это замечательное свойство простейшего потока является
другой формой проявления свойства отсутствия последействия.
Это свойство означает, что любая сколь угодно подробная ин-
формация о том, -как себя вел поток в прошлом (до произволь-
ной точки S), не дает нам никаких сведений о том, что произой-
дет после этой точки. Другими словами, будущее развитие про-
цесса появления точек не зависит от того, как этот процесс про-
текал в прошлом. Данное свойство намного облегчает исследо-
вание различных задач, связанных с анализом потока событий.
Вычислим характеристическую функцию интервала между
двумя соседними событиями в простейшем потоке с парамет-
ром X:
оо оо
g(x) = eltx\e-udt = —^— ( (\-1х)е-^~1х^М= —— . (1.4.14)
J \ — lx J X — ix
о о
В последующем изложении будем опираться на это выражение,
утверждая, что поток Пальма является простейшим, если харак-
теристическая функция интервала между соседними событиями
равна —• Это утверждение основывается на однозначности
связи между характеристической функцией и плотностью распре-
деления.
20
§ 1.5. ДРУГИЕ СТАЦИОНАРНЫЕ ПОТОКИ ПАЛЬМА
1. Регулярный поток событий
Регулярный поток представляет собой последовательность
событий, разделенных строго одинаковыми интервалами
(рис. 1.5.1). Плотность распределения интервала ме?кду любыми
событиями может быть представлена в виде
/(/) = 8(/-тД
где 6(т) —известная дельта-функция.
Напомним основные свойства дельта-функции:
0-{-8
1. С <Р(т)8(т)д1т=<Р(0), , (1.5.2)
0-а
где <р(т)—любая функций, не-
прерывная в точке т=0.
В выражении (1.5.2) величина
е может быть любым положи-
тельным числом. В частности, если <р(т) == 1, то получим
o+t
(1 5.1)
l^t
—
t
О
Рис. 1.5.1
2. 6(т)=0 при т=#0. (1.5.3)
3. тб(т)^0. (1.5.4)
Так как интервал между соседними точками строго постоянен
и равен mti то, очевидно, что математическое ожидание этого
интервала равно /И/, а дисперсия
Dt=Q. (1.5.5)
Для нахождения плотности распределения интервала, на ко-
торый случайным образом падает точка S (см. рис. 1.5.1), вос-
пользуемся соотношениями (1.2.3), (1.5.1) и (1.5.4):
Г W= — f (0= — §-Z~OT< + m< 8 8(tmt).
mt mt mt
(1.5.6)
Таким образом, наличие случайной точки S на каком-либо
из интервалов между соседними событиями не изменяет закона
распределения этого интервала: интервал остается по-прежнему
неслучайным и равным mt.
Найдем закон распределения времени 0 от случайной точки S
до наступления
(1.3.2) и (1.5.2)
очередного события. На основании выражений
получим
& >
1 — j b (t — mt) dt
о
mt
— при & cz (0, тД
О при 9 ф(0, т^,
(1.5.7)
21
где Фе (О, mt) означает выполнение неравенства 0<Ф<ть
а выражение Ф^;(0, mt) означает, что Ф^/nt или Ф^О. Таким
образом, случайная величина 0 распределена по закону равно-
мерной плотности на интервале (0, mt). Найдем числовые харак-
теристики случайной величины 0 [см. (1.3.5), (1.3.7) (1.5.5)]:
0 2 1 2mt 2
з™, 12
(1.5.8)
(1.5.9)
Характеристическая функция интервала между соседними
событиями в регулярном потоке будет иметь вид [см. (1.2.4),
(1-5.2)]
g(x) = M [е^г]= J ettJb(i-mt)dt=e,mtx . (1.5.10)
— оо
Регулярный поток событий сравнительно редко используется
при решении прикладных задач теории массового обслуживания.
Это объясняется тем, что такой поток событий обладает очень
большим («неограниченным») последействием, так как, зная
лишь один момент наступления события в регулярном потоке,
можно восстановить все прошлое этого потока и предсказать все
его будущее.
2. Нормальный поток событий
«Нормальным потоком» будем называть поток Пальма, для
которого интервалы между событиями распределены по нормаль-
ному закону:
_ 2_ У
f(t) = —2 1 (1.5.11)
V 2л а/
Заметим, что, строго говоря, интервал между событиями не
может быть подчинен нормальному закону, Так как он представ-
ляет собой не отрицательную величину, а область определения
нормального закона (—оо, +оо). Однако еЬли границы практи-
чески возможных значений случайной величины не выходят за
пределы положительной области, например, выполняется условие
(1.5.12)
ь
то можно считать интервал распределенный нормально (вероят-
ность отрицательных значений практически равна нулю).
22 :
Заметим, что описанный выше регулярный поток событий
можно рассматривать как предельный случай нормального по-
тока при —>0. Действительно, при at—Ч) имеем
Нот——е 2 1 (1.5.13)
e/-° У2л а,
т. е. при Gt—М) нормальная плотность распределения переходит
в дельта-функцию.
Найдем плотность распределения интервала Т* между дву-
мя соседними событиями, на который случайным образом пада-
ет точка S (см. рис. 1.2.2):
1 у-*"/¥*
/*(/)=-L_/(0 =---------*-=—е 2 °' ’ (/>0). (1.5.14)
mt ' nttV2л at
Определим числовые характеристики интервала Т* [см. (1.2.1),
(1-2.2)]:
(1.5.15)
mt mt
W[T2])2
mt ntf
Величина М[Г3] для нормального закона будет
М [7'3]=а3 = \t3f (t) dt = 3mrf + m3.
С учетом последнего равенства получаем
О[Г]=За3 + т3----(°' + ,”')2 4---^-(/п2-/>Д(1.5.16)
mt mt mt
Закон распределения случайной величины 0 (см. рис. 1.3.1) —
промежутка времени между точкой S и следующим за этой
точкой событием, будет [см. (1.3.2)]:
1 _ф* ( *~mt \
?(§)=_L1£W =-------'——L (0 > о), (1.5.17)
mt
где
х -J—
ф’(•«)=—L f е 2 dt (1.5.18)
/2«_1
— нормальная функция распределения.
23
Числовые характеристики случайной величины 6 найдем из
выражений (1.3.5) и (1.3.7)
2 mt
2 2 4
Ш61 = -___________= ____________ZL
3z”« 4m2 2 4ot2
12
(1.5.19)
(1.5.20)
При выполнении условия (1.5.12) эта величина не может быть
отрицательна.
Характеристическая функция интервала между соседними со-
бытиями в нормальном потоке имеет вид
1 I2 &
g(x)=\ е"* -е М ) dt = e!m‘x~^~. (1.5.21)
У 2л
3. Поток Эрланга
Поток Эрланга получается путем особого преобразования
(«разрежения») простейшего потока. Это преобразование осу-
ществляется путем выбрасывания некоторых событий из про-
стейшего потока (рис. 1.5.2).
Рис. 1.5.3
Рис. 1.5.2
В верхней части рисунка изображен простейший поток 77.
Предположим, что дз него выбрасывается каждая вторая точка
(событие). Оставшиеся невыброшенными события составляют
новый поток событий, который называется потоком Эрланга 1-го
порядка Эь Если выбрасывать два события подряд и оставлять
в потоке каждое третье событие, то получим поток Эрланга 2-го
порядка Э2 (рис. 1.5.3) и т. д.
Теперь можно дать следующее общее определение: потоком
Эрланга k-го порядка называется поток Пальма, у которого ин-
тервалы между событиями представляют собой сумму (£+1) не-
зависимых случайных величин, распределенных одинаково по
показательному закону с параметром X. Параметр X представля-
ет собой интенсивность исходного простейшего потока 77. Вели-
чина k может принимать значения 0, 1,2, ... При k=0 получаем
24
исходный простейший поток /7, так как никакого преобразования
мы не делаем.
Можно доказать, что плотность распределения случайной ве-
личины Г-интервала между двумя соседними событиями в пото-
ке Эрланга £-го порядка равна
(*>0). (1.5.22)
Для дальнейших расчетов нам понадобится ввести в рассмот-
рение специальную функцию
/7*
P(k, а)=~-е~а. (1.5.23)
Напомним, что вероятность P(k, а) равна вероятности того,
что случайная величина X, распределенная по закону Пуассона
с параметром а, примет значение k:
P(k, a)-=P(X = k). (1.5.24)
Таким образом:
Л(/)=хр(а, к/).
Функция распределения случайной величины Т будет иметь
вид
/ k ;
Л (0= 5 A W dt=1 “Ее~и-
О л = 0 ’ /
Если ввести в рассмотрение функцию /
k к /
/?(£, е~а=- У* Р(п, а\ fl.5.26)
л=0 л = 0 /
то выражение для функции распределения примет вид/
F(f)=\-R(k, U). / (1.5.27)
Функция R(k, а) равна вероятности того, что случайная величи-
на X, распределенная по закону Пуассона с параметром а, при-
мет значение не большее k: /
R(k, a) — P(X^.k). / (1.5.28)
Таблицы функции R(k, а) даны в приложении. /
В дальнейшем изложении будем часто пользоваться введен-
ными функциями P(k, а) и R(k, а), поэтому советуем читателю
/ 25
запомнить их определения. Между функциями P(k, а) и R(k, а)
существуют следующие соотношения:
dR^ a).= —p(k, а); (1.5.29)
R(k\)^{P(k, x)dx; (1.5.30)
а
P(k, d)=R(k. a) —A?(£—1, a), (1.5.31)
в справедливости которых читатель может убедиться самостоя-
тельно.
При больших значениях параметра а (а>20) для вычисления
функции R(k, а) можно пользоваться следующим приближенным
выражением:
R(k, а)^Ф* P + 0’L~" V (1.5.32)
\ Va )
X _ р
где Ф* (х)=—-— 2 dt — нормальная функция распреде-
ли Л
ления.
, Помимо этого, полезно знать следующие свойства функций
\Р (k, a), R (k, а)-.
ПтР(0, a)=l; 11тР(£, a)=0; lim/?(Ar, а)=1; 11тR(k, d)= 1.
аДп a->0 (k =# 0) a->0 Л-><»
Рассмотрим случайную величину X, распределенную по за-
кону Пуассона с параметром а, и найдем наивероятнейшее зна-
чений А*. Это значение определяется из условия
\ Р(&*, а)-=шахР(&, а).
\ к
Для\гого чтобы выполнялось это равенство, требуется сов-
местное выполнение двух неравенств:
\ P(k* — 1, a)<P(k\ a);
\ P(£* + l, a)^P(k\ a).
Из первого неравенства имеем |
\ a**-1 ak*
\ (Л* — 1)! л*! ’
откуда \
\ a >k*.
26
Из второго неравенства
л**+1 а**
—-----е~а < -— е~а,
(k* + 1)! k*\
откуда
Объединяя эти два неравенства, получим
а — 1
где Л’ — целое неотрицательное число.
Рассмотрим положительное число а и обозначим [а] его целую
часть («антье»), т. е. наибольшее целое число, заключенное в а.
Например, если а=7,85, то [а]=7; если а=0,3, то [а]=0; если
а — целое число, то [а]=а. Тогда (если а — нецелое число)
наивероятнейшее значение k* будет определяться из равенства
Л*=[а]. Если а<1, то Л* = 0; если а — целое число, то имеются
два наивероятнейших значения: kx*=a и ft2*=a—1. При этом
Р(а, а)=Р(а — 1, а).
Вернемся к рассмотрению потока Эрланга k-vo порядка. Чис-
ловые характеристики интервала Т между двумя соседними со-
бытиями в этом потоке будут
оо (
(1.5.0)
J Л /
0 /
оо /
Dt=\(t- mt)2fk (/) dt=А±1. (10.34)
0 - /
Плотность распределения интервала времени Т*, на который
случайным образом падает точка S (см. формулу (1.2.3)], через
функцию P(k, а) выразится следующим образом: /
/;(0 = ^Д(/)=—4—= W + U (1.5.35)
к -г 1 /
X /
Таким образом, случайная величина Т* будет подчинена за-
кону Эрланга (Л-Ы)-го порядка. Числовые характеристики слу-
чайной величины Т* будут /
Л4[Т*] = * + 2 ; / (1.5.36)
D[T*}=-^~ . / (1.5.37)
27
Выразим плотность распределения случайной величины 0
(см. рис. 1.3.1)—интервала времени между точкой S и ближай-
шим событием [см. (1.3.2), (1.5.25), (1.5.33)] через функцию
R (т, а):
-('-2-TH
т1 ----L =
mt k + 1
k
’е—X
п=0
Математическое ожидание случайной величины 0 определим
по формуле (1.3.5):
(1.5.39)
Сопоставляя выражения (1.2.15), (1.3.7) и (1.5.37), можно найти
величину Z>[0]:
£)|91= Л±2_Л±А
1 J Х2 12 ’
Найдем характеристическую функцию интервала времени
между двумя соседними событиями в потоке Эрланга &-го по-
рядка:
Л+1
(1.5.40)
J
о
Закатим, что при достаточно большом k (практически при
&>5) пЬток Эрланга £-го порядка можно считать приближенно
нормальным с параметрами (1.5.33) и (1.5.34). Это следует из
того, что потоке Эрланга Л-го порядка интервал между сосед-
ними событиями представляет собой сумму (£+1) независимых
случайных\величин, распределенных одинаково по показатель-
ному зако , а такая сумма, согласно центральной предельной
теореме, npi\A->oo асимптотически нормальна.
Рассмотренный нами поток Эрланга получается путем выбра-
сывания из остейшего потока k точек подряд и оставления
каждой (k+ 1\-й точки. Такое преобразование приводит к тому,
что интенсивность потока Эрланга А-го порядка Х& уменьшается
в (£+1) раз по\сравнению с интенсивностью исходного простей-
шего потока с интенсивностью X:
*— — «.II
mt & -f- 1
(1.5.41)
28
Введем новое преобразование простейшего потока, состоящее
из такого же «разрежения», как выше, но после этого поток «сжи-
мают» так, чтобы его интенсивность была равна интенсивности
первоначального простейшего потока. Для этого достаточно ин-
тервал времени Т между двумя соседними событиями в потоке
Эрланга /5-го порядка уменьшить в (/5+1) раз. Назовем такой
поток нормированным потоком Эрланга k-го порядка, В этом по-
токе случайный интервал времени Т между двумя соседними
событиями будет
• (1-5-42)
Плотность распределения случайной величины Т будет
иметь вид
Л(0= (1-5.43)
где
Т*=(А + 1)Х.
Математическое ожидание величины Т равно
М[Г]=-^- = -Ь (1.5.44)
k -г 1 к
т. е. интенсивность нормированного потока Эрланга /5-го поряд-
ка равна —— и равна интенсивности исходного ПрОСТеи-
^И [Г]
шего потока событий.
Дисперсию величины Т определим из выражения /
D [7]== _*±2------------!---=-----1--. (15.45)
1 j (Л+1)2 X2 (*4-1)2 X2(fe+ 1) Г
Таким образом, при k—>оо интенсивность потока не изменяется,
а дисперсия D[T] стремится к нулю, т. е. поток приближается
к регулярному. Этот вывод подтверждается анализом характе-
ристической функции величины Т (см. 5-е свойство ^характери-
стических функций в § 1.2): /
~ ч ( х \ f \*+1 /
—ZT 7
Найдем предел этого выражения при k—>-оо: /
tx
Umgft(x) — lim /------V+1 =/”Г. (1.5.46)
й-оо ZX I /
V_T+t7 /
29
Это выражение с точностью до обозначений совпадает с ха-
рактеристической функцией интервала между событиями ре-
гулярного потока [см. (1.5.10)]. Следовательно, при достаточно
большом k нормированный поток Эрланга k-ro порядка будет
сколь угодно близок к регулярному потоку.
Таким образом, с помощью нормированного потока Эрланга
можно построить целую гамму потоков с различным последей-
ствием начиная от полного отсутствия последействия (6 = 0)
вплоть до регулярного потока (соответствующего k=<x>). Заме-
тим, что при k>5 рассматриваемый нормированный поток (так
же как и ненормированный) можно считать нормальным, но с па-
раметрами (1.5.44) и (1.5.45).
Для нормированного потока Эрланга k-ro порядка закон
распределения участка времени Т*, на который случайным обра-
зом падает точка S, имеет вид
/*W=^-^r^=MA + l)P(A + l, Х(А + 1)0, (1.5.47)
т. е. тоже представляет собой закон Эрланга, но (&+1)-го по-
рядка с параметром Xfe = X(£+1).~Следовательно, числовые
характеристики случайной величины Т* можно найти по форму-
лам, аналогичным (1.5.36) и (1.5.37):
* + 2-.; (1.5.48)
1 J X(fe+1)
£)[7'*1 = _А+±==—(1.5.49)
(Xft)2 Х2(й+1)2
Платность распределения случайной величины 0 — остатка
до наступления очередного события в нормированном
ланга А-го порядка — определяется по формуле, анало-
5.38):
времен
потоке
гичной
Числовые х
ственно
y)=x/?(fc, Х(*4-1)0- (1.5.50)
актеристики случайной величины 0 равны соответ-
k + 2 k + 2 .
—
А + 2
- (V
2хл 2Ш+1)’
6 + 6 _ (£ Ч- 2) (Л Ч- 6)
12 Х2 (k + 1)2 12
(1.5.51)
(1.5.52)
Напомним, что величина X в формулах (1.5.43) — (1.5.52) равна
интенсивности исходного простейшего потока событий.
30
§ 1.6. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ПОТОКОВ СОБЫТИЙ
В большинстве исследований прикладного характера делается
предположение, что фигурирующие в них потоки событий являют-
ся пуассоновскими. Это объясняется не только тем, что введение
пуассоновских потоков событий намного упрощает исследование
и облегчает нахождение решения, а еще и тем, что пуассоновские
потоки событий (или весьма близкие к ним по структуре)
часто имеют место в действительности, так как в опреде-
ленном смысле они являются предельными для различных пото-
ков. Например, если накладывать друг на друга («складывать»)
большое число различных по структуре потоков событий, то сум-
марный поток в весьма широком классе условий будет близок
к пуассоновскому. С другой стороны, если взять произвольный
поток и из него случайным образом выбрасывать события, то по-
сле нескольких таких разрежений полученный поток событий бу-
дет также близок к пуассоновскому *. На практике очень часто
фактически имеет место сложение или случайное разрежение
потоков событий, поэтому пуассоновские потоки событий нахо-
дят широкое применение при решении различных прикладных
задач.
1. Предельная теорема для суммарного потока
Предельная теорема для суммы нескольких потоков имеет
такое же значение, как и центральная предельная теорема для
суммы нескольких случайных величин. Центральная предельная
теорема утверждает сходимость закона распределения суммы
независимых случайных величин к нормальному закону прд уве-
личении числа слагаемых. Предельная теорема для суммарного
потока утверждает сходимость суммы независимых^ р^динар-
ных, стационарных потоков_к простейщеА^1^току.П ус-
ловия, налагаемые на суммируемые потоки, приблизительно та-
кие же, как и условия центральной предельной теоремы: скла-
дываемые потоки должны оказывать более или менео одинаково
малое влияние на суммарный поток. Другими словами, среди
суммируемых потоков не должно быть потоков с очень большой
интенсивностью (по сравнению с суммарной интенсивностью всех
остальных); интенсивности складываемых потоков не должны
становиться по мере увеличения номера потока исчезающе ма-
лыми; кроме этого, должны быть наложены некоторые несущест-
венные ограничения на последействие внутри каждого потока,
которые мы не будем уточнять, так как книга носит прикладной
характер. Здесь важно отметить, что сходимость суммарного по-
тока к простейшему осуществляется очень быстро. Практически
можно считать, что сложение четырех-пяти стационарных, орди-
* Ниже будет дано более подробное разъяснены^понятий сложения и раз-
режения потоков. /
31
парных, независимых потоков, сравнимых по интенсивности,
достаточно для того, чтобы суммарный поток был близок к про-
стейшему.
Остановимся несколько подробнее на понятии «сложение.»
потоков. «Сложение» двух потоков П\ и П2 состоит в том, что все
моменты появлений событий в этих потоках относятся к одной
оси 0/ (см. рис. 1.6.1), на которой отмечаются моменты появле-
ния событий в суммарном потоке /7 = /71 + /72-
Рис. 1.6.1
При сложении п потоков интенсивность суммарного потока
определяется следующим образом:
п
о-6-1)
/=1
где Xj — интенсивность /-го потока событий.
Таким образом, для выяснения всех свойств суммарно-
го потока событий достаточно знать лишь интенсивности сумми-
руемых потоков событий и практически не требуется знать внут-
реннюю структуру этих потоков.
Как указывалось выше, для
сходимости суммарного потока
событий к простейшему требуется
взаимная независимость склады-
ваемых потоков. Поясним поня-
тие независимости потоков на
примере двух потоков. Рассмот-
рим участок времени ть наложен-
ный на поток событий П\. Участок
Т] может иметь произвольную
длительность начало его может быть в произвольной точке t\
оси времени ol (см. рис. 1.6.2).
Таким же образом выберем участок времени тг в потоке /72.
Случайное числе событий в потоке 77ь наступающих на участке
времени ть обозначим Хр Случайное число событий в потоке П2,
наступающих на\участке времени ?2, обозначим %2- Потоки со-
бытий ГЦ и П2 называются независимыми, если случайные вели-
чины Xi и Х2 независимы. Короче это можно сформулировать
следующим образом: два потока называются независимыми, ес-
ли число событий,\ попадающих на любой участок времени
32 \
в первом потоке не зависит от того, сколько событий попало на
любой участок времени во втором потоке.
На практике часто потоки возникают в результате сложения
не строго независимых, а слабо зависимых потоков событий. Ис-
следования, проведенные методом статистических испытаний, по-
казывают, что и в этом случае (при достаточном числе слагае-
мых) суммарный поток также оказывается близок к простейшему.
До сих пор мы рассматривали только сложение стационар-
ных потоков событий. Оказывается, если складываемые потоки
не стационарны, то предельное свойство также имеет место: по-
лучается суммарный поток, близкий к нестационарному пуассо-
новскому с интенсивностью
п
о-6-2)
* 7 = 1
где Zj(/)—переменная интенсивность /-го потока. При этом для
любого момента времени t интенсивности всех пото-
ков должны быть соизмеримы.
Из всего вышеизложенного следует, что многие потоки собы-
тий, возникающие на практике и фигурирующие в задачах мас-
сового обслуживания, можно приближенно считать пуассонов-
скими.
Так, например, поток космических частиц является практиче-
ски пуассоновским, так как частицы порождаются очень боль-
шим числом звезд, испускающих эти частицы независимо друг
от друга. Поток машин на загородном шоссе будет также прак-
тически пуассоновским потоком, так как он состоит из отдель-
ных машин, выезжающих на шоссе с различных улиц и дорог.
Поток самолетов, осуществляющих посадку на аэродром, также
близок к пуассоновскому, несмотря на то, что его стремятся сде-
лать строго регулярным (зйранее планируют время приземления
каждого самолета). Это объясняется тем, что самолеты прибыва-
ют к аэродрому не в строго заданное время (раньше или позже)
и тем самым вносят элемент случайности в поток приземлений
(каждый самолет независимо от других) и т. д.
Заметим, что пуассоновский поток обладает устойчи-
востью, состоящей в том, что при суммировании независимых
пуассоновских потоков получается снова пуассоновский поток,
причем интенсивности складываемых потоков суммируются. До-
кажем это свойство, которое понадобится нам в дальнейшем.
Рассмотрим участок времени произвольной продолжительно-
сти т, начало которого находится в произвольной точке /, нала-
гаемой на все складываемые потоки (рис. 1.6.3). Введем в рас-
смотрение случайную величину Xj — число событий, наступив-
ших на участке времени т, в потоке П$ (/=1, 2, ..., п). Так как
все потоки пуассоновские, то случайная величина Xj распреде-
лена по закону Пуассона с математическим ожиданием
2—1964 33
aj=a}(f, %)= J
t
где Xj(O —интенсивность потока Ilj.
Характеристическая функция случайной величины Xj, распре-
деленной по закону Пуассона с параметром аД/, т), будет
g)(x)=M[eixXi]=^
^Le-aielxb = ea^-eix\ (1.6.3)
k\ 4 -
Рассмотрим сумму п пуас-
соновских потоков и в каждом
из этих потоков возьмем оди-
наковый интервал длительно-
сти т.
Тогда для того, чтобы дока-
зать, что в результате сумми-
рования п независимых пуас-
соновских потоков получается
пуассоновский поток, доста-
точно показать, что случайная
величина
п
Х=^Х, (1.6.4)
;=1
подчинена закону Пуассона с параметром
/ + т /4-т п п
а = j J
t t j=i j=i
(1.6.5)
Найдем характеристическую функцию g(x) случайной вели-
чины X. Так как потоки Пх, П2, ..., Пп независимы, то случайные
величины Xt, Х2, ..., Хп тоже независимы и, следовательно [см.
(1.2.6), (1.6.3) и (1.6.5)]:
п
n п . -2м1-е") . ,,
£(х)=гил*)=гкв'(1-е i=1 =e^-eix)a.
j=l
Сравнивая это выражение с выражением (1.6.3), убеждаемся,
что случайная величина X подчинена закону Пуассона с пара-
метром а, что и требовалось доказать.
Таким образом, складывая независимые пуассоновские по-
токи, мы снова получаем пуассоновский поток.
34
2. Предельная теорема для редеющих потоков
Потоки событий, встречающиеся на практике, часто подвер-
гаются операции «разрежения». Она состоит в том, что под влия-
нием случайных причин те или иные события выпадают из по-
тока. Например, поток космических частиц, прежде чем достичь
уровня земли, редеет за счет столкновения этих частиц с атома-
ми атмосферы; поток самолетов, прорывающихся через систему
ПВО противника, редеет за счет поражения части этих самоле-
тов; поток готовых изделий тоже редеет за счет выбраковывания
части этих изделий в от-
деле технического контро-
ля. В отличие от потока
Эрланга &-го порядка, ко-
торый получался путем
строго закономерного раз-
режения простейшего по-
тока (k точек выбрасыва-
лось, а (&+1)-я точка
Рис. 1.6.4
оставлялась), в приведенных выше примерах осуществляется
случайное разрежение исходного потока событий, когда каж-
дое событие с определенной вероятностью р исключается из пото-
ка независимо от того, исключены другие частицы или нет.
Рассмотрим подробнее такое случайное разрежение. В каче-
стве исходного потока событий П рассмотрим стационарный
поток Пальма. К этому потоку событий применим операцию раз-
режения, состоящую в том, что каждое событие, независимо от
других, переносится из исходного потока в разреженный поток
Пр с неизменной вероятностью р (следовательно, выбрасывается
с вероятностью ^=1—р; рис. 1.6.4).
Такую операцию разрежения будем называть «операцией Rp»
и обозначим Rp{n}:
np=Rp\n}.
Допустим, что в исходном потоке Пальма интервал между со-
седними событиями Т имел характеристическую функцию g(x).
Найдем характеристическую функцию интервала Тр между со-
седними событиями в разреженном потоке Пр.
Для отыскания этой характеристической функции проведем
преобразования, связанные с анализом случайного числа случай-
ных слагаемых. Рассмотрим последовательность случайных
величин Xit Х2, Х3, .... Суммой п случайных слагаемых будем на-
зывать выражение вида
1=1
где п — вполне определенное неслучайное число.
2*
35
Теперь представим себе опыт, в результате которого сумми-
руется не определенное число слагаемых п, а случайное число
слагаемых У. Тогда суммой случайного числа случайных слагае-
мых будет выражение
1=1
где случайная величина У может принимать только положи-
тельные целочисленные значения (1, 2, 3 ...). Число возможных
значений случайной величины У может быть либо ограничено
некоторым конечным числом п, либо равно бесконечности.
Вернемся к исследованию случайной величины Тр. Очевидно,
что случайная величина Тр может быть представлена как сумма
случайного числа случайных слагаемых
тр=-^т„
где случайные величины 7\(i=l, 2, ...) взаимно независимы и
каждая имеет характеристическую функцию g(x).
Случайная величина Z представляет собой число просумми-
рованных интервалов в исходном потоке П и подчинена закону
Паскаля:
p^Z=k) = pqk~'i (k=l, 2,...), (1.6.6)
где ?=1— р (0</?<1).
Для нахождения характеристической функции gT (х) случай-
_ р
ной величины Тр выдвинем гипотезу, состоящую в том, что слу-
чайная величина Z = k. В предположении, что эта гипотеза имела
место, получим выражение для условной характеристической
функции [ем. (1.2.7)]:
gTplk(x)=(s(x»k.
Следовательно, безусловная характеристическая функция вели-
чины Тр будет
g Тр (•*)=2 РЯ*"1 (g (*))* = у J] (g (х)яУ =
k=l к = 1
Р qg (X) _ pg(x) О -
я i W 1 — qg (х) ’
V 1
так как 0<<?<1 и |g(x) | ^1.
36
Найдем числовые характеристики случайной величины Тр.
Применяя формулы (1.2.9) и (1.2.10) и учитывая, что
ОО оо
(1М)
---k=0 k=0
D[Z]=Af[Z2]-(WD2=£ =
fe=l
(1.6.9)
*=I
получим
/„« ( Pg'(x)(l — qg(x))+pg(x)qg'(x)\ _ g' (0)
(STp (z))„»=^--------
откуда
I M[Tp]^-ig'r (0)=_^L.
\ / p p
Ho \
-te'(O)=(Af[r]. 1
Следовательно [см. (1.6.8)]: "
_M[Tp\=^M[r\-M[Z]. (1.6.10)
Найдем дисперсию случайной величины Тр.
D[Tp\=-g’T W + (g'r (°))2=
р р
_ _ (Pg" (X) (1 — qg (х))2 -4- 2 (1 — gg (х)) qg' (x)pg' (х) \ ,
\ (1 — 4g(x))i Л=о ‘
+ (g' (О))2 = -Г(0Н(г' (°)>2i _ (0))2 л =
р р ’ р
=D{T]-M [Z] -|-(Af [T])2D [Z]. (1.6.11)
Зная характеристическую функцию gT (х) интервала Тр,
р
можно по формуле (1.2.11) найти плотность распределения
Л (0.
р
Анализ формулы (1.6.10) приводит нас к естественному вы-
воду, что интенсивность разрежейного потока Пр будет равна
интенсивности исходного потока П, умноженной на вероятность
сохранения события в потоке р:
Х_=—— =---------5----=Хр, (1.6.12)
, р . М [Тр] М [Г] М [Z] г 4
где X — интенсивность исходного потока 77.
37
Введем новое преобразование RP потока П, заключающееся
в том, что поток подвергается сперва преобразованию /?р, а за-
тем сжимается так, чтобы интенсивность потока Пр была равна
интенсивности исходного потока П. Для этого достаточно слу-
чайную величину Тр умножить на р:
тр=трр. (1.6.13)
В этом случае характеристическая функция интервала между
соседними событиями Тр в потоке ПР=#Р{П} (см. пятое свой-
ство характеристической функции в § 1.2) имеет вид
RP {g(x)\ = gr . •
р \ — qg (х)
Нетрудно убедиться, что
М[Гр] = М[Т];
D[Tp]=D[T]p+M[T]^.
(1.6.14)
(1.6.15)
(1.6.16)
Теперь можно перейти к предельной теореме для редеющих
потоков. Смысл этой теоремы состоит в том, что если последо-
вательно разрежать стационарный ординарный поток Пальма
достаточно большое число раз, то такой многократно разрежен-
ный поток будет близок к простейшему. Предположим, что
первое разрежение сохраняет событие в потоке с вероятностью
Pi>0, второе — с вероятностью р2>® и т. д. Обозначим Л интен-
сивность исходного потока Пальма. Предположим, что вслед за
каждым разрежением происходит сжатие потока с тем, чтобы
его интенсивность оставалась неизменной. Обозначим п после-
довательных таких преобразований символом /?<”>:
*(л) (/71=RPn .. RPl {77} • • •}}. (1.6.17)
Сначала покажем, что последовательное двойное разрежение
со сжатием потока П с вероятностями р\ и р% эквивалентно
одному «разрежению со сжатием» с вероятностью p = т. е.
RPt {RP1 {n\}=RPtPt {Z7}.
(1.6.18)
Действительно, преобразование RPi [см. (1.6.14)] дает характе-
ристическую функцию
Тогда
RpAgj (*))=
(л)а= Р.ИР.» .
Тр. 1— <lig(P\x)
P2gv (Ргх) ,
TPi_______P\Pjg (Р\ Р2Х)
^—42gT„ (Р2Х) 1— (1— PlP2)g(PiP2x)
Pl
(1.6.19)
(1.6.20)
38
Отсю да
RwlgWI = ,
где
п
P{n} = PiP2--Рп=П Pi-
1=1
(1.6.21)
(1.6.22)
Преобразуем выражение (1.6.21):
/<<я) {g(x)] =--------------------------------------
[1 — g (р(п}х)} + g (р(п}х)
(1.6.23)
Найдем предел этого выражения при неограниченном увеличе-
нии числа преобразований (га—>-оо). В этом случае р<”)—>Ю и в
знаменателе (1.6.23) получится неопределенность вида -у- . Рас-
кроем эту неопределенность:
Hm = lim -^(a_4L=_xg40)=-±
р(")-0 />(я) „С") л 1 ,Х
1
Следовательно:
Ит/е(л)(£(х))=—— =-А-
X К — IX
Т+ 1
(1.6.24)
Сравнивая это выражение с (1.4.14), видим, что. у предель-
ного потока интервалы между соседними событиями распределе-
ны по показательному закону. Так как исходный поток был по-
током Пальма и всякое преобразование Rp оставляет его потоком
Пальма (интервалы остаются независимым^), то предельный
поток будет также потоком Пальма с показательно распределен-
ными интервалами, т. е. простейшим потоком. Исследования
показывают, что на практике уже 4—5-кратное разрежение (при
р<0,8) дает поток, близкий к простейшему, даже если исходный
поток был регулярным. Рассмотрим случай, когда разрежению
подвергается простейший поток с интенсивностью Л. При разре-
жении без сжатия (7?р) преобразованный поток остается про-
стейшим с параметром Хр [см. (1.6.7), (1.6.24)]:
g (Л)=. ^(х)—------------------------= —!£.— . (1.6.25)
Р V 1 — qg (х) \ l — ix]\ X — ix) 1р — ix
Если же простейший поток с параметром X подвергается
«разрежению со сжатием», то получается простейший поток с
тем же параметром Л.
39
§ 1.7. ЗАДАЧИ И УПРАЖНЕНИЯ
1.7.1. Поток Эрланга А-го порядка является частным слу-
чаем так называемого гамма-потока, у которого интервал между
соседними событиями является случайной величиной, подчинен-
ной гамма-распределению с параметрами‘а и 0:
Йа/а~1
где
ОО
Г (а) = J x^xe~xdx
о
— известная гамма-функция. При а = &+1 получаем закон рас-
пределения Эрланга А-го порядка. Найти характеристики этого
потока.
Решение
Найдем числовые характеристики случайной величины Г,
подчиненной гамма-распределению:
л noua—1 „
mt= \t -------e-^dt=— ;
' ' Г(«) ?
о
= mJ2 pa/a~1 e-^dt=— .
* JV V Г (a) ₽2
0
Следовательно, интенсивность потока будет \
a
Характеристическая функция интервала Т между событиями
имеет вид
g (х)== \ eitx -—-----------------Y. г
3 Г (a) \ )
о
Плотность распределения интервала Г*, на который случай-
ным образом падает точка S, определяется по формуле (1.2.2):
Г(0=—/(0= —
mt “
tf ta-
Г(«)
e~V.
Воспользовавшись известным свойством гамма-функции:
аГ (а) = Г (a-I-1),
получаем
40
Г(0=
Г(а+1)
е~^.
Таким образом, случайная величина Т* также подчинена гамма-
распределению с параметрами (а+1); р. Следовательно, число-
вые характеристики случайной величины Т* будут
Характеристическая функция случайной величины Т* имеет
вид ' . , I
Закон распределения остатка времени 0 найдем по формуле
(1.3.2): .
» йО/“— I
1 - f
____________________о 22____________
'mt_________________а_______________Г (а) ’
т
где у (а, х)= ( —неполная гамма-функция,
о
Математическое ожидание случайной величины 0 определим по
формуле (1.3.5):
Для определения дисперсии величины 0 воспользуемся фор-
мулой (1.3.7):
о|«1=- +м'<°> у„
3mti V J
( 02 / fl \а |2
_______1 03 / fl \а ( 0X2 \ fl— iX /х=о/
3mti 0x3\fl — ix )x=Q 4m2t
Найдем производные:
Ф - ^)-а = - «(« +1) (а + 2) (р - /х)-“-3 • г.
Следовательно:
D [91__ (а + 1) (а 2
л 1 1 р2.12
41
1.7.2. Моменты прибытия вагонов метро на остановку обра-
зуют поток, приближенно являющийся потоком Пальма, причем
интервал Т между поездами подчинен закону равномерной плот-
ности с характеристиками mt — 2 мин, о<=0,05 мин.
Определить вероятность р того, что время ожидания пасса-
жиром очередного поезда не превысит /=1,5 мин, если пассажир
приходит на станцию, не зная расписания движения поездов.
Решение.
Плотность распределения времени ожидания 0 определяется
по формуле (1.5.17), следовательно, искомая вероятность будет
/?= U (0)4/0= — (1 - F (0)) 4/0,
J mt J
о о
где F(t)—функция распределения случайной величины Т, ко-
торая имеет вид
при /<а,
при a <J<ib,
при />^.
Величины а и b находим из условия
2 Уз
откуда
«=1,91; b = 2,09.
Следовательно:
1.5
р= у ^(1 — F(t))di = 0,75.
о
1.7.3. Станок производит шарики для подшипников. Средняя
производительность одного станка Л] (шариков в единицу вре-
мени). В цехе имеется пг таких станков (т>5). Шарики от стан-
ков поступают в единый поток, где некоторые из них выбраковы-
ваются. Средний брак составляет / процентов. Доброка-
чественные шарики поступают в цех сборки подшипников,
бракованные — ссыпаются в бункер, вмещающий k шариков.
Найти закон распределения времени Т, через которое бункер
будет заполнен бракованными шариками.
42
Решение.
Так как станков много, то общий поток произведенных шари-
ков можно считать простейшим с интенсивностью X=%i/n.
Поток бракованных шариков будет также простейший, так
как разрежение общего потока происходит случайным образом
(вероятность выбраковки шарика равна р=//100). Интенсив-
ность простейшего потока бракованных шариков будет
Хб=Хр.
Обозначим число бракованных шариков, поступивших в бункер
за время г, отсчитываемое от
начала заполнения бункера,
через X(t). Для фиксирован-
ного момента t случайная
величина X (t) подчинена
закону Пуассона с парамет-
ром a=fat.
Очевидно, случайная ве-
личина Т определяется слу-
чайным моментом выполне-
ния равенства (рис. 1.7.3а)
X(T)=k. Функцию распреде-
ления случайной величины Т в
ловия
этом случае можно найти из ус-
k
У7 (/)=Р(7'</) = 1 —р (7’>/)=1 — Y^e~a=X~R(k'
/=0
т. е. случайная величина Т будет подчинена закону Эрланга
й-го порядка с параметром Хб (см. 1.5.27). Так как величина k
(число шариков в бункере) обычно достаточно велика, то можно
считать, что случайная величина Т будет приближенно подчине-
на нормальному закону с параметрами (см. (1.5.33) и (1.5.34):
*4-1
лб
1.7.4. По условиям предыдущего примера определить вероят-
ность р переполнения бункера, если в цехе имеется два бункера
Для бракованных ^шариков, которые заполняются последова-
тельно. Время, потребное для доставки бункера с бракованными
шариками в другой цех для опорожнения бункера и возвраще-
ния пустого бункера на место, равно t\. Считать, что в началь-
ный момент работы цеха оба бункера пустые.
43
Ответ
jP=P(r</1)=l-/?(A, Х^).
1.7.5. Производится воздушная разведка подвижной цели.
Установлено, что время пребывания цели на одном месте под-
чинено «сдвинутому» — показательному закону:
/(/)=
при
при
t > а.
1<~а
О
величины а и а положительны, a 1 (х) —известная единич-
ная функция.
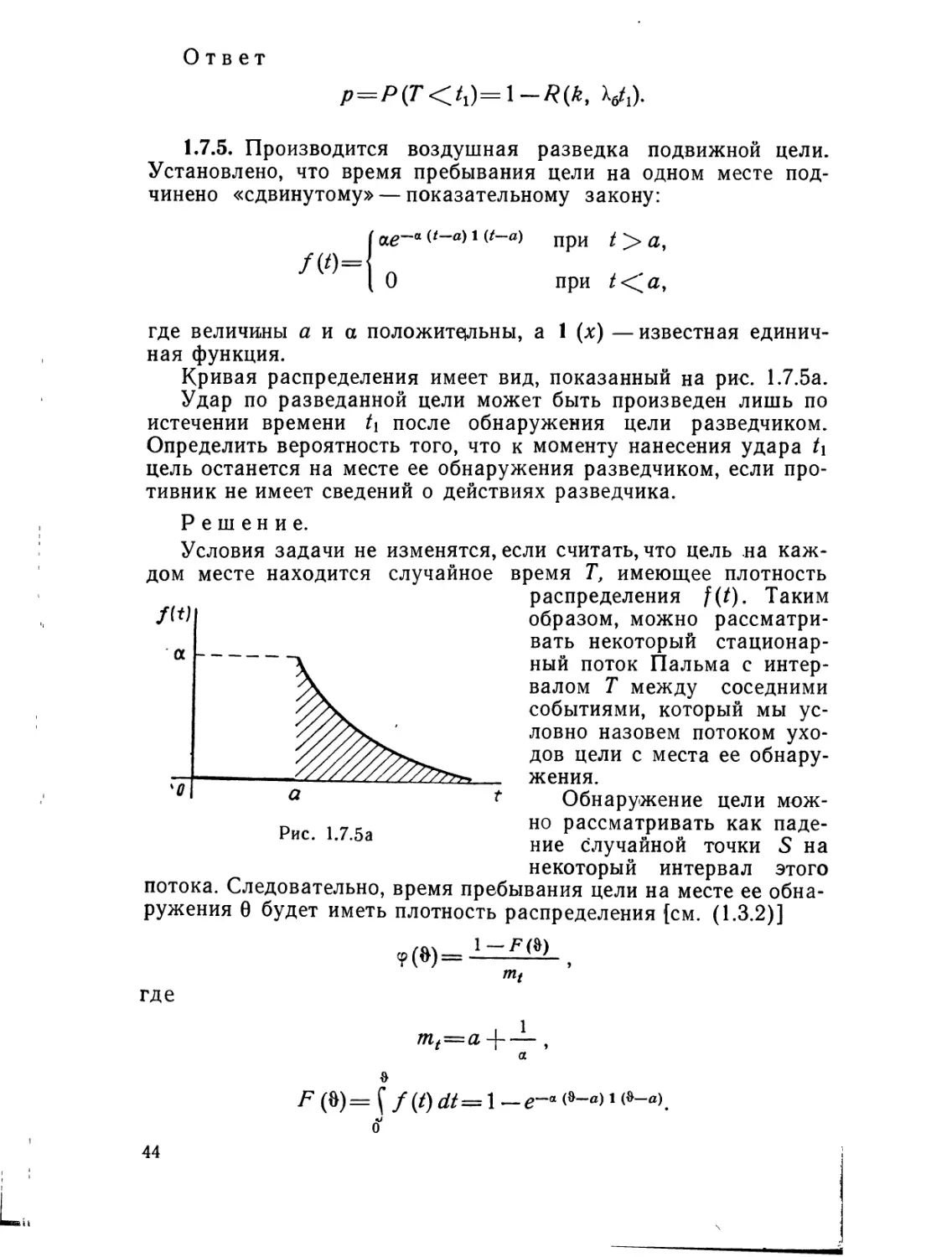
Кривая распределения имеет вид, показанный на рис. 1.7.5а.
Удар по разведанной цели может быть произведен лишь по
истечении времени t\ после обнаружения цели разведчиком.
Определить вероятность того, что к моменту нанесения удара t\
цель останется на месте ее обнаружения разведчиком, если про-
тивник не имеет сведений о действиях разведчика.
Решение.
Условия задачи не изменятся, если считать, что цель на каж
дом месте находится случайное
время Т, имеющее плотность
распределения f(t). Таким
образом, можно рассматри-
вать некоторый стационар-
ный поток Пальма с интер-
валом Т между соседними
событиями, который мы ус-
ловно назовем потоком ухо-
дов цели с места ее обнару-
жения.
Обнаружение цели мож-
но рассматривать как паде-
ние случайной точки S на
некоторый интервал этого
потока. Следовательно, время пребывания цели на месте ее обна-
ружения 0 будет иметь плотность распределения [см. (1.3.2)]
где
, 1
mt—a -|----,
а
а
F (&) = ( f (/) dt = 1 - е~а <»-«)1
О
44
(Л>0).
Искомую вероятность найдем из условия
ОО t!
/, о
a [Z] 1 (a - /1) + al (6 — a)] + 1 — e~a 1 (<’~a)
1 + aa
График этой функции представлен на рис. 1.7.56.
Рис. 1.7.56
Глава 2
МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
§ 2.1. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
*(Г)
Рис. 2.1.1.
t
При анализе работы систем массового обслуживания при-
ходится сталкиваться со своеобразными случайными процессами.
Договоримся, что случайным процессом будем называть процесс,
который в ходе опыта протекает так, что заранее (до опыта) у
нас нет возможности в точности предсказать, как именно будет
протекать этот про-
цесс. Последователь-
ность конкретных со-
стояний, которые слу-
чайный процесс прини-
мает в результате
опыта, с их продолжи-
тельностями, будем на-
зывать реализацией
процесса.
Рассмотрим некото-
рую физическую систему X, д которой протекает случайный
процесс, состоящий в том, что система X с течением времени слу-
чайным образом изменяет свои состояния. Обозначим состояние
системы X в момент времени t через X(t). Состояние X(t) может
характеризоваться какой-нибудь одной величиной (параметром)
или совокупностью таких параметров. Конкретную реализацию
случайного процесса обозначим через x(t).
В качестве примера рассмотрим работу автомата по продаже
газированной воды. В некоторые промежутки времени автомат
будет свободен, а в другие — занят. Условимся для определен-
ности считать, что если автомат в момент времени t свободен,
то Х(/)=0, а если занят, то Х(/) = 1. Одна из возможных реали-
заций случайного процесса x(t) показана на рис. 2.1.1.
В данном примере работа автомата характеризуется одной
случайной величиной X(t), которая в любой момент t равна
46
либо 0, либо 1 (автомат свободен, автомат занят). При этом,
если в момент /о=О автомат был свободен, то, вообще говоря,
нельзя предсказать заранее, когда его займут первый раз (Л),
когда он после этого освободится (^), когда его займут вторич-
но (/з) и т. д.
Случайная величина X(t), рассматриваемая как функция
времени, представляет собой случайную функцию аргумента /,
изменяющуюся скачкообразно в случайные моменты времени.
В качестве второго примера рассмотрим два автомата по
продаже воды. Процесс X(t) может случайным образом в ка-
кие-то моменты t переходить из состояния в состояние:
хо,о — оба автомата свободны;
хЬо — первый автомат занят, второй свободен;
%o,i — первый автомат свободен, второй занят;
— оба автомата заняты.
В данном случае процесс характеризуется двумя параметра-
ми (индексами), которые могут принимать значение 0 или 1.
Характерным для тех случайных процессов X(t), которые нам
предстоит рассматривать, является то обстоятельство, что физи-
ческая система, состояния которой описываются случайным про-
цессом X(t), может в любой момент времени t находиться только
в одном из них. Например, один автомат по продаже воды
может находиться в состоянии х0— свободен или в состоянии
— занят. Если в данный момент времени t автомат свободен,
то имеет место событие
^(/)=х0;
если он занят, то имеет место событие
X(t)=xv
Одной из основных задач изучения случайных процессов,
протекающих в системах массового обслуживания, является
отыскание вероятностей того, что в момент времени t система
находится в том или ином состоянии. Не описывая случайный
процесс исчерпывающим образом, эта вероятность все же дает
достаточно полное представление о нем.
Таким образом, объектом нашего изучения будут случайные
процессы, протекающие в системах массового обслуживания и
описывающие изменения состояний этих систем во времени. Мы
будем рассматривать только системы, которые имеют конечное
или счетное множество возможных состояний*. Такие системы
будем называть системами с дискретными состояниями. Возмож-
* Счетным множеством называется множество, элементы которого можно
расположить в определенной последовательности (перенумеровать). Счетное
множество может быть как конечным, так и бесконечным. Примером беско-
нечного счетного множества может служить множество всех натуральных
47
ные состояния системы массового обслуживания будем обозна-
чать %о, хп (для систем с конечным множеством состоя-
ний) и Xq, хь х2, ..., xk, ... для систем с бесконечным множеством
состояний.
Будем считать, что переход системы из состояния в состоя-
ние осуществляется скачком (мгновенно).
Рассмотрим систему с конечным числом состояний х0, ...»
хп. В любой момент времени t может иметь место одно из
(п+1) событий
X{t)=xL (/ = 0, 1, 2,..., п), (2.1.1)
которые образуют полную группу несовместных событий. Собы-
тие X(t)=Xi состоит в том, что система в момент времени t на-
ходится в состоянии Xi. Вероятность этого события обозначим
pz(/)=P(^(/)=xz) (z = 0, 1, 2,...,п). (2.1.2)
Так как события X(t)=Xi (i=0, 1, 2, ..., п) образуют полную
группу несовместных событий, то для любого момента времени
t выполняется условие
' л
2>(0=1, (2.1.3)
z =о
которое называется «нормировочным».
Дискретным случайным процессом X(t) будем называть про-
цесс, протекающий в системе с дискретными состояниями, число
которых конечно (или счетно). Такой процесс удобно интерпре-
тировать с помощью графа (схемы) возможных состояний с ука-
занием возможных переходов из состояния в состояние, кото-
рые обозначаются стрелками. На рис. 2.1.2 показан граф
возможных состояний для автомата по продаже воды. Прямо-
угольники символизируют состояния, а стрелки — переходы из
состояния в состояние*.
Процесс удобно представлять себе, как блуждание точки,
изображающей систему, по этой схеме, с мгновенными переско-
ками из состояния в состояние по соответствующей стрелке,
происходящими в случайные моменты времени.
Вообще граф возможных состояний будем изображать в виде
нескольких прямоугольников, изображающих состояния системы,
соединенных стрелками, обозначающими возможные переходы
непосредственно из одного состояния в другое, причем направ-
ление стрелки будет указывать направление перехода.
' * Переход будем считать «возможным», если система, находящаяся в со-
стоянии, откуда берет начало стрелка, может перейти из этого состояния непо-
средственно в то состояние, куда направлена стрелка (не попадая в другие
состояния).
48
На рис. 2.1.3 показан граф состояний системы, состоящей
из двух автоматов по продаже воды. Состояния %о,о и %i,i не
соединены стрелками, так как непосредственных пере-
ходов между этими состояниями нет (практически невозможно
строго одновременное занятие или освобождение обоих автома-
тов). Это же замечание относится и к состояниям x0,i и %i,o.
Состояние, из которого система не может перейти ни в какое
другое, называется «состоянием без выхода» *. Например,
электрическая лампочка может быть в трех состояниях: выклю-
чена Xq, включена Xi и перегорела х2 (рис. 2.1.4). Очевидно,
состояние х2 есть состояние без выхода.
Рис. 2.1.2 Рис 2.1.3 Рис. 2.1.4
Состояние Хг будем называть соседним по отношению к со-
стоянию Xj, если возможен непосредственный переход из состоя-
ния Xj в состояние Хг.
Если в числе состояний есть только одно состояние хт без
выхода, то при достаточно длительном протекании процесса
система рано или поздно окажется в этом состоянии:
11m pm(t)=L (2.1.4)
/-►оо
Так как для любого момента времени t выполняется нормировоч-
ное условие (2.1.3), то в этом случае
lim p.(t) = Q (2.1.5)
/-► оо
Если в числе состояний есть несколько состояний без выхода:
ТО
lim Y рт (/)=!,
t —► оо
т. е. через достаточный период времени система с практической
достоверностью окажется в одном из состояний xmi, Хт2, xms.
* Иногда это состояние называют поглощающим.
49
На рис. 2.1.5 изображен граф состояний системы: состояния Xi
и х2 представляют собой состояния без выхода. В этом случае
11m (МО+МОМ-
00
Могут быть случаи, когда несколько состояний представляют
собой «группу состояний без выхода». Так, на рис. 2.1.6 изобра-
жен граф состояний, в котором состояния х, и х2 представляют
собой группу состояний без выхода.
Если имеется одна группа состояний без выхода, в которую
входят состояния хт., хт.,..хт , то
s
11m У рт (/) = 1.
/-> оо
Рис. 2.1.5
Рис. 2.1.6
Если имеется k групп состояний без выхода:
Хт*, ..., Хт\ — первая группа состояний без выхода;
х<т\, Хт*,..., х(т^ —вторая группа состояний без выхода;
хт\ Хт*,..., Xml -k-я группа состояний без выхода, то
к
k Sj
Другими словами, после достаточного периода времени
система с практической достоверностью будет находиться в
одной из групп состояний без выхода.
На рис. 2.1.7 показан граф состояний системы, у которой две
группы состояний без выхода: первая группа имеет два состоя-
ния Xi, х2; вторая группа — тоже два состояния х4, х$. При этом,
если известно, что в какой-то момент времени t\ система была
в определенной группе состояний без выхода, то для любого
момента времени t>t\ система будет продолжать там нахо-
диться.
Состояние, в которое система не может перейти ни из какого
другого, называется состоянием без входа. Например, на
50
рис. 2.1.5; 2.1.6; 2.1.7 состояние х0 является состоянием без входа.
Очевидно, если состояние без входа будет Xi, то
lim pz(/) = 0.
/-►оо
Анализ любой системы массового обслуживания следует
всегда начинать с рассмотре-
ния всех состояний, в которых
эта система может быть, и с со-
ставления графа состояний с
указанием возможных перехо-
дов. Такой порядок анализа си-
стемы значительно облегчает
исследование и делает его бо-
лее наглядным.
Рис. 2.1.7
§ 2.2. ДИСКРЕТНЫЕ МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Рассмотрим один из важных с прикладной точки зрения
класс дискретных случайных процессов — дискретные марков-
ские случайные процессы с непрерывным временем *.
Пусть имеется дискретный случайный процесс, протекающий
в системе с возможными состояниями
Обозначим условную вероятность того, что в момент /=/о+т
система будет в состоянии если в момент to она была в со-
стоянии х^ через pij (to, т).
Дискретный случайный процесс X(t) называется марков-
ским, если вероятность Pij (to, т) зависит только от указанных
в обозначении параметров (i, j, to, т), т. е. от того, в каком со-
стоянии была система в момент to, в какое состояние она должна
перейти через время т.
Другими словами, все вероятностные характеристики марков-
ского процесса в будущем (при t>tQ) зависят лишь от того, в
каком состоянии этот процесс находится в настоящий момент
времени tQ и не зависят от того, каким образом этот процесс
протекал до момента t0 (в прошлом). Короче можно сказать
так: для марковского процесса «будущее зависит от прошлого
только через настоящее».
Различают два типа марковских случайных процессов: с дис-
кретным временем и с непрерывным временем. Марковским
* «Марковскими» называют процессы без последействия потому, что их
впервые изучил А. А. Марков (1856—1922).
51
случайным процессом с дискретным временем называется про-
цесс, у которого переходы из одного состояния в другое возмож-
ны в строго определенные заранее моменты времени /2, tk,...
Такие процессы редко встречаются при анализе систем
массового обслуживания, поэтому мы их рассматривать не будем.
Марковским случайным процессом с непрерывным временем
называется процесс, у которого переход (перескок) из одного
состояния в другое возможен в любой момент времени t. Можно
доказать следующее важное утверждение: если все потоки собы-
тий, переводящие систему из состояния в состояние, являются
пуассоновскими, то случайный процесс, протекающий в системе,
будет марковским с непрерывным временем *. Таким образом,
марковские случайные процессы с непрерывным временем тес-
нейшим образом связаны с пуассоновскими потоками событий.
В первой главе было показано, что стационарные и нестацио-
нарные пуассоновские потоки событий часто встречаются на
практике. Соответственно часто встречаются процессы марков-
ские или близкие к марковским процессам с непрерывным вре-
менем.
Для того чтобы описать'дискретный марковский процесс с
непрерывным временем, нужно знать следующие характеристи-
ки: перечень возможных состояний с указанием возможных не-
посредственных переходов из состояния в состояние, интенсив-
ности всех потоков событий, под влиянием которых осуществля-
ются эти переходы, и, в общем случае, состояние системы в
начальный момент при t=0.
Таким образом, для исследования процесса нужно:
1. Указать все состояния, в которых может находиться си-
стема.
2. Составить граф состояний, т. е. указать пути возможных
непосредственных переходов системы из состояния в состояние.
3. Для каждого возможного перехода указать соответствую-
щую интенсивность потока событий, переводящего систему
из состояния Хг непосредственно в состояние х$.
4. Указать, в каком состоянии находится система в началь-
ный момент времени (при t = 0).
Рассмотрение марковских случайных процессов, протекающих
в системах со счетным множеством состояний, будем начинать
всегда с описания самих состояний и составления графа состоя-
ний, на котором у каждой стрелки проставляется интенсивность
соответствующего пуассоновского потока событий. Граф состоя-
ний с интенсивностями пуассоновских потоков событий полно-
стью определяет процесс, протекающий в системе, если указано
начальное состояние (или начальные состояния) системы.
На рис. 2.2.1 показан граф системы с двумя состояниями
* Справедливо и обратное утверждение: если процесс, протекающий в си-
стеме, является марковским с непрерывным временем, то все потоки событий,
переводящие систему из состояния в состояние, являются пуассоновскими.
52
Рис. 2.2.1
x0, Xj; переход системы из состояния х0 в Xi происходит под
воздействиём пуассоновского потока событий с интенсивностью
Ao,i(O*> из *1 в х0— с интенсивностью М,о(О-
В дальнейшем договоримся, что если переход из состояния
хк непосредственно в состояние Xi невозможен, то соответствую-
щей стрелки на графе состояний указывать не будем и интен-
сивность соответствующего потока событий бу-
дем считать равной нулю: Удобно
также считать, что для любого k интенсив-
ность Xfe,fe(0=0-
Системы, в которых протекают марковские
случайные процессы с непрерывным временем,
будем _ называть пуассоновскими системами.
В дальнейшем будем рассматривать главным образом пуассо-
новские системы.
§ 2.3. СОСТАВЛЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДЛЯ ВЕРОЯТНОСТЕЙ
СОСТОЯНИЙ
Основное преимущество пуассоновских систем в отношении
их исследования состоит в том, что для этих систем вероятности
состояний описываются с помощью обыкновенных линейных диф-
ференциальных уравнений.
Чтобы продемонстрировать методику вывода этих уравнений,
рассмотрим простую систему с двумя состояниями х^, хь граф
которой изображен на ри.с. 2.2.1. Составим уравнения, опреде-
ляющие вероятности p0(t) и pi(t) того, что система в любой
момент времени t будет находиться в состоянии х0 и Xi соответ-
ственно. Для этого рассмотрим момент времени t и дадим ему
малое приращение А/. В этом случае вероятность ро(^+|А/) есть
вероятность того, что в момент времени (/+А0 система находит-
ся в состоянии х0. Это событие может иметь два исхода:
А — система в момент времени t была в состоянии х0 и за
время А/ из него не вышла;
В — система в момент времени t была в состоянии х\ и за
время А/ перешла в состояние х0.
В силу ординарности пуассоновских потоков событий вероят-
ность осуществления нескольких переходов за время А/ пред-
ставляет собой величину высшего порядка малости по сравне-
нию с А/ (О (А/) ).
Найдем вероятность события А. Это событие будет иметь
место, если в момент времени t система будет находиться в со-
стоянии х0 (вероятность этого р0(/)) и за время А/ не наступит
ни одного события в потоке с интенсивностью Xo,i(O- Условная
вероятность этого (в силу отсутствия последействия) равна [см.
(1.4.2) и (1.4.3)]:
53
/+д/
- ( хо.1(0<//
е \
Следовательно:
- f
Р{А)-—р0{1)е ‘ . (2.3.1)
Считая величину А/ малой, a Ход (0 — непрерывной функцией,
получим
Р (Д) = р0 (t) (1 - Ход (/) Д/ + О (А/)), (2.3.2)
где О (А/)—величина высшего порядка малости по сравнению
с АЛ
Событие В будет иметь место, если система в момент време-
ни t будет в состоянии х, и в потоке событий с интенсивностью
%1,о(О за время А/ наступит хотя бы одно событие, а в потоке
событий с интенсивностью Ход (0 за это же время Л/ не наступит
ни одного события. Опираясь на те же формулы (1.4.2), (1.4.3)
и считая функцию Xi,o(Z) непрерывной, получим
(t+м \ t+м
- J Xl,0<*>" I - J Ход(/>Л
1-е ‘ Je ‘ =
=A0(MWO(aO)- (2.3.3)
Применяя теорему сложения вероятностей, будем иметь
ро (/+Д/)=(1 - Х0|1 W М Ро (0 + ко (0 A/Pi (0 + 0 (Д/), (2.3.4)
где О (А/) представляет собой сумму всех членов, порядок ма-
лости которых выше АЛ
Проведя элементарные преобразования в выражении (2.3.4),
получим
Ро(7 + ДО-А>(О= _Хо1(/)а(/) + х1,о(/)а(0 + -^- .
дг д*
Переходя к пределу при А/—И), найдем уравнение
lim pa(t + M)-pn(t) = _Ч] (/)ро (/) (/).
Д/->0 М
Так как предел левой части есть производная функции p<At),
то окончательно дифференциальное уравнение для po{t) примет
вид
-М-=^(/)= -Хо.1(/)/’о(О + м.о(О А(0- (2.3.5)
54
Следует обратить внимание на то, что при выводе этого диф-
ференциального уравнения использовались оба свойства пуассо-
новского потока событий: ординарность и отсутствие последей-
ствия.
Очевидно, пользуясь аналогичными рассуждениями и учиты-
вая для каждого состояния все возможные переходы, связываю-
щие это состояние с соседними, можно получить столько обык-
новенных линейных дифференциальных уравнений, сколько
имеется возможных состояний системы.
Для нашего примера второе уравнение для р\ (t) будет
(2.3.6)
at
Естественно, для любого t должно соблюдаться условие
P^Pitf)=\. (2.3.7)
Таким образом, вероятности состояний р,(/) для дискретной
системы, в которой протекает марковский процесс с непрерыв-
ным временем, определяются системой обыкновенных линейных
дифференциальных уравнений. Другими словами, если все по-
токи событий, переводящие систему из состояния в состояние,
являются пуассоновскими, то вероятности состояний определя-
ются обыкновенными линейными дифференциальными уравне-
ниями *.
В^оятности состояний марковского процесса находятся
интегрированием соответствующей системы дифференциальных
уравнений при определенных начальных условиях. Если система
в начальный момент времени находится заведомо в одном опре-
деленном состоянии хт, то при t—Q вероятность этого состояния
равна единице: рт (0) = 1, Pi (0) =0 при i=#/n. В общем случае
могут быть заданы. вероятности всех состояний в начальный
момент, отличные от 0 и 1, при непременном соблюдении условия
п
2а(0)=1. (2.3.8)
1=0
Существует определенный методический прием, намного об-
легчающий вывод дифференциальных уравнений для вероятно-
стей состояний [19].
Продемонстрируем этот прием на конкретном примере. До-
пустим, что система имеет четыре возможных состояния: xQ,
х2, х3, и что переход системы возможен из любого состояния в
любое. Граф состояний такой системы показан на рис. 2.3.1. На
этом рисунке около каждой стрелки, указывающей возможность
* Заметим, что если процесс, протекающий в системе, не является марков-
ским процессом с непрерывным временем, то обыкновенных дифференциальных
Уравнений для вероятностей состояний составить нельзя.
55
и направление перехода, проставлены интенсивности пуассонов-
ских потоков событий, переводящих систему из состояния в со-
стояние по данной стрелке. Напомним, что интенсивность пуас-
соновского потока событий, переводящего систему из состояния
Xi в состояние Xj, мы договорились обозначать функция
для любого момента времени t является неотрицательной.
Условимся для краткости граф состояний, на котором простав-
лены не только стрелки переходов,
но и интенсивности соответствую-
щих потоков событий, называть
«размеченным графом состояний».
Если составлен размеченный
граф состояний, то для составления
дифференциальных уравнений для
вероятностей pi(t) (i=0, 1, ..., п)
можно предложить простое мне-
моническое правило.
Производная dpi(t)jdt вероятно-
сти пребывания системы в состоянии
Xi равна алгебраической сумме не-
скольких членов; число членов этой
Рис. 2.3.1
суммы равно числу стрелок на гра-
фе состояний системы, соединяющих состояние Xi с другими
состояниями. Если стрелка направлена в состояние х^ <о член
берется со знаком плюс; если стрелка направлена из состоя-
ния х^ то со знаком минус. Каждый член суммы равен произве-
дению вероятности того состояния, из которого направлена
стрелка, на интенсивность потока событий, переводящего систе-
му по данной стрелке. Число отрицательных членов равно чис-
лу стрелок, направленных из состояния х^ число положительных
членов равно числу стрелок, направленных в состояние Xi.
Пользуясь этим правилом, составим дифференциальные урав-
нения для вероятностей состояний системы, размеченный граф
состояний которой приведен на рис. 2.3.1:
—~— = — (41 (0 + 2 (0 + 4з (0) Ро (0++о (0 Pi (0 +
+ 4о (^) Р2 (*) + 4о (0 Рз
_ (х110 (/) 4- 4,2 (0+4,з (0) (0+41 (0 Р0 (0+
+41 (0 Рч (0+^з,1 (0 Рз (£);
= - (4,о (0+4.1 (0+Х2,з (0) р2 (0+><0,2 (0 р0 (0 +
+4Д0 МО+4,2 (0 МО;
dp3^ = — (4,о (0+4,1 (0 + 4,2 (0) Рз (0 Ч- 4,з (0 Ро (0 4
44з (0 Pi (044,з (0а (0-
56
При составлении этой системы дифференциальных уравнений
рекомендуется смотреть на граф состояний: это существенно
облегчает запись уравнений. Систему (2.3.9) можно короче за-
писать так:
з з
JSj£L=- S р* &+S ® (2-3-10)
J=O /=0
Напомним, что hh,h(t)=Q.
Полученный результат можно обобщить на случай, когда
система может иметь произвольное (п+1) число состояний
(х0, •*+). Система уравнений для такой системы будет
иметь вид
п п
+ (*=0,1, «)•
7=0 1 = 0
(2.3.11)
Для того чтобы проинтегрировать эту систему дифференциаль-
ных уравнений, нужно задать начальные условия
До(О),Л(О), р2(0),...,л(0). (2.3.12)
На эти начальные условия накладываются естественные огра-
ничения:
0<а(0)<1;
п
2^(o)=i.
й=0
(2.3.13)
Если условия (2.3.13) соблюдены, то для любого момента
времени t решение системы (2.3.11) должно соответствовать
нормировочному условию
п
2 Pk(t)= 1. (2-3.14)
й = 0
так как в любой момент времени t система будет достоверно
находиться в каком-нибудь одном из своих состояний *.
Отметим еще раз, что систему обыкновенных дифференциаль-
ных уравнений для вероятностей состояний (2.3.11) можно со-
ставить только для пуассоновской системы, т. е. для си-
стемы, в которой переход из состояния в состояние осуществляет-
ся под воздействием пуассоновских потоков событий. При этом
* В формулах (2.3.10) и (2.3.11) некоторые функции (/) могут быть
равны нулю для любого момента времени /, когда переход из состояния Xj
в состояние Xj невозможен.
57
интенсивности Mj(0 в системе (2.3.11) могут быть любыми не-
отрицательными функциями времени. Это означает, что потоки
событий, переводящие систему из состояния в состояние, явля-
ются пуассоновскими, не обязательно стационарными (простей-
шими).
Таким образом, допущение о марковском характере процес-
са, протекающего в системе с конечным (или счетным) числом
состояний приводит к необходимости анализа системы обык-
новенных линейных дифференциальных урав-
нений. В настоящее время аппарат обыкновенных линейных
дифференциальных уравнений разработан достаточно подробно.
Это является одной из причин широкого применения пуассонов-
ских потоков событий при анализе различных случайных
процессов, протекающих в системах массового обслуживания.
Если не делать предположения о том, что процесс, протека-
ющий в системе массового обслуживания, является марковским,
то аналитическое исследование работы такой системы требует
привлечения более сложного математического аппарата, с кото-
рым инженер либо не знаком вовсе, либо знаком, но весьма
поверхностно. К тому же в большинстве задач прикладного ха-
рактера замена непуассоновских потоков событий пуассоновски-
ми с теми же интенсивностями приводит к получению решения,
которое мало отличается от истинного, а иногда и вовсе не
отличается. При этом погрешность решения, как правило, нахо-
дится в пределах точности исходных данных, которые зачастую
известны весьма приближенно. Специальное моделирование раз-
личных задач, проведенное методом Монте-Карло [3], показало,
что в большинстве случаев эта погрешность ограничена Зн-5%
и лишь в редких случаях доходит до 104-12%, что вполне прием-
лемо при решении прикладных задач. Данное положение объяс-
няется тем, что потоки событий, протекающие в реальных си-
стемах, в силу предельных теорем теории потоков по своей
структуре весьма близки к пуассоновским.
Однако, как показал А. Д. Соловьев, имеются особые усло-
вия, когда погрешность может достигать значительных величин.
Поэтому при решении сложных задач, когда нет уверенности в
том, что замена реальных потоков пуассоновскими потоками
приведет к малым ошибкам, нужно рекомендовать проверять
аналитическое решение методом Монте-Карло (методом стати-
стических испытаний). При этом решение, полученное с помощью
пуассоновских систем, можно рассматривать как первое прибли-
жение. Это сокращает проведение расчетов методом Монте-
Карло.
В качестве простого инженерного критерия небольшого отли-
чия реального стационарного потока от пуассоновского можно
рассматривать близость математического ожидания и дисперсии
числа событий, наступающих на определенном участке времени
в реальном потоке.
58
Сделаем следующее замечание. Выше для составления диф-
ференциальных уравнений, описывающих вероятности состоя-
ний, мы пользовались размеченным графом состояний системы.
Любому размеченному графу состояний однозначно соответ-
ствует система дифференциальных уравнений, и наоборот. Таким
образом, информация, заключенная в размеченном графе и си-
стеме дифференциальных уравнений одна и та же. Однако граф
обладает большей наглядностью. Поэтому в дальнейшем, говоря
о различных системах массового обслуживания, мы *в основном
не будем писать дифференциальных уравнений, а будем ограни-
чиваться размеченным графом. Слово «размеченный» для крат-
кости будем опускать.
§ 2.4. ЭРГОДИЧЕСКИЕ МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ.
ТЕОРЕМА МАРКОВА. СТАЦИОНАРНЫЙ РЕЖИМ РАБОТЫ СИСТЕМЫ
Рассмотрим дискретные марковские случайные процессы с
непрерывным временем, которые обладают так называемым
эргодическим свойством. Будем называть процесс эргодическим*
если по истечении достаточно продолжительного промежутка
времени т вероятности со-
стояний системы прак-
тически не зависят от
того, в каком состоя-
нии она находилась в на-
чальный момент времени
/о и не зависят от са-
мого промежутка вре-
мени т.
Пусяъ имеется система с состояниями (х0, ...» *п). Для
просторы будем считать число состояний п конечным *. Допус-
тим, что система в момент времени tQ была в состоянии хг-. Обо-
значим через pi,j(tQ* т) условную вероятность того, что система в
момент времени / = /о+т будет в состоянии xj, если в началь-
ный момент времени /0 она была в состсяний Xi (рис. 2.4.1).
В сооответствии с определением марковского процесса можно
записать
PijVo, x)=P(^(/0 + x)=xy.|^(/0) = xi). (2.4.1)
Назовем процесс транзитивным, если для любой пары состоя-
ний Xi, Xj и любого /0 найдется такое т>0, при котором вероят-
ность
(2.4.2)
* Случаи бесконечного (счетного) числа состояний будут также рассмот-
рены в дальнейшем.
59
Это значит, что граф состояний не должен иметь ни одного
отдельного состояния без выхода и без входа и ни одной группы
состояний без выхода и без входа. Другими словами, из л ю б о-
г о состояния, например Хг, можно найти путь, по которому мож-
но добраться до любого другого состояния, например Xj
в том числе, и вернуться в исходное. Это утверждение вовсе не
означает, что каждое состояние системы должно непосредствен-
но соединяться с каждым другим состоянием.
На рис: 2.4.2 приведен граф состояний транзитивной системы,
а на рис. 2.4.3 —нетранзитивной системы, так как состояние х3
на рис. 2.4.3 является состоянием без выхода.
Рис. 2.4.2
Рис. 2.4.3
Возвращаясь к ранее рассмотренным графам состояний, мож-
но сказать, что на рис. 2.1.2; 2.1.3; 2.2.1 и 2.3.1 приведены тран-
зитивные системы, а на рис. 2.1.4, 2.1.5, 2.1.6, 2.1.7 — нетранзи-
тивные.
Очевидно, транзитивность процесса (достижимость любого
состояния из любого другого) является необходимым условием
того, чтобы этот процесс обладал эргодическим свойством. Если
процесс не транзитивен, то система по истечении достаточного
времени окажется в одной из групп состояний без выхода и^и в
одном из состояний без выхода. Однако для того, чтобы процесс
был эргодическим, этого недостаточно. Нужно, чтобы процесс
кроме того, протекал однородно во времени, т. е. чтобы
вероятность перехода из состояния Xi в состояние xj за время т
не зависела от того, в какой момент времени tQ система находи-
лась в состоянии Xi, а зависела лишь от величины т. Назовем
марковский случайный процесс однородным, если это условие
выполняется:
Pl,j(to, ^=pt,j($- (2.4.3)
Для того чтобы марковский случайный процесс был однород-
ным, нужно, чтобы все потоки событий, переводящие систему из
состояния в состояние, были стационарными пуассоновскими,
т. е. простейшими потоками. В дальнейшем системы, в которых
60
протекает однородный марковский случайный процесс, будем
называть простейшими системами.
Теорема Маркова утверждает, что любой транзитивный одно-
родный марковский процесс с конечным числом состояний обла-
дает эргодическим свойством, т. е. предел
Um р. у(т)=р. (0< Z < «; 0 < J < п) (2.4.4)
существует и не зависит от L Другими словами, по истечении
достаточно большого времени функционирования системы веро-
ятность того, что она будет в состоянии Xj не зависит от того,
в каком состоянии она находилась в начальный момент времени
/0 и практически не зависит от времени т, т. е. при достаточно
большом т вероятности pj будут достаточно близки к своим пре-
дельным значениям. Режим работы системы, при котором веро-
ятности Pj нахождения системы в состоянии Xj (j=0, 1, 2, ..., п)
не зависят от времени, называется стационарным режимом. Сле-
довательно, любой процесс, обладающий эргодическим свойст-
вом, имеет предельный стационарный режим, который практи-
чески наступает после достаточно продолжительного времени
функционирования («работы») системы. Этот режим не зависит
от того, в каком’ состоянии система находилась в начальный
момент времени.
Таким образом, для того чтобы марковский процесс, проте-
кающий в системе с конечным числом состояний, обладал эрго-
дическим свойством, нужно, чтобы 1) граф состояний не имел ни
одного состояния без выхода и б£з входа и ни одной группы
состояний без выхода и без входа; 2) все потоки событий, пере-
водящие систему из состояния в состояние, были простейшими.
Такие системы будем называть простейшими эргодическими
системами. Основное внимание в книге будет уделено изучению
стационарных режимов работы простейших эргодических систем.
Для всякой простейшей системы (в том числе и эргодической)
интенсивности пуассоновских потоков событий не зависят от вре-
мени и системы дифференциальных уравнений (2.3.11) превра-
щается в систему (п+1) обыкновенных линейных дифференци-
альных уравнений с постоянными коэффициентами:
п п
(*=0’ ’’ 2-•••>«)• (2-4-5)
;=0 :=0
Рассмотрим эргодическую простейшую систему, работа кото-
рой описывается уравнением (2.4.5).
Все время работы системы можно разбить условно на два
интервала: интервал (ОА) и интервал (^п, сю) (рис. 2.4.4), при-
чем для моментов времени />/п можно практически считать
вероятности рг постоянными. Интервал времени (О, /п) обычно
называется интервалом переходного режима работы системы,
61
интервал (tn, оо) — интервалом стационарного режима работы
системы, а величина tu — временем переходного режима систе-
мы. Время переходного режима системы можно определить из
следующего условия:
для любого t>ta
1/^(0 —Р;1О (7=0, 1,..л),
где величина 8>0 назначается исследователем.
Это условие эквивалентно тому, что вероятность Pj(t) пре-
бывания системы в момент t>tu в состоянии Xj мало отличает-
Переходный режим Стационарный режим
работы система работы систрмь
ся от вероятности
пребывания системы в
этом состоянии в ста-
ционарном режиме
(£—изо). Чем меньше
выбрана величина 8,
тем будет больше вре-
мя переходного режима
/п. Время tn зависит
Рис. 2.4.4.
также от начальных условий (2.3.13), при которых интегрируется
система уравнений (2.3.11).
По истечении достаточного времени, когда система войдет
в стационарный режим работы, в соответствии с равенством
Рис 2.4.5
(2.4.4) вероятности состояний практически не будут зависеть от
времени.
Имеем
11гп^>
at
Система дифференциальных уравнений (2.4.5) превращается
при этом в систему (п-Н1) алгебраических уравнений:
(2А6)
j=o 1=0
Пользуясь системой (2.4.6), можно определить значение pk
(fe=0, 1, ..., п) с точностью до постоянного множителя, но эта
62
неопределенность устраняется, если учесть нормировочное
условие
2^=1- (2-4.7)
й=0
В прикладных задачах часто ограничиваются изучением
лишь стационарных (установившихся) режимов работы систе-
мы. В дальнейшем основное внимание будет уделено рассмотре-
нию стационарных режимов работы.
Выше мы рассмотрели эргодическое свойство как свойство
независимости вероятностей состояний от времени и начальных
условий при t—х».
Однако эргодическому свойству можно дать- и несколько
иную трактовку, которая поможет решать различные приклад-
ные задачи.
Пусть система, в которой происходит эргодический процесс,
находится в стационарном режиме, в ходе которого она время
от времени попадает в состояние Xj и через некоторое случайное
время выходит из него. Изобразим на оси 0/ зачерненными уча-
стками промежутки времени, в течение которых система нахо-
дится в состоянии Xj, а незачерненными — промежутки, в тече-
ние которых она находится вне этого состояния (рис. 2.4.5).
На рисунке случайная величина Гр —это время пребывания
системы в состоянии xj первый раз; — время пребывания
системы вне состояния xj первый раз; =T\i)— время
первого цикла обращения системы; ...; 7’/^ —время пребывания
системы в состоянии л,/-й раз; — время пребывания системы
вне состояния Xj i-й раз; /УР=7'И)4-0/Л — время z-ro цикла.
Вследствие того, что система обладает эргодическим свойст-
вом, она рано или поздно попадет в состояние Xj, затем выйдет
из него, вновь попадет в состояние Xj, опять выйдет из него
и т. д. Другими словами, система будет «блуждать» по своим
состояниям^ иногда попадая в состояние Xj.
Рассмотрим достаточно большое число циклов N и возьмем
отношение суммарного времени нахождения системы в состоянии
Xj к общему времени всех N циклов:
(n \ ( N \—1
27?’> . (2.4.8)
Z = 1 / \/=1 J
Можно доказать, что при неограниченном увеличении числа
Циклов N отношение (2.4.8) будет сходиться по вероятности к
вероятности события ру.
(2.4.9)
63
С другой стороны, в силу однородности рассматриваемого
процесса случайные величины (Т^ (i=l, 2, 2V) распределены
одинаково, а так как процесс марковский, то они независимы.
То же самое можно сказать и о случайных величинах
(f=l, 2. Af). Поэтому при достаточно большом числе циклов
N можно написать следующее приближенное равенство:
n
Г/0) NM mTU)
л01
/=1
где mTW— среднее время пребывания системы в состоянии xj;
mH(i)—среднее время цикла.
Приближенное равенство (2.4.10) выполняется тем точнее,
чем большее число циклов имело место, т. е.
mTU)
(2.4.11)
Сравнивая (2.4.11) с (2.4.9), приходим к следующему важно-
му равенству:
тМ
Р;=----
тн^
(2.4.12)
т. е. вероятность пребывания системы в состоянии Xj (при рас-
смотрении стационарного режима работы) равна отношению
среднего времени пребывания системы в состоянии xj к среднему
времени цикла. Так как для любого i имеет место равенство
Hp’=7P+9P, (2.4.13)
ТО
т1^=тТч^т^ . (2.4.14)
и выражение (2.4.12) можно записать в следующем виде:
тта>
Pj
1 тги> +
(2.4.15)
где /пв(д — среднее время пребывания системы вне состояния Xj.
Таким образом, вероятность р, можно трактовать как среднее
относительное время пребывания системы в состоянии Xj. Из
этого равенства следует, что для отыскания среднего времени
/птО) пребывания системы в состоянии х, достаточно знать ве-
64
роятность пребывания системы в этом состоянии pj и среднее
время пребывания системы вне этого состояния и на-
оборот.
Равенством (2.4.15) будем часто пользоваться. Напомним
еще раз, что это равенство имеет место только для простейших
эргодических систем, находящихся в стационарном режиме
работы.
§ 2.5. ПРОЦЕССЫ ГИБЕЛИ И РАЗМНОЖЕНИЯ
Для большинства систем массового обслуживания, которые
будут рассмотрены в этой книге, граф состояний имеет вид, по-
казанный на рис. 2.5.1. Для этих систем характерно то обстоя-
тельство, что каждое состояние (кроме двух крайних) имеет
только два соседних состояния. Крайние состояния (крайнее ле-
вое и крайнее правое) имеют только по одному соседнему со-
стоянию.
Рис. 2.5.1
Таким образом, граф состояний можно представить
в виде цепи состояний, соединенных между собой стрелками
переходов. Другими словами, из любого состояния хь (кроме
крайних: k=^n) возможен переход только в два соседних
с ним состояния: Хн-\ (предыдущее) и a+i (последующее). Из
крайнего левого состояния хо возможен переход только в состоя-
ние X], а из крайнего правого состояния хп — только в состоя-
ние Хп-1.
Процессы, описываемые с помощью такого графа состояний,
в литературе принято называть «процессами гибели и размно-
жения». Такое название они получили потому, что впервые были
применены в биологии для анализа численности популяций, рас-
пространения эпидемий и при исследовании других проблем. Так,
например, если считать, что состояние х& соответствует числен-
ности популяции, равной k, то переход системы из состояния Ха
в состояние ха+1 происходит при рождении одного члена популя-
ции, а переход в состояние xk-i — при гибели одного члена попу-
ляции. Число п может быть как конечным, так и бесконечным.
Конечное число членов популяции может иметь место в том
случае, когда имеются физические ограничения на максимальную
численность популяции, например, при анализе развития микро-
организмов в каком-либо запаянном стеклянном сосуде. При ана-
лизе численности популяций в естественных условиях можно
практически считать, что нет ограничений на эту численности^
3—1964 65
На самом деле, такие ограничения есть в силу ограниченности
размеров земного шара, но на практике эти ограничения не до-
стигаются.
Систему дифференциальных уравнений для вероятностей со-
стояний процесса гибели и размножения можно записать с по-
мощью правила, приведенного в § 2.3:
-^P-=-Vo(O+^i(O;
—А— = _ рк (/) рк_г (/) -j_ +j рк+j (/)
-1М>я(0+*л-1(0 Pn-iii).
at J
Эта система уравнений справедлива как для постоянных ин-
тенсивностей потоков, так и для случая, когда интенсивности
потоков являются некоторыми функциями времени:
(А = 0, 1,..., д-1); (*=1, 2,...,«).
Для интегрирования этой системы дифференциальных уравнений
нужно задать начальные условия
п
Ро(О); А(0);..., ^„(0); 2 Л(0)=1- (2.5.2)
й=0
Если число состояний п в системе конечно, то для любого момен-
та времени выполняется нормировочное условие
п
(2.5.3)
л=о
Иногда рассматривают процесс размножения (чис-
того размножения), когда переход из состояния в состояние
возможен только слева направо. Граф процесса размножения
доказан на рис. 2.5.2. •
Рис. 2.5.2
Если переход возможен только справа налево, то такой про-
цесс называется процессом гибели (чистой гибели). Граф
процесса гибели показан на рис. 2.5.3.
66
Для того чтобы написать дифференциальные уравнения для
вероятностей состояний процесса размножения достаточно в
системе (2.5.1) положить все параметры |Ыг=0 (/=1, ..., п). Ана-
логично, если требуется написать дифференциальные уравнения
для вероятностей состояний процесса гибели, достаточно в си-
стеме (2.5.1) положить все параметры (& = 0, 1, ..., п—1).
Рассмотрим несколько подробнее случай, когда у процесса
гибели и размножения все параметры являются положительными
постоянными величинами. Это означает, что величины не
зависят от времени, но зависят от индексов. Такой процесс ги-
бели и размножения, описываемый с -помощью графа, изобра-
женного на рис. 2.5.1, будет обладать эргодическими свойствами,
так как оба необходимых для этого условия выполняются;
Рис. 2.5.3
1) граф состояний не имеет ни одного состояния без выхода
и без входа и ни одной группы состояний без выхода и без
входа;
2) все потоки событий, переводящие процесс из состояния в
состояние, являются простейшими, так как параметры являются
постоянными (во времени) величинами.
Будем называть такой процесс простейшим процессом гибели
и размножения.
Таким образом, для простейшего процесса гибели и размно-
жения с конечным числом состояний п всегда существует стацио-
нарный режим работы *. Для определения предельных вероят-
ностей для стационарного режима, который наступит в процессе
гибели и размножения после достаточного периода времени
функционирования, можно записать систему (п+1) однородных
алгебраических уравнений [см. (2.4.6)]:
— + + н=0 (k=\, — 1);} (2.5.4)
- НЛл + \Р«-1 = 0. ]
Для решения этих уравнений введем следующие обозначения:
«ft= — \,Pk+ H>+iP*+i (£ = 0, —1). (2.5.5)
3*
Случай, когда и=оо, будет рассмотрен ниже.
6?
Тогда уравнения (2.5.4) примут вид
«о=О;
«ft—«4_1=0; (2.5.6)
— и„_1=0.
Анализ полученной системы уравнений показывает, что имеет
место равенство
«й=0 (£=0, 1,...,я-1), (2.5.7)
следовательно [см. (2.5.5)]:
Pt+i=--*- рк (А=0, 1,..., л-1). (2.5.8)
Таким образом, мы получили возможность с помощью рекур-
рентной формулы (2.5.8) выразить значение любой вероятности
через все предыдущие.
Рк+г —---Pk—--------p*-i= ...
...=р0 П—(*=0. V--. (2.5.9)
/=о W+I
Найденное выражение для всех вероятностей состояний про-
цесса гибели и размножения зависит от вероятности ро и пара-
метров потоков. Вероятность ро можно определить из нормиро-
вочного условия (2.5.3):
л—1 Л—1 £
До+22/,*+1=До+Ро22 П ~~
г n H'J+l
Л=0 й=0 /z= 0
откуда
(2.5.10)
Итак, совокупность формул (2.5.9) и (2.5.10) дает возмож-
ность, определить все вероятности состояний процесса гибели и
размножения для конечного числа состояний п.
В случае, когда число состояний не ограничено (п=оо), ста-
ционарный режим может не существовать даже при постоянных
68
(не зависящих от времени) параметрах щ. Это объясняется
тем, что могут иметь место условия, при которых нет никаких
ограничений на рост популяции, и процесс все время «будет
двигаться направо».
Для того чтобы нормировочное условие
2 ^(0=1
й=0
выполнялось, достаточно расходимости ряда (см. 20):
УГР. (2.5.11)
Г. I- 11
Если ряд (2.5.11) расходится, а ряд
П—— (2.5.12)
сходится, то существует стационарный -режим
pft=llmpft(0.
/->оо
Условие (2.5.12) всегда выполняется, если начиная с некоторого
k справедливо неравенство
< х < 1.
W+1
(2.5.13)
В дальнейшем изложении будет дано физическое обоснование
и приведены примеры, когда наличие постоянных интенсивностей
потоков еще не гарантирует существование стационарного режи-
ма в процессах гибели и размножения.
Если рассматривается процесс чистого размножения, то нор-
мировочное условие
ft=0
выполняется только в случае, когда ряд
(2.5.14)
69
расходится [22]. В противном случае имеет место неравенство
*=0
откуда
оо
рку)=ру)>о-
k=Q
Последнее неравенство означает, что за время t имеется
конечная вероятность p(t) того, что в процессе чистого размно-
жения произойдет сколь угодно большое (бесконечное) число
переходов. Такие процессы-имеют место при рассмотрении явле-
ний типа «взрыва».
В процессах чистого размножения при отсутствии ограниче-
ний на число состояний (п=оо) стационарный режим не сущест-
вует. В этом случае будет иметь место постоянное «движение»
системы в сторону состояний, находящихся «справа».
В начале этого параграфа указывалось, что процессы функ-
ционирования большинства рассматриваемых в книге систем
массового обслуживания можно представить как процессы гибе-
ли и размножения. Из этого следует, что основные соотношения
и формулы для этих систем массового обслуживания могут быть
получены из формул этого параграфа как различные частные
случаи процесса гибели и размножения. Однако такое методи-
ческое построение книги привело бы к более формальному
изложению материала и не дало бы возможности раскрыть
физический смысл, вкладываемый в те или иные соотношения и
формулы.
Так как книга имеет прежде всего прикладной характер, по-
этому все соотношения и формулы мы будем выводить из физи-
ческих условий работы той или иной системы массового обслу-
живания, а не как частные случаи формул этого параграфа. При
этом мы будем широко использовать общие результаты, полу-
ченные для процессов гибели и размножения.
§ 2.6. ОПРЕДЕЛЕНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ
НАХОЖДЕНИЯ В ГРУППЕ СОСТОЯНИЙ
При рассмотрении различных задач теории массового обслу-
живания зачастую требуется найти закон распределения времени
пребывания системы в группе состояний. Например, при рассмот-
рении системы с очередью требуется определить закон распреде-
ления времени наличия в системе очереди, которое отсчитывается
от момента возникновения очереди до момента, когда последняя
заявка, стоящая в очереди, уйдет из нее (т. е. очередь будет
ликвидирована).
70
Как уже указывалось, граф состояний большинства рассмат-
риваемых в книге систем X имеет вид, показанный на рис. 2.6.1.
Такая система имеет (п+1) состояний, переход возможен
непосредственно только в «соседние» состояния. Переход «через
состояния» невозможен вследствие ординарности пуассоновского
потока событий. Процессы, описываемые такими системами, на-
зываются процессами гибели и размножения (см. § 2.5).
Рис. 2.6.1
НайДем закон распределения времени Т непрерывного пре-
бывания системы в группе состояний
xh Х/+1, ..., Xj-\, Xj (Z—О, 1, 2,..., n; У = 0, 1, 2,..., n; /<_/)
при условии, что в начальный момент времени Z=0 система на-
ходилась й каком-то одном из этих состояний. Для определенно-
сти будем считать этим состоянием xt. Очевидно, нахождение
закона распределения времени Т эквивалентно отысканию зако-
на распределения времени блуждания системы по состояниям
xit ..., х,- до первого выхода за пределы этих состояний, если
в начальный момент времени t=0 система была в состоянии
хг(г^/^/). Для отыскания этого закона применим следующий
Рис. 2.6.2
прием: представим себе некоторую подсистему X, состояния ко-
торой изображены на графе (рис. 2.6.2). Эта подсистема имеет,
кроме исследуемой группы состояний хг-, ..., Xj, еще два смежных
состояния «слева» и «справа», в которые она может только ухо-
дить, но из которых она не может возвращаться. Этой подсисте-
ме соответствует система дифференциальных уравнений:
71
p'i-i(i)='ki,i-ipl(ty,
Pt(fr= — (^./+i+^z,/-i) Р((0+^г+1,/Д/+1Ю‘,
pit (f)~ —P-o+i i) Ph(t)-\-'^k—i,kPk—i (z)4-
-{-^ft+i,ft/>*+i(0 (/ <^k < /);
(2.6.1)
Pi(t}= — O-jj+i-H/.z-i) Ы0+>/-»./Р;-» (0;
pj+i(0=x;j+ip)(^
Так как в начальный момент времени Z=0 известно, что
система находится в состоянии xj(z^Z^j), то интегрировать
уравнения (2.6.1) нужно при начальных условиях
А(0)=1; Л(0)=0 (/</</; k^ly (2.6.2)
Найдем функцию распределения F(t) времени Т пребывания
системы X в группе состояний х<, .... Xj. Она равна вероятности
того, что это время Т будет меньше, чем t, т. е. что к моменту
времени t система не будет находиться в группе состояний
Xi...Xj, а будет находиться либо в состоянии xt_i, либо в состоя-
нии Xj+i. Следовательно:
^(О=Л_1Ю+?У+1(О (*>0). (2.6.3)
Так как производная dF(t)ldt существует, то плотность рас-
пределения непрерывной случайной величины Т будет равна *
/W= '£<'>_. fo-'0» + fH?. (2.6.4)
J к 7 dt dt 1 dt v
Воспользовавшись системой уравнений (2.5.1), получим
/(/)=Xz,Z-1pz(/)+X7J+1^(/) (/> 0). (2.6.5)
Хотя система X отличается от системы X, но закон распреде-
ления времени пребывания ее в группе состояний Хг, ..., %; будет
тот же, как и? у системы X.
Действительно, поскольку мы предполагаем, что в начальный
момент t = 0 система X находится в одном из состояний группы
(xz, ..., Xj) и рассматривается только время до первого вы-
хода из этой группы состояний, то совершенно все равно, как
* Непрерывность случайной величины Т следует из того, что рассматри-
ваемый марковский случайный процесс является процессом с непрерывным
временем и счетным числом состояний.
72
Ж[Г21 =
система X ведет себя за пределами этой группы и как она в нее
возвращается.
Таким образом, для отыскания плотности распределения вре-
мени Т пребывания системы в группе состояний xt-, Xj нужно
проинтегрировать систему (2.6.1) без первого и последнего урав-
нений при начальных условиях (2.6.2) и найти вероятности
Pi(t) и pj(t) *. После этого по формуле (2.6.5) найдем плотность
распределения времени Т.
Зная плотность распределения случайной величины Т, можно
найти ее числовые характеристики:
математическое ожидание
М [Т] =7= J if(t)dt=\lti-i f tpi(f)dt+l},j+1 J ipj(i)di; (2.6.6)
ООО
второй начальный момент
оо оо со
% = J PptWdf+Xjj+i. J Рр}(2.6.7)
о о о
дисперсию
Z>[7']=a2 -(7)2=Л4 [Л]-(Л4 [Г])2. (2.6.8)
Если требуется найти закон распределения времени Т пребы-
ванйя системы в группе состояний «правее» х< (включая само
состояние xt(Z>0)), то граф состояний подсистемы X будет
иметь вид, показанный на рис. 2.6.3. Интегрировать систему
дифференциальных уравнений, соответствующих такому графу
I состояний, нужно при начальных условиях pi(0) = l; рь(0) = 0
(i^/^n, k=£l). Плотность распределения случайной величины Т
найдем из выражения
f (/). (2.6.9)
at
При необходимости отыскать закон распределения времени
Т пребывания системы в группе состояний левее Xj (включая
само состояние х3 (/<п)) нужно решать систему дифференциаль-
ных уравнений, соответствующую графу состояний, изображен-
ному на рис. 2.6.4.
Начальными условиями для решения этой системы уравнений
бУДУт £r(0)=l; 7*(0)=0 k^l).
* Заметим, что этим способом можно отыскивать закон распределения
времени пребывания в группе состояний и в случае, когда интенсивности пото-
ков являются переменными.
73
Плотность распределения случайной величины Т в этом случае
найдем по формуле
/(П=-^й^(0=Ч/+1М0- (2.6.10)
at
Таким образом, решая определенную систему уравнений,
можно найти закон распределения времени нахождения в группе
состояний. Однако зачастую нам не требуется находить закон
распределения времени пребывания системы в группе состояний
Рис 2.6.3
Рис. 2.6.4
%г, х^, а требуется лишь найти математическое ожидание этого
времени. Мы ограничимся при этом лишь случаем, когда либо
j = n, i^l; либо r = 0, a j^n—1 и интенсивности всех потоков со-
бытий постоянные.
Рассмотрим граф состояний, изображенный на рис. 2.6.5.
Будем искать среднее время пребывания системы в состояниях
Рис. 2.6.5
Рис. 2.6.6
xif ..., Xn(i^l). Очевидно, закон распределения времени нахож-
дения системы в состояниях Хг, ..., хп не зависит от того, какой
конкретный вид имеет граф состояний системы «слева» от со-
стояния Хг. Следовательно, для решения задачи можно рассмот-
реть более простой граф состояний подсистемы, изображенный
на рис. 2.6.6.
При постоянных значениях всех интенсивностей потоков со-
бытий для подсистемы, граф состояний которой изображен на
рис. 2.6.6, существует стационарный режим. Обозначим через
Tit ..., п время пребывания в группе состояний хг-, ..., хп, отсчиты-
ваемое от момента попадания в состояние Хг до следующего
очередного момента попадания в состояние Хг-ъ через Ti-i —
время однократного пребывания в состоянии Хг-\ и через л?, ..., п—
вероятности нахождения системы, граф состояний которой
изображен на рис. 2.6.6, в состояниях х^ ..., хп.
74
При t—>-оо и постоянных интенсивностях потоков событий
можно найти вероятность щ, ..., п, решая соответствующую си-
стему алгебраических уравнений.
Система алгебраических уравнений, определяющих вероят-
ность ж, .... п=1—ж-ь имеет вид
0= —рi-it-iPi',
о= — 4-^/j-i) Pj-\-^j-ijPi-i-t^j+ijPj+i i);
0= —Хл,л—1Рп 1,пРп—1-
Эту систему нужно решать совместно с нормировочным условием
2 р^-
Вероятность
.........................п=2 р]'
7=1
' KZ-1~ 1 — .....n~Pl-V
С другой стороны, на основании эргодического свойства
имеем
(2.6.11)
где ti_A = —----------среднее время нахождения системы
1 i-\,i
в состоянии
ti..—искомое среднее время нахождения
я/,п
системы в группе состояний Xi..х„.
Аналогично находится среднее время to, г пребывания систе-
мы В СОСТОЯНИЯХ Хо, —, Xi (i^n—1).
Заметим, что для нахождения среднего времени пребы-
вания системы в группе состояний нам нужно решать не систему
дифференциальных уравнений, а систему алгебраических
уравнений, что значительно облегчает задачу.
Примеры решения задач с применением формул (2.6.11),
(2.6.12) будут рассмотрены в следующих главах, где будут ана-
лизироваться конкретные системы массового обслуживания.
Во многих случаях можно приближенно считать, что закон
распределения времени Т,-,..., п пребывания в группе состояний
75
Xi,—,xn ('рис. 2.6.6) является иоказательным. Здесь время
Л, ...» п отсчитывается от момента попадания системы в состоя-
ние Хг до следующего очередного момента перехода в состояние
Xi-i. Возможность такого приближенного допущения основана
на том, что вероятность определяемая графом состояний,
изображенным на рис. 2.6.7, является монотонно убывающей
функцией времени t. Это справедливо только в случае, если в
начальный момент система находится в состоянии
А(0) = 1; й(0)=0 (2.6.13)
Расчеты показывают, что такое приближение вполне допусти-
мо с инженерной точки зрения.
Обозначим приближенную плотность распределения времени
пребывания в группе состояний
приближенное выражение для
Рис. 2.6.7
х,, хп через f{....n(t). Тогда
этой плотности распределения
будет иметь вид
Л...,л(/)=Хе-^ (/>0),
(2.6.14)
где
ti,.... п — среднее время пребывания в группе состояний х».хп,
определяемое по формуле (2.6.12).
Метод отыскания закона распределения времени пребывания
в группе состояний, изложенный в этом параграфе, может быть
применен и в случае, если граф состояний системы имеет произ-
вольный вид, отличный от того, который показан на рис. 2.6. L
Этот метод может быть применен и для отыскания законов рас-
пределения времен пересечения марковским процессом заданного
уровня.
§ 2.7. ЗАДАЧИ И УПРАЖНЕНИЯ
2.7.1. Для системы, граф состояний которой изображен на
рис. 2.6.1, найти закон распределения времени нахождения в
крайнем «левом» состоянии Хо, если в начальный момент система
находилась в этом состоянии.
Решение
Для нахождения закона распределения воспользуемся гра-
фом состояний, изображенном на рис. 2.7.1а.
Дифференциальное уравнение будет иметь вид
^- = -Wo(O-
at
76
Его нужно решать при начальном условии ро(О)=1:
Ро(/)=е-хо.1' (/>0).
Плотность распределения времени Т будет
/(0= (*>0).
at
Мы получили показательный закон распределения, что естест-
венно. Числовые характеристики этого закона будут равны
УИ[7-]=—,
Л0,1
О[7'1=— .
Если требуется найти закон распределения времени пребыва-
ния в крайнем «правом» состоянии хп, то соответствующий граф
состояний будет иметь вид, показанный на рис. 2.7.16.
Рис. 2.7.1
Следовательно, и в этом случае закон распределения будет
показательный, но с параметром Лп, п-ь
2.7.2. Решить пример 2.7.1 при условии, что параметр X0.i за-
висит от времени
Ход (/)=а (1 —- sin <о/).
Решение
Дифференциальное уравнение имеет вид
= _ а (1 — sin и/) /70(/).
at
Его нужно решать при начальном условии ро(О) = 1:
t
— {ЧНОЛ _ г cos <><-!]
Po(z)=e ° “ -I (Z>0).
Очевидно, при и a=Xo,i получим решение предыдущей
задачи. Таким образом, f(t) =а(1 —sin a>t) е “> + 2
77
2.7.3. Граф состояний системы имеет вид, показанный на
рис. 2.7.3а. Требуется определить закон распределения времени Т
пребывания в состояниях х0, ..., хп-г при условии, что при /=0
система находилась в состоянии х0.
Решение
Граф состояний подсистемы X для определения закона рас-
пределения времени Т будет иметь вид, показанный на рис.
Рис. 2.7.3а
2.7.36. Соответствующая этому графу состояний система уравне-
ний будет
-^-=-Wo(O;
at
(о <*<«).
dt
Начальные условия, при которых нужно интегрировать эти урав-
нения, имеют вид:
Ро(О) = 1; Л(°)=° (0<*<л).
Рис. 2.7.36
В соответствии с решением
задачи 2.7.1 решение перво-
го уравнения можно записать
так:
А)(0=е-м-
Тогда для отыскания вероятности p\{t) получим уравнение
^a_==_xj1(Z)=Xoe-M.
Преобразование Лапласа для этого уравнения будет
s И- Ао
где pi(s) —изображение функции
78
Следовательно:
рг (s)=----------------------*£--
(S + W+М 1
П (5 + Ъ)
/=0
Оригинал для изображения pi (s) будет иметь вид
Р^=К *-------------•
А1 — Л0
Для отыскания вероятности pz(t) получим уравнение
^rL+x2p2(/)=k1^1(/).
« at
Преобразование Лапласа для этого уравнения будет равно
$р2 («) + Х2^2 (5) = Х1Pl («) = — W,
П 4- X/)
/=о
откуда
p!(s)=,_w_.
П (<$ + X/)
/=о
Соответствующий этому изображению оригинал будет иметь вид
~ (/)______кХ. + (Xt — Хо) i~Xg/
(Хо—^^(Х! —Х2)(Х2 —Хо)
Выражения для p\(t) и p2(t) можно переписать в следующем
виде:
х л-1 k —\jt
А(0=(-1)йП\Е~Г-£------------ (^=1, 2).
/=0 >=о П (Х;-ХА)
л=о h + 1
То, что означает, что рассматривается произведение
только различных параметров, т. е. при h= j нужно полагать
X j—Xh = 1 •
Можно показать, что выражение для вероятности Pk(t) будет
рИ0=(-1)*п\-£ „ е — (*=Ъ 2,..., п-1).
1=0 j=o Y\aj-h)
h=Q h* i
79
Тогда искомая плотность распределения случайной величи-
ны Т запишется так:
л-1 "-1 -хл
at л—1
/=0 /=0 П(Х/-*л)
л=о * + >
Закон распределения, имеющий такую плотность, называется
обобщенным законом Эрланга (п—1)-го порядка (п=1, 2, ...).
Его числовые характеристики будут равны
п—1
1=0
л—1
O[r|=L^-
1=0
При Хо=М=... =Xn-i = A, получим закон Эрланга (л—1)-го по-
рядка:
(XQ"-» х/
для которого
D [Т]=~ .
1 J W
состояний системы имеет вид, показанный на
2.7.4. Граф
рис. 2.7.4а. Сравнить между собой законы распределения двух
случайных величин То и Ть где
Рис. 2.7.4а
Рис. 2.7.46
То — время нахождения в группе состояний х0 и хь если в
начальный момент /=0 система была в состоянии х0;
Tj — время нахождения в группе состояний х0 и хь если в
начальный момент t=0 система была в состоянии хь
Решение
Граф состояний подсистемы X для отыскания законов рас-
пределения времени То и Л представлен на рис. 2.7.46.
80
(О;
Соответствующая этому графу система дифференциальных
ура нений имеет вид
dt
dt
- (*+h)a0+*a>(O-
Преобразование Лапласа для этих уравнений при отыскании за-
кона распределения величины То(Ро(0) = 1; Pi(0)=0) запишет-
ся так:
(s+x)Po(«)-l1Pi(s)=s;
(s + X + |i) pi ($)-Xpo(s)=O.
Решая эту систему относительно изображения pi($), получим
— , ч Is Is
' 14 ’ s2 4-(214-р.) 4-12 (s4-a)(s4-0 ’
откуда
~ e~bt — e~at
а— b
где
-21 4- р — 41р. 4- р2
-——————————
2
&21 4~ р + V 41р. 4- р2
(2.7.4)
корни уравнения х2+ (2Х+р,)х+.Х2 = 0, взятые с обратным знаком.
Тогда искомая плотность распределения случайной величины
То будет
/о(/)=-^-=Хл(0=Х2
at
e~bi — e~at
a— b
Нетрудно убедиться в том, что условие
(/>0).
выполняется.
Действительно:
-Ы _e-at
a — b
I2 Г 1 11 I2 1
at=---------------1 —---=1,
а — b I b a J ab
о
2
J /о(/)Л=1
о
81
так как произведение корней равно свободному члену. Найдем
математическое ожидание То:
^[7'о]=/о=-^т-
\ te~btdi — \ te~atdt
-6 о
Х2
а — b
Г------Ll^x2
[ Z>2 а?- J
а 4- b _ _ 2 । fi
— Т Х2
При отыскании закона распределения случайной величины Тi
начальными условиями будут /?о(0)=0; pi(0) = l. В этом случае
преобразование Лапласа для дифференциальных уравнений при-
мет вид
(«+>•) А («)-!* А («)=0;
(« + >• + р) A (s)-X/70(s)=s.
Решая эту систему относительно Pi(s), получим
А СО
S(S + k)
s2 4* s (2k -f- fi) 4~ A.2
откуда
px (/)= e at * bi
a — b
где а и b находятся из формул (2.7.4).
Следовательно:
fdt)=XPl(t)=.x\^-e-»4
[ а — b
b-Л
b — a
e~bt
Математическое ожидание времени 7\ будет равно
м [Fj]=/, = (/) dt = X
О
оо *
^^-\te-btdt = хГ-а~Х —
b — a J [а — b eft
о J
^—^-\te-aidt +
а— b J
о
b — \ 1
b — a b'2
Сравнивая это выражение с выражением для математического
ожидания случайной величины То, убеждаемся в том, что для
любых Х>0 и р,>0 значение 70>?ь
82
Это объясняется тем, что система будет блуждать по состоя-
ниям х0 и Xi в среднем больше, если она в начальный момент
находится в состоянии х0. На рис. 2.7.4в показаны графики
плотностей распределения f0(t) и fi(t) при Х=р.= 1.
2.7.5. Через систему ПВО прорывается группа самолетов,
состоящая из т постановщиков помех и одного бомбардировщика.
Огонь сначала ведется по постановщикам помех, а затем по бом-
бардировщику. Поток пусков
ракет можно считать пуассо-
новским с интенсивностью X;
вероятность поражения одной
ракетой одного самолета (лю-
бого) равна р. После пораже-
ния самолета огонь мгновенно
переносится на следующий са-
молет. Время нахождения са-
молетов в зоне обстрела ПВО
равно т. Определить вероят-
ность того, что за время обстре-
ла т бомбардировщик будет по-
ражен.
Решение.
Группа налетающих само-
летов может быть в следующих
состояниях: Xt — сбито i само-
летов (г=0, 1, 2,..., т+1).
Граф состояний системы по-
казан на рис. 2.7.5а.
Величина Х( определяется
следующим образом: Xi = Xp.
Этот граф с точностью до обозначений совпадает с графом,
изображенным на рис. 2.7.36-
Рис. 2.7.5а
Следовательно:
= <
di----------ml
где pm+i (t) — есть вероятность того, что к моменту t бомбарди-
ровщик будет поражен.
Тогда искомую вероятность найдем по формуле
Pm+i(х)= "dPm+d\ (° dt== 1 ~
О
где /?(т, а) —табулированная функция (см. приложение).
83
Например, при Х=’1 ——; т=16 мин; р = 0,5; т=10 получим
мин
рот4_1(т)=1-/?(10,8)=1-(1-0,184) = 0,184.
вестна интенсивность пуассоновского
водящего систему из состояния х0.
Рис. 2.7.6а
2.7.6. Граф состояний системы приведен на рис. 2.7.6а. Из-
потока событий Х(/), пере-
Известно также, что при
выходе системы из со-
стояния Хо она с веро-
ятностью qi оказывает-
ся в состоянии Xi
2, ..., п). Определить
а) интенсивность пуас-
соновского потока со-
бытий, переводящего
систему из состояния
xQ в состояние Xi и
б) вероятность pi(t) того, что к моменту t система будет в со-
стоянии х^ если в момент (/=0 система была в состоянии х0.
Ответ
( - J К (х) dx
a) 6)pz(/)=j \-(т) е 0 dt.
о
При k(/)=k=const получим:
a) б)
2.7.7. Граф состояний системы имеет вид, показанный на
рис. 2.7.7а. Требуется найти закон распределения времени ТОд
нахождения системы в состояниях х0, в стационарном режиме,
если интенсивности всех потоков равны 1 .
сек
Решение
В соответствии с графом состояний система из группы со-
стояний х0, Xi может попасть только в состояние х2. Попав в со-
стояние х2, система с вероятностью V2 перейдет в состояние х0,
либо с вероятностью V2 — в состояние х3 (а оттуда в состояние
*1). Следовательно, блуждание в группе состояний х0, Xi с равной
вероятностью V2 может начаться из состояния Хо или из состоя-
ния хь Граф состояний подсистемы X, с помощью которого мож-
но найти искомый закон распределения времени Тод блуждания
по состояниям Хо, Xi, представлен на рис. 2.7.76.
64
Этот граф с точностью до обозначений интенсивностей пото-
ков событий совпадает с графом, изображенным на рис. 2.7.46.
Следовательно, и решение с точностью до обозначений будет
таким же, как и в примере 2.7.4.
Рис. 2.7.7а Рис. 2.7.76
Рис. 2.7.7в
Таким образом, если блуждание начинается из состояния xQr
то плотность распределения времени To,i будет равна
з- /5 , з + /Г ,
е----*-- -е--------
--------- (*>о).
Если блуждание начинается из состояния хь то плотность рас-
пределения времени ТОд будет равна
С учетом того, что блуждание в состояниях х0; может с веро-
ятностью V2 начаться из состояния х0 и с вероятностью V2 — ив
состояния Xi, получим следующее выражение для плотности
распределения времени блуждания в состояниях %о; Xi-
/o.i(0 = 4-[/o(0+/iW] =
85
График этой функции представлен на рис. 2.7.7в,
Математическое ожидание времени пребывания в состояниях
хо> Ху будет равно
ОС
~С 5
/о,1 = yfo.i(f)dt = — сек.
о
2.7.8. Автомашина при ее эксплуатации может находиться в
следующих состояниях:
х0 — исправна;
Xi — неисправна, проходит осмотр, ко-
торый проводится с целью опре-
деления вида ремонта;
х2 — неисправна, проходит капиталь-
ный ремонт;
х3 — неисправна, проходит средний ре-
монт;
х4 — неисправна, проходит текущий ре-
Рис. 2.7.8а
монт.
Граф состояний автомашины показан на рис. 2.7.8а. Среднее
время межремонтного пробега равно to. Среднее время осмотра
машины равно t\. После осмотра автомашина подвергается капи-
тальному ремонту с вероятностью q2, среднему ремонту с веро-
ятностью q3 и текущему ремонту с вероятностью q^ (?г + <7з+?4=
= 1). Среднее время проведения капитального ремонта равно t2,
среднее время проведения среднего ремонта равно t3, среднее
время проведения текущего ремонта равно /4. Определить веро-
ятность того, что машина будет исправна (для стационарного
режима), вероятность того, что время простоя машины будет не
более t и среднее время простоя машины.
Решение
Найдем интенсивности потоков, переводящих автомашину из
состояния в состояние:
Хо,1=т~ '> to Х1.2=4г; >-1.з=4г; ^1,4=^; tl tl h
Х2,0=-7~" » *2 Л3,о = — ; а4,0 = — • ^3 ^4
Считая, что все потоки простейшие с выше указанными
интенсивностями, найдем вероятность ро того, что машина будет
исправна для стационарного режима. Решйм соответствующую
систему однородных алгебраических уравнений:
О — — Ход pQ -|- ^2,0р2 Хз.оРз “Ь ^4»0
8б
0= —(^1,2 "b ^"1,3 ~b ^1,4) Р\ Н”^О,1Ро>
0= —^'2,0Pi 4- ^XfiPx'i
0= — ^•з.оРз'Ь^.зА’р
0= — Х4.0Р4-НмА-
Решение этой системы уравнений, удовлетворяющее нормиро
вочному условию
1^=1.
£=о
имеет вид [см. (2.5.10)]
1
А)=----------к------'/--х--------к---
Л0,1 Л л1,2 л1,3
1 + ~4 ( + X + X
VI \ Л2,0 Л3.0
2j Ч/
7=2
=->-к Pl~ Ра <;=?, з, 4).
24; Чо2 Ч;
J = 2 j=2
Таким образом, вероятность того, что машина исправна, нами
найдена.
Для отыскания вероятности того, что время простоя машины
будет не более t, требуется найти
закон распределения времени про-
стоя, т. е. закон распределения вре-
мени 71,2,3,4 пребывания в состоя-
ниях Xi, х2, х3, х4.
Граф подсистемы X, с помощью
которого можно отыскать закон рас-
пределения времени 7\, 2, з, 4, показан
на рис. 2.7.86.
Соответствующая этому графу
состояний система дифференциаль-
ных уравнений имеет вид
Рис. 2.7.86
dp\(t) _
dt
4
7 = 2
^-=-хг,о^(О+хмЛ(/)
dt
(1=2, 3, 4);
dPo (0
dt
87
Начальные условия для решения этой системы определяются
из соотношения
Л(0) = 1; А(0)=0 (zVl).
Для сокращения записи введем обозначение
4
^2 + Уз + ^4
J = 2
С учетом начальных условий и принятого обозначения вероят-
ность p\(t) определится по формуле
Pi(t)=e 1 •
Вероятность pi(t) найдем из выражения
t
dt=-——[е х’и — е-^*].
j М — л/0
При равенстве Х/,0=Х1 будем иметь
р.^=\и1е^ (i=2, 3, 4).
Вероятность ро(О найдем, интегрируя последнее дифферен-
циальное уравнение системы:
?о (о=J 2Х/-°^ (z)dt=2 Xz’° f di"
~ " о
1=2
О 1=2
В случае, когда Xf,о =£ Хь имеем
М0=£х/,° Х1До
4
I \ е at — \е at
Lo i
\',0 M
kl.i
/=2 Х1~Х/-О
В случае, когда XZ,O=X1 (1=2, 3, 4), имеем
a (o=2Xi-z
1=2 0 1=2 1
Если для некоторых значений i величина Хг-,о=М> а для дру-
гих значений i Xi,o#=Xi, то выражение для ро(О (в соответствии
с правилами интегрирования дифференциальных уравнений)
В8
будет представлять линейную комбинацию полученных решений.
Например, если Z,i,o=M, Л2,0=7^1 и Лз,о=#А,ь то можно записать
следующее выражение для вероятностей po(t):
-т2- I1 ~(М+ 1)е~м1 У Х/,о—X
ГТ А1~Л/.о
I —о
L Ai.O *1 J
Таким образом, функция распределения случайной величины
Т112, з,4 найдена, так как
Р (Т1, 2,3, 4 < /) = F1, 2.3, 4 (0= Ро (/).
По условию задачи вероятность того, что простой машины
продлится не более времени t, и равна найденной функции рас-
пределения случайной величины Т^г.з, 4-
Для нахождения среднего времени простоя Л, 2,3,4 можно при-
менить два приема. Первый прием заключается в том, чтобы вос-
пользоваться найденным законом распределения случайной ве-
личины Ti.2,3,4:
6, 2, 3, 4 = t dF 1, 2, 3, 4 (tf)= ^1,0 tPi (f) dt.
0 i=2 0
Однако если требуется найти только математическое ожида-
ние t\, 2,з,4, то можно обойтись и без закона распределения, а
воспользоваться эргодическим свойством. В соответствии с гра-
фом состояний, изображенным на рис. 2.7.8а, среднее время
пребывания в состоянии х0 равно
Л0,1
С другой стороны, на основании эргодического свойства для
стационарного режима работы системы имеет место равенство
^0 / I / ’
го -г *1, 2, 3, 4
откуда выражение для среднего времени простоя машины будет
~~Т __1 Р®
*1,2, 3,4— *0---- ,
Ро
89
где ро определяется из выражения (2.7.8):
2.7.9. Исследуется процесс чистого размножения, граф кото-
рого приведен на рис. 2.7.9а. Ограничений на число состояний
Рис. 2.7.9а
никаких нет. Плотность потока, переводящего процесс из состоя-
ния xk в состояние (&=0, 1, 2, ...), определяется формулой
ХЛ--=Хоа*(а>О) (£=-0, 1, 2,...).
Определить при каких значениях а возможно явление «взры-
ва» и найти выражение для вероятности Pk(t) того, что к момен-
ту t процесс будет в состоянии xk, если в момент ^=0 он был
В СОСТОЯНИИ Xq.
Решение
Найдем, при каких условиях ряд (2.5.14) расходится:
ОС п п
У — —- ИтУ — = 11111 у —=
Xj£ Л-*ОО Х^ Л-*ОО Xq6Z
Л = 0 Л = 0
п
= 2-limy J_ =
Хо ак
л=о
й=0
‘-f-Г1
1 11m----------———
X/ —► оо 1
о 1 — —
а
Последнее выражение имеет конечное значение при а>\.
Следовательно, для того чтобы ряд 2 Т" расходился, нужно
А=0 k
соблюдать условия 0<а^1. Таким образом, явление «взрыва»
возможно при а>1. «Взрыв» в данном примере означает, что
имеется конечная вероятность того, что система за любое, даже
малое, время Д^>0 перейдет в состояние со сколь угодно боль-
шим k.
Для отыскания вероятности Pk(t) можно воспользоваться
решением задачи 2.7.3. Действительно, граф, изображенный на
рис. 2.7.36, до состояния Xk совпадает с любым участком графа,
90
изображенного на рис. 2.7.9а. Следовательно, в этом примере
вероятность pk(t) будет определяться из выражения
k 1 л Г й Т 1
A(0=(-l)ft (*=1,2,...);
,-А Я-A
С учетом того, что Xh=Xoaft, получаем следующее выражение
для вероятности Ph(t):
*-! * -
1=0 >=<>’ .П
цл=о
-(-~W 2 ----- (^-=1,2,...).
' -° П (а>-аА)
Л = 0
Глава 3
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МАССОВОГО
ОБСЛУЖИВАНИЯ
§ 3.1. КАНАЛ ОБСЛУЖИВАНИЯ; ВРЕМЯ ОБСЛУЖИВАНИЯ;
ПОТОК ОБСЛУЖИВАНИИ; ПОТОК ЗАЯВОК;
ДИСЦИПЛИНА ОБСЛУЖИВАНИЯ
Основным параметром любой системы массового обслужива-
ния является число каналов обслуживания, которое мы будем
обозначать буквой п. Каналом обслуживания называется вся
совокупность технических устройств, обеспечивающих обслужи-
вание одной заявки.
Рассмотрим несколько примеров:
1. Автомат продажи газированной воды является каналом
обслуживания. Если рядом стоят п автоматов, то можно гово-
рить об n-канальной системе массового обслуживания.
2. Рассматривается работа столовой самообслуживания. Ка-
налами обслуживания являются места раздачи пищи. Если в
столовой два места раздачи, то столовую можно рассматривать
как двухканальную систему массового обслуживания.
3. Рассматривается система противовоздушной обороны
(ПВО). Каналом обслуживания является совокупность всех тех
устройств, которые обеспечивают стрельбу по одной цели (радио-
локационная станция наведения снарядов и пусковые установки,
которые обеспечивают запуск снарядов, наводимых этой радио-
локационной станцией).
В дальнейшем при рассмотрении конкретных задач будем
указывать ту совокупность устройств, которая называется кана-
лом. Работа каждого канала характеризуется тем временем,
которое затрачивается на обслуживание одной заявки. В общем
случае это время является случайным. Так как мы договорились
рассматривать в этой книге простейшие пуассоновские системы,
то время обслуживания Г1Х одной заявки одним каналом должно
быть распределено по показательному закону с параметром ц.
Это эквивалентно тому, что на выходе непрерывно занятого
канала будет простейший поток обслуженных заявок с парамет-
92
ром g. Поясним это положение. Допустим, что на входе такого
канала всегда имеется очередь из необслуженных заявок
(рис. 3.1.1). Например, имеется много желающих напиться у
автомата для продажи воды. Каждая заявка обслуживается
независимо от других случайное время Т^, распределенное по
показательному закону с параметром ц, и заявка не покидает
систему во время обслуживания (если желающий пить дождется
своей очереди, то он напьется воды обязательно). Тогда на вы-
ходе такой системы будет появляться поток обслуженных заявок,
Обслуженные
заяВки
0 — 000 ф
---------------/ Ч
Очередь к каналу Канал
обслуживания обслуживания
Рис. 3.1.1
при этом интервалы времени между ними (Ть Т2, T3i ...) будут
независимы и распределены одинаково по показательному закону
с параметром ц, т. е. поток обслуженных заявок будет простей-
шим с интенсивностью ц. В дальнейшем канал обслуживания
будем характеризовать интенсивностью потока обслуживаний ц.
Следует обратить внимание читателя на тот факт, что рассмат-
ривается лишь случай, когда на входе канала всегда имеется
очередь. Если же это условие не выполняется (очередь то появ-
ляется, то исчезает), интенсивность выходного потока будет
меньше, чем ц.
В общем случае параметр потока обслуживаний может зави-
сеть от времени (ц(0)- Это эквивалентно тому, что на выходе
занятого канала будет не простейший поток обслуженных зая-
вок, а пуассоновский поток с интенсивностью р, (t).
Следовательно, можно представить себе, что обслуживание
происходит так, как будто на заявку, поступившую в канал, на-
правляется поток обслуживаний с интенсивностью ц. Факт
обслуживания имеет место, как только в этом потоке обслужи-
ваний наступает первое событие. Такая постановка задачи очень
удобна в методическом отношении, особенно, если поток обслу-
живаний пуассоновский. В дальнейшем будем всегда гово-
рить о «потоке обслуживаний», действующих на заявку, не-
смотря па то, что каждая заявка может быть обслужена только
один раз.
Рассмотрим несколько подробнее, в чем состоит допущение
о показательном распределении времени обслуживания. В соот-
ветствии со свойством простейшего потока это допущение экви-
валентно тому, что если в какой-то момент времени tQ происходит
93'
Рис. 3.1.2
обслуживание заявки, но заявка еще не обслужена, то закон
распределения оставшегося времени обслуживания не зависит
от того, сколько времени продолжалось обслуживание до этого
момента /0 (рис. 3.1.2). Доказательство этого положения было
изложено в § 1.4 [см. формулу (1.4.13)].
Такое положение на практике возникает тогда, когда обслу-
живание осуществляется рядом попыток, в каждой из которых с
некоторой вероятностью р заявка может быть обслужена. Это
приводит к тому, что поток «попыток»
разрежается случайным образом. В § 1.6
было показано, что если поток Пальма
многократно разрежать случайным обра-
зом, то такой поток будет стремиться к
простейшему, а следовательно, интервал
времени между двумя удачными попытка-
ми будет распределен по показательному
закону. Это утверждение справедливо,
если вероятность р мала.
Подобная картина наблюдается при обстреле цели, когда
стрельба ведется до ее поражения. Аналогичная ситуация возни-
кает при ремонте сложного радиотехнического устройства, когда
«наугад» начинают искать неисправность и т. п. Во многих прак-
тических задачах время обслуживания распределено по закону,
сильно отличающемуся от показательного. Однако расчеты по-
казывают, что приближенная замена этого закона показатель-
ным не приводит к большим погрешностям и большинство
формул теории массового обслуживания остаются приближенно
справедливыми, даже если время обслуживания не показа-
тельное.
В дальнейшем будем без специальных оговорок предполагать,
что поток обслуживаний каждого канала является простейшим с
интенсивностью ц. Интенсивность обычно определяют через сред-
нее время обслуживания одним каналом одной заявки
Н = (3.1.1)
+
Как правило, будем считать, что все каналы имеют одинако-
вую интенсивность потока обслуживаний р (иногда величину р
называют интенсивностью обслуживания). В этом случае нет
необходимости различать каналы (первый, второй и т. д.). По-
мимо этого, будем считать, что заявка может обслуживаться
любым из п каналов, т. е. любой из п каналов «доступен» для
заявки
Следующим важным параметром системы массового обслу-
живания является интенсивность (плотность) потока заявок X.
(Сам поток заявок будем считать простейшим). Здесь уместна
напомнить, что заявки различаются лишь моментом поступления-
94
на обслуживание, а интенсивность потока заявок X определяется
через средний интервал между поступлением двух заявок
следующим образом:
*=—- • (3.1.2)
h
Помимо этих параметров: числа каналов п, интенсивности
обслуживания заявки каждым каналом р, и интенсивности по-
ступления заявок в систему X, эффективность работы системы
массового обслуживания будет зависеть от дисциплины (алго-
ритма) обслуживания. Алгоритм обслуживания определяет по-
рядок распределения заявок между свободными каналами: по-
ведение заявок, попавших в систему на обслуживание; закон
образования очереди; поведение заявки, попавшей в очередь,
и т. п. Например, покупатель, попавший в большой универсаль-
ный магазин, может долго искать нужный отдел, в то время как
в другом магазине при хорошо поставленной информационной
службе и хороших указателях покупатель будет тратить на это
меньше времени. Далее, при наличии нескольких одинаковых
отделов покупатель может стоять в очереди в одном отделе, в
то время как другой отдел будет свободен. Каждый отдел, в
силу ограниченности помещения, допускает обслуживание опре-
деленного числа покупателей и наличие определенной очереди.
Покупатели, не дождавшиеся своей очереди, могут покидать
магазин. Некоторые покупатели стараются купить товар без
очереди и т. п.
При решении различных задач методами теории массового
обслуживания нужно ясно представить себе весь порядок обслу-
живания. Лишь после того, как сформулирован алгоритм обслу-
живания, можно приступать к решению поставленной задачи.
§ 3.2. РАЗОМКНУТЫЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Системы массового обслуживания можно делить на «разомк-
нутые» и «замкнутые». На вход разомкнутой системы массового
обслуживания извне поступает некоторый поток заявок, причем
источники этих заявок в систему не входят и их состояния ана-
лизу не подвергаются. Примером разомкнутой системы может
служить счетчик Гейгера, регистрирующий космические части-
цы, или (с некоторым приближением) АТС, на которую посту-
пают вызовы.
В замкнутой системе массового обслуживания число источ-
ников заявок ограничено и интенсивность поступления заявок
зависит от состояний источников, обусловленных работой самой
системы. Примером замкнутой системы массового обслуживания
может служить рабочий, обслуживающий несколько станков, яв-
ляющихся источниками заявок.
95
Рассмотрим л-канальную разомкнутую систему массового
обслуживания (СМО) с отказами, на вход которой подается про-
стейший поток заявок с интенсивностью X (рис. 3.2.1).
На выходе такой системы в стационар» м режиме (если он
существует) будут два потока;
— поток обслуженных заявок с интенсивностью
— поток необслуженных заявок с интенсивностью Лн.
000
Поток
заявок
Рис. 3.2.1
Поток
обслуженных
заявок
0 0
Поток
необслуженных
заявок
При этом будет выполняться очевидное равенство, которое назы-
вается «уравнением расхода» для разомкнутой системы:
Х=Х0 + Хн. (3.2.1)
Разделим обе части равенства на величину X:
(3.2.2)
А А
Очевидно, отношение Хо/Х есть не что иное, как вероятность РОбс
того, что заявка, поступившая на вход такой системы, будет об-
служена или, короче, вероятность обслуживания заявки
Робс = ^. (3.2.3)
Вероятность Рн необслуживания заявки, очевидно, равна
Рн=^-. (3.2.4)
А
В дальнейшем при анализе стационарных режимов работы
системы будем широко пользоваться уравнениями (3.2.1) —
(3.2.4).
Иногда интенсивность потока обслуженных заявок Хо назы-
вают абсолютной пропускной способностью системы, а вероят-
ность обслуживания заявки РОбс — относительной пропускной
способностью системы.
Заметим, что если поток заявок был простейший, то потоки
обслуженных и необслуженных заявок в общем случае не будут
простейшими.
96
Следующей важной характеристикой разомкнутой системы,
находящейся в стационарном режиме, является сроднее, число
занятых каналов Тс. Для системы без «взаимопомощи» между
каналами, когда заявка может обслуживаться только- однимка-
налом, интенсивность потока обслуженных заявок определяется
формулой
Х0 = |лТ. (3.2.5)
Для доказательства этой формулы будем рассуждать следую-
щим образом. Пусть в момент времени t занято случайное число-
каналов У. Мгновенная интенсивность потока обслуженных
заявок будет равна Уц,, а среднее число обслуженных заявок в
единицу времени
Х0 = Ж [УИ] = ИЛ1 [У] = Д (3.2.6)
Рассмотрим произвольно выбранный канал и найдем веро-
ятность л3.к того, что в произвольно выбранный момент времени
этот канал будет занят (индекс «з.к» означает «занят канал»).
Так как все каналы работают в одинаковых условиях, то
k =
откуда
*з.к
С другой стороны, на основании эргодического свойства вели-
чина Лз.к может быть получена из выражения
Тсз.к = ._. , (3.2.9)
^з.к + ^п.к
где F3.K — среднее время, протекающее от момента занятия ка-
нала заявкой до его освобождения;
?з.к — среднее время, протекающее от момента освобожде-
ния канала до его занятия новой заявкой (индекс
«п.к» означает «простаивает канал»).
Из (3.2.9) имеем
4к=7п.к-2Ьк_ , (3 210)
1 Лз.к
7п.к=/7.к--^Лз-к • (3.2.П)
Лз.к
Напомним, что формулы (3.2.7) — (3.2.11) справедливы толь-
ко для стационарного режима работы системы.
Рассмотрим вопрос о среднем числе заявок, находящихся
в системе. Заявка, находящаяся в системе, может быть либо в
4—1964 97
^з.кЯ, .. (3.2.7)
=— . (3.2.8)
П !
очереди, либо на обслуживании. Обозначим среднее число зая-
'вок, находящихся в очереди, через г и среднее число обслужи-
ваемых заявок при стационарном режиме работы системы —
через s. Очевидно, среднее число заявок I, находящихся в систе-
ме, будет равно
. . 7=<Н-г. (3.2.12)
Обозначим среднее время нахождения заявки в системе через t.
Очевидно:
~t=7r + is, • (3.2.13)
где tr — среднее время нахождения заявки в очереди и
is — среднее время нахождения заявки на обслуживании.
Так как мы рассматриваем стационарный режим, то уравнение
расхода (3.2.1) имеет место. С другой стороны, среднее число
(заявок, находящихся в системе, будет равно
7=\7==л7г4-)<='Ч-Г (3.2.14)
Докажем справедливость формулы (3.2.14). Пусть имеется
эргодическая система массового обслуживания X, работающая
в стационарном режиме. Тогда на нее поступают заявки, обра-
зующие поток с интенсивностью X, и покидают заявки также по-
током с интенсивностью Х=ЛО+ХН (см. рис. 3.2.1).
О t t
Рис. 3.2.2
Возьмем очень длинный промежуток времени длиной Т (мы
его потом устремим к бесконечности) и зафиксируем некоторый
'момент времени /, принадлежащий этому промежутку
(рис. 3.2.2).
Обозначим L(t) случайную функцию, равную числу заявок
в системе в момент времени t.
На основании эргодического свойства среднее число заявок
в системе
M[L (t)]=7
может быть найдено как предел интеграла
т
: 7=lim — L(t)dt.
т ;
о
&8
Перенумеруем заявки, которые успевают побывать в системе
за время (О, Т), т. е. те, время пребывания которых в системе
пересекается с промежутком (О, Т):
1, 2,..., k....
Очевидно:
к
где случайная функция Lh(t) определяется следующим образом:'
М0=
0,если в момент t k-я заявка (уже или еще) не находится
в системе;
1,если в момент t k-я заявка находится в системе.
Отсюда
т т т
7==lim -М L(t)dt=Vim у'j V^(/)Л=11тУ Д Lb(t)dt.
1 T-I-OO 1 •) 1 J
0 0 к к О
Т
Докажем, что выражение Lk(f)dt
k 6
приближенно равно сумме времени пребывания в системе всех
перенумерованных заявок.
Действительно, предположим, что k-я заявка пришла за вре-
мя (0, Т) и ушла за это же время.
Тогда
j* Lk(t)dt—ik,
6
где — время пребывания k-я заявки в системе.
Выражение
^\Lk(t)dt
k 6
отличается от суммы времени пребывания в системе всех заявок
2’-
к '
только за счет тех заявок, которые:
1) за время (0, Т) пришли, но ушли позже;
2) за время (0, Т) ушли, но пришли раньше;
3) пришли раньше начала, а ушли позже конца промежут-
ка (0, Т).
4* 99
Предположим, что Т—*оо, а среднее время пребывания за-
явки в системе ограничено. Тогда, очевидно, третью категорию
заявок можно отбросить, а двумя первыми пренебречь, так как
участки времени длиной Зат, на которых этот «краевой эффект»
сказывается, будут малы по сравнению с полной длиной отрезка
(О, Т) (рис. 3.2.3).
Следовательно, математическое ожидание числа заявок равно
т
О к
где суммирование распространяется на все заявки, пришедшие
за время (О, Т).
Основной иуасоюн ? *
W” длиной 34>9eKm
Рис. 3.2.3
При достаточно большом числе заявок «(Г), приходящих за
время (О, Т), на основании закона больших чисел
к k
где t — среднее время пребывания заявки в системе, а
7^ —
k
Но величина п(Т)1Т приближенно равна интенсивности потока
заявок X; отсюда
7=к й.
При Т—>-оо это приближенное равенство становится точным.
Рассмотрим другое доказательство формулы (3.2.14). Иссле-
дуем два возможных способа работы эргодической системы мас-
сового обслуживания в стационарном режиме.
1. Система массового обслуживания работает по принципу
«кто позже пришел, тот не может покинуть систему раньше того,
кто пришел раньше».
Перенумеруем все входящие заявки (рис. 3.2.4). Обозначим
время пребывания первой, второй, третьей и т. д. заявок в систе-
ме через Т\, Т2, Т3. Эти величины представляют собой систему
МЮ
одинаково распределенных (в общем случае зависимых) случай-
ных величин.
Рассмотрим произвольную заявку и предположим, что время
ее пребывания в системе Т приняло значение, лежащее в интер-
вале (t,t+dt)-,
P(Tc(t, / + f {t)dt.
За время пребывания t заявки в системе в нее поступит в
среднем W заявок, т. е. к моменту выхода заявки из системы в
ней будет находиться в среднем М заявок.
2 3
3 4-
Рис. 3.2.4
? # ^вх Входящий
t поток
~ т Выходящий
6 7 8 t поток
Тогда полное математическое ожидание числа заявок в си-
стеме будет
О
и формула (3.2.14) доказана.
2. Система работает по принципу «заявка, поступившая в
систему позже, может уйти из нее как раньше тех заявок, кото-
рые поступили в систему до нее, так и позже» (рис. 3.2.5).
5 6 7
1 2 3 4
+
О
+
О
5 2 7
V 5' 6'
^вх Входящий
I поток
^вых Выходящий
+ поток
Рис. 3.2.5
Перенумеруем заявки в выходящем потоке событий в соот-
ветствии с порядком выхода заявок из системы (рис. 3.2.6).
Относительно вновь перенумерованного выходного потока
заявок 77'вых можно сказать, что заявки в нем выходят строго
друг за другом.
101
Опять выдвинем гипотезу, состоящую в том, что время пребы-
вания произвольной заявки в системе Т попало в интервал
(t,t+dt):
P(Tc(t, i-\-dt))^f(t)dt.
Так как в потоке 77'вых заявки следуют строго друг за другом,
то за время t в системе накопится в среднем М заявок. Следова-
тельно, и в этом случае формула (3.2.14) тоже имеет место.
Вернемся к аналиву разомкнутых систем массового обслужи-
вания.
4-
Q
-----т-------н
# r t г | т т входящий
1’ 2' 3’ 4' 5' 6' 7' t nomo*
Рис. 3.2.6
Сравнивая выражения (3.2.12) и (3.2.14), можно записать
следующую формулу для среднего времени нахождения заявки
в системе:
7= = (3.2.15)
В дальнейшем будет доказана справедливость формулы,
определяющей среднее время ожидания заявки в очереди
7,,= 7. (3.2.16)
Сопоставляя формулы (3.2.14) и (3.2.16), можно убедиться
в том, что среднее время обслуживания заявки определяется по
формуле
7,=^ . (3.2.17)
А
Разомкнутые системы массового обслуживания будут рас-
смотрены в гл. 4, 5, 6.
Глава 4
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
С ОТКАЗАМИ
Система массового обслуживания называется системой с от-
казами (потерями), если заявка, пришедшая в момент, когда все
каналы заняты, немедленно получает отказ и покидает систему
(теряется).
Рассмотрим n-канальную разомкнутую систему массового
обслуживания, на вход которой подается простейший поток зая-
вок с интенсивностью Л. Поток обслуживаний каждого канала —
простейший с интенсивностью р. Если заявка застает все каналы
занятыми, то она покидает систему необслуженной (получает
отказ).
При наличии свободных каналов могут рассматриваться раз-
личные алгоритмы распределения заявок по каналам: строгое
(неслучайное) распределение заявок по свободным каналам или
же случайное (хаотическое) распределение заявок по каналам.
Кроме того, могут иметь место случаи, когда заявка, принятая к
обслуживанию, по тем или иным причинам, не дождавшись конца
обслуживания, покидает систему, т. е. остается необслуженной
(случай «нетерпеливых» заявок). Могут иметь место случаи не-
полного обслуживания заявки, выхода канала из строя и т. п.
Общим для всех этих систем является то обстоятельство, что
заявка получает отказ, если все каналы заняты.
Перейдем к анализу различных систем массового обслужива-
ния с отказами. Рассмотрение каждой системы будем начинать
с постановки задачи и заканчивать сводкой основных расчетных
формул.
Хотя большинство систем, рассматриваемых в книге, являет-
ся частными случаями схемы гибели и размножения, тем не ме-
нее с целью развития навыков анализа этих систем будем каж-
дую систему изучать достаточно подробно.
103
§ 4.1. КЛАССИЧЕСКАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
С ОТКАЗАМИ (СИСТЕМА ЭРЛАНГА)
Постановка задачи. На вход n-канальной системы
массового обслуживания подается простейший поток заявок с
интенсивностью X. Интенсивность простейшего потока обслужи-
ваний каждого канала ц. Если заявка застала все п-каналов
занятыми, то она получает отказ (покидает систему необслужен-
ной). Если заявка застала свободным хотя бы один канал, то она
принимается к обслуживанию любым из свободных каналов и
обслуживается до конца (заявки «терпеливые»).
Рис. 4.1.1
Описанная выше система названа нами классической потому,
что с рассмотрения такой системы Эрлангом и начала разви-
ваться теория массового обслуживания. Эрланг рассмотрел ра-
боту такой системы на примере работы автоматического теле-
фонного узла связи. В этом случае поток заявок представляет
собой поток вызовов со стороны абонентов. Длительность обслу-
живания характеризуется длительностью коммутации и длитель-
ностью разговора. Число каналов п равняется максимально воз-
можному числу одновременно осуществляемых разговоров.
Анализ работы любой СМО будем начинать с рассмотрения
возможных состояний системы и составления размеченного гра-
фа состояний системы с указанием интенсивностей потоков,
переводящих систему из состояния в состояние.
Рассмотрим следующее множество состояний системы:
Хо — все каналы свободны, ни одна заявка не обслуживается;
Xi — занят ровно один канал (какой — неважно), обслужи-
вается одна заявка;
xk — занято ровно k каналов (каких именно — неважно), об-
служивается k заявок;
хп — все п каналов заняты, обслуживаются п заявок*.
Граф состояний данной СМО с отказами представлен на
рис. 4.1.1. Как и ранее, возможность перескока «через состояния»
не рассматривается, так как все потоки ординарны.
* Можно было бы рассмотреть и более обширное множество состояний
с указанием, какие именно каналы заняты, но в этом нет необходимости, так
как все каналы одинаковы.
104
Поясним порядок определения интенсивностей потоков собы-
тий на рис. 4.1.1. Когда система находится в состоянии х0, на нее
действует поток заявок с интенсивностью X, переводящий систему
в состояние Хь Если система находится в состоянии хь то на нее
действует уже два потока событий: 1) поток заявок с интенсив-
ностью X, который стремится перевести систему в состояние Хг и
2) поток освобождений канала («поток обслуживаний»), кото-
рый стремится перевести систему в состояние х0. Интенсивность
этого потока равна ц.
Рассмотрим случай, когда система находится в состоянии
xft(£=l, 2, п—1). В этом состоянии на систему действует опять
два потока:
1) поток заявок с интенсивностью X, который стремится пере-
вести систему слева направо, т. е. в состояние хь+г,
2) поток освобождений всех k занятых каналов с интенсив-
ностью йр, который стремится перевести систему справа налево
в состояние х^-ь
Если система находится в состоянии хп, то на нее действует
только один поток событий с плотностью пр, переводящий систе-
му справа налево в состояние хп_ь
В соответствии с мнемоническим правилом составления си-
стемы дифференциальных уравнений для вероятностей состояний
(см. § 2.3) получим
^10 = _ (Х _|_ Рк (/)+\Рк_х (/)+
at
+ (А + 1)РФ*+1(О (* = 1, 2,..., п-1),
-^-=-«нрй(0+^л-1(0.
Система (4.1.1) обычно интегрируется при начальных условиях
а>(0)=1;
ДДО)=О (* = 1, 2,..., п),
(4.1.2)
что соответствует случаю, когда система в начальный момент
при /=0 свободна. Решение системы (4.1.1) при начальных усло-
виях (4.1.2) удовлетворяет нормировочному условию
п
k = Q
(/>0).
(4.1.3)
105
Уравнения (4.1.1) называются уравнениями Эрланга. Заме-
тим, что выражения (4.1.1) — (4.1.3) справедливы и для случая,
когда потоки событий не являются простейшими, а представляют
собой нестационарные пуассоновские потоки. В этом случае пара-
метры Х=Х(/), р,=|л(/) являются некоторыми функциями вре-
мени. В дальнейшем мы, как правило, не будем выписывать систе-
му дифференциальных уравнений для вероятностей состояний,
так как читатель, зная мнемоническое правило составления этих
уравнений и глядя на граф состояний, может без труда самостоя-
тельно их записать.
Вернемся к анализу нашей системы и рассмотрим стационар-
ный режим работы при t.—х». Такой режим существует (см.
§ 2, 4), так как наша система эргодична.: в ней нет групп состоя-
ний без выхода или без входа и все потоки простейшие.
Тогда при t—н» система дифференциальных уравнений
(4.1.1) превратится в систему алгебраических уравнений:
0=—kpo + ^i;
0=4H^+^-i+(H1)lW+i (*=1, 2,..., га-1);
(4.1.4)
0= — гар.ря + Хрл_1,
которые нужно решать совместно с нормировочным условием
(4.1.3).
Для решения системы (4.1.4) введем обозначения такие же,
какие были введены при анализе схемы гибели и размножения:
Ut— —^pi-i-j-i^Pi (/=1, 2,..., га). (4.1.5)
С учетом (4.1.5) уравнения (4.1.4) примут вид
«1=0;
Uk}-i — ик—0 (k=\, 2,..., га—1);
(4.1.6)
и„=0.
Анализируя систему (4.1.6), убеждаемся в том, что
«. = 0 (/=1, 2,..., га). (4.1.7)
Следовательно:
X / X \2 1 / х \з 1
Р1=—Ай ^з=( —I ~vPn
рь \ н / * \ |* / О»
106
и вообще
(> \ь 1
у) ^ро (* = 0, 1, 2,..., п). (4.1.8)
Для нахождения вероятности р0 воспользуемся нормировоч-
ным условием
п п
Л=0 Л=0
откуда
(4.1.9)
Окончательно получим следующие формулы для вероятностей
состояний:
f—Г
\ р- /
Ръ =---ГГ-Г (*=0’
( Л г
п —
у? 1х '
k\
которые называются формулами Эрланга:
Введем обозначение
а = —. (4.1.11)
р-
Величина а равна среднему числу заявок, поступающих в систе-
му за среднее время обслуживания одной заявки в одном канале.
Преобразуем выражение (4.1.10) к виду, удобному для вы-
числений. С этой целью используем обозначение (4.1.11) и умно-
жим числитель и знаменатель дроби (4.1.10) на величину е“а:
—
— е а
k\ Р (k, а)
А = —---------=~------г ,
(4.1.12)
Л = 0
где P(k,a) и R(n, а) табличные функции пуассоновского распре-
деления (см. приложение).
107
Подробнее эти функции были рассмотрены в § 1.5.
Найдем характеристики работы классической системы массо-
вого обслуживания с отказами. Вероятность обслуживания за-
явки Робе очевидно, равна вероятности того, что заявка, посту-
пившая в систему, застанет свободным хотя бы один канал:
Р обе 1 Рп 1
_ Р (п, а) Р (л, а) — Р (п, а) Р (п — 1, а)
Р(п, а) Р(п, а) P(nt а)
.(4.1.13)
С другой стороны, вероятность обслуживания заявки равна отно-
сительной пропускной способности системы
Робс=~=-^ = —, (4.1.14)
Л Л а
где Хо — плотность потока обслуженных заявок (абсолютная
пропускная способность СМО), a k — среднее число занятых ка-
налов.
Отсюда
1=^аРобс = а/?(л~ Ь а) . (4.1.15)
Р(п, а)
Выражение для среднего числа занятых каналов k можно полу-
чить и непосредственно через вероятности
п
п п 2 ^Р а)
А—V kpk = y 6 Р(*’ а) . (4.1.16)
Р(п, а) Р(п, а)
Л = 0 k^O
Сравнивая (4.1.15) и (4.1.16), убеждаемся в том, что
2 kP(k, a)—a/?(re — 1, a). (4.1.17)
*=0
Это соотношение нам потребуется в дальнейшем изложении.
Вероятность того, что канал занят, будет равна отношению
среднего числа занятых каналов k к общему числу каналов п:
k а Р(п — 1, а)
п п Р(п, а)
(4.1.18)
Введем в рассмотрение случайную величину Т3.к — время
занятости канала, равную длине промежутка времени, начинаю-
щегося с момента поступления заявки в канал до следующего
непосредственного момента освобождения канала. Время заня-
тости канала Т3.к по условию распределено по показательному
108
закону с интенсивностью р. Следовательно, среднее время заня-
тости канала t3,K будет равно
/;.K = M[T,K] = -L. (4.1.19)
Временем простоя канала Тп.к называется длина промежут-
ка времени, начинающегося с момента освобождения канала до
его занятия следующей заявкой. Среднее время простоя канала
/п.к определяется из следующего выражения, имеющего место
для эргодической системы, находящейся в стационарном режиме:
^э.к = -?3-к_ , (4.1.20)
^З.К + А1.К
т. е. вероятность занятости канала равна отношению среднего
времени занятости канала к сумме среднего времени занятости
канала и среднего времени простоя канала (см. 2.4.15).
Сравнивая выражения (4.1.19) и (4.1.20), получим
Г = Г 1~Яч-к — 1 nR(n, a) — aR(n—\, а) д „р
Л3.к X R(n, а)
Вероятность полной загрузки системы, т. е. вероятность того,
что все каналы будут заняты, равна
^п.з-^=4г - росс- (4.1.22)
К(л, а)
Введем в рассмотрение время полной загрузки системы Гп„ъ
время, протекающее с момента занятия заявками всех п кана-
лов до момента освобождения хотя бы одного канала, т. е. время
однократного пребывания в состоянии хп. Время полной загрузки
системы Тп.з распределено по показательному закону с парамет-
ром пр. Это следует из того, что граф состояний подсистемы для
определения закона распределения времени пребывания в состоя-
нии хп имеет вид, показанный на рис. 4.1.2. Соответствующие
дифференциальные уравнения нужно решать при начальных ус-
ловиях рп(0) = 1, рп-1(0) =0. Следовательно, среднее время пол-
ной загрузки системы будет
Гп.з=Л1[Гп.,] = —. (4.1.23)
Л (Л
Время неполной загрузки системы Тн.з равно длине проме-
жутка времени, протекающего от момента перехода системы из
состояния хп в состояние хп-1, до следующего момента, возвраще-
ния системы в состояние хп. Граф состояний подсистемы для
определения закона распределения времени неполной загрузки
системы имеет вид, показанный на рис. 4.1.3. Систему дифферен-
169
циальных уравнений, соответствующую графу состояний, изобра-
женному на рис. 4.1.3, нужно решать при начальных условиях
р„_1(0)=1, рД0)=0 (/#=«-1).
Функция распределения времени Тн,3 определяется из ра-
венства
^Н.Э (0 — Р (Т'н.З Pn(t\ (4.1.24)
где вероятность pn(t) определяется из решения системы диффе-
ренциальных уравнений, соответствующей графу состояний, изо-
Рис. 4.1.2 Рис. 4.1.3
браженному на рис. 4.1.3. Система дифференциальных уравнений
должна решаться при начальных условиях
/?я_1(0)=1; Л(0)=ь0 (Л^п-1).
Плотность распределения времени неполной загрузки системы
равна
/н.з(0=4- = (0- (4-1.25)
* dt dt
Среднее время неполной загрузки системы FH<3 найдем на
основании эргодического свойства: вероятность лп.з того, что
система полностью загружена, равна отношению среднего вре-
мени полной загрузки системы к сумме средних времен полной
и неполной загрузки системы:
‘ _____ ^п.з
. , “п,3 — __ »
^н.з *4* ^п.з
откуда
Под простоем системы будем понимать такое ее сочетание,
когда все каналы простаивают.
Вероятность простоя системы лп.с, очевидно, равна вероятно-
сти того, что все каналы свободны, т. е. вероятности пребывания
системы в состоянии х0:
^п.с — Ро- (4.1.27)
-НО
Время простоя системы Тц.с распределено по показательному за-
кону с параметром X, так как граф соответствующей подсистемы
имеет вид, показанный на рис. 4.1.4. Следовательно, среднее
время простоя системы равно
7п.с = 4- . (4.1.28)
Л
Среднее время пребывания заявки в системе t определяется'
из условия
где I — среднее число заявок, находящихся в системе, равное
среднему числу занятых^ каналов k или среднему числу
обслуживаемых заявок s,
откуда
/=—
X
(4.1.29)
Для того чтобы найти закон распределения времени Т нахож-
дения заявки в системе, воспользуемся следующими рассужде-
ниями:
а) если система полностью загружена (вероятность этого
равна лп.з), то время пребывания очередной заявки в системе
равно нулю;
б) если система неполностью загружена
(вероятность этого равна лн.з=1—лп.з), то
время пребывания очередной заявки в системе
распределено по показательному закону с
параметром р, так как заявка будет при-
нята к обслуживанию одним из кана-
лов.
Рис. 4.1. 4
Случайная величина Т относится к случай-
ным величинам смешанного типа, функции распределения кото-
рых имеют как участки плавного возрастания, так и скачки.
У случайной величины Т имеется единственный скачок в точке
f = 0. Следовательно, плотность 'распределения времени Т пребы-
вания заявки в системе будет иметь следующий вид:
/ (0 = ^П.з8 (/) + *н.зК-!1/1 (0. (4.1 -30)
где 3 (/) — дельта-функция;
!(/)—- ( 3 (/)dt — единичная функция.
—
111
Функция распределения времени Т пребывания заявки в систе-
ме определяется из выражения
t
F(t)= J /(/)rf/=l(/)h.3+(l-n>')^]. (4.1.31)
Напомним, что в данном случае единичная функция (единич-
ный скачок) имеет следующее определение:
О при t <. 0;
1 при t > 0,
Дельта-функция равна
8(/)=Л ’W-
at
График функции распределения F(t) представлен на рис. 4.1.5.
Предлагаем читателю самостоятельно проверить справедли-
вость формулы (4.1.29), вы-
оо
7= J
числив математическое ожи-
дание времени t по формуле
где f(t) определяется из вы-
ражения (4.1.30).
В дальнейшем при фор-
мулировке условий задач
будем для краткости число каналов п, интенсивность потока за-
явок X и интенсивность потока обслуживаний р называть пара-
метрами системы и перечислять всегда в указанной последова-
тельности (п, X, ц).
Основные расчетные формулы
Вероятность того, что занято ровно k каналов:
р а>
* R(n, а) ’
где а = Х/р.
Среднее число занятых каналов
R (Л, а)
112
Вероятность обслуживания заявки (относительная пропуск-
ная способность системы)
jrj k ^0 i
Робе — = — = 1 рпу
а к
где до — плотность потока обслуженных заявок (абсолютная
пропускная способность системы).
Вероятность того, что канал (любой) занят:
^ЗЖ--
П
Вероятность того, что система полностью загружена:
^П.З Рп == 1 Робе — 1 ♦
а
Среднее время занятости канала
Среднее время простоя канала
"7____~ 1 яз.к
*п.к —*з.к
Л3.к
Среднее время полной загрузки системы
Среднее время неполной загрузки системы
Т 1 1 ЛП. 3
4Н.З--*з.с •
лп.з
Среднее время простоя системы
Среднее время пребывания заявки в системе
Задачи и упражнения
4.1.1. Рассматривается двухканальная система массового
обслуживания с отказами и параметрами (n=2, X, ц). Найти за-
кон распределения времени неполной загрузки системы в стаци-
онарном режиме.
113
Решение
Граф состояний подсистемы для определения плотности
распределения /н.з(0= имеет вид, показанный на рис.
dt
4.1.1а.
Выпишем систему дифференциальных уравнений для опреде-
ления плотности распределения /н.з (/):
-W)Wi(0;
at
at
at
Начальные условия для интегрирования системы следующие:
^(0)=1; Д0(0)-0; й(0) = 0.
Дифференциальные уравнения будем решать с помощью преоб-
разования Лапласа. Уравнения для изображений будут иметь
вид:
(s-R)p0(s)-M ($)=0;
(« + х + [*•) («) - *До («) = 5,
гдерД$)—изображение функции pt(t) (i=0,l).
Решая эту систему уравнений, получим
, \ $ (s -I- X)
п ($) —--------L---
или
Р\ (5) ,
($ 4-а) ($ 4- Ь)
где
__21 Ч- р ~ 41р. р.2 . __ 21 4- р. । 4Хр 4~ р.2
“ 2 |/ 4 ’ 2 Г у 4 ‘
Изображению Pi(s) соответствует оригинал Pi(/):
Рх ^=-^4 e-at+-~- е-»‘.
а — b b — а
График плотности распределения времени неполной загрузки
системы /н.3(/)=кр1(/) для случая 1х = 4; Ь=1 показан на
рис. 4.1.16 сплошной линией.
114
Математическое ожидание времени неполной загрузки систе-
мы для этого случая будет
оо оо
м [Гн.з]=4.з = \tfH.3(t)dt= \t
О о
ЛГ4-.; 2
3 ' 3
+ — e-2i dt— —
1 з 2
На рис. 4.1.16 пунктиром показана плотность распределения
/н.з (0 случайной величины, распределенной то показательному
закону с математическим ожиданием, равным 3/2.
Читателю предоставляется самостоятельно убедиться в том,
что величина /н.3, определяемая по формуле (4.1.26) для и = 2,
и Х=1, получается тоже равной 1,5. Отметим, что если
требуется найти только среднее время неполной загрузки систе-
мы, то лучше пользоваться формулой (4.1.26).
Рис. 4.1.1а
4.1.2. Рассматривается работа районной автоматической те-
лефонной станции (АТС), которая обеспечивает не более 120
переговоров одновременно. Средняя длительность переговоров
— = 1 мин. Вызовы на станцию поступают в среднем через
1
0,5 сек, т. е. ~ =0,5 сек. Требуется найти характеристики рабо-
ты АТС: k\ Рo6cj ^з.ю ^з.к> ^п.к? £п.з5 ^Н.Зт
Решение
АТС представляет собой 120-канальную систему массового
обслуживания с отказами. Параметры системы следующие:
п = 120; Х=2[—1;
Lсек J
[Л = —Г—1; а=—=120.
60 [ сек J р.
115
Среднее число занятых каналов будет равно (см. (4.1.15)]:
k — аРобс^а
R(n—], а)
R(n, а)
120/?(119, 120)
/?(120, 120)
Воспользуемся приближенной формулой (1.5.32):
* = 120
/119 + 0,5—120
ф* ( ----2—------
\ у 120
/120 + 0,5— 120
ф* / ------------
\ ]/120
112.
Вероятность обслуживания
₽-=т=ъно-931-
Вероятность того, что канал занят, будет равна
К3.к = —— 0,931.
п
Среднее время занятости канала
/з к = _ = ] мин = 60 сек.
Среднее время простоя канала
‘ ^п.к ~~ ^з.к ~4,5 сек.
Лп.К
Среднее время пребывания заявки в системе (с учетом того, что
разговор может и не состояться)
- k 112
t= —=—=56 сек.
х 2
Вероятность полной загрузки системы
лп.з = 1 — Ро6с =. 0,069.
Среднее время полной загрузки системы
4.з=—— =0,5 сек.
Пр
Среднее время неполной загрузки системы
4.з=4.3 =13,5 сек.
Лп.з
116
4.1.3. Рассматриваются две системы массового обслуживания
с отказами, на которые подается одинаковый поток заявок с
интеисивностью Л:
1) /i-канальная с производительностью каждого канала у,.
2) одноканальная с производительностью канала пц.
Таким образом, общая потенциальная производительность
обеих систем одинаковая. Определить, для какой системы веро-
ятность обслуживания заявки будет больше.
Решение
Для первой системы
р(П Ppf—1, я)
Л(л, а)
где
X
а= —
Р-
Для второй системы
- ”. .
/?fl, —)
\ п /
Покажем, что для любых Х>0; ц>0 и п>1 вероятность
Робе *>-Р1бс , т. е. что всегда выгоднее «дробить» каналы на ряд
менее производительных, но так, чтобы общая производитель-
ность всех каналов оставалась неизменной.
Имеем
л—1 k
рф
•* обе
п k
kl
k = 0
1—=-г--.
i + ^ " + "
п
Чтобы доказать, что Робе >Робс , достаточно доказать, что
л-1 ъ
Л=0
ak
j
а
п
Л=0
117
Преобразуем неравенство
Л=0 k=0 fe=0
ИЛИ
fe=xO fe=0 fc=0
откуда
что имеет место для любого а>0 и любого и>1.
Найдем приращение А вероятности обслуживания заявки за
счет «дробления» общей производительности между п каналами:
г>(1) п(2) _ а —2, а)
a — "обе — /обе =-------—------ •
а -f- п R (п, а)
Так, при а—10 и га = 10 имеем
Д = 0,51 ~ 0,667 = 0,286,
1 — 0,417
Робс=-^—= 0,5,
1 +1
/>&=0,5 Ч-Д=0,786.
Следовательно, вероятность обслуживания при дроблении на
10 каналов увеличивается почти на 60%.
Однако дробление общей производительности не всегда мо-
жет быть выгодно, так как в этом случае увеличивается время
пребывания заявки в системе. Действительно, для первой систе-
мы (п каналов с производительностью каждого канала ц) сред-
нее время пребывания заявки в системе равно
Т k(l) 1 /?(и —1, а)
i (1) =--=--------------.
Л р. R (П, а)
Для второй системы (один канал с производительностью пр)
среднее время пребывания заявки в системе равно
118
Покажем, что для любых Х>0, р. > О и /г>1
1 R(n — 1, «) 1 (в* л )
откуда
(я \
о, —
, П
R(n, а) п ( а \
К II» |
\ п )
или
Р$с> — Р^с. (4.1.32)
п
Выше уже была доказана справедливость неравенства
Робе >Роьс. Следовательно, и неравенство (4.1.32) тем более
будет иметь место. Таким образом, при дроблении общей произ-
водительности увеличивается вероятность обслуживания, но
вместе с ней увеличивается также и среднее время пребывания
заявки в системе в основном за счет уменьшения потерь заявок.
4.1.4. Рассматривается СМО с отказами с параметрами
(n, X, ц). Обслуживание одной заявки приносит среднюю прибыль
Сь создание одного канала обслуживания требует среднего рас-
хода С2, эксплуатация одного канала в единицу времени требу-
ет среднего расхода С3.
Определить, при каких соотношениях стоимостей Сь С2 и С3
система будет рентабельна и через какое время t она начнет при-
носит^ прибыль.
Решение
Будем решать задачу в предположении, что система находит-
ся в стационарном режиме. Тогда за время t эксплуатации
системы она принесет среднюю прибыль.
где Х0^ХРобс=Х --абсолютная пропускная способ-
ность системы. За это время будет израсходована в среднем стои-
мость
C72/z —Н •
Прибыль такая система начнет приносить через время Л оп-
ределяемое условием
119
откуда
/=——
С^О — С3Л
Условие рентабельности системы очевидно, следующее:
Ci\) —С3я>0
или
> C3zz.
Преобразуем это выражение (с учетом того, что k — X - ——-а^):
v а)
Cl П R(nt а)
Сз к R(n — 1, а)
(4.1.33)
Таким образом, для фиксированных значений X, р, Сь Сз
существует область значений числа каналов п, в которой система
рентабельна. Максимальное число каналов пШах определяется из
условия
__nniax^ (лтах»
” Х^(лтах-1, а)
Область рентабельных значений числа канала п определяется из
выражения
1 /Zmax
при условии выполнения неравенства (4.1.33).
Заметим, что область рентабельных значений числа
каналов п для некоторых значений параметров X и ц и стоимо-
стей С\ и Сз вообще может не существовать. Так, например, при
сз
не существует такого целого положительного числа п, для кото-
рого выполняется условие
1>„ *<"'> ,
R(n — 1, 1)
так как минимальное значение правой части будет иметь место
при п= 1; это минимальное значение равно 2:
R(lt 1) 7
Я(0, 1)
При увеличении п отношение
R(n, 1)
R(n — \, 1)
120
монотонно уменьшается, имея свой предел, равный единице, а
выражение
п *fal>
Я(л-1, 1)
монотонно возрастает, оставаясь все время больше 2.
Следовательно, при проектировании систем массового обслу-
живания можно подсчитать, будет ли такая система рентабельна
и через какое время t она начнет приносить прибыль. Прибыль
С, принесенная такой системой к моменту t\>t (при условии, что
система рентабельна), определяется из выражения
С=Ci\) (/i — f) — С3 (/j — t) п = (/х — /) [Ci\) — пС3].
4.1.5. Есть возможность спроектировать две системы массово-
го обслуживания с отказами: в первой системе производитель-
ность каждого канала равна во’ второй — ц2(щ>ц2). По
условию спроектирован-
ная система должна обес-
печивать вероятность об-
служивания заявки Робе
при интенсивности потока
заявок %. Определить,
сколько потребуется ка-
налов n*i при производи-
тельности канала pi и ка-
налов п*2 при производи-
тельности канала р2.
Решение
Для ответа на постав-
ленный вопрос нужно по-
строить графики зависи-
мости вероятности обслуживания Робе от числа каналов пх и п2.
На рис. 4.1.5а приведены такие графики. Вероятность РОбс оп-
ределена только при целых положительных значениях аргумен;
тов П1 и п2. Однако для удобства построения на рисунке изо-
бражены непрерывные кривые. По таким графикам легко опре-
делить потребное число каналов. В рассматриваемом случае
ti\* =4; п2* = 6. Читателю предлагается самостоятельно доказать,
что при одинаковом числе каналов п и интенсивности потока за-
явок % та система будет лучше, для которой производительность
канала выше, т. е.
Я(л —1, а1)^Я(л —1, а2) _ X
---------- ----------- , 1 АС --
Л (я, “1) Я («» «2> Н
X
а2=-----.
1*2
4.1.6. Найти основные характеристики системы массового
обслуживания с отказами при неограниченном числе каналов
(п = оо).
121
Решение
При п = оо вероятность того, что будет занято ровно k кана-
лов, найдем из выражения
^=lim а),
л-оо R (п, а)
т. е. эти вероятности будут распределены по закону Пуассона.
Среднее число занятых каналов k будет равно
-г 1. R (п — 1, а)
£ = lima —------—-- — а.
л-ОС R(nt а)
Вероятность обслуживания будет равна единице:
Робс = Ь
Вероятность того, что канал занят, равна нулю:
-3.к = Ит —=0.
Л-> -хз Т1
Среднее время пребывания заявки в системе равно
т .. k 1
/=11ш— — —,
а само время Т пребывания заявки в системе распределено по
показательному закону с параметром р,.
§ 4.2. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ
И НЕДОСТОВЕРНЫМ ОБСЛУЖИВАНИЕМ
Постановка задачи. На вход n-канальной системы
массового обслуживания поступает простейший поток заявок с
интенсивностью X. Интенсивность простейшего потока обслужи-
ваний каждого канала р.. Если вновь прибывшая заявка застала
все п каналов занятыми, то эта заявка получает отказ и покида-
ет систему необслуженной. Если вновь поступившая заявка за-
стала свободным хотя бы один канал, то она принимается к
обслуживанию и обслуживается до конца (заявки «терпеливые»).
Однако заявка, прошедшая обслуживание в канале, оказывается
фактически обслуженной не достоверно, а с вероятностью р.
Такая система отличается от классической системы массового
обслуживания с отказами, рассмотренной в § 4.1, только тем, что
заявка, побывавшая на обслуживании в канале, выходит из нее
обслуженной лишь с вероятностью р. Это схематически показано
на рис. 4.2.1 (на рисунке изображена схема, а не состояния).
Такую систему можно представить условно как двухступенча-
тую систему массового обслуживания: в первой ступени заявка
122
принимается к обслуживанию (или не принимается); во вто-
рой— обслуживается (или не обслуживается). При этом полное
обслуживание обеспечивается лишь в том случае, если заявка
пройдет оба этапа обслуживания. Первая ступень обслуживания
работает так же, как классическая СМО с отказами, рассмотрен-
ная в § 4.1. На вторую ступень обслуживания поступают лишь
те заявки, которые были обслужены первой ступенью. Обслу-
живание второй ступенью осуществляется мгновенно, но не до-
стоверно, а с вероятностью р.
v_______ Поток
Рис. 4.2.1
необслуженных
заявок
Граф состояний такой системы остается таким же, как и в
случае классической системы массового обслуживания с отказа-
ми (см. рис. 4.1.1.). Следовательно, вероятности состояний опре-
деляются по тем же формулам, что приведены в § 4.1. Все вре-
менные характеристики работы системы остаются такими же, как
и для СМО с отказами. Отличие состоит лишь в том, что вероят-
ность обслуживания будет определяться как произведение веро-
ятности того, что заявка будет принята к обслуживанию (1—рп),
на вероятность «успешного» обслуживания р;
Робс = (1 ~рп) P = R(2, (4.2.1)
Р(л, а)
Абсолютная пропускная способность системы будет
• (4.2.2)
К(п9 а)
Основные расчетные формулы
Среднее число занятых каналов:
k=g “> ,
R(n, а)
где
а = Х/р..
Вероятность обслуживания заявки (относительная пропускная
способность)
ро6с=_1±р=(1_^)>=А.
Л Л
123
Вероятность того, что взятый наугад канал занят:
k
Вероятность того, что система полностью загружена:
“п 3 Рп 1 ?
Среднее время занятости канала
Г ——
*з.к
р-
Среднее время простоя канала
^п,к ^з.к
^з.с
1 Лз.к
лз.к
Среднее время полной загрузки системы
t =—5—
*з,с
Пр.
Среднее время неполной загрузки системы
"7 “7 1 яп.ч
ГП.З fH.3 _
Яп.з
Среднее время пребывания заявки в системе
7=—.
Задачи и упражнения
4.2.1. Рассматривается круглосуточная работа пункта прове-
дения профилактического осмотра автомашин. Этот пункт состо-
ит из четырех каналов (четырех групп проведения осмотра). На
осмотр каждой машины затрачивается в среднем 1/р = 0,5 часа.
При осмотре группа выявляет дефекты с вероятностью р = 0,8.
На осмотр поступает в среднем 192 машины в сутки: А,=
= 192-----=8------. Машина считается «обслуженной», если
сутки час J
в ней выявлен дефект. Если машина, прибывшая на пункт
осмотра, не застает ни одного канала свободным, она покидает
пункт несбслуженной и вновь эксплуатируется.
Определить характеристики работы пункта профилактическо-
го осмотра.
124
Решение.
Работу пункта проведения профилактического осмотра мож-
но рассматривать как работу СМО с отказами и недостоверным
обслуживанием с параметрами
я = 4;
Х=8—— ;
час
/7-0,8;
X
а,—— = 4.
V
Характеристики работы системы следующие: среднее число
занятых каналов
= Д<3. 4> =2J6
Я(П, а) Я (4, 4)
вероятность выявления скрытого дефекта
Ро5с=(1 -Рп) Р^-27Х\а} Р=0,55.
R(n, а)
Абсолютная пропускная способность пункта
Х0=ХРобс=4,40 — .
час
Полная абсолютная пропускная способность, считая все осмот-
ренные машины:
Х=—= 5,50—.
р час
Вероятность того, что канал занят:
7ГЗЖ = —=0,69.
п
Среднее время простоя канала \ J
/пк—/з к 1 о,234 часа.
лз.к
Вероятность того, что все группы будут заняты осмотром:
ТГ..з=/7я = 0,312.
125
Среднее время неполной занятости системы (простоя хотя бьв
одной группы)
f„.3= — -—^=0,275 часа.
fV Яп.З
Рис. 4.2.2а
вынужден садиться на запасной
4.2.2. Производится дозаправка самолетов горючим в возду-
хе. В районе дозаправки находятся 3 самолета-заправщика. Са-
молет, нуждающийся в дозаправке, выходит в район, где дежу-
рят заправщики, с вероятностью р=0,9. Если самолет вышел в
район дозаправки и свободен хотя бы один из заправщиков, то он
производит дозаправку, на что
уходит в среднем 10 мин. Если
самолет выходит в район доза-
правки, но все самолеты-за-
правщики заняты, то этот са-
молет остается недозаправлен-
ным. Во всех случаях, когда
самолет недозаправлен, он вы-
нужден садиться на запасной
аэродром. Определить вероят-
ность того, что самолет будет
аэродром, если самолеты подхо-
дят к району дозаправки со средним интервалом в 150 сек.
Р еш ен и е
Эта система несколько отличается от той, которая рассмат-
ривается в данном параграфе. Схематически работу такой систе-
мы можно представить в виде двух этапов обслуживания: на
первом этапе производится мгновенный отбор на обслуживание
(с вероятностью р заявка мгновенно направляется на обслужи-
вание), на втором этапе отобранные заявки подвергаются обслу-
живанию. Схема такого обслуживания представлена на
рис. 4.2.2а (на рисунке изображена схема, а не состояния).
Таким образом, такая система представляет систему массо-
вого обслуживания с отказами, на вход которой поступает про-
стейший поток заявок с параметром Хр.
Следовательно, вероятность обслуживания для рассматривае-
мой системы будет определяться по формуле
Р обе
__Р(и — 1, ар)
R(n, ар)
Все остальные характеристики системы будут такими же>
как и у системы массового обслуживания с отказами, параметры
которой п; Хр; ц.
Таким образом, система дозаправки самолета в воздухе мо-
жет рассматриваться как СМО с отказами с параметрами
о 0,9 г 1 1 1 г 1 1
Л = 3; А =----------1; ---- ----I.
150 [ сек J 600 [ сек J
126
Следовательно, вероятность Р незаправки самолета будет
Pd6c=l —-(2> 3’ 6) =0,411.
• /?(л, ар) Я(3, 3, 6)
§ 4.3. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ
И ПОЛНОЙ ВЗАИМОПОМОЩЬЮ МЕЖДУ КАМАЛАМИ
Постановка задачи. На вход n-канальной системы
массового обслуживания поступает простейший поток заявок с
интенсивностью Л. Интенсивность простейшего потока обслужи-
ваний каждого канала р. Если заявка застает все каналы сво-
бодными, то она принимается на обслуживание и обслуживается
всеми п каналами одновременно. Предполагается, что такое об-
служивание возможно и производительность обслуживания при
этом увеличивается в п раз (т. е. интенсивность суммарного по-
тока обслуживаний равна пр,). После окончания обслуживания
все п каналов освобождаются одновременно *.
Если вновь прибывшая заявка застает в системе одну заявку,
то она принимается на обслуживание. В этом случае часть кана-
лов продолжает обслуживать первую заявку, а остальные кана-
лы приступают к обслуживанию вновь прибывшей заявки. Рас-
пределение каналов по заявкам может производиться любым
образом. В дальнейшем мы увидим, что для пуассоновской си-
стемы характеристики обслуживания не зависят от того, как мы
делим общее число каналов; важно, чтобы все каналы участво-
вали в обслуживании. Если прибывшая новая заявка застает в
системе две обслуживаемые заявки и п>2, то каналы распреде- ’
ляются по всем трем заявкам, и т. д.
Если вновь прибывшая заявка застает в системе k заявок
(k=\, 2, ..., п—1), то она принимается к обслуживанию и все п
каналов перераспределяются произвольным образом между
k +1 -заявками, но так, чтобы все каналы участвовали в обслу-
живании.
Если вновь прибывшая заявка застает в системе п заявок,
то она получает отказ и не обслуживается. Попавшая на обслу-
живание заявка обслуживается до конца (заявки «терпели-
вые»), Каждая заявка, принятая к обслуживанию, обслуживает- I
ся достоверно.
Если обслуживание какой-либо заявки окончено, то освобо-
дившаяся группа каналов присоединяется к обслуживанию ос-
тальных заявок, находящихся в системе. Таким образом, при на-
личии в системе хотя бы одной заявки все п каналов все время
будут заняты.
Требуется найти характеристики работы такой системы мас-
сового обслуживания.
* Другими словами, имеется точная информация о результатах обслужи-
вания.
127
Будем нумеровать состояния системы по числу заявок, нахо-
дящихся в системе:
хо — в системе нет заявок (все каналы свободны);
хк — в системе имеется k заявок, они обслуживаются п канала-
ми, общая производительность обслуживания равна пр,
каналы распределяются произвольно между заявками.
Граф состояний такой системы показан на рис. 4.3.1. При
наличии хотя бы одной заявки в системе интенсивность потока
обслуживаний будет равна
как бы не распределялись ка-
налы по заявкам.
Глядя на этот граф состоя-
ний, можно составить систему
дифференциальных уравнений,
которая справедлива и для пе-
ременных параметров X, р.
Рис. 4.3.1
(Читателю предлагается самостоятельно написать такую си-
стему).
Рассмотрим стационарный режим работы системы (X=const,
p=const, t—>оо), который существует, так как система облада-
ет эргодическим свойством (см. § 2.4). В этом случае работа
СМО будет описываться системой алгебраических уравнений:
o=-^+«i*w
0=—(Х4-Я|х)рй+Х/7л_1 + «р/7*+1 (£=1, 2,..., п. — 1); (4.3.1)
0= —пу.рп 'крп-г-
Для решения этой системы введем обозначение
ut= — \pi-i — nppi (г=1, 2,..., п). (4.3.2)
С учетом (4.3.2) уравнения (4.3.1) примут вид:
«1 = 0;
Uk+i — uk=0 (£=1, 2,..., «);
«„=0,
откуда
«z = 0 (/= 1,2,..., «).
Следовательно:
Рь=(—) Ро (* = 0, 1,..., «).
\ Пр /
(4.3.3)
(4.3.4)
(4.3.5)
128
Введем обозначение
= (4.3.6)
Пр. п
Величина к равна среднему числу заявок, поступающих в
систему за среднее время обслуживания одной заявки всеми п
каналами.
С учетом принятого обозначения получим
Ph=*kPo- (4.3.7)
Вероятность ро найдем из нормировочного условия
п п п *
__ _ __________ 1 „л+1
У Р*=:£ *кРо=Ро£ = =1.
Л = 0 Л = 0 л=о
откуда
До=-Ц^Г- (4.3.8)
1—х.л+1
Следовательно:
-1 —— (А=0, 1, 2,..., п; х^=1). (4.3.9)
1—хл+1
Это выражение справедливо для любых значений х#=1. При х=1
имеет место неопределенность, раскрывая которую, получим
р6=—— (*=0, 1, 2.............п; Х=1), (4.3.10)
п + 1
т. е. все состояния будут равновероятны.
Вероятность обслуживания заявки определяется из выра-
жения
Робе =1 — Pfl~
1 - Xя
1 - хл+1
п
П 4- 1
при X #= 1,
при Х=1.
(4.3.11)
Найдем среднее число заявок I, находящихся в системе:
п п
7=2>*~Г^г£ <4-3-,2>
*=о 1 А *=0
5—1964 129
Для вычисления суммы, входящей в выражение . (4.3.12), вос-
пользуемся методом дифференцирования рядов:
У ^‘=У х—х* = х-^-У х* =
fa fa
Л = 0 *=0 Л=0
_ д 1 1 — [и (1— х)4- 1]
dx 1 — х (1 — х)2
Следовательно, среднее число заявок, находящихся
ме, будет равно
-j 1 — х * 1 — хл [л (1 — х) 4- 1] * 1 — хя [л (1 — х) 4- 1]
— 1— хл+^Х (1—х)2 —
При х=1 получим [см. (4.3.10)]
п п
7=у kpk=—— У k=—— п.(п + .1) =4- . (4.3.15)
4- ™ л + 1 Li л 4- 1 2 2 4
Л=0 Л=0
Среднее число занятых каналов k определяется так:
(4.3.13)
в систе-
. (4.3.14)
k=tl(\ — р0)=
хп
при х =/= 1;
Л2
при Х = 1.
(4.3.16)
Для этой системы вероятность того, что любой отдельный ка-
нал будет занят, равна вероятности того, что все каналы будут
заняты:
*з.к=1-/?о=— • (4.3.17)
Л
Время простоя канала Тп.к распределено по показательному
закону с параметром X, так как граф состояний для определения
закона распределения времени Тпк имеет вид, показанный на
рис. 4.3.2.
Среднее время простоя канала будет равно
Тп.к=4-- (4.3.18)
А
Среднее время занятости канала определяется на основании
эргодического свойства:
4,к^=7п.к , Яз* . (4.3.19)
цю
Закон распределения времени занятости канала определяет-
ся с помощью графа состояний, имеющего вид, указанный на
рис. 4.3.3.
Соответствующую этому графу состояний систему дифферен-
циальных уравнений нужно интегрировать при начальных усло-
виях
Pi'(0)=l; Д*(0)=0 (А^1). (4.3.20)
Рис. 4.3.2 Рис. 4.3.3
Вероятность полной загрузки системы равна вероятности того,
что в системе обслуживается п заявок:
тсп.3 = рЛ. (4.3.21)
Закон распределения времени полной загрузки системы Гп,3
будет показательным с параметром пц, так как граф состояний
для определения этого закона имеет вид, показанный на
рис. 4.3.4.
Рис. 4.3.4 Рис. 4.3.5
Следовательно, среднее время полной загрузки системы будет
7п.з=— , (4.3.22)
откуда (на основании эргодического свойства) среднее время
неполной загрузки системы, когда в системе имеется число зая-
вок меньше, чем п, равно
(4.3.23)
Яп.З
Закон распределения времени неполной загрузки системы опре-
деляется с помощью графа состояний, изображенного на
рис. 4.3.5.
Систему дифференциальных уравнений, соответствующих это-
му графу состояний, нужно интегрировать при начальных усло-
виях
ря_1(0)=1; ^(0)=0 (Л>п-1).
(4.3.24)
131
5*
Среднее время нахождения заявки в системе определяется из
равенства [см. (4.3.14) и (4.3.15)]:
1 1 — х” [п(1—х)+ 1]
Лр. (1—x^+^fl-x)
при х =# 1;
при х=1.
(4.3.25)
Расчеты показывают, что функцию распределения времени
пребывания заявки в системе довольно хорошо можно аппрокси-
мировать выражением
_ [ -*н.з~И|
F (/) = 1кп.з + 7Гн.з\ 1 — е 1 7J !(/)*,
(4.3.26)
где Лп.з=1—Лн.з — вероятность полной загрузки системы.
/
Основные расчетные формулы
Вероятность того, что занято ровно k каналов:
Pk=
k 1 — х
хл---------
при
где
1
л 4- 1
при
х=1,
Пр.
Вероятность обслуживания заявки
1 — х”
1—ХП^1
при х =/= 1;
Р обе---‘ 1 Рп-------
при х— 1.
х =
п
( Среднее число заявок, находящихся в системе:
1 — хл[п(1 —х) 4- 1] , 1
X------1 при х=/= 1;
__ (1—х)(1 —хя^1) к
i /=
при х=1.
* Эта формула получается при сохранении в аппроксимированной функ-
ции F(/) величины скачка при ^=0 и математического ожидания таким же,
как и для функции F(t).
132
Среднее число занятых каналов
при х =# 1;
при х=1.
Вероятность того, что канал занят:
k
ЯЗ.К--- •
п
Вероятность того, что система полностью загружена:
ЯП.З---Рп----
— %П-И
1 — ХЛ Т1
1
п+ 1
при х =# Г,
при Х=1.
Среднее время полной загрузки системы
Среднее время неполной загрузки системы
2 _ Л 1 Яц.з
*Н.З---:^з.с
Лп.З
'Среднее время нахождения заявки в системе
Задачи и упражнения
4.3.1. Указать, какая система имеет большую пропускную
способность: 1) система массового обслуживания с отказами и
без взаимопомощи или 2) система массового обслуживания с
отказами и полной взаимопомощью, если параметры обеих си-
стем (n, X, ц) одинаковы (п>1).
Решение
Очевидно, введение взаимопомощи должно привести к увели-
чению абсолютной и относительной пропускной способности си-
стемы и формального доказательства можно было бы и не при-
водить. Однако методические приемы, употребленные при
.доказательстве, помогут нам решать другие задачи.
133
Перейдем к решению задачи. Покажем, что если
Р(12
* обе
_R(n— 1, я) .
R(n, я)
р&
1—хп
1—+
где
а
х =----,
п
то Робе 1> Робе, т. е. СМО с отказами и взаимопомощью имеет
большую пропускную способность, чем СМО с отказами и без
взаимопомощи.
Рассмотрим три различных случая:
Случай 1.
Х=—=1 (а=я).
п
Докажем, что
р£ > р£.
т. е.
п 7? (/? — 1, п)
' л+1 R (п, п)
Перепишем это неравенство в виде:
п п) — Р (п, П)
п 4- 1 R (п, п)
откуда
nR(n, я)ХЛ+1)[#(я, п) — Р(п, п)]
и
(п+1)Р(п, п)>/?(п, п\
тогда
п п
(«+1)Р(п, n)=^P(n, n)>VP(k, «),
Л=0 *=0
п
так как каждый член суммы Р(га, я), кроме последнего,
л=о
п
.больше каждого члена суммы P(k, п) [см. (1.5.24)], а по-
; Л = 0
следние члены сумм равны.
134
Рассмотрим другой случай.
Случай 2. х<1. В этом случае 1 —хя>0 и
]_хл+1> 0.
Проведем доказательство:
1—Xя а) — Р(п, я)
1— хя+1 R(n, а)
ИЛИ
(1-хя)/?(л, а)>(1 -хя+1)[/?(л, а)-Р(л, а)].
Заметим, что если х<1, то 1 — хя+1 > 1 — хя>0, откуда
(1-хя)[Я(л, а)-Р(га, а)]>(1-хя+1)Р?(/г, а.)-Р(п, а)].
Но
(1—хя)/?(«, а)>(1 —хя)[/?(«, а) — P(rit а)]>
>(1-*«+!)[/? (П> а)-Р(п, а)].
Таким образом, и во втором случае доказано, что
РЙ>Р&.
Предоставим читателю самостоятельно доказать это неравен-
ство и в третьем случае, когда х>1 (рекомендуется воспользо-
ваться неравенствами 1 — хп+1<1 —х"<0).
Таким образом, система со взаимопомощью всегда имеет
большую пропускную способность, чем система без взаимопо-
мощи.
4.3.2. Обслуживание заявок производится системой массового
обслуживания с отказами, параметры системы n, X, у,. Обслужи-
вание каждой заявки приносит среднюю прибыль С целью
увеличения доходов от обслуживания предлагается провести ре-
организацию, состоящую в том, что система будет допускать взаи-
мопомощь между каналами. На преобразование СМО с отказами
в СМО с отказами и взаимопомощью требуется израсходовать
стоимость Сг. Переоборудование занимает время тп. Определить,
по истечении какого времени t после начала переоборудования
вновь организованная СМО с отказами и взаимопомощью начнет
приносить прибыль.
Решение
Задачу будем решать при условии, что время установления
стационарного режима в системах мало по сравнению со време-
нем переоборудования тп и временем /(<>тп). Начало отсчета
135
для времени тп и t одно. В этом случае можно записать следую-
щее уравнение:
Ctf>t= -С2 + С1Х{(2)(/-тп),
Л (1) 7? (л — 1, а)
где Хо = а —— абсолютная пропускная способность
СМО с отказами;
Xq2) = Х—--------абсолютная пропускная способность
1 — хл+х
СМО с отказами и взаимопомощью;
X
а =— ,
Р-
X
х=---- .
Пр.
Решая это уравнение, получим время t, по истечении которого
реорганизация начнет приносить прибыль:
— ( ^2 + ^1тп^
1 —хЛ+1 Д 1 \ 1 —
7?(л — 1, Ot)
7? (и, а)
hi
4.3.3. При решении предыдущего примера стоимость содержа-
ния канала без взаимопомощи и стоимость содержания канала со
взаимопомощью предполагалась одинаковой. На самом деле это
может быть не так. Рассмотрим случай, когда на содержание
одного канала СМО с отказами без взаимопомощи в единицу
времени расходуется стоимость С3, а на содержание одного канала
СМО с отказами и взаимопомощью в единицу времени расхо-
дуется стоимость С4>С3. Преобразование СМО с отказами в
СМО со взаимопомощью потребует единовременных затрат С2, а
время переоборудования -будет равно тп. Средняя прибыль при
обслуживании одной заявки равна Обе рассматриваемые
СМО: с отказами без взаимопомощи и с отказами и взаимопо-
мощью имеют одинаковые параметры (n, X, ц). Определить усло-
вия рентабельной работы обеих СМО и при каких условиях с
экономической точки зрения есть смысл переходить от СМО с
отказами и без взаимопомощи к СМО с отказами и взаимопо-
мощью между каналами. Указать время t после начала переобо-
рудования, по истечении которого вновь созданная СМО со
взаимопомощью начнет приносить прибыль.
Решение
Рассматривается стационарный режим работы. Для СМО с
отказами и без взаимопомощи условие рентабельности будет
иметь вид
С3л,
где Хо(1) — абсолютная пропускная способность СМО с отказами
и .без взаимопомощи.
136
Условие рентабельности состоит в том, что средняя прибыль
от обслуживания должна покрывать средние расходы на содер-
жание системы массового обслуживания [см. (4.1.33) в примере
4.1.4]. Тогда
С3 \R (п — 1, а)
С\ ' nR(n, а)
Условие рентабельности для СМО с отказами и взаимопо-
мощью определяется по формуле
4"^ > С4п,
откуда с учетом (4.3.11)
С4 к(1—х”)
Ci л (1 —• хЛ+1)
при % #= 1;
с4 х
Cj п + 1
при х=1.
С экономической точки зрения переход от СМО с отказами и
без взаимопомощи к СМО с отказами и взаимопомощью может
быть оправдан только в том случае, если прибыль в единицу вре-
мени, получаемая от СМО с отказами и без взаимопомощи, будет
ниже, чем прибыль в единицу времени, получаемая от СМО с от-
казами и взаимопомощью:
^,)С1-С4п>Х^)С1-С3п
или
откуда
ХР^сС1-С4п
ХРобсСj — Czti,
Р<2’ _ р(1> > п
* обе * обе .
CjA.
(С4-С3).
(4.3.27)
В примере 4.3.1 было показано, что вероятность обслуживания
для СМО с отказами и взаимопомощью Робе всегда больше ве-
роятности обслуживания СМО с отказами и без взаимопомощи
Робе- Поэтому левая часть неравенства (4.3.27) всегда положи-
тельна. Правая часть неравенства также положительна по усло-
вию задачи. Следовательно, решение о переходе на обслужива-
ние со взаимопомощью зависит от конкретных значений парамет-
ров системы п, X, ц, а также от коэффициентов стоимости Сь
С3, С4.
Предположим, что условие (4.3.27) данной задачи выполняется
и обе системы рентабельны. Тогда время t, по истечении которого
вновь созданная СМО с отказами и взаимопомощью начнет при-
" 137
носить прибыль большую, чем система с отказами, определится из
уравнения
- C3n)t= - С2+(X^’Ci - С4п) (t - тп),,
откуда
С2 К 1—хЛ ^4
х /?(я - 1, Я) С3 п
R(n, a) Ci
Рассмотрим численный пример. Допустим, что на переобору-
дование СМО требуется время тп=1 [месяц]. Обе СМО имеют
параметры
га = 6;Х = 15——; <л = 3—,
месяц месяц
откуда
15 е
а = = 5,
3
— = 0,833.
п
Стоимостные характеристики заданы отношениями
-^-=6;
Ci
_^.==1>5[—!—1 ;
Ci L месяц J
-^-=1,85 Г——1 .
Ci [ месяц J
Проверяем, являются ли обе
вычисления:
Х(1) = Х а) = 2.
° П R (п, а)
СМО рентабельными. Проводим
Х(2)^2_ 1~*я.
П I -------
2,38.
Убеждаемся в том, что
С3 X — 1, а)
Cl п R(nt а)
и
С4 X 1—
п 1 — хя+1
Следовательно, обе СМО рентабельны.
138
Выясним, целесообразно ли переоборудование, для чего про-
верим, выполняется ли условие (4.3.27) данной задачи:
Р$с - Робе=0,95 - 0,8=0,15;
f (7Г“ТЧ=0’14’
следовательно, условие (4.3.27) данной задачи выполняется, так
как 0,15>0,14.
Подсчитаем, через какое время t переоборудованная система
начнет приносить прибыль:
/=3,02 [месяца].
4.3.4. Доказать, что среднее время пребывания заявки в СМО
с отказами и полной взаимопомощью с параметрами п, Л, ц
всегда меньше среднего времени пребывания заявки в СМО с
отказами и без взаимопомощи и теми же параметрами (n, X, ц).
Решение
Для системы с отказами и взаимопомощью среднее время
нахождения заявки в системе определяется по формуле
7(2) = —*
где
[п(1-х)+1]
(1— х)(1 — Хп+1)
п
,т
при х =!= 1,
при х=1
среднее число заявок, находящихся в СМО. Для системы с отка-
зами и без взаимопомощи среднее время нахождения заявки в
системе определяется из выражения
х
где
R{n—\, а)
R(n, «)
— среднее число заявок, находящихся в СМО, равное среднему
числу занятых каналов, так как каждый канал может обслужи-
вать только одну заявку.
Для доказательства того, что
7<2) <7(0
достаточно доказать, что I(2) < Л(1).
139
Рассмотрим вначале случай, когда х=1, т. е. когда a=n>L
В этом случае должно выполняться неравенство
и . R(n — \, п)
2 R (п, п)
или
/?(п, я)<2/?(я —1, я).
Вспомним, что
/?(п, п)= 2
й-0
тогда
п п—\
2 p{k, «)<22 «),
£=0 Л=0
откуда
2 2^(^. и)>°-
Л = 0 /?=0
Произведя почленное вычитание, получаем
л—2
^P(k, ti)±P(n-\, ri)—P(nt л)>0
Л=0
или
R(n — 2, п)-\-Р(п — 1, п) — Р(п9 п)>0.
В § 1.5 при рассмотрении потока Эрланга было доказано, что
для любого целого числа п>0 имеет место равенство
P(n—1, п) = Р(п, п).
Следовательно, окончательно имеем
R(n — 2, п)>0.
Это неравенство выполняется для любого п>1, так как функция
л*—2
R(n — 2, п) = 2 п)> т- е- равна сумме вероятностей, которые
k=0
больше нуля.
Рассмотрим теперь случай, когда х<1. В этом случае нужно
доказать, что
r l-x"[l + n(l-x)] R(n-1, а)
(1—х)(1 — R (п, а)
140
В примере 4.3.1 было доказано, что при х<1
\ Р& > А
т. е. выполняется неравенство
I R(n — 1, а) | . 1 —х”
R (л, а) 1 1 — хл+1
Пользуясь этим неравенством, получим
1 — хя[/г(1 —х) + 1) 1—х«
х------------------ < а---------.
(1 — х)(1 ХЯ+*) 1 ХЯ +1
Имея в виду, что а=хп, сокращая последнее неравенство
на---------, получим
1—Хя+1 J
1 -X
откуда
1 —хя— Лхя-|-Пхл+1 — п?-п—
или
1 — хя<^л(1 —х),
но (1—х)< (1—Xя),
откуда
1 — хл п (1 — х) < п (1 — Xя),
что всегда выполняется, так как взаимопомощь имеет смысл
только при числе каналов п>1.
Предлагаем читателю самостоятельно доказать справедли-
вость неравенства
/(2><Л(1> Для случая х>1.
§ 4.4. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ
и частичной взаимопомощью между каналами
Постановка задачи: На вход n-канальной системы
массового обслуживания поступает простейший поток заявок с
плотностью X. Плотность простейшего потока обслуживаний каж-
дого канала р.. Если поступившая на обслуживание заявка за-
стает все каналы свободными, то она принимается на обслужи-
вание и обслуживается одновременно I каналами (/<л). При
этом поток обслуживаний одной заявки будет иметь интенсив-
ность /ц..
141
Если поступившая на обслуживание заявка застает в системе
одну заявку, то при п^21 вновь прибывшая заявка будет при-
нята к обслуживанию и будет обслуживаться одновременно /
каналами. 1
Если поступившая на обслуживание заявка застает в системе
I заявок (:=0, 1, 2,...), при этом (i+l)/^n, то поступившая
заявка будет обслуживаться / каналами с общей производитель-
ностью /р. Если вновь поступившая заявка застает в системе /
заявок и при этом выполняются совместно два неравенства
(/+1)/>и и j<n, то заявка будет принята на обслуживание.
В этом случае часть заявок может обслуживаться / каналами,
пр пр пр
Рис. 4.4.1
другая часть — меньшим, чем I, числом каналов, но в обслужи-
вании будут заняты все п каналов, которые распределены между
заявками произвольным образом. Если вновь поступившая заяв-
ка застает в системе п заявок, то она получает отказ и не обслу-
живается. Попавшая на обслуживание заявка обслуживается до
конца (заявки «терпеливые»).
Как и при анализе системы массового обслуживания с отка-
зами и полной взаимопомощью между каналами (см. § 4.3),
будем классифицировать состояние системы по числу заявок,
находящихся в системе:
Xi — в системе имеется i заявок (/=0, 1, 2, ..., Л), где —
целая часть числа и//. Каждая заявка обслуживается одновре-
менно / каналами с общей производительностью /ц;
Xj — в системе имеется / заявок (j=h +1, ..., п), в обслужива-
нии принимают участие все п каналов, распределяясь между
заявками приблизительно равномерно. Граф состояний такой
системы показан на рис. 4.4.1.
Этому графу соответствует система дифференциальных урав-
нений для вероятностей состояний, которая справедлива и для
переменных параметров X и р (желающие могут составить эти
уравнения).
Рассмотрим стационарный режим работы системы для случая
Л=const, р = const и t—>оо, который существует, так как система
обладает эргодическим свойством (см. § 2.4). В этом случае
142
\
можно выписать систему алгебраических уравнений и решать ее
так, как это мы делали до сих пор. Однако можно поступить
проще и воспользоваться теми решениями, которые были уже
получены.
Заметим, что граф состояний системы до состояния Xh с точ-
ностью до обозначений параметров потоков совпадает с графом
состояний классической системы массового обслуживания с от-
казами; изображенными на рис. 4.1.1. Следовательно [см. (4.1.8)]:
^=-7(7-У^ <4-4Л)
Н \ZfxZ
Граф состояний системы начиная от состояния Xh и кончая со-
стоянием хп совпадает с точностью до обозначений с графом
состояний системы массового обслуживания с полной взаимопо-
мощью, изображенным на рис. 4.3.1. Таким образом [см. (4.3.5)]:
Введем обозначения:
(4.4.2)
(4.4.3)
С учетом (4.4.3) выражение (4.4.1) окончательно примет вид
•^-Ро (* = 0, 1, 2,..., Л);
ah
Kti-h_Lp0 (k = fl, Л-1-1,. .., п).
М
(4.4.4)
Вероятность р0 найдем из нормировочного условия
" Л " / Л „Л " \
Л = 0 Л=0 й=Л4-1 \Й=О ’ ’ * = Л + 1 /
откуда
1
po=~T—k---------=(4А5)
k=Q Л=1
143
С учетом (4.4.5) выражение (4.4.4) окончательно
--------------------------- (fc==Q
R (Л, at) + Р (h, at) х —--
1 —х
Xfe—АР(й, аг) ... .
---------------v ”------------- (k = fl,. . ., n).
l—x"-* V 7
R (h, at) + P (h, aft x —----
1 --X
пример вид
(4.4.6)
I
Для сокращения дальнейшей записи
введем обозначение
Р=
____________1-------------
1—хя"л
R (h, at) + p (h, at) x —-_
1 — x
при х =/= 1;
(4-4.7)
1
/? (Л, аг) + Р (fl, at) (п — Л)
при Х= 1.
Найдем характеристики работы системы. Вероятность обслу-
живания заявки будет равна
Робе = 1 -рл= 1 - px"-A Р.(Л, а,). (4.4.8)
Среднее число заявок I, находящихся в системе [см. (4.1.17)
и (4.3.13)]:
л h п
’l=^kpk=Yik?p^k' аЛ+ £ ^Рх‘-Ар(л> “«)=
fe=0 Л=0 Л = Л+1
= pazP(A—1, аг) + р/Р(Л°‘~
гл h
= pazP(A—1,аг)-[-
kyfi — kr.k
L*=0 Л=0
+ р7>(Л, «г)-^—[1+А(1-х)-х«-'>[«(1-х)4-1П. (4.4.9)
Среднее число занятых каналов k найдем из выражения
h л
—klpk-±-n У* /?j=ZpazP(A—1, а;)4-«рР(Л, аг)х^-^-----.
k=0 k=h+l
(4.4.10)
Вероятность того, что отдельный канал будет занят:
к3.к=—. (4.4.11)
п
144
Вероятность занятости всех каналов системы определим из
выражения
I п
«з.в.к = У Р»=рР(Л, at)"4~*"~*. (4.4.12)
1 -X
Л = Л4-1
Это выражение справедливо, если Л<у-, т. е. nil не является
целым числом. Если h—пЦ, то
Л , -
1— ХП“Л+1
*з.в.к = У р*=рР(Л, аг)-------------.
k = h
В случае, если х=1, во всех выражениях, где имеет место неоп-
ределенность, ее нужно раскрыть:
1 _4n—h
lim х--------=/z— й; (4.4.13)
х->1 1—х 4
11m -^—[1 +Л(1 -х)-х«-*(Л (1 -х)+1)]=(”~/1)(” + А+1);
х—>1 (1 — Х^ z
(4.4.14)
1 _~п—Л + 1
lim-— --------=«-й + 1. (4.4.15)
х—>1 1 — X
Закон распределения времени Тз.в.к занятости всех каналов для
случая, когда h<nll определяется с помощью графа состояний,
изображенного на рис. 4.4.2.
Рис. 4.4.2
Соответствующая этому графу состояний система дифферен-
циальных уравнений должна интегрироваться при начальных
условиях рм-1(0) = 1; pfe(0) =О(А#=Л+1). Плотность распределе-
ния времени занятости всех каналов системы находится из
выражения
/з.в.к(/) = п^Л+1 (/) (/>0). (4.4.16)
Закон распределения времени простоя хотя бы одного из кана-
лов, если Л<п//, определяется с помощью графа состояний, изо-
браженного на рис. 4.4.3. Соответствующая этому графу состоя-
145
ний система дифференциальных уравнений должна интегриро-
ваться при начальных условиях рл(О) = 1; рь(О) =0(^#=Л).
Плотность распределения времени простоя хотя бы одного канала
системы найдем по формуле
(4.4.17)
Л.Х.К (0 = ^(0 (*>0).
Рис. 4.4.3
Для отыскания среднего времени занятости всех каналов си-
стемы 7'з.в.к, т. е. времени ее однократного пребывания в состоя-
ниях Хд+1, ..., хп (см. рис. 4.4.1),
составим дополнительный граф
состояний, изображенный на рис.
4.4.4. Этот граф состояний с точ-
ностью до обозначения состояний
Рис. 4.4.4. соответствует графу, изображен- ному на рис. 4.3.1. Тогда в соот- ветствии с формулой (4.3.9) веро-
ятность ph+k будет определяться из выражения
JjX. (*=°-1............-*'> <44-|8>
Следовательно, вероятность пребывания системы в группе со-
стояний Xh+i> Хп (см. граф на рис. 4.4.4) будет
~ 1__~п—h
^З.в.К = ^ХЛ+1..х,,= 1—= х x_^n_h+1 • (4.4.19)
Тогда, в соответствии с формулами (2.5.11) и (2.5.12), будем
иметь
_________ ^з.в.к
^3. в. К_ J Э
^з.в.к +
откуда среднее врёмя занятости всех каналов равно
7 _Д_ *З.В.К . Л х(1 —х,"-*) _ 1 1 — t.n-h (4.4.20)
1 X Пр. 1 X
Если х=1, то 7 — 1 п—h *з.в.к р. п (4.4.21)
146
Теперь можно _найти среднее время простоя хотя бы одного ка-
нала Ьистемы /п.х.к, т. е. среднее время пребывания системы в
состояниях Хо, Xi, Xh, из простой формулы
^з.в.к
^з.в.к
^З.в.к "Г ^п.х.к
откуда
1 _
_ _ 1 1 — рР (Л, а/) х —---------
4 _4 1 « 3 ,в,к_ 1 1 Ъ
*п.х.к--*З.В.К ----------— "Г- • "
Яз.в.к Л рР (Л, а/)
Если х=1, то
: _J_ 1 —pP(/t, аг)(и-Л)
П-* Х-К К ' рР(Л, аг)
(4.4.22)
(4.4.23)
где р — вычисляется по формуле (4.4.7).
Напомним еще раз, что формулы (4.4.20) — (4.4.23) справед-
ливы только для случая, когда число каналов п не делится без
остатка на величину/ •
Если число п делится на число I без остатка = то рас-
смотренные выше формулы принимают такой вид:
1
И(Л
1
р-
1 —%«—*+!
1 -Z
ti h Ч- 1
п
при х =f= 1;
при х=1.
(4.4.24)
1 1 — рР(Л, а;)х(1— хл—й+1)(1—х)—1
X рР(Л, а,)
= 1
X рР (Л, at)
(4.4.25)
Можно показать, что система массового обслуживания с час-
тичной взаимопомощью и отказами имеет большую пропускную
способность, чем система массового обслуживания без взаимо-
помощи (естественно при одинаковых параметрах системы n, X,
р,), но меньшую, чем система с полной взаимопомощью между
каналами при тех же параметрах n, X, р.
Вероятность полной загрузки системы равна
к„.з=ря. (4.4.26)
Время полной загрузки системы Гп.3 распределено по показа-
тельному закону с параметром пр, потому что граф состояний, с
147
помощью которого определяется это время, имеет вид, показан-
ный на рис. 4.4.5.
Следовательно, среднее время полной загрузки системы равно1
7„.3=— . (4.4.27)
Пр.
На основании эргодического свойства можно найти среднее
время неполной загрузки системы
7н.з=7п.з-—"-3- . (4.4.28)
Л-п.з
Среднее время пребывания заявки в системе определяется из
выражения
•*n-f
7.-=Х
(4.4.29)
Рис. 4.4.5 где I — среднее число заявок, (находящихся в
системе и определяемых по формуле (4.4.9).
Функцию распределения времени Т пребывания заявки в
системе можно аппроксимировать выражением
u г ( -"-Hl
^(0=Ьп.з + ^.зк1-е 1 Л1(0. (4-4.30)
где Лн.з=1—лп.з — вероятность неполной загрузки системы.
Эта формула получена так же, как и формула (4.3.26).
Основные расчетные формулы
Вероятность того, что все каналы свободны:
—— - при х =# 1; R(h, a{) + P(h,
Ро= 1 X Р (0, <*z) 1 —— при >-=1, 1 R (h, at) + Р (Л, аг) (И - Л)
где
И»
Вероятность того, что занято ровно k каналов:
Вероятность обслуживания равна
Ро6с=1-рп=1-^^-До-
Среднее число заявок /, находящихся в системе:
(atR(h-l, аг)Ро I „ x[l + ft(l-x)-x«-*[n(l-x)-|-l]]z .
Р(0, a,) ±Ph (1 —х)2 (
(х=1)
Р (0, а{) ' ' й 2 ' ’ ' V '
Среднее число занятых каналов k равно
laiR(h—1, а/) । 1 — хя~Л , ....
— -------—— Д04- Пр л -------(к =£ 1).
_ Р (0, аг) ° 1 Л 1 - х V '
k =
^(оГог) ”г) + О^1)-
Вероятность полной загрузки системы
КП.З-рп*
Среднее время полной загрузки системы
Пр
Среднее время пребывания заявки в системе
7=—.
Задачи и упражнения
4.4.1. Определить, на сколько увеличится вероятность обслу-
живания для СМО с отказами, параметры которой равны п=10,
Х=8[—5-1; р.=0,8|—!-|, если обеспечить взаимопомощь в пре-
[мин] [мин]
делах группы из двух каналов (/=2).
Решение
Для СМО с отказами без взаимопомощи вероятность обслу-
живания определяется по формуле (4.1.13):
,(i) R(n — 1, я)
ОбС R (п, а)
149
В нашем случае п=10, а=10
рП)___________________ & (9> Ю) _л усг
₽"“- «(10, 10) - °’ 95'
Для системы с частичной взаимопомощью имеем
«=Ю; х=— = 1; аг=—=5; й=|—1 = 5.
лр. L / J
Для этой системы в случае, когда х=1, вероятность обслужи-
вания определяется по формуле (4.4.7) и (4.4.8):
Р&=1--------Р(5’ 5) =0,883.
Л (5, 5)+5Р(5, 5)
Таким образом:
Роб’с - Р$с ==0,883 — 0,795 =0,088.
4.4.2. Для условий, приведенных в предыдущем примере,
найти среднее время нахождения заявки в системе для обоих
случаев: СМО с отказами и без взаимопомощи и СМО с отказа-
ми и частичной взаимопомощью.
Решение
Для отыскания среднего времени нахождения заявки в си-
стеме можно воспользоваться формулой
Г=—.
х
и
с
Среднее число заявок, находящихся в СМО с отказами, будет
равно среднему числу занятых каналов
= = а .pWc=7,95.
Среднее число заявок находящихся в СМО с отказами
частичной взаимопомощью, определяется по формуле (4.4.9)
учетом формулы (4.4.14):
Т2) =-----------5---------М (Л -1, at) + Р (Л, at) X
R (hai) Р {h, al)(n-h) 1 1 v U • 4 1
X-^(«+* + 1)1=6,2.
Следовательно, среднее время нахождения Заявки в СМО
отказами и без взаимопомощи равно
7<i)==_i!2.=Zi95_=0 995 м
X 8
с
а для системы с взаимопомощью
7<2)=7(2) ,Х-1 = = 0 775 мин
8
150
Таким образом, в данном случае система с частичной взаимо-
помощью обслуживает заявки с большей вероятностью и бы-
стрее.
§ 4.5. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ
И СЛУЧАЙНЫМ РАСПРЕДЕЛЕНИЕМ ЗАЯВОК ПО ВСЕМ КАНАЛАМ
(ЗАНЯТЫМ И НЕЗАНЯТЫМ)
Постановка задачи. До сих пор мы рассматривали
различные системы с отказами, когда вновь поступившие заявки
распределялись только по свободным каналам. Сейчас рассмот-
рим случай, когда вновь поступившая заявка направляется с
равной вероятностью 1/п в любой из п каналов, безотносительно
к тому, занят канал или нет. Если заявка направлена в свобод-
ный канал, то она принимается к обслуживанию и обслуживает-
ся показательное время с параметром р. Если заявка направлена
в занятый канал, то она покидает систему необслуженной. Оче-
видно, что если вновь прибывшая заявка застанет все каналы
занятыми, то она не будет обслужена и получит отказ. Но она
может получить отказ и при наличии свободных каналов.
Входной поток заявок, как и в предыдущих параграфах,
простейший с интенсивностью X. Заявка, попавшая в канал на
обслуживание, «терпеливо» ждет конца обслуживания. Заявка,
принятая к обслуживанию, обслуживается достоверно.
Примером такой системы массового обслуживания может
служить система ПВО при нарушенном управлении в распреде-
лении целей между каналами обстрела.
Такую СМО будем кратко называть «системой с отказами и
случайным распределением заявок».
Рассматриваемая система массового обслуживания может
находиться в следующих состояниях:
%о — система свободна; вновь поступившая заявка обязатель-
но будет обслужена;
xk — в системе занято k каналов (0<&<п), которые обслужи-
вают k заявок; вновь поступившая заявка попадет в один
n~k
из свободных каналов с вероятностью ------ и в этом
п
случае будет обслужена;
хп — все п каналов заняты; вновь поступившая заявка полу-
чает отказ.
Граф состояний этой системы показан на рис. 4.5.1. Этому-
графу состояний соответствует система дифференциальных урав-
нений для определения вероятностей состояний, справедливая
как для постоянных параметров X и ц, так и для переменных-
151
(Читателю рекомендуется написать эту систему дифференциаль-
ных уравнений.)
Проанализируем установившийся режим, который имеет ме-
сто при постоянных параметрах %=const, р=const и t—>оо
(система обладает эргодическим свойством).
Рис. 4.5.1
Выпишем систему алгебраических уравнений для определения
вероятностей состояний в стационарном режиме:
о=—М+нл;
о = — fx ——— Ap.'j pk 4- к -—ръ-\ 4-
\ л J п
+(* + 1)М>А+1 (0<Л<п),
(4.5.1)
о=— Рп-1-
п
Выражая последовательно вероятности pi, рг, —, Рь, — через
Ро, получим
X
Pi = ~Pq.
л-1
^=тгтП (24г-)/’о (0<^<«);
f=o '
(4.5.2)
152
Преобразуем выражение для вероятности pk\
* СТ ( п — I \ V
^=тгтП ---------До= —
Л! Z=0 ' ' J
= (— ) СпРо = пРо (0 < k < п),
\ р.п )
(4.5.3)
где
X
х=-----
пр.
ck__ п\
п~ k\ (n~k)\
(4.5.4)
Вероятность ро определим из нормировочного условия:
п п
/?=0 Л=0
откуда
1
А>=ТГТ
(4.5.5)
Таким образом, окончательно получим [см. (4.5.3) и (4.5.5)]:
__
Рк (1 + %)"
(4.5.6)
Найдем среднее число занятых каналов к (в данном случае
оно совпадает со средним числом обслуживаемых заявок):
п п п
k = '^kpk = p(j^t k-».kCn = рах ^Сп —
*=0 k=Q k=Q
-Р^-~ • (4-5.7)
дх 14-х
Вероятность обслуживания заявки получим из выражения
Вероятность того, что отдельный канал будет занят, опре-
делим из формулы
___ k ____ "*•
з.к : ; »
п 14-х
(4.5.9)
153
откуда среднее время простоя канала будет
j ____/ 1 — яз.к П
*п.к—*з.к —~
Лз.к Л
(4.5.10)
Среднее время полной загрузки системы равно/п.з =——
ГЦ1
(см. граф состояний на рис. 4.5.1). Вероятность того, что
система будет полностью загружена, равна ^п.3=р„—
(1 + хя) ’
следовательно, среднее время неполной загрузки системы
можно найти по формуле
/н.3=/п.8±^. = 4-1(1 +х)"-х"]. (4.5.11)
Я-п.з Л
Среднее время нахождения заявки в системе определяется по
формуле
- Г 1 1
/=—=---------
k р. 1 -|- х
Ввиду небольшого объема данного параграфа не будем при-
водить сводку расчетных формул.
Задачи и упражнения
4.5.1. Доказать, что классическая система массового обслу-
живания с отказами, рассмотренная в § 4.1, параметры которой
п, X, р, имеет вероятность обслуживания Робе большую, чем ве-
роятность Робе для GMO с отказами и случайным распределе-
нием заявок с теми же параметрами (n, X, р.) (п>1).
Решение
Вероятность обслуживания Pole определяется по формуле
(4.1.13):
Вероятность обслуживания Р$с определяется из выражения
(4.5.8):
Требуется доказать, что
/? (л — 1, а) I
(л, а) 14-Х
__ а
Преобразуем это неравенство, имея в виду, что х=— •
п
154
R(tl—1, a)-(-—/?(« —1, a)
Л
или
R(tl—\, a.)> — [R(n, a)-/?(n-l, a)],
a
При рассмотрении потоков Эрланга в § 1.5 было показано, что
R(n, a) — R(n — 1, a)=P(«, а).
Кроме, того:
— Р(п, а) — — — е~л=Р(п — 1, а),
а ал!
С учетом двух последних равенств получим
R(n-1, a)>P(/z-l, а),
или
R(n — 2, a)-f-P(n-l, a)>P(n—1, а),
откуда
R(n — 2, а)>0,
что выполняется для любых а и п. Таким образом, доказано, что
/>обс>/>обс для любых параметров (п, %, р,).
4.5.2. Рассматриваются две системы массового обслуживания:
1) СМО с отказами с параметрами п, Л, ц и 2) СМО с отказами
и случайным распределением заявок по каналам с теми же пара-
метрами (n, X, р). Доказать, что среднее время пребывания за-
явки в системе _в первом случае будет больше, чем во втором,
если л>1, т. е. /<1)>А2).
Решение
Для СМО с отказами имеем
(1) k 1 /? (л — 1, а) 1 R(jl— 1, a)
X X R (n, a) p. R (/?, a)
Для СМО с отказами и случайным распределением заявок
получим
-^(2) k 1
X X(1 4- х) р. 14-х
Следовательно, для того чтобы выполнялось неравенство
7(1) >7(2),
достаточно выполнения неравенства
R(n—\, a) 1
R (nt a) 14-х
155
Справедливость этого неравенства_была показана в предыду-
щем примере. Уменьшение времени Л2> (по сравнению с временем
Z(1)) связано с тем, что вероятность обслуживания заявки системой
с отказами больше, чем у системы с отказами и случайным рас-
пределением заявок. Если же рассматривать условное среднее
время пребывания в системе, вычисленное при условии, что
заявка принята к обслуживанию, то для обеих систем оно будет
одинаковым, равным 1/р.
§ 4.6. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ,
ВЗАИМОПОМОЩЬЮ И ОТСУТСТВИЕМ ИНФОРМАЦИИ
О РЕЗУЛЬТАТАХ ОБСЛУЖИВАНИЯ
Постановка задачи. На вход n-канальной системы
массового обслуживания подается простейший поток заявок с
интенсивностью X. Каждый канал обслуживает заявку в течение
случайного времени распределенного по показательному за-
кону с параметром ц. При этом обслуживание заявки заканчи-
вается успешно с вероятностью р. Информация о том, закончи-
лось ли обслуживание успешно или безуспешно, в СМО не
поступает. Если к моменту прихода новой заявки занято k кана-
лов (£=0, 1, 2, ..., п—1), то оставшиеся (и — k) каналов присту-
пают к обслуживанию вновь прибывшей заявки. Таким образом,
если заявку начали обслуживать (п — k) каналов, то вероятность
ее обслуживания будет равна
1 —(1 . (4.6.1)
Каждый канал, начавший обслуживать заявку, обслуживает
ее случайное время, по истечении которого он освобождается,
в то время как другие каналы могут еще продолжать обслужи-
вание. *
Заявки «терпеливые», т. е. время обслуживания заявки не
ограничено.
Примером такой системы может быть система ПВО, когда
нарушено целераспределение и каждую вновь поступившую в зо-
ну обстрела цель обстреливают все свободные каналы. Каждый
канал обстреливает цель некоторое время и за это время пора-
жает ее (независимо от других каналов обстрела) с вероят-
ностью р.
Рассмотрим подробнее работу такой системы. Допустим, что
в момент £=0 все каналы были свободными. В этом случае пер-
вую пришедшую заявку будут обслуживать все и каналов и ве-
роятность ее обслуживания будет равна 1 — (1—р)п. Если к мо-.
менту прихода новой заявки все п каналов заняты, то она полу-
чает отказ. Постепенно каналы, занятые обслуживанием первой
заявки, будут освобождаться (все в общем случае в разное вре-
мя). Если к моменту t свободен хотя бы один канал, и в этот
момент прибывает новая заявка, то она принимается на обслу-
156
живание всеми свободными к этому моменту каналами. Таким
образом, если в системе обслуживанием занято k каналов
(k=l, 2, п), то нельзя точно указать, сколько заявок обслужи-
вается. Можно лишь утверждать, что число обслуживаемых зая-
вок S находится в пределах
(k=\, 2,..., «). (4.6.2)
Анализ работы системы начнем с введения состояний
системы, которые в данном случае будем связывать с числом за-
нятых каналов: xh—обслуживанием занято ровно k каналов,
(п—k) каналов свободны (6 = 0, 1, 2, ..., п); в этом случае число
заявок в системе не больше k.
X
Рис. 4.6.1
Из состояния xk система может перейти в состояние Хь-ъ
если освободится канал. Интенсивность потока освобождений
равна йц. Система из состояний xk может перейти в состояние хп,
если придет новая заявка. Интенсивность потока заявок %. Если
система находится в состоянии хп и прибывает новая заявка, то
последняя получает отказ.
Граф состояний такой системы показан на рис. 4.6.1.
Этому графу состояний соответствует система дифференци-
альных уравнений для вероятностей состояний:
^^-=-Хр0(/) + |гД1(/);
= - (). + Л|Х) рк (0 + (* -Н) (О (0<А<«);
at
(4.6.3)
at
*=0
Начальные условия для интегрирования этой системы обычно
берут такими: ро(О) = 1, pfe(0) =0(£#=0). Напомним, что в этой
системе уравнений параметры X и р могут быть некоторыми
157
функциями времени, т. е. потоки событий могут быть нестацио-
нарными пуассоновскими потоками.
Найдем решение этой системы для случая Х= const и
p=const Последнее уравнение системы (4.6.3) можно перепи-
сать в следующем виде:
(4-6.4)
at
так как для любого t выполняется нормировочное условие
п
(4.6.5)
Л = 0
Преобразование Лапласа для уравнения (4.6.4) при началь-
ном условии Рп(0) =0 будет иметь вид
(s + «|i-|-X)/7„(s)=k,
откуда
'рЛ$=-- х (4.6.6)
s 4- 4~
Следовательно:
А. (*)=—4т(1 (4.6.7)
пр. + А
Уравнение для определения вероятности pn-i(0 запишется
так:
1Р1=^1= -(Х + (и-1) ix)^-! (/) +(4.6.8)
at
С учетом (4.6.6) преобразование Лапласа для уравнения
(4.6.8) при начальном условии pn-i(0)=0 примет вид
(* + Х + (п-1)г0 ~рп-1 (s) = -, (4.6.9)
s -|- пр. 4- А
откуда
р„_1 (s)=-------------------- . (4.6.10)
' (s+n!i+X)(s + (n—1)(л + Х) v '
Переходя далее к pn-2, Рп-з и т. д., можно убедиться, что
тп—1
х П р.(л —о
^(S)^-—, (4.6.11)
П (S 4- (n-i)p- +*)
1 = 0
158
откуда по формулам обращения для преобразований Лапласа
получим
П (п —0 m-i
Рп-т (/) = ———-------------F X П (й — О £_(Л|Х+Х)/ X
П (Х + !Л(Л-»)) 1=0
1=0
"у (-1)^ 1
X 4- р,(п—у) (т— /)!
L;=o
ml (X + р. (л — т))
п. (4.6.12)
Вероятность po(t) найдем из условия
Ро^=^-^Рп-т(1). (4.6.13)
т=0
Рассмотрим стационарный режим работы при t—>-оо. В этом
случае получим следующие выражения для вероятностей со-
стояний:
т—1
П (п — о
11т р„_т (i) = р„-т =---—--------- (0</п<п), (4.6.14)
/->оо Ш
П (X + ?(п — /))
1=0
lim Pn(t) = pn=~—2— .
t-+<x> X -f- Ир.
Обозначим, как прежде,
х
— = а
Р-
(4.6.15)
(4.6.16)
и разделим числитель и знаменатель выражения (4.6.14) на ве-
личину Нт-Г
т—1
а П (П-1) а--------
рп~т = -^----------=т (0<т<п). (4.6.17)
П (а+ (« — «)) П (а + (и —г))
1=0 1=0
Обратим внимание на то, что последнее выражение справедливо
и для /п=0, в чем можно непосредственно убедиться [см. (4.6.15)].
Дальнейшие преобразования связаны с введением гамма-
функции Г(х). Напомним ее свойства:
г (х и-1) . „
х= —-------- при х > О,
Г(х) н
й! = Г(п-(-1) при п=1, 2, 3,... .
(4.6.18)
159
С учетом выражения (4.6.18) вероятность рп-т {см. (4.6.17)]
будет иметь вид
ал! Г (а 4- л — т)
Рп т (п — т)1 Г (ал-|-1) 4 7
Если обозначить число занятых каналов k=n—т, то
(4.6.19) можно будет записать так:
Г(а + *} (0<Л<га).
(4.6.19)
формулу
ал!
Рк~ ~k\
(4.6.20)
Вероятность ро найдем
из условия
Рк'
Л=1
(4.6.21)
Если а
(4.6.20)
является целым положительным числом, то
упрощается (см. (4.6.18)]:
«я! (« + fe— 1)! c°71-i ,п . .
формула
где
Pk—
k\ (а + п)!
с:
(4.6.22)
Ст
п
л!
т\ (п. — т)\
Можно убедиться в том, что формула (4.6.22) справедлива для
любого целого числа k (£=0, 1, 2, ..., п), т. е. что
п
>а
Вычисление вероятностей ph удобно проводить с
таблиц биномиального распределения В (п, т, р) *
В (п, т, p) = C™pmqn'~n\
ПОМОЩЬЮ
(4.6.23)
где
q = \-p\
п.
Действительно:
В л, т,
Ст \
п — :
п, т,
(4<6.24>
2 J
* Таблицы биномиального распределения можно найти в [23].
Л=0
т
£
2
п
п, И,
160
откуда
ра-1 В fa + k~ 1, а— 1,
л=-^=-‘=-Ц-------------«-*+1. 2.).
®+я В ( о + П, а,
(4.6.25)
Напомним, что последнее выражение справедливо только при
целом положительном а. Если а не целое, то при большом чис-
ле каналов п(и>10) можно приближенно провести линейную
интерполяцию: сначала найти решение для (а] — целой части а,
а затем для числа [a]+1 и после этого линейно интерполировать
на величину а.
Найдем различные характеристики работы системы. Для оп-
ределения вероятности обслуживания проведем следующие рас-
суждения. Выдвинем гипотезу о том, что к моменту поступления
очередной заявки система находилась в состоянии х&. Вероят-
ность этой гипотезы будет р^. В этом случае очередную посту-
пившую заявку будет обслуживать (п—k) каналов и вероят-
ность ее обслуживания будет равна 1—(1 —p)n~h. Следователь-
но, полная вероятность обслуживания заявки будет
k п
Робс=2(1-(1-р)'’-й)^=1-^ s fh (4-6-26)
6=0 6=04
где q — \—р.
В частном случае, когда вероятность р = 1:
/>обс = 1-Л,= 1-------. (4.6.27)
/гр. 4- п 4- « 14-х
Сравнивая эту формулу с формулой (4.5.8), можно заметить, что
при р = ^рассматриваемая система и система с отказами и слу-
чайным распределением заявок имеет одинаковую пропускную
способность.
Вероятность того, что система будет полностью загружена,
определим из формулы
— (4.6.28)
а 4- п
(эта формула справедлива для любого а>0). Время полной за-
грузки системы распределено по показательному закону с па-
раметром рц, следовательно, среднее время полной загрузки сис-
темы
6-1964
161
откуда среднее время неполной загрузки системы можно найти
из выражения
Для отыскания закона распределения времени неполной за-
грузки системы составим граф состояний подсистемы X, пока-
занный на рис. 4.6.2.
Л.
Рис. 4.6.2
Систему дифференциальных уравнений, соответствующих это-
му графу состояний, нужно интегрировать при условии, что в мо-
мент t—О, система находится в состоянии xn-i, т. е.
р„_1(0)=1; pk(0)=0 (fe=#n-l). (4.6.30)
Покажем, что время простоя системы в этом случае также
распределено по показательному закону с найденным выше па-
раметром Х= =— .
1н.з.
Выпишем систему дифференциальных уравнений, соответст-
вующих графу состояний подсистемы X, изображенной на
рис. 4.6.2:
at
^(0 = _(X+(n_w)tx)~n_m(z)+
at
-j- (n - m +1) pn_m+i (/) (и=2,3.n). j
(4.6.31)
1'62
Преобразование Лапласа для этой системы уравнений
чальных условиях (4.6.30) будет иметь вид
(s 4" 1) I*) Р"—1 (s)=
(S X 4~ (^ — Я1) Н-) Рп—т {$) =
=(п — т-}-1)р/>л_т+1($) (т = 2, 3,...,'n). ।
Решая последовательно эти уравнения, получим
рп—\ ($)=--------------;
s + X + (п — 1) р.
при на-
(4.6.32)
(4.6.33)
tn—1
Sfl"1-1 П (п — I)
Pn—m(s)=— (ш = 2, 3,..., я).
П (S-F-X+(л —Of»)
i=i
Можно убедиться, что сумма изображений всех этих вероят-
ностей состояний имеет вид
7-1
п п s-pi-1 П(п—О
S * .. 4-S ----------—--------=“• t4’6-34)
“ S + A-b(n—])|А "X S 4- а
Я=1 . /=2 П (<+* + (« —01»)
/=1
Следовательно, оригинал для этой суммы равен
(4.6.35)
Преобразование Лапласа является линейной однородной опе-
рацией, для которой выполняется свойство суперпозиции:
если
п
1=1
__ п
и /z(s) есть изображение функции ft(t\ то /(s)=^/f (s)
i=i
есть изображение функции /(/). Следовательно, сумма вероят-
ностей p0(t), pn-i(t) будет равна
2 P-"W=e~U- (4.6.36)
т = 1
6*
163
В соответствии с графом состояний, изображенным на
рис. 4.6.2, плотность распределения времени неполной загрузки
системы будет определяться по формуле
/«.з(М2^-«(0=^>0), (4.6.37)
m = l
что и требовалось показать.
Среднее число занятых каналов будет равно
п
*=2 Ьр* (4.6.38)
Л = 0
Вероятность того, что канал занят< найдем по формуле
V (4.6.39)
п
i ____
Среднее время занятости канала /З.к по условию равно
7з.к^—, (4.6.40)
р. ' •
откуда на основании эргодического свойства среднее время про-
стоя канала можно' вычислить так:
7п.к^7и 1~Яз-к (4.6141)
Л-з.к
Найдем среднее время пребывания заявки в системе. Допу-
стим,, что к моменту прихода очередной заявки система была в
состоянии xk(k<n). Вероятность этой гипотезы равна Pk. В этом
случае очередную заявку .начнут обслуживать (и—k) каналов.
Обслуживание будет продолжаться до тех пор, пока для всех
(п—k) каналов не кончится время обслуживания, которое осу-
ществляется каждым каналом независимо от других (при этом
заявка с некоторой вероятностью может быть и не обслужена;
вероятность этого равна (1—p)”_fe). Следовательно, обслужива-
ние будет продолжаться до тех пор, пока оно не закончится
у того канала, который обслуживает заявку максимальное вре-
мя среди всех п—k каналов. Таким образом, время обслужива-
ния будет определяться из формулы
Т(„_*)=max (Т;, Тъ..., Tn-k\ (4.6.42)
где Т<(» = 1, 2, ..., п—k)—система независимых случайных вели-
чин, распределенных одинаково по показательному закону с па-
раметром ц.
164
Известно [19], что закон распределения максимума (п—k)
независимых одинаково распределенных случайных величин
имеет вид
= ./JZ), (4.6.43)
где /] (Z>0) —плотность распределения случайной
величины ^(«=1, 2, 3,..., п — А);
Л(0-Функция распределения той же слу-
чайной величины.
Следовательно, плотность распределения максимума (п—k)
случайных величин, распределенных одинаково по показательно-
му закону с параметром р, будет иметь вид
/(л_й) (Z)=(/i —Л)(1 — •fxe“p'z (/>0), (4.6.44)
а функцию распределения этого времени можно найти по фор-
муле
(/)==(!—e_i‘/)'’'"*(Z> О, k<n). (4.6.45)
Если вновь прибывшая заявка застает все каналы занятыми
(вероятность этого равна рп), то она немедленно получает от-
каз, следовательно, плотность распределения времени нахожде-
ния заявки в системе будет равна
/(о)=Ш ‘ ’ (4-6.46)
где 6(Z)— дельта-функция (см. § 1.5), а функцию распределения
найдем по формуле
Л<»(0=1(0, (4-6.47)
где
1(Z) = ( Z(t)dt — единичная функция.
Таким образом, безусловная плотность распределения време-
ни нахождения заявки в системе будет иметь вид
/0=2/<«-*) (о р* (*>о).
Л=0
(4.6.48)
Найдем математическое ожидание времени пребывания заяв-
ки в системе:
__ — оо п—1 Л—1 во
t=J tf (Z) dt= J t £ /(я_4) (Z) pkdt = 2 P$f<*-*) (0 di, (4.6.49)
0 ft=0 fe=0 0
так как (см. [21])
Z8(Z) = 0.
165
Найдем интеграл вида
J (/) dt= J t (п - k) (1 - е-^)п~к~у p.e-*‘dt=
о о
=(«-*)"s'1 (-1 )т Jt{е-^Уег^dt=
m=0 0
л-й-1
= («-Л) 2
т=0
Исходя из последнего выражения, получим следующую фор-
мулу для среднего времени нахождения заявки в системе:
л—I л—1
7=!7-S РЛч-k) £ (-l^C^-l
£=0 лг=0
----!---. (4.6.50)
(т +1)2 v '
С учетом формулы (4.6.20) выражение для среднего времени на-
хождения заявки в системе окончательно примет вид
л—1 л—й—1
7=-s^-r,r(:+‘)„ s (-d-с—,
р. Л! Г (а + п + 1)
Л=0 т=0
--------.(4.6.51)
(m+1)2 v
При целом положительном числе а получим
п—1 ра—1 п—k—1
-Г 1 Ьа+Л-1
XJ га
, п ^а+л
£ = 0 т = 0
--------. (4.6.52)
(т +1)2 v '
>лг
<n.—k— 1
Зная среднее время пребывания заявки в системе, можно найти
среднее число заявок, находящихся в системе:
(4.6.53)
Основные расчетные формулы
Вероятность того, что занято ровно k каналов:
= дл Г(яЧ- .
Pk~~ k\ Г(а-Нг + 1) ’
Ро=1--2^’
Л = 1
X
где а = —
166
При а целом положительном числе эти формулы принимают вид
Pft=^±U_(0
С«+л
Вероятность обслуживания
п
Робс=1-^ •
»=0 ч. ' .
где q=\—p.
В частном случае при р = 1 (<7=0)
Вероятность полной загрузки системы
тсп.э = Рп= —~- •
a -f- п
Среднее время полной загрузки системы
1 —L
*з.с--
пр-
, Среднее время неполной загрузки системы
7 —L
*н.з--•
Л
Среднее число занятых каналов
* = 2 kP»-
*=0
Вероятность того, что канал занят
k
*З.К -- •
' п
Среднее время занятости канала
7 __L
*З.К-
р-
Среднее время простоя канала
“7 _ 1 1 — Яз.к
1 П. к-
Р* Л3,к
167
Среднее время пребывания заявки в системе
/7—1
*7__ 1 уч ап!
Л=0
Г(а + Л)
Г(а + п + 1)
1
И 4- 1)2 *
/п=0
В частности, при а целом положительном числе
//“1 ра—1
7—— V
а га
Л=0 а+«
1
(т + 1)2
Среднее число заявок в системе
7=Гх.
Задачи и упражнения
4.6.1. Рассматривается система ПВО с нарушенным управле-
нием*. Нарушение управления состоит в том, что каждую вле-
тающую в зону обстрела цель обстреливают все свободные к это-
му времени каналы. Обстрел цели каждым каналом длится слу-
чайное время, распределенное по показательному закону
с параметром ц. За это время каждый канал поражает цель с ве-
роятностью р независимо от других каналов, принимающих
участие в обстреле. Определить характеристики работы системы,
если параметры системы ПВО следующие: п=4; Х = 4——;
мин
ри=1—; р=0,5.
мин
Решение
В рассматриваемом примере величина
х л
а=—=4 —целое число.
Вероятности различных состояний системы будут равны:
Рз
Ч.+2 20 . у _ 35
с« ~ 70 ’ Р* " Рк 70
л=о
168
Вероятность поражения налетающего самолета
я 4
Po6c=l-^S = 2*^=0,247.
Q \ ~ /
Л = 0 *=о
Вероятность полной загрузки системы
«п.з=^^=0,5.
а 4- п
Среднее время полной загрузки
/п.3= —— = 0,25 мин.
пр
Среднее время неполной загрузки
/н.3=—= 0,25 мин.
* X
Среднее число занятых каналов
^=3>2-
fe=0
Вероятность того, что канал занят:
^з.к=—=0,8.
п
Среднее время занятости канала
т 1 1
t3.K =-= 1 мин.
Среднее время простоя канала
7П K=J__Lz2^2i=o,25 мин.
Iх ЛЗ.К
Среднее время пребывания заявки в сцстеме
л ра—1 л—ft—1
/= —У ——-1- У (-l^C^-i- -1—=0,429 мин.
и гл (т + 1)2
* = 1 а+я т=0
Среднее число обстреливаемых самолетов / = /Х=1,75.
4.6.2. Сравнить по пропускной способности систему ПВО, рас-
смотренную в предыдущем примере, с системой ПВО, работаю-
щей как СМО с отказами и вероятностью успешного обслужива-
ния р (см. § 4.2), если параметры системы n, X, р, р одинаковы
(такие же как в задаче 4.6.1).
169
Решение
Для СМО с отказами и вероятностью успешного обслужива-
ния р относительная пропускная способность определяется по
формуле (4.2.1):
Р{^ = Р
/?(Я—1, я)
Л(п, а)
0,5-—3,4- =
R (4, 4)
0,397.
Таким образом, система массового обслуживания с отказа-
ми и вероятностью успешного обслуживания р при данных зна-
чениях параметров п, Л, ц, р имеет большую пропускную способ-
ность.
4.6.3. Рассматривается си-
стема массового обслуживания
с отказами и недостоверным об-
служиванием (см. § 4.2) и си-
стема массового обслуживания
с отказами, взаимопомощью и
отсутствием информации о ре-
зультатах обслуживания, кото-
рая анализируется в этом па-
раграфе.
Показать, что при малом значении параметра Л система мас-
сового обслуживания, рассматриваемая в этом параграфе, имеет
большую пропускную способность, чем СМО, рассмотренная
в § 4.2; при большом значении параметра Л — наоборот. При
этом предполагается, что остальные параметры (п, р, р) одина-
ковы для обеих систем.
Решение
При малом значении, параметра Х(ХСц) у обеих систем веро-
ятность ро того, что все каналы свободны, будет близка к едини-
це. Тогда практически каждая заявка, поступающая на вход сис-
темы, рассмотренной в этом параграфе, будет обслуживаться
всеми «каналами и вероятность ее успешного обслуживания при-
ближенно будет равна 1 — (1—р)п, в то время как каждая заяв-
ка, поступающая на вход системы, рассмотренной в § 4.2, будет
обслуживаться одним каналом и вероятность успешного ее об-
служивания будет равна р.
При большом значении параметра X и в той и в другой сис-
теме практически будут заняты все каналы, т. е. рп~1- В этом
случае абсолютная пропускная способность системы, рассмот-
ренной в § 4.2, будет равна пр,р, а вероятность обслуживания
npcplK Для системы, рассмотренной в этом параграфе, вероят-
ность обслуживания будет практически равна нулю:
п
2 (1 - (1 - ру-к) pk^(s-(1 - ру-п) рп=о-
k = Q
170
Это следует из того, что
п—1
i-pn=2^~°-
й=0
Таким образом, для обеих систем, рассмотренных в § 4.2 и
4.6, существует тг!кое значение параметра %* (при прочих оди-
наковых параметрах), когда обе системы имеют одинаковую
пропускную способность. При %<Х* СМО, рассмотренная в § 4.6,
будет иметь большую пропускную способность, чем СМО, рас-
смотренная в § 4,2, а при X>Z* — наоборот. На рис. 4.6.3а по-
казаны графики зависимости относительных пропускных способ-
ностей систем, рассмотренных в § 4.2 (/’обе) и § 4.6 (Робе).
Глава 5
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
С ОЖИДАНИЕМ
До сих пор рассматривались системы массового обслуживания
с отказами; характерной особенностью таких систем было то, что
любая поступившая заявка либо немедленно принималась к об-
служиванию, либо немедленно получала отказ и покидала сис-
тему.
В этой главе будут рассмотрены системы массового обслужи-
вания с ожиданием, в которых заявка, заставшая все каналы за-
нятыми, не получает немедленного отказа, а может стать в оче-
редь и ожидать освобождения канала, который может ее обслу-
жить.
Системы с ожиданием бывают «чистого» или «смешанного»
типа. В чистой системе с ожиданием число мест в очереди и вре-
мя ожидания в ней ничем не ограничены: каждая заявка рано
или поздно будет обслужена. Для такой системы понятие «от-
каз» не имеет смысла.
В системе с ожиданием смешанного типа возможны как от-
казы, таки ожидание заявки в очереди. Отказы (отсутствие обслу-
живания) могут быть связаны или с ограниченным числом мест
в очереди, или с ограниченным временем ожидания, которым
располагает заявка.
В этой главе рассмотрим систему массового обслуживания
смешанного типа с ограниченным числом мест в очереди т.
Очевидно, при т = 0 получим как частный случай ранее рассмот-
ренную систему с отказами, а при т—*оо чистую систему с ожи-
данием.
При рассмотрении систем массового обслуживания с ожида-
нием необходимо учитывать систему правил., регламентирующих
порядок образования и обслуживания очереди (так называемую
«дисциплину очереди»). Необходимо указать, является ли оче-
редь общей, или образуется к каждому каналу отдельно; каков
порядок вызовов заявок из очереди и т. д.
Будем называть порядок вызовов заявок из очереди естест-
венным, если заявки обслуживают по принципу «кто раньше стал>
172
в очередь, тот и раньше обслуживается». Можно рассмотреть
обслуживание с приоритетом, когда определенного вида заявки
обслуживаются в первую очередь. Например, самолетам, иду-
щим на посадку, в первую очередь предоставляют взлетно-поса-
дочную полосу (ВПП). Если нет самолетов, идущих на посадку,
разрешается использование ВПП взлетающими самолетами.
Другим примером системы массового обслуживания с приорите-
том может служить система обслуживания населения городским
транспортом: пассажиры с детьми и инвалиды обслуживаются
вне очереди. Могут рассматриваться и такие случаи, когда заяв-
ка вызывается из очереди на обслуживание в случайном порядке.
Поведение заявок в очереди также входит в понятие «дис-
циплина очереди». Заявки в очереди могут «терпеливо» ждать
начала обслуживания, а могут и уходить из системы, не дождав-
шись своей очереди. В этой главе будут рассматриваться только
«терпеливые» заявки. Случай «нетерпеливых» заявок будет рас-'
смотрен в шестой главе.
§ 5.1. КЛАССИЧЕСКАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
С ОЖИДАНИЕМ
Постановка задачи: На вход n-канальной системы
массового обслуживания поступает простейший поток заявок
с плотностью X. Плотность простейшего потока обслуживаний
каждрго канала р. Если вновь поступившая заявка застает сво-
бодным хотя бы один канал, она принимается на обслуживание
и обслуживается до конца (заявки «терпеливые»). Если заявка
застает все каналы занятыми, она становится в очередь и «тер-
пеливо» ждет своего обслуживания.
Дисциплина очереди естественная: кто раньше пришел, тот
раньше и обслуживается *; максимальное число мест в очере-
ди т. Если заявка застает все т мест в очереди занятыми, то
она получает отказ и исключается из обслуживания. Каждая за-
явка может обслуживаться только одним каналом (взаимопомо-
щи между каналами нет). Величины n, X, ц, т будем называть
параметрами системы массового обслуживания с ожиданием.
Состояния рассматриваемой системы будем связывать с чис-
лом заявок, находящихся в системе (обслуживаемых и ожидаю-
щих в очереди):
' xk — в системе имеется k заявок (£ = 0, 1, 2, ..., п), они об-
служиваются k каналами, очереди нет;
хп+г — в системе имеется п + r заявок (г=1, 2, ...,zn), п из
них обслуживаются в п каналах и г заявок находит-
ся в очереди.
*Необходимо иметь в виду, что для пуассоновских систем дисциплина
очереди влияет лишь на закон распределения времени пребывания заявки в,
очереди. При этом никакие вероятностные характеристики самой системы, ни
даже среднее время пребывания заявки в очереди не зависят от дисциплины
очереди.
173
Таким образом, система имеет п + т+1 состояний. Граф со-
стояний рассматриваемой системы показан на рис. 5.1.1.
Этому графу состояний соответствует система дифференци-
альных уравнений для вероятностей состояний, которая справед-
лива и для переменных X и ц. Обычно эту систему дифференци-
альных уравнений интегрируют при начальных условиях
Ро(О)=1; р;(0)=0 (7 =^0), (5.1.1)
т. е. когда в момент t=0 система свободна от заявок.
Рис. 5.1.1
Заметим, что рассматриваемый нами граф состояний СМО
с ожиданием (рис. 5.1.1) с точностью до обозначений сов-
падает с графом состояний системы массового обслуживания
с отказами и частичной взаимопомощью между каналами, изо-
браженным на рис. 4.4.1. Поэтому при анализе стационарного
режима работы СМО с ожиданием, когда к=const, р,=const,
m<oo, t—>оо, можно воспользоваться результатами § 4.4. Сле-
довательно [см. (4.4.6)], имеем
Рл=~Ро(к=О, 1, «); Рп+r=*гРп (г = 0, 1. 2,..., т).
k\
п т
Используя нормировочное условие ^ + 2 ^л+/'==^ получим
Л=0 Г=1
Pk=
(5,1.2)
где
X
а =—
V-
(5.1.4)
174
Пр.
(5.1.5)
Эти формулы получаются из формул (4.4.2), (4.4.3) и (4.4.6) пу-
тем замены величин:
/р. — величиной ц;
h — величиной п;
п — величиной п+т.
(сравните графы на рис. 4.4.1 и рис. 5.1.1). В формулах (5.1.2)
и (5.1.3) величина х=#1.
Для сокращения дальнейших записей введем обозначения:
-------:-------------—— при х =# 1;
1 — хт
R (Л, а) 4- Р (п, а) х
1 5
-------------------- при х = 1.
R(n, п) 4- Р(п, п)т
(5.1.6)
Заметим, что если нормировочное условие записать в виде
л—1 т
2 Рк + ^Рп+г=\,
k=0 г=0
то величина р будет определяться так:
1
1 _ Zm+1
R(n- 1, a)4-P(«, а)—--------
1 — х
1
при х =/= 1;
(5.1.7)
R (п— 1, п) 4- Р(п, п) (т 4- 1)
при х—1.
Из этого, в частности, вытекают следующие равенства:
R(n— 1, a)~|-P(n, а)-1~~~х +1 = /?(п, а) +
1-X
1__~т
a)x~(* =!= 1);
(5.1.8)
/?(« — !, п)-\-Р(п, п)-\-Р\п, п)т> ,
в справедливости которых для любых положительных а и к
и любых положительных целых п и т можно непосредственно
убедиться.
Вероятность обслуживания заявки равна вероятности того,
что заявка, поступившая на обслуживание, застанет свободными
хотя бы один из каналов или хотя бы одно место в очереди:
Робс= 2 /,л=1 —а)=1 — *тРп- (5.1.9)
л=о
175
С другой стороны:
Робе = -*7-,
л
где
*=2 ^*+л2Дя+г
Л = 0 г = 1
среднее число занятых каналов.
Следовательно, среднее число занятых каналов будет
k=— Робс = а(1-/.^п). (5.1.10)
р-
Вероятность того, что канал занят, равна
*з.к=— • (5.1.11)
п
Вероятность того, что система полностью загружена, равна ве»
роятности того, что в системе заняты все каналы:
т ) т
Лп.з =2 Рп+г=рР(п., а) 2 ъг=рп 1 ~ x"*+1. (5.1.12)
“ " 1 X
г=0 г=0
При рассмотрении классической системы массового обслужи-
вания с отказами мы приводили граф состояний для определения
времени неполной загрузки системы (см. рис. 4.1.3), который бу-
дет справедлив и для рассматриваемой СМО с ожиданием при
определении закона распределения времени неполной загрузки
системы.
Поэтому среднее время неполной загрузки СМО с ожиданием
будет равно среднему времени неполной загрузки ^н.з, опреде-
ляемому для СМО с отказами [см. (4.1.26)]:,
(5.1.13)
=_1_ 7?(п—1, я)
Пр. Р (п, а)
Рис. 5.1.2
Закон распределения времени полной загрузки системы опре-
деляется графом, который изображен на рис. 5.1.2. Этот граф
аналогичен графу, изображенному на рис. 4.3.3, с помощью ко-
торого определялся закон распределения времени полной заня-
тости СМО с отказами и полной взаимопомощью, рассмотренной
в § 4.3.
176
Среднее время полной загрузки СМО с ожиданием определим
на основании эргодического свойства [см. (5.1.12) и (5.1.13)]:
/. ___4. Лп.З
*П.З — *Н.З ~
1 ЛП.З
(5.1.14)
Рассмотрим величину Тн.о — время наличия очереди в систе-
ме. Это время отсчитывается начиная от момента образования
очереди до следующего очередного момента ликвидации очереди.
Закон распределения времени наличия очереди в системе опре-
деляется с помощью графа, изображенного на рис. 5.1.3. Соответ-
Рис. 5.1.3
ствующую этому /графу состояний систему дифференциальных
уравнений нужно интегрировать при начальных условиях
Рп+1(0) = 1; р^(0)=0 при й#=п+1. Функция распределения вре-
мени наличия очереди определяется из выражения
Среднее время наличия очереди можно найти с помощью гра-
фа состояний, изображенного на рис. 5.1.4. Этот граф с точ-
ностью до обозначений совпадает с графом СМО с отказами и
полной взаимопомощью, изображенным на рис. 4.3.1.
Рис. 5.1.4
Следовательно:
1 —X
хг------
1 _ + 1
рп+г--
(Х=1).
Таким образом, среднее время наличия очереди^ (т. е. среднее
время пребывания системы в группе состояний ...» *n+m)
определяется по формуле
1
---X ------------
X 1 — х
^Н.О---
лп
\—Рп
Т>п
(5.1.15)
177
Для нахождения среднего времени занятости канала прове-
дем следующие рассуждения. Допустим, что к моменту оконча-
ния обслуживания заявки в рассматриваемом канале в системе
нет очереди.
Вероятность этой гипотезы обозначим
Рн.О^^ 1 Рн.О,
где рн.о — вероятность наличия очереди в системе.
Если в системе очереди нет к моменту окончания обслужи-
вания, то среднее время занятости канала будет равно 1/ц. Если
к моменту окончания обслуживания в системе будет очередь (ве-
роятность этой гипотезы рн.б), тр среднее время занятости кана-
ла будет равно-------|-/н.о- Применяя формулу полного матема-
тического ожидания, можно найти среднее время занятости ка-
нала:
Аз.К==(1 /?Н.о) ЬРн.оГ 1“ Рн.О^Н.О- (5.1.16)
Iх \ Iх ) V-
Вероятность наличия очереди определяется по формуле
т т
Рн.0 = ^ Pn+r—^i Рп*Г = Рп*~^~' (5.1.17)
Г=1 Г=1
Среднее время простоя канала найдем из выражения
7п.к=7з.к , Язж (5.1.18)
1 — Яз.к
Рассмотрим другие характеристики очереди. К таким харак-
теристикам относится прежде всего среднее число завок г, на-
ходящихся в очереди и ожидающих обслуживания, которое оп-
ределяется из следующего выражения [см. (5.1.3), (5.1.6) и
(4.3.13)]:
т
~г = % + 1] 1)- (5-1.19)
Г=1
При х= 1 это выражение примет вид
т
7=2 грР(п, а)=рР(Л, п) = Л . (5.1.20)
Г=1
В этом выражении р определяется из второго равенства в фор-
муле (5.1.6).
178
I Найдем закон распределения времени пребывания заявки
в (очереди Точ, для чего найдем вероятность того, что это время
больше некоторого фиксированного интервала t, т. е. найдем
Р(7'оч>0 (/>0).
Будем рассматривать только стационарный режим работы. Вы-
двинем гипотезу, состоящую в том, что система находится в со-
стоянии Xk (k = 0, 1, 2, ..., п+т). Тогда по формуле полной
вероятности
п+т
Р(Л>ч>0= S ^Р(Гоч>/|хД (5.1.21)
£=0
где P(T'04>t\xk) —условная вероятность пребывания в очереди
в течение времени, большого, чем /, при усло-
вии, что к моменту поступления очередной
заявки система находилась в состоянии
Очевидно, вероятность Р(Точ>/|х&) =0 при k<nt так как
в этом случае есть свободные каналы и заявка немедленно при-
нимается на обслуживание. Кроме того, вероятность
Р(Т0Ч>1\хп+тп) =0, так как в этом случае заявка получает отказ
и тоже в очередь не становится. Следовательно:
т—1
/’Гоч > 6=’S Pn+rP(T04>t I х„+г). (5.1.22)
г=0
(т—г) сВоВодных
мест 6 очереди
г заяВок В очереди
| j I
t—10Ы01- .
Каналы
одслужибания
2 1
Рис. 5.1.5
Вероятность того, что время ожидания в очереди ТОч будет боль-
ше, чем t, при условии, что перед данной заявкой имеется оче-
редь, в которой стоят г заявок (r=0, 1, 2, ..., т—1) (см.
рис. 5.1.5) равна вероятности того, что за время t будет обслу-
жено не более г заявок, при этом обслуживание производят всея
каналов. При наличии очереди, когда все п каналов заняты, по-
179
ток обслуженных заявок будет простейший с параметром пи,
следовательно: Г
Р(Точ > t |хл+г)=У f^Le-^=R(r> (5.1 J3)
“ л!
Л = 0
С учетом этого выражения, а также выражений (5.1.22), (5.1.3)
и (5.1.5) получим
т—1 г
P(T04>t)= S
г=0 *=0
Изменим порядок суммирования:
m—1 т—1 т—1
P{T04>t}.= pne-^ S *r=A.S
Л=0 r=k k=0
-m—1
= Pn— V X* —___ (jn _ ], __
1 — x k\
Ljfc = O J
= Pn
1 — x
При x= 1 получим
e-^-WR(rn--\, k/)-y™/?(m—1, np/) . (5.1.24)
m-1
P(T04>f)=Pne-^ J Sn^-(m_k)=
k=Q
m—1
— pn mR(tn — \, n^t)— ke-nv-f =
*=o
kA
= pn[mR(jn—l, n^f) — n^tR(m — ‘2, пр/)] (m> 1), (5.1.25)
n
так как kP(k, a)=aR(n—], a) (n>0).
*=o
Заметим, что при f<0
P(T04>t)=l,
так как время ожидания заявки в очереди есть величина неотри- 4
нательная. При /=0 имеет место скачок
Р(Гоч>0)=
Рп
1 — хт
1 — х
(^1);
(х=1).
(5.1.26)
180
Вероятность противоположного события T04^t будет равна
P(TO4<f)=\-P(TO4>t). (5-1.27)
Типичный график этой зависимости показан на рис. 5.1.6.
Функция распределения случайной величины Точ определяет-
ся так:
Роч(О=р(Гоч<t)=\-P(Точ>t)-P(Точ=1). (5.1.28)
Вероятность P(T04 = t) имеет смысл только при / = 0. График
функции распределения показан на рис. 5.1.7.
Мы видим, что случайная величина Точ является случайной
величиной смешанного типа, так как функция распределения
имеет скачок и интервал непрерывного возрастания. Для вычис-
ления различных начальных моментов случайной величины Точ
можно воспользоваться следующей формулой:
оо
(5.1.29)
J Ot
о
С помощью этой формулы при &=1 можно получить выраже-
ние для математического ожидания времени нахождения в оче-
реди:
Для нахождения функции--------—Р (Гоч > /) можно использо-
dt
вать следующий прием. Время ожидания Тг данной заявки в оче-
реди при условии, что перед ней стоит в очереди г заявок (см.
рис. 5.1.5), равно сумме (г+1) времени обслуживания в предпо-
ложении, что работают все п каналов. Так как работают все ка-
налы, то время, протекающее между вызовами двух очередных
заявок из очереди, распределено по показательному закону с
параметром пр. Следовательно:
г+1
Tt (r=0, 1,..., /п~1), (5.1.30)
Z = 1
181
где Ti(i=l, г +1)—независимые случайные величины, рас-
пределенные одинаково по показательно-
му закону с параметром пр.
С подобной суммой мы сталкивались раньше в § 1.5 при изу-
чении потока Эрланга. Там было показано, что сумма
(5.1.30) подчинена закону Эрланга r-го порядка, т. е. [см.
(1.5.22)] плотность распределения величины Тг будет иметь вид
g_niu (5.1.31)
.Теперь по формуле полной вероятности можно найти функ-
цию --Lp(T04>ty.
Ot
m—1 m—1
--^р(ТоЧ>^=Х frtf)pn+r=^
r=0 r=0
= pnn^n^R (m -1, M). (5.1.32)
Заметим, что
co oo m—1
0 0 r=0
m— 1 oo m—1
=Pn j tre~n^dt=-- j *rpn=
r=0 0 r=0
m—1
SI — xm ,
Pn+r — Pn “7 < 1 •
1 —x
r=0
Этот интеграл не равен единице, так как он не учитывает то-
го обстоятельства, что заявка вообще может не находиться в оче-
реди: получит немедленный отказ или немедленно будет приня-
та к обслуживанию.
Единице будет равно следующее выражение:
ОО L
(Точ >t)dt+P (Точ=0)=1,
J 01
о
где
1____________________________________
Р(Точ=0)=-1-рп-!—^
1 — х
есть вероятность того, что время пребывания в очереди будет
равно нулю.
182
Если ввести в рассмотрение дельта-функцию д(х) (см. § 1.5),
то можно записать выражение для плотности распределения вре-
мени ожидания в очереди /Оч(0- Напомним, что дельта-функция
обладает следующими основными свойствами:
8(х)=0 при х=^0;
е
J ?С*)8(ХМ*=<Р(0)»
—е
если ф(х) непрерывна в точке х=0;
8 (х) <|» (х) = 0;
если ф (х) — нечетная функция.
Плотность распределения времени пребывания заявки в оче-
реди имеет вид
(т — 1, К/) -|- 8 (г) X
[1 ________~т т
1 - А.-ттт-](*¥= D;
pn\R(m-l, X/)4-8(/)(l —pnm)(z=l),
где
Если требуется_определить лишь среднее время нахождения
заяйки в очереди £оч, то закон распределения времени Точ отыс-
кивать не требуется. Покажем это (см. гл. 3). Допустим, что время
ожидания данной заявки в очереди попало в элементарный ин-
тервал (t, t+dt). Вероятность этой гипотезы приближенно рав-
на fo4(t)dt. За время пребывания заявки в очереди за этой за-
явкой образуется очередь, в которой в среднем будет находить-
ся М заявок. Следовательно, полное математическое ожидание
числа заявок, находящихся в очереди, будет определяться из
выражения
00
r=Jx//O4(0^=Wo4. (5.1.35)
О
откуда формула для определения среднего времени ожидания за
явки в очереди примет вид
(5.1.36)
183
Среднее время нахождения заявки в системе
7=-^±*-=-^-, (5.1.37)
где l=r+k — среднее число заявок, находящихся в системе.
Таким образом, для отыскания среднего времени ожидания
заявки в очереди требуется лишь знание среднего числа заявок,
находящихся в очереди. Таковы основные характеристики време-
ни пребывания заявок в очереди.
Рассмотрим теперь случай, когда вероятность успешного
обслуживания заявки, побывавшей на обслуживании, равна
р<1. Все характеристики системы, кроме вероятности РОбс, оста-
ются неизменными. Вероятность обслуживания заявки в этом
случае определяется по формуле
Робс = /?(1 — Рп+т)- (5.1.38)
Абсолютная пропускная способность будет равна
\)== *Робс — ^-р (1 Рп+т)- (5.1.39)
Обратим внимание читателя на то, что при рассмотрении ста-
ционарного режима работы СМО с ожиданием мы ограничились
лишь случаем ограниченного числа мест в очереди (т<оо). При
неограниченном числе мест в очереди (тп = оо) стационарный ре-
жим работы системы существует только при условии, что
х = —<1. (5.1.40)
П[Л.
Это условие указывает на то, что среднее число заявок, обслу-
живаемых в единицу времени всеми п каналами, должно быть
больше среднего числа заявок, поступающих в систему в единицу
времени. Если это условие не выполняется и число мест в оче-
реди не ограничено (zn = oo), то стационарного режима работы
наблюдаться не будет. Это можно объяснить следующим обра-
зом. При х=-----> 1 система все время (неограниченно) будет
лр.
двигаться «вправо», т. е. перемещаться в сторону состояний с
большим числом г, и очередь будет неограниченно возрастать.
Однако стабилизации этого движения «вправо» не наступит, так
как система не справляется с потоком заявок, что приводит к
постоянному увеличению очереди. Заметим, что если х^1, то
для любого конечного г
lira pn+r{f)=Q, (5.1.41)
/->оо
так как система рано или поздно пройдет это состояние и практи-
чески в него уже не вернется.
184
Поэтому
11m ^r(Z) =0. (5.1.42)
z-o« dt ' ’
Однако в этом случае уравнения (5.1.2) и (5.1.3) уже будут
несправедливы.
Рассмотрим встречающийся на практике частный случай,
когда имеется всего один обслуживающий канал и т мест в
очереди. В этом случае “величинах [см. (5.1.4) и (5.1.5)] будет
равна величине а и вероятность того, что в системе будет k зая-
вок (одна заявка обслуживается, а остальные ожидают в очере-
ди), будет равна
2,...,« + 1). (5.1.43)
Это выражение получается, если в выражениях (5.1.2) и (5.1.3)
положить п=1 и х=а.
Вероятность обслуживания определяется из выражения
P^=\-Pm+i=±-^. (5.1.44)
Среднее число занятых каналов (или вероятность того, что
единственный канал будет занят) равно
^обс 1 — аотт1 с
k = = . (5.1.45)
р, 1 — а"*+2
Среднее число заявок, находящихся в очереди, будет
т т + 1 т+1 т+1
г=в Л=1 Л=1 Л=1
=--------f Г(т +1) а”»+24- ~ п,я+1)1 _ а (1 - а^+М . (5.1.46)
1_«я»+2 ][' 1 1— a J 4 ZJ V ’
Среднее время ожидания в очереди равно
<5Л-47)
Л
При неограниченном числе мест в очереди (/п = оо) стацио-
нарный режим существует только при условии а<1. В этом
случае получим следующее выражение для вероятности наличия
k заявок в системе:
Л=а*(1-а) (& = 0, 1, 2,...).
Такое распределение вероятностей называется распределени-
ем Паскаля. Оно уже встречалось у нас в гл. 1.
185
Вероятность обслуживания в этом случае будет равна едини-
це, вероятность того, что канал занят, будет [см. (5.1.45)]:
тс3.к = Л = а. (5.1.48)
Среднее число мест в очереди найдем по формуле
оо со
(k-\)pk= -±~. (5.1.49)
г=0
Среднее время ожидания в очереди равно
*оЧ = V = — ~Г— • (5.1.50)
X. [Л 1 — а
Среднее время нахождения заявки в системе найдем по формуле
L+L_
JX-------------------------------X
'• ' (5.1.51)
Закон распределения времени ожидания в очереди определим из
выражения (5.1.27) при условии, что п=1; х=а и
Um/?(zn — 1, Х/)=1;
lim xm=lim ат=О,
Я1->оо
так как а<1.
при t > 0;
при <<:о,
(5.1.52)
откуда функция распределе-
ния Л, (0 будет иметь вид
^оч (*) = 1 - «г-н1-»»' (/ > 0).
(5.1.53)
График функции распределе-
ния времени ожидания в очере-
ди имеет вид, показанный на
рис. 5.1.8.
Основные расчетные формулы
Вероятность того, что занято ровно k каналов, а очереди нет:
Р,=----------Р(‘'Д> , '• 2....»>
R (п, «) 4- Р (п, а) х
1 — х
136
где
„ 1 >
а = —, х—------.
р пр
Вероятность того, что все каналы заняты и в очереди имеется
г заявок:
pn+r=rfpn (r=0, 1, 2,..., /п).
При х=1 (а = п) получим
л=_------------------------- (£ = о,
Л (л, л) + тР(п, п)
Рп+г=Рп (г=0, 1, Д..., т).
Вероятность обслуживания равна
Р обе--------------------- 1 рп'
Среднее число занятых каналов (среднее число обслуживае-
мых заявок)
А = а(1— хтрл).
Среднее число заявок, находящихся в очереди:
рлХ 1-х”»[л(1-х) + 1] _J_ п.
r=
(1-х)’-
Среднее время нахождения заявки в очереди
7 =-
04 к
Среднее время нахождения заявок в системе
F+
к
Задачи и упражнения
5.1.1. Показать, что для любого т>0 и любых параметров
(п, к, р.) СМО с ожиданием имеет большую пропускную способ-
ность, чем СМО с отказами и с теми же параметрами (n, X, р).
Решение
Вероятность обслуживания заявки для СМО с отказами равна
п(1) _R (п — 1, а) _1 Р(п, а)
* обе — 7 1 г» /
R (п, а)
R(n, а),
187
Вероятность обслуживания заявки для СМО с ожиданием равна
Р&=1 -X---------:—.
1 — xw
Р (п, «) + Р (п, а) X —-
1 —х
Рассмотрим первоначально случай, когда х=1 (а=л), и по-
кажем, что
Р(о<1с-Р&с>0.
Разность вероятностей в этом случае равна
।________Р (п, л)______Г j Р (л, л)
R (т, л) + тР (п, л) |_ Р (п* л)
1 1
=Р(п, п)
п(2) пМ_Р(п>а)
* обе *обе — ~ “
R (п, а)
_ R (п, п) R (п9 п) + тР (л, п) J
так как знаменатель первой дроби в квадратной скобке меньше
знаменателя второй дроби.
Рассмотрим общий случай, когда х#=1:
1 — хот
R (л, а) 4- Р (л, а) X --— R (л, а) хт
___________________1 — х____________
1 — хт
R (п> а) + р (л, а) х —-
1 — х
Для того чтобы эта разность была положительна, нужно,
чтобы был положителен числитель последней формулы; покажем,
что он положителен:
/?(п, а)-|-Р(п, а)х ~х----/?(п, а)хт=
1 — X
1 _
[/?(«, а)(1-х)-хР(«, а)] =
= -—— [R(n, а)1.
1 — х
1_xm
Отношение------- положительно при любом значении х. По-
1 — х
кажем, что разность, стоящая в квадратных скобках, тоже поло-
жительна:
/?(п, а)-х/?(/г-1, а)=/?(п, а)---а) =
п
п
==Р(0, а) + Рр(*. а)( 1 ——^>0,
Я V П/
так как каждый член суммы не отрицателен (k^n).
183
Таким образом, мы показали, что при одинаковых парамет-
рах (п, Л, р.) система с ожиданием имеет большую пропускную
способность, чем система с отказами. Это достигается за счет
увеличения времени нахождения заявки в системе, т. е. за счет
того, что заявка будет ожидать в очереди.
5.1.2. Рассматриваются опять две системы: 1) система с отка-
зами с параметрами п, К, pi ,и 2) система с ожиданием с пара-
метрами п, Z, р2, т. При этом p,i>p2, т. е. производительность
каждого канала системы с
отказами больше, чем про-
изводительность каждого ка-
нала системы с ожиданием.
Считдя число каналов п
и число мест в очереди т за-
данными, определить, при
каких значениях параметра
X система с отказами будет
иметь большую пропускную
способность, чем система с
ожиданием, и наоборот. Рис. 5.1.2а
Р е ш е н и е
Рассмотрим характер изменения абсолютной пропускной спо-
собности для СМО с отказами (М1’) и для СМО с ожиданием
(Хо(2)) (рис. 5.1.2а) в зависимости от интенсивности потока зая-
вок Z при условии, что pi>p2. При большой интенсивности по-
тока заявок Л все каналы будут практически заняты и в этом
случае' пропускная способность обеих систем будет определяться
лишь общим числом каналов п и производительностью канала р.
Так как по условию ри >Иг, а число каналов у них одинаковое, то
при Z—>оо Хо(1)>Ло(2)- При К—Ч) абсолютная пропускная способ-
ность обеих систем будет тоже стремиться к нулю (заявок очень
мало), а относительная пропускная способность для обеих си-
стем будет одинаковой:
lim РЙс=НтР^с = 1,
Х-0 X—о
так как любая заявка будет принята к обслуживанию.
В примере 5.1.1 было показано, что в случае одинаковых па-
раметров (п, %, х) пропускная способность СМО с ожиданием
(при т>0) всегда выше пропускной способности СМО с отка-
зами. Следовательно, ограниченное (небольшое) увеличе-
ние производительности обслуживания канала СМО с отказами
можно «компенсировать» увеличением числа мест т в очереди
для СМО с ожиданием, т. е. всегда можно подобрать такую про-
изводительность канала обслуживания ри>И2 Для системы с от-
казами, когда пропускная способность обеих систем будет оди-
наковой.
189'
На рис. 5.1.26 показаны графики абсолютной пропускной
способности СМО с отказами (М’О и СМО с ожиданием (М2))
при значении параметров п=5; т=5, щ=2, р,2=1- Анализируя
графики на рис. 5.1.26, приходим к выводу, что при Z<X*«5
пропускная способ-
ность СМО с ожидани-
ем немного выше за
счет того, что у нее есть
места для ожидания не-
смотря на то, что про-
изводительность кана-
лов СМО с ожиданием
в 2 раза ниже произво-
дительности каналов
СМО с отказами:
Ц1/Ц2=2. Однако при
Х>^,*, когда СМО с
ожиданием почти пол-
ностью загружается,
начинает сказываться наличие большей производительности
СМО с отказами. Так, например, при %=8 вероятность того, что
в системе с ожиданием будет очередь, равна [см. (5.1.17)]
1__„т
Роч=^-т-^-=0,865,
1 — X v
/
т. е. практически система бу-
дет полностью загружена,
достигнув своей максималь-
ной производительности, рав-
ной иц2—5, в то время как
СМО с ожиданием еще не
достигла своей максималь-
ной производительности,
равной ПЦ1 = 10.
5.1.3. Определить то число- мест в очереди zn*, при котором
абсолютная пропускная способность СМО с ожиданием W2)(m*)
отличалась бы от предельной абсолютной пропускной способно-
сти системы Хо(2) (при неограниченном увеличении числа мест в.
очереди т—>оо) на заданную величину А.
Решение
Абсолютная пропускная способность СМО с ожиданием
(Xo(2)(zn)) есть неубывающая функция числа мест в очереди т
(рис. 5.1.3а), имеющая определенный предел при оо:
k^2)= Um Хо2) (^).
т->оо
190
При от = О она равна абсолютной пропускной способности СМО с
отказами (Хо(1)=Хо(2Ч0))- Естественно, что при решении постав-
ленной задачи величина Д должна быть ограничена условием
д<х[>2)-х^.
Абсолютная пропускная способность системы Х^Ч/п) при не-
ограниченном увеличении числа т зависит от того, какое значе-
х
ние имеет параметр х=—.
Л (Л
Рассмотрим два случая:
1 х<1.
В этом случае [см. (5.1.9) и (5.1.2)]
^2)=ИтХ^2)(от)=ПтХРобс(от)=
/71—>ос /И->00
Таким образом, величина Д при х<1 равна
Д=X — Хо (от*)=X — ХРобс (от*)='^т*р„ (от*)=
--1______х”** Р (л, а)
_________Д . --- — ,
1—х“*
Я (л, а) + Р (п, а) х —;-
1 -X
Из этого выражения после простых преобразований можно найти
величину от* как функцию величин Д, п, а, х:
«)4-j°)*1 [р(л, а)Г1 +
w*=__Ш---------Lz2lJL----L_
Igx
Д
X
Полученное из последнего выражения число нужно округлять до
ближайшего большего целого числа, так как число мест в очере-
ди от* должно быть целым.
2. х^1.
В этом случае при от=оо стационарного режима не сущест-
вует, однако абсолютную пропускную способность системы мож-
но определить исходя из того, что система будет полностью за-
гружена:
X^2) = lim Xq2) (от)=Л|1.
191
Величина Д при х:>1 будет равна
Д = Л[х—ко2)(/п*) = й|х—X 1— ит*
откуда
д
Р(п, п)-------------------— R(n, и)
т'=----------------------- (х=1, а=п),
д
— Р(п, п)
Л
1 ----X
Р (л, а)х
R (п, а) +---------------
1 ----X
т
Р(П, +
\ Л х
1g х
(х>1).
1 ----X
Полученное значение т*
большего целого числа.
Во всех формулах этого
летворять условию
нужно округлить до ближайшего
примера величина Л должна удов-
д<42>-х">=
Rin— 1, ot)
R(nt а)
, R(n — 1, а)
пр —X —-------
L R(n, i)
1).
К 1
§ 5.2. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
С ОЖИДАНИЕМ И ПОЛНОЙ ВЗАИМОПОМОЩЬЮ
МЕЖДУ КАНАЛАМИ
Постановка задачи. На вход п-канальной системы
массового обслуживания поступает простейший поток заявок с
интенсивностью X. Интенсивность простейшего потока обслужи-
ваний каждого канала р. Если заявка застает все каналы свобод-
ными, она принимается на обслуживание и обслуживается все-
ми п каналами одновременно, при этом производительность
увеличивается в п раз. После окончания обслуживания все ка-
налы освобождаются одновременно. Если вновь прибывшая за-
явка застает в системе одну заявку, то она принимается на об-
служивание: часть заявок обслуживает первую заявку, часть
приступает к обслуживанию второй заявки. Разделение каналов
приблизительно равномерное. Если в системе обслуживалось k
заявок (&=0, 1, ...» п—1), то вновь прибывшая заявка прини-
мается на обслуживание и все А+1 заявок обслуживаются ti
каналами, распределяясь произвольно между заявками, но так^
что все каналы заняты обслуживанием, т. е. порядок обслужива-
ния тот же, что и в СМО с отказами и полной взаимопомощью,
192
рассмотренной в § 4.3. Если в системе имеется п заявок (каждая
из них обслуживается одним каналом), то вновь прибывшая
заявка встает в очередь и ожидает освобождения хотя бы одного1
из каналов. Если в системе имеется п+г заявок (п из них обслу-
живается и г ожидают в очереди; r=0, 1, 2, ..., т—1),.то вновь
прибывшая заявка становится в очередь. Максимальное, число
мест в очереди т. Если вновь прибывшая заявка застает в оче-
реди т заявок, то она получает отказ и исключается из обслу-
живания. Попавшие в систему заявки (на обслуживание или в
очередь) обслуживаются до конца (заявки «терпеливые»). Вели-
чины п, X, ц., т будем называть параметрами СМО.
Рис. 5.2.1
Состояния рассматриваемой системы будем связывать с чис-
лом заявок, находящихся в системе:
Xk — в системе имеется k заявок (&=0, 1, ..., п), они обслужи-
ваются всеми п каналами, общая производительность
обслуживания пр;
хп+г — в системе имеется п+r заявок (r=0, 1, ..., т), п из них
обслуживается п каналами (каждый канал обслуживает
одну заявку), г заявок ожидает в очереди.
Граф состояний такой системы показан на рис. 5.2.1. На осно-
вании этого графа состояний можно составить систему диффе-
ренциальных уравнений для вероятностей состояний, которая
справедлива не только для постоянных, но и для любых перемен-
ных параметров %(/) и р(/). Читатель может составить такие
уравнения самостоятельно, воспользовавшись мнемоническим
правилом, изложенным в § 2.3.
Рассмотрим стационарный режим работы системы (при
X=const, |i = const, m<oo, t—»-oo), который существует, так как
система обладает эргодическим свойством (см. § 2.4).
Заметим, что граф состояний рассматриваемой системы с
точностью до обозначения максимального числа возможных со-
стояний совпадает с графом состояний СМО с отказами и полной
взаимопомощью, изображенным на рис. 4.3.1. Следовательно,
вероятность пребывания в /-м состоянии (1=0, 1, 2, ..., k.п, ...,
п+г, ..., п + т) будет определяться по формулам, аналогичным
(4.3.9), (4.3.10):
ч.1 —— при х =# Г,
]____хл+т+1
М . 1
---------------- при Х= 1,
. п 4- т + 1
7—1964
(5.2.1)
193
где
к
х =------- .
Пр.
Среднее число заявок, находящихся в системе, найдем из вы-
ражения
л+/п
~i= j] ipt=
1=0
[(n + m)(l-х) + 1] ф
(1_ХЯ + 'П + 1)(1 —х)
i±i («=!).
(5.2.2)
Вероятность обслуживания заявки равна вероятности того,
что заявка, поступившая на обслуживание, застанет свободным
хотя бы одно место в очереди:
. ППЫ v —f— 1 •
Робе— Pl—1 pn+m 1=0 ПРИ X । %n+m+l n + m < _ - ttГЧЫ ’ a/ 1 (5.2.3)
HUM л — 1 •
, n 4- m 4- 1
среднего числа занятых каналов
восполь-
Для нахождения
зуемся равенством
РобС = ^,
А
откуда
Л — лР обе-----
Г 1 — ч п +т
а ----------- при х =И= 1;
J _ ^л-Ь/л + 1
п 4- т .
П------------ при х=1,
L п 4- т + 1
(5.2.4)
где
к
а = — .
Р-
Среднее число обслуживаемых заявок определяется формулой
п п+т
’s=YilPi+n J] Pl=
1=0 l = n+l
----*- ( 2——jO-t-1) _|_ ft [xn _ 1);
1 —. I 1 X J
(5.2.5)
194
Вероятность того, что канал занят:
(5.2.6)
Вероятность того, что система полностью загружена:
т т т
r=G г=0 г=0
При х=1 получим
т 4- 1
п Н- т 4- 1
(5.2.7)
(5.2.8)
Рис. 5.2.2
Время простоя канала Тп.к распределено по показательному
закону с параметром X, так как граф состоя-
ний для определения закона распределения
времени Тп.к имеет вид, показанный на рис.
5.2.2. !
Среднее время простоя канала равно
г __L
*П.К ----------------------
Л
На основании эргодического свойства среднее
сти канала найдем из выражения
4.к=4.к-; Яз^- • (5.2.10)
J Я3,к
Закон распределения времени занятости канала определяется
с помощью графа состояний, показанного на рис. 5.2.3. Систему
(5.2.9)
время занято-
Рис. 5.2.3
дифференциальных уравнений, соответствующую этому графу
состояний, нужно интегрировать при начальных условиях
Л(0)=1; Р;(0) = 0 (/=#1). (5.2.11)
7* 195
Закон распределения времени неполной загрузки системы Т'н.з
определяется с помощью графа состояний, изображенного на
рис. 4.3.5, так как этот закон для СМО с ожиданием и полной
взаимопомощью будет таким же, как и для СМО с отказами и
полной взаимопомощью, рассмотренной в § 4.3. Следовательно,
среднее время неполной загрузки системы будет определяться
1см. (4.3.23), (4.3.22), (4.3.21) и (4.3.39)] по формуле
— I 1 <y/I + 1 1 1
1—- = ----5—— (*¥=1). (5.2.12)
ии „--------------------------1—х-лц х«(1 — х) v ’ ' ’
1 —х’+1
При х= 1 получим
Гн.з = —. (5.2.13)
р-
Среднее время полной загрузки системы можно найти на
основании эргодического свойства:
7п.з=Гн.з • Яп-3 , (5.2.14)
1 Лп.з
Рис. 5.2.4
где Лп.з — вероятность полной загрузки системы определяется по
формуле (5.2.7) при х#=1 или по формуле (5.2.8) при х=1.
Закон распреде-
ления времени пол-
ной загрузки систе-
мы можно найти с
помощью графа со-
стояний, изображен-
ного на рис. 5.2.4.
Соответствующую этому графу состояний систему дифферен-
циальных уравнений нужно интегрировать при начальных усло-
виях
Л,(0)=1; рЛ(0) = 0 (А#=/г). (5.2.15)
Рассмотрим основные параметры очереди в такой системе
массового обслуживания. Найдем среднее число заявок г, нахо-
дящихся в очереди:
т т
г=1 г=0
т
= Рп^”Г=рпъ + П (х Ф 1), (5.2.16)
г=0
196
где
р„=хя —1~х , (5.2.17)
1 — л»
вероятность того, что в системе будет ровно п заявок, но очереди
не будет.
При х= 1 получим выражение, аналогичное выражению
(5.1.16):
7=рп-т(т+}) , (5.2.18)
где
_ 1
п -h т -|- 1
Заметим, что при любых значениях х должно выполняться ра-
венство
Z=s + r,
т. е. среднее число заявок в системе равно сумме среднего числа
обслуживаемых заявок и среднего числа заявок, ожидающих в
очереди.
При наличии очереди рассматриваемая система работает
таким же образом, как и система, исследованная в предыдущем
параграфе. Поэтому среднее время пребывания заявки в очереди
будет равно
704 = V’ (5.2.19)*
Л
где величина г определяется в зависимости от значения х либо из
выражения (5.2.16), либо из выражения (5.2.18).
Закон распределения времени нахождения в очереди найдем
таким же образом, как это мы делали в предыдущем параграфе:
m—1 т = 1 г
р(точ>*)= у pn.rp(T()4>t\xn.r)=у *Ря
r = 0 r=0 A?=0
R(tn-1, W)-xm/?(/n-l, n^)](*¥= 1), (5.2.20)
1 — X
где pn определяется из выражения (5.2.17).
При х=1 получим
Р(Т0Ч > f) — pn\mR(tn — 1, n^i) — n^tR(tn —2, Лц/)], (5.2.21)
где
_ 1
л + m + I
*Вывод этой формулы был дан в § 3.2.
197
Вероятность того, что время нахождения в очереди будет рав-
но нулю, равно вероятности того, что поступившая заявка будет
либо немедленно принята на обслуживание, либо застанет все
места в очереди занятыми:
р (Л>ч=о)=у} pk+p„+m=i- рп+г—
k=0 г=0
При х= 1 получим
Р(Гоч = 0)^1
тп_____________ п 4- 1
п 4- т -f- 1 л 4- 4- 1
(5.2.23)
Функцию распределения времени Точ найдем из выражения
Роч (') = Р (Лч </)=!-/> (7'0Ч > /)- Р (Точ = f). (5.2.24)
В этом выражении для любых моментов времени /=/=0 вероят-
ность P(T04=t) —0. График функции распределения имеет вид,
показанный на рис. 5.1.7.
Плотность распределения времени нахождения в очереди
определяется выражением, аналогичным выражению (5.1.37):
/оч(/) =
рппре-<п»---*>‘Р (тп — 1, Х/) +
+8(/)(1-^15т-)(х¥=1);
рп\Р (m -1, X/) + 8 (/) (1 - рпт) (х = 1, X=яи).
(5.2.25)
Если число мест в очереди ничем не ограничено (т=оо), то
стационарный режим существует только при х<1. Об этом под-
робно говорилось в предыдущем параграфе. В этом случае веро-
ятность того, что в системе будет ровно I заявок (/^0), опре-
деляется из выражения
Р/ = ^(1-х), (5.2.26)
которое представляет собой известное распределение Паскаля.
Вероятность обслуживания при т = оо равна единице
(^обс=1); среднее число занятых каналов будет равно
)fe = 2fo£c-=2_=a. (5.2.27)
р. у.
198
Вероятность того, что канал занят, равна
«з.к = 1-А)=—=*• (5.2.28)
п
Вероятность того, что система будет полностью загружена,
найдем из выражения
7Гп.з=^^ pn+r= 1 Аь=хЯ* • (5.2.29)
г=0 Л=0
Среднее число заявок в очереди равно [см. (5.2.16)]
• (5 2-30)
(1 — х)2 (1 — х)2 1 — %
Среднее число заявок в системе найдем из выражения
1=2 iPi=Yi 1*‘(1 -х )==“тЬ~ • (5-2-31)
1=0 1=0
Среднее цремя пребывания заявки в очереди
— 7 1
^=Т=т4---------------. (5.2.32)
Л Л 1 — X
Вероятность того, что время ожидания в очереди будет боль-
ше t, определим из выражения (5.2.20) при т,—>оо:
^оч >0=*яе-Я|И1-х>/ (*>.0). (5.2.33)
Вероятность того, что время пре-
бывания в очереди будет равно ну-
лю, найдем из выражения (5.2.22)
при т—ню и х<1:
Р(Точ=0) = 1-*п, (5.2.34)
Следовательно, функция распре-
деления времени нахождения заяв-
ки в очереди равна
роч(*)=Р(точ < ^-P(r04>t)-P(T04=t).
График этой функции распределения имеет вид, показанный
на рис. 5.2.5.
199
Среднее время пребывания заявки в системе найдем из вы-
ражения:
' 1 l-x^m[(W-|-W)H-z)+ 1]
(1-*л+'п+1П1—> Г (5.2.35)
X X п 4- т , . ч
------ (х — 1).
2Х V 7
При т -> оо и х<4 получим
7=4- = —--------—. (5.2.36)
X пр. 1 — х
Основные расчетные формулы
Вероятность того, что в системе будет k заявок:
где
X
х=-----
пр.
Вероятность обслуживания заявки
Р обе----
1___ъп+т
—— --------— (X 1):
1 — %л+/«+1
п+.т (х=1).
п 4- т 4- 1
Среднее число занятых каналов
k =
] ___+
2х_____________
] хл + т+1
п 4- т
П--------:----
п 4- т + 1
(х= IX
Среднее число обслуживаемых заявок
1
1 —х
5 =
1 — хя \п (1 — х) 4 1] . г и ,- । 1 п
.х---------— ---------- + ях Iхл — х +тI lx 1);
j _х«4-/»+1 I 1 - • L J (\ / /*
п (п 4- 1) . 1 1
—---------- 4- пт -------------
2 J п -Ь т + 1
200
Среднее число заявок в системе
х 1—хп+Я1[(п-Ьм)(1—х) + 1] 1)
у_ (1— хп+я,+1)(1 — х)
“ Ь±^- (х=1).
2 ’
Среднее число заявок, находящихся в очереди:
М-х»Н1-хН1] (х^1);
1 — xn+'n+1 (1 — х)
т(т+\) (х=П.
ь 2 (п 4- т 4- 1)
Вероятность того, что канал занят:
k
^З.К--- ’ •
п
Вероятность того, что система полностью загружена:
| +/Л + 1
т 4- 1
п 4- т + 1
(*¥= 1);
(х=1).
Среднее время простоя канала
Среднее время занятости канала
Т ____Т лз.к
*З.К-*п.к ~
1 Л3.к
Среднее время неполной загрузки системы
— . 1~х'1 (х =£
_ nji (1—х)
- (*=1).
^Н.З---
Среднее время полной загрузки системы
V _____~ ^п.з
*П.З--*н.з Т
1 Яд. 3
201
Среднее время нахождения заявки в системе
t=-L
Среднее время нахождения заявки в очереди
t =—
04 к
Задачи и упражнения
5.2.1. Доказать, что СМО с очередью и полной взаимопомо-
щью между каналами (/п>0) имеет большую пропускную спо-
собность, чем СМО с отказами и полной взаимопомощью между
каналами при условии, что параметры обеих систем (n, X, р)
одинаковы.
5.2.2. Доказать, что СМО с очередью и полной взаимопомо-
щью между каналами имеет большую пропускную способность,
чем СМО с очередью и отсутствием взаимопомощи при условии,
что параметры обеих систем (n, X, р, т) одинаковы.
5.2.3. Рассматривается СМО с ожиданием и частичной
взаимопомощью, когда каналы могут помогать друг другу,
объединяясь в группы, наибольший состав которых равен 1<п.
Подобная система с отказами рассматривалась в § 4.4. При за-
нятии всех каналов очередная пришедшая заявка не получает
Рис. 5.2.3а
отказ, а может стать в очередь, число мест в которой равно т.
Составить размеченный граф состояний системы и найти основ-
ные характеристики работы такой системы.
Решение.
Граф состояний имеет вид, показанный на рис. 5.2.3а. На
этом графе величина h= -y-j равна целой части отношения
-у-. Этот граф с точностью до обозначений совпадает с графом
состояний системы массового обслуживания с частичной взаимо-
помощью (см. рис. 4.4.1) или системы массового обслуживания
с ожиданием (см. рис. 5.1.1.)
202
Следовательно:
Pi=-----------—-----------------(Z=0, 1, 2,.... А);
l_xn-ft+m
R (h, ai) + P (h> ai) * —:-
1 — X
Pi=^PhU=b n±m),
где
X
“z= —,
Zp.
X
x =----------------------------- .
np.
Для краткости рассмотрим только случай, когда х=#1.
Вероятность обслуживания найдем по формуле
Робе = 1 — Рп+т = 1 — Рн • *n~h+m.
Среднее число занятых каналов будет
k=aPo6c.
Среднее число заявок, находящихся в очереди:
т т т
Г = rph-7.n+r=y.nph
л=1 г=1 г=1
Среднее число заявок в системе
п+т h п+т
Т= s /„=2"<+S --------•"гм~1Т)
/=0 /=о j=h (h, at) 4- Р (Л, «/) X---
1 — х
। 1 x»+m[(„ + m)(1 x)+1]
Среднее число обслуживаемых заявок
s=l—г.
Среднее время ожидания в очереди
203
и среднее время пребывания заявки в системе
(При необходимости можно определить и другие характери-
стики системы с частичной взаимопомощью).
§ 5.3. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
И ПРИОРИТЕТОМ В ОБСЛУЖИВАНИИ
Зачастую при рассмотрении систем массового обслуживания
приходится иметь дело с заявками определенного типа, которые
должны обслуживаться в первую очередь. Примером такой
системы массового обслуживания является аэродром с одной
взлетно-посадочной полосой (ВПП). Самолетам, идущим на по-
садку, ВПП предоставляется в первую очередь, т. е. они пользу-
ются Приоритетом в обслуживании по сравнению с самолетами,
которые используют ВПП для взлета. Аналогичную картину
мы наблюдаем на автозаправочной станции (АЗС), где обычно
рейсовые автобусы обслуживаются в первую очередь.
В системах массового обслуживания с приоритетом могут
быть различные варианты дисциплины обслуживания.
Системами с абсолютным приоритетом называются такие
системы, в которых заявка, обладающая приоритетом, немедлен-
но принимается к обслуживанию каналом, занятым обслужива-
нием заявки без приоритета в обслуживании. Например, если на
АЗС прибывает рейсовый автобус, а в это время заправляется
легковая машина, то ее заправка прекращается и начинается
заправка автобуса. После того, как заявка, обладающая приори-
тетом, будет обслужена, и других заявок, обладающих приори-
тетом, нет, возобновляется прерванное обслуживание заявки, не
обладающей приоритетом. Здесь возможны различные вариан-
ты: заявка, обслуживание которой было прервано, начинает об-
служиваться заново; прерванное обслуживание заявки начинает-
ся с того места, где оно было прервано; заявка, обслуживание
которой было прервано, вообще теряется.
Системами с относительным приоритетом называются такие
системы, в которых заявка, не обладающая приоритетом, обслу-
живается до конца, после чего принимаются к обслуживанию за-
явки, обладающие приоритетом (если такие имеются).
Из всех возможных систем массового обслуживания с прио-
ритетом здесь будет рассмотрена только одна, самая простая, а
именно, одноканальная СМО с абсолютным приоритетом.
Постановка задачи. Рассматривается одноканальная
система с абсолютным приоритетом, на вход которой подаются
два независимых простейших потока заявок с интенсивностями
М и Xj. Заявки первого потока (интенсивность которого равна
204
Xi) обладают приоритетом в обслуживании. Число мест в очере-
ди для заявок обоих видов не ограничено. Если канал обслужи-
вает заявку первого потока, то интенсивность простейшего потока
обслуживаний равна рь Если канал обслуживает заявку вто-
рого потока, то интенсивность простейшего потока обслужива-
ний равна р2. В этом случае нет различия между двумя вариан-
тами дисциплины обслуживания:
а) прерванное обслуживание заявки начинается с того места,
где оно было прервано;
Рис. 5.3.1
б) заявка, обслуживание которой было прервано, начинает
обслуживаться заново.
Это объясняется тем, что интервал времени всего обслужива-
ния и интервал остатка времени обслуживания распределены
одинаково по показательному закону с параметром р,2.
Рассмотрим случай, когда число мест в очереди для заявок
обоих видов (с приоритетом и без приоритета) не ограничено.
Состояния системы будем связывать с числом заявок z, облада-
ющих приоритетом, и числом заявок j, не обладающих приорите-
том, находящихся в данный момент t в системе. Рассмотрим раз-
личные состояния системы:
Хо,о — в системе нет никаких заявок;
%оз — в системе имеется / заявок, не обладающих приоритетом
/= 1, 2, ...), и нет заявок, обладающих приоритетом; из
этих / заявок одна обслуживается и / — 1 заявок ожидают
в очереди;
205
Xito — в системе имеется i заявок, обладающих приоритетом
0 = 1, 2, ...), и нет заявок, не обладающих приоритетом; из
этих i заявок одна обслуживается и i — 1 заявок нахо-
дится в очереди;
xi>} — в системе имеется i заявок, обладающих приоритетом
0=1, 2, ...), и / заявок, не обладающих приоритетом
(/=1, 2, ...), из i заявок, обладающих приоритетом, одна
заявка обслуживается, а остальные I — 1 ожидают в оче-
реди; до тех пор, пока все заявки, обладающие приори-
тетом, не будут обслужены, заявки, не обладающие при-
оритетом, не обслуживаются.
Размеченный граф состояний системы показан на рис. 5.3.1.
Ввиду некоторой необычности этого графа по сравнению с
теми, которые были рассмотрены ранее, составим систему диф,-
ференциальных уравнений для вероятностей состояний:
—~— = — 014" М Ро.о (0 + н Р1,о 0)4*ftjPo.i (0;
at
—~— = ~0i 4"\i4_l,'i)/,/.oO)4“^iP*-i.oO)4'
4~ НРж.оО) 04>0);
--= “ 014" ^2 4" 0) 4" KPOJ-l 0) 4"
+ НгРо.жОНнРиО) (J > 0);
(5.3.1)
— — Oi 4*^2 + Hi)PzJ (0J-i. 0) 4~
+ X1P/-ij0)4-HiPi+u (t) (i>0, />0).
Эту систему дифференциальных уравнений обычно интегри-
руют при начальных условиях
Рол (0)=1; Pt;(0)=0 (при z 0 или /=И=0) (5.3.2)
(в начальный момент система свободна).
Решение системы уранений для любого момента t удовлетво-
ряет условию
2 2 (5.3.3)
z=o j=0
Введем обозначения
а1=А; (5.3.4)
н
«2=—. (5.3.5)
И2
206
Величина cti равна среднему числу заявок, обладающих приори-
тетом, поступающих в систему за среднее время обслуживания
одной такой заявки, величина <хг соответственно используется
для заявок, не обладающих приоритетом.
Можно доказать, что стационарный режим работы системы
существует только в случае, когда
ai + ct2<l- (5.3.6)
Так как величины cq и «2 положительны, то при этом также
должны выполняться условия
«1< 1; )
(5.3.7)
a2 <С 1 • J
Найдем стационарный режим работы системы с приоритетом,
для чего нужно в уравнениях (5.3.1) положить все производные
равными нулю.
Допустим, что нам удалось решить полученную систему алге-
браических уравнений и вероятности pij (i=0, 1, 2,..., /=0, 1, 2...)
найдены. Тогда вероятность р/1) того, что в системе будет ровно
i заявок, обладающих приоритетом (безотносительно к тому,
сколько имеется там заявок, не обладающих приоритетом), мож-
но найти по формуле
= (5-3.8)
;=о
Вероятность того, что в системе имеется ровно / заявок,
не обладающих приоритетом (безотносительно к тому, сколько
имеется там заявок, обладающих приоритетом), будет
^=2 р^- <5-3-9)
1=0
Так как рассматриваемая нами система является системой с
абсолютным приоритетом, то рассмотрение вопросов обслужи-
вания заявок, обладающих приоритетом, можно проводить без
учета наличия заявок, не обладающих приоритетом. Одноканаль-
ная система без ограничения числа мест в очереди была рас-
смотрена в конце § 5.1. Следовательно:
(1-сч) (/=0, 1,2,...). (5.3.10)
Для нахождения вероятностей применим метод произво-
дящих функций и введем в рассмотрение производящую функ-
цию вида
<р(*. У)=2 (5.3.11)
1=0 /=0
207
Отметим некоторые свойства этой производящей функции:
1. v=2 2^=1;
/=0 7=0
2. <р(0, 0)^2 V phJ0{.Qi=pM-
1=0j=0
з. ?(х,
z=o;=o i=o j=o
= yj >=у} хЩ (1 - di)= .
1 = 0 1=0
(5.3.12)
(5.3.13)
(5.3.14)
Среднее число заявок, не обладающих приоритетом и находя-
щихся в системе, найдем так:
ОО ОО ОО ✓ ОО 00 \
?=Ё Ё 7',>j=S Ё Ё p'-’yt) =
- j=0 1=0 П \ у i^O j=0 Jy = l
=(4-<р(1- у)) • (5-3-15)
\ оу ./у=1
После этих предварительных замечаний найдем производя-
щую функцию (р(х,у), для чего в уравнениях (5.3.1) положим все
производные равными нулю. Далее, первое уравнение системы
(5.3.1) умножим на х?у°—\, второе уравнение на х{у°=х\
третье уравнение — на x°yi=yi и четвертое уравнение — на
x*yi и все эти уравнения сложим, перебрав все возможные зна-
чения i и /. Проделав это и проведя некоторые простые преобра-
зования, получим
+ + 2 (Н-Н2)РО./У' + 112РО.О +
1=0 7=0 j=0
ОО ОО ОО оо
+Х12 2 2 2 р^х‘у’+
i = l 7=0 1=0 7=0
2 ^.^+^2 p^^yj- (5.3.16)
1=0 j=l 7 = 0
Двойные суммы, входящие в выражение (5.3.16), могут быть
выражены через функции ф(х, у). Проведя соответствующие пре-
208
образования выражения (5.3.16), получим следующую формулу:
ф/х у\ (х — 1) — fi2* (у — 1)] ? <0, у) + у^х (у — 1) ? (0, 0) /53
^\ху (1 — х) + \2Ху (1 — у) + У2У (х — 1)
Найдем корни xj и х2 знаменателя этого выражения, считая,
что 1^£/<0:
„ Xj + Х2 (1 — у) + !Х1 ч- к2 (1 — t) + p-i)2 — 4Х1р.1 „ 1Я.
._Xj + X; (1 — 0 + (1] + V (Xj 4- Х2(1 -у) + р.])-— 4Х1[Л1 (КЗ 19)
2 2Xj '
Это даст нам возможность (после некоторых довольно гро-
моздких преобразований, которые мы опускаем) получить следу-
ющее выражение для производящей функции:
?(х, у)=-------a-aHi-aiXi)--------- (5.3.20)
Л (l-a1Xj-a2f/)(l-aix1x)
где
a = aj-l-a2. (5.3.21)
Обратим внимание на то, что величина Xi зависит от переменной
у. При y = l Xj = l.
Для нахождения отдельных вероятностей состояний можно
воспользоваться следующими формулами:
Ро,о=<р(О, 0)=1 -а; (5.3.22)
Воспользуемся выражением производящей функции <р(х, у)
[см. (5.3.20)] для отыскания закона распределения числа заявок,
не обладающих приоритетом в обслуживании и находящихся в
СМО:
то. (5-з-24)
/=о;=о ;=о
откуда
Н-гг^1’ У)) • <5-3-25)
1 / \ dyl Jj=O
При вычислении производных по выражению (5.3.25) нужно
иметь в виду, что величина Xi является функцией у [см. (5.3.18)].
209
Среднее число заявок, обладающих приоритетом в обслужи-
вании и находящихся в очереди, определяется из выражения,
аналогичного выражению (5.1.48):
7 <ai)?
1 1-а,
(5.3.26)
Среднее время пребывания заявки, обладающей приоритетом,
в очереди равно
7ОЧ1==41- =— . (5.3.27)
Х1 М-11 — 64
Среднее время пребывания заявки, обладающей приорите-
том, в системе (в очереди и на обслуживании) найдем по фор-
муле
Л=4к=?оч> +—=— (r±- + 1)=-LrL-’ (5Л28>
Х1 н \1—а1 / 1 — Я1
Среднее число заявок, не обладающих приоритетом и нахо-
дящихся в системе, найдем из выражения (5.3.15):
fo (1, u) \
dy )y-
^2xl
dXi 1
«1 —— + «2
(l-a)----------------
(1 Jy=l
а1 Г Г" + “2
Iх! — XjXj
(1 — atjjq — a2J')2
При = получим
а2
1 — а
а1 I
1 —ai J
(5.3.29)
а1
/2=
а______1
(1-а) (1-aj) (l_2ai)(l-aj)
(5.3.30)
Среднее время нахождения в системе заявки, не обладающей
приоритетом, равно _
72=-^-=Гоч, + —, (5.3.31)
Х2 «12
откуда среднее время ожидания в очереди для заявки, не обла-
дающей приоритетом, будет
7 _ h 1 _ 1 н 1 —ai 1 _
*ОЧ2-1 1 -
*2 Н-2 Н-2 L 1 — a J
^--^- + a
= _L . м A-gi-------. (5.3.32)
H2 l-a
210
Задачи и упражнения
5.3.1. Рассматривается функционирование большого аэродро-
ма с единственной взлетно-посадочной полосой (ВПП). В сред-
нем за сутки взлетает 240 самолетов и садится тоже 240 самоле-
тов. При посадке самолет занимает ВПП в среднем в течение
3 мин, а при взлете 1,5 мин. Определить характеристики работы
аэродрома в стационарном режиме.
Решение
Аэродром можно рассматривать как одноканальную систему
с приоритетом. Самолету разрешается взлет с аэродрома в том
случае, когда нет самолетов, идущих на посадку. Поток самоле-
тов, идущих на посадку, можно рассматривать как поток заявок,
обладающих приоритетом в использовании ВПП. Характеристи-
ки. такой системы с приоритетом следующие:
Х1 = Х2=240—!—=— — .
сутки 6 мин
Характеристика обслуживания •
мин ’
2 1 1*2=- • 3 мин
Следовательно: „ Х1 — 1 • 1 Н 2
Л2 1
О2 = — = —
^2 4
Условие ai + ct2<l выполняется.
Среднее число самолетов, ожидающих в воздухе, пока осво-
бодится ВПП, равно
1 1 —ai 1—0,5
Среднее время пребывания самолета в воздухе перед по-
садкой
4ч,=—= — 6=3 мин.
1 Xi 2
Среднее время, затрачиваемое самолетом на посадку:
/| = /Оч1"-|-= 3 3:=; 6 мин.
211
Среднее время ожидания разрешения на взлет для самолета,
находящегося на аэродроме, равно
+ " , 2-Н- + 0'75
, 1m.i1 — ai 3 0,5 ч ~ г-
/ОЧ0 = — —----1---—------!-------=16,5 мин.
2 1-« 2 0,25
Среднее число самолетов, ожидающих на аэродроме разреше-
ния на взлет, найдем по формуле
г2 = к2/ОЧл = —• 16,5 = 2,75.
6
Среднее время, проходящее от момента готовности самолета
ко взлету с аэродрома до момента осуществления взлета, равно
/2 = /оч2 ~~I-~~ 16,5 1,5 = 18 мин.
Среднее число самолетов, готовых ко взлету, но находящихся
на аэродроме, равно
Z2=k2/2=-l_-18= 3.
Таким образом, мы видим, что несмотря на довольно большое
число посадок и вылетов за сутки (240) можно считать, что
аэродром будет функционировать нормально: самолетам, иду-
щим на посадку, не придется долго ждать в воздухе освобожде-
ния ВПП.
Замечание. Задача решена приближенно. При реальном функ-
ционировании аэродрома самолеты, идущие на посадку, не име-
ют полного (абсолютного) приоритета: если взлетающий само-
лет уже бежит по ВПП, то его взлет не прекращается. Однако
приближение не вносит сколько-нибудь заметных изменений в
полученное в задаче решение.
5.3.2. Анализируется работа междугороднего переговорного
пункта в небольшом городке. Пункт имеет только один телефон-
ный аппарат для переговоров. Переговоры бывают двух видов:
обычные и срочные. При проведении срочного переговора обыч-
ный переговор прерывается. В среднем за сутки поступает 180
заявок на обычные переговоры и 60 — на срочные переговоры.
Средняя длительность переговоров обоих видов (с учетом вы-
зова абонента в другом городе) составляет 5 мин. Определить
характеристики работы переговорного пункта в стационарном
режиме.
212
Решение
Переговорный пункт можно рассматривать как одноканаль-
ную систему массового обслуживания с приоритетом. Ее харак-
теристики следующие:
?_601 1 ? _ 180 _ 1 1
1 24-60 24 мин ’ 2 24-60 8 мин '
11 X] 5 Х2 5
р*1 = Р'9=----;-а1=—=- —; а2=—=—.
5 мин 1 pq 24 р2
Условие наличия стационарного режима выполняется
(a = ai + ct2= — <Й .
6 /
Среднее число ожидающих срочного переговора будет равно
7 = J^2L~o,o5.
1 1 —a.
Среднее время ожидания срочного переговора
^ОЧ1 = —=1,20 мин.
Среднее время ожидания обычного переговора
— - 04 4-a
Г0Ч2= —-------------= 32,9 мин.
Р2 1 —a
Среднее число ожидающих обычного вызова
Г2 = \/оч2 = 4,11.
Среднее число людей, находящихся на переговорном пункте (за
исключением обслуживающего персонала):
1=+ 4 —“k^2^2=s^i ( ^o4i Н-~1“ ^2 б^°ч2 "4"—^ = 4,20.
\ Р1 / \ р-2/
Таким образом, мы видим, что приобретение за дополнитель-
ную плату права на срочный переговор сокращает время ожида-
ния в очереди приблизительно в 27 раз.
Глава 6
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
С РАЗЛИЧНЫМИ ОГРАНИЧЕНИЯМИ НА ВРЕМЯ
ПРЕБЫВАНИЯ ЗАЯВКИ В СИСТЕМЕ
До сих пор мы рассматривали такие СМО, когда заявки, по-
пав в систему, «терпеливо» ожидали конца обслуживания.
Однако на практике имеют место случаи, когда заявки по тем
или иным причинам, не дождавшись окончания обслуживания,
покидают систему. Будем называть такие заявки «нетерпеливы-
ми». Их «нетерпеливость» может проявиться либо при нахожде-
нии заявки в очереди, либо при нахождении заявки на обслужи-
вании, либо и в очереди и на обслуживании.
С тем, чтобы остаться в рамках марковских случайных про-
цессов с непрерывным временем, нужно сделать допущение, со-
стоящее в том, что на заявку, находящуюся в системе, действует
пуассоновский поток уходов из системы. Будем считать, что
параметр этого потока различен в зависимости от того, находится
ли заявка на обслуживании или ожидает в очереди. Интенсив-
ность потока_уходов заявки из очереди обозначим v, а интенсйв-
йоСТь"потока ухо дов'из~каналов обслуживания — т). Для некото-
рых случаев эти параметры могут быть равны. Иногда эти интен-
сивности называют параметрами «нетерпеливости»: параметр v
есть параметр «нетерпеливости» при нахождении в очереди, а
параметр rj — параметр «нетерпеливости» при нахождении на об-
служивании.
Примером системы массового обслуживания с ограниченным
временем пребывания заявки в системе является радиолокаци-
онный комплекс определения параметров полета самолетов по
трассе. Этот комплекс имеет определенную зону, в пределах
которой он может «обслужить» самолет, т. е. измерить различ-
ные параметры движения самолета и передать эту информацию
на самолет или в другое место. Если за время пребывания само-
лета в зоне действия комплекса его параметры не успеют изме-
рить, то самолет покинет зону «необслуженным».
Другим примером может служить работа конвейера по сбор-
ке. На каждом рабочем месте собираемый агрегат находится
214
ограниченное время, по истечении которого этот агрегат перево-
дится на другое рабочее место. Если за отведенное время все
операции не будут выполнены, агрегат не будет обслужен на
этом месте.
Наиболее типичным примером работы системы массового об-
служивания с ограничением времени пребывания заявки в систе-
ме является работа системы противовоздушной обороны (ПВО).
Система ПВО имеет вполне определенную зону обстрела, в пре-
делах которой самолет (заявка) может быть поражен (обслу-
жен). Следовательно, самолет, попав в зону обстрела, находится
там ограниченное время (проявляет «нетерпение»).
§ 6.1. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ,
ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ ЗАЯВКИ В СИСТЕМЕ
И УПОРЯДОЧЕННЫМ ОБСЛУЖИВАНИЕМ
Постановка задачи. Рассматривается работа n-ка-
нальной системы ПВО с ограниченным временем пребывания
заявки в системе. Алгоритм работы системы следующий: если к
моменту поступления заявки в систему свободен хотя бы один из
Рис. 6.1.1
и каналов, то эта заявка принимается к обслуживанию только
одним (любым) из свободных каналов. Если к моменту поступ- rj
ления заявки в систему все каналы заняты, то данная "заявка
остается нёобслуженной. На занятый канал действует пуассонов-
ский поток освобождений с интенсивностью ц*. Эта интенсив-
ность слагается из интенсивности потока обслуживаний одного
канала р, и интенсивности потока уходов заявки из-под обслужи-
вания, которую обозначим буквой т):
[х*=и4-1). (6.1.1)
Величина т) характеризует интенсивность уходов заявок из
системы (не дожидаясь конца обслуживания). Интенсивность
потока заявок равна X.
В любой момент времени t рассматриваемая система может
находиться в одном из следующих состояний:
х0— в системе нет ни одной заявки (свободны все каналы);
Xj — одна заявка находится в системе и она обслуживается од-
ним (любым) из п каналов;
xh — ровно k заявок (1<&<п) находятся в системе и все они
обслуживаются (каждая заявка одним каналом);
хп — ровно п заявок обслуживается п каналами.
215
Граф возможных состояний такой системы с указанием пара-
метров потоков событий, переводящих систему из состояния в со-
стояние, изображен на рис. 6.1.1. В соответствии с приведенным
на этом рисунке графом и мнемоническим правилом, указанным
в § 2.3, система дифференциальных уравнений для вероятностей
состояний будет иметь вид
-^£L=-XPo(O+1xVi(O;
(О < k < /г);
(6.1.2)
^-=-йН>я(0+Хрл-1(/).
at
Эту систему дифференциальных уравнений обычно интегри-
руют при следующих начальных условиях:
До(О)=1; Рй(0)=0 (£=1, 2,..., п)
(в начальный момент времени при t—О система свободна). Для
любого момента времени t выполняется нормировочное условие
п
2^(0 = !. (6.1.3)
k=Q
Граф, изображенный на рис. 6.1.1, с точностью до обозначений
совпадает с графом состояний классической системы массового
•обслуживания, приведенным на рис. 4.1.1. Поэтому вероятности
состояний системы в стационарном режиме могут быть найдены
ло формулам, аналогичным (4.1.12):
рк=—^’ g*} (k=0, 1, 2,..., n), (6.1.4)
где
P(k. а*) и /?(п, а*)—табличные функции пуассоновского рас-
пределения.
Для рассматриваемой системы вероятность обслуживания
заявки уже не может быть определена как вероятность того, что
заявка, поступившая в систему, застанет свободным хотя бы
•один из каналов. Это лишь необходимое условие обслуживания.
Для того чтобы заявка была обслужена, нужно, чтобы к мо-
216
менту поступления ее в систему был свободен хотя бы один из
каналов и чтобы за время обслуживания заявка не покинула
систему.
Для отыскания вероятности обслуживания заявки восполь-
зуемся выражением
Робс = -^ . (6.1.6)
Л
Среднее число занятых каналов k подсчитывается по форму-
ле, аналогичной (4.1.15):
k = a* я*>, (6.1.7)
R (п, a*) 4 !
откуда [см. (6.1.5) — (6.1.7)]
Робс = JL а* " к”*» = **> . (6.1.8)
X R(n, а*) 1*4-1) Я(л, а*) v 7
При т] = 0 рассматриваемая система превращается в СМО с
отказами, анализ которой был проведен в § 4.1. Продолжим ис-
следование системы с ограниченным временем пребывания за-
явки в системе.
Плотность потока обслуженных заявок будет равна
Х0=РобсХ=(*а* (6.1.9)
Я (И, а*)
Вероятность того, что канал (любой) будет занят, равна
k a* R(n— 1, а*)
П П R(nt а*)
(6.1.10)
Время занятости канала по условию распределено по показа-
тельному закону с параметром р*. Следовательно, среднее время
занятости канала будет
7 __1
i-Э.К-----—
(6.1.11)
Среднее время простоя канала определим на основании эрго-
дического свойства:
j. ____1 1 Яз.к
*11. К *з.к
^з.к
(6.1.12)
Среднее время, в течение которого заняты все каналы (сред-
нее время полной загрузки системы), равно
Гп.з=~, (6.1.13)
217
откуда среднее время неполной загрузки системы найдем по фор-
муле /и.з = /п.з 1 Яп-3 , (6.1.14) яп.з
где Р (п, а*) 1 "•-л-
— вероятность того, что в системе заняты все каналы (система
полностью загружена).
Ввиду небольшого объема этого параграфа не будем здесь
приводить сводку основных расчетных формул.
Задачи и упражнения
6.1.1. Рассматривается работа радиолокационного комплекса
измерения параметров движения самолетов по трассе. Система
состоит из двух станций, каждая из которых может измерять
параметры движения самолетов («обслуживать» самолеты) в пре-
делах зоны протяженностью в а = 50 км. Скорость самолетов на
трассе v = 1000 км!час.
Параметры движения самолета измеряются в среднем в тече-
ние одной минуты. Если самолет, влетевший в зону измерения
параметров, застает обе радиолокационные станции занятыми,
то его параметры не измеряются. В среднем за один час в зону
измерения параметров влетает 30 самолетов. Определить раз-
личные характеристики работы такой системы.
Решение
Рассматриваемый радиолокационный комплекс состоит из
двух каналов обслуживания (п = 2), на вход которого подается
поток заявок с интенсивностью Х = 30—— =—---—. Параметр
час 2 мин
«нетерпения» ц определяется из формулы
v 1000 on 1 1 1
т\ =——------— 20------=-------.
а 50 час 3 мин
Интенсивность потока обслуживаний каждого канала равна
р,= 1---. Следовательно:
мин
♦ ' 11 1 4 1.
U = U -г- 71 = 1 -I-—----
r г ‘ 1 3 3 мин
а* = А =.0,375.
pL*
Таким образом, радиолокационный комплекс можно рассмат-
ривать как двухканальную систему массового обслуживания с
218
отказами ограниченным временем пребывания заявки в системе
и упорядоченным обслуживанием.
Вероятность того, что параметры самолета будут измерены,
определяются по формуле (6.1.8):
D , _
* обе— ‘
Р + 1
R(n — l, a*) = Q>715
7? (Л, а*)
Среднее число занятых каналов
1=_Р^== 0,358.
И
Вероятность того, что канал занят:
^3^ =—=0,179.
п
Среднее время занятости радиолокационной станции (канала)
Т 1 3
/З.к=--—---- мин.
р* 4
Среднее время простоя радиолокационной станции
А1.к= А).к 1 ~Яз,к =3,44 мин.
Из.к
§6.2. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ. С ОЖИДАНИЕМ,
ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ ЗАЯВКИ В СИСТЕМЕ
И УПОРЯДОЧЕННЫМ ОБСЛУЖИВАНИЕМ
Постановка задачи. Рассматривается п-канальная
система массового обслуживания, которая отличается от рас-
смотренной в § 6.1 лишь тем, что заявка, заставшая все каналы
занятыми, может быть в дальнейшем обслужена, если за время
пребывания ее в очереди освободится хотя бы один из каналов.
Максимальное число мест в очереди обозначим буквой т.
Если в системе находятся k заявок (&г^п), то все они обслу-
живаются (каждая заявка одним каналом). Если в системе на-
ходятся (и+г) заявок (r^m), то п из них обслуживаются, а г
находятся в очереди на обслуживание.
Если в системе находится п + т заявок, то п из них обслужи-
ваются, а т — ожидают обслуживания. Если заявка, поступив-
шая в систему, застала в ней (п+\т) заявок, то она получает
отказ и обслуживанию не подлежит при любых условиях.
Находясь в очереди, заявка может проявлять «нетерпение».
Обозначим интенсивность потока уходов заявки из очереди вели-
чиной v, которая в общем случае может отличаться от интенсив-
ности потока уходов заявки из-под обслуживания т) (см. § 6.1).
В частном случае, если заявка ведет себя статистически одина-
219
ково, находясь как в очереди, так и на обслуживании, интенсив-
ности v и т] могут быть равными.
На рис. 6.2.1. показан граф состояний такой системы. Мы
видим, что до состояния хп этот граф совпадает с графом систе-
мы с отказами и ограниченным временем пребывания заявки в
системе, изображенным на рис. 6.1.1. Далее, в схеме имеются
другие состояния, характеризующие наличие того или другого
Рис. 6.2.1
числа заявок «в очереди» на обслуживание. Для определенности
поясним все состояния:
Хо — в системе нет ни одной заявки (все каналы свободны);
xfe — ровно k заявок (£=1, 2, ..., п) находятся в системе и все
• они обслуживаются (каждая заявка одним каналом);
хп+г — ровно п+г заявок (г=1, 2, ..., т—1) находятся в систе-
ме, из них п обслуживаются (каждая заявка одним ка-
налом) и г ожидают обслуживания;
*п+т — обслуживается п заявок, т заявок ожидают обслужи-
вания.
Пользуясь графом, изображенным на рис. 6.2.1, можно выпи-
сать систему дифференциальных уравнений для вероятностей
состояний системы с ожиданием и ограниченным временем на-
хождения заявки в системе:
at
- (X+^k) рк (/) + Х^_х (/) + (*+!) (О
at
(0<£<п);
at
-P-nZ(t) = - (X+цр* + г>) рП+г (/)+\рп+г-1 (/) +
at
+(np.*+(r + l)v)p„+r+i(/) (0<г</и);
= - («р* + т») рп+т (/)+\рп+т-х (0-
(6.2.1)
220
Напомним, что в этих уравнениях параметры р,* = р.+т], X, v
могут быть любыми неотрицательными функциями времени.
Рассмотрим стационарный режим работы такой системы с
ожиданием, когда параметры р, т), Z, v являются постоянными и
система работала достаточно долго для того, чтобы переходной
процесс затух. Тогда вместо системы дифференциальных урав-
нений (6.2.1) мы получим систему алгебраических уравнений.
Эту систему можно получить из системы (6.2.1), если положить
все производные равными нулю. Решая последовательно такую
систему алгебраических уравнений, можно получить следующие
выражения для
жиме:
вероятностей состоянии в установившемся ре-
Рк=^£-Ро (6.2.2)
k\
-------Ро=~——-------------Рп, (6-2.3)
7=1 X v /
определяется так же, как и в § 6.1:
(а*)п
где величина а*
Введем новые обозначения
у = —; (6.2.5)
§ = (6.2.6)
Величине у можно дать такое истолкование: это есть среднее
число заявок, которое находилось бы в системе, если бы ни одна
из них не обслуживалась. В этом случае заявки покидают систе-
му только за счет своего «нетерпения».
Величина 6 есть среднее число циклов обслуживания всеми и
каналами, приходящееся на среднее время пребывания заявки
в системе в случае' если она не обслуживается.
Величину pQ найдем из нормировочного условия:
откуда
V («*)* „ _i_V (а*)л ir „ — 1
Ъ~^~Ро 2j~i г Ро ’
й=0 г=1 П(8+У)
/=1
1
Ро = ~-----------------т-------- •
у, (а*)* (а*)п -у тг
+ л! Zi г
Л-° r-1 J-J + у,
/=1
(6.2.7)
(6.2.8)
221
Умножим знаменатель и числитель правой части (6.2.8) на
е~а* и с учетом обозначений (1.5.23) и (1.5.26) получим
_а»
Ро=------------------------------• (6.2.9)
т г
R (П, а*) + Р (п, а*) У-1------
П0+Л
/=1
Подставим выражение (6.2.9) в (6.2.2) и (6.2.3):
рк=--------------------------------(k = 0, 1,..., га), (6.2.10)
R (п, а*) + р (п, а*) 2 -----
Г=1 П (б +/)
7=1
тг
Р (П, а*)---!----
П (« + /)
рп+г=------------------------------(г=1, 2,..., гаг). (6.2.11)
R (п, а*) + Р (п, а*) 2 ~~--
Г=1 П(8+7)
/=1
Дальнейшие преобразования связаны с необходимостью введе-
ния в рассмотрение гамма-функции Г(х). Напомним ее опреде-
ление
Г(л)=( е~Ч*-'(Н. (6.2.12)
о
Нам потребуется использовать следующие два свойства гамма-
функции:
1) для любого действительного положительного х
Г(х+1)=хГ(х); (6.2.13)
2) для любого неотрицательного целого х
Г(х+1)=х! (6.2.14)
На основании первого свойства гамма-функции можно на-
писать следующее равенство:
И(§+;)= r.g..±/yi- . (6.2.15)
222
Рассмотрим выражение П—!—— при условии, что вели-
/=1 (6+-,)
чина б я в л я е тс я целым неотрицательным числом.
В этом случае [см. (6.2.14) и (6.2.15)]
тгг (& + 1) _ 7'8!
Г(8+г + 1) (8 +г)!
П (8 +/)
7=1
т
(6.2.16)
Это выражение преобразуем к виду
7'-Ы 7* 8+'-е-М! 78+' _т 1
(8 + г)! (8 -|- г)| (8 +г)! fS
— е •
S!
Р (8 + г, т)
.(6.2.17)
Р(Ъ. 7)
После этого легко вычислить сумму, входящую в знаменатель
выражений (6.2.10) и (6.2.11):
5 7)~S p<z’ Т)
/=0 /=0
Р(8, 7)
/? (от + 8, 7) — # (6, 7)
Р(8» 7)
(6.2.18)
Таким образом, при целом неотрицательном 6 окончательно по-
лучим следующие выражения для вероятностей состояний:
________________Р (k, а*)-
о, мгс * Р(т + ъ, 7)-/?(8, 7)
/? (п, а*) + Р (п, а*)----------------
(О <£<«),
(6.2.19)
Р (п, а*)
Рп+Г =
R (п, а*) + Р (п, а*)
Р(Ъ + г, 7)
Р(8. 7)
/? (от + 8, 7) — /? (6, 7)
Р (8. 7)
(0<г</п). (6.2.20)
В случае, если величина б не является целым числом, можно
воспользоваться следующим приближенным приемом, который
дает вполне удовлетворительную точность. Любое положитель-
ное число б может быть записано следующим образом:
8 = [8] + {8},
(6.2.21)
где [б] — целая часть числа б,
{6} — дробная часть числа б.
223
L
Например, число 7,75 может быть записано так:
7,75=[7,75] + {7,75} =7+0,75
После этого вычисляются вероятности рк (или рп+г) для двух
значений [б] и [б]+1. Затем производится линейная интерполя-
ция на величину {б}.
Расчеты показывают, что такая линейная интерполяция впол-
не достаточна. При больших значениях б (б^ 10) можно обой-
тись и без линейной интерполяции, а просто число б округлять
до ближайшего целого числа и расчеты производить по этому
числу. В дальнейшем будем предполагать, что число б является
целым.
Найдем основные характеристики такой системы. Начнем с
математического ожидания числа занятых каналов k:
н т
k=-- kpk+.^Прп+Г =
к=0 г=1
*О, , DZ +'6- 7) — (V7)
aR (п, а*) + пР (п, а»)-------------
"" о/ Р(т + 6, Т)-Л(5, 7)
R(n, а») + Р(П, а ) -------------
(6.2.22)
Вероятность обслуживания будет равна
Робс =--^у- •
К
Найдем среднее число заявок, «ожидающих» обслуживания г
[см. (6.2.20) и (6.2.17)]:
т
™ 7Г6!
(6.2.23)
„ * /?(»г + В, 7) — /?(й, 7)
R (п, а*) + Р (п, а*)-------------------------L,?..,17
Р (8> 7)
Для вычисления суммы, входящей в числитель выражения
(6.2.23), применим метод дифференцирования рядов:
V г — Y _L у = V — 8’ 7)~#(8. 7)] =
4J (8 +г)! 07 (6 + г)! * У 67 ( 7) J
Г=1 Г=1
_ R(m±\V-_RbV ( 8) . Г ! _ Р(т + 8. 7) 1 (6 2 24)
^(8,7) L Р(8, 7) J
224
Таким образом, окончательное выражение для среднего числа
заявок, находящихся в очереди на обслуживание, будет иметь
вид
(₽_(» + ..7)-«<»,7)^ 7)11
г =--------1-----Я. (6.2.25)
Я(п. -) + Я(„. ,.)«И + М)-'?<».7>
Р(6, 7)
Если по условиям задали величина т достаточно велика, то
выражения (6.2.22) и (6.2.25) можно упростить, имея в виду
следующие предельные соотношения:
lira/?(т4-8, у)=1;
11п1Р(7п4-8> т)=о.
(6.2.26)
Рис. 6.2.2
Вероятность того, что канал (любой) будет занят, опреде-
ляется ,из выражения ,
k
. „ ^з.к--
п
Вероятность того, что система будет полностью загружена,
определяется по формуле [см. (6.3.20)]:
т т
=-₽£vS₽<’+^’=
(6.2.27)
теп.з
г-1
Рп
7)
Р?(//г + 8, у)-Я (8-1, у)], (6.2.28)
- 8—1 _ т
2Р<Г’ Л)+У)р (8 + п Y)-J] Р(г, у) =
_ Рг
Р(Ъ, 1)
(при 8=0 полагать /?(8—1, у) =0). •
Закон распределения времени неполной загрузки системы
определяется с помощью графа состояний, изображенного на
рис. *6.<2.2. Систему дифференциальных уравнений, соответствую-
щую этому графу состояний, нужно интегрировать при началь-
ных условиях
рл-1(0)=1; д*(0)=0. (Л ^=/г—1).
8—1964
(6.2.29)
.225
Плотность распределения времени простоя системы будет
/п.с(0=хЛ(0 (/>0).
Среднее время неполной загрузки системы будет таким же,
как и у системы с отказами и ограниченным временем пребыва-
ния заявки в системе [см. (6.2.14) и (6.2.15)]:
Р(п,а*)
1________/?(п, «*)
П|Л* Р(п, а*)
(6.2.30)
Л(Я, «*)
Для определения закона распределения времени полной за-
грузки системы составим граф состояний, изображенный на
рис. 6.2.3.
Рис. 6.2.3
Систему дифференциальных уравнений, соответствующую
этому графу, нужно интегрировать при начальных условиях
рп (0)=1; ~рк (0)=о (k ф п).
(6.2.31)
Плотность распределения времени занятости системы найдем
из выражения
Среднее время полной загрузки системы определим на осно-
вании эргодического свойства
4.з=^.з , Яп— , (6.2.32)
1 - Лп.з
где /н.з и Яп.з определяются из выражений (6.2.30) и (6.2.28) со-
ответственно.
Применяя рассуждения, аналогичные тем, которые были
проведены в § 5.1 при выводе формулы (5.1.15), найдем среднее
время занятости канала:
^З.К— ~Т--(“Рн.О^Н.О, (6.2.33)
JJL*
где рн.о — вероятность наличия очереди в системе, которая опре-
деляется из выражения
226
nr
Ря.о= Рп+Г
m
+ Y)=
P(0, 7) AJ
r=l
__ Rjm + Ъ, 7)— /?(B, 7) .
~Pn P(6,i)
(6.2.34)
tn.o — среднее время наличия очереди.
Среднее время наличия очереди /н.о определяется с помощью
графа подсистемы X, приведенного на рис. 6.2.4.
Рис. 6.2.4
В соответствии с формулами (6.2.3)—(6.2.6) вероятность
рп+г для стационарного режима будет определяться по формуле
Рп+г=Рп-------------(г = 1, 2,..., rti).
S П (В +J)
j=i
Величина рп определяется из нормировочного условия
г=1
откуда
-_____________________________1__________
&п т Г г Ч—1
г=1 Ь=1
При целом положительном значении 6 получим [см. (6,2.18)]
1 1
рп=-------------------------------------------------=
чз/пмГ + д<”+д-;<,">
г=1 и=1 I
=________Р(Ъ, 7)______.
R (т + В, 7) —/?(6—1, 7) ’
р Р(В + г>7)
Рп+Г Я(т + 8, т) —Я(В—1, 7)
8»
227
Среднее время пребывания в состоянии хп (см. граф на
рис. 6.2.4) будет
Ч=т-
Следовательно, среднее время наличия очереди, т. е. пребы-
вания системы в группе состояний хп+1, ..., хп+т, примет вид
7Н.О=^ =— ;?<w + 8> Т) (6.2.35)
Хп ~Рп * />0.7)
Среднее время простоя канала найдем на основании эргоди-
ческого свойства
7п.к=4.к-^-, (6.2.36)
1 — Лз.к
где Лз.к определяется из выражения (6.2.27).
Не повторяя всех рассуждений, которые проводились в § 5.1,
запишем выражение для среднего времени пребывания заявки
в очереди:
4.=у-, (6.2.37)
где г —среднее число заявок, находящихся в очереди, опреде-.
ляемое выражением (6.2.25).
Для отыскания закона распределения времени пребывания
заявки в очереди введем в рассмотрение гипотезу, состоящую в
том, что в системе к моменту прихода очередной заявки имелось
в очереди г заявок (r=0, 1, ..., т). Вероятность этой гипотезы
равна по определению рп+т- В этом случае время нахождения
вновь поступившей заявки в очереди будет определяться из вы-
ражения
rr=min(9p -Г,),
где б, — время, потребное для'освобождения хотя бы одного
канала при условии, что в очереди имеется г заявок
(будут ли эти заявки обслужены или нет, нас не ийте-
ресует);
Т, J— время пребывания заявки в очереди В случае, если эта
заявка не будет передана на обслуживание.:
Случайная величина Т, подчинена показательному закону с
параметром v[/, (t)=ve~',t (f>0)]. Случайная величина 0Г пред-
ставляет собой сумму независимых показательно распределен-
ных случайных величин
(6.2.38)
/=6
226
с параметрами zip,*, np*+v, np*4-rv соответственно. Извест-
но, что закон распределения суммы независимых показательно
распределенный случайных величин является обобщенным зако-
ном Эрланга r-го порядка и в данном случае имеет вид [19}
Л; (&)= И (пи* 4- zv) V --------------(& > О,). (6.2.39)
<=° ;=оу П (Z-у) Г>°
i=o
При г=0 имеем
(&>0). (6.2.40)
Тогда закон распределения минимума двух независимых слу-
чайных величин можно найти из выражения [19]
оо оо
л (0=5 А (»)•/* (0^+5 А(0Л (»)^=
t t
yi >* + (/+ i)v ен«р-*+а+1)4<
' & nii* + jv '
/=0 V n (l-j)
1=0 (l+j)
При r=Q получаем закон распределения минимума двух не-
зависимых показательно распределенных случайных величин с
параметрами пр* и v соответственно. Этот закон также будет
показательным:
/0 (/)=(пр* -j- v) е-^*+^ (I > 0).
(6.2.42)
Условное математическое ожидание времени нахождения
заявки в очереди при условии, что в очереди имеется г заявок,
равно
tT=\tfT(f)dt=—-^±1_-(r=0, 1,..., /п-1). (6.2.43)
J Лр* + (г + 1) V
Безусловную плотность распределения времени нахождения
заявки в очереди можно найти следующим образом:
n+m—1 л—1
/(0= ЛЮр«+г+^(0 Рй+рл+ш
г-0 1й=0
(/>0). (6.2.44)
229
Наличие в составе плотности /(/) дельта-функции указы-
вает на то, что время ожидания в очереди представляет собой
смешанную случайную величину с одним скачком при t=0. Ти-
пичный график функции распределения времени ожидания пока-
зан на рис. 6.2.5.
Среднее время пребывания
заявки в системе определяется
по формуле
+ С ; (6.2.45)
величины Лиг находим по
формулам (6.2.22) и (6.2.25)
соответственно.
Основные расчетные формулы
Вероятность того, что занято ровно k каналов и очереди нет:
= ______________P(k, а*)_____________,
Рк~ /?(т4-8, т) —/?(8, т) ’
R (п, а*) + Р(п, а*) -—----5—~
РФ. V
где •
а* = — ;
[1*
н*==11 + 7|'>
8 = — целое число;
к
у= —
V
Вероятность того, что все п каналов заняты обслуживанием
п заявок и в системе есть еще г заявок в очереди:
о/ „ Р(* + г, т)
р (п> а ) —ttsz—;—
Dr+r=-------------------Р- --------------(Г — 0,1,2,.. .,"/п).
+ + 7)~ 7)
R (п, а*) + Р (П, а*)-'-~-------~
Р(«. т)
Вероятность обслуживания заявки
Р(т + 8, 7) — R(t>, 7)
«*Р (п - 1, а*) + пР (П, а*)-—-----------
р______£___________________________________________
Х О/ *>., 0/ * Л(m+ 6.7)-Л(6,'7)
R(n, а*) + Р(п, а»)----- - —
230
Средйее число занятых каналов
k = — Робе
f1
Среднее число заявок в очереди
(/г (? + >, .7) -/го. т) R
~~ Ц Р(8, 7) П °' + Ч PQ.7) JJ
dz . О/ 7)-/г(». 7)
/г (П. “*) + Р (п, а*) ----------
Вероятность того, что канал занят:
Г
тсз.к— •
П
Вероятность наличия очереди
„ _ „ /г(/» + «. 7)-ЛО. 7)
Рн.°-Рл — .
Среднее время наличия очереди : ,
7 _ 1 /?(т + », 7)—/гр. 7)
х />(8,7)
Среднее время занятости канала . у
/з.к== ““F Рн.о/н.О"
рЛ
Среднее время простоя канала I
7 _~ 1 яз.к
*П.К-*з.к •
Лз.к
Среднее время пребывания заявки в системе ।
у Г~+Т
X
Задачи и упражнения
6.2.1. Показать, что система массового обслуживания с ожи-
данием и «нетерпеливыми» заявками имеет большую пропускную
способность, чем система массового обслуживания с отказами и
нетерпеливыми заявками при одинаковых параметрах п, р, п, "к
(параметры т и v могут быть любыми).
231
§ 6.3. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ,
ОГРАНИЧЕННЫМ ВРЕМЕНЕМ НАХОЖДЕНИЯ ЗАЯВКИ В СИСТЕМЕ
И ВЗАИМОПОМОЩЬЮ МЕЖДУ КАНАЛАМИ
В отличие от систем, рассмотренных в этой главе, когда одну
заявку мог обслуживать только один канал, в данном параграфе
будет исследован случай взаимопомощи между каналами ана-
логично тому, как это было сделано в § 4.4.
Постановка задачи. Имеется n-канальная система
массового обслуживания; каждый канал имеет интенсивность
потока обслуживаний ц. Заявка доступна к обслуживанию лю-
бым каналом. Если в системе находится одна заявка, то она
принимается к обслуживанию и обслуживается .одновременно I
каналами. При этом предполагается, что суммарный поток об-
служиваний будет иметь интенсивность Zp,. Если Вновь поступив-
шая заявка застанет в системе i заявок (i=0, 1, 2, ...), при этом
(Z-f-l)Z^n, то эта вновь поступившая заявка принимается к
обслуживанию и обслуживается одновременно I каналами. Если
вновь поступившая заявка застает в ней j заявок и при этом
(/ + l)Z>n и ]<п, то эта заявка-будет принята к обслуживанию.
В этом случае часть заявок может обслуживаться I каналами, а
часть — меньшим, чем I, числом каналов. В обслуживании всегда
будут участвовать все п каналов. Заявки в системе находятся’
ограниченное время («нетерпеливые» заявки). Параметр «нетер-
пения» равен т|.
Если вновь поступившая в систему заявка застает все каналы
занятыми, она становится в очередь. Как только освободится
один из каналов, заявка будет назначена на обслуживание, если
за время ожидания в очереди она не покинет систему. Таким об-
разом, уход заявки из очереди может быть по двум причинам:
либо заявку возьмут на обслуживание, либо она уйдет из очереди,
не дождавшись обслуживания. Всего имеется т мест в очереди.
Если заявка находится в очереди, то ее параметр «нетерпения»
будет V.
Если вновь поступившая заявка застает в системе п обслу-
живаемых заявок и т заявок в очереди, то она получает отказ.
В частном случае при 1=п получим систему с полной взаимопо-1
мощью между каналами.
Состояния системы будем классифицировать по числу заявок,
находящихся в системе массового обслуживания:
Xi — в системе имеется i заявок (i=0, 1, 2, ..., А, где А=
— целая часть числа -р) , каждая заявка обслуживается
одновременно I каналами с общей производительностью
Zp;
Xj — в системе имеется / заявок (/=А+1, А+2, ..., п); в обслу-:
живании этих / заявок участвуют все п каналов, распреде-
232
ляясь более или менее равномерно между всеми j заяв-
ками;
Хп+г — в системе имеется п+r заявок, п из них обслуживается п
каналами и г стоят в очереди на обслуживание (г=0,
1,т).
Граф состояний такой системы показан на рис. 6.3.1. (1а этом
графе величина p,* = p,+j]. Читателю предоставляется возмож-
Рис. 6.3.1
ность составить систему дифференциальных уравнений, соответ-
ствующуюэтому графу состояний.
Проанализируем подробнее случай, когда величина Л=-у-
является целым числом, равным h. Введем обозначение
+ (6.3.1)
С учетом этого обозначения и принимая во внимание, что ~ =
=h — целое число, граф состояний системы со взаимопомощью
будет иметь вид, представленный на рис. 6.3.2.
Заметим, что с точностью до обозначений параметров потоков
и номеров состояний граф на рис. 6.3.2 левее состояния хп
(включая само состояние хп) совпадает с графом, изображенным
на рис. 6.2.1. Следовательно, для нахождения вероятностей со-
стояний системы со взаимопомощью можно воспользоваться фор-
мулами (6.2.3) и (6.2.4):
(«;>г
Р1=~7Г-Ро
(6.3.2)
(«1)й
Яс-
V~h
j—h / Л[Л
П (—£+А
fc=i' Ч
233
где
(6.3.4)
х__=_х
Jp-H и.*.
Рис. 6.3.2
Заметим также, что конец графа правее состояния хп на
рис. 6.3.2 такой же, как и конец графа на рис. 6.2.1 правее состоя-
ния» хп. Поэтому
Рп+г = Ра'
(О < г < т),
(6.3.5)
где
(»*)
n—h
п
*=1
(6.3.6)
Для упрощения дальнейших выкладок введем обозначения:
X у——; (6.3.7)
8=2^ ; (6.3.8)
Ф=—; ?=—. (6.3.9) (6.3.10) .
234
С учетом этих обозначений получим [см. (6.3.2) — (6.3.6)]:
(а*)1
Pi=-^—Po (0<г<й);
pj=~- ро --------------(А < j < «); (6-3-п)
П (? + k)
) Л=1
Рп+г=-----------Рп (0 < г < т). (6.3.12)
П (8 + *)
Л=1
Для простоты будем считать величины <р и 6 целыми числами.
В этом случае получим [см. (6.2.16) и (6.2.17)]:
Pj=— рй (h < j < n); (6.3.13)
h\ ™ P(<t, ф) >’ '
Р.„=Р.Р(рР'^ (0<г<и). (6.3.14)
Величину ро найдем, исходя из нормировочного условия:
h п т
Zu 2^я+,,в1'
1=0 j=h+\ r=l
/
Используя^ выражения (6.3.2), (6.3.13), (6.3.14) с учетом фор-
мулы (6.2.18), получим
P(<f+j-h,V ,
р°е 2j п М е 2j Р(ьФ) •
L/=o ;=л+1
, е—* P(<f + n-h, Ф) yi Р(Ъ + г, т)1 =
л Р(?, ф) jj Р(8, 7)
r=l J
=^[s(*. .;)+Р(Л, °;)'г,"~'1+;^)~Я(т^) +
A-Dth ~«V P^^-n — h, |) Ж/п + 8, 7) — /? (8, Т)1_1
+ ( ’ Р р(ъ ф) • р(8(17) ] «
235
откуда
Р(0, ар
Ро=----------------;--------------------------
, Р(Л,арГ
/?(Л, а;) + ^—jy (n — ft + <р, ф) —ф) +
Р(0, ар
(6.3.15)
Р(*.
й);
(6.3.16)
(6.3.17)
(6.3.18)
Р {I. «Р
Pi——т-Ро (0</<
Р(0, а,)
_ Р(Л, ар _ р (<f+j- Л, ф)
Pi — Г- Ро----7Г7 ГТ----
Р(0, <ф Р(ъ Ф)
„ _ Р(Л’ п Р(? + п-Л,ф) Р(» + Л 7) /л
П+Г P(Q,at) ° Р(Т> Ф) Р(М)
В случае, если величины <р и 6 не являются целыми числами,
можно применить следующий приближенный прием: сосчитать
вероятности для величин [<р]; [ф]+1; [6]; [б]+1 и провести линей-
ную интерполяцию. Напомним, что [х] есть целая часть числа х.
HaiUieM характеристики системы. Среднее число занятых ка-
налов А (см. (6.3.16) — (6.3.18) и (4.1.17)] будет равно
h / п j т . \ Л
1-iPi + n ( У] Р/+ У pn+rj=~--^— ар + •
р(?+/-л, ф)+
Р(0, ар ° Р(Ъ Ф) Р(8. 7) L 1
Р(0, ар
, Р (Л. а*) P(^ + n~h, ф)
’Г Р (0, а*) Р° Р(Ъ Ф)
Следовательно, вероятность
Р обс==
1=0
Ч=л+1
Р(Л, а*)
Ро
Р(0, а*) Ф)
. р (0, <)
R (п — h + <р, Ф) — R (?, Ж)
Ро
Р(т, Ф)
Г/?(т + 8, 7)—/?(8, у) | (6 3.19)
Р0. 7)
обслуживания заявки будет
. (6.3.20)
X
236
\Найдем среднее число заявок г, находящихся в очереди Гем.
(6.2.23) и (6.2.24)]:
TAJ Я+Г Р(0,а*) Рй Р(Ч, М-Р (М) 2Г ( +Г’ Y)~
Г=Ъ 1 г=0
— Р(,1> “*> р P(<f + n-h, Ф) I R(m + b, f)-R(b, 7) _
Р(0, а]) ° Р(<Р, Ф)Р(5, 7)1 Р(8. 7)
~И Г + 7)1] . (6.3.21)
L ^(®.7) JJ '
Вероятность того, что канал занят, найдем из выражения
*з.к=—, (6.3.22
п
где К определяется из (6.3.19).
Вероятность того, что система полностью загружена, равна
_ ____VI „ Р(А’ gi) Р(<? + л—Л, Ф)7?(т 4- 8, 7) — 7)
2> n+r P\oTfy Р° p(f>M Р(ъ,1)
(6.3.23)
Среднее время нахождения заявки в очереди будет
V V=-^, (6.3.24)
где г определяется из формулы (6.3.21).
Ввиду небольшого объема этого параграфа сводку основных
формул приводить не будем.
§ 6.4. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ
ВРЕМЕНЕМ НАХОЖДЕНИЯ ЗАЯВКИ В ОЧЕРЕДИ
И НЕОГРАНИЧЕННЫМ ВРЕМЕНЕМ НАХОЖДЕНИЯ ЗАЯВКИ
НА ОБСЛУЖИВАНИИ
Отличие системы, рассматриваемой в этом параграфе, от си-
стемы, рассмотренной в § 6.1, состоит лишь в том, что заявка
проявляет «нетерпение», только находясь в очереди. Попав же
на обслуживание, заявка «терпеливо» дожидается конца обслу-
живания. В качестве примера такой системы может рассматри-
ваться система дозаправки самолетов в воздухе: самолет может
ждать дозаправщика ограниченное время, но, начав заправку,
самолет-дозаправщик проводит ее полностью.
237
Другим примером является работа парикмахерской: клиент
может быть «нетерпелив», пока стоит в очереди, но, дождавшись
своей очереди, терпеливо ждет пока его побреют или постригут.
Постановка задачи. На вход n-канальной системы
массового обслуживания поступает пуассоновский поток заявок
с интенсивностью X. Каждый канал обладает производительно-
стью р,. Взаимопомощь между каналами отсутствует: каждая
заявка обслуживается одним каналом. Заявка, попавшая на об-
служивание, обслуживается до конца. Если все п каналов заня-
Рис. 6.4.1
ты, то заявка становится в очередь. Число мест в очереди т.
Находясь в очереди, заявка проявляет нетерпение. Параметр
«нетерпения» при нахождении в очереди равен v. Если заявка
застае^ в очереди все т мест занятыми, то она получает отказ.
Состояния такой системы мы будем связывать с числом зая-
вок, находящихся в системе:
Хь — в системе имеется k заявок (О^&^п); все они обслужи-
ваются; каждая заявка обслуживается одним каналом;
хп+г — в системе имеется п+r заявок (O^r^/п); п из них об-
служиваются (каждая заявка одним каналом) и г ожи-
дают в очереди.
Граф состояний системы приведен на рис. 6.4.1. Этот граф
состояний с точностью до обозначений совпадает с графом со-
стояний системы, приведенным на рис. 6.2.1. Поэтому можно для
определения вероятностей состояний воспользоваться формулами
(6.2.19) и (6.2.20):
Рл=
Р (k, а)
R(n, а) + Р(п, а)
R (т + а, "() — R (з, 7)
Р(Ъ 7)
(Л=о, 1, 2,..., п);
(6.4.1)
., т),
(6.4.2)
(6.4.3)
238
\ <з = ^; (6.4.4)
\ У = — . (6.4.5)
Напомним, что при выводе формул (6.4.1) и (6.4.2) предпо-
лагалось, что величина а является целым числом. Если величина
а не является целым числом, то можно проводить линейную
интерполяцию так, как это указывалось в § 6.2.
Среднее число занятых каналов определяется по формуле,
аналогичной (6.2.22):
, R(m + c, 7) — R(c, 7)
aR (п — 1, а) 4- пР (п, а) ----------------------------
----------------------------
R (т 4- а, 7) — R (а, 7)
R (п, а) + Р (п, а) —-----------—--------—-
Р (°, 7)
(6.4.6)
Р(°, 7)
Вероятность обслуживания заявки найдем из выражения
Робс=^-. -(6.4.7)
Л
Среднее число заявок, находящихся в очереди, будет равно
[см. (6.2.25)]:
------1------------------------L-----Р('^> 1 . (6.4.8)
r.z к 4- а, 7) — /?(а, 7)
R (П, а) + Р (П, а) -р-~^----
Вероятность того, что канал занят, определим из выражения
«з.к=—; (6.4.9)
вероятность того, что система полностью загружена, равна
«п.з = У] Рп+г= [/?(« + ’, у) —/?(а—1, у)]. (6.4.10)
г=0
Среднее время неполной загрузки системы определим по фор-
муле [см. (6.2.30)]:
t Р (я, а)
7„.з = —--------R(n' а) = — b а) . (6.4.11)
лр. Р (п9 а) пр. Р (п, а)
R(n, а)
239
Среднее время полной загрузки системы будет /
7п.3=Асз Ян-3 . (6.4.12)
1 -Лн.з /
Среднее время'занятости канала будет равно I
^з.к = 'е— Н- Рн.о'^н.о, (^.4.13)
где Рн.о — вероятность наличия очереди в системе;
/н.о — среднее время наличия очереди.
Вероятность наличия очереди определяется по формуле
т
+ . (6.4.14)
Т)
Г=1
Среднее время наличия очереди определяется по формуле, ана-
логичной (6.2.35):
7ao=J_^±^kl£l2Ll). (6.4.15)
* т)
Среднее время простоя канала равно
?п.к=73.к --!ж- . (6.4.16)
1 ^з.к
Среднее время ожидания заявки в очереди находим из фор-
мулы
70Ч=^ • (6.4.17)
Л
Закон распределения времени ожидания заявки в очереди
можно определить по формулам (6.2.41) и (6.2.44), заменив в
них величину ц* величиной ц, а вероятности Pk и Рп+г найти из
выражений (6.4.1) и (6.4.2) соответственно. Среднее время пре-
бывания заявки в системе равно
7=d—^±±J-. (6.4.18)
X X
Ввиду небольшого объема этого параграфа не будем приво-
дить сводку основных расчетных формул.
Задачи и упражнения
6.4.1. После выполнения задания самолеты производят доза-
правку в воздухе. В районе дозаправки постоянно дежурят
4 самолета дозаправщика. Среднее время дозаправки одного
240
самолета равно — = 10 мин: Плотность потока самолетов, нуж-
\ 14 1
дающихся в дозаправке, %=0,4 ----. Если самолет, нуждаю-
\ мин
щийся в дозаправке, застает все заправщики занятыми, он
может! некоторое время ожидать освобождения заправщиков в
районе дозаправки. Среднее время ожидания дозаправки —=
=20 мин. Самолет, не дождавшийся дозаправки, производит по-
садку На запасной аэродром. Если самолет дозаправлен, он
производит посадку на основной аэродром. Определить вероят-
ность того, что отдельно взятый самолет будет дозаправлен, и
другие характеристики системы, обеспечивающей заправку са-
молетов в воздухе: среднее число дозаправляемых самолетов,
среднее время ожидания дозаправки.
Решение
Систему, обеспечивающую дозаправку самолетов в воздухе,
можно рассматривать как систему массового обслуживания,
разобранную выше. Параметры этой системы равны:
«=4;
Х=0,4 1 ;
мин
v=0,05—;
мин
т = оо (так как нет никаких ограничений на очередь);
X л
а= —=4;
а=-^-=8;
v
X Q
у=—=8.
У
Среднее число дозаправляемых самолетов, вычисленное по
формуче (6,4.6), равно
k=3,93.
Вероятность того, что самолет будет дозаправлен, равна
po6c=J^_=0,834.
241
Среднее число самолетов, ожидающих дозаправки самолета
в йоздухе, определяется по формуле (6.4.8): /
7=2,90, /
т. е. около трех самолетов будут ожидать в воздухе дозаправки,
вероятность того, что самолет покинет район дозапр^ёки, не
заправившись, равна '
s Ровс=1 -Робс = 0,166.
Среднее время ожидания самолета в «очереди» на заправку
будет равно [см. (6.4.16)]
/оч=—=7,25 мин.
X
Среднее время, потребное на осуществление дозаправки, оп-
ределяется по формуле (6.4.18):
j I 1* “1~ k 1 *7 1
t=----—-------=17,1 мин.
X X
6.4.2. Производится дезинфекция (специальная санитарная
обработка) сельскохозяйственной техники, прежде чем ее допус-
тить к работам в дафВм районе. Специальная обработка произ-
водится для того, чтобы в данный район не была занесена инфек-
ция (например, ящур). Любая машина может быть обработана
в одном из п=10 пунктов дезинфекции. Пропускная способность
каждого пункта р=0,1 Каждая машина, прошедшая дезин-
фекцию, остается зараженной с вероятностью pi =0,1. По усло-
виям обработки каждая машина может ожидать дезинфекции
(находиться в очереди) в среднем v=20 мин. Машина, попавшая
на обработку, проходит ее до конца. Определить вероятность Q
того, что отдельная машина, поступившая на обработку, останет-
ся зараженной, если среднее число машин, поступающих на об-
работку в единицу времени, равно Х=1——•
Решение
В этой задаче систему дезинфекции машин можно рассмат-
ривать как систему массового обслуживания, исследованную
выше в этом параграфе. Найдем параметры системы:
«=10;
а=—= 10;
р
242
\ /
\ а = —=20;
\ у=—=20;
т=оо'(так как нет никаких ограничений яа очередь).
Тогда среднее число обслуживаемых машин будет опреде-
ляться по формуле (6.4.6):
£=8,8.
Вероятность того, что машина пройдет обработку, будет:
po6c=J±_ =0,88.
Л.
Полная вероятность Р того, что машина будет продезинфе-
цирована, равна:
P=Po6c(\-Pl)=0,792.
Искомая вероятность Q того, что машина останется зараженной,
будет равна:
Q= 1—/>=0,208.
§ 6.5. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ
ВРЕМЕНЕМ НАХОЖДЕНИЯ ЗАЯВКИ НА ОБСЛУЖИВАНИИ
И НЕОГРАНИЧЕННЫМ ВРЕМЕНЕМ НАХОЖДЕНИЯ ЗАЯВКИ
В ОЧЕРЕДИ
В этом параграфе будет рассмотрена система, в которой,
заявки проявляют «нетерпение», находясь только на обслужи-
вании. Примером такой системы может служить конвейер с на-
копителем. В накопителе (в очереди) детали могут находиться
неограниченное время. Из накопителя детали поступают на кон-
вейер. Время же обработки детали на конвейере ограничено вре-
менем прохождения конвейера через рабочее место.
Постановка задачи. На вход n-канальной системы
массового обслуживания поступает простейший поток заявок с
плотностью X. Каждый канал обладает производительностью р.
Взаимопомощи между каналами нет: каждая заявка обслужи-
вается одним каналом. Находясь на обслуживании, заявка про-
являет «нетерпение». Параметр «нетерпения» равен т). Если все п
каналов заняты, заявка становится в очередь, где ждет неограни-
ченное время (в очереди заявки ведут себя «терпеливо»). Число
мест в очереди т. Если заявка застает все места в очереди за-
нятыми, то она получает отказ.
Состояния рассматриваемой системы будем опять связывать
с числом заявок, находящихся в системе:
243
Xk — в системе имеется k заявою все они обслужи-
ваются; каждая заявка обслуживается одним каналом;
хп+г — в системе имеется п^-r заявок (0<г^т); п из них обслу-
живается (каждая заявка одним каналом) и т ожидают
в очереди.
Граф состояний рассматриваемой системы показан на рис.
6.5.1. Величина ц* на этом графе определяется из выражения
(6.5.1)
Этот граф с точностью до обозначений совпадает с графом си-
стемы, изображенном на рис. 5.1.1. Поэтому для определения
А АЛ* ЛА
Рис. 6.5.1
вероятностей состояний рассматриваемой системы можно вос-
пользоваться результатами, полученными в § 5.1:
------------Р№д,> (6-5-2>
R (П, а*) -|- Р (л, а*) х* —--
1 — х*
ря+г = (х’Г/,„=--------(х*ГР(Я, “7 (0 < г <7/1), (6.5.3)
1 ““ (Y'*
R (п, а*) + Р (п, а*)х*-----
1 —х*
где
ЛЦ* П (ft + 1))
Во всех выражениях этого параграфа предполагается, что
х*=И=1. При х* = 1 получается неопределенность, которую чита-
телю предлагается раскрыть самостоятельно (см. § 5.1).
Вероятность обслуживания равна вероятности того, что вновь
прибывшая заявка не получит отказа (1 — рп+т), умноженной
244
на\ вероятность того, что за время нахождения на обслуживании
она будет обслужена |—-—):
\ + l /
Ровс=(1 - Рп+т) -^— = [1 -(x’)VJ- (6-5.6) ч
(а +1 р + 1)
Вероятность обслуживания можно определить и через сред-
нее число занятых каналов k:
А>бс=^-,
откуда [см. (6.5.6)]
^=2- ро6с==__2_ [1 -(»ГРЯ]=«’ [1 ~^}тРп\. (6-5.7)
Iх р- + ’)
Вероятность того, что канал занят, равна
^з.к = — . (6.5.8)
п
Вероятность того, что система полностью загружена, опреде-
лим по формуле
1=^L. (6.5.9)
XJ 1 — X*
1 r=0
Среднее время неполной загрузки системы найдем по фор-
муле, аналогичной формуле (5.1.13):
Среднее время полной загрузки системы найдем на основании
эргодического свойства:
7п.8=7и.» , "д-8 - • (6.5.11)
1 ЯП.з
Среднее время занятости канала найдем из выражения [см.
(5.1.16)]
^з.к== т—h Рн.о^н.о, (6.5.12)
[А*
где ри,о — вероятность наличия очереди в системе;
^н.о — среднее время наличия очереди.
Вероятность наличия очереди определяется по формуле
т
S. 1 — (х*)да
(6.5.13)
245
Среднее время наличия очереди определим по формуле, ана-
логичной формуле для среднего времени наличия очереди для
системы с ожиданием [см. (5.1.15)]:
7 • 1 * 1 — (х*)ш
А,.о=—* —f-
X 1 — X*
(6.5.14)
Среднее время простоя канала найдем по формуле
7п.к=7з.к-~Яз-к • (6.5.15)
Лз.К
Средняя длина очереди г равна
т
. (6.5.16)
Г=1
Среднее время ожидания в очереди найдем из выражения
• (6-5.17)
Л
Закон распределения времени нахождения в очереди определяет-
ся таким же образом, как это было сделано в § 5.1.
Среднее время пребывания заявки в системе определяется по
формуле
7=-L=A+r . (6.5.18)
X X
В рассматриваемой системе при неограниченном увеличении
числа мест в очереди, (т—>-оо) стационарный режим существует
только при величине х*=—^—<1. Подробное объяснение этого
И|1*
факта было изложено в § 5.1.
Ввиду небольшого объема этого параграфа не будем приво-
дить сводку основных расчетных формул.
§ 6.6. ИССЛЕДОВАНИЕ СИСТЕМЫ ПВО КАК СИСТЕМЫ МАССОВОГО
ОБСЛУЖИВАНИЯ .
Рассмотрим работу n-канальной системы ПВО (рис. 6.6.1),
на вход которой поступают самолеты противника. Самолеты,
пролетающие в пределах полосы налета, могут быть обстреляны
любым из п каналов данной систем ПВО.
Ширина полосы налета b определяется возможностями об-
стрела всеми п каналами любой цели в пределах полосы налета.
Предполагается, что если самолет летит вне пределов полосы
налета (слева или справа), то эти самолеты не могут быть об-
стреляны ни одним из п каналов данной системы ПВО.
246
Глубина зоны обстрела а определяется рубежом перехвата*
и рубежом прекращения огня, которые являются одинаковыми
для всех п каналов. Если обозначить через dmia среднюю даль-
ность перехвата и через dmta — среднюю дальность прекращения
стрельбы, то можно записать следующее приближенное выра-
жение для глубины зоны обстрела а:
Л ~ rfmax-' ^min- (6.6.1)
Необходимо отметить, что характеристики зоны обстрела а и
Ь зависят также от скорости налетающих самолетов v, высоты их
полета h и т. п.
Рис. 6.6.1
При анализе системы ПВО в качестве канала обслуживания
рассматривается канал наведения. Под каналом наведения бу-
дем понимать всю совокупность средств, обеспечивающих стрель-
бу по воздушной цели. Например, канал наведения может со-
стоять из радиолокационной станции наведения и одной пусковой
установки. Если одна станция наведения обеспечивается одно-
временно тремя пусковыми установками, то каналом наведения
будет эта станция и три пусковых установки. Иногда несколько
каналов могут обстреливать одну цель. В этом случае будем
говорить о том, что в такой системе ПВО существует «взаимопо-
мощь» между каналами.
Одной из основных характеристик системы ПВО является
эффективная скорострельность одного канала р. Допустим, что
станция наведения обеспечивается одновременно g пусковыми
* Рубежом перехвата называется условная линия, пролетев которую само-
лет может быть обстрелян.
247
установками, а каждая пусковая установка производит в сред-
нем р, выстрелов в единицу времени. Тогда эффективная скоро-
стрельность одного канала определится так:
(6.6.2)
где р — средняя вероятность поражения цели одной выпущенной
по ней ракетой.
При рассмотрении работы системы ПВО существенным яв-
ляется вопрос о получении информации о результатах стрельбы.
Здесь возможны различные случаи.
Самым простым является случай, когда канал обстреливает
цель в течение времени /Об, после чего обстрел цели прекращает-
ся независимо от того, поражена цель или нет. Считая, что каж-
дый из каналов производит пуассоновский поток^ эффективных
(успешных) выстрелов с параметром j*’ можно прйблйженйб
вычислить вероятность поражения”цели'одним каналом по фор-
муле
' (6.6.3)
Если считать, что каждый канал производит регулярный по-
ток выстрёлов 'с'параметром gp, то вероятность поражения цели
"одним’таким каналом можно приближенно вычислить по фор-
муле ' ,
P^l-tl-p)^. (6.6.4)
Необходимо отметить, что формула (6.6.3) проще в обращении,
а по точности мало уступает формуле (6.6.4).
Если цель обстреливалась одновременно k каналами и каж-
дый из k каналов поражает цель независимо от других, то ве-
роятность поражения цели будет равна
рА=1-(1-ЛЛ
В рассматриваемом случае время обстрела ТОб должно быть
меньше или по крайней мере равно времени пребывания цели в
зоне обстрела Т3. Среднее время пребывания цели в зоне обстре-
ла будет
М[Г3]=7з=-^-, " (6.6.5)
где v — скорость полета самолета при условии, что он обстре-
ливается.
i Случай, когда ТОб = 7’з, характерен для системы ПВО, когда
\ само время Т3 мало и нет возможности выяснить, поражена ли
/ цель или нет за время ее обстрела, т. е. когда цель находится в
7 зоне обстрела очень малое время.
248
Другой способ обстрела имеет место тогда, когда есть воз-
можность получить и использовать информацию о поражении -2
цели. Допустим, что йремя, проходящее между моментом пора- ?
жения цели и моментом прекращения огня, есть случайная вели-
чина Ти с математическим ожиданием М(7'и]=ги. Если за начало
отсчета времени считать момент входа самолета в зону обстре-
ла, то при наличии свободных каналов это начало отсчета совпа-
дает с началом обстрела цели. В общем случае время пребыва-
ем
Рис. 6.6.2
ния в зоне обстрела будет случайной величиной Т3 с математи-
ческим ожиданием Л1[7'3]=/3. Цель будет не поражена, если
время, потребное для ее пораженйя Тп, будет больше времени
пребывания щели в зоне обстрела Т3 (рис. 6.6.2а). Если
ТП<Т3 (рис. 6.6.26), то цель будет поражена. Время обстрела
цели ТОб (или время занятости канала) в этом случае будет
Гвб=ш1п(Гв4-Тя, Т3), (6.6.6)
так как при всех условиях обстрел ведется до тех пор, пока цель
находится в зоне обстрела. Если величина Тя велика, то с боль-
шой вероятностью будет выполняться равенство 7'0б = 7'3, т. е. мы
приходим к первому случаю обстрела цели, когда стрельба
ведется в течение всего времени пребывания цели в зоне обстре-
ла (типично для системы ПВО, у которой время Т3 мало).
Таким образом, вероятность поражения цели при условии, что
она обстреливается одним каналом, будет определяться как
вероятность выполнения неравенства Ти<Т3:
Pi=P(Tn<T3\ (6.6.7)
Имея в виду принятое допущение о пуассоновском характере
системы, будем считать, что среднее время, затрачиваемое на
поражение цели, равно
[Tn]=-L, (6.6.8)
р-
а поток эффективных выстрелов является пуассоновским с пара-
метром р. Далее, в силу того, что мы условились рассматривать
249
только пуассоновские системы, будем считать, что время пребы-
вания самолета в зоне обстрела Т3 является показательным с па-
раметром т):
— • (6.6.9)
<з а
В этом случае можно доказать справедливость формулы
Л=Р(ГП<Т3)=—. (6.6.10)
Если, кроме того, допустить приближенно, что сумма случай-
ных величин Гп+Ти распределена по показательному закону с
математическим ожиданием tn+tH, то можно доказать [21], что
время занятости канала Тп« будет также подчинено показатель-
ному закону с параметром
(6.6.11)
1 + iA
Таким образом, поток освобождений канала ПВО, определяе-
мый выражением (6.6Л1), имеет интенсивность р*. Если время
передачи информации /и мало, то выражение (6.6.11) примет вид
^*=1*4-1). (6.6.12)
Можно дать следующее объяснение формуле (6.6.12). Поток
освобождений канала слагается из двух потоков: потока пора-
жающих выстрелов с параметром р. и потока уходов непора-
женных самолетов из зоны обстрела с параметром т). Другими
словами, канал освобождается либо по причине поражения само-
лета, либо по причине выхода самолета из зоны обстрела непора-
женным.
Если время передачи информации велико по сравнению со
временем пребывания цели в зоне обстрела (типично для систе-
мы ПВО, у которой время Т3 мало), то
!»* = •»!. (6.6.13)
Наконец, при анализе работы системы ПВО необходимо знать
характеристики налета. Будем считать, что налетающие самоле-
ты образуют пуассоновский поток с интенсивностью X, который
определяется так:
(6.6.14)
где / — средний линейный интервал между самолетами.
250
1. Система ПВО с отказами и упорядоченным обслуживанием *
В § 6.1 была рассмотрена система массового обслуживания
с отказами и «нетерпеливыми» заявками, когда канал мгновенно
освобождается, либо при обслуживании заявки (поражение са-
молета), либо при уходе заявки из системы (непоражение само-
лета). Другими словами, в этом параграфе был рассмотрен
случай, когда величина ц* = ц+т), т. е. когда среднее время пере-
дачи информации о поражении самолета tK мало. Если время
передачи информации велико, то обстрел цели будет длиться
практически в течение всего времени нахождения самолета в
зоне обстрела, тогда ц*=т]. В этом случае среднее число занятых
каналов будет определяться по формуле
: „ «(”->.-)
k=-— ------->—. (6.6.15)
1 «(”• -)
\ 1 /
Вероятность поражения цели (относительная пропускная спо-
собность) нужно находить по фор муле
Робс=Р1—Ц-------(6.6.16)
Я[л,—)
ГДв
(6.6.17)
Абсолютная пропускная способность Ао определяется по фор-
муле
Х0=ХРобс. (6.6.18)
Все остальные параметры определяются через k так же, как
в случае р*=р,+т]. _
Если среднее время передачи информации /и сравнимо с вели-
чиной I/р., а среднее время обстрела /ос<— , то среднее число
занятых каналов, будет определяться по формуле (6.1.7), с той
разницей, что параметр ц,* определяется по формуле (6.6.11).
Вероятность поражения самолета РОбс в этом случае нужно на-
ходить по формуле (6.6.16), где Pi уже подсчитывается по фор-
муле (6.6.3) или (6.6.4).
* Упорядоченное обслуживание состоит в том, что заявки (цели) строго
распределяются по свободным каналам (нет случайного распределения заявок
и нет взаимопомощи).
251
Таким образом, в этом случае характеристики системы ПВО
будут вычисляться по следующим формулам:
Л(Л, а*)
♦ •
а“ ’
>?=-ПГ7“+1|;
_р /?(«-!, а*) .
Роб'-Р! Л(пИ ,
Р1=1-е"’хГ°б;
Xq=XP обо
Все остальные параметры системы подсчитываются так же,
как и в случае, когда р,* = р+т|, и время обстрела ограничивает-
ся лишь пребыванием самолета в зоне обстрела. В дальнейшем
ограничимся лишь случаем, когда время передачи информации
мало и параметр освобождения канала определяется по формуле
+ (6.6.19)
Среднее время пребывания заявки в системе (связи самолета
с_ системой ПВО) для любого времени прохождения информации
определяется по формуле
7= А . (6.6.20)
Ввиду небольшого объема этого параграфа мы не будем при-
водить список основных расчетных формул.
Задачи и упражнения
6.6.1. Радиолокационный канал наведения может наводить
ракеты, пущенные с одной установки или с двух установок. Всего
имеется 2g установок, эффективная скорострельность каждой из
них р. Требуется определить, при каком способе организации си-
стемы ПВО с отказами и упорядоченным обслуживанием она
будет более эффективной:
а) если каждому каналу наведения будет придана одна уста-
новка (всего будет n=2g каналов с эффективной скорострель-
ностью каждого канала р);
б) если каждому каналу наведения будут приданы две уста-
новки (всего будет n=g каналов с эффективной скорострельно-
стью каждого канала 2ц).
252 '
Решение
В случае а имеем [см. (6.1.8)]
Аналогичные вычисления проводим и для случая б:
2fi + т)
*(* -^тг)
Можно показать, что для любых конечных значений р, т), % и
положительном g Робе < Робе, т. е. всегда выгоднее объеди-
нять каналы. Так, если — =ц=т] и £=3, получим
L6
L «(S. з> с0 474;
2 Л(6, 3)
РФ
• обе
2 /?(2, 2)
3 Л(3, 2)
0,528,
т. е. эффективность увеличивается приблизительно на 11 % • Слу-
чай б по существу эквивалентен наличию взаимопомощи, поэто-
му он эффективнее.
6.6.2. Система ПВО с отказами и упорядоченным обслужива-
нием характеризуется следующими данными:
— скорострельность каждой пусковой установки
~ 1 1
ц, =-------;
3 мин
— вероятность поражения цели одной ракетой р =0,570;
— станция наведения обеспечивается двумя пусковыми уста-
новками (g=2);
— длина полосы обстрела а=35 км;
— скорость налетающих самолетов
о = 1300 км/час;
— средний линейный интервал между самолетами 1=7 км;
— общее число каналов наведения п=2.
Определить вероятность поражения цели и другие характе-
ристики системы ПВО.
253
a =
Решение
Рассчитаем параметры работы системы:
И=£РФ=0,380 —— ;
• мин
•>] = —=0,620—— ;
а мин
мин
Х=—=2—J— ;
мин
— =2.
JX*
Вероятность поражения любой отдельной цели
Ро6с = о,225.
l»*Ju Л(п, a*)
Среднее число занятых каналов
£=_fW =1д8
*
Вероятность того, что канал занят:
ks.k= —=0,59.
п
Среднее время занятости канала
t3.K =--= 1 MUH.
р,*
Среднее время простоя канала
к=4 к ^М- = 0,695 мин.
Лз.к
6.6.3. Определить, насколько увеличится эффективность си-
стемы ПВО, рассмотренной в задаче 6.6.2, если увеличить длину
зоны обстрела и взять ее равной не 35 км, а довести ее до 72 км.
Все остальные характеристики системы ПВО остаются теми же,
как и в задаче 6.6.2.
Решение
Рассчитаем параметры системы
u.=guo=0,380 —-— ;
мин
254
ij = —=0,302 —;
а мин
. u* = u.-]-Tiq=:::0»682—-— ;
мин
к=— = 2—— ;
1 мин
а* = —^3.
Вероятность поражения отдельной цели (самолета) будет равна
Ро5с = Ji- 7?<"-?!_5.!)=о>262.
pi* R(n, а*)
Среднее число занятых каналов
£=—Робе =1,38.
(А
Сравнивая полученный результат с тем, который был получен
в примере 6.2.2, видим, что значительное увеличение зоны обстре-
ла (почти в два раза) не приводит к существенному увеличению
эффективности системы ПВО: вероятность поражения цели уве-
личивается всего на 14%.
6.6.4. Определить эффективность системы ПВО, рассмотрен-
ной в примере 6.6.2, при условии, что число каналов системы
ПВО увеличится в два раза и станет равным 4.
Решение
= JL А>(,г— 1, »*) = 0,380 R(3, 2) 0 344
°бс (л* R(n, а*) 1 Л(4, 2)
Заметим, что при неограниченном увеличении числа каналов
(п—>-оо) получим
lim Po5c(«) = — Um b a7.^Ji_ =0,380.
|X* n—~ ’ R(n, a*) p*
Если в условиях примера 6.6.3 (когда мы увеличили зону
обстрела почти в два раза) взять очень большое число каналов
(п—>оо), то получим
lim Po6c(«)=JJ =-^-=0,557.
л—~ jx* 0,682
Таким образом, увеличение числа каналов приводит к замет-
ному росту эффективности системы ПВО. Однако даже неограни-
ченное число каналов в системе ПВО без взаимопомощи не мо-
жет обеспечить поражения самолета с большой вероятностью.
255
Это объясняется тем, что даже4 при условии обстрела каждой
налетающей цели одним каналом, она не будет поражаться с
большой вероятностью, так как за время пребывания цели h зоне
обстрела по ней делается мало выстрелов. Дальнейшее увеличе-
ние эффективности рассматриваемой системы ПВО без взаимо-
помощи каналов может быть обеспечено путем увеличения
эффективной скорострельности каждого канала.
6.6.5. Рассмотрим сцстему ПВО, которая отличается от систе-
мы ПВО, исследованной в задаче 6.6.2, лишь тем, что скоро-
стрельность каждого канала увеличена примерно в 4 раза и до-
ведена до ц=1,21------. Определить, насколько увеличится
эффективность такой системы по сравнению с системой, разо-
бранной в задаче 6.6.2.
Решение
Рассчитаем параметры новой системы ПВО:
=^/?=1,38—
мин
т]=— =0,620——
а мин
• 1 о 1
мин
х=—=2—;
/ мин
а =--= 1;
га=2.
Вероятность поражения отдельной цели
робс=JJ- а*)=0 550.
pi* R(n,«)
Таким образом, при увеличении скорострельности каждого
канала примерно в 4 раза эффективность системы ПВО увели-
чивается почти в 2,5 раза. Надо отметить, что вообще значитель-
ное увеличение эффективности системы ПВО достигается в ос-
новном при увеличении эффективной скорострельности каждого
канала системы ПВО.
6.6.6. Предлагается рассмотреть систему ПВО с отказами и
нарушенным управлением: каждая появляющаяся в зоне обстре-
ла цель передается на обстрел в любой из п каналов (занятый
или свободный) с равной вероятностью 1/п. Другими словами,,
система ПВО работает так же, как и система массового обслу-
256
живания с отказами и случайным распределением заявок по
всем каналам (см. § 4.5) с той лишь разницей, что заявка (цель)
находится под обслуживанием (обстрелом) ограниченное время:
интенсивность потока освобождений равна р*=р+%]. »
Р ешение
Не повторяя подробно всех выкладок, приведенных в § 4.5,
запишем сразу результат.
Вероятность того, что в системе ПВО занято ровно k каналов
(обстреливается k самолетов, каждый самолет обстреливается
одним каналом):
Рь—/1 1 *wi —О’
(1 + х*)л
где
Среднее число занятых каналов Е равно
т Лх*
к=-------.
14-**
Вероятность поражения самолета (обслуживания заявки)
po6c=-M^_!L —1—
X [** 1 + х*
Вероятность того, что канал будет занят:
Среднее время простоя канала
- 1 1—Я3.к _ 1)
*п.к- “ —_____—. .
Р-* Яз,к Л
Среднее время занятости канала
7______L
гз.к— •
[Л*
Среднее время пребывания заявки в системе
. - k 1 1
/=—--------------.
X ft* 1 + **
8*—1964
257
2. Система ПВО с ожиданием и упорядоченным
обслуживанием
Рассмотрим случай, когда самолет, влетевший в зону обстре-
ла и заставший все каналы занятыми, не получает отказа и в
дальнейшем может быть еще обстрелян.
За самолетом, влетевшим в зону обстрела и заставшим все
каналы занятыми, осуществляется слежение с помощью спе-
циальных станций. Если освобождается канал, то эта станция
передает самолет на обстрел при условии, что самолет еще на-
ходится в зоне обстрела. Эта система ПВО аналогична системе
массового обслуживания с ожиданием, с ограниченным числом
заявок в очереди и с ограниченным временем пребывания заявки
в системе, рассмотренной в § 6.2.
В общем случае время нахождения самолета в зоне обстрела
может зависеть от того, обстреливается самолет или нет. При
обстреле самолета может быть включен форсаж и т. п. Поэтому
параметр, характеризующий время пребывания самолета в зоне
обстрела при условии, что он не обстреливается, обозначим бук-
вой V. Величина v обратно пропорциональна среднему времени
пребывания в зоне обстрела. Параметр v подсчитывается по фор-
муле
(6.6.21)
> а
где vB.o — скорость полета самолета при условии, что его не
обстреливают;
а — глубина зоны обстрела.
В частном случае, если все параметры полета не зависят от
того, обстреливается самолет или нет, параметр v=rj [см. (6.6.9)].
Задачи и упражнения
6.6.7. Определить, насколько увеличится вероятность пора-
жения цели системой ПВО, рассмотренной в задаче 6.6.2, если в
нее ввести две специальные станции, следящие за целью (/п=2).
Определить различные характеристики такой системы ПВО при
условии, что необстреливаемый самолет имеет скорость он.о =
= 840 км/час.
Решение
Помимо тех параметров системы, которые были подсчитаны
при решении задачи 6.6.2, нужно рассчитать еще следующие
параметры:
v = -^=0,4—— ;
а мин .
. 8=_2£_=5;
У
258
В нашем случае 6 целое число, поэтому можно воспользовать-
ся формулой (6.2.22) для подсчета вероятности поражения само-
лета данной системой ПВО:
*о/ 1 *1. О/ R (т + Ъл) — R (Ъ, t)
*R (п— 1, а*) + пР (п, а*) ------—-----------
________________________________* (о> 7)_____
D, D/„ *1 /?(т + 8, т) —Я(8, 7)
R (п, а*) + Р (п, а*)-----~~------------
0,285.
Следовательно, введение двух специальных станций, следя-
щих за целями, увеличивает вероятность поражения цели на ве-
личину
Д=0,285—0,225=0,060,
что составляет около — 21 %.
Если неограниченно увеличивать число специальных станций,
следящих за целями, то вероятность обслуживания в нашем слу-
чае будет равна
lim Робе (/и)=0,295,
т->оо
т. е. увеличится всего на 3,5%. Следовательно, дальнейшее уве-
личение числа специальных станций, следящих за целями, не
приводит к заметному увеличению эффективности системы ПВО.
Найдем другие характеристики системы:
^Среднее число занятых каналов
k=— Робе =1,50.
При неограниченном увеличении т~получим
lim Л(/и)=1,55.
Среднее число занятых станций подслеживания (среднее
число заявок в очереди)
+ 7)~Ж&, 7) Г + 7)7
«<». ..>+₽(», 7,
Р(1. 7)
Среднее число занятых станций при т->-<х> равно
lim г (т)=1,07.
17*
259
Вероятность того, что будет занята хотя бы одна специальная
станция (вероятность наличия очереди) равна
D — п + 7)-Р(б,т)_03б4
Рч.а-Рп р(5 7) -и,<$04.
При неограниченном увеличении числа специальных станций
получим
limpH.o(/n)=0,466. -
Среднее время наличия очереди
7 ___ 1 + т) Я (8,?)__0717 ыин
/к-°~ х 7чм)“0,717 ман-
Um 4.о(т)—1,13 мин.
Вероятность того, что канал занят:
гс3.к=—=0,750;
л
Ит ^з.к (/п)=0,775.
/71-♦оо
Среднее время занятости канала стрельбой
4.к=— 4-Рн.о/н.о=1,27 мин; lim 1,53 мин.
It* т->~
Среднее время простоя канала
4.к=4.к г~Язл =0,424 мин;
Лз.к
lim 4.к [гп)=0,444 мин.
т-*<»
6.6.8. Рассматривается работа четырехканальной системы
ПВО с двумя специальными станциями, следящими за целями с
такими же параметрами, как и в задаче 6.6.7. Определить, на-
сколько увеличится эффективность такой системы ПВО по срав-
нению с рассмотренной в задаче 6.6.7.
Р еш ен не
Вероятность поражения самолета определяется по формуле
(6.2.22):
=0^390.
Эффективность увеличилась на Д=0,390—0,285=0,105, что
составляет около 27%.
260
При неограниченном увеличении числа специальных станций,
следящих за целями т-хх>, получим
lim Розе (/и)=0,446.
Сравнивая результаты решения этой задачи с результатом, по-
лученным в задаче 6.6.4, убеждаемся в том, что введение двух
специальных станций, следящих за целями, в четырехканальной
системе ПВО приводит к большему повышению эффективности
по сравнению со случаем неограниченного увеличения числа ка-
налов: 0,390>0,380.
3. Система ПВО с ожиданием и взаимопомощью между
каналами
Аналогичная система рассматривалась в § 6.3. При рассмот-
рении системы ПВО взаимопомощь между каналами состоит в
том, что одну цель могут одновременно обстреливать I каналов,
при этом эффективная скорострельность увеличивается в I раз.
' Задачи и упражнения
6.6.9. Рассматривается четырехканальная система ПВО
(п=4) с ожиданием (т=2) и взаимопомощью между каналами
(Z=2). Характеристики системы ПВО следующие:
— скорострельность каждой пусковой установки
~ 1 1
w=---------;
3 мин
— вероятность поражения цели одной ракетой
jp=0,570;
— станция наведения обеспечивается двумя пусковыми уста-
новками (g=2);
— длина полосы обстрела а=35 км-,
— скорость налетающих самолетов при условии, что они не
обстреливаются:
ин.о=840 км1час;
— скорость налетающих самолетов при условии, что они об-
стреливаются:
о =1300 км)ч.ас;
— средний линейный интервал между самолетами 1=7 км;
— число канадов п=4;
— число станций, подслеживания т=2;
9—1664 261
—максимальное число взаимодействующих каналов 1—2.
Определить пропускную способность системы ПВО.
Решение
Рассчитаем параметры работы системы:
l»=g|xp=0,380 —— ;
мин
т(= —= 0,620—
а мин
(х» = 1х-[-Т1 = 1—— ;
мин
v= 2н^=о,4—— ;
а мин
Х=—= 2 —;
/ мин
Ь О
а =----=2;
pi*
8 = Л£!1 = 5;
X с
у=— = 5;
а‘=------^1,45;
ф=—=3,23;
^^=4,45.
ftv-i
?=-------
Т) К)
Вероятность р0 того, что будут свободны все каналы, можно
найти по формуле (6.3.15). Ввиду того, что в нашем случае вели-
чина <р не целое число, нужно расчет всех функций R(m,a) и
Р(т, а) произвести для значения [<р]—4 и (<р]+1 = 5, а затем
итоговые формулы проинтерполировать на <р=4,45. Можно про-
водить и интерполяцию самих функций /?(/и, а) и Р(т, а) на
Ф=4,45. Остановимся на последнем способе*. Найдем значение
следующих функций (см. (6.3.15)]:
* Расчеты показывают, что в обоих случаях погрешность весьма мала.
262
/?(«-Л+ф, <]>)=*/? (4—2+4,45; 3,23)^/?(4-2+4; 3,23)+
+ (#(4-2+5; 3,23)-А>(4-2+4; 3;23)]-0,45 - 0,966;
/?(<Р, ф)=/?(4,45; 3,23)=/?(4; 3,23)+[Я(5; 3,23)-/?(4; 3,23)] X
X 0,45 =0,727;
Р(га+<Р—й; ф)=Р(4—2+4,45; 3,23)=Р(6; 3,23)+
+ [Р(7; 3,23)-Р (6; 3,23)]-0,45=0,0574;
Р(<Р, <|>)=Р(4,45; 3,23)=Р (4; 3,23)+[Р(5; 3,23)-Р(4; 3,23)] X
X 0,45=0,151;
Р(0, aJ)=P(0; 1,45)=0,224;
Р(Л, ар=Р(2; 1,45)=0,252;
J Р(8, у)=Р(5, 5)=0,176;
/?(Л, а*)=/?(2; 1,45)=0,810;
/?(/п+8, у)=/?(7,5)=0,867;
/?(8, y)=/?(5,5)=0,616.
Теперь можно найти вероятность ро [см. (6.3.15)]:
ро=О, 166.
•Для определения среднего числа занятых каналов k найдем
значение функции R(h—1, a/*):
? /?(й-1, ap=/?(l; 1,45)=0,167. .
Теперь по формуле (6.3.19) найдем среднее число занятых
каналов й:
6=3,73.
Вероятность поражения цели будет равна
Робс =-5^=0,709.
Л
Сравним полученную вероятность поражения цели с вероят-
ностью поражения цели при отсутствии взаимопомощи при про-
чих равных параметрах (см. задачу 6.6.2). Мы видим, что нали-
чие взаимопомощи между каналами в данном случае резко по-
вышает эффективность системы ПВО: вероятность увеличивается
на величину
Д=0,709 - 0,390 = 0,319,
т. е. приблизительно на 82%.
9* 263
6.6.10. Провести качественное сравнение пропускной способ*
ности рассмотренных в этой главе’ систем ПВО при различных
интенсивностях налетающих самолетов к (исследовать стацио-
нарный режим работы).
Решение
Для краткости будем называть систему ПВО с отказами и
упорядоченным обслуживанием, рассмотренную в § 6.1, первой
системой ПВО; систему ПВО с отказами и случайным распре-
делением целей, рассмотренную в задаче 6.6.6, второй системой
ПВО; систему ПВО с ожиданием и упорядоченным обслужива-
нием, рассмотренную в § 6.2,— третьей системой ПВО и систему
ПВО с ожиданием и взаимопомощью, рассмотренную в этом
параграфе,— четвертой системой ПВО.
Будем считать все параметры рассматриваемых систем
(п, р, Л, т|, т, v) одинаковыми. Обозначим вероятность пораже-
ния налетающего самолета для первой системы ПВО Робе' ; для
второй—Робе , для третьей—Робе , для четвертой—Р(»бс,
абсолютные пропускные способности рассматриваемых систем
ПВО — М1’; kffi М3); М4) соответственно; будем рассматривать
эти величины как функции интенсивности налетающих самолетов
Л при прочих равных параметрах (п, р, т|, т, v).
На рис. 6.6.10а показана зависимость вероятности поражения
самолета для различных систем ПВО от плотности налетающих
самолетов Z.
Для любых систем без взаимопомощи между каналами (т. е.
когда одну цель может обстреливать только один канал)
Р<9с(0)=11ш Р&(Х)=—— (1=1, 2, 3).
Х-»-0 (А + ч
Другими словами, когда рассматривается малая плотность
налета, практически одиночный самолет, вероятность его пора-
264
жения равна вероятности того, что за время пребывания его в
зоне обстрела цель будет поражена. Поэтому, если рассматри-
ваются различные системы ПВО без взаимопомощи при малой
интенсивности налета, вероятность поражения цели практически
не зависит ни от числа каналов в системе ПВО, ни от наличия
станций подслеживания. Если рассматривается система ПВО со
взаимопомощью с максимальным числом взаимодействующих
каналов I (1=2, 3, .... ,п) *, то
P<4>c(0)=lim Р&(Х)= .
Х-0 /|А + 1J
Эту формулу можно обосновать следующим образом: при налете
одиночного самолета его будут обстреливать одновременно I
каналов. Таким образом, общая эффективная, скорострельность
будет равна /ц.
Следовательно, при малой интенсивности налета система
ПВО со взаимопомощью имеет определенное преимущество по
сравнению со всеми другими системами ПВО без взаимопомощи,
которые обладают одинаковой вероятностью поражения цели.
Для любого Х>0 существует следующее соотношение между
вероятностями поражения самолета для различных систем ПВО:
Р& (X) > Р^обс (X) > Р& (X) > Р^е (X).
Однако при очень больших плотностях налета (при X—>оо)
разность между этими вероятностями будет стремиться к нулю,
так как
11m Робе (Х)=0 (/=1, 2, 3, 4).
ОО
Это означает, что при больших плотностях налета все рассмат-
риваемые системы будут практически иметь одну эффектив-
ность. Для разъяснения этого положения рассмотрим графики
зависимостей абсолютных пропускных способностей всех систем
ПВО, приведенные на рис. 6.6.106.
Для рассматриваемых систем ПВО существуют следующие
соотношения для абсолютных пропускных способностей:
44) (X) > х£» (X) > Х^> (X) > (X) (X > 0);
при X->0 имеем
Х^(0)=11тХ^(Х)=0 (i=l, 2, 3, 4),
так как в этом случае нет потока налетающих самолетов и сред-
нее число сбитых самолетов равно нулю;
* Максимальным числом взаимодействующих каналов называется такое
число каналов, которое может одновременно обслуживать одну цель.
265
при Л->оо получим
11m (Х)=лц(1 = 1, 2, 3, 4),
к->ео
так как при болыцой плотности полета все п каналов всегда
будут практически заняты и общее среднее число сбитых самоле-
тов в единицу времени будет определяться только общим числом
каналов п и эффективной скорострельностью каждого канала р.
Таким образом, методы теории массового обслуживания сле-
дует применять тогда, когда интенсивность потока налетающих
самолетов X не очень велика (по сравнению с величиной пр), но
и не очень мала (по сравнению с параметром р для систем без
взаимопомощи и с величиной /ц для системы со взаимопо-
мощью) .
Это замечание касается не только систем ПВО, но и любых
систем массового обслуживания. Поэтому, прежде чем исследо-
вать подробно систему массового обслуживания, следует прове-
сти качественный анализ. При этом можно дать следующие прак-
тические рекомендации:
если для систем без взаимопомощи
10 ’
или для систем со взаимопомощью
Х<-^- ,
10
то можно практически считать параметр X малым;
если
10пр.»
то можно практически считать парамерт X большим.
266
6.6.11. Рассмотрим вопрос о выборе рационального интерва-
ла между самолетами при преодолении системы ПВО. В этом
параграфе были рассмотрены различные системы ПВО. При
этом для любой системы ПВО вероятности поражения отдельно-
го самолета РОбс при прочих равных условиях тем меньше, чем
больше плотность налега. Таким образом, при планировании на-
лета нужно уменьшать средний интервал между самолетами /,
стремясь сделать его по возможности небольшим. Однако умень-
шение интервала / приводит к повышению требований к технике
пилотирования. Кроме этого, при малых интервалах / возможно
поражение одним и тем же снарядом двух или более соседних
самолетов, особенно если.радиус поражения Рп снарядов ПВО
сравним с интервалом между самолетами I. Налицо противоре-
чие: с одной стороны, при увеличении плотности налета % (умень-
шении интервала между самолетами I) вероятность поражения
самолета РОбс уменьшится за счет того, что система ПВО пере-
гружается, но с другой стороны, увеличивается вероятность по-
ражения одним и тем же снарядом соседних самолетов при на-
личии значительного радиуса поражения /?п- Следовательно, для
каждой системы^ ПВО (с ее характеристиками) и каждого типа
налетающих самолетов существует рациональный (оптималь-
ный) интервал I между самолетами, при котором полная веро-
ятность^ поражения самолета Р будет минимальна. Обозначим
полную вероятность поражения отдельного самолета Р; вероят-
ность непоражения Q= 1—Р.
Очевидно, полную вероятность непоражения самолета можно
определить как вероятность произведения двух событий:
Q=P(A-B),
где А — цепоражение самолета теми снарядами, которые наво-
дились по нему самому;
В — непоражение самолета теми снарядами, которые наво-
дились по соседним самолетам.
События А и В, строго говоря, зависимы, однако эта зависи-
мость небольшая и приближенно можно считать, что
Q=P(A).P(B)=Po6cPB, (6.6.22)
где Р(Л) =РОбс — вероятность непоражения самолета, вычис-
ленная как ранее (см. § 6.1 и § 6.3);
Р(В)=Рв — вероятность непоражения самолета теми сна-
рядами, которые наводились по соседним са-
молетам.
Вероятность Рв зависит от строя, в котором летят самолеты, и от
радиуса поражения снаряда Rn.
Допустим для простоты, что самолеты летят кильватерной
колонной со средним интервалом I. На рис. 6.6.11а изображен
267
такой поток самолетов (по оси абсцисс откладывается рассто-
яние) .
Самолеты, проходящие систему ПВО и не пораженные сна-
рядами, которые наводились на эти самолеты, изображены на
рисунке кружочками; самолеты, которые поражаются наводимы-
ми на них снарядами, изображены крестиками, остальные само-
леты, на которые снаряды не наводились, также изображены
кружочками.
Рис. 6.6.11а
Рассмотрим стационарный режим работы системы ПВО. Ес-
ли плотность налета была %, то линейная плотность налета (сред-
нее число самолетов на единицу длины Лл) будет равна
Хл=-у- Цкм. (6.6.23)
Связь между интенсивностью налета X и линейной интенсив-
ностью налета Хл следующая:
хл=—, (6.6.24)
V
где v — скорость налетающих самолетов.
Введем в рассмотрение случайную величину X — линейное
расстояние между самолетом, обозначенным на рис. 6.6.11а кру-
жочком, и ближайшим самолетом по направлению полета, поме-
ченным крестиком. Другими словами, случайная величина X —
это расстояние между самолетом, который не поражается наво-
димыми по нему снарядами, и центром ближайшего по направ-
лению полета взрыва. Если поток самолетов во времени был
простейший пуассоновский, с интенсивностью X, то и поток само-
летов, изображенный на рис. 6.6.11а будет также простейшим с
интенсивностью Лл.
Рассмотрим любой из самолетов, обозначенных на
рис. 6.6.11а кружочками. Для нахождения закона распределения
случайной величины X введем в рассмотрение ряд гипотез:
Но — ближайший (по направлению полета) впереди летящий
самолет был поражен снарядами, которые по нему наводи-
лись;
Hi — ближайший впереди летящий самолет не был поражен сна-
рядами, которые по нему наводились, а следующий за ним
самолет был поражен снарядами, которые наводились по
нему;
268
Hk — первые k впереди летящих самолетов не были поражены
снарядами, которые по ним наводились, а Л+1 впереди
летящий самолет был поражен снарядами, которые по нему
наводились и т. д.
Очевидно:
РРобе(1 -Робе)4(Л=о, 1, 2,...). (6.6.25)
Если имела место гипотеза Hk, то в этом случае случайная
величина X подчинена распределению Эрланга k-ro порядка с
параметром Лл, т. е. условная плотность распределения случай-
ной величины X равна
Л(х)= (х>0). (6.6.26)
Тогда безусловную плотность распределения случайной величи-
ны X можно найти по формуле
00 оо
л=о л=о
х е“Хл’г=КРо6се“хлробслг(х > 0). (6.6.27)
Следовательно, закон распределения расстояния между само-
летом, не пораженным наводящимися по нему снарядами и бли-
жайшим по направлению полета взрывом, является йоказатель-
ным с параметром ЛлРОбс-
Очевидно, такие же рассуждения можно провести о законе
распределения случайной величины Y — расстояния между са-
молетом, не пораженным наводящимися по нему снарядами, и
ближайшим к нему взрывом в направлении, обратном направле-
нию полета самолета (см. рис. 6.6.11а).
Вероятность Рв поражения самолета подорвавшимися снаря-
дами, которые наводились по другим самолетам, можно найти
следующим образом:
РВ=Р(Х> Ra)-P (У > ^^е-^ЛбЛ. (6.6.28)
Используя выражения (6.6.22), (6.6.24) и (6.6.28), окончательно
получим формулу для определения полной вероятности непора-
жения самолета системой ПВО с учетом возможности пораже-
ния самолета взрывом снаряда, который наводился на другие
самолеты:
“—2 7? Р
Q=(l-Po6c)e - о* (6.6.29)
Рассмотрим пример определения оптимального интервала.
Для простоты будет анализировать систему ПВО с отказами и
269
упорядоченным обслуживанием (см. § 6.1). Для этой системы
вероятность РОбс определяется по формуле
(6.6.30)
О _ Iх /?(л—1, Я*)
обе ~ " •
(Л* /?(л, а»)
С учетом (6.6.30) выражение (6.6.29) можно переписать так:
а»)
Q=[ 1 — б-2 F‘ /?(«.«»> . (6.6.31)
L Iх* Л(л. <**) 1
Если число каналов п=1, то формулу (6.6.31) можно записать в
следующем виде:
Q(k)= vl~A е v (6.6.32)
р- 4-1 + X
Напомним, что
В выражении (6.6.32) нужно подобрать такую величину М°\
которая бы обращала полную вероятность непоражения самоле-
та Q в максимум:
Q(0)=maxQ(X). (6.6.33)
*
При решении этой задачи нужно помнить о том, что величина А.
ограничена сверху величиной %в, которая определяется условия-
ми безопасности полета, а снизу — величиной Хн, определяемой
временем всего налета. Поэтому нахождение максимума функ-
ции (6.6.33), как правило, нужно проводить численными мето-
дами.
В качестве примера рассмотрим систему ПВО (п, Л, ц, tj) ;
величина ц принята за единицу измерения плотности потоков со-
бытий: р=1. Величина т]= радиус поражения J?n=2,5 км; а
протяженность зоны обстрела а =10 км. В соответствии с форму-
лой (6.6.24) имеем
о 2°
fl = 271= —,
а
откуда
__ 0,5 4- К 1,5+Х
“ 1,54-Х
При %—Ч), что соответствует случаю налета отдельных само-
летов:
Q (0)=lim Q (Х)=—=0,333.
Х-о 3
270
Вк
При Л—>-оо, что соответствует очень большой плотности на-
лета:
Q(oo)=limQ(k)=0,368.
к->ОО
На рис. 6.6.116 показан график зависимости Q(X) для рас-
сматриваемого случая. Из графика видно, что рациональной
плотностью является Х=1 4- 2,5. С тактической точки зрения же-
лательно брать плотность потока меньшей, так как более редкий
налет легче осуществлять.
Полная вероятность непоражения самолета Q(0) будет поряд-
ка 0,4, значит, вероятность поражения P<°>«0,6.
Глава 7
ЗАМКНУТЫЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
До сих пор мы рассматривали системы массового обслужива-
ния, на которые поступал поток заявок с интенсивностью А, при-
чём эта интенсивность А не зависела от состояния СМО, а сами
источники заявок находились вне системы и нами не рассматри-
вались.
В данной главе рассмотрим другие системы массового обслу-
живания, где интенсивность потока заявок зависит от состояния
СМО, а сами источники заявок являются не внешними, а внут-
ренними элементами СМО. С такими случаями мы встречаемся,
когда .СМО обслуживает ограниченное число «клиентов» (источ-
ников заявок), сравнимое по количеству с числом каналов об-
служивания. Находясь под обслуживанием, данный «клиент»
(источник заявок) перестает подавать заявки, а после конца
обслуживания снова становится источником заявок. Классиче-
ским примером такой системы является работа группы наладчи-
ков в ткацком цеху: станки являются источниками заявок, а на-
ладчики — каналами обслуживания. Интенсивность поступления
заявок на обслуживание зависит от того, сколько станков в дан-
ный момент работает и сколько станков обслуживается или
ожидает обслуживания.
Такие системы, в отличие от рассмотренных ранее, будем на-
зывать замкнутыми системами (так как источник заявок здесь
является элементом системы).
Рассмотрим несколько примеров работы замкнутых систем
массового обслуживания.
Первый пример: допустим, что на аэродроме базируется m са-
молетов (источников заявок), и имеется п мест проведения ре-
монтных работ (каналов обслуживания). Обычно п<т, т. е.
число мест проведения ремонтных работ меньше общего числа
самолетов, приписанных к данному аэродрому. На каждом само-
лете после выхода из строя каких-то его элементов или налета
определенного числа часов требуется проводить ремонтные ра-
боты.
272
Будем считать, что каждый самолет, находящийся в эксплу-
атации, «генерирует» поток заявок на ремонтные работы, интен-
сивность которого обозначим %, а находящийся в ремонте или
ожидающий его — не генерирует потока заявок, так как не экс-
плуатируется. Тогда общий поток заявок на ремонтные работы
будет зависеть от числа самолетов, которые в настоящий момент
эксплуатируются. Например, если эксплуатируются все т само-
летов, то интенсивность потока заявок на ремонтные работы
будет равна тХ. Если эксплуатируется только k самолетов из
т, то интенсивность потока заявок
равна М.
Таким образом, интенсивность
потока заявок существенно зави-
сит от того, какое число самоле-
тов находится в эксплуатации,
т. 'е. зависит от состояния СМО.
В качестве второго примера
можно рассмотреть работу гара-
жа, в котором имеется т автома-
шин и п мест ремонта. При по-
ломке машины ее направляют в
ремонт. В ремонт могут направ-
на ремонтные работы будет
ляТься машины, нуждающиеся в
профилактическом ремонте. Рис. 7.1.1
Рассматривая работу различ-
ных систем с ограниченным числом источников заявок (замкну-
тых систем массового обслуживания), полезно иметь в виду об-
щую схему изменения состояний каждого технического устрой-
ства (ТУ) (источников заявок), изображенную на рис. 7.1.1.
Будем считать, чТо каждое ТУ, подавшее заявку на обслужива-
ние, немедленно снимается с эксплуатации.
Состояние «техническое устройство работает» состоит в том,
что данное ТУ не нуждается в обслуживании. В примере с аэрод-
ромом это состояние состоит в том, что самолет эксплуатируется
и не нуждается в проведении ремонтных работ. В примере с гара-
жом это состояние состоит в том, что машина работает нормаль-
но и не нуждается в ремонте или профилактическом осмотре.
Находясь в этом состоянии, ТУ генерирует поток заявок с интен-
сивностью X.
В случае отказа (поломки) ТУ его направляют на обслужи-
вание (ремонт, наладка, производство регламентных работ, про-
филактика и т. д.). Если имеются свободные места для обслужи-
вания техники, то ТУ принимается на обслуживание и обслужи-
вается. Если свободных мест для обслуживания техники нет, то
техника вынуждена простаивать (ожидать обслуживания). По-
сле освобождения мест обслуживания техника принимается на
обслуживание. Места обслуживания будем называть каналами
обслуживания. При нахождении ТУ в состояниях «техническое
273
устройство ожидает обслуживания», «техническое устройство
обслуживается», оно (ТУ) не генерирует потока .заявок (не мо-
жет выйти из строя, поломаться).
Так как мы условились рассматривать только, пуассоновские
системы массового обслуживания, то будем считать, что каждый
канал обеспечивает пуассоновский поток обслуживаний с интен-
сивностью ц, а каждое техническое устройство (самолет, авто-
машина и т. д.) порождает пуассоновский поток отказов с интен-
сивностью Д, если ТУ находится в состоянии -«работает».
Обозначим через т общее число ТУ, подлежащих обслужива-
нию, R(t) — случайное число ТУ, ожидающих очереди на обслу-
живание в момент времени t, S (/) — случайное число обслужива-
емых ТУ в момент времени t и H(t)—случайное число заявок,
не нуждающихся в обслуживании в момент времени /.
Для любого момента времени t имеет место равенство
или, переходя к математическим ожиданиям:
лг =7(0+«(0+^(0-
Для стационарных режимов работы замкнутых систем получим
( m=r-\-s-\-h,
где г — среднее число ТУ, ожидающих очереди на обслужи-
вание;
среднее число обслуживаемых ТУ;
h — среднее число ТУ, не нуждающихся в обслуживании.
Последнее уравнение будем называть уравнением расхода
для замкнутой системы. Величины в этом уравнении не зависят
от времени.
Вероятность того, что ТУ не будет нуждаться в обслужива-
нии (или коэффициент использования), определяется по фор-
муле .
т т
Вероятность того, что ТУ будет нуждаться в обслуживании,
равна
c=i-$=Z±L.
т
Вероятность того, что ТУ находится на обслуживании, най-
дем по формуле
т
Тогда вероятность того, что ТУ находится в. очереди (ожидает
обслуживания), определится по формуле' .
^-=С-ф.
т
Введем в рассмотрение следующие временные характери-
стики:
/Оч — среднее время однократного пребывания заявки (ТУ)
_ в очереди;
/обе — среднее время однократного обслуживания заявки
(ТУ) (или, просто, среднее время обслуживания);
/р — среднее время однократной работы ТУ, т. е. среднее
время, протекающее с момента окончания последнего
обслуживания до появления очередной «неисправно-
сти» (подачи очередной заявки).
Тогда на основании эргодического свойства будут выполнять-
ся следующие равенства: • • - ...............
?оч + Л>бс + ip
^оч + ^обс 4"
£___£ _______ ^оч______
^оч 4- ^обс 4" ip
Среднее время полного цикла обращения * технического уст-
ройства найдем из выражения /ц=^Оч4-/абс4-<р.
§ 7.1. ЗАМКНУТАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
БЕЗ ВЗАИМОПОМОЩИ МЕЖДУ КАНАЛАМИ..................
Постановка задачи: имеется т одинаковых техниче-
ских устройств, каждое из которых может в некоторые случай-
ные моменты времени нуждаться в обслуживании (отказать,
выйти из строя и т. п.). Поток отказов каждого ТУ пуассонов-
ский с интенсивностью X. В качестве ТУ могут рассматриваться
станки, самолеты, автомашины и т. д. Каждое ТУ может обслу-
живаться одним из п каналов. Интенсивность пуассоновского
потока обслуживаний каждого канала р. Если к моменту отка-
за ТУ все п каналов будут заняты, то это ТУ станет в очередь
* Время полного цикла обращения слагается из времени однократного
пребывания ТУ в очереди, времени обслуживания и времени однократной
работы ТУ.
275
на обслуживание. Дисциплина очереди естественная: «кто
раньше пришел, тот раньше обслуживается» *.
Состояния системы будем связывать с числом отказавших
технических устройств:
— отказало ровно k ТУ (&=0, 1, га) и все они нахо-
дятся на обслуживании (ремонтируются, проходят
регламент);
хп+г — отказало п+r ТУ, из них га обслуживается и г ТУ
ожидает в очереди (г=1, 2, ..., гаг—га).
Граф состояний системы с указанием плотностей потоков, пе-
реводящих систему из состояния в состояние, показан на
рис. 7.1.2.
В соответствии с этим графом можно записать систему диф-
ференциальных уравнений для вероятностей состояний системы:
ар°.^ = — mkpo(t)+vpi(ty,
at
+ X(/n-^ + l)^_1(0+(*+l)^A+1(f)(A=l,2,...,ra-l).
-^Е=_[(щ-«)к+«и]дл(/)4-
+ (гаг—га+1) Хря_1 (/) 4- п^рп^ i (/);
= _ [(яг-я-г)к+пи]ря+г(/)4.
at
+ (гаг—га —r + l)Xjp„+r(Z)4-ra|i.pn+r+i (r= 1, 2,...,/га—га);
at
Напомним, что в системе уравнений (7.1.1) параметры Л и
ц. могут быть любыми неотрицательными функциями времени и
га гаг.
Рассмотрим стационарный режим работы системы при Л=
=const, p,=const и оо. В этом случае вместо системы диф-
ференциальных уравнений (7.1.1) можно получить систему алге-
браических уравнений, для чего достаточно в системе (7.1.1)
* Дисциплина очереди влияет лишь на закон распределения времени ожи-
дания в очереди, но не влияет на среднее время ожидания в очереди и другие
интегральные характеристики системы.
276-.
j
L
। положить все производные равными нулю. Решая полученную
I таким образом систему алгебраических уравнений, получим
I ^=-^Чг(-У^=с»а^<> <Л=0’<7Л2>
11 л! (/И — я)! \ /
В где
I . а=— . (7.1.3)
I Iх
жА Оп-**ОА (я-А)А (т-п+/)Л (т-п)Х.
Рис. 7.1.2
Выражение Cmkak можно вычислить по таблицам биномиаль-
ного распределения:
pft „ _ В (т> Р) (7 1
С“ ’ (7.1.4)
где
р=—— (0<р<1);
! + “ (7.1.5)
7=1 — Р\
В (т, k, p)=Ckmpkqm~k.
Вероятность pn+r(r=O, 1, 2.. т—п) подсчитывается по
формуле
ml пл. г
Р^г=-—-.---------7Г “ Ро =
пТп\ (т — п — г)!
п)Р(т-п-.г, у) (г=о i 2 т_п1 (7Л.б)
Р(0, п)Р(т, X) F0V 7 v
где
Р(т, а)——е_<?;
ml
Z=-^=-. (7.1.7)
Л а
Величину ро находят из нормировочного условия
277
п > m—л
Ja+2 - (7.i.8>
fe=O r=l
откуда [см. (7.1.2), (7.1.4) и (7.1.6))
1
n0=----------------------------------
R (m, n9 P) P(n, n)R(m — n—\t x) /? j g\
qm + P(0, n)P(m9 x) ’ 1 ’ 7
где
R(m, n, ^)=2 B(m, k, p)=^ Cbmp*q*-*, (7.1.10)
Z?=0 Л=0
/л m &
Rfa 7)=^P(k, a)=J] ^-e-o. (7.1.11)
*=o k=0
Таблицы последней функции приведены в приложении. Таким
образом, получим окончательные выражения для вероятностей
состояний:
р^ в(т,^,~)-Ро (*=0’ 2>---«);
рп+г= Р (п, п) Р (т — (п + г), х)Ро (г=0 ъ т_п)
Р Р(р, п)Р(т,т) *
1
р —-------------------------------- в
° (т> л> р) П) — ч)
qm + Р (0, п)Р (т, х)
Найдем среднее число обслуживаемых ТУ k:
kpk+n Pn+r=^-^ kB(m, k, р) +
jS й=0
. nppP (т, п) R(m — n — 1, х)
+ Р(0, п)Р(т. х)
(7.1 :i2)
(7.1.13)
Среднее число технических устройств, ожидающих очереди на
обслуживание, можно найти так:
т—л
?= у; гр.„- г»-
г=0
— z/?(m-/z-l, х)]-
(7.1.14)
278
Следовательно, среднее число простаивающих (не работающих).
ТУ будет
7=1+г. (7.1.15)
Наиболее выпукло характеризует работу такой системы ве-
роятность £ того, что определенное (любое) ТУ в любой момент
времени t будет работать. Иногда величину £ называют коэффи-
циентом использования (или коэффициентом оперативного ис-
пользования) техники. Величина g подсчитывается по формуле
5=1- —, (7.1.16)
тп
Чем 'больше коэффициент тем более интенсивно работает
техникНу тем меньше она простаивает.
Зачастую интерес представляет коэффициент простоя техни-
ки (вероятность того, что ТУ будет простаивать):
С=1-5—. (7.1.17)
тп
Среднее время простоя ТУ /п можно найти исходя из следую-
щих соображений. Вероятность того, что ТУ будет работать,
можно вычислить на основании эргодического свойства по фор-
муле
(р +
где (р=-^- сРеДнее время безотказной работы ТУ. Следова-
тельно:
Н-у-. (таяв)
Время простоя Тп слагается из времени ожидания в очереди
Точ и времени обслуживания
Тв=Точ+Тобс. (7.1.19)
Воспользуемся теоремой сложения математических ожиданий
для отыскания среднего времени ожидания ТУ в очереди:
7П=Ж [ТП]=Л4 [Точ] 4-Л4 [Тобс]=7оч+7о6с. (7.1.20)
Среднее время обслуживания ТУ (Обс равно 7/р, следовательно
[см. (7.1.18)]:
7оч=7п-7обс=4- -^г-- — - (7-1-21)
Л 5
279
Найдем закон распределения времени ожидания в очереди
Гоч- Случайная величина Гоч представляет собой смешанную
случайную величину, функция распределения которой
терпит разрыв в точке t=0, так как существует определенная ве-
роятность того, что это время будет равно нулю:
п—1
Р(Гоч=0)=^Рк. (7.1.22)
*=о
Определим условную плотность распределения времени ожи-
дания в очереди fr(t) при условии, что к моменту отказа данно-
го ТУ система будет находиться в состоянии хп+г, т. е. в очереди
будет находиться г технических устройств —п—1)
и все п каналов будут заняты обслуживанием. В этом случае ус-
ловная плотность распределения будет
e-nv.t (/>0), (7.1.23)
т. е. (7.1.23) представляет собой закон Эрланга г-го порядка
с параметром пр. Это объясняется тем, что очередная заявка бу-
дет обслужена лишь после того, как все п каналов проведут
(г+,1) циклов обслуживания.
Следовательно, безусловная плотность распределения време-
ни ожидания в очереди будет иметь вид
л—1 т—п—1
/оч(П=8(/)2]л+ S ^^е-^Рп+г (/>0). (7.1.24)
k=0 k=0
Заметим, что среднее время нахождения в очереди можно
найти и по более сложной формуле, чем (7.1.21):
00
А>ч= J if04^dt.
— оо
Эту формулу мы используем не для нахождения среднего време-
ни ожидания в. очереди, которое легко вычисляется по формуле
(7.1.21), а для отыскания одного специального интеграла, вы-
числение которого нам потребуется в дальнейшем.
Подставим в последний интеграл выражение для плотности
распределения (7.1.24). Имея в виду, что
j /8 (/)<#=О,
280
получим
Pn+r
e-.f, dt.
Введем обозначение
ср (пр., r)= -М-2. е-^* dt.
о
(7.1.25)
Тогда с учетом второго равенства в формуле (7.1.12) получим
ОТ—Л—1
~‘" = РПп>Р<2 г> S + Х)т(<4*. г).
г=0
Сравнивая это выражение с формулой (7.1.21), видим, что у нас
есть возможность вычислить сумму, входящую в последнее вы-
ражение, по формуле
от—Л—1
г=0
11. (7.1.26),
р- J
Эта формула может быть применена для вычисления средне-
го времени нахождения в очереди для других замкнутых систем.
Время простоя ТУ есть сумма времени нахождения в очереди
Точ и времени обслуживания ТОбс [см. (7.1.19)]. Случайные вели-
чины Точ и Тобс независимы, поэтому плотность распределения
времени простоя можно найти как композицию двух законов [см.
(7.1.24)]:
/п(0=[^/оч(/-т)^ (/>0).
о
Зачастую имеется всего один канал обслуживания техники
(n=i). В этом случае многие формулы значительно упрощают-
ся. Состояние Xi — это такое состояние, когда отказало одно тех-
ническое устройство и оно находится на обслуживании. Граф
состояний рассматриваемой системы показан на рис. 7.1.3. Ве-
роятность pi найдем из второй формулы выражения (7.1.12) при
п—1 и г=0:
(7.1.27)
Р (т, И.)
так как при п= 1 Р (п, п) =Р (0, п). Заметим, что при п=1
281
Вероятность того, что в- очереди будет г технических уст-
ройств, можно найти по формуле
P(m-(r + l), х)
Вероятность ро найдем из нормировочного условия
т т
z=o
откуда
(7.1.28)
Р(т, у) Р(т, х) Ро Р(т, Х)
z=o
(7.1.29)
п — Р (т' •
,,J Л(«. х) ’
>• 2....
где pi — вероятность того, что в обслуживании нуждается I
технических устройств (/=0, 1, 2, ..., т), т. е. I техни-
ческих устройств простаивает.
тХ
(т-я+Г)А (т-я)А
(ст-Дг+ПА (ст.-Дг)Л
Рис. 7.1.3
1
Среднее число простаивающих технических устройств будет
?(да~/. х)=—1—yi[/n-(m-/)]P(/n-/, х)=
Л(да, х) /?(да,х)2^1
т^Р(т — Ц х) =
z=o z=o
Х)-У}/Р(Л X) =
— т—х =т — хО~Ро)-
л R(m,x)
Zf=o
1
R(m, у.)
1
я (да. х)
(7.1.30)
282
Среднее число обслуживаемых технических устройств $ , рав-
ное среднему числу занятых каналов Л» будет
У=Л= 1 — 7?0= 1 — (yw> х) (7.1.31) х
Среднее число ТУ, ожидающих в очереди г, будет [см. (7.1.30)
и (7.1.31)]
r=Z-A = m-(z+l)^^^=m-(x + l)(l-^). (7.1.32)
R \mf X)
Коэффициент использования техники £ (или вероятность того,
что техническое устройство будет работать) определим из выра-
жения
R(m-1, у)
т 1 R(m, j)
т
$=1-—=1
т
— X Яри-1, х)_ X /1 ч
т R(m,f_) ™ Р°'
Среднее время простоя ТУ будет [см. (7.1.18) и (7.1.27)]
(7.1.33)
j__-j 1 — 5__1 т _____1 т — х(1—р0)____1 I
₽ 5 k X . Р 1—Ро V- 1 — Ро’
— (1 — Ро) । .
т (7.1.34)
Среднее время нахождения ТУ в очереди найдем из выраже-
ния [см. (7.1.21), (7.1.29), (7.1.32) и (7.1.34)]
7—7 7 1 1 1 г /71ое>
-оч = tn “ ‘обе ---------------= --------. (7.1 .35)
(Л 1—Ро Р- Р 1— Ро
Плотность распределения времени простоя ТУ будет иметь вид
f /а_V e—v-*n — V
f^-2j k\ е*Р*~Ъ k\ в R(m,t) ~
Л = 0 Л=0
, т—1 , . . т—1
1 VI {[Lt)k Xm~k (\t)k т\
k\ (т — k)l R(mt4)m\ Ы (т—k)\
Л=0 ' л=о
= Г) у с‘ [р (Of [q (ОГ-*, (7.1.36)
R(m, x)k(0]m U l*v,J *
*=0
28а
где
(7.1.37)
1 ~t“ лг
q(t)=\-p(t). (7.1.38)
Заметим, что из свойства биномиального распределения следу-
ет, что
2 1 - Рт. (7.1.39)
*=0
С учетом этого выражения получим формулу для плотности рас-
пределения времени простоя [см. (7.1.36) — (7.1.39)]:
/ к/ \д
Л(0=jrr^ibJS). =|ИГ^
к 1 + к/ )
1 ( М )”*
+к/Г-(т (7.1.40)
» (i + к/ 7
Плотность распределения времени ожидания в очереди будет
[см. (7.1.24), (7.1.36) —(7.1.40)]
Л1—1 k
/оч(0=8(ОРо + 5 ^-е^р^^р.А-
*=1
= Р0 U(/)+V-e~^[(1 }. (7.1.41)
Основные расчетные формулы
Вероятность того, что все ТУ работают нормально:
1
р =---------------------------------------,
R(т, п, р) Р(п, n)R(m— n~ 1,
+ Р(0, п)Р(т, у.)
где
284
^ = 1—р;
к
“=—;
р
А к
Вероятность того, что отказало ровно k ТУ и все они обслужи- ’
ваются (очереди нет):
д.^Р).р0 *=(0, 1, 2,..., п).
Вероятность того, что отказало («4 г) ТУ — п из них обслу-
живается и г ожидает в очереди:
_ Р(п, л)Р(т —(п + г), х) z 0 , )
Рп+г— —т -т- г Ръ \г—и, 1,..., т — п).
Р(0, п)Р(т, х)
Среднее число обслуживаемых ТУ (среднее число занятых
каналов)
п
kB (т, k, р} । P(n, ri)R(m — п—1, X)
’ П Р(0, п)Р(т, х)
k = Po
-к=0
Среднее число ТУ, ожидающих в очереди:
р<£У(£ z> z)l
Среднее число простаивающих ТУ
I=k 4- г.
Вероятность того, что ТУ будет простаивать (коэффициент
простоя техники):
т
Среднее время безотказной работы ТУ
W-
Среднее время простоя ТУ
7 =7 £ 1 7
п рс-с к т_у
285;
Среднее время пребывания ТУ в очереди
7 =_L_£______L
04 X 1-С (л '
Задачи и упражнения
7.1.1. На аэродроме имеется 24 самолета и один заправщик
горючим. Заправка длится в среднем — =0,5 часа. Полеты
спланированы так, что каждый самолет совершает в среднем
два вылета в сутки. Определить среднее время простоя самолета,
связанное с его заправкой горючим, если после каждого полета
он требует заправки.
Решение
Рассматривается замкнутая система СМО при га=1; /п=24;
,11.. „1
Х=-------; р.=2----.
12 час час
Следовательно:
Х=т -у-=24.
Л
Далее, вероятность того, что заправщик будет свободен, равна
[см. (t.1.29), (1.5.31), (1.5.32)]
Р(т, х) Я (24, 24) _
Ро~ Р(т, х) “Я(24, 24)
ф* / 24 + 0,5-24 \ / 23 + 0,5-24 \
« -1_____15 I 1 15--------------L =0,149,
/ 24 + 0,5 — 24 \
ф* I I I ' . I
\ Кй /
где
X____
Ф*(х)=—[в 2 di
]/2л J
— оо
— нормальная функция распределения, таблицы которой приве-
дены в [2].
Заметим, что точное значение Р^т’ =0,147.
Я (т, х)
Среднее число заправляемых и ожидающих заправки самоле-
тов будет равно [см. (7.L32)]
7=т-^[\-р0] = 2,7.
286
Среднее число самолетов, ожидающих заправки [см. (7.1.31)]:
г=Т—Г=Г—(1—р0) = 1,85.
Среднее время простоя самолета
/=— Г-----—-----1 1=2,04 часа,
n X Lx(i — «о) J
а среднее время ожидания заправки равно
/Оч=/П—А>бс=2,04—0,5=1,54 часа.
7.1.2. В гараже имеется 30 автомашин и три станции обслу-
живания, где проводятся профилактические и ремонтные работы.
В среднем каждая машина в течение месяца трижды нуждается
в проведении ремонтных работ. Машина при выполнении ремонт-
ных работ находится на обслуживании в среднем одни сутки. Оп-
ределить вероятность того, что отдельно взятая автомашина не
будет нуждаться в проведении ремонтных работ, и найти сред-
нее время, потребное для проведения ремонтных работ и ожида-
ния этих работ.
Решение
Опять рассматривается замкнутая система СМО с парамет-
рами
га=3; /га=30; Х=— =0,1-------; |х = 1------.
30 сутки сутки
Имеем:
Х=— =30;
Л. х
а=—=0,1;
р = —°—=0,91;
Г Ц-а
^ = 1—р=0,09;
п
R(m, п,рУ==у>с^=г 4
дт 2J
fe=0
Р(л, л)/?(/л—л—1, х) |6 5
P(0rn)P(m, х)
ПЬ формуле (7.1.12) находим
р0= ----------------------------=0,0336.
R (т, nt р) Р (п, п) R(m — п— 1, %)
" + Р(0, л)Р(т, х)
287
По формуле (7.1.13) определим среднее число занятых каналов й:
7=2,48. '
Среднее число автомашин, ожидающих ремонтных работ, будет
равно [см. (7.1.14)]
7=2,08.
Среднее число автомашин, нуждающихся в проведении ремонт-
ных работ, будет
7=7 4-7=2,48 + 2,08 = 4,56.
Вероятность того, что отдельно взятая машина не будет нуж-
даться в проведении ремонтных работ, равна
5 = 1 — С= 1--=0,848,
т
т. е. в среднем около 85% всех машин не будут нуждаться в про-
ведении ремонтных работ.
Среднее время проведения ремонтных работ и ожидания ре-
монтных работ будет равно
, /п= —---Ё—суток.
Среднее время ожидания в очереди будет
^оч-^п--— — 0,79 суток,
р-
§ 7.2. ЗАМКНУТАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
С ЧАСТИЧНОЙ ВЗАИМОПОМОЩЬЮ МЕЖДУ КАНАЛАМИ
В отличие от системы, рассмотренной в предыдущем пара-
графе, где техническое устройство (ТУ) могло обслуживаться
только одним каналом, в этом параграфе будет рассмотрена сис-
тема, в которой возможна частичная взаимопомощь между ка-
налами. Например, если имеется шесть групп обслуживания са-
молетов, то один отказавший самолет будут обслуживать сразу
две группы; два отказавших самолета будут обслуживать уже
четыре группы: две группы — один самолет, две группы — второй
самолет. Если в обслуживании нуждаются три самолета, то все
они будут обслуживаться, каждый двумя группами. Если же
в обслуживании нуждаются четыре самолета, то все шесть групп
будут принимать участие в обслуживании самолетов; при этом
два самолета будут обслуживаться каждый двумя группами и
два самолета будут обслуживаться каждый одной группой и т. д.
288
Предполагается, что при обслуживании одного самолета двумя
группами производительность увеличивается вдвое.
Постановка задачи: Имеется т одинаковых ТУ,
каждое из ^которых может в случайные моменты времени отка-
зать (выйти из строя). Поток отказов каждого ТУ пуассоновский
с плотностью к. Каждое отказавшее ТУ может обслуживаться од-
ним из п каналов. Плотность пуассоновского потока обслужива-
ний каждого канала ц. Если отказало не более
Л=[у] (7.2.1)
технических устройств, то каждое отказавшее ТУ обслуживается
одновременно I каналами (напомним, что [х]— целая часть чис-
ла х). При этом производительность обслуживания каждого ТУ
равна 1р. Величина I равна максимальному числу каналов, кото-
рое может обслуживать одно ТУ.
Если число отказавших технических устройство / лежит в
пределах
h < j <п,
то в обслуживании участвуют все п каналов, распределяясь бо-
лее или менее равномерно между всеми / отказавшими ТУ, при
этом каждое ТУ обслуживается одновременно не более чем I ка-
налами.
тК (rn-i)k (m-h+l)k (m-h)k
(m-n-r+пк (m-n-r)K Л.
пр пр
Рис. 7.2.1
Хт
яр
Если отказало k технических устройств то ров-
но п ТУ обслуживается (каждое ТУ обслуживается одним ка-
налом) и k—п ожидает очереди на обслуживание.
Состояния системы будем связывать с числом отказавших ТУ:
Xi — отказало ровно I ТУ (i=0, 1, ..., ft) и все они нахо-
дятся на обслуживании (ремонтируются, проходят ре-
289
гламент и т. п.); каждое ТУ обслуживаемся одновре-
менно/ каналами;
Xj — отказало ровно / ТУ (j=h+l, ..., п.—1) и все они на-
ходятся на обслуживании; в обслуживании участву-
ют одновременно все п каналов, распределяясь про-
извольно между отказавшими ТУ, но так, что все п.
каналов заняты обслуживанием;
хп+г — отказало ровно n+r ТУ (r=0, 1, ..., т — п); из них
п обслуживается (каждое ТУ одним каналом) и г
ожидает в очереди на обслуживание.
Граф состояний системы показан на рис. 7.2.1.
Сравнивая граф этой системы с графом, изображенным на
рис. 7.1.2, можно убедиться в том, что с точностью до обозначе-
ний они совпадают. Следовательно, можно воспользоваться фор-
мулами (7.1.12) для вероятностей состояний при стационарном
режиме работы рассматриваемой системы:
Р/=В(ОТ,У(,))Ро (/=0, 1,..., А); (7.2.2)
?(0
Р(Л, -/.) (у=А, А+1,..., «); (7.2.3)
7 Р(0, h)P(m, х) . '
, рп+г== ^Р^-(п + г),Г) ^(г=0,1..., т—п);(7.2.4)
, Р(0, h)P(m, х) °
где
/’и>=-ггг(?«>=1<т.3.5>
«,=4-; (7.2.6)
/р.
Z = -^-; (7.2.7)
А
Ро=---------------5; (7.2.8)
• ™ R(m, h,pw) + P(h, h)R(m — h—\, х)
Р(0, h)P(m, х)
В(/П, /, Р(1)) = СтРщЯ(1~1',
R(m, А, р(0) = 2
л=о
Найдем среднее число обслуживаемых ТУ $:
h п т—п h
s=yjPi+ V JPj+пУ, P^r=-^-^iB(т, i, Pw)±
iTo j=h+l r=l 1=0
290
+ р,Х(рг~? E x)+
P(0, h)P(m, 1) ы
„ /=*+1
m—n
+ np0 V p(m-(« + r), x). (7.2.9)
P (О, Л) P (tn, x)
r-1
Проведем следующие преобразования:
2 хИ^/РИ-Л *>“2 jP{tn — j, x)=
;=л+1 7=o 7=o
n h
= 2 — J)]P(m~J> — Z).-=
;=o ' 7=o
j=0 7=0 -
x)=m 2P(y’ *>“ 2 p(7’X) -
i=o l_7=o ' ’
m m—n—1
-^JPU, z)+ 2 x)-/n
7=0 >=o
m—ft—1
J=0
rn—n—1
m
/=0
m—ft—1
2 P(7’z) +
J=0 7=0
+ y.jP{J, z)- 2 Z)==^[7?(/«-A-l, x)-
7=0 7=0
— R(m — n — 1, Z)] — x[7?(/n — h — 2, x)—R(m — n — 2, x)]. (7.2.10)
Далее
2"'P(m-(n + r), x)=m 2+1)P(r, ri = R(m-(n + 1), x) (7.2.11)
r=l r=0
С учетом выражений (7.2.10) и (7.2.11) среднее число обслужи-
ваемых ТУ будет равно
ft
7==Д2_У’/Т?(т1 -----й>---------[m[R(m-h-\, х)~
qm V ^( ,/ 1 Р (0, Л) Р (т, х) I
— R(m—п— 1, х)] —х[^(»1 —Л —2, х) — R{m — п, — 2, х)]} +
Ч----яРоР(/>’ Л)— R(т - (п 4-1), х).
Р(0, h)P(m, х)
(7.2.12)
291
Среднее число ТУ, ожидающих очереди на обслуживание,
можно найти из выражения
т—л т—п
j j ГР(П~(П + Г),
Г=1 г=1
т—п
Г = 1
= Ро
Р (h, h)
Р(0, h)P(m, х)
т—п
(т — п) yj Р(т — п — г, х1-
т—п
- J] (т — п — г)Р(т — п — г, х)
PoPlh, h)
Р(0, h)P(m, х)
Х[(/и — n)R(m—п— 1, х)—//?(/п — п — 2, x)L (7.2.13)
Тогда среднее число простаивающих технических устройств
будет
(7.2.14)
Вероятность того, что ТУ будет работать, равна
Х-=1------ .
т
Среднее время простоя ТУ будет
7=1
4П Jp J
(7.2.15)
(7.2.16)
где /р — -----среднее время работы ТУ.
Плотность распределения времени ожидания в очереди най-
дем из выражения, аналогичного выражению (7.1.24):
(h л—1 \ т—п—1
Sa+ S ^)+ S !!t7rLe-^^(t>o).
1=0 j=/i+i / r=o (7.2.17)
Используя тот же прием, который был применен в предыду-
щем параграфе при непосредственном определении среднего вре-
мени нахождения в очереди, из формулы
t04= J tfw(t)dt
292
получим такое выражение (см. (7.1.25), (7.1.26) и (7.2.4)];
т—л—1
Е (» + Н, ЙЛ. г). (7.2.18)
г=0 '
Сумму, входящую в это выражение, можно вычислить по
формуле (7.1.26). Следует обратить внимание, что при вычисле-
нии правой части выражения (7.1.26) нужно пользоваться фор-
мулами § 7.1 для вычисления величины ро [см. (7.1.9)] и величи-
ны | [см. (7.1.13) —(7.1.16)].
Для нахождения среднего времени обслуживания одного ТУ
можно воспользоваться равенством
4=А>ч-Но5с, (7.2.19)
откуда
/обс = ^п — А,ч.
Ввиду небольшого числа формул не будем приводить сводки
основных расчетных формул.
Задачи и упражнения
7.2.1. Рассматривается работа аэродрома, к которому припи-
сано 20 самолетов. На аэродроме имеется 4 ангара для ремонта
и профилактического осмотра самолетов. (Число каналов обслу-
живания п—4). Оборудование ангаров допускает «взаимопо-
мощь» при ремонте самолетов только между двумя ремонтными
группами (1=2). Каждый самолет в среднем через 5 суток дол-
жен либо ремонтироваться, либо проходить профилактический
осмотр: -----—V Ремонт или профилактика осуществ-
\ 5 сутки/
ляется в среднем в течение суток |р. = 1-|. Определить па-
\ сутки)
раметры работы аэродрома с точки зрения ремонта и проведения
профилактического осмотра самолетов.
Решение
Работу аэродрома можно рассматривать как работу замкну-
той системы массового обслуживания с параметрами:
й=4; m = 20; Z=2; h = \—1 = 2; Х=0,2—— ;
L Z J сутки . ;
1>=1—2; х= — =20; а,= —=0,1;
сутки X 1 /р.
Лп= 0,1 =0,091; #,..=0,909.
1 + 0,1 . ,
10—1964
293
По формуле (7.2.8) можно найти вероятность того, что все са-
молеты будут находиться в эксплуатации.
Предварительно определим значение следующих функций:
^-^-^=3,90; Р(й, й)=0,271;
Р(0, Л)=0,135; Р(т, х)=0,0888;
R(m — h—l, х)=0,270.
Следовательно:
" Р(Л, Л)/?(т —Л—1, х)
+ Р(0, h)P(m, х)
Среднее число обслуживаемых самолетов [см. (7.2.12)] равно
7=2,80.
Среднее число самолетов, ожидающих обслуживания [см.
(7.2.13)]:
7=0,937.
Среднее число обслуживаемых и ожидающих обслуживания са-
молетов (т. е. самолетов, которые не находятся в эксплуатации)
7=7+7=3,74.
Вероятность того, что отдельно взятый самолет будет нахо-
диться в эксплуатации: _
$ = 1---1- =0,813,
т
т. е. около 81% самолетов будет эксплуатироваться, а 19% —
ожидать ремонта или находиться в ремонте.
Среднее время простоя самолета
— _ 1 _с
ta=tf—^-=1,15 суток.
Среднее время ожидания ремонта найдем по формуле
(7.2.18):
/0 ч=0,36 суток,
откуда среднее время ремонта самолета будет
70бс=7и—7с,=0,79 суток.
294
7.2.2. Условия задачи такие же, как и предыдущей. Требуется
определить, насколько взаимопомощь увеличивает эффективность
обслуживания.
Решение
Для решения задачи найдем сначала характеристики обслу-
живания без взаимопомощи, для чего применим формулы § 7.1.
По формуле (7.1.9) найдем вероятность того, что все само-
леты будут эксплуатироваться, имея в виду, что при отсутствии
взаимопомощи параметры системы следующие:
щ = 20; и = 2; и = 1 —J;
сутки
Х=0,2 —— ;
сутки
а= —=0,2;
р-
р= 0,2 =0,167;
г 1+0,2
4 = 0,833;
Х=20.
Отсюда [см. (7.1.9)]
^0=0,0205.
Среднее число обслуживаемых самолетов [см. (7.1.13)]
£=7=3,13.
Среднее число самолетов, ожидающих обслуживания, найдем
по формуле (7.1.14)
7=1,01.
Среднее число обслуживаемых и ожидающих обслуживания
самолетов
Г=£"Д-7=4,14.
Вероятность того, что самолет будет находиться в эксплуа-
тации:
$=1-—=0,793.
т
Сравнивая системы со взаимопомощью (задача 7.2.1) и без
взаимопомощи, видим, что в данном случае взаимопомощь не
приводит к серьезному увеличению эффективности обслуживания.
Ю* 295
§ 7.3. ЗАМКНУТАЯ СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ
С ПОЛНОЙ ВЗАИМОПОМОЩЬЮ МЕЖДУ КАНАЛАМИ
Постановка задачи. В отличие от системы, рассмот-
ренной в § 7.2, где техническое устройство (ТУ) могло обслужи-
ваться несколькими, но не всеми каналами одновременно, в этом
параграфе будет рассмотрена система, в которой возможна вза-
имопомощь между всеми п каналами. Например, если имеется
две бригады, обслуживающие самолеты, то один отказавший са-
молет будут обслуживать сразу две бригады, два самолета бу-
дут обслуживать тоже две бригады: каждая бригада будет об-
служивать по одному самолету. При этом предполагается, что
Рис. 7.3.1
если одно ТУ обслуживается сразу h каналами, то производи-
тельность увеличивается ровно в h раз. Занятые каналы обслу-
живания могут распределяться произвольным образом между
обслуживаемыми ТУ, лишь бы все они участвовали в обслужива-
нии. Таким образом, если отказало хотя бы одно ТУ, то все п ка-
налов заняты обслуживанием. В остальном рассматриваемая си-
стема работает так же, как и система, исследованная в §7.1 и 7.2.
При анализе такой системы массового обслуживания введем
следующие состояния:
х0 — все ТУ работают; каналы обслуживания свободны;
xk — отказало ровно k технических устройств (k= 1, 2, ..., п),
все эти k технических устройств обслуживаются п ка-
налами, которые распределяются приблизительно рав-
номерно между каналами;
хп+г — отказало ровно п+r технических устройств (г = 0, 1,
2, ..., (ш — и)); из этого числа ТУ п обслуживается п
каналами и г ожидает в очереди на обслуживание.
Граф состояний рассматриваемой системы показан на
рис. 7.3.1.
Этот граф состоянии с точностью до обозначений совпадает
с графом состояний системы, рассмотренной в § 7.1 и изобра-
женной на рис. 7.1.3. Следовательно, при определении вероятно-
стей состояний этой системы можно воспользоваться формулой
(7.1.29):
296
л=£ЙЙг(4=0’b2.........я,; (7А1)
Pn+r= PKw~(n+/)> х) (г=0, 1, 2,..., т -л), (7.3.2)
х)
где
Х=-?- . (7.3.3)
Среднее число простаивающих ТУ будет равно [см. (7.1.30)]
7=2 ^+r)pn+r=m-^(\-p^. (7.3.4)
*=0 г=1
Среднее число обслуживаемых ТУ можно найти по формуле
п т—п
*"=У kpk + n У Рп+г = ——-
LJ £4 R(m, х)
Л=0 Г=1
kP(m — k, х)-Н
т—п п
+ п У Р(/тг-(п^г), х) = ’ [т[Р(т, х)-
r=l J
-R(m-n-\, x)]-xR(m-l, x)-^(m-«-2, x)J +
4-пР(т — п — 1, х)Ь (7.3.5)
Для нахождения среднего числа ТУ, ожидающих в очереди г,
можно воспользоваться равенством
Z=
откуда
r=l— s.
(7.3.6)
Вероятность того, что ТУ будет работать, найдем по формуле
5 = 1-—=— (1-Ро). (7.3.7)
т т
Среднее время простоя будет [см. (7.1.34)]
7=7 1=1= п р ? _ 1 1 - -Z- 0 -Ро) т 1 Z - . (7.3.8)
X — (1 - Ро) т пр. 1—Ро
297
Плотность распределения времени ожидания в очереди най-
дем по формуле, аналогичной формуле (7.2.17):
л—1 т—л—1
J ^^е-^рп+г. (7.3.9)
й=0 г=0
Среднее время ожидания в очереди
оо 7Л—Л—1 ОО
70, = ^/0Ч(/)^= 2 Pn+r
О г=0 О
т—л—1 rm-л тл—л—1
= ~k Е ('•+D/>.«=~ -
r=0 L г=о г=0
г т—п
=тр-^>^Ер^<:7,>-*- =
г=0
= — \7-(т-п-+ (7-ЗЛ0)
лр L R(mt х) J
Среднее время обслуживания одного ТУ можно найти по фор-
муле
7обс=7п-7оч: (7.3.11)
Ввиду небольшого объема этого параграфа не будем приво-
дить сводку основных расчетных формул.
Задачи и упражнения
7.3.1. Рассмотрим те же условия, что и в задаче 7.1.2, но при
этом допустим наличие взаимопомощи между всеми каналами.
Параметры системы остаются теми же. Найти те же характери-
стики системы, что и в задаче 7.1.2.
Решение
По формуле (7.3.1) найдем вероятность ро того, что ни один
самолет не будет нуждаться в проведении ремонтных работ:
PSa^L=0,152.
° 1)
По формуле (7.3.5) находим среднее число ремонтируемых
самолетов
s=2,18.
.298
Далее, по формуле (7.3.4) найдем общее число простаиваю-
щих самолетов l=s+r:
7=4,00.
Следовательно, среднее число самолетов, ожидающих ремон-
та, будет равно
7=7—7=1,82.
Вероятность того, что отдельный самолет не будет нуждаться в
ремонте, равна
(• = 1— =0,867.
т
Среднее время проведения ремонтных работ и ожидания ре-
монта
t„=-у- 1 = 1,53 суток.
Среднее время ожидания в очереди будет равно
/оч=*п—А>бс=0,53 суток—12,7 часа,
т. е. снизилось приблизительно на 30% по сравнению со случа-
ем, когда взаимопомощи между каналами нет (см. задачу 7.1.2).
Приложение
Таблицы распределения Пуассона
В приложении приведены таблицы * значений функции
R(m, d)—\—R(m, а),
где
т k
R(m,
Л=0
— распределение Пуассона.
Вероятность
„т
Р(т, а)=— е~а
т\
определяется по табличным значениям следующим образом:
Р(гп, a) = R(m, a) — R(m — 1, a)=R(m — \, a) — R(m, а).
При а>20 вычисление можно проводить по приближенной
формуле
j R (т, а)« Ф* /и + 0’5_~а\ t
I Va )
где
х _
ф»(х)=—— е 2 dt
нормальная функция распределения, таблицы которой приведе-
ны в [2].
Таблица была специально рассчитана на ЭЦВМ В. К. Томшиным.
R (m, a)
а т 0,05 0,10 0,15 0,20
0 4,87706-2* 9,51626-2 1,39292-1 1,81269-1
1 1,20910-3 4,67884-3 1,01858-2 1,75231-2
2 2,00670-5 1,54652-4 5,02862-4 1,14848-3
3 2,49740-7 3,84611-6 1,87136-5 5,68401-5
4 5,58051-7 2,25809-6
т а 0,25 0,30 0,35 0,40
0 2,21199-1 2,59182-1 2,95312-1 3,29680-1
1 2,64990-2 3,69363-2 4,86711-2 6,15519-2
2 2,16150-3 3,59950-3 5,50893-3 7,92633-3
3 1,33370-4 2,65812-4 4,73350-4 7,76251-4
4 6,61223-6 1,57857-5 3,27367-5 6,12429-5
5 2,74333-7 7,84101-7 1,89379-6 4,04227-6
2,28902-7
а т 0,45 0,50 0,55 0,60
0 3,62372-1 3,93469-1 4,23050-1 4,51188-1
1 7,54392-2 9,0204(1-2 1,05728-1 1,21901-1
2 1,08793-2 1,43877-2 1,84641-2 2,31153-2
3 1,19535-3 1,75162-3 2,46580-3 3,35807-3
4 1,05904-4 1,72116-4 2,66027-4 3,94487-4
5 7,85413-6 1,41650-5 2,40520-5 3,88566-5
6 5,00368-7 1,00244-6 1,87100-6 3,29359-6
7 1,28202-7 2,45331-7
т а 0,65 0,70 0,75 0,80
0 4,77954-1 5,03415-1 5,27633-1 5,50671-1
1 1,38624-1 1,55805-1 1,73359-1 1,91208-1
2 2,83423-2 3,41416-2 4,05054-2 4,74226-2
3 4,44783-3 5,75346-3 7,29217-3 9,07986-3
4 5,64977-4 7,85535-4 1,06468-3 1,41131-3
5 6,02060-5 9,00264-5 1,30554-4 1,84342-4
6 5,52255-6 8,88364-6 1,37886-5 2,07462-5
7 4,44794-7 7,69360-7 1,27805-6 2,04954-6
8 1,05181-7 1,79876-7
понимать следующим образом:
♦Запись выражения 4,87702-2 нужно
4,87706—2—4,87706 • 10-2.
301
R (тп, a)
0,85 0,90 0,95
0 5,72585-1 5,93430-1 6,13259-1
1 2,09282-1 2,27518-1 2,45855-1
2 5,48787-2 6,28569-2 7,13381-2
3 1,11310-2 1,34587-2 1,60744-2
4 1,83464-3 2,34412-3 2,94931-3
5 2,54280-4 3,43495-4 4,55539-4
6 3,03725-5 4,34008-4 6,06919-5
7 3,18605-6 4,81730-6 7,10545“б
8 2,97499-7 4,76648-7 7,42060-7
тп a 1,0 1,1 1,2 1,3
0 _ 6,32121-1 6,65129-1 6,98806-1 7,27468-1
1 2,64241-1 3,00971-1 3,37373-1 3,73177-1
2 8,03014-2 9,9г 837-2 1,20513-1 1,42888-1
3 1,89882-2 2,57418-2 3,37690-2 4,30955-2
4 3,65985-3 5,43529-3 7,74579-3 1,06630-2
5 5,94185-4 9,67858-4 1,50023-3 2,23061-3
6 8,32417-5 1,48828-4 2,51113-4 4,03579-4
7 1,02498-5 2,01235-5 3,69793-5 6,42745-5
8 1,12578-6 2,42660-6 4,85923-6 9,13742-6
9 1,12006-7 2,63652-7 5,76561-7 1,17319-6
10 1,37836-7
a ni^ 1,4 1,5 1.6 1,7
0 7,53403-1 ; 7,76870-1 7,98103-1 8,17316-1
1 4,08167-1 4,42175“i 4,75069-1 5,06754-1
2 1,66502-1 1,91153-1 2,16642-1 2,42777-1
3 5,37253-2 6,56425-2 7,88135-2 9,31894-2
4 1,42533-2 1,85759-2 2,36823-2 2,96148-2
5 3,20115-3 4,45598-3 6,04029-3 7,99943-3
6 6,22315-4 9,25991-4 1,33576-3 1,87508 -3
7 1,06548-4 1,69565-4 2,60440-4 3,87734-4
8 1,62888-5 2,77352-5 4,53762-5 7,16738-5
9 2,24852-6 4,09692-6 7,14252-6 1,19734-5
10 2,82875-7 5,51168-7 1,02514-6 1,82439-6
1,35333-7 2,55895-7
302
Я (т, а)
а т 1,8 1,9 2,0 2,1
О 8,34701-1 8,50431—1 8,64665-1 8,77544-1
1 5,37163-1 5,66251-1 5,93994-1 6,20385-1
2 2,66379—1 2,96280-1 3,23324-1 3,50369-1
3 1,08708-1 1,25298-1 1,42877-1 1,61357-1
4 3,64067-2 4,40814-2 5,26530-2 6,21261-2
5 1,03780-2 1,32192-2 1,65636-2 2,04491-2
6 2,56945-3 3,44614-3 4,53381-3 5,86212-3
7 5,61527-4 7,93458-4 1,09672-4 1,48603-3
8 1,09754-4 1,63446-4 2,37448-4 3,37306-4 .
9 1,93877-5 3,04436-5 4,64989-5 6,92703-5
10 3,12354-6 5,17316-6 8,30907-е 1,29829-5
11 4,62125-7 8,08257-7 1,35546-6 2,23711-6
2,08194-7 3,56595-7
2 а т 2,2 1,9 2,0 . j 2,1
8,89197-1 8,99741-1 9,09282-1 9,17915-1
1 6,45430-1 6,69146-1 6,91559-1 7,12703-1
2 3,77286-1 4,03961-1 4,30291-1 4,56187-1
3 1,80648-1 2,00653-1 2,21277-1 2,42424^1
4 7,24963-2 8,97507-2 9,58686-2 1,08822-1
5 2,49098-2 2,99757-2 3,56725-2 4,20210-2
6 7,46135-3 9,36193-3 1,15941-2 1,41873-2
7 1,97756-3 2,58884-3 3,33862-3 4,24670-3
т а 2,2 2,3 2,4 2,5
8 4,69520-4 6,41578-4 8,61979-4 1,14025-3
9 1,00888-4 1,43944-4 2,01542-4 2,77352-4
10 1,97888-5 2,94875-5 4,30368-5 6,16266-5
11 3,56896-6 5,55602-6 8,45391-6 1,25982-5
12 5,95333-7 9,69114-7 1,53732-6 2,38391-6
13 2,60421-7 4,19634-7
303
R (m, a)
m a 2,6 2,7 2,8 2,9
0 9,25726-1 9,32794-1 9,39190-1 \ 9,44977-1
1 7,32615-1 7,51340-1 7,68922-1 7,85409-1
2 4,81570-1 5,06376-1 5,30546-1 5,54037-1
3 2,63998-1 2,85908-1 3,08063-1 3,30377-1
4 1,22577-1 1,37092-1 1,52324-1 1,68223-1
5 4,90372-2 5,67317-2 6,51103-2 7,41738-2
6 1,71701-2 2,05695“2 2,44106-2 2,87167-2
7 5,33376-3 6,62117-3 8,13074-3 9,88451-3
8 1,48695-3 1,91363-3 2,43278-3 3,05783-3
9 3,75653-4 5,01365-4 6,60087-4 8,58122-4
10 8,67147-5 1,20054-4 1,63732-4 2,20207-4
11 1,84202-5 2,64590-5 3,73867-5 5,20294-5
12 3,62309-6 5,40024-6 7,90616-6 1,13865-5
13 6,63669-7 1,02649-6 1,55652-6 2,31995-6
1,82990-7 2,86585-7 4,41898-7
m a 3,0 3,1 3,2 3,3
0 9,50213-1 9,54951-1 9,59238-1 9,63117-1
1 8,00852-1 8,15298-1 8,28799-1 8,41402-1
2 5,76810-1 5,98837-1 6,20096-1 6,40574-1
3 3,52768-1 3,75160-1 3,97480-1 4,19662—1
4 1,84737-1 2,01811-1 2,19387-1 2,37410-1
5 8,39179-2 9,43338-2 1,05408-1 1,17123-1
6 3,35085-2 3,88042-2 4,46191-2 5,09656-2
7 1,19045-2 1,42125-2 1,68298-2 1,97771-2
8 3,80299-3 4,68323-3 5,71414-3 6,91181-3
9 1,10249-3 1,40092-3 1,76189-3 2,19454-3
10 2,92337-3 3,83409-4 4,97168-4 6,37845-4
11 7,13871-5 9,66543-5 1,29249“4 1,70836-4
12 1,61496-5 2,25761-5 3,11374-5 4,24082-5
13 3,40243-6 4,91130-6 6,98688-6 9,80731-6
14 6,70902-7 9,99804-7 1,46676-6 2,12282-6
15 2,89132-7 4,32236-7
304
R (m, d)
a m 3,4 3,5 : 3,6 3,7
0 9,66627-1 9,69803-1 9,72676-1 9,75276—1
1 8,53158-1 8,64112-1 8,74311-1 8,83799-1
2 6,60260-1 6,79153-1 6,97253-1 7,14567-1
3 4,41643-1 4,63367-1 4,84784-1 5,05847-1
4 2,55818-1 2,74555-1 2,93562-1 3,12781-1
5 1,29458-1 1,42386-1 1,55881-1 1,69912-1
6 5,78532-2 6,52881-2 7,32734-2 8,18092-2
7 2,30739-2 2,67389-2 3,07893-2 3,52407-2
8 8,29274-3 9,87366-3 1,16714-2 , 1.37028-2
9 2,70873-3 3,31494-3 4,02427-3 4,84834-3
10 8,10171-4 1,01939-3 1,27129-3 1,57218-3
11 2,23343-4 2,88992-4 3,70322-4 4,70202-4
12 . 5,70746-5 7,59583-5 1,00030-4 1,30425-4
13 1,35891-5 1,86030-5 2,51798-5 3,37188-5
14 3,02831-6 4,26413-6 5,93266-6 8,16087-6
15 6,34536-7 9,18400-6 1,31334-6 1,85658-6
16 2,73998-7 3,98708-7
a m 3,8 3,9 4,0 4,1
0 9,77629-1 9,79758-1 9,81684-1 9,83427-1
1 8,92620-1 9,00815-1 9,08422-1 9,15479-1
2 7,31103-1 7,46875-1 7,61897-1 7,76186-1
3 5,26515-1 5,46753-1 5,66530-1 5,85818-1 "
4 3,32156-1 3,51635-1 3,71163-1 3,90692-1
5 1,84444-1 1,99442-1 2,14870-1 2,30688-1
6 9,08924-2 1,00517-1 1,10674-1 1,21352-1
7 4,01074-2 4,54015-2 5,11336-2 5,73121-2
8 1,59845-2 1,85328-2 2,13634-2 2,44918-2
9 5,79928-3 6,88962-3 8,13224-3 9,54027-3
10 1,92889-3 2,34880-3 2,83977-3 3,41016-3
11 5,91853-4 7,38870-4 9,15230-4 1,12530-3
12 1,68457-4 2,15643-4 2,73718-4 3,44642-4
13 4,46947-5 5,86754-5 7,63292-5 9,84338-5
14 1,11022-5 1,49486-5 1,99325-5 2,63300-5
15 2,59209-6 3,57960-6 4,89343-6 6,62165-5
16 5,70944-7 8,08417-7 1,13365-6 1,57137-6
2,48998-7 3,53364-7
305
R (т, а)
т а 4,2 4,3 4,4 4,5
0 9,85004-1 9,86431-1 9,87723-1 9,88891-1
1 9,22023-1 9,28087-1 9,33702-1 9,38901-1
2 7,89762-1 8,02645-1 8,14858-1 8,26422-1
3 6,04597-1 6,22846-1 6,40552-1 6,57704-1
4 4,10173-1 4,29562-1 4,48816-1 4,67896-1
5 2,46857-1 2,63337-1 2,80088-1 2,97070-1
6 1,32536-1 1,44210-1 1,56355-1 1,68949-1
7 6,39433-2 7,10317-2 7,85794-2 8,65865-2
8 2,79322-2 3,16984-2 3,58029-2 4,02573-2
9 1,11270-2 1,29058-2 7,48899-2 1,70927-2
10 4,06880-3 4,82495-3 5,68824-3 6,66867-3
11 1,37386-3 1,66608-3 2,00756-3 2,40428-3
12 4,30629-4 5,34158-4 6,57981-4 8,05138-4
13 1,25893-4 1,59751-3 2,01199-4 2,51588-4
14 3,44727-5 4,47550-5 5,76390-5 7,36606-5
15 8,87489-6 1,17894-5 1,55280-5 2,02826-5
16 2,15547-е 2,92993-6 3,94754-6 5,26998-6
17 4,95376-7 6,88990 -7 9,50240-7 1,29605-6
3,02578-7
а т 4,6 4,7 4,8 4,9
0 9,89948-1 9,90505-1 9,91770-1 9,92553-1
1 9,43710-1 9,48157-1 9,52267-1 9,56065-1
2 8,37361-1 8,47700-1 8,57461-1 8,66669-1
3 6,74294-1 6,90316-1 7,05770-1 7,20655-1
4 4,86766-1 5,05391-1 5,23741-1 5,41788-1
5 3,14240-1 3,31562-1 3,48994-1 3,66499-1
6 1,81971-1 1,95395-1 2,09195-1 2,23345-1
7 9,50510-2 1,03969-1 1,13334-1 1,23138-1
8 4,50720-2 5,02559-2 5,58169-2 6,17612-2
9 1,95271-2 2,22059-2 2,51412-2 2,83448-2
10 7,77653-3 9,02234-3 1,04168-2 1,19708-2
11 2,86263-3 3,38938-3 3,99166-3 4,67696-3
306
Продолжение
а т 4,6 4,7 4,8 4,9
12 9,78974-4 1,18314-3 1,42160-3 1,69863-3
13 3,12448-4 3,85498-4 4,72650-4 5,76031-4
14 9,34469-5 1,17718-4 1,47297-4 1,83121-4
15 2,62865-5 3,36142-5 4,31837-5 5,47700-5
16 6,97791-6 9,16727-6 1,19498-5 1,54626-5
17 1,75321-6 2,35313-6 3,13079-6 4,13280-6
18 4,18018-7 5,73884-7 7,79051-7 1,04858-6
2,53174-7
7? (m, а)
т а 5,0 5,2 5,4
0 9,93262-1 9,94483-1 9,95483-1
1 9,59572-1 9,65797-1 9,71094-1
2 8,75348-1 8,91213-1 9,05242-1
3 7,34974-1 7,61935-1 7,86709-1
4 5,59507-1 5,93872-1 6,26689-1
5 3,84039-1 4,19087-1 4,53868-1
6 2,37817-1 2,67607-1 2,98329-1
7 1,33372-1 1,55078“1 1,78341-1 *
8 6,80936-2 8,19350-2 9,73498-2
9 3,18281-2 3,96744-2 4,87549-2
10 1,36953-2 1,76989-2 2,25137-2
11 5,45309-3 7,31050-3 9,63164-3
12 2,01885-3 2,80885-3 3,83471-3
13 6,97990-3 1,00819-3 1,42675-3
14 2,26254-4 3,39368-4 4,97971-4
15 6,90082-5 1,07512-4 1,63609-4
16 1,98690-5 3,21584-5 5,07618-5
17 5,41625-6 9,10915-6 1,49162-5
18 1,40161-6 2,45047-6 4,16255-6
19 . 3,45128-7 6,28090-7 1,10624-6
2,81041-7
307
R (m, a)
m a 5,6 5,8 6,0 6,2
0 9,96302-1 9,96972-1 9,97521-1 9,97971-1
1 9,75594-1 9,79413-1 9,82649-1 9,85389-1
2 9,17612-1 9,28489-1 9,38031-1 9,46382-1
3 8,09378-1 8,30037-1 8,48796-1 8,65771-1
4 6,57850-1 6,87282-1 7,14944-1 7,40823-1
5 4,88139-1 5,21685-1 5,54320-1 5,85887-1
6 3,29742-1 3,61609-1 3,93697-1 4,25787-1
7 2,03025-1 2,28974-1 2,56020-1 2,83984-1
8 1,14322-1 1,32814-1 1,52763-1 1,74086-1
9 5,91300-2 7,08439-2 8,39240-2 9,83793-2
10 2,82222-2 3,49014-2 4,26209-2 5,14410-2
11 1,24873-2 1,59499-2 2,00920-2 2,49848-2
12 5,14434-3 6,78996-3 8,82748-3 1,13158-2
13 1, £8122-3 2,70323-3 3,62849-3 4,79668-3
14 7,15977-4 1,01016-3 1,40035-3 1,90967-3
15 2,43619-4 3,55503-4 5,09099-4 7,16366-5
16 7,82932-5 1,18191-4 1,74878-4 2,53961-4
17 2,38331-5 3,72252-5 5,69174-5 8,53199-5
18 6,88992-6 1,11363-5 1,75973-5 2,72323-5
19 1,89616-6 3,17235-6 5,18041-6 8,27742-6
20 4,97908-7 8,62798-7 1,45535-6 2,40140-6
3,91054-7 6,66580-7
m a 6,4 6,6 6,8 7,0
0 9,98338-1 9,98640-1 9,98886-1 9,99088-1
1 9,87704-1 9,89661-1 9,91313-1 9,92705-1
2 9,53676-1 9,60032-1 9,65562-1 , 9,70364-1
3 8,81081-1 8,94850-1 9,07194-1 9,18235-1
4 7,64930-1 7,87296-1 8,07969-1 8,270C8-i
5 6,16256-1 6,45327-1 6,73023-1 6,99292-1
6 4,57671-1 4,89161-1 5,20084-1 5,50289-1
7 3,12679-1 3,41918-1 3,71514-1 4,01286-1
8 1,96785-1 2,20443-1 2,45230-1 2,70909-1
308
Продолжение
т а 6,4 6,6 6,8 7,0
9 1,14201-1 1,31361-1 1,49816-1 1,69504-1
10 6,14107-2 7,25671-2 8,49339-2 9,85208-2
11 3,06965-2 3,72908-2 4,48251-2 5,33496-2
12 1,43156-2 1,78887-2 2,20968-2 2,69998-2
13 6,25115-3 8,03850-3 1,02081-2 1,28114-2
14 2,56454-3 3,39481-3 4,43360-3 5,71720-3
15 9,91591-4 1,35159-3 1,81583-3 2,40658-3
16 , 3,62410-4 5,08757-4 7,03279-4 9,58183-4
17 1,25542-4 1,81540-4 2,58258-4 3,61784-4
18 4,13222-5 6,15611-5 9,01393-5 1,29852-4
19 1,29535-5 1,98841-5 2,99704-5 4,44026-5
20 3,87548-6 6,13068-6 9,51298-6 1,44955-5
21 1,10886-6 1,80818-6 2,88867-6 4,52643-6
22 3,04019-7 5,11427-7 8,41159-7 1,35446-6
3,89075-7
R (т ,а)
т а 7,2 7,4 7,6 7,8
0 9,99253-1 9,99389-1 9,99500-1 9,99590-1
1 9,93878-1 9,94865-1 9,95696-1 9,96394-1
2 9,74526-1 9,78129-1 9,81243-1 9,83930-1
3 9,28083-1 9,36847-1 9,44629-1 9,51223-1
4 8,44484-1 8,60475-1 8,75061-1 8,88330-1
5 7,24103-1 7,47443-1 7,69319-1 7,89749-1
6 5,79644-1 6,08038-1 6,35379-1 6,61593-1
7 4,31059-1 4,60667-1 4,89958-1 5,18791-1
8 2,97332-1 3,24349-1 3,51808-1 3,79559-1
9 1,90350-1 2,12265-1 2,35149-1 2,58891-1
10 1,13324-1 1,29323-1 1,46487-1 1,64770-1
11 6,29058-2 7,35255-2 8,52301-2 9,80299-2
12 3,26553-2 3,91171-2 4,64340-2 5,46487-2
13 1,59012-2 1.953С8-2 , 2,37532-2 2,82600-2
14 7,28478-3 9,17805-3 1,14408-2 1,41183-2
15 3,14891-3 4,07068-3 5,20249-3 6,57745-3
309
Продолжение
а т 7,2 7,4 7,6 7,8
16 1,28776-3 1,70853-3 2,23929-3 2,90127-3
17 4,99514-4 6,80292-4 9,14573-5 1,21455-3
18 1,84215-4 2,57574-4 3,55246-4 4,83635-4
19 6,47325-5 9,29364“5 1,31515-4 1,83576-4
20 1,17190-5 3,20205-5 4,64976-5 6,65535-5
21 6,97150-6 1,05549-5 1,57293-5 2,30879-5
22 2,14505-е 3,33464-6 5,10029-6 7,67733-6
23 6,34158-6 1,01161-6 1,58808-6 2,45115-6
24 2,95331-7 4,75877-7 7,52640-7
Я (/и, а)
т а 8,0 8,2 8,4 8,6
0 9,99665-1 9,99725-1 9,99775-1 9,99816-1
1 9,96981-1 9,97473-1 9,97886-1 9,98233-1
2 9,86246-1 9,88239-1 9,89953-1 9,91424-1
3 9,57620-1 9,63000-1 9,67740-1 9,71907-1
4 9,00368-1 9,11260-1 9,21092-1 9,29946-1
5 8,08764-1 8,26406-1 8,42723-1 8,57772-1
6 6,86626-1 7,10438-1 7,33007-1 7,54324-1
7 5,47039-1 5,74591-1 6,01348-1 6,27229-1
8 4,07453-1 4,35347-1 4,63106—1 4,90603-1
9 2,83376-1 3,08481-1 3,34080-1 3,60049-1
10 1,84114-1 2,04450-1 2,25699-1 2,47772-1
11 1,11924-1 1,26900-1 1,42934-1 1,59992-1
12 6,37972-2 7,39075-2 8,49993-2 9,70836-2
13 3,41807-2 4,04814-2 4,75644-2 5,54669-2
14 1,72570-2 2,09033-2 2,51035-2 2,99024-2
15 8,23101-3 1,02006-2 1,25253-2 1,52454-2
16 3,71803-3 4,71549-3 5,92183-3 7,36731-3
17 1,59426-3 2,06972-3 2,65891-3 3,38191-3
18 6,50369-4 8,64420-4 1, К 622-3 1,47777-3
19 2,25940-4 3,44240-4 4,63028-4 6,15893-4
20 9,39685-5 1,30966-4 1,80288-4 2,45288-4
21 3,34079-5 4,76875-5 6,71916-5 9,35159-5
22 1,13859-5 ( 1,66474-5 2,40094-5 3,41869-5
23 3,72603-6 5,58091-6 8,23857-6 1,20030-5
24 1,17275-6 1,79985-6 2,71876-6 4,05383-6
25 3,55707-7 5,59667-7 8,64107-7 1,31929-6
26 4,14788-7
310
R (m, a)
m a 8,8 9,0 9,2 9,4
0 9,99849-1 9,99877-1 9,99899-1 9,99917-1
1 9,98523-1 9,98766-1 9,98969-1 9,99140-1
2 9,92683-1 9,93768-1 9,94693-1 9,95485-1
3 9,75566-1 9,78774-1 9,81580-1 9,84033-1
4 9,37902-1 9,45036-1 9,51420-1 9,57122-1
5 8,71613-1 8,84309-1 8,95926-1 9,06529-1
6 7,74390-1 7,93219-1 8,10835“l 8,27267-1
7 6,52166-1 6,76103-1 6,99000-1 7,20829-1
8 5,17719-1 5,44347-1 5,70391-1 5,95765-1
9 3,86260-1 4,12592-1 4,38924-1 4,65142-1
10 2,70577-1 2,94012-1 3,17974-1 3,42356-1
11 1,78030-1 1,96992-1 2,16815-1 2,37430-1
12 1,10162-1 1,24227-1 1,39261-1 1,55238-1
13 6,42206-2 7,38508-2 8,43759-2 9,58072-2
14 3,53532-2 4,14663-2 4,83087-2 5,59035-2
15 1,84018-2 2,20357-2 2,61875-2 3,08971-2
16 9,08408-3 1,11059-2 1,34679-2 1,62059-2
17 4,26077-3 5,31957-3 6,58426-3 8,08251-3
18 1,90271-3 2,42640-3 3,06597-3 3,84030-3
19 8,10550-4 1,05595“3 1,36239-3 1,74153-3
20 3,30001-4 4,39253-4 5,78734-4 7,55100-4
21 1,28629-4 1,74952-4 2,35420-4 3,13557-4
22 4,80795“5 6,68293-5 9,18526-5 1,24898-4
23 1,72607-5 2,45202-5 3,44256-5 4,77940-5
24 5,96051-6 8,65436-6 1,24119-5 1,75949-5
25 1,98283-6 2,94264-6 4,31086-6 6,24001-6
26 6,36544-7 9,65505-7 1,44434-6 2,13478-6
27 4,67597-7 7,05550-7
m a 9,6 9,8 10,0 10,2
0 9,99932-1 9,99945-1 9,99955-1 9,99963-1
1 9,99282-1 9,99401-1 9,99501-1 9,99584-1
2 9,96161-1 9,96738-1 9,97231-1 9,97650-1
311
Продолжение
a m 9,6 9,8 10,0 10,2
3 9,86174-1 9,88040-1 9,89664-1 9,91076-1
4 9,62205-1 9,66729-1 9,70747-1 9,74312-1
5 9,16185-1 9,24959-1 9,32914-1 9,40112-1
6 8,42553-1 8,56735-1 8,69859-1 8,81974-1
7 7,41572-1 7,61209-1 7,79779-1 7,97257-1
8 6,20394-1 6,44217-1 6,67180-1 6,89244-1
9 4,91138—1 5,16812-1 5,42070-1 5,66829-1
10 3,67052-1 3,91955-1 4,16960-1 4,41966-1
11 2,58759-1 2,80719-1 3,03224-1 3,26183-1
12 1,72124-1 1,89876-1 2,08444-1 2,27768-1
13 1,08148-1 1,21395-1 1,35536-1 1,50550-1
14 6,42788-2 7,34580-2 8,34585-2 9,42916-2
15 3,62024-2 4,21392-2 4,87404-2 5,60357-2
16 1,93566-2 2,29564-2 2,70416-2 3,16475-2
17 9,84360-3 1,18981-2 1,42776-2 1,70146-2
18 4,77002-3 5,87745-3 7,18651-3 8,72259-3
19 2,20653-3 2,77207-3 3,45434-3 4,27110-3
20 9,76056-4 1,25043-3 1,58826-3 2,00085-3
21 4,13553-4 5,40333-4 6,99652-4 8,98149-4
22 1,68097-4 2,24017-4 2,95738-4 3,86899-4
23 6,56456“5 8,92390-5 1,20124-4 1,60170-4
24 2,46651-5 3,42046-5 4,69510-5 6,38107-5
25 8,92865-6 1,26311-5 1,76819-5 2,44960-5
26 3,11824-6 4,49958-6 6,42457-6 9,07257-6
27 1,05232-6 1,54813-6 2,25518-6 3,24592-6
28 3,44007-7 5,15123-7 7,66115-7 1,12336-6
3,76807-7
R (т, a)
m a 10,4 10,6 10,8 11,0
0 9,99970—1 9,99975-1 9,99980-1 9,99983-1
1 9,99653-1 9,99711-1 9,99759-1 9,99800-1
2 9,98007-1 9,98311-1 9,98570-1 9,98789-1
3 9,92302-1 9,93365-1 9,94287-1 9,95084-1
312
Продолжение
т а 10,4 10,6 10,8 11,0
4 9,77468-1 9,80259-1 9,82723-1 9,84895-1
5 . 9,46613-1 9,52473-1 9,57745-1 9,62480-1
6 8,93131-1 9,03384-1 9,12784-1 9,21386-1
7 8,13673-1 8,29050-1 8,43417-1 8,56808-1
8 7,10377-1 7,30557-1 7,49771-1 7,68015-1
9 5,91013-1 6,14554-1 6,37396-1 6,59489-1
10 4,66874-1 4,91591-1 5,16031-1 5,40111-1
11 3,49506-1 3,73100-1 3,96872-1 4,20733-1
12 2,47787-1 2,68432-1 2,89630-1 3,11303-1
13 1,66413-1 1,83088-1 2,00536-1 2,18709-1
14 1,05963-1 1,18470-1 1,31806-1 1,45956-1
15 6,40507-2 7,28068-2 8,23207-2 9,26039-2
16 3,68079-2 4,25549-2 4,89181-2 5,59244-2
17 2,01417-2 2,36919-2 2,76976-2 3,21905-2
18 1,05124-2 1,25838-2 1,49654-2 1,76865-2
19 5,24160-3 6,38656-3 7,72806-3 9,28946-3
20 2,50079-3 3,10205-3 3,81992-3 4,67108-3
21 1,14343-3 1,44415-3 1,81002-^3 2,25193-3
22 5,01775-4 6,45344-4 8,23345-4 1,04235-3
23 2,11634-4 2,77199-4 3,60035-4 4,63858-4
24 8,59059-5 1,14601-4 1,51546-4 1,98715-4
25 3,36031-5 4,56600-5 6,14782-5 8,20522-5
26 1,26820-5 1,75532-5 2,40655-5 3,26949-5
27 4,62345-6 6,51865-6 9,10049-6 1,25854-5 _
28 1,63029-6 2,34129-6 3,32826-6 4,68659-6
29 5,56887-7 8,14383-7 1,17860-6 1,69012-6
30 4,04732-7 5,91419-7
т а 11,2 11,4 11,6 11,8
0 9,99986-1 9,99989-1 9,99991-1 9,99992-1
1 9,99833-1 9,99861-1 9,99885-1 9,99904-1
2 9,98976-1 9,99134-1 9,99268-1 9,99381-1
3 9,95774-1 9,96369-1 9,96883-1 9,97326-1
313
Продолжение
а т 11,2 11,4 11,6 11,8
4 9,86808-1 9,88491-1 9,89968-1 9,91264-1
5 9,66726-1 9,70527-1 9,73925-1 9,76957-1
6 9,29240-1 9,36397-1 9,42908-1 9,48819-1
7 8,59261-1 8,80814-1 8,91508-1 9,01388-1
8 7,85291-1 8,01607-1 8,16979-1 8,31426-1
9 6,80794-1 7,01279-1 7,20919-1 7,39698-1
10 5,63758-1 5,86904-1 6,09489-1 6,31460-1
11 4,44595-1 4,68371-1 4,91982-1 5,15349-1
12 3,33375-1 3,55764-1 3,78391-1 4,01174-1
13 2,37555-1 2,57017-1 2,77033-1 2,97538-1
14 1,60899-1 1,76608-1 1,£3051-1 2,10188-1
15 1,03663-1 1,15498-1 1,28104-1 1,41472-1
16 6,35972-2 7,19565-2 8,10183-2 9,07941-2
17 3,72011-2 4,27583-2 4,88890-2 5,56177-2
18 2,07769-2 2,42661-2 2,81835-2 3,25577-2
19 1,10952-2 1,31707-2 1,55422-2 1,82362-2
20 ‘ 5,67348-3 6,84639-3 8,21022-3 9,78651-3
21 2,78190-3 3,41317-3 4,16020-3 5,03859-3
22 1,30982-3 1,63415-3 2,02473-3 2,49198-3
23 5,92976-4 7,52365-4 9,47708-4 1,18546-3
24 2,58450-4 3,33520-4 4,27149-4 5,43082-4
25 1,08583-4 1,42527-4 1,85509-4 2,39882-4
26- 4,40251-5 5,87833-5 7,78454-5 1,02276-4
27 1,72454-5 2,34250-5 3,15469-5 4,21368-5
28 6,53349-е 9,02916-6 1,23661-5 1,67925-5
29 2,39648-6 3,37009-6 4,69375-6 6,47997-6
30 8,52000-7 1,21965-6 1,72712-6 2,42371-6
31 4,28845-7 6,17050-7 8,79721-7
/? (т, а)
т 1 а 12,0 12,2 12,4 12,6
0 9,99994-1 9,99995-1 9,99996-1 9,99997-1
1 9,99920-1 9,99934-1 9,99945-1 9,99954-1
2 9,99478-1 9,99559-1 9,99628-1 9,99686-1
I
4
314
Продолжение
т а 12,0 12,2 12,4 12,6
3 9,97708-1 9,98037-1 9,98319-1 9,68562-1
4 9,92400-1 9,93393-1 9,94262-1 9,95021-1
5 9,79659-1 9,82064-1 9,84200-1 9,86097-1
6 9,54178-1 9,56026“ 1 9,63406-1 9,67356-1
7 9,10496-1 9,18875-1 9,26570-1 6,33624-1
8 8,44972-1 8,57645-1 8,69475-1 8,80494-1
9 7,57608-1 7,74644-1 7,90810-1 8,06114-1
10 6,52771-1 6,73383-1 6,63266-1 7,12394-1
М 5,38403-1 5,61075-1 5,83307-1 6,05042-1
12 4,24035-1 4,46896-1 4,69682-1 4,92322-1
13 3,18464-1 3,39743-1 3,61302-1 3,83071-1
14 2,27975-1 2,46366-1 2,65308-1 2,84745-1
15 1,55584-1 1,70420-1 1,85953—1 2,02151-1
16 1,01291-1 1,12511-1 1,24453-1 1,37108-1
17 6,29664-2 7,09533-2 7,65940-2 8,89001-2
18 3,74165-2 4,27861-2 4,86912-2 5,51544-2
19 2,12798-2 2,46968-2 2,85231-2 3,27757-2
20 1,15977-2 1,36672-2 1,60189-2 1,86771-2
21 6,06515-3 7,25777-3 8,63540-3 1,02179-2
22 3,04737-3 3,70345-3 4,47382-3 5,37315“3
23 1,47288-3 1,81811-3 2,23018-3 2,71904-3
24 6,85(34-4 8,59731-4 1,07097-3 1,32564-3
25 3,07756-4 3,92042-4 4,95997-4 6,33364-4
26 1,33351-4 1,72587-4 2,21781-4 2,83030-4
27 5,58377-5 7,34265-5 9,58444-5 1,24208-4
28 2,26176-5 3,02208-5 *4,00725-5 5,27381-5
29 8,87139-6 1,20446-5 1,62253-5 2,16856-5
30 3,37290-6 4,65260-6 6,36841-6 8,64358-6
31 1,24445-6 1,74393-6 2,42566-6 3,34262-6
32 4,46278-7 6,34886-7 8,97839-7 1,25536-6
33 4,58414-7
315
R (m, a)
m a 12,8 13,0 13,2 13,4
0 9,99997-1 9,99998-1 9,99998-1 9,99998-1
1 9,99962-1 9,99968-1 9,99974-1 9,99978-1
2 9,99736-1 9,99777-1 9,99812-1 9,99842-1
3 9,98771-1 9,98950-1 9,99103-1 9,99234-1
4 9,95683-1 9,96260-1 9,96762-1 9,97199-1
5 9,87778-1 9,89266-1 9,90582-1 9,91744-1
6 9,70914-1 9,74113-1 9,76986-1 9,79561-1
7 9,40077-1 9,45972-1 9,51347-1 9,56240-1
8 8,90738-1 9,00242-1 9,09042-1 9,17176-1
9 8,20567-1 8,34138-1 8,46996-1 8,59015-1
10 7,30749-1 7,48318-1 7,65095-1 7,81079-1
11 6,26232-1 6,46835-1 6,66814-1 6,86139-1
12 5,14748-1 5,36895-1 5,58705-1 5,80122-1
13 4,04979-1 4,26955-1 4,48932-1 4,70843-1
14 3,04619-1 3,24868-1 3,45432-1 3,66247-1
15 2,18978-1 2,36323—1 2,54353-1 2,72809-1
16 1,50465-1 1,64507-1 1,79212-1 1,94554-1
17 9,88792-2 1,09535-1 1,20867-1 1,32871-1
18 6,21958-2 6,98331-2 7,80810-2 8,69509-2
19 3,74828-2 4,26687-2 4,83559-2 5,45654-2
20 2,16665-2 2,50118-2 2,87374-2 3,28671-2
21 1,20261-2 1,40814-2 1,64057-2 1,90215-2
22 6,41713-3 7,62245-3 9,00670-3 1,05883-2
23 3,29562-3 3,97177-3 4,76033-3 5,67507-3
24 1,63081-3 1,29431-3 2,42482-3 2,93183-3
25 7,78426-4 9,66037-4 1,19167-3 1,46145-3
26 3,58792-4 4,51828-4 6,65608-4 7,03644-4
27 1,59854-4 2,04350-4 2,59534-4 3,27546-4
28 6,89114-5 8,24173-5 1,15242-4 1,47556-4
29 2,87710-5 3,78256-5 4,95642-5 6,43887-5
30 1,16445-5 1,55625-5 2,06660-5 2,72405-5
31 4,57290-6 6,20699-6 8,36092-6 1,11829-5
32 1,74425-6 2,40345-6 3,28509-6 4,45879-6
33 6,47080-7 9,05085-7 1,25477-6 1,72839-6
34 4,66520-7 6,52290-7
316
R (m, a)
m a 13,6 13,8 14,0 14,2
0 9,99999-1 9,99999-1 9,99999-1 9,99999-1
1 9,99682-1 9,99985-1 9,99988-1 9,99990-1
2 9,99867-1 9,99888-1 9,99906-1 9,99921-1
3 9,99347-1 9,99443-1 ' 9,99526-1 9,99596-1
4 9,97579-1 9,97909-1 9,98195-1 9,98443-1
5 9,92769-1 9,93673-1 9,94468-1 9,-95167-1
6 9,81668-1 9,83930-1 9,85772-1 9,87415-1
7 9,60687-1 9,64723-1 9,68380-1 9,71690-1
8 9,24680-1 9,31591-1 9,37945-1 9,43777-1
9 8,70270-1 8,80789-1 8,90601-1 8,99736-1
10 7,96271-1 8,10681-1 8,24319-1 8,37199-1
11 7,04783-1 7,22728-1 7,39960-1 7,56469-1
12 6,01096-1 6,21582-1 6,41542-1 6,60939-1
13 4,92623-1 5,14212-1 5,35552-1 5,56590-1
14 3,87249-1 4,08376-1 4,29563-1 4,50751-1
15 2,91711-1 3,11006“i 3,30640-1 3,50557-1
16 2,10503-1 2,27025-1 2,44082-1 2,61634-1
17 1,45537-1 1,58852-1 1,72799-1 1,87357-1
18 9,64510-2 1,06586-1 1,17357-1 1,28761-1
19 6,13160-2 6,86245-2 7,65049-2 8,49687-2
20 3,74243-2 4,24310-2 4,79084-2 5,38759-2
21 2,19515-2 2,52182-2 2,88441-2 3,28512-2
22 1,23865-2 1,44210-2 1,67122-2 1,92807-2
23 ' 6,73068-3 7,94272-3 9,32758-3 1,09024-2 -
24 3,52571-3 4,21770-3 5,01989-3 5,94523-3
25 1,78221-3 2,16149-3 2,60759-3 3,12956-3
26 8,70226-4 1,07012-3 1,30865-3 1,59178-3
27 4,10856-4 ’ 5,12305-4 6,35131-4 7,83015“4
28 1,87733-4 2,37383-4 2, £8371-4 3,72857-4
29 8,30963-5 1,06558-4 1,35797-4 ’ 1,72021-4
30 3,56610-5 4,63785-5 5,99286-5 7,69p86“ 5
31 1,48506-5 1,95889-5 2,56656-5 3,34139-5
32 6,00619-6 8,03586-6 1,06756-5 1,40910-5
33 2,36122-6 3,20459-6 4,31621-6 5,77624-6
34 9,Q3237-7 1,24366-6 1,69764-6 2,30361-6
35 , 4,70507-7 6,50209-7 . 8,94725-7
317
R (m, a)
a tn 14,4 14,6 14,8 15,0 I
0 9,99999-1 9,99(99-1
1 9,99991-1 9,99993-1 9,99994-1 9,99995-1
2 9,99934-1 9,99944-1 9,99953-1 9,99961-1
3 9,99655-1 9,99708-1 9,99751-1 9,99789-1
4 9,98658-1 9,98844-1 9,99004-1 9,99143-1
5 9,95782-1 9,96321-1 9,96793-1 9,97208-1
6 9,88879-1 9,90182-1 9,91340-1 9,92368-1
7 9,74680-1 9,77378-1 9,79810-1 9,81998-1
8 9,49121-1 9,54011-1 9,58479-1 9,62554-1
9 9,08227-1 9,16105-1 9,23400-1 9,30146-1
10 8,4f340-i 8,60761-1 8,71485-1 8,81535-1
11 7,72251 -i 7,87305-1 8,01635-1 8,15248-1
12 6,79745-1 6,97934-1 7,15487-1 7,32389-1
13 5,77276-1 5,975 3-1 6,17411-1 6,36782-1
14 4,71879-1 4,92891-1 5,13731-1 5,34346-1
15 3,70699-1 3,91010-1 4,11432-1 4,31910-1
16 2,79636-1 2,98043-1 3,12807-1 3,35877-1
17 2,02501-1 2,18201-1 2,34427-1 2,51141-1
18 1,40793-1 1,53441-1 1,66692-1 1,80528-1
19 9,40244-2 1,03377-1 1,13930-1 1,24781-1
20 6,03512-2 6,73501-2 7,48852-2 8,29709-2
21 3,72609-2 4,20940-2 4,73697-2 5,31064-2
22 2,21474-2 2,53331-2 2,88586-2 3,27442-2
23 1,26849-2 1,46(36-2 1,69471-2 1,94646-2
24 7,00748-3 8,22119-3 9,60164-3 1,11648-2
25 3,73727-3 4,44132-3 5,25315-3 6,18491-3
26 1,92607-3 2,31878-3 2,77785-3 3,31190-3
27 9,60102-4 1,17104-3 1,42102-3 1,71579-3
28 4,63317-4 5,72574-4 7,03838-4 8,60724-4
29 2,16638-4 2,71277-4 3,37829-4 4,18451-4
30 9,82314-5 1,24646-4 1,57264-4 1,97314-4
31 4,32298-5 5,55877-5 7,10587-5 9,03128-5
32 1,84791-5 2,40798-5 3,11888-5 4,01558-5
33 7,67884-6 1,01399-5 1,33078-5 1,73572-5 -
34 3,10459-5 4,15398-5 5,52425-6 7,29901-6
35 1,22262-6 1,65:98-5 2,23295-6 2,98834-6 jr
36 4,69838-7 6,44315-7 8,79852-7 1,19222-6 g
318
R (m, a)
a m 15,5 16,0 16,5 17,0
0 1 9,99997-1 9,99298-1 9,99299-1 9,99999-1
2 9,99975-1 9,99984-1 9,99990-1 9,99993-1
3 9,99859-1 9,99907-1 9,92938-1 9,99959-1
4 9,99413-1 9.S9600—1 9,99728-1 0,99815-1
5 9,98930—1 9,98616-1 9,99032-1 9,99325-1
6 9,94456-1 9,95294-1 9,97119-1 9,97938-1
7 9,86554-1 9,90000-1 9,92610-1 9,94567-1
8 9,71213-1 9,78013-1 9,83310-1 9,87404-1
, 9 9,44810-1 9,56702-1 9,66259-1 9,73875-1
10 9,03884-1 9,22604-1 9,38126-1 9,50876-1
11 8,46217-1 8,73007-1 8,95927-1 9,15331-1
12 7,71731-1 8,0(878-1 8,37902-1 8,64976-1
13 6,82919-1 7,25489-1 7,64256-1 7,99127-1
14 5,84593-1 6,32473-1 6,77458-1 7,19167-1
15 4,82989-1 5,33255-1 5,81981-1 6,28546-1
16 3,84560-1 4,34038-1 4,83519-1 5,32262-1
17 3,94816-1 3,40656-1 3,87954-1 4,35977-1
18 2,17536-1 2,57651-1 3,00353-1 3,45042-1
19 1,544^2-1 1,87751-1 2,24278-1 2,63678-1
20 6,05633-1 1,31832-1 1,61516-1 1,94519-1
21 6,95704-2 8,92266-2 1,12203-1 1,38534-1
22 4,41627-2 5,82409-2 7,52187-2 9,52720-2
23 2,70401-2 3,66857-2 4,8(863-2 6,32960-2 _
24 1,59817-2 2,23155-2 3,04452-2 4,0c 463—2
25 9,12553-3 1,31186-2 1,84061-2 2,52445-2
26 5,03819-3 7,45892-3 1,07659-2 1,51741-2
27 2,69176-3 ' 4,10506-3 6,09692-3 8,83352-3
28 1,39284-3 2,18857-3 3,34554-3 4,98385-3
29 6,28589-4 1,13120-3 1,78010-3 2,72715-3
30 3,39823-4 5,67263-4 9,19103-4 1,44836-3
31 1,60545-4 -2,76201-4 4,60833-4 7,47080-4
32 7,36733-5 1,30670-4 2,24537-4 3,74528-4
33 3,28699-5 6,01094-5 1,06390-4 1,82607-4
34 1,42684-5 2,69044-5 4,90532-5 8,66463-5
319
Продолжение
т а 15,5 16,0 16,5 17,0
35 6,03056-6 1,17250-5 2,20232-5 4,00369-5
36 2,48372-6 4,97862-6 9,63442-6 1,80269-5
37 9,97883-7 2,06125-6 4,10969-6 7,91422-6
38 8,32879-7 1,41080—6 9,39012-6
39 6,95887-7 1,41807-6
40 5,79952-7
R (т, а)
т а 17,5 18,0 18,5 19,0
2 9,99996-1 9,99997-1 9,99998-1 9 , 99999-1
3 9,99973-1 9,95982-1 9,99988-1 9,99992-1
4 9,99875-1 9,99916-1 9,99943-1 9,99962-1
5 9,99532-1 9,99676-1 9,99777-1 9,99846-1
6 9,98530-1 9,98957-1 9,99262-1 9,99480-1
7 9,96026-1 9,97107-1 9'97903-1 9,98487-1
8 9,90548-1 9,92944-1 9,94759-1 9,96127-1
9 9,79896-1 9,84619-1 9,88298-1 9,91144-1
10 9,61255-1 9,69634-1 9,76344-1 9,81678-1
11 9,31599-1 9,45113-1 9,56240-1 9,65327-1
12 8,88351-1 9,08331-1 9,25246-1 9,39439-1
13 8,30133-1 8,57402-1 8,81139-1 9,01601-1
14 7,57360-1 7,91923-1 8,22856-1 8,50250-1
15 6,72458-1 7,13347-1 7,50972-1 7,85206-1
16 5,79596-1 6,24950-1 6,67857—1 7,07966-1
17 4,84003-1 5,31352-1 5,77408-1 6,21639-1
18 3,91066-1 4,37755-1 4,84446-1 5,30516-1
19 3,05466-1 3,49084-1 3,93932-1 4,39393-1
20 2,30566-1 2,69280-1 3,10206-1 3,52826-1
21 1,68149-1 2,00876-1 2,36447-1 2,74503-1
22 1,18499-1 1,44910-1 1,74422-1 2,06861-1
23 8,07220-2 1,01110-1 1,24533-1 1,50983-1
24 5,31763-2 6,82602-2 8,60767-2 1,06746-1
25 3,38943-2 4,46083-2 5,76190-2 7,31256-2
26 2,09160-2 2,82339-2 3,73703-2 4,85570-2
320
Продолжение
т а 17,5 18,0 18,5 19,0
27 1,25042-2 1,73176-2 2,34961-2 3,12680-2
28 7,24679-3 1,03000-2 1,43293-2 1,95362-2
29 4,07422-3 5,94428-3 8,48148-3 1,18499-2
30 2,22356-3 3,33083-3 4,87533-3 6,98185-3
31 1,17883-3 1,81334-3 2,72327-3 3,99823-3
32 6,07489-4 9,59754-4 1,47911-3 2,22670-3
33 3,04507-4 4,94161-4 7,81626-4 1,20672-3
34 1,48560-4 2,47671-4 4,02114-4 6,36741-4
35 7,05871-5 1,20904-4 2,01514-4 3,27321-4
36 3,26835-5 5,75212-5 9,84284-5 1,64016-4
37 1,47560-5 2,66861-5 4,68855-5 8,01566-5
38 6,50001-6 1,20800-5 2,17922-5 3,82269-5
39 2,79536-6 5,33875-6 9,88896-6 1,77997-5
40 1,17459-5 2,30517-6 4,38372-6 8,09670-6
41 4,82789-7 9,73363-7 1,89965-6 3,60022-6
42 8,05478-7 1,56609-6
43 6,67293-7
R (т, а)
а т 19,5 20,0 а т 19,5 20,0
2 9.S9S99—1 24 1,30319-1 1,56773-1
3 9,99995-1 9,99997—1 25 9,12816-2 1,12185-1
4 9,99975-1 9,99983-1 26 6,20038-2 7,78868-2
5 9,99895-1 9,99928-1 27 4,08588-2 5,24807-2
6 < 9,99635-1 9,99745-1 28 2,61327-2 3,43335-2
7 9,98912—1 9,99221-1 29 1,62307-2 2,18182-2
8 9,97150-1 9,97913-1 30 9,79444-3 1,34747-2
9 9,93333-1 9,95005-1 31 5,74580-3 8,09176-3
10 9,85888-1 9,89188-1 32 3,27867-3 4,72743-3
11 9,72691-1 9,78613-1 33 1,82081-3 2,68844-3
12 9,51245-1 9,60988-1 34 9,84690-4 1,48904-3
13 9,19077-1 9,33872-1 35 5,18851-4 8,03663-4
14 8,74271-1 8,95136-1 36 2,66621-4 4,22899-4
15 8,16024-1 8,43487-1 37 1,33536-4 2,17081-4
16 7,45035-1 7,78926-1 38 6,52942-5 1,08756-4
17 6,63606-1 7,02972-1 39 3,11731-5 5,32047-5
18 5,75392-1 6,18578-1 40 1,45391-5 2,54289-5
19 4,84856-1 5,29743-1 41 6,62782-6 1,18798-5
20 3,96583-1 4,40907-1 42 2,95471-6 5,42785-6
21 3,14616-1 3,56302-1 43 1,28899-6 2,42694-6
22 2,41963-1 2,79389-1 44 5,50775-7 1,06289-6
23 1,80366-1 2,12507-1 45 4,56639-7
321
ЛИТЕРАТУРА
1. Гнеденко Б. В., Коваленко И. Н., Лекции по теории массо-
вого обслуживания, КВИРТУ, Киев, 1963.
2. В е н т ц е л ь Е. С., Теория вероятностей, изд. 3, изд-во «Наука»»
1964.
3. Б у с л е н к о Н. П., Шрейдер Ю. А., Метод статистических испы-
таний, ГИФМЛ, 1961.
4. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д., Математи-
ческие методы в надежности, изд-во «Наука», 1965.
5. Гнеденко Б. В., Курс теории вероятностей, ГИФМЛ, 1961.
6. К о ф м а н А., К р ю о н Р., Массовое обслуживание, теория и при-
ложения, изд-во «Мир», 1965.
7. Д и т к и н В. А., Прудников А. П., Справочник по операционному
исчислению, изд-во «Высшая школа», 1965.
8. М о р з Ф. М., К и м б е л л Д. Е., Методы исследования операций»
изд-во «Советское радио», 1966.
9. В е н т ц е л ь Е. С., Введение в исследование операций, изд-во «Совет-
ское радио», 1964.
10. Чуев Ю. В. и др. Основы исследования операций в военном деле»
изд-во «Ьоветское радио». 1965.
11. Феллер В., Введение в теорию вероятностей и ее приложения»
изд-во «Мир», 1964.
12. X и н ч и н А. Я., Работы по математической теории массового обслу-
живания, ГИФМЛ, 1963.
13. Кокс Д., С м и т У., Теория очередей, изд-во «Мир», 1966.
14. К л и м о в Г. П., Стохастические системы обслуживания, изд-во
«Наука», 1966.
15. Розенберг В. Я., Прохоров А. И., Что такое теория массового
обслуживания, изд-во «Советское радио», 1962. »
16. Риордан Дж., Введение в комбинаторный анализ, ИЛ, 1963.
17. Бусленко Н. П., Голенко Д. И., Соболь И. М., Сраго-
в и ч В. Г., Шрейдер Ю. А., Метод статистических испытаний (метод
Монте-Карло), Физматгиз, 1962.
18. Дунин-Барковский И. В., Смирнов Н. В., Теория вероят-
ностей и математическая статистика в технике, ГИТТЛ, 1955.
19. Вентце ль Е. С., Овчаров Л. А., Теория вероятностей, изд-во
«Наука», 1969.
20. Г н е д е н к о Б. В., Коваленко И. Н., Введение в теорию мас-
сового обслуживания, изд-во «Наука», 1967.
21. Больщев Л. Н., Смирнов Н. В., Таблицы м*атематической ста-
тистики, изд-во «Наука», 1965.
22. С а а т и Т. Л., Элементы теории массового обслуживания и ее при-
ложения, изд-во «Советское радио», 1965.
322
Стр.
ОГЛАВЛЕНИЕ
Предисловие ..................................................... 3
Глава 1. Потоки событий.......................................... 7
§ 1.1. Основные определения ................................. 7
§ 1.2. Закон распределения участка времени, на который падает
точка ....................................................... 9
§ 1.3. Закон распределения времени до наступления очередного
события ................................................... 14
§ 1.4. Пуассоновский поток событий.......................... 17
§ 1.5. Другие стационарные потоки Пальма.....................21
§ 1.6. Предельные теоремы для потоков событий................31
§ 1.7. Задачи и упражнения...................................40
Глава 2. Марковские случайные процессы с непрерывным временем . . 46
§ 2.1. Дискретные случайные процессы......................... 46
§ 2.2. Дискретные марковские случайные процессы с непрерывным
временем ....................................................51
§ 2.3. Составление системы обыкновенных дифференциальных урав-
нений для вероятностей состояний.............................53
§ 2.4. Эргодические марковские случайные процессы. Теорема Мар-
кова. Стационарный режим работы системы . ............59
§ 2.5. Процессы гибели и размножения.........................65
§ 2.6. Определение закона распределения времени, нахождения
. в группе состояний..........................................70
§ 2.7. Задачи и упражнения....................................76
Глава 3. Основные понятия теории массового обслуживания..........92
§ 3.1. Канал обслуживания; время обслуживания; поток обслужи-
ваний; поток заявок; дисциплина обслуживания.................92
§ 3.2. Разомкнутые системы массового обслуживания.............95
Глава 4. Системы массового обслуживания с отказами.'.............ЮЗ
§ 4.1. Классическая система массового обслуживания с отказами
(система Эрланга) ..........................................104
§ 4.2. Система массового обслуживания с отказами и недостоверным
обслуживанием ..............................................122
§ 4.3. Система массового обслуживания с отказами и полной взаи-
мопомощью между каналами....................................127
§ 4.4. Система массового обслуживания с отказами и частичной
взаимопомощью между каналами................................141
§ 4.5. Система массового обслуживания с отказами и случайным
распределением заявок по всем каналам (занятым и незаня-
тым) .......................................................151
§ 4.6. Система массового обслуживания с отказами, взаимопомощью
и отсутствием информации о результатах обслуживания . . .156
323
Стр.
Г лава 5. Система массового обслуживания с ожиданием..........172
§ 5.1. Классическая система массового обслуживания с ожиданием 173
§ 5.2. Система массового обслуживания с ожиданием и полной
взаимопомощью между каналами...............................192
§ 5.3. Система массового обслуживания с ожиданием и приорите-
том в обслуживании . . ....................................204
Глава 6. Система массового обслуживания с различными ограничениями
на время пребывания заявки в системе...........................214
§ 6.1. Система массового обслуживания с отказами, ограниченным
J временем пребывания заявки в системе и упорядоченным
обслуживанием ..........................,.....................215
§ 6.2. Система массового обслуживания с ожиданием, ограниченным
временем пребывания заявки в системе и упорядоченным об-
служиванием ...............................................219
§ 6.3. Система массового обслуживания с ожиданием, ограниченным
временем нахождения заявки в системе и взаимопомощью
между каналами ................. . . .............../. . . 232
§ 6.4. Система массового обслуживания с ограниченным временем
нахождения заявки в очереди и неограниченным временем на-
хождения заявки на обслуживании............................237
§ 6.5. Система массового обслуживания е ограниченным временем
нахождения заявки на обслуживании и неограниченным вре-
менем нахождения заявки в очереди .........................243
х § 6.6. Исследование системы ПВО как системы массового обслужи-
J вания .................................................. 246
Глава 7. Замкнутые системы массового обслуживания . . . ..... . । . 272 •
§ 7.1. Замкнутая система массового обслуживания без взаимопо-
мощи между каналами . .:...................................275
§ 7.2. Замкнутая -система массового обслуживания с частичной взаи-
мопомощью между каналами...................................288
§ 7.3. Замкнутая система массового обслуживания с полной взаи-
помощью между каналами................................... 296
Приложение. Таблицы распределения Пуассона....................300
Литература ................................................. 322
Лев Александрович Овчаров
ПРИКЛАДНЫЕ ЗАДАЧИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Редактор И. А. Суворова Художник Л. А. Витте
Техн, редактор В. Й. Орешкина Корректор В. Е. Блохина
Г—64546 Сдано в набор 11/IX 1968 г. Подписано в печать 23/IV 1969 г.
Формат 60X90716 Печ. л. 20,25 Уч.-изд. л. 16,39
Бум. л. 10,13 Бумага № 1 Тираж 7500 экз. Зак. 1825
Цена 97 коп. ' Тем. план 1968 п № 371
___________Издательство «Машиностроение», Москва, К-51, Петровка, 24. /
Московская типография № 8 Главполиграфпрома » '
Комитета по печати при Совете Министров СССР,
Хохловский пер., 7. Зак. 1964.
97 коп.
Москва,К’51, Петровка,24