ОГЛАВЛЕНИЕ
Предисловие................................................  5
Глава 1. Микрокалькуляторы с обратной бесскобочной ло-
гикой вычислений............................................7
1.1.	Функциональные возможности микрокалькуляторов с
обратной бесскобочной логикой вычислений ....'.	7 •
1.2.	Система команд и кодов программируемого мнкрокаль-
 кулятора Электроника БЗ-34 ..........................14
1.3.	Основы программирования микрокалькуляторов ... 17
1.4.	Специальные приемы программирования микрокальку-
ляторов .......................................... . 21
1.5.	Погрешности вычислений на микрокалькуляторах . . 27
1.6.	Инструкция по вводу и пуску программ для микро-
калькуляторов .........................................28
Глава 2. Микрокалькуляторы с алгебраической логикой вы-
числений ..................................................33
2.1.	Общие сведения.....................................33
2.2.	Клавиатура и язык микрокалькуляторов с алгебраиче-
, ской лргикой.........................................37
2.3.	Элементарное программирование микрокалькуляторов
с алгебраической логикой ............................. 44
2.4.	Специальные вопросы программирования микрокальку-
ляторов с алгебраической логикой . .-..................46
2.5.	Работа с библиотекой программ пользователя .... 49
2.6.	Операторы управления цифровым магнитофоном и
принтером..............................................51
2.7.	Ввод, редактирование н перевод программ............53
Глава 3. Программирование простых вычислений , , , , 5э
3.1.	Операции с действительными числами.................56
3	2.	Вычисление определителей и операции с . матрицами 57
3.3.	Вычисление факториалов н комбинаторика.............61
3.4.	Операции с комплексными числами....................62
Г л а в-а 4. Вычисление элементарных функций, многочленов и
цифровых последовательностей ......	... 64
.	4.1. Гиперболические и обратные гиперболические функции 64
4.2.	Непрерывные дроби...............................  .65
4.3.	Вычисление многочленов по схеме Горнера...........65
4.4.	Вычисление рядов и сложных числовых послёдователь-
ностей .	...................................65
4.5.	Вычисление многочленов Лагерра, Лежандра, Лагран-
жа, Эрмита и Чебышева и их коэффициентов .’ ... 68
4.6.	Элементарные функции комплексной переменной , . 74
Глава 5. Программная реализация основных численных ме-
тодоа ...................................._	....... 'У
5	1. Решение систем линейных уравнений . . . . . . . 79
5.2.	Интерполяция и экстраполяция функций одной пере-
менной .-•••'.........................................
5.3.	Интерполяция и экстраполяция функции двух перемен--
5.4.	Вычисление корней нелинейных уравнений	....	88
5*5.	Поиск экстремумов функций одной	переменной	.-	.	.	96
5.6.	Решение алгебраических уравнений.................97
5.7.	Численное дифференцирование.....................100
5.8.	Вычисление частных производных	н коэффициентов	
чувствительности -	 102
5.9.	Численное интёгрирование........................105
5.10.	Решение дифференциальных уравнений.............11'1
5.11.	Спектральный анализ............................120
5.12.	Статистические расчеты и реализация метода Монте-
Карло .................................................133
5.13.	Приближение функций............................140
5.14.	Сглаживание эмпирических данных................146
Глава 6. Вычисление специальных функций....................	150
6.1.	Интегральная показательная н родственные ей функции 150
6.2.	Интегральные синус и косинус.......................152
6.3.	Гамма-функции......................................1-54
6.4.	Функции Бесселя . '. ..............................156
6.5.	Интегралы Френеля.................................  163
6.6.	Эллиптические интегралы .......................  .	164
* 6.7.	Дилогарнфм .....................................166
6.8.	Функции Дебая.....................................  166-
6.9.	Интеграл вероятности и связанные с ним функции . .167
6.10.	Функции плотности вероятности и распределения слу-
чайных величин........................................170
6.11.	Гипергеометрические функции . , ................175
Глава 7. Примеры расчета электрических и электронных
цепей и устройств................................’.........176
7.1.	Расчет индуктивных элементов .	,	...............176
7.2.	Расчет емкостей..................................183
7.3.	Расчет линий передачи и задержки.................185
7.4.	Расчет выпрямителя...............................190
7.5.	Пересчет параметров транзисторов.................191
7.6.	Расчет малосигнальиых усилительных	каскадов	.	.	193
7.7.	Моделирование нелинейных цепей	второго	порядка	195
Приложение 1. Инструкция по применению встроенной биб-
лиотеки программ пользователя для микрокалькуляторов
TI-58C/59...........................'..................198
Приложение 2. Библиотека внешних программ для микро-
калькуляторов TI-58C/59 ............................. 205
Приложение 3. Пакет программ с особыми приемами про-
грамЯирования для микрокалькуляторов Электроника БЗ-34 216
Список литературы.........................................221
Указатель алгоритмов и численных методов ....... 223
в. п. дьяконов
СПРАВОЧНИК
ПО РАСЧЕТАМ
НА МИКРО-
КАЛЬКУЛЯТОРАХ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ литературы
19S5 ,
ББК 22.18
ДЭЗ
УДК 519.6
Справочник по расчетам на микрокалькуляторах. Дьяко-
нов В. П.— М.: Наука. Главная редакция физико-математической
литературы, 1985. — 224 с.
Описаны современные отечественные и зарубежные микрокаль-
куляторы для инженерных и научных расчетов. Дано математиче-
ское и программное обеспечение их. В справочник включено около
300 программ, главным образом для отечественных программируе
мых микрокалькуляторов Электроника БЗ-34, Электроника МК 54 и
Электроника МК-56. Основное вниманнё уделено конкретной реали-
зации основных численных методов и вычислениям специальных
функции.
Для широкого круга читателей.
• \
Рецензент: кандидат технических наук Н. П. Брусенцов
Владимир Павлович Дьяконов,
СПРАВОЧНИК ПО РАСЧЕТАМ НА МИКРОКАЛЬКУЛЯТОРАХ
Редактор Л. Г. Силкова
Техн, редактор С. Я. Шкляр Корректор Н. Б. Румянцева
ИБ № 12576
Сдано в набор 01,08.84. Подписано к печати 10.06.85. Т-13683. Формат 84Х1087м.
Бумага тип. № 3. Гарнитура литературная. Печать высокая. Усл. печ. л. 11,76.
Усл. кр.-отт. 11,97. Уч.-изд, л. 15,5. Тираж 220 000 экз. Заказ № 282. Цена 80 коп.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ленинградская типография № 2 головное предприятие ордена Трудового
Красного Знамени Ленинградского объединения «Техническая книга» им.
Евгении Соколовой Союзполнграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли. 198052. г. Ленинград,
Л-52, Измайловский проспект, 29
1702070000—102
053(021-85	48-80	© Издательство «Наука».-
' '	Главная редакция
физико-математической
литературы, 1985
ПРЕДИСЛОВИЕ
Заметно уступая универсальным ЭВМ в предельной сложности
решаемых задач и скорости вычислений, миниатюрные и дешевые
электронные калькуляторы позволяют решать большинство повсе-
дневных научных и технических задач достаточно быстро, бесшумно,
в любое время и в любой обстановке, с высокой надежностью и точ-
ностью. Современные программируемые микрокалькуляторы имеют
функциональные возможности, недавно присущие лишь большим
ЭВМ: прямую и косвенную адресацию, организацию безусловных и
условных переходов, подпрограмм и циклов, микропрограммное вы-
числение элементарных и отдельных специальных функций вводом
одной команды, встроенные модули профессиональных программ
пользователей, накопители на магнитных картах, печатающие
устройства — принтеры и т. д.
Однако эффективное и грамотное использование программируе-
мых микрокалькуляторов, как и ЭВМ других классов, требует глу-
бокого знания языков их программирования, основ вычислительной
математики, умелого выбора алгоритмов и численных методов рас-
четов, практических навыков в переводе “программ с одного языка
программирования на другой, а главное — наличия Отлаженных па-
кетов и библиотек программ.
Справочник содержит данные о конструкции н характеристиках
массовых отечественных и зарубежных микрокалькуляторов, языках
и особенностях их программирования, алгоритмах вычислительных
процедур и численных методах их реализации Основной материал
справочника, в отличие от книг [6—8], ориентирован на научно-тех-
нические и инженерные расчеты общего характера. Исключением
является лишь последняя глава, иллюстрирующая типовые электро-
радиотехнические расчеты и дополняющая книгу автора [8]. Основ-
ное внимание в справочнике уделено программной реализации разно-
образных численных методов и вычислениям специальных математи-
ческих функций, использующихся в самых различных областях науки
И техники. Ввиду ограниченного объема справочника математиче-
ское обеспечение микрокалькуляторов дается в основном в виде
конечных формул, входящих в Инструкции по использованию про-
грамм.
В справочник включена обширная библиотека программ (их
свыше 250) для массовых отечественных программируемых микро-
калькуляторов с обратной бесскобочной логикой вычислений Элек-
троника БЗ-34. Они пригодны для их функциональных аналогов
Электроника МК-54 и Электроника МК-56, а также (после неслож-
ного перевода) для, микрокалькуляторов HP-llC, НР-15С, НР-21С,
НР-67 и др. фирмы Hewlett Packard (США). Описано также
свыше 50 программ для одних из наиболее сложных программируе-
мых микрокалькуляторов с алгебраической логикой Т/-58С и 77-59
фирмы Texas Instruments (США). Знакомство с нн.мн позволит чи-
тателям разобраться с множеством программ, описанных в зарубеж-
ной литературе, и получить навыки в переводе программ.
При подборе и разработке программ для основной части спра-
вочника в первую очередь учитывались их наглядность, возмож-
ность простой структурной проверки и соответствие программ алго-
ритму расчетов и оригиналам (для переводных программ). Во всех
программах использованы только регламентированные (т. е. указан-
ные в инструкции по эксплуатации [25, 26] операторы). Некоторые
нерегламентированные операторы (см. § 1.6) и особые приемы про-
граммирования позволяют сократить длину программ, уменьшить
время вычислений и. повысить предельную сложность решаемых за-
дач. Основанные на этом программы для калькуляторов Электро-
ника БЗ-34 даны в приложении 3 (в том числе несколько программ
из кн6ги‘[29], опубликованной после сдачи рукописи справочника
в набор).
Справочник рассчитан на научных работников, инженеров и сту-
дентов вузов и техникумов. Он полезен и тем, кто впервые присту-
пает к Ойвоенйю более сложной вычислительной техники, в частно-
сти персональных ЭВМ.
Обилие числового и программного материала в справочнике,
из-за крайне сжатого изложения, создает условия для отдельных
неточностей и опечаток. Автор выражает глубокую признательность
Н. П. Брусенцову, В. В. Козлову и другим, своими замечаниями, со-
ветами и пожеланиями способствовавшим работе автора иад книгой,
и с благодарностью ожидает замечаний, советов и пожеланий по
улучшению материала справочника, которые следует высылать по
адресу: 117071 Москва В-71, Ленинский пр., 15, Главная редакция
физико-математической литературы издательства «Наука», редакция
математических справочников.
В. П. Дьяконов
Глава 1
МИКРОКАЛЬКУЛЯТОРЫ С ОБРАТНОЙ
БЕССКОБОЧНОЙ ЛОГИКОЙ ВЫЧИСЛЕНИЙ
1.1. Функциональные возможности
микрокалькуляторов с обратной бесскобочной
логикой вычислений
•
Микрокалькуляторы. — специализированные на выполнение по-
вседневных расчетов ЭВМ личного пользования. Их основой (рис. 1.1)
является специальное устройство для проведения логических и ариф-
метических операций — микропроцессор (МП). Хранение двух чисел
(операндов) осуществляется с помощью запоминающих устройств —
Рнс. 1.1. Функциональная схема микрокалькулятора
операционных регистров X и У. Результат вычислений поступает в
регистр X и индицируется в десятичной форме с помощью индика-
тора [дисплея).
В современных микрокалькуляторах с операционными регистра-
ми X и Y объединены еще несколько регистров (Z, Тит. д), об-
разуя стек (магазин). Перемещение чисел в стеке вверх (X —> Y,
Y->-Z, Z->T и т. д.) или вниз (X *- Y, Y -<-Z, Z*-T и т. д.) напо-
Рис. 1.2. Внешний вид мик-
рокалькулятора Электрони-
ка БЗ-19М с обратной бес-
скобочной логикой вычисле-
ний
минает перемещение патронов в ма-
газине пистолета.
К МП подключаются также по
стояпное запоминающее устройство
(ПЗУ) и оперативные запоминаю-
щие устройства (ОЗУ) данных и про-
грамм. ОЗУ данных представляет
собой от одного до нескольких сотен
регистров памяти, подобных регист-
рам X или Y. Пользователь может
обратиться к любому нз них, задав
его номер (адрес). ОЗУ программ
хранит команды, задаваемые про-
граммой, которую вводит пользова-
тель. В ПЗУ хранятся команды (ми-
кропрограммы) для выполнения ос-
новных операций. У непрограммируе-
мых  микрокалькуляторов ОЗУ про-
грамм отсутствует. Иногда ОЗУ дан-
ных и программ объединяются,
т е. часть ОЗУ используется для
хранения данных, остальная часть—•
для хранения программ.
Управление всеми блоками от
клавишного пульта пли автоматиче-
ски по программе осуществляется
устройством управления. Через него
к МП могут подключаться некоторые
дополнительные устройства: модуль с программами пользователя
(МПП), накопитель информации на магнитной карте (НМК), печа-
тающее устройство — принтер и др.
Для проведения сложных расчетов весьма удобной оказалась
бесскобочная логика вычислений, предложенная польским математи-
ком Лукасевичем Микрокалькуляторы с обратной бесскобочной ло-
гикой вычислений имеют специальную клавишу для ввода и переме-
щеиия чисел в стеке вверх	1		4- Е	или	4- ENTER	
*) Иногда регистры Y, Z, Т и т д. на функциональной схеме
микрокалькулятора указываются под регистром X. В этом случае
•(enter — ввод). Арифметические операции при этом выполняются пз
схеме: ввод числа а, ввод оператора (команды) f, ввод числа Ь,
ввод оператора соответствующей операции * (* — знак операции:
_ X ИЛ13 -2_) , Сокращенно эта схема выглядит так: a f b*.
Из отечественных непрограммируемых микрокалькуляторов лишь
одна модель — Электроника БЗ-19М относится к рассматриваемой
группе микрокалькуляторов. Она имеет стек из трех регистров X, Y
и Z. Функциональные возможности микрокалькулятора очевидны из
надписей на пульте управления (рис. 1.2). Габариты этого микро-
калькулятора 86 X 167 X 41 мм, масса 400 г, питание от сети и
аккумуляторов (4 элемента Д-0,55).
Микрокалькуляторы Электроника БЗ-19М, как и другие, рас-
смотренные в книге, оперируют с числами, представленными в пока-
зательной форме х = ЛЫ0Б, где М — нормализованная мантисса и
Е — ±99 — порядок числа. Функции, обозначения которых даны над
клавишами, вводятся" после нажатия префиксной клавиши F и со-
ответствующей клавиши. Например, функция In х вычисляется после
in
набора х и нажатия клавиш F н | —	. Результат заносится в ре-
гистр X.
Обратная бесскобочная логика вычислений особенно удобна при
вычислении сложных выражений, требующих выполнения заданной
последовательности операции, например:
(а X 6) + (с X . aft>Xcf^X+...
(a — Ь)Цс + rf) ...	affc —	..
e lg (^7“) •••	b fc + frf ± F 1g f a X ...
Операции с тремя числами a, b и с могут выполняться после их
ввода, например:
(«+6)Хс cft)fa + X
> (о X 6) + с с f Ь f а X +
В этих примерах отчетливо видны особенности обратной бесско-
бочной логики вычислений: ввод чисел в порядке, обратном их ис-
пользованию, и разделение их при вводе оператором f, выполнение
подряд двух операторов арифметических действий, отсутствие ско-
бок. Более детальное описание дается в следующих параграфах этой
главы. 4
Применение обратной бесскобочной логики в программируемых
микрокалькуляторах позволяет заметно уменьшить число шагов
программы, .особенно если при вызове очередного числа предше-
ствующие числа автоматически смещаются в верхние регистры стека,
стрелка на клавише ENTER обращена острием вниз. Однако такое
обозначение встречается очень редко.
Характеристики отечественных программируемых микрокалькуляторов
Таблица 1.1
Параметр	Тип ЭВМ				
	Электроника				
	БЗ-21	МК-46	Б 3-34	МК-56	Ж-54
Число разрядов мантиссы/порядка	7,8/2	7.8/2	8/2	8/2	8/2
Число регистров операционного блока	2	2	4	4	4
Регистр восстановления результата предшествующей операции	Нет	Нет	Есть	Есть	Есть
Число добавочных	регистров (ячеек) памяти	6 + стек на 6 чисел	6 + стек на 6 чисел	14	14	14
Максимальное число шагов про- граммы	60	66 \	98	98	98
Вычисление функций х: l/x, х2, ех, In x, sin x, cos x	Есть	Есть	Есть	Есть	Есть
Вычисление функций x: tg x, arctgx, arcsinx, arccos x, 10*, 1g x	Нет	Нет	Есть	Есть	Есть
Представление углов	Радианы „	Радианы	Радианы, градусы	Радианы, градусы, грады *)	Радианы, градусы, грады *)
Адресация	Прямая	Прямая	Прямая и косвенная	Прямая и косвенная	Прямая и косвенная
Время выполнения арифметиче- ских операций ие более, с	0,5	0,5	0,5	0,5	0,5
Габариты, мм	185X100X48	280x240x90	185X100X48	208X205X60	167X78X36
Масса, кг	0,39	2,5	0,39	1,з	0,25
Питание	Универсаль- ное	Сеть	Универсальное	Сеть	Универсальное
Оформление	Переносное	Настольное	Переносное	Настольное	Переносное
*) Град—мера измерения углов, равная 1/100 части прямого угла.
а при выполнении операций — в нижние регистры. Тогда операция
(ц + b) X с выполняется символически так: cba-\- X- Для сравнения
укажем, что у микрокалькуляторов с алгебраической логикой- (см.
главу 2) те же вычисления символически записываются в виде
(а + Ь)Х.с =. Таким образом, в программе они займут 8 шагов,
тогда как в первом случае только 5.
Указанные обстоятельства привели к массовому применению
программируемых микрокалькуляторов с обратной бесскобочной ло-
гикой вычислений. К этой группе относятся отечественные програм-
мируемые микрокалькуляторы, технические характеристики которых
даны в табл. 1.1.	.	.
Микрокалькуляторы Электроника БЗ-21, Электроника МК-46
условно можно отнести к первому поколению программируемых
микрокалькуляторов. Они имеют ограниченный набор команд и вы-
числяемых по ним функций, небольшое предельное число шагов про-
граммы, а главное — только прямую адресацию (см. ниже). Особен-
ности вычислений и программирование этих микрокалькуляторов
детально описаны в книгах [6—9] и поэтому далее не рассматри-
ваются.
Гораздо большими функциональными возможностями обладают
программируемые микрокалькуляторы второго поколения: Электро-
ника БЗ-34, Электроника Л1К-54 и Электроника МК-56 (настольная
микро-ЭВМ). Эти Микрокалькуляторы, а также подобные модели
зарубежных фирм (см. табл. 1.2 с параметрами широко распростра-
ненных калькуляторов фирмы Hewlett Packard (HP) США), удовле-
творяют важнейшим требованиям, предъявляемым к современным
микро-ЭВМ индивидуального пользования, ориентированным. на на-
учно-технические расчеты. В их числе:
—	простота в работе и обслуживание одним пользователем, как
правило, неспециалистом в области программирования,
—	малые габариты и масса, питание от автономного источника
и сети переменного тока,
—	простота языка программирования, ввода и редактирования
программ,
—	вычисление по встроенным микропрограммам важнейших эле-
ментарных функций аргумента х (1/х, х2, 'у/х, ух или Xs1, ех, 10',
1п х, 1g х, sinx, cosx, tgx, arcsin x, arccosx, arctgx и др.),
—	достаточное число регистров памяти с произвольным досту-
пом (не менее 10),
—	достаточное максимальное число шагов программной памяти
(л100 и выше),
—	развитые программные возможности (наличие команд прямой
и косвенной адресации, организации-условных и безусловных пере-
ходов, подпрограмм и циклов),-
возможность выполнения всех операций с клавишного пульта,
Таблица 1.2
Характеристики зарубежных м крокалькуляторов с обратной бесскобочной логикой вычислений
для инженерных и научных расчетов (в,,модели, помеченные знаком*, встроен принтер)
Параметр 	Тип ЭВМ							
	HP-I5C	НР-25С	НР-29С	НР-55	НР-91*	» НР-67	НР-97’	НР-41С '
Программируемость	Есть	Есть	Есть	Есть	Нет	Есть	Есть	Есть
Число регистров памяти	64	8	30	20	16	26	26	320
Число шагов программы	448	49	98	49	• —	224	224	2249
Вычисление функций I/JC, -у/х In х, Igx, ех 10х	Есть	Есть	Есть	Есть	Есть	Ехть	Есть	Есть
Тригонометрические и обратные им функции	Есть	Есть	Есть	Есть	Есть	Есть	Есть	Есть
Гиперболические и обратные им функции	Есть	Нет	Нет	Нет	Нет	Нет	Нет	Нет
Статистические" расчеты	Есть -	Есть	Есть	Есть	Есть	Есть	Есть	Есть
Число разрядов мантиссы/порядка	10/2	8/2	8/2	10/2	10/2	10/2	10/2	10/2
Запоминание программ при выклю- чении	Есть	Есть	Есть	Нет	Нет	Нет	Нет	Есть
Запись на магнитные карты	Нет	Нет	' Нет	Нет	Нет	Есть	Есть	Есть
Число флажков/меток	10/25	Нет	-Нет	Нет	Нет	4/10	4/10	56
Косвенная адресация	Есть	Нет	Нет	Нет	Нет	Есть	Есть	Есть
Подключение принтера	Нет	Нет	Нет	Нет	Есть	Есть	Есть	Есть
Габариты, мм	128X80X15	130X68X30	130X68X30	152X81X34	229X203X64	152X81X34	229X203X64	144X79X33
— низкая стоимость, делающая микро-ЭВМ доступными для ши-
рокого круга пользователей (инженерно-технических и научных ра-
ботников, студентов и т. д.).
Развитие современных программируемых микрокалькуляторов с
обратной бесскобочной логикой вычислений идет по следующим на-
правлениям: увеличение числа регистров памяти и шагов программы
(см., например, модель НР-41С — табл. 1.2), использование дополни-
тельных ОЗУ, ПЗУ с записями программ (твердотельных и в виде
цифровых магнитофонов с записью программ на миниатюрные маг-
нитные карты), обеспечение работы с внешним периферийным обо-
рудованием (кассетные магнитофоны, принтеры, устройства сопря-
жения с телефонной сетью и др.).
У некоторых последних зарубежных моделей таких микрокаль-
куляторов существенно расширен набор функций, выполняемых мик-
ропрограммно. Так, микрокалькуляторы НР-15С имеют емкость про-
граммной памяти на 448 шагов, выполняют различные операции с
-матрицами (размер до 8X8), решают- системы из 2—7 линейных
уравнений, выполняют операции с комплексными числами, вычис-
ляют определенные интегралы, проводят статистические расчеты и
др. У микрокалькуляторов с буквой С в названии (НР-15С, НР-41С
и др.) программа и данные в регистрах памяти сохраняются после
отключения питания, что дает большие удобства при отладке слож-
ных программ и проведении трудоемких вычислений.
Для отечественных программируемых микрокалькуляторов базо-
вой является .модель Электроника Б3;34. Микрокалькуляторы Элек-
троника МД-54 и Электроника МД-56 полностью совместимы с этой
моделью-по языку программирования и системе команд. Эта совме-
стимость предусматривается и у новых моделей (Электроника МД-52,
Электроника МД-61 и др.), имеющих расширенный набор микропро-
грамм, встроенные ПЗУ и ОЗУ, разъемы для подключения перифе-
рийных устройств.
Отечественные и . зарубежные (серии HP) микрокалькуляторы
имеют простой символьно-кодовый язык программирования с тща-
тельно продуманной системой команд. Это означает, что операции
-вводятся нажатием клавиш с изображенными на них символами и
им присваиваются коды в виде чисел и знаков, отображаемых дис-
плеем в ходе ввода программ и их редактировании*). Наиболее
.распространенные операции (ввод чисел в регистры памяти и их
вызов, безусловные переходы и обращения к подпрограммам с кос-
венной адресацией и др.) выполняются одношаговыми операторами,
что заметно сокращает общее число шагов программ. Не составляет
*) У микрокалькуляторов НР-41С операторы, в том числе бук-
венные, отображаются алфавитно-цифровым жидкокристаллическим
Дисплеем.
труда перевод программ для отечественных микрокалькуляторов на
язык программирования калькуляторов серии HP и наоборот.
Символьно-кодовое программирование имеют также некоторые
настольные микро-ЭВМ: Электроника ДЗ-28, 15ВСМ-5, Искра-124,
Искра-125 и др. [11, 12]. Микро-ЭВМ Электроника ДЗ-28 с емкостью
ОЗУ 16 или 32 кбайт им.еет емкость программируемой памяти до
32 256 шагов и допускает с пульта прямое обращение к 166 деся-
тичным регистрам памяти (ср. с 98 шагами и 14 регистрами у ми-
крокалькулятора Электроника БЗ-34). Время вычисления иа ней
примерно в 100 раз меньше,’ чем у микрокалькуляторов. Особенно-
сти программирования данной ЭВМ на символьно-кодовом языке
описаны в [8]. Эти микро-ЭВМ программируются н иа языке высо-
кого уровня бейсик [12, 13].
Микро-ЭВМ Искра-124 имеет емкость программной памяти на
180 шагов, 10 регистров памяти и 3 стековых регистра. Время вы-
полнения операций сложения и вычитания около 0,02 с, умножения
и деления 0,1 с, извлечения квадратного корня 0,3 с и вычисления
функций около 1 с.
Микро-ЭВМ Искра-125 имеет блок отображения информации иа
электронно-лучевой трубке, обеспечивающей индикацию результатов
вычислений и вводимой программы. Емкость ОЗУ 1 кбайт, постоян-
ного ЗУ 4 кбайт. Предусмотрены прямое н косвенное обращение к
256 регистрам памяти и возможность записи программ и данных на
магнитную ленту накопителя.
Символьно-кодовое программирование этих микро-ЭВМ в прин-
ципе подобно программированию микрокалькуляторов. Однако си-
стема символов клавиатуры и кодов операторов у них иная.
1.2.	Система команд и кодов программируемого
микрокалькулятора Электроника БЗ-34
Внешний вид программируемого микрокалькулятора Электрони-
ка БЗ-34 приведен на рис. 1.3. В верхней части передней панели его
расположен 12-разрядиый люминесцентный индикатор, под которым
располагаются выключатель питания и, переключатель Р — Г (ра-
дианы — градусы).
Пульт управления микрокалькулятором имеет 30 клавиш с двой-
ным или тройным управлением. Основная операция, вводимая кла-
вишей, обозначена символом прямо на клавише. Операции, обозна-
ченные символами красного цвета над клавишами, вводятся после
нажатия префиксной клавиши F, а операции, обозначенные симво-
лами черного цвета под клавишами, вводятся после нажатия пре-
фиксной клавиши К, которая используется также для ввода опера-
ций косвенной адресации.
Отметим назначение специальных символов:
АВТ — перевод в режим автоматических вычислении,
ПРГ —перевод в режим программирования,
л — вызов числя л = 3,1415926,
Рис. 1.3. Внешний вид программи-
руемого микрокалькулятора Элек-
троника БЗ-34 с обратной бесско-
бочной логикой вычислений .
(ераций для организации циклов.
Q— поворот стека для вывода чисел из него в регистр X,
. Бх — вызов числа из регистра восстановления результата пред*
шествующей операции, «
Сх — сброс содержимого
операционного регистра X на
нуль,
CF — сброс действия пре-
фиксной клавиши -F,
0 х,— 0, х^ 0 и
х Ф 0 — ввод операций услов-
ных переходов,
БП — ввод операции безус-
ловных переходов,
ПП — ввод подпрограмм,
П—-запись чисел в реги-
стры памяти,
ИП — вызов чисел из реги-
стров памяти,
ШГ — смещение программы
на один шаг в направлении
ввода,
X —	г
• ШГ — смещение програм-
мы на один шаг против на-
правления ввода,
/—/ — смена знака мантис-
сы или порядка,
В/0 — установка програм-
мы на нулевой шаг и ввод
операции возврата из подпро-
граммы,
С/П — ввод операции оста-
новки и пуска вычислений по
программе,
БО, LI, L2 и L3 — ввод
НОП — ввод операции нейтрализации ошибочно введенной в
Программу команды,
А, В, С и Д — обозначение регистров памяти с номерами 10, 11,
12 и 13,
t — смещение чисел в стеке вверх на одну ступень.
При включении микрокалькулятора автоматически устанавли-
вается режим автоматических вычислений и обнуляются все регист-
ры памяти и операционные регистры. Сброс ошибочно введенного
числа выполняется нажатием клавиши Сх. В этом,режиме микро-
калькулятор обеспечивает выполнение арифметических операций, вы-
числение функций, отмеченных в табл. 1.1, вызов числа л, запись
чисел в 14 регистров памяти и вызов их из этих регистров, запись
чисел в регистры стека и управленце их продвижением, изменение
знака мантиссы и порядка числа х в регистре X, обмен содержимого
регистров X и Y, восстановление результата предшествующей опе-
рации и проведение сложных последовательных вычислений пц_об-
ратной бесскобочной схеме вычислений.
Все эти вычисления могут проводиться вручную или по введен-
ной программе. Различие заключается лишь в том, что вводимые
подряд с клавиатуры числа разделяются операцией В связи с
идентичностью ручных вычислений и вычислений по программе
правила их проведения подробно описаны в следующем параграфе,
посвященном организации вычислений по программе.
Таблица 1.3
 Операция	Код	Операция	Код	Операция	Код	Операция	Код
0	00	ПО ч	40	Kx^OO	70	КПП0	-0
9	09	П9 ’	49	Kx^09	79	КПП9	-9
	0-	ПА	4 —	Kx^OA	1-	КИПА	— —«
/-/	0L	ПВ	4L	Kx^OB	7L	кппв	— f,
ъп	0C	ПС ’	4C	Kx#=0C	7С	КППС	-с
Сх	or	ПД	4Г	Кх^ОД	7Г	кппд	— р
4	0E	FBx	0	КБ ПО	80	кпо	L0
+	10	С/П	50	...	...		...
—	11	БП	51	КБП9	89	КП9	L9
X	12	B/0	52	КБПА	8-	КПА	L “
4-	13	ПП	53	ЦБПВ	8L	КИВ	LL
XY	14	КНОП	54	ЦБПС	8С	КПС	LC
1'10*	15	Fx#.O	57	КБПД	8Г	кпд	1_Г
Бе*	16	FL2	58	Кх > 00	90	кипо	го
Fig	17	Fx>00	59	...		...	...
F hl	18	Fx==0	5E	Кх>09	99	КИП9	Г9
F arcsln	19	Fx<0	SC	Кх>0А	9-	КИПА	Г —
F arccos	1~	FLO	5Г	Кх> 0В	9L	кипв	Г" [_
F arctg	1L	FL1	5L	Кх>0С	9С	кипе	, ГС
F sin	1C	FL3	5-	Кх>0Д	9Г	КИПД	гг
F cos	1Г	ИП0	60	Кх<01	□	Кх=00	Е0
Fig	IE	...	...	...		...	...
Fa	20	ИП9	69	Кх<09	С9	Кх=09	Е9
	21	ИПА	6-	Кх<0А	С-	Кх=0А	Е—
Fx2	22	ИПВ	6L	Кх<0В	CL	Кх=0В	HL
Fl/x	23	ИПС	6C	Кх<0С	сс	Кх=0С	ЕС
	24	ИПД	6p	Кх<0Д	СГ	Кх=од	Ег
После перевода в режим программирования (нажатием клавиш
F и ПРГ) каждая операция или команда вводится нажатием соот-
ветствующих клавиш и кодируется определенным символом. Все
операции микрокалькулятора и их коды даны в табл. 1.3. Коды
имеют вид цифр и знаков, отображаемых семисегментными элемен-
тами индикатора в процессе.ввода программы и ее редактирования.
1.3. Основы программирования микрокалькуляторов
Рассмотрим основные понятия программирования микрокальку-
ляторов Электроника БЗ-34.
Ввод и представление чисел. Числа-операнды вводятся в микро-
калькулятор нажатием соответствующих клавиш. Порядок числа
вводится нажатием клавиши ВП. Знак минус вводится нажатием
клавиши /—/ после ввода мантиссы или порядка числа. Числа,
большие 1, но меньшие 108, представляются в обычном виде, на-
пример 9725 или 14,1256. Числа за этими пределами представляются
в экспоненциальной форме М- 10е, где М — нормализованная мантис-
са с первым знаком оу 1 до 9, Е — порядок числа (до ±99). Нор-
мализация числа происходит при записи чисел в любой регистр
(см. ниже).
Операторы. Совокупность символов, обеспечивающих по про-
грамме выполнение одной из элементарных операций, называется
оператором. Операторы вводятся нажатием одной или нескольких
клавиш. Например, вычисление е* сводится к набору числа х и на-
жатию клавиш F и е'. В программе это соответствует оператору Fe*,
который занимает один шаг (см. ниже). Некоторые операторы яв-
ляются двухшаговыми.
Регистры. Для хранения чисел и результатов вычислений служат
регистры памяти. По своему назначению они подразделяются на три
типа. Первый тип — операционные регистры X и Y, в которые вво-
дятся два операнда двухместных арифметических операций. Второй
тип регистров — регистры  памяти — служит для записи исходных
данных и промежуточных результатов вычислений. Эти регистры
обозначаются буквами А, В, С, Д и цифрами 0 ± 9 (всего 14 ре-
гистров). Кроме того, еще два таких регистра Z и Т объединяются
с регистрами X и Y, образуя стек. К третьему типу регистров отно-
сится регистр восстановления результата предшествующей опера-
ции X.
Структура стека и перемещение в нем чисел при различных опе-
рациях показаны на рис. 1.4: а) операция f, б), ввод числа х в ре-
гистр X после операции f, в) вызов в регистр X числа л или числа
из регистра N (см. ниже), г) обмен содержимым регистров X и Y
Xs±Y, д) одноместная операция (Г), например вычисление е*,
е) двухместная арифметическая операция (2). ж) кольцевое переме-
щение чисел в стеке — оператор F0, з) вызов числа из регистра
XI — оператор ГВ*. В дальнейшем операторы X F и F 0 будут
указываться упрощенными символами XY и F. .
Ввод чисел в регистры памяти. Число можно ввести в регистр
памяти N набором и нажатием клавиш П и N. Здесь N— символ
Рис. 1.4. Перемещение чисел в регистрах стека при основных опера-
циях
регистра (А, В, С, Д, 0 4-9). В программах ввод соответствует one*
ратору ПЛ.
Вызов чисел из регистров памяти. Вызывается число из реги-
стра памяти N нажатием клавиш ИП и N (оператор ИПЛ').
Шаги программы и их адреса. Каждому оператору в программе
соответствует свой шаг. Шаги последовательно нумеруются двух-
значными десятичными числами от 00 до 97 (всего 98 шагов)',
В режиме программирования (после нажатия клавиш F и ИРГУ
номера шагов высвечиваются в правом конце индикатора. Операто-
ры в программе удобно записывать построчно, по 10 операторов в
каждой строке. В этом случае положение оператора в программе
позволяет легко найти номер шага, именуемый его адресом.
Прямая адресация. Непосредственное указание адреса (номера
шага программы или символа регистра памяти) называется прямой
адресацией. Так, описанный выше ввод чисел в регистры и их вызов
проводились с использованием прямой адресации.
Косвенная адресация. Если адрес указан содержимым одного
из регистров памяти, то адресация будет косвенной. Косвенная адре-
сация вводится нажатием клавиши К. Например, при выполнении по
программе оператора КП5 число х — РХ будет записано -в регистр
памяти, номер которого указан содержимым регистра 5. Аналогично,
оператор КИПА обеспечивает вызов числа из регистра с номером,
указанным содержанием регистра А, в регистр X. Числам 0 4-13
в регистре адресации соответствуют регистры 04-9, А(10), В(11),
С(12) и Д(13).
Модификация адресов при косвенной адресации. Если в качестве
регистра адресации, в котором хранится адрес обращения, взять
один из регистров 7, 8, 9, А, В, G или Д, то при выполнении опе-
раторов косвенной адресации содержимое регистра адресации не
изменяется. Если регистр адресации имеет номер 0, 1, 2 или 3, то
при каждом выполнении операторов косвенной адресации содержи-
мое регистра адресации уменьшается на 1, а при регистрах адреса-
ции 4, 5 или 6 увеличивается на 1. Таким, образом, происходит
модификации адресов.
Безусловные прямые и косвенные переходы. Для построения
разветвляющихся программ используются безусловные переходы.
Безусловный переход на шаг программы с 'адресом N вводится опе-
ратором БП N. Например, во фрагменте програм?.<ы
ИПА ИПВ + БП 17	..................
....................................  ИПС	X С/П
после выполнения операции (а + Ь) при а = РА и & = РВ происхо-
дит безусловный переход на адрес 17, т. е. (а + Ь) умножается на с
•’(с = PC), после чего вычисления останавливаются (оператор С/П).
Для простоты пропущенные операторы обозначены точками. Одно-
шаговая команда КБП/И обеспечивает безусловный косвенный пере-
ход по адресу, указанному содержимым регистра адресации М
{М = А, В, С, Д, 0 4-9).
Условные прямые и косвенные переходы. Переход к адресу N
может проводиться по данным анализа содержимого х регистра X
на выполнение одного из условий: х < 0, х = 0, х 0 или х# 0.
.Такие переходы вводятся операторами Ех < 0, Fx = 0, Fx 0 и
Fx 0, после которых указывается оператор — адрес перехода N.
Если условие перехода не выполняется, то происходит переход на
шаг программы с адресом N, если выполняется — адрес перехода
игнорируется и выполняется следующая за ним часть программы.
.Одношаговая команда Кх < ОМ, Кх = 0/W, Кх 0/И или Кх =/= ОМ,
где М—символ регистра адресации (М = А, В, С, Д, 0 4- 9) обес-
печивает условный переход по адресу, указанному содержимым ре-
гистра М. .
Подпрограммы. Повторяющиеся фрагменты программ можно
оформить в виде подпрограммы, которая должна начинаться с ад-
реса N и кончаться оператором возврата из подпрограммы В/0. Об-
ращение к подпрограмме из любого места программы задается двух-
шаговой командой, содержащей операторы ПП и N.
Пусть подпрограмма имеет п шагов и повторяется т раз. Тогда
она в программе займет п + 1 шагов. Кроме того, придется дать т
обращений к подпрограмме, что займет 2т шагов. Без введения
подпрограммы вычисления займут т-п шагов. Следовательно, если
2т п + 1 <Zm-n или п> (2m-j-l)/(m—1), то введение подпро-
граммы сокращает общее число шагов программы. Однако число
операций при этом возрастает, растет и время вычислений. Можно
использовать до пяти подпрограмм, вложенных друг- в друга. Одио-
шаговая команда КППЛ/ обеспечивает косвенное обращение к под-
программе с адресом N, определяемым содержимым регистра адреса-'
дни М (М = А, В, С, Д, 0 4- 9).
 Организация циклов. Для организации циклов циклических про-
грамм служат операторы построения счетчиков FLO, FL1, FL2 и
FL3 в регистрах 0, 1, 2 и 3. После этих операторов указывается
адрес перехода N. При выполнении этих операторов содержимое
соответствующего регистра-счетчика уменьшается на 1. Если оно не
равно нулю, то происходит переход по адресу N, а если оно ста-
новится равным 0 — переход идет к шагу программы, следующему
вслед за оператором N. Одношаговые команды KLOM/KLIM, KL2AI
и KL3AI обеспечивают косвенные переходы с адресом ЛА, указанным
содержимым регистра адресации М.
Остановка и пуск программы. Для остановки программы в нуж-
ном месте вводится оператор С/П. Нажатие клавиши с этим сим-
волом ведет .к запуску программы. Для запуска программы с нуле-
вого адреса нажимаются клавиши. В/0 и С/П.	।
Ввод и редактирование программы. Программа вводится нажа-
тием соответствующих клавиш после перевода калькулятора в ре-
жим программирования (нажатием клавиш F и ПРГ). При этом на
индикаторе отображаются коды трех последних операций и адрес
последующей операции, например:
Показания индикатора	10 6L	6—	10
Операторы	+ ИПВ ИПА
Направление ввода программы ------------------>
При ошибочно нажатой префиксной клавише -F сброс ее дей-
ствия производится нажатием клавиши CF. Для установки програм-
мы на заданный адрес используются клавиши сдвига, программы на
один шаг вправо ШГ или влево ШГ. С их помощью можно устл-
ловить программу на шаг с ошибочно набранным оператором и
исправить его. Для этого (в режиме автоматических вычислений
.дюсле нажатия клавиш F и АВТ) можно использовать команды' БП
и N (установка программы на шаг с адресом N). Двухшаговые
команды, набранные ошибочно, заменяются новыми полностью (т. е.
с вводом обоих операторов). На место лишнего оператора встав»
ляется оператор КНОП (иет операции).
Индикация некорректных операций. При выполнении некоррект*
пых операций (деление на 0, переполнение разрядной сетки ЭВМ,
возведение х = 0 в степень у, вычисление квадратного корня из от-
рицательного числа, вычисление 1/х при х = 0 и т. д.) вычисления
останавливаются и на индикаторе. появляется символ ЕГГОГ (от
английского слова error — ошибка). После этого можно проводить-
ввод чисел и продолжать вычисления.
Представление углов. Аргумент тригонометрических функций
можно выражать в градусах или радианах. Для этого служит пере-
ключатель ' Р — Г (радианы — градусы).
Примеры для контроля программ. Составленные и отлаженные
программы должны сопровождаться контрольным примером (или
примерами, если программа разветвляющаяся). Приступать к основ-
ным вычислениям можно только после проверки программы по кон-
трольному примеру. Если будет обнаружена ошибка, следует про-
верить правильность ввода программы по кодам основных операций
(см. табл. 1.3)-. При отладке программ бывает полезно проверить
вычисления по шагам; для этого в режиме автоматических вычисле-
ний нажимается клавиша ПП.
Л
1.4.	Специальные приемы программирования
микрокалькуляторов
Операторы косвенной адресации обеспечивают дополнительные
возможности, не отмеченные в инструкции к пользованию микро-
калькуляторами. Так, при вводе числа х (1 < х < 108) в регист-
ры 7, 8, 9, А', В, С и Д и последующем выполнении операторов КП7И
млн КИПМ происходит автоматическое отбрасывание дробной части
числа х. Например, введя в. регистр X число х = 421,756 и выполнив
операторы П9 КИП9 ИП9, получим результат в виде числа
00000421. При любой последующей операции это число приобретает
обычный вид числа 421. Таким образом, всего два оператора ПМ н
КИПМ обеспечивают выделение целой части х.
Если регистр М — 0, 1, 2 или 3, то наряду с отбрасыванием
дробной части при выполнении оператора КИПМ или КПМ проис-
ходит уменьшение целой части числа в регистре М на 1, а если
Л1 = 4, 5 или 6а то происходит увеличение целой части на 1. Эго
позволяет строить счетчики вида п — (п — 1) и п —	вводом
-сего одного оператора КИГШ или КПМ, причем текущие значе-
и’ш п заносятся в регистр Л4 и могут в дальнейшем без модифика-
дни вызываться оператором ИПМ. Повторяя операторы КИПА! или
КПМ а раз, можно организовать построение счетчиков вида
п=(п— а) и п=(и+«). Предпочтение следует отдавать оператору
КИПЛ4, так как при использовании оператора КПМ в регистры, но-
мера которых соответствуют и, будут заноситься результаты пред-
шествующих операций.
Для последовательного ввода до N(1 = 13 чисел ais, ап, ..., at
в регистры 1, 2, ..., 9, А, В, С и Д можно использовать цикличе-
скую программу с косвенной адресацией к регистрам при вводе в
них чисел:	•
Если n=N0
I 'Ir
N ПО О С/П КПО ИПО 1 — Fx = 0 02 ...
•fr Если n<N„|
Здесь N=(Nt) 4-1). Если N > 9, адрес 02 в конце программы надо
заменить на 03. При каждом цикле меняется на —1 адрес в регист-
ре адресации 0 и соответственно каждое новое число попадает в
новый регистр: Д, С, В, А, 9, ..., 1. После ввода всех чисел про-
исходит выход из цикла.
Еще один фрагмент программы обеспечивает ввод до 8 чисел
в регистры 6, 7, 8, 9, А, В, С и Д
Если n=N0
I 4г
5 П4 8 ПО С/П КП4 FL0 04' ...
Если	8	| г
В этом фрагменте номера регистров, в которые заносятся числа,
формируются в регистре 0 при выполнении оператора FL0.
Отметим, что ввод No чисел фрагментом программы с прямой
адресацией
П1 С/П П2 С/П ПЗ С/П П4 С/П и т. д.
занимает (2N0—1) шагов, т. е. 15 шагов при No=8 я 25 при Мо=13,
что существенно больше, чем прн организации ввода с использова-
нием косвенной адресации.
В общем случае программы могут быть линейными, разветвляю-
щимися и циклическими. Примером линейной программы является
программа вычисления функции	—
у = (sin sinft)/ппft	(1.1)’
с вводом i в регистр X. Отведем под запись и и f регистры 8 и 9
'п = Р8, f = Р9, t = РХ). Будем записывать программу с нулевого
адреса. В полном виде программа имеет вид (внизу дано размеще-
ние чисел в регистрах X, Y, Z, Т и XI стека после ввода п, f nt и
выполнения программы по шагам):
Адрес	00	01	02	03 04	05	06	07	08	09.
Код	20'	68	69	12 12	18	И	0	13	50
Оператор	Fji	ИП8	ИП9	X X	X	Fsin	FBx	4-	С/П
Т 0	п	f	t	t t	t	t	t	t	t
Z п	f	t	л	t t	t	t	t	t	t
Y /	t	л	n	л t	t	t	sin sinft	t '	t
X t	л	n	f	nf я/if nnft		sin nnft nnft		У	У
XI 0	t	t	t	f nf	stnf	Jinft	nnft	ntlft	nnft
При вычислении по этой программе используются все регистры
стека. Перед пуском программы нажимается клавиша В/0 и про-
грамма устанавливается на нулевой адрес. После этого вводятся
исходные данные. Перемещения чисел в стеке даны под программой.
При п — 2, f = 1000 и t = 1,2-10“4 получаем т/= 9,0790883-1 О*1.
Эту .программу можно записать несколько иначе, выполняя опе-
рации умножения по мере ввода каждого нового сомножителя:
Fji X ИП8 X ИП9 X Fsin FBx 4- С/П
Обычно такой способ предпочтителен, так как слабее загружает
стек и предотвращает потерю числа из регистра Т при случайных
переполнениях стека.
.В дальнейшем адреса и коды приводиться не будут. Адрес легко
определяется положением команды при записи программы построчно
с десятью операторами в каждой строке. Коды нужны только при
проверке программ неопытными пользователями, так как на пер-
вых порах ошибочное нажатие клавиш не редкость. Если пользова-
тель критически оценивает свою пунктуальность при вводе программ,
он может составить дополнительную таблицу кодов нужной про-
граммы, используя табл. 1.3. Прн некотором навыке коды операций
быстро запоминаются.
Теперь рассмотрим простейшую разветвляющуюся программу.
Нетрудно заметить, что при t = 0 значение у по (1.1) определять
нельзя, так как (sinnnft)/nnft дает неопределенность вида 0/0, а
деление на 0 относится к некорректным операциям. При вводе / = 0
вычисления по описанным программам приводят к появлению знака
ошибки ЕГГОГ. Между тем значение sin х/х = 1 при х = 0. Следо-
вательно, более точно определять у по двум формулам
у = 1	при t — 0,	(1.2)
у = (sin wft)lnnft при t 0.
Переход от одной из них к другой можно осуществить, используя
условные переходы по условиям х = 0' или х 0. Тогда получим
такую программу:
Fx = 0 04	1	С/П Fn ИП8 ИП9 XXX
Fsin FBx 4- С/П
Если ввести t = 0, то условие t = х = 0 выполняется, адрес
перехода 04 игнорируется и на индикацию выводится 1. Если
t = х =£ 0 условие не выполняется и происходит переход по адре-
су 04, т. е. вычисление по второй формуле (1.2). Отметим, что при
вводе каждого нового значения t надо нажимать клавиши В/0 и
-С/П.
Модифицируем программу так, чтобы после ввода каждого зна-
чения t требовалось нажимать только клавишу С/П:
Fx = 0	06	1	С/П БП 00	Fn	ИП8 ИП9 X
X	X	Fsin	FBx 4- БП	03
Допустим введено 1=0. Тогда после пуска будет выдано^зиачение
у = 1. Набрав новое, значение t и нажав клавишу С/П, мы обеспе-
чим безусловный переход (команда БП 00) на' адрес 00. Если /¥=0,
то условие t — х = 0 • не выполняется и продолжение программы
пойдет с адреса 06. После деления sin jinfl на mft (операция с адре-
сом 14) происходит безусловный переход на адрес 03 (операторы
БП 03), т..е. к команде остановки вычислений С/П.
Рассмотрим пример составления программы с подпрограммой и
косвенной адресацией регистров памяти. Пусть надо вычислить вы-
ражение
(1.3)
Будем руководствоваться следующим- алгоритмом:
. 1. Значение л/2 вычислим один раз в начале программы, что
сократит общее время счета.
2. Вычисление похожих членов аеях^2, />еад^2 и- cenz^2 офор-
мим подпрограммой.
3 Так как при выполнении п. 2 значения х, а, у, b, z и с долж-
ны вызываться поочередно, то это целесообразно сделать, используя
косвенную адресацию регистров памяти и разместить х, а, у, b, z
н с последовательно в регистрах 7, 8, 9, А, В и С.
Тогда получим программу в виде
Fji _	2	4-	П6 6	П5	ПП 15	ПП	15
—	ПП	15	4- С/П	КИП5	Fx2. ИП6	X	Fe*
КИП5 X В/0
Запись числа 6 в регистр адресации 5 задает вызов первого
числа, х из регистра 7 при первом обращении к подпрограмме. Оно
начинается с операции косвенной адресации КИП5 по адресу 15.
При выполнении этого оператора содержимое регистра 5 (число 6).
увеличивается на 1. Следовательно, происходит вызов числа х из
регистра 7= (6+1). Далее х возводится в квадрат, умножается йа
л/2=Р6 и вычисляется елл:^2. Затем (оператор КИП5 по адресу 20)
происходит вызов числа а из регистра 8, так как содержимое регист-
ра 5, указывающее на номер регистра, из которого вызывается опе-
ранд, вновь увеличивается на- 1. Подпрограмма заканчивается умно-
жением ел*^2 на а и возвратом (оператор В/0) к основной про-
.грамме. Аналогично (со сменой пар «/, 6 и z, с) происходят второе
и третье выполнение подпрограммы.
Сравним эту программу с программой вычисления (1.3) без
подпрограммы:
Fn 2	П6	ИП7	Fx2	X	Fe*	ИП8	X*
ИП9 Fx2	ИП6 X	Fe*	ИПА	X	—	ИПВ	Fx2
ИП6 X Fex ИПС X -F С/П .
Нетрудно заметить, что в данном случае введение подпрограм-
мы сократило общее число шагов программы на. '4 шага. Однако
время вычисления при введении подпрограммы несколько увеличи-
вается. Действительно, при х = 3,	100, у = 2, b = 5, z = 4 и
с = 0,01 получим результат f,= 1,6775483-10-1 за время около 15 с
по первой и около 12 с по второй программе,
Теперь рассмотрим составление циклических программ. Пусть
надо вычислить функцию
для х— 1, 2, 3,- ... Один из простейших вариантов программы вы-
числения f(x) имеет вид (0=Р4)
КИП4 ИП4 Fe* 1 + ИП4 1 + -F F In
С/П БП 00
Первые два оператора обеспечивают увеличение содержимого
регистра Р4 х на 1 при каждом пуске программы. Последующие
операторы (с адресами 03—10) служат для вычисления f(x). Опера-
торы БП 00 обеспечивают переход к началу программы. Таким об-.,
разом, при нажатии клавиши С/П происходит циклическое вычисле-
ние f (х), причем при каждом цикле х возрастает на 1. Нажимая
клавишу С/П (перед первым пуском В/0 и С/П), будем получать
f(l} = 0,6201145, /(2) = 1,0283157, /(3) = 1,6622929 и т. д.
Вычисления можно автоматизировать в еще большей степени.
Пусть надо автоматически вычислить до 12 значений /(х) для 
х = 1, 2, 3,	, 12 с записью-результатов без вмешательства опе-
ратора в регистры 1, 2.....9,	Д. В, С. В этом случае требуется
Дополнительно решить две задачи: организовать до п 12 циклов
вычислений и предусмотреть автоматический выбор регистров для
записи результатов. Первая задача решается использованием опера»
тора организации цикла, например в регистре 0 — FLO. Вторая —*
использованием косвенной адресации. Один из вариантов такой про-
граммы следующий (и = РО):
НПО ПД Fex 1	+ ИПД 1 + -н Fin
КПД FLO 00 С/П
В начале программы содержимое регистра счетчика 0 (при пер-
вом пуске и) переписывается в регистр адресации РД — операторы
ИПО ПД. Затем (операторы с адресами 01—09) вычисляется f(x).
Оператор КПД обеспечивает запись f(x) в тот регистр, номер ко-
торого указан содержимым регистра Д. Оператор FL0 обеспечивает
возврат к началу программы (адрес 00) и уменьшение на 1 содер-
жимого регистра 1. Циклы продолжаются, пока содержимое регист-
ра 0 не станет равным 0. Введя, например, п = 10, спустя минуту
счета получим /(1) =0,6201145. Извлекая из регистров 2, 3, ..., 9, А
другие значения f(х), получим: f(2) =1,0283157,f(3) = 1,6622929, ...,
f (10) =7,6021501.
Большое число конкретных примеров программирования чита-
тель найдет в последующих разделах книги. Однако внимательное
знакомство с приведенными простыми примерами поможет разо-
браться в алгоритмах вычислений, реализованных в более сложных
программах. Эти примеры иллюстрируют также большие функцио-
нальные возможности косвенной адресации и операторов организа-
ции циклов.
Следует обратить внимание на то, что в некоторых микрокаль-
куляторах' первых выпусков нельзя по программе производить смену
знака вычислений и заканчивать подпрограммы следующими опера-
торами: Fsin, Feos, Ftg, Farcsin, Farccos, Farctg, Fe*, Fig, Fin,
Fx2, Fl/x, FV~, Fn, F10* и Fxa. Если по условию задачи надо про-
вести смену знака результата, то при умножении и делении это
можно сделать, присвоив знак минус одному из сомножителей, либо
делимому, либо делителю. Например, если надо вычислить число
•—ab (а — РА, b = РВ), то фрагмент программы должен быть
ИПА /—/ ИПВ X или ИПА ИПВ /—/ X, а не ИПА ИПВ X /—/•
Отмеченные выше операции допустимо проводить перед засылкой
результата в какой-либо неиспользованный регистр памяти (в том
числе в регистр Y командой }).
 Описанные в книге программы составлены с учетом этого огра-
ничения с тем, чтобы они были пригодны для любых микрокальку-
ляторов данного типа. В выпускаемых в дальнейшем микрокальку-
ляторах эти ограничения отсутствуют,, что несколько упрощает со-
ставление программ.
Для уменьшения времени вычислений нециклических программах
рекомендуется выносить за пределы цикла фрагменты программ,
вычисляющие члены уравнений, которые ие меняются от цикла к
циклу. Полезно также нормирование уравнений и приведение их к
возможно более простому виду.
1.5. Погрешности вычислений на микрокалькуляторах
Получаемый в результате вычислений результат у отличается ог
точного {/о. Абсолютная погрешность вычисления
А» = |Д{/| = |{/о — у},
а относительная
б« = Д«/|{/о|.
Поскольку значения yD не всегда заранее известны, иногда за-
дают Ау независимо. Например, если &у = ±2, то при уз = 5 имеем
^=:5±2 = 3 4-7, а при у„ = 100 у = 100 ± 2 = 98 4- 102. Часто
задают у числом верных знаков результата. Верными называют
знаки, если представленный ими результат имеет абсолютную по-
грешность не более 1/2 младшего разряда. Например, если , результат
у = 50,0124 задан тремя верными знаками, то можно принять, что
49,95 < у < 50,05. • , •
Поскольку результат вычислений микро-ЭВМ выдает с конечным
числом знаков, ему всгда присуща погрешность округления. Обычно
ее считают равной ±1 последнего разряда.
При вычислении элементарных и специальных функций наблю-
дается методическая погрешность. Она связана с тем, что такие вы-
числения проводятся разложением функций в ряд или непрерывную
дробь с конечным числом членов. Отбрасываемые члены создают по-
грешность результата, оцениваемую остаточным членом R. Эта по-
грешность обычно зависит от аргу$дента х (см. табл. 1.4 для микро-
калькуляторов Электроника БЗ-34).
При вычислении функций нескольких переменных у =
г= f(xi, xz, Хз, ..., хЛ) относительная погрешность вычисления
где S; — коэффициент чувствительности ^относительному изменению
б, t-го параметра.
Погрешность, получаемая в результате проведения операций над
приближенными числами, называется операционной погрешностью.
Операционная погрешность арифметических операций равна сумме
погрешностей чисел, над которыми проводятся эти операции. Суще-
ствуют определенные правила уменьшения этой погрешности. Так,
суммировать числа рекомендуется с меньших значений. При умноже-
нии следует умножать меньшее число на большее. Если промежу-
точный результат при этом yi > 1, его надо умножить на меньшее
		Таблица 1.4
Функция	Допустимые значения x	Максимальная относительная погрешность
sin X	1.10-49</x/<109	З-Ю-7 ‘
cos X	1.10-49</x/<109	3-10—7
igx	i-io-"<i x l<io9	З-Ю-7
arcsin x	1 X I< 1	З-Ю-7
arccos x	1 x 1<1	З-Ю-7
arctg X	1 • 10	< | X J < 9,9999999.1099	З-Ю-7
хУ	x>0	1-10—е 
e*	1 x |<100 In 10	4-10—7
x1 2 *	|x|<1050	1-10—7
10х	I x | <99,999999	4.10-7
\fx	x¥-0	I-IO-7
я	x>0	1-ю-4
Inx	x>0	З-Ю-7
Igx	x>0	3-10-7
из оставшихся чисел, если у, < 1, то надо умножить на большее.
Операции умножения и деления целесообразно чередовать друг с
другом, избегая переполнения операционного регистра X. Следует
избегать вычитания близких чисел, так как результат может попасть
в область машинного нуля, что может привести к 'большим погреш-
ностям, например, при последующем умножении даже на большое
число.
Для уменьшения операционной погрешности полезно проводить
преобразования функций с учетом отмеченных выше правил. Напри-
мер, у'= (а-|-Ь)2— а2 при b а следует представить в виде
у — 2аЬ + 62, что позволит избежать вычитания близких чисел
(а 4-6)2 и Ь2. К таким преобразованиям относится также нормиро-
вание уравнений, степенных полиномов и других функций, проводи-
мое так, чтобы вычисления велись с числами, далекими от машин-
ного нуля или бесконечности.
1.6. Инструкция по вводу и пуску программ
для микрокалькуляторов
1. Перед использованием программ следует внимательно ознако-
миться с_ алгоритмом вычислений н правилами работы с программой.
2. Включив микрокалькулятор, переводим его в режим про-
граммирования, нажав клавиши F и ПРГ, затем вводим программу,
нажимая указанные в ней клавиши, , 
3.	Нажав клавиши F, АВТ и В/0, переводим калькулятор в ре-
зким автоматических вычислений Я устанавливаем программу иа ну*
левой шаг.
4.	В точном соответствии с инструкцией вводим исходные дан*
ные: обозначение вида xt=PN означает ввод х, прямо в регистр W,
обозначение х;=РХ означает ввод х, в регистр X с фиксацией ввода
нажатием клавиши С/П. Для ввода x,=PY нажимаем клавишу f.
5.	Пускаем программу, нажав клавишу С/П. Вычисления сопро-
вождаются миганием индикатора. Если время счета не оговорено,
результат должен появиться - спустя 30—40 с. Обозначения^ вида
у, РХ, Zi -> РХ и так далее указывают на то, что результат yi
появляется на индикаторе регистра X (для получения затем z, надо
нажать клавишу С/П и т. д.). Обозначение yi PN означает,' что
результат заносится в регистр 7V (результат нз регистра N вызы-
вается нажатием клавиш ИП и N). Если программа зациклилась,
счёт прерывается нажатием клавиши С/П.
6.	Программу следует проверить по контрольному примеру. Если
его результат ошибочен, необходимо внимательно проанализировать
программу по кодам (см. табл. 1.3) и уточнить правильность ввода
исходных данных. Иногда полезно провести вычисления по шагам,
что позволяет выявить и затем устранить ошибки.
7.	Приведенные в основном тексте справочника программы при*
годны для микрокалькуляторов Электроника БЗ-34, Электроника
МК-54 и Электроника МК-56 с учетом эквивалентности символов:
f — B.f, ИП=П->х, П = х—»-П, arcsin = sin-1, arccos = cos-’,
arctg = tg-1, A = a, В = 6, C= с, Д = d и XY = Х-» Y.
Внимание! Операторы косвенной адресации КИП| (код fE)»
КП| (код LE), КБП| (код 8Е) и т. д. аналогичны операторам
КИПО, КПО, КБПО и т. д. с регистром адресации 0. Однако при их
исполнении содержимое регистра 0 не модифицируется. Операторы
К7- (код 34), ..., КД (код 3—) обеспечивают вызов одной коман-
дой знака ошибки ЕГГОГ. Оператор ВП при х — 0 = РХ засылает
этот регистр 1. Поскольку данные операторы не регламентированы,
программы с их применением даны отдельно в приложении 3. При
завершении выполнения циклов с операторами FLO ~ FL3 в адрес-
ном регистре остается число 1 (т. е. при последнем их исполнении
вычитание 1 не происходит).
Глава 2
МИКРОКАЛЬКУЛЯТОРЫ С АЛГЕБРАИЧЕСКОЙ
ЛОГИКОЙ ВЫЧИСЛЕНИЙ
2.1. Общие сведения
Микрокалькуляторы с алгебраической логикой выполняют вычис-
ления в более естественном виде благодаря использованию клавиш
рвода скобок
и равенства
В таких микрокалькуляторах числа вводятся в стек при нажатии
клавиши с открывающимися скобками, а выводятся — при нажатии
клавиши с- закрывающимися скобками. Число скобок, иногда только
круглых, может быть от 1 до 16 и определяется числом регистров
в стеке. Такие калькуляторы подразделяются на: 1) непрограмми-
руемые, 2) программируемые с обычной алгебраической логикой,
3). программируемые по системе AER (Algebraic Expression Reserve —
алгебраическое выражение условий) и 4) программируемые на упро-
щенной версии языка высокого уровня бейсик.
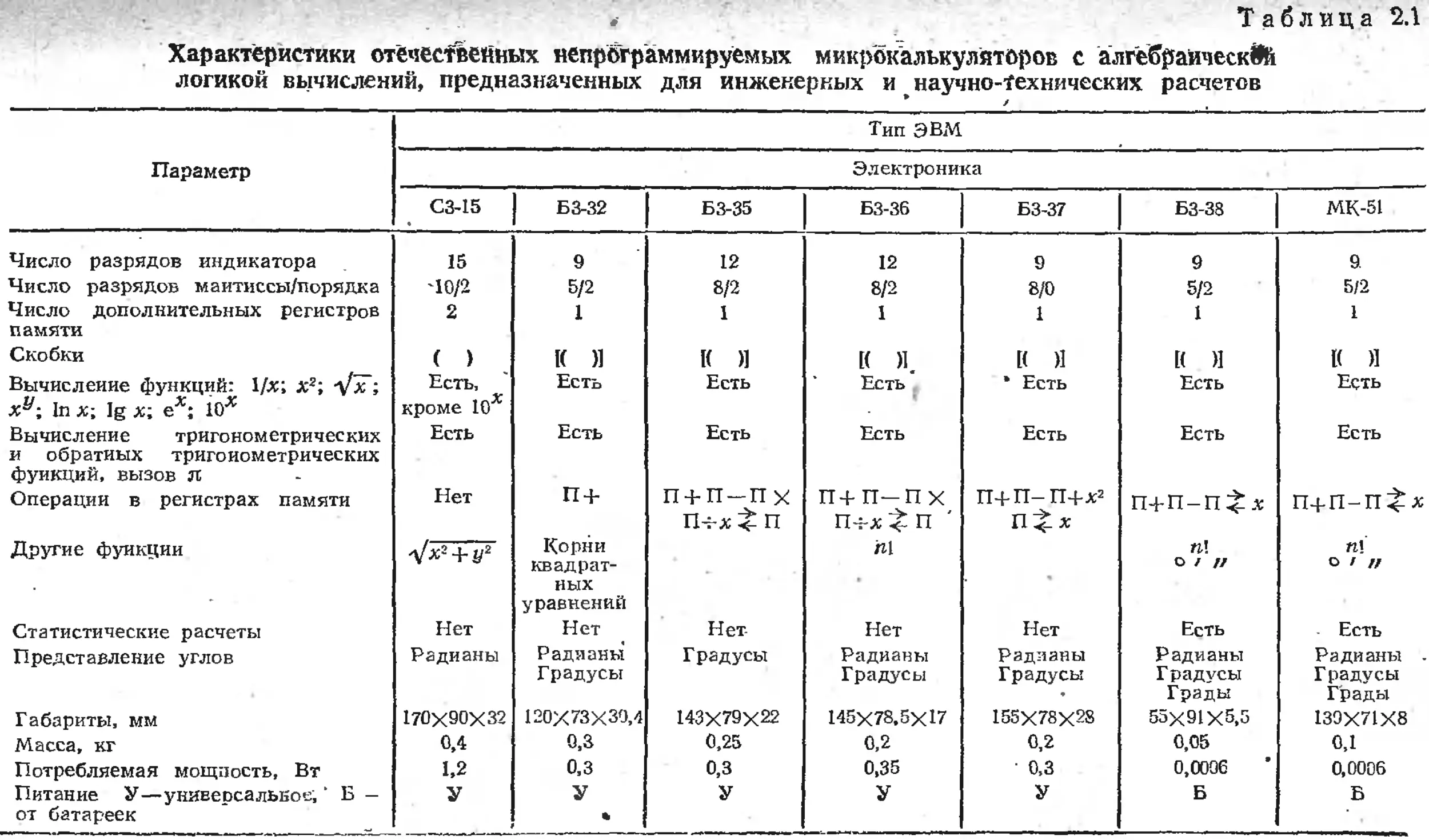
В табл. 2.1 даны характеристики отечественных непрограммируе-
мых микрокалькуляторов для научных и инженерных расчетов.
В функциональном отношении они различаются мало. Поэтому рас-
смотрим наиболее современную модель миниатюрного микрокаль-
кулятора Электроника БЗ-38 с наибольшим числом выполняемых
операций. Этот калькулятор (рис. 2.1) имеет тройное управление
большинством клавиш, достигаемое применением двух функцио-
нальных (префиксных) клавиш Fi и Fa. Общий сброс осуществля-
ется клавишей С, сброс ошибочно набранного числа осуществляется
клавишей СК. Имеется один дополнительный регистр памяти (ввод
чисел в него задается нажатием клавиш Fi ЗП, а вызов — нажа-
тием клавиш F2 ИП). Скобки [(и)] двойные.
Для непрограммируемых микрокалькуляторов очень полезно со-
ставлять программы вычислений. Так, обозначая операнды’числа в
кружках, вычисление выражения а + (Ь + (с d)) = ? можно вы-
полнить по такой программе:
® + ( ® + (© + ©.))
Таблица 2.1
Характеристики отёчествейных непрограммируемых микрокалькуляторов с алгёбрайческвй
логикой вычислений, предназначенных для инженерных и научно-технических расчетов
	Тип ЭВМ						
Параметр	Электроника						
	СЗ-15	Б 3-32	Б 3-35	БЗ-36	БЗ-37	63-38	МК-51
Число разрядов индикатора	15	9	12	12	9	9	9
Число разрядов маитиссы/порядка	'10/2	5/2	8/2	8/2	8/0	5/2	5/2
Число дополнительных регистров	2	1	1	1	1	1	1
памяти Скобки	( )	К )1	К )1	к я	к я	[( я	к я
Вычисление функций: 1/х; хг; VT;	Есть,	Есть	Есть	Есть	• Есть	Есть	Есть
xv-, In х. Ig х; еж; 10*	кроме 10х						
Вычисление тригонометрических и обратных тригонометрических	Есть	Есть	Есть	Есть	Есть	Есть	Есть
функций, вызов л Операции в регистрах памяти	Нет	П+	П + П —П х	п+п-пх	П+П- П+х2	П+ П - П х	П+П-П< х
Другие функции		Корни квадрат-	Пч-х $ П	Пч-х -< П	п х	п\ ъ / V	п\ О / //
	<хг + д2			Л1			
		пых					
		уравнений					
Статистические расчеты	Нет	Нет	Нет-	Нет	Нет	Есть	Есть
Представление углов	Радианы	Радианы	Градусы	Радианы	Радианы	Радианы	Радианы -
		Г радусы		Градусы	Градусы	Г радусы	Градусы
						Грады	Грады
Габариты, мм	170X90X 32	120X73X30,4	143X79X22	145X78.5X17	155X78X28	55x91x5,5	139X71X8
Масса, кг	0,4	0,3	0,25	0,2	0,2	0,05	о,1
Потребляемая мощность, Вт	1,2	0,3	0,3	0,35	 0,3	0,0006	0,0006
Питание У—унивеосалькое, ‘ Б —	У	У	У	У	У	Б	Б
от батареек		*					
Подставляя вместо a-~b числа 2, 3, 4 и 5, получим результат 29.
Нередко с помощью непрограммируемых микрокалькуляторов можно
лести вычисления по программам, составленным для программируе-
мых микрокалькуляторов (если к этому вынуждает их отсутствие).
- Одноместные операции выполняются указанием их оператора по-
сле набора числа х. Например, sin 30° вычисляем, набрав чиыц» 30
и нажав клавиши Ft sin (указываем только действующую надпись
на клавише или над ней).
Рис. 2.1. Внешний вид микрокалькулятора Электроника БЗ-38 С ал-
гебраической логикой вычислений
Приведем примеры более сложных вычислений:
1.	Вычисление гиперболического косинуса chx = (е+1/е*)/2
@ Fa е” + Г, 1/л?	4-	@	« '
Для х — 1 получим ch(l) = 1,5430806.
2.	Вычисление обратного гиперболического косинуса arch х ==
«= In (х + V-’c2 — 0
@	li	ЗП	+	[(	МП	_ -
1	)]	Fi	У	=»	Fl lrl
Этот пример иллюстрирует применение регистра памяти. Для х — 5
получим arch(2)= 1,3169678.
3.	Вычисление числа сочетаний Сд = 91/(3! (9 — 3)!)
®	F2	п»	*	[(	[(	@ F2	п!	Я
X	[(	@	®	Л "i	Я	=*
Получим Сд = 84.
4.	Для пяти чисел 7, 8, 8, 9 и 9,5 найти среднее и дисперсию.
Ввод проводим по программе:
И © х ® Уг х, (8) га
JC (э) F& ®	“
Нажав клавишу с надписью справа х, получим к = 8,3, нажав кла-
вишу с надписью справа-n, получим' п ==. 5 (число введенных чисел),
нажав клавишу F2 и клавишу с надписью сверху оп, получим
сп — 0,8717797, и, нажав клавишу F2 и клавишу с надписью свер-
ку Ол-1, получим ои-1 = 0,9746794. Также можно вычислить
£ х = 41,5 и У х2 = 348,25.
5.	Найти корни квадратного уравнения х2 + рх + q — 0 по фор-
р	/ р2	„
мулам Xii2=—g ± А/ -----------q. Программа вычислений имеет
вид
@ Г?	, (?)	- ©= F(
Ft ЗП @	“ F1 - ИИ S
: 1'1	№1 Гх /-/	|3
Корни получаем после исполнения операторов =	. Если
,р = 2,736 и q = —5,219, то имеем Xi — 1,294785 и хг = —4,030785
В этой программе член р/2 становится константой после исполнения
подряд операторов — и —.
6.	Найти, сколько граммов радия
-ln2f/r
останется после его радиоактивного распада за время t — 2000 лет,
если исходная масса тв = 125 г, а период его полураспада Ti/2—
1620 лет. Программа вычислений m(i) в общем виде следующая:
® „ Д	hi х @ +
е* *	-
© “ Д Л/
Для приведенных данных m(t) — 53,12122 г.
Сложные и многократно повторяющиеся вычисления удобно про-
водить на программируемых микрокалькуляторах. Отечественные
программируемые микрокалькуляторы с алгебраической логикой
вычислений к моменту подготовки данной книги находились в стадии
разработки. Поэтому далее рассмотрены основные типы широкорас-1
прбстравениых зарубежных калькуляторов (табл. 2.2). ,
t	T а б л и ц a 2.2
Характеристики зарубежных программируемых микрокалькуляторов с алгебраической логикой вычислений
Параметр	Тип ЭВМ						
	SR-52	SR-56	TI-58C	TI-59	FX-502P	FL-5100	FL-5101
Фирма (страна) изготовитель	TI	TI	TI	TI	Casio	Sharp	Sharp
	(США)	(США)	(США)	(США)	(Япония)	(Япония)	(Япония)
Число регистров памяти	20	10	60	}00	22	25	12
Число шагов программы	100	224	480	960	256	80 членов формул	48 членов формул
Функции ух.	In х. 1g X, ех, 10х, 1/х,	Есть	Есть	Есть	Есть	Есть	Есть	Есть
ВЫЗОВ It							
Тригонометрические и обратные тригоно- метрические функции	Есть	Есть	Есть	Есть	Есть	Есть	Есть
Статистические расчеты	Есть	Есть	Есть	Есть	Есть	Есть	Есть
Гиперболические функции	Нет	Нет	Нет	Нет	Нет	Есть	Есть
Число разрядов мантиссы/порядка	10/2	10/2	10/2	10/2	10/2	10/2	10/2
Запоминание программ и данных	Нет	Нет	Есть	Нет	Нет	Есть	Есть
Логика вычислений (О — обычная или ARE}	о	о	о	О	о	ARE	ARE
Запись программ на магнитные карты	Есть	Нет	Нет	Есть	Нет	Нет	Нет
Подключение принтера	Нет	Нет	Есть	Есть	Нет	Нет	1 Нет
Встроенный модуль с библиотекой про- грамм пользователя	Нет	Нет	Есть	Есть	Нет	Нет	Нет
Габариты, мм	90X160X40	80X150X30	162X80X36	162X80X36	141X71X9.6	175X70X9,8	175X70X9.3
Масса, г	350	235	350	350	72	120	ПО
Питание У — универсальное» Б — от бата- реек	У	У	У	У	Б	Б	Б ,
Калькуляторы этого класса обычно имеют иерархию операций,
(г. е. выполнение их в определенном порядке: 1 — вычисление матема-
(гическнх функций, 2 — вычисление функций ху и V* \или ух и
*_Л
Vу)> 3 — умножение и деление, 4 — сложение и вычитание и 5 —
окончание вычислений (оператор = ). Так, при наличии иерархии
выражение 2 + 3X4 вычисляется как 2+(3X4) =14, а при от-
сутствии ее как (2 + 3) X 4 = 20. Наличие иерархии позволяет бо-
лее экономно использовать скобки и сокращать длину программ, ко-
торая обычно бывает несколько больше, чем у калькуляторов с об-
ратной бесскобочной логикой вычислений.
Калькуляторы EL-5100 и EL-5101 фирмы Sharp (Япония) реа-
лизуют метод программирования AER. Его суть заключается в фор-
мульном представлении программ. Например, вычисление функции
f(A, В, С) = 0,5 АВ sin С
Выполняется по такой программе, вводимой в режиме AER [23]:
2nd ]( )=ДВС f( )=5ABsinC
Вначале резервируются переменные А В С в виде букв, а затем
записывается формула для вычисляемой функции.
Вычисления сводятся к вводу исходных данных по подсказке
калькулятора путем нажатия клавиши СОМР. Первое ее нажатие
ведет к появлению на дисплее сообшения А = ? (надо ввести Д),
второе к сообщению В = ? (надо ввести В), третье к сообщению
С = ? (вводим С). Нажав- клавишу СОМР, еще раз получим значе-
ние f(Д В С). При системе AER число нажатий клавиш существен-
но меньше, чем при обычной алгебраической логике .вычислений.
Микрокалькуляторы с системой программирования AER явились
шагом к разработке наиболее совершенных микрокалькуляторов,
программируемых на языке высокого уровня бейснк [13]. Его осо-
бенности заключаются в выражении сложных операторов в виде
сокращенных английских слов (INPUT — ввести, LET—присвоить,
PRINT — напечатать, GOTO — идти к строке, GOBUS — идти к под-
программе, RETURN — возврат из подпрограммы, END — конец
и т. д.), возможности ввода словесных комментариев, диалоговом
режиме общения с пользователем. Так, программа вычисления
функции F = ](А, В, С) на бейсике имеет наглядный и не требую-
Ший^ особых пояснений вид:
10	INPUT	'	ВВЕДИТЕ	А,	В, С' А,. В, С
20	LET	F	= 0.5 *	А	* В * S1N (С)
30	PRINT	F	: GOTO	10	: END !
Подробное описание микрокалькуляторов, программируемых на
бейсике (см, табл, 2.3),. и самого языка выходит за рамки данной
Характеристики микрокалькуляторов, программируемых на языке бейсик
Таблица 2.3
Параметр		.	,	j—		—		 Тип ЭВ*М				
	Р С-1210	РС-1211	РС-1500	ZX80 *) ZX81	ZX *) Spectrum
Фирма (страна) изготовитель	Sharp (Япония)	Sharp (Япония)	Sharp (Япония)	Sinclair (Англия)	Sinclair (Англия)
Объем ПЗУ, кбайт	Данных нет	Данных нет	16	16	16
Объем ОЗУ, кбайт	Данных нет	Данных нет	3,5+ 3,5	16	16/48
•Число регистров памяти	26/40	178	Данных нет	Данных нет	Данных нет
Число шагов программы	400	400+1024	Данных нет	Даиных нет	Данных нет
Встроенный дисплей	24 знака	24 знака 1	7 X 156 точек	Нет	Нет
Вывод информации и а стандарт- ный телевизор	Нет	Нет	Нет	Есть (цифры, буквы, графика)	Есть (цифры, буквы, графика, 8 цветов)
Периферийные устройства: П — принтер, Т — телевизор, КМ t— кас- сетный магнитофон, ВПЗУ —внеш- нее ПЗУ	и	п	п км ПЗУ	т Км П'	Т км п Дисковый накопи- тель на 100 кбайт
Размеры, мм	175X71X15	175X71X15	196X86X 25,5	229X178X51	233X144X30
Масса, г	163	163	375	340	300
*) Модели ZX относятся к простейшим персональным Э8М. Они не имеют встроенного дисплей и для отображения программ
и данных должны подключаться к стандартному телевизору—цветному для ZX Spectrum.-
книги, поскольку они ближе к сложным персональным ЭВМ, чем
к,- обычным программируемым микрокалькуляторам. Нередко подоб-
ные микрокалькуляторы оснащаются многочисленным периферийным
оборудованием. Так, один из наиболее сложных калькуляторов
RL-H1000 ННС фирмы Panasonic (США) имеет следующее перифе-
рийное оборудование: акустический телефонный модем для передачи
данных по телефонным линиям со скоростью 110 или 300 бит/с (раз-
рядность от 5 до 8, предусмотрен контроль четности), внешняя про-
граммируемая память на 8 кбайт с автономным питанием, устрой-
ство термопечати с шириной строки на 16 символов, адаптер к теле-
визору для отображения 16—32 символьных строк, адаптер для
подключения одного-двух кассетных магнитофонов для записи дан-
ных и программ, последовательный интерфейс для передачи данных
со скоростью от 110 до 9600 бит/с, драйвер управления до 6 пери-
ферийных устройств ввода-вывода и т. д. Следует отметить, что
стоимость подобных калькуляторов (учитывая микроминиатюриость
всего комплекса оборудования) выше стоимости персональных ЭВМ
и даже мини-ЭВМ. Поэтому широкого распространения они пока не
получили.
В то же время ряд широко распространенных современных мо-
делей микрокалькуляторов (например, TI-58C, TI-59, HP-67, НР-97
и др.) также приобрел присущие ЭВМ черты: встроенные библио-
теки программ пользователя, встроенные магнитофоны для запи.си
данных и программ, периферийные (иногда встроенные) устройства
печати — принтеры. Причем это сочетается с умеренной стоимостью
И доступностью.
2.2. Клавиатура и язык микрокалькуляторов
с алгебраической логикой
С клавиатурой и языком современных микрокалькуляторов'с ал-
гебраической логикой можно ознакомиться иа примере широко рас-
пространенных моделей программируемых микрокалькуляторов высо-
кого класса TI Programmable 58С и 59 (Т1-58С?59). Пульт управле-
ния их (рис. 2.2) содержит 45 клавиш, которыми вводятся 108 опе-
раций. Это достигается с помощью клавиши двойной операции 2nd
(она нажимается, если выполняется операция, обозначение которой
находится над основной клавишей) и клавиши инвертирования опе-
рации INV (см. ниже). В программах нажатие клавиши 2nd не
указывается, так как иа него прямо указывает расположение функ-
циональной надписи; основной клавиши. Например, нажав клавишу
? Ibg	iqg
In х , вводим оператор In х. нажав клавиши 2nd и 1п х ,
, вводим оператор In х, нажав клавиши 2nd и
HIIIHIHII
Texas Instruments *
□ .1ЕЗЧ5
Б1
16	A'	.17	B'	18	c'	19	D'	10	E'	
11	A	12	ГЧ	13	C I	M	D 1	ffi	E	
		27		28	log	29	CP	20		
	,2nd.	22	INV	23	1пг|	24	CE |	25	CER	
36	Pgm 37		P—R	38	sin	39	COS	30	tan	
	LRN	32	x*t	33	X2-	34	vs	35	\/x	
	Ins	47	CMs	48	E-xc	49	Prd.	40	Ind.	
	SST	n	| STD	43		44	sun|	45		
	Del	57	Eng-	58	Fix	59	I nt	50	|г1	
	BST	52	[ТГ	53	ГП	54	T|	55	-T-	
ш 66	Pause 67		x=t	68	Nop	69	Op	60	Deg	
II 61	GTO	°7L	1	“I	8	]O9	9	I65	X	
Ш К	Let	77	xit	78	1 +	7S	X	70	Rad.	
I 71	SBR	oa|	4	05	5	105	6	J75	—	
Ш66	Stflg 87 If fig 88 D- MS					89	V	80	Grad.	
11е<	RST	Cl	1	02	2	Iю	3	85	+	J
и 96		97	Dsz	SB	Ad.v	99	Prt	so List		
1191	R/S	00	0	93	•	S4	+/<-	95	=	
11 Key Code Н Overlay					T1 Programmable 58C Solid. State Software Constant Memory					
										
Рис. 2.2. Внешний вид программируемого микрокалькулятора TI-58C
с алгебраической логикой вычислений
log
In X
вводим оператор log(logx), нажав клавиши INV 2nd
Вводим оператор 10х и т. д.
Операторы ввода чисел. К ним относятся цифры 0, 1 ... 9, раз»
делительная точка . , оператор смены знака мантиссы или порядка
+/—, оператор ввода порядка ЕЕ и оператор вызова числа
я = 3,141592653590 (выводится 10 знаков из 13 используемых при
вычислениях).
Операторы стирания (сброса). Общий сброс вводится операто-
ром CLR. При этом устанавливается на 0 содержимое регистра X,
устанавливается стандартная форма представления чисел, прекра-
щается индикация ошибок (мигание индикатора). Содержимое ре-
гистров памяти сохраняется.
Оператор СЕ (clear entry — стирание ввода) обеспечивает только
стирание числа в регистре X (за исключением числа л). Стирание
программы обеспечивается вводом вручную оператора СР (clear
program — стирание программы), а очистка всех регистров памяти
осуществляется оператором CMs (clear memory — стирание памяти).
Оператор СР в программе обеспечивает стирание содержимого ре-
гистра сравнения /.
Операторы прямых и обратных функций. Операторы прямых
функций вводятся нажатием основных клавиш, обратных функций —
после нажатия клавиши INV.
Прямая функция	Обратная функция	
ЕЕ	(ввод порядка) Eng	(ввод инженерного формата) Fix	(ввод ограничения числа знаков) log	(десятичный логарифм) In х	(натуральный логарифм) уК	(у в степени х) Int	(выделение целой части х) sin (sin х) cos (cos x) tan (tgx) Prd (умножение в регистре) SUM (суммирование в регистре) D. MS (преобразование угла в градусы с десятичными долями) Р + R (преобразование полярных коор- динат в декартовы)	INV 1NV INV INV INV INV INV INV INV 1NV INV INV INV INV	ЕЕ	(сброс порядка) Eng	(сброс инженерного	фор- мата) Fix	(сброс ограничения	числа знаков) iog	(функция у— ,10 х) In х	(функция у—ех) ук	(корень степени х из	числа У) Int	(зыде-лгние дробной	части X) sin (arcsin х) cos (arccosx) tan (arctgx) Prd (делеийе в регистре) SUM (вычитание в регистре) D. MS (преобразование	угла в градусы, минуты, се- кунды) р > Р (преобразование декарто- вых координат в полярные)
Прямая функция	Обратная функция
S+ (накопление с суммированием) х	(среднее значение) list (печать программа) SBR (обращение к подпрограмме) x=t (условие перехода) x^t (условие перехода) if fig (проверка, подъема флага) st fig (поднять флат) Dsz (скачок, если Write (запись программы)	INV Е-р (накопление с вычитанием) 1NV х	(стандартное отклонение) INV list (печать данных .из регист* ров) INV SBR (возврат из подпрогра'ммы) INV x=t (х=#0 INVx>f (х<0 INV if fig (проверка спуска флага) INV st fig (опустить флаг) INV Dsz (скачок, если INV Write (считывание программы)
Операторы установки формата чисел. Нормальный формат соот-
ветствует выводу десяти знаков мантиссы в виде десятичного числа
с фиксированной запятой. При вводе порядка оператором ЕЕ уста-
навливается научный (экспоненциальный) формат чисел х — М • 10е,
где Ж — нормированная мантисса, содержащая € знаков, и £—поря-
док, содержащий два знака. Например:
Мантисса	Порядок
—	2. 5786431	—	16
Знак	Знак
маитиссы	порядка
Диапазон чисел лежит в пределах от ± 1 • 10 до хм =
= 9,9999999 • 1099.
Инженерный формат вводится оператором Eng. При этом поря-
док чисел равен 0 или кратен трем. Например, разделив 1 на 3, по-
лучим .3333333333- Нажав клавиши ЕЕ и =, получим 3.3333333 — 01,
нажав далее клавиши 2nd и Eng, получим 333.33333 — 03.
Формат с фиксацией числа знаков после запятой N устанавли-
вается вводом оператора Fix N. Например, при N — 2 предшествую-
щий результат получим (после нажатия клавиш 2nd Fix 2) в виде
333.33 — 03.
Операторы арифметических операций. К ним относятся опера-
торы сложения +, вычитания —, умножения X, деления 4-, ввода
открывающих (и закрывающих.) скобок и знака равенства =, Допу-
стим ввод до девяти пар скобок.
Операторы алгебраических функций. К операторам алгебрам
четких функций относятся вычисление натурального логарифма in х,
десятичного логарифма log (1g х), функции е* —INVlnx, функции
10’ — INV log, квадрата х — х2, квадратного корня Vх, функций уя
х	X
и Vy - 1NV ffx. За исключением функций д* н V*/ остальные
функции вычисляются после ввода числа х в регистр X. Например,
нажав клавиши 2 INV In х, получим е2 — 7.389056099.
Для вычисления функции у* вводится число х, исполняется опе-
ратор у*. вводится число у и исполняется оператор =. Для вычис-
X
ления функции 's/y — y^* вводится число у, затем исполняется опе-
ратор 1NV у\ вводится число х н исполняется оператор =. Напри»
мер, для вычисления и/б4 = 4 нажимаем клавиши 6 4 1NV у* 3 = .
Тригонометрические и обратные тригонометрические функции.
Эти функции вычисляются при представлении углов в градусах
(оператор Deg), радианах (оператор Rad) и градах (оператор Grad).
Синус, косинус и тангенс вычисляются вводом операторов sin,
cos и tan *). Если после них исполняется оператор 1/х, то вычисля-
ются косеканс esc х == 1/sin х, секанс secx — 1/cosx и котангенс
eotx=l/tgx. Аргумент может находиться в пределах ±36 000",
±200зг радиан в ±40 000 град.
Обратные тригонометрические функции вычисляются, если перед
операторами вводится оператор INV. Результат прн этом представ-
ляется в следующих пределах:
arcsin х
arcsin (— х)
arccos х
arccos (— х)
arctg х
arctg (— x)
0 4- 90°, rt/2 радиан, 100 град,
0 4---90°, — л/2 радиан, —100 град,
0 4- 90°, л/2 радиан, 100 град,
90 4- 180", л/2 -г- л радиан, 100 4- 200 град,
0 4- 90°, зт/2 радиан, 100 град,
0 4- — 90°, — л/2 радиан, — 100 град.
Арккосеканс arccsc х, арксеканс arsec х и арккотангенс arcot ж
вычисляются с помощью операторов 1/х INV sin, 1/х INV cos и
1/х INV tan.	х
Если угол задан в градусах, минутах и секундах, то его можно
преобразовать в градусы с десятичными долями с помощью -опера-
тора D.MS. Например, угол 24° 17'29" вводим в виде 24.1729 и,
нажав клавиши 2nd и D.MS, получим <р = 24.29138889°. Обратное
преобразование производится вводом оператора INV D.MS (нажи-
маются клавиши INV 2nd и D.MS).
Операторы выделения абсолютного значения, целой и дробной
частей чисел. Абсолютное значение (модуль) дробного числа х вы-
деляется при исполнении оператора |х|. Операторы Int и INV Int
обеспечивают выделение целой и дробной частей числа х.
Операторы управления регистрами памяти. Запись чисел в ре-
гистр XX (XX — двухзначное число —адрес регистра) производится
операторами вида STO XX (store — записывать).' Вызов числа из
регистра XX производится операторами RCL XX (recall — вызвать).
*) Обозначение. функций соответствует приведенным в [26].
Обмен содержимым между регйстрами X и XX производится при
исполнении оператора Exc XX (exchange — менять). Оператор х t
обеспечивает обмен между регистрами X и t.
Операторы арифметических операций в регистрах памяти.
С содержимым регистров X и XX можно выполнять арифметические
операции с занесением результата в регистр XX. Такие операции
вводятся операторами: сложение SUM XX, умножение Prd XX, вы-
читание INV SUM XX и деление INV Prd XX.
Пример. Разделить число 12, хранящееся в регистре 00, на
число 2,5 — RX.
Нажимаем клавиши 1 2 STO 00 (ввод числа. 12 в регистр
00) 2 . 5 INV 2nd Prd 00. Теперь, нажав клавиши RCL 00, вызы-
ваем из регистра 00 результат — число 4,8. При этих операциях со-
держимое регистра X не меняется.
Преобразования систем координат. Пусть в системе полярных
координат (Р) имеется радиус-вектор с ‘ длиной R и углом 0
(рис. 2.3,а). Нужно найти координаты х и у в декартовой системе
Рис. 2.3. К преобразованию координат: из полярных в декартовы (а)
и из декартовых в полярные (б)
координат (рис. 2.3, б). Для этого служит оператор Р -> R. Обрат-
ное преобразование выполняется с помощью операторов INV P->-R
(означает R^P). Для проведения этих преобразований использует-
ся регистр t. Порядок преобразований следующий:
	Р-		R->P
Вводим	R.		X
Исполняем оператор	х<-	t	x^t
Вводим	е		У
Исполняем оператор	р +	R.	INV Р -> Р.
Получаем	У		е
Исполняем оператор!.	X	У	x^t
Получаем	X		ft
Угол 0 вычисляется в пределах	—90° sg 0	270° или
—л/2 рад	0 Зл/2 рад или —100 град С' 0	300 град.
Пример. R = 5, 0 = 25°, найти у н х.
Нажимаем клавиши 5 х sst t 25 2nd Р -> R и получаем у
:= 2.113091309, нажав клавишу получим х = 4.53Г538935.
Операторы управления вычислениями по программе. Стирание
программ {clear program) в ОЗУ производится оператором СР. Пе-
ревод в режим программирования (обучения ЭВМ) и наоборот
ООО
079
159
239
319
399
479
559
639
719
799
873
959
Шаги	Номера
программы	.регистров
a) TI-59
Банк.1
6анк2
БаикЗ
Ванк4
99
89
79
69
29
- 19
09
00
59
49
39
Лрограм
иная
память
Используе-
мые
регистры
памяти
Номера
регистров
TI-58C
9
Рнс. 2.4. Структура ОЗУ
производится нажатием клавиши LRN {learne — учить). Останов вы-
числений по программе и пуск программы производятся вводом опе-
ратора R/S {run —stop). В программе этот оператор обеспечивает
останов вычислений для выдачи результата. В режиме счета он ис-
пользуется для пуска программы с того адреса, на котором опа
остановилась.
Оператор RST -{reset — возврат к нулю) обеспечивает переход
на нулевой адрес (000) программы. Кратковременный останов (на
«0,5 с) вычислений по программе обеспечивается вводом в нее опе-
ратора Pause {пауза).
Распределение объема ОЗУ. Емкость ОЗУ может распределять-
ся пользователем между регистрами памяти и шагами программы
(рис. 2.4). Каждые 10 регистров памяти занимают в ОЗУ место для
80 шагов программы.
Число десятков регистров N задается пользователем с помощью
операторов N Ор 17. При нажатии клавиш N 2nd Ор 17 на индика-
торе высвечиваютси максимальный адрес программы н максималь-
ный номер регистра памяти. Например, если N = 3, то на индика-
торе будут цифры 239.29 (239 — максимальный номер шага и 29 —«
максимальный номер регистра памяти). Переполнение памяти, отве-
денной под регистры или программу, индицируется как ошибка ми-
ганием дисплея.
Операторы статистических расчетов. Простейшие статистические
расчеты могут выполняться микропрограммно после очистки регист-
ров оператором CMs. Для ввода чисел, подлежащих статистической
обработке, служат клавиши 2nd S +, нажимаемые после ввода
каждого числа х,. Если какое-то число введено ошибочно, его исклю-
чают повтором набора и нажатием клавиш INV 2nd S +. Среднее
значение ряда введенных чисел х можно вызвать на индикацию,
нажав клавиши 2nd к. Дли вычисления дисперсии, коэффициента
парной корреляции н параметров линейной регрессии (см. § 5.12 и
5.13) служат специальные операторы Ор 11 -т- Ор 15 (см. далее).
Их использование поясняет пример в приложении 1 (описание про-
граммы ТИЛ-01).
2.3. Элементарное программирование
микрокалькуляторов с алгебраической логикой
Элементарное программирование микрокалькуляторов с алгеб-
раической логикой мало отличается от такового для микрокалькуля-
торов с обратной бесскобочной логикой вычислений. Очевидные от-
личия заключаются в использовании операторов ввода скобок (до
9 пар) и оператора — (они достаточно очевидны), а также в учете
приоритета операций. Рассмотрим несколько типовых примеров.
1. Вычисление
e = a-|-6x(c — d) =,?	(2.1);
при а = POO, b — R01, с — Р02 н d — ДОЗ с занесением результата
в регистр Д04 выполняется по программе
RCL	00	+	RCL	01	X (	RCL 02- —
RCL	03	)	=	STO	04 R/S
2. Иногда можно сократить программу, исключив скобки и соз-
дав приоритет выполнения операций вводом оператора ==. Напри-
мер, (2.1) можно вычислить по программе:
RCL	02	—	RCL	03	=	X RCL 01 +
RCL	00	=	STO	04	R/S
В данном случае сначала вычисляем (e — d), умножаем результат
на Ъ и прибавляем затем а, ,
- 3. Вычисление
у = 7,06 • 10- эе^ = 7.06  IO3 X (ехр(2 X х)) = ?	(2.2)
формально выполняется по программе (я = R00):
7-0	6	ЕЕ	3	+/—	X (	(
2 X RCL	00	)	INV	1п х	)	=	R/S
Для х = 2 получаем у — 3,8546294- Юг*.
4.	Введя число 7,06-10^3 в регистр R01 н несколько изменив
порядок вычислений (2.2), можно заметно сократить программу;
2 X RCL 00 = INV In х X RCL 01
= R/S
5.	Вычисление
y.= x-(lnx+l)=?	(2.3)
формально требует запоминания х для последующего ввода его в
скобки н вычисления In х:
STO 00	— ( RCL 00 In х + 1 )
= R/S
Для х — 3 получим у = 0,9013877113.
6.	Вычисление (2.3) можно выполнить по более простой про-
грамме:
— ( 1п «• + 1 ) = R/S
учитывая, что после исполнения: операторов — и ( число я сохра-
няется в регистре X. Этот прием можно использовать,, если после
оператора ( стоит оператор вычисления математической функции или
оператор СЕ.
Операторы безусловных переходов. Безусловные переходы зада-
ются к метке N (вводится любой клавишей, имеющей код) или
трехзначному адресу п пп с помощью операторов GTO N (двухша-
говых) и GTO п пп (трехшаговых). Символ GTO (go to) означает
«идти к». Например, переход к началу программы задается опера-
тором GTO 0 00. Такой переход дает и специальный оператор RST.
Операторы условных переходов. Имеется четыре типа операто-
ров условных переходов.
Операторы	Условие перехода
x~^t N	или п пп	x^t,
x — t N	или п пп	x — t,
INV x^t N нли п пп	х < t,
INV x — t N или п пп	X t.
Здесь t — содержимое регистра сравнения t. Если условие перехода
выполняется, то- происходит переход к метке W нли адресу - п пп.
Если условие • не  выполняется, происходит выполнение оператора,
указанного после метки или адреса п пп. Оператор х т* I обеспечи*
вает обмен содержимого регистров Хи/, например для ввода I
Оператор СР в программе обеспечивает очистку регистра t (t = О J
Пример. Вычислить	,
у — sin xjx
У = 1
Программа
СР Rad x — t 0 18
00	=	R/S	1 R/S
при X =/= 0,
при х — 0.
STO 00 - sin -5- RCL
при x = 0 (в регистре t число 0) обеспечивает условный переход по
адресу 013, т. е. вывод на индикацию числа 1. Если х ф О, то вы-
числяется sin х/х.
Операторы ввода подпрограмм. Подпрограмма, начинающаяся
с адреса ппп, выполняется при исполнении трехшагового оператора
SBR п пп (SBR сокращение слова subroutine — подпрограмма). Если
подпрограмма начинается операторами ввода метки Lbl N (см. ниже),
то она выполняется при исполнении двухшагового оператора SBR N.
В конце подпрограммы вводится оператор INVSBR (возврат из
подпрограммы) *). Число вложений подпрограмм друг в друга нз
должно превышать 6.
2.4. Специальные вопросы программирования
микрокалькуляторов с алгебраической логикой
Операторы ввода меток. Метки (labels) вводятся операторами
вида Lbl N, где Л' — символ любой клавиши, кроме цифровых,
имеющей код (общая метка). Очень удобны 10 меток, вводимые
клавишами верхнего ряда и обозначенные буквами А, В, С, D, Е,
А', В', С', D' и Е'. Ввод такого символа обеспечивает выполнение
программы с адреса, следующего за операторами метки.
Пример. Вычислить (2.1), обозначив переменные a, b, с, d и е
метками А, В, С, D и Е.
Программа при этом будет иметь вид
Lbl	A	STO	00	R/S	Lbl	В	STO	01	R/S
Lbl	С	STO	02	R/S	Lbl	D	STO	03	R/S
Lbl	E	RCL	02	—	RCL	03	=	X	RCL
01	+	RCL	00	=	R/S
Теперь числа А, В, С и D можно вводить в любом порядке, указав
после ввода соответствующий буквенный символ. Например, если
А=2, В = 5, С = 4 и D = 3, ввод можно выполнить так: 3 D 5 В
2 А 4 С. Теперь, указав символ Е, получим е = 7.
*) В программах оператор INVSBR сокращенно обозначен как
ISBR.
Операторы организации циклов. Циклы организуются операто-
рами Dsz X N и Dsz X п пп, где X — номер регистра R* (от О
до 9). При каждом исполнении этого оператора. от содержимого
Rx > 0. отнимается 1, а к содержимому 0 прибавляется. 1,
после чего, если =/= 0, происходит переход к метке N или к ад-
ресу п пп. Если Rx = 0, метка N (или адрес' п пп) игнорируется И
выполняется следующий за ними оператор.
Пример. Вычислить ряд
т
Л=1
Программа имеет вид (т = RX; п — RX):
CMs	STO	00	R/S	STO	01	RCL	00	ух	RCL
01	=	SUM	02	Dsz	0	0	06	RCL	02
R/S RST
Здесь оператор Dsz 0 0 06 организует в регистре R00 счетчик
k — (k—1) с начальным значением k = т и цикл вычисления kn;
начинающийся с адреса 0 06 и кончающийся оператором Dsz 0 0 06.
При k = 0 программа выходит из цикла, и содержимое суммирую-
щего регистра R02 вызывается на индикацию. Для т = 5 и п — 6
получим у = 20 515 при времени счета 5 с.
Операторы установки и контроля флагов. Флаг — специальный
указатель перехода в программе (аналог флагу в руках регулиров-
щика уличного движения). Флаг имеет номер у = 0, 1, 2, .... 9.
Подъем флага выполняется вводом оператора St fig у, а спуск—*
оператором INV St fig у. Проверка условия установки флага в нуж-
ном месте программы обеспечиваетси исполнением оператора
If fig у N или If fig у п пп. Если флаг у поднят, то осуществ-
ляется переход к метке N или к шагу программы п пп. Если флаг у
опущен, такой переход не происходит. При исполнении операторов
INV If fig у N или INV If fig у п пп переход происходит, если
флаг у опущен, и не происходит, если он поднят.
Пример. Составить программу перевода мер длины в соот-
ветствии с формулами:
1 км = 1С00 м; 1 м = 3,28084 фут; 1 миля = 5,280 фут. Один
из вариантов такой программы имеет вид
ЕЫ	А	X	1	0	0	0	Stflg	0	СТО
С	ЕЫ	В	INV	Stflg	0	LbL	С	X	3
2	8	0	4	INV	Ifilg	0-	=	-н
5	2	8	0	Lbl	=	=	ISBR
Здесь, если вводятся километры (метка А),' флаг у = 0 подни*
мктся, если метры (метка В) — флаг у = 0 опускается. В зависи-
мости' от этого пересчет ведется по той или иной формуле. Пусть
надо узнать, сколько миль в 75 км. Вводим число 75 и указываем
метку А. Получим 46,6 мили. Теперь выясним, сколько футов в
1,78 м. Вводим 1,78 и указываем метку В. Получим 5,84 фута (ре-
зультаты округлены на третьей цифре).
Специальные операторы Ор. Командой вида Ор пп, где
пп = 00 4- 39 вводятся 40 специальных операторов'.
пп Назначение оператора Ор пп.
00-4-08 Управление печатью принтера (описаны далее).
09	Запись в ОЗУ программы из блока ML (см. далее).
J0	Вычисление сигнум-функцин (у = 1 при х > 0, у — 0
при х = 0 и у = —1 при х < 0, причем y-^RX).
11	Вычисление дисперсии и наклона прямой при линейной ’
регрессии.
12	Вычисление у(0) при линейной регрессии.
13	Вычисление коэффициента корреляции.
14	Вычисление у по заданному х	при линейной	регрессии.
15	Вычисление х по заданному у	при линейной	регрессии,
16	Проверка распределения памяти.
17	Установка заданного распределения памяти.
18	Подъем флага у — 7, если нет	ошибки.
19	Подъем флага у = 7, если есть	ошибка.
20 4- 29 Увеличение содержимого регистра R00 4- R09 на 1.
30 4- 39 Уменьшение содержимого регистра R00 4- /?09 на 1. .
Операторы косвенной адресации. К ним относятся следующие
операторы (XX — номер регистра адресации):
Оператор	Код	Назначение оператора
STO Ind*) XX	72 XX	Запись в регистр памяти R
RCL Ind XX	73 XX	Вызов из регистра па-
«*-		мяти R
EXC Ind XX	63	Обмен R X
(INV)SUM Ind XX	(22) 74 XX	Суммирование или вычи- тание в регистре памяти R
(INV)Prd Ind XX	(22) 64 XX	Умножение и деление в регистре памяти
GTO Ind XX	83 XX	Безусловный переход
Pgm Ind' XX	62 XX	Обращение к программе
Op Ind XX	84 XX	Выполнение оператора Ор
SBR Ind XX Fix Ind XX	71 40 XX	Обращение к подпрог- рамме
	58 40 XX	Задание числа цифр после запятой
		
*) Операторы косвенной адресации		STOInd, RCLInd и т. д. в.
программах сокращенно обозначаются как STOI, RCLI и т. д.
(INV) x=t Ind XX
(INV) Ind XX
(INV) St fig Ind XX
(INV) If fig Ind
XX N или n tin
(INV) Dsz X Ind XX
IV или n nn
(22) 67 40 XX
(22) 77 40 XX
(22) 86 40 XX
(22) 87 40
XX, W или n nn
(22) 97 40
XX, N или n nn
Условные переходы
Подъем (спуск) флага
Анализ положения
флага
Организация циклов
Напомним, что при косвенной адресации адреса программы, но-
мера регистров и номера флагов указываются содержимым регистра
адресации XX. Для модификации его могут использоваться опера-
торы Ор 20 4- Ор 39 и Dsz. Например, в программе
CMs	+	1	STO	00	=	x^.t RCL	00	R/S
STOI	00	Op	20	RCL	00	INV x — t	0	09
R/S ...	........... ..........................
обеспечивается запись N чисел последовательно в регистры памяти
от Л01 до RN с использованием косвенной адресации (регистр ад-
ресации 00) и модификацией адреса, обеспечиваемой исполнением
оператора Ор 20. ,При пуске программы в регистр t вводим число N,
а в регистр R00— число 1. Для N — 5, нажав клавиши RST и R/S,
получим на индикаторе номер числа, которое надо вводить — но-
мер 1. Введем Xi = 12 и, нажав клавишу R/S, получим новый но-
мер 2. Вводим Хг = 7 нт. д., например х3 == 7, х4 = 9 и х5 = 1,5.
Теперь нетрудно убедиться, что эти числа окажутся записанными
в регистрах R014-R05. В этой программе выход из цикла осу-
ществляется по условию х0о = t — N. Если хсо =/= N происходит пе-
реход на адрес 0 09 (начало цикла с оператором записи в регистры
памяти с косвенной адресацией).
2.5.	Работа с библиотекой программ пользователя
В микрокалькуляторы TI-58C/59 встроен смеппый модуль с биб-
лиотекой программ пользователя ML (Master Library). Он представ-
ляет собой твердотельное постоянное запоминающее устройство ем-
костью около 40 кбит, в котором может храниться библиотека из
нескольких десятков простых программ либо сложная программа
с числом шагов до 5000. Смена блока ML позволяет мгновенно пе-
реориентировать микрокалькулятор на выполнение различных про-
фессиональных вычислений: научно-технических, деловых (экономи-
ческих), статистических, биологических и т. д.
Типовой блок ML (модуль 1) содержит 25 программ, в основ-
ном, реализующих научно-технические расчеты. Перечень этих про-
грамм и инструкции по их применению даны'в приложении 1.
Программы ML могут использоваться самостоятельно. В этом
случае они вводятся с клавиатуры нажатием клавиш 2nd Pgm тт,
где пгт — двухзначный номер программы ML. Следует отметить, что
введенная таким образом программа ML не занимает ту часть ОЗУ,
которая отводится под-внешние (вводимые пользователем) про-
граммы. Поэтому число шагов программ ML- может превышать до-
пустимое" для внешних программ. Однако при работе с программа-
ми ML используется часть регистров памяти (их номера указаны в
описании'Программ ML), что должен учитывать пользователь при
составлении своих (внешних) программ.
Программы ML можно переписать в ОЗУ вводом команд
2nd Pgm тт Ор 09. Это возможно, если число шагов программы
ML — тт меньше максимального числа шагов программной памяти
(480 у TI-58C и 960 у TI-59). Такая перезапись позволяет детально
проанализировать программу ML — тт и изменить ее. Запись нз-
лененной программы в блок ML невозможна, что обеспечивает за-
щиту программ ML.
В программах ML широко используются метки, которые делят
каждую программу на части, имеющие самостоятельное значение.
1рограмму ML — тт полностью или частично можно использовать
з качестве подпрограммы, входящей во внешние программы, состав-
ляемые пользователем. И напротив, внешние программы можно ис-
пользовать в качестве подпрограмм для программ ML. Эти воз-
можности реализуются операторами:
Fgm	mm	N	Обращение к части программы ML — тт, поме-* ченной меткой AL
Pgm	mtn	SBR N	Возврат .из подпрограммы ML—mm к выполнен нню внешней программы.
Pgm	mm	R/S	Обращение к программе ML—mm с остановкой.
S3R	n	tin	Обращение из программы ML—mm к подпро-* грамме, внесенной в ОЗУ с адреса п пп.
SBR	N		Обращение к подпрограмме в ОЗУ, помеченной меткой N.
Такое комбинированное использование программ нередко позво-
ляет реализовать вычисления, которые потребовали бы составления
программ с общим числом шагов до 5000.
Поясним комбинированное использование программ ML и внеш-
них программ на примере вычисления выражения
.6
f (a, b) = V2x + 1 dx + bea — I + bea,
a
содержащего интеграл lt который вычисляется npv. 4 «ммой ML—09
численного интегрирования. Из ее. описания выясняем использование
регистров памяти: jROI = a, R02 = Ь, /?03 = п, R04 = I, R05 = п.'
Программа, вводимая в ОЗУ, имеет вид:
Ввод	Фрагмент программы-	Пояснения
а Ъ с	Pgm 09 A R/S Pgm 09 В R/S Pgm 09 С Pgm 09 D	Ввод а по программе ML-09. Ввод b по программе ML— 09. Ввод с no программе ML—09. Вычисление Z no программе ML—09.
	RCL 01	INV In X X RCL 02	+	RCL 04 R/S	Вычисление be4* + / п остановка основ- ной программы
	Lbl	A'	(	STO	06 RCL	06	X	2	+ 1	)	V*~	INVSBR	Подпрограмма в ОЗУ для вычисления подынтегральной функции V2x+ 1 .
В этой программе 4 раза части программы /И £—09 исполь-
зуются в качестве подпрограмм для выполнения основной програм-
мы. С другой стороны, заключительный фрагмент программы — вы-
числение f (х) = -\/2х -^^используется в качестве подпрограммы для
вычисления интеграла по программе ML—09. Для а = 0, b — 1 и
с — п — 8 получим f(a, b) = 2,398713896.
2.6.	Операторы урравления цифровым магнитофоном
и принтером
В микрокалькулятор TI-59 встроен миниатюрный магнитофон
для записи данных и программ с двух сторон магнитных карт
(длина 7,62 см). Данные вводятся оператором, вида п 2nd Write,
где п — номер банка данных (п — 1, 2, 3 или 4). Запись программ
выполняется вводом оператора 2nd Write. Считывание данных про-
изводится оператором п INV 2nd Write, а программ—INV 2nd
Write. При этом недопустима установка формата Fix (сброс его вы-
полняется вводом оператора INV 2nd Fix).
К микрокалькуляторам TI-58C и Т1-59 могут подключаться ми-
ниатюрные принтеры РС-100А и РС-100С. Вывод данных на печать
обеспечивается вводом в программу оператора Prt (от слова print —
печать). Его работа иллюстрируется следующим примером,.
Пример.
Образец печати программы			Образец печати данных
Адрес	Код	Оператор	
000	85	+	3
001	03	3	6
002	95	«я	9
003	99	PRT	12
004	• 81	RST	15
005	00	0	18
При вводе перед оператором Prt (PRT) оператора Adv увели-
чивается пробел между строками. Распечатка текста (листинга)
программы (см. пример выше) обеспечивается вводом с пульта опе-
ратора List.
Предусмотрена возможность печати алфавитно-цифровых сим-
волов в любом месте строки. Строка разбивается иа 20 знакомест,
устанавливаемых вводом операторов O'pl -i-Ор4:
0 1 2 3 4 5.6 7 8 9 10 И 12 13 14 15 16 17 18 19
Ор1 Ор2	ОрЗ	Ор4
Каждый из 64 символов задается кодом:
Вторая цифра кода .
		0 -	1	2	3	4	, 5 4*	6	7	
	0	Пробел	0	1	2	3	4	3	6	
	1	7	8	9	А	В	С	D	Е	
«$ g	2	—	F	&	Н	I	J	К	Е	J2 Ч О ей
<0 В-	5	м	К	□	Р	а	К	S	Т	х: з: О
zf	4	•	и	V	w	X	Y	Z	+	ш £
rt со ш	5	X		-г	•7Г	е	(	)	9	а> <а «о
EZ	6	1	%	ь ч	/	==	//	X	X	с? ez
	7	г		-5-	! Печатаемые		I д символы		и	Е	
Коды	СИМВОЛОВ		указываются			перед		вводом		операторов
Ор1 Ор4. Допустим, нужно напечатать фразу INPUT X, Y, Z,
Распределяем знакоместа строки печати:
Символ INPUT X , Y , Z
Код	24 31 33 41 37 00 44 57 45 57 46 00 00 00 00 00 00 00 00 00
Программа печати данной фразы имеет вид:
Оператор	Показания дисплея	Пояснения
CLR Ор 0'3	0.	Сброс регистра принтера
2431334137 Ор 01	2431334137	Печать слова INPUT
0044574557 Ор 02	0044574557	Печать знаков .X, Y
4690000000 Ор 03	4600000000	Печать знака Z
0000000000 Ор 04	ооэооооооо	Печать пробелов
Таким образом, при работе с принтером оператор имеет возмож-
ность вывода на печать не только цифр, но и специальных знаков
и словесных комментариев. С помощью оператора Ор 07 можно пе-
чатать символом * простые графики,- При этом результат вычис-
лений надо нормировать так, чтобы содержимое регистра X не пре-
вышало 20 (зона печати разбивается на 20 знакомест). Так, печать
синусоиды знаками * производится с помощью программы:
Lbl A	RCL	01	sin	+	1	=	X	9
9	=	Ор	07	1	8	SUM	1	А
Амплитуда синусоиды нормирована, так что печать в строке зани-
мает 18 интервалов.
Оператор Ор 08 обеспечивает вывод на печать текста (листин-
га программы), как и оператор List Оператор WW INV List обес-
печивает распечатку содержимого десяти регистров памяти, начиная
с номера NN в виде (NN — 20):
Образец печати данных
Содержимое регистра	Номер регистра	Содержимое регистра	Номер регистра
12,73964896	20	0.	26
148,9657318	21	0.	27
0.	22	0.	28
9.1786109-15	23	0,000124564	29
-1,2256434 08	24		
0.	25		
2.7.	Ввод, редактирование и перевод программ
Перед вводом новой программы иногда полезно стереть старую,
нажав клавиши 2nd СР, н очистить все регистры памяти нажатием
клавиш 2nd и CMs. Для ввода программы нажимается клавиша
LRN. На дисплее насвечивается символ 00000 (первое число—номер
шага или адрес, второе — код). После этого вводится программа
соответствующим нажатием клавиш.
Пр и м е р. Введем программу вычисления факториала Е1 =1
= 1.-2-3 ... £ с учетом значения 0! = 1:
Lbl	Е	STO	О	СР	x = t	A Lbl	В	RCL
О	X	Dsz	О	В	Lbl	Al	=	R/S
Более детально процесс ввода виден из подробного описания
программы:
Показания дисплея		Оператор	Пояснения
Адрес	Код		
ООО	76	Lbl	Ввод
 001	15	Е	метки Е
002	42	STO	Запись числа Е
(ЮЗ	09 •	 0	в регистр R00
004	29	СР	Сброс на 0 регистра t
PQ5	67	x=t	Сравнение Е с 0 = t
096	11	А	Если Е = 0, переход к метке А: задание 0! — I
007	76	 Lbl	Ввод
033	12	В	метки В
009	43	RCL	Вызов
010	03	0	содержимого регистра 7?00
он	65	X	Операция умножения
012	97	P3Z	Выполнение оператора организации Цикла с воз«
013	00	0	вратом по метке В
014	12-	в	
015	76	Lbl	Ввод
016	И	•А	метки А
017	01	1	Вывод числа 1
018	95		Фиксация конца вычислений
019	91	R/S	Останов вычислений
Коды операций нанесены на прозрачной пластмассовой наклад-
ке с прорезями для клавиш (см. рис. 2.2). Если при вводе про-
граммы или при ее редактировании допущена и обнаружена оши-
бочная операция, ее стирают нажатием клавиш 2nd Del (от слова
delete — стирать). Пропущенный оператор можно вставить: он вво-
дится после Нажатия клавиш 2nd 1ns (от слова insert — вставлять).
При этом автоматически меняются адреса всех последующих опе-
раторов (уменьшаются или увеличиваются).
Просмотр программы по шагам производится при нажатии кла-
виш SST (шаг вперед) и BST (шаг назад). Переход в режим вы-
числений происходит после нажатия клавиши LRN. Если пуск про-
граммы проводится с нулевого Адреса, нажимаются клавиши RST
(установка нулевого адреса) и R/S (ran/stop—пуск/стоп). Пуск с
адреса п пп обеспечивается вводом оператора GTO п пп, пуск с
метки N (кроме буквенных) производится вводом оператора GTO N.
Пуск с буквенных Меток А, В, G, D, Е, А', В', С', D' и Е' произ-'
водится указанием нужной буквы путем нажатия соответствующей
клавиши (для букв AV-Е' перед этим нажимается клавиша 2nd).
Провести вычисления по шагам можно, нажимая в режиме сче-
та клавишу SST. Результаты вычисления на каждом шаге выво-
дятся на индикатор.
Важным источником программного обеспечения микрокалькуля-
торов является перевод программ. В справочной [6—9] и периоди-
ческой литературе описано множество программ для различных мо-
делей микрокалькуляторов с разной логикой вычислений и симво-
ликой клавиатуры. Это затрудняет перевод программ и требует
детального знакомства с языком программирования различных мо-
делей калькуляторов. Тем не менее самостоятельное составление
сложных программ более трудоемко, чем перевод готовых программ.
Здесь та же ситуация, что и с написанием или переводом литера-
турных произведений.
Обычно при переводе учитываются следующие обстоятельства:
1.	Легким является перевод с простого языка программирова-
ния на более сложный. Обратный перевод значительно труднее.
2.	Формальный перевод заменой символов (ИП на RCL, П на
STO, БП на GTO, ПП на SBR и т д.) возможен, если модели
калькуляторов имеют одинаковую логику вычислений и систему
команд. Так, весьма простым является перевод программ с языка
отечественных микрокалькуляторов Электроника БЗ-34 (MK-54t
МК-56) на язык калькуляторов серии HP (HP-65, HP-67, НР-97
и др.) и наоборот.
3.	При различиях в логике вычислений они должны быть вни-
мательно изучены и учтены при переводе. Особых трудностей такой
перевод ие вызывает, но требует повышенного внимания.
4.	Наиболее важной обычно является детальная и конкретная
реализация алгоритма вычислений в найденной программе. Поэтому
нередко проще разобраться в частях алгоритма, а затем вбепроиз-
зестн их на языке используемого микрокалькулятора с учетом всех
гго функциональных возможностей.
Для читателей, желающих освоить технику перевода, полезно
знимательно ознакомиться с реализацией важнейших численных ме-
'одов на различных калькуляторах. Основной материал данной книги
тосвящен программному обеспечению массовых отечественных про-
раммируемых микрокалькуляторов Однако в приложениях 1 и 2
ложно найти ряд примеров составления программ (от простейших
Ю сложных) для микрокалькуляторов TI-58C и TI.-59. Сопоставле-
ще их с программами для отечественных микрокалькуляторов явит-
:я хорошей школой для освоения техники перевода и использования
[рограмм, описанных в зарубежной литературе. Кроме того, язык
калькуляторов TI-58C/59 типичен для большинства зарубежных мо-
делей, а также для некоторых отечественных моделей.
Глава 3
ПРОГРАММИРОВАНИЕ ПРОСТЫХ
ВЫЧИСЛЕНИИ
3.1. Операции с действительными числами
Программа 3.1. Выделение целой части чисел	Ю8)'.
Ввод: х = РХ *) (М = 7, 8, 9, А, В, С или Д).
ПМ КИПА! ИПА1 С/П
Программа 3.2. Выделение дробной части чисел х(0 < х < 10е)’«
Ввод: х — РХ.
1 1 + ПЛ4 КИПА! XY ИПЛ4 — С/П
Программа 3.3. Усечение числа х(0 < х < 108) с погрешностью
е == 1 • 10~п. Ввод: е = РД, х = РХ.
ИПД пс кипе ИПС ИПД X с/п
Для е= 1-10-2' и х — 123,4567 получим результат 123,45.
Программа 3.4. Округление числа х любого знака с коррекцией
последней цифры результата (она сохраняется, если последующий
знак х меньше 5 и увеличивается на 1, если он больше 5). Вводз
в = 1-10~в = РД, х = РХ. .
f	Fx<0	04	/-/	П9	FBx	ИПД	-*	ПС
КИПС	XY	ИПС	-	Fl/x	2	-	Fx<0	23	ИПС
1	+	ПС	ИПС	ИПД	X	ИП9	-х	С/П
Для х — ±12,345678 и е = Ы0~’2 получаем округленное зна-
чение х0 — ±12,35, а для х = ±12,344999 округленное значение
х = ±12,34. 
Программа 3.5. Выделение модуля |х| числа х. Ввод: х = РХ,
........ Fx<0 /-/ ... ... ...
Здесь N — адрес шага после оператора /—/.
Программа 3.6. Преобразование угла, выраженного в радианах
<р, в угол, выраженный в градусах <р°, минутах <р' и секундах
*) Операция ввода числа х в регистр Х(х->РХ) обозначается
х = РХ, Операция вывода числа у в регистр X обозначается у-+-
-PX.J	:
Бвед:ф = .РХ.	.
Fit	-s-	1	8	О	ПП	19	ИП8	6	0
ПП	19	ИП8	6	О	x	C/п	БП	00	X
ПП	27	ИП9	1	-	С/П	B/0	1	+	П9
КИП9	XY	ИП9	—	П8	B/0
Для <p = 2 рад, нажав трижды клавишу С/П, получим <р° = 114,
ф' = 35 и <р" = 29,616, т. е. <р = 114° 35'29,616".
Программа 3.7. Перевод угла, выраженного в градусах, мину*
тах и секундах в угол
Нй+’'UMw'
выраженный в радианах. Ввод: <р°, ф' и	ф" в	регистр	X.
П8	С/П	П9	С/П	ф	6	0-s-	ИП9	+
6	О	-s-	ИП8	+	ПО	1	8	0	н-
Fn	X	С/П	БП	00
Для ф = 114° 35' 29,616", вводя 114°, 35' и 29,616", получим
Ф = 2. Кроме того, из регистра 0 можно -вызвать значение фграя =
.= 114,59156°.
3.2. Вычисление определителей
и операции с матрицами
Программа 3-8. Вычисление определителя второго порядка:
.	1®1=Р8 61 = Р91	,	 ,
А —|Й2 = Р5 />2 = Р6’| й1*2 'а2*ь
ИП8 ИП6 X ИП5 ИП9 X - С/П
15	41
1,5 3| = 9-
Программа 3.9. Вычисление определителя третьего порядка:
а1==Р7 Z>] == Р8
а-2 = Р4 b2 = Р5
а3 = Р1 />з = Р2
с, = Р9
с2 = Р6
с3 = РЗ
= Ci (a2Z>,3 — a3b2) + с2 (аЛ —-Д|6з) 4~ Сз (аг/>2 — a2bt).
ИП4 ИП2	X	ИП-1	ИП5	х -	ИП9	X	И.П1
ИП8 X	ИП7	ИП2	X	— ИП6	X	+	ИП7
ИП5 X	ИП4	ИП8	X	— МПЗ	X	+	С/П
При мер.							
		:'2 6	—3	•			
		1 1 4	—Г	= 1’0.			
		' 1 3	2*				
Время счета около 10 с.
Программа 3.10. Вычисление определителя четвертого порядкам
at Оз «з = =	РА РВ PC	bl Ьг Ьз bt	= Р7 = Р4 = Р1	О О м О- Си Си II II II — N СП "Ч* 43 43 43 43 QO ю сч си си си II II II -< N СО Си «и	= Oj Ai —	“Ь	— d\D\9
где					i
				bz Cz ^2	dz Cz dz
			Ai =	Ьз £з	== 0,3 Сз dz 9
				bi ^4	Oi Ci di
				#2 bz	Oz bz Cz
			(?! =	Оз Ьз &3 t	~ аз Ьз Сз •
				Oi bi di	Oi bi Ci
Сх	по		ПП	54 ИП7 ПА	XY П7 ИПВ ИП4
ПВ	XY		П4	ИПС ИП1 ПС	XY П1 ПП 54
ИП8	ПА		XY	П8 ИПВ ИПс	5 ПВ XY П5 ИПС
ИП2	ПС		XY	П2 ПП 54	ИП9 ПА XY П9
ИПВ	ИП6		ПВ	XY П6 ИПС ИПЗ ПС XY ПЗ	
ПП	54		ИПО	С/П ИП4 ИП2 X ИП1 ИП5 X	
—	ИП9		X	ИП1 ИП8 х	ИП7 ИП2 X —
ИП6	X		+	ИП7 ИП5 X	ИП4 ИП8 X —
ипз	X		+	С/П X ИПО + ПО ИПА В/0	
После ввода программы и исходных данных, нажав клавишу
С/П, получим значение А(. Вводим at — РХ и, нажав клавишу С/П,
ПОЛуЧИМ Bi. ВВОДИМ -т-61 = РХ И ПОЛуЧИМ С|, ВВОДИМ С( = РХ и
получим Di, наконец вводим —= РХ и получим Д.
Пример:
6	3	0	3
л—	4	4	2	1
Д—0442
7	7	8	5
Получаем: At=8, Вх = 16,	С|	— 52,	£)|=72. Вводим: 0^ = 6,
— bi — — 3, Ci = 0, — di= — 3. Окончательно Д = — 216.
Определители более высокого порядка могут вычисляться пу-
тем разложения на определители 2, 3 и 4-го порядка. Однако более
рационально проводить такие вычисления на настольных или уни-
версальных ЭВМ по стандартным программам.
С помощью микрокалькуляторов легко проводить операции над
матрицами с числом элементов, не превышающим числа регистров
памяти (16 у Микрокалькулятора Электроника БЗ-34, включая ре-
гистры Z и Т стека). Поясним это примерами.
Пусть надо сложить неограниченно^., число матриц с числом
строк 4 и столбцов 3.
Удобно эту'операцию представить в виде
я? da
Я4 Яд
Д1 Яд
Яо а10
я9
Я6
Яд
Яц
Ь1
bi
bi
bo
ba
ba
ba
bio
bg
be
ba
bit
m7 ma mg
mt m5 me
mi m2 tn3
m0 mio mi
где индексы у элементов матриц заменены номерами регистров, с
которые эти элементы заносятся (РЮ = РА, Р11 = РВ).
Программа 3.11. Сложение матриц размера 4X3. Ввод:
«о 4- Яц = РО 4- Р11, Ьо 4- Ьц — РХ ... Результат /и0 4-/Пц зано-
сится в регистры Р0 4-Р11.
7	С/П	ИП7	+	П7	8	С/П	ИП8	+	ПЗй
9	с/п	ИП9	+	П9	4	С/П	ИП4	+	П4
5	с/п	ИП5	+	П5	6	С/П	ИП6	+	П6
1	с/п	ИП1	+	П1	2	С/П	ИП2	+	П2
3	с/п	ИПЗ	+	ПЗ	0	С/П	НПО		ПО
1	0	С/П	И ПА	1	ПА	1	1	С/П	ипв
+	пв	БП	00						
При использовании этой программы сначала в регистры РО 4-
•4-Р11 вводятся числа первой матрицы. Затем, после нажатия кла-
виши С/П, построчно вводятся значения элементов второй матрицы.
При этом программа всякий раз подсказывает номер числа матри-
цы. Например 7, 8 и 9, при вводе первой строки. Если матриц не-
сколько, то в той же последовательности вводятся значения элемен-
тов последующих матриц. Проверить программу можно, присвоив
значениям .элементов складываемых двух матриц номера регистров
(получим их удвоение).
Часто возникает необходимость в умножении матриц. Произве-
дением матрицы А размера т X п на матрицу В размера п X Р яв-
ляется матрица С = АВ размера т X Р, элемент С,у которой, рас-
положенный в ij клетке, равен сумме произведений элементов 1-ой
строки матрицы А на соответствующие элементы /-го столбца мат-
рицы В:
п
С1/ = аПЬц + ai2b2j + ••• +ainbnj==^ialkbkj-
Таким образом, число столбцов матрицы А должно быть равно чис-
.лу.строк матрицы В.
Программа 3.12. Умножение матрицы А размера 3 X 4 иа мат-
рицу В размера 4X2. Ввод элементов матрицы В и вывод значе-
ний элементов матрицы С соответствуют указанным в формуле.
«11 «21 «31	«12 «22  «32	«13 «23 «33	«14 «24 «34	X		6ц=Р7 Ь12==Р8		=5=1	п	еъ	л СО	№ II	II	II 15	Ч	-U W	СП	ср Га СО	КЗ	>-* КЗ	КЗ	КЗ II	II	II Ч	-я	-1? J=t	О	сз	*
						&21 === Р4 &22	II II II 45 45 45 > to сл			
						6з1 = Р1 Ьзг				
						Ьц = Р0 &42				
ПП ипд	16 ПС		ИПЗ ПП		П9 ИПД 16	0		ПВ С/П	ПП 1	16	ИПЗ П6 С/П	ИП7	
X X 3	ПЗ ипз С/П		F, + 4		ИП8 X ПЗ F, ИП1 х		ПД ИП5 ипз	Я. X +	С/П 4 ИП4 ИПД +' ПД ПЗ F, ИП2	
X	ипд		+		ПД 4		С/П	4	ИП0 х ИПЗ	
+ ПЗ F, ИПА х Работу этой программы можно							ипд + проверить		ПД В/0 на примере:	
2 О’ 5 1 0 0	2 0 4 1 2-1	— +	Ч3 5 3-24	=3 -3-		4+1 -3 = 17	2-3 + 0-		1+3-0+1-5 = 11	
=	5-14-1-2 + 2				•	4 + 0 • 3 = 15	5-3+1-		1+2-0 + 0-5=16	
	0 • 1 + 0 • 2 + 4					4+1-3=19	0-3 + 0-		1 +4-0 + 1 -5 = 5	
Введем элементы матрицы В. Нажав клавишу С/П, получим на
индикаторе цифру 1, указывающую на ввод первого элемента пер-
вой строки йц матрицы А. Вводим его, затем нажав клавишу С/П,
получим цифру 2 — надо вводить а^. Введя, таким образом по-
строчно все элементы матрицы А, получим на индикаторе цифру О,
указывающую на конец вычислений. Из регистров 9, 6, 3,' В, С и Д
вызываем результат вычислений — числа 17, 15, 19, 11, 16. и 5.
Иногда нужны обратные матрицы Л-1, удовлетворяющие уело-,
вию А-А~1 = 1. Правила обращения матрицы А в обратную матри-
цу описаны в [4—7]. На микрокалькуляторе легко провести об-
ращение квадратных матриц размера 2X2 и 3 X3. Обращение мат-
риц большего размера можно проводить, разбивая их на блоки
меньшего размера.
z Программа 3.13. Обращение матрицы размера 2X2. Ввод:
«и = Р7 «21 = Р8
«|2==Р4	«22 Р5
Обращенная матрица заносится на место исходной.
ИП4	ИП8	X	П2	ИП7	П9	ИП5	X	ИП2	—
П2	ИП5	XY	-J-	П7	ИП9	ИП2	П5	ИП4
ИП2	/-/	4-	П4	ИП8	ИП2	/-/	->	П8	С/П
БП 00
•Для контроля программы можно выполнить следующие вычис-
ления:	»
_ I 7 8 |	д-11	1,6666666 —2,6666666 I
А~ I 4 5 Г	А — | —1,3333333 2,3333333 [’
Программа 3.14. Обращение матрицы размера 3X3. Ввод:
<7[ 1 = Р7 П12 == РЗ П1з = Р9
a2i — Р4 а22 = Р5 а2з — Р6
G31 = Р1  П32 = Р2 Сзз = РЗ
Обращенная матрица заносится на место исходной.
3	ПО	ИП4	ИП7 +	ПД	ИПД	/-/	ПС	ИП5
ИПД.	ИП8	X	— ПА	ИП6	ИПД	ИЛ9	X	—
ПВ	ИП1	ИП7	4- ПД	ИПД	/-/ 	П6	ИП2	ИПД
ИП8	X	—	П4 ИПЗ	ИПД	ИП9	X	—	П5
ИП8	ИП7		П1 ИП9	ИП7	4-	П2	ИП7	Fl/x
пз •	ИПА	П7	ИПВ П8	ИПС	П9	FLO	02	С/П
Работу программы можно проверить					на примере:			
	4 8 0		0,08333333 —0,08333333	0,66666666
Л =	8 8 8 2 0 1	; А ' =	0,08333333 0,04166667 —0,16666666 0,16666666	—0,33333333 . —0,33333333
Повторное обращение матрицы А~1 даст матрицу А е неболь-
шими операционными погрешностями.
3.3. Вычисление факториалов и комбинаторика
Программа 3.15. Вычисление факториала п! 1-2-3 ... -п с
исключением заведомо известного значения 0! — 1 при п — РХ
ПО. 1 НПО X FLO 02 С/П
Пример. 10! = 3628800 вычисляется за 10 с.
Программа 3.16. Вычисление факториала п! для любых п, вклю-
чая 0, при п = РХ.
ПО Fx^O 11	1 ИП0 X FLO 0’4 С/П БП
00 1  БП 08
Примеры. 0! = 1, 11 = 1, 3!-== 6, 10! = 3628800, 20!==
= 2,432902-1018 (время счета /с ~ и со-
программа 3.17. Вычисление факториала п! больших чисел (при
и > 10 верны пять первых знаков результата) по уточненной фор-
муле Стирлинга [1, 2]:
n! = пп exp [- п +	(1 - з^)]-	(3.1)
Ввод: п = РХ при максимальном п = 56.
П9- f	Fx®	1	ИП9	3	0
1	2	-г-	ИП9	ИП9	-
Fn X	ИП9	X	F-x/"	X	С/П
X Fl/x -
Fev X 2.
БП 00
Примеры. 10! = 3628711,6 (точно 3628800)',	20! =1
= 2,4328826-1018 (время счета 12 с), 56! = 7,1100172-1074.
Программа 3.18. Вычисление факториала п! при п 12 по точ-
ной формуле, а при п >• 12 — по формуле (3.1).’'
ПО	1	3	— Fx<0	20	ИПО	Fx=A0	17	1
ИПО	X	FLO	10 С/П	БП	00	1	БП	14
ИПО		Fx®	1	ИПО	3	0	X	Fl/x	—
1-	2		ИПО 4-	ИПО	—	Fe*	X	2
Тл	X	ИПО	X F <	X	БП	14		
Примеры. 3! = 6, 10! =. 362880, 15! = 1,3076567-1012.
Программа 3.19. Расчет числа перестановок Рп — п!, числа раз*
мещений из п элементов по т:
А™ = п!/(п - т)!
и числа сочетаний из п элементов по т:
С™ = «!/((« - т)! ml).
Ввод: п — РХ, т = РХ. Вывод: mt -> Р4, Рп = nt -> Р5, (и — т) !->
-> Р6, А™	-> РА,	wn •	->РС	= РХ.					
П9	С/П	П8	пп	26	П4	ИП9	ПП	26	П5
ИП9	ИП8	—	пп	26	П6	ИП5	XY	4-	ПА
ИП4	4-	ПС	С/П	БП	00	ПО	1	ипо	X
FLO	28	В/0							
Для п-	= 10,	т —	5 получим		(спустя 30		с	счетй)	/">5 - с10 “
А*о = 30240 и PlQ = 3628800.
3.4. Операции с комплексными числами
Программа 3.20. Преобразование комплексного числа из алгеб-
раической формы Z — а jb в тригонометрическую Z — Ме^ф, где
A4 = Vo2 + ^2 н <р = arccos(а/|Л4)) при b J и <р =1
— —arccos(а/|Л1|) при b < 0 (—180° ср 180°). Ввод: а = РХ,
Ь = РХ. Вывод: результата Л4->РХ, <р (в градусах)~>Р¥. Пере-
ключатель Р—Г в положении Г.
ПА	С/П	ПВ	ИПА	ф	Fx2	ИПВ	Fx2	+	FV
П8	4-	Farccos	П9	ИПВ	Fx < 0	20	ИП9	/—/	П9
ИП9	ИП8	С/П	БП	00
Примеры. Для Z = —1 +/-1 М — 1,4142135 и <р = 135°,для
Z = — I—/! М = 1,4142135 и ф==—135°, для Z = —1 + / 0
А1 = 1 и ср = 180°.
' Арифметические операции над комплексными числами ’ в алгеб-
раической форме выполняются по формулам:
Zo = Zi + Z2 = (oi + а2) + / (61 + 62)
,Z0= Zi • Z2 — (ata2 — btbi) + j (aj62 + 6jn2)
7 __ Z,	aia2 + 6i62 , . Ьха2 — ахЬг
-z	2 . .2	* 1	2 , «.2
Z2 O2+62	C2 + &2
Программа 3.21. Арифметические операции (сложение — код 0,
умножение — код 1 и деление — код 2) над дарами комплексных
чисел Z, = Oi +/&! и Z2 = a2 + jb2. Ввод: аь bt, а2, 62 в регистр X,
код операции в регистр Х,.п3, 63, код в регистр X и т. д. Результат
Zo =	По + jbo'. По		Р4 =. РХ, 60->		 Р5 =	РУ.			
П4	С/П	П5	С/П	П2	С/П	ПЗ	0	С/П	Fx Ф 0
52	1	—	Fx?b0	30	ИП2	Fx2	ипз	Fx2	+
П8	ИП2	ИП8		П2	ИПЗ	/-/	ИП8	-~-	ПЗ
ИПЗ	ИП5	X	ПО	ИП4	ИПЗ	X	П1	ИП2	ИП5
X	ИП1	+	П5	ИП2	ИП4	X	ипо	--	П4
БП	03	ИП5	ИПЗ	+	П5	ИП4	ИП2		П4
БП	03								
Пример. Вычислить
(5-/-3) (3 +j-2)
(5 + /-3)(2-/.4)
F (0,5+ / • 1).
Zo
Вводим 5, —3, 3, 2, 1 (код умножения), 5, 3, 2 (код деления), 2,
—4, 2 (код деления), 0,5, !,• 0 (код сложения). Получим Zo =
= 1,1588235 + / • 1,4647059.
Программа 3.22. Последовательное умножение и деление ком-
плексных чисел в тригонометрической форме:
Zo = Z,Z2 =	Zo = -fL =
Ввод: Mi, <pb M2, <p2, код операции (1 для умножения и 2 для де-
ления). Результат Zo — Мое!<*>": Л40->РХ = Р6, <p0-->PY = P7.
П6	С/П	П7 ‘	С/П	П8	С/П	П9	0	С/П	t
1	—	Fx 0	24	ИП7	ИП9	—	П7	ИП6	ИП8
-j-	П6	БП	03	ИП7	•ИП9	+	П7	ИП6	ИП8
X	П6	БП	03						
Пример.		. Вычислить							
Z,Z2 2елз0° • 6ел20°
4е-'-«°
Вводим 2, 30, 6, 20, 1 (код умножения), 4, —40, 2 (код деле-
ния). Получаем Zo = Зе'’90° (Л40 =3, <р0 = 90°). Перед вводом кода
в программах 3.21 и 3.22 индицируется цифра Q.
Глава 4
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ,
МНОГОЧЛЕНОВ И ЦИФРОВЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
4.1. Гиперболические
и обратные гиперболические функции
Программа 4.1. Вычисление гиперболического синуса shx=j
(е* — 1/е*)/2. Ввод: х — РХ.
Fe* f Fl/x -2 4- С/П
Для х — 1 имеем sh(l) — 1,1752012.
Программа 4.2. Вычисление гиперболического косинуса ch х =]
[е= (е* + l/ez)/2. Ввод: х — РХ.
Fe* f Fl/x + 2 4- С/П
Для х — 1 имеем ch(l) — 1,5430806.
Программа 4.3. Вычисление гиперболического тангенса thx=a
= sh x/Vl 4* sh2 x . Ввод: x = PX.
Fex f Fl/x — 2 4- f Fx2 1 4-
FV 4- С/П
Для х=1 получаем th(l) — 0,76159417. Для вычисления
cthx==l/thx перед оператором С/П ввести оператор Fl/x.
Программа 4.4, Вычисление обратного гиперболического синуса
arsh х = In (х + V1 + я2 ) при х = РХ в диапазоне значений от
»—оо до 4-оо.
t Fx2 1 + F/ 4- .Fin С/П
Для х— 1 имеем arsh (1) = 0,88137355.
Программа 4.5. Вычисление обратного гиперболического коси-
нуса arch = In (х 4* Vx2 — 1) лля х~ РХ > 1
t Fx2 1 /-/ 4- F V 4- F In С/П
Для x = 2 получаем arch (2) = 1,3169579.	1
Программа 4.6. Вычисление обратного гиперболического танген-
са arth х— In V(x ~F 1)/(1 — х) для х = РХ в диапазоне значений
от —1 до 4-1.
fl XY 4- FBx 1 XY — 4- F-V"
Fin С/П
При x — 0,7615942 получим arthx = 1,0000001.
Программа 4.7. Вычисление обратного гиперболического котан-
генса arcth х = In Vl + 2/(х — 1 j длях = РХ>1.
f 1 - 2 XY 4- 1 -}-	Fin
С/П
Для x= 1,3130352 получим arcth x — 1,0000001.
В некоторых микро-ЭВМ, например Электроника ДЗ-28, ЭТИ
функции вычисляются микропрограммно. •
4.2. Непрерывные дроби
Программа 4.8. Вычисление непрерывных дробей вида
г		’
-——
—к
“, + -STF
а2 ’ а3 ’ ''"J'
Ввод: а1П, bm, am_t, bm_t, аь bt, ав в регистр X.
f С/П XY 4 f С/П -}- БП .00
Пример. f = Гб; 4-;	=6,8765432.
• L 4 7 5 J
г Непрерывной дробью можно представить некоторые дробно-ра-
цноиальные функции, что упрощает их вычисления [1—5].
v Программа 4.9. Вычисление дробно-рациойальной функции
с, .	15 — 21х2 4- х* Г — х2 — х2 — х21
fW=-------I5=6F—= [1; “Г-;	-5~J-
Ввод: х — РХ.
П9	ИП9 /-/	X	П8 5	4-3	4-	ИП8
XY	4-	1	4-	ИП8 XY 4- 1	4-	С/П.
БП 00
г Для х = 0 имеем f(0) = I, для х = 1 f(l) — —0,5555554, для
X = 2 f (2) = 5,8888889.
4.3. Вычисление многочленов по схеме Горнера
Программа 4.10. Вычисление многочлена действительного пере-
менного степени п^П по схеме Горнера Р(х) = а0 4- aix 4-  •*
i.. +апхп =(. ..(апх^-ап-^х	^-,ai)x^-xB. Ввод:' а0 = PC,
Й1 _ ап — Р1 4- Рп, х = РХ (при смене х вводится только новое
значение х и нажимается клавиша С/П).*)
ПД........... ПО	ИПп	f	XY , ИПД X	КИПО
4-	ИПО Fx = 0 .05	XY	ИПС	+ С/П . БП	00
Для многочлена Р(х) = 0+1x4- 2х2 + Зл:3 + 4х4 (и = 4) по-
лучим Р(1) = 10, Р(2)=98 и т. д. Эту программу нетрудно при-
способить для вычисления многочленов только с чгт-ными или не-
четными степенями.
Программа 4.11. Вычисление многочлена комплексного перемен-
ного Z = а + jb степени п 10 по схеме Горнера. Ввод: ае — Р0,
Я1 = Pi, ..., as = Р9, Сю = РА, a — PY и b = РХ. Результат
P(Z) = с + jd: с-*РХ, d->- PY.
ПС	XY	ПВ	ИПА	X	ИП9	+	ИПС	ИПА	X
ПД	XY	ИП8	ПП	42	ИП7	ПП	42	ИП6	ПП
42	ИП5	ПП	42	ИП4	ПП	42	ИПЗ	ПП	42
ИП2	ПП	42	ИП1	ПП	42	ИПО	ПП	42	С/П
БП	00	ИПД	ИПС	X	—	XY	ИПВ	X	+
XY	ИПС	X'	ИПД	ИПВ	X	+	ПД	XY	В/0
Для многочлена P(Z) = 1 + Z + 2Z2 + ... + 8Z8 (fle = аю — 0)
при Z=l+j-l получим P(Z)— 144 — j-113 при времени счета
tc » 70 с. При усложнении ввода исходных данных и нормировке
(делении на Сю) степень многочлена можно повысить до п = 13,
а при действительной переменной х — до 16 [7].
4.4.	Вычисление рядов и сложных числовых
последовательностей
В основе вычислений рядов и сложных числовых последователь-
ностей лежат циклические программы с циклами, вычисляющими
главный член последовательности. Изменение этого члена задается
последовательностью чисел, формируемых счетчиками вида i =1
==.«’+ 1 или i — i— 1. Такие счетчики создаются операторами кос-
венной адресации вида КИПА? ИПА? ' или операторами организации
циклов FLO, FL1 или FL3. Проиллюстрируем методику составления
таких программ на конкретных примерах.
Программа 4.12. Вычисление суммы целых чисел
S = I = I 4“2 + з-р •••	— 1) Ч~ я.
*) На место многоточия вводится число п3 состоящее из двух
цифр, например, 5 вводится как 0 и 5. ,
Ввод: х = РХ
. I	I
ПО О ИПО + FLO 02 С/П
Главный член последовательности—сами числа I, которые создают-
ся в регистре Р0: п, п — 1 ... 3, 2, 1 и суммируются в регистре X
по мере выполнения каждого цикла. Число 0 (оператор по адресу
01) служит для обнуления накапливающего регистра X перед вы-
полнением циклов. Взяв п = 10 и нажав клавиши В/0 и С/П, по-
лучим S — 55‘.
В некоторых случаях текущее значение главного члена легко
найти с помощью рекуррентных соотношений. Так, при вычислении
последовательности
S== £ п!= 1 + 1 - 2+ 1-2-3+ 1.2-3.4+' ... + (ft — 1)1 4-я!
i = l
каждый последующий член равен предыдущему, умноженному на
текущее значение i, т. е. i! = (i— 1) !i.
Программа 4.13. Вычисление суммы факториалов 8(п!). Вводз
п = РХ.
П7	0	П9	П6	1	П8	КИП6	ИП6	ИП8	X
П8	ИП9	+	П9	ИП6	ИП7	— .	Fx = 0	06	ИП9
С/П БП 00
В этой программе п вводится в регистр 7, накопление сумм про-
исходит в регистре 9, текущие значения i формируются в регист-
ре 6. Регистр 8 используется для запоминания, предшествующего
значения главного члена последовательности. Счет останавливается
при i — n = 0. Взяв п = 4 = РХ, получим 8(га!) = 33.
Программа 4.14. Вычисление произведения факториалов Р («!) =.
I— 1 • (1 -2) • (1- 2-3) ... /!“... (га — l)!ft!. Ввод: п = РХ.
П7	0	П6	1	П8 П9	КИП6	ИП6	ИП8	X
П8	ИП9	X	П9	ИП6 ИП7	—	Fx = 0	06	ИП9
С/П БП 00
В этой программе для вычисления главного члена — факториа-
ла— также используется рекуррентное соотношение i! — (i—1)!/.
Для n = 4 — РХ получим Р(п’) = 288.
Программа 4.15. Вычисление последовательности
т
У =^kn.
fe=l-
Ввод: т и п в регистр X.
П7	С/П	П9	0	П4	П8	КИП4.	ИП4	ИП9	XY
; FxV	ИП8	+	П8	ИП7	ИП4	-	Fx = 0	06	ИП8
С/П БП 00
Главный член последовательности в этом случае К", где К =
= 1, 2, 3, ..., т. Для /л = 20 н п — 4 значение у = 722665,91
(точное значение 722666),. а » 2 мин.
Если знаки главного члена должны попеременно меняться, вво-
дится умножение его в каждом цикле на — 1. Вычисление рядов с
бесконечным числом' членов заменяется суммированием конечного
числа членов с контролем значений каждого из них. Если они ста-
новятся меньше малого-числа е, задающего погрешность вычисле-
ний, последние останавливают.
Приведенные выше рекомендации широко используются в про-
граммах вычисления специальных функций по их разложению в
ряды.
4.5.	Вычисление многочленов Лагерра, Лежандра,
Лагранжа; Эрмита и Чебышева и их коэффициентов
Широко распространенные в научно-технических расчетах диф-
ференциальные уравнения второго порядка часто имеют решения
в виде ортогональных многочленов Лагерра, Лежандра, Эрмита и
Чебышева [1—3]. В [6] описан пакет программ вычисления их ко-
эффициентов на микрокалькуляторе Электроника БЗ-21. Приведен-
ные ниже программы получены переводом этих программ. Во всех
программах степень многочлена h вводится в регистр X (после на-
жатия клавиш..F, АВТ и В/0). Каждое нажатие клавиши С/П ве-
дет к выдаче очередного коэффициента многочлена до тех пор,
пока не высветится цифра 0, указывающая на конец вычислений.
Программа 4.16. Вычисление коэффициентов многочлена Ла-
герра.
П2	0	ПЗ	ИП2	Fn	X	Feos	П8	С/П	НПЗ
П9	1	4-	ПЗ	ИП9	ИП2	—	Fx2	ИП8	X
НПЗ	/-/	4-	БП	07
Для п — 5,	нажимая	клавишу С/П	до	появления цифры	0, бу-
дем получать коэффициенты многочлена Лагерра
L5(x) = — lxs + 25х4 — 200л3 + 600х2 — бООх + 120
в виде последовательности чисел —1, 25, —200, 600, —600, +120
и 0 (конец вычислений). Переключатель Р — Г в положении Р.
Программа 4.17. Вычисление коэффициентов многочлена Ле-
жандра.
П2	1	П6	П8	+	ПЗ	2	П7	X	3
•*—	П5	П4	ИП8	X	ИП6	ч-	П8	ИП6	1
+	П6	ИП4	2	—	Fx < 0	12	ИП8	С/П	ипз
1	—	П9	1	—	ПЗ	ИП9	X	ИП8	X
ИП7	Ч-	ИП5	/-/	ч-	П8	ИП7	2	-	+ ’	П7
ИП5	2	——-	П5	БП	27				
Для п = 5 получим коэффициенты многочлена
Р5 (х) = 7,875xs “ 8,75х3 + 1,875х. -	(4.1)
Программа 4.18. Вычисление коэффициентов многочлена Эрмита.
П2	1	ПЗ	П8	+	П4	2	П5	ИП8	~С/П
ИП4	1	—	П9	1	—	П4	ИП9	X	ИП8
X	ИП5	/-/	4-	П8	ИП5	2	+ '	П5	БП
08
Для п —.8 получим коэффициенты многочлена
Д8(х) = lx8 — 28х® + 21 Ох4 — 420х2 + 105.
Программа 4.19. Вычисление коэффициентов многочлена Чебы-
шева по формуле
П2	Тп(х)=^		пр Е П8	(-1)			• X	П4
	2	П4			ПЗ	ИП4 2		
ИПЗ	1	П5	—	ПЗ	Fx = 0	06 , ИП4	с/п	/-/
ИП2	X	4	-4-	П9	ИП5	X	с/п	ИП9	ИП8
*“—	П4	ИП8	1	П5	+	П8	П7	2	—
П6	ИП7	ПО	1	+	П7	ИП9 ИП2	—	ИП5
X 22	П5	ИП6	1	—	П6	Fx = 0 40	ИП4	БП
Для п = 8 = РХ получим округленные коэффициенты много*
(члена Чебышева 8-й степени:
Г8(х) = 128х8 - 25бх® + 160х4 - 32х2 + 1.
Вычисление значений ортогональных многочленов можно орга-
низовать непосредственно по их разложениям в степенные ряды,
примеры которых приведены выше. Однако в этом случае для каж-
дого многочлена с заданным п придется составлять свою програм-
му. Более рационально воспользоваться известными рекуррентными
соотношениями [2].
Программа 4.20. Вычисление значений Бп(х) многочлена Ла-
Герра
т е* <Р(х”е-*)
11' ' п1 ' dxn
По рекуррентной формуле (i0(x) = 1; Бц(х) = 1 — х):
X/+i (х) = -7-^-г [(2/ + 1-х) Li	(x)J (i = 1,2, ..., n-1).
I T I
Ввод: п = РД, х — РХ.									
П7	1	XY	—	П9	1	П8	П6	ИП6	ИП8
/-/	X	ИП6	2	X	1	+	ИП7	—	ИП9
JI8	X	+	ИП6	1 .	+	П6	-т*	П9	ИП6
ИПД	—	Fx>	0 08	ИП9	С/П	БП	00		
Для х = 3 имеем 1,2(3)==—0,5; Бз(3)= 1; Б4(3)= 1,375
(/с » 25 с).
Программа 4.21. Вычисление значений Рп(х) многочлена Ле«
жандра
2-п ап (. _ Л
Рп (х) = (-!)"	- • °
п' '	'	' п! <1х
по рекуррентной формуле (Р0(х) = 1. Pi(x)= х);
Pi+i И = -4гг К2/ + В xPi “ iPi~' (х)1	= *'2	п~ В- 1 ~г 1
Ввод: п — РД, х = РХ.
П7 П9	1 П8 П6 ИП6 /-/ ИП8 X ИП6
2 X	1	+ ИП7 X ИП9 П8 X +
ЙП6 1	+ П6 4- П9 ИП6 ИПД — Fx>0
05 ИП9 С/П БП 00
, Для х = 2 имеем Р2(2)=5,5, Р3(2) = 17, Pt(2) = 55,375.
Программа 4.22. Вычисление значений Нп(х) многочлена Эрмита
"лИ---- ( ’} е Jvn >
по рекуррентной формуле (ДоТВ ~ В Д1(х)=2х):
Д/+1 (*) — 2x111 (х) —	(х)	(2=1,2...п — 1).
П7	2	X	П9	1	П8	П6	ИП6 2	X
ИП8	/-/	X	ИП7	2	X	ИП9	П8 X	+
П9	КИП6	ИП6	ИПД		Fx;	5 0 07	ИП9 С/П	БП
00								
Для х—3 получим Л/2(3)= 34, Я3(3) = 180, 7/4(3)= 876.
Многочлены Чебышева первого рода Тп(х) == cos (ftarccosx)’’
и второго рода Un(x)= sin((n+ l)arccosx)/sin(arccosx) несложно
вычислить непосредственно по приведенным формулам (ввиду про-
стоты их программы не приводятся).
Особый интерес представляет вычисление коэффициентов интер«
поляционных полиномов Лагранжа, которые применяются для ин*
терполяции функции у(х), заданной рядом ординат уо-^-Уп при абс-.
циссах Хо 4- хп. В качестве нулевого узла можно яспользовать лю-
бой узел, например, при трех узлах и нулевом центральном узле
значения функций будут обозначаться; у-х = y(x-i), у0 — у(х0)п
y+i = £/(x+i). Полином Лагранжэ может записываться в двух фор-,
мах.
Первая форма имеет вид [1]:
п
у (х) = До (х) ув + л (х) iji + ... + Ап (х) Уп = у Ат (х) Ут, (4.2)
о
где коэффициенты определяются из формулы
Дт (х) ~
(х — х0) (х — Xi) :. (х — Хпг_1) (х — хт+1) ..  (х — хп)
(хт хо) (хт . Х1) — (*/7i хт—1) (хт хт+>) • • • kxm xni
Ввиду сложности этого выражения на микрокалькуляторах зна-
чения Ат (х) можно вычислять раздельно для полиномов с п 5
при п + 1 ординатах. При нормировке
х — хо + ph.
где h — разность абсцисс соседних узлов, *
р=(х —х0)/й,	(4.3);.
и будем вычислять значения нормированных коэффициентов Лагран-
жа Дт(р). Ниже дан пакет программ, позволяющих вычислить
Дт(р) для п+1, равного 3, 4, 5 нли 6 по формулам, приведенным
В [3].
Программа 4.23. Вычисление коэффициентов полинома Лагран-
жа прн трех ординатах y-i, ув, у+р.
	Дт (р) — ( О	т+1	 (1	р (р2 — 1)	 + т)! (1 — т)! (р — т) ‘
ПД	Fx2 1	-	ИПД	X ПС 0	П6 ПП
27	2	П1	пп	27	/-/ ПО	ПП 27
2	4- ПА 3	с/п	БП 00 кипе ИПС ИПД
ИП6	-	2	+	4-	В/0
Для р =. 0,45 = РХ, нажав клавишу С/П, получим цифру 3
'(указание на 3 ординаты). 'Коэффициенты полинома заносятся в
регистры Д-1 = —0,12375->Р1, До = 0,7975 РО, Д-н = 0,32625
ГЭ-РА.
Программа 4.24. Вычисление коэффициентов полинома Лагран-
жа прн четырех ординатах y-t, ув, У+i н р+г’-
	Дт(р) = (-1),гг+2			р(р2- (1 + ту. (2		1)(Р—2) — т)1 (р — т)		
ПД	Fx2	1	—	ИПД	X	ИПД 2	—	X
ПС	0	П6	ПП	39	6	/-/	4-	П1	ПП
39	2		по	ПП	39	2	/-/		ПА
ПП	39	6	-i-	ПВ	4	С/П БП	00	кипе
ЙПС	ИПД	ИП6	—	2	+	В/0		
Для р = 0,15, нажав клавишу С/П, получим, цифру 4 (число
ординат). Коэффициенты полинома заносятся в регистры: А-, =;
-=—0,0393125--Р1, До = 0,9041875--Р0, Д+1 = 0,1595625 -+ РА н
А +2 = -0,0244375 РВ.
Программа 4.25. Вычисление коэффициентов полинома Лагран-
жа при пяти ординатах у-2, y-i, ув, У+i п р+2:
	Ат (р) = (-1)т+2-				р(р2 (2 + т)!	— 1)(рг —4) (2 — гЛ)1 (р — т) ’			(4-4)
ПД	Fx2	ПС	1	—	ИПС	4	—	X	ИПД
х	ПС	0	П6	ПП	47	2	4	-Т-	П2
пп	47	6	/-/	“Г	П1	ПП	47	4	-4-
по	ПП	47	6,	/-/	-4-	ПА	ПП	47	2
4	-4-	ПВ	5	С/П	БП	00	кипе	ИПС	ИПД
ИП6	—•	3	+	•V-	В/0				
Для р = 0,3, нажав клавишу С/П, получим цифру 5 (число ор-
динат). Коэффициенты полинома заносятся в регистры: Д-2 =
= 0,0193375 Р2, Д_, = -0,13685 Р1, Ав = 0,889525 — Р0,
А+1 =.0,25415 — РА и А+2 = -0,0261625—РВ.
Программа 4.26. Вычисление коэффициентов полинома Лагранжа
при шести ординатах у~2, У-i, ув, y+i, У+2 и у+в:
	^т(-р)=(-1)'"+			3 Р<РЯ~ 1)(р2 —4)(р —3) (2 + т)1 (3 — т)\{р — т)					
ПД	Fx2	П8	1	—.	ИП8	4	—.	х	ИПД
3	—	х	ИПД	X	П8	0	П6	пп	63
1	2	0	/-/	-4-	П2	ПП	63	2	4
-4-	П1	пп	63	1	2	/-/	-Т-	по	пп
63	1	2	-4-	ПА	ПП	63	2	4	/-/
-4-	ПВ	пп	63	1	2	0	-4-	ПС	6
С/П	БП	00	КИП6	ИП8	ИПД	ИП6	—	3	+
-4-	В/0								
Для р = 1,45 = РХ, нажав клавишу С/П, получим цифру 6
(число ординат). Коэффициенты полинома заносятся в регистры:
Д_2 =-0,011356897 —Р2,	Д_, = 0,079961829--₽1, . Ав =
= -0,27021584 — Р0, Д+1 = 0,8706955 РА, Д+2 = 0,35619361 —
— РВ и Д+3 = -0,025278255-- PC.
Во второй форме записи интерполяционного полинома Лагранжа
у. (х) = Вв (у) + Bl (у) (х — хв) + В2 (у) (х — х0) (х — Х1) +' . • •
... + Вп (у) (х — х0) (х — xi) ... (х — х„_i)	(4.5)
коэффициенты Вв(у)~ Вп(у), или сокращенно Вв -Р Вп, являются
функциями ординат ув 4- у„ [1].' Алгоритм их вычисления по схеме
Эйткена поясняется табл. 4.1. При известных В0~-Вп вычисление
у(х) для любого х можно провести по схеме Горнера.
Таблица 4.1
X	и	4- 	г		S
Х»-»Р0 Xt-»P1	Ус “> Р А = Bq	. Xl-~X0 = В!->РВ		
Х2->Р2	£/2“>РС	У2 — Уа Х^:—Хо = g2->PC	4г—41 . Х'2~ Xi i=	Bz~^PC	
Xj->P3	1/3-».РД	l/з —l/o =д- « <7з->РД	<7-> — Хз — Xi = га->РД	Гя — Ъ  -Х3 — Хз = sA~B !->РД
Программа 4.27. Вычисление коэффициентов Во, В{ и В2 по
вводимым в регистр X значениям х0, ув, xb yit х2 и у2.
по	С/П	ПА	С/П	П1	с/п	ПВ С/П П2	С/П
ПС	ИПВ	ИПА	—	ИИ1	ИПО	—	-4г	ПВ	ИПС
ИПА	—	ИП2	ИПО		4-	ИПВ — ИП2	ИП1
—	4-	ПС	0	С/П	БП	00	
Для	хв —	1,3, у в =	= 0,934,	XI =	1,4, Vi	= 0,9523,.х2 = 1,5	и у2 =.
'=0,9661 получим цифру 0 (окончание-вычислений). Коэффициенты
полинома заносятся в регистры: Вв — 0,934 РА, Bi — 0,183 -> РВ
и В2 = —0,225-»-PC.
Программа 4.28. Вычисление коэффициентов Во, Bi, В2 и В3.
Ввод: х0 -4- Хз — Р0 4- РЗ, ув 4- Уз РА 4- РД; результат Во ~В3->-. — РА 4- РД.	
ИПВ ИПА — ИП2 4-	ПС —	ИПЗ 4-	ПД	-	ИП1	ИПО	—	4-	ПВ	ИПС	ИПА ИПО	-	4-	ИПВ	—	ИП2	ИП1	— ИПД	ИПА	—	ИПЗ	ИПО	—	4-	ИПВ ИП1	—	4-	ИПС	—	ИПЗ.	ИП2	— 0	С/П
Для Хо =	= 1,3, Xi — 1,4, Ха = 1,5, хз•= 1,6, ув = 0,934,	=*1
'= 0,9523, у2 — 0,9661 н уз = 0,9763. получим, нажав клавишу С/П,
цифру 0 (указывает на конец счета). Коэффициенты полинома за-
носятся в регистры: Во = 0,934 РА, Bi — 0,183-»- РВ, В2 =
= —0,225-»-PC и В3 = 0,15^РД.
Программа 4.29. Вычисление коэффициентов Во, Вь В2, В3 и В4,
Ввод: хв 4- х4 = Р0 4- Р4, у0 = Р9 и tji 4- yt =. РА± РД; .результат
Во -»- Р9, Bi ± Bt -> РА ± РД..	.
ИПА ИП9 -			ИП1	ИПО — •		ПА	ИПВ	ИП9
—	ИП2	ИП0	—	4- ИПА	—	•ИП2	ИП1	-г—
-Г-	ПВ	ИПС	ИП9	— ИПЗ	ИПО	—	—	ИПА
	ИПЗ	ИП1	—	4- . ипв	—	ИПЗ	ИП2	—
	ПС	ипд	ИП9	— ИП4	ИПО	—	ч-	ИПА
	ИП4	ИП1	—	+ ИПВ	—	ИП4	ИП2	—
	ИПС	—	ИП4	ИПЗ —		ПД	0	С/П
Для Хо =		= 2,2,	Xi = 2,3, х2 — 2,4,		Хз =	2,5, х4	= 2,6,-	уо ==:
= 0,4860966, уi = 0,4892759, у2 = 0,4918025, y3 = 0,4937903 и у a ='
= 0,4953388 получим, нажав клавишу С/П, цифру 0, указывающую
на конец вычислений. Результаты: Во = 0,4860966, Bi = 3,1793-Ю-2,
В2 =-3,2635-10~2, В3 — 1,89833-10-2 и В4 = -5,99965 10-».
4.6.	Элементарные функции комплексной
переменной
паи.
В приведенных ниже программах комплексная переменная. обо-
значена как Z = х + jy, где х — Р8 и у — Р9. Результат вычисле-
ния функции f(Z)=« + /u (н-»-РХ = Р5, u->PY = P6). Кон-
трольные примеры приведенного ниже пакета программ вычисления
элементарных функций комплексной переменной даны для числа
2 = 3 + /-2. Формулы для вычисления функций комплексной пе-
ременной взяты из [1—3].
Программа 4.30. Возведение комплексного числа в квадрат;
Z2 = (х2 — у2) + / • 2ху.
ИП8 Fx2 ИП9 Fx2 П5 ИП8 ИП9 2 X
X П6 ИП5 С/П
Имеем f (Z) = 5 + /• 12.	4
Программа 4.31. Обращение комплексного числа: -
1 _ х' _ у
Z х2 + у2 1 х2 + у2’
ИП8	ф	Fx2 ИП9	Fx2	+	П7 4- П5 ИП9
/-/	ИП7	4- _ П6	ИП5	С/П
Имеем f(Z)= 0,23076923 — /-О,'15384615.
Программа 4.32. Обращение квадрата комплексного числа:		
1	х2 — у2	2ху
Z2	(х2 + у2)2	1 (X2 + у2)2 •
ИП8 Fx2 ИП9	Fx2 —	ИП8 Fx2 ИП9 Fx2 +
Fx2 П7 4-	П5 ИП8	/-/ ИП9 2	XX
ИП7 4- П6	ИП5 С/П	
Получаем f(Z) = 2,9585798-10~2.—		/г.7,1005917-10-2,
: Программа 4.33. Обращение разности комплексного числа Z
L?= х + jy с числом (а + /6):
1________________х — а	_ ._____У — Ь_____
Z — (а + lb) ~ (х — а)2 + (у — Ь)2	1 (х — а)2 + (у — 6)2 ’
ИП8	ИПА	—*	t	Fx2	ИП9	ИПВ	-	Fx2	+
П7	-г-	П5	ИПВ	ИП9	-	ИП7	4-	П6	ИП5
С/П
•' Для а = 2= РА, 6 = 1 = РВ находим /(Z, а, Ь) = 0,5 — /-0,5.
Программа 4.34. Вычисление квадратного корня из комплексного
числа:
'	^/-.^yg+Z.
ИП8	Fx2	ИП9	Fx2	+	F/	П7	ИП8	+	2
-г-	F<	П5	ИП7	ИП8	—	2	-=-	F V	П6
ИП5 С/П
’' Имеем /(Z) = ±1,817354± /-0,55025048..
' Программа 4.35. Вычисление ez:
ez = e* cos у + jex sin y.
Переключатель P — Г в положении P.
„ ИП8 Fex П7 ИП9 Feos X П5 ИП7 ИП9 Fsin
X П6 ИП5 С/П
Имеем f (Z) = —8,3585327 + / 18,263726.
Программа 4.36. Вычисление In Z:
In Z =	In (x2 + y2) + j ( arctg 4- 2/гл~),
£	\ x	J
где k — 0, ±1, ±2, ... Переключатель P — Г в положении P.
ИП8	Fx2	ИП9	Fx2	+	Fin	2	т П5 ИП9
ИП8	-?	F arctg	П6	IIП5	С/П	•
Находим f(Z) = 1,2824746+ /• 0,58800261.
Программа' 4.37. Вычисление синуса комплексной переменной:
sin Z = sin х ch у	+ /’ cos x sh y.
ИП9	Fe*	t	Fl/x	+2-7-	ИП8	F	sin	X
П5	ИП9	Fex	f	Fl/x	— 2	-т-	ИП8	Feos
•[ X	П6	ИП5	С/П
Получаем /(Z) = 0,53092084 —/-3,5905644.
Программа 4.38. Вычисление косинуса комплексной переменной:
cos Z = cos x ch у — j sin x sh y.
ИП9	Fe*	f	Fl/x	+	2	-т-	ИП8	F cos	X
П5-	ИП9	Fex	f	Fl/x	—	2	->	ИП8 .	/—/
F sin	X 	П6	ИП5	С/П
Находим f(Z) = —3,7245453 —/-0,51182233.
Программа 4.39, Вычисление тангенса комплексной переменной:
	L_	sin 2x	, .	sh 2y		
		cos 2x + ch 2y	‘ ' cos 2x + ch 2y ’
ИП9	2	X Fe* ф	Fl/x + 2	4- ИП8
2	X	F cos + П6	ИП8 2 X F sin ИП6
	П5	ИП9 2 X	Fex ф Fl/x -	2
•—	ИП6	4- П6 ИП5	С/П -
Имеем f (Z) == -9,8843723 • 10~3 + /  0,96538587.
Программа 4.40. Вычисление гиперболического синуса комплекс-
ной переменной:
sh Z = sh х cos у + j ch x sin y.
ИП8	Fex	f	Fl/x	—	2	4-	ИП9	F cos	X
П5	ИП8	Fex	f	Fl/x	+	2	+	ИП9	F sin
X-	П6	ИП5	С/П
Находим f(Z) =—4,168907 + /-9,1544984.
Программа 4.41. Вычисление гиперболического косинуса ком-,
плексной переменной:
•	' ch Z = ch х cos у + j sh x sin y.
ИП8	Fe*	f	Fl/x	+	2	4-	ИП9	Feos	X
П5	ИП8	Fe*	f	Fl/x	~	2	4-	ИП9	F sin
X	П6-	ИП5	С/П
Имеем f(Z) = —4,1896257 + /.-9,1092272.
Программа 4.42. Вычисление гиперболического тангенса ком-,
плексной переменной:
th 7 = sll2% . • sin 2у
ch 2х + cos 2 г/ ‘ ch 2х + cos 2у
ИП8	2	X	Fex	f	Fl/x	+2	4-	ИП9
2	X	Feos	+	П6	ИП8	2	X	Fe*	ф
Fl/x	-	2	4-	ИП6	4-	П5	ИП9	2	X
F sin	ИП6	4-	П6	ИП5	С/П
Получаем f (Z) = 1,0032386 — /-3,7640263-10~3.
Обратные тригонометрические функции комплексного перемен-
ного вычисляются по следующим формулам:
arcsin Z — arcsin В + j in [Л + -у/А2 — 1],
arccos Z = arccos В — j In [Д + № — 1 ],
arctgZ- — arctg	) + 4 In ( х2 + {«/ - I)2 )’
A=-|'7(x + I)2 4- у2 +-g-V(* —l)2 + «/2
и	.____________.	-_______
B = У V(x+ l)2 + {/2 —2 V(x-l)24V.
Программа 4.43.. Вычисление арксинуса комплексной перемен-
ной.
ИП8	1	+	Fx2	ИП9	Fx2	П7	+	F V	2
U-	П6	ИП8	J	—	Fx2	ИП7	+	F V"	2
u-	П5	+	ПЛ	ИП6	ИП5	— .	ПВ	F arcsin	П5
ИПА	Fx2	1	—	F V"	ИПА	+	F In	П6	ИП5
С/П
Для Z — х + jy = 3 + j-2 получаем arcsin Z — 0,9646583 -f-
;+ /-1,9686379.
Программа 4.44. Вычисление арккосинуса комплексной перемен-
ной.
ИП8	1	+	Fx2	ЙП9	Fx2	П7	+	F V"	2
~	П6	ИП8	1	-	Fx2	ИП7	+	F V"	2
4-	П5	+	ПА	ИП6	ИП5	—	ПВ	F arccos	П5
ИПА	Fx2	1	-	F V"	ИПА • +	Fin	|	/-/
П6	ИП5	С/П
 Для Z = 3 + /-2 находим arccos Z — 0,60613793 — /•1,9686379.
Программа 4.45. Вычисление арктангенса комплексного пере-
. менного.
ИП8	2	X	1	ИП8	Fx2	П7	—	ИП9	Fx2
—	4-	F arctg	2	4- 	П5	ИП7	ИП9	1	+
Fx2	+	ИП7	ИП9	1	-	Fx2	+	4-	Fin
4	4-	П6	ИП5	С/П
С учетом допустимой области определения Z для Z = 0,3 +
4- / 0,2 получим arctg Z — 0,30187467 + /-0,18499461.
Для вычисления обратных гиперболических функций комплекс-
ной переменной воспользуемся связью с обратными тригонометри-
ческими функциями; arsh Z = —/arcsin(jZ), arch Z = ±j arccos Z и
arth Z = —/ arctg (jZ).
Программа 4.46. Вычисление обратного гиперболического синуса
Комплексного переменного.
ИП9	/-/	I	+	Fx2	ИП8	Fx2	П7	+	F V
2		П6	ИП9	/-/	I	—	Fx2	ИП7	+
fV'	2		П5	+	ПА	ИП6	ИП5	—	ПВ
F arcsin		/-/	П6	ИПА	Fx2	1	—	F V“	ИПА
	F In	П5	С/П						
Для Z — 3 + /-2 получим arsh Z = 1,983387 4* /-0,5706528.
Программа 4.47. Вычисление обратного гиперболического коси-
нуса комплексной переменной.	у									
ИП8	1 .	+	Fx2	ИП9	Fx2	rt7	+	F V’	2
	П6	ИП8	1	—	Fx2	ИП7	+	F V'	2
-J-	' П5	+	ПА	ИП6	ИП5	—	ПВ	F arccos	П6
ИПА	Fx2	1	—	F V"	ИПА	+	F In		/-/
П5	ИП6	XY	С/П						
Для Z = 3-f-/-2 имеем archZ = Т1,9686379±/-0,60613793.
Программа 4.48. Вычисление обратного гиперболического тан-
генса комплексной переменной.
ИП9	/-/	2	X	1	ИП9	Fx2	П7	—	ИП8
Fx2	—	-4-	F arctg	2	/-/	-4-	П6	ИП7	ИП8
1	+	Fx2	+	ИП7	ИП8	1	—	Fx2	+
-4-	F In'	4	-J-	П5	ИП6	XY	С/П		
Для Z = 0,3 + /-0,2 находим arth Z — 0,29574995 + /-0,2154745.
Программа 4.49. Вычисление отношения многочленов f (Z) =
— A(Z)/B(Z) комплексной переменной при степени A (Z) п С 3,
и B(Z)/n<4 [7]. Ввод: Ьо -г-	= Р0;-е- Р4, а0'=Р5, .... а3 =
= Р8, 0 = Р9 x=.PY и у = РХ. Результат: п->РА=РХ, и->
-> РВ = PY.
ПВ	XY	ПА	ИП7	ИП8	ПП	47	ИП6	ПП	54
ИП5-	+	ПС	ИП9	пд-	ИПЗ	ИП4	ПП	47	ИП2
ПП	54	ИП1	ПП	54	ИП0	+	t	Fx2	ИП9
Fx2	+	-4-	ПА	ИП9	FBx	-4-	ПВ	ИПС	П9
'ИПД	ПП	55	ИП9	С/П	БП	00	t	ИПВ	X
П9	F,	ИПА	X	+		ИПВ	X	ИПА	ИП9
X	+	ИП9	XY	П9	F,	ИПВ	X	XY	ИПА
X	XY	—	B/0						
Для f(2 + /- I) = (Z2 + 2Z+ 1)/(3Z3 + 2Z2 + Z + 0,5) полу-
чим « = 0,1863999 и « = — 0,12612384 прн tc » 70 с.
Гл а в а 5
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ
ЧИСЛЕННЫХ МЕТОДОВ
5.1. Решение систем линейных уравнений
Решение Систем линейных уравнений выполняется по програм*
мам, описанным в [28].
Программа 5.1. Решение системы из п 4 уравнений
[«И «12 ... «щ	г *1 т	г 61 1
............... . ... =1 ...	(5.1)
аМ аП2 • • • аПП J L Хп J	I 6n J
ИЛИ (61 = сц, 1+1)
= «/./+!’ <5-2>
1=1
где 4=1,2		, ...» п методом оптимального исключения переменных.						
В ВО!	i: и = Р0, коэффициенты			ац = РХ,	' «1.1+1	= РХ	(построчно, не	
обращая внимания			на вывод	промежуточных		результатов и		завер-
шая	ввод каждого коэффициента нажатием клавиши						С/П).	Вывод:
Xi->	РХ (Xi-	->РД, >	'2 PC, Х3	-> РВ и х4 -» РА)				
П4	1	4	П2 ИПО	П1	С/П	ИП4	-5-	КП2
FL1	06	.1	4 ПЗ	ИПО	П1	FL1	23	кипз
С/П	БП	19	Сх КП2	FL1	24	КП2	ИПО	ИП2
	П1	П2	ИПЗ -	F%t4=0	42	С/П	ПП	84
БП	28	кипо	ИПО ПЗ	С/П	КИП2	—	П4	С/П
КИП2 -		ИП4	4- КП1	FL3	49	ИП1	ИПО	+
ПЗ	1	4	П1 П2	КИП1	/-/	пп	84	ИПЗ
	ПЗ	ИП1	— Fx=	0 65	ИПО	П1	КИПЗ	КП2
FL1	78	БП	12 ИПО	XY	f •	кипз	X	КИП1
+	КП2	F,	FLO 86	F,	ПО	В/0		
	Для системы из		трех уравнений (п =		= 3)			
		Г4	0,24 -	-0,08-1 Г	Xi "I	Г 81		
		I 0,09	3	-0,15 •	х2 1 =	= | 9 I		(5.3)
		L 0,04	—0,08	4 J L	Хз J	1.20 J		
Получим Xi = 1,9091983, х2 = 3,1949644 и х3 = 5,0448073 при tc «
« 2 мин. Более простые программы для решения систем из 2 и 3
уравнений описаны в [6—8].
Программа 5.2. Решение систем из п < 11 уравнений в полуав-
тематическом режиме по методу Жордана с циклической переста-
новкой строк и применением вычислительного бланка (см. пример,
ниже).
ф	Сх	XY	ИП1	-т-	ПО	XY	1	ПС	XY
С/П	ИПД	ИПС	1	+	ПС	—	Fx>0	.26	XY
КИПС	ИПО	X	—	БП	10	XY	ИПО	БП	02
Пример. Решить систему
-4—2 -3	Ир1!	Г 13‘ 0	5	—2	3	х2	16 2-3	4	—2	* х3	—	0	*	 - г о з	1 L Xi	L —4. Вычислительный бланк для решения системы уравнений (5.4)						
 О	1=1	/=2	/=з	7=4	/=5	м
в	4 0 2 1	-2 5 -3 0	3 -2 ' 4 -3	1 3 -2 1	13 16 0 —4	19 22 . 1 -5
1	1	5 -2 0,5 -0,5	-2 2,5 ' -3,75 0,75	3 -2,5 0,75 0,25	16 -6,5 -7,25 3,25	22 -8,5 -9,75 4,75
2		1 1	1.7 -.3,55’ 0,55 -0,4	-1,3 0,45 0,56 0,6	-о,1 -8,85 4,85 3,2	0,3 -11,95 .6,95 4,4
3	-		1 1 1	-2,2647059 0,97058823 0,29411765 -0,76470588	-9,0588235 4,8823529 3,1764706 -0,58823529	-11,323529 6,8529412 4,4705882 0,17647058
4				I 1 1 1	Xi = 1,0000001 Хг—2 *3=2,9999999 *,=3,9999999	2,0000003 3 3,9999998 4,9999997
Графа для р =Д бланка заполняется коэффициентами уравне-
ния, вводится п — РД. Далее последовательно заполняются графы
для р = 1, 2 и т. д. Для этого вводится первый столбец в регистры
1, 2, ..., п (сверху вниз).. Затем вводится первый элемент следую-
щего столбца и нажимаются клавиши В/0 и С/П — высвечивается О,
Далее вводятся остальные элементы в регистр X и нажимается кла-
виша С/П (после ввода последнего элемента клавиша С/П нажи-
мается дважды). Полученные результаты вписываются в графу под
вводимым .столбцом, а в графе слева снизу дописывается 1. После
.заполнения бланка для р — п .получаем Xi, х2, ,.,, хи и контроль-
ные суммы.
У некоторых -микрокалькуляторов (НР-15С, TI-58C, . TI-59
и др.) решейие систем из п (6 -Ь 10) уравнений реализовано мик-
ропрограммно или с помощью встроенных программ пользователя.
- 5.2. Интерполяция и экстраполяция функций
одной переменной
Интерполяция заключается в на-хбЛсденни значений функции
у(х), заданной п узлами, в промежутках между ними. При этом
функция заменяется тем или иным полиномом Р(х), значения кото-
рого в узлах совпадают со значениями у(х). Ниже дан пакет про-
грамм, реализующих интерполяцию с помощью полинома Лагранжа
{3]. Коэффициенты интерполяционного полинома при произвольном
расположении узлов вычисляются методом Эйткена (см. § 4.5).
С помощью приведенных ниже программ можно производить и
экстраполяцию, т. е. вычисление у(х) при х, выходящем за пределы
интервала интерполяции.
Программа 5.3. Линейная интерполяция при п — 2 по формуле
У (х) = Ус + (х — хб) (z/i — ус) /h.	(5.5)
Ввод: h — Р9, Хс, Ус, yi и (после индикации цифры 0) х в ре-
гистр X.
ПО’	С/П ПА	С/П	ИПА	-	ИП9	4- ПВ	0
С/П	ИПО -	ИПВ	X	ИПА	+	БП 10
Для h — 0,01, х0 = 2,47, уо = 0,4932443 и «Л = 0,4934309 полу-
чим у(2,475) = 0,4933376 (интерполяция). Набрав новое значение
к = 2,485 и нажав клавишу С/П, получим «/(2,485) = 0,4935242
(экстраполяция).
Программа 5.4. Квадратичная интерполяция при п = 3 по фор*
'муле
у(х) == Во 4" Bi(x — Хо)-Ь В2(х %о) (л" *1)	15-6)
при произвольном расположении узлов. Ввод в регистр X: х0, Ус,
х1, У1, х2, у2 и х (после пуска программы и индикации цифры 0).
Коэффициенты Во, Bj и В2 после вычисления заносятея в регистры
А, В -и С.
ПО	С/П	ПА	С/П	П.1	С/П	ПВ	С/П	П2	С/П
ПС	ИПВ	ИПА	-	ИП1	ИПО	—	4- '	ПВ-	ИПС
ИПА	—	ИП2	ИПО	—	*4-	ИПВ	—	ИП2	ИП1
—	4-	ПС	О	С/П	П8	'	ИП1	-	ИПС	X
ИПВ	+	: •	ИП8 	ИПО	-	X	ИПА	+	БП	34
Для х0 = 1,3, у а = 0,934, Xj = 1,4, у\ — 0,9523, х2 = 1,5 и у2 =
= 0,966 Г получим у(1,43) =0,9569125. При смене х набираем только
его новое значение и нажимаем клавишу С/П.
Программа 5.5. Квадратичная интерполяция при равноотстоящих
узлах по формуле
y(x0 + ph) р(р2	«/_, + (1	р2) уо + Р	(р+1) 2	У+Р	(5.7)
где р = (х —хо)/Л. Ввод: h = Р9, х0, у-i, у о,	У+1 и 1	[после	иидика-
ции цифры 0) х в регистр X. П8 С/П П1 С/П П2 С/П ПЗ	0	С/П	П7
ИП8 — ИП9 -г- П6 1	—	ИП6	X	2
• 4- ИШ X 1	ИП6 Fx2 —	ИП2	X	+
ИП6 1	+ ИП6 X 2	4-	ИПЗ	X	+
БП 08 Для h — —0,1, Хо = 1,4, уо — 0,9661, «/1 =	= 0,9523	1 и у2	= 0,934,
нажав клавиши В/0 и С/П, получим цифру 0. Введя х = 1,43 и на-
жав клавишу С/П, получим «/(1,43) = 0,9569125— интерполяция на-
зад (h < 0).
Программа 5.6. Интерполяция при четырех произвольно распо-
ложенных узлах при п — 4 по формуле
У W = [ [Вз (х — х2) + B?J (х — xi) + ZJi] (х — хо) + Во. (5.8)
Ввод: х0 4- xs = Р0 4- РЗ, «/о 4- Уз = РА 4- РД и х = РХ (после пу-
ска программы и индикации цифры 0). Коэффициенты В04-В3 за-
носятся в регистры			А-РД.					
ИПВ ИПА		—	ИП1 ИПО	—	•4"	ПВ	ИПС	ИПА
	ИП2	ИПО	—	"Г"	ИПВ	—	ИП2	ИП1	—
-г-	ПС	ИПД	ИПА —	ипз	ИПО	—	4-	ИПВ
—	ИПЗ	ИП1	—	ИПС		ИПЗ	ИП2	—
	ПД	0	С/П П9	ИП2	—	ИПД	X	ИПС
+	ИП9	ИП1	X	ИПВ	+	ИП9	ИПО	
X	ИПА	+	БП 43					
	Для Хо	= 1,3,	Xi = 1,4, х2	= 1,5,	Хз =	1,6, Уо	= 0,934,	=
= 0,9523, {/2 = 0,9661 и «/3 = 0,9763 получим р(1,43) = 0,95687155
при точном значении -0,9569.
Программа 5.7. Интерполяция при четырех равноотстоящих» уз-
лах по формуле	।
и(х , рйч~,. Р(Р~1).(р-2)	 (Р2~1)(Р~ 2)	_
6	А/_1Т	2 »о
р(р+1)(р^-2)	р(р2-1)	.
-	2	^+1 +	6 7 ^+2- ( 1
Ввод: h = Р9, y-i, Уо,		У+1, J/+2, *о и х в регистр X.						
П1	С/П . П2 .	С/П	ПЗ	С/П	П4	с/п	П8	С/П
П7	ИП8 —	ИП9	4-	П6	2	—	2	4-
П5	3	4-	ИП6	1	—	X	ИП6	/-/	X
ИП1	X ИП6	Fx2	1	—	ПА	ИП5	X	ИП2
х	+ ИП6	.1	+	ИП6	X	ИП5	X	ИПЗ
’ X БП’ 	— ИПА 09	ИП6	X	6		ИП4	X	+
Для приведенного выше примера при h — 0,1, у-i = 0,934, у0 =3
== 0,9523, у+1 = 0,9661, у+2 = 0,9763, х0 = 1,4 и х = 1,43 получим
«/(1,43) = 0,9568716.'
Программа 5.8, Интерполяция при пяти произвольно располо-
женных узлах по формуле
у(х) = [[[В<(х — Хз) + Bs](x — х%) + В2](х — -^i) 4* BJ(x — Хо)+ Во,
Ввод: хо 4- х,. = Р0 Р4, уй = Р9, «д 4- f/4 = РА 4- РД и х = РХ
(после пуска и индикации цифры 0). Коэффициенты Во, Bi4-B2 за-
носятся в регистры 9, А 4- Д.
ИПА	ИП9 ИП2	ИПО	ИП1	ИПО	ИПА			ПА ИП2	ИПВ иш	ИП9
Ч-	ПВ	ИПС	ИП9	—	ИПЗ	ИПО	—	4-	ИПА
<— -	ИПЗ	ИП1	—	—	ИПВ	—	ИПЗ	ИП2	—
	ПС	ИПД	ИП9	—	ИП4	ИПО	—	4-	ИПА
i—	ИП4	ИП1	—	4-	ИПВ	—	ИП4	ИП2	—
ч-	ИПС	—	ИП4	ИПЗ	—	Ч-*	ПД	0	с/п
П8	ИПЗ	—	ИПД	X	ИПС	+	ИП8	ИП2	—
X ИПО В	ИПВ + - X табл. 5.1 даны У		ИП8 ИП1 — ИП9 + БП значения функции (X) = Фо (X) = '\/2ы			X 69 X 0	ИПА 2 а/	+	ИП8
Таблица 5.1
X	У	в	B-+PN
х»=2,2	у,=0,4869963	В„=4,860986-10~*	Р9
Х1=2,3	Vl=0,4892759	в1 =3,1793-10 “ 2	РА
X,—2,4	£/-2—0,4918025	в2= -3,2635-10“2	РВ
Хз=2,5	» £/3= 0,4937903	В,,= 1,89833-КГ"2	PC
Х,=2.6	yt— 9,4953388	В.,= -5.99965-10“2	 РД
в узлах интерполяции и вычисленные .по данной программе значения
Во, В\ -t-Вь. При х — 2,45 получим «/(2,45) = 0,49285719 при точном
значении 0,4928572.
Программа 5.9. Интерполяция при пяти равноотстоящих узлах
по формуле
Il /v -1 nh\ —		(р2 — 1) р (р	-2)	(р— 1)р(р2 —4)			
»	• P‘L)		24	У-2		6	- у	-1Т
	.(р2	— 1) (р2 — 4)	(р+1)р(р2		-4)	</+1 +	
	i	4	»0	6			
			4--^	1) р(р + 2) 24		У+2-	(5.10)
Ввод: h	= Р9,	У-2, У-t, Уо, У-\л, У+2, Хо и		х в регистр		X.	
П1	С/П	П2 С/П	ПЗ С/П	П4	С/П	П5	С/П
П8	С/П	П7 ИП8	— ИП9	-4-	П6	Fx2	ПД
1	—	4	~	ПА  ИП6	2	—	X	ИП6
X	6	-т-	ИП1	х ипд	4	—	ПС	6
ч-	пв	ИП6 х	ИП6 1	—	X	ИП2	X
—	ИПА	ИПС х	ИПЗ X	+	ИП6	1	+
ИП6	X	ИПВ х	ИП4 X		ИП6	2	+
ИП6	X	ИПА X	6	4-	ИП5	X	+	БП
11							
Для приведенного выше примера, взяв хо = 2,4 и уо=0,4918025,
для х == 2,45.получим у (2,45) = 0,49285719.
Программа 5.10. Интерполяция при шести равноотстоящих узлах
по формуле
g_2+
р (р — 1) (р2 —- 4) (р — 3)	(р2 - 1) (р2 - 4) (р - 3)	,
т	24	 ^-1	12
, р(р+1)(р2-4)(р-3)	р(р2“1)(р + 2)(р—3)	,
1- .	12	У+х	24---------+
 Р(Р2— 1)(р2—4)
+	120	' ^+3"
Ввод: xQ = Р8, h = Р9, у..2 = Р2, «/_t == Pl, у0 = Р0, j/+1 = РА,
У+2 — РВ, у 1-3 — Р(			2 и х = РХ.						
П7	ИП8	—	ИП9	-i-	П7	Fx2	1		ПЗ
2	4	ч*	ПД	ИП7	3	—	X	ИП7	/-/
х 	П4	ИП7	2		X	5	-4-	ИП2	X
ИП7	Fx2	4	—	П5	ИП7	3		X	1
s
ИП7
ИП4
X
00
	П6	ИП7	"X	ИП7	1	—	X	2
ИП1	X	+	ИП6	ИПЗ	X	ИПО	х	
1	+	ИП7	X	ИП6	х	ИПА	X	+
ИП7	2	+	X	ипв	X	+	ИП7	ипд
ИП5	X	5	-Г	ИПС	X		С/П	БП
' Для контроля этой программы воспользуемся табулированными
данными функции Р(х). нормального распределения вероятностей [3]
ррИ х_2 = 0,5, х-i = 0,6, х0 = 0,7, х+1 = 0,8, х+2 = 0,9, х+3 — 1,0
(т е- Хо=О,-7 и /г=0,1). Для этих- значений.х имеем «/_2==0,6914625,
tyj, '= 0,7257469, Уо = 0,7580363, y+t = 0,7884446', у+2 = 0,8159399
и у+3 = 0,8413447. Введя эти данные п положив х — 0,86 = РХ,
найдем р(0,86) — 0,80510553 при известном точном значении
0,80510547 и 1 мин.
Программы, обеспечивающие интерполяцию функции </(х) при
произвольном расположении узлов, могут использоваться и для об-
ратной интерполяции, т. е. нахождения значений х при заданном у.
Для этого значения х, .в узлах интерполяции заносятся в регистры,
отведенные под запись у,, а значения y-i — в регистры, отведенные
под запись X, в узлах.
Приведенные выше программы обеспечивают минимальное время
интерполяции благодаря вычислению коэффициентов полиномов Ла-
гранжа по готовым формулам с заранее вычисленными членами,
содержащими факториалы. Однако при этом для каждого п прихо-
дится использовать свою программу.
В [22] описаны универсальные программы для. интерполяции по-
линомами Лагранжа и Ньютоца {п 6 при произвольном и п 10
при равномерном расположении узлов), а также кубическими сплай-
нами. Однако время интерполяции по ним велико (в 3—4 раза
больше, чем по описанным выше программам). Поэтому подобные
программы удобнее использовать для представления (аппроксима-
ции) функций степенными полиномами (см. § 5.13).
5.3.	Интерполяция и экстраполяция функций
двух переменных
Часто встречаются функции f(x, у) двух переменных у и х. -Огра-
Вичившись доступными для микрокалькуляторов Электроника БЗ-34
методами интерполяции и экстраполяции функций / (х, у) с постоян-
ным шагом h = Лх и k — &у [3], введем наряду с параметром
р = (х — xo)/h
Параметр,
- fi==.(j(—po)/fe.
Точку (хо, у о) условно обозначим как 0, а значение функции для
нее foo — f(XD,yt>). Тогда fi0 = f(%i,у»), foi = f(xD,yt), fa = f(xl,yl)t
fo-i — f (x0,y-i) и т. д.
U.\
An
Tpo
0 ’
Ao

B)
Рис. 5.1. Расположение узлов при интерполяции функций двух пере->
менных при трех (а), четырех (б) й шести (в) точках
Программа 5.11. Интерполяция и экстраполяция функции f(x,y]
двух переменных х и у по формуле для трех точек (рис. 5.1,а):
f (х, у) = (1 — р — у) foo + pf ю + yfoi
с погрешностью О(Л2), пропорциональной h2. Ввод: h = Р8, k = Р9
и далее в регистр X: х0, Уо, foo, foi, fio, х и у (при повторных пусках
программы для новых х и у вводятся только последние).									
ПО	С/П	П1	С/П	П2	С/П	ПЗ	с/п	П4	С/П
П5	С/П	П6	ИП1	—	ИП9	-V-	П6	ИП5	ИПО
—	ИП8		П5	1	XY	—	ИП6	—	ИП2
X	ИП5	ИП4	X	+	ИП6	ИПЗ	X	+	БП
09
Для контроля программы рассмотрим значения (см. табл. 5.2)’
функции последействия [5]
f(x, y)— е-г/2г2-г-хе
Таблица 5.2
X У	0J	0,7	1,о
0,00	2,500	1,429	1,000
0,05	2,487	1,419	0,955
0,10	2,456	1.400	0,981
Для выбранных узлов имеем h = 0,3, k — 0,1, хо = 0,4, уо = 0,
foo = 2,5, foi = 2,456 и fю = 1,429. Введя эти данные и придавая
х и у различные, отмеченные ниже значения, получим f (0,7; 0,05) =
= 1,407 при точном значении 1,4.19, f (0,7; 0,1) = 1,385 при точном
значении 1,4; f (0,4; 0,05) — 2,478 при точном значении 2,487 В 11 А*
в узлах интерполяции расчетные значения f(x,y) совпадают с ис-
ходными. Время вычисления одного значения f(x,y) около 12 с.
Программа 5.12. Интерполяция и экстраполяция функции f(x,y}
двух переменных х и у по формуле для четырех точек (рис. 5.1, б)а
- f(x,y) — (1 — р) (1 ~ ?)foo + р(1 — q)fio + <7(1 — p)fol 4- pqfii
с погрешностью О (/г2), пропорциональной h2. Ввод: h = Pl, k = Р2
и далее, после нажатия клавиши С/П, в регистр X значений х0, уо,
foo, foi> flO> f*i> x и У’	,
4'	П4	6	ПО	С/П	КП4	FLO	04	С/П	ПЗ
С/П	П4	ИП6	—	ИП2		П4	ИПЗ	ИП5	—
ИП1		ПЗ	1	ИПЗ	—	ПВ	1	ИП4	—.
ПС	X	ИП7	X	ИПВ	ИП4	X	ИП8	X	+
ИПС	ипз	X	ИП9	X	+	ИПЗ	ИП4	X	ИПА
X	+	БП	08						
Для проверки этой программы воспользуемся данными табл. 5.2,
Введя ft = 0,3 = Pl и fe = 0,l = P2, нажимаем клавишу С/П —•
высвечивается цифра 6, указывающая на ввод шести параметрона
Хо — 0,4, уо = 0, foo = 2,5, f01 = 2,456, fio = 1,429 и fn — 1,4. При
вводе их в регистр X нажимается клавиша С/П. Далее, после ввода
в регистр X текущих значений х и у, получим значение f{x,y).
Например, будем иметь / (0,4; 0,05) = 2,478 при точном значении
2,487, f(0,7; 0,05)= 1,4145 при точном значении 1,419, f(0,5; 0,08)=»
= 2,1118001 и т. д.
Программа 5.13. Интерполяция н экстраполяция функции f(x,y)
двух переменных х и у по формуле для шести точек (рис. 5.1, в) а
f (*> У) = 9 ^2—~ ~1 + ~Р2-------~	10	+ РУ ~ Рг ~~ 92) foo+
р(р—2?+l)f	<7(<7-2р+1) t	с
4--------2------',0 --------2------'°* + Pq'11
с погрешностью O(/t3), пропорциональной h3. Ввод h = Pl, k = Р2
и далее, после нажатня клавиши С/П и высвечивания цифры 8, в
регистр X: хо, у о, foo, fio,				fo -1, f-	-10, fob	Аь х	и У-		
4	П4	8	ПО	С/П	КП4	FLO	04	С/П	ПЗ
С/П	П4	ИП6	—	ИП2		П4	ИПЗ	ИП5	—
ИП1		ПЗ	ИП4	1	—	ИП4	X	ИП9	X
•ИПЗ	1	—	ИПЗ	X	ИПА	х	+	ИПЗ	ИП4
X	ПД	1	+	ипз	Fx2	—	ИП4	Fx2	—
2	X	ИП7	X	+	ИПЗ	ИП4	2	X	—
1	+	ИПЗ	X	ИП8	X	+	ИП4	ИПЗ	2
X	—	1	4-	ИП4	X	ИПВ	X		ИПД
ИПС	X	2	X	+	2	-5-	БП	08	
Для контроля этой- программы вновь воспользуемся, данными
табл. 5.2; взяв в качестве-центральной точки точку хо=0;7, </о—0,05,
Тогда исходными будут следующие данные: Л. = 0,3, k — 0,05
хо=.О,7, у0 = 0,05, fa— 1,419,. fa = 0,995, f0-i = 1,429, f_I0’=’-
= 2,487, fa = 1,4 и fu = 0,981. Введя указанные далее значения х
и у, получим f (1,0) = 1 при точном значении 1, f (0,4; 0) = 2,502 при
точном; значении 2,5, f(0;5; 0,03) = 2,0658579 и т. д. Время счета
около 25 с.
5.4.	Вычисление корней нелинейных уравнений
Нелинейное, в частности трансцендентное, уравнение
F(x)=0	(5.12)'
имеет один или несколько корней х — gz, обращающих F (х) в нуль.
Их нахождение сводится к оценке интервала изоляции корня [a, fc]
(т. е. интервала, в котором находится один корень) и его последую-
щему сужению до тех пор, пока приближенное значение корня xi
в этом интервале не станет отличаться от точного на заданную
малую величину к Ниже дан пакет программ вычисления корней
функции F(x) различными методами [4—8]. Вычисление F (х) оформ-
ляется фрагментом программы, вписываемым в текст основной про-
граммы на место многоточия.
Программа 5.14. Определение корня (5.12), приведенного к виду
х = f (х), методом простых итераций, реализованным выражениями-!
хп+1 = f (хп)	пока (х„+1 — х„) 2 > е2.
Ввод: данные f (х), е2 = PC, начальное приближение хо = РХ.
ПД ................................................  ИПД
XY ПД — Fx2 ИПС — Fx < 0 01 ИПД С/П
Отметим, что метод простых итераций схедится, если в интер-
вале [a, fe], f'(x) < 1.
Пример. Найдем корень уравнения
F(x) = х — sin х — 0,25 = 0.	(5-13),
Приведем его- к виду
х = f (х) = sin х + 0,25.	(5.14J,
Поскольку f'(x)= cosx < 1, то метод простых итераций применим
для решения- (5.14). При k = 0,25 = Р9 фрагмент программы для
вычисления /(х) имеет вид: ЙПД F sin ИП9 + , Для Хо = 1,2 и
в2 = 1  10-6 получим х = 1,1718537 при tn 22 с,
Программа 5.15. Реализация метода простых итераций с оста-
новкой по критерию машинного нуля, т. е. при Xn+i = %п с точностью
до последнего знака. Ввод: данные f (х), х0 = РХ.
ПД .........
....... ИПД XY ПД - Fx = 0 01 ИПД С/П
Для приведенного выше примера получим х — 1,1712298 при
tc « 60 с.
Высокую скорость сходимости-итерационного.процесса-имеет ме-
тод Ньютона (касательных)., реализуемый итерационным уравнением
вида
х,i-i-i == хп F(-x„)/F'(хп).	(5.15),
Сходимость обеспечивается при выборе начального приближения хо,
удовлетворяющего условию
F(x0)-F"(x<1)>0.	•	(5.16)'
В качестве Хо выбирается тот конец интервала, [а, 5], иа котором
знаки Г(х) и F"(x) совпадают.
Программа 5.16. Реализация метода Ньютона е остановкой вы-
числений по критерию машинного нуля. Ввод: данные Г[хг,)/Р'(х)
прн хп = РД, Хо = РХ.
ПД ... . .............................................
... ИПД XY — ПД FBx Fx = 0 01 ИПД С/П
Программа 5.17. Реализация метода. Ньютона с остановкой вы-
числений по критерию (хл-н — хп)2 < б2. Ввод: данные F(x„)/F( (хп\
прн Хп = РД, е2 — PC, Хо = РХ.
ПД ...'....................................ИПД XY
— ПД FBx Fx2 ИПС — Fx<0 01 ИПД С/П
Для контроля двух последних программ вычислим корень урав-
нения (5.13). В этом случае
F (х) __ х — sin х — 0,25
F' (х)	1 — cos х
и фрагмент программы, вычисляющий F(x)/F'(x), имеет вид
(0,25=Р9):
ИПД ф Fsin — ИП9 — 1 ИПД Feos —•
Поскольку F"(x) = sin х > 0 и Г(х)>0 при х — Ь, то надо
взять хо-=6.=; 1,3. По программе 5.16: получим х= 1,1712297 при
t « 30 с.
Если нахождение производной F' (х) затруднено или нежела-
тельно, можно использовать модифицированный метод Ньютона, реа-
лизуемый выражением
Хп+1 — Хп — F(Xh)IK,
где К —константа, близкая к среднему значению F'(x) в интервале
[а, Ь].
Программа 5.18. Реализация модифицированного метода Ньюто-
на с остановкой вычислений по критерию машинного нуля. Ввод:
данные F(x„) при хп = РД, К = РВ, хо = РХ.
ПД.............................................. ИПВ
ИПД XY - ПД FBx Fx = 0 01 ИПД С/П
Для приведенного- выше примера при К — 0,64 получим х ==
= 1,1712297 при времени счета «35 с. Фрагмент программы вы-
числения F(x„) имеет вид: ИПД f F sin — ИП9 —.
Вычисление корней (5.12) возможно также методом хорд. При
этом методе каждое новое значение х находится как точка пересе-
чения хорды, проведенной через точки F(a) и F(b) функции F(x),
с осью абсцисс, причём одна из этих точек фиксируется — та, для
которой знак F(x) совпадает со знаком F"(x). Условие сходимости
этого метода аналогично (5.16). Если неподвижен конец хорды о
х — а, то
F (хге) ,	\
'	X„+1 - х„ - F{Xn}_F(a} - а),
а если неподвижен конец хорды с х = Ь, то
F (хп)	,
Xn+i-x„ f(6)_f(x„)
Полученное значение xn+J присваивается значению b в первом слу-
чае и а во втором, что обеспечивает сужение интервала [и, Ь]. Вы-
числения прекращаются при (хл-ц— х„)2	е2.
Программа 5.19. Реализация метода хорд прн неподвижном кон-
це а. Ввод: данные F(xn), а = РА, е2 = РД, b = РХ.	,
ПВ	ИПА	ПП	28	ПС	ИПВ	ПП	28	ф	ИПС
-	-е-	ИПВ	ИПА	-	X	ИПВ	XY	—	ПВ . .
FBx	Fx2	ИПД	-	Fx<0	05	ИПВ	С/П	...	В/0 ’
Программа 5.20. Реализация метода хорд при неподвижном кон-
це Ь. Ввод: данные F(x„), b = РВ, е2 = РД и а = РХ.
ПА	ИПВ	ПП	28	ПС	ИПА	ПП	28	f	ИПС
-	-ь	ИПВ	ИПА	—	X’	ИПА	XY	+	ПА 
FBx	Fx2	ИПД	-	Fx < 0	05	ИП/\	С/П	...	В/0
В этих программах вычисление А(х„) оформляется подпрограм-
мой, причем значения хп заносятся в начало подпрограммы. Пусть
надо вычислить корень уравнения
F(x) = х3 — 0,2х2 - 0,2х - 1,2 = ((х - 1/5)х - 1/5)х - 1,2,	'
лежащий в интервале [1; 1.5]. Вычисление значений F(x) и F"(x)’
показывают, что их знаки одинаковы при х = а = 1. Следовательно,
над© использовать программу 5.19, дополнив ее программой вычис-
ления F(x):
ПО 5 Fl/x - ИПО X 5 Fl/x - ИПО
XI. 2 “
Введя о = 1 = РА, е2 — 1 • Ю~*6 = РД и Ъ = 1,5 = РХ, получим
х = 1,1712297 при tc « 2 мин.
Для контроля программы 5.20'найдем корень уравнения (5.13),
введем в нее программу вычисления функции F(x) (0,25.= Р9):
j psin__ ИП9 — . Для b — 1,3, е2 = 1-Ю-1® и а — 1,1 получим
~ _ j э 1712297 при времени счета около 1 мин.
При методе хорд абсциссы а и b выбираются по обе стороны
от корня. Если их взять с одной стороны, реализуется метод секу-
щих. Недостатком методов хорд и секущих является реализация их
по одной из двух итерационных формул (по двум программам)'.
На практике предпочтение часто отдается методам, не требую-
щим анализа F(x) на сходимость. К таким методам относится ком-
бинированный метод секущих — хорд. В его основе лежит итера-
ционная формула Ньютона (5.15), но точное-значение производной
F'(x)  заменяется приближенным — множитель после Г(хл):
' ,n+1 = x„-F(x„)TI^§b--
Метод дает сходимость при произвольном выборе в пределах отрез-
ка [о, 5] нулевого хв и первого xt приближений.
Программа 5.21. Реализация комбинированного метода секу-
щих— хорд. Ввод: данные F(x„), х0 = РА, Xi = РВ и е2 = Р0.
ИПА	ПП	34	ПС	ИПВ	ПП	34	ПД	ИПА	ИПС
	ИПД	ПС	XY			ИПА	ИПВ	—	X
+	ИПВ	XY	ПВ	XY	ПА	—	Fx2	ИПО	—
Fx<0	04	ИПВ	С/П	...	...	...	...	...	В/0
1 В табл. 5.3		даны	результаты		вычисления		корня	(5.13)	по про
грамме 5.21. Фрагмент программы вычисления F(xnj при х„, заноси-
Таблица 5.3
	*1	X	Время счета #с, с
1,1=а	1,15	1,1712297	50
1.1=а	1,3==Ь	1,1712297	80
1,3=6	1,1 = а	1,1712297	80
1,3=6	1,25	1,1712297	80
1,1=а	1.2	1,1712297	50
мом в его начало и 0,25 =;Р9, имел вид: f Fsin — ИП9 —, Вы-
числения велись при е2 = 1  10-*6.
Гарантированную сходимость при простой программной реали-
зации имеет метод деления отрезка пополам. В нем интервал [а, Ь]
делится пополам, затем выбирается тот полуинтервал, в котором
F(x) переходит через нуль, он делится вновь пополам и т. д., пока
ширина суженного интервала не станет меньше е [4, 5].
Программа 5.22. Реализация метода деления отрезка .пополам.
Ввод: данные F (х) при х-»-РА, а = РА, (Ь — а)== РВ, любое число
со знаком, совпадающим со знаком F(a), п = PC и е2 = РД.
ИПВ- 2	4-	ПВ	| ИПА	+	ПА	4г	Fx2
ИПД - Fx<0 46 ИПА 'С/П ...............................
ИПЙ. XY	ПС	х	Fx	< 0 00	ИПВ	/-/	БП	01
Решим для контроля этой программы уравнение
Д.(//д) = Е - t/д - RIB (evC/«—1) = 0,
определяющее падение напряжения на диоде х = С/д, подключен-
ным через резистор R к источнику напряжения Е. Тогда при £=Р1,
RIB — P2 и v=P3 фрагмент программы, вычисляющий F(x)=F((7fl)I
имеет вид
ИПА ИПЗ X Fex 1 - ИП2 X ИПА +
" ИП1 XY - *
Для £ = 0,5 В; IBR = 1 -10~3 В; v = 20 1/В; K = F(0)=0,5,
а — 0, 6 = 0,5 В и е2= 1-Ю-6 получим Ua = 0,271-72852 при
А » 2 мин и при е2 = 1 • 10~14 (7Д = 0,27174234 В при А « 4 мин.
Из этого примера видно, что сходимость метода деления отрезка
пополам медленная, ибо функция F(x)=F((7fl) относительно про-
стая.
Гарантированную сходимость имеет также метод случайных
проб (Монте-Карло). В нем приближениям Хо, Xi, хг, ..., хп задают
случайные значения в интервале [а, 6], каждый раз сужая этот ин-
тервал. Например, если значения F(a)>0 и F(x„)>0 функции
F(x), то а присваивается значение х«, если F(x„)< 0, то 6 присваи-
вается значение хп н т. д. до тех пор, пока разность 6 — о не станет
меньше е. Генерация случайных чисел с равномерным распределе-
нием описана далее в § 5.12.
Программа 5.23. Реализация метода случайных проб. Ввод: дан-
ные F(x„) при хп = PC, начальное случайное число Vo =. Р0.
(Vo < 1), а= РА, 6 = РВ, е = РД.
ИПО 3	7	X	1	+	ПС	кипе	XY	ИПС
— по	ИПВ	ИПА	—		ИПА	+	ПС	• - °
. •  . ...	. . .		N	ИПС	ПА	БП	(М+2)	ИПС
ПВ ИПВ	ИПА	—	ИПД	-	Fx<0	00	ИПА	с/п
в этой-программе ЛГ —число, дающее номер шага команды ИПС
после записи в программу фрагмента, вычисляющего F(x„). Для
„педшествующего примера при Vo = 0,1234567, £==0,5 В = Pl,
/ д = 1 • IO-3 В = Р2, v = 20 1/В = РЗ, а = 0,2 В = РА, b =
2-03 в = РВ и в — 1-Ю'3 = РД получим Uu — 0,27144498 В при
tc я» 70 с. Фрагмент программы вычисления F(xn) имеет при этом
ВИД’ ИПЗ X Fe* 1 ~ ип2 х ИПС + ИП1
XY -
Процесс формирования значений хо, xlt Хг, ,.., хп можно упо-
рядочить, в частности, формируя эти значения поразрядно [8]. На-
пример, можно формировать значения хп с шагом
Xn^Xn-l+^XN'	<517>
вычисляя каждый, раз F(xn}. Если F{x„)ILxn 0, даем хп очеред-
ное приращение Дхл. Дели F(xn)/&Xn < 0, то делим Дхл на некото-
рое число —7? (показатель разрядности), т. е. получаем новое зна-
чение
ДхЛ, = -ДхЛ,_1/7?.
Если (Длл/)2 > е2, вычисляем хп по формуле (5.17), если (Дхл/)2=^е2,
заканчиваем счет. При R = 10 метод поразрядного приближения
становится методом подекадного приближения [8], причем результат
вычислений автоматически усекается (точными являются все
цифры результата).
Программа 5.24. Реализация метода подекадного приближения.
Ввод: данные F(xn) при хп -> РА, Хо — РА, Лх( = РВ и е2 = PC.
ИПА ИПВ + - ПА ......................................
.................ИПВ	ч- Fx<0 00 ИПВ /-/	1
0 ч- ПВ Fx2 ИПС — Fx < 0 00 ИПА С/П
Для- приведенного выше примера при Л 7/л = &xt =0,1 Ви
е2 = 1 • 10~® получим t/д = 0,272 В при tc еи 65 с.
Ввиду невысокого быстродействия мнкро-ЭВМ индивидуального
пользования значительный интерес представляют методы решения
нелинейных уравнений, обеспечивающие повышенную скорость схо-
димости итерационных процессов.
Корень уравнения (5.12) можно найти путем обратной интер-
•поляцни/экстраполяции. При этом в интервале [a, 7>] задается N зна-
чений. абсцисс хп и вычисляется N ординат Е(х«). Записав значе-
ния хп в регистры, отведейные в программах интерполяции с произ-
вольно расположенными узлами (§ 5.2) под запись ординат, а зна-
чения 7(х„) — в регистры, отведенные под запись абсцисс, найдем
сразу приближенное значение корпя Xi. После этого можно сузить
^интервал [а, &] и повторить расчет.
Программа 5.25. Реализация метода нахождения корней с по-
мощью квадратичной обратной ннтерполяции/эКсТфаполяции-. Ввод!
данные F(x) при х, заносимом в начало подпрограммы, Хо = РА,
Xt — РВ И %2 = PC.
ИПА	ПП	46	ПО	ИПВ	пп	46	П1	ИПС	ПП
46	П2 •	ИПВ	ИПА	—	игл	ИПО	—	4-	ПВ
ИПС	ИПА	—	ИП2	ИПО	—	ч-	ипв	—	ИП2
ИП1	—		ПС	ИП1	/-/	ипс		ипв	+
ИПО	/-/	X .	ИПА	+	С/П	...	...	...	В/0
1 Пусть надо найти напряжение на стоке мощного МДП-транзи-
стора (рис. 5.2, а и б) из решения уравнения
р ___rj
Дз) = 0,	(5.18)
если зависимость тока стока /с от напряжений на стоке Uc и затво-
ре Ua описывается выражением
re (Uc, U3) = s(u3—u0 — uty [G;pUcKua-uo- ьиз) _ J (519)
где S — крутизна, р и & — параметры аппроксимации вольт:амперной
характеристики.	,
Рис. 5.2. Каскад на мощном МДП-транзисторе (а) и графическое
определение положения его рабочей точки (б)
Подставляя (5.18) в (5.19), получим окончательно
(Uc) = EC-UC- RCS (bUz3 -U3 +	- 1].
(5.20)
При Ес = Р4, U3 = Р5, Sflc = Р6, р=Р7, b = Р8 н До =+1 В
вписываемый в подпрограмму фрагмент вычисления функции F(Ud
имеет вид:
ф ИП7 X ИП8 ИП5 Fx2 X 1 + ИП5
- П9 •«- Fex 1	— ИП& X ИП6 X
+ ИП4 XY -
. Для Ес = 40 В, 1Л>--= 10 В 5^ = Ю В, р = I,' b = 0,02 1/В,
Ut0 = х0 = 4 Д, t/cl = xl = 5 11, Uc2 = х2 = 6 В получим Ос =
= 4,8762113 В при точном значении £ = 4,876727 В и времени счета
а 40 с. Таким образом, уже при одном цикле интерполяции (7с
определено с точностью до 4-х верных знаков, что более чем доста-
точно. для практических расчетов.
Автоматическое ..уточнение корня лри методе обратной иитерпо-
ляции/экстраполяцпи можно выполнить различными способами.
Так, для данного примера лучшим оказался следующий способ: ле-
вая граница интервала изоляции корня берется равной Хо = 0 (при
этом F(UC(I) = Ес), значение xi = к и х2 = xi -|- Ах, где Дх=АВ,с =
.= const (например 1 В).
Программа 5.26. Расчет Uc для схемы рис. 5.2, а методом обрат-
ной интерполяции/экстраполяции с автоматическим уточнением кор-
ня. Ввод: начальное значение Uc — РВ, Uo = Р0, Ес — Р4, в2 = Р5,
=	Р6, р =	Р7, b	= Р8 н U3 = РХ.				
П9	Fx2	ИП8	X ИПО +	ИП9	—	П9	ИПВ
ПП	57	П1	ИПВ 1	+	ПС	пп	57	П2
ИПВ	ИП1	ИП4	- ПД	ИПС	ИП2	ИП4	—
4-	ИПД	—	ИП1 ИП2 -	4-	ИП1	X	ИПД
+	ИП4	/-/	X' ИПВ XY	пв	—	Fx2	ИП5
—	Fx <’0	09	ИПВ С/П БП	00		ИП7	X
ИП9	4-	Fe*	1	- ИП6	X	ИП9		+
ИП4	XY	—	В/0				
' Пр	и UcO =	5 В,	е2=1-10_10, U3 =	10 в	и указанных		выше
Других	данных	F(Uc	) получим Uc = 4,8767272		В, при U3		= 6 в
Uc = 6,522966 В, при ТА = 4 В Uc = 13,381808 В, при U, = 2 В
'Uc — 30,8 В. При повторных вычислениях вводится только значение
U3 = РХ и нажимается клавиша С/П. Время вычисления одного
значения Uc около 2 мин.
Ускоренную сходимость при сложных уравнениях (5.12) имеет
также метод Эйткена — Стеффенсона. При его реализации уравне-
ние (5.12) приводится к виду х = f(x), вычисляется первое прибли-
жение для х — хо'. xi = f(xo), затем второе: х2 = /(Х1). По ним
находится уточненное значение корня [2]
- х = (х^х-2 — Xj)/(x0 — 2х, + х2).	(5.21)
Ойо присваивается хо, после чего процесс повторяется до тех пор,
пока разность (х— хо)2 не станет равной или меньшей е2. В про-
грамме следует предусмотреть контроль знаменателя (5.21) на нуле-
вое значение, которое может возникать при равенстве Хо, Xt и xi
в конце итераций. Если такая ситуация возникает, следует перейти
К выдаче значения х0 = х.
Программа 5.27. Реализация метода Эйткена — Стеффенсона.
Ввод: данные f(x) при хп-+ РХ, е2 = РВ и х0 = РО.
ИПО	ПП	33	ПА	ПП	33	ф	ИПО	X	ИПА
Fx2	-	XY	ИПО	+	ЙПА	2	X	~	Fx^O
31'	-j-	ИПО	XY	ПО	—	Fx2	ИПВ	—	Fx < О
00	ИПО	С/П	..........................В/0
Программу 5 27 можно проверить вычислением корня уравнения
(5.14). При Хо = 1,2 и Е2‘=1-10~в получим х= 1,1714285 при
tc & П с.
5.5. Поиск экстремумов функции одной переменной
Поиск экстремумов функций нескольких переменных
F(x, у, г, ...) относится к довольно сложным вычислительным за-
дачам, алгоритмы которых детально оинсаны в [24]. Реализация
простейших из них на программируемых микрокалькуляторах дана
в [7], но требует чрезмерно больших затрат времени. Поэтому поиск
экстремумов функций несколь-
ких переменных целесообразно
выполнять на настольных ми-
кро-ЭВМ. В связи с этим огра-
ничимся описанием поиска эк-
стремумов функции одной
переменной.
Пусть некоторая целевая
функция F(x-) имеет экстрему-
мы при изменении х. Задача
их поиска близка к решению
нелинейных уравнений и сво-
дится к определению интервала
[а, Ь], в котором находится экстремум, и его сужению. Будем искать
максимум Р(х), так как функция f(x), имеющая минимум, сводится
к функции F(x) умножением /(х) на —1. Будем решать эту задачу
Рнс. 5.3. Иллюстрация к поиску
экстремума функции А(х)
методом поразрядного приближения.
Поскольку при однократном прохождении экстремума (х ме-
няется с шагом Ах) знак приращения F(x) может не изменяться
(см. рис. 5.3), то следует перед дроблением Ах предусмотреть
возврат назад на два шага после изменения знака прираще-
ния Р(х).
Программа 5.28. Определение максимума F(x). Ввод: данные
А(х), Хо = РА, Ахо = РВ, е/4 = РО. Значения х — х^и F (хд)
в точке максимума заносятся в регистры РХ = РД и PC соответ-
ственно, текущее значение х РЛ,
ПП	29-	ПС	ИПА	ИПВ	+	ПА	ПП	29	ИПС
XY '	ПС	—	Fx>0	03	ИПВ	2	/—/	-4-	ПВ
Fx < о	23	/-/	ИПО	—	Fx < 0	03	ИПА	С/П	...
...	........................................... В/0
Для F(x) = 10х—2х2, вписав в программу фрагмент вычисле-
ния F(x) вида
1 О ИПА X FBx Fx2 2 X -
прн х0 = 0,. Дхо — 1 и е/4 = 2,5 • Ю~4 найдем (нажав клавиши В/0 и
С/П) Хм = 2,5 при tc « 190 с. Из регистра С вызываем значение
Д(хм) = 12,5.
' 5.6. Решение алгебраических уравнений
Решение алгебраических уравнений выполняется по приведенным
ниже программам, которые описаны также в [7, 27].
Программа 5.29. Вычисление корней квадратного уравнения
а2х2 + Я1Х + Оо = 0	(5.22)'
по формулам xlt 2 = —ai/(2a2) ± V(“i/(2a2))2 — а0/а, . Ввод: Со =«
= Р0, at = Pl и й2 = Р2. Вывод результатов (после нажатия кла-
виш В/0. и С/П): 7->-РХ, xi->PY, x2-»-P7, если корни веществен-
ные, и 4 -*.РХ, tn -> PY и d Р4, если корни xt, 2 = d ± jm ком-
плексно сопряженные.
ИП1'	/-/	ИП2	-4-	2	.	±	.	П4	Fx2	ИПО	ИП2
-4-	—	Fx <	0	18	/-/	FV	4	-С/П	FV"	ПЗ
ИП4	+'	П7	ИП4	ИПЗ	-	7 .	С/П
Для	уравнения	2х2— 5х—10 = 0	получим	х( =—1,3117376 и
х2 = 3,8117376, а для уравнения х2 + 2х + 15 = 0 ’получим xj, 2 —
==— 1 ±/-3,7416573.
Программа 5.30. Решение квадратного уравнения (5.22) с умень-
шенной погрешностью вычисления вещественных корней (меньший
по модулю вещественный корень вычисляется по формуле х2 =
= —Oo/(xia2), где Xi — больший по модулю корень). Ввод: оо = PC,
Bi = РВ, и о2 = РА. Вывод результатов (после нажатия В/0 С/П):
7 РХ, xi -> Р7, х-i Р8, если корни вещественные, и 4->РХ, d->-P4,
tn -> Р5; если корни Xi, 2 = d ± jm комплексно сопряженные.
ИПС	ИПА	-4-	П9	ИПВ	/-/	ИПА	2	X	±
П4	Fx2	—	Fx < 0 31	/-/	F'V"	ИП4	Fx < 0 23
XY	-	0	+	П7	ИП9	XY	-г-	П8	7
С/П	П5	4	С/П
Для уравнения; Зх2 + 2ООО0Х + 12 = 0 получим по этой про-
грамме х( = —6666,666 и- х2-= —6,0000006  10~Л По программе 5.29
Ki = —6666,666 и X2 = —6,66666666-10~* (точное значение Хг =>’
= 6-10-‘).
Программа 5.31. Решение кубического уравнения
Xs + а3х2 + Ojx + Оо = 0	(5 23)'
выделением вещественного корня х, делением (5.23) иа (х— х) и
вычислением корней полученного квадратного уравнения. Ввода
ое = РО, Hi = Р1, о2 = Р2, 1 + |омакс| = РХ (здесь |амакс| — взя-
тое по модулю значение коэффициента с максимальным численным
значением). Вывод результатов (после нажатия клавиши В/0 и
С/П): 7 -> РХ, Xi Р7, Хз -> Р8 и хз -> Р9 (если корни веществен-
.ные) и 4РХ,- d-> P4, zn->P5 плексно-сопряженных корней).					и хз->Р9		(если	есть пара ком	
ПА	Сх	XY	FBx	1	1	ИП2	+	П6	X
ИП1	+	ПЗ	X	ИПО	+	Fx <	0 22	F,	ИПА
+		F,	ИПА	2	ч-	ПА	—	 П9	—
Fx = 0	03	ИП6	1-1	2	4-	П4	Fx2	ИПЗ	—
Fx <0	47	/-/	fV	П5	4	С/П	fV	П5	ИП4
+	П7	ИП4	ИП5	—	П8	7	с/п		
Для уравнения х3-—6х2 + Их — 6 — 0 найдем корни. Xi =
= 2,9999996; х2 = 2,0000006 и хз — 0,99999982, а для уравнения
Xs— 6х2 + 21х -г 52 — О получим Xi, 2 = 1 ±/-3,4641015 и хз = 4.
Программа 5.32. Вычисление корней алгебраического уравнения
четвертой степени
х4+03Х3 + О2Х2+-О1Х-|-оо = 0	(5.24)
путем разложения на два квадратичных множителя. Ввод: о0 4- Оз=
= Р0 4- РЗ, 2(1 + |а.макс|) — ДА. Вывод результатов (после нажатия
клавиш В/0 И С/П): xj -> РХ, Хг -> PY, если корни Xi. 2 действитель-
ные, и ЕГГОГ, если корни комплексно-сопряженные (тогда, нажав
клавишу С/П, получим d->PX и m-^-PY). Для вычисления анало-
гичным образом Хз, 4 нажимается клавиша С/П.
ИПЗ	/-/	2	4-	ПД	ИПД	Л-	К	ИПЗ	+•
П6	X	ИП2	+.	П5	X	ИП1	+	Fx = 0	65 .
ИШ	ИПЗ	4-	Г-	Fx2.	ИПО	—	Fx>0	65	F V"
4-	П7	ИПД	2	-4- .		Fx2	ИП7	—	Fx<0
50	/-/	F V'	0	-7-	Сх	F, :	XY	БП	54'
fV	+ :'	4-	FBx	С/П	ИПЗ	/-/	ИПД	—	ПД
ИПО	ИП7		БП	31'	XY	ИП6	+	Fx =/: 0	84
4-	П7		ИП5	—	X	ИПО	+ •	Fx < 0	84
ИПД ПД	ИПА FBx	—,	ПД • Fx = 0	ИПА 05	.2 ИП7	БП	ПА.. . 32	ИПД	+
Для уравнения х1 + 9х3 + 31х2 + 59х + 60 = 0 получим xt, г =э
— 1 ± /-1,9999999 (А ~ 7 мин)-и хз = —3 и х4 — —4 (А» 10 с).
Из регистров Д и 7 можно вызвать значения коэффициентов квадра-
тичных множителей (—2 и 4,9999998) *). Для х3 и х4 получаем
значения —3 и —4 (tc » 10 с).
Программа 5.32. Решение алгебраического уравнения пятой сте-
пени
х5 + а4х‘ + взх3 + агх2 + aix + а0 = 0	(5.25)
выделением вещественного корня и приведением к уравнению четверо
той степени. Ввод: По «к = РО 4- Р4, 2(1 + |с„акс |) = РА = РВ.
Вывод результатов (после нажатия клавиши В/0 и С/П): 1. Xi->PX,
jc2->PY и хз-*РД, если корни Xi, г. з действительные, 2. ЕГГОГ,
если корни xi, 2 комплексно сопряженные. В случае 2, нажав кла-
вишу^ XY, получим di, г, .нажав клавиши XY /—/ F V . получим
/П1,2-(хз->РД). Далее, нажав клавиши БП . 76 С/П, получим]
1. х4->РХ, Xs->PY или 2. ЕГГОГ (нажав клавишу XY, получим
di, s, далее,		нажав клавиши XY /—/ F V ,				получим Л??4,		s).	
Сх’	ПС	XY	FBx		f	ИП4	+	П8	X
ИПЗ	+	П7	X	ИПС	Fx = 0	63	F,	ИП2	+
П6	X	ИП1	• +	,П5 '	X	ИПО	+	Fx <	0 34
F,	ИПА	+		F,	ИПА	2	4-	ПА	—
П9	—	Ег=	0 03	ИПС	Fx = 0	76	ИПВ	ПА	ПС
ИП9	ПД	ИП5	по	ИП7	ПЗ	ИП8	П4	/-/	2
4-	БП	35	F,	ИП6	+ '	XY	ИП8	+	4-
П5	f	ИП7	—	БП	25	ИПО	ИП5	4-	П5
И.П4	/-/	ИП9	—	П9	2	4-	t	Fx2	ИП5
—	fV~	+	4-	FBx	С/П				
Для уравнения xs + 8х4 + 31.x3 + 80х2 + 94х + 20 — 0 получим
хт. 2 — — 1 ± /-3,0000178, х3 = —3,7320507, х4 = —0,2679458 и xs =
= —2,000032 (при времени счета около 13 мни).
Уравнения более высоких степеней (и 5= 6) могут быть сведены
к уравнениям меньшей степени, описанным выше (для п == 2, 3, 4
и 5), выделением вещественного корня прн нечетных п и разложе-
нием на множители с пониженной степенью. Однако в этом случае
вычисления приходится проводить по нескольким программам [7, 27),
что ведет к значительному росту времени вычислений и снижению
их Достоверности. Поэтому решение алгебраических уравнений со
степенью л > 6 целесообразно проводить на более быстродей-
ствующих настольных ЭВМ (либо на микрокалькуляторах с боль-
шим объемом памяти) по единым программам.
*) После вычисления первой пары корней.
5.7.	Численное дифференцирование
Численное дифференцирование гладкой функции у = f (х), за-
данной ординатами yt и абсциссами xi, изменяющимися с шагом
h —	— const, заключается в приближенном нахождении произ-
водной у'(х). Для этого у = f(х) заменяется интерполяционным
полиномом, аналитическое выражение для производной которого не-
трудно найти. Таким образом выводятся формулы численного диф-
ференцирования [2—5], используемые в поивепенном ниже пакете
программ. Отметим, что в них связь р и х соответствует (4.3).
Программа 5.34. Нахождение производной при трех ординатах!
У' W = .[(р “ 1/2) У-t —2рУо+Ьр + 1/2) P+il/Л.
Ввод: h — Р9, у-i, уо, yi, хо и х в регистр X (при смене-.только х
вводится новое значение х = РХ).
П1	С/П	ПО.	С/П	ПА	С/П	П8	С/П	П7	ИП8
—	ИП9	+-’	ПД	2	Fl/x	—	ИП1	X	ИПД
2	X	ИПО	X	-	ИПД	2	Fl/x	+	ИПА
X	4*	ИП9	+-	БП	07 .
Для h = 0,02, у-, = 0,3555325, ув = 0,3520653, y+i = 0,3484925,
Хо = 0,5 и х = 0,49 получим у’(х) = —-0,17336, для х = 0,52 полу-
чим р'(х) =—0,18128 при точном значении у'(х) =—0,1812161.
Программа 5.35. Нахождение производной при четырех ордина-
тах;
,", .	1 / Зр2 — 6р + 2
----y-t +
, Зр2 —4р —I Зр2-2р —2	: Зр2—1 X
+ ~------------Уо ~ —----g----Р+1 4---^-g----Р+2 J.
Ввод: h = Р9 и' (после нажатия клавиш ’В/0 и С/П и индикации
цифры i.	О р-1, Уо, У+1,		у+2, Хо и х в регистр X.						
0	П6	5	ПО	4	С/П	КП6	FL0	05	С/П
П7	ИП5	—	ИП9		•ПД	Fx2	3	X	ПС
. ипд	4	X	—	1	—	2		ИП2	X
ИПС	ипд	6	X	—	2	4-	6	- “4*	ИШ 
X	—	ИПС	ипд	2	X	—	2	—	2
	ИПЗ	X	—	ИПС	1 .	—	6	-4-	ИП4
X	4-	ИП9	-г-	БП	09				
Дополнив		данные	предшествующего			примера значением			Р+2 —
= 0,344818, получим для х — 0,51 значение у'(х) =—0,1786483, а
для х = 0,52 значение р'(х).= —0,1812155 при точном значении
—0,1812161,
Програг . 2р3 — 5р	л-ма 5.3€. Нахождение производной при пяти ординатах: ( 2р3 — Зр2 — р Ч~ 1	4р3 — Зр2 — 8р 4
	С	12	6	"'/-1'4- 4р3 + 3р2 —8р —4 „	, 2р3 + 3р2—р —1	\
1	6	?Т1 •	12	£/~Ь2 J- Ввод: y-z — Р2, у-i = Р1, уо = Р0, y+i .= РА, у±2 = РВ, h = Р9, Хо — Р8 и х -	РХ. П6	ИП8	-	ИП9	4-	П7	2	X	3	- ИП7	X	1	-	ИП7	X	1	+	Я	2 4-	ИП2	X	ИП7	4	X	3	-	ИП7	X 8	—	ИП7	X	4	+6	4-	ИП1	X —	ИП7	Fx2	2	X	5	—	ИП7	X	2 4- ИПО X + ИП7 4X3	+ ИП7 X	8	—	ИП7	X	4	-	6	4-	ИПА X	-	ИП7	2	X	3	+	ИП7	X	1 —	ИП7	XI	-	1	2	4-	ИПВ.	X +	ИП9	4-	С/П	БП	00	
' Для y-z = 0,35889029, y-t = 0,35553253, у0 = 0,35206533, у+1=*
•«= 0,34849251, у+2 = 0,34481800, хо = 0,5, h = 0,02 и х = 0,51 полу-
чим у'(х) = —0,1786488, а для х — 0,5 получим у'(х)= —0,17603265
при точном значении —0,17603266. В этом и двух предшествующих
примерах вычислялись производные функции у (х) = Z (х) = е_*2/2/
/V2:rc нормального распределения вероятностей по округленным
данным таблиц [3].
Если нужно найти у'(х) только в узлах интерполяции, формулы
численного дифференцирования резко упрощаются. Например, при
трех ординатах и р = 0
у' (х0) = (у+t — г/— i) /2ft,	(5.26)
а при пяти ординатах и р = О
у'(хо) = (у-2 — 8t/~i + 8p+i — г/+2)/12й.	(5.27)'
Иногда, используя эти формулы, целесообразно вычислять
у'.(х — Хо) аналитически заданной функции, производную которой
нежелательно или сложно найти в аналитическом виде. При .этом
вычисления ординат р(х) оформляются подпрограммой.
Программа 5.37. Вычисление производной функции y = f(x),
заданной аналитически по формуле (5.26). Ввод: данные f(x), hfxo=*.
.= PC н хо = РХ.
ПД	ИПС	XY 4-	ПВ	ИПД ИПВ' -	ПП 29
ПА	ИПД	ПП 29	с/п	ИПД ИПВ +	ПП 29
ИПА	—	2	4-	ИПВ	4- с/п БП	00	...
.	...	. . . . ...	...	... . •.• •••	В/0
Так как значения хо могут меняться в широких пределах, то
задается не абсолютное изменение х, а относительное Дх/хо = Л/х®.
Значение /г/х0 для гладких функций на практике легко оценивается.
Пусть надо вычислить производную функции у(х) = Z(x) —)
_ е-хг/2 д/2л в точке хо = 0,5 при /г/хо — 0,01. В текст программы
вписываем подпрограмму вычисления Z (х): Fx2 2 /—/ -i- Fe* Fit 2 X
F V~ *-. Нажав клавиши В/0 и С/П, получим значение
Z (0,5) — 0,35206532, еще раз нажав клавишу С/П, получим
Z'(0,5) — —0,1760005 при точных значениях Z(0,5) = 0,35206533 и
Z'(0,5) = —0,1760327 соответственно.
Программа 5.38. Вычисление производной аналитически задан-
ной функции f(x) в точке х = х0 по пяти ее ординатам с помощью
формулы (5.27). Ввод; Л/х о — PC и хо = РХ.
ПД	ИПС	XY		ПВ	ИПД	ИПВ	2	X	—
пп	56	ПА	ИПД	ИПВ	—	ПП	56	8	X
ИПА	XY	—	ПА	ИПД	ПП	56	С/П	ИПД	ИПВ
+	ПП	56	8	X	ИПА	+	ПА	ИПД	ИПВ
2	X	+	ПП	56	ИПА	XY	—	1	2
4-	ИПВ	J-	С/П	БП	00	...	...		В/0
Для приведенного выше примера получим Z(0,5) = 0,35206532
и Z'(0,5) =—0,1760325.
5.8. Вычисление частных производных
и коэффициентов чувствительности
Нередко необходимо найтн частные производные функции
7(х, у, z, ...) нескольких переменных при х — хо, у = у о, z = Zo
и т. д. В отличие от численного дифференцирования по одному па-
раметру, при вычислении частных производных необходимо выбирать
Один изменяемый пйрамётр и фиксировать значения остальных пара-
метров. Это можно обеспечить с помощью косвенной адресации ре-
гистров памяти, отведенных под ввод соответствующих параметров.
Например, если хо = Р1, уо — Р2, zo — РЗ и т. д., то программу
можно составить так, чтобы указание номера регистра (кода пере-
менной), например цифры 2, при вычислении df/dy и т. д. непосред-
ственно указывало на то, по какому параметру выполняется диффе-
ренцирование. В конце вычисления параметру присваивается исход-
ное значение.	\
Программа 5.39. Вычисление частных производных аналитически
заданной функции f(x, у, г, ...) по трем ее ординатам. Ввод;
h — PC, данные f (х, у, г, ...),. коды переменных.
ПД КИПД	ПА.	„ИПС	—	КПД	ПП	27	ПВ	ИПА
ИПС<+ ,	КПД	ПП .	.27	ИПВ	-	2 ; ,	4-	ИПС	.
4- ИПА	КПД	XY	С/П	БП	00	...	...	В/0
Пусть надо найти частные производные функции
f (х, у, г) = 2хг + у2 — За2 — Зху — 2xz,	(5.28)
ПрИ ххо — 0, у = у о = 0 и г = г0 = I. Фрагмент программы вы-
числения функции f(x, у, г) при х — Р1, у = Р2 и г — РЗ:
ИП1	Fx2	2 X	ИП2	Fx2	+	ИПЗ	Fx2	3
X	—	ИП1	' ИП2	X	3	X	—	ИП1	ИПЗ
X 2 X •-
Вводим программу с этим фрагментом и исходные данные:
h = 0,001 — PC, 0 = Pl, 0 = Р2 и 1 = РЗ. Для вычисления df/dx
набираем цифру 1 (код переменной х) и, нажав клавишу С/П, по-
лучим результат df/dy — —2 при аг 20 с. Набрав цифру 2 "(код
переменной у) и нажав клавишу С/П, получим df/dy = 0. Наконец,
набрав цифру 3 (код переменной г), получим df/dz= —6. Эти зна-
чения полностью совпадают с точными.
Программа 5.40. Вычисление частных производных аналитически
заданной функции f(x, у, г, ...) по пяти ее ординатам. Ввод:
h = PC, данные f (х, у, z, ...), коды переменных.
ПД	КИПД	ПА '	ИПС -		кпд	пп	53	ПВ	ИПА
ИПС	+	кпд	пп	53	ИПВ	—	8	X	ПВ
ИПА	ИПС	2	X	—	кпд	пп	53	ИПВ	4-
ПВ	ИПА	ИПС	2		+	кпд	ПП	53	ипв
XY	—	1	2	—	ИПС	-Г-	ИПА	кпд	XY 
С/П	БП	00	...	...	...	...	...	...	В/0
Работу этой программы можно проверить по приведенному выше
примеру.
Нередко переменные функции f(x, у, г, ...) имеют резко отлич-
ные исходные значения. В этом случае целесообразно задание отно-
сительного изменения h/p каждой переменной р (р — х, у, г, ..
Программа 5.41. Вычисление частных производных аналитически
заданной функции f (х, у, г, ...) по трем ее ординатам при задании
относительного приращения h/p каждого параметра. Ввод: h/p — Р9,
данные f(x, у, г, ...), коды, переменных.
ПД	КИПД	ПА		ИПС х —	кпд	пп	34
ПВ	ИПА		ИПС	X +' кпд	пп	34 .	ИПВ
—	2		ИПС	-Т-	ИПА —	ПВ	ИПА	кпд
ИПВ	С/П	БП	00			...	...	В/0
Для приведенного выше контрольного примера получим при h/p =»’
= 0,01, хо = 1, уо = 2 и го = 3 значения df/dx — —8, df/dy = 1
и df/dz = —20, которые также совпадают с точными значениями.
Общее абсолютное приращение функции нескольких переменных
при изменении каждой из них
(х, у, z,...) =-^-Лх 4--^p-Ap 4-Az 4-...
' ' и ' дх ду ° dz
Частные производные при приращениях Дх, Др, Дг и г. д. назы-
ваются абсолютными коэффициентами чувствительности функции к
изменению соответствующего параметра.
В практике научно-технических расчетов предпочитают использо-
вать безразмерные относительные коэффициенты нестабильности по
каждому параметру, например:
е ..	цт
х дх/х дх_>о Дх/х
и т. д. В этом случае легко вычисляются относительные общие при-
ращения функции
-Af------r = Sx — 4-Sp — + S2~4- ...
f (xo,-Po> Zo, ...) x0 y y0 Zo
Приведенные выше программы легко приспособить для вычисления
относительных коэффициентов нестабильности.
Программа 5.42. Вычисление значения функции f(x, у, г, ...) и
относительных коэффициентов нестабильности при трех ординатах
функции. Ввод: /г/р = PC, данные f(x, р, г, ...), коды переменных.
Значение f(Xo, у о, zB, ...) ~>РА.
ПД-	КИПД	ПА f	ИПС	X	—	КПД	ПП	37
’	ПВ	ИПА	4 ИПС	X	4-	КПД	ПП	37	ИПВ
—	ИПС	4-2	-	ПВ	ИПА	КПД	ПП	37
ПА ИПВ XY 4- С/П БП 00	......... В/0
Для иллюстрации вычислим коэффициенты относительной неста-
бильности периода повторения импульсов, формируемых' релаксаци-
онным генератором на однопереходном транзисторе
/П = ДС In (1 - Tl)"’,
где Р=1-105 Ом — величина времязадающего резистора, С —
= 1-10-8 ф — емкость времязадающего конденсатора, rj = 0,66—
к-даффициент деления.
Вписываемая в программу 5.41 подпрограмма вычисления
tn(R, С, ц) при R = Pl, С = Р2 и ч = РЗ имеет вид;-
1 ИПЗ — Fl/x Fin ИП1 X ИП2 X
Введя значения R, С, ц и /г/р—0,1, набираем код 1. Нажав клавишу
С/П, спустя /с == 25 с получим SK — 0,99999999. Набрав код 2 и
нажав клавишу С/П, получим Sc — 0,99999999 и, наконец, набрав
код 3, получим 1,8224953. Из регистра А можно вызвать ис-
ходное значение /п — 1,0788096-10~? с,	,
Программа 5.43. Вычисление значения функции / (х, у, г, ...) и относительных коэффициентов нестабильности при пяти ординатах								
функции. Ввод: hip — PC, данные f(x, у, z, ..						.), коды переменных.		
Значение/ (хо, у о, Zo, ПД КИПД ПА		...)-> РА. ПП 53		2	пп	57	ПВ	пп
52	’ ПП	58	8	/-/	ПП	48	+	ПП	59
8	ПП	48	2	X	+	ПП	59	ИПВ	XY
—	ИПС -т-	1	2		ПВ	ИПА	кпд	ПП '
59	ИПВ ХУ .	ПА	—-	С/П	БП	00	х	ИПВ
-f*	ПВ	ИПА	Ф	ИПС	X	В/0	X	—	КПД
• • •	... ...	...	•..	.«•	•. .			В/0
Для предшествующего примера при /г/р = 0,01 получим
= 0,9999949, Sc = 0,9999949,	= 1,7993745 и tn = 1,0788Э96Х
х ю~3 с при / яз 50 с.
5.9. Численное интегрирование
Основная задача численного интегрирования сводится к нахо-
ждению значения собственного определенного интеграла
6
I=^f(x)dx.	(5.29)
а
В общем случае интервал интегрирования [a, fe] разбивается ва
т частей. В свою очередь каждая из них делится на п частей, в
пределах каждой части у — f (х) аппроксимируется полиномом, инте-
грирование которого возможно по достаточно простым формулам
[1—5]. Приведенные ниже программы отличаются степенью поли-
нома и числом ординат f(x), вычисляемых па каждой из т частей.
Последний член приводимых формул характеризует погрешность
интегрирования.
Программа 5.44. Численное интегрирование методом прямоуголь-
ников по формуле
/ =
т-1
1=0
т-1
i=0
b — а
т

где h = (6 — a)jm. Ввод: данные f(x), т, Ь и а в регистр X. Теку-
щие значения х->РЛ, регистры 0, А, В и С заняты.
ПЭ	0	ПС	С/П	ПВ	С/П	ПА	—	ИПС	-»-
ПЭ	...... ИПС	+	ПС	ИПА	ИПО	+	ПА
ИПВ	-	Fx>0	11	ИНС	ИПО	X	С/П	БП	00
Пусть надо вычислить значения интегралов, приведенных в
табл. 5.4.
Таблица 5.4
Интеграл и его точное значение	Про- грамма	Метод	m	Результат	Время счета, мин
•	5.44	Прямоугольников	16	0,88939982	1.7
			64	0,90313381	7
5 г»	5.45	Прямоугольников	16	0,90797012	1.7
г X /—х<-р16		модифицированный	64	0,90748612	7
1	5.46	Трапеций	16	0,906642285	1.5
=0,9074539			64	0,9073897	6
	5.47	Симпсона	8	0,9074589	2.2
			32	0,9074541	10
	5.44	Прямоугольников	16	1,3757033	1,4
			64	1,3929898	5,5
1	5.45	Прямоугольников	16	1,3987863	1,5
7=^V2x+t Лс=		модифицированный	64	1,3987217	6
0	5.46	Трапеций	16	1,3985799	1.5
= 1,3987175			64	1,3987089	6
	5.47	Симпсона	4	1,3987137	1.2
			8	13987172	2.5
Для первого интеграла фрагмент программы, вычисляющей f(x),
имеет вид (число 16 вводим в регистр 8):
ИПА ф Fx2 X FBx Fx2 ИП8 + ч-
Для второго интеграла фрагмент программы, вычисляющий f(x),
следующий:
ИПА 2X1 + FV" ф
Результаты вычислений для различных т даны в табл. 5.4.
Программа 5.45. Численное интегрирование модифицированным
методом прямоугольников
т-1
/.==. Л £ f + 0,5ft) +	г (g),
где /"(!)'— значение-второй производной f(x)' в точке X = §, где
f"(x) максимальна;. Ввод аналогичен описанному для программы 5.44.
ПО	0 .	ПС	С/П	ПВ	с/п	ПА 	—	ИПО
ПО	2	Ч-	’ ИПА	+	ПА	...	. . .	. » • . . •
	• « •	♦ . .	ИПС	+	ПС	ИПА	ИПО	+ ПА
ИПВ	—	FxJ	&0 16	йпс	ИПО	X	с/п	БП 00
Данные контрольных примеров см. в табл. 5.4.
Программа 5.46. Численное интегрирование методом трапеций:
m-t
, h у	. Л2 (Ь — а) .
.	1	2 / 	*"	12
1=0
Ввод аналогичен описанному для программы 5.44. Регистры О, А, В
и С заняты, текущее значение					РА.				
ПО	С/П	ПВ	пп	41	ПС	ИПВ	С/П	пп	41
ИПС	4-	2	ч-	ПС	ИПВ	ИПА	—	ипо	-4-
ПВ	ипо	1	—	ПО	ИПА	ИПВ	4-	пп	41
ИПС	4*	ПС	FLO	25	ИП.С	ипв	X	С/П	БП
00	ПА	• . .	.. •	. •		• • •	. . .	. . .	В/0
В приведенных выше программах п = 1. Для повышения точ-
кости интегрирования каждый из т отрезков разбивается на п ча-
стей, так что на нем f(x) задается «4-1 ординатами. Это позволяет
повысить степень полинома, аппроксимирующего f(x).
Программа 5.47. Численное интегрирование методом парабол
(Симпсона) при п = 2:
ь
I=\l(x)dx=4-[f (°) + 4И« + Л) + 2/ (а 4- 2Й) 4-
J
а
	4* 4/ (а 4- Зй) 4- .							mhs 90	
Ввод: гистр	данные X. .	/(*)	при	РВ,	2т (четные		числа)	, b н	а в ре*
по	С/П	ПВ	С/П	ПА	ПП	44	ПС	ИПВ	ИПА
ПВ	.—	ипо	-Л-	ПА	ПП	44	1	ПП	32
4	пп	32	2	БП	18	ИПС	3	-Г-	ИПА
X	С/П	X	ИПС	-F	ПС	FLO	40	БП	26
ИПЕ	1 ИПА	4-	ПВ		•. •	• •. •	...	• • .•	В/0.
Как видно , из табл. 5.4, из простых методов интегрирования ме-
тод Симпсона дает наиболее высокую точность — ошибка пропорцио-
нальна Л5 [3|. Он применяется наиболее ча'сто. Однако, если иод-
программа вычисления /(х) вписывается в программу, то примене-
ние более точных.методов (с и>2) позволяет сократить время ин-
тегрирования (при заданной точности). В приводимых ниже програм-
мах h — (b— a) In, а интервал [я, 6] соответствует при пг — 1 ин-
тервалу [хо, хп], в пределах которого равномерно расположены абс-
циссы хо, xi, х.2, .	х„. Предусмотрена возможность разбивки ин-
тервала [а, 6] па т интервалов [хо, х„].
Программа 5.48. Численное интегрирование методом Ньютона —<
Котеса при п = 4 (формула. Водэ):
хг
J f (х) dx == -Ц- (7ув + 32y, + 12p2 + 32ya + 7yt) - -Ц- /VI (g).
Ввод: данные f(x) при x->PA, m, b и а в регистр X (регистры О,
А, В и С заняты).
ПО	0	ПС	С/П	t	С/П	ПА	—	ИПО	—
4	-Z-	ПВ	пп	26	FLO	13	ИПС	ИПВ	X
2	X	4	5	Ч-	С/П	ИПА	пп	58	7
ПП	50	3	2	ПП	50	1	2	ПП	50
3	2	ПП	50	7	X	ИПС	+	ПС	В/0
X	ИПС	+	ПС	ИПА	ИПВ	+	ПА	>. •	-В/0
Программа 5.49. Численное интегрирование методом Ньютона
Котеса при п = 6:
J f (х) dx =	(41 г/о + 216р! + 27у2 + 272j/s + 27у< +
*"	9/г9
+ 216^ + 41^)--^-/VIII (g).
Ввод см. в программе 5.48.
ПО	0	ПС	с/п	f	с/п	ПА	—	ИПО	-т-
6	—	ПВ	пп	25	FL0	13	ИПС	ИПВ	X
1	4	0	Ч-	С/П	ЙПА	ПП	70	4	1
ПП	62	2	1	6	ПП	62	2	7	ПП
62	2	7	2	ПП	62	2	7	ПП	62
2	1	6	ПП	62	4	1	X	ИПС	4-
ПС	В/0	X	ИПС	+	ПС	ИПА	ИПВ	+	ПА
• • •	• • •	• • •	• • •	  •	• • •	• • •	...		В/0
Программа 5.50. Численное интегрирование методом Уэддля для
п = 6:
хе
47b1
f (х) dx == ~Л(Уо + 5f/i. + у2 + брз + yt + 5(/9. + ув) + тут™ ZV1 (В).
О
Ввод см. в программе 5.48.
ПО	0	ПС	с/п		с/п	ПА	—	ИПО Ч-	
6	ч-	ПВ	пп	26	FLO	13	ИПС	ИПВ	X
3	X	1	0	-Т-	С/П	ИПА	пп	59	I
ПП	51	5	пп	51	1	ПП	51	6	ПП
51	1	ПП	,51	5	ПП	51	ИПС	+	ПС
В/0	X	ипс'	+	ПС	ИПА	ИПВ	+	ПА	. • .
• • •	• • •	• • •	. • • 4	 • •	• •	• « в	. а в .	а . •	. В/Э-
При интегрировании методом Чебышева интеграл (5.29) подста-
Л0ВКОЙ
* = —i— + —— *	(5.30)
+ *
Z= р(/)Л = -|-£/(/.).	(5.31)
-1 .1=1
производится из условия, что выражение (5.31)
вида /, tz, ts, .... tn, т. е. для полиномов
приводится к виду
Выбор значений Л
будет точным для
вплоть до л-й степени. Для микро-ЭВМ представляют интерес слу-
чаи, когда п = 2 (/1, 2 = Т V3/3 = ТО,57735 для i = 1, 2) и п — 3
(А, э = F д/Т/2 = Т 0,707107 для 1=1,3 И. t2 = 0 для I = 2).
Программа 5.51. Интегрирование методом Чебышева для п — 2.
Ввод: данные f (х) при х, заносимом в начало фрагмента вычисления
f(x), tn, b и а в регистр X (регистры 0, 1, 2, А, В, С и Д заняты).
ПО	3	Ру-	FBx	-Т-	ПД	0	ПС	с/п	
с/п	П1	-	ИПО	-4-	П2	ИП1		ИП2	+
П1	XY	пп	30	FL0	16	ИПС	ИПВ	X	с/п
ПВ	+	2	—	ПА	ИПВ	-=—	ПВ	ИПД	/-/
ПП	44	•ИПВ	ИПД	X	ИПА	+	...	 . •	
• ..	...	...	• ..		.. .	ИПС		ПС	В/0
Программа 5.52. Интегрирование методом Чебышева при п = 3«
Ввод см. в программе 5.51.
ПО	2		FBx -г-		ПД	о	ПС	с/п	
с/п	П1	•—	ИПО	-4-	П2	ИП1	1	ИП2	+
m	XY	пп	34	FL0	16	ИПС	ИПВ	X	2
X	3	—	С/П	ПВ	+	2	*4“	ПА	ИПВ
—	ПВ	ИПД	1-1	ПП	51	ИЛА	ПП	54	ИПВ
ИПД	X	ИПА	+	...	. . о	ИПС	+	ПС	В/0
При интегрировании методом Гаусса также выполняется под-
становка (5.30), причём
+ 1	п
J	(5 32)
-1	1=1
а выбираются как корни полинома Лежандра. Абсциссы h распо-
ложены неравномерно из условия наилучшего приближения J (У) по-
линомом Лежандра. При этом (5.32) оказывается точной для поли-
номов до (2л — 1) й степени.
При п _ 2, i=l, 2 имеем At 2 = 1 И Т V1/3 =а
= ТО,57735027, при n==.3,’l = 1, 2, 3 имеем Д1, з = 5/9, Аг = 8/9,
/t 3 = + V6/5 = =F 0,77459667 и t2 — 0.
Программа 5.53. Интегрирование методом Гаусса при п = 2,
Ввод см. в программе 5.51.									
ПО	3	Fl/x	F<	ПД	0	ПС	С/П	t	С/П
П1	—	ИПО		П2	ИП1		ИП2	+	П1
ХУ	пп	27	FLO	15	ИПС	С/П	ПВ	+	2
	ПА	ИПВ	—	ПВ	ипд	/-/	ПП	41	ИПВ
ипд	X	ИПА	+	ПП	52	ИПВ	X	ИПС	+
ПС	В/0	...	•..	...		...	• • • X	...	В/0
Программа 5.54. Интегрирование Ввод см. в программе 5.51.						методом	Гаусса при		п = 3.
ПО	0		6	F<	ПД	0	ПС	С/П	t
С/П	П1	—	ипо		П2	ИП1	t	ИП2	+
П1	ХУ	ПП	28	FL0	16	ИПС	С/П	ПВ	+
2	-4-	ПА	ипв	— _	ПВ	ипд	/-/	ПП	48
ИПА	пп	63	8	ПП	54	ипв	ипд	X	ИПА
+	пп	63	5	X	ИПВ	X	9	-j-	ИПС
+	ПС	В/0	...	- • •	• • •	• • .	. . •	...	В/0
Погрешности, присущие методу численного интегрирования Гаус»
са при п = 2, 3, определяются остаточными членами [5]
Из табл. 5.4 и 5.5 следует, что с ростом пит точность инте-
грировання растет. Обычно для получения требуемой точности на-
ходят 1 при разных т (2, 4, 8, 16 и т. д.). Точными считают совпа-
дающие знаки результата. Кроме точности при проведении интегри-
рования надо учитывать сложность программы, число занятых ею
регистров памяти и наличие у подынтегральной функции особенно-
стей, например вида 0/0, оо/оо или f(x) -> 00. Если есть особенность
при х-*-а или х-+Ь, то предпочтение отдается методу Гаусса, т. к.
у него абсциссы f(x) никогда не попадают на концы интервала [а, 6].
Если особенность появляется в середине интервала [а, 6], предпочти-
тельней использование методов с равномерным и легко предсказы-
ваемым положением абсцисс (Симпсона, Ньютона1—Котеса, УэддляЧ.
Интегрирование таблично заданных функции обеспечивается по
следующей программе. Число интервалов разбиения л при 'вычисле-
ниях по этой программе должно быть четным.
Т а б л и ц а 5.5
Интеграл и его точное значение	Про- грамма	Метод	т	Результат /	Время счета, мин
	5.48	Бодэ	4	0,907455186	2
	5.49	Ньютона — Котеса	4	0,90745414	3
5		прн и=6			
л -X3 ХЧ-16 djc=a	5.50	Уэддля	4	0,90745401	3
1	6.51	Чебышева при п—2	8	0,90745077	2,5
=0,907X539	. 5.52	Чебышева при п=3	8	0,9074528	3
	5.53	Гаусса при я=2	4	0,90737764	1,5
	5.54	Гаусса при п=3	4	0,90745631	2,5
	5.48	Бодэ	4	1,3987174	2
	5.49	Ньютона — Котеса	4	1,3987175	3
1		при			
д/1+2х dx—	5.50	УэддлЯ	2	1,3987174	2
0	5.51	Чебышева прн п=2	8	1.3987176	2,2
= 1,3987175	5.52	Чебышева прн л=3	8	1,3987175	2,6
	«.53	Гаусса прн п=2	4	1,3987198	1,6
	5.54	Гаусса при п=3	4	1,3987174	2
Программа 5.55. Интегрирование таблично заданных функций
методом Симпсона. Ввод: h = Р8, число интервалов разбиения п,
ординаты j/o, j/i, ..., уп в регистр X. .
ПО	С/П	П9	С/П	КИПО	XY	4	X'	ИП9	+
П9	С/П	ф	ИП9	+.	+	FLO	02	FBx	ИП8
X	3	4-	С/П	БП.	00 '
Если h — 0,25, п = 4, уо = 3, yt = 4, у2 — 5, уз = 6 и «Л = Т->
получим I = 5.
5.10. Решение дифференциальных уравнений
Решение обыкновенного дифференциального уравнения (вида
К.ош‘и)
у' — dyjdx = f (х, у)	' (5.33)'
заключается в нахождении функции у(х), удовлетворяющей урав-
нению (5.33) прц известных начальных условиях х« и уо = у(хе).
При одношаговых методах решения каждое новое, значение yi+.t
находится по известному предшествующему, значению yi. Этим ме-
тодам..присуще «самостартование», а..также возможность изменение
шага й = х,ц — х, в процессе вычислений.. Реализация численных!
методов решения (5.33) заключается в разложении функций у(х) в
ряд Тейлора,' у которого берется некоторое число членов, опреде-
ляющее порядок п метода [1—8]. Погрешность решения (5.33) про-
порциональна hn+l.
Программа 5.56. Решение дифференциального уравнения про-
стым методом Эйлера (первого порядка):
Ввод: данные f(xz, yt) при х,-->-РВ, у;->РС, хо = РВ, уа = PC и
/г = РД. 
ИПВ ИПД + ПВ .......................................
ИПД X ИПС + ПС ИПВ С/П БП 00
Для контроля этой и последующих программ решим простое
дифференциальное уравнение
у' — dyjdx — —у/г,	(5.34)
аналитическое решение для которого известно:
У(х) = ехр(—х/г).
Фрагмент вычисления f(x, у) — —у/х имеет вид:
ИПС /—/ ИП9
Введя исходные данные: хз = 0, уз = 1, h = 0,1 и t = 1 = Р9, на-
жав клавиши В/0 и С/П, получим xt — 0,1. Нажав клавишу XY, из
регистра Y вызываем yi — 0,9. Далее, нажимая поочередно клавиши
С/П и XY, будем получать значения xz = 0,2, у2 = 0,81, хз = 0,3,
уз = 0,729 и т. д.
Для повышения точности вычислений шаг h целесообразно де-
лать малым, а вывод результатов производить с большим шагом
Н = Nh. Это реализует следующая программа.
• Программа 5.57. Реализация простого метода Эйлера с выдачей
результатов с шагом Н = Nh. Ввод: данные f(x, у) при х->РВ и
у->-РС, N = РА, хз = РВ, у» = PC и Л = РД.
ИПА ПО	ИПВ	ИПД	+	ПВ	.......... ИПД	X
ИПС +	ПС	FL0'	02	ИПС	ИПВ С/П БП	00
Для приведенного выше примера и N = 5 будем получать
Xi = 0,5, yi = 0,59049, xz = 1, у2 = 0,34867844, хз = 1,5, уз =
= 0,20589114 и т. д.
Программа 5.58. Решение дифференциального уравнения моди-
фицированным методом Эйлера (второго порядка):
У i+i = Vi + kf (xt + Л/2; у*+0.5),
где
1//+0,5 = Vi + N (xit уj)/2.
Ввод: данные f(x, у} при ^-->Р0 и #->PA, х0 = РВ, j/0 — PC н
ft = РД. Вывод: X; -* РХ = РВ, yt -> PY = PC.
ИПВ	ПО	ИПС	ПА	ПП	33	ИПД	X	2	4-
ИПС	+	ПА	ИПВ	ИПД	2	4-	+	ПО	ПП
33	ИПД	х	ИПС	+	ПС	ИПВ	ИПД	+	ПВ
С/П БП 00	.................................в/0
' Для ранее приведенного примера имеем Xi = 0,Г, yi = 0,905,
Хг = 0,2, у г = 0,819025, х3 = 0,3', уъ = 0,74121763 и т. д.
Простейшей реализацией методов прогноза и коррекции явля-
ется усовершенствованный метод Эйлера — Коши, В нем сначала
вычисляется приближенное значение
= + Vi)
простым методом Эйлера (прогноз). Затем оно корректируется с по-
мощью формулы
{/,-+! = yt + у h [f (xt, yt) + f (xf+1, y;+1)].
Программа 5,59. Решение дифференциального уравнения усовер-
шенствованным методом Эйлера — Кошн. Ввод: данные f(x, у) при
х—>РВ, j/->PA, хо ~ РВ,' уо - PC и h = РД. Вывод: х/->-РХ
,= РВ, j/f->PY = PC.
ИПС	ПА	пп	29	по	ИПД	X	ИПС	+	ПА
ИПВ	ИПД	+	ПВ	пп	29	ИПО	+	2	ч-
ИПД	X	ИПС	+	ПС	ИПВ	С/П.	БП	00	...
• •.	. • •	•..	•. •	. . .	...	...	.. .	...	В/0
Для использованного выше примера имеем Xi — 0,1, у± = 0,905,
Хг — 0,2, уг = 0,819025, х3 = 0,3, уз — 0,74121763 и т. д.
Программа 5.60. Решение дифференциального уравнения мето-
дом Рунге — Кутта 4-го порядка:
Vt+l = Vi + (*I + 2/<2 + 2*3 +
где
К, = Л/ (хр yt)-, К2 = hf(x{ + Л/2, yt + ^]/2);
К3 = hf (xi + й/2, у{ + ЗД; К4 = hf (х/ + Л, у. + К3).
Ввод: данные f(x, у) при х->-Р0 и j/->PB, Л/2 = РА, хо = РЦ
Уо — РХ (регистры 0, А, В, С и Д заняты)'. Вывод: Xi~>PX — Р0,
jq->PY —РВ.
ПВ	ПС .	3	X	ПД	ПП	34	ПД	ПП	30
+	ПД	пп	34	+	ПД	F,	ИПВ	+	ПВ
ПП	30	3	4-	ПВ	ИПО	С/П	ИПВ	БП	01
ИПА	ИПО	+	по=	...		> . •		ИПА	X
t .	ИПС	+	ПВ	F,	л	1	ИПД	+	В/0
Для  указанного ранее контрольного примера будем иметь Xi ==)
= 0,1, </4 = 0,9048376, Х2 = 0,2, у2 = 0,81873086, Хз = 0,3; у3 =1
= 0,7408184 и т. д.
В табл. 5.6 дано сравнение результатов решения уравнения (5.34)
методами Эйлера и Рунге — Кутта. Хотя точность последнего суще»
ственно выше., время вычисления также возрастает. Поэтому, если
погрешность решения дифференциального уравнения относительна
велика (порядка единиц процентов), то применение даже простого
метода Эйлера вполне возможно (табл. 5.6).
Таблица 5.6
X	Метод *)				Точное решение
	Эйлера простой	Эйлера модифици- рованный	Эйлера — Кошн	Руиге— Кутта	
0	1	1	1	1	1
0,1	0.9 .	0,905	0,905	0,9048375	0,90483743
0,5	0,59049	0,60707576	0,60707578	0,6065309	0,60653064
1,0	0.34867844	0,36854098	0,368541	0,36787976	0,36787944
1,5	0,20589114	0,2237323	0,22373232	0,22313042	0,22313016
.2,0	0,12157667	0; 1'3582248	0,13582247	0,13533549	0,13533529
'*) Время вычи^еНий "указанными методами' составляет на одном шаге					
соответственно 5, 13, 12 н 30 с.
К многошаговым методам решения дифференицальных уравне-
ний относится метод Адамса. В нем по ряду предшествующих зна-
чений у'(х) с помощью полинома Лагранжа вычисляется очередное
значение у(х). В- зависимости от числа предшествующих значений
11’(х) порядок метода- Адамса может быть различным. Достоинство
метода — вычисление очередного значения у1+1 требует- лишь одного
обращения к функции f(x, у), что заметно ускоряет'счет при слож-
ных f(x, у). Однако метод Адамса лишен возможности «самостарто-
вания», так как предварительно надо найти, ряд предшествующих
значений у'(х) какими-либо другими методами.
Программа 5.61. Реализация метода Адамса второго порядка:
!h+i == У1 + h Vi-1)/2-
Ввод: данные у’.=1{к,'у) при %->-РА и.{/->РВ, (хо + Л)=РА,
Vi = РВ, j/g = PC и h = РД. Вывод: xi -» РХ = РА, yt -> PY= РВ.
ПП	23	ЙПС XY	ПС	3 X '	-	ИПД	/-/
X	2-ИЦВ.	4-	ПВ ИПА	ИПД	+	ПА
С/П БП 00	...	'................. ...	’В/0
Решим уравнение (5.34) при Хо — 0, у о == 1, т = 1 и h — 0,1.
'Для старта воспользуемся результатом расчета yt — 0,905 при
Ki = 0,1, вычисленный по методу Эйлера — Коши. Имеем также
=—Уо/Х=—1- Введя эти данные, будем получать значения Xi
и yi, начиная с 1 = 2, приведенные в табл. 5.7.
Таблица 5.7
X	Метод *)				Точное зн ачение
	Адамса 2	Адамса 3	Адамса 4	Эйлера — Адамса 2/2	
0					L	1
0,1	—	—	—	0.905	0,90483743
0,2	0,81925	—-	—-	 0,81923	0.81873072
O.3	0,7416125	0,74078578			0.7416125	0,74081822
0,4	0,67133313	0.6702644	0,67032315	0.67133313	0,67032004
0,5	0,60771379	0,60645471	0,60653567	0,60771379	0,60653064
1,0	0,36940619	0,36775653	0,36789008	0,36940619	0,36787944
1,5	0,22454802	0,22300898	0,22314117	0,22454802	0,22313016
2,0	0,13649423	0,13523351	0,13534472	0,13649423	б,'13533529
*) Время вычисления указанными методами на одном шаге составляет
соответственно 8, 10, 13 и 10 с.
Программа 5.62. Реализация метода Адамса третьего порядка:
У1+1 = Ui + h {^y'i т + 5^_2)/12.
Ввод: данные у' = f(x, у) при х->-Р0 и j/->PA, (хо + 2/г) = Р0,
yi — РА, у{ — РВ, у'д *= PC и h — РД. Вывод: х;->РХ = Р0,
z/z-^PY = РА.
ИПС	5	X	ИПВ	ПС	1	6	х4	—	П1
ПП	33	ПВ	2	3	X	иш	+	ИПД	X
1	2	—-	ИПА	+	ПА	ИПО	ИПД	+	ПО
с/п	БП	00	I . .		• •.	• • •	...		В/0
Для контроля этой программы по приведенному выше примеру
воспользуемся дополнительно результатами, полученными методом
Рунге — Кутта: уг = 0,81873086, у{~ — 0,9048375 и у'а = — 1. Ре-
зульуяты вычислений даны в табл. 5.7.
Программа 5.63. Реализация метода Адамса четвертого порядка:
Vi+l = Vi + h (&Уi — Styi-i + 37/4„2 — 9//f_3)/24.
Ввод: данные y'—f(x, у) при *-*Р1 « К**Р0. (•*<> +3ft) Р1,
у3 = р0> у'2 = ра, у{ = РВ, = PC и ft = РД. Вывод: Xl-> РХ =.
= Р1, у.--	PY = РО-
ИПС	/-/ 9 X ИПВ ПС 3	7 х +
ИПА	ПВ 5	9	X — П2 ПП 40 ПА
5	5 X ИП2 + ИПД X 2	4	—
ИПО	+ ПО ИП1 ИПД + П1 С/П БП 00
...		В/0
Результаты вычислений контрольного примера-решения (5.34)’	
по этой программе даны в табл. 5.7. Значения у:) — — 1, yi =
= —0,904837, у-2——0,81873086 и j/3 = 0,7408184 взяты из решения
дифференциального уравнения (5.34) методом Рунге — Кутта.
Как видно из сравнения табл. 5.6 и 5.7, метод Адамса дает су-
щественный выигрыш во времени вычислений на одном шаге по
сравнению с одношаговыми методами аналогичного порядка. Это
достоинство можно сочетать ,с возможностью «самостартованпя»
одношаговых методов, что иллюстрируется следующей программой.
Программа 5.64. Реализация комбинированного метода Эйле-
ра-Адамса. Ввод: данные у' — f(x, у) при х-*РА и у-»-РВ,
Хо = РА,	, уо — РВ	и ft =	РД.	Вывод:	>-РХ=РА,	#/->PY = РВ.
ПП	44 ПС	ПП	33	ПП 44 ИПС	+ ипд
X	2	-4-	ИПО	+	ПВ ИПА С/П	ПП 44
ИПС	XY ПС	3	X	2	I-/	= ПП
33	БП 17	ипд	X	ИПВ по +	ПВ ИПА
ипд	+ ПА	В/0		...	... В/0
При	нажатии клавиш		В/0	и С/П эта программа	сначала вычис-
ляет j/j->PB.h у0->РС усовершенствованным методом Эйлера.
Затем при нажатии только клавиши С/П значения xi н tjt вычисля-
ются методом Адамса. Если по ходу вычислений надо сменить шаг ft,
новое значение h заносится в регистр Д и нажимаются (как при
первом пуске) клавиши В/0 и С/П (далее только С/П). Результаты
вычислений приведены в табл. 5.7.
Помимо описанного ранее метода прогноза и коррекции (усовер-
шенствованного метода Эйлера — Коши) на микрокалькуляторах
просто реализовать двухшаговый метод [6], базирующийся на фор-
мулах прогноза
V*i+i =yi + 2hl (xz, yt)	(5 35)
и коррекции
= +	+	^+i)l	<536)
Программа 5.65. Реализация метода прогноза (5.35) и коррек-
ции (5.36) второго порядка. Ввод: данные у’ — j(x, у) при РВ,
^-*P1, f (JC1, У1) = РО, уо = РА, Xi = РВ, yi = PC и h = РД. Вы-
вод: xi	->РХ	= РВ,	PY — PC.						
ИПВ	ипд	+	ПВ	ИПО	ипд	X	2	X	ИПА
пп	30	ИПО	1	ипд	X	2		ИПС	ПП
30	по	ИПС	ПА	ИП1	ПС	ИПВ	С/П	БП	00
	П1		...	...	...		•..		В/0
Возьмем для старта данные модифицированного метода Эйлера
(см. выше контрольный пример): х0 = 0, уа — 1,	= 0,1, yi =
с= 0,905, f(.Xi, yt) = —у tlx — —0,905 при х = 1 и h — 0,1; нажи-
мая клавиши С/П (при первом пуске В/0 и С/П) и XY, будем полу-
чать данные: х2 = 0,2, у2 = 0,8188, х3 — 0,3, у3 — 0,740798, Х4 = 0,4,
yt — 0,67022608 и т. д. '
Точность методов прогноза и коррекции можно несколько по-
<21
высить, уточнив окончательное значение	по результа-
там вычисления y^j при прогнозе и при коррекции по форму-
ле [6]
«4+1 =	(5-37)
Программа 5.66. Реализация метода прогноза и коррекции с
уточнением результата по формуле (5.37). Ввод и вывод см. в про-
грамме 5.65.
ИПВ	ИПД	+	ПВ	ИПО	ипд	X	2	X	ИПА
+	ПП	37	ИПО	+ '	ипд	X	2		' ИПС
ПА	+	4	X	ИП1	+	5	+	пс	ПП
37	ПО	ИПС	ИПВ	С/П	БП	00	П1	...	В/0
Воспользовавшись для старта этой программы значениями
yi = 0,9048375 и f (xt, yt) = —0,9048375, найденными методом Рун-
ге — Кутта, будем получать следующие данные: х2 = 0,2, у2 =.
= 0,8187217, хз = 0,3, у3 = 0,7408034, Xt = 0,4, yt = 0,67030034
и т. д.
Недостатком всех описанных выше методов является возникно-
вение числовой неустойчивости решения при большом шаге h. Так,
при решении дифференциального уравнения (5.34) неустойчивость
возникает при h х, поэтому следует брать It < т. Неустойчивость
отсутствует у так называемых неявных методов, у которых yi'+t на-
ходится по значению f(x?, yt+t). Детальное рассмотрение этих спе-
циальных методов выходит за рамки данной книги. Отметим лишь,
что сочетание ивного и неявного методов Эйлера приводит к выра-
жению
j/f+i = yt + й[#(х„ yi) + (1 — A)f(xit 4ч+1)],	(5.38)
причем при А — 1 реализуется явный метод Эйлера, при А — О —
неявный, а при 0 < А < 1 — комбинированный [16]. При этом не-
устойчивость отсутствует, если 0 < А < 0,5. Погрешности ивного и
неявного методов по модулю близки (пропорциональны Л2), но по
знаку различны. Поэтому при А 0,5 имеет место значительно
меньшая погрешность, чем у этих методов, используемых в отделы
ПОСТИ.	. '			' !
В общем случае уравнение (5.38) решается итерационным мето*
дом. Однако иногда его можно разрешить относительно t/z+i в яв«
ном виде. Приведем пример.
Рис. 5.4. Интегрирующая 7?С-цепь (а) и пример расчета ее реакции
на заданное входное воздействие (б)
, Реакция и (Г) интегрирующей ЛС-цепи (рис. 5.4) на воздействие
eft) определяется’ из решения дифференциального уравнения
и' «)--% = e(t) — u
' dt т
где т = RC. Для такого.уравнения из (5.38) при x—e(t) и у.=и(1)
имеем
= «» 4-
[*(*<)-“d Ah
1	" т
(1-A)[e(/f+,)-«;+i]ft
‘	т
Разрешим последнее уравнение относительно ui+i и получим
_ 4+ [*(',) - «,] AW + (1 - л)«(//+1) Л/Т
z+‘	1 + (1 - А) й/т	’	(5'39)
Программа' 5.67. Вычисление реакции /?С-ц'епи на воздействие
e(t) комбинированным (явным и неявным) методом Эйлера (5.39).
Ввод: данные e(t) при /-> РВ, А = РА, /о = РВ, йа = PC, ft = РД
И т = RC = Р9. Вывод: 4 -^РХ, in -> PY = PC и e(ti) -> Р6.
ИПВ	ПП • 42	ИПС		ИПА	X	ИПД	ИП9	-1-
П8	X ИПС	:+-	П7	ИПВ	ИПД	+ 	ПВ	ПП
42 ;	ИП8 X	1	,ИПА	т—	X	ИП7	+	1
ИЦА	т- ИП8	X	1	+	-4-	ПС	ИПВ	С/П
БП	00	...		. •.	. . .	.  •	. •«	П6	В/0
Пусть надо найти реакцию ДС-цепи на двухэкспоненциальный
Ймпульс
е (/) = UB — е-Цъ).
Для этого в программу вписываем фрагмент вычисления е(/) в
виде подпрограммы (n = Р1, т2 = Р2. UB — РО).
ИПВ /-/ ИП1 4- Fe* ИПВ /-/ ИП2 -т- Fe*
— ИПО X
Введя исходные данные А = 0,5, fB = 0, ив — 0, h — 0,2,
UB — 10, т = 1, Ti = 1 и- т2 = 0,5, получим /1 = 0,2, u(ti) =
;== 0,1349188, /2 = 0,4, и(/2) = 0,44620789, ts = 0,6, u(ts) = 0,7910869
и т. д. (рис. 5.4, б). Единицы измерения /, т, Ti, т2,' UB и и — секун-
ды и вольты.
Системы дифференциальных уравнений первой степени решаются
описанными выше методами. Остановимся на решении часто встре-
чающихся систем из двух дифференциальных уравнений вида
=	1/. z), z = —= <р(х, у, z).	(5.40)
Решение системы (5.40) простым методом Эйлера сводится к вычис-
лениям j//+i и Z/+1 по формулам Эйлера.
Программа' 5.68. Реализация простого метода Эйлера для си-
стемы из двух дифференциальных уравнений вида (5.40). Ввод: дан-
ные f(x, у, z) и ф(х, у, z) при х->-РА, у -> РВ й z~>PC, хо = РА,
уо = РВ, Zo = PC и h = РД. Вывод: xt -► РХ = РА, yi PY = РВ
и z, -> PC.
........................	ИПД	х	ИПВ	+	ПО
.............	...	...	...	ИПД	х	ИПС	+
ПС ИПО ПВ	ИПА	ИПД	+	ПА	С/П	БП	00
Модифицированный метод Эйлера (второго порядка) для си-
стемы (5.40) реализуется выражениями
=	+	yi’ Zi\ yi + \ = Vl + hf +	y’i+l’
ZI+1 = Z/ + 44’(X«’ У1' Zl\ Zi + l = Zi +	(*i + 4’ Vi' Zi + 1)
и следующей программой.
Программа 5.69. Реализация модифицированного метода Эйлера
для системы (5.40). Ввод: данные f(x, у, г) и <р(х, у, z) при Р0,
РА и z — PC, Л/2 = Р9, хв = Р0, ув = РА = РВ, z0 — PC =»
.== РД. Вывод: xt ч- РХ = Р0, у, -> PY = РА. и zi -> PC.
ПП	24	X	П9	FBx	ИПО +	ПО	ПП	24
XY	—	П9	ИПО	+	ПО ИПС	ПД	ИПА	ПВ
ИПО С/П БП 00	............. ...............
ЙП9 X ' ИПВ + П1 ...................................
ИП9 X ИПД + ПС ИП1 ПА 2 ИП9 В/0
Для проверки двух последних программ решим систему диффе-
ренциальных уравнений
-^ = 2,
dx dx \ х ) х J
определяющих табулированные функции Бесселя л-го порядка [1, 2,
6]. При й/2 = 0,025, п — 1, хо = 0,2,	= 0,09950083 и г0 = 0,49235
будем получать данные, приведенные в табл. 5.8 (даны выборочно).
Таблица 5.8
Х1	Метод		Точное решение У (*)==/ (х)
	Эйлера простой	Эйлера модифицированный	
0,2	0,09950083	0,09950033	0,09950083
0,3	0,14855151	0,14832009	0,14831881
0,4	0,19867502	0,19603182	0,19602657
0,5	0,24350396	0,2422791	0,2422684
1	0,44633959	0,44008729	0,44005058
2	0,59549752	0,57069725	0,57672480
4	-0,074593343	-.0,06634331	—0,066044332
4,5	-0,25419072	-0.23126802	-0,231060431
Дифференциальные уравнения и-го порядка сводятся к систе-
мам из п уравнений первого порядка, которые решаются описанны-
ми выше методами (см. приложение 3 и [29j).
5.11. Спектральный анализ
Периодическая функция, зависящая от времени, с периодом
Т — J/(0> удовлетворяющая условиям Дирихле [1,2], может быть
разложена в ряд Фурье
т
У (0 = -у- + (йл cos + t>n Sin	(5.41)
n=l
ИЛИ
m
y{t)^=~+ An cos (nwi/ — q>n),	(5.42)
n~l
где n — номер гармоники, <0i = 2л/( — угловая частота повторений,
fi — частота повторения первой гармоники; ао, а„ и Ьа — коэффици-
снял ряда Фурье- Точное представление y(t) возможно прн т->ео,
однако на практике обычно используются укороченные ряды Фурье
с конечным значением т.
Программа 5.70. Вычисление y.(t) по разложению в ряд Фурье
"(5.41) с m 6. Ввод; ао 4? а6.= РО 4-Р6; 6» 4-6» = Р7 4-Р9;
bi 4- Ь6 — РА 4- PC, t/T = РХ. При смене t/T очищается, операцион-
ный блок (нажатием клавиш Сх ftf) и вводится новое значение t/T.
Переключатель Р'— Г устанавливается в положение Р1
рл	X	2	X	ПД		F cos	ИП1	X	XY
F sin	ИП7	X	+	+	2	ИПД	X	A 1	F cos
ИП2	X	XY	F sin	ИП8	X	+	+	3	ИПД
X		F cos	ИПЗ	X	XY	F sin	ИП9	X	+
+	14	ИПД	X		F cos	ИП4	X	XY	F sin
ИПА	X	+	+	5	ИПД	X		F cos	ИП5
X	XY	Fsin	ИПВ	X	+	+	6	ИПД	X
Ф	F cos	ИП6	X	XY	F sin	ИПС	X	+	+1
ИПО	2	4-	+	c/n	БП	00			
Если нас интересует				только	форма	P(0.	то член Co/2		может
быть отброшен^ Тогда регистр 0. можно использовать для вычисле-
ния номеров гармоник п = 1, 2, ..., т (т 6) и организации кос-
венной адресации вызова ап и, Ьл из регистров памяти. Использова-
ние квадратных скобок объясняется в описании программы 5.71.
Программа 5.71. Вычисление y(t) по разложению в ряд Фурье.
(5.41) без члена со/2. Ввод: ct = Pl, = Р2, ..., с5 = Р9, Ьъ =:
= РА, се — РВ, be — PC (вводятся коэффициенты. до ат, Ь'т. вклю-
чительно), т = РХ и t/T — РХ. При изменении . t/T  повторяется
ввод только m и t/T.				Переключатель Р — Г в положении Р.					
л. i	2	X	1	+	ПО	0	с/п	Fn	х
2	X	ПД	0		XY	ипд	ИПО	1	—
2	4-	X		F sin	кипо	х	XY	F cos	КИПО
X	+	+	ИПО	1	—	Fx =0	15	XY	с/п
БП 00
Для контроля этих программ вычислим значение: ряда (5.41)
при. т = 3 и следующих данных: а0 = 0, at,= --5,23, с2 = 0,. сз =
~ 5,1, &1 = 25,3, Ьг 0 и Ьз — 3,47. Так как т — 3.< 6, то из про-
граммы 5.70 можно исключить фрагмент, заключенный в квадратные
скобки. Введя коэффиценты с„, 6, с помощью программ 5.70 и
5.741, будем получать следующие значения- у(г/Т): р(1/24) =
=7,5562347, ^(8/24)=29,625443, у( 13/24) =-7,5562351, */(20/24) =
=ч —29,625444 и т. д. Время счета около 32- с.
‘Программа 5.72. Вычисление */(<) по разложению (542) без
члена  ао/2. Ввод: Ai = Pl, (ft = Р2, ..., Л = Р9, cps = РА,. Ав =
= РВ,.<рв = PC (вводятся Ап.в фл до. Ат и ф/л включительно), ш..=;
— рх и ЦТ = РХ. При изменении ЦТ повторяется ввод только nt
и ЦТ.
ж 1	2	X	1	+	по	0	С/П	Fn	X
2	X	ПД	0		XY	ИПД	ипо	1	—
2	Ч-	X	кипо	—	F cos	кипо	X	+	ипо
1	—	Fx = 0	15	XY	С/П	БП	00		
х = Xjw cos <0[Г + х0, применяется
Рис. 5.5. Иллюстрация к ме-
тоду пяти ординат
Пример: для А = 25,9, <pi = —0,203 рад, Аг — 0, <ра = Q,
Аз = 6, <р3 = 0,973 рад, вводя т = 3 и разные ЦТ, будем получать
р(0) = 28,745108,. г/(1/24) = 29,047034,	{/(3/24) = 15,364754,
у(7/24)= -12,728526 и т. д.
При исследовании систем с малой нелинейностью зависимости
{/.(х), где х — входное воздействие в виде гармонического сигнала
метод пяти ординат [6—8]. С его
помощью по пяти ординатам у(х)
(рис. 5.5) определяются среднее
значение у0 и амплитуды первых
4-х гармоник зависимости' y(t)i
Уо — [(1/1 + Уо) + 2 (1/2 + 1/4)]/6.
У«П = [(1/1 - Уз) + (1/2 - 1/4)]/3,
1/мг = [(1/1 + 1/б)/2 — Уз]/2,
УмЗ = [1/м1 — (1/2 — /МЖ
У «14 — У «а — Уо + 1/3-
Коэффициент нелинейных ис-
кажений
л/fУм2 + Уыз Ч" y«ii/y«il'
Программа 5.73. Реализация метода пяти ординат. Ввод: {/i=P9,
уг = РА, уз — РВ, {/I = PC и {/5 = РД. Вывод: {/0	Р0, {/Mi 4- {/м1 -*
^Р1Ч-Р4, Кг — РХ.
ИПА	ИПС	+	2	X	ИП9	ипд	+	П6	+
6	ч-	по	ИП9	ипд	—	П8	ИПА	ИПС	—’
+	3	4-	Ш	ИП6	2	—	ИПВ	—	2
4-	П2	Fx2	ИП1	ИПА	—	ИПС	+	2	ч-
ПЗ	Fx2	+	ИП2	ИПО	—	ИПВ	+	П4	Fjc2
+	fV"	ИП1	4- .	С/П					
Пустй зависимость [7С (С73) каскада на мощном МДП-траизисто-
ре задана значениями: 46,6(1); '38,9(3,5); 32(6); 26(8,5) и 21(11).
причем t/CI С/с5 ^ {/, 4- {/5. Введя эти значения, получим /<г..=1
— 7,0177955-10-2, у0 — Uc0 — 32,9 В, {/м1 = t/c„i = 12,833333 В,
i/мг =. Ucmz — 0,9 В, {/мз =. t/смз — —0,0333335 В, ущ = Ucw — 0.
Если нелинейная функция у(х) при воздействии x = xMcos«>i£
задана 12-ю ординатами, то коэффициенты «0/2, «„ и Ьп ряда (5.41)
могут быть определены методом 12 ординат по следующей методи-
ке [11:
1.	Записываем 12 ординат функции у(1) и определяем почленно
их суммы si и разности по схеме:
t/i=Pl	р2=Р2	г/3=РЗ	У1 = Р4	р5 = Р5	i/e=P6
ffi2=PC ylt=PB PA у8= Р9' уа=°Р8 — Р7
So-*PC	S|->P1	s2-»-P2	s3->P3	s4P4	s5-> P5	s6-> P6
dt->PB	d2->PA	d3->P9	d4->P8	JS->P7
2.	Вычисляем суммы Oi и разности di по схеме:
So	St	$2	S3
Se	S5	$4
Oo-’-PC	Ot->P1	o2->P2	o3-»-P3
d0 -> Р6	d,	P5	d2 ->	Р4
3.	Вычисляем	суммы	0!	и разности т],	по	схеме:
•	+	d2	d3
d3	dt
01->PB	02->PA	03 -> P9
T]i -» P7 T]2 -> P8
4. Находим значения коэффициентов 2ct по формулам:		bi-i-b5, ao-i-as и значение
.	0,/2+ 0з+ 02 УЗ/2 Ь'~ '	6	..fl0 =	-Ь о>2 4" 0*1 -Ь СГз в 12
. hi + т>г) УЗ/2 . ь2 -  6	а, =	6g/2 -Ц- др Ц- д] *^/3 /2 6
Ь е»~ез Ьз- 6--		о0 — сг2/2 + О|/2 — од
	^2	6
, Уз z bt = —2~ (Th — Т]2);	а3 =	д0 — дг . 6	’
0, /2 + 03-02 УЗ/2		Оо —о2/2—о,/2 + <Тз_
Ьь		 6	—	6
	,а5~-	дг/2 + д0 - д, УЗ/2 . 6
„ do + Oi — (o, + O3)
2o6-----------g ——.
И Этн расчеты на микрокалькуляторе Электроника БЗ-34 реали-
зуются двумя согласованными программами.
Программа 5.74, «. Подготовка данных для расчета методом
12 ординат. Ввод: У\ 4- у а — Р1 4- PC.
ИП1	ИПВ	—	ПВ	ИП1	FBx	+	П1	ИП2	ИПА
—	ПА	ИП2	FBx	+	П2	ИПЗ	ига	—	П9
ИПЗ	FBx	+	ПЗ	ИП4	ИП8	—	П8	ИП4	FBx
+	П4	ИП5	ИП7	—	П7	ИП5	FBx	+	П5
ИПС	ИП6	—	П6	ИПС	FBx	+	ПС	ИП1	ИП5
—	П5	ИП1	FBx	+	П1	ИП2	ИП4	—	П4
ИП2	FBx	+	П2	ИПВ	ИП7	—	П7	ИПВ	FBx
+	ПВ	ИПА	ИП8	—	П8	ИПА	FBx	+	ПА
3	F V	2	4-	ПД	2	С/П			
В- конце этой программы значение -д/З /2 заносится в регистр Д,
а на индикацию выводится цифра 2, указывающая на окончание
вычислений и необходимость ввода второй программы.
Рис. 5.6. Иллюстрация к методу Берга
Программа 5174, б. Расчет bt 4- Ь5, а0 4- as и 2ав.
ИПВ	2	4-	ига	+	ПО	ИПА	ипд	X	+
пп	92	ИП7	ИП8	+	ипд	X	ПП	92	ИПВ
ИП9	ПП	91	ИП7	ИП8	—	ИПД	X	ПП	92
ИПО	ИПА	ИПД	X	ПП	91	ИПС	ИП2	+	П9
ИП1	ИПЗ	+	П8	+	2.	4-	ПП	92	И! 14
2	•"	ИП6	+	П7	ИП5	ипд	X	ПА	+
ПП	92	ИПС.	ИП2	2	4-	.—	ПВ	ИП1	2
4-	ИПЗ	—	ПД	+	ПП	92	ИП6	ИП4	ПП
91	ИПВ	-ИПД	,-ПП	91	ИП7	ИПА	пп	91	ИП9
ИП8		6		С/П	В/0 •				
Пусть у ~’f(x) задана следующими ординатами fl]: yt = 1,
~у2 = 4, уз — 5, у4 = 4, у$ — 3, ув = 3,5, у7 = 3,5, уа = 3,	.= I,
01(| = 0,5, уц = 0,2 и J/12 = 0. Расчет по программе 5,74, с дает
Оо = 3,5, о, = 7,7, <т2 = 11,5, о3 = 6, 0| = 0,3, 02 — 4,5, 03 = 4,
6а = —3,5, 6| — —5,3, б2 = ~2,5, r]i=’J,3 и т]2 — 2,5. Расчет по
программе 5.74,6 дает Ь, =='1,3411057, Ь2 = 0,54848275, Ь3 =
₽ —6,1666666, bi = —0,17320508, &5 = 0,042147616, aQ = 2,3916666,
«, = —1,5566557, а2 = —0,73333333, с3 = —0,16666666, а, =
= ->0,016666666, а5 = тЧ0;О26677:566 .и 2аа = 0,21666666. Данные
вычислений по этим программам и приведенные в [1J полностью
совпадают. Отметим, что обозначения ап и Ьп в [1] соответствуют
Ьп и ап, принятым в (5.41).
Часто нелинейная функция у = f (х) может быть представлена
двумя отрезками прямых (рис. 5.6). Тогда действующая часть вход-
ного воздействия
х (t) — хм cos со/ + Хо
характеризуется углом отсечки
0 = arccos [(хс — Х0)/хм].
Спектр выходных косинусоидальных импульсов для этого случая
вычислен Бергом (6—8] и задается относительными средним^ значе-
нием а0 и амплитудами гармоник:
Уо	sin 0 — 0 cos 0	i/M( 0 — sin 0 cos 0
‘Я® Ум	«(1 — COS О) *	-Ум ~~ 71 (1 — COS 0) ’
_____ умп ___ 2 sin «0 cos 0 — n cos n0 - sin 0
а«— я • л («2 — 1) (1 — cos 0)
' Программа 5.75. Расчет коэффициентов cto, ос, и а„ Берга. Ввод:
« и 0 (в градусах) в регистр X. Переключатель Р — Г в положе-
нии Р.
/по	С/П	Fn	X	1	8	0	-4-	П9	“F cos
117	1	—	Fn	X	П8	ИПО	Fx = 0	28	ИП9
ИП7 X 		ИП9	F sin	—	ИП8	4-	В/0	ИПО	Fx2
1	—	П5	Fx = 0	44	ИП9	F sin	ИП7	X	ИП9
ЧТ—	ИП8	=	В/0	ИПО	ИП9	X	F cos	ИП9	F sin
X	ИПО	X	ИПО	ИП9	X	F sin	ИП7	X	
2	X	ИПб	-4-	ИПО	4-	ИП8	4-	В/0	
	. » Найдем	а0 при	0 = 30°.	Введя	« =	0 = РХ,	а затем	0 =	30 ==:
= РХ, получим ао(ЗО) = 0,11059842. Аналогично: ос0(90) =
>= 0,31830985; O.j (30);— 0,21522308; «2(90)= 0,2122066 и т. .д.
В общем случае для функции у(0, представленной рядом Фурье
(5.41), коэффициенты ап и Ъп определяются выражениями [6—8];
т
ап = -у- у (0 cos n&xt dt	(5.43)
б
и
Т
ьп = у-\у (О sin naj dt.	(5.44)
о
Для ряда (5.41)
Ап (о) == Уа„(<й)2 + «>„(а>)2	(5.45)
определяет амплитудно-частотную характеристику спектра (АЧХ), а
<Рл («) = — arctg [bn (a)fan (о)]	(5.46)
фазо-частотную характеристику (ФЧХ), Отметим, что здесь со =3
=- 2nf = 2nnft —- 2rtn/T.
Если функция y(t) задана N ординатами yi с разбиением перио-
да Г = l/ft на равные отрезки времени Д1, то для численного ин-
тегрирования (5.43) и (5.44) можно использовать метод прямо-
угольников. Тогда будем иметь
ап = yi cos innfti Д1,	Ч (5.47)
1-1
N
bn = yi sin 2nnhi Kt.	(5.48)
1-1
Если y[t)— непериодическая функция, определенная иа конеч-
ном интервале времени [0, to], то она характеризуется спектральной
плотностью
S (/о) = Sc (о) + jSs (со) = S (о) е^ (а‘,	(5.49)
где
1-
Sc (о) — у (/) cos at dt,	(5.50)
Го
' Ss (со) == ( у (0 sin со dt.	(5.51)
о
Интегрирование. (5.50) и (5.51) методом прямоугольников с
учетом условия /о = N&t дает
N
sc = Л/ У у, cos (2 л/ AZZ),	(5.52)
«=1 •
Ss = Ы У yi sin (2л/ Д«).	(5.53)
i-1
Сравнивая (5.52) с (5.47) и (5.53) с (5.48), нетрудно заметить,
что при / = «/1
N
=	= C°S Д^’	(5.54)
- j «1
/V
ДГ ==	S'n (2Я// Д^’	(5.55)
г«=1
Эти соотношения позволяют строить единые программы спек-
трального анализа, как периодических, так и непериодических функ-
ций y(t). После определения (5.54) и (5.55) находится АЧХ спектра
«(/)	Л„(/)Л/	VSc(/)? + Ss (/)2
“дГ = —----------= — -	—-	(5 5&>
и ФЧХ
<₽(/) = arctg [Ss(/j/Sc(/)J.	(5.57)
Для удобства вычислений программы спектрального анализа
строятся так, чтобы по мере ввода у, индицировался номер i орди-
наты yt. Кроме того, если начиная с некоторого номера i > U орди-
наты yi = 0, следует предусмотреть возможность прерывания вы-
числений.
Программа 5.76. Спектральный анализ. Ввод: Д/ = РА, гм = РВ,
f — РХ и (после  нажатия'клавиш В/0 и С/П и высвечивания циф-
ры 1) Уъ Уг, '{/м в регистр-X. Переключатель Р-— Г в полож е-
нии Р. Вывод: S->PX = P6, <p-*PY = P7, NAs/2-»-P8, NAC!2-+
-► P9.
Fn П9	X КИИ6	2 ИП6	X С/П	ИПА П7	X ИПС	ПС ИП6	0 X	П6 П5	П8 F sin
X	ИП8	+	П8	ИП5	F cos	ИП7	X	ИП9	+
П9 .	ИПВ	ИП6	—	F* =	0 11	ИП8	ИП9	4-	F arc g
I	8	0	/-/	X	рл	4-	П7	ИП8	Fx2
ЙП9	Fx2	+	fV	ИПА	X	П6	С/П	БП	00
-Вычислим		S(/)	и ф-(/)	для.	прямоугольного		импульса с		ампля-.
тудой, равной 1 (условная единица);, длительностью 1 мкс и перио-
дом повторения Т — 4 мкс. Взяв N — 32, yt задаем восемью еди-
личными отсчетами (остальные нулевые). Вводим М — 4-10г"в/32с=]
= 0,125-10-6 с = РА, >м = 8 = РВ и частоту f = 2,5-10? Гц = РХ,
Нажав клавиши В/0 и С/П, получим на индикаторе цифру 1, ука-
зывающую на необходимость ввода первого значения yi = y\= 1.
Введя t/i=l, нажимаем клавишу С/П и после обработки первого
отсчета (за время около 10 с) получим на индикаторе цифру 2
н т. д. После ввода последнего ненулевого отсчета Уе = 1 программа
автоматически переходит к вычислению S = 9,0176423-10-7, tp =
= —50,624991°, Nb/2 = 5,5765853 (вызывается из регистра 8) и
Aa/2’= 4,5765856' (вызывается из регистра 9).
Иногда для периодических функций y(t) удобно использовать
разложение в ряд Фурье по синусам:
, N
«/(()= Ло + У Ап sin (2лп</7’)-
П=1
(5.58)
Для такого ряда при А/ = T/N
N	N
л=уAsn=У, yisin
i=l	i=X
N
Acn = l^lL yi C0SAn = '\!Asn + Acn •
1=1
<pn == arctg (Actl/Asn).
Программа 5.77. Вычисление коэффициентов ряда Фурье (5.58).
Ввод: А = РВ, n, yt, уг, yN в регистр X. Вывод: Ал-*РХ = РЗ,
<р„ (в градусах) -+• PY = Р4, <р„ (в радианах)-> Р5, Asn->Р6, Ас„-+-
->-Р7, AsN/2 ->-Р8 и AcN/2 Р9. Переключатель Р — Г в положе-
нни Р.									
ПА	0	П6	П8	П9	ИПА	Fx = 0	25	КИП6	ИП6
С/П	ИП8	-р-	П8	ИПВ	ИП6	—	Fx =	008	ИП8
ИПВ	-4-	С/П	БП	00	2	X	Fn	X	ИПВ
"V*	ПА	КИП6	ИП6	С/П	ПД	ИПА	ИП6	X	ПС
Fsin	X	ИП8	+	П8	ИПД	ИПС	F cos	X	ИП9
+	П9	ИПВ	ИП6	—	Fx = 0	32	ИП9	ИП8	-4-
F arctg	П5	1	.8	0<	X	Fir		П4	ИП8
2	X	ИПВ	-4-	П6	Fx2	ИП9	2	X	ИПВ
Hr	П7	Fx2	+	fV“	ПЗ	БП	22		
Пусть надо найти спектральный состав функции y(t), пред-
ставленной на рис. 5.7 при п 3. Поскольку y(t\ симметрична от-
носительно оси абсцисс, то До = 0 и Az = 0‘. Следовательно! доста-
точно найти А), Аз, ф1 и ф3- Зададим «/(/) при N — 24 только но-
ложительными ординатами: yt = 7, у2 = 11, у3 = 13,5, ул = 15,4,
^5=17,4, р6 = 20,5, р7 = 25,4, ys = 32,5, р9 = 27,7, р10 = 19,2*
уи — Ю и у а — 0. Введя N = .24 = РВ и и = 1 = РХ, нажимаем
клавишу С/П. Высвечивается цифра 1, указывающая на необходи-
мость ввода у\. Вводим У\ = 1 — РХ, нажимаем клавишу С/П
и т. д. После ввода у12 = 0 и нажатия клавиши С/П высвечивается
число 13. Теперь прерываем ввод, за-
даем /V/2=12 = PB и нажимаем
клавиши БП 57 С/П. Получим At —
= 25,836556, нажав клавишу XY, по-
лучим ф|=—11,407519°. Кроме того,
из регистров, указанных в инструкции
к программе, получим <р,=—0,1990988
рад, 4SI = 25,326161, АС1 =
==.—5,1101083, AslM/2 = 151,95697 и
AciNI^ = —30,66065.
Проведя аналогичные действия
для п = 3, получим Аз — 6,1575834,
<Рз = 56,131231°, <рз = 0,9796748 рад,
Аз = 3,431579,	Аз = 5,1127416,
Рис. 5.7. Зависимость y(t)
AssN/2 = 20,58945, ЛсзА//2 = 30,67645. Полученные результаты прак-
тически аналогичны приведенным в [15], оттуда взят данный пример.
При использовании программ 5.76 и 5.77 усеченный m 2./V чле-
нами ряд Фурье дает приближение к y(t) с минимальной средне-
квадратической погрешностью. Однако эта погрешность значительна
в силу двух причин: функция y(t) трактуется как-решетчатая и ин-
тегрирование выражений (5.43) и (5.44), содержащих быстроосцил-
лирующие множители, методом прямоугольников сопряжено с боль-
шими погрешностями.
Для повышения точности спектрального анализа целесообразно
аппроксимировать у(1) ступенчатой линией и -сместить ее на поло-
вину шага Д/, добавив Д//2 к текущему времени. Кроме того, можно
вычислять интегралы в (5.43) и (5.44) на каждом отрезке по точ-
ным аналитическим формулам. Так, для ап в этом случае получим
выражение
N i &.t
an==-T^Lyi S coS[2nnb(/+49]4Wl C+jt)]-
i=l (i-l)Ai
После аналитического вычисления интеграла находим оконча-
тельно [8]:
N
А- =	у yi cos (2лп[, Mi).	(5.59)
М 2	\ лпд М J Lj
j=»l
Аналогичво (5.59) получим
N
Ss „ bnN _ ( sin nnF' Ы А у
д7	2	\ nnfi Д< ) L-i
i=l
yi sin (2лп/| Д/i).
(5 60)
От (5.43) и (5.44) формулы (5.59) и (5.60) отличаются нали-
чием корректирующего множителя, ..существенно повышающего точ-
ность вычисления аг и Ъ„.
Повторное умножение на корректирующий множитель соответ-
ствует кусочно-линейной аппроксимации у(1).
Программа 5.78. Спектральный анализ повышенной точности с
вычислением ап и Ьп по формулам (5.59) и (5.60). Ввод: Д/ = РА,
iM = РВ, fРХ (после нажатия клавиш В/0 и С/П и высвечивания
цифры 1) уъ уг, ..., у» в регистр X. Переключатель Р—Г- в поло-
жении Р. Вывод: S(f)-»- РХ = Р0, A>(f)~* Р7, <₽(/)-> Р8 (в радиа-
нах), <р (f)-> Р9 = PY (в градусах), л/Д/ -> PC, sin nf Lt Inf Д/ -> P4,
W&/2-’-P5, Na/2-+P6, нескорректированные значения Nb/2~>P1,
,Vc/2->P2.
Fn	X	ИПА	X	ПС	0	П6 ?	П1	П2	КИП6
ИП6	С/П	ПД	ИП6	ИПС	X	2	X	ПЗ	F sin
X	ИП1	+	П1	ИПЗ	F cos	ИПД	X	ИП2	+
П2	ипв	ИП6	—	Fx = 0	09	ИПС	Fsin	ИПС	ч_
14	ИП1	X	П5	Fx*	ИП2	ИП4	X	П6	Fx2
F	F V	П7	ИПА	X	ПО	ИПб	ИП6	ч-	F arctg
	/-/	П8	1	8	0	X	Fit	ч-	П9
ИПО	С/П	БП	00						
Описанный метод спектрального анализа повышенной точности
дает весьма малую погрешность особенно в том случае, когда сту-
пенчатая аппроксимация y(t) точна, например, при вычислений спект-
ра прямоугольных импульсов. Так, для примера, приведенного к про-
грамме 5.76, вычисления по программе 5.78 при f — 2,5-106 Гц дают
8(f) = 9,0031637-10~7, (₽(/)=—50,624991°	(—0,8835728 рад),
A,(f) = 7,202531, аА'/2 = 4,5692374, WV/2 = 5,5676318 (нескорректи-
рованные значения равны 4,5765854 и 5,5765854, корректирующий
множитель равен 0,99835443). Из табл. 5.9 видно, что погрешность
значения 8(f) не превышает 1-10-7.
Недостатком программ 5.76 4- 5.78 является необходимость по-
вторного ввода всех ординат yt при смене п или f. Кроме того, даже
при iu — 10 время вычисления S(f) и <p(f) значительно — около 2—•
3 мии. При 1м ^10 можно организовать запоминание yi в регист-
рах .памяти, используя косвенную адресацию к . ним, — см. пример
ниже. У микрокалькуляторов Т1-58С/59 с большим числом регист-
ров памяти можно организовать запоминание до 30 и более
(у Т159) отсчетов yt, что исключает необходимость их повторного
а б л иц a 5.9
Частота f кГц	S(f)		Точное значение S(f)
250	9,0031637-10“7	-50,624991°	9,0031632-1.0—7
500	6,366198 -I0-7	78,750007°	6,3661977-10~ 7
750	3,0010541-IO-7	28,124997°	3,0010544-10—7
1000	1,5835548-10~14	—	0
1250	1,8006325-10—7	-73,124981°	1,8006326-10—7
ввода. Такое число отсчетов достаточно для большинства практи-
ческих задач.
Важным приложением спектрального анализа является расчет
АЧХ и ФЧХ линейных систем по их переходным характеристикам
Рис. 5.8. К аппроксимации a(t)
'(ПХ), заданным в конечном интервале времени (О, /0]. Связь ПХ а(/)
с АЧХ и ФЧХ дается известными выражениями
где	A = а (0) + Ас (со) + jAs (со), fo	(5.61)
	Ас (®) = а' (t) cos (at dt, 0 tn	(5.62)
	(®) •= a' (f) sin co/ dt.	(5.63)
	0	
	d(f)-=Vdc(n2 + As(D2,	(5.64)
	ф (Л = arctg [A, (f}/Ac (f)J	(5.65)
Для повышения точности вычислений заменим a'(t) ступенчатой
кривой, смещенной во времени на —Д//2. Это означает, что ПХ e(f)
аппроксимируется кусочно-линейной функцией — рис. 5.8. При этом
в пределах каждого отрезка времени
а' (/)
Да (/) а;— аг_,
Д/ “ ДГ ’
(5.66)
Воспользуемся описанным выше приемом — интегрированием
(5.62) и (5.63) в пределах каждого шага по точным аналитическим
формулам. Тогда будем иметь [8J:
Л	sinn/AZ л/Д/	N (at — ai^i) cos	(2/ — 1)>	(5.67)
_ sin nf At л*и>~ nfM	w •	(a. — at_j) sin stf Af (2z — 1). z-i	(5.68)
Для микрокалькуляторов Электроника БЗ-34 объем памяти поз-
воляет запоминать до II значений at (три оставшихся регистра ис-
пользуются как служебные). Ввод и вывод д< в процессе вычислений
для упрощения программы целесообразно организовать с помощью
косвенной адресации.
Программа 5.79. Расчет АЧХ и ФЧХ по ПХ, заданной 11-ю ор-
динатами. Ввод: яю = PY, До, Де, .... До, )Д( в регистр X. Пере-
ключатель Р — Г в положении Р. При смене ft-.t после расчета A(fj
и ЧР(/) вводится только новое значение /ДА
1	1	no	XY	С/П	—	кпо	FBx	ИП0	1
—	Fx = 0	03	С/П	Fn	X	ПВ	1	1	no
0	ПС	ПД	ИП0	1,	—	2	X	1 -	—
ИПВ	X	Ф	F sin	XY ’	F cos	кипо	XY	FBx	J'/
ИПС	+	ПС	F,	X	ИПД	+	ПД	ИП0	1
—	Fx = 0	23	ИПС	Fx2	ипд	Fx2	+	F-V	ИПВ
•	ИПВ	F sin	X	С/П	ИПС	Fx<0	70	1	8
0	no	ИПД	ИПС	-T-	ПВ	Fx>0	81	ИП0	/-/
no	ИПВ	F arctg	1	8	0	/-/	X	Fn	—
ИП0	—	БП	13						
В этой программе с помощью анализа знаков Ac(f) и A(f)
обеспечивается представление углов <р(/) в расширенном до ±180°
диапазоне.
Пусть надо построить АЧХ и ФЧХ системы, ПХ которой по-
казана на рис. 5.9, а. Введя программу, нажимаем клавиши В/0 0
С/П. Набираем Дю = 1 и, нажав клавишу f, дв •= 1,02. Нажав кла-
вишу С/П и дождавшись обработки отсчета (он вновь выводится
на индикатор), вводим as == 1,08 и т. д. После ввода До и нажатия
клавиши С/П высвечивается цифра 0. Вводим /Д( — 0,01 и, вновь
нажав клавишу С/П, через время «2 мин получим результат
A (/)= 1,0088276; нажав еще раз клавишу С/П, получим
= —6,1442791°. Значения A(f) и <р (f) для разных /Д/ даиы в
табл. 5.10. Графики рассчитанных зависимостей А(/) и ф(/) показа-
ны на рис. 5.9,
Рис. 5.9. Переходная характеристика (слева) и рассчитанные по ней
АЧХ и ФЧХ (справа)
Таблица 5.10
f А«	A (f)	ф <f>
0,01	1,0088270	—6,1442791
0,02	1,0331342	-.12,82609 -
0,05	1,1341967	—38,690029
0,1	1,0438064	-96,20238
0,125	0,83008103	-125,96085
0,15	0,56762792	-151,63527
0,2	0,23672042	-160,43524
0,3	0,15961459	-198,81658*)
0,5	0,050929582	-269,99994 *)
, *) От показаний индикатора отнимается 180°, так как <р(Л) вышло за
пределы определения отрицательных углсз.
. \ 5.12. Статистические расчеты и реализация метода
Монте-Карло
 Совокупность N некоторых величин Xi (например, данных экс«
перимента) характеризуется начальными и центральными момен"
<гами А-го порядка [1-=—10]
W	N
w=4- X Mk w=4 Е k=L 213> 4> • ••’
i=i	i=i
Центральный момент Mi (х) ~ Q, Обычно k 4.
Для исключения запоминания всех xt Mk рассчитываются по зна-*
чеииям
. 9
Л12 = т2 — т\,
М3 = т3 — 3mjm2 + 2m|,
M4 = «4 — 4mlm3 + 6m|m2 — 3m|. 
Наиболее вероятное (среднее) значение числа в массиве
N
1--1
Вероятная степень отклонения Xi от х — дисперсия
N
c=g2==4-X^-^2=m2-
Величина o—'s/D является стандартным отклонением (или средне-
квадратичной погрешностью).
Рис. 5.10. Функции плотности распределения при разной асиммет-
рии (а) и эксцессе (б)
Для нормального распределения вычисленная дисперсия являет-
ся смещенной. Несмещенная дисперсия
П0 = 4_1 = М21У/(1У-1).
Характер скошенности функции плотности распределения р(-к),
(рис. 5.10, а) определяется значением асимметрии
N
1 = 1
При Д = 0 кривая р(х) симметрична, при / >0 вытянут ее пра-
вый участок спада, а при Л<0-—левый участок спада (рис. 5.10, а).
Показателем остроты пика р(х) (рис. 5.10.6)’, в сравнении с
нормальным распределением, является эксцесс
£• = —Ц-У (xf-x)* = ^-3
AD2 Zu V i )	Л12
i=i	*
Программа 5.80. Вычисление начальных и центральных момен-
тов, среднего, дисперсии, асимметрии и эксцесса. Порядок ввода и
вывода результатов дан в контрольном примере (см. ниже).
ИП6	С/П	П6	ИП1	+	П1	ИП6	Fx2	ИП2	+
П2	ИП6	Fx2	ИП6	X	ипз	+	ПЗ	ИП6	Fx2
Fx2	ИП4	+	П4	FLO	00	ИП1	ИПА	-4-	П1
С/П	ИП2	ИПА	-i-	П2	ипз	ИПА	-i-	ПЗ	ИП4
ИПА	—	П4	ИП2	ИП1	Fxz	—	пв	с/п	ИП1
Fx2	2		ИП2	О	X	—	ИП1	X	ИПЗ
+	ПС	ИП2	2	X	ИП1	Fx2	—	ИП1	
3	X	4	—	ипз	—	ИП1	X	4	X
ИП4	+	ПД	ИПС	ИПВ.		Fx2		F	ч-
С/П	ипд	ИПВ	Fx2	-4-	3	—	С/П		
Допустим, надо найти статические характеристики массива из
JV = 10 случайных чисел: 9, 8, 10, 9, 11, 12, 10, 10, 9 и 11. После
ввода программы вводим N = 10 в регистры 0 и А и обнуляем ре-
гистры 1, 2, 3, 4, 5 и 6. Нажимаем клавиши В/0 и С/П — иа инди-
каторе высвечивается цифра 0. Вводим последовательно все значения
Xi, нажимая клавишу С/П после обработки каждого отсчета (время
обработки около 10 с). После ввода последнего xt нажатие клавиши
С/П ведет к выдаче значения х — 9,9. Еще раз нажав клавишу С/П,
получим 1,29. Для определения Do умножим D на N/(N—1),
нажав клавиши ИПА X ИПА 1----------Ь (значение N хранится в ре-
гистре А). Получим Do = 1,4333333. Далее, нажав дважды кла-
вишу С/П, получим А — 0,19656579 и Е — —0,752539. Значения
mi -т- тк можно вызвать из регистров 1 -4- 4, а Л1г, и Л14 — из
регистров В, С и Д.
По вычисленным значениям к, D, А и Е можно в первом при-
ближении судить о возможных законах распределения чисел хга. Так,
для наиболее часто встречаемого нормального закона А=0 и £=0.
Можно принять закон распределения за нормальный, если значе-
ния А и Е в 2—3 раза меньше значений вспомогательных коэффи-
циентов [2];
U —	/	6(М-1)		_	/ 24/V (N - 2) {N - 3) ~
3 V (А + 1) (А + 3) ’ Ut Л/ (А - 1Д (А + 3)(./V + 5) ’
Программа 5.81. Вычисление вспомогательных коэффициентов
U3 и I/4. Ввод: N — РХ.
ПО	1	—	6		ИПО	1	+	4-	ипо
3		"4”	F V	С/П	ИПО	2	4	X	ипо
2	—	X	НПО	3	—	X	ИПО	1	—
Fx2	—	ипо	5	БП	07				
Для N — 10 получаем U3 — 0,61450986 и = 0,92244356.
Часто случайные величины X и У с нормальными - законами
распределения описывают некоторую функциональную зависимость
У(Х). Взаимосвязь (корреляция) между ними может быть установи
лена с помощью выборочного коэффициента корреляции
N	N w
Е XY - Е х Е
7V = I	W.I W = 1
Программа 5.82. Вычисление выборочного коэффициента корре-
ляции. Ввод: N — РХ, затем после нажатия клавиш В/0 и С/П
высвечиваются значения Xi,				, У1( Х2, У2,		..., Хм,. У»		в регистр X.	
ПО	П1	0	ПЗ	П4	П5	П6	П7	П9	ИП9
С/П	П8	ИП7	+	П7	ИП8	Fx2	ИП6	+	П6
ИП8	С/П	П9	ИП5	+	П5	ИП9	Fx2	ИП4	+
П4	ИП8	ИП9	X	ИПЗ	..+	ПЗ	FLO	09	ИП6
ИП7	Fx2	ИП1	4-	—	ИП4	ИП5	Fx2	ИП1	
—	X	F V	П2	ИПЗ	ИП7	ИП5	X	ИШ	
—	ИП2	4-	П2	С/П	БП	00			
Пример. Найти г для N — 5 значений У(Х): 2(0,95), 4,05(2,1)’,
5,8(3), 8,1 (4,1) и 9,2(4,9). Введя N и попарно значения X и У, по-
лучим г = 0,99872802.
Выборочный коэффициент корреляции может принимать значе-
ния от —1 до 4-1. Близость г к 1 указывает на то, что величины
X и У коррелированы.
Нередко массив случайных чисел характеризуют гистограммой
их распределения, т. е. количеством чисел, попадающих в интервалы
с границами dt, dt, ..., dK. Гистограммы интегрального распределе-
ния строятся путем подсчета числа попаданий в интервалы
(—оо, dt], (—00, ds] и т. д.
Программа 5.83. Обработка массива случайных чисел xt, х2, ...
..., xN для построения гистограмм. Порядок ввода и вывода дан
ниже в контрольном примере.
по	ИПО	С/П	ПО	ИП8	—	Fx <	:о 13	ИГП	1
	П1	В/0	ИПО	И ПЭ		Fx <	:о 23	ИП2	1
-г	П2	В/0	ИПО	ИПА	—	Fx <	: о зз	КПЗ	1
	ПЗ	В/0	ИПО	ИПВ	—	Fx <	: о 40	КИП4 В/0	
ИПО	ИПС	—	Fx < 0	47	КИП5	В/0	ИПО ипд		—
Fx <	0 54	КИП6	В/0	ИП7	1	+	П7	В/0	кноп
иш	С/П	И112	+	С/П	ИПЗ	+	С/П	ИП4	+ 
с/п	' ИП5	+	С/П	ИП6	+	С/П	ИП7 +		с/п
0	Fl/x	С/П							
Пусть нужно -построить гистограмму для 20 случайных чисел:
2,5, 5,15; 3,05;-1,1; 1,7; 3,6; 4,7; 4,65; 6,8; 5,6; 2,3; 2,9; 3,2; 3,8; 4,2,
3,5; 4,8; 5,7; 4,9 и 7,5, Вводим программу, затем границы dj = 1 =
== Р8, dz = 2=P9, ds — 3 = РА, ds = 4 = РВ, d6 = 5 = PC и
de — 6 = РД и записываем 0 в регистры 0 4- 7. Нажимаем клавиши
В/0 и С/П (высвечивается 0), после чего последовательно вводим все
вначения Хд Из регистров 1 Ч- 7 вызываем числа 0, 2, 3, 5, 5, 3 и 2,
характеризующие число попаданий Xi в интервалы с 1-го по 7 й
Нажав клавиши БП 60 и С/П, переходим к вычислению данных для
построения гистограммы интегральной функции распределения. По
мере нажатия клавиши С/П (до появления знака ЕГГОГ, сигнали-
вирующего конец вычислений) будем получать числа 0; 2; 5; 10; 15;
18 и 20 —число попаданий х в интервалы (—оо, di], (—oo.dz], ...
(—о°, d6]. На рис. 5.11 построены гистограммы данного примера.
Рис. 5.11. Гистограммы распределения случайных чисел (а) и инте-
гральной функции распределения (б)
Для построения гистограмм с большим числом интервалов (до
12—13) можно вписать значения di, dz, ..., dw непосредственно в
программу либо формировать их в программе (см. пример ниже).
Пусть нужно построить гистограмму напряжений стабилизации
кремниевых стабилитронов типа Д814А — Д814Д, изготовляемых по
единой технологии с разбивкой на группы по значениям UiT, Такая
разбивка, естественно, требует знания статистического разброса UCT.
Ограничимся рабочим диапазоном UCT = 6-4- 15,5 В и составим про-
грамму, позволяющую группировать Ucr в 13 интервалах с шириной
каждого' из них А Пет — 1 В.
Программа 5.84. Обработка значений Utt для построения гисто-
граммы на 13 интервалах (—°°; 5 В), [5; 6 В), [6; 7 В), ..., [15; 16 В)
и [16 В; оо). Ввод: Un — РХ (после нажатия клавиш В/0 и С/П).
1	3	ПО	О	КПО	ИПО	Fx = 0	03	1	ПД
ИПО	С/П	ПО	ИПО	ИПД	4	+	—	Fx < 0	26
КИПД	1	+	КПД	БП	08	ИПД	1	+	ПД
БП 13
Пусть для UCT имеем значения: 9,3г 10,5; 9,7; 5,6; 6,1; 15,5; 11,2;
8,9; 12,2; 8,3; 7,8; 9,2; 13,8; 9,05; 10,3. По окончании ввода из регист-
ров 1 4- 9, А, В и С вызываем данные для построения функции
р(Ист) — числа: 0; 1; 1; 1; 2; 4; 2; 1; 1; 1; 0; 1.
В основе ряда статистических расчетов лежит метод Монте-Кар-
ло. Он заключается в многократном расчете выходных параметров
у — f(xi, yi, Zi, ...) системы под воздействием входных параметров
X/, yi, Zi, ... с заданными законами распределения. В результате по-
лучается информация о работоспособности системы, разбросе ее вы-
ходных параметров, законах их распределения и т. д.
Основой реализации метода Монте-Карло . является генерация
случайных чисел с равномерным в интервале [0; 1] распределением.
Путем соответствующих преобразований можно получить иные за-
коны распределения.
Программа 5.85. Формирование случайных чисел с равномерным
распределением мультипликативным способом
V„+1 = D[KVn),	(5.69)’
где К = 8/ + 3 и О (A Vn)—дробная часть KVn (в программе взято
/ = 5 и К — 8-5 — 3 = 37). Ввод: начальное случайное число
V’o < 1 = PY.
3	7 X 1 + ПД КИПД XY ИПД —
С/П БП 00
Так, введя Го = 0,1234567 = PY, нажимая клавишу С/П, будем
получать числа: 0,5678979; 0,012222; 0,452214; 0,731918 и т. д. Время
генерации одного числа 4 с.
Программа 5.86. Формирование до 9000 неповторяющихся слу-
чайных чисел с равномерным распределением по формуле (см. [9])j
Уп+1 = Д(11Р„ + л).
Ввод: Vo < 1 = PY.
1	1 X Fsi + ПД КИПД XY ИПД -
С/П БП 00
Для Vo = 0,002 — PY, нажимая клавишу С/П, будем получать
числа: 0,1635926; 0,9411112; 0,493816 и т. л.
Программа 5.87. Формирование случайных чисел с равномерным
распределением по (5.69) преобразованием их в интервал [а, 6]:
Хп = а -р (Ь —~ и) Vп-
Ввод: а = РА, b = РВ, Vo = Р0.
ИПО	3	7	X	1	+	ПД	КИПД	XY	ИПД
—	ПО	ИПВ	ИПА	—	X	ИПА	+	С/П	БП
00
При а — 2, 6 = 3 и Vo — 0,1234567, нажимая клавишу С/П, бу-
дем получать числа: 2,5678979; 2,012222; 2,452214 и т. д.
Случайные числа с некоторыми законами распределения можно
долучать с помощью простых формул преобразования [8, 10]. Наи-
более часто встречается необходимость в генерации случайных чи-
сел с нормальным распределением. Пару таких чисел Rn и R", имею-
щих 0=1их = Я = О, можно получить из пары чисел Vn-i и Va
с помошью формул
J R'n = ^/2ln(l/Vn) cos (2^,,), R" = V2ln(‘/^) sin (2nI\_l)-
,	(5.70)
Программа 5.88. Генерация чисел с нормальным распределением
fn ==s R + RnO	(5 71)
с заданным R и а по формулам (5.69) —(5.71). Ввод: Vo = Р0,
Й = РВ	и	а = PC. Переключатель	Р — Г	в	положении Р.
ИПО	3	7	X	1	+	ПД	КИПД	XY	ИПД
—	ИПО	2	X	Рл	X	F sin	XY	ПО	Fl/x
Fin	2	X	F<	X	ИПС	X	ИПВ	+	С/П
БП 00
При Vo — 0,1234567; R~ 1 и а = 0,1, нажимая клавишу С/П,
будем получать следующие числа: 1,0744877; 0,8771866; 1,0096652
и т. д. Время выдачи одного числа около 11 с.
Следует отметить, что реализация метода Монте — Карло на
микрокалькуляторах из-за большого числа вычислений весьма тру-
доемка и рациональна, если f(xi, yi, ...) является функцией не бо-
лее 2—3-х переменных. Поэтому данный метод более рационально
применять при расчетах на быстродействующих микро-ЭВМ. При
втом нужно особое внимание уделять проверке необходимых зако-
нов распределения случайных чисел, которые нередко заметно отли-
чаются от принимаемых при расчете, что может приводить к зна-
чительным погрешностям.
5.13. Приближение функций
Пусть некоторая функция yt(xt) задана N парами значений абс-
цисс xi и ординат yt. Пусть далее приближенно известен аналити-
ческий вид функции у(х) и нужно найти основные параметры ана-
литической функции, которая с минимальной среднеквадратической
погрешностью приближалась бы к исходной функции yi(xi). Ниже
дай ряд программ, обеспечивающих такое приближение по методу
наименьших квадратов [1, 2, 17] при произвольном расположении
абсцисс xt. Исходные данные во всех программах вводятся в ре-
гистр X в следующем порядке: N, xt, yt, Хг, уг, .... Xn, уц. '
Программа 6.89. Вычисление коэффициентов £>« и £>i линейного
приближения
У — Ьа + btx
по формулам:
. N N	N
X xi Е	yt-N Е xtVi
.	<-! i=l	Ы
~	/ N	X2	N *
\i-1	/	£-1
				/ N		N X			
		6о	-1		bl		1-		
				\£=1		f=l >			
П1	ПО	0	П4	П5	П6	П7	ИП1	ИПО	
1	+ -	С/П	П2	С/П	ПЗ	ИП6	+	П6	ИПЗ
ИП4	+	П4	ЙП2	Fx2	ИП5	+	П5	ИП2	ИПЗ
X	ИП7	+	П7	FLO	07	ИП4	Fx2	ИП1	ИП5
X	—	П8	ИП4	ИП6	X	ИП1	ИП7	X	•и»
ИП8		-ИА	С/П	ИП6	ИПА	ИП4	X		ИП1
4-	ПВ	С/П							
Пусть уi — f(xt) задана N — 5 значениями yi(xt'j: 5,5(2), 6,3(4)’,
7,2(6), 8(8) и 8,6(10). Введя эти данные, получим £>, = 0,395 и
6о=4,75. Следовательно, функция у(х) имеет вид у = 4,75 + 0,395х.
Программа 5.90. Вычисление коэффициентов £>0 и bt гиперболи-
ческого приближения
у = £>о + £>i/x
из решения системы уравнений:
N	N
i-l	i=i
ПО	П7	0	ПЗ
1	+	С/П П9
N	N  N
£>0	1/л:£ +£>12^ l/^i «= У*( Уj/Xf
i-l	i-i
П5	П6	П8	ИП7 ИПО —
С/П П2	ИП6 + П6 ИП9
Fl/x	ИП8	+	П8	ИП9	Fx2	Fl/x	ИП5	+	П5
ИП2	ИП9		ИПЗ	"Т	ПЗ	FLO	07	ИП7	ИП5
X	ИП8	ИП8	X	—	ПО	ИП6	ИП5	X	ИПЗ
ИП8	X	—	ПА	ИПЗ	ИП7	X	ИП6	ИП8	X
—-	ПВ	ИПА	ИПО		С/П	ИПВ	ИПО		С/П
Пусть у =s= f(x) задана N — 8 значениями yt(xt): 12,2(1), 6,8(2),
5,2(3), 4,6(4), 3,9(5), 3,7(6), 3,5(7) и 3,2(8). Введя эти данные, по-
лучим Ьо — 1,9357621 н bi = 10,160173. Следовательно, функция
у = f(x) имеет вид у 1,936+ 10,16/х.
Программа 5.91. Вычисление параметров bt и Ьо степенного при-
ближения функцией
у = Ьахь'
по формулам:
N	N	N
У 1п *1 In yt — N У in xt In у(
L i-1	i = l	i = l
01 = z N \2 N	•
(E InxJ ~N E(Inx/)2
ПО	П7	0	ПЗ	П4	П5	П6	ИП7	ИПО	—•
1	+	с/п	П1	F In	П8	ИПЗ	+	-ПЗ	ИП8
Fx2	ИП4	+	П4	ИП1	С/П	П2	F in	П9	ИП5
+	П5	ИП8	ИП9	X	ИП6	+	П6	FLO	07
ИПЗ	ИП5	X	ИП7	ИП6	X	—	ИПЗ	Fx2	ИП7
ИП4	X	—	~	ПВ	ИП5	ИПЗ	ИПВ	X	—
ИП7		Fe*	ПА	с/п	ИПВ	с/п			
Пусть функция yi = f(x;) задана W = 6 значениями yi(xi): 3(1),
12(2), 27(3), 48(4), 75(5) и 108(6). Тогда получим ba = 2,9999996
н bt = 2. Следовательно, y(x) имеет вид у Зх2.
Программа 5.92. Вычисление параметров а и Ь приближения
показательной функцией
j/ = 10a+6x
путем решения системы уравнений:
N	N	N	N	N
aN + b =	а^Х1 + Ь £ xj = £ (х, 1g У £	.
1=-Г	£=1	х=1	i=l
ПО	П7	0	ПЗ	П5 П6	П8	ИП7 ИПО —
1	+	С/П	П9	С/П П2	F 1g	П1 X ’ ИПЗ
4-	ПЗ	ИП1	ИП6		П6	ИП9	ИП8	+	П8
ИП9	Fx2	ИП5	+	П5	FL0	07	ИП7	ИП5	X
ИП8	ИП8	X	—	ПО	ИПб	ИПб	X	ИПЗ	ИП8
X		ПА	ипз	ИП7	X	ИПб	ИП8	X	—
ПВ	ИПА	ИПО		С/П	ИПВ	ИПО	-г-	С/П	
Пусть при N = 6 yi(xi) имеет значения: 5(1), 9(2)', 12(3), 20(4),
32(5) и 50(6). Введя ,эти данные, получим а == 0,51880038 и 6 =*
= 0,19641628, т.е. у(х) имеет вид Ьг~Ю0>519+0Д9ь\
При приближении функцией
у = ехр(а + М
в программе 5.92 достаточно заменить оператор Fig по адресу 16
на оператор F In.
Программа 5.93. Вычисление параметров Ь1 и Ьо приближения
экспоненциальной функцией
у = 60ехр (&\х)
ио формулам:
по	П7	0	ПЗ	П4	П5	П6	ИП7	ИПО	—
1	+	С/П	П1	Ипз	+	ПЗ	ИП1	Fx2	ИП4
+	П4	ИП1	С/П	F In	П8	ИПб	+	П5	ИП8
ИП1	X	ИПб	+	П6	FLO	07	ИПЗ	ИПб	X
ИПб	ИП7	X	—	ипз	Fx2	ИП4	ИП7	X	—
	ПВ	ИП5	ИПЗ	ИПВ	X	—	ИП7	—	Fe*
ПА	С/П	ИПВ	С/П						
Пусть функция yi(xi) задана N = 9 значениями yi(xi); 3,5(2)’,
5(3), 6,2(4), 9(5), 13(6), 16(7), 23(8), 30(9) и 40(10). Тогда полу-
чим Ьо == 1,9394789 и bt = 0,30528351. Следовательно, функция у(х)'
имеет вид у^ 1,94 ехр (0,3053х).
Программа 5.94. Вычисление параметров а и & приближения по-
казательной функцией
/	У =
из системы уравнений:
	7/			N				N	
Л 1g а	+ 1g й£ Xi = i-1		i = l	yL, lgaj>i 4=1		4- 1g й	4=1	= Х( 1=1	Xt 'g уД
ПО	П7	0	ПЗ	П5	П6	П8	ИП7	ИПО	«—
1	+	с/п	П9	С/П	Fig	П1	ИП6	+	П6
ИП9	ИП8	+	П8	ИП9	Fx2	ИП5	+	П5	ИП9
ИП1	X	ИПЗ	+	ПЗ	FLO	07	ИП7	ИП5	X
ИП8	ИП8	X	—	ПО	ИП6	ИП5	X	ИПЗ	ИП8
X	—	ПА	ИПЗ	ИП7	X	ИП6	ИП8	X	—.
ПВ с/п	ИПА	ИПО	-г-	F10*	С/П	ИПВ	ИПО		FlO*
Пусть функция yi(xi) задана W = 5 значениями tji(xi)-. 6(1),
7(2), 8,7(3), 10,4(4) и 12,4(5). Введя эти данные, получим а —
= 4,9419892 и b = 1,2029501. Следовательно, у(х) имеет вид
4,942- 1,203х.
Программа 5.95. Вычисление параметров а и b приближения
логарифмической функцией
У = a + b Igx
из системы уравнений:				N		N	Л'		
	N	N							
aN + b	tlg			а У lg^ + Й £ (lg^)2 =				X (Vi >g xi)-	
	i=i	i	= 1 .			1=1			
ПО	П7	0	ПЗ	П5	П6	П8	ИП7	ИП0	—
1	+	с/п	П9	С/П	П2 ’	ИП6	+	П6	ИП9
Fig	П1	ИП8	+	П8	ИП9	Fig	Fx2	ИП5	+
П5	ИП1	ИП2	X	ИПЗ	+	ПЗ	FLO	07	ИП7
ИП5	X	ИП8	ИП8	X	—	ПО	ИП6	ИП5	X
ИПЗ	ИП8	X	—	ПА	ИПЗ	ИП7	X	ИП6	ИП8
X	—	ПВ	ИПА	ИПО		С/П	ИПВ	ИПО	
С/П									
Пусть yi		— f (х<) задана			N = 6	значениями		Й-М	: 1(1),
1,451(2), 1,716(3),			1,903(4), 2,048(5) и			2,167(6). Введя эти			данные,
получим	а = 0,99993157 н			b =	1,4997935. Следовательно,				функция
у(х) имеет вид: у о			i 1 + 1,5 1g х.						
Параметры а и			b логарифмического приближения функцией						
				у = «	+ b In х				
могут также определяться по последней программе, если в ней one'
ратор Fig по адресам 20 н 26 заменить на оператор Fin.
Параметры bo, bt и Ь? приближения параболической функцией
у = Йо "Ь biX Ьгх2
определяются из решения системы нз трех уравнений:
N	N	-N
b0N + bl £ Xt + b2 £ x2 = £ Vi>
i=i	i=i	/=1
N	N	NN
b0 E xi + bi £ x2 + b2 J] x? = £ xiVi,	(5.72)
i=l	i=l .	i = l	i=l
N	N	NN
bo E *2i + fci E x3i + ь2 Ё xi = E x2iyi-
i=l	i=l	i = l	i = l
Программа 5.96. Вычисление коэффициентов ba, bi н h2 при па-
раболической аппроксимации [7]. Ввод: 0 = Р1=г=Р2 = ... = Р9
и yi — PY, Xi = РХ (после ввода каждой пары yi, xi нажимаем
клавиши В/0 и С/П, время счета около 50 с). По окончании ввода
нажимаем клавишу С/П и получаем 6о-*-Р7, hj->-P8 и h2->P9
(время счета около 60 с).									
ПА	XY	ПВ	1	ПС	ПД	ПП	79	ипз	П4
5	ПД	ПП	81	ИПВ	ПС	ПП	79	С/П	ПП
26	ПП	32	ПП	37	С/П	ИПб	ИП4		ПП
74	П6 -	ИПЗ	ИП2	ПП .	73	ПЗ	ИП8	ИП7	ПА
ПП	73	П7	ИП9	ИПА	ИП4	ПП	74	П8	ИПА
ИП1		П9	ИПб	ИП4	ПП	73	ПА	ИП4	ИП1
ч-	П5	ИП2	ИП1	-4-	П4	ИПА	П2	ИПЗ	П1
ИП6	ПЗ	В/0	ИП2	X	ИП1	-4-	—	В/0	ПП
83	ПП	83	ИПС	кипд	+	КПД	ИПС	ИПА	X
ПС	ИПД	1	+	ПД	В/0				
Для yi(xi), равных 3,76(2), 4,44(4), 5,04(6), 5,56(8), 6(ГО),
6,36(12) и 6,64(14), получаем ho = 3, bi = 0,4 и bz = —0,01.
Часто используется приближение yi(xi) интерполяционными по-
линомами. Значения  -у (х) в узлах в этом случае точно совпадают
со значениями yt(xi), но в промежутках между ними погрешность
может быть большей, чем при приближении по методу наименьших
квадратов. Кроме того, в этом случае степень полинома п одно-
значно' определяется числом ординат.
Интерполирующая функция может быть представлена полино-
мом Ньютона:
п i
у (х) = b0 + Е bi П (х - х ).	(5.73)
i=l /=0
Для практики удобнее представление в виде
п
У W = Е aixi = а0 + а1х + v2 + • • • + апхП’ <5-74>
-которое можно получить, воспользовавшись следующим алгорит--
мои, реализованным в программе 5.97 [22]:
1.	Задаем j — 0 и Ьп = 0.
2.	Прибавляем 1 к j.
3.	Вычисляем
— ПРИ / + / = «,
I? I	J
[	при / + / < п,
4.	Если / = n + 1, принимаем а1 — Ь^+^ и заканчиваем вы-
числения, в противном случае идем к п. 2.
Программа 5.97. Вычисление коэффициентов bt и а, степенных
многочленов (5.73) и (5.74) при п J- 1	6. Ввод: у, = РХ f, xt =
= PX (i = 0, 1, .... п). Получаем: b0 -г Р7..66->Р2, Для по-
лучения а0 -* Р7, ..., as -> Р2 нажимаем клавиши БП 40 С/П. Для
получения у(х) вводим п + 1 = Р9 для каждого х = РХ и на-
жимаем клавишу С/П. Для смещения начала отсчета х в точку
хj = ха + Д вводим Д — РД = PC — ... =Р(14 — п), (7 — п) =
= Р1 и нажимаем клавиши БП 40 С/П (аа-> Р7, ... а5-> Р2).
ПД	XY	П7	7	Ш	1	4	по	С/П	П8
п,	ИП8	КИПО	—	XY	ИПО	5	1 1 1	ПО	F,
кипо	—	XY	4-	ИПО	6	+	по	’ 6	—
HF1	—	Fx = 0	10	F,	КП1	ИПЗ	кпо	БП	05
иш	1	+	П8	7	+	ПО	6	—	П1
9’	—	Fx=H= 0	79	КИПО		F,	• f	КИП1	XY
киш	X	—	ИП1	2	+	П1	F,	КП1	F,
ИП1	ИП8	—	Fx = 0	56	ИПО	2	БП	45	С/П
f	ИП9	П1	Сх	ИП8	по	F,	X	кипо	+
ИПО	2	+	FL1	85	F,	БП	79		
Пример. Найти bt и су многочленов, аппроксимирующих за-
висимость yt(xi), заданную табл. 5.1. Введя yi(xi), получим: bt> —
= 0,4860966, bi = 0,031793, b2 = —0,032635, Ьз = 0,0189833,	=
= —0,00599965, ио=—0,16166365, с, =0,79047151, я2=—0,36226819,
Оз = 0,07538001 и =—0,00599965. Далее можно найти для
х = 2,45 у (2,45) = 0,49285713.
Максимальную степень многочлена можно повысить с 5 до 9,
если абсциссы xi расположены равномерно с шагом h относительно
значения хе-
- Программа 5.98. Вычисление коэффициентов су многочлена
(5.73), at и функции y(z), где z = x— хс, по формуле (5.74) [22].
Ввод: уц = Р0, yi — Pl, ..., Уп = Рп и п = РХ. Нажав клавиши
В'/0 и С/П, получаем ао->РО, ai->-Pl, .... Оп-*-Рп. Далее вводим
= рх и, нажимая клавишу С/П, - получаем 0о, Oi....ап->РХ
(Bo, at, а2, .... а„ заносятся также в регистры РО, Pl, Р2,	Рл)'.
Для определения по формуле (5.74) для каждого г вводим
п _ рд, z = х — хо = РХ и нажимаем клавиши							БП 78 С/П.		
ПА	Сх	ПД	кипд	ПВ	ипд	1	+	ПС	ИПД
1	+	ПД	ипв	кипд ПВ		XY	—•	ИПС	-г*
кпд ипд		ИПА	—	Fx=0	09	ИПС	ПД	ИПА	—
Fx=	=0 03	ИПА	1	—	ПС	ПВ	ИПВ	1	+
ПД	кипв	КИПД ИПС		X	—	кпв	ипв	1	+
ПВ	ИПА	—	Fx=0	37	ИПС	1	—	Fx=0	35
ПД	С/П	ПВ	 КИПД ИПС			кпд	С/П	ИПС	ИПВ
X	ПС	ипд	1	+	пд	БП	63	t	1
1	Сх	1	F,	X	кипд	+	ИПД	1	—-
ПД	Fx<0 83 - Для указанного		F, выше	С/П БП 78 примера получим ссо			= 0,4860966,		cci —
= 0,0035472167, а2 = —0,0003899, а8 = 2,2583333-10-’, а8 =.
= —6-10-7, а0 = 0,4860966,	= 3,5472167-10"2, а2 = —0,3899-10"2,
а3 = 0,022583333, аз = -6 - 10-8. Для х — 2,45 (г = 0,25) получаем
у(х) = 0,49285719.
5.14. Сглаживание эмпирических данных с ошибками
Нередко функция yi(xi) задается значениями yi при равноот-
стоящих абсциссах X/. Значения yi могут содержать случайные от-
клонения. По ряду yi, используя усреднение на основе интерполя-
ционных формул, можно уточнить значения ординат, т. е. провести
сглаживание зависимости yi(xi). Сглаженные ординаты записы-
ваются в виде у>.
Программа .§.99. Линейное сглаживание по трем ординатам а
помощью формул:
У о = (5у0 + 2^1 — i/s)/6,	i = 0,
^ = (^-1 + ^ + ^+1)/3’	1<»</V-1,.
Мы = n + %Un—i ~~ ^дт-г)/®’	’ “
Ввод: уз = Р7, yi = Р8, у2 = Р9 и далее (после нажатия клавиш
В/0 и С/П) у3,	yv ....	VN в регистр X. Вывод yQ, yv у£,	уN в
регистр X. ИП7 5	X	ИП8 2	X + ИП9 — 6
-4- С/П	ИП7	ИП8 ИП9 +	+	3	-г- С/П
П6 ИП8	П7	ИП9 П8 ИПб П9 БП 12 ИП9
5 X	ИП8	2	X + ИП7 -	6 -~
с/п ( После ввода уа, Уз		и у2 нажимаем клавиши В/0 и С/П и полу-
чаем уз, Еще раз нажав клавишу С/П, получаем yt. Теперь вводим
у, и,-нажав клавишу С/П, получаем уг и т. д. После ввода послед»
него значения yN и получения b'N_i нажимаем клавиши БП 29 и
С/П и получаем yN. Результаты сглаживания для функции 10х
прн х = 0,1 -j- 1 даны в табл. 5.11.
Таблица 5.11
«1	Сглаживание по трем ординатам	Сглаживание по пяти ординатам	(очное значение у=10х
0.9	0,97	0,992	1
2,12	1.98	1,995	2
2,92	3,0633333	2,998	3
4,15	8,99	4,038	4
4,9	5,05	4,998	5
6,1	5,9733333	6,014 '	6
6,92	7,0566666	7,024	7
8,15	8,04	8.004	8
9.05	9	8,957	9
9.8	9,825	9,91	10
Программа 5.100. Линейное сглаживание при пяти ординатах
по формулам;
Уо = (3^0 + 2^1 4- у— у4)/5,	i = 0,
Si = (4j/0 + 3У1 + 2у2 + г/з)/Ю,	х	i = 1,
{У 1-2 + Уi-i + «I + Уш + ^г+2)/5-	2<z < N ~ 2>
Ук-i ~ (Уц-з + 2^w-2 + 3^w-i + 4f/w)/10’	i = N-i,
$N ~ (3^W + 2^JV-I + yN-2 ~ Ум-з)/5’	1 ~ N-
Ввод: ya — P5, у I — P6, уг = P7, уз = P8, yt = P9, ys, yt, ..,, y„
в регистр X (см. пояснения в контрольном примере).
ИП5	3	X	ИП6	2	X	+	ИП7	+	ИП9
—	5	•4-	с/п	ИП5	4	X	ИП6	3	X
+	ИП7	2	X	+	ИП8	+	1	0	"Т"
С/П	ИП5	ИП6	+	ИП7	+	ИП8	+	ИП9	+
5	-t-	С/П	П4	ИП6	П5	ИП7	П6	ИП8	117
ИП9	П8	ИП4	П9	БП	31	ИП9	4	X	ИП8
3	X	+	ИП7	2	X	+	ИП6	+	1
0	•4"	С/П	ИП9	3	X	ИП8	2	X	+
ИП7	+	ИП5	—	5	4-	С/П			
Проведем сглаживание значений ^/приведенных в табл. 5.1!«
Введя уо — уз и нажав клавиши В/0 и трижды С/П (с перерывами
на время счета), получим So, уь уг, Далее вводим у$ и получаем у9
н т. д. Аналогично получаем yt, -у5, .... yN_^- После ввода ум
нажимаем клавиши БП 56 С/П и получаем y^_v затем еще раз
нажимаем клавишу С/П и получаем у^ (числовые данные см. в
табл. 5.11).
Для функций yi(xi), заметно отличающихся от линейных, ис-
пользуется нелинейное сглаживание с помощью полиномов высоких
степеней т. При т = 3 необходимое число ординат составляет 7.
Программа 5.101. Нелинейное сглаживание при семи ординатах
по формуле
St “ (^£-3 + a&Si-2 + ‘Vl-l + аЬ&1 + аВ^£+1 + аС^;+2+аДУ(+з)>
где индексы у коэффициентов а соответствуют номерам регистров,
из которых берутся их численные значения.. Ввод; уо-i-!/e=P0-j-PS
Таблица 5.12
1	Р7	Р8	Р9	РА	РВ	РС	РД	Пуск программы
0	39	8	-4	-4	1	4	—2	В/0 с/п
1	8	19	16	6	-4	-7	4	В/0 с/п
2	-4	16	19	12	2	-4	1	В/0 С/П
3	-4	6	12	14	12	6	-4	В/0 с/п
4	-4	6	12	14	12	6	-4	с/п
...	...		...	...	...	...	...	с/п
N—2	1	-4	2	12	19	16	-4	В/0 С/П
N — 1	4	-7	-4	6	16	19	8	В/0 С/П
N	-2	4	1	-4	-4	8	39	В/0 с/п
Т а б л и ц а 5.13
1	У1	(сглаженные)	у точные
0	0,7	0 70142857	0,69314717
1	1,03	1,0807142	1,0986122
2	1,39	1,383	1,3862944
3	1,64	1,6242857	1,6094379
4	1,76	1,7995238	1,7917594
5	1,99	1,9509523	1,9459101
6	2,04	2,0733333	2,0794415 '
7	2,22	2,1914285	2,1972245
8	2,28	2,3028571	2,3025851
9	2,42	2,412619	2,3978952
и далее в соответствии с табл. 5.12 и указаниями контрольного при-
мера.
ИПО	ИП7	X	ИП1	ИП8	X	+	ИП2	ИП9	X
+	ИПЗ	ИПА	X'	+	ИП4	ИПВ	X	+	ИПЗ
ИПС	X	+	ИПб	ИПД	X	+	4	2	-4-
С/П	ИП1	ПО	F,	ИП2	П1	F,	ИПЗ	П2	F,
ИП4	ПЗ	F,	ИПб	П4	F,	ИПб	П5	F,	П6
БП	00								
Пусть нужно 'провести нелинейное сглаживание функций
представленных в табл. 5.13. Вводим уо-т-ув в регистры 0-5-6 н ai
для i = 0 согласно табл. 5.12. Нажав клавиши В/0 и С/П, получим
у0 — 0,70142857. Далее, не меняя значения у0 -т- уе, вводим значе-
ния at для i = 1, 2 и 3. Получим у\, yz и уз. После этого, не ме-
няя значений я(, набираем очередное-значение yL = y^ у %,	yN-
Нажимая в конце'набора только клавишу С/П, будем получать зна-
чения у4, у5, ..., Уы_г- Для получения yN_T и 3N вводим но-
вые ai и при каждом пуске нажимаем клавиши В/0 и С/П. Данные
сглаживания приведены в табл. 5.13.
К процедурам сглаживания относится также регрессивный ана-
лиз (приближение функций), описанный в § 5.13. Спектральный ана-
лиз (§ 5.11) обеспечивает сглаживание с помощью усеченного три-
гонометрического ряда Фурье. Ряд других программ, сглаживания
(в том числе с одной, двумя и тремя произвольными функциями)
описан в [29].
Глава 6
ВЫЧИСЛЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
6.1.	Интегральная показательная
и родственные ей функции
Программа 6.1. Вычисление интегральной показательной функ-
ции разложением в ряд:
оо	оо
f е—х”
Ei(x) — — Vp \ -Ц—= у + In х + ) —j-.	(6.1)
J I	fvfhl
—X	n=l
Ввод:	постоянная		Эйлера у — 5,7721566-10“				* = РД,	0 < х = РХ.	
П9	1	П8	П5	0	П4	П6	КИП4	ИП4	ИП5
X	П5	ИП4	X	ИП9	ИП8	X	П8	XY	ч-
ИП6	+	ИП6	XY	П6	—	Fx = 0	07	ИП6	ИПД
+	ИП9	F 1п	+	ПО	С/П	БП	00		
Для x — 0,5 получим ££(0,5) — 0,4542199 при tc ял 1 мин, для
х = 5 получим ££(5) = 40,185274 при tc ял 2 мин.
Программа 6.2. Вычисление функции £t(x) разложением в ряд:
т2-"' —№
X	п>1
Ввод: у = 5,771566-10"1 = РД, х = РХ.
П9	1	П8	П5	0	П4	П6	киш	ИП4	ИП5
X	П5	ИП4	X	ИП9	/-/	ИП8	X	П8	XY
ч-	ИП6	+	ИП6	XY	П6	—	Fx = 0	07	ИП6
/-/	ИПД	—	ИП9	Fin	—	ПО	С/П	БП	00
Для х — 0,5 получим £, (х) = 0,5597736 прн /с « 1 мин, для
х — 5 получим Ei(x)= 1,1481-10-’ при tc ял 2,5 мин.
Программа 6.3, Вычисление функции
1
для п — О, 1, 2, 3, ... по рекуррентной формуле
En+i (х> = 7 [е”’“х£л(х)]'	« = 1. 2, 3.... (6.3)
при Ео(х)= е~х1х и Ei(x), вычисляемом разложением в ряд (6.2)',
Ввод:	у=5,7721566-10-‘=РД, х=РХ. Вывод: п->РХ,	£„(х)	-> PY.
П9	/-/ Fe* ИП9 4- ПО 0	П4	П6	С/П
1	П8 П5 КИП4 ИП4 ИПб X	П5	ИП4	X
ИП9	/-/ ИП8 X	П8 XY 4-	ИПб	+	ИПб
XY	П6 - Fx = 0 13 ИПб /-/ ИПД	—	ИП9
F In	- ПО 1	П4 С/П КИП4 ИП9	/-/	Fe*
ИПО	ИП9 X ~	ИП4 1	— •	4-	по	ИП4
С/П БП 46 Для х — 0,5 будем получать п = 0,		1 £о(О,5) =	
= 1,2130612 (1,2130612), n=l, £t (0,5) = 0,5597736 (0,559773595),
п = 2, Ег(0,5)= 0,32664384 (0,3266439), ... п = 10, £10(0,5) =
= 0,063458298 (0,06344583) и т. д.
Программа 6.4. Вычисление £п(х) по заданному значению
£т(х) при п > т. Ввод: х = РХ, Ет(х) = РХ и т = РХ. Вывод:
п-> РХ, £„(%)-> PY.
П5	С/П	П6	П9 С/П	П4	КИП4	ИПб	/-/	Fex .
ИПб	ИПб	X	- ИП4	1	—	4-	П6	ИП4
С/П БП 06
Эту программу легко проверить по примеру, приведенному для
программы 6.3.
Программа 6.5. Вычисление функции
оо
an(x)=^ tne~xtdt, n = 0, 1, 2, ...
1
по рекуррентной формуле
ап W = [е Л + nan-i w]/x
при а0(х) = (ехр(—х))/х. Ввод: х = РХ. Вывод результатов: n-^-PXj
a„(x)-*PY = Р0.
П9	/-/	Fex	П8 ИП9 >	ПО 0	П4 С/П
КИП4	ИП4	ИПО	X ИП8 +	ИП9 4-	ПО ИП4
С/П	БП	10			
Для х = 2 имеем а0 (2) = 0,067667645, ai(2) = 0.10150147,
a2(2) = 0,16916911........a6(2)=	5,5994975 и т. д.
Программа 6.6. Вычисление функции
I
₽n(x) = ( ine~xtdt, n = 0, 1, 2............
-1
по рекуррентной формуле
₽„ (х) = [(-1)”е*-е х 4- прге_( (х)]/х
при р0(х) = (ет — е~*)/х. Ввод х = РХ. Вывод результатов: п->РХ,
Р„(х)-* PY = РО.
П9	Fe*		Fl/x		ИП9 4-	ПО	0	П4
С/П	1	П8	КИП4	ИП4	ИПО X	ИП9	/-/ Fe*
—	ИП9	Fe*	ИП8	/-/	П8 X	+	ИП9 4-
ПО	ИП4	С/П	БП	13			
Для	х = 4	ПОЛ)	.'ЧИМ Р(	>(4) =	J 3,644957,	₽*(4)	= -10,242876,
р2(4) = 8,5235195, рз (4) =—7,2614757 и т. д.
Если промежуточные значения Еп(х), ая(х) или ря(х) не нуж*
ны, можно составить программы с остановкой вычислений по задан*
ному значению п. Примером является приведенная ниже программа.
Программа 6.7. Вычисление функции ая(х) для заданных х и п.
Ввод: х = РХ и (после высвечивания цифры 0) и = РХ.
П9	/—/	Fe*	П8	ИП9	4-	ПО	0	С/П	П7
ИПО	П6	0	П4	КИП4	ИП4	ИП6	X	ИП8	+
ИП9	4-	П6	ИП7	ИП4	—	Fx = 0	14	ИП6	БП
. - 08
Пусть надо вычислить ав(2). Введя х = 2 и и = 6, получим
се6 (2) = 5,5994975.
Интегральная функция
х
11 (х) = Vp = Ei (In х), х > 1,
о
вычисляется по программе 6.1 при нводе вместо х значения 1пх
6.2.	Интегральные синус и косинус
(включая гиперболические)
Программа 6.8. Вычисление интегрального синуса разложением
в ряд:
	Si (х) =		X С sin t J t	dt=-	Z/ (2n + 1) <2n 4- 1)1				(6.4)
			0		n<=0				
Ввод: х	= РХ	(х <	: ю) .						
П6	П7	П8	Fx2	2	/-/	d-	П9	0	П4
КИП4	ИП4	2	X	1	+	Fx2	П5	ИП4	2
X	1		ИП9	X	ИП7	X	ИП4	4-	ИП5
	П7	ИП8 +		П8	FBx	—	Fx=0	10	ИП8
С/П	БП	00							
Контрольные примеры: Si (0,1)= 0,099944467 (lefts 30 с) и
Si(10) = 1,6583514 (tc fts 4 мин).
Программа 6.9. Вычисление интегрального синуса при большая
х > 8 асимпотическим разложением:
Ввод: х — РХ. Переключатель Р — Г в положении Р.
П8	Fx2	Fl/x	П9 .	1	2	X	Ф	Ф	1
—	X	1	+	4	X	ИП9	X	2	—
ИП8	F cos	X	ИП8	-4-	П7	ИП9	2	0	X
Ф	Ф	1	—	X	1	+	1	2	X
ИП9	X	2	—.	ИП8	F sin		ИП9	X	ИП7
+	Fat	+	2	4-	С/П	БП	00		
Для х= 10 получаем Si(10)’= 1,6583685 при tc « 20 с.
Программа 6.10. Вычисление интегрального косинуса разложе-
нием в ряд:
Ci (х) = у + 1пх + C0S*~ -df = Y-Hnx4-	С6-ч. 5)
0	n=I
Ввод: у = 5,7721566-10~‘ = РД, х = РХ.
П9	Fx2	П8	0	П4	П5	1	ПЗ	П7	КИП4
ИП4	2	X	П6	1	—	ИП6	X	ИП7	/-/
X	П7	ИП6	X	ИПЗ	ИП8	X	ПЗ	XY	
ИП5	+	ИП5	XY	П5	—	Fx = 0	09	ИП5	ИП9
Fin	+	ИПД	+	С/П	БП	00			
' Для х — I имеем Ci(l) = 0,33740392 (tc fts 1 мин).
Интегральные гиперболические синус и косинус можно разло-
жить в ряды:
ч. . . . f sh f V x2n+1
Shi (х) —	t dt—^ (2n + 1) (2n 4-1)1 ’
0	n»o
oo
, ,	. ,	. f chf — 1 o , ,	, V x
Chi (х)=¥+1пхЧ-	----Д = уЧ-1пх+2, 7адГ27-
о	• n=I
1 Они вычисляются по программам 6.8 и 6.10, если оператор /—/ по
адресам 05 и 19 заменить оператором КНОП (нет операции).
Функции этого параграфа могут вычисляться и по программам
численного интегрирования. Однако при этом время вычислений
больше.
6.3.	Гамма-функции (включая неполные)
Вычисление гамма-функций
СО
Г (х) = e",fl dt
о
ввиду сложности разложения в ряд цёлесообразно выполнять по
аппроксимациям [3].
Программа 6.11. Вычисление Г(х) при х 1 по формуле Стир-
линга с коррекцией последнего члена [3, 6];
Г(х)= д/^-е-УН(х),
где
г] , х_, , 1	,	1	0,7
W ~ "* 12х + 288ха	288х3 '
с преобразованием
Г(х) = Г(х + 1) /х при х < I,
Г (— х) = — л/[хГ (х) sin их] при х < 0.
Ввод: х = РХ. Переключатель Р — Г в положении Р.
П9	Fx < 0	21	/-/	П9 ПЦ	25	Fn	ИП9	X
F sin	X	ИП9 X	Fl/x Fn	/-/	X	С/П	БП
00	ПП	25 БП	18 f	t	1	+	X
П8	11П9	2	4-	t П7	1	Fcx	4-	Fxy
ИП8	4-	П8 Fir	2 X	ИП7	4-	F V	ИП8
X	П8	0	7	ИП7	4-	1	XY	—
2	4	-Г-	ИП7	-5-	1	+	1	2	
ИП7	-г*	1 +	ИП8 X	В/0			
Контрольные примеры. Г(0,5				) = 1,7724781		(«с	« 22 с)»
точное	значение	Vn = 1,7724538, Г(1,2) = 0,91817537,					Г(4,7) =
= 15,431423, Г(		-3,2) = 0,68905558 (tc ж		25 с).			
Программа		6.12. Вычисление Г(х +		1) при	X <	1 С	погрет-
ностью	не более	2-10~7 аппроксимацией					
Г (х + 1) = (((((((&sx + bi) х + &6) х + Ь5) х + bi) х + Ьз) х 4-
Ввод: bt = —57719165 = Pl, b2 = 98820589 = P2, fcs=—89705694 =
= P3, bt = 91820688 = P4, fc5 = —75670408 = P5, d6 = 482I9934 =
.₽ P6, bi = —19352782 = P7, bs = 3586835 = P8 и x = PX.
ПД 8	ПО	ИП8	f	XY	ИПД	X КИП0	+
ИПО Fx==0	05	XY	1	ВП	8	4-1	+
С/П БП 00
При x = 0,2 T(l,2) = 0,9181689 (точное значение 0,91816874),
при x = 0,8 Г(1,8) = 0,9313837 (точное значение 0,931383771);
22 с.
Неполные гамма-функции представлены соотношениями [3]:
X
Р(а’
о
х
Y (а, к) = Р (а, х) Г (а) =	dt,
о
оа
Г (а, х) = Г (а) — у (а, х) — е~ fta~1 dt.
X
Все эти функции могут быть определены через функцию
X
у* (а, х) = х~аР (а, х) = -А_- у (а, х) =	е-'/а-1 dt. .
о
Программа 6.13. Вычисление функции у* (а, х) разложением е
ряд
оа
Г (а) у’(а, х) = У	а 0, - 1, - 2, ...
Z_j (а + п) nl
«=о
Ввод:	а= РХ	и х == РХ.			
П8	С/П	П9	1 ПЗ	П5 0	П6	П4	КИП4
ИП4 ИП5		X	П5 ИП8	ИП4 + ’ X	П7	ИП9
/-/	ИПЗ	X	ПЗ XY	4- ИП6 +	ИГ16	XY
П6	—	Fx==0 09 ИП8	Fl/x ИП6 +	ПО	С/П
г п	ример.	Найти у*(1; 4) и	у* (—0,5; —3). Вводим		а = 1 и
х — 4,	получаем Г(1)у*(1; 4) =		0,2454211 при /с	« 2,5	мин. Но
Г(1)= Г(1 -|-0)= 0! = 1, следовательно, у*(1; 4)= 0,2454211. Для
второго случая, введя а — —0,5 и х — >—3, получим
р(__0,5)у*(—0,5; —3) = 10,495471. По описанным выше программам
или таблицам [3] находим Г (—0,5). В данном случае Г (—0,5) ==
= — 2'л/л. Следовательно, у* (—0,5; —3) = 10,49547j/(—2 -y/tst) =
= — 2,9607177.
6.4.	Функции Бесселя (включая модифицированные)'
Функции Бесселя являются решениями дифференциального
уравнения [1, 2]
, d2w dw . . ,	п	,сс.
z2-^5- + z-^-+(z2 —v2) а>=0.	(6.6)
при z = (х + ]{/). Ограничимся вычислением функций' Бесселя для
действительных г = х и целых v = n (порядок функций). Двум
независимым решениям (6.6) соответствуют функции Бесселя пер-»,
вого /я(х) и второго Ул(х) рода.
Программа 6.14. Вычисление JK(x) разложением в ряд
Jn (х) =	4(	5	1	(х/2)2	, 1(«4-1) 1	(х/2)* 21 («4-1) («4-2)		(6.7)
Ввод: п	= Р5,	, X —	РХ.				
П9	0	П4	1	П6 ИП5	Fx=A0 17	П8	ИП6
X	П6	ИП8	1	— Fx =	= 0 08	ИП9	2	-4-
ПО	Fx2	П9	ИП5	ИПО Fx»	ИП6 4-	П7	П8
КИП4	ИП4	ИП5	4-	ИП4 X	ИП9 Ч-	ИП7	/-/
XY	ч-	П7	ИП8	4- П8	FBx -	Fx = 0	30
ИП8	с/п	БП	00				
Имеем Jo(0,5) = 0,93846981 (<с к 40 с); Jo(4) = —0,397149761
J30(20) = 1,2401602-10-“ (tc at 3 мин).
Ряд для У„(х) весьма сложен [3]. Кроме того, вычисления Jn(x)
и У„(х) разложением в ряд занимают много времени. Поэтому це-
лесообразно вычисление Jo(x), Ji(x), У«(х) и Yi(x) аппроксимацией
с последующим вычислением Jr.(x) и Yn(x) по рекуррентным фор-
мулам.
Программа 6.15. Вычисление Jo(x) и Уо(х) аппроксимацией!
Jo (х) = 1 - at (х/3)2 4- а2 (х/3)4 - а3 (х/3)6 +
-к а4 (х/3)8 - а5 (х/3)1» + я6 (х/3)12
для —3 к -С 3 с погрешностью до 5-Ю-8 и
Уо (х) = | In ~ Jo (х) + b0 + bt (х/3)2 - Ь2 (х/3)4 +
4- Ьз (х/3)6 - bt (х/3)8 4- Ь5 (х/3)1» - Ье (х/3)13
для 0<х<Зс погрешностью до 1,4 10-8. Ввод: щ = 2,2499997 =ч
= Р1, а2 = 1,2656208 = Р2, а3 = 0,3163866 = РЗ, а4 = 0,0444479 =»•
= Р4, Д5= 0,0039444 = Р5, а«=0,00021 ==Р_6, Ьо=3,6746691-1О-‘^|
-=P7, bt = 6,0559366-10-1 = Р8, b2 = 7,4350384-10-’ = Р9, 6S =
 = 2 5300117-10-’ = РО, bi = 0,4261214-10-’ = РА, 65
-= 0,0427916-		Ю~’ = РВ, be = 0,0024846-10-* = PC и х = РХ.							
1	3	-X-	Fx2	ПД	1	ипд	ипр	X	ИП5
	ипд	X	ИП4	+	ИПД	X	ипз	—	ипд
X	ИП2	+	ипд	X	ИП1	—	ипд	X	+
с/п	2	X	Fat	-т-	ИПД	F<	3	X	2
	Fin	X	ИП7	+	ипн	ИПС	ипд	X	—
ипд	X	ИПА	—	йпд	X	ипо	+	ипд	X
ИП9	—	ИПД	X	ИП8	+	ипд	X	+	с/п
БП 00
Контрольные примеры (н скобках даны точные значе-
ния результатов). 70 (0,5) = 0,9384698 (0,9384698072); УДОД) =
= —0,44451888 (—0,4445187335); /о (1) = 0,7651977 (0,7651976865);
Уо (1) = 0,088256943 (0,0882569642); /о (2) = 0,2238908 (0,2238907791);
Уо (2) = 0,51037568 (0,5103756726).
Программа 6,16. Вычисление функций Ji(x) и.УДх) аппрокси-
мацией:
для —3 sg х < 3 с погрешностью менее 1,3-10~s и
хУ\ (х) = х In (-0 7i (х) — 60 + bi j + b2 (3-) —
для 0<х<3 с погрешностью меиее 1,1-10'7. Ввод} =
= 5,6249985-10“’ = Р1,	а2 — 2,1093573-10-* = Р2,	as =
= 0,3954289-10-’ = РЗ,	а4 = 0,0443319-10-’ = Р4,	б5 =
= 0,0031761-10-’= Р5, Со=О,0001109-10-* = Р6, 6о=О,6366198 =
= Р7, б/= 0,2212091 = Р8, Ь2 = 2,1682709 = Р9, Ь3 = 1,3164827=
= Р0, bi = 0,3123951 = РА, 65 = 0,0400976 = РВ, 66 = 0,0027873 =
= PC и х = РХ.									
4			3	-5-	Fx2	ПД	ИПб	X	ИП5
—	ипд	X	ИП4	+	ипд	X	ипз	—	ипд
X	ИП2	+	ИПД	X	ИП1	—	ипд	X	2
Fl/x	+	X	С/П	XY	X	FBx	2	-г-	Fin
X	2	X	Fn	-4-	ИПС	ИПД	X	ИПВ	—
ипд	X	ИПА	+	.ИПД	X	ИП0'	—	ипд	X
ИП9	+	ипд	X	ИП8	+	ИПД	X	+	ИП7
	ипд	F V	3	X		С/П	БП	00	
Для х — 0,5 и 3 получим (в скобках даны точные значения)!
//(0,5) = 0,24226846	(0,2422684577), У, (0,5) = —1,4714725
(—1,4714723^27), Л (3) = 0,33905898	(0,3390589585), У^З) —
= 0,3246744 (0,324674448).
Программа 6.17. Вычисление функций Бесселя 7„(х) и Ув(х) по
рекуррентному соотношению
2„
где В означает 7, У или любую линейную комбинацию этих функ-
ций, коэффициенты которых не зависят от х и и. Ввод: х, Bn~i(x)
и В„(х) в регистр X. Вывод: п -*• РХ, BB(x)->PY.
П7	С/П	П8	С/П	П9	0	П4	КИП4	ИП4	2
v	X	ИП9	X	ИП7	4-	ИП8	—	ИП9	П8	XY
П9	ИП4	1	+	С/П	БП	07
Введя х — 1, Уо(1)= 8,8256943-10-2 и У1(1)=—7,8121282-10-’.
нажимая клавиши С/П и XY, будем. получать следующие резуль-
таты (в скобках даны точные значения):
п = 2  У2 (1) = — 1,6506825	(—1,65068261)
и = 3	У3 (1) = —5,8215172	(-5,8215)
и = 4	У4(1) = — 33,27842	(—33,278) и т д.
При х S’3 функции 70(х) и Уо(х) могут вычисляться с по-,
мощью аппроксимаций:
70 (х) = x-1/2focos0o и Уо (х) = x-,/2f0 sin е0.
где
вычисляется с погрешностью менее 1,6-10“я и
е._^.+ Ц|)+Ц|)Ч».(|у+<)’+
вычисляется с погрешностью менее 7-10~8. Значения коэффициен-
тов ан 4- ав и bt> 4- Ъе указаны в табл. 6.1.
Функции Л(х) и У1(х) при х>3 находятся по аппроксимации!
7i (х) = x~1/2/l cos6l и У1 (х) = x-1/2f, sin ©i,
Таблица 6.1
п	Функция Бесселя			
		Ко (х)		У1 (X)
	ап	Ьп	tl	»п
0	х79788456	-78539816	79788456	—2,3561945*13s
I	—77 ’	-4166397	156	12499612
2	-552740	-3954	1659667	5650
3	-9512	262573	17105	-637879
4	137237	-54125	-249511	74348
6	-72805	-29333	113653	79824
6	14476	13558	-20033	-29166
5-[«•+“ (7)+“'(J) + ‘й (7) +”’(1) +
вычисляется с погрешностью менее 4-10-8 и
»—[ь+ь(|)+ц4у+щу+Ц4у+
вычисляется с погрешностью менее 9-10~8. Значения коэффициентов
Со 4- «в и Ьо -г- Ьо даны в табл. 6.1.
Программа 6.18. Вычисление функций Бесселя Jo(x), Уо(х),
Jifje) и Yi(x) аппроксимациями (6.8)-г-(6.11) для х 3. Ввод: см.
в инструкции к программе (после ее текста). Переключатель Р—Г
в положении Р.
Fl/x	3	X	ПД	ИП6	X	ИП5	+	ипд	X
ИП4	+	ипд	X	ипз	+	ипд	X	ИП2	+
ипд	X	ИП1	+	ипд	х	7	9	7	8
8	4	5	6	+	1	вп	8		ИПД
3	-4-	Fl/x	F V'	-4-	ИПС	ИПД	х	ИПВ	+
Ипд	X	ИПА	+	ипд	X	ИПО	+	ипд	X
ИП9	+	ипд	X	ИП8	+	ипд	X	ИП7	+
1	ВП	8	-4-	ипд	3	—	Fl/x	+	ПД
F cos	XY	X	с/п	XY	ипд	F sin	X	С/П	БП
00				-					
Для вычисления функций Уо(х) и /о(х) вводятся коэффициен-
ты at 4- ав = Pl -j- Р6 (значение ад занесено в текст программы).
(—0,01969407393),	/о(Ю) = —0,24593577
Уо(10) = 0,055671124	(0,0556711673), Л(4) =
Ьо -4- bs = Р7 Ч- Р9, Ьз = Р0,	4-= РА Ч-PC (см. табл. 6.1).
Затем вводится' значение х = РХ, нажимаются клавиши В/0 и С/П
(получим Je(x)) и С/П (получим У0(х)), При смене х = РХ нажи-
мается дважды только клавиша С/П. Для вычисления Ji(x) и У4(х)
все операции повторяются заново с вводом значений коэффициентов
аппроксимаций для этих функций.
Контрольные примеры (в скобках даны точные значе-
ния функций Бесселя). 70(4) =—0,3971498 (—0,3971498098), У0(4) =
= —0,01694076
(—0,245937644),
= —0,066043332 (—0,0660433280), У!(4) = 0,3979257 (0,3979257106),
7, (10) = 0,043472698	(0,043727462), У4 (10) = 0,24901544
(0,2490154242).
Решениями дифферениального уравнения
„ d2w . dw . , ,	п
z2 —г-?- + z —----(z2 + v2) w = 0
rfz2 dz
являются модифицированные функции Бесселя 7v(z) и Kv {г). Как и
прежде ограничимся вычислением этих функций для действительных
z = к и целых v= п.
Функции 1п(х) имеют разложение в ряд
nl V27 L1+ 1! (n + 1) + 2l(n+ 1) (n + 2) + ---J(6-12)
и могут вычисляться по программе 6.14, если в ней оператор смены
знака /—/ по адресу 39 заменить оператором КНОП (нет операции).
Тогда получим /0 (2) = 2,2795892, h (2) = 1,5906368, /о (10) =
= 2815,7168.
Программа 6.19. Вычисление модифицированных функций Бессе-
ля /о (х) и 11 (х) при —3,75 < х < 3,75 аппроксимацией:
/о (X) = 1 + att2 + й2г4 + a3te + ait8 + д6Р° + aet'2
с погрешностью не более 1;6-10~’ и
х-ih (х) = 0,5 + bit2 +- b-J* + b3t8 + bit8 + b5P° + fe6Zlz
с погрешностью не более 8-10~°, причем t — х/3,75, а также функции
/,,(х) по рекуррентному соотношению
/п+1 W ~ 2п1п + In-l	п 2'
Ввод: at = 3,5156229 = Pl, аг = 3,0899424 = Р2, as = 1,2067492 =
= РЗ, а4 = 0,2659732 = Р4, д5 = 0,0360768 = Р5, ае = 0,0045813
(вписан в программу), bt = 0,87890594 = Р7, Ь3 — 0,51498869 = Р8,
bs = 0,15084934 = Р9, Ь4 = 0,02658733 = Р0, Ьз = 0,00301532 = РА,
Ь6 = 0,00032411 = РВ и х = РХ. Вывод:	РХ = Р6, 1п[х) -> PY.
ПС			7	5		Fx9	ПД	О	Пв
ипд	4	5	8	1	3	ВП	7	!Ч	X
ИП5	+	ипд	X	ИП4	4-	ИПД	X	ИПЗ	4-
ИПД	X	ИП2	4-	ипд	X	ИП1	4-	ипд	X
1	+	ипд	ИПВ	X	ИПА	4-	ИПД	X	ИПО
+	ипд	X	ИП9	+	ИПД	X	ИП8	4-	ипд
X	ИП7	+	ИПД	X	2	Fl/x	4-	ИПС	X
XY	ПД	0	С/П	F,	F,	КИП6	F,	ИП6	с/п
XY	2	/-/	X	ИПС	-4-	XY	X	FBx	XY
ипд	+	XY	ПД	XY	БП	76			
Для к = 2, нажимая клавиши С/П и XY, будем получать: п = О,
/о (2) = 2,2795853, п = 1./Д2) = 1,5906369, п = 2, /2 (2) =0,6889484
и т. д.
Программа 6.20. Вычисление h(x} или Ii(x) по аппроксимациям
(х > 3,75)
„t/2 -X, tv\~n  а‘ I а* I аз I at I “5 , Об , «7 , ав
х е /о, i W — «о + —+ -р- + "р"+тг+'7Г+7Г+7Г»
где / = х/3,75, с погрешностью'не более 1,6-10-1 для функции /о(х)
и 2,2-10"’ для h(x). Ввод для вычисления /о(х): ао — 0,39894228 =
= РА, ai = 0,01328592 = Pl, о2 = 0,00225319 = Р2, а3 =».
= -0,00157565 = РЗ, а4 = 0,00916281 = Р4, а5=-0,02057706=Р5;
ав = 0,02635537 = Р6, с7 = —0,01647633 = Р7, as = 0,00392377 =
= Р8, х — РХ. Ввод для -вычисления h(x) в регистры, указанные
выше: а0 = 0,-39894228, at = —0,03988024, а2 = —0,00362018, аз =;
= 0,00163801, с4 =—0,01031555, а5=0,02282967, а6 =—0,02895312,
а? = 0,01787654, аз = —0,00420059 и х = РХ.
ПД	3	,	7	5	~	ПС	8	ПО	ИП8
ф	XY	ИПС	-j-	КИПО	+	ИПО	Fx = 0	11	XY
ИПА	+	ИПД	F /	v	ИПД	Fe* ,	X	С/П	БП
00
Для х = 10 получим Zo (10)= 2815,7168 (точное значение
2815,7166), /ДЮ) = 2670,9884 (точное значение 2670,9884).
Программа 6.21. Вычисление модифицированных функций Бес-
селя Ко{х) при 0 гС х 2 по аппроксимации
<»•(*) = — 1п (у) /0 (х) — аа + а{ (у) + а2 (у) +
1
с погрешностью не более 8-Ю-9. Ввод: flo = 0,57721-566 — РА,
li>(x) = РВ, ai = 0,42278420 = Pl, а2 = 0,23069756 = Р2, аз =
= 0,03488590 = РЗ, а4 = 0,00262698 = Р4, а5 — 0,00010750 =. F 5,
Об .= 0,00000740 = Р6, х = РХ.
ПД	2	4-	Fx2	ПС	6	ПО	ИП6	f	XY
ИПС	X	КИПО	+	ИПО	Fx = 0	09	XY	ИПА	—
ИПД	2	4-	Fin	ИПВ	X	—	С/П	БП	00
Для л = 0,5, учитывая, что /о (0,5)= 1,0634834, получим
Ко (0,51= 0,9244191.
Программа 6.22. Вычисление модифицированных функций Бес»
селя Ki(x) при 0 < х =С 2 по аппроксимации
xKi (х) — х 1п (х/2) Ц (х) + 1 +	(х/2)2 + а2 (х/2)4 + а3 (х/2)8 +
+ at (х/2)8 + а5 (х/2)18 + а6 (х/2)12
с погрешностью не более 8-10~®. Ввод: at = 0,15443144 — Pl, 02 =>
= —0,67278579 = Р2, а3 = —0,18156897 = РЗ, а4 = —0,01919402=
= Р4, а5 = —0,00110404 = Р5, а6 = —0,00004686 = Р6, Л(х) = РВ
и х = РХ.
ПД 2 4- Fx2 ПС 6	- ПО ИП6 | XY
ИПС	X	КИПО +	ИПО	Fx = 0	09	XY	1	+
ИПД	+	ИПД 2	4-	Fin	ИПВ	X	+	С/П
БП 00.
Для х = 0,5 и /1(0,5) = 0,2578949 получаем Ki(0,5) = 1,6564404
при точном значении 1,656441.
. Программа 6.23. Вычисление модифицированных функций Бес-
селя Ко(х) и Ki(x) для х 2 по аппроксимации
e*xI/2KOj 1 (х) — aQ + at (2/х) -f- а2 (2/х)2 + а3 (2/х)3 +
+ at (2/х)4 + а5 (2/х)5 + ав (2/х)8
с погрешностью не более 8-10~® для Ло(х) и 2,2-10-7 для Ki(x).
Ввод для вычисления Ло(х): а0 = 1,2533141 = РА, at =
= —0,07832358 = Pl, а2 = 0,02189568 = Р2, а3 = —0,'01062446 =.
= РЗ, at = 0,00587872 = Р4, а5 = —0,00251540 = Р5, с6 ==
= 0,00053208 = Р6 и х = РХ. Ввод для вычисления Л\(х) в ука-
занные выше- регистры: ао = 1,2533141; ai = 0,23498619; а2 =;
= —0,03655620, as = 0,01504268; а4 = —0,00780353; а5 =
= 0,00325614; а6 = —0,00068245 и х = РХ.
ПД	2	XY	4-	ПС	6	ПО-	ИП6	ф	XY
ИПС	X	КИПО	+	ИПО	Fx = 0	09	XY	ИПА	+
ИПД	Fex	4-	ИПД	F<	+	С/П	БП	00
Для х=5 и 10: Ао(1О) = 1,7780061-10-5, Ао(5) = 3,6910982-Ю-8;,
А1(10)= 1,8548772-10-5 и Ai(5) = 4,0446133-10-®.
6.5.	Интегралы Френеля
Программа 6.24. Вычисление интеграла Френеля С(х) разло»
вкением в ряд при х < 3 (х — РХ):
	X C (x) ~ cos 0		OO (л«2/2) dt = £ n=0			(-1)» (n/2)2” 4n+1 (2«)l(4ft-l-1)		
П9	П8	Fx2	Fn	X	Fx2	4	4-	П7	0
П4	КИП4	ИП4	2	X	ПЗ	1 —	ИПЗ	X
из	ИП4	4	X	3	—	П0 4	+	ИП0
XY	—	ИПЗ		ИП7	X	ИП8 /-/	X	П8
ИП9 00	+	П9	FBx	—•	Fx =	= 0 11 ИП9	С/П	БП
Примеры. С (0,5) = 0,49234422; С (1) = 0,77989341 и С (2) =»'
»= 0,48825334 (время вычисления от 50 до 160 с).
Программа 6.25. Вычисление интеграла Френеля S(x) по раз-
ложению в ряд при х < 3 (х — РХ);
-	X s W - J p		OO sin (л/?/2) dt = n=i		(—1)" (n/2)2ft+1 (2n + 1)1 (4ft + 3)			xlln+3.	
П8	Fx2	Fn	X	2		П9	Fx2	П5	ИП9
ИП8	X	3		П7	П8	0	П4	КИП4	ИП4
2	X	П6	1	+	ИП6	X	П6	ИП4	4
X	1	—	П9	4	+	ИП9	XY	—-	ИП6
	ИП5	X	ИП7	/-/	X	П7	ИП8	+	П8
FBx	—	Fx	= 0 18 ’	ИП8	С/П	БП	00		
Примеры. S(0,5)= 0,064732433, S(l) = 0,43825912 и S(2)=-
1*= 0,34341539 (время вычисления от 50 до 165 с).
• С интегралами Френеля связаны вспомогательные функции
f W = [у - s w] cos (jy) - [у - C (x)] sin (^y ),
g (x) = [y — C (x)J cos (jy J + [у - s (x)J sin [-yj -
Программа 6.26. Вычисление f(x) и g(x) по аппроксимациям
f i \	I atx	. .	1
X 7W = 2 + atx + a.x2 И S W = 2 + blX + Ь2хг + Ь3х*
С погрешностью менее 2-10-3 (0 x oo), а также
I o , . ’ 1	,, . * (nx2 X .	. ( xx2 X
, S(x) = --f(x)cos^—J-g(x)s,n^-yJ,
C(x) = j + f (x) sin (-y) — g (x) cos (Др)-
Ввод: ао = 0,926 = Pl, а, = 1,792 = P2, a2~ 3,Ю4 = РЗ, б, =»
= 4,142 = P4, b2 = 3,492 = P5, b3 = 6,67 = P6 и x — РХ. Вывод
результатов: /(x)->PA, g(x)->PB, C(x)->PC и S(x)-*PX = РД.
Переключатель P — Г в положении Р.
П9	ИП1	X	1	+	ИП9	ИПЗ	X	ИП2	+
ИП9	X	2	+	4-	ПА	ИП9	ИП6	X	ИП5
+	ИП9	X	ИП4	+	ИП9	X	2	+	Fl/x
ПВ	ИП9	Fx2	Fn	X	2		П8	F sin	ПД
ИПА	X	ИП8	F cos	П8	ИПВ	X	—	2	Fl/x
+	ПС	FBx	ИПА	ИП8	X	—	ИПВ	ипд	X
“г-	ПД	С/П	БП	00-					
Имеем S(0,5) = 0,06567349 и С (0,5) = 0,49256592 (/с = 23 с).
Программа 6.27. Вычисление С(х) и S(x) тори больших х Э> 1 по
асимптотическим разложениям:
г 1лЛ___ I	, sin(nx2/2) f,	3	\	cos (лх2/2) (,	5
W 2+	лх	V	(лх2)2 )	п2х3	V	(лх2)2,’
- , , __ 1 cos (лх2/2) Z	3	\	sin (лх2/2) /	5	\
2	лх	V	OiJTJ	л2х3	V	(РРр)
с погрешностью менее 5/(л4хт) (при х 4 верны ие менее пяти зна-
ков результата). Ввод: к = РХ. Вывод результатов: С(х)->РХ,
S(x)-*PX. Переключатель Р — Г в положении Р.
	Fn	X	П8	X	П9	2		F cos	П7
FBx	F sin	П6	ИП9	Fx2	3	XY	ч-	1	—
ИП6	X	ИП8		П5	ИП9	Fx2	5	XY	4"
1	—	ИП7	X	ИП9	ч-	ИП8	ч-	2	Fl/x
+	ИП5	—	С/П	ИП7	/-/	f	ИП6	/-/	П7
XY	БП	12							
Для х = 4 имеем С(4) = 0,49841993 и S (4) = 0,42051702.
6.6.	Эллиптические интегралы
Программа 6.28. Вычисление полного эллиптического интеграла
первого рода по его разложению В ряд:
л/2
A(m)=\ (1- m sin2.6)~1/2dO =» *
Ввод: tn = РХ. 7
П9	0	П5	1	П4	П6	П8	КИП5	КИП5	ИП4
ИП5	ч-	Fx2	ИП9	X	ИП6	X	П6	КИП4	КИП4
ИП6	ИП8	+	ИП8	XY	П8	—	Fx = 0	07	ИП8
Fn	X	2	Ч*	С/П	БП	00			
Примеры (в скобках даны точные значения результатов).
К(0,1) = 1,6124415 (1,61244135), К(0,2) = 1,6596237 (1,659623599),
К(0,5)= 1,8540744 (1,85407468). Время вычисления одного значения
К(т) в этих примерах от 1 до 2,5 мин.
Программа 6.29. Вычисление полного эллиптического интеграла
второго £(т)^=	рода по его разложению в ряд:							... j.
	1 К |сч	(Я	т /	' 1 - 3> .2-4/	|2 т2 L з	1 ЬЭ — »£* W СП сл	k2 т3 1 5	
			1 1					
Ввод: т	= РХ.							
П9	0	П5	П8	1	П4	П6 КИП5	КИП5	ИП4
ИП5		Fx2	ИП9	X	ИП6	X П6	ИП4	4*
П7	КИП4	КИП4	: ИП7	ИП8	+	ИП8 XY	П8	—-
Fx = 0	07	1	ИП8	—	Ел	X 2	-4-	с/п
БП	00							
Примеры		(в скобках		даны	точные значения		результатов).	
£(0,1) = 1,5307576 (1,530757637), £(0,2) = 1,4890351 (1,489035058);
£(0,5) = 1,3506438 (1,35064388). Время вычисления от 1 до 2,5 мин.
Эллиптические интегралы общего вида (неполные):
ф
£ (<р \ а) = F (<р | m) = (1 — т sin2 0)-1/2 dQ,
о
ф
Е (<р [ tn) — (1 — т sin2 0)I/2 d0
о
могут вычисляться по программам численного интегрирования. Так,
для вычисления £(ф]вг) можно воспользоваться программой 5.54
интегрирования методом Гаусса, вписав в нее фрагмент вычисления
подынтегральной функции (m = Р9):
Fsin Fx2 ИП9 X 1 XY — FV* Fl/x.
При tn — 0,5 = P9, ф = nj2 = 6 и o = 0, деля отрезок инте«
грирования на 8 частей, получим F(«/2|0,5) = 1,8540742 при tc «
5 мин. Для вычисления £(<p|/w) достаточно убрать оператор
Fl/x и конце приведенного фрагмента.
6.7.	Дилогарифм
Программа 6.30. Вычисление дилогарифма по его разложению
вряд(х=РХ):
=	= £ (-»)"-(>С7г1)П-. 0<х<2.
1	п=1
fl	П8	—	П9	0	П6	П7	КИП6	ИП9
. /-/ ИП8	X	П8	ИП6	Fx2	~	ИП7	+	ИП7
XY П7	—	Fx = 0	08	ИП7	С/П	БЯ	00
Примеры (в скобках указаны тачные значения результатов)’.
/(0,1) = 1,2997151 (1,299714723), /(0,5) = 0,58224055 (0,582240526);
время вычисления составляет 6,5 и 2,5 мин.
При точности, меньше предельной, и малых х время вычисления
дилогарифма можно существенно уменьшить, используя для этого
программы численного интегрирования.
6.8.	Функции Дебая
Функции Дебая
X .	. X
п , . _ п ( tndt ( ntn
п Х хп J ?-1 “j х"(е*-1) ’
n=i, 2, 3, ....
ввиду сложности разложения  в ряд целесообразно вычислять по
программам численного интегрирования. Так как при t = 0 подын-
тегральная функция имеет особенность 0/0, то целесообразно ис-
пользовать метод Гаусса.
Организация единой программы (для всех п) нецелесообразна,
так как вычисление микрокалькуляторами функций х" и 1п опера-
цией вида х» занимает много времени. Ниже дан пример вычисле-
ния функции Dt(x). Подобным образом могут вычисляться функции
Дебая прн других п.
' Для вычисления функции Di(x) воспользуемся программой 5.54,
нпис.ав в нее фрагмент вычисления функции 4/4/х4(е'— 1);
П8 Fx2 Fx2 ИП8 Fe* 1 - v 4 X
ИП9 Fx2 Fx2 -j-
Быполивв ввод (m = PX, x = b — P9 и a = 0), для m = 2 и x = 1
получим (1) == 0,6548742 при точном значении 0,654874, а для
m — 4 и x = 10 £>4(10) = 0,00967427 при точном значении 0,009674,
6.9.	Интеграл вероятности
/ и связанные с ним функции
К важнейшим функциям теории вероятности относятся плот-
ность Гауссовского стандартного распределения
ф (х) = р (х) = е	(6.13)
и функция распределения (интеграл вероятности)
X
'Площадь между кривой ф(х) и осью абсцисс слева от верти-
кали, проходящей через точку (х, 0)
X.
П(х) = -)=Г	(6.15)
— oo
Полагая t ^2 — и и y — xl'y/b, получим [!]:
__у
ф {у) = ф = д/f- е du- (6.16)
Эта функция связана с II (х) простым соотношением
ф(-~0+1=2П(х).	(6.17)
Программа 6.31. Вычисление функции Ф({/) И (у = РХ):							разложением		в ряд
Ф (У) = У		|сч | К	(У/2)2 1!3		, (г//2) 1	215	4	(г//2)6 , 317		...).	(6.18)
П9	Fx2	2	/-/	-X-	П6	2	Fn		F <
ИП9	X	П7	П8	0	П4	КИП4	ИП4	2	X
1	+	П5	ИП4	2 	X	1	—	ИПб	X
ИП4		ИП5	—	ИП7	X	П7	ИП8	+	П8
FBx	—	Fx = 0	16	ИП8	с/п	БП	00		
Примеры. ф (0,1 )= 0,079655675 вычисляется за 33 с, Ф(1)=^
== 0,6826895— за 80 с и Ф (4) = 0,99993495 — за 5 мин.
Программа 6.32. Вычисление Ф(у) при у > 4 асимптотическим
разложением (у = РХ):
П9	Fx2	П8	2	/—/	Ге*	2 Fn	4-
FV	X	ИП9	4-	П9	3	ИП8	-5-1	XY
—	ИП8	4-	1	—	ИП9	X	1 +	С/П
БП CO
Пример. Ф(4) — 0,9999365 вычисляется за 10 с.
Программа 6,33. Вычисление Ф({/) при любых у разложением
(6.18) для у	< 4 и (6.19) при у 4..
П9 4	—	Fx < 0 52	ИП9 Fx2 2	/г-/ 4-
П6 2	Fn 4-	F V ИП9 X П7	П8 0
П4 КИП4	ИП4 2	X 1	+ П5	ИП4 2
X 1	— ИП6 X ИП4 4- ИП5 4- ИП7
X П7	ИП8 +	П8 FBx — Fx = 0 21 ИП8
БП 81	ИП9 Fx2	П6 2	/-/ 4-	Fe« 2
Fax 4-	F V X	ИП9 4- П9 3	ИП6 4-
1 XY	- ИП6 4-	1	— ИП9 X 1
+ с/п	БП 00
При у --	= 0,Г получим Ф (0,1)= 0,079655675, а при у = 4
Ф(4) = 0,9999365.	
Функцию П(х) можно вычислить по соотношению (6.17). Для	
этого в конце вычислений нажимаем на клавиши f 1 + 2 4-. Так,
для х ~ 0,1 имеем П(0,1)= 0,53982785.
Если в описанные программы перед оператором С/П ввести
фрагмент
ИП8	1	+	2	4-	ПО	ИП9 Fx2	2	/—/
4-	Fe*	2	Frt	X	FV' П1	ИПО
то будут вычисляться функция П(х)->Р1 = РХ и ее производная
П' (х) — е~*г/2/У2л-> PY.Например, для х = 0,1 получим П(0,1)=ч
= 0,53982785 и П'(0,1 )= 0,39695256.
Функцию Ф(х) можно рассчитывать также с помощью про-
грамм, вычисляющих Ф({/). Для нахождения Ф(х) надо вместо у
ввести значение х ^2 • Например, чтобы вычислить Ф(х) при х = 0,5
перед пуском программы надо нажать клавиши 0 , 5 f 2 F V" Х>
Получим Ф (х) = Ф (0,5) = 0,52049986. Для ускоренного вычисления
функции Ф(х) предложен ряд аппроксимаций [2, 3].
Программа 6.34. Вычисление Ф(х) при х>0 аппроксимацией
с погрешностью менее 2,5-10~5
ф (х) = 1 - (Л (ai + X (о2 + а3к)))/ех1,	(6.20)
где Л = 1/(1 + рх). Ввод: р = 0,47047 = Р0, а{ = 0,3480242 = Р1а
а2 — —0,0958798 = Р2, а3 = 0,7478.556 = РЗ и х = РХ.
t ИПО	X	1	+	FA/x	П9	ИПЗ	X	ИП2
+ ИП9	X	ИП1	+	ИП9	X	XY	Fx2	Fe«
4-1	XY	—	С/П	БП	00
— Имеем Ф (0,1) — 0,1124832, ф(0,5) — 0,5264876, Ф(1) = 0,8427168
и 'Ф(З) = 0,9999776. Время счета одного значения Ф(х) около 10 с.
При х <. 0 вычисления можно выполнить, используя соотношение
Ф(-х) = 1 -Ф(х).	"
Упростив коэффициенты в (6.20), эту формулу можно записать
в виде
Ф (х) = 1 [(Л (348 + Я (-96 + 748A)))/eJc2] 103	(6.21)
и проводить расчет по программе с одним запятым регистром па-
мяти.
Программа 6.35. Вычисление Ф(х) по формуле (6.21) с погреш-
ностью порядка 1 • 10-4. Ввод х = РХ.
	Г	0		4	7	X	1	+	Fl/x
П9	7	4	8	X	9	6	—	ИП9	X
3	4	8	+	ИП9	X	1	ВП	3	
XY	Fx2	Fe*	4-	1	XY	—	С/П	БП	00
Для х = 0,1 и 1 имеем Ф(0,1) = 0,1123962, Ф (1 )= 0,8426262.
Программа 6.36. Вычисление Ф(х) аппроксимацией
Ф (х) = 1 — (fliX + а2Т? Ц- а3Л3" +	+ п5Л5)/е';2,
где Л = 1/(1 + Оех) с погрешностью не более 1,5-10~7. Ввод: а, =;
= 0,2548295 = Pl, а2 = -0,28449673 = Р2, а3.= 1,4214137 = РЗ.
«4 = -1,453152 = Р4, а5 = 1,0614054 = Р5, о6 = 0,3275911 = Р6 и
х = РХ.
П9	ИП6	X	1	+	Fl/x	П8	5	ПО	ИП5
f	XY	ИП8	X КИПО	+	ИПО	Fx = 0	11	XY
ИП9	Fx2	Fe*	4-1	XY	-	С/П	БП	00
Для х = 0,1 и 2 имеем Ф (0,1)= 0,1124632, Ф(2)= 0,9953221.
Программа 6.37. Одновременное вычисление функций Ч'(х) по
формуле (6.13), П(х) с погрешностью до 1-10~5 аппроксимацией
П (х) = 1 - ф (х) (а,Л - а2№ + e3V),
где ?. = 1/(1 + рх), а также функций
со J X И If -л	e-«72rf/ = 1 _П(х) e~t21zdt^2U (x) ~ 1.
Ввод: р — 0,33267 : Р9, '°1 = 0,4361836 — PI, а2 — 0,1201676 — Р2;
Оз'= 0,937298 = РЗ  и х = РХ. Вывод: Л->- Р8, Ф(х)-> РХ = РД,
п(х)-*	РХ = РВ, Q(x)-»PX = PC и Л(х)-^РХ = РА.								
П7	ИП9	X	1	+	Fl/x	П8	ИП7	Fx2	2
/-/	ч-	Fex	2	Far	X	F V"	ч- 	ПД	С/П
1	ИПЗ	ИП8	X	ИП2	—	ИП8	X	ИП1	+
ИП8	X	ипд	X	—	пв	с/п	1	ИПВ	—
ПС 00	с/п	ипв	2	X	1	—	ПА	С/П	БП
Для к — 1 получим ’P(l) = 0,24197072 (точное значение
9,2419707245), П(1) =0,8413513 (точное значение 0,8413447), Q(l) =
= 0,1586487 и А(1) = 0,6827026.
. Программа 6.38. Вычисление функций V(x)b П(х), Q(я) и Д(х)'
€ гримененнем аппроксимации
П (х) = 1 - ¥ (х) (а(Л + а2Л2 + ... + М5),
где X = 1/(1 + рх), с погрешностью  не более 1-10~7. Ввод: р =
= 0,2316419 = Р9, а( = 0,31938153 = Р1, а2 = —0,35656378 = Р2,
а3 = 1,7814779 = РЗ, а4= —1,821256 = Р4, а5 = 1,3302744 = Р5 н
х = РХ. Вывод см. в программе 6.37.
Т77	ИП9	X	1	+	Fl/x	П8	ИП7	Fx2	2
/-/	ч-	Fe*	2	Far	X	F V	ч-	ПД	С/П
5	ПО	ИП5		XY	ИП8	X	кипо	+	ИПО
Fx = 0	24	XY	ипд	/-/.	X	1	+	ПВ	С/П
1	ИПВ	—	ПС	С/П	ИПВ	2	X -	1	—
ПА	С/П	БП	00						
Для	х =	1 получим		^(1)	= 0,24197072,		П(1) =	= 0,8413448,	
Q (1) = 0,1586552, А (1) = 0,6826896.
6.10. Функции плотности вероятности
и распределения случайных величин
Частота появления случайной величины х в интервале dx:
p{x) — dF(x)ldx
определяет плотность вероятности случайных величин. Интеграл
X
F (х) = р (х) dx
— оо
задает функцию распределения случайных величин.
Для многих законов распределения р(х) п F(x) задаются про-
стыми формулами [10] и составление программ для их вычислений
не' представляет трудностей. Ниже дан пакет программ вычисления
р:(х) н F(x) для тех законов, у которых вычисления р(х) и F(x)
требуют специального подхода.
Программа 6.39. Вычисление p(x)=4f(x) (6.13) и П(х) (6.15)
для гауссовского стандартного распределения аппроксимацией
П (х) = 1 — (1 4- cix 4- сгх2 4- ... 4-с6х®)~16/2
с погрешностью до 1,5-10-7. Ввод: Ci = 49867347- 10_» = Р1, сг ==
.= 21141006-10-»= Р2, с3 = 3277626-10-»= РЗ, с4 = 38004-10“»=
= Р4, с5 = 48891 • 10-» = р5> Св = 5383.)0-е == Рб и х = РХ (при
смене х вводится только новое значение х).
П9	Fx <	:o 04	/-/	ПА	Fx2	2	/-/ ’	"4“	Fe*
Гл	2	X	F V*	4-	П8	С/П	6	-no	ИП6
	XY	ИПА	X	КИП0	4-	ИП0	Fx = 0	21	XY
1	4-	1	6	/-/	XY	FXy	2	/-/	-4“
1	4-	ИП9	Fx>0	50	XY	П7	С/П	БП	00
XY	1	XY	—	БП	46				
Для х = 0,5 р(х) = 0,35206532, П(х) = 0,6914625, а для х = — 1
р(х)= 0,24197072 и F(x)= 0,1586552. При х < 0 используется фор-
мула П(х)= 1 —П(|х|).
Программа 6.40. Вычисление
р (х) = ехр £—]/и f W = п 0 g " )
для нормального (гауссовского) распределепия с дисперсией а.									
Ввод: Ci 4- с6		(см. программу 6.39), т = PC, а — РД и х = РХ.							
ИПС	—	ипд	-4**	П9	Fx<0	08	/-/	ПА	Fx2
2	/-/	-4“	Fe*	Fn	2	X	F V		ИПД
-4-	П8	с/п	6	ПО	ИП6		XY	ИПА	X
КИПО	4-	ИПО	Fx = 0	27	XY	1	4-	1	6
/-/	XY	FxV	2	/-/	-4**	1	4-	ИП9	Fx>0
56	XY	П7	С/П .	БП	00	XY	1	XY	—
БП	52							>	
' Для т = 1,5 и о = 0,5 р(1) = 0,48394144, F(l) = 0,1586552 и
р(2) = 0,48394144 и >(2) = 0,8413448.
Программа 6.41. Вычисление
, . 1gе Г (1g х — ш)21 р, ч /Igx —
р (х) =---£-=- exp I — -i-s-----— I и F (х) = П I —----------1
хад/2л L 2о2 J	ко/
для логарифмического гауссовского распределения, Ввод'см. в про-
грамме 6.40.
ПЭ	Fig	ИПС —	ипд		ПВ	Fx<0	10	/-/
ПА	Fx2	2	/-/	•А»	Fe*	1	Fe*	F Is»	X
ИП9	•4-	ИПД -5-	Fit	2	X	F	-=•	П8
С/П	6	ПО ИП6	f	XY	ИПА	X	КИПО	+
ИПО	Fx =	0 35 XY	1	+	1	6	/-/	XY
Fx»	2	/-/ -	1	+	ИПВ	Fx>0	64	XY
П7	С/П	БП 00	XY	1	XY		БП	60
Для т		— 1 и а — 0к1	р(8) = 0,13541585,			F(8) =	0,1662477 и	
р(10)	= 0,17325843 и F(10).=		-0,5.					
Программа 6.42. Вычисление						-		
Р (*) —		1 ( F 1 ехр а V 2л 1 L	(х — т)2 1 2а2 J		+ ехр£	_ (* + »02T) 2ff2 JJ		
и								
		F(x) = H (А	— m \ О )	+ п	fx + m 1 G	) 1		
для распределения модуля гауссовской случайной величины: Ввод
см. в программе 6.40 (х > 0).
П9	ИПС	—	ИПД		П7	ИП9	ИПС	+	ИПД
—	ПВ	Fx2	2	/-/	—	Fe*	ИП-7	Fx2	2
/-/	ч-	Fe*	+	ипд	ч-	Fit	2	X	F V"
=	с/п	ИП7	Fx<0	36	/-/	ПП	59	ИП7	Fx>0
44	XY	БП	48	XY	1	XY	—	ПА	ИПВ
ПП	59	ИПА	+	1	——•	С/П	БП	00	П8
6	ПО	ИП6	t	XY	ИП8	X	КИПО	+	ИПО.
Fx=0	64	XY	1	+	1	6	/-/	XY	Fx”
2	/-/	н-	1	+	В/0				
Для т	= 2 и	с = 1	P(l) =	0/24640257,		F(l) =	0,1573054 и		Р(3)=:
= 0,24197221 и Г(3) = 0,8413445. •
Программа 6.43. Вычисление
р(х)=Ле-Л'х-'г1/2
И
е-х | х-|х у2(	_ 00 < х < р,
1 — е-*’1 *~и 1/2, р < х < оо,
F (х) =
для распределения Лапласа. Ввод: р = РО, X = Р1 и х — РХ.
П2	ИПО	— .	Fx<0	06	/—/	ИП1	/-/	X	Fe*
2	4-	ПЗ	ИП1	X	С/П	ИП2	ИПО	—	Fx<0
25	ИПЗ	С/П	БП	00	1	ИПЗ	—	БП	22
Для р = 1 и X = 2 р(—0,5)= 0,049787072, F(—0,5) = 0.024893536И
р(1,5) = 0,36787944 и f (1,5) = 0,8160603. 4
Программа 6.44. Вычисление р(х) =±xme~*/ml для показательно-
степенного распределения. Ввод: т = РА, х = РХ > О.
П9	ИПА	ПО	Fx =/=	О	12	1	ИПО	X	FLO	06
,БП	13	1	П8	ИПА	ИП9	FxU	ИП9	/-/	Fe*
X	ИП8	4-	П7	С/П	БП	00
Для х —	т = 3 р(3)	= 0,22404176,	а для	х = т = 1	р(1)=«
== 0,36787944.
Программа 6.45. Вычисление
₽W==2dhF И FW = 4 + Tthax
для распределения sch2x. Ввод:	а = РА, х = РХ. Вывод	результа«
тов; р(х) -> РХ, F(x) -> PY. П9 ИПА X П6 Fe*	t Fl/x — 2	
f Fx2 1	+ F/	2	4-2	Fl/x
+ П8 ИП6 Fe* f	Fl/x + Fx2 Fl/x	ИПА
X 2	X П7 С/П	БП 00	
Для а = 1 и х = —1 р(х)= 0,20998718 и F(x) = 0,11920292,
Программа 6.46. Вычисление
.пут-па г,+
у/nN Г(ЛГ/2) k ЛМ
для распределения Стыодента с применением для гамма-функций
формулы Стирлинга, т. е. [6]
Р (*) д/— Ввод: N — РО,	(tf + 2)	fN + 3\N	(6W + 19)	X/	
	17,08	VW4-2,	(W+ 1) (6У+ 13) z' х — РХ (при первом пуске х = Р9).			-0V+B/2
ИПО |		3	+ ИПО 2	+	Ч-	Fx«
X ИПО	2	+ X 1	7 ,	0	8
-> F V	ИПО	6	X П8 1	9	+	X
ИПО 1	+	-S- ИП8 1	3	+	“Г'’	П8
ИП9 П9	Fx2	ИПО 4-	1	+ ипо	1	+
2	/-/ Для Л' = 3 Программа	4- XY Fx'J ИП8 X С/П и х = 2 получим р(х) = 0,067514971. 6.47. Вычисление		БП	41
хяе-х/Р
Р ~ ₽а+’Г(а+ 1)
ДЛЯ гамма-распределения при целых а, когда Г(а+. 1)=ос!. Ввод:-
а — РА, р == РВ и х = РХ (при первом пуске х — Р9). ••
ИПА	ПО	Fx¥=O	|1	1	ИПО	X	FLO	05	БП
12	1	П6	ИПА	1	+	ИПВ	Fx»	ИП6	X
П5	ИП9	П9	ИПА	XY	Fx*	ИП9	ИПВ	/-/	4-
Fe*	X	ИП5	4-	П7	С/П	БП	22
Для а = 0, ₽ = 1 и х = 0,2 р(х) = 0,81873072-
Программа 6:48. Вычисление
р (х) = xw“1e“x!/2/2/v/2-Ir (N/2)
для /-распределения с применением для Г (А/2) формулы Стирлин
га, т. е.
, ,	Axw_1e-*'/2	, , N
р (х) ~ -г,-;.;—" —---а------------> гДе « == 1 + — •
2ni~ ^2п/а (а/е) (1 + 1/( 12а))	2
Ввод: N — РО, х = РХ (при первом пуске х =. Р9).
ИПО	2	4-	П7	2	Fx»	Fit	2	X	ИП7
1	+ '	П7	4-	F V	X	1	ИП7	1	2
X	Fl/x	+	X	ИПО		П8	ИП7	1	Fex
	ИП7	XY	РхУ	ИП8	X	П8	ИП9	П9	ИПО
1	—	XY	Fx»	. ИП9	Fx2	2	/-/	4-	Fe*
X	ИП8	4-	П7	С/П	БП	38			
Для А = 1 и х = 0,1 р(х) — 0,79449834.
Программа 6.49: Вычисление
р (х) = xNI2~le~xl2/2NI2r (А/2)
для распределения /2 с применением соотношения
Г(А/2) = 2Г(1 + N/2)/N = 2Г (a) IN
И формулы Стирлинга для Г (а), что дает
Ах^2-*е-ж/2
р (х) ~ ---==----------------------,
2“ V2n/a (а/е)« (1 + 1/(12а))
где а = 1 — N/2.
Ввод: N = Р0, х — РХ (при первом пуске х = Р9).
ИПО	2	”7“	1	+	П7	2	Fx»	Fn	2
X	ИП7	4- F V"	X	ИПО		1	ИП7	1
2	X	Fl/x +	X	П8	ИП7	1	Fe*	
ИП7	XY	РхУ ИП8	. X	П8	ИП9	П9	ИПО	2
	1	—J XY	Fx»	ИП9	2	/-/		Fe*
*	ИП8	4- С/П	БП	37				
Для	N =	20 и х = 10	р(х)=.	0,01813276,				
Программа 6.50. Вычисление плотности распределения Эрланга
К-го порядка (А — целое число)
о(х)==	Х**--хКе- р W Г(/(+ 1)	Лх _	—		 V А!	Ке-Лх	
Ввод: X = РА, К = РВ, х = РХ х = Р9).	(при	первом	пуске	программы
ИПВ ПО Fx =/= 0 11	1	ИПО	X	FLO	05 БП
12	1	П6	ИПВ 1	+	ИПА	Fx»	ИП6 ~
П5	ИП9 П9	ИПВ XY Fe* X ИП5	X П7	рхУ С/П	ИП9 БП	ИПА 22	1-1 X
Для /( = 3 и X = 2 имеем = 0,39073354.	р(0,5) = 0,12262644			н p(2)=j
' 6.11. Гипергеометрические функции
Программа 6.51. Вычисление гипергеометрического ряда по раз«
ложению [29]
N ri-1	-1
»=1 4=0	J
Ввод: а, b, с и х в регистр X.
П2	С/П	ПЗ	С/П	П4	С/П	Fn	Fe*	ПО	Fig
ИПО	1	——	П1	ИП2	+	X	ИШ	ИПЗ	+
X FLO	ИП1 10	ИП4 С/П	+	—	ИПО	-г-	X	1	+
Для а — Ь = с — 1 и х = 0,8 получим Г(1; 1; 1; 0,8) = 4,978539
’(точно 5). Погрешность вычисления 6 < 0,5% при —0,1 х 0,8.
Программа 6.52. Вычисление вырожденной гипергеометрической
функции по разложению [29]
w р-1	"I
ф(0, с, х)=1 + £ IJJ (1+“ jV+’n j + е"+г
1 = 1 *-/=0	J
Ввод: а,	сих	в регистр X.					
П2	С/П	ПЗ С/П	Fn	Fe*	ПО	Fig	ИПО 1
—•	Ш	ИП2 +	X	X	ИП1	ИПЗ	+ -F
ИПО		1 +	FLO	08	С/П		
Для а = с — 1 и х = 5 получим Ф(1,1,5) == 148,41315 (точно
148,41316). Погрешность вычисления 6<1-10“4 при 0,<а<си
<—5 х 10, ~ 2 мин.
Глава 7'
ПРИМЕРЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ
И ЭЛЕКТРОННЫХ ЦЕПЕЙ И УСТРОЙСТВ
7.1. Расчет индуктивных элементов
Индуктивность проводов, катушек н других индуктивных эле-
ментов L(w, xi, х2, ..., хп) в справочной литературе обычно задает-
ся функцией числа витков w и конструктивных параметров х2, ...
..., хя [14]. Одиако чаще требуется найти w (или какой-либо па-
раметр Xi, х2, х„У по заданной L = £0. Если L(w,х2, ...
хя) разрешима в виде ш = (£, Xi, х2, ..., х„), расчет сводится
К формульному счету. В противном случае w определяется числен-
ными методами решения нелинейного уравнения
£о— L(w,. хь х2, ...., ха) = 0.
В приведенных ниже программах Lo задана в наногенри, а гео-
метрические размеры катушек — в сантиметрах.
Рис. 7.1. Виток в свободном
пространстве
Рис. 7.2. Однослойная ка-
тушка
Программа 7.1. Расчет индуктивности’ круглого витка со сред-
ним диаметром D и диаметром провода d по формуле L =ч
i.«=.2n£)(ln(8D/d)- 1,75). Ввод: D = РХ, d == РХ.
f С/П -т-	8	X	Fin	1	,	7	5
- X 2	X	Fit	X	С/П	БП	00
Для D = 2 см, d = 0,1 см получим L = 41,785364 иГи.
Программа 7.2. Расчет числа витков- w однослойной катушка
заданной длины I (рис. 7.2) из уравнения
Lo — L(Aw + B/w — С) — 0,
,.де д = (stP)2/(Z + 0,45Р); В = 3^lDjd и С = 4Р. Ввод: D । = Р5, = Р6 и Ео = РХ.										= Р4,
П7	Fn		ИП4	X	Fx2	0		4	5	ИП4
-X	ИП5		+	•	ПА	ИП5	ИП6	-т-	ИП4	X
3			5	X	ПВ	ИП4	4	X	ПС	0
П2	1		0	ПЗ	ИП2	ИПЗ	4*	П2	ИПА	X
ИПВ ИП2				+	ИПС	—	ИП2	/-/	X	ИП7
	Fx<	:о	34	ИП2	ИПЗ	—	П2	С/П	ИПЗ	1
0	-г-		ПЗ	БП	34					
Для D = 2 см, / == 2 см, d = 0,05 см и Lo = 5- 10s нГи, нажав
(трижды клавишу С/П (с перерывами на время счета), получим
w — 18,9. Если сечение катушки не круглое и имеет вид правиль-
ного многоугольника, то в приведенных выше формулах берется
D — Do cos2 (л/(2п)).
Рис. 7.3. Тороидальная катуш- Рис. 7.4. Тороидальная катуш-
ка круглого сечения i ка прямоугольного сечения-
Программа 7.3. Расчет w однослойной тороидальной катушки
круглого сечения (рис. 7.3):
w = дД0/2л (р — д/р2 — Р2).
Ввод: D, Dj и Ео в регистр X.
П9 С/П	П8	С/П	1	2	-5- Fm	-4-	ИП9
1 Fx2	ИП8	Fx2	-	FV'	— 4-	FV	БП
03
Для D =3 см, Di. = 1 см, Lo — Ю5 нГн получим w=304,56901.
Программа 7.4. Расчет w тороидальной однослойной катушки
прямоугольного сечения (рис. 7.4):
w — '\ZLol2hA'ti(D2IDi).
Ввод: Р2, Dlt h. и Lo в регистр X.
П9 С/П	П8 С/П П7	С/П	ИП7	-2	4-
ИП9 ИП8	-j- F 1п -т-	F V	БП	05
Для Рг = 3 см, Di = 1 см, Л= 1 и Lo ss 1-108 иГн получим
w ~ 213, 33533.
. Программа 7.5. Расчет w многослойной тороидальной катушки
'круглого сечения (рис. 7.3):
1,75).
Ввод: D, Dt и Lo в регистр X.
П9 С/П П8 . С/П	ИП9	8	X ИП8	ч-	F In
1,75	—	ИП9	X Рл	X	2
X + F/ С/П БП 03
w=aJlo!'2mD (in-—
Для D = 4 см, 7>1 = 0,8 см
= 453,00673.
и Lo = 107 нГи получим w =)
Рис. 7.5. Многослойная
короткая цилиндрическая
катушка
Программа 7.6. Расчет w многослойной короткой цилиндриче-
ской катушки (рис. 7.5):
w = Vi-o (ЗР + 9/ + 10с)/25лР2.
Ввод: D, I, с и £0 в регистр X.
П9	С/П	. П8	С/П	П7	С/П	ИП9	3	X	ИП8
9	X	+	ИП7	1	0	X	+	X	2
5	f	Ря	4-	ИП9	Fx2	ч-	F V	БП	05
Для D == 2,5 см, I — с = 1 см и Lo = 2 • 10s нГн получим w =9
= 103,90895.
Программа 7.7. Расчет ш катушки на кольцевом ферромагиит»
ном сердечнике:
w = VLo (d„ +.rfB)/4pft (dH — rfE) при dn/dB < 1,75,
w = V^-o/2pftin (dH/dE)	при d„/dB>l,75,
где dH и de — наружный и внутренний диаметры сердечника, h — его
1сота. П9	Ввод: С/П	dE, de, h, ц и Lo в регистр X.							
		П8	с/п	П7	с/п	П6	с/п	П5	ИП9
ИП8	——	П4	1		7	5	—-	Fx < 0	38
ИП9	ИП8	+	ИП5	X	4		ИПб	"Д'"	ИП7
ч-	ИП9	ИП8	—		FV	БП	07	ИП5	2
07	ИПб	 *т*	ИП7	4-	ИП4	F In	-j-	F<	БП
Для rfH = 4:см,.rfa = 2 см, h = 1. см, ц = 1000 п Lo = 2-.107 нГя
получим w = 120,11223, а для dB = 3 см н этих же данных полу*
чим w — 187,08286.
Программа 7.8. Расчет w катушки на
броневом сердечнике (рис. 7.6):
w = ^Lo (4 + В)! 19,74ц-
где
А = (Л, + й2)
1 1
d*-d* + 4-4
В = -*-*---In
h2 —
da + d.<
dj + d2
Рис. 7.6. Катушка на
броневом сердечнике
и нажимается клади*
Ввод (после нажатия клавиш В/0 и G/П):
db d2, dz, dt, hu hi, ц и La в регистр X.
При смене La набирается новое значение £0
ша С/П.
8	ПО	0	С/П	КПО	ИПО	1	——•	Fx = 0	02
С/П	П8	ИП4	Fx2	ИП5	Fx2		Fl/x	ИП6	Fx2
ИП7	Fx2	—	Fl/x	+	ИПЗ	ИП2	+	X	ПА
ИП5	ИП4	+	ЙП7	ИП6	+		F in	ИП2	ИПЗ
—		ПА	+	ИП8	X	ИП1	—	1	9
»	7	4		FV	БП	10			
Для di — 1 см, d2 = 2 см, d3 = 4 см, dt — 5 см, hi — 3 см,
h-г = 4 см, ц — 10 и Lo = 5-105 нГн получим w = 103,26144. Для
Lo — 1 • 105 нГн w — 46,179922.
Рис. 7.7. Сердечники из элементов’ П- (а) и Ш-образиой формы (б)'
i
Программа 7.9. Расчет w катушек с замкнутым сердечником
(рис. 7.7):
w = VLolm (1 + И di/alm)/4itiiFc,
где Fc — площадь поперечного сечения сердечника, 1т — средняя дли-
на магнитной линии. Ввод: Fc, lm, a, di, ц -и Lo в регистр X. При
смене Lo набирается новое значение LB и нажимается клавиша С/П.
ПЭ	С/П	П8	С/П	П7 С/П	П6	С/П	П5	с/п
ИП8	X	4	4-	Fn	ИП9	-j-	ИП5	4-
ИП5 ИП6 X ИП7 ИП8 1	+ X
F< БП 09
Для	Fc = 1	cms,	Im =v	10 см, a — 1,5 cm, di	= 0,05	cm, g	='
== 1000	и	Lo = 5-107 иГи получим	w —	415,23228. Для	=
= 1-107 нГн получим w = 185,69752.
Программа 7.10. Расчет w тонкопленочной катушки (рис. 7.8)
с заданными размерами Лн и Лвн:
w e <Л» + Лвн) ,п Лн - Лвк)]} ’
где ki = 2,33 и kt = 4 для круглой катушки и kt = 12,05 и fo =1
= 8 — для квадратной (k, п k2 — коэффициенты, учитывающие гео-
«) #/
Рис. 7.8. Тонкопленочные катушки с витками круглой (а) и квадрат-*
ной (б) формы
метрическую форму витка). Ввод: kt, kz, Лн, Лвн и Lo в регистр X,
При вводе нового значения Z.o нажимается только клавиша С/П.
П9	С/П	П8	С/П	П7	С/П	П6	С/П	ИП9	4-
ИП7	ИП6	+	П5	4-	ИП5	ИП8	X	ИП7	ИП6
-	-т-	F 1п	4-	3	t	-5	4-	XY	Fx»
БП 07
Для ki = 2.33, kz — 4, А„ — 1 см, ЛВн = 0,5 см и /.о = 200 иГн
получим w = 6,5669484. Для Lo = 500 нГн и w = 11,379616.
Программа 7.11. Расчет w тонкопленочной катушки (рис. 7.8)
с заданным шагом I из решения уравнения
L--k' (l+?sr) '"-'‘“'"Ь ('+“”)]“»
Ввод: kt, k2, Лвн, I и Lo в регистр X. Для круглой катушки kt = 2,33
и kz = 4, для квадратной kx = 12,05 и kz = 8.
П7 С/П П9 С/П П4 С/П П5 С/П П6 =0
П2 1 ПЗ ИП2 ИПЗ + П2 ИП4 2	. X ’
ИП2	4-	ИПб		1	+•	П8	ИП9	X	Fin
ИПб	X	ИП8	X	ИП7	X	П8	8		3
	ИП2	Fx*	ИП8 /-/		X	ИПб	+	Fx <0	13
ИП2	ИПЗ	—	П2	С/П	ИПЗ	1	0		ПЗ
БП 13 Для kt =		2,33,	kz =	4, у4вн =	0,2 см	, Z =	0,05 см	И До =	100 нГн
получим w = 7,14, нажимая три раза (с перерывами на время сче-
та) клавишу С/П.
Дроссель фильтра обычно выполняется на П или Ш-образном
сердечнике для стальных пластин (или ленты). Он должен обеспе-
чить, заданную индуктивность До при токё_7о, текущем через обмот-
ку дросселя.
_ Расчет дросселя выполняется по методике (8) с помощью двух
программ.
Программа 7.12. Расчет ширины стержня а, поперечного сечения
Q, оптимального зазора Zz/2, коэффициента М, относительной длины
воздушного зазора 1г (в % от 1т), эффективной магнитной, прони-
цаемости материала сердечника pz и толщины набора с. Ввод: 10 =$
й= PG, Lq = Pl.
ИПО	Fx2	ИП1	X	П9	F<	FV	2		6
X	С/П	Fx2 .	Г		5	X	С/П	ИПА	
ПС	ИП9	ИП2	—	ИП4		П5	Fx2	1	5
вп	3	X	П9	ИПб	3	3	0	X .	ИП9
—	П6	ИПб	/-/	4	0	1	X	Fe*	1
1	4	X	5	0	+	П7	ИПб	ИП4	X
2	0	4"	С/П						
Пусть нужно рассчитать дроссель, имеющий До = 3-10~’ Гн при
рабочем токе 1о — 15 А. Введя 1а и До и, нажав клавиши В/0 и С/П,
находим а = 2,6 \/д0/ц== 1,3252545 см. Еще "раз нажав клавишу
С/П, находим Q — 1,5а2 = 2,6344491 см2. По нормали Н0.666.002
«Магнитопроводы ленточные» выбираем подходящий сердечник
ШЛ 16X16. Вводим в машину его уточненные данные: а — 1,6 см=]
;= РА, Ь =. 1,6 см = РВ, h = 4 см = РЗ, 1т = 13,7 см = Р4 и Q=»'
If= 2,65 = Р2 = РХ. Нажав- клавишуС/П, получим: Л1=До/о/(ас/т)=»
«= 1,859248 • 10~3 -> Р5, Zz% = ЗЗОМ - 15 • 103А12 = 0,56169979 мм ->
->Р6, pz = 114ехр(-40Ш)4-50== 104,08949->-Р7,	с=<?/а =
»=• 1,65625 см PC н IJ2 = Zz%Zm/20 = 0,38476435 мм -> РХ. Пере-
ходим к следующей программе.
Программа 7.13. Расчет диаметра провода d, числа витков w;
омического сопротивления г и коэффициента заполнения окна медью
йм. Ввод (после выполнения программы 7.12): допустимая плотность
Дока б = Р8.	.
ИПО	ИП8 +	FV	1	1	3	X	П9
с/п	ИП1 ИП4	X	1	,	2	6	4-	ИП7
	ИП2 4-	FV"	1	‘ВП 4	X	ПД	С/П
ИПА	ипс +	2	X	ИПВ Frt	X	+	ИПД
X	2	2	5	ВП 4	/-/	X	ИП9
Fx2	П9 4-	С/П	ИП9	ипд X	8	ВП	3
/-/	X ипв	•т*	ИПЗ	4- С/П			
Введя 6 = 3 А/мм2 и нажав клавиши В/0 и С/П, найдем
rf= 1,13^/^/6 = 2,5267567 мм. Нажав ещё раз клавишу С/П, полу-
чим w == 104 VWm/(l>26iiz«c) ==34,388184, далее, дважды нажав
клавишу С/П, получим' г — 2,25- 10~4tci[2(« -}- с) -KnB]/d2 =j
= 1,398411b 10-2 Ом и Ам = 8-10-3 wtP/(bh) = 0,27443915..
Исходными данными при расчете силового трансформатора яв-
ляются: габаритная мощность Рт, максимальная индукция в сер-
дечнике В,п, число стержней сердечника с обмотками а, допустимая
плотность тока 6, коэффициент заполнения окна сердечника медью
kK, к. п. д. трансформатора т), напряжения U\ и U2 и токи /1 й /а
первичной и вторичной обмотки. Порядок технического расчета си-
лового трансформатора следующий.
1.	Находим произведение сечений стали Ост и окна Qo сердеч-
ника
ОстОо = г/0,022/
Подбираем подходящий тип сердечника и уточняем для него зна-
чения Ост и Qo.
2.	Определяем э. д. с. одного витка е — 4,44-10~* /BmQo-tko.
3.	Находим число витков вторичной обмотки w2 = Ui/e.
4.	Находим приближенное число витков первичной обмотки Wi =i
= Ui/e.
5.	Определяем диаметр провода вторичной обмотки (без изо-
ляции) rf2 = 1,13 V/2/6.
6.	Определяем диаметр провода первичной обмотки (без изо-
ляции) dl = 1,13 V/i/6-
7.	Находим длину провода первичной обмотки li =1
= а>1[2(а + с)4~nh]-10-2, где а—ширина сердечника, b — ширина
окна ис — толщина набора.
8.	Рассчитываем падение напряжения иа активном сопротивле-
нии первичной обмотки ДЦ =2,25. Ю-2/]/]/^2.
9.	Уточняем число витков первичной обмотки a>i = (6Л — &Ui)'e,
Программа 7.14. Расчет силового трансформатора. Ввод: fBm =1
= Pl, 6 = Р2, т] = РЗ, s = Р4, ke — Р5, kK = Рб и далее в соот-
ветствии.с табл. 7.1.	'
Таблица 7.1
Ввод	РГ=РХ	а=РА, Ь=Р.В с==РС	(72=РХ			/,=РХ	-	-	-
Вывод	^ст^о	е	W2	Ю1			е	AC/j	
ИП1	"Г	ИП2 -4-		ИПЗ	-4-	ИП4	_u	ИП5 -4-	
ИП6		4	5	X	С/П	ИПА	ИПС	X	ИП1
X	ИП5	X	4	4	4	ВП	6	/-/	X
no	С/П	ИПО -i-		С/П	П7	ИПО	-4-	П8	С/П
ИП2	4-	FV- 1		В	1	3	X	С/П	П9
ИП2	-—	FV" 1			1	3	X	ПД	С/П
ИПА	ИПС	+	2	X	ИПВ	Fit	X	+	ИП8
X	1	0	0	ч-	С/П	ИП9	X	0	
0	2 ’	2	5	X	ипд	Fx2	-4-	С/П	/-/
ИП7	+	ИПО 4-		С/П					
Пусть нужно рассчитать силовой трансформатор при следующих
исходных данных: fBm = 60 Гц-Тл (f = 50 Гц, Вт = 1,2 Тл), б =
i= 2 A/мм2,' т) = 0,96, s = 2, kc = 0,95, k„ = 0 32 и Рг = 215 Вт.
Пустив программу нажатием клавиш В/0 и С/П, получим Q„QO =
= 138,13218 см2. Выбираем магнитопровод ленточный ПЛ -25X50 —
65, имеющий QctQo = 140 см4 (а = 2,5 см, b — 2 см и с = 5 см).
Введя эти данные в регистры А, В и С, получим (нажав клавишу
С/П) е= 0,31635 В. Далее, введя U2 — 450 В,- получим w2•=
.== 1422,4751; введя U\ = 127 В, получим Wi = 401,45408; введя
'72 = 0,475 А получим d2 = 0,55069387 мм; введя /, = 1,7 А, полу-
чим rfi = 1,0418085 мм и, далее, h — 85,442214 м, Д1Л —
.= 3,0111205 В и (i'i = 391,93576.
7.2. Расчет емкостей
Расчет емкостей конденсаторов обычно проводится при их раз-
работке. Конструкторы электротехнической и электронной аппара-
туры используют их как готовые элементы. Характерное исключение
'составляют пленочные конденсаторы гибридно-пленочных интеграль-
ных микросхем.
Расчет пленочных конденсаторов с заданной емкостью С, числом
обкладок т, толщиной его диэлектрика d и относительной диэлек-
трической проницаемостью е сводится к определению удельной ем-
кости Со = 0,0885 е(т — l)/d и площади обкладок S = С/Со. После
втого по заданному отношению сторон Q = А/В прямоугольника об-
кладок находятся стороны А == VQS и B^^SIQ.
Программа 7.15. Расчет пленочного конденсатора. Ввод: m .= Р1,
dt — Р2, е — РЗ, Q = Р4 и С — РХ. Вывод результатов: Со~>Р0,
А, -> РА, В -> РВ, 3 -> PC = РХ.
ИПЗ	ИШ	1	—	X	ИП2	4-0	,0
8	8	5	X	ПО	-г	ПС ИП4	X FV
ПА	ИПС	ИП4	-Ь	FV"	ПВ	ИПС С/П	БП 00
Для т — 3, d = 0,01 см, е = 4,7, Q = 2 и С = 100 пФ полу-
чим Со = 83,19 пФ/см2, Л =. 1,5505273 см, В — 0,77526366 см и
3 = 1,2020675 см2.
Расчет емкости проводников в свободном пространстве прово-
дится по формуле
С = kiel/lg(kzx/d),
где значения klt k2 и наименование параметра х указаны в табл. 7.2,
I — длина провода и d — его диаметр.
Таблица 7.2
Емкость
ki ki L Наименование х
Между двумя проводами вдали от
земли
Расстояние между прово-
дами
Между горизонтальным проводом
и .землей
Высота подвески
Между вертикальным проводом и
землей при расстоянии от земли
до нижнего конца
’ ft > //4
Длина провода
Между вертикальным проводом и
землей при расстоянии от земли
до нижнего конца
h < 114
Длина провода
0,24	1,15
Между проводом и корпусом при
вводе провода через отверстие
0,24	2
Диаметр отверстия
Программа 7.16. Расчет емкости проводника в свободном про-
странстве. Ввод: ki = Pl, k2 — Р2, в = РЗ, I = Р4, d = Р5 и
х = РХ.	'	~
ИП2	X	ИП5	4-	Fig - ИП1	ИПЗ X ИП4 X
ХУ	Ч-	С/П	БП	00
Для ki = 0,24, k2 = 4, в = 1, t — Г03 см, d = 0,2 см н к =>:
= 200 см получаем £ = 66,62854 пФ.
Иногда некоторый конструктивный параметр х, определяющий
емкость Со, можно определить из решения нелинейного уравнения
С(х)-Со = О
численными методами (см. пример ниже).
Программа 7.17. Расчет расстояния х между центрами двух ша-
ров по заданной емкости Со между ними при С(х) вида
Ввод: Со, диаметр шаров D и е в регистр X.
П9	С/П	П8	С/П	П7	ИП8	ТО	1	0	П5
ИП0	ИП5	+	ТО	Fx2	4	X	ИП8	Fx2	—
П4	ИП8	X	2	•4.	ИП6		ИП4	ИТО	2 е
X	ИП8	X	—	—	1	+	0	»	2
7	8	X	ИП7	X	ИП8	X	ИП9	—	Fx<0
10	ИП6	ИП5		П6	С/П	ИП5	1	0	—
П5	БП	10							
В этой программе х > D (при х = D шары соприкасаются в
С(х)->со) возрастает поразрядно. Для Со — 5 пФ, D = 10 см и
е = 1 получим х = 12,259 см, нажав пять раз клавишу С/П с пе-
рерывами на время выдачи каждой цифры.
7.3. Расчет линий передачи и задержки
Линии передачи могут быть проводные, коаксиальные, полоске*
вые и др. Полосковые несимметричные (рис. 7.9, а) и симметричные
(рис. 7.9, б) линии широко используются в радиоэлектронной аппа*
ратуре. Расчет линий обычно сводится к определению некоторого
V/
Рис. 7.9. Полосковые несимметричные (а) и симметричные (б) линии
конструктивного параметра х по заданному входному сопротивле-»
нию линии Zo, а также определению фазовой скорости V. Для длин-
ных линий существенна оценка потерь на единицу геометрической
длины линии.	''
Для некоторых линий
 _ г£> _ exp (/л Vе/бо)
Х d	k
(7.3)
где е — относительная диэлектрическая проницаемость диэлектрика,
d — диаметр внутреннего проводника, a D и k определяются сле-
дующим образом:
1.	Для линии в виде круглого проводника, расположенного в
середине между проводящими плоскостями, расположенными на рас-
стоянии D друг от друга, k — 1,27.
2.	Для линии в виде круглого проводника, помещенного в экран
с квадратным сечением и стороной D, k = 1,08.
3.	Для линии в виде круглого проводника, помещенного в экран
круглого сечения с диаметром D, k — 1 (коаксиальная линия).
4.	Для линии в виде круглого проводника, расположенного на
биссектрисе прямого угла, образованного двумя полубесконечнымя
проводящими плоскостями, на расстоянии D/2 от каждой плоскости,
1,4.
Программа 7.18. Расчет х по формуле (7.3):
в FV" 7Л X 6 0 4- Fex ( 4-
Вычисленне (7.3) по этой программе проводится вручную.
Пример. Для воздушной коаксиальной линии в = 1, k= 1
и Z. = 100 Ом получим х = Dfd — 5,2944895.
Программа 7.19. Расчет ширины полоски W и vic (где с — ско-
рость света в вакууме) несимметричной полосковой линии
(рис. 7.9, а) по формулам .
W = 1,25 Г----f---------пу-г - /1,
Lexp [Zn (в -ь 1,41) ^/87] J
v/c = 1 /[о,475е + 0,67)%] •
Ввод: Zj,, h„ /пев регистр X. Вывод результатов: v/c-^PX, и,-
->PY = РД.
П7	С/П	П8	С/П	П9	С/П	П6	1	,	2
5	ИП8	5	. ,	9	8	X	ИП6	1
4	1	+	F<	ИП7	X	8	7	4-	FeK
ИП9 — X ПД ИП6 0,47
5	X	0,	6	7	4-	FV-	Fl/Х	С/П
БП 00
Для = 75 Ом, h = 1 мм, / = 0,05 мм и в — 4,7 получим
v/c == 0,58696727 и (нажав клавишу XY) № = 0,82501461 мм.
Программа 7.20. Расчет v/c и ширины полоски Ц7 симметричной
полосковой линии (рис. 7.8,6) по формулам
W = 0,59 Г-----4А- .-_ _ 2,1/1 v/c = 1/д/е,
L exp (Zn Ve/60)	. J
Ввод: Z.i, b, 1 и е в регистр X. Вывод: о/с -	> РХ,	IV->	PY.
П7 С/П П8 С/П П9 С/П	П6	0	, 5
9 ИП8 4 X ИПб FV	ПД	ИП7	X 6
0	4-	Fex 4- ИП9 2	>	1	X -
X ИПД Fl/x С/П БП 00			
Для Z.n = 50 Ом, b = 2,5 мм, t = 0,5 мм и в = 4,7 получим
г/с — 0,46126561 и (нажав клавишу XY) IV = 0,34932508 мм.
Для ряда линий передачи выражение для Zn неразрешимо или
трудно разрешимо относительно конструктивного параметра х, опре-
деление которого является целью расчета. Тогда, задав требуемое
значение ZJl0, его можно найти из решения нелинейного уравнения
2л0 —Хл(х) = 0,
например, методом подекадного приближения с выдачей каждой
очередной цифры результата нажатием клавиши С/П.
Программа 7.21. Расчет диаметра d внутреннего проводника
коаксиальной линии, смещенного отосительио внешнего проводника
с отверстием, имеющим диаметр D, на расстояние Z, из уравнения
			60	ъ D2 + d2- 	=- arch	 Vb	2dD			4/2 _	0.	
Ввод: D, 1, 2ло и в в			регистр X.					
П5	С/П	П6	С/П П7	С/П		6	0- -	XY
	П4	0	П2 0		1	ПЗ	ИП2	ИПЗ
+	П2	Fx2	ИПб Fx2	+	ИПб	Fx2	4	X
—	2	Ч-	ИП2 4-	ИПб	ч-		Fx2	1
1-1	4-	FV	+ Fin	ИП4	X	ИП7	—	Fx<0
18	ИП2	ИПЗ	— П2	С/П	ИПЗ	1	0	
ПЗ	БП	18						
Для D = 1 см, I = 0,25 см, Z.,l0 = 100 Ом и в = 1 получим,
нажав четыре раза клавишу С/П (с перерывами на время выдачи
очередной цифры результата), d = 0,1403 см.
Программа 7.22. Расчет параметра х = a/d линии в виде двух
одинаковых проводников с диаметром d, расположенных на расстоя-
нии а друг от друга из уравнения
„	120
7ЛО------т=~ arch х — о.
-уе
Ввод: ZJ|O и	в в регистр X.							
П9	С/П	F< 1	2	0	XY		П8	0
П2	1	ПЗ ИП2	ИПЗ	+	П2		Fx2	1
/-/	+	FV +	Fin	ИП8	X	ИП9	XY	—
Fx < о	13	ИП2 ИПЗ	—	П2	С/П	ИПЗ	1	0
Ч*	ПЗ	БП 1	3					
Для ZM = 300 Ом и е = 1 получим, нажав клавишу С/П че-
тыре раза, х = 6,132.
Программа 7.23. Расчет параметра х — D/d линии в виде круг-
лого проводника с диаметром d,. расположенного иа расстоянии О
от проводящей плоскости, из уравнения
2ЛО------arch х = 0.
•уе
Ввод: Zno	и e в регистр		X.					
ПО	с/п	F<	6	0	XY		ПВ	0 П2
1	0	ПЗ	ИП2	ИПЗ	+	П2		Рхг 1
/-/	+	FV-	+	Fin	ИП8	X	ИП9	XY —
Fx<0	13	ИП2	ИПЗ	—	П2	С/П	ИПЗ	1	0
	ПЗ	БП	13					
Для Z„o = 300 Ом и е = 1 получим х = 74,2, нажав клавишу
С/П три раза.
Программа 7.24. Расчет расстояния а между двумя проводни-
ками линии в виде двух одинаковых проводников с диаметром d,
расположенных на расстоянии D от проводящей плоскости, из урав-
нения
	2Л0	120 Vs	- Г arch — — L d				= 0.	
Ввод: D, d, 2яо и е в регистр X.								
П9	С/П	П8	С/П	П6	С/П FV“	1	2	0
XY		П5	0	П2	1 ПЗ	ИП2	ИПЗ	+
П2	ИП8			Fx2	1 /-/	+	FV	+
Fin	ИП2	2		ИП9	4- Fx2	1	+	FV*
Fin	—	ИП5	X	ИП6	XY -	Fx <0	17	ИП2
ИПЗ 17	—	П2	с/п	ИПЗ	1	0	ПГ	ПЗ	БП
Для D = 1,5 см, d — 0,1 см, Z.,o = 200 Ом и е = I получим
а — 0,275 см после четырех нажатий клавиши С/П.
Программа 7.25. Расчет расстояния а между двумя проводни-
ками линии с разными диаметрами dt и г/г, расположенными в сво-
бодном пространстве, из уравнения
60	4а2 —df — df
Zno------т=- arch----——------г- = 0.
-ye	2rfl d2
Ввод: dt> dz, 2ло и e в регистр X,
П9	с/п	П8	с/п	П7	С/П	FV	6	0	XY
-Г*	П6	0	П2	I	ПЗ	ИП2.	ИПЗ	+	П2
Fx2	4	X	ИП9	Fx2		ИП8	Fx2	•—а	2
Ч- .	ИП9	ИП8	-е-	t	Fx’	1	I—J	4-
FV	4-	Fin	ИП6	X	ИП7	XY	—	Рх<1Ю	16
ИП2	ИПЗ	—	П2	С/П	ИПЗ	1	0	-* *	ПЗ
. БП 16
ДЛя dt — 0,1 см, = 0,95 см, Хло = 300 Ои и 8 = 1 получим
а — 0,434, нажав клавишу С/П четыре раза.
Для получения больших /л используются коаксиальные линии,
внутренний проводник которых выполнен в виде спирали, содержа-
щей п витков на 1 см длины линии. Для этой линии
£я == ХЛКГ у, V = VKF у,
где 7Л1< и ок — волновое сопротивление и фазовая скорость коакси-
альной линии с обычным внутренним проводником, имеющим диа-
метр d (как и у внешнего диаметра спирали), Fw—поправочный
коэффициент, имеющий вид
Программа 7.26. Расчет п для линии со спиральным проводни-
ком с внешним диаметром d, расположенным внутри проводящего
экрана с внутренним диаметром D, из уравнения
— Fw (п) = 0,
где F№(n) определяется выражением (7.4). Ввод: FVl? d и D в
регистр X.
П6	С/П	П8	С/П	П9		Fx2	1	XY	—
ИП8	Fit	X	Fx2	X	2		ИП9	ИП8	4-
Fin	-s-	П7	0	П2	1	ПЗ	ИП2	ИПЗ	+
П2	Fx2	ИП7	X	1	+	FV~	ИП6	XY	—•
Fx < 0	27	ИП2	ИПЗ	—	П2	С/П	ИПЗ	1	0
	ПЗ	БП	27						
Дпя FWa = 4, d — 0,5 см и D — 1 см получим п = 3,35.
Искусственные линии задержки строятся на основе БС-фильтров
нижних частот. По заданным волновому сопротивлению Х.л, вре-
мени задержки t3 и длительности фронта на выходе линии /ф опре-
деляются число ее звеньев ж= ^i(/3/^),,s и значения индуктивно-
сти L и емкости С звеньев С = 13/Б2л2л, L = t^ZJkzn, где kt = 1,1
и kz = 1,07 для линий на фильтрах Л-типа и kt'= 0,94 и k2 = 1,2
для линий на фильтрах /И-типа.
Программа 7.27. Расчет параметров п, С и L искусственных ли-
ний задержки. Ввод: ki = Pl, fe=P2, Z„,	11 /ф в регистр X.
После получения п число ячеек округляется в сторону увеличения,
уточненное значение вводится в регистр X,
П7	С/П	П9	С/П	П8	-j-	1	,	5	XY
Вх«	ИП1	X	С/П	П6  ЙП9	ИП2	ИПб 4- ,
П5	ИП7	С/П	ИПб ИП7	X	С/П	БП	00
Для kt = 0,94, ki = 1,2,	= 600	Ом.	t3 =	1-10~в с н =='
= 0,05-10~в с получим « = 84,07614. Округляем до п = 85 и на-
бираем уточненное значение п. Получим С = 1,6339869-10~11 Ф и
L = 5,8823529-IO-6 Гн.
7.4. Расчет выпрямителя
Рассмотрим расчет т фазной схемы выпрямителя, работающего
на конденсатор фильтра (см. мостовую схему для т = 2 на
рис. 7.10). Угол отсечки 0 диодов определяется из решения транс-
цендентного уравнения
tg 0 — 0 == nrlmRn = А,	(7.5)'
где г — внутреннее сопротивление открытых вентилей и обмотки
трансформатора, Ru— сопротивление нагрузки.
Рис. 7.10. Мостовой выпрямитель
. После нахождения 0 определяются вспомогательные коэффици-
енты:
К(0) = sin 0— 0cos0, Г(0) = я(1—соз0)/Л’(0),
1 л,д. Vn[0(l + cos 20/2)— 3 sin 20/4]
V2 cos 0	К (0)
с помощью которых определяются требуемое напряжение U2 =
== UaB(Q) на вторичной обмотке трансформатора, пиковое значение
тока вентиля Iът === /о/7(9)/щ, действующее значение тока вентиля
/в = й(9)/о/т, ток вторичной обмотки /2 —V2/B и емкость кон-
денсатора фильтра С —	4- -^-^/26iIBf/?H, где f—частота сети
и kaB — коэффициент пульсаций выходного напряжения.
Программа 7.28. Расчет выпрямителя,работающего иа емкость.
Ввод: г — Pl, Ru == Р2, т = РЗ, f = Р4, kne = Р5 и в = Р6. Вы-
вод результатов: 0->РО, Л(0) = РА, B(0)->PB, F(Q) PC,
£>(0) -» РД и С->РХ. Переключатель Р — Г в положении									Р.
ИП1	ИП2		ИПЗ	ч-	Fit	X	П9	0	ПО
1	П8	ипо	ИП8	+	ПО	Fig	ИПО	—	ИП9
—	Fx>0	12	ИПО	ИП8	—	ПО	ИП8	3	4-
П8	ИП6	—	Fx < 0	12	ИПО	F sin	ИПО	F cos	П7
ИПО	X	—	ПА	2	FV-	ИП7	X -	Fl/x	ПВ
1	ИП7	—	Fit	X	ИПА	-Ч-	ПС	ИПО	2
X	П8	F cos	2 '	4-	1	+	ИПО	X	3
ИП8	F sin	X	4	4-	—	Fjt	X	F-<	ИПА
	ПД	ИПЗ	Fl/x	ипо	Fn	4-	+	2	4-
ИП4	4-	ИП2	ч*	ИП5	4-	с/п			
Пусть г =		= 100 Ом, R„ =		1000 Ом, т		= 2,/ =	= 50 Гц, ft,, в		= 0,1,
— 150 В и 7о == 0,15 А. Введя первые пять параметров и задав
е == 10-*, получим: С = 7,29187-10~5 Ф, 6 = 0,7200122 рад, К(6) =
= 0,11809036, В (0)— 0,94055459, F (0) = 6,6029987 и В(0) =
= 2,2940527. Следовательно, U2 = 150-0,94055459 = 141,08319 В,
7ВИ = 0,15-6,6029987/2 = 0,4952249 А, /» = 0,15-2,2940527/2 =
= 0,17205395 А и /2 = ^21В = 0,24332101 А.
7.5. Пересчет параметров транзисторов
Нередко нужно найти физические параметры транзистора (со-
противления эмиттера гэ, базы ге, коллектора г„ и коэффициент пе-
редачи тока эмиттера а гт/гк) по Л-параметрам транзистора, ха-
рактеризующим его как четырехполюсник. Пересчет ведется по фор-
мулам табл. 7.3 [20] и реализуется одной программой.
Таблица 7.3
Пара- метр	Схема с общей базо^	Схема с общим эмиттером
гэ	А11б“(1+А21б) А12б/А22б	А12э/А22Э
гб	А12б/А22б	АПЭ—/112Э 0 + А21э)/А22Э
гк	(* ~ А12б)/А22б	(* + А2|э)/А22Э
гт	~(А12б +А21б)/А22б	(А|2Э + А21э)/А22э
а	“ (А12б + А21б)/(1 —А12б)	(А12Э + А21э)/(* + А21э)
Программа 7.29. Расчет физических параметров по Л-парамет-
рам. Ввод: Ли — РА, hl2 = РВ, h2l = PC, h22 = РД и код (0 для
схемы с обшей базой и 1 с общим эмиттером) в регистр X. Вывод
результатов: гб -* Pl, гэ-> Р2, гк -> РЗ, гт -*• Р4 и а -> Р6 — РХ.
П5 ИПА 1 ИПС 4- ИПВ X ИПД 4- . -
П2 ИПВ ИПД -j- Ш ИПВ ИПС + П9 ИПД
-Я-	П4	ИП5	Fx=0	44	1	ИПВ'	- ИПД	
ПЗ	ИП4	/-/	П4	ИП9	1-г	1	ИПВ —	
П6	С/П	БП	00	ИП1	ИП2	ХУ	П2 ХУ	П1
1	ИПС	+	ИПД		ПЗ	ИП9:	1	ИПС	+
	П6	БП	41					
Пример. Для ftue — 25 Ом, ftne = 0,25-10~3, Лгю = —0,98 и
Лгав. = 3- IO-® См, введя код 0 = РХ, получим г6 — 83,333333 Ом,
г» = 23,333333 Ом, гк — 333.250 Ом, гт = 326583,33 Ом и а =.
= 0,97999499. Для Лцэ = 2800 Ом, ft12s = 210-3, hU3 = 60 и
Ла2в = 5-10~6 Ом, введя код 1 = РХ, получим ге = 360 Ом. r3 =i
= 40 Ом, гк = 1 220 000 Ом, гт — 1 200 040 Ом и а = 0,983639347
Обратное преобразование физических параметров в ft-парамет-
ры проводится ио формулам [20], приведенным в табл. 7.4.
Таблица 7.4
Пара- метр	Схема		
	С общим эмиттером	С общей базой	С общим коллектором
*11	Г +	Vk	О-а)гбгк	г .	Гэгк
	° ГЭ + ГК flrK	э	гб + гк	6 1 гэ’|'гк-огк
*12	гэ	гб	гк~агк
	г9 + гк~агк	'к + 'б	r3 + rK~arK
h	агк-г3	'б + огк	гк
П2\	гэ + гк-сгк	гб + гч	гэ + гк-«гк
h	1	1	I
"22	гЭ + гк~огк	гк + гб	гэ + гк-сгк
Программа 7.30. Расчет ft-параметров биполярного транзистора
по физическим параметрам. Ввод: гв — Р1, гэ — Р2, гк= РЗ и
а — Р4, Вывод результатов: Лц->РА, fti2->PB, ft2i->PC = PX и
Лгг->РД.'При первом пуске подучаем параметры схемы с общим
эмиттером, при втором — схемы с общим коллектором и при
третьем — схемы с общей базой»
ИШ	ипз	+.	Fl/x	П9	ИП2	ИПЗ	+	ИПЗ	ИП4
X	П7	—	Fl/x	П8	ПД	ИП2	X	ПВ	ИП2
ипз	ИП8	X	X	ИП1	+	ПА	ИП7	ИП2	—
ИП8	X	ПС	С/П	ИПЗ	ИП7	—	ИП8	X	ПВ
ипз	/-/	ИП8	X	ПС	С/П	1	ИП4.	—	иш
X	ИПЗ	X	ИП9	X	ИП2	+	ПА	ИП9	ПД
ИП1	X	ПВ	ИП1	ИП4	ИПЗ	X	+	ИП9	/-/
X	ПС	С/П							
V Пример. Для г6 — 400 Ом, гэ=25 Ом, гк = Ю6 Ом и а=0,985
получим при первом нажатии клавиши С/П Лц3 = 2063,8935 Ом,
й12э = 1,6638935-10-3, Аги = 65,55574 и Л32т= 6,655574-10“5 См.
При втором нажатии клавиши С/П получим Лик = 2063,8935 Ом,
Л12к =0,9983361, Лги =—66,55574 и Лггк = 6,655574-10-5 См. При
третьем нажатии клавиши С/П получим Лив = 30,997601 Ом,
/г126 = 3,9984006-10-4, Л21(;=-0,98500599 и Л226=9,9960015-1Л~7См.
V
,	7.6. Расчет малосигнальных усилительных каскадов
На рис. 7.11 представлены три упрощенные схемы усилительных
каскадов иа биполярных транзисторах. Цепи питания (по постоян-
ному току) ие показаны. Эквивалентные схемы этих каскадов даны
ва рис. 7.12.
Рис. 7.11.-Упрощенные схемы каскадов с общей базой (а), общим
эмиттером (б) и общим коллектором (в)
Рис. 7.12. Эквивалентные схемы каскадов с общей базой (а), общим
эмиттером (б) и общим коллектором (в)
Основными параметрами усилителей в области средних частот
являются входное сопротивление Двх = ХЛх/Лх, коэффициент усиле-
ния по току Ki — Кык/Ibx, коэффициент усиления по напряжению
Kv = UBaJUBX, сквозной коэффициент усиления по напряжению
Ке — UBBa/EBX и выходное сопротивление RBBix = ДУВых/ДЛых при
Д/вых, задаваемом изменением нагрузки. Рассмотрим расчет этих
параметров [20].
Для каскада с общей базой (рис. 7.11, а и рис. 7.12, а):
к =________(М'М________
и 'э ('к + 'б + «в) + V« (!-«)+ 'б*н ’
к _________(^'бИн_________
£	(«и + ’’э) ('к + 'б + «и) + Vk (!-“) + 'б*н’
^вых /к + /б(1
+ Г6 А
'э + 'б + tfj
Программа 7.31. Расчет параметров каскада с общей базой.
Ввод: г6 = Pl, гэ = Р2, гк = РЗ, RB — Р4, R„ = Р5 и а = Р6.
Вывод результатов: R„-> РО = РХ,	/(,.-> РА, R,->PB, R ->
kJ	1	вх
PC и R вых		->рд.							
ИП6	ИПЗ	X	ИП1	+	П7	ИПЗ	ИП1	ИП5	+
+	П8	-Т-	ПВ	1	ИП6	—	ИПЗ	X	ИП5
+	П9	ИП1	X	ИП4	ИП2	+	ИП8	X	+
Fl/x	ИП7	X	ИП5	X	ПО	ИП7	ИП5	X	ИП2
ИП8	X	ИП1	ИП9	X	+	ч-	ПА	ИП9	ИП8
	ИП1	X	ИП2	+	ПС	1	ИП7	ИП2	ИП1
+	ИП4	+	4-	—	:ИП1	X	ИПЗ	+	ПД
ИПО	С/П								
Найдем параметры усилителя на транзисторе, имеющем пара-*
метры: г6. = 400 Ом, г3 — 25 Ом, гк — 10е Ом и а — 0,98, если
RB = 100 Ом и RM — 5000 Ом. При этих данных получим 7G
= 139,51899, Ке = 36,130459, Ki = 0,97513427, RBX = 34,94629 Ом
и Rbmx = 253428,6 Ом.
Для каскада с общим эмиттером (рис. 7.11,6 и рис. 7.12, б)'а
п . гэ (rK + Rh)	к  ________(агк — г3)
. вх	б + rK(I-o) + rs + RH'	А/	MI-^ + ts + Rh’
„	.	_______ (Ofк гэ) Кн__________
и~ Гэ ('к + *н) + 'б К1 - 'к + 'э + V
IZ __ ____;~ К ~ /~э)	__
' Е rArK + ^ + (^ + r6)l^-a'frE+>-3+^\'
 •  Лвых^ Гк (1 - п) +*•»( 1 + 	Y
.	: А :Л.Т'б.Т/?и/
Программа 7.32. Расчет параметров каскада с общим эмитте-
ром. Ввод и вывод результатов см. в программе 7.31.
ИПб X	ИПЗ ИП2	X +	ИП2 ИПб	+	П7 П8	1 ИП4	ИПб ИП1	+	ИПЗ Пэ
ИП8	X	ИПЗ	ИП5	+	ИП2	X	ПС	+	Fl/x
ИПб	ИП7	/-/	X	ПВ	X	ПО	ипв	ИП1	ипз
X	ИПС	+		ПА	ИП7	/-/	ИП8		пв
ИП2	ИП5	ипз	+ 	X	ИП8	—	ИП1	+	ПС
ИПЗ	ИПб	X	ИП2	—	ИП9	ИП2	+		1
+	ИП2	X	1	ИПб	—	ИПЗ		+	ПД
ИПО	С/П								
Найдем параметры каскада с					общим	эмиттером при гб =			400 Ом,
гэ — 25 Ом, гк — 10° Ом, = 1000 Ом, 7?к = 5000 Ом и а — 0,98.
Для этих данных получим Ки — —139,45851, Ке— —81,447388,
— —39,15984, 7?вк = 1403,996 Ом и 7?вых = 37217,544 Ом.
Для каскада с общим коллектором (рис. 7.11, в и рис. 7.12, а) 1
П _	1_____ГК (ГЭ + fi.)___ г/ _ _____________ГК_________
вх б-Г гк(1-а) + гэ + Ян’	гк(1 -а)+гэ + Ян’
is __ ________________Г К^Н_________________
Ке = гк ('э + /?н) + (Гб + /?Кн)Н[гк (1 - а) + гэ + /?н] ’
^вых = ГЭ + (гб + Ru) гк + Гб + 7?и •
Программа 7.33.			Расчет параметров каскада с					общим кол лек-	
тором.	Ввод и	вывод	результатов		см. в	программе 7.31.			
1	ИПб	—	ипз	X	П8	ИП2	ИП5	+	П9
+	П7	ИП1	ИП4	+	ПД	X	ИП9	ИПЗ	X
ПВ	+	ИПЗ	ИП5	X	ПА	XY	—	ПО	ИПА
ИП1	ИП7	X	ИПВ	+	—	ПА	ИПЗ	ИП7	ч-
ПВ	ИПЗ	ИП9	X	ИП7	-t-	ИП1	+	ПС	ипд 
ипз	X	1	ИПб	—	X	ипд	ИПЗ	+	
ИП2	+	ПД	ипо	с/п				*	
Найдем параметры каскада					с общим коллектором при Гб =>				
!= 400	ОМ, Гэ =	= 25	Ом, гк 	= 10е	Ом,	/?н =	104 Ом,	, /?н =	500 Ом
и а = 0,98. Получим К и = 0,93771684, Ке = 0,67708474, Kt ==
= 48,421071, RBX = 25978,562 Ом и /?вых = 230,85906 Ом.
7.7. Моделирование нелинейных цепей
второго порядка
В радиоэлектронике важное место занимают нелинейные цепй,
описываемые нелинейными дифференциальными уравнениями вто-
рого порядка, К ним относятся релаксационные и £С-геиераторы.
Микро-ЭВМ являются удобным инструментом для математического
моделирования таких цепей (рис. 7.13,а).
Цепь рис. 7.13, а описывается системой дифференциальных урав-
неиий
di  Е — IR — и	6)
dt L
~ =	,	(7.7)
dt G
относительно переменных состояния — тока i и напряжения и. Фор-
ма колебаний в первую очередь зависит от нелинейной зависимости
7 (и), описывающей статическую вольтамперную характеристику не-
линейного прибора НЭ (рис. 7.13,6). Далее предполагается, что
Рис. 7.13. Цепь с нелинейным элементом (ери его W-образная вольт-
амперная характеристика (б)
инерционность НЭ учитывается его емкостью, составляющей часть
общей емкости С.
Пусть в качестве НЭ применен туннельный диод, W-образиая
вольт-амперная характеристика которого описывается выражением
I (и) = Аие~““ + D (е₽“ - 1), ~	(7.8)
где параметры A, a, D и р выражаются через напряжение L>i при
пике тока /п, обратный ток и тепловой потенциал <рг в соответ-
ствии с формулами А — eln/Ui; а — i/Ur, D — I и р = 1/т<рт, где
т — поправочный множитель (т » 2).
Используя программу решения системы из двух дифференциаль-
ных уравнений (7.6) и (7.7) с учетом (7.8), получим програм-
му 7.34, позволяющую найтн зависимость i(£) и u(t).
Программа 7.34. Расчет зависимостей i(() и u(f) автоколеба-
тельного релаксатора на туннельном диоде. Ввод: А = Р2, а = РЗ,
D == Р4, Р = PS, Е - Рб, R = Р7, L = Р8, С = Р9, h = РВ,
uo = PC, Д/ — h = РД и to = РА. Вывод результатов: t„ -> РХ,
«(/„)-> PY и «(/„)-> PC.
ИП6 ИПВ	ИП7 X	—	ИПС	—	ИП8 4-	ИПД
X ИПВ + ПО ИПВ ИПС ИПЗ /-/ X Fe*
ИПС X	ИП2 X	-	ИП5	ИПС	X Fe*	1
—	ИП4	X	-	ИП9	4-	ИПД X	ИПС +
ПС	ИПО	ПВ	ИПА	ИПД	+	ПА С/П	БП .00
' При А = 0,2718 В (диод с 7о = 10-10~3 А и {Д = 0,1 В)\
а =10 1/В, Р=1-10-« А, Р = 20 1/В, £ = 0,3 В, £=10 Ом,
£= 100 IO-9 Гн, C = 1010~13 Ф, to = O, ио = 0, Д = 0 и Ы
— 0,1 • 10~9 с, нажимая клавиши С/П, XY и ИПС, будем получать
следующие данные:
trit с	i Un), А	и (tn.), В
ЫО-10	З-Ю-4	о
2- 10“10	5,97-Ю-4	З-Ю-3
3-10“10	8,8803-10~4	1,0569807 • 10“3
4-Ю“10	1,1780927- 10“3 7,0946111 • 10~3
5 • 10“10 1,4592172 • 10“3 9,130329 • 10“4 и т. д.
Внимательный просмотр значений u(tn) обнаруживает харак-
терную для моделирования таких систем периодическую численную
Рис. 7.14. Временные зависимости /(/) (внизу) и u(t) (вверху) ре-
лаксатора (рис. 7.13, а)- на туннельном диоде
неустойчивость решения. При выбранном Д/ она проявляется только
тогда, когда рабочая точка туннельного диода попадает на крутые
участки вольтамперной характеристики. Усредняя значения и (У,
получим приведенные на рис. 7.14 графики зависимостей i(t) и н(/),
которые хорошо описывают реальную форму колебаний. Для умень-
шения численной неустойчивости следует уменьшать шаг Д/.
Приложение 1
ИНСТРУКЦИЯ ПО ПРИМЕНЕНИЮ
ВСТРОЕННОЙ БИБЛИОТЕКИ
ПРОГРАММ ПОЛЬЗОВАТЕЛЯ
ДЛЯ МИКРОКАЛЬКУЛЯТОРОВ TI-58C/59
Программа МТ-01. Диагностика, статистические вычисления,
линейная регрессия и управление принтером. Диагностика прово-
дится командами 2nd Pgm 01 SBR = (спустя примерно 15 с ис-
правный микрокалькулятор выдает цифру 1). Контроль модуля МТ.1
библиотеки программ проводится командами 2nd Pgm 01 SBR 2nd
R/S( должны получить цифру 1). При вводе операций 2nd Pgm 01
SBR CLR калькулятор готов к проведению линейного регрессивного
анализа. После ввода операторов '2nd Pgm 01 STO 00 подключен-
ный к микрокалькулятору принтер готов к работе.
Статистические расчеты, вычисление коэффициентов и bi ли-
нейной регрессии (§ 5.13) и коэффициента парной корреляции вы-
полняются по программе ML-01 в следующем порядке:
1.	Подготовка к вычислениям задается командами 2nd Pgm 01
SBR CLR.
2.	Вводятся значения Xi, yt, х2, y2, ..., Хп, уи в следующем
порядке для каждой пары чисел xi и ус xi х -=t t yt 2nd 2 +
3.	Находим среднее значение у, нажав клавиши 2nd х, и сред-
нее значение х, нажав клавишу х ч=ь t.
4.	Находим стандартное среднеквадратическое отклонение
нажав клавиши INV 2nd х, и вх, нажав клавишу х t. 
5.	Находим дисперсию £>и, нажав клавиши 2nd Ор 11, и дис-
персию Dx, нажав, клавишу
6.	Находим параметр Ьо линейной  регрессии, нажав клавиши
2nd Ор 12, затем, нажав клавишу x^t, находим параметр bt.
7.	Коэффициент корреляции г = тах/оу находим, нажав кла-
виши 2nd Ор 13.
8.	Для значения х находим у — bo + btx, нажав клавиши
2nd Ор 14.	.	- .
9.	Для значения у находим х = (у — b0)lbt, нажав клавиши
2nd Ор 15.
Для массива yt(xt): 2(0,95), 4,05(2,1), 5,8(3), 8,1 (4,1) и 9,2(4,9)
находим &0 = 0,2112006713, Ь| = 1,86671074, г = 0,9987280191. Для
х = 5 получим у — 9,544754373, а для у = 5 получим х =>
.= 2,565367641.
В программе Л1Л-01 заняты регистры R01 — У у, R02 — у\
R03 = N, R04 = У х, R05 — У х2, R06 = У ху, R09 и регистр I.
Программа ЛН.-02. Вычисление детерминанта матрицы А, вы-
числение обратной матрицы Л-1 и решение системы линейных урав-
нений Ах з= В.
Размер матрицы А (п X н)	2X2	зхз	4X4	5X5	6X6	7X7	8X8	9X9
Максимальный номер ре- гистра для вычисления Л”1	13	19	27	37	49	63	79	97
Максимальный номер ре- гистра для решения систе- мы уравнений Ах = В	15	22	31	42	55	70	87	-
Вычисление детерминанта матрицы
ап Я|2 ... ащ
у] _	°21	°22 • • ‘ °2/1
П/ll О«2 • • • Пдп
производится командами 2nd Pgm 02 n А 1 В
он	R/S a.2i	R/S	...	ani	R/S	Щз
• •• R/S	ctifi	R/S	а2п	R/S	...
R/S а22 R/S
Пдп R/S С.
Пример. Для матрицы
л =
8 0
8 8
0 1
4
8
2
(п — 3) получим детерминант |Д[= 96.
Решение системы уравнений проводится после вычисления де-
терминанта с помощью команд 1 D (ц R/S Ьг R/S ... bn R/S CLR
Е 1 2nd A' R/S (получаем х,) R/S (получаем xz) R/S (получаем
Хз) ... Для системы уравнений
4 8 0
8 8 8
2 0 1
Xl
Хг
Хз
получим xi = 4, Хг ~
1,5 илз =
2.
4
4
6
Вычисление обратной матрицы проводится с помощью ко-
манд CLR 2nd В' 1 2nd С' R/S (получаем afi1) R/S (получаем а^*)
R/S (получаем a^i*) и т’ д- .(выводим элементы других
столбцов).
В программе заняты регистры R014-R08 (Д = R06, п = R07)
и следующие до указанного выше максимального номера.
Программа Л1/-03. Сложение и умножение матриц. Первая
часть программы вычисляет сумму матриц А и В, умноженных на
постоянные множители Xi и Х2:

«и ... а1п
+ ^2
бц ... Ь\п
Си ••• Ст
ат\ • • • атп
Ьт\ ... Ьтп
с ml • •  стп
Ввод: 2nd Pgm 03 m А л А 1 В Оц R/S a2i R/S ... amt R/S aw
R/S a22 R/S ... CmK R/S 1 С (ввод матрицы В) Xt D X2 D CRL E 1
2nd A' R/S R/S ... R/S (выводим по столбцам элементы матри-
цы С). Работу программы можно проверить иа примере:
] 2	3 0 1	I 4 0	-1 |_| -6	3	2 1
I 1	0 5 j	I 3 2	6 | | -5	—4	-7 Г
Вторая часть
двух матриц:
программы
служит для вычисления произведения
Дц
Дц ... б|р
Си
С;р
ат\ • • • Clmn
Ъп\
bap
Cmi ... Сщр

Повторяем операции ввода «элементов матрицы А. Далее вво-
дим команды 1 2nd В' blt R/S ... bnp R/S (ввод по столбцам мат-
рицы В) 1 2nd D' R/S R/S ... R/S (вывод по столбцам элементов
матрицы С). Заняты регистры R01-T-R08 (т = R03, п = R04,
Xi — R05, Х2 = R06) и последующие с номерами до R2mn+i—для
первой части программы и до Лпл+гА+т— для второй части про-
граммы.
Программа Л17.-04. Действия с комплексными числами X—a+jb
и У = с + jd. Результат — комплексное число Z — е + jg. Ввод:
2nd Pgm 04 а А b А с 2nd A' d 2nd А'. Далее вводятся следую-
щие команды-.
Действия, выполняемые над комплексными числами	X+Y	X~Y XxY	X/Y	yX	logy X	X л/у
Команды для получения е	В	2nd В' С	2nd С	D	2nd D'	E
Команды для получения g	t	x%t x^t	X$t		X<-t	X
Завершение вычислений: 2nd Е' (ввод новых X и У).
Пример. Вычислить
Вводим команды 2nd Pgm 04 2 А 3 А 1 2nd А' 1 +/— 2nd А' С
х t (получаем результат умножения комплексных чисел, заклю-
ченных в квадратные скобки) 2nd Е' 1 А 1 A D (получаем е =
= —1,05842350В) х t (получаем g — 4,09577726).
В программе заняты регистры Р01 AJ04 (числа а, Ъ и резуль-
таты е и g заносятся в регистры -Д01 и /?02).
Программа МА-05. Функции комплексного переменного X =
— а + jb. Результат У = с -|- jd. Ввод: 2nd Pgm 05 а А & А. Да-
лее вводятся- следующие команды.
Вычисление полярного радиуса г н угла 6: В (получаем г)
х t (получаем 0).
Функции комплексного не- ’ ременного Команды для получения с Команды для получения g	X2 С xtt	dx D xtt	l/x E	InX 2nd A'	eX 2nd B' .xtt
Пример. Вычислить е<2+'3). Вводим команды.2nd.Pgm 05 2 А
3 А 2nd В' (получаем с = —7,315110095) х t (получаем d —
= 1,042743656). Распределение регистров памяти см. в программе
МА-04.
Программа ME-Ofi. Вычисление тригонометрических и обратных
тригонометрических функций комплексного переменного X = а + jb.
Результат Z — с 4- jd. Ввод: 2nd Pgm 06 а А b А. Далее -вводятся
следующие команды.
Тригонометрические и обратные тригонометрически’е функции комплексного переменного	Команды для получения с	Команды для получения . X
sin X	В	xt-t
cos X	с	xtt
tgX	D	xtt
arcsin X	2nd В' *)	xtt
arccos X	2nd С'	xtt
arctg X	2nd D'	xt-t
♦).Если b <0, вводятся **) Если b <0, вводятся	операторы +•/— STO02. операторы +/— STO 01.	
Пример. Вычислить sin (3 +/-2). Вводим команды 2nd Pgm
06 3 А 2 А В .(получаем с—.0,5309210863) х t {получаем d =*
.= —3,5905645). Распределение регистров памяти см. в -программе
МА 04.
Программа Л1/.-07. Вычисление значений полинома
р (х) = я0 + fli* + «2*2 + ... + апхп.
Ввод: 2nd Pgm 07 я А О В a0 R/S ai R/S ...ап R/S х С (полу-
чаем Р(х)).
Пр и м е р. Вычислить значение полинома
Р(х) = 0 + 1х + 2х2 + Зх3 + 4х4
для х = 1 и х = 2. Вводим команды 2nd Pgm 07 4 А О' В О R/S 1
R/S 2 R/S 3 R/S 4 R/S 1 (значение х) С (получаем Р(1)= 10) 2
(новое значение х) С (получаем Р(2)= 98).
Программа Л1/.-08. Вычисление корней уравнения F(x) = 0 с
 погрешностью е в интервале [я, 6] изменения х с начальным ша-
гом Дх. Вычисление F(x) оформляем подпрограммой, помеченной
меткой Lbl А' и заканчивающейся оператором INVSBR.-Текущее
значение х заносится в начало подпрограммы. Ввод: данные F(x)
2nd Pgm 08flA6BAxCeDEE... (нажимаем клавишу Е
каждый раз для выдачи нового значения корня до тех пор, пока
не получим число 9.9999999-10" (переполнение, означающее, что
корней больше нет).
Пример. Найти корни уравнения F(x)— 4sinx-|- 1—х в ин-
тервале [—3,3] с начальным шагом Дх = 0,5 и погрешностью
е = 0,01. Решение состоит из следующих частей.
1. Ввод подпрограммы вычисления F(x): RST LRN 2nd Lbl 2nd
A' ( STO 10 2nd sin X 4 + 1 - RCL 10 ) 1NVSBR LRN.
I 2. Ввод программы ML-08: 2nd Pgm 08.
3. Установка значений x в радианах: 2nd Rad.
4. Ввод исходных данных я, Ь, Дх и е: 3 +/— А 3 В . 5 С . 01
D Е (получаем х4 = —2,20793125) Е (получаем х2 = —0,33984375)
Е (получаем хз = 2,69921875) Е (получаем число 9.9999999-10",
т.е. больше корней нет).
Распределение регистров памяти: а, я + Дх = Д01, b — R02,
Дх = ДОЗ, R04 4- R08 заняты, е — R09, остальные регистры сво-
бодны.
Программа Л1Т-09. Численное интегрирование аналитически за-
данной функции f(x) методом Симпсона. Подынтегральная функция
f(x) в выражении 
/ = f (х) dx
а
должна вычисляться подпрограммой, начинающейся меткой Lbl А'
и заканчивающейся оператором INVSBR (текущее значение х за-
носится в начало подпрограммы). Далее ввод выполняется коман-
дами: 2nd Pgm 09 а А b В- п С D (получаем I), где п число ин-
тервалов разбиения [я, 6]'
Пример. Вычислить
1
I = д/2х + 1 dx
О
при п = 8. Вводим подпрограмму вычисления f (х) — ^Чх 4- I .
RST LRN 2nd Lbl 2nd А' X 2 + 1 = ^~х INVSBR LRN. Далее вво-
дим программу Л4/.-09: 2nd Pgm 09 0 (ввод я) А 1 (ввод 6) В 8
(ввод n) С D (получаем I = 1,398713896).
Использование регистров памяти: а — R01, b — R02, h = R03,
/ == R04, п = R05 (остальные регистры свободны).
Программа ML-10. Численное интегрирование методом Симп-
сона функции f(xi), заданной четным числом п ординат f0, Л,
h> • - •» fn. Ввод: 2nd Pgm 10 п A h В 0 С /0 R/S ... fn R/S D (полу-
чаем I). Для h = 1 и f, = 1, 8, 27, 64 и 125 получим I = 156. Рас-
пределение регистров памяти: заняты регистры R014-R05, причем
h == R03, I = R04, п = R05, ординаты /о, ft, , fn заносятся в
регистры от Roe для /о до RK+e для fn. Число ординат ограничи-
вается допустимым числом свободных регистров памяти.
Программы ML-11 ч- ML-13 предназначены для проведения эле-
ментарных вычислений (углы и стороны треугольников, сегменты
окружностей и т. д.). Поэтому подробное описание их опущено.
Программа ML-14. Вычисление функций Z(x) и Q(x) нормаль-
ного распределения вероятности с х — (т — у.)/о. Значение
Z (х) = е~*г/2/д/2:п , Q(x) площадь под кривой Z(x) при т х.
Ввод: 2nd Pgm 14 х А (получаем Z(x)) В (получаем Q(x)). Пло-
щадь под кривой Z(x) при т <_ х вычисляется как Р(х) = 1 —Q(x).
Пример. Для х — 0,5 получим Z (х) = 0,3520653268; Q (х) =
[= 0,3085375322 и Р(х) = 0,6914624678. Распределение регистров:
Z(x)= R01, R02 занят, х = R03.
Программа ML-15. Генерация случайных чисел. Ввод: 2nd Pgm
15 2nd Е' Хо (начальное число от 0. до 199017) Е. Далее в соот-
ветствии со следующими режимами работы.
। 1. Генерация случайных чисел с равномерным распределением
в интервале [«,&]: а А b В С С ... С (получаем.ряд случайных
чисел).
2. Генерация случайных чисел с нормальным распределением и
заданным средним значением х и о: х А о В 2nd С' 2nd С' ...
... 2nd С' (получаем ряд случайных чисел).
. 3. Вычисление х и о для чисел, полученных по п. 2: 2nd х
(получаем х) INV 2nd х (получаем о) RCL 03 (получаем Л’).
4. Генерация случайных чисел с равномерным распределением в
интервале [0, 1]: SBR 2nd D.MS SBR 2nd D.MS ... SBR 2nd D.MS
и т. д. (получаем ряд случайных чисел).
Пример. Для хо — I, Х=1 и <т = О,1 получим следующий»
ряд чисел с нормальным распределением: 1,093261476; 1,068422521;
0,8696010813; 0,9655443104; 0,8812833351 и т. д. Распределение ре-
гистров памяти: заняты регистры «01 -4- «11 (У, у = «01,УУ=«02,
N. = «03, У х = «04, У*2 = «05, хо = «О9, a, x = RW и Ь, -сг =
= «11).
Программа М£-16. Вычисление факториала п! перестановок
Р“ и» сочетаний С” «691). Ввод:- 2nd Pgm 16 и А г В С (полу*
чаем и!) или D (получаем «J?) илн Е (получаем С”).
Пример. Для п = 10 и г = 4 имеем п! = 3628800, Р\° =
=5040 и 0$° = 210 (при вычислениях Р^ и с|° повторить ввод п
и г). Распределение регистров памяти: п = «01, г =.«02, ДОЗ занята
п\, Р, С = «04.
Программа ML-17. Усреднение данных по мере их ввода:
теР = ("гй + "гй+1+ •" +mk+n-№	А=1,2,3,...
Ввод: 2nd Pgm 17 2nd Е'n A mi В Иг В m3 В и т. д. (получаем
/Пер). Распределение регистров памяти: заняты «01 4-«06, п — «02.
Программы М£-18 и М£-19 служат для проведения деловых
расчетов (займы, ренты, накопления и т. д). Описание этих про-
грамм не приводится, поскольку оно не соответствует профилю
книги.
Программа М£-20. Вычисление дня недели и числа дней между
двумя датами. Даты задаются двухзначными числами месяца MMt
дня DD и (через точку) года- YYYY. Нельзя задавать DD >31,
ММ > 12 и YYYY'< 1582. Ввод: 2nd Pgm 20 и далее в соответ-
ствии с режимом использования программы,
1. Число дней между двумя датами: MMDD.YYYY (ввод первой
даты) A MMDD.YYYY (ввод второй даты) В С (получаем число
дней).
2. День недели, соответствующий определенной дате:
MMDD.YYYY (ввод даты) D (получаем день недели: 0 — суббота,
1 — воскресенье, 2 — понедельник 3 — вторник, 4 — среда, 5 — чет-
верг и-6— пятница).
Пример. Найти, какой день педели соответствует" дате 1 ян-
варя 1984 г. (ММ=01, £>£>=01). Вводим; 2nd Pg’m 20 0101.1984 D
(получим-число- 1, т.е. этот день — воскресенье). Распределение ре-
гистрой памяти: заняты «01 4-«05, ММ = «01, DD = «02 и
YYYY = «03.
Программа ML-21. Игра с цифрами Hi-LO Game.
Программа М£-22 Деловые расчеты, связанные с платежами.
Программа MZ.-23; Операции с переводом мер измерения вре-
мени- И-' углов-.
Программа MZ.-24. Перевод мер длины.
Программа Л1£-25. Перевод мер измерения температуры и веса.
Программы Л1£-21 4- ML-25 реализуют элементарные вычисле-
ния общего характера, выходящие за рамки тематики данной книги.
Поэтому они подробно не описываются.
Приложение 2
БИБЛИОТЕКА ВНЕШНИХ ПРОГРАММ'
ДЛЯ МИКРОКАЛЬКУЛЯТОРОВ TI-58C/59
Контрольные примеры см. в соответствующих программах для
калькулятора Электроника БЗ-34*).
Программа Л!. Вычисление значений многочлена Чебышева
1-го рода. Ввод: п — R01, х — RX.
INV cos X RCL 01 = cos R/S RST
Программа П2. Вычисление значений многочлена Чебышева
2-го рода. Ввод: п — R01, х = RX.
INV cos STO 00 X	( RCL 01 +	1
)	— sin 4- RCL 00 sin == R/S RST
Программа ПЗ.. Вычисление значений многочлена Эрмита. Ввод:									
1 == (п —	1)= RX, x =		 RX.						
STO 01		R/S STO 04			X	2	=	STO	03
1	STO 02		STO 05		RCL	05	X	RCL	02
+/	— +	RCL 04		X	RCL	03	STO	02	=
X	2		STO 03		Op	25	Dsz	1	0
15	R/S RST								
Программа		П4.	Вычисление		значений		многочлена		Лагерра
Ввод: i =	= (« —	1)= RX, x =		RX.					
STO	01	R/S	STO	07	+/-	+	1	STO 08	
STO	06	s=s	STO	09	RCL	06	X	RCL 08	
+/-	+	(	RCL	06	X	2	+	1	—
RCL	07	)	X	RCL	09	STO 08		=	4-
Op	26	RCL	-06	==	STO	09	Dsz	1	0
15	R/S	RST							
Программа П5. Вычисление .значений многочлена Лежандра,
Ввод: i — (п — 1) = RX, х — RX.
STO	01	R/S	STO 07	STO	09	1	STO	08
STO	06	RCL	06	+/“	X	RCL	08	+	(
*) Время вычислений на микрокалькуляторах TI-58C/59 в
7 раз ‘меньше, чем для микрокалькуляторов .Электроника БЗ-34.
RCL	06	X	2	+	1	)	X	RCL	07
X	RCL	09	STO	08	=	-j-	Op	26	RCL
06	=	STO	09	Dsz	1	0	12	R/S	RST
Программа ПбС-Вычисление гиперболических функций действи-
тельного переменного х — RX.
a)	shx (sh 1 = 1,1755201194):
INV	Inx	—	1/х	=	4-	2	=	R/S	RST
6)	ch x (ch 1 — 1,543080635):
INV	Inx	+	1/x	==	4-	2	=	R/S	RST
в)	thx (th 1 = 0,761594156)
INV	Inx	x2	+	1	=	4-	2 =	1/x
+/-	+	1	=	R/S	RST
г)	Для вычисления cth x перед оператором R/S следует поста-
вить оператор 1/х.
Программа П7. Вычисление обратных гиперболических функций
действительного переменного х — RX.
a)	arshx (arsh 1 = 0,881373587):
+ ( х2 + 1 ) Vx" = Inx R/S RST
6)	arch x (arch 2 = 1,316957897) вычисляется по программе П7
а) с заменой знака + по адресу 003 на знак —.
в)	arthx (arth 0,5 = 0,5493061443):
1/х	—	1	=	-г-	2 = 1/х + 1
=«	Vх	In х	R/S	RST
г)	arcth х (arcth 2 = 0,5493061443):
-	1	=	4-	2 = 1/х + 1 =
Vx	Inx R/S RST
Программа П8. Вычисление гиперболических функций комплекс-
ного переменного Z — а + jb. Ввод: а = RX, b = RX. Вывод ре-
вультата f(Z) — с + jd: c-*-RX, d-*-RX.
a)	sh Z = sh(3 + /-2) = —4,16890696 + j-9,154499147;
STO 02	R/S	+/—	STO	01	Pgm	06	В	x^t
R/S x^t	+/—	R/S	RST
6)	chZ = ch(3 + j-2) = —4,189625691 + /-9,109227894:
STO 02	R/S	+/—	STO	01	Pgm	06	C	R/S
x^Lt R/S RST
в)	thZ = th(3 + /-2) = 1,003238697 — j-0,0037640256:
STO	02	R/S	4-7—	STO	. 01 Pgm 06 D
R/S	x^t	+/-	R/S	RST
Программа П9. Вычисление обратных гиперболических функций
комплексного переменного Z = а + jb. Ввод и вывод см. в про-
грамме П8.
a)	arsh Z == arsh(3 + /-2) = 1,98338703 + / 0,5706527843:
STO 02	R/S +/— STO 01 Pgm 06 B' x^t
R/S x^t +!- R/S RST
6)	arch Z = arch(3 +./-2) = +1,968637926 ± /•0,6061378224:
STO 01 R/S STO 02 Pgm 06 C' ,x^.t R/S
x^t R/S RST
в)	arth Z = arth(0,3 + /-0,2) = 0,2957499202 + /-0,2154744937:
STO. 02	R/S	+/- STO 01 Pgm 06 D' x^lt
R/S x^tt +!— R/S	RST
Программа. П10. Интерполяция по формуле Лагранжа для трех
Точек. Ввод: y-i, у0, у+1, h, х0 и х в регистр X.
STO	00	R/S	STO	01	R/S	STO	02	R/S	STO
03	R/S	STO	04	R/S	—	RCL	04	=	+
RCL	03	—	STO	05	X	(	RCL	05	—
1	)	X	RCL	00	•4-	2	+	(	1
—	RCL	05	X2	)	X	RCL	01	+	RCL
05	X	(	RCL	05	+	1	)	X	RCL
02		2		GTO	0	14			
Программа ПИ- Интерполяция по формуле Лагранжа для пяти
точек. Ввод (после нажатия клавиш RST и R/S): у-г, y~i, ув, y+t,
у+г, li, х0 и х в регистр X.
CMs	7	STO	00	R/S	STOI	0	Dsz	0	0
04’	0	R/S	—	RCL	01	=s	4-	RCL	02
==	STO	08	(	RCL	08 '	X2	—	1	)
STO	09	X.	RCL	08	X	(	RCL	08	—
2	.)	X	RCL	07		2	4	—	(
RCL	08	—	1	)	X	RCL	08	X	(
RCL	08	X2	.—	4	)	STO	10	X	RCL
0.6	4-	6	+	RCL	09	X	RCL	10	X
RCL	05 		4		(	RCL	08	+	1
)	X	RCL	08	X	RCL	10	X	RCL	04
	6,	+	RCL	09	X	RCL	08	X	(
RCL	.08		2	)	X	RCL	03	-Г-	2
4 ' 1	ss	GTO	O'	12					
Программа П12, Вычисление .корней нелинейного, уравнения
Г(х)~ 0 методом подекадного приближения. Ввод: данные F(x),
Хо — R00, Axi — Rbl, е = 02.
CP	RCL	01	SUM	00	SBR	A	4-	RCL	01
=	0	00	1	0	+/-	INV	Prd	01
RCL	02	x^it	RCL	01	|x|	x>/	0	00	RCL
00 R/S Lbl A ..............................ISBR
Программа П13. Вычисление корней нелинейного уравнения
f(x) = 0 комбинированным методом секущих — хорд. Ввод: данные
F(x), Хе = R00, xt — R01, е — R02, R03 занят.
RCL	00	SBR	А	X^t	RCL	01	SBR	A	STO
03	RCL	01	—	RCL	03	X	(	RCL	01
	RCL	00	)		(	RCL	03	—	x^t
)	=	x^t	RCL	01	STO	00	x^t	STO	01
	RLC	00	=	|x|	x^Lt	RCL	02	INV	
0	00	RCL	01	R/S	Lbl	A	• • •	• * •	ISBR
Программа П14. Численное дифференцирование таблично за-
данной функции в трех точках. Ввод: f-j, /о, Ли, h, хе и х в ре-
гистр X.
STO	00	R/S	STO	01	R/S	STO	02	R/S	STO
03	R/S	STO	04	R/S	—	RCL	04	=	4-
RCL	03	=	STO	05	(	RCL	05	—	•
5	)	X	RCL	00	—	2 .	X	RCL	05
X	RCL	01	+	(	RCL	05	+	•	5
)	X	RCL	02		4-	RCL	03	=s	GTO
0	14
Программа П15. Численное дифференцирование таблично за-
данной функции в пяти точках. Ввод: /_2, f-i, fo, f+i, f+z, h, x0 и x
в регистр X. Перед вводом нажать клавиши RST и R/S (высвечи-
вается число 7).
7	STO	00	R/S	STOI	0	Dsz	0	0	03
0	R/S	—	RCL	01		—•	RCL	02	=s
STO	08	X2	X	3	==	STO	10	RCL	08
X2	X	RCL	08	X	2	=	STO	09	(
RCL	09	—.	RCL	10	—	RCL	08	+	1
)	X	RCL	07	4-	1	2	—	(	2
X	RCL	09	—	RCL	10	——	8	X	RCL
08	+	4	)	X	RCL	06	4-	6	+
(	RCL	09	—	5	X	RCL	08	)	X
RCL	05 '	4-	2	—	(	2	X	RCL	09
+	RCL	10	—	8	X	RCL'	08	—	4
)	X	RCL	04	~	6	+	(	RCL	09
4-	RCL	10	—	RCL	08	—	1	)	X
RCL	03	4-	1	2	=5	4-	RCL	02	=3
GTO	0	11							
Программа П16. Вычисление частных производных и относи-
тельиых коэффициентов нестабильности по трем ординатам функции
f(Xi). Ввод: данные f(x), kxilxi — R01, коды xt (в виде номеров
регистров, отведенных под переменные xt). Вывод результатов:
Si->RX, df/dxi R04, f (х/о) ->• R05, регистры R00 4- R05 заняты.
STO	00	RCLI	00	STO	02	X	RCL	01	+
STO	03.	RCL	02	=F	STOI	00	SBR	A	STO
04	RCL	02	—	RCL	03	=	STOI	00	SBR
А	INV	SUM	04	RCL	02	STQI	00	SBR	A
STO	05	RCL	04	-r-	2	4-	RCL	03	X
STO	04	RCL	02	4-	RCL	05		R/S	RST
Lbl	А	• a a	a a a		• • •	• • •	• • •	a • a	ISBR
Программа П!7. Вычисление частных производных и относи-
тельных коэффициентов нестабильности по пяти ординатам функции
f(x). Ввод и вывод результатов см. в описании программы П16.
STO	00	RCLI	00	STO	02	—	RCL	01	X
RCL	02	X	STO	03	2	SBR	В	STO	04
RCL	02	—	RCL	03	SBR	В	X	8 .	=s
INV	SUM	04	RCL	02	+	RCL	03	SBR	В
X	8	=	SUM	04	RCL	02	+	2	X
RCL	03	SBR	в	INV	SUM-	04 -	RCL	02	SBR
В	STO	05	RCL	04	4-	1	2	4-	RCL
03	=	STO	04	X	RCL	02	-4-	RCL	05
	R/S	RST	Lbl	B	=	STOI	00	.,.	ISBR
Программа П'18. Численное интегрирование методом Гаусса
"(п — 3). Ввод: данные f(x), Ь, а и т 'в регистр X. Заняты регистры
ЛОО 4- Л07. Подпрограмма вычисления f(x) должна начинаться со
знака равенства = и заканчиваться операторами X INVSBR (см,
конец программы). Текущее значение х получается после исполне-
ния первого оператора == подпрограммы.
CMs	—	R/S-	STO	01		4-	R/S	STO	00
=3	SUM	07		6	y/x	STO	03	Lbl	в
RCL	01	+	RCL	07	—	STO	02	RCL	01
x=	-X.	2	+	STO	04	RCL	01	—	STO
05	(	RCL	04	X	RCL	03	)	SBR	A
5	==	SUM	06	RCL	05	SBR	A	8	=
SUM	06	RCL	04	X	RCL	03	+	RCL	05
SBR	A	5	==	SUM	06'	RCL	02	STO	01
Dsz	0	В	RCL	06	X	RCL	04	—	.9
	R/S	Lbl	A	=	a a •	a a a	• a a	X 	ISBR
Программа 'П19. Решение дифференциального уравнения пер-
вого. порядка методом Рунге —Кутта. Ввод: данные f(x,y) при
х->/?00, у заносим в начало подпрограммы (после знака =),
Хо — R00, h/2 — R03 и уо — RX. Заняты регистры /?00 ч- R04.
STO	01	STO	02	SBR	SBR	STO	04	RCL	03
SUM	00	RCL	04	SER	E	SUM	04	SBR	E
SUM	04	x t	RCL	03	SUM	00	x^t	X	2
SBR	E	RCL	04	X	RCL	03	-4-	3	+
RCL	01	=	R/S	RST	Lbl	E	X	RCL	03
+	RCL	02	SBR	SBR	SUM	04	ISBR	Lbl	SBR
=a	• • •	• ..	• • •	• • •		• • •	• • •	=s	ISBR
Программа Н20. Гармонический анализ методом пяти ординат
(§ 5.11). Ввод: j/i Ч- уо = R01 4- R05. Вывод результатов: г/о->/?10,
1/м1 -►/?!!, j/mz-*7?12, у,,.з-+1Ш, г/м4-*/?14, Лг->2?Х.
RCL	 05	+	RCL	01	+	2	X	(	RCL
04	+	RCL	02	)		4-	6	—	STO
10	RCL	05	—	RCL	01	+	RCL	04	—
RCL	02	=		3	=	STO	11	RCL	05
+	RCL	01	—	2	X	RCL	03		—
4	=	STO	12	RCL	11	—	RCL	04	+
RCL	02	=	4-	2	=	STO	I3	RCL	12
—	RCL	10	+	RCL	03	=	STO	14	X2
+	RCL	13	X2	+	RCL	12	X2	—	
—-	RCL	11	=	R/S					
Программа П21. Расчет (p(f) и S(f) см. § 5.11. Ввод:
4 2nd Ор 17 N и затем yi, у2, ..., у к (при вводе отсчетов yt инди-
цируется их текущий иомер), Д1 и f (IV 32 ненулевых yi). .
CMs	+	1	STO	0	=S	STO	33	x t	RCL
0	R/S	STOI	00	Op	20	RCL	0	INV	x — i
0	11	0	R/S	STO	39	R/S.	STO	38	X
RCL	39	=	X	Jt	=	STO	37 '	Rad	sin
—	RCL	37	=	STO	36	0	STO	35	STO
34	1	,STO	00	RCL	00	X	2	=	X
RCL	37	=	STO	38	sin	X	RCLI	00	s=
SUM	35	RCL.	38	COS ;	X	RCLI	00	=3	SUM
34	Op	20	RCL	00	INV	x= t	0	54 -	RCL
36, ,	Prd	35	Prd	34	Deg.	RCL	34	x^t	RCL
35	INV	P-> R	+/-	INV	Eng	R/S	x^t	X	RCL
39	=	STO	37	RCL	33:i		RCL	37	Eng
GTO	0 :•	26							
Программа П22. Расчет амплитудно- и фазо-частотной характе-
ристик по переходной. Ввод: 4 2nd Ор 17 и далее /V, at, а2, ...
..., nN, At и f (N < 32)
CMs	+	1	STO	0	s=3	STO	32	x^f	RCL
0	R/S	STO	39	—	RCL	38	=	STOI	00
RCL	39	STO	38	Op	20	RCL	0	INV	x =>/
0	И	0	R/S	STO	39	R/S	STO	38	X
RCL	39	=	X	л	==	STO	37	Rad	sin
-4-	RCL	37	=	STO	36	0	STO	35	STO
34	1	STO	00	RCL	00	X	2	=	—
1	=	X	RCL	37	—	STO	33	sin	X
RCLI	00	=	SUM	35	RCL	33	cos	X	RCLI
00	=	SUM	34	Op	20	RCL	00	INV	x = t
0	64	RCL	36	Prd	35	Prd	34	Deg	RCL
34	x^t	RCL	35	INV	P-> R	+/-	R/S	x^t	STO
31	RCL	32	x^t	RCL	31	GTO	0	36	
Программа П23. Статистическая обработка. Ввод (после нажа-
тия клавиши RST) х,- — RX. Вывод результатов (после нажатия
клавиши A)		: x, D, Do,		A, E, U3 и U4 (mi -4- m4->-R01					-4-R04,
/v->	R00, M2->-R12, M3			-*R13,		R14,	Do-+	R15, A	— R16.
E^	R17, Us	-+R18, U4 — R19).							
CMs	Lbl	В	STO	09	SUM	05	X2	SUM	06
X2	SUM	08	-4-	RCL	09	=	SUM	07	Op
20	RCL	09	R/S	GTO	В	Lbl	A	RCL	05
	RCL	00	=	STO	01	R/S	RCL	06	-4-
RCL	00	=	STO	02	RCL	07	-4-	RCL	00
s=	STO	03	RCL	08	-4-	RCL	00	s=	STO
04	RCL	02	—	RCL	01	X2	=	STO	12
R/S	X	RCL	00	—	(	RCL	00	—	1
)		STO	15	R/S	RCL	03	—	3	X
RCL	01	X	RCL	02	+	2	X	RCL	01
Vх	3	=3	STO	13	4-	RCL	12	yK	(
3	-4-	2	)	=	STO	16	R/S	RCL	04
—	4	X	RCL	01	X	RCL	03	+	6
X	RCL	01	X2	X	RCL	02	—	3	X
RCL	01	X2	X2		STO	14	-4-	RCL	12
X2	—	3	=	STO	17	R/S	6	X	(
RCL	00	—	1	)	-4-	(	RCL	00	+
1	)	-4-	(	RCL	00	+	3	)	
V*"	STO	18	R/S	2	4	X	RCL	00	X
(	RCL	00	—	2	)	X	(	RCL	00
—	3	)	-4-	(	RCL	00	—	1	)
X2	“T"	(	RCL	00	+	3	)		(
RCL	00	+	5	)		•V*"	STO	19	R/S
Примечание. После вычисления статистических характерна
стик .массива партии чисел Xt можно вернуться к вводу новой пар-
тии, набрав ее первое число и нажав клавишу. В.
Программа П24. Генерация случайных чисел с повышенной
скоростью (в 3—4. раза выше, чем по программе ML-15).
1. Для чисел с равномерным распределением в интервале [0, 1 ].
Ввод: Vo — RX < 1.
X 1 1 + Л = INV Int R/S RST
Для Vo = 0,123456789, нажимая клавишу R/S, будем получать
V, = 0,4996173326, V2 = 0,6373833121, V» = 0,1528090865, V4 =
= 0,8224926048, Vs = 0,189011306 и т, д. (время генерации одного
числа менее 1 с).
2. Для чисел с равномерным распределением в интервале [a, t>J.
Ввод: Vo = R01 < 1, а = R02 и b = R03.
RCL 01	X	3	7	=	INV	Int	STO	01
X ' (	RCL	03	-	RCL	02	)	+	RCL
02	=	R/S	RST
Для Vo = 0,123456789, a = 1 и- b = 2 получим Xi= 1,567901193,
X2 = 1,012344141, X3 = 1,456733217, Xt = 1,899129029 и т..д. (вре-
мя выдачи одного числа 1,5 с).
,3. Для чисел с нормальным распределением. Ввод: Vo =:
= R01 < 1, <т = R02 и R = R03. Перед пуском нажать-клавиши
2nd и Rad.
RCL	01	X	3	7	=х	INV	Int	х^	It RCL
01	X	2	X	п		sin	Х_	(	x^t
STO	01	1/х	In X	X	2	)	V-X	X	RCL
02	+	RCL	03	=	R/S	RST			
Для Vo’= 0,1234567, о = 0,1 н R = 1 получим, нажимая кла-
вишу R/S, Rt = 1,074487657, R2 = 6,8771869012, Rs = 1,00966529,
Rt — 1,023339944, Rs = 0,7849199467 и т. д. (время выдачи одного
числа 2 с).
Программа П25 *). Вычисление коэффициентов -Ьо и /ц прибли-
жения гиперболической функцией у = b + Ь-,./х. Ввод (после нажа-
тия клавиш RST и R/S): xt, у±, х2, у-л, ...,' xN, yN в регистр X
(после ввода каждой пары х,-, высвечивается номер I). Вывод
результатов: после нажатия клавиши А получим коэффициент Ьо,
после нажатия клавиши x^t — коэффициент bi. Для вычисления
у(х) набираем х = RX, нажимаем клавишу В.и т. д.
*) В программах П25 4- П29 приближение нелинейной функцией
осуществляется с помощью линеаризирующих преобразований [17]
и линейной регрессии, выполняемой оператором Ор 12 и програм-
мой ML-1,
Pgm 01 SBR CLR
R/S £ + GTO R/S
В 1/x Op 14
Lbl R/S R/S 1/x x^>t CLR
Lbl A	Op	12 R/S	Lbl
R/S
Программа П26. Вычисление коэффициентов bQ и bt приближен
кия степенной функцией у — 60хЬ|. Ввод и вывод результатов см.
в программе	П25.
Pgm 01	SBR CLR' Lbl R/S R/S log x^t CLR
R/S log	У + ' GTO R/S Lbl A Op 12 INV
log x^>	t x^t R/S Lbl В log Op 14	INV
log R/S	
Программа П27. Вычисление коэффициентов Ьо и bt приближе-
У — Mf- Ввод
Ния показательной функцией
см. в программе П25.
и вывод результатов
Pgm	01	SBR	CLR Lbl	R/S	R/S	x t	CLR	R/S
log	z+	GTO	R/S ' Lbl	A	Op	12	INV	log
X^-t	INV	log	R/S	Lbl	В	Op	14	INV
. log. R/S
Программа П28. Вычисление коэффициентов Ьо и 'bt приближе-
ния экспоненциальной функцией у .= Ьо ехр/Ьрс). Ввод и вывод ре-
зультатов см. в программе П25.
Pgm	01	SBR	CLR	Lbl	R/S	R/S		CLR	R/S
inx		GTO	R/S	Lbl	A	Op	12	INV	In X
x^.t	x^t	R/S	Lbl	В	Op	14	INV	In X	R/S
Программа П29. Вычисление коэффициентов Ьо и bt приближе-
ния логарифмической функцией у = bo + bilogx. Ввод и вывод
результатов см. в программе П25.
Pgm	01	SBR	CLR	Lbl	R/S	R/S	log	x^t	CLR
R/S	£ +	GTO	R/S	Lbl	A	Op	12*	R/S	Lbl
В	log-	Op	14	R/S
Программа ПЗО. Вычисление коэффициентов а и b приближе-
ния показательной функцией у = 10(с+6*). Ввод (после нажатия
клавиши RS Г)xi, yi, х2, у2, .... хк, у к в регистр X. Для получе-
ния а нажать клавишу А, для получения b — нажать клавишу R/S.
CMs	Lbl	E	STO	09	SUM	08	X	R/S	STO
02'	log	SIJM	06	=	SUM	03	RCL	09	X2
SUM	0Б	Op	20	RCL	02	R/S	GTO	E	Lbl
A	RCL	00	X	RCL	05	—	RCL	08	X2
—	STO	07	RCL	06	X	RCL	05	—	RCL
оз'	X	RCL	08	=	STO	10	RCL.	03	X
RCL	00	—	RCL	06	X	RCL	08	=	STO
11	RCL	10	4-	RCL	07	=	R/S	RCL	11
4-	RCL	07	=	R/S
Программа П31. Вычисление коэффициентов bo, bt и b2 при»
ближеиия параболической функцией у = b0 + bix + b2x2. Ввод:
RST 2nd CMs и далее xt, yi, х2, у2, хц, у к в регистр X. Вывод
результатов: нажав клавиши 2nd Е', получим Ьо, нажав клавишу
R/S дважды,, получим сначала Ь±, затем Ь2.
STO	24	SUM	09	SUM	11	X2	SUM	10	SUM
12	SUM	14	X2	SUM	16		RCL	24	=
SUM	13.	SUM	1Б	RCL	24	X	R/S	STO	25
SUM	30	=	SUM	31	X	RCL	24	=	SUM
32	Op	28	RCL	2Б	R/S	RST,	Lbl	E'	X
Pgm	02	A	1	Pgm	02	В	Pgm	02	C
1	Pgm	02	D	RCL	’30	SBR	D'	RCL	31
SBR	D'	RCL	32	SBR	D'	CLR	Pgm	02	E
1	Pgm	02	A'	SBR	D'	R/S	SBR	D'	R/S
SBR	D'	R/S	Lbl	D'	Pgm	02	R/S	ISBR	
Программа П32. Вычисление коэффициентов ас, ai, .... ак ин»
терполирующего многочлена Ньютона и коэффициентов полинома
у(х) = ао 4- а-,х + а2х2 + • . + апхп при равномерном расположении
узлов yt(xi) с шагом h. Ввод (после нажатия клавиши RST):
Уо - R0, yi = R1, .... yn—Rn (и < 1Б)и п — RX. Нажав кла»
вишу R/S, получаем 0-»-RX, a0->R0, at-»-Rl, a„-*Rn. Вво-
дим h — RX и, нажимая n +1 раз клавишу R/S, получаем
ао, fli, ..., ап (они заносятся в регистры RO-j-Rn). Для вычисления
y(Z),	где Z = x — Хо. нажимаем				клавишу А (получаем 0-				>RXJ,
вводим Z И, STO 16		нажав клавишу R/S, получаем y(Z)-+RX. 0	STO ’ 19	RCLI 19 STO						17	RCL
19	+	1	=	STO	18	1	SUM	19	RCL
17	—	RCLI	19	STO	17		+/-	4-	RCL
18	=	STOI	19	RCL	19	X^t	RCL	16	INV
x = i	0	16	RCL	18	STO	19	x^ t	RCL	16
INV	x — t	0	05	RCL		—	1	=	STO
18 	STO	17	RCL	17	+	1	—	STO	19
RCLI	17	—	RCLI	19	X	RCL	18	=	STOI
17. .	1	SUM	17	RCL	17	xltt	RCL	16	INV
x — t	0	63	0	x t	RCL	18	—	1	—
INV	x — t	0	Б9	STO	19	R/.S	STO	17	RCLI
19	~T-	RCL	18	=	STOI	19	R/S	RCL	17
Prd	18	1	SUM	19	GTO	1	09	Lbl	A
RCL..	00.	STO	>8	0	R/S	STO	1'7	RCL	16
STO	00	RCLI	00	=	X .	RCL	17	+	Dsz
0	1	42 .	RCL	18..		GTO	1	35	
Программа ПЗЗ; Решение системы из двух дифференциальных
уравнений методом Рунге — Кутта. Ввод: хо = R00, у0 = R01 =
= R02, Zo — R03 = R04, h/2 — R07, данные у'(х, у, г) и z'(x, у, г)
при X	-»-R00,	y->R02 и z->		R04.					
SBR	SBR	STO	06	+	RCL	03	—	STO	04
x^i	STO	05	+	RCL	01	=	STO	02	RCL
07	SUM	00	SBR	SBR	SUM	06	SUM	06	+
RCL	03	=	STO	04 	x^t	SUM	05	SUM	05
+	RCL	01	=	STO	02	SBR	SBR	SUM	06
SUM	06	X	2	+	RCL	03	=	STO	04
х^ t	SUM	05	SUM	05 .	X	2	+	RCL	01
—	STO	02	RCL	07-	SUM	00	RCL	00	R/S
SBR	SBR	+	RCL	06	=	4-	3	+	RCL
03	=	STO	03	STO	04	R/S	X^Lt	+	RCL
05	=		3	+	RCL	01	=	STO	or
STO	02	R/S	RST	Lbl	SBR	. . .	. . .	X	RCL
07	=	x X t	/	...	X	RCL	07	=	ISBR
Для примера к программе 5.69 при хо = 0,2, у0 = 0,0995008326
и 2о = 0,49235 получим при h = 0,1«
X	z	У
0,3	0,4831085134	0,1483051274
0,4	0,4702289079	0,1960019786
0,5	0,4538403861	0,2422342378
0,6	0,4340847683	0,2866579678
0,7	0,4111281313	0,3289445709
0,8	0,3851618702	0,3687833162
0,9	0,3564017201	0,4058838367
1,0	0,3250861121	0,4399784873
Программа П34. Решение системы из трех дифференциальных
уравнений методом Руиге — Кутта. Ввод: х0 = R00, у0 =; R01 =
I— R02, г0 — R03 = R04, w0 = R05 — R06, Л/2 = Rl 1, данные
у'(х, у, г, ш), г'(х, у, г, w) и w'(х, у, г, w) при x-»-R00, y-*-R02,
z->-R04 и ki->-R06. Вывод результатов: х, ш, г и у в регистр X.
SBR	SBR'	STO	09	+	RCL	05	=	STO	06 
X^Lt	STO	08	+	RCL	03		STO	04	RCL
10	STO	07	+	RCL	01	=	STO	02	RCL
11	SUM	00	SBR	SBR	SUM	09	SUM	09	+
RCL	05	=	STO	06	x^f	SUM	08	SUM	08
•4-	RCL	03	=	STO	04	RCL	10	SUM	07
SUM	07	+	RCL	01	=5	STO	02	SBR	SBR
SUM	09	SUM	09	X	2	+	RCL	05	=
STO	06	X^t	SUM	08	SUM	08	X	2	+
RCL	03	=	STO	04	RCL	10	SUM	07	SUM
07	X	2	+	RCL	01	=	STO	02	RCL
11	SUM	00	RCL	00	R/S	SBR	SBR	+	RCL
09	=		3 •	+	RCL	0Б	=	STO	-05
STO	06	R/S	x^t	+	RCL	08	=	4-	3
+	RCL	03	=	STO	03	STO	04	R/S	RCL
10	+	RCL	07	==	—	3	+	RCL	01
==	STO	01	STO	02	R/S	RST	Lbl	SBR	...
		...	. . .	...	X	RCL	11	=2	STO	10 .
. . .	...	. . .	• . •	. . .	X	RCL	11	—	x^t
•. -	• ••	...	...	.. 	X	RCL	11	=	ISBR’
Для	системы								1
	dy dx	= z;	dz _ dx	— 6z -	-Hy-	Gw,	dw dx	= y	
при	Xo = 0,	Ze = —	-11, ye =	3, Wo	= 0 и	h —	0,1 получим:		
X	z	У	w	w (точное)
0,1	—8,13280	2,05030	fljSBOlO	0,2513
0,2	—6,98340	1,34971	0,41830	0,41833
0,6	—2,26691	0,19219	0,62202	0,62206
1,0	—0,26380	—0,31568	0,55062	0,55064
2,0	<0,17508	—0,22660	0,24987	0,24988
3,0	0,08865	—,0,09425	0,09697	0,09697
4,0	0,03523	—,0,03523	0,03629	0,03629
5,0	0,01329	—0,01338	0,01343	•0,01343
Точное решение w (х) = 2е~*— е~2х — е~3*.
Время счета по программам ПЗЗ и П34 составляет около 20 и
2Б с иа каждый шаг. Программы П32—34 наглядно иллюстрируют
возможности программируемых микрокалькуляторов с повышенной
емкостью запоминающих устройств.
Приложение 3
ПАКЕТ ПРОГРАММ С ОСОБЫМИ ПРИЕМАМИ
ПРОГРАММИРОВАНИЯ для микрокалькуляторов
ЭЛЕКТРОНИКА БЗ-34
Программа П3.1. Вычисление факториала п! при п = РХ, вклей
чая случай п = 0 (см. программу 3.16).
ВП ПО 1 ИПО X FLO 03 С/П
Программа П3.2. Вычисление .значении многочлена степени
п 12 по схеме Горнера, Ввод: ао — РД, ai~a„ — Pl^j- Prz и .дач
лее для каждого к п — РО и к = РХ (см. программу 4.10)’.
ф ф Сх КИПф + X FLO 03 ИПД +
С/П БП 00 •
Программа ПЗ.З. Решение системы из п 13 нелинейных урав-
нений Xi — Fi(Xi) модифицированным методом Зейделя [29]. Под-
программа должна заносить Х1->РД, х2-»-РС, ..., Xis-*-Pl. Ввод;
начальное значение Xi В/0 С/П, начальное значение х2 С/П и т. д.,
затем число итераций т = РХ БП 09 С/П (получаем х}) С/П (по-
лучаем х2) и т. д.
ПД	1	3	ПО	XY	С/П	КП0	БП	ОБ	ПО
ПП	21	FLO	10	1	4	ПО	КИПО	С/П	БП
17	...	...	............................ В/0
Для системы xi = V[*i (х2 + 5) ~~ 1]/2 5 х2 = V*i + 3 In xt под-
программа имеет вид
ИПС Б -J- ИПД X 1 -	2	4- FV
ПД ф Fin 3	X + FV" ПС
При начальных Xi = 4, х2 =: 2,Б и т = 6 получим xi = 3,7607299
(точное значение 3,7568) и х2 — 2,7811093 (точное значение 2,7798)
при tc ~ 70 с.
Программа П3.4. Поиск экстремума функции F(x) одной пере-
менной х методом ее квадратичной аппроксимации в интервале
Xi + h. Ввод: данные F(x) при х заносимом в начало подпрограм-
мы, h = РВ, е2 = PC, начальное значение х — xi = РХ. Результат:
Хм->РХ, F(xM)->Pl. Заняты регистры 0, I, А, В и С. Программа
вычисляет Xi — хм для аппроксимирующей F(x) параболы до тех
пор, пока (х<+1 — X;)2 не станет меньше е2.
ПА	ИПА	ИПВ —		ПП	58	по	ИПА	ПП	58
Ш	ИПА	ИПВ	+	пп	58		ИПА	2	X
ИПВ	—	X	ИПА	2	X	ипв	+	ИПО	X
+	ИП1	4	X ,	ИПА	X	—	XY	ИПО	+
ИП1	2	X	—	i-	2	4- •	ИПА	XY	ПА
1—	Fx2	ИПС	—	Fx < 0	01	ИПА	С/П	...	В/0
Для F(x) = 10х —2x2+'0,lxs при xt = 3;-ft ='0;1; е2= 1-10-®
получим хм = 3,33375 и Г(хм) — 14,814815 при tc ж 90 с.
Программа П3.5. Минимизация гладких • функций А(х,-) сл<9
переменными методом координатного, спуска, .Ввод: данные F(xi)
при x;-»Pi, 1-10" = P0, (e/9)2 = PA, 1 = РВ, &x = PC = РД,
x;(0) = Pi. Результат: F(xiMaH) ->PX — РО, x, мин-»-Pi.
кипв	ипд	+ .	КПВ	  «	. • •	ИПО	XY	по	XY
—	Fx>0	00	ипд	/-/	3 ‘	4-	ПД	Fx2	ИПС
3		Fx2	—	Fx<	:о оо	ипс	ПД	п	ИПВ
1	+	ПВ	—	Fx <	:о  оо	1	ПВ	ИПА	ИПС
9		ПС	ПД	Fx2	—	Fx>0	00	ИПО	с/п
Для /7(х1-) = exp(xi + x2 + хз)/(*1х|х|) ПРИ e=l-10*4, Ax =•'
= x/(0)—0,5 и n — 3 получим F(xiM„H) = 3,7354517; Xi мин —;
=.1,0001271; Хгмин = 2,0001018; xs мин — 3,0002796 (tc ~ 21 мин).
Программа П3.6. Минимизация выпуклых функций п 10 пере-
меииых методом спирального спуска. Ввод: данные F (х,) при Xi->Pi,
1-10" = Р0, (е/5)2 = РВ, 1= PC, Ах = РД и х,(0) = Pi. Резуль-
тат: F (Xi мин) —> РХ = Р0, Xj мин “* Pi.
кипе	ипд	+	кпе	... ...	. . .	...	
	ИПО	XY	ПО	XY	-	Fx>0	00	n
1	+	ПС	—	Fx < 0 00	1	ПС	ИПВ
/-/	5	—	ПД	Fx2	-	Fx>0	00	ИПО
ИПС
ИПД
С/П
Для примера к программе П3.6 получим F(xi мин) = 3,7354523;
>;i мнн = 0,999872; х’г MHH = 2,000672; хз мнн = 3,001184 (А « 15 мни).
Программа П3.7. Численное интегрирование методом Симпсона
с заданной погрешностью е. Ввод: данные f(x), лее Ь ПВ а ПА — П7 В/0 С/П.							(15е)2 = РД		и да-
ИПВ	ПП	58	П9	ИПА	ПП	58	ИП9	+	П9
ИП7	2	-4-	П7	ИПА	+	П8	0	ПС	ИП8
ПП	58	2	X	ИПС	+	ПС	ИП7	2	X
ИП8	+	П8	ИПВ	—	Fx>0	19	ИПС		ИП9
+	П9	+	3	-т-	ИП7	X	ИП6	XY	П6
—	Fx2	ипд	—	Fx < 0	10	ИП6	С/П	...	В/0
При в « 1,5	= 1 мин,	10-5 второй что дает / =		интеграл 1,3987138.	табл. 5.4 вычисляется за				tc
Программа П3.8. Решение системы из двух дифференциальных
уравнений = f(x, у, г), и г' = g(x, у, z) методом Рунге — Кутта
[29]. Подпрограмма должна вычислять z'~>-РЗ и у'->-РХ при
х —>Р6, у-»-РА и z-*PB (свободны регистры 0, 1, 2; для записи
промежуточных результатов можно использовать регистры 3, 4, 5).
Рвод: хо = Р6, Л/2 = Р7, Зуо = PC = РХ и (после иажатия кла-
виш В/0 и С/П) 3zo = РД = РХ. Вывод результата по мере нажа-
тия клавиши С/П: yit zb t/2, г? ... в регистр X.
В/0	3		П8	ПА	С/П	ипд	3	Ч-	П9
пв	с/п	пп	28 . .	ПП	24	пп	46	ПП	28
ипв	ИПА	пп	39	ИПб	ИП7	+	П6	ПП	55
ИП7	X	П5	ИПЗ	ИП7	X	П4	ИП9	ИП8	ИПЗ
+	ПА	XY	ИП4	+	ПВ	ипд	ИП4	+	пд
ИПС	ИПб	+	ПС	В/0			.. .	...	Е/0
Для системы у' — ху + z и г' = х + уг при х0 = у о = zo = 1,
/i=0,l будем получать yi иг;: 1; 1; 1,2275429; 1,2284363; 1,5224128;
1,5320161 и т. д. (/с « 70 с иа одну пару yt, zi).	,
Программа П3.9. Решение дифференциального уравнения 2-го
порядка у" = f (x, у, у') методом Рунге — Кутта [29]. Подпрограм-
ма должна заносить у” РХ при х Р6, у РА и у' -> РВ (сво-
бодны регистры 0 4-3, промежуточные результаты можно заносить,
в регистры 4 и 5). Ввод: h/2 — Р7, х0 = Р6, 3(/о = PC, 3y'Q —
.= РД = РХ. Выводы результатов: ylt у2, у3 и т. д. в регистр X.
В/0	3	—	П9	ПВ	ИПС	3	—-	П8	ПА
С/П	пп	27	ПП	23	пп	45	пп	27	ИПВ
ИПА	пп	38	ИПб	ИП7	+	П6	пп	54	ИП7
X	П4	ИПВ	ИП7	X	П5	ИП9	ИП8	ИПб	+
ПА	XY	ИП4	+	ПВ	ИПС	ИПб	+	ПС	ипд
ИП4	+	пд	В/0	. . .	. • •	• •«	...	• . .	В/0
Для уравнения у" = — (—=- + А при Л/2 = 0,05; х0 = у0 = у0 = 1
4 \Л/У )
будем  получать yv. 1; 1,1077563; 1,2321001; 1,3747563 и т. д.
(/с « 70 с на шаг).
Программа П3.10. Решение дифференциального уравнения 3-го по-
рядка у"’ = f(x, у, у', у”) методом Рунге — Кутта 2-го порядка
[29]. Подпрограмма должна заносить у"' -> РХ при х->-Р7, </-*Р5
</'-*РЗ и у"->Р1 (свободны регистры Ач-Д, для промежуточных
результатов можно использовать регистр 9). Ввод: h — Р8, Хо = Р7,
у0 = Р6, у'й = Р4, у" = Р2. Результат: yi, у2, у3, ... и т. д. в ре-
гистре X.
В/0:	ИП2.	Ш	ИП4	ПЗ	ИПб	П5	С/П	пп	14
ИП7	ИП8	+	П7	7	ПО	ПП	37	П9	ИПЗ
 :ПП	26	•	ИП1	ПП	26	ИП9	ИП8	X	2	-т-
 -ф	кипо	+	КП[	+	кпо	В/0	• 1 •	...	В/0
Для уравнения у'" — ху(2у" — 3/2)/(у')2 при хо = 2; уо — 3,0625;
^/' = 3,5 и . у" 3,75 будем получать: yv 3,4313; 3,8405; 4,2936;
4,7938 .и а. д. при tc « 45 с на 1 шаг (й = 0,1).
^Программа JI3.1.1; Решение дифференциального уравнения 4-го по-
рядка y'v — f(x, у, у‘, у", у”') методом Рунге — Кутта 2-го по-
рядка	[29]. Подпрограмма должна заносить уп					'->РХ	при X	-Р9,
	у'-+Р5, у	"-►РЗ И	у'"	— Р1	(свободны регистры Д			и С,
промежуточные результаты			можно заносить в			регистр В).		Вводз
h = РА, де» = Р9,		уь = РВ,	Уо =	= Р6,	Уо=Р4.	Уо —	Р2 Резуль-	
тат: yi.	Уг, у3 ... и	т. д. в регистр		X.				
В/0	ИП2 П1	ИП4	ПЗ	ИП6	П5	ИП8	П7	С/П
ПП	16 ИП£	1 ИПА	+	П9	9	ПО	ПП	42
ПВ	ИП5 ПП	31	ИПЗ	ПП	31	ИП1 '	ПП	31
ИПВ	ИПА X	2	-т-	t	кипо	+	КПф	+
кпо	В/0		> • •	• • •	• • •	• ’• •	• • •	В/0
Для уравнения	при й=0,1; х0 = 3,
Уп — 9, Уп = 9, у" = 7,5 и у”' — 4,5 будем получать уг. 9,937; 10,955?
12,056; 13,246 и т. д: при tc ~ 55 с на 1 шаг.
Программа П3.12. Вычисление 5 смежных гармоник по схеме
параллельного спектрального анализа. Ввод: (после иажатия клавиш
В/0 и СП и индикации цифры 0) иомер начальной гармоники
Пн = PC, 2n/N — РД (или 360/2V, если переключатель Р — Г в по-
ложении Г), номер начального ненулевого отсчета 1Я — Р¥,У; = РХ
С/П у. j = РХ С/П и т. д. Вывод результатов (после ввода по-
следнего отсчета): Л>->Р0, aiW/2-»-Pi, 6i/V/2.->P2, asNI2~*P9
и 65/V/2->-PA.
1	0	ПО.	Сх	КП|	FLO	03	ПО	с/п	ПВ
ИПО	+	ПО	пп'	69	•ИП1	+	Ш	F,	ИП2
+	П2	пп	69	ИПЗ	+	ПЗ	F,	ИП4	+
П4	ПП	69	ИП5	+	П5	F,	ИП6	+	Пб
ПП	69	ИП7	+	П7	F,	ИП8	+	П8	ПП
69	ИП9	+	П9	F,	ИПА	+	ПА	F,	ИПС
5	—	ПС	F,	1	+		БП	08	F,
f	ИПД	X	ИПС	X	ИПС	1	+	ПС	F,
F cos	FBx	F sin	ипв	X	XY	ИПВ	X	В/0	
Для N =		= 32 и	Ую -F ।	У17 = 1	(остальные у.		= 0)	введя	1 Пц = I,
2л/32	= РД	И 1н =	= 10 получим:		Ао =	8 (сумма всех		Уд,	a iN/2 ==
= -6,3622798; btN/2 = 3,4007106; a3N/2 = 2,8477578; 62/V/2 =:
= —4,2619737; a3N/2 = -0,23875957; b3N/2 = 2,424179; aiN/2 =
= 1 • IO-8; faN/2 = 6>7. ю-T; asN/2 == _1Д595353;	b3N/2 =
= —0,95160494. Число вводимых отсчетов yi при использовании
программы не ограничено.
СПИСОК ЛИТЕРАТУРЫ
-1. А нг о А. Математика для электро- и радиоинженеров/Пер.
с франц.; под ред. К. С. Шнфрина. — М.: Наука, 1965.— 772 с.
2.	Корн Г„ Корн Т. Справочник по математике для научных
работников и инженеров. —М.: Наука, 1984. — 832 с.
3.	Справочник по специальным функциям с формулами, графи-
ками н математическими таблицамн/Под ред. М. Абрамовица и
И. Стигана.— ,М.: Наука, 1979. — 832 с.'
4.	Б а х в а ло в Н. С. Численные методы. — Мл Наука, 1973.—
632 с.
5.	Демидович Б. П., ,М а р о и И. А. Основы вычислитель-
ной математики. — М.: Наука, 1970. — 644 с.
.6	. Трохнменко Я. К-.-Лю б н ч Ф. Д. Инженерные расчеты
на микрокалькуляторах. — Киев: Техника, 1980. — 383 с.
7.	Т р о х н м е и к о Я. К.; Л ю б и ч Ф. Д. Радиотехнические
расчеты на микрокалькуляторах. — М.: Радио н связь, 1983. — 256 с.
8.	Дьяконов Вг П. Расчет нелинейных и импульсных
устройств на программируемых микрокалькуляторах;—М.: Радио
и связь, 1984. — 176 с.
9.	Цветков А. Н. Прикладные программы для мнкро-ЭВМ
Электроника БЗ-21. — М.: Финансы н статистика, 1982.— 127 с.
10.	Г о р я н и о в В. Г., Журавлев А. Г., Тихонов В. И.
Статистическая радиотехника: Примеры н задачи. — М.: Советское
радио, 1980. — 544 с.
11.	Вычисления на электронных клавишных вычислительных ма-
шинах ряда Искра/Б. А. Баклан, А. Бухштаб, М. Е. Левин н др.
М.: Статистика, 1978,— 160 с.
12.	Иванов В. И., Иванов Е. А., Муреяко Л. Л. Мало-
габаритные вычислительные комплексы индивидуального, пользова-
ния. — Радиотехника, 1983, № 1, с. 24.	‘
13.	Уорт Т. Программирование на языке бейснк./Пер. с англ.;-
под ред. В. Ф. Шаиьгина. — М.: Машиностроение, 1981. — 225 с.
14.	Мей и ке X., Гуид л ах Ф. Радиотехнический справочник:
В 2-х т. —:М.: Госэнерговздат, 1961. Т. 1. — 416 с.
15.	Бессонов. Л. А. Теоретические основы электротехники.—
М.: Высшая школа, 1964. — 750 с.
16.	Ильин В. Н. Основы автоматизации схемотехнического
проектирования. — М.: Энергия, 1979. — 392 с.
17.	Львовский Е. Н. Статистические методы построения эм-
пирических формул. — М.: Высшая школа, 1982. — 224 с.
18.	В о л к о в Е. А. Численные методы, — М.: Наука, 1982. —
256 с, ’
19.	Харкевич А. А. Основы радиотехники. — М.: Связьиздат,
1962.— 560 с.
20.	С и горский В. П., Петренко А. И. Основы теории
электронных схем. — Киев: Вища школа, 1971. — 568 с.
21.	Дьяконов В. П. Вычисление амплитудно- и фазо-частот-
ных характеристик по переходным с помощью микро-ЭВМ индиви-
дуального пользования. — Изв. вузов. Приборостроение. 1983, № 4,
с. 69.
22.	Т р о х и м е и к о Я. К., Л ю б и ч Ф. Д. Искусство програм-
мирования программируемых микрокалькуляторов, 7. Интерполиро-
вание табличных моделей. — Изв. вузов. Радиоэлектроника. 1983,
№ 12, с. 40.
23.	В а р л а м о в Р. Г. Эксплуатация и ремонт современных
микрокалькуляторов. — М.: Легкая и пищевая промышленность,
1983.- 120 с.
24.	Щуп Т. Решение инженерных задач на ЭВМ. — М.: Мир,
1982. — 238 с.
25.	Микрокалькулятор Электроника БЗ-34. Руководство по экс-
плуатации. — Светловодск, 1980. — 156 с.
26.	П Programmable 58С/59. Personal Programming. Master
Library. — Dallas: Texas Instr. Inc., 1979.
27.	T p о x и м e н к о Я. К., Л ю б и ч Ф. Д. Искусство програм-
мирования программируемых микрокалькуляторов, 8. Численное ре-
шение нелинейных уравнений.—Изв. вузов. Радиоэлектроника, 1984,
№ 1, с. 50.
28.	Трохименко Я. К., Лю бич Ф. Д. Искусство програм-
мирования программируемых микрокалькуляторов, 10. Численное
решение систем уравнений. — Изв. вузов. Радиоэлектроника, 1984,
№ 3, с. 43.
29.	Цветков А. Н., Епанечников В. А. Прикладные про-
граммы для микро-ЭВМ «Электроника БЗ-34», «Электроника .МК-56»
и «Электроника МК-54». — М.: Финансы и статистика, 1984, — 175 с.
УКАЗАТЕЛЬ АЛГОРИТМОВ И ЧИСЛЕННЫХ МЕТОДОВ
Анализ спектральный 120
.---повышенной точности 129
Аппроксимация полиномом 144
Вычисление АЧХ 131
— многочленов 65
— определителей 57
— перестановок 62
— производных 102
•	— размещений 62
—	рядов 66
—	факториала 61
Гамм а-функции 154
— — неполные 156
Гистограмма, построение 136
Дилогарифм 166
Дроби-непрерывные 65
Емкость шаров 185
Задача Коши III
Метод Адамса 114
—	Адамса — Эйлера 115
—	Горнера 65
—	деления пополам 92
—	интегрирования Гаусса ПО
---- трапеции 107
—	— Уэддля 108
---- Чебышева 109
—итераций 88
----Ньютона 89
—	Коши 113
—	Монте — Карло 133
—	подекадного приближения 93
— решения дифференциальных урав*
нений неявный 117
—	Рунге — Кутта 113
—	секущих-хорд 91
—	случайных проб 92
— Стеф фенсон а. 95
—	хорд 90
—	Эйлера 112
—	Эйткена 73
Методы интегрирования Ньютона —
Котеса 168
----прямоугольников 105
— прогноза-коррекции 116
Многочлен Лагерра 68
—	Лагранжа 71
—	Лежандра 68
Многочлены комплексного переменно*
го 66
—	ортогональные 68
—	Чебышева 69
—	Эрмита 69
Модуль, выделение 56
Интеграл вероятности 167
Интегралы Френеля 163
— эллиптические 165
Интегральный косинус 152
— синус 152
Интегрирование таблиц Ш
— численное 105
Интерполяция 81
—	обратная 93
—	таблиц 81
Обработка статистическая 133
Основы программирования 17, 44
Преобразование координат 42
— углов 56
Логика алгебраическая 30
—. — обратная бесскобочная 8
Матрицы, обращение 60
—, сложение 59
—, умножение 59
Расчет выпрямителя 190
— дросселя 181
— емкости 183
— индуктивных элементов 176
— линий передачи 185
— трансформатора 182
— усилителей 193
Релаксатор, моделирование 196
Сглаживание данных 146
Случайная величина, распределение
17Q
Транзистор, параметры 191
Функции Бесселя модифицированные
159
—	гиперболические 64
•	обратные 64
---комплексного переменного 77
—	Дебая 166
— интегральные показательные 150
— комплексного переменного 74
—, приближение 140
Уравнения алгебраические, корни 87
— дифференциальные, решение 111
— системы 119
—	линейные, системы 79
—	нелинейные, решение 98-
Формула интегрирования Бода 156
Функции Бесселя 156:
Числа комплексные 62
—, округление 56
— случайные, генерация 138
—. усечение 56
Экстраполяция 81
Экстремум, поиск 97