Алгебра и начала анализа в таблицах. 7-11 классы - Чекова А.М.

Author: Чекова А.М.
Tags: общее школьное образование общеобразовательная школа алгебра математика
ISBN: 966-8902-11
Year: 2006
Similar
Геометрия в таблицах. 7-11 классы
Алгебра и начала математического анализа. 11 класс
Алгебра. 7 класс. Задачник
Алгебра. 7 класс. 2 часть
Text
                    ПОДАРОК
Чек > »АМ
ГЕОМЕТРИЯ
7*11 классы
к i
УДК 373.167.1:512+512 (075.3)
ББК 22.14 я 721
Чекова А.М. Алгебра и начала анализа в таблицах. 7-11 классы. Учебн. пособие - X.: КраТна мр!й ™, 2006. - 256 с.
Пособие содержит основные теоретические вопросы курса алгебры 7-11 классов согласно действующей программе по математике.
Материал пособия подан в справочной форме, чаще всего в виде таблиц, что поможет учащимся наглядно увидеть правила и их иллюстрации, лучше понять алгоритмы.
В рубрике «Ученическая страничка» рассмотрены решения типичных задач каждой темы, что поможет учащимся лучше усвоить изученный материал, научит их правильно и вкратце записывать условия и решения заданий.
Будет полезна для учащихся и рубрика «Страничка абитуриента» (11 класс). С ее помощью старшеклассники смогут решать сложные задания и подготовиться к поступлению в высшие учебные заведения.
Пособие предназначено для учащихся 7—11 классов, учителей, абитуриентов.
Учебное издание
Чекова Алла Михайловна
Алгебра и начала анализа в таблицах 7-11 классы
Редактор Дудник Н.В.
Корректор Ольховская М. А. Компьютерная верстка Мажитова Р.Р. Дизайн обложки Терлецкий А. В.
Подписано в печать 05.01.2006 р. Формат 60x90/8.
Бумага офсет. Печать офсет.
Издатель Халимон Ю.А.
Регистр, свид. ДК № 961 от 19.06.2002 г.
61146, г. Харьков, а/я 2656, тел. 58-50-70
ISBN 966-8902-11 -4
© Чекова А. М., 2006.
© Терлецкий А. В., худож. оформл., 2006.
© КраТна мр!й™, 2006.
Ц-
ЭТО УЖЕ НУЖНО ЗНАТЬ
МНОЖЕСТВА ЧИСЕЛ
Определения	Примеры
— множество натуральных чисел (употребляемых при счете).	1,2,3...28.
Z — множество целых чисел (нуль, натуральные числа и противоположные им отрицательные числа).	-23,0,17. .
Q — множество рациональных чисел (которые можно пред- т	ч ставить в виде —, где т - целое, п - натуральное число). п	-10, 25, 1—; 2; 7,5; 13 3
ОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
Действия	Свойства		
	Переместительное	Сочетательное	Распределительное
Сложение: а + Ь = с (а,Ь— слагаемые; с — сумма).	а + b = Ь + а.	а + (6 + с) = (а + Ь) + с.	
Вычитание: а-Ь = с (а —уменьшаемое, Ь — вычитаемое, с — разность).	а-Ь = -{b-а).	а - (b - с) = а - b + с; (а - Ь) - с = а - b - с.	 !* М
Умножение: а-Ь-с (а,Ь —сомножители, с — произведение).	a-b-b a.	(a-b)-c = a-(b-c)	(а + Ь)-с = ас + Ьс, (а-Ь)с = ас - Ьс.
Деление: а:Ь-с (а —делимое; Ь —делитель; с — частное).	а _ 1 Г" а	деление числа на произведение: с: (ab) = (с: а): 6 = (с: 6): <7; деление произведения на число: (ab): с = (<7: c)b = (b : с)а.	деление суммы (разности) на число: (a + b) _а Ь С	с с
СВОЙСТВА О И 1
ab = 0, если <7 = 0, или b = 0, или а = b - 0;
“ - 0 только при <7 = 0, b * 0.
а + 0 = а; а-0 = а; 0-а = -а]
а + {-а) = 0; а - а = 0;
(а и -а противоположные числа).
1 , , 1
а- — = 1; {а и--обратные).
а а
W Считают, что 0 делится на любое число, но делить на нуль нельзя!
ПРИЗНАКИ ДЕЛИМОСТИ
Признаки
На 2 — делятся числа, последняя цифра которых 0,2,4,6,8 - это четные числа, их записывают п = 2к,к— натуральное. Нечетные числа не делятся на 2, их записывают: п = 2к +1 ,к — целое неотрицательное.
На 3 — делятся числа, сумма цифр которых делится на
На 4—делятся числа, число из двух последних цифр ко-торых делится на 4.___________________________
На 5 — делятся числа, последняя цифра которых 0 или 5.
На 8— делятся числа, у которых число, выраженное тре-мя последними цифрами данного числа, делится на 8.
На 9— делятся числа, сумма цифр в записи которых де-лится на 9.__________________________________________
На 11 —делятся числа, суммы цифр на четных и нечетных местах которых дают разность, которая делится на 11.
Примеры
258:2; так как 8 : 2;
344:2; так как 4 : 2;
456:3; 4+5+6=15,15:3.
12316:4; (16:4).
105:5; 30:5.
-1256:8; (256:8).
351:9; 3+5+1=9, (9:9).
1727:11 т. к. 7 + 7 = 14;
1 + 2 = 3;
14-3 = 11; (11:11).
ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
Определения	Примеры
Простые числа делятся сами на себя и на 1, т. е. имеют два делителя.	17, (17:1 и 17:17).
Составные числа имеют более двух делителей.	18, (18:1; 18:2,18:3,18:6,18:9,18:18). 18 имеет шесть делителей: 1, 2, 3, 6, 9, 18.
не является ни простым, ни составным числом.	
ОБЫКНОВЕННЫЕ ДРОБИ
Правила	Примеры
ОСНОВНОЕ СВОЙСТВО ДРОБИ	
Значение дроби не изменится, если числитель и знаменатель дроби умножить или разделить на одно и то же число (выражение), не равное нулю.	а	ас	22	2	4	8	2 — =	• 	= — ~ ~ ' 	= — b	Ьс	33	3	6	12	3
Сократить дробь — значит разделить числитель и знаменатель дроби на общий делитель.	ас а 21 3 _ — = —; —--.7—общий делитель чисел 21 be b 28 4 и 28
	СРАВНЕНИЕ ДРОБЕЙ		
Из двух дробей с одинаковыми знаменателями та дробь больше, у которой числитель больше.	2 П '	,, — < —, т.к. 2 < 11. 17 17
Если знаменатели разные, то нужно дроби привести к общему знаменателю и сравнить их как дроби с равными знаменателями.
Из двух дробей с равными числителями та дробь больше, у которой знаменатель меньше.
2	3	2	16	3 21	16	21	2	3
-	и	-	= —;	- = —;	—<	—, т.е.	-
7	8	7	56	8 56	56	56	7	8
13 13
17 15 ’
т.к. 15 <17.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Если знаменатели равны, то числители складываются (вычитаются), а знамена-тель сохраняется.______________________
Если знаменатели разные, то дроби приводят к общему знаменателю и складывают (вычитают) как дроби с равными знаменателями.
а с ad + cb _ ad+ cb b d bd db bd
При сложении (вычитании) смешанных чи- 1	5	1 5	3 + 20	23
сел нужно сложить (вычесть) их целые и g+ + +g + 6~ + 24	24'
дробные части.__________________________|_________ _________________________
_____________________________УМНОЖЕНИЕ ДРОБЕЙ	 При умножении дробей умножают числи- а с _ ас тели и знаменатели.__________~b ~d~~bd	t
При умножении смешанных чисел превращают их сначала в неправильные дроби, а потом умножают.
2	3 32 59 4-59
2 — 7 —=-------=-----
15	8	15 8	15-1
Если в произведении один из множителей - целое число, то его представляют в виде дроби со знаменателем 1.
1 . „ „ „1	1 4 27 22 1-4-9-11
-•4-2 7 • 3 — =---------=----------
3	’	7 3 1 10 7	11-5-7
36-11 396 И
35 ” 35 ” 35'
ДЕЛЕНИЕ ДРОБЕЙ
При делении двух дробей деление заменяют умножением первой дроби на дробь, обратную второй дроби. ас ad a-d
ВОЗВЕДЕНИЕ ДРОБИ В СТЕПЕНЬ
Возведение дроби в степень: при возведении дроби в степень возводят числитель и знаменатель этой дро-би в данную степень.___________________________
При возведении смешанного числа в степень сначала превращают его в неправильную дробь, а потом возводят в степень.
ПРОПОРЦИИ
Определение. Пропорция — это равенство двух отношений. — = — или а: Ь - с: d b d
Члены пропорции: a,d —крайние члены, Ь,с —средние члены.
____________________Свойства___________________
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних ее членов.________________________________________
Каждый член пропорции является четвертым пропорциональным членом по отношению к трем остальным.
_______Примеры
ad = be.
ПРОЦЕНТЫ
Определение. Процент - это сотая часть некоторого числа (принимаемого за единицу).
100
Нахождение процента от числа
р% от числа а = -J—
100
15 Решение:-----180 =
100
15-180 ------= 27. Ответ: 27.
100
Нахождение числа по его проценту
Если р°/о от какого-то числа равно Ь ,то всё число равно
, р 6-100 о:---=-------.
100 р
Найти число, 22% которого равны 33.
Решение: Искомое число — х —это решение уравнения:
22 100
22	33 100
— ;х =	---; а: = 150. Ответ: 150.
100	22
Нахождение процентного отношения двух чисел
Число а составляет от числа Ъ
- • 100% .
Сколько процентов составляет число 24 от числа 120?
Решение: искомое число процентов — х.
х	24-100
---120 = 24; х — ——--; х = 20(%). Ответ: 20%.
100	120
Изменение числа, выраженное в процентах
.1-
Число а увеличивалось на р% , Р% л , Р°/о V
а +----а = а(1 Ч—  );
100%	100%
Число а уменьшилось на р% р% а 100%
р°/о
100%
Цена товара а = 120 грн увеличилась на 5%. Новая цена товара:
120 +----120 = 120 1 +
100	V
120-21	ч
--------= 126 (грн).
20
Ответ: 126 грн.
20
КООРДИНАТНАЯ ПРЯМАЯ
__________________Правила_________________
На координатной прямой изображается множество всех действительных чисел.
0 - начало координат.____________________
Числа, обозначенные на координатной прямой справа от точки 0, являются положительными, а слева - отрицательными.
Примеры
МОДУЛЬ ЧИСЛА
___________Определения___________
Модулем положительного числа на-зывается само это число._________
Модулем отрицательного числа называется число, ему противоположное._
Модуль нуля равен нулю.
Примеры
а -b =АВ.
-12 = 12 =12..
_________________________СВОЙСТВА модуля
Модуль любого числа - неотрицательное число, а > 0.
ГЕОМЕТРИЧЕСКИМ СМЫСЛ МОДУЛЯ
На координатной прямой модуль - это расстояние от начала координат до точки, изображающей данное число.
Модуль разности двух чисел а и Ь— это расстояние между двумя точками а и b на координатной прямой.
Модули противоположных чисел равны, -а = а .
Величина числа не превосходит величину его модуля.
И
= а2к
Модуль произведения равен произведению модулей сомножителей. |a-Z>| = |а|-|б|;
/7
Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю).
СЛОЖЕНИЕ И ВЫЧИТАНИЕ
___________________Правила____________________
При сложении двух чисел с одинаковыми знаками их модули складываются, а перед суммой ставится их общий знак. _______________________________
При сложении двух чисел с разными знаками от большего модуля вычитают меньший и ставят знак того числа, у ко-торого больший модуль.________________________
Вычитание двух чисел заменяется сложением уменьшаемого и противоположного вычитаемому числа.
Примеры
-13 + 21 = 8; 20-37 = -17.
УМНОЖЕНИЕ И ДЕЛЕНИЕ
При умножении двух чисел модули их умножают, а знак ставят по указанной схеме:
При делении двух чисел модуль первого числа (делимого) делят на модуль второго числа (делителя), а знак ставят по схеме умножения.
ПОДОБНЫЕ СЛАГАЕМЫЕ
Определения
Подобными слагаемыми называются слагаемые, которые равны, или отличаются только ко-эффициентами._____________________________
Привести подобные слагаемые — значит сложить их коэффициенты, а буквенную часть оставить неизменной.
Примеры
Па-2Ь + 4а-Па + с-1Ь = = (11 + 4-12)а + (-2-7)6 + с = — За - 9Ь + с.
СКОБКИ
Правила
Примеры
Скобки в выражениях вводятся для изменения обычного порядка действий:
1)	возведение в степень (справа налево);
2)	умножение или деление (слева направо);
3)	сложение или вычитание (слева направо).
13 + (7-3)2 = 13 + 42 = 13 + 16 = 29; (113 +17): (123-121) = 130:2 = 65, (200 - 28) - (17 + 53) = 172 - 70 = 102.
______________________ РАСКРЫТИЕ СКОБОК__________________________
Если перед скобками стоит «+», то скобки опус- ... +(а + 6) = ... +а + />. каются, а знаки слагаемых в скобках не меняются._________________
Если перед скобками стоит знак «-», то скобки ... -(а + д) = ... -а-Ь. опускаются, а знаки слагаемых меняются на противоположные.
УРАВНЕНИЯ.
§1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ. ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ
УРАВНЕНИЕ И ЕГО КОРНИ
Определения	Примеры
Уравнение - это равенство, содержащее переменную. Корень уравнения - это значение переменной, при котором уравнение обращается в верное равенство.	3(х-4) = 24, при х = 12 3(12-4) = 24 3-8 = 24 24 = 24 х = 12 - корень уравнения.
Решить уравнение - это значит найти его корни или доказать, что их нет.	3(х-4) = 24, х = 12.
Равносильные уравнения - это уравнения, которые имеют одни и те же корни.	3х = 36 и 3(х-4) = 24; их корень х = 12.
НЕКОТОРЫЕ СВОЙСТВА УРАВНЕНИЙ
________________Свойства________________
В любой части уравнения можно привести подобные слагаемые.
Если из одной части уравнения перенести слагаемые в другую часть и поменять при этом знаки слагаемых на противоположные, получим уравнение, равносильное данному.
При делении (умножении) обеих частей уравнения на одно и то же число, отличное от нуля, получим уравнение, равносильное данному.
___________Примеры
Зх - 4 + 5х = 36
Зх + 5х = 36 + 4
8х = 4 + 36
8х - 40.
Разделим обе части уравнения
8х = 40 на 8:
х = 5 — это уравнение равносильно 8х = 40, их корень 5.
ЛИНЕЙНОЕ УРАВНЕНИЕ
_____________Определения______________
Уравнение вида ах = Ь, где х— переменная, а и Ь— некоторые числа, называется линейным уравнением.
____________Примеры___________
4 - 5х = 6 - 2(х + 2) , используя свойства уравнений:
4-5х = 6-2х-4,	-5х + 2х = 6-4-4,
ах = -Ь.
Решение линейных уравнений
5х + 4 = 0,
а*0; х =------единственный корень.
__________а________________________
а = 0; Ох = -Ь — нет корней.
— корень.
Ох = -10
нет корней -10 на 0 разделить не-
а = 0; 6 = 0. 0 х = 0 — бесконечное множество корней.
возможно.
7х = 7х, 7х-7х = 0, Ох = 0,
...... 	—	 ।		»« ! I	 <
х — любое число.
ах + b = 0 ;
______________ ВИДЫ ВЫРАЖЕНИИ__________________________ ______________________________________________________Определения_Примеры Выражение - правило, задающее совокупность действий, которые нужно выполнить в определенном порядке над значениями переменных и постоянных, чтобы получить зна-чение этого выражения.________________________________
Числовое выражение - выражение, состав-
ленное из чисел с помощью знаков действий (21-13)2--\ и скобок.__________________________________________________
Выражение с переменными - это выражение, составленное из чисел и переменных с 1,5х2-(28^-127) :3. помощью знаков действий и скобок._______
Подставив в выражение значение переменных, получим числовое выражение.
Найдя значение этого числового выражения, получим значение выражения с переменной.
если х- 2;у -5,5, то 1,5х2 - (28^-127) :3 = = 1,5-22— (28 • 5,5 —127) • 3 = = 1,5-4-(154-127)-3 = = 6-27:3 = 6-9 = -3.
ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ
Определения	Примеры
Тождество - это равенство, справедливое при всех допустимых значениях входящих в него переменных.	За-4 + 5а = 8а-4.
Тождественное преобразование выражения - это замена одного выражения другим, тождественно равным ему.	Зх-4 - х + 2 и 2х = 6 - тождественно равны.
ИЗВЕСТНЫЕ ТОЖДЕСТВА
_______________Свойства_________________
a + b = b + a;ab = ba переместительное свойство.
(a + b) + c = a + (b + c); (ab)c = а(Ьс) сочетательное свойство.
a(b +c) = ab+ac распределительное свойство.
Примеры
17 + 13 = 13 + 17;5-3 -3-5 .
(17 +13) + 33 = 17 + (13 + 33);
(2-8)-4 = 2-(8-4)._________
7-(11 + 13) = 7•! 1 + 7-13 .
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. РЕШИТЬ УРАВНЕНИЕ.				Зх-2(8-5х) = 12х.		
Решение. Раскроем скобки. Перенесем слагаемые и поменяем их знаки на противоположные, приведем подобные слагаемые.				Зх-16 4- 10х = 12х; Зх4-10х-12х = 16; х = 16. *		
Ответ: 16.	_						
2. РЕШИТЬ УРАВНЕНИЕ.				2х-3 х-ь2_ 3x4-3 4 ' 2 ~ 4		
Решение. Домножим левую и правую части на 4 -общий знаменатель. Выполним уже известные преобразования, а именно: разделим числитель на знаменатели.				4-(2х-3) 4-(х4-2) _ 4-(Зх4-3) 4'2'4 2х - 3 4- 2 (х 4- 2) = Зх 4- 3 ; 2х - 3 4- 2х 4- 4 = Зх 4- 3; 2х 4- 2х - Зх = 3-44-3; х = 2.		
Ответ: 2.						
3. РЕШИТЬ УРАВНЕНИЕ.			. 4х -1 6x4-2	1 1.	= — . 2	3	6			2. Зх + 2 + 4/(2х-1) = 11х-2.
Решение.			3(4х-1)-2(6х4-2) = -1; 12х-3- 12х-4 = -1; -7 = -1, что невозможно			Зх 4- 2 4- 8х — 4 = 11х - 2; 11х-2 = 11х - 2; 0-х = 0.
Ответ:			нет корней;			любое число.
4. РЕШИТЬ ЗАДАЧУ.	Автомобиль проехал за три дня 2299 км, причем за второй день он проехал на 48 км больше, чем за первый, а за третий - на 31 км больше, чем за второй день. Сколько километров проезжал автомобиль каждый день?					
Решение. 1 способ.	Пусть за первый день автомобиль проехал х км, тогда за второй -(х + 48) км, а за третий день (х + 48 + 31) = (х + 79) км. За три дня вместе по условию - 2299 км.					
Составим уравнение и решим его:	х + х + 48 + х + 79 = 2299; Зх + 127 = 2299; Зх = 2172; х = 724. За первый день автомобиль проехал 724 км, за второй день -724 4- 48 = 772 (км), за третий день -7724-31 = 803 (км).					
Ответ: 724 км, 772 км, 803 км.						
Способ оформления задачи таблицей						
Решение. II способ. ч.		1 день - ? х км II день-? (х 4-48) км	1 III день-? (х4-48 4-31) км			_ 2299 км	
		х4-х4-48-1-х4-484-31 = 2299, Зх = 2172; х = 724.			1 день - 724 км; II день-7244-48 = 772 км; III день - 7724-31 =803 км.	
Ответ: 724 км, 772 км, 803 км.						
. ЦЕЛЫЕ ВЫРАЖЕНИЯ
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Определения
п раз
ие N, п>2
_______________Примеры__________
З3 =3-3-3 = 27; (-5)2 = (-5)-(-5) = 25;
71 = 7; 0" = 0; 1” = 1; п е N;
0° — не определено;
СВОЙСТВА СТЕПЕНЕЙ
ni+n а
(ab)n = ап-Ьп
(2-3)4 = 24-З4 = 16-81 = 1296
Полезные замечания
Любая степень числа д>0 положительное.
есть число
5и>0; (1,2)7 >0.
При возведении в четную степень отрицательного числа в результате получаем знак «+», в нечетную степень -знак «-».
(-3)4 = (-3)(-3)(-3)(-3) = З4 = 81; (-3)4 > 0 (_3),=(-3)(-3)(-3) = -27;(-3)’<0.
Удобные приемы вычислений со степенями
а) ЗЗ2 = (11 -З)2 = 112-32 =121-9 = 1089;
б) 42’5 =42-42 = 16-74 = 16-2 = 32;
ОДНОЧЛЕНЫ И ДЕЙСТВИЯ над ними
__________Определения_________
Одночленом называется произведение чисел, переменных и их натуральных степеней, а также сами числа, пе-
Примеры
0; За2ху3;
12
13
ab3; т; х6 — одночлены.
ременные и их степени.
Число 0 называется нулевым одно-
членом.___________________________
Степенью одночлена называется сумма показателей переменных, входящих в одночлен. Если одночленом является число, не равное нулю, то его степень считается равной нулю.
Число 0 степени не имеет._________
Если в запись одночлена входит переменная х в степени к(хк), то говорят, что этот одночлен имеет по х (или отно-сительно х) степень к.____________
Одночлен записан в стандартном виде, если первый его множитель есть число, коэффициент одночлена, а дальше стоят переменные в некоторых степенях, расположенные по алфавиту (латинскому или греческому).______
Одночлены называются подобными, если они равны между собой или отличаются только своими коэффициентами.
За5Ь2с3 - одночлен десятой степени (5 + 2 + 3= 10);
5ох3 - одночлен четвертой степени (1 +3) = 4;
7 - одночлен нулевой степени (7х°).
5ох3 - одночлен третьей степени тельно переменной х.
4а2 Ь3 у3; 6а5Ь2с6; -3xy3z4; 4a2Z>J/3 в стандартном виде.
2
4а b ;-1;За b а b - подобные одночлены
Сложение и вычитание
Умножение
Действия над одночленами________________
За3 +ab + b2 +5а3 -ЗаЬ = Ъа3 -2ab + b2.
Возведение в степень
Деление
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. вычислить.
Решение.
Ответ: -1.
2. ВЫЧИСЛИТЬ.
Решение.
ч
(~2)5 • 77 265-210
146	134-84___________________________________________________
(-2)5-77-(2-13)5-2'° (-2)5-77:25-2‘°-135 _ -25+5+'° -77 • 135 _ -220-77-135
(2• 7)6 -134 • (23)4	26 • 76-134-2’2	~ 26+|2-76-В4 ~ 2|8-76-134
—22-7-13
=	= -4 • 7 • В = -364
111
Ответ: -364.
3. УПРОСТИТЬ ВЫРАЖЕНИЕ.
Решение.
(4я26)5(16я&3)4(-24а3&7)3
(4а25)5(16а63)4(-24 <Л7)3 =
= 45 (а2 )5 У164 а4 (Ь3 )4 (-24 )3 (а3 )3 (Z?7 )3 =
= (22)5а10&5(24)4а4612(-1)3(24)3Л21 = -238№
Ответ: -238а23638.
4. ВПИСА ТЬ ПРОПУЩЕННЫЕ ОДНОЧЛЕНЫ ТАК, ЧТОБЫ ПОЛУЧИЛОСЬ ТОЖДЕСТВО.
Решение.
(?)б.(?)6=-64х15
(-64х)15 =-2бх|2х13 = 26(х2)6(-х)3 = (2х2)6(-х)3
Ответ: (-64х)15 = (2х2)6(-х)3 - тождество.
5. ПРЕДСТАВИТЬ, ЕСЛИ ВОЗМОЖНО, В ВИДЕ КВ АДР А ТА ОДНОЧЛЕНА.
Решение.
Ответ:
6. ПРЕДСТАВИТЬ, ЕСЛИ ВОЗМОЖНО, В ВИДЕ КВАДРА ТА ОДНОЧЛЕНА.
Решение.
-9a6Z>14
-З2 (а3)2(67)2 =-(За367)2- это выражение является противо-
положным квадрату одночлена.
Ответ: представить в виде квадрата одночлена нельзя.
§ 3. МНОГОЧЛЕНЫ. ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ
ВИДЫ МНОГОЧЛЕНОВ
______________Определения______________
Многочленом называется алгебраическая сумма нескольких одночленов.___________
Многочлен, состоящий из двух членов, назы-вается двум леном._____________________
Многочлен, который состоит из трех членов, называется трехчленом._________________
Одночлен считается частным случаем многочлена; Если все члены многочлена записаны в стандартном виде и выполнено приведение подобных слагаемых, то получен многочлен стандартного вида.
____________Примеры
5ху2 - Зур2, + 4ху.
\5d~m1n.
ДЕЙСТВИЯ с многочленами
Определения
СЛОЖЕНИЕ И ВЫЧИТАНИЕ
При сложении и вычитании многочленов пользуются правилами раскрытия скобок.
УМНОЖЕНИЕ И ДЕЛЕНИЕ
Чтобы умножить одночлен на многочлен, умножают каждый член многочлена на одно-член и результаты складывают.___________
Чтобы умножить многочлен на многочлен, умножают каждый член первого многочлена на каждый член второго многочлена и полу-ченные произведения складывают._________
Чтобы разделить многочлен на одночлен, надо разделить на этот одночлен каждый член многочлена и полученные частные сложить.
Примеры
6х(х3 - 2) = 6х • х3 - 6х • 2 = 6х4 - 12х..
(2а - Ь) • (За - 4Ь) - 6а2 - 8ab - 3ab + 4/г = = 6а2 -1 \ab + 4£>2.
12а b
i
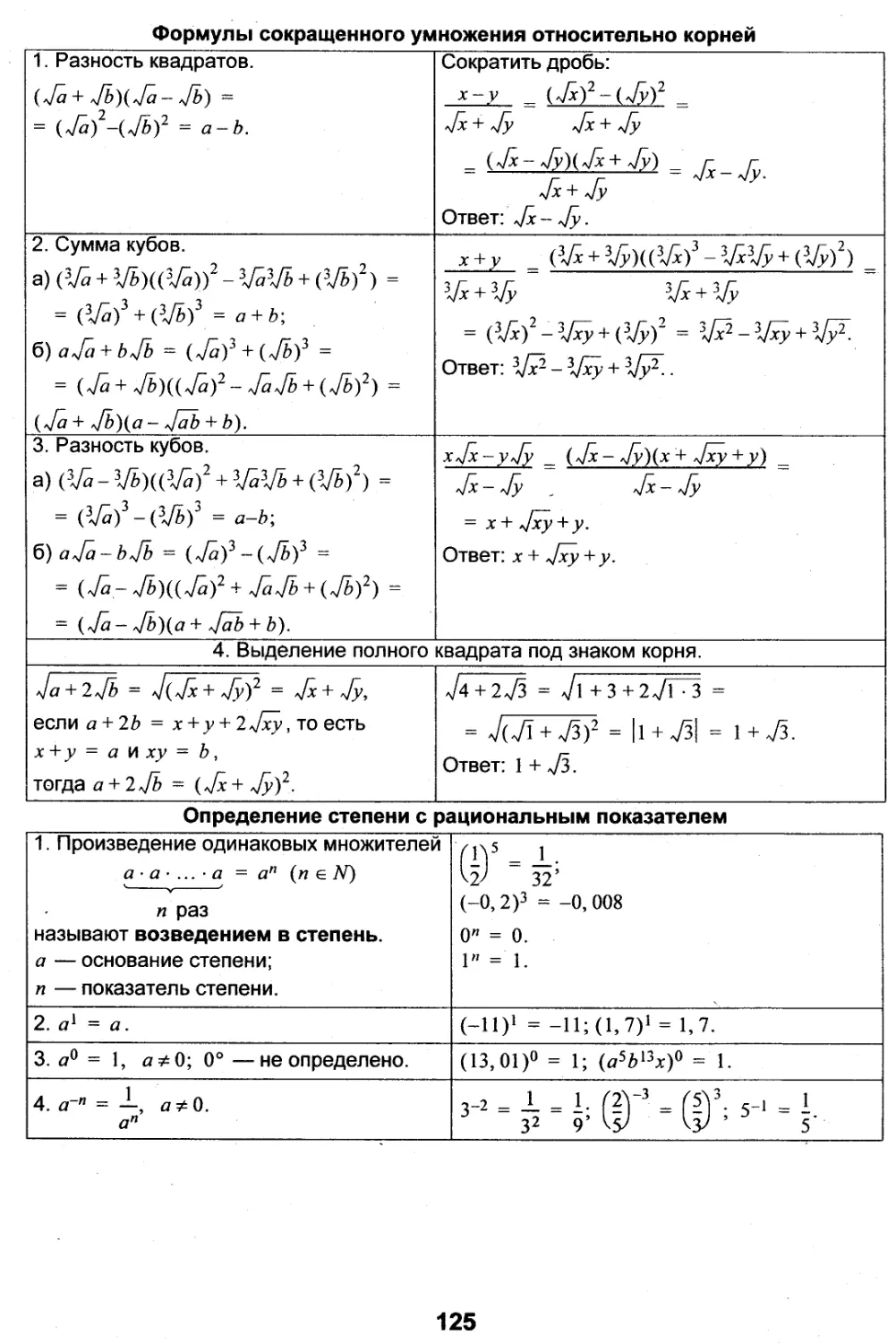
§ 4. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Квадрат су м м ы
{а + b)2 - а" + 2аЬ + Ь2
Квадрат разности
(о - b)2 — а2 - 2аЬ + Ь2
Разность квадратов
а2 -Ь2 = (а-Ь)(а + Ь)
Куб суммы
(а + ЬУ = а2 + За2Ь + ЗаЬ2 + Ь3
Куб разности
(а - Ь)3 - а3 - За2Ь + ЗаЬ2 - Ь* *
Сумма кубов
а3 + Ь3 - (а + b)(a2 - ab + Ь2)
Разность кубов
а3 - Ь3 = (а - Ь)(а2 + аЬ + Ь2)
§ 5. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ
Разложение многочлена на множители — это преобразование алгебраической суммы одночленов в произведение. Существует три основных способа.____________
ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ:____________________
а)	найти общий множитель;	18«5Ь2 -14д463 = 2а* Ь2 (9а -1Ь).
б)	разделить на него каждый член многочлена и полученную сумму взять в скобки;
в)	записать произведение общего множи-
теля на полученную сумму.______________________________________________
Если при вынесении за скобки общий мно- -ay + by + су = -у(а - Ь - с). житель выносится со знаком «минус», то знаки слагаемых в скобках меняются на противоположные.
СПОСОБ ГРУППИРОВКИ:
а)	объединить члены многочлена в такие группы, которые имеют общий множитель;
б)	вынести этот общий множитель за скобки.
2а + Ьс + 2Ь + ас = (2а + 2b) + (Ьс + ас) -= 2(а + Ь) + с(Ь + а) - (а + Ь)(2 + с).
_________ИСПОЛЬЗОВАНИЕ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
Для разложения многочлена на множители ?5х2-4v2 = (5х-2у)(5х + 2у). используют известные формулы.	,	"	,
•	х~ +1 бху + 64 у' = (х + 8 у)(х + 8j>) = (х + 8 у)~.
‘1
УЧЕНИЧЕСКАЯ СТРАНИЧКА
РАЗЛОЖИТЬ МНОГОЧЛЕН НА МНОЖИТЕЛИ.
Решение.
1. Выделим общий множитель 9у и вынесем 9а* 1 2у + 18аЬу его за скобки.	,
2. Применим формулу квадрата суммы чисел аиЬ. = 9у(а + Ь) 

Ответ: 9y(a + bf.
Решение.
1.	Выделим общий множитель. Для этого заменим знак выражения (у-х).
2.	Вынесем (x-j/) за скобки.
3.	Применим формулу разности квадратов для
2
а2
Решение.
1. Вынесем -х2 за скобки.
2. Применим формулу квадрата разности.

9
Ответ: -х- бх —

Решение.
1.	Применим формулу разности квадратов.
2.	Упростим выражение в скобках.
Ответ: (5Ь-а)(5а-Ь).
5. 4т2 -20тп + 25п2 -36.
Решение.
1. Применим формулу квадрата разности.
2. Применим формулу разности квадратов.
4/и2 ~ 20m/? + 25п2 — 36 — 4w2 - 20 тн + 25/7" - 36

Ответ: (2/и-5и-б)(2ю-5и + 6).
Решение.
1. Применим формулу разности кубов.
2. Упростим выражение в скобках.
§ 6. РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИИ
С ДВУМЯ ПЕРЕМЕННЫМИ
Определения
Линейным уравнением с двумя переменными х и у называется уравнение вида: ах + Ьу + с = 0,
________________Примеры______
Зх + 4у + 5 = 0 — линейное уравнение
где х и у - переменные, а,Ь,с — некоторые числа.____________
Решением уравнения с двумя переменными называется любая пара чисел (х;у), обращающая уравнение в тождество. Решить уравнение с двумя переменными — значит найти все пары чисел (х;у), которые явля-ются его решением.__________
Множество точек, координаты которых удовлетворяют уравнению ах + Ьу + с = 0, называются его графиком.
Графиком уравнения
ах + Ьу + с = 0 является прямая.
х + 2у = 5 — линейное уравнение.
Пара (1;2) — решение уравнения, так как при x = l;j = 2, получаем 1 + 2-2 = 5; 5 = 5 — верное равенство, пара (2;1) — не является решением, так как при х = 2;^ = 1 получаем 2 + 21 = 5.
4 = 5 не является тождеством, т. е. пара (2;1) не является решением уравнения х + 2у = 5.
1)	Если коэффициент Ь при у не равен нулю, то у можно выразить через х: ах + Ьу + с = Ъ,
Ьу = -ах+с, У--—Х-— —это линейное уравнение.
Ь Ь
2)	Если 6 = 0, ах + б7 + с = 0 принимает вид
Q
ах + 0у + с = 0, ах + с = 0, приа^0,х =— ,и
а
графиком уравнения будет прямая, параллельная оси ординат и пересекающая ось абсцисс в точке
_ с
а
3)	При а = 0имеем 0х+6у + с = 0,Ьу + с = 0, у = -- — b
это прямая, параллельная оси абсцисс и пересе-
кающая ось ординат в точке у = --.
Ь
4)	Если а = 0 и 6 = 0, то уравнение принимает вид Ох+Qy + с = 0, тогда при с = 0 равенство верно при всех х и у, при с * 0 - неверно ни при каких х и у, т.е. при а = 6 = с = 0,в этом случае графиком линейного уравнения ох + 6у + с = 0 является вся координатная плоскость.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. ПОСТРОИТЬ ГРАФИК УРАВНЕНИЯ.
4х + 2_у+ 3 = 0.
Так как а* О, Ь*О, с*О, то графиком уравнения является прямая, которую можно построить по двум точкам: х = 0,х = 1, у = -1,5 Иу = -3,5.
2. ПОСТРОИТЬ ГРАФИК УРАВНЕНИЯ.
0х + 2у + 3 = 0.
Так как а = 0, то 2у = -3, у =--это прямая, параллель-
ная оси абсцисс, проходящая через точку с координатами
3.	ПОСТРОИТЬ ГРАФИК УРАВНЕНИЯ.
х + Оу + 0 = 0.
Так как 6 = 0 и с = 0, то х = 0,— это прямая, перпендикулярная оси абсцисс и являющаяся осью ординат.
§ 7. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИИ С ДВУМЯ ПЕРЕМЕННЫМИ
____________Определения_____________
Системой уравнений называются два или несколько уравнений, у которых требуется найти все общие решения.
Уравнения системы записываются столбиком и объединяются фигурной скобкой.
Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными.
Систему двух линейных уравнений с двумя переменными обычно записывают в виде:
Примеры
2x-3j = 9,
Решением такой системы уравнений является множество упорядоченных пар
Пара чисел (3;-1) является решением
системы
Решить систему уравнений — значит найти все ее решения или доказать, что решений нет.
Если система имеет конечное число решений, то она называется определенной. Если система имеет бесконечное число решений, то она называется неопределенной. Две системы называются равносильными, если они имеют одинаковое множество решений.____________________________
Если система из л-линейных уравнений содержит п неизвестных, то возможны следующие три случая: - система не имеет решений; - система имеет только одно решение; - система имеет бесконечно много шений.
6х-8у = 11.
— решений нет;
Система
ре-
Зх - 4у = 13,
единственное решение (7;2);
не имеет решении, если
к’
2 w2 2
имеет единственное решение, если
^6х-8у = 30.
-4 15 _
• — = —, бесконечно много решении.
-8 30
i
2	2
имеет бесконечное число решений, если
а. Ь, с,

2
г

УЧЕНИЧЕСКАЯ СТРАНИЧКА
Типы систем
1)1 Ни одной точки, 1 ни одной точки.
Примеры
Ох + Оу - 1, 0х + 0у = 2.
Число решений
Система не имеет решений.
2)1 Вся плоскость, I ни одной точки.
Ох + 0}> = О, Ох + 0 у = -1.
Система не имеет решений.
3)1 Вся плоскость, 1 вся плоскость.
I I 		—
Ох + Оу = О, Ох + Оу = 0.
Любая пара чисел -решение системы
4)1 Ни одной точки, 1 прямая.
5)1 Вся плоскость, прямая.
Ох + Оу - 6, (2х + Зу = 5.
Ох + Оу = О, ' 2x + 7v = 5.
Система не имеет решений.
6)1 Две пересекаю-X щиеся прямые.
х + у = О, [х + Зу = 4.
Решение системы - координаты любой точки прямой.
Единственное решение - координаты точки пересечения прямой.
7ь Две параллельные I прямые.
Система не имеет решений.
8)1 Две совпадающие I прямые.
х + у = 0, -
2х + 2у = 0.
Координаты любой точки прямой являются решением системы.
СПОСОБЫ РЕШЕНИЯ СИСТЕМ
Способ подстановки
Решить систему уравнений:
Решение.
Выразим из первого уравнения переменную х = 15-3у и подставим во вто-
рое уравнение, а второе уравнение системы оставим без изменения, получим систему, равносильную данной.
Решим второе уравнение системы:
Подставим полученное значение переменной у в первое уравнение системы:
Ответ: (6;3).
х = 15 - Зу, ' 3(15-3у)-4у = 6.
45 - 9у - 4у - 6;
-13у = 6-45;
-13у = -39;
У = 3. *
Графический способ
Для решения системы графическим способом строят графики всех уравнений, входящих в систему. Координаты точек пересечения являются решением этой системы.
Графический способ удобен для нахождения числа решений системы (т.е. сколько точек пересечения графиков, столько решений имеет система), но неудобен в вычислении координат точек (т.к. получаются приближённые значения координат).
Решить систему уравнений.
(2х + Зу = 15, [3х-4у = -3.
Построим графики обоих уравнений:
1)2х + 3^ = 15
2
Зу = 15-2х; у = 5—х
3
это прямая, проходящая через точки с координатами (0;5); (3;3);
2)3х-4у = -3
4у = 3х + 3, у = ^х + ^, 4	4
это прямая, проходящая через точки с координатами (-1;0); (3;3);
3) графики этих функций пересекаются в точке с координатами (3;3).
Ответ: (3;3).
противоположные числа.
____________________________Способ сложения___________________________
Способом сложения удобно решать системы, у которых коэффициенты при одной из переменных -Решить систему уравне-ний._
Решение.
Коэффициенты при переменной у - противоположные числа, поэтому сложим почленно оба уравнения системы.
2х + 2_у + х - 2у = 15-3, упростим это уравнение:Зх = 12, получим х = 4.
Вернемся в систему Р= 4,	Подставим значение
х-4 во второе
уравнение системы и решим его.
Ответ: (4;3,5).


§1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
ДРОБНЫЕ РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
Различают целые и дробные рациональные выражения. Целое выражение не содержит деления на переменную. Дробное выражение содержит деление на выражение, в которое входит переменная.
______Правила_______
Значения переменных, при которых выполняются математические действия, записанные в рациональном выражении, называются допустимыми значениями переменных.
Примеры
------у этой рациональной дроби при х = 8 в знаменателе х-8
получаем х-8=8-8=0, поэтому допустимыми значениями
данной дроби являются все числа, кроме х = 8.
Чтобы найти допустимые значения рациональной дроби, нужно приравнять знаменатель к нулю, то есть найти корни полученного уравнения и из всех чисел исключить корни полученного уравнения.
Найти допустимые значения выражения-----.
Зх-х*
Приравняем знаменатель к нулю и решили это уравнение: Зх-х2=0, вынесем х за скобки: х(3-х) = 0, произведение равно нулю, если хотя бы один из множителей равен нулю, то есть х = 0, или 3 - х = 0.
Допустимыми значениями переменной являются все числа, кроме х = 0 или х = 3.
Ответ: х — любое число, кроме 0 и 3.
ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ДРОБЯМИ
Правила
Примеры
СОКРАЩЕНИЕ ДРОБЕЙ
Сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Это действие обусловлено основным свойством дроби.
Для того, чтобы сократить дробь, нужно: а) разложить числитель и знаменатель дроби на множители;
б) выбрать общий множитель в числителе и знаменателе дроби;
в) разделить числитель и знаменатель дроби на общий множитель.
Сократить дробь:
Зх -18х2 15х2 - 90х3 ’
а)	разложим числитель и знаменатель дроби на множители, для этого вынесем
общий множитель за скобки:
Зх(1-6х) 15х2(1-6х)
б)	выберем общий множитель в числителе и знаменателе это: Зх(1 — 6х);
в)	сократим дробь на Зх(1-6х).
Ответ:
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
Сумма (разность) двух дробей с одинаковыми знаменателями равна дроби с тем же знаменателем и с числителем, равным сумме (разности) числителей исходных дробей.
За -4 7 - 4а _ За- 4 + 7-4а _ 3 - а . а -1 ’ а — 1	а — 1	а -1
За-4 _ 7-4а _ За-4-(7-4а) _
а -1 а -1	а — 1
_ За-4-7 + 4а _ 7а-11
а -1	а -1
При сложении (вычитании) двух рациональных дробей с разными знаменателями нужно привести дроби к общему знаменателю и выполнить сложение (вычитание) дробей с одинаковыми знамена-
1 За	1(с + 3а)	За	с + 3а-3а	1
с с1+3ас с с(с + 3а)	с(с + 3а)	с + За
телями.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ
Произведение двух рациональных дробей равно дроби, числитель которой равен произведению числителей, а знаменатель равен произведению знаменателей умножае-мых дробей.__________________________
Частное от деления двух рациональных дробей заменяется произведением дроби делимого на дробь, обратную делителю.
А- - 1 4х + 1 _ (х-1)(4х + 4) _ (х-1)4(х + 1) _ х+1 х —1 (х + 1)(х —1) (х + 1)(х-1)
х Зх2 х(5а-10) а2-4 ‘ 5а-10 “ (а2-4)3х2 ”
5х(а-2)	5
(а - 2)(а + 2)3х2 Зх(а + 2)
Удобнее перед умножением или делением рациональных дробей разложить их чис лители и знаменатели, если это возможно, на множители.________
ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ В СТЕПЕНЬ
Степень рациональной дроби равна дроби, у которой числитель есть степень числителя, а знаменатель — степень знаменателя.
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Множество целых чисел (Z) - это множество, состоящее из натуральных чисел, числа нуль и чисел, противоположных натуральным.
Поэтому понятие степени а", где п- натуральное число, можно расширить, если рассмотреть случаи п = 0 и п — целое отрицательное число. 
Примеры
число, то а"
___________Определение____________
Если и п- целое отрицательное

а
Полезно запомнить
0° - не определено.
- не определено
-п
Свойства степени с целым показателем
„/и а	— а	СЛ а LZ1 II LA 11 LA 1 IQ 1 I i	a ~ a a s
а	• * II 1 LU 1 м	am-n=—(a *0) a" V	7
(ат)" = ат"	(З’1 2)3 * * =3“б; (з2)’3 =3~*	I \n	/ n \m . a =l<7 I	I ,
(ab)n =an-bn	1 • m i гч II гг> 1^	 еп g	an-bn=(ab)"
\ь) ьп	LU I м 1 IQ II Ю | LU II bJ LU IQ	IQ II	bn UJ
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. выполнить
ДЕЙСТВИЯ.
Рекомендация. Подоб-
ные задания лучше делать
по действиям — вероят-
ность ошибки меньше!
Решение.
Ответ: 1.
2. ДОКАЗА ТЬ ТОЖДЕСТВО.
Доказательство.
Упростим левую часть равенства:
- числитель:
- знаменатель:
тождество доказано:
3. СОКРА ТИТЬ ДРОБЬ.
Разложим числитель и знаменатель дроби на множители способом
ax + ay-bx-by
ах -ay-bx + bx
ax + ay-bx-by а(х + y)-b(x +у) _ (х + у)(а -Ь) _х + у ax-ay-bx + by а(х-у)-Ь(х-у) (х-у)(а-Ь) х-у
группировки:
Ответ:
______х-у_________
4. СОКРА ТИТЬ ДРОБЬ.
Для разложения на множители в числителе вынесем общий множитель за скобки, а в знаменателе, применив формулу суммы кубов и вынеся общий множитель за скобки, получим:
Ответ: ——— .
(а + Ь)~
t
Л
a2b + ab2
a3+b3+3ab(a +Ь)
a2b + ab2 _	ab(a + b)
a3 + b3 + 3ab(a + Ь) [а + Ь)(а2 - ab + b2) + 3ab(a + Ь)
_________ab(a + b)________ gb _ ab
(а + b}[a2 - ab + b2 + 3ab} a2 +2ab + b2 (а + Ь)2
5. СОКРА ТИТЬ ДРОБЬ.
Чтобы разложить на множители числитель и знаменатель дроби, применим способ группировки.
Для этого представим а2 + За + 2 как а2 + а + 2а + 2, аналогично представим знаменатель: а2 + 6а + 5 = а2 + а + 5а + 5, а2 + За + 2 _ а' + а + 2а + 2 _ а(а +1) + 2(а +1) _
Ответ:
а + 2
а + 5
6. УПРОСТИТЬ АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ.
а2 + 64 а4 -16 а4 -4а’ +16 аг + 4
Применим формулу разности кубов и разности квадратов в числителях дробей:
а6+64 _ а4-16 _ (д2) +43 _ (а2)~~42 а4-4а2+16 а2+4 а4-4а2+16 а2+4
(а2 +4)(а4-4а2 +1б) (а2-4)(а2+4)
а4-4а2+16	а2+4
-сг + 4-(а2 -4) = а2 +4-а2 +4 = 8.
Ответ: 8.
7. УПРОСТИТЬ
ВЫРАЖЕНИЕ.__________
Иногда для преобразования алгебраических выражений применяют способ последовательных преобразований или одновременно нескольких преобразований. Говорят: «Упростим “цепочкой”». Пользуясь этим методом, надо быть пре-дельно внимательным.
Ответ: 1.
8. ВЫПОЛНИТЬ ДЕЙСТВИЯ.
Используем значение степени с отрицательным показателем:
3~2Л .
27~'х ’____________
3~УЧ> 27b _ 33Ь _ ЗЬ
27~'х 32ах 32ах ах
ЗЬ
Ответ: —
ах
9. УПРОСТИТЬ ВЫРАЖЕНИЕ.
Решение.
Ответ:
10. ПРЕДСТАВИТЬ ВЫРАЖЕНИЕ В ВИДЕ ДРОБИ.______________
Используем формулу разности квадратов и значение степени с отрицательным показателем:
(5а 1 + Ь 2)’(5<я 1 -Ь 2).
Ответ:
§2. КВАДРАТНЫЕ КОРНИ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
КВАДРАТНЫЕ КОРНИ И ИХ СВОЙСТВА
_______________Определения_______________
Квадратным корнем из числа а называют число, квадрат которого равен а.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Арифметический квадратный корень из числа а обозначается знаком 4а ;
а называется подкоренным выражением. Действие, при помощи которого находится арифметический квадратный корень, называется извлечением квадратного корня.
Равенство 4а =Ъ верно, если: 1) 6>0; 2) 62 = а.
При а < 0 4а не имеет смысла, ибо квадрат любого числа не может быть отрицательным.___________
При любом а, если 4а имеет смысл, верно равенство: (4а Г = а .
Примеры
-- wZ j
г = 5;х, = -5 — квадратные корни.
725 =5;
5 — арифметический квадратный корень.
781=9.
V- 25 не имеет смысла.
(^)!=9;(VTf
СВОЙСТВА арифметического квадратного корня
4б-х = 41б-4х = 4
36 Тзб 6 з
16 ” 716 -4-2‘
Для любого значения а верно равенство:
Вынесение множителя из-под знака корня.
Внесение множителя под знак корня.
УРАВНЕНИЕ х = а2
Если а < 0, то уравнение не имеет корней;
Если а = 0, то уравнение имеет один корень х = 0;
Если а > 0, то уравнение имеет два корня: х} = 4а; х-, = -4а . v
7125 = 73• 25= 5Тз . юТ2 = 7100-2 = 7200.
х2 =-25, нет корней; х2 = 0, х = 0________
х2 = 144;
х, = 12; х2 = -12;
х2 = 7;
X] = 7?;х2 = -7? .
действительные числа
Числа, которые можно записать в виде дроби —, где т — целое число, п — нату-п
ральное, называются рациональными. Это все целые и дробные числа (положи-7	3/-
тельные и отрицательные). Например, —; - —; -75. Все остальные числа называ-
ются иррациональными. Рациональные и иррациональные числа составляют мно-жество действительных чисел.____________________________________________
N — множество натуральных чисел; Q — множество рациональных чисел;
Z — множество целых чисел; R — множество действительных чисел.
Квадратный корень из рационального числа мо-жет быть: а) целым числом;_________________
б) десятичной дробью;
в) бесконечно непериодической десятичной дробью или бесконечно периодической десятичной дробью.
16
49
8?
121
= 0,57142857...
= 0,818181...
Во всех случаях, описанных выше, квадратный корень является рациональным числом.
3-т, если 3-т
0, если и?-3 = 0, т-3.
г) бесконечно непериодической десятичной дробью(в этом случае квадратные корни яв-ляются иррациональными числами)._
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. НАИТИ КОРНИ.
Решение.
Ответ:
2. ВЫЧИСЛИТЬ.
Решение.
3 - ту если т < 3
Ответ:	если т>3
0, если т-3.
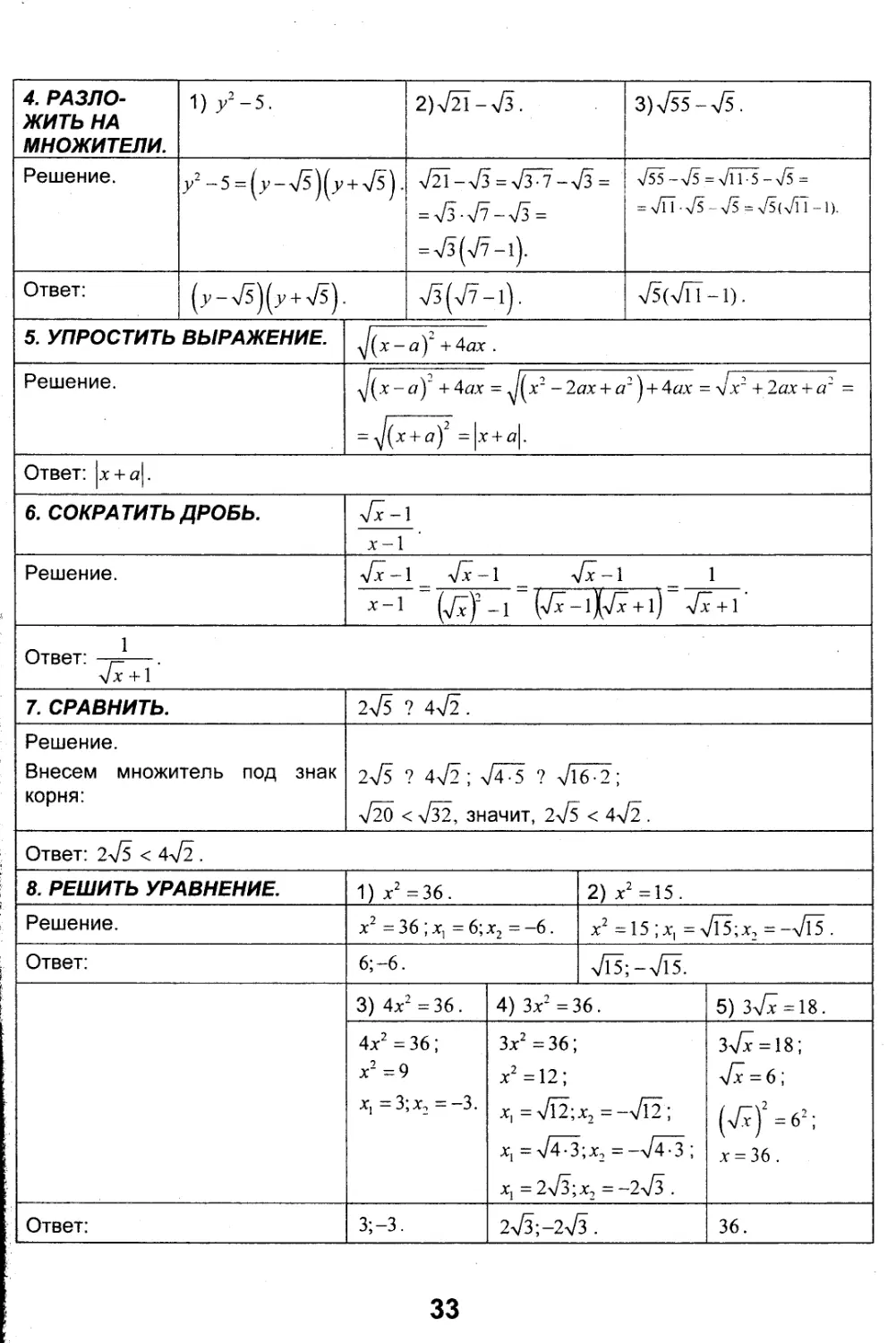
3. РАЗЛОЖИТЬ НА МНОЖИТЕЛИ.
Решение.
Ответ:
Ответ: х + а .
6. СОКРА ТИТЬ ДРОБЬ.
4. РАЗЛОЖИТЬ НА МНОЖИТЕЛИ.
Решение.
5. УПРОСТИТЬ ВЫРАЖЕНИЕ. ft
Решение.
Решение.

Ответ:
7. СРАВНИТЬ.
2>/5 ? 4V2.
V5(VTT-1) -
Решение.
Внесем множитель под знак корня:
2^5 ? 4^2 ; VT5 ? 716-2;
720 < х/32, значит, 2\/5 < 4л/2 .
Ответ: 2 71 < 472 .
8. РЕШИТЬ УРАВНЕНИЕ.
Решение.
Ответ:
Ответ:
§3. КВАДРАТНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КВАДРАТНЫХ УРАВНЕНИЙ
КВАДРАТНЫЕ УРАВНЕНИЯ
Определения
Уравнение вида ах2 + Ьх + с = 0, где х - переменная; а,Ь,с— некоторые числа, причем а*0, называют квадратным уравнением; а - первый коэффициент, Ь - второй, с - свободный член.
Примеры
2х2 + Зх-1 - 0;
х2 - 2х + 4 = 0.
Если в этом уравнении хотя бы один из коэффициентов равен нулю, то данное уравнение называют неполным квадратным уравнением. Неполные квадратные уравнения бывают трех видов:
1) ах2 = 0; 2) ах2 + Ьх = 0; 3) ах2 + с - 0.
1) ох2 =0 при = 0, с = 0;
х2=0;
х = 0
уравнение имеет только один корень.
2) При с = 0, ах + Ьх = 0;
x(ax + Z>) = 0;
X] = 0 или (ox + Z?) - 0; х, =
а уравнение всегда имеет два корня.
3) При Ь = 0 ,
ах2 + с - 0;
а
так как с^О.то - — 0, тогда : а
а) если —>0 а
то уравнение имеет два
кор-
5х2 = 0;
Ответ: 0.
4х2 + Зх = 0;
х(4х + 3) = 0;
х-- 0 или 4х + 3 = 0;
Х~ 4
Ответ: 0,--.
4
9х2-4 = 0;
Ответ:
5
16х2+9 = 0;
б) если < 0 , то уравнение не имеет корней. а
16
нет корней.
Если а = 1, то квадратное уравнение называют приведенным.
Ответ: нет корней. х2 - х + 30 = 0.
Полные квадратные уравнения ах2 * + Ъх + с = 0, а * 0, решаем по формуле:
где D - Ь2 -4ас называют дискриминантом данного квадратного
уравнения.____
Если D < 0, то уравнение не имеет действительных корней.
2х2 + 5х + 6 = 0;
D - 25 -48 = -23;
Если D = 0, то уравнение имеет два одинаковых
корня: Х| = х2 = ——.
2а
D<Q, следовательно, уравнение
не имеет действительных корней. 4х2 + 4х +1 = 0;
£ = 16-16 = 0, £ = 0, следовательно, уравнение имеет два одинаковых корня:
4	1
х, = х-, = — = —. '	8	2
Ответ: -0,5.
Если D > 0, то уравнение имеет два разных
корня: хх =
2х’ +Зх + 1 = 0;
£ = 9-8 = 1;
Ответ: -0,5; -1.
Для квадратного уравнения ах2 + 2кх + с = 0, второй коэффициент которого — четное число, формулу корней удобно записать так:
а
где £, = к2 - ас.
Теорема Виета
ах2 +Ъх + с = Ъ, а *0 , хх х2 = —, х, + х, = — а	а
в приведенном квадратном
уравнении
Уравнение вида ах4 + Ьх2 + с = 0, где а * 0, 6*0 называется биквадратным уравнением.
Формула разложения квадратного трехчлена на множители:
ах2 +bx + c = a(x-X])(x-x2).
Зх2 + 8х-3 = 0;
£, =16 + 9 = 25;
Ответ: 2; 3.
2х4 + Зх2 + 4 = 0.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. НАИТИ ВСЕ КОРНИ УРАВНЕНИЯ. Решение.
1) Их2-99 = 0.
3) 4х2

Ответ:
2. НАИТИ ВСЕ КОРНИ УРАВНЕНИЙ.
Решение.
I способ.
II способ.
Ответ:
3. РАЗНО-ЖИТЬ КВАД-РА ТНЫЙ ТРЕХЧЛЕН НА МНОЖИТЕЛИ.
Решение.
Преобразуем данное уравнение. Най-дем неизвестный множитель. Их2 =99;
Вынесем общий множитель за скобки.
D > 0, т.е. уравение имеет два разных корня:
-(-3)-V25
х = 0; или
следовательно, уравнение имеет два одинаковых корня:
D = 72 - 4-1-10 = 49 - 40 = 9
D>0, следовательно, уравнение имеет два разных корня:

2 —
По теореме Виета:
2 “
По теореме Виета:
9

5

По формуле сокращенного умножения имеем:
2
следовательно, имеем уравнение:
4х2 - 19х +12 = 0; = (-19)2 -4-4-12 = 361 -192 = 169;
-(-19) + V169	-(-19)-V169
х, =----г—------; х, =----—------;
19-13
следовательно
Разложим числитель и знаменатель на множители:
Разложим числитель на множители:
Ответ:
4. СОКРА ТИТЬ ДРОБЬ.
Решение.
Ответ:
-1 + V49
5. РЕШИТЬ ГРАФИЧЕСКИ КВАДРАТНОЕ УРАВНЕНИЕ (ДВУМЯ СПОСОБАМИ)._______________________
I способ.
Построим график функции:
По теореме Виета:
тогда:
тогда:
2
Корнями этого уравнения будут абсциссы точек пересечения графика функции у = х2 - 2х - 3 с осью Ох.
у = х2 - 2х - 3 - парабола.
Область определения функции: все числа.
Найдем координаты вершины параболы:
О ~ ’ Ло ” 2а
(1; -4) - вершина параболы.
а = 1 > 0, ветки параболы направлены вверх. Абсциссы точек, в которых парабола пересекает ось Ох, являются корнями уравнения:
II способ.
Корнями этого уравнения будут абсциссы точек пересечения графиков функции у = х2иу = 2х + 3.
Построим трафики функций: у = х2- пари бола; у = 2х + 3- прямая
X	0	-2
У	3	-1
Графики пересекаются в точках (-1; и и(3;9), а абсциссы этих точек и будут корнями уравнения xt = -1; х, = 3.
Ответ:-1; 3.
6. РЕШИТЬ УРАВНЕНИЕ.
Решение.
Введем новую переменную: тогда получим уравнение: по теореме Виета имеем: дробь равна нулю, когда числитель — нуль, а знаменатель отличный от нуля.
(х: +3)2-14(х2 +з) + 24 = 0 .
у2 - 14у + 24 = 0;
у, = 12; у, = 2, получим: х2 + 3 = 12; х2 + 3 = 2
х2=9; х2=-1 - нет корней.
Ответ: -3; 3.
7. РЕШИТЬ УРАВНЕ-
НИЕ_______________
Решение.
Запишем в виде:
приведем к общему
знаменателю:
упростим:
дробь равна нулю, когда числите!и.
- нуль, а знаменатель отличный <>t
нуля. Имеем:
х = -1 — посторонний корень
Ответ: 2.__________
8. НАИТИ ВСЕ КОРНИ УРАВНЕНИЯ._________
Решение.
Ответ: нет корней.
9. РЕШИТЬ ЗАДА ЧУ.
2х2+Зх + 12 = 0.
D = 32 - 4-2-12 = 9 - 96 = -87, D< 0, следовательно, уравнение не имеет корней.
Из города А в город В вышел пешеход. Расстояние АВ рав но 10 км. Через 30 мин после него из города А в город В от правился велосипедист, скорость которого на 6 км больше; скорости пешехода. Велосипедист, обогнав пешехода и достигнув города В, вернулся в город А в то же время, когда пешеход достиг города В. Определить скорость пешехода.
РЕШЕНИЕ.
Пусть пешеход шел со скоростью х км/час, тогда расстояние 1Л 10
в 10 км он прошел за — ч. Велосипедист ехал со скоро-
стью (х + 6) км/ч и проехал расстояние 20 км от А до В и 20
назад за----ч. По условию задачи, пешеход вышел на 30
х + 6
мин раньше, т.е. он затратил для прохождения пути на -ч больше, нежели велосипедист. Составим уравнение 10	20 _ 1
х х + 6 2
10-2(х + 6)-20-2х-х(х + 6) Л 20х + 120-40х-х2-6х Л
-----------------------= 0; ------------------— 0;
2х(х + 6)	2х(х + 6)
-х2 -26х + 120 2х(х + 6)
Jx2 + 26х-120 = 0, -2х(х + 6) Ф 0;
х2 +26х-120
-2х(х + 6)

х = -30 не удовлетворяет условию задачи (скорость не может быть отрицательной), следовательно, скорость пешехода 4 км/ч.
Ответ: 4 км/ч.
Для решения этой задачи можно составить уравнение с помощью такой табли-
цы:
Пешеход
Велосипедист
Расстояние, км_______Скорость, км/ч.
10	х
20	х + 6
Время, ч.
10
х
20
х + 6
Г
ч
Ш. РЕШИТЬ УРАВНЕНИЕ ВЫДЕЛЕНИЕМ КВАДРАТА ДВУЧЛЕНА.
Решение.
Выделим квадрат двучлена:

Ответ: 8; 2.
§4. ФУНКЦИИ
И ИХ ГРАФИКИ
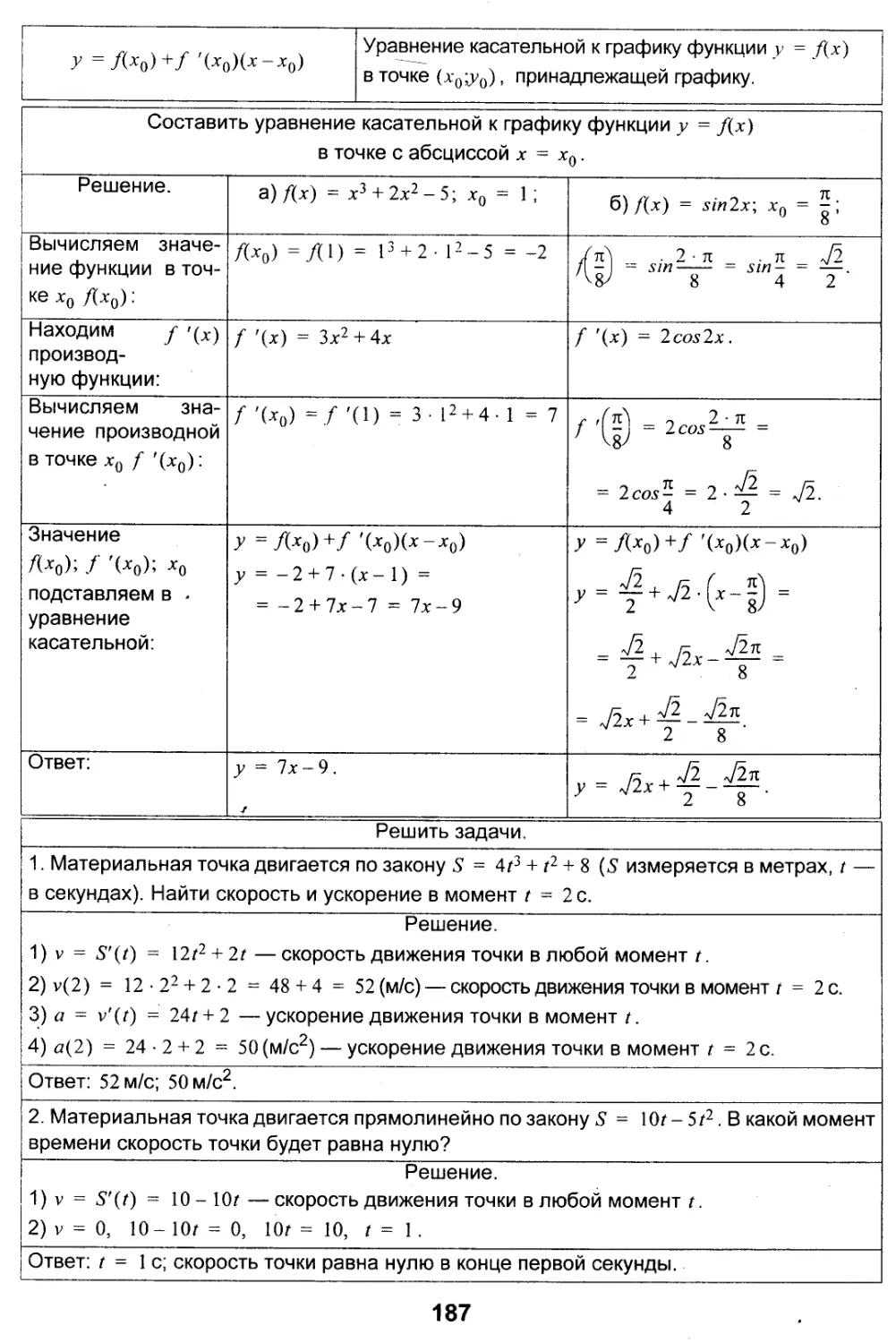
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
Функция обозначается или одной буквой f (или) f (х), или равенством у = f(x), где х - независимая переменная или аргумент, у - зависимая переменная или значение функции,/(х0) - значение функции f вточкех0. <__ __        . .   и-__  I	I I I ~ 1  *   _ 
_____________Область определения и множество значений функции________________ Область определения функции (D) - множество тех значений, которые может при-нимать аргумент.______________________________________________________________
Множество значений функции (Е) - это множество тех значений, которые может принимать сама функция при всех значениях аргумента из области определения. Например: /(*) = ~77-
Л* I
Область определения (0;0): х-1^0; х*1, х —любое число, кроме х = 1.
___________________________ГРАФИК
Определение. Графиком функции у = f(x) называется множество точек плоскости с координатами (х;у), где первая координата х «пробегает» всю область определения функции /(х), а вторая координата — это соответствующее значение функции f в точке х.
ФУНКЦИИ
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
1. Аналитический способ: функция задается с помощью математической формулы._____________________________
2. Табличный способ: функция задаётся с помощью таблицы.
	1	2	3	4	5
У	2	4	6	8	10
3. Описательный способ: функция за-дается словесным описанием._____
4. Графический способ: функция зада-ется с помощью графика.
Функция Дирихле: /(х) = 1 для рациональных х, /(х) - 0 для иррациональных х.
ЛИНЕЙНАЯ функция и ее график
Линейной функцией называют функцию вида у = кх+Ь, где к и Ь — некоторые
числа, х — независимая переменная._______________________
Свойства Значения переменных
1. Область определе- х — любое действительное число х <= R.
ния.________________
2.	Множество значений.
3.	Точки пересечения с осями координат.
4.	Возрастание и убывание.
5.	Графиком линейной функции является прямая.
к — угловой коэффициент прямой.
1) При к * 0; у — любое действительное число, у е R.
2) При к = 0', у = Ь.
1)	При к*0, х = -—\ у = 0 — точка пересечения с осью Ох. к
2)	к = 0, тогда у = Ь — прямая, параллельная оси Ох, пере-
секает Оу в точке (0;Z>) и совпадает с осью Ох при Ь = 0.
3)	у = Ь, х = О — точка пересечения с осью Оу, т.е. (0;Z>).
1)	При к > 0 функция возрастает на всей области определения.
2)	При к < 0 функция убывает на всей области определения.
3)	При к = 0 функция постоянная.______________________
1) При Ь = 0 (у = кх) — прямая, проходящая через начало координат_______________________________________________
2) При Ь*0 (у = кх + Ь) — прямая, не проходящая через начало координат (которая получается из прямой у = кх параллельным переносом вдоль оси Оу на b единиц).
Взаимное размещение графиков линейных функций
I
f
г и
Если к^к2, графики функций у = к}х + Ь1 и у = к2х + Ь2 пересекаются в одной точке.
Если к{ = к2, 6, * Ь2, графики функций у = к{х + Ь{ и у = к2х + Ь2 параллельны.
£

£
Эти графики полезно запомнить
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. НАЙТИ КООРДИНАТЫ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГР А ФИКОВ ФУНКЦИЙ С ОСЯМИ КООРДИНАТ.
Решение.
Чтобы найти точку пересечения графика с осью Ох, необходимо решить уравнение:
-24	-24 + х
у = 0, то есть--+1 = 0;------= 0, если
х	х
-24 + х = 0; ч
х Ф 0, |х = 24.
График пересекает ось Ох в точке (24; 0). С осью Оу график пересекается при условии, что абсцисса точки пересечения х = 0, но область определения этой функции исключает это значение, поэтому график данной функции не пересекает ось Оу.
Ответ: (24; 0).
2. НАЙТИ КООРДИНА ТЫ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКОВ ФУНКЦИЙ С ОСЯМИ КООРДИНАТ.
Решение.
Чтобы найти точку пересечения с осью 0х,
решим уравнение:
Для того, чтобы найти точку пересечения графика с осью 0у, нужно найти значение у при'х = 0.
0 _	_
Зх-10х-2 5х + 1
= 0, то есть
При х = 0 у =
-7х-2 = 0,
- точка пересе-
Точка пересечения графика с осью
чения графика с осью 0х.
Ответ: —;0 ;(0;2).
3. РЕШИТЬ ГРАФИЧЕСКИ УРАВНЕНИЕ.
4-х = 2х + 10.
Чтобы решить это уравнение графически, нужно построить графики функции у = 4-х и у = 2х + 10. Абсцисса точки пересечения этих графиков является решением данного уравнения. Рассмотрим функцию у = 4-х и построим ее график. Областью определения этой функции является множество значений х < 0.
Составим таблицу:____________________
X	0	-1	-4	-9
У	0	+1	2	
Графиком функции у = 2х + 10 является прямая, проходящая через точки (0;10); (-4; 2). Графики пересекаются в точке (-4; 2). Корень уравнения х = -4.
Ответ: -4.
ПРЯМАЯ ПРОПОРЦИОНАЛЬНОСТЬ
Определение. Функция у = кх при к*0 называется прямой пропорциональностью. к — угловой коэффициент. Эта функция является частным случаем линейной функции у = кх + Ь, при Ь = 0. Поэтому её графиком является прямая, проходящая че-рез начало координат.
1. Если к>0, то график функции у = кх 2. При к<0 график функции расположен расположен в I и III координатных углах.
во II и IV координатных углах.
Характерная точка (о;о).
ОБРАТНАЯ
___________Определения___________ Обратной пропорциональностью называется функция, которую можно за-
/с
дать формулой у = —, где к — число,
не равное нулю.
Число к называется коэффициентом пропорциональности.______________
Графиком обратной пропорциональности является кривая, которая называется гиперболой.
Гипербола состоит из двух отдельных частей, симметричных относительно
Графики
начала координат, и проходит через точки (1;£) и
Свойства функции у = _
1. Область определения обратной пропорциональности^_____________________
2. Область значений обратной пропорциональности:
Значения переменных х —любое число, кроме нуля (х^О)
у — любое число, кроме нуля {у ф 0).
3. При к > 0 график функции расположен в I и III координатных четвертях.
4. При к<0 график функции расположен во II и IV четвертях.
Если к > 0 , то х > 0 соответствует у > 0;
х < 0 соответствует у < 0;
Если к < 0 , то х>0 соответствует ^<0;
х < 0 соответствует у > 0.
ФУНКЦИИ у = хг; у = X3. ИХ ГРАФИКИ И СВОЙСТВА
График функции у-х является параболой. Парабола состоит из двух веток, симметричных относительно оси ординат.
Некоторые свойства функции у = х2
1. Любому х можно найти соответствующее значение у, причем у>0; при х = 0 и у = 0.
2. Противоположным значениям х соответствует одно и то же значение у: (-х)2 = х2 = у
*2 = 5;, у2 = 52 = 25, поэтому график имеет симметрию относительно оси Оу . V
Г рафиком функции у = х3 является кубическая парабола. Кубическая парабола имеет симметрию относительно начала координат.
Некоторые свойства функции у - х
1. Любому значению х соответствует значение у, причем у & R (множеству действительных чисел) при х = 0 ; у = 0 ; если х > 0, то у >0; если х < 0, то _у<0.
2. Противоположным значениям х соответствуют противопо-/	\3 з
ложные значения у: (-х) = -х
х, =-5; ух =(-5)3 =-125.
*2 =5; у2 = 53 = 125,
поэтому график имеет симметрию относительно начала ко-ординат.
Точка с координатами (0;0) называется вершиной параболы.
Г рафик расположен в I и III координатных углах.
Графики функций у = 4х и у = х2 при х>0 симметричны относительно прямой у = х.
___________	ФУНКЦИЯ у = Л
Область определения функции у = 4х - множество неотрицательных действительных чисел: х > 0 (потому что корень можно извлечь только из неотрицательного числа),__________________________________________
Если х = 0, то у = 0, поэтому график функции у = 4х проходит через начало координат.
Если х > 0, то у > 0, поэтому график функции расположен в первой координатной четверти. Большему значению аргумента соответствует большее значения функции, действительно:
х, =4, тоу} ~ V? -2;
х2 = 9, тоу2 = у/9 = 3, то есть х2 > Х] и у2 > ух.
Таким образом, функция у = 4х является возрастающей.

§1. НЕРАВЕНСТВА
ВИДЫ ЧИСЛОВЫХ НЕРАВЕНСТВ
Определения		Примеры	
Если а меньше Ь или а больше Ь, то записывают так а < Ь или а>Ь. Такое выражение называется неравенством.	7<10; -8<-5; 13>4; 6,3 >-10,2.
Число а больше числа Ь, если разность а - Ь положительное число, число а меньше Ь, если разность а-Ь — отрицательное число.	а — Ь = 7,02 , то а > b ; а-Ь = -9,5 , то а <Ь .
На координатной прямой большее число изображается точ-	а<Ь
кой, лежащей правее, а меньшее — точкой, лежащей левее.	а	b
Знаки >, < называются знаками строгих неравенств.	а <Ь', Ь> а .
Знаки >, < — знаки нестрогих неравенств.	а < b > а.
> — знак больше или равно ( не меньше).	5 > 5; -17,5 >-131,1.
< — знак меньше или равно (не больше).	5 < 5; -17,5 < 0,13 .
а>Ь и c>d — неравенства одного знака.	15 >4,3; -9 >-17.
а>Ьи c<d- неравенства противоположных знаков.	6,2 > -»; 2 <10,2.
СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ
1. Если а >b, то Ь<а ; если а <b , то b > а.
13>5, то 5<13; -12,9<4, то 4 >-12,9.
2.	Если а>Ь и 6 > с, то а>с (свойство транзитивности).
3.	Если, g>Z>, то а + об + с.____________________
4.	Если а >Ь и с - положительное число (с>0), то ас > Ьс. Это свойство имеет следующий смысл: если обе части верного неравенства умножить на одно и то же по-ложительное число, то получится верное неравенство.
5.	Если а < Ь и с отрицательное число (с < 0), то ас > Ьс. Это свойство имеет следующий смысл: если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак исходного неравенства на противоположный, то получится верное неравенство.____________________
6.	Если а>Ь и с> d ,то a + ob + d.
Если почленно сложить два верных неравенства одного знака, то получится верное неравенство.__________
7.	Если a,b,c,d —положительные числа, причём а >Ь и с > Ь, то ac>bd. Если почленно перемножить верные неравенства одного знака, левые и правые части которых положительные числа, то получится верное нера-венство._________________________________________
8.	Если а>Ь и c<d,TO a-c>b-d
17>8; 8>5, то 17>5. 14>9, ТО 14 + 8>9 + 8. 7,2>-5; 4>0, то 7,2-4>-5-4, т.е. 28,8 >-20.
6,9 >3,5;
6,9(-2) и 3,5(-2) ;(-2 < 0), то -13,8 <-7.
+7,0 > 3 + -1,7 <3 4.3>-7; -1,3<0.
-2,0 <3
3 1	3	1
18> 15; ->-, то 18 -> 15 —;
8 5	8	5
18-3 151 г3 , ---->----; 6->3.
8	5	4
9.	Если а > 6 > 0, то — <-	а b____________________________________________
10.	Если а>Ь>Ъ, то для любого натурального числа п выполняется неравенство а" >Ь" 
12>7; 5<9;
12-5>7-9, то 7>-2.
„ „ 11
8 > 4, то - < - .
8 4
ЧИСЛОВЫЕ ПРОМЕЖУТКИ
Вид промежутка	Геометрическое изображение	Обозначения			Записать с помощью неравенств
Интервал		У//////Л	_ а	Ь		(а;б)		а < х < b .
Отрезок		ААААААА.	 a	b		 « а;Ь		а < х < b.
Полуинтервал		АААААА.	_ a	b		(а;&		а < х < b.
Полуинтервал	77777777* a	b				а < х < b.
Луч		АААА-А	. а		а; +оо		х> а.
Луч		АААААА^ ' *		-oo;Z?		х < b.
Открытый луч		АААААА a		а;+оо		х > а.
Открытый луч	АААААА , ь		-оо;б)		х < b. 4
На практике не всегда используют термины «интервал», «отрезок», «полуинтервал», «луч», а заменяют их общим названием «числовой промежуток».
ЛИНЕЙНЫЕ неравенства
________________________________Определения_________________________________
Линейным называется неравенство вида ах>Ь (или, соответственно, ах <Ь, ах>Ь,ах<Ь), где я * 0, и Ь*0 — числа.
Решением неравенства с одной переменной называется множество таких значений переменной, которые обращают его в верное числовое неравенство.
1.	Если а > 0, то решение неравенства ах > Ь имеет вид х > —.
а
2.	Если а < 0, то решение неравенства ах > Ь имеет вид х < —.
3.	Если а = 0, то неравенство ах>Ь принимает вид Ох>Ь, т. е. оно не имеет реше-ния при Ь > 0 и верно при любых х, если Ь<0.___________________________
При решении неравенств используются следующие свойства.
Свойства	Примеры
1.	Если из одной части неравенства пе- 4(^-1) + 7<1-3(^ + 2);4>--4 + 7<1-Зу-6; ренести в другую слагаемое с противо- 4v + 3 <i_<+4_7 положным знаком, то получится равно- у сильное ему неравенство._______________________
2.	Если обе части неравенства умножить Ту < -8; или разделить на одно и то же положи- г , г тельное число, то получится равносиль- I ’ т. ное ему неравенство.	. 8


3.	Если обе части неравенства умножить -Зх + 8 < 2х - 2; - Зх - 2х < -8 - 2, или разделить на одно и то же отрица- -5х<-10.	'///////~
тельное число, изменив при этом знак неравенства на противоположный, то по-лучится равносильное ему неравенство.
ОЦЕНКА СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО
2.
о.
О’
Ответ:
Ответ:
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ
Доказать неравенство можно на основании определения: если а>Ь, то а-Ь>0 и если I
1. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
2. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
9z-36z-10z-21z < -4-:
7 У//////.
Так как числитель дроби 4 > 0, то неравенство 4 > р справедливо
2
4х-1 < -1; или 4х-1
при любых х и у, значит, х2 + у2 > 2ху при любых х и у.
1. ДОКАЗА ТЬ
НЕРАВЕНСТВО.___________
Доказательство.
Найдем разность левой и правой частей неравенства:
Выражение называют средним арифметическим чисел а и Ь , а выражение 2
4аЬ — средним геометрическим.
2. ДОКАЗАТЬ НЕРАВЕНСТВО.
Среднее арифметическое двух положительных чисел не । меньше их среднего геометрического. х+-у >./^.	'
Доказательство.
Найдем разность левой и правой частей неравенства:

XV =
и ^>0, значит, при х
ху 
§2. СИСТЕМЫ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
___________Определения_____________
Если необходимо найти общие решения двух или более неравенств с одной переменной, то это значит, что надо решить систему двух или более нера-венств с одной переменной.
Решением системы называются такие значения переменной, которые являются решениями сразу всех неравенств, входящих в данную систему._________
Решить систему неравенств с одной переменной — значит найти все ее решения или доказать, что их нет.
Примеры
г4х + 4>0,
Значения
являются решением не-
равенства 4х + 4 > О и 6-4х >0.
Ответ:
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. РЕШИТЬ СИСТЕМУ НЕРАВЕНСТВ._______
Решение.
отсюда
Ответ: (-1,5;4).
2. РЕШИТЬ ДВОЙНОЕ НЕРАВЕНСТВО.
Решение.
Решением двойного неравенства является решение системы двух неравенств.
Ответ: (-1;2).
3. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
Решение этого неравенства сводится к решению двух систем.
или
или
////Л
2
Решений нет
§3. КВАДРАТИЧНАЯ ФУНКЦИЯ
КВАДРАТНЫЙ ТРЕХЧЛЕН И ЕГО КОРНИ
Выражение 2х2 * * * * -5х + 3 является многочленом второй степени с одной переменной. Такие многочлены называют квадратными трехчленами.
___________Определения___________ Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю. Для того, чтобы найти корни квадратного трехчлена ах2 +Ьх+с, надо решить квадратное уравнение ах2 + Ьх + с = 0.
Если %! и х2 — корни квадратного трехчлена ах2 + Ьх + с = 0, то ах2 + Ьх + с = а (х-х,)• (х-х2У.
Квадратичной функцией называется функция, которую можно задать формулой у = ах2 + Ьх + с, где х — независимая переменная, а,Ь,с — некоторые числа, причем д*0._______________________
Г рафики функций у = ах2 + Ьх + с и у = ах2 — равные параболы, их можно совместить параллельным переносом, т.к. функцию у = ах2 + Ьх + с можно представить В виде у = а(х + т) -п.
_______________Примеры__________________
Найти корни трехчлена: 2х2 -5х + 3
Решим уравнение: 2х2 - 5х + 3 = 0
D = 25 - 24 = 1
5±V1	5±1	,	3 ,1
х =-----;х =---;х, = 1;х, = — = !—.
4	4	2 2	2
Значит, квадратный трехчлен имеет два корня: 1 и 1,5 .
2х2 -5х + 3 = 2(х-1)-(х-1,5) = (х-1)'(2х-3),
Примеры квадратичной функции: у — х2 ,у — —х2 ,у = х2 +2,у = (х-4)2. Их графики — равные параболы, только по-разному расположены на координатной плоскости._____________________________
Функцию у = 2х2-4х + 10 можно записать так: j/ = 2(x-l)2 + 8.
1	2	1	1 / 7	.	1 /
— х —х —1 = — х +4х + 4| = —(х + 21 .
4	4V	' 4V 7
Значит, график функции у = ах2+Ьх + с есть парабола, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов — сдвига вдоль оси х и сдвига вдоль оси у. Отсюда следует, что график функции у - ах2 + Ьх + с
-	w	\	Ь -Ь2 + 4ас
есть парабола, вершиной которой является точка (т;п), где т =-, п =------
2а 4а
Осью симметрии параболы служит прямая х = т, параллельная оси у. При а > 0
веткипараболы направлены вверх, а при а < 0 — вниз.
1. Функция у - f(x) четная или нечетная, если ее область определения симметрична относительно нуля и для каждого значения х из области определения /(-х)=/(х).
2. Если график функции симметричен отно-
сительно оси у, то функция является чет-
ной. Если график функции симметричен от-
носительно начала координат, то функция
является нечетной.
ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИИ_________________________
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = mf(x)
у = w/(x), где т >0,т ф 1, если задан график функции у- f (х).
Ординаты точек графика функции ^ = w/(x) получаются умножением на т соответствующих ординат точек графика функции у = /(х). Такое преобразование графика функции у = /(х) называется растяжением от оси х с коэффициентом т , если т > 1, и сжа-тием к оси х, если 0 < ти < 1.____________________________________
у = -/(х), если задан график функции у = /(х).
При одном и том же значении х ординаты точек графика функции у = /(х) и функции у = -/(х) отличаются только знаком. Значит, график функции у = -/(х) можно4 получить из графика у = /(х) преобразованием симметрии последнего относительно оси х. у = mf(x), где т < 0,т -1, если задан график функции у = /(х).
Так как w/(x) = -|m|/(x), то график функции y = mf(x) может быть получен при помощи растяжения (сжатия) графика функции у = /(х) от оси х с коэффициентом ри| и последующим преобразованием симметрии относительно х.
1) Построим график функции у = 4х .
2)	Увеличим ординату каждой точки этого графика в 2 раза, получим у - ijx . г
3)	Если ординату каждой точки уменьшим в 2 раза, то получим у = —4х.
симметричен графику Jx относительно оси х.
1. Чтобы построить график функции у = f{x}+n, нужно график функции у = /(х) перенести на п единиц в направлении оси у, если п>0 (вверх), или в противоположном направлении (вниз), если п < 0.
2. Чтобы получить график функции у = f(x-m), достаточно график функции у = /(х) перенести на м единиц в направлении оси х (вправо), если т>0, или на -и? еди-ниц в противоположном направлении (влево), если т < 0. 
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Чтобы построить график квадратичной функции, нужно:______
1)	найти координаты вершины параболы и отметить ее в координатной плоскости;
2)	построить еще несколько точек, принадлежащих параболе;
3)	соединить отмеченные точки плавной линией.______________________
ПОСТРОИТЬ ГРАФИК ФУНКЦИИ. I у = х2 * * 5 6 7-2х-Ъ.
Найдем координаты вершины параболы.	Ь -2 ,
2а
Найдем координаты точек пересечения графика с осью х, т.е. найдем нули функции.
(1;-9) — вершина, параболы. х2 -2х-8 = 0
0 1	2
-9
-S
(4;0) (~2;0) — координаты точек пересечения с осью х.
х = 0; у = -8, (0;-8) — точка пересечения графика с осью у.
J' -к	п2	О о г
х = 1 —ось симметрии.
Сформулируем свойства функции у = х2 -2х-8.
2. Если х = 0, то у = -8; (0;-8), график пересекает ось у в этой точке.
4. Противоположным значениям аргумента соответствуют равные значения функции.
График функции симметричен относительно прямой х = 1.
5. Функция убывает в промежутке (-оо; 1] и возрастает в промежутке [!;+<»).
6. Наименьшее значение, равное - 9, функция принимает при х = 1.
7. Наибольшего значения функция не имеет.
§4	. КВАДРАТНЫЕ НЕРАВЕНСТВА
РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ
Определения
Примеры
Неравенство ВИДа ах2+Ъх + с>Ъ (ах2 +Ъх + с<6], где а,Ь,с — некоторые числа, а*0 и х — переменная, называется квадратным.
Для решения квадратных неравенств используют эскиз графика функции
параболы.
й-Л Л
X
10
у = Зх2 - 7х -10 график — парабола, ветки направлены вверх, ось 0х пересекает в точках
х, =-1;х, = —.
Решение любого квадратного неравенства можно свести к одному из шести случаев таблицы.
число.
ах2 + Ьх + с > о: решений нет;
ах2 + Ьх + с <0'.х — любое
любое число;
ах2+Ьх+с < о: решений нет.
ах' + Ьх+с < о: решений нет.
ах2 + Ьх + с > о: решений нет;
о.
Решением неравенства ах2 + Ьх + с > 0 являются значения х, для которых точ-Д ки параболы расположены над осью 0х.
Решением неравенства ах2 + Ьх + с > о являются значения х, для которых точ-ки параболы расположены под осью 0х._______________________________
Алгоритм решения квадратных неравенств вида ах2 + Ьх + с>0, или ах2 +Ъх + с<Ъ.
Решить неравенство
1.	Определяем направление ветвей параболы, соответствующей функции у = ах2 + Ьх + с.
2.	Находим корни квадратного трехчлена ах2 + Ьх + с (решаем уравнение ах2 + Ьх + с = 0).
3.	Строим эскиз графика функции
1. а = -3; ветки направлены вниз.
2. Зх2 - 7х -10 = 0; Z) = 169; х, =-1;
-1
10
10
4. Выбираем значения переменной, которые соответствуют решению не-
5. Записываем ответ.
5. Ответ: (~оо;
ло
¥
РЕШЕНИЕНЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Решить неравенство.
Если левая часть неравенства является произведением, а правая часть— 0, т.е.
/(х)>0(/(х)<0) и /(x) = (x-a)(x-Z>)...(x-c), где а,Ъ,с—некоторые числа, то такие неравенства решают методом интервалов Алгоритм решения неравенств методом интервалов
1.	Найти ОДЗ функции у = /(х).
2.	Найти нули функции j
2. Нули функции: (х+6)(х + 1)(х-4) = 0;
3.	Нанести нули на ОДЗ.
4.	Определить знаки и функции /(х) в каждом интервале, на которые разбивается ОДЗ нулями функции.
5.	Записать ответ.
3. Нанесем нули на ОДЗ:
Ответ: (-oo;-6)U(-l;4).
Если все множители функции у = /(х) вида (х-я), то есть линейные, то знаки на промежутках из ОДЗ можно чередовать справа налево с « + » на «-»,
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1
1. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
По теореме Виета х1 = -3;х2 = 5.
'/////,
Ответ:
При рассмотренном способе решения неравенства не определяют координаты вершины параболы. Важно лишь знать, куда направлены ветки параболы — вверх или вниз, и каковы абсциссы точек ее пересечения с осью х. 2. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
По теореме Виета:
X
х—любое число.
£) = 9-16 = -7<0, т.е. уравнение не имеет корней. Покажем схематически расположение параболы в координатной плоскости:
Ответ:
3. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
Множитель (0,2-х) представим в виде (х - а):
(0,2 -х) = -(х-0,2)
х(0,2-х)(х+5) < 0.
-х(х-0,2)(х + 5)<0,х(х-0,2)(х+5)>0.
1. ОДЗ: х е R.	—	+—	+
2. Нули функции:	-^//////$	vz////// х
Ответ: (-5;0)и(0,2;+оо).
4. РЕШИТЬ НЕРАВЕНСТВО.
Такие неравенства решают методом интервалов;_____________________
Решение.
Преобразуем неравенство.
Знаки этой дроби совпадают со знаками произведения.
Ответ: (-оо;-8)и(4;+оо).
5. РЕШИТЬ НЕРАВЕНСТВО.
Решение.
Знаки данного неравенства совпадают со знаками неравенства.
Ответ: (-оо;-1)и(3;+<ю).
1. ОДЗ: х -8, т.к. х + 8 0, то
3. (х-4)(х + 8)> 0.
W///z X
(х + 1)(3-х)(х-2)2 <0.
-(х + 1)(х-3)(х-2)2 <0 (х + 1)(х-3)(х-2)2 >0. (х + 1)(х-3) > 0,
1. ОДЗ: х g R.
2. Нули: X] = -1;х2 = 2;х3 = 3.
3.
§5. УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ. СИСТЕМЫ УРАВНЕНИЙ
УРАВНЕНИЕ И ЕГО КОРНИ
________________Правила_________________
Уравнения называются целыми, если у них левая и правая части являются целыми выражениями.______________________________
Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого — многочлен стандартного вида, а пра-вая — нуль._____________________________
Если уравнение с одной переменной записано в виде Р(х) = 0, где Р(х) — многочлен стандартного вида, то степень этого многочлена называют степенью уравнения._____________________
Некоторые уравнения третьей или более высокой степени нетрудно решить с помощью разложения многочлена на множители.
Примеры
(Зх2 -22х-16 = 0)
Уравнение х2 - 2х3 +1 = О является уравнением третьей степени.
Решить уравнение.
х3-8х2-х + 8 = 0,?(х-8)-(х-8) = 0 , Л
(х-8)(х-1)(х + 1) = 0. Уравнение имеет
три корня: X! = -8; х, = 1; х3 = 8 .
УЧЕНИЧЕСКАЯ СТРАНИЧКА
РЕШЕНИЕ УРАВНЕНИЙ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
И ВВЕДЕНИЯ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ
Уравнения, степень которых выше двух, иногда удается решить, введя некую пе-ременную или с помощью разложения на множители.________________________________
16х3 - 32х2 - х + 2 = 0.	____________________________
х-2 = 0 или 4х-1 = 0
1. РЕШИТЬ УРАВНЕНИЕ.
Решение.
Разложим левую часть уравнения на множители.
(16х3-32х2)-(х-2) = 0; 16х2 (х-2)-(х-2) = 0; (х-2)(16х2-1) = 0;
(х-2)(4х-1)(4х + 1) = 0,
или 4х + 1 - 0;
х = 2 или 4х = 1; или 4х - -1;
Ответ:-11-4’4’
2. РЕШИТЬ УРАВНЕНИЕ.
Решение.
Обозначим х2 + 2х через у: Тогда уравнение сведется к уравнению с переменной^ :
х2 + 2х = у;
у(у-2) = 3;у2-2у-3 = 0, по теореме Виета: у{ = -1,у, =3.
Получим х2 + 2х = -1, или х2 + 2х = 3
х2+2х + 1 = 0,	ИЛИ х2 +2х-3 = 0
(х+1)2 = 0, xt= -3;х2 = 1 (по теореме Виета).
Ответ:-3;-1;1.
Метод введения новой переменной позволяет легко решать уравнения четвертой степени, имеющие вид ах4+Ьх2+с = 0. Уравнения вида ах4 + Ьх2 + с = 0, гдеа^О, яв-ляющиеся квадратными относительно х2, называют биквадратн ы миура внениями.
3. РЕШИТЬ БИКВАДРА ТНОЕ УРАВНЕНИЕ.
Решение.
Введем новую переменную, обозначив х2 через у:
Получим квадратное уравнение с переменной у:
х2 = у.
1
4у2-5у+1 = 0. Решив его, найдем, что _у,=- и у, =2.
Значит, = 1 или х2 = 2, тогда х = _ 11, х = /1 и
2	1 V2 V2
4. РЕШИТЬ БИКВАДРА ТНОЕ
Уравнение._____________
Решение.
х4-Зх2-4 = 0.
Пусть х2 = у, получим у2 - Зу - 4 = 0.
По теореме Виета
у} = -1;у2 = 4, тогда х2 = -1— корней нет,
Ответ: -2; 2.
СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Систему уравнений можно решить тремя способами:
1. Графический способ.
1. РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ, ИСПОЛЬЗУЯ СПОСОБ ПОДСТАНОВКИ.
2.Способ подстановки. З.Способ сложения.
Решение.
< (7 + 2.у) _у + ,у: = -2, х = 7 + 2у.
'2у2 + 7у+у2 = -2,
х = 7 + 2у.
Зу2 + 7у + 2 = 0, D = 49-24 = 25 = 52,
Ответ:
.У 1 + У 6
Подставим выраженное значение х во второе уравнение системы
| '6,Ь”	|	\6г	| \v(l+n
—	—	  ।	^3 ***•	)
у	1 + Х	6
ОДЗ:у*0;.у*-1
бу + 6-6у = у(1 + .у); у(1 + .у) -6 = 0;
У2+У-6 = О. П = 1 + 24 = 25 = 52;
~*4 i 5 .	_ о.  
у — _ , У[ ~	У2 ~~ ^5
х -1 + у\х, = —2; х2 = 3 (-2;-3);(3;2).
2.	РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ СПОСОБОМ
СЛОЖЕНИЯ.
хг-2уг =14,
х2+2/ =18 ’
2х2 = 32, х2 = 16 , х, = -4 , х, = 4.
J	4*
Находим у: (-4)2 - 2у2 = 14; -2у2 = -2; у2 = 1; у{ = -y/i;y2 = VI.
Ответ: (^;Vf);(4;Vi)-
3.	РЕШИТЬ ЗАДА ЧУ
Решение.
Диагональ прямоугольника равна 10 см, а его периметр ра-вен 28 см. Найти стороны прямоугольника.____________
Пусть АВ = х см, ВС = у см. Периметр равен 2(х+у) см, а по условию 28 см. Получаем первое уравнение системы: 2(х + ^) = 28или(х + у) = 14. АС = 10 см по условию, тогда по теореме Пифагора: х2 +у2 = 102— получаем вто-
рое уравнение системы.
Имеем систему: <
х = 14-у, ^(14-j)2+r =100;
Подставим выраженное значение х во второе уравнение: 196 - 28^ + у2 + у2 -100 = 0; 2у2 - 28у + 96 = 0 или у2-14у + 48 = 0
Г» = 49-48 = 1;^ = 7±1;^ = 8;у2 = 6;
х = 14- у;Х\ = 14-8 = 6;х, =14-6 = 8.
Ответ: 6 см и 8 см.
4.	РЕШИТЬ ЗАДА ЧУ.
Решение.
Из пункта М в пункт N, расстояние между которыми равно 18 км, вышли одновременно два туриста. Один из них прибыл в пункт N на 54 мин позже, чем другой. Найдите скорость каждого туриста, если известно, что скорость одного из них на 1 км/ч меньше, чем скорость другого._________________
Пусть скорость одного из них х км/ч, а другого —у км/ч, т.к.
скорость одного из них на 1 км/ч меньше, чем скорость другого, получаем первое уравнение: у - х = 1. Второй турист
прибыл в пункт М на
18
7“ ю ’
54 мин позже, — получим другое
уравнение:
54	9
т.к. — ч = —ч .
60	10
Решив систему:
9
5
5
< 18_18_2.
х v 10
получим: р = 5км/ч, а х = 4 км/ч.
Ответ: 5 км/ч и 4 км/ч.
§6. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
________________Определения_______________
Числовая последовательность задана, если любому натуральному числу п поставлено в соответствие некоторое число а,,.
Примеры
3; 10; И; 13; 16; 20;...
4; 7; 10; 13; 16;...
Последовательность задают при помощи формулы п -го члена, тогда нетрудно вычислить любой ее член.
Последовательность (а„) задана формулой а,, = n3,neN, 1; 8; 27; 64;...
Последовательности бывают конечные и бесконечные. Последовательность (ап) называется возрастающей (убывающей), если для любого номера п справедливо неравенство:а„+1 >ап(а„+1 <ап), где ап — предыдущий член, ял+|— последующий член по-
следовательности._______________________________
Числовая последовательность(ап), каждый член которой, начиная со второго, равен предыдущему, к которому прибавлено одно и то же число, называется арифметической прогрессией. Это число обозначают буквой d и называют разностью арифмети-ческой прогрессии.______________________________
Первые члены арифметической прогрессии будут: ах,ах +d‘,ax + 2d;ax +3d;...
Формула и-го члена арифметической прогресии: ап = а, + d(n -1),и е N.
Последовательность (а„) является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому соседних с ним членов, то есть:
= а"~' + Q"*1 , где п > 2, и е N .
Сумма двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равна сумме крайних членов.
Формула суммы первых п членов арифметической прогрессии:
„ а.+а	2a.+d(n-l}
S„ = —*-- п, ил и S' =------- n,neN.
”	2	"	2
2; 4; 6; 8; 10; 12;...— возрас-
тающая.
— убывающая.
1; 3; 5; 7; 9—арифметическая прогрессия
ах = l',d = 2.
30; 25; 20; 15; 10; 5;...
ах = 30; <7 - -5 .
-50;-40;-30;-20;...
€7t = -50;<7 10._______________
а6 = -50 + 10(6-1) = -50 + 10-5 = 0 =0.
4;7;10;13;16;...
4 + 16
2
•5 = 50
или
УЧЕНИЧЕСКАЯ СТРАНИЧКА
РЕШЕНИЕЗАДАЧ
1.	Написать 4 первых члена последовательности, заданной формулой «-го члена. Найти а°. О
Решение.
п
» ПЛ 1
8
8 28 32
Л
Ответ: а) 1,3,5,7

8 32
2.	Найти 16-й член арифметической прогрессии (а„), в которой первый член равен 5, разность равна 2._______________________________________________________
Решение.
16
3.	Найти первый член арифметической прогрессии (а„), у которой а21 = 291,t7 = 11. Решение.
а„
„ -сци-1); п = 27; а21 = 291; d = 11;
= 291-286;^ =5 . Ответ: 5.
4.	Найти разность арифметической прогрессии (о,,), у которой^ =28; о Решение.
п = 21,а,| м I
-52-28 -80 -------=----= -4. Ответ: -4.
21-1	20
5.	Найти номер члена арифметической прогрессии (я„), который равен 46, если
Решение.
/Г 1 ’	_ /7
—:—>«- —
и
on J п л 46-32 ,	14
ап = 46, <я, = 32; d = 0,4; п =-+1 = —
6.	Найти первый член и разность арифметической прогрессии(а„), если:<^
Решение.
I
п
; а9 = а{+Ы, следовательно,
2а, + 4d = 24
получим систему:
3d = 15,’
а, = 12 — 2^7;
Ответ: а, = 2\d = 5.
7. Найтих, если! + 4+7+...+х = 51.__
Решение.
1+4+7+...+х = 51;
1 + 4 + 7 + ...— возрастающая арифметическая прогрессия (ап), где d = 3; о, = 1.
В нашем уравнении ап = х, Sn = 51. ап =ai+d(n-l), х = 1 + 3(п-1);
х = Зп — 2.
чения:
 п; Подставляем известные зна-
51 =---п :102 = (1 + х)«; и =-;
2	к ’	1 + х
102
х = 3-----2;х + х2 =306-2 — 2х,х*-1;
1 + х
х2 +Зх-ЗО4 = О;
X] = 16;х2 = -19— не удовлетворяет условию задачи,ап >0.
Следовательно, ап =16. Ответ: 16.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.
РЕШЕНИЕ КОМБИНИРОВАННЫХ ЗАДАЧ
Определения
Примеры
Числовую последовательность (6Л), каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, называют геометрической прогрессией. Это число обозначают q и называют знаменате-лем геометрической прогрессии._____________
Первыми членами геометрической прогрессии будут:
Формула п -го члена геометрической прогрессии:
2; 4; 8; 16; 32; 64;... 6, =2, q = 2.
1111
* — * _•
’ 2? 4’ 8* 16
1	1	1	1	,	„	л
—;	—;	—;	~;	1;	2;	4;...
16	8	4	2
6, =—; ^ = 2;510= —•210‘1= —-29 =32.
1	16	10	16	16
Ьп =	> neN._____________________
Последовательность (Ьп) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов:
A2 =A-in>2,neN.
3, 9, 27, 81, 243;...
Z>32=Z>2-V.e.
272 =9-81
729 = 729
Формула суммы п первых членов геометрической прогрессии:
_ b„q -Ь,	b.- b„q
S„ = —---1 ИЛИ S= —-----—
"	q-1	1-q
neN,q*l	n&N,q*l
1) 3,9,27,81,243,... q = 3
2’4’8’16
31-2 _ 31	1-5
32 ”16” 16’
Если (b„) - бесконечно убывающая геомет-ь рическая прогрессия (|^|<1), то ее сумма вы-
числяется по формуле:
1-?
1111 - 1 1
2 4 8 16	1 2	2
УЧЕНИЧЕСКАЯ СТРАНИЧКА
РЕШЕНИЕ ЗАДАЧ
1. Найти знаменатель геометрической прогрессии	если:	
а) 64 = 20, Ь5 =30.	б) ^442 "" 25, 6441 “ 30.
Решение. q=^-, q=^_-, ?=—; q=~. 4 h	b’	20	2 Г<	*Т	Решение. q = ^iL-	25 = 5	5 Ьп 4 Ь^’4 30 б’4 6’
Ответ: 2. 2	Ответ: <? = -. 4 6
2. Вычислить пятый член геометрической прогрессии (bn).	
а) 2; 6; 18;...	^<-1. J- I23- о) 5 ; 3	1 3	5 25
2; 6; 18;... Ьх =2, 9 = 3; Решение. =Z>1	= 65 = 2-34 = 2 - 81 = 162.	Решение, ь =5--о = з--5- =—= 2-а = 1-1	з’4	5	3 5	3	5 16 5’q 5’ l	L 4 t	J Гз?	16 81	16-27	432 5	5	3 \5;	3 625	625	625
Ответ: 162.	Ответ: 432. 625
3. Найти первый член геометрической прогрессии (bn}, в которой:
Решение. Ь„=Ь} -qn';
486 486
3s " 243
Решение.
<?8’
8
- = 4-36 =4-729 = 2916.
Ответ: 2.
Ответ: 2916.
2
4. Найти сумму членов геометрической прогрессии (b„}, в которой: b} = 1, q = -
Решение.
16
81 _ 65 . 1
"LL> ♦
81 3
81 1 27
Ответ: 2—
27
5. Найти сумму п членов геометрической прогрессии (bV в которой:
Решение. bg =b} -q\
7 b>	384 7
q = 7~> q =—; q =128; q = 2
b{	3
Решение.
п__,

Ответ: 2; 765.
Ответ: IjsZ.

6. Определить первый и последний члены геометрической прогрессии, в которой:
=2047, д = 2,п = \\.________________________________________
S -Ь' b М^1). ь 2047(2-1) _ 2047 _ 2047
Решение. 11"	q-\ ’	^"-1 ’	2"-1	~ 2048-1 ~ 2047
Ь, =1; Ьи = h -ql°; b.. = 1-210 = 1024.
Ответ: 1; 1024.
7. Между числами 27 и 729 поместить два числа, которые вместе с данными соста-вили бы геометрическую прогрессию.
Решение.
1\; Ь2; Ь,- b,-... bx =2Т, Z>4 =729; b^b{ -q3-
---=
27
Ь2 =27-3 = 81; Ь3 =81-3 = 243.
Ответ: 81, 243.
8. Написать геометрическую прогрессию (b„}, в которой Ь5 -Ь} =15, Ь4 -Ь2 =6. Решение.
Ответ:-16; -8; -4; -2; -1;...	1; 2; 4; 8; 16; 32;....
9. Сумма первых трех членов арифметической прогрессии равна 12. Если к третьему члену прибавить 2, то данные числа составят геометрическую прогрессию. Найти эти числа.
Решение.
— 8;	О1 — 2;
<я3 =0;	а3 = 6;
8; 4; 0;...или 2; 4; 6;...
Ответ: 8; 4; 0 или 2; 4; 6.
§7. ЭЛЕМЕНТЫ ПРИКЛАДНОЙ МАТЕМАТИКИ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Математическими методами решают не только абстрактные математические задачи, но и многие прикладные задачи. Прикладными задачами в математике называют задачи, условия которых содержат нематематические понятия. Решая при-
кладную задачу математическими методами, сначала создают ее математиче-
скую модель.______________________________________
Задача 1. Сколько досок нужно, чтобы настелить пол в комнате длиной 7,5 м и шириной 5 м, если длина доски 6 м, а ширина 0,25 м?
Решение. Поверхность пола имеет форму прямоугольника. Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину: 7,5-5 = 37,5 (м2); поскольку доска тоже имеет форму прямоугольника, то ее площадь: 6-0,25 = 1,5 (м2). Чтобы узнать, количество досок, надо: 37,5:1,5 = 25 (досок). Ответ: 25 досок.
Задача 2. 30%-ный раствор борной кислоты смешали с 15%-ным и получили 450 г 20%-го раствора. Сколько граммов каждого раствора было взято?_________________
Решение. Пусть х г взяли 30%-го раствора, а у г -15%-го.
Тогда масса смеси будет 0,Зх + 0,15.у, а это (450-0,2) г.
Получаем систему: [х + _у = 450,
О,Зх + 0,15>> = 450-0,2
Пусть х = 450 - у, тогда 0, Зх 4- 0,15 у = 450 • 0,2;
0,3(450-у) + 0,15у = 90;
135-0,3^ + 0,15^ = 90;
Данная задача прикладная, поскольку в ней говорится о поверхности пола - нематематическом понятии. Решая задачу, мы заменили ее другой: вместо поверхности пола рассмотрели прямоугольник. Задача нахождения площади прямоугольника — модель данной прикладной задачи._______
Эта задача также прикладная, поскольку раствор борной кислоты -нематематическое понятие. Система уравнений -математическая модель данной задачи.
0,15у = 45; .у = 300, значит, 15%-го раствора было 300 г, а 30%-го: 450-300 = 150 (г).
Ответ: 150 г, 300 г.
Моделью называется специально созданный объект, отображающий свойства исследуемого объекта. Уменьшенные модели самолета, автомобиля, здания - примеры физических моделей. Математические модели создают, используя математические понятия и отношения: геометрические фигуры, числа, выражения и т.п. Математическими моделями в большинстве случаев бывают функции, уравнения,
неравенства, их системы.__________________
Решение прикладной задачи математическими методами осуществляется в три этапа:
1) создание математической модели данной задачи;
2) решение соответствующей математической задачи;
3)анализ ответа.
Схематически эти этапы можно изобразить так: Л-+5-+С-+П;
А - данная прикладная задача, В - ее математическая модель, С - ответ для модели,
D - ответ для данной прикладной задачи А .
Чтобы создать соответствующую модель, нужно знать не только математику, но и ту отрасль науки или производства, с которой связана данная прикладная задача. Если модель составлена неправильно, то неправильными будут и решение задачи, и ответ. Важным является также последний этап решения прикладной задачи. Ответ С может быть точным для задачи В, ответ для прикладной задачи А почти всегда может быть только приближенным. Поэтому его следует записывать соот-ветственно с правилами приближенных вычислений.
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
___________Определения________________
При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая, следующая за этим разрядом, цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая, следующая за этим разрядом, цифра меньше 5, то последнюю оставшуюся цифру не изменяют.____________________
Приближенные значения появляются не только при округлении чисел, чаще они возникают при различных измерениях (длин, масс, температур и т.д.). Пусть а - приближенное значение числа а. Тогда модуль разности точного и приближенного значения чисел а и а, т.е. [а -о|, называется абсолютной погрешностью приближенного значения числа а, а отношение абсолютной погрешности к модулю приближенного значения называется относительной погрешностью приближенного значения. Относительную погрешность обычно выражают в процентах. Если точное значение величины неизвестно, то неизвестна и абсолютная погрешность ее приближенного значения. В таком случае указывают границу абсолютной погрешности - число, которого не превышает абсолютная погрешность._____
Приближенные значения можно записывать и без границ. При этом договорились записывать их так, чтобы все их цифры, кроме последней, были верными, а остальные (сомнительные) отличались от верных не более чем на единицу.
Примеры______________
Округлить число а = 2471,05624 с точностью до: а) десятков; б) единиц; в) десятых; г) сотых; д) тысячных.
Решение, а) а « 2470; б)а « 2471; в)а «247i,i;	г)а» 2471,06;
д) а «2471,056.
Все найденные значения в примере называются приближенными значениями числа а = 2471,05624 •
Взвесив деталь, масса которой равна 54,12705 г, на йесах с ценой деления шкалы 0,1 г, получили приближенное значение массы 54,1 г. Найти абсолютную и относительную погрешности этого приближенного значения.
Решение: Абсолютная погрешность равна 54,12705-54,1 = 0,02705, относительная погрешность равна
-в2705 • 100% = 0,05% . Если
54,1
х — 4,273 ±0,002, т.е.
4,271 <х<4,275, то граница абсолютной погрешности равна 0,002.
Например, когда пишут х = 6,428 м, то понимают, что х = 6,428 ±0,001 м. Если у - 3,247 ± 0,002 кг, то говорить у = 3,247 кг не принято, такой результат желательно округлить: у = 3,25 кг.
Верной цифрой приближенного значения называют цифру любого разряда, если абсолютная погрешность не превосходит единицы этого разряда.
В таблице плотности вещества указано, что приближенное значение плотности кислорода р (в кг/м* 3) равно 1,429. В записи 1,429 все цифры верные. Значит, абсолютная погрешность меньше или равна 0,001.
1) у = 73± 1; 72 < у < 74; 2) /7 = 1,429 + 0,001; 1,428<р< 1,430
3) у = 6,5 ± 0,1; 6,5 - 0,1 < у < 6,5 + 0,1; 6,4 < у < 6,6.
Напомним, что десятичными знаками числа называют все его цифры, стоящие справа от десятичной запятой.
В приближенном значении 0,02085 пять десятичных знаков и четыре — значащие цифры: 2; 0; 8; 5.
Значащими цифрами числа называют все его цифры, кроме нулей слева и нулей
справа, стоящих на местах цифр, замененных при округлении.
При сложении и вычитании прибли-женных значений в результате следует оставлять столько десятичных знаков,
1) 4,24 + 1,5-5,7;4,24-1,5 = 2,7.
2)х «17,2 ;у«8,407',х+у = 17,24+8,407 = 25,607;.г+_у *25,6.
3)х « 6,784; у « 4,91; х-у ~ 1,874; х-у ~ 1,87.
сколько их имеет компонент действия с наименьшим чис-
лом десятичных знаков._____
При умножении приближенных значе-ний в результате следует сохранять столько значащих цифр, сколько их имеет множитель с наименьшим чис-лом значащих цифр. Подобным прави-лом пользуются и при делении приближенных значений.
Перемножим (разделим) данные приближенные значения.
1)8,23	2) х «563,2;
х 1,5
4ПТ Ответ: 12,3.
823
12,345*12,3
У «32;
х:у «17,6;
Ответ: х: у «18.
СЛОЖНЫЕ ПРОЦЕНТЫ
Понятие сложного процента встречается при увеличении (уменьшении) числа на р% несколько раз (ежегодно, ежемесячно, ежедневно) без изъятия прироста, т. е. каждый год начисляется процент с учетом наращенной величины. Вычислять сложные проценты удобно с помощью таблицы, если ввести коэффициент увеличения (уменьшения)-к							
	1-й год	2-й год	3 - й год				п — Й ГОД
Ежегодное увеличение на р% (к = 1 +	) 100							
Было	а	ка	к2 а				
Приросло за год	-Р—а 100	-^—ка 100	Р /2 	к а 100				
Стало	100 = I +——= ка < 100)	ка +	• ка = 100 - |+_^_ ка~к~а V юоJ	к\	,+-р-.к 100 1+—1 100 )	:~а = к^а - kJa	h •		к" а
Ежегодное уменьшение на р% (k = i	—) 100							
Было	а	ка	к2а				
Уменьшилось за год	-Р-.а 100	_Р—.ка 100	Р /2 	к а 100				
Стало	р а——а- 100 - (1 ——)а - ка 100	Р ка	ка - 100 = (1 --^—)ка = к2 а 100	к	100 1 Ж	:'а = к2а - к3а	« • •	кпа
Первоначальный вклад в банк составил ЗООгрн. За год начисляется 3% годовых. Найти сумму/
вклада через 5 лет. Решение.
X я р
100;
а = 300; р = 3; п = 5.
Ответ: «348грн.
100
= 300(1,03)5 « 300 • 1,159 « 348(грн).
РАСЧЕТЫ
_____________Определения_______________
Процент - это одна сотая часть целого.
1% = 0,01; 25% = 0,25; 50% = 0,5; 100% = 1.
Часто приходится решать задачи на проценты бухгалтерам и работникам банка. Вложенный в Сбербанк начальный капитал под р% го-
довых через п лет превратится в наращенный
капитал, д
____________Примеры______________
Из сахарной свеклы при переработке получается 16% сахара. Сколько нужно взять свеклы, чтобы получить 48 ц сахара?
48
48:0,16 = 300 (ц) или —100 = 300 (ц).
16
Из 35 учеников класса на уроке присутствуют 28. Найти процент посе-
Это формула сложных процентов. Она находит применение не только в финансовых во-
щаемости.
28:35-100 =
просах; ею пользуются для определения численности населения страны или города,
28 100
35
Ответ: 80%.
4 Л 00
5
= 80%
роста поголовья скота и в других вопросах.
Подобные понятию процента промилле и проба.
Промилле - это одна тысячная (f/oo-O.OOl).
Пробами характеризуют сплавы драгоценных металлов. Так, золото 875 -й пробы - это сплав, в 1000 г которого содержится 875 г
Латунь - сплав 60% меди и 40% цинка. Сколько меди и цинка нужно сплавить, чтобы вышло 500 г латуни?
1) 500 0,6 = 300 г (меди);
2) 500 0,4 = 200 г (цинка).
чистого золота.

§ 1. Тригонометрические функции и их свойства
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки (вершины угла).
Угол можно рассматривать как фигуру, образованную вращением луча около своей начальной точки 0. Причем вращение против часовой стрелки называют положительным, а по часовой стрелке — отрицательным.
Полный оборот луча вокруг начальной точки образует полный угол (окружность).
Оси координат Ох и Оу разбивают окружность (полный угол) на четыре четверти.
Связь между радианной и градусной мерами угла
Углы измеряются в градусах и радианах.
1° — это угол, который равен
1 360
части полного оборота
1° = 60' (60 минут);
Г = 60" (60 секунд)
луча вокруг своей начальной точки в положительном направлении (против часовой стрелки).
1 радиан — это центральный угол, которому соответствует длина дуги, равная радиусу этой окружности.
Г = 180; 1 радиан = —• 1OU	п
Г радусы	0°	30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
Радианы	0	л 6	л 4	л 3	л . 2	2л 3	Зл 4	5л 6		Зл 2	2л .. ..   - 
Определения тригонометрических функций и их простейшие свойства
Через прямоугольный треугольник (для острых углов)
Через произвольную окружность (R — радиус окружности)
Через единичную окружность (/?=!)
sin а = у ордината точки Рп
COSO. = X —
абсцисса точки Р„
у sma tga. = < = ------
х cos о.
х cos a ctgo. = - = —------
у sin a
Наглядное представление тангенса и котангенса в единичной окружности
ордината соответствующей точки оси тангенсов.
СВ— ось котангенсов
СВ || Ох
t хв
ctgo. = — = ХВ —
абсцисса
соответствующей точки
оси котангенсов.
Знаки тригонометрических функций
sin а.
coso.
tga., ctgo.
Значения тригонометрических функций некоторых углов
a	в град.	0°	30°	45°	60°	90°	180°	270°	360°
	В рад.	0	л 6	4			Я	Зя 2	2л
sin а		0	1 2	J2 _ 1 2 J2	2	1	0	-1	0
cos а		1	~2	72 2	2	0	-1	0	
tga		0	1!	1		в	0		0
ctga		в		1		0	а*	0	ж
Четность и нечетность
Функция у = f(x) называется четной, если для любых значений х и (~х) из области определения соблюдается равенство: Д-х) = f(x).
График четной функции симметричен относительно оси ординат.
Функция у = f(x) называется нечетной, если для любых х и (-х) из области определения соблюдается равенство: Д-х) = -Дх)
График нечетной функции симметричен относительно начала координат.
У f
cos(-x) = cosx —четная;
sin(-x) = —sinx —нечетная; rg(-a) = -tga — нечетная;
ctg(—a) = —ctga — нечетная.
Периодичность тригонометрических функций
Функция у = Дх) называется периодической с периодом 7V 0, если для любого х из области определения
у = sinx	Т = 360° = 2л
у ~ COSX	Т = 360° = 2л
у = tgx	Т = 180° = л
180° =
У = ctgx
Свойства периодических функций
1. Если число Т — период функции, то и число п • Г, где (п g Z), — также период этой функции (Т — наименьший период).
sinx = sin(x + 2л«), п е Z tg(x) = tg(x + nn), п е Z.
2. Если функция у = fix) периодическая с периодом Т, то функция у = af{kx + Ь) — также
периодическая с периодом
постоянные числа и к ф 0).
Формулы приведения
Соотношения, у которых значения тригонометрических функций аргументов
± а, л ± а,	± а, 2л±а выражаются
через sina,cosa,tga,ctga, называются формулами приведения.
sin 1940° = szn(360° • 5 + 140°) =
= sznl40° = .$7и(180°-40°) = sin 40°.
389л cos----
18
cos
18
18
—cos—л
18
(	7	( 7 >	7л
= -cos Л-----л = -cos------Л = cos-----.
к	18 > v 18 >	18
Основные формулы приведения
X				 п + а	7i - а	2л - а	71 2	Я x - а 2	3л , ~ + о 2	3 л 2 “а
sinx	—sin а	sin о.	-sin a	cos a	COSO	-cos a	- cos а
COSX	-cos а	-cos a	cos a	-sin a	sin о	sin о	-sin a
tgx	tga	-tga.	-tga	-ctga	ctga	-ctga	ctga
ctgx	Ct go.	-ctga	-ct go	-tgo	tga	-tga	tga
Формулы дополнительных углов
Два угла называют дополнительными, если их сумма равна ^(90°).
Основные тригонометрические тождества
sin а + cos а — 1.
Упростить выражения:
. ~ sina tga = ----
cosa
----— = sec a. cos a
—.— • sin a = 1;
. 2 sin a
sec a - ----
cosa
6) cos ft-cos Pszzz’p = cos P(l~sz>z“p) = э 2	4
= cos'ft • cos P = cos P;
X . 4	.	. 2	2	. 2	. .
cosa  seco. — 1.
. cosa
ctga = ----
sina
= sin a(sin a + cos a) + (l-sin a) =
2	2
= sin a + cos a - 1;
10.
coseca = ----
sina
—— = cosec a. sin~a
sina  coseca = 1.
tga  ctga ~ 1.
cos a _ 1 - sin a _ (1 - sz>za)(l + sina) _ 1 — sina 1 - sina
1 - sin а
n\	,	,	•	sina ,	.
Д) cosa  tga + sina = cos a --+ sina =
cosa
= sina + sina = 2sina.
Формулы сложения
sin(a + P) =
= sina  cos ft + cosa  sinft.
sz«(a-p) =
= sina  cos ft- cosa • sinft.
cos (a + P) =
= cosa • cos ft - sina • sznp.
cos (a- P) =
- cosa • cosp + sina • sinft.
1. Вычислить sin 75°.
Решение: sin!5° — sz«(30° + 45°) =
= sz>7 30° cos 45° + cos30°sz>z45o =
Ответ:
tg(a + ft) = ‘Sa + ttf 8{ N 1 - tgatgft
Я
a,p,a + P Ф - + Ttk, к e Z.
2. Вычислить cos 15°.
Решение: cos 15° = cos(45°-30°) =
tga ~ ‘g$
1 + ?gazgp
= cos45°cos30° + cos45°sz'h30° =
crg(a + P)
ctgactgft - 1 ctga + cfgP
Ответ: ^=(73 + 1).
а,р,а+Р^л&, к e Z.
3. Упростить tg - + a = ------- = -—
ctg(a - P)
ctgactgft + 1 ctgft - ctga
a,p,a - p Ф nk, kcZ.
Тригонометрические функции кратных аргументе
sin2a = 2sina • cos a = ——22
cos2a - cos a-sin а = 2cos~a-l =
= 1 - 2sin а =
t _ 2tga tg2a = ---
ctga - tga
etg a- 1
sin3a = 3sina- 4 sin a =
i
= 4swa • sin\ - - a • sin\ - + a
= 3cos asina.
sinx = 2 sin-cos-, 2	2
 e ~ . 5x 5x
sin5x - Ism — cos—, 2	2
4	2
cos st = cos 4t-sin 4t.
1. Упростить выражение.
,	sina cos a
d) tga - ctga=-------:—=
cos a sina
2	2	2	2
_sin a - cos a _ cos a —sin a
sinacosa 1 ~ .
- • 2sinacosa 2
-cos2a n ~ =-2------=-2 ctg2 a.
sin 2 a
6) cos 10a + sin 5a _
sin 10a
7	Э	Э
_ cos~5a- sin~5a + sin~5a
sin 10a
2<	1	<
_ cos 5 a _ 1 cos 5 a
2sin5acos5a 2sin5a
cos3a = 4cos a-3cosa =
= 4 cos a • cos - - a
cos a-3cosasin a.
2. Найти значение выражения. cos 15° - sin 15°.
Пусть cos 15°-sin\5° = a, тогда a2=co5215° + $7и"15° - 2sin 15°cas 15°=
3tga-tg a =
5
= 1 -sin30° = 1 -1 = 2	2
следовательно, a2 = a = ±—, 2	72
cos 15° i sin 15° —положительные числа,
cos 15° > sin 15° , поэтому a =
72
Ответ: —.
72
Формулы понижения степени
.2	1 - оо52а
sin a = ---------
2л
cos а
sin
1 - COSX ---z---: cos
1
Преобразование суммы и разности тригонометрических функций в произведение
sina + sin ft = 2sin------<-cos
Преобразовать в произведение:
а) со548° - cos 12° =
sin a - sin P = 2 sin-----cos
cos a + cos ft — 2 cos--- cos
э . 48°+ 12° . 48° - 12°
= -2 sin-------sin--------- =
2	2
= -2sz«30osj«18° = -2--sin\%° = -sin\V>-, 2
cos a - cos Р = -2 sin
6) sinx + cos2x - sin3x - sinx - sin3x + cos2x =
= -(sin3x - sinx) + cos2x =
, . о szw(a + P) tga + rgP = ---
cos a • cosp
= -2sinxcos2x + cos2x = cos2x(l -2sinx) =
2cos2x  2sin
rga-rgP = —
cos a • cos p
ctga + ctgft
sin(a + P) sin a  sin ft
.	„ . (л x< (л ,x}
= 4 cos 2x sin! — - - 605 — + - .
<12 2>	<12 2/
в) (tga + tgft)ctg(a + p)+(Zga - tgft)ctg(a - p)= _ sin (a + p) cos (a + P) sin(a - P) cos (a - P) _ cosacosft 5z>?(a+P) cosacosft 5z>?(a-P)
a,P Ф nk, к g Z.
cos(a + р),оо5(а-P)_oo5(a + Р)+бо5(а-Р) cos a cos P cos a cos P	cos a cos P
ctga - ctgft =
sin (ft - a) sin a • sin ft
a,P £ nk, к e Z.
_ 2 005 a 605 P cos a cosP
Ответ: 2.
1 + cosa = 2cos
1 - cosa - 2sin —.
Полезно запомнить
sin a-sin р = sin(a + р)5/и(а- Р)
2	2
cos а - cos Р = sin (а + Р)$;и(Р - а)
2	2
sin a-cos Р = -со.у(а + Р)со$(а-р)
2.2
COS CL—sin а = cosZa.
Введение вспомогательного угла
Преобразование произведения тригонометрических функций в сумму
sina-sinfi = ^(сол(а - Р) - cos(a + Р)).	sin43°cos 19° = „.•„/ЛОО	1 П О \ I „ • / Л О О । 1 п о \
cosa-cosfi - -(с<м(а~Р) +cas(a +Р)).	II о с "	о h Н • Г)	| 1	II **	г >:	о к	ЧС К h I	о ? II	II
5«аеИ₽ = 1(™(а-₽) + «Л(а + ₽)).	2	' 2 = — соу19°. 2
Формулы половинного аргумента
sin —
cos —
Выразить через функции вдвое большего аргумента:
1 - cos2a. А	1
с , 11 + cos 10a б) cos 5 а = ± I-----------
tg-g
1 - cos a _ sina
1 + cosa cosa
1 - cosf>a --------- или л?3а
1 + cos6a
1 - cos 6 a. s/иЗа
a 1 - cos a tg— = ----:----
2 sina
--------- или ctg- =
, а 5 4
1 - cos —
sin —
. а , /1 + cosa. sina. ctg— = ± /-------- — -------
2 у 1-cosa 1 - cosa
a * 2лк, к e Z.
ctg— = ----:—
2 sina
Тригонометрические функции, их графики и свойства
Функция
Свойства
График
Область определения Множество значений
у = sinx
кривая — синусоида
D(sinx} - R
E(sinx) = [-1; 1 ];
sinx
у = cosx
кривая — косинусоида
D(cosx) = R
cosx
Четность или нечетность функции
нечетная: sin(-x) = -sinx симметрия графика относительно начала координат’.
четная: cos(-x) = cosx симметрия графика относительно оси Оу.
Периодичность
T= 2л; cos (x + 2n) = cosx.
Точки пересечения с осями ординат: а) с осью Ох: б) с осью Оу:
KO-
а) sinx = 0, х - пк, к е Z, 6) /(0) = sinQ = 0 точка (0;0).
б) ДО) = со50 = 1 точка (0;1).
Промежутки зна-копостоянства
Промежутки монотонности: а) функция возрастает на каждом из промежутков;
б) функция убывает на каждом из промежутков.
Экстремумы
Асимптоты графика
Функция
Свойства
График
Область определения Множество значений Четность или нечетность функции Периодичность
sinx > 0 при х е (2я&; я + 2 л к); sinx < 0 При х е (я + 2яЛ; 2я + 2яА), к е Z.
- - + 2я&;- + 2я&
X + 2я&;-я + 2я&
2	2
^ + 2яЛ 2
к е Z,
У max
=   —	Этт ]г
тт о
У m in
не имеет
У = tgx
кривая — тангенсоида
E(tgx) = R.
нечетная: tg(-x) = -tgx симметрия графика относительно начала координат.
COSX > 0 при х е (- 2 + 2я£;2 + 2я*) ;
COSX < 0 ПрИх 6 + 2яЛ;|п + 2лА, к € Z.
[-я + 2я£;2я&], к е Z.
[2яЛ;я + 2я&], к е Z.
% max
max
min
min
= 2лк, к е Z,
не имеет
у = ctgx
кривая — котангенсоида
t{ClgX) -
нечетная: ctg(~x) = -ctgx симметрия графика относительно начала координат.
Точки пересечения с осями координат: а) с осью Ох; б) с осью Оу. Промежутки знакопостоянства
a)zgx = 0 :х = пк, к е Z:(nZr;0), б) ДО) = rgO = 0 точка (0;0).
tgx > 0 при х G
к е Z.
3)ctgx = 0:х =
- + пк' к е ZI- + пк',0
б) пересечения с Оу нет.
ctgx > 0 при х е
ctgx < 0 При А €
к е Z.
Промежутки монотонности: а) функция возрастает на каждом из промежутков;
б) функция убы-вает на каждом из промежутков. Экстремумы
максимума и минимума не
имеет.
у = sinx - 1
Асимптоты графика
вертикальные асимптоты
х | к € Z.
(л£;л + пк), к е Z
максимума й минимума не имеет.
вертикальные асимптоты
х = пк, к е Z.
Построение графиков тригонометрических функций
1.	Для построения графика функции У ~ Лх) +а нужно график функции у = f(x) сдвинуть вдоль оси Оу на а единиц вверх, если а > 0, и на а единиц вниз, если а < 0.
2.	Для построения графика функции У = fix + о) необходимо график функции у = Дх) сдвинуть вдоль оси Ох на а «пиниц вправо при а < 0 и на а единиц влево при а > 0.
у = sinx - 1
у = sinx сдвигают вдоль оси Оу на единицу вниз.
у = sinx сдвигают вдоль оси Ох на - единиц
6 вправо.
3.	Для построения графика у = -f(x) необходимо график функции у = Дх) отобразить симметрично относительно оси Ох.
4.	Для построения графика у = Д-х) необходимо график функции у = f(x) отобразить симметрично оси Оу.
5.	Для построения графика у = Дх)| необходимо положительную часть графика у = f(x) оставить неизменной, а отрицательную часть отобразить симметрично относительно оси Ох.
6.	Для построения графика функции У = /(Ы) можно рассмотреть соотношение:
ч [Дх) , еслих>0 /(*) = 1
Д-х) , если х < О
Отсюда следует, что при х>0 необходимо строить график функции у = Дх), а для х < 0 надо построить график, который будет симметричен для уже построенного графика относительно оси Оу.
7.	Для построения графика у = kf(x) необходимо ординаты всех точек графика у = Дх) умножить на к, оставив при этом неизменными абсциссы. Причем при к > 1 график у = kf(x) получают из графика у = Дх) растяжением его от оси Ох ь к раз, а при 0 < к < 1 — с помощью
сжатия к оси Ох в - раз. Эти деформации к
графика у = Дх) выполняют в перпендикулярных направлениях к оси Ох.
у = -sinx
8.	Для построения графика у = f(kx),k>0 необходимо все абсциссы графика
у = Дх) разделить на к, оставив орди-
наты неизменными. То есть при к>\ график у = f(kx) получают из графика
У = f(x) < сжимая его к оси Оу в к раз, а
= sin2x
-1 у = sin2x г
при 0 < к < 1 растягивают график у = Дх)
от оси Оу в - раз. Эти деформации
графика у = Дх) выполняют в направлениях, перпендикулярных к оси Оу.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
	Представить в виде произведения.
л . 5а , . За 1. sin— + sin	 3	2	. 5а , .За ~ . 10а + 9а 10а-9а Л . 19а а sin— + sin— = 2 sin	cos	 = 2 sin	cos —. 3	2	2-3-2	2-3-2	12	12
Ответ:	n . 19a a	> 2sm	cos— .	'
г	12	12
2.5zna + sin2a + sin3a	*	!	• о /М _i • Q	'	j	 5	Ct sina. + sin2a + sin3a = sina + 2sin—cos— = 2	2 ~ . a a , о . 5a а э a( • a , . 5aA
№	= 2sin-cos — + 2sin — cos- = 2cos—\ sin- + sin— -2	2	2	2	2<	2	2> = 2cos— • 2 sin—1 cosa = 4cos—cosasin —. 2	2	2	2
Ответ:	. a	.3a 4 cos—cos asm — . 2	2
2	2 3. sin a-cos Р	.2	2n 1 - cos2a 1 + cos2Q sin a - cos p _	„		—*- - H	2	2 cos2a + cos2Q	, , n. . 				= -cas(a + p)cay(a-p).
Ответ:	2	2
	sin a-cos p = -cos(a + p)cas(a-p).
4. sin а + cosfi	sina + cosP = sina + sin(90° - P) = \ . a + 90° - P a - 90° + p = 2 sin	'-cos	. 2.2
Ответ:	.и о o • а + 90°~Р	a-90° + p szHa + cosp = 2 sin	f-cos	*-. 2	2
5. 3 - 4szn2a	-5 л • 2	лР .2) Л/77^12	• 2 к 3—4sin а = 4 - — sin а = 4	—sin а = . <4	J кк 2 >	> 1 - cos— - 1 + cos2а = 4\ sin -~~sin2a\~ 4			 = к 3	>	2 С л	2 71^	а • f I	f 7С = 2\cos2a-cos— = 4sin а + - sin - — а .
Ответ:	V	3'	к 37	<3	/ _ л-2	. . ( , лк . f Я	к 3-4sin а - 4sin а + - sin --а . к 3>	<3	)
6. 3 - ТЗ/ga	3 - 7з tga = 7з (7з - tga) = 7з ug- - rga^ = 7з _ aj 2 7з _ а) 71	cos а cos - cos а 3
Ответ:	2 Тз sin	- aj 3 - 73 tga ~
*	cos а
Полезные тождества
sin а+ cos а = 1 —sin 2а - -(3 + cos4a)
sin а + cos a
\ -~sin^2a - -(5 - cos4a)
sin a + cos a = —(cos 4а + 14cos4a + 17) 32
7. Вычислить.
. 4	,	4
sin a + cos a,
Решение.
если sina + cos a - — 72
то
то есть
sin~a + 2sinacosa + cos~a = 1 + sin2a
, тогда
sin a + cos a = 1
Ответ:
8. Доказать тождество.
4	4
sin а + cos a - 1 _ 2 . 6 ,	6	, “ з
sin g + cos g — 1
Доказательство.
4	4	l--5ZM* 22g-l
sin g + cos g - 1 _	2__________ _
. 6 ,	6	, “	3	2	~
sin g + cos g - 1	1 - - sin g - 1
4
9	9
1 - 2sin~acos'a - 1	-2 _ 2
2	2	—3 ~ 2
1—3 sin "g cos g — 1	J J
Тождество доказано.
9.	Доказать тождество.
Доказательство.
sin2(a - 30°)+ sin (а + 30°) -- sin2а = 0, 5
9	9	9
sin" (a - 30 ) + sz«'(g + 30°) - sin~a =
1 - cos(2a- 60°) + 1 - cos(2g + 60°) - 1 + cos2a _
2
1 - 2cos2acos60° + cos2a _ 1 - cos2a + cos2a _ 1
2	2	2’
0,5 = 0,5. Тождество доказано.
10. Доказать тождество.
2	2
sin За-sin a _ 7	~
cos~3a - cos5acosa = 2cos2a
Доказател ьство.
Поскольку sin23a - -—CO5^a> sin2a
1 + cos 6g
cos5acosa - -(cos4a + cos6a), to
sin 3a-sin a
cos 3g- cos 5 a cos a
cos2a- cos 6a 1 - cos4a
sin4asin2a
1 - cos4a
2sin2acos2asin2a -	~
----------------= 2 cos 2a.
2 sin 2 a Тождество доказано.
11. Вычислить.
sin268°-sin238°-
- 0,5 szn 106° + 3
Решение.
• 2zroo 1-COS 136°	. 2«O0	1-COS 76
Учтем: sin 68 = ---------------; sin 38 = -------r----
2	2
sin'68° - sin“38° = ~(cos!6° - cos 136°) = 2V
= sin 106 ° sz’zz 30° = -sin 106°.
2
Тогда szzz268°-sin238° — 0,5sin 106° + 3 =
= jszrz 106°-0,5szn 106°+ 3 = 3.
Ответ:
12. Вычислить.
3(cos20° — szh20°)
J2sin25°
Решение.
3(cos20° - szh 20°) _ 3(cos20° - cos70°)
J2sin25° 6sin45°sin25°
J2sin25°
Jlsin25°
Ответ:
13. Вычислить.
(Zgl4° +ctg23°')cos 14°szh14°.
Решение.
rgl4° =
sin 14°
cos 14°’
cos28° szh 28 °
(Zgl4° + ctg28°)cos 14° sin 14° =
sin 14°szh28° + cos 14°cos28°
cos 14°szn28°
cos 14°szh 14°
4
cos 14° • cos 14° • sin 14° _ s/и 28 ° _ 1
cos 14°szh28°	2szh28°	2
14. Вычислить.
.2Л	2 л
sin -cos -
Решение.
В знаменателе:
4 2л 2 2л .2 2л - cos------cos------sin ---
4 2л 2 2л .2 2л
— cos-----cos —— sin -----
5	5	5
,	2 2лГ 2 2л , .2 2 лЛ ,	2 2л .2 2л
= 1 - cos — cos — + sin — = 1 - cos — = sin ----
5 v 5	5>	5	5
В числителе:
 2 л 2 Л	1л.2л 2л	1.2	2л
sin -cos -	-	-4 sin -cos -	=	-sin	—.
5	5	4	5	5	4	5
-sin
„	4
Получим:------
2 sin
Полезные тождества
sina • szn(60° - a)szn(60° + a) = -s/иЗа
Вычислить.
sin 10os/h50°s/h70° =
cosacos(60° - a)cos(60° + a) = -cos3a
= szn 10°s/n(60° - 10°)szh(60°+ 10°) -
-sin3 • 10° = -sin3Q° =
15. Существует ли выражение---с——
sin6a-sin2a
при каждом из указанных значений а:
cos 2 • —
12
COS-
12
sin6 ----sin2  —
12	12
sin— sin-
Ответ: да.

Л /V cos2 • -
О
^-0.
я у- /V	*	/ L
sinv • — sin2 • -
sin-it - sin-
Ответ: да.
2 /и • -
cosit
——- не имеет смысла.
sin6  — sin2  -
Ответ: нет.
16. Упростить выражение.
sin a
cos a
sin a • cos a
cos a • sin" a
sin a cos a
cos asin~a
cos
sin a - cos a
sm acos a - cos asm a
asm а 9 sin~acos a(sin a-cos a)
cos a - sin a
cos “a - sin~a
2	. 2
cos a - sm a
2	12	„
sin acos a(sin a-cos~a)(sin a +cos a)
cos a - sin a
— • 4 sin acos a = —sin 2a.
cos а - sin a
Построить графики функций.
1) Строим график функции у =
2) Сжимаем график у = sinx в
sinx.
2 раза
к оси Ox, получим график у =
-sinx.
3) Поднимем график у = -sinx
на единицу
вверх вдоль оси Оу, получим график
18.	у = 2sinx — 1
1)	Строим график функции у = sinx.
2)	Г рафик функции у = sinx растягиваем в
2 раза от оси абсцисс.
Получим график функции у = 2sinx.
3)	График функции у = 2sinx переносим параллельно вдоль оси ординат на одну единицу вниз. Получим график данной функции у = 2sinx- 1.
1) Строим график функции у = tgx.
2) Г рафик функции у = tgx сместим вдоль оси абсцисс на - единицы влево. Получим
график данной функции у =
1)	Строим график функции у = cosx.
2)	Г рафик функции у - cosx растягиваем в
2 раза от оси ординат.
Получим график функции у = cos-.
3)	График функции у = cos- сжимаем
в 3 раза к оси Ох и получим график данной
функции у = -COS
21.	у = \sin2х|
1)	Строим график функции у = sinx.
2)	Г рафик функции у = sinx сжимаем к оси ординат в 2 раза, получим график функции у — sin2x.
3)	Часть графика у = sin2x, которая расположена под осью абсцисс, отобразим симметрично оси Ох.
Получим график функции у = \sin2x .
. 1
у - sin-x
22.	у = sin |2х|
1)	Строим график функции у = sinx для х > 0.
2)	Сжимаем полученный график в 2 раза к оси Оу, получим график функции у = sinlx.
3)	Отобразим полученную кривую симметрично оси Оу, получим график функции у = 5z«|2x|.
23.	Построить график функции у = 2sin
лЛ
6>
Построение.
1)	Преобразуем функцию.
у = 2 sin
2)	Построим график у = sinx.
у = sinx
3)	Построим график функции у = sin-x
у - sinx ОТ ОСИ Оу.
растяжением графика
4) Построим график функции у = 2sin-x
растяжением графика^ = sin-x от
оси Ох.
5) Построим график функции
смещением графика
у = 2sin-x на - вправо вдоль оси Ох.
СТРАНИЧКА АБИТУРИЕНТА
1. Доказать тождество.
a)	sin3a = 3sina-4sin а.
sin3a = sin(2a + а) = sin2acosa + cos2asina =
-	2sinacos a + (cos a-sin a)sina =
-	2sin(\ - sin а) + (I-2sin a)sina = о- n  3	.	.	_ . 3	. 3
= 2sina-2sin a + sina-2sin a = 3stna-4sin a.
6)	sin3a =
з	13
sin3a = 3sina- 4sin a = 4iz«a - -sin a
= 4szna5jn(60° - a) sin (60° + a).
= 4sina(sin~60° - sin a) =
л .	1 - cos 120° - 1 + cos2a
= 4 sina-------------------
= 2sina(cos2a- cos\20°
= 4sinasin(60° - a)szn(60° + a).
2.	Представить в виде произведения.
1 + sina + cosa.
1 + sina + cosa = 2cos — + 2sin—cos— =
л
--a	,	.
= 4cos — sin-cos-- = 2a/2cO5 —cos( 7 - 77 ].
2	4	2	2	<4 2)
Ответ:
1 + sina + cosa
3.	Найти сумму: S = cosa + cos2a + cos3a + ... + cosna..
Решение.
Аргументы слагаемых составляют арифметическую прогрессию с d = 1.
Домножим каждое слагаемое на 2sin-, где d — разность прогрессии.
2Ssin— = 2sin—cosa + 2sin—cos2a + 2sin — cos3a + ... + 2 sin —cosna =
2	2	2	2	2
_ . 3a	. a , . 5a . 3a . 7a	. 5a
= sin----sin—+ sin--sin— + sm----sin— + ...
2	2	2	2	2	2
,	. (2« + l)a . (2и-1)а	.a, . (2n+l)a	~ . па (и+1)а
+... sin --* sin  -----— = - sin —+ sin ---= 2 sin — cos *---—.
2	2	2	2	2	2'
Ответ:
sin—
. na sin — cos
4.	Доказать тождество. rg* 2 *10° + tg25Q° + rg270° = 9.
tg210° + rg250° + rg270° = f—5-----11 + f—\-----I4 * *) + [—1-11 =
cos 10° 7 4cos 50°	7 Vos 70°	7
_ cos250°cos270° + cqs210ocos270° + cqs210ocos250° - _
cos210°cos250°cos270°
= 4 (1 -CQ580°)(l - cos40°) +(1 - cos40°)(l + cos20°) + (l + cos20°)(l - cos80°) _ 3 (4cos 10°cos(60° - 10°)cos(60° + 10°))2
g
После раскрытия скобок в числителе получим -. В знаменателе используем формулу
4
косинуса тройного угла.
(4cosl00cos(60°-100)cos(60°+10°))2 = cos230° = | .
Тождество доказано.
5.	Вычислить. crg70° + 4cos70°.
Решение.
~no , , neo cos70 +4cos70 sin70 sin20 +2sin4Q
*70° + 4 cos 70 ° = -------ztt-------- = --------Z77---
sinlQ	sin70
2coslQ°sin3Q° + sin4G° cos 10° + sin4Q° _ sinS0° + sin40°
sin70°	sin7Q°
s/n 70° 2 sz>? 60 ° cos 20 ° cos 20 °
Ответ:
6.	Задача. Если sina = Asin(a + Р), то доказать, что /g(a + р) =
5шР cos Р - А '
Доказательство.
Пусть a = (a + р) - р, тогда sz«((a +р)-р) = Л$/и(а + р) или sin(a + P)cosP~ cos(a + P)szhP = Jszn(a + P).
Разделим обе части равенства на cos (а + Р) * 0,
получим: tg(a + P)cosP -sinfi = Atg(a + Р);
rg(a + P) =
S’z'nP cos P - A
7. Доказать тождество.
1 + sina	fa , n\
------- = tg\---h “ cosa---\2 4/
Доказательство.
1 + sin a _ 1 + cos (90° -a) cosa soi(90°-a)
2 cos 45
2sin\ 45° - - cos 45° -
8. Вычислить без таблиц и калькулятора szn 18°.
Решение.
Учтем, что s/n36° = cos54° и 36° = 2 • 18°, а 54° = 3 • 18°, тогда 2sz«18°cosl8° = 4cos^ 18°-3cos 18°,
2sfwl8° = 4cos218°-3,
2sz«18° = 4(1 -sw218°)-3,
2sm18° = 4-4szh218° - 3,
4szn 18° + 2sin 18° - 1 = 0,
sin 18° =
Ответ:
-1 + 75
4
§2. Тригонометрические уравнения
Обратные тригонометрические функции
Определения
Арксинусом числа а называется угол (число)
Примеры
ar с sin- =	arc sin-— = rj
из промежутка
синус которого равен а.
ardsin(-\) = --; arcsinO = 0.
pre sina = ср
sin у - a
Арккосинусом числа а называется угол (число) из промежутка [0;л], косинус которого равен а.
prccosa~=
cosy = a
Арктангенсом числа а называется угол (число)
из промежутка
, тангенс которого равен а.
ar с cos- = -; arccos-^— =
arccos(-\) = л; ar с cosQ = -
Yirctga = ф|
arctgft = л.
rg(p = а
Арккотангенсом числа а называется угол (число) из промежутка (0;л), котангенс которого равен а.
\arcctga = ф
arcctg(~V) = ——; arcctgO — -
#ф = а
arcctg J3 = 7;
Простейшие свойства обратных тригонометрических функций
sin(arcsina) — а|
аг с cos {-а) = = п — arccos а
cos (arc cos а) = а
arccos (cost?) = ф, если ф е [0;л]
а = aretga, Р = arctg(-a), Р = -а, то есть prctg(-a) = |= —arctg а tg(arctg а) ~ а|
а = arcctg а, Р - arcctg(-a), Р = л - а, то есть arcctg(-a) = = л - arcctg а \ctg(arcctg а) - а arcctg(ctg а) = а, если а е [0;л].

arcsina + arccosa = ? 2	arctg a + arcctg a = -
Тригонометрические уравнения
sinx = а
|а| > 1
Решений нет.
|д| < 1
х = (—\)narcsina + пп, neZ. sinx = 01; х = пк, к е Z.
1) sinx - 3 —решений нет.
2) sin3x = 0,6
Зх = (~V)narcsinO,6 + пп, n е Z;
х = (—\)n^arcsin0,6 + n е Z.
5
к е Z.
n е Z.
|со5х = а]
|а| > 1
Решений нет.
|а| < 1
х = ± arccosa + 2пк, к е Z.
1) cosx = -17 — решений нет.
n е Z.

5
- + пк, к е Z.
COSX
= 2пк,
х-- = 2ли, n е Z; х = -т + 2л», n е Z.
4	4
tgx = а\
х = arctg а + лЛ, к g Z tgx = 0; х = пк, к е Z.
[ctgx = а
х = arcctg а + пк, к е Z ctgx = 0; х = ^ + пк, к &Z.
2х = arcctg-+ пп, n е Z;
n е Z.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Решение тригонометрических уравнений
Уравнения, приводимые к квадратным
Уравнения вида: asin х + bsinx + с = 0; asin x + bcosx + c = 0; acos х + bsinx + с = 0;
atgx + bctgx = 0 и другие — не являются алгебраическими, но их можно привести к алгебраическим, введя новую переменную, относительно тригонометрической функции получится квадратное уравнение.
Решить уравнение.
1) sin~x - 4 sinx - 5 = О
пусть sinx = t, тогда sin х
2
4sin x-4sinx-3 = О,
Г sinx = 5
пусть sinx = у, тогда sin х = у
Ответ: -- + '2ли,
= 16;
Уг = -
sinx =1,5; Г0
sinx —
Ответ: (-1)
п e Z.
Решение уравнений вида 2	2
acos х + bsinx + с = 0; asin x + bcosx + c = 0; a tg^j
Решить уравнение.
2sin x-cosx-\ = 0;
1) .Приведем уравнение к одной функции, используя одну из формул:
2	2	2	2
sin х = 1 — cos x,cos х = 1 - sin x;
2	2
cos x = 1 - sin x:
2
cos2x = 2cos x-1 = l-2sin~x',
2
2 • (1 - cos x) - cosx -1=0.
tga =	ctga = —
ctga	tga
2) Выполним тождественные преобразования, приведем к квадратному относительно одной из тригонометрических функций:
2 - 2cos~x - cosx - 1 = 0;
2
- 2cos х - cosx +1=0;
9
2cos~x + cosx -1=0.
3) Произведем замену:
cosx = r;
t <1,
4) Решим полученное квадратное уравнение относительно t :
5) Вернемся к замене и решим уравнение:
cosx = -1; х = Ti + lnn, neZ1,
1 cosx =
2
9
neZ.
6) Запишем ответ.
Ответ: л + 2 ли, п е Z; ± - + 2л», п е Z.
Однородные уравнения
Уравнения вида: asinx + bcosx = 0; asin х + bsinxcosx + ccos x = 0;
. 3 , , . 3	,	.	2 , ,	3 Л
asm x + bsin xcosx + csinxcos x + acos x = 0 называют однородными относительно sinx и cosx. Сумма показателей степеней каждого слагаемого должна быть одинаковой. Эта сумма называется степенью однородного уравнения (£).
Решаются однородные уравнения делением на cos х, где к — степень однородного уравнения.
1) 2 sinx-3 cosx - 0 (однородное 1-степени) cosxф 0, разделим на cosx.
2tgx -3 = 0,
tgx = 2'
п е Z. ч
Ответ: arctg- + ли,
п е Z.
2)cos x-3cosxsinx + 1 = 0, 2	2	2
cos х - 3 cosxsinx + cos x + sin x = 0 ,
(однородное 1-степени)
2	2
2 cos x - 3 cosxsinx + sin x = 0,
2	2
cos x * 0, разделим на cos x.
sinx , cosx
. 2 Sin X
2 COS X
2 - 3tgx + tg2x = 0,
пусть tgx = у, тогда у1 -Зу + 2 = 0.
У i = И r?gx = 1;
уг = 2; \-tgx = 2;
Ответ: - + nn,
n e Z; arctg2 + nm,
х = arctg2 + пт.
m И n e Z.
m e Z
Уравнения, решаемые разложением на множители
Одним из наиболее используемых методов решения тригонометрических является метод разложения на множители.
Для решения этим методом используют: вынесение общего множителя способ группировки, формулы сокращенного умножения, а также тригонометрические формулы.
уравнении
за скобки, различные
1) sin х - sinx = 0
Вынесем общий множитель sinx за скобки: sinx(sinx-l) = 0 ~sinx = 0 -sinx —1=0
'-sinx = 1
Tin,
Ответ: ял; - + 2пт, п,
Используем формулу разности квадратов: tgx(tgx ~ 1 )(tgx + 1) = 0.
’ tgx = 0, tgx = 1,
.tgx = -1;
Ответ: лп;
пп
9
Тригонометрические уравнения вида ^cosx +bsinx = с Такие уравнения можно решать введением вспомогательного угла.
Пусть с * 0 а2 + Ь2 0, тогда равносильное ему уравнение:
cosx +
sinx =
поскольку
то существует такой угол у, для которого siny = • а (1); cosy =
siny cos х+ cosy sinx =
arc sin
где у выводится из формул (1) и (2). Решить уравнение.
Решение.
7<т2 + Ь2 = 79 + 16 = 5. Разделим уравнения на 5: -sinx + -cosx
Пусть siny = cosy = - тогда получим уравнение:
sinx cosy + cosx siny = 1;
к e Z, если siny > 0, cosy > 0, тогда угол у можно взять:
у = arcsin- (или arccos-}.
Ответ:
-arccos- + - + 2пк, keZ.
Примечание. Если 7д2 + Ь2 < с, то уравнение не имеет решения. Например: Isinx + 3cosx = 4, 74 + 9 < 4, поэтому решени^нет.
Решить уравнение.
Решение.
Найдем значение Ja2 + Ь2:
Разделим обе части уравнения на 7«2 + Ь2:
Зная, что siny =	, найдем
7а2 + Ь2
значение у:
arc sin -
Запишем данное уравнение в виде
Решим полученное уравнение:
Запишем ответ:
- + 2лл.
Решить уравнение.
Удобно решать уравнение
asinx + bcosx = с с помощью формул:
sinx = -<
cosx
5x
= 0
Тогда данное уравнение приводится
к
квадратному относительно tg-.
л , 2пп
10 ~5~’
Необходимо помнить, что при решении таким способом могут быть потеряны корни вида х = n + 2itk, поэтому в данное уравнение необходимо лодставить х = л, если получится верное равенство, тогда к ответу прибавим корни вида
5х
Ответ: £ +
10	5
2пт ---, w
2пт
Различные способы решения тригонометрического уравнения sinx - cosx = 1.
1-й способ. Приведение уравнения к однородному относительно синуса и косинуса.
sinx - cosx = 1
Разложим левую часть по формулам двойного аргумента, тригонометрической единицей:
а правую часть заменим
2sin-cos—cos - + sin - = sin - + cos -,
= О
2 sin-cos — 2 cos -
cos-\ sin---COS-
= 0,
cos- - 0,
sin— cos- - 0;
COS- = 0;
sin— cos-
0 — однородное уравнение первой степени.
cos-*0, потому что если cos- = 0,
sin- = 0, что
противоречит тождеству
cos J + sin - = 1, поэтому делим обе части уравнения на cos-.
Получим: tg- — X = 0; tg- = -1;
Ответ: х = л + 2лЛ; к g Z;
или х - - + 2ли; п g Z.
2-й способ. Разложение левой части уравнения на множители.
sinx - cosx - 1
sinx-(\ + cosx) = 0;
Так как (1 + cosx) = 2cos -, .asinx - 2sin-cos~, 4	7	2	2	2
TO 2sin-cos--2cos - = 0; cos-\ sin--cos-\ = 0, 2	2	2	2< 2	2>
получили уравнение, которое рассматривали в первом случае.
3-й способ. Преобразование разности (или суммы) тригонометрических функций в произведение
- cosx = 11
Запишем уравнение в виде sinx-sin№-x) = 1.
По формуле разности двух синусов получим 2sin[x-^]cos-
—, а дальше — как в предыдущем случае.
4-й способ. Приведение к квадратному уравнению относительно одной из функций
sinx - cosx = 1
Так как sin х + cos х - 1 , то sinx = ±V1 - cos х,
/2	I
sinx - cosx =1	<Х>	±л/ 1 - cos х - COSX = 1, ±л/ 1 - cos'x = 1 + cosx
Возведем обе части уравнения в квадрат: 1 - cos1 х = 1 + 2 cosx + cos1 х-, 2cos~x + 2cosx = 0;
cosx(cosx + 1) = 0
'cosx = 0;
-cosx +1=0;
Я ,	—9
х = - + яг, г е Z
_х = я + 2яи, п е. Z.
Возведение в квадрат
могло привести к появлению посторонних корней, поэтому
необходима (обязательно) проверка. Выполним ее. Полученные корни равносильны
объединению трех корней.
я + 2яи;
- - + 2лт.
и х2 совпадают с полученными ранее, поэтому не являются посторонними.
Проверим:х
sin
- cos\-~ + 2пт\ = sin
Тогда х3 = - - + 2яти, т е Z — посторонний корень.
Ответ: х = + 2я&, к е Z; х = я + 2ял, п е Z.
5-й способ. Возведение в квадрат обеих частей уравнения. | sinx — cosx = 1 ~|
(sinx — cosx)2 = I2; sin x —2sinxcosx + cos1 x = 1; 1-sin2.x = 1; sin2x = 0;
2x = лк; x = -k‘, к e Z.
2
Проверим, не получили ли посторонних корней.
= 2лл,
- + 2л&,
Проверка показывает, что Xj и х4 — посторонние корни.
Ответ: - + 2ли, и е Z;
6-й способ. Графическое решение.
sinx - cosx = 1
Запишем уравнение в виде sinx = 1 + cosx.
Построим графики функций у{ = sinx; у2 = 1 + cosx.
Абсциссы точек пересечения этих графиков будут корнями данного уравнения.
Решить уравнение.
cosx - sinx = а.
Решение.
Заменим равносильным уравнением: Исследуем вероятные случаи решения:
при — < 1, то есть а е [~J2;J2]
уравнение корней не имеет.
Ответ:
- - ± arccos— + 2л£, к е Z, если а е [-72;72];
Решение тригонометрических уравнений с использованием формул понижения степени Часто тригонометрические уравнения решаются с помощью формул понижения степени: 2	1 + cos2x .2	1 — cos2x
cos х = ------: sin x = -—z---.
Решить уравнение.
Понизим степень:
Домножим левую и правую части уравнения на 2: 1 - cos2x + 1 - cos6x = 2.
Выполним упрощение: cos2x + cos6x = 0.
Преобразуем левую часть в произведение: 2cos4xcos2x = 0.
~cos4x = 0;
-cos2x = 0;
2х — - + пт, т е
п е Z,
пт
Ответ: J + —, п е Z; 8	4
т е Z.
Решить уравнение, ч
1) Понизим степень тригонометри-ческих функций:
1 + cos2x . 1 + cos4x . 1 + cosbx , 1 + cos8x —	......_ -j---------[_		,,
2	2	2	2
2) Домножим левую и правую части на 2 и выполним упрощение:
(cos2x + со$4х) + (со$6х + cos8x) = 0.
3) Разложим левую часть уравнения на множители:
2cos3xcosx + 2 coslx cosx = 0, cosx(cos3x + coslx) = 0, 2cosxcos5xcos2x = 0.
4) Решим полученное уравнение:
cosx = 0, или cos5x = 0, или cos2x = 0,
10
5) Запишем ответ:
10
Решение дробно-рациональных уравнений относительно тригонометрических функций
Для решения уравнений такого типа используют условия равенства дроби нулю и условие равенства произведения выражений с переменными нулю.
/Я*) = 0;
kg(x)*0.
-/(х) = 0;
-g(x) - 0.
tyf(x)-g(x) = 0
Решить уравнение.
2sin x-3sinx _ „
1 + cosx
sin2x + sin6x _ q 1 — sin2x
Решение.
Решение.
2
\2sin x-3sinx = 0;
11 + cosx^O;
2sin4xcos2x = 0;
sinx(2sinx- 3) = 0; cosx *-l;
4sin2xcos 2x = 0;
sinx = 0;
S \-sinx = 1,5;
sinx
cosx*-].
cosx * -1.
х Ф л + 2ли, п е Z.
sin2x = 0;
•s Lcos2x = 0;
2х - пп, п е Z
и е Z
У1
2х Ф - + 2ли.
На единичную окружность нанесем числа х = ли, п е Z и выберем те, которые удовлетворяют условию л + 2ли, и е Z.
х = 2ли, и е Z.
sin2x Ф 1;
У*
Ответ: 2ли, и е Z.
Ответ: —, и е Z. - - + ли, и е Z.
2	4
Эти серии решений можно объединить и записать так:
т
3) tg2x • sin\x = 0
ОДЗ:х^ + —, neZ
4	2
4) sinxcos2x - sin3x = 0.
sinxcos2x - sin(x + 2x) = 0,
sinxcos2x - sinxcos2x - cosxsin2x = 0 ,
cosxsin2x = 0,
Ответ: —, и е Z. 2
Ответ:
СТРАНИЧКА АБИТУРИЕНТА
Уравнения вида
a(sinx± cosx) + bsinxcosx = с решаются с помощью замены t = sinx ± cosx, так как
Решить уравнение:
sin2x + Y2(sinx + cosx) - 12 = 0.
Решение.
Замена: sinx + cosx = t.
1 + 2sin2x — t2
то |z| < л/2; тогда sinxcosx = ±
и

sin2x =
получим квадратное уравнение относительно переменной г.
Необходимо помнить, что возможно появление посторонних корней, поэтому необходимо сделать проверку полученных корней.
После подстановки получим уравнение:

~ t = 1, Г sinx + cosx = 1
-t = -13; \-sinx+ cosx = -13;
т е Z
х = 2тст, п,т g Z
Ответ:
- + 2ли, n g Z; 2nm,
1. Решить уравнение.
sin(ncosx) = 0 ticosx = Tin, n g Z cosx = n.
'cosx = 1, cosx = -1, .cosx = 0;
У А л
= 2nk,
Ответ: -т
2. Решить уравнение. ctg(sinx) = л/3 .
sinx = - + Tin,
sinx =
, m g Z.
Ответ: (— \)marcsin[ -) + urn,
Нестандартные приемы решения тригонометрических уравнений
Для овладения нестандартными приемами и методами решения тригонометрических уравнений необходим следующий теоретический материал.
Теорема 1. Если на некотором множестве чисел верны неравенства Дх) < a, g(x) < Ь, то на множестве М уравнение Дх) + g(x) = а + Ь равносильно системе уравнений:
= b.
Теорема 2. На любом множестве действительных чисел уравнение f 2(х) + ф2(х) = 0 равносильно системе уравнений:
f(x) = 0;
ф(х) = 0.
Теорема 3. Если на некотором множестве действительных чисел верны неравенства Дх)>я; <р(х)<а, то на множестве М уравнение Дх) = ф(х) равносильно системе уравнений:
f(x) = а\
. ф(х) = а.
Теорема 4. Если [Дх)| > а; |ф(х)| < Ь, то уравнение Дх) • ф(х) = ab равносильно совокупности систем уравнений:
f(x) = а;
ф(х) = Ь.
= -а;
^ф(х) = -Ь.
1. Решить уравнение.
Решение.
sinx • sin5x = 1.
Так как |sznx| < 1, |sz>z5x| < 1, то (теорема 4):
sinx = 1;
sinSx = 1.
sinx = -1; sin5x - -1.
Ответ:
2. Решить уравнение.
sinx + sin2x = 2.
Решение.
sinx\ <1, |sz’rt2x| < 1	2=1 + 1 (теорема 4);
sin2x = 1
следовательно, система не имеет решении.
3. Решить уравнение.
sinx + sin 9х = 2.
sinx
+ 2пп, п е Z
(а);
Решение.
sin9x = 1
я , 2тти
18	9
П G Z (б).
Корни (а) изображаются одной точкой единичной окружности, корни (б) — девятью точками. Значит, если система совместима, то ее корнями могут быть лишь корни (а)
7t	f 9 ТС	'Х	9 ТГ	7Т
х — - + 2ял, п s Z. Проверим это: sin9x = sin — + 18я& = sin— = sin-
Ответ:
х = - + 2ял, п g Z.
4.	Решить уравнение.
.2001 ,	2000
Sin X + COS X
Решение.
Так как |s7>?x| < I,
. 2001 sin
2000
X - Т1П ИЛИ X =
1	• 2001
cosx < I sin
. 2001 sin x -
2000
1 COS
2000 COS
sin х; sinx = 0; I cosx = 0; ±I
COS X?
пп. п е
- + пп или х = 2ли или л + 2пп

Ответ:
ял; - + 2лл, n g Z.
2
5.	Решить уравнение.
. 8	5
sin x - COS X =
Уж
Г . 8	.2
Sin X = sin X
5	1
^-COS X - COS X
Решение.
sinx
Ответ:
cosx - 0;
k	7
71 + 2яи,
1
n e Z.
6.	Решить уравнение.
. 11»	1999
sin Зх - cos
Решение.
।	11	1999
sinx\ < 1; sin Зх < 1; cosx| < 1; cos 5х < 1;
. 11,	1999»	».	. 11,	, .	1999-
sin Зх - cos эх = 2 , sin Зх - 1 , cos эх = -

24° - пп
45лп = -я; 45» = -!;» =	; 0, так как п е Z.
Ответ:
Использование области определения функции при решении уравнений
Теорема. Пусть Дх) = g(x). Z>(/), D(g) — области определения функций Дх) и g(x). Рассмотрим общую часть этих множеств. ОДЗ уравнения. Если' ОДЗ — пустое множество, то уравнение не имеет корней. Если ОДЗ — конечное множество, то корни уравнения можно найти подбором.
Например: sin
Проверка: sinO = sinO, х = 0 —корень уравнения.
Ответ:
0.
Использование области значений функции при решении тригонометрических уравнений
1. Решить уравнение.
2cosx = 3 - cos2x.
Решение.
E(2cosx) = [-2;2]; £(3 - cos2x) = [+2;4], значит, решениями уравнения могут быть только такие числа х, для которых одновременно левая и правая части равны 2.
2cosx = 2;
< cosx = 1, cos2x = 1; k	7
x = 2тгп, n e Z.
Ответ:
2лл, п е Z.
2. Решить уравнение.
2 cosx = Дх - 3 + Дх + 3 .
2cosx = fix) => Дх - 3 + Дх + 3 = ф(х)
Область значений Дх) и ф(х): 2cosx е [-2;2]. ОДЗ функции ф(х): х е [3;+оо] Ф(3) = Дб", ф(х) — возрастает, тогда ф(х) е [Дб;+оо].
Но значения функции Дх) и ф(х) не пересекаются: [—2;2] п [Дб;+<ю].
Ответ:

Графическое решение уравнений и
Если графики функций у = Дх) и у = g(x) легко построить, то уравнение Дх) = g(x) можно решить графически. Абсциссы точек пересечения графиков функций будут корнями уравнения.
1. Решить графически уравнение.
Решение.
Обе части данного уравнения являются четными функциями, а поэтому, если х0 является корнем этого уравнения, то и число -х0 будет его корнем. Значит, чтобы найти все его корни, достаточно найти неотрицательные решения уравнения.
cosnx =

Учитывая, что 0 < х < 3 , х =
Графически легко установить, что уравнение не имеет корней.
Ответ:
2. Решить уравнение.
Решение.
/Ж 7///Z/7 >
ZL 1	2 5л 3 7л 4 19л
6	6	6	6
Проверкой убеждаемся, что числа х = 1 уравнению системы.
или х = -1 удовлетворяют и первому
Ответ:
3. Решить уравнение.
2 cos х + 3 sinх = О
при
х2 - Зх + 2 х2 - 7х + 12
Решение.
Найдем промежутки, к которым относится х.
х2-Зх + 2 х2-7х+ 12
О ОДЗ: х Ф 3; х 4.
(х2 - Зх + 2)(х2 - 7х + 12) < 0;
(х-1)(х-2)(х-3)(х-4) < 0; х g (1 ;2) и (3;4), или
Г1 <х<2;
3 < х < 4.
2cos x + 3sinx = 0, 2-2sin x + 3sinx = 0, sinx = у, 2^2 - Зу — 2 = 0.
sinx — 2,
1 sinx- —;
n e Z.
Используем условие
уччтем x e (1;2) u (3;4) получим x = -n.
Ответ:
§ 3. Тригонометрические неравенства
Простейшие тригонометрические неравенства — это неравенства вида:
sinx $ a, cosx £ a, tgx £ a, ctgx £ a.
Для решения простейших тригонометрических неравенств можно пользоваться графиками соответствующих тригонометрических функций.
Решить неравенство.
sinx
Ответ:
— + 2ли;-л + 2ли
1 cosx > --.
2
Ответ:
tgx>-\.
Ответ:
Ctgx < л/3 .
Ответ:
— +	+ Tin , п е Z.
Для решения тригонометрических неравенств очень удобно пользоваться единичной окружностью, на которой множество решений изображается в виде одной или нескольких дуг окружности.
Напомним: ось синусов совпадает с осью Оу, ось косинусов — с осью Ох, ось тангенсов — это прямая х = 1, а ось котангенсов — это прямая у = 1.
Решениями неравенств вида sinx > а , cosx > а является множество всех действительных чисел, если а <-1. Решениями неравенств sinx < а и cosx < а является множество всех действительных чисел, если а > 1.
sinx >-1,2. Ответ: х е R .
cosx <7,5 . Ответ: х е R .
sinx >1,2. Ответ: 0.
cosx < -3 . Ответ: 0.
Решить неравенство.
sinx
Ответ:
7 + 2пк < х <	+ 2пк, к е Z.
6	6
1 cosx > --.
2
Ответ:
— —- + 2пк < х
3
2пк
+ 2пк, к е Z.
Решение простейших неравенств вида tgx % a, ctgx % а.
1.	Функция у = tgx определена при х * + пп, п е Z.
Функция у = ctgx определена при х ф пп, п е Z. Период этих функций равен л.
2.	Так как областью значений функций у tgx и ctgx является множество всех
действительных чисел, то неравенства tgx £ а и ctgx % а всегда имеют решения.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Решение простейших тригонометрических неравенств cosx % а; sinx £ а.
При решении неравенств вида sinx % a, cosx % ас помощью тригонометрической окружности необходимо помнить:
1) записывая промежуток, который является решением неравенства, следят, чтобы слева было меньшее число, а справа — большее, что соответствует на окружности движению против часовой стрелки;
2) ответ записывают с учетом периода.
Решить неравенство.
1.	Проверим, имеет ли решение данное неравенство.
2.	Нарисуем единичную окружность и на соответствующей оси отложим отрезок, равный а.
3.	Через полученную точку на оси проведем прямую, параллельную другой оси, и отметим точки ее пересечения с единичной окружностью.
4.	Запишем соответствующую дугу.
Ответ:
Решить неравенство.
1.	Начертим единичную окружность и соответствующую ось, на которой отметим отрезок, равный а.
2.	Через полученную точку на оси и начало координат проведем прямую и обозначим точки ее пересечения с единичной окружностью.
3.	Запишем дугу соответственно данному неравенству.
sinx
Так как --
то решения есть.
или —л + 2ли <%<-- + 2ли, п е Z .
rgx<-l
Так как tgx<-\, то нужно записать дугу
или дугу о , которые отличаются на пе-
7 л
риод л. - - + пп
или - + ЯП

Ответ:
Неравенства вида \sin(ax +b)>c, cos(ax + b)
Решить неравенство: 2sin\ - - Зх < tg- .
\6	3
Обозначим выражение ах + Ь через t и решим полученное неравенство.
Решение.
-2sin Зх--
3 (применили нечетность функции);
sin[ Зх - -
Заменим Зх-- = t. Решим неравенство sint>-
Проведем прямую у =	, отметим точки пересечения с окружностью и дугу,
соответствующую решению неравенства.
Неравенству sint'z-— удовлетворяют все значения t двойного неравенства:
4л
тогда
Ответ:
2яи я
Решить неравенство.
Замена ах + b = t:
Проведем прямую t - с:
Отметим точки пересечения прямой с единичной окружностью и соответствующую дугу:
Запишем соответствующие значения t в виде неравенства с учетом периода:
Вернемся к замене и решим полученное неравенство:
Ответ:
Тригонометрические неравенства, приводимые к квадратным
Если тригонометрическое неравенство в результате тождественных преобразований приводится к виду:
или
то вводят подстановку: у = sint,{y = cost), причем [у| < 1.
Получают неравенство вида: ay* 1 2 + by + с > 0 или ay2 + by + с < 0.
Решив алгебраическое неравенство, возвращаются к подстановке. Решают простейшее тригонометрическое неравенство, полученное в результате подстановки.
Решить неравенство 2sinx + sinx -1 < 0 .
Решение.
Пусть sinx = у, тогда 2у2 +у - 1 < 0, решаем это неравенство:
'//////Л
1	1
2
5
Неравенство сводится к решению системы:
sinx
sinx
Ответ:
_ JI
2
х ф - + 2ли,
- + 2пп
Решить неравенство.	cos2x + 5sinx — 3 < 0 .	
Выполним тождественные преобразования, приведем к одной функции:	2 — 2sin х — 5sinx — 2 < 0 .	
Введем подстановку:	у = sinx.	
Решим алгебраическое неравенство:	-2y2 + 5y-2<0. 2y2-5y + 2>0, Z/Л// 1	2 2	' 4: Л V NJ 1	NJ •	4»
Вернемся к подстановке, решим совокупность или систему простейших тригонометрических неравенств.
Ответ:
sinx
sinx
—л + 2ля
Решение тригонометрических неравенств другими методами
1. Решить неравенство.
| sinx
cosx
Решение.
Так как sinxl > 0 и |со5%| > 0, то возведем обе части неравенства \sinx при этом получим неравенство, равносильное данному.
|5Z«x|2 > |сО5х|2 ; (sinx)- > (cosx)2 ",
sin х - cos х > 0;
cosx в квадрат,
Ответ:
cos х-sin х<0; cos2x<$ (II и III четверти единичной окружности);
2. Решить неравенство.
sinx — 2
Asin х - 1
Обозначим sinx = t, получим:
/(1 -8f)(2r- 1)(2/ + l)>0
4/2-1
4z2-1
0, 4/2-1
0;
Используем метод интервалов. Получим:
i о
77///Л

sinx
Решив каждое из неравенств, получим:
— — + 2пп
2лп, п е Z,
sinx < 0
л + 2лк
arc sin - + 2л/и
- + 2л/п,
9
sinx
л - arcsin-+ 2лр, peZ.
Решением данного неравенства является объединение совокупности.
решении неравенств
Ответ:
3.	Решить неравенство.
sinx > cos х .
Решение.
Данное неравенство равносильно следующему: sin х + sinx - 1 > 0 или
sinx —
sinx
• sinx -
> 1, поэтому sinx +
О, при х е R, а
О, то есть решениями данного неравенства будут решения неравенства
Ответ: arcsin--- + 2пк<х<л-arcsin---- + 2пк, к е Z .
2	2
4. Решить неравенство.
Решение.
2cos2x + sin2x > tgx
Для решения неравенства используем универсальную подстановку.
sinx =
; cosx =
Перепишем данное неравенство в виде
tg3x + 2tg2x - tgx - 2 < 0 ,
ИЛИ
2bj£^ + 2-ieL_-,^>0, или
1 + tg2X 1 + tg2X
(tgx - 1) • (tgx + 1) • (tgx + 2) < 0 .
t г
7///7£ ~7////////А
Отсюда
tgx > -1 , тогда
Tin
-ar
I
I I
5. Доказать, что sinx + *8Х > 0 при всех допустимых значениях х. cosx + ctgx
Доказательство.
sinx • 1 Ч---
.. cos
Имеем ----------------
fl 4. 1
cosx • 1 н---
v sin
0 (sinx*Q\ cosx*0).
СТРАНИЧКА АБИТУРИЕНТА
Тригонометрические неравенства
Решение тригонометрических неравенств сводится к тому, чтобы с помощью преобразований привести неравенство к виду Дх) > 0 или Дх) < 0, где Дх) — некоторая тригонометрическая функция.
1. Решить неравенство.
. 2
. sm х cosx >--------- .
2 - cosx
Решение.
Перенесем все члены неравенства в левую часть и приведем к общему знаменателю:
sin X cosx - -------
2 - cosx
2 cosx — cos x - sin x
2 — cosx
2cosx- cos x-sin x>0 ; 2cosx-l>0; cosx>~. Получим простейшее неравенство, решением которого является дуга
М2М{, то есть неравенство
cosx > - соблюдается на
промежутке - - + 2лк <х<- + 2пк.
Ответ:
2. Решить неравенство.
Решение.
Неравенство определено при х*^ + пк и эквивалентно неравенству sin* cos х
Установим sinx = t, причем
1
что t < 1, получим t- -7- > 0 и t
Следовательно, sinx
отсюда - + 2пк<х < —• + 2пк. Учитывая,
1
окончательно найдем - + 2тск < х
— + 2ък.
3. Решить неравенство.
cosx > sin(x - 1) при условии 0 < х < 2п.
Решение.
Неравенство эквивалентно неравенствам: cosx- sin(x - 1) > 0 ;
2sin\ х -
О , поэтому — + - + 2лк < х
Окончательно получим — + -
Для решения тригонометрических неравенств можно использовать метод интервалов.
4. Решить неравенство.
cosx + cos3x > 0 .
Составим алгоритм решения:
1)	Разложим левую часть неравенства на множители: 2cos2xcosx>0 .
2)	Найдем область определения функции: у = 2cos2xcosx, х е R .
3)	Найдем нули функции:
у = 2 cos 2х cosx
~cos2x = 0;
Lcosx = 0;
п е Z,
4) На единичную окружность нанесем область определения и нули функции.
Определим знак функции на полученных промежутках:
-п--]: ср = 0; Яф) =
cosO  cosQ = 1 > 0;
: Ф = -; .у(ф) = cos — cos-
п е Z .
Приведенный пример имеет одну особенность. Серии х} и хк могут совпадать на единичной окружности.
Если точки разных серий совпадают, то их называют кратными. Точки, повторяющиеся в четном числе серий, называют точками четной кратности, а повторяющиеся в нечетном числе серий, —точками нечетной кратности. Волнистая линия, проходящая от точки хк, после встречи с точкой нечетной кратности должна перейти в другую область (то есть, если была за границами единичной окружности, то теперь будет в середине нее, и наоборот).
Точка четной кратности не дает линии возможность перейти в другую область.
Прокомментируем этот случай на примерах:
5. Решить неравенство.
sinx • sin3x > q cosx • sin2x
sinx • sin 3x q cosx • sin2x
sinx • sin3x • cosx • sin2x > 0
Нули функции у = sinx • sin3x • cosx • sin2x
sinx = 0;
sin3x = 0;
cosx = 0;
sin2x = 0;
Ответ:
л + 2лп, n e Z
4л
6. Решить неравенство.
tgx • sin3x q cosx • sin2x
Решение.
Рассмотрим систему уравнений и набор значений х, следующих из нее:
'tgx = 0,
X + лп,
sin3x = 0, cosx = 0, sin2x - 0,
Рис.4.
При записи ответа заметим, что интервалы А и С, В и D центрально симметричны. Это и отражено на рис.4. Поэтому их можно объединить одной записью.
Ответ:
7. Решить неравенство.
• Л	Л /Л
sin- • сох- > 0 .
Решение.
Найдем наименьшее общее кратное знаменателей дробей — число
12 — и произведем в исходном неравенстве замену у = р-. Тогда 1
оно приобретет вид sin3y • cos4у > 0 . Решение последнего неравенства проводится так же, как и предыдущих. Из системы уравнений
rsin3y = О,
получаем
-cos4y = О
*
Рис.5.
Г
На тригонометрической окружности
отметим все точки, представляющие серии
значений у{ и у2. Пусть ср = -. Тогда
. Зл 4л sin— • cos —
Значит, точку хк надо взять на луче Оу в середине окружности. Линия, начинающаяся в
точке хк, перейдет из внутренней части окружности на внешнюю в каждой из отмеченных точек (см. рис.5). Все области, имеющие на рис.5 знак «+», дают искомые значения у, из которых умножением на 12 получим необходимые интервалы для значений х.
Для решения тригонометрических неравенств вида ~^пх’ cosxl > о (<о, > 0, < 0) мож-Q(sinx, cosx)
но использовать метод секторов.
В методе секторов каждому множителю вида (Дх) - а), где Дх) — одна из функций sinx
или cosx , и -1 < а < 1, в тригонометрической окружности соответствуют два угла х, и х2
(Дх,) =/U2) = я), разделяющие окружность на два сектора. При переходе через X] и х2 функция (Дх) - а) изменяет знак.
Необходимо помнить!
1. Множители вида (sinx-а) и (cosx-а) , где |я| > 1, сохраняют знак для всех значений х. Такие множители числителя и знаменателя отбрасывают, изменяя (если а> 1) при каждом отбрасывании знак неравенства на противоположный.
2. Множители вида (sinx+1) и (соух±1) также отбрасывают, причем если это множители знаменателя, то в систему неравенств добавляют неравенства вида sinx* + \ и cosx* + \ . При отбрасывании множителей вида (sinx-l) или (cosx-1) знак неравенства изменяют на противоположный.
8. Решить неравенство.
2 sin x - sin x - sinx > g
Решение.
Раскладывая числитель и знаменатель на множители, запишем неравенство в виде sinx(sinx- l)(2sinx+ 1) > g Эквивалентная система неравенств:
sinx
0;
sinx * 1.
2 ZE
7л
6
о
11л
6
При х = - левая часть первого неравенства положительная. Значит,
в секторе 0 <х< знак левой части «+». Для других секторов проводим чередование
знаков. Учитываем, что х * -.
Ответ: - + 2 ли < x < - + 2ли
5
5
2пп,
При решении неравенств, содержащих sinx, cosx , tgx и ctgx одновременно, или содержащих тригонометрические фунции разных аргументов, необходимо найти общий период функций, входящих в неравенства, и, используя разные тождественные преобразования, разложить неравенство на простейшие множители.
9. Решить неравенство.
sin2xsin3x — cos2xcosЗх > sin 10х.
Решение.
Имеем: -cosSx > sinlOx , 2sin5xcos5x + cos 5x < 0,
Пусть 5х = t. Тогда cost[sint +
7л , »
— + 2ли;
— + 2пп
Л
7я
6
Зя э
1л
6
Ответ:
Гл 2лл	7л , 2ли
—	। < Y < - -—
10	5	30	5
Зл . 2ли
L10
1 л 2ли
30	5
10. Решить неравенство. *
sin xcos3x + cos xsin3x >
Решение.
Воспользуемся формулами sin3x = 3sinx-4sinix, cos3x = 4cosJx-
Имеем: (3sinx — sin3x)cos3x + (cos3x + 3cosx)sin3x >
1
sinxcos3x + cosxsin3x > — , sin4x > —. Пусть 4x = t,
получим sint —
Ответ. — + — < x < — + —, n &Z.
12	2 o 2
11. Решить неравенство.
Решение.
ОДЗ: cosx*0 , cos2x^0. Используя формулу tg2x =
2 tgx
запишем в области
определения неравенства эквивалентное неравенство:
12. Решить неравенство.
Решение.
Тут общий период функций Т=2п. Решаем неравенство в тригонометрической окружности, отмечая все углы, при которых числитель и знаменатель превращаются в ноль или не определены.
- + 2лп
4л , ~ — + 2ли
Зя
13. Решить неравенство.
cos 2х
cos х
Решение.
cos 2х 3sinx
2cos 2х - 3sin2x
2sin 2x + 3sin2x — 2
cos~x cosx
Период sin2x eT = л.
12
5 л .12
14. Решить неравенство.
Решение.
Запишем неравенство в виде 7 - 4sinx < 3\2sinx - 1 .
sinx > -
sinx > -
sinx — 1
sinx
sinx
sinx < -
э

5
2sin x-3sinx-2>0.
Ответ:

§ 4. Степенная функция
Иррациональные уравнения и неравенства
Определения
Примеры
Корнем и-ой степени из числа а называется такое число, и-ая степень которого равна числу а (число п — натуральное число).
nJa —корень; п — показатель; a — подкоренное выражение.
V32 = 2, 25 = 32;
1/729 = 3, З6 = 729;
V-125 = -5, (-5)3 = -125;
V^768 = -4, (-4)5 = -768.
Арифметическим корнем я-ой степени из неотрицательного числа называется такое неотрицательное число, и-ая степень которого равна a.
1/81 =3 — арифметический корень;
1/-243 = -3 — неарифметический корень;
725 = 5; 79 = 3 — арифметические корни.
Показатели корней вида n = 2k + \ используют для обозначения любых корней.
Показатели корней вида n = 2k используют для обозначения арифметических корней. Показателем корня может быть любое натуральное число, но показатель корня n = 1 не рассматривается.
Свойства корней
1. Корень четной степени из отрицательного числа не определен.
21/а = Ь, если a > 0.
7-9 — не существует.
2. Корень нечетной степени определен из любого числа.
з. ”76 = о.
Действия с корнями «-ой степени
1.	Произведение корней л-ой степени.
n/a-n/b = nJTb a>0; b>0
127128 • 12732 = 127128  32 =
nJab = nfa-nfb a>0; b>0.
2.	Частное корней «-ой степени.
3.	Степень корня.
("Та/ = "Та* а > 0; к — целое; п — натуральное.
(2570?25)5 = 23 •(1/6/25/ = = 25 • 0,25 = 8.
1/а* = (\!a)k а > 0; к — целое; п — натуральное.
4. Корень из корня.
mJ^/a =	= mnJa а > 0, т,п— натуральные.		4J372 = ХЦ2. -а
5. Приведение корня к новому показателю.		
npJamP — п*]ат	12л/2б = J2; ,2лДЙ = 3Js.	= пР^атр
а > 0; т, п,р —	75 • 3j25 = 6^53 • 6^252 =	а > 0; т,п,р —
натуральные.	= л/s3 • 54 = 6л/57 - 5 • 6Т5	натуральные.
6. Внесение множителя под корень.
anJb = nJa"b а > 0; b > 0.
7.	Извлечение корня четной степени.
2,7<з2” = Ы
а > 0; п — натуральное.
7(-22)2 = |-22| = 22; *Jb*c4 = |Z>||c|4A
8.	Извлечение корня нечетной степени.
натуральное.
37(-3)3 = -3; sjlPc* = bc\jb3c4.
V-128 = -V128 = -2.
натуральное.
9.	Формула сложного радикала.
Формулы сокращенного умножения относительно корней
1.	Разность квадратов, (л/а + л/б)(л/а - л/b) = = (Та)2-(л/б)2 = а-Ь.
Сократить дробь:
= (Jx- Jy)(J~x + Jy) Jx + Jy Ответ: Jx - Jy.
2.	Сумма кубов.
а)	(3Ja + У^)((У«))2 - 3Ja3Jb + (У&)2) =
= (V«)3 + (37^)3 = а + й;
б)	aja + bjb = (У?)3 + (7/>)3 =
= (Та + л/Ь)((л/а)2 - JaJb + (7б)2) = (л/g + Jb)(a- Jab + b).______________
3.	Разность кубов.	~
а) (3Ja - 3Jb)((Уд)2 + 3Ja3Jb + (Уб)2) =
= (Уд)3 - (3Jb)3 = a-b;
b)aja-bjb - (Ja)3 ~(Jb)3 =
= (Ja - Jb)((Ja)2 + J~aJb + (Jb)2) =
x+y = (3Jx + з/уХСУх)3 -3Jx3Jy + (Уу)2)
Г	I ° r~
Ух + Уу	Ух + У у
= (Ух)2 - Jxy + (Jy)~ — Jx3 — 3Jxy + 3Jy3.
Ответ: Ух^ - 3Jxy + Jy3..
xjx—yjy = (Jx- Jy)(x + Jxy+y) Jx- Jy , Jx- Jy
= x+ Jxy + y.
Ответ: x +Jxy + y.
= (Ja - Jb)(a + Jab + b).
4. Выделение полного квадрата под знаком корня.
j$ + 2ji = 71 +3 + 2jl==3 =
= J(J\ + J3)2 = |i + 7з| = 1 + J3.
Ответ: 1 + Ji.
Ja + lJb = J(Jx + Jy)2 = Jx + Jy, если a + 2b = x + y + 2 Jxy, то есть x+y = а и xy = b, тогда a + 2jb = (Jx+Jy)2,
Определение степени с рациональным показателем
1. Произведение одинаковых множителей а • а • ... • а = ап (п е N) —— • - . . •> п раз называют возведением в степень. а — основание степени; п — показатель степени.	Y-Y = — • V2/	32’ (-0,2)3 = -0,008 0" = 0. Iй = 1. х
2. а1 = а.	(-11)1 = -HjCI,?)1 = 1,7.
3. а° = 1, а*0; 0° —не определено.	(13,01)° = 1; (a5b[3x)Q = 1.
4. а~п = —, а -ф- 0. ап	*—' 1 II 1 in  СП иТГс^ II cThZ II СП II СП
1
5. ап = nJa, а > 0; п > 2; п е N.
ап = "Ja"1, а > 0, п & N, п>2, т е Z.
6254 = 1/625 = 5
1 1
3/8 = 83 = (23)3 = 2
3
164 = 1/163 = 1/(23)4 = 23 = 8.
Свойства степеней
Ь 0, а Ф 0
b 0, а ф О
Степенная функция
Функция вида у = ха, где х — независимая переменная (аргумент), а а — любое действительное число, называется степенной функцией.
Свойства	функции у = ха (а =
у = х^к \ У1 ж i\ 1 V -1	(к е /V). /\ у 1 0	1	*х
1. Область определения.' при всех действителы	
	2. Облает
у > 0 (у — неотрицательное число).	
При х = 0 у =	3. Нули 0, то есть график фун
= п — натуральный показатель)	
у =	1 У -1 	Г" у I X [/ . 		  .	4	 ...	.	. . .	(к е N). / 1 0.1 -1
Функция у = хп определена ныхзначенияхх (хе/?).	
ъ значения.	
у е R (у — любое действительное число).	
функции. кции проходит через начало координат.	
4.	Интервалы знакопостоянства.
Функция положительная при х * 0.
При х > 0 функция положительная (у > 0).
При х < 0 функция отрицательная (j < 0).
5.	Четность и нечетность.
Функция четная, график ее симметричен Функция нечетная, график ее симметри-чен относительно начала координат.
относительно оси Оу.
6.	Интервалы возрастания и убывания функции.
При х < 0 функция убывает. При х > 0 функция возрастает.
Функция возрастает при х е R.
-
7.	Наибольшее и наименьшее значения функции.
Наименьшее значение у = 0 , при х = 0 ;| Функция не имеет ни наибольшего наибольшего значения не имеет.
наименьшего значений.
, ни
a — нецелое положительное число
у = ха (а > 0, а — нецелое) у
a — нецелое отрицательное число
у = ха (а < 0, а — нецелое)
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1.	Вынести множители из-под знака корня.
•	Представим множители подкоренного выражения в четвертой степени:
•	Извлечем корень четвертой степени из произведения и дроби и упростим полученное выражение:
так как^>0; а>0.
Ответ:
За
2.	Избавиться от иррациональности в знаменателе дроби.
Для этого можно использовать формулы сокращенного умножения применительно к корням. Домножим числитель и знаменатель на выражение, дополняющее знаменатель до разности квадратов:
Домножим числитель и знаменатель дроби на неполный квадрат суммы:
Ответ:
3.	Вычислить.
3) 1 = TS-2
7 75 + 2	(а/5 + 2)(75-2)
Решение.
п 632-272 = (63-27)(63 + 27) = 36
’	5	5	X
2) — • /36 • 18 = 12 • 6 _3 •	= 12 • 18 .
72
3) 1/12 -18 = 3/23 • З3 = 6.
Ответ:
4. Вычислить.
(4 77 - 7Й9 - 4 73 + 751 )(4 7? + JT19 + 4 л/3 + УЯ ) .
Решение.
1) Разложим на множители первую скобку:
= 4(77-Тз)-717(77-7з) = (4-717)(Т7 - Тз).
2) Разложим на множители вторую скобку:
3) Используем формулу разности квадратов:
= 4(77+ 73) +717(77+ 7з) =
= (4 + 717X 77 + 73).
3) (4-7П)(77 + 73)(Т7-73X4 + 717) =
= (42-(7й)2)((77)2-(7з)2) =
= (16-17X7-3) =-4.
Ответ:
5. Вычислить.
Решение.
Внесем множитель под корень:
(721 - 2) 725 + 2784 = 7(^1-2)2(25 + 2ТЙ) = = 7(25-4ТП)(25 +4721) = 7252 - (16 • 21) = = 7289 = 17.
Ответ:
17.
6. Упростить выражение.
Вычислить при т = 3 .
Решение.
1) Вынесем множители из-под знака корня и разложим выражение на множители:
т
2) Выполним деление:
Ответ:
При т = 3
~(т3 - 18) = -(27-18) = 6.
7. Упростить выражение.
Вычислить при а = 95 .
Решение.
Ответ:
0,9.
8. Построить график функции.
Найдем ОДЗ функции:
Найдем область определения функции:
Функция имеет значение при х = 3, у = ДЗ) = 0.
Ответ:
точка (3;0).
9. Построить график.
Найдем ОДЗ функции: Преобразуем функцию:
Построим график функции:
10. Построить график.
Найдем ОДЗ функции: Преобразуем функцию:
Построим график функции:
Иррациональные уравнения
Область определения иррациональных уравнений
Уравнение, в котором есть неизвестное под знаком корня или неизвестное имеет в степени дробь, называется иррациональным.
При решении таких уравнений необходимо помнить, что:
• в уравнении корни четной степени являются арифметическими, это значит, что значение корня неотрицательное, кроме этого, подкоренное выражение положительное;
• все корни нечетной степени определены для любого подкоренного выражения, причем значение корня имеет тот же знак, что и подкоренное выражение. Значит, решение иррациональных уравнений необходимо начинать с нахождения области определения уравнения, если в него входят корни четной степени.
Область определения иррационального уравнения — это множество всех действительных значений х, при которых одновременно имеют смысл выражения, входящие в уравнение.
Корни уравнения, не удовлетворяющие исходное уравнение, называются посторонними.
Для того чтобы исключить полученные в результате неравносильных преобразований посторонние корни, необходимо сделать проверку корней.
К появлению посторонних корней могут привести, но необязательно, такие преобразования, как возведение обеих частей уравнения, которые равны по абсолютным значениям, но могут отличаться знаком, в квадрат или в другую четную степень.
Обратите внимание, что формальное использование свойств корня
2”Jab = 2nJa2nJb или 2nfe = может W 2nJb
привести к сужению области определения уравнения в целом, что недопустимо.
1) Jx^3 = -2.
Jx-3 > 0 всегда, корней нет.
Ответ: 0.
х-4 = 49;
к	7
Ответ: 53.
Это уравнение решено методом равносильных преобразований, то есть с учетом области определения уравнения.
3) л/3 -х = *j2x + 1
3-х = 2х + 1
Зх = 2
2
3
- — корень уравнения.
Проверка: /3 - -
Ответ: |.
Это уравнение решено без учета области определения уравнения, поэтому сделана проверка полученного результата.
4) д/x + 5 = х - 1
Jx2-3x-4 = 0;
Ответ: 4. Уравнение решено методом равносильности .
Основные методы решения иррациональных уравнений
1.	Возведение обеих частей уравнения в степень и избавление от радикалов.
Решить уравнение 79-х = х + 3.
Решение.
Так как в уравнении слева корень четной степени, то 9-х>0=>х<9. Кроме того, правая часть уравнения должна быть положительной, поскольку слева имеем арифметический корень. Значит, х + 3>0=>х>-3 и тогда область значений переменной такая: х е [—3 ;9]. Возведем в квадрат обе части уравнения:
9-х = (х + З)2 => х2 + 6х + 9 + х-9 = х(х + 7) = 0 =i> х, - 0; х2 = -7 ,
но х2 = -7 g [-3 ;9]. Значит, уравнение имеет только один корень х = 0.
Ответ: х = 0.
2.	Отделение квадратного корня используется в тех случаях, когда это упрощает решение уравнения.
Решить уравнение 7* + 2 + 73 -х = 3.
Решение.	“
Область определения уравнения
5
5
1
Отделим один квадратный корень: Тх + 2 = 3 - 73 -х.
Возведем обе части уравнения в квадрат:
х + 2 = 9-673 -х + 3 - х => 5 - х = 37з-х. Еще раз возведем в квадрат:
25-	10х + х2 = 9(3-х) =>х2-х-2 = 0=>Xj = -I; х2 = 2. Оба корня принадлежат области определения уравнения, но убедиться в том, что эти решения являются корнями уравнения, можно и проверкой.
Ответ: Xj = -1; х2 = 2.
3.	Отделение кубического корня.
Решить уравнение 37х- 1 + \]х-2 - 372х - 3 = 0.
Решение.
Областью определения уравнения являются все действительные числа. Отделим один из корней и возведем обе части уравнения в куб:
З37(х - 1 )(х - 2)(37(х — 1) 4- V(x - 2» = О

Возведем еще раз в куб: х- 1 = -(х - 2) => 2х - 1 - 2 = 0; 2х = 3, х = |.
Ответ: х = 1, 5.
4.	Введение новой переменной.	-
Один из распространенных способов, используемый для решения иррациональных и других уравнений, — введение новой переменной. По этому способу определенное выражение, входящее в уравнение и содержащее неизвестное, для упрощения решения обозначают одной буквой, и сначала решают полученное уравнение относительно новой переменной. Например, решение уравнения 7х2 - 6х + 9 + 7х2-6х + 18 = 9 значительно упрощается, если х2-6х + 9 обозначить, например, через 'у. х2-6х + 9) =^)>0. Тогда х2-6х+18 = у + 9, и данное уравнение приобретает вид Jy + Jy + 9 = 9. Решив его известным способом, получим у = 16. Вернемся теперь к осуществленной подстановке.
6х 7
Имеем: х2-6х + 9 = 16;х2--------- 0; Х| = -1, х2 = 7. Оба корня удовлетворяют
начальному уравнению.
Иррациональные неравенства
Иррациональными называют неравенства, у которых переменная стоит под знаком радикала, причем рассматриваются только арифметические корни, если корень четной степени.
Основным методом решения иррациональных неравенств является метод приведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. Но необходимо помнить.
1.	Возведение обеих частей неравенства в нечетную степень с сохранением знака неравенства всегда является равносильным преобразованием.
2.	Если обе части неравенства на некотором множестве X определены и имеют только положительные значения, то можно возвести обе части неравенства в квадрат или другую четную степень с сохранением знака исходного неравенства, поскольку получим неравенство, равносильное исходному на множестве X.
3.	Для иррациональных неравенств вида
2tljf(x) < q(x) > где q(x) < 0, возводить в четную степень обе части неравенства нельзя. Необходимо учитывать дополнительные условия.
Приведем методы решения простейших иррациональных неравенств:
1) 2” +	< q(x) о/(х) < q2n + 1 (х);
2) 2" + к/Дх) > q(x) «>/(х) > q2" + 1 (х) ;
f/(x) > о,
3)	< ЯМ < q(x) > О,
Л*)<?2"(*);
4) 2nJf{x) > q(x)
jq(x)<0,
f^(x)>0, Дх) > q2n(x).
Примечание. Чтобы избежать ошибок при решении неравенств общего вида, необходимо прежде всего найти область определения исходного неравенства, а потом осуществлять равносильный переход на области определения или на ее части.
1) Jx^5>3.
Решение.
Ответ: (14;+оо).
2) ,/х-5 > -3 .
Решение.
х — любое число из области определения, то есть:
х- 5 > 0
х > 5.
Ответ: [5;+оо).
3) Jx^5 < 3 .
Решение.
Необходимо учесть область определения.
х < 14;
5 <х< 14.
Ответ: [5; 14).
4)- Jx^5 <-3 .
Решение.
7х-5 > 0 всегда, тогда неравенство решений не имеет.
Ответ: 0.
5. V* - 5 < -3 . Решение.
х - 5 < -27
х < -22.
Ответ: (-<ю;-22).
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1.	Решить уравнение.
Решение.
Найдем область определения уравнения: для этого предположим, что все подкоренные выражения больше или равны нулю:
5
Зйачит, область определения состоит только из одной точки х = 2. Проверим, будет ли это значение решением исходного уравнения: 711-2 + 3 - J2^2 - 79-2 + 7 + Т2--2 = J25-J25 = 0.
Как видим, х = 2 — решение исходного уравнения.
Ответ:	V2.
2.	Решить уравнение.	= 0
Решение.
Найдем область определения уравнения:
Значит, общих точек нет и исходное уравнение не имеет решения.
Ответ:
3.	Решить уравнение.
Решение.
Область определения уравнения
5
Если проанализировать уравнение, то два положительных выражения в сумме не могут равняться нулю, значит, корень х е 0.
Ответ:
4.	Решить уравнение. * 1
; оо . Уединим квадрат-
Решение.
Область определения уравнения 1 + 5х>0=>х>-
ный корень: 71 + 5х = 1 - х. Допустим, что 1 - х > 0 => х < 1; тогда область определения г 1 1 •
такая: хе --;1 . Возведем в квадрат обе части уравнения:
1 + 5х = 1-2х + х2=>х2-7х = 0=>Xj = 0; х2 = 7. Поскольку возводили в квадрат, то могут появиться посторонние корни, и поэтому надо сделать проверку или выбрать корни, принадлежащие области определения.Проверка:
1) х = 0, 1-71=0=>х = 0 — корень;
2) х = 7, 1 - 71 +35 + 7 =>х = 7 — не является корнем уравнения.
5. Решить уравнение.
Зх + 2 + х2 — 4х - 4 .
Решение.
Запишем уравнение в виде 7х2 - Зх + 2 = -(х - 2)2.
Слева л/х2 - 2х + 2 > 0, справа — (х - 2)2 < О. Очевидно, решение возможно только при х = 2. Значение х = 2 превращает уравнение в тождество.
Ответ:	ПТ
Решить уравнение.
1) Для решения иррациональных уравнений можно пользоваться методом рассуждений в общем виде. Например: 2'i//(x) = ф(х) Заменим уравнение равносильной ему системой:
/(х)>0
s ф(х) > О
(1)
(1)
/(’х) = (р2”(х)
2) Решим систему (1):
Ответ:
Решить уравнение.
1) Пользуясь определением арифметического корня, запишем данное уравнение в виде
|/(х)| = ф(х):
Данное уравнение равносильного совокуп-
ности двух систем: [Дх)| = ф(х) <=>
f ф(х) > О, 1Лх) = 0;
Гф(х)>0, Дх) = ф(х)
,х -5х + 6 = 2-х;
f2-x>0,
Решить уравнение вида nJf{x) = V<p(x) 
1. а) Если п = 2к-\, то данное уравнение запишем в виде Дх) = >-(х);
б) если и = 2к, то данное уравнение заменим равносильной ему системой:
Дх) > 0;
1 (р(х) >0;
= ф(х).
2. Решим уравнение (1) или систему (2).
В данном уравнении п = 2, поэтому имеем случай б):
В данном случае удобно решить уравнение Дх) = у(х) и выполнить проверку:
х2-Зх-4 = х2-5х + 6; х = 5.
Проверка:
Ответ:
Решить уравнение.
1) Введем новую переменную:
лДх2 - 8х + 12 = х2 - 4х - 6.
-8х+12 = -(2х2-8х+ 12)- 12;
2)	Найдем значение новой переменной, решив полученное уравнение (1):
3)	Вернемся к исходному неизвестному:
4)	Решим полученные уравнения (2) и (3):
У *]1х2 8х + 12 , у = ^у2- 12; у2-1у-1А = 0.
У1 = 6’ У2 = ~4’ ‘72х2-8х+ 12 = 6;	(3)
.( 72х2-8х+ 12 = -1) (2), корней нет. л/2х2 - 8х + 12 = 6;
2х2 - 8х + 12 > 0;
.2х2-8х+ 12 = 36;
2х2 - 8х + 12 > 0 всегда;
(D<0, а = 2>0)) х2 - 4х- 12 = 0;
Решение иррациональных неравенств вида 2nJ(f(x))2n £ g(x)
Решить неравенство.
1)	Пользуясь определением арифметического корня, запишем данное неравенство в виде	g(x):
*
2)	Рассмотрим случай, когда выражение, стоящее под знаком модуля, неотрицательное:
(1) g(x)
3)	Решим систему (1):
4)	Рассмотрим случай, когда выражение, ящее под знаком модуля, отрицательное:
Дх) < 0
g(x)
5)	Решим систему (2):
6)	Запишем ответ, объединив результаты, полученные в п.З и п.5.
Ответ:
Решить неравенство.
сто-
2 или х
1. а) Если п = 2к— 1, то данное неравенство (1) запишем в виде Дх) > g(^xy, б) если п = 2к, то данное неравенство заменим равносильной ему системой:
В данном примере п = 2, поэтому имеем случай б):
1
Ж>0;
/(*) > 0;
(1)
2. Решим неравенство (1) или (2).
2х< 10.
3. Запишем ответ:
Решение иррациональных неравенств вида	< g(x)
Решить иррациональное неравенство.
1) Заменим неравенство равносильной системой:
(1)
<g(x)>0	(1)
Лх) < ё2п(х)
2) Решим систему (1):
Lx>0;	0<х<4
3) Запишем ответ:
0<х<4
Решение иррациональных неравенств вида 2'7?(х) > g(x)
Решить иррациональное неравенство.
1) Рассмотрим случай, когда Дх)>0 и g(x) > 0:
Дх)>0
<g(x)>0	(1)
Лх) > s2n(x)
2) Решим систему (1):
(2)
3) Рассмотрим случай, когда /(х)>0 и
g(x) < 0:
|g(x) < 0
(2)
4-х>0;
х + 2 < 0.
х < -2
4) Решим систему (2):

5) Запишем ответы, объединив результаты, полученные в п.2 и п.4:
Ответ:
(-оо;-2) U (—2 ;0).
Решение иррациональных неравенств вида Jf{x) + b > bf^ + c
Решить иррациональное неравенство.
1)	Введем новую переменную:
2)	Найдем значение новой переменной, решив неравенство (1):
3)	Вернемся к начальной неизвестной:
4)	Решим полученные неравенства (2), (3):
5)	Запишем ответ:
л/2х2 — 8х + 12 < х2 - 4х - 6 .
^2х2-8х+ 12 < 1(2х2 - 8х + 12) - 12
у = 72х2 - 8х + 12;
У < |у2 “ 12.
у2-2^-24>0 (1)
у2 - 2у - 24 > 0 у < -4, у > 6 .
л/2х2 - 8х + 12 < -4 (2), решений нет.
л/2х2-8х + 12 >6 (3).
2х2-8х+12>0 fx2-4x + 6>0 12х2-8х- 12 >36 1х2-4х-12>0 х2 - 4х + 6 > 0 — всегда, х2-4х-12>0; х<-2, х>6.
х < -2 или х > 6.
СТРАНИЧКА АБИТУРИЕНТА .
Способы приведения иррациональных уравнений к рациональным
Уравнения вида nJf(x) = mJg(x)
Обе части возведем в степень к = НСК (п, т) — наименьшее общее кратное чисел п и т.
1. Решить уравнение.	/9 . = а _ v
Решение.
1-й способ. Возведем обе части уравнения в квадрат.
2х + 3 = 36-12х + х2, х2-14х + 33 = 0, х{ = 3, х2 = И. Сделаем проверку и убедимся, что х = 11 — посторонний корень, а х = 3 удовлетворяет уравнению.
2-й способ. Исходное уравнение равносильно системе
5
J

5
Последняя система имеет единственный корень х = 3 .
Ответ:
2. Решить уравнение.
Решение.
Возводим обе части уравнения в степень 6 = НСК (2,3).
(х-1)3 = (х + 3)2, х3-4х2-Зх-10 = 0. Подбором находим xt = 5. Дальше х3-4х2-Зх-10 = (х-5)(х2+х + 2). Уравнение х2+х + 2 = 0 корней не имеет. Проверкой убеждаемся, что х = 5 — корень заданного уравнения.
Уравнения вида J/(x) ± */g(x	) = й(х) (или =Jh(x))
3. Решить уравнение.	Jx + 2 + л/Зх -2 = 4.
Решение.
Возводим обе части уравнения в квадрат.
Снова возводим в квадрат Зх2 + 4х - 4 = 64 - 32х + 4х2, х2 - 36х + 68 = 0. Находим X) = 2, х2 = 34. Проверкой убеждаемся, что только значение х = 2 удовлетворяет исходному уравнению (для х = 34 при повторном возведении в квадрат было нарушено правило совпадения знаков).
Ответ:
4.	Решить уравнение.
Решение.
Возводим обе части уравнения в квадрат:
"У"''	" 'V	* * ^5
4(25-х2) - (И — х)2, 5х2-22х + 21 = 0. Имеем Xj = 3, х2 = 1,4.
Корень Xj = 3 удовлетворяет исходному уравнению. Проверка корня х2 = 1,4 затруднена. Но он удовлетворяет ОДЗ, и в процессе решения не было нарушено правило совпадения знаков обеих частей уравнения при возведении в квадрат.
Вывод: х =1,4 —тоже корень.
Ответ:
Уравнения вида 37/(x) ± Vg(*) = /г(х) или 37/(х) ± VgW = 3Jh(x)
При решении уравнений такого вида необходимо возвести обе части в куб по формуле (Va±Vd)3 = а ± b ± 3\[аЬ(\fa ± \[b) и для выражения, стоящего в правой части этой формулы в скобках, использовать условие исходного уравнения. Необходимо отметить, что иррациональное уравнение, возникающее при этом, не равносильно заданному. Оно следует из исходного уравнения, но исходное уравнение не всегда является следствием этого уравнения. Поэтому рациональное уравнение, которое появляется, может иметь посторонние корни, и проверка заданного иррационального уравнения обязательна.
5.	Решить уравнение.
Решение.
После возведения обеих частей уравнения в куб получим:
Имеем: 37(8-х)(х + 1) = 2 или х2-7х = 0, откуда xt = 0, х2 = 7.
Проверкой убеждаемся, что оба корня превращают заданное уравнение в тождество.
Ответ:
6.	Решить уравнение.
Решение.
Возведение в куб обеих частей дает:
Зх + 24 - 2х - 6 - 3 З7(3х + 24)(2х + 6)(373х + 24 - Ц2х + 6) =
Используя заданное условие, после преобразований получаем:
V(3x + 24)(2х + 6)х = 6 или х3 + 11х2 + 24х-36 = 0. Выделяя в кубическом уравнении целые корни, находим X, = 1, х2 3 =-6. Проверкой исходного уравнения убеждаемся,
что значение х = -6 является посторонним корнем.
Ответ:
Метод введения новых переменных
7.	Решить уравнение.
374х + 48 - Зл/4х - 17 = 5 .
Решение.
Обозначим 3«/4х - 17 = у, тогда 4х = у3 + 17. Уравнение приобретает вид \1у3 + 65 = 5 + у, откуда _у2 + 5у + 4 = 0. Корни этого уравнения = -1, у2 = -4. Возвращаясь к
подстановке, находим Xj = 4,
47
Ответ:
47
Метод приведения иррационального уравнения к системе уравнений
8.	Решить уравнение.
34х + 7 + V28 -х = 5 .
Решение.	7
Обозначим 37х + 7 = a, 3j28 - х = Ь , тогда, по условию, а + b = 5. Кроме того,
а3 + Ь3 = х + 7 + 28 -х = 35. Получаем систему уравнений:
а3 + Ь3 = 35	f(а + b)3 - ЗаЬ(а + Ь) = 35 аЬ = 6
[а + 6 = 5	ка + Ь = 5	а + b = 5
Находим два корня а1 = 2, Ь1 = 3; а2 = 3, Ь2 = 2. Возвращаясь к подстановке
х = а3-7 или х = 28 - Ь3, получаем: х{ = 1, х2 = 20.
Ответ:
9.	Решить уравнение.
Пусть 8 - х = а4 И 89 + х =
1; 20.
Решение.
Ь4. Получаем систему уравнений:
(а + b = 5 [а4 + Ь4 =
97.
2 2
Поскольку а4 + b4 = (а2 + 62)2 - 2а b = ((а + b}2 - 2аЬ)2 - 2а2Ь2, то получим уравнение
(25 - 2аЬ)2 - 2а2Ь2 = 97, откуда ab = 6 или ab = 44
то есть <
а + Ъ - 5 ab = 6
или <
ab = 44.
Вторая система не совместима, первая система имеет два корня: а = 2; Ь = 3 или
а = 3; b = 2. Итак, х = -8 или х = -73.
Ответ:
-8; -73.
Метод выделения полного квадрата
Для использования этого метода надо знать формулы сокращенного умножения и формулу «сложного радикала».
10. Решить уравнение.
х + 2 + з72х-5 - 7л/2.
Решение.
Сделаем подстановку 72х- 5 = у > 0.
Тогда х =
При у > 0 имеем: j+1+^ + З = 14, у = 5. Решив уравнение 72*-5 = 5, находим
Ответ:
11. Решить уравнение.
15.
Решение.
Выделим полный квадрат в подкоренных выражениях:
Имеем:
Значит, заданное уравнение равносильно уравнению: 7* - 1 - 2 + 7* - 1 - 3 = 1. Решим его методом интервалов:
5

с = 10;
5
5
Ответ:
Иррациональные уравнения с параметрами
12. Решить уравнение.
х-а = 2х- 1, где а — параметр.
Решение.
Заданное уравнение равносильно системе:
Корни квадратного уравнения
5-79- 16а
--------- являются
9
действительными числами при а <	. При а > корней нет.
Учтем неравенства х > а и х > -:
5 + A-Jfo > а, 79- 16а > 8а-5.
Если а< —, то 8а-5<0 и неравенство 79- 16а > 8а-5 верно для всех допустимых 16 о	9
значении а. Значит, х, является корнем исходного уравнения при а < —. 16
2) х2 =	16д >1 79- 16а < 1, а>- (а < —Y
2	8	2	2 <	16>
Если - < а < —, то 5~ V9 ~ 16g > а.
2	16	8
Итак, х2 является корнем исходного уравнения при - < а < —.
2	16
Ответ: — j-~16-, если а <	~ ^9~ 16- , если - < а < —; 0, если а > — .
8	2	8	2	16	16
13. Решить уравнение.	г—; , /т—; _ „ гпо „
*jx — 1 + —х — а, где а — параметр.
Решение.
Очевидно, а>0. Обозначим Jx-1 = Ь, 75-х = с. Тогда приходим к системе уравнений:
Так как а > 0 и по смыслу b > 0, с > 0, то необходимо а > 2 . Из последней системы находим:
Очевидно, допустимое множество значений параметра а имеет вид 2<а<78. Возвращаясь к подстановке х = b2 + 1 или х = 5 - с2, определяем корни уравнения. Имеем при 2 < а < 78:
Подставляя значения х, (или х2) в исходное уравнение, можно получить тождество:
Ответ: 3 ± ^78-а2, если 2 < а < 78; 0, если а < 2 или а > 78.
Иррациональные неравенства
Напомним, что решение иррациональных неравенств сводится к решению равносильной
совокупности систем рациональных уравнений.
[/(х) > О
/(х) > О
ЕСЛИ 7/W < q(x), ТО <! q(x) > О
ЕСЛИ 7/(х) >	, ТО ( q(x) > О
f(x) > о
Дх) < (?(х))2.
Дх) > (<7(х))2
^(х)<0.
или <
14. Решить неравенство.
 _ --- 1 ___ - - _ - -
Решение.
Данное неравенство равносильно совокупности двух систем:
2х — 8 < 0;
х2 - 5х + 4 > 0;
х2 - 5х + 4 > (2х - 8)2.
Ответ:	(-°°;1 ]	u(4;5).
15. Решить неравенство.	J2x - 1 - Jx - 1 < J 6 - х.	
Решение.
1)	Запишем неравенство в виде: 72х- 1 < Jx- 1 + j6-x.
2)	Учитывая область определения, имеем равносильное неравенство:
2х - 1 < х - 1 + 2 J(x - 1 )(6 - х) + 6 - х,
J(x- 1)(6-х) > х - 3.
3)	Полученное неравенство равносильно совокупности двух систем:
(х - 1 )(6 -х) > (х - З)2.
2х2- 13х+ 15 <0.
=> 1 <х < 5.
Ответ:
16. Решить неравенство.
Решение.
1) Введем новую переменную: Jx-4 = у > 0, тогда х = у2 + 4.
2) Неравенство принимает вид: Jy2 + 4у + 4 - Jy2 -4у +4 > 3. |у + 2| - ly -2j > 3 .
При у £ 2, имеем у + 2-у + 2>3', 4 > 3.
Неравенство верно для всех у > 2;
При 0<у<2,
При - <у < 2 неравенство верно, значит, |у + 2| - |у- 2| > 3 верно при у >
Вернемся к переменной х: Jx-4 >
Ответ:
25
17. Решить неравенство.
8 + 2х + х — 4 > 16-х2 х + 1 X - 1 J х2 _ 1
Решение.
Находим ОДЗ для функции, стоящей под знаком корня:
Рассмотрим каждый из полученных промежутков отдельно.
Q 2 у
1) 1 < х < 4. На этом промежутке 2-> О,
х + 1
Тогда исходное неравенство принимает вид 2а2-b2-ab>0.
Так как а* 0, то разделим неравенство на а2. Получим z2 + z-2<0, где z = ->0. а
Решая полученное неравенство, находим -2 < z < 1. Приходим к двойному нера-
венству 0 <
, которое на промежутке 1 < х < 4
равносильно системе
неравенств:
Решением последней системы является множество 2 < х < 4.
Q
2) -4 < х < -1. На этом промежутке---< О,
х + 1
Пусть =	=
N х+ I ух — 1
Тогда исходное неравенство принимает вид - 2а2 + b2-ab>0. Так как Ь * 0, то разделим неравенство на Ъ2. Имеем: 2z2 + z- 1 < 0, где z = у > 0. Находим -1 < z < -.
и	2
Полученное двойное неравенство 0< р—% •	1 < 1 на промежутке -4<х<-1
л/ х + 1 4 - х 2
равносильно системе неравенств:
Решением последней системы является множество
~ /.-9- 7481Y
10	> '
Ответ:
и(2;4].
I
Иррациональные неравенства с параметром
18, Решить неравенство.
Ja2 + х2 >х + а - 1, где а — параметр.
Решение.
При любом значении а, если правая часть х + а- 1 <0, то есть х< 1 - а, заданное
неравенство верно. При х > 1 - а равносильная система неравенств имеет вид:
Рассмотрим возможные случаи.
<2а- 1.
(1)
П __ 1
1)	а > 1, тогда 1 - а < х < --. Объединяя с множеством х <
2а-2
1 - а, получаем х
2а- 1
2а-2
2)	а = 1. х > 0 — решение системы (1). Объединяя со множеством х < 1 - а (а = 1), находим: х —любое число.
3)	а < 1. Решение системы (1) х > 1 - а. Присоединив х < 1 - а, имеем: х — любое число.
Ответ:
1; (—оо;+оо), если а< 1 .
19. Решить неравенство.
х - <7 > Jx + a2, где а — параметр.
Решение.
Данное неравенство равносильно системе неравенств:
Определим расположение на числовой оси точек -а2, а, 2а + 1 и 0 в зависимости от
значения параметра а. Некоторые-из этих точек могут совпадать при а = -1; и 0.
Поэтому необходимо исследовать четыре промежутка.
1)	Пусть а <-1. Тогда нетрудно установить, что расположение точек такое:
Решением системы (1) является множество х > 0.
3) Пусть —5- < а < 0. Тогда:
4) Пусть а > 0. Тогда:	о
Ответ: (0;+<ю), если а <-1; [~а2;2а + 1) о (0;+оо), если -1 < а <	[-а2;0) и(2а+1;+оо), если--<<7<0; (2а + 1;+оо), если а > 0.
20.	Построить график функции.
1)	Найдем область определения функции: D(y) = [ 1 ;+оо).
2)	Преобразуем подкоренное выражение:
Если а/х + 1 > Jx—\, то у = 7* + 1 - л/т-1 + -Ух - 1, у - -Ух + 1
3)	Построим график функции:
21.	Построить график функции.
1) Область определения функции: D(y) = (0;+оо).
2) Упростим выражение, задающее функцию:
3) Построим график:
если х е (0; 1 ]
если х> 1.
§5. Показательная функция. Показательные уравнения и неравенства
Показательная функция
Свойства
Функция у = ах.
1)	Область определения D(y).
х <=R-, D(y) = R.
2)	Множество значений Е(у).
у>0‘, Е(у) = (0;+оо).
у>0; Е(у) = (0;+<х>). р
Показательная функция приобретает только положительные значения
и все г,
График не пересекает ось Ох.
3)	Значения у для х = 0.
4)	Значения у
График пересекает ось Оу в точке (0; 1).
для х > 0.
0 < ах < 1, при х > 0.
а
5)Значения у для х < 0.
6) Монотонность.
х<0; 0<у< 1.
0 < ах < 1, при х < 0.
Возрастает на всей числовой прямой (большему показателю соответствует большая степень).
х < 0; у > 1. ах > 1, при х < 0.
Убывает на всей числовой прямой (большему показателю соответствует меньшая степень).
Следствие. Если две степени одного и того же положительного числа, отличного от 1,
равны, то равны и их показатели. Если аь = ас, то b = с.
Основные показательные тождества
Показательные уравнения и неравенства
Уравнения (неравенства), в которых неизвестное входит в 'показатель степени, называются показательными.
Например: 2х-3 = 32; 5* "1 > 1.
Простейшие показательные уравнения (неравенства) — это уравнения (нера-
венства) вида: ах = Ь\ ах >Ь; а <Ь \ а > 0; а * 1; b > 0.
Решение простейших показательных уравнений (неравенств)
Я*) = £(*)
/(х) > g(x)
Ях) < g(x)
приравниваем показатели при разных основаниях
знак неравенства не изменяется
знак неравенства изменяется на противоположный
Общего способа решения таких уравнений (неравенств) не существует. Рассмотрим некоторые типы и способы решения показательных уравнений (неравенств).
I.	Простейшие и те, которые приводятся к ним следующим путем:
а)	приведение к одному основанию;
б)	вынесение общего множителя за скобки;
в)	деление обеих частей на степень.
II.	Показательные уравнения (неравенства), приводимые к алгебраическим:
а)	приведение к квадратному путем замены;
б)	однородные.
III.	«Нестандартные» показательные уравнения (неравенства).
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Построение графиков показательных функций
1.	Построить график функции у = -2х.
Решение.
Сначала построим график функции у = 2х, потом симметрично отобразим его относительно оси Оу.
График функции у = -2х на рис.1.
2.	Построить график функции у = 2|х|. Решение.
Для х > 0 строим график у = 2х.
Симметрично отображаем его относительно оси Оу.
Объединение этих графиков и будет искомым графиком.
График функции у = 2^ на рис.2.
3.	Построить график функции у = 3 х-1
Решение.
Пусть х - 1 > 0, тогда у = 3 х-1
• 3 х. Г рафик функции у
при
х> 1 изображен на рис.З.
Пусть х- 1 < 0, тогда у = 3lx~Ч = 3“(х-1> = 3~х+1
Здесь
График функции у = 3 •
при х < 1 изображен на рис.4
(при х = 0 у = 3
= 3). График функции у = з!х-11 изображен на рис.5.
Решение показательных уравнений
1. Решить уравнение.	7х-1 = 49.	7х-1 = 1.	7Х~’ = -7.	7х”1 = 0.	7х = 14.
Решение.	7х-1 = 72; х — 1 =2; х = 3.	7х-1 = 70. х — 1 =0; х = 1.	Функция у - 7f приобретает только положительные значения, поэтому уравнение не имеет корней.		х = /og714. и
Ответ:	х = 3.		хе 0.		х = 7og714.
дх
О
2. Решить неравенство. Решение.
х — любое число.
веющая функция.
для всех
возрастающая функция.
О
неравенство не имеет решений, поскольку 4' > 0 для всех х е R.
Ответ:
Приведение показательных уравнений (неравенств) к простейшим путем приведения к общему основанию
1. Решить уравнение.
	Решение.
Приведем обе части уравнения к основанию 5:
10
0, 04 =	= 5~2.
100	25
Уравняем показатели степеней при разных основаниях:
Решим полученное уравнение:
Запишем ответ.
Ответ: 2.
2. Решить неравенство.
Решение.
Приведем обе части неравенства к общему основанию:
Установим, является ли функция с данным основанием возрастающей или убывающей: Учитывая монотонность функции с данным основанием, составим неравенство из показателей степеней:
Решим полученное неравенство:
13
возрастающая.
Запишем ответ.
Ответ: —; + оо .
Приведение показательных уравнений (неравенств) к простейшим путем вынесения общего множителя за скобки
Показательные уравнения (неравенства) вида
Ао • атх +к° + Ах  атх + к{ + ... + Ап  атх +кп = М
Ао  атх + к° + А\ • атх + к1 + ... +А„- атх + к" % М приводятся к простейшим путем вынесения за скобки общего множителя атх + к‘, где kt — наименьшее из чисел к0, кх, к2...кп.
При делении степеней с одинаковыми основаниями основание остается неизменным, а показатели — вычитаются.
х-5-(х-8) = ох-5-х+8 — оЗ —
1. Решить уравнение.
1 = 20.
Решение.
Вынесем за скобки общий множитель (множитель с наименьшим из наличных показателей):
237^-1(2 + 3) = 20.
Выполним действия в скобках:
23^-1 . 5 = 20.
Разделим левую и правую части уравнения на выражение в скобках:
Приведем к одному основанию:
Уравняем показатели и решим полученное уравнение:
Запишем ответ.
Ответ: 1.
2. Решить неравенство.
3 • 4х + 2 • 4х+1 + 3 • 4х + 2 < 236 .
Решение.
Вынесем общий множитель за скобки:
4Х(3 + 2 • 4 + 3 • 42) < 236.
Выполним действие в скобках:
4х • 59 < 236.
Разделим левую и правую части неравенства на 59:
Решим полученное неравенство (помня о монотонности функции с данным основанием):
Запишем ответ.
4х <4
4 > 1, у = 4х — возрастающая.
х< 1.
Ответ: (—со; 1 ].
Приведение показательных уравнений (неравенств) к простейшим путем деления левой и правой частей на одну из степеней
Показательные уравнения (неравенства) вида апх = Ьпх апх ё* (а*Ь) приводятся к
простейшим путем деления обеих частей на Ьпх или апх (Ьпх 0; апх * 0).
1. Решить уравнение.
Решение.
Разделим обе части уравнения на 3 х2 -z 0:
Приведем обе части к одному основанию, используя свойства:
Приравняем показатели и решим полученное х-2 = 0;
уравнение:	= 2
Запишем ответ:	Ответ: 2
2. Решить неравенство.	— 5^-3 < 73-
Решение.
Домножим обе части неравенства на 7х-3 > 0: Приведем к одному основанию: ах  Ьх = (а  Ь)х, а° - 1 .
.ух-3 < 7З-х.ух-3
35х"3<7°;
35х-3<1;
35х"3
<35°.
Решим показательное неравенство:
Запишем ответ.
35 > 1, у = 35г — возрастающая.
х-3 <0;
х < 3.
Ответ: (—оо;3).
Приведение показательных уравнений (неравенств) к квадратным путем введения новой переменной
Показательные уравнения (неравенства) вида Аа2х + Вах + С = 0 (Аа2х + Вах + С I 0)
приводятся к квадратным путем замены ах = t, / > 0 (показательная функция приобретает только положительные значения).
ах + У = ах • аУ
Справедливы следующие свойства степеней: ах~у = —
аУ
ахУ = (ах)У = (аУ)х
Решить уравнение.
Решение.
Выполнив тождественные преобразования, приведем уравнение к квадратному:
Сделаем замену:
Замена Зх+2 = t, t > О тогда 32х + 4 = г2.
Решим полученное квадратное уравнение относительно t:
3t2-t-2 = 0;
~ 1;	=	— не удовлетворяет условию
Вернемся к замене и решим показательное уравнение:
Запишем ответ.
г>0.
3-V + 2 = 1; х + 2 = 0; х = -2.
Ответ: -2.
Решить неравенство.
Решение.
Преобразуем левую часть неравенства:
Сделаем замену:
Решим полученное неравенство, учитывая, что t>0:
t2- 3r + 2<0;
Ь>0,
Вернемся к замене и решим показательное неравенство:
Запишем ответ.
(г-1)(г-2) <0; \>0,
1<t<2.
2 > 1; у = 2х
возрастающая.
Ответ: [0;1].
Приведение показательных уравнений (неравенств) к квадратным путем почленного деления на одну из степеней
Показательные уравнения (неравенства) вида Аа2х + В(а -Ь)х + С  Ь2х = О
( Аа2х + В(а • b)x + С- Ь2х< 0) являются однородными. Решаются такие уравнения (неравенства) почленным делением, как правило, или на а2х^0, или на Ь2х*0
(я2х>0; Z?2x>0).
Решить уравнение.
3 • 16х + 2-81х = 5 -36х. р g
Решение.
Запишем уравнение так:
Разделим обе части на 42х * 0: д2х	2х
4^ ~ Ч? ’
3 -42х + 2-92х-5 • (4 • 9)х = 0.
уравнения
Сделаем замену:
(4 • 9)х = 4х • 9х
42%	4*. 4х
t>0.
Решим полученное квадратное уравнение:
It2 — St + 3 = 0;
Вернемся к замене и решим совокупность показательных уравнений:
Запишем ответ.
Ответ: 0; -.
2
Решить неравенство.
ПИ.	,	,	
2 • 4х > 6х + 3 • 9х
Решение.
Запишем неравенство в виде:
Разделим обе части неравенства на 32х> 0 :
Сделаем замену:
Решим полученное неравенство, учитывая, что г>0:
/>0;
[2г2-г-3 £0.
Вернемся к замене и решим показательное неравенство:
— убывающая функция.
Запишем ответ.
Ответ: (-со;-1 ].
Преобразование уравнения к виду f(x) = g(x), где в одной части — возрастающая функция, в другой — убывающая.
У такого уравнения если есть корень, то он единственный. Единственный корень можно найти подбором, или доказать, что уравнение не имеет решений.
Решить уравнение.
Решение.
Разделим обе части уравнения на 7х * 0:
Функция у =
— убывающая;
х = 1 — единственный корень.
у = 1 — постоянная.
Графики этих функций пересекаются не более чем в одной точке.
Запишем ответ.
Ответ: 1.
СТРАНИЧКА АБИТУРИЕНТА
1. Решить уравнение.
2* * х + 2 х = 2 cos 2х.
Решение.
Оценим левую и правую части уравнения:
2cos2x < 2.
Заменим уравнение равносильной системой:

2cos2x = 2.
Решим первое уравнение системы:
2х = у; у + ^ = 2; у2-2у+ 1 = 0;
Проверим, удовлетворяет ли корень х = 0 второму уравнению системы:
2cos2 -0 = 2;
Значит, х = 0 — решение системы значит, и данного уравнения.
Ответ:
2. Решить уравнение.
Решение.
Сделаем замену:
Уравнение приобретет вид:
Решим полученное уравнение как квадратное относительно у:
Зу2 + (Зх- 10)^ +3-х = 0.
= -Зх+ 10 ± 7(3х- 10)2 - 12(3-х) 6
- Зх + 10 ± л/9х2 - 48х + 64 _
6
- Зх + 10 + (Зх - 8)
6
У1 = 3-х или у =
Вернемся к замене:
2х = 3-х левая часть уравнения — воз-
растающая функция, правая — убывающая;
х = 1 — единственный корень.
--- .. . --
Ответ:
3. Решить уравнение.
Решение.
Это уравнение показательно-степенное. Для нахождения его корней надо рассмотреть четыре случая.
1)	х + 1 = 1 (основание равно 1), откуда х = 0. Проверка I-4 = I2; 1 = 1
х = 0 — корень.
2)	х + 1 = -1 (основание равно -1), откуда х = -2; (-1)-2 = (-1)2
х = -2 — корень.
3)	х + 1 =0 (основание равно 0), откуда х = -1. Выражение О-4 не имеет смысла,
х = -1 не является коренем.
4)	х2+х-4 = 2 (показатели равны), Xj =2; х2 = -3. Проверкой убеждаемся, что 2; - 3— корни данного уравнения.
Ответ:	1-3; -2; 0; 2.
4. Решить неравенство.	(х - 2)х2 ~6х + 8 > 1
Решение.
Данное неравенство равносильно совокупности двух систем. Решим каждую из систем.
0<х-2< 1;
[х2 - 6х + 8 < 0.
хе(2;3)и(4; +оо).
Ответ:
(2;3) U (4; + оо).
5. Решить неравенство.
Решение.
Сделаем замену Iх = у.
Данное неравенство равносильно системе неравенств:
Ь-4>0;
V2-6y > 0;
=> v(j- 6)>0;
j2-6y<(y-4)2.
у2-6у<у2-8у + 16.
<j(j-6)>0;
j<8.
\?У< 16.
6<у<8.
Вернемся к замене:
6<2*<8, 2> 1; у = 2х — возрастающая функция log26<x<3.
Ответ:
[/og26;3).
6. Решить неравенство.
Решение.
Разделим обе части неравенства на5х>0:
f
Рассмотрим функцию
/3\ х /д\ X
Дх) = 1-1 + 1-1 - 1, которая определе-
на для всех х е R и убывающая:
Найдем корень уравнения Дх) = 0:
х = 2 — единственный корень уравнения.
Дх) — убывающая функция, поэтому,
Ответ:
если х < 2 ,то Дх) >Д2) = 0, если х > 2, то Дх) <Д2) = 0.
(-°о;2].
§ 6. Логарифмическая функция. Логарифмические уравнения и неравенства
Логарифмом числа b по основанию а называется показатель степени, в которую надо возвести основание а, чтобы получить число Ь.	
Обозначается logab.	Читается: логарифм Ь по основанию а.'
<2>0; атИ; Ь>0
I	*
показательное равенство ax = Ь
.................
х — показатель степени;
а — основание степени;
Ь — степень числа а.
логарифмическое
равенство х = logab
х — логарифм числа Ь
по основанию а;
а — основание логарифма; Ъ — число, стоящее под знаком логарифма.
Примеры:
25 = 32	5 = log232;
log — = -4 о 2 4 = т'
5 2 16	1<
З4 = 81 <=> Zog381 = 4;
log\ 125 = -3
125.
al°Sab = b, а > 0; а Ф 1; Ь>0. основное логарифмическое тождество.	Вычислить:
	2/о^7 = 7.
	2~l°sJ = —!— = 1. 2'°^	7’
	4/02,7 _ 22‘1о£->1 = (2/og27)2 = 72 = 49*
	2! + /0227 = 21 • 2/og2? = 2 • 7 = 14.
Логарифмы по основанию 10 называются десятичными и обозначаются 1g lOte* = b.	/glO = 1
	Zg 100 = 2
	ZglOOO = 3
	igO, 1 = -1
	ZgO, 01 = -2
	ZgO, 001 = -3
Свойства логарифмов
1)	l°gbb = 1 > так как Ь1 - Ь.
Логарифм числа по тому же основанию равен 1.
Примеры
2)	l°ga^ = °> так как л° = 1 •
Логарифм единицы по любому основанию равен 0.
3)	loga(bc) = logab + logac, с > 0, b > 0
Логарифм произведения равен сумме логарифмов.
Логарифм дроби (частного) равен разности логарифмов числителя и знаменателя.
5) logabn = nlogab, b>0
Логарифм степени равен произведению показателя и логарифма основания.
loganJb '= -logb, b> 0
n
Zog9l = 0;
log^x = 0 => х = 1.
/gl5 = Zg(3 • 5) = Zg3 + Zg5;
Zg20 + Zg5 = Zg(20-5) = ZglOO = 2.
з
Zog - = Zog33-Zog35 = 1 — Zog35;
3 5
Zog38-Zog = log ^8:^ = Zog327 = 3.
3 2/	3^ Z/7
_________________________£__________________
Zog381 = Zog334 = 4 • log^3 - 4 • 1 =4;
Zg8 = Zg23 = 3Zg2;
**
Zg5749 = IgV = |Zg7;
3lgb = Igb3.
n
n
m
log$ = log j2 = 2/og22 = 21 = 2;
22
2
logj^fi = log ,33 = 2 • | • 1 = ^. ^2	3	J
Нахождение логарифмов заданных чисел или выражений называется логарифмированием.	
Прологарифмировать выражения по произвольному основанию а.	
Используем правило: логарифм произведения:	1) х = ЗаЬс; logo* = loga3 + logab + logac.
Логарифм произведения и частного:	log^ = logaa + logab - loga3 .
Логарифм произведения и степени: и	3) x = 2w8 • k6 ; logx = log 2 + Slogam + blogk.
Нахождение чисел (выражений) по данному логарифму числа (выражения) называется потенцированием.	
Пропотенциировать выражение и найти х.	
Сумму логарифмов заменим логарифмом произведения:	a) Igx = lg2 + Iga + Igc; /gx = /g(2 • a • c); x = lac.
Запишем правило, обратное логарифму частного и степени:	6) ^Sx ~ 2lga-Slgb\ _ <7 2 x ~ ~b5'
1.	Область определения: D(y) = (0;+оо). Выражение, которое логарифмируется — положительное. График не пересекает ось Оу.
2.	Множество значений: Е(у) = R.
3.	При х = 1 логарифмическая функция у = logjc приобретает значение, равное 1.
Г рафик пересекает ось Ох в точке (1 ;0).
а > 1
у - /og^x — возрастающая; большему числу соответствует больший логарифм;
Если 0 < х < 1, то logjc < 0; если х > 1, то logjc > 0.
Логарифмы чисел, больших 1, положительны. Логарифмы чисел, меньших 1, отрицательны.
0<а< 1
у = logjc — убывающая; большему числу соответствует меньший логарифм;
если 0 < х < 1, то logjc > 0; если х > 1, то logjc < 0.
Логарифмы чисел, больших 1, отрицательны. Логарифмы чисел, меньших 1, положительны.
Следствие. Из равенства логарифмов по одному основанию двух чисел следует
равенство самих чисел logjc = logj> => х = у а > 0; а * 1.
Логарифмические уравнения
Логарифмическими называются уравнения, содержащие переменную под знаком логарифма.
Например: /og2(3x-2) = 4.
Решение логарифмических уравнений основывается на определении логарифма, свойствах логарифмической функции и свойствах логарифма.
Основные методы решения логарифмических уравнений
1) l°g<J{x) = b f(x) = аь л>0; а;* 1.
f{x)b = g(x)
2) l°gfa&x) = Ь
Дх)>0
Дх)* 1
g(x) > О к
3) loga Дх) = loga g(x)
<Дх) = g(x) Дх) > о
Дх) = g(x) или г & 7 .g(x) > о
g(x) = Л(х),
g(x) = Л(х),
4) logAx^g(x) = logAx}h(x)
< g(x) > О, /(х) > о,
й(х) > О,
Дх) > О,
или <
Дх) * 1;
Дх)*1.
7«ga(/(x)g(x)) = loga h(x),
5) i°ga Дх) + loga g(x) = loga h(x)
Дх) > 0, g(x) > 0,
[h(x) > 0.
a
6) loga Дх) - loga g(x) = loga A(x) о Дх) > 0,
7) "logа Лх) = loSa h(x)
loga Лх)П = loga Л(Х)
Дх) > 0,
Д(х) > 0.
logalAx)  g(x)) = loga\f(x)\ + /ogo|g(x)|
loga \ = l°SMx)\ - loga\g(x)
a g(x)
loga(Ax))2n = 2nloga\f[x)
Логарифмические неравенства
Неравенства, содержащие переменную под знаком логарифма, называются логарифмическими.
Например: log2(x2 - Зх + 2) > 1.
При решении логарифмических неравенств помни:
1)	общие свойства неравенств; .
2)	свойство монотонности логарифмической функции;
3)	область определения логарифмической функции.
Основные методы решения логарифмических неравенств
Дх) > а
3) loga Дх) < b
а > 1
Дх) < аь
Дх) > О
< Дх) < аь Дх) > О
Дх) > а
5) logg{xflx) > ъ
l°gа Дх) > loga Й(х)
8)
0<а< 1 loga f(x) > loga h(x)
Дх) > g(x)^
0<g(x)<l ^x)<g(x)h Дх) > о
6) logg(xflx) < b
Дх) > О
Дх) > g(x)b
Дх) > й(х) |Д(х) > О
J{x)<h(x)
Дх) > 0
9)
loga ДХ) < loga h(x)
10)
loga Лх) < loga h(x)
J{x)<h(x)
Дх) > 0
<Л* *)>И(х) Д(х)>0
11) logg(xflx) < logg(x)h(x)
g(x) > 1
*Дх)<й(х)
Дх) > 0
0<g(x)< 1 'Ax)>g(x) g(x) > 0
1Дх)>й(х)
12) /о^(хДх) > logg(x)h(x)
Д(х) > 0
0<g(x)<l
<Дх)<Дх) Дх) > 0
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. Найти.
logfi.
Решение.
Обозначим /og48 через х:
Перейдем к показательному равенству:
/og48 = х.
4х = 8.
Приведем к основанию 2 и решим показательное уравнение:
2х = 3;
Ответ:
2.	Решить уравнение.
Решение.
Запишем показательное равенство и выполним вычисления:
Ответ:
3.	Найти х.
logx125 = I.
Решение.
По определению логарифма имеем:
*
х2 = 125.
Возведем обе части в степень
Ответ:
4.	Доказать.
х = 25.
al&b = blsa.
Доказательство.
Запишем очевидное равенство: V
Правило, обратное логарифму степени:
Igblga = Iga  Igb. lgalsb = igblga
Из равенства логарифмов при равных основаниях имеем:
algb = ijlga
3
5. Зная, что lg2 = a- lg3 = b; lg5 = с, выразить через a,b,c lg6; lg3Q; lg\6.
Решение.
Применим правила логарифмирования произведения степени:
6. Вычислить.
Ig6 = Zg(2 • 3) = Ig2 + lg3 = a+.b\ lg30 = lg5 + lg6 = a + b + c;
lg!6 = lg24 = 4lg2 = 4 • a.
log9S  log2527.
Решение.
Перейдем к основанию 10:
^5.^ =
Zg9 lg2S
Используем свойство logabm = mlogab и сократим дробь:
Ответ:
log95  logls22 = - .
7. Вычислить.
Zog308, если lg5 = a, lg3 = b.
Решение.
Перейдем к основанию 10:
Применим правила логарифмирования степени, произведения, частного:
2 = 1°
5
Подставим lg5 = a; lg3 = b:
los^ lg3Q Zg(3 • 10) Ю 3/g—
= 3lZ2 = 3l%2 =	5
Zg3 + ZglO Zg3+1 Zg3 + 1
= 3(ZglO-Zg5) = 3(1-Zg5) = Zg3 + 1 Zg3 + 1
= 3(1 -g) b + 1
Ответ:
Основные методы решения логарифмических уравнений.
Применение определения логарифма
1. Решить уравнение.	Zog2(x- 3) = 4.
Решение.	
По определению логарифма имеем:	х-3 = 24.
Решим полученное уравнение:	х-3 - 16; х = 19.
Запишем ответ:	19.
2. Решить уравнение.
Заменим равносильной системой по
схеме Zog^x)g(x) = b
= g(x)
VW>0
Дх) * 1
Решим квадратное уравнение, выберем корни, удовлетворяющие условию
Запишем ответ:
1. Решить уравнение.
Решение.
Метод потенцирования
Заменим равносильной системой:
Решим уравнение и выберем те корни, которые удовлетворяют усло-
вию х
Запишем ответ:
2. Решить уравнение.
Число 2 представим в виде десятичного логарифма:
Сумму логарифмов заменим лога-рифмом произведения выражений: Заменим равносильной системой, учитывая ОДЗ:
0
Ответ:
Решение.
Zg(x-9) + Zg(2x-1) = 2.
Решение.
Zg(x-9) + Zg(2x-1) = ZglOO.
Zg((x-9)(2х-1)) = ZglOO.
(х-9)(2х - 1) = 100;
2х2- 19х + 9 = 100;
2х - 1 >0.
13.
Приведение логарифмического уравнения к алгебраическому путем замены
Решить уравнение:
Решение.
Сделаем замену Igx = t :
Решим полученное квадратное уравнение относительно г.
Вернемся к замене, решим совокупность логарифмических уравнений:
Запишем ответ:
Igx - t, х > О
t2 - 4 - 3f;
r2 + 3r-4 = 0;
'Igx = -4,	Гх = 10-4,
-Igx =1;	Lx = 10;
10; 0,0001.
~х = 0,0001;
-х = 10.
Приведение логарифмического уравнения к одному основанию
t
Решить уравнение.
16
Решение.
Приведем все логарифмы к основанию 2:
х > 0.
Приведем подобные слагаемые:
Разделим левую и правую части уравнения
на - и решим полученное уравнение:
4
Запишем ответ:
Логарифмирование обеих частей уравнения
Решить уравнение.
х^х =	.
Решение.
Найдем ОДЗ:
Прологарифмируем обе части уравнения по основанию 10, использовав свойство логарифма степени и частного:
Решим квадратное уравнение относитель-но lgx\
Решим совокупность логарифмических уравнений:
Запишем ответ:
х>0.
Igx • Igx = ZglOO-Zgx;
lg2x = 2- Igx;
lg2x + Igx-2 = 0.
Гх = 0, 01
Lx = 10.
0,01; 10.
Применение монотонности при решении логарифмических уравнений
Решить уравнение.
log5(x + 3) = 3-х.
Решение.
Установим монотонность функций в левой и правой частях:
Подбором найдем корень:
Запишем ответ:
у = log5(x + 3) —возрастающая функция;
у = 3-х —убывающая.
х = 2, проверка: logs5 = 3-2; 1 = 1; х = 2 —корень.
Решить неравенство.
Решение логарифмических неравенств log2(x2 + Зх) < 2 .
Решение.
Запишем число 2 в виде логарифма с основанием 2:2 = log24:
log2(x2 + Зх) < /og24.
Установим монотонность функции:
Заменим равносильной системой:
2 > 1; у = log2t — возрастает.
Решим каждое неравенство и найдем общее решение:
Запишем ответ:
Решить неравенство.
[-4;-3)и(0;1].
logx-^x- 1)<2.
Решение.
Запишем ответ:
Решим совокупность двух систем неравенств:
Решить неравенство.
Решение.
Заменим logQ s х = t, методом интервалов решим неравенство:
Вернемся к замене и ре-шим систему логарифмических неравенств с учетом ОДЗ:
Запишем ответ:
Решить неравенство.
Сумму логарифмов заменим логарифмом произведения с учетом ОДЗ:
Составим систему неравенств с учетом ОДЗ и того, что
У = logo 4 * — убывающая функция:
Запишем ответ:
Решить неравенство.
7///////Л
учитывая ОДЗ х > О
О О
Решение.
(3 - 2x)Zog0 < 0.
Решение.
Данное неравенство решим методом интервалов.
Найдем ОДЗ:
Нули функции у = (3 -2x)Zog0> ре:
На числовую прямую нане-сем ОДЗ и нули функции.
Установим знак функции на каждом промежутке
Запишем ответ:
(3 - 2х) • log
СТРАНИЧКА АБИТУРИЕНТА
1. Вычислить.
Решение.
Перейдем к основанию 10 и сократим дроби:
Ответ:
lg3 lg4 lg9 IglO IglO
2. Вычислить.
Zog616, если Zog172 = а.
Решение.
Ответ:
= а; отсюда log 62 =
а
4<я
4а
3. Решить уравнение.
/g(2x) = -lg{x-\5y.

Найдем ОДЗ: ч
В показателе четная степень:
Решение.
lg(2x) = lg\x- 15
2х = |х - 15
Раскроем модуль на области определения уравнения:
15;
15;
15
Запишем ответ:
4. Решить уравнение.
lg(x -2)6 = 0.
Решение.
Используем свойство логарифма степени, если показатель четный:
По определению модуля:
Запишем ответ:
5. Решить уравнение.
5/°И* + х/оНг = 04 Решение.
ОДЗ:
Используем основное логарифмическое тождество:
х > 0.
х1о& + Xiog}x = о, 4;
2х/о^х = 0,4; 0,4:2 = 0,2 = 5’1.
Прологарифмируем обе части по основанию 5:
Решим полученное уравнение:
Запишем ответ:
6. Решить уравнение.
х = 5-‘.
1
О
5
xlog^x(2x + 3)log3x + 6 = 0.
Решение.
Замена log^x = t, х > 0:
Решим квадратное уравнение:
Вернемся к замене:
Ответ:
хг2-(2х + 3)г +6 = 0 — квадратное относительно t. №
_ 2х + 3 ± 7(2х + 3)2-4-х • 6 _
?1>2	2х
_ 2х + 3 + (2х - 3) 2х
t = 2 или t = |.
log^x = 2; х = 9.
log,x = у = log,x — возрастающая х
функция;
у = | — убывающая, х = 3 — единственный корень.
3; 9.
Применение основного логарифмического тождества
уравнение.
log2(9 —2х) = 10^<3-х).
Решение.
правой части используем logab = h-
По определению логарифма: Квадратное уравнение отно-сительно 2х:
Ответ:
2. Решить уравнение.
По определению логарифма имеем:
4/о£43 = з
Решим показательное уравнение:
Ответ:
3. Решить неравенство.
Преобразуем правую часть:
Неравенство запишем так:
log 2(9- 2 х) = 3-х.
2х = 1; 2х = 8, откуда
х = 0; или х = 3 — не принадлежит ОДЗ.
x-l+/og43 = /og4(5x-4x J).
Решение.
4 х -1+	= 5Х _ 4Х - i
4-х-1.4/0543 = 5Х-4Х-1. з . 4Х-1 = 5x._4.x- 1;
з . 4х- 1 + 4х-1 = 5х; 4.4х- 1 = 5Х.
4х = 5х; х = 0.____________________________
0.
(/oW)2 < logsm^sinx).
Решение.
0 < sinx < 1 .
logsinx(4sin х) = 2log . 2 + 3log  sinx = kJ f f * WV	J И I 'V
= 2log  2 + 3. O sinx
l°g2sinx2 < 2l°gSinx2 + 3 
Замена log. 2 = г. u*f *Л
5
sinx
sinx
0 < sinx
2лп
Ответ:
0 < sinx
0 < sinx
sin x;
0 < sinx

5
5
4

4
 *





$»s&£2Si
 
о₽й- ^г>°^ <V9e5\\9°*

. бХ


69®
*


»»P'T ^5'’^ fi ^O*’ -O.0*
it
;<>*
. 4P*'a** c

6^®
-
e
e^
o9^

*♦*
1V^

w
>&>>>§

:ди//ж


»ж
w
§ 1. Модуль. Предел. Непрерывность. Производная
Модуль числа
Модуль положительного числа равен самому числу.
Модуль отрицательного числа является числом, ему противоположным. |-5| = -(-5) = 5.
Модуль нуля равен 0.
|0| = 0.
а, если а > 0, = s 0, если <2=0,
—'Ciу если <2 < 0
<2, если а > 0,
-а, если а < 0
если <2 > 0,
-а. если а < 0 к *
если <2 > 0, если а < 0.
Геометрический смысл модуля
Предел функции
Понятие предела
Пример 1.
Рассмотрим таблицу значений функции у = х2 в точках, которые
на числовой прямой расположены достаточно близко к числу 2 (и
в самой точке 2).
X	1,98	1,99	2,00	2,01	2, 02
X2	3,92	3, 96	4, 00	4, 04	4,08
х2 - 4	0, 08	0, 04	* 0	0, 04	0, 08
Чем ближе аргумент х к числу 2 (пишут х -> 2), тем ближе значение функций к числу 4 (/(%) -> 4).
Записывают так: Нт х2 = 4. х—>2
Пример 2.
В общем случае НтДх) = В означает: если х-> а, то Дх)
о
Дх)
Дх) - в
Число В называется пределом функции Дх) при х, стремящемся к а, если для любого положительного числа е найдется такое положительное число 5, которое при всех х ф а, удовлетворяющих неравенству |х - а Если Нт Дх) = В, то В —единственная.
5, выполняется неравенство: Дх) - В\
Теоремы о пределах
( Нт Дх), Нт g(x) - существуют)
Нт с = с (с - постоянная величина)
Нт с f(x) = с Нт f(x)
Примеры
Нт 5 = 5.
Нт (/(x)±g(x)) = Нт fix) ± Нт g(x) а	х —> я	х —> а
Нт (х2 - 4х + 2) = Нт х2 - 4 Нт х+ Нг^ 2 =
Нт (fix)  g(x)) = Нт ffx)  Нт g(x)
Нт Дх)
'.Г*0 , ч( Нт %(х) * 0)
П/И g(x) х-»а

Нт х = а
: —> а
Нт - = О
Нт х =
Нт
Нт
Нт
V -*• 2Х - 1
Если	= о, то Нт =
*-»а	ха Дх)
Если Нт f(x) = оо, то Нт -------- = 0.
х -> a	x-ta f(.x)
А
Если Нт Дх) = 0 и Нт g(x) ~ оо, то Нт -4—- = 0. х->а	х~>а	x-»a;L'(v)
Способы вычисления пределов
1. Для любого многочлена Р(х): Нт Р(х) - P(xq).
2. Если число х0 входит в область определения дробно-рациональной функции 7?(х), ТО Пт R(x) = R(xq) .
Нт
Если в результате подстановки х = а получили выражение ( J , то:
а) попробуем разложить числитель и знаменатель на множители и сократить дробь;
1) Пт
Нт
= Нт
2) Нт
Нт
— Нт
3) Нт
Пт
- Нт
б) если дробь нельзя сократить, то в этом случае нужно числитель и знаменатель дроби домножить на выражение, сопряжённое со знаменателем (или числителем’/ а потом сократить дробь;
Пт
Пт
= Пт
х > О
о
в) если под знаком предела стоят тригонометрические фунци'И или обратные тригонометрические функций- т0 приводим к первому замечательному пределу:
7. sinx Пт----
если Пт f(x) --х —> О
1 » О III / I J lim — л ->0 /(х)
2
sin3x 3sin3x
---- = Нт---------
ОХ	х->0 Зх
sin3x ,
sin8x — sin 12х
0
>• — 2sin2xcos 10х _
10х	x->0	10x
sin2x  cos lOx _
2x
j. arcsinx lim--------- =
г->0 х
lim	= 1
>0 X
lim cosx ~ 1
> 0
lim sinx = 0
.• —> о
Iim sJs2^. цт cos =
: —> 0 2х	х —> 0
Непрерывность функции
Функция fix) называется'непрерывной в точке х0, если она в ней определена, предел, функции в точке х0 существует и равен значению функции в этой точке.
По этому определению ставятся три условия:
1)	функция должна быть определена в точке х = х0;
2)	функция f(x) имеет предел в точке х0;
3)	Пт fix) = _Дх0).
х->х0
Пример: Дх) = т-—; у = —; х e (-а>;3) и (3 ;+оо) х ф 3 .
Данная функция не будет непрерывной в точке х0 = 3, поскольку она не определена при х = 3 .Те точки, в которых эти условия не выполняются, называются точками разрыва, х = 3-точка разрыва.
Примеры функций, которые имеют точки разрыва
у = [х] — целая часть х
У*
Точки разрыва — все целочисленные то»4ки.
О — точка разрыва.
Если функция Дх) непрерывна в каждой точке некоторого промежутка /, то ее называют непрерывной на промежутке 1.
В школьном курсе математики:
График функции, непрерывной на промежутке, — непрерывная линия на этом промежутке.
Свойства
Иллюстрация
Формулировка
Т Если непрерывная на отрезке [a, Z>] функция принимает на концах этого отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю.
Пример использования f(x) = 4х3 + х - 1 — непрерывная функция (многочлен);
ДО) = -1<0; Д1) = 4>0, поэтому на интервале (0;1) существует точка х, в которой функция равна 0 (это точка х0 = о )•
2. Функция f(x), непрерывная на отрезке [а, Ь], принимает все промежуточные значения между значениями этой функции в крайних точках, то есть между Да) и /(/>)•
3. Если на интервале (а, Ь) функция Дх) непрерывна и не превращается в ноль, то на этом интервале функция сохраняет постоянный знак.
Дх) = Зт — непрерывная функция. Если х е [2;3], то З2 = 9, З3 = 27 . Поскольку 9 < 15 < 27, то существует точка х0, в которой Дх0) = Зх° = 15 (как известно, х0 = 7og315).
На этом свойстве основыва-ется метод интервалов решения неравенств вида Дх)г 0 .
Решим неравенство Дх)гО , где Дх) — произвольная функция.
1.	Найдем область определения функции Дх): D(f).
2.	Определим все нули функции, то есть решим уравнение Дх) = 0.
3.	Разбиваем на промежутки область определения нулями функции .
4.	Определим знак функции на каждом промежутке.
Примеры функций, непрерывных на всей области определения
	Функция	Область определения
1.	у ~ X	X 6 (-со;+оо)
2.	у = Хп	х е (-оо;+оо)
3.	1 У х-а	х Ф а
4.	У = Я	х>0
5.	,	(а > 0\ У = toga* 1 J	х > 0
6.	у - sinx	х е (-оо;+оо)
	у = cosx	X 6 (~оо;+оо)
8.	У = tgx	Л ,	г, х Ф - + ли, п е Z
9.	у = ctgx	х Ф як, к е Z
10.	у = arcsinx] у = arccosx	- 1<х<1
11.	у = ах	х е. (—оо;+оо)
Приращение аргумента и функции
Дх = х{ -х0 — приращение аргумента в точке х0;
Xj = х0 + Дх — начальное значение аргумента х0 получило приращение Дх;
Ду = ДДх) =Лх1)-/(х0)—приращениефункции в точке х0;
&У = f(x0 + д*) -/(*о) •
Производная функции у = f(x)
У =
О
Производной функции у = Дх) в точке х называется предел отношения приращения функции в точке х к приращению аргумента, когда приращение аргумента стремится к нулю (можно обозначить у' или f '(*) ) Операция нахождения производной называется дифференцированием.
Касательная к графику функции и геометрический смысл производной
Касательной к кривой в данной точке М называется предельное положение секущей MN, когда точка N стремится вдоль кривой к точке М.
f 'Ы = tg<j?
к — угловой коэффициент касательной.
к = tg<? = f 'ЗД.
У = /Ы+f \x0)(x-xQ) — уравнение касательной к графику функции у = Дх) в точке с абсциссой х0.
Значение производной в точке х0 равно тангенсу угла наклона касательной к графику функции в точке с абсциссой х0 (и равно угловому коэффициенту касательной).
Механический смысл производной
Производная характеризует скорость изменения функции при изменении аргумента; в частности: производная времени является мерой скорости изменений, используемой по отношению к различным физическим величинам. Например, мгновенная скорость v неравномерного прямолинейного движения является производной от функции, выражающей зависимость пройденного пути S от времени г.
5 = S(t) — зависимость v = S'(t) — скорость пря- а = v\t) — ускорение пройденного пути от времени; молинейного движения; прямолинейного движения.
Таблица производных некоторых функций
Элементарные функции	Сложные функции
с' = 0 (с-const)	
(кх + Ь)' = к х' = 1 (-х)' = -1	
(ха)' = аха-1 (а е R)	(«“)' = а • иа“1 • и'
(х2)’ = 2х	и2 = 2и • и'
г _	1 2л/х	(Л)' = ~ и' 2 Jи
Тк II 1	г** 1 1 1 л 1 1 —
(sinx)' = cosx	(sinu)' = cosn • w'
(cosx)' = -sinx	(cosu)' = —sinu’u'
(tgx)’ ~	2 COS X	(tgu)' ~	2 W cos и
(ctgx)' - sin x	(ctgu)' -	2 -u' sin и
,	 V	1 {arcsinx) “ 	 7i -x2	(	• V -	1 {arcsinu) =	- и Vi — и2
(	V	1 {arccosx) = - .		<	V	1	, {arccosu) = - 	• и J\-u2
1 (arctgx)’ - 1 +xz	(arctgu)' ~	u' 1 + W“
(arcctgx)' = - 1 + xz	(arcctgu)' = -	 u' 1 + u2
Правила дифференцирования
(с • м(х))' = си'(х) (с — постоянная).
Постоянный множитель можно выносить за знак производной.
Производная суммы
Производная суммы функций, которые дифференцируются, равна сумме их производных.
Производная произведения
Производная частного (и\, _ u'v -v'u i
Производная сложной функции (функции от функции) (m(v(x)))' = w'(v(x)) • v'(*)
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. Найти.	,. 1 - cosx х—>0	Х“
Решение.	
1 - cosx = 2 sin - .
выражение
2sin- • sin-2	2
hm----------
О X•X
2 sin -
1 - cosx	2
hm--------- = hm---------
: -> 0 x2 x-> О X2
Воспользуемся тем, что
sin-
/•	2
hm------
sin-  sin-
=2 Нт —---------
sin-
Нт —-
sin-
 Нт----
Ответ:
2. Найти.
Нт
Решение.
Домножим числитель и знаменатель дроби на выражение, сопряженное с числителем.
В числителе «свернем» формулу разности квадратов.
Сократим на х - 5.
Нт
Нт
= Нт
= Нт
Нт
Нт
: 0
Ответ:
Нт
3. Исследовать функцию у = Дх) на непрерывность в точке х = х0:
sinx если x * 0, Я*) = i *
б) Дх) = х2-4; х0
О, если х = 0.
Решение.
1)«0) = 0.
2) lim f^x} ~ lim ^2. = 1. x—>0	x-»0 x
3) limf(x)*f(0).
x —> 0
Ответ: функция не является
непрерывной в точке х0 = 0.
1)/(3) = 5.
2) Нт Дх) = Нт (х2 - 4) = 5 .
3) limf(x) = ДЗ).
Ответ: функция непрерывна в точке х0 = 3.
4. Решить неравенство.
Решение.
Рассмотрим функцию: Дх) =
log-,(x + 1)
2) Нули функции Дх): —-—;— = 0;х+1 = 1;х = 0.
3) Разбиваем D(f) на промежутки и определяем знак функции Дх) на каждом из них:
4) Решением исходного неравенства будут промежутки, где Дх) > 0; то есть х 6 (—1 ;0) и (1;+оо).
Ответ:
(-1;0) и (1;+оо).
Приращение функции
&У = Дхо + Дх) -/(хо)
Приращение аргумента
Дх = х-х0
Дх>0
Вычислить приращение функции Дх) в произвольной точке.
а) Дх) = 2х2 + Зх-5;
Решение.
Фиксируем произвольное значение аргумента х0 и находим Дх0):
Зададим аргументу х приращение Дх и найдем Дх0 + Дх):
х = х0 + Дх.
Дх0 + Дх) = 2(х0 + Дх)2+3(х0 + Дх) - 5 = 2(х^ + 2х0Дх + (Дх)2) + Зх0 + 3 Дх - 5 = =2х^ + 4х0Дх + 2(Дх)2 + Зх0 + 3Дх - 5.
Находим приращение функции
ДДх) = Д*о + Ах)-Дх0)
Ответ:
ДДх) = (2xq + 4х0Дх + 2(Дх)2+Зх0 + ЗДх - 5) - (2xq + Зх0 - 5)
=4х0Дх + 2(Дх)2 + ЗДх=Дх(4х0 + 2Дх + 3).
ДДх) = Дх(4х0 + 2Дх + 3).
б) Дх) = sin2x\
Решение.
Фиксируем произвольное значение аргумента х0 и находим Дх0): Зададим аргументу приращение Дх и находим Дх0 + Дх): Находим приращение функции ДДх) = Дх0 + Дх)-Дх0)
= х0; Дх0) = sin2xQ.
х = х0 + Дх; Дх0 + Дх) = sin2(х0 + Дх).
ДДх) = szh2(x0 +Дх)-$/и2х0 =
2х0 + 2Дх - 2х0	2х0 + 2 Дх + 2х
=2 sin------------cos —------------
2	2
=2 sin Ах cos (2х0 + Дх).
Ответ:
ДДх) ~ 2sinAxcos(2xQ + Дх).
Используя определение, вычислить производную функции у = f(x) в точке х = х0.
а) Дх) = Зх2 - 5х + 1; х0 = 2.
Фиксируем произвольное значение аргумента х и задаем аргументу
Решение, х; х + Дх
приращение Дх:
Вычисляем приращение функции
Д/ = Ах + Дх) —Дх):
Находим отношение приращения функции к приращению аргумента Д/ _ Дх + Дх) -Дх).
Дх	Дх
Д/ = (3(х + Дх)2 - 5(х + Дх) + 1) - (Зх2 - 5х + 1) =
=6хДх + 3(Дх)2 - 5Дх = Дх(6х + ЗДх - 5).
Л/ _ Дх(6х + ЗДх - 5)
Дх	Дх
= 6х + 3 Дх - 5 .
Вычисляем производную
f '(х) = lim	г
Дл->0 Дх
f '(х) - Нт (6х + ЗДх-5) - 6х-5. Д.г О
Вычисляем f '(х0) :
Ответ: _________________
f '(2) = 6 -2-5 = 7.
f '(2) = 7.
б) Дх) = а/7х - 5 ; х0 = 2.
Решение.
Фиксируем произвольное значение аргумента х и задаем аргументу приращение
Дх:
Вычисляем приращение функции
Д/ = Дх + Дх) -Дх):
Находим отношение приращения функции к приращению аргумента
х; х + Дх.
Д/ = л/7(х + Дх) - 5 - л/7х- 5 =
=л/7х + 7Дх- 5 - 77х - 5.
Д/ _ Jlx + 7Дх - 5 - л/7х - 5
Дх	Дх
Вычисляем производную
f '(х) = Пт
Дх —> О Дх
Нт +	~ $ ~7Х + $
А* -* °Дх( Jlx + 7Дх - 5 + 77х-5 )
Вычисляем f '(2):
Ответ:
Рассмотрим различные способы вычисления производной.
Постоянный множитель вынесем за (5Х2)' = 5 (х2)' = 5 -2х = 10х знак производной:
Используем формулу: (хау = а-х^х23)' = 23-х23"1 = 23-х22.
Запишем сначала в виде степени с отрицательным показателем, а потом
(х-9)' = -9 -х-9-1 = -9х-ю =
используем формулу (ха)' = ах01-1:
Используем теорему о производной суммы (и + v)' = и' + v':
Используем теорему о производной произведения (м • v)' = u'v + v'u:
Используем теорему о производной
частного	v v,t0:
v~
Используем формулу (sinu)' = cosu-u''.
(sinx + Jx)' = (sinx)' + (Jx)' = cosx +— 2a/x
(4x • cosx)' = (4x)' • cosx + (cosx)' • 4x =
- 4cosx-4x • sinx.
f2x + 3Y _ (2x + 3)' sinx - (sinx)’  (2x + 3)
sinx	sin2x
_ 2sinx - (2x + 3)cosx
. 2 Sin X
(sp?14x)' = cos 14x • (14x)' = cos\4x • 14 =
= 14cosl4x.
Ggw)' = —•w' cos ~u
Сначала выделим целую часть, а затем найдем производную сложной
1
функции вида -:
_____________и____________________
Сначала запишем в виде степени с отрицательным показателем, а затем найдем производную сложной функции:
(4х-5)7
4
У = /(*о)+/ '(Хо)(х— х0)
Уравнение касательной к графику функции у = Дх) в точке (xojyo), принадлежащей графику.
Составить уравнение касательной к графику функции у = Дх) в точке с абсциссой х = х0.
Решение.	а)/(х) = х3 + 2х2-5; х0 = 1;	б) Дх) = sin2x; х0 =
Вычисляем значение функции в точке х0 Дх0):	/(х0) = Д1) = I3 + 2 - I2 - 5 = -2	тсА	* 2 ’ л	* л	2 / - - sm	 = sin- = —. <8>	8	4	2
Находим	f '(х) производную функции:	f '(х) = Зх2 + 4х	f '(х) = 2cos2x.
Вычисляем значение производной в точке х0 f '(х0): 4	f '(*о) =/ '(О = 3 • 12 + 4- 1 = 7	i w	€15 §	II 4^ 1 Я	bJ 11	s Ю	ЬО 00 • bo bOl j	II bOl • 1
Значение f	хо подставляем в -уравнение касательной:	У = f(xQ)+f '(х0)(х-х0) у = -2 + 7 • (х- 1) = = -2 + 7х-7 = 7х-9	II Z	II	II	II * Ъп i	>	>	+ bOl !	bJl	bOl OO bOl	^7^	H .	oc m	X a	OQia,	и 11	II	H © 1 1 i
Ответ:	у = 7х - 9. У	/X , J2 */2it У= 72x+ 2 - 8 •
Решить задачи.
1.	Материальная точка двигается по закону S = 4г3 +12 + 8 (S измеряется в метрах, t в секундах). Найти скорость и ускорение в момент t = 2 с.
Решение.
1)v = S'(0= 12/2 + 2г — скорость движения точки в любой момент t.
2)	v(2) = 12 • 22 + 2 • 2 = 48 + 4 = 52 (м/с) — скорость движения точки в момент t = 2 с.
3)	а = v'(t) = 24г + 2 — ускорение движения точки в момент t. *
4)	а(2) = 24-2 + 2 = 50 (м/с2) — ускорение движения точки в момент t = 2 с.
Ответ: 52 м/с; 50 м/с2.
2.	Материальная точка двигается прямолинейно по закону S = Юг - 5г2. В какой момент времени скорость точки будет равна нулю?
Решение.
1)	v = S’(t) = 10- Юг —скорость движения точки в любой момент t.
2)	у = 0, 10- Юг = 0, Юг =10, t = 1.
Ответ: t = 1 с; скорость точки равна нулю в конце первой секунды.
3.	Тело двигается вертикально по закону Л(/) = 2 + 9t- 5/2. Определить скорость тела в момент его приземления, если h выражается в метрах, t — в секундах.
Решение.
1)	v(/) = h'(f) = 9-10/ (м/с) — скорость движения тела в момент времени /.
2)	В момент приземления тела
h(t) = 0; h(t) = 2 + 9/-5/2;
2 + 9/-5/2 = 0, 5/2-9/-2 = 0.
D = (-9)2-4-5 (-2) = 81 +40 = 121.
9—11	—2	1
Значение /1 = - --- = — = -- не подходит по условию задачи, т.к. речь идет о
9+11	20	„, х
моменте времени после начала движения; /9 = ——— = — = 2 (с).
ю ю
В момент приземления тела / = 2 с.
3)	v(2) = 9-10-2 = 9-20 = -11 (м/с).
Ответ: -11м/с.
4.	Скорость v тела, двигающегося в вертикальном направлении, изменяется по закону v = 9-10/ (м/с). Определить скорость тела в момент приземления, если оно в начальный момент находилось на высоте 2 м от земли.
Решение.
1)	а = v’(/) = -10 (м/с2); т.к. ускорение постоянно, то тело движется по квадратичному at2
закону: h = — + vot + h0.
2)	v0 = v(0) = 9- 10 • 0 - 9 (м/с). — 10/2
3)	h = —-y—+ 9/+2 = -5/2 + 9/ + 2.
Отсюда легко найти время приземления тела / = 2 с и скорость в момент приземления v = -11м/с.
Ответ: -11 м/с.
5.	При торможении маховик за / секунд поворачивается на угол ср = 5 + 6/ — /2 (ср — в радианах). Найти: угловую скорость со вращения маховика в момент / = 2с; угловое ускорение в момент времени /; момент времени /, когда вращение закончится.
_______решение
1)	Угловой скоростью со называется скорость изменения угла ср за время А/. Угловая скорость — это производная от угла поворота ср за время /: со = ср'(/) = 6-2/.
2)	со(2) = 6-2 -2 = 6-4 = 2(рад/с) — угловая скорость в момент t - 2с.
3)	Угловое ускорение — это производная от угловой скорости за время /:
£ = <о'(/); £ = -2рад/с2.
4)	В момент остановки маховика:
со = 0; со = 6-2/; 6-2/ = 0, 2/ = 6, t - Зс.
В конце третьей секунды угловая скорость будет равна нулю, и вращение закончится.
Ответ: со = 2рад/с; £ = -2рад/с2; t = Зс.
СТРАНИЧКА АБИТУРИЕНТА
1Я*)1 = ь
Ь<0,
х е 0, Дх) = О, ~Лх) = ь, -Лх) = -ь.
Решить уравнение.
5х2 - 3 = 2.
Решение.
Данное уравнение равносильно совокупности двух уравнений:
Ответ: ±1;
И»
I способ
’\Лх) * О, \ЛХ) = g(x),
to < О, 1-Л*) = g(x).
= g(x)
II способ lg(x)>0, Vw = g(x), lg(x)>0, l/(x) = -g(x).
Решить уравнение.
= 2x - 1.
Решение.
Уравнение равносильно совокупности систем уравнений:
Ответ: 1;
Решить уравнение.
|Зх-4| = 4х2 + Зх-2.
Ответ: х =
Решить уравнение.
Зх-4>0,
Зх-4 = 4х2 + 3х —2;
Решение.
2х2 + Зх - 3 = О
-з±Узз
4
|х| - 2|х + 1
= 5.
Решение.
Нули подмодульных выражений:
|х| —
Ответ: уравнение не имеет решений.
И» =		g(*)l
1 способ Возвести левую и правую части в квадрат и решить полученное уравнение.		II способ ’/(*) = g(x); -f{x) = -g(x).
Решить уравнение.
Решение.
Возведем обе части в квадрат и решим полученное уравнение:
-12x-28x = 49-9,
-40x = 40,
Ответ: х = -1.				
Решить уравнение.	|2х2 - 4		4 - Зх2	•
Решение.
Ответ:
I дх),	если /(x) > 0
I-Дх), еслиДх)<0
Решить уравнение.			х2+х- 12		= х2 + х - 12 .
Решение. 					
Используем определение модуля:	х2 + х — 12 > 0 (х + 4)(х- 3) > 0				t	3	X
Ответ:	х е (-оо;-4] и [3;+оо).				
Решить уравнение.	]cosx| = -cosx.				
Решение.					
Используем определение модуля:	cosx < 0 + 2пп <х < ^7 + 2пп, п g Z. 2	2				
Ответ: «А	л , . Зл , _ — + 2л»;— + 2л» 2	2	J	* , » е Z.			
1Дх)
а
f(x) < g(x)
/(*) > -g(x)
Решить неравенство.
Решение.
Заменим двойным неравенством:
Ответ:
Решить неравенство.
Решение.
(х- 4)(х + 1) < 0;
Дх + 4)(х-1) > 0;
п иш_____,
-4-114	>
х е (1;4)
Ответ:
(1;4).
/(х) >g(x)
> g(x)
-fix) < -g(x)
Решить неравенство.
Решение.
-(х-4)(х + 3)>0
-X 6 0
Ответ:
Решить уравнение.
|4 -х| + |2х - 2
Решение.
Точки Xj = 1 и х2 = 4 разбивают числовую ось на три интервала.
у = 4 -х
Здесь пункт в) можно было не выполнять, т.к. по условию 5-2х>0, следовательно,
Ответ:
Решить уравнение.
|х - а\ = Зх - 1, где а — параметр. Решение.
Равносильная совокупность систем:
Корни уравнений х
. Из условия Зх - 1 > 0 найдем а.
Отметим, что при а = -
Ответ:
, если а <
,если а
Решить уравнение.
= |2х - д|, где а — параметр.
Решение.
Обе части уравнения неотрицательны, поэтому обе части уравнения возведем
в квадрат. Имеем (х + а)2 = (2х-а)2, отсюда Зх2-6ах = 0. Находим х, =0, х2 = 2а.
Ответ: 0; 2а.
Решить неравенство.
х - а = 0 при х =
|х — д| < 2х — 1, где а — параметр. Решение.
а. Данное неравенство равносильно совокупности систем неравенств
О,
0.
а',
Рассмотрим каждую систему отдельно.
1—а при а = - Если а<-
то размещение точек а,
- на числовой оси 2

следующее:	а	j_a
2 Решением системы является множество х > 1 - а.
Если а > -, то получим
Следовательно, решением системы является множество х > а.
5
а
при а = -. Если а < -, то решений нет, так как первое и третье неравенства не
совпадают. Если а > -, то размещение точек следующее:
Получим
Ответ:
х<а. Объединяем решения двух систем неравенств.
,если а
Решить неравенство.
|3х — 1| < |4х - а\, где а — параметр. Решение.
Возведем обе части неравенства в квадрат:
0.
Найдем дискриминант левой части.
Имеем: Dx = (4а-3)2-7(а2- 1) = 9а2-24а+16 = (За-4)2.
Следовательно, корни квадратного трехчлена:
, то есть х

Рассмотрим размещение корней Xj и х2 на числовой оси в зависимости от значения
параметра а. а - 1
при а = -
этом случае заданное неравенство имеет вид Зх -1
4х- -
или
. в

-|3х- 1|. Оно выполняется, при х * -.
Ответ:
если а
5
Вычислить производную функции.
Имеем: у' =
• 2 sinx • (s/их)' =
2 sinx cosx =
sin2x.
f
Вычислить площадь треугольника, ограниченного осями координат и касательной к
графику функции у = -------- в точке х0 =
1 1
Решение.
Составим уравнение касательной: у' = 1'	у' =--------, у'(1) = -1.
(2х- I)2	(2х- I)2
Уравнение касательной имеет вид у-\ = -1 (х- 1)<=>у = -х + 2. Полученная прямая пересекает координатные оси в точках X! = О, У[ = 2, у2 = 0, х2 = 2. Поскольку
координатные оси взаимно перпендикулярны, то треугольник является прямо
угольным. Оба катета равны 2. Имеем SA = - • 2 • 2 = 2.
Ответ: SA = 2.
К параболе у = Зх2 - 5х + 8 в некоторой точке проведена касательная под углом 45° к оси абсцисс. Найти точку касания.
Решение.
Пусть М(х0,у0) является точкой касания. Точка М принадлежит кривой у = Зх2 - 5х + 8, следовательно, имеем у0 = Зх^-5х0 + 8 (1). По условию у'(х0) = 1 (rg45° = 1). Но у’ = 6х-5. Следовательно, _у'(х0) = 6х0-5, 6х0-5 = 1 (2).
Решая систему уравнений (1) и (2), находим: х0 = 1, у0 = 6.
Ответ: М(1,6).
4“ 1
Составить уравнение касательной к графику функции у = ---- в точке пересечения
его с осью абсцисс.
Решение.
X3 + 1
Находим точку пересечения графика с осью Ох. Допустим, у = 0, тогда —— = 0. Отсюда х3 + 1 = 0, то есть х = -1. Следовательно, М(-\, 0).
Находим к: у' = f—tT)' = fx2 + -V = 2х- —=> y'(-l) = -2-1 = -3. v X 2	\	х2
Следовательно, к = -3 . Отсюда вытекает, что уравнение касательной — это у = 0 = —3(х—(-1)) = —3(х+ 1).
Ответ: у = -3(х+ 1).
Тело, выпущенное вертикально вверх, двигается по закону Л(/) = 8/-5/2. Найти скорость тела в момент столкновения с землей.
Решение.
На земле h = 0, то есть 0 = 8r- St1. Отсюда t
-. То есть тело столкнется
с землей через - с. Находим скорость тела: v =
h', то есть, v = (8/- 5/2)' = 8-10/.
~	8	о 10-8
Следовательно, при t = - с имеем v = 8---—
= -8 (м/с).
Ответ: -8 м/с.
-F-
Материальная точка двигается прямолинейно по закону S = 60/-5/3. Через какое время после начала движения точка остановится? Найти расстояние, пройденное точкой до остановки.
Решение, ч
К моменту остановки скорость точки равна нулю. Находим v: v = (60/-5г3)' = 60- 15/2. Решим уравнение 60- 15/2 = 0, то есть, /2 = 4=>/j 2 = ±2. После начала движения, как выяснилось, точка остановится через = 2 с. Расстояние, пройденное точкой до остановки, составит S = 60 • 2 - 5 • 23 = 120-40 = 80 м.
Ответ: 2 с, 80 м.
Найти сумму: 1 + 2 • - + 3 •
П"
Решение.
Рассмотрим функции g(x) = 1 + 2х + Зх2 + ... + ЮОх"
100
f(x) — сумма геометрической прогрессии. v-./'l-vlOOx	V.101
Ях) =
j\ 100
]\ 101
Ответ: -(9-205 • 3~").
§2. Применение производной
Возрастание и убывание функции на промежутке
Функция
У = Лх) возрастает на промежутке (а, Ь)
*1 <х2^/(х,)</(х2) для всех х,,х2 е (а, Ь)
Функция
У = убывает на промежутке (а, Ь)
Х1 <х2=>/(х,)>/(х2) для всех Х[, х2 е (а, Ь)
Достаточный признак возрастания, убывания функции
Если
/'«>0
ДЛЯ всех X е (а, Ь),
функция у = f(x) возрастает на промежутке (а, Ь).
Если
/’(х)<0
для всех х е (а, Ь),
функция у = /(х) убывает на промежутке (а, Ь).
Если функция непрерывна в конце промежутка, то его можно присоединить к промежутку возрастания (убывания) функции.
Достаточное и необходимое условие постоянства функции
Если
f '(х) = О для всех х е {а, Ь),
функция у = Дх) постоянная на промежутке (а, Ь).
Критические точки функции
У = /U) — непрерывная функция.
х0 — внутренняя точка ее области определения.
Если
f ’Uo) = 0 или f '(х0) не существует,
х0 — критическая точка.
f W = о
О х0 х
Точки экстремума
х0 — точка максимума
Вблизи точки х0 Дх0) — наибольшее значение.
х0 — точка минимума
Вблизи точки х0 /(х0) — наименьшее значение.
х0 —точка максимума
х0 —точка минимума
— максимум функции
точки экстремума
/(х0) — минимум функции
Если
экстремумы функции
Необходимый признак экстремума
х0 — точка экстремума,
существует.
существует
Точки экстремума нужно искать только среди критических точек, но не каждая точка, в которой f *(х0) = 0 или не существует, является точкой экстремума.
/’(х0) - 0, но хоне является точкой экстремума.
не является точкой экстремума.
Достаточный признак экстремума функции
Первый признак
Если х0 — критическая точка, f '(х0) = 0 или f '(х0) — не существует.
Если при переходе через х0 производная f '(х) изменяет знак с «+» на «-»,
Хо
Если при переходе через х0 производная / '(х) изменяет знак с «-» на «+»,
О
Второй признак
то
— точ ка
минимума.
х0 — точка максимума.
х0 — точка максимума.
9
х0 —точка минимума.
существует
X
I
о не существует
X
Наибольшее и наименьшее значения функции, / непрерывной на отрезке
Свойство
Если функция Дх) непрерывна на отрезке и имеет на нем конечное число критических точек, то она принимает свои наибольшее и наименьшее значения на этом отрезке или в критических точках, которые принадлежат этому отрезку, или на концах отрезка.
Примеры
Я*) =
Wi& = f(b) [a.oj
та та
/(x) = Я*)
/(х) =
И =
Если функция у = /(х) на промежутке х имеет только одну точку экстремума х = а и если это точка максимума, то f(a) — наибольшее значение функции на данном промежутке.
А если х = а — точка минимума, тогда Да) — наименьшее значение функции на этом промежутке.
Выпуклость и вогнутость кривой
Кривая, выпуклая на (а, Ь).
Кривая, вогнутая на (а, Ь).
Кривая размещена ниже любой своей касательной.
Кривая размещена выше любой своей касательной.
Достаточные признаки выпуклости и вогнутости
f (х) > о на (а, Ь).
Кривая, вогнутая на (а, Ь).
f"(x)<0 на (а, Ь).
Кривая, выпуклая на (а, Ь).
Для построения графика целесообразно проанализировать, какой вид имеет график
функции на интервале (а, Ь) в зависимости от знаков первой и второй производных.
Точка перегиба (*оЛ*о)) •
В точке (х0;/(х0)) существует касательная, при переходе через эту точку выпуклость меняется на вогнутость (или наоборот).
Достаточный признак точки перегиба
В точке (х0 Лхо)) существует касательная, у"(х0) = 0 (или не существует) и при переходе через точку х0 У' изменяет знак.
(хо;/(хо)) — точка перегиба.
Для построения точки перегиба необходимо установить связь между существованием производной в точке х0 и существованием касательной к графику функции
Точки разрыва функции и их характер
Для элементарных функций точка разрыва — это такая точка, в которой функция не определена, но определена вблизи этой точки.
Виды точек разрыва
х0 — точка разрыва, • который устраняется.
х0 — точка конечного разрыва.
х0 — точка бесконечного разрыва.
Дх0) - не существует;
Нт f(xQ) =
х —> х0 - О
= Нт f(x) = А.
х —> х0 + О
Нт fix) = А;
х хй-0
Нт f(x) = В;А*В.
х -> х0 + 0 '
Нт f(x) = + оо;
х —> х0 - О
Нт Дх) = А.
х —> х0 + О
Нт Дх) ~ +оо;
х -> х0 - О
Нт f(x) = -оо.
х —> х0 + О
Асимптоты графика функции
Прямая I называется асимптотой графика функции у = Дх), если расстояние от точки М графика до прямой стремится к нулю при удалении точки М по кривой в бесконечность.
М СО
Вертикальная
о
Виды асимптот
Горизонтальная
Наклонная
Нт Дх) = оо.
Нт Дх) = у0.
: —> оо
к = Нт ;
b = Нт |Дх)-£х].
Если Дх) можно представить в виде Дх) = кх + Ь + а(х), где а(х) 0, когда х -> оо, то прямая у = кх + Ь является асимптотой: при к = 0 — горизонтальной, а при к * 0 — наклонной.
График функции может иметь вертикальные асимптоты в точках разрыва (бесконечного) или на границах области определения функции.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. Найти промежутки возрастания и убывания функции: Найдем область определения функции: D(y): Найдем производ-ную функции и разложим ее на множи-
тели, если это возможно:
Найдем знак производной методом интервалов:
Выберем промежутки, где f '(х) > 0, / '(х) < 0:
Запишем промежутки возрастания (убывания) функции с учетом непрерывности функции на концах промежутка:
D(y) = R.
f '(х)>0, х е (-1 ;1)
f '(х) < 0, если
х е (-оо;-1)и(1;+оо).
возрастает на [-1 ;1]; убывает на (—«>;—1 ], [!;+<»).
и
б) у =
+ 6х
D(y) = (-00;2) и (2; +оо).
, = (2х + 6)(х - 2)-(х2 + 6х) • 1 (х-2)2
= х2-4х- 12 = (х + 2)(х-6) (х-2)2	(х-2)2
f '(х) > 0, если X е (-оо;-2) о (6;+оо), f '(х)<0, если х е (-2;2) и (2;6).
функция возрастает на каждом из промежутков (-ос;-2] и [6; +оо);
убывает на каждом из промежутков [-2;2) и (2;6].
2. Найти критические точки функций:
Найдем область определения функции 7
у = Лх) £>(у):
Найдем производную функции / '(х):
Найдем точки, где: а) производной не существует;
б) производная равна О f '(х)= 0:
Проверим, будут ли дан-ные точки внутренними точками области опре-
деления и сделаем вы-
вод: -Ответ:
а) /(х) - х3 - Зх2 + 5 .
D(y) = (—оо;+оо).
/ '(х) = Зх2 - 6х = = Зх(х- 2).
f '(х) = О, х = 0; х = 2, f '(х) существует при всех хе R.
О е D(y) 2 е Р(у).
х = 0; х - 2 —
критические точки.
б) Лх) =
Зх-2 2х + 3 ’
f '(х) =
6х + 9 - 6х + 4
(2х + 3)2
13 (2х + 3)2
'(х) не существует, если х = -
f '(х) = 0;хе 0.
функция критических точек не имеет.
3. Найти точки экстремума и экстремумы функции: Находим область определения функции:
а) Дх) = 2x -x .
б) Дх) =
6х +18х
ММ
Находим производную:
Находим критические точки:
а) в которых производная не существует;
б)Д(х) = 0:
Определим знак производной на каждом из интервалов, на которые критические точки разбивают область определения: Найдем точки экс-тремума, учитывая характер изменения знака производной: Найдем экстрему-мы функции:

/ '(х) существует для всех
f '(х) не существует, если х = 0 х — —4,5 — не является внутренней областью определения
х = -1 —точка максимума, х — 0 — точка минимума, х = 1 — точка максимума.
точка максимума, х = 0 — точка минимума.
min = /(0) = о,
max j \	/
„„ -Л1) “ I-
max J *
= ДО) = 0.
min J 4 * * 7


j1
4. Исследовать функцию с помощью
производной и построить ее график:
Найдем область определения функ-ции Дх):
Найдем производную функции:
Найдем критические точки функции. Для этого: а) определим, в каких точках производная не существует;
б) решим уравнение f '(х) = 0:
a) f '(х) существует во всех точках числовой прямой;
X] = -1,х2 = 1 —критические точки.
Определим знак производной на каждом из интервалов, на которые критические точки разбивают область определения, найдем промежутки возрастания, убывания функции Дх):
Найдем точки экстремума функции:
Найдем экстремумы функции:
х = -1 —точка минимума,
1 — точка максимума функции.
Для уточнения формы графика найдем значения функции в нескольких дополнительных точках:
Начертим график функции:
ДО) = 0, Д2) - -2, Д-2) = 2.
5.	Найти наибольшее и наименьшее значения функции у = х - Зх“ - 45х + 225 на отрезке [0;6].
Находим D(y):
Находим производную у':
D(y) - R.
у' - Зх -6х-45 = 3(х -2х-15) =
Находим критические точки (в которых г'(х) = 0 или не существует):
Выбираем тё^ которые принадлежат данному отрезку:
Вычисляем значение функции у = Дх) в этих критических точках и на концах отрезка:
Сравниваем получённые результаты и выбираем среди них наибольший и наименьший и записываем ответ:
у' существует для всех х е R
х = 5 принадлежит отрезку [0;6].
ДО) = 225,
Д5) = 50,
У(6) = 63.
max у(х) = у(0) = 225, [0;6]
То-6]	= у^ = 50 
6.	Найти множество значений функции Дх) = х -Зх + 3 , если хе [-1;1 ]. _____
Данная функция определена и непрерывна на множестве R.
f '(х) = Зх2-6х = Зх(х-2). f '(х) = 0; если х = 0 или х = 2. Отрезку [-1;1 ]
принадлежит одна критическая точка х = 0.
ла\ - о. л 1\ - 1. лчч - 1 тах /(х) = 3; min Дх) = -1.
Учитывая непрерывность функции /, получим [-1;3].
Ответ:
7.	Число 64 записать в виде суммы двух положительных слагаемых, чтобы сумма их квадратов была наименьшей.
Решение.
Пусть одно слагаемое будет х, тогда другое — 64-х.0<х<64.
2	2
Рассмотрим функцию /(х) = х +(64-х) на [0;64].
/ (х) = 2х2 - 128х - 4096 — квадратичная функция. Она имеет одну точку экстрему-ма
х = — = 32 —точку минимума. Эта точка принадлежит отрезку [0;64]. с*»
Д32) </(0) </(64). Значит, функция принимает наименьшее значение при х = 32.
Искомые слагаемые 32 и 32.
Ответ: 32 и 32 .
8.	В правильной четырехугольной призме длина диагонали боковой грани равна 6л/з см. При какой длине высоты объем призмы будет наибольшим?
Решение.

I
А
90°.
Из теоремы Пифагора DC = 7108-х2.
2
Рассмотрим функцию: У(х) = (108-х )х = 108х-х
108 -х > 0; 0 <х
Исследуем данную функцию на экстремум на промежутке (0;67з):
V\x) = 0; если х = 6,
если 6 < х < 673 , то И'(х) < 0.
Значит, х = 6 —точка максимума.
И(6) — наибольшее значение функции на промежутке (0;б7з).
Ответ: объем призмы будет наибольшим, если ее высота 6 см.
Построение графиков функций
Прежде чем приступить к решению заданий, отметим, что при построении графика не обязательно анализировать все элементы поведения функции. Построение графиков функций целесообразно начинать с исследования поведения непрерывной функции, используя первую производную.
Отметим, что областью изменения многочлена нечетной степени является множество всех действительных чисел. Для многочленов четной степени и других рассматриваемых функций E(f), как правило, определяется после проведения исследования. Поэтому сначала не следует уделять особое внимание нахождению £(/). £(/) — множество значений функции.
Алгоритм построения графика функции
1.	Найти область определения функции, точки пересечения с осями координат.
2.	Исследовать функцию на четность или нечетность и на периодичность.
3.	Найти интервалы возрастания и убывания функции и точки экстремума.
4.	Построить график функции.
9.	Построить графики функций.
у = 9х2(1-х) (сложность 1).
1)	Область определения £)(у):
у = Зх - 5х + 4 (сложность 2).
Точки пересечения с осями координат: х = 0=>у = 0; у =	= 0; х2 = 1.
2) Функция непериодическая.
3) Найдем интервалы возрастания и убывания функции и точки экстремума: у' = 18х-27х2;
Нули функции уточним позднее.
2) Функция непериодическая.
3) у' = 15х4-20х3;у' = 0=>х« = 0;
у' = 9х(2-3х);у' = О
у(0) = 0;у
V
max
max	min
Уточним точку пересечения с Ох:
У
о
2	у
у - sin х - cosx (сложность 3).
sin x-cosx - 0; cos x+cosx-1 = 0;
cosx
;cosx} =
0,7; cosx2 =
-1 (не подходит);
cosx = 0, 7=>Xj = 40° + 360° • п 2) Функция четная.
= 320° + 360° • п = 1,8л + 2лп.
3) у' = 2sinx • cosx + sinx',
Будем искать решение на отрезке [0,2л].
Находим sinx = 0
- 2л; cosx = -
0 => sinx\ 2 cosx +
О
4я
2л
2л
min
min
max
min
max

СТРАНИЧКА АБИТУРИЕНТА
Использование производной для доказательства тождества
" 11 ------ 	 — -----" .» 
1.	Доказать тождество: sin2x + cos\х - ?) cos[ х + ?
Решение.
Рассмотрим функцию Дх) = sin х + cos
cos2x + cos
/(х) = 2sinxcosx — sin2x ~ sin2x — sin2x = 0.
/(х) = 0 для всех хе/?, значит, Дх) — постоянная; Дх) = С.
Вычислим значение функции Дх) при любом значении х, например, х = 0.
ДО) = sin^O + cos(-^]cos- = 0+ ;;•- = 7 .
то есть, верно тождество sin х + cos\x-
Использование производной для доказательства неравенств
Чтобы доказать неравенство Дх) > 0 при х > 0, достаточно, чтобы ДО) > 0 и /(х) > 0 при
1.	Доказать, что sinx < х для всех х > 0.
Решение.
Рассмотрим функцию Дх) = х - sinx.
f '(х) = 1 - cosx> 0 для всех хе/?. Значит, Дх) возрастает на /?. Если х>0, то
Дх) >ДО), то есть х - sinx > 0; или sinx < х.
2.	Доказать, что при 0 < х < - справедливо неравенство: 2х + —
Решение.
Рассмотрим функцию Дх) = 2х + —
О
На промежутке (0;1] данная функция убывает, поэтому при 0<х<- справедливо
Значит, Дх) > 5, то есть 2х + —
3.	Доказать, что х + - > 2 при х > 0.
Решение.
На промежутке (0;+<ю) х = 1 — точка максимума, Д1) — наименьшее значение функции Дх) = х + р Д1) = 1 + 1 = 2. Значит, Дх)>2, то есть других точек
экстремума нет. То есть х + - > 2, если х > 0.
4. Исследовать функцию и построить ее график.
1) D(y) : (-оо;+оо);
х = 0=>у = 0; у = 0 => 3 V? -х2 = 0;
л/х"(3 - л/*4) = 0; Xj = 0;
х2 з - ±I/х3 « ±2, 3 .
2) Функция четная.
ох , о 2 “з 0	,	2(1 -хЦх)
3)у = 3 -х -2х; у =	.
В этом примере ищем не только такие точки, где у' = 0, но и такие, где у' не существует.
Имеем у' = 0 => 1 -х\/х - 0 => Х] 2 ± 1;
у' не существует => х = 0. Если х -> 0, то у'->оо, то есть' в точке (0;0) касательная к графику функции вертикальная.
Я±1) - 2;у(0) = 0; : (-оо;2].
4)
б) у = 3^/х-х.
1) D(y): (-оо;+оо);
х = 0 => у = 0;
у - 0=>Xj = 0; X] 9 = ±727.
2) Функция нечетная.
2
3)У = зЛ ’-1;
у(±1) = ±2;у(0)= О, £(у): (-оо;+со).
4)
§3. Интеграл и его применение
Первообразной для функции Д F(x), если для всех х из этого проме				x) на заданном промежутке называется функция жутка выполняется равенство F'(x) = Дх)
/(X)	F(x)	Доказать, что F(x) является первообразной для Дх) на заданном промежутке.		
2х	x2, x e R	F'(x) = (х2)' = 2х = Дх), х е R.		
	2Jx	F'(x) = (2лУх)' = 2 • -Д- = -у: = Дх), х е (0;+оо) . 2jx Jx		
X2		F'(x) =	= -f—3) = *4 = Дх), x g (-<x>;0) VJ (0; + oo). \ X/	v	xL	
sinx	-cosx	F'(x) = (-cosx)' = -(-sinx) = sinx = f(x), x e R.		
cosx	sinx	f(x) = (sinx)' = cosx = f(x), x e R. 		
1 2 COS X	tgx	1	TC F'(x) = (tgx)’ = —для всех x, кроме x = - + nn, n e Z. COS X		
1 . 2 Sin X	-ctgx	f 1 \	1 F(x) = (-Ctgx)' - -I- 2 ) =	2 = f(x) для всех X, sin x	sin x кроме x = nn, n e Z.		
к к — число	kx	F'(x) = (кх)' = к = f(x), x g R. 4		
X	x~ 2	F'(x) =	• 2x = x = Дх), x g R.	
X2	*5 XJ	F'(x) =	(y)' = 1 ’ ^x2 = X2 = f(x), x G R.	
xa a^-1	Xa + 1 a + 1	F'(x) =	(xa+ ? + 1-	)' = —-— • (a + 1) • ха = ха = Дх), х g R, а ф -1. '	а + 1
Операция нахождения
первообразной функции — интегрирование.
Интегрирование — операция, обратная дифференцированию.
Основное свойство первообразной
Если Г(х) первообразная для Дх),
F(x)+ с — первообразная для Дх).
с — произвольная постоянная.
Каждая из функций у = 2х2; у = 2х2 + 2; у = 2х2-2 является первообразной для функции у = 4х.
Геометрическая интерпретация основного свойства первообразной
Г рафики всех первообразных данной функции можно получить
х из любого путем параллельного переноса вдоль оси Оу..
F(x) + с — общий вид первообразной для f(x).
2х2 + с — общий вид первообразной для 4х.
Три правила нахождения первообразной
Если
F(x) — первообразная для /(х), Н — первообразная для h,
F(x) + Н(х) — первообразная для /(х) + Л(х).
Если
F(x) — первообразная для /(х),
kF(x) — первообразная для к -Дх); к = const.
Если F(x) — первообразная для Дх),
-F(kx + b) — первообразная для к
flkx + b) ;
к и Ь — постоянные; к ф 0.
Функция	A*	Общий вид первообразных
х4 _|_ -7	x4 4- 1 x- 7 4	1 ,	X5 , X-6 ,	X5 1	,
	4+1+-7+	г 1 ии <4. с 1 LA | !	1 С •
12-47 = 12-х-10	r- 10 + 12x~——	1	Х“9	1 + с = 12х — Л + с = 12х +	+ с.
X10	- 10 +	1	-9	9х9
	3	
1	2	2 Гзи. •	2	,
г ,	2 .	— + sinx + c	= - л/Х3 + Sinx + С = = тХл/х + sinx + с.
л/х + cosx = х + cosx		3	3
	2	
5 . 2	5 • (-ctgx) +	1 и 1
sin X		
л 2	1	, _u -tgx + c = 4	+ с . 4
4 cos х		
10-х16	V.16+ 1 10 -	+	= 10 X17 !
	16 + 1	с	17
22	„	.I	r-ll	22	-2
— = 22 • x-12	22 • -— + c			,, + с - ,, + с.
y12 A	— 1 1	11-х11	хи
1 х~10 +	1	।
4-10 C	4Ox10 C'
\0 • 2jx + c = 20jx + c.
— = 10-х-1/3
Ifx
cos4x
-sin4x + c. 4
1 cos2(7x + 6)
|rg(7x + 6) + c.
15
(8x + 2)9
Совокупность всех первообразных функции Дх) на промежутке называется неопределенным интегралом от функции f на этом промежутке.
Обозначается: |Дх)сЬс, читается:
интеграл эф от икс по дэ икс.
f — знак интеграла, Дх) — подинтегральная функция,
f(x)dx — подинтегральное выражение, х— переменная интегрирования.
Если F(x) — одна из первообразных Для f,
пишут:
\f(x)dx = F(x) + с.
ycf(x)dx - ky\x)dx, к = const;
постоянный множитель можно
выносить за знак интеграла.
|(Д*) ± g(xY)dx = |Дх) ± \g(x)dx;
интеграл от суммы функций равен сумме интегралов от каждой функции.
Таблица неопределенных интегралов
Пример
. [0<& = с, с — постоянная.
. |хаб& =
J(3x2 + x + V)dx = j3x2dx + jxdx + jldx =
. \sinxdx = - cosx +
. tcosxdx — sinx + c
t dx .	.
dx . 2 sin X
1. \cos(k.x + b)dx =
JrgWx =	= jl ~ ™=
COS X	COS X
= —Ц- -	= tgx-x + c.
COS X
2. j(&x + b)adx —
dx
dx	.	,
---- = arc sinx + c
fix) — непрерывная на промежутке Z;
F(x) — первообразная для f на промежутке I;
F(b)-F(a) — приращение первообразной.
Число F(b)-F(a) называется определенным интегралом от а до Ь от функции Дх) a g I, b е I.
ь
а) [Дх)ййс; читается: интеграл от а до b эф от икс дэ икс;
а
I б)
F(6)-F(a) = F(x)*
[/(x}dx = F(x) формула Ньютона-Лейбница
a
a
f(x) — подинтегральная функция; f(x)dx — подинтегральное выражение а — нижний предел интегрирования; Ь — верхний предел интегрирования;
х — переменная интегрирования.

у
-X
Вычислить интегралы.
Чтобы вычислить определенный интеграл
pc2dx = — о
O’’ _ 1 A _ 1 — — - _ (J _ -
о
• •?
[f(x)dx, нужно найти
a
одну из первообразных для функции Дх), в полученное выражение вместо х сначала подставить верхний, а потом нижний предел интегрирования, а потом от первого результата вычесть второй.
\cosxdx = sinx
О
о = sinn-sinQ = 0-0 = 0.
2	5
э
\4sinxdx = (—4cosx) ~
4 2V
cos-
4/V cos-

4
f!
• ч'
'l'
ч
Основные свойства определенных интегралов
5
1)	j(/(x)±g(x))Jx = [f(x)dx± jg(x)dx; а	а	а

b	b
2)	\kj{x)dx = k\f{x)dx 'i (k - постоянная)
a	a
Л
b	с	b
3)	ty[x)dx = [f(x)dx+ [f(x)dx; (/(x) - интегрирована
a	a	c
•И
‘Г
-•Я • .4

о	а
4) F/(x)tZx = -Mx)dx;
214
у

Геометрический смысл определенного интеграла
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной непрерывной функции / на отрезке [а;6], осью Ох (у = 0), прямыми х = а, х = b.
$ABCD = $А.Х№ а
b
Если функция /{х) непрерывна и неотрицательна на отрезке [а;£], то интеграл [flx)dx
равен площади криволинейной трапеции, ограниченной графиком данной функции.
Площадь фигуры, заштрихованной на рисунке, равна:
Вспомни графики.
у = кх + Ъ, к> О
Построить график функции у = 2х2 - 12х + 19.
“	Решение.
1) хо =	= 3 • 2) у0 = И*о) = Я3) = 1 •
3) Строим параболу вида у = 2х2 (ветви вверх, поскольку а = 2 > 0) с вершиной в точке (3; 1) (пересечение с осью Оу в точке с = 19).
Вычисление площади трапеции с помощью интеграла
Объемы тел
!
В общем случае
Для тел вращения
Если тело расположено между двумя перпендикулярными к оси Ох плоскостя-
ми, которые проходят через точки х = а и
х = Ь, то
где 5(х) — пло-
щадь сечения тела плоскостью, которая
проходит через точку х е [<?;/>] и
Если тело получено в результате поворота вокруг оси Ох криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции у = fix) на отрезке [а;/?] и прямыми х = а и х = 6, то ' ь
V = л j/ ~(x)dx. а
перпендикулярна оси Ох.
ь
V =	,
а
Механический смысл интеграла
Если функция v = /(г) определяет мгновенную скорость движения тела в каждый ь
момент времени t на [а-,Ь], то определенный интеграл равен пути, пройденному а
за отрезок времени t = b - а.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Для функции /(х) = —— найти первообразную, график которой проходит через точку cos х
1
Решение.
Найдем общий вид первообразной:
Координаты точки М подставим в равенство первообразной:
Найдем постоянную с:
Ответ:
F(x) - tgx + с.
F(x) = tgx - 1 .
Вычислить интеграл.
Решение.
Представим подинтегральное выражение в виде суммы дробей, разделив почленно числитель на х2. Используем формулу интеграла суммы:
Найти интеграл.
Решение.
Представим подинтегральное выражение в виде степени с дробным показателем:
dx -
13
Найти f(x-3)Jx, если при х = 2 первообразная функции равна 9.
Решение.
dx;
Ответ:
Вычислим интеграл:
Найдем постоянную с:
Вычислить площадь фигуры, ограниченной линиями.
1.	Строим заданные линии и штрихованием отмечаем фигуру, площадь которой надо найти. Ус тановим, является ли эта фигура криволинейной трапецией:
2.	Записываем формулу для вычисления площади искомой фигуры:
£ $ABCDE~ &ABDE
b	b
= [Jxdx- (2dx. a	a
$OA C + $A CB
a	b
= |x2<Zr-J(2-x)dx.
0	a
3.	Находим пределы интегрирования:
2 - x = 0; x = 2.
у = x2, x2+x-2 = 0, у = 2-x\ и x = 1, x = -2;
4.	Вычислим искомую площадь по формуле (1):
9	9
S = j^/xdx- ^2dx =
4	4
= |(27-8)-2(9-4) = *,
5.	Ответ:
о Используя геометрический смысл интеграла, вычислить ^25-x2dx.  -5 Решение.
Рассмотрим функцию у = J25 - х2. Найдем ее область определения: 25-х2>0, -5<х<5. Значит, на отрезке [—5;0] функция определена и принимает о
неотрицательные значения. Поэтому значение интеграла [ J25 -x2dx равно площади -5
фигуры, ограниченной линиями у = 725-х2, у = 0, х = -5, х = 0.
Если у>0, то у2 = 25-х2 — уравнение полуокружности с центром в О(0;0) и радиусом 5.
о ______
Значение выражения Г J15 -x2dx равно - площади круга (см. рис.),
4
тоесть5лов =
СТРАНИЧКА АБИТУРИЕНТА
1.	Найти общий вид первообразной для функции Дх) = |х - 1|. Решение.
если х < 1, если х > 1.
На промежутке (-оо;1) первообразная имеет вид F,(x) = х
X2
На промежутке [1;+оо): Г2(х) = — ~х + с2. F2(l) = ГД1);
если х < 1,
если х > 1.
Ответ: Г(х)
если х < 1,
если х > 1.
2.	Вычислить интеграл tj2x-x2dx.
1
9
Решение.
Искомый интеграл равен половине площади сегмента дуги в — радиан.
4л
Ответ: - +
3.	Найти площадь фигуры, ограниченной линией
, касательной к ней
у - 1 ~ СО5 2х- -
в точке с абсциссой х = 7 и прямой у = — - -
Решение.
X е (-оо;1).
Уравнение касательной имеет вид:
у - 2 = 0 — уравнение касательной.
Точка А имеет координаты А -;2 .
Найдем координаты точки D :
d(-и2).
Найдем координаты точки С:
Значит, В\— л ;2]. 42 >
Искомая площадь 5 =	+ S2,
S2 — площадь \BCD .
где — площадь криволинейного треугольника АВС,
л ми 8’
Ответ: 5 =
4.	Найти первообразную для функции /(х) = Зх2-х+ cosnx, график которой проходит
через точку М
Решение.
Первообразной для функции Зх2 является х3, для функции х — функция -х2, а для
функции cos их — функция -sinnx. Поэтому функция х3 - — + -sinnx — первообразная
для функции f(x), следовательно, [(Зх2 -х + cositx)dx = х3_-— + -sinnx + с.
J	у ~ 42 д
Среди этих первообразных условию задачи удовлетворяет та, для которой
5
, то есть F(x) = х3 - — + -sirnix.
5.	Вычислить интеграл jcos 4х<Ух.
о Решение.
Запишем подинтегральную функцию cosx в виде
4 fl + COSixX1 1/1.-» n ,	2_ ч if. о . 1 + cos4x\
cos х = ------- = -(1 + 2cos2x + cos 2x) = - 1 + 2cos2x +--- =
К 2	> 4V	' 4V	2 J
3 , 1	_ , 1	.
= - + -cos2x + -cos4x.
8 2	8
4	3	11
Первообразной для функции cos x является функция F(x) = -x + -sin2x + d-sin4x.
8	4	32
Я
Применив формулу Ньютона-Лейбница, имеем [cos 4xdx = F(n)-F(0) = о
/	a
6. Найти все положительные числа а, для каждого из которых [(2 - 4х + Зх2)<& < а. о
Решение.
Первообразной для функции Дх) = 2 - 4х + Зх2 является функция F(x) = 2х - 2х2 + х3.
Поэтому |(2-4х + Зх2)б/х = F(a)-F(0) = 2а —2а2 + а3 о
и неравенство из условия задачи можно записать так: 2а-2а2 + а3<а, а3 - 2а2 + а < 0, а(а - 1 )2 < 0. Поскольку по условию задачи а > 0, то среди положительных чисел неравенство а(а- 1)2<0 удовлетворяет только одному числу: а = 1 .
Ответ: а = 1.
7. Вычислить объем тела, образованного поворотом плоской фигуры, ограниченной
1
графиком функции у - cosx на промежутке
Решение.
и осью абсцисс, вокруг оси абсцисс.
По формуле вычисления объема тела вращения находим:
ТТ	7T	Я
1 - cos2х
sinlx

о
о
8. Вычислим объем тела, образованного вследствие поворота около прямой у = 1 плоской фигуры, которая ограничена графиком функции у = I + sinx и касательными к этому графику, проведенными в точках с абсциссами х = 0 и х = л.
Решение.
Искомый объем равен объему тела, образованного поворотом около оси абсцисс плоской фигуры, которая ограничена графиком функции у = sinx и касательными, проведенными к этому графику в точках с абсциссами х = 0 и х = л.
Равенство касательных у = х и у = л-х. Поскольку фигура поворота симметрична
я
относительно прямой х = -, то искомый объем:
2
1 — cos2x\ ,	~ (xJ х , sinlx
--------- dx = 2 л — - - ч-----.—
9
•;
О
О
о
<1

• 4
§4. Производная и первообразная показательной, степенной
и логарифмической функций
Формулы дифференцирования
/ - х (е ) ~ е {ax)' = aIna	(0, 3 х)' - 0, 3x/«o,3 .
(Inx)’ = " X	{log^y =	. '	xlnl *
(logax)' u	x • Ina	d P
Если n = y{x), to (e ) = e * и	(e^)' = е/х-{/хУ = e/x--±- =	. 2a/x 2vx
(a")' = auIna • u'	(7x+l)' - 7 х +l • Ini  (x2+ 1)' = 2x-7x’+l • bfl.
{lnu)' = - • u'	{ln{cosx))' = 		 {cosx)' = - ' ' = -tgx.
u	cosx	cosx
{log u)' -	-и' ulna	1	3 (/ogs(3x+ 1))' = 	1	3 = -—X-— . 5	(3x+1)-/m5	(3x+ \)ln5
{ ax,	a- 1	, (w ) = aw • и	11 NJ] и 73	+ X NJ 11 to 73 1 1 >—* to W I *— 1 • NJ bO 1 UJ i to *
Таблица интегралов
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1.	Под каким углом кривая у = 1пх пересекает ось Ох ?
Решение.
Найдем точку пересечения оси Ох с графиком функции у = 1пх: 1пх = 0; х = 1 .
Вычислим угловой коэффициент касательной в точке х0 = 1; к = у' (х0) •
у' = {1пхУ = -; У(1) = | = 1. Найдем угол, который образует касательная с Ох:
tga = У(х0); tga. = У(1) =
1; а = 45° — искомый угол.
Ответ: 45°.
2.	Исследовать на монотонность функцию у = — - 3 /и(х - 2).
Решение.
1) О(у): х - 2 > 0; х>2; хе(2; + оо).
3) у' существует для всех х е D(y);
у' = 0; если х = 3; х = -1.
4) Знак производной на каждом из интервалов области определения покажем на рисунке.
5)У>0, х g (3; + оо); у <0; х е (2;3).
(х-3)(х+ 1)
Функция возрастает на промежутке [3;+оо), а убывает на (2;3].
Ответ: [3;+оо) —промежуток возрастания, (2;3] —промежуток убывания.
3.	Исследовать функцию у = х • е на экстремум.
Решение.
D(y) = R’,y' = (хех)’ = х'ех + х(еху = е + хех = ех(1+х), + у'
у' = 0; х = -1 -,у' существует для всех х е R.	-i - у
х = -1 — точка минимума.
У min = Х-1) = е1 = (график функции на рисунке). ГШП	'
Ответ: у . - —.
* Jmin р С1
4.	Найти наибольшее значение функции у = 23-х на отрезке [4;6]. _____
t 	%	\f	%
У = 2	• (3-х)' = -2	= —.
2
Поскольку у < 0 для всех х е R, то функция не имеет критических точек.
у(4) = 23’4 = 2-1 = |; у(6) = 23"6 = 2-3 = max у(х) = у(4) = 2	8 [4;6]	2
Ответ: max у(х) = у(4) = -
[4;6]	2
5. Построить графики функций.
Поскольку х > 0, то с осью Оу график не пересекается, у = О
V' - О
2) Функция четная.
3)У =
3) Нуль функции: х = 1.
У
2
вертикальные асимптоты
у = 1п4; у = О
у' = О
Находим нуль функции:
max
6. Вычислить площадь фигуры, ограниченной линиями у = -\лу = 1-х
у' = 0 => х = О Е(у): (~<х>;1п4).

Построим заданные линии и заштрихуем фигуру, площадь которой нужно найти.
= eabcd-SABCD.
Пределы интегрирования:
24-6,5-6/и6 = 17, 5-6/л6.
СТРАНИЧКА АБИТУРИЕНТА
1. Найти производную функции у = х .
Решение.
Прологарифмируем левую и правую части по основанию е.
Iny = xlnx.
Найдем производную левой и правой частей равенства.
2. Вычислить площадь фигуры, ограниченной графиком функции и у = 2jx и касательной, проведенной к графику функции у = 1 + 1пх в точке с абсциссой х = 1. Решение.
Уравнение касательной у=1 + 1(х-1) = х.
Искомая площадь равна S = ty2jx-x)dx = -о
Ответ:
3. Найти наименьшее и наибольшее значения функции у = е
 sin2x
на промежутке 0;-
Решение.
= е • (-2л/3) • sin2x + 2cos2x • е 2 = е 2'fi'\-2j3sin2x + 2cos2x) = — 4е
sin2x-
-cos2x
= -4е
sin\ 2х- - = 0;
Ttn
п
промежутку 0;- принадлежит точка
12’
Я0) = е 2^’° • sinQ = 0;
sinn = 0;
sin-
0.
max
0;?
Ях) =
, т in
0:?’
у(х) = у(0) = у! -1 = 0
4. Найти наибольшее значение функции у = 9 • 3х • 3 Решение.
у = 32-3Х-3-Х‘ = 3~х+х+2; D(y) = R;
у1 = 3-х+х + 2./„3.(_ 2х+1);
I
0;
Следовательно,
= ~ — точка максимума, 9
З4
max ~	’
-
Ответ: З4.
1
5. При каких значениях а уравнение ах1 = Inx имеет один корень? Решение.
Построим график функции Дх) =
Inx
2 '
1) D(f) = (0; + оо) .
2)/<х) =
3) f(x) = 0; Inx -
4)
V - т ах
2e
Уравнение имеет один корень при а < 0 и при а = —
§5. Комплексные числа и действия с ними
Комплексные числа
Число, которое удовлетворяет равенству х2 = -1, обозначают буквой i и называют
I
мнимой единицей. Таким образом, i2 = -1.
Числа вида а + Ы, где а и Ь — любые действительные числа, i — мнимая единица, называются комплексными.
a — действительная часть комплексного числа,
Ы — мнимая часть комплексного числа, Ь — коэффициент при мнимой части.
Числа вида 0 + Ы называют чисто мнимыми числами. О + Ы = Ы.
Числа вида а + 0/ отождествляют с действительными числами a + Oz = a\ 0 = 0 + 0/. О — единственное комплексное число, которое является и действительным, и чисто мнимым.
Комплексные числа вида a + bi и а-Ы называют сопряженными.
Комплексные числа вида а + Ы и -а-Ы называют противоположными.
Два комплексных числа а + Ы и c + di называют равными, если равны их действительные части и коэффициенты при мнимых частях
7 .	I а = с
а + Ы = с + di <^> < b = d к
Понятий «больше», «меньше» для комплексных чисел не существует.
5 + 2/ — комплексное число.
5 — действительная часть.
2/ — мнимая часть.
2 — коэффициент при мнимой части.
—12/ — чисто мнимое число.
—12/ = 0+ (-12/).
7 — действительное число.
7 = 7 + 0/.
- 2 + 3 / и — 2 — 3 /, 6 / и —6 z, 3 и -3 .
-л/2-7з/ и л/2 + ТЗ/.
Найти действительные числа х и у из уравнения (х-у) + (2x + y)i = -3 + 3/.
Решение.
На основании равенства комплексных чисел имеем:
Действия над комплексными числами в алгебраической форме (а + Ы) Сложение
(а + Ы) + (с + di) = (а + с) + (b + d)i,
(а + Ы) + (а-Ы) = 2а — сумма двух взаимно сопряженных комплексных чисел является действительным числом.
(5+ 2/)+ (2-3/) =
= (5 + 2) + (2 + (-3))z = 7-z (1-2/) + (1 + 2/) = 2".
Вычитание
(исходя из определения, вычитание рассматривается как действие, обратное сложению).
(a + bi)-(c + di) = (а - с) + (b - d)i.
/
(10 + 2z)-(3-4z) =
= (10-3) + (2-(-4))z = 7 + 6/.
Умножение
(а + bi)  (с + di) = ас + adi + bci + bdi2 = = (ас - bd) + (ad + bc)i.
Умножение комплексных чисел выполняется как умножение многочленов с учетом, что /2 = -1 .
(а + bi) • (а - bi) = а2 - (bi)2 = а2 + Ь2 — произведение двух взаимно сопряженных выражений является числом действительным.
(5 + 2/)(3-4/) = 15-20/ + 6/-8/2 = = 15 + 8- 14/ = 23- 14/
(5-3/)(5 + 3/) = 25 + 9 = 34.
Разложить на комплексные множители а4 + Ь2 = (а2 + Ы)(а2 - bi).
а2 + b2 = (а + bi)(a - Ы).
Деление
(действие, обратное умножению)
а + i (с + di * 0). Умножим числитель и знаме-с + di
7-i _ (7-i)(3-i) 3 + i (3 + /)(3 - /)
натель на число, сопряженное со знаменателем
а + bi _ (а + bi)(c - di) _ с + di с2 + d2
_ (ас + bd) + (-ad + bc)i _ ас + bd be-ad. c2 + d2	c2 + d2 c2 + d2
Степени мнимой единицы
/о = 1; /' - /;	/2 = -1;	/3 = -/; /4 = 1;	/17 = /4-4+1 = ZJ - /
i4k = l;/44r+ 1 = i-^k+2 = -l;/4* + 3 = /.4Л = |	.39 = .9.4 + 3 = .3 = .
• £ £ £ * к = 0;±l;±2 i т.д.
Возведение в степень
21 -7/-3/+/2, 21 - 10/- 1
9+1	10
20- 10/ = 20 _ 10/ =
10	10 10 л
(а + Ы)п = (а + Ы) • (а + Ы)  ... • (а + bi),neN <_________________________________/
п раз
Извлечение корня
(а > 0).
знак «+» в скобках, если Ь > 0, знак «-» в скобках, если Ь < 0.
— арифметический корень
Геометрическое изображение комплексных чисел. Модуль и аргумент комплексного числа
Первый способ.
Комплексное число а + Ы геометрически изображают точкой М(х;у) в прямоугольной системе координат: х = а; у = Ь.
У ж
М(а,Ь) b----т
[Ь	М(а;Ь) <-» а + Ы
о 1 а	X
Ось абсцисс, на которой размещены точки, соответствующие действительным числам (а + Oz), называется действительной осью.
Ось ординат, на которой размещаются все мнимые числа, называется мнимой осью.
О = 0 + Oz — изображается началом координат.
Второй способ.
Комплексное число а + Ы изображается в сис-
теме координат радиус-вектором ОМ О(0;0); М(а;Ь).
A (4;2)->4 + 2z;
В (0;3)->0 + 3z = 3z;
У (5;0)-> 5 + 0z.
Построить векторы, которые изображают слагаемые и сумму комп-
лексного числа (- 5 + 4z) + 5 .
Слагаемым соответствуют —> —> радиусы-векторы О А и ОМ,
а сумме — радиус-вектор ОС.
Длина вектора, изображающего комплексное число, называется модулем этого
комплексного числа и обозначается буквой г. Из рисунка видно, что г = Ja2 + Ь2.
Модуль действительного числа совпадает с его абсолютным значением.
Сопряженные комплексные числа а + Ы и а-Ы имеют один и тот же модуль.
Модуль чисто мнимого числа равен абсолютному значению коэффициента.
Комплексные числа Z, которые имеют один и тот же модуль |Z| = г, соответствуют
точкам комплексной плоскости, которые расположены на окружности с радиусом г и с центром в начале координат.
Найти модули комплексных чисел 2 - z; - z; 2z.
Решение.
Угол <р между положительным направлением оси абсцисс и вектором ОМ, изображающим комплексное число а + Ы, называется аргументом комплексного числа (0<ф<360°).
L
Аргумент ф комплексного числа а + Ы связан с а и Ь формулой tg ф = -;
аргументом действительного положительного числа является 0°; действительного отрицательного числа — 180°; аргументом мнимых чисел Ы является 90°; аргументом чисел -Ы является 270°.
Для нуля аргумент не определен.
Найти аргумент комплексного числа - 3 + 3 /.
Решение.
Найти аргументы чисел а)1; 6)3/; в)-2; г)—2/.
Тригонометрическая форма комплексного числа
Z = а + Ы — алгебраическая форма записи комплексного числа.
У ж,
М(а;Ь)
а = ГСО5ф
Записать числа
в тригонометрической форме. Решение.
Ф — II четверть;
tg
Z = а + Ы = гсо5ф + irsiny =
= 2(cosn + isirnt;
= г(со5ф + isimp) — это выражение называется тригонометрической формой комплексного числа z.
<P
cos - + isin-.
Записать число в алгебраической форме.
4 cos - + isin
Действия над комплексными числами в тригонометрической форме
Сложение и вычитание комплексных чисел удобнее выполнять в алгебраической форме. Для остальных операций более удобна тригонометрическая форма.
Умножение
+ jsintpj) • r9(cos<p7 + zsm<p7) = = Гу  г2(со5(ф1 + ф2)+ is™(ф 1 + Фг))-
2(cos36° + isin36°)  3(cos54° + isin54°) =
= 2 • 3(cos(36° + 54°) + ш«(36° + 54°)) =
= 6(cos90° + isin90°) - 6i.
Деление
г](солф1 + isin(py) _ 	_______	.	__ емче
г2(со$ф2 + isin<p2)
г.
= — (со5(ф[ - ф2) + isin((py - ф2)).
г2
3(cosn + isinn)
cos - + isin-
= 0, 6 cos я - -
+ isin
0,6
= (-0,3 + 0,373г).
Возведение в степень
(г(со$ф + isin<p))n = rn(cosn<p + isinny) — формула Муавра.
(2(cos20° + ш«20°))3 =
= 2J(cos60° + isin60°) — 8 • + i *
= 4 + 473/.
Извлечение корня и-ой степени
nJr(costy + ш«ф) =
Найти VT.
Решение.
пг( ф + 2Ъс . . . ф + 2^я^ = *]г\ cos?----+ isin^----- .
' П	п '
'Тг — арифметический корень
к = 0; 1; 2; ...п - 1.
Корень степени п в множестве комплексных чисел имеет п различных значений. Все значения '76 равны между собой и равны 0.
Все п значения корня и-ой степени изображаются точками на окружности с центром в начале координат, радиус 4
которой равен nJr. Эти точки — вершины правильного «-угольника.
1 = cos0° + isinO.
з/T (	0 + 2кя.. . 0 + 2&тЛ
= JI • cos-------+ isin------ .
v 3	3 >
к = 0; 1; 2;
к = 0; Uq = 1 • (cosO + isinO) = 1;
Ответ:
УЧЕНИЧЕСКАЯ СТРАНИЧКА
1. Решить уравнение в множестве комплексных чисел: х4 + 16 = 0.
Решение.
Прибавим и отнимем 8х2. х4 + 8х2 + 16 = (х2 + 4)2 Разложим на множители разности квадратов:
Заменим равносильной совокупностью квадратных уравнений:
Ответ:
2. Решить уравнение: Z3 = - +
Правую часть запишем в тригонометрической форме и используем формулу извлечения корня я-ой степени:
Ответ:
х4 + 8х2+ 16-8х2 = О, (х2 + 4)2-8х2 = 0.
(х2 + 4 - л/8х)(х2 + 4 + а/8х) = 0;
= 2^2 + 78- 16.
"х2-2л/2х + 4 = 0;	Х{'2	2
х2 + 2Т2х + 4 = 0	_ -2J2 + 78- 16
Х3,4	о ’
_ 2^2±2^2i
Х1>2	2	’
_ -2Т2±2Т2/ х3,4	й	’
Решение.
COS
- + 2.ля cos---------
7л , . . 7л. — + ism— ,
/V |	•	* /V .
0 = cos - + I Sin - , Zj =
cos-----+ isin
7л ... 7л 13л	. 13л
cos— + ism —; cos-+ ism---
3. Решить уравнение: x3 + 1000 = 0.
Решение.
Левую часть разложим на множители как сумму кубов:
(х+ 10)(х2 - 10х+ 100) = 0;
‘х + 10 = 0;
-х2- 10х+ 100 = 0;
ю ± 7-300
2
-х = -10;
-х - 5±573/.
Ответ:
-Ю;
4.	Какое множество точек комплексной плоскости задают условия:
a) |Z+z| = 1; б) 1 <|Z+2| <2; в) |Z- 1 -j| = |Z + 1 + z|?
Решение.
а)	условию |Z+z| = 1 удовлетворяют те и только те точки плоскости, которые равноудалены от точки Zx = -i на расстояние, равное 1. Такие точки лежат на окружности с центром в точке Zx = -i R = 1 (рис. 1);
б)	кольцо между концентрическими окружностями радиусов 1 и 2 с центром в точке Z] = -2, включая эти окружности (рис. 2);
Геометрическое решение.
в)	|Z—(1 + z)| = |Z—(— 1 -z)| — это условие задают те и только те точки плоскости, которые равноудалены от точек Zt = 1 + i и Z2 = - 1 - i. Множество точек плоскости, равноудаленных от двух данных точек, — это прямая, перпендикулярная отрезку, который соединяет данные точки и проходит через его середину.
Аналитическое решение.
(х - 1) + (у - 1 )z| = |(х + 1) + (у + 1 )/|, приравнивая модули, получаем:
СТРАНИЧКА АБИТУРИЕНТА
1. Записать число в тригонометрической форме.
Л .	. Л ,	Л ... Л
a) cos — - isin- , о) - cos- + isin-.
Решение.
IV . . л
a) cos—isin- = cos
+ isinl—- = cos— + isin
cos — + i sin — .
2. Решить уравнение |Z| + Z = 13 - 6i.
Решение.
26
Ответ: Z = 5— - 6/.
§6. Элементы комбинаторики
Множество
Множество — одно из основных понятий математики,
которое не подлежит формальному определению.
В математике понятие множество используется для описания совокупности предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, которые не входят в эту совокупность. Например, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств. Множества обычно обозначаются большими буквами А,В,Х... . Тот факт, что объект а является элементом множества А, записывается так: а е А и читается «47 принадлежит множеству А », «47 входит в множество А ». Запись a <£ А означает, что a не является элементом множества А. Множество натуральных чисел, расположенных между числами 21 и 22, не содержит ни единого числа. Такое множество называется пустым множеством. Пустое множество обозначается знаком 0. Множества А и В называются равными, если они складываются из одних и тех же элементов. В этом случае пишут А = В. В школьном курсе математики приняты стандартные обозначения числовых множеств: ЛГ — множество натуральных чисел, Z — множество целых чисел, Q — множество рациональных чисел, R —множество действительных чисел.
Задача 1. Записать с помощью фигурных скобок множество натуральных чисел, расположенных на луче между числами 10 и 15. Какие из чисел 0;10;11;12;15 и 50 принадлежат этому множеству?
Пусть А — множество натуральных чисел, расположенных на луче между числами 10 и 15.
А = {11 ;12;13;14};
0 й А, 10 g А, 11 е А, 12 е А, 15 <£ А, 50 £ А.
Задача 2. Сравните множество решений уравнения х2-5х + 6 = 0 и множество простых чисел, меньших пяти.
х2-5х + 6 = 0. Х| =2их, = 3
(по теореме Виета).
Множество простых чисел х < 5 — это {2;3}.
Ответ: эти два множества равны.
Задача 3.
Записать множество двузначных чисел, расположенных на луче левее девяти.
Ответ: 0.
Подмножество
NcZ;
(a',b) cz [4?;Z>]
[a-,b]	(a-,b ], потому ЧТО 47 e [a;b].
Если любой элемент множества А принадлежит также множеству В, то множество А называется подмножеством множества В. Это записывают так: А с. В или В =>А. В этом случае говорят, что множество А содержится в множестве В или множество В содержит множество А. Если в множестве А найдется хотя бы один элемент, не принадлежащий множеству В, то А не является подмножеством множества В \ A <zВ.
Из определения подмножества следует, что любое множество является подмножеством самого себя, то есть справедливо 4 с. А.
Пересечение множест
Множество, состоящее из всех элементов, при-
[a\b] п (]
, так как а е [я;/?].
надлежащих и множеству А, и множеству В,
называется пересечением множеств А и В и
обозначается А пВ.
Объединение множеств
Множество, состоящее из всех элементов, принадлежащих или множеству А, или множеству В, называется объединением множеств Л и В и обозначается А о В.
а)х = {0;1;3;5}; у = {1;2;3;4} хсуу = {1;3}.
б)А п 0 = 0;
{0;1;3;5} u {1 ;2;3;4} = {0;1 ;2;3;4;5}.
Для конечного множества А через т(А) обозначим число его элементов. Число элементов пустого множества, очевидно, равно нулю. Для любых конечных
множеств А и В справедливо равенство: т(А о В) = 7и(Л) + ти(В)-т(Л п В) (1)
Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти баллов получили 180 человек, а выдержали этот экзамен 210 абитуриентов (то есть не получили «2 »).
Сколько человек получили оценки «3 » и «4 »?
Пусть А — множество абитуриентов, выдержавших экзамен, В —множество абитуриентов, получивших оценку ниже пяти баллов, по условию т(А) = 210, т(В) = 180, ди(ЛиВ) = 250. Абитуриенты, получившие оценки «3 » и «4», образуют множество А п В. По формуле (1) находим
от(ЛпВ) = т(А) + т(В) - т(А и В) = 140.
Размещения
Пусть имеется множество, содержащее и-элементов. Каждое его упорядоченное подмножество, состоящее из А:-элементов, называется размещением из п -элементов по к -элементов.	Л 4 = 4(4-1)(4-2) = 4-3 -2 = 24; А*о = 10(10-1)(10-2) = = 10-9-8 = 720; Л26 = 6 • 5 = 30.
В комбинаторных задачах необходимо уметь подсчитать число всех размещений из и-элементов по Zr-элементов. Для обозначения этого числа применяется специальный символ Акп (читается: «число размещений из п по к» или «А из п по Л». А$ = 1. А — первая буква французского слова «arrangement», что означает «размещение, приведение в порядок».	Используя знак факториал, записать: 1! = 1 2! = 1 - 2 = 2 3! =3-2-1 = 6 4! = 4 • 3 • 2 • 1 = 24 5! = 5 - 4-3 - 2- 1 = 120.
В общем случае на вопрос о числе размещений из «-элементов по А:-элементов дает ответ такая формула:
то есть число размещении из п -элементов по к -элементов равно произведению к последовательных натуральных чисел от п до п - к + 1 включительно.
20!+20!
14! 15! = 16!+ 16!
20!	14! 15!
16!
16 • 16 = 256.
Формулу (1) удобно записывать в другом виде. Будем для краткости произведение «(«- 1)(«-2)...3 -2-1,то есть произведение всех натуральных чисел от п до единицы, обозначать символом п\ (читается «эн факториал»).
Умножим и разделим произведение, стоящее в правой части формулы (1) на (п-ку. Тогда получим:
л к А п


Вычислить:
В седьмом классе изучается
14 предметов. Сколькими способами можно составить расписание занятий на субботу, если в этот день недели должно быть 5 разных уроков?
Решение.
Л514 = 14 • 13 • 12 • 11 • 10 = 240240.
или (2)
О!
О!
, если
условиться, что 0! = 1.
Перестановки
Размещения из «-элементов по «-элементов называются перестановками из «-элементов.
Перестановки являются частным случаем размещения. Так как каждая перестановка содержит все «-элементы множества, то разные перестановки отличаются друг от друга только порядком элементов. Число перестановок из «-элементов обозначают через Рп. Р — первая буква французского слова «permuta-tion» — «перестановка». В общем случае число перестановок из «-элементов Рп = Апп , следовательно, его можно найти по формуле (1) или по формуле (2), предположив в каждой из них к = п.
Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1,2,3,4, 5, 6 при условии, что в числе цифры не повторяются?
Решение: 5! = 5 • 4 • 3  2 • 1 = 120.
Действительно, формула (2) дает:
Р = Ап =	= «I
п п («-«)! О!
Из формулы (1) находим:
Рп=Апп =
Итак, число перестановок из «-элементов равно «!.
Таким образом, в множестве, содержащем «-элементов, установить определенный порядок последовательности элементов или, как говорят, упорядочить такое множество можно «! способами.
Найти «, если
= 240Л к„+А  к < «. Рп - к
Применяя формулу для числа перестановок и формулу (2) для числа размещений, перепишем данное уравнение следующим образом:
(” + 5)! _ 240	(» + 3)!
(п-к)\ (п + З—к—Зу. Полученное уравнение равносильно квадратному уравнению (« + 5)(« + 4) = 240, где « = II; « = -20. При « = -20 левая и правая части уравнения не имеют смысла, тогда « = И .
Ответ: « = 11.
Например, список учеников клас-са, в котором 20 человек и нет однофамильцев, можно составить 20! = 2432902008176640000 способами.
Сочетания
Пусть имеется множество, состоящее из «-элементов. Каждое его подмножество, содержащее к -элементов, называется сочетанием из «-эле-ментов по к-элементов. Число всех сочетаний из «-элементов по А:-элементов обозначается
символом Ск (читается: «число сочетаний из
« по Ь или «цэ из « по А ». С — первая буква французского слова «combinasion» — «сочета-ние». = 4; Cj = 10.
В общем случае число сочетаний из «-
элементов определяется формулой:
следующей
Сколько экзаменационных комиссий, состоящих из 7 членов, можно образовать из 14 преподавателей?
Решение. Очевидно столько, сколько существует семиэлементных подмножеств у четырнадцатиэлементного подмножества. По формуле (4) находим:
Г1 _ 14- 13- 12 - 11 • 10-9-8 _
С14	-7.
14- 13-12- 11 -10-9-8
7-6-5-4-3-2 - 1
= 3432.
«!
(n-k)lkl
(3).
Формулу (3) можно записать в другом, более удобном для вычислений виде. Сократив
числитель и знаменатель дроби на («-£)!,
^1, п(п - 1)(« - 2)...(« - к+ 1)
получим С* = —--------------77--51-------1
к\
(4), т.е. число сочетаний из «-элементов по
к -элементов равно произведению всех
натуральных чисел от « до «- к +1 включительно, деленному на А!.
1)^4” = т(т - 1)(»? - 2)...(w - п + 1);
2) Р = А'" = т(т- 1)(ю-2)...3 -2-1 = 1 • 2 • 3...(w- l)w = т! число всевозмож-
ных перестановок из т -элементов равно произведению натуральных чисел от 1 до т;
т(т - 1	-2)...(т - п + 1)
•2-3...
100 -99-98 1-2-3
= 161700.
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Комбинаторные задачи
Задача 1. В классе 30 учеников. Сколькими способами могут быть выбраны староста и его заместитель, если каждый учащийся может быть избран на одну из этих должностей?
Решение. Так как по условию задачи каждый учащийся может быть выбран старостой, то, очевидно, существует 30 способов выбора старосты. Заместителем может быть каждый из оставшихся 29 человек. Любой из 30 способов выбора старосты может осуществляться вместе с любым из 29 способов выбора заместителя старосты. Поэтому существует 30 -29 = 870 способов выбора старосты и его заместителя. Значит, A j0 = 30 -29 = 870.
Задача 2. Для дежурства в классе в течение недели (кроме воскресенья) выделяли 6 учащихся. Сколькими способами можно установить очередность дежурства, если каждый учащийся дежурит один раз?
Решение. В понедельник может дежурить любой из выделенных шести человек, во вторник может дежурить любой из 5 человек. Следовательно, расписание дежурств на первые два дня недели можно составить 6-5 = 30 способами. К среде остаются 4 человека, которые еще не дежурили, и поэтому на среду дежурного можно выбрать 4 способами. Каждый из этих способов может комбинироваться с любым из 30 способов выбора дежурных на понедельник и вторник. Поэтому существует 6-5-4 = 120 способов и т.д.
.Ясно, что число способов, которыми можно установить дежурство, равно
Р. = 1 • 2 • 3 • 4 • 5 • 6 = 720
Задача 3.
Для проведения экзамена создается комиссия из двух преподавателей. Сколько разных комиссий можно составить из пяти преподавателей?
Решение. Cj =	= 10.
Ответ: 10 комиссий.
Задача 4.
На плоскости дано п точек, три из которых не лежат на одной прямой за исключением т точек, которые лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?
Решение. С%-С^ —треугольников. Задача 5.
Нужно распределить работу в шести классах между тремя учителями, чтобы каждый из них работал в двух классах. Сколькими способами можно это сделать?
Решение.
Ответ: 90 способами.
Решая сложные комбинаторные задачи, часто приходится пользоваться следующими двумя правилами.
1. Если некоторый выбор можно выполнить т разными способами, а для каждого из этих способов некоторый выбор можно выполнить п разными способами, то число способов для выполнения последовательности этих выборов равно произведению тп.
2. Если некоторый выбор можно выполнить т разными способами, а другой выбор п разными способами (отличными от предыдущих), то общее число способов, которыми можно выполнить любой из этих выборов, равен сумме т + п.
Бином Ньютона
Хорошо известные формулы
(а + Z>)2 = <з2 + 2аЬ + Ь2
(а + Ь)2 = а3 + За2Ь + ЗаЬ2 + Ь2
можно записать так:
(a + b)2 = с^а2 + c^ab + с^Ь2,
(а + b)2 = с9а3 + c\a2b + clb2 + clb2, **	J	«Г'
поэтому
(а + Ь)п = с^ап + с^ап~^Ь + ... + скап~кЬк +
+ ... + с”Ь"— это равенство известно как
формула бинома Ньютона.
Можно его записать так:
1)(х + я)7 * * = х1 + 7ах6 + 21«6х5 + 35а6х4 + +З5а4х3 + 21а5х2 + 7а6х + о7.
2) Найти приближенное значение степени 0,975.
Решение.
0,975 = (1 -0, ОЗ)5 = (1+(-0,03)5)= = 1 -5 0,03 = 10 0, ОЗ2- 10 0, 033 + +5  0, ОЗ4 - 0, 035. Найдем сумму первых трех членов, получим 0,659 с погрешностью 0,001.
3) Для освещения зала может быть
включена каждая из 10 ламп. Сколько
существует разных способов освеще-
ния зала?
Решение. Очевидно столько, сколько
существует подмножеств у десятиэле-
ментного множества, т.е. 210 = 1024.
Основные правила комбинаторики
1. Правило суммы.
Если объект А может быть выбран т способами, а объект В может быть выбран другими п способами, то выбор одного элемента — или А, или В— может быть осуществлен т + п способами.
Задача 1. В одной вазе лежат 5 яблок, а в другой — 8 мандаринов. Сколькими способами можно выбрать яблоко или мандарин?
Решение. Одно яблоко можно выбрать пятью способами, а один мандарин — другими восьмью способами. Тогда яблоко или мандарин можно выбрать N = 5 + 8 = 13 способами.
2. Правило произведения.
Если объект А может быть выбран т способами и после каждого такого выбора объект В может быть выбран п способами, то выбор пары объектов А и В в указанном порядке может быть осуществлен тп способами.
Эти правила могут быть распространены на случай выбора из трех и более множеств.
Задача 2. В магазине имеется три вида ручек и два вида карандашей. Сколько разных комплектов, содержащих ручку и карандаш, можно приобрести в этом магазине?
Решение. N = 3 • 2 = 6 разных комплектов.
Задача на совместное применение суммы и произведения.
Задача 3. Сколько чисел, имеющих не больше трех знаков, можно составить из цифр 1, 2,3,4, 5 так, чтобы цифры в числах не повторялись?
Решение. Нам надо узнать, сколько можно составить однозначных, двузначных или трехзначных чисел. По правилу суммы их будет: Л' = JVj + N2 + N3.
Nj = 5;N2 = 5 • 4 = 20^V3 = 5-4-3 = 60.
Следовательно, N = 5 + 20 + 60 = 85 . Ответ: 85 .
§7. Начала теории вероятности
Основные понятия тёории вероятности
Раздел математики, который изучает закономерности массовых случайных событий, ] называется теорией вероятности.
Исходным понятием теории вероятности является понятие события.
Событие — это явление, о котором можно сказать, что оно происходит или не 1 происходит, в зависимости от природы самого события.	i
События обозначаются большими буквами латинского алфавита А,В, С,... Любое событие происходит вследствие испытания.
Например, подбрасываем монету — испытание, появление герба — событие; достаем лампу из коробки — испытание, она бракованная — событие; вынимаем наугад шарик из ящика — испытание, шарик оказался черного цвета — событие.
Случайным событием называется событие, которое может произойти или не произойти во время данного испытания. Например, вынимая наугад одну карту из колоды, вы взяли туз; стреляя, стрелок попадает в цель.
Теория вероятности изучает только массовые случайные события.
Достоверным называется событие, которое вследствие данного испытания обязательно произойдет: (обозначается Е).
Невозможным называется такое событие, которое вследствие данного испыта-ния не может произойти: (обозначается U).
Например, появление одного из шести очков во время одного броска игрального кубика — достоверное событие, а появление 8 очков — невозможное.
Равновозможные события — это такие события, каждое из которых не имеет никаких преимуществ в появлении чаще другого во время многочисленных испытаний, которые проводятся с одинаковыми условиями.
Попарно несовместимые события — это события, два из которых не могут произойти вместе.
Вероятность случайного события — это отношение числа событий, которые благоприятствуют этому событию, к общему числу всех равновозможных несовместимых событий:
Р(Л) » М,
N
где А — событие;
Р(А) — вероятность события;
N — общее число равновозможных и несовместимых событий;
N(A) — число событий, которые благоприятствуют событию А .
Это — классическое определение вероятности случайного события.
Классическое- определение вероятности имеет место для испытаний с конечным числом равновозможных результатов испытания.
Пусть сделано п выстрелов по мишени, из которых оказалось т попаданий. Отноше-ние
/Л
ИЦА) = — называется относительной статистической частотой наступления события А.
Следовательно, ИЦА) — статистическая частота попадания.
Таблица 1
Количество выстрелов, п	10	20	30	40	50	60	70	80	90	100
Количество попаданий, т	8	17	26	33	41	49	56	65	. 72	81
ИЦА) = -п 	 		 _ _	0,8	0, 85	0, 86	0, 83	0, 82	0, 82	0,8	0,81	0,8	0,81
При проведении серии выстрелов (табл.1) статистическая частота будет колебаться около определенного постоянного числа. Это число целесообразно принять за оценку вероятности попадания.
Вероятностью события А называется то неизвестное число Р, около которого собираются значения статистических частот наступления события А при возрастании числа испытаний.
Это — статистическое обозначение вероятности случайного события.
Операции над событиями
Под элементарными событиями, связанными с определенным испытанием, понимают все неразложимые результаты этого испытания. Каждое событие, которое может наступить в результате этого испытания, можно рассматривать как некоторое множество элементарных событий.
Пространством элементарных событий называется произвольное множество (конечное или бесконечное). Его элементы - точки (элементарные события). Подмножества пространства элементарных событий называются событиями.
Все известные отношения и операции над множествами переносятся на события.
Говорят, что событие А является частным случаем события В (или В является результатом А), если множество А является подмножеством В. Обозначают это отношение так же, как для множеств: А с В или В z> А. Таким образом, отношение А а В означает, что все элементарные события, входящие в А, входят также в В, то есть при наступлении события А наступает также событие В. При этом, если АсВ и В А, то А = В.
Событие А, которое происходит тогда и только тогда, когда событие А не происходит, называется противоположным событию А . Поскольку в каждом испытании происходит одно и только одно из событий — А или А, то Р(А) + Р(А) = 1, или
Р(А) = }-Р(А).
Объединением или суммой событий А и В называется событие С, которое происходит тогда и только тогда, когда или происходит событие А, или происходит событие В, или происходят А и В одновременно. Это обозначается С = А и В или С = А+В.
Объединением событий А,, А2,Ап называется событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из данных событий. Обозначается объединение событий Ах и А2 и ... и А, или О Ак, или А{ + Л, + ... + Ап.
к - I
Пересечением или произведением событий А и В называется событие D, которое происходит тогда и только тогда, когда события А и В происходят одновременно, и обозначается D = А п В или D = А • В.
Совмещением или произведением событий Ах,А2,...,Ап называется событие, которое происходит тогда и только тогда, когда происходит и событие Ах, и событие А2, и т.д. , и событие Ап. Обозначается совмещение так: Ах пА-> п ... пАп или Д Ак, или 1
Если события А и В не могут произойти одновременно, то такие события называют несовместимыми.
Значит, для несовместимых событий, и только для них, Ar>B = U.
Также АоЕ = A, Au U = A, AnU = U ,то есть невозможное событие U играет роль нуля, а достоверное событие Е играет роль единицы, то есть, U = 0, Е= 1.
Разностью А\В событий А и В. называется событие F, которое происходит тогда и только тогда, когда происходит событие А и не происходит событие В, то есть F = А\В.
Определение операций объединения, пересечения, разности событий можно проиллюстрировать с помощью колец Эйлера;
Из статистического определения вероятности события вытекает, что вероятность события всегда есть число положительное или нуль. Следовательно, имеем такие свойства вероятности:
2)P(U) = 0-,
3) 0 < Р(А) < 1 для любого события.
Вероятность суммы событий
Вероятность суммы двух событий равна сумме вероятности этих событий без вероятности их произведения.
Если А и В — некоторые события, то Р(А + В) = Р(А) + Р(В) - Р(А  В).
Данная теорема называется теоремой сложения вероятностей.
Из этой теоремы вытекает результат для несовместимых событий А и В; если А п В = U то Р(А - В) = 0. Поэтому для несовместимых событий |Р(Л + В) = Р(Л) + Р(В], то вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.
есть
Если А,. А
т — попарно несовместимые события, то
Эта теорема справедлива для событий, связанных с одним и тем же испытанием.
Условная вероятность и независимость событий
Пусть имеем события А и В, и Р(В) * 0. Условной вероятностью события А событие В, называется число Р(А/В) =
при
условии, что наступило
|Р(Л • В) - Р(А/В) • Р(В)].
Если А = В, то PiB/B)
События А и В называются независимыми, если 1Р(Л  В) = Р(А) • Р(В) .
Р(А • В) Р(В)
или
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Если события Я и В независимы, то независимы также события А и В.
Случайные события А, В, С независимы в совокупности, если они попарно независимы и |Р(Л • В • С) = Р(Л)-Р(В)Р(С)|.
Случайные события А, В, С, D независимы в совокупности, если независимы в сово-
купности любые три из них и Р(А B C D) = Р(А)  Р(В)  Р(С) • P(D).
Независимые испытания. Схема Бернулли
Пусть при осуществлении п независимых испытаний событие А наступило т раз. Обозначим вероятность наступления события через Рп(т). Тогда
— формула Бернулли.
т = 0, 1,2, ..., п .
Здесь Стп — количество случаев осуществления события А ,
т
( н
= —-—'—р = Р(А), q =	= 1 -р-
Случайная величина. Закон ее распределения
Случайной величиной называется функция, заданная на множестве результатов
данного эксперимента или в пространстве элементарных событий.
Например, количество аварий автотранспорта в течение суток в любом городе
зависит от случая.
Совокупность результатов опыта называется пространством элементарных событий эксперимента.
Законом распределения случайной величины X называется функция, которая
каждому значению х случайной величины X ставит в соответствие вероятность Р(Х = х). В общем случае закон распределения случайной величины записывается так, как показано в таблице 2.
Таблица 2
хк	*1	Хэ	• * «	Хп
Рк	Pl	Р2	ь • * •	Рп
Здесь х,,х2, ...,х„ — все различные значения случайной величины X, а
Рк = Р(Х = хк), к = 1,2, ...,п —вероятности, с которыми X принимает эти значения.
События {X = х(},..., {X = хп} попарно несовместимы, их сумма является достоверным событием. Поэтому сумма вероятностей этих событий д, +р2+ ••• +рп = 1- Данное равенство можно использовать для проверки закона
распределения случайной величины.
Математическое ожидание
Пусть случайная величина имеет закон распределения, обозначенный в таблице 2.
Сумма произведений значений случайной величины на соответствующие вероятности называется математическим ожиданием (или средним значением) случайной
величины X
и обозначается символом MX
MX = Х]Р1 +х2р2+ ... +Хпрп = ^хкрк к
Свойства
1.	Для произвольной случайной величины X и произвольного числа с имеет место равенство: М(сХ) = сМХ.
2.	Математическое ожидание постоянной равно самой постоянной: Мс = с.
3.	Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин: М(Х + Y) = МХ+ MY. Аналогично М(Х- Y) = MX-MY.
4.	Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: М(Х У) = MX • MY.
Дисперсия случайной величины
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: DX = М(Х- MX)2.
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии: <j(%) = JDX.
Свойства дисперсии случайной величины
1. DX = MX2 - (MX)2 .
2. Если с — постоянная, toD(X+c) = DX', D(cX) = c2DX; De = 0.
3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(X+ Y) = DX+DY.
Выборочной дисперсией называется выражение S2 = у (х,-х)2—, где . ,	п
I = 1
xj,x2, ...,хт —наблюдаемые различные значения случайной величины; п1,...,пт —их частоты, п = И] + п2 + ... + пт — общее количество наблюдений, х — выборочное среднее.
_	'	п, п->	п
Выборочным средним называется величина х = х, — + х0— + ... + х — и ~ п	п
или х =
Выборочная дисперсия является средним всех квадратов отклонений результатов наблюдений от их среднего значения х.
Величина S, которая равна корню квадратному из выборочной дисперсии, называется выборочным средним квадратичным или стандартным отклонением.
Случайные величины называются независимыми, если для любых х и у выполняется равенство: |P((Z = х) • (У = у)) = Р(Х = х) • Р(У = у)|.
Случайные величины ...,Хп называются независимыми в совокупности, если
события (Хх =Х]),..., (Хп = х„) независимы в совокупности для любых х,, ...,х„.
Закон больших чисел
Если случайные величины Х{,. ..,Хп независимы и имеют одно и то же математическое ожидание и одну и ту же дисперсию, то их среднее арифметическое при достаточно большом п с вероятностью, как угодно близкой к единице, как угодно мало отклоняется от а.
Это простейший частный случай теоремы П. Л. Чебышева.
Следствие (теорема Бернулли)
Пусть к — количество наступления события Ави независимых испытаниях, р — вероятность наступления этого события в каждом испытании. Тогда для любого е>0:
1, когда п
УЧЕНИЧЕСКАЯ СТРАНИЧКА
Классическое определение вероятности Использование формул комбинаторики для вычисления вероятностей
1.	В корзинке находятся 4 белых и 7 черных шариков. Какова вероятность того, что наугад вынутый шарик окажется белого цвета?
Решение.
Используем формулу Р(А) =	. Пусть А —событие, которое означает, что наугад
взятый шарик белого цвета; таких шариков 4, поэтому N(A) = 4 — число всех равновозможных событий, которые благоприятствуют событию А; число всех
равновозможных элементарных событий ¥ = 11. Поэтому Р(А) = —
2.	Из полного набора костей домино наугад выбирается одна кость. Какова вероятность появления кости, сумма очков на которой равна шести?
Решение.
Испытание состоит в том, что вынимается одна кость из полного набора домино. Поскольку она выбрана наугад, то все результаты испытания равновозможны, причем они несовместимы. В полном наборе домино 28 костей, следовательно, ¥ = 28. Пусть А — событие, которое означает, что сумма очков на выбранной кости равна шести. Событию А благоприятствуют 4 результата испытания, а именно: появление костей, на 4
которых нанесены очки 0-6, 1-5, 2-4, 3 - 3. Следовательно, Р(А) = — ~ 0,143 .
3.	Какова вероятность того, что при бросании игрального кубика выпадет четное число очков?
Решение.
Пусть А — событие, которое означает, что при бросании кубика выпадет четное число очков. В этом эксперименте мы имеем 6 равновозможных результатов: события А{, А2, Л3,Л4, А5, А6. Нас интересует вероятность события А. Этому событию благоприятствуют три результата эксперимента: А-,, А. и А^. Следовательно,
N = 6, N(A) = 3 , поэтому искомая вероятность Р(А) = 7 = 
6	2
4.	Подбросили две монеты. Какова вероятность того, что на каждой монете выпадет герб?
Решение.
Возьмем одну монету медную, одну серебряную и обозначим: Г — событие, которое означает, что на обеих монетах выпал герб; Ц — на обеих монетах выпала цифра;
А{ — событие, которое означает, что на серебряной монете выпал герб, на медной
монете выпала цифра; А-, — на медной монете выпал герб, на серебряной монете — цифра. Эти четыре события равновозможны. Следовательно, равно-возможность результатов эксперимента — 4, то есть N = 4. Нас интересует вероятность события Г. Ему благоприятствует только один результат, то есть N(A) = 1. Значит, искомая
вероятность Р (Г)
5.	Подбросили два игральных кубика и подсчитали сумму выпавших очков. Что вероятнее получить в сумме: 7 или 8 ?
решение
Пусть А — событие, которое означает, что сумма выпавших очков равна семи1. Этому событию благоприятствуют следующие 6 результатов: 1-6, 2-5, 3-4, 4-3, 5-2 и 6 - 1, следовательно, N(A) = 6. Число всех равновозможных событий N = 36, по-скольку каждое из 6 очков, которые могут выпасть на первом кубике, может быть в паре с любым из 6 очков, которые могут выпасть на втором кубике. Поэтому Р(А) = 77=7-36	6
Пусть В — событие, которое означает, что сумма выпавших очков равна восьми. Этому событию благоприятствуют следующие 5 результатов:
2-6, 3-5, 4-4, 5-3, 6-2. То есть N(B) = 5. Поэтому Р(В) = Следова-36
тельно, сумма очков 7 является более вероятным событием, чем сумма очков 8.
6.	В ящике лежат 20 одинаковых на ощупь шариков. Из них 12 белых и 8 черных. Наугад вынимают два шарика. Какова вероятность того, что оба шарика белые? что они разного цвета?
1 1
J
1
Решение.
Число всех равновозможных событий N = С$о, то есть из 20 шариков выбираем 2. Пусть В — событие, которое означает, что оба шарика белые. Поскольку белых шариков 12 и среди них нам нужно выбрать 2 шарика, то N(B} = Cj2 — число всех равновозможных результатов, которые благоприятствуют наступлению события В. Следовательно, искомая вероятность:
Р(В> _ С12 _ 121-2118! _ 11-12 _ 13 ” С,20 ~ 7- Ю120!	19-20 “ й'°’35'
Пусть А — событие, которое означает, что взятые шарики разного цвета. Этому событию благоприятствуют результаты, при которых первый шарик можно вынуть 12 способами, а второй — 8 способами, при этом любой шарик из 12 (белый) может комбинироваться с любым черным, то есть, использовав правило произведения, получим N(A) = 12-8.
12-8-2! 18!	12-8-2	48 Л с
------- — — » 0, 5 . 19-20-95
Поэтому искомая вероятность: Р(А) = ——
С20
20!
7.	В одном ящике находятся 8 белых и 12 красных шариков, в другом — 15 синих и 5 черных шариков. Из каждого ящика наугад вынимают по одному шарику. Какова вероятность того, что вынули красный и черный шарики?
Решение.
Пронумеруем все шарики: а}, а2, ...,а8 — белые; а9, а10,..., о,0 — красные (в пер-вом ящике), Ь{, Ь2,..., 615 —синие; &16, Z>17,..., Z?20 —черные (в другом ящике). В ре-зультате эксперимента получаем события (az, Z>z) = «вынутый шарик и вынутый шарик />( ». Эти события образуют множество результатов данного эксперимента. Поскольку шарики вынимаются наугад, то эти события равновозможны. По правилу произведения, число этих событий N = 20 • 20 = 400. Событию, интересующему нас, благоприятствуют результаты опыта, для которых выполняются неравенства: 9 < i < 20 и 16 < i < 20. Их число (по правилу произведения) при событии А, которое означает, что вынули красный и черный шарики, равно N = 12-5 = 60. Следовательно, ,,(Л) - J55 = й = °-15
8.	На соревнования по баскетболу приехали 18 команд, которые путем жеребьевки разделены на две группы по 9 команд в каждой; 5 команд обычно занимают первые места. Какова вероятность того, что все лидирующие команды попадут в одну группу? Какова вероятность того, что две лидирующие команды попадут в одну группу, а три — во вторую?
Решение.
Обозначим события: А — «все 5 лидирующих команд попали в одну группу»; В — «2 лидирующие команды попали в одну группу, 3 —во вторую». Из 18 команд группы по 9 команд могут быть образованы С?8 способами, то есть N = С^8. Событию А благоприятствует столько событий, сколькими способами 5 лидирующих команд могут образовать девятки с четырьмя командами из 13 оставшихся команд. Поэтому как первая, так и вторая девятки могут быть образованы Cf3 способами. Поэтому
/У(Л) = 2Cf3.
Следовательно, искомая вероятность
Р(А)-2С‘>з_2- 13!#9!_ ЛГ-5 • 6 • 7_1
k Ct 419118! X 3 -Л- 14  15 • 16 • 17 -И 34 1 о
Аналогичные рассуждения подсказывают, что число приятствуют событию В, равно: N(B) = Cj  С]3 + Cj  Cf3
событий, которые благо-
С 5 ' ^13 + ^5 ’ С13
Поэтому искомая вероятность: Р(В) =
СУ е18
12
17’
9.	Случайная величина X принимает значения 1,2,3,4, причем Р(Х = 1) = 0,4; Р(Х = 2) = 0,3; Р(Х = 3) = 0,2. Найти Р(Х=4); Р(У>2); P(Z<3); Р(1, 5 <Х< 3,7).
Решение.
Поскольку Р(Х = \) + Р(Х = 2) + Р(Х = 3) + Р(Х = 4) = 1, то
Р(% = 4) = 1 -(0,4+ 0,3 + 0,2) = 0, 1.
Р(Х>2) = Р(Х = 3 ИЛИ X = 4) = Р(2Г = 3) + Р(Х=4) = 0,2 + 0, 1 =0,3.
Аналогично Р(Х<3) = Р(Х= 1) + Р(Х = 2) + P(Jf = 3) = 0,4 + 0,3 + 0,2 = 0,9.
P(1,5<Z<3, 7) = Р(Х= 2) + P(Z= 3) = 0,5.
10.	Количества очков, выбиваемых при одном выстреле каждым из двух стрелков, имеют соответственно законы распределения:
а)	б)
хк	8	9	10
Рк	0,4	0,1	0,5
хк	8	9	10
Рк	0,1	0,6	0,3
Какой из двух стрелков стреляет лучше?
Решение.
Если Xi (z = 1,2) — количество очков, которое выбивает первый стрелок при одном
выстреле, ТО МХ{=8 • 0,4 + 9 • 0, 1 + 10 • О, 5=9,1; MY2=8 • 0,1 + 9 • 0, 6 + 10 • 0, 3=9,2 .
Среднее количество очков, которое выбивает второй стрелок при одном выстреле, несколько больше, чем у первого. Следовательно, второй стрелок стреляет лучше, чем первый.
11.	Из ящика, в котором находятся 4 шарика, пронумерованные числами 0,1,2,3, наугад бер^г два шарика. Составить закон распределения суммы номеров двух вынутых шариков.
Решение.
В этом испытании возможны такие результаты: (0,1); (0,2); (0,3); (1,2); (1,3); (2,3).
Здесь (0,1) означает, что первым вынули шарик с номером 0, а вторым — с номером 1.
Вероятность элементарных событий одинакова, то есть равна - (поскольку образовалось 6
6
пар шариков, а достать пару можно только одним способом). Найдя серии номеров двух шариков, можем составить таблицу.
Результаты испытания	0;1	0;2	0;3	1;2	1;3	2;3
Вероятности элементарных событий	1 6	6	6	6	6	1 6
Суммы номеров	1	2		3	4	
Все результаты испытания одинаково вероятны. Выпишем теперь все различные значения случайной величины — суммы номеров двух шариков — и подсчитаем соответствующие вероятности. Вероятность pi находится сложением вероятностей всех элементарных событий, которые соответствуют значению х-. Получим таблицу:
хк		2		4	
Рк	1 6	1 •—*	1 3	1 6	1 6
12.	При сборке прибора для точной подгонки определенной детали необходимо сделать несколько попыток. При этом деталь, забракованная при сборке одного прибора, уже не используется при сборке других. Для установления количества дета-лей, которыми необходимо обеспечить рабочего, было проведено 100 наблюдений. Оказалось, что в 7 случаях понадобилась одна попытка, в 16 —две, в 55 —три, в 21 —четыре и в одном случае — пять попыток. Найти среднее количество деталей, необходимых для сборки одного прибора.
Решение.
Ответом на вопрос задачи является математическое ожидание количества деталей, необходимых для сборки одного прибора. По результатам 100 наблюдений можно подсчитать выборочное среднее количество деталей, необходимых для сборки одного прибора:
100
Таким образом, рабочему для сборки одного прибора нужно приблизительно три детали.
13.	Найти математическое ожидание случайной величины X, равной числу очков, которые выпадают на игральном кубике при одном броске.
Решение.	"
Величина X принимает каждое из целых значений от 1 до 6 с вероятностью -, поэтому
14.	Мишень разделена на восемь равных пронумерованных секторов и установлена так, что может вращаться вокруг горизонтальной оси. При достаточно большой угловой скорости стрелок не может различить цифры, написанные на секторах. Он вынужден стрелять наугад. При попадании в первый сектор стрелок выигрывает 1 грн, во второй сектор — 2 грн, в третий сектор — 3 грн и т.д. Стоит ли ему принимать участие в этой игре, если за каждый выстрел он должен платить 5 грн?
Решение.
Поскольку мишень вращается, то попадание здесь — чистая случайность. Случайная величина X выражает возможные выигрыши. Она может принимать значения 1,2,3,..., 8. Поскольку все сектора одинаковые, то каждое из этих значений —
случайная величина — принимает с одинаковой вероятностью -.
=4, 5 (грн). Следовательно,
8	8	8
математическое ожидание выигрыша — 4,5 грн, а стоимость выстрела 5 грн. Стрелять много раз невыгодно.
15.	В цеху установлено два разных станка, изготовляющих одинаковые детали. Количество бракованных изделий, которые могут изготовить эти станки за сутки, имеют соответственно законы распределения а) и б): а)	б)
Ук	0	1	2	
Рк	0,6	0,2	0,15	0, 05
Ук	0	1	2	
Рк	0,5	0,25	0,2	0, 05
1) Найти среднее количество бракованных деталей, которые изготовляет первый станок за 10 дней.
2) Каково среднее количество бракованных деталей, изготовленных цехом за сутки? Решение.
Пусть X и Y — количество бракованных деталей, которые изготовляют, соответ-ственно, первый и второй станки за сутки, MX = 0,65; MY = 0,8. За десять дней пер-вый станок изготовляет 10^ бракованных деталей. М(1 ОХ) = 10 MX = 6, 5. Цех за сутки изготовляет X+Y бракованных деталей: М(Х + У) = MX + MY = 0,65 + 0,8 = 1,45 .
16. Количество яиц, которое фермер отправляет на рынок каждую неделю, имеет такой закон распределения:
хДдес.)	5	6	7	8
Рк	0,1	0,4	0,3	0,2
Цена одного десятка яиц может равняться 2 грн,’ 2,5 грн, Згрн с вероятностями 0,1; 0,6; 0,3 соответственно. Найти средненедельную выручку фермера от реализации яиц.
Решение.
Пусть X — количество яиц (в десятках), которые отправляет фермер каждую неделю на рынок, Y — цена одного десятка. Тогда XY — недельная выручка фермера. Нужно найти M(XY). Случайные величины X и Y независимы, поэтому M(XY) = MX-MY. Поскольку MX = 5-0,1 + 6-0,1+7-0, 3 + 8-0,2 = 6,6(грн), MY = 2 • 0,1 + 2, 5 • 0, 6 + 3 • 0, 3 = 2,6 (грн), то M(XY) = 6,6  2,6 ~ 17,2 (грн).
§8. Введение в статистику
Начальные сведения о математической статистике
Раздел прикладной математики, в котором исследуются количественные характеристики массовых явлений, называется математической статистикой (от лат. «status» — «состояние»). Математическая статистика — наука о математических методах систематизации, обработки и использования статистических данных для научных и практических выводов.
1 Решить задачу.
нешение.
Построим столбча-
2. Решить задачу.
Восьмиклассники одной школы написали контрольную работу по математике. Из них на «11» — 5, на «10 » — 8, на « 9 » — 25 ,
на « 8 » — 30, на « 7 » — 15, на «1 —6 » — 19.
Количественные характеристики проведенной контрольной работы можно представить в виде таблицы:
Оценки	11	10	9	8		1-6
Кол-во учеников	5	8	25	30	15	19
Наглядно изобразить эти данные можно с помощью столбчатой диаграммы.
Столбчатые диаграммы в статистике называют гистограммами.
Швейной мастерской надо знать, сколько мужских пальто и каких размеров надо сшить. Как это выяснить?
Решение.
По частотной таблице (размеры пальто) по-
спросить всех слишком дорого и долго. Поэтому делают выборку: опрашивают выборочно несколько десятков или сотен людей. Допустим, что, опросив 50 мужчин, их размеры записали в таблицу:
50	42	48	50	46	48	52	44	50	50
50	50	44	54	44	50	50	46	50	48
42	50	50	54	52	54	54	42	48	52
44	48	50	52	50		46	52	52	52
48	48	46	48	52	46	50	50	54	46
Это — выборка 50 значений (данных). Для удобства ее группируют в классы (по размерам) и отмечают, сколько значений выборки содержит каждый класс.
Размер пальто	42	44	46	48	50	52	54
Кол-во мужчин	3	4	5	9	15	8	6
Такие таблицы называют частотными. В них числа второй строки — частоты; они показывают, как часто встречаются в выборке те или другие ее значения. Относительной частотой значения выборки называют отношение его частоты к числу всех значений выборки.
В рассмотренном примере частота размера 44 равна 4, а относительная частота — 8%.
Выборки характеризуют центральными тенденциями: средним значением, модой и медианой. Средним значением выборки называют среднее арифметическое всех ее значений. Мода выборки — те ее значения, которые встречаются чаще всего. Медиана выборки — это число, «разделяющее» пополам упорядоченную совокупность всех значений выборки.
3. Решить задачу.
Найти центральные тенденции выборки:
1,3; 1,8; 1,2; 3,0; 2, 1; 5; 2,4;
1,2; 3,2;
1,2; 4; 2,4.
Решение.
Упорядочим выборку: Мода данной выборки равна 1,2.
Среднее значение выборки:
Медиана выборки:
1,8; 2, 1; 2,4; 2,4;
1,2+ 1,2+ 1,2+ 1,3 + 1, 8 + 2, 1 + 2, 4 + 2, 4 + 3, 2 + 3, 8 + 4 + 5
12
29,6	296	35
“ ЛГ ~ L20 “ Т?
2, 1 +2, 4 _ 4, 5 _ 45 _ 9
2	2	20	4'
4. Решить задачу.
Найти центральные тенденции выборки:
Решение.
Упорядочим ее:
Мода данной выборки равна 5 , потому что 5 встречается чаще всего.
Среднее значение выборки:
1, 1,2, 3,3, 4, 4, 5, 5, 5, 6.
Медиана выборки равна 4, поскольку число 4 «разделяет» упорядоченную выборку пополам.
Если упорядоченная выборка имеет парное число значений, тогда ее медиана равна полусумме двух ее средних значений.
Содержание
7 класс Г	-
Это уже нужно знать................................................          .....4
§ 1.	Уравнения. Уравнения с одной переменной. Выражения и их преобразования.......10
§ 2.	Целые выражения............................................                  13
§ 3.	Многочлены. Действия с многочленами...................................       16
§ 4.	Формулы сокращенного умножения....................................  ........17
§ 5.	Разложение многочлена на множители...........................................17
«
§ 6.	Решение линейных уравнений с двумя переменными...........................    19
§ 7.	Системы линейных уравнений с двумя переменными.............................. 21
ч-ч
’	8 класс
§ I.	Рациональные выражения........................    '......................    26
§ 2.	Квадратные корни. Действительные числа.................................     31
§ 3.	Квадратные уравнения. Решение задач с помощью квадратных уравнений...........34
л
4. Ф	ункции......................................'...............................40
л
9 класс
i
§ I.	Неравенства.........................................................         46
§ 2.	Системы неравенств с одной переменной....................................    49
§ 3.	Квадратичная функция.......................................             .....50
§ 4.	Квадратные неравенства.................................................      53
§ 5.	Уравнения, сводящиеся к квадратным. Системы уравнений.......................;.. 56
§ 6.	Числовые последовательности............................................      59
§ 7.	Элементы прикладной математики.....................................      ....65
7	10 класс
§ 1.	Тригонометрические функции и их свойства................................     70
§ 2.	Тригонометрические уравнения............................    ;............... 92
§ 3.	Тригонометрические неравенства...........................................    109
§ 4.	Степенная функция. Иррациональные уравнения и неравенства.............. :....123
§ 5.	Показательная функция. Показательные уравнения и неравенства.............    149
§ 6.	Логарифмическая функция. Логарифмические уравнения и неравенства.............161
ь	Л	.
• to + 4 ’ 11 класс
§ 1.	Модуль. Предел. Непрерывность. Производная....................    :..........176
§ 2.	Использование производной...'..........................................     197'
§ 3.	Интеграл и его применение................................................... 210
§ 4.	Производная и первообразная показательной, степенной и логарифмической функций.......................................        225
§ 5.	Комплексные числа и действия с ними....................................      230
§ 6.	Элементы комбинаторики...........................................            237
§ 7.	Начала теории вероятности..............................................      244
§ 8.	Введение в статистику................................................        255