В.И.ЛОКАЙ
М.К.МАКСУТОВА
В.А.СТРУНКИН
Газовые
турбины
двигателей
летательных
аппаратов
ТЕОРИЯ, КОНСТРУКЦИЯ и РАСЧЕТ
ТРЕТЬЕ ИЗДАНИЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено
Министерством высшего и среднего специального образования СССР
в качестве учебника
для высших технических учебных заведений
Москва
«МАШИНОСТРОЕНИЕ». 1979
ББК 39.55
Л73
УДК 629.7.036:621.438.001.2(075.8)
Рецензент: кафедра теории воздушно-реактивных двигателей МАИ
Локай В. И. и др.
Л73 Газовые турбины двигателей летательных аппаратов:
Теория, конструкция и расчет: Учебник для втузов.—3-е
изд., перераб. и доп./В. И. Локай, М. К. Максутова,
В. А. Стрункнн.—М.: Машиностроение, 1979.—447 с.,
ил.
В пер.: 1 р. 40 к.
31808-192
Л — -192-79 3606030000
ББК 39.55
6Т5.1
038(01)-79
@ Издательство «Машиностроение», 1979 г.
Светлой памяти дорогого учителя
проф. Георгия Сергеевича
ЖИРИЦКОГО посвящается
ПРЕДИСЛОВИЕ
Книга представляет собой учебник по курсу газовых турбин
для авиационных втузов, который базируется на общенаучных
(математика, физика и др.) и общеинженерных (механика, термо-
динамика и теплопередача, газовая динамика, сопротивление ма-
териалов, детали машин и др.) дисциплинах. В книге содержатся
теория, методы расчетов и проектирования, а также обзор конст-
рукций газовых турбин, применяющихся в авиационных газотур-
бинных, жидкостных ракетных двигателях, а также во вспомога-
тельных авиационных силовых установках (турбостартеры, энер-
гоузлы и др.). В данном курсе детально изучаются газовые турби-
ны как таковые. Вместе с тем чётко обозначена их авиационная
направленность, обосновано место и значение газовой турбины в
общей компоновке ГТД, турбонасосных агрегатов ЖРД, вспомо-
гательных силовых установок. Тем самым обеспечивается преемст-
венность курса газовых турбин с последующими специальными
дисциплинами (теория. ВРД, конструкция ВРД, теория и конст-
рукция ЖРД и др.).
Многолетний опыт показывает, что изучение теории и конструк-
ции турбомашин в едином курсе дает возможность студенту вы-
полнять полноценный курсовой проект и учебно-исследователь-
скую работу независимо от проработки курсов теории ВРД и кон-
струкций авиадвигателей, которые изучаются на последующих
семестрах обучения.
В книге очень кратко рассмотрен цикл и наиболее распростра-
ненные принципиальные схемы базовых и вспомогательных авиа-
ционных газотурбинных двигателей. Достаточное внимание уделе-
но физике явлений при течении газа в каналах, тепловому процес-
су и газодинамике турбин. Изложена методика аналитического
расчета турбин по средним теплоемкостям, в том числе с помощью
газодинамических функций. Кроме того, в объеме, необходимом
для практического использования, изложен эффективный метод
расчета турбин с учетом переменных теплоемкостей. В приложении
к книге приведены таблицы термодинамических функций, облег-
чающие выполнение расчетов.
С необходимой полнотой изложены теория и расчеты простран-
ственного потока в ступени; характеристики турбины и методы
расчета на нерасчетных режимах.
3
Значительное место отведено достижениям и перспективам раз-
вития систем охлаждения газовых турбин. Приведена классифика-
ция систем охлаждения и указаны области целесообразного их
применения. В книге обобщены результаты исследований законо-
мерностей теплообмена в элементах проточной части, на дисках и
в охлаждающих каналах.
Даны методы расчета температурных полей охлаждаемых де-
талей в стационарных и нестационарных условиях. Изложены ме-
тоды расчета температурных напряжений в охлаждаемых деталях
турбин. Приведены методы оценки влияния охлаждения на потери,
параметры рабочего процесса и характеристики турбин.
В разделах, посвященных конструкции газовых турбин, приве-
дены типовые конструкции узлов и основных деталей турбин, а
также современные методы расчетов на прочность и колебания
лопаток, дисков, валов как специфических деталей турбины, обыч-
но не рассматриваемых в курсе «Детали машин». Все частные рас-
четные методики представлены в виде, удобном для ,их програм-
мирования на ЭВМ. Тем самым обеспечивается их использование
в виде подсистем будущего автоматизированного оптимального
проектирования турбин и ГТД в целом.
Третье издание книги базируется на предыдущем втором изда-
нии. Вместе с тем, материал книги существенно переработан, с
учетом замечаний и пожеланий читателей второго издания кнцги,
В новом изложении широко использованы новейшие работы со-
ветских и зарубежных специалистов по газовым турбинам, в том
числе научные и учебно-методические разработки коллектива ка-
федры и проблемной лаборатории турбомашин Казанского авиа-
ционного института.
Предисловие, введение, гл. I, II, III, VII, IX, X и приложение I
подготовлены В. И. Локаем; гл. IV, V, VI, VIII, — М. К. Максуто-
вой; вторая часть книги (гл. XI—XX) и приложения II, III —
В. А. Стрункиным.
Авторы выражают глубокую благодарность сотрудникам кафед-
ры турбомашин КАИ за помощь в оформлении материалов, вклю-
ченных в книгу.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Рц— центробежная сила [Н]*
Е—	модуль упругости [Н/м2];
G — расход [кг/с]; модуль сдвига [Н/м2];
Н — высота полета [м, км]; перепад тепла [Дж/кг];
—	адиабатный перепад тепла [Дж/кг];
/ — момент инерции [м4]; энтальпия [Дж/моль];
Н — удельная работа [Дж/кг]; потери [Дж/кг]:
Яо — удельная адиабатная работа газа в диапазоне от ро*» Г«* до Ръ(р1)
[Дж/кг];
—	то же от ро*, Го* до ръ* [Дж/кг];
М — момент силы [Н м],
М — число Маха;
N — мощность [Вт]:
Nu— число Иуссельта,
Р — сила [Н];
Рг — число Прандтля;
Q — количество тепловой энергии [Дж];
Р— газовая постоянная [Дж/(кг К)]; радиус [м];
Re — число Рейнольдса;
S — энтропия газа [Дж/К];
Sh — число Струхаля;
Г — температура [К], период колебаний [с]; кинетическая энергия при коле-
баниях [Дж]:
Г/ — температура торможения потока на рабочих лопатках в относительном
движении [К];
W — момент сопротивления [м3];
Y — характеристика Парсонса;
а — скорость звука [м/с]; коэффициент температуропроводности [м2/с];
b — длина хорды профиля [м];
с — абсолютная скорость газа [м/с];
сР — теплоемкость при постоянном давлении [Дж/(кг К)];
d — средний диаметр колеса турбины [м]; диаметр [м];
f— площадь Поперечного сечения [м2];
g — ускорение свободного падения [м/с2];
h — высота лопаточных решеток [м];
i — энтальпия газа [Дж/кг];
к — коэффициент теплопередачи [Вт/(м2 • К)]; показатель адиабаты;
I — длина [м];
5
m — масса [кг]:
п — частота вращения [с-1];
р — давление газа [Па];
q — удельное количество тепловой энергии [Дж/кг]; приведенный расход;
г — радиус [м];
s — осевая ширина лопатки [м]; толщина стенки [м];
t — шаг решетки [м];
и — окружная скорость [м/с]; периметр [м];
v — скорость [м/с]; удельный объем газа [м3/кг];
w — относительная скорость газа [м/с];
х — отношение и1с&л\ координата [м];
у - толщина диска, прогибы, координата [м];
z — число сопел, лопаток, ступеней; координата [м];
а— угол наклона абсолютной скорости газа; коэффициент теплового линей-
ного расширения; коэффициент возврата тепловой энергии; коэффици-
ент теплоотдачи [Вт/(м2 • К)];
Р — угол наклона относительной скорости газа;
Руст — угол установки профиля в решетке;
у — различные угловые величины;
6 — зазор [м]; угол атаки;
е — степень парциальности; относительное удлинение;
0 — безразмерная температура лопатки; отношение среднего диаметра обло-
пачивания к высоте лопатки;
? — коэффициент потери энергии в сопле;
*П — к. п. д.; динамическая вязкость [Н • с/м2];
*qe — эффективный к. п. д.;
— внутренний к. п. д.;
Ли — окружной к. п. д.;
1 — привеченная скорость; коэффициент теплопроводности [Вт/(м2К)];
ц— молекулярная масса; коэффициент расхода; коэффициент Пуассона;
v— кинематическая вязкость [м2/с]; частота колебаний [Гц];
л — степень повышения (понижения) давления;
р — плотность [кг/м3];
рст — степень реактивности;
о — коэффициент восстановления давления; нормальное напряжение в мате-
риале [Н/м2];
т — время [с]; касательное напряжение в материале [Н/м2]; отношение темпе-
ратур в цикле;
В — коэффициент потерь энергии на рабочих лопатках; радиальное удлинение;
Ф — скоростной коэффициент сопел;
ф — скоростной коэффициент рабочих лопаюк;
(О — угловая скорость [рад/с]; угол отклонения струи газа;
Г — циркуляция [м2/с];
Q — угловая скорость прецессии вала [рад/с];
Индексы
* — адиабатно заторможенный поток;
О — вход в ступень;
1	— выход из соплового аппарата и соответствующие этому сечению геомет-
рические размеры;
6
2	— выход из рабочих лопаток;
ад — адиабатные (к. п. д., скорость);
в — воздух; втулка (турбины);
г —газ:
е — эффективные (мощность, работа, к п. д.);
к —корневой (радиус);
кр — критический (перепад);
л — лопатки (потери на лопатках);
м — механические (к. п д, потери);
н — направляющая (лопатка),
охл — охлаждаемый;
п — периферийный;
с — сопла.
т — турбины (к. п. д); параметры за турбиной;
ут — утечка;
а — осевое направление;
/ — внутренний (перепад, к. п. д.);
г —радиальный;
/ — теоретический, тангенциальный;
и — окружные (к. п. д., работа, направление);
ц — центробежный.
ВВЕДЕНИЕ
В настоящее время ГТД являются основным типом базовых
авиационных силовых установок и интенсивно внедряются в дру-
гие отрасли техники (судостроение, железнодорожный и автомо-
бильный транспорт и др.). Главными достоинствами ГТД (по срав-
нению с другими типами силовых установок) являются: малая
удельная масса и возможность получения больших мощностей
(10 МВт и более) в малых габаритах.
Для достижения приемлемой экономичности ГТД необходимо,
чтобы к.п.д. турбины и компрессора, составляющих неотъемлемую-
часть ГТД, а также температура газа перед турбиной были доста-
точно высокими.
«Современные авиационные турбины с воздушным охлаждением
надежно работают с температурой газа порядка 1500 ... 1600 К.
Обнадеживающие результаты получены в экспериментальных ГТД
с температурами газа перед турбиной 1750 ... 1800 К.
В перспективе ставится задача создать так называемые стехио*
метрические ГТД — с начальной температурой газа 2200 ... 2300 К.
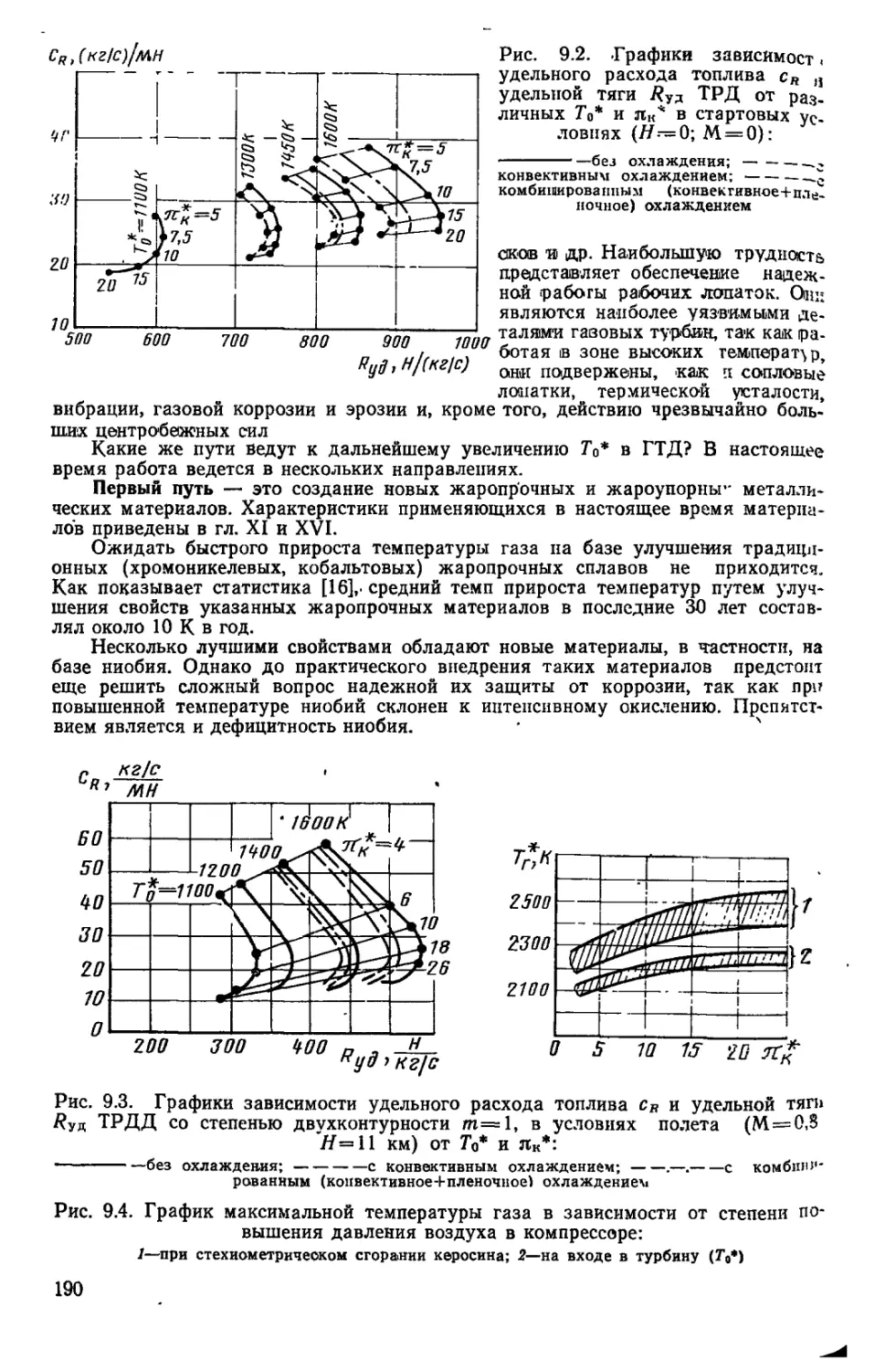
Повышение температуры газа перед турбиной по годам графически
показано на рис. 0.1, относящемся к авиационным ГТД в старто-
вых условиях.
Большое распространение в авиации получили так называемые
вспомогательные силовые установки (турбостартеры, энергоузлы
привода электрических генераторов и насосов и т. п.).
Одним из первых изобретателей, построивших газовую турбину
(1892 г.), был русский инженер П. Д. Кузьминский. Его турбина [6]
была радиального типа и работала на парогазовой смеси при не-
прерывном горении в камере сгорания, т. е. по циклу р=const.
В 1908 г. другой русский инженер В. В. Караводин построил и
успешно испытал пульсирующую бескомпрессорную газовую тур-
бину периодического сгорания (цикл u«const).
Над создание^ газотурбинных двигателей работали талантли-
вые инженеры и изобретатели Н. В. Герасимов, А. П. Горохов,
М. Н. Никольский и др. Лауреат Ленинской премии В. И. Базаров
еще в 1923—1924 гг. предложил схему авиационного газотурбин-
ного двигателя, принципиально не отличающегося от современных
ТВД.
8
Рис 0.1. Рост температуры газа перед тур-
биной авиационных ГТД по годам развития
Одним из пионеров советского
газотурбостроения является проф.
В. М. Маковский. В 1925—1935 гг.
им была спроектирована, а в 1939 г.
под его руководством на Харьков-
ском турбогенераторном заводе по-
строена оригинальная охлаждаемая
турбина для работы по циклу р =
=const на продуктах подземной га-
зификации углей.
В области теории, в первую
очередь, следует отметить научные
труды проф. Н. Е. Жуковского, пос-
вященные реакции втекающей и вы-
текающей жидкости (1882—1886 гг.)
и теории судов, приводимых в дви-
жение силой реакции вытекающей
воды (1908 г.). Эти работы явились началом теории реактивных
двигателей. Теория работ Н. Е. Жуковского по вихревой теории
гребного винта, теории крыла и воздушного винта (1912—1918 гг.)
легла в основу теории турбомашин.
Значительным событием явилось опубликование в 1929 г. в жур-
нале «Техника воздушного флота» статьи акад. Б. С. Стечкина
«Теория воздушно-реактивных двигателей». Эта работа получила
всемирное признание и послужила основой современной теории
этих двигателей. Дальнейшее развитие эта теория получила в ра-
ботах профессоров Н. В. Иноземцева, И. И. Кулагина, М. М. Мас-
ленникова, С. П. Шляхтепко и других авторов.
Выдающийся вклад в развитие ГТД внес ученый и конструк-
тор, акад. А. М. Люлька. В 1935 г. им была разработана схема
ТРД, а в 1941 г. — получено авторское свидетельство на один из
наиболее широко применяемых в настоящее время ТРДД. Под ру-
ководством генерального конструктора А. М. Люльки создан ряд
современных реактивных двигателей.
Переходя непосредственно к теории газовых турбин, следует
отметить монографию проф. В. М. Маковского «Опыт исследования
турбин внутреннего сгорания» (1925 г.) и книгу проф. В. В. Ува-
рова «Газовые турбины»1. В этой книге впервые в отечественной
литературе были систематизированы работы по теории газовых
турбин и оригинально разработаны наиболее важные вопросы тео-
рии турбин.
1 У в а р о в В. В. Газовые турбины: Ч. 1.— М.—Л.; ОНТИ, Главная ре-
дакция энергетической литературы, 1935. — 212 с.
9
Ценным вкладом в науку о газовых турбинах являются труды
по авиационным лопаточным машинам профессоров Г. С. Жириц-
кого, К. В. Холщевникова, В. X. Абианца, Г. Н. Абрамовича,
Г. Ю. Степанова, М. Е. Дейча, Л. А, Симонова, Ю. Н. Нечаева и
других советских ученых.
Работы, выполненные в ряде научно-исследовательских орга-
низаций и вузов: ЦИАМ цм. П. И. Баранова, ЦАГИ, ЦКТИ, МВТУ,
МЭИ, МАИ и др. позволили довести до высокой степени совершен-
ства проточную часть газотурбинного двигателя.
Существенное значение для создания современных высокотемпе-
ратурных ГТД имели исследования в области систем охлаждения
газовых турбин, выполненные профессорами К. М. Поповым,
А. М. Зысиной-Моложен, Е. П. Дыбаном и др., исследовательски-
ми организациями ЦИАМ, МВТУ, ИТТ АН СССР, ЦКТИ, КАИ
и др.
По конструкции и расчету на прочность газовых турбин и газо-
турбинных двигателей большая заслуга принадлежит профессорам
Г. С. Скубачевскому, Р. С. Кинасощвили, И. А. Биргеру и другим
советским ученым.
Надежные и высокоэффективные конструкции газовых турбин и
ГТД в целом созданы моторостроительными конструкторскими
бюро и под руководством выдающихся конструкторов и ученых
А. М. Люльки, А. А. Микулина, С. К. Туманского, В. Я. Климова,
В. А. Добрынина, Н. Д. Кузнецова, П. А. Соловьева, И. И. Ивчен-
ко, П. А. Колесова, С. Д. Колосова, С. П. Изотова, В. А. Лотаре-
ва и др.
В настоящее время советская школа авиадвигателестроения по
праву занимает передовые позиции в мировой авиационной тех-
нике.
Указывая на достижения советской науки в области газотур-
бостроения, следует упомянуть также о значительном вкладе в
эту область зарубежных ученых, исследовательских институтов и
моторостроительных фирм. Большой вклад в теорию газовых тур-
бин и авиационных ГТД внесли капитальные работы В. Траупеля,
Б. Эккерта, И. Крушика и др., такие научные центры, как NASA
(США), NGTE (Англия) и др.
• \
Часть первая
ТЕРМО- И АЭРОДИНАМИКА ГАЗОВОЙ ТУРБИНЫ
Глава I
ТИПЫ И СХЕМЫ ДВИГАТЕЛЕЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
§ 1.1. ОСНОВНЫЕ ТИПЫ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ
Принципиальная схема и цикл работы ГТД со сгоранием при
постоянном давлении приведены на рис. 1.1. Компрессор К заса-
сывает атмосферный воздух, повышает его давление и направляет
в камеру сгорания КСГ, в которую через форсунку впрыскивается
жидкое топливо, подаваемое из бака Б насосом Н. Выделяемая при
сгорании топлива тепловая энергия повышает температуру рабоче-
го тела — газа. Из камеры сгорания, давление в которой постоян-
но, газ входит в турбину Т, где его давление снижается до атмос-
ферного • давления и выходит наружу. Повышение давления
воздуха в компрессоре требует затрат механической работы. При-
расширении газа в турбине получают механическую работу на валу.
Так как мощность турбины оказывается больше требуемой на при«
вод компрессора и вспомогательных агрегатов, то появляется избы-
точная мощность, которая может быть использована потреби-
телем.
Графически тепловой процесс*двигателя, работающего по схе-
ме, приведенной на рис. 1.1, изображен в координатах р—v на
рис. 1.2. Термический к.п.д. газотурбинного двигателя, работающе-
го по описанной схеме в земных условиях и параметрах газа (рз,
Тз), применяемых в настоящее время, сравнительно низок (0,22 ...
... 0,27). В авиационных ГТД при полетах на высоте, где температу-
ра воздуха на входе в двигатель (Т\) значительно меньше, чем в
земных условиях, термический к.п.д. при прочих равных условиях
оказывается более высоким (0,32 ... 0,42). Это благоприятное сте-
чение обстоятельств является одной из причин первоочередного и
быстрого внедрения ГТД в авиацию.
Газотурбинные двигатели используются в летательных аппара-
тах для различных целей. В качестве основных двигателей само-
летов используются мощные ГТД с тягой, измеряемой десятками
тонн. Наряду с ними созданы средние, небольшие и совсем мини-
атюрные, так называемые «ранцевые» ГТД, имеющие тягу всего
несколько сотен ньютонов и предназначенные для индивидуальных
полетов человека на платформе. Малоразмерные ГТД используют-
ся в авиации в качестве вспомогательных машин — турбостарте-
ров, турбоэлектрогенераторов.
11
Рис. 1.1. Принципиальная схема ГТД при p=const:
К—компрессор; КС Г—камера сгорания; Г—турбина; Б—бак с топливом. Я—насос- Я—потре-
битель; /—вход в компрессор; 2—вход в камеру сгорания, 3—вход в турбину. 4—выхлоп
Рис. 1.2. Схема цикла теплового процесса ГТД со сгоранием при р—const в ди-
аграмме р—v:
1—2—повышение давления в компрессоре; 2-3- -подвод тепловой энергии в камере сгорания;
3—4— расширение газа в турбине; 4—5—расширение газа в реакгивнсм сопле (силовой тур-
бине)
Газовые трубины применяются в жидкостных ракетных двига-
телях' (ЖРД) для привода насосов подачп горючего и окисли-
теля.
Воздушные турбины, использующие скоростной напор летатель-
ного аппарата приводят в действие топливные насосы в прямоточ-
t ных ВРД, вращают буксировочные лебедки и т. п.
Любой из авиационных ГТД включает в себя газогенератор-
ную часть, преобразующую потенциальную энергию топлива в так
называемую свободную энергию Несз, и устройство, трансформи-
рующее эту свободную энергию в полезный технический эффект —
тягу R или мощность Ne двигателя.
Рис. 1.3 схематично иллюстрирует, как на базе газогенератор-
ной части ГТД (см. рис. 1.3, а) и с помощью различных преобра-
Рис. 1.3. Принципиальные конструктивные схемы ГТД различных типов в зави-
симости от устройства преобразователя свободной энергии:
а—газогенераторная часть ГТД, б—турбореактивный двигатель: ^—турбовинтовой двигатель,
г—двухконтурный турбореактивный двигатель; д—турбовальный двигатель; К—компрессор;
КСГ—.камера сгорания- Г—турбина; PC—реактивное сопло; В—воздушный винт- Р—редуктор;
ТВ—турбина винта (вентилятора); Кц—компрессор второго контура, СТ—силовая турбина
12
зователей свободной энергии могут быть получены различные типы
двигателей. Если всю свободную энергию Не св использовать в реак-
тивном сопле (PC) двигателя для ускорения струи газа, получа-
ется турбореактивный двигатель (ТРД), принципиальная конст-
руктивная схема которого показана на рис. 1.3, б; при срабатыва-
нии всей или большей части Явсв в дополнительной турбине (ТВ),
соединенной через редуктор с воздушным винтом (В), получается
другой основной тип двигателя — турбовинтовой ТВД (см. рис.
1.3, в); если мощность, развиваемая дополнительной турбиной, рас-
ходуется на привод компрессора (вентилятора) второго контура
(Ап), а оставшаяся часть свободной энергии идет на разгон струи
газов в реактивном сопле первого (внутреннего) контура, то Такой
двигатель называется двухконтурный турбореактивный двигатель
ТРДД (см. рис. 1.3, г). Наконец, если израсходовать всю Hecs в
так называемой тяговой или,силовой турбине (СТ), то получится
типичная конструктивная схема турбовального двигателя ТВаД
(см. рис. 1.3, д), используемого на вертолетах, транспорте, кораб-
лях, в стационарных ГТУ п во вспомогательных авиационных сило-
вых установках.
§ 1.2. ГАЗОТУРБИННЫЕ ДВИГАТЕЛИ
И ТУРБИНЫ ВСПОМОГАТЕЛЬНОГО НАЗНАЧЕНИЯ
На летательных аппаратах для вспомогательных целей приме-
няют как малоразмерные ГТД, так и собственно газовые турбины.
Принципиальная схема малоразмерного ГТД, используемого в ка-
честве турбостартера, т. е. для запуска основных ГТД, показана на
рис. 1.4. Газовые турбины, как таковые, применяют, например, в
турбонасосных агрегата? (ТНА) жидкостных ракетных двигателей
п в прямоточных воздушно-реактивных двигателях (ПВРД). Одна
из схем ТНА, турбина которого работает по открытой схеме (ра-
бочее тело выбрасывается в атмосферу), показана на рис. 1.5. Тур-
, Рис. 1.4. Схема газотурбинного стартера:
1—вал силовой турбины; 2—свободная силовая турбина; 3—турбина привода цечтробежх’зго
компрессора; 4—камера сгорания. 5—центробежный компрессор; 6—вход воздуха; 7—выпуск
газов
Рис. 1.5. Схема турбонасосного агрегата ЖРД:
1 насос для горючего; 2—турбина с двумя ступенями скорости; 3—соединительная муфта;
'	4—насос для окислителя
13
Рис. 1.6. Схема ТНА в ЖРД с дожиганием газа после турбины:
/, 5—насосы для горючего « окислителя; 2—активная газовая турбина; 3—газопровод от тур-
бины к камере сгорания; 4—камера сгорания ЖРД, 6—газогенератор
бина ТНА такой схемы имеет ряд особенностей. Рабочее тело для
нее готовится в специальном газогенераторе, обеспечивающем тре-
буемое давление и температуру. Ввиду того что отработавшие в
турбине газы выбрасываются в атмосферу, расход газа делают не-
большим, а для получения необходимой мощности срабатывают в
такой турбине очень большие перепады давлений. В результате
турбины получаются, как правило, сверхзвуковые. Для эффектив-
ного срабатывания большого теплоперепада при умеренных обо-
ротах рабочего колеса часто эти турбины выполняют с двумя сту-
пенями скорости (колеса Кертиса), как это и показано на рис. 1.5.
В мощных ЖРД, работающих при высоком давлении в камере
сгорания, турбины ТНА работают при небольших перепадах дав-
лений; в этих ЖРД газ после турбины дожигается в камере сгора-
ния двигателя и турбина работает по закрытой схеме. Принципи-
альная схема такой установки показана на рис. 1.6. Расход рабочего
тела в таких турбинах сравнительно большой. Турбины выполняют
непарциальными, дозвуковыми, активного .типа. К.п.д. турбин, ра-
ботающих по замкнутой схеме, получается, как правило, выше,
чем по открытой. Рабочим телом в турбине привода топливного
насоса ПВРД, также как и в турбинах привода буксировочных
лебедок, служит воздух, сж^аемый за счет скоростного напора
при полете летательного аппарата,-
Турбины пороховых стартеров, при-
меняемых для запуска авиационных
ГТД, работают на продуктах сгора-
ния пороха, а воздушных старте-
ров — на сжатом воздухе, который
подается или от аэродромных источ-
Рис 1.7. Схема малоразмерного ТВаД с от-
бором сжатЬго воздуха за компрессором:
/—вспомогательные агрегаты; 2—центробежный
компрессор; 3—заслонка регулирования отбора
воздуха, 4—камера сгорания; 5—одноступенчатая
осевая турбина
14
ников питания или от автономного энергоузла, устанавливаемого
на самолете и представляющего собой малоразмерный турбоваль-
ный ГТД. Принципиальная схема такого ТВаД показана на рис.
1.7. Компрессор 2 и турбина 5 сбалансированы так, что за ком-
прессором можно отбирать до */з поступающего в него воздуха.
Отбираемый воздух используется также в системе кондициониро-
вания на стоянках самолета, при неработающих основных двига-
телях.
В параграфах 1.1 и 1.2 определено назначение и место газовой
турбины в авиационных ГТД и других типах газотурбинных уста-
новок.
Остановимся теперь более подробно на принципе действия га-
зовой турбины.
Глава II
ПОНЯТИЕ О ГАЗОВОЙ ТУРБИНЕ
§ 2.1. ПРИНЦИП ДЕЙСТВИЯ ОСЕВОЙ ТУРБИНЫ
Газовая турбина предназначена для преобразования тепловой
энергии газа в механическую работу на валу. Это преобразование
осуществляется за два этапа. Вначале потенциальная энергия газа
в виде повышенного давления и температуры преобразуется в кине-
тическую энергию движущегося газа. С этой целью газ расширяют
в соплах турбины, где он приобретает большую дозвуковую или
даже сверхзвуковую скорость. На втором этапе газ, проходя по
каналам между лопатками рабочего колеса, отдает часть своей
энергии ротору, который таким образом приводится во вращение и
совершает механическую работу. Преобразование потенциальной
энергии газа в кинети-
ческую может происхо-
дить не только в соп-
лах, но и в каналах ра-
бочего колеса, где оба
этапа преобразования
энергии происходят в
рабочем колесе одно-
временно. Типичная
схема турбины осевого
типа приведена на рис.
Рис. 2.1. Схема одноступен-
чатой осевой турбины:
/—обойма; 2—подшипник; 3—вал;
4—диск; 5—рабочие лопатки; 6—
решетка сопловых лопаток; 7—
корпус турбины
Э, 1, 2—расчетные сечения про-
точной части 6a, бг—зазоры
осевой с! радиальный
15
2.1. Расчетные сечения проточной части турбины принято обозна-
чать (см. рис. 2.1): 0 — перед турбиной (перед сопловым аппара-
том); 1—за сопловым аппаратом (перед рабочим колесом); 2 —
за решеткой рабочих лопаток (за турбиной).
Диск 4, тем или иным способом соединенный с валом 3, несет
на ободе решетку рабочих лопаток 5. Газ входит в сопловую решет-
ку 6 и расширяется в ней от начального давления р0 до давления
pi, которое в частном случае может равняться и давлению р2 на
выходе из турбины (например, атмосферному). Решетка сопловых
лопаток укреплена в корпусе 7. Вал опирается на подшипники,
один из которых 2, находящийся в обойме 1, показан на схеме.
В правой части рис. 2.1 показано в развертке на плоскость цилинд-
рическое сечение на среднем диаметре решеток сопловых (заштри-
хованы) и рабочих (зачернены) лопаток. Там же показаны диа-
граммы изменения давления и скорости газа по длине проточной
части турбины.
При расширений газа в соплах скорость его возрастает от на-
чальной величины со до Сь Это преобразование подчиняется урав-
нению энергии
dq=di-^-d(-^\-}-dHe-\-dz,	(2.1)
где dq — энергия теплообмена с внешней средой; di — изменение
, / с2 \
энтальпии газа в рассматриваемом процессе; d 1—1 — изменение
кинетической энергии потока; dHe — внешняя механическая рабо-
та, совершаемая газом; d,z — изменение' энергии положения (в га-
зовых турбинах работой гравитационных сил пренебрегают, dz=0).
Поток в турбомашинах в общем случае существенно неравно-
мерный как по окружности, так и по радиусу проточной части. Од-
нако в теории удобно рассматривать осредненный равномерный
поток, а все особенности, вносимые фактической неравномерностью,
учитывать экспериментальными поправочными коэффициентами.
(Подробнее об этом см. § 3.1). Такой подход, как показывает опыт,
облегчая расчеты, дает в то же время хорошее совпадение расчет-
ных данных с действительными. Всюду в дальнейшем, за исключе-
нием особо оговоренных случаев,, будем оперировать с осредненны-
ми значениями параметров.
Для случая энергетически изолированного процесса расшире-
ния газа в соплах- (d^=0; dHe=0) из (2.1) следует, что
c1=yr‘2(io ч),	(2-2)
2
где i0*=.i0+ ~—начальная энтальпия адиабатно заторможенно-
го потока газа.
16
5
Рис. 2.2. Развертка на плоскость ступени осевой турбины (треугольники скоро-
стей, эпюра давлений по профилю рабочей лопатки, распределение давлений р и
скоростей w по сечению канала) (а) и план скоростей (б):
спинка; 2—«вогнутая часть
В дальнейшем всюду состояние газа на входе в турбину будем
выражать через параметры адиабатно-заторможенного потока:
^=Ро(1+±^М2о)*-1=А)(1
Т*й=Тй(\ + ~-^\ = -
. .	. и
—— Хо) *"1.
Л 4“ 1	/
_1о_________
Л—1 ^2\’
(2.3)
(2-4)
где Мо=— и Хо= ——число Маха и приведенная скорость по-
Ло	Скр	-
тока при входе его в сопловой аппарат;	ад=У kRT^ — скорость
звука при температуре Тй газа; Скр = 1 / 2—-—Т??*—критическая
у л+1
скорость при температуре То* газа; k — показатель адиабаты; /? —
газовая постоянная.
В других поперечных сечениях проточной части турбины, как
правило, используются статические (термодинамические) пара-
метры газа.
Итак, со скоростью, Направленной под некоторым углом оы
(рис. 2.2). к фронтальной плоскости сопловой решетки, газ попа-
дает на решетку рабочих лопаток, движущихся с окружной скоро-
стью
u—stdn,
(2.5)
где d — диаметр, измеряемый по середине высоты лопаток; п —
частота вращения турбины.
17
Вектор относительной скорости Wi газа при входе на рабочие
лопатки находят, вычитая из вектора абсолютной скорости. Ci век-
тор скорости и переносного движения. Из соотношений косоуголь-
ного треугольника следует, что
__________________________________________ V
Wi = с? й2— 2й^1 cos вр	(2.6)
Из межлйпаточных каналов газ выходит с некоторой скоростью
гс'2, которая может быть и больше и меньше a?i. При проходе через
каналы рабочей решетки газ меняет свое направление. Вследствие
поворота струи, а также (в большинстве случаев) ее ускорения
возникает сила, приложенная к лопаткам, которая создает крутя-
щий момент и производит механическую работу на валу турбины.
Возникновение этой силы объясняется тем, что на обеих сторо-
нах лопатки образуется разное давление. Одна из составляющих
этой силы направлена параллельно фронтальной поверхности ре-
шетки по направлению скорости и. На рис. 2.2 приведена пример-
ная эпюра давлений по обе стороны лопатки: давление на вогну-
той поверхности существенно выше, чем на выпуклой (спинке).
Заштрихованная площадь эпюры давлений в известном масштабе
эквивалентна величине силы, приложенной к лопатке. Давление за
рабочей решеткой р2 меньше давления или равно ему. Как по-
казано ниже, эти давления обычно непостоянны на высоте лопатки.
Давление на вогнутой поверхности лопатки больше р2, тогда как
на значительной части спинки — оно меньше. Если давление на
профиле меньше р2, то это давление часто называют разреже-
нием.
Характер эпюры объясняется действием инерционных (массо-
вых) сил при повороте струи газа в межлопаточном канале — сил,
которые прижимают частицы газа к вогнутой поверхности лопатки,
создавая на ней повышенное давление. Таким образом, по ширине
канала давление резко изменяется от минимального на спинке до
максимального на вогнутой поверхности. В соответствии с этим
меняются и скорости газа по сечению канала (см. эпюру скорости
w на рис. 2.2).
Возникающая при повороте струи газа сила, приложенная к ло-
патке, может быть определена по закону сохранения количества
движения в проекции на ось и (см. рис. 2.2).
Окружное усилие, создаваемое на лопатках (Н),
Ра=т(с1и — с2а),	(2.7)
где т — секундная масса.
Применяя эту формулу к решетке лопаток, для которой а2 <90°,
и, следовательно, скорость с2и имеет направление, обратное ciu,
получим
Pe=/n(Cie4-c2e)-
В обоих случаях, когда аг<90° и когда «2>90°, углы 01 и 02 <90°
и, следовательно, Ciu=u+Wicos ₽ь с2и = и—K)2cos02-
18
Подставив эти выражения в формулу (2.7) получим
Ра—т(Wi cos	cos р.2)w2u).	(2.8)
Векторы скоростей и их составляющие, входящие в формулы
(2.7), (2.8), определяют из треугольников скоростей. Треугольник,
составленный из векторов Ci, Wi, и, называют входным, — из векто-
ров с2, w2, и — выходным.
В реальных ступенях входной и выходной треугольники скоро-
стей имеют неодинаковую высоту по оси турбины. Высота (с2о)
выходного треугольника обычно больше, чем входного (с10). Одна-
ко в ряде случаев в теории турбомащин методически удобнее опе-
рировать с равновысокими треугольниками (с2а=с1а).
Обычно треугольники скоростей рисуют из одной -вершины, как
показано па рис. 2.2, бив таком случае называют планом скоро-
стей турбинной ступени. Планы скоростей дают наглядное • пред-
ставление о кинематике турбинной ступени, облегчают понимание,
а в некоторых случаях (см. рис. 2.5) и решение вопросов теории
турбомашин.
§ 2.2. ПОНЯТИЕ О РЕАКТИВНОСТИ ОСЕВОЙ СТУПЕНИ
Комплект сопловой и рабочей решеток образует ступень про-
точной части турбины. В зависимости от характера расширения га-
за в ступени различают активный и реактивный процессы. Актив-
ный характерен тем, что давление pt за сопловой решеткой равно
давлению р2 за рабочими лопатками, и потенциальная энергия газа
преобразуется в кинетическую только в соплах турбины. При реак-
тивном процессе расширение газа начинается в соплах и продол-
жается в рабочей решетке, поэтому po*>pi>p2- Таким образом,
отличительными признаками реактивного процесса являются: пре-
образование потенциальной энергии газа в кинетическую не только
в сопловой, но и в рабочей решетках; непре-
рывное падение давления газа как в сопловых
каналах, так и между рабочими лопатками
(см. рис. 2.1).
Положим, что при адиабатном расширении
газа от давления р0* до Pi тепловой перепад
составляет HOi~io* — lit, а при расширении от
Pi до Р2—H02=iit—1’2. Эти перепады показаны
на диаграмме IS (рис. 2.3).
Термодинамической степенью реактивности,
или просто степенью реактивности, называется
отношение адиабатного перепада тепла в ра-
бочей решетке к суммарному адиабатному пе-
репаду тепла от ро* до р2 в обеих решетках,
составляющих ступень турбины, т. е.
Q=/>02/^0,	(2.9)
где Hq,—
Рис. 2 3. Адиабатное расширение газа'в ступени
осевой турбины в диаграмме £—S
19
Хотя на рис. 2.3 показан тепловой процесс турбины без потерь,
но указанное выше определение реактивности относится и к турби-
не, в которой расширение газа сопровождается потерями. Если
Яо2=О, то и с>=0. Такие ступени турбины называются активными.
Существуют турбины, у которых сопловой аппарат вовсе отсут-
ствует и газ расширяется только на рабочих лопатках. Для такой
турбины До2=Яо и g=l. Таким образом, степень реактивности сту-
пени может изменяться от нуля до единицы. Реактивность ступени
турбины не остается постоянной по высоте проточной части. В за-
зоре 6в (см. рис. 2.1) между сопловой и рабочей решетками от ча-
стицы газа массой dm на поток действует центробежная сила
dC\=dm-^—, а за рабочими лопатками — сила dc2=d/n—
где г — радиус, на котором находится частица dm-, ciu, с2и — ско-
рости закрутки потока.
Для радиального равновесия частицы необходимо, чтобы в по-
токе существовал радиальный градиент давления, т. е. чтобы дав-
ления pt и р2 возрастали по высоте лопатки. Особенно интенсив-
ным должен быть рост давления pt в связи с тем, что ctu>c2u.
Скорость сги значительно меньше (см. рис. 2.5У и может даже рав-
няться нулю (при осевом направлении скорости с2). Поэтому дав-
ление р2 по высоте лопатки растет незначительно и может даже
оставаться постоянным. Разность pt—р2 увеличивается по высоте
лопатки, а в соответствии с этим возрастают теплоперепад Дог на
рабочих лопатках и степень реактивности. В основании лопаток
она может быть даже отрицательной, когда давление pt<p2.
Ступень, называемая активной, имеет на самом деле положи-
тельную реактивность на периферии лопатки и отрицательную у ее
корня. Таким образом, реактивность неразрывно связана с длиною
лопатки и радиусом рассматриваемого сечения. Если радиус спе-
циально не оговаривается, то имеется в виду степень реактивно-
сти на среднем диаметре d (см. рис. 2.1). У реактивных ступеней
авиационных ГТД обычно q=0,25 ... 0,45.
В активной турбине на среднем диаметре (если пренебречь по-
терей скорости при проходе газа через рабочую решетку) Wt = w2;
в реактивной турбине вследствие расширения газа на рабочей ре-
шетке скорость w возрастает, т. е. ау2>®ь
Кинетическая энергия, не использованная в турбине (см. рис.
2.5), пропорциональна скорости с2.
§ 2.3. ОДНОСТУПЕНЧАТЫЕ ОСЕВЫЕ ТУРБИНЫ
На рис. 2.1 приведена схема одноступенчатой турбины, проточ-
ная часть которой состоит из сопловой и рабочей решеток. Если
в меридиональной плоскости поток газа движется параллельно или
почти параллельно оси турбины, то такая турбина называется
осевой. Характер изменения давления газа на решетках показы-
вает, что эта схема относится к реактивной ступени турбины. Реак-
тивную ступень изображает также схема на рис. 2.2 (w2>nPi).
20
Рис. 2.4. Решетка и треугольники скоростей активной осевой турбины
Рис. 2.5. Треугольники скоростей активной ступени осевой турбины при различ-
ных отношениях и/сх и углах а2:
а— а2<90°; б—а2=-90°; в— ай>90°
На рис. 2.4 приведены поперечный разрез (развертка'* по ре-
шеткам активной ступени турбины и относящиеся к ней треуголь-
ники скоростей. Если pi=p2 и &y2=to1 (без учета потерь), то при
одинаковой высоте рабочих лопаток на входе и выходе межлопа-
точный канал активной решетки должен иметь постоянное попереч-
ное сечение и, в частности, равные углы 01 и р2, что и отражено на
рис. 2.4.
Для активной ступени при wi=w2, Pi = p2 треугольники скорЬс-
тей можно начертить совмещенными так, как на рис. 2.5.
Работа газа на лопатках активной ступени эквивалентна изме-
С?— Со
неншо кинетической энергии  -—— (см. § 6.7). Чем меньше ско-
рость с2, тем большее количество кинетической энергии преобразо-
вано в механическую работу, тем-меньше выходные потери турби-
ны с^/2.
Как видно из рис. 2.5, наименьшая скорость с2 при данных ct
и угле ai получается в случае а2=90°. Из отношения скоростей,-при
котором выходная потеря минимальна (см. рис. 2.5, б), находим
(для а2=90°), что 2zc=cicosai, откуда u/ci = cosси/2. Величину от-
ношения скоростей u/ci, при которой достигается минимум выход-
ных потерь, принято называть оптимальной. Величина u/cj играет
важную роль в теории турбин.
Так как угол выхода газа из сопловой решетки в активных сту-
пенях обычно мал (at=14 ... 18°), то н/с^О.5. Соблюдение это-
го отношения скоростей обусловливает быстроходность газовых
•турбин. Так, если газ выходит из соплового аппарата со скоро-
стью С1 = 700 м/с (что вполне реально), то окружная скорость долж-
на составлять и=350 м/с.
и	cos а 1
При отступлении от условия—= направление скорости с2
отклоняется от осевого, выходные потерн увеличиваются, а меха-
ническая работа, снимаемая с вала турбины, при прочих равных
условиях снижается. В реактивных ступенях турбин также имеется
вполне определенная величина отношения и/су ,при которой ско-
рость с2 минимальна и направлена по оси. Отношение u/ct тем
больше, чем выше степень реактивности ступени (см. § 6.10). При
степени реактивности'q=0,5 минимальные выходные потери соот-
ветствуют приблизительно величине «/c1 = cosai,i т. е. вдвое боль-
шей, чем в активной турбине. Отсюда следует,' что реактивные
турбины должны быть еще более быстроходными, чем активные.
(При одинаковом теплоперепаде окружная скорость в ступени с
2=0,5 должна быть примерно в 1,5 раза больше, чем в ступени с
2=0.)
Одноступенчатая турбина в современных авиационных силовых
установках применяется довольно редко. Обычно это имеет место
лишь в тех случаях, когда степень повышения давления рабочего
тела в цикле не превосходит 5 ... 6, или на первый план выступа-
ют простота конструкции, малая масса и габариты, а не к.п.д. тур-
бины. Основная область применения одноступенчатых турбин в ле-
тательных аппаратах — это'турбонасосные агрегаты ЖРД и все-
возможные вспомогательные силовые установки (турбостартеры,
турбогенераторы бортовой электросети и т. п.).
Предельным адиабатным тепловым перепадом, который эффек-
тивно (с минимальными потерями) может быть сработан в осевой
одноступенчатой турбине обычной конструкции, является
«300 кДж/кг (подробнее см. § 7.1). В тех случаях, когда эконо-
мичность турбины не играет особой роли, можно применять одно-
ступенчатую турбину с адиабатным тепловым перепадом, сущест-
венно большим указанного выше. При этом, однако, величина u/ci
получается меньше оптимальной и возникают повышенные потери
энергии с выходной скоростью.
§ 2.4. РАДИАЛЬНЫЕ ТУРБИНЫ
В радиальных турбинах газ движется в основном по радиусу
турбины; В зависимости от направления движения (к центру; от
центра) различают центростремительные (рис. 2.6, а) и центробеж-
ные (см. рис. 2.6, б) турбины. К центростремительным турбинам
относят и так называемую радиально-осевую турбину, показанную
на рис. 2.6, в. В этом случае в процессе преобразования энергии
газ движется вначале в сопловом аппарате (лопатках) 1 от пери-
ферии к центру, затем в рабочих лопатках 2 колеса постепенно
22
рис. 2.6. Схемы проточных частей ради-
альных газовых турбин:
центростремительная; б—центробежная; в—ради-
ально-осевая (для всех типов турбин); /—сопловые
лопатки; 2—рабочие лопатки; 3—диск турбины
разворачивается и на завершающем
этапе движется по оси, как в осевой
турбине.
На рис. 2.7 показаны схемы лопа-
точных решеток перечисленных выше трех типов радиальных тур-
бин, а также входные и выходные треугольники скоростей. В соп-
ловых решетках радиальных турбин расширение газа происходит
также, как в осевых, и подчиняется тем же законам. За счет сни-
жения давления от ро на входе до pi на выходе из решетки поток
газа разгоняется от скорости с0 до сь величина которой может быть
определена по формуле (2.2).
Принципиальное отличие рабочего процесса в радиальных тур-
бинах по сравнению с осевыми заключается в том, что преобразо-
вание энергии на рабочих лопатках сопровождается здесь непре-
рывным изменением окружной скорости от величины «1 на входе
до «2 на выходе из решетки.
Таким образом, относительная скорость w в радиальных турби-
нах изменяется как в связи с расширением газа в рабочем колесе,
так и под действием инерционных сил, которые в центростреми-
тельных турбинах замедляют, а в центробежных ускоряют течение
газа в межлопаточных каналах. Основное преимущество радиаль-
ных турбин перед осевыми одноступенчатыми турбинами — боль-
шой теплоперепад. Главный их недостаток — относительно неболь-
шая пропускная способность (малый расход газа). Именно по этой
причине в крупных авиационных двигателях радиальные турбины
не применяются.
Ввиду малости диаметральных габаритов и необходимости соб-
людения оптимального соотношения скоростей (окружной и газа)
частота вращения радиальных турбин получается очень высокой —
500 ... 700 с-1 и более.
Рис. 2.7. Решетки и треугольники скоростей радиальных турбин:
а—центростремительной; б-чцентробежной; в—радиально-осевой
23
Воздушные радиальные турбины с периферийным расположсни-
•ем на диске рабочих лопаток по типу рис. 2.6, а и б широко ис-
пользуются для привода агрегатов ГТД самолетов и вертолетов
(в частности, внутрибаковых насосов), аварийных пожарных насо-
сов. Их применяют также в качестве бортовых источников электро-
питания ракет и др.
§ 2.5. МНОГОСТУПЕНЧАТЫЕ ОСЕВЫЕ ТУРБИНЫ
Предельный тепловой перепад Но, который может быть эффек-
тивно преобразован в механическую работу на валу одноступенча-
той осевой турбины, во многом зависит от того, какая окружная
скорость (и) может быть допущена на лопатках турбины без их
поломки. В большинстве современных авиационных ГТД на сред-
нем диаметре «<400 м/с. При этом тепловой перепад ограничива-
ется значениями Но—25О ... 300 кДж/кг; скорости газа в проточ-
ной части остаются дозвуковыми, а к.п.д. турбины достаточно вы-
соким.
В случаях, когда заданный теплоперепад превосходит указан-
ные предельные значения, обычно применяют многоступенчатые
турбины, которые по принципу рабочего процесса делятся на тур-
бины со ступенями давления и турбины со ступенями скорости.
Многоступенчатая турбина в принципе может быть и комбиниро-
ванной: первые ступени работают как ступени скорости, а после-
дующие как ступени давления.
Турбины со ступенями давления
В конструктивном плане турбина со ступенями давления пред-
ставляет собою ряд последовательно включенных друг за другом
одноступенчатых турбин, принцип действия которых описан в § 2.3.
На рис. 2.8, а для примера показана схема двухступенчатой тур-
бины. В каждом ряде сопловых и рабочих лопаток происходит пре-
образование энергии давления в кинетическую энергию. В резуль-
тате по длине проточной части турбины давление газа р0 от ступе-
ни к ступени падает, как показано в нижней части рис. 2.8, и за
последней решеткой достигает величины pz' за турбиной (в част-
ном случае равно атмосферному pz' = pa)- Там же показан график
изменения величины абсолютной скорости газа (с): в сопловых
решетках она растет, а в рабочих — в соответствии с отводимой
.работой — уменьшается.
Если переработать весь заданный тепловой перепад Но в одно-
ступенчатой реактивной турбине, то в соответствии с формулами
((2.2) и (2.9) скорость выхода газа из сопел будет
C1=V2(1-q)H0. ’	(2. 101
При больших величинах Но скорость ci получается настолько
большой, что величина окружной скорости и, необходимая для
поддержания оптимального отношения скоростей (M/ci)opt, оказы-
вается недопустимой по условиям прочности лопаток.
24
Ряс 2 8. Схема (а) двухступенчатой
2. “обины со ступенями давления, разверт-.
ка решеток и треугольников скоростей
/л) изменение параметров потока (в) по
' 7’ длине проточной части:
1 сопловой аппарат I ступени; 2—рабочие ло-
I ступени; 3, 4—сопловые и рабочие ло-
паТ	патки II ступени
Если же теплоперепад Но раз-
делить, например, поровну между
z ступенями турбины, то при q=
= const скорость выхода газа из
сопел будет
(2-11)
т. е., снизится в раз. Во
столько же раз, очевидно, умень-
шится и потребная окружная ско-
рость и лопаток турбины, если
считать величину («/cjopt одина-
ковой во всех ступенях.
Таким образом, одним из дос-
тоинств турбин Со ступенями дав-
ления является то, что они позво-
ляют срабатывать весьма боль-
шие (теоретически любые) тепло-
вые перепады при допустимых по
условиям прочности окружных
скоростях лопаток. Другое их
важное преимущество по сравне-
нию с другими типами турбин состоит в том, что с ростом числа
ступеней к. п. д. турбины не только не падает, но даже возрастает
(подробнее об этом см. гл. VII).
К недостаткам турбин со ступенями давления относятся утяже-
ление их и увеличение длины. Наличие нескольких ступеней услож-
няет конструкцию, технологию изготовления и трудоемкость. Тур-
бины со ступенями давления являются самым распространенным
типом турбин в авиационных ГТД и в других типах ГТД и ГТУ,
где на первый ‘план выступает, требование получения высоко-
го к. п. д.
В современных ТРД чаще всего применяются двухступенчатые
турбины, хотя встречаются и трехступенчатые; в ТВД наиболее
распространены трех- и четырехступенчатая конструкции. В верто-
летных и других типах ТВаД встречаются турбины с числом сту-
пеней до шести и более; в ТРДД — турбины трех-, четырех- и пя-
тиступенчатые (до восьми ступеней).
25
Турбины со ступенями скорости
Турбина со ступенями скорости включает сопловой аппарат,
два-три ряда рабочих лопаток и соответственно один-два ряда на-
правляющих лопаток. Конструктивно обычно рабочие лопатки
располагают на одном диске с развитой ободной частью, как по-
казано на рис. 2.9. В сопловом аппарате 1 турбины срабатывается
Практически весь располагаемый теплоперепад. Ввиду этого выход-
ная скорость газа (с,) — сверхкритическая. Некоторая малая
(5 ... 10%) доля теплоперепада распределяется между рабочими
2, 4 и направляющими 3 лопатками, чтобы улучшить их обтекание
(в решетках с ускорением потока потери меньше). Таким образом,
турбины со ступенями скорости относятся к турбинам активного
типа, которые, как показано в § 2.3 на примере одноступенчатой
турбины, для эффективного срабатывания теплоперепада требуют
существенно меньших7 окружных скоростей, чем турбины реактив-
ные. К тому же при коротких лопатках, характерных для практи-
чески применяемых турбин со ступенями скорости, активные сту-
пени способствуют снижению потерь от утечек газа в радиальных
зазорах бг над рабочими лопатками.
Большая скорость газа Ci и ограниченная прочностью лопаток
и дисков частота вращения ротора обуславливают в I ступени тур-
бины низкие величины параметра u/ci по сравнению с оптимальным
его значением. Поток газа на выходе из такой ступени имеет боль-
шую скорость С2 и закрутку в сторону, противоположную враще-
нию колеса, что видно из треугольников скоростей на рис. 2.9. Для
дальнейшего преобразования кинетической энергии выходной ско-
рости с2 в механическую работу на валу 5 (см. рис. 2.9) газ разво-
рачивают в направляющем аппарате 3 в сторону вращения колеса
Рис. 2.9. Схема турбины с двумя ступенями скорости, развертка на плоскость
цилиндрического сечения лопаток по среднему диаметру, треугольники скоростей
и графики изменения давлений и скорости газа:
<1—сопловой аппарат; 2, 4—рабочие лопатки; 3—направляющие лопатки; 5—вал; 6—диск; 7—
корпус
26


с2=с7'^/=й^
рис. 2.10. Треугольники скоростей турбины
с двумя ступенями скорости без учета по-
терь (симметричные лопатки)
и подают на рабочие лопатки 4 II
ступени турбины. Если по выходе из
II ступени скорость Сг окажется все
еще значительной, можно поставить
III ступень и т. д., пока скорость на
выходе не достигнет приемлемой величины. Таким образом, можно
свести выходную потерю энергии к минимуму, даже при малом
значении u/ci. Практически, однако, больше двух ступеней скоро-
сти не делают. Анализ работы таких турбин показывает, что с уве-
личением числа их ступеней максимальное значение к. п. д. пада-
ет и выгода от использования скорости с% не компенсирует утяже-
ление, усложнение и удорожание турбины.
В правой части рис. 2.9 показана развертка на плоскость ци-
линдрического сечения по среднему диаметру d проточной части
турбины с двумя ступенями скорости, треугольники скоростей и
графики изменения давления и скорости газа. Видно, что скорость*
с2 от ступени к ступени сильно уменьшается и достигает миниму-
ма, когда поток направлен по оси турбины. Если предположить, что
турбина работает без потерь, осевая скорость потока во всех ре-
шетках одинакова (с1а=с2а=с1<г=С2а) и что лопатки всех решеток
симметричны, т. е. Pi=>p2; 02=0/; pi'=₽2', то треугольники скорос-
тей можно совместить так, как показано на рис. 2.10:
 При минимальной скорости c2mtn из прямоугольного треуголь-
ника со сторонами clt 4и, Сгтш следует, что для двухступенчатой
турбины 4m=cicos си или ( —| = —При трех ступенях ско-
\ ci /opt 4
/ и
рости, рассуждая аналогично, можно получить, что —
, \ С1
и т. д. В общем случае для турбины со ступенями скорости при
числе ступеней z
а \cr.cK cosai	<2.12)
Ci /opt 2г
Таким образом, главное достоинство турбин со ступенями ско,-
рости состоит в том, что они могут достаточно эффективно срабо-
тать большие тепловые перепады при малых окружных скоростях.
Например, при заданном тепловом перепаде оптимальная окруж-
ная скорость в турбине с двумя ступенями скорости будет в два
раза меньше, чем в одноступенчатой активной турбине, и примерно
в 1,5 раза меньше, чем в двухступенчатой турбине (q=0,5) со сту-
пенями давления. Турбины со ступенями скорости получили широ-
кое распространение в установках вспомогательного назначения:
турбонасосных агрегатах ЖРД, вспомогательных энергоузлах са-
молетов, для привода аварийных пожарных насосов и т. п. В ГТД
___COS CQ
opt 6
27
самостоятельного назначения, где на первый план выступает тре-
бование высокого к.п.д., эти турбины не применяются. Иногда сту-
пени скорости применяют в качестве первых ступеней многост\ -
пенчатых турбин.
§ 2.6. ОСНОВНЫЕ ТРЕБОВАНИЯ К ГАЗОВЫМ ТУРБИНАМ
В зависимости от типа и назначения газовой турбины выдвига-
ются те или иные основные требования к ней. В числе требований,
которые предъявляются к авиационным турбинам, важнейшими
являются:' высокая надежность в течение всего ресурса; высокий
к.п.д.; минимальные габариты и масса; хорошая приспособляе-
мость к условиям эксплуатации (нерасчетным режимам).
Надежность и ресурс газовых турбин
Требование высокой надежности применительно к деталям га-
зовой турбины авиационных двигателей является абсолютным. Пра-
вильным конструированием и выбором материалов и запасов про-
чности должна быть обеспечена безусловная гарантия надежной
работы всех деталей турбины в течение всего времени, предусмот-
ренного техническими условиями на эксплуатацию. Поломка или
обрыв сопловой или рабочей лопатки турбины влечет за собою
обычно выход из строя двигателя. Разрыв диска турбины или по-
ломка вала может стать причиной тяжелой аварии всего летатель-
ного аппарата. Методы обеспечения надежной работы турбин рас-
сматриваются во второй части книги. Газовые турбины современ-
ных ГТД имеют гарантийный ресурс, т. е. время работы до первого
ремонта, составляющий нередко 5 ... 10 тыс. ч.
К- п. д. турбин
Эффективным к.п.д., или просто к.п.д. газовой турбины т)‘т* по
заторможенным параметрам, называют отношение механической
работы, снимаемой с вала турбины Ят, к адиабатному теплопере-
паду Но* (см. рис. 2.3), т. е.
(2.13)
Достижение высокого к.п.д. в авиационных газовых турбинах
является непременным условием совершенства двигателя в целом.
Это объясняется весьма существенным влиянием к.п.д. турбины на
топливную экономичность ГТД. Каждый процент улучшения к.п.д.
турбины снижает расход топлива в современных ТРД и ТРДД на
0,7 ... 0,9%, а в ТВД и ТВаД на 1,3 ... 1,8%. К.п.д. турбины ока-
зывает влияние также на массу и габариты ГТД, поскольку от его
величины, даже сильнее, чем экономичность, зависит удельная (по-
лучаемая от 1 кг/с воздуха) тяга двигателя. При выполнении всех
28
требований теории оптимального проектирования авиационных тур-
бин, которые излагаются в последующих главах книги, удается по-
дучить г|т*=0,91 ... 0,94.
Габариты и масса турбин
Получение минимальных габаритов и массы является основным
требованием для любой авиационной конструкции. Выполнение это-
го требования в ГТД в значительной степени зависит от габаритов
и массы турбокомпрессорной части двигателя, составляющей
65 ... 70% массы всего двигателя. Узел турбины обычно дает от
1/4 до 1/3 массы двигателя. Чтобы иметь минимальные габариты и
массу авиационных турбин, приходится применять большие скоро-
сти газа в проточной части; уменьшать число ступеней за счет по-
вышения нагрузки на каждую из них; использовать лопатки с боль-
шим удлинением ft/d=20 ... 25% и, наконец, применять наиболее
жаропрочные, жаростойкие сплавы и эффективные системы охлаж-
дения лопаточных аппаратов и дисков. Охлаждение горячих частей
позволяет иметь высокую начальную температуру газа перед тур-
биной, что благоприятно как для снижения массы и габаритов узла
турбины, так и для улучшения удельных показателей ГТД в целом.
Удельная масса современных турбин авиационных ГТД состав-
ляет 4 ... 7 г/н тяги в ТРД и ТРДД и 40 ... 50 г/кВт мощности в
ТВД.
Приспособляемость газовых турбин.
к нерасчетным режимам эксплуатаций
Газовые турбины выполняются в металле по размерам, полу-
ченным на основе термодинамических, газодинамических и прочно-
стных расчетов, при каком-то одном сочетании внешних атмосфер-
ных условий (рн, Ти, Мн) и исходных внутренних параметров (То*,
ро*, Р2, «) двигателя. В процессе эксплуатации все эти величины
существенно изменяются при изменении скорости и высоты полета,
тогда как геометрия турбины остается неизменной.
При плохой приспособляемости турбины к нерасчетным усло-
виям работы может сильно снижаться ее к.п.д. со всеми вытекаю-
щими отсюда последствиями для двигателя. Поэтому при проекти-
ровании стремятся так выбрать расчетный режим турбины и рас-
пределить теплоперепад по ее ступеням, чтобы во всем возможном
диапазоне нерасчетных режимов турбина имела высокий к.п.д. и
чутко реагировала на воздействие органов регулирования и управ-
ления.
29
Глава 111
ОСНОВЫ ТЕОРИИ РАСШИРЕНИЯ ГАЗА В СОПЛОВЫХ
И РАБОЧИХ ЛОПАТОЧНЫХ РЕШЕТКАХ ТУРБИН
§ 3.1. ОБЩИЕ СВЕДЕНИЯ
В задачу настоящей главы входит получение расчетных формул для опреде-
ления параметров потока в контрольных сечениях ступени турбины (см. рис. 2.1);
перед сопловым аппаратом (сечение 0—0); в осевом зазоре между соплами и ра-
бочим колесом (сечение 1—1) и за рабочим колесом (сечение 2—2). Указанные
параметры служат основой для расчета расхода газа или проходных сечений
проточной части, теплоперепадов в решетках, полезной работы, потерь коэффи-
циентов теплоотдачи и др.
В общем случае поток газа в указанных сечениях ступени турбины сущест-
венно неравномерен. На входе в сопловой аппарат I ступени турбины сказывается
влияние камеры сгорания: поток сильно турбулизирован; поле температур су-
щественно неравномерно по высоте и по окружности. За сопловым аппаратом
проявляются дополнительные воздействия, усиливающие неравномерность потока.
Из-за конечной толщины выходных кромок сопловых лопаток возникают вихре-
вые следы, а у концов решетки из-за вторичных течений так называемые «пар-
ные вихри». (Подробно эти явления рассматриваются в гл. IV). В результате
полные давления оказываются неодинаковыми как по шагу решетки, так и по
высоте. Из-за закрутки потока от центробежных сил статическое давление в осе-
вом зазоре также не остается постоянным, а увеличивается с увеличением ради-
уса.
По аналогичным причинам, а также из-за периодической нестационарности
потока, обусловленной вращением лопаток, поле скоростей остается существенно
неравномерным и за рабочим колесом.
Таким образом, в расчетных сечениях ступени турбины фактически сущест-
вует какое-то весьма сложное, имеющее пространственный и неустановившийся
характер поле скоростей и неравномерное nojfe всех других параметров. Расчет
таких течений во всех подробностях применительно к проточной части турбома-
шин наталкивается пока что на непреодолимые математические трудности. Ввиду
этого в инженерной практике используются расчеты, базирующиеся на различ-
ных упрощающих допущениях.
Если, например, с самого начала отказаться от изучения течения во всех
деталях и подробностях и в контрольных сечениях ступени турбины оперировать
не с истинными, а с некоторыми осредненными, среднеинтегральными параметра-
ми, то расчет основных величин, характеризующих течение, сразу же становится
элементарном. При таком подходе теория расширения газа в сопловых и лопа-
точных решетках сводится к хорошо изученной теории одномерных течений,одно-
родных потоков газа.
Следует только помнить, что осреднение всегда связано с утратой части ин-
формации о потоке и влечет за собой погрешность в расчетах. Скажем, если]
воспользоваться среднеинтегральной температурой газа при расчете температурь^
металла сопловых лопаток вместо того, чтобы учесть истинное распределение;
температур газа за камерой сгорания, то все лопатки будут иметь одинаковую]
расчетную температуру. Информация о том, какие лопатки нагреты больше, какие<
меньше, окажется утерянной, а погрешность расчетов составит десятки процентов.)
Принципиально аналогичная картина имеет место и при расчете параметров по-,
тока. Чтобы отличия в искомых величинах, рассчитанных по одномерной теории»]
и среднеинтегральных в неоднородном потоке были минимальными, необходимо^
придерживаться определенных правил осреднения. Наиболее строго эти вопросы]
рассмотрены акад. Л. И. Седовым 1.	:
1 Седов Л. И. Методы подобия и размерности в механике. М., Наука, 1967.
428 с
30
В одномерной теории турбомашин средние скорости газа в контрольных се-
ниях (сг) всегда понимают как интегральные значения количеств движения,
отнесенные к единице массы, т. е
J QCaCidF
cZcp = Q »	(3- 1)
е р__площадь проходного сечения; q — плотность; са, Ci — местные скорости
(осевая и проекция на ось i); G — масса газа.
k Выбор количества движения в качестве опорной величины диктуется тем
соображением, чго только в этом случае оказывается справедливой простая те-
орема сложения скоростей
Т =. w 4- o’	(3.2)
и простой переход от абсолютных скоростей с к относительным w при известной
окружной (переносной) скорости и.
Следовательно, только в этом случае возможно построение треугольников и
планов скоростей, существенно упрощающих и делающих наглядной теорию
турбомашин.
Можно показать [18], что, например для энергетически осредненных скоростей
faaC^dF
(3.3)
указанная теорема сложения скоростей (3.2) недействительна и поэтому этими
скоростями нельзя пользоваться при построении треугольников скоростей.
В элементарной теории осевых газовых турбин все расчеты привязывают к
среднему диаметру d (см. рис. 2 1) ступени турбины, т. е. оперируют с окружны-
ми скоростями мСр на среднем диаметре. Строго говоря, это несовместимо с ус-
ловием осреднения скоростей по  количеству движения, при котором
\§cau.dF
4 = F Q •	(3.4)
В общем случае м=з4=ыСр. Различие между и и иСр тем меньше, чем короче
длина h лопаток, характеризуемая обычно величиною ^=d/h. При 0>6, что-
обычно имеет место в первых ступенях турбин авиационных ГТД, разница между
и и цСр составляет менее 1% и практически не отражается на точности расчетов.
В последних ступенях турбин могут достигаться величины 0=3,5... 4 и одно-
мерная теория, базирующаяся на использовании величин иСр, может вызвать
заметные (2... 4%) погрешности. Повысить точность расчетов в этом случае мож-
но, например, разбиением высоты проточной части на отдельные кольцевые эле-
менты.
Заметим еще, что и чисто радиальной турбомашине (см. рис. 2.6) одномерная
теория, базирующаяся на осреднении скоростей по количеству движения, всегда
точна, так как здесь в контрольных сечениях понятия и и «Ср совпадают.
Итак, расчеты расширения газа в соплах, в сопловых и рабочих решетках
турбин, определение параметров газа в предварительных расчетах одно- и много-
ступенчатых газовых турбин, как впрочем и при расчетах течения во всех других
узлах ГТД, можно выполнять по одномерной теории поступательных течений
однородных потоков.	,
§ 3.2. ОДНОМЕРНАЯ ТЕОРИЯ ТЕЧЕНИЯ ГАЗА
В СОПЛАХ И СОПЛОВЫХ РЕШЕТКАХ
При расширении газа в соплах и сопловых решетках от началь-
ных параметров р0> T$, cQ до конечных h, Ci происходит
Уменьшение давления (р), температуры (Т), энтальпии (I), уве-
личение скорости газа (с) и энтропии (S).
31
Определение скорости и других параметров газа за соплами
Адиабатный (без потерь) процесс расширения газа
По уравнению сохранения энергии для одномерного, установив-
шегося течения газа
dqm=di+d(^y*iHe,	(3.5)
где qsa — количество подведенной к газу или отведенной от него
во внешний источник тепловой энергии; Не — механическая рабо-
та, совершаемая газом.
В соплах газ не производит механической работы, т. е. Яе=0;
в адиабатном процессе расширения газа <?вн = 0 и на основе (3.5)
d(-y)+<tf=O.	(3.6)
Отсюда после интегрирования в пределах от начальных (0) до
конечных (1) параметров
си—1^2 (Zo—iu) -f- <?о.	(3.7)
Подстрочный индекс t указывает на то, что соответствующие
параметры являются теоретическими, относящимися к адиабатно-
му расширению газа без потерь.
В газовых турбинах авиационных двигателей принято опериро-
вать^ адиабатно заторможенными параметрами газа на входе в
сопловой аппарат турбины, т. е. с условными параметрами, кото-
рые были бы в потоке при адиабатном торможении скорости с0 до
нуля (рис. 3.1). Параметры адиабатно заторможенного потока
связаны со статическими параметрами р, Т и I известными из
газодинамики формулами
/?*= р(1М2)*-1 =
^(i-^-X2) *-*;	(3.8)
Г=1'+Т’	(ЗЛ0)
Рис. 3.1, Адиабатный процесс расширения газа в соплах
в диаграмме S
32
где М и X — число Маха и приведенная скорость потока: М=с/а:
^==с/скР; а — скорость звука при температуре Т газа:
a^VkRT-,
(3.11)
— критическая скорость при температуре Т* газа:
В общем случае
(& 12)
(3.13)
С учетом формулы (3.10) теоретическая скорость на выходе из
сопловой решетки
C1<=/2(^-Zu)=1,415 /(/;-/«). 1	(3.14)
Наконец, если учесть, что адиабатный теплоперепад в соплах
Яш (см. рис. 3.1) равен адиабатной работе расширения газа,
т. е.
й-П
,	(3.15)
/о / J
к— 1
—V 2/701 —
(3.16)
Другие параметры газа на выходе из соплового аппарата най-
дутся с помощью уравнений адиабаты и состояния газа:
л-1	, п_
(3.17)
Формулы (3.16, 3.17) получены при условии постоянства пока-
зателя адиабаты k в процессе расширения газа. Фактически изо-
барная теплоемкость ср и показатель адиабаты k зависят от пара-
метров состояния газа и в первую очередь от температуры газа.
Поэтому при точных, численных расчетах надо пользоваться, на-
пример, вместо (3.16) формулой (3.14), а величины г0* и ilt нахо-
дить из таблйц термодинамических функций (см. приложение I),
рассчитанных с учетом зависимости cv(T).
Действительный процесс расширения газа (с учетом потерь)
При наличии вязкости действительный процесс течения газа
через сопло сопровождается трением и выделением тепла, вследст-
вие чего температура и энтальпия протекающего газа повышают-
ся. Действительный процесс расширения газа в сопле происходит,
2
/
1337
33
Рис. 3.2. Процесс расширения газа в
сопловом аппарате в диаграммах:
а—(Г—S); б— (i-~S)
таким образом, не по адиабате
A0*Ait (рис. 3.2, а), а по некото-
рой условной политропе A0*Ai,
причем в конечной точке процес-
са этальпия ii>iit.
Действительная скорость на
выходе из сопла Ci, очевидно, ста-
нет меньше теоретической с«. Ес-
ли для случая течения без потерь
кинетическая энергия струи была
См/2=1о—1и, то в действитель-
ности она будет Ci2/2 = i0*—А*
Таким образом, потеря кинетической энергии в сопле составит
2	2
/7с—	£	—11 llt’ '
(3.18)
На рис. 3.2, а величина Яс изображается площадью AuAiDC.
Сопоставление адиабатного и действительного процессов расши-
рения газа особенно наглядно на диаграмме i—S (см. рис. 3.2, б).
Отложив вверх от точки Ан (конца адиабатного расширения) от-
резок АцВ~Не, определим в точке Ai состояние газа на выходе из
сопла. Следует подчеркнуть, что потеря кинетической энергии Нс
оказывается меньше работы трения в соплах qr. Объясняется это
тем, что часть работы трения в процессе расширения после превра-
щения в тепловую энергию вновь превращается в кинетическую
энергию. Эта часть работы трения, измеряемая площадью АдМЙп
(см. рис. 3.2, а), называется возвращенным теплом Нъ. Таким об-
разом, если тепловая энергия газа, которая может быть полезно
преобразована в кинетическую энергию, для случая без потерь изо-
бражается площадью A0*CGE на диаграмме Т—S, то в действи-
тельном процессе она уменьшается до величины площади AfCHF
(косая штриховка по контуру).
Отношение действительной скорости истечения газа из сопел к
теоретической
<p=Cj/cw	(3.19)
принято называть коэффициентом сохранения скорости в соплах,
или просто скоростным коэффициентом сопел.
Величина ф определяется опытным путем (см. § 4.6). Таким
образом, действительная скорость истечения
Cj=<p£i<,	(3.20)
где cit — определяется по формулам (3.14) или (3.16).
34

С использованием коэффициента <р потери кинетической энер-
гии в соплах находятся по формуле
Л2 л	£
(3-21>
Л	л
Исходя из формулы (3.15), можно также записать
Яе=(1-^)ЯМ,	(3.22)
или, используя понятие реактивности ступени турбины [см. форму*
лу (2.9)],
tfc==(l-?2)(l-Q)#o.	(3.23)
где Но — адиабатный тепловой перепад в ступени.
Очевидно, в действительном процессе расширения газа по срав-
нению со случаем истечения без потерь претерпят изменение и дру-
гие параметры газа, такие как температура, плотность, удельный
объем.
При заданном перепаде давлений в сопловом аппарате (от р0*
до pi) и известных потерях Нс действительная температура газа
за соплами определится по формуле	‘
----(3.24)
где Tlt — теоретическая температура газа в конце адиабатного
расширения (см. рис. 3.2), может быть найдена также по таблицам
термодинамических функций.
Плотность газа и его удельный объем находим из уравнения сос-
тояния газа
б1=-§г’ ^=T=VL-	(3’25)
Л'1	Qi Pi
Определение площади проходного сечения сопел
и сопловых решеток
Адиабатный процесс
В установившихся условиях площадь поперечного сечения f,
скорость с, плотность е и расход газа G связаны уравнением не-
разрывности
£?=Q/c=const,	(3.26)
откуда	f =	(3.27)
При расширении газа в сопловом аппарате от давлений ро* до
Pi скорость постепенно увеличивается, а плотность уменьшается.
В соответствии с законами их изменения должна изменяться и
площадь проходного сечения.
• 2*
35
Рис. 3.3. Графики изменения площади поперечного сече-
ния и параметров газа по длине сопла при сверхкритичс-
ском перепаде давлений (без потерь; Мкр= 1)
Качественный анализ характера измене-
ния сечения сопла f в направлении движения
газа можно выполнить на основе известного
из газовой динамики уравнения Гюгонио (ади-
абатный процесс расширения):
1).	(3.28)
f ct
При дозвуковых скоростях течения газа, когда
М<1, для ускорения потока (4-rfcj) требуется
уменьшение сечения канала (—df), т. е. сопло
должно суживаться по ходу газа. При М=1 сечение должно быть
неизмененным (df=O). При сверхзвуковых скоростях течения, ког-
да число М>1, ускорение потока (+dct) возможно только при
увеличении проходного сечения сопла (j-df), т. е. сопло должно
расширяться в направлении течения. Физически это объясняется
тем, что в дозвуковой области скорость потока нарастает быстрее,
чем уменьшается плотность, а в сверхзвуковой — наоборот: плот-
ность уменьшается быстрее, чем растет* скорость (рис. 3.3). Ха-
рактер изменения площади сечения сопла по длине х для рассмот-
ренных случаев показан в верхней части рис. 3.3.
Для случая течения без потерь площадь любого сечения сопла
может быть определена по формуле (3.27). Подставляя в нее ско-
рость из формулы (3.16), написанной не для конечного давления
Pi, а для текущего по ходу газа давления р, и используя уравне-
k
ние адиабаты Po!p=(ToT)k~i, найдем площадь произволь-
ного сечения сопла
(3.29)
Если рассчитать по формуле (3.29) кривую изменения ft в
функции 8=р/ро*, то она примет вид, показанный в верхней ча-
сти рис. 3.3.
Вначале при уменьшении р от р0* до р1(р величина ft уменьша-
ется, достигает при р/Ро*=Ркр/Ро*=8кр минимального значения, а
затем возрастает.
Величину екр называют критическим отношением давлений, а
Ркр=8крРо* — критическим давлением.
Величина екр легко определяется из формулы (3.29). Обозна-
чим выражение, заключенное в квадратные скобки под корнем
формулы (3.29), через Ф. Очевидно когда Ф=Фтах-
36
Используя обычный прием отыскания максимума функции из
2-й	1_
_	2 ft -J-1 fe ___л
<?Ф/г9с- 0, получаем — sKp-— екр=0,
< . „ л
„«уда	=.,	=	У"-	(3’30)
При /г=1,4 еКр=0.528; при k= 1,333 екр=0,541.
Скорость газа в минимальной сечении сопла, т. е. по достиже-
нии в нем давления ркр, называется критической (с1ф) и определя-
ется по формуле (3.12).
При k= 1,4 <^=1,08)/*!^Го—ро®о,
(р0* в Па, Я в Дж/(кг- К)).	__
Для воздуха при /?=287,3 Дж/(кг*К); cKP=18,3i/"Го ; для
продуктов сгорания при k= 1,333 и R=288,4 Дж/(кг-К) Скр=
= 1,07 У₽7’о*= 18,15 УГО*.
Формулу (3.12) легко привести к виду
^Р=УЖГР, '	(3.31)
где ГкР=Го--------температура в критическом сечении.
н k 4- 1
Выражение (3.31) представляет собой скорость звука в среде с
температурой ТКР. Таки/и образом, при адиабатном расширении га-
за критическая скорость' равна скорости звука в газе при том его
состоянии, которого он достигает в минимальном сечении сопла:
для воздуха при/?= 1,4 <\р== 20,1]/Гкр; для продуктов сгорания
при 'k= 1,333 скр= 19,6УТ^.
Минимальное сечение сопла при адиабатном расширении най-
дется из формул (3.29) и (3.30):
При k=1,4 р=0,683; при Л=1,333 р=0,673.
Таким образом, если отношение- давлений Р1/ро*^®кр, следует
применять суживающиеся сопла; если же отношение давлений
Р1/ро*<«кр, то вслед за суживающимся участком должен быть
- - расширяющийся участок сопла.
Следует заметить, что косой срез на выходе из сопел (см. рис.
; 2.4) в известной степени может заменить расширяющийся участок
сопла. Поэтому к сделанным рекомендациям о выборе типа сопла
следует внести поправку, которая излагается в § 3.7.
37
Действительный процесс
Анализ изменения проходного сечения сопла в действительном
процессе с учетом потерь удобно выполнять с использованием за-
конов политропного расширения газа.
Если считать, что процесс расширения газа протекает по ус-
ловной политропе Ao*Ai (см. рис. 3.2) с показателем п, то нетруд-
но установить связь между скоростным коэффициентом сопел ф и
показателем политропы п. В политропном процессе
Я—1
l\fT*0=(Pl>p$n .	(3.34)
Пусть текущие параметры р и Т в процессе адиабатного расши-
рения получили элементарное приращение. Тогда на основе урав-
нения адиабаты
ft_1
/ p+gp \	=Т_+_й7\д>	/3. 35}
\ Р 1 т	}
Разлагая левую часть равенства (3.35) в ряд Маклорена и огра-
k— 1 dp_________________________________________________ dTax
ничиваясь двумя членами разложения, получим —--------~ у *
Если считать коэффициент ^=clct=C\lcu величиной постоянной
для всего процесса расширения, то из уравнения энергии di=
=—d(c2/2) следует, что с?Тад=е/Т/ф2, и тогда k~1'
После интегрирования получаем	. s
т	ft—1 >
(3.36)
. Т* \ ро )
Сопоставляя выражения (3.36) и (3.34), можем написать
—	(3.37)
п	k
или	.	(3.38)
&— 1
Формулы (3.37) и (3.38) тем точнее, чем выше значение ф. За«
метим еще, что при расширении газа n<k.
Теперь на основе формулы (3.27), замечая, что
Ci=<pl/ 2-H-RTl 1-(4)=" к	(3.39)
г п— 1	[ \Ро / J
получим для действительного процесса'
38
Рис. 3 4. График изменения скорости газа с и скоро-
сти звука а при адиабатном (0 и действительном ис-
течении из расширяющегося сопла
Изменится, очевидно, и критическое от-
ношение давления, которое на основе фор-
мулы (3.40) для течения с потерями примет
вид
(3.41)
х
Отметим еще, что в действительном про-
цессе скорость звука о в каждом из сечений станет больше (так
как увеличится средняя температура от трения), а скорость потока
с меньше. Поэтому в минимальном сечении расширяющегося сопла
скорость потока уже не будет равна местной скорости звука. Равен-
ство это наступит где-то за узким сечением сопла, как это видно
на рис. 3.4 в точке А'.
Расчетную формулу для определения величины минимального
сечения сопла в действительном процессе можно получить так же,
как это было сделано при выводе выражения (3.32).
Будем иметь
/га1п=------/ ..  ' •	(3.42)
¥Ро]/ п\——У1-1	•
г \Л 1 j
Отсюда следует, что при прочих равных условиях сечение сопла
/шт в действительном процессе должно быть больше, чем в адиа-
2
й + 1
2____
\п + 1
вышение составляет 4—5%.
]й-1
зррр- раз. В реальных соплах это пре-
1П—1
Расход газа через сопло
Адиабатный процесс
При течении газа без потерь расход его Gt через суживающее
сопло с заданным проходным сечением может быть определен по
формуле, вытекающей из (3.29) ,
Pofi , f 2 л , pi \|- / Р1ДПГ
о '	1 _ \ Ро /	\ Ро /
(3.43)
При пользовании формулой (3.43) следует иметь в виду, что
Давление не в среде, куда вытекает газ, а в выходном (наимень-
39
Рис. 3.5. Графики зависимости рас-
хода газа через суживающееся со»
пло от давления на срезе сопла рь
шем) сечении сопла, или, как
принято говорить, в устье-
сопла. При снижении давле-
ния в среде за соплом, па
сравнению с начальным ро*>
снижается и давление в устье
сопла pi, а расход газа Gt растет. Однако такой процесс продолжа-
ется только до того момента, пока давление в среде ра не снизится
до величины рКр='8крРо*.
При дальнейшем снижении давления в среде (ро<ркр) давле-
ние в устье сопла будет оставаться неизменным (pi=pKp), а следо-
вательно, не будет меняться и расход газа через сопло (G( =
= Gt шах). Физически это явление объясняется тем, что по дости-
жении критического перепада давлений на выходе из суживающе-
гося сопла устанавливаются звуковые скорости (рассматривается
случай без потерь). Поскольку малые возмущения в среде распро-
страняются со скоростью звука, то дальнейшие изменения давле-
ния в среде не могут проникнуть к сечению в устье сопла. Харак-
тер изменения расхода газа через сопло при изменении давления в
среде за соплом показан на рис. 3.5.
Теоретический расход газа через суживающееся сопло при
сверхкритическом перепаде давлений (pi/po*^eKp) является мак-
симально возможным и находится по формуле (3.43), если в ней
заменить pi/po* на еч>в1^ГГ'Г~1* фоРмУла примет вид
где ,р — находится по формуле (3.33).
По этой же формуле определяют расход газа через расширяю*
щееся сопло с подстановкой fmin вместо fi.
Действительный процесс расширения газа
Расход газа при течении с потерями может быть рассчитан на
основе формулы (3.40), по законам политропного расширения.
На практике действительный расход газа G предпочитают опре-
делять по формулам адиабатного расширения (3.43), (3.44), а ре-
альность процесса учитывать с помощью коэффициента расхода
^=0^.	(3.45).
Таким образом,
G=pOt.	(3.46)
40
Рис 3 6. Диаграмма i—S к расчету коэффициента восстановления полного дав-
ления в соплах
Рис. 3.7. График зависимости коэффициента восстановления полного давления в
лопаточных решетках в зависимости от приведенной скорости Xi и скоростных
коэффициентов <р, ф
Коэффициент расхода ц учитывает не только потери от трения,
но и все другие отличия реального процесса от адиабатного, вклю-
чая и неравномерность потока по сечению. Ввиду этого наиболее
достоверные величины р получают опытным путем.
Если известны скоростной коэффициент сопел qp и так называе-
мый коэффициент восстановления полного давления <т, то коэффи-
циент расхода может быть определен по формуле
к-1
р=<ра к .	(3.47)
В курсах газодинамики для величины a=pi*/po* выведена фор-
мула
Соотношение величин pi* и р0* показано в диаграмме i — S на рис.
3.6, а зависимость о от М и <р на рис. 3.7.
Использование в расчетах таблиц
газодинамических функций (ГДФ)
В предварительных расчетах, в том числе при определении расхода газа
через сопловой аппарат, часто пользуются таблицами ГДФ. Их применение су-
щественно упрощает расчеты, связанные с процессом расширения газа.
41
Расход газа через сопло G—fcp.
Если в сечении f достигаются критические параметры и рКр), то расход
газа становится максимальным: Сгаах~/£крркр.
Отношение плотности тока в потоке газа ср к максимально возможной плот-
ности тока при адиабатном изменении состояния газа Скрркр называется приве-
денным расходом и обозначается
Q	Q Q*
Заменяя----=—---------
Qkp	Q* Окр
женного потока) в формуле
CQ G
Ч —	— —
^крУкр	<Лпах
(3.48)
(♦ — указывает на параметры адиабатно затормо-
(3.48) и выражая отношение плотностей q/q* че-
□	/	ь 1 JL
рез приведенную скорость X, получим /1 __------->2
Q*	\	k+l	)
Так какх	Q* Окр	_(т* \a=i_(k + l V кр /	\ 2	4	1 1	>	(3.49)
то		[2	k+1	,	nJL 1 г *•	(3.50)
Значения q, так же как и р/р*, Т/Г*, р/р*, приводятся в таблицах в функ-
ции приведенной скорости 1 для различных показателей адиабаты k (см, на-
пример [6]).
Из выражения (3.48) теоретический расход газа через сопло Gt=qGmiXX~
Г k
~qcKppKpf и поскольку [см. (3.12)] скр = \/ 2 -—-~#7q» то с. учетом фор-
у К I
мулы (3.49) можно получить
(3.51)
Действительный расход газа через суживающиеся сопла с выходным сече-
нием fi и коэффициентом расхода ц найдем по формуле
Ро
G = ^fiq~r=--	(3.52)
В сопловых аппаратах авиационных турбин скоростной коэффициент имеет
k—1
высокие значения (<р^0,97). Если при этом %1<1, то %* ив соответствии
с формулой (3.47) р«<р. Для этого случая вместо (3.52) можно записать
(7 <&fiq (Хи)
Pq
(3.53)
Более удобной в практических расчегах является формула, которую можно
получить на основе рис. 3.6. Действительный расход газа при расширении по
линии At*Ai (условная изоэнтропа, эквивалентная реальному процессу)
Р*1
о = ₽Л’мк^Т'.
42
Или, так как Ti*=To*. Pi*=aoPo*. то
4.
Pq
G == mfiq (Xi) ac	(3.54)
V TQ
Здесь коэффициент oc может быть оценен по графикам (см. рис. 3.7), для чего
предварительно следует задаться величиною Х_в пределах 0,9 ... 0,95; g(Xi) на-
ходится по перепаду давлений pi/pi*; /п=₽ )/7? (для продуктов сгорания керосина
при 6= 1,33, #=288,4 Дж/(кг  К), т=0,0396).
' г Если заданным является расход газа G, то на основе формул (3.52) ...
(3.54) рассчитывают площадь проходного сечения. Например, для сопел и
сопловых решеток расчетным является выходное» сечение (1—1), (см. рис. 2.1),
поэтому	'	___
1 GVK
/1 =------------------	(3.55)
В заключение подчеркнем, что таблицы ГДФ рассчитаны по формулам
(3.8), (3.9), (3.13), (3.50), предполагающим постоянство показателя адиабаты k
в процессе расширения газа. Фактически величина k зависит от температуры и,
следовательно» изменяется в процессе расширения газа. В связи с этим в окон-
чательных расчетах надо пользоваться более точными методами. Один из таких
методов описан в § 3.6.
Расширение газа в соплах при условиях,
отличающихся от расчетных
В процессе эксплуатации турбины параметры ро*, Го*,- pi не остаются посто-
янными. При изменении любого параметра газа изменяется расход газа G ч&рез
сопло в соответствии с изменением теплового перепада. Рассмотрим этот вопрос
подробнее: вначале применительно к суживающимся, а затем расширяющимся
соплам. Ограничимся адиабатным процессом расширения газа, так как основные
выводы остаются справедливыми и для действительного процесса.
Если отношение pi/po*>eKP, то изменение теоретического расхода газа сле-
дует определять по формулам (3.43), (3.51); если Р1/Ро*^8кр — по форму-
ле (3.44).
Построив графические зависимости расхода газа от р0* и pi, получим кри-
вые, приведенные на рис. 3.8 и 3.9.
Рис. 3.8. График зависимости расхода газа через суживающееся сопло от на-
чального давления
Рис, 3 9. График ^зависимости расхода газа через суживающееся сопло от проти-
водавления pi
43
Рис. 3.10. Схемы истечет ,
газов из суживающихся с»
пел при изменении против^
давления за соплом
На рис. 3. 8 показана зави-
симость G от ро* при постоян-
ных pi и То*. При po* = pi рас-
ход равен нулю (точка В). От
этой точки до точки А расход
изменяется в соответствии с
формулами (3.43), (3.51). От
точки Л, соответствующей кри-
тическому отношению давле-
ний (Р1/ро*) = еКр, расход G
прямо пропорционален началь-
ному давлению, как это следует
из формулы (3.44). Чем ниже
противодавление ph тем на
большем протяжении ' линия
имеет прямолинейный характер.
На рис. 3.8 даны три кривых
G=f(po*): ВС — для противо-
давления pi\ ВС —для pi'; ОС
для pi = 0 (точкой А.' отмечено
начало прямолинейного участка
кривой ВС).
На рис. 3.9 показана зависимость G от pi при постоянных и 7V Прг
изменении pi от нуля до ркр=екрро* расход газа остается постоянным (лини;
ЛВ) и равным Gmax; при дальнейшем повышении давления расход уменьшается
достигая нуля при pi=po*. Изменение расхода газа на участке ВС подчиняется
формуле (3.43). При другом начальном давлении pQ' изменение расхода газа в
функции pi изобразится кривой Л'В'С', причем расход газа достигает макси-
мальной величины Стах. Так как при критическом отношении давлений расход
газа прямо пропорционален давлению р0*, то точки В и В' лежат на прямой
OB'.
На рис. 3.10 приведены схемы, иллюстрирующие процесс истечения таза из
суживающегося сопла при изменении противодавления. При pi^pKp расшире-
ние происходит по кривой АВ, причем газ вытекает из сопла резко очерченной
струей; линии, ограничивающие струю, параллельны осн сопла (см. рис 3.10, а).
При изменении pi в пределах от р0* до ркр расход газа меняется по кривъ-j MN.
При р1<ркр спектр струи принимает вид, показанный на рис 3.10, б. От кромок
сопла отходят волны разрежения, границами которых являются характеристи-
ки CBi и DCi. Попадая на свободную границу CCi или ВВ4, характеристики от
ражаются от нее с обратным знаком, и волны разрежения CDDi и DCC\ пере-
ходят в волны сжатия DDiCi и CCJ)i. В результате в пределах клипа CDE
давление падает от ркр до pi'<pKp, а в пределах клина EC\Di — возрастает
почти до критического. Характер изменения давления по оси показан пунктиром
на рис. 3.10, г.
В соответствии с этим меняются скорости газа. В сечениях CD и CjDi они
равны критической. От сечения CD до точки % скорость возрастает, достигая
максимального значения в потоке. От точки Е к сечению CiZ>t скорость пада-
ет. Сверхзвуковые скорости сохраняются, следовательно, в любом сечении струи
между CD и CiDi (см. рис. 3.10, б).
При давлении р4, существенно меньшем критического, спектр потока прини-
мает вид, показанный на рис. 3 10, в. В ядре потока образуются прямой скачок
уплотнения EF и криволинейные скачки СЕ и DF, причем дозвуковые скорости
сохраняются только в ядре потока между линиями EEi и FF\. Чем ботьше пере-
пад давлений (р11Р—р4), тем больше «разбухает» струя при выходе из сопла.
По мере отдаления от среза сопла спектр потока принимает вид, аналогичный
рис. 3.10, б, и колебания давления в струе затухают.
рис. 3.11- Кривые характера
^течения газа из расширяю-
щегося сопла на нерасчет-
ных режимах
Расход газа при всех
давлениях р^ркр остается
постоянным (Стах)* Вместо
конечного давления может
изменяться начальное дав-
ление. В этом случае для
нормальной работы сопла
также необходимо, чтобы
pi/Po* > екр. В противном
случае возникают описанные
выше явления. Таким обра-
зом, суживающиеся сопла
хорошо приспосабливаются
к нерасчетным режимам во
всем диапазоне (pi/p0*) >
еКр. Расширяющиеся
сопла работают нормально лишь при том отношении давлений piP/po*, на кото-
рое они рассчитаны.
Кривая АВС расширения газа по длине сопла Лаваля на расчетном режиме
изображена на рис. 3.11. В минимальном сечении сопла достигается критичсс-
в кое давление рКр, в выходном — pip, равное давлению окружающей среды ра.
' Если давление в окружающей среде pi"<piP (или за счет изменения началь-
ного давленияРа/Р*^ < Р1р/Ро)>.то процесс истечения из сопла аналогичен при-
веденному на рис. 3.10 случаю для суживающегося сопла, когда pi<pKp. В вы-
ходном сечении сопла сохраняется расчетное давление pi, а давление р/' уста-
навливается по оси сопла лишь на некотором расстоянии от него в результате
постепенного затухания волн расширения и сжатия, образующихся в струе.
Схематически этот процесс изображен линией CD на рис. 3.11.
Если противодавление повышается по сравнению с расчетным piP. то режим
работы сопла существенно нарушается. При сравнительно небольшом превыше-
нии р! над р1Р (или в случае, когда pi/po* станет больше* Pip/ро* за счет паде-
ния р0“) от выходных кромок сопла отходят косые скачки уплотнения, в резуль-
тате пересечения которых в потоке устанавливается давление, превышающее
внешнее. Скорость потока остается сверхзвуковой. При дальнейшем повышении
Pi в ядре потока возникает криволинейный скачок уплотнения, преобразующий
сверхзвуковую скорость в дозвуковую. При некотором давлении pi' расширение
газа следует по линии АВС с прямым скачком давления СЕ, занимающим все
выходное сечение.
При давлении большем, чем р/, скачки давления перемещаются вглубь соп-
ла. Такие скачки показаны в виде BiE\, В[2Е2. За скачком устанавливается дозву-
ковая скорость, а давление продолжает повышаться в расширяющейся части
сопла (работающей как диффузор) до величины противодавления.
Обычно возникновение скачка давления в расширяющейся части сопла свя-
зано с местным отрывом потока от стенок. При этом в месте отрыва образуют-
ся вихри и может происходить подсос газа из окружающей среды. Таким обра-
зом, режимы работы сопла, при которых pi/po*>piP/Po*, связаны с большими
потерями.
В случае повышения противодавления до величины, большей критического'
Давления, в минимальном сечении сопла все же сохранится давление р1;р и рас-
ход газа по-прежнему составит Gmax. Лишь при некотором достаточно высоком
противодавлении р1т перемещающийся вглубь сопла скачок достигает минималь-
ного сечения и исчезает. Параметры потока в минимальном сечении сохраняют-
ся критическими, но перехода в сверхзвуковую область не происходит; измене-
ние давления в сопле подчиняется кривой АВЕз, причем вся расширяющаяся
часть сопла работает как диффузор.
45
Если при давлении pim .расход газа еще сохраняется Gmax, то при даль-
нейшем росте противодавления расход газа начинает снижаться. Сопло в этом
случае работает с дозвуковыми скоростями и характер изменения давления в
нем показан линией АЕ^
Давление р1т можно определить по следующей формуле Форнера [И]:
Plm == Pq I екр + (1 — ®кр)
(3.56)
где
Из сказанного ясно, что расширяющиеся сопла менее приспособлены к из-
менению режима, чем суживающиеся. Особенно вредно отражается на к.п.д. рас-
ширяющихся сопел повышение противодавления, вызывающее скачки уплотнения
и отрыв потока от стенок сопла.
Поэтому при проектировании турбин следует избегать применения расши-
ряющихся сопел. В турбинах авиационных ГТД расширяющиеся сопла не приме-
няются. Их используют во вспомогательных силовых установках, при больших
тепловых перепадах, в тех случаях, когда на первый план выдвигаются малая
масса и габариты, а не к.п.д. турбины.
§ 3.3. ОДНОМЕРНАЯ ТЕОРИЯ РАСШИРЕНИЯ ГАЗА
В КАНАЛАХ ВРАЩАЮЩИХСЯ ЛОПАТОЧНЫХ РЕШЕТОК
Общие сведения
Ступень турбины состоит из двух лопаточных решеток (сопловой и рабо-
чей), в межлопаточных каналах которых и происходит расширение газа. В об-
щем случае газ расширяется последовательно в обеих решетках (реактивный
процесс). В частном случае только в сопловой (активный процесс).
Разобранная в предыдущих параграфах одномерная теория истечения газа
из сопел и сопловых решеток приложима и к решеткам рабочих лопаток турби-
ны. При этом, однако, следует оперировать не с абсолютными (с), а с относи-
тельными скоростями (до) газа. Математически это сводится к рассмотрению дви-
жения в системе координат, синхронно вращающейся вместе с рабочим колесом.
В относительном движении траектории частиц газа в межлопаточных каналах
приблизительно совпадают с обводами профиля лопаток, как это имело место
и в сопловых решетках.
В абсолютном движении элементарные частицы газа совершают в рабочей
решетке весьма сложное движение. Траектория этих частиц может быть полу-
чена вычислением их пути за последовательные малые промежутки времени, на
основе построения мгновенных треугольников скоростей (cT==aH“«), в те же про-
межутки времени (рис. 3.12).
Силы, действующие на элементы поверхности вращающихся лопаток и на
поток, различны, так как траектории частиц неодинаковы. Не совпадают и зако-
газа в абсолютном и относительном движе-
ниях.
Характер относительного движения в ра-
бочей решетке не только количественно, но
и качественно отличается от абсолютного.
Так, ускоренному (конфузорному) течению
в относительном движении (w2>tth) соот-
ветствует существенно замедленное (диффу-
зорное) в абсолютном движении (см.
>рис. 3. 12).
Рис. 3.12 Схема траектории частиц газа
во вращающейся лопаточной решетке осе-
вой турбины в абсолютном (1) и относи-
тельном (2) движениях
номерности изменения параметров
46
В абсолютном движении в рабочей решетке от газа отбирается работа, е?
тносительном — решетка предполагается неподвижной (ц=0), газ не соверша-
0 механической работы и, следовательно, уравнение энергии по форме должно
е1меТь такой же вид, как и в неподвижных сопловых решетках. Уравнение нераз-
рывности в относительной (вращающейся) системе координат имеет формально
такой же,вид, как и в абсолютной. Это позволяет рассчитывать проходные сече-
ния и расход газа через рабочие решетки по относительным скоростям газа, т. е.
по формулам, опять-таки по форме совпадающим с аналогичными формулами,
пслХтьзуемыми в неподвижных сопловых решетках.
Подытожив выше сказанное, можно сделать следующие выводы:
1) переход к относительному движению при анализе расширения газа во
вращающихся лопаточных решетках турбин существенно упрощает расчеты, по-
скольку в этом случае получающиеся формулы по форме в точности совпадают с
формулами для неподвижных соплойых решеток (§ 3.2);
2) для расчета параметров потока и расширения газа в каналах вращаю-
щихся решеток рабочих лопаток необходимо:
а)	в сечении (1—1) (см. рис. 2.1) перед вращающейся решеткой осущест-
вить переход от абсолютных скоростей газа (с±) к относительным (oh);
б)	выполнить расчет расширения газа в «застопоренной» рабочей решетке в
относительном движении, в соответствии с заданным перепадом статических
давлений от pi до р2;
в), в сечении (2—2) за рабочим колесом совершить обратный переход от от-
носительного движения (скорости о>2) к абсолютному (скорости с2).
Формулы для расчета расширения газа
в решетке рабочего колеса турбины
Рассматриваем действительный (с учетом потерь) процесс рас-
ширения газа. Как и в сопловом аппарате, расчет ведется по сред-
нему диаметру d ступени турбины (см. рис. 2.1).
Так как значение частоты вращения п турбины обычно извест-
но, то переносная (окружная) скорость на входе в решетку лопа-
ток
=	(3.57)
Поскольку осреднение скоростей в неоднородном потоке в за-
зоре между сопловым аппаратом и рабочим колесом выполнено из
условия неизменности количеств движения в осредненном однород-
ном и/Действительном неоднородном потоках (см. § 3.1), то спра-
ведлива простая теорема соотношения скоростей Wi = Ci—и±. Сле-
довательно, осредненную относительную скорость tea можно опре-
делить из входного треугольника скоростей
= ус\ + «1 — 2^ cos als	(3.581
где он — угол наклона вектора скорости ci к фронтальной плос-
кости решетки.
Теперь можно рассчитать параметры адиабатно заторможенно-
го в относительном движении потока газа на входе в рабочую рс-
47
Рис. 3.13. Процесс расширения газа в сопло-
вой и лопаточной решетках реактивной ступе-
ни на диаграмме i—S
шетку. Для этого предварительно о
ределяем скорость звука
число	и далее по форм
лам, аналогичным (3. 8) ... (3. 10), ц
ходим:
А = Pl (1	Ml,	(3.59)
+	(3.60)
*	W-,
(3.61)
После определения числа MW1 величины p„lt T*Wl, qI, и т. гй
можно также определить по таблицам ГДФ. Процесс действителы
ного расширения газа в ступени турбины показан нарис. 3.13 жира}
ной линией.
Уменьшение относительной скорости w2 на выходе из решетки
ио сравнению с теоретической w2< при адиабатном расширении без
потерь характеризуют коэффициентом сохранения скоростд в ра-
бочей решетке:
ф=ад2/да2г	(3.621
Величину скоростного коэффициента ф находят по опытным
данным’(см. § 4.6). Теоретическую (без учета потерь) скорость га-
за на выходе из решетки определяют по уравнению энергии, в от-
носительном движении аналогичному уравнению (3.6):
й(^)+л=о.
(3.63)
Отсюда после интегрирования от входных с индексом «1» до
выходных с индексом «2» параметров получаем
®2< = V 2 (/t — i2()	(3. 641
Тепловой перепад —i2t=H02 эквивалентен адиабатной работе рас;
ширения газа от давления pi до р2, т. е.
.	г	.	Д-11
*—1	L	\Р\) J
(3.65^
и, следовательно,
w2/=JZr2//02 + ®?='|/
r R— 1
(3. 66}’
48
Наконец, с учетом формулы (3.61) можно записать, что
Я7'«1
k— 1
Л-1
(3.67)
В приближенных расчетах можно пользоваться любой из пере-
деленных (3.64) ... (3.67) формул. В точных, окончательных рас-
1етах следует, применять формулу (3.64), а величины ц и i2t нахо-
дить из таблиц термодинамических функций (см. § 3.6 и приложе-
на I).
Таким образом, осредненная скорость газа в относительном
цвижении на выходе из решетки рабочих лопаток
w2=^w2t.	(З.,68)
Потери кинетической энергии газа в решетке рабочих лопаток
по аналогии с формулой (3.21)
,, Wo, — W9 „ wlf
--2 - -(1-ф2)-^.
(3.69)
С учетом формулы (3.66) можно также записать, что
/	«.2 \
(3.70)
(3.71)
или, используя понятие реактивности ступени qct,
Я,=(1-^)(вяЯ0+4).
\	X* /
Величины Ня, Я02, Но показаны на рис. 3.13.
Температура, плотность и удельный объем газа в конце дейст-
вительного расширения в лопаточной решетке найдутся по очевид-
ным формулам (см. рис. 3.13):
7,2=7'2/+—=7'1	+—;
ер \ Pi) ер
„ — Рг • 7) — 1 — ^2
02 ЛГ2 ’ 2	02 Р2 ’
Площадь проходного сечения на выходе из рабочей решетки при
заданном расходе газа найдем из уравнения неразрывности в от-
носительном движении:
(3.72)
02®2 Sin 02 ’
где ay2sinip2=te’2a — осевая составляющая относительной скорости
газа. Если известна площадь проходного сечения f2, то из формулы
(3.72) можно найти расход газа через рабочую решетку.
49
Температура и давление адиабатного заторможенного поток:
газа на выходе из рабочей решетки в относительном движении рае
считываются по формулам, аналогичным (3.59) ... (3.60):
где
/ Ь 1	' *
Т*  Т /l I 1 М2 \ Т '	®"2
1 w,— I 21 Ч ~ Мо>2 I — 1 2 ~	7--->
\
 мю, = -^, а2=уЫ$\.
(3.7^
(з.?4
• Важно подчеркнуть, что в соответствии с уравнением энергий
в энергоизолированнбм процессе 7'Х,=^Х1 = 7'Х (см. рис. 3.13).
Обратный переход к абсолютному движению за решеткой ло}
паток осуществляется по теореме сложения скоростей (см. выход-]
ной треугольник скоростей на рис. 2.2).
Абсолютная скорость газа за решеткой рабочих лопаток
С2 =	+ «2 — ‘2u2w2 cos 32,
(3. 751
где и2 — окружная скорость на среднем диаметре d2 в выходном
сечении рабочей решетки; f}2 — угол выхода потока, в относитель-
ном движении.
абсолютном движении осредненный угол а2 найдем из три-
гонометрических соотношений выходного треугольника скоростей.
Например, при агОО0
[W9  о
--=- sin р2
с2
На рис. 3.13 изображен процесс расширения газа в реактивной
ступени. Поскольку в i—S диаграмме с увеличением "энтропии изо-
бары расходятся, то сумма адиабатных
теплоперепадов (Т/О1 + #о2) >#о« Физи-
чески это объясняется тем, чго вслед-
ствие потерь в соплах энтальпия газа
перед рабочими лопатками больше, чем
при адиабатном расширении. Часть по-
терь трения в рабочих лопатках, мгно-
венно преобразуясь в тепловую энер-
гию, так же увеличивает суммарный
располагаемый теплоперепад.
Рис. 3.14. Схема рабочего процесса в сопловой
и лопаточной решетках активной ступени на
S	.	диаграмме i—S
50
рабочий процесс в активной ступени турбины показан на рис.
3.14. Для активного процесса (р=0) характерным является равен-
ство давлений pi=p2. В связи с этим w2I=a>i,
®2
<|>==W2®’i и //л=(дУ1 — гг>|)(2=(1 — ф2)-у~;
Температура газа за решеткой в э'гом случае находится по фор-
муле T2-Ti~\-H я1ср.
Параметры газа Т2, q2, Vz и скорость w2 в конце расширения за
рабочей решеткой можно рассчитать и по законам политропного
расширения, как это было сделано в сопловой решетке.
Определим показатель условной политропы расширения газа
от давления pti до р2 по формуле, аналогичной (3.37):
п * — ф2 1
п	k ’
или	п—-----—------.
1-^р-ф2
Тогда
, л—1	. й—1..
тп=т* / Рг \ « —т* ( Р2 \ * *
/ 2 — 7 Wi I # J —i wi I " I
\	/	\ Pwi /
и, как обычно,
Действительный теплоперепад газа в рабочей решетке
.п— 1
(3.76)
а относительная скорость на выходе из решетки
§ 3.4. ОСОБЕННОСТИ РАСШИРЕНИЯ ГАЗА
В ОХЛАЖДАЕМЫХ СОПЛОВЫХ И РАБОЧИХ РЕШЕТКАХ
С повышением температуры газа перед турбиной для обеспече-
ния надежной работы элементы проточной части часто приходится
охлаждать (подробнее об этом см. гл. IX). Отвод тепловой энергии
от газа в процессе его расширения в сопловых и рабочих решетках
вызывает снижение располагаемой работы и уменьшение скорости
истечения. Связанные с этим дополнительные потери энергии при-
нято называть термодинамическими потерями от охлаждения. Вве-
дение охлаждения вызывает и другие виды дополнительных потерь
51
' То At
л
'ос
/АНОС |
It ОХЛ
т
4/
T1t охл
_75
Т10ХЙ
&10ХЛ
a b С



Рис. 3 15. Процесс расширения газа
охлаждаемой сопловой решетке в
аграмме T—S
энергии. Они связаны с конструк.
тивн.ым,и особенностями выбран-
ной системы охлаждения и рас-
сматриваются отдельно в гл. IX.
Отвод тепловой энергии от газа в
систему охлаждения отразится,
очевидно, и на параметрах газа
за решеткой.
На рис. 3. 15 показан для при-
мера процесс расширения газа в
охлаждаемой сопловой решетке
на диаграмме Т — S. Сплошными
линиями Л0*Л1< и Ао*А[ изобра-
жен процесс расширения газа без
охлаждения (теоретический и с
потерями. от трения соответственно); пунктирными линиями
Ло*Лиохл и Л0*Дюхл — процесс расширения газа с охлаждением.
Видно, что температура газа на выходе из решетки ' снижается:
в действительном процессе с до Локл, в теоретической — с T,t
ДО ТИ охл-
Рассмотрим более детально процесс расширения газа в соплах
с охлаждением, но без трения. Тепло охлаждения q0X!i с. отводимое
через стенки сопловых лопаток, изображается на диаграмме T—S
площадкой А0*Аи ох^аЬА0*, которую можно представить в виде фор-
мулы, состоящей из двух слагаемых (см. рис. 3.15): <7охл.с = <7с^-
+ДЯос, одно из которых <7° не отражается на располагаемом теп-
лоперепаде газа, а лишь’снижает его температуру на выходе из
решетки. Второе слагаемое Д#ос, равное площади А0*Аи охлАиАо*
(горизонтальная штриховка), напротив, целиком идет на уменьше-
ние кинетической энергии истечения газа из сопел. Величину Д// ,
pi
можно рассчитать по формуле Д/70с= f (®~ v^dp, где v — удель-
ный объем газа в адиабатном процессе; оОхл — удельный объем
газа в процессе расширения без потерь от трения, но с охлажде-
нием.
Аналогичная картина наблюдается и в охлаждаемом процессе
расширения газа с потерями от трения (см. рис. 3.15). Величинаq<‘
идет на снижение температуры газа за решеткой, а Д/7ос умень-
шает кинетическую энергию потока. Положение точки А10хл
изобаре pi определяется соотношением дополнительных термоди-
намических потерь от охлаждения и трения. Обычно при воздуш-
ном охлаждении точка Аюхл располагается между точками At 1
Ап. Однако при глубоком охлаждении и малых потерях от трения
точка Аюхл может совпасть и даже оказаться левее точки Alt.
52
Параметры газа за охлаждаемыми сопловыми решетками мож-
0 определить по закономерностям политропного расширения и
‘.равнению первого закона термодинамики, записанному в виде
dqcV~ dqow—di — vdp,	(3.78)
где <frp, <7охл — тепло трения и охлаждения; i = cpT; v\p — текущие
параметры вдоль линии расширения.
Опуская промежуточные выкладки (желающие могут их найти,
например, в (6]), приведем окончательные расчетные формулы.
Показатель условной политропы расширения газа в соплах с
охлаждением определяется из формулы
—(3.79)
гдетс~ -------коэффициент интенсивности охлаждения сопло-
вой решетки; #Охл.с—— относительный теплоотвод в систему
«о
охлаждения сопел; Но — адиабатный теплоперепад в ступени; рст—
реактивность ступени на среднем радиусе.
Величина тепловой энергии, отводимой от газа в систему
охлаждения <?Охл с, зависит от глубины охлаждения, конфигурации
решетки, распределения коэффициентов теплоотдачи и температур
по профилю и других факторов. Подробно эти вопросы рассмотре-
ны в гл.IX.
Для охлаждаемой решетки рабочих лопаток'коэффициент ин-
—	w?
тенсивности охлаждения	, где дохл.д=<7охл.л/Яо;
2/7 о
<7охл л — тепловая энергия, отводимая в систему охлаждения, а по-
казатель условной политропы
(3.80)
П и	/2
При внутреннем воздушном охлаждении тс обычно не превосхо-
дят величин 0,015 ... 0,025, а тл2>0,05 ... 0,15.
После определения показателей условной политропы пс и пл
Расчет параметров потока выполняется по формулам политропного
расширения, приведенным в § 3.3.
Например, скорость истечения газа из охлаждаемой сопловой
решетки с учетом выражения (3.39) примет вид
clma=V2H^' '	(3.81)
где
^Аохл‘	^ЛоХЛ ?охл.с
«с— 1
(считается, что скоростной коэффициент в охлаждаемой
^аждаемой решетках остается одинаковым).
и неох-
53
Температура газа в этом случае будет равна
«с-1	”,-1
Т _____Т1* /	.	-г*	___р* / Р2	\	п
* 1охл	* О I	< I ’ 2охл	* I *	I •
\ Pq /	\ Pwt /
Если ступень активная, то
Т	1	— Уохл.л
1 2охл~* 1охл Т"	•
(3.82)
В заключение отметим, что в этом параграфе рассмотрен вари,
ант охлаждения без выпуска охладителя в проточную часть тур{
бины. Если же воздух после охлаждения деталей смешивается с ос!
новным рабочим телом, то это обстоятельство должно быть учтена
в расчетных формулах. Параметры смеси газа с воздухом за ре-
шеткой для случая выпуска воздуха из кромок-лопаток могут быть
найдены из совместного решения уравнений сохранения: расхода,
энергия и количества движения.-Ввиду громоздкости получаемых
выражений они здесь не приводятся. В перфорированных лопатках,
когда воздух выпускается в проточную часть в различных местах
по обводу профиля, надежные данные могут быть получены только
из опытов.
§ 3.5. РАСШИРЕНИЕ ГАЗА В КОСОМ СРЕЗЕ
ЛОПАТОЧНОГО КАНАЛА
Если конфузорная решетка лопаток работает с докритическим
отношением давлений, то в сечении АВ (рис. 3.16) достигается ко-
нечное давление р\, и на протяжении косого среза среднее давле-
ние в потоке можно считать неизменным.
Если же в конфузорной решетке (или в единичном сопле с ко-
сым срезом) отношение давлений (pi/po*) <ек₽, то в сечении АВ
устанавливается критическое давление, а в косом срезе расшире-
ние газа продолжается и достигается сверхзвуковая скорость исте-
чения. Косой срез выполняет роль расширяющейся части сопла
Лаваля.
54
г
3.17. График сопоставления угла откло-
^П<ия в косом срезе сорла по уточненному ме-
не*оду [30] и по приближенной формуле (3.86)
В сверхзвуковой решетке (рис.
316, б), работающей при расчетном
режиме, конечное давление pt дости-
гается в сечении АВ, и на протяжении
косого среза средние давление и ско-
рость газа не меняются. Если же дав-
ление за решеткой ра окажется меньше
расчетного pi, то в косом срезе проис-
ходит расширение от pi до ра с соот-
ветственным возрастанием сверхзвуко-
вой скорости.
Так как единичные сопла и решетки
лопаток всегда имеют ко-
сой срез, то возможность расширения газа в косом срезе как сопло-
вых, так и рабочих решеток должна учитываться при конструиро-
вании турбины.
Рассмотрим явления, происходящие при расширении в косом
срезе. В расчетном выходном течении АВ суживающегося канала
(см. рис. 3.16, а), работающего при . сверхкритическом перепаде
давлений, господствует критическое давлёние ркр. За этим сечением
давление падает до pi: в точке В — сразу, вдоль стенки АС — по-
степенно. За сечением АВ газ приобретает сверхзвуковую ско-
рость, и расширение его происходит тйк же, как при обтекании
сверхзвуковым потоком тупого угла в точке В. Точка эта является
источником возмущений, от нее отходит пучок характеристик, из
которых вдоль? BD устанавливается конечное давление рь Среднее
направление потока отклоняется от оси канала, что обусловливает-
ся наличием повышенного (по сравнению с pi) давления вдоль,
степки AD и расширением газа (ширина отклоненной струи боль-
ше, чем в сечении АВ).
По мере понижения давления pi (или отношения pi/po*) точка
В приближается к точке С. Если последняя характеристика при-
близительно совпадает со срезом ВС, то расширительная .способ-
ность косого среза является исчерпанной. Истечение газа из косого'
среза расширяющегося сопла показано на рис. 3.16, б для случая,
когда давление за соплом меньше расчетного pi. Первая характе-
ристика BD наклонена к оси потока под углом 6i=arcsin (1/M.i).
Расчетное давление pi господствует не только в сечении АВ, но
и в части косого среза, ограниченной характеристикой BD. Расши-
рение газа до давления ра может закончиться как в пределах косо-
г° среза, так и за ним: на рис. 3.16, б показан случай, когда послед-
няя характеристика BE лежит в пределах косого среза. Расшири-
тельная способность косого среза в расширяющихся соплах огра-
ничивается таким давлением ра, при котором последняя характе-
ристика из точки В приблизительно совпадает со срезом ВС. Так
Как расширение газа в косом срезе такого сопла начинается ПОЗ-
55-
же, чем в срезе суживающегося сопла, то его расширительная сг0,
собность оказывается меньше.
Состояние газа при выходе из косого среза после расширения в
нем можно определить по обычным термодинамическим соотношу
ниям. Дополнительно необходимо определить лишь средний уго.ч
•отклонения струн со после расширения в косом срезе. Задача sia
решается обычно применительно к каналу, образованному тонки-
ми и плоскими выходными кромками (см. рис. 3.16, а), в котором
поле скоростей и давлений можно считать однородным.
Выберем в потоке на некотором расстоянии от сопла сечение НЕ
(см. рис. 3.16, а) и запишем для сечений АВ и НЕ уравнение не-
разрывности:
Cy.Qj.p/' sin a1=c1Q1Z sin (ax w),	(3. 83)
где шаг решетки t~BC (толщиной кромок пренебрегаем), QKp и
61 —плотности газа в сечениях АВ и НЕ. Из уравнения (3.83) сле-
дует, что
sin (a!-|-o))=C|Cp—р sin aj.	(3. 84)
значения Скр, QKp, ci, Qi могут быть найдены по соответствующим
•формулам § 3.3 с учетом потерь при расширении.
Полагая потери одинаковыми для суживающейся части канала
и для косого среза, вместо уравнения (3.84) можно написать
sin(a1+«>)=^,	(3.85)
0 (М)
г
где Л1=фХи; Ли — приведенная скорость при адиабатном течении,
ее можно определить из таблиц ГДФ по отношению давлений
Р1/ро*.
Таким образом, угол отклонения в. косом срезе суживающихся
сопловых решеток
cof==arcsin	(3. 86)
Этой приближенной формулой широко пользуются в практике
турбостроения.
Более точные методы определения угла <о при значительных
сверхкритических перепадах, хорошо подтверждающиеся опытны-
ми данными, подучены Г. Ю. Степановым и М. Е. Дейчем. На
рис. 3.17 дано сопоставление величины со, рассчитанной при £=
= 1,333 по формуле (3.86) и методу Г. Ю. Степанова (пунктир).
Из кривых следует, что во всем практически интересном интервале
изменения сверхкритических перепадов (до 1,3) оба метода
дают близкие результаты. Разница увеличивается с ростом Xi И
уменыйением угла ai, но' во всех случаях не превосходит 1°.
56
формулами (3.84).... (3.86) рекомендуется пользоваться пр»
= (Pi/Po*) >0,3. Для расширяющегося сопла вместо формулы
(Й5) имеется следующая:
, ClnVl
sin «i=----sin а1э	(3. 87}
где йр, — скорость и удельный объем в расчетном сечении АВ
сопла (см. рис. 3.16).
По формуле (3.87) можно определить угол отклонения в косом
срезе расширяющихся сопел при понижении давления за соплом
рв до величины ниже расчетного р1р. Этот случай обычно встреча-
ется при расчете сверхзвуковых турбин на переменных режимах.
Как указывалось выше, расширительная способность косого
среза ограничена тем давлением, которое можно получить в сече-
нии ВС (см. рис. 3.16, а и б). Предельно возможный перепад дав-
ления в сопле достигается в том случае, если последняя характе-
ристика совпадает с линией ВС (конечно, приблизительно, так как
характеристика эта является криволинейной). При этом, как изве-
стно, угол а/ (который в этом случае обозначен ащр) равен углу
8!=arcsin (1/Mi),	(3.88)
т. е.	sin а1пр= 1/МР	(3.89)
Используя формулу (3.84) и имея в виду, что М1=С1/2!. можем
написать
скр .	ai
------sin 04=—.
VKp	Ci
Для приближенной оценки pimm — давления вдоль характерис-
тики, совпадающей с линией ВС, — пренебрежем потерями при рас-
ширении, тогда можно воспользоваться формулой (3.31):
и	sin at (=_®L.	(3.90).
\ Plmin / скр
Так как a^—VkRTi, cKP=V kRT^,
TO	—-1 /	__(Plmtn \~2fe~
Скр У 7кр \ Ркр /
Подставив последнее соотношение в формулу (3.90) и решив ее
относительно р< mln. найдем
2fe	к	2k
Amm=PKp (sin а/+1 =ро )ft-1 (sin ai)ft+1, , (3.91)
Или
2k
eim1n=^i7ia-=eKp(sin a,)»*1,
Po
(3.92)
r^e eKp — определяется формулой (3.30) i
57
Для случая с потерями, в том числе и от охлаждения, рассу,Кч
дая аналогично, можем получить
,	_ . п
2л

(3.93)
где п — показатель условной политропы расширения газа от р
ДО' pi min.
Таким образом, угол отклонения потока увеличивается от нуля
до йпр, а угол выхода потока — от си до ащр. При этом осевая сос-
тавляющая скорости cl в соответствии с формулой (3.89) делается
равной ai, а окружная составляющая с1и достигает максимума.'
Дальнейшее понижение давления внутри решетки становится не-
возможным.
При расширении газа за пределами косого среза, т. е. от Pinua
до более низкого давления, угол отклонения потока ш продолжает
возрастать. При этом окружная составляющая скорости Ciu оста-
ется неизменной, а осевая Cia станет больше скорости звука и бу-
дет возрастать. Очевидно, реализоваться этот случай может толь-
ко при расширении проточной части за сопловой решеткой, что сле-
дует из уравнения Гюгонио [см. формулу (3.28)].
В соответствии с изложенным на рис. 3.18 изображено измене-
ние скоростей и углов потока при различных степенях расширения
от ei = eKp ДО нуля. В этом случае как для течения без потерь, так
и при наличии потерь достигается скорость
Рис. 3.18. Схема изменения скоростей и углов потока-при изменении давлен^
на выходе из соплового аппарата
Рис. 3.19. График характера изменения скоростного коэффициента ф при нерас-
четных режимах истечения из сопел:
/—суживающегося; 2—суживающегося с косым срезом; 3—расширяющегося
58
В заключение надо отметить, что использование косого среза
я расширения в нем газа представляет известные выгоды при
Дпоектировании турбин. Часто отношение давлений pi/po* в сопло-
ом аппарате лишь немного меньше критического. Использование
8 этом случае косого среза суживающихся сопел для достижения
Вверхкритической скорости целесообразнее, чем применение рас-
щйряющихся сопел: упрощается конструкция соплового аппарата;
с увеличением отношения давлений pi/po* в меньшей степени ухуд-
шается к.п.д. суживающихся каналов, чем расширяющихся.
На рис. 3.19 показано изменение скоростного коэффициента сопел
в зависимости от отношения давлений ei=pi/po*- Расширяющееся
сопло рассчитано для ,81 = 0,1.
Анализ рис. 3.19 показывает, что в соплах с косым срезом ве-
личина <р сохраняется практически неизменной во всем диапазоне
от Р1/Ро*=|вкр ДО Р1/ро* = 0,25. Желательно, однако, чтобы угол от-
клонения потока в косом срезе был не слишком велик, по крайней
мере a/ai<;0,l ... 0,15. Поэтому при больших перепадах давлений,
когда pi/po*<0,25, приходится применять расширяющиеся сопла
и мириться с тем, что на нерасчетных режимах у таких сопел ф,
резко уменьшается (см. рис. 3.19).
§ 3.6. РАСЧЕТ ТЕПЛОВЫХ ПРОЦЕССОВ В ТУРБОМАШИНАХ.
С УЧЕТОМ ПЕРЕМЕННЫХ ТЕПЛОЕМКОСТЕЙ ГАЗА
Как уже указывалось (см. § 3.2), предварительные термо- и газодинамиче-
ские расчеты газовых, турбин, также как и других узлов ГТД (компрессоры,
камеры сгорания, теплообменники, входные и выходные устройства) можно вы-
полнять в предположении постоянства некоторых средних для данного конкрет-
ного процесса изобарных теплоемкостей и показателей адиабаты, т. е. ср ср =
—const; ЛСр = const.
‘ Причем под средней теплоемкостью понимают величину сР = отно-
шения тепловой энергии &q (подведенной или отведенной) к приращению тем-
пературы рабочего тела АТ. В пределе при Ад—>0 и АТ—>0 выражение для
ср ср обращается в истинную теплоемкость cp=dq/dT, являющуюся одной из
важнейших теплофизических характеристик газа.
В диапазоне изменения параметров состояния рабочего тела, имеющем прак-
тическое значение для ГТД, величина ср практически не зависит от давления.
Напротив, влияние температуры на истинную теплоемкость весьма существенно.
Так, при увеличении температуры с 273 до 1800 К, ср воздуха возрастает на 1/4,
а продуктов сгорания почти на 1/3. Экспериментальные данные сР(Т) аппрокси-
ь i=n
мируют обычно степенным полиномом: сР (Т) = 2	(л=5... 7; ai — постояв*
z=o
ные).
/г=л \
В таком случае dq == cp(T)dT = I 2 а'1^ )	» а конечное приращение
тепловой энергии в процессе между состояниями газа, характеризуемого темпе-
Ратурами Л и Т2,
г.
= $ МП	(Т1-Г?) +01-г?) +...
Т,
59
Возвращаясь теперь к понятию средней теплоемкости, будем иметь
а0 (Т2 - Л) + (Tl - Т>) +	(73- Г3)
Срс₽ = 77" =	:	(г2—то	=
= а0 +	+ 7*1) +	(7*f + ^2^1 + ^i) + • • •	(3-94)
Ограничиваясь двумя первыми членами, получим вместо (3.94)
Срср ~ «о + *2^ (Л 4- Тз).	(3.95)
В большинстве справочников приводятся данные средних теплоемкостей,
подсчитанные именно по формуле (3.95). Кроме неточностей, связанных с заме-
ной формулы (3.94) на (3.95), пользование средними теплоемкостями ведет к ус-
ложнению расчетов. Связано это с необходимостью применять последовательные
приближения, так как одно из крайних значений температурного интервала зари-
нее не известно. Кроме того, следует иметь в виду, что при использовании сред-
них теплоемкостей теплоперепад в турбине всегда оказывается заниженным, а
напор в компрессоре завышенным, поэтому удельная свободная энергия газоге-
нератора, представляющая собой разность работ в турбине и компрессоре (не-
большая разность больших чисел) получается с существенной ошибкой.
Применение средних теплоемкостей является также источником ошибок при
расчете расхода рабочего тела через турбину.
Существует несколько методов для выполнения тепловых расчетов с пере-
менными теплоемкостями. Широкое распространение получил метод с использо-
ванием J—S диаграмм. Однако он не обеспечивает требуемой в настоящее время
точности и поэтому все меньше используется в расчетной практике.
Наиболее удобным для учета переменных теплоемкостей оказался метод, ба-
зирующийся на термодинамических соотношениях _между абсолютной темпера-
турой Т, энтальпией / и относительным давлением р(Т), при изоэнтропном изме-
нении параметров состояния газа. В основе метода лежит основополагающая за-
висимость, вытекающая из начал термодинамики и заключающаяся в том, что.
для рабочих тел, подчиняющихся уравнению состояния идеальных газов, в пзо-
энтропных процессах с переменной теплоемкостью величина относительного дав-
ления р=р/рбаз зависит только от абсолютной температуры газа.
Действительно, из первого закона термодинамики
dq=^di — vdp	(3.96)
для энергоизолированного (бй/=О) изоэнтропного процесса в расчете на мол»
газа (J=|u;	р — молекулярная масса рабочего тела) получается
dJ = pepdT = Vdp,	(3.97)
где	’— истинная мольная теплоемкость газа при постоянном давлении
С учетом уравнения состояния идеального газа
v = —	(3.98)
Р
вместо (3.97) можно записать
(3.W
|1Л Т р '	'
где р/? — универсальная газовая постоянная; для идеальных газов р/?^'
==8314,2 Дж/(моль К).
60
Интегрирование уравнения (3.99) между некоторыми базовыми (рбаз, Гбаз)
текущими (р, Г) параметрами дает
£ С Wp(T)dT
_	р	г
р(Т) = -^~ — е гбаз	,	(3.100)
Рбаз
е p(D действительно является функцией» только абсолютной температуры Т.
Из второго закона термодинамики
dS>^.	(3.101)
Дчя энергоизолированпого, пзоэнтропного процесса dS=dqjT. Отсюда с учетом
выражения (3 96) и уравнения состояния следует, что
\^CpdT dp
	-	(3.102)
Интегрируя это уравнение в пределах от базового состояния до двух фик-
сированных состояний рабочего тела (например, в точках 1 и 2) в изоэнтропном
процессе (52—Si=0), получим после потенцирования
1 Тр ^Cp(T)dT
Й# J f
ро » е ^баз
—=---------------------.	(3. ЮЗ)
1 9
Р-Я J т
т
е баз
Сопоставляя теперь числитель и знаменатель правой части равенства (3.103)
с выражением (3.100). получаем основное расчетное соотношение метода в виде
чрезвычайно простой формулы:
7(Г2) = Х7’1)^.	(3.104)
__
Для практического применения этой формулы в расчетах функцию р(Т) за-
ранее табулируют, или представляют в виде ленточных номограмм, в зависимо-
сти от абсолютной температуры Т. Основой для определения численных значе
ний функции р(Т) служит формула (3.100).
Величина истинной мольной теплоемкости	выражается при'этом на
основе экспериментальных данных для соответствующего рабочего тела степен-
ными полиномами 4—5-й степени.
При тех же значениях аргумента Т вычисляются также значения мольной
энтальпии по очевидной формуле
т
J=J6a3+ J ^p(T)dT.	(3.105)
^баз
Если в тепловом процессе участвует не один газ, а смесь газов, то строго
'оворя, таблицы должны быть составлены для каждого из газов рабочего тела,
а итоговые численные расчеты выполнены по таблицам в соответствии с сосга-
зом смеси на основе закономерностей смешивания газов. Для воздуха и пр оду к-
сгорания углеводородных топлив, используемых в современных авиационных
можно ограничиться приближенным учетом влияния состава газа на ис-
гипную мольную теплоемкость и на соотношения величин Т, J, р(Т).
Можно показать, что в наиболее практически важном диапазоне величин ко-
эффициента избытка воздуха а=3 ... 10 молекулярная масса указанных рабо-
61
чих тел изменяется весьма мало и ее можно считать постоянной цсм=29. В Тп.
же диапазоне а газовая постоянная /?См = —М~ СМ ' =286,7 Дж/(кг«К).
Рем
В приложении I приведены таблицы Г, J, р(Т) термодинамических функций
для воздуха (а=оо) и продуктов сгорания различного состава (<х=1, 2, 3, 4, 7
15). Такой набор значений а позволяет выбрать таблицу, ближайшую к заданно!
му а, и, не прибегая к интерполяции, вести расчет с высокой (0,1 ... 0,2%) тОч,
ностью.
Пример 1. Расширение газа в турбине.
Продукты сгорания, состав которых характеризуется величиной ц=28,9 кг/моду
и коэффициентом избытка воздуха а=2,85, расширяются в турбине от полного
давления ро*=28,6-105 Па до р2=2,2-105 Па. Температура торможения газа перем
турбиной Го*=16ООК, внутренний к.п.д. турбины т)т*=0,92.	।
Требуется определить параметры состояния газа за турбиной и внутреннюю^
работу 1 кг газа, передаваемую на вал турбины.	t
Решение.
1. При Го*=16ОО К из таблиц приложения I для а=3 (ближайшее к а==/
= 2,85 значение)
yj =52404,4 кДж/моль; ~р (Гд) = 978,363.
2. По формуле (3.104)
—	__. по	2,2*105
Р (Г2) = Р (tJ)	= 978,363	= 75,259.
1	3. Из таблиц в строке со значением р(Тъ)=75,259 находим
/2ад == 26627,4 кДж/моль; Г2ад = 871,6 К.
4.	Адиабатный теплоперепад в * турбине при падении давления от р0* До р»
Яая.т = J*o— У2ад = 52404,4 — 26627,4 = 25777 кДж/моль.
5.	Энтальпия в конце действительного расширения газа составит
У2 = yj— 1)*Яад1 = 52404,4 — 0,92-25777 = 28689,56 кДж/моль.
6.	В строке, где /2 =28689,56 кДж/моль, находим действительную темпер^
туру газа 72=933 К.
Остальные параметры (р, п) находятся из уравнения состояния
= 0,8197 кг/м3; v2 = 1,22 м3/кг.
7.	Внутренняя удельная работа турбины в расчете на 1 кг газа

//ад.т!*	25777-0,92
р.	28,9
= 820,45 кДж/кг.
Примечание. При £ср= 1,33=const в аналогичных условиях получилось
бы (//T)jfe -=1,зз = 795,358 кДж/кг, т. е. ошибка составляет 3%.
ср
Пример 2. Определение параметров газа и размеров проходного сечения н*
выходе из турбины.
Из предварительного расчета одновального ТРД известны исходные данные
для расчета турбины: коэффициент избытка воздуха а=3,2; расход газа G?^
=92 кг/с; давление и температура газа перед турбиной ро*=12*1О5 Па; Го**!
= 1300 К; потребная работа на валу турбины Ят = 358*103 Дж/кг; наружны»
диаметр турбины dn=0,93 м, приведенная скорость на выходе из турбины ХС2=*
=0,56; внутренний относительный к.п.д. турбины т1т* = 0,91.
Требуется определить параметры газа, площадь проходного сечения и высо"
ту рабочих лопаток на выходе из турбины.
62
1. По величине То* из_таблиц для а=3 (ближайшее а=3,2) находится
t *^41494,783 кДж/моль и р(Т0*) ==395,458.
Jo 2. По величине |а#т=29 • 358 • 103= 10382 Дж/моль (р,=29, так как а>3)
определяется	—ji/7T=41494,783—10382 = 31112,783 кДж/моль, а по вели-
пине Л* и3 таблицы находится температура торможения газа за турбиной Т2*=
1004 К и р(Т2*) = 133,576.
„	-	10382
3.	Определяется /2аг = Jo— —— = 41494,783— — Q— = 30086 кДж/моль
Чт	9
и в строке таблицы, где J = ^ал’ находится Т^&1==97^ К н~р (7’2а1)=П7,953.
4.	По формуле (3.104) определяется давление торможения за турбиной
р2 = р*0	= 12-105. -^’^3 = 3,579-105 па.
2	0 р (То)	395,458
5.	По температуре Т2*=1004К и а=3,2 из справочника находим значение по-
казателя адиабаты knc т = 1,32.
6.	Вычисляется величина
с2	ь
*	лисг Т 1
= 31112,783 — 0,5621004-8314,2 = 29623,366 кДж/моль
2,32
(pR=8314,2 Дж/(моль-К) — универсальная газовая постоянная.
7.	Из таблицы по величине Д находится статическая Температура за турби-
ной 7’2=960,45 К и значение функции р(Т2) = 111,364.
8.	По формуле (3.104) находится статическое давление за турбиной
Р2 -= р*2 = 3,579-105- 111’364 = 2 984.юг Па
2р(т2)	133,576
и далее плотность газа
№	29-2,984-105
рТ?Т2 ~ 8314,2-960,45
= 1,0837 кг/мз.
9.	Выбирается угол выхода потока газа из турбины а,=86° и по уравнению
расхода рассчитывается площадь
F2 =
_____ - — = 0.2655 м2,
_______ Л___„„ Л 2 (31112,783 - 29623,366)-103
1,0837-0,99761/ —ь-----------—-----1--------
Имея в виду, что средний диаметр на выходе из турбины’d2T=dn--<ft2, вы-
сота рабочих лопаток ра выходе из турбины определится из формулы
/.2	_________________
Рг 0,93 Г 0,932	0,2655
2 у 4 л ~ 2 ~ у 4	3,14	=
= 0,465 — 0,3629 = 0,1021 м= 102,1 мм.
63
Таким образом, применение метода Т—J—р(Т) функций не только повы
ет точность (учитывается зависимость теплоемкостей от температуры), но и уПр^
щает тепловые расчеты, сво^я их к простым арифметическим действиям, облег',
чает использование ЭЦВМ.
Глава IV
ОБТЕКАНИЕ РЕШЕТКИ ЛОПАТОК ГАЗОМ
§ 4.1. ОБЩИЕ СВЕДЕНИЯ
В осевых турбинах применяются’ кольцевые решетки, в которых ось лопат-
ки направлена приблизительно по радиусу турбины (рис. 4.1, о).
При исследовании аэродинамических качеств решетки по предложению
Н. Е. Жуковского обычно считают, что газ в ней движется концентрическими
слоями, причем трение газа между слоями отсутствует.
Сделав цилиндрическое сечение по решетке на любом радиусе г и развер.
нув это сечение на плоскость, получают плоскую решетку профилей бесконечно
малой высоты (см. рис. 4.1, б), в которой можно исследовать процесс течения
газа на данном радиусе облопачивания. Такую элементарную решетку будем в
дальнейшем называть решеткой профилей, опуская последнее слово, когда оче-
видно, о какой решетке идет речь элементарной или конечной длины.
Возможность применения гипотезы цилиндрических сечений подтверждается
многочисленными экспериментами. Следует, однако, иметь в виду, что эта гипо-
теза не может быть применена к сечениям, близким к основанию и к периферия
лопаток, где на течение газа влияют торцовые стенки (так называемые «конце*
вые> поверхности) и радиальные зазоры (на периферии).
Ограничиваясь в ряде случаев исследованием потока в плоскости на том
или ином радиусе облопачивания, рассмотрим в дальнейшем также особенности
пространственного потока через решетку.
На рис. 4.2 показан профиль турбинной лопатки в решетке. Линия тпр
профиля соответствует вогнутой поверхности лопатки. С другой стороны канал
ограничен спинкой лопатки.
/
Рис. 4.1. Схема-кольцевой решетки:
а—решетка; б—развертка на плоскость цилиндрического сечения решетки
Рис. 4.2. Схема профиля лопатки и канала в решетке
64
Средней линией профиля называется кривая, представляющая собой гсомег-
Уое место центров окружностей, вписанных в профиль.
Р11Че^орд°й профиля b называется расстояние между крайними точками средней
лияИф’онтальной линией решетки называется линия, проведенная через одноимен-
точки профилей. Линию, перпендикулярную к ней, называют осью решетки.
нЫесеВых турбинах ось решетки параллельна оси турбины.
В 0 углом установки профиля называется угол руСт между хордой профиля и
Апонталыюй линией решетки.
ФР Шириной решетки s называется расстояние между крайними точками про-
. «я измеренное в направлении оси турбины (аксиальной).
* Шаг решетки t представляет собой расстояние между одноименными точка-
соседпих профилей, измеренное в направлении фронта решетки.
М Высота или длина лопатки h измеряется по радиусу осевой турбины между
е концевыми поверхностями.
е Наименьшая ширина канала в конфузорной решетке определяется разме-
ром о- , ,
Е Величины t h, а часто рассматриваются в их относительном значении, т. е,
в виде отношения этих размеров к длине хорды Ь.	|
Применительно к сопловым решеткам линейные ее размеры будем снабжать
индексами 1-(/ь	применительно к рабочим решеткам-индексом 2.
Геометрическими углами входа в сорловую решетку и выхода из нее обычно
считаются углы аогеом и atreoM между касательными к средней линии у ее кон-
цов и фронтом решетки. В рабочей решетке те же углы обозначаются’р1ГСом »
02геом	л <
Средние величины углов потока обозначим соответственно ао и щ (₽i и
Углом атаки считаем разность между а0геом и а0 или для сопловых лопатою
6=fСбогеом—-Оо; ДЛЯ рабОЧИХ ЛОПаТОК 6=01геом—Pi.
При нулевом угле атаки будем условно считать вход в решетку <безудар^
ним».
Затылочным углом профйля называется угол у между касательными в точке
е канала в выходном сечении и в точке f на выходной кромке. При плоском
очертании косого среза у=0.
§ 4.2. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ПО ПРОФИЛЮ
Вследствие криволинейности линий тока к частицам газа при-
ложены центробежные силы, которые вызывают повышение давле-
ния в канале от спинки лопатки к вогнутой поверхности соседней ей
лопатки. В связи с этим расстояние между линиями тока увеличи-
вается в указанном направлении, а скорость газа вдоль линии тока
падает при переходе от спинке к вогнутой части поверхности.
Максимальное давление наблюдается в месте разветвления по-
тока на входной кромке лопатки — критической точке профиля.
В ней линия тока нормальна к профилю, скорость равна нулю, а
полное давление (при несжимаемой жидкости) для сопловой ре-
*	Сп	»	W?
шетки р0=р0-|7е_ и для рабочей	(
Если учитывать сжимаемость, то для определения полного
Давления надо пользоваться формулой (3.8).
Условимся считать положительными давления, которые превы-
шают давление за решеткой, отрицательными — давления, мень-
шие. чем за решеткой. Эпюра давлений на вогнутой поверхности
изображается кривой с положительными ординатами (см. рис. 2.2)'i
На большей своей части; лишь вблизи выходной кромки могут Haff--
Ждаться отрицательные давления. На всем протяжении спинки>
3	1337	Q5.
эпюра давлений в большинстве случаев отрицательна; положите.^
ные величины давления наблюдаются лишь вблизи входной кром.
ки. Разность давлений на обеих поверхностях создает подъемную
силу и, следовательно, в турбине — окружное усилие, приложен,
ное к рабочей лопатке. Следует отметить, что это усилие создается
главным образом разрежением на спинке, так как избыточное дав.
ление на вогнутой поверхности ограничивается полным давлением
газа.
Вместо эпюры давлений часто рассматривают эпюру скоростей
по профилю и обе эти эпюры строят в прямолинейных координатах.
По оси абсцисс откладывается длина (или относительная длина)
развертки профиля, по оси ординат — относительные давления
Р= -~Г '	(4.1)
ci
61 2
или относительные скорости
c=dcb	(4.2)
где р и с — статическое давление и скорость газа в произвольной
точке профиля; рх и сх — статическое давление и скорость газа за
решеткой.
Применительно к рабочей решетке
(4-3)
е2Т
и	w=^/w2*-	(4.4)
Вместо относительной скорости по оси ординат откладывают
иногда приведенные скорости % или М.
Характер эпюр давления и скорости при обтекании решетки иде-
альной несжимаемой жидкостью показан на рис. 4.3, где точка О
является точкой разветвления потока. Распределение давления по
профилю можно найти из опыта. Для этого при продувке решетки
лопатки (см. § 4.4) дренируют по всему периметру профиля, т. е. в
них просверливают отверстия, к которым присоединяют мано-
метры.
На рис. 2.2 осью абсцисс эпюры служит ширина лопатки. Эпю-
ра приобретает вид замкнутой кривой и удобна для вычисления
окружного усилия, эквивалентного по величине заштрихованной
площади. На участках профиля, где давление повышается (диффу-
зоркость), может произойти отрыв потока от профиля, являющий-
ся одной из существенных причин возникновения потерь в решет-
ках.
Распределение давлений по профилю зависит от ряда факторов'-
1) от угла поворота газа в канале решетки, равном 180°—([31 +
+ fe) (применительно к рабочей решетке). С увеличением угла
66
Рис 4.3. Эпюра распределения давлений по
г ’ профилю активного типа
ворота возрастает подъемная сила
профиля за счет разрежения на
спинке. Это обусловливает увеличе-
ние диффузорности на спинке по на-
правлению к выходной кромке и,
следовательно, возможность отрыва;
2) от шага решетки, с увеличени-
ем которого подъемная сила профи-
ля также возрастает за счет разре-
жения на спинке; при больших ша-
гах отрыв потока вблизи выходной
кромки неизбежен;
3) от угла атаки. Как правило,
отрицательные углы атаки (боль-
шие углы входа) вызывают провал
давления на вогнутой поверхности,
положительные углы — на спинке.
За этими провалами давление резко
повышается и наблюдается отрыв потока;
4) от скорости газа (числа М в потоке). С увеличением М подъ-
емная сила профиля возрастает. Особенно интенсивно меняется
давление на спинке, причем с возрастанием М диффузорный эф-
фект в выходной части спинки увеличивается.
Характер обтекания профиля существенно меняется, если в ка-
нале возникает местная скорость звука. Возникающие при этом яв-
ления описаны в § 4.6. Распределение скоростей или давлений по
.профилю лопатки можно найти расчетным путем по заданным раз-
мерамфешетки и параметрам газа перед и за решеткой.
Ряд известных теоретических методов расчета базируется на
конформном отображении профилей и позволяет довольно точно
рассчитать обтекание решетки идеальной несжимаемой жидкостью.
В расчетной практике большее распространение получили приб-
лиженные методы расчета течения в криволинейных каналах или
так называемые «канальные» методы расчета, детально разрабо-
танные А. Н. Шерстюком и также дающие возможность построить
эпюру скоростей по стенкам канала, т. е. по профилю лопатки.
§ 4.3. СИЛЫ, ДЕЙСТВУЮЩИЕ В РЕШЕТКЕ ПРОФИЛЕЙ
При протекании газа через решетку на каждую лопатку со сто-
роны газа действует сила Р, причина возникновения которой ука-
зана в § 2.1. Составляющие этой силы в осевом п тангенциальном
направлениях обозначим Ра и Ри.
Для определения величины этих сил выделим часть потока
fbed (рис. 4.4), ограниченную двумя линиями тока fd и Ьс, расстоя-
иие между которыми равно шагу решетки t, и линиями fb и cd, па-
раллельными фронту решетки. Эти линии должны быть так удале-
3*	67
Рис. 4.4. Схема сил, действующих в решетке
яы от решетки, чтобы в сечениях по fb и cd можно было считать
равномерными поля скоростей и давлений газа.
Так как линии тока fd и Ьс эквидистантны, то равнодействую-
щие сил давления, приложенные вдоль этих линий, равны друг дру-
гу и направлены в противоположные стороны. Следовательно, в
тангенциальном направлении на поток действует лишь сила Ru,
приложенная к лопатке. По уравнению Эйлерй Ru=G(w2u—wlu),
где обозначения соответствуют рабочей решетке, причем под wlu и
w2u понимают алгебраические величины скоростей; G— секунд-
ный расход газа через сечения fb и cd. Направление силы Ru сов-
падает с направлением скорости w2u.
Очевидно, сила Ри, с которой поток действует па лопатку в тан-
генциальном направлении, равна по величине и направлена проти-
воположно силе Ru, т. е.
Ри = — Ra=Q	—®2в)«	(4.5)
Направление силы Ри положительно, если оно соответствует
направлению окружной скорости лопаток. Так как wiu=c\u—и<
w2u=c2u—и, где также фигурируют алгебраические значения ско-
ростей, то
Ра = °(.С1и — С2и)-	(4-б>
В турбинных решетках обычно а>2и отрицательна, так что при
пользовании формулой (4.5) надо ставить знак плюс, в формуле же
(4.6) знак минус сохраняется для случая угла а2>90°, в противном
случае (о2<90°) перед с2и появляется знак плюс (см. рис. 2.4).
По условию равновесия сил, действующих на поток в осевом
направлении, можно написать Ra+th(p1—p2) = G(w2a—wIe), где
Ra — алгебраическая величина силы, действующей на поток от
лопатки; h — высо'га лопатки.
68
Сила Ра, с которой поток действует на лопатку, равна и прямо
1ротивоположна силе Ra, т. е.
Ра = “ Ра = (Pi -Pi^ + O (Wla - ™2а)-	(4. 7)
В этой формуле величина Wja может быть заменена равной ей
, а ^2а — величиной С2а.
Положительным направлением силы Ра будем считать направ-
ление, совпадающее с осевой скоростью газа, т. е. на рис. 4.4 —
вертикальное вниз. Расход газа равен
(4-8)
где р — средняя плотность газа;
„д=.,.+»2.	(4.9)
— средняя величина осевой скорости.
В таком случае из формул (4.8) и (4.9) находим
С учетом уравнения (4.8) формулу (4.5) приводим к виду
Pe=Q (w18—w2e) wjh,	(4.11)
а формулу (4.7) —	1
(4-12)
Величина P=tfP«-|-7-a представляет собой силу, приложенную
к лопатке.
§ 4.4.	ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ РЕШЕТОК
Целью экспериментального исследования решетки обычно является:. 1) опре-
деление среднего угла' выхода газа из решетки, 2) определение скоростного ко-
эффициента (ф, ф) или коэффициента потерь энергии (£, £); 3) определение ко-
эффициента расхода (g); 4) снятие эпюры давлений по профилю; 5) определе-
ние сил,'действующих на реп/етку в целом или на отдельную лопатку; ж 6) изуче-
ние спектра потока; 7) изучение ряда специальных вопросов, относящихся, на-
пример, к трехмерному исследованию решетки. Первые шесть пунктов из этих
исследований могут быть осуществлены на установке для статической продувки
решеток Сравнительные _опыты по определению основных характеристик реше-
ток на статической установке и на экспериментальной турбине показали удов-
летворительную сходимость обоих методов исследования. Простота и удобство
экспериментирования на статических установках заставляют в отдельны^ случа-
ях отдать предпочтение этому методу перед исследованием на эксперименталь-
ной турбине.
При конструировании плоской решетки выдерживают принцип геометричес-
кого моделирования и равенство чисел М. для модели и натуры. Равенство чи-
сел Рейнольдса обычно не удается выдержать: впрочем, обычно турбинные ре-
шетки й в натуре и при продувке работают с такими высокими числами Ре,
величина которых незначительно сказывается па коэффициенте потерь в решетке."
Завершающий этап исследования решетки производят обычно на эксперимен-
тальной одноступенчатой турбине, к которой предъявляются следующие требо-
вания:
1)	на входе в проточную часть турбины и на выходе из нее должно быть
с°здано равномерное поле давлений и скоростей;
69

Рис. 4.5. Кривые изменения параметров потока па выходе из решетки по шагу
лопаток
Рис. 4.6. Кривые изменения по высоте лопатки средних по шагу параметров по
'	тока на выходе из решетки
2)	конструкция турбины должна допускать удобное траверсирование потока
по шагу и по высоте лопаток с'определением направления потока (в npocipaih
стве), статического и полного давления газа перед сопловой решеткой, в зазоре
между сопловой и рабочей решетками, за рабочей решеткой; измерять темпера-
туру газа необходимо по крайней мере перед проточной частью и за ней:
3)	должно быть предусмотрено измерение расхода газа через турбину, уте-
чек через уплотнения, развиваемой на валу мощности, числа оборотов;
4)	должно быть предусмотрено надежное измерение мощности, поглощаемой
трением ротора турбины, с тем, чтобы можно было определить так называемую
внутреннюю мощность турбины (мощность, развиваемую газовым потоком) и ра-
боту на окружности колеса;
5)	конструкция турбины должна допускать легкую смену облопачивания, из-
менение осевых и радиальных зазоров.
Экспериментальные турбины работают обычно на сжатом воздухе. Облопа-
чивание турбины выполняют в натуральную величину или по принципам не-
метрического моделирования, причем необходимо сохранять существующее в на-
туре отношение djh — среднего диаметра облопачивания к высоте лопатки.
При траверсировании решетки на турбине или в статической установке из-
меряют локальные значения параметров газа по шагу и по высоте лопаток Как
уже указывалось, в различных точках какого-либо поперечного сечения потока
давления, скорости, направления линий тока неодинаковы. Это иллюстрируется
рис. 4.5 и 4.6, где показан характер изменения величин pi*, pi, at по шагу и
осредненных по шагу величин aicp и /?1ср — по высоте решетки при се стати-
ческой продувке.
Причины такого изменения параметров (которые выравниваются по мере'
удаления от фронта решетки) поясняются в следующих параграфах. Здесь отме-
тим, что указанное'изменение параметров потока заставляет измерять их в бол»'
шом числе точек по сечению.
Осредненные параметры решетки приближенно можно найти как среднеариф'
метические величины из ряда замеров, например,
“1СР= пЦ"1’
IL
70
Пля более точного осреднения надо использовать формулы, основанные на
нениях неразрывности, импульсов и энергии. Подсчет по этим формулам
уравн доемок. Чем определение среднеарифметических величин.
^°Ледсредненные параметры решетки являются их оценочными характеристи-
ками.
§ 4.5.	ПОТЕРИ В РЕШЕТКЕ
Потери энергии в турбинных решетках можно разделить на две
группы: профильные и концевые (рис. 4.7).
Профильные потери наблюдаются в так называемой элементар-
ной решетке, выделенной на каком-либо радиусе облопачивания
двумя цилиндрическими поверхностями с бесконечно малым рас-
стоянием между ними. Эти потери обусловливаются:
1)	трением в пограничном слое, образующемся на профцле ло-
паток;
2)	вихреобразованием в зоне за выходными кромками;
3)	отрывом потока от поверхностей профиле;
4)	скачками уплотнения, возникающими в межлопаточном кана-
ле при переходе сверхзвуковой скорости в дозвуковую.
Следует заметить, что в научно-технической литературе встре-
чается и другая номенклатура разделения потерь. Так, например,
из трения в пограничном слое на профиле лопаток выделяют поте-
ри в косом срезе и т. п. Потери на отрыв потока и потери, связан-
ные с возникновением скачков уплотнения (волновые), необяза-
тельны и наблюдаются только в определенных случаях. Неизбеж-
ными профильными потерями являются трение и вихреобразование
за выходными кромками. Профильные потери в чистом виде мож-
но обнаружить только при продувке неподвижных решеток с отно-
Рис. 4.7. Структурная схема потерь в решетках
71
сительно длинными лопатками. По середине высоты таких решето^
вторичными течениями, о которых говорится ниже, можно прене,
бречь и определять профильные потери методами, описанными fi
§ 4.4.,
Концевые потери вызываются наличием концевых поверхностей
ограничивающих решетку по высоте.. Для рабочих лопаток турби!
ны концевыми поверхностями служат цилиндрическая или кониче-
ская поверхность у корня лопаток и внутренняя поверхность бан.
дажа, а при отсутствии его — внутренняя поверхность корпуса
турбины. Концевые потери вызываются: трением в пограничном
слое, образующемся на концевых поверхностях; образованием
вторичных или индуцированных течений в канале между лопатка-
ми, обусловленных неравномерным полем давлений по сечению ка-
нала; перетеканием газа с вогнутой стороны лопатки на спинку че-
рез радиальный зазор между лопатками и корпусом турбины (если
лопатки не снабжены бандажом). Концевые потери можно опреде-
лять при продувке решетки траверсированием потока по высоте ло-
патки.
Но во вращающихся решетках добавляются еще потери: от ра-
диального течения газа; от нестационарности потока.
Каждый из видов потерь в решетке характеризуется соответст-
венным коэффициентом, который представляет собой отношение аб-
солютной величины потерь к теоретической работоспособности газа,
выходящего из решетки. Так, например, коэффициент потерь на
трение £тр=#тр/#о, где ДТр — выражена в Дж/кг, а Но (для сопло-
вой решетки) равна
Коэффициент потерь энергии £ в сопловой решетке, определя-
емый формулой (3.21), представляет собой сумму
где индексы означают: «пр» — профильные потери; «к» — конце-
вые; «кр» — кромочные.
Мы положили здесь £пр=£тр + вкр, так как срывные и волновые
потери не всегда наблюдаются. При их наличии коэффициент про-
фильных потерь соответственно возрастает. Потери от радиально-
го течения газа и от нестационарности потока на вращающихся
решетках можно учесть умножением суммы (ьпр-Нкр) на коэффи-
циент, больший единицы. К. п. д. решетки г) = 1—*. Для оценки
профильных потерь пользуются «профильным» к. п. д.: т|Пр=1—£щ>-
Если при отношении d!h<i (8 ... 10) лопатки можно выполнить не-
закрученными (постоянного по высоте профиля), то в соответствии
с § 5.1 в ступени возникают так называемые веерные потери. Они
объясняются тем, что профили лопаток, выбранные расчетом по
среднему диаметру, не подходят к параметрам потока в других се-
чениях по высоте лопаток. Оптимальную величину шага лопаток
также не удается выдержать по всей высоте решетки. Вопрос о ве-
личине веерных потерь рассматривается в § 5.4.
72
§ 4.6.	ПРОФИЛЬНЫЕ ПОТЕРИ
Потери на трение
При течении через решетку вязкой жидкости на поверхности ло-
даток образуется пограничный слой, характер изменения толщины
которого и эпюра скоростей в нем показаны на рис. 4.8. Набегаю-
щий поток разветвляется в точке а. От этой точки на лопатке об-
оазуется ламинарный пограничный слой, протяженность его (до
точки перехода в турбулентный слой) зависит ог ряда факторов
(параметров набегающего потока, кривизны профиля и др.). На
вогнутой поверхности толщина слоя постепенно возрастает, причем
на участках уменьшающейся кривизны возможен переход ламинар-
ного слоя в турбулентный или даже отрыв его. В той части канала
на вогнутой поверхности, где скорость потока интенсивно возраста-
ет, толщина слоя уменьшается.
На спинке в связи с возрастанием скорости ламинарный слой
быстро переходит в турбулентный. Толщина слоя сначала возрас-
тает, и при резком уменьшении кривизны профиля здесь создаются
благоприятные условия для отрыва слоя. Далее в связи с ростом
скорости толщина слоя уменьшается, а затем на выходной части
спинки благодаря дпффузорности (см. § 4.2) пограничный слой
быстро набухает. Из-за значительного градиента давления вдоль
потока у спинки могут появиться обратные течения (см. рис. 4.8),
что приводит к отрыву слоя и образованию вихрей.
Сопротивление трения зависит прежде всего от характера погра-
ничного слоя (ламинарный он или турбулентный). Так как при ла'
минарном слое потери меньше, стремятся проектировать лопатки
так, чтобы точка перехода ламинарного слоя в' турбулентный нахо-
ходилась дальше от входной кромки профиля. Положение этой
точки приближенно можно определить расчетом. Чаще всего точка
перехода на спинке профиля совпадает с точкой минимального дав-
ления или находится в начале диффузорной
области.
В области ламинарного пограничного слоя
и турбулентного с гладкими стенками толщи-
на пограничного слоя и потери на. трение
уменьшаются с ростом числа Рейнольдса. При
турбулентном течении с шероховатыми стенка-
ми наблюдается автомодельность по числу Re
и потери на трение зависят только от степени
шероховатости поверхности лопатки.'
В турбинных решетках за характерный раз-
мер при определении Re 'принимается хорда
профиля, за скорость — теоретическая ско-
рость выхода из решетки; коэффициент вязко-
сти определяется по состоянию газа в конце
Рис. 4.8. Схема пограничного слоя при обтекании
профиля
73
изоэнтропного расширения. Различные авторы по разному оцени-
вают величину Re, при которой процесс обтекания решетки можно
считать автомодельным по этому критерию. Разноречивые
данные отдельных исследований объясняются различными
условиями испытания и разнородностью испытанных про-
филей. М. Е. • Дейч указывает, что автомодельность насту-
пает при меньших числах Re в случае значительной степени
турбулентности набегайщего потока, при углах pjCipireoM, а также
в решетках с малой конфузорностью [4]. Тем не менее можно счи-
тать, что автомодельность по числу Re в турбинных решетках с
тонкой кромкой наступает при Rei> (5 ... 6) 105 [4]. Чистота обра-
ботки спинки лопатки соответствует 7—8-му классу. Так как на
вогнутой поверхности скорости меньше, чем на спинке, то вогнутук»
поверхность можно обрабатывать с еще меньшей чистотой (при-
близительно по 6-му классу).
Необходимо, однако, иметь в виду, что повышенная чистота
обработки профиля совершенно необходима с точки зрения проч'
ности лопатки. Поэтому ббщедринята обработка всей поверхности
профиля по 8—9-му классам чистоты.
Турбины современных крупных ГТД работают при числах Re^
ajI-105 и более; для этих турбин как коэффициенты <р, ф. так и
к. п. д. турбины в целом можно считать почти независимыми от
Re. Число Рейнольдса, однако, сказывается на к. п. д. мелких тур-
бин, а также при работе турбин в высотных условиях, где сущест-
венно возрастает кинематическая вязкость газа.
Коэффициент потерь от трения существенно зависит от углов
входа в решетку (ао или 01) и выхода из нее (at или fj2). Эта зави-
симость, по данным (34], представлена на рис. 4.9. График построен
на основе экспериментальных данных, полученных при продувках
прямых решеток из профилей, аэродинамически отработанных и
74
I'nc. 410. График зависимости коэффициента потерь на трение от режима ра-
боты
Рис. 4.11. Схема вихревого следа за выходной кромкой лопатки
рекомендуемых для использования в сопловых и рабочих венцах
дозвуковых и околозвуковых турбин. Зависимость относится к ре-
шеткам с оптимальным шагом и нулевой толщиной выходной кром-
ки и значениям чисел X2t«0,8 для сопловой Лси или рабочей Xw2! и
Re>4-105.
Из графика видно, Что особенно большие коэффициенты потерь
имеют место в решетках с большими углами поворота потока и ма-
лыми конфузорностями канала (малыми значениями отношения
sm Pt/sin ₽2).
Коэффициент потерь на трение возрастает с уменьшением ско-
рости выхода из решетки и равен [58]
Стр=Стро (1 + ДСгро),	(4.13)
где Стро — коэффициент потерь на трение при %2i=0,8 и определя-
ется из графиков на рис. 4.9; ДСтро — поправочный коэффициент,
зависящий от приведенной скорости истечения газа из решетки
^2<(Хсп или lw2t), определяется графиком на рис. 4.10.
При <0,5 пропадает эффект сжимаемости газа и коэффи-
циент потерь на трение в этом диапазоне приведенной скорости не
зависит от Л2ь Минимальное значение Стр соответствует ^«0,9 ...1.
Рост Стр с уменьшением Х2< вызван снижением градиента давления,
а следовательно, ростом толщины пограничного слоя [4].
Увеличение Стр при Х2«>0,9 объясняется волновыми потерями.
Кромочные потери. Направление потока за решеткой
Как указано выше, за выходными кромками лопаток образует-
:я вихревой след, схематически показанный на рис. 4.11. Вихреоб-
Разование за кромками объясняется отрывом потока при сходе его
с кромок; при этом после отрыва давление со стоооны вогнутой по-
верхности лопаток падает, а со стороны спинки возрастает. При
Удалении от решетки неравномерность потока по шагу постепенно
Уменьшается, давление в следе повышается, а пограничные слои,
75
Рис. 4.12. График влияния чисел Re и М на профильные потери в решетках е
различной толщиной выходных кромок по данным МЭИ:
--------0,162;------------------2Гвых- 0,085
ь	ъ
стекающие с обеих сторон межлопаточного канала, сближаются до
тех пор, пока ядро потока не исчезнет, приблизительно это расстоя-
ние z= (1,3 ... 1,9) t. При выравнивании поля средняя скорость по-
тока уменьшается, а его статическое давление возрастает. Возника-
ют потери, в известной степени аналогичные потерям от внезапно-
го расширения..
Как показали теоретические и опытные исследования Н. М. Мар-
кова и Г. Ю. Степанова, эксперименты в КАИ и в других организа-
циях, коэффициент кромочных потерь £кр и направление потока из
решетки в дозвуковой области слабо зависят от сжимаемости газа.
Для £цР справедлива формула
^=(0,36...0,4) /ят- ,	. (4.14}
t SIH di
где гВых — радиус выходной кромки.
Опытные исследования показывают также, что с увеличением
толщины выходной кромки область практической автомодельности
по числу Re смещается в область более низких чисел Re, о чем сви-
детельствует график на рнс. 4.12. [4].
Направление потока на выходе из решетки, определяемое углом
«I для сопловых лопаток и углом 02 для рабочих лопаток, в основ-
ном зависит от геометрии решетки и режима работы. В первом при-
ближении (см. рис. 4.2)
ai(W=ai3$(W==arcsinlfl//k	(4-
Влияние режима на углы ср л 02 учитывается графиком на рис.
4.13.	В результате
а1 = а1эф + д«-	"	(4.16)
76
Отрыв потока от поверхности профиля.
Влияние угла атаки на потери в решетке
Отрыв потока от поверхности лопаток является одной из наи-
более существенных, хотя и не всегда имеющих место, потерь при
обтекании решетки. В местах отрыва образуются вихри, обуслов-
ливающие значительные потери энергии. При отрыве сужается про-
ходное сечение канала, что может повлечь за собой уменьшение
пропускной способности решетки и, следовательно, уменьшение
расхода газа через турбину по сравнению с принятым в расчете.
Отрывы потока могут наблюдаться на входной части профиля,,
особенно когда угол атаки существенно отличается от нуля. Так.
при положительном угле атаки отрыв может произойти на спинке,
а при'отрицательном — на вогнутой поверхности, причем.в обоих
случаях вблизи входной кромки, как показано на рис. 4.14. Резкое
изменение кривизны профиля, как это часто наблюдается на спин-
ке лопатки при переходе криволинейного очертания в плоское у
входной кромки, почти всегда вызывает отрыв1 потока.
На эпюре давлений по профилю отрыв потока характеризуется
обычно наличием диффузорного участка с последующим участком
постоянного давления. На диффузорном участке профиля с повы-
шением давления падает скорость газа. ПрА тонком пограничном
слое и не слишком значительной диффузорности частицы газа и
пограничном слое могут продолжать свое движение за счет кине-
тической энергии соседних слоев, в противном случае при значи-
тельном градиенте давления направление движения частиц в пог-
77
Рис. 4.14. Схема срывов потока на
обусловленпых углами атаки	*
граничном слое изменяется (как пока-
зано на нижней эпюре скоростей на
рис. 4. 8) и происходит отрыв потока
от стенки канала.
Таким образом, для безотрывного
обтекания благоприятны профили с
плавно изменяющейся кривизной; при
этом радиус кривизны должен посте-
пенно возрастать от входа к выходу.
Типичная зависимость скоростного ко-
эффициента ф от угла Pi и, следова-
тельно, от угла атаки для двух профилей: активного (Л) с тонкой
входной кромкой и реактивного (С) с большим радиусом скругле-
ния входной кромки, показаны на рис. 4. 15. Кружочками на кри-
вых помечены расчетные углы входа.
Отрыв потока и связанное с ним вихревое движение внутри
межлопаточного канала представляют собой настолько сложное
явление, что сколь-либо точное аналитическое определение потерь,
связанных с этим, оказывается невозможным.
В связи с изложенным в практике расчетов получили распрост-
ранение полуэмпирические и эмпирические формулы, основанные
на обобщении опытных данных по исследованию большого числа
решеток. К их числу относятся формулы, предложенные А. Н. Шер-
стюком и Г. Ю. Степановым. Детальные опыты по изучению влия-
ния угла атаки на профильные потери были проведены в КАИ.
При обобщении опытных данных оказалось эффективным вве-
дение понятий об относительном угле атаки (угол атаки в долях от
геометрического угла входа):
g  Й  31геом 31  |31
31геом 31геом	31геом
и об относительном снижении к. п. д. (т] = ф2) решетки (снижение
к. п. д. в долях от'к. п. д. при расчетном угле входа)
А- Д’*! Чр— Ч - т!
Дт] = — --------= 1----*— .
Чр	*qP
На рис. 4.16 показаны основные результаты опытов КАИ, обоб-
щенные в виде зависимости Дт}=/(б) (сплошная линия). Точками
нанесены результаты обработки опытных данных советских и зару-
бежных авторов, полученные при продувке 10 решеток, составлен-
ных из различных профилей активного и реактивного типов, но
примерно с одинаковым относительным шагом t/b ^0,6 и радиусом
скругления входной кромки гвх/^~3 ... 4%.
Установлено, что на зависимость потерь в решетке от угла ата-
ки существенное влияние оказывают шаг решетки и радиус скруг-
ления входной кромки профиля. Редкие решетки оказываются бо-
78
Рис. 4.15. График влияния угла входа потока в решетку fi на скоростной коэф-
фициент ф
Рис. 4.16. График влияния относительнЬ-
го угла атаки 6 на относительные поте-
рн At]
лее чувствительными к изменению угла атаки, чем решетки с ма-
лым шагом. Увеличение радиуса скругления входной кромки делает
решетку более атакоустойчивой.
Подводя итог всему вышеизложенному, можно сделать следую-
щие выводы.
1.	Положительные углы атаки («удар» в вогнутую часть лопат-
ки), существенно ухудшающие условия обтекания спинки профиля,
где скорости потока велики, вызывают значительно большие поте-
ри, чем углы атаки отрицательные («удар» в спинку), ухудшающие
течение на корытце.
2.	Уровень потерь в решетке при нерасчетных углах натекания
•потока определяется не абсолютной величиною угла атаки б, а от-
носительной 6=6/Pip. В связи с этим, при прочих равных условиях,
решетки с большим углом входа оказываются менее чувствитель-
ными к изменению угла атаки, чем решетки с малыми углами
входа.
3.	На характер зависимости потерь от угла атаки оказывает
влияние относительный шаг решетки. Уменьшение относительного
шага улучшает атакоустойчивость, увеличение — ее ухудшает.
4.	Увеличение радиуса скругления входных кромок приводит к
повышению атакоустойчивости решетки. Однако следует помнить,
что максимальный к. п. д. решетки (на расчетном режиме) при этом
уменьшается.
5.	Максимальные к. п. д. решетки достигаются при углах атаки,
близких к нулю. Следует подчеркнуть, что, как показывают опыты,
Для решеток с малыми углами входа (Pip<3(F) минимум потерь
' обычно достигается при небольших отрицательных углах атаки
б= —(0,1 ... 0,15). Физически это объясняется тем, что наряду с
79
увеличением (небольшим) потерь отрыва, уменьшаются (~
потери трения на входной кромке.	;
6.	Угол потока на выходе из решетки р2 практически не зависит
от угла атаки в широком диапазоне его изменения.
Анализ большого числа (более ста) характеристик решеток
опубликованных в советской и зарубежной литературе, с различны-
ми геометрическими и режимными параметрами позволил предло-
жить .следующую эмпирическую зависимость £31]:
.ДП = 14,6 (0,5-rK)5|i|2,37? arcctg [7,7 (?opt-0,75)] х
X arcctg [6,9 (Z* — 0,65)] K~l,	(4.17)
где гвх=Гвх/Ь — относительный радиус входной кромки;
= t[topt— относительный параметр шага; I — шаг решетки; iopt —
оптимальный шаг решетки (см. § 4.9); Лг — приведенная теоретиче-
ская скорость потока на выходе из решетки (Zcit Для сопловых ло-
паток и — для рабочих); К — параметр, учитывающий различ-
ный характер обтекания профиля при положительных и отрицатель-'
яых углах атаки:
/С==1-|- [6 In (2— 1 signg>] (0,5-7„) (1-0,3582) х
х arcctg [5,3 (7орт—0,75)].
В заключение отметим, что все вышеизложенное относится к
плоским турбинным решеткам. С известным приближением ука^
ванными зависимостями можно пользоваться и для элементарны^
решеток, расположенных на различных радиусах реальной кольце-
вой решетки. В турбинной ступени, как показывают опыты, потери,
вызванные углом атаки, выше аналогичных потерь в решетке, о
чем более подробно см. в § 8.3.
Волновые потери
Скорость газа на выходе из решетки может быть звуковой или
сверхзвуковой; сверхзвуковая обычно достигается в косом срезе
сопла или в решетках с расширяющимися каналами. Возможно,
однако, достижение в лопаточных каналах звуковой или сверхзву-
ковой скорости даже в том случае, если скорости на входе в решет-
ку и на выходе из нее являются дозвуковыми. Это может наблю-
даться при достаточно большой дозвуковой скорости входа в решет-
ку на спинке профиля в месте максимума отрицательного давления.
Большой шаг решетки и значительная кривизна профиля способ-
ствуют образованию здесь сверхзвуковых скоростей.
Число М на выходе, при котором где-либо в канале достигается
скорость звука, называется критическим (Мг*), а момент появле-
ния звуковой скорости — волновым кризисом.
Если основной поток в канале движется с дозвуковой скоро-
стью, то появление местной сверхзвуковой скорости связано с даль-
нейшим ее переходом в дозвуковую. Переход этот совершается при
помощи скачка уплотнения и сопровождается потерей энергии.
80 .
Рис. 4 17. Кривые изменения критических значений чисел М2* для реактивной
решетки в зависимости от относительного шага решетки
Рис 4.18. Схема вихревых течений в межлопаточном канале, имеющем радиаль-
ный зазор:
/—верхний парный вихрь; 2—поток, переходящий в соседний канал; 3—вихревая пелена. 4—
канавка
Из опытов известно, что сверхзвуковые скорости возникают не
только на спинке профиля, но и в области, примыкающей к выход-
ной кромке, где этому способствует пониженное давление за вы-
ходной кромкой. Опытное определение критических величин М2*
показывает, что они существенно зависят от геометрических разме-
ров решетки.
В частности, в соответствии со сказанным выше, значение кри-
тической скорости уменьшается с увеличением шага решетки и кри-
визны сцинки в косом срезе.
На рис. 4.17 показаны кривые изменения критических значений
М2* для реактивной решетки в зависимости от. относительного ша-
га t=t]b. При малых величинах шага сверхзвуковые зоны образу-
ются сначала у выходных кромок, при больших — на спинке про-
филя. Имеется такое значение t, при котором звуковые скорости
Достигаются одновременно и на выходной кромке, и на спинке (в
Данном случае £ = 0,74). Хотя возникновение скачков уплотнения
в канале связано с волновыми цотерями, однако, они невелики, и
не всегда переход через критическое число М2* вызывает падение
к. п. д. решетки.
§ 4.7. КОНЦЕВЫЕ ПОТЕРИ
Потери от трения в пограничном слое на концевых поверхно-
стях имеют тот же характер, что и описанные в § 4.6. Значение их в
общем балансе потерь становится заметным лишь в лопаточных ка-
I
81
налах малой высоты. Зато на к. п.д. решетки существенно влия.
ют вторичные течения, обусловленные разностью давлений на вог-
нутой поверхности лопатки и на спинке соседней лопатки.
Наличие градиента давления между вогнутой поверхностью ц
спинкой вызывает в пограничном слое, гдедоток подторможен, вто-
ричные токи от средней по высоте части вогнутой поверхности к
торцам лопатки, затем по концевым поверхностям к спинке сосед,
ней лопатки и по спинке от торцов лопатки к среднему ее сечению.
Течение это схематически показано на рис. 4.18 линиями 1.
Попадая на спинку лопатки, вторичные токи увлекаются основ-
ным потоком к выходному сечению решетки, в результате чего в
верхней и нижней частях спинки пограничный слой набухает и в
двух местах срывается со спинки, образуя так называемый «пар-
ный» вихрь. Оба вихря вращаются в противоположных направле-
ниях соответственно направлению перетекания воздуха на конце-
вых поверхностях.
Вторичные течения в канале, с одной стороны, приводят к пере-
распределению давления; повышению у торцов лопатки на спинке и
понижению на вогнутой поверхности; с другой стороны, вызывают
значительные потери энергии потока, в.связи с чем характер изме-
нения полного давления по высоте решетки принимает вид кривой,
показанной на рис. 4.6. При этом наибольшие потери возникают на
спинке лопаткп.
Как видно из рис. 4.6, в местах образования парного вихря на-
блюдается увеличение выходного угла оц, что объясняется оттесне-
нием линий тока от поверхности спинки в местах вспучивания пог-
раничного слоя и отрывом потока от спинки на некотором расстоя-
нии от выходной кромки, большем, чем в средней части лопатки.
Уменьшение углов потока непосредственно у концевых поверх-
ностей объясняется существенным сокращением зоны отрыва в этих
местах и перетеканием в пограничном слое, как бы прижимающим
поток к спинке лопатки. Абсолютная величина концевых погерь не
зависит от высоты лопаток до тех пор, пока при уменьшении высо-
ты лопаток не начинается взаимодействие парных вихрей. Смыка-
ние зон пространственного обтекания лопатки может начаться при
Л=Л/6«1; при меньших значениях Л концевые потери резко воз-
растают с уменьшением этого отношения. Относительная величина
концевых потерь в любом случае возрастает с уменьшением высоты
лопатки или увеличением длины хорды. Эта зависимость оправды-
вает рекомендации по уменьшению ширины коротких лопаток, с
тем чтобы увеличить отношение Л.
Значение концевых потерь зависит от величины профильных по-
терь, и, на основании опытных данных, их соотношение может быть
представлено в следующем виде [9]:
Г-=—(4'18)
1 + £> Л — А
где h=hja — отношение высоты лопатки к горлу решетки;
А== 1,0 ... 1,2 и В = 0,4 ... 0,5 — постоянные коэффициенты.
82
Большие значения А и меньшие В соответствуют - решеткам с
малыми профильными потерями (£пр=0,02 ... 0,03). Для подавля-
ющего большинства решеток профилей, применяемых в авиацион-
ных турбинах, Д = 1,0 ... 1,1, а В=0,5.
Концевые потери уменьшаются, если на торцевых поверхностях
проточной части решеток по всей их ширине выполнить специаль-
ные канавки 4 вблизи спинки лопатки (см. рис. 4.18) [4].
В сверхзвуковых решетках концевые потери существенно мень-
ше, чём в дозвуковом потоке, где численные значения коэффициен-
тов профильных и концевых потерь имеют одинаковый порядок.
Для коротких сверхзвуковых лопаток при й/(/^0,013 в Ленин-
градском кораблестроительном институте (ЛКИ) рекомендуют сле-
дующую формулу для определения концевых потерь:
СкоГО= А О,9°3 — •	(4-19)
— 4-0,003
d
По данным, приведенным в работе [24], эта формула справедли-
ва и для дозвуковых активных решеток с короткими лопатками.
В кольцевой решетке концевые потери несколько перераспреде-
ляются по высоте канала. Увеличение шага решетки по направле-
нию к периферии вызывает увеличение градиента давлений в попе-
речном сечении канала. Это обусловливает интенсификацию
периферийного вихря и смещение его по направлению к середине
высоты лопатки. По той же причине вихрь’ в основании канала ос-
лабляется и приближается к корню лопатки.
-Все изложенное выше в этом параграфе относится к решеткам
без радиальных зазоров между лопатками и концевыми поверхно-
стями. Таковыми являются сопловые решетки и решетки рабочих
лопаток,’перекрытых на периферии лентой, приклепанной к лопат-
кам, или полками, фрезерованными (штампованными) заодно с ло-
патками (лопатки с бандажом).
Если рабочие лопатки турбины не имеют бандажа, то концевой
поверхностью с этой стороны, отстоящей от лопаток на величину
радиального зазора, служит корпус турбины. В этом случае через
радиальный зазор перетекает газ от вогнутой поверхности к спинке
той же лопатки, как показано на рис. 4.18.
По вогнутой поверхности лопатки, в области ее вершины части-
цы газа, подторможенные в пограничном слое на профиле, движут-
ся вверх и к выходной кромке. Одна часть их образует верхний пар-
ный вихрь 1. Другая часть 2 попадает в зазор над лопаткой, а из
него — в соседний канал. Здесь этот поток газа сворачивается в
вихревую пелену 3, которая уносится основным потоком. По мере
приближения к выходной кромке все большее количество газа, пе-
ретекающего через зазор из соседнего канала, участвует в вихре-
вом движении.-Ось вращения вихревой пелены несколько отклоня-
ется от верхней торцовой стенки. Этот дополнительный вихрь не
Перемешивается с верхним парным вихрем, а оттесняет его от спин-
ки лопатки, причем оба вихря вращаются во взаимно противопо-
83
ложных направлениях. Вихревая пелена 3 взаимодействует с пог.
раничным слоем на профиле, вызывая его*перераспределениеповц.
соте лопатки.
Характер изменения полного давления pl (Picp) и угла
Рз(сИср) на выходе из решетки показан на рис. 4.6. В связи с утеч-
кой газа через зазор полное давление и угол выхода у вершины до-
патки резко падают. Течение газа через зазор обусловливается
также разностью давлений по обе стороны решетки (при наличии
реактивности на периферии ступени).
Непосредственное определение дополнительных концевых по-
терь, вызванных радиальным зазором, зачруднптсльнб. Их можно
найти только как разность в потерях решетки с радиальным зазо-
ром и без зазора. Величина коэффициента дополнительных конце-
вых потерь приблизительно такая же, как и коэффициента конце-
вых потерь в решетке без радиального зазора.
§ 4.8. ПОТЕРИ, СВЯЗАННЫЕ С ВРАЩЕНИЕМ РЕШЕТКИ
Как было отмечено в § 4.5, во вращающихся решетках возника-
ют дополнительные потери, вызванные действием центробежных
сил на частицы газа и йестацпонарностью потока.
1. Центробежные силы только частично уравновешиваются си-
лами давления, изменяющимися по высоте лопатки (см. § 5.2).
В большинстве же случаев йоток в радиальном направлении не
уравновешен, особенно в межлопаточных каналах; вследствие этого
в каналах возникают радиальные течения (отличные от рассмот-
ренных в § 4.7), на образование которых тратится часть энергии
потоку.	-
В то же время следует отметить, что вращение кольцевой ре-
шетки без бандажа несколько снижает потерн от перетекания газа
через радиальный зазор, так как направление относительно скоро-
сти корпуса турбины противоположно направлению перетекающе-
го потока.
2. Нестациоиарность потока обусловлена непрерывным измене-
нием взаимного расположения сопловой и рабочей решеток, а так-
же изменением параметров газа в потоке, выходящем из сопловой
решетки (эти изменения неравномерны как по шагу,, так и по высо-
те решетки). В осевом зазоре между решетками роток не успевает
выровняться и, поступает на рабочую решетку неравномерным.
При числе сопловых лопаток z и частоте вращения вала п пара-
метры газа перед решеткой меняются с периодом v=Zi/i.
Периодичность изменений потока при входе на решетку может
быть охарактеризована числрм Струхаля: Sh=vL/a), где v — часто-
та изменения параметров газа перед решеткой; L — характерная
длина (например, шаг решетки или толщина выходной кромки);
w — скорость газй.
Зависимость к. п. д. решетки от числа Струхаля пока не уста-
новлена, но опытные данные показывают, что при малом осевом за'
84
зоре увеличение числа Sh на 20% может привести к снижению
к. п. Д. турбины на 1%. С ростом осевого зазора влияние числа Sh
на к. п. д. падает [9].
§ 4.9. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
РЕШЕТКИ НА К.П.Д.
Шаг решетки
Шаг профилей в решетке оказывает существенное влияние на
ее характеристики. С уменьшением шага возрастают профильные
потери в связи с увеличением поверхности трения, омываемой еди-
ницей количества газа.
С увеличением шага давление на вогнутой поверхности профи-
ля лопатки возрастает, на спинке — падает. Это, с, одной стороны,
вызывает увеличение концевых потерь, а с другой — способствует
отрыву потока на спинке, где разность давления на выходе из ре-
шетки и минимального давления возрастает. Кроме того, сниже-
ние давления на спинке при увеличении шага может вызвать появ-
ление.волновых потерь.
Очевидно, для каждого типа решетки должен существовать оп-
тимальный шаг, при котором к. п. д. решетки достигает максимума.
Величина этого шага определяется из условия такой оптимальной
нагрузки профиля, при которой потери минимальны, и, в частности,
отрыв потока происходит только на выходной кромке, а волновые
потери отсутствуют.
На рис. 4.19 показана зависимость к. п. д. решетки (учитываю
щсго только профильные потери) от величины относительного ша
га. Кривые 1, 2, 3, 4 относятся к различным профилям, изображен
ным на рисунке. Оптимальный относительный ша1 для этих профи
лей колеблется в пределах 0,55 .. .0,65.
Многочисленные экспериментальные данные различных авто
рой показали зависимость оптимального шага от режимных и гео
метрических параметров про-
филя и решетки, таких как уг-
лы на входе в решетку и выхо-
де из нее, толщцны выходной
кромки и профиля, скорость
потока на выходе и др.
По выбору оптимального
шага широкое распространение
получила формула В. И. Дыш-
левского [1]. Здесь приводится
Рис. 4 19. График зависимости про-
фильного к п.д. решетки от относи-
тельного шага для различных про-
филей при р1 = 50® (опыты КАИ):
z-p2=36c; 2— ^2=32°, 3—Р2=ЗО,Э°; 4—.0^34°
85
формула, предложенная А. Г. Клебановым и Б. И. Мамаевым
[25], которая при .определенных условиях дает согласованные
данные с формулой В. И. Дышлевского, но учитывает большее чис-
ло параметров, влияющих на величину оптимального шага:
^opt ~ (A^)opt=(1 + 4>Pt) A'Kp/opto,	(4.20)
где iopt — относительный оптимальный шаг решетки; i0pto — отно-
сительный оптимальный шаг решетки при нулевой толщине выход-
ной кромки приЛ(=0,8
/ор10=(Ы21_0,869)34г- — +1,604 для 1	1,5,
\ К	/ /0 К
7	0,327 0,994 । 1 о 1 л гл 1 е
^opt0^/<'(l>37i3/'fl—л:0’385	1’314 ДЛЯ 1,5,
sin	sin а0
/< = —— —для рабочих лопаток; К=--------------—для сопловых
Sin р2	Sin а1
лопаток; 9=[18O — (Р1.+-Р2] — —угол поворота потока в радиа-
нах; Ккр — поправочный коэффициент, учитывающий толщину вы-
ходной кромки
Ккр = 1 15«вых + (3,75iopt0 0,6) авых;
—	2/*	__
-$вык == —~ — относительная толщина выходной кромки; A*Opt —
ь
поправочный коэффициент, учитывающий влияние режима работы
Aiopt= — 0,625k? 4-0.48Х, + 0,016;
Xt — приведенная скорость на выходе из решетки, равная Xcit для
сопловой решетки и Хш2< — для рабочей.
При выборе величины шага надо учесть конструкцию лопаточ-
ного замка с точки зрения его прочности и возможности размеще-
ния необходимого числа на диске.
Отметим, что только при величинах шага, близких к оптималь-
ным, угол выхода из решетки можно определить по формулам, при-
веденным в § 4.7. Как при увеличении, так и при уменьшении шага
средний угол выхода газа из решетки возрастает, особенно резко —
при увеличении шага.
Влияние поворота струи в решетке на к.п.д.
При увеличении угла поворота струи в решетке, т. е. уменьше-
нии суммы углов (₽i + p2), возрастает разность давлений между
вогнутой стороной лопатки и ее спинкой. При этом увеличивается
протяженность диффузорного участка на спинке, возрастает опас-
ность отрыва потока и увеличиваются концевые потери вследствие
интенсификации вторичных течений. Поэтому к. п. д. решетки т]==
=Ф2(ф2) = 1—£ с уменьшением суммы углов ,01 +р2 (или ao+ai)
уменьшается.
-86
Повышение конфузорности решетки ослабляет влияние угла по-
ворота, так как способствует непрерывному нарастанию скорости
в межлопаточном канале и устойчивости течения (см. рис. 4.9).
Влияние ширины лопатки на к.п.д. решетки
Уменьшение (до известного предела, конечно) ширины лопатки
s приводит к увеличению относительной высоты (отношение высо-
ты к ширине или к хорде профиля), что вызывает уменьшение кон-
цевых потерь. Что касается профильных потерь, то из-за уменьше-
ния числа Re они могут возрастать. В результате при произволь-
ном снижении ширины лопаток суммарный'коэффициент потерь мо-
жет даже увеличиваться. Это свидетельствует о наличии оптималь-
ной ширины решетки, которая зависит и от режима работы.
При выборе ширины рабочих лопаток необходимо помнить о
том, что уменьшение ширины повлечет за собой увеличение числа
лопаток и может вызвать трудность в размещении их на диске.
Кроме того, в узких лопатках по прочностным и технологическим
соображениям не всегда удается выдержать оптимальные толщи-
ны входной и выходной кромок.
Лопатки авиационных ГТД выполняются в I ступенях с шири-
ной s= (0,25 ... 0,4) h, в последних — s можёт составлять всего
0,15ft (21]. В турбинах ТНА ЖРД и вспомогательных турбинах
slhw 1 из-за малой высоты лопаток.
Входная и выходная кромки
При дозвуковых скоростях входа целесообразно скруглять
входную кромку не очень малым радиусом. Так, по опытам в КАИ,
оптимальный радиус скругления входной кромки должен лежать в
пределах (0,025 ... 0,04) ft.
По опытам ЦКТИ с активным профилем, в котором радиус
скругления входной кромки менялся от 0,07Стах до 0,ЗЗСтах, где
Стах — максимальная толщина профиля, наивыгоднейшими оказа-
лись радиусы от 0,15Стах до 0,ЗЗСтах. Для турбин, работающих
преимущественно на переменном и/с\, желательно выбирать боль-
шой радиус скругления, так как с увеличением радиуса входной
кромки к. п. д. решетки более устойчив к изменению угла атаки
(см. § 4.6).
В решетках, работающих на сверхзвуковой скорости входа,
входную кромку следует выполнять заостренной в такой степени, в
какой это допускают соображения прочности. Выходная кромка
лопатки, как указывалось в § 4.6, должна быть выполнена возмож-
но более тонкой. В лопатках крупных авиационных турбин с хор-
дой профиля 50.. 100 мм толщина 2гвых выходной кромки состав-
ляет обычно 1 ... 1,5 мм. Радиус скругления выходной кромки ра-
бочих лопаток у выполненных турбин составляет обычно (0,015 ...
•.. 0,02) ft. Более низкие цифры не всегда возможны по соображени-
ям прочности. Для сопловых лопаток можно допустить ГВ|,1х=
=7 (0,007... 0,015) ft.
87
Применение бандажа и проволочных связей
на рабочих решетках
Из сказанного в § 4.7 ясно, что применение бандажа на рабочей
решетке ликвидирует дополнительные концевые потери. Кроме то-
го, бандаж позволяет уплотнить радиальный зазор и, следователь-
но, снижает потери на перетекание через этот зазор, вызванное раз-
ностью давлений по обе стороны решетки (см. § 6.4).
В опытах, проведенных в ЦКТИ В. Т. Тырышкиным, получено,
что при относительной величине радиального зазора б2/й=0,02
к. п. д. безбандажной турбины на 2,5% меньше, а при б2/Л = 0,03 —-
на 4% меньше, чем у турбины, лопатки которой выполнены
с бандажом.
Для отстройки от резонанса при вибрации лопаток иногда ло-
патки прошивают проволочной связью. По тем же опытам ЦКТИ
применение такой связи (диаметром 3 мм) снизило к. п. д. ступе-
ни приблизительно на 1 % •
Влияние конусности решетки на эффективность
Турбинные ступени с большой степенью расширения газа в ме-
ридиональном сечении имеют коническую форму с углом раскры-
тия проточной части ук у корня и уп на периферии (см. рис. 7.5).
Скос потока приводит к дополнительным гидравлическим потерям.
На рис. 4.20 {9] приведена зависимость относительного коэффици-
ента концевых потерь от угла раскрытия проточной части, позволя- .
кидая оценить дополнительные потери, вызванные конусностью сту-
пени. Здесь £к=— относительный коэффициент концевых потерь;
СкО
?к — концевые потери при у>0; ^ко — концевые потери при у=0.
Как указано в работе [9], на основании опыта доводки турбин
авиационных двигателей углы ук и уп у соседних решеток не дол-
жны различаться более,* чем на 8.. 12°. При этом обеспечивается
плавное изменение обводов проточной части и практически отсутст-
вие дополнительных потерь.
§ 4.10.	ОЧЕРТАНИЕ ПРОФИЛЯ ЛОПАТКИ И ФОРМА КАНАЛА
Профилирование лопаток должно проводиться таким образом, чтобы обес-
печить расчетные параметры потока на входе и выходе из решетки, а также
уменьшить возможность отрыва потока от поверхности профиля. Кроме тою»
форма лопатки должна удовлетворять требованиям прочности и простоты тех-
нологической обработки лопатки.
Имеющиеся профили в атласах турбинных профилей ЦИАМ, МЭИ, ЦАГИ,
ЦКТИ им. Крылова не всегда удовлетворяют всем перечисленным требован^/’Л
с учетом переменности геометрии профилей по высоте лопатки (см. гл. V)»
В связи с этим в ряде случаев появляется необходимость в построении профи»’я
для конкретной проектируемой турбины.
Один из возможных способов построения профиля лопатки — это получение
его по заданному закону распределения скоростей. Другой способ построения
профиля основан на богатом опытном, материале с последующей расчетной или
экспериментальной проверкой распределения параметров по профилю, о кото-
рых было сказано в § 4.2 и § 4.4. Для второго способа построения профиля
лопатки выработался ряд изложенных ниже положений. Чтобы уменьшить воз-
88
р {с 4.20. График, влияния конусности решетки на вто-
'	ричные потери
ожность отрыва потока от поверхности профиля, его
бедует выполнять прстоянной кривизны или с радиусом
коивизны, постепенно увеличивающимся от входа в ка-
нал к выходу из него. Вогнутая поверхность лопатки ча-
сто описывается одним радиусом, что существенно упро-
щает обработку этой поверхности. Спинку всегда при-
ходится делать переменной кривизны; ее иногда строят
п0 точкам, лежащим на отрезке параболы, лемнискаты
или Другой подходящей кривой: в любом случае кри-
визна профиля должна уменьшаться от входа в решетку к выходу из нее. Если
вогнутая поверхность также описывается какой-либо параболической кривой, то
указанное выше правило сохраняет и здесь свою силу. Особенно опасны пере-
ходы от плоской к криволинейной поверхности и обратно, что раньше применя-
лось при профилировании активных лопаток.
Наряду е очертанием профиля эффективность решетки характеризуется и
формой канала между лопатками. Желательно, чтобы канал по ходу газа плав-
но сужался или (при активном облопачивании) оставался с неизменным попе-
речным сечением. Для проверки в капал вписывается ряд окружностей, как по-
казано на рис. 4.21, ось канала выпрямляется, а из соответствующих точек на
этой оси описываются окружности того же диаметра. Касательные к этим
окружностям (см. рис. 4.21, правая фигура) определяют ширину выпрямленного
канала и позволяют убедиться в плавности изменения этой ширины. Расширение
выходной части канала, безусловно, не допускается; при этом надо учесть также
возможное уширение канала в радиальном направлении. В активных решетках
расширение входйЬй части канала с последующим сужением выходной части в
некоторых случаях более благоприятно, чем постоянная ширина.
В дополнение к изложенным выше общим требованиям к профилю лопатки-
надо упомянуть еще о величине затылочного угла у (см. рис. 4.2), который во
избежание отрыва потока не следует делать большим. Какие-либо предельные
цифры для величины этого угла пока указать трудно, но обычно его делают ье
более 10 ... 15°.
Если сверхзвуковая скорость развивается в косом срезе, то затылочный угол
рекомендуется выполнять возможно малым, доводя его прн М2> 1,3 до нуля.
Все сказанное выше относится к профилированию сопловых и рабочих лопаток
в дозвуковом потоке; ширина сопловой лопатки обычно на 20 ... 40% больше
ширины рабочей.
У существующих сопловых лопаток относительная максимальная толщина
Профиля	ах — Сщах/^~0,1 -	•	~
Для рабочих лопаток могут быть рекомендованы следующие значения Стах:
а) у корня Стах=0,2^... 0,3 (большая величина для активных профилей);
б) в среднем сечении Стах = 0,1 ... 0,15; в) на периферии Стах = 0,04'... 0,05.
Если поток является сверхзвуковым на входе в рабочую решетку ча-
сто наблюдается в турбинах ТНА ЖРД), то перед решеткой возникают или пря-
мые скачки уплотнения, или система косых скачков; в обоих случаях входная
кромка профиля выполняется заостренной, с минимальным углом заострения,
а входная часть спинки — прямолинейной.
При проектировании лопатки наиболее целесообразно пользоваться завод-
скими нормалями профилей или профилями, рекомендуемыми научно-исследо-
вательскими организациями. Это тем более удобно, что для таких профилей ука-
зываются желательные величины шага, угла установки, угла атаки и приводятся
опытные материалы по исследованию данной решетки, которые позволяют уста-
новить идентичность угла выхода р2 с заданным и найти к.пд. решетки (или
коэффициент -ф).
В МЭИ М. Е. Дейчем и А. В. Губаревым разработан ряд активных про-
филей для работы в широком диапазоне чисел Mci, которые разбиты авторами
на три группы: А, Б и В.
89
Рис. 4.21. Схема конфузорного межлопа-
точного канала
К группе А относятся профили, пред-
назначенные для работы до Mwi = o,9.
Группа Б включает профили для работы
с Mwi = 0,85... 1,3. Профили для работы
в сверхзвуковой области Mwi=l,3... 1,9
(Xwi — l,6) составляют группу В.
Профили группы А имеют криволи-
нейные входные и выходные участки и
увеличенный радиус закругления входной
кромки по сравнению с выходной, канал
должен быть конфузорным или постоян-
ного сечения. Как показали опыты ВТИ
и МЭИ [5], в коротких лопатках с большим поворотом потока не выгодно кон-
фузорное течение из-за потерь от вторичных течений. Профили, образующие
решетку с диффузорно-конфузорным каналом, имеют меньшие потери. Такие про-
фили разработаны в МЭИ и включены в группу А с обозначением Ак. От основ-
ных профилей группы А профили Ак отличаются вогнутой поверхностью (рис.
4.22). Если в исходных профилях йтМ<1 и ai/a2>l, то в новых решетках (груп-
па Ак) ат/ах>\ и ai/a2>l.
Профили группы А могут оказаться пригодными для второй турбины со
ступенями скорости в ТНА ЖРД. Профили* группы Б выполнены с прямолиней-
ными заостренными входными и выходными кромками и с плавно суживающими-
ся межлопаточными каналами При Mwi>l перед решеткой поток тормозится
в прямом скачке, затем расширяется до Mwi=l в горле с переходом в сверх-
звуковую область в косом срезе. Для Mwl^l,35 потери в прямом скачке не
превышают 2%. Профили группы Б могут быть использованы в рабочем колесе
II ступени и в направляющем аппарате турбины со ступенями скорости T1IA
Для значительных сверхзвуковых скоростей на входе в решетку наимень-
шие потери можно достичь специальным профилированием. В связи с тем, что
при больших скоростях потери в головном скачке оказываются значительными,
в профилях группы В предполагается ступенчатое или плавное торможение на
входе; в первом случае входной участок состоит из ломаных линий, во-втором—
спннка на входе вогнутая Опыты, проведенные в КАИ, показали, что решетки
для работы с Mwi=2,4 имеют малые потери при организации на входе трех
косых скачков. Профили МЭИ группы В имеют прямолинейный входной участ ж
с одним головным скачком на входе. .	й
При любом способе организации потока на входе желательно, чтобы сред-
няя криволинейная часть канала была суживающе-расширяющейся. Здесь но-
ток сначала тормозится, затем ускоряется. Минимальное сечение располагается
внутри канала. Выходная часть может быть выполнена прямолинейно или пост-
роена методом характеристик.
Подробное изложение метода построения сверхзвуковых решеток имеется в
литературе, например, в книге [5]. В настоящее время в ряде организаций pa J-
Рис. 4.22. Схемы типов профилей активных рабочих турбин, предложенных
МЭИ.
а—профиль типа А; б—профиль типа Б; в—профиль типа В (метод ступенчатого профили-
рования); г—профиль типа В (метод прямого скачка)
90
оаботаны новые профили турбинных лопаток активного и реактивного типа для
различных чисел Mwi (до 1,9) с малой величиной профильных потерь. С профи-
лями можно познакомиться в атласах МЭИ, ЦКТИ и др.
§ 4.11.	ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СОПЛОВОЙ
И РАБОЧЕЙ РЕШЕТОК
Осевой зазор
При выборе взаимного расположения сопловых и рабочих лопа-
ток необходимо обращать внимание на величину осевого зазора
между решетками и соотношение между высотами сопловых и рабо-
чих лопаток.
Чем больше осевой зазор между сопловой и рабочей решетка*
ми, тем более выровнившимся поступает поток на рабочие лопат-
ки, т. е. тем меньше в них потери от нестационарности потока; од-
нако при большом осевом зазоре приходится считаться с трением о
поверхности, ограничивающие зазор. По-видимому, в каждом част-
ном случае должен существовать оптимальный осевой зазор, вели-
чина которого тем больше, чем неравномернее поле скоростей на
выходе из сопловой решетки.
Однако, кроме указанных выше факторов, надо считаться еще с
утечкой- газа или подсосом его через осевой зазор в корневом сече-
нии и через радиальный зазор на периферии. Поэтому при выборе-
зазора надо учитывать, является он «открытым» или «закрытым»
(когда имеются лабиринтовые уплотнения, препятствующие утечке
газа или подсосу газа). Отсутствие уплотнения вызывает размыв
потока у концевых поверхностей проточной части и утечку газа как
на периферии, так и у основания лопаток, если в струе давление вы-
ше, чем в пространстве, ограничивающем ее. Это всегда наблюда-
ется на периферии лопаток, и газ, прошедший через осевой зазор,
проходит далее через радиальный зазор и работы не совершает.
В основании лопаток, где часто между корпусом и диском тур-
бины подается охлаждающий воздух, утечка газа наблюдается ре-
же. Зато при пониженном давлении в осевом зазоре у основания
лопаток (причины понижения давления здесь пояснены в § 1.2) мо-
жет происходить подсос газа (или воздуха) в проточную часть осо-
бенно интенсивный в том случае, если входная высота рабочих ло-
паток h2 больше высоты сопливых hi. При открытом зазоре увели-
чение осевого зазора приводит к снижению к. п. д. турбины.
Иначе обстоит дело с закрытым зазором, т. е. перекрытым по
концевым поверхностям. Перекрытие зазора ограничивает и раз-
мыв струи, и подсос, и утечку газа. В зависимости от величины за-
зора в уплотнении изменение величины осевого зазора в известных
пределах не оказывает заметного влияния на к. п. д. ступени.
Опытами в МАИ было установлено, что имеется некоторое опти-
мальное значение осевого зазора (ба) ' при величине 6а меньше оп-
тимального неравномерность потока, вытекающего из сопел, обус-
ловливает пониженный к. п. д. рабочей решетки. При больших ве-
91
Рис. 4 23. Схемы форм перекрыши
личинах осевого зазора, как ука.
зано выше, возрастает сумма по-
терь на выравнивание поля ско-
ростей и давлений и на трение. На
основе этих опытов рекомендуется
величина 6а= (0,25 ... 0,32) Ь, что
для современных турбин ГТД мо-
жет составить 20 ... 40 мм и бо-
лее.
Перекрыта лопаток
/
В активных турбинах высота рабочих лопаток h2 должна быть
больше высоты* сопловых лопаток Ль Такое превышение Л2 над hx
возможно и в реактивных ступенях. В этом случае проточная часть
ступени в меридиональном сечении может быть выполнена пли ко-
нической или с уступом (рис. 4.23).
Величину уступа на периферии и у корня лопатки принято на-
зывать соответственно верхней и нижней перекрышей. С уступом
могут быть и безбандажные ступени.
Влияние верхней перекрыши Дп на экономичность ступени опре-
деляется, главным образом, двумя факторами: утечкой поверх ло-
паток или бандажа и изменением условий входа в рабочую решет-
ку. Увеличение верхней перекрыши, вызванное появлением внезап-
ного расширения, уменьшает количество перетекаемого через ради-
альный зазор газа и ухудшает обтекание верхней части рабочих ло-
паток.
Многочисленные исследования по выбору’оптимальной верхней
перекрыши в обандаженных ступенях показали, что AnOpt тем вы-
ше, чем больше открытый осевой зазор и степень реактивности на
периферии.	,
По опытам, проведенным на турбомоторном заводе (ТМЗ) [5],
допустимо бтклонение верхней перекрыши от ее оптимальной вели-
чины на 25% в сторону уменьшения и на 50% в сторону увеличения
перекрыши.
По экспериментальным данным И. И. Кириллова и А. А. Клим-
цова, перекрыша в’ необандаженных лопатках сильно снижает кон-
цевые потери энергии (при Дп=Дп/Л2=0,02 концевые потери сни-
зились в два раза по сравнению с Дп=0) и с этой точки зрения же-
лательно отдавать предпочтение проточной части с уступом.
Испытания активной турбины по влиянию нижней перекрыши
Дк, ^проведенные на ТМЗ, показали слабую зависимость к. п. д.
от Дк.
Максимальный к. п. д. получается при нулевой нижней пере-
крыше. Дополнительные опыты с подсосом газа также не показали
влияния Дк.
92
Qnp
г,о
и
1.2
j 0,0-0,2 О 0,2 0,0 0,6 L=~
•-Нез перегородки
о-перегородка с 3=0,16
•-	,,	С 8=0,2
а-	,,	с 3=0,05
л-	6ориант„Ва
X - перегородка.
вариант „Г

Рис. 4.24. График зависимости профильных потерь от формы, размеров и места
расположения перегородок
§ 4.12.	ВЛИЯНИЕ СТОЕК, РАСПОЛОЖЕННЫХ ПЕРЕД
СОПЛОВЫМ АППАРАТОМ, НА ПОТЕРИ В РЕШЕТКЕ
Во многих газотурбинных двигателях перед сопловым аппара-
том располагаются силовые стойки, которые приводят к росту по-
терь в сопловых лопатках. По опытам работы [9], величина по-
терь зависит от толщины стоек и места расположения их по шагу
сопловых лопаток. Из рис. 4.24 [9] видно, что наибольшие потери
возникают при центральном расположении стоек относительно
межлопаточного канала и растут с увеличением толщины стоек.
Таким образом, скоростные коэффициенты сопловых и рабочих
лопаток, равные <р (Ф)=У'Преш= V1 — С> зависят от геометрии
самих решеток, от режима их работы и могут быть определены по
изложенным в этой главе зависимостям и графикам.
У существующих турбин авиационных газотурбинных двигате-
лей потери в сопловых решетках составляю! 6... 4%, а в рабочих
лопатках — 8... 6%, что соответствует <р=0,97 .. .0,98 и ф—
==0,96 ... 0,97.
В турбинах турбонасосных агрегатов ЖРД и во вспомогатель-
ных турбинах потери в решетках значительно больше, чем в соот-
ветствующих решетках авиационных ГТД, и соответствуют <р=
=0,94 ... 0,95 и ф=0,88 ... 0,92.
93
Глава V
ОСНОВЫ РАСЧЕТА ПРОСТРАНСТВЕННОГО ПОТОКА
В ПРОТОЧНОЙ части турбины
§ 5.1.	ОСОБЕННОСТИ ПРОСТРАНСТВЕННОГО ПОТОКА
В ПРОТОЧНОЙ ЧАСТИ ТУРБИНЫ
В предыдущих параграфах книги неоднократно отмечалось, чТо
поля скоростей и давлений газа при проходе газа через решетку
неравномерны как по шагу решетки, так и по высоте ее. Отмеча-
лось также действие инерционных сил на частицы газа в проточ-
ной части, обусловливающих, в частности, переменную реактив-
ность по высоте лопаток. Однако при этом предполагалось, что ли-
нии тока в меридиональном разрезе турбины представляют собой
прямые линии, параллельные оси турбины и являющиеся образу-
ющими цилиндрических поверхностей тока. Развертка каждой из
таких поверхностей представляла собой плоскость, в которой лежа-
ли векторы абсолютной и относительной скоростей, приложенных к
частице газа. Другими словами, рассматривался двухмерный поток
на том или ином радиусе проточной части. В порядке исключения
рассматривались вторичные течения в канале и обусловленные ими
концевые потери в решетке.
В настоящей главе рассмотрены особенности трехмерного пото-
ка в ступени турбины. Эти особенности вызваны: 1) изменением
окружной скорости по высоте решетки; 2) возникновением инерци-
онных радиальных сил /\т—си2!г, приложенных к частицам газа
по направлению к'периферии ступени (Ат — элемент массы на ра-,
диусе г, си — тангенциальная составляющая скорости); 3) возмож-
ной непараллельностью меридиональных линий тока оси турбина
(рис. 5.1), вызывающей появление радиальной составляющей ско-
роста потока сг (рис. 5.2); 4) возможной кривизной меридиональ-
ных линий тока (рис. 5.3) и появлением в связи с этим сил, кото-
рые могут быть направлены как к оси, так и к периферии турбины.
Изменение окружной скорости по высоте лопатки даже в пред-
положении постоянства вектора абсолютной скорости q выхода из
сопловой решетки вызывает переменность от-
носительной скорости Wi и угла входа Pi на ра-
бочие лопатки (рис. 5.4). Это обстоятельство,
очевидно, диктует необходимость изменения по
высоте решеткй и входного угла Р1геом лопат-
ки, т. е. необходимость закручивать входную
кромку лопатки в сторону увеличения угла
Pi геом от основания к вершине.
Но на величину угла Pi влияет и'другое об-
стоятельство. Центробежные силы, приложен;
ные к частицам газа вследствие закрутки пото-
ка, создают переменное по высоте канала дав-
Рис. 5 1. Схема конической проточной части
94
Рис. 5.2 Схема проточной части и составляющие скорости потока
ление газа, повышающееся от основания к вершине лопаток. Как
указано в § 2.2, это создает переменную по высоте лопатки реак-
тивность, возрастающую от основания к вершине лопаток.
В связи с изменением реактивности по высоте решетки меняют-
ся и скорости газа, в частности, уменьшается, что вызывает еще
более резкий рост .угла |Ji и еще более резкое изменение скорости
Wi по сравнению с тем случаем, когда учитывается только измене-
ние окружной скорости. В решетках с относительно короткими ло-
патками описанными явлениями пренебрегают, ведут расчет тур-
бины по среднему диаметру и выполняют лопатки с постоянным по
высоте профилем.
При отношении среднего диаметра облопачивания к высоте ло-
патки dcpfh<z8 ... 10 пренебрежение влиянием инерционных сил
и переменностью окружной скорости часто ведет к заметному па-
дению к. п. д. ступени, вызванному веерными потерями (см. § 4.5).
Поэтому в настоящее время во всех турбинах (а в газовых — почти
с первых лет их применения в авиации) профилируют лопатки с
учетом переменных по высоте как реактивности, таю и окружной
скорости.
В советской литературе первым указал на целесообразность та-
кого профилирования В. В. Уваров. Он разработал методику газо-
динамического расчета длинных лопаток для потенциального по-
тока без потерь.
§ 5.2.	УРАВНЕНИЕ РАДИАЛЬНОГО РАВНОВЕСИЯ ЧАСТИЦ ГАЗА
Для изучения пространственного потока в проточной части тур-
бины следует рассмотреть в первую очередь поля скоростей и дав-
лений газа в сечениях 0—0, 1—1 и 2—2 (см. рис. 5.1 ... 5.3), т. е. пе-
ред сопловыми лопатками, в зазоре между сопловой и рабочей ре-
шетки и, наконец, за рабочими лопатками. Параметры перед соп-
ловой решеткой могут меняться по радиусу, в большинстве же слу-
95.
Рис. 5.3. Схема цилиндрической проточной части с криволинейной линией тока
Рис. 5.4. Входной треугольник скоростей
чаев статическое и полное давления газа можно считать постоян-
ными по высоте лопатки, т. е. p0=const, ро*== const.
Движение идеального газа в зазоре между сопловым annapai
том и рабочим колесом (сечение 1—1), а также за рабочим коле-
сом (сечение 2—2) подчиняется уравнению движения Эйлера, ко-
торое, как известно из курса газодинамики, в цилиндрической сис-
теме координат имеет вид
1	- I ___________J_ др .
Л	\dt ~*да где	e”t' dr	'	е	да ’
4св_дсв’ , дси„	,дси _______др сисг .
dt	di *~да	а~Г где dr	'	Q	где	г '
2
dCr_дсг.дсг . \ dct_f, । дсг „_______1_ др , Д»
dt dt 'да а~1~ где а ‘ dr r Q дг г ’
(5. Г
В связи с тем, что решить систему (5.1) очень трудно, упростим
уравнения следующими допущениями:
«Ч	Л
1)	течение газа в ступени установившееся, т. е. —-=0;
dt
&
2)	поток в сечении 1—1 и 2—2 осесимметричный, т. е. —=0;
3)	коэффициенты восстановления давления ос и °л постоянны
по высоте лопатки;
4)	изменение параметров вдоль осевого зазора незначительно,
и скорость (или с2) и давление pi (или р2) на выходной кромке
соплового аппарата (рабочих лопаток) и на входной рабочих лопа-1
ток (сопловых лопаток следующей ступени) одинаковы.
Принятые допущения позволяют исключить из рассмотрения
первое уравнение системы (5.1), так как оно тождественно обраща-,
ется в нуль, а из второго следует, что движение газа в зазоре под-:
чиняется закону rcu=const.
96
Третье уравнение, называемое уравнением радиального равно*
весия, с учетом изложенных допущений принимает вид
2
дсг	। дсг_  си______1 dp
да а~Г дг т г	0 dr'
Здесь заменено на —, так как ^-=0 и —^-=0.
dr	dr	да	гд9
Применим уравнение (5.2) для сечения 1—1.
Как известно [см. формулу (2.3)],
k -р 1
(5.2)
k
pi
*
Pl
Следовательно, с учетом того, что pi*=po*oc=const, можно за*
писать
dpi 2k . Г. k-
p\	A+l L k-\
С другой стороны,
81__81 gi _Г| k~ 1
8* Pl L * + l
1
1
Pi
Тогда
1 dpi^P^
91 dr Qi
dp\___ 2k
p\dr ' k + 1
dr	dr
»_4 dXciu ] } d^cir 1
dr V cltt dr + clr dr ]•
Подставив последнее равенство в уравнение (5.2) и поделив обе
части равенства на скр2, получим
d^clr •>	^clu	। i dfrfia	। > ^cla	i2 ^0	/к Qu
~ZT~ Kcla--------Vkcla~y~~Vkcla~J- N>lr-^T‘ I0- °)
da	r	dr	dr	T(flr
Уравнение (5.3) представляет собой преобразованное уравнение
(5.2) для сечения 1—1, справедливое для любого закона изменения
температуры То* по радиусу.‘При постоянстве ТР* по г уравнение
(5.3) приобретает вид
2
dc\r „ __ clu । „ dcia । dcitt
~Т— с1а — ~—Г с1а~Г,—Гс1в-Т7
da	г	dr dr
Аналогичные уравнения получим для сечения 2—2 за рабочим
колесом. Они несколько сложнее, чем уравнения (5.3) и (5.3'), так
как давление р2* в отличие от ро* не может быть принято постоян-
ным по высоте лопаток, а закон изменения температуры Т2* по г
не отвечает соответствующему закону изменения температуры То*.
4	1337	97
(5.3')
Переменность рг* и Т2* по г вызвана тем, что при проходе через ра.
бочие лопатки 1 кг газа передает колесу энергию
Hu=-^-R(To-T2),
R—‘ 1
которая в общем случае не постоянна по радиусу.
Статическое давление газа за рабочим колесом равно
А=тг/^=
Ро	\1 о /
(5.4)
откуда
(T2\k=id(T^)
dr c л k — 1 IT J J dr
Так как
02. —в а /И\»-1
-тг— .	,
Оо но/
то
1 dP2
02 dr k— 1
Отношение температур
вом
. “(К/гд
dr 2{k— 1) K₽ dr
Т2/Т0* может быть.выражено

(5-5)
тождест-
Здесь
Т2
k— 1-21	k— 1 .2
(5.6)
4
.	2k »
k + iRTi TT\RT(>
Совместное решение равенств (5.4), (5.5) и (5.6) приводит к
следующей зависимости:
1 dp2	& (^и/скр)	1 <Лс20 _ d (^и^Скр) 1	Л£20О
---------Т c20~r Tr h20a dr
. d\.c2pu	1	<^с20и
Mor dr	Mo.
Теперь уравнение радиального равновесия (5.2) для сечения
2—2 принимает вид
2	e2 . ч2
^2-----2k	’	—
(5.7)
^(?2Qr
да	г
./Яв\
d I Т~ I
\ С*р / , rfXtaoa
dr	dr
I d\c20u 1	XC20r dT°
A,20«	-ys- dr 
(5.8)
* + 1

9B
Для случая постоянной температуры газа То* по радиусу урав-
нение (5.8) упростится п может быть записано через абсолютные
значения скоростей:
2 х
аа	г аг аг аг
Уравнения радиального равновесия (5.3) и (5.3') за сопловым
аппаратом и соответствующие уравнения (5.8) и (5.8') за рабочим
колесом отличаются членом, учитывающим изменение работы Ни
по радиусу.
Часто ступени турбины проектируют с постоянной Ни по г.
В этом случае изменение скоростей сх и С2 подчиняется одному
уравнению. При переменной температуре То* по радиусу идентич-
ность уравнений (5.3) и (5.8) получается при постоянстве по ради-
усу величины Ни1сК92.
В зависимости от изменения углов щ и 02 по радиусу меняется
пропускная способность отдельных сечений соплового аппарата и
рабочего колеса, что вызывает искривление линий тока в меридио-
нальном направлении. За выходными кромками лопаток поток га-
за в меридиональной плоскости стремится вернуться к цилиндри-
ческому или коническому течению в зависимости от формы ограни-
чивающих поверхностей у корня и периферии лопаток. Искривле-
ние линий тока в уравнениях (5.3) и (5.8) учитывается левыми их
членами, и при цилиндрических линиях тока они обращаются в
нуль. При цилиндрической проточной части в меридиональной пло-
скости радиальные составляющие скоростей газа в контрольных
сечениях также равны нулю, а следовательно, и последние члены
правых частей уравнений (5.3) и (5.8). Если в сечении 2—2 за ра-
бочим колесом искривлением линий тока можно пренебречь, то за
сопловым аппаратом при отдельных видах закрутки его необходи-
мо учитывать.
Величину отклонения по радиусу линии тока в сечении 1—1 по
сравнению с сечением 0—0 позволяет определить уравнение нераз-
рывности, проинтегрированное в интервале от гк до текущего г\-.
Дгх=Д-^---М*	(5.9)
2п ’и J coQo
гк
где Дг1=г1—г0, а скорости и плотности в сечениях 0—-0 и 1—1 от-
вечают одним линиям тока.
Подынтегральное отношение C1<t0- выразим через парамет--
_	соОо
ры среднего сечения:
CioQi ClacpQicp СрсрОрср	Cia(?i
CqQo	СрсрОоср CqCo	CiecpQicp
При переменной по радиусу температуре газа перед сопловым
аппаратом температурная неравномерность погока сохраняется
4*
99
вдоль всей проточной части турбины и температура То* может быт
принята одинаковой для соответствующих размеров г0 и гь Пс
этому
ClaQl ____Г
• л
HacpQlcp
£4-1Г1ср
и (при постоянных по радиусу р0* и ро)
Тогда
^1лсрб1ср -
Mo ^ocpQocp
где
___gpQo
^ОсрОоср
1
а-1
^lacpQlcp -	-
Z *cla 1
c0cpW0cp
Т» ____1
1а ср
j_*~ 1ч 2.
. £+bcl
k 4-1 clc₽
tg«! .	_ Xgi __
tg BlCp	Xglcp
1 + tg2«l ".
l + tg2aicP ’
M2 _ A+lMc₽
Mglcp--	-	-	'
1
fe+1 clc₽
(5.10.
Здесь и далее «ср» — индекс, характеризующий параметры на
среднем диаметре. Черта над параметром означает отношение его.
к такому же параметру на среднем диаметре.
Совместное решение уравнений (5.9) и (5.10) дает
A7l=^sZ^_J_^^nIeri+!!^LX
Гер 2г г CocpQocp • L 2
/_я	(5П1
\	Sin2«i /J	'	♦
Отношение ^lcp.t входящее в уравнение (5.11), близко м
сова
единице.
100
Найде! нию тока ном случа Прибл!	1ное по всей высоте значение Ari позволяет построить ли- в меридиональной плоскости, которую в каждом отдель- е можно выразить аналитической зависимостью. именно линия тока может быть выражена синусоидой: . .	. / я а \ r=r^Lrx sin 		. \ 2 /
Радиа., чае равна	тьная составляющая скорости в любой точке в этом слу.- „ dr л Ди	/я а \ п сг=—			 cos	] С„ r	dt	2 S]	\ 2 S1 ) а
И	/ Л \2 Д — Cla ——= — (—1 Дг, — при a=slt ди	\2s\J	/*ср
или	dXcir	 „ / д V ди	\2$i /	/*ср
Здесь	z — S1 и д7 — Afi /*Ср	/ср
В связ нуж!	и с приближенностью задания формы линии тока для ю ввести поправочный коэффициент К и тогда (5.12) Х^1д да	^*ср\2$1/
Совмес ==^<cla/t{s С	:тная запись уравнений (5.3) и (5.12) с заменой Xciu= ii приводит к следующему виду:
	(5.13) \2«1/	tg2air ( tg2ai / Ida ‘Я3«1
При за ния (5.11) стей по Bi ча: по вы( ходимый г	данном законе распределения угла ai по радиусу уравне- и (5.13) позволяют построить эпюру приведенных скоро- лсоте лопатки. Может быть поставлена и обратная зада- >ранной эпюре приведенных скоростей определяется необ- (акон распределения угла сц по г.
§ 5.3. РАЗЛИЧНЫЕ МЕТОДЫ ЗАКРУТКИ ЛОПАТОК
Из изложенного выше ясно, что параметры газа в любом попе-
речном сечении проточной части переменны по высоте решеток.
В связи с этим, а также вследствие изменения окружной скорости
по радиусу облопачивания профиль лопатки должен меняться по
высоте решетки, если желательно выдержать оптимальный угол
атаки при входе на решетку.
В уравнения (5.11) и (5.13) могут быть подставлены любые за-
висимости ai=ai (г) и найден соответствующий характер измене-
вия или- Ciu по радиусу, а следовательно, Кс1а(с1а) и Xci (ci)•
Аналогичное решение получается для сечения 2—2 с помощью
Уравнения (5.8) при условии дс2г1да=0. При помощи перечислен-
ии
ных уравнений можно определить как параметры газа в сечениях
1—1 и 2—2, так и углы входа и выхода газа на любом радиусе об-
лопачивания. Необходимое изменение этих углов и вызывает за.
крутку лопаток, которая дает возможность получить желательный
характер пространственного потока в решетке.
В общем случае закон изменения угла си по радиусу можно
представить в виде
tgai=rmtgaicp-	(5.14)
В этом случае унифицируются различные методы закрутки, что
важно при использовании ЭВМ для выбора оптимального вида за-
крутки лопаток для того или иного типа турбины. Но и в этом слу-
чае совместное решение уравнений (5.11) и (5.13) представляет
определенные трудности. Поэтому проведем решение методом пос-
ледовательного приближения.
Закон изменения приведенной скорости kcia по радиусу, необ-
ходимый для определения Aq [уравнение (5.11)], в первом прибли-
жении найдем из уравнения (5.13) в предположении цилиндрично-
сти линййтока, т. е. Д/'1==0:
dr_____। d^eia /1 _i_____1 \ _ d (tg ai) __q
r tg2 ai Tcia \ tg2ai ) tg3 a!
Проинтегрируем уравнение (5.15) с использованием
(5.14) в интервале от текущей г до r= 1:
In kcie= — (1 — т) In г 4-	In
z/и
-1
1 4- rm tg2 СС{ср 2т
1 4* tg2C&lcp
1 + tg2 Й1
1 + tg2alcp ’
или
(5.15)
условия
(5.16)

1

Зависимость (5.16) справедлива для любого постоянного значе-
ния т, отличного от нуля. Для я?=0 зависимость Xcia по г может
быть найдена из уравнения (5.15):
\ia =-COS’a, •
Г
Для значений аюр^ЗО0 и —1^/п^1 с достаточной
точности можно принять
1 -Ь Г2” tg2 a]Cp	-2т sin» е1ср
1 + tg2 aiep
Тогда	Xcie = _(i—От) cos» а.	•
f
степенью
(5.18)
Отсюда видно, что если Ао на входе в сопловой аппарат постоян-
на по радиусу, как это и было принято вначале наших рассужде-
ний, то цилиндрические линии тока для несжимаемой жидкости воз-
можны только при /п=1. При /п<1 приведенная скорость Хс1а уве-
102
ичивается к корню лопаток и уменьшается к периферии, что вы-
ЛЫВает искривление линий тока так, как это показано на рис. 5.3.
при такой форме линий тока уменьшается радиальный градиент
скорости по сравнению с тем, который получается в результате ре-
шения уравнения (5.18).
В связи с этим для определения из равенства (5.11) закон
изменения Xcia п0 г зададим в виде
U=i/r’;	(5-19)
где <7=(1— w)cos2aicP—б.
Величина 6 учитывает кривизну линий тока и определится при
решении уравнения радиального равновесия. В частном случае
при /п=1 для несжимаемой жидкости значение 6=0. При течении
сжимаемого газа линии тока искривляются выпуклостью к перифе-
рий за счет повышенной плотности потока у периферии лопаток,
что вызывает увеличение радиального градиента давления и, как
следствие, уменьшение Хс10 от корня к периферии. В этом случае б
будет величиной отрицательной.
В связи с тем, что радиальный градиент —4 с  не может изме-
dr
нить знака из-за возникшей кривизны линий тока, то при всех зна-
чениях т обязательно соблюдается неравенство 6<(1—m)cos2aiCp.
Итак, при выбранных законах изменения Zcia и а, по выражени-
ям (5.19) и (5.14) из уравнения (5.11) найдем относительный про-
гиб линии тока:
ДГ1=-(Гп~Г191(Г1~7к)	(1 —Mgicp)-M2clCp/ncos2aicp]. (5.20)
Теперь совместное решение уравнений (5.19) и (5.12) приводит
к следующему приближенному значению 6:
(дд J \2
——1 sin2a’lcpcos2a1Cp (1 — т —*М^
—------------------------------------------
ClCp) 1 ~г
mcos2alcp
(лЛ \ 2	I	(/•	1 р
-JTJ sin 2alcp (1 _ M2clcp) 11 + -*-^=— m cos2aiep
(5.21)
По опытным данным КАИ, К»0,5.
Окружная составляющая приведенной скорости Aciu равна
==‘5n’	1—( l-m) sin* alc — s'	(5.22)
rt	1ср
Абсолютная приведенная скорость
(5-23)
sin aiCp	1ср
Таким образом, ясно, что в зависимости от значения т может
существовать множество методов закрутки. Рассмотрим некоторые
из них, применяемые в практике турбостроения.
103
Постоянство циркуляции по высоте лопаток
Хотя этот метод закрутки, предложенный В. В. Уваровым, раз.
работай применительно к потенциальному потоку несжимаемой
жидкости, он широко применяется в практике конструирования
проточной части турбины в предположении постоянства температу.
ры То* по радиусу.
Циркуляция вокруг контура сопловой лопатки постоянна в том
случае, когда ciur=ciu cprcp=const
или	ёи7=1.	(5.24)
Для несжимаемой жидкости (Mcicp=0) постоянство циркуля-
ции выдерживается при т=1 {см. формулы (5.22) и (5.21)], т. е.
tga1=7tgalcp.	(5.25)
В этом случае
с1а=1 и c?=l+cos2alcp ^-1—.	(5.26)
Из закона изменения ai = ai(r) и c1==ci(r) при постоянной цир-
куляции по радиусу видно, что с увеличением радиуса возрастает
угол щ, уменьшается скорость cit растет давление газа Pi за счет
окружной составляющей Сш при неизменной Cja. В случае несжи-
маемой жидкости расход ее равномерен по высоте лопатки и ли-
нии тока цилиндрические, что соответствует принятому ранее допу-
щению. Как известно, в турбинной ступени мы имеем дело с
сжимаемым газом, плотность которого, следуя за давлением, повы-
шается к периферии и падает к корню. Пропускная способность
верхних сечений лопаток растет, и линии тока искривляются выпук-
лостью к периферии. Величину искривления Ди можно найти по
уравнению (5.11), а затем и эпюру скорости Ci = Ci(r). Она должна
оказаться с более резким изменением tj, чем по уравнению w (5.26)
за счет дополнительной центробежной силы, появившейся от иск-
ривления линий тока.
Как показывают экспериментальные исследования, в турбин-
ных ступенях, закрученных по закону постоянства циркуляции, ра-
диальный градиент давления dp]dr меньше расчетного. Поэтому
при расчете закрутки лопаток по закону rcu=const пренебрегают
влиянием плотности на форму линий тока в меридиональной плое-
кости, поток принимают цилиндрическим и.относительные скорости
определяют по формулам (5.24) и (5.26). Расхождение расчетных
и действительных параметров газа вызвано внутренним взаимодей-
ствием струек потока; влиянием радиального зазора над рабочими
лопатками, под действием которого снижается степень реактивно-
сти на периферии; отрывом потока в корне лопаток, из-за чего воз-
растает угол ai в корневой зоне.
Циркуляция вокруг рабочих лопаток r2=2n(eiU'±c2u)r. Так
как по высоте лопаток clur остается неизменной, то постоянство
104
циркуляции по радиусу будет обеспечено при с2иг-с2а сргОр
„И	<5'27’
Также как и для сечения 1—1, примем линии тока цилиндриче-
скими и тогда из уравнения (5.8х) получим
tga2=rtg a2cp.	(5.28)
В случае осевого выхода в среднем сечении (а2Ср=90°) он дол-
исен быть обеспечен по всей высоте лопатки. По полученным зако-
нам изменения абсолютных скоростей сг и с2, углов щ и а2 по ради-
усу для правильного проектирования рабочей лопатки необходимо
найти характер изменения углов и р2: первый — чтобы обеспе-
чить безударный вход на лопатку; второй — чтобы обеспечить выб-
ранный закон изменения угла а2. Из треугольников скоростей
(5.29)
Clacp
^1иср -
-ИсрГ
tg
(5.30)
лопа-
И
, о с1а	'С1аср
tg Р1=---------------------------
С1Ц—11 ^1всргср	г
~	— “ср ~
Г	'ср
С2д ___ g2qcp
а—с2и _ С2иср
ГИср--у-
(в случае а2<90° перед с2и ставится знак плюс).
Так как в практике газо- и паротурбостроения закрутка
ток по закону постоянства циркуляции является одним из наиболее
распространенных методов, на ней и остановимся более подробно.
Скорости и направления потока в различных сечениях облопа-
чивания найдем по соотношениям (5.24) ... (5.30). Давление на
любом радиусе в зазоре между соплами и лопатками можно опре-
делить из уравнения
__ k
'	2 k~ 1
k
откуда
Г /
RT*q 1 - (ЦХ *
\ро J
сп
Pi = Po
2,—
(5.31)
Аналогично давление р2 при выходе из рабочих лопаток на ра-
диусе г определяется формулой
_ „‘Гт
Р2=Ро 1—
(5.32)
л k
где в числителе стоит сумма изоэнтропных работ в соплах и рабо-
чих лопатках (без учета прироста теплоперепада на лопатках, обус-
ловленного потерей в соплах). Давления р1 и р2 можно определить
и с помощью таблиц термодинамических функций.
105
Ju=Jo-^ или Jlt=JUcp-^sf^- — l}cos2aicp и J2t
2	2 t 2	2
где	cas=cif-K®2/-®i.
По таблицам для значений и J2( найти p(Tlt) и p(T2t).
или Pi^p^ Тл~\ и р*=ра Т/FT- (5,33)
Р \J 0j	PVltCf)	„ Р\То)
Так как направление скорости с2 обычно близко к осевому, то
можно считать в большинстве случаев p2=const(r) и пользовать-
ся формулой (5.32) лишь для углов а2, значительно (на 20° и бо-
лее) отличающихся от 90°.
Степень реактивности ступени QCi=Ho2/ffo можно вычислить
на каждом радиусе по скорости газа, найденной из треугольни-
ков *:
/И»2 \2	2
,	I — I —
6И = р1\2Ф /®2\2	2=	4^	*	(5‘
I — ]	[ -2- J __	1 ।  1___________
\ Т /	\ Ф /	<р2 (да2— ф2да2)
ТО
где
В том случае, если поток на выходе из рабочего колеса имеет
осевое направление, можно пользоваться более простой формулой
для определения qct. Тепловой перепад в соплах //01=(1—рСт)Яо.
а на среднем радиусе облопачивания Я01ср=(1—Ост.ср)Яо, где Яо в
рассматриваемом случае постоянно по высоте ступени.
Из этих двух уравнений находим, что
6ст = 1 - (1 - QC г ,ср )	= 1 - (1 - & ,ср) Д
"01ср	С1ср
(скоростной коэффициент <р принят постоянным по высоте).
Та к как с? = {+ <& = ( j cos2 «юр+ CicP si п2 aIcp,
Сст=1 —(1 —е«.сР)Я,	(5.35)
cos2 aicp t .
=—--------f- Sin2 alcp.
(5.36)
Так как степень реактивности уменьшается к корню лопатки,
желательно чтобы у корня она оставалась все же положительной
или равнялась нулю.
1 Формула (5.34) приближенная, так как в знаменателе стоит величина,
несколько большая (в связи с возвратом тепла) адиабатного перепада тепла в
ступени.
106
Если принять на внутреннем радиусе $ст.к=0, то на среднем ди-
аметре реактивность определяется по уравнению (5.35):
0=1-(1-Си.ср)^	(5.37)
_. _ _1__ ._____________1___________
Qcr.cp 1 у 1	/	\2
А	/	г<4> 1	. „
I COS CCicp-I + Sin2 CCicp
\	FK7
Характерной особенностью данного вида закрутки является то,
что отношение u/ci в любом сечении лопаток остается оптималь-
ным, если оно выбрано наивыгоднейшим в каком-то сечении, так
как увеличение u/ci с ростом радиуса соответствует повышению
степени реактивности. На самом деле, при с2и Ср=0 закрутка пото-
ка за рабочим колесом отсутствует по всей высоте лопатки.
Формула для расхода газа через ступень принимает интеграль-
ную форму, так как плотность газа по высоте проточной части яв-
ляется переменной.
Элементарный расход газа через сопловой аппарат
dQ=2nrQlcladr.
На рсновании формулы (5.10)
[м2	/	д2	\ "I
1	I	mlcp	I	1	С1	I
1Т 9	I	1 ~ 2	II*
2	'	с1ср	/ J
Для данного вида закрутки
2	2.2	2.2
1 - -£-= 1 -Cla + C1“cP7C.^ptci<«.=cos2 а1ср (1 -
м2
ei=eicP 1+-^-^ cos2a1(
и интегральный расход газа равен
м»ср C0S2 а
у	®1ср
(5.38)
Тогда
Q — 2 nCjgQicpFcp
rdr~
К
(5.39)
2^1aQlcprcp^l Ч”
Meicp cos2 aicp I J rK
2	F« — гк
Так как 2nCiaQicprcpfti представляет собой расход газа, найден-
ный по среднему сечению, то
(5.40)
G=Glcp H
(1 Гп
t ° гк
гп ----
Следует отметить, что при О2=90° и с2а=const расход газа
Иожно значительно проще и точнее определить по состоянию га-
107
за за рабочими лопатками: G=ndA2Q2c2a, так как Q2 при указан-
ных выше условиях практически постоянен по радиусу. Формула
эта дает вполне достаточную степень точности и в том случае, ког-
да а2¥=90°, но лежит приблизительно в пределах 70 ... 110°.
Постоянная величина угла си
Этот метод закрутки кажется целесообразным, так как на пер-
вый взгляд представляет возможность выполнять сопловые лопат-
ки незакрученными.
Необходимо отметить, что углом си определяется истинное сред-
нее направление потока в зазоре между сопловыми и рабочими
лопатками. Так как величина этого угла зависит от отношения a/t,
переменного по высоте лопатки, а при больших скоростях и от ве-
личины М, то геометрический угол профиля соплсвой лопатки при
соблюдении данного закона закрутки не может быть постоянным
по высоте.
Пренебрегая незначительным изменением угла щ по высоте в
решетке из широких лопаток постоянного профиля, можно все же
рассчитать параметры потока в сечении 1—1, применяя уравнения
настоящего метода закрутки, приведенные ниже.
В случае узких длинных сопловых лопаток с постоянным про-
филем по высоте, изменение угла си близко к закону tgai=rtgaicp.
При желании сохранить постоянным угол сц по высоте в таких ре-
шетках сопловую лопатку нужно подкрутить.
Закон закрутки сопловых лопаток с постоянным углом ai так-
же, как и предыдущий метод, широко применяется в практике тур-
бостроения. Его принято рассматривать в предположении цилинд-
ричности линий тока (Дп=Дг2=0). В этом случае воспользуемся
уравнением (5.17)
i ___	1
cl	—cos* ax '
Ас1Ср Г
При постоянной температуре газа То* перед сопловым аппара-
том
~с — С1 —	1
1 dep 7СО8’“*’
Так как const, то 
Cla = -cos>a, И <:>e=-cos«al *	(5.41)
Г	Г
Абсолютная скорость ct падает от корня к периферии как за
счет окружной составляющей, так и за счет осевой. При течении
несжимаемой жидкости изменение с1а приводит к перераспределе-
нию расхода газа по высоте, и линии тока искривляются выпукло*
стью к корню лопаток.
В сжимаемом газе повышенная плотность в периферийных сече-
ниях уменьшает кривизну линий тока и при Лсь равном 0,7... 0,9
108
(в зависимости от щ, djh), поток в меридиональной плоскости ста'
новится цилиндрическим.
Закрутка рабочих лопаток производится из условия постоянст-
ра работы Ни, что предопределяет закон изменения скорости c2tt:
— Ci«cp с1вср ±
62в—-cos’s, ----=------- (о» 42)
Уравнение радиального- равновесия за рабочим колесом имеет
вид (5.8')
tg2 а2—+tg aj (tg а2)+ ~
Г	С2и	<>2и
В этом равенстве заменим tga2 через с2и и c2a: tga2=c2a/c2u>
тогда
^-d (с2иг)-|_<?2а^С2а==0’
Интегрирование равенства в интервале от 1 до г с учетом зако-
на изменения с2« дает нам зависимость с2а от радиуса:
I Ctacp I 1	1 О СО82«1 /, , g2acp \ /	1_____j
+ 4ср b2008*'* l+coS2aj\ * С1иср Д7Н-«о»’«.
(5.43)
По уравнениям (5.34) и (5.35) не трудно найти углы 01 и р2.
Интегральный расход газа
С	сл -
G=2.-t \ re1cierfr=2nclfl cpQicprcpX Ci0-Si- г dr.
г	J Olcp
к	г
гк
Для данного вида закрутки .
7 __	1 и Qi ______1 > ^cicp /,_________1	\
la -cos* 41 п	। о t —2 cos* «ц | ’
Г	Vlcp	x \ r f
тогда	,
q .Qcp_ [(и MM n~co8,gt-n~co841
L \	2 /	2 —• cos2 аг
M2 72—3,cos« at 72—3cos«at1
__2 rlcp ' n______rK	I
2	2 —3cos2ai Г
Последняя зависимость может быть заменена следующей при-
ближенной формулой:
G=Gcp [1 — (1 — глгк) cos2 04 [sin2	( cos2 a!— —2--1lL
*	L	2 \	3 JJ
(5.44)
109
Ступени с уменьшенным градиентом реактивности
В рассмотренных выше методах закрутки лопаток скорость газа в осевом
зазоре уменьшается от корня к периферии, что ведет к увеличению статичес-
кого давления pi по радиусу, а следовательно, и реактивности.
Увеличение реактивности по радиусу приводит к повышенным радиальным
перетеканиям на периферии и возможной отрицательной реактивности у корня.
Поэтому понятно стремление ряда исследователей спроектировать ступень с
постоянной реактивностью по радиусу или с пониженной разностью Дрст=рст п—
Рст к, где рстп и рст к соответственно реактивность на периферии и у корня.
Так как изменение давления по радиусу происходит за счет инерционных
сил Д/п —»то для уравновешивания их необходимы другие силы, направленные
в обратную сторону. Такие силы появятся, если линии тока направить не по
прямым, параллельным оси турбины, а по криволинейным поверхностям, подчи-
са
няющимся определенному закону (см. рис. 5.3), и будут равны Дт —, где Я —
•
радиус кривизны линии тока. На этом принципе и основаны все предложенные
методы закрутки ступени с уменьшенным градиентом или даже постоянной ре
активностью по радиусу.	е
М. Е. Левина и Л. И. Слободянюк получили расчетным путем для актив-
ной ступени с постоянной нулевой реактивностью по всей высоте лопами
меридиональный профиль проточной части на периферии, показанный на рис. 5 5.
Там же приведен характер изменения составляющих скоростей газа в каналах
проточной части. Постоянство давления в этом зазоре было проверено опытами
на передвижной кольцевой решетке. В опытах Ю. И. Митюшкина также подт-
верждено выравнивание реакции по высоте ступени при меридиональном ее про-
филировании. Другим путем снижения градиента давления в межвенечном зазоре
является наклон сопловых лопаток вогнутостью к оси
турбины. В этом случае появляется радиальная со-
ставляющая сила, с которой лопатка действует на
газ, в результате чего наблюдается искривление ли-
ний тока и, как следствие выравнивание давления pi
по радиусу. Такие решетки были испытаны в Мо-
сковском* энергетическом институте (МЭИ), в Ленин-
градском кораблестроительном (ЛКИ). Необходимо
обратить внимание на то, что наклон лопаток улуч-
шает вибрационные характеристики, о чем более под-
робно сказано в § 13.7.
В МЭИ взамен наклоненных лопаток предложено
применение криволинейных (саблевидных) лопаток,
пример которых дан на рис. 5.6. В таких лопатках
можно осуществить произвольный закон изменения
реактивности по радиусу.
Рис. 5.5. Схема ступени с постоянной реактивностью
Рис. 5.6. Схема саблевидных лопаток ‘
ПО
Третьим пунктом снижения радиального градиента давления в межвенечном
зазоре является специальная закрутка соплового аппарата с уменьшением угла
3	*	tg aicP\
ai от корня к периферии, т. е. при т<0 (например, по закону tgcq =—=—Г
В этом случае периферийные сечения сопловой решетки не способны пропустить
то количество газа, которое вошло в них; газ устремляется к оси турбины, ли-
нии тока искривляются, что и уменьшает радиальный градиент давления.
При уменьшении угла oti от корня к периферии пренебрежение кривизной
линии тока недопустимо, так как ее влияние на градиент давления соизмеримо
%
С влиянием инерционных сил Д/и —.
Геометрия ступени с уменьшением угла оь к периферии существенно отли-
чается от геометрии ступеней, закрученных по закону ai = const или tgai =
=7tgaicp(^ur=const). В последних типах закрутки геометрия сопловой лопат-
ки очень слабо меняется по высоте, но сильно закручены рабочие лопатки.
С уменьшением ои к периферии, наоборот, закрученным оказывается сопловой
аппарат, а диапазон изменения угла pi по радиусу сокращается. Закрутка лопа-
ток рабочего колеса при таком методе может быть выполнена или по закону
Ни=const, или p2=const. Соответствующей закруткой соплового аппарата можно
достичь полного выравнивания давления у корня и на периферии, но в этом слу-
чае требуется сильное изменение угла ai по г и в длинных лопатках он становит-
ся недопустимо малым на периферии. С другой стороны, по мере выравнивания
реактивности по высоте лопатки увеличивается неравномерность потока по ра-
диусу на выходе из ступени, и возрастают выходные потери.
§ 5.4. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ ЗАКРУТКИ ЛОПАТОК
Характер изменения некоторых параметров при различных ме-
тодах закрутки лопаток указан при рассмотрении этих методов.
Критериями для сравнения между собой различных законов зак-
рутки являются: пропускная способность ступени, характер изме-
нения степени реактивности по высоте лопатки, характер измене-
ния углов лопаток Щгеом, ₽1гсом, Рггеом и к. п. д. ступени.
Пропускная способность ступени может быть охарактеризова-
на коэффициентом
а
л</А101срС1дср
представляющим собой отношение расхода газа через ступень к
расходу, вычисленному по параметрам на среднем диаметре ступе-
ни. Расчеты показывают, что пропускная способность ступеней,
спроектированных по различным методам закрутки, практически
одинакова, и коэффициент 1.
Изменение степени реактивности по высоте проточной части за-
висит от угла си на среднем диаметре и закона его изменения по
радиусу. По мере увеличения угла а1ср и с уменьшением его к пе-
риферии падает разница AqCt = Qct.ii—Qct.k. Для наиболее распрост-
раненных методов закрутки лопаток по законам rcu = const и си =
= const характерны наиболее резкие изменения степени реактив-
ности С Практически ОДИНакОВЫМ Диапазоном AQCT = QcT.n—Qct.k-
На рис. 5.71 дана зависимость реактивности рст.к у корня лопат-
ки от реактивности qct на среднем диаметре для различных отно-
1 Заимствован из работы [21].
111
Рис. 5.7. График зависимости степени реак-
Г .г	- —	J/»
ре-
по
по
тивности у корня рк от отношения d/h
различных законах закрутки и различных
активностях на среднем диаметре:
------------rcu=const;---«i-const
шений d/h и двух методов закрутки:
закону постоянства циркуляции и
закону ai = const (при расчетах угол си
был принят в 30°). При малых значе-
ниях d/h в основании лопаток появля-
ется значительная отрицательная реак-
тивность. Чтобы избежать ее, надо на-
значить высокую степень реактивности
на среднем диаметре, например, при
d/h=^ величина Qct должна быть 0,4
ПрИ Qct.k ~ 0.
Как уже отмечалось, многочислен-
ные экспериментальные данные, полу-
для незакрученных и закрученных по
ченные в ряде организаций
закону ai = const или cMr=const ступеней, показали меньшую раз-
ность Дрст=бст.п — Qct.k по сравнению с расчетной. Отклонение
Aqct от Aqct. расч увеличивается с увеличением радиального зазора,
ухудшением уплотнения корневой зоны, увеличением величины
верхней и нижней перекрыши.
Характер изменения угла щ по радиусу зависит от вида закрут-
ки лопаток и наибольшее увеличение к периферии наблюдается
при закрутке лопаток по закону постоянства циркуляции.
Угол р2 обычно уменьшается примерно с такой же интенсивно-
стью, с какой растет по высоте лопаток угол си. В турбинных сту-
пенях со сравнительно короткими лопатками, когда d/h>§, измене-
ния углов си и 02 незначительны, что позволяет профилировать ло-
патки с постоянными углами сигеом и 02геом. Технологическая
целесообразность такого профилирования очевидна.
Угол резко растет по высоте решетки. На рис. 5.8 показана
зависимость угла pt от г для турбинных ступеней. Наиболее интен-
сивно меняется угол Pi для закрутки rcu = const.
Интенсивность изменения угла 0! по высоте решетки создает оп-
ределенные трудности при профилировании лопаток. Поэтому часто
допускают на вершине отрицательный, а в основании — положи-
тельный углы атаки, чтобы угол 01геом не менялся в столь широких
пределах, как угол '01. Положительный угол атаки в корневом се-
чении оказывается целесообразным и потому, что действительный
угол 0! всегда больше расчетного. Поэтому при проектировании
турбинной ступени в корне лопаток расчетный угол 0iK допускают
на 5... 7° меньше угла <02к, а профилируют лопатку с углом
₽1^.геом=|02к«
В ступенях, закрученных с уменьшением угла <xi к периферии,
угол 01 по радиусу изменяется незначительно или остается постоян-
ным.
112
Рис 5 8. График изменения угла pf
Г для различных законов закрутки
К. п. д. ступени является,
очевидно, важнейшим критери-
ем сравнения различных мето-
дов закрутки. Как известно из
гл. П, к. п. д. ступени зависит
от различных факторов, в том
числе от отношения u/ci или
til Сал *•
При любом методе закрутки
окружная скорость возрастает
по высоте лопатки, а скорость
d уменьшается (за исключени-
ем случая QcT=const). Поэто-
му отношение u/ci всегда растет от корня лопатки к периферии.
В то же время в связи с ростом реактивности растет по высоте ло-
патки и оптимальная величина и/d. Как отмечалось выше, для за-
крутки по закону постоянства циркуляции при изоэнтропном тече-
нии оптимальной величине u/ci в одном сечении по высоте проточ-
ной части соответствует оптимальное же значение u/ci в любом дру-
гом сечении. Таким образом, достаточно выбрать оптимальное m/ci
для среднего диаметра облопачивания, чтобы во всех цилиндриче-
ских сечениях ступень работала с благоприятным отношением и/Сь
Это правило в меньшей степени, но выдерживается и в ступенях с
постоянным углом <Х1 по радиусу. При отрицательном градиенте
угла си по высоте решетки (пг<0) поле скоростей на выходе из
ступени неравномерно по радиусу, что приводит к неравномерно-
сти давления и к повышенным выходным потерям.
На к. п. д. влияют потери в решетках, которые в свою очередь
зависят: 1) от угла атаки при входе на рабочие лопатки (при всех
видах закрутки он может быть выбран оптимальным); 2) от ради-
альных составляющих скорости газа, которые (практически) отсут-
ствуют при закрутке по методу rcM=const и ai=const
Влияние многочисленных факторов на к. п. д. облопачивания
лучше всего учесть сравнительными испытаниями.
На рис. 5.9 приведены результаты испытаний четырех турбин-
ных ступеней с длинными лопатками (0=3,5), проведенных в КАИ.
Ступени отличаются типами закрутки лопаток при одинаковых
профилях в среднем сечении. Как видно из графиков, метод закрут-
ки лопаток оказывает влияние на эффективность ступени и наи-
больший выигрыш в к. п. д. r]f (учитывающий потери в решетках,
выходные потери, от радиального зазора и потери на трение диска о
газ) по сравнению с цилиндрическими (незакрученными) лопатка-
ми наблюдается в турбинных ступенях, лопатки которых закруче-
* 1	является для реактивной ступени фиктивной скоростью, соот-
ветствующая ей кинетическая энергия с^л/2 эквивалентна адиабатическому пере-
паду тепла в ступени; для активной ступени сад=Сц.
113
Рис. 5.9. График изменения внутреннего к.п.д. в функции н/сад для различных
законов закрутки
ны по закону постоянства циркуляции. Метод закрутки оказывает
слабое влияние на к. п. д. в заторможенных параметрах г^*, кото-
рый отличается от тн тем, что не учитывает выходные потери. Это
свидетельствует о том, что расхождение в к. п. д. ц; вызвано боль-
шей или меньшей степенью неравномерности потока на выходе из
рабочего колеса (выходной потерей).
Графики на рис. 5.9 построены для турбинных ступеней с отно-
сительным радиальным зазором над рабочими лопатками &rlh2=
=0,02. Как показали опыты, с увеличением зазора выигрыш от за-
крутки падает, кроме того уменьшается преимущество _ступеней
закрученных по закону постоянства циркуляции, и при 6=S,//?2>
>0,05 к. п. д. ступени с обратной закруткой лопаток выше к. п. д
всех остальных ступеней.
Обращает на себя внимание более пологая характеристика тур-
бинной ступени с цилиндрическими лопатками по сравнению с за-
крученными. Это объясняется более слабой зависимостью скорост-
ного коэффициента ф у цилиндрических лопаток по сравнению (
закрученными от и/сад.
Экспериментальные исследования по оценке влияния закрути
лопаток' на эффективность турбинной ступень
проводились и проводятся в ряде организаций
Качественная картина влияния закрутки н£
к. п. д. турбины отвечает графикам на рис. 5.9.
Рис. 5.10. Схема совмещенных профилей сопловой лопатю
на различных радиусах меридионального сечения:
/—корневое; 2—среднее; 3—п евиферийное
114
Количественную оценку дать затруднительно, так как она зависит
^уг ряДа Факторов, как отношения dfh=Q (с увеличением 0 влияние
закрутки снижается и полностью пропадает при 0^10), степени
реактивности на среднем диаметре, относительной ширины лопа-
ток, перепада давлений на ступень и т. п., и степень влияния каж-
дого из них нельзя считать окончательно выясненной.
§ 5.5. ПОСТРОЕНИЕ ЛОПАТОК ПЕРЕМЕННОГО ПРОФИЛЯ
По высоте лопатки намечают ряд поперечных сечений, в которых произво-
дят -расчет параметров профиля и его построение. Крайними являются обычно
сечения, отстоящие на 2 ... 4 мм от радиальных границ потока, так как про-
фильная часть (перо) лопатки переходит в замковую часть с большим радиусом
закругления, а на периферии лопатка часто заостряется. Расстояние между
крайними сечениями делят обычно на четыре части, и для этих сечений на основе
расчета, подобного приведенному в § 53, строят профили лопатки по той или
иной методике, например, по описанной в § 4.10.
Кроме углов входа и выхода, при построении каждого профиля надо при-
нимать во внимание ширину и толщину профиля. Ширина рабочих лопаток
может оставаться постоянной или уменьшаться к периферии (в этом случае
ширину сопловых лопаток можно увеличивать к периферии, чтобы сохранить осе-
вой зазор неизменным по высоте; уширение сопловых лопаток целесообразно с
точки зрения сохранения по высоте оптимального шага t—t]b). Толщину профи-
ля следует уменьшать от основания к периферии для снижения напряжений в
корневом сечении. В сильно нагруженных лопатках максимальную толщину
периферийного профиля доводят до 0,25 толщины профиля в основании, причем
абсолютная толщина периферийного профиля должна быть не менее 2 ... 3 мм.
Профиль сопловых лопаток можно сделать переменным, повернув неизмен-
ный профиль вокруг центра входной кромки, как показано на рис. 5.10. При
этом ширина профиля увеличивается к периферии.
Характер профилей рабочих лопаток (в трех сечениях) показан па рис. 5.!1
и 5.12 \ В этих профилях вогнутая поверхность описана дугами двух радиу-
сов, подобранных так, чтобы поверхность можно было фрезеровать конической
фрезой, поворачивая лопатку вокруг оси. Средняя линия профиля представляет
собой параболу.
Рис. 5.11. Схемы профилей рабочей лопатки
1 Рисунки заимствованы из работы [21].
115
Рис. 5.12. Схема совмещения профилей (см. рис 5 ] 01
в различных сечениях:	'
Проекция оси поворота лопатки; 2—проекция оси Фоезы
На рис. 5.11 под профилями показаны разверт-
ки каналов, из которых видно, что в корневом сече"
нии не удалось избежать небольшой диффузорности
при входе.
 При совмещении профилей (см. рис. 5.12) стре,
мятся к тому, чтобы центры тяжести всех сечений ле-
жали на одной радиальной линии, проведенной из
центра вала через ось замка и центр тяжести корне-
вого сечения. Иногда центр тяжести лопатки в целом
смещают относительно указанной выше радиальной
линии в сторону к вогнутой поверхности корневого
сечения (см. рис. 5.12). Этим создается изгибающий
момент от центробежной силы (§ 12.3),уравновеши-
вающий момент от давления газов.
Для облегчения механической обработки входную и выходную кромки по
высоте желательно выполнять прямолинейными; кромки могут также вписывать-
ся в цилиндр, конус или другие поверхности вращения.
Радиусы входных и выходных кромок обычно уменьшаются к периферии
(часто по линейному закону).
На рис. 11.10 показана типичная лопатка переменного профиля с елочным
хвостовиком (см. § 11.2) и заостроенным профилем на периферии до 1 мм но
всему контуру. Относительно осей х—х и у—у можно указывать координаты
профиля в различных сечениях.
Глава VI
К. П. Д. СТУПЕНИ. РАСЧЕТ СТУПЕНИ
§ 6.1.	ПОТЕРИ В ТУРБИНЕ
Потерями в турбине (ступени) называют разность работы иде-
альной турбины, работающей без потерь с адиабатическим расши-
рением газа, и работы на валу действительной турбины. Потери
сводятся к следующим видам: 1) потери в сопловой решетке; 2) по-
тери в решетке рабочих лопаток; 3) выходная потеря; 4) потери на
утечку; 5) потери от охлаждения горячих частей турбины; 6) по-
тери вентиляционные и на трение диска в газе; 7) механические
потери.
Первые три вида потерь относятся к так называемым потерям
на венце турбины. По сравнению с другими потерями по величине
они являются основными и более всего влияют на к. п. д. турбины.
За исключением механических потерь, все остальные относятся к
внутренним потерям, происходящим внутри корпуса турбины и не-
посредственно влияющим на состояние или на расход газа *.
1 Исключение составляют потери на трение диска в газе, которые, как пра-
вило, не влияют на состояние или на расход газа в турбине (см. § 6.5).
116
Дополнительные потерн от охлаждения горячих частей турбины,
оказывающие влияние на рабочий процесс ступени и ее к. п. д., де-
тально рассмотрены в § 9.8.
Механические потери (турбины и компрессора вместе) в боль-
шинстве случаев относятся к числу потерь ГТД в целом и учитыва-
ются при определении к. п. д. двигателя. Здесь о механических
потерях следует говорить лишь тогда, когда турбина не находится
на одном валу с компрессором, а последний имеет самостоятель-
ный привод.
Потери в сопловой и рабочей решетках рассмотрены в гл. IV.
Рассмотрением в следующем параграфе выходной потери заканчи-
вается изучение общих законов преобразования энергии на венце
турбины..
§ 6.2.	ВЫХОДНЫЕ ПОТЕРИ
Потеря эта вызвана тем, что газ на выходе из рабочих лопаток
обладает некоторой скоростью Сг, а следовательно, и кинетической
энергией (на 1 кг газа)
//e=d/2.
Так как в данной ступени эта часть кинетической энергии газа
осталась неиспользованной, то ее надо отнести к числу потерь да-
же в том случае, если она используется в последующей ступени для
создания реактивной тяги самолета. В любом из этих случаев ра-
бота, развиваемая данной ступенью, снижается на величину вы-
ходных потерь. Однако следует подчеркнуть, что для авиационного
ТРД или ТВД кинетическая энергия газа, выходящего из лопаток
турбины, используется в реактивном сопле, и поэтому величина Я»
для ГТД в целом не является потерей.
В тех ступенях, за которыми выходная скорость не использует-
ся, она рассеивается и теряется от удара струи газа о неподвижные
детали турбины; при этом теплосодержание выходящего из турби-
ны (или отдельной ступени) газа повышается на величину Нв.
Как указано в § 1.3, выходная потеря зависит от отношения
«М и лишь при определенной его величине достигает минимума.
В этом случае скорость с2 имеет осевое направление: c2=utg р2;
Нв = —. Адиабатическая работа в ступени HQ=c2aJ2, где
Сад —фиктивная скорость, смысл которой пояснен в § 5.4. По отно-
шению к адиабатической работе выходные потери составляют
/7о	/
Если, например м/сад=0,55; р2=30°, то Нв /Яо=О,1, т. е. выход*
ные потери в этом случае составляют 10% от адиабатического пе-
репада тепла.
Конечно, в ТРД кинетическая энергия газа на выходе из турбин
Не может рассматриваться как потеря, так как она используется в
НТ
реактивном сопле для получения тяги. Однако и в этом случае по
ряду особенностей работы двигателя необходимо стремиться к ог-
раничению выходной скорости. Выбор выходной скорости определя-
ется соображениями прочности лопатки последней ступени турбц.
ны: чем меньше с2, тем длиннее лопатка, тем больше напряжение
в ней.
§ 6.3.	ПОТЕРИ НА УТЕЧКУ ЧЕРЕЗ ЛАБИРИНТНЫЕ УПЛОТНЕНИЯ
Потери на утечки вообще можно разбить на две группы: 1) по-
тери через уплотнения ротора в тех местах, где может перетекать
газ (или охлаждающий воздух); 2) потери на утечку через ради-
альный зазор рабочих лопаток, а в многоступенчатых турбинах —
и сопловых лопаток.
В газовых турбинах для снижения утечек применяются исклю-
чительно лабиринтные уплотнения, схема устройства и принцип
действия которых представлены на рис. 6.1.
Весь перепад давлений распределяется между несколькими ла-
биринтными камерами. При проходе через первую щель давление
газа падает до величины р'. В камере А, куда попадает газ, ско-
рость, возникшая в результате расширения газа, полностью или
частично теряется вследствие удара о стенки и вихреобразования,
а теплосодержание газа, понизившееся при расширении, вновь дос-
тигает начальной величины. В следующей щели давление газа па-
дает до величины р"‘, в камере В скорость газа теряется, теплосо-
держание вновь достигает начальной величины и т. д.
На рис. 6.2 приведено описанное изменение состояния газа на
диаграмме г—S. Линии AAt', BBt', CCt' изображают адиабатное
расширение газа в щелях от статических давлений pi, р', р",..
линии А/В,, Bt'C — повышение теплосодержания, вызванное поте-
рями /7П при расширении в щели и частичной потерей скорости в
камерах. Над точками А, В, С отложена величина кинетической
энергии газа Со2/2 (не потерянной полностью) при входе в щель.
Так как при расширении газа в лабиринте работа не производится
и точки Д*, В*, С* лежат на линии .по-
стоянного теплосодержания, то в конеч-
ном итоге расширение в лабиринте пред-
ставляет собой процесс дросселирования
(i*=const; 7’*=const).
Очевидно, с увеличением числа лаби-
ринтов перепад давлений в каждом из них
уменьшается; это вызывает снижение ско-
рости газа, а значит и расхода газа через
лабиринт.
Так как для каждой из щелей спра-
ведливо уравнение Gv=fc, то, имея в ви-
ду одинаковый расход газа через каждую
щель и одинаковую величину проходного
А В С
Рис. 6.1. Схема лабиринтного уплотнения
118
Рис. 6 2. Диаграмма i—S теплового процесса в лабиринтном уплотнении
сечения (разницей диаметров на рис. 6. 1 можно пренебречь), по-
лучаем соотношение clv=Glf= const.
По мере расширения газа его удельный объем возрастает, сле-
довательно, должна возрастать от щели к щели и скорость газа,
т. е. перепад тепла в ступени лабиринта должен увеличиваться,
как это показано на рис. 6.2. Точки Д', В', С' на этой фигуре долж-
ны лежать на одной кривой, удовлетворяющей условию c(v=const.
Кривые c/v — const, построенные для различных значений G/f, на-
зываются кривыми Фанно.
Так как скорость газа в щели не может превысить критическую,
а наибольшая скорость возникает в последнем лабиринте, то кри-
тическая скорость, если она вообще достигается, может возникнуть
лишь в последнем лабиринте; во всех предыдущих щелях скорость
газа всегда меньше критической.
Приближенная теория лабиринтного уплотнения, разработан-
ная Стодолой, получила широкое распространение в практике тур-
бостроения. Определение утечки газа через лабиринтное уплотне-
ние основывается на следующих предположениях: 1) скорость, при-
обретаемая газом на проходе через лабиринтную щель полностью
Дросселируется в лабиринтной камере; 2) в пределах одного лаби-
ринта газ принимается несжимаемым. Тогда
у v •' у v	У RT*	V 7
где	.
р’ +Р"
Суммарная запись утечки, записанной для каждой щели в фор-
ме уравнения (6.1) в случае докритической скорости в последнем
лабиринте, т. е. при Р2/Рх>екр, где рх — давление в последней ла-
биринтной камере (см. рис. 6.1), дает:
Gvr = p./ |/ —	(6.2)
\	2
119
где f — площадь поперечного сечения щели лабиринта; рь р2 __
соответственно давления газа перед и за лабиринтом; oi — удель-
ный объем газа перед лабиринтом; z — число лабиринтов; р — Ко.
эффициент расхода.
Если же р2/Рх<еКр, то формула (6.2) справедлива для первых
(z—1) лабиринтов:
[1 - (Дг/А)2]
(z-1)
С другой стороны, расход газа через уплотнение можно найти
по формуле, вытекающей из (3.44):
Из совместного решения двух последних формул находим
и
°ут	V1 [jJ2(z_1) + 1]
р — —— P1 — -
/₽2(г-1) + 1
(6.3)
(6-4)
Критическая скорость в последн.ем лабиринте установится в
том случае, когда р2/рх<рКр/рж=екр.
Критическое давление Лр=екрРл=екр
Pi
/₽2(г-1) + 1
екр
Таким образом, при —	---------
н н A PW-D + 1
в последнем лабиринте наблюдается критическая скорость и для
определения утечки через лабиринт можно использовать формулу
(6.3).
Если	> екр/К?2 (* - 1)+ 1»
то расчет должен быть произведен по формуле (6.2).
Коэффициент расхода р зависит от конструкции лабиринта, ока-
зывающей влияние на степень дросселирования потока в камере,
от формы и шага гребня.
Представим коэффициент расхода р в виде произведения: р =
— ц'К, где К — коэффициент, учитывающий конструкцию лаби-
ринтного уплотнения. На рис. 6.3 показаны различные типы лаби-
ринтных уплотнений и приведены значения К для них из опытов
С. М. Шляхтенко. Коэффициент р' зависит от формы гребня и ра"
вен 0,7... 0,9. Меньшие значения относятся к гребням с острыми
кромками, большие — к закругленным.
Так как газ, расширившийся в соплах и ушедший затем через
переднее концевое*уплотнение вала, не отдал своей кинетической
120
Рис. 6.3. Схемы различных типов лабиринтных уплотнений
энергии лопаткам, то потери на утечку, отнесенные к 1 кг рабоче-
го газа, могут быть выражены формулой
(6.5)
где Ни — полезная работа на венце турбины.
§ 6.4.	ПОТЕРИ НА УТЕЧКУ ЧЕРЕЗ РАДИАЛЬНЫЕ
ЗАЗОРЫ ЛОПАТОК
Сопловые лопатки
газ с одной стороны соп-
В многоступенчатых турбинах по внутреннему диаметру сопло-
вых лопаток всегда имеется зазор, через который перетекает газ
под действием разности давлений по обе стороны сопловой решет-
ки. Применительно к этому случаю дана схема на рис. 6.4.
Перед диафрагмой поток газа G делится на две части: часть
Gc проходит через сопловую решетку, часть GyV' перетекает через
лабиринт диафрагмы (в частном случае
ловой решетки на другую может пере-
текать через щели).
Расход газа через сопловую ре-
шетку
Gc=^adh1clt sin aiQh. (6. 6)
Расход газа через лабиринт диаф-
рагмы можно определить' по формуле
(6.2) ил'и (6.3). Его удобно предста-
вить как долю теоретического -расхода
через сопло с тем же проходным сече-
нием л</Лабб1, что и в лабиринте, т. е.
^ут = Рлабя^лаб^1см0и>	(6.7)
Рис. 6.4. Схема перетекания газа через ради-
альные зазоры в проточной части
121
где р,Лаб — определяют из уравнения (6.7) с подстановкой в левую
часть расхода, определенного по формуле (6.2) или (6.3).
Заменяя в уравнении (6.6) коэффициент расхода ц близким к
нему по значению скоростным коэффициентом <р и обозначая
<?лаб=^лаб/с!; = найдем
	__ У sin си °ут	Р-лаб<-габБ1	*	( •
Потери на утечку	, Оут HyTGc + G;T “	•	(6-9) °ут
Тем, что количество газа GyT' может еще совершить работу за
счет расширения на лопатках, пренебрегаем.
Подставляя в формулу (6.9) уравнение (6.8), найдем
//ут---
Ни
у sin а1!
Ила б	лаб
(6.10)
Рабочие лопатки с бандажом
Протекание газа через радиальный зазор наиболее просто пред-
ставляется в ступени с обандаженными рабочими лопатками, когда
поток перед рабочим колесом разделяется на две части: первая,
основная часть, поступает в каналы рабочего колеса, другая, зна-
чительно меньшая, протекает через зазор мимо венца рабочих ло-
паток.
По данным Н. М. Маркова, зазор мало'влияет на характер по-
тока, протекающего через каналы рабочего колеса, и потеря от за-
зора обуславливается, в основном, утечкой газа. Величина утечки
Gy/' зависит от степени реактивности на периферии и относитель-
ной .величины зазора. Некоторое влияние на GyT" оказывает и ре-
рекрыша.
Утечка газа лимитируется или осевым зазором б^, если он мень-
ше радиального, или радиальным зазором бг, когда он меньше осе-
вого.
Величину Gy7 принято определять через минимальное сечение
(8’ Ъли бг) в предположении нулевой скорости на входе в зазор.
Коэффициент расхода оценивается экспериментально.
В МЭИ [5] минимальный зазор заменяют некоторым эквивалент
ным зазором, учитывающим б/ и бг, а также и коэффициенты рас
хода через эти зазоры
1 / 1
I/ 2	2*2
у н	Mr
122
рис. 6.5. Вспомогательный
график для подсчета потерь
на утечку газа через ради-
альный зазор
где hi и |Л2 — коэффициен-
ты расхода соответствен-
но в осевом и радиальном
зазорах; z2— число лаби-
ринтов радиального уп-
лотнения.
В первом приближении
можно принять Ц1=0,5 ир,2=0,8. Тогда
38КВ
и потеря от утечки:
«1 S1U (Г1
где — коэффициент, зависящий от qCt.cp и d/h, определяемый
из рис. 6.5 [5J.
В авиационных ГТД обандаженные рабочие лопатки выполня-
ют с лабиринтным уплотнением, радиальный зазор в котором зна-
чительно меньше осевого. Поэтому можно принять 8ЭКВ= 0,88г//72.
По опытам, проведенным в КАИ, все предложенные формулы
по определению потери на утечку в обандаженных лопатках дают
заниженное значение Яут ПРИ малой реактивности на периферии
из за пренебрежения динамическим напором на входе в зазор.
Во всех проведенных экспериментах по влиянию радиального
зазора замечается снижение реактивности, особенно на периферии,
притом реактивность меняется пропорционально относительной
утечке.
Рабочие лопатки без бандажа
При отсутствии бандажа характер потока в области радиально-
го зазора является значительно более сложным, чем в обандажен-
ных лопатках. Под действием перепада давлений между вогнутой
поверхностью и спинкой лопатки газ перетекает через зазор со сто-
роны высокого давления на сторону низкого. Это приводит к нару-
шению структуры потока в верхней части лопаток, и влияние зазо-
ра сказывается не только на утечке газа, но и на характере его те-
чения. Авторами, изучающими структуру потока, замечено, что из-
менение радиального зазора вызывает деформацию потока за ра-
бочим колесом в периферийной части лодаток, притом с увеличени-
ем зазора углубляется зона деформации. В основном с увеличени-
ем зазора в деформированной зоне за счет энергообмена с пото-
123.
ком, протекающим в зазоре, возрастают угол аг и полное давле-
ние рг*.
Необходимость оценки потерь, вызванных радиальным зазором
и сложность течения газа сквозь зазор вынуждают искать эмпири-
ческие зависимости 7/ут" от бг-
Болыпая часть методов расчета потерь на утечку основывается
на том, что газ, протекающий сквозь зазор, не совершает работы и
для ступени является потерянным. Так как действительная карти-
на не соответствует расчетной схеме, то для совпадения расчета с
экспериментом авторами теоретического расчета вводятся экспери-
ментальные коэффициенты пропорциональности [9]:
ц-„=^-нл=к<, п’ я„;
Q	*2^2 Sin Р2
(6.12)
где Kg=0,5 ... 0,7 — коэффициент расхода. Большие величины со-
ответствуют лопаткам с более тонкими концевыми сечениями.
На основе анализа опубликованного экспериментального мате-
риала и большого числа формул для Яут" в работе А. Е. и О. Е. За-
рянкиных предложена следующая зависимость для определения
потерь на утечку газа через радиальный зазор необандаженной ло-
патки:
//;т= 1,37(1 + 1,6ц) (1 + —) ЬгНи.	(6.13)
\	6 /
Результаты опытов в КАИ совпали с этой рекомендацией.
§ 6.5.	ПОТЕРИ НА ТРЕНИЕ ДИСКА И НАРУЖНОЙ
ПОВЕРХНОСТИ БАНДАЖА
Потери на трение диска вызываются тем, что частицы окружаю'
щего газа под влиянием трения о поверхность диска приобретают
вращательное движение и при этом они отбрасываются к перифе-
рии и замещаются другими частицами. Вследствие этого в меридио-
нальном сечении турбины возникает циркуляционное движение га-
за между диском и корпусом; у поверхности диска частицы газа
движутся к периферии, а у поверхности корпуса — к центру. На
создание этого движения и вращательного затрачивается энергия
колеса турбины.
В литературе имеется обширный материал по определению по-
терь от трения диска о газ. Здесь остановимся на рекомендации
МЭИ [5].
Мощность трения ATP« QtZ5co3.
Работа, затрачиваемая на трение одним килограммом газа, рав-
на Нтр—А/тр/ •
Пренебрегая разницей между сг и сад при определении расхода
и помня, что dK=d—h2, получим
Н„=	Но,	(6.14)
Ч \ сад/
124
Рис. 6.6. Вспомогательный график для
подсчета потерь трения диска о газ
где Fi = wtdhi sin oti — выходная
площадь сопловой, решетки; е —
парциальность ступени; B=f(sl/dK,
Reu) — коэффициент, значения ко-
торого даны на рис. 6.6; s' — рас-
стояние от боковой поверхности ди-
ска до стенки камеры; Reu=udK/v.
Потери трения наружной поверх-
ности бандажа о газ могут быть оп-
ределены по той же формуле, но с
другим коэффициентом пропорцио-
нальности и на диаметре dt=d+h2:
Hipt=6-10-3-^- Ш3/70,	(6.15)
\саХ/
где sa — осевая ширина бандажа.
В мощных турбинах с малым отношением d/h потерями на тре-
ние можно пренебречь; в парциальных турбинах с большим d/h эти
потери могут доходить до 3%.
§ 6.6.	ПОТЕРИ, ВЫЗВАННЫЕ ПАРЦИАЛЬНОСТЫО СТУПЕНИ
При парциальном подводе газа к рабочему колесу в турбине
возникают дополнительные потери, вызванные следующими причи-
нами: 1) вентиляционным действием тех рабочих лопаток, на кото-
рые в данный момент не поступает струя рабочего газа и которые
перемешивают и перемещают инертный газ, окружающий колесо;
2) трением поверхностей не работающих частей рабочей решетки;
3) падением (при уменьшении степени парциалыюсти) реактивно-
сти ступени и неравномерностью ее по дуге подвода газа; 4) подсо-
сом рабочей струей инертного газа из осевого зазора с одной сторо-
ны соплового сегмента и утечкой газа из проточной части с другой
его стороны, что приводит к размыканию рабочей струи. Ориенти-
ровочно можно принять [5]:
е2=е1-|-0,01;	(6. 16)
5) прерывистостью поступления газа на парциальное колесо, т. е.
явлениями, происходящими в межлопаточном канале, который от-
ходит от рабочей струи газа, или в канале, подводящем к соплу, но
заполненным еще инертным газом. Поясним п. 5. В межлопаточ-
ном канале, заполненном рабочим газом, но отошедшим от сопла,
нормальное протекание струи нарушается, и газ, находящийся в ка-
нале, производит работу с пониженным к. п. д. При подходе к соп-
лу лопаток, на которые в предыдущий момент газ не поступал,
часть энергии струи тратится на ускорение частиц инертного газа,
который находился в межлопаточных каналах и который струя ра-
бочего газа выталкивает.
125
Рис. 6.7. График влияния относительных осевого
и радиального зазоров на потери от парциального
подвода газа
Потери, вызванные причинами пп. 1 о
в литературе принято называть потерями
на чистую вентиляцию.
Потери, вызванные причинами, ука-
занными в пп. 3 ... 5, называют потерями
на выколачивание или потерями на кон-
цах дуг подвода газа. Потери из-за нерав-
номерности параметров потока по длине
всей дуги подвода могут быть отнесены
сюда условно, и большая их часть при оп-
ределении потерь на выколачивание не
учитывается.
Деление потерь, вызванных парциальностью, на вентиляцион-
ные и на выколачивание совершенно условно и раздельное опреде-
ление их недостаточно надежно, так как все факторы, влияющие
.на потери из-за парциальности, взаимосвязаны.
Из большого числа рекомендованных формул по определению
потерь, вызванных парциальностью, по опытам, проведенным в
КАИ, наиболее достоверной оказалась формула, приведенная в
книге В. Траупеля [18]:
с 1—* и ( и
t sin Ctj Cl \ Сад
2  0,3г a s
• сад &
Яо>
(6.17)
где z — число дуг подвода газа; s — ширина рабочих лопаток; С —
коэффициент, который выбирается равным: а) для открытого коле-
са С=0,04 ... 0,52 hz/d; б) для колеса, прикрытого в неактивной
своей части, С=0,019... 1,1 (0,125—h^d)2.
Уравнение (6.17) справедливо при малых осевых зазорах и
обандаженных лопатках. При повышенном осевом зазоре и в без-
бандажных лопатках потери значительно повысятся. Ориентировоч-
но для оценки влияния зазоров можно рекомендовать кривые, при-
веденные на рис. 6.7, откуда по данной величине зазора определя-
ются коэффициенты Sa и Sr, на которые нужно умножить Нвеит
По рекомендациям МЭИ (5] и В. Траупеля [18], для расчета по-
терь от парциальности в турбине с двумя ступенями скорости мож-
но предложить следующую формулу:
Явеи= Г 1,41С	JL Я0)	(6.18)
L asinaj Cj \сад/ « сад hid J
где SsA — сумма произведений ширины на высоту трех решеток:
двух рабочих и одной направляющей.
В связи с тем что потери на трение диска и бандажа ощутимы
в парциальных турбинах, их часто суммируют с потерями, вызван-
ными парциальностью, и обозначают Ятв=Ятр.д +Я1Р» 4-Явеят-
126
В прикрытых колесах границы кожуха должны быть выбраны с
учетом размыва струи и переноса газа вращающимся колесом [5].
Так, Для одноступенчатой турбины рекомендуется смещать край
кожуха по направлению вращения на величину не менее, чем s/=
= l,2(6actgai + l,05s«/caB), и с другой стороны соплового сегмента
со сдвигом по вращению на величину ре более, чем Sz'=
=0,6(6octgai + l,05su/can—6Kctg02), где ba — полный осевой зазор;
s — ширина рабочей решетки; 6К — осевой зазор между рабочей ре-
шеткой и кожухом (рис. 6.8).
При проектировании турбины большое значение имеет правиль-
ный выбор соотношения высоты лопатки и парциальности при од-
ном и том же значении их произведения еЛ1, которое определяется
выбранным диаметром d и углом щ, а также заданным расходом.
С увеличением парциальности е уменьшается высота лопаток, в
связи с чем падают потери, вызванные парциальностью, но с дру-
гой стороны, возрастают концевые потери. Следовательно, для каж-
дого значения eAt должно существовать оптимальное соотношение
между парциальностью и высотой лопаток, определяемое мини-
мальной суммой концевых потерь и потерь, вызванных парциаль-
ностью.
Так как величина концевых потерь в решетках с короткими
равна
0,003
Ск°вд=	j	,
—-------+ 0,003
d е
лопатками
(6. 19)
а потери, вызванные парциальностью, определяются формулой (6.17), то на ос-
яовании этих равенств .можно заключить, что оптималь-
ная степень парциальности увеличивается с ростом отно-
в , еА1
шении ufc^ и комплекса — и с уменьшением угла ai.
а
На рис. 6.9 приведен ориентировочный график для
определения e0Pt в зависимости от и/сад и — , полу-
де
четный решением равенств (6.17) и (6.19). При построе-
нии этого графика угол ои принят равным 17°, а отно-
шение s2/&2 — равным 1, что при сравнительно длинных
лопатках (25... 30 мм) неверно. Как показывают расче-
ты и опытные данные {5], отклонение от eopt, а следова-
тельно, и от hi на 15... 20% не сказывается заметно на
к. in. |д. Резкое отклонение от eopt может привести к по-
тере в к. п. д. до 6%.
Рис. 6.8. Схема расположения защитного кожуха в парциальной турбине
Рис. 6.9. График оптимальной парциальности ступени в зависимости от отноше-
ний и/сад и shi/d
127
§ 6.7. РАБОТА ГАЗА НА ЛОПАТКАХ ТУРБИНЫ
В соответствии с формулой (4.6) момент сил, действующих на
лопатки турбины (как осевой, так и радиальный) при протекании
1 кг газа, Л4= (псщ—г2с2и), где гь г2 —радиусы середины высоты
входной и выходной кромок лопатки осевой турбины.
Для радиальной турбины эти радиусы показаны на рис. 2.6.
Работа, совершаемая газом на лопатках,
Ня=М<л=(й1<?1в—«2С2в),	(6.20)
где со — угловая скорость вращения.
Если в последнюю формулу подставить
с1+а1—^	с2 + а2~ ®2
ztjti cos ot! =—-—£-— и а2с2 cos а2——-—,
то уравнение работы газа на лопатках примет вид
+	(6-20
Первая пара слагаемых в этом уравнении характеризует ис-
пользование кинетической энергии, созданной в сопловом аппара-
те, вторая — работу, полученную в результате ускорения газа в ра-
бочих каналах (в активном процессе эта работа отрицательна),
третья — работу центробежной силы, действующей на 1 кг газа
при изменении окружной скорости от и\ до и2.
В центростремительной турбине работа центробежной силы от-
рицательна («2<«1) и увеличивает Ни, в центробежной турбине —
положительна и уменьшает Ни. В осевой турбине ы2 может быть и
больше, и меньше, и равна щ.
В последнем случае для осевой турбины
Ня—(ci — С2 + — ®»i) == U (w 1 cos ?! 4-	cos ?2).	(6.22)
Здесь и далее перед ay2cos р2 знак «минус» сменен на «плюс» пото-
му, что вектор щ2и в турбинах всегда отрицателен.
 Чтобы найти зависимость скорости w2 от Wi для случая u2#=«!.
надо написать уравнение энергии в относительном движении газа
а>?	w|
через рабочее колесо: —/7Ц4-#02=7777 > откуда
2
®2 = ф 1^2/702-4-2^14-«2 —И11	(6.23)
ИЛИ .	ЧО2 = ф ]/\>ст	w? 4" «2 — И? .	(6. 24)
§ 6.8. НОМЕНКЛАТУРА К.П.Д. ТУРБИНЫ (СТУПЕНИ)
Под коэффициентом полезного действия турбины (ступени) по-
нимают отношение работы, совершаемой турбиной, к располагае-
мой работе, т. е. к максимально возможной работе турбины, не
имеющей потерь.
128
рис. 6.10. Тепловой процесс сту-
пени на диаграмме i—S
Располагаемую работу тур-
бины можно понимать по-раз-
ному. С одной стороны, макси-
мально возможная работа тур-
бины без потерь эквивалентна
адиабатному перепаду тепла
Но от начальных параметров
газа в заторможенном состоя-
нии (ро*> То*) до конечного
давления р2 (рис. 6.10).
С другой стороны, целесо-
образно учитывать то обстоя-
тельство, что газ, покидающий
рабочие лопатки турбины, обладает скоростью с2; кинетическая
энергия Н3=с22)2 может быть использована в реактивном .сопле
двигателя или в следующей ступени многоступенчатой турбины.
Поэтому располагаемым теплоперепадом можно считать также ве-
личину
Яо= i*t=Ho-^ н*	(6- 25>
•	Т2
где отношением Т2</Т2 учитывается разница между величинами
Нв и
Так как	1, то в дальнейшем полагаем Но*=Но—с22[2.
В связи с изложенным различают две системы к. п. д., вычис-
ленных по статическим параметрам на выходе, т. е. отнесенных к
работе.Но, й вычисленных по параметрам торможения на выходе,
т. е. отнесенных к работе Но*.
Если из величины Но вычесть величину потерь в сопловой и ра-
бочей решетках, то определится работа турбины с гидравлическими
потерями, но без учета выходной потери: Н=Но—(пс+Нл). От-
ношение
(6.26)
называется адиабатным или лопаточным к. п. д., характеризует
степень совершенства проточной части турбины и представляет со-
бой к. п. д. системы двух решеток. К перепаду Но* в параметрах
торможения этот к. п. д. не относят.
Вычитая из Но все три вида потерь на венце турбины — в соп’
лах, на рабочих лопатках и выходных — находим работу на лопат-
ках или окружную работу турбины:
Ни=Но-(Яс+/Л+ЯД	(6.27)
^та величина Ни для активной турбины точно, а для реактив-
ной — приблизительно совпадает с вычисленной по формуле Эйле-
Рй. Ну—^2u^2*
5	1337	12Й
Отношение окружной работы к располагаемой называется ок-
ружным к. п. д. В зависимости от того, что понимать под распола-
гаемой работой — Но или Но*, различают два коэффициента
ЧЖ=ЯЖ/ЯО и ч\и^=Ни!Но.	(6.28)
Если от работы на венце отнять остальные внутренние потери
турбины, т. е. на трение диска в газе, на вентиляцию и на утечки,
то получим внутреннюю работу турбины (ступени): -
(6.29)
Ей соответствует внутренняя мощность турбины (ступени):
Nt=GHt.	(6.30)
Отношение внутренней работы к располагаемой называется
внутренним к. п. д.
и t|*=#z/#o.	(6.31)
Особенности определения к. п. д. охлаждаемой ступени рассмот-
рены в § 9.9.
Если учесть, наконец, механические потери, то с вала турбины
может быть снята работа He=Hi—Ны, называемая эффективной
работой или работой на валу. Ей соответствует эффективная мощ-
ность
Ne=QHt.	(6.32)
Так как турбйна и компрессор находятся на одном валу, под
Ям понимают обычно совместные механические потери турбины и
компрессора.
Механическим к. п. д. т]м называется отношение эффективной
работы (мощности) к внутренней:
(6.33)
Отношение же эффективной работы к располагаемой называ-
ется эффективным к. п. д.:
<6 М)
Но	о
Очевидно, что
Пе = 'Пг’1м-	(б-35)
На рис. 6.10 показан на диаграмме Ь—S тепловой процесс сту-
пени с произвольной степенью реактивности.
Состояние газа при входе в ступень характеризуется точкой
До*, на выходе из сопел — Ль на выходе из рабочих лопаток — Лг-
.Если выходная скорость за турбиной теряется, то состояние газа
:на выходе из турбины (после потери этой скорости) определяется
точкой Дз. В случае использования скорости с2 в реактивном сопле
или в следующей ступени турбины статические параметры газа на
130
выходе из данной ступени определяются точкой А2', а параметры
заторможенного потока — Л2*.
Превращенный в механическую работу внутренний теплопере-
пад	—(/7с+Ял+Яв+Ятв + //ут). Здесь поставлен не знак'
равенства потому, что сумма адиабатных перепадов в сопловой и
рабочей решетках больше располагаемого на ступень перепада:
AoAif-j- Л1Л2< ЛоЛ^.
Это объясняется использованием в рабочей решетке части по-
терь в сопловом аппарате. Поэтому же, как указано выше, окруж-
ная работа Ни, вычисленная по разности располагаемой работы и
потерь на венце, с одной стороны, и tio формуле Эйлера, с другой,
для реактивной ступени оказывается неодинаковой. Хотя разница
между величинами, подсчитанными по обеим формулам, пренебрег
жимо мала, принципиально правильный результат для Ни дает
формула Эйлера, а для Hi — величина Я<= («iCiu—u2c21t) —
-- (^Т.в + //уг) .
Внутренний к. п. д. может быть найден непосредственно из ди-
аграммы i—S: r\i=Hi/H0; i\i*=Hi/H0*.
§ 6.9.	АДИАБАТНЫЙ К.П.Д.
Как сказано в предыдущем параграфе, этот к. л. д. учитывает
лишь потери в сопловой и рабочей решетках и характеризует газо-
динамическое совершенство проточной части:
^0~(^+Ял)-=1-Сс-Сд)	(6.36)
«О
где ^=ЯС/ЯО; t,a=HJl/Ho.
Найдем зависимость адиабатного к. п. д. от отношения скоро-
стей и/сх.
Потери в соплах от этого отношения не зависят, следовательно,
максимальное значение т]ад соответствует минимуму коэффициен-
та £л.
Как известно, потери в рабочей решетке осевой турбины На=
= ^/2+Ног).
При заданном теплоперепаде Яог в рабочей решетке потери в
ней минимальны, если достигают минимума £ и wt. Скорость wt
очевидно, минимальна тогда, когда имеет осевое направление, т. е.
входной треугольник скоростей является прямоугольным. Так как '
при этом и коэффициент потерь энергии £ близок к минимальной
величине (с точки зрения суммы углов pi + р2), то наибольший ади-
абатный к. п. д. соответствует величине w/ci=cosai независимо от
степени реактивности.
Конечно, из этого не следует, что надо выбирать отношение
w/ci равным cos ai, т. е. приблизительно единице, но во всяком слу-
чае при этом отношении скоростей гидравлические потери в про-
точной части минимальны.	’
5*	/	131
§ 6.10.	ОКРУЖНОЙ КПД. ТУРБИННОЙ СТУПЕНИ
Общие формулы
По определению окружной коэффициент полезного действия
*1и=Я«/Я0 или 1\и*=Ни/Н0* ‘.
Работа на лопатках турбинной ступени /fu=a1ciui±u2c2u. Рас-
полагаемую работу представим в виде кинетической энергии газа,
имеющего скорость сад.
Таким образом,
Я0=^д/2; M=(ca2«-d)/2;
_2(«1С1В ±ае2и) .
Чи--------Тг-----»	(6.37)
Сад
• _ 2 (В1С1в ± и2с2в)	„й
Т|в-------- 5	•	(О. ОО)
Преобразуем эти формулы. Как известно, Ci=q> - QCT)A/0
ИЛИ	=	—Ост = (р'сад» '	(6.39)
где	<pz=<p/'l —qct.	(6.40)
Из выходного треугольника скоростей
c2a=w2 cos 32—(6.41)
Для скорости w2 используем выражение (6.24), в которое вмес-
то tW]2 подставим Ci2+«i2—2utCicos аь а скорость Ci заменим вели-
чиной ф'Сад [формула (6.39)]. Тогда формула (6.37) принимает вид
riu=2x ^'cosai+S(^cosp2)Ap'2+d2x2—2/xcosa1-|-()CT —Jxj] .
(6.42)
Здесь приняты обозначения: u2/«i = <?; uJcA}S=:x.
Окружной к.д.п. центростремительной турбины
В центростремительной турбине, схема которой приведена на
рис. 2.7, всегда 3<1. Для таких турбин, помимо степени реактив-
ности, большое значение имеет отношение скоростей С\г1с2а, которое
находится в пределах 0,9... 1,1. От этого отношения зависит мери-
диональный профиль колеса.
Для каждых значений х и выбранных «и, <р, ф, с^/с^а существуют
оптимальные величины 02 и аг, соответствующие максимальному
iju. Реактивность является функцией этих величин. Зависимость
Tiumax, «г и qct от х представлена на рис. 6.11 для различных значе-
ний d=‘U2/Ui при ai=15°; ф=0,85; с1г/с2о=1. Угол р2 принят опти-
мальным, но ограничен условием 02^15°. Переломы кривых выз-
ваны ограничением р2.
132
Рис. 6.11. График зависимости т)и тах,
as. ₽ст радиально-осевой турбины от
xssUj/Сад, и	(при <р=0,95; ф=
^=0,85; а. = 15°;	== 11	^15с;
pci^pmtn)
Как видно_ из рис. 6.11, с
уменьшением d возрастают мак-
симальный к. п. д. и оптимальное
значение х. Это связано с тем,
что с изменением d соответству-
ющим образом меняется реактив-
ность Qct И СКОРОСТЬ W2.
Сделанные выводы справедли-
вы для различных вариантов рас-
чета турбины, когда при заданном
угле ai и различных меня-
ется угол рь В турбине с радиаль-
ными лопатками (Pi=9(r) опти-
мальная величина «i/Сад лежит в
0,3	0,5	0,7	0,9 х
пределах 0,65 ... 0,7 независимо от степени реактивности.
При анализе кривых на рис. 6.11 нужно помнить о том, что все
расчеты проведены при ф=0,85 естественном для радиальных
турбин, но заниженном для осевых. Не подходит также для осевой
турбины и отношение cir/c2a=l.
Окружной к.п.д. осевой ступени
Осевая ступень представляет собой частный случай радиальной
турбины с одинаковыми диаметрами d\ и d2, т. е. с 5=1. Как вид-
но из формулы (6.42), для такой ступени
Лв=2х'[<р' cos «ц cos & УУ2 jc2—fy'x cos ai+QcT ~(6.43)
Сопоставляя формулы (6.37) и (6.38), .находим
(6.44)
1-4
сал
—-Л С?	W? + «2±-2ttW2COS ₽2 п Л	Л
Здесь	-----j--------—у2-\-х2—2ху cosfe, (6.45)
сад	сад
W2
где	z/2= 2 =ф2(?'2_(_Л2_ 2х<р'COSdi+Qj.	(6.46)
сад
На рис. 6.12 по формулам (6.43) и (6.44) построены кривые
Ли и т]и* в функции от и/сад для различных Qct- При этом были
приняты: ai=20°; <р=0,95; ф=0,97. Угол 02 определялся из усло-
вия, чтобы отношение c2a/cia, характеризующее соотношение меж-
133
Рис. 6.12. График зависимости к.п.д. т]« и т]«* от а/сад при различных рст я
При ПОСТОЯННЫХ ф, ф, Ol, Cja/Cla:
-	T)u*—сплошная ЛИНИЯ; пунктирная линия
ду высотами сопловых и рабочих лопаток, составляло 1,2 при qct=
=0,5 и 1 для qct=0 и QCT=0,3.
Оптимальная величина и/сад возрастает с увеличением qCt осо-
бенно заметно, если выбирать и/сад по величине к. п. д. т]и. Выби-
рая и/сад по оптимальной величине т]и*, следует отметить, что для
реактивной (<>ст=0,3 ... 0,5) ступени и/с^ можно варьировать в
весьма широких пределах от 0,4 до 0,9 без заметного влияния на
к. п. д. То обстоятельство, что для qct=0,3 и 0,5 кривые т]и* сли-
ваются, объясняется различным значением отношения c2o/cia- При
одинаковом отношении осевых скоростей взаимное расположение
сплошных кривых получается примерно таким же, как и пунктир-
ных.
Кривые для активной ступени доведены до и/сад=0,8, так как
при больших значениях и/сад угол Рг начинает превышать 90°, что
нереально.
На рис. 6.12 построены также кривые угла az, из которых вид-
но, что осевой выход (аг=90о) имеет место при х«0,44, если
qc,=:0, х=0,55, если qCt=0>3, х=0,65, если qct=0,5. Конечно, при
других величинах угла Рг, отличающихся от тех, которые положе-
ны в основу данного расчета, величины х, соответствующие осево-
му выходу, окажутся ицыми.
134
Йз приведенных на графике кривых видно, что с увеличением
степени реактивности возрастает максимальный окружной к. п. д.
В действительности это расхождение значительнее, так каксумень*
шением конфузорности каналов рабочего колеса (т. е. уменьшени-
ем степени реактивности) снижается значение скоростного коэффи-
циента ф (см. гл. IV), принятого в расчетах величиной постоянной.
Но при этом нельзя забывать о том, что возросшее оптимальное
отношение ulc^ с увеличением степени реактивности может быть
реализовано увеличением или числа оборотов ротора (что не всег-
да удается) или диаметра колеса.
К.п.д. т)и активной осевой ступени
В этом случае сад=с1/'ф, и формула (6.37) с учетом равенства
(6.41) принимает вид
Пв=(С1 со® ®1+w2 cos ₽2—и) =~ ср2 (cos ах — — V1+ф
(6.47)
так как cicos щ—w=o>icospi и в активной турбине а>2=фи>1.
Для нахождения оптимального ц/ci, при котором т|и достигает
dt\	л. COS ₽2
максимума, приравняем к нулю ----'—, считая <? и Ф —посто-
d (u/Ci)	cos рх
явными.
Тогда получим cosai—2«/cj=0; (M/cI)opt=cos ai/2, что соответ-
ствует выводу, сделанному4® начале книги (см. § 2.3).
Максимальное значение к. п. д. при этом
Пвтах=?2 (1+Ф С-^ .	(6.48)
\ COS Рх/ 2
Как видно из значений Яитах, (u/ci)opt и формулы (6.47), при
работе на u/ci, отличном от cos сц/'2, снижение rju подчиняется сле-
дующей параболической зависимости:
Чв _ 4ulci fa a/ci \
Чатах COS ai \ COS tfi J
или	1----3s-=( 1 -	(6.49)
Чатах A	cos (Ii /
Такая зависимость i)u от u/ci объясняется влиянием выходной
потери, как показано на рис. 6.13.
Величину к. п. д. т|и можно записать так:
_ Я0-(Яе + Ял + Яв)
Че----------77	1 ’с Ч» Чв>
«О
где буквой £ обозначено отношение тех или иных- потерь к распо-
лагаемой работе.
Определив £с, £л и £в для различных и/q и вычитая их из еди-
ницы (см. рис. 6.13), получим параболическую кривую т)и.
135
Рис. 6.13. График зависимости окружного
к.п.д. активной ступени от (при посто-
янных Ct, <р, ф, at и при Pa=Pi)
Надо отметить, что относитель-
ные потери в соплах £с=1—<р2 не
зависят от отношения u/d, потери
же на лопатках £л= (1—
увеличиваются с уменьшением «/сь
так как, во-первых, возрастает wu
а во-вторых, уменьшается скорост-
ной коэффициент ф вследствие
уменьшения суммы углов 0i+₽2.
Относительная выходная потеря
£в=Ф2С22/С12 достигает мини-
мума при осевом направлении <ъ, что соответствует ————
Ci 2
при ф=1. Так как в рабочем колесе потери наблюдаются всегда и
уменьшаются с увеличением и/сь то выходная потеря достигает
минимума при u/ci несколько меньшим оптимального значения, но
сумма ^с+Сл+?в минимальна при —=	-.
с\ 2
Из формулы (6.46) следует, что наивыгоднейшим углом ои (при
прочих постоянных величинах) является 0°. Однако, не говоря уже
о конструктивной невозможности получить такой угол, следует
учесть, что с уменьшением он снижается как коэффициент <р, так и
в связи с уменьшением углов ,р< и р2 — коэффициент ф.
Обычно для активных ступеней выбирают ai = 16 ... 20°, дово-
дя его при малых объемных расходах газа до 12°.
§ 6.11. ОКРУЖНОЙ К.П.Д. ТУРБИНЫ
СО СТУПЕНЯМИ СКОРОСТИ	'
Понятие о турбине со ступенями скорости дано в § 2.5. На
рис. 2.9 приведены схема облопачивания и треугольники скоростей
при двух ступенях скорости. На рис. 6.14 треугольники скоростей
вычерчены из одной вершины 0.
Рис. 6.14. Треугольники скоростей турбины с двумя ступенями скорости
136
Ступени скорости выполняют обычно чисто активными, однако
по соображениям, указанным ниже, иногда допускают небольшие
перепады тепла и на рабочих лопатках, т. е. допускают работу с
некоторой степенью реактивности. В этом случае работа адиабати-
ческого расширения в турбине представляет собоц сумму Но=
= #014"^(й+^0н+^<я» где Яо1 — адиабатная работа в соплах:
Но2 — на рабочих лопатках первой ступени; — в направляю-
щих лопатках; //02 — на рабочих лопатках второй ступени.
Скорости газа определяются по следующим формулам:
®2=Ф )Ав?-|-2//о2;

(6.50)
(6.51)
(6.52)
(6.53)
где ф, фн, ф' — скоростные коэффициенты соответственно рабочих
лопаток первой ступени, направляющих лопаток, рабочих лопаток
второй ступени. В соответствии со
значениями теоретических скоро-
стей на выходе из решеток опре-
деляются потери на венцах.
Выходная потеря
'2
(6>54)
Для активного облопачивания
формулы для скоростей и потерь
значительно упрощаются, так как
Я02, Яод и /У® равны нулю.
Диаграмма i—S теплового
процесса активного колеса изоб-
ражена на рис. 6.15, где кроме
Указанных выше потерь, отложе-
ны потери на трение и вентиля-
цию Ятв1.
1 Величина Ят.в отложена условно. I
жпС’ ДиагРамма *—5 теплового
Роцесса активной турбины с двумя сту-
пенями скорости
137
Работа на венце колеса Кертиса складывается из работ отдель-
ных ступеней. Работа каждой ступени определяется по формуле
(6.20), поэтому
/7и = И(С1и + С2а“Ьс1и + с2(<4’’• • •)	(6.55)
или Яв=«(дах cos cos&4-W1 coscos&+•••)• (6.56)
Знак минус в уравнении (6.55) ставится при «2>90° (соответст-
венно а/). Из рис. 6.14 видно, что большая часть работы колеса
Кертиса‘приходится на I ступень. При активном облопачивании
двухступенчатого диска на I ступень приходится обычно 75 ... 80%
всей работы, на II — 20 ... 25%. При трех ступенях скорости по-
следняя ступень загружена еще меньше и обычно производит лишь
около 10% всей работы.
Окружной к.п.д. турбины со ступенями скорости
п  Ни  и 2 (cla i с2а)
Т,““ н0 7Г0
(6.57)
Формула эта может быть приведена к сравнительно простому
виду лишь для активного колеса без использования выходной ско-
рости, для которого
. Яа== 2y2aS(CiB±C2a) ,	(6.58)
С1
Пользуясь треугольниками скоростей, величину 2 (ciu ± с2а)
можно привести к такому виду [6]: 2(^iB ± с2а)=ас1 cos ах — Ьи,
где	а = 1+пф+тффи+;	(6.59)
Ъ—2 пф+/лфн+п 'ф'+/плффн+/дл'ФнФ'+/плл'ФФяФ'; (6.60)
; л'=-^4 .	(6.61)
COS 0t2	COS Pl	COS Pj
К подобному же виду можно привести 2 (cia ± с2а) Для трех и
большего числа ступеней; при этом коэффициенты а и b принимают
более сложный вид, но во всех случаях
•a/£«l/z,	(6.62)
где z — число ступеней. Это соотношение выдерживается точно при
^ = ^=^'=1 и равенстве углов: p2='₽i; ai=aa; Рг'=1р1'.
* Теперь формула (6.67) принимает вид
= 2y2(flC1COSgl-M«_=2(p2 L да. _ j .	(6.63)
•	q	\	«1 / ci
Для определения величины u/сь соответствующей максималь-
ному т]и, приравняем нулю первую производную от выражения
(6.63). Получим acoscti—26«/ci=0, откуда
«,'c1=(a/6)(coisa1/2).	(6.64)
138
Рис. 6.16. График окружного к.п.д. т]« турбины с различным числом ступеней
скорости
(6.65)
С учетом соотношения (6.62)
и ^cosai
ci ~ 2z
В § 2.5 показано, что это значение оптимального u/ci выдержи-
вается точно в турбине без потерь с симметричными лопатками
(Р1=₽2 и т. д.). Характер изменения т)и в функции u/ci показан на
рис. 6.16, где для сравнения приведены графики tiu одно-, двух- и
трехступенчатого активных колес. Графики построены для трех
углов ai=10, 17 и 25° в следующих предположениях: 'Pi=p2,‘ !₽/=
= fe';	а/—аг; а1"=аг"; ф=фн==фн'=0,95. Коэффициенты
ф приняты меняющимися в функции Pi +1Р2-
Абсолютные цифры к.п.д. на рис. 6.16 сильно занижены: в сов-
ременных одноступенчатых турбинах т]и- достигает 0,85, в двухсту-
пенчатых турбинах — 0,8 (которая достигается лишь при наличии
некоторой реактивности).
Из рис. 6.16 видно, что с увеличением числа ступеней скорости
быстро снижаются как к.п.д. турбины, так и оптимальное «/сь При
а/с1<0,25 («1=17°) к.п.д. двухступенчатой турбины оказывается
выше одноступенчатой, а при w/ciC0,12 к.п.д. трехступенчатой тур-
бины выше двухступенчатой. Так как в последнем случае разница
в к.п.д. невелика, а по абсолютному значению к.п.д. при малых
а/С1 очень низок, то нет смысла применять число ступеней больше
Двух: каждая добавочная ступень вызывает дополнительные потери
(в направляющих и рабочих лопатках), а прирост полезной рабо-
ты ничтожен.
139
Рис. 6.17. График влияния реактивности
на к.п.д. турбины со ступенями скорости
Рис. 6.16 дает некоторые указания
и по выбору угла <ц. Для одноступен-
чатой турбины наивыгоднейшим углом
<ц (из трех намеченных) является 10°,
хотя к. п. д. при этом и незначительно
отличается от случая ai=17°, в трех-
ступенчатой — 25°. Таким образом, с
увеличением числа ступеней влияние
скоростного коэффициента лопаток на
выбор угла си становится все бол.ее заметным. Поэтому в турбинах
Кертиса вообще применяют большие углы щ, чем в одновенечных
колесах.
Для получения приемлемых к.п.д. углы ip2, а/, р2' целесообраз-
но выбирать небольшими, соответственно меньшими, чем pi, a2, Pi'.
Нижний предел для величины этих углов обусловливается как
уменьшением коэффициентов ф, так и неблагоприятным влиянием
малых величин этих углов на высоту лопаток (см. ниже).
Применение реактивности вызывает, с одной стороны, повыше-
ние к.п.д., а с другой — увеличение оптимального u/ci. На рис. 6.17
приведены кривые T)u=/(w/cJ для двухступенчатых колес Кертиса
с различными степенями реактивности; цифры на кривых показы-
вают относительную величину теплоперепада в процентах от обще-
го теплоперепада, причем первая — на рабочих лопатках I ступе-
ни, вторая — на направляющих лопатках и третья — на рабочих
лопатках II ступени.
Обычно как на рабочих лопатках каждого ряда, так и в направ-
ляющих лопатках допускают перепад не более 10 ... 15% от сум-
марного теплоперепада колеса, так как более значительные пере-
пады при парциальном облопачивании вызывают большие утечки
газа через зазоры.
Низкие значения к.п.д. турбин со ступенями скорости препятст-
вуют их широкому распространению. В авиации двухступенчатые
колеса Кертиса применяются лишь для ТНА ЖРД.
§ 6.12.	ВНУТРЕННИЙ К.П.Д. И ВЫБОР ОТНОШЕНИЯ и/сад
Как известно, внутренний к.п.д.
_ Н» (^Т.В + ^ут)	_	«	(с. сеч
П1=---------------=Яв-Ст.в- СуТ,	(6.бб)
^0
где Ст.в=//т.в///0; Сут=/7ут///0.
В авиационных ТРД и ТВД величина £ут относительно неве-
лика, а вентиляционные потери отсутствуют. Поэтому максималь-
ный внутренний к.п.д., характеризующий в конечном счете эконо-
мичность турбины, достигается практически при том же отноше-
нии ulctm, что и максимальный окружной коэффициент (см.
§6.10).
140
Рис. 6.18. График зависимости к.п.д. t]« и qi
от «/свд
В небольших турбинах вспомога-
тельного назначения, а также в парци-
альных турбинах для ТНА ЖРД поте-
ри на утечку, трение и вентиляцию
оказываются более существенными,
поэтому их влияние на оптимальное'
значение и/сад необходимо учитывать.
Относительные (Нчр/Н0) потери на'
трение диска и бандажа, как видно из
формул (6.14) и (6.15), (&г.д+Ст.б)«
~ (и/Сад)®.
Относительные потери на вентиляцию из уравнения (6.17)
Св~(я/сад)«, где 2<а<3.
Поэтому r)i=i1u—/Си/сад), где/(u/Сад) =Ст.в+£ут.
Имея графическую зависимость к.п.д. от и/сад и вычитая из
ординат кривой т]и ординаты кривой Kulc^, получаем кривую
внутреннего к.п.д. (рис. 6.18). Очевиднб, для турбины надо выбрать
такую величину ulc^, при которой T]i достигает максимума. Учи-
тывая пологость кривой т]<=/(«/сад) вблизи максимума, следует
выбрать величину iz/сад несколько меньшей ее оптимальной вели-
чины. Это позволяет при заданном теплоперепаде снизить окруж-
ную скорость, что повышает надежность работы турбины, а при
заданном числе оборотов снизить диаметр турбины, что уменьшает
габариты и массу двигателя.
В соответствии со сказанным следует выбирать: для одноступен-
чатых турбин ТРД и ТВД u/сад= 0,4 ... 0,5 (при любой степени
реактивности); для одноступенчатых турбин без использования
выходной скорости и/сад=0,4... 0,6 (соответственно при реактив-
ности g=0 ... 0,5); для радиальной центростремительной турбины
с радиальными лопатками и1/сад=0,2 ... 0,25; для двухвенечного
колеса Кертиса с небольшой реактивностью и/сад=0,25 ... 0,3.
§ 6.13.	КОЭФФИЦИЕНТ НАГРУЗКИ ТУРБИННОЙ СТУПЕНИ
Одним из характерных параметров турбины является коэффи-
циент нагрузки р, под которым понимается отношение работы на
окружности колеса к квадрату окружной скорости на соответствую-
щем радиусе:

(6.67)
Так как Ни = и(с1и±С2и),
с1и ± С2и
г-------------
и
(6. 68)
141
Коэффициент нагрузки можно выразить через окружной к.п.д,
ступени:
=2^®.	±—	(6.69)
«2 Hq U2 2 (И/Сад)2	k '
2(и/сл)2 (1 Свых)'
(6.70)
Каждой ступени соответствует свое оптимальное значение коэф-
фициента нагрузки, отвечающее максимальному к.п.д.и зависящее
от геометрии ступени, соотношения скоростей Cijc^a, степени реак-
тивности. Так, для активной ступени, в которой (w/ci)Opt=cosai/2,
«оптимальное значение pOpt~2. Реактивной ступени с q = 0,5 соот-
ветствует pOpt~ 1.
При проектировании ступени в ряде случаев целесообразно ис-
ходить из окружной скорости, несколько меньшей оптимальной, что
приводит к уменьшению диаметральных габаритов турбины без за-
метного снижения к.п.д. При этих условиях коэффициент нагрузки
увеличивается.	•
Для авиационных ГТД при осевом выходе потока из ступени
р, = 1,34 . .. 1,4. При «2=70 ... 65° коэффициент нагрузки ц® 1,75...
... 1,85. Расчетный и экспериментальный анализ показал, что из-
менение р в диапазоне 1,2 ... 1,7 оказывает слабое влияние на
к.п.д. ступени [9].
§ 6.14.	ОСОБЕННОСТИ РАСЧЕТА СТУПЕНИ ТУРБИНЫ
В зависимости от назначения турбины могут меняться требо-
вания, предъявляемые к данному типу турбины, параметры в зада-
нии для расчета и порядок расчета. Для всех авиационных турбин
предъявляется безусловное требование минимальных массы и га-
барита. Сокращая габариты и массу двигателя, приходится допус-
кать пониженный ресурс его работы, который особенно мал у ра-
кетных двигателей.
Турбины ТРД и ТВД должны обладать возможно более высо-
ким к.п.Д.; это требование не всегда предъявляется к вспомога-
тельным турбинам малой мощности, где общий расход топлива
невелик. В турбинах ТНА обычно жертвуют коэффициентом полез-
ного действия в пользу габаритной и массовой характеристик, учи-
тывая, что расход топлива на ТНА составляет малую долю расхо-
да топлива ракетой. Турбины ТРД и ТВД обладают характерной
особенностью, не присущей другим типам газовых турбин (в том
числе стационарных и судовых): выходная потеря турбины ZB ис-
пользуется для создания тяги в реактивном сопле. Поэтому в тео-
рии авиационных ГТД величина Яв не рассматривается как потеря.
Это позволяет допускать завышенные выходные скорости сг, что
благоприятно сказывается на высоте лопаток. Тем не менее нужно
помнить о том, что с повышением выходной скорости при заданном
полезном теплоперепаде возрастает адиабатный перепад (по ста-
тическим параметрам) на турбину, а следовательно, и оптимальная
142
окружная скорость и. Кроме того, из-за роста скоростей потока по>
тракту ступени увеличиваются потери в сопловом аппарате и в ра-
бочем колесе, что приводит к снижению к.п.д. не только в стати-'
ческих параметрах, но и в заторможенных.
В турбинах ТРД рекомендуется выбирать %сг=0,5 ... 0,6. В тур-
бинах ТВД ХС2 может достигать значения 0,7 [9]. Допускать приве-
денные выходные скорости %с2>0,7 нецелесообразно, так как в этом-
диапазоне значений % прирост скорости оказывает слабое влияние
на высоту лопаток. Если рассматриваемая ступень является по-
следней, то непременным требованием при этом является'
приблизительно осевой выход газа из турбины (угол аг должен сос-
тавлять 82 ... 90°), в противном случае при входе в реактивное'
сопло надо ставить спрямляющий аппарат, в котором происходит
определенная потеря энергии.
Для промежуточных ступеней аг может дох<}дить до 70°.
Особенности расчета ступени турбины для ТРД
Так как турбины всех авиационных ТРД представляют собой
многоступенчатые турбины со ступенями давления, детальный рас-
чет которых приведен в гл. VII, здесь отметим только особенности
расчета отдельной ступени многоступенчатой турбины.
Заданием для расчета ступени являются начальные параметры
газа ра*, То*, расход газа через ступень G, число оборотов п, конеч-
ное давление рг> а также ориентировочные высоты лопаток. Все эти
величины для ступени известны из газодинамического расчета дви-
гателя и прикидочного расчета многоступенчатой турбины. Для де-
тального расчета ступени необходимо выбрать степень реактивно-
сти на среднем диаметре и угол выхода потока из сопловой решет-
ки. Скорость газа на выходе из сопловых аппаратов ступеней тур-
бины авиационных двигателей близка или превышает скорость
звука, поэтому угол выхода потока из сопловых лопаток может
быть определен с помощью уравнения расхода (3.51) при q(Ku) = 1:
G1/*RT* I
sin <ij=---;—2- / (2л</Л1<р₽).	(6.71)
Ро I
Для первых ступеней турбин ai=15 ... 20°. В последней ступени
угол aj может доходить до 30° и превышать его.
Степень реактивности на среднем диаметре в ТРД обычно рав-
на 0,2 ... 0,4. При малых qct может возникнуть отрицательная
степень реактивности в основании лопаток, большие qCt требуют
высоких отношений и/сад и, следовательно, большой окружной ско-
рости и. Оптимальной степенью реактивности на среднем диаметре
является тот случай, когда в корневом сечении степень реактивно-
сти равна 0.
Радиальный градиент степени реактивности наибольший в сту-
пенях, лопатки которых закручены по закону постоянства циркуля-
143
ции, поэтому при выборе степени реактивности на среднем диамет-
ре будем ориентироваться на этот вид закрутки. Тогда
бет з ,	»	(6* 72)
1 + 'к *1» а1ср
где rK=rK[rcv. Значение qCt получено из условия рк=0.
Выбранные qCt и он позволяют определить параметры газа на
выходе из сопловых лопаток Л, Qi с помощью таблиц термоди-
намических функций, скорость Wt и угол pi в относительном дви-
жении — из входного треугольника скоростей, построенного по
скоростям съ и и углу at.
В случае сверхкритического истечения газа из сопел угол <ц,
найденный по формуле (6.71) равен углу а/, а угол си, которому
должен удовлетворять профиль сопловой решетки, находится по
формуле (3.85).
Скорость газа на выходе из рабочих лопаток в относительном
движении w2 определяется формулами (3.53) и (3.55). Параметры
газа за ступенью р& Тъ <?2 находятся с помощью таблиц термо-
динамических функций.
Направление потока на выходе из лопатки рабочего колеса в
относительном движении, характеризуемое углом р2, может быть
определено из уравнения расхода:
sin₽>=^b--	<6-73’
ЛаЛ2^2б2
Значения углов и 02 необходимо сопоставить как в среднем
сечении, так и в корневом, причем ₽2ср< Picp, а в корневом сечении
желательно ргк«1₽1к-
В связи с тем что в корневой зоне действительный угол ащ
больше расчётного, на внутреннем радиусе допускается расчетный
угол Р1К иметь меньше угла Ргк на 5 ... 6° [9]. В этом случае при
профилировании геометрический угол ₽1К.геом выполняется равным
углу р2к.
Значения углов р1к и ргк в корневом сечении для лопаток, за-
крученных по закону постоянства циркуляции, соответственно равны
p1(C=arctg-------------;	(6.74)
<?lcp COS ttlcp-ttcpf*K
q	»	Hcw2cp sin p2cp	yj-x
P2K=arctg-----------------------=5-.	(6.75)
®2cp COS p2cp — Вер + исрГK
Если окажется, что р2к—iPiK>5 ... £°, необходимо в среднем
сечении лопаток увеличить угол щ или уменьшить угол р2 за счет
прироста отношения Л2/Ль Значения w2, р2 и и определяют выход-
ной треугольник скоростей, а следовательно, скорость с2 и угол а2.
При расчете последней ступени турбины нужно следить за тем, что-
бы направление потока за рабочими лопатками в абсолютном дви-
жении было близко к осевому (а2 = 84 ... 86°).
144
Полученные параметры газа в среднем сечении позволяют най-
ти работу на окружности колеса Ни, к.п.д. ступени г]и* и рас-
считать закрутку потока по высоте лопатки в соответствии с вы-
бранным законом закрутки (см. гл. V), определить потери на утеч-
ку газа через радиальный зазор лопаток, потери на трение и, как
следствие, внутренний г],* и эффективный т]й* к. п. д. ступени.
Расчет турбины без использования выходной скорости
В летательных аппаратах к таковым относятся турбины турбонасосных ai-
регатов ЖРД, турбины турбостартеров и различных вспомогательных установок.
Кроме того, без использования выходной скорости работают турбины всех судо-
вых, стационарных и транспортных установок.
Существенным отличием этого расчета от предыдущего является то, что
давление на выходе из турбины здесь задано и выходная скорость с2 должна
быть по возможности минимальной.
Таким образом, для расчета должны быть заданы: полное давление газа
перед турбиной р0* (или статическое давление р0 и скорость входа с©); полная
или статическая температура газа перед турбиной То* (Го); давление выхода из
турбины р2; расход газа G или мощность турбины Ne\ физические константы га-
за: k, R. Число оборотов п может быть задано, но может быть и предостав-
лено выбору конструктора.
Расчет турбины можно вести при помощи таблиц термодинамических функ-
ций, газодинамических функций, термодинамических формул и, наконец, при по-
мощи диаграммы Z—S. Рассмотрим методику расчета по термодинамическим
формулам. Эту методику рекомендуется применять лишь в том случае, если для
данного газа нет таблиц термодинамических или газодинамических функций.
1.	Адиабатная работа газа при расширении от р0* до р2 (Дж/кг):
.	Г	/	к*-1!
Н0=**Т*0 .
1 L	\PqJ J
2.	Задаемся степенью реактивности рст: для турбин с короткими лопатка-
ми (турбокомпрессоры наддува, турбостартеры, мелкие вспомогательные тур-
бины) следует выбирать рСт = 0 ... 0,2. В турбинах ТНА с большой степенью
понижения давлений и высокими сверхзвуковыми скоростями степень реактив-
ности, как правило, равна нулю. Мощные турбины ТНА выполняются с полным
облопачиванием при рст =0,2 ... 0,4. С уменьшением реактивности снижается
температура рабочей лопатки, что может существенно повлиять на выбор вели-
чины рст.
3.	Адиабатная работа расширения в соплах (Дж/кг): /Ли—(1—Рст)Я0.
4.	Скорость, эквивалентная адиабатной работе газа (м/с): сад = у/Г2//0.
5.	В соответствии с величиной рст и пунктирными кривыми на рис. 6.14
задаемся отношением и/с&л=х. Обычно х=0,4 ... 0,5. Исключение составляют
турбины ТНА и вспомогательные воздушные турбины, в которых из-за больших
скоростей газа не удается выйти на оптимальное отношение ufc^ и значение
«го для одноступенчатой турбины составляет х>0,2.
6.	Окружная скорость: и=хсад не должна превышать 400 м/с (в зависи-
мости от температуры газа и длины лопаток, пока, впрочем, неизвестных).
и
7.	Средний диаметр облопачивания (м): d = —. Если число оборотов не
ял
задано, то его можно здесь определить, исходя из диаметра облопачивания, кото-
рый выбирают по габаритным соображениям с последующей проверкой длины
лопаток.
8.	Скорость газа »а выходе из сопел: = у]/2#0г В турбинах с коротки-
ми лопатками <р=0,95 ... 0,96.
Для сверхзвуковых сопел небольшой высоты ф=0,94 ... 0,95.
145
9.	Угол ai выбирают: для активных ступеней ai=15 ... 20°, для реактив-
ных at = 18 ... 25° (правильность выбора контролируется высотой лопаток ha
10.	Давление на выходе из сопел (Па):
*01
Л—l*7®/
Pi = Pol 1
' k
11. Температура газа там же (К):
Л =
?2/*01
—Л ’
k—\R
*	12. Соответствующий удельный объем (мв/кг) :
RT\
V!	.
Pl	<
13.	Расход газа через турбину (если он не задан):
(i = A-.
VA)
В зависимости от размеров и параметров турбины т)е может колебаться в
широких пределах 0,6 ... 0,85 (меньшим цифрам соответствуют малые расхода
газа и сверхзвуковые скорости не только Ct, но и Wi). В активных турбинах
можно принять т)в=т1«—(0,03 ... 0,07). Большие значения дополнительных по-
терь относятся к парциальным турбинам. Окружной к.п.д. активной турбины
(см. § 6.10)
Л Л и ( и/С1 \L , COS 02 \
= 2^>2--COS ai I 1 —----) I 1 + Ф-г— ) .
Cl	\ COS СС1 J \ COS 01 /
Скоростной коэффициент ф следует выбирать по материалам § 4.9. ф-=
=0,88 ... 0,92. В первом приближении p2=0t.
14.	Высота сопловой решетки на выходе (м):
t	Gvi
»1 =—з—•— •
cpafc! sm tri
Причем парциальность обычно вводится лишь в том .случае, если при полном
облопачивания hi оказывается меньше 7 ... 12 мм (см. § 6.6).
15.	Полагая в первом приближении h2=hi, проверим величину Q—dfh^ и
напряжение (для лопатки постоянного профиля из материала с плотностью р=
=0,008 кг/см») ар=0,016н2/0 (см. § 12.2).
Если эти величины выходят за пределы допустимых, можно уменьшить ок-
ружную скорость или увеличить угол at. В то же время, поскольку речь идет
о турбинах для летательных аппаратов, нежелательны большие значения 0
(свыше 5 ... 6) и малые напряжения в лопатках. В турбинах ТНА из-за малого
расхода газа значение 0 может доходить до 30 при больших запасах npoi-
ности.
16.	Относительная скорость входа на лопатки (м/с):
wi = a* — 2cja cos aj.
17.	Температура потока, заторможенного на входе в рабочую решетку (К):
*	w?
= Л +------!----
146
18.	Приведенная скорость

Wi
k ,
обычно меньше единицы, но у турбин ТНА может быть > 1.
19.	Угол входа на рабочие лопатки:
п . a sin ai
Bi = arcsin-------------------------------.
Wi
20.	Работа адиабатного расширения в рабочей решетке (Дж/кг):
21.	Скорость выхода из рабочих лопаток:
,	w2 = Ф + 2/Л)2-
22.	Температура газа на выходе из рабочих лопаток (К):
Г2 = Т’,
____
23.	Соответствующий удельный объем (м3/кг):
/?Т2
V2 = —- -
Р2
24.	Зададимся высотой рабочей лопатки на выходе (мм):
Л2 =	+ (0... 10); но < L3A1.
25.	Определим угол
А	.	G№
р2 = arcsin —-—— ,
623tu2^2**2
где ег==«1+0,01.
Расход 6л собственно через решетку для турбин со степенью реактивно-
сти менее 15% можно принять равным G. Для турбин со значительной степенью
реактивности следует учесть утечку через радиальный зазор по методике, изло-
женной в § 6.4 (формула (6.12) для лопаток с бандажом и (6.13) для лопа-
ток без бандажа).
Угол Рг надо определить в предположении, что Сл —G, а затем найти
угол Рг во втором приближении. Однако необходимо, чтобы р2 < Pi, или по край-
яей мере р2<Р1гвом, где ₽1геом может быть несколько больше (до 5°), чем
Угол Pi. При определении»угла р2 можно варьировать как высоту лопатки Аг,
так и диаметр который не обязательно должен равняться (L
26.	Выходная скорость газа (м/с):
С2 ==:	4- м2— 2aw2 cos ₽2-
27.	Угол
. W2 SIH
а2 = arcsin----------.
<*2
^айденные величины скоростей «ч, cz и углов Pi и аг рекомендуется проверить
построением треугольников скоростей.
147
28.	Окружная работа (Дж/кг):	•
Ни — и (»1 cos -|-W2COS₽2).
29.	Потерн на трение [см. формулы (6.14) и (6.15)] Ятр=Ят.д+Ят «•
30.	Потери от парциального подвода газа Няеят определяются по форму*
ле (6.17).	’	3
31.	Внутренняя работа турбины (Дж/кг): Я<=Я„—(Ят.в+Яу1).
32.	Внутренний к.п.д. турбины тц=Я</Я».
33.	Эффективный к.п.д. т]е=т]мг]1> где обычно t)M=0.95 ... 0,99 (0,95 — для
турбин малой мощности: менее 75 кВт).
Если найденная величина т)« не совпадает с принятой в начале расчета, при-
чем последняя является вполне достоверной (основанной на результатах испы-
таний аналогичной турбины), то необходимо изменить принятые коэффициенты
<р и ф. Если же значения этих коэффициентов достоверны, то необходимо най-
денную величину т]е положить в основу расчета, т. е. найти новое значение рас-
хода газа 6 и по нему пересчитать высоту сопловых и рабочих лопаток.
34.	Для случая, когда задан расход газа, определяется мощность турбины
(Вт): Ne=GH^„.
§ 6.15. ОСОБЕННОСТИ РАСЧЕТА ТУРБИН
СО СТУПЕНЯМИ СКОРОСТИ
Колесо со ступенями скорости (число которых обычно не превы-
шает двух) можно рассматривать как частный случай одноступен-
чатой турбины; весь перепад или большая часть его, срабатывае-
мая в турбине, реализуется в соплах, а два ряда рабочих лопаток
располагаются на одном диске.
Как указано в § 6.11, колеса Кертиса выполняются часто ак-
тивными, особенно в том случае, когда парциальность турбины ма-
ла (турбины для ТНА небольшой мощности).
Если колесо Кертиса работает с реактивностью (что желатель-
но при парциальности е>0,4 ... 0,5), то работу адиабатного рас-
ширения Но делят между всеми решетками лопаток, в которых про-
исходит расширение газй. Реактивность возрастает от первой ре-
шетки к последней, не превышая величины 10 ... 15% в одной ре-
шетке и приблизительно 25% суммарно по всем решеткам (в том
числе и направляющей). Степень реактивности относится к вели-
чине Но так, что, например, реактивность направляющего аппара-
та Он=Яон/Яа, где Яон — адиабатная работа расширения в направ-
ляющей решетке. Задавшись степенью реактивности каждой из ре-
шеток, нетрудно определить работу Н<п, и Нсиъ каждой из них,
а следовательно, и давление газа за любой решеткой. Целесооб-
разность назначения той или иной реактивности для данной решет-
ки проверяют в дальнейшем соотношением высот лопаток и плав-
ностью меридионального профиля проточной части. При сверх-
звуковом натекании газа на лопатки следует проектировать чисто
активные решетки (qct=0).
Скорости и величины потерь определяют по формулам § 6.11.
Там же показаны треугольники скоростей турбины и тепловой про-
цесс на диаграмме i—S. При построении треугольников скоростей
приходится задаваться величинами выходных углов каждой чз
решеток. Обычно их принимают равными или нй несколько граду-
148
Рис. 6.19. Схема проточной части колеса Кер*
тиса
сов меньше входного угла данной ре-
шетки, причем разность углов часто
возрастает от первого ряда рабочих
лопаток к последнему.
Правильность выбора углов прове-
ряют по проточной части турбины, ко-
торую ограничивают цилиндрическими поверхностями или кониче-
скими (рис. 6.19). Возможна также комбинация цилиндрических и
конических поверхностей (например, рабочие решетки ограничива-
ются цилиндрическими поверхностями, направляющие — кониче-
скими) .
Выходные высоты решеток определяются по формулам: для ра-
бочей лопатки I ступени
h___	О»2
SIH ₽2
для направляющей лопатки
Gv\
Ня=----^2—г ;
tadc1 sin ctj
для рабочей лопатки II ступени
------------------------------------------------------------б»2
j	«2_:—1—;—~7 •
Sin 02
Здесь удельные объемы соответствуют: о2 — точке Л2 диаграм-
мы i—S (см. рис. 6.15); о/ — точке At'; = точке Л2'.
При аналитическом расчете эти объемы определяются по дав-
лениям и температурам, а температуры находятся так же, как это
показано в случае одноступенчатой турбины. Желательно, чтобы
... 2,5.
Параллельно с построением треугольников скоростей рекомен-
дуется строить схему проточной части, в которой в качестве высот
лопаток в первом приближении принимают осевые составляющие
скоростей Л/с1о вместо hi, А/с2а вместр й2, А/с'1а вместо hi, А/сз»
вместо й2'. Здесь Л — любая постоянная, заменяющая масштабный
коэффициент (см. рис. 6.14). Это позволит на этой стадии расчета
проверить целесообразность выбора степеней реактивности решеток,
углов (аь р2, а/, р/) и в случае необходимости внести корректи-
вы. Характер проточной части, определенной по высотам лопаток»
найденных в конце расчета турбины, будет лишь незначительно от-
личаться от предварительного построения, в котором пренебрегают
незначительным влиянием переменности удельного объема на вы-
ходе из отдельных решеток.
К.п.д. ступеней скорости, образованных современными типами
профилей, достаточно высок, и при околозвуковых скоростях г];
Достигает 75 ... 80%.
149-
Глава VII
ТЕПЛОВОЙ ПРОЦЕСС ТУРБИН СО СТУПЕНЯМИ
ДАВЛЕНИЯ И ЕГО РАСЧЕТ
§ 7.1.	ОБЩИЕ СВЕДЕНИЯ
Понятие об этих турбинах дано в § 2.5.
Наибольший тепловой перепад, который можно эффективно сработать в од-
ной ступени, не превышает Яо~ЗОО кДж/кг. Это объясняется тем, что: а) ско-
рости газа на выходе из сопловых и рабочих лопаток приближаются к крити-
ческим (A^wl;	а возрастание волновых потерь снижает к.п.д. ступени;
б)	окружные скорости вращения колеса турбины при соблюдении оптимального
по к.п.д. отношения скоростей (г//сад) opt приближаются к предельно допусти-
мым по прочности рабочих лопаток величинам «=380 ... 400 м/с.
Здесь уместно заметить, что в последние годы появились отдельные образ-
цы особо мощных высокотемпературных авиационных ГТД, турбины которых
имеют «>500 м/с и, следовательно, способны эффективно сработать в одной
ступени существенно большие теплоперепады (до Яо=600 ... 700 кДж/кг). Это-
му способствуют ряд факторов: большие диаметральные габариты позволяют
выполнять турбины с относительно короткими (Л/d=0,06 ... 0,07 против
0,12 ... 0,15 в обычных ГТД) лопатками; высокая температура газа отодвигает
критические режимы («кр=]/"?о) с их повышенными волновыми потерями, в об-
ласть больших скоростей газа.
В обычных условиях в одной ступени целесообразно ограничиваться тепло-
перепадом даже меньшим, чем 300 кДж/кг, а именно 200 ... 250 кДж/кг. Боль-
шие теплоперепады следует делить между несколькими ступенями. При этом
уменьшается потребная окружная скорость, повышается к.п.д., уменьшается диа-
метр ротора при данном числе оборотов, а при данном диаметре — уменьшает-
ся число оборотов.
Как показано в § 2.5, при заданном теллоперепаде окружная скорость тур-
бины со ступенями давления приблизительно обратно пропорциональна корню
квадратному из числа ступеней г. Если для турбины задано определенное число
оборотов, то диаметр ротора уменьшается пропорционально Vz.
Применение многоступенчатой конструкции оказывает благоприятное влия-
ние на к.п.д. турбины по следующим причинам:
1)	небольшой перепад тепла в ступени позволяет иметь умеренные числа М
в проточной части. Умеренные скорости газа и небольшой диаметр ротора обус-
ловливают значительную длину лопаток, а это снижает потери на венце, а так-
же относительные потери от утечки через радиальные зазоры лопаток. Таким
образом, к.п.д. отдельных ступеней оказывается выше, чем в том случае, если
бы весь теплоперепад был сработан в одной ступени;
2)	выходная скорость из каждой ступени, кроме последней, используется в
следующей ступени (выходные потери последней ступени в авиационных ГТД
используются на создание тяги);
3)	прирост энтальпии газа, происходящий вследствие внутренних потерь в
предыдущих ступенях, частично используется для полезной работы следующих
ступеней. В результате к.п.д. многоступенчатой турбины в целом оказывается
более высоким, чем средний к.п.д. отдельной ступени (см. ниже).
Недостатком многоступенчатой конструкции является сохранение высокой
температуры газа в нескольких ступенях из-за медленного срабатывания тепло-
вого перепада. В случае высокотемпературных турбин последнее обстоятельство
усложняет охлаждение проточной части, так как потребуется охлаждать несколь-
ко рядов лопаток и дисков.
Применение многоступенчатой конструкции связано с утяжелением турби-
ны и увеличением ее длины. Наличие нескольких ступеней усложняет конст-
рукцию, технологию изготовления и трудоемкость. К тому же при большом
числе ступеней может возникнуть необходимость установки дополнительной опо-
ры (за турбиной). Однако, несмотря на эти недостатки, многоступенчатые тур-
150
бины получили широкое распространение как в авиационных ГТД, так и в дру-
гих типах ГТУ, где на первый план выступает требование получения высоко-
го К.П.Д.
В многоступенчатых турбинах применяются почти исключительно реактивные
ступени, причем целесообразно степень реактивности рСт повышать от ступени
к ступени по мере роста длины лопаток, что благоприятно для к.п.д. Малая ре-
активность в первых ступенях снижает потери на утечки. Вместе с тем, во из-
бежание отрицательной реактивности в корневых сечениях лопаточных решеток,
в первых ступенях назначают рст > 0,2. Реактивность в последних ступенях не-
редко составляет рСт=0,4 ... 0,5.
§ 7.2.	ОТЛИЧИТЕЛЬНЫЕ ОСОБЕННОСТИ ТЕПЛОВОГО
ПРОЦЕССА МНОГОСТУПЕНЧАТОЙ ТУРБИНЫ
Параметры расширения газа в предыдущей ступени многосту-
пенчатой турбины являются начальными для следующей за ней
ступени. Важной отличительной особенностью теплового процесса
в многоступенчатой турбине является использование энергии вы-
ходной скорости предыдущих ступеней. Для этого необходимо, од-
нако, соблюдение ряда условий:
1)	из рабочих лопаток газ должен попадать непосредственно
в сопла следующей ступени без резких изменений поперечного се-
чения;
2)	лопатки соплового аппарата ступени, в которой используется
выходная скорость газа предыдущей ступени, должны быть спро-
филированы так, чтобы газ входил на них с оптимальным углом
атаки (0 ... —5°). Для этого входная кромка сопел должна быть
очерчена приблизительно под углом аз к фронтальной линии ре-
шетки. Обычно угол атаки постепенно увеличивают от —2° в сопло-
вом аппарате второй ступени до —5° в последней, что способствует
снижению профильных потерь.
Другой особенностью рабочего процесса многоступенчатой тур-
бины является значительное увеличение объемного расхода газа
при переходе от I к последней ступени. В этих условиях, чтобы ог-
раничить резкое увеличение высоты сопловых и рабочих лопаток,
приходится увеличивать углы потока и осевые скорости. Радиаль-
ные градиенты давлений в зазоре между сопловым аппаратом и ра-
бочим колесом при этом уменьшаются при переходе от первой к
последней ступени.
Рассмотрим процесс расширения га-
за в многоступенчатой турбине (трех-
ступенчатой) в диаграмме Т—S (рис.
7.1). Адиабатный процесс расширения
газа изображается вертикалью АцАц,
действительная (условная) линия рас-
ширения — кривой AqA2; точки Ао, А2
указывают состояние адиабатно затор-
моженного газа на входе и на выходе
из турбины. В J ступени турбины газ
Рис. 7.1. Схема процесса возврата тепловой
энергии в диаграмме Т—S
151
расширяется по линии Аоа[. Потери в этой ступени изображаются
площадью DaltaiE, однако для турбины в целом потерянным явля-
ется лишь тепло, измеряемое площадью AUKED. Количество тепла,
соответствующее площади ацСиКАгь присоединяется к располагае-
мому теплоперепаду следующих ступеней. Подобным же образом
при расширении газа во II ступени добавочное количество тепла,
измеряемое площадью d^MK, увеличивает располагаемый тепло-
перепад в последующих ступенях и т. д.
Легко видеть', что сумма адиабатных перепадов тепла в отдель-
ных ступенях (S^oct) окажется больше адиабатного теплопере-
пада в турбине в целом (Ho—io— lit)'
Если обозначить через Q площадь а^а^й^МАц, по которой из-
меряется количество добавочного тепла, то сумма адиабатных теп-
лоперепадов в ступенях турбины 2/7oCt=/7o-|-Q-
Обычно полагают
2^=(14-ав)№,	(7.1)
где ав — коэффициент возврата тепла.
Сопоставляя два последних уравнения, находим
aB—Q/Ho7	(7.2)
Обозначая через г|<* внутренний к.п.д. по заторможенным пара-
метрам турбины в целом, можно написать, что внутренний тепло-
перепад в турбине Hi=x\i*Ho*. С другой стороны, для отдельной
ступени /7/ет=т|*ст//ост'
Суммируя внутренние теплоперепады во всех ступенях и пола-
гая Т|*ст одинаковым для всех ступеней, находим
5 Н1а = Н(^П1ет 3 //Зст = Т1‘сТ (ЯЗ + Q).
Следовательно, Я/7/о=11*ст(1+ив) Но,
откуда	Т)*=(1+ав)т1*сг.	(7.3)
Это подтверждает ранее высказанное положение о том, что
к.п.д. турбины со ступенями давления в целом вышр среднего к.п.д.
отдельных ее ступеней.
Коэффициент возврата тепла ав тем выше, чем больше степень
расширения в турбине (лт*), чем больше потери в отдельных сту-
пенях турбины и чем больше число ступеней г турбины. Влияние
большого числа ступеней на коэффициент возврата тепла видно из
рис. 7.1. Сумма площадей вида ОиС^КАм и dia^MK. с увеличением
числа таких площадей возрастает, стремясь в пределе к площади
Коэффициент возврата тепла можно оценить, сравнивая тепло-
перепады политропного На* и адиабатного Но* расширения. Сог-
452
ласно формуле (7.2) при бесконечно большом числе ступеней (ког-
да площади ЛоАгАц)
(7.4)
где
*— 1 L \ Ро /
В турбине с числом ступеней г величина ав<ав«> и пропорцио-
нальна отношению (г—1)/г. Таким образом, для конечного числа
ступеней найдем
(7.6)
Иллюстрацией формулы (7.5) служит рис. 7.2.
С увеличением числа ступеней коэффициент возврата тепла ав
возрастает от 0,5авво при двух ступенях до 0,9аВОо при десяти сту-
пенях. В большинстве случаев для турбин авиационных ГТД
ав«0,02 ... 0,03.
Формула (7.3) с достаточной для практических целей точностью
отражает также соотношение между лопаточными к.п.д. турбины в
целом и отдельных ее ступеней, т. е.
Т)^«(14-а^т] ист*	(7.6)
В заключение подчеркнем, что в приведенных выше соотноше-
ниях располагаемые теплоперепады в ступенях и в турбине в це-
лом определялись по адиабатно заторможенным параметрам на
входе и выходе из турбины. Если, как это часто делают при расче-
те многоступенчатых турбин, за располагаемую работу принимать
) адиабатно заторможенного
теплоперепад от параметров (роь Тм)
потока на входе в турбину (сту-
пень) до статических (р2т, Т2т) —
яа выходе, то разница между адиабат-
ным перепадом турбины в целом (//От)
и суммой адиабатных теплоперепадов
в отдельных ступенях (2770Ст)
Рис. 7.2. График коэффициента возврата теп-
ловой энергии в функции отношения давлений
и внутреннего к.п.д. ступени »)*„
153
Рис. 7.3. Схема идеального (без
потерь) процесса расширения га-
за в трехступенчатой турбине со
ступенями давления в диаграмме
i—S
будет еще большей. Объяс-
няется это тем, что в этом
случае при суммировании
располагаемых теплоперепа-
дов по ступеням энергия вы-
ходной скорости, за исклю-
чением последней ступени
(с2т/2), учитывается факти-
чески дважды: во-первых,
как часть работы расшире-
ния рассматриваемой п-й
ступени; во-вторых, как на-
чальная кинетическая энер-
гия [(со/2)п+1 = (с1/2)„] по-
следующей («+1)-й ступени.
Особенно наглядно это по-
ложение иллюстрируется
(без потерь) процессе расши-
s
в диаграмме i—S при идеальном
рения газа.в многоступенчатой турбине (рис. 7.3). Из рис. 7.3 еле
дует, что суммарный располагаемый тепловой перепад ступеней
y/70CT=^oi+^on + ^oin при таком подходе к расчету оказы-
л=2-1
вается замышенным на величину (cz/^)n по сравнению с
I л=-0
адиабатным теплоперепадом Но турбины в целом. Обозначая йак
и раньше Но—Но—с1т12 (см. рис. 7.3) и учитывая, что для любой
’	n~z	n=z
ступени //ост=^ГОст+Сгст/2, получим 2 ^Ост = ^ /'/’ст +
л-1	л—1
Л>=1
•В действительном процессе с потерями, из-за возвра-
та части тепла трения в процесс, в соответствии с формулой (7.1)
л—г
2 Ност=Но(1-\-а,^ Таким образом, в рассматриваемом случае
п—1
при распределении теплоперепада по ступеням надо исходить
не из величины Я0*(1 + ав) [см. формулу (7.1)], а из
л=з	n=>z
я0С1=я;(1+Ов)+2
Л = 1
Сумма внутренних теплоперепадов останется, конечно, прй
этом неизменной, такой же как и в случае использования в расче-
154
те теплоперепадов по заторможенным параметрам, а к.п.д. (t){T, T]iCTr
Лист), отнесенные к статическим параметрам на выходе — меньше.
§ 7.3. РАСЧЕТ ТУРБИНЫ СО СТУПЕНЯМИ ДАВЛЕНИЯ
Газодинамический расчет турбины со ступенями давления сос-
тоит из трех этапов.
На первом этапе выполняется так называемый предваритель-
ный расчет. Он включает выбор основных параметров турбины, та-
ких как диаметр, число оборотов, число ступеней, выходная ско-
рость и др.
В процессе предварительного расчета намечается меридиональ-
ный контур проточной части турбины. Все выбранные величины
должны быть увязаны с конструктивными особенностями двига-
теля (ТРД, ТРДД, каскадность компрессора и др.) и с парамет-
рами приводимых турбиной агрегатов. К.п.д. турбины, естествен-
но, выбирается таким же, как и в тепловом расчете двигателя. На
первом этапе расчета оцениваются также размеры и прочность
лопаток первой (наибольшие температуры) и последней (наиболь-
шие напряжения) ступеней турбины, а также намечается распре-
деление теплового перепада по ступеням турбины. Если в процессе
расчета компрессора ГТД выполнялось согласование параметров
компрессора и турбины, на основе безразмерного, комплексного
параметра проф. К. В. Холщевникова [21], то полученные при этом
величины (Di, п, z, Хт и др.) используются и в расчете турбины.
Второй этап расчета заключается в детальном поступенчатом
расчете турбины на среднем радиусе. В процессе этого расчета
определяются и уточняются геометрические размеры проточной ча-
сти, к.п.д., мощность и параметры потока в характерных сечениях
и на выходе из турбины.
Третий этап включает расчет пространственного потока в сту-'
пенях турбины с целью достижения наибольших величин к.п.д. и
получения исходных данных для профилирования сопловых и ра-
бочих допаток по высоте ступени (закрутки лопаток).
Предварительный расчет турбины
Выбор основных параметров многоступенчатой турбины пред-
ставляет собой важную и в то же время сложную задачу, решае-
мую обычно путем вариантных расчетов. Ниже изложены основные
рекомендации, которыми руководствуются в предварительном рас-
чете турбин авиационных ГТД.
Наружный диаметр турбины (Z)T) авиационных ГТД
следует выбирать с учетом размеров компрессора и диаметральных
габаритов двигателя в целом (к моменту детального расчета тур-
бины они уже известны из теплового расчета двигателя и предва-
рительного расчета компрессора). Главная цель, которая пресле-
дуется при выборе диаметра турбины, — это обеспечение минималь-
ной ее массы. При заданной частоте вращения ротора п уменьше-
155
яие диаметра против некоторой оптимальной величины ведет к
снижению окружных скоростей и; для поддержания к.п.д. на высо-
ком уровне приходится снижать теплоперепад на ступень; это при
заданной работе в турбине в целом ведет к увеличению числа сту-
пеней и может вызвать увеличение массы турбины. Значительное
увеличение диаметра также не желательно (возрастает масса дис-
ков). По статистическим данным, в двигателях с осевым компрес-
сором наружный диаметр турбины обычно равен наружному диа-
метру ротора компрессора или несколько превышает его (на 10...
... 15%). В ТРДД при этом имеется в виду диаметр компрессора
внутреннего контура. В двигателях с центробежным или комби-
нированным компрессором наружный диаметр турбины равен или
на 10 ... 20% меньше диаметра крыльчатки компрессора.
Частота вращения (п) турбины или групп ступеней (в
многовальной схеме) выбирается в соответствии с частотой враще-
ния приводимых ими агрегатов. В то же время оно должно быть
увязано с диаметром турбины, так как по условиям прочности де-
талей ротора окружная скорость на среднем диаметре I ступени
(u=ndn) не должна превышать 350 ... 380 м/с; в последней сту-
пени — 260 ... 300 м/с. При многовальной схеме выбор частоты
вращения и окружных скоростей производится раздельно для каж-
дого из роторов.
Число ступеней z турбины выбирается исходя из типа и
назначения двигателя. При выбранной окружной скорости и задан-
ном теплоперепаде от числа ступеней z зависит отношение (и/сад)ст-
В свою очередь отношение (ы/сад) ст влияет на к.п.д. турбины и угол
выхода потока. При выборе числа ступеней турбины удобно ориен-
тироваться на так называемую характеристику Парсонса:
Г =	(7.7)
сад.т
где 2и2 — сумма квадратов средних окружных скоростей всех сту-
пеней; сад.т — скорость, соответствующая располагаемому адиабат-
ному теплоперепаду турбины.
Величина Y для многоступенчатой турбины играет ту же роль,
что и отношение и/сад (см. § 6.10) для одноступенчатой турбины.
Чем больше число ступеней, тем больше при прочих равных усло-
виях величина У. Для случая, когда окружная скорость во всех сту-
V «V*
пенях равна Y = —1, откуда
са*.т
В турбинах ТРД величина Y обычно выбирается в пределах
0,52 ... 0,54; в ТВД и ТРДД — 0,55 ... 0,6. Большее значение Y и
связанное с этим большее число ступеней турбины в этом случае,
объясняется тем, что в этих двигателях к.п.д. турбины сильнее влия-
ет на экономичность, чем в ТРД.
156
В турбинах авиационных ГТД, обычно бывает заданным не адиа-
батный До, а эффективный теплоперепад Не. В этом случае число
ступеней турбины удобно оценить по средней величине коэффициен-
та нагрузки ступени р, (см. § 6.13).
Полагая Не=Ни, можно получить, что
2 = 7/г/р.срйср,	9)
где Мер — среднее (по ступеням) значение окружной скорости на
среднем диаметре; ц,Ср — среднее значение коэффициента нагрузки
ступеней турбины (для ТРД цср = 1,4 ... 1,5; для ТВД и ТРДД рСр=
= 1,3... 1,4).
При выборе числа ступеней турбины можно также ориентиро-
ваться на статистические данные выполненных авиационных ГТД,
приведенные в работах [9, 5] и в табл. 7.1.
Таблица 7.1.
Тип двигателя	Степень повышения давления воздуха в компрессоре я*	Число ступеней турбины Z
ТРД	4,5...5,0 6...10 11...15 15 и более	1 2 2...3 3
ТРДД а) со степенью двухконтурностн т=0,7...1,5 ’ б) т=4... 5 в) /и=6... 8	9...10 И...19	f 20...27 20...27	2...3 3...5 5...6 7...8
ТВД и ТВаД	4...5 ' 5...8 9...16	2 3 4...6
Выходная скорость из турбины выбирается обычно
в следующих пределах (в долях от критической скорости лкр.т=
1/2—-—: в ТРД Ад®=СзтА^кр.т=0,5 ... 0,55; в ТРДД
г k 4-1	/
Дат = 0,45 ... 0,65; в ТВД Аат=0,5 ... 0,7; в вертолетных ТВД Х2т =
= 0,4 ... 0,6.
При малых скоростях газа (Агт^О.Зб) недопустимо увеличива-
ются высота лопаток последних ступеней и напряжения в них;
затрудняется профилирование лопаток проточной части, обеспечи-
вающее высокий к.п.д. (это в особенности относится к корневым ре-
чениям). При правильном выборе А2т в последней ступени отно-
шение ft=d!h должно быть больше 3 ... 3,5. У выполненных двига-
157
Рис. 7.4. Зависимость коэффициента по-
тери полного давления Д/>*//£,. в затур.
бинном устройстве от %зт и угла выхода
потока из турбины:
7-(Х2=75\ 2—80°; 5-85°; 4—90°
телей отношение d/h составляет*
у ТВД и ТРДД 3 ... 4; у ТРД
4 ... 5; в первых ступенях авиа-
ционных двигателей всех типов
обычно 7,5 ... 9.
При больших величинах А^т вы-
сота и напряжение в лопатках
последних ступеней уменьшаются, но появляются свои трудности.
Снижается к.п.д. турбины и двигателя в целом, так как возраста-
ют потери в последних ступенях и в реактивном сопле (в особенно-
сти, если поток за турбиной окажется закрученным, что иллюст-
рируется на рис. 7.4) [9]. Во избежание больших потерь от закрут-
ки потока в реактивном сопле и сохранения запаса работы турби<
ны на нерасчетных режимах угол потока на выходе из последней'
ступени турбины должен находиться в пределах а2т=84 ... 90°.
- В зоне высоких А2т мощность турбины очень вяло реагирует на
изменение режима работы двигателя из-за слабого изменения ра-
боты газа на-лопатках и скорости. с[и вблизи критических режимов
(см. рис. 3.18). К тому же расход газа, определяемый обычно'
узким сечением соплового аппарата, останется при этом практичес-'
ки неизменным.
Меридиональный профиль проточной части
многоступенчатых турбин при выбранном значении Dr (на выходе
из последней ступени турбины) может быть выполнен по-разному;
Общим, однако, является то, что площадь проходного сечения дол-
жна непременно увеличиваться по ходу газа несмотря на некоторое
увеличение осевых скоростей {(c2aT/c2ai) «1,3 ... 1,4]. Это объясня-
ется тем, что приращение удельного объема по длине L турбины'
оказывается больше соответственного приращения осевой скорости
са газа.
Профили проточной части многоступенчатых турбин, наиболее
часто встречающиеся в двигателях, показаны на рис. 7.5. Если счи-
тать, что максимальный диаметр и окружные скорости на перифе-
рии (в точке А на рис. 7.5) в последней ступени во всех схемах
одинаковы, то проточцая часть с dH=const при заданной частоте
вращения позволяет получить наибольшие окружные скорости во
всех ступенях. Это позволяет выполнить турбину с меньшим чис-
лом ступеней. Кроме того, она обусловливает цилиндрическую, т. е.
относительно простую форму корпуса, а меридиональные линии то-
ка в ней согласованы с направлением потока на входе в реактив-
ное сопло. Преимуществом такой проточной части является также
и то, что радиальные зазоры остаются неизменными при осевых
смещениях ротора. Недостатком этой схемы, как впрочем и схемы
158
Рис. 7.5. Схемы меридионального сечения проточной части турбины со ступени*
,	ми давления:
а—с постоянным наружным диаметром (dH=dT=const); б—с постоянным средним диаметром
(rf^const); в—с постоянным внутренним диаметром (dB=const)
(см. рис. 7.5, в) с постоянным внутренним диаметром dB=const,
является большой угол ув внутренней конической поверхности. Во
избежание больших потерь необходимо, чтобы ув^8 ... 12°. Вели-
чина у в схеме с постоянным средним диаметром d=const получает-
ся Меньше. Угол раскрытия проточной части у=ув=ун можно оце-
нить по формуле, полученной из очевидных геометрических соотно-
шений, при d=const:
у=arctg (. h2-L± ^-k^ ) ,	(7.10)
где Лсют и hit — выходные высоты первой сопловой и последней
рабочей решетки соответственно; бт — радиальный зазор в послед-
ней ступени турбины;
z	z
(«р.л+8а) + 2 ($с+80ст)> £т — Длина турбины; $р.л, $с —
1	п
ширина рабочей и сопловой решеток; бо, бает — осевые зазоры пе-
ред и за рабочим колесом.
При углах раскрытия проточной части больше 12° поток не ус-
певает приспособиться к сильному изменению геометрии. Вероят-
ность отрыва потока от внутренней конической поверхности осо-
бенно велика (см. рис. 7.5, а), так как в корневых сечениях обыч-
но мала степень реактивности, а крутизна наклона поверхности
здесь наибольшая.
На рис. 7.5, в лопатки первых ступеней получаются наиболее
длинными, что важно при проектировании небольших турбин. Эта
схема обладает и некоторыми технологическими преимуществами,
так как позволяет выполнять диски и замки нескольких ступеней
одинаковыми.
В современных авиационных ГТД форма проточной части тур-
бин обычно выполняется комбинированной. Например, в первых сту-
пенях выдерживается d=const, а в последних dB=const. Нередко
все три диаметра dR, dB и d непостоянны по длине турбины (см.
Рис. 20.3).
К.п.д. турбины в предварительном расчете при-
ходится задаваться. Как уже указывалось, он должен выбираться
159
таким же, как и в тепловом расчете двигателя: для ТРД ти*=-
=0,9 ... 0,91, для ТВД и ТРДД тн* = 0,92 ... 0,94.
Проверка прочности рабочих лопаток первой
и последней ступеней турбины производится по упрощенным фор-
мулам, исходя из максимального суммарного напряжения разры-
ва и изгиба в корневом сечении лопаток от действия центробеж.
ных и газовых сил (см. гл. XI), в Н/м2:
ое=2,66л -^-Ф,	(7.Ц)
где бл — плотность материала лопатки 0=£?/&; Ф — коэффициент
формы лопатки. Выбирается по рекомендациям гл. XII или прибли-
женно в пределах 0,46 ... 0,55. Иначе формулу (7.11) можно за-
писать так:
ав=8,2рл/7п2Ф,	(7.12)
где площадь кольцевого сечения на выходе из турбины
, -С^	^25,2..	(7.13)
₽/>2т? (х2> sin а2	P^q (Х2) sin а2
(?=0,673; =288,4 Дж/(кг-К)).
Напряжения в корневом сечении рабочих лопаток I ступени сле-
дует определять непосредственно по формуле (7.11), так как в
предварительном расчете параметры за I ступенью, необходимые
для расчета F, еще неизвестны. В тоже время величина в в I сту-
пени ГТД всех типов примерно одинакова: 0=7,5 ... 9.
Для оценки запасов прочности в лопатках по заданному ресур-
су работы двигателя и температуре в пограничном слое лопаток
оценивается предел длительной прочности в материале одл. Проч-
ность лопатки считается приемлемой, если отношение ow/aB ока-
жется не менее 1,5 ... 2, в противном случае следует изменить
геометрические соотношения диаметра и длины лопаток или при-
менить охлаждаемые лопатки. Современные высокотемпературные
ГТД, как правило, имеют одну или две ступени с охлаждаемыми
воздухом лопатками (особенности теплового расчета охлаждаемых
турбин изложены в § 9.9).
Температура в корне лопаток последней и
промежуточных ступеней в первом приближении Тл=
=t,Tw*, где 5=0,95;
।	°2г
1 w 1 2т "1--------7----< 2т И----------7-----
«2т — окружная скорость на среднем диаметре в выходном сечении
соответствующей ступени.
Учитывая что 7*2т=7'о---—--->
160
где Hi — внутренний теплоперепад соответствующих ступеней,
окончательно получим
Гл«0,95 (То---
(1.14)
Для лопаток I ступени удобнее следующая формула [15]:
Тл sTo — 0,95 —---(—CcT-0S ai — 1
2-А-Л \
(<р=0,96 ... 0,98; ест = 0,2 ... 0,25; ai=14...18°; ы/сад=0,45 ...
...0,5).
Распределение теплового перепада между
ступенями производится в зависимости от конкретных требо-
ваний, предъявляемых к двигателю, и от его схемы.
Большие теплоперепады в первых ступенях приводят к значи-
тельному снижению температуры газа в них, чем облегчается ра-
бота последующих ступеней. Это обстоятельство особенно должно
учитываться при проектировании высокотемпературных охлаждае-
мых турбин, где благодаря такому распределению теплоперепадов
может быть сокращено число охлаждаемых решеток, уменьшена
глубина охлаждения и, как результат, снижены затраты воздуха
на охлаждение и соответствующие потери. По этим причинам в пер-
вых ступенях высокотемпературных ГТД проточную часть целесо-
образно делать с постоянным наружным диаметром (окружные
скорости получаются наибольшими, что и позволяет эффективно
сработать в них повышенные теплоперепады).
При увеличенном теплоперепаде на последних ступенях получа-
ется более плавное очертание меридионального профиля проточной
части (возрастают скорости в последних ступенях). Кроме того,
при прочих равных условиях несколько увеличивается к.п.д. турби-
ны, поскольку к.п.д. последних ступеней обычно выше, чем у пер-
вых (меньше углы поворота потока, меньше влияние радиальных
зазоров и концевых потерь в длинных лопатках). Турбины с уве-
личенным тепловым перепадом на последних ступейях обладают и
еще одним немаловажным преимуществом. При работе на крейсер-
ских и нерасчетных режимах, когда теплоперепад в турбине умень-
шается по сравнению с расчетным, перераспределение теплопере-
пада по ступеням затрагивает главным образом последние ступени.
В результате нагрузка ступеней примерно уравнивается и турбина
на крейсерском режиме (п<праоч) имеет даже более высокий к.п.д.,
чем на расчетном (рис. 7.6), что особенно важно для двигателей,
предназначенных для дальних транспортных и пассажирских само-
летов и вертолетов.
Общей тенденцией для турбин ГТД является увеличение реак-
тивности от I ступени к последней. Нередко’ чтобы избежать от-
6	1337	161
Рис. 7.6. График влияния расчетного распределе-
ния теплоперепада по ступеням ' турбины на ее
к.п.д. при уменьшении числа оборотов:
/—повышенные теплоперепады в первых ступенях; 2—по-
вышенные теплоперепады в последних ступенях; 3—число
оборотов 1на крейсерском режиме
рицательной реактивности в корне лопа-
ток, на последней ступени в среднем се-
чении принимают реактивность qCt =
=0,4 ... 0,45.
После выбора всех основных параметров турбины с учетом из-
ложенного выше производится детальный поступенчатый расчет
по методике, изложенной в § 6.14, и расчет закрутки лопаток (см.
гл. V).
Глава VIII
РАБОТА ТУРБИНЫ НА НЕРАСЧЕТНЫХ РЕЖИМАХ
ХАРАКТЕРИСТИКИ ТУРБИНЫ И ИХ ИСПОЛЬЗОВАНИЕ
§ 8.1.	ТИПИЧНЫЕ ИЗМЕНЕНИЯ ПАРАМЕТРОВ ТУРБИНЫ
В ГАЗОТУРБИННЫХ ДВИГАТЕЛЯХ
Газовая турбина рассчитывается на заданную тягу (ТРД) или
мощность (ТВД) Двигателя при работе его в определенных усло-
виях. Однако в период эксплуатации меняются тяга двигателя,
скорость и высота полета, температура атмосферного воздуха;
вследствие этого параметры турбины отклоняются от расчетных.
Связь между параметрами теплового процесса двигателя в целом
рассматривается в курсе теории авиадвигателей. В курсе газовых
турбин мы разбираем влияние некоторых параметров двигателя на
тепловой процесс собственно турбины.
В процессе работы двигателя возможны изменения следующих
параметров турбины: давления газа перед турбиной ро*; темпера-
туры газа перед турбиной То*; расхода газа G; давления газа за
Турбиной р2\ частоты вращения турбины л; мощности турбины Nf,
к.п.д. турбины щ. Из перечисленных семи основных параметров
турбины независимыми являются только четыре, которые целиком
определяют оставшиеся три параметра; расчет турбины на пере-
менный режим заключается в их нахождении.
Расчеты, относящиеся к высотным и скоростным характеристи-
кам двигателя, можно выполнять (особенно для ТРД) с определе-
нием изменившегося теплоперепада и расхода газа, но в предпо-
ложении постоянного к.п.д. турбины. При существенном отклонении
теплоперепада и числа оборотов от расчетных значений на нор-
мальном режиме следует проводить детальный расчет турбины;
методы расчета изложены ниже.
162
§ 8.2.	КРИТЕРИИ ПОДОБИЯ ПРОЦЕССОВ В ТУРБИНЕ
При испытании турбины не всегда удается выдержать все па-»
раметры рабочего режима, поэтому характеристики турбины удоб-
нее рассматривать в функции безразмерных величин, представляю-
щих собой комплексы отдельных параметров.
. Определим безразмерные величины, которые могут служить
критериями подобия, и необходимое количество их для определения
режима работы турбины. Режимы работы турбины подобны в том
случае, если обеспечено геометрическое, динамическое и кинемати-
ческое подобие. Кроме того, для обеспечения подобия в сходствен-
ных точках необходимо равенство показателя адиабаты k. Под гео-
метрическим подобием понимается соответствие всех геометричес-
ких размеров сравниваемых турбин (равенство углов, пропорцио-
нальность соответствующих размеров, идентичная шероховатость
поверхности).
При рассмотрении подобных режимов рдной турбины условие
геометрического подобия, естественно, выдерживается. Динамиче-
ское подобие считается обеспеченным в том случае, если по тракту
проточной части турбины подобны поля всех одноименных физи-
ческих величин (давления, температуры и др.). Под кинематиче-
ским подобием понимается .геометрическое подобие линий
тока как в абсолютном, так и в относительном движениях. При-
нимая за контрольные сечения проточной части турбины выходные
сечения соплового аппарата и рабочего колеса, можно сказать, что
условием кинематического подобия является подобие треугольни-
ков скоростей. Для подобия сложных процессов постоянство отно-
шений однородных величин оказывается недостаточным и требует-
ся неизменность отдельных безразмерных комплексов, составлен-
ных из различных величин, характеризующих изучаемое явление.
Эти безразмерные комплексы в теории подобия называются крите-
риями подобия. При выявлении подобных режимов работы турби-
ны течение газа принимается установившимся. Но при условии ус-
тановившегося течения жидкости на режим работы турбины оказы-
вает влияние большое количество факторов: сжимаемость жидко-
сти, теплоотдача в корпус и теплообмен в жидкости, вязкость жид-
кости и т. д. Каждый из этих факторов учитывается определенным
критериев подобия, одновременное постоянство которых характе-
ризует подобные режимы.
При испытании турбин невозможно удовлетворить требованию
постоянства всех критериев подобия, характеризующих режим ра-
боты турбины. Поэтому на практике приходится принимать за по-
добные режимы такие, у которых постоянны только отдельные кри-
терии подобия, наиболее сильно влияющие на исследуемое явле-
ние. В существующих турбинах при рассмотрении течения газа до-
пустимо пренебречь теплоотдачей в корпус и теплообменом в
Жидкость, а также изменением показателя адиабаты k от измене-
ния температуры.
в*
163
Критериями, характеризующими режим работы турбины, явля-
ются число М, учитывающее сжимаемость газа, и число Re, учи-
тывающее вязкость газа:
М=—	: Re=— ,
О- V kRT	*
где с — скорость газа; а — скорость звука; d — характерный ли-
нейный размер, например хорда профиля; v — коэффициент кине-
матической вязкости.
Большое число опытов, поставленных в различных организаци-
ях, показало, что существующие турбины работают в автомодель-
ной области по числу Re. Поэтому подобие режимов работы тур-
бины, автомодельных по числу Re, полностью определяется равен-
ством чисел М в соответствующих точках проточной части турбины.
Если предположить равенство числа М на выходе из соплового ап-
парата в абсолютном движении
МС1=—^1—,
VMTi
то угол выхода потока из соплового аппарата ai и скоростной ко-
эффициент -ф остаются неизменными.
В самом деле, так как в соответствии с формулой (3.9)
то	-^i-= const; -^-=const.
Ро	во
Дополнительное условие равенства числа М на выходе из соп-
лового аппарата в переносном движении
I
М_= ———=const
Уыгт\
обеспечит подобие треугольника скоростей на входе в рабочее ко-
лесо, т. е. постоянства угла pi и числа
М«,=———=const.
/ШТ '
Угол выхода потока из рабочего колеса Ра и скоростной коэф-
фициент ф зависят от геометрии решетки рабочих лопаток и чисел
-M-wi и Mw2:
Г ПР	М«. ————
где	----•
V kRTa,
164
Из уравнения энергии в относительном движении осевой ма-
шины
——/?Г2
2	1k —1	2	'k—1	2
имеем
1
т2	_	2	Wl
Ti	~	k—\	2
2	3
Казалось бы, что для подобия режима работы в турбине требу-
ется постоянство чисел Mci, Mu и Mw>. Но анализируя уравнение
неразрывности, записанное относительно входного и выходного се-
чений рабочего колеса в относительном движении, можно видеть,
что условие подобия определяется двумя числами М..
Действительно, AiWiQisinPi=ft2^aQ2sinfJ2- Отсюда имеем
W2 02  &1 ' sin Pl
W1 Q1 Л2 sin p2
Так как
sin Pi _
sin P2

то для данной турбины MW1=F(MO,I).
Следовательно, условие неизменности MW1 гарантирует посто-
янство MWl.
Итак, постоянство двух чисел М—Mci и Ми или Мв и Mw,
и т. д. обеспечивает подобие режима работы турбины. Эти крите-
рии подобия могут быть заменены двумя другими критериями или
их комбинацией, как например: pi/po* и Ми или Р2/Р0* и Ми или
«/ci=Mu/Mcl и pslpo* и т. д. В настоящее время в теории газовых
турбин в качестве критериев подобия широко используются газо-
динамические функции, основой которых является приведенная
скорость X, однозначно связанная с числом М формулой (3.13). По-
этому она также может служить критерием подобия.' Критерием
расхода является приведенный расход q (k) = cg -, критерием
Акрбкр
мощности — произведение
Степень реактивности, выраженная через газодинамические
ФУНКЦИИ, QCT= I Xi/Асал’ ГДе %с ад= ^ад/^-кр»	= ^и/^кр*
Окружной к.п.д. на подобных режимах остается неизменным.
Часто критерии подобия заменяются размерными параметра-
ми, определяющими подобие режима. Так, критерий
К
и
Акр
и
165
заменяется параметром «/VTo, а при сравнении режимов работы
одной турбины — параметром njVTo.
В качестве параметра расхода, вместо критерия q(k) примени-
"1 /” -W.*
G у Tq
ют, например, величину —-----или (в случае одной турбины)
___	Pq fl
gVt^ „
----;—.Справедливость этого параметра видна из формулы (3.54):
Л
-------(Xi),
Fo
ГДе <м(М) — величина безразмерная й явлйется критерием подо-
бия, а т зависит от R, k и в данном случае величина постоянная.
Кроме величины. --------, за характерный расходный параметр
Ро
можно принять его комбинацию с другими параметрами подобия,
О« ®	Си
как, например, —. или--------, или — и т. д.
Р2	Р2
Параметр подобия мощности можно получить из уравнения
N^QH^t—Q	/-^aVK.
k~1 L \ / I
Если обе части равенства поделить на ро VVo, то
Nt
РоУТо
Отсюда видно, что параметром подобия мощности может слу-
Nt
жить величина »-,/—» или сочетание ее с другими параметрами,
Роу 7о
как, например, NfGTo* и т. п:
Так как M=95,5Af/n, то за параметр подобия момента может
быть принято отношение М/р0*.
Таким образом, два критерия подобия или параметра, пропор-
циональные им, как, например, перепад давлений в турбине pz/po*
и параметр njVTo целиком определяют остальные ее параметры,
GiVrl Nt
как параметры расхода и мощности----;—, й степень реак-
Ро PoV То
ТИВНОСТИ Qct, К.П.Д. Tji И Т]<*.
166
§ 8.3.	ЗАВИСИМОСТЬ ОТДЕЛЬНЫХ ВИДОВ ПОТЕРЬ
ОТ РЕЖИМА РАБОТЫ ТУРБИНЫ
Значения отдельных видов потерь в турбине в значительной
мере зависят от режима ее работы. Основное изменение претерпе-
вают потери в рабочем колесе (в связи с появлением углов атаки
на нерасчетных режимах): выходные потери и потери, вызванные
утечкой газа через радиальный зазор. Так как потери с выходной
скоростью легко определяются "Из выходного треугольника скорос-
тей и в конкретной турбине зависят от отношения и!слл, реактив-
ности и Мад, то в данном параграфе рассмотрим зависимость по-
терь от угла атаки и потерь на утечку от режима работы турбины.
Эти виды потерь могут быть определены только эксперименталь-'
ним путем.
Влияния угла атаки на характеристики турбинной ступени
В § 4.6 подробно рассмотрено влияние угла атаки на потери в
неподвижной турбинной решетке. В реальной ступени к потерям,
имеющим место в неподвижной решетке, добавляются, потери из-за
нестационарности набегающего на лопатки потока, обусловленной
непрерывным пересечением рабочими лопатками закромочных сле-
дов сопловых лопаток.
На рис. 8.1 для примера приведены результаты сравнительных
испытаний плоских решеток и турбинных ступеней при различных
значениях углов атаки. Из графиков видно превышение потерь в
турбинной ступени по сравнению с потерями в неподвижной ре-
шетке. Анализ результатов испытаний показал, что разница меж-
ду изменением относительного к.п.д. ф2= (ф/фр)2 (индекс «р» отно-
сится к параметрам на расчетном режиме) рабочей решетки, испы-
танной на турбине и в статических условиях, пропорциональна из-
менению относительного числа Струхаля Sh, которое для конкрет-
ной турбинной ступени может быть заменено отношением «/ci [32]:
где Дф2=Дт] изменение к.п.д. от угла атаки в неподвижной турбин-
ной решетке, определяемое равенством (4.17); К. — коэффициент,
зависящий от геометрии проточной части
ступени, по опытам КАИ К.=0,95 ... 1,2.
Меньшие значения относятся к ступени с
Цилиндрическими лопатками, большие — с
закрученными.
Рис 8.1. График изменения относительного к.п.д ра-
бочей решетки ф2 в зависимости от относительного
угла атаки б:
"^ — плоская решетка;-реальная ступень; 0-7вх=
Ьгвху&=0,°5; X—Гвх=0,12
Рис 8.2. График характеристик
ступеней при различных значений
радиального зазора;
—  —дт=О*. О—62=0,018; —  -------
"бг=0,03; •—6^=0,048
Влияние режима работы
турбины на потери на утеч-
ку газа через радиальный,
зазор
Известные эмпирические
зависимости для определе-
ния потерь, вызванных утеч-
кой газа в радиальный за-
зор над рабочими лопатка-
ми, приведенные в § 6.4, по-
лучены для расчетного ре-
жима работы турбинной сту-
пени.
На рис. 8.2 в качестве примера приведены графики, полученные
по результатам экспериментального исследования турбинной ступе-
ни с обандаженными рабочими лопатками, характерные для боль-
шого числа турбинных ступеней, испытанных при различных значе-
ниях радиального зазора. Обращает на себя внимание эквидис-
Пг
тантное смещение кривых — с изменением радиального зазора
6Г. Это свидетельствует о том. что переход к новому режиму ра-
боты турбины оказывает одинаковое влияние на степень реактив-
ности ступеней с различными величинами радиального зазора.
На самом деле окружной к.п.д. т|ц=2—Г-122- ± ^2. ] (индекс «0»
отвечает условию дг=).
Внутренний к.п.д. (в пренебрежении потерями на трение диска)
1)/=т1в —Cyr=2a,cM(c1Bii/ca4 + с2<а/сал), так как наличие радиального
зазора и потери в нем приводят к уменьшению изменения момента
количества движения, в основном за счет уменьшения составляю-
щей с2и.
Параметр	± а
и/сел V сад сад I U/Cai и1саи
==2[д7—'j + д(—'П ,
I t. \ сад }	\ сад / J
где Af С1ЦО-С1В и д /_£2д\	С2а0~.Ч8..
\ сад / ^ад	\ сад /	^ад
о Сут	I
Практическое постоянство отношений ~— с изменением и/см
свидетельствует о неизменности Д(с1и/сад) и А(с2и/сад) ДДЯ данН°'
168
го радиального зазора и, следовательно, об идентичном влиянии
режима на параметры газа в ступени при различных радиальных
зазорах.
Таким образом, потери на утечки газа через радиальный зазор
рабочих лопаток на нерасчетных режимах [33]
<8-2)
где индекс «р» отвечает расчетному режиму. Потери на утечки на
расчетном режиме определяются формулами, приведенными в
§ 6.4.
§ 8.4. ХАРАКТЕРИСТИКИ ТУРБИНЫ
Графическая зависимость параметров турбины, определяющих
ее работу, называется характеристикой турбины.
Необходимость в характеристиках турбины вызвана потребно-
стью расчета совместной работы турбины с другими агрегатами,
как, например, с компрессором (ТРД и ТВД), насосом (ТНА), вин-
том (ТВД) и т. д.
Характер изменения параметров турбины с изменением внеш-
них условий работы всей машины определяется не только самой
турбиной, но и агрегатом, работающим совместно с турбиной.
Координатами характеристики турбины могут быть как абсо-
лютные параметры (нормальные характеристики), так и безраз-
мерные (универсальные характеристики). Безразмерные характе-
ристики в настоящее время получили широкое распространение.
Неудобство нормальных характеристик заключается в том, что
они изображаются большим числом кривых и не дают возможно-
сти проводить сравнительную оценку отдельных режимов. В уни-
версальных характеристиках все многообразие режимов работы
турбины может быть охарактеризовано не четырьмя параметрами,
как в нормальных характеристиках (например, расходом газа, на-
чальными параметрами ро*, То* и частотой вращения двигателя п),
а только двумя безразмерными, что показано в § 8.2. Особенно
Удобны безразмерные параметры при рассмотрении совместной ра-
боты турбины с компрессором и реактивным соплом в ТРД или
винтом в ТВД.
Наиболее распространенной характеристикой турбины является
зависимость к.п.д. и реактивности ступени от отношения ujc^ или
“Сад при постоянном отношении давлений р2/ро* или рг*/ро*.
Для многоступенчатых турбин параметры и/с^ и и/с^ заменя-
ются параметрами Парсонса:
Y — -	— и I * —
Сал-Т	сад.т
На рис. 8.3 и 8.4 1 для примера показаны характеристики одно-
ступенчатой и двухступенчатой турбин соответственно в указанных
1 Рис. 8.4 заимствован из работы [16].
169
Рис. 8.3. График зависимости к,п.д. и реактивности ступени от отношения а/сад
Рис. 8.4. График зависимости к.п.д. двухступенчатой турбины от параметра У*
Рис. 8.5. Графики характеристик турбины:
*	1^0 П Ря
зависимость Чр “П/ и---от —^-2- и —т
Р° и То РО
170
t
координатах. Характеристики турбины могут быть построены так-
,/ Р2 \
:?ке в координатах-— ; т)/ = /(	I при постоянных значениях
Ро	\ Ро /
п
/?0'
В указанных координатах изображена характеристика турбины
на рис. 8.5. Как видим, на рис. 8.3 .. ._8.5 по существу приведены
зависимости параметра расхода —степени реактивности qct
Ро
и к.п.д. rji и тц* в функции от перепада давления рз/Ро* и парамет-
ра чисел оборотов «'VjTo, так как при p2/p0* = idem отношение ulc^
пропорционально njV^То- Проанализируем влияние pzlpa* и я/Т*о
на остальные параметры турбинной ступени.
Изменение параметра частоты вращения n/VТо
При постоянном отношении давлений рг/ро* увеличение пара-
метра То вызывает увеличение степени реактивности еСт, а
G 1/г*
'ледовательно, некоторое уменьшение параметра расхода	——9
Ро
при докритическом истечении газа из соплового аппарата (см. рис.
8.3 и 8.5). Объясняется это следующим. Если предположить, что с
изменением ft/j/"То степень реактивности сохраняется неизменной,
то с увеличением n/l^To при сохранившейся_С1/УГТо (наше пред-
положение рст — const) уменьшается Wi/]^То, что повлечет за со-
>ой уменьшение То, а следовательно, и Снижение пропускной
пособности рабочего колеса. Так как расход газа через сопловой
шпарат и через рабочее колесо одинаков, то снижение расхода га-
ia через рабочее колесо должно привести к уменьшению его через
'опловой аппарат, что возможно только при увеличении степени
п
реактивности. Треугольники скоростей для двух значений
и \
.jTp) изображены на рис. 8.6.
Такое изменение параметра расхода и степени реактивности с
’величением я'Р^То продолжается до тех пор, пока угол pi не до-
стигает 9О'Л_При pi>90° приведенная скорость Wi/V"То растет с ро-
стом л/VТо и параметр расхода увеличивается, а реактивность
йадает.
171
Рис. 8.6. Треугольники скоростей при различных числах оборотов:
*	— —при номинальном числе оборотов;------—при повышенном числе оборотов
Максимальный параметр расхода достигается в том случае,
когда критический режим наблюдается в сопловом аппарате, как
показано на рис. 8.5. При увеличении значения nl\f То, когда воз-
растает степень реактивности, возможно возникновение критичес-
кого режима в рабочем колесе, а в сопловом аппарате устанавли-
вается докритический режим. В этом случае критический параметр
расхода будет меньше того параметра расхода, который достига-
ется при критическом режиме в сопловом аппарате, причемТо[р%
будет тем меньше, чем больше Го.
Как видно из треугольников скоростей, изменениеnj\fГо влечет
за собой появление углов атаки: положительных с уменьшением и
отрицательных с увеличением njV^То, что приводит к уменьшению
ф и, как следствие, к увеличению реактивности и уменьшению пара-
метра расхода.	__
При сравнительно небольших изменениях л/V Го приведенный
расход газа меняется незначительно и может быть принят величи»
ной постоянной. Рассмотренная зависимость О V Го/ро от л/V Г о
справедлива при докритическом истечении газа из соплового аппа-
рата и рабочего колеса.
В случае сверхкритического перепада в сопловом аппарате и
докритического на рабочих лопатках на расчетных числах частоты
, вращения рост п/ VГо вызывает также увеличение степени реактив-
ности, но без изменения Q V^о/Го и приведенной скорости газа
«b/VГо. Вследствие уменьшения расширения_в косом срезе сопел
угол а/ уменьшается. Дальнейший рост n/VТо может привести к
докритическому истечению из сопел, и тогда увеличение л/V Г о бу-
дет сказываться на параметре расхода.
При сверхкритическом истечении из рабочего колеса на расчет-
ных значениях njVГо увеличение л/VГоприводит к росту степени
реактивности, а при докритическом истечении из сопел и к умень-
172
шению параметра расхода, несмотря на сохранение критического»
режима в горле рабочих лопаток; это объясняется тем, что из-за'
уменьшения температуры торможения в относительном движении
падает критическая скорость.
Коэффициент полезного действия тц как одноступенчатой, так и
многоступенчатой турбины падает с уменьшением числа оборотов
вследствие увеличения потери с выходной скоростью на рабочих
лопатках. Так как расчетное отношение (и/сад)р несколько ниже
оптимального, то при некотором увеличении числа оборотов воз-
можно незначительное повышение т)< с последующим уменьшени-
ем. Зависимость т]<* от выражается сравнительно пологой,
кривой.
В практике эксплуатации турбин большое значение имеет мо-
мент, развиваемый на валу турбины: M=N/<o = 95,5N/n и зависи-
мость параметров момента М/р0*, мощности и к. п. д. от
п/V То при постоянных значениях отношения р^ро*.
При угле aj<9(F окружное усилие на лопатках Pu = G(ciu4-c2u)
и крутящий момент Af = Pud/2=G(clu + c2M)d/2, где d — диаметр
облопачивания.
То же самое выражение, записанное в параметрах подобия, име-
ет вид
jM G Т'^Т’о f Ciu । c2u \ d	/a i\
7T=^(y?;+F7;)T'	_	<8-3’
С изменением п/У To ( равносильно изменению и)УГо) в срав-
нительно широком диапазоне О УTolpo изменяется незначительно,
в такой же мере меняетсяиа^УГои несколько интенсивнее изменя-
ется Ci/VТо. Причем, какговорйлось выше, возрастание п/УГо
вызывает уменьшение оУТо/ро,	~Т*о и с^УТо.	__
Так как при постоянном отношении pzlpo* изменение T*Q
равносильно изменению и, в дальнейшем будем рассматривать за-
висимость М и N от частоты вращения двигателя.
В первом приближении допустим, что при постоянном значении
Рз/Ро*, расход газа, степень реактивности и скорость газа не зависят
от оборотов. Тогда треугольники скоростей примут вид, изобра-
женный на рис. 8.7. За исходный принят треугольник, скорости ко-
торого с индексом «р».
Из рис. 8.7 видно, что Ci=cip = const; а>2=ге/гр —const, а следова-
тельно, ciu — ciuP=const; с2и — с2ир+ир—и.
Тогда формула (8.3) может быть записана так:
^=<?kiBp+^up+«p-«]y •	(8-4)
173
Рис. 8.7. Приближенные треугольники скоростей при переменном числе оборотов
Рис. 8.8. График зависимости мощности ступени и крутящего момента от числа
оборотов
Так как в формуле (8.4) все.величины, кроме и, постоянны, tg
зависимость М от и или п изображается прямой линией. Макси-
мальный вращающий момент соответствует неподвижному ротору,
когда и=0, т. е. Mmax = G[ciup+c2up+«p]d/2.
На основании линейной зависимости М от п можно записать
(рис. 8.8, тонкая сплошная линия):
(8.5) ’
Лр	|_	пр -
ГДе p.=Mmax/Mp.
Полагая в формуле (8.5) М=0, находим максимальное число
оборотов, которое не может быть превзойдено при разбеге ротора:
Лтах=/1р“ j •
Мощность, развиваемая турбиной, равна N—Ma или на основа-
нии уравнения (8.5)
# = #₽ —[p-(F-l)—]•	<8-6)
Пр L	npJ
Зависимость мощности от частоты вращения по этому уравне-
нию изображается параболой (см. рис. 8.8, сплошная линия).
Приравнивая нулю первую производную уравнения (8.6), нахо-
дим частоту вращения ротора, соответствующую максимальному
значению мощности:
nNmai—,l9	1')" “О.бЛшах-
При ЭТОМ
\т =N ---------
7VP4((i_1)
174
Из последних двух формул ясно, что, вообще говоря, макси-
мальное значение Nmax имеет место не при выбранных, расчетных
значениях частоты вращения пр.
Как уже указывалось, действительный момент несколько отли-
чается от прямой, изображенной сплошной линией на рис. 8.8, и по-
казан здесь пунктирной вогнутой линией. Такое отклонение дейст-
вительного момента объясняется ростом скоростей Ci и ®2 и рас-
хода G с уменьшением частоты вращения ротора п (что вызывает
увеличение и момента Л1) и, наоборот, падением cb w2, G с увели-
чением п, что вызывает уменьшение М.
Мощность N отклоняется от параболы, приведенной на рис. 8.8
сплошной линией, в соответствии с отклонением момента М от ли-
нейного закона.
Изменение отношения давлений р2/р0*
Изменение отношения давлений рг/ро*, как и при истечении из
сопел, сказывается на приведенном расходе газа через турбину
лишь в том случае, если скорость газа в проточной части турбины
меньше критической.' Известно, что при докритическом истечении'
из сопел приведенный расход газа меняется по закону эллипса (см.
рис. 3.9); при докритическом протекании газа через турбину зави-
симость параметра расхода газа от перепада давлений в ступени
близка к закону эллипса и отклоняется от него из-за меняющейея
реактивности. Если же скорость газа не слишком отличается от
критической, то приведенный расход газа при небольших измене-
ниях перепада давлений остается практически постоянным.
Необходимо помнить о том, что на абсолютное значение расхода
газа G влияние ро* и р2 различное: если отношение р2/ро* меняется
за счет изменения р2, то зависимость расхода _газа от отношения
рг/ро* аналогична зависимости комплекса оУта/ро; при измене-
нии р0* расход газа меняется сильнее комплекса G Tolpo в ро*
раз.
Параметр работы, равный Но/То*, уменьшается с увеличением
Рг/ро* (уменьшением перепада давлений), поэтому и параметр
мощности Nj^pa'VТо) падает.
Однако с уменьшением рг/ро* (увеличением перепада давлений)
параметр мощности возрастает лишь до определенного предела.
В одноступенчатой турбине, например, с понижением рг/ро* возрас-
тают тепловые перепады как в соплах, так и на рабочих лопатках.
При достижении критической скорости начинается расширение в
косых срезах сопел или рабочих лопаток. По использовании расши-
рительной способности косых срезов прирост тангенциальных сос-
тавляющих скоростей газа си прекращается (см. рис. 3.18) и, сле-
довательно, параметр мощности турбины более не растет.
Влияние ра/ро* на реактивность двоякое. С одной стороны, с
Уменьшением рг/Ро* возрастает ЛЭд, а следовательно, и Ль что при
175
неизменном Хв/ А приводит к уменьшению и)с&л и, как следст-
1 1/ I	•
вие, к снижению реактивности. С другой стороны, с увеличением
Аад (уменьшением ра/р0*) газ переходит в область большей сжи-
маемости, и пониженная плотность газа на выходе из рабочего ко-
- леса по сравнению с плотностью его за сопловым аппаратом при-
водит к снижению пропускной способности рабочих лопаток, что
и вызывает рост реактивности.
В сказанном убеждает следующее.
•Степень реактивности
Т
I
1
—(8.7)
+-1
?21 —~	~)
т 1 2	2 1
\ С1	«I /
Как видно из равенства (8.7), влияние р^Ро* на qCt зависит от
изменения значения отношений wjci и Wzttci при отклонении ра/ро*
от расчетной величины.
Отношение —-=!-]-------2—cos <Xi возрастает с уменьшением
pdp* (растет Cj/j/Toпри неизменной скорости «// То). Изменение
отношения ^-зависит от реактивности ступени и степени сжимае-
<?i
мости газа.
Запишем уравнение неразрывности для сечений 1—1 и 2—2:
у	-	Wo fl Qi
flClQl = f 2^202 ИЛИ —2==^- -J- .
Cl ft Q2
Отношение плотностей газа в двух сечениях qJiQz можно пред-
ставить в виде
0l= 1
02
л-1
ИЛИ
Ql
«2
1
л—1
, *
1	* х2 1
fe+l clt
k— 12
+^iecTM2j4
Л-1
(8.8)
Здесь Xcit и Хад приведенные скорости, равные Лси=Си/Скр; Хад=
= Сад/Скр; Мад — ЧИСЛО М., соответствующее скорости Сад и связан-
ное с Лад отношением
_±_Х2
Ма' k- 1 2
1 — -—-х2
176
Таким образом, в ступенях, работающих на несжимаемом газе
^практически Мад^0,5), отношения плотностей Q1/Q2, а следователь-
но, и W2IC1 не меняются с изменением рг/ро* и степень реактивности
падает с уменьшением рг/ро*- В активных ступенях, работающих
при Мад>0,5, уменьшение qgt со снижением рг/ро*(Мад) значитель-
нее, так как при отрицательной степени реактивности, возникшей
в результате увеличения wjc\, значениеуменьшается.
В реактивных турбинных ступенях при Мад>0,5 отношение w^Cy
возрастает с уменьшением ра/р«* за счет влияния сжимаемости газа
и с определенного момента прирост ^2tjc2 становится больше рос-
та w^lc^ и степень реактивности увеличивается с уменьшением
pdpn*. Турбинные ступени авиационных ГТД всегда реактивны и
работают на числах Мад>1. Поэтому в них уменьшение отношения
давлений pdpo* вызывает рост реактивности.
Из входного треугольника видно, что из-за возросшей приведен-
ной скорости ХС1 появляется положительный угол атаки, и, следова-
тельно, уменьшается скоростной коэффициент ф, что в свою оче-
редь приводит к дополнительному увеличению реактивности.
Так как на расчетном режиме отношение (и/сад|р выбирается
близким к оптимальному, когда О2р = 82 ... 84°, то с увеличением
р2/ро* отношение и!сая становится меньше расчетного, в то время
как (н/сад)орг увеличивается из-за возросшей реактивности.
Угол аз падает и выходная потеря увеличивается, что приводит
к понижению к.п.д. т|х-.
Увеличение рг/ро* вызывает уменьшение параметров расхода,
мощности и реактивности ступени. К.п.д. вначале незначительно
возрастает или сохраняет прежнее значение, затем при дальней-
шем увеличении р^ро* падает. Рост к.п.д. объясняется тем, что
расчетное отношение (и/сад)р выбирается, как правило, несколько
меньше оптимального: последующее уменьшение к.п.д. вызывается
увеличением выходной потери и уменьшением ф с появлением зна-
чительного отрицательного угла атаки.
К.п.д. в заторможенных параметрах, наиболее характерный
для ГТД, зависит главным образом от атакоустойчивости профи-
лей рабочих лопаток и слабо меняется в значительном диапазоне
отклонения р2/ро* от расчетного.
В многоступенчатой турбине изменение pdpn* влияет в первую
очередь на тепловой перепад последней ступени, в предшествую-
щих же ступенях изменение перепадов не столь значительно. Если
же какая-либо ступень работает со сверхкритической скоростью, то
изменение рг/ро* сказывается только на тепловом перепаде после-
Дующих ступеней.
Характеристики турбины^ построенные в координатах d}/~Tolpo,
Л» в функции Pzlpv* То, не всегда удобны из-за незначитель-
но изменения параметра расхода Gp^Го/Роот параметра часто'-
177’
Рис. 8.9. График характеристик турбины в координатах Gn/po*; Не/п*
ты вращения n/V Го, отчего линии постоянных значений п/у То
располагаются в очень узком диапазоне характеристики; они могут
быть перестроены в другие координаты. Так, например, взамен па-
раметра G VTo/Ро может быть применен параметр Gn/p0*, предста-
вляющий собой произведение
Gn___Q Угр п
Ро~ Ро V^O
При исследовании совместной работы турбины с компрессором
в системе ТРД одной из удобных форм изображения характеристик
являются координаты, предложенные акад. Б. С. Стечкиным:
Gn/po*, Hein2. В этих координатах наносятся линии постоянных зна-
чений ро*/р2- На рис. 8.9 изображена характеристика турбины к
указанных координатах. Удобство координат акад. Б. С. Стечкина
заключается в том, что они могут быть общими для турбины и ком-
прессора, так как Gr = GB; Неч — Нек, пт —пк = « и давление за комп-
рессором равно давлению перед турбиной.
178
Для теоретических исследований работы турбины могут быть
рекомендованы характеристики, построенные в координатах Ли,
^ад с линиями постоянных значений XCl, Xw, и нанесением допол-
нительно линиц постоянного значения к. п. д. Характеристика тур-
бины, построенная в одних координатах, без труда может быть пе-
рестроена в другие. Характеристики многоступенчатых турбин име-
ют ту же форму, что и у одноступенчатых. Изменение общего пере-
пада давления в турбине р2/р0* при постоянном параметре частоты
вращения п/УТо вызывает перераспределение теплового перепа-
да между ступенями. Впрочем, существенно меняется лишь пере-
пад в последней ступени: он уменьшается с повышением отношения
р2/ро* и возрастает с его понижением. Доказательством этому мо-
гут служить рассуждения, аналогичные рассуждениям о зависимо-
сти степени реактивности qct от отношения Рг/ро* в одноступенча-
той турбине.
§ 8.5. ПОСТРОЕНИЕ ХАРАКТЕРИСТИК ТУРБИНЫ
Характеристики турбины могут быть получены как опытным, так
и теоретическим путем. При снятии характеристики турбины опыт-
ным путем замеряют следующие величины: начальное давление ро*
и температуру То*; давление и температуру газа за турбиной р2
и Т2; расход газа G; частоту вращения ротора турбины п; момент
на валу турбины М; направление и скорость потока за турбиной а2
и с2. В экспериментальных турбинах дополнительно замеряют па-
раметры газа в зазоре между сопловым аппаратом и рабочим ко-
лесом, а также направление потока (угол ai). Замер этих величин
позволяет построить характеристику турбины в любых удобных
координатах.
Существует ряд методов построения характеристики турбины
теоретическим путем. Все они базируются на уравнениях энергии
и неразрывности и отличаются друг от друга выбором контрольных
сечений и первоначально заданными параметрами. Расчет отдель-
ных точек характеристики отличается от первоначального расчета
турбины при проектировании тем, что в последнем случае известны
все параметры рабочего газа и определяются размеры проточной
части турбины. При расчетечточек характеристики произвольными
являются только некоторые параметры газа, а остальные окажутся
обусловленными геометрией проточной части. Как показано в § 8.2,
Режим работы ‘турбины целиком определяется двумя параметрами
подобия или четырьмя абсолютными параметрами газа.
Рассмотрим метод расчета характеристики турбины в критериях подобия при
помощи таблиц газодинамических функций. В качестве контрольных сечений
принять выходные сечения соплового аппарата и рабочего колеса. Это объясня-
йся постоянством углов выхода потока щ и 02 и большей точностью расчета,
ак как выходные скорости из решетки более чувствительны к изменению режи-
,а> чем входные, особенно в сопловом аппарате.
Прежде чем перейти к расчету отдельных точек характеристики турбины,
“Пишем основные уравнения турбины в газодинамических функциях.
179
Рис. 8.10. Процесс расширения в турбине на диа-
грамме i—S
Уравнение ‘расхода в газодинамических функ~
циях может быть «представлено уравнением Гем
формулу (3.54)]
° Vто/р*о =	(АС1)	(8.9)
или	Q УTq/p*0 = mfi<fack q ,	(8.10)
где m —
s+i
— (——У-1,a /i =rtrfA16in at.
H \k + l)
При существующих значениях скоростного ко-
fe-i
эффвдиента величину с можно представить
уравнением
**' -1 - Ы *’' ° -,!) -1 - Ы х’> (i -1) -	(8- п>
Л-1
£
Для значений <р>0,97’ и Xci<l можно положить ffc = 1,н тогда вместо
формулы (8.11) имеем уравнение	ч
,	(8.12)
Уравнение расхода применительно к рабочим лопаткам по аналогии с урав-
нением (8.10) записывается в газодинамических функциях так:
г—	*Z-J
а V ТМ>, = «ЛК* я (*«,,/).	(8-13)
Цю/	ф ж
где kWs/ ss -------.	......1	=;	и Tw — соответственно давление и
температура торможения перед рабочим колесом в относительном движении
(рис. 8.10).
Так как Гр(Т0*—Tw*) =(ci2*—0У12)/2 и ayi2==»?i2d-u2—2i«4 cos a*,
TO — =	1 —^-|(2kalci cosaj —X2),
(8.14)
где Xe =----.. =.
J/
180
Отношение давлений
♦	♦	♦	/ ♦ \
Ро	Ро	Pi	\ Л) /
(8.15)
На основании равенств (8.9), (8.13) ... (8.15) уравнение неразрывности в
газодинамических функциях принимает вид
ft-Н
/1? (Хс1) = /2+v2t»-l) q <г/ .	(8.16)
Известное равенство с|д == Су -г wf* — wj = Ч- 2a<?i cos cq — a2 c^(l—
—^2), представляющее собой уравнение энергии без учета тепла, возвращенного
газу за счет потерь на трение газа, в газодинамических функциях запишется
так:
^ал =	+ 2Ud cos «И - k2 + k2u (1 - ?2),	(8.17)
где	/ v
®2/
Отношение температур торможения Тъ*1Ти* (см. рис. 8.10) можно найти
из равенства Cp(Tw*—-Т2*) = (ш22—с22)/2, где с22—a’22+u2—2aw2 cos р2.
Тогда
и=8=1_^
т*„	* + 1
а отношение
7*2	*Г&_____________1	] г
—=V»= р - — (2k„kel cos ai - k2)j 11
k____1
= 1- 2 ——	cos сц 4-	cos ₽2 —k£).
Л •J"' 1
Отношение давлений торможения
Pi	Pi	p*vt	Pwt	Pt	.
~=—----;---;—«л.
7^0	Pwa	Pwi	Pl	Po
(8.18)
(8.19)
Приведенная скорость на выходе из ступени
и*и \с2 Vrt =z
находится из уравнения выходного треугольника
= t^-9 — гкакяй Vv cos fe + к2.
181
Приведенная адиабатная скорость Х*д, соответствующая параметрам тор-
>можсния на выходе из ступени и связанная с p^lp^ равенством
/ * \5zzl
Ш к . i
1.1 ~А £+1а*>
\ А)
жожет быть определена приведенными скоростями Хад и Хсг. Так как
«ли
Pz	Pz	Р2
Ро	р2 Ро '
„	—1±р
fe~ 1,2
Л + 1Кс2
“12 — >2
. *2___Лад Л<?2
Лад	jfe —. 1 л
1	__1}2
1 Ь 1 кс2
1
(8,20)
1 — У&
k~ 1 >2
k+l а*
2 G-zAcl 4*	$2 ~~	(8.21)
^ад
Если пренебречь различием в отношениях и Т2/Г2/, то по аналогии
с равенством с^. = с|д — с| можно записать
ад ад с*
Окружной К.П.Д. турбины
?2
1 — —
То
%—	гр
1-^
То
1-4
.	То
 чв =----г
1-4
То
Внутренний к.п.д.
1 — уВ
)*2
£+1 ах
2	«
(^iAei cos <xi -f* у* cos р2 *“*"	• (8.22)
Чд
Щ ~~~ Сут — Стр.п,
~ Кут 4- Стр.д) ^ад^ад.
(8.23)
(8.24)
Характеристику турбины необходимо рассчитывать как для докритическьх,
так и для сверхкритических режимов в сопловом аппарате или в рабочем колесе.
В общем случае в турбине возможны четыре категории режимов работы: 1) до-
критический в сопловом аппарате и рабочем колесе; 2) сверхкритический в
сопловом аппарате с расширением в косом срезе сопел и докритический в ра-
бочем колесе; 3) докритический в сопловом аппарате и сверхкритический в рабо-
чем колесе с расширением в косом срезе рабочих лопаток; 4) сверхкритическпй
в сопловом аппарате и рабочем колесе.
182
Уравнение энергии, записанное в форме (8.17), справедливо как для до-
критического, так и для сверхкритического режимов работы турбины. Приведен-
ные скорости Ad и Л«2, входящие в эти уравнения, в зависимости от режима
могут быть больше или меньше единицы. При сверхкритической скорости в соп-
ловом аппарате угол at должен соответствовать направлению потока после от-
клонения в косом срезе сопел.
Уравнение неразрывности (8.16) может быть также записано через сверх-
критические скорости, но в этом случае необходимо учитывать увеличение пло-
щадей fi или f2 в зависимости от места наступления критического режима за
счет расширения в косом срезе. В то же время максимальный расход газа опре-
деляется приведенной скоростью в горле решетки и сохраняется постоянным с
дальнейшим понижением давления за решеткой. Поэтому при сверхкритическом
расширении расход газа может быть определен по максимальной скорости в гор-
ле решетки. Для адиабатного процесса расширения максимальная скорость в гор-
ле решетки равна звуковой, при расширении с потерями (ф или ф меньше еди-
ницы) — меньше звуковой. Критическую скорость в горле решетки можно най-
ти из условия максимального расхода, при котором, как видно из уравнения
(8.9), выдерживается условие
Выполнив дифференцирование и обозначив %ci через 1кр, придем к следую-
щему биквадратному уравнению:
(ОА \Р	А 1 1
1-у2 + —-)х2р’ + т2_д_ = 0.	(8.25>
Уравнение (8.25) можно заменить упрощенной приближенной формулой, при
пользовании которой ошибка составляет менее 1°/о при ф > 0.86:
Акр = ? 1 ~	2	*	(° 
Опираясь на изложенные выше зависимости, предлагаем следующий порядок
построения характеристики. Задаемся рядом значений njY Т$. По выбранным
значениям «//г; находим
Для £=1,33 и Я=288 Дж/(кг К) Xtt = 0,173d—
V А
Для каждого значения 7* задаемся рядом значений pi/po*.
По выбранным значениям pi/po* при помощи таблиц газодинамических
Функций находим =f(pi/p0*); <7(Xcit), М= <Mcir]_?(Xi).
По уравнению (8.13) находим параметр Т'о/Ро. точек» У которых
.	Г (£______1) (1__<р2) 1
Ас1>Х1Кр, где Х1кр = ср| 1 —------------- 1, величина в уравнении берет*
ся по значению X=XiKp.
Находим отношение температур торможения v [уравнение (8.14)]. При
верхкритическом истечении из сопла, когда Xci>XiKp поток за соплами повора-
ивается за счет расширения в косом срезе сопел.
183.
k___1
При определении v — 1 — ——-(2XaXci cos cci — X^) для случая Xci>XdKy не-
»4‘1
обходимо учитывать поворот потока и считать не на cos ai, а на cos а/. Угол
а/ можно наДги по приближенной формуле (3.85), но с учетом потерь при рас-
ширении
sin а
“'“Тм-	(8-27>
М2кр \
По формуле (8.16) определяем ^(Xw2e)- Если окажется, что q (XW2f)>^~^“J
Х2кр (jfe_i)(i_ ф2)
где —j— = 1--------------, то это свидетельствует о наступлении критиче-
т	2
ского режима в рабочем колесе раньше, чем в сопловом аппарате, и о невозмож-
ности пропустить через колесо выбранное количество газа. Предельным значени-
ем pi/po* при выбранном л/ ]/"у* является случай, когда
я а»2«)=я
По значению g(Xw2t) при помощи таблиц газодинамических функций нахо-
✓^2кр \
дим Xw2t; kw2. Для случая q	J задаемся рядом значений Xw2, пре-
вышающих Хгкр.
По формуле (8.17) подсчитываем Хад.
По значению Хад при помощи таблиц газодинамических функций определя-
•ем В(Хад), т(Хад).
По формулам (8.21) и (8.22) находим iqtt и т]и*.
Определяем параметр:
Не (НС1 cos at + cos [i2 — И2) „ и ч
=-----------------п*	(1 - Cyi) *
«ли = 2 (kekcj cos ai + kek®2 К* cos ₽2 - k®)	(1 — Сут)
/ а \2
Так как л2 — I —~,
\ яЛ /
то	= (rtrf)2 (Y- cos cti 4- -cos ₽2 - 1) (1 - Сут) Чм =
\ ха	ха	f
= 9,86rf2 cos ki 4- cos ₽2 - 1) (1 - Сут) Чм. (8.28')
\ хи	ха	у
где £ут— коэффициент потерь на утечку; т]м — механический к.п.д.
В результате расчета можно построить характеристику турбины в любых,
удобных для данного случая, координатах. В турбинах авиационных ГТД, как
правило, в сопловом аппарате наблюдается критический режим. Поэтому при
расчете приближенных характеристик двигателя изменение расхода газа прини-
мается пропорциональным ро* и обратно пропорциональным j/"T'J, Кроме тог©!
в связи с тем что в узком интервале режима к.п.д. т]* меняется незначительно,
его принимают обычно величиной постоянной. Для детального расчета подобные
допущения не могут быть рекомендованы. .
Характеристика многоступенчатой турбины может быть получена продолже-
нием предложенного выше расчета характеристики одноступенчатой турбины.
184
В этом случае можно использовать для расчета I ‘ступени пп. 1 ... 8 приведен-
ного выше расчета. Далее устанавливается следующий порядок расчета.
Находится отношение T^ITq* пи формуле (8.19). По уравнению (8.20) опре-
деляется /?2*/Ро*. По значению р2*/ро* при помощи таблиц газодинамических
функций определяется Хад. Для И ступени начальными параметрами являются
Г2* и рг*. Параметры II ступени будем снабжать штрихом: T'Q* ~ Т2 и р'о = р^
В связи с этим
, хв gVK	pS
хй = —- И--------— =-----------~yvl.
У?* P(t	Pq P2
По найденному значению Gy T'q/p'qhb формулы (8.12) определяется £ (x'u)»
Далее расчет II ступени ведется тем же методом, что и I.
Отношение давлений торможения двух ступеней
(Р2 \	Р2	Р2 р2
Ро /т	Ро	Ро Pq
Отношение температур торможения
К.п.д. турбины (двух ступеней)
Чв = [(ХВХС1 cos -ь ХвХш2 Vv COS ₽2 — x|) +
Хад.г
+ (XX1 Cos al + XuX®2 pVCOS ₽2 — Х^) V&] ,
a == т|и(1 — £Ут).
Значение ХаДвГ можно определить при помощи таблиц газодинамических
функций по отношению (рг*/ро*)т-
Значение	представляющее собой квадратный корень числителя
выражения для qu*, можно определить при помощи таблиц газодинамических
функций: по величине Tj = Т2 /TQ найти соответствующую ей X, которая и равна
Параметр Не/п3 для двухступенчатой турбины определяется формулой ана-
логичной формуле (8.28): Не[п2— (Нс/п2)т+ (Нв1пг)ц.
§ 8.6. ПОСТРОЕНИЕ ХАРАКТЕРИСТИКИ
МНОГОСТУПЕНЧАТОЙ ТУРБИНЫ
ПО ХАРАКТЕРИСТИКАМ ОТДЕЛЬНЫХ СТУПЕНЕЙ
В § 8.5 указан способ построения характеристики Многоступен-
чатой турбины, путем последовательного расчета характеристики от
ступени к ступени. Возможны случаи, когда характеристики отдель-
ных ступеней известны. Тогда характеристику турбины можно по-
строить по характеристикам отдельных ступеней, но без учета не-
равномерности потока на выходе из предыдущей ступени.
185
Предположим, что для двухступенчатой турбины имеются ха-
рактеристик,. обеих ступеней в координатах ---—; — при по-
'	Ро Ро
стоянных значениях —.Кроме того, для всех точек известны
V То
к.п.д. т]и* ступеней.
В тех же координатах необходимо построить характеристику
турбины.
Для обеих ступеней турбины общими параметрами являются
расход газа Gi=Gn=G и частота вращения ni=nn=n- Давление
и температура торможения на выходе из I ступени являются соот-
ветственно давлением и температурой торможения на входе во II
ступень, т. е. Рц — Рои и Тц = 7’оп»
Тогда
Выбрав точку на характеристике I ступени с координатами
-	, п/V То и (р2*/ро* )т, найдем соответствующую ей точку на
Ро
характеристике II ступени, для чего необходимо определить отно-
шение температур (Тг*/То*)1.
Из уравнения (8.21) [ —| =1 —Tlei | 1— — | > где/ | =
\	/1	\ ?о /I \ т0 /I
/ о* Х*-1
I ”2	\~ь-	-	,
=1—— I * , и может быть определено при помощи таблиц газо-
• v '1
* i Р2
динамических функций по et (кад) = I —— .
\Ро )
Найденное отношение (Т2*/То*)г позволяет подсчитать значения
| и^/Кт^п по формулам (8.29) и (8.30), а отношения
Ро
давлений (р2*/ро*)п и Лип будут найдены из характеристики II
ступени турбины.
186
Окружной К.П.Д. турбины

ЗдеСЬ ТItITо—Т (Хад)> а Лад—
Отношение
По аналогии с отношением (T2*/T0*)i
Следовательно,
Если турбина содержит в себе больше двух ступеней, то харак*
теристика такой турбины строится аналогичным методом.
§ 8.7. РЕГУЛИРОВАНИЕ ТУРБИНЫ ПОВОРОТОМ
ЛОПАТОК СОПЛОВОГО АППАРАТА
Одним из эффективных методов регулирования турбины являет-
ся поворот сопловых лопаток, что позволяет в нужном направле-
нии менять характеристику турбины.
Регулируемые сопловые аппараты (РСА) в настоящее время
нашли применение во вспомогательных турбинах и в тяговых тур-
бинах автомобильных газотурбинных двигателей. В авиационных
ГТД такой вид регулирования турбины до настоящего времени
применения еще не получил из-за конструктивных трудностей, свя-
занных с высокой температурой газа перед турбиной, но безусловно
является перспективным.»
Принцип регулирования поворотом сопловых лопаток заключа-
ется в изменении угла выхода потока из решетки ai, что сказыва-
ется на расходе газа, степени реактивности и соотношении скорос-
тей газа в абсолютном и относительном движении. Так, при умень-
шении угла ai уменьшается выходная площадь соплового аппара-
та, в результате чего с одной стороны падает степень реактивно-
сти, с другой — уменьшается расход газа пропорционально умень-
шению выходной площади соплового аппарата ft при сверх- или
187
(^т )a.i=var
(Пт)а.1 = уаг
Рис. 8.11. График изменения лт* при регулировании сопловым аппаратом тур-
бины
Рис. 8.12. График изменения к.п.д. по приведенному расходу при регулировании
сопловым аппаратом турбины
околокритическом истечении газа из сопловых лопаток (что харак-
терно для турбин авиационных ГТД). При докритическом истече-
нии из сопел расход газа падает слабее уменьшения площади Д
из-за снизившейся степени реактивности. Рост скорости ci (в связи
с уменьшением степени реактивности) происходит за счет окруж-
ной составляющей Сщ при уменьшении cia. Относительная скорость
Wi возрастает также за счет окружной составляющей, в результа-
те чего появляется положительный угол атаки на рабочие лопат-
ки или уменьшается отрицательный угол атаки в зависимости от
режима работ ступени. Так как скорость w2 уменьшается без изме-
нения направления, то при сохранении неизменной окружной ско-
рости и наблюдается увеличение угла аг. Таким образом, с умень-
шением угла си рост ст и уменьшение с2и оказывают ' различное
влияние на окружную работу Ни. Как показывают расчеты, при-
рост работы Ни должен наблюдаться в области низких значений
и!Сад. При высоких значениях и/сад возможно даже снижение Ни
с уменьшением угла
Испытания турбин с РСА показывают снижение к.п.д. турбины
с изменением угла он в обе стороны от расчетного значения. Такое
расхождение с расчетом объясняется тем, что в расчетах не всегда
учитывается дополнительное влияние угла атаки на скоростной ко-
эффициент рабочих лопаток ф, а также потери на утечку газа через
радиальный зазор между корпусом и сопловыми лопатками, увели-
чивающийся с поворотом лопаток.
Как правило, турбина работает совместно с выходным устрой-
ством, роль которого в авиационных газотурбинных двигателях
выполняет реактивное сопло. Так как выходное сечение сопла не
меняется с поворотом лопаток соплового аппарата, то при неиз-
менном суммарном перепаде давлений поворот лопаток приводит
к перераспределению перепадов давлений на турбине и в выходном
устройстве. С уменьшением угла ai перепад давления на турбине
188
возрастает в основном за счет соплового аппарата. В многоступен-
чатых турбинах также наблюдается перераспределение перепадов
давлений между ступенями и выходным устройством при регулиро-
вании положением лопаток соплового аппарата. При уменьшении
угла ai возрастает перепад давлений в данном сопловом аппарате,
что вызывает рост перепада давлений во всей турбине с уменьше-
нием перепада давлений в выходном устройстве.
На рис. 8.111 показано примерное изменение лт*=Ро*/Р2* от из-
менения площади выхода из соплового аппарата в многоступенча-
той турбине. На рис. 8.12 приведено изменение к.п.д. турбины с
уменьшением расхода газа, вызванного уменьшением угла аь
Глава IX
ОХЛАЖДЕНИЕ ДЕТАЛЕЙ ТУРБИНЫ
§ 9.1. ОБЩИЕ СВЕДЕНИЯ
Главнейшими показателями, характеризующими совершенство авиационных
ГТД, являются: удельная тяга (ТВД — мощность), удельный расход топлива
и удельная масса.
С ростом температуры газа То* перед турбиной или с увеличением т=
= Т0*/Та (Т« — температура атмосферного воздуха) и при соответственном воз-
растании степени повышения давления в компрессоре лк* удельные параметры
ГТД улучшаются. Сказанное иллюстрируется графиками на рис. 9.1 ... 9.3.
Сплошные линии относятся к неохлаждаемым ГТД, пунктирные и штрихпунктир-
ные — к охлаждаемым (с учетом потерь от охлаждения). Легко видеть, что
с увеличением То* особенно резко возрастает удельная тяга (мощность) авиа-
ционных ГТД, а следовательно, снижается удельный расход рабочего тела,
уменьшаются габариты и масса.
В ТВД и ТРДД с большой степенью
двух-контурностн (т>3), с ростом
То* засиетно уменьшается удельный
расход топлива.
Уровень максимальных темпера-
тур газа при сжигании углеводород-
ных топлив •иллюстрируется рис. 9.4.
С повышением температуры газа
снижается надежность работы ряда
элементов газовой турбины: сопел, ди-
1 Рис. 8.П и 8.12 заимствованы
кз работы [16].
Рис. 9.1. Графики зависимости удель-
ного расхода топлива Се и удельной
ощности ТВД от различных То*
Лк в стартовых условиях (Я=0;
М==0):
охлаждения.---------с впут-
с кп^л 0Нвективным охлаждением:------—
моинированным (конвективное-{-пле-
ночное) охлаждением
189
CRt(KZlC)/MH
'4 Г
2.0
10
500	600	700	800	900	1000
Ryd^/(^lc)
Рис. 9.2. Графики зависимост <
удельного расхода топлива cR
удельной тяги Яуд ТРД от раз.
личных То* и Лк* в стартовых ус.
ловпях (Я —0; М = 0):
----------без охлаждения;--------_г
конвективным охлаждением;--------
комбинированным (конвекгивное+пле-
ночное) охлаждением
сков и др. Наибольшую трудность
представляет обеспечение надеж-
ной срабогы рабочих лопаток. Они
являются наиболее уязвимыми де-
талями газовых турбин, так как ра-
ботая в зоне высоких температур,
они подвержены, как п сопловые
лопатки, термической усталости,
вибрации, газовой коррозии и эрозии и, кроме того, действию чрезвычайно боль-
ших центробежных сил
Какие же пути ведут к дальнейшему увеличению То* в ГТД? В настоящее
время работа ведется в нескольких направлениях.
Первый путь — это создание новых жаропрочных и жароупорны- металли-
ческих материалов. Характеристики применяющихся в настоящее время материа-
лов приведены в гл. XI и XVI.
Ожидать быстрого прироста температуры газа на базе улучшения традици-
онных (хромоникелевых, кобальтовых) жаропрочных сплавов не приходится.
Как показывает статистика [16],-средний темп прироста температур путем улуч-
шения свойств указанных жаропрочных материалов в последние 30 лет состав-
лял около 10 К в год.
Несколько лучшими свойствами обладают новые материалы, в частности, на
базе ниобия. Однако до практического внедрения таких материалов предстоит
еще решить сложный вопрос надежной их защиты от коррозии, так как npv
повышенной температуре ниобий склонен к интенсивному окислению. Препятст-
вием является и дефицитность ниобия.
Рис. 9.3. Графики зависимости удельного расхода топлива cR и удельной тяги
/?уД ТРДД со степенью двухконтурности т=1, в условиях полета (М=0,8
Я= 11 км) от То* и Лк*:
----------без охлаждения;--------с конвективным охлаждением;----.—.---с комбини-
рованным (копвективное+пленочное) охлаждением
Рис. 9.4. График максимальной температуры газа в зависимости от степени по-
вышения давления воздуха в компрессоре:
1—при стехиометрическом сгорании керосина; 2—на входе в турбину (То*)
190
Второй путь — это разработка керамических и металлокерамических мате-
риалов. Керамические материалы обладают прекрасными антикоррозионными
Свойствами, механические свойства их почти не изменяются при нагреве до 1550 К,
д температура начала плавления превышает 3000 К. Плотность этих материалов
в 1,5 ••• 3 раза меньше, чем у сталей и жаропрочных сплавов, что резко умень-
шает напряжение от центробежных сил в лопатках и дисках турбин. Наиболь-
шие надежды в настоящее время возлагают на горячепрессованный и спекаемый
кремниевый нитрид Si3N4 и кремниевый карбид (SiC).
F Существенным недостатком керамических материалов является чрезвычай-
ная трудность их механической обработки, а также затруднения, возникающие
при разработке креплений керамических лопаток к дискам или барабанам, а
также повышенная их чувствительность к вибрациям и ударным, нагрузкам.
Третий путь —это охлаждение горячих частей турбины. С внедрением воз-
душного охлаждения среднегодовой темп прироста температуры газа перед тур-
биной возрос до 25 К, т. е. более чем в два раза (см. рис. 0.1) по сравнению с
периодом, когда применялись неохлаждаемые ГТД.
г В настоящее время воздушное охлаждение деталей турбины широко при-
меняется в авиационных ГТД. Одновременно ведется интенсивная работа по
усовершенствованию систем охлаждения горячих частей турбины и в первую
очередь сопловых, рабочих лопаток и дисков. В современных авиационных Г ГД
в качестве хладагента используется исключительно воздух. Вместе с тем продол-
жаются настойчивые попытки использовать в качестве охладителя жидкости, в
том числе и в авиационных ГТД.
§ 9,2. СПОСОБЫ ОХЛАЖДЕНИЯ ГОРЯЧИХ ДЕТАЛЕЙ ТУРБИНЫ
Горячие детали можно охлаждать воздухом или жидкостями, в
зависимости от этого различают воздушное и жидкостное охлаж-
дение. По характеру движения и использования охладителя систе-
мы охлаждения можно подразделить на открытые и замкнутые.
В открытых системах охладитель используется однократно. После
отбора тепла от охлаждаемых элементов он выпускается в проточ-
ную часть турбины (рис. 9.5). Основным достоинством открытых
систем охлаждения являются относительная простота конструкции
и малая масса.
Отбираемый за компрессором или из промежуточной его ступе-
ни воздух прогоняется через специальные каналы, выполненные в
•охлаждаемых деталях (внутреннее конвективное охлаждение), ли-
бо обдувает их снаружи (пленочное охлаждение). Для форсирова-
ния охлаждения, в особенности при больших скоростях полета и
высоких лк* в компрессоре, охлаждающий воздух может предвари-
тельно охлаждаться за счет хладорееурса топлива или в специ-
альных турбоХолодильных машинах.
Исследования последних лет показали, что открытые системы
комбинированного воздушного охлаждения при рациональной кон-
струкции лопаток могут обеспечить повышение начальной темпе-
ратуры газа вплоть до предельной (см. рис.
у-4). Недостатком таких систем является
сравнительно большая затрата энергии на
нспрерывную подготовку и подачу охлади-
теля. Кроме того, с увеличением высоты Н
Рис. 9.5. Схема открытой системы охлаждения:
отбор воздуха; 2—отбор тепла при охлаждении; 3—вы-’
пуск охлаждающего воздуха
191
и скорости v полета эффективность системы охлаждения ухудщд,
ется. Это связано с уменьшением пропускной способности системы
охлаждения и изменением (увеличением) температуры охладителя
с ростом скорости полета. Увеличение лк* компрессора также ве-
дет к росту температуры воздуха и снижению эффективности сис-
темы охлаждения.
К открытым системам охлаждения относят:
а)	охлаждение теплоотводом в сопряженные детали, которые в
свою очередь охлаждаются воздухом (см. рис. 9.11, поз. /);
б)	внутреннее охлаждение деталей воздухом, паром или воздуш-
но-жидкостными смесями, протекающими в специально выполнен-
ных открытых каналах (см. рис. 9.11, поз. 4, рис. 9.13 ... 9.17);
в)	пленочное (заградительное) охлаждение воздухом, вдувае-
мым через специально выполненные отверстия-перфорации на по-
верхность горячих деталей, соприкасающуюся с газом (см. рис.
9.11, поз. 5). Пленочное охлаждение в комбинации с внутренним
охлаждением- считается наиболее перспективной для достижения
максимальных температур;
г)	охлаждение, осуществляемое продавливанием охладителя
через специальные пористые или многослойные перфорированные
материалы, из которых в этом случае изготовляются детали, под-
вергающиеся наибольшему нагреву (см. рис. 9.11, поз. 6, рис. 9.19).
К открытым системам охлаждения относится также струйное
жидкостное охлаждение рабочих лопаток (см. рис. 9.11, поз. 3).
В качестве охладителя здесь могут применяться жидкости, воз-
душно-жидкостные смеси, а также пар. Охладитель в виде сильно
распыленной струи подается через две-три форсунки, устанавливае-
мые в плоскости соплового аппарата и за рабочим колесом (впрыск
против потока).
В замкнутых системах охладитель используется многократно.
Циркулируя в замкнутом контуре, охладитель выполняет роль про-
межуточного теплоносителя, отбирая тепло от нагретых деталей и
отдавая его в радиаторе-холодильнике. В качестве промежуточного
теплоносителя в таких системах могут использоваться различные
газы (углекислый газ, гёлий) под высоким давлением, а,также
жидкие теплоносители (некоторые органические соединения, жид-
кие металлы’: натрий и его сплав с калием и др..).
Замкнутые системы охлаждения открывают возможность при-
менения высокоэффективных охладителей без больших затрат на
их прокачку и восполнение. Кроме того, такие системы позволяют
осуществить весьма глубокое охлаждение деталей.
К недостаткам замкнутых систем охлаждения относятся: ухуД-
шепие эксплуатационной надежности установки, значительное ус-
ложнение конструкции, увеличение массы, трудность осуществле-
ния надежных уплотнений (особенно в местах перехода от вращаю-
щихся частей к неподвижным) вследствие чрезвычайно высоких
требований к герметичности системы (нарушение герметичности
приводит к невосполнимой утечке охладителя из системы, и, каХ
следствие, выводу ГТД из строя). Кроме того, эти системы нужда"
192
ютСя в специальных устройствах для рассеивания тепла охлажде-
НИЯ (рис. 9.6).
В схеме на рис. 9.6 тепло рассеивается во внешнем радиаторе.
Эта схема удобна в транспортных и авиационных ГТД, где для
охлаждения радиатора используется набегающий поток атмосфер-
ного воздуха. Съем тепла в радиаторе может осуществляться так-
же топливом, направляющимся в камеру сгорания. Это может
оказаться перспективным при больших скоростях полета, ког-
да из-за скоростного напора температура торможения наружного
воздуха приблизится к допустимой температуре деталей и рассеи-
вание тепла обычным способом окажется затруднительным или
невозможным.
Охлаждающая способность топлива ограничена той предельной,
температурой нагрева топлива, при которой нарушается нормаль-
ная работа топливной аппаратуры камеры сгорания или происхо-
дит закупорка трубок радиатора.
Жидкостное охлаждение лопаток в авиационных ГТД пока не
применяется. Вместе с тем этот способ охлаждения по-прежнему
находится в поле зрения исследователей и конструкторов. Можно
отметить три основных направления поисковых и опытно-конструк-
торских работ по созданию систем жидкостного
паток:
а)	с использованием принципа «термосифо-
на» [6] (рис. 9.7). Тепло отбирается от лопатки
1 прбмежуточным жидким теплоносителем й 
передается воздуху, в автономных радиаторах
5, расположенных под лопатками;.
б)	с применением испарительно-конденсат-
ного принципа «тепловой трубки» (рис. 9.8).
Тепло отбирается от лопатки 1 испаряющимся
охлаждения лен
Рис. 9.6. Схема замкнутой системы охлаждения с рассеиванием тепла во внеш-
нем радпаторе:
с 3®пас®м охлаждающей жидкости; НВД—насос высокого давления (подкачивающий):
лавныи насос; Р—внешний радиатор; /—отбор тепла; 2 и 3—вход и выход внешнего ох-
лаждающего воздуха
Рис. 9.7. Схема автономного термосифонного охлаждения рабочих лопаток:
часть лопаток; 2—глухие каналы в лопатке; 3—каналы охлаждения в замке;
алы промежуточного теплоносителя в холодильнике; 5—автономный радиатор-хол о-
дильншк; 6—первичный охладмггель (воздух, пар и т. п.)
1337
193
Рис. 9.8. Схема охлаждения сопловой лопатки по испарительно-конденсатному
принципу «тепловой трубки»:
/—сопловая лопатка; 2—радиатор в наружном контуре ГТД; 3—фитиль тепловой трубки
A-A
Рис. 9.9. Схема лопатки при циркуляционном жидкостном охлаждении
Рис. 9.10. Схема жидкостного охлаждения рабочей лопатки турбины:
/—•форсунки для подачи воды; 2—заплечию» на диске для поддержания уровня свободной
поверхности; 3, 4—входные отверстия; 5—охлаждающие каналы в лопатке; б—сборная по-
лость; 7—©ылускное сопло; 8—щелевой вэдосборгпик
промежуточным жидким теплоносителем, и передается воздуху в
радиаторе 2. Сконденсированная жидкость возвращается в горячую
зону по фитилю 3 капиллярными силами;
в)	циркуляционные системы с принудительной прокачкой ох-
лаждающей жидкости [6] (рис. 9.9). Основную трудность в созда-
нии таких систем' составляют уплотнения в местах перехода от не-
подвижных к вращающимся деталям.'
Одна из американских фирм ведет упорные работы по созда-
нию циркуляционной водяной системы охлаждения рабочих лопа-
ток, отличительной особенностью которой является отсутствие слож-
ных уплотнений (рис. 9.10). Вода подается через форсунки 1 к
входным отверстиям 3, 4 в диске, проходит по каналам 5 меЖДУ
194
оболочкой и силовым стержнем лопатки, после чего собирается в
сборной полости 6 у вершины лопатки и сбрасывается через сопло '
7 в районе радиального зазора. Почти полное улавливание воды и
пара осуществляется щелевым водосборником 8, расположенным
в корпусе турбины. Свободное зеркало жидкости устанавливается
на радиусе заплечиков 2 или на большем радиусе.
§ 9.3. КРАТКАЯ ХАРАКТЕРИСТИКА РАЗЛИЧНЫХ СПОСОБОВ
ВОЗДУШНОГО ОХЛАЖДЕНИЯ ЛОПАТОК ТУРБИНЫ
Основные схемы открытого охлаждения рабочих лопаток газо->
вых турбин показаны на рис. 9.11.
Охлаждение рабочих лопаток отводом тепла в диск (см.
рис. 9.11, поз. /), с конструктивной точки зрения, является одним
из самых простых. Отбор тепла охлаждения осуществляется воз-
духом, который обдувает ротор (диск) или продувается через спе-
циальные каналы или монтажные зазоры в замковых соединениях
рабочих лопаток.
Вследствие теплопроводности температура пера лопаток, осо-
бенно в наиболее нагруженной корневой части, снижается и появ-
ляется возможность соответственно увеличить То*’. Возможности
этой схемы охлаждения весьма ограничены. Расчеты, проведенные
с учетом изменения механических свойств жаропрочных материа-
лов от температуры, показывают, что способ охлаждения отводом
тепла в диск позволяет поднять температуру газа в ГТД с корот-
кими {h=30 ... 40 мм) лопатками не более чем на 50 ... 60 К. При
этом расход охлаждающего воздуха составляет 0,7 ... 1,3% от рас-
хода газа. Основная область применения — ГТД с короткими ло-
патками.
При парциальном охлаждении (см. рис. 9.11, поз. 2) рабочих ло-
паток охладитель подается через часть дуги, занимаемой сопловы-
ми каналами. При вращении рабочие лопатки омываются попере-
менно то рабочим газом высокой температуры, то охлаждающим
агентом с низкой температурой. Вследствие больших чисел оборо-
тов чередование волн нагрева и охлаждения не успевает отразить-
1	2	3
РИс- 9.Ц. Классификация схем открытого охлаждения рабочих лопаток газовых
,	турбин. Охлаждение:
воеЬП40О^?°Д01М » Диск; 2—парциальное; 3—струйное (жиДкоснное или воздушно-жидкост-
’ внУтреннее воздушное (конвективное); 5—щелевое (шлейочмое); 6—эффузионное (по-
ристое)»
7*
195
Рис. 9.12. Схема парциального, корневого охлаждения
рабочих лопаток турбин малоразмерных ГТД с регене-
ратором:
/—газ, 2—воздух на охлаждение (отбирается после регенерато-
ра); 3—воздушные сопла», 4—рабочие лопатки
ся на температуре в глубине металла и устанавливается некоторая
средняя практически неколеблющаяся температура лопатки.
Разновидностью парциального охлаждения является схема,
предназначенная в особенности для регенеративных ГТД и пока-
занная на рис. '9.12. Воздушные сопла 3 расположены здесь по
всей окружности прикорневой зоны проточной части. Воздух на
охлаждение в больших количествах отбирается из-за регенератора
ГТД} т. е. достаточно подогретый, чтобы совершать полезную рабо-
ту на турбине. В то же время этот поток воздуха 2 достаточно хо-
лодный и надежно изолирует корневую часть 4 рабочих лопаток и
диск от воздействия потока горячего газа 1.
Принципиальная схема внешнего струйного охлаждения пока-
зана на рис. 9.11, поз. 3. Через форсунки, расположенные в подво-
дящей трубке, вблизи выходного сечения сопел, жидкость или воз-
душно-жидкостная смесь впрыскивается в поток газа. Попадая на
рабочие лопатки, охладитель снижает их температуру. Основное
достоинство рассматриваемого типа охлаждения заключается в
том, что оно практически не требует измейения конструкции лопа-
точных аппаратов и в то же время позволяет резко снижать сред-
нюю температуру лопаток.
Основные недостатки этого способа охлаждения:
а)	требует больших расходов охлаждающей жидкости;
б)	приводит к неравномерному охлаждению пера лопаток.
Особенно резкое снижение температуры лопаток наблюдается
при подаче жидкости в пределах от (0,5 ... 0,6) до (1,0 ... 1,5) %
от расхода газа. При этом средняя температура лопаток снижает-
ся до 0,7 ... 0,5 от Т X (температуры газа в относительном дви-
жении) .
Из-за центробежного эффекта наибольшая температура ока-
зывается у задних кромок лопаток и в корневых сечениях, т. е. как
раз в местах наибольших напряжений.
Как уже указывалось, большое распространение в современных
высокотемпературных ГТД получило внутреннее воздушное ох-
лаждение рабочих лопаток (см. рис. 9.11, поз. 4).
При внутреннем воздушном охлаждении воздух проходит через
систему образованных внутри лопаток каналов, после чего обычно
сбрасывается в проточную часть. В зависимости от характера дви-
жения охладителя выполняются конструкции с продольными охла-
ждающими каналами, с поперечными охлаждающими каналами и
«смешанные. Типичными представителями лопаток с продольными
охлаждающими каналами являются литые рабочие лопатки первых
ступеней турбин ТРД «Олимп» и ТРДД «Спей» (Англия), пока-
занные на рис. 9.13, а и б.
196
__ n g’]3 Схема рабочих лопаток английских
РИС. * •	ГТД:
а—«Олимп»; б—«Спей»
Воздух входит параллельно во все
каналы, протекает к периферии и сме-
шивается с газом в радиальном, зазоре.
В нижней части рис. 9.13 показана
форма и расположение охлаждающих
каналов в среднем сечении лопаток.
Система мелких каналов в лопатке
«Олимп» обеспечивает более эффек-
тивное их охлаждение. Несмотря на то,
что эти лопатки почти вдвое длиннее
(/i=125 мм), чем лопатки «Спей», а
начальная температура газа (То*«
«1400 К) и расход охладителя
(^охл=2%) примерно одинаковы, их
ресурс (10 тыс. ч.) даже превосходит
ресурс лопаток «Спей». Основное дос-
тоинство продольной схемы охлажде-
ния — более простая технология изго-
товления лопаток.
Следует отметить, что хотя в среднем при удачной конструкции
таких лопаток эффективность их охлаждения оказывается доста-
точно высокой, однако наблюдается значительная неравномер-
ность температуры металла как по высоте, так и по профилю.
К примеру, в лопатках (см. рис. 9.13, б) средняя по сечению тем-
пература лопатки снижается у корня на 240 ... 260 К; в средине
высоты — на 200 ... 220 К и на' периферии на 100 ... 120 К. Осо-
бенно нагретыми оказываются входная и выходная кромки (~ на
100 К выше средней), тогда как центральная часть — ниже сред-
ней примерно на 50 К. Это объясняется не только трудностью раз-
мещения охлаждающих каналов в непосредственной близости от
кромок, но и специфичным распределением коэффициентов тепло-
отдачи по обводу профиля (см. рис. 9.27).
Таким образом, перегретыми оказываются как раз те участки
профиля, которые в работе наиболее нагружены (к напряжениям
от центробежных сил добавляются наибольшие напряжения от из-
гиба лопаток). Именно это обстоятельство, наряду с общим стрем-
лением к созданию конструкций с улучшенной эффективностью
охлаждения, привело к появлению петлевых схем (рис. 9.14), де-
флекторных лопаток с поперечным течением охладителя (рис. 9.15),
е развитой внутренней теплообменной поверхностью (рис. 9.15 и
у-16) и наконец лопаток с комбинированным (конвективное-)-пле-
ночное) охлаждением (рис. 9.17).
В лопатке выполненной по рис. 9.14 холодный воздух поступает
каналы 1 и 3 вблизи кромок, интенсивно их охлаждает, затем
Разворачивается на 180° и движется к корню лопатки по централь-

Рис. 9.14. Петлевая схема охлаж-
дения рабочих лопаток ГТД «Ко-
нуэй»:
1, 2, 5—охлаждающие каналы; 4—отвер-
стия для удаления пыли
"Рис. 9.15. Схема рабочей лопатки
с поперечным течением воздуха:
/—тело лопатки; 2—щели для выпуска
воздуха; 5—ребра; 4—дефлектор; 5—от-'
верстия в дефлекторе; 5—опорные и
натравляющие пояски дефлектора; 7—
охлаждающий канал
ному каналу 2. В результате
неравномерность температур
(АГ) между кромками и
центральной частью сечения
уменьшается (в лопатке
ГТД «Конуэй» ДГ=75 К по
сравнению с ДГ= 150 Кв
лопатке ГТД «Спей»). В пе-
риферийной части лопатки
имеются небольшие отвер-
стия 4-для удаления из охла-
дителя посторонних включе-
поперечным течением охла-
дителя является рабочая лопатка по патенту К. В. Туманского.
Для выравнивания температур в районе ^ромок в конструкции,
показанной на рис. 9.15, внутренняя поверхность в районе входной
кромки оребрена и охлаждающий воздух через впускные отверстия
5 в дефлекторе подается в виде отдельных струй прежде всего в
зону входной кромки (где коэффициент аг наибольший, см. § 9.5).
За дефлектором весь воздух смешивается и вытекает через специ-
альные щели 2 в районе задней кромки, интенсивно ее охлаждая.
Подобная организация течения воздуха приводит к значительному
выравниванию поля температур в поперечном сечении лопаток и
снижению общего уровня температуры металла вследствие более
полного использования хладоресурса воздуха (коэффициент тепло-
отдачи воздуха ав в зоне удара о стенку входной кромки много-
кратно увеличивается (см. рис. 9.34)]. К недостаткам лопаток
описанного типа относятся значительные конструктивные и техно-
логические трудности, связанные с размещением дефлектора. Кро-
ме того, сам по себе дефлектор во вращающихся лопатках является
слабым звеном и о его прочности следует заботиться также тща-
тельно, как о прочности лопаток. Применительно к рабочим лопат-
кам высокотемпературных ГТД большого ресурса применение деф-
лектора нежелательно.
Существенное повышение эффективности внутреннего охлаж-
дения лопаток достигается с помощью различных* интенсификато-
ров: закручивателей, волнистых каналов, штырьков-турбулизато-
ров, устройств, создающих пульсирующее течение охладителя,
198
Рис 9.16. Схемы литых рабочих
лопаток (22] с ребрами-турбулиза-
-	торами:
„—продольное течение охладителя (тур-
2УЧизаторы в виде штырьков / и ре-
Jln 9 каплеобразной формы <?); б—по-
моечное течение охладителя (турбули-
заторы цилиндрического сечения 4)
л т. п. На рис. 9.16 показаны
лопатки с турбулизаторами,
которые одновременно вы-
полняют роль ребер жестко-
сти (см. рис. 9.16, а поз. 2).
Часть турбулизаторов может
быть выполнена в виде
штырьков 1, что еще боль-
ше увеличивает внутреннюю
теплообменную поверхность.
Заменой круглого сечения турбулизаторов на каплеобразное суще-
ственно снижается гидравлическое сопротивление и увеличивается
пропускная способность каналов охлаждения.
При начальной температуре газа перед турбиной То* более
1450 ... 1550 К и лк* в компрессоре более 15 схемы ох-лаждения с
чисто внутренним конвективным охлаждением лопаток уже не в
состоянии обеспечить длительную их работу. В этих случаях при-
ходится применять более сложные, комбинированные схемы охлаж-
дения, где наряду с внутренним используется также внешнее пле-
ночное (заградительное) охлаждение (см. рис. 9.11, поз'. 5).
На рис. 9.17 показаны схемы двух лопаток такого типа, приме-
няющиеся в авиационных ГТД (США). Система комбинированного
охлаждения (см. рис. 9.17, а) рабочих лопаток I ступени турбины
ТРДД TF39, по данным фирмы, обеспечивает ресурс рабочих лопа-
ток 1 ступени турбины 15000 ч, при Го* = 158О К и расходе охлаж-
дающего воздуха на
эту_решетку в количест-
ве Сохл«3,5%. Литые
лопатки из кобальтово-
го сплава имеют доста-
точно равномерное по-
ле температур в сече-
ниях, со средней темпе-
ратурой менее 1170 К.
Рис. 9.17. Схемы рабочих ло-
паток авиационных ГТД с
комбинированным (внут-
реннее конвективноеЧ-внеш-
нее пленочное) охлажде-
нием:
а—л остатки I ступени
ТРДД TF39;
б—то же ТРДД JT9D
199
Перфорации для выпуска охладителя на наружную поверхность
лопатки в районе входной и выходной кромок, а также все внут-
ренние каналы в лопатках выполнены электрохимическим и элект-
роэрозионным способами.
Заслуживают быть отмеченными следующие оригинальные мо-
менты: подвод воздуха на охлаждение передней и задней частей
лопаток выполнен раздельно (см. рис. 9.17, а, поз. 1 и 6), что об-
легчает дозированное распределение охладителя; вблизи передней
и задней кромок выполнены ребра с перфорациями 3 и 4, что по-
зволяет осуществить струйное охлаждение стенок и дополнительно
турбулизировать поток охладителя перед подачей его на наруж-
ную поверхность через наклонные отверстия 2; петлевое течение
воздуха вдоль лопатки способствует более эффективному исполь-
зованию его хладоресурса; для предотвращения засорения каналов
и перфораций в стенках и удаления пыли в двойной торцевой
стенке выполнены небольшие очистительные отверстия 5, через ко-
торые отводится пыль и часть воздуха в радиальный зазор.
Литые, из кобальтового сплава, рабочие лопатки одной из по-
следних модификаций ТРДД JT9D (см. рис. 9.16, б) предназначе-
ны для работы при То* = 1620 ... 1640 К. Продольные каналы вол-
нообразной формы имеют очень развитую внутреннюю теплообмен-
ную поверхность. Заградительное охлаждение кромок, осуществляе-
мое подачей воздуха через множество перфораций, способствует
выравниванию температурного поля по сечению лопатки.
Пленочное (заградительное) охлаждение сопловых и рабочих
лопаток (см. рис. 9.11, поз. 5) в комбинации с интенсивным внут-
ренним охлаждением получает дальнейшее развитие во вновь про-
ектируемых ГТД, рассчитанных на еще большую начальную тем-
пературу газа. На рис. 9.18 показана одна из возможных схем соп-
ловых лопаток с развитым пленочным охлаждением наружной
поверхности и интенсивным охлаждением внутренней поверхности.
Раздельная подача воздуха в переднюю и заднюю часть лопаток
способствует снижению его расхода и позволяет в задней части ло-
паток использовать более холодный воздух из промежуточной сту-
пени компрессора. Дефлектор со множеством мелких отверстий
(«душ») реализует струйное натекание воздуха на внутреннюю
поверхность, что интенсифицирует теплосъем; рационально распо-
ложенные многочисленные перфорации в стенке лопатки создают
заградительную пленку воздуха в зонах наибольших коэффициен-
тов теплоотдачи (см. рис. 9.27). Большие надежды возлагаются на
пленочное заградительное охлаждение рабочих лопаток, изготов-
ленных по принципу так называемой гильзовой конструкции
(рис. 9.19) с несущим стержнем и профилирующей гильзой (обо-
дочкой).
Несущий стержень 1, выполненный за одно с ножкой лопатки 2,
имеет на поверхности пера, на некотором расстоянии друг от дрУ*
га, ребра. С ребрами стержня скрепляется пайкой или термодиф-
фузионным способом гильза 4, образующая внешний контур ло-
патки.
200
Ояс 9.18. Схема охлаж-
«₽яйя сопловой лопатки
г ступени высокотемпера-
турного ^авиационного
t 2—дефлекторы типа «душ»
Годней и задней частей
допатки
РИС. 9.19. Сйема гильзо-
вой рабочей лопатки с
оболочкой из проницае-
мых материалов:
/—стержень; 2—ножка ло-
патки; 5—пазы, ^проница-
емая оболочка («гильза»)
Оболочка лопатки выполняется из про-
ницаемых материалов (пористых, много-
слойных перфорированных) и таким обра-
зом реализует заградительное охлаждение.
Отличительной конструктивной особенностью таких лопаток явля-
ется то, что стержень лопатки, воспринимающий основные усилия,
находится в облегченных температурных условиях (защищен от
действия газов гильзой). В то же время гильза защищена от горя-
чих газов пленкой воздуха и несет небольшие силовые нагрузки.
Основные результаты детального исследования гильзовых ра-
бочих лопаток с непроницаемой оболочкой, включая испытания на
опытной турбине с температурой газа до 1470 К, показаны на
рис. 9.20. Там же показана конфигурация испытанных лопаток и
схема расположения термопар (светлые кружочки). При подаче 2%
воздуха средняя температура стержня составляет ~0,7 от Тт*, т. е.
снижается до ~ 1070 К.
В лопатках с гильзой из пористых и многослойных проницаемых
листовых материалов (см. рис. 9.11, поз. 6) на наружной поверхно-
сти образуется низкотемпературный теплозащитный слой из вду-
ваемого воздуха с низкой теплопроводностью. Благодаря этому
несколько уменьшается и конвективная теплоотдача от, газа к по-
верхности лопаток. Кроме того, проявляется так называемый
«атмосферный эффект» — наличие в составе воздуха углекислоты
(СгО) и водяного пара (Н2О) с их большой теплопоглощательной
способностью снижает радиационный поток тепла от газа к стен-
кам лопаток.
Результаты детального исследования [39] лопаток, выполненных
из перфорированного многослойного материала, показывают, что
при рациональном, программированном их расположении от-
верстий в слоях металла можно: во-первых, за счет большого
внутреннего теплосъема добиться примерно в 1,5 ... 1,6 раз боль-
шего использования хладоресурса воздуха, чем в самых совершен-
ных лопатках канальной конструкции; во-вторых, практически со-
хранить аэродинамическое совершенство профилей на уровне лучших
беременных охлаждаемых турбин; в-третьих, за счет относи-
тельно большого диаметра отверстий устранить губительный недо-
201
Рис. 920. Результаты опы-
тов по исследованию гиль-
зовых лопаток с воздушным
охлаждением £11]:
а—схема лопатки: б-^кривые от-
носительных температур /—га-
за; 2—гильзы; 3—стержня: в—за-
висимость 7'/7’*Ср стержня от
GB; 4—вершина; 5—корневое се-
чение
статок пористых мате-
' риалов, заключающий-
ся в быстрой засоря-
емости пор пылью и
окалиной. Это достига-
ется выполнением в
листовом материале от-
верстий диаметром
100 ... 200 мкм, тогда
как предельные разме-
ры пыли в очищенном
воздухе составляют
15 ... 30 мкм, а толщи-
на слоя окалины, как
показали опыты, обычно не превосходит 15 ... 20 мкм.
Предел прочности уже созданных многослойных материалов из
тонких (0,3 ... 0,4 мм) перфорированных листов металла оказыва-
ется всего на 20 ... 30% ниже, чем у исходного материала. Счита-
ется, что такая прочность пригодна для создания лопаток обычной
конструкции, а не только гильзовой, с силовым стержнем.
На рис. 9.21 показана одна из возможных структур многослой-
ного перфорированного материала. В опытных образцах выступы
на листах (см. рис. 9.21, поз. 1) получены методом фототравления.
В серийном производстве выступы могут быть образованы уже в
процессе изготовления (прокатки) ленты.
На рис. 9.21, б показано поперечное сечение стенки из четырех
слоев листового материала с перфорациями. Отверстия в смежных
листах расположены так, что
на наружную поверхность стен-
ки воздух вытекает с малыми
углами (у = 15 ... 35°) к нап-
равлению основного потока
газа.
Рис. 9.21. Схема строения многослой-
ного перфорированного материала:
а—вид на выступы / промежуточных лис-
тов (2—отверстия для воздуха); б—сече-
ние стенки по каналам для прохода возду-
ха; 3—охлаждающий воздух; 4—плоскости
терм одиф фу знойного сращивания (или пай-
ки1) листов; 5—пав. 6-^нисправление выпу-
ска воздуха
202
Подводя итог, можно сказать, что при дальнейшем усовершен-
ствовании технологии изготовления проницаемых материалов и
конструкции самих лопаток ГТД с воздушным охлаждением смогут
успешно работать при температурах газа перед турбиной до 2000 К
и более и при этом расходовать не более 2 ... 3% воздуха на один
ряд лопаток.
§ 9.4. ОСНОВНЫЕ ЭТАПЫ РАСЧЕТА ВОЗДУШНОГО
ОХЛАЖДЕНИЯ СОПЛОВЫХ И РАБОЧИХ ЛОПАТОК
ГАЗОВЫХ ТУРБИН
В задачу разрабатываемой системы охлаждения входит обеспе-
чение надлежащей работоспособности всех деталей. Однако, как
показывает опыт, основную трудность составляет разработка эф-
фективного охлаждения прежде всего лопаточных венцов. Хотя
главная цель охлаждения рабочих и сопловых лопаток одинакова,
конкретные задачи, которые приходится решать при этом, сущест-
венно различны. Это предопределяется коренным несовпадением
условий, в которых находятся сопловые лопатки с одной стороны
и рабочие лопатки с другой.
Сопловые лопатки работают в зоне максимальных температур
газа: при сравнительно большой (100 ... 250 К) неравномерности
температур как на высоте, так и в особенности по окружности про-
точной части (рис. 9.22, а). В то же время воспринимаемые сопло-
выми лопатками нагрузки (изгибные) обычно невелики. Рабочие
лопатки, напротив, несут весьма большие нагрузки от газовых,
центробежных и термических сил, но омываются газом меньшей,
чем сопловые лопатки, температуры. К тому же окружная нерав-
номерность температуры газа автоматически осредняется из-за
большой (150 ... 250 с-1) частоты вращения лопаток. Что же ка-
сается неравномерности температуры газа по высоте лопаток, то
она в известной степени поддается управлению и ей обычно при-
дают профиль (см. рис. 9.22, б), выгодный как для к.п.д. турбины
(наибольшие температуры в ядре потока), так и для запасов проч-
ности охлаждаемых деталей (более низкие температуры в корневых
сечениях и вблизи корпуса).
Способ охлаждения лопаточных венцов должен быть рациональ-
ным в данных конкретных условиях. Это означает, что он должен
обеспечивать необходимое снижение их температуры наиболее про-
Рис. 9.22. .Схема характера
неравномерности темпера-
турного поля газа на входе
* турбину в окружном (а)
н радиальном (б) направле-
ниях:
’ 2. 3—радиальная неоавномер-
1ость в трех типах реальных
ГТД <^тах -1510 К; Г*.св -
-1310К; л^тах(ч>)~200К;
дгттахГЛ)-И5К)
203
Рис. 9.23. График предела
ных возможностей разлив
ных способов воздушного
охлаждения лопаточных ац.
паратов турбины (условна
старта):
—.-----идеальный вариант без
затрат энергии на охлаждение’
7—внутреннее конвективное ох-
лаждение; 2—внутреннее конвек-
тивное охлаждение с устройст-
вами для интенсификации внут-
реннего теплосъема (штырьки
ребра и'т п.); 3—комбинация
внутреннего конвективного с
пленочным охлаждением кромок,
4—комбинация конвективного с
пленочным с предварительным
охлаждением воздуха на 50. .
. .70 К; 5—оболочка из равно-
мерно проницаемых -материалов-
6—оболочка при программиро-
ванной проницаемости по обводу
профиля (1 ... 4— по данным
натурных ГТД; 5 . . б^по опыт-
ным данным)
стыми конструктивны-
ми и технологическими
приемами и при этом
обязательно минималь-
ными количествами
охлаждающего воздуха.
Подчеркнем, что спо-
соб охлаждения лопа-
точных венцов существенно влияет на конструкцию турбины в це-
лом и поэтому обоснованный его выбор является одним из важных
вопросов при проектировании' системы охлаждения. При выборе
способа охлаждения турбинных лопаток следует пользоваться све-
дениями по эффективности, достоинствам и недостаткам различ-
ных схем, изложенными в параграфах 9.2 и 9.3, а также в специ-
альной литературе [3, 8, 22]. .Для тех же целей могут служить гра-
фики на рис. 9.23. По оси ординат отложены величины удельного
свободного теплоперепада газогенераторной части ГТД *.
С ростом То* величина Явуд резко увеличивается (см. пунктир-
ную кривую 1 на рис. 9.23, относящуюся к неохлаждаемому ГТД).
Каждой точке этой кривой соответствует своя оптимальная степень
повышения давления лк*. Однако одновременно с ростом уве-
личиваются и дополнительные затраты энергии (см. § 9.8) на
функционированные системы охлаждения (см. ДЯОХЛ на рис. 9.23).
В результате прирост Яеуд от повышения температуры газа снижа-
ется (см. кривые 2 ... 7 на рис. 9.23). Кружочками на кривых по-
мечены ориентировочные границы, до которых целесообразно при-
менение того или иного способа охлаждения. При расчете графиков
принято, что механические свойства материала позволяют не
1 Деуд — теплоперепад 1 кг рабочего тела, который может быть преобра-
зован в полезный технический эффект (тягу, мощность) двигателя.
204
,хлаждать рабочие лопатки при температурах до 1200 К и сопло-
jbie лопатки до 1300 К. Температура охлаждающего воздуха TBt
финята в соответствии с лк* в рассматриваемой точке, кривой 1.
Проектирование и расчет системы охлаждения лопаточных вен-
Ров турбины включает ряд этапов. Вначале делают предварнтель-
ый расчет, в процессе которого выполняется:
а)	оценка суммарных напряжений as и средних температур Тя
и неохлаждаемых лопатках (см. формулы 7.11, 7.12, 7.14, 7.15);
б)	расчет допустимых температур Тяоа стенок лопатки, исходя
|з Заданного ресурса и запасов прочности К (для авиационных
ГТД на стадии предварительного расчета следует принимать
— = 1,8...2,2. Свойства материалов, необходимые для опре-
ла
деления <тх, имеются в табл, приложения II);
в)	определение потребной глубины охлаждения сопловых А70ХЛ.с
и рабочих ДТ'охл.п лопаток (ЛТоХЛ.с=Тс ТдоЛ.с; ЛТохл.л=Тя,—~
—7доп.л);
г)	расчет потребных расходов охлаждающего воздуха для ох-
лаждения деталей до допустимых температур.
Параметры воздуха (рв*, Тв*) считаются при этом известными
из теплового расчета ГТД (воздух на охлаждение отбирается из-за
компрессора или из промежуточных его ступеней). Уточненный
расчет потребных расходов охладителя выполняют параллельно с
детальным поступенчатым тепловым расчетом охлаждаемой турби-
ны (см. § 9.7 и 9.9).	_
В первом приближении величину Сохл необходимо знать уже на
самой ранней стадии проектирования ГТД — при тепловом расче-
те двигателя и согласовании параметров турбины и компрессора
между собою, а также в начале детального расчета турбины при
определении расхода газа через сопловой аппарат I ступени.
В двигателях большого ресурса (т>3000 ч) при серийно используе-
мых материалах сделать это можно, ориентируясь на следующие
статистические рекомендации:
а)	при То* до 1250 К для охлаждения ножек рабочих лопаток и
дисков требуется -—0,5% воздуха;
б)	лопаточные решетки можно не охлаждать, если максималь-
ная температура торможения газа составляет: перед сопловыми ло-
патками Тс*^1270К; перед рабочими лопатками Тл*^1170К;
в)	превышение температуры торможения газа перед лопаточны-
ми решетками на каждые 100 К, по сравнению с цифрами, указан-
ными в п. «б», требует: при внутреннем конвективном охлаждении
°>8 ... 1,2% воздуха на каждый ряд; при комбинированном (кон-
вективное+пленочное охлаждение кромок) — 0,6 ... 0,9%; при
заградительном (пористое, многослойные перфорированные мате-
риалы) — 0,4 ... 0,6% на каждый охлаждаемый венец.
Графики на рис. 9.24 иллюстрируют эти рекомендации и отра-
жают фактические величины Сохл в серийных и опытных охлаждае-
мых авиационных ГТД большого ресурса всех типов, в диапазоне
'° =1300... 1700 Килк*= 12 ... 28. Обычно при То* до 1350 К охлаж-
205
Рис. 9.24. Графическое определение относительного количества воздуха, необхо-
димого для охлаждения сопловых и рабочих лопаток авиационных ГТД:
1~внутреннее конвективное охлаждение: 2—комбинированное (конвективное+лленочное) О'
лаждение; 3—-пористое и проницаемое (многослойные перфорированные материалы) охлаж-
дение
Рис. 9.25. График зависимости расхода воздуха Сохл, необходимого для охлаж
дения рабочих лопаток I ступени высокотемпературного ГТД от Тдоп.д:
------------конвективное охлаждение;-----------заградительное охлаждение; Гв*=
=650 К; 2—Тв*=700 К; 3-7^ *=800 К
даются только сопла I ступени; при То* до 1400 ... 1450 К — сопла
и рабочие лопатки I ступени; при То* ДО 1500 К — три первых ло-
паточных венца; при То*>16ООК— четыре и более. Кривые 1 на
рис. 9.24 соответствуют в основном внутреннему конвективному ох-
лаждению (при Го*>1400К из-за окружной неравномерности тем-
пературы газа приходится применять пленочное охлаждение кро-
мок сопловых лопаток); кривые 2 относятся к комбинированном}
охлаждению сопел, а на верхней границе — и рабочих лопаток
кривые 3 нанесены по результатам опытов с пористыми и много-
слойными перфорированными материалами. Расслоение кривых
определяется рядом причин, основная из которых — различная тем-
пература охлаждающего воздуха Тв*.
Нижние кривые соответствуют меньшим значениям Тв*. На рис-
9.25 показано влияние Тв* и допустимой в среднем температурь*
металла (ГДОп.л) рабочих лопаток I ступени турбины- на потреб-
ный расход охлаждающего воздуха.
Из рис. 9.25 следует, например, что если ТДОп.л=1150 К, то при
Тв* = 800 К конвективное охлаждение (сплошная кривая 3) требует
<?охл=3,9%, тогда как при Тв*=650К — всего <?охл=2,75%, т.е-
снижение температуры воздуха на 150 К ведет к снижению его раС'
хода ~ на 1/3. Весьма существенно сказывается на расходе во3'
духа и качество материала. Так, если при неизменной величии®
Тв*=800К окажется возможным увеличить Тдов.л ДО 1250 К (яа
100К), то потребный расход охладителя снизится примерно 1,3
206
30°/о- Резкого (в 2 раза) снижений (70хл можно добиться переходом
t заградительному охлаждению (см. пунктирные кривые на1
рис. 9.25).
После выбора расходов охладителя выполняется этап конструи-
рования охлаждаемых лопаток. Одновременно распределяется ох-
ладитель по каналам и определяются в первом приближении их
проходные сечения. Площади выпускных щелей в лопатке прибли-
женно рассчитываются на основе уравнения неразрывности по фор-
муле
(9.1)
р	@охл______
где Сохл — расход охлаждающего воздуха; ц. — коэффициент рас-
хода (отношение действительного расхода через систему охлаж-
дающих каналов к расходу при адиабатном течении без потерь и
подогрева); /п = 0,0404; рВЬ1Х — давление на выходе из охлаждаю-
щих каналов; Т№> Рв* — температура и давление воздуха на вхо-
де в канал; У(Лад.в) —'газодинамическая функция расхода, опреде-
ляемая по перепаду давлений рвых/р*х; для лопаток с продольными
охлаждающими каналами (по типу рис. 9.13, б) ц=0,6 ... 0,7; для
дефлекторных лопаток с поперечным течением охладителя (по ти-
пу рис. 9. 14, б) ц=0,35 ... 0,45.
При конструировании охлаждаемых лопаток следует учитывать
опыт создания уже реализованных и зарекомендовавших себя в экс-
плуатации конструкций, а также технологические возможности
производства, новейшие достижения в этой области и условия экс-
плуатации (пыль, коррозионные среды и т. п.).
В заключение выполняется детальный поверочный расчет скон-
струированной системы охлаждения. Он включает: определение
температурных полей в лопатках и гидравлический расчет про-
пускной способности охлаждающих каналов с учетом всех реаль-
ных воздействий (подогрев воздуха, массовые силы, сужение —
расширение и поворот каналов и т. п.). Расчленение поверочного
расчета носит условный характер, поскольку обе части такого рас-
чета тесно связаны между собой и влияют друг на друга. Методи-
ка поверочного расчета охлаждаемых лопаток и необходимые для
этого дополнительные сведения рассматриваются в гл. X.
§ 9.5. ГРАНИЧНЫЕ УСЛОВИЯ ТЕПЛООБМЕНА МЕЖДУ ГАЗОМ
И ЭЛЕМЕНТАМИ ПРОТОЧНОЙ ЧАСТИ ТУРБИНЫ
Точность поверочного расчета систёмы охлаждения горячих эле-
ентов проточной части (определение потребных расходов охлаж-
Дающего агента, температурных полей, тепловых потоков и допол-
Ительных потерь от охлаждения, запасов прочности и т. п.) зави-
207
Рис. 9.26. Диаграмма распределения коэффициентов аг по дли-
не проточной части ТРДД:
О'-’Рредиие по обводу профиля величины аг на среднем диаметре рабочих лопаток;
ф—средние величины аг в сопловых решетках
Рис. 9.27. Эпюра распределения местных коэффициентов теплоотдачи по обводу
профиля турбинных лопаток
сит прежде всего от точности определения граничных условий теп-
лообмена со стороны газа (аг) и со стороны охладителя (<хв)-
При этом следует иметь в виду, что интенсивность теплоотдачи
существенно не одинакова, как по длине проточной части (рис. 9.26),
так и по обводу профиля в лопаточных решетках (рис. 9.27).
Например, из рис. 9.26 (проточная часть ТРДД: лк* = 16; То*-
==1500 К) следует, что величина аг меняется от 700 ... 1300
Вт/(м2 • К), в районе стенок камеры сгорания до Ог=2000 Вт/(м2 • К)
в соплах и аг=3000 Вт/(м2*К) по обводу профиля рабочих лопа-
ток и в осевом зазоре I ступени. Характер распределения коэффи-
циентов теплоотдачи по профилю турбинных лопаток [3] (см. рис.
9.27) свидетельствует о почти пятикратном колебании величин аг-
Таким образом, для надежного расчета деталей в высокотемпера-
турных охлаждаемых ГТД должны быть известны локальные зна-
чения величин, т. е. распределение коэффициентов теплоотдачи по
всей поверхности проточной части. Определение коэффициентов
теплоотдачи может выполняться как аналитически, так и по опыт-
ным критериальным зависимостям.
Расчетный метод определения коэффициентов
теплоотдачи
Аналитический расчет величин аг вдоль контура лопатки базируется
эпюре скоростей, предопределяющей развитие теплового пограничного слоя
обтекании профиля. Эпюра скоростей w, в свою очередь, может быть получена н-
основе расчета потенциального обтекания профиля в рцшетке, или определена экс-
208
периментально. Например, если в процессе опытов найдено распределение ста-
тических давлений
\ 6 /
81 ~2
где х — текущая координата по обводу профиля; Ь — хорда;	Q —ско-
рость, давление и плотность на входе в решетку, то
гж=^=/г^.
_ W1
Эти величины wx и закладываются в расчет.
Существует несколько методов аналитического расчета местных значений аг.
В зарубежной практике, например, распространение получил метод Патанкара —
Сполдинга [40]. В нашей стране приближенный метод разработан Л. М. Зысиной-
Моложен [8]. Главное преимущество этого метода по сравнению с другими за-
ключается в том, что он позволяет единообразно рассчитывать тепловой погра-
ничный слой при всех трех режимах течения (ламинарном, переходном и турбу-
лентном). Метод Л. М. Зысиной-Моложен основывается на приближенном
решении вдоль поверхности интегрального уравнения сохранения энергии в погра-
ничном слое несжимаемой жидкости:
dbT 1 dwx д** _ «гх _
dx v>x dx x cpQwx
(9.2)
где 8 = \ —i1 —  -----------—r | dy — условная толщина потери энтальпии;
J wx 7CT—J
Niijf
Stx=——-—— число Стантона; Nux, Rex, Prx — местные числа Нуссельта,
RexPrx
Рейнольдса и Прандтля соответственно; у — координата поперек пограничного
слоя. Не останавливаясь на изложении самого хода решения *, приведем сводку
конечных расчетных формул.
Для ламинарного течения в пограничном слое (от точки разветвления пото-
ка на входной кромке до начала переходной области)
Nur = 0,297 Re
(9.3)
1-0,5
wxdx
V V
о J
где v — коэффициент кинематической вязкости. Для участков с переходным по-
граничным слоем
Nux = 3,43-10-4 Rex
wxdx л
—----+0,047
v
" 0,11
(9.4)
где xB — координата начала переходной области. Для участков профиля с тур-
булентным течением в пограничном слое
'	Nnx \9
2,915.10-3 -~Ч
/
wxdx
v
— координата конца переходной области.
3 [22] ^0ДР°бный вывод расчетных формул содержится в работе [8], а также
Nu
= 0,0255 Rex
(9.5)
209
Интегралы в формулах (9.3) ... (9.5) рассчитывают любым из известных
численных методов.
В заключение укажем, что формулы (9.3) ... (9.5) получены при ряде ог-
раничений: несжимаемый поток; ТСт/Тг*«1; изотермическая поверхность и др
Для приближения к реальным условиям в работах [8, 22] и др. предлагается
корректировать результаты расчетов с помощью поправочных коэффициентов,
так что
Nux = NuXo»I1,	(9.6)
где «я = «мевегиевренеиз“- поправки на влияние тех или иных факторов.
При удачном выборе координат начала (хн) и конца (хк) переходной об-
ласти результаты расчетов по методу проф. Л. М. Зысиной-М сложен подтверк-
даются экспериментальными данными.
На практике, в особенности на стадии предварительных расчетов, предпочи-
тают определять величины аг по участкам профиля, на основе ’опытны^ уравне-
ний подобия.
Опытные данные по теплообмену в неподвижных
турбинных решетках
Средний (по обводу профиля) коэффициент теплоотдачи аг.сР
изучался в опытах многих отечественных и иностранных исследо-
вателей.
Приближенно влияние основных геометрических параметров
решетки на теплообмен может быть учтено полученным ’ в КАИ
критерием подобия [27]:
5 —: Sin Pl
г Sin ₽2
____________«2________________Л05
_	8i — 8">
t sin (Pl -I- P2) cos2-^=-
(9 .7)
где pi, p2 — углы потока на входе и выходе из решетки; s=s/b:
t = tlb\ s — ширина; t — шаг; b — хорда решетки. '
В сопловых решетках используются углы ао и aj.
На основе обобщения (рис. 9.28) большого числа опытных дан-
ных КАИ (9 решеток) и опытов других авторов'[6] получено сле-
дующее универсальное уравнение:
Nucp=0,206 Re2°'V0'58	(9.8)
(определяющий размер — хорда Ь; определяющие параметры га-
за — температура и скорость потока на выходе из рабочей или
сопловой решетки).
Формула (9.8) с точностью 10% охватывает подавляющее боль-
шинство опытных данных. Она справедлива для решеток активного
и реактивного типа при изменении Re2 от 105 до 106; $г — от 1,3 до
6 и ТСт/Тт* — от 0,5 до 1,2; степени турбулентности ети®2 ... 6%;
М2^0,9 и углах атаки 6«0.
210
Рис. 9.28. График к обобщению опытных данных по теплоотдаче от газа к про-
фильной части неподвижных турбинных лопаток:
светлые значки — по опытам КАИ; темные — по данным других авторов.-по форму-
ле (9.8)
На основе (9.8) средний по обводу профиля коэффициент теп-
лоотдачи
0^=0,206	Re0,6V°’58,	(9.9)
где для сопловых решеток
Re=Rex=C1^cgl ; для рабочих— Re=Rea = W2^g2 .
41	42
С увеличением температуры газа его излучение возрастает и
при Тг*>1500 ... 1600 К становится существенным. Так, при
Г/дагОООК энергия, передаваемая радиацией от продуктов сгора-
ния керосина к лопаткам, составляет 10% и более от конвектив-
ного потока тепла. Таким образом, в высокотемпературных ГТД
вместо величины аг следует использовать
«;=агеи8л,	(9- Ю)
где еизл=Р/Сковв; Q, Сконв — суммарный и конвективный потоки
тепла. Поскольку основными источниками излучения продуктов сго-
рания является двуокись углерода (СОз) и водяной пар (НгО), то
приближенно
8изл« 1+50Г ±L(i+e+924-e3),	(9.11)
«г
где Тг* = 10~3Гг*; 0 = 7'ст/ТР*; ТСт — средняя по обводу профиля тем-
пература поверхности лопатки (Тст~Тд0П); ег=5со,-|-Рен,о — сте-
пень черноты газа при Тг*-, р = 1,1 ... 1,2; при выводе формулы
(.9.11) степень черноты стенок лопаток принята ®с.г=0,55.
Влияние угла атаки б на средний коэффициент теплоотдачи ис-
следовалось рядом авторов. Установлено, что это влияние может
быть значительным [3]. В практических расчетах для определения
211
аг.ср при различных углах атаки можно пользоваться формулой [6)
полученной на основе обобщения опытных данных КАИ и других
авторов:
ar.cp(8)=ar.cp(0)es,	(9.12)
где 68 =0,97-|-0,78(б—0,2)2; 6—6/f3ir — относительный угол атаки.
Специальными опытами установлено, что формула (9.12) сох-
раняется и во вращающихся турбинных решетках.
Зависимость (9.12) справедлива для решеток активного и реак-
тивного типов при:
8=— 0,5...-f-0,4; ^=(2,25...7,25) %; ReBX=(l,5.. .4)-105.
У концов лопаток в решетке наблюдается возрастание среднего
коэффициента теплоотдачи, что объясняется влиянием вторичных
течений («парный вихрь»).
На основе опытов КАИ и Уолкера и Маркленда [41] для оценки
влияния на аг.Ср концевых явлений на участке приблизительно
0,1/г от периферии и корня можно рекомендовать соотношение:
®г.конд=(1>06... 1,15)аг.ср.	(9.13)
Местные (по обводу профиля) коэффициенты теплоотдачи
Формулами (9.8), (9.13) определяется некоторый средний по
обводу профиля коэффициент теплоотдачи. В действительности, как
уже указывалось ранее, аг не остается постоянным.
На рис. 9.27 показано изменение аг по профилю лопатки в опы-
тах КАИ. Такой характер распределения аг по профилю объясня-
ется состоянием пограничного слоя. Высокие значения аг входной
кромки — это следствие тонкого ламинарного пограничного слоя.
По мере нарастания толщины пограничного слоя аг уменьшается, а
затем вновь увеличивается, когда возникает турбулентное течение.
Для'наиболее характерных участков профиля коэффициенты
теплоотдачи в лопатках можно рассчитывать на основе следующих
рекомендаций, полученных при анализе распределения значений аг
по обводу профиля в решетках различной геометрии.
Входная кромка
В точке торможения и разветвления потока на входной кромке
a^^-Re?'5	(9.14)
2гвх
(расчет ведется по параметрам на входе в решетку; характерный
линейный размер — удвоенный радиус входной кромки гвх).
. Среднее значение коэффициента теплоотдачи по обводу входной
кромки профиля
ar.M=0,63-^-Re?’5	(9.15)
2гвх
212
/Reie=f^-BX-fCo ;Relw=1Р1Гвх-<<?1— характерные параметры те же, что
и в формуле (9.14); обвод кромки — протяженность между точками
сопряжения со спинкой и вогнутой частью).
Выходная кромка
Средний по обводу выходной кромки [3] коэффициент .тепло-
отдачи
«г.вых=3,25 • Ю-з 3г2 Reo,93	(9 1б)
%	*	2гвых
Протяженность выходной кромки приблизительно до 0,16 от кон-
ца профиля. Расчет ведется по параметрам на выходе из решетки;
определяющий размер — удвоенный радиус выходной кромки.
Спинка и -корытце лопатки
Распределение «г вдоль выпуклой и вогнутой-частей профиля
зависит от структуры пограничного слоя на этих участках.-На ос-
нове анализа большого числа опытных и расчетных данных по
теплообмену можно принимать:
— при активной решетке (qCt~0 ... 0,15)
®г.вып (1•..1,1) Of .ср»
«г.вога ~ (0,85.. .0,95) Of.cp;
— при реактивной (qCt>0,2) решетке
®г.вогн	(1 • • ♦ 1 »2) (ХГаСр,
«глып (0,75.. .0,95) Ог.ср»
Ог.вып (1,2... 1,4) <ХГаСр
(9.17)
(9.18}
(ог.шп занимает протяженность 0,6 ... 0,7 длины спинки от точки
сопряжения с входной кромкой,	— остальную часть).
В высокотемпературных ГТД величины аг, рассчитанные по
формулам (9.12) ... (9.18), должны быть скорректированы на
влияние радиации газа по формулам (9.10), (9.11).
Теплообмен между газом и элементами
вращающейся лопаточной решетки
Многими исследователями была замечена значительная интен-
сификация теплообмена между газом и элементами вращающейся
Решетки по сравнению с теплоотдачей в неподвижных условиях.
Специальные исследования показали, что основными причина-
ми, вызывающими возрастание интенсивности теплоотдачи во вра-
щающихся решетках по сравнению с неподвижными, являются:
воздействие на течение центробежных и кориолисовых (от вторич-
ных течений) сил; периодическая нестационарность потока за соп-
213
Рис. 9.29. График зависимости коэффй
циента интенсификации средней по
филю теплоотдачи от частоты вращец^
(числа $и):	’
точки—опытные данные на роторах с раалЛ
ным облопачиванием;---------кривая по
муле (9.20)
лами и повышенная в связи с
этим степень турбулентности в
потоке газа.
В интенсивно охлаждаемых
лопатках проявляется также дей-
«твие подъемных сил (из-за неизотермичности поперек потока).
Детальное исследование теплообмена во вращающихся решет-
ках выполнено в КАИ [30], МВТУ и ЦИАМ.
Количественное влияние на теплообмен центробежных и корио-
лисовых сил, возникающих во вращающейся решетке, а также пе-
риодической нестационарности потока может быть учтено введени-
ем в структурное уравнение, полученного в КАИ, числа подо-
бия [27]:
Sa----7
(9.19)
где и — окружная скорость на среднем радиусе; о>2 — относитель-
ная скорость потока на входе в решетку; Q=dlh (здесь а — сред-
ний диаметр; h — высота решетки).
Основные результаты опытов по изучению влияния вращения на
теплообмен, выполненные на различных решетках, представлены
на рис. 9.29.
Таким образом, в условиях вращения
®г.ср.вращ ®г.ср®вр>
где коэффициент интенсификации
Sep = 1+0,85^.	(9.20)
Диапазон изменения Su в опытах составлял от 0 до 0,22. Здесь
уместно отметить; что в первых ступенях турбин авиационных ГТД
•обычно Su=0,1 ... 0,15. Аналогичные зависимости получены '
для отдельных элементов профиля лопаток. Интенсификация тепло-
обмена на этих участках во вращающихся решетках может быть
рассчитана как [27]
eBP=l+/?S2,	(9-21)
где Rnq берутся из табл. 9.1.
При реальном соотношении величин (Rer; ReB; Тг*; Тв* и др.) в
авиационных ГТД в стартовых условиях возрастание интенсивно-
сти теплоотдачи во вращающихся решетках составляет обычно
30 ... 40% по сравнению с неподвижными.
:214
Таблица 9.1
М ПО пор.	Участок профиля в решетке и формула		я
1	Входная кромка (9.15)	0,2	0,17
2	Выходная кромка (9.16)	0,87	0,37
3	Спинка и вогнутая часть профиля	0,8	0,42
4	Торцевая поверхность меж лопаточного канала (у корня лопаток)	1,1	0,59
Теплообмен на лопатках турбины
при заградительном их охлаждении
Закономерности теплообмена на участках профиля лопаток со>
вдувом охладителя на наружную поверхность до конца еще не изу-
чены. Имеющиеся опытные данные получены в основном на плас-
тинах. Поэтому приводимые ниже расчетные рекомендации следует
рассматривать лишь как первое приближение.
Удельный тепловой поток, передаваемый от газа в стенку при
заградительном (пленочном, пористом) охлаждении, можрт быть
рассчитан формально также, как и в случае течения однородного'
газа возле сплошной стенки, т. е.
д=а(Те—Т^),
(9.22}
где а — коэффициент теплоотдачи; Те* — эффективная («грею-
щая») температура; Тот — температура стенки.
Однако численные значения величин q при прочих равных усло-
виях будут существенно меньше, чем в случае сплошных лопаток.
Объясняется это рядом причин.
При пленочном охлаждении (см. рис. 9.18) из-за изменения ха-
рактеристик пограничного слоя коэффициент теплоотдачи а=аг.Пл-
лишь на коротком (Дхнач=^^!-= 4...s')начальном участке 1 (рис.
\	Sg	/
9.30) значительно (в 1,2 ... 1,6 раза) превосходит величину аг
сплошных лопаток.
На остальных участках защи-
щаемой поверхности 2 и 3 аг.Пл
лишь немногим- отличается от аг
(см. рис. 9.30). В то же время эф-
фективная температура Те* резко
Рас. 9.30. Расчетная схема пленочного
охлаждения:
твруи5оЬНЫ® Уча<:ток (с поверхностью контак-
y^acTtwrfJ0,111*1*0 охладитель); 2—переходный
Участок ^1}?ремешивание воздуха с газом): 3—
оьгетрого затухания эффективности
пленочного охлаждения
Рис. 9.31. График зависимости эффективности пленочного охлаждения:
/—по опытам на пластине [22]; 2—-пю опытам на двух лопаточных решетках
Рис. 9.32. График осредненной по параметру вдува зависимости отношения ко-
эффициентов теплоотдачи на поверхности лопаток при вдуве (аГПл) и без вду.
ва (аг) от относительного расстояния (xfse) до сечения вдува:
Z—Rer=6.10s; твд=0,45 .. .0,85; 2—Rer=3.105; л*вд=0,3 . ..1,0 (обе кривые относятся к двух-
рядному шахматному расположению перфораций с углом наклона отверстий к поверхности
35 ... 45е)
уменьшается, в особенности на участках 1 и 2. Последнее и предоп-
ределяет снижение величины q.
Кроме того, при пленочном охлаждении проявляется так назы-
ваемый «атмосферный» эффект. Содержащиеся в воздухе углекис-
лота (12%) и водяные пары (Н20~13°/о) снижают радиационные
потоки тепла от газа к стенке лопаток. По имеющимся оценкам
можно принимать, что при пленочном охлаждении ®изл.пл = (0,65...
... 0,75) визл. где еИзл определяется по формуле (9.11).
При использовании пленочного охлаждения следует иметь в
виду, что защищающее действие пленки быстро затухает. Уже при
®=х/з^50 ... 80 (se — ширина щели) эффективность пленочного
охлаждения т]пл=С0,4 (см. рис. 9.31):
Т*— т*
Я-=г.г_/ 	(9.23)
1 г 1 в.вх
Т*п Т„м — местные температуры торможения газового потока и
воздуха в точке вдува.
При пленочном охлаждении эффективная температура Те*=ТВл
численно равна той температуре, которая установилась бы на по-
верхности абсолютно нетеплопроводной стенки (Лст=0) в данных
конкретных условиях. По этой причине Тпл иногда называют «адиа-
батной температурой стенки».
На основе (9.23)
7’ил=^‘-(Т*г-г:.вх).	(9.24)
Таким образом, в расчетах температурных полей лопаток с
пленочным охлаждением вместо о&г надо использовать величину
аг.пл и вместо Гг* температуру Гпл. Величины ТПл и аг.пл с необхо-
димой точностью аналитическому расчету пока не поддаются. ДлЯ
их определения используют опытные данные. Например, на
рис. 9.31 и 9.32 показаны результаты опытов, полученные при пр0-
1216
дувке лопаточных решеток и пластин с пленочным охлаждением,
в' диапазоне изменения параметра интенсивности вдува
=s_Cb№«.=:0,3...1. . Числа Рейнольдса Rer= (2,5 ... 6) • 10s; чис-
"вд QrWr
ла Маха на выходе из решетки до 0,85.
Наиболее систематизированные рекомендации по определению
величин аг.пл и т]пл содержатся в работах [22] и [14]. По этим реко-
мендациям:
1.	На начальном участке (см. рис. 9.30, поз. /):
«г.пл=«геге1т>	(9.25}
где Вт=0,9 ... 1 — учитывает скачок температуры на поверхности
стенки в сечении вдува; *im=f(x/se) отражает влияние собственно
вдува. Для наиболее распространенного двухрядного, шахматного
расположения отверстий eim может определяться по рис. 9.32.
2.	На переходном участке (см. рис. 9.30, поз. 2):
®г.пл == ®ге2т’	(9-26)
где ,егт может определяться по опытной формуле [26]:
в2т=8195^;|5Кео^^вд0’55“1’2\	(9.27)
где Re03M= [qbj р,в — плотность и динамическая вязкость
воздуха, определяемые по температуре пленки Твл
9.24)].
3.	За переходным участком (обычно при — >50)
se /
1,1)аг.
(см. формулу
®Г.ПЛ ~ (0,9 . . .
Определение эффективной температуры
при пленочном охлаждении
На начальном участке (см. рис. 9.30, поз. 1)
7"ПЛ ~ В.ВХ>	. (9.28)
На переходном участке (см. рис. 9.30, поз. 2)
7’nJIss7’r—[1,37(1 —ет)Л~°>285—едискр] (т;-	(9.29)
гДе — поправка 1 на угол вдува у: при у=40 ... 60° и /пВд=
’•0,6 ... 0,8; 8Т =0,15 ... 0,25; 8ДИскр — поправка на дискретность
Расположения отверстий, например, при двухрядном шахматном
Расположении тВд=0,6 ... 0,8; 8диыф=0,15 ... 0,2 и
_____	n«= 1,37(1-ет)-0,175.	(9.30)
1 Кроме перечисленных здесь поправок ет и еДЯскр в специальной литера-
*Уре предлагаются и другие поправки для уточнения расчетов, применительно
. /Конкретным условиям (см. [14, 22], Lander R. D., Fish R. W., Sou M. The
yernal Heat Transfer Distribution on film cooled Turbins Vanes. — AIAA Pa-
per- - 1972, N 72—9, pp. 1—10.
217
На участке развитого турбулентного течения (см. рис. 9.30
поз. 3)	’
Г1И=Г:-[6,72А-‘>.®(1-ет)-8дискр](т;-Т‘в.и).	(9.31)
Протяженность характерных участков при пленочном охлажде.
нии зависит от многих факторов: твд, Rpr, ReB, ТВ* = ТВ*/ТГ, геомет-
рии мест вдува и др. Приближенно, по рекомендациям [12, 14],
начальный участок располагается в области А<2; переходный
2СА<10,
где (	А«Ке70,85/п^1’3Гв'1,28л	(9.32)
Rer = --	; х= — ; х — расстояние от рассматриваемой точки
1)г
до сечения вдува; se — ширина щели вдува; при дискретных от-
верстиях эквивалентная ширина se=^-^—\	— проходное се-
чение отверстий; I — расстояние между крайними в ряду отверстия-
ми) . При двухрядном расположении отверстий каждый ряд рассчи-
тывается отдельно, либо вносится экспериментальная поправка [22].
Обычно протяженность начального участка Дх=-*Нач =4 ... 8;
— _ Se
переходного от х = (4 ... 8) до х = 50 ... 80.
Теплообмен на поверхности лопаток из пористых
или многослойных перфорированных материалов
Тепловой поток от газа в стенку может определяться при порис-
том охлаждении по формуле [24]
7пор=аг.пор (ррт^г СртГ<х)'1	(9.33)
где аг.пор=Ог.пор/срг — обобщенный коэффициент теплоотдачи при
пористом охлаждении; по опытам для турбулентного режима тече-
ния в основном потоке (охладитель — воздух)
®г.пор (®г/^рг)о о, 19qbwb;	(9.34)
(аг/сРг)о — отношение коэффициента теплоотдачи сплошных лопа-
ток к изобарной теплоемкости газа при прочих равных условиях;
е	W2
срг7’г=срг7’г-|- г~-	— эффектная энтальпия газа; г — коэффици-
ент восстановления полной температуры (для лопаток г«0,9 •••
... 0,95); СргТст — энтальпия смеси, имеющей температуру стенки,
а состав внешнего потока. Формула (9.34) хорошо обобщает опыт-
ные данные при (аг.пор/срг) ^0,1 [24].
Таким образом, в основе расчета теплообмена на поверхности
лопаток при заградительном (пленочном, пористом) охлаждении
лежат закономерности, полученные на сплошных лопатках, тем са-
мым в известной степени учитываются основные особенности гео-
метрии решеток и характера течения в потоке газа, а также влия-
218
яе вращения лопаток на закономерности теплообмена (см. форму-
(У 9.21 и табл. 9.1). В тоже время ряд важных для такого способа
охлаждения особенностей пока не изучен. К ним относятся: кривиз-
на поверхности; поперечный к основному течению наклон отвер-
тий; расстояние между рядами отверстий (при двухрядном шах-
матном расположении перфораций); месторасположение и протя-
женность переходной области и др.
Коэффициент теплоотдачи между газом
и торцовой поверхностью межлопаточных каналов [3]
Коэффициенты теплоотдачи от газа к торцевой поверхности
межлопаточных каналов (амл.к) надо знать для расчета темпера-
туры полок лопаток и количества тепла, отводимого в сторону ди-
ска (в рабочих решетках) и в корпус турбины (в районе соплового
аппарата).
Обобщение опытов на решетках с малой (qct=0,1 ... 0,2) сте-
пенью реактивности, характерной для корневых сечений рабочих
лопаток, приводит к зависимости
аг.млж=0,032 А (1+0,7S?0-54) ReF.	(9.35)
Хг
Формула подтверждена в диапазоне: ReCp«Re2 до 2,5-105;
Гст/Тг*=0,85... 1; Ма<0,9; SP= 1,3... 2,4. Физические параметры
определяются по температуре на выходе из решетки; характерный
линейный размер — хорда профиля. Менее точной (±13%), но бо-
лее универсальной, обобщающей многочисленные опыты КАИ и
других авторов на различных решетках активного и реактивного
типа (Sr= 1,3... 5,5) является следующая зависимость:
аг=0,065 — Recp8S70>54,	(9.35а)
Х2
где^Квср « Rei + Re2. Величины Sr определяются в соответствую-
щем сечении по формуле (9.10).
Имеются достаточно подтвержденные опытные рекомендации
Для определения аг и на других участках проточной части: на кор-
пусе в районе осевых и радиальных зазоров турбины; в лабиринтах
и Др. Интересующиеся могут найти эти сведения в специальной
литературе (см. например [3, 14, 22] и др.).
§ 9.6. ГРАНИЧНЫЕ УСЛОВИЯ ТЕПЛООБМЕНА
в ОХЛАЖДАЮЩИХ КАНАЛАХ СОПЛОВЫХ И РАБОЧИХ ЛОПАТОК
В связи с большим разнообразием геометрических форм охлаж-
Дающих каналов в сопловых и рабочих лопатках турбин исчерпы-
ающие сведения по определению коэффициентов теплоотдачи от
ХЛаДителя к стенке в литературе отсутствуют. Ниже приводятся
^счетные рекомендации лишь для некоторых форм каналов, ис-
°льзуемых в современных авиационных ГТД.
219
Сопловые лопатки	*
В высокотемпературных авиационных ГТД широко применяют-
ся сопловые лопатки с дефлектором (рис. 9.33). На участке 1 та-
кой лопатки входная кромка охлаждается струями воздуха, выте-
кающими из отверстий (круглых, овальных, щелевых) в носике де-
флектора. Опыты свидетельствуют, что местные коэффициенты теп-
лоотдачи ав при этом могут возрастать в 5 и более раз по сравнению
с величинами ав при стабилизированном течении в трубах и тех же
числах ReB. Вместе с тем из-за чрезвычайной чувствительности та-
кой системы охлаждения к геометрическим соотношениям (dCTp, h,
В), к соосности отверстий со средней линией входной кромки ло-
патки, а также к газодинамическим характеристикам струй надеж-
ных данных для расчета величин <xBi в литературе не имеется. Для
оценки местных и средних значений aBi на основе иностранных ис-
точников в книге [8] приводятся критериальные зависимости.
В зоне «пятна» натекания струи (ReB>2000; ft=ft/dCTp<14)
Nurfcip= 1,2 ReSJ (й)-0'62.	(9.36)
По мере удаления от границы «пятна» струи величина <хв быст-
ро убывает (рис. 9.34) и на расстоянии A//dCTp= 10 уменьшается
примерно в 3 раза. Оценку локальных значений ав по обводу вход-
ной кромки на участке 1 можно выполнить по рис. 9.34.
Средняя теплоотдача на участке шириною х от центра «пятна»
[в] (*ч,Р>200°; *>8)
•	Nu„ps;O,36Re0/2,	(9.37)
где ReJC=^£^; wx=w„p -i / -Z-;wCTP — скорость струи на Bbixo-
V	у Л
де из носика дефлектора.
Рис. 9.33. Принципиальная схема охлаждающих каналов в дефлекторной сопло-
вой лопатке и основные обозначения:
1, 2—участки охлаждения входной кромки (/вх), корытца (ZK) и спинки Ксп) лопатки; 3—
участок воздушной полости за кормой дефлектора (/з); 4—участ.>к выпускных каналов
5—участок струйного охлаждения через перфорированную стенку дефлектора
Рис. 9.34. Кривая снижения интенсивности теплоотдачи по мере удаления от
границы «пятна» натекания струи:
/—граница струи
220
Нередко на внутренней поверхности входной кромки сопловых
лопаток для увеличения теплообменной поверхности выполняют
оребрение (по типу рабочих лопаток на рис. 9.15). Сведений о за-
кономерности теплообмена при струйном натекании на ребристую
поверхность не встречается.
В первом приближении можно пользоваться формулами (9.36)
и (9.37).
На участке 2 (см. рис. 9.33) спинка и корытце лопатки охлаж-
даются воздухом, протекающим в щелевом канале между стенкой
лопатки и дефлектором. Характерными особенностями течения на
этом участке являются высокая степень турбулентности, достигаю-
щая 30... 40% [22], и односторонний подвод тепла. По опытным
данным [9, 14, 22], коэффициент теплоотдачи на этих участках
спинки и корытца в диапазоне ReB=0,6- (103... 10б) можно опре-
делять по формуле1
/ т* \0>55
а„=0,023 Re2’8PrW—)	(9.38)
^экв	\Тсх !
где <4кв=2дщ (бщ — высота щели) —гидравлический диаметр; оп-
ределяющая скорость — среднерасходная в рассматриваемом сече-
нии канала; определяющая, температура — Гв* в данном сечении.
Для локального теплообмена при
-^-<20; г,
^экв
—0,33
Для среднего коэффициента теплоотдачи, вдоль участка /Сп
(спинки) или/к (корытца) при 1^/зс/<4кв^4 sz= 14-1,7/—1 °’25;
/ I х-0,9	^экв7
при Жкв)>5 Н 4-4,2(.
\ «экв /
С целью интенсификации охлаждения того или иного участка
спинки или корытца применяют струйное натекание воздуха через
специально выполненные перфорации в дефлекторе 5 (см.
рис. 9.33).
По данным [22], в зоне струйного охлаждения в условиях сно-
сящего потока наблюдается усиление теплоотдачи в 2... 3 раза по
сравнению с рассчитанной по формуле (9.38).
На участке 3 (см. рис. 9.33) происходит смешивание потоков
охладителя, вытекающего в закормовую область дефлектора из ще-
лей вдоль спинки и вогнутой части. Характер течения и теплообме-
на в этой зоне предопределяется формой кормовой части дефлек-
1оРа, внезапным расширением сечения, с последующим конфузор-
ным каналом. Местное значение коэффициента теплоотдачи в кон-
Че участка 3 (перед входом в выпускные каналы) приближенно
ЭпРеделяют по формуле (9. 38), где вместо 1Х подставляется длина
-'Частка 3. Местные значения ав в других сечениях участка 3 можно
' Ранний переход к турбулентному течению обусловлен сильной турбулиза-
" потока, на участке 1 и односторонним подогревом воздуха в щели [9].
221
оценить линейной интерполяцией величин ав в конце участков
2 и 3.
На участке 3 в сопловых лопатках, также как в рабочих (см.
рис. 9.16, б) нередко выполняют ребра овальной или прямоуголь-
ной формы. Эти ребра увеличивают теплосъемную поверхность и
одновременно служат турбулизаторами потока. Интенсивность теп-
лоотдачи в зоне турбулизаторов возрастает при этом, по данным
[22], в 1,3 ... 1,6 раза так, что на участке 3 aB,pe6p~(l,3...1,6)aBii.
Из лопаток воздух выпускается в проточную часть турбины че-
рез щелевые, овальные, реже круглые отверстия (см. рис. 9.33, уча-
сток 4). Отверстия располагают либо непосредственно в кромке
лопатки, либо вблизи нее, обычно на корытце (см. рис. 9.18).
Специальными опытами [22] было установлено слабое влияние
формы и размеров охлаждающих каналов на теплообмен при тур-
булентном режиме течения, что всегда имеет место в реальных
ГТД. Поэтому расчет величин ав на участке 4 можно выполнять
по формуле (9. 38).
В дефлекторных сопловых лопатках с продольным течением ох-
ладителя в щелевом, канале, образованном дефлектором и стенкой
лопатки, коэффициент теплоотдачи можно находить по формуле
(9. 38). Часто дефлектор таких лопаток помимо опорных выступов
имеет множество выштамповок, выполняющих роль турбулизато-
ров. В последнем случае величины ав могут быть оценены по дан-
ным для пластинчатых теплообменников [4, 24], либо в первом
приближении приниматься в 1,2... 1,3 раза больше, чем подсчи-
танные по формуле (9. 38), при тех же ReB.
Рабочие лопатки
Основное отличие в характере течении в охлаждающих каналах
рабочих лопаток по сравнению с сопловыми вызывают возникаю-
щие в результате вращения ротора массовые силы: центробежные
и кориолисовы. Из-за неодинаковости массовых сил в продольных
и поперечных сечениях охлаждающих каналов возникают интенсив-
ные вторичные течения, вызывающие вихри. В результате тепло-
отдача и гидравлические сопротивления изменяются по сравнению
со статическими условиями. Этот фактор- давно обнаружен многи-
ми отечественными [3] и зарубежными исследователями. Для
лопаток с продольными охлаждающими каналами (течение от кор-
ня к периферии см. рис. 9.13) влияние частоты вращения на интен-
сивность теплоотдачи изучалось в опытах КАИ 1. Установлено, что
в этом случае средний коэффициент теплоотдачи
ав.вр = ав£вр>	(9-39)
где ав определяется по формуле (9. 38); коэффициент интенсифи-
кации
£	ReB=^-; А=16,1; «=0,7; />=0,38;
в₽ 1 DoP ’ в 1ПЗ
1 Опыты проводили А. С. Лиманский и Э. И. Гунченко.
222
критерий подобия, отражающий воздействие массовых сил 5вр=
9— _Л;	—средний диаметр турбины; wB — относи-
~~ -О?в0Лл	Яд
тельная среднерасходная скорость воздуха; h — высота лопатки
(канала); ~h.A=~-',dK —гидравлический диаметр канала.
В среднем для начального участка охлаждающего канала (при-
корневая зона лопатки йлл= — =О...ЗО; dK —диаметр канала)
^4=^^= 1,2... 1,3,
«В.Н
т. е.	авр.нач=(1>2---1>3)ав нач-	(9.40)
Для всего канала увеличение внутреннего теплообмена в про-
дольных каналах при частотах вращения, характерных для первых
ступеней турбин авиационных ГТД [SBp= (1,5... 2,5) • 10-2], со-
ставляет 1,25... 1,40. Данные о влиянии частоты вращения на теп-
лоотдачу в охлаждающих каналах лопаток при других способах
охлаждения в литературе не встречаются, поэтому такие исследо-
вания крайне необходимы и актуальны. Поскольку неучет возмож-
ной интенсификации теплоотдачи во вращающихся охлаждающих
каналах ведет к увеличению запаса прочности лопаток, то до полу-
чения опытных данных расчет ав можно выполнять по рекоменда-
циям для статических условий.
В лопатках с продольным течением охладителя наличие на стен-
ках лопатки штырьков (см. рис. 9.16, а) или ребер жесткости при-
водит как к увеличению теплообменной поверхности, так и к интен-
сификации теплоотдачи за счет дополнительной турбулизации пото-
ка. Существенное влияние на величину теплоотдачи оказывает в
этом случае, как показывают опыты [22], геометрия оребрения и
форма каналов. В среднем теплоотдача в таких лопатках возраста-
ет в 1,3... 1,6 раза по сравнению с получаемой по формуле (9.38).
При наличии в канале цилиндрических штырьков величины ав мо-
гут быть рассчитаны по данным поперечно-омываемых трубных
пучков. При этом величина ав на стенке лопаток между штырька-
ми принимается на 10 ... 20% большей, чем на гладкой поверхно-
сти. В лопатках с отдельными продольными каналами в связи с не-
избежным поворотом потока на входе на 90° поток с самого начала
можно считать турбулентным и рассчитывать местные величины ав
по формуле (9. 38). В лопатках с петлевыми каналами расчет мест-
ных величин ав можно также выполнять по формуле (9.38), но при
этом следует иметь в виду, что при развороте на 180° пограничный
слой полностью разрушается. Так что в каждом канале после пово-
рота местные ав следует рассчитывать в предположении, что турбу-
лентный пограничный слой развивается заново. Таким образом, при
петлевом и многопетлевом течении охладителя следует применять
формулу (9.38), отсчитывая каждый раз величину 1Х от входа в
Данный канал.
223
§ 9.7. ЭФФЕКТИВНОСТЬ ВОЗДУШНОГО ОХЛАЖДЕНИЯ
СОПЛОВЫХ И РАБОЧИХ ЛОПАТОК ГАЗОВЫХ ТУРБИН
И ВЫБОР РАСХОДА ВОЗДУХА НА ОХЛАЖДЕНИЕ
Суммарное количество охлаждающего воздуха, которое необ-
ходимо отобрать из компрессора и прогнать через систему охлаж-
дения, складывается из количеств воздуха, требующихся для сни-
жения температуры отдельных деталей проточной части.
Относительный расход воздуха на охлаждение (в долях от рас-
хода воздуха на входе в компрессор — бв) СОхл= Сохл/<?в.
Чем меньше G0M для получения заданного уровня температур,
тем экономичнее при прочих равных условиях система охлаждения^
тем, как говорят, она эффективнее. Эффективность охлаждения ло-
паток турбин часто характеризуют безразмерной температурой
_ Гг-Гл
t=—i-----»—, показывающей, какая часть располагаемого перепа-
Т’г Л,.вх
да температур (Г*— Твлх) в системе охлаждения фактически ис-
пользована. На рис. 9.35 показано протекание т от (?в различных
лопаток. Очевидно, что та лопатка, у которой величина т больше,
имеет при прочих равных условиях и более эффективную систему
охлаждения.
Для ГТД одинакового класса и размерности величина т являет-
ся удобной характеристикой для сопоставления и выбора наиболее
эффективного способа охлаждения. Следует, однако, помнить, что
зависимости температуры лопаток, а следовательно, и величины т
от Св неоднозначны. Кроме она зависит от режимных условий
со стороны газа и охладителя, геометрических параметров решетки
и др.
Как показано в работах [3, 28], более полной характеристикой
эффективности охлаждения лопаточных аппаратов турбин являет-
ся так называемый удельный коэффициент расхода охлаждающего
воздуха:
’л	срв
(9.41)
где безразмерная температура в отличие от величины т выражает-
ся формулой
Рис. 9.35. График зависимости безразмерной
температуры лопаток т от относительного рас-
хода охлаждающего воздуха GB:
У—лопатка с тремя каналами и петлевой схемой те-
чения охладителя (см рис 9 14); 2—лопатка с про-
дольными каналами (см. гис. 9.13, б); 3—литая ло-
патка с дефлектором и поперечным течением охла-
дителя; 4—то же, что и 3, но с внутренним оребрени-
ем входной кромки
224
Очевидно, что
т==——.
1 + вл
В формуле (9.41)
7- * -
1 — ВАл
(9.43)
(9.44)
— коэффициент, учитывающий термосопротивление стенок лопаток;
&ел<0,8; СрГ, Срв — изобарные теплоемкости газа и воздуха; аг*
я ав* — критерии конвективного переноса тепла в решетке со сто-
роны газа и воздуха соответственно.
Коэффициенты аг* и <хв* пропорциональны критерию Станто-
на 1 и по физическому смыслу указывают на соотношение интен-
сивности теплоотдачи и удельной энтальпии потока со стороны газа
я воздуха соответственно. При внутреннем конвективном охлажде-
нии величина аг* обычно составляет: для сопловых лопаток ас*=
=0,01... 0,015; для рабочих — ал*=0,02... 0,025.
Удельный коэффициент расхода охлаждающего воздуха g ука-
зывает, сколько требуется воздуха в долях от расхода газа, чтобы
снизить в данных условиях температуру поверхности лопатки в
среднем на 1 градус при температурном напоре со стороны охлаж-
дения в 1 градус. Чем меньше g, тем лучше используется хладоре-
сурс воздуха, т. е. тем меньшими количествами воздуха достигает-
ся заданный уровень температур.
На рис. 9.36 показаны приведенные к эталонным условиям
опытные величины удельного коэффициента расхода охлаждаю-
щего воздуха gm сопловых и рабочих лопаток различных отечест-
венных и зарубежных авиационных ГТД. В качестве эталонных
условий, сообразуясь с реальными значениями величин авиацион-
ных ГТД, приняты [28]: число Рейнольдса в газовом потоке
Rer.3T= 106; число Прандтля Рг=0,73; отношение температур воз-
духа и газа Тв*/Тг*=0,5; Ддот=Г, относительный шаг решетки
Гэг=0,7; угол выхода потока из решетки уЭт=35°; относительный
перийетр профиля лопаток йг.ет=2,6; число S„^ =0,1 [см. фор-
мулу (9.19)]; 5г.эт=2,5 [см. формулу (9.7)]; число Рейнольдса
в каналах охлаждения ReB8T=104 *; комплекс в формуле (9.41)
f(aB*)OT=l,5.
Опытными кривыми рис. 9.36 удобно пользоваться при деталь-
ном поступенчатом расчете турбины для уточнения величин Сохл, с
и Сохл. л- Как показано в работах [3, 6], отклонения числа ReB от
эталонного значения слабо отражаются на комплексе f(aB*). С уче-
том этого на основе формулы (9.41) можно получить
» 25c/Cyiger
«г (тХ)0’25^0’58
Re °’84 7 sin у
7 г	7*<on
7доп
(9.45)
4 Критерий Стантона St=Nu/(Re Pr).
8	1337
225
где gw — выбирается по рис. 9.36; для сопловых лопаток с учетом
окружной неравномерности температур газа ДТЯ= (100 ... 250) X
1 Т г= Тс max ~ 0,98 (Го-)- КГ а)', с=1; y=aj; 1;
Т в.вх.с = Т к -f- КГ ком.
(подогрев в коммуникациях подвода воздуха Д7’КОм= 10... 30 К;
7К* — температура за компрессором или в месте отбора воздуха
на охлаждение).
Для рабочих лопаток; с= l + 0,8S2’42; у=02; Кут= 1,05 ... 1,15;
температура воздуха на входе в охлаждающие каналы лопаток в
относительном движении: при подаче воздуха под покрывной деф-
лектор рабочего колеса (см. рис. 10.13)
ТВ.ВХ.Л —А^ком 4 п-------------’ (®—djh,)',
при струйном подводе охладителя (см. рис. 10.13, в), с предвари-
тельной подкруткой в направлении вращения, так что угол нате-
Рис. 9.36. Обобщенные данные по эффективности внутреннего конвективного воз-
.душного охлаждения рабочих (1 ... 7) и сопловых (8 ... 13) лопаток в эта-
лонных условиях. Рабочие лопатки ГТД:
:RB 201 Е22]; 2—экспериментальная гильзовая КАИ [31]; 3—с поперечным течением охлаДЯ'
-теля (по типу рис. 9.15); 4—с большим числом мелких (0=0,15 мм) отверстий [5J; 5—«Спей»
[221; б—«Олимп» [5]; 7—RB.2O7 122] Сопловые лопатки; 8—JT9D 9—«Олимп» [221; /0—«Спей’
[22]; //—«Конуэй» [22]; /2-с продол иными каналами 151; 13—RB.207 1221;--—средни6
значения для сопловых лопаток;-----------«по экспериментам на плоских решетках
226
каяия воздуха в относительном движении равен 90° к плоскости
вращения
Из сопоставления двух последних формул видно, что в схемах
с подкруткой охладителя температура охладителя на входе оказы-
вается существенно, на величину д2 ~	% 80... 150К, меньше,
Срв
чем без подкрутки.
Порядок действий при пользовании формулой (9.45) следую-
щий. На основе расчета варианта с неохлаждаемой ступенью выби-
раются необходимые геометрические параметры решетки. Затем
рассчитываются числа Rer и Sr (формула 9.7), а также оценива-
ется допустимая по условиям прочности температура Тяоп.
Далее^ в зависимости от выбранной в первом приближении ве-
личины Сохл (см. рис. 9.24) и предполагаемой конструкции ох-
лаждаемых лопаток по кривым рис. 9. 36 находится величина g^.
Наконец, по формуле (9.45) рассчитывается во втором прибли-
жении требуемый расход охлаждающего воздухй на данный ряд
лопаток.	_
Окончательно уточненные значения С0Хл определяют на стадии
совместного гидравлического расчета пропускной’ способности и
температурных полей в деталях (см. гл. X).
§ 9.8. ДОПОЛНИТЕЛЬНЫЕ ПОТЕРИ ЭНЕРГИИ
В ОХЛАЖДАЕМЫХ ТУРБИНАХ
Как следует из всего ранее изложенного, охлаждение являет-
ся вынужденным дорогостоящим мероприятием, которое, не говоря
о конструктивных усложнениях, всегда требует для своего функ-
ционирования затрат энергии. Поэтому введение охлаждения
можно считать оправданным лишь в том случае, если получаемый
при этом выигрыш (за счет повышения температуры газа) по
сравнению с неохлаждаемым низкотемпературным вариантом су-
щественно перекрывает появляющиеся дополнительные затраты
энергии.
Дополнительные потери энергии в охлаждаемых ГТД склады-
ваются из: а) дополнительный гидравлических (профильных) по-
терь, снижающих кинетическую энергию движущегося газа,
°) Дополнительных термодинамических потерь, уменьшающих рас-
полагаемый адиабатный теплоперепад; в) дополнительных потерь
энергии, возникающих при смешивании охладителя, сбрасываемо-
г° в проточную часть турбины, с газом; г) дополнительных затрат
Мощности на подготовку и прокачку охладителя через систему
Охлаждения.
Очевидно, что величина дополнительных потерь в первую оче-
₽еДь будет зависеть от глубины охлаждения и тех количеств теп-
а> которые потребуются отвести от деталей для обеспечения за-
8*
227
данного уровня их температур и от расходов охлаждающего воз-
духа [3].
Оценка дополнительных потерь, перечисленных в пп. «а» ... «г>
необходима уже на самой ранней стадии проектирования: при теп-
ловом расчете ГТД и в предварительном термодинамическом рас-
чете турбины.
Дополнительные профильные потери от ох-
лаждения появляются по ряду причин, имеющих различную
физическую природу. Исследования ЦИАМ показали, что отвод
тепла от пограничного слоя сопловых лопаток вызывает некоторое.
увеличение потерь на трение. Однако величина этих потерь даже
при сравнительно глубоком охлаждении (до Тст/Гг*=0,7 ... 0,8)
пренебрежимо мала. Во всяком случае при воздушном охлажде-
нии сопел ее можно не учитывать. В рабочих лопатках эти потери
возрастают более существенно. Объясняется это изменением плот-
ности погранслоя, что в сильном поле центробежных сил приво-
дит к интенсификации вторичных течений. Детальное опытное ис-
следование этого явления на одноступенчатой газовой турбине
выполнено в МВТУ Э. А. Манушиным. Им установлено, что при
глубоком охлаждении в диапазоне изменения окружных скоростей
в натурных турбинах 11*.охл/т1г.иеохл== 0,995...0,985 (меньшие значе-
ния характерны для жидкостного охлаждения).
Другая причина возрастания профильных потерь в охлаждае-
мых решетках объясняется вынужденным отступлением от той оп-
тимальной геометрии профиля и лопаточных решеток, которые
были теоретически и опытно отработаны для неохлаждаемых тур-
бин. В первую очередь это касается радиусов входной и выходной
кромок (-^?охл^ 1,5./?нвохл) > шага (^охл^”1Д • • • 1»15^неохл)> ширины
и максимальной толщины профиля и др., а также мест выпуска
охладителя в проточную часть. В результате скоростные коэффици-
енты сопловых и рабочих решеток уменьшаются. Для рациональна
спроектированных охлаждаемых воздухом решеток можно прини-
мать, что Дфохл=Ч> — Фохл== (5 -. - 7) • 10-3; Дфохл=Ф— фохл=
= (6 ... 8) • 10-3. При глубоком жидкостном охлаждении Дфохл =
= (10 ... 12) • 10-3.
Еше более существенно возрастают дополнительные профиль-
ные потери от охлаждения при выполнении лопаток из проницае-
мых материалов или с большим числом перфораций. При вдуве
воздуха пограничный слой набухает и потери заметно растут.
В среднем, при SB=2 ... 3% на одну лопаточную решетку, при
перпендикулярном к поверхности выдуве Дфохл= Дфохл— (13 • • •
... 17) • 10~3; при угле выдува меньше 45° Дфохл=Дфохл= (Ю • • ’
. .. 14) • IO-3.
Дополнительные термодинамические потери
•в охлаждаемых решетках детально рассмотрены в
§ 3.4. Эти потери проявляются в конечном счете в уменьшении ско-
ростей истечения газа из охлаждаемых решеток, при заданном пере'
паде давлений в них, а значит и в снижении удельной окружно
работы газа. Следует сразу оговориться, что дополнительные тер
228
лодинамические потери в системах воздушного охлаждения, исполь-
зуемых в настоящее время в авиационных ГТД, столь малы (ско-
рости газа уменьшаются на 0,2... 0,3%), что ими часто пренебре-
гают. Однако, как показывают расчеты, с увеличением глубины
охлаждения и, в особенности в связи с возможным переходом к
проницаемому охлаждению и стехиометрическим температурам
газа, эти потери возрастают в 3 ... 4 и более раз. Практически учет
дополнительных термодинамических потерь выполняют в процессе
поступенчатого расчета турбины по формулам, приведенным в
§ 3. 4.
Дополнительные потери энергии от смешива-
ния газа с выпускаемым в проточную часть охла-
дителем существенно зависят от места расположения и конст-
руктивного оформления выпускных отверстий. Например, если от-
верстия размещены на выходных кромках лопаток, скорость и угол
потока смеси на выходе из решетки могут быть приближенно опре-
делены на основе уравнения импульсов в проекции на осевое (ось
а) и окружное (ось и) направления.
Для сопловых лопаток
С1с«=е1г ]/(xce sin	cosaj)2;
aia<=arctg (—tg а^ ;
\ *ся /
Для рабочих лопаток
«’2сМ=®2г sin	cos ftj)2;
' Раем—arctg p^tgpA
\ хл« 1
Здесь:
-	- Sin aiB
1 + ^охл.ссв -
sin air
1 4“ ^охл.с
- cos 0C1B
1 + ^охл.с^в _
cos air
*c« =--------------------------

1 4“ ^охл.с
- Sin р2в
1 + ^охл.л^в .
SIH p2r
*л a	i .7^	’
1 4" ^охл,л
—	- COS Р2в
1 + ^охлл^в Q
COS P2r
*лв= ГТй ’
1 С'охл.л
ёв=с1в/с1г;
(9.46)
(9-47)
(9.48)
(9.49)
(9.50)
(9.51)
(9.52)
(9.53)
cib, Cir, w2B, ц/jjr — скорости воздуха и газа в абсолютном и отно-
сительном движении, в выходном сечении сопловых и рабочих ре-
шеток соответственно; am, an — углы потока воздуха и газа на вы-
229
ходе из соплового аппарата; р2в> ргг — то же на выходе из рабочего
колеса в относительном движении.
Помимо снижения скоростей потока за решеткой, подмешивание
охладителя уменьшает и температуру смеси. На основе известных
из термодинамики формул смешивания газов температура тормо-
жения смеси будет: за сопловой решеткой
/ т* \1,52
. , I 2 в.вых.с |
1 + ^в.с \	/
-г* тА ‘	'	10	}
* 1см— * 0	==	—/ О^с’
1 4- бв.с
за рабочей решеткой в относительном (w) движении
/ т* \1,52
т . г* I в-вх-л ]
1 4' ^в.л I т* I
' 11CMW *	__
1 2см w —л 1см w---------“	—* 1смтохл*
1 + Ов.л
(9.54)
(9.55)
Здесь <?в.с и Gb.ii — относительные расходы охлаждающего воз;
духа в сопловой и рабочей решетках; Г*см» — адиабатно затормо-
женная температура потока смеси перед рабочей решеткой в отно-
сительном движении.
При выводе формул (9. 54), (9. 55) принято, что отношение изо-
еРв / тЛ9’26
барных удельных теплоемкостей воздуха и газа —-	I —£)
Ср г \ ‘ Г '
Дополнительные затраты энергии на подготов-
ку и прокачку воздуха через систему охлаждения слагают-
ся в основном из двух составляющих. Первая из них (Явр) имеет
место только при охлаждении рабочих лопаток и объясняется уве-
личением энергии вращательного движения воздуха по мере пере-
мещения его от радиуса подачи к периферии лопаток («насосный*
или «компрессорный эффект»). В расчете на 1 кг/с охладителя
//вр =	- «вх^а вх) >	(9.56)
где t, — коэффициент, учитывающий компенсацию потерь; лри вы-
пуске в радиальный зазор (£=0,75 ... 0,8) из-за уменьшения потерь
на утечку; цри выпуске из кромок (£=0,6 ... 0,7) из-за реакции
струи, увеличивающей окружное усилие на лопатках. В первом слу-
чае щ=ивер (на периферии лопаток), во втором Mf=uCJ>; сиВх.~~
окружная составляющая скорости воздуха на входе («подкрутка*) -
Практически затраты энергии на «компрессорный эффект» учиты-
вают при расчете внутреннего к. п. д. охлаждаемой ступени.
Вторая составляющая — затрата мощности на сжатие воздуха в
компрессоре — составляет наибольшую долю всех дополнительных
потерь от охлаждения. Отобранный из компрессора воздух после
охлаждения горячих деталей вводится в газовый тракт турбины И
при дальнейшем расширении частично компенсирует работу
230
|/в03Вр). затраченную на его сжатие (ЯМтр). Так что потеря рабо-,
в расчете на 1 кг/с охладителя составит
^Лиы = ^затр ^возвр==^за»р (1 РвЬ *	(9.57)
где рв^^возвр/Язатр — коэффициент возвращенной работы.
В охлаждаемых авиационных ГТД с рационально спроектиро-
=днной системой охлаждения цв достигает значений 0,6... 0,8.
С помощью соотношения (9. 57) и ранее высказанных рекомен-
даций по учету других видов дополнительных потерь от охлажде-
ния, по формулам теории ВРД [16] нетрудно вычислить удель-
ные показатели охлаждаемого ГТД [6].
Детальные расчеты показывают, например, что каждый процент
воздуха, отбираемого из компрессора на охлаждение в авиацион-
ном ТВД, снижает удельную мощность АГвтвд на 1,2 ... 1,6% и уве-
личивает удельный расход топлива на 0,4... 0,7% по сравнению с
идеальным случаем (без потерь на охлаждение).
Результаты расчета удельных параметров современных и пер-
спективных авиационных ГТД с воздушным охлаждением турбины
(пунктир и пунктир с точкой) и без охлаждения (сплошные линии)
оказаны на рис. 9.1 (ТВД), 9.2 (ТРД) и 9. 3 (ТРДД).
Анализ графиков позволяет заключить, что хотя дополнитель-
<ае потери от охлаждения заметно снижают удельные показатели
ГТД (сравните взаимное протекание штриховых и сплошных ли-
ний) , все же итоговая выгода от повышения температуры газа перед
урбиной оказывается весьма существенной. Особенно резко уве-
нчивается удельная тяга (мощность) ГТД, а. в ТВД снижается
п удельный расход топлива.
Потери на сжатие охлаждающего воздуха в компрессоре отно-
сят к дополнительным потерям от охлаждения двигателя в целом
и учитывают при расчете его удельных показателей (сд, /?уд и т. д.)
в процессе теплового расчета ГТД.
§ 9.». ОСОБЕННОСТИ ТЕРМОГАЗОДИНАМИЧЕСКОГО
РАСЧЕТА ОХЛАЖДАЕМЫХ ТУРБИН (СТУПЕНЕЙ)
Ограниченный объем книги не позволяет изложить во всех де-
алях методику теплового расчета охлаждаемых турбин и тем бо-
'te привести численный пример их расчета *. Поэтому здесь приве-
тны лишь основные особенности и руководящие указания по рас-
чету.
т Главные отличия в методике расчета охлаждаемых воздухом
Урбин от неохлаждаемых вызваны особенностями протекания ра-
'Чего процесса в охлаждаемых турбинах.
Г Расход рабочего тела не остается постоянным по длине про-
чной части охлаждаемых ступеней, а возрастает от венца к вен-
мере выпуска охладителя в проточную часть и перемешива-
 ч-ов Локэй В. И., Сальников Г. М. Термогазодинамический расчет
“°и турбины с. воздушным охлаждением. Уч. пособие. — КАИ, 1978.
231
ния с основным потоком [на входе в турбину Gr; на входе в рещет
ку рабочих лопаток первой ступени (Ог-|-Оохл.с); на входе gQ
II ступень (С?г+<?охл.с+Оохл.л) И. т. д.].
2.	Параметры рабочего тела в расчетных сечениях должны оц.
ределяться как с учетом отвода тепла д0Хл в процессе расширения
газа (см. § 3.4), так и с учетом газодинамического [см. формулу
(9.46) ... (9.49)] и термодинамического [см. формулы (9.54) ..
...(9.55)] смешивания газа с охладителем. После определения
параметров смеси относительная скорость рабочего тела на входе
в рабочую решетку и абсолютная на выходе определяются, как
обычно, из треугольников скоростей.
Например,
®1см=у4с?см+«1-- 2е1смИ! cos а1си;	(9.58)
^2сМ = ’|/Г®'2см + ^ + 2®>2ем»2	(9.59)
3.	При расчете многоступенчатой охлаждаемой турбины за на-
чальные параметры последующей ступени принимаются параметры
торможения потока смеси газа с охладителем на выходе из пре-
дыдущей ступени p*w =/?2СМ/; T*0l+1 =T*2ctti-, c0/+l=c2cMZ и т. д.
4.	Дополнительные потери энергии от охлаждения (см. § 9.8)
снижают к. п. д. охлаждаемых ступеней и турбины в целом. Это
вынуждает как в тепловом расчете ГТД, так и в предварительной
расчете турбины задаваться меньшей величиною Л’.охл =т1*—
— (1,5...3) 10-2, что равносильно назначению несколько повышен-
ных адиабатных теплоперепадов на ступень и турбину для полу-
чения заданной мощности.
При расчете внутреннего к. п. д. охлаждаемой ступени (л’о.м,)
и многоступенчатой турбины в целом ('г)*охл) необходимо, с одно®
стороны, учесть все дополнительные потери, перечисленные в § 9.8,
а с другой — скорректировать выбранный в предварительном рас-
чете располагаемый адиабатный тепловой перепад турбины. Это
необходимо сделать потому, что фактические параметры (р<*, Т?)>
найденные в расчетных сечениях при детальном поступенчатом
расчете, не совпадают с выбранными. Кроме того, надо учесть
энергию, вносимую охладителем при подмешивании к рабочему
телу.
Как уже указывалось, затраты мощности на сжатие охлажД2'
ющего воздуха удобно учитывать при тепловом расчете ГТД ®
целом.
Все остальные виды дополнительных потерь от охлаждения, 3*
исключением затрат на «насосный эффект», учитываются при РаС'
чете величины удельной работы рабочего тела на окружности коЛе'
са (Эйлеровой работы) ЯиСт.охл- Ее определяют по формУ^,
(6.22), где, однако, скорости рабочего тела находят с учетом ре*\
мендаций § 9.8. Насосную работу ЯВр рассчитывают по формг\
(9.56). Теперь о коррекции располагаемого теплового перепад
232
ступени. Так как в процессе детального расчета ступени парамет-
pbi торможения, а следовательно, и адиабатные теплоперепады в
ступени и в турбине в целом будут отличаться от намеченных в
предварительном расчете значений, то их надо привести в соответ-
ствие с фактическими параметрами рабочего тела, т. е. найти
#ост.расч и //от.расч- Кроме того, необходимо определить распола-
гаемые теплоперепады каждой порции выпускаемого в проточную
часть воздуха (за соплами, за рабочими лопатками), т. е. //аД.в.с»
/7ад.в.л и т. д. от параметров в месте выпуска до параметров за сту-
пенью (турбиной).
' Таким образом, внутренний относительный к. п. д. по затормо-
женным параметрам охлаждаемой воздухом ступени следует рас-
считывать по формуле
------- ^/ст.охл ^вр^охл.л________/л
Чст.охд __________________________-5->	(У- Ov)
*0 ст.расч "Ь (^охл^ад.в)ст
где Сохла=<?03Ui.,^- .<?охлл=^г:2—относительный расход воздуха
на охлаждение решетки рабочих лопаток в долях от расхода возду-
ха на входе в компрессор; Gr — расход газа на входе в данную
ВОХЛ г
ступень; (Сохл^ад.в)ст	— суммарный адиабатный теплоперепад
1
воздуха, выпускаемого в проточную часть ступени в расчете на
1 кг/с рабочего тела на входе в ступень; л01л — число охлаждае-
мых решеток.
Аналогично для каскада охлаждаемой турбины (в ТРДД) или
турбины в целом
гст	гохл	__,
Hl СТ.ОХЛ-- 2 ^ВР ^охл
JL________________1___________
лохл___
^От.расч + 2 (^охл^ад.в)т
1
(9.61)
где zCT — число ступеней турбины (включая и неохлаждаемые);
гоХд — число ступеней с охлаждаемыми рабочими лопатками;
— общее число рядов охлаждаемых решеток (сопловых и ра-
бочих).
233
Глава X
РАСЧЕТ ТЕМПЕРАТУРЫ ДЕТАЛЕЙ ТУРБИНЫ
И ГИДРАВЛИЧЕСКОГО СОПРОТИВЛЕНИЯ
СИСТЕМЫ ИХ ОХЛАЖДЕНИЯ
Общие сведения
Температурные поля в деталях турбины предопределяют запасы
прочности. Температуры необходимо знать для определения градиентов темпе-
ратуры и связанных с ними термических напряжений; количеств тепла, отводи-
мого от газа в систему охлаждения; подогрева воздуха в каналах и параметров
смеси (газч-воздух) после/сброса охладителя в проточную часть.
Гидравлические сопротивления предопределяют пропускную
способность системы охлаждения. Детальные сведения о потерях полного давле-
ния необходимы для правильного назначения начального давления охладителя
(Ров*); распределения воздуха по каналам системы охлаждения; определения
располагаемой работы воздуха после выпуска его в проточную часть (от пол-
ного давления в месте выпуска до статического давления на срезе сопла 'ГТД
см. § 9.9).
Как уже указывалось, температурный и гидравлический расчеты существен-
но взаимосвязаны между собою. Без знания достоверного распределения воздуха
по каналам невозможно с приемлемой точностью рассчитать температуру охлаж-
даемых деталей. С другой стороны, температуры стенок существенно влияют на
подогрев воздуха, а значит, и на пропускную способность системы в целом и
отдельных ее каналов. Практически обе эти задачи решают параллельно мето-
дом последовательных приближений.
В начале выполняется гидравлический расчет. Он базируется на суммарном
(на всю деталь) расходе воздуха и на размерах проходных сечений охлаждаю-
щих каналов, назначенных в предварительном расчете (см. § 9.4) при эскизном
проектировании системы охлаждения.
Подогрев воздуха на этой стадии гидравлического расчета оценивается
приближенно. Например, в лопатках ДГ*^А(Гд0п.л~ Г* вх), где при чисто внут-
реннем конвективном охлаждении ЛКонв = 0,45 ... 0,6; при комбинации внут-
реннего конвективного с пленочным Лпл = 0,65 .. 0,75.
В итоге такого гидравлического расчета получают уточненное в первом при-
ближении распределение воздуха по каналам. Затем на основе этих данных рас-
считывают температурные поля и уточненные подогревы охладителя в каждом
из каналов	При несовпадении Д71*- с принятыми в гидравлическом
расчете значениями вновь выполняется гидравлический расчет с учетом найденных
значений ДГвр уточняется во втором приближении распределение охладителя
по каналам и, наконец, рассчитываются во всех деталях температурные поля в
лопатках. Обычно двух-трех приближений в инженерных расчетах оказывается
достаточно.
Заключительным этапом расчетов является оптимизация системы охлажде-
ния, в процессе которой на базе подробных расчетов добиваются желаемого
распределения температур при минимальных расходах охладителя. Кроме рас-
четов на номинальном режиме система охлаждения рассчитывается также на
двух предельных режимах и на переходных нестационарных режимах. В качест-
ве предельных режимов в авиационных ГТД выбирают: полет на предельной
высоте, где ухудшается эффективность охлаждения; полет с максимальной ско-
ростью у земли, когда возрастают нагрузки на лопатки от газовых сил и тем-
пература охлаждающего воздуха. Переходные режимы — это пуск и останов
двигателя, когда резко за короткое время изменяются граничные условия.
Детальные расчеты системы охлаждения выполняют для всех охлаждаемых Де'
талей. Ниже рассматриваются только наиболее ответственные детали: сопловые,
рабочие лопатки и диски турбин.
234
§ 10.1. ОСНОВЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА СИСТЕМЫ
ОХЛАЖДЕНИЯ СОПЛОВЫХ И РАБОЧИХ ЛОПАТОК
Гидравлический расчет базируется на известном из прикладной
газодинамики принципе независимого воздействия возмущений.
Суть его состоит в том, что при течении воздуха с дозвуковыми ско-
ростями в разветвленных сетях с разделениями и слияниями пото-
ков суммарные потери энергии можно находить простым суммиро-
ванием потерь в отдельных типовых элементах.
Так, если потери энергии выражать в единицах полного давле-
ния р*, то суммарные потери полного давления
/=л
^2 = 2^*'	(10. 1)
1-1
где — потери подного давления в каждом из п характерных
по типу сопротивлений элементов охлаждающих каналов.
В свою очередь величины Apt* включают:
а) местные потери давления Дрм* (вход, выход и др.), — на-
пример:
«	w2 / М2 \
Дрвх=ск(?и^- 1+-Г ;	(10.2)
*	/ М2 \
-=Ч i+	(Ю- 3)
2 \	4 /
где ?bi, £вых — коэффициенты гидравлического сопротивления входа
и выхода из каналов, определяемые по справочным данным [14];
q, w, М — плотность, скорость н число Маха; члены в скобках фор-
мул (10.2) и (10.3) —поправка на сжимаемость потока;
б)	затраты энергии на преодоление сил трения, например, в пря-
мом канале [22]:
Рвх
-|-1п-£2£-1+-£!2--1],	'	(10.4)
Рвых J Рвых J
где Стр=ктр —--коэффициент гидравлического сопротивления
du
трения; А^р — коэффициент трения; /к, dK — длина и гидравлический
Диаметр канала. Изменение вязкости при течении с подогревом
,	/ 1 + дг* \0,м.
Учитывается приближенно членом I—-—-1 ’
в)	тепловое сопротивление из-за увеличения удельного объема
ВозДуха при подогреве его от стенок канала £тр=0) [22]:
fMl+^)(l+-^)-(l--^)l: (10-5)
1 1_А>ых \	? вх / \	4 /	\	4 /J
235
1
Рис. 10.1. Сопловая лопатка с поперечным течением охладителя (по типу
рис. 9.38) I
а—конструктивная схема; б—поперечное сечение: в—эквивалентная гидравлическая расчет*
ная схема; /-^3; 2—3—сопротивления входа и трения в дефлекторе; 3—узловая точка слия-
ния (Gi+G2) и разделения (Ga, G6, GB, Gr, Од) потоков; а, б. в,	д—однотипные сопро-
тивления коротких каналов в носике дефлектора; 4—узловая точка слияния «и разделения
(Gs, Ge) потока; 4—5 и 4—6—потери при струйном натекании и повороте потока в полости <
входной кромки; 5—7 и 6—8—-потери входа, трения и выхода из каналов вдоль спинки и
вогнутой части профиля; 7—9 и 8—9—потери смешивания и поворота потока в полости 9;
9—узловая точка слияния (G7+G8) н разделения (G10. ,. G1B) потоков* (9—10) ... (9—/5)—соп-
ротивления входа, трений и выхода при течении в каналах выходной кромки
г)	изменение полного давления из-за подвода (течение от цент
ра), или отвода (течение к центру) механической энергии во вра^
щающихся каналах:
dpt=^~ г dr,
(10.6)
где и — угловая скорость вращения; г —- текущий радиус. Прибли-
женно после интегрирования (10.6) в предположении изотермиче-
ского течения
.( 2	2 \
V вых~гвх/
е 2₽г“
^Рт Рвх
(10.7)
Число уравнений типа (10. 1) равно числу п входящих в систе-
му охлаждения лопатки типовых элементов.
236
рис. 102. Рабочая лопатка тур-
бины с петлевым течением ох-
ладителя и продольным распо-
ложением охлаждающих ка-
налов:
конструктивная схема; б—сече-
ние по охлаждающим каналам; в—
дивалентная гидравлическая рас-
четная схема
/—узловая точка разделения пото-
ка "воздуха (G2, G3); 1—2 и 1-Я—
сопротивления входа, трения и по-
ворота потока на криволинейном
участке каналов охлаждения: 2—4 и
3—5—потери трения и выхода из
Продольных каналов; 4—6 и 5—6—
потери смешивания и поворота по-
тока на 180°; 6—узловая точка слия-
ния потоков (G4+G5); 6—7—потери
входа и трения в обратном прямоли-
нейном канале; 7—6—потери пово-
рота, трения и выходные в криволи-
нейном выпускном канале
' Для точек системы охлаждения, в которых происходит разделе-
ние и слияние потоков, так называемых узловых точек, можно за-
писать еще уравнения сохранения массы:
2о.=о.	(10-8>
В установившихся условиях сумма притоков воздуха к узлу и отто-
ков воздуха от узла равна нулю.
Число уравнений типа (10.8) равно числу т узловых точек.
Система из (n+m) алгебраических уравнений является замкнутой
(число уравнений равно числу неизвестных) и в принципе позволя-
ет найти все искомые величины (Gt, Py^j)-
Часто, однако, аналитическое решение такой задачи оказывае-
тся невозможным и приходится прибегать к различным приближен-
ным методам: численному, с помощью ЭВМ, аналоговому, графо-
аналитическому.
Основное назначение поверочного гидравлического расчета на
заключительной стадии проектирования — это определение действи-
тельного распределения воздуха по каналам охлаждения и суммар-
ного расхода воздуха через сконструированную систему охлаж-
дения.
Первым шагом, в любом методе гидравлического расчета, явля-
ется анализ физической модели системы охлаждения, расчленение
ее на типовые элементы, для которых имеются справочные данные
По Коэффициентам гидравлического сопротивления и составление
Так называемой эквивалентной гидравлической расчетной схемы.
°на включает все узловые точки и типовые элементы в той же по-
следовательности, как и в натуре (рис. 10. 1 и 10.2).
237
§ 10.2. ПОВЕРОЧНЫЙ ГАДРАВЛИЧЕСКИЙ РАСЧЕТ
СИСТЕМЫ ОХЛАЖДЕНИЯ РАБОЧЕЙ ЛОПАТКИ
Наглядным и в то же время обеспечивающим приемлемую точ-
ность является графоаналитический метод гидравлического рас-
чета, разработанный Е. П. Дыбаном и И. Т. Швецом в ИТТф
АН УССР [22].
Рассмотрим существо этого метода применительно к сопловой
лопатке с продольным течением воздуха (рис. 10.3), при заданных:
суммарном расходе GBs и параметрах на входе рвх, Гвг Эквива-
лентная гидравлическая расчетная схема такой лопатки изображена
на поз в (см. рис. 10.3). При параллельном расположении типо-
вых элементов (1—4, 2—5 и 3—6) между двумя узловыми точками
(0 и 7) падение давления во всех каналах, очевидно, будет одина-
ковым и равным перепаду давлений между узловыми точками, т. е.
^>1-4= Д/>2-5= Дрз-6= Д/?0-7.	(10. 9)
Расходы воздуха в каналах будут различными, но в узловых точ-
ках одинаковыми:
Ob(0) = Gs(7)-	(10.10)
Расчет течения воздуха через каждый типовой элемент начи-
нается от той узловой точки, в которой давление известно (в рас-
сматриваемом случае точка 0).
Рис. 10.4. Кривые к определению расхода воздуха по каналам охлаждения гра-
фическим методом:
2, 3—характеристики каналов; 4—суммарная зависимость GB=f(P*); Gi. G2, Gs—искомые
расходы
Рис. 10.3. Схема сопловой лопатки с продольным течением охладителя (я.и б) и
соответствующая ей эквивалентная гидравлическая расчетная схема (в):
0, 7—узловые точной; 1—4, 2—5, 3—6—сопротивления входа, трения и выхода из каналов ох-
лаждения
238
Для каждого из каналов применяются формулы (10.1) ....
... (10. 5) и аналитически рассчитываются потери полного давле;-'
ния. Поскольку для использования формул (10. 1) ... (10. 5) дотгж-
ны быть уже известны расходы воздуха, которые еще только пр<ед,-
стоит найти, то метод дополняется графическим приемом. Суть его
состоит в следующем: а) назначается несколько (3...4) произ-
вольных значений расхода воздуха GBj через рассчитываемый ка-
нал в диапазоне реально возможных величин; б) для каждого из’
этих расходов аналитически рассчитываются потери полного давле-
ния Др»* и выходное давление р^ых=р‘х— Др*; в) строится гра-
фическая зависимость Pna—fi(GB) (рис. 10.4, поз. /). Аналогич-
ные действия повторяются для каждого из каналов (см.
рис. 10.4).
‘ Графическая зависимость суммарного расхода Ова от давле-
ния РвЫХ находится суммированием характеристик по расходам от-
дельных каналов, при фиксированных значениях рв«х (см. рис. 10_ 4,
поз. /). Заданному суммарному расходу воздуха GBs- на кривой 4
соответствует точка А, определяющая фактическое давление . р*ыж
и потерю Дра =Рвх—Рвых"
Изобара, проведенная из точки А до пересечения с кривыми/, 2„
3 в точках В, С, D позволяет найти истинные расходы через каж-
дый из каналов, а именно Gb Gz, G3 (см. рис. 10.4).
Детальные указания по применению графо-аналитического ме-
тода расчета в более сложных схемах охлаждения имеются в ра-
боте [22], а примеры расчетов в [14].
§ 10.3. ПРИБЛИЖЕННЫЙ ПОВЕРОЧНЫЙ РАСЧЕТ ТЕМПЕРАТУРЫ
СОПЛОВЫХ ЛОПАТОК И ПОДОГРЕВОВ ВОЗДУХА
В КАНАЛАХ ИХ ОХЛАЖДЕНИЯ
" Общие сведения
Расчет температурных полей Т (х, у, г, т) в охлаждаемых дета-
лях турбин требует в общем случае решения нестационарной про-
странственной, нелинейной задачи теплопроводности:
дх \ дх ] ду \ ду )' дг \ дг ] dt
где х, у, 2 — координаты; Х=%(Т), ср и р — коэффициент теплопро-
водности, удельная теплоемкость и плотность материала лопатки;
т— время. К уравнению (10.11) должны быть присоединены на-
чальные условия в виде
Т(х, у, z, т0)=/(х, У, z)	(10.. 12)
239
и переменные по времени т и координатам граничные условия со
стороны газа и охладителя. Чаще всего на стадии поверочного рас-
чета используют граничные условия третьего рода:
«г (Т'г—7'я-о)=—	у, z, т);	(10.13)
\ОП /n~Q
. <Хв (Гя_о-г:)= -X =Л(X, у, z, т),	(10.14)
\(т Jn^Q
где аг, ав — коэффициенты теплоотдачи на газовой и воздушной
сторонах; Тг*, Гв* — температуры восстановления газа и воздуха;
п — нормаль к поверхности; fit f2 — известные заданные функции.
Для тел сложной формы, какими являются сопловые и рабочие
лопатки турбины, точного аналитического решения такой задачи
пока не найдено. Поэтому практически температуры в охлаждае-
мых лопатках отыскивают различными приближенными числен-
ными или аналоговыми (электротепловым, гидротепловым) мето-
дами, а также опытным путем.
Среди численных методов наибольшее распространение в прак-
тике получили так называемые конечно-разностные методы (см.
§ 10.6). К числу недостатков этих методов относится существенная
их трудоемкость. Даже в тех случаях, когда требуется определить
температуру всего в нескольких точках (например, на кромках ло-
паток), задачу приходится решать в полном объеме, т. е. рассчи-
тывать температуры во всех узлах аппроксимирующей сетки.
В этом плане большим шагом вперед являются усиленно разраба-
тываемые в последние годы так называемые вероятностные методы
решения задач теплопроводности [8]. Эти методы обладают уни-
кальным свойством, позволяющим рассчитать температуры в зара-
нее выбранных точках, не рассчитывая всего поля температур.
Поверочные расчеты температур, на стадии увязки с гидравли-
ческим расчетом целесообразно выполнять упрощенными метода-
ми, базирующимися на одномерной теории теплопроводности,
в установившихся условиях. Ниже излагаются разработанные в
КАИ способы таких расчетов, применительно к охлаждаемым соп-
ловым и рабочим лопаткам [6]. Методика одределения температу-
ры сопловых лопаток зависит от конструктивных особенностей их
охлаждения (продольное, поперечное течение охладителя, наличие
дефлектора и др.).
Для простоты рассмотрим вначале тонкостенные лопатки, в ко-
торых передачей тепла по стенке за счет теплопроводности можно
пренебречь. Будем считать, что расход воздуха и его распределе-
ние по элементам определены в гидравлическом расчете и для дан-
ного расчета являются заданными (см. § 10.2).
Температура сопловых лопаток с продольным
течением охладителя
Расчетная схема лопатки по типу рис. 10.3, б представлена на
рис. 10.5, а. Охлаждающий воздух движется вдоль образующей
240
рис. Ю-5- Ci ем а воздушного
охлаждения сопловых лопа-
ли с продольным (а) и с
поперечным (6) течением ох-
лаждающего воздуха
тремя отдельными по-
токами: вблизи вход-
ной и выходной кромок
н в центральной (в дан-
ном случае оребренной
изнутри) части лопат-
ки. Необходимая дози-
ровка воздуха по ка-
налам достигается со-
ответствующими раз-
мерами выпускных ще-
лей.
Сопловая лопатка
разбивается на п уча-
стков высотою как
показано на рис. 10.5, а. В среднем сечении каждого из таких уча-
стков выделяются элементы: входная кромка (вх), спинка (сп),
вогнутая часть (вогн) и выходная кромка (вых). Тогда, например,
для входной кромки /-го участка, если пренебречь излучением, те-
плопроводностью по стенкам и теплопередачей через перегородки I
и II (см. рис. 10.5) между каналами, уравнение теплового баланса
можно записать в виде
или
Чт1—
f ®г.вх/ (7'cmaxi 7'ст|)
= f ав/стг	TBl)dFBi,
(Ли)
(10.15)
(10.16)
где FTi и FBi — соответственно поверхности стенки лопатки на
i-м участке, омываемые газом и воздухом.
В уравнении (10.16) в общем случае все величины переменны.
При оценке температуры элементов принимаем постоянными по
всей поверхности рассчитываемого Z-го элемента: коэффициент теп-
лоотдачи от газа к стенке входной кромки аг> (см. формулу 9.15);
коэффициент теплоотдачи от стенки к охлаждающему воздуху ав«
(см. §9.6); искомую температуру стенки ТСт», а также температу-
ру восстановления газа Те шах I-
С учетом этих допущений
г/ (T'cmaxZ	(10. 17)
241
Элементарное количество тепла, отводимое охлаждающим воз.
духом,
^7в/==Ов/ (T'cti T'bi) dFBi=CrBiCp-uidTti,	(10.18^
где TBt — температура торможения охлаждающего воздуха, пере,
менная по высоте Д/,- участка входной кромки; GBz — расход возду.
ха через охлаждающий канал у входной кромки (в соответствии с
найденным в гидравлическом расчете).
Разделяя в уравнении (10. 18) переменные и интегрируя по-внут.
ренней поверхности z-ro участка входной кромки, найдем
(T’cTf —	 CCbZ^bZ
7ctZ ^*в I	^в1Срв!
И
@в№рв1
(10.19)
где TB'i и T^i—соответственно температуры торможения охлаж-
дающего воздуха на входе в i-й участок входной кромки и на выхо-
де из него.
Подогрев воздуха на г-м участке входной кромки лопатки, оп-
ределенный на основе формулы (10.19), будет:
ДГв*/« Т*\- TBi=(Тстz - TBl) (1 - e"*i')	(10.20)
_	r
Соответственно тепловая энергия, передаваемая воздуху,
^=Ов^вгА7'^=Овг^вг(Лте-7'в;)(1-е-й10. (10.21)
Теперь с учетом выражений (10.17), (10.16) и (10.21) напишем
аг;Гг/(7':тах/-Тст/)=Ов£срвг(Тстг-7’в,Э(1-е-#10, (10.22)
откуда искомая температура стенки входной кромки на l-м участке
Т rcmaxZ + A2z7bZ (1 е *0	поч
Гст z —	/	>	(10,26’
1+*2Z\1 —е и)
где
^2Z =
GbI^PbI
®rZ^* rZ
По уравнению (10.23) определяется средняя по толщине стен-
ки температура входной кромки на i-м участке. При чисто конвек-
тивном охлаждении в тонкостенных лопатках градиент температу-
ры по толщине стенки не превышает 10 К. При значительной тол-
щине стенок (дст), глубоком охлаждении и больших тепловых пото-
ках ((f) температуры стенок со стороны газа (Tcti) и со стороны
охладителя (Тстг) могут различаться между собой более сущест-
венно. Для этого случая с учетом термосопротивления стенки вме-
сто равенства (10. 22) приближенно можно написать
ariF TltTcmui ^'ctli)~^Bl^pBl	^'в1)(1	6
242
Кроме того,
Лти-Л12/=^^-=аг/(7':тах/-ТС11/)^ ,
Лет/	Лет/
ОТКуДа 7’cTli=^rmax» ^2/ (Tct2i — ^в/)(1— С *1Г)>	(10.24)
7'ст2£ = ^'сг1/ 0- + BiCTf)	с max i В1СТ/,	(10. 25)
где В1„г = аг,-ет<-критерий Био, характеризующий соотношение
Лет
внутреннего (в стенке) и внешнего (со стороны газа) термических
сопротивлений; Тстц и Тст а — температуры, которые найдем из
совместного решения уравнений (10.24) и (10.25).
Формулами (10. 23) ... (10. 25) в рассматриваемой конструкции
лопатки можно пользоваться для оценки температуры и других
элементов профиля на i-м участке. При этом при расчете темпера-
туры спинки и вогнутой части профиля следует исходить из поло-
винного расхода воздуха через центральный канал; коэффициент
теплоотдачи ан от газа к спинке и корытцу определять с учетом ре-
комендаций гл. IX; внутреннюю теплообменную поверхность —
с учетом оребрения, а коэффициент теплоотдачи к воздуху — с по-
правкой на термосопротивление ребер [22].
При расчете 7, выходной кромки аг следует определять по фор-
муле (9. 16), а коэффициент теплоотдачи со стороны воздуха аВ£ по
формуле (9.38). Заметим, что в сопловой лопатке с продольным
охлаждением обычно не удается разместить охлаждающий канал
в непосредственной близости от конца тонкой выходной кромки.
В этом случае распределение температур Т{ по длине кромки (от
внутренней стенки канала до ее конца) следует производить по осо-
бой методике, например, как указано в работе [3].
Для каждого из элементов профиля расчет ведется начиная с
первого участка последовательным переходом ко второму, третьему
и так далее. При этом за температуру воздуха на входе в (/+1)-й
участок принимается его температура T^'i на выходе из г-го участ-
ка, т. е.
7,:,(Я.1)=7’В*; + ДГВ\	(10.26)
Для центрального канала температура воздуха предварительно
Усредняется, т. е.
Т\i=.	(ю. 27)
Найденные таким образом температуры стенки лопаток сравни-
ваются с допустимыми, а суммарные подогревы воздуха в каждом
каналов — с принятыми в гидравлическом расчете ДГВ*. При
существенном расхождении сравниваемых величин расчеты выпол-
няются во втором приближении и т. д.
243
Температура сопловых лопаток с поперечным
течением охладителя
Как уже указывалось, более равномерное температурное поле
по сечению сопловой лопатки получается в конструкциях с попе-
речным течением о'хладителя (см. рис. 9. 15 и 9.33).
Расчетная схема такой сопловой лопатки показана на
рис. 10.5, б.
В соответствии с эпюрой распределения теплоотдачи аг< по про-
филю сопловой лопатки ее контур разбивается на участки так, что-
бы в пределах каждого из них аг< можно было считать приблизи-
тельно постоянным.
В простейшем случае выделяются четыре элемента: входная и
выходная кромки, спинка и корытце.
Температура входной кромки. При тех же, что и ранее, допуще-
ниях из уравнения тецлового баланса (?г~7в) следует
г.вх С max Твх.кр) = ав^в (Т'вх.кр Т'в.вх)-
Отсюда средняя по обводу профиля температура входной
кромки
»г	шах "Ь	оох
^вх.кр— 1 + Кз ,	(10.28)
Дв /1 — ^ст,вх V
«г.вх \ Явх /
бет. вх и 7?вх — толщина стенки и внешний радиус входной кромки;
аг. вх—определяется по формуле (9.15); <хв — коэффициент тепло-
отдачи на внутренней поверхности входной кромки может быть рас-
считан по рекомендациям [14] или по критериальной зависимо-
сти (9.36), если имеет место струйное натекание.
При необходимости вместо средней по толщине стенки темпе-
ратуры можно приближенно рассчитать ее значения на газовой и
воздушной стороне также, как это сделано в сопловых лопатках с
продольными каналами.
Подогрев воздуха во входной кромке рассчитывается на основе
уравнения теплового баланса:
дг:.вх = ?^^ (Гс‘ Иах- Г^).	(10. 29)
ОвСрв
Разделение расхода воздуха GB между щелевыми каналами
спинки (бв.сп) и корытца (GB.BOrH) считается заданным, в соответ-
ствии с результатами гидравлического расчета в первом приближе-
нии (см. § 10.1). Температура воздуха на входе в щелевые кана-
лы с учетом подогрева его (ДГв.вх) во входной кромке
г:.'сп=7'в*.'вогн=г:.вх+дг:.вх.	. (ю.зо)
244
Изменение температуры спинки и вогнутой части профиля по ко-
ординате у (см. рис. 10. 5, б) с учетом принятых ранее допущений
описывается дифференциальным уравнением
^^^-+/n(7’:max-r)=0,	(10.31)
dy
те т —г* - агДв— (здесь Лс — высота сопловой лопатки; GB'=
®в^₽в Or + ®в
== GB. сп при расчете спинки и GB'= GB. вогн при расчете корытца).
Решение уравнения (10.31) принимает вид
Тд=Т*т!а-(Т*етах-Т^0)е-ту, '	(10.32)
у	агЛ: max "Ь ав (Т’в.вх + АТ’в)	, <л
где	Т у _0=-----——------------.	(10.33)
Яг -f- <хв
Коэффициенты теплоотдачи на газовой стороне определяются по
формулам (9. 17) и (9.18); на воздушной — из критериальных за-
висимостей при течении в щелевых каналах (см. рекомендации
гл. IX).
Подогрев воздуха при течении его в щелевых каналах между
дефлектором и стенкой лопатки можно рассчитать по формуле
ДГВ=_(10.34)
где	q—hc Г аДГстах—Ty)dy.	(10.35)
Воспользовавшись формулой (10.32), взяв интеграл и проде-
лав соответствующие преобразования, найдем
Д7'^1)=(г:та1-Тр_о) -^^(1-e-w.),	(10.36)
«в
где для спинки: аг=аг. сп> У\—Усп! для корытца аг=аг.вогн, У1=
=Увогн (Усп, Увогн—протяженность спинки и вогнутой части про-
филя от входной до выходной кромок).
Температура выходной кромки. Приближенную оценку распре-
деления температуры по длине выходной кромки (по координа-
те у) в случае сплошной выпускной щели или частого расположе-
ния выпускных отверстий можно выполнить по формуле, анало-
гичной (10.32):
Л,вЫх.кр = Л* max- (т: „тх- Т	е~^У,	(10. 37).
где	аг?ь.х.кр^в.т .	(10 38)
аг.вых.кр 4” С’В.Щ
<?В — суммарный расход воздуха через лопатку; <хг. вых. «р и а», щ —
коэффициенты теплоотдачи в районе выходной кромки со стороны1
газа (формула 9.16) и стороны охлаждающего воздуха (в щели).
245.
Температура основания кромки ТОсн приблизительно может при.
миматься равной среднему арифметическому значению температур
спинки и корытца в том же сечении, или более точно по формуле
типа (10.33).
Подогрев воздуха на протяжении выходной кромки может быть
подсчитан по формуле, аналогичной (10.36):
дт:.вых« (T^max-ToJ аг.ВЫх + «,.щ 0 _	(Ю. gg
Okie	'
Суммарный подогрев воздуха по всей лопатке
(10.40)
Найденные величины подогревов воздуха сопоставляют с при-
нятыми в гидравлическом расчете. В случае существенного их не-
совпадения гидравлический расчет, а затем и расчет температур
повторяют. Обычно двух приближений оказывается достаточно.
§ 10.4. ПРИБЛИЖЕННЫЙ ПОВЕРОЧНЫЙ РАСЧЕТ
ТЕМПЕРАТУРЫ РАБОЧИХ ЛОПАТОК
Попытки получения аналитических решений для распределения
•температур по высоте рабочих лопаток приводят к весьма гро-
моздким вычислениям с учетом непостоянства определяющих па-
раметров: температуры газа Т*\ коэффициентов теплоотдачи От,
ав; коэффициента теплопроводности %; площади поперечного сече-
ния /; периметров профиля С7Г и охлаждающих каналов £/в. Ниже
излагается простой и достаточно точный инженерный метод расче-
та Т(х) в лопатках турбин, с помощью ЭВМ. Метод базируется
на условном расчленении лопатки (см. рис. 10.9) на произвольное
число п небольших участков, в пределах каждого из которых мож-
но считать постоянными: Тт*(х), аг(х), ав(х), Ли/. Для каждого
участка (i) применяются известные простые решения, с последу-
ющей их стыковкой на границах участков.
Сплошные лопатки, охлаждаемые теплоотводом в диск
Введем обозначения:	Т=^-, х^-,
На основе уравнения теплового баланса для элементарного
участка высотою dxi (рис. 10.6, a) q\— 42+4?=®, уравнений
•Фурье q= — и Ньютона аг£7г(7г*— T)dx=qT получаем
dx
& Г) _ /С2 (f;_ г) = 0.	(10.41)
с1л
Отсюда распределение безразмерной температуры по высоте
любого i-ro участка	_
Тг = f*rl - AfM' -	(Ю. 42)
246
a
Рис. 10.6. Расчетная схема:
а—сплошные лопатки, охлаждаемые теплоотводом в диск; б—лопатки с продольными ох-
лаждающими каналами
При числе участков разбиения п число произвольных постоян-
ных A;, Bi будет 2п и для их отыскания требуется 2п краевых ус-
ловий. При х=0 температура в корне лопатки Тк известна (зада-
на) поэтому из (10. 42) следует, что
Aj+В^Л-Гк-	(Ю.43)
При х = 1 с достаточной для практических целей точностью
можно в первом приближении принимать температуру на вершине
лопатки Тя=Тгп, в связи с чем из (10.42) следует, что
A„4-B„e-2ft"=0.	(10.44)
Остальные 2(п— 1) уравнения найдутся при стыковке решений
на границах смежных участков. Здесь должно быть равенство тем-
ператур Ti+i—Ti и тепловых потоков Qi+i=Qi- На основе (10.42)
и уравнения Фурье получим систему уравнений
(Ле‘г«4-5е-^сг)г+1 _ (Ае^ст4-Ве-^ст)( - Дсг=0;
[>/£ (Ае*'«— Be_fe*CT)]/+i — [л fk (Aeix”—Ве-Ъ’=г)] i=0;
^СТ Тг(/ + 1) Ур/, *^ст +1»
где I последовательно принимает значения от 1 до (п— 1). Прак-
тически задачу следует решать в два приближения. В первом %
назначают по известным температурам Тк и Тп; во втором — по-
температурам участков из первого приближения.
(10.45)
247
Уис. 10.7. Графики сопоставления результатов расчетов температуры сплош-
ных лопаток (а) и с продольными охлаждающими каналами (б) с замерами в
опытах:
'Т=Т.10-з—средняя в сечении температура лопатки (А—по опытам; •-—по расчету в
два приближения); Гг*—температура торможения газа в пограничном слое лопаток (•—по
замерам;-----------------------------аппроксимация)
На рис. 1Q. 7, а показано протекание температур в лопатке, ох-
.лаждаемой теплоотводом в диск, при переменной по радиусу тем-
пературе газа.
Аналогично описанному можно рассчитывать и температуру уд-
.линенных ножек рабочих лопаток.
Лопатки с продольными охлаждающими каналами
Уравнение теплового баланса для элемента dxt (см. рис. 10.6, б)
qP+qi— qz — <^=0. Развертывая слагаемые этого уравнения по
-	тт	d^T । art/r Г™,»	a3Ua
.законам Фурье и Ньютона, получим —-Ч——- \Тг—Т-----------х
X/ L	arUT

Введем новые переменные jp=—;т=Тг—Т
л	dtUr
делах каждого участка будем считать постоянными
Х’=Л1/Г2^;	8=Т-7’в.
)и в пре-
величины:
X/
Тогда получим

4^—№т=0.
(10.46)
Решение этого уравнения для любого i-ro участка
тг=Аге*л-|-Ве
(10.47)
.где А<, Bi — произвольные постоянные, находимые, как и в случае
сплошных лопаток, из краевых условий на концах лопатки и на
стыках ®ст смежных участков. При числе участков разбиения Я
общее число произвольных постоянных будет 2л. Для их отыска-
248
/ dT’ \
-В при 1-^=4 <0 ; (10.49)
ния имеется 2и краевых условий: а) в корневом сечении лопатки
(г=1) при xi=0 т=Т1=тк и из (10.47) следует, что
Л1-{-2?1 = Тк = 7,г.к-Т’к-'Мк»’	(10.48)
б) на периферии лопаток («=1), при i=n известно количество
тепла QT, поступающего в торец лопатки fv, и на основе закона
Фурье из (10.47) получаем. .
-Дле*«±Ве"*«=-^---------
в) остальные 2(п— 1) уравнений получаем также, как и в случае
сплошных лопаток, из условий согласования решений на стыках
(хст) смежных участков. Эти уравнения полностью совпадают с
уравнениями (10.45), только на стыках участков вместо ДСт сле-
дует подставить величину
Дст.охл =	г(/+1) — 7’ri) — (/fy+l&Z+l —
Практически, как и для сплошных лопатой, задача решается с
помощью ЭЦВМ методом последовательных приближений. В пер-
вом приближении можно принимать QT=0; с^—ав(Тср, Г^ср); Х=Х
(Тср); Тср^7\4-100/<; Г1Ср=Тв*.вх+ 100/G
После определения в первом приближении произвольных постоян-
ных и температур на стыках участков находятся средние в преде-
лах каждого из участков температуры стенки Гср< лопаток. Далее
по уравнению теплового баланса
Т’в/) U3idXi=QaiCpvidTvi
уточняется подогрев воздуха (ДГВ;) и средняя температура возду-
ха Г* Срг в пределах каждого участка:
Д7,:/=(Гср/-КВх/) (1-е-*»); 7,:.cpZ=n.Bxz+0,5Ar:/,
где ku= a*iU*^xi дХ/ =	— протяженность t-ro участка.
ОвСрв	Л
По найденным значениям ТСрг и Гв.сР/ уточняются величины ко-
эффициентов теплоотдачи aBi=aB(.Tcv, Tcv.Bi) и коэффициентов теп-
лопроводности ^=%(7'с1й). Описанный процесс уточнения гранич-
ных условий теплообмена aBz и Гв.Ср/ повторяется 2... 3 раза, пос-
ле чего) полагая Bz+1 = 8j —ДГВ/’ расчет по формулам (10.47) ...
... (10. 49) выполняется во втором приближении. Обычно двух при-
ближений оказывается достаточным. На рис. 10. 7, б показано изме-
нение по х средних в сечении температур охлаждаемых лопаток,
рассчитанных описанным методом.
Распределение температур по сечению рабочей лопатки
Температурное поле в сечении охлаждаемых лопаток необхо-
димо знать для оценки запасов прочности и термических напряже-
249
поо
woo
900
800
15 13 11 0 7 5 3 1 3’5'7941’13’ &
l Развертка профиля J

Рис. 10.8. Результаты расчета температуры по обводу профиля охлаждаемой
лопатки по одномерной теории:
а—сечение лопатки с указанием распределения аг; б—температура в расчетных точках
[Тг*=1206 К; Тв*=572 К; <ZB=1435 Вт/(м».К)!
ний. На стадии увязочных расчетов оценку распределения темпе-
ратур по сечению лопатки можно выполнить сведением плоской за-
дачи [Т(у, z)] к системе одномерных задач по нормали к стенке.
При этом в сечении лопатки выделяются участки, конфигурация
которых с известным приближением может быть заменена геомет-
рическими элементами, точные решения для которых известны
(полый цилиндр, пластина, стержень и т. п.).
После независимого друг от друга определения температур в та-
ких участках (в предположении, что передачи тепла между ними
нет) при необходимости может быть выполнено последующее со-
гласование и корректирование результатов на сопрягающихся уча-
стках.
Для этой цели по результатам расчетов на отдельных участ-
ках строятся изотермы. Причем на границах участков эти изотермы
соединяются между собой плавными линиями.
На рис. 10. 8 для примера показаны результаты такого расчета
температур по контуру сечения лопатки.
Температура в точке 1 (на газовой стороне при гЛ=г2) опреде-
лена по формуле дЛя цилиндрической стенки при граничных усло-
виях третьего рода
/. Гх
I In —	.
Т{Г^Т'.+К	-П2 + -2-
\	2авГ1
(10.50)
k — коэффициент теплопередачи через цилиндрическую стенку;
И, г2 — внутренний (по воздуху) и внешний (по газу) радиусы
входной кромки; гх — текущий радиус; Лст — коэффициент тепло-
проводности стенки; аг. вх, ав — коэффициенты теплоотдачи со сто-
роны газа и воздуха.
2$о
Температура в точке 15 (на конце выходной кромки) и по ее-
длине определена по формуле распределения температур в стерж-
не постоянной толщины:
ew____________
mk ССг.вых^кр
тК 4- ссг.ВЫх1кр
e-w
тк 4- «г.вых^кр
е-т + еш --------------
тк— <Хг.вых*кр
т(!/)=т:-(т;-тосн)/—
\ ет + е
. (Ю.51)
// — координата, отсчитываемая от конца кромки в сторону охлаж-
дающего канала; Zkp— длина выходной кромки; X — коэффициент
теплопроводности кромки; S — средняя толщина кромки; ТОсн —
температура в основании кромки; аг. 8Ых— коэффициент теплоот-
дачи от газа к выходной кромке [см. формулы (9.16), (9.21)].
Температуры в точках контура вдоль спинки и вогнутой части
профиля и по толщине стенки могут быть найдены по формулам
теплопроводности плоской стенки
г(х)=г:+А(г:-г:)р^^+—(ю.52)
\ Xcf «в /
или	Т(х-)=Тг-к(Т*-Ю (—+— V
\Хст аг /
где k=-------------;
1 1
---I- -S- +-
“г Хст ав
х— координата по толщине бСт стенки, отсчитываемая со стороны
газа; аг, ав коэффициенты теплоотдачи со стороны газа и воздуха.
На рис. 10. 8, а показаны также заложенные в расчет коэффи-
циенты теплоотдачи со стороны газа, найденные по рекомендациям
§ 10.5. ДЕТАЛЬНЫЙ РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
В ОХЛАЖДАЕМЫХ ЛОПАТКАХ ТУРБИН
В СТАЦИОНАРНЫХ УСЛОВИЯХ
Общие сведения
Уравнения (10.11) ... (10.14) для установившихся условий при-
Цимают вид: уравнение теплопроводности
Т"(кТ')+Л(Х^)+/’(кА=0;	<10<53)
дх \ дх ] ду \ ду ) dz \ дг )
гРаничные условия
аг(7’;-7’я_0)=-х(^ , Ов(Тя.0-Т:)=-к(^ .
\ ОН /п-Ъ	\оп }п—Ъ
251
Рис. 10.9. Схема к расчету температур в сече-
нии лопатки по методу О. И. Голубевой
Хотя эта система и проще, чем (10.11)
... (10.14), но для тел сложной формы ащь
литического решения также не имеет. Прак-
тически для определения температур в этом
случае используют различные численные и
аналоговые (например, ЭТА — электротеп-
ловая аналогия) методы. Выбор того или
иного метода диктуется как конкретной
целью расчетов, так и наличием вычисли-
тельного оборудования (универсальные бы-
стродействующие ЭВМ; сеточные электро-
интеграторы, аналоговые ЭВМ и др.).
Наибольшее распространение в расчетной практике в двигателе-
строении получили так называемые конечно-разностные методы
[8] в совокупности с ЭВМ и их разновидность: метод элементар-
ных тепловых балансов [13]. В установившихся условиях эффек-
тивным оказался разработанный впервые О. И. Голубевой метод,
базирующийся на формуле Грина [29]. Главные его достоинства
заключаются в том, что он позволяет, во-первых, рассчитывать по-
верхностные (контурные) температуры (Ттах, Гты). не решая за-
дачи в целом и, во-вторых, после определения поверхностных тем-
ператур определять температуру любой наперед заданной точки
тела, опять-таки без того, чтобы решать задачу в полном объеме.
В результате сокращается трудоемкость расчетов. Рассмотрим суть
этого метода подробнее. Предполагая -^-==0 и Х(Г) =const вместо
(10.53), приходим к уравнению Лапласа для плоскости
	*£+«L=0.	(10.54)
dl/2 1 <Jz2	V
Далее с помощью формулы Грина для замкнутой области $ (се-
чение лопатки) дифференциальное уравнение Лапласа сводится к
интегральному уравнению Фредгольма второго рода. Его решение
проще, чем уравнения Лапласа, ибо выполняется интегрированием
по линиям контура, ограничивающего заданную область (сечение
лопатки). Формула Грина, отражающая свойства гармонических
функций, которые удовлетворяют уравнению Лапласа, в нашем
случае связывает значение температуры Гм» произвольной точки
Mo(i/o> zo), лежащей внутри рассматриваемого сечения лопатки
(рис. 10.9), с температурами (Tv) и их нормальными производны-
ми точек, лежащих на контуре U лопатив, т. е.
\dN /
(1O-SS)
и
252
где г — радиус-вектор от фиксированной точки Л10(уо, Zo) до теку-
щей i-й точки контура с координатами (г/i, Zi); М — внешняя нор-
маль в i-й точке контура; dU — элемент дуги контура;
= dy — элементарный угол, под которым элемент дуги контура
dU видён из точки Мо, в которой определяется температура. На ос-
(дТц \	а..
нове граничных условий величина	о=-^-(Г* — Гу),
где аи=аг, Т*=Тт* для точек, лежащих на газовом контуре и
аг,=а01л, Т*=Г*ХЛ для контуров охлаждающих каналов.
Формула (10.55) справедлива для всех точек области, включая
ее границы. Для определения температур в любой i-й точке кон-
тура вместо (10. 55) получаем
Tui =
a.
-i- \T^-\\nra-^{T^-Tv)dU .
J	J А
L<y)
(10.56)

Интегралы, входящие в уравнение (10.56), вычисляют прибли-
женно, с приемлемой для практики точностью. Для этого контур ло-
патки и контуры охлаждающих каналов разбивают на достаточно
большое число (п — по газовой стороне и m — по воздушной) от-
резков. В пределах каждого такого отрезка контура принимаются
постоянными: ay, X, Г* и Ту.
Если теперь интегралы в (10.56) заменить приближенными
суммами, то в итоге получается конечная система линейных алгеб-
раических уравнений, не содержащих интегралов. Порядок системы
уравнений (n+tn) зависит от числа участков п и tn, на которые
разбивается контур. Обычно хорошая точность достигается при раз-
бивке (вычерченных в масштабе 10:1 или 20:1) внешнего контура
на 50... 100 участков и каждого из внутренних контуров на
5... 8 участков. После указанных замен система (п+т) уравнений
в краткой записи принимает вид
Л+/П
2 (ФЛ-Фг/Г:/-фв/г;/-2л7’(й))=0.	(10.57)
й-1
Здесь индекс указывает, для какой точки составляется урав-
нение (см. рис. 10.9), а индекс — на участок, которому при-
надлежат коэффициенты
\ br^(npn Л<дг, ay=ar, при k~>m, ay==aoM),
(»)	W
п
Vnr^’
(*)
л+m
^=^2 $ 1п/уД4.	(10.58)
£-п+1 (к)
253
Вычисление коэффициентов ф в (10.58) может выполняться лю-
бым приближенным способом отыскания определенных интегралов.
Далее решается система (10.57) с помощью ЭВМ и в результате
получаются (п+т) контурных температур в срединах участков
разбиения.
В промежуточных контурных точках температуры определяют
интерполяцией.	»
В любой точке М сечения (s) температура может быть найде-
на на основе'уравнения (10.57). Для этого в члене 2лТ(Д) вместо
средней температуры T(ft) следует подставить искомую и решить
уравнения относительно этой температуры:
1
‘ 2л
Ti
(10.59)
где Тил — уже известные средние температуры на участках кон-
тура 1, 2,..., (п+/п); коэффициенты ф«, фгг-, фВг имеют те же
значения, что и при определении контурных температур.
Изложенный метод, разработанный в 1947 г. О. И. Голубевой,
когда еще не существовало ЭВМ, был в дальнейшем усовершенст-
вован (учет переменных at/) и Л(Т) [8]; учет at/, ЦТ) и осреднен-
ных по сечению продольных потоков тепла, т. е. при —— =7^0 [29]) и
дх
реализован программами для ЭЦВМ «БЭСМ» и М-222.
Программы позволяют определять температуры в 100... 200 точ-
ках контура и в любом (без ограничения) числе внутренних точек
сечения, при этом машинное время расчета составляет 15... 30 мин.
Дальнейшим шагом в развитии этого метода явилось разрабо-
танное в КАИ 1 приближенное решение трехмерной задачи тепло-
проводности. Метод расчета позволяет учитывать переменность ве-
личин TT*(F), Tb*(F), а (Г), К(Т) и реализован программой для
ЭЦВМ М-222. Поверхность лопатки, соприкасающаяся с газом и
охладителем, в этом методе разбивается на ряд плоских элементар-
ных площадок, в пределах которых ар, Тт* и Тв* принимаются по-
стоянными. Поверхностные температуры в средине площадок раз-
биения определяются в результате решения системы линейных ал-
гебраических уравнений. После этого можно найти температуры в
любой внутренней точке объема лопатки. Первое приближение вы-
полняется при X(T)=const, второе — при к=к(Т1), где Ti— тем-
пературы, найденные в первом приближении.
При числе площадок разбиения п= 100 время формирования и
решения системы уравнений на ЭЦВМ М-222 составляет 25.. •
... 35 мин. Последующее определение температуры в любой внут-
ренней точке требует 15... 20 машинного времени.
1 Локай В. И., Гунченко Э. И. Объемное поле стационарных тем-
ператур в охлаждаемых лопатках турбины. — Инженерно-физический журнал;
т. 33, № 4.—Минск: 1977, с. 687—693.
254
§ 10.6. ДЕТАЛЬНЫЙ РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
В ОХЛАЖДАЕМЫХ ЛОПАТКАХ ТУРБИН
В НЕСТАЦИОНАРНЫХ УСЛОВИЯХ (ПУСК.
ОСТАНОВКА, ПЕРЕХОДНЫЕ РЕЖИМЫ)
Наибольшее распространение в практике расчетов нестационар-
ных температурных полей в лопатках и других деталях турбин ГТД
получили так называемые конечно-разностные методы. Они могут
успешно применяться и для определения установившихся темпера-
тур, когда процессы переноса тепла описываются дифференциаль-
ными уравнениями эллиптического типа, но наиболее эффективны
при решении нестационарных задач теплопроводности (дифферен-
циальные уравнения параболического типа).
Детальное описание конечно-разностных методов решения за-
дач теплопроводности имеется в специальной литературе [3, 8, 13].
Суть этого метода состоит с том, что исходная непрерывная физи-
ческая система заменяется некоторой дискретной системой (сетка
с множеством узловых точек), а частные производные — конечно-
разностными соотношениями. Так, например, одномерный нестацио-
нарный тепловой процесс в теле описывается параболическим диф-
ференциальным уравнением в частных производных:
дт	д^т
—=а--------,
дх	дх2
где а=-----коэффициент температуропроводности.
CQ
Используя равномерную сетку по х(Дх) и разлагая функцию Т
в ряд Тейлора, получаем аппроксимирующее (сеточное) уравнение
в конечных разностях:
(10.60)
Т1х,(т + Д-с)]—ТСх.т) = Т[(х — Дх),т] — 2T (x,t) 4- У[(х 4- Дх) ,т] .
айх	(Дх)2
+ е(Д-С, Дх2),	(10.61)
'Де Дт, Дх — приращения независимых переменных; е(Дт, Дх3) —
погрешность аппроксимации.
Если ячейки сетки по координате х и по времени т выбрать до-
статочно малыми, то отбрасывая е—>0, получаем расчетное конеч-
но-разностное уравнение для любого узла сетки в виде
r,(,+4t)=(l -^)г^+-^-(Г(ж-дж),х+Г(х+джм. (Ю.62)
Уравнения типа (10.62) позволяют определить температуру во всех
/злах сетки в момент времени (т+Дт) по известным температурам
5 предыдущий момент времени т. Таким образом, по своей сути
Меленные конечно-разностные методы являются экстраполяцион-
ными и потому требуют особого внимания к вопросам сходимости и
Устойчивости получаемых решений. В частности, из . уравнения
255
(10.62) следует, что для получения устойчивого решения необхо-
димо, чтобы
0<(1 —2аДт)/Дх2< 1.	(10.63)
Условие сходимости конечно-разностного метода связано с по-
грешностью аппроксимации дифференциального уравнения сеточ-
ным уравнением и сводится к требованию, чтобы эта погрешность
равномерно стремилась к нулю при неограниченном измельчении
сетки (Ат—>-0; Ах—И)).
Условие устойчивости решения связано с погрешностями округ-
лений при выполнении численных операций. Требование устойчиво-
сти решения сводится к тому, чтобы ошибки округления убывали,
или по крайней мере не увеличивались в процессе счета.
Принцип экстраполяции, лежащий в основе конечно-разностных
методов, приводит также к тому, что всегда при нарастании теп-
лового потока по времени определяемые температуры оказывают-
ся несколько заниженными, а при снижении — завышенными по
сравнению с истинными. Однако эти расхождения обычно не пре-
вышают 1... 2%.
Расчет нестационарных температурных полей
в сечении охлаждаемых лопаток методом
элементарных тепловых балансов (метод А. П. Ваничева)
Метод элементарных тепловых балансов представляет собой раз-
новидность конечно-разностных методов. Рассчитываемое тело коор-
динатными поверхностями разбивается на ряд правильных геомет-
рических элементарных объемов. При определении температур в се-
чении лопатки шаг по координате х принимается равным 1, а по
координатам у и г (рис. 10. 10) бу и 6z соответственно. В частном
случае квадратной сетки dy=6z. В пределах каждого из таких эле-
ментарных объемов теплофизические характеристики (коэффици-
ент теплопроводности Л и удельная теплоемкость с) принимаются
постоянными, а изменение температуры по времени линейным. Тем-
пературы в узлах сетки определяются в пооведовательные моменты
времени из уравнений теплового баланса тех элементов, которые
примыкают к рассматриваемой узловой точке. Для внутренних то-
чек тела потоки тепла по координатным осям записываются по
уравнению Фурье/у=— Xдля граничных (соприкасающихся с
газом или охладителем) — по соотношениям Ньютона у=
=o.F(T* — Т) и Фурье; приращение или убыль тепловой энергии в
рассматриваемой точке за элементарный промежуток времени — по
изменению теплосодержания (у=с(>ДУ-^-) . Далее дифферента-
\	dn /
лы (dT, dn, dr) в полученных уравнениях заменяются конечными
приращениями (AT, Ay, Az, Дт). В результате получаются разност-
ные уравнения, которые и решаются численно относительно иско-
мых температур.
256
Рис. 10.10. Расчетная схема сечения охлаждаемой лопатки турбины;
at б, в, г, д, е, ж, з—характерные узловые точим
В зависимости от способа замены конечными разностями произ-
водных по времени и по координатам различают явный и неявный
методы вычисления температур.
Например, при решении одномерного уравнения (10.60) явным
методом Titk+i=fi(Ti'k; Л+i.fe), т. е. температура в /-Й точ-
ке в (&+1)-й промежуток времени выражается через температуру
самой точки и температуры соседних точек в данный k-й момент
времени;
в неявном методе —
7’/.#+1=Л1(Л; Л-ь т^-, (Л-ь Л+Л+iL	(Ю.64)
т.. е. искомая температура выражается не только через температу-
ры в данный k-й момент времени, но еще и через температуры со-
седних точек в следующий (&+1)-й промежуток времени. Посколь-
ку эти температуры ei^fe неизвестны, то в неявном методе на каждом
шаге по времени Дт приходится решать систему линейных алгебраи-
ческих уравнений. В результате сильно увеличивается громоздкость
расчетов и их трудоемкость.
К другим недостаткам неявного метода относятся ненаглядность
и невозможность вмешаться в процесс вычислений практически до
получения конечных результатов, а также то, что при переменных
граничных условиях, что имеет место в турбинах, точность расчетов
существенно снижается. По указанным причинам, несмотря на аб-
солютную устойчивость решения, неявный метод в расчете охлаж-
даемых лопаток турбин применяется редко. Опыт сравнительных
расчетов показывает, что жесткие ограничения по устойчивости ре-
шения явным методом и необходимость в связи с этим иметь весьма
малые шаги по времени в итоге все же приводят к существенной
экономии машинного времени по сравнению с неявным методом.
9	1337	'	257
a
I Рис. 10.11. Схема я графики к расчету перепадов температур АТ
в сечении лопатки:
а—перепады по толщине стенки лопатки в местах /—5 (см. контур лопатки в верхней час-
ти); -*•>-мгновеннбе возрастание граничных условий;-------возрастание по линейному
закону за время т=10 с; б—изменение температуры газа по времени в случае возрастания
граничных условий по линейному закону
Главная причина этого состоит в том, что в явном методе расчетные
уравнения независимы друг от друга и от времени. Решение на-
глядно и допускает контроль и внесение исправлений на любом
этапе расчетов. Особенно выгоден этот метод при значительной
продолжительности теплового процесса и переменных граничных
условиях.
Если воспользоваться прямоугольной аппроксимирующей сеткой
постоянного шага, то вся совокупность узловых точек сечения ох-
лаждаемой лопатки может быть представлена характерными типа-
ми узлов, показанных в укрупненном масштабе на рис. 10.10 (см.
поз. а...з).
Уравнение теплового баланса для элементарного объемчика,
представленного внутренней узловой точкой (рис. 10.10, поз. а),
принимает вид1
-Л+kty.l AZiLAr-lk+Agz. 1 дг—
2 а Ъг	2	В®
-	. 1 AZm. дт._^+1в8г. 1 ?Z±L Дт==C1(h8!/Sz. 1. дТр (10.65)
г t. 2	bz	2	Ъу
1 В разработке алгоритма расчета принимал участие'В. В. Жуйков. Он
сжтавил программу для ЭЦВМ М-222.
258
Или, в краткой записи для любой i-й внутренней узловой точки,
—Дт
yi
7-1 L
(гтг) Н^ДП-
»	/и!
(Ю. 66)
Для граничной узловой точки, например, типа в (см. рис.
10. 10) уравнение теплового баланса принимает вид
_21±А Ьу	дт + ajy (Тп - 7\) Дт=cl9liy Ц-	(10.67)
Л	Ъ2	2
В краткой записи, для любой i-й граничной точки, в соответ-
ствии с поз. б... з на рис. 10. 10:
j-m
-д* У	Т-^-аДГ*—7'/)Д//Дт=(срДУ’Д7’)Р
L 2	\ А» Jijj
(10.68)
В разностных уравнениях (10.66), (10.68) обозначено: m —
число соседних узловых точек в направлении осей z, у; Kit Л3 — ко-
эффициенты теплопроводности элементов, представляемых i-й и /-Й
узловыми точками; Д— объем элемента, представляемого дан-
ной узловой точкой. Для узловых точек: типа а — ^Vi=6z6y-1; ти-
па б, в, г	(ЪгЪу-1); типа д, е—ЬУ}—— (Ъг&у-1); типа ж,
2	8
з—ДУг=— (Szby-1); Д/jj — расстояние от рассматриваемой i-й и
до соседней /’-и узловой точки; Fit j — площадь поперечного
сечения соответствующего элемента (при тепловом потоке вдоль
оси у AFitj=6z-1; в направлении оси z Д/\	1); Д/<— пло-
щадь теплообмена гарничного элемента с омывающей его средой;
a»', Т<”— коэффициент теплоотдачи и температура омывающей сре- .
Ды на участке i-ro элемента; Д7\13— разность температур между
i-й точкой и соседними с нею узлами; ДГ< — приращение темпера-
туры рассматриваемой узловой точки за время Дт; сг-, — удель- •
ная теплоемкость и плотность материала при температуре i-й точки.
Для одномерного случая условие устойчивости решения имеет
вид неравенства (10.63). Оно указывает на то, что при использо-
вании явного метода вычисления температур шаг по времени Дт не
может выбираться произвольно, а должен быть связан с шагом по
координате Дх. Для двухмерной задачи из условия устойчивости ,
Решения получается
CQ(M2
(10.69)
9*
259
Поскольку теплопроводность жаропрочных металлов и сплавов
в рабочем диапазоне температур достаточно точно аппроксимиру-
ется линейным законом %=%о+ЬТ, то вместо (10.69)- имеем
- г('мл •	(10'70)
2Xmax^l+(Wj
где lmax=A,o+b7’imax; Л max — максимальная в данный момент вре-
мени температура в расчетном сечении лопатки. Выполнение усло-
вия (10.70) для точки с максимальной температурой означает од-
новременно выполнение этого условия и во всех других точках
сечения.
Формулы (10.66) ... (10.70) позволяют с помощью ЭВМ полу-
чить подробное поле температур в охлаждаемых лопатках турбин
в нестационарных условиях.
Разработанная в КАИ программа для ЭВМ М-222 позволяет
производить расчет при числе узловых точек N^3700 и числе уча-
стков, на которых задаются граничные условия М^100. Затраты
машинного времени при #=1500, М=100, Дт=5-10-3 с и продол-
жительности теплового процесса т=25 с составляют 80 мин.
Для примера на рис. 10.11 показаны рассчитанные описанным
способом градиенты температур по толщине стенки охлаждаемой
сопловой лопатки в условиях пуска ГТД из холодного состояния.
Максимальные перепады температур в стенке, достигающие при
внезапном нарастании температуры газа величин 80 К, существен-
но снижаются при плавном, в течение 10 с, выходе на режим.
§ 10.7. ОХЛАЖДЕНИЕ ДИСКОВ ТУРБИН
Способы охлаждения дисков
Диски турбин ГТД являются высоконагруженными деталями.
Охлаждение дисков имеет целью отвести тепло, передаваемое из
проточной части через нижние полки лопаток, удлиненные ножки
и замковую часть обода, ь- тем самым обеспечить необходимый по
условиям прочности тепловой режим диска. В современных ГТД
температура дисков на периферии достигает 850 ... 950 К; в цент-
ральной части (у ступицы) Тц=500... 650 К; перепад температур
по радиусу диска составляет ДГд^250 ... 350 К, по его толщине
60... 100 К, в ободе (замковой части) — 100... 150 К.
В большинстве конструкций газовых турбин применяется при-
нудительное воздушное охлаждение дисков. Можно указать три ос-
новных типа принудительного воздушного охлаждения, различные
комбинации которых используют в конструкциях авиационных
ГТД:
1) радиальный обдув диска (рис. 10.12, а) —воздух подводит-
ся к центральной части диска, прогоняется вдоль боковой поверх-
ности и у периферии через уплотнение осевого зазора просачи-
вается в проточную часть. Обдув может быть как односторонний,
так и двухсторонний. При обдуве с двух сторон поле температур
260
Рис. 10.12. Схемы охлаждения дисков турбин:
а—радиальный обдув диска; б—струйный обдув диска: в—продувкой воздуха сквозь мон-
тажные зазоры хвостовиков и под полками лопаток; г—комбинированное охлаждение
(струйный и радиальный обдув); д—радиальный обдув под вращающимся дефлектором
по толщине диска получается более равномерным. Достоинства
этого способа — простота конструкции, надежность работы и хоро-
шая вентиляция всей полости между диском и корпусом. Недостат-
ки: требует больших, чем при других способах, расходов охлажда-
ющего воздуха и ему присущи невысокие величины коэффициен-
тов теплоотдачи у периферийной, наиболее нагретой части диска;
2) струйный обДув диска (см. рис. 10.12,6). Отбираемый от
компрессора воздух подается к поверхности диска в виде отдель-
ных струй через большое число сопел, обычно вблизи периферий-
ной его части, и затем, также как в первом случае, сбрасывается
в проточную часть. Основное достоинство этого метода — высокие
значения коэффициентов теплоотдачи в зоне удара струи о поверх-
ность диска и интенсивный отвод тепла в наиболее нагретой зоне.
Последнее способствует некоторому снижению градиентов темпе-
ратур по радиусу диска. Недостатки: при отдельных струях и недо-
статочном уплотнении осевого зазора возможно проникновение го-
рячего газа в полость охлаждения; при большом числе струй или
кольцевой струе ухудшается вентиляция полости под струей, что
ухудшает охлаждение диска у ступицы;
3) продувка воздуха через монтажные зазоры хвостовиков ло-
паток (см. рис. 10. 12, в) или под полками лопаток с удлиненной
ножкой. Имевший широкое распространение в ГТД способ охлаж-
дения дисков радиальным обдувом воздухом, подаваемым в полость
между диском и вращающимся вместе с ним покрывным дефлекто-
ром (см. рис. 10. 12, д), существенно утяжеляет ротор. Детальные
исследования КАИ [3] показали, что наиболее эффективным яв-
ляется комбинированное охлаждение полотна диска, включающее
следующие элементы: (см. рис. 10.12,г) обдув струями, натекаю-
щими нормально к поверхности диска (в относительном движении)
1 его периферии; радиальный обдув полости, расположенной ниже
. адиуса струйного обдува; надежное уплотнение осевого зазора,
еспечивающее подачу основной массы воздуха под полки лопа-
261
ток; принудительная вентиляция полости с тыльной стороны диска.
Этот способ наиболее экономичен и обеспечивает пониженную раз-
ность температур по радиусу и по толщине диска.
§ 10.8. ПРИБЛИЖЕННЫЙ РАСЧЕТ РАСПРЕДЕЛЕНИЯ
ТЕМПЕРАТУР ПО РАДИУСУ ДИСКА
В УСТАНОВИВШИХСЯ УСЛОВИЯХ
Из уравнения теплового баланса q\— q2— ?охлл—7охлп=0
(рис. 10. 13) получается [6] дифференциальное уравнение распре-
деления температур' Т по радиусу г диска переменной толщины у,
охлаждаемого с обеих сторон:
—+(—+— —) —-^-(Г-Гохл)=0.	(10.71)
dr* ' \ г 1 * .« dr) dr yh '
Здесь, в случае несимметричного охлаждения левой (Л) и пра-
•> /Г7\	®Л ”1" ®П т, Т*	”1*
вой (П) сторон диска: аохл   - и /Охл =-----
2	«л + ап
— осредненные значения коэффициента теплоотдачи и температуры
охладителя.
Решение уравнения (10.71) с учетом изменения всех парамет-
ров по радиусу (у, А, аохл> Тохл ) оказывается весьма громоздким,
а упрощения [6] могут вызвать существенное искажение резуль-
татов. Ниже излагается простой, и в тоже время обеспечивающий
необходимую точность метод решения с, помощью ЭВМ рассмат-
риваемой задачи *. Метод базируется на условном расчленении дис-
ка произвольного профиля (вместе с ободом) на п — участков-ко-
лец постоянной толщины y=const (см. рис. 10.13) так, чтобы в
пределах каждого из таких колец можно было принять постоян-
ными: Л=const; а0Хл=const; Г0Хл == const.
Введем новые переменные: 6 = 10~3(Т—f=r!r06 н обо-
значим m — r0o у , где гОб — периферийный радиус обода
диска. Тогда вместо (10.71) получаем, например, для i-ro участка
(10.72)
dr? * rt dn
Это модифицированное уравнение Эйлера — Бесселя имеет ре*
шение в виде
= ЛЛ (яг,Г/)+BtK0	(10.73)
где lo(miri), Ко(ггцъ) —функции Бесселя первого и второго роДа
нулевого порядка по мнимому аргументу; Д{, В, — произвольные
постоянные, которые находят из граничных условий. При числе уча*
стков п число произвольных постоянных At и Bi будет 2п. Для их
1 Впервые этот метод был предложен Кноршильдом еще в 1940 г., но ввпдУ
его громоздкости при ручном счете, он не пблучил распространения.
262
Рис 10.13. Схема к расчету температур
по радиусу диска произвольного про-
филя
отыскания имеется 2п.уравнений,
вытекающих из 1раничных усло-
вий.
1. На внутреннем радиусе дис-
ка (г=го) обычно известна тем-
пература центра Гд= 10-% и тог-
да с помощью (10.73) получаем
Aj/o (mir о) ~Ь ВДо (wxr о)=®ц»
[0ц=1О-з(Гц-7’^,.1а)]. (10.74)
Поскольку при Г(г*0, Ko(^iro)-»-
->оо, то без существенной погреш-
ности можно принимать Bt=0 и
д __	9“_	.
1 /оОих'о) •
2. На внешнем радиусе обода,
при г=1, из предварительных
расчетов известен тепловой поток
Qoe (может быть задана также
Ь+1
&ОХЛП
т*
1 о хял
n
n-1
НННН, П1)
 >a
^охл.л
гохлл
Чохл.п
41
Чохл.л
ь
/	Уг>^2
(9 бала) *-
t?
JI
e
температура обода 70б) и из уравнения (10.73) получаем по закону
Фурье .
2лу„Мгя [ЛЛ (тп) - ВпК\ (/»„)] -	0.	(10.75)

2
7
3. Еще 2(п—1) уравнений получаются из согласования реше-
ний на границах смежных участков, где при r/+i=n должно со-
блюдаться равенство температур Ti+i=Ti и равенство радиальных
тепловых потоков Qi+i=Q<. Из (10.73) получаем
\AI0(mr)-\-BKz(tnr)~\-T охл];— [A/q (л1г)-|-В/Со(л1г)-}-7'охл]/4.1=0
(10.76)
и (укт\ [А/1 (лгг)—ВК\	[А/1 (mr)—BKi (лгг)],+1 =0,
(10.77)
где i — последовательно принимает значения от 1 до (п— 1); Ц,
Ai —функции Бесселя первого порядка, соответственно первого и
второго рода по мнимому аргументу; 7'оХЛ= 10-3Гох»-
После решения на ЭВМ системы уравнений (10.74) ... (10.77)
и определения произвольных постоянных А< и Bf распределение
температур 7\- по радиусу г< каждого из п участков находится по
Уравнению (1Q.73) последовательным переходом от первого к
'МУ кольцу. Практически эту задачу приходится решать в несколь-
ко приближений. Поскольку величины X,, вохл <, Т'охл/ зависят от
тУп°тЫХ темпеРатУР 7*<» т0 в начале расчета значениями темпера-
УР Ti приходится задаваться, например, на основе параболиче-
263
Рис. 10.14-. Схема и график результатов расчета температур Т по радиусу- диска
турбины осевой турбины ГТД. Заданные граничные условия:
°охл’ — -~тОха
ской зависимости Т1(г) =Тц(г0) +0,Зг?. По температурам первого
приближения Т< i уточняются граничные условия аохл п, Гохлн и
величины kii и расчет повторяется во втором приближении. Двух-
трех приближений оказывается вполне достаточно. На рис. 10.14
показаны результаты расчета температур в диске с комбинирован-
ным охлаждением, описанным методом: струйный и радиальный об-
дув полотна с левой (Л) стороны, принудительная вентиляция поло-
сти с правой (П) стороны плюс продувка воздуха под полками ло-1
паток с удлиненными ножками.
§ 10.9. ДЕТАЛЬНЫЙ РАСЧЕТ НЕСТАЦИОНАРНЫХ
И СТАЦИОНАРНЫХ ТЕМПЕРАТУР В ДИСКЕ ТУРБИНЫ
Диски турбин, имея достаточно большую массу, обладают зна
чительной тепловой инерцией. С повышением, температуры газа пе
ред турбиной и все более жесткими требованиями ко времени пере
хода с одного режима работы двигателя на другой (пуёк, холосто»
ход, крейсерский и максимальный режимы и т. п.) градиенты тем’
пературы в дисках и ободе на переходных режимах (в нестацио
парных условиях) становятся весьма большими. Вызываемые-этими
градиентами температурные напряжения при многократном цикли-
ческом повторении могут явиться причиной усталостных поломок
дисков. Поэтому, наряду с расчетом стационарных температур, не-
обходимо располагать информацией о температурных полях в дис-
ках в неустановившихся условиях.
264
Рис. 10.15. Схема разбивки сечения
диска на элементарные участки при
численном расчете температур:
А—выделяемый сектор диска; £5—диск ра-
диальной турбины; В—(диск осевой турби-
ны
Подробный инженерный
расчет температур диска мож-
но выполнить методами элект-
роаналогии [22] или численным
методом1 аналогично тому, как
это делалось при расчете не-
стационарных температур в се-'
чении охлаждаемых лопаток
(см. § 10.6).
В полярной системе коорди-
нат (г — радиус; <p, z — угло-
вая и осевая координаты) тем-
пературное поле в тела.х с осе-
вой симметрией ^~=О описывается уравнением нестационарной
теплопроводности [13]:
в
Л 8 А
L
со-----
* дт
(10.78)
Для тел сложной формы в меридиональном сечении, каковыми
являются диски осевых и радиальных турбин, аналитического ре-
шения уравнения (10. 78) пока не имеется. Для отыскания числен-
ных значений температур Г(г, z, т) при переменных по координа-
там и времени граничных условиях и с учетом зависимости A=X(T)
наиболее эффективным оказывается конечно-разностный метод
элементарных тепловых балансов, детально рассмотренный в
§ 10. 6.
Для составления расчетных уравнений из диска мысленно вы-
резается сектор с углом: Дф=1 рад (рис. 10.15, поз. А). Диамет-
ральное сечение тела диска (до оси) аппроксимируется прямо-
угольной (в .частном случае квадратной) сеткой (см, рис. 10.15,
поз. Б и В).
Для каждой из узловых точек, подобно тому, как это делалось
при расчете температур в сечении охлаждаемых лопаток (см.
§ 10. 6), составляются уравнения теплового баланса. По форме эти
уравнения как для внутренних, так и для граничных узловых Точек
в точности совпадают с уравнениями (10.66), (10.68), т. е. имеют
вид:
1 Разработка метода выполнена совместно с В. В. Жуйковым. Им же сос-
тавлена Программа для расчетов на ЭЦВМ М-222.
265
Рис. 10.16. Схемы типичных узловых точек при разбивке сечения диска на эле-
ментарные участки
для любой i-й внутренней узловой точки (т=4)
(10-га’
7=1
для i-й граничной точки (0<т^2)
-Д<,(10.80)
7=1	1 J
Фактическое отличие уравнений (10.79) и (10.80) от уравнений
(10.66) и (10.68) состоит в том, что размер элементарного °бъ®м«
чика в окружном направлении не остается постоянным для любой
узловой точки, а является функцией радиуса, т. е. йг=6г, а 6?
s=f(r). Это накладывает свой отпечаток на вычисление величин-
263
элементарных объемов ДУ<; площадей сечений и поверхностей
в характерных узловых точках. Набор узловых точек, с помо-
щью которых можно с достаточной для практических целей точно-
стью аппроксимировать сечение дисков любой сложной конфигура-
ции, приведен на рис. 10. 16. Формулы для расчета величин ДУ<,
и Д/f в типичных узловых точках сведены в табл. 10.1.
Примечание. Величина у в табл. 10.1 принимает значения: у=1 — для
граничных узлов, помеченных на рис. 10.16 знаком (+); у=—1—для узлов,
помеченных знаком (—).
Условие устойчивости решения конечно-разностных уравнений
(10. 79) ... (10. 80) можно привести к виду
(10.81)
4Хщах
где по-прежнему Лтах=Хо+6Гтах; Т’тах — максимальная темпе-
ратура в расчетном сечении диска в данный момент времени; 6 —
наименьший размер сетки (бг или 62).
Для произведения расчетов в КАИ разработана программа для
ЭЦВМ М-222. При подготовке исходных данных для расчета пред,
полагается: в дисках осевых турбомашин равномерное по окруж-
ности распределение граничных условий по периферийной поверх-
ности с некоторым условным коэффициентом теплоотдачи, учитыва-
ющим как фактическую теплоотдачу газа, так и теплопроводность
по металлу лопаток (ножек) [38]; в дисках радиальных турбин
лопатки, дискретно расположенный на боковых поверхностях дис-
ка, отсутствуют (отсечены), а их влияние учитывается симметрич-
ным по окружности на данном радиусе условным коэффициентом
теплоотдачи [38].
В заключение укажем, что описанный метод позволяет выпол-
нять решение при задании граничных условий III рода (аг-, Л*),
II рода (qi) или любых их комбинаций.
На рис. 10.17 для примера показаны рассчитанные описанным
методом градиенты температур в диске радиальной турбины од-
ного из натурных ГТД. Как видно (см. рис. 10. 17, а), подогрев ди-
ска осуществляется неодинаково. В области ступицы, где толщина
диска наибольшая, прогрев диска идет медленнее. При приближе-
нии к периферии прогрев диска осуществляется более интенсивно.
Если в стационарных рабочих условиях (т>300 с) разность темпе-
ратур между периферией и центром диска составляет 240 К, то в
процессе выхода на режим через 40 с после запуска она достигает
435 К; через 60 с — 475 К; через 120 с — 385 К. Существенно изме-
няется по времени разность температур ДТ=ГП—-Тя и по толщине
Диска (см. рис. 10.17, б). Максимальная разность температур меж-
ду газовой и воздушной сторонами диска на фиксированном радиу-
се равняется 161 К и достигается через т=37 с после пуска. На
стационарном режиме (т>300 с) на этом же радиусе значение ДГ
снижается до 126 К.
Основные меры борьбы с большими ДГ в дисках ГТД — это уве-
личение времени перехода с режима на режим, использование для
267
Таблица lo.i
Тип узла	Объем элемента 4 Г,	Площадь поверхности теплообмена с окружающей средой Л/1	Площадь с нормального вому потоку по оси г	ечения к тепло- **l-k по оси z
а	Г/82		82 M+Y-y	гг8
б	Г/»2	J3 2 + Y 12	Ъг[ -/2	82 M+Yy	П8
в	П»2	63 —-—4-Y	 2	8	8rZ	82 n8 + Y-2"	—
г	Г/62		—•	г/8
д'	Зг/82	583 8 +Y 48	м(1+П)+,!^	.	82 M + Yy	—
е	Зг/52	83 8 +Y24 t	* (1+Г2)+,нй^2)	—	08
	5гг82	583 8 +Y 48		82 n» + YT	О»
3	5r/82	83 8 ~Y24	2	О	62 г/8 + ут	О»
и	Л82	83 4 +Y12	8/2^гг + у-j-j	82 П-8 4-y —	
к	r,82 4		—	о»
л	Зг/82	83 4 +Y 16	82 П» — Y V О	82 П8+ут	Г/8
268
у
Рис. 10.17. Графики распределения нестационарных температур по радиусу и
толщине диска радиально-осевой турбины
дисков'материалов с большим коэффициентом теплопроводности,
организация рационального охлаждения (более интенсивное охлаж-
дение периферийной части диска), наконец, изоляция диска от. про-
точной части продувкой воздуха под полками лопаток со специаль-
но выполненной удлиненной ножкой (см. рис. 20.1).
В турбинах кратковременного действия (ТНА ЖРД, турбостар-
теры и др.), где время работы исчисляется от нескольких десятков
секунд до нескольких минут, нестационарный режим является ос-
новным тепловым режимом конструкции. В таких турбинах тепло-
вая инерция дисков может быть использована полезно. Отбирая
тепло от лопаток и аккумулируя его, диск турбины в течение не-
которого времени замедляет прогрев лопаток и тем самым позво-
ляет несколько увеличить рабочую температуру газа или обороты
турбины.
Часть вторая
КОНСТРУКЦИЯ ТУРБИН И ИХ ДЕТАЛЕН.
РАСЧЕТЫ НА ПРОЧНОСТЬ
Глава XI
КОНСТРУКЦИЯ ДЕТАЛЕЙ ПРОТОЧНОЙ ЧАСТИ ТУРБИН
§ 11.1. СОПЛОВЫЕ АППАРАТЫ И КОРПУСЫ ТУРБИН
Сопловые аппараты турбин ГТД представляют собой ряд равно-
мерно 1 расположенных по окружности сопловых лопаток, наруж-
ного и внутреннего колец. Выходная кромка лопаток направлена
по радиусу или под небольшим углом к нему (см. § 13.7). Профиль
поперечного сечения сопловых лопаток выполняется с учетом тре-
бований, о которых сказано в гл. IV.
При изготовлении лопаток допускается отклонение от теорети-
ческого профиля сечения до ±0,2 мм. Выходную кромку выполня-
ют более тщательно, с точностью до ±0,05 мм по толщине, так как
с утолщением выходной кромки ухудшается к. п. д. турбины и уве-
личиваются вибрационные напряжения в рабочих лопатках (см. гл.
XIII). При уменьшении же толщины выходной кромки возрастает
опасность ее обгорания.
При запуске и остановке двигателя температура основной части
сплошной лопатки и ее кромок изменяется с разной скоростью, что
приводит к значительным, переменным по знаку, термическим на-
пряжениям и в итоге к образованию трещин на кромках. Чтобы
избежать этого, часто лопатки выполняют полыми с примерно по-
стоянной толщиной стенок по контуру (см. рис. 20.2).
Профильную часть лопатки обрабатывают по классу шерохова-
тости V 7... 9. Высокий класс шероховатости затрудняет газовую
коррозию лопаток и образование термоусталостных трещин, т. е.
увеличивает надежность и срок службы лопаток.
По высоте лопатки профиль иногда выполняют неизменным.
Переменный по радиусу угол выхода потока получают поворотом
сечения вокруг выходной или входной кромки. Ширину лопатки
пли ее хорду выбирают в основном по прочностным или конструк-
тивным соображениям (см. так же § 4.9). По конструкции сопло-
вые аппараты разделяются на разъемные и неразъемные. Каждая
из этих конструкций* может быть выполнена с охлаждаемыми и не-
охлаждаемыми лопатками. В любой конструкции необходимо обес-
печивать возможность свободных температурных деформаций соп-
лового венца, особенно — возможность радиального удлинения
лопаток.
1 В некоторых конструкциях турбин лопатки располагают неравномерно п0
окружности (см. § 13.7).
270
Рис. 11.1. Сопловой аппарат I ступени турбины двухвального ТРДД:
/ и 5—выступы (центрирующие элементы наружной полочки); 2 и 6—штифты; 5—лента: 4 и
12—внешнее и внутреннее кольца; 7—сегмент; S—дефлектор; 9—лопатка; 10 и 15—внутренняя
и наружная полочки; 11—буртик; /3—компенсатор; 14—выштамповки
В турбинах современных газотурбинных двигателей, как прави-
ло, применяют разъемные конструкции сопловых аппаратов. Осо-
бенно это относится к первым ступеням турбин, сопловые лопатки
которых имеют наиболее высокую температуру. Температура от-
дельных (неохлаждаемых) лопаток может превышать среднемассо-
вую температуру газа перед турбиной вследствие неравномерности
температурного поля по окружности. Разъемная конструкция соп-
лового аппарата позволяет сравнительно легко заменять одну или
несколько дефектных лопаток. В неразъемных конструкциях — ли-
тых или сварных — такая замена практически исключается. Кроме
того, в процессе длительной эксплуатации в сварных узлах могут
появиться трещины. Преимущества неразъемных сопловых аппара-
тов заключаются в'болыпей жесткости, сравнительной простоте и
технологичности конструкции.
В турбинах турбонасосных агрегатов ЖРД применяются от-
дельные сопла, сопловые сегменты и полностью облопаченные соп-
ловые аппараты.
Охлаждаемые лопатки имеет сопловой аппарат 1 ступени турбины двухваль-
ного ТРДД, показанный на рис. 11.1 (см. так же рис. 20.2).
' Литые пустотелые лоцатки 9 имеют наружные 15 и внутренние 10 полочки,
па наружной полочке имеются конический 1 и Г-образный 5 выступы, которы-
ми лопатки входят в соответствующие проточки во внешнем кольце 4. Усилие
газов на лопатку передается на внешнее кольцо призонными штифтами 2, а ьа
ниутреннее кольцо 12 буртиками 11, входящими в Проточки на кольце. Внут-
реннее кольцо имеет тонкостенный изогнутый элемент, необходимый для ком-
271
\
Рис. 11.2. Сопло турбины ТНА:
1—винт; 2—литой корпус; 3—сопло; 4—про-кладка
пенсации неодинаковых температурных расшире-
ний кольца и полок лопаток, — компенсатор 13,
Свободное термическое расширение лопаток в
радиальном направлении обеспечивается зазором
а, в осевом — зазором б, в окружном — зазором
между полками соседних лопаток. В наружном
кольце соплового аппарата радиальными штифта*
ми 6—фиксируются двенадцать кольцевых сегмен-
тон 7, образующих трактовое кольцо, которое ог-
раничивает проточную часть над ipa-бочими лопат-
ками Свободное расширение сегментов в окруж-
ном направлении обеспечивается за счет зазор о-в
между ними, в осевом—за счет зазора в. Внутрь
лопатки вставляется и завальцовывается тонкое
стенный дефлектор 8. Охлаждающий -воздух пос-
тупает сначала внутрь дефлектора через отвер-
стия в наружном кольце и ленте 3, затем через
отверстия в передней кромке дефлектора в щеле-
вую полость между, дефлектором и лопаткой.
В црюточную часть воздух выходит через щелевые каналы вблизи выходной
кромки. Расчетный зазор между лопаткой и дефлектором обеспечивается сфери-
ческими выштамповками 14 в дефлекторе.
Примерами конструкции неохлаждаемых сопловых аппаратов могут служить
второй и последующие сопловые аппараты турбин, приведенных на рис. 20 1 i
20.2. Отдельное сопло турбины ЖРД показано на рис. 11.2.
Сопло 3 свободно вставляется (по ходовой посадке) в отверстие литого
корпуса 2. Для правильной установки сопла относительно ротора служит вит
1, который входит в продольный паз на сопле. Зазор между срезом сопла в
ротором регулируемся прокладкой 4. Для уменьшения теплоотдачи в корпус
сопло центрируется в нем по двум узким пояскам, часть поверхности которыз
сфрезерована (сечение А—А). Выходное сечение сопла квадратное. Расширяю*
щаяся часть имеет форму пирамиды, узкая часть которой постепенно переходи!
в круглое минимальное сечение.
Один из трех сопловых сегментов турбины показан на рис. 11.3. Сегмен‘1
отлит из серого чугуна и механически обработан.
Корпусы турбин ГТД ограничивают проточную часть турбиг
снаружи и являются составным элементом общей силовой схемы
двигателя. К корпусам крепятся выхлопные устройства и проме-
жуточные сопловые аппараты в многоступенчатых конструкциях
турбин. В случае расположения заднего подшипника за турбиной
через корпус турбины передаются также нагрузки от ротора. В не-
которых конструкциях корпус турбины используется для подвески
двигателя на самолете (см. рис. 20.3). Иногда корпус одноступен-
чатой турбины и наружное кольцо соплового аппарата выполня-
ются за одно целое.
Корпусы многоступенчатых турбин представляют собой цилинд-
рические, конические или ступенчатого профиля оболочки, имею-
щие, как правило, разъемы в плоскостях, перпендикулярных оси
турбины. В большинстве случаев наружные кольца сопловых
аппаратов являются составными частями корпусов многоступен-
чатых турбин. Для увеличения жесткости корпусов их выполняют
иногда с кольцевыми ребрами. Центровку отдельных частей кор-
пусов производят при помощи цилиндрических буртов или призоя-
272
Рис. 11.3. Сопловой сегмент ТНА
ными болтами. При большой разнице температурных деформаций
отдельных частей корпуса отверстия под болты выполняют эллип-
тическим# с расположенной радиально большой осью. Корпусы
турбин с большим расходом газа изготовляют сварными из листо-
вого материала. Точеные фланцы приваривают газовой или кон-
тактной сваркой. Соединение контактной сваркой хуже, так как
утяжеляется конструкция; кроме того, после длительной эксплуата-
ции появляются трещины в сварочном шве.
При эксплуатации ГТД наблюдается усадка корпусов турбин.
Это явление состоит в следующем. Внутренняя поверхность корпу-
са нагревается до 950 ... 1000 К, температура же наружной,поверх-
ности, соприкасающейся с холодным воздухом, на несколько сот
градусов ниже. Большие градиенты температуры в корпусе, и осо-
бенно во фланцах, вызывают значительные напряжения растяже-
ния на внешней поверхности и напряжения сжатия на внутренней
поверхности корпуса. Эти напряжения могут оказаться выше пре-
дела текучести сильно нагретого материала и вызвать в нем пла-
стические деформации. После выключения двигателя корпус осты-
вает, и его внутренний диаметр оказывается меньше первона-
чального.
Усадка фланцев сопровождается короблением корпуса, приводит
к возникновению больших натягов в местах центровки соединяе-
мых частей корпуса, что затрудняет его разборку, а также умень-
шает с течением времени радиальный зазор между корпусом и тор-
гами рабочих лопаток. Для уменьшения коробления фланцев и
273
предупреждения их усадки между отверстиями под крепежные
болты делают фрезеровки.
Более радикальным средством борьбы с усадкой и короблением
корпусов является охлаждение их внутренней поверхности возду-
хом, отбираемым из камеры, сгорания. Воздух, минуя жаровые
трубы, попадает в полость, образованную снаружи корпусом,
а изнутри кольцами сопловых аппаратов и трактовыми кольцами
или развитыми полочками сопловых лопаток. Менее эффективно,
но конструктивно проще внешнее охлаждение корпуса турбины.
В этом случае для охлаждения используется воздух, текущий во
втором контуре ТРДД (см. рис. 20. 2), или забортный воздух, по-
даваемый действием скоростного напора в полость между корпу-
сом и специальным наружным тонкостенным кожухом.
Охлаждение корпусов необходимо также для уменьшения ради-
альных зазоров между ними и рабочими лопатками. Эти зазоры
изменяются при переходе двигателя с одного режима на другой.
Так, например, при запуске двигателя тонкие стенки корпуса про-
греваются быстрее массивного ротора и радиальный зазор между
, лопатками и корпусом турбины увеличивается. При остановке дви-
гателя корпус омывается сравнительно холодным воздухом из
компрессора (который продолжает вращаться по инерции или бла-
годаря авторотации) и остывает быстрее, чем ротор. В этом слу-
чае радиальный зазор уменьшается и может произойти заклини-
вание двигателя. Чтобы этого не произошло, должен быть правиль-
но назначен монтажный («холодный») радиальный зазор.
Из схем изменения зазора в зависимости от режима работы тур-
бины с неохлаждаемым и охлаждаемым (пунктирные линии) кор-
пусами видно преимущество охлаждаемого (рис. 11.4). При мень-
шем зазоре на рабочих режимах к. п. д. турбин с охлаждаемыми
корпусами увеличивается. Существующие турбины ГТД имеют
монтажный радиальный зазор, равный 0,002 ... 0,003 внешнего диа-
метра ступени.
Рис. 11.4. Схема изменения радиального зазора в зависимости от режима ра-
боты турбины:
а—при холодном двигателе; б—при запуске, в—при рабочем режиме; г—при остановке Д^г(*
гателя
Рис. 11,5 Схемы вставок для уменьшения радиального зазЪра:
а—металлокерамические; б—сотовые
274
в некоторых конструкциях для уменьшения радиальных зазоров
применяют специальные металлокерамические вставки (рис.
11.5, а). Они состоят из двух слоев: наружного — опорного, обес-
печивающего необходимую прочность вставки, и внутреннего —
сравнительно мягкого, легко срабатываемого при задевании его ра-
бочими лопатками. При эксплуатации турбин наблюдаются случаи
•выкрашивания вставок. Преимущество в этом отношении имеют
.-сотовые вставки, соединяемые с корпусом высокотемпературной
пайкой (см. рис. 11.5,6).
§ 11.2. РАБОЧИЕ ЛОПАТКИ
•
Рабочая лопатка — одна из наиболее ответственных деталей га-
зовой турбины. Она работает в условиях высоких температур и
напряжений и должна отвечать требованиям прочности, газовой
динамики и технологии.
В общем случае в конструкции лопатки можно выделить сле-
дующие элементы: рабочую часть, или перо 1, хвостовик 2, верх-
нюю (бандажную) и нижнюю полочки 3 и 4, удлиненную ножку 5
(рис. 11.6). Охлаждаемые лопатки могут иметь дефлектбр (см.
рис. 9. 15).
Рабочая часть выполняется с постоянным или переменным про-
филем по высоте. Профили строятся для нескольких расчетных се-
чений; между ними обеспечивается плавный переход. При изготов-
лении лопаток допускается отклонение от теоретического профиля
не более 0,15 мм.
Центры тяжести расчетных сечений располагаются или на одном
радиусе, лежащем в плоскости симметрии хвостовика, или смеща-
ются от него. В первом случае центробежные силы вызывают толь-
ко растяжение лопатки, во втором — смещение рассчитывают та-
ким образом, чтобы момент, возникающий от центробежных сил,
был направлен против момента от газовых усилий и тем самым
разгружал лопатку от напряжений изгиба (см. § 12.4). Лопатки
изготовляют методом точного литья по выплавля-
емым моделям или фрезерованием предваритель-
но отштампованной заготовки. Направление воло-.
кон в штамповке должно быть продольным для
увеличения прочности лопаток. Окончательно перо
лопатки получают шлифованием, электрохимиче-
ской размерной обработкой и полированием абра-
зивной лентой до 7 ... 9-го, а в менее ответственных
турбинах — до 6-го класса шероховатости. Следы
от механической обработки (трещины, риски, цара-
пины) снижают усталостную прочность лопаток,
т. е. уменьшают срок ее службы.
Рис. 11.6. Рабочая лопатка турбины:
^Рабочая часть лопатки (перо); 2—хвостовик; 3—верхняя (бандаж-
мая) полочка: 4—нижняя полочка; 5—удлиненная ножка
7
275
Рис. И.Л Схемы различных типов
бандажных полок
Хорду рабочих лопаток,
как и сопловых, выбирают
главным образом по соображе-
G	о	в ниям прочности. Чтобы умень-
шить напряжения от центро-
бежных сил, площадь поперечного сечения лопатки уменьшают от
корня к периферии. Обычно fCp= (0,55 ... 0,6) /к, /п= (0,2 .. ,0,3)fHt
где fcp, /п, /к — площади среднего, периферийного и корневого се-
чений.
Периферийная часть пера лопаток в некоторых конструкциях
переходит в полочки, образующие в собранной турбине бандаж
(см. рис. 11.6, 11.10), наличие которого снижает потери на утечку
(ей. § 6.4), концевые потери и уменьшает опасность поломок ло-
паток от вибрации (см. § 13. 7).
Различная конфигурация бандажных полок показана на рис.
11.7. Наличие скошенных поверхностей, отмеченных стрелками, по-
зволяет при сборке создать натяг между полками и этим устранить
соударения и наклеп во время вибрации лопаток *. На поверхности
полок выполняют гребешки (см. рис. 11.6), образующие лабиринт-
ное уплотнение над рабочими лопатками. Бандажная полочка, рас-
положенная на максимальном радиусе лопаток, создает значитель-
ную центробежную силу, которая увеличивает напряжения в кор-
невом сечении пера на 20 ... 25%. Для уменьшения этой силы при-
меняют «экономные», полочки по типу в на рис. 11.7. Однако это
связано с некоторым уменьшением к. п. д. турбины.
У лопаток ГТД с полкой более толстые профили в периферий-
ных сечениях: f= (0,25 ... 0,35)fK.
В современных авиационных ГТД применяется исключительно
соединение лопаток с диском типа «елочки» (см. рис. 11.6, 20.1,
20.2) 1 2. Хвостовик лопатки п соответствующий паз в диске изобра-
жены на рис. 11. 8.
Шаг«зубьев s, угол клина <р, угол между рабочей и нерабочей
поверхностью зубьев у и угол между рабочей поверхностью зуба
1 В процессе эксплуатации
происходит износ контактных гра-
ней, уменьшение первоначального
натяга и даже появление зазора
между полками. Основная причи-
на этого явления — смещение по-
лок друг относительно друга на
переходных' режимах работы дви-
гателя.
2 На соединение этого типа
разработан ОСТ 1.10975—73.
Рис. 11.8. Схема геометрии
елочного соединения
276
Таблица 11.1
Sif-0,008, мм		Т±30'	₽±15'	Количес сво пар зубьев ¥
1,8; 2,0; 2,2; 2,4; 2,6; 2,8; 3,0; 3,2; 3,5	20°	65°	115°	2
1,8; 2,0; 2,2; 2,4; 2,6; 2,8; 3,0; 3,2; 3,5; 4,0; 4,5; 5,2; 6,0	30°	55°	105 е	От 2 до 5
		65°	115°	
	40 е	55°	105°	
	50°			
и средней линией т — т профиля гребенки р приведены в
табл. 11. 1.
В выполненных конструкциях размер Л= (0,46... 0,55)s, раз-
мер. Л1= (0,45... 0,5) h, радиус впадины г= (0,16... 0,2)з. Радиус
перехода первого зуба лопатки в ножку для уменьшения концент-
рации напряжений делается больше, чем остальных, и равным
1,0... 1,2 мм. Количество пар зубьев выбирается в основном по со-
ображениям прочности соединения. При большом числе сравни-
тельно узких лопаток в один паз устанавливают две лопатки, как
показано на рис. 18. 3 (вид Л).
При холодном состоянии двигателя между лопатками и диском
имеется зазор Д= (0,05... 0,06) s, который равен разности разме-
ров Kt в диске и на лопатке. Этот зазор обусловливает качку кон-
ца лопатки в тангенциальном направлении а^Д— ив осевом
L
направлении п2«0,6Д—. Здесь L — длина всей лопатки; q— чис-
ло пар зубьев; I — средняя длина зубьев (в направлении оси тур-
бины). Свободная индивидуальная посадка лопаток в диск устра-
няет возможность возникновения высоких температурных напря-
жений в ободе и лопатках (см. § 15.2) и позволяет легко Заменить
лопатки в случае необходимости.
Ухудшение теплоотвода от ло-
паток в диск при наличии зазоров
в соединении можно компенсиро-
вать продувкой охлаждающего
воздуха через эти зазоры (рис.
И.9, б).
Нижние полочки лопаток пре
филируют внутреннюю границу
Рис. 11.9. Схема осевой фиксации лопа-
ток с елочным замком:
7—КОЛЬЦО
277
Рис. 11.10. Рабочая лопатка турбины
ТНА с Т-образным хвостовиком
VS Остальное
газового тцакта турбины и за.
щищают обод диска от нагре-
ва газом. Между полочками в
сборе обеспечивается зазор для
их свободного температурного
расширения. Для облегчения
полок в них выполняют фрезе-
ровки (см. рис. 11.6, 20.2).
Для уменьшения температу-
ры зубьев елочного соединения
и обода диска применяют ло-
патки с удлиненной ножкой
(см. рис. 11.6, 20.1). Через по-
лости, образованные наружной
поверхностью диска и полками
хвостовиков лопаток, проходит
охлаждающий воздух.
Газовые усилия, действую-
щие на лопатку в осевом нап-
равлении, в несколько  раз
меньше силы трения, обуслов-
ленной центробежной силой. Поэтому для фиксации лопаток в осе-
вом направлении пользуются главным образом отгибными пластин-
ками (см. рис. 11.9, а и в). Используются для этой цели также де-
тали ротора, выполняющие другие функции. Так, например, на рис.
11.9, б перемещению лопатки в сторону лабиринта препятствует
кольцо 1, которое служит для подвода охлаждающего воздуха, про-
дуваемого через зазоры в замке.
В турбинах для привода насосов ЖРД литые лопатки, сегмен-
ты лопаток или даже целые венцы приваривают к диску. В неко-
торых случаях диски малых турбин отливают заодно с лопатками.
Такие соединения достаточно просты, улучшают охлаждение, ис-
пользуя теплоотвод в диск, и уменьшают разброс собственных ча-
стот колебаний лопаток данного диска. Однако в такой конструк-
ции уменьшается демпфирование колебаний лопаток (см. § 13.6).
Замена отдельных лопаток здесь затруднена (дефектную лопатку
вырезают и приваривают новую). Следует заметить, что даже при
сравнительно небольшом числе запусков турбин с такими колеса-
ми вследствие возникновения больших переменных по величине и
знаку температурных напряжений в ободе возможно возникнове-
ние радиальных трещин, вызванных термической усталостью ме-
талла.	, •
В турбинах ТНА кроме елочного распространено также Т-об-
разное соединение (рис. 11. 10). В турбинном диске протачивают
фасонную канавку, в которую, вставляют лопатки через специаль-
ный вырез в ободе. В этот вырез после установки всех лопаток
278
вставляют специальные детали (см. рис. 14.3, поз. J и 2). Толщи-
на хвостовика (по окружности диска) равна шагу лопаток на этом
диаметре. Прочность Т-образного хвостовика достаточна лишь для
коротких лопаток при не очень больших окружных скоростях. К то-
му же центробежная сила лопаток создает значительные напря-
жения изгиба в боковых частях обода диска (см. § 12.6). Приме-
ры конструкций охлаждаемых лопаток ГТД приведены в гл. IX.
§ 11.3. МАТЕРИАЛЫ, ПРИМЕНЯЕМЫЕ ДЛЯ СОПЛОВЫХ
АППАРАТОВ И РАБОЧИХ ЛОПАТОК
Сопловые и рабочие лопатки являются наиболее нагретыми
деталями. Рабочие лопатки при этом подвержены высоким напря-
жениям на разрыв и не столь значительным, но не менее опасным
I напряжениям на изгиб, переменным по величине и вызывающим
i усталость материала. На переходных режимах работы турбины в
лопатках возникают большие знакопеременные термические напря-
жения. .
При температуре выше 900 ... 1000 К существенно уменьшается
предел кратковременной прочности — <ув материалов, применяе-
мых для изготовления лопаток. Кроме того, при длительном
действии нагрузки в условиях высокой температуры металл
пластически деформируется при напряжениях даже меньших пре-
дела текучести <jT — это явление называется ползучестью. В ус-
ловиях ползучести металл разрушается при напряжении, меньшем,
чем предел кратковременной прочности при данной температуре,
так как с увеличением времени приложения нагрузки разрушаю-
щее напряжение падает. Отсюда следует, что при высоких темпе-
ратурах величины от и ов не могут служить критериями прочности.
Таковыми следует считать предел длительной прочности и предел
ползучести.
Предел длительной прочности о* —это напряжение,
которое при данной температуре Т вызывает разрушение металла
через определенный промежуток времени т.
Предел ползучести *<з,г/т —это напряжение, которое при
данной температуре Т за время т вызывает определенную пласти-
: ческую деформацию е (в процентах). Таким образом, обозначение
, предела длительной прочности, например <Jioo°=210 МН/м2 озна-
чает, что при температуре 1000 К и нагрузке 210 МН/м2 материал
разрушается через 100 ч.
Обозначение предела ползучести, например 4,2/100= 140 МН/м2
означает, что при температуре 1000 К и нагрузке 140 МН/м2 через
100 ч образец из данного материала удлинится на 0,2% от своих
первоначальных размеров. Под деформацией может пониматься
или общая (упругая плюс пластическая) деформация, или только
остаточная пластическая деформация. В справочниках это особо
оговаривается. Часто верхние индексы в обозначениях пределов
279
Рис. 11.11. Диаграмма ползучести
длительной прочности и ползучести опус-
кают, а соответствующую температуру
указывают отдельно.
На рис. 11.11 представлены кривые
пол-з у чести, показывающие изменение
относительней деформации е образца в
функции времени т при постоянных нап-
ряжениях ст и одинаковой температуре.
Каждая кривая соответствует постоян-
ным напряжениям, причем О1<ст2<стз<;
<СТ4<СТб.
Начальную упругую деформацию, которую образец получает в
начале нагружения (при т=0), обозначим через во, пластическую
деформацию, вызванную ползучестью, — через вп. Очевидно, что
е=во+вп=о!Е+еп.
Как видно из графика, процесс ползучести состоит из трех ста-
дий. В первой из них (ab) деформация быстро возрастает. Ско-
рость ползучести v=d&ldx уменьшается вследствие упрочнения
металла, вызванного наклепом при деформации. Это .стадия
неустановившейся ползуче.сти. Длительное действие вы-
сокой температуры уравновешивает эффект упрочнения, и с неко-
торого момента (точка Ь) уменьшение скорости деформации пре-
кращается.
Вторая стадия ползучести (6с) —стадия установившейся
ползучести — характеризуется приблизительно постоянной ско-
ростью ползучести; она сохраняется до тех пор, пока на испытуе-
мом образце не появится шейка. В третьей стадии (cd) скорость де-
формации непрерывно возрастает до тех пор, пока не наступит
разрушение образца (точка d). В этой стадии процесса напряже-
ние уже не является постоянным вследствие изменения попереч-
ного сечения образца за счет образования шейки или в связи с
развитием трещин в металле. Точка d соответствует пределу дли-
тельной прочности.
Третья стадия может отсутствовать: .разрушение происходит в
точке Ci (кривая /) и сопровождается «хрупким» изломом в про-
тивоположность «вязкому» разрушению с образованием шейки.
При достаточно больших напряжениях может отсутствовать вторая
стадия (кривая 5).
На рис. 11. 12 показаны кривые ползучести сплавов на никеле-
вой основе ЭИ437Б и ЖС6-К, откуда видно, что с увеличением на-
пряжения или температуры деформация увеличивается. При по-
мощи кривых ползучести можно определить пределы ползучести.
Так, например, точка а характеризует предел ползучести «02/100=
=300 МН/м2.
Деформацию ползучести на первых двух стадиях часто аппро-
ксимируют зависимостью
в„=2(7’, т)«{П	(Ц.1)
280
а—сплав ЭИ437Б;
Рис. 11.12. Диаграмма ползучести:
Г=923 К:-------7М023 К; б—сплав JKC6-K: Т=1073 К:
Т=1173 К
где Й(Т, т) —некоторая функция температуры и времени, харак-
терная для данного материала; п — коэффициент, зависящий от
температуры. Значения Йип могут быть найдены соответствую-
щей обработкой экспериментальных кривых ползучести.
Связь между пределом длительной прочности о» и временем до
разрушения тр удовлетворительно описывает уравнение
•	Ч;=А<т,	Д11.2)
где А и т — постоянные для данного материала и температуры ко-
эффициенты.
Простой и удобной для графического представления является
зависимость оч от параметра жаропрочности P=T(C+lgTp), пред-
ложенного Ларсоном и Миллером. Приближенно можно считать,
что постоянная С=20.
На рис. 11.13 представлена указанная зависимость для некото-
рых материалов [20] *. Пунктиром показан порядок определения
предела длительной прочности.
Следует подчеркнуть, что наличие наклепа, образующегося при
фрезеровании или шлифовании абразивным кругом поверхности
лопаток, заметно снижает их длительную прочность. Поэтому пред-
почтительнее ленточное шлифование и электрохимическая оконча-
тельная обработка лопаток [17]. Таким образом, материал рабо-
чих лопаток должен быть жаропрочным, т. е. хорошо сопро-
тивляющимся ползучести и выдерживающим длительное воздейст-
вие высоких температур и нагрузок.
1 Отличие зпачег:’.'! г\, определяемых по рис. 11.13 и приведенных в при-
ложении, объясняется заметным разбросом результатов испытаний материалов
на длительную прочность.
281
Рис. 11.13. Номограмма для определения пределов длительной прочности мате*
риалов
Сопловые и рабочие лопатки омываются газами, имеющими вы-
сокую температуру и содержащими, кроме кислорода, такие агрес-
сивно действующие вещества, как пары воды, углекислый газ, сер-
нистый ангидрид и др. Это способствует развитию газовой корро-
зии, приводящей в конечном итоге к разрушению лопаток. Особен-
но опасно присутствие в газах ванадия и в меньшей степени —
серы.
Поэтому топливо газотурбинных двигателей должно очищаться
от вредных примесей, а материалы сопловых и рабочих лопаток
должны быть не только жаропрочными, но и жаростойкими,
т. е. устойчивыми против коррозии в атмосферных условиях и газо-
вой среде при рабочей температуре.
Кроме основных требований жаропрочности и жаростойкости,
материал лопаток газовых турбин должен обладать малой чувстви-
тельностью к концентрации напряжений, должен иметь высокие
значения предела усталости при рабочих температурах, противо-
282
стоять термической усталости, удовлетворительно обрабатываться,
по возможности меньше содержать дефицитных материалов и быть
дешевым. Материалы, применяемые для изготовления литых лопа-
ток, должны обладать хорошими литейными свойствами. Однако
удовлетворить всем требованиям одновременно невозможно.
Поэтому при выборе металла для лопаток в первую очередь ори-
ентируются на его жаропрочность и жаростойкость. Такие мате-
риалы можно разбить на две основные группы:
1) хромоникелевые стали аустенитного класса с добавкой воль-
фрама, молибдена, марганца, титана и других элементов;
2) сплавы на никелевой основе 1 с большим содержанием хрома
(10... 20%), а также вольфрама (до 7%), молибдена (до 8%),
алюминия (до 5%) и титана (до 3,5%). Эти сплавы также относят-
ся к аустенитному типу 2.
Из материалов первой группы можно указать, например, сталь
10Х11Н20ТЗР, в ряде случаев заменяющую сравнительно дорогой
никелевый сплав ХН77ТЮР, содержащий около 80% никеля.
Лопатки, работающие ’при высоких напряжениях и температу-
рах, изготавливают из деформируемых сплавов на никелевой ос-
нове ХН77ТЮР, ХН70ВМТЮ, ХН55ВМТКЮ, ЭП220, ЖС6-КП и
др. Первый из них рекомендуется применять при температуре ло-
паток до 1020 К, ЖС6-КП  наиболее жаропрочный — до 1150...
... 1250 К. Для литых сопловых и рабочих лопаток ГТД применя-
ют сплавы ЖСЗ, ЖСЗ-ДК, ЖС6-К и др. Сопловые лопатки также
штампуются из ХН77ТЮР, 20Х23Н18 и других материалов. Для
увеличения жаростойкости и ресурса лопаток их подвергают али-
тированию или хромоалитированию. Дефлекторы охлаждаемых
лопаток изготавливают из высокопластичных материалов. Внешнее
и внутреннее кольца и другие детали сопловых аппаратов изготав-
ливают из хромоникелевых сталей 20Х23Н18, 1Х18Н9Т (ЭЯ1Т),
малолегированной "стали ЭИ415, а в высокотемпературных двигате-
лях— из стали 10Х11Н20ТЗР и из сплава ХН77ТЮР.
Основные механические и физические свойства некоторых мате-
риалов для рабочих и сопловых лопаток приведены в приложе-
нии II.
Лопатки турбин ЖРД при температурах 1000 ... 1300 К йзготав-
ливают из тех же материалов, что и лопатки ГТД. При более низких
температурах применяют нержавеющие стали 1Х18Н9Т, 1Х18Н9ТЛ
(литейная), 2X13.
В качестве материала для соплового аппарата турбины ТНА
известной немецкой ракеты V-2 (см. рис. 11.3) был использсУван се-
рый чугун, а для рабочих лопаток — алюминиевый сплав типа АК4
(см. §20.2).
1 За границей применяются также сплавы на кобальтовой основе.
2 Аустенитные стали представляют собой однородные твердые растворы на
Железной основе с осрбым кристаллическим строением. Сходное строение имеют
и твердые растворы па никелевой и кобальтовой основе, которые поэтому также
Называются аустенитными.
283
Исключительно высокую длительную прочность имеют сплавы
на молибденовой, а также ниобиевой основе. Однако они в значи-
тельной степени подвержены газовой коррозии, против которой не
найдены еще надежные методы защиты при длительной эксплуа-
тации. • ;
Глава XII
РАСЧЕТ ЛОПАТОК НА ПРОЧНОСТЬ
§ 12.1.	ОБЩИЕ СВЕДЕНИЯ
Расчет лопаток на прочность заключается в определении действующих на-
пряжений и сравнении их с допустимыми или, точнее, в определении запасов
прочности и сравнении их с принятыми нормами.
Кроме того, в лопатках, работающих длительное время при температуре вы-
ше 500° С, оценивается допустимость пластических деформаций, возникающих
в результате ползучести металла. Обычно расчет производят для взлетного ре-
жима работы двигателя и для режима работы на расчетных высоте и скоро-
сти полета. При полете самолета зимой на малых высотах с максимальной ско-
ростью расход воздуха через двигатель и, следовательно, расход газа через тур-
бину достигают максимального значения, напряжения изгиба в лопатках также
будут максимальными. Поэтому прочность лопаток ГТД на этом режиме также
должна быть проверена.
В настоящей главе рассматривается статическая прочность лопаток, испы-
тывающих действие центробежных сил и сил давления газа. Эти нагрузки вы-
зывают в пере и хвостовике лопатки растяжение и изгиб. В хвостовике, кроме
того, возникают напряжения от смятия и среза. Напряжениями кручения,^кото-
рые также могут возникнуть в лопатке, обычно пренебрегают.
В закрученных лопатках под действием центробежных сил появляется де-
формация, уменьшающая угол закрутки. При этом в передней и задней кром-
ках возникают сжимающие, а в средней части профиля ,— растягивающие уси-
лия, которые-накладываются на равномерно распределенные по сечению растяги-
вающие напряжения от центробежных сил.
В охлаждаемых лопатках неравномерное температурное поле обуславливает
иногда значительные температурные напряжения. Эти напряжения возникают
также в сравнительно толстых неохлаждаемых лопатках при запуске или оста-
новке двигателя, когда температура кромок лопатки значительно отличается от
температуры ее средней части.
При запуске в кромках возникают сжимающие напряжения, при остановке—
растягивающие. Это вызывает термическую усталость материала лопаток. Кроме
того, высокие сжимающие напряжения в кромках сопловых лопаток могут при-
вести к местной потере устойчивости и короблению.
§ 12.2.	РАСЧЕТ ЛОПАТОК НА РАСТЯЖЕНИЕ
ЦЕНТРОБЕЖНЫМИ СИЛАМИ
Схема лопатки переменного профиля приведена на рис. 12. 1.
Обозначим площади сечений лопатки: /к — корневого; fCp —
среднего; fn—на периферии; f—на произвольном радиусе (гк+*)-
Центробежная сила бесконечно малого элемента лопатки на радиу-
се (гк+х)
Qi»2/ (rK -f-х) dx.
284
Рис. 12.1. Схема к расчету лопатки на растя-
жение
Центробежная сила лопатки, располо-
женной между радиусами (rK4-jc) и
(Гк + Л)>
h
(12.1)
X
Напряжение растяжения в сечении на
расстоянии х от места заделки лопатки в
диск
°р=~7‘•	(12.2)
Интеграл в выражении (12.1) определяется аналитическим,
графическим или численным способами.
Если лопатка имеет бандажную полочку, то формула (12.2)
должна быть записана так:
д 	+ РЦ.6
"	f
Здесь центробежная сила полочки Рц.в определяется выраже-
нием
^’ц.б==0(о21/Г6гб>
где q — плотность; со — угловая скорость вращения; Уб — объем
полочки; гс — радиус центра тяжести полочки.
Выше указывалось, что лопатки профилируются в нескольких
сечениях по высоте. Зная площади расчетных сечений, напряжения
в лопатке можно определить следующим образом.
Центробежная сила в i-м сечении (см. рис. 12.1) равна этой си-
ле в (i— 1)-м сечении, сложенной с центробежной силой участка
лопатки между сечениями. Таким образом,
Х1-\ + XI
2
или 0p/=ep((_1)2t=L_|__L 00)2(1-].
(12.3)
Отсчет сечений ведется от периферии к корню лопатки, а коорди-
ната х отсчитывается от корневого сечения. В нулевом, периферий-
ном сечении fo=fn’> <»о=ап=^н^ • Если бандаж (полочка) отсут-
/п
ствует, то оо=0.
В некоторых случаях изменение площади по высоте лопатки
можно с достаточной точностью аппроксимировать законом
А	_	/=Л[1-(1-/п)^].
ГДб fn = frJfw X=^x!h.
(12.4)
285
Коэффициент т может быть найден из уравнения (12.4), напи-
санного для среднего сечения: zn=3,3221g ——,
где 7ср=/ср//к-
Подставив уравнение (12.4) в (12.1) и (12.2), получим после
интегрирования выражение для безразмерного напряжения:
(I2-5)
где5)=й/й.
На рис. 12.2 эта зависимость изображена кривыми для различ-
ных т при /п=0,25 и 0=4,5. На этом же рисунке нанесена зави-
симость <Тр(«) для лопатки постоянного профиля при 0=4,5.
По кривым видно, что напряжения в корневом сечении (х=0)
убывают с уменьшением коэффициента т. Однако при т<0,8 мак-
симальное напряжение имеет место не в- корневом сечении, а не-
сколько выше.
В связи с изменением температуры и, следовательно, прочност-
ных характеристик материала по длине лопатки опасным сечением
часто является не корневое, а лежащее выше (см. § 12.9). С этой
точки зрения распределение напряжений при /п<0,8 оказывается
нежелательным. Для напряжений в корневом сечении (я=0) с уче-
том (12. 5) можно получить формулу
ар.к = 2е^-Ф,
(12.6)
где Ф=2ор,к/0 — коэффициент формы лопатки: На рис. 12.3 при-
ведена зависимость Ф от /п, 0 и т. Видно, что величина Ф зависит
-главным образом от отноше-
ния площадей /п- Для ло-»
’патки постоянного сечения
/п=1 и Ф=1. Таким обра-
зом, коэффициент формы Ф
есть отношение напряжений
(в корневом сечении) в ло-
патках с переменной и пос-
тоянной площадью по высо-
те. Для лопатки ГТД обыч-
но коэффициент Ф=0,5-
0,55.
Формулу (12.6) МОЖНО
преобразовать также к виду
Рис. 12 2. Кривые изменения без-
размерной величины напряжения
растяжения по двине лопатки
286
рис. 12.3. График зависимости ко-
эффициента формы лопатки Ф от
величин fn, 9 и т
epJt=2flQFn20, (12.7)
где F=tndh — площадь попе-
речного сечения проточной
части за ступенью турбины.
 В формулы (12.6) и
(12.7) следует подставлять
q в кг/м3, и в м/с, F в м2, и
в об/с. Тогда напряжения
0рк получим в Н/м2. В ло-
патках с бандажной полоч-
кой напряжения в корневом сечении больше в 1,1 ... 1,1} раза, при-
чем тем больше, чем меньше 0 и абсолютная длина лопатки.
Окружная скорость на среднем диаметре в современных турбинах
ГТД достигает 380 ... 400 м/с, а напряжения <Тр.к=3*108 Н/м2=
=300 МН/м2*. В некоторых турбинах и^500 м/с.
§ 12.3.	РАСЧЕТ ЛОПАТОК НА ИЗГИБ
Изгиб рабочей лопатки силами давления газов
При расчете лопатки на изгиб ее рассматривают как консоль-
ный стержень с жесткой заделкой в основании и распределенной
по длине нагрузкой. Лопатку с бандажной полочкой рассматривают
по такой же схеме. Это допущение идет в запас прочности *. Напра-
вим оси: х — вдоль радиуса; и — по направлению окружной ско-
рости; а — по оси турбины в направлении потока газа. Необходимо
учитывать, что силы давления газов неравномерно распределены
по длине лопатки и, кроме того, *в закрученной лопатке изменяют-
ся как моменты сопротивления, так и положение главных цент-
ральных осей инерции сечений. Поэтому для расчета разобьем ло-
патку несколькими сечениями на s участков (рис. 12.4) и пронуме-
руем их, начиная с вершины лопатки.
Используя данные расчета закрутки лопаток (см. § 5. 5), постро-
им вспомогательные графики изменения по высоте лопатки скоро-
стей Ciu, С2и, С1а, С2а, ДЭВЛвНИЙ ри р2, ПЛОТНОСТИ Q2 И ШЭГа ЛОПЭТОК
^2- Составляющие скоростей будем считать положительными, если
их направление совпадает с положительным направлением осей и
и а. Выпишем значения указанных величин в середине каждого
участка.
Расстояние от основания лопатки до середины i-ro участка обо-
значим Xfcp. Тогда расход гаЗа (кг/с) через данный участок, при-
* Напомним, что МН/м2» 10 кгс/см2 в системе МКГСС.
1 В процессе длительной эксплуатации двигателя часто образуется зазор
между полками соседних лопаток.
287
№
Рис. 12.4. Схема к расчету лопатки на изгиб силами давления газов
Рис. 12.5. Схема изгибающих моментов, действующих в сечении лопатки
(12.8)
холящийся на одну лопатку, G,= (£2062)^21 Ах{, где Ах,— длина
i-ro участка.
Составляющие сил давления (в Н), воздействующие на
i-й участок,
Pul = Ql (С1«“
Pai = Gi	+
Будем считать эти силы положительными, если их направление сов-
падает с положительным направлением осей и и а.
- Найдем изгибающие моменты сил давления газов относительно
осей и и а (рис. 12. 5) в нижнем сечении n-го участка (сечение
п — «на рис. 12.4). Определим их как сумму моментов от сил каж-
дого участка, лежащего выше этого сечения (Н • м):
Л/аг(хп)=-2^в/(х/ср-л-я);
м
п
(*л) =	(#/ ср	-*л)> ’
х‘=»1
(12.9)
где хп — расстояние от сечения п—п до основания лопатки в м.
Изгибающий момент считаем положительным тогда, когда он стре-
мится осуществить поворот по часовой стрелке, если смотреть от
положительного направления оси к началу координат. Поэтому в
первом уравнении (12.9) перед суммой поставлен знак минус.
Если в сечении п — п между осью максимального момента инер-
ции т) и осью а (см. рис. 12.5) имеется угол а, то изгибающие мо-
менты относительно главных центральных осей инерции можно oft*
288
(12.10)
ределить по формулам:
(х„)=Ma sin а—М„ cos а,
М^(хя)=cos а Ми sin а.
Положение главных центральных осей инерции можно найти по ме-
тоду, излагаемому в курсах сопротивления материалов. Однако при
практических расчетах ось максимальной жесткости £ проводят па-
раллельно хорде лопатки. В этом случае угол а равен углу уста-
новки профиля РуСТ.
Обозначим момент инерции сечения лопатки относительно оси g
через а относительно оси т| через /щах-
Тогда напряжение в произвольной точке профиля, вызванное
изгибом от сил давления газов,
Лф ^6
•^min ^max

(12.11)
В формулу (12. 11) координаты точки g и т] следует подставлять с
учетом их знака. Напряжения изгиба определяют для трех наибо-
лее удаленных от центральных осей характерных точек профиля
А, В u С, показанных на рис. 12. 5. Обычно наибольшие напряжения
изгиба имеют место на входной кромке профиля в точке А, коор-
динаты которой и т]а отрицательны. Так как момент Маг и, сле-
довательно, момент М [ отрицательны, то оба слагаемых в формуле
(12.11) для точки А получаются положительными.
Изгибающие моменты и соответствующие напряжения удобно
определять, записывая результаты в специальный бланк
(табл. 12.1).
В прикидочных расчетах определение напряжений от изгиба в
корневом сечении лопатки можно упростить. Обычно реактивность
в корневом сечении близка к нулю и, следовательно, угол установ-
ки руСТ близок к 90°. В этом случае М[ л;Маг; «А1иг. Кроме
того, М$ <Af£, a Jmax^>/min. Поэтому вторым членом в формуле
(12.11) можно пренебречь. Тогда

Лп1п
(12.12)
Окружное усилие Ри, приложенное к середине лопатки (прихо-
дящееся на одну лопатку),	где Мк=—--------крутящий
-2*2^	2ЛП
Момент турбины в Н • м; — внутренняя мощность турбины в Вт;
п — частота вращения об/с; d — средний диаметр в м.
Следовательно, изгибающий момент
Мта= ------------*L-.
2 2л6пг2
(12. 13)
10 1337
289
Таблица 12.1
К определению изгибающих моментов
	№ участка					
	1	2	3	4	5	6
X} ср >	о,1	0,086	0,064	0,042	0,020	0,004
Хд, М	0,097	0,075	0,053	0,031	0,009	0
Put, Н	5,9	26,4	30,4	33,0	28,6	7,8
Pat, Н	8,9	29,5	22,9	16,3	12,3	4,5
(*1ср — Хп), м	0,003	0,025	0,047	0,069	0,091	0,1
(Л2ер — хп), м	—	0,011	0,033	0,055	0,077	0,086
(хзср — ха), м	—	—	0,011	0,033	0,055	0,064
(Х4ср	Хд), М	—	—	—	0,011	0,033	0,042
(xgcp Хд), м	—	—	—	—	0,011	0,020
(Xficp — хп), м	—	—	—	—	—	0,004
^eiUiep — ха), Н-м	0,018	0,148	0,277	0,407	0,537	0,590
Лй(*2ср —*л). Н-м	—	0,290	0,871	1,451	2,032	' 2,271
^вз(хзер — хп), Н-м	—	—	0,334	1,003	1,672	1,944
ЛмСЧср — хп), Н-м	—	—	—	0,363	1,089	1,385
^и5(*5ер — xtt), Н-м	—	—	—	—	0,315	0,572
Риб(Хбср — хп), Н-м	—	, —	—	—	—	0,031
Мта(ха), Н-м	-0,018	-0,438	—1,482	—3,224	-5,645	-6,793
Лп(*1ср — Хп), И-“	0,027	0,223	0,419	0,615	0,810	0,890
Ра2(Х2с9— Хп), Н-М	—	0,324	0,974	1,622	2,271	2,538
Раз {Хзср — хп), Н-М	—	—	0,252	0,756	1,260	1,466
Ра4(х4ер — Х„), Н-М	«	—	—	0,179	0,538	0,685
• Раб^Хбпр — Ха), Н-М	—	—	—	—	0,135	0,246
Раб(Х(*р — ха), Н-м	—	—	—	—	—	0,018
<(хя),Н-м.	0,027	0,547	1,645	3,172	5,014	5,843
а°	36°30	45°30	54° ‘	62°48	73°	77’20
Л4£, Н-м	-0,033	-0,699	-2,177	-4,334	-6,873	—7,934
М^, Н-м	0,001	0,084	0,463	1,350	3,164	4,225
290
Изгиб рабочих лопаток центробежной силой
Центробежные силы могут вызвать не только растяжение, но и
изгиб лопатки. Это будет в том случае, если центры тяжести всех
сечений лопатки не лежат на одном радиусе.
Для определения изгибающих моментов от центробежных сил,
как и при расчете на изгиб от сил давления газов, разобьем ло-
патку на s участков сечениями, перпендикулярными радиусу OD,
проходящему через центр тяжести корневого сечения (рис. 12. 6) Ч
Пронумеруем участки, начиная с вершины лопатки, и обозна-
чим: fi ср и &Xi — площадь профиля в середине i-ro участка и его
длина; ср и bicp — координаты центра тяжести l-го участка, на-
зываемые выносами оси лопатки; Xi ср — расстояние от середины
l-го участка до основания лопатки.
Эти величины можно подсчитать как средние арифметические
значения соответствующих величин для верхнего и нижнего сече-
ний участка. Координаты центра тяжести сечения п — п обозначим
через ап и Ьп. Будем их считать положительными, если они направ-
лены в сторону положительных осей а и и. Начало координат рас-
положим в центре тяжести корневого сечения.
Составляющие центробежной силы f-го участка, действующие в
радиальном и окружном направлениях, подсчитаем по формулам:
Рix=	срДяДГк + Х^ ср) ; Piu==Q4>^fi	ср-
Последняя формула получена с учетом того, что (см. рис. 12. 6)
Piu=Pixtg б, Уде tg б=bi Ср/ (гк+Х{ ср).
Изгибающие моменты от -центробежных сил в нижнем сечении
n-го участка (см. рис. 12.6, сечение п — га), лежащем на расстоя-
нии хп от основания лопатки, найдем суммированием моментов
(с учетом знака координат а и Ь) от сил каждого участка, лежа-
щего выше этого сечения:
я	п
Ма (•£«) ~	$1 cP 2 с₽
i-1	Z=1
п
(л:л) = Pix {ci i Cp	лл).
/•=*1
(12.14)
По формулам (12. 10) и (12. 11) определим напряжения от из-
гиба центробежными силами о а в точках А, В и С (см. рис. 12. 5).
Для подсчета этих напряжений можно составить таблицу, анало-
гичную табл. 12. 1.
После определения напряжений, вызванных растяжением и из-
гибом лопатки газовыми и центробежными силами, можно найти
суммарные напряжения:
3.=0р_;-^+0р.	(12.15)
При этом необходимо учитывать знаки напряжений.
1 Если имеется бандажная полочка, то ее принимают за первый участок.
10*
291
На рис. 12.7 показано изменение по длине лопатки растягива-
ющих ор и суммарных напряжений в характерных точках сечения
лопатки ГТД (аА, Ов, ос)- В корневом сечении лопаток ГТД на-
пряжения изгиба (<тиР4-(Га ) обычно составляют примерно 30% от
напряжений растяжения <гр.к.
Учитывая (12.6) и (12.7), суммарные напряжения в корневом
сечении можно приближенно подсчитать по формулам
или
а2к«2,6р^-Ф.
”ак ~ 8,2qF/i2®.
(12.16)
(12.17)
,	§ 12.4. РАЗГРУЗКА ЛОПАТКИ ОТ ИЗГИБАЮЩИХ МОМЕНТОВ
Выбирая соответствующим образом координаты а и b центров
тяжести сечений, можно добиться нужной компенсации моментов
от сил давления газов моментами от центробежных сил и тем са-
мым уменьшить напряжения, вызванные изгибом лопатки (см. рис.
12.6). При этом надо иметь в виду, что полной разгрузки лопатки
от изгибающих моментов можно добиться лишь на одном каком-
либо режиме работы двигателя, так как моменты от газовых и цен-
тробежных сил по-разному изменяются с изменением режима.
Так, например, если изгибающие моменты скомпенсированы в
•каком-либо сечении (или по всей высоте) лопатки на стендовом ре-
жиме, то с подъемом на высоту при тех же оборотах двигателя
моменты от центробежных сил остаются прежними, а моменты от
>сил давления газов уменьшаются в связи с уменьшением плотно-
292
сти (рг) рабочих газов. По этой же причине при полете с большой
скоростью’ у земли и при тех же оборотах двигателя изгибающие
моменты от сил газов возрастают, и \ компенсация также нару-
шается.
В связи со сказанным, рекомендуется определять выносы оси
лопатки из условия частичной компенсации на режиме максималь-
ного расхода газа через турбину:
Л#(х)=-М£(л);
Л#(х)=-МЯ(*)-
Коэффициенты компенсации ki и Л2 следует принимать исходя из
обеспечения необходимого запаса прочности лопатки с учетом раз-
личных режимов работы двигателя (см. ниже, § 12.10). В выпол-
ненных двигателях значения ki и k2 находятся в пределах
0,3... 1,0.
Рассмотрим изгиб лопатки, у которой выносы оси изменяются
по линейным законам:
(12.18)
(12.19)
где по-прежнему а<Ср» 6«ср и х<ср— координаты центра тяжести
/-го сечения (см. рис. 12.6); ап и Ьп — координаты центра тяжести
периферийного сечения лопатки.
Координаты ,ап и Ьп найдем, применив условия компенсации
(12.18) к корневому сечению (х=0), в котором обычно напряже-
ния изгиба от сил давления газов .максимальны.
Подставляя выражения (12.19) в формулы (12.14) и исполь-
зуя соотношения (12.18), получим
. А2<(0)
Лп~ h>s ’
Pix Xi ср
i-l

ИР.5
6Я=—А—
*1<(0)
VI P<**<cp
с₽
i—l
При бесконечно большом
(12.20) принимают вид
числе участков лопатки
формулы
*2<(0)
w2z*к^ц.т^пр 4“ °2Q^ol
*l<(0)
a>2/* кХц,тС?пр
(12.20)
(12.21)
293
Здесь хц.т — расстояние от корневого сечения до центра тяже-
* ’
сти профильной части лопатки; Gnp и Jo= x2fdx — масса профиль-
ной части лопатки и момент инерции относительно корневого се-
чения.	'
Формулы для подсчета этих величин в случае изменения пло-
щади сечений лопатки по закону (12.4) приведены в § 12.5.
Определив значения ап и Ьп, по формулам (12.19)* находим ко-
ординаты центра тяжести i-ro участка лопатки. Затем, при помо-
щи выражений (12.14), определяем изгибающие моменты от цент-
робежных сил и соответствующие им напряжения изгиба в расчет-
ных сечениях по высоте лопатки.
Следует заметить, что при рассмотрении вопроса о компенса-
ции изгибающих моментов мы считали лопатку абсолютно жест-
кой. В действительности под действием сил давления газов лопат-
ка прогибается, что приводит к возникновению изгибающих
моментов от центробежных сил. Вти моменты обратны по знаку
изгибающим моментам от сил давления газов.
Указанная естественная разгрузка лопатки от изгибающих мо-
ментов проявляется в большей степени в высоконагруженных (на
растяжение) длинных лопатках последних ступеней турбин. Точный
учет эффекта естественной разгрузки приводит к сложным расче-
там, которые здесь не приводятся.
§ 12.5. ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ ПРОФИЛЯ,
МАССЫ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ,
ЕЕ ЦЕНТРА ТЯЖЕСТИ И МОМЕНТА ИНЕРЦИИ
Под элементами профиля лопатки мы понимаем здесь площадь, координаты
центра тяжести и моменты инерции профиля. Для определения этих элементов
профиль вычерчивается в увеличенном масштабе (лучше всего 10 : 1, для боль-
ших размеров профиля — 5:1).
Площадь профиля можно вычислить по формуле Симпсона, известной из
математики и приводимой в большинстве справочников, или приближенно, если
начертить профиль на миллиметровой бумаге.
Центр тяжести профиля можно определить аналитическими методами (на-
пример, по формуле Симпсона), но проще всего опытным путем. Для этого про-
филь вырезают из тонкого картона (ватмана) и подвешивают последовательно -в
нескольких точках на булавке. Из этих точек опускают отвес па тонкой нити
и на профиле проводят отвесные линии. Пересечение этих линий находится в
центре тяжести профиля S. Через точ-
ку S проводят главные центральные оси
инерции, за которые часто принимают
(как указано выше) ось параллельную
касательной к кромкам, и ось т), перпен-
дикулярную к ней.
Моменты инерции профиля. Наряду
с известными из механики аналитичес-
кими и графическими методами опреде-
ления момента инерции плоской фигуры,
можно рекомендовать следующий прос-
Рис. 12 8. Номограмма для определения
момента инерции профиля лопатки
294
*оЙ, хотя и приближенный метод, основанный дта применении специальной номо-
граммы. Принцип ее построения описан в работе [7]. Здесь приведем правила
пользования номограммой, образец который дан в приложении III. Номограмму на-
кладывают на профиль, вычерченный в масштабе т: 1, подобранном так, чтобы
весь профиль поместился в пределах номограммы (рис. 12.8). При этом цент-
ральная линия номограммы должна совпадать с осью, относительно которой
определяется момент инерции.
Момент инерции подсчитывают по формуле (мм4)
100
J = —	-4* 6SC2 Ч- 121с3 Ч- 24Sc4 + 60Zc5 + 1202с6),	(12. 22)
да
где 2С1» 3^2— сумма отрезков в мм, заключенных между контурными линия-
ми профиля на первом (на рис. 12.10 aa'4’55'4-cc'4-</rf,4-z/"rf",4-ee,4-jy/); Sc2 на
втором и S с3 на третьем участках номограммы и т. д.
Цифра 100 — масштаб данной номограммы. В других аналогичных номо-
граммах она может быть иной.	*
Масса профильной части лопатки может быть подсчитана по формуле
л
mnp = Q Г fdx, где интеграл определяется в общем случае численным или гра-
о I
фическим способом; р — плотность материала лопатки.
Если закон изменения площади по высоте лопатки подчиняется уравнению
(12.4), то
mnp=Q/KA(l--^V7-).	(12.23)
у /И т 1 /
Если лопатку разбить сечениями на участки (см. рис. 12.5), то, пользуясь
обозначениями § 12 2. массу лопатки можно определить суммированием масс
а
отдельных участков: тпр = Q 2 ЛсрД-*ь где s — число участков.
Z-1
Координаты центра тяжести профильной части лопатки с переменным про-
филем, показанные на рис. 12.6, можно подсчитать по формулам
•s
6 2 У/ср-Я/срА^/
Q У У/срЛ/ерА*/
Z-1
Лц.т --------------------
/Япр
5
9 2 /zcp^Zcp^Xz
JMiip
Обозначения здесь те же, что и в § 12.2. Если площадь изменяется по высоте
лопатки согласно уравнению (12.4), то координата
л
Хц.т --------=- 4 ---------------------- ( 1Z. ZD)
А	—	1	*
295
Момент инерции профильной части лопатки относительно корневого сечения
определяется по формуле Jq = х? //Срд-*/-Грсли плошадь профиля лопатки
изменяется по ее высоте согласно закону (12.4), то
А	_
Jo = \ X2fdx =	(Ц- - А) .	(12. 26>
J	\ о т + о /
о
§ 12 6. РАСЧЕТ НА ПРОЧНОСТЬ СОЕДИНЕНИЙ
ЛОПАТОК С ДИСКОМ
Замковые соединения лопаток являются одним из наиболее от-
ветственных элементов газовой турбины. Недостаточная прочность
их часто является причиной поломок и аварий турбин.
Однако точный расчет соединений оказывается затруднитель-
ным вследствие сложности конфигурации их элементов, многооб-
разия нагрузок и других факторов, влияющих на напряженное сос-
тояние соединения (различные физические и упругие свойства
материалов лопатки и диска, неодинаковые температуры, пласти-
ческие деформации, ползучесть и т. п.).
Ниже приводится упрощенная методика расчета двух типов,
соединений: Т-образного, применяемого в турбинах ЖРД, и елоч-
ного, преимущественно применяемого в современных ГТД.
Т-образный тип соединения (рис. 12.9). Введем следующие обо-
значения: />ц = Ркл + Рц.б — сумма центробежных сил профиль-
ной части лопатки и бандажной полочки (если таковая, имеется);
Рц.х — центробежная сила всего хвостовика (между сечениями
М—N и х—х); Рц.х — центробежная сила части хвостовика, ог-
раниченной линиями MN и АВ; Рц.х —.центробежная сила участ-
ка ABCD.
Наибольшее растягивающее напряжение возникает в сечении
А—В хвостовика:
Вц + В ц.х
(12.27)
где fi — площадь сечения А—В хвостовика.
Напряжения среза в сечениях А—D и В—С хвостовика
Тср----,	(12.28)
2/г
где f2 — площадь сечения А—D.
По площадкам abed и eghf возникают напряжения смятия, рав'
ные
	(12.29)
где t3 — площадь abed (при подсчете надо учесть действительную1
площадь прилегания хвостовика за вычетом фасок или галтелей)-
296
Рис. 12.9. Схема к расчету Т-образного сое-
динения
В ободе диска от центробежных сил
лопаток и самого обода возникают напря-
жения растяжения и изгиба. При расчете
напряжений, как показывает детальное
исследование, можно пренебречь кривиз-
ной обода и рассматривать его как пло-
скую балку.
Круговое сечение по х—х площадью
4лгг1 нагружено центробежной силой
всех лопаток с хвостовиками, т. е.
22(Рц+Рцх), и центробежной силой Рц.ов
части обода над сечением х—х.
Таким образом,
2
*2 ( Рц + Рц.х ) + ~Z~ Рц.об
Силу Рц.об внесли с коэффициентом 2/3, так как обод представляет
собой кольцо, и его центробежная сила вызывает не только ради-
альные напряжения, но и тангенциальные (см. § 15.1).
Каждая из двух сил Р, изгибающих обод, определяется выра-
жением
* р_______ (Рд + Рц.х) I 2 |р'
f'---------- ——.Л'ц.об,
Z	и |
где Рд.об —центробежная сила кольца BEFG, которая, как и в
предыдущем случае, вводится с коэффициентом 2/3.'
Изгибающий момент в сечении х—х М—Рт.
Момент сопротивления этого сечения' (кривизной обода прене-
брегаем)
3
На.пряжение изгиба <ya=M/W.
Суммарное напряжение в. сечении х—х
О—КТр + Оп-
Наконец, должно быть определено напряжение среза в сечении
обода F—G
•	~П~ (Рд + Рц.х) + “7“ Рц.ов
<е₽=—-----------—-------2-------.	(12.31)
Соединение елочного типа (рис. 12.10). Расчет ведем только на
центробежную силу всей лопатки Рц.л, которую будем считать дей-
ствующей по осн хвостовика:
1—0
297
NO
Рис, 12.10. Схема елочного хвос-
товика лопатки
где Рц,п и Рц.б — центробеж-
ные силы пера лопатки и
бандажной полочки; Рц ,• —
.центробежная сила i-ro уча-
стка хвостовика; п — число
зубьев с одной стороны хво-
стовика.
Условие равновесия
сил, действующих в на-
правлении оси хвостовика,
^ц.л — 2= 0(где (=1.........k, п) дает нам одно уравнение
i-i
для определения п неизвестных сил Rf. Следовательно, мы имеем
дело с (л—1) раз статически неопределимой системой. Раскрытие
неопределимости требует рассмотрения деформации зубьев, что
приводит к довольно сложным и громоздким расчетам.
Поэтому при расчете елочных соединений приближенно счита-
ют, что нагрузка, приходящаяся на единицу длины зуба, одинако-
•	р
ва для всех зубьев и равна --5, где Ц — длина Z-го зуба.
22 h
ial
Тогда сила Rk, действующая на Л-й зуб, пропорциональна его
ширине:
я
2 2 11
1-1
(12.32)
Усилие Gj, разрывающее'хвостовик в сечении В—В (см. рис.
12.10), определим по формуле
Oj=P«.n+P„.e + 2	(12.33)
i-0	i-0
где /?о=0.
Разрывающее напряжение в j-м сечении
=,
ailf
где ajlj' — площадь /-го сечения хвостовика.
Разрывающее напряжение в сечении А—А
__Р Ц.п + Рц.б + ^ц0
__Т,------------- »
(12.34)
(12.35'
298
Рис. 12.11. Схема усилий, действующих на зуб
елочного хвостовика
где Рцо — центробежная сила нулевого
участка хвостовика, лежащего выше се-
чения по первым впадинам (см. рис.
12.10). В действительности в сечении
Д—А кроме разрывающих напряжений
действуют напряжения, вызванные изги-
бающим моментом, равным алгебраиче-
ской сумме моментов от сил давления га-
за, обтекающего лопатку, и от центробеж-
ной силы лопатки, которая не проходит
через центр тяжести сечения. Эти допол-
нительные напряжения, которые на неко-
торых режимах могут составить 30% от
разрывающих напряжений (см. § 12.4), .
учитываются при подсчете запасов проч-
ности (см. формулу (12.57)].
Определим напряжения, возникающие в'зубе. Сила, действую-
щая нормально к рабочей поверхности зуба (рис. 12.11),
cos ₽
(12.36)
где (У=кр/2+ р—90° — угол давления.
Напряжения смятия на рабочей поверхности зуба найдем, учи-
тывая уравнения (12.32) и (12.36):
зсм=-^-=-------д - ,	(12.37)
2с cos р' 2 h
где с — ширина контакта зубьев (за вычетом радиусов и фасок).
Напряжение среза
% — AGcCos(p'—у/2) __ Рц.л costf' —?/2)	,12
**	Ь'1к	п	cos р'	' '	7
2Ь' 2 It
Изгибающий момент в основании зуба M=Nbf, где плечо f си-
лы Nk относительно середины основания
/=-----------------— sin (£—90°).
, 2cos(p —90°)	2	’
Момент сопротивления основания зуба
Учитывая полученные выражения, определим напряжения от из-
гиба в зубе:
а =	------ЗРцл г .. Г----*----Sin (р- 90е)] . (12.39)
Wk	* [cos(p — 90е)	J v 1
2^2 COS P' 2 U
Z-l
299
Рис. 12.12. Схема к расчету замкового
выступа диска
Формулы (12.37) .. .(12.39)
действительны для любого зу-
ба, что является следствием
принятого нами допущения о
распределении нагрузки меж-
ду зубьями.
Более строгие расчеты по-
казывают, что наиболее нагру-
женными (при Ц—const) яв-
ляются первая и последняя па-
ра зубьев *.
На распределение нагрузки между зубьями большое влияние
оказывает разность температур хвостовика лопатки и замкового
выступа диска, а также разница в величинах коэффициентов ли-
нейного расширения материалов лопатки — ал и диска — ад. Если,
например, хвостовик лопатки имеет более высокую температуру,
чем обод диска или ал>ад, то в рабочем состоянии шаг зубьев ло-
патки окажется больше, чем у диска. Это приведет к тому, что пер-
вая пара зубьев окажется еще более нагруженной.
Указанные особенности работы елочного соединения следует
иметь в виду при его конструировании и выборе материалов лопат-
ки и диска.
В зубьях выступа диска возникают такие же по величине нап-
ряжения, что и в зубьях лопатки, ввиду практически одинаковой их
геометрии.
Разрывающее усилие в /-м сечении по впадинам замкового выс
тупа диска (рис. 12.12) Q;=2 2^ + 2 где — центробе^г-
f-i i-i
ная сила Z-ro участка выступа.
Соответствующее напряжение на разрыв в j-м речении
(12.40)
где djl" — площадь /-го сечения. Напряжения на разрыв в сечении
В—В
qp= PM.±_gsA . . '	(12.41)
п
где ^ц.в=2	—центробежная сила выступа диска. В сечении
В—В, также как и в сечении А—А хвостовика лопатки, действует
изгибающий момент, который при реальном проектировании следу-
ет учитывать.
' 1 Здесь имеется аналогия с работой резьбового соединения. Надо заметить,,
что напряжения меняются также по длине каждого зуба.
300
§ 12.7.	РАСЧЕТ БАНДАЖНОЙ ПОЛОЧКИ
Точный расчет на изгиб бандажной полочки (рис. 12.13), пред-
ставляющей собой пластинку переменной толщины, три стороны
которой свободны, в четвертая, криволинейная, защемлена, весьма
затруднителен.
Приближенно напряжения от изгиба полки центробежной си-
лой найдем следующим образом. Проведем сечение А—В и найдем
центробежную силу Рц.п отсеченной части полки, приложенную в
ее центре тяжести (точке Е): P^i^qVabcdRe®2, где g — плотность
материала лопатки; Vabcd — объем отсеченной части полки; /?я —
радиус, соответствующий точке Е; а> — угловая скорость вращения
лопатки.
Тогда изгибающий момент в сечении А—В будет
МИ=А.Л	(12.42)
где h — расстояние ЕЕ от точки Е до сечения А—В.
Напряжение изгиба
(12.43)
где W — момент сопротивления полки изгибу в сечении А—В.
Аналогично определяются напряжения и в нескольких других
характерный сечениях полки, например, К—А4 и т. п.,
Если на полке имеются гребешки 1 лабиринтного уплотнения
(см. рис. 12.13, б), то их объем должен быть учтен при вычислении
Vabcd, а момент сопротивления W в формуле (12.43) должен соот-
ветствовать точке N (методы определения W в этом случае извест- .
ны из курса сопротивления материалов). Наличие гребешков замет-
но уменьшает напряжения изгиба в полке, поэтому в некоторых кон-
струкциях лопаток на полках имеются специальные гребешки, не
участвующие непосредственно в работе лабиринтного уплотнения
(они в этом случае играют роль ребер жесткости). Зазор между
такими гребешками и корпусом турбины дол-
жен быть достаточно большим (бблыпим, чем
в лабиринтном уплотнении), чтобы они не ис-
тирались в процессе эксплуатации двигателя.
§ 12.8.	ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИИ ЛОПАТКИ
С УЧЕТОМ. ПОЛЗУЧЕСТИ МЕТАЛЛА
Определение деформации лопатки необхо-
димо для подсчета радиального зазора, изме-
няющегося с переходом двигателя с одного ре-
жима на другой (см. § 11.1).
Деформация лопатки, т. е. изменение ее
длины, складывается из деформации растяже-
Рис. 12.13. Схема к расчету бандажной полки:
с—бандажная полка: б—сечение полки с гребешком лабиринтно-
го уплотнения; /—гребешок
301
ния |р, температурной деформации £т, а также пластической де-
формации |п, вызванной ползучестью металла.
Первые две составляющие в общем случае неравномерно нагре-
той лопатки определяются формулами
а	л
=	(12.44)
о	о
А	Л
$T=J	— J atdx,	(12.45)
где ep и :&r — соответствующие относительные деформации; Е — мо-
дуль упругости; t—TC9— Гя — разность температур: средней по се-
чению лопатки — Тср и нормальной (комнатной) — Тп.
Деформацию ползучести найдем, учитывая зависимость (11.1),
л
$n=j2(r,t)3»</x.	(12.46)
Полученные формулы значительно упрощаются, если принять
температуру лопатки постоянной, равной среднему ее значению:
А	А
$т=а/Л; $п=2(Т,т)^Мх.	(12.47)
о	о
Интегралы в формулах (12.44) ... (12.47) определяются чис-
ленным или графическим способом.
Общая деформация лопатки
Л=5Р+$г+еи.	(-12-48)
Для определения радиального зазора необходимо произвести
подсчет деформаций диска (см. § 15.5, 16.4, 16.6) и корпуса тур-
бины.
§ 12.9.	ПОНЯТИЕ О РАСЧЕТЕ НЕРАВНОМЕРНО
НАГРЕТЫХ ЛОПАТОК
Как указывалось в § 12.1 в неравномерно нагретой лопатке турбины (сопло-
вой и рабочей) возникают температурные напряжения. Эти напряжения тем
больше, чем больше при прочих равных условиях разница между максимальной
и минимальной температурой в сечении лопатки. Поэтому особо больших значе-
ний температурные напряжения могут достигать в охлаждаемых лопатках, а так-
же в неохлаждаемых при запуске и выключении двигателя (см. § 12.1). Расчеты
показывают, что в ряде случаев возникающие на этих режимах напряжения
могут превышать предел текучести материала. Напряжения в неравномерно на-
гретой лопатке, с учетом зависимости величин £ и а от температуры, опреде-
ляются по формуле, полученной И. А. Биргером и Н. Н. Малининым на осно-
вании гипотезы плоских сечений
4-Г f Р“ I-
М Edf J E-tfdf j E&df / '
/ j Eatdf j Ewtdf , \ E&tdf \
4“ с I i 4-1 ~~2	4- c	— ar ],
К J Edf J Elpdf J E?df /
(12. 49)
302
Рис. 12.14. Эпюры распределения темпера-
туры (а) и напряжений (б) и области плас-
тической деформации (а) в сопловой ло-
патке
Здесь Рц — центробежная сила в данном
сечении лопатки; ЛЦ и ЛЦ —суммарные из-
гибающие моменты от действия центробеж-
ной силы и газовых сил; Е и, а — модуль
упругости и коэффициент линейного расши-
рения в точке сечения с координатами £ и
г). Первая часть формулы .(Г2.49) определя-
ет напряжения, вызванные внешними сила-
ми, а вторая—температурные напряжения.
Оси 0g и От]—главные, центральные оси
термоупругой жесткости. Они выбираются
так, чтобы выполнялись следующие равен-
ства:
f£grf/=O; J.£i)rf/= 0;	=0.	,
7	/	/
(12. 50)
Начало координат 0 называется термоупругим центром сечения.
Положение термоупругого центра сечения 0 и осей 0g и От] находят по той
же методике, что и положение центра тяжести сечения и главных, центральных
осей инерции. Разница будет только в том, что в используемые при этом инте-
гралы по площади сечения входит модуль упругости Е, переменный по сечению.
Расчеты по формуле (12.49) получаются достаточно громоздкими и требуют при-
менения ЭВМ.
На рис. 12.14 для примера показано распределение температуры по сечению
сопловрй лопатки в момент запуска двигателя. Этому температурному полю
соответствуют напряжения, подсчитанные по формуле (12.49), которые представ-
лены на рис. 12.14, б. В части сечения эти напряжения (полученные в предпо-
ложении только упругих деформаций) превышают предел текучести материала,
из которого была изготовлена лопатка. Следовательно, в этом случае возникают
пластические деформации в области сечения, заштрихованной на рис. 12.14, в.
Наличие пластических деформаций приведет к перераспределению напряже-
ний по сечению лопатки. Действительные напряжения можно найти, например,
методом переменных параметров упругости, изложенным ниже в гл. XVI..
Как уже указывалось выше, при определенных условиях значительные зна-
копеременные пластические деформации приводят к термоусталостным явлениям
в лопатках турбин.
§ 12.10. КРИТЕРИИ И ЗАПАСЫ ПРОЧНОСТИ ЛОПАТОК
Заключительным этапом расчета лопаток на статическую проч-
ность является сравнение действующих в них напряжений с допус-
тимыми или определение соответствующих запасов прочности. Как
уже указывалось, критерием прочности материалов при высоких
температурах является предел длительной прочности оч. Таким об-
разом, запас статической прочности лопаток при высокой темпе-
ратуре .
(12.51)
Для лопаток, температура которых не превышает 550 ... 650 К,
когда еще не проявляется явление ползучести, критерием прочно-
сти следует считать предел прочности, соответствующий данной
температуре.
303
Рнс. 12.15. Кривые изменения запаса проч-
ности по длине лопатки
Интересно отметить следующее
обстоятельство. Если рабочая лопат-
ка охлаждается, например, тепло-
отводом в диск, то ее температура
изменяется по длине, как показано
на рис. 12.15.
В соответствии с этим предел
длительной прочности увеличивает-
ся к основанию лопатки быстрее,
чем растет напряжение В итоге
наименьший запас прочности может
оказаться не в основании лопатки,
где достигает максимума напряже-
ние «в» а ближе к середине ее.
Сказанное выше относится к случаю, когда температура газа по
длине лопатки не изменяется. Однако, как правило, она имеет наи-
большую величину приблизительно на середине длины лоратки, и.
здесь оказывается ее опасное сечение.
В лопатках последних ступеней многоступенчатых турбин с не-
охлаждаемыми дисками изменение температуры и, следовательно,
предела длительной прочности по длине лопатки обычно невелико.
Тогда опасным становится корневое сечение.
Как указывалось выше, расчет лопаток на прочность произво-
дится на нескольких характерных режимах работы двигателя. На
каждом из этих режимов пб формуле (12.51) определяются част-
ные запасы прочности (где z=l; 2;...; z— номер режима).
При этом предел длительной прочности принимается соответст-
вующим температуре лопатки на данном режиме (см. гл. X) и сум-
марному времени наработки на этом режиме в течение всего ресур-
са. Это время (в процентах от ресурса) зависит от назначения дви-
гателя. Запас прочности лопаток с учетом работы двигателя на всех
z режимах (К\) определяется на основе гипотезы линейного сумми-
рования повреждений [17]. Под повреждением понимается отноше-
ние времени работы п на каком-либо i-м режиме ко времени т, Р.
через которое наступает разрушение при напряжениях ог{ и темпе-
ратуре Ti, соответствующих данному режиму.
В соответствии с указанной гипотезой
V—= 1	(12.52)
Согласно зависимости (11.2)
xip=AaTmi.	(12.53)
Времени соответствует разрушающее напряжение оРазр> за кото-
рое следует принять предел длительной прочности при температу-
ре Tit поделенный на искомый коэффициент запаса Kt.
304
Следовательно,
'•	' t12-54)
Подставив выражения (12.53) и (12.54) в уравнение (12.52) с уче-
том равенства (12.51), получим уравнение
которое можно решить, например, графически. Входящая сюда ве-
личина т может ориентировочно выбираться в пределах 6... 10 в
зависимости от материала и температуры. Чем выше жаропроч-
ность материала и ниже температура, тем больше т. Если принять
т одинаковым для всех режимов (равным, например, значению
его на режиме с минимальным Kti), то из уравнения (12.55) по-
лучим
В рабочих лопатках выполненных ГТД минимальное значение К,
находится в пределах 1,5 ... 2,0.
В двигателях для дозвуковых пассажирских самолетов (и в не-
которых других случаях) минимальное значение частного запаса
прочности имеет место на взлетном режиме. На остальных режимах
запасы значительно больше. Тогда оказывается, что запас прочно-
сти Kt лишь незначительно меньше запаса прочности на взлетном
режиме Kt, вм, т. е. Ktf&K %, вм- На взлетном режиме наработка
этих двигателей равна примерно 5% или 1/20 всего срока службы.
Поэтому расчетный ресурс лопаток будет превышать в 20 раз вре-
мя, соответствующее пределу длительной прочности, принятому
при подсчете Kt, вал-
Так, например, если запас прочности лопаток двигателя для
гражданской авиации определен по пределу длительной прочности
0200, то за расчетный ресурс этих лопаток можно принять 200X
Х20=4000 ч.
Критерии прочности елочных хвостовиков в настоящее время не-
достаточно разработаны. Обычно напряжения в замке сравнивают
с пределом длительной прочности.
Запас прочности по разрывающим напряжениям в сечении А—А
хвостовика лопатки (см. рис. 12.10) или в сечении В—В выступа
диска (см. рис. 12.12)
(12.57)
Лв®р
где at—предел длительной прочности материала лопатки (или
диска) при температуре в данном сечении; ар — разрывающее нап-
305
ряжение, определяемое по формулам (12.35) или (12.41);
= 1,5 — коэффициент, учитывающий концентрацию напряжений и
некоторые напряжения от изгиба в сечении А—А,
Расчетная величина Лр должна быть не менее 2,5 ... 3,0 для ло-
паток и 2,0 ... 2,5 для дисков.
Запасы прочности в зубьях: на изгиб Ки=1,9 ... 2,6; на срез
Кср=1,8 ... 2,5; на смятие Ксм=0,8 ... I,!1.
Глава XIII
КОЛЕБАНИЯ ЛОПАТОК
§ 13.1. ОСНОВНЫЕ ПОНЯТИЯ
Опыт эксплуатации газовых турбин показывает, что большом
процент аварий связан с усталостными поломками лопаток. Эти
поломки, как правило, вызываются резонансными колебаниями ло-
паток, характеризующимися совпадением частоты возмущающей
силы с собственной частотой колебаний лопатки.
Собственной частотой колебаний называется частота свободных
(собственных) колебаний лопатки, выведенной из положения рав-
новесия кратковременной действующей силой. При резонансе рез-
ко возрастает амплитуда колебаний лопатки и, следовательно, нап-
ряжения в ней. Это видно из рис. 13. i, где показана зависимость р
(отношения амплитуды вынужденных колебаний к статическому
прогибу под действием максимального значения возмущающей си-
лы) от а (отношения частоты этой силы к собственной частоте), а
также от коэффициента х, учитывающего силы сопротивления ко-
лебаниям. Чем меньше эти силы, тем меньше величина %.
Лопатка имеет бесчисленное множество форм колебаний. На
рис. 13.2 формы колебаний лопатки изображены в порядке возрас-
тания собственных частот. Пунктирными линиями показаны так
называемые узлы, т. е. места лопатки, которые при колебаниях
данной формы остаются неподвижными. Положение узлов можно
определить следующим образом. Если на горизонтально располо-
женную (достаточно плоскую) лопатку насыпать равномерный слой
песка и привести ее в колебания с одной из указанных частот, то
через некоторое время песок останется лишь в местах, указанных
пунктиром. Расположение узлов и деформация оси лопатки при
первой, второй и третьей формах изгибных колебаний показано на
рис. 13.2, а, б и в. На рис. 13.2, г и д изображены первая и вторая
крутильные формы колебаний. При этом ось лопатки не изгибает-
ся, а сечения лопатки закручиваются вокруг нее. Строго говоря, в
1 Значения КСм<1 допускаются вследствие условности сравнения напряже-
ний смятия с пределом длительной прочности на разрыв.
306
Рис. 13.2. Форма колебаний лопаток
Рис. 13.1. График зависимости 0 (отношение амплитуды вынужденных колеба-
ний лопатки к ее статическому прогибу) от а (отношение частоты возмущающей
силы к частоте собственных колебаний)
закрученных лопатках с несимметричным профилем центры тяже-
сти и жесткости сечений не совпадают, поэтому имеют место сов-
местные изгибно-крутильные колебания. При колебаниях по рис.
13.2, а, б и в преобладают изгибные деформации, а по рис. 13.2, г
и д — крутильные.
Рассмотренные первые пять форм колебаний не связаны с де-
формацией профиля поперечного сечения лопатки. Такие формы ко-
лебаний называют стержневыми; для их расчета можно применять
теорию стержней или балок. Существуют более сложные, так на-
зываемые пластиночные формы колебаний (см. рис. 13.2, е, ж). Для
их расчета требуется применять теорию пластинок или, точнее, обо-
лочек. На практике обычно рассчитывают первые две изгибные и
две крутильные частоты. Из-за сложной конфигурации лопаток оп-
ределение высших частот расчетным путем возможно лишь с помо-
щью вычислительных машин.
(	§ 13.2. ПРИЧИНЫ КОЛЕБАНИИ ЛОПАТОК
5
Силы,, вызывающие колебания лопаток (возмущающие силы),
связаны с действующим на них газовым усилием, неравномерным
по окружности колеса.
В парциальных турбинах ЖРД рабочая лопатка, двигаясь ми-
мо сопла или соплового сегмента, полностью нагружается газовым
усилием; пройдя сопло, она разгружается от этого усилия и лопатка
получает zcn импульсов в секунду, если число сопел (сегментов)
обозначить z0, а частоту вращения турбины п.
307
Подобные же возбуждающие колебания импульсы, хотя и мень-
шей интенсивности, лопатка ГТД получает, проходя мимо кромок
сопловых лопаток, против которых полное давление газа в потоке,
выходящем из сопел, несколько падает. При числе сопловых лопа-
ток Zi частота возмущающей силы будет Z|/i.
Значительная неравномерность газового потока по окружности
обусловливается и конечным числом камер сгорания, форсунок и
т. п. Силовые стойки за компрессором или за турбиной также вы-
зывают периодические усилия, действующие на рабочие лопатки.
Кроме того, колебания лопатки могут быть вызваны неуравнове-
шенной силой ротора. При перекосах осей вал'ов турбины и комп-
рессора лопаткам передаются колебания с частотой, равной удво-
енному числу оборотов. При ошибке в зацеплении шестерен
редуктора ТВД лопаткам турбины также передаются периодиче-
ские возмущения, кратные числу оборотов.
. Таким образом, частота возмущающей силы в общем случае
составляет vB=in, где i — любое целое число, называемое гармо-
никой.
Ниже показано, что при неравномерности действующих на ло-
патку сил всего в несколько процентов динамические напряжения
изгиба на резонансном режиме могут превышать статические нап-
ряжения от изгиба в десятки раз. Поэтому при проектировании и
доводке двигателя необходимо стремиться к максимальному вырав-
ниванию полей давлений и температур перед рабочими лопатками
турбины.
§ 13.3. ЧАСТОТА КОЛЕБАНИЙ ЛОПАТКИ,
ПОСТОЯННОГО ПРОФИЛЯ
Изгибные' колебания
Определим статическую частоту колебаний v лопатки постоян-
ного профиля. Под статической частотой понимается частота коле-
баний лопатки на'неподвижном колесе (или лопатки, зажатой в
тисках).
Для вывода дифференциального уравнения колебаний восполь-
зуемся известным уравнением упругой линии стержня:
Д/^-=-Ж(х),	(13.1)
ох*
где М (х) — изгибающий момент в любом поперечном сечении;
J — момент инерции относительно какой-либо главной централь-
ной оси сечения. Считаем, что колебания относительно главных
осей происходят независимо друг от друга.
. Дважды дифференцируя уравнение (13.1), находим
Д/-^-=?(х).	(13.2)
308
Распределенной нагрузкой q(x) в случае свободных колебаний
являются силы инерции (принцип Д’Аламбера):
(13.3)
где f — площадь сечения лопатки, q — плотность материала.
Подставляя значение'q(x) в равенство (13.2) и вводя относи-
тельную координату х=—, запишем уравнение колебаний
h
_^L_|_e^L-^£-=0.	(13.4)
дх* ТЧ W	v '
Представим решение этого уравнения в виде
y=Y(х) sin (Xt-|-<po),	(13.5)
где Y(x) —функция распределения амплитуды колебаний по дли-
не лопатки; X — круговая частота изгибных колебаний; <ро — фаза
колебаний.
Подставляя в уравнение (13.4) соответствующие производные
от у, получим
ylV-a*r=0,	(13.6)
где	a4=eZ^l.
Таким образом, секундная частота колебаний
v=— =	(13.7)
2л 2яЛ2 у qf	4
Общее решение уравнения (13.6) можно записать так:
Y (x)=Cl(cosax-|-chax)-{-C2(cosax—ch ax)-f-
-J-C3(sin ax-|-sh ax)-f-C4(sin ax—sh ax), (13.8)
где постоянные C\... Ct определяются граничными условиями.
В защемленном конце при x=0 равны нулю прогиб У(0)=0 и
угол наклона касательной к упругой линии У'(0)=0. Отсюда сле-
дует, что С1 = С3=0.
На свободном конце консольной лопатки при х = 1 равны нулю
изгибающий момент EIY" и перерезывающая сила E1Y'". Следова-
тельно,
— С2 (cos a-]-ch a)—C4(sin a-f-sh a)=0;
C2(sjn a—sh a)—C4(coisa-|-cha)=0.
Исключение величин C2 и C4 приводит к так называемому час-
тотному уравнению задачи:
cosa-cha= —1.	(13.9)
Для лопатки с бандажной полкой при х==1 приближенно можно
309
принять, что изгибающий момент EJY" и прогиб У равны нулю.
Частотное уравнение в этом случае
tga=tha.
(13.10)
Уравнения (13‘.9) и (13.10) имеют бесконечно большое число
корней. Каждому из них соответствует одно зцачение собственной
частоты, определяемое формулой (13.7), например:
Обозначение корня..................ai ctj a3 сц a5
Консольная лопатка ................ 1,875 4,694 7,855 10,996 14,137
Лопатка с бандажной полочкой .	. . 3,927 7,068 10,210 13,352 16,493
Откуда видно, что частоты собственных колебаний лопатки с
бандажной полочкой выше, чем консольной.
Крутильные колебания
Частота i-й формы крутильных колебаний консольной лопатки
v=.(2f~1L-i /	(13.11)
4А у	к f
чении, который приближенно можно определить по формуле
C = \h.3ds,
(13.12)
где s — длина средней линии профиля; h — толщина профиля, за-
меренная по нормади к средней линии; f — площадь сечения;
л= f rW==A+A .— полярный момент инерции сечения.
§ 13.4. ЧАСТОТА КОЛЕБАНИЙ ЛОПАТКИ
ПЕРЕМЕННОГО ПРОФИЛЯ
Изгибные колебания
Частоту колебаний лопатки переменного профиля с учетом дей-
ствия центробежной силы можно определить энергетическим мето-
дом, хотя и приближенным, но достаточно простым. Сущность это-
го метода состоит в следующем. Определяем потенциальную энер-
гию П деформации лопатки в максимально отклоненном положе-
нии и работу W, совершенную центробежной силой лопатки при ее
выпрямлении. Затем находим максимальную кинетическую энер-
гию массы лопатки К, соответствующую моменту ее прохождения
через недеформированное положение (когда потенциальная энер-
гия изгиба отсутствует). По закону сохранения энергии, если пре-
310
небречь работой сил внешнего и внутреннего (в металле) трения \
n-\-W=K.	(13.13)
Это равенство дает возможность определить частоту собствен-
ных колебаний, входящую в формулу для кинетической энергии.
Прогибы лопатки при ее колебаниях подчиняются зависимости
У—Y(х) sin (kv-f-^o).	(13.14)
Скорость любой точки лопатки
v=^-—YY cos(Jcr-|-®0).
Максимальная скорость достигается в
ложении, когда cos (Ат+фо) — 1 '
‘	®тах==^<Г"
Кинетическая энергия лопатки
*	л	।
недеформированном по-
ft
/(=4- \ v2msidm=-J-qA2 fY2dx.
о	о
В максимально отклоненном положении при sin (Ах 4-фо) = 1
У=У(х). При этом изгибающий мрмент в любом сечении лопатки
М (х)= — EJ & —, а максимальная потенциальная энергия дефор-
мации
(13.15)
h	h
EJ f dW
2 J \ dx*
0
элемента ло-
произведеншо
dx.
(13.16)
о
Работа центробежной силы
патки при выпрямлении равна
силы йРц>на путь г, пройденный точкой прило-
жения этой силы (рис. 13.3). При этом прене-
брегаем работой, составляющей dP^ и центро-
бежной силы, и полагаем, кроме того, cosa= ”
= 1 ввиду малости этого угла. При колебаниях
лопатки в осевом направлении £?РЦ и и а точно
равны нулю.
Из рис. 13.3 следует, что z=s—х. Длина
кривой, как известно, определяется формулой
s=j y^l-j-K'2dx. Разложим в ряд Vl-J-X'2»
тогда уг1-|-К,2=
1 Это допущение практически не сказывается
частоте собственных колебаний.
на
Рис. 13.3. Схема колеблющейся лопатки
, d-Рци.
Мц-созапар*
. л
311
Пренебрегая ввиду малости производной У' ее степенями выше
второй, получим
s=jc-|—Таким образом,	dx.
о	о
Так как центробежная сила элемента лопатки dPu=Qco2f (гк+
4-х)dx, то работа центробежной силы
Л	к	х
W^zdPK^-L^\f(rK+x)\
О	0	0
Используя выражения (13.13) и (13.15) ... (13.17), получим
*
2
dxdx. (13.17)
(13.18)
Первый член в правой части выражения (13.18) представляет
собой квадрат статической частоты колебаний, что легко видеть,
если положить <в=0. Второй член — это квадрат частоты колеба-
ний вращающейся лопатки, не обладающей силами упругости
(£7=0).
Таким образом,
где
Vx=]/V24-Bn2,
ft
(13.19)
(13.20)
п — частота вращения в об/с.
Чтобы определить частоту по формуле (13.18), необходимо
знать точное выражение функции У(х) —амплитуды прогибов ло'
патки в каждой ее точке. Так как эта функция для лопатки произ-
вольного профиля заранее не известна, воспользуемся принципом
Релея. Согласно этому принципу использование в указанной фор-
муле любой произвольной зависимости У(х), но удовлетворяющей
геометрическим граничным условиям [для защемленной консоль-
312
Рис. 13.4. График для выбора коэффициента В
ной лопатки У(0) = У'(0) =0], приводит
всегда к значению частоты, большему дейст-
вительного. Таким образом, определив час-
тоту по формуле (13.18) для нескольких
форм кривой, удовлетворяющих этим усло-
виям, надо остановиться на той из этих
форм, которая дает наименьшее значение
частоты.
Интегралы, входящие в • выражение
(13.18), подсчитываем численным или гра-
фическим способом. Модуль Е оставлен под знаком интеграла, так
как в неравномерно нагретой лопатке он изменяется по высоте.
Обычно, однако, в расчетах его считают величиной постоянной, со-
ответствующей средней температуре лопатки.
Если рассчитана или определена экспериментально статическая
частота vo лопатки при нормальной температуре, то частота коле-
баний лопатки на различных режимах работы двигателя может
быть определена по формуле

(13.21)
где Eq и Ет — модуль упругости материала при нормальной и ра-
бочей температурах.
Для ориентировочного выбора коэффициента В в формулах
(13.19) и (13.21) при определении частоты первого тона лопатки
переменного профиля может служить график, приведенный на рис.
13.4. Кривая 1 относится к лопатке постоянного профиля и построе-
на по формуле
5=0,7850-0,592.	(13.22)
Кривая 2 — к лопатке переменного профиля с минимальным
практически встречающимся отношением	Для различных
Л
лопаток величина коэффициента В ориентировочно лежит в зашт-
рихованной на графике области.
Если лопатка установлена по углом руст к окружному направ-
лению, то величина В в формулах (13.19) и (13.21) должна б*ыть
заменена величиной
5I»5—sin8₽yet.	(13.23)
В случае закрученной лопатки за угол руот можно принимать
угол установки профиля в середине лопатки.
Применим формулу (13.18) для расчета лопатки, у которой пло-
щадь поперечного сечения и минимальный момент инерции изменя-
ются по законам, аналогичным формуле (12.4):
/=Л(1-аР”);
j=jK(l-^₽),
313
где	л 1 J^n/Ук’ & 1 *Л1АЛс» х—х/ИУ.
Воспользуемся при этом уравнением упругой линии в виде
Y=cxq,
где c=const, a q— параметр, определяемый далее из условия ми-
нимума частоты.
Подставляя принятые функции f, J и Y в формулу (13.18), полу-
чим после интегрирования
/1	Ь \
V2 — Е1к.	— й ~2д + р—з) 
V* (2«)2q/kA4	1	д	-
2^ -j- 1	2$г -]- т 4-1
( 1 - а \ •
4-Л2 _£-----1 ZJL---2£---2£+т---------j_ 1 \	(13 24)
,	2^—1 I 1	1 _ д I
2^ -f-1	ж -|-1	/
Задаваясь несколькими значениями q (в пределах 1,6...2,2),
строим график зависимости vR от q. По нему определяем минималь-
ную величину уд, которую и следует принять за искомую. Для расче-
та частоты колебаний лопатки с бандажной полочкой можно при-
нять уравнение упругой линии в виде
Г=с(х’-х2).
По формуле (13.24) можно определить частоту только первого
тона колебаний.
Частота, определённая по энергетическому методу, превышает
действительную на 2 ... 5% в зависимости от того, насколько удач-
но выбран вид функции У(х). Для лопаток с малой жесткостью
Л/q (Л — длина лопатки; р — радиус инерции сечения) расхожде-
ние между расчетным vpac4 и экспериментальным уэксп значениями
частот получается более значительным. На рис. 13.5 сплошными
линиями показана зависимость отношения частот ф—Уэксп/урасч от
гибкости Л/р, полученная в опытах с двумя типами лопаток, отли-
чающихся креплением их к ди-
ску [7].
Расхождение между ука-
занными частотами объясняет-
ся, с одной стороны, тем, чтс
Рис. 13.5. Кривые к определению соб-
ственной частоты колебаний лопато*
1 В лопатках с елочным хвостовиком иногда за расчетную длину принимаю'
расстояние от сечения по первым впадинам замка (см. рис. 12.11 сечение А—At
до периферийного сечения лопатки.
314
при выводе дифференциального уравнения колебаний мы прене-
брегли влиянием перерезывающих сил на прогиб лопатки. С другой
стороны, — заделку лопатки в‘замке нельзя считать абсолютно
жесткой, даже в случае изготовления лопаток за одно целое с дис-
ком (например, отливкой). В связи с этим истинная частота коле-
баний получается обычно меньше вычисленной по приведенным
выше формулам, особенно для коротких лопаток.
Пунктирной линией на рис. 13.5 показана зависимость отноше-
ния частот, вычисленных с учетом и без учета влияния перерезы-
вающих сил от гибкости лопатки. Видно, что главную роль в сни-
жении действительной частоты по сравнение с расчетной играет
нежесткая заделка лопаток.	*
Крутильные колебания
Для определения частоты первого тона крутильных колебаний
лопаток переменного профиля можно применить энергетический
метод. Поступая так же, как при выводе формулы (13.18), получим
1
Г, (йФ \2 _
\ GJKI —=- ] dx
J \dx )
о__________
1 _
f ItfWdx
V2=-----1—
(2я)2 еЛ2
(13.25)
Функция Ф(х) может быть принята в виде Ф(х)=сх^.
При построении кривой v=v(^) значения q следует выбирать в
пределах 0,6 ... 1,0. 
Достаточная для практики точность получается при использо-
вании функции	_
Ф(х)=с(2л:-л:2),	(13.26)
являющейся решением задачи о кручении консольного стержня пос-
тоянного профиля распределенным моментом постоянной интенсив-
ности.
§ 13.5.	РЕЗОНАНСНАЯ ДИАГРАММА КОЛЕБАНИИ ,
Число оборотов, при которых имеют место резонансные колеба-
ния лопаток, удобно определять при помощи диаграммы (рис. 13.6).
По формуле (13.21) или по экспериментальным данным строят
кривые собственных частот в функции числа оборотов. Так как
лопатки на одном и том же колесе изготовлены с технологически-
ми отклонениями и имеют поэтому различные частоты (с разбро-
сом до 10%), то на диаграмме каждому тону колебаний соответст-
вуют две кривые — максимальной и минимальной частот лопаток
данного колеса. Между ними лежат частоты остальных лопаток.
Снижение частоты с увеличением числа оборотов объясняется
уменьшением модуля упругости при высоких температурах. Повы-
шение частоты за счет действия центробежных сил не компенсиру-
ет падение ее из-за нагрева лопатки. Собственная частота лопаток
последних ступеней многоступенчатых турбин, имеющих сравни-
315
Рис. 13.6. Резонансная диа-
грамма колебаний лопаток
Ь^МН]мг
тельно невысокие тем-
пературы, может расти
с увеличением частоты
вращения.
Из начала коорди-
нат диаграммы прове-
дены лучи , соответст-
вующие различным
частотам возмущаю-
щих сил: Ьп, 2*и,...,
21-П.
Абсциссы точек пе-
ресечения лучей с кри-
зыми соответствуют
резонансным числам
частот вращения, Так,
например, при частотах
вращения nAi пв и пс
имеет место резонанс
возмущающей силы,
обусловленной наличи-
ем девяти камер сгора-
ния (9-я гармоника)
соответственно е часто-
тами 1й изгибной, 1-й крутильной и 2-й изгибной форм колебаний.
Вследствие разброса частот отдельных лопаток эти резонансные
числа частот вращения лежат в пределах заштрихованных участ-
ков диаграммы. Для уменьшения ширины этих участков лопатки
должны изготавливаться с малым разбросом собственных частот.
Наиболее опасен резонанс в области максимальных значений
частот вращения, где наибольшее значение имеют динамические и
статические напряжения, а механические характеристики материа-
ла лопаток снижаются из-за высокой температуры.
В верхней части рис. 13.6 показано изменение по оборотам ди
намических напряжений в колеблющейся лопатке, получение
экспериментально (тензометрированием). Видно, что с. помощь*
резонансной диаграммы можно установить причину сильных коле
баний лопатки на отдельных режимах работы турбины.
§ 13.6.	НАПРЯЖЕНИЯ В ЛОПАТКЕ
ПРИ РЕЗОНАНСНЫХ КОЛЕБАНИЯХ
Совершенно избежать резонансных режимов работы лопато!
при эксплуатации двигателя нельзя, поэтому необходимо найт!
величину напряжений при резонансе и наметить меры, уменьшаю
щие их. Определить расчетом эти напряжения практически невоз
можно, в основном, из-за отсутствия данных о величине и распре
316
делении по высоте лопатки возмущаюищх сил и сил сопротивления
колебаниям. Поэтому на примере изгибных колебаний лопатки пос-
тоянного профиля выясним, какие основные факторы влияют на
величину искомых напряжений. Положим, что амплитуда возмуща*
ющей силы одинакова по высоте лопатки и составляет |-ю часть
равномерно распределенной статической нагрузки’. Тогда макси-
мальное динамическое напряжение в корневом сечении лопатки при
резонансе составляет [7]
вд=2л-^-^,	(13.27)
где <тиг — статические напряжения от изгиба силами давления га-
зов (без учета разгрузки центробежными силами); Сп — коэффи-
циент, зависящий от крепления концов лопатки и номера формы ко-
лебаний; б — логарифмический декремент колебаний, учитываю-
щий силы сопротивления.
Значения коэффициента Сп для первых трех форм изгибных ко-
лебаний защемленной лопатки будут следующие: консольная лопат-
ка— С] = 0,4440, (?2=0,0394, С3=0,0084; лопатка с бандажной по-
лочкой — 01=0,1120, С2=0,0330, С3=0,0064.
Отсюда видно, что в лопатках с бандажной полочкой значения
коэффициента Сп, а следовательно, и напряжений <тд заметно мень-
ше, чем в консольной лопатке. С повышением номера формы (то-
на) колебаний при той же интенсивности возмущающей силы ди-
намические напряжения резко падают.
Логарифмическим декрементом колебаний называется натураль-
ный логарифм отношения двух смежных амплитуд затухающих ко-
лебаний. Такие колебания возникают в реальной лопатке под дей-
ствием кратковременно приложенной силы. Под действием разно-
го рода сопротивлений (трение в металле и замковом соединении,
воздействие газового потока на колеблющуюся лопатку) колеба-
ния со временем затухают. Величина 6 зависит от химического сос-
тава и термической обработки материала лопатки и ее конструк-
ции, от напряжений и температуры лопатки, а также от времени
эксплуатации турбины. В реальных лопатках б изменяется & пре-
делах 0,01 ... 0,06. Отсюда следует, что даже малая возмущающая
сила, составляющая лишь небольшую часть от сил давления газов,
способна вызвать при резонансных колебаниях напряжения, значи-
тельно превышающие статические напряжения изгиба.
Так, например, если интенсивность возмущающей силы состав-
ляет всего 5% от интенсивности статической нагрузки (|=0,05), а
статическое напряжение в консольной лопатке циг=30 МН/м2, то
при 6=0.035 ад=2л^^-•0,05-30= 120 МН/м2.
Таким образом, в данном случае динамические напряжения превы-
шают статические напряжения от изгиба силами давления газов в
4 раза. Особенно большой величины достигают динамические нап-
ряжения в парциальных ступенях.
317
Заметим также, что максимальные динамические напряжения
возникают в корневом сечении лопатки, а также между узлами ко-
лебаний (т. е. в точках А, Б, В см. рис. 13.2).
§ 13.7.	ОБЕСПЕЧЕНИЕ НАДЕЖНОСТИ
ЛОПАТОК ПРИ КОЛЕБАНИЯХ
• Из предыдущего параграфа ясно, какую серьезную опасность
представляют для прочности лопаток резонансные колебания, ког-
да тд;=Ув. Избежать резонанса можно изменением частоты возму-
щающей силы vB или собственной частоты колебаний лопатки vA.
Выше указывалось, что частота возмущающих сил пропорцио-
нальна секундному числу оборотов турбины:
vB=in,
где i — любое целое число.
Наибольшей интенсивностью обладают возмущающие силы,
вызванные наличием отдельных камер сгорания, различными стой-
ками в газовоздушном тракте (в том числе и расположенными за
ступенью), сопловыми лопатками и т. п. Поэтому изменить частот^
возмущающей силы можно изменением числа этих элементов или
числа оборотов турбины. Изменения собственной частоты колеба-
ний лопатки можно добиться изменением конструкции лопатки, т. е.
Изменением законов распределения площади и моментов инерции
по длине лопатки.
Отстраиваться от резонансных режимов часто приходится после
изготовления двигателя при его доводке. В этом случае прибегают,
например, к подрезке выходных кромок лопаток. В современном га-
зотурбинном двигателе имеется большое число разнообразных ло-
паток, обуславливающих широкий спектр собственных частот и
разнообразных возмущающих сил с различной частотой. Это при-
водит к тому, что не удается полностью избежать резонансных ре-
жимов в пределах рабочих частот вращения двигателя — от обо-
ротов малого газа до максимальных. Поэтому главной задачей
обеспечения надежности облопачивания при колебаниях является
устранение резонанса из областей длительных режимов работьа
двигателя и уменьшение динамических напряжений, возникающих
при резонансе.	I
Из формулы (13.27) следует, что динамические напряжения1
можно снизить, если:
1)	уменьшить напряжения от изгиба силами давления газов,,
увеличив моменты сопротивления лопатки:
2)	уменьшить неравномерность потока по окружности. Для это-
го нужно добиться лучшего распределения параметров потока за
камерой сгорания, отнести по возможности дальше от лопаток раз-
личные силовые стойки, увеличить осевой зазор в турбине и т. п.;
3)	ввести бандажирование лопаток, если это допустимо по ус-
ловиям статической прочности, при этом ограничивается амплитуда,
колебаний лопаток и особенно тонких выходных кромок;
318.	'
Рис. 13.7. График зависимости относительных
динамических напряжений в рабочих лопатках
от параметра С
4)	увеличить различные силы соп-
ротивления колебаниям (применить
материалы, имеющие большие декре-
менты колебаний, или использовать
конструктивное демпфирование), т. е.
теми или иными конструктивными ме-
роприятиями искусственно увеличить
работу трения при колебаниях лопа-
ток.
Уменьшить динамические напряжения при резонансе с гармони-
кой i='zi можно также, применив конструкцию соплового аппара-
та с неравномерно расположенными по окружности лопатками.
Лопатки разбиваются на 3 ... 4 группы, в которых шаг решетки
незначительно отличается от оптимального. Это нарушает равно-
мерную последовательность импульсов от аэродинамических сле-
дов за сопловыми лопатками и приводит к снижению амплитуды
Zi-й гармоники возбуждения. Однако следует иметь в виду, что в
этом случае несколько увеличиваются возмущающие силы с гармо-
никами, близкими к Zi. Эти гармоники можно выявить расчетом,
еслц разложить в ряд Фурье эпюру полных давлений за сопловым
аппаратом.
К снижению динамических напряжений приводит и наклон соп-
ловых лопаток к радиальному направлению в сторону корытца.
При этом рабочая лопатка не одновременно по всей высоте, а пос-
тепенно, пересекает след за сопловой лопаткой, что в итоге умень-
шает амплитуду возмущающей силы. На рис. 13.7 показана зависи-
мость динамических напряжений в рабочих лопатках от параметра
С, характеризующего наклон сопловых лопаток. Здесь: ад и од0—
соответственно, напряжения при наклонных и радиально установ-
ленных сопловых лопатках; параметр С подсчитывается по форму-
ле [26]
(13.28)
У яг,сД
~90 02— 1
где у — угол между наклонной кромкой сопловой лопатки и ради-
альным направлением (на среднем диаметре турбины) в градусах.
Из рисунка следует, что увеличение наклона приводит к сниже-
нию напряжений при колебаниях по 1й изгибной форме, но может
увеличить напряжения, при резонансе с более высокими формами.
Отметим также, -что применение наклонных сопловых лопаток сни-
жает шум турбины и уменьшает градиент давления по высоте ло-
патки (см. § 5.3).
Помимо определения запасов прочности по статическим напря-
жениям, проверяются также запасы усталостной прочности в про-
фильной части и'ножке лопаток на рабочих режимах двигателя по
319
формуле Kv=®vl<(Jx, где cr« — предел выносливости материала ло-
патки с учетом концентрации напряжений, температуры и асиммет-
рии цикла нагружения, т. е. влияния постоянных растягивающих
напряжений на усталость металла; од— максимальное переменное
напряжение, возникающее в лопатке.
Имеющиеся в литературе данные не позволяют пока надежно
определять при проектировании турбины величины av и <тд. Пра-
вильное суждение о запасе усталостной прочности можно сделать
лишь после экспериментальных исследований на работающем дви-
гателе.
Величина К» должна быть не менее 3,0 ... 4,0. При определении
величины <т„ исходным является предел выносливости <j_i при сим-
метричном цикле нагружения (когда отсутствует постоянная сос-
тавляющая напряжений). Эта характеристика металла обычно и
указывается в справочных материалах.
Предел усталости уменьшается с увеличением концентрации
напряжений, поэтому эффективным средством борьбы с поломками
лопаток от вибрации являются тщательная их полировка, увеличе-
ние радиусов перехода пера в нож.ку, скругление кромок, увеличе-
ние радиусов впадин замков, снижение наклепа при механической
обработке пера и хвостовика упрочнением поверхности (например,
обдувкой микрошариками) и т. п.
О чувствительности к концентрации напряжений того или иного
материала можно судить, сравнив значения пределов выносливо-
сти гладких (о_1) и надрезанных (o-i) образцов.
Глава XIV
КОНСТРУКЦИЯ ТУРБИННЫХ дисков И РОТОРОВ
§ 14.1.	КОНСТРУКЦИЯ ДИСКОВ И СПОСОБЫ
СОЕДИНЕНИЯ ИХ С ВАЛОМ
Диски газовых турбин в общем случае состоят из обода, полот-
на и ступицы (рис. 14.1, 14.2). Обод представляет собой уширенную
периферийную часть диска, служащую для крепления на нем рабо-
чих лопаток. В сечении обод может быть постоянной ширины, су-
живающимся к периферии или к центру диска (см. рис. 11.9). В ря-
де конструкций обод диска имеет буртики для лабиринтного уп-
лотнения или выступы 1 (см. рис. 14.2) для крепления других дета-
лей ротора. Полотно диска в большинстве случаев выполняют в се-
чении коническим. Такие диски технологичны и имеют достаточно
благоприятное распределение напряжений при малой массе. Иног-
да центральную часть диска выполняют с постоянной толщиной по
радиусу, а периферийную — конической.
320
Диски постоянной толщины не приме-
няют ввиду больших напряжений, возни-
кающих в них при вращении турбины.
При необходимости в полотне диска
выполняют отверстия для охлаждающего
воздуха или для болтов крепления дис-
Рис. 14.1. Схема диска трехступенчатой турбины ТВД
Рис. 14.2. Схема диска турбины высокого давления двухвального ТРДД
ков к валу и между собой. Для крепления дисков и деталей уплот-
нения служат также фланцы 3 (см. рис. 14.2) и специальные высту-
пы, в которых для уменьшения массы диска делают выборки (см.
.рис. 14.1).
Диски с центральным отверстием имеют, как правило, ступицу
2 (см. рис. 14.2),, уменьшающую значительные напряжения на
внутренней поверхности (см. § 15.3). В конструкции дисков ГТД
часто предусматриваются специальные буртики 1 (см. рис. 14.1)
для крепления при сборке турбины специальных приспособле-
ний — съемников.
Для уменьшения концентрации напряжений в местах соедине-
ний обода, ступицы, фланцев и др. с полотном диска выполняются
галтели с достаточно большими (10... 20 мм и более) радиусами.
На рис. 14.3 приведен двухвенечный диск (колесо Кертиса) тур-
бины ТНА ЖРД. Диск и лопатки выполнены из алюминиевого
сплава. Для крепления лопаток в ободе диска проточены две коль-
цевые канавки Т-образного сечения. Лопатки вставляются через
специальные пазы, один из которых показан на рис. 14.3, справа.
После постановки всех лопаток в паз вставляют специальный клин
1 и пробку 2, которую затем расклепывают. Для надежности проб-
ку фиксируют стопорным винтом 3.
В центре диска имеется отверстие, в которое с напряженной по-
садкой вставляют две стальные шлицевые втулки, скрепляемые
заклепками (8 шт.). Заклепки ставят с глухой посадкой. Полотно
диска несимметричное. Одна его поверхность перпендикулярна к
11	1337
321
Рис. 14.3. Схема двухвеиечного диска
турбины ТНА ЖРД
оси диска, другая — кониче-
ская на периферии и криволи-
нейная у втулки. Это несколько
упрощает технологию изготов-
ления диска, но вызывает в
нем дополнительные напряже-
ния от изгиба. В данной конст-
рукции диск имеет невысокую
температуру и незначительный
ресурс, поэтому рост напряже-
ний неопасен.
Несимметричные диски, име-
ющие высокую температуру и
предназначенные для длитель-
ной работы, в результате пол-
зучести «выпрямляются», т. е.
их срединная поверхность стремится обратиться в плоскость. При
этом со временем изменяются осевые и радиальные зазоры в тур-
бине, а материал диска испытывает большие пластические дефор-
мации, которые могут привести его к разрушению. Поэтому диски
ГТД и ТНА, работающие при высокой температуре, как правило,
выполняют симметричными (если не учитывать различных флан-
цев, буртиков и т. п.).
, В некоторых конструкциях дисков ГТД обод выполняют несим-
метричным с целью разгрузки полотна от изгибающих моментов.
Из рис. 14.4 видно, что изгибающий момент М от газовых сил, дей-
ствующий на- лопатки и передаваемый на диск, может быть час-
тично или полностью (на одном режиме) скомпенсирован момен-
том Ра, где Р — суммарная центробежная сила лопаток и разрез-
ной части обода диска, а а — расстояние от плоскости симметрии
полотна до плоскости действия силы Р.
Диски являются наиболее нагруженными деталями газовых
турбин. Максимальные напряжения в них достигают 500 МН/м2 и
более.
В сравнительно тонких дисках значительной величины могут
достигать переменные напряжения, вызванные вибрацией. В связи
с этим для уменьшения концентрации напряжений поверхность дис-
ков должна быть чисто обработана (по 7 ... 9-му классу), не иметь
резких переходов, края отверстий в диске должны быть скруглены
и т. п. Высокие требования предъявляются также к качеству заго-
товок (поковок) дисков.
Способы соединения дисков с валом весьма разнообразны. Сое-
динения могут быть разъемными и неразъемными.
Из разборных соединений наиболее часто применяются флан-
цевые различной конструкции (см. рис. 14.1, 14.2, 20.1, 20.2). Дис-
ки центрируются по наружной или внутренней цилиндрической по-
322
Рис. 14.4. Схема диска турбины с несимметричным ободом
всрхности фланца вала. Крутящий момент пере-
дается призонными втулками или болтами.
Конструкция соединения должна обеспечивать
по возможности меньшую передачу тепла по ва-
лу от диска к подшипнику. Для этой цели слу-
жат кольцевые канавки 1 (см. рис. 14.4). В тур-
бине, показанной на рис. 20.2, диск с валом сое-
динен на значительном удалении от подшипника
с помощью танкой перемычки. Это снижает тем-
пературу подшипника.
В некоторых двигателях диск соединяется с
валом шлицевым хвостовиком, отъемным (см.
рис. 18.3) или изготовленным заодно с диском.
В роторе турбины, показанном на рис. 18.3,
диск центрируется по коническим участкам при-
зонных болтов. Для удержания болтов при сбор-
ке служат стопорные кольца.
Соединение алюминиевого диска с валом турбины ТНА ЖРД,
показанное на рис. 14.3, осуществляется при помощи стальных вту-
лок, имеющих прямоугольные шлицы. Крутящий момент от диска к
втулкам передается через заклепки, работающие на срез.
Большим распространением пользуется неразъемное соединение,
осуществляемое радиальными штифтами (см. рис. 14.4). Штифты
сажают с прессовой посадкой в совместно обработанные отверстия
в соединяемых деталях.
Крутящий момент и осевая сила передаются штифтами, работа-
ющими на срез, и частично трением. Это соединение достаточно на-
дежно, технологично, сохраняет центровку при температурных де-
формациях диска и_вала. При переборках ротора балансировка его
изменяется незначительно. К недостаткам такого соединения мож-
но отнести сравнительную сложность замены диска или вала. В не-
больших турбинах вал и диск могут быть выполнены заодно, сое-
динены контактной сваркой или сваркой трением.
§ 14.2.	РОТОРЫ МНОГОСТУПЕНЧАТЫХ ТУРБИН
Роторы многоступенчатых турбин бывают: дисковой или сме-
шанной — барабанйо-дисковой конструкции. Соединение дисков
между собой и с валом в многоступенчатых турбинах может быть
неразъемным и разъемным. Неразъемные роторы проще по конст-
рукции, технологичнее, обладают большей жесткостью. При пере-
борках двигателя их балансировка нарушается в меньшей степени,
чем в разъемных роторах. Однако при неразъемном роторе услож-
няется конструкция и сборка турбины, увеличивается диаметр ла-
биринтных уплотнений между ступенями, что снижает к. п. д. тур-
бины. Поэтому обычно неразъемные роторы применяют в турбинах,
имеющих число ступеней не более двух.
Наибольшее распространение в турбинах современных ГТД
11*
323
нашли разъемные роторы. Диски соединяются между собой и с ва-
лом с помощью фланцев. Крутящий момент передается призонны-
ми втулками, болтами, штифтами (см. рис. 20.1, 20.2) или торцевы-
ми треугольными шлицами (см. рис. 20.3). Эти элементы служат
также и для центровки дисков.
В осевом направлении-фланцы соединяются болтами или при-
жимаются к фланцу вала гайками 4 и 7, имеющимися на валу (см.
рис. 20.2). При соединении с помощью треугольных шлицев диски
могут стягиваться одним центральным болтом.
В некоторых конструкциях турбин на валу между дисками ус-
танавливаются специальные кольцевые детали, на которых наре-
заются гребешки лабиринтного уплотнения, уменьшающего пере-
течку газов мимо сопловых аппаратов (см. рис. 20.2).
Для уменьшения числа соединений в роторе целесообразно кре-
пить сразу два диска к одному фланцу вала. В этом случае соеди-
нение располагается между дисками, что уменьшает также осевые
габариты турбины (см. рис. 20.1 ... 20.3).
В многоступенчатых конструкциях относительно тонкие диски,
подверженные изгибу и вибрации, дополнительно соединяются меж-
ду собой вблизи обода тонкими кольцевыми перемычками (см. рис.
20.3).
В одновальных многоступенчатых турбинах диски могут выпол-
няться без центрального отверстия. В многовальных турбинах с
концентрично расположенными валами диски имеют центральное
отверстие и развитую ступицу.
Глава XV
РАСЧЕТ НА ПРОЧНОСТЬ БАРАБАНОВ И ДИСКОВ
§ 15.1.	РАСЧЕТ РОТОРА БАРАБАННОГО ТИПА
В некоторых роторах газовых турбин применяют конструктив-
ные элементы, представляющие собой цилиндрические или близкие
к цилиндрическим барабаны с малой по сравнению с радиусом тол-
щиной стенки.
Барабан рассчитывают как свободно вращающееся кольцо ма-
лой толщины. Увеличение жесткости барабана за счет имеющихся
на концах утолщений, фланцев, дисков и т. п. не принимают обыч*
но во внимание; это идет в запас прочности.
Выделим из барабана элемент длиной у, ограниченный ради-
альными сечениями, составляющими между собой бесконечно ма-
лый угол <&р (рис. 15.1). На элемент, массу которого обозначим
dm, при его вращении действует центробежная сила инерции
dPu== dmra>2=Qrdyydra2.
Вызываемые этой силой тангенциальные напряжения чтгк в по-
перечном сечении кольца площадью у 6 обуславливают результиру-
324
Рис. 15.1. Схема к расчету напряжений в барабане
ющие силы (в предположении равномерного распределения напря-
жений) N—y6otK.
Из условия равновесия c/PIl=22Vsin ^-=2V4/<p, откуда
(к/фг/6г2со2=ybatmdff.
Следовательно, o<K=Q(r<o)2=Qa2.	(15.1)
Напряжения в барабане, таким образом, пропорциональны
плотности материала и квадрату окружной скорости. Для стали
(в МН/м2) <rt к=0,008 и2, где и — скорость в м/с.
Величины напряжений составляют: «=100; 150; 200; 250 м/с и
о(к=80; 180; 320; 500 МН/м2 соответственно.
Из чего следует, что окружные скорости порядка 150 м/с явля-
ются предельными для стальных барабанов газовых турбин, и толь-
ко при применении жаропрочных материалов и эффективном ох-
лаждении скорость может достигать 200 м/с.
Высокие температуры и окружные скорости в авиационных ГТД
затрудняют применение для многоступенчатых реактивных турбин
роторов барабанной конструкции, используемых в стационарном
турбостроении. Это объясняется в значительной мере и теми высо-
кими добавочными напряжениями, которые вызывают центробеж-
ные силы лопаток, расположенных на барабане.
Положим, что на единице площади цилиндрической поверхно-
сти барабана на радиусе г от лопаток и их креплений действует
напряжение <гга	где — центробежная сила всех лопа-
ток на участке у барабана.
На выделенный элемент действует сила dPn.a=rdq>y<jra. Под-
ставляя ее в уравнение равновесия элемента, получим суммарное
напряжение в барабане
e«=Qa2+-7-are.	(15.2)
О
При больших значениях отношения радиуса барабана к его тол-
щине добавочные напряжения от лопаток становятся соизмеримы-
ми с напряжениями от центробежных сил собственно барабана или
даже превышают их.
325
§ 15.2.	ОБЩИЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ДИСКОВ
НА РАСТЯЖЕНИЕ
Для определения напряжений в диске выделим бесконечно ма-
лый элемент толщиной у, ограниченный радиусами г и r+dr и пло-
скостями, проходящими через ось вала и составляющими между
собой угол dtp (рис. 15.2). Масса этого элемента dm—Qrydqdr.
Центробежная сила dP^dmrw^—Qr^aPyd^dr.
К поверхностям элемента приложены следующие усилия: 1) ра-
диальная сила di/?, приложенная к внутренней поверхности элемен-
та: 2) радиальная сила dR', приложенная к наружной поверхности
элемента; 3) тангенциальные силы dN, приложенные к боковым по-
верхностям элемента.1
Обозначим радиальное напряжение через ог, тангенциальное че-
рез ot и, считая их равномерно распределенными по толщине эле-
мента, находим величины указанных выше сил: dR=yrdyar-, dR'=
= (y+dy) (r+dr)d(p(<Tr+dor); dN=ydrat,
Отметим, что напряжения <jr и являются нормальными
(растягивающими или сжимающими), так как действуют перпенди-
кулярно соответствующим площадкам. В силу осевой симметрии
рассматриваемой задачи касательных напряжений в диске не
возникает. Касательные напряжения, вызванные крутящим момен-
том, действующим на диск, обычно малы и ими пренебрегают.
Сумма проекций всех сил, приложенных к элементу, на ради-
альное направление должна равняться нулю (см. рис. 15.2), т. е.
dPa+dR’— dR—2dN sin ^-=0.
Подставляя сюда выражения для сил и пренебрегая бесконеч-
но малыми величинами высшего порядка, получим уравнение
равновесия в таком виде:
—уъ+$г№у=0.	(15.3)
dr
Для определения двух напряжений аг и а* уравнения (15.3) не-
достаточно. Второе, необходимое уравнение получим, рассматривая
деформацию элемента.
Под влиянием напряжений и температуры радиус кольца г уд-
линяется на величину g, а радиус (r+dr) —на величину (g + dg)
(см. рис. 15.2). Следовательно, полное удлинение элемента dr сос-
тавляет dg, а относительная радиальная деформация
(16.4)
Относительная деформация в окружном направлении
= 2л (г+ 5)-^^ _5_	(15. 5)
*	2лг	г	v
где g=8tr.
326
Рис. 15.2. Схема к расчету напряжений в диске
Дифференцируя это выражение, на-
ходим
JL—е I г
dr '
„	di
Подставляя сюда значение-
dr
из
равенства (15.4), получим уравне-
ние совместимости деформ а-
ц и й:
г	— 8г=0.
dr п *
На основании закона Гука
е, =4-(в,—1*3/)+а/;
е/=4(Л—1*3,0+аЛ
С,
(15.6)
(15.7)
где, ц — коэффициент Пуассона; а — коэффициент линейного рас-
ширения металла; t—T—— разность температур диска Т и нор-
мальной (комнатной) температуры Тн. При постоянной (по ради-
усу) температуре Тн напряжения в диске принимаем равными ну-
лю, а его размеры — исходными для расчета. Заменив 8Г и 8/ их
выражениями (15.7) и считая при дифференцировании величины
Е, а и р,, независящими от радиуса, уравнению (15.6) можно при-
дать такой вид:
(15-8)
Из уравнения (15.8) следует, что напряжения ог и at связаны
друг с другом и не могут выбираться произвольно.
Система двух дифференциальных уравнений (15.3) и (15.8) поз-
воляет определить искомые напряжения аг и и( в зависимости от
радиуса.
§ 15.3. ДИСК ПОСТОЯННОЙ ТОЛЩИНЫ (y=const)
Уравнение (15.3) в случае диска постоянной толщины можно
записать так:
а^г-^+^+ег^».	(15.9)
Дифференцируя, находим
+=г^т+2^+2в™г-	(15.10)
ar ar£ аг
Подставив выражения (15.9) и (15.10) в уравнение (15.8), полу-
чим следующее дифференциальное уравнение:
£[“ (гЧ)]“НЗ+|»)вл»’-£а.^-.	(15.11)
327
Рис. 15.3. Кривые изменения безразмерной величины напряжений по радиусу
равномерно нагретого вращающегося диска
Дважды интегрируя уравнение (15.11), находим
(15.12:
ri
где Л1 и А3 — постоянные интегрирования; г,- — внутренний радиус
диска (для сплошного диска г<=0).
Напряжение о4 определяется из уравнения (15.9) с учетом вы-
ражения (15.12):
(15.13)
ri
Постоянные Ai и А2 находятся из граничных условий. На внеш-
нем радиусе (г=га) радиальное напряжение <тг равно напряже-
нию ога, вызванному центробежной силой лопаток.
На внутреннем радиусе диска с отверстием при г=г< напряже-
ние аг равно нулю или напряжению сжатия он, которое возникает
в диске при посадке на вал с натягом (orri<0). Величина напря-
жения ori изменяется в зависимости от режима работы турбины и
может быть определена на каждом режиме только при рассмотре-
нии совместной деформации диска и вала [7].
Если диск сплошной, то А3=0 и при г=0 напряжения а,0=<тг0.
На рис. 15.3 и 15.4 показано изменение напряжений в дисках:
сплошном и с центральным отверстием. На рис. 15.3 графики пост-
роены для вращающегося с угловой скоростью со и равномерно
нагретого диска; на рис. 15.4 — для неподвижного неравномерно
нагретого диска, в котором закон изменения величины t по радиусу
принят параболическим:
/=/04-ATf—У*,	(15.14J
Vai
328
Рис. 16.4. Кривые изменения безразмерной величины напряжений по радиусу не-
равномерно нагретого неподвижного диска
где ДТ=ТО—То — разность температур на периферии и в центре
диска; п—2 — показатель параболы.
По оси абсцисс отложены напряжения, отнесенные к величине
@ы2га2 — на рис. 15.3, и к величине ЕаДТ — на рис. 15.4.
Из рисунков видно, что в обоих случаях нагружения тангенци-
альные напряжения ati на контуре отверстия примерно вдвое боль-
ше напряжений в центре сплошного диска. Поэтому диски с отвер-
стием, как правило, выполняют со ступицей — уширенной частью
диска вблизи отверстия (см. рис. 14.2).
В неравномерно нагретом диске, при Та>Т0, на его периферии
возникают отрицательные (сжимающие) тангенциальные напря-
жения, вызванные стремлением диска на этих радиусах расширить-
ся больше, чем это допускают внутренние, более холодные участки
диска. Эти напряжения вдвое превышают напряжения в центре
сплошного диска при той же величине ДГ.
При выключении ГТД обод диска турбины остывает быстрее
его центра. В этом случае величина ДТ становится отрицательной и
напряжения аг и <тг меняют свой знак на обратный. Поэтому при
эксплуатации ГТД в дисках турбин возникают знакопеременные
напряжения, которые могут вызвать появление трещин при сравни-
тельно небольшом числе циклов запуск—останов. Это так называе-
мое явление малоцикловой усталости.
Можно иначе определить постоянные Д! и Д2- Будем считать,
что диск равномерно нагрет (2=0) и напряжения на внутреннем
радиусе диска ог='ог,-;
Записав выражения (15.12) и (15.13) для радиуса r=ri, найдем
значения постоянных Л! и А2:
Л1	।	1	* 1 -f* р. л 2
ъ	2
Тогда формулам (15.12) и (15.13) можно придать следующий
329
0 1 + 3[л— 2 (1 + (x) m2 4- (1 — и)
C=q№.	(15.21)
Отметим, что-все коэффициенты а и р — безразмерные величи-
ны, а С имеет размерность напряжения.
Формулы (15.15) и (15.16) применены в методике расчета дис-
ка произвольного профиля, изложенной в следующем параграфе.
Для облегчения вычислений по формулам (15.15) и (15.16) на
рис. 15.5 дана графическая зависимость коэффициентов ar, at, рг,
Pt, ас и рс от отношения радиусов т—г^г, где O^/n^l.
§ 1S.4. РАСЧЕТ НА РАСТЯЖЕНИЕ ДИСКА
ПРОИЗВОЛЬНОГО ПРОФИЛЯ
Ниже приводится метод поверочного расчета на растяжение
диска произвольного профиля. Размеры диска и условия его рабо-
ты заданы.
При проектировании диска новой турбины обычно исходят из
определенных конструктивных соображений, и основываются'на
анализе работы дисков, удовлетворительно зарекомендовавших се-
бя в эксплуатации.
Задачу проектирования во многом облегчает знание основных
свойств напряженного состояния дисков. О них сказано в конце
этого параграфа.
Диск произвольного профиля (рис. 15.6) всегда можно разбить
на ряд участков постоянной толщины. Число участков должно быть
не менее 7 ... 10. В местахх резким изменением толщины диска ра-
диальная протяженность участков должна быть меньше, чем в мес-
330
Рис. 15.6. Схема к расчету диска произвольного профиля на растяжение
тах с медленным изменением. Толщину каждой ступеньки выбира-
ют равной толщине истинного профиля в середине данного участка.
Таким образом, например, отрезок ab равняется отрезку Ьс. Нуме-
рация участков идет от центра к периферии.
За расчетный наружный радиус диска следует принимать в слу-
чае елочного соединения лопаток с диском радиус га (см. рис. 15.6),
при Т-образном — радиус г2 (см. рис. 12.9).
Напряжение tjra, действующее на внешнем радиусе диска, при
елочном соединении подсчитывают по формуле
_ __~ ^*Ц.п + -Рд.6 + Рц.х + Рц.в	( 1 Е ОМ
Ю	^гаУа	’	( •	)
где Рц.п, Рц.б, Рц.х, Рц.в — центробежные силы, соответственно, пе-
ра, бандажной полки, хвостовика лопатки и замкового выступа дис-
ка; уа — ширина обода на радиусе ra; г — число лопаток.
Для Т-образного соединения напряжение ага определяют по
формуле
»«=«₽—,	(15.23)
Уа
где Пр — напряжение, подсчитываемое по формуле (12.30).
В дисках ГТД изменение температуры по радиусу можно при-
нять в виде
7=7'о+ДР(—Г»
\ га/
где AT=Ta~TQ; Та и То — температуры на радиусе га и в центре
331
диска; л=3 для охлаждаемых дисков; л=2 для неохлаждаеМых
дисков.
Для диска I ступени турбины обычно Та=750. „800 К, То=
= 550... 600 К.
Заменим принятую зависимость ступенчатым графиком, как по-
казано на рис. 15.6. В пределах каждого участка температура ос-
тается постоянной, равной ее значению в середине участка. По этой
температуре находим значения Е и а, постоянные в пределах уча-
стка. Как показывают расчеты, коэффициент Пуассона мало влия-
ет на величину напряжений в дисках, поэтому примем его постоян-
ным и равным 0,3.
С учетом сделанных допущений расчет диска в пределах каждо-
го участка можно произвести по формулам (15.15) и (15.16).
Условимся обозначать напряжения на радиусе rn-i, действую-
щие со стороны (л—1)-го участка, через	1> и ацп-i)» а со сто-
роны л-го участка — через arn и Ctn (см. рис. 15.6). Установим
связь между этими напряжениями.
Рассмотрим равновесие цилиндрической поверхности m—m ра-
диуса rn-i. Предполагая равномерное распределение напряжений
по толщине (п—1)-го и л-го участков, найдем, чтоо,я1/я=о^я_1)^я_ь
откуда
агп^п_1}-^.	(15.24)
Уп
С другой стороны, радиальные удлинения £ (л—1)-го и л-го
участков на радиусе rn-i должны быть одинаковыми. Тогда, приме-
няя формулы (15.5), (15.7) и (15.24), найдем значение напряже-
ний atn‘
atn -----3< (В—1) "4“ И1 f	) °г(в—1) (<Мч ап—ifn— №п-
сч-1	\ Уп сп-1 /
(15.25)
Расчет диска ведется в следующем порядке. Неизвестное пока
тангенциальное напряжение на внутреннем радиусе первого участ-
ка обозначим через он- Радиальные напряжения в центре сплош-
ного диска равны тангенциальным, т. е. <jrl=ion. Если диск имеет
центральное отверстие, то радиальные напряжения на внутреннем
радиусе первого участка равны нулю или известному напряже-
нию — Ori. При посадке диска на вал с натягом это напряжение
оказывается сжимающим, т. е. отрицательным.
Так как -напряжения на внутреннем радиусе г0 первого участка
(см. рис. 15.6) известны, то по формулам (15.15) и (15.16) опреде-
ляем напряжения он и он на внешнем радиусе и этого участ-
ка. При этом mi—ro/ri, a Ci=iQ(o2ri2. Для сплошного диска
0г1 = (аГ1_1_®н)3н — ас/ч =-^i3/!— Bi; 3<i=(?riH"?fl)3/i— Рс/н =
= Kiaa— Ц.
332
Напряжения на внутреннем радиусе и второго участка согласно
формулам (15.24) и (15.25) равны:

а,2 —— зГ]=—	—— Bi=A^/i — Bj;
У2 У2	У2
с;+„(ja._&. л; 1	- Г	£;+„(л_ &.) й;+
\ У2 El! J L^l	\У2 El/
+(а^2 — ctj/J В2] ~ Ktfti ~ ^2-
Переходя, таким образом, от участка к участку, убедимся, что
на любом радиусе
ат—Аяац Вя\
8tn~K ifltl	л»
°rn— Anati — В ni
atn—KnPfk~ £л-
(15.26)
(15.27)
Рекуррентные формулы для коэффициентов Ап, Вп и др. имеют
следующий вид:
л  ‘Уп-l д' .
Ул
Вп=Ул=^в'п-1\
Уп
Ka=^-Kn-i+v>	AU;
&п—1	\ Уп ^n—l J
Ln=~^~ L'n-i+*	- Щ B'„-i+(a^„-a„_i^i)E„;
Ея-1	\ Ум Ец—1/
Ая=а,я Ая -|- o-tn^n!
Вп = ^гцВц + О/ л^ л + асСц ;
= Р/л^л!
^п= ?гл^л+ Рм^лЧ" РСд^Л"
(15.28)
Из формул (15.26) и (15.27) видно, что величины Ап, Кп, Ап',
Кп безразмерные, а Вп, Ln', Вп', Ln' имеют размерность напряже-
ния.
Для сплошного диска при r=0 ari=|Oii=Aiori—В4; Он=
=Х1<гн—М, откуда А1==4; Bi=0; Ki = l; Li=Q,
На внутреннем радиусе диска, напрессованного на вал,
Ori=Aioti—Bi; a(i = XiO*i—£ь следовательно, Ai=0; Bl=]orri|;
Л1 = 1; £i=0.
Для диска со свободным отверстием Ai=0; ’ Bi=0;
/<! = !; £1=0.
По формулам (15.28) последовательно определяем все коэффи-
циенты.
333
На внешнем радиусе диска га согласно первому уравнению
(15.27) <Jra=Aa<Jti—Ba, откуда
яга + В а
ап =
(15.29)
где Ога — напряжение, действующее на внешней цилиндрической
поверхности диска; Аа' и Ва' — коэффициенты для внешнего ради-
уса последнего участка.
Подставляя полученное значение ati в, уравнения (15.26) и
(15.27), находим значения напряжений ог и ot на внутреннем и
внешнем радиусах каждого участка.
На радиусах стыка участков диска, имеющих действительно (по
чертежу) разную толщину, получаются по два значения напряже-
ний: радиальных ar(n-i) и агя; тангенциальных—ацм_1) и at„.
В этом случае эпюры напряжений на указанных радиусах будут
изменяться скачком от o'r(n-1) ДО огя и от до atn (рис. 15.7).
Если же скачок в толщине участков получается только в резуль-
тате схематизации профиля диска, то за напряжения на радиусе
стыка участков можно принять средние напряжения:
аЦп-1) + вгп Ai-1 + Ап  Вп-1 + Ва _
2	2
ср  ° t (п-1) +	^п-1 + 4г
°/п-------------------------
ср__
ат —
1л
— ап
2
(15. зо;

т *<п
2
2
2
334
н	ra	У	Т	t	а-106	Wn—1	m	аг==₽.		ас	₽с	г С	асС		£-10“5	Еа	/ -1 Еп А	£
						«п										Еп-1		
«1 ST* ж	мм		к		1/К	—	—	—	—	—	л	МН/м»				—		
1	2	3	4	5	б	7	s	9	10	и	12	13	14	15	16	17	18	
1	50	33	604	зи	16,6	—	0	0,500	0,500	0,412	0,237	35,1	14,5	8,3	1,85	—		
2	64	50	621	328	16,8	0,659	0,781	0,805	0,194	0,181	0,071	57,6	10,4	4,1	1,83	0,989	—0,098	
3	100	29	644	351	17,1	1,724	0,640	0,704	0,295	0,264	0,119	140,5	37,1	16,7	1,82	0,994	0,218	
4	136	22	692	399	17,7	1,318	0,735	0,770	0,229	0,211	0,087	259,9	54,8	22,6	1,78	0,978	0,102	
5	150	18	735	442	18,3	1,222	0,906	0 911	0,088	0,086	0,029	316,1	27,2	9,2	1,74	0,977	0,073	
6	158	16	757	464	18,5	1,124	0,949	0,950	0,049	: 0,048	0,015	350,8	16,8	5,3	1,72	0,988	0,040	
7	166	18	786	493	18,9	0,888	0,951	0,952	0,047	0,046	0,014	387,2	17,8	5,4	1,70	0,988	—0,029	
8	174	24	791	498	19,0	0,750	0,954	0,955	0,044	0,044	0,014	425,4	18,7	6,0	1,70	1,000	—0,074	
£
Продолжение табл. 15.1
	Ча 1 а 1	А	В	К	L	Д'	В1		и	*г		аг	•f		
СО is	^8*														
се & S	МН/м*	—		—	МН/м»	—	МН/м»	—				МН/м	2		
	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33
1	—	1	0	1	.0	1	1 14,5	1	8,3	389,0	389,0	374,5	380,6	—-	—
2	63,6	0,659	9,6	0,89	70,5	0,704	31,9	0,845	62,7	247,1	• 275,9	242,3	266,1	—•	д«.
3	89,5	1,215	55,0	0,995	158,9	1,150	122,8	1,060	144,9	417,7	228,2	324,6,	267,4	376,3	186,7
4	188,7	1,516	161,9	1,154	343,0	1,433	258,4	1,237	324,1	427,9	106,0	299,1	157,2	332,3	77,1
5	178,6	1,751	315,8	1,314	514,4	1,712	360,7	1,353	506,0	365,5	—2,9	305,5	20,5	324,6	—15,9
6	85,2	1,926	405,8	1,408	600,2	1,901	432,4	1,433	596,1	343,7	—52,4	307,1	—38,4	290,1	—105,1
7	124,7	1,690	384,4	1,360	701,0	1,674	417,2	1,375	691,8	273,0	—171,8	234,2	—156,6	204,9	—177,7
8	24,5	1,255	312,9	1,250	685,1	1,255	348,4	1,250	674,4	175,6	—198,7	140,0	—188,0	—	
Расчет сведен в табл. 15.1.
Напряжение <jta на внешнем радиусе диска найдем по второму
уравнению (15.27). По результатам расчета строятся кривые рас-
пределения напряжений ог и ot по радиусу диска.
Радиальное удлинение на внешнем радиусе га, необходимое для
подсчета радиального зазора между корпусом турбины и рабочи-
ми лопатками, можно определить, используя формулы (15.5) и
(15.7):
Ъ = V (ata - №га) +	(15- 31)
с
Индексом «а» здесь помечены соответствующие величины на
радиусе га.
Отметим некоторые особенности напряженного состояния дис-
ков.
1.	Напряжения, вызванные только центробежными силами ди-
ска (T=const), не зависят от модуля упругости Е, пропорциональ-
ны квадрату угловой скорости, т. е. квадрату числа оборотов и
плотности материала диска.
2.	Температурные напряжения (<о=0)^при одинаковом законе
распределения температуры по радиусу ’пропорциональны разно-
сти температур обода и центра диска ДТ (см. формулу (15.14)]. Эти
напряжения пропорциональны также величинам Е и а (если пос-
ледние неизменны по радиусу).
3.	Если наружный радиус диска изменить в К. раз при сохране-
нии тех же зависимостей у [—) и t(—)> то температурные нап-
ряжения останутся прежними, а напряжения от центробежных сил
изменятся в К2 раз.
4.	Суммарные напряжения в диске сохраняют свои значения
при изменении толщины диска в одинаковое число раз на вбех ра-
диусах, если напряжение ога при этом не изменяется.
§ 15.5.	ПРИМЕР РАСЧЕТА ДИСКА ПРОИЗВОЛЬНОГО ПРОФИЛЯ
Определить напряжения, вызванные вращением и неравномерным нагревом,
в диске, изображенном на рис. 15.7. Частота вращения диска /2=12500 мин-1.
Напряжение ага=140 МН/м2. Материал диска ХН77ТЮР (ЭИ437Б); его плот-
ность р=8200 кг/м3.
Изменение температуры по радиусу показано на рис. 15.7. Разность темпе-
ратур между поверхностью обода и центром ДТ=200К. Профиль диска заменен
восьмью участками постоянной толщины. На периферии диска, где резко изме-
няются его толщина и напряжения аг и ст*, радиальные размеры ступенек посто-
янной толщины выбраны меньше, чем в центральной части. Это увеличивает точ-
ность расчета.
Результаты расчета приведены в табл. 15.1. Распределение напряжений по
радиусу диска показано на рис. 15.7.
§ 15.6.	РАСЧЕТ КОЛЕСА РАДИАЛЬНОЙ ТУРБИНЫ
На рис. 15.8 изображено колесо радиальной центростремительной турбины.
Ввиду сложной конструктивной формы такого колеса точный расчет его на проч-
ность представляет большие трудности [2].
337
Рис. 15.8. Схема колеса радиально-осевой турбины и кривые напряжений в нем
Приближенный расчет может быть произведен по методике, изложенной в
§ 15.4. При этом жесткость лопаток, т. е. их способность воспринимать нагруз-
ки, не учитывается. Масса лопаток считается равномерно распределенной по
окружности. Следовательно, масса элементарного кольца высотой dr, выделен-
ного на радиусе г, может быть записана так:
1 + т;----]%$>rydr,
2я,гу /
где р — плотность материала колеса; z — число лопаток.
Остальные обозначения ясны из рис. 15.9.
Введем обозначение
Опр = Q11 4-	)•	(15.32)
\ 2ягу /
Тогда центробежная сила dPn элемента этого кольца длиной rdq> (ф —
центральный угол) определится по формуле
аРц == Qap<&rtyd<pdrt
использованной в § 15.2.
Следовательно, для расчета на прочность диска радиальной турбины с уче-
том присоединенной массы лопаток можно использовать методику § 15.4. Особен-
ность в данном случае заключается в том, что приведенная плотность рпр изме-
няется по радиусу. Это следует учитывать при определении величины С=рпрХ
входящей в формулы (15.15) и (15.16) (графа 13 табл. 15.1).
Распределение напряжений ог и в диске радиальной турбины показано
на рис. 15.8 тонкими линиями; жирными линиями нанесены значения этих напря-
жений, вычисленные с учетом жесткости лопаток.	>
Из сравнения кривых следует, что при учете жесткости лопаток несколько
увеличиваются максимальные тангенциальные напряжения на внутренней поверх-
ности диска и заметно (на 30 ... 50%) снижаются максимальные радиальные
напряжения в его центральной части.
В колесе возникают также термические напряжения, вызванные как нерав-
номерным нагревом диска по радиусу, так и разностью температур лопаток и
диска. Картина распределения напряжений значительно изменяется, если сечение
полотна диска несимметрично. Это обычно наблюдается в колесах с лопатками,
расположенными на одной стороне диска. В этом случае в нем помимо напря-
жения растяжения, возникают также напряжения изгиба. В результате напряже-
ний аг и а* на стороне диска, где размещены лопатки, могут в 2 ... 4 раза
превышать напряжения на свободной стороне диска.
338
Рис. 15.9. Эпюры нагрузок, изгибающих диск
§ 15.7. РАСЧЕТ ДИСКА НА ИЗГИБ
Диск газовой турбины кроме растяжения подвержен также из-
гибу, который вызывают: 1) разность давлений Др по обе стороны
диска, где Др=р'—р" (см. рис. 15.9); 2) действующие на диск от
лопаток перерезывающая сила Qn и изгибающий момент Мл, при-
ходящиеся на единицу длины окружности внешнего радиуса диска
Га, 3) градиент температуры по толщине диска.
В дисках малой толщины по сравнению с наружным диаметром
или в сравнительно толстых дисках при достаточно большой разно-
сти температур боковых поверхностей напряжения от изгиба могут
достигать 'значений, соизмеримых с напряжениями растяжения.
Будем считать, что на радиусе Г\ в месте соединения с валом
(или соседними дисками) диск жестко защемлен (см. рис. 15.9).
Для расчета заменим профиль диска участками постоянной толщи-
ны. При этом можно использовать ту же схему, что и в расчете ди-
ска на растяжение. Необходимо только изменить нумерацию участ-
ков. Положим, что в пределах участка величины Др и ДТ (разность
температур боковых поверхностей диска I и II) постоянны. Эти ве-
личины будем считать положительными, если давление и темпера-
тура на поверхности I больше. От участка к участку величины Др и
ДТ могут изменяться.
Для дальнейшего упрощения расчета заменим действие на диск
распределенной по радиусу разности давлений Др системой сосре-
доточенных сил Рп, приложенных на внешних радиусах участков.
(Это допущение идет в запас прочности. Чем меньше радиальная
протяженность участков, тем точнее расчет).
339
Величину Рп найдем по формуле
P4=A^(r’+1-r’),	(15.33)
где Дрп — разность давлений на среднем радиусе л-го участка.
При такой схематизации нагрузки перерезывающая сила Sn в
пределах каждого участка остается постоянной. Расчет сил Sn
удобно вести от периферии к центру. Для периферийного Л-го уча-
стка Sh==5a+Pfe, где 5Л — осевая сила, передаваемая на диск от
лопаток. Силу Ръ. подсчитываем по формуле (15.33), полагая
rk+l = l'a. Величину 5Я МОЖНО подсчитать, суммируя усилия Pai
(см. формулу 15.8) и умножая результат на число рабочих лопа-
ток. В эту величину должна входить также осевая сила, действую-
щая на кольцевой участок диска между наружным (расчетным)
радиусом га и радиусом корневого сечения рабочих лопаток г^. Эту
силу можно подсчитать по формуле (15.33).
Для остальных участков, при n^k—1,
5п=5я+1+Рл.	(15.34)
Эпюра перерезывающих сил показана на рис. 15.9. Изменение
температуры по толщине диска примем линейным.
В излагаемом методе влиянием растяжения на изгиб пренебре-
гаем.
Рассмотрим изгиб кольца постоянной толщины. Вырежем из не*
го элемент двумя цилиндрическими сечениями с радиусами г и
r+dr и двумя осевыми плоскостями, отстоящими на угол dm (рис.
15.10).
На единицу длины окружности радиуса г цилиндрической по-
верхности ab действуют перерезывающая сила Q и изгибающий мо-
мент Мг.
IS
Очевидно, Q=——, откуда
2 л г
Qr= —=const.	(15.35)
Момент Мг является результирующим моментом от нормаль-
ных.к поверхности ab напряжений ог, распределение которых по
толщине диска оказывается линейным, если принять так называе-
мую гипотезу жесткой (или прямой) нормали. Согласно этой гипо-
тезе любая нормаль к средней плоскости диска (см. рис. 15.9, 0—0),
проведенная до нагружения диска, остается прямой, нормальной к
изогнутой в результате изгиба срединной поверхности 0'0.
На поверхности cd действует сила Q+dQ и момент Mr+dMr.
На гранях Ьс и ad из-за осевой симметрии задачи перерезывающие
силы равны нулю. Нормальные к этим граням напряжения at так-
же линейно распределены по толщине (см. рис. 15.10 сеч. А—А).
Их результирующие моменты Mt, приходящиеся на единицу длины
вдоль радиуса, равны по абсолютному значению.
Положительные направления сил, напряжений и моментов по-
казаны на рис. 15.10. Справа на рисунке изображены векторами
340
Рис. 15.10. Схема к расчету диска на изгиб
моментц, действующие на поверхности элемента. Условно к центру
элемента приложен также момент (приходящийся на единицу дли-
ны в окружном направлении) от сил Q и Q+dQ, который равен
Qdr (с точностью до малых величин высшего порядка).
Рассмотрим равновесие элемента относительно окружного нап-
равления под действием приложенных к нему моментов.
На грань ab действует момент A4rrrf<p; на грань cd— (Л4Г+
+dMr) (r+dr)dq>; на каждую из граней Ьс и ad—Mtdr; на элемент
в целом — Qfdrdtp.
Так как суммарная проекция моментов Mtdr на окружное нап-
равление равна 2Mtdr sin dq!2=Mtdrdq, то уравнение равно-
весия примет вид
г \-Mr-Mt-\-Qr=0.	(15.36)
Второе уравнение для определения моментов Мг и Mt получим,
рассматривая деформации изгиба кольца.
Из теории изгиба пластин имеем формулы (с учетом принятого
здесь правила знаков для Mr, Mt, w и ДТ)
\ г аг аг*	/
где D==	----цилиндрическая жесткость; w — прогиб дис-
ка в направлении оси; F==-^~; а — коэффициент линейного рас-
ширения.
Из этих формул найдем значения производных
dw_=rMt-^rMt_ , F	(1б g8)
dr	(1 —|*з)О	v
_d2w = Mr-y.Mt. I Р	.(15.39)
dr*	(1 —|*2)D 1	'
341
Дифференцируя уравнение (15.38) с учетом, что AT=const и
d^w
|x=const, и приравнивая два выражения для —— , приходим к
dr*
уравнению совместности деформаций:
+	(1+|*)ЛГ,-О.	(15.40)
Из уравнений (15.39) и (15.36) с учетом условия (15.35) полу-
чим дифференциальное уравнение
г^М^ЗгМ'г-----(14-[*)Qr= -	(15.41)
Решение этого уравнения
(15.42)
Г2 4Л
где —внутренний радиус кольца [для n-го кольца (см. рис. 15.9)
Л=гЛ-11.
Из уравнения (15.36)
^=Сх+ -^-+А[(1_!*)+(1 + 1л)1пг//г].	(15.43)
Г* т
Как и в расчете диска на растяжение, найдем постоянные Ci и
считая известными значения Mri и Mti на радиусе г<.
Тогда формулам (15.42) и (15.43) можно придать такой вид:
Mr—arMrl-}-atMtt — oqS;	(15.44)
.	(15.45)
В этих формулах коэффициенты ar, at, ₽г и pt те же функции вели-
чины /и=Г(/г, что и в выражениях (15.15) и (15.16). Они подсчи-
тываются по формулам (15.17) и (15Л8) или находятся по графи-
кам, показанным на рис. 15.5.
Коэффициенты
(H^ln/nl;	(15.46)
₽{г=-77[(1-1‘)112:^- + (1 + н)1п/п1.	(15.47)
4Л l	z	j
Для их определения можно воспользоваться рис. 15.5.
По своему виду уравнения (15.44) и (15.45) схожи с уравнени-
ями (15.15) и (15.16). Поэтому методика расчета диска на изгиб
имеет много общего с методикой расчета на растяжение, изложен-
ной в § 15.4.
По уравнениям (15.44) и (15.45) находим моменты Mr(n-i) и
М/(Я_1) на периферии (п—1)-го участка, полагая т=^=±- .
га
По условию равновесия поверхности радиуса rn-i
Мга^М\^.	(15.48)
342
_	«, dw	t «\
Значения производной--на радиусе rn-i для (n—1) и n-го
dr
участков должны быть равны между собой.
Применяя формулы (15.38) и (15.45), получим
MtK	fl—2«_)X(n-1)-(l-{*2)£>«(Fn-F„_1).
Un—1 *
(15.49)
71—1
Так как на внутреннем радиусе первого участка диска по усло-
вию закрепления =0» то из формулы (15.38)
Л4п=|*Л1г1-(1-Яад-	(15.50)
Переходя последовательно от участка к участку по формулам
(15.50), (15.44), (15.45), (15.48) и (15.49), найдем, что
МГП=АпМЛ Bnl 1	Zjg 51»
Мгп~Ац.Мг^—Вп\	(15
Рекуррентные формулы для коэффициентов системы уравнений
(15.51), (15.52) имеют следующий вид:
A„=X_i;
Ва—Вп—\\
Кп=-^Кп-л+?.(\--£-} A;_i;
Dn-l	\	£>n-l /
Dn~l	\	Д1-1 /
Ая=агяАя-(-а/л7<’я;	(15.53)
Вп=ЪгпВп + at п^п +	п 1
Кп=%лАп+^аКп,
L* = РлА + &л Д’. + Рвл^Я-
Здесь коэффициенты Ап, К.п, Ап' и Кп — безразмерные, а Вп,
Ln, Вп' и Ln имеют размерность силы (Н).
Для рассматриваемой схемы диска из формул (15.50) и (15.51)
следует, что
Ах=1; 51=0; ^=1*; Z1=(l-lb2)D1Ft.	(15.54)
По формулам (15.53) последовательно определяем’ все коэффи-
циенты.
На внешнем радиусе га имеем Мл= Aa'Mri—Ва', откуда
•	(15.55)
343
По формулам (15.51) и (15.52) находим значения моментов на
радиусах стыка участков. При резком изменении толщины сосед-
них участков эпюра момента Мг, согласно формуле (15.48), не пре-
терпевает разрыва, а на эпюре Mt будет скачок. Если в -реальном
диске изменения толщины на стыке участков нет, то среднее значе-
ние Af<n на радиусе гп найдем по формуле
- - ^(«-1) ^<я-_ ^«-14* К‘п м J
2	2	2
-. (15.56)
После того как определены моменты Мг и Mt, найдем напряже-
ния изгиба
----------±6Л1Г-	__
°rmax___________________> e/max—	•
(15.57)
Положительные напряжения (растягивающие) действуют на
стороне I, отрицательные (сжимающие) — на стороне II (см. рис.
15.9). Эти напряжения должны быть сложены с напряжениями,
найденными в результате расчета диска на растяжение (§ 15.4).
В формулах (15.57) значения моментов Мг и Mt и толщины дис-
ка должны приниматься соответственно номеру участка. Таким об-
разом, на стыке участков с резким изменением толщины будет
иметь место скачок напряжений or max. несмотря на равенство мо-
ментов Мгп и Mr(n-i)' Изложенный здесь метод расчета дисков на
изгиб и расчет на растяжение (§ 15.4) обеспечивают достаточно
удовлетворительную точность определения напряжений в сравни-
тельно тонких (по отношению к наружному диаметру) дисках.
Для расчета толстых дисков и определения концентрации напря-
жений, возникающих в местах резкого изменения толщины, в нас-
тоящее время разработан метод конечных элементов (МКЭ)1. Рас-
чет по этому методу требует использования ЭВМ с высоким быст-
родействием и большой памятью.
Алгоритмы и программы расчета методом конечных элементов
дисков осевых и колес радиально-осевых турбин (с учетом нали'
чия лопаток) разработаны и используются в КАИ и других органи-
зациях.
1 Зенкевич О. Метод конечных элементов в технике. — М.: Мир, 1975.
Глава XVI
РАСЧЕТЫ ДИСКОВ НА ПРОЧНОСТЬ С УЧЕТрМ
ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ.
МАТЕРИАЛЫ ДЛЯ ИЗГОТОВЛЕНИЯ ДИСКОВ.
КРИТЕРИИ И ЗАПАСЫ ПРОЧНОСТИ
§ 16.1. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
НА КРАЯХ ОТВЕРСТИЯ В ДИСКЕ
На краях отверстий, которые сверлят в полотне диска, напри-
мер, для выравнивания давлений по обе стороны диска или для
прохода охлаждающего воздуха (рис. 16.1), возникает значитель-
ная концентрация напряжений.
Максимальные радиальные напряжения возникают в точках В,
максимальные тангенциальные — в точке А. Эти напряжения могут
в два-три раза превышать напряжения в аналогичном диске без
отверстия.
Анализ характера разрушения дисков с эксцентричными отвер-
стиями показывает, что в случае расположения отверстия в зоне,
где ог>0< (в сплошном диске), диск разрушается по кольцевому
сечению b—b (см. рис. 16.1).
Если отверстие расположено в зоне, где Ог<<гг, то разрыв диска
происходит по сечению а—а под действием высоких тангенциаль-
ных напряжений. В этом случае происходят более серьезные раз-
рушения диска.
Таким образом, отверстия по возможности следует располагать
в области малых тангенциальных напряжений.
Для случая ОгСое теоретический коэффициент концентрации
напряжений можно определить по формуле [7J
_ з °г__________—
о*	at	п
(16-1)
где аг и ot — напряжения в сплошном диске (без эксцентричного
отверстия) в точке A; Ot max— местное напряжение в той же точке
диска с отверстием; d — диаметр отверстия; п — наименьшее рас-
стояние между краями отверстий по окружности.
Несмотря на то, что напряжения на краях отверстий, вычислен-
ные по теоретическому коэффициенту концентрации напряжений,
могут превысить предел текучести материала, они не всегда опас-
ны: в дисках из достаточно плас
тичных материалов они вызыва-
ют местную пластическую дефор-
мацию, вследствие которой нап-
ряжения передаются соседним
слоям металла и распределяются
между ними. Необходимо только,
Рис. 16.1. Схема отверстия в полотне
• диска
345
чтобы отверстие имело возможно малый диаметр, было чисто обра-
ботано (не менее чем по 7-му классу чистоты) и кромки отверстия
были тщательно скруглены возможно большим радиусом (см.
рис. 16.1).
§ 16.2. РАСЧЕТ ДИСКА С УЧЕТОМ ПЛАСТИЧЕСКИХ
ДЕФОРМАЦИЙ
Диски авиационных газовых турбин в целях снижения массы
проектируют сравнительно тонкими. Такие диски иногда имеют
области, в которых напряжения превышают предел упругости (про-
порциональности). В этих областях возникают местные пластиче-
ские деформации, которые приводят к иному распределению напря-
жений по радиусу диска, нежели при наличии только упругих де-
формаций.
Диски, в которых наряду с упругими имеют место пластические
деформации, будем называть упругопластическими. Изла-
гаемая ниже методика их расчета базируется на теории малых уп-
ругопластических деформаций [2, 10]. Преимуществом данной мето-
дики является возможность распространения изложенного выше ме-
тода расчета дисков, находящихся в упругом состоянии, для расче-
та дисков, в которых возникают пластические деформации, и дис-
ков, работающих в условиях ползучести (см. § 16.4). Единый во
всех трех указанных задачах алгоритм решения удобен и при руч-
ном счете и в особенности при расчете с помощью ЭЦВМ.
Основные зависимости теории малых
упругопластических деформаций
Рассмотрим диаграмму деформирования при чистом растяже-
нии (рис. 16.2). До напряжения, равного пределу упругости се, для
большинства металлов, как известно, имеет место линейная зависи-
мость между напряжением а и деформацией &:
о=Еь,	(16.2)
где модуль упругости материала Е численно равен тангенсу угла а,
т. е. £=tga. Для напряжений, соответствующих точке а, при кото-
рых уже возникают пластические деформации, очевидно, можно за-
писать по аналогии
«»Г»,	(16.3)
где £'=tg р.
Принципиальная разница зависимо-
стей (16.2) и (16.3) состоит в том, что мо-
дуль упругости Е одинаков для всех то-
чек упругого равномерно нагретого тела
и не зависит от степени деформации.
В противоположность этому величина Е'
зависит от степени деформации и поэто-
му различна в каждой точке тела, испы-
тывающего пластические деформации.
Рис. 16.2. Диаграмма деформирования
346
В общем случае объемного напряженного состояния упругого
тела также имеется зависимость, аналогичная (16.2),
(16.4)
где	=^~ V (°i—°2)2+(°2 — «з)*+ (°з—oi)2; '	(16.5)
Ь = V (ei- e2)2+(s2- е3)2+ (е3- 61)2.	(16.6)
О
Величина ot называется интенсивностью напряжений,
8< — интенсивностью деформаций. В формулах (16.5) и
(16.6) сгь 02 и оз — главные напряжения; вь щ и ез — главные отно-
сительные удлинения.
Обширные эксперименты и теоретические исследования дают
возможность записывать закон пластической деформации для лю-
бого объемного напряженного состояния в виде
,	(16.7)
В этой зависимости Е' та же величина, что и в формуле (16.3).
Это важное обстоятельство позволяет при расчете любого объем-
ного напряженного состояния (упругого или упругопластического)
пользоваться диаграммой о—в, полученной в опытах на чистое
растяжение.
Следует заметить, что закон (16.7) справедлив лишь в случае
простого нагружения или достаточно близкого к нему. Под прос-
тым нагружением понимают такой процесс, когда действующие на
тело нагрузки возрастают пропорционально их общему параметру,
например, квадрату числа оборотов в случае растяжения диска *.
В рассматриваемой теории при пластических деформациях ма-
териал считается несжимаемым. Отсюда следует, что коэффициент
Пуассона у,=0,5.
Для дисков (плоское напряженное состояние) зависимость
компонентов деформации от компонентов напряжений выражается
следующими формулами: -
е,=-^-(а,—0,5^) 4-а/;
С.
at.
С
(16.8)
Формулы (16.8) аналогичны формулам (15.7), записанным для
у=0,5. Разница заключается в том, что величина Е' зависит от де-
формации и температуры в данной точке диска, так как вид диаг-
раммы деформирования а—& определяется температурой испыта-
ния (см. рис. 16.2).
Подробными исследованиями установлено, что напряжения в
упругом диске при ц=0,3 и 0,5 практически одинаковы. Следова'
1 Более строгий расчет требует учета истории нагружения диска и может
быть выполнен по методу, изложенному в работе [17].
347
тельно, при расчете дисков можно пользоваться формулами (16.8)
как для пластической, так и для упругой областей.
Очевидно, что уравнение равновесия (15.3) действительно и для
дисков, имеющих области пластических деформаций.
Таким образом, установлена аналогия между основными урав-
нениями, необходимыми для расчета упругих и упругопластических
дисков.
Расчет дисков с учетом пластических деформаций
Исходя из сказанного выше, для расчета дисков, имеющих об-
ласти пластических деформаций, можно принять тот же метод, что
и для расчета дисков, находящихся в упругом состоянии (§ 15.4).
Основная, принципиальная разница будет заключаться в том,
что при расчете диска, находящегося в упругом состоянии, модуль
упругости Е — известная в каждой точке диска величина, завися-
щая только от температуры, а Е' зависит, кроме того, и от степени
деформации в данной точке, которая заранее неизвестна. Поэтому
расчет упругопластических дисков ведут методом последователь-
ных приближений. Профиль диска по-прежнему заменяют участка-
ми постоянной толщины.
Методом, изложенным в § 15.4, диск рассчитывают как упру-
гий. Полученные напряжения принимают за нулевое приближение.
Коэффициент ц при этом берут равным 0,5. Изменение у скажется
только на коэффициентах ас и рс, значения которых при у=0,5
приведены на рис. 15.4 пунктирными линиями.
В качестве нулевого приближения можно принять и упругие
напряжения, вычисленные при у=0,3. Однако расчет первого и
последующих приближений выполняется для у=0,5.
По значениям аг и на среднем радиусе каждого участка вы-
числяют at. Для дисков формула (16.5) принимает вид
о/ =	— araz.	(16.9)
Пусть значению о< какого-либо участка диска соответствует
точка Оо> которая лежит на продолжении начального, линейного
отрезка диаграммы деформирования о—8 (рис. 16.3) *.
Деформации ео, соответствующей точке Oq, на диаграмме дефор-
мирования отвечает напряжение характеризуемое точкой d0.
Если провести луч Odo, то E'=ig ?i=«rf0/8o«
Аналогичные вычисления выполняют для каждого участка дис-
ка. Полученные значения Е' принимают за новые значения моду-
ля упругости на каждом участке. После этого выполняют новый
расчет диска как упругого. В результате получают напряжения ог
и ot в первом приближении. По ним снова по формуле (16.9) под-
считывают значения для среднего радиуса каждого участка.
Пусть этим напряжениям в рассматриваемом участке отвечает
точка ai, лежащая на продолжении луча Odo.
1 В неравномерно нагретом диске кривые деформирования и, следовательно,
угол а будут различными для каждого участка диска.
348
По деформации ei и напряжению ад,, соответствующему точ-
ке d\, определяют новые значения Е' для данного участка: Е'=
=tg р2=ад,/ех.
По полученным таким образом для каждого участка значениям
Е' выполняют расчет диска как упругого во втором приближении
и т. д.
Процесс последовательных приближений для рассматриваемого
участка изображается линией а0> ai, «2,...»а. Точка а пересечения
этой линии с диаграммой деформирования соответствует действи-
тельным напряжениям (оа) и деформации (ев), возникающим в се-
редине данного участка упругопластического диска.
Кривые, изображающие процесс последовательных приближе-
ний для других участков данного диска, могут по виду отличаться
от кривой do,' - • •>
Так, если действительные напряжения в каком-либо участке
диска, находящегося в упругопластическом состоянии больше, чем
полученные в нулевом приближении, то процесс последовательных
приближений для этого участка изобразится кривой 6о,Если
же напряжения не превышают предела упругости, то указанный
процесс изобразится совокупностью точек Со,.... с, лежащих на ли-
нейном участке диаграммы деформирования.
При определении напряженного состояния диска расчет можно
закончить, когда напряжения двух последующих приближений бу
дут практически одинаковыми. Для этого обычно бывает достаточ-
но двух-трех приближений. Для правильного подсчета радиально-
го зазора между рабочими лопатками и корпусом, для определения
посадки диска на вал в рабочем состоянии или для сравнения воз-
никающих пластических деформаций с допустимыми для данного
материала может потребоваться определение деформированного
состояния диска. В этом случае расчет следует закончить, когда,
кроме напряжений, будут практически одинаковыми значения в<
двух последующих приближений в каждой точке диска.
Радиальные удлинения диска,
га, можно определить, используя
формулы (15.5) и (16.8):
= т- (°<« 0,5вгв) -|- aafara,
(16.10)
где Еа определяется действитель-
ными значениями о, и е, на внеш-
нем радиусе (например, точкой а
на рис. 16.3).
После расчета диска можно
определить границы между упру-
гой и пластической областями.
Для этого, нужно построить гра-
например, на внешнем радиусе
°	ео £i sa e(et)
Рис. 16.3. Диаграмма о—в к расчету дис-
ка с учетом пластических деформаций
349
фики изменения по радиусу диска интенсивности напряжений и
предела упругости ав и найти точки их пересечения. При
‘имеют место деформации упругие, при Ог>ое — пластические де-
формации.
Порядок расчета упругопластического диска
1.	Для расчета диска должны быть заданы схема разбивки на участки и
размеры диска, число его оборотов, величина напряжений на внешнем и внут-
реннем радиусах ога и вп, плотность материала, закон изменения по радиусу
температуры, модуля упругости, коэффициента линейного расширения и, нако-
нец, кривые деформирования материала диска в диапазоне температур в диске. _
Эти кривые приведены в справочных руководствах. Весь расчет выполняют на
бланке, аналогичном табл. 15.1. Вначале заполняют столбцы 1 ... 15.
2.	По методике, изложенной в § 15.4, производят расчет диска как упругого
(нулевое приближение). При этом заполняют графы 16 ... 33. В дополнительную
графу 34 записывают значение о,, подсчитанное по формуле (16.9) для значе-
ний ог и О/ в середине каждого участка.
3.	Вычисляют напряжения в первом приближении. Для этого при помощи
кривых деформирования по величинам Of определяют значения Е для каждого»
участка, принимая их за модуль упругости в тех же участках, и в графах
16 ... 33 вновь выполняют расчет диска как упругого.
4.	По величинам ог первого приближения и кривым деформирования под-
считывают новые значения Е' для каждого участка и так же, как в предыду-
щем пункте, определяют напряжения во втором приближении и т. д.
5.	Процесс последовательных приближений заканчивается, если значения
напряжений (или Е' при определении деформированного состояния диска) двух
последующих приближений практически совпадают.
6.	При необходимости определения радиальных удлинений в каком-либо
сечении используют формулу (16.10), записанную для данного сечения.
На рис. 16.4 для примера показано распределение напряжений в диске, вы-
численных с учетом (сплошные линии) пластических деформаций и без их учета
(пунктирные линии).
Видно, что напряжения, подсчитанные с учетом пластических деформаций^
изменяются по радиусу диска менее резко, чем это следует по расчету в пред-
положении только упругих деформаций. Действительные максимальные танген-
циальные напряжения на внутреннем радиусе в данном примере на 20% меньше.
Этим объясняется то обстоятельство, что в ряде случаев диски с отверстием
удовлетворительно работают при напряжениях на внутреннем радиусе," превы-
шающих предел текучести.
§ 16.3.	РАСЧЕТ ДИСКА С УЧЕТОМ ПОЛЗУЧЕСТИ МЕТАЛЛА
Понятие о ползучести металлов при одноосном напряженном
состоянии приведено в § 11.3. Явление ползучести наблюдается и
в дисках газовых турбин, работающих при температуре выше
650 ... 750 К. Ползучесть приводит с течением времени к перерас-
пределению напряжений в диске.
Расчеты по определению напряжений в дисках с учетом ползу-
чести базируются на различных гипотезах, приближенно описыва-
ющих механизм ползучести.
Так как деформации ползучести являются пластическими, та
удобно и в данном случае применить теорию малых упругопласти-
ческих деформаций, о которой кратко сказано в § 16.2.
Если воспользоваться гипотезой старения в формулировке
Ю. Н. Работнова, согласно которой а=/(е, т), где е — полная де-
350
Рис. 16.4. Кривые напряжений в диске, находящемся в упругопластическом сос-
тоянии
формация, то для расчета диска с учетом ползучести металла мож-
но применить метод, изложенный в § 16.2.
Особенность такого расчета заключается в том, что диаграммы
о—8 для различных значений времени различны. Построение этих
диаграмм, называемых изохронными кривыми, ясно из рис. 16.5.
Слева на фигуре изображена диаграмма ползучести, снимаемая
при испытаниях материала в условиях одноосного растяжения при
постоянных напряжениях (oi=const; о2=const и т. д.) и одинако-
вой температуре. Справа перестроением получена диаграмма
для той же температуры и времени x=xv.
Аналогичные диаграммы можно построить для любых других
значений температуры и времени. Принимая их за диаграммы
Ci—8i, можно определить распределение напряжений и деформаций
в диске для соответствующих значений времени по методу, изло-
женному в § 16.2 *.
В период установившейся ползучести напряжения в диске оста-
ются неизменными, а деформации в каждой точке радиуса диска
растут пропорционально времени. Поэтому расчет напряжений при
установившейся ползучести можно сделать для одного значения
времени ти (см. рис. 16.5). Дальнейший расчет при х>ху заключи'
ется лишь в определении деформаций в интересующих точках дис-
ка, например, на периферии его или в месте соединения диска с ва-
лом (см. рис. 14.4). Это необходимо в первом случае для подсчета
1 Использование кривых ползучести, полученных при постоянных напряже-
ниях, для расчета диска, в котором напряжения изменяются с течением вре-
мени, является в этом случае одним из допущений.
351
Рис. 16.5. Построение изо-
хронных кривых с_ помощью
диаграммы ползучести
радиального зазора между рабочими лопатками и корпусом турби-
ны, во-втором — для определения посадки в соединении.
Учитывая зависимости (15.4) и (15.6), можно записать
5=-^^-°’5зг)+ГО/’	(16.11)
где Е" — величина, аналогичная Е' (.§ 16.4).
В этой формуле с течением времени (в период установившейся
ползучести) изменяется только Е". Так как <т<(т) =Еу"ъ,у=const и
«i=«iv+ATtg6 (см. рис. 16.5), то
+ At). (16.12)
ЕуЧу	\ Чу /
Подставляя выражение (16.12) в (16.11), получим
5=—(1 +	Дт) (а, - 0,5а,) -J- rat,	(16.13)
в; \ чу /
где <тг, at, ety и Ev" — соответственно напряжения, интенсивность
деформации и величина Е" на радиусе г.для времени т«; 6 — угол
наклона кривой ползучести, соответствующей интенсивности нап-
ряжений ау на том же радиусе в период установившейся ползуче-
сти; Дт=т—Ху.
Ползучесть заметно сказывается на распределении напряже-
ний по радиусу диска. С течением времени оно становится более
равномерным, т. е. максимальные напряжения в диске уменьша-
ются.
§ 16.4.	МАТЕРИАЛЫ ДЛЯ ИЗГОТОВЛЕНИЯ ДИСКОВ
Диски газовых турбин реактивных двигателей работают в усло-
виях высоких температур и напряжений. В ряде случаев температу-
ра достигает 800 ... 900 К. К центру диска температура снижается
до 500 ... 600 К. В последних ступенях многоступенчатых турбин
температура в центре неохлаждаемых дисков достигает 850 К.
Напряжения в отдельных точках дисков доходят до предела теку-
чести материала, т. е. до 500 МН/м2.
Поэтому требования к материалам дисков в основном те же,
что и к материалам рабочих лопаток. В отношении жаропрочности
и жаростойкости к материалам дисков требования несколько ниже,
352
так как их максимальная температура на 150 ... 300 К меньше тем-
пературы лопаток.
Учитывая сказанное в конце § 15.4, для дисков следует выбирать
материал с большим коэффициентом теплопроводности (это сни-
жает значения ДТ) и с малым коэффициентом линейного расшире-
ния а.
Для дисковых материалов желательна по возможности большая
пластичность, соответствующая наиболее рациональному использо-
ванию их. В газотурбинных двигателях диски турбин изготовляют-
ся из сравнительно дешевых аустенитных сталей 37Х12Н8Г8МФБ,
ЭИ696М, ХН35ВТЮ и сплавов на никелевой основе ХН77ТЮР,
ЭИ437БУВД (улучшеный, вакуумно-дуговой выплавки) и ЭИ698.
Вследствие большого (80%) содержания никеля стоимость этих
сплавов высокая, поэтому применение их должно быть обосновано.
Для дисков и других нагруженных деталей ротора турбины, ра-
ботающих при температуре до 800К, применяется также сравни-
тельно дешевая сталь перлитного класса ЭИ415. Эта сталь в отли
чие от аустенитных имеет хорошую теплопроводность, низкий ко-
эффициент линейного расширения и легко обрабатывается реза-
нием.
Диски турбин ТНА, при невысоких (до 650К) начальных тем-
пературах рабочего газа, изготовляют из легированных конструк-
ционных сталей или даже алюминиевых сплавов типа АК4. При
высоких температурах можно применять те же материалы, что и
для дисков ГТД. В этом случае следует учитывать малый ресурс
турбин ТНА. Имеются конструкции ТНА, в которых диски (иногда
заодно с лопатками) отлиты из материала типа ЖСЗ-ДК или
ЖС6-К, а также из титановых сплавов (при температуре до 850К).
Химический состав, основные механические и физические характе-
ристики указанных здесь материалов приведены в приложении II.
§ 16.5.	КРИТЕРИИ ПРОЧНОСТИ ДИСКОВ. ЗАПАСЫ ПРОЧНОСТИ
Оценка прочности дисков газовых турбин сложная и оконча-
тельно не решенная задача. Сложность ее обусловлена изменени-
ем напряжений и температуры по радиусу диска и во времени, яв-
лением ползучести, работой материала в условйях плоского напря-
женного состояния при наличии концентраторов напряжений й т. п.
В настоящее время можно считать установленным, что критери-
ем кратковременной прочности дисков является равенство больше-
го из напряжений ог или Ц/, определенного с учетом пластических
деформаций (назовем его атах) в каком-либо сечении пределу
прочности ов материала в этом сечении (с учетом температуры).
Критерий длительной прочности можно сформулировать аналогич-
но, если указанное наибольшее Напряжение, подсчитанное с учетом
ползучести металла, сравнивать с пределом длительной прочности
материала при температуре на соответствующем радиусе диска.
Учитывая сформулированные выше критерии, можно оценить
прочность дисков из малопластичных материалов по величине за-
пасов прочности:
12	1337
353
при кратковременном режиме
;	(16.14)
°тах
при длительном режиме
*»==— •	•	(16.15)
°тах
Рекомендуется Кт= 1,6 ... 2,0.
Так как ав и а* уменьшаются к периферии диска (из-за увели-
чения температуры), следует выяснить распределение запасов
прочности по радиусу диска и определить их минимальные значе-
ния.	f
Для дисков с высокой пластичностью пользуются и другими
критериями прочности. Считается, что диск разрушится при крат-
ковременных испытаниях, если область пластических деформаций
распространится на весь диск, и в каждой точке его сечения напря-
жения Oi станут равными пределу прочности ав, соответствующему
температуре металла в данной точке. Раз£ушение диска при этом
произойдет по его меридиональному сечению. Найдем разрушаю-
щее число оборотов, соответствующее условию <т(==ов.
На рис. 16.6, а изображены нагрузки, действующие на полови-
ну диска при предельной (разрушающей) частоте вращения ив.
На радиусе га к диску приложены напряжения (<тга)в от лопаток и
замковых выступов диска.
В сечении диска диаметральной плоскостью АВ действуют нап-
ряжения ц<=.ав.
Рассмотрим равновесие выделенной части диска.
Центробежная сила инерции половины диска
Рл = Je J dPn Sin <Р= С QwByr2dr sin фй?<₽=2€<од/пРоф.
Го и	о
(*а
где •/проф=] yr2dr.
Го
Равнодействующая сил, приложенных к внешнему контуру ди-
ска.
Я =J (®гЛ УаГ^ч sin ср=2 (ага)вуага. (16.16)
Уравнение равновесия
Рл+Я=2 \\ydr.	(16.17)
fo
4
Подставляя сюда значения Рд, R и учитывая, что (<’fe)B=«re--.
ю2
тде Ста — напряжение на радиусе га при каком-либо значении и
354
Ряс. 16.6. Схемы к определению разрушающих оборотов диска
(например, при расчетной скорости вращения), получим формулу
предельного значения частоты вращения диска (в об/мин):
Лв = ^==_32_1/Г_	Д--------.	(16.18)
Я	f	гаУа + 6^проф
При длительной работе нагретого диска разрушающее число
оборотов определяют по аналогичной формуле с заменой ав на <гт •
Запас по разрушающим.оборотам:
. при кратковременной работе
+ Q®2/ проф ’
(16.19)
при длительной работе
J
+ е“2/проф ’	(16. 20)
В практике эксплуатации дисков имели место случаи, разруше-
ния дисков не по меридиональному, а по цилиндрическому сечению.
Такие диски имели резкие сужения профиля. Радиальные напряже-
ния в области сужения оказываются больше тангенциальных и
при увеличении числа оборотов напряжения аг на каком-либо ра-
диусе г* (см. рис. 16.6, б) становятся равными пределу текучести,
а затем и больше его. В этом случае напряжения <jt во внешней
части диска (г>г*) растут быстрее, чем во внутренней. Эти напря-
жения становятся также больше предела текучести, т. е. область
пластических деформаций распространяется на все сечение внеш-
ней части.
При достижении условия о/ = <тв во всех точках сечения диска,
лежащего выше радиуса г*, наступает разрушение диска. Внешняя
часть диска разрывается по нескольким радиальным сечениям и
отрывается от внутренней по цилиндрическому сечению радиуса г*.
12»
355
Часто это сечение проходит через центры отверстий в полотне ди-
ска.
Чтобы найти разрушающее число оборотов, рассмотрим пре- '
дельное равновесие половины внешней части диска (см. рис.
16.6,6).
Это уравнение составим аналогично уравнению (16.17), доба-
вив в правую часть равнодействующую сил, приложенных к внут-
реннему контуру. Эта сила /?' находится по уравнению (16.16) с за-
меной (Ога) в на <гв* — предел прочности, соответствующий темпе-
ратуре на радиусе г*.	.
Если учесть также ослабление сечения отверстиями, то вели-
чина

где z и d — соответственно число и диаметр отверстий.
В итоге предельная частота вращения
»	30
Пв— —
я
*	/ zd
^raya + (>J*
(115.21)
а запас по разрушающим оборотам
.ОгаГаУа + б"2/*
(16.22)
где. J*=^aуr2dr.
Вычисление Кв* следует выполнить для нескольких значений
г* в-области, где аг>Оь Минимальное из значений Кв или Кв*
должно превышать 1,35 ... 1,4.
'	Глава XVII
КОЛЕБАНИЯ ДИСКОВ
§ 17.1. ФОРМЫ КОЛЕБАНИЙ ДИСКОВ
В газовых турбинах могут иметь место резонансные колебания
.дисков. Опасность возникновения этих колебаний становится тем
«больше, чем меньше толщина диска по сравнению с его диаметром.
356
Рис. 17.1. Схемы форм колебаний диска
Чтобы выяснить условия их возникновения, рассмотрим вначале
формы собственных колебаний дисков. Если покрыть равномерным
слоем сухого мелкого песка горизонтально расположенный невра-
щающийся диск и возбудить в нем изгибные колебания, то при
совпадении частоты возмущающей силы с одной из собственных
частот диска на нем образуются так называемые песочные фигу-
ры. Песок удерживается лишь на неподвижных частях диска —
узлах и сбрасывается с колеблющихся (рис. 17.1).
Различают колебания без узловых линий — так называемые
«зонтичные» (см. рис. 17.1,а), колебания с узловыми диаметрами
или «веерные» (см. рис. 17.1,6), колебания с узловыми окруж-
ностями (см. рис. 17.1, в) и комбинацией узловых окружностей и
диаметров.
Наиболее опасными являются обычно колебания с двумя (см.
рис. 17.1,6), тремя и четырьмя узловыми диаметрами. При этих
колебаниях прогиб диска, по окружности изменяется пропорцио-
нально sin fop, где k — число узловых диаметров; <р — угловая коор-
дината, отсчитываемая от узловой линии. На рис. 17,2 показана
развертка окружности АБВГ диска, колеблющегося с двумя узло-
выми диаметрами (см. рис. 17.1,б).
Колебания с одним узловым диаметром (£=1) в диске, закреп-
ленном в центральной точке (что возможно, конечно, только теоре-
тически), не могут возникнуть, так как инерционные силы в этом
случае приводятся к моменту, который не компенсируется внут-
ренними усилиями, однако, при совместных колебаниях с валом
деформация диска, соответствующая k=l, может иметь место (см.
гл. XIX). Колебания с узловыми окружностями и «зонтичные» мо-
гут возникнуть, если, например, со стороны вала или потока газа
на диск будет действовать периодическая осевая сила, частота
которой совпадает с соответствующей собственной частотой диска.
Рис. 17.2. Деформация обода при
колебаниях диска
357
Можно показать, что «веерные» колебания невращающегося
диска (стоячие волны) следует рассматривать как наложение двух
цепей так называемых бегущих волн. Эти волны распространяют-
ся по окружности диска в разные стороны с одинаковой угловой
скоростью.
Бегущая волна проходит путь, равный длине волны, за время Тг
соответствующее одному периоду колебаний. Этот путь, как виДно
из рис. 17.2, измеряется величиной радиан. В то же время 7=
л *
=,l/v, где v — секундная частота колебаний. Поэтому угловая ско-
рость бегущей волны
(-17.Д)
2я
«>6=v -г- •
R
Таким образом, частота вращения каждой из цепей волн относи-
тельно неподвижного диска (в об/с)
„___<26 у
6	2л	k
Облопаченный диск колеблется как единая система диск — ло-
патки. В этом случае при одном и том же числе узловых диаметров
имеются различные формы резонансных колебаний, соответствую-
щие формам колебаний отдельной лопатки. С увеличением числа
узловых диаметров частота системы диск — лопатки приближается
к парциальной частоте лопатки данной формы (например, первой
изгибной, второй изгибной и т. д.). Это положение иллюстрирует
рис. 17.3.
Лодатки на колеблющемся диске не только изгибаются, но еще
и закручиваются вокруг своей оси, т. е. совершают изгибно-кру-
тильные колебания. В этом можно убедиться, рассматривая пере-
мещение лопатки, расположенной в точке Д на рис. 17.2. Лопатка,
расположенная в точке Г на узловом диаметре, совершает только
крутильные колебания, а в точке Е — только изгибные. Формы ко-
лебаний дисков с закрученными лопатками еще более сложные,
так как такие лопатки изгибаются также и в плоскости диска.
г § 17.2. КОЛЕБАНИЯ ВРАЩАЮЩИХСЯ ДИСКОВ
Если диск вращается с частотой вращения п, то по отношению
к неподвижному наблюдателю вперед бегущая волна (т. е. волна,
распространяющаяся в направлении вращения диска) совершает
(в с-1) пв= —+п, а назад бегущая волна пн= —— п, где vK —
k	k
душамтеская частота собственных колебаний вращающегося дис-
ка, которая, как показано ниже, отличается от частоты неподвиж-
ного диска.
В соответствии с формулой (17.1) частоты колебаний, соответ-
ствующие бегущим волнам, определяются как произведение часто-
ты вращения, совершаемой волной, на число волн, укладывающихся
358 •
V
Рис 17.3. Кривая зависимости частоты колебаний
диска с лопатками от числа узловых диаметров
на окружности диска, т. е. на число узло-
вых диаметров. Таким образом,
vb=*«b=v1+^;	(17-2)
va=^kna=vt — kn.	(17.3)
При отрицательном значении vH назад
бегущая волна движется со скоростью,
меньшей скорости вращения диска, вслед-
ствие чего -эта волна переносится диском
вперед..
Колебания дисков вызываются теми же силами, что и колеба-
ния лопаток. Совпадение частоты силы, -возбуждающей колебания
диска, с частотой вперед или назад бегущей волны приводит к явле-
нию резонанса, которое сопровождается увеличенными перемен-
ными напряжениями изгиба в диске.
Как показывает практика, наиболее опасна работа диска при
таких оборотах, когда частота назад бегущей волны равна нулю.
Эти обороты называются критическими и определяются из
формулы (17.3), записанной для случая vH=0: Пкр—VjJk-
При критических оборотах для возбуждения колебаний с боль-
шой амплитудой достаточно приложить к диску в одной точке по-
стоянную (по времени) незначительную силу.
Эта сила возникает в парциальных турбинах; она может воз-
никнуть и в полностью облопачённой турбине, например, из-за мест-
ного изменения энергии потока, вызванного наличием конструктив-
ных элементов, погрешностями изготовления, сборки и т. п.
Форма изгиба любой окружности диска при критических оборо-
тах представляет собой неподвижную в пространстве синусоиду с
числом полных волн на длине окружности, равным k.
Таким образом, эти колебания вращающегося диска характерны
неподвижными в пространстве узловыми диаметрами.
§ 17.3. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ СОБСТВЕННЫХ
КОЛЕБАНИЙ ДИСКОВ
Наиболее надежно частоту собственных колебаний диска газовой
турбины можно определить экспериментальным путем.
Расчетное значение частоты может быть найдено энергетическим
методом (примененном в § 13.4), распространенным на систему
диск — лопатки *. При этом определяются потенциальная и кинети-
ческая энергии собственно диска и расположенных на нем лопаток.
Кроме того, для определения частоты колебаний диска в рабочих
условиях тд необходимо учесть также работу внутренних сил, воз-
1 Расчеты в данном случае отличаются большой трудоемкостью, и мы огра-
ничиваемся в отношении их лишь ссылкой на литературу [7].
359
пикающих в диске при вращении и неравномерном его нагреве.
Напряжения, вызванные вращением, пропорциональны квадрату
частоты вращения и, температурные напряжения пропорциональны
разнице температур периферии и центра диска ДТ (см. § 15.3).
В соответствии с этим квадрат частоты собственных колебаний
диска в рабочих условиях
у2л=у2г+Вп?-СЬТ,	(17.4)
где Ут — частота собственных колебаний неподвижного диска с уче-
том изменения по радиусу модуля упругости; В и С — коэффици-
енты, зависящие от размеров и материала диска и лопаток, коли-
чества лопаток и числа узловых диаметров.
Из формулы (17. 4) следует, что при вращении диска его собст-
венная частота увеличивается. При неравномерном нагреве частота
уменьшается, что объясняется как уменьшением модуля упругости
материала диска при нагреве так и преобладающим влиянием
значительных сжимающих, т. е. отрицательных, температурных на-
пряжений в ободе диска, действующих в области максимальных
прогибов диска при его колебаниях.
При увеличении разности температур ДТ частота собственных
колебаний диска падает и становится равной нулю при
V?- + В«2	_ ~
ДТкр=-^—------.	(17.5)
Эта разность температур называется критической.
С учетом выражения (17.5) формулу (17.4) можно записать
так:
*д=(^+^2)(1-~) •	(17.6)
Частота ут связана с частотой неподвижного диска при нор-
мальной температуре Та соотношением
vr=V|/^,	(17.7)
V Етп
где Ет — модуль упругости, соответствующий средней температуре
диска.
Таким образом, частота собственных колебаний диска в рабочих
условиях может быть как больше, так и меньше частоты невра-
щающегося диска при нормальной температуре.
§ 17.4. РЕЗОНАНСНАЯ ДИАГРАММА КОЛЕБАНИЙ
И ОБЕСПЕЧЕНИЕ НАДЕЖНОЙ РАБОТЫ ДИСКА
Для определения числа оборотов, опасных с точки зрения коле-
баний диска, удобно построить диаграмму (рис. 17. 4).
1 Аналогичное явление наблюдалось при колебаниях нагретой лопатки (см.
§ 13.4).
360
Рис. 17.4. Диаграмма колебаний дис- у, у,
ка	1000
По оси абсцисс откладыва-’
ют частоту вращения диска, по
оси ординат — частоту колеба- 750
ний диска. По формуле (17.6)
строят кривые va=f(n) для
различного числа узловых диа- доо
метров k. Например, кривая ab
определяет частоту колебаний
при k=2.	ZJ0>
Далее по формулам (17.2)
и (17.3) строят кривые частот
бегущих вперед и назад волн.
Так, кривые ас и ad определи- °
ют частоты vB и vh бегущих впе-
ред и назад волн при двух уз-
ловых диаметрах.	-230
В точках е и f равны нулю
частоты назад бегущих волн
соответственно при двух- и трехузловой формах колебаний. Эти
точки определяют наиболее опасные для диска критические скоро-
сти вращения, которых следует, безусловно, избегать.
Резонансные явления будут иметь место также при частотах
вращения, определяемых точками пересечения лучей возмущающих
частот с линиями va, vB или vH. Так, при частоте вращения, соответ-
ствующей точке g, возникает резонанс возмущающей частоты 1Ц-
об
(от неуравновешенности ротора) с частотой бегущей назад волны
двухузловой вибрации. Точка h определяет резонансную частоту
вращения для назад бегущей волны при наличии возмущающей
частоты 2-^-'‘ (вызванной парциальным подводом газа) и трехуз-
об
ловой формы колебаний. В точке с совпадают частота бегущей
вперед волны при k=2 и возмущающая частота 3-^-.
об
Диаграмма позволяет выбирать безопасные режимы (по часто-
там вращения турбины) или произвести «настройку» (т. е. измене-
ние профиля) диска для безопасной работы турбины на эксплуата-
ционных режимах.
Запрещается работать на критических скоростях вращения и не
рекомендуется работать на частотах вращения, соответствующих
резонансным частотам вращения первой кратности.
, Интервал между рабочим и критическим значениями частоты
вращения должен составить не менее 15% от рабочей частоты вра-
щения при k=2 и не менее 10% — при £=3 и 4 [7].
• 361
Глава XVIII
КОНСТРУКЦИЯ И РАСЧЕТ НА ПРОЧНОСТЬ
ТУРБИННЫХ ВАЛОВ
§ 18.1. КОНСТРУКЦИЯ ТУРБИННЫХ ВАЛОВ
И ПРИМЕНЯЕМЫЕ МАТЕРИАЛЫ
Конструкция вала турбины в основном определяется мощно-
стью и схемой двигателя, типом и расположением опор, а также
способом соединения вала с диском турбины и валом компрессора
(или насоса в ТНА ЖРД) •
Валы ГТД выполняются пустотелыми и опираются, как прави-
ло, на подшипники качения: один из них — шариковый — воспри-
нимает радиальную и осевую нагрузки, другой — роликовый — не-
сет только радиальную нагрузку и для уменьшения изгибающих
моментов, действующи^ на вал, а также для повышения критиче-
ских оборотов (см. § 19.1), располагается по возможности ближе
к диску турбины. В высокооборотных маломощных ГТД, турбо-
стартерах и ТНА ЖРД применяются также подшипники сколь-
жения.
От осевого перемещения валы фиксируются только в одной опо-
ре. В противном случае на вал и подшипники будут действовать
дополнительные осевые нагрузки,, вызываемые главным образом
неодинаковыми температурными деформациями вала и корпуса при
работе турбины. Разность этих деформаций может достигать не-
скольких миллиметров.
Мощность с вала турбины на вал компрессора или насоса в
большинстве случаев передается при помощи эврльвентных и реже
прямоугольных шлицев.
Обычно ротор турбины опирается на роликовый подшипник,
расположенный перед или за турбиной в специальной опоре. В двух-
вальных ГТД внутреннее кольцо подшипника ротора турбины вы-
сокого давления может быть установлено на вал турбины низкого
давления. Аналогичное конструктивное решение, упрощающее си-
ловую схему двигателя, используется и в трехвальных двига-
телях.
В случае расположения подшипника за турбиной целесообразно
разделение вала на две части, одна из которых (передняя) соеди-
няется с диском I ступени, другая (задняя) — с диском последней
ступени. В одноступенчатых турбинах эти части вала присоединя-
ются с двух сторон диска и крепятся общими болтами. Такая кон-
струкция позволяет применять диски без центрального отверстия.
Сравнительно короткая задняя часть вала (цапфа) может быть
откована заодно с диском.
Передним концом ротор турбины опирается на вал компрессора
(рис. 18. 1) или жестко соединяется с последним диском компрес^
сора, образуя единый ротор турбокомпрессора, вторая опора кото-
рого располагается перед компрессором. Возможно и непосредст-
362
♦
Рис. 18.1. Схема муфты, соединяющей валы турбины и компрессора
венное соединение диска турбины с валом компрессора при помо-
щи специального шлицевого хвостовика (см. рис. 18. 3).
Пример конструкции узла соединения вала турбины и компрессора приведен •
на рис. 18.1. Передача крутящего момента осуществляется здесь эвольвентными
шлицами. Благодаря наличию зазоров между ними соединение удовлетворитель-
но работает при некотором перекосе осей. Шлицы являются также передней
опорой вала турбины, т. е. воспринимают радиальную нагрузку. От осевого пе-
ремещения вал турбины 10 удерживается пустотелым болтом 6, ввернутым в
вал компрессора 7. На головке болта имеются торцевые шлицы 9, используе-
мые при его заворачивании. После соединения валов болт фиксируется пружин-
ным замком 4. Для разъединения валов снимают вначале диски турбины, если
они не имеют центрального отверстия. Внутрь вала вставляют специальный ключ,
которым сдвигают влево по направляющей втулке 1 замок 4, сжимая пружину 2.
При этом шлицы 5 разъединяются, а шлицы 3 остаются в соединении, так как
их длина больше. После этого отворачивается болт 6 и освобождается вал
турбины. Шлицевой дистанционной втулкой 8 регулируется осевой зазор между
ротором и корпусом турбины.
В турбине низкого давления, показанной на рис. 20.1, крутящий момент
передается эвольвентными шлицами на рессору 16, соединяющую валы турбины
и компрессора. Осевое усилие, действующее на ротор, воспринимается стяжным
болтом 1, головка которого упирается в вал компрессора.
• Соединение валов турбины (см. рис 20.2) и компрессора высокого давления
двухвалщюго ТРДД показано на рис. 18.2.
Па переднем конце вала турбины 8 имеются наружные шлицы 4, передаю-
щие крутящий момент. Осевое усилие воспринимается гайкой 10, навернутой на
стяжную втулку 5, которая ввернута в вал компрессора 3 до упора в подшип-
ник 1, являющийся передней опорой вала турбины низкого давления. Гайка
законтрена шлицевым замком 11, который фиксируется от осевого перемещения
пружинным кольцом 12. Дистанционными кольцами 2 и 9 регулируется осевое
положение ротора турбины. Сферические кольца 6 и 7 обеспечивают нормаль-
ную работу соединения при перекосе осей валов.
На рис. 18.3 приведена конструкция ротора турбины высокого давления двух-
вального ТРДД. На диске турбины 10 закреплены 134 рабочие лопатки 13, рас-
положенные попарно в каждом пазу (вид Л). От осевого перемещения лопатки
зафиксированы пластинчатыми замками 12. К диску крепится шестью болтами
шлицевой хвостовик 15. Конические призонные участки болтов служат для цент-
рирования диска и передачи крутящего момента. Болты .от выпадения при сбор-
ке турбины зафиксированы в хвостовике пружинными кольцами 14, вставлле-
мыми в кольцевые канавки на болтах.
Передний конец хвостовика центрируется на заднем валу компрессора 5
по цилиндрическому пояску 4. Второй центрирующей опорой является упорное
кольцо 7, которое, в свою очередь, центрируется на валу компрессора. Переда-
ча крутящего момента с хвостовика на вал осуществляется эвольвентными
шлицами 6. Хвостовик затянут на валу гайкой 8, удерживаемой от отворачи-
вания контровочным кольцом 9, которое центрируется в диске турбины. На на-
363
вала компрессора установлено внутреннее кольцо ролико-
мн Подбором толщины кольца 2 можно регулировать осевой
I) турбины и деталями корпуса.
(яановлено наружное кольцо роликового подшипника 1, явля-
(Р/ турбины низкого давления (см. рис. 20.1).
Й подшипника отводится через отверстия в валу 5 и радиаль-
\1Г7 и 18 (показано стрелками).	’
^У^тора производится перестановкой лопаток и балансировоч-
1 дения турбинных валов применяются стали
’!“МА, а при повышенной температуре отдельных
20ХЗМВФ (ЭИ415) или ЭИ691, механические
1* приведены в приложении II.
^мя усталостной прочности вал необходимо обра-
ПЧе чем по 6-му классу шероховатости, а посадочные
^пники — по 7-му или 8-му. С этой же целью еле-
цких переходов поверхностей, посадки на вал дета-
тягом и т. п. (см. § 18. 2).
И, определяются расчетом его на прочность (см.
ическое число оборотов (см. гл. XIX). В ряде слу-
Вид А
чаев при расчете на критическую частоту вращения диаметр вала
получается больше, чем по расчету на прочность.
§ 18.2. РАСЧЕТ ВАЛА НА ПРОЧНОСТЬ
На вал турбины действуют: крутящий момент; осевое усилие;
центробежная сила неуравновешенной массы ротора; масса ротора;
инерционные силы и гироскопический момент, возникающие при
эволюциях самолета; усилия от шестерен, если они имеются на-
валу.
Крутящий момент можно представить двумя составляющими: -
постоянной, соответствующей передаваемой валом внутренней мощ-
ности турбины, и переменной, вызванной пульсацией давления воз-
духа за компрессором, неравномерной по времени работой форсу-
нок и другими причинами. В соответствии с этим в сечениях вала
возникают постоянные тт и переменные га касательные напря-
жения.
Величина тт определяется по формуле (в МН/м2)
__Л1к10-б
т ’
(18.1)
где AfK= --50^ — крутящий момент, Н-м;
п	32
момент сопротивления изгибу сечения полого вала с наружным
диаметром D и внутренним d, м8; Nt — внутренняя мощность, кВт;
п — частота вращения вала, мин-1.
Переменную составляющую крутящего момента можно принять
равной 5... 10% от AfK. Следовательно,
тЛ==(0,05...0,10)тЯ1.	(18.2)
Осевое усилие вызывает растягивающие напряжения, которые
также можно рассматривать состоящими из двух слагаемых: посто-
янной
=	> МН/м2	(18.3/
и переменной
®ai=(0,05...0,10)aml,	(18.4)
где Ро — осевое усилие, определяемое согласно § 6.18, Н; f — пло-
щадь поперечного сечения вала, м2.
Центробежная сила неуравновешенной массы ротора (Н) Рн=
=треш2, где /пр— масса ротора, кг; е — расстояние от центра тя-
жести ротора до оси вала, м.
Величина mve (неуравновешенность ротора) задается техниче-
скими условиями и составляет от 2-Ю-5 для маленьких роторов
турбостартеров и вспомогательных турбин до 50-10-8 кг-м для
крупных турбин ТРД и ТВД.
365
Сила Рн вызывает в валу постоянные напряжения От2, так как
вектор этой силы вращается синхронно с ротором,
«л,2=-^-.	(18.5)
Изгибающий момент Afp от силы Ри определяется в соответст-
’вии с расчетной схемой вала.
Центробежная сила инерции, возникающая при полете самоле-
та по криволинейной траектории с радиусом кривизны R,
Pj^mpRQ^kGp,	(18.6)
где й — угловая скорость вращения самолета, с-1; k — коэффици-
ент перегрузки; бр — сила тяжести ротора, Н.
Учитывая, что скорость полета v=QP, находим
V
Гироскопический момент, возникающий при тех же условиях,
что и сила Pj, будет максимальным, когда векторы скоростей ю и
О взаимно перпендикулярны. При этом (в Н * м)
Л4г=/л<о2,	(18.7)
где Jx — полярный момент инерции ротора, кг-м2 (см. § 19.7).
Сила тяжести ротора, инерционные силы, гироскопический мо-
мент и усилия от шестерен вызывают в сечениях вала вследствие
его вращения переменные напряжения изгиба оа2-
Указанные нагрузки в -общем случае не лежат в одной плоско-
сти, поэтому их надо разложить по двум взаимно перпендикуляр-
ным плоскостям — вертикальной А и горизонтальной Б, построить
эпюры изгибающих моментов Afui и Ми2 в этих плоскостях, а за-
тем геометрически суммировать их по формуле
МЯ=У М2и1-]-МЪ.	(18.8)
Тогда (в МН/м2)
При полете самолета по криволинейной траектории, лежащей в
горизонтальной плоскости Б, рассмотренные выше нагрузки дейст-
вуют, как показано на рис. 18.4, а. Эпюры изгибающих моментов
Ми1 и МШ2 для данной схемы вала приведены на рис. 18.4, б и в.
Максимальный изгибающий момент будет в опоре В и может быть
подсчитан по формуле
Митах=/(H4r+GpZ)2+(P;Z)2.	(18.10)
Если производится маневр в вертикальной плоскости А, то
Л4итах=V	(18.11)
Соответствующие этому случаю эпюры Mui и Afu2 показаны на
рис. 18, д и е.
. 366
Рис. 18.4. Схемы нагрузок, действующих на вал турбины
Таким образом, в сечениях вала возникают постоянные и пере-
менные нормальные и касательные напряжения. Вследствие этого
вал необходимо рассчитывать на статическую прочность под дейст-
вием максимальной кратковременной нагрузки и на выносливость,
как это делается в курсах деталей машин.
Расчет на статическую прочность
Для прочности вала турбины наиболее опасным является ре-
жим плоского штопора (к—2... 4; 0=2,5... 3,0).
Используя формулы (18.1), (18.9) и (18.10), определим запас
статической прочности:
п
(18.12)
где п,=—-—; «г=—;
=	+	°e = °al4'9e2-
В приведенных выражениях <гт и тт — пределы текучести соот-
ветственно при растяжении и при кручении. Как известно, тт=
=0,6ат:
В валах турбин запас статической прочности должен быть не
менее 1,4... 1,6.
В прикидочных расчетах диаметр вала можно определить из
формулы (18.1), принимая тт=300... 400 МН/м2.
Расчет на выносливость
Этот расчет обычно выполняют для режима выхода самолета из
пикирования (Л=8...1О; 0=0,5... 0,6). Большое влияние на
прочность вала в условиях действия знакопеременных нагрузок
367
оказывает концентрация напряжений в местах резкого изменения
диаметра вала, в резьбе, в местах расположения шпоночных пазов,
шлицев, поперечных отверстий и т. п. Поэтому проверять усталост-
ную прочность вала следует как в сечениях с максимальными на-
пряжениями, так и в местах расположения указанных конструктив-
ных элементов.
Запас прочности по сопротивлению усталости вычисляют по фор-
муле
Пх =-------—-------
*
—	+ ’Мт
ЕВ
где «<,= —----------
аа + 4'aam
ЕР
о-i и т-i — пределы выносливости гладких образцов при перемен-
ном изгибе и кручении (см. приложение П); можно принять т_1 =
= (0,6... 0,7)ia_i; ka и kt —эффективные коэффициенты концент-
рации напряжений; в — масштабный фактор, учитывающий абсо-
лютные размеры вала; р — коэффициент, учитывающий состояние
поверхности (чистоту обработки, поверхностное упрочнение); фо ==
=0,25...0,3 и фт=0,1 — коэффициенты, учитывающие свойства
материала.
Значения коэффициентов k„, kt, е и р приведены в специальной
литературе *.
Запас прочности, определяемый по формуле (18.13), должен
быть не менее 1,5 ... 1,8.
Следует отметить, что расчет на выносливость выполнен в
предположении непрерывного одновременного действия макси-
мального крутящего момента и инерционных, массовых и других
сил. Очевидно, что это допущение идет в запас прочности.
§ 18.3. ОПОРЫ РОТОРОВ ТУРБИН
Как уже указывалось, в авиационных газовых турбинах приме-
няются преимущественно подшипники качения. Они имеют меньший
коэффициент трения (0,002... 0,006), требуют по сравнению с под-
шипниками скольжения меньших расходов масла, которое необхо-
димо главным образом для охлаждения. Подшипники качения ме-
нее чувствительны к чистоте и температуре масла, вследствие этого
масляная система ГТД упрощается. В турбонасосных агрегатах
ЖРД ввиду малой длительности их работы широко применяется
консистентная смазка подшипников качения. Это уменьшает мас-
су, сложность ТНА и увеличивает их надежность. Подшипники тур-
бин являются ответственными узлами ГТД; заметный процент ава-
рий, поломок и дефектов двигателей связан с нарушением нормаль-
ной работы подшипниковых узлов.
* Справочник машиностроителя. — Т. 3. — М.: Машгиз, 1952.—с. 1080.
368
Одним из решающих факторов в обеспечении надежной работы
подшипника является правильная организация его смазки и ох-
лаждения. Увеличение рабочей температуры приводит к снижению
твердости материала подшипника и уменьшению срока его службы.
Для уменьшения рабочей температуры турбинные подшипники
охлаждают маслом.
В турбонасосных агрегатах ЖРД для смазки и охлаждения под-
шипников часто используют компоненты топлива, например, ке-
росин.
Расход масла на турбинный подшипник ГТД зависит от нагруз-
ки, числа оборотов и размеров подшипника, температуры окружа-
ющей среды.
Масло к подшипнику следует подводить в таком количестве,
чтобы обеспечить температуру колец не' выше 400 ... 420 К. В неко-
торых конструкциях температура подшипников достигает 500...
530 К. В современных ГТД на турбинные подшипники подается до
13 л/мин масла на охлаждение. Правильно организованный под-
вод и отвод масла в значительной мере увеличивает срок службы,
подшипника. Масло к подшипнику подводят в большинстве случаев
при помощи одной или нескольких форсунок или жиклеров (см.
рис. 20.1 и 20. 2), а также через отверстия в наружном кольце.
Для’ более равномерного распределения температуры по под-
шипнику и увеличения срока его службы в некоторых ГТД число
форсунок доводят до шести, располагая их по три с двух сторон
подшипника, равномерно по его окружнрсти.
Струя масла из форсунки направляется в зазор между сепара-
тором и внутренним кольцом и центробежными силами отбрасы-
вается к наружному кольцу, охлаждая, таким образом, все эле-
менты подшипника.
Большое внимание при конструировании опоры должно быть
уделено отводу масла от подшипника. Для того чтобы масло не
перегревалось в подшипнике, необходимо с обеих его сторон вы-
полнять по возможности большие полости, причем каждая из них
при помощи отверстий или специальных каналов в корпусе опоры
должна сообщаться с откачивающей магистралью масляной систе-
мы ГТД.
Для предотвращения утечки масла из полости подшипника в
проточную часть двигателя или во внутренние полости, ограничен-
ные горячими стенками камеры сгорания, а также для защиты под-
шипника от подогрева горячими газами применяют бесконтактные
или контактные уплотнения.
Наибольшее распространение в турбинах ГТД нашло бескон-
тактное лабиринтное уплотнение (рис. 18. 5, а). Оно может работать
при высоких окружных скоростях и больших перепадах давлений
по обе стороны уплотнения. Гребешки лабиринтов могут быть на-
резаны как на вращающихся, так и на неподвижных деталях.
Кромки гребешков выполняют шириной 0,3... 0,5 мм и оставляют
их не скругленными. Радиальный зазор б выбирают в пределах
0,2 ... 0,3 мм. Для уменьшения этого зазора и, следовательно, про-
369
Рис. 18.5. Типы уплотнений
течек газа через уплотнение на его гладкую неподвижную поверх-
ность часто наносят специальное мягкое покрытие, допуская при
эксплуатации врезание в него гребешков лабиринта.
Турбинные подшипники нагреваются в значительной мере горя-
чими газами, прорывающимися через уплотнения. Поэтому уплот-
нения следует конструировать так, чтобы не допустить или свести
к минимуму количество этих газов.	,	4
Так, например, в турбине ТРДД, изображенной на рис. 20.2, имеется четыре
лабиринтных уплотнения. В полость А между двумя из них подается вторичный
воздух из камеры сгорания, который идет далее на схлаждение деталей тур-
бины Часть его проходит через наружное лабиринтное уплотнение в проточную
часть турбины, препятствуя прорыву газов в полость Л, и далее, к подшипнику.
В полость В по трубопроводу 12 подается воздух из второго контура двига-
теля. Повышенное давление в этой полости препятствует утечке масла из по-
лости подшипника. Воздух, прошедший через внутрейний лабиринт в полость
подшипника, отводится через центробежный суфлер в реактивное сопло. Воздух,
прошедший через лабиринты в полость Б (вместе с незначительным количест-
вом масла, просочившегося через внутренний лабиринт), отводится в проточную
часть второго контура двигателя.
Для уменьшения подогрева подшипника теплом, идущим от дис-
ка, на валу под подшипником иногда нарезают шлицы или уста-
навливают подшипник на втулку, имеющую небольшую поверх-
ность контакта с валом лишь по посадочным пояскам.
Более герметичным является контактное уплотнение. Пример
такого уплотнения с металлическими кольцами показан на рис.
18. 5, б. На валу закрепляют кольцедержатель 1, в канавки которого
устанавливают разрезные упругие кольца 2 из чугуна, бронзы или
стали. Наружный размер колец в свободном состоянии несколько
превышает внутренний диаметр стакана 3, расположенного в кор-
370
пусе опоры. После сборки уплотнения кольца прижимаются к внут-
ренней, цементируемой поверхности стакана силой упругости, кото-
рая удерживает их ot проворачивания при вращении вала.
Кольца выполняются шириной 2... 3 мм, ширина канавок на
0,05... 0,15 мм больше. Кольцо в работе под действием разницы
давлений по обе стороны его прижимается к боковым поверхностям
канавок, обеспечивая уплотнение.
Уплотнения с бронзовыми кольцами удовлетворительно рабо-
тают при окружных скоростях 60... 80 м/с, с кольцами из хроми-
стого чугуна — до 100 м/с при температуре 440 ... 450 К. Для пре-
дотвращения быстрого износа боковые поверхности канавок коль-
цедержателя азотируют, а у колец подвергают пористому хромиро-
ванию. С этой же целью при большой разнице давлений в масляной
и газовой полостях к трущимся поверхностям подводят масло че-
рез отверстия в кольцедержателе и кольцах.
Высокую герметичность и надежность при длительной эксплуа-
тации обеспечивают графитовые уплотнения. Они могут работать
при более высокой (до 800 ... 815 К) температуре, чем уплотнения
с металлическими кольцами, и окружных скоростях до ПО м/с.
На рис. 18.5, в приведено торцевое уплотнение. Цельное гра-
фитовое кольцо 3 прижимается пластинчатой пружиной 6 к упор-
ному кольцу 4, зажатому на валу 2. От проворачивания графитовое
кольцо фиксируется в корпусе опоры штифтами 5. Для устранения
перетечек между втулкой корпуса и графитовым кольцом примене-
но статическое уплотнение круглым кольцом 1 из маслостойкой
резины. Для повышения допустимой рабочей температуры статиче-
ское уплотнение может быть обеспечено металлическими разрез-
ными кольцами. Графитовое кольцо в этом случае запрессовывает-
ся в металлическую обойму.
Уплотнение, показанное на рис. 18. 5, г, состоит из трех кольце-
вых сегментов 1, стягиваемых пружиной 2. Штифт 3, ввернутый в
кольцо, фиксирует его в корпусе от проворачивания. Между сег-
ментами имеются небольшие зазоры, обеспечивающие плотное при-
легание к валу при износе сегментов. От выпадания из корпуса уп-
лотняющее кольцо удерживается крышкой 4. В ТНА ЖРД сегмен-
ты изготавливаются из чугуна. Два таких уплотнения могут уста-
навливаться последовательно. Полости между кольцами при необ-
ходимости суфлируются.
Масляные полости подшипника ротора турбины, показанного на
рис. 18. 3, изолируются передним и задним уплотнениями. Перед-
нее уплотнение — контактное. Основными его элементами являются
разрезные графитовые кольца 20, 21 и 23. Кольцо 20 прижимается
к распорному стальному кольцу 19 давлением воздуха. Кольца 21
и 23 прижимаются, соответственно, к стальным кольцам 18 и 19
пружиной 22. Заднее уплотнение комбинированное — контактное,
аналогичное переднему, и лабиринтное 16.
Уплотнение подшипника ТНА ЖРД фирмы «Вальтер», приве-
денное на рис. 18. 5, д — комбинированное. Утечка масла из поло-
сти подшипника устраняется применением контактных сальниковых
371
уплотнений 1. Для предотвращения попадания компонента топли-
ва (смеси метилового спирта с гидразингидратом) в полость под-
шипника служит торцевое графитовое уплотнение. Графитовое
кольцо 4, впрессованное в обойму 3, постоянно прижимается пру-
жиной 6 к втулке 5, сидящей на валу. От проворачивания обойма
3 фиксируется винтами 2. Резиновая мембрана 7 устраняет перете-
кание жидкости через зазор между корпусом и обоймой 3 и обес-
печивает ее осевое перемещение при износе графитового кольца.
На рис. 18.5, е изображено манжетное уплотнение. Манжету,
изготовляемую из специальной резины, фторопласта-4 (пластмас-
сы, стойкой в азотной кислоте) или других материалов, укрепляют
в корпусе или на валу стальными кольцами и прижимают к поверх-
ности трения свернутой в кольцо спиральной пружиной. Если упру-
гость манжеты достаточно велика, пружину можно не ставить.
Манжетные уплотнения работают при окружной скорости не более
25 м/с.
§ 18.4. ВЫБОР ПОДШИПНИКОВ
В авиационных газовых турбинах, являющихся высокооборотны-
ми машинами, применяются подшипники легких серий прецизионно-
го (А) и сверхпрецизионного (С) классов точности. Основные
типы подшипников и их размеры приведены на рис. 18.6
В опорах, воспринимающих радиальные и осевые нагрузки, при-
меняются одинарные или сдвоенные радиально-упорные шарико-
вые подшипники. Беговые дорожки колец могут быть образованы
одним радиусом, несколько большим, чем радиус шарика, или дву-
мя. В первом случае (см. рис. 18. 6, а) шарики касаются .колец в
двух точках, во втором (см. рис. 18. 6, б) — в четырех. Четырехто-
чечные подшипники имеют больший угол контакта (12... 16°) и,
следовательно, могут воспринимать более высокие нагрузки.
С целью повышения работоспособности подшипника увеличива-
ют число шариков в нем. В этом случае для обеспечения сборки
* Бейзельман Р. Д., Цыпкин Б. В., Перель Л. Я. Подшип-
ники качения. Справочник. — М : Машиностроение, 1975.— с. 574.
372
подшипника одно кольцо, внутреннее или наружное (см. рис.
18.6, б), делают разъемным.
Роликовые подшипники (см. рис. 18.6, в) воспринимают толь-
ко радиальную нагрузку и допускают осевые смещения колец.
С буртиками, удерживающими ролики, можно выполнять внутрен-
нее или наружное кольцо.
В некоторых случаях для снижения габаритов и окружных ско-
ростей подшипника его применяют без внутреннего кольца
(см. рис. 20. 3).
Кольца подшипников и тела качения изготовляют из шарико-
подшипниковых хромистых сталей ШХ15 и ШХ6 или ШХ9. В под-
шипниках, предназначенных для работы при высоких температу-
рах; эти детали изготовляют из специальных хромоникельмолибде-
новых или вольфрамовых сталей.
Сепараторы подшипников изготовляют из бронзы БрАЖМц
10-3-1,5, алюминиевых сплавов АК4 и Д1-Т, а также из чугуна.
На вал или втулку подшипники устанавливают обычно по плот-
ной подшипниковой посадке 1-го класса точности П\п и затягива-
ют гайкой. Для установки в корпус опоры применяют скользящую
подшипниковую посадку 1-го класса точности Сщ для возможно-
сти поворота наружного кольца и равномерного его износа 1. Если
корпус опоры выполнен из алюминиевого сплава, то перед уста-
новкой подшипника в него запрессовывают и фиксируют от воз-
можного поворота стальную втулку или стакан.
В турбинах ТНА при малом ресурсе подшипники устанавли-
ваются непосредственно в алюминиевый корпус (см. рис. 20.4).
Внутренний диаметр подшипника выбирают в соответствии с
размером вала в опоре. При этом необходимо проверить подшип-
ник на быстроходность.
Подшипники качения в ГТД удовлетворительно работают, если
окружные скорости, соответствующие окружности центров тел ка-
чения, не превышают 50... 80 м/с. Параметр dn (где d — диаметр
вала, мм, а п — частота вращения вала, мин-1) достигает
(1,0... 2,0) • 106.
Расчетная долговечность выбранного подшипника может быть
приближенно определена по известной формуле (в ч)
лрасч \ Чэкв '
где Прасч — расчетная частота вращения вала, мин-1; С — работо-
способность подшипника, определяемая по каталогу 2; QaKB — экви-
валентная условная нагрузка, Н.
Значение Q3kb определяет по формуле
i^z
Q3Kb=2(«A)0,3Qp	(18.15>
__________ i~l
1	Следует помнить, что поля допусков подшипниковых посадок отличаются
от таковых для обычных посадок.
2	В системе единиц СИ величину С следует брать примерно в 10 раз боль-
шей, чем в системе единиц МКГСС.
373
Рис. 18.7. Зависимость коэффициента Kt
от температуры подшипника
\
тде z — число режимов работы турбины; а< — относительная про-
должительность работы на i-м режиме, включая расчетный (оче-
i=z	ч
видно, что VV=1|; ?/ = ——------относительные частоты враще-
j	прасч
ния на i-м режиме; Qi— приведенная условная нагрузка на под-
шипник на i-м режиме.
Величину Q для каждого режима подсчитывают по формуле
Q=(/?+/n4)/<-KWo	(18.16)
где R и А — соответственно радиальная и осевая нагрузка на под-
шипник, Н; — коэффициент, учитывающий вращение кольца;
при вращении внутреннего кольца он равен единице; при враще-
нии наружного — 1,35; Кб — коэффициент безопасности, учитыва-
ющий динамичность действующей нагрузки; для турбин Кб=1;
Kt — коэффициент, учитывающий влияние рабочей температуры
подшипника на его долговечность; величина его определяется по
графику рис. 18.7; т — коэффициент, учитывающий неодинаковое
влияние радиальной и осевой нагрузок на долговечность подшип-
ника.
Значение коэффициента т изменяется от wt=3 g1 (при чисто
радиальной нагрузке) до т=—±— при чисто осевой. Здесь р —
2,8 tg 3
угол контакта шарика с дорожкой качения (см. рис. 18.7), выпол-
няемый в пределах 12... 26°.
Полученное по формуле (18.14) значение долговечности под-
шипника не должно быть меньше ресурса проектируемого ГТД.
Глава XIX
КОЛЕБАНИЯ ТУРБИННЫХ ВАЛОВ
§ 19.1. ПОНЯТИЕ О КРИТИЧЕСКОЙ ЧАСТОТЕ
. ВРАЩЕНИЯ ВАЛА
Хотя при обработке вала и дисков стремятся добиться возмож-
но более точной их балансировки, однако математически точного
совпадения центра тяжести ротора с геометрической осью вала
374
Рис. 19.1. Схемы положения центра тяжести диска при частоте вращения:
а—меньше критической; б—больше критической
Рис. 19.2. График зависимости относительной величины прогиба вала от угловой
скорости вращения
можно достичь лишь случайно. Обычно центр тяжести расположен
эксцентрично относительно оси вала. Вследствие этого возникает
неуравновешенная сила инерции тем большая, чем выше число обо-
ротов вала.
Рассмотрим действие этой силы на невесомый вал с одним дис-
ком, массу которого будем считать сосредоточенной в его центре
тяжести. Ось вала выберем вертикальной, чтобы не учитывать
влияние начального прогиба вала под действием силы тяжести
диска.
Положим, что центр тяжести диска находится в точке 5 на рас-
стоянии е от оси вала (рис. 19. 1,а). При вращении возникает цен-
тробежная сила Р, вызывающая прогиб вала. Величина прогиба у
зависит как от величины силы Р, так и от размеров и материала
вала и расположения диска относительно опор.
Так как вращение происходит вокруг вертикальной оси вала
АО'В, то центробежная сила Р=т(у+е)<й2, где т — масса дис-
ка, кг, у и е — прогиб и эксцентриситет, м, а со — угловая скорость
вращения вала, с-1.
В то же время Р—су, где с — жесткость вала, Н/м, т. е. сила в
Н, которая при данных условиях вызывает прогиб вала в точке
крепления диска на 1 м. Таким образом,
т(у-{-е]ш2=су и у= '.	(19.1)
с — т^2
На рис. 19. 2 изображена зависимость — («>), построенная по
е
формуле (19. 1). При угловой скорости
шк=1/ —,	(19.2)
375
называемой критической, знаменатель в формуле (19.1) становит*
•ся равным нулю, а прогиб вала бесконечно большим.
Полагая т=— (G — сила тяжести диска, Н, a g=9,81 м/с1 2),
S	,
находим критическую частоту вращения вала (в мин-1):
д 30шк==_30_	/^с_=29 9 /_с_	(19 з)
к л л у g У a v ’
Прогиб реального вала при критических оборотах будет хотя и
большой, но конечной величиной вследствие различных сопротив-
лений, возникающих при колебаниях вала и демпфирующих эти ко-
лебания. К этим сопротивлениям относятся внутренние силы тре-
ния, возникающие при деформации вала, трение диска об окружаю-
щую среду, трение в подшипниках и т. п.
Прогиб вала при критических оборотах определяется формулой
где £ — коэффициент, учитывающий сопротивления.
Отсюда видно, что прогиб вала и, следовательно, напряжения
в нем тем меньше, чем меньше дисбаланс ротора те и критическая
скорость вращения.
Как видно из рис. 19.2, при оборотах вала, больших критиче-
ских, его прогиб отрицателен, т. е. направлен в сторону, противопо-
ложную эксцентриситету е, отсчитываемую от 0 (см. рис. 19.1, б).
При увеличении оборотов в закритической области величина
прогиба уменьшается и стремится к значению |е|, т. е. центр тяже-
сти S приближается к оси АО'В. При этом колебания вала умень-
шаются и турбина работает тем спокойнее, чем выше частота вра-
щения *.• Колебания вала при п=пк наблюдаются и при отсутст-
вии эксцентриситета е. В этом идеальном случае полного уравно-
вешивания вала (е=0) центробежная сила P=my<s?. Так как при
критическом числе оборотов с=тю2, то Р=су, т. е. центробежная
сила диска равна упругому противодействию вала при любом про-
гибе вала; следовательно, при критическом числе оборотов диск в
любом положении находится в состоянии неустойчивого равнове-
сия. Колебания в этом случае могут быть вызваны случайной на-
грузкой.
Описанное явление, наблюдаемое и в опыте, полностью соответ-
ствует теории колебаний. Если полностью уравновешенный ротор
(е=0) привести в колебательное движение, то уравнение этого дви-
жения примет вид
(19.5)
aw
где у отсчитывается от равновесного положения, т. е. от положе-
ния, соответствующего статическому прогибу вала.
1 В реальном вале при достижении оборотов, соответствующих второму,
третьему и т. д. тону колебаний, амплитуда вновь возрастает (см. § 19.2).
376
Уравнение это можно переписать так:
1 *
(19.6)
где A2=c/m.
Как известно, интеграл уравнения {19.6)
jr=AcosXr-|-B sin К,	(19-7)
где постоянные А и В зависят от начальных условий движения.
Уравнение (19.7) соответствует гармоническим колебаниям с
периодом Т =-^-=2л l/" — и круговой частотой
К Ус
X=Vclm.	(19.8)
Эта частота совпадает по величине с критической угловой ско-
ростью вращения [см. формулу (19.2)].
Таким образом, при критическом числе оборотов имеет место
явление резонанса, при котором круговая частота возмущаю-
щей, неуравновешенной силы, равная угловой скорости вращения,
совпадает с круговой частотой собственных колебаний.
Опасна для турбины лишь частота вращения, близкая к кри-
тической и равная ей. По обе стороны от критической частоты вра-
щении (с достаточным удалением от нее) вал работает спокойно.
Валы, работающие при частоте вращения, большей критической,
называются гибкими. Валы, работающие при частоте вращения,
меньшей критической, называются жесткими.
Предшествующие выводы остаются справедливыми и для гори-
зонтального вала. Горизонтальный вал под действием силы тяже-
сти диска прогибается на'величину у0 (рис. 19.3). Вращение про-
исходит вокруг упругой Линии вала АО"В (а не АО'В). Прогиб у
вызывается действием центробежной силы, которая по-прежнему
равна m(z/+e)co2. Все предыдущие выводы сохраняют поэтому силу
и для горизонтального вала; критическое число оборотов от распо-
ложения оси вала не зависит.
Статический прогиб вала под действием силы тяжести диска G
определяется по формуле у0= G/с, или
-L=—
G у0
Подставляя отношения (19.9) в формулу (19.3), находим
«К=-Д^- -	(19.10)
Таким образом, критическую частоту вращения легко опреде-
лить по статическому прогибу ротора под влиянием силы тяжести.
Жесткость вала с определяется по известной формуле сопротив-
ления -материалов
(19.9)
c=k^~,
P
(19.11)
377
Рис. 19.3. Схема вращения прогнувшегося вала
Рис. 19.4. Значения коэффициента k для &вух
схем однодискового ротора
где k — коэффициент, зависящий от взаимного расположения опор
и точки приложения силы; J — момент инерции сечения, м4; I — рас-
стояние между опорами, м.
На рис. 19.4 указаны значения коэффициента k для двух слу-
чаев расположения диска относительно опор.
Из формул (19.3) и (19.11) находим
«к=29,9|/^-.	(19.12)
У Gi3
Это соотношение наиболее удобно для практического использо-
вания.
Отметим, что все приведенные выше формулы являются прибли-
женными. Они не учитывают массу вала, гироскопический момент
диска, податливость опор и ряд других факторов, о влиянии кото-
рых на критическое число оборотов сказано в следующих пара-
графах.
§ 19.2.	ЧАСТОТА КОЛЕБАНИИ ВАЛА ПОСТОЯННОГО
ДИАМЕТРА БЕЗ ДИСКОВ
Рассмотрим вал постоянного сечения без дисков, свобЬдно ле-
жащий на двух опорах. Для определения его критической скорости
(йк (равной круговой частоте собственных колебаний) может быть
использовано решение (13.8) дифференциального уравнения коле-
баний призматического стержня (13.6). Граничные условия в дан-
ном случае: У(0) = У"(0) = У(1) = У"(1) =0. Равенство нулю Y"
объясняется отсутствием изгибающих моментов на опорах [см.
формулу (13.1)]. Из этих условий следует, что Ci=C2=0; С3=С4.
Если обозначить через Л величину Са+С4, то уравнение упругой
линии вала примет вид
K=4sinax,	(19.13)
где х=хЦ— относительная координата вдоль вала.
378
Частотное уравнение задачи (оно вытекает из условия
У(1)=0)
, t	sina=O,	(19.14)
откуда	а=1л,	(19.15)
где i — любое целое число (1, 2, 3,...).
Критическая скорость [см. формулу (13.7)] «
(19.16)
где m—qfil — масса вала.
Критическое число оборотов при колебаниях первого тона
^=®Ье=295
л
EJ
Gal3
(19.17)
где GB — сила тяжести вала, Н.
В соответствии с уравнением (19.13) и формулой (19.15) при
колебаниях вала первого тона (i=l) упругая линия представля-
ет собой половину волны синусоиды, при колебаниях вала второго
тона (i=2) на длине вала размещается две полуволны с узловой
точкой посредине вала и т. д.
§ 19.3.	ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЯ КРИТИЧЕСКОЙ
ЧАСТОТЫ ВРАЩЕНИЯ ВАЛА ПОСТОЯННОГО
ДИАМЕТРА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ДИСКАМИ
Для приближенного определения критической частоты враще-
ния вала с диском (с учетом массы вала) может служить фор-
мула
где п0 — критическая частота вращения гладкого вала (без дис-
ка), определяемая по формуле (19.17); п.\— критическая частота
вращения невесомого вала с диском, подсчитываемая по формуле
(19.12); «к — искомая критическая частота вращения реального
вала с диском.
Отсюда
п^пА/ --------------,'	(19.19)
к ¥	1+(П1/Яо)2	k '
Из формулы (19. 19) видно, что учет массы вала уменьшает
расчетную критическую частоту вращения по сравнению с часто-
той, получаемой по формуле (19.12). Обычно поэтому раз-
ница между частотами вращения п\ и пк невелика.
Формулу (19. 18) применяют и для многоступенчатых турбин с
379
постоянным диаметром вала. В этом случае она записывается сле-
дующим образом:
____J___।___L_ । _L
„2	~ „2 ~ „2	„2
nK	Zig flj rtj n3
(19.20)
где ti\, иг, «з — критические частоты вращения вала с одним первым
диском, с одним вторым диском и т. д.
Частоту вращения п0 определяют по формуле (19. 17), а Ль л2,
Лз — по формуле (19.12) с тем или иным коэффициентом k, зави-
сящим от расположения данного диска относительно опор. Степень'
точности формул (19.18) и (19.20) оценивается различными авто-
рами в 3... 10%> причем истинное значение критической частоты
вращения обычно больше, чем найденное по этому методу.
В авиационных турбинах встречаются как жесткие, так и гиб-
кие валы. Если применяется гибкий вал, то критический режим
приходится на малые обороты, когда возбуждающая неуравнове-
шенная сила невелика и не вызывает больших прогибов [см. фор-
мулу (19.4)]. В случае необходимости применяются демпферы,
ограничители колебаний и т. п.
Для обеспечения прочности вала и уменьшения вибрации всего
двигателя разница между рабочей и критической частотами вра-
щения ротора должна составлять не менее 20... 25%.
§ 19.4.	ЭНЕРГЕТИЧЕСКИЙ МЕТОД РАСЧЕТА ВАЛА
Обычно валы газовых турбин имеют переменный по длине диаметр и нагру-
жены одним или несколькими дисками. Для определения критической частоты
вращения таких роторов существует ряд методов, из которых вначале мы оста-
новимся на энергетическом, применявшемся нами при исследовании колебаний
лопаток. При пользовании этим методом учитывают, что критическая угловая
скорость вращения равна круговой частоте собственных колебаний ротора, и
исходят из условия равенства максимальных значений потенциальной и кинети-
ческой энергии ротора за период колебания. •
Для определения энергии надо знать кривую прогиба вала при колебании.
Вполне удовлетворительный по точности результат получается, если за кривую
прогиба вала принять его упругую линию, возникающую под действием стати-
ческой нагрузки i.
Пусть Gi, Gz, G3 — силы тяжести дисков, Н: у^г у2, уз — прогибы под
дисками, м (рис. 19 5). .
Потенциальная энергия деформации вала, соответствующая максимальному
отклонению от положения равновесия,
Я — — (Gi#ii + Gflfa + G&3 -г ...) -	(19.21)
Расстояние центров тяжести дисков от положения равновесия в любой мо-
мент во время колебания равны:
!У1 sin Хт; $2 sin Хт; y# sin Хи...,
где А — круговая частота колебаний; т — время.
1 Абсолютные значения прогибов вала при колебаниях несколько отличают-
ся от значений статических прогибов.
380
Рис. 19.5. Расчетная схема вала «многоступенчатой
турбины
Когда диски яроходят через положение равновесия, скорости их достигают
наибольшего значения:
/ ду \
I	А; jfo*. - -
\ /max
Кинетическая энергия ротора в этот момент
2	>2
|	(^гУ? + ^2*^1 + ^3^1 + ...). (19.22)
'max Zg
Приравнивая выражения (19.21) ц (19.22), определяем круговую частоту
колебаний, т. е. критическую угловую скорость:
К
А = (i)K =
и критическую частоту вращения (об/мин)
30сок
лк =----=29,9
л
(19.23)
Отметим, что для определения первой критической скорости (частоты коле-
баний первого тона) необходимо выбирать соответствующую форму упругой ли-
нии вала, характерную наибольшими (по сравнению с другими формами) стре-
лами прогиба.
Так, для консольного вала наибольшие прогибы и, следовательно, первое
значение критической частоты вращения получается при форме упругой линии
(рис. 19 6, а), соответствующей случаю, когда силы направлены в противопо-
ложные стороны. Форма упругой линии (см. рис. 19.6, б) с односторонним'
направлением сил соответствует второй критической скорости. Поэтому при рас-
чете консольных или многоопорных в$лов (число опор более двух) следует при-
нимать направление действующих сил взаимно противоположным в двух сосед-
них пролетах.
Определять прогибы вала удобнее всего рекомендуемым в курсах сопротив-
ления материалов графическим методом, заключающимся в следующем.
Пусть задан вал, схематически изображенный на рис. 19.7, а. Вал состоит
из трех участков с моментами инерции /ь /2, /з и нагружен четырьмя силами
тяжести Gi, G%, Gs, G*.
Вал вычерчиваем в определенном масштабе по длине, равным 1 : т, т. е. 1 см
на чертеже изображает т см натуры. Под схемой вала строим эпюру изгибаю-
щих моментов (см. рис. 19.7, б). Относящийся к ней многоугольник сил показан
на рис. 19 7. в. Масштаб сил примем р в Н/см (т. е. 1 см чертежа соответствует
Р в ньютонах). Полюсное расстояние Hi выбираем произвольно. В масштабе
сил опо составляет рЯ* ньютонов.
Изгибающий момент в любой точке вала можно найти, умножив соответст-
вующую ординату эпюры z, измеренную в масштабе длин т, на полюсное рассто-
яние Яь измеренное в масштабе сил р, т. е.
М = mzpH\.
Для учета переменной жесткости сечений вала принимаем один из его уча-
стков (с наибольшим моментом инерции /осн) за основной и увеличиваем ор-
динаты других участков эпюры в отношении моментов сечений вала /осн/Л, где
381
Ji — момент инерции Z-го участка ва-
ла 4. Таким образом, на ’первом уча-
стке вала ординаты эпюры изгибаю-
щих моментов увеличены в 70си/Л
раз, на третьем участке — в 7о<.н//з
раз.
Для построения упругой линии
полагаем вал находящимся под наг-
рузкой, измеряемой площадью эпюры
изгибающих моментов.
Рис. 19.6. Схема консольного вале
Рис. 19.7. Схема графического расчета вала
Делим эпюру на ряд участков (заштрихованных в противоположные сторо-
ны) и в центре тяжести каждого из них прикладываем силу Л, равную площади
этого участка в Н • см2. Если площадь участка в масштабе чертежа равна f, то
сила R=m2fPHt.
Необязательно изменять контур эпюры изгибающих моментов, как это сде-
лано на рис. 19.7, б. Абсцисса центра тяжести участка не меняется при пропор-
циональном увеличении ординат участка. Поэтому можно умножить на /ОСн/Л
площадь участка, не увеличивая ординат эпюры.	\
чМногоугольник сил (см. рис. 19.7, г) для построения упругой линии строим
в масштабе 1 см=^ Н • см2.
Полюсное расстояние должно равняться (Е7)ос« или в выбранном мас-
штабе
---------
Так как обычно эта величина получается большой и не м'ожет быть отложена
на чертеже, уменьшаем ее в произвольное число г раз.
Таким образом,
„ (^Оосн
П2 —--------
qr
При этом прогибы вала окажутся выполненными на чертеже не в масштабе
1 : т, а в увеличенном масштабе 1 : mfr.
Построив упругую линию (см. рис. 19.7, д), найдем прогибы вала у^ г/г»
Уз, #4 под точками приложения сил. Снятые с чертежа величины прогибов умно-
жим на mfr, определив этим истинные прогибы вала. Далее вычисляем величины
^Gy и ^Gyi, а затем по формуле (19.23) — критическое число оборотов.
1 От участка к участку может изменяться также модуль упругости Е
(в случае составного’ ротора или изменения температуры по длине вала). Тогда
ординаты эпюр умножаются на отношение (EJ) Qcnf(EJ) i.
382
При этом значения у тдфъълягм. в метрах и считаем их положительными не-
зависимо от действительного знака прогиба.
.При определении критического значения частоты вращения вала, выполнен-
ного заодно с диском, момент инерции вала на протяжении толщины диска
можно считать бесконечно большим
В изложенном выше расчете не учитывается гироскопический эффект вра-
щающихся дисков, о котором сказано в § 19.5... 19.81 2.
Особенности расчета вала с консольно
расположенным диском
Отметим некоторые особенности расчета валов, имеющих консольные участки.
На рис. 19.8 изображен вал переменного диаметра с диском, расположен-
ным на консоли. Вал разбит на пять участков, длины которых указаны на чер-
теже
Рис. 19.8. Схема к расчету вала с консольно
расположенным диском
1 Принимать этот участок за исходный при изменении эпюры моментов не
следует.
2 Энергетический метод расчета критических чисел оборотор вала с учетом
гироскопического момента изложен в работе [7].
383
Рис. 19.9. Схема ротора с двумя консолями
Согласно сказанному выше силы тяжести Git G2* с одной стороны, и
Gs ... G5 — с другой, отложены как на схеме вала, так и на многоугольнике
сил во взаимно противоположных направлениях.
Построение веревочного многоугольника, как обычно, начинается с точки Л.
Из этой точки проводят линию, параллельную лучу а на силовом многоуголь-
нике, затем последовательно проводят линии, параллельные лучам b> ct d и е.
Из точки F, находящейся на линии приложения крайней справа силы G5, про-
водят линию, параллельную лучу f, до точки В, лежащей на вертикали, прохо-
дящей через правую опору. Замыкает эпюру линия АВ. Полученную эпюру изги-
бающих моментов приводят к максимальному моменту инерции (в данном при-
мере — к J3). Момент инерции пятого участка принят бесконечно большим.
Дальнейший расчет производят обычным образом. Строят веревочной многоуголь-
ник, соответствующий силам & ... /?8 и определяют упругую линию вала. Осе-
вую линию вала, от которой должны отсчитываться прогибы у^ ... проводят
через точки С и D. В формулу (19.23) эти прогибы подставляют положитель-
ными независимо от их направления.
Если вал имеет две консоли (рис. 19.9), то после построения многоугольника
сил из точки А влево до линии действия силы Gi, проводят линию АЕ, парал-
лельную лучу а. Из точки пересечения Е вправо проводят последовательно ли-
нии, параллельно лучам b ... g. Затем проводят линию FB, параллельную лучу Л.
Замыкает эпюру линия В А. Эпюру изгибающих моментов приводят к жесткости
какого-либо участка (в нашем случае четвертого) и определяют упругую линию
вала. Осевую линию проводят через точки С и D на вертикалях под опорами
вала.
384
§ 19.5.	ВЛИЯНИЕ ГИРОСКОПИЧЕСКОГО МОМЕНТА ДИСКОВ
НА СОБСТВЕННЫЕ ЧАСТОТЫ КОЛЕБАНИЙ ВАЛА
Вращение ротора в каждой его точке происходит вокруг каса-
тельной (£ — g на рис. 19.10) к упругой линии вала с угловой
скоростью со. При наличии возбуждающих сил упругая линия мо-
жет вибрировать в двух взаимно перпендикулярных плоскостях.
В, результате сложения колебаний каждая точка упругой линии
может иметь прямолинейную, эллиптическую или круговую траек-
торию движения. При движении по окружности упругая линия
вращается с угловой скоростью Q вокруг геометрической оси вала,
т. е. прямой линии АВ, проведенной через центры подшипников.
Вообще говоря, скорость и направление вращения упругой ли-
нии не зависят от скорости и направления вращения ротора.
При совпадении направлений скоростей а и Q имеем случай
прямой прецессии; если же вращение ротора и его упругой
линии происходит в противоположных направлениях, то имеет ме-
сто обратная преце'ссия. Когда абсолютные значения ® и
Q совпадают, прецессия называется синхронной, в противном
случае — несинхронной.
Прецессионные движения обусловливаются наличием внутрен-
них и внешних сил, вызывающих колебания изогнутой оси вала.
К внутренним силам прежде всего следует отнести неуравно-
вешенную силу ротора, круговая частота которой равна угловой
скорости вращения его. Эта сила, всегда имеющаяся в реальном
роторе, возбуждает прямую синхронную прецессию. Неодинако-
вая в горизонтальном и вертикальном направлениях жесткость
опор, а также статический прогиб вала приводят при вращении
его к появлению внутренних сил, которые могут возбудить обрат-
ную синхронную прецессию.
К внешним силам относятся периодические силы газов, дейст-
вующие на облопаченный диск; переменные усилия, возникающие
в шестернях и муфтах, соединяющих валы; воздействие друг на
друга соосных валов, вращающихся с различными скоростями в
двухроторных ГТД, и т. д. Эти силы могут вызывать прямую и об-
ратную прецессию как синхронную, так и несинхронную.
Резонансной частот ой вращения будем называть
такую, при которой частота какой-либо внешней или внутренней
силы совпадает с собственной часто-
той колебаний вращающегося вала.
Наибольшую опасность представля-
ет работа на такой частоте, при ко’
торой частота возмущающей н е-
уравновешенной силы ро-
тора совпадает с собственной час-
тотой колебаний вращающегося ва-
Рис. 19.10. Схема к расчету вала с учетом
гироскопического момента диска
13	1337	385
ла. Это значение частоты вращения, как уже указывалось, называ-
ется критическим и должно определяться в первую очередь.
При наличии прецессионных движений вала на элементарную
массу диска (см. рис. 19.10) действует центробежная ДРЦ и корио-
лисова AQ силы, которые в сумме дают силу
P=mQ1 2y	(19.24)
и изгибающий момент
M=AJKQ2a,	(19.25)
приложенные к валу в точке О {15] *.
В этих формулах т — масса диска; /д — экваториальный мо-
мент инерции диска относительно диаметра, проходящего через
точку О; А=1—y —коэффициент прецессии, характеризующий
величину и знак гироскопического момента, действующего на вал
при прецессионном движении. Здесь Jx — полярный момент инер-
ции относительно оси диска, которая в данном случае совпадает
с касательной £ — g.
Для тонких турбинных дисков /Ж/7Д=2. Как следует из формул
(19.24) и (19.25), при прямой синхронной прецессии (А=—1) ги-
роскопический момент отрицателен, т. е. уменьшает прогиб вала и,
следовательно, увеличивает, его собственную частоту и критические
обороты.
При обратной синхронной прецессии (А=3) гироскопический
момент положителен, т. е. увеличивает прогиб вала и снижает его
собственную частоту 2.
Из сказанного следует, что критическая угловая скорость вра-
щения с учетом гироскопического момента дисков отличается от
круговой частоты собственных колебаний невращающегося вала.
§ 19.6.	КРИТИЧЕСКАЯ И РЕЗОНАНСНАЯ ЧАСТОТЫ
ВРАЩЕНИЯ ВАЛА С УЧЕТОМ ГИРОСКОПИЧЕСКОГО
МОМЕНТА ДИСКА
Рассмотрим круглый невесомый вал на двух опорах с диском
между ними (рис. 19. И).
Пусть кривая АОВ — деформированная при колебаниях ось ва-
ла, центр тяжести диска находится в точке О, система координат
хуг— неподвижная, система gijg— подвижная, причем Og направ-
лена по касательной СО к линии АОВ в точке О.
Будем считать далее, что координата х центра тяжести при
колебаниях не изменяется. Тогда положение рассматриваемой си-
стемы определится координатами центра тяжести диска у =0^0 и
z=OOi и углами аир, где а=2_0С£>— угол между касательной
СО и плоскостью ху; ^=Z-OiCiF — угол между проекцией каса-
1 Полагаем, что центр тяжести диска совпадает с точкой О. Направление
силы AQ (см. рис. 19.10) соответствует обратной прецессии.
2 При обратной синхроной прецессии Д<2>ДРЦ.
.386
Рис. 19.11. Схема к выводу урав^
нений движения вала
тельной на плоскость ху
(Р1С1) и осью х. Диск вра-
щается с угловой скоростью
о), направленной по часовой
стрелке, если смотреть с по-
ложительного направления
оси 0% к ее началу.
Чтобы составить четыре!
уравнения движения (необ-
ходимых для определения
четырех неизвестных у, г, а
и р), воспользуемся уравнениями Лагранжа второго рода, приво-
димых в курсах теоретической механики:
(19. 26)
где 77 и К — потенциальная и кинетическая энергия колеблющейся
системы; <р< — обобщенная координата (в нашем случае у, z, а и р);
т — время.
Для определения потенциальной энергии П рассмотрим изгиб
вала в плоскостях хг и ху под действием силы Р и момента А7.
Ввиду малости углов аир можно принять, что угол а равен углу у
между проекцией касательной ОС на плоскость хг (О2С2) и осью х.
Тогда потенциальная энергия изгиба в плоскости xz
П^у^+ТИа),	(19.27)
а в плоскости ху
(19-28)
Известно, что при малых деформациях
z=anP-|-
а :=== 021^ “|“ 022^^»
где 0ц, 012, аги агг — коэффициенты влияния.
Первый индекс при коэффициентах означает номер деформации
(прогиб—1, угол поворота — 2), второй — номер • единичной на-
грузки (сила— 1, изгибающий момент — 2). Таким образом, ац —
прогиб в точке О от действия единичной силы; 0]2 — прогиб в точке
О от действия единичного момента; 021 — угол поворота сечения ва-
ла в точке О от действия единичной силы; а22—угол поворота се-
чения вала в точке О от действия единичного момента.
Определение этих коэффициентов дано в следующем параграфе.
По известной из сопротивления материалов теореме взаимности
перемещений ai2=a2i.
13*	387
(19.29)
Из уравнений (19.29) находим
Р ~~ СцХ С12®)
М= — С21Х + С22О>
где коэффициенты
г _	«22
Сн— г- >
«11«22 — «12
с12 =---------—J“ = c2i;
«11«22 - «12
- _ «И
с22---------------Т
«11«22 — «12
(19.30)
(19.31)
называются коэффициентами жесткости системы.
Подставив уравнения (19.30) в формулу (19.27), найдем выра-
жение для потенциальной энергии изгиба вала в плоскости xz 
/7j=-у (cuz2—2ci2za+с22а2).
(19.32)
Так как вал симметричный, то аналогично запишется и выраже-
ние для потенциальной энергии изгиба вала в плоскости ху
/71=-^(С11У2-2С12У₽+^).	'	(19.33)
Суммарная потенциальная энергия изгиба вала
/7=/714-/72.	(19.34)
Кинетическая энергия данной системы определяется выраже-
нием
/C=-i-m(z'2+y'2)+K1,	(19.35)
где К\.—~ Jx<oa4--y-т — масса диска.
Подставляя найденные значения для П и К, в уравнения (19.26),
получим систему из четырех уравнений для определения неизвест-
ных z, у, а и
otz" 4- cuz—с12а—0;
т^+сцу-Сц^О-,
/да"-/Лш?'+С12а-С122=0;	1 J
J 4- Jx«>aZ-|_C22p“Ci2P=O. '
Частное решение этой системы уравнений будем искать в виде
z=a sinQt; y=acosQt; |	(19 37)
a=isin£2r; bcosSr. j
-388
Здесь Q — собственная час-
тота колебаний вращающегося
вала, равная угловой скорости
вращения его упругой линии
(относительно оси ЛОВ), или
скорости прецессии. Из уравне-
ний (19.37) видно, что поло-
Рис. 19.12. Диаграмма прецессионных движений вала
Рис. 19.13. Схемы форм упругой линии при колебаниях вала с одним диском
жительные направления скоростей w и Q совпадают.
Подставив выражения (19.37) в систему (19.36), получим
(сп—mQ2) а — саЬ=0; — с12а + (<?22 — /д22+7Л<о2) b=0.
Исключая отсюда величины а и Ь, придем к уравнению частот
2
2*— -Ll <023_ рп	д24—а>2 4- С11С22~С12 = о. (19.38)
7д	\ /и	Jд т	mJ»
Это уравнение можно записать в виде
а4-/—+—1а24- —1С22~—q(q2-Sil). (19.39)
\ т	/	m/д	/д \	т )
или иначе (22—2?) (22—21)2 (22 — 2о),
где Qi и-Я2 — собственные частоты невращающегося вала, т. е. кор-
ни уравнения (19.39) при со=0; 20=1/ — .
у т
На рис. 19.12 показана диаграмма прецессионных движений ва-
ла, т. е. зависимость его собственной частоты Q от скорости вра-
щения ю.
Рассматриваемая система имеет две формы собственных коле-
баний, изображенных на рис. 19.13. Форме а соответствует нижняя
кривая на рис. 19.12, форме б — верхняя.
Нижняя кривая расположена между асимптотами 0=0 и
2=р/~верхняя — между асимптотами.2= р/"и 2=-^- ш
для тонких дисков
389
Правый квадрант (см. рас. 19.12) соответствует области пря-
мой прецессии (знаки юий одинаковы), левый — области обрат-
ной прецессии (знаки © и й различны).
Из рассмотрения кривых й(©) следует, что при прямой прецес-
сии гироскопический момент увеличивает собственную частоту ко-
лебаний вала, при обратной — уменьшает ее. Это подтверждает
сказанное в § 19. 5.
Если на рис. 19.12 провести лучи й=Аю, где k — любое целое
число, отвечающее частотам возмущающих сил, то точки пересече-
ния их с кривыми собственных частот определят резонансные ско-
рости вращения.
Неуравновешенная сила ротора имеет частоту, равную его угло-
вой скорости вращения (k=l). Луч й=® пересекает только ниж-
нюю кривую й(и) в точке а, которой соответствует критиче-
ская скорость вращения ©к-
При	имеются две резонансные скорости вращения
\ ' Д /
(точки b и с), при которых возникает прямая несинхронная пре-
цессия.
В области обратной прецессии при любом значении k имеем две
резонансные скорости. Так, точкам d и е отвечают резонансные ско-
рости при обратной синхронной прецессии. Одна из них по вели-
чине меньше, другая больше критической скорости.
Представляющую наибольший интерес критическую скорость,
при которой Й—со, можно определить, если в уравнении (19.38)
величину й заменить на со. При этом получим биквадратное урав-
нение
2	>
I ^С22-С12 = (?> Н9.40)
\ /д /	[\ /д / т л J mh
имеющее лишь один положительный вещественный корень, отвечаю-
щий критической скорости.
Заменяя в уравнении (19. 38) й на —со, получим уравнение
2
fl-b^'jco4—[(1-I-—) —+ ———=0 , (19.41)
\ ^д / L\ л / /И	?д J	®^д
которое имеет два положительных вещественных корня, определя-
ющих две резонансные скорости обратной синхронной прецессии.
Аналогично, полагая в (19.38) й=±/гсо, можно найти скорости
прямой или обратной несинхронной прецессии.
Изложенный в данном параграфе метод расчета вала на коле-
бания при помощи коэффициентов влияния позволяет не только
более точно, чем при графическом расчете, определить критическое
число оборотов (в связи с учетом гироскопического момента), но и
дает возможность исследовать прецессионные движения вала, не-
которые из которых также представляют опасность для его проч-
ности.
Недостатком этого -метода является сложность применения его
для расчета валов с большим числом дисков. В этом случае урав-
390
Рис. 19.14. Схема и эпюры к
определению коэффициентов
влияния
нение (19.40) для опреде-
ления критических скоро-
стей (их будет тогда не-
сколько) имеет порядок
2п относительно со2, где
п — число дисков.
Если, однако, в много-
ступенчатой турбине дис
ки расположены доста-
точно близко друг к дру-
гу и скреплены между со-
бой, как показано, напри-
мер, на рис. 20.1, 20.2, то
вал такой турбины можно
рассчитать по уравнениям
(19.40) и (19.41), понимая под т массу
всех дисков с лопатками, сосредоточенную в общем центре тяже-
сти, а под 1Х и /д — соответствующие моменты инерции этой
массы.
Следует также заметить, что рассматриваемым здесь методом
нельзя учесть влияние массы вала на критическое число его обо-
ротов
§ 19.7. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЛИЯНИЯ
И МОМЕНТОВ ИНЕРЦИИ
Определение коэффициентов влияния
Коэффициенты влияния ан, 012=021 и а,,, входящие в формулы (19.19) и
(19.31), найдем при помощи интеграла Мора:
Г
ail = \~^TdXi
012 = 021
С МрМм .
\~£Td3C'
(19.42)
Л22 = 5“ёГ'/х
о
В этих формулах, приводимых в курсах сопротивления материалов, МР и
Мм <— изгибающие моменты соответственно от единичной силы и единичной
пары, приложенных к валу в месте расположения диска.
Для вычисления интегралов вал разбиваем на участки, в пределах которых
остаются неизменными жесткость вала, а также закон изменения момента по
длине участка.
Масса вала учитывается в методе, изложенном в книге [7] § 8.2.
391
Так, например, для вала, изображенного на рис. 19.14, в пределах участка
..	^5— Й	х
между опорами Мр1~'—;—xt Мм, ~	; на консольном участке Л1Р2==
,	*з
— 1ъ—Мм2=1.
Подставим эти выражения в формулы (19.42) и введем обозначения:
* = Т R+"77 <Ч- •*?)+ ~7Г ("з - -1) ];
*2 =	-j4(i - *3)3 - (1 - *4)3];
Ъ - V -у- [О - хз)2 - (1 - *4)2];
Z /4
Й4=__(Ж4_ хз)
J4
Тогда, считая жесткость £7, бесконечно большой,
(19.43)
«и =«/5(02*1 + *й);
(19-44)
^22 *= а
Определение моментов инерции
Полярный момент инерции диска подсчитывают по частям. Обычно диск
можно разбить на части, представляющие собой цилиндр, полый цилиндр, усе-
ченный конус. Полярный момент инерции цилиндра относительно его оси
j;=q
aR4h
2 ‘
(19.45)
усеченного конуса
Полярный момент инерции полого цилиндра
/',=с-^-(Л4-н),
nh Я5— г5
х = ° 10 R — r
(19.46)
(19.47)
* В этих формулах: h — высота цилиндра (конуса); R — наружный радиус
цилиндра или радиус большего основания конуса; г — внутренний радиус ци-
линдра или радиус меньшего основания конуса.
Полярный момент инерции лопаток	где т — масса одной ло-
патки; z — число лопаток; п »— радиус центра тяжести лопатки.
Суммарный момент инерции /х = 2 ? х*
Экваториальный момент инерции /д==Л»/2. Эта формула дает удовлетвори-
тельную точность лишь для тонких дисков. Для дисков значительной толщины
(по сравнению с диаметром, например, для радиальных турбин) или роторов мно-
гоступенчатых турбин
/д=2</;+'ив2)’
(19.48)
392
где /д' — экваториальный момент инерции той или иной части диска (ротора)
массой т\ е — расстояние от центра тяжести этой массы до общего центра тя-
жести диска.
§ 19.8. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ
НА КРИТИЧЕСКУЮ ЧАСТОТУ ВРАЩЕНИЯ ВАЛА
При определении критической частоты вращения мы пренебре-
гали влиянием ряда различных факторов, хотя некоторые из них
при определенных соотношениях не могут считаться второстепен-
ными. Рассмотрим вкратце эти факторы.
Влияние упругости опор и корпуса
Выше, определяя частоты изгибных колебаний вала, мы счита-
ли, что он опирается на абсолютно жесткие опоры, расположенные
в массивном корпусе. Тонкостенный корпус и опоры газотурбинного
двигателя имеют сравнительно небольшую массу и обладают за-'
меткой гибкостью. В этом случае указанное допущение приводит
к значительному расхождению расчетной и действительной вели-
чин критической частоты вращения.
Критическую частоту вращения ротора на упругих опорах (без
учета гироскопического момента диска) можно подсчитать по фор-
муле, аналогичной (19.9):
,	29,9	29,9
К УУ К|Ио + '«1
(19.49)
где yo=G[c — прогиб собственно вала в точке крепление диска;
— смещение этой точки, вызванное деформацией опор; G — сила
тяжести диска; с — жесткость вала, определяемая по форму-
ле (19.1ф).
Величину yi, например, для ротора, изображенного на рис.
19. 15, найдем следующим образом. Перемещение у упругой опоры
с жесткостью с0 под действием реакции R y=R/c0.
Так как У1==у1—^-, а	, то
' (19,50)
где ^=а!1.
Пользуясь выражениями (19.9), (19.49) и (19.50), найдем,
что
(19.51)
Зависимость-^-, определяемая формулой (19.51), представле-
лк
на на рис. 19. 15. Из рассмотрения кривых следует, что при жест-
кости опоры, сравнимой с жесткостью вала, критическая чаето-
393
Рис. 19.15. График влияния жест-
кости опор на критическую часто-
ту вращения вала с диском между
опорами
та вращения вала заметно
снижается. Если опоры име-
ют неодинаковую жесткость
в двух взаимно перпендику-
лярных направлениях, то
для вала с одним диском бу-
дут два различных значения
критических чисел оборо-
тов.
Надежное значение жесткости опор можно получить лишь экс-
периментальным путем. Ориентировочно жесткость опор с0^
(0,05 ... 0,2) • 109 Н/м, причем жесткость подшипников качения
для вала диаметром 60... 80 мм составляет (0,3 ... 1,0) • 109 Н/м.
Пример упругой (обладающей пониженной жесткостью) опоры
показан на рис. 19.16. Между наружным кольцом подшипника и
корпусом опоры установлен пакет из нескольких гибких колец.
В пакете последовательно чередуются гладкие кольца 1 и кольца 2,
имеющие двухсторонние выступы. При сборке пакета кольца уста-
навливаются так, чтобы выступы располагались в шахматном по-
рядке, как показано на рис. 19.16 справа. Под нагрузкой кольца
между выступами изгибаются и их суммарная деформация обуслов-
ливает повышенную гибкость опоры. Введение упругих опор позво-
ляет сместить первую критическую скорость в область малых зна-
чений частоты вращения, где амплитуда возбуждающей колебания
неуравновешенной силы мала. Это обеспечивает безопасный много-
кратный проход ротора через критическую частоту вращения.
Данная опора обладает также демпфирующими свойствами. При
деформации упругих колец имеет место трение выступов о поверх-
ности гладких колец. Часть энергии колебаний тратится на выдав-
ливание масла из малых щелей-зазоров между кольцами. Поэтому
такие опоры правильнее называть упругодемпферными. Вместо ко-
Рис. 19 16. Схема упругодемпферной опоры
394
Рис. 19.17. Схема упругодемпферной опоры
типа «беличье колесо»:
/—жиклер: 2—обойма-. 3—окна: 4—корпус опоры;
5—уплотнительные разрезные кольца; 6—рессора,
7—гайка
лец, изготовление которых достаточ-
но сложно, можно применить набор
из кольцевых разрезных пластин,
образующих упругий пакет.
Упругодемпферная опора типа
«беличье колесо» изображена на
рис. 19.17. Наружное-кольцо зажи-
мается гайкой 7 в стакане рессо-
ры 6.
Фланцевым соединением рессора скреплена с обоймой 2, кото-
рая в свою очередь крепится к корпусу опоры 4. В цилиндрических
оболочках, соединяющих фланец и стакан рессоры и фланцы обой-
мы, прорезаны параллельно оси окна 3, узкие перемычки (балочки)
между которыми являются упругими элементами. Варьируя разме-
рами балочек, можно получить необходимую жесткость опоры.
Между стаканом рессоры и корпусом опоры имеется небольшой
зазор, в который подается под давлением масло. Зазор уплотнен с
двух сторон разрезными кольцами 5. Образованная таким обра-
зом масляная полость является демпфирующим элементом. Через
жиклер 1 подводится масло к подшипнику.
Если ротор вращается на упругих опорах, расположенных в
корпусе, имеющем конечную жесткость (иногда сравнимую с жест-
костью ротора), то-возникают связанные колебания системы ро-
тор — корпус. В этом случае критические значения частоты вра-
щения несколько повышаются, однако они остаются меньшими, чем
критические значения частоты вращения ваш на жестких опорах.
Кроме того, появляются дополнительные значения частоты враще-
ния, при которых наблюдается значительная вибрация двигателя.
Некоторые из них могут быть меньше, чем критические значения
частоты вращения ротора на жестких опорах. Однако напряжения
в вале, возникающие в этом случае, оказываются малыми. Под-
робно вопрос совместных колебаний ротора и корпуса рассмотрен
в специальной литературе.
Влияние конструкции ротора
Роторы турбины ГТД являются, как правило, составными. Флан-
цевые и штифтовые соединения уменьшают жесткость вала и, сле-
довательно, критическую частоту вращения.
Наоборот, диски, различные втулки и кольца, посаженные на
вал с натягом, повышают жесткость и критическую частоту враще-
ния ротора.
Если диск, сидящий на валу, достаточно тонок, то при колеба-
ниях он не остается плоским, а изгибается относительно диаметра,
перпендикулярного плоскости колебаний. Это также в некоторых
395
случаях заметно снижает собственную частоту колебаний ротора и,
следовательно, его критическую частоту вращения.
В авиационных ГТД широко применяется трехопорная схема ро-
тора, когда турбина и компрессор соединены муфтой (см. рис.
18.1), которую можно принять за шарнирную опору для ротора
турбины. В этом случае колебания роторов турбины и компрессо-
ра становятся взаимосвязанными и, строго говоря, следует опре-
делять критическую частоту вращения ротора двигателя в целом.
Для этого можно применить, например, метод,  изложенный в
§ 8.2 книги [7]. Особенно заметно снижается частота колебаний
ротора турбины, если частота колебаний компрессора и турбины»
вычисленные независимо друг от друга, близки между собой, а кон-
сольный участок вала компрессора превышает 0,1... 0,15 от длины
вала турбины.
Влияние осевой силы, перерезывающей силы
и крутящего момента
Влияние осевой силы, всегда действующей на турбинный вал, на
частоту собственных колебаний 1-го тона учитывается формулой
и>к=<ок1/Г 1 ±	»	(19.52)
Г	-Тир
где ©к — низшие частоты собственных колебаний при наличии
продольной силы и без учета ее влияния; Р — величина осевой си-
лы; РКр — критическая сила при продольном изгибе вала.
При силе, растягивающей вал, под корнем уравнения (19.52)
берется знак плюс, при сжимающей — знак минус, т. е. растягива-
ющая сила повышает, а сжимающая снижает критическое число
оборотов. В большинстве случаев эта поправка пренебрежимо мала.
Столь же незначительно влияние перерезывающей силы и кру-
тящего момента, которые, вообще говоря, снижают критическую
частоту вращения вала.
Глава XX
КОНСТРУКЦИИ ТУРБИН
§ 20.1. ТУРБИНЫ ГТД
На рис. 20.1 изображена трехступенчатая турбина двухвального
ТРДД АИ-25.
Первая ступень турбины приводит компрессор высокого давле-
ния, две последующих — компрессор низкого давления. Сопловые
лопатки I ступени охлаждаемые, внутри них завальцован дефлек-
тор. Вторичный воздух из камеры сгорания проходит к лопаткам
396
00
58
• Рис. 20.1. Схема турбины двухвального ТРДД АИ-25:
/—стяжной болт; 2, /0—подшипники; 3—форсуночное кольцо; 4, //-втулки- 5, 0—контактные
уплотнения;	12—трубки; 7—кожух; 3—вал турбины низкого давления; 13—балансировочные
Грузы; 14—труба; 15—отверстия; 16— рессора
через отверстия 15. Выход воздуха из лопатки осуществляется че-
рез отверстия вблизи выходной кромки. Сопловые лопатки II и
III ступеней, а также рабочие лопатки всех трех ступеней — неох-
лаждаемые. Рабочие лопатки имеют бандажные полочки с высту-
пами лабиринтного уплотнения.
Ротор турбины высокого давления описан в § 18.1.
Вал турбины низкого давления опирается на два роликовых
подшипника, один из которых 2 установлен внутри вала ротора вы-
ского давления, другой 10 — в задней опоре двигателя. К фланцу
вала 8 с двух сторон присоединяются призонными болтами диски
II и III ступеней. Осевое усилие воспринимается стяжным болтом
1, соединенным с валом компрессора низкого давления. Грузы 13
служат для балансировки ротора низкого давления.
Уплотнения 5 и 9 — контактные, аналогичные показанным на
рис. 18.2.
Масло к подшипнику 2 подается через форсуночное кольцо 3.
В его кольцевую проточку масло попадает из вращающейся масло-
подводящей трубки 6 через радиальные сверления во втулке 4 и
валу 8.
Трубка 6 опирается на кожух 7, закрепленный на валу. Узел
перехода масла из неподвижной трубки 12 к вращающейся труб-
ке 6 уплотнен бронзовой втулкой 11.
Отвод смазки от подшипника 2 производится через отверстия в
валу ротора высокого давления (см. § 18.1). Охлаждение роторов
турбины осуществляется вторичным воздухом, как показано стрел-
ками. Со стороны реактивного сопла диск III ступени охлаждается
воздухом, поступающим через трубу 14 от III ступени компрессора
высокого давления. Наружный корпус турбины охлаждается возду-
хом второго контура.
На рис. 20.2 показана четырехступенчатая турбина двухваль-
ного ТРДД. Обе турбины — высокого и низкого давления — двух-
ступенчатые. Первая ступень турбины высокого давления имеет
охлаждаемые сопловые (см. рис. 11.4) и рабочие лопатки. Для
обеспечения подвода воздуха к рабочим лопаткам служит дефлек-
тор 9, который крепится к переднему фланцу диска (см. рис. 14.2).
На периферии дефлектор дополнительно соединен с ободом диска
замком пушечного типа. В полость между дефлектором и диском
через отверстия 11 и фрезеровки во фланце диска подается вто-
ричный воздух из камеры сгорания. Через отверстия в ободе диска
и контровочном замке 10, фиксирующем лопатки от осевого пере-
мещения, воздух попадает в радиальные отверстия, выполненные в
теле лопаток, и выходит в радиальный зазор над бандажными пол-
ками лопаток.
Через щели между диском, лабиринтом 1 и валом турбины вы-
сокого давления 2 вторичный воздух попадает в полость между дис-
ками I и II ступеней. Часть его охлаждает боковые поверхности
дисков и выходит в проточную часть турбины; другая его часть
идет далее на охлаждение задней стороны диска II ступени и на
охлаждение с двух сторон диска III ступени. Диск IV ступени ох-
398
Рис. 20.2. Схема турбины двухвального ТРДД с охлаждаемыми рабочими лопатками:
/—лабиринт; 2—вал турбины высокого давления; 3, 6—призониые штифты; 4, 5, 7—гайки: 8—силовые стойки- 9—дефлектор; /0—контровочный
замок; //—отверстия; 12—труба
399
лаждается воздухом второго контура, подводимым по полым сило-
вым стойкам 8 задней опоры и через отверстия в ее стенках. Сна-
ружи корпус турбины охлаждается воздухом второго контура.
Валы турбин высокого и низкого давлений опираются на ро-
ликовые подшипники, установленные в упругодемпферных опорах
(см. рис. 19.17). Узел соединения валов турбины и компрессора
высокого давления показан на рис. 18. 2.
Крутящий момент с дисков II, III и IV ступеней передается на
соответствующие валы призонными штифтами 3 и 6. К фланцам
валов диски прижимаются гайками 4, 5 и 7 через распорные втулки
и детали лабиринтных уплотнений.
Пятиступенчатая турбина трехвального английского ТРДД
RB.207 приведена на рис. 20.3 [23]. Двигатель развивает тягу на
взлетном режиме ~211 кН. Степень двухконтурностй равна 5. Тем-
пература газа перед турбиной 1422 К.
Турбины высокого и низкого давления — одноступенчатые.
Между ними располагается передняя опора 2, в корпусе которой
закрепляются фланцами, выполненными заодно с наружными коль-
цами, роликовые подшипники первого и второго роторов. В задней
опоре 8 расположен роликовый подшипник трехступенчатой турби-
. ны вентилятора. Все подшипники не имеют внутренних колец. Опо-
ры коробчатого сечения сварены из листового материала.
Передняя опора соединена с наружным корпусом турбины фре-
зерованными стойками 10, которые проходят через широкие полые
сопловые лопатки II ступени 9 и фиксируются в корпусе призон-
ными втулками. Задняя опора соединена с корпусом сварными об-
текаемыми стойками. К наружному кольцу задней опоры приваое-
ны узлы крепления двигателя к самолету.
Крутящий момент передается с диска I ступени на вал, соеди-
ненный с диском последней ступени компрессора с помощью ради-
альных треугольных шлицев и болтов. Аналогичным способом сое-
динены диски III и IV ступеней, а также вал турбины вентилятора
с диском IV ступени.
Диск и вал II ступени, диски IV и V ступеней и задняя цапфа,
ротора турбины вентилятора соединены призонными болтами. От
изгиба и вибрации тонкий диск II ступени подкреплен коническим
силовым кольцом 3, диски IV и V ступеней соединены между собой
с помощью тонких кольцевых перемычек 5 и 7.
Сопловые лопатки всех ступеней отлиты заодно с верхними и
нижними полочками, которые имеют кольцевые бурты и радиаль-
ные выступы, входящие в соответствующие кольцевые проточки и
пазы в корпусе турбины и фиксирующие лопатки в окружном, ра-
диальном и осевом направлениях.
Сопловые лопатки I ступени охлаждаются вторичным воздухом.
Для охлаждения лопаток II ступени подводится воздух от III сту-
пени компрессора высокого давления.. Для интенсификации охлаж-
дения служит дефлектор 11. Подвод вторичного воздуха для ох-
лаждения рабочих лопаток I ступени производится через коллек-
тор 1, прикрепленный к внутреннему кольцу соплового аппарата.
400
Рис 20.3. Схема пятиступенчатой турбины английского ТРДД RB 207:
/—коллектор; 2—передняя опора; 3—силовое кольцо; 4, 6—отверстия; 5, 7—перемычки; Я—
задняя опора; 9—сопловые лопатки II ступени; 10—стойки; //—дефлектор
В коллекторе создается предварительная закрутка потока возду-
ха для обеспечения осевого входа на лопатки.
Охлаждение дисков осуществляется воздухом от компрессора,
который проходит через кольцевую щель между диском I ступени
и валом II ступени, отверстия в задней цапфе I ступени, передней
опоре, фланцах валов Пступени и турбины вентилятора, а также
в нижнем кольцевом элементе крепления диска IV ступени.
Выход охлаждающего воздуха в проточную часть турбины про-
исходит через лабиринтные уплотнения и отверстия 4 и 6 в верх-
них кольцевых перемычках дисков III и IV ступеней.
§ 20.2. ТУРБИНЫ ПРИВОДА НАСОСОВ ЖРД
В ЖРД с небольшой и средней тягой (порядка нескольких де-
сятков килоньютонов), которые имеют обычно невысокое давление
в камере сгорания, применяются преимущественно активные (час-
то парциальные) турбины, работающие с малым отношением и/сад
(например, 0,2). Это объясняется их простотой, малой удельной
массой, способностью работать с высокими частотами вращения
401
при высоких температурах газов. Низкие к. п. д. турбин (порядка
40%) в таких ЖРД не играют большой роли, так как турбина ТНА
расходует незначительный процент запаса топлива в ракете. Дав-
ление газа перед турбиной обычно бывает в пределах 2,0...
... 5,5 МН/м2, но в отдельных случаях достигает 10 МН/м2. На-
чальная температура газов, как правило, меньше, но в некоторых
конструкциях ТНА она выше, чем в ГТД.
В двигателях больших космических ракет с тягой в несколько
сотен или даже тысяч килоньютонов максимально возможное увели-
чение к. п. д. турбины крайне желательно. Увеличение к. п. д. тур-
бины на несколько процентов в таких ракетах означает весьма
заметное снижение их начальной массы при заданной конечной
массе или значительное увеличение полезного груза при заданной
стартовой массе ракеты. Поэтому в больших ЖРД находят при-
менение многоступенчатые турбины как активные со ступенями
скорости или давления (число которых достигает шести), так и ре-
активные.
Некоторые ЖРД выполняют по схеме с дожиганием газа, про-
шедшего через турбину в основной камере сгорания двигателя.
Давление и температура газа перед турбиной таких двигателей
может достигать весьма высоких значений.
Следует заметить, что газовые турбины в ракетостроении при-
меняются не только в ТНА, но используются также для привода
генераторов, холодильных и гидравлических насосов и других аг-
регатов различного назначения.
На рис. 20.4 показана турбина ТНА известной немецкой ра-
кеты V-2. Турбина развивает мощность 342 кВт при 3800 мин-1 и
расходе газа 2,13 кг/с. Давление газа на входе 2,58 МН/м2, на вы-
ходе— 0,175 МН/м2; начальная температура газа 660 К. Средний
диаметр турбины 447 мм.
Рабочий газ (продукты разложения 80%-ной перекиси водоро-
да) подводится к патрубку 6, а затем по распределителю 7 к четы-
рем сопловым сегментам 8 (см. рис. 11.3). После выхода из коле-
са Кертиса 3 (см. рис. 14.3) газы собираются в спиральном кор-
пусе турбины 1, имеющем выходной патрубок с фланцем 9. Кор-
пус турбины справа присоединяется к корпусу спиртового насоса
10 при помощи шпилек 12 и четырех призматических сухарей 13,
которые обеспечивают центровку корпусов при их температурных
деформациях. В корпусе спиртового насоса расположены два ша-
риковых подшипника (один из них не показан на рисунке), в ко-
торых вращается вал 11.
К крышке корпуса 2 слева также сухарями крепится корпус
кислородного насоса. .Мощность на его вал передается при помо-
щи упругой муфты, ведущая половина которой 4 сидит на тех же
прямоугольных шлицах вала 11, что и колесо турбины. Цилиндри-
ческий участок 5 вала служит для центрирования вала кислород-
ного насоса. Контактные уплотнения (на рис. 20.4, узлы I и II)
показаны на рис. 18.5, г и е.
402
Рис. 20.4. Схема турбины ТНА немецкой ракеты V-2:
/—корпус турбины: 2-чкрышка корпуса; 3—колесо Кертиса; 4—ведущая половина муфты; 5—
Цилиндрический участок вала; патрубок; 7—распределитель; 8—сопловой сегмент; 9— вы-
ходной патрубок, 10—корпус насоса; //—вал; 12—шпилька. /3—сухарь
403
§ 20.3. ТУРБИНЫ ВСПОМОГАТЕЛЬНЫХ УСТАНОВОК
В настоящее время газовая турбина широко применяется в
авиационных вспомогательных установках: для привода генерато-
ров и насосов, в турбостартерах и турбохолодильниках, в аэро-
дромных установках для производства сжатого воздуха и т. п.
В качестве рабочего тела используются продукты сгорания керо-
сина, пороха, продукты разложения перекиси водорода, сжатый
воздух и т. п.
Конструкция таких турбин весьма разнообразна: они выпол-
няются одно- и многоступенчатыми, осевыми и радиальными.
Принципы конструирования небольших осевых турбин в основном
те же, что и турбин ГТД.
Пример конструкции радиально-осевой турбины вспомогатель-
ной установки с полезной мощностью 37 кВт показан на рис. 20.5.
Колесо турбины / при помощи болта 2 присоединяется через
кольцо 3 к колесу центробежного компрессора 4, сидящего кон-
сольно на валу 5.
На кольце 3 имеются форсунки, которые вращаются вместе с
ротором. Топливо к форсункам подается из трубки 6 через полость
между болтом и валом.
Применение вращающихся форсунок и радиально-кольцевой ка-
меры сгорания 7 позволяет обеспечить равномерное распределение
параметров газа на входе в турбину и выполнить установку ком-
пактной с небольшой удельной массой.
Рис. 20.5. Схема вспомогательной установки с радиально-осевой турбиной BMW-'
6002:	•
/—колесо турбины; 2—болт-. 3—кольцо; 4—колесо компрессора; 5—вал; б—трубка для лодмИ
да топлива; 7—камера сгорания	Я
ПРИЛОЖЕНИЯ
Приложение I
ТАБЛИЦЫ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИИ
Сухой воздух (а=оо) Т=210... 1770 К
т, к	J, кДж/моль	AJ, кДж/моль		Др
210	6080,714	« 292,000	0,4040	0,0674
220	6372,714	291,120	’	0,4714	0,0783
230	6663,834	290,200	0,5497	0,0881
240	6954,034	290,620.	0,6378	0,0977
250	7244,654	290,200	0,7355	0,1074
260	7534,854	290,618	0,8429	0,1189
270	7825,472	290,622	0,9618	0,1311
280	8116,094	290,620	1,0929	0,1424
290	8406,714	291,040	1,2353	0,1552
300	8697,754	291,020	1,3905	0,1694
310	8988,774	291,470	1,5599	0,1831
320	9280,244	291,030	1,7430	0,1987
330	9571,274	291,500	1,9417	0,2145
340	9862,774	291,800	2,1562	0,2310
350	10154,574	292,300	2,3872	0,2473 •
360	10446,874	292,300	2,6345	0,2661
370	10739,174	292,330	2,9006	0,2850
380	11031,504	293,130	3,1856	0,3058
390	11324,634	293,140	3,4914	0,3262
400	11617,774	294,000	3,8176	0,3462
410	11911,774	293,900	4,1638	0,3724
420	12205,674 -	294,400	4,5362	0,3932
430	12500,074	294,800	4,9294	0,4187
440	12794,874	295,300	5,3481	0,4435
405
Г, к	J, кДж/моль	AJ, кДж/моль	Р(Г)	
450	13090,174	296,000	5,7916	0,4716
460	13386,174	296,500	6,2632	0,4991
470	13682,674	296,900	6,7623	0,5272
480	13979,574	297,300	7,2895	0,5574
490	14276,874	297,800	7,8469	0,5903
500	14574,674	298,500	8,4372	0.6180
510	14873,174	299,400	9,0552 z	0,6521
520	15172,574	299,500	9,7073	0,6895
530	15472,074	300,200	10,3968	0,7256
540	15772,274	301,100	11,1224	0,7626
550	16073,374	301,100	11,8850	0,8061
560	16374,474	302,300	12,6911	0,8420
570	16676,774	302,800	13,5331	0,8847
580	16979,574	303,600	14,4178	0,9248
590	17283,174	304,000	15,3426	0,9728
600	17587,174	304,900	16,3154	1,0226
610	17892,074	305,700	17,3380	1,0697
620	18197,774	306,100	18,4077	1,1132
630	18503,874	306,900	19,5209	1,1662
640	18810,774	307,400	20,6871	1,2207
650	19118,174	308,200	, 21,9078	1,2768
660	19426,374	308,734	23,1846	1,3342
670 i	19735,474	309,400	24,5188	1,3812
680	20044,874	310,300	25,9000	1,4526
690	20355,174	310,800	27,3526 •	1,5142
700	20665,974	311,900	28,8668	1,5700
710	20977,874	312,000	30,4368	1,6406
720	21289,874	313,200	32,0774'	1,7135
730	21603,074	313,700	33,7909	1,7804’
740	21916,774	314,500	35,5713	1,8483
750	22231,274	314,900	37,4196	1,9263
760	22546,174	316,100	39,3459	2,0064
770	22862,274	316,600	41,3523	2,0887
780	23178,874	317,000	43,4410	2,1521
I

406
Продолжение прилож. I
Г, к	Л кДж/моль	А/, кДж/моль	Р(Г)	Ар
790	23495,874	318,300	45,5931	2,2478
800	23814,174	318,200	47,8409	2,3240
810	24132,374	320,000	50,1649	2,4247
820	24452,374	319,500	52,5896	2,5165
830	24771,874	320,800	55,1061	2,5971
840	25092,674	321,200	57,7032	2,6916
850	25413,874	322,000	60,3948	2,8027
860	25735,874	322,400	63,1975	2,9174
870	26058,274	323,300	66,1149	2,9885
880	’	26381,574	323,700	69,1034	3,1070
890	26705,274	324,500	72,2104	3,2293
900	27029,774	324,600	75,4397	3,3192
910	27354,374	325,800	78,7589	3,4464
920	27680,174	326,200	82,2053	3,5576
930	28006,374	326,600	85,7629	3,6911
940	28332,974	327,500	89,4540	3,7855
950	28660,474	327,900	93,2395	3,9456
960	28988,374	328,700	97,1851	4,0194
970	29317,074	329,200	101,2045	4,2099
980	29646,274	329,500	105,4144	4,3597
990	29975,774	330,400	109,7741	4,4348
1000	30306,174	330.900	114,2089	4,6413
1010	30637,074	331,200	118,8502	4,7445
1020	30968,274	332,100	123,5947	4,9043
1030	31300,374	332,500	128,4990	5,0374
1040	31632,874	333,300	133,5364	5,2030
1050	31966,174	333,300	138,7394	5,4057
1060	32299,474	334,200	144,1451	5,5473
1070	32633,674	334,600	149,6924	5,7251
1080	32968,374	335,400	155,4175	5,8325
1090	33303,674	335,900	161,2500	6,0515
1100	33639,574	335,800	167,3015	6,1587
1110	33975,374	336,300	173,4602	6,5097
1120	34311,674	337,500	179,9699	6,5821
ИЗО	34649,174	337,100	186,5520	6,8228
407
Продолжение прилож. I
г, к	Jt кДж/моль	AJ, кДж/моль	Р(Г)	Др
1140	34986,274	338,400	193,3748	6,9800
1150	35324,674	338,300	200,3548	7,2321
1160	35662,974	338,800	207,5869	7,3940
1170	36001,774	339,200	214,9809	7,5549
1180	36340,974	339,600	222,5358	7,7673
1190	36680,574	340,000	230,3031	8,0934
1200	37020,574	340,900	238,3965	8,2074
1210	37361,474	341,300	246,6039	8,4312
1220	37702,774	341,300	255,0351	8,7194
1230	38044,074	341,700	263,7545	8,9548
1240	38385,774	341,700	272,7093	9,1938
1250	38727,474	343,000	281,9031	9,3697
1260	39070,474	342,500	291,2728	9,6117
1270	39412,974 '	343,400	300,8845	9,9290
1280	39756,374	343,800	310,8135	10,1827
1290	40100,174	344,200	320,9962	10,3636
1300	40444,374	344,200	331,3598	10,6196
1310	40788,574	345,100	341,9794	11,0411
1320	41133,674	345,100	353,0205	11,2298
1330	41478,774	345,900	364,2503	11,5005
1340	41824,674	345,400	375,7508	11,7743
1350	42170,074	346,800	387,5251	12,2354
1360	42516,874	346,300	399,7605	12,3369
1370	42863,174	347,100	412,0974	12,6199
1380	43210,274	347,200	424,7173	63,0062
1390	43557,474	347,600	437,7235	13,3008
1400	43905,074	347,500	451,0243	13,5978
1410	44252,574	348,400	464,6221	14,0079
1420	44600,974	348,400	478,6300	14,2032
1430	44949,374	348,900	492,8332	14,6246
1440	45298,274	349,200	507,4578	15,0586
1450	45647,474	349,300	522,5164	15,2577
1460	45996,774	350,100	537,7741	15,7033
1470	46346,874	350,000	553,4774	16,0307
1480	46696,874	350,100	569,5081	16,4950
408
Продолжение прилож. I
J, КДж/МОЛЬ	AJ, кДж/моль		Ар
47046,974	350,500	586,0031	16,6951
47397,474	351,400	602,6982	17,1708
47748,874	351,300	619,8690	* 17,3664
48100,174	351,300	637,2354	17,8530
48451,474	351,800	655,0884	18,3532
48803,274	351,800	673,4416	18,7079
49155,074	352,600	692,1495	19,0639
49507,674	353,000	71К2134	19,4206
49860,674	352,600	730,6340	19,9511
50213,274 50566,674	353,400	750,5851 771,4360	20,8509
50919,674	353,000	792,1363	20,7003
' 51273,974	354,300 .	813,3921	21,2558
51628,074	354,100	835,0258	21,6337
51982,074	354,000	857,2351	22,2093
52336,774	354,700	880,0350	22,7999
52691,474	354,700	903,0253	22,9903
53046,574	355,100	926,6163	23,5910
53402,074	355,500	950,6046	23,9883
53757,674	355,600	974,9895	24,3849
54113,174	355,500	1000,2301	25,2406
54469,074	355,900	1025,8886	25,6579
54825,474	356,400	1051,9617	26,0737
’ 55181,874	356,400	1078.6981	26,7364
55538,174	356,300	1105,8594	27,1613
55895,374	357,200	1133,4436	27,5842
56252,574	357,200	1161,7159	28,2723
56609,774	357,200	1190,6933	28,9774
56967,474	357,700	1219,8318	29,1385
Продукты сгорания (а=1) 7=270... 1770 К			
7821,076	305,300	1,0000	0,1420
8126,376	305,670	1,1420	0,1566
8432,046х	306,130	1,2986	0,1720
409
Продолжение прилож. I
г, к	J, кДж/моль	А/, КДж/М?ЛЬ	Р(Т)	&р
300	8738,176	306,900	1,4706	0,1882
310	9045,076	307,800	1,6588	0,2054
320	9352,876	308,600	1,8642	0,2231
330	9661,476	309,500	2,0873	0,2418
340	9970,976	309,900	2,3291	0,2614
350	10280,876	310,700	2,5905	0,2829
360	10591,576	311,600	2,8734	0,3064
370	10903,176	311,900	3,1798	0,3317
380	11215,076	312,900	3,5115	0,3566
390	11527,976	313,600	3,8681	0,3829
400	11841,576	314,500	4,2310	0,4123
410	12156,076	315,300	4,6633	0,4429
420	12471,376	315,800	5,1062	0,4746
430	12787,176	317,000	5,5808	0,5075
440	13104,176	317,400	6,0883	0,5414
450	13421,576	318,700	6,6297	0,5763
460	13740,276	319,500	7,2060	0,6138
470	14059,776	320,300	7,8198	0,6524
480	14380,076	320,800	8,4722	0,6942
490	14700,876	321,600	9,1664	0,7373
500	15022,476	322,500	9,9037	0,7843
510	15344,976	323,300	10,6880	0,8306
520	15668,276	324,100	11,5186	0,8807
530	15992,376	325,000	12,3993	0,9328
540	16317,376	325,900	13,3321	0,9864
550	16643,276	326,800	14,3185	1,0418
560	11970,076	327,700	15,3603	1,1023
570	17297,776	328,600	16,4626	1,1612
580	17626,376	329,500	17,6238	1,2257
590	17955,876	330,400	18,8495	1,2923
600	18286,276	331,300	20,1418	1,3612
610	18617,576	331,600	21,5030	1,4373
620	18949,176	332,500	22,9403	1,5108
630	19281,676	333,800	24,4511	1,5924
410
Продолжение прилож. I
г, к	/, кДж/моль	А/, кДж/моль	Р(Г)	Ар
640	19615,476	335,000	26,0435	1,6705
650	19950,476	336,300	27,7140	1,7505
660	20286,776	337,100	29,4645	1,8395
670	20623,876	337,900	31,3040	1,9313
680	20961,776	338,800	33,2353	2,0261
690	21300,576	340,000	35,2614	2,1238
700	21640,576	340,900	37,3852	2,2243
710	21981,476	342,100	39,6095	2,3277
720	22323,576	343,000	41,9372	2,4338
730	22666,576	343,800	44,3710	2,5427
740	23010,376	344,600	46,9137	2,6655
750	23354,976	345,500	49,5792	2,7928
760	23700,476	346,300	52,3720	2,9247
770	24046,776	347,200	55,2967	3,0478
780	24393,976	348,000	58,3445	3,1731
790	24741,976	348,800	61,5176	3,3159
800	25090,776	350,100	64,8335	3,4475
810	25440,876	350,900	68,2810	3,5976
820	25791,776	351,700	71,8786	3,7524
830	26143,476	352,200	75,6310	3,9116
840	26495,676	352,600	79,5426	4,0754
850	26848,276	353,400	83,6180	4,2437
860	27201,676	354,700	87,8617	4,4166
870	27556,376	356,000	92,2783	4,6163
880	27912,376	356,800	96,8946	4,8004
890	28269,176	357,600	101,6950	4,9891
900	28626,776	358,500	106,6841	5,1823
910	28985,276	359,200	111,8664	5,3801
. 920	29344,476	360,200	117,2465	5,5822
930	29704,676	361,000	122,8287	5,7887
940	30065,676	361,800	128,6174	5,9996
950	30427,476	362,600	134,6170	6,2469
960	30790,076	363,500	140,8639	6,5030
970	31153,576	363,900	147,3669	6,7321
980	31517,476	363,900	154,0990	6,9655
411
Продолжение прилож. г
Г, к		А/, кДж/моль	Р(П	Ар
990	31881,376	364,300	161,0645	7,2416
1000	32245,676	365,200	168,3061	7,5267
1010	32610,876	366,400	175,8328	7,7787
1020	32977,276	366,800	183,6115	8,0345
1030	33344,076	367,700	191,6460	8,2941
1040	33711,776	368,500	199,9401	8,6530
1050	34080,276	369,400	208,5931	8,9272
1060	34449,676	370,100	217,5203	9,2572
1070	34819,776	370,600	226,7775	9,5966
1080	35190,376	371,100	236,3741	9,8893
1090	35561,476	371,800	246,2634	10,2440
1100	35933,276	372,300	256,5074	10,5471
1110	36305,576	373,100	267,0545	10,9808
1120	36678,676	374,000	278,0353	11,2990
ИЗО	37052,676	374,300	289,3343	11,6889
1140	37426,976	375,300	301,0232	12,0889
1150	37802,276	376,000	313,1121	12,4995
1160	38178,276	376,900	325,1116	12,8426
1170	38555,176	377,300	338,4542	13,2681
1180	38932,476	377,700	351,7223	13,7041
1190	39310,176	378,200	365,4264	14,1506
1200	39688,376	378,900	379,5770	14,6078
1210	40067,276	379,400	394,1848	. 15,0758
1220	40446,676	379,800	409,2606	15,5545
1230	40826,476	380,300	424,8151	16,0441
1240	41206,776	381,100	440,8592	16,4394
1250	41587,876	381,900	457,2986	16,9433
1260	41969,776	382,700	474,2419	17,5710
1270	42352,476	383,200	491,8129	17,9872
1280	• 42735,676	383,600	509,8001	18,5234
1290	43119,276	384,400	528,3235	19,0704
1300	43503,676	385,200	547,3939	19,6281
1310	43888,876	385,300	567,0220	20,1968
1320 •	44274,176	385,700	587,2188	20,7761
1330	44659,876	386,100	607,9949	21,5112
412
Продолжение прилож. I
Г, к	Jt кДж/моль		AJ, кДж/моль		Ар
1340	45045,976		386,900	629,5061	22,1221
1350	45432,876		387,400	651,6282	22,8997
1360	45820,276		387,700	674,5279	33,3829
1370	46207,976		388,200	697,9108	24,0272
1380	46596,176		388,600	721,9380	24,6825
1390	46984,776		389,100	746,6205	25,3486
1400	47373,876		389,800	771,9691	26,2092
1410	" 47763,676		389,900	798,1783	26,9090
1420	48153.576		390,300 -	825,0873	27,4235
1430	48543,876		390,700	852,5108	28,1323
1440	48934,576		391,100	880,6431	• 29,0605
1450	49325,676		391,600 •	909,7036	30,0196
.	1460	49717,276		392,300	939,7232	30,7866
1470	50109,576		392,800	970,5098	31,5645
1480	'	50502,376		393,200	1002,0743	32,5911
1490	50895,576		393,700	1034,6654	33,4051
1500	51289,276		394,400	1068,0705	34,2298
1510	51683,676		394,500	1102,3003	35,0649
1520	52078,176		394,900	1137,3652	35,9101
1530	52473,076		395,300	1173,2753	36,7652
1540	52868,376		395,700	1210,0405	37,6300
1550	53264,076		396,200	1247,6705	38,5041
1560	53660,276		396,600	1286,1746	39,6922
1570	54056,876		397,000	1325,8668	40,9174
’ 1580 1590	54453,876 54851,276		397,400 397,800	1366,7842 1408,6397	41,8555 42,8031
1600	55249,076		398,200	1451,4428	43,7595
1610	55647,276		398,700	1495,2023	45,0786
1620	56045,976		398,600	1540,2809	46,0725
1630	56444,576		398,700	1586,3534	47,0741
1640	56843,276		399,100	1633,4278	48,4712
1650 -	57242,376		399,900	1681,8990	49,5111
1660	57642,276		400,300	1731,4101	50,5579
1670	58042,576		400,800	1781,8630	52,0345
1680	58443 376		400,700	1834,0025	53,5539
413
Продолжение прилож. I
г, к	J, кДж/моль	AJ, кДм/моль	Р(Г)	Др
1690	58844,076	400,800	1887,5564	54,6703
1700	59244,876*	401,200	1942,2267	55,7938
1710	59646,076	401,600	1998,0205	56,9232
1720	60047,676	402,000	2054,9437	58,0584
1730	60449,676	402,000	2113,0021	59,6987
1740	60851,676	402,400	2172,7008	60,8711
1750	61254,076	402,400	2233,5719	62,5763
1760	61656,476		2296,1482	
1770	62058,976	402,500	2359,9344	63,7862
	Продукты сгорания (а=2) Т=		=270... 1770 К	
270	7823,204	298,200	* 1,0000	0,1378
280	8121,404	298,100	1,1378	0,1516
290	8419,504	298,600	1.2894	0,1657
300	8718,104	299,000	1,4551	0,1805
310	9017,104	299,400	1,6356	0,1962
320	9316,504	300,300	1,8318	0,2132
330	9616,804	300,200	2,0450	0,2300
340	9917,004	301,100	2,2750	0,2478
350	10218,104	301,500	2,5228	0,2684
360	10519,604	301,900	2,7912	0,2884
370	10821,504	302,400	3,0796	0,3111
380	11123,904	302,700	3,3907	0,3332
390	11426,604	303,600	3,7239	0,3564
400	11730,204	304,100	4,0803	0,3824
410	“ 12034,304	304,800	4,4627	0,4092
420	12339,104	304,900	4,8719	0,4369
430	12644,004	306,500	5,3088	0,4655
440	12950,504	306,100	5,7743	0,4947
450	13256,604	307,400	6,2690	0,5261
460	13561,004	308,200	6,7951	0,5584
470	13872,204	308,600	7,3535	0,6007
480	14180,804	309,100	7,9542	0,6181
414
Продолжение прилож. I
Г, к	/, кДж/моль 1	AJ, кДж/моль	Р(Г)	Ар
490	14489,904	* 309,800	8,5723	0,6640
500	14799,704	310,800	9,2363	0,7040
510	15110.504	311,100	9,9403	0,7428
520	15421,604	311,600	10,6831	0,7878
530	15733,204	312,800	11,4709	0,8289
540	16046,004	313,200	12,2998	0,8736
550	16359,204	314,500	13,1734	0,9227
560	16673,704	315,300	14,0961	0,9734
570	16989,004	315,800	15,0695	1,0184
580	17304,804	317,000	16,0879	1,0753
590	17621,804	317,000	17,1632	1,1304
600	17938,804	318,200	18,2936	1,1734
610	18257,004	318,300	19,4670	1,2534
620	18575,304	319,900	20,7204	1,3190
630	18895,204	320,400	22,0394	1,3759
640	19215,604	321,600	23,4153	1,4389
' 650	19537,204	322,000	24,8542	1,5091
660	19859,204	322,900	26,3633	1,5685
670	20182,104	324,100	27,9318	1,6551
680	20506,204	324,500	29,5869	1,7243
690	20830,704	325,800	31,3112	1,8019
700	21156,504	326,200	33,1131	1,8894
710	21482,704	327,100	35,0025	1,9632
720	21809,804	328,300	36,9657	2,0644
730	22138,104	328,700	39,0301	2,1322
740	22466,804	330,000	41,1623	2,2487
750	22796,804	330,400	43,4110	2,3294
760	23127,204	331,300	45,7404	2,4321
770	23458,504	331,600	48,1725	2,5499
780	23790,104	332,900	50,7224	2,6233
890	24123,004	333,400	53,3457	2,7461
800	24456,404	334,600	56,0918	2,8603
810	24791,004	335,400	58.9521	2,9634
820	25126,404	335,800	61,9155	3,0824
415
Продолжение прилож. I
г, к	J, кДж/моль	AJ, кДж/моль	Р(Г)	др
830	25462,204	336,700	64,9979	3,2203
840	25798,904	336,700	68,2181	3,3303
850	26135,604	337,900	71,5484	3,4928
860	26473,504	338,400	75,0412	3,5909
870	26811,904	339,600	78,6321	3,7437
880	27151,504	340,500	82,3758	3,8823
890	27492,004	341,200	86,2581	4,0236
900	27833,204	341,800	90,2817	4,2113
910	28175,004	342,500	94,4930 *	4,3167
920	28517,504	343,400	98,8097	4,4903
930	28860,904	344,200	103,3000	4,6443
940	29205,104	344,200	107,9443	4,8013
950	29549,304	344,700	112,7456	4,4607
960	29894,004	344,700	117,7063	5,1790
970	30238,704	344,500	122,8853	5,3477
980	30583,204	346,800	128,2330	5,5805
990	30930,004	347,600	133,8135	5,6626
1000	31277,604	349,100	139,4761	5,9358
1010	31626,704	350,300	145,4119	6,1534
1020	31977,004	351,200	151,5653	6,2684
1030	32328,204	350,100	157,8337	6,5277
1040	32678,304	350,900	164,3614	6,7976
1050	33029,204	351,800	171,1590	6,9147
1060	33381,004	352,200	178,0737	7,1941
1070	33733,204	352,600	185,2678 5,1	7,4846
1080	34085,804	353,000	192,7524	7,6486
1090	34438,804	354,300	200,4010	7,9041
1100	34793,104	354,200	208,3051	8,2158
1110	35147,304	354,700	216,5209	8,3845
1120	35502,004	355,500	224,9054	8,7091
ИЗО	35857,504	356,400	233,6145	8,9347
1140	36213,904	356,400	242,5492	9,2764
1150	36570,304	357,600	251,8256	9,5108
1160	36927,904	357,600	261,3364	9,8075
1170	37285,504	358,500	271,1439	10,1109
416
Продолжение прилож. I
г, к	J, кДж/моль	AJ, КДж/моль		
1180	37644,004	358,804	281,2548	10,3535
1190	38002,804	359,300	291,6083	10,7347
1200	38362,104	359,800	302,3430	11,0576
1210	38721,904	360,500	313,4006	11,3126
1220	39082,404	360,600	324,7132	11,7208
1230	39443,004	360,900	336,4340	12,0637
1240	39803,904	361,800	348,4977	12,3300
1250	40165,704	361,900	360,8277	12,6803
1260	40527,604	363,000	373,5080	13,0364
1270	40890,604	363,100	386,5444	13,4003
1280	41253,704	363,900	399,9447	13,8643
1290	41617,604	364,300	413,8090	14,1478
1300	41981,904	364,700	427,9568	14,5296
1310	42346,604	365,200	442,4864	15,0229
1320	42711,804	366,000	457,5093	15,3151
1330	43077,804	365,600	472,8244	>	15,7154
1340	43443,404	366,400	488,5398	16,2376
1350	. 43809,804	366,800	504,7774	16,8975
1360	44176,604	367,300	521,6749	17,0908
1370	44543,904	367,700	538,7657	17,5226
1380	44911,604	368,000	556,2883	17,9603
1390	45279,604	368,600	574,2486	18,5401
1400	45648,204 	368,500	592,7887	18,8570
1410	46016,704	369,300	611,6457	19,4569
1420	46386,004	369,400	631,1026	20,0757
1430	46755,404	369,700	651,1783	20,2504
1440	47125,104	370,200	671,4287	21,0396
1450	47495,304	370,600	692,4683	21,5345
1460	47865,904	371,000	714,0028	22,0347
1470	48236,904	371,500	736,0375	22,7146
Д480	48608,404	371,800	758,7521	23,2356
1490	48980,204	372,300	781,9877	23,5760
1500	49352,504	372,300	805,5637	24,6692
1510	49724,804	373,100	830,2329	24,6368
1520	50097,904	373,500	854,8697	25,5706
14	1337
417
Продолжение прилоак. I
Г, к	J, кДж/моль	ДУ, кДж/моль	Р(Т)	Др
1530	50471,404	373,600	880,4403	25,9180
1540	50845,004	373,900	906,3583	26,8959
1550	51218,904	374,400	933,2542	27,2515
1560	51593,304	374,400	960,5057	27,8197
1570	51967,704	375,200	988,3254	28,8595
1580	52342,904	375,200	1017,1849	29,4613
1590	52718,104	376,000	1046,6462	29,8188
1600	53094,104	375,700	1076,4650	30,6683
1610	53469,804	376,800	1.107,1333	31,5420
1620	53846,604	376,500	1138,6753	32,1711
1630	54223,104	376,500	1170,8464	32,5257
1840	54599,604		1203,3721	
1650	54976,504	376,900	1237,3709	33,9988
1660	55354,204	377,700	1271,4519	34,0810	1
1670	55731,904	377,700	1306,4715	35,0196
1680	56110,004	378,100	1342,4556	35,9841
1690	56488,204	378,200	1379,4309	36,9753
1700	56366,804	378,600	1417,0982	37,6673
1710	57245,304	378,500	1456,1293	39,0311
1720	57624,304	379,000	1494,8580	38,7287
1730	58003,704	379,400	1534,2634	39,4054
• 1740	58383,504	379,800	1575,0702	40,8068
1750	58763,304	379,800	1616,5902	41,5200
1760	59143,104	379,800	1659,5867	42,9965
1770	59523,404	380,300	1702,9423	43,3556
	Продукты сгорания (а=3)		270 ... 1770 К	
270	7823,983	295,600-	1,0000^	0,1365
280	8119,583	296,100	1,1365	0,1499
290	8415,683	296,100	1,2864	0,1637
300	8711,783	296,400	1,4501	0,1780
310	9008,133	296,500	1,6281	0,1936
320	9304,683	297,800 ’	1,8217	0,2097
330	9602,483	297,300	2,0314 ’	0,2264
340	9899,783	298,200	2,2578	0,2442
418
Продолжение прилож. I
г, к	/, кДж/моль	А/, КДж/моль		Ар
350	10197,983	298,500	2,5020	0,2636
360	10496,483	298,600	2,7656	0,2829
370	10795,083	299,400 •	3,0485	0 3042
380	11094,483	299,900	3,3527	0,3260
390	11394,383	300,200	3,6Ш	0,3493
400	11694,583	300,700	4,0280	0,3724
410	11995,283	301,500	4,4004	0,3991
420	12296,783	301,900	4,7995 '	0,4244
430	12598,683	302,300	5,2239	0,4528
440	12900,983	302,800	5,6767	0,4807
450	13203,783	304,000	6,1574	0,5106
460	13507,783	304,100	6,6680	0,5414
470	13811,883	305,200	7,2094	0,5727
480	14117,083	305,300	7,7821	0,6086
490	14422,383	306,100	8,3907	0,6437
500	14728,483	307,000	9,0344	0,6774
510	15035,483	307,300	9,7118	0,7185
520	15342,783	307,800	10,4303	0,7563
530	15650,583	308,700	11,1866	0,7945
540	15959,283	309,400	, 11,9811	0,8451
550	16268,683	310,300	12,8262	0,8889
560	16578,983	311,200	13,7151	0,9336
570	16890,183	311,500	•	14,6487 -	0,9791
580	17201,683	312,800	15,6278	1,0293
590	17514,483	313,300	16,6571	1,0847
600	17827,783	314,000	17,7418	1,1337
610	18141,783	314,100	18,8755	1,1969
620	18455,883	315,800	20,0724	1,2482
630	18771,683	316,100	21,3206	1,3102
640	19087,783	i317,000	22,6308	1,3685
650	19404,783	317,900	23,9993	1,4396
660	19722,683	318,200	25,4389	1,4950
670	20040,883	319,500	26,9339	1,5697
14*
*
Продолжение прилож. I
				
Г, к	Л кДж/моль	AJ, кДж/моль	p(J)	Ар
680	20360,383	320,400	28,5036	1,6364
690	20680,783	320,800	30,1400	1,7093
700	21001,583	321,600	31,8493	1,7941
710	21323,183	322,400	33,6434	1,8624
720	21645,583	323,300	35,5058	1,9483
730	21968,883	324,500	37,4541	2,0279
740	22293,383	325,000	39,4820	2,1186
750	22618,383	325,800	41,6006	2,2020
760	22944,183	326,200	43,8026	2,2866
770	23270,383	327,000	46,0892	2,4061
780	23597,383	327,500	48,4953	2,4729
790	23924,883	328,700	50,9682	2,5867
800	24253,583	329,600	53,5549	2,6921
810	24583,183	330,400	56,2470	2,7866
820	24913,583	330,800	59,0336	2,8962
830	25244,383	331,300	61,9298	3,0233
840	25575,683	332,100	64,9531	3,1238
850	25907,783	332,900	68,0769	3,2576
860	26240,683	333,300	71,3345	3,3619
870	26573,983	334,200	74,6964	3,5203
880	26908,183	335,400	78,2167	3,6297
890	27243,583	335,800	81,8464	3,7390
900	27579,383	336,500	85,5854	3,9304
910	27915,883	. 337,300	89,5158	4,0247
920	28253,183	337,600	93,5405	4,1832
930	28590,783	339,100	97,7237	4,3232
940	28929,883	338,800	102,0460	4,4654
950	29268,683	339,300	106,5123	4,6352
960	л 29607,983	340,800	111,1475 .	4,8100
970	29948,783	341,300	115,9577	4,9628
980	30290,083	341,700	120,9205	5,1460
990	30631,783	341,700	126,0665	5,2743
1000	30973,483	342,500	131,3408	5,4950
1010	31315,983	343,800	136,8358	5,6234
420
Продолжение при лож. I
Г, к	J, кДж/моль	AJ, кДж/моль	Р(Г)	Ар
1020	31659,783	343,800	142,4592	5,8950
1030	32003,583	344,300	148,3542	6,0289
1040	32347,883	345,400	154,3831	6,2370
1050	32693,283	345,900	160,6201	6,4120
1060	33039,183	346,400	167,0321	6,6279
1070	33385,583	346,700	173,6600	6,8910
1080	33732,283	347,600	180,5510	7,0770
1090	34079,883	348,000	187,6289	7,2657
1100	34427,883	348,800	194,8946	7,5470
1110	34776,683	348,800	202,4416	7,6941
1120	35125,483	350,100	210,1357	9,0367
ИЗО	35475,583	350,100	218,1724	8,1877
1140	35825,683	350,900	226,3601	8,4949
1150	36176,583	- 350,900	234,8550	8,7016
1160	36527,483	351,800	243,5566	9,0239
1170	36879,283	352,600	252,5805	9,2377
* 1180	37231,883	352,600	261,8182	9,4506
1190	37584,483	353,400	271,2688	9,8565
1200	37937,883	353,900	281,1253	10,0804
1210	38291,783	354,200	,291,2057	10,3030
1220	38645,983	354,300	301,5087	10,7394
1230	39000,283	354,700	312,2481	10,9732
1240	39354,983	355,500	323,2213	11,2816
1250	39710,483	356,000	334,5029	11,5161
1260	40066,483	356,300	346,0190	11,8301
1270	40422,783	356,800	357,8491	12,2345
1280	40779,583	357,600	370,0836	12,5648
1290	41137,183	357,600	382,6484	12,8092
1300	41494,783	358,500	395,4576	13,2379
1310	41853,283	358,900	-	408,6955	13,6812
1320	42212,183	359,300	422,3767	13,8376
1330	42571,483	359,300	436,2143	14,2910
1340	42930,783	359,700	450,5053	14,6521
1350	43290,483	360,100	465,1574	15,3498
1360	43650,583	361,000 4	480,5072	15,3994
421
Продолжение прилож. Г
Г, к	J, кДж/моль	AJ, кДж/моль		
1370	44011,583	361,000	495,9066	15,8930
1380	44372,583	361,400	511,7996	16,2807
1390	44733,983	361,800	528,0803	16,5476
1400	45095,783	362,200	544,6279	17,1956
1410	45457,983	362,600	561,8235	17,4717
1420	45820,583	362,700	579,2952	18,0150
1430	46183,283	363,100	597,3102	18,4334
1440	46546,383	363,400	615,7436	18,8562
,1450	46909,783	364,000	634,5998	19,2822	‘
1460	47273,783	364,300	653,8820	.19,7140
1470	47638,083	364,700	673,5960	20,4680
1480	48002,783	364,800	694,0640	20,9259
1490	48367,583	365,100	714,9899	21,2171
1500	48732,683	365,600	736,2070	21,8466
1510	49098,283	366,400	758,0536	22,3152
1520	49464,683	366,400	780,3688	22,6023
1530	49831,083	366,400	802,9711	23,4472
1540	50197,483	366,900	826,4183	23,9360
1550	50564,383	367,600	850,3543	24,4279
1560	50931,983	367,700	874,7822	24,9224
1570	'51299,683	367,700	899,7046	25,6324
1580	51667,383	368,500	925,3370	26,3626
1590	52035,883	368,500	951,6996	26,6632
1600	52404,383	368,900	978,3628	27,1785
1610	52773,283	369,400	1005,5413	28,1716
1620	53142,683	369,300	1033,7129	28,4715
1630	53511,983	369,800	1062,1844	29,2558
1640	53881,783	369,800	1091,4402	30,0614
1650	54251,583	370,100	1121,5016	30,3590
1660	54621,683	371,100	1151,8606	31,1808
1670	54992,783	370,600	1183,0414	31,7450
1680	55363,383	371,400	1214,7864	32,8841
1690	55734,783	371,000	1247,6705	33,1844
1700	56105,783	371,500	1280,8549	•	34,0669
1710	56477,283	371,800 *	1314,9218	34,3515
422
Продолжение прилож. I
Г, к	J, кДж/моль	AJ, кДж/моль	Р(Г)	Др
1720	56849,083	372,300	1349,2733	35,8867
1730	57221,383	372,300	1385,1600	35,8592 ’
1740	57593,683	372,700	1421,0192	36,7875
1750	57966,383	372,700	1457,8067	38,0843
1760	58339,083	373,100	1495,8910	38,3724
1770	58712,183		1534,2634	
	Продукты сгорания (а=7) 7=270 ... 1770К			
270	7824,845	292,700	1,0000	0,1350
280	8117,545	293,100	1,1350	0,1479
290	8410,645	293,200	1,2829	0,1608
300	8703,845	293,100	1,4437	0,1758
310	8996,945	293,600	1,6195	0,1897
320	9290,545	293,900	1,8092	0,2054
330	9584,445 *	294,000	2,0146	0,2220
340	9878,445	294,400	2,2366	0,2391
350	10172,845	294,300	2,4757	0,2576
360	10467,145	295,300	2,7333	0,2762
370	10762,445	295,600	3,0095	0,2964
380	11058,045	295,700	3,3059	0,3173
390	11353,745	296,500	3,6232	0,3395
400	11650,245	296,500	3,9627	0,3614
410	11946,745	297.300	4,3241	0,3867
420	12244,045	297,300	4,7108	0,4095
430	12541,345	298,100	5,1203	0,4374
440	12839,445	298,600	5,5577	0,4637
450	13138,045	299,000	6,0214	0,4918
460	13437,045	299,900	6,5132	0,5207
470	13736,945	300,600	7,0339	0,5518
480	14037,545	300,700	7,5857	0,5820
।	490	14338,245	301,100	8,1677	0,6184
।	500	14639,345	301,900	8,7861	0,6501
510	14941,245	302,800	9,4362	0,6842
520	15244,045-	302,700	10,1204	0,7238
530	15546,745	304,500	10,8442	0,7622
423
Продолжение прилож. I
г, к	J, кДж/моль	Д/, кДж/моль		Др
540	15851,245	304,400	11,6064	0,8015
550	16155,645	305,300	12,4079	0,8446
560	16460,945	306,100	13,2525	0,8858
570	16767,045	306,100	14,1383	0,9277
580	17073,145	307,800	15,0660	0,9812
590	17380,945.	308,200	16,0472	1,0254
600	17689,145	308,200	17,0726	1,0741
610	17997,345	309,^00	18,1467.	1,1241
620	18306,445	310,700	19,2708	1,1795
630	18617,145	‘ 310,700	20,4503	1,2367
640	18927,845	311,600	21,6870	• 1,2903
650	19239,445	312,000	22,9773	1,3503
660	19551,445	312,800	24,3276	1,4059
670	19864,245	314,000	25,7335	1,4747
680	20178,245	314,500	27,2082	1,5326
690	20492,745	315:400	28,7408	1,5981
700	20808,145	315,700	30,3389	1,6795
710	21123,845	316,600	32,0184	1,7414
720	21440,445	317,400	33,7598	1,8197
730	21757,845	318,300	35,5795	1,8832
740	22076,145	319,100	37,4627	1,9830
750	22395,245	319,500	39,4457	2,0401
760	22714,745	320,300	41,4858	2,1356
- 770	23035,045	320,800	43,6214	2,2244
780	23355,845	 321,600	45,8458	2,3046
790	23677,445	322,400	48,1504	2,3854
800	23999,845	323,700	50,5358	2,4915
810	24323,545	323,700	53,0273	2,5887
820	24647,245	324,600	55,6160	2,6747
830	24971,845	324,900	58,2907 '	2,7894
840	25296,745	326,300	61,0801	2,8786
				
424
Продолжение прилож. I
г, к	J, кДж/моль	AJ, кДж/моль		Др
850	25623,045	326,200	63,9587	3,0143
860	25949,245	327,000	66,9730	3,0918
870	26276^-245	327,900	70,0648	3,2176
880	26604,145	328,700	73,2824	3,3478
890	26932,845	329,200	76,6302	3,4453
900-	27262,045	330,000	80,0755	3,5810
910	27592,045	330,400	'83,6565	3,6808
920	27922,445	330,800	87,3373	3,8427
930	28253,245	332,100	91,1800	3,9630
940	28585,345	332,000	95,1480	4,0721
950	28917,345	332,962	99,2201	4,2226
960	29250,307	333,338	103,4427	4,3774
970	29583,645	334,600	107,8201	4,5368
980	29918,245	334,200	112,3569	4,6469
990	30252,445	335,400	117,0038	4,8390
1000	30587,845	335,800	121,8428	4,9807
1010	30923,645	336,700	126,8235	5,1540
1020	31260,345	336,700	131,9775	5,2685
1030	31597,045	337,500	137,2460	5,4789
1040	31934,545	338,400	142,7249	5,6635
1050	32272,945	338,800	148,3884	5,8171
1060	32611,745	339,100	154,2055	6,0083
1070	32950,845	339,700	160,2138	6,2040
1080	33290,545	340,400	166,4178	6,3647
1090	33630,945	340,900	172,7825	6,5669
1100	33971,845	341,300	179,3494	6,7735
1110	34313,145	341,700	186,1229	5,9405
1120	34654,845	342,500	193,0634	7,1992
ИЗО	35997,345	343,400	200,2626	7,3721
1140	35340,745	343,000	207,6347	7,5938
1150	35683,745	343,800	215,2285	7,8203
1160	36027,545	343,800	223,0488	8,1044
1170	36371,345	345,000	231,1532	8,2334
1180	36716,345	345,500	239,3866	8,4697
425
Продолжение прилож.
т, к	J, кДж/моль	А/, кДж/моль	Р(Г)	д,
1190	37061,845	345,500	247,8563	8,8283
1200	37407,345	346,300	256,.6846	8,9593
1210	37753,645	346,700	• 265,6439	9,2087
1220	38100,345	346,800	274,8526	9,5279
1230	38447,145	346,700	284,3805	9,7905
1240	38793,845	347,600	294,1710	10,0575
1250	39141,445	348,400	304,2285	10,2565
1260	39489,845	348,400	314,4850	10,5274
1270	39838,245	348,800	325,0124	10,8798
1280	40187,045	349,300	335,8922	11,1641'
1290	40536,345	350,100	347,0563	11,3700
1300	40886,445	350,500	358,4263	11,6573 *
1310	41236,945	350,500	370,0836	12,1245 '
1320	41587,445	350,900	382,2081	12,2491
1330	41938,345	351,300	394,4572	12,6417
1340 ’	42289,645	351,800	407,0989	12,9500
1350 ♦	42641,445	351,700	420,0489'	13,4619
1360 .	42993,145	352,600	.433,5108	13,5843
1370	43345,745	353,100	447,0951	14,0100
1380	43698,845	353,000	461,1051	14,3395
1390	44051,845	353,400	475,4446	14,5597
1400	44405,245	353,900	490,0043	15,0056
1410 •	44759,145	354,200	505,0099	15,4652
1420	45113,345	354,300	520,4751	15,8152
1430	45467,647	354,700 ’	536,2903	16,1685
1440	45822,345	355,100	552,4588	16,3940
1450	46177,445	355,500	568,8528	16,8805
1460	46532,945	356,000	585,7333	17,3814
1470	46888,945.	356,300	603,1147	17,8972
1480	47245,245	356,400	621,0119	18,1339
1490	47601,645	356,400	639,1458	18,5119
1500	47958,045	357,200	657,6577	19,2039
1510	48315,245	357,200	676,8616	19,2837
1520	48672,445	358,000	696,1453	19,6683
1530	49030,445	357,600	715,8136	20,3934
426
Продолжение прилож. I
г, к	J, кДж/моль	AJ, кДж/моль	р(Г)	Др
1540	49388,045	358,500	736,2070	20,9743
1550	49746,545	358,500	757,1813	21,0343
1560	50105,045	358,800	778,2156	21,6185
1570	50463,845	359,300	799,8341	22,4084
1580	50823,145	359,300	822,2425	22,8416
1590	51182,445	359,700	. 845,0841	23,0762
1600	51542,145	360,200	868,1603	23,5011
1610	51902,345	360,500	891,6614	24,3480 ‘
1620	52202,845	360,600	916,0094	24,8476
1630	52623,445	361,000	940,8570	24,9713
1640	52984,445	360,500	965,8283	25,9165
1650	53344,945	361,400	991,7448	26,3774'
1660	53706,345	362,200	1018,1222	26,5979
1670	54068,545	361,800	1044,7201	27,5395
1680	54430,345		1072,2596	
1690	54792,645	362,300	1100,5251	28,2655
•1700	55154,445	361,800	1129,2756	28,7505
1710	55517,045	362,600	1158,2436	28,9680
1720	55880,145	363,100	1187,9548	29,7112
1730	56243,145	363,000	1218,7087	30,7539
1740	56606,645	363,500	1249,3955	30,6868
1750	56970,145	363,500	1281,1498	31,7543
1760	57334,045	363,900	1313,7113	32,5615
1770	57697,945	363,900	1346,4801	32,7688
Приложение И
МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ, ПРИМЕНЯЕМЫХ ДЛЯ ДЕТАЛЕН ТУРБИН
	Марка материала	Термообработка"	т	°т	%	&	ф	ю 1 о	Предел длительной прочности			о о о" D	7 0	к 1 о	0	НВ	X	а*10в	в.1О»	Примечания
			к	МН/м*		%		МН/м*							кг/м®	МН/м»	В г/ (м«К)	1/К	м»/с	
(/	Л18Н9Т (ЭЯ1Т)	Закалка с 1320К	293	280	620	41	63	1,88	а0,8	ql	°5	—	—	—	7900	1490— 1920	16,0	16,0	4,4	
		в воде или н.а воз- духе	550	210	480	32	64	1,65									16,2	17,0	4,6	
																				
			650	190	455	31	65	1,60	—		—	—ч	—	—	—	—	17,6	17,5	4,7	
			750	190	455	30	65	1,50	440	426	390	—	—	—	—	—	18,9	18,0	4,8	
			850	180	410	25	62	1,45	356	338	318	—-	—	—	—	—	20,2	18,6	4,9	
			950	165	290	26	60	1,25	276	264	230	—	—	—	—	—	21,6	19,0	5,1	
			1050	ПО	190	34	59	0,95	140	130	100	—*	—	—	-—	—	23,3	19,3	5,4	
	О §	Закалка с 1460К	293	627	1010	13,7	12,0	1,89		<4	а5	—-	510	350	7800	2550— 3400	12,6	17,1	—	Сталь пригодна для работы при
		в воде; старение																		
	е	при 1070К — 8ч	650	550	805	12,5	22,4	1,61	—	—-	-—•	—	—	—	—	—	19,7	19,0	—	870—920К. Хоро- шо обрабатывает-
	£00		750	500	742	11,8	22,8	1,50	710	680	600	—	—	—	—	.—	21,5	19,6	—	ся резанием. Сва-
			850	478	710	9,6	23,4	1,45	500	470	420	250	400	280	—	—	23,5	20,0	—	ривается хорошо
	О		950	435	535	11,6	32,0	1,19	350	330	290	170	350	250	—	—	25,6	20,4	—	j
			1050	290	385	7,7	17,0	1,17	242	228	200	82	250	210	—	—	27,3	20,7	——	
	10Х11Н20ТЗР	Закалка с 1470К	293	695	1000	23	26	1,60	а100	q200	q50Q	-	—	—	7900	2530—	15,1	15,1	4,6	Хорошо обраба-
-	(ЭИ696)	— 2 ч; охлажде-														2800				тывается резанрем.
		ние на воздухе; старение	при	850	675	910	21	26	1,25	560	540	520	400	350		—	—	23/6	17,8	5,4	Жаропроч н ост ь высокая	при
		1020K — 16 ч; ох- лаждение на воз- духе	950 1000 1050	630 480	765 .594 460	14 16 24	.16 22 42	1,19 1,16 1,12	416 312 170	320 270 150	370 226 120	344 226 100	292	290	—	—	24,8 25,5 26,5	18,1 18,4 18,8	5,3 5,3 5,3	870—Ю20К. Не- чувствительна к надрезу при рабо- чих температурах
ХН77ТЮР		Закалка с 1350К	293	700	1080	20	21	2,10	q100	q200	q500	—	370	220	8200	2550—	12,6	12,6	3,5	Жаропрочность
(ЭИ437Б)		— 8 ч; охлажде-														3200				высокая при 970—
		ние на воздухе+	850	650	954	25	35	1,65	760	660	610	440	312	246	—			22,8	18,1	4,8	—1020К. Применя-
		+ старение	при				23														ется для лопаток
		970 К — 16 ч; ох-	950	610	886		31	1,49	476	440	400	290	370	233	—	—	24,5	19,0	4,8	и дисков ГТД
		лаждение на воз-	1050	496	602	19	44	1,28	290	260	200	165	290	238	-			27,4	20,1	5,0	
		духе																		
			1100	380	432	17	45	1,00	162	134	104	—			—	—	28,9	20,7	5,2	
ХН70ВМТЮ		Закалка	с	293	,725	1100	14	13,7	1,86	q100	q3QQ	q500	—	350	250	8400	2700—	8,4	12,0	2,6	Жаропрочность
(ЭИ617)		1470 К+закалка с														3400				высокая. Сплав
		1I320K; старение	950	672	935	8	11,1	1,60	520	490	430	350	375	291					21,3	15,0	3,0	пригоден для ра-
		при 1070 К—16 ч;			795															боты при 1120—
		охлаждение	на	1050	596		6	12,2	1,54	330	310	270	202	365	298	—	—	23,8	15,7	4,7	—1170К. Удовлет-
		воздухе	1150	470	528	8	18,5	1,36	140	110	84	100	290	215	—	—	26,6	16,3	5,1	ворительно обра- батывается реза-
			1250	—	210				60											нием	
о		Закалка	с	293	750	1000	6	9	2,22	q100	q2Q0	q500		—	—	8500	3000—	8,8	10,1	—	Не разрушается
H-t		1490 К+закалка с														3400				при длительных
§	Й СП	1320 К -1- старение при 1120 К — 8 ч;	950	700	900	8	10	1,86	750	700	650	630	346	—	—	—	22,2	14,0	—	выдержках	до 1170К. Использу-
CQ Ю		охлаждение	на	1050	625	830	9	11	1,79	440	410	365	410	356	—.	—	—	24,0	14,3	—	ется до '1170—
X X	X Qz	воздухе	1150	450	610	11	И	1,69	240	210	180	200	330	—	*—	—	26,3	14,6	—	122ОК
			1200	330	440	16	18	—	155	130	110	110	—	—,	—	—	27,4	14,9	•—	
& Q		Закалка	с	293	730	1000	10	11	2,26	qlQ0	q2QQ	q50C	—		—	8400	3000—	8,0	12,0		Рекомендуется
Ж ь	£	1490 К+закалка с														3400				для лопаток, рабо-
< « Ю к X	СЧ СЧ C Ф.	1320 К + старение	950	—	940	10	. 15	1,92									19,3	14,2	—	тающих до 1220К;
§
Продолжение приложения И
Марка материала	Термообработка	т	ffT	%		Ф	F.10”5	Предел длительной прочности			j** 8 5-	7 о		Q	HB	X	a* 10®	a-10®	Примечания
		к	МН/м1		%		МН/м»							кг/м8	МН/м8	Bl/ (M-K)	l/K	M»/C	
	при 1220 К — 2 ч;	1050	—	915	8	И	1,89	§00	—	—	370	—	 —	—	—	21,0	14,8	—	кратковременно —
	охлаждение	на	1150	400	730	8	11			315					320									23,1	15,5	—	при более высокой
	воздухе		350			12		230			280								температуре
		1200		585	9		—		—	—		—	—	—	—	—	15,9	—	
		1250	—	446	10	13	—	—	—	—	—	—	—	—	—	—	16,4	—	
ЖС6-КП	Закалка	с	293	800	1250	10	14	2,00	<*100	q2QQ	q500			430			8250	3200—	9,6	11,5	—.	Применяется для
	1490К -4 ч; ох-														3500				штампованных ра-
	лаждение на воз- духе + отжиг при	950	760	1110	15	21	1,66	770	740	710	—	420	—	—	—•	19,4	13,7	—	бочих лопаток при 1170—1270К
	1320К — 2 ч; ох-	1050	750	1020	12	16	1,59	530	500	430	420	400	—	—	—	21,2	14,2	—	
	лаждение на воз- духе	1150	520	820	10	15	1,34	350	340	240	220	370	—	—	—	23,1	14,9	—	
		1200	380	640	5	9	1,25	260	230	155	120	330	—	—	—	24,1	15,3	—	
		1250	290	510	9	14	1,18	180	165	105	—	270	—	—	—	25,2	—	—	
ЖС6-К		293	850	1000	1.5	6,5	2,00	<*100	q2QQ	q500	—	270	—	8100	3200—	8,4	11,0	2,4	Применяется для
															3500				литых сопловых и
		450	840	940	2.0	8,0	1,70									17,5	13,1	4,0	рабочих лопаток
		850	840	930	2.4	7,6	1,65,					—				19,4	13,8	4,4	при 1100—1270 К
		950	840	920	1,8	8,8	1,60	790	750	720	—	—	—	—	—	21,1	14,1	4,5	
		1050	830	910	1,1	6,0	1,53	550	520	460	390	—	—	—1	—	22,7	14,6	4,4	
	•	1150	580	780	1,8	3,4	1,30	360	350	250	210	260	—	—	—	24,8	15,1	4,4	
		1250	350	550	4,2	5,8	1,21	190	175	110	80	—	—	—.	—	27,1	15,8	—	।
		1350	200	270	8,8	17	1,05| 65		50	—	60	—	—	—	—	—	—	—	
				1		|						1		1	1			1	
37Х12Н8Г8МФБ (ЭИ481)	Закалка	с 131 ОК в воде; двойное старение; 920К — 16 ч; 1070К — 16 ч; ох- лаждение на воз- духе	293 750 800 850 900 950 1000	630 496 484 468 424 388 350	1000 693 662 632 584 500 436	18,0 13,2 12,7 12,2 11,7 12,4 13,1	35 38 39 40 42 46 48	1,74 1,32 1,27 1,24 1,21 1,23 1,17	<*100 620 560 490 410 320 240	tf2QQ 610 550 460 390 290 230	1 дзос 600 540 440 360 270 210	। — 250 240 235 200 174	1	1 1 1 1 1 1	1	1 1 1 1 1 1	7850	3100- 3400	16,3 22,7 23,6 24,4 25,1 25,7 26,4	15,3 18,0 18,3 18,5 18,8 19,0 19,3	1	1 1 1 1 1 1	Применяется для дисков, работаю- щих при Т <920К, и крепежных де- талей. Хорошо об- рабатывается реза- нием
20ХЗМВФ (ЭИ415)	Закалка	с 1320К в масле; от- пуск при 970К	293 450 550 650 700 750 800 850	760 712 710 678 652 624 580 415	890 810 800 752 676 648 605 532	13 12 10 9 11 12 11 10	49 54 40 34 44 45 44 31	2,11 2,04 2,00 1,91 1,87 1,82 1,76 1,69	а100	с200	а300	1 III 1 1 § 1	1 Illi 1 1 1	1 1 1 1 1 1 1	1	7800 •	1 о SS | 1 | | | | | 		38,5 33,6 31,8 30,8 30,3 30,0 29,5 29,3	12,2 12,5 12,6 12,7 13,4	—	Применяется для дисков и деталей роторов, работаю- щих при Т< <820К. Наиболее жаропрочный ма- териал из числа мало- и среднеле- гированных сталей. Дешевле,	чем 37Х12Н8Г8МФБ (ЭИ481), хорошо обрабатывается резанием.	Для сварки требует ус- ложненной техно- логии	
								600 540 460 380	580 530 440 290	540 500 410 220									
18ХНВА	Нормализация при 1190—1250К и отпуск	293	850	1150	11	50	2,00	—	—	—		520	—	7850	3310— 3380	36,0	11,0	—	Цементирует^ Азотируется
40ХНМА	Закалка	с 1120К в масле, от- пуск при 850К (2 ч), охлаждение на воздухе	293	950	1100	.12	50	2,05	—	—	—	—4	550	—	7850	3210— 3750	46,1	11,7	—‘	Азотируется
Номограмма для определения мам
П= 120\	-------- —	;
432
ПРИЛОЖЕНИЕ Ht
ента инерции профиля лопатки
43
Приложение IV
ТАБЛИЦЫ ОСНОВНЫХ ГАЗОДИНАМИЧЕСКИХ ФУНКЦИИ
А		•-Р/Р*	я (X)	Г (А)	м
		л=	=1,40		
0	1,000	1,0000	0,000	0,000	0,000
0,10	0,9983	0,9942	0,1571	0,1580	0,0914
0,20	0,9933	0,9768	0,3102	0,£f76 .	0,1830
0,30	0,9850	0,9485	0,4557	0,4804	0,2760
о.31	0,9840	0,9451	0,4697	0,4970	0,2850
0,32	0,9819	0,9415	0,4835	0,5135	0,2957
0,33	0,9819	0,9379	0,4972	0,5302	0,3040
0,34	0,9807	0,9342 >	0,5109	0,5469	0,3134
0,35	0,9796	0,9303	0,5243	0,5636	0,3228
0,36	0,9784	0,9265	0,5377	0,5804	0,3322
0,37	0,9772 •	0,9224	0,5509	0,5973	0,3417
0,38	< 0,9759	0,9183	0,5640	0,6142	0,3511
0,39	0,9747	0,9141	0,5769	0,6312	0,3606
0,40	0,9733	0,9097	0,5897	0.6482	0,3701
0,41	0,9720	0,9053	0,6024	0,6654	0,3796
0,42	0,9706	0,9008	0,6149	0,6826	' 0,3892
0,43	0,9692	0,8962	0,6272	0,6998	0,3987
0,44	0,9677	0,8915s	0,6394	0-,7172	0,4083
0,45	0,9663	0,8868	0,6515	0,7346	0,4179
0,46	0,9647	0,8819	0,6633	0,7521	0,4275
0,47	0,9632	0,8770	0,6750	0,7697	0,4372
- 0,48	. 0,9616	0,8719	0,6865	0,7874	0,4468
0,49	0,9600	0,8668	0,6979	0,8052	0,4565
0,50	0,9583	0,8616	0,7091	0,8230	0,4663
0,51	0,9567	0,8563	0,7201	0,8409	0,4760
0,52	0,9549	0,8509	0,7309	0,8590	0,4858
0,53	0,9532	0,8455	0,7416	0,8771	0,4956
0,54	0,9514	0,8400	0,7520	0,8953	0,5054
0,55	0,9496	0,8344 '	0,7623	0,9136	0,5152
0,56	0,9477	0,8287	0,7724	0,9321	0,5251
0,57	0,9459	0,8230	0,7823	0,9506.	0,5350
0,58	0,9439	0,8172	0,7920	0,9692	0,5450
0,59	0,9420	0,8112	0,8015	0,9880	0,5549
0,60	0,9400	0,8053	0,8109	• 1,0069	0,5649
434
^^^^^^^wt-^^^^OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOtoOOOOOOO
»т- >— *-* *-* *- о о о о о о о ооо оЪ^фЪЪфЪю'ооооооооодааоооаоооооч^чччччччччЪЪ о о о> о> о о о
СЛ^СОЬЭ*-ОСООО«^О5СЛ4Ь.СОКЭ»^ОООО-Ч05О14*СОЬО>-‘О<ОаОМОСЛ^СОЬОь-ОСООО1ЧОСЛ>(*СОЮн-ОСООО>ЧОСЛ4*СОГО|—
ООООООООООООООООООООООООООООООрОООООО 0*0 оооооооооооооооо
*4 М ^4 *4 М “4 00 оо Q0 ОО ОО 00 ОО 00 ОО ОО 00 ОО ОО 00 00 00 ОО 00 ОО ОО 00 00
чаососо(Осоооо*-н->-мк)ис>зссид^>^слслсло(7)а)ч
о w“Ч О4*ооюсдсоьоооаоооао оэсосо о со ьэ сл оо ю сл оо о
WOOh24 WSK)0>OW4£>K)^Cft4<O£JOOC)<O
OOOOOOQOQOQOQOOOQOQOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCO
чччооаоооюсодюоаоо*-.- кэьэююьэсосрсосо
СООСОЬЭСЛ^<ООО0>ОО>—Q0O>00»—СООООСЭЬОСЛМСО»—СОСлОО
CO"4<X>^K)COMWOChbO'4Co-4tOQ>OCO*4CO ЬЭ 4* 01*4000
&
t
СЛОО О ЮКЭ
t
CQ
К
ч
000000000000000^-000000000000000000000000000000000000000
сОООСОСООСООООООООО О О OOcOOCOCOcOCOOOOOOOCOOOOcOOOCOOOOOOOOQOOOQOQOQOaoOOOOOOOO
^•400QOOOOOOOOOOOOOOOOOOOOOOO'OOOOOQD*4M*4000CnCn4*4*CQWbOt-‘H--OtOcC>OD-414C»Cni4*CA3b2'--
ООООК>СЛОООЮИ*СЛООООООООООООСЮ*ЧСЛЙ*ЬОО"ЧСЛЮОС»ЮОСЛ>— О) Н- 0>ь-ОЭ©СлООЬЭОО№01“ЧОЬЭ4*СЛ*4аО$0
СЛООООа>ООО4*н-*4ООС0СЛООСС>СлО»— О “Ч t— Wb004*004*c0>— K)OQiOOOOOrf*QOOOO»— СО 4* to 00 Оо СО СО СЛ 00 00
NShDbDtsDNDNDbObObObObOtsO
Ъэ Vo ьэ ьо bO *>—	о о о о'
ЬОСООООО-Ч4*н- ООСЛЬЗО
О Сл со W со со 4* СЛ -4 со н-<
КЭЬО*-»— — Н-ОООО
N3O00O4^N3OQ0O4*h0
tON2tObOtObOCo4*4*4*CH
M4*boboaoooK)b-cooo
w->— н-1—1F-1000000000000000000000000000000000000000
§
Продолжение прилож. IV
Продолжение прилож. IV
А	«	-г—Г/Г*	ч-р!р*	q (X)	Г (X)	м
1,16	0,7757	0,4111	0,9698	2,3588	1,2023
1,17	0,7719	0,4040	0,9659	2,3911	1,2157
1,18	0J679	0,9396	0,9620	2,4238	1,2292
1,19	0,7640	0,3898	0,9577	2,4570	1,2428
1,20	0,7600	0,3827	0,9531	2,4906	1,2566
1,21	0,7560	0,3757	0,9484	2,5247	1,2708
1,22	0,7519	0,3687	0,9435	2,5593	1,2843
1,23	0,7478	0,3617	0,9384	2,5944	1,2974
1,24	0,7437	0,3548	0,9331	2,6300	1,3126
1,25	0,7396	0,3479	0,9275	2,6660	1,3268
1,26	0,7354	0,3411	0,9217	2 7026	1,3413
1,27	0,7312	0,3343	0,9159	2,7398	1,3558
'	1,28	0,7269	0,3275	0,9096	1,7775	1,3705
1,29	0,7227	0,3208	0,9033	2,8158	1,3853
1,30	0,7183	0,3142	0,8969	2,8547	1,4002
1,31	0,7140	0,3075	0,8901	2,8941	1,4153
1.32	0,7096	0,3010	0,8831	2,9343	1	1,4305
1,33	0,7052	0,2945	0,8761	2,9750	1,4458
1,34	0,7007	0,2880	0,8688	3,0164	1,4613
1,35	0,6992	0,2816	0,8614	3,0586	1,4769
1,36	0,6917	0,2753	0,8538	3,1013	1,4927
1,37	0,6872	0,2690	0,8459	3,1448	1,5087
1,38	0,6826	0,2628	0,8380	3,1889	1,5248
1,39	0,6780	0,2566	0,8299	3,2340	1,5410
1,40	0,6733	0,2505	0,8216	3,2798	1,5575
1.41	0,6687	0,2445	0,8131	3,3263	1,5741
1,42	0,6639	0,2385	0,8046	3,3737	1,5909
1,43	0,6592	0,2326	0,7958	3,4219	1,6078
1,44	0,6544	0,2267	0,7869	3,4710	1,6250
1,45	0,6496	0,2209	0,7778	3,5211	1,6423
1,46	0,6447	0,2152	0,7687	3,5720	1,6598
1,47	0,6398	0,2095	0,7593	3,6240	1,6776
1.48	0,6349	0,2040	0,7499	3,6768	1,6955
1,49	0,6300	0,1985	0,7404	3,7308	1,7137
1,50	0,6250	0,1930	0,7307	3,7858	1,7321
		А=	=1,33		
0	1,0000	1,0000	0,0000	0,0000	0,0000
0,10	0,9985	0,9944	0,1582	0,1591	0,0927
0,20	0,9943	0,9774	0,3123	0,3195	0,1858
0,30	0,9873	0,9496	0,4584	0,4827	0,2797
0,31	0,9864	0,9463	0,4724	0,4992	0,2892
0,32	0,9855	0,9428 *	0,4863	0,5158	0,2986
0,33	0,9846	0,9393	0,5001	0,5324	0,3081
0,34	0,9836	0,9356	0,5137	0.5491	0,3176
0,35 ‘	0,9827	0,9319	0,5273	0,5658	0,3271
0,36	0,9817	0,9281	0,5407	0,5826	0,3366
0,37	0,9806	0,9241	0,5539	0,5994	0,3462
0,38	0,9796	0,9201	0,5670	0,6162	0,3557
0,39	0,9785	0,9159	0,5799	0,6332	0,3653
0,40	0,9773	0,9118	0,5928	0,6501	0,3749
0,41	0,9762	0,9075	0,6055	0,6672	0,3845
0,42	0,9750'	0,9030	0,6179	0.6843	0,3941
436
Продолжение прилож. IV
ООООООООООООООООО’-Ч’-”-'’-*’--'—
437
ОООООООООООООООООООООООООООООООООООООООООООООООООООООО
<O <0 <D .ЧЧЧЮ.® ЧЬЛЛ	<30a000Q000Q0Q0Q0Q0C?a5oJSSo>O>
ооооооооооооооосоооосюооооосюооооооооооаГоооооооооооооо
Продолжение прилож. IV
X		—Pip*	q (X)	Г (X)	м
0,97	0,8667	0,5619	0,9989	1,7778	0,9653
0,98	0,8640	0,5547	0,9995	1,8018	0,9768
0,99	0,8612	0,5476	1,0000	1,8261	0,9884
1,00	0,8584	0,5404	1,0000	1,8506	1,0000
1,01	0,8555	0,5332	1,0000	1,8754	1,0117
1,02	0,8527	0,5260	0,9995	1,9003	1,0234
1,03	0,8497	0,5188	0,9989	1,9255	1,0352
1,04	0,8468	0,5116	0,9981	1,9509	1,0471
1,05	0,8439	0,5045	0,9972	1,9766	1,0590
1,06	0,8409	0,4973	0,9958	2,0025	1,0710
1,07	0,8379	0,4902	0,9944	2,0286	1,0830
1,08	0,8348	0,4830	0,9926	2,0550	1,0951
1,09	0,8317	0,4759	0,9907	2,0818	1,1073
1,10	0,8286	0,4688	0,9886	2,1087	1,1196
1,11	0,8255	0,4617	0,9862	2,1360	1,1319
1,12	0,8223	0,4546	0,9835	2,1635	1,1443
1,13	0,8192	0,4475	0,9806	2,1913	1,1567
1,14	0,8159	0,4405	0,9777	2,2194	1,1693
1,15	0,8127	0,4335	0,9744	2,2478	1,1819
1,16	0,8094	0,4265	0,9709	2,2765	1,1946
1,17	0,8061	0,4196	0,9674	2,3055	1,2073
1,18	0,8028	0,4126	0,9634	2,3349	1,2202
J,19	0,7994	0,4057	0,9593	2,3646	1,2331
1,20	0,7961	0,3986	0,9545	2,3940	1,2461
1,21	0,7926	0,3920	0,9506	2,4249	1,2592
1,22	0,7892	0,3852	0,9459	2,4556	1,2723
1,23	0,7857	0,3784	0,9410	2,4867	1,2856
1,24	0,7882	0,3716	0,9357	2,5181	1,2990
1,25	0,7787	0,3649	0,9305	2,5500	1,3124
1,26	0,7752	0,3583	0,9252	2,5821	1,3259
1,27	0,7716	0,3516	0,9193	2,6147	1,3396
1,28	0,7680	0,3450	0,9135	' 2,6477	1,3533
1,29	0,7643	0,3385	• 0,9075	2,6811	1,3671
1,30	0,7606	0,3320	0,9014	2,7149	1,3820
1,31	0,7570	0,3255	0,8949	2,7492	1,3950
1,32	0,7532	О',3191	0,8883	•2,7838	1,4091
1,33	0,7495	0,3128	0,8816	2,8190	1,4234 -
1,34	0,7457	0,3065	0,8749	2,8545	1,4377
1,35	0,7419	0,3002	0,8677	' 2,8905	1,4521
1,36	0,7380	0,2940	0,8606	2,9271	1,4667
1,37	0,7342	0,2878	0,8531	2,9642	1,4814
1,38	'	0,7303	0,2817	0,8455	3,0017	1,496о
1,39	0,7264	0,2757	0,8381	3,0398	1,5110
1,40	0,7224	0,2697	0,8303	3,0784	1,526о
' 1,41	0,7184	0,2637	0,8221	3,П76	1,5412
1,42	0 7144	0,2578	0,8140	3,1573	1,5564
1,43	0,7104	0,2520	0,8060	3,1977	1,5719
1,44	0,7063	0,2463	0,7976	3,2386	1,5875
1,45	0,7022	0,2406	0,7891	3,2802	1,6031
1,46	0,6981	0,2349	0,7805	3,3222	1,6188
1,47	0,6940	0,2294	0,7718	3,3649	1,6349
1,48	0,6898	0,2238	0,7629	3,4083	1,6510
1,49	0,6856	0,2184	0,7540	3,4524	1,6672
1,50	0,6813	0,2138	0,7449	3,4972	1,6836
СПИСОК ЛИТЕРАТУРЫ
I.	Абианц В. X. Теория газовых турбин реактивных двигателей. М., Машино-
строение, 1965, 310 с.	4
2.	Биргер И. А. Круглые пластинки' и оболочки вращения. М., Оборонгиз,
1961. 368 с.
3.	Высокотемпературные охлаждаемые газовые турбины. [Сб., статей/Под
ред. В. Л. Иванова и В. И. Локая]. М., Машиностроение, 1971 232 с.
4.	Дейч М. Е. Техническая газодинамика. М., Энергия, 1974. 592 с.
5.	Дейч М. Е. Трояновский Б. М. Исследования и расчеты ступеней осевых
турбин. М., Машиностроение, 1964. 628 с.
6.	Жирицкий Г. С. и др. Газовые турбины двигателей летательных аппара-
тов. /Жирицкий Г. С., Локай В. И., Максутова М. К., Стрункин В. А. М., Маши-
ностроение. 1971. 620 с.
7.	Жирицкий Г. С., Стрункин В. А. Конструкция и расчет на прочность дета-
лей паровых и газовых турбин. М., Машиностроение, 1968, 520 с.
8.	Зысина-Моложен Л. М., Зысин Л. В., Поляк М. П. Теплообмен в турбома-
шинах. Л., Машиностроение, 1974. 335 с.
9.	Копелев С. 3., Тихонов Н. Д. Расчет турбин авиационных двигателей. М.,
Машиностроение, 1974. 264 с.
10.	Малинин Н. Н. Прикладная теория пластичности и ползучести. М., Маши-
ностроение, 1975. 399 с.
И. Масленников М. М., Шальман Ю. И. Авиационные газотурбинные двига-
тели. М., Машиностроение, 1975. 576 с.
12.	Митрохин В. Т. Выбор параметров и расчет центростремительной турби-
ны. М., Машиностроение, 1974. 227 с.
13.	Основы теплопередачи в авиационной и ракетно-космической технике.
/Под ред. В. К. Кошкина. М., Машиностроение, 1975. 623 с
14.	Расчетные и экспериментальные методы определения теплового состояния
основных узлов газовых турбин с воздушным охлаждением. /Под ред. Ё. П. Ды-
бана, М. М. Иващенко, Л. А. Коздобы. — [Руководящие указания ЦКТИ—ИТТФ
АНУССР]. Вып. 29, т. 2. 1972. 224 с.
15.	Скубачевский Г. С. Авиационные газотурбинные двигатели. М., Машино-
строение, 1974. 520 с.
16.	Теория воздушно-реактивных двигателей. /Под ред. С. М. Шляхтенко. М.,
Машиностроение, 1975. 568 с.
17.	Термопрочность деталей машин. /Под ред. И. А. Биргера, Б. Ф. Шорра.
Машиностроение, 1975. 455 с.
18.	Траупель В. Тепловые турбомашины. Т. 1. М,—Л., Госэнергоиздат, 1961.
342 с.
19.	Уваров В. В. и др. Локомотивные газотурбинные установки. М., Машгиз,
1962. 548 с.
20.	Химушин Ф. Ф. Жаропрочные стали и сплавы. М., Металлургия, 1969.
749 с.
21.	Холщевников К. В. Теория и расчет авиационных лопаточных «машин. М.,
Машиностроение, 1970. 610 с.
22.	швец И. Т., Дыбан Е. П. Воздушное охлаждение деталей газовых тур-
бин. Киев, Наукова думка, 1974. 487 с.
439
23.	Абианц В. X. Состояние и тенденции развития современных авиационных
газовых турбин. — Изв. вузов. Авиационная техника, 1970, № 1, с. 5—16.
24.	Емин О. Нм Шварцман П. И. Общий метод определения оптимальных па-
раметров турбин с малым объемным расходом. — Йзв. вузов. Авиационная техни-
ка, 1969, № 1, с. 70—76. .
25.	Клебанов А. Г., Мамаев Б. И. Оптимальный шаг турбинной решетки. —
Теплоэнергетика, 1969, № 10, с. 56—60.
26	Ковалев А. А., Стрункин В. А., Курцева И. И, К вопросу о влиянии не-
равномерности потока на колебания лопаток турбомашин.—[Труды КАИ]. Вып.
151. Казань, 1972, с. 11—20
27.	Локай В. И. К вопросу обобщения опытных данных по теплообмену в ох-
лаждаемой проточной части высокотемпературных газовых турбин. — Изв. вузов.
Авиационная техника, 1968, № 3, с. 67—78.
28.	Локай В. И. Исследование эффективности воздушного охлаждения лопа-
ток газовых турбин. — Теплоэнергетика, 1970, № 7, с. 13—17.
29.	Локай В. И. Расчет температурного поля охлаждаемых турбинных ло-
паток при переменных граничных условиях и зависимости теплофизических
свойств материала от температуры. — Изв. вузов. Авиационная техника, 1969,
№ 3, с. 80—90.
30.	Локай В. И., Трушин В. А. Исследование теплообмена между газом и
элементами проточной части газовой турбины в условиях вращения. — Из-
вестия АН СССР. Энергетика и транспорт, 1970, № 1, с. 94—100
31.	Максутова М. К., Вавилов Г. А. Влияние угла входа потока на профиль-
ные потери турбинной решетки. — [Труды КАИ]. Вып. 153. Казань: 1973. с. 33—40.
32.	Максутова М. К., Вавилов Г. А., Тарасов В. Н. Влияние угла атаки на ха-
рактеристики осевой турбинной ступени. — Изв. вузов. Энергетика, 1974, № 8,
с. 74—78.
33.	Максутова М. К., Вавилов Г. А., Тарасов В. Н. К расчету характеристики
осевой турбинной ступени при различных значениях радиального зазора. — Изв.
вузов. Авиационная техника, 1974, № 1, с. ПО—116.
34.	Мамаев Б. И., Клебанов А. Г. Профильные потери в турбинной решет-
ке. — Теплоэнергетика, 1970, № 6, с. 38—42.
35.	Стрункин В. А. О колебаниях неравномерно нагретых дисков турбома-
шин.—-Изв вузов. Авиационная техника, 1958, № 1, с. 165—170.
36.	Barnes I. F. Advances in Engine Technologiy: Cooled Turbines. — Aircraft
Eng., 1969, vol. 41, NIO, pp. 18—21.
37.	Halls G. A. Air Cooling of Turbine Blades and Vanes. — Aircraft Eng.,
1967; vol 39, N 8, pp. 4—14.
38.	Hertsel I. F. Predicting of Effects of Mass-transfer Cooling on the Blade-
Row Efficiency of Turbine Airfoils. — AIAA Paper, 1972, N 11, pp. 1—7.
39.	Helms H. E. Stoichiometrie Gas Turbines Development Problems. — The
international Symposium on Air Breathing Engines; Marseille..— France, 1972.
pp. 19—23.
40.	Mountain A. R., Barnes I. E. Journal of the RAS. — Aug., 1963, pp. 29—36.
41.	Patancar S. V. Spalding Heat and Mass Transfer in Boundary Layers:
Morgan—Grampian—London: 1967, p. 128.
42.	Malker L. A. and Markland E. Heat Transfer to Turbine Blading in the
Presence of Secondary Flow. — Int. J. Heat-Mass Transfer. — London: 1965, vol. 8,
pp. 729—748.
Предметный указатель
А
Адиабата 33, 35
Аппарат направляющий 26
— сопловой 15, 96, 270
Б
Бандажные полки 83, 88, 275
Балансировка ротора
Безразмерные комплексы 163
В
Вал гибкий 377
— жесткий 377
Вихрь закромочный 75
— парный 82
Воздушное охлаждение 195
Вставки (металлокерамические —
сотовые) 275
Вторичные течения 82
Входная кромка лопаток 66, 87, 212
Высота лопаток 65
Выходная кромка лопаток 67, 87, ^13
Г
Геометрия решеток 64
Главные центральные оси
инерции 288
Горловина (горло) решетки 39, 65,
Градиент давления 73, 104
Грина формула 252
Д
Давление 94
— статическое 65, 96
— торможения (полное) 17, 32
Движение
— абсолютное 46,- 47	*'
—	относительное 46, 47
Двигатель газотурбинный
—	турбовальпый 13
—	турбовинтовой 13
—	турбореактивный 13
—	турбореактивный
двухконтурный 13
Диаграммы резонансные 315
— р—v 12
- — TS 34
— IS 19, 23, 48
Диаметр гидравлический 221
— средней ступени 15, 100
Диск турбины 260 261
— постоянной толщины 321, 327
— произвольного профиля 330
Диффузорный участок профиля 66, 77
Ж
Жаропрочность металла 281
Жаростойкость металла 282
Жесткость вала 377
Жидкостное охлаждение 194
3
Заградительное охлаждение 199, 215
Закон постоянства циркуляции 104
Запас прочности вала 367, 368
----- диска 354
----- лопаток 303
И
Интенсивность деформаций 347
— напряжений 347
К
Колебания вала 374
— диска 356
— лопатки 306
Колесо турбины осевой 96, 99
---- радиальной 337
Косой срез решетки лопаток 54
Корпус турбины 15, 272
Коэффициенты влияния 387, 391
Коэффициент полезного действия
лопаточной решетки 78
— *---ступени турбины
адиабатный 129
-----------внутренний 130, 233
-----------механический 130
-----------окружной 130, 133
“----------эффективный 28, 130
Коэффициент восстановления
441
давления 41
— нагрузки 141
— Пуассона 327, 332
—	расхода 40, 207
—	теплоотдачи от газа к
лопатке 208, 211
—	теплоотдачи от лопатки
к охладителю 220, 222
—	теплопередачи 250
—	формы лопатки 286
— компенсации напряжений 293
Л
Логарифмический декремент
колебаний 317
Лопатка активная 78, 89
— направляющая 137, 149
— охлаждаемая 108, 201
— рабочая 76, 89
— переменного сечения 115
— реактивная 115
— сопловая 76, 220, 236
М
Метод Ваничева (элементарных
балансов) 256
Многоступенчатая турбина
24, 151, 185
Момент изгибающий 288
— инерции 290, 294
— количество движения 128
— крутящий 173, 174
Мощность турбины
— внутренняя 130
— эффективная 130
Н
Напряжения в диске 326
— в замке 286, 297
—	в рабочей лопатке 291
—	в вале турбины 365
— термические 302
Несжимаемый поток 67, 104
Нестационарный процесс 255, 264
О
Обороты критические валы 376
--- диска 359
Окружное направление 67
— усилие 18, 66
Охлаждаемая турбина 227
Опоры упругодемпферные 394
Осевой зазор 15, 70, 91
Осесимметричный поток 96
Осреднение потоков 30, 70
Относительная высота лопатки 87
Отношение давлений критическое 36
— скоростей 21
Отрыв пограничного слоя 71, 73
П
Параметр Ларсена-Миллера 281
Параметры адиабатно-
заторможенного потока 17
Парсонса характеристики 169
Парциальность 125
Перекрыша лопаток 92
План скоростей (треугольники) 17
Плотность тока (безразмерная)
42, 103
Прецессия вала 385
Потери в турбине вентиляционные 126
— вторичные 71, 82
------ в соплах 116
------ в рабочих лопатках 116
------от смешивания потоков 229
------охлаждения 227
Предел длительной прочности 279
— ползучести 279
Приведенный расход 42
Приведенная скорость 33
Профиль (меридиональный)
проточной части 160
Р
г Работа адиабатного раширения
' газа в турбине 19
Работа, турбины внутренняя 130
----на окружности колеса
(Эйлерова) 70, 129
----располагаемая 128, 129
----эффективная 130
Радиальный зазор (именение
по режимам) 121, 274
Радиус кривизны (профиля) 78, 89
Разрушающее число оборотов 354,
355
Реактивность (ступени) 19, 95
Режим работы турбины
нерасчетный 162
----подобный 163
----расчетный 162
Резонанс 306, 318
Релея принцип 312
Решетка профилей 64
---- кольцевая 64
---- плоская 17, 64
Ротор барабанно-дисковый 323
— дисковый 323
С
Сверхзвуковой поток 89
Сила, действующая на профиль ч
67, 69
— инерции 94
— центробежная 84, 94, 285
.— подъемная 66
Скоростной коэффициент решетки
(сопловой, рабочей) 34, 49, 93
442
Скорость абсолютная 31, 50
— звука 33, 67
—	истечения 16
—	относительная 94
—	переносная (окружная) 17
—	критическая 33
Сопловая решетка 31
Средняя линия профиля 65
Ступень турбины активная 20, 135
— реактивная 20
Т
Термодинамические функции 62
Турбина активная 135
—	одноступенчатая 116
—	осевая 133
—многоступенчатая 25
---со ступениями давления 24, 150
---------скорости 26, 136, 148
—	парциальная 125
—	радиальная 22
—	радиально-осевая 23
У
Угол атаки 65, 80
— затылочный 65, 89
—	отклонения 56
—	поворота потока 66
— потока на выходе из решетки
65, 76
—	установки профиля 65
Удельная теплоемкость газов 59
Уравнение Гука 327
—	движения 96
—	количества движения 68
—	Лагранжа 387
—	Лапласа 252
—	моментов количества движения
128
—	неразрывности 99
—	первого закона термодинамики
53, 60
—	радиалыюго равновесия 95
—	Эйлера 96
—	энергии 16, 48
—	энтропии 61
Э
.Энтальпия 16
Энтропия 61
Эпюра распределения давлений 15, 65
---скоростей 15, 66
---температуры газа на входе
в турбину 203
—	изгибающих моментов 366
Ф
Фиксация осевая рабочих
лопаток 278
Фронтальная линия 65
X
Характеристики турбины 162
Хвостовик рабочей лопатки 275
—	елочный 276	»
------Т-образный 278
Хорда профиля 65	t
Ц
Цикл ГТД 12
Циркуляция потока 104
Ч
Частота вращения 171
—	собственных колебаний 306
Число Маха 17, 164
—	Нуссельта 209
—	подобия теплоотдачи во
вращающихся лопатках 214, 223
—	Прандтля 225
—	Рейнольдса 66, 73’
—	Стантона 225
Ш
Шаг л^ешетки 65, 85
---относительный 65, 86
Ширина решетки 65, 85
ОГЛАВЛЕНИЕ
Стр.
Предисловие .......................................................... 3
Условные обозначения.................................................. 5
Введение...............................................................8
Часть перв ая
Термо- и аэродинамика газовой турбины
Глава I. Типы и схемы двигателей летательных аппаратов................11
§ 1.1.	Основные типы газотурбинных двигателей.....................11
§1.2.	Газотурбинные двигатели и турбины вспомогательного назна-
чения ............................................................13
Глава И. Понятие о газовой турбине....................................15
§ 2.1.	Принцип действия осевой турбины............................15
§ 2.2.	Понятие о реактивности осевой ступени......................19
§ 2.3.	Одноступенчатые осевые турбины ... *.......................20
§ 2.4.	Радиальные турбины.........................................2%
§ 2.5.	Многоступенчатые осевые турбины............................24
§ 2.6.	Основные требования к газовым турбинам.....................28
Глава III. Основы теории расширения газа в сопловых и рабочих лопаточ-
ных решетках турбин...............................................30
§ 3.1.	Общие сведения.............................................30
§ 3.2.	Одномерная теория течения газа в соплах и сопловых решетках 31
§ 3.3.	Одномерная теория расширения газа в каналах вращающихся
лопаточных решеток................................................46
§ 3.4.	Особенности расширения газа в охлаждаемых сопловых и ра-
бочих решетках....................................................51
§ 3.5.	Расширение газа в косом срезе лопаточного канала ....	54
§ 3.6.	Расчет тепловых процессов в турбомашинах с учетом перемен-
ных теплоемкостей газа.......................................-	.	59
Глава IV. Обтекание решетки лопаток газом.............................64
§ 4.1.	Общие сведения...........................................  64
§ 4.2.	Распределение давления по профилю..........................65
§ 4.3.	Силы, действующие в решетке профилей........................67	‘
§ 4.4.	Экспериментальное исследование решеток.....................69
§ 4.5.	Потери в решетке...........................................71
§ 4.6.	Профильные потери........................................  73
§ 4.7.	Концевые потери..........................................  81
§ 4.8.	Потери, связанные с вращением решетки......................84
§ 4.9.	Влияние геометрических параметров решетки на к. п. д. . . .	85
§ 4.10.	Очертание профиля лопатки и форма канала...................88
§ 4.11.	Взаимное расположение сопловой и рабочей решеток ...	91
§ 4.12.	Влияние стоек, расположенных перед сопловым аппаратом, на
потери в решетке...................................................93
444
Стр.
Глава V. Основы расчета пространственного потока в проточной части тур-
бины ...........................................................  94
§ 5.1.	Особенности пространственного потока в проточной части тур-
бины ..............................................................94
§ 5.2.	Уравнение радиального равновесия частиц газа................95
§ 5.3.	Различные методы закрутки лопаток..........................101
§ 5.4.	Сравнение различных методов закрутки лопаток...............111
§‘5.5. Построение лопаток переменного профиля.....................115
Глава VI. К. п. д. ступени. Расчет ступени............................116
§ 6.1.	Потери в турбине...........................................116
§ 6.2.	Выходные потери............................................117
§ 6.3.	Потери на утечку через лабиринтные уплотнения	.	.	.	.	118
§ 6.4.	Потери на утечку через радиальные зазоры лопаток	«	121
§ 6.5.	Потери на трение диска и наружной поверхности бандажа	,	.	124
§ 6.6.	Потери, вызванные парциальностью ступени .	. ’	.	.	.	.	125
§ 6.7.	Работа газа на лопатках турбины............................128
§ 6.8.	Номенклатура к. п. д. турбины (ступени)....................128
§ 6.9.	Адиабатный к. п. д.........................................131
§ 6.10.	Окружной к. п. д. турбинной ступени.......................132
§ 6.11.	Окружной к. п. д. турбины со ступенями скорости .... 136
§ 6.	12. Внутренний к. п. д. и выбор отношения и/с&д.............140
§ 6.13.	Коэффициент нагрузки турбинной ступени....................141
§ 6.14.	Особенности расчета ступени турбины.......................142
§ 6.15.	Особенности расчета турбин со ступенями скорости ....	148
Глава VJJ. Тепловой процесс турбин со ступенями давления и его расчет 150
§	7.1.	Общие сведения...............................150
§ 7.2.	Отличительные особенности теплового процесса многоступенча-
той турбины.......................................................151
§	7.3.	Расчет турбины со	ступенями давления......155
Глава VIII. Работа турбины на нерасчетных режимах, характеристики тур-
бины и их использование...........................................162
§ 8.1.	Типичные изменения параметров турбины в газотурбинных дви-
гателях ...........................................................162
§ 8.2.	Критерии подобия процессов в турбине........................163
§ 8.3.	Зависимость отдельных видов потерь	от режима работы турбины 167
§ 8.4.	Характеристики турбины......................................169
§ 8.5.	Построение характеристик турбины	.	.	'..................179
§ 8.6.	Построение характеристики многоступенчатой турбины по ха-
рактеристикам отдельных ступеней...................................185
§ 8.7.	Регулирование турбины поворотом лопаток соплового аппарата 187
Глава IX. Охлаждение деталей турбины.................................189
§ 9.1.	Общие сведения............................................189
§ 9.2.	Способы охлаждения горячих деталей турбины................191
§ 9.3.	Краткая характеристика различных способов воздушного охлаж-
дения лопаток турбины...........................................195
§ 9.4.	Основные этапы расчета воздушного охлаждения сопловых и
рабочих лопаток газовых турбин..................................203
§ 9.5.	Граничные условия теплообмена между газом и элементами про-
точной части^турбины............................................207
§ 9.6.	Граничные условия теплообмена в охлаждающих каналах соп-
ловых и рабочих лопаток ....................................... 219
§ 9.7.	Эффективность воздушного охлаждения сопловых и рабочих ло-
паток газовых турбин и выбор расхода воздуха на охлаждение 224
§ 9.8.	Дополнительные потери энергии в охлаждаемых турбинах .	. 227
§ 9.9.	’Особенности термогазодинамического расчета охлаждаемых тур-
бин (ступеней)..................................................231
445
Стр.
Глава X. Расчет температуры деталей турбины и гидравлического сопротив-
ления системы их охлаждения....................................234
§ 10.1.	Основы гидравлического расчета системы охлаждения сопловых
и рабочих лопаток..............................................	235
§ 10.2.	Поверочный гидравлический расчет системы охлаждения рабо-
чей лопатки......................................................238
§ 10.3.	Приближенный поверочный расчет температуры сопловых лопа-
ток и подогрев воздуха в каналах их охлаждения ....	239
§ 10.4.	Приближенный поверочный расчет температуры рабочих лопаток 246
§ 10.5.	Детальный расчет температурных полей в охлаждаемых лопат-
ках турбин в стационарных условиях...............................251
§ 10.6.	Детальный расчет температурных полей в охлаждаемых лопат-
ках турбин в нестационарных условиях (пуск, остановка, пере-
ходные режимы)...................................................255
§ 10.7.	Охлаждение дисков турбин.................................260
§ 10.8.	Приближенный расчет распределения температур по радиусу дис-
ка в установившихся условиях...................................  262
§ 10.9.	Детальный расчет нестационарных и стационарных температур в
диске турбины....................................................264
Часть втор ая
Конструкция турбин и их деталей. Расчеты на прочность
Глава XI.	Конструкция деталей	проточной	части турбин...............270
§ 11.1.	Сопловые аппараты	и	корпусы	турбин......................270
§ 11.2.	Рабочие лопатки........................................  275
§ 11.3.	Материалы, применяемые для сопловых аппаратов и рабочих
лопаток..........................................................279
Глава XII. Расчет лопаток на прочность.............................................................................284
§ 12.1.	Общие сведения.......................................................................................  284
§ 12.	2.	Расчет лопаток на	растяжение центробежными силами .	.	. 284
§ 12.3.	Расчет лопаток на	изгиб ...............................................................................287
. § 12.4.	Разгрузка лопатки	от изгибающих	моментов...............................................................292
§ 12.5.	Определение элементов профиля, массы профильной части ло-
патки, ее центра тяжести и момента инерции'.......................294
§ 12.6.	Расчет на прочность соединений лопаток с диском .... 296
§ 12.7.	Расчет бандажной полочки...............................................................................301
§ 12.8.	Определение деформации лопатки с учетом ползучести металла 301
§ 12.9.	Понятие о расчете неравномерно нагретых лопаток .... 302
§ 12.	10. Критерии и запасы прочности лопаток..................................................................303
Глава XIII. Колебания лопаток......................................................................................306
§ 13.	1. Основные понятия......................................................................................306
§ 13.2.	Причины колебаний лопаток..............................................................................307
§ 13	3. Частота колебаний лопатки постоянного профиля .	.	. « i 308
§	13.4.	Частота колебаний лопатки переменного профиля.310
§	13.5.	Резонансная диаграмма колебаний.........................................315
§	13.6.	Напряжения в лопатке при резонансных колебаниях . .	.	. 316
§	13.7.	Обеспечение надежности лопаток при колебаниях.313
Глава XIV. Конструкция турбинных дисков и роторов................................................................320
§ 14.1.	Конструкция дисков и способы соединения и\ с валом .	.	.	320
§ 14.2.	Роторы многоступенчатых турбин........................................................................323
Глава XV. Расчет на прочность барабанов и дисков......................324
§ 15.1.	Расчет ротора барабанного типа.............................324
§ 15.2.	Общие формулы для расчета дисков на растяжение .... 326
§ 15.	3. Диск постоянной толщины (у=const).........................327
§ 15.4.	Расчет на растяжение диска произвольного профиля ....	330
s 15.5. Пример расчета диска произвольного профиля.................337
446
Стр.
§ 15.6.	Расчет колеса радиальной турбины..............................
§ 15.7.	Расчет диска, на изгиб..................'..................339
Глава XVI. Расчет дисков на прочность с учетом пластичности и ползуче-
сти. Материалы для изготовления дисков. Критерии и запасы прочности 345
§ 16?	1.	Концентрация напряжений на краях отверстий в диске	.	.	.	345
§ 16.2.	Расчет диска с учетом пластических деформаций..........346
§ 16.3.	Расчет диска с учетом ползучести металла...............350
§ 16.4.	Материалы для изготовления дисков......................352
§ 16.5.	Критерии прочности дисков. Запасы прочности............353
Глава XVII. Колебания дисков..........................................356
§ 17.1.	Формы колебаний дисков.....................................356
§ 17.2.	Колебания вращающихся дисков...............................358
§ 17.3.	Определение частоты собственных колебаний дисков	.	.	.	359
§ 17.4.	Резонансная диаграмма колебаний и обеспечение надежной	ра-
боты диска	360
Глава XVIII. Конструкция и расчет на прочность турбинных валов	. 362
§ 18.1.	Конструкция турбинных валов и применяемые материалы. .	. 362
§ 18.2.	Расчет	вала на прочность...................................365
§ 18.3.	Опоры	роторов турбин......................................368
§ 18.4.	Выбор	подшипников.........................................372
Глава XIX. Колебания турбинных валов..................................374
§ 19.1.	Понятие о критической частоте вращения вала................374
§ 19.2.	Частота колебаний вала постоянного диаметра без дисков . . 378
§ 19.3.	Определение значения критической частоты вращения вала по-
стоянного диаметра с одним или несколькими дисками .	. . 379
§ 19.4.	Энергетический метод расчета вала..........................380
§ 19.5.	Влияние гироскопического момента дисков на собственные ча-
стоты колебаний вала ............................................. 385
§ 19.	6. 'Критическая и резонансная частоты вращения вала с учетом ги-
роскопического момента диска.......................................386
§ 19.7.	Определение коэффициентов влияния и моментов инерции . . 391
§ 19.8.	Влияние различных факторов на критическую частоту вращения
вала...............................................................393
Глава XX. Конструкция турбин........................................  396
§ 20.1.	Турбины ГТД..............................'.................396
§ 20.2.	Турбины привода насосов ЖРД................................401
§ 20.3.	Турбины вспомогательных установок..........................404
Приложения..........................................................  405
Г. Таблицы термодинамических функций............................405
П. Механические и физические характеристики материалов, применяе-
мых для деталей турбин.....................................428
III.	Номограмма для определения момента инерции профиля лопатки 433
IV.	Таблицы основных газодинамических функций......................434
Список литературы.....................................................439
Предметный указатель....................-.............................441
ИБ Xs 1902
Виктор Иосифович Локай, Махфузя Каримовна Максутова,
Валентин Александрович Стрункин
ГАЗОВЫЕ ТУРБИНЫ ДВИГАТЕЛЕЙ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Редактор Г. Д. Журавлева	Корректор С. Я. Голубева
Технический редактор В. Я. Орешкина	Переплет художника А. Я. Кдрамышкина
Сдано в набор 24.10 78.	Подписано в печать 20.02.79.	Т-01081
Формат 60X90'/ie	Бумага типографская № 3	Гарнитура литературная
Печать высокая. Усл. печ. л 28,0	Уч -изд. л 31,2
Тираж 4800 эка.	Заказ 1337	Цена 1 р. 40 к.
Издательство «Машиностроение» t 107885, Москва, ГСП-6, 1-Й Басманный пер, 3
Московская типография № 8 Союзиолиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли,
Хохловский пер., 7.