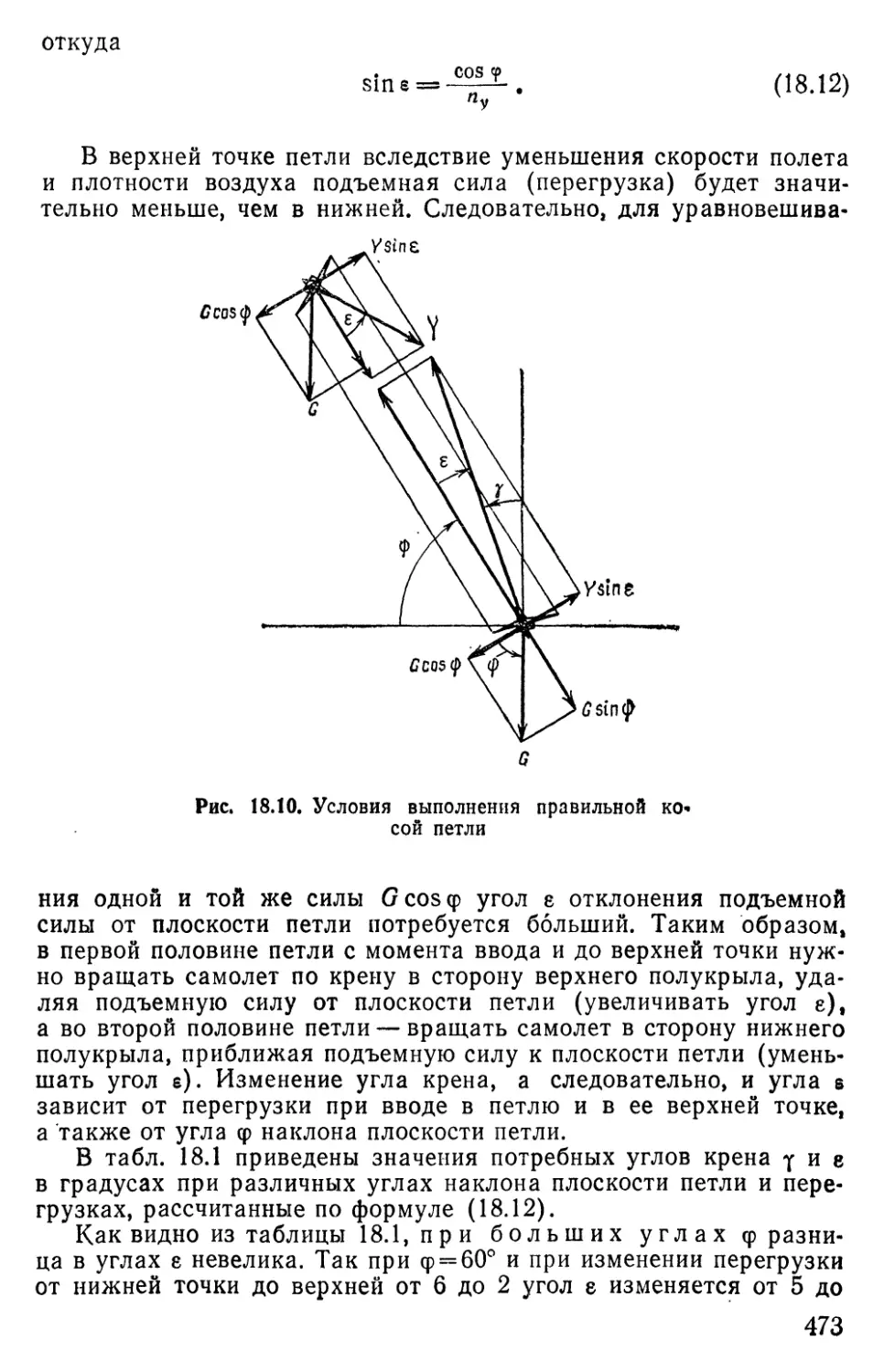
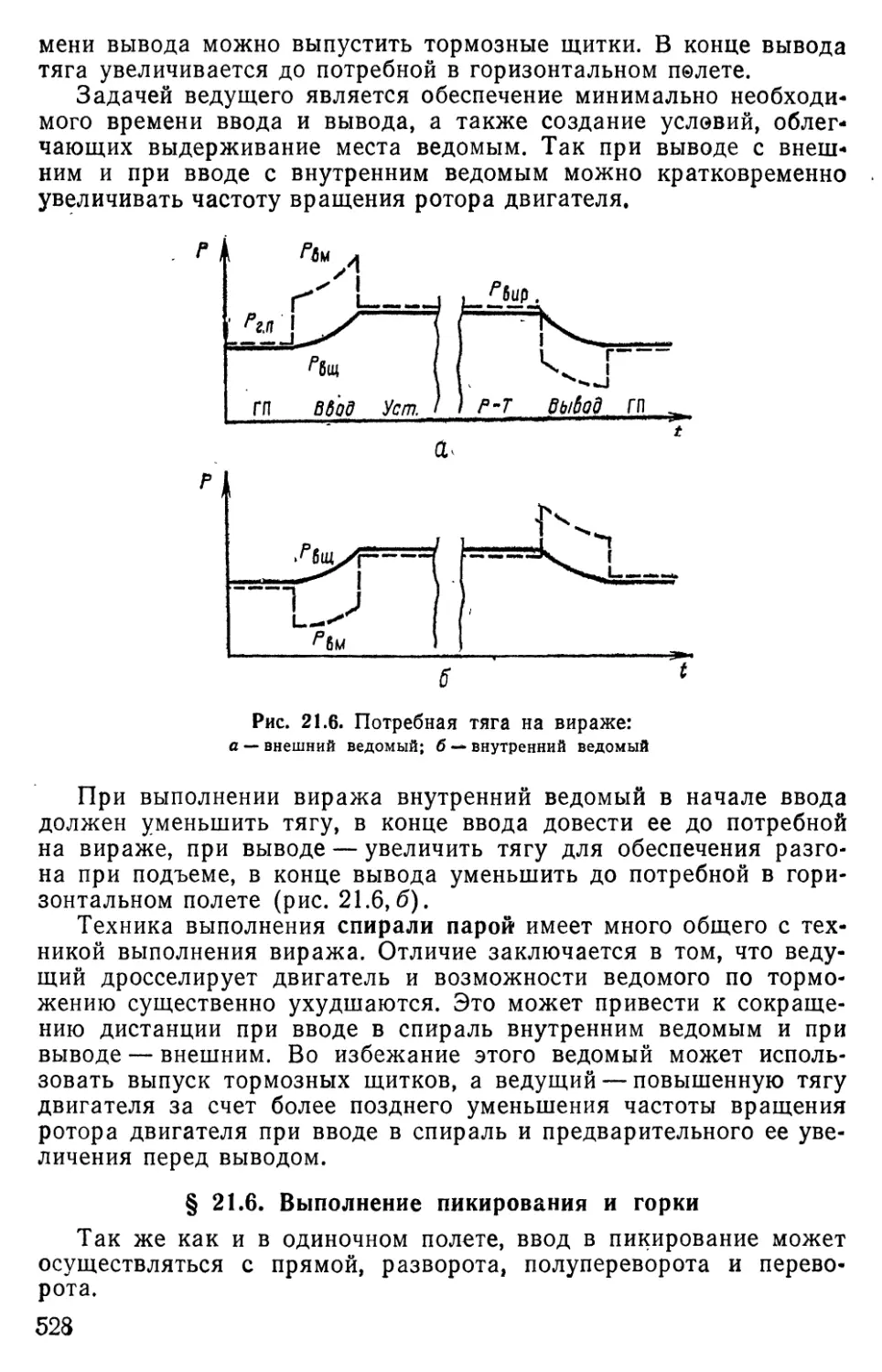
Text
МИНИСТЕРСТВО ОБОРОНЫ CCCR
АЭРОДИНАМИКА
И ДИНАМИКА ПОЛЕТА
МАНЕВРЕННЫХ
САМОЛЕТОВ
МИНИСТЕРСТВО ОБОРОНЫ СССР
ВОЕННО-ВОЗДУШНЫЕ СИЛЫ
АЭРОДИНАМИКА
И ДИНАМИКА ПОЛЕТА
МАНЕВРЕННЫХ
САМОЛЕТОВ
Утвержден главнокомандующим Военно-воздушными силами
в качестве учебника для курсантов В В АУЛ
и летного состава строевых частей
Под редакцией профессора,
доктора технических наук Н. М. ЛЫСЕНКО
МОСКВА
ВОЕННОЕ ИЗДАТЕЛЬСТВО
1984
УДК 533.6(07)'
Авторский коллектив: Е. С. Г а л а ш е в, Н. М. Лысенко, С. А. Микоян,
В. И, В е к р а с о в, Ю. Н. Нечаев, М. И. Ни шт, М, И. Радченко,
Г. Ф. Сивков
Учебник предназначен для курсантов высших военных авиационных учи-
лищ летчиков и летного состава строевых частей ВВС, эксплуатирующих ма-
невренные самолеты.
В книге рассматриваются основы аэродинамики маневренных самолетов,
особенности их силовых установок, устойчивость и управляемость, критические
режимы, летно-технические и маневренные свойства самолетов.
Особое внимание в работе уделяется раскрытию физической сущности рас-
сматриваемых явлений и обоснованию действий летчика на различных этапах
и режимах полета.
ПРЕДИСЛОВИЕ
Учебник обеспечивает теоретическую часть дисциплины «Аэро-
динамика и динамика полета» высших военных авиационных учи-
лищ летчиков, поэтому авторы стремились излагать материал по-
следовательно с необходимыми математическими выкладками. Для
удобства пользования учебником летному составу в процессе пла-
новых занятий и самостоятельной подготовки авторы вынуждены
были включить в него некоторые сведения по характеристикам
двигателей и системам управления, необходимые для лучшего по-
нимания практической аэродинамики.
Под практической аэродинамикой обычно понимается при-
кладная часть аэродинамики и динамики полета, а также теории
двигателей и систем управления. Она рассматривает те явления
и процессы, происходящие в полете, знание которых необходимо
летчику для сознательного освоения техники пилотирования са-
молета, безаварийного и наиболее эффективного использования
его тактико-технических возможностей.
Аэродинамикой называется наука, изучающая законы дви-
жения газов и их силовое воздействие на поверхность обтекаемых
тел.
Аэродинамика развивается в двух направлениях: теоретиче-
ском и экспериментальном. Оба направления, развиваясь, взаим-
но дополняют друг друга. Экспериментальная аэродинами-
ка рассматривает явление таким, какое оно есть на самом деле,
а не его упрощенную модель, и обобщает результаты опытов.
Теоретическая аэродинамика имеет дело, как правило,
с математическими моделями явления. Модели разрабатываются
на базе физических экспериментов или теоретических гипотез. Пра-
вильность моделирования проверяется экспериментом. Теоретиче-
ское и экспериментальное изучение явлений обтекания дает необ-
ходимый материал для уточнения гипотез и построения новых
более точных моделей обтекания.
Целью экспериментальной и теоретической аэродинамики яв-
ляется получение аэродинамических характеристик, т. е. совокуп-
ности величин, характеризующих взаимодействие летательного ап-
парата с воздушной средой в конкретных условиях полета.
К аэродинамическим характеристикам в первую очередь относятся
действующие на самолет силы и моменты.
Авиация за сравнительно короткий промежуток времени со-
вершила большой путь в своем качественном и количественном
1*
3
развитии. Решающее влияние на развитие аэродинамики оказали
работы русских ученых Николая Егоровича Жуковского (1847—
1921 гг.) и Сергея Алексеевича Чаплыгина (1869—1942 гг.).
Среди многочисленных замечательных работ Н. Е. Жуковского
следует особо выделить одну — «О присоединенных вихрях»,
впервые опубликованную в 1906 г. В ней Николай Егорович опи-
сал открытый им механизм возникновения подъемной силы крыла
и тем самым заложил основы теоретической аэродинамики.
Н. Е. Жуковский наряду с теоретическими исследованиями зани-
мался и аэродинамическим экспериментом. Несмотря на отсут-
ствие какой-либо помощи со стороны царского правительства,
Н. Е. Жуковский проводил систематические опыты по обширной
программе. В проведении аэродинамических исследований ему
помогала большая группа талантливых учеников, ставших впо-
следствии крупнейшими специалистами в различных областях
авиационной науки: А. Н. Туполев, Б. Н. Юрьев, Б. С. Стечкин,
В. П. Ветчинкин и др.
Лишь Октябрьская революция открыла неограниченные воз-
можности в развитии авиационной науки и техники. Уже в первые
годы существования социалистического государства был создан ряд
авиационных научно-исследовательских и испытательных инсти-
тутов, специализированных конструкторских бюро, высших учеб-
ных заведений. Н. Е. Жуковский, которого В. И. Ленин назвал
«отцом русской авиации», возглавил Центральный аэрогидроди-
намический институт (ЦАГИ), который сейчас является всемирно
известным авиационным научным центром. Он был ректором пер-
вого высшего авиационного учебного заведения, переименован-
ного после его смерти в Военно-воздушную академию им. Н. Е. Жу-
ковского.
Долгое время совместно с Н. Е. Жуковским работал С. А. Чап-
лыгин, которого по праву считают основоположником аэродина-
мики больших скоростей (газовой динамики). Он вместе с
Н. Е. Жуковским считается создателем теоретических основ авиа-
ции. С. А. Чаплыгин после смерти Н. Е. Жуковского возглавил
советскую школу аэродинамиков.
Бурное развитие авиации происходит совместно с ростом ко-
личества научных исследований. Исследовались и решались новые
проблемы, связанные с увеличением скорости, дальности и высоты
полета самолетов.
За последнее время в связи с бурным развитием ЭВМ (элек-
тронных вычислительных машин) большой памяти и быстродей-
ствия все более широкое применение находят численные методы
определения и исследования аэродинамических характеристик.
Появилась возможность проведения широких исследований и ана-
лиза в сжатые отрезки времени. Наибольших успехов в этой обла-
сти достигли ученые-аэродинамики Военно-воздушной инженерной
академии (ВВИА) им. проф. Н. Е. Жуковского и ЦАГИ им. проф.
Н. Е. Жуковского.
Динамикой полета называется наука, изучающая дви-
4
жение летательных аппаратов в воздухе. Подобно теоретической
механике в динамике полета решаются две взаимосвязанные за-
дачи: прямая — по заданным силам и моментам найти траекто-
рию и закон движения, и обратная — по заданной траектории и
закону движения определить потребные силы и моменты.
Важнейшей задачей динамики полета является определение
летно-тактических характеристик самолета и характеристик устой-
чивости и управляемости, от которых зависят пилотажные свой-
ства самолета.
Основоположником динамики полета является также Н. Е. Жу-
ковский. В первом законченном труде по динамике полета «О па-
рении птиц», доложенном в 1891 г., Н. Е. Жуковский рассмотрел
маневрирование по различным траекториям и предсказал воз-
можность движения по петлеобразным траекториям. В 1913—
1916 гг. Н. Е. Жуковский опубликовал в двух статьях «Динамика
аэропланов в элементарном изложении» лекции, читанные им
военным летчикам. В них были изложены вопросы расчета лет-
ных характеристик самолета, рассмотрены первые и вторые ре-
жимы полета, устойчивость самолета, введены понятия наивы-
годнейшей и экономической скоростей и другие вопросы.
Большая заслуга в развитии динамики полета принадлежит
ближайшему ученику Н. Е. Жуковского В. П. Ветчинкину, ко-
торый начиная с 1916 г. систематически проводил научные иссле-
дования в области динамики полета. В опубликованных им кни-
гах «Динамика полетов» (1927 г.) и «Динамика самолета»
(1933 г.) изложены фундаментальные вопросы полета самолета.
Значительное место в этих работах занимают вопросы расчета
разгонов самолета, пикирования, вцражей, спиралей, петли Не-
стерова, взлета и посадки. В 1935 г. В. П. Ветчинкин опублико-
вал исследования некоторых вопросов динамики полета реактив-
ного самолета.
Крупные исследования в области динамики полета выполнены
и выполняются в ЦАГИ, ВВИА им. Н. Е. Жуковского и других
организациях.
В Военно-воздушных силах продолжателем работ Н. Е. Жу-
ковского и В. П. Ветчинкина стал известный советский ученый
В. С. Пышнов, который наряду с научными исследованиями в об-
ласти динамики полета создал ряд учебников по динамике полета,
сыгравших большую роль в воспитании летчиков и авиационных
инженеров.
В 1932 г. впервые в Советском Союзе был издан учебник для
летного состава «Практическая аэродинамика самолета», в напи-
сании которого принимал участие В. С. Пышнов. Им написан
фундаментальный учебник «Аэродинамика самолета», изданный
сначала отдельными четырьмя частями (1934—1938 гг.), затем
единым учебником (1943 г.). Его исследования штопора на Все-
мирном конгрессе инженеров в 1929 г. получили всеобщее при-
знание, а его труды, посвященные динамическим свойствам само-
лета, актуальны и в настоящее время,
5
Большой вклад в развитие динамики полета внес профессор
Б. Т. Горощенко, результаты исследований которого нашли отра-
жение в опубликованных им учебниках по динамике полета «Аэро-
динамика скоростного самолета» (1948 г.), «Динамика полета
самолета» (1954 г.), «Динамика полета» (1958 г.).
Коммунистическая партия и Советское правительство уже в
первые годы существования нашего социалистического государства
проявляли заботу о развитии отечественной авиации вообще и
истребительной (маневренной) авиации в частности. Первый со-
ветский истребитель И-1 был создан под руководством Н. Н. По-
ликарпова в 1923 г. А в 1925 г. под руководством Д. П. Григо-
ровича создан истребитель И-2. В последующие годы под руко-
водством А. Н. Туполева создается первый цельнометаллический
истребитель И-4 (АНТ-5). В этот период началась специализация
конструкторов. Проектированием истребителей занимается кол-
лектив, возглавляемый Н. Н. Поликарповым. Им создаются
истребители И-15, на котором в 1935 г. был поставлен рекорд
высоты, И-16, И-17 с пушкой, стреляющей через винт.
В конструкторском бюро А. И. Микояна с участием М. И. Гу-
ревича была создана целая плеяда самолетов-истребителей, в чис-
ле которых серийно выпускались МиГ-3, один из первых реактив-
ных истребителей МиГ-9, МиГ-15, МиГ-17, первый сверхзвуковой
истребитель МиГ-19, МиГ-21, Е-166, Е-266 и другие. На самоле-
тах конструкторского бюро А. И. Микояна установлен ряд миро-
вых рекордов скорости и высоты полета. Отличным истребителем
в период Великой Отечественной войны был самолет-истребитель
Як-3 конструкции А. С. Яковлева. В этом же конструкторском
бюро созданы реактивный истребитель Як-15, взлетевший в один
и тот же день (24 апреля 1946 г.) с самолетом МиГ-9, и целый
ряд других истребителей.
Под руководством С. А. Лавочкина разработаны и созданы
истребители ЛАГГ-3, Ла-5, Ла-7, Ла-11, первый советский реактив-
ный истребитель со стреловидным крылом Ла-160. На самолете
Ла-176 в январе 1949 г. впервые в нашей стране была превышена
скорость звука и установлен мировой рекорд скорости. Серийно
выпускался также реактивный самолет Ла-15.
Один из замечательных советских конструкторов П. О. Сухой
участвовал в создании истребителя И-4 под руководством А. Н. Ту-
полева. Впоследствии возглавляемое им конструкторское бюро
создает ряд отличных самолетов истребителей, истребителей-пе-
рехватчиков, истребителей-бомбардировщиков. В их числе Су-7Б
и др.
Большую роль в испытаниях, доводке, развитии истребительной
авиации, разработке методов ее боевого применения сыграли за-
мечательные военные летчики, летчики-испытатели. Трудно пред-
ставить современную авиацию без новаторства таких выдающихся
русских летчиков, как П. Н. Нестеров, К. К. Арцеулов, М. М. Гро-
мов, В. П. Чкалов, В. К. Коккинаки, С. П. Супрун, В. А. Степан-
ченок, Н. М. Стефановский и многих других, в раскрытии манев-
6
ренных возможностей, освоении больших высот и дальностей по-
лета, разработке методов вывода самолета из штопора, в испы-
тании новой авиационной техники.
В годы Великой Отечественной войны особенно ярко прояви-
лось мастерство таких летчиков-истребителей, как трижды Героев
Советского Союза А. И. Покрышкина и И. Н. Кожедуба, дважды
Героев Советского Союза Д. Б. Глинки, В. Д. Лавриненкова,
Б. Ф. Сафонова, Н. М. Скоморохова и многих других.
Большой вклад в развитие реактивной истребительной авиации
в послевоенный период внесли такие выдающиеся военные лет-
чики-испытатели, как С. Н. Анохин, Ю. А. Антипов, Г. Т. Бере-
говой, В. Г. Иванов, В. С. Ильюшин, А. Г. Кочетков, С. А. Микоян,
Г. А. Седов, А. В. Федотов, Ю. М. Шиянов, А. А. Щербаков и др.
Опыт боевых и учебно-боевых полетов убедительно показывает,
что глубокое знание аэродинамики и динамики полета эксплуа-
тируемых самолетов помогает летчику разобраться в сущности
возникающих в полете явлений и позволяет ему полнее исполь-
зовать возможности авиационной техники при соблюдении усло-
вий безопасности полетов.
Учебник написан по заданию главнокомандующего ВВС ав-
торским коллективом в составе полковника-инженера Е. С. Г а л а-
ш е в а, профессора, доктора технических наук Н. М. Лысенко,
Героя Советского Союза, заслуженного летчика-испытателя, кан-
дидата технических наук генерал-лейтенанта авиации С. А. Ми-
кояна, летчика первого класса полковника-инженера В. И. Не-
красова, заслуженного деятеля науки и техники, профессора,
доктора технических наук генерал-майора-инженера Ю. Н. Н е ч а-
е в а, профессора, доктора технических наук генерал-майора-ин-
женера М. И. Н и ш т а, старшего научного сотрудника, доктора
технических наук полковника-инженера М. И. Радченко,
дважды Героя Советского Союза, доцента, кандидата технических
наук генерал-майора-инженера Г. Ф. Сивкова.
Авторы благодарны профессорско-преподавательскому составу
КВВА им. Ю. А. Гагарина и Харьковского ВВАУЛ, давших цен-
ные замечания по рукописи. Авторы признательны также майору-
инженеру А. Н. Малиновскому, выполнившему художественное
оформление иллюстраций.
Часть первая
АЭРОДИНАМИКА МАНЕВРЕННОГО САМОЛЕТА
ВВЕДЕНИЕ
Различают внешнюю аэродинамику, т. е. обтекание воздухом
различных тел, в том числе самолета и его частей, и внутреннюю,
т. е. течение воздуха (газа) в каналах и других устройствах, на-
пример во входных и выходных устройствах двигателей, в их ло-
паточных машинах и т. п.
Основной задачей аэродинамики самолета является изучение
его обтекания, т. е. физической картины течения воздуха около
самолета, и получение его аэродинамических характеристик, т. е.
совокупности величин, характеризующих взаимодействие самолета
с воздушной средой в конкретных условиях полета. Основной за-
дачей аэродинамики двигателя является изучение физических
процессов, происходящих в газе при работе двигателя, и получе-
ние характеристик двигателя, т. е. совокупности величин, харак-
теризующих эти процессы и взаимодействие газа с элементами
двигателя. Поскольку и работа двигателя, и обтекание самолета
сопровождаются взаимодействием воздуха (газа) с твердыми те-
лами, то аэродинамика двигателя имеет много общих закономер-
ностей с аэродинамикой самолета.
Как известно из физики, воздух (газ) обладает определенными
физико-механическими свойствами. Его состояние определяется
термодинамическими параметрами, к которым относятся плот-
ность р, давление р, температура Т, внутренняя энергия единицы
массы и, энтальпия единицы массы I.
Окружающая землю оболочка называется атмосферой. Она
представляет собой механическую смесь газов. Состав атмосферы
изменяется с высотой: на уровне моря в нее входят 78% азота,
21% кислорода и 1% других газов и водяных паров.
Состояние атмосферы, характеризуемое давлением, плотностью
и температурой, зависит от времени года и суток, географических
координат, метеорологических условий и т. п. и существенно из-
меняется по высоте. Поэтому атмосфера представляется в виде
слоев: тропосферы, стратосферы, мезосферы, термосферы и экзо-
сферы. Полеты современных самолетов проводятся в нижних слоях
атмосферы: в тропосфере, простирающейся в среднем до высоты
11 км, и в стратосфере, верхняя граница которой достигает вы-
8
соты порядка 50 км. В тропосфере сосредоточено до 90%" всей
массы атмосферы. В тропосфере с поднятием на высоту давление,
плотность и температура воздуха уменьшаются. В стратосфере
давление и плотность продолжают падать, а температуру до вы-
соты 25 км принято считать постоянной и равной —56,5°С
(216,5 К), хотя в действительности она может отличаться от этого
значения.
К настоящему времени параметры атмосферы земли изучены
в широком диапазоне высот, вплоть до космического простран-
ства. Для практического использования эти параметры осреднены
и сведены в таблицы и графики стандартной атмосферы
(ГОСТ 4401—73). Характеристики этой условной атмосферы соот-
ветствуют некоторому среднему по времени и географическим ко-
ординатам состоянию действительной атмосферы.
Воздух имеет молекулярное строение и его взаимодействие с
телами происходит посредством соударения частиц друг с другом
и с поверхностью тела. В нормальных условиях у поверхности
земли в 1 мм3 воздуха содержится 2,7 • 1016 молекул. Средняя
длина свободного пробега молекул между двумя соударениями
составляет /о==6,3*1О~5 мм. В этих условиях передача импульсов
от молекулы к молекуле происходит на очень малых расстояниях,
неизмеримо меньших по сравнению с размерами тел. Поэтому
Л. Эйлер ввел гипотезу сплошности, т. е. предположение о том,
что воздух является сплошной средой, заполняющей простран-
ство без каких-либо пустот и промежутков. В этом случае можно
говорить о давлении, плотности и т. д. в точке и считать, что
параметры воздуха всюду изменяются непрерывно.
На больших высотах (Я>100 км) плотность воздуха сильно
падает, длина свободного пробега молекул возрастает, поэтому
к разреженным газам применять гипотезу сплошности нельзя.
Критерием, по которому можно судить о сплошности среды, яв-
ляется число Кнудсена
Кп = 4»
где L — длина тела.
При Кп<10-3 среда считается сплошной.
Важнейшим свойством воздуха является его сжимаемость,
т. е. способность изменять плотность при изменении давления.
Количественно сжимаемость характеризуется отношением прира-
щения плотности Др, обусловленного изменением давления на
величину Др, т. е. отношением Др/Др. Но из физики известно, что
скорость звука
Следовательно, величина скорости звука в воздухе является
характеристикой его сжимаемости. Чем меньше сжимаемость
9
среды, т. е. отношение Лр/Др, тем больше скорость звука а в ней
и наоборот.
Как будет показано ниже, изменения давления и плотности
воздуха зависят от скорости его движения V: чем больше ско-
рость, тем они больше. Поэтому для движущегося воздуха ха-
рактеристикой проявления сжимаемости является число Маха
м=4.
Чем больше число М, тем сильнее проявляется сжимаемость
воздуха. В несжимаемой среде Др = 0 и при любых скоростях
М = 0, так как а = оо. В сжимаемой среде при малых скоростях
(малых числах М) изменение плотности мало и влиянием сжи-
маемости можно пренебречь (считать среду несжимаемой). При
больших скоростях (больших числах М) сжимаемость воздуха
надо учитывать.
По влиянию сжимаемости воздуха различают следующие ско-
рости полета: малые дозвуковые, большие дозвуковые, трансзвуко-
вые (околозвуковые), сверхзвуковые и гиперзвуковые.
При малых дозвуковых скоростях (М<0,4) влиянием
сжимаемости в большинстве случаев можно пренебречь, считая
среду несжимаемой. К большим дозвуковым (0,4<М<<|
<Мкр) относятся скорости полета, при которых влияние сжимае-
мости необходимо учитывать, но скорости обтекания частей са-
молета меньше скоростей звука. Число Мкр соответствует такому
числу М полета, при превышении которого около самолета появ-
ляются сверхзвуковые скорости обтекания. Трансзвуковые
скорости — это скорости, близкиеж скорости звука (Мкр^М^1,2)«
При сверхзвуковых скоростях число М>1, а гиперзву-
ковыми называются большие сверхзвуковые скорости (условно
принимают М>5-?-7).
При движении воздуха, как и жидкостей, происходит дефор-
мация их частиц. Способность жидких и газообразных еред сопро-
тивляться деформациям сдвига называется вязкостью. Физи-
ческой причиной проявления вязкости является межмолекулярное
взаимодействие. Вследствие этого взаимодействия при относитель-
ном перемещении слоев воздуха в нем возникают распределенные
касательные силы трения т. Эти силы зависят от вязкости возду-
ха, определяемой динамическим коэффициентом р, и градиента
скорости ДУ/Дп, т. е. от изменения скорости по направлению,
нормальному к направлению относительного перемещения слоев
воздуха. Характеристикой относительной степени проявления вяз-
кости является число Рейнольдса
п VL
Re = —,
где L — характерный линейный размер тела (длина, диаметр),
v = p/p — кинематический коэффициент вязкости. Число Рейнольд-
10
са характеризует соотношение между силами трения и силами
инерции. С увеличением Re роль вязкости уменьшается. Если газ
невязкий (v = 0, Re = oo), то касательные силы трения отсутствуют,
а действуют только силы давления. Невязкий газ будем в даль-
нейшем называть идеальным. Реальный газ, в том числе воздух,
всегда обладает некоторой вязкостью,
11
Раздел I
ОСНОВЫ АЭРОДИНАМИКИ
МАНЕВРЕННОГО САМОЛЕТА
Глава!
ОБЩИЕ СВЕДЕНИЯ О МАНЕВРЕННЫХ САМОЛЕТАХ
§ 1.1. Назначение маневренных самолетов
Маневренность характеризует способность самолета изменять
вектор скорости по величине и направлению, иначе говоря, изме-
нять скорость и направление полета.
К маневренным относятся самолеты, у которых прочность кон-
струкции позволяет создавать нормальную перегрузку больше
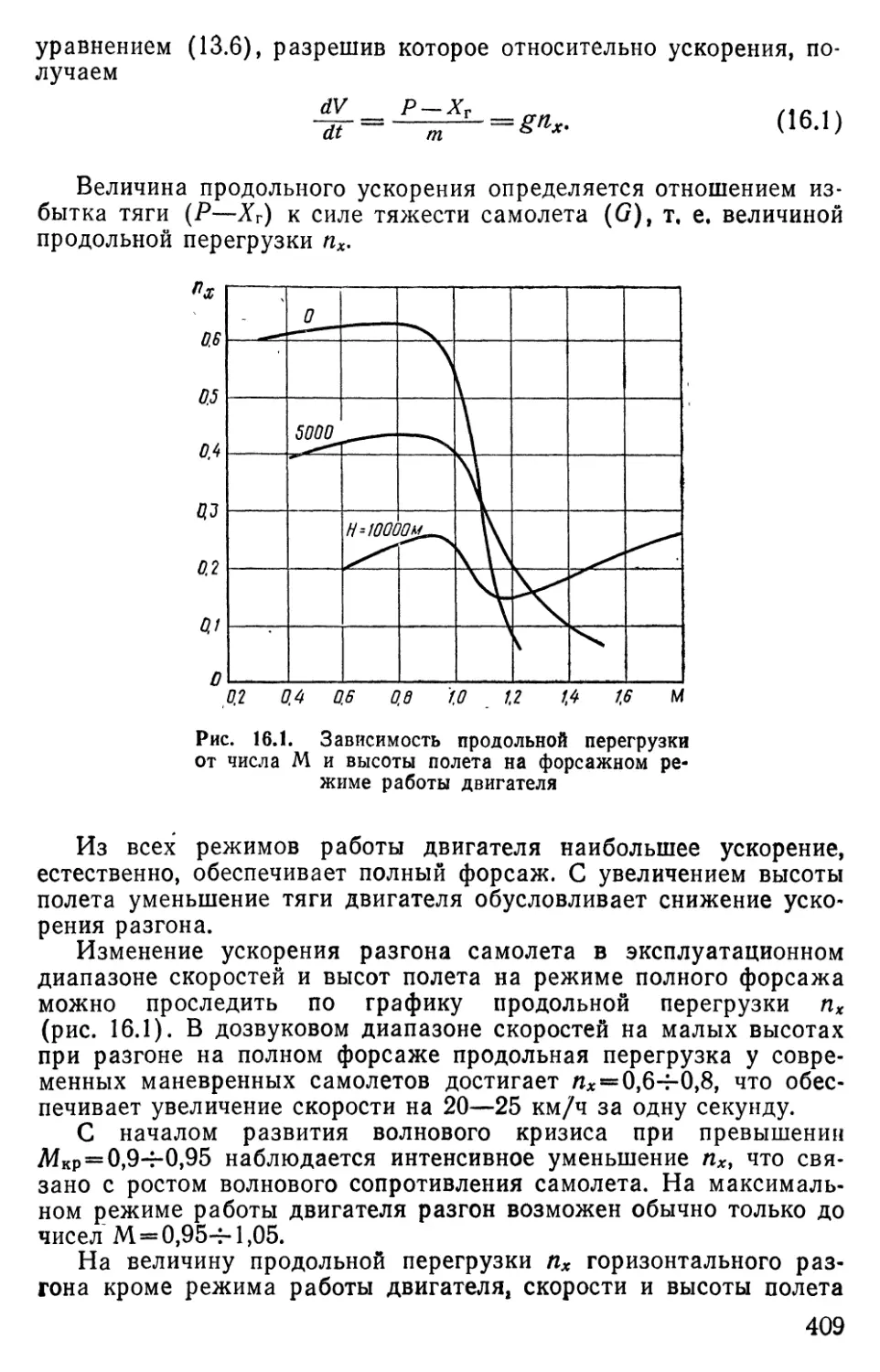
пяти. Наиболее характерными представителями маневренных са-
молетов являются самолеты-истребители. Они предназначены для
уничтожения летательных аппаратов противника главным обра-
зом на дальних подступах к прикрываемым войскам и объ-
ектам.
• Выполнению задачи завоевания господства в воздухе путем
ведения воздушного боя способствуют высокие летно-технические
свойства современных истребителей, оснащение их эффективным
оружием, использование средств радиоэлектроники и автоматизи-
рованного управления и наведения. Они способны вести боевые
действия днем и ночью, в простых и сложных метеоусловиях.
Несмотря на появление ракетного вооружения, не утратил
своего значения маневренный воздушный бой, которым, как пра-
вило, заканчивается воздушный бой при неудачной атаке ракет-
ным оружием. В ближнем воздушном бою, при прочих равных
условиях, победа определяется преимуществом в маневренных ха-
рактеристиках.
Маневренными являются также самолеты истребительно-бом-
бардировочной авиации. Они предназначены для уничтожения ма-
лоразмерных и подвижных целей, но могут привлекаться и для
борьбы с авиацией и беспилотными средствами противника в воз*
духе.
12
Летчик-истребитель должен быть способен самостоятельно в
единоборстве с сильным противником выполнить поставленную
перед ним боевую задачу. Для этого он должен уметь искусно
применять различные тактические приемы, обладать высоким лет-
ным мастерством, безупречно знать технику, быть отважным и
бесстрашным, глубоко верить во всепобеждающую силу ленин-
ских идей.
§ 1.2. Основные части самолета и их назначение
Самолет включает следующие основные части (рис. 1.1): кры-
ло, оперение, фюзеляж, силовую установку, систему управления
и шасси. Кроме того, на самолете может размещаться различное
Рис. 1.1. Маневренный самолет нормальной (классиче-
ской) схемы:
J крыло; 2 •** элерон; 8 закрылок; 4 стабилизатор; 5
киль; 6 руль направления; Z — фюзеляж
оборудование, вооружение и т. п. Крыло, фюзеляж, оперение и
шасси образуют планер самолета.
Крыло 1 является основной несущей поверхностью самолета
и служит для создания подъемной силы, необходимой для под-
держания самолета в воздухе. На крыле располагаются органы
поперечного управления (элероны 2, интерцепторы), взлетно-по-
садочная механизация (закрылки 3, предкрылки, отклоняемые
носки), главные ноги шасси, пилоны для подвески вооружения
(ракет, бомб) и топливных баков, иногда двигатели. Внутренние
объемы крыла обычно используются для размещения топлива,
оборудования, шасси в убранном положении и т. п.
Оперение (горизонтальное и вертикальное) обеспечивает
устойчивость и управляемость самолета. Горизонтальное опере-
ние обычно состоит из управляемого стабилизатора 4 или стаби-
лизатора и руля высоты и служит для обеспечения продольной
устойчивости и управляемости, а в некоторых случаях — управ-
ляемости и по крену. Вертикальное оперение включает киль 5
и руль направления 6 и обеспечивает устойчивость и управляе-
13
мость в путевом отношении. Для увеличения эффективности вер-
тикального оперения иногда устанавливают форкили или подфю-
зеляжные кили (гребни). Горизонтальное оперение в некоторых
случаях устанавливается на киле.
Рис. 1.2. Маневренный самолет схемы «утка»
Фюзеляж 7 самолета служит для соединения крыла и опе-
рения и размещения в нем экипажа, оборудования, вооружения,
двигателя, топлива, грузов. Обычно фюзеляж имеет форму, близ-
кую к форме тела вращения.
Рис. 1.3. Маневренный самолет схемы «бесхвостка»
В зависимости от расположения оперения и управляющих по-
верхностей (рулей) различают три основные схемы самолетов:
нормальную, схему «утка» и схему «бесхвостка». В нормальной
схеме горизонтальное и вертикальное оперения расположены по-
зади крыла (рис. 1.1). В схеме «утка» оперения разнесены: вер-
тикальное оперение находится сзади, а горизонтальное — впереди
крыла (рис. 1.2). В схеме «бесхвостка» отсутствует горизонталь-
ное оперение, а управляющие поверхности по тангажу (элевоны)
расположены на крыле и одновременно используются и как эле-
роны (рис. 1.3),
14
Силовая установка обеспечивает создание силы тяги,
необходимой для перемещения самолета в воздухе.
В качестве двигателей на маневренных самолетах применяются
газотурбинные двигатели, которые обычно устанавливаются в фю-
зеляже.
Система управления предназначена для изменения про-
странственного положения самолета. В систему управления вхо-
дят командные рычаги КРУ (ручка управления или штурвал, пе-
дали), органы управления (рулевые поверхности), проводка, со-
единяющая КРУ с органами управления, рулевые приводы, за-
грузочные механизмы и другие агрегаты. Ручка управления со-
единяется с органами продольного и поперечного управления,
а педали —с органами путевого управления.
Шасси самолета представляет собой систему его опор и обес-
печивает взлет, посадку и передвижение по аэродрому. Шасси
воспринимает статистические и динамические нагрузки и имеет
упругие элементы (пневматики колес и амортизаторы), смягчаю-
щие удары и поглощающие кинетическую энергию самолета при
взлете, посадке и рулении по земле.
В зависимости от расположения на самолете различают шасси
с носовым колесом, с хвостовым и велосипедного типа с подкрыль-
евыми стойками. Наиболее распространены на современных са-
молетах шасси с носовым колесом, когда центр масс самолета
расположен впереди основных колес. Шасси современных само-
летов для уменьшения сопротивления делаются убирающимися
в полете в фюзеляж, крыло или специальные гондолы на крыле.
§ 1.3. Стандартные оси координат. Углы атаки и скольжения.
Угловые скорости вращения
При изучении аэродинамики самолета наиболее часто исполь-
зуются две прямоугольные системы координат: скоростная Oxyz
и связанная Oxxy\Z\ (рис. 1.4), начало которых О совмещено с
центром масс.
В скоростной системе скоростная ось Ох направлена вдоль век-
тора скорости полета самолета V, ось подъемной силы Оу пер-
пендикулярна направлению полета и лежит в плоскости симмет-
рии самолета, а боковая ось Oz перпендикулярна первым двум
осям и направлена в сторону правой половины крыла. При изме-
нении ориентации самолета относительно вектора скорости V ско-
ростная система координат изменяет свое положение относительно
самолета.
Связанная система координат жестко скреплена с самолетом,
неподвижна относительно последнего и поворачивается вместе
с ним. В ней продольная ось Oxi направлена вдоль оси самолета
вперед, нормальная ось Oyi лежит в плоскости симметрии, попе-
речная ось Ozi перпендикулярна плоскости симметрии и направ-
лена в сторону правой половины крыла.
15
Положение самолета относительно вектора скорости полностью
определяется двумя углами: углом атаки а и углом скольжения р
(рис. 1.4). Углом атаки самолета называется угол между про-
дольной осью Oxi (осью самолета) и проекцией вектора скорости
на плоскость симметрии. Углом скольжения называется угол
между вектором скорости и плоскостью симметрии самолета. При
Рис. 1.4. Связанная и скоростная системы коор-
динат
а=0 р есть угол между вектором скорости и осью самолета, и на-
оборот, при р = 0 а есть угол между вектором скорости и осью
самолета. Положительные направления отсчета углов аир по-
казаны на рис. 1.4.
Движение самолета в общем случае определяется вектором
поступательной скорости V и вектором скорости его углового вра-
щения со. Проекции этого вектора на связанные оси координат
обозначаются и юг (рис. 1.4) и называются соответственно
угловой скоростью крена, рыскания и тангажа. Угловые скорости
вращения считаются положительными, если при виде с конца ко-
ординатной оси вращение направлено против хода часовой стрел-
ки (рис. 1.4).
§ 1.4. Крылья маневренных самолетов и их геометрические
характеристики
Аэродинамические свойства крыла в значйтельной степени
определяются его формой и размерами. Геометрическая форма
крыла характеризуется его формой в плане, профилем, попереч-
ной формой и закрученностью,
16
Форма крыла в плане характеризуется проекцией кры«
ла при виде сверху. Различают крылья простой и сложной фор-
мы в плане. Наиболее простую форму в плане имеют крылья с
прямолинейными кромками: прямоугольные, трапециевидные,
стреловидные и треугольные (рис. 1.5).
Рассмотрим стреловид-
ное крыло (рис. 1.5,в). Его
размеры характеризуются
размахом /, корневой Ьо и
концевой Ьк хордами и пло-
щадью S.
Хордой называют от-
резок прямой линии, соеди-
няющей носик и хвостик се-
чения крыла. Под корне-
вой хордой понимают хор-
ду в центральном сечении
крыла (в плоскости его сим-
метрии). Концевой назы-
Рис. 1.5. Крылья простой формы в плане:
а — прямоугольное; б — трапециевидное;
в — стреловидное; г — треугольное
вается хорда, взятая в кон-
цевом сечении крыла. За
размах крыла принимает-
ся расстояние между плос-
костями, параллельными плоскости симметрии и касающимися
концов крыла. Площадью крыла считается площадь его проек-
ции на плоскость, перпендикулярную плоскости симметрии и про-
ходящую через корневую хорду:
(1.1)
где Ьср = -у- (60 + Ьк) — средняя геометрическая хорда крыла.
В эту площадь входит часть крыла, занятая фюзеляжем.
Форму в плане крыльев с прямолинейными кромками можно
определить тр^мя безразмерными параметрами: удлинением X,
сужением г) и углом стреловидности %.
Удлинением крыла называется отношение квадрата его
размаха к площади:
Х = 4-. (1.2)
(1.1) Х = -^,
°Ср
С учетом формулы
т. е. удлинение крыла
представляет собой соотношение его размаха и средней хорды.
Сужение крыла представляет собой отношение длины кор-
невой хорды к длине концевой хорды, т. е.
(13)
Углом стреловидности крыла по передней кромке
называется угол между передней кромкой крыла и плоскостью,
17
Рис. 1.6. Геометрические характери-
стики профиля
с=
а
перпендикулярной корневой хорде крыла (рис. 1.5,в). Понятие
угла стреловидности применяется и по отношению к задней кром-
ке крыла. Удлинение, сужение и угол стреловидности крыльев
современных маневренных самолетов изменяются в широких пре-
делах (1,5^Х^5; 0^х^75°). У прямоугольных
крыльев т]=1 и х=0, У треугольных т] = оо (рис. 1.5,я и г).
Рассечем крыло плоскостью
АА, параллельной его плоскости
симметрии (рис. 1.5,в). Контур
сечения при этом образует фи-
гуру, которая называется про-
филем крыла в данном сече-
нии (рис. 1.6). Форма профиля
определяется координатами ув и
г/н, т. е. расстояниями его верх-
ней и нижней дужек от хорды.
Толщиной профиля в
рассматриваемой точке хорды на-
относительной толщиной
профиля — отношение максимальной толщины к хорде, т. е.
~с=Ста*/Ь. Кривизной профиля считается величина
/= -i-(ув4- ун), а относительной кривизной — отноше-
ние максимальной кривизны к хорде, т. е. f=fmax/&.
Положение максимальной толщины и максимальной кривизны
профиля определяется координатами хс_и Xf и характеризуется
безразмерными величинами хс = хс1Ь и xf = xflb.
Важной геометрической характеристикой профиля является
радиус закругления носка г, т. е. радиус вписанный в носок про-
филя окружности (рис._1.6), и соответствующий безразмерный
относительный параметр r^r/b.
Для профилей маневренных самолетов с=0,03ч-0,09; f=040,02;
7С=0,34-0,5; *7=0,24-0,4; г^=0ч-0,03.
Поперечная форма крыла при виде спереди (сзади) харак-
теризуется углом поперечного V и оценивается углом ф (рис. 1.5,в).
При положительном поперечном V (ф>0) концы крыла подняты
вверх, при отрицательном (ф<0)—опущены вниз. У современ-
ных самолетов со стреловидными крыльями обычно ф<0. Иногда
поперечное V может иметь только часть крыла — концевая или
корневая.
Закрученность крыла создается аэродинамической или
геометрической круткой. Аэродинамическая крутка достигается
набором крыла из разных профилей в сечениях по размаху. Гео-
метрическая крутка осуществляется деформацией крыла, т. е. по-
воротом его сечений друг относительно друга. Одним из примеров
такой деформации является коническая крутка, когда носок крыла
отгибается вниз по конической поверхности.
18
§ 1.5. Особенности крыльев сложной формы в плане
и крыльев изменяемой в полете стреловидности
В последние годы на самолетах начали широко применяться
Крылья сложной формы в плане: с изломом передней кромки»
с переменным по размаху углом стреловидности по передней
Кромке (с криволинейной передней кромкой) и с изменяемой в
полете стреловидностью (рис. 1.7).
Рис. 1.7. Крылья сложной формы в
плане:
а — с криволинейной передней кромкой;
б — с изломом по передней кромке (с
наплывом); в — гибридное крыло; г —с
изменяемой в полете стреловидностью
Рис. 1.8. Зависимость
геометрических харак-
теристик крыла изменяе-
мой в полете стреловид-
ности от угла стреловид-
ности консоли
Форма в плане крыла с переменным по размаху углом стре-
ловидности по передней кромке (рис. 1.7, а) определяется обычно
заданием координат передней и задней кромок.
Крыло с изломом передней кромки (рис. 1.7,6) характеризу-
ется двумя углами стреловидности —%] и Центральная часть
крыла называется наплывом и характеризуется (кроме угла xi)
размахом /ь корневой хордой Ьо и хордой в изломе bv.
Разновидностью крыла сложной формы в плане является так
называемое гибридное крыло (рис. 1.7,в), имеющее концевую
часть малой стреловидности и наплыв с криволинейной передней
кромкой.
У крыльев с изменяемой в полете стреловидностью (рис. 1.7, г)
имеются неподвижная корневая часть — центроплан или наплыв
и подвижная концевая часть, которая в полете может поворачи-
ваться относительно некоторой оси. При повороте концевой части
назад увеличивается ее стреловидность, уменьшается размах
19
крыла, его площадь, удлинение и относительная толщина, и на-
оборот. Изменение относительной толщины поворотной части свя-
зано с изменением размеров ее хорд, так как профиль рассматри-
вается в сечении, параллельном плоскости симметрии, а умень-
шение площади крыла при повороте консоли на увеличение стре-
ловидности объясняется тем, что при этом часть крыла входит
в центроплан.
На рис. 1.8 качественно показано изменение геометрических
параметров крыла изменяемой в полете стреловидности при по-»
вороте концевой части назад, на увеличение угла стреловидно-
сти х2. Индекс «О» относится к исходному крылу с минимальным
углом стреловидности концевой части, а индекс «%» — к крылу с
текущим значением угла ее стреловидности. Видно, что при пово-
роте концевой части наиболее сильно изменяется удлинение кры-
ла, особенно при больших углах стреловидности %2.
Таким образом, при повороте назад крыло изменяемой стрело-
видности из толстого нестреловидного крыла большого удлинения
преобразуется в тонкое стреловидное крыло малого удлинения, ;
§ 1.6. Органы управления и механизации маневренных
самолетов
Управление самолетом обеспечивается специальными рулевы-
ми органами, при отклонении которых возникают аэродинамиче-
ские моменты, поворачивающие самолет в соответствующую сто-
рону.
Для изменения крена самолета используются элероны и ин-
терцепторы, установленные на крыле, или дифференциально от-
клоняемый стабилизатор (режим «ножниц»). Элероны на левой
и правой половинах крыла и левая и правая половины стабили-
затора в режиме «ножниц» отклоняются в разные стороны. Для
накренения самолета влево левый элерон (хвостик левой поло-
вины стабилизатора) отклоняется вв^рх, а правый (хвостик пра-
вой половины стабилизатора)—вниз, и наоборот. Интерцепторы
обычно устанавливаются на верхней стороне крыла и отклоняются
поочередно только вверх: для накренения влево — на левой по-
ловине крыла, и наоборот. Обычно управление самолетом по кре-
ну обеспечивается следующими способами: только одними элеро-
нами, элеронами совместно с интерцепторами или дифференциаль-
но отклоняемым стабилизатором, дифференциально отклоняемым
стабилизатором совместно с интерцепторами.
Для поворота самолета влево-вправо вокруг нормальной оси
используется руль направления, устанавливаемый на киле. Для
поворота самолета влево он отклоняется влево, и наоборот. За-
метим, что при отклонении органов поперечного управления (эле-
ронов, интерцепторов, «ножниц» стабилизатора) возникает сопут-
ствующий разворачивающий момент, а при отклонении руля на-
правления — кренящий момент.
20
Для поворота самолета вокруг поперечной оси используются
руль высоты, управляемый стабилизатор или элевоны. Для созда-
ния момента на кабрирование (для поднятия носа самолета) руль
высоты (элевоны, хвостик управляемого стабилизатора) откло-
няется вверх, для создания момента на пикирование (для опуска-
ния носа самолета) — вниз.
Для улучшения взлетно-посадочных характеристик самолетов
используются органы механизации задней кромки крыла (закрыл-
ки) и передней кромки крыла (предкрылки, отклоняемые носки) г
Рис. 1.9. Закрылки:
а — простой: б — щелевой; в — выдвижной; г — двухщелевой
Закрылком называется отклоняющаяся вниз хвостовая часть
крыла (рис. 1.9). При отклонении закрылка изменяется кривизна
крыла. Различают простые (рис. 1.9,а), щелевые (рис. 1.9,б), вы-
движные (рис. 1.9,в), многозвенные (рис. 1.9,а) закрылки.
Рис. 1.10. Предкрылок
Рис. 1.11. Отклоняемый носок
Предкрылок — это небольшое крылышко, которое устанавли-
вается вдоль передней кромки крыла и в полете выдвигается впе-
ред (рис. 1.10). Эффективным средством механизации острой пе-
редней кромки крыльев современных самолетов являются откло-
няемые носки (рис. 1.11). Отклонение носка изменяет кривизну
профиля вблизи передней кромки.
В настоящее время используются также органы управления и
механизации, обеспечивающие непосредственное управление си-
лами, действующими на самолет. Для торможения самолета в
полете применяются тормозные щитки, а на посадке — тормозной
21
парашют или интерцепторы, отклоняемые одновременно на обеих
половинах крыла. Для изменения подъемной силы в полете на
некоторых самолетах используются спойлеры — поверхности, по-
добные интерцепторам, но отклоняемые на небольшие углы, или
флапероны (закрылки-элероны), отклоняемые на небольшие углы.
§ 1.7. Схемы и компоновка маневренных самолетов
Под аэродинамической компоновкой самолета понимаются
внешние формы и размеры его отдельных частей и их взаимное
расположение. Требования к выбору внешних форм самолета и
a ff s
Рис. 1.12. Схемы расположения крыла:
а —• низкоплан: б — среднеплан; в — высокоплан
*его отдельных частей весьма сложны и противоречивы. При этом
следует учитывать, что форма и размеры частей самолета, их
взаимное расположение влияют не только на аэродинамические,
но и на другие свойства самолета: на его массу, центровку, проч-
ность, технологию изготовления, эксплуатационные характеристи-
ки и т. п. Это значительно затрудняет выбор аэродинамической
компоновки самолета в соответствии с предъявляемыми к нему
требованиями и приводит, как правило, к компромиссным, не луч-
шим с точки зрения аэродинамики решениям.
Анализ тенденций развития и условий боевого применения по-
казывает, что непрерывно расширяется диапазон скоростей и вы-
сот полета, усложняются форма и конструкция маневренных са-
молетов и их оборудования. Современные маневренные самолеты
летают со скоростями от весьма малых (практически нулевых у
вертикально взлетающих самолетов) до скоростей, превышающих
3000 км/ч, как на предельно малых высотах, так и на очень
больших (//>25 км). Такой широкий диапазон используемых ско-
ростей и высот полета, большое количество решаемых боевых задач
обусловили создание значительного числа разнообразных аэро-
динамических компоновок современных маневренных самолетов.
В большинстве случаев маневренные самолеты выполняются
по нормальной схеме (рис. 1.1). В зависимости от места располо-
жения крыла на фюзеляже по высоте различают следующие схе-
мы самолетов: нйзкоплан (рис. 1.12,а), среднеплан (рис. 1.12,6),
высокоплан (рис. 1.12,в).
На выбор аэродинамической компоновки маневренного само-
лета определяющее влияние оказывает диапазон используемых
скоростей полета. В зависимости от этого различают дозвуковые,
околозвуковые и сверхзвуковые маневренные самолеты.
22
Для аэродинамической компоновки дозвуковых самолетов ха-
рактерно применение нормальной схемы, прямоугольных или тра-
пециевидных крыльев большого удлинения (Х>5) с достаточно,
толстым (с=0,08-г-0,12) несимметричным профилем, с фюзеля-
жем небольшого удлинения (Лф<7).
Для аэродинамической компоновки околозвуковых маневрен-
ных самолетов характерно наличие стреловидного крыла и опе-
рения стреловидности %<45° и удлинения %>3 с умеренной тол-
щиной (с<0,08) симметричного профиля и удлиненного фюзе-
ляжа (Хф>7).
Переход к сверхзвуковым скоростям полета еще больше из-
менил аэродинамическую компоновку маневренного самолета..
Крыло (оперение) стало еще более стреловидным (х>45°) или
треугольным, малого удлинения (Х<3), тонким (с 0,04),.
с острой передней кромкой. Фюзеляж стал заостренным, увели-
чилось его удлинение (Хф>9). В компоновке сверхзвукового ма-
невренного самолета стали шире применяться схемы «утка»
(рис. 1.2) и «бесхвостка» (рис. 1.3), а также крылья сложной'
формы в плане и изменяемой в полете стреловидности (рис. 1.7),
Глава 2
ОСНОВНЫЕ ЗАКОНЫ АЭРОДИНАМИКИ
§ 2.1. Основные понятия аэродинамики.
Общая картина обтекания тела
Выделим в движущемся воздухе (потоке) небольшую частицу,,
которая в некоторый момент времени t находилась в некоторой
точке А с координатами х, у, г. Через бесконечно малый проме-
жуток времени dt координаты рассматриваемой частицы изменя-
ются также на бесконечно малые величины dx, dy, dz, и в момент
времени t+dt частица окажется в точке Ai с координатами x+dx,
y+dy, z+dz. По определению составляющие скорости частицы
будут равны:
у — — • у — — • ]/ —
v* dt ’ vy dt ’ v‘~ dt'
В общем случае движения воздуха они зависят от времени и
координат рассматриваемой точки.
Ускорением движущейся частицы воздуха на-
зывается изменение ее скорости в единицу времени, поэтому со-
ставляющими ускорения являются величины dVx/dt, dVy/dt,
dVz/dt. В общем случае они также являются функциями коорди-
нат и времени.
Изучаемое в аэродинамике движение воздуха может быть
установившимся и неустановившимся. Если параметры воздуха
23
(скорость, давление, плотность, температура и др.) в каждой
точке пространства с течением времени не изменяются, то такое
движение воздуха называется установившимся (стационар-
ным). В противном случае движение воздуха является неуста-
новившимся.
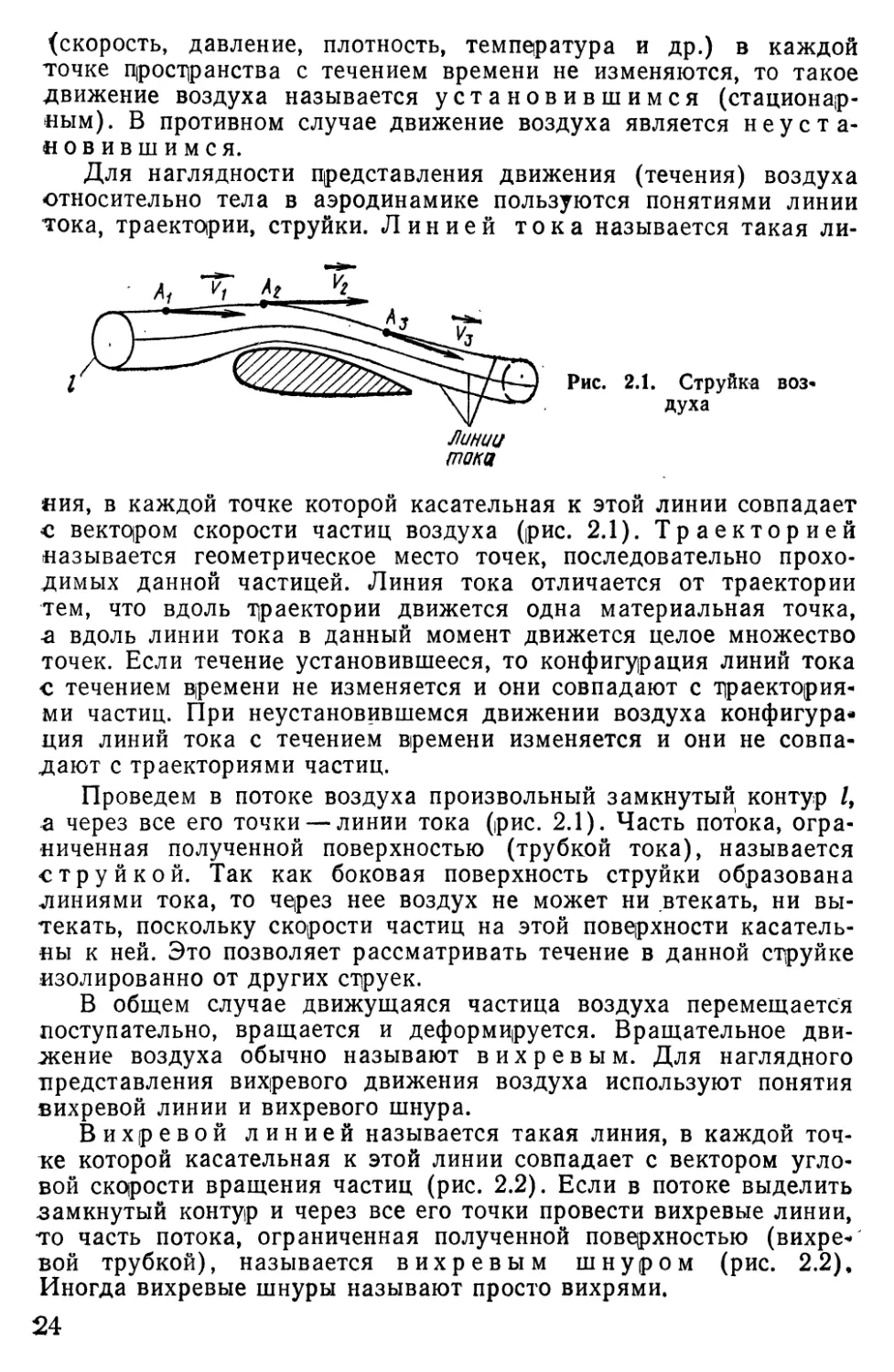
Для наглядности представления движения (течения) воздуха
относительно тела в аэродинамике пользуются понятиями линии
тока, траектории, струйки. Линией тока называется такая ли-
/ у
Рис. 2.1. Струйка воз*
\ духа
Линии
токи
яия, в каждой точке которой касательная к этой линии совпадает
с вектором скорости частиц воздуха (рис. 2.1). Траекторией
называется геометрическое место точек, последовательно прохо-
димых данной частицей. Линия тока отличается от траектории
тем, что вдоль траектории движется одна материальная точка,
я вдоль линии тока в данный момент движется целое множество
точек. Если течение установившееся, то конфигурация линий тока
с течением времени не изменяется и они совпадают с траектория-
ми частиц. При неустановившемся движении воздуха конфигура-
ция линий тока с течением времени изменяется и они не совпа-
дают с траекториями частиц.
Проведем в потоке воздуха произвольный замкнутый контур /,
а через все его точки — линии тока (рис. 2.1). Часть потока, огра-
ниченная полученной поверхностью (трубкой тока), называется
струйкой. Так как боковая поверхность струйки образована
линиями тока, то через нее воздух не может ни втекать, ни вы-
текать, поскольку скорости частиц на этой поверхности касатель-
ны к ней. Это позволяет рассматривать течение в данной струйке
изолированно от других струек.
В общем случае движущаяся частица воздуха перемещается
поступательно, вращается и деформируется. Вращательное дви-
жение воздуха обычно называют вихревым. Для наглядного
представления вихревого движения воздуха используют понятия
вихревой линии и вихревого шнура.
Вихревой линией называется такая линия, в каждой точ-
ке которой касательная к этой линии совпадает с вектором угло-
вой скорости вращения частиц (рис. 2.2). Если в потоке выделить
замкнутый контур и через все его точки провести вихревые линии,
то часть потока, ограниченная полученной поверхностью (вихре-
вой трубкой), называется вихревым шнуром (рис. 2.2)t
Иногда вихревые шнуры называют просто вихрями.
24
Наличие в потоке струек и вихревых шнуров позволяет по-
лучать аэродинамические спектры обтекания тел путем введения
в поток видимых частиц и фотографирования картины течения.
Рассмотрим вихревой шнур произвольной формы (рис. 2.3).
Пусть S — площадь произвольного сечения шнура. Обозначим че-
рез <0д составляющую угловой скорости вращения частиц, нор-
'Вихребые линии
Рис. 2.3. Определение напри,
жения вихревого шнура
Рис. 2.2. Вихревой шнур
мальную к сечению S. Тогда напряжением вихревого шнура на-
зывается величина
r = 2J Jov/5.
S’ "
(2.1)
Из определения следует, что напряжение вихревого шнура яв-
ляется количественной характеристикой интенсивности вращения
в нем частиц воздуха: если Г=0, то движение воздуха является
безвихревым, и наоборот. Для идеальной (невязкой) среды спра-
ведлива теорема Гельмгольца: напряжение вихревого шнура по
его длине не изменяется (r=const). В вязкой среде вихревое дви-
жение затухает вследствие влияния сил трения.
Рассмотрим в потоке воздуха некоторый замкнутый контур /
(рис. 2.4). Циркуляцией скорости по этому контуру называется
следующий криволинейный интеграл
(2.2)
где Vi — проекция вектора скорости на направление касательной
к контуру I в рассматриваемой точке.
Если контур I охватывает один или несколько вихревых шну-
ров, то согласно теореме Стокса циркуляция скорости по этому
контуру не зависит от его формы и равна напряжению охваты-
ваемых им вихревых шнуров
(2.3)
25
В идеальной среде в соответствии с теоремой Томсона цирку-
ляция скорости по произвольному замкнутому контуру с течением
времени не изменяется, т. е.
/,(/) = Г ф = const. (2.4)
Отсюда следует, что если в некоторый момент времени цирку-
ляция скорости по замкнутому контуру равна нулю (движение
Рис. 2.4. Определение циркуляции скорости
по замкнутому контуру
•безвихревое), то она будет равной нулю и в последующие моменты
времени (безвихревое движение сохранится) .
В аэродинамике часто используется принцип обратимости дви-
жения. При этом считают физическую картину обтекания тела
_ воздухом и его взаимодействие с
-...т.-г—телом независящим от того, дви-
IZ, —z.—*1 жется ли тело с некоторой ско-
—• ростью в неподвижной среде или
Ж i на неподвижное тело набегает
поток с той же скоростью. Прин-
Рис. 2.5. Общая картина обтекания цип обратимости широко исполь-
тела зуется при проведении экспери-
ментальных исследований в аэро-
динамических трубах.
В соответствии с принципом обратимости движения рассмотрим
•общую картину обтекания воздухом некоторого тела со скоростью
V (рис. 2.5). Весь поток около тела можно условно разделить на
три области.
1. Тонкий слой 7, прилегающий к поверхности тела, в котором
воздух вследствие вязкости сильно тормозится; имеют место боль-
шие градиенты скорости, необходимо учитывать силы трения.
2. Спутный след за телом 77, в котором градиенты скорости
также велики; при исследовании течения в этой области тоже
•следует учитывать силы трения.
3. Область течения 777, в которой градиенты скорости невели-
ки, касательные напряжения малы; здесь в большинстве случаев
можно пренебрегать влиянием вязкости и считать воздух идеаль-
ным.
26
Указанные особенности потока около тела позволяют общую*
задачу исследования обтекания тела разбить на три этапа. На
первом этапе можно не учитывать тонкий слой I и считать весь
воздух идеальным, при этом определяются нормальные силы дав-
ления. На втором этапе проводится расчет слоя I и определяются
касательные силы трения, при этом нормальные силы давления
считаются известными. И, наконец, на третьем этапе параметры
спутного следа и его влияние на попавшие в спутный след дру-
гие тела, например самолеты, могут изучаться отдельно.
В аэродинамике часто приходится судить о силах и моментах,
действующих на реальные объекты, по результатам исследования
их геометрически подобных моделей в аэродинамических трубах.
Рассмотрим самолет и его геометрически подобную модель. На-
помним, что у геометрически подобных тел сходственные линей-
ные размеры пропорциональны, а соответствующие углы равны.
Расположим их совершенно одинаково по отношению к вектору
скорости набегающего потока V, т. е. обеспечим кинематическое
подобие при их обтекании. Пусть на самолет и модель действуют
соответственно аэродинамические силы R и /?м. Так как размеры
модели меньше размеров самолета, то Опыт показывает,
что величина аэродинамических сил пропорциональна скоростному
pV2 и ° О
напору # = -4)- и некоторой характерной площади S, например
площади крыла. Выразим реальные силы через безразмерные
аэродинамические коэффициенты:
K = CR-^S-, = (2.5)
Здесь р, V, S — плотность газа, скорость и характерная пло-
щадь при полете реального самолета, рм, VM, SM — плотность газа,
скорость и характерная площадь при испытании модели.
В аэродинамике, как правило, определяют не силы, а их аэро-
динамические коэффициенты, так как силы можно найти путем
простого умножения коэффициентов на скоростной напор и харак»
терную площадь.
Пусть в обоих случаях используется один и тот же газ — воз-
дух (р=рм) и одинаковы скорости (V = VM). Тогда при наличии
геометрического и кинематического подобия Cr = CRm. В общем
случае среда и скорости могут быть разными (р=/=рм, V=0=VM).
Тогда для равенства аэродинамических коэффициентов необхо-
димо соблюсти не только геометрическое и кинематическое, но и
динамическое подобие, т. е. подобие по ряду критериев, напри-
мер по числам Маха, Рейнольдса и др.
Для получения аэродинамических характеристик самолетов в
настоящее время широко используется математическое модели-
рование и расчеты на ЭВМ. В этих расчетах, например, реаль-
ный самолет может заменяться системой тонких базовых поверх-
ностей, при этом каждой точке на поверхностях присваиваются
реальные условия обтекания (величины скоростей, их ориентация
27
по отношению к поверхности самолета и т. п.). Результаты рас-
четов аэродинамических характеристик самолетов с использова-
нием указанного математического моделирования хорошо согла-
суются с экспериментальными данными.
§ 2.2. Уравнение постоянства расхода
Уравнение постоянства расхода является следствием закона
сохранения массы, сформулированного впервые М, В, Ломоносо-
вым в. 1748 г.
Рис. 2.6. Вывод уравнения неразрывности
Рассмотрим струйку идеального газа (рис. 2.6) и выделим в
ней несколько сечений 1—1, 2—2, 3—3. Обозначим площади се-
чений, плотности газа и скорости в этих сечениях соответственно
Sb pi, Vi; S2, р2, V2; S3, р3, V3- Из определения струйки следует,
что через ее стенки газ протекать не может. Поэтому через лю-
бое сечение в единицу времени проходит одна и та же масса
газа
ГП1 = т2 = тг — т, (2.6)
где т — секундная масса газа.
Выразим секундную массу газа через плотность, скорость и
площадь сечения:
m — pVS. (2.7)
На основании уравнений (2.6) и (2.7) получим pi ViS^paVzSa3»
= р3 V3S3.
Поскольку сечения 1—1, 2—2, 3—3 были выбраны произволь-
но, то вдоль струйки
рУ5= const. (2.8)
Полученное уравнение называется уравнением постоян-
ства расхода или уравнением неразрывности. Оно
справедливо при любых скоростях движения газа. Из него сле-
дует, что
Произведение pV называется удельным массовым рас-
ходом газа и зависит от скорости (рис. 2.7), При увеличении
28
0 а /
Рис. 2.7. Зависимость удельного рас-
хода от скорости течения воздуха
скорости это произведение сначала растет, достигает максималь-
ной величины цри звуковой скорости (У=а), а затем падает из-за
уменьшения плотности газа.
Из формулы (2.9) следует, что площадь сечения струйки за-
висит от удельного массового расхода
с_ const
РУ •
При увеличении скорости удельный расход сначала увеличи-
вается (рис. 2.7), а площадь сечения струйки уменьшается. При
V=a удельный расход достигает
максимальной величины, а пло-р/
щадь сечения струйки минималь-'
на. При дальнейшем увеличении
скорости рУ уменьшается, а пло-
щадь сечения струйки растет
вследствие сильного падения
плотности.
Таким образом, при дозвуко-
вых скоростях увеличение скоро-
сти возможно в сужающемся ка-
нале, а при сверхзвуковых — в
расширяющемся. В самом узком
сечении канала имеет место кри-
тический режим, при котором ско-
рость потока равна местной ско-
рости звука (Укр = Якр). Поэтому
для получения сверхзвукового
потока площадь его сечения дол-
жна вначале уменьшаться, а затем увеличиваться. Канал такой
формы называется соплом Лаваля (по имени шведского инжене-
ра, впервые его применившего).
При малых скоростях движения газа его можно считать не-
сжимаемым, а плотность его постоянной по длине струйки. Тогда
из уравнения (2.8) имеем
VS — const. (2.10)
Следовательно, в несжимаемом газе цри увеличении скорости
струйка сужается, и наоборот.
§ 2.3. Уравнение сохранения энергии и его различные формы
Рассмотрим струйку газа, изображенную на рис. 2.6, и приме-
ним к ней закон сохранения энергии. Пусть lt — теплосодержание
(энтальпия) единицы массы газа в сечении 1—1, Vi2/2 — ее ки-
нетическая энергия, a lz и Уг2/2 — аналогичные величины в сече-
нии 2—2. Как показывают исследования, потенциальной энергией
положения струйки по сравнению с этими величинами можно пре-
29
небречь. Запишем для сечений струйки 1—1 и 2—2 уравнение
сохранения энергии:
h + ~2~ = z'2 "+ ~2~ — ^вН — Уо"' (2.11)
Здесь /Вн — работа, совершаемая газом (или над ним) между се-
чениями 1—1 и 2—2, qBH — внешнее тепло, подводимое к газу (от-
водимое от него) на участке 1—1 и 2—2.
В аэродинамике самолета обычно рассматриваются процессы,
в которых не совершается внешняя работа (/вн = 0) и нет тепло-
обмена, т. е. процессы адиабатические (^вн = 0), в отличие от тео-
рии турбореактивных двигателей, где имеет место и то и другое.
Учитывая это, из выражения (2.11) имеем:
• V2
+ “2~ = *2 + -у.
Так как сечения 1—1 и 2—2 выбраны произвольно, то уравнение
сохранения энергии для струйки запишется в виде
172
i + — const. (2.12)
Полученное уравнение справедливо как для идеального, так
и для вязкого газа при любой его температуре и при условии, что
процесс адиабатический и не совершается внешняя работа.
Получим другие формы записи уравнения сохранения энергии.
Будем считать, что для рассматриваемого газа справедливо урав-
нение состояния
-^ = RT, (2.13)
где /? — газовая постоянная, которая зависит от молекулярного
веса газа. Если Ср и Cv — удельные теплоемкости газа при по-
стоянном давлении и постоянном объеме, то
R = Cp-Cv. (2.14)
Для воздуха при отсутствии диссоциации R = 288 м2/с2/С
В этом случае энтальпия газа является функцией только его тем-
пературы:
i = CpT. ♦ (2.15)
Введем в рассмотрение показатель адиабаты
k = ^. (2.16)
Из формулы (2.16) найдем Cv и подставим в выражение (2.14)
30
Отсюда
следовательно,
i = T^\RT’ (2.17)
С учетом (2.17) уравнение (2.12) принимает вид:
—Lr/?r + -y-«const. (2.18)
Воспользуемся уравнением состояния (2.13), Тогда из (2.18)
имеем
_А_ = const. (2.19)
Из физики известно, что скорость звука в газе выражается
формулой
a = VkRT=yk-^. (2.20)
Поэтому имеем еще одно выражение для уравнения сохране-
ния энергии:
/72 V2
4--^- = const. (2.21)
Поскольку при обтекании самолета струйки воздуха могут рас-
ширяться или сужаться, то в соответствии с уравнениями (2.18),
(2.19) и (2.21) от сечения к сечению могут измениться темпера-
тура, плотность, давление и местная скорость звука в воздухе.
Уравнения сохранения энергии в форме (2.12), (2.18), (2.19)
и (2.21) получены в общем случае для сжимаемого газа. Для
несжимаемого газа можно получить это уравнение в более про-
стой форме. Для этого воспользуемся уравнением (2.12) и учтем,
что согласно формуле (2.14)
Ср = /?+Си. (2.22)
С учетом выражений (2.15) и (2.22) из уравнения (2.12)
имеем
RT -|- CVT 4- -у- « const. (2.23)
В несжимаемом газе CVT=const вдоль струйки, поэтому урав-
нение (2.23) можно переписать в виде
R7 4- X- — const
31
или с учетом уравнения состояния (2.13):
п V2
+ -п - = const,
р *
Так как в несжимаемом газе p = const, то окончательно имеем
р + = const. (2.24)
Уравнение сохранения энергии для несжимаемого газа в фор-
ме (2.24) было впервые получено Д. Бернулли и носит название
уравнения Бернулли.
Из уравнения Бернулли следует, что цри увеличении скорости
давление в несжимаемом газе уменьшается, и наоборот. Сравни-
вая уравнения (2.19) и (2.24), видим, что в сжимаемом газе из-
менение скорости приводит к большему изменению давления, чем
в несжимаемом, вследствие одновременного изменения плотности.
Если скорость в струйке обращается в нуль (V=0), т. е. поток
полностью тормозится, что имеет место на лобовых частях само-
лета, то давление в этих точках максимально и равно давлению
заторможенного потока р*. С учетом этого из выражения (2.24)
имеем
р + ^=р\ (2.25)
где р— статическое давление потока, pV2/2— скоростной напор,
р* — полное давление (давление заторможенного потока).
Уравнение Бернулли широко используется в аэродинамике и
в авиационной технике. В частности, с его помощью, измерив в
потоке статическое и полное давления и зная плотность воздуха,
можно определить скорость несжимаемого потока (потока воз-
духа при малых скоростях). Это используется для измерения
скорости на самолетах.
§ 2.4. Распространение возмущений в воздухе
При своем движении в воздухе тела вносят в поток возмуще-
ния, которые представляют собой изменения газодинамических
параметров (скорости, давления, плотности, температуры и др.).
Любая точка поверхности тела является источником возмущений.
Различают слабые и сильные возмущения. Если параметры газа
изменяются на малую (точнее говоря, на бесконечно малую) ве-
личину, то такие возмущения называются слабыми. Слабые
возмущения представляют собой волны сжатия-разрежения и
распространяются в газе со скоростью звука а. Примерами сла-
бых возмущений являются звуковые волны. Слабые возмущения
возникают при обтекании тонких тел, шероховатостей, бесконеч-
но малых изломов поверхности и в других случаях.
Характер распространения возмущений зависит от соотноше-
ния между скоростью потока и скоростью звука. Предположим,
32
что точечный источник возмущений находится в неподвижной
среде (V = 0, рис. 2.8,а). В этом
пространяются со скоростью а во
волн, радиус которых с течением
времени t увеличивается по за-
кону
г = at. (2.26)
Если источник действует непре-
рывно и продолжительное время,
то возмущения охватывают всю
область, занятую газом.
В движущемся газе волны
возмущения сносятся потоком со
скоростью V и это смещение
s = (2.27)
При дозвуковой скорости
(V<a, рис. 2.8,6) возмущения
против потока распространяются
медленнее, чем по потоку: на-
встречу потоку со скоростью а—V,
по потоку — со скоростью a+V.
При неограниченном времени
действия источника возмущений
они также заполняют все окру-
жающее источник пространство.
При звуковой скорости (V = at
рис. 2.8, в) во все моменты вре-
мени смещение волн возмущений
в соответствии с выражениями
(2.26) и (2.27) равно их радиусу
(s = r), поэтому волны против
потока не распространяются и с
течением времени заполняют по-
лупространство, лежащее справа
от плоскости /С—К, проходящей
случае слабые возмущения рас-
все стороны в виде сферических
Рис. 2.8. Распространение слабых
возмущений:
а — в покоящемся воздухе; б — в дозву-
ковом потоке; в — в звуковом потоке;
г — в сверхзвуковом потоке
через источник.
В сверхзвуковом потоке (У>а, рис. 2.8, е)*волны возмущения
сносятся потоком быстрее, чем растет их радиус (s>r). В резуль-
тате возмущения охватывают только часть пространства, лежащую
внутри конуса возмущений ВОВ'. Действительно, рассмотрим
сферическую волну (рис. 2.8,г). За время t ее существования центр
волны сместился на расстояние s = Vt от источника возмущений О,
а ее радиус стал г—at. Проведем касательную О В к этой волне
и определим угол ее наклона р, к оси потока OO'z
. O'D г а 1
8in^ — OQ' ~ s ~ V ~ М
2-21
33
или
arcsin-—-. (2.28)
Следовательно, угол наклона касательной к волне возмущения
в любой момент времени один и тот же, не зависит от времени
и определяется только числом М. Поэтому в сверхзвуковом по-
токе возмущения распространяются внутри конической поверхно-
сти, образованной вращением касательной ОВ вокруг оси 00'.
Линии О В и ОВ' называются характеристиками, а угол р —
углом наклона характеристик. Рассматриваемый ко-
нус называется конусом возмущений, или характеристиче-
ским конусом, или конусом Маха. Из формулы (2.28) следует,
что при увеличении числа М угол наклона характеристик (полу-
раствора конуса ц) уменьшается, уменьшаются размеры возму-
щенной области.
На характеристиках (образующих конуса возмущений) нор-
мальная к ним составляющая скорости невозмущенного потока Vn
равна скорости звука. Действительно, из рис. 2.8, а имеем
Vn = V sin fl ==!/-!-= а.
При переходе через характеристику параметры воздуха изме-
няются непрерывно, т. е. на бесконечно малые величины.
Аналогичная картина наблюдается при движении со сверхзву-
ковой скоростью источника слабых возмущений в неподвижной
среде.
§ 2.5. Физическая природа скачков уплотнения.
Течения расширения
При обтекании сверхзвуковым потоком тел конечных разме-
ров, при повороте сверхзвукового потока на конечные углы, при
взрывах и т. д. возникают сильные возмущения, которые вызы-
вают изменения газодинамических параметров на конечные ве-
личины и распространяются со скоростями, большими скорости
звука. Образование сильных возмущений в газе происходит вслед-
ствие наложения волн слабых возмущений.
При обтекании газом тела каждая точка его поверхности яв-
ляется источником слабых возмущений. Непрерывное изменение
скорости, давления, плотности и температуры приводит к обра-
зованию слабых волн возмущения, которые в сверхзвуковом по-
токе накладываются друг на друга, в результате в газе образуется
ударная волна (скачок уплотнения), на которой скачкообразно
возрастают давление, плотность и температура, а скорость скач-
кообразно уменьшается. Обычно движущееся сильное возмущение
называется ударной волной, а неподвижное — скачком
уплотнения. Однако природа их одинакова.
34
Поясним физическую сущность скачка на примере обтекания
затупленного тела (рис. 2.9). В лобовой его части поток тормо-
зится. Уменьшение скорости потока согласно уравнению сохра-
нения энергии (2.21) приводит к возрастанию местной скорости
звука, т. е. скорости распространения слабых возмущений. По-
этому слабые возмущения от поверхности тела распространяются
Рис. 2.9. Образование скачка уплотнения перед
телом
вперед. По мере удаления от тела скорость их распространения
уменьшается, так как увеличивается местная скорость потока. На
некотором расстоянии от тела местная скорость звука становится
равной местной скорости потока (К = а). В этом месте волны ела-
бых возмущений останавливаются, накладываются друг на друга,
в результате образуется скачок уплотнения (рис. 2.9). Скачки
уплотнения возникают в сверхзвуковом потоке во всех
случаях, когда имеется торможение газа и повышение дав-
ления.
Форма скачков уплотнения зависит от конфигурации тела, его
ориентации относительно потока и числа М. По форме различают
прямые, косые и криволинейные скачки, а по их положению от-
носительно тела — присоединенные и отошедшие (отсоединен-
ные) .
Фронт прямого скачка уплотнения располагается перпендику-
лярно к набегающему потоку. За прямым скачком направление
скорости не изменяется. Прямые скачки являются отошедшими,
если они располагаются на некотором расстоянии от тела.
У косых скачков фронт располагается относительно набегаю-
щего потока под углом р<90° (рис. 2.10). Косые скачки образу-
ются при обтекании заостренных тел (клиньев, конусов и т. п.)
и являются присоединенными. Направление потока за такими
скачками обычно совпадает с направлением поверхности обтекае-
мого тела.
При обтекании сверхзвуковым потоком затупленных тел и тел
с большим углом полураствора со (рис. 2.11) образуются ото-
шедшие криволинейные скачки уплотнения. Вблизи оси такой
скачок близок к прямому, по мере удаления от нее угол наклона
2* 35
скачка 0 уменьшается, а интенсивность скачка падает. Достаточ-
но далеко от тела скачок уплотнения превращается в характери-
стику с углом наклона р =
Рис. 2.10. Косой присоединенный
скачок уплотнения (фотография)
Рис. 2.11. Криволинейный ото-
шедший скачок уплотнения
(фотография)
Рассмотрим сверхзвуковое течение газа с расширением при
обтекании выпуклой криволинейной поверхности (рис. 2.12).
В соответствии с уравнением расхода (2.8) расширение сверхзву-
кового потока вызывает увеличение
его скорости (числа М) вследствие
интенсивного падения плотности, свя-
занного с уменьшением давления и
температуры. При этом каждая точка
(/, 2, <?) криволинейной поверхности
является источником слабых возму-
щений и из нее исходит характеристи-
ка (рис. 2.12). В результате поворот
сверхзвукового потока происходит на
веере характеристик, которые расхо-
дятся вследствие увеличения числа М
Рис. 2.12. Сверхзвуковое тече-
ние расширения около выпук-
лой криволинейной поверхно-
сти
и уменьшения в соответствии с урав-
нением (2.28) угла их наклона ц. Поэтому скачок разрежения не
образуется, а параметры газа плавно изменяются при переходе
через характеристики. Аналогичная картина наблюдается и при
обтекании сверхзвуковым потоком выпуклого угла.
Таким образом, увеличение скорости (разгон) сверхзвукового
потока происходит плавно, а уменьшение ее (торможение) только
с образованием скачка уплотнения.
36
Рассмотрим обтекание верхней поверхности профиля дозвуко-
вым потоком (М<1, рис. 2.13). Нетрудно видеть, что площадь
сечения струйки сначала уменьшается до некоторого минималь-
ного значения, скорость возрастает, а давление падает. Затем
струйка опять расширяется, скорость течения в ней уменьшается,
а давление возрастает. При
некотором числе М невоз-
мушенного потока, называ-
емом критическим
(Мкр), скорость обтекания
в самом узком сечении ста-
новится равной местной
скорости звука (VM = aM).
Последующее расширение
струйки при М>Мкр вызы-
Рис. 2.13. Образование местного скачка
уплотнения
вает разгон потока, ско-
рость обтекания на этом участке становится сверхзвуковой и по-
является сверхзвуковая зона Поскольку в целом поток
является дозвуковым и за профилем так же, как и перед ним
число М<1, то в кормовой части профиля происходит торможе-
Рис. 2.14. Скачки уплотнения около модели са-
молета (фото)
ние сверхзвукового потока с образованием скачка уплотнения
(рис. 2.13). Указанный скачок принято называть местным, имея
в виду, что он замыкает местную сверхзвуковую зону, обра-
зующуюся при обтекании тел дозвуковым потоком с числом
М^> Мкр-
При полете самолета со сверхзвуковой скоростью у его поверх-
ности образуется сложная система скачков уплотнения и зон раз-
режения (рис. 2.14). На некотором расстоянии от самолета скачки
объединяются в две ударные волны — головную и кормовую, ко-
торые перемещаются в пространстве вместе с самолетом. Если
полет происходит на не очень большой высоте, то эти волны
могут достичь поверхности земли и при пролете самолета наблю-
датель на земле может ощущать их как взрыв. Это явление
получило название сверхзвукового «хлопка» или звукового
удара.
87
§ 2.6. Изменение параметров воздуха на скачках
уплотнения
Рис. 2.15. Косой скачок уплотнения
V„ = И sin Р;
^„1 = ^1 sin ф — о>);
Рассмотрим косой скачок уплотнения (рис. 2.15). Условимся
параметры потока перед скачком обозначать V, р, р, Т, а сразу же
за скачком — соответственно 1Л,
Pi, pi, Ть На скачке изменяется
величина и направление скоро-
сти. Угол между векторами ско-
рости до и после скачка называ-
ется углом поворота пото-
ка и обозначается со. Разложим
скорости до и после скачка уп-
лотнения на нормальные (Vn,
Vni) и касательные (I/., I/ ) со-
ставляющие. Из треугольников
скоростей (рис. 2.15) имеем
V = V cos р;
^1=1/1 COS ф —О>).
(2.29)
Применим закон сохранения массы (уравнение расхода) к тече-
нию газа на скачке (рис. 2.15). Если S и Si — площади струйки
до и после скачка, то в соответствии с уравнением (2.8) plA£ =
= Pi V iSp
Из рис. 2.15 имеем:
S __ Si
sin 8 sin (Р — w) *
Учитывая это и соотношения (2.29), можно получить уравнение
расхода на скачке в виде
Р^ = рУщ. (2.30)
Применим второй закон Ньютона к движению воздуха вдоль
скачка. Изменение количества движения секундной массы возду-
ха т равно т (Ух — Но вдоль скачка давление воздуха не
меняется, поэтому
Отсюда следует, что при переходе через скачок касательная со-
ставляющая скорости не изменяется, т. е.
= (2.31)
Повышение давления на скачке происходит вследствие умень-
шения нормальной составляющей скорости. Применим теорему об
изменении количества движения секундной массы воздуха m==pVrt
при прохождении ее через единичную площадку скачка. Импульс
сил давления на этой площадке равен pi—р, а изменение количе-
ства движения секундной массы т при движении по нормали
к скачку т(Уп — Vnl) == рУп(Уп — Ия1). Следовательно,
—/> = Р^Л(И„ — (2.32)
При переходе через скачок выполняется закон сохранения энер
гии и поэтому справедливы уравнения (2.12), (2.18), (2.19)
(2.21).
Используя уравнение со-
хранения энергии на скачке в
виде (2.19) и формулы (2.29) —
(2.32), после достаточно слож-
ных преобразований можно
получить соотношение нор-
мальных скоростей на скачке
= (2.33)
Для прямого скачка ((о =
~0; р = 90°), как следует из
выражения (2.29), Vx = 0, по-
этому
Гя1/я1 = а2. (2.34)
Так как Vn>a, то
т. е. на прямом скачке уплот-
нения сверхзвуковой поток
тормозится до дозвуковой ско-
рости.
За криволинейным (ото- Рис. 2.16. Изменение параметров
шедшим) скачком уплотнения потока на скачке
(рис. 2.11) наблюдается сме-
шанное течение. Вблизи оси скачок близок к прямому, скорость
за скачком дозвуковая. По мере удаления от оси угол наклона
скачка уменьшается, скорость за скачком падает менее интен-
сивно и может оставаться сверхзвуковой.
Вследствие уменьшения скорости давление, температура и
плотность воздуха за скачком возрастают и тем сильнее, чем
больше число М и угол наклона скачка. На рис. 2.16 показаны
зависимости отношений Pi/p, Т\/Т и pi/p от параметра Msin 0.
При увеличении этого параметра отношение давлений и темпера-
тур растет неограниченно, а отношение плотностей имеет предел,
равный 6. Ограниченный рост плотности за скачком связан с тем,
что при увеличении давления за скачком одновременно растет
температура, а это препятствует неограниченному уплотнению
среды.
Если сравнить полное давление р* до скачка и р\ после скач-
ка, то оказывается, что /?*</>*, хотя температуры торможения,
как следует из формулы (2.18), одинаковы при V=
39
= Vi = O). Дело в том, что на скачке происходит увеличение тем-
пературы газа (Ti>T) и часть кинетической энергии потока пе-
реходит в тепло. Поскольку превратить это тепло обратно в ки-
нетическую энергию за скачком не удается, то происходят не-
Рис. 2.17. Изменение коэффициента
сохранения полного давления на
скачке
Рис. 2.18. Фотография системы
скачков во входном устройстве
двигателя
обратимые потери полного давления. Эти потери оцениваются
коэффициентом сохранения полного давления
° = (2.35)
Коэффициент а<1 и зависит от параметра Msinp (рис. 2.17).
Наибольшие потери полного давления наблюдаются на прямых
скачках (sin р= 1). Уменьшение полного давления на входе в дви-
гатель приводит к уменьшений) его тяги. Для увеличения о вход-
ные устройства двигателей выполняют таким образом, чтобы за-
менить прямой скачок системой косых (рис. 2.18).
§ 2.7. Пограничный слой и сопротивление трения
Рассматривая общую картину обтекания тела воздухом
(рис. 2.5), установили, что вблизи поверхности тела имеется тон-
кий слой воздуха (пограничный слой), в котором интенсивно про-
является вязкость и поток тормозится. Непосредственно на по-
верхности тела скорость равна нулю, а по мере удаления от по-
верхности скорость возрастает и на некотором расстоянии, рав-
ном толщине пограничного слоя б, становится практически равной
той скорости, которую имел бы невязкий газ.
Различают ламинарный и турбулентный пограничный слои.
В ламинарном слое течение слоистое (без перемешивания
слоев), в турбулентном — с интенсивным перемешиванием.
Турбулентный пограничный слой всегда толще ламинарного, так
40
Рис. 2.19. Профили скоростей в ла-
минарном и турбулентном погра-
ничных слоях
как вследствие перемешивания слоев в этом случае большая мас-
са воздуха испытывает влияние вязкости и торможение.
Важной характеристикой пограничного слоя является профиль
скоростей, т. е. изменение скорости по толщине слоя. Вследствие
перемешивания слоев и обме-
на кинетической энергией тур-
булентный слой имеет более
выпуклый профиль скоростей,
чем ламинарный (рис. 2.19).
Наличие градиента скорости
по толщине пограничного
слоя вызывает появление ка-
сательных напряжений трения,
которые в ламинарном слое
определяются по формуле
Ньютона
< = |^. (2.36)
На рис. 2.20 показано изме-
нение давления, температуры,
плотности и напряжения тре-
ния по толщине пограничного
слоя. Видно, что давление
по толщине пограничного слоя
постоянно, температура и на-
пряжение трения при приближении к стенке возрастают, а плот-
ность падает.
Рис. 2.20. Изменение параметров воздуха по толщине погра-
ничного слоя
Характер пограничного слоя по длине обтекаемого тела может
изменяться: в головной части он обычно ламинарный, а затем
превращается в турбулентный (рис. 2.21). Такой пограничный слой
принято называть смешанным. Координата хт точки перехода за-
висит от числа Рейнольдса
- _ Хт_ _ ReKp
L ~ Re *
(2.37)
41
Здесь ReKP — известное из опыта критическое число Рейнольд-
са, L — длина тела. При увеличении числа Re координата хт
уменьшается, т. е. увеличивается протяженность турбулентного
Рис. 2.21. Смешанный пограничный слой
участка (хт = 0 соответствует полностью турбулентному погранич-
ному слою, хт=1 — полностью ламинарному).
По длине тела толщина пограничного слоя б возрастает, а на-
пряжение трения т уменьшается.
Рис. 2.22. Зависимости коэффициен-
та двустороннего трения пластины
от числа Re
Пусть при обтекании поверхности с площадью S вязким га-
зом возникает сила трения ХТр. Коэффициентом трения называется
безразмерная величина
с, “4г- <2-38)
о У2
где q = -Ч,----скоростной напор.
Коэффициент С; зависит от характера пограничного слоя (ко-
ординаты хт), числа Re и числа М, На рис, 2.22 приведены зави-
42
симости коэффициента Cf от числа Re и параметра хт для не-
сжимаемой среды (М = 0). При увеличении числа Re в случае
хт = const роль вязкости уменьшается и коэффициент Cf падает.
Заметим, что при одинаковых условиях в турбулентном погранич-
ном слое коэффициент Cf всегда больше, чем в ламинарном,
вследствие больших градиентов скорости у стенки (рис. 2.19).
Рис. 2.23. Отрыв потока с обтекаемой поверх-
ности
Поэтому при увеличении числа Re в случае смешанного погра-
ничного слоя точка перехода смещается вперед (хг уменьшается)
и коэффициент Cf может возрасти (рис. 2.22).
При обтекании тела по
его длине скорость и давле-
ние воздуха могут изме-
няться. Рассмотрим течение
в пограничном слое (рис.
2.23), когда градиент дав-
ления положительный
(Др/Дх>0) и давление в
направлении движения воз-
духа возрастает (Рз^>Р2> Рис. 2.24. Волновой срыв потока
>Pi), а разность давлений
действует против потока и тормозит его. Так как вблизи стенки
кинетическая энергия частиц мала, то под действием противо-
давления эти частицы могут останавливаться и даже двигаться
навстречу основному потоку. Это вторичное течение отжимает
от поверхности тела основной поток и может вызвать его отрыв
(рис. 2.23). Поскольку в турбулентном пограничном слое скорости
у стенки больше, чем в ламинарном (рис. 2.19), то турбулентный
слой более устойчив к отрыву, чем ламинарный.
Одной из причин преждевременного обрыва потока с обтекае-
мой поверхности может явиться взаимодействие пограничного
слоя и местного скачка уплотнения (рис. 2.24). При наличии по-
граничного слоя скачок до поверхности тела не доходит, так как
43
в пограничном слое скорости резко уменьшаются и вблизи стенки
становятся дозвуковыми.
При переходе че)рез скачок давление увеличивается (p{>pY
Повышенное давление передается на дозвуковые слои воздуха,
непосредственно прилегающие к поверхности тела, и вызывает
обратное течение газа в пограничном слое. Это противотечение
отжимает основной поток,
Рис. 2.25. Х-образный скачок (фотогра-
фия)
в результате возникает срыв
потока (волновой срыв).
Струйки перед прямым
скачком искривляются, по-
ток как бы обтекает вогну-
тый угол, появляется допол-
нительный косой скачок. На
косом скачке происходит
поворот потока вверх, что
способствует отрыву потока
от стенки. Образуется си-
стема скачков, имеющая
форму буквы X (лямбдаоб-
разный скачок).
В ламинарный слой ска-
чок входит незначительно
из-за интенсивного умень-
шения скорости. Образуется достаточно толстый дозвуковой
подслой (без скачка), в котором наблюдается обратное
течение, срыв потока и образование Х-скачка (рис. 2.25). Те-
чение с отрывом неустойчиво и сопровождается тряской (коле-
баниями) конструкции из-за вибрации скачка по поверхности.
В турбулентном пограничном слое дозвуковой подслой очень тон-
кий вследствие более равномерного распределения скоростей, по-
этому отрыв потока и Х-скачок обычно не возникают.
§ 2.8. Аэродинамический нагрев
При обтекании летательного аппарата воздух может как тор-
мозиться, так и ускоряться. Как следует из уравнения сохранения
энергии (2.18), при торможении потока его температура возра-
стает. Наибольшие температуры воздуха наблюдаются там, где
скорости наименьшие: на головных частях фюзеляжа и подвесок
вооружения, на передних кромках крыла, на выступающих частях
конструкции и т. п.
Выведем формулу для определения температуры полностью
заторможенного потока Т*. Из уравнения (2.18) имеем
44
отсюда
Т* = Т р Ч g . (2.39)
Но в соответствии с формулой (2.20) kRT — a"1. Тогда
П = Т'(1 + А^1^.
Учитывая, что = М, окончательно получим
7'‘ = 7'(1 + ^М2), (2.40)
где Т — температура окружающей среды. Заметим, что форму-
ла (2.40) справедлива в условиях постоянной теплоемкости газа
(£ = const) и отсутствия диссоциации. При температуре воздуха
Т>650 К получаемые по ней результаты следует рассматривать
как оценочные.
Как следует из выражения (2.40), температура Г* тем больше,
чем больше число М. Повышение температуры газа становится
ощутимым на сверхзвуковых скоростях. Так, при числе М = 3 тем-
пература торможения может достигать 700 К, а при входе косми-
ческого аппарата в атмосферу земли с первой космической ско-
ростью (7=7,91 км/с) — 8000 К.
Как известно, торможение сверхзвукового потока происходит
сначала на скачке уплотнения, а затем в пограничном слое. Основ-
ное повышение температуры имеет место на скачке уплотнения,
особенно если он близок к прямому. Аэродинамический нагрев
приводит, во-первых, к изменению характеристик пограничного
слоя и сопротивления трения и, во-вторых, к нагреву и снижению
прочности конструкции самолета.
С ростом числа М увеличивается температура в пограничном
слое и коэффициент динамической вязкости ц, а плотность возду-
ха уменьшается. В результате увеличивается толщина погранич-
ного слоя и уменьшается коэффициент трения.
От нагретого при торможении воздуха тепло передается в кон-
струкцию самолета. Сильнее всего подвержены нагреву лобовые
части, однако нагреваются и боковые поверхности вследствие по-
вышения температуры в пограничном слое. При этом снижается
прочность материала конструкции, ухудшаются условия работы
оборудования, в частности головок самонаведения ракет. Поэтому
для современных маневренных самолетов иногда ограничиваются
максимальные числа М полета по условиям аэродинамического
нагрева элементов конструкции или подвесок вооружения.
На интенсивность аэродинамического нагрева, кроме числа М,
влияют высота полета Н, характер пограничного слоя, тип за-
тупления передних кромок и его диаметр, стреловидность крыла,
удаление от передних кромок и другие факторы.
45
При увеличении высоты полета уменьшается плотность возду-
ха, а следовательно, и количество подводимого к самолету тепла.
В ламинарном пограничном слое меньше трение и меньше тем-
пература воздуха, чем в турбулентном. Чем больше диаметр затуп-
ления носовой части, тем меньше удельный тепловой поток, при-
ходящийся на единицу площади поверхности, тем меньше ее
температура. Кроме того, в этом случае скачок является отошед-
шим и часть тепла между скачком и телом рассеивается.
При наличии стреловидности передней кромки нагрев также
уменьшается, так как на скачке тормозится не весь поток, а его
составляющая, нормальная к линии передней кромки. По мере
удаления от передней кромки напряжение трения уменьшается,
снижается и температура воздуха.
Кроме затупления передних кромок на летательных аппара-
тах, особенно космических, применяются и другие способы борьбы
с аэродинамическим нагревом — жаропрочные материалы, тепло-
защита и т. п. В качестве теплозащитных (абляционных) мате-
риалов используются различные смолы (фенольные, эпоксидные)
с тугоплавкими наполнителями (асбест, кварц, графит). Этими
смолами обмазываются поверхности летательного аппарата, наи-
более подверженные нагреву. При нагреве смолы плавятся, испа-
ряются и уносятся потоком, а между нагретым воздухом и по-
верхностью аппарата создается изолирующая газовая пленка.
§ 2.9. Принципы измерения скорости и числа М
Принципы определения скорости и числа М в полете основаны
на измерении давления заторможенного потока и статического
давления невозмущенного потока. Эти давления измеряются спе-
Рис. 2.26. Измерение числа М полета:
а — на дозвуковых скоростях; б — на сверхзвуковых скоростях
циальной трубкой — приемником воздушных давлений (ПВД),
принципиальная схема которого показана на рис. 2.26, а. Внут-
ренняя трубка является приемником давления заторможенного по-
тока, так как ее отверстие, встречающее поток, расположено в
области точки полного торможения (V = 0). Отверстия на боко-
46
вой поверхности являются приемниками статического давления
невозмущенного потока р.
Для измерения скорости используется уравнение сохранения
энергии. Из уравнения (2.25) для несжимаемого газа при малых
скоростях полета имеехм
Р*-Р = -^- =Я- (2.41)
Отсюда видно, что измеряемая ПВД разность давлений про-
порциональна скоростному напору. Но скоростной напор зависит
не только от истинной скорости полета самолета V, но и от плот-
ности воздуха р. Если бы плотность воздуха была неизменной, то
скоростной напор однозначно определялся бы значением скоро-
сти. Так как при изменении высоты полета плотность воздуха из-
меняется, то указатель скррости регистрирует истинную воздуш-
ную скорость V только при нормальных атмосферных условиях,
при которых плотность равна р0. Именно при этих условиях про-
изводится градуировка шкалы указателя скорости.
В других условиях указатель показывает так называемую ин-
дикаторную скорость Vi, которая определяется по фактическому
скоростному напору q и плотности р0. Следовательно,
9=4^-<2-42)
Отсюда находим связь между истинной и индикаторной скоро-
стями:
V = VtV^-. (2.43)
Это соотношение используется для градуировки шкалы истин-
ной скорости полета.
По значению индикаторной скорости летчик косвенно может
судить о величине угла атаки в горизонтальном полете.
В сжимаемом дозвуковом потоке для измерения скорости ис-
пользуется уравнение сохранения энергии в виде (2.39).
Запишем уравнение состояния (2.13) для заторможенного воз-
духа и для невозмущенного потока:
Отсюда
р* _ р* г*
“р Р т •
Процесс торможения дозвукового потока является изэнтропи-
ческим, поэтому
Р* Р
(р*)й р» ’
47
откуда
(2.45)
Подставив выражение (2.45) в (2.44) и проведя несложные
преобразования, получим
л
= (2-46)
Учитывая (2.39), имеем
ь
р‘=р <2-47)
В соответствии с уравнением состояния
р
поэтому
k
р*=/>(1 +<2-48)
Вычтем р из левой и правой частей выражения (2.48):
k — \
kp
к
рУ2
(2.49)
-1
Из формулы (2.49) видно, что в сжимаемом дозвуковом потоке
величина скоростного напора дсж М<1 зависит не только от истин-
ной скорости V и плотности воздуха р, но и от статического дав-
ления р.
Учитывая связь (2.43) между истинной и индикаторной ско-
ростью, скоростной напор можно представить в виде
+ - vt)m -'] <2-50)
Так как kR.T=a2, то из выражения (2.47) имеем
А
р* — Л _l k~ 1
V — V "г 2 в2 J ’
Но = М. Поэтому
(2.51)
На основании этой зависимости тарируется указатель числа М
на дозвуковых скоростях (М<С1).
На сверхзвуковых скоростях (М>1) перед приемником воз-
душных давлений образуется криволинейный скачок уплотнения
(рис. 2.26, б) и прибор измеряет отношение p*Jp. Связь между
числом М и отношением давлений на сверхзвуковых скоростях
является более сложной, чем на дозвуковых. Запишем отноше-
ние р*/р в виде
Рх Р\ р* р*
р р* р р
(2.52)
Здесь коэффициент сохранения полного давления ст (рис. 2.17)
определяется только числом М, так как в критической точке (по
оси трубки) скачок уплотнения можно считать прямым, поэтому
0 = 99° и sin 0=1. Отношение р*/р, как показано выше, зависит
тоже только от числа М. Поэтому и на сверхзвуковых скоростях
число М. однозначно определяется отношением давлений р*1р-
Подставив в формулу (2.52) значения ст и р*/р и учитывая,
что M2=V2/a2, можно получить формулы для определения
#сж м>1= Р* ~Р как чеРез истинную V, так и через индика-
торную Vi скорости. Соответствующие выражения являются весь-
ма сложными и здесь не приводятся. Из них следует, что ско-
ростной напор <7сжМ>1 также зависит от статического давле-
ния р.
Таким образом, в сжимаемом потоке как на дозвуковых, так
и на сверхзвуковых скоростях скоростной напор, измеряемый при-
бором, зависит от статического давления. Поскольку прибор гра-
дуируется в земных условиях при р=ро, то на других высотах
в его показания необходимо вводить поправки на сжимаемость
бКж и 6МСЖ. Не следует думать, что эти поправки учитывают
все влияние сжимаемости. Они учитывают лишь различную сте-
пень проявления сжимаемости на -различных высотах (при раз-
личных статических давлениях).
Реальные условия работы ПВД вносят в измерения скорости и
числа М погрешности, которые вызываются воздействием на по-
ток самого ПВД и искажением поля статических давлений в месте
установки прибора вследствие влияния самолета при его обтека-
нии. В показания прибора приходится вводить так называемые
аэродинамические поправки 6Va и бМа. Для уменьшения аэроди-
намических погрешностей ПВД по возможности выносятся из
возмущенной зоны (например, вперед) и на них применяются спе-
циальные компенсаторы.
Градуировка шкал указателей скорости и числа М по сред-
ним характеристикам приборов, которые вследствие производст-
венных допусков могут отличаться от фактических, вызывает не-
обходимость введения инструментальных поправок бГинстр и
бМцнстр-
49
Таким образом, если приборы показывают некоторые значения
скорости Vnp и числа Мпр, то индикаторная скорость и действи-
тельное значение числа М будут равны:
VI = ИПр + инстр»
М = Мпр + 8МСЖ + 8Ма + 8Минстр.
(2.53)
Глава 3
АЭРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ
§3.1. Картина распределения давления на крыле
Рис. 3.1. Картина распреде-
ления давления в сечении
крыла
Суммарные аэродинамические силы являются результатом дей«
ствия касательных сил трения и нормальных сил давления, рас-
пределенных по поверхности крыла. Рассмотрим обтекание неко-
торого сечения крыла несжимаемым
потоком и изучим картину распреде-
ления нормального давления в этом
сечении (рис. 3.1).
Выделим в потоке элементарную
струйку воздуха непосредственно у
поверхности крыла в рассматривае-
мом сечении и проследим изменение
вдоль нее параметров воздуха (рис.
3.1,а). При приближении к перед-
ней кромке струйка расширяется,
скорость в ней уменьшается (поток
перед крылом тормозится), а давление
возрастает по сравнению с давлением
невозмущенного потока роо. В неко-
торой точке Л, которая называется
критической, поток полностью тормо-
зится (V = 0), а давление максималь-
но и равно давлению заторможенного
потока р*.
При обтекании верхней поверхно-
сти крыла площадь сечения струйки
сначала уменьшается, скорость потока
возрастает, а давление падает. Затем
струйка опять расширяется, скорость
в ней уменьшается, а давление повышается. На нижней поверх-
ности крыла при положительном угле атаки струйки сужаются
в меньшей степени или даже расширяются, скорости меньше,
а давления больше, чем на верхней поверхности. За счет разности
давлений на нижней и верхней поверхностях крыла и создается
подъемная сила. х
5G
Построим в масштабе векторы давлений по нормали к поверх-
ности крыла в ряде точек. В результате получим диаграмму дав-
лений в рассматриваемом сечении крыла (рис. 3.1,6, сплошная
линия). Для сравнения там же штриховой линией показана ве-
личина статического давления невозмущенного потока рго.
Изменение давления р в рассматриваемой точке крыла при
его обтекании по сравнению с давлением невозмущенного потока
рт можно характеризовать коэффициентом давления
В каждой точке обтекаемого крыла получается определенное
значение коэффициента давления. Откладывая в некотором мас-
штабе величины р по нормали к поверхности крыла, получим кар-
тину распределения коэффициентов давления в сечении крыла
(рис. 3.1, в). Такое представление наглядно, но весьма сложно.
Поэтому на практике величины р обычно откладывают по нор-
мали к хорде крыла в сечении в тех ее точках, на которые прое-
цируются соответствующие точки поверхности крыла (рис. 3.1, а).
При этом отрицательные значения р, соответствующие разреже-
нию потока, откладываются вверх, а положительные — вниз.
При безотрывном обтекании крыла несжимаемым потоком с
ростом угла атаки уменьшение давления на верхней поверхности
происходит в большей степени, чем увеличение давления на ниж-
ней. Действительно, из уравнения Бернулли для двух сечений
струйки
для коэффициента давления получим
Следовательно, в критической точке (V = 0) давление ограни-
чено (pmax=l). С другой стороны, разрежение потока может про-
исходить теоретически до полного вакуума (р = 0), тогда
(ЛпДред = При малых скоростях обтекания pV2J2 <с
<^ртп величина разрежения потока может быть весьма большой,
поэтому на малых скоростях основную роль в создании подъем-
ной силы играет разрежение на верхней поверхности крыла.
И наоборот, при больших скоростях (особенно сверхзвуковых)
и возрастает роль нижней поверхности в создании
подъемной силы.
51
§ 3.2. Полная аэродинамическая сила й момент
и их составляющие. Аэродинамические коэффициенты
При движении самолета в воздухе на него действуют каса-
тельные силы трения и нормальные силы давления. Эти распре-
деленные по поверхности самолета аэродинамические силы можно
Рис. 3.2. Полная аэродинамическая сила самолета и
ее составляющие:
а— в скоростной системе координат; б — в связанной системе
координат
свести к результирующей (суммарной) силе R, которую принято
называть полной аэродинамической силой. Сила R создает отно-
•ф
сительно центра масс самолета момент М,_ под действием кото-
рого самолет может крениться вправо (влево), изменять углы
атаки и скольжения.
52
Вместо полной аэродинамической силы и момента обычно рас-
сматривают их составляющие, т. е. проекции на оси координат.
Рассмотрим составляющие силы /? в скоростной (рис. 3.2, а) и
в связанной (рис. 3.2, б) системах координат.
Проекциями силы R на оси скоростной системы координат яв-
ляются сила лобового сопротивления X, подъемная сила У и бо-
ковая сила Z. Сила X всегда направлена против вектора скорости
Рис. 3.3. Аэродинамический момент самолета и
его составляющие в связанной системе коор-
динат
движения самолета, а положительные направления сил У и Z
совпадают с положительными направлениями осей Оу и Ог.
Проекциями силы R на оси связанной системы координат яв-
ляются продольная сила Хь нормальная сила У1 и поперечная
сила Zb Продольная сила Х\ в отличие от силы лобового сопро-
тивления X может быть направлена как против, так и в сторону
движения самолета.
В аэродинамике наиболее часто рассматривают проекции век-
тора момента М на оси связанной системы координат (рис. 3.3).
Их обозначают Мх, Му, Мг и называют соответственно моментом
крена, моментом рысканья и моментом тангажа. Проекции мо-
ментов считаются положительными, если момент Мх кренит са-
молет вправо, Му разворачивает влево, Mz поднимает нос само-
лета, т. е. положительные моменты вращают самолет против ча-»
совой стрелки, если смотреть из конца координатной оси
(рис. 3.3).
Величины аэродинамических сил и моментов зависят от мно-
гих факторов: от формы и размеров самолета, скорости и высоты
полета, углов атаки и скольжения, угловых скоростей вращения
и др. В соответствии с формулой (2.5) введем безразмерные ко-
53
эффициенты пропорциональности (аэродинамические коэффици-
енты) и через них выразим составляющие силы и момента. В ско-
ростной системе координат имеем:
X = CxqS\ Y = CyqS- Z = CzqS, (3.1)
где Сх, Су, С? — соответственно коэффициенты лобового сопротив-
ления, подъемной и боковой сил, 6? = pV2/2— скоростной напор,
S — площадь крыла.
Рис. 3.4. Определение связи между коэффициен-
тами сил в связанной и скоростной системах
координат
В связанной системе координат силы выражаются через коэф-
фициенты следующим образом
Xx = CXiqS-, Yx = CyqS\ Z^C^qS, (3.2)
где Сх, Суг Cz —коэффициенты продольной, нормальной и
поперечной сил.
Аналогично через безразмерные коэффициенты выражаются и
составляющие момента
Мх = mxqSl-, Му = myqSl\ Mz = mzqSb, (3.3)
где тх, ту, тг — коэффициенты момента крена, рысканья и тан-
гажа соответственно, I — размах крыла, Ь — его хорда.
Безразмерные аэродинамические коэффициенты сил и моментов
недеформирующегося в полете самолета не зависят от скоростного
напора и размеров самолета, но зависят от его формы, углов
атаки и скольжения, угловых скоростей, критериев подобия, ха-
рактеризующих сжимаемость воздуха и его вязкость, т. е. от
чисел М и Re.
Между аэродинамическими коэффициентами сил в скоростной
и связанной системах координат существует связь. Установим ее
применительно к случаю полета без скольжения (0 = 0), когда
Cz — CZ=Q (рис. 3.4). Пусть известны коэффициенты CXi и
Суг Тогда на основании рис. 3.4 имеем
Сх = Сх cos а 4- Cyi sin а; Су = Су> cos а — sin а. (3.4)
54
При малых углах атаки с достаточной точностью можно счи-
тать, что cos а 1, a sin а ~ а. Тогда
Сх = Сх+Суъ Су = Су. (3.5)
§ 3.3. Зависимость коэффициентов аэродинамических сил
от углов атаки и скольжения
Подъемная сила самолета связана с действием нормальных
сил давления и определяется разностью давления на нижней и
верхней поверхностях частей самолета и прежде всего крыла. При
увеличении угла атаки струй-
ки на верхней поверхности су-
жаются, поток ускоряется, его
давление уменьшается, а на
нижней поверхности, наоборот,
струйки расширяются, поток
тормозится, давление его воз-
растает. В результате увели-
чивается коэффициент подъем-
ной силы самолета (рис. 3.5).
Исследования показывают,
что при малых углах атаки
коэффициент Су линейно зави-
сит от угла атаки а (соответ-
ствует безотрывному режиму
обтекания). При плавном об-
Рис. 3.5. Зависимости коэффициен-
тов подъемной силы и силы лобо-
вого сопротивления самолета от уг-
ла атаки
текании самолета поток пово-
рачивает на угол а, при этом изменение количества движения
пропорционально Vsina или при малых углах атаки—Va. Следо-
вательно, импульс сил (в данном случае нормальных) прямо про-
порционален углу атаки а.
С увеличением угла атаки увеличивается разрежение на верх-
ней поверхности самолета и растет положительный градиент дав-
ления Др/Дх. При некотором угле атаки ан. с на верхней поверх-
ности самолета (например, в кормовой части крыла) возникает
местный отрыв потока и линейная зависимость коэффициента Су
от а нарушается, рост Су замедляется (рис. 3.5). Дело в том, что
при срыве потока с верхней поверхности на ней уменьшаются ско-
рости и разрежения. Угол ан. с и коэффициент Cytt.c соответствуют
началу срыва потока (точка /). При дальнейшем увеличении угла
атаки коэффициент Су растер до некоторого максимального зна-
чения С у max, соответствующего критическому углу атаки акр. При
а>аКр коэффициент Су уменьшается, так как срыв потока быстро
распространяется на все крыло или большую его часть. При от-
рицательных углах атаки зависимость Су от а качественно та-
кая же, как при а>0, но при этом обычно С\/<0.
В общем случае для самолета кривая зависимости Су от a
может быть смещена относительно начала координат (рис. 3.5),
55
а угол «о, при котором С^ = 0, называется углом нулевой подъем-
ной силы.
На линейном участке зависимости Су от а можно записать
Су = С*(а-а0), (3.6)
где Сау = дСу1да —производная коэффициента подъемной силы по
углу атаки. Производная Су зависит от формы самолета и крите-
риев подобия и на линейном участке зависимости Су от а не за-
висит от угла атаки.
На рис. 3.6 для сравнения
приведена зависимость коэф-
фициента нормальной силы
самолета от угла атаки.
Вследствие роста сопротивле-
ния этот коэффициент на боль-
ших углах атаки возрастает.
Сопротивление самолета
обусловлено действием как
нормальных сил давления,
Рис. з.б. Зависимости коэффициен- так и касательных сил трения,
тов нормальной и продольной сил поэтому при любых углах
самолета от угла атаки атаки Сх>0 (рис. 3.5). С
увеличением угла атаки
коэффициент лобового сопротивления самолета интенсивно воз-
растает. Что касается коэффициента продольной силы Сх, то
его зависимость от угла атаки более сложная (рис. 3.6).
Заметим, что коэффициенты Сх, Сх, Су и СУ1 самолета срав-
нительно слабо зависят от угла скольжения р.
Рассмотрим зависимость коэффициента боковой силы Cz от
угла скольжения. Боковая сила на самолете создается в основ-
ном вертикальным оперением и корпусом, которые при скольже-
нии работают принципиально так же, как крыло при наличии
угла атаки. Поэтому зависимость коэффициента Сг от угла сколь-
жения р качественно такая же, как зависимость Су от а. При
малых углах скольжения она линейная. Поскольку самолет сим-
метричен относительно плоскости Оху, то зависимость Cz от р
проходит через начало координат и на линейном участке ее мож-
но представить в виде
сг=с%,
(3.7)
где = дСг/д$ —производная коэффициента боковой силы по
углу скольжения. Эта производная зависит от формы самолета
и числа М и на линейном участке зависимости Сг от р не зависит
от угла скольжения.
Качественно так же, как и коэффициент Cz, коэффициент по-
перечной силы С зависит от угла скольжения. Заметим, что
коэффициенты Cz и CZj сравнительно слабо зависят от угла атаки
(обычно несколько уменьшаются при его увеличении),
55
§ 3.4. Поляра и аэродинамическое качество
Рассмотрим коэффициент лобового сопротивления самолета.
Пусть Су = 0. Тогда и Су 0. Обозначим через Сх* коэффициент
лобового сопротивления,при Су = 0. Так как это имеет место при
малых углах атаки (а—*0), то в этом случае из выражений (3.5)
имеем:
сх = с .
л Х\ х0
При отсутствии подъемной силы (Су = 0) сопротивление созда-
ется силами трения и силами давления, поэтому
Со,= Сгтр Схдавл> (3.8)
Если Су^О, то из-за разрежения потока на носовых частях
самолета и прежде всего на носке крыла (рис. 3.1, в) при его
обтекании возникает подсасывающая сила Т, направленная впе-
ред. Введем безразмерный коэффициент этой силы Ст = Т/д8. При
а>0 для коэффициента лобового сопротивления в этом случае
в соответствии с формулой (3.4) получим
Сх = (С — Cr) COS а СУ1 sin а.
При малых углах атаки можно полагать cosa ~ 1; sina ~ а;
Су, поэтому
Сх = СХя + С^-Ст. (3.9)
Допустим, что зависимость Си от а для самолета проходит че-
рез начало координат, т. е. ао=0 и на линейном участке Су — СуЯ.
При этом угол атаки а = Су/Су. Тогда выражение (3.9) можно
переписать в виде
Как,показывают исследования, при увеличении угла атаки ко-
эффициент подсасывающей силы Ст увеличивается пропорцио-
нально Су. Следовательно, на линейном участке зависимости Су
от а величина Сг/Су не зависит от угла атаки, как и 1/С“.
Обозначим
Тогда
СХ = СХ' + АС’. (3.11)
Первое слагаемое С характеризует лобовое сопротивление
при отсутствии подъемной силы и называется коэффициентом
лобового сопротивления при нулевой подъемной
силе. Второе слагаемое характеризует сопротивление, обуслов-
57
ленное подъемной силой, и называется коэффициентом ин-
дуктивного сопротивления CXi Чем больше подъемная
сила, тем больше это сопротивление.
Зависимость коэффициента лобового сопротивления Сх само-
лета от коэффициента подъемной силы Су называется полярой
первого рода. Обычно поляра представляется графиком
Рис. 3.8. Поляра второго рода
(рис. 3.7). Если у самолета ао = О, то на линейном участке зави-
симости Су от а поляра описывается уравнением квадратной па-
раболы (3.11). На рис. 3.7 эта зависимость показана штриховой
линией. В других случаях уравнение поляры первого рода имеет
более сложный вид.
При изучении динамики полета требуется знание сил в свя-
занной системе координат. Зависимость коэффициента осевой силы
Сх от коэффициента нормальной силы называется поля-
рой второго рода (рис. 3.8). Поляра второго рода прибли-
женно описывается зависимостью
СЛ=С„-СГ. (3.12)
Если подсасывающая сила отсутствует (например, передние
кромки острые), то Сх Сх>.
В аэродинамике самолета при оценке его аэродинамического
совершенства важнейшее значение имеет аэродинамическое
качество — отношение коэффициента подъемной силы к коэф-
фициенту лобового сопротивления
# = (3.13)
58
Нетрудно видеть, что аэродинамическое качество зависит от
угла атаки (рис. 3.9). С увеличением а качество вначале растет,
так как растет коэффициент Су, а коэффициент Сх изменяется
мало (рис. 3.5), достигает максимального значения /(max, а затем
падает вследствие интенсивного роста сопротивления. Угол атаки,
Рис. 3.9. Зависимость аэродинамического каче-
ства самолета от угла атаки
коэффициенты Су и Сх, при которых имеет место К max, называют-
ся наивыгоднейшими.
Если известно уравнение поляры, то для Ктах можно получить
аналитическое выражение. Воспользуемся уравнением (3.11).
Тогда
к — Су
CXi + АС2у ’
Найдем наивыгоднейший коэффициент подъемной силы С^наив.
Для этого возьмем производную и приравняем ее нулю, т. е.
dK АСу наив 2ЛСу наив
dCy- (С,0+^наив)2
Отсюда
(3.14)
наив |/ д’;
Схнаив = Сх° + АС* наив = 2СХ<.
(3.15)
Подставляя эти значения в формулу для качества, получим
гг ____________________ Су наив _ 1
шах Сх наив 2 JZАСХ>
(3.16)
59
Как следовало ожидать, чем больше коэффициенты Сх и Л,
определяющие величину коэффициента сопротивления, тем мень-
ше максимальное аэродинамическое качество. Если ао = О, то наи-
выгоднейший угол атаки определяется по формуле
Сунаив 1 , / сх
анаив = —= -q |/ (3.17)
Обычно максимальное аэродинамическое качество самолета
реализуется при сравнительно небольших углах атаки (анаив =
= 4-7-6°).
§ 3.5. Зависимость коэффициентов аэродинамических
моментов от углов атаки и скольжения
Аэродинамические моменты создаются аэродинамическими си-
лами, шоэтому зависимости коэффициентов этих моментов от углов
атаки и скольжения имеют много общего с рассмотренными выше
зависимостями коэффициентов сил от углов атаки и скольже-
ния.
На рис. 3.10 представлена типичная для самолетов со стрело-
видными крыльями зависимость коэффициента момента тангажа
mz от угла атаки а. При малых углах атаки коэффициент tnZl
как правило, линейно зависит от а, а при больших углах атаки
эта линейность нарушается вследствие влияния срыва потока. По-
скольку при возникновении срыва изменяется не только величина
аэродинамических нагрузок, но и закон их распределения по по-
верхности самолета, то нелинейная зависимость mz от а может
быть более сложной, чем зависимость Су от а. В частности, срыв-
ные явления в обтекании самолета приводят к «выполаживанию»
зависимости т2 от а, т. е. значительному уменьшению или замед-
лению роста пикирующего момента при увеличении угла атаки
(рис. 3,10).
60
На линейном участке зависимости т2 от а можно записать
^г = ^(а-а0 J, (3.18)
где /п“ = dmzlda —производная коэффициента момента тангажа
по углу атаки, ао т — угол нулевого момента тангажа (в общем
случае ао /пУ=ао).
Рис. 3.11. Зависимость коэффициента момента танга-
жа от коэффициента подъемной силы
Так как коэффициенты тг и Су однозначно определяются углом
атаки, то, исключая а, можно получить зависимость тг от Су
(рис. 3.11), которая широко используется при изучении динамики
полета. Характер зависимости тг от Су аналогичен характеру за-
висимости тг от а: при малых значениях Су эта зависимость ли-
нейная, а при больших — обычно нелинейная. Значение коэффи-
циента тг при 0^ = 0 обозначим тг. Тогда при малых значе-
ниях Су можно записать
ГПг == тг, + т^У’ (3-19)
где т^у == дтг1дСу — производная коэффициента момента танга-
жа по коэффициенту Су.
Производные и т%у зависят от формы самолета, положе-
ния оси приведения (например, центра масс) и числа М и не
зависят (на линейном участке) от угла атаки и коэффициента Су.
Коэффициент mz* зависит от формы самолета и числа М. Заме-
тим, что коэффициенты тг, т* и тсгУ сравнительно слабо за-
висят от угла скольжения р.
При движении самолета со скольжением вследствие несим-
метричного обтекания возникают моменты крена Мх и рыска-
ния Му. Их коэффициенты зависят от угла скольжения. При ма-
61
лых углах скольжения зависимости тх и пгу от р линейны, по-
этому коэффициенты тх и ту могут быть представлены в виде:
тх = т^; (3.20)
= (3.21)
где т?х ~дтх/д^ ni^ = д/пу/д$ —производные коэффициентов
тх и ту по углу скольжения. Величины т?х и на линейном
участке не зависят от угла |3, но зависят от формы самолета,
числа М, угла атаки.
§ 3.6. Центр давления и аэродинамический фокус.
Средняя аэродинамическая хорда
Центром давления (ц.д.) называется точка на продоль-
ной оси самолета, через которую проходит линия действия полной
I
Рис. 3.12. Определение средней аэ-
родинамической хорды (САХ)
аэродимической силы самолета.
Аэродинамическим фо-
кусом самолета (по углу
атаки) называется точка на
продольной оси самолёта, в ко-
торой приложено приращение
подъемной силы, вызванное ма-
лым изменением угла атаки. Ины-
ми словами, момент тангажа от-
носительно оси, проходящей че-
рез фокус, остается неизменным
при малых изменениях угла ата-
ки. В общем случае фокус не
совпадает с центром давления.
Введение понятия фокуса на-
ряду с понятием центра давления
обусловлено тем, что центр дав-
ления для самолета может зна-
чительно изменять свое положе-
ние при изменении угла атаки, в
то время как фокус сохраняет
неизменным свое положение, осо-
бенно на малых углах атаки.
Координаты центра давления
хц. д, фокуса хр и центра масс
Хц. т обычно отсчитываются от
носка средней аэродинамической
хорды (САХ). Средняя аэродинамическая хорда —
это осредненная по площади хорда крыла
».='’c„=4Vw's- (3-22)
где Ь'— хорда сечения крыла.
62
Таким образом, САХ представляет собой хорду некоторого пря-
моугольного крыла, эквивалентного по площади рассматривае-
мому крылу произвольной формы в плане (рис. 3.12). Введение
САХ упрощает сравнительный анализ аэродинамических харак-
теристик самолетов, имеющих крылья различной формы в плане.
Найдем положение центра давления и фокуса самолета на сред-
ней аэродинамической хорде. Рассмотрим самолет под углом ата-
Рис. 3.13. Определение положения центра давления и
фокуса на САХ
ки (рис. 3.13). В центре давления приложена нормальная сила Уь
которая относительно центра масс создает момент тангажа
^-^„-xj. (3.23)
При изменении угла атаки меняется величина нормальной силы
и положение центра давления хц.д, что затрудняет определение
момента тангажа по выражению (3.23). Определение этого момен-
та удобнее производить, воспользовавшись понятием аэродинами-
ческого фокуса, положение которого (координата Хг) и момент
Мго относительно которого не зависят от угла атаки (в пределах
плавного обтекания). Следовательно,
Мг = 4- Kj (хц. т — xF).
При не очень больших углах атаки подъемная сила практиче-
ски равна нормальной (У ~У1), поэтому можно записать:
Мг = Мг>+ Г(хц.т-хД (3.24)
Выразим подъемную силу и момент через аэродинамические ко-
эффициенты Y = CvqS\ Мг = m^Sb^ Мге = tn^qSb^ и введем
безразмерные координаты хЦеТ = -у^-; хР==-^-. В результате
получим:
тг — тг, + Су 'Лц. т ~ (3.25)
63
Между положением фокуса и центра давления существует
связь. Для ее установления определим момент относительно фо-
куса
— Y (хц> д хР)
или в безразмерном виде
Рис. 3.14. Зависимости координат центра давле-
ния и фокуса от угла атаки
Если т,г< = 0, то фокус совпадает с центром давления (хР =
= -'-ц. д)-
Построим на одном графике (рис. 3.14) зависимости Су, тг,
Хц.д и xF от угла атаки а. На линейном участке зависимостей Су
и тг от а положение фокуса не зависит от угла атаки (xp=const).
-При а = ао имеем Су = 0 и хц.д—*-±оо (в этом случае на самолет
действует пара сил). При увеличении угла атаки и коэффициента
подъемной силы по абсолютной величине центр давления стре-
мится к фокусу (Лц. д -> Хр).
Координаты центра давления и фокуса по углу атаки зависят
от формы самолета и числа М.
64
Аналогично вводятся понятия бокового центра давления и фо-
куса по углу скольжения. Под боковым центром давле-
ния понимается точка приложения боковой силы, а под фоку-
сом по углу скольжения — точка приложения ее прира-
щения при изменении угла скольжения р. Поскольку самолет сим-
метричен относительно плоскости Оху, то фокус по углу скольже-
ния совпадает с боковым центром давления.
Глава 4
АЭРОДИНАМИКА ЧАСТЕЙ САМОЛЕТА
§ 4.1. Теорема Н. Е. Жуковского о подъемной силе крыла
Теорема Н. Е. Жуковского о подъемной силе устанавливает
связь между подъемной силой и циркуляцией скорости.
2 з .
’
Рис. 4.1. Вывод формулы Н. Е. Жуковского
Рассмотрим обтекание крыла бесконечного размаха несжимае-
мым потоком невязкого воздуха (рис. 4.1). У такого крыла кар-
тина течения во всех сечениях одинакова, поэтому достаточно ис-
следовать подъемную силу, приходящуюся на единицу размаха
крыла.
Выделим в движущемся относительно крыла воздухе на до-
статочно большом удалении от крыла контур 1—2—3—4' Пусть
отрезки 1—2 и 3—4 этого контура перпендикулярны невозмущен-
ному потоку, а отрезки 2—3 и 4—1 параллельны ему. Вычислим
циркуляцию скорости по выделенному контуру
= Л-2 + ^-З + Л-4 + Л-Z*
Так как стороны рассматриваемого контура расположены на
достаточно большом расстоянии от крыла, то можно считать, что
течение воздуха вдоль линий 1—2 и 3—4 отсутствует. Поэтому
Л-2= Л-4 О*
3—21 65
Определим циркуляцию скорости на отрезках 2—3 и 4—li
=
Тогда
/=,1 (V^-V^dl.
Представим скорости на отрезках 2—3 и 4—1 через скорость
невозмущенного потока V и возмущенные крылом скорости:
^2-3 = ^ + ^2-3’ ^4-1 + V4-r
С учетом этого циркуляция скорости по контуру 1—2—3—4
'= J ("г-.М)
Найдем подъемную силу к^рыла. В соответствии с третьим за-
коном Ньютона она равна силе, действующей на воздух вдоль
оси Оу. Пусть р2_3 и p4_j — давления, действующие на верхний
и нижний участки контура. Тогда подъемная сила, приходящаяся
на единицу размаха, будет
= f (Р4-1 Р2-3) dt-
Для несжимаемого воздуха, движущегося вдоль отрезков 2—3
и 4—/, запишем уравнение Бернулли (2.24):
Р2_3 Ч--§---= COnst;
Р 4—1 + —= const.
Отсюда найдем разность давлений:
- Р^, = f (Ии - И-,) = f + v<^ (У>-> ~
Учтем, что
^2-3 Ч" 4—1 = Ч~ ®2-3 Ч~ V4-r V2-3 4-1 = ®2-3 ^4—1'
Тогда
Р4-1 Рг-З = (^2-3 + ~2~ (V2-3 ^4-7)
Й
У = J dl + 4- J dl.
В соответствии с уравнением (4.1) первый интеграл в полу*
ценном выражении представляет собой циркуляцию скорости по
рассматриваемому контуру.
66
Будем неограниченно удалять отрезки 2—3 и .4—1 от крыла.
Тогда добавочные скорости и т^__7 будут стремиться к нулю,
при этом будет стремиться к нулю и второй интеграл, а первый
интеграл в соответствии с теоремой Стокса будет оставаться ко-
нечной величиной, не зависящей от формы контура.
Следовательно, для подъемной силы получаем выражение
r=pV/. (4.2)
Это и есть формула Н. Е. Жуковского. В соответствии с ней
подъемная сила крыла, приходящаяся на единицу размаха, в
установившемся потоке идеального несжимаемого воздуха равна
произведению плотности, скорости невозмущенного потока и цир-
куляции скорости вокруг крыла.
Согласно теореме Стокса циркуляция скорости по любому
замкнутому контуру равна напряжению охватываемых им вихре-
вых шнуров (/ = Г), поэтому
Г=рУГ. (4.3)
Следовательно, с точки зрения воздействия на поток крыло
эквивалентно некоторой системе вихрей.
В этом заложена идея о замене крыла системой вихрей, кото-
рые Н. Е. Жуковский назвал присоединенными (скрепленными
с крылом) в отличие от свободных вихрей, находящихся в потоке.
Теорема Н. Е. Жуковского не только объяснила механизм обра-
зования подъемной силы на крыле, связанный с циркуляцией ско-
рости, но и положила начало нового метода исследования в аэро-
динамике путем моделирования крыла вихрями (вихревого ме-
тода). К настоящему времени теорема Н. Е. Жуковского уси-
лиями многих ученых доказана для сжимаемого воздуха, для не-
установившегося движения, для самолета в целом и для других
более сложных случаев.
§ 4.2. Влияние геометрических параметров крыла
на его аэродинамические характеристики
Проанализируем влияние удлинения X, угла стреловидности х
и сужения т] на аэродинамические характеристики крыла.
Важной характеристикой крыла является распределение подъ-
емной силы по размаху, которое характеризуется коэффициентом
подъемной силы сечений С'у. У крыла бесконечного,размаха во
всех его сечениях условия обтекания и картина распределения
давления одинаковы, поэтому коэффициент Су по размаху не
изменяется (рис. 4.2, z = 2zi//— безразмерная координата). На
крыле конечного размаха из-за разности давлений на нижней и
верхней поверхностях воздух перетекает через боковые кромки
с нижней поверхности на верхнюю (рис. 4.3). Это вращательное
движение воздуха продолжается и за крылом, образуя два кош
3* 67
цевых вихря, которые можно наблюдать в аэродинамических тру-
бах и в полете.
Вследствие концевых перетеканий воздуха давления на ниж-
ней и верхней сторонах крыла стремятся выравняться (давление
на нижней стороне уменьшается, а на верхней возрастает). Это
Рис. 4.2. Влияние удлинения крыла
на распределение коэффициентов
подъемной силы сечений по размаху
выравнивание давления наблюдается не только непосредственно на
концах крыла, но и распространяется на его срединные сечения.
В результате наибольшее значение коэффициента С'у у прямо-
угольного крыла имеет место в корневом сечении, при приближе-
Рис. 4.3. Перетекание воздуха через боковые
кромки крыла конечного размаха
нии к концам крыла коэффициент С уменьшается, а непосред-
ственно на концах обращается в нуль (рис. 4.2). Чем меньше
удлинение ^рыла X, тем значительнее уменьшение коэффициента
С'у сечений, так как влияние концевых перетеканий воздуха
распространяется на относительно большую часть площади
крыла.
Рассмотрим влияние угла стреловидности крыла х на распре-
деление Су по размаху. Разложим вектор скорости набегающего
потока V на две составляющие: нормальную к передней кромке
68
Vn=Vcos% и тангенциальную VrT==I/sinX (рис. 4.4). Проана-
лизируем поведение струек газа на поверхности стреловидного
крыла. Возьмем вначале сечение, удаленное как от конца крыла,
так и от его центральных сечений. При движении частиц воздуха
в этом сечении тангенциальная составляющая скорости VT
остается неизменной, а изменяется т
лишь нормальная составляющая
Vn, при этом изменяется как вели-
чина, так и направление полной
скорости потока.
При приближении к передней
кромке поток тормозится, нормаль-
ная скорость Vn уменьшается и по-
ток поворачивает к концевым сече-
ниям. Далее поток на верхней по-
верхности разгоняется вследствие
сужения струек, нормальная ско-
рость возрастает и достигает макси-
мальной величины в точке наи-
большей толщины, а струйки раз-
ворачиваются к центральным сече-
ниям. По мере приближения к зад-
ней кромке поток опять тормозится
вследствие расширения струек, ско-
рость Vn уменьшается, а струйка
опять разворачивается к концевым
сечениям, к исходному направлению
невозмущенного потока. В результа-
те линии тока в рассматриваемом
Рис. 4.4. Особенности обтека-
ния стреловидного крыла
сечении стреловидного крыла име-
ют вид, изображенный на рис. 4.4.
Описанная картина течения воздуха, определяемая эффектом
скольжения потока, наблюдается только в средней части полу-
крыльев (область //), в центральном и концевых сечениях проис-
ходит распрямление струек (области / и ///). При этом в области/
имеет место расширение струй на верхней поверхности в передней
части крыла, увеличение на ней давления и падение коэффициента
Су, а в области /// под влиянием внешнего потока — поджатие
струй, уменьшение давления на верхней поверхности и возраста-
ние коэффициента С'у (рис. 4.5). Чем больше угол стреловидности
крыла, тем сильнее проявляются эти эффекты (срединный и кон-
цевой), тем более значительно перераспределяется подъемная
сила по размаху стреловидного крыла.
Качественно аналогично стреловидности влияет на распреде-
ленные характеристики крыла его сужение. Уменьшение хорд к
концам крыльев с сужением ц приводит к увеличению коэффици-
ентов Су в концевых сечениях. Если при этом крыло имеет
стреловидную переднюю кромку, то дополнительное влияние на
69
распределение Су по размаху оказывает и стреловидность крыла
У треугольных крыльев (т] = оо) коэффициент Су в концевых се
чениях теоретически стремится к бесконечным значениям (в дей
ствительности он ограничен из-за срыва потока).
Рис. 4.5. Влияние угла стреловид-
ности крыла на распределение коэф-
фициентов подъемной силы сечений
по размаху
Рис. 4.6. Зависимость коэффициен-
та Су крыла от его удлинения X
Рассмотрим влияние геометрических параметров крыла на его
суммарные аэродинамические характеристики: коэффициенты
подъемной силы, лобового сопротивления и координату фокуса.
Рис. 4.7. Зависимость безразмерной
координаты фокуса крыла от его
удлинения
Несущие свойства и положение
фокуса у крыльев сильно зависят
от удлинения. У крыла бесконеч-
ного удлинения (Z = oo) коэффи-
циент Су имеет наибольшее зна-
чение, теоретически равное в не-
сжимаемом потоке 2л, а фокус
у этого крыла располагается на
расстоянии одной четверти хорды
от ее носка (л> = 0,25). С умень-
шением удлинения возрастает
влияние перетекания воздуха че-
рез боковые кромки и коэффи-
циент Су уменьшается (рис. 4.6), а фокус смещается вперед (коор-
дината Xf уменьшается, рис. 4.7).
Смещение фокуса вперед при уменьшении удлинения объяс-
няется тем, что в этом случае крыло все больше удлиняется по
потоку, увеличивая область перетекания потока и выравнивания
давлений на нижней и верхней поверхностях крыла. Поскольку
основная деформация струй (поворот потока) при обтекании
70
крыла осуществляется в его носовой части, то аэродинамическая
нагрузка все больше сосредотачивается вблизи передней кромки.
Как было показано выше, эффект скольжения у стреловидных
крыльев наиболее сильно проявляется в средней части полукрыль-
ев, где при увеличении угла стреловидности х подъемная сила
уменьшается, так как уменьшается нормальная составляющая
Рис. 4.8. Влияние удлинения и уг-
ла стреловидности крыла на коэф-
фициент Су
Рис. 4.9. Зависимость безразмерной
координаты фокуса крыла от угла
стреловидности
скорости Vn, которая и определяет эпюру давления в сечении.
Что касается корневого и концевых сечений стреловидного кры-
ла, то уменьшение подъемной силы в корневых сечениях в извест-
ной мере компенсируется ее увеличением в концевых. Поэтому
влияние угла стреловидности % на коэффициент зависит от
удлинения: чем меньше удлинение крыла, тем меньше роль сред-
ней части половин крыльев, тем слабее зависит коэффициент С*
от угла %, и наоборот (рис. 4.8).
Как известно, при увеличении стреловидности нагрузка в кор-
невых сечениях крыла уменьшается, а в концевых, сдвинутых на-
зад,— увеличивается (рис. 4.5). Поэтому фокус крыла при уве-
личении его стреловидности смещается назад (координата xf воз-
растает, рис. 4.9).
При изменении сужения г] нестреловидного крыла аэродина-
мическая нагрузка перераспределяется по размаху, поэтому ко-
эффициент С® изменяется незначительно, а фокус при увеличе-
нии т] несколько смещается назад вследствие роста коэффициен-
та Су в концевых сечениях.
Относительная толщина крыла сравнительно слабо влияет на
его аэродинамические характеристики при малых дозвуковых ско-
71
ростях, а кривизна профиля и крутка крыла оказывают влияние
на угол «о и коэффициент тг .
Исследования показывают, что форма крыла при малых ско-
ростях слабо влияет на коэффициент определяемый в этом
случае в основном силами трения, но оказывает существенное
Рис. 4.10. Влияние удлинения крыла
на его поляру
Рис. 4.11. Влияние угла стреловид-
ности крыла на его поляру
влияние на коэффициент А и, следовательно, на коэффициент со-
противления Cxi, обусловленного подъемной силой. С уменьшением
удлинения и увеличением угла стреловидности коэффициенты А
и CXi возрастают, так как уменьшаются несущие свойства
и подсасывающая сила (Ст) из-за уменьшения разрежения на
передней кромке. При наличии у крыла сужения подсасывающая
сила также уменьшается и коэффициенты А и CXi возрастают.
На рис. 4.10 и 4.11 показано влияние удлинения и стреловидности
крыла на его поляру.
§ 4.3. Влияние чисел М и Re на аэродинамические
характеристики крыла
Рассмотрим влияние сжимаемости (числа М) на обтекание и
аэродинамические характеристики крыла. Начнем этот анализ с
обтекания профиля. На рис. 4.12 приведены фотографии потока
около профиля и диаграммы распределения коэффициентов дав-
ления по его верхней (рв) и нижней (рн) поверхностям при раз-
личных числах М. При малых числах М влияние сжимаемости
несущественно (при изменении давления плотность практически
не изменяется). Поэтому картина распределения коэффициентов
72
давления по профилю одинакова (М = 0-ь0,4 на рис. 4.12,а). При
дальнейшем увеличении числа М начинает сказываться уменьше-
ние плотности. На верхней поверхности профиля при положитель-
ном угле атаки скорость возрастает, давление падает, следова-
тельно, в сжимаемом потоке уменьшается плотность. За счет
уменьшения плотности вследствие неразрывности потока проис-
ходит дополнительное увеличение скорости, а следовательно, до-
полнительное уменьшение давления (М = 0,6 на рис. 4.12,а). На
нижней поверхности, наоборот, поток тормозится, давление и
плотность возрастают и за счет увеличения плотности происходит
дополнительное уменьшение скорости, а следовательно, дополни-
тельное увеличение давления. Чем больше число М, тем больше
дополнительно изменяются давления на нижней и верхней поверх-
ностях профиля. В результате увеличивается коэффициент подъ-
емной силы.
Такая картина обтекания наблюдается при М<Мкр. Если
М>МКр, то вблизи поверхности крыла возникает область сверх-
звукового течения, которая заканчивается местным скачком уплот-
нения (рис. 4.12,6, М = 0,75). В сверхзвуковой зоне скорость по-
тока и разрежения возрастают, а за скачком резко уменьшаются.
При положительном угле атаки (а>0) местный скачок вначале
появляется на верхней поверхности. С увеличением числа М раз-
меры сверхзвуковой зоны возрастают, а скачок на верхней поверх-
ности смещается к задней кромке. При некотором числе М сверх-
звуковая зона обтекания и местный скачок появляются на нижней
поверхности и на ней в сверхзвуковой зоне уменьшается давление
из-за увеличения скорости потока (рис. 4.12, в, М = 0,8). При уве-
личении числа М скачок на нижней поверхности быстрее сме-
щается к задней кромке, чем на верхней (рис. 4.12, г, М = 0,85).
При некотором числе М<1 нижний скачок стабилизируется вбли-
зи задней кромки (рис. 4.12,6, М = 0,9). Последующее увеличение
числа М. вызывает дальнейшее смещение верхнего скачка к зад-
ней кромке. При числе М, несколько большим 1, верхний скачок
оказывается на задней кромке, а перед профилем образуется ото-
шедший головной скачок (рис. 4.12,е, М=1,05). Пик разрежения
на верхней поверхности смещается к задней кромке, возрастает
давление на передней кромке (за головным скачком). На сверх-
звуковых скоростях (М>1) увеличение числа М приводит к
уменьшению углов наклона скачков и размеров возмущенной об-
ласти. Из-за сильного уменьшения плотности (рис. 2.7) безраз-
мерные аэродинамические коэффициенты падают.
Как видно из рис. 4.12,6 и в, при увеличении числа М>Мкр
в передней части профиля коэффициенты разрежения на верхней
поверхности уменьшаются. Это объясняется тем, что в этой обла-
сти течение является сверхзвуковым и происходит сильное умень-
шение плотности.
Такой характер обтекания профиля сжимаемым потоком, осо-
бенно при М>Мкр, получивший название волнового кризиса, су-
щественно влияет на аэродинамические характеристики. За счет
73
Рис. 4.12. Фотографии потока и диаграммы распределения
влияния сжимаемости коэффициент возрастает (рис. 4.13)
тем сильнее, чем больше число М. Для его оценки у крыла бес-
конечного размаха можно использовать формулу
f?a__
у 1Л1 - М2 *
Рис. 4.13. Зависимость коэффициента С* про-
филя от числа М
При М>Мкр этот рост становится более интенсивным вслед-
ствие дополнительного разрежения потока в сверхзвуковой зоне
на верхней поверхности. При появлении сверхзвуковой зоны и
74
коэффициентов давления по профилю при различных
числах М
местного скачка на нижней поверхности рост С® при увеличе-
нии М замедляется и затем вследствие более быстрого смещения
нижнего скачка к задней кромке коэффициент падает. После
стабилизации нижнего скачка на задней кромке при увеличении М
коэффициент Су снова возрастает вследствие расширения сверх-
звуковой зоны сверху. При М=1 коэффициент С“ достигает мак-
симального значения, а при увеличении М на сверхзвуковых ско-
ростях монотонно уменьшается вследствие сильного уменьшения
плотности. Для тонкого профиля на сверхзвуковых скоростях
Са—
у ум2 — 1 ’
(4.5)
Что касается подъемной силы Y==CySpV2/2) то она с увеличе-
нием числа М возрастает как на дозвуковых, так и на сверхзву-
ковых скоростях вследствие роста скоростного напора.
Как было показано выше, при М>Мкр с увеличением М зоны
разрежения смещаются на профиле к задней кромке. Это вызы-
вает появление дополнительного так называемого волнового со-
противления (рис. 4.14). Действительно, смещение назад зоны
разрежения как на верхней, так и на нижней поверхностях про-
филя (рис. 4.12, б) приводит при М>Мкр к появлению составляю-
щей от сил давления, направленной назад, на увеличение
сопротивления.
75
При наличии волнового сопротивления коэффициент С опре-
деляется по формуле
Рис. 4.14. Зависимость коэффициента CXq профиля
от числа М
Вследствие уменьшения разрежения на носке профиля умень-
шается подсасывающая сила, возрастает коэффициент А (рис. 4.15)
и сопротивление, обусловленное подъемной силой. В результате
Рис. 4.15. Зависимость коэффициен-
та Л крыла от числа М
роста коэффициентов Сх и А при М>Мкр резко уменьшается
максимальное аэродинамическое качество Ктах (рис. 4.16).
Рис. 4.16. Зависимость максимального аэродинамиче-
ского качества крыла от числа М
76
Вследствие смещения к задней кромке зон разрежения при
М>МКр фокус также смещается назад (рис. 4.17). На сверхзву-
ковых ^скоростях фокус занимает более заднее положение (у про-
филя л> = 0,5), коэффициент Сх при увеличении числа М посте-
пенно уменьшается вследствие уменьшения коэффициентов дав-
Рис. 4.17. Зависимость без-
размерной координаты фокуса
крыла от числа М
Рис. 4.18. Влияние относительной толщи-
ны крыла на зависимость его коэффициен-
та Сх от числа М
ления, а коэффициент А продолжает расти вследствие уменьшения
коэффициента С* (рис. 4.13). Максимальное аэродинамическое
качество при этом продолжает несколько уменьшаться.
Коэффициент волнового сопротивления профиля на сверхзву-
ковых скоростях определяется по формуле
<4-7)
где с — относительная толщина профиля, k — коэффициент, зави-
сящий от его формы. Волновое сопротивление профиля при М>1
зависит от формы носка. Если носок острый, то образуется при-
соединенный скачок (рис. 2.10), если закругленный, то скачок
отошедший (рис. 2.11). А за отошедшим скачком давление повы-
шается в большей степени, чем за присоединенным, поэтому про-
филь с закругленным носком имеет большее волновое сопротив-
ление, чем с острым.
На критическое число М и явления волнового кризиса сущест-
венное влияние оказывает толщина крыла, его стреловидность и
удлинение. С уменьшением относительной толщины и удлинения
и увеличением стреловидности число Мкр возрастает (так как
уменьшаются скорости обтекания крыла и разрежения на его по-
верхности), а волновое сопротивление уменьшается (рис. 4.18—
4.20), при этом аэродинамические характеристики крыла и само-
лета в целом по числам М изменяются более плавно; в меньшей
77
степени изменяются коэффициенты и А, максимальное аэро-
динамическое качество /Стах, уменьшается смещение фокуса на-
Рис. 4.19. Влияние удлинения
крыла на зависимость его
коэффициента CXq от числа М
Рис. 4.20. Влияние угла стреловидности
крыла на зависимость его коэффициента
С Vq от числа М
Аэродинамические характеристики крыльев на сверхзвуковых
скоростях зависят от характера обтекания их кромок. Рассмотрим
стреловидное крыло (рис. 4.21). Кромка крыла называется до-
звуковой, если нормальная составля-
ющая скорости меньше скорости зву-
ка (Vn<.a), звуковой, если Vn = a, и
сверхзвуковой, если 14>а. Проведем
из вершины крыла конус возмущений
с углом полураствора р, = агс sin 1/М.
Если кромка крыла находится внутри
конуса возмущений, она является до-
звуковой, если вне, сверхзвуковой.
Звуковая кромка совпадает с образу-
ющей конуса (характеристикой). Дей-
ствительно, нормальная к характери-
стике скорость потока равна скорости
звука. Поэтому при любом числе М>
>1 боковая кромка всегда дозвуко-
вая, а характер обтекания передней и
задней кромок зависит от их стрело-
видности. Показанное на рис. 4.21
крыло имеет дозвуковую переднюю и
сверхзвуковую заднюю кромки. При
изменении числа М характер обтека-
ния кромок может изменяться.
Перетекание потока с образованием подсасыващей силы воз-
можно только на дозвуковой кромке. Сверхзвуковая кромка не
обтекается, поток на ней раздваивается и подсасывающая сила
на ней не образуется.
Вязкость воздуха (число Re) при малых углах атаки оказы-
вает заметное влияние лишь на коэффициент сопротивления тре-
78
ния гфыла (рис. 2.22), т. е. на коэффициент Сх (при увеличе-
нии Re коэффициент Сх несколько уменьшается), а на других
характеристиках (Су, TcF и т- п.) практически не сказывается.
Ниже будет рассмотрено влияние вязкости (числа Re) на обте-
кание крыла при больших углах атаки.
Анализируя аэродинамические характеристики крыльев в ши-
роком диапазоне чисел М, можно сделать следующие выводы. На
малых дозвуковых скоростях целесообразно иметь нестреловид-
ное крыло большого удлинения с закругленной передней кромкой.
П,ри переходе к трансзвуковым скоростям необходимо уменьшать
удлинение и относительную толщину, увеличивать стреловидность
и переднюю кромку выполнять закругленной. На сверхзвуковых
скоростях выгодно применять крылья малого удлинения и боль-
шой стреловидности, с малой относительной толщиной, с^ за круг-
ленной передней кромкой, если она дозвуковая, и с острой, если
она сверхзвуковая. На больших сверхзвуковых скоростях форма
Крыла в плане существенно не влияет на его аэродинамические
характеристики.
Таким образом, для каждого числа М необходимо иметь свою
оптимальную форму крыла. Это можно в определенной степени
обеспечить применением крыла изменяемой в полете стреловид-
ности.
§ 4.4. Аэродинамические характеристики крыльев
на больших углах атаки
Как показано в гл. 3, при увеличении угла атаки начиная с
некоторого угла анс. характер зависимостей аэродинамических ко-
эффициентов от угла атаки изменяется вследствие срыва потока,
при этом в большинстве случаев уменьшаются подъемная сила и
аэродинамическое качество, возрастает сопротивление, могут су-
щественно изменяться моментные характеристики по сравнению
со случаем безотрывного обтекания. Причиной отрыва потока с
крыла является взаимодействие положительного градиента дав-
ления по хорде с пограничным слоем (рис. 2.23). Характер этого
взаимодействия определяется геометрической формой крыла (фор-
мой профиля и формой гфыла в плане), углом атаки, состоянием
пограничного слоя (числом Re), числом М и другими факторами.
При этом отрыв потока может происходить как с поверхности
крыла, так и с его кромок. При отрыве потока с верхней поверх-
ности крыла на ней существенно уменьшается разрежение, а сле-
довательно, и коэффициент подъемной силы крыла. Отрыву пото-
ка с поверхности крыла способствует образование местных скач-
ков, которые вызывают волновой срыв (рис. 2.24).
У крыла бесконечного размаха картина распределения давле-
ния и структура пограничного слоя во всех сечениях одинакова,
одинаковы и градиенты давления. Поэтому отрыв потока начи-
нается во всех сечениях одновременно при одном и том же угле
79
атаки. У крыла конечнего размаха в различных его сечениях кар-
тины распределения давления и структуры пограничного слоя
различны, поэтому отрыв потока происходит неодновременно.
Кроме того, наличие концевых перетеканий воздуха с нижней
Рис. 4.22. Определение области сры-
ва потока на крыле конечного раз-
маха
поверхности на верхнюю умень-
шает разрежение и положитель-
ные градиенты давления на верх-
ней поверхности и срыв потока
затягивается на большие углы
атаки.
Рассмотрим, как влияет фор-
ма крыла в плане на место воз-
никновения отрыва потока. До-
пустим, что известны характери-
стики профилей в сечениях кры-
ла, т. е. известна зависимость Су
от а в сечениях. В этом случае
можно построить распределение
коэффициентов подъемной силы
сечений С^н с, соответствующих
началу срыва потока в этих се-
чениях, по размаху (рис. 4.22).
Задаваясь углами атаки щ, а2,...»
ап, можно построить распределе-
ние коэффициентов Су по раз-
маху. В сечениях, гдеСу>С'н с>
имеет место срыв потока (заштри-
хованная область на рис. 4.22).
Пользуясь указанным приемом, определим наиболее вероятные
места возникновения срыва на крыльях различной формы.
У прямоугольных крыльев наибольшие значения коэффициента
Су имеют место в корневых сечениях (рис. 4.2). В этих сечениях
обычно начинается срыв потока. При увеличении угла атаки
срыв быстро распространяется на всю верхнюю поверхность.
Уменьшение удлинения приводит к затягиванию срыва на боль-
шие углы атаки (углы ан.с и акр увеличиваются).
У стреловидных крыльев наибольшие значения коэффициента
Су смещаются к концевым сечениям крыла (рис. 4.5), а коэффи-
циент Сун ск концам уменьшается из-за увеличения положитель-
ного градиента давления и перетекания пограничного слоя и его
утолщения вследствие наличия течения вдоль крыла (рис. 4.4).
Поэтому срыв потока начинается на концах стреловидного крыла
(концевой срыв).
У треугольных крыльев коэффициенты Су возрастают от кор-
невых сечений к концевым, а коэффициенты Сун с, наоборот, убы-
вают не только вследствие увеличения положительного градиента
давления и перетекания пограничного слоя, но и вследствие зна-
80
чительного уменьшения числа R'e = VT>'/v из-за уменьшения
хорд. Поэтому на треугольных крыльях концевой срыв наблю-
дается даже при сравнительно малых углах атаки.
Рис. 4.23. Образование носовых вихрей на треугольном
крыле
Тангенциальное течение от середины к концам стреловидных и
треугольных крыльев приводит к тому, что начавшийся на кон-
цах срыв потока при увеличении угла атаки сравнительно мед-
ленно распространяется затем на центральную часть этих
крыльев.
У тонких крыльев малого удлинения и большой стреловидно-
сти (например, треугольных) обтекание передних кромок анало-
гично обтеканию боковых кромок прямоугольных крыльев
(рис. 4.3). При этом отрыв потока уже на малых углах атаки про-
исходит по всей передней кромке и сопровождается образованием
спиралевидных вихревых жгутов (рис. 4.23). В этих вихревых
жгутах имеется значительное разрежение потока. В отличие от
этого при отрыве потока с передней кромки нестреловидных
крыльев (например, прямоугольных) устойчивые вихри не обра-
зуются.
Срыв потока с крыла приводит к значительному изменению
действующих на него аэродинамических сил и моментов. Если
при отрыве потока не образуются устойчивые вихри, то, как пра-
вило, такое обтекание сопровождается уменьшением подъемной
силы (наблюдается «вредный» отрыв). При наличии устойчивых
вихрей за счет разрежения в них несущие свойства крыльев по-
вышаются («полезный» отрыв). На рис. 4.24 приведены получен-
ные расчетом зависимости коэффициента нормальной силы С
от угла атаки а для случаев «вредного» отрыва (рис. 4.24, а, пря-
81
моугольное крыло) и «полезного» отрыва (рис. 4.24,6, треуголь-
ное крыло), штриховыми линиями — для безотрывного обтекания,
сплошными — для отрывного.
Рис. 4.24. Зависимости коэффициентов нормальной
силы от угла атаки:
а — прямоугольное крыло («вредный» отрыв); б — треугольное
крыло («полезный» отрыв)
Сопротивление крыла при отрыве потока возрастает, особенно
заметно при отрыве с передних кромок вследствие практически
полной потери подсасывающей силы. Однако наиболее сильное и
неблагоприятное влияние оказывает срыв потока с крыльев на
их моментные характеристики, особенно для стреловидных и тре-
угольных крыльев. Концевой срыв приводит к уменьшению подъ-
емной силы концевых сечений и всего крыла (соответствует от-
валу зависимости Су от а в точке 1 на рис. 3.5). Это равносильно
появлению дополнительного кабрирующего момента и приводит
к смещению фокуса крыла вперед. Смещение фокуса может быть
значительным, так как уменьшение подъемной силы в концевых
сечениях происходит на большом плече. Поэтому изменение коэф-
фициента момента тангажа тг (рис. 3.10) оказывается более зна-
чительным, чем изменение коэффициента подъемной силы.
Проанализируем, как влияют числа М и Re, т. е. сжимаемость
и вязкость потока, на аэродинамические характеристики крыла
при больших углах атаки. Как известно, при увеличении числа М
возрастает разрежение и положительный градиент давления на
верхней поверхности крыла, поэтому срыв потока начинается при
меньших углах атаки, уменьшаются коэффициенты Суа. с и Сутах.
При М>Мкр образование местного скачка способствует появле-
нию волнового срыва.
83
Число Re, характеризующее вязкость воздуха, влияет на срыв-
ное обтекание крыла через характеристики пограничного слоя.
При увеличении числа Re точка перехода ламинарного погранич-
ного слоя в турбулентный смещается вперед, протяженность тур-
Рис. 4.25. Влияние числа Re
на коэффициент подъемной
силы
булентного участка возрастает.
Поскольку турбулентный слой бо-
лее устойчив к отрыву, то отрыв
потока происходит при больших
положительных градиентах дав-
ления, т. е. на больших углах ата-
ки. Вследствие этого при увели-
чении числа Re величины аКр и
Су max крыла возрастают (рис.
4.25). Однако это увеличение не
может быть беспредельным. При
некотором числе Re точка пере-
хода смещается на переднюю
кромку, весь пограничный слой
гребень
Рис. 4.26. Аэродинамический
гребень на стреловидном
крыле
становится турбулентным. Дальнейшее увеличение числа Re уже
не влияет на характеристики пограничного слоя и рост «Кр и Сутзх
прекращается. Заметим, что на отрыв потока с передних кромок
число Re практически не влияет, поскольку он не связан с по-
граничным слоем.
Для борьбы с неблагоприятными последствиями срыва потока,
особенно на стреловидных и треугольных крыльях, принимаются
специальные меры. К ним относятся:
1) аэродинамическая крутка крыла, т. е. установка в конце-
вых сечениях профилей с большими значениями коэффициен-
тов с;нс;
2) геометрическая крутка крыла, которая достигается поворо-
том концевых сечений на меньшие местные углы атаки;
3) установка перегородок (аэродинамических гребней) на стре-
ловидных и треугольных крыльях (рис. 4.26), которые препятст-
вуют перетеканию пограничного слоя к концам крыла и умень-
шают коэффициенты С’у концевых сечений;
4) применение запилов, уступов, зубьев на передней кромке
крыла (рис. 4.27), которые вызывают образование над верхней
поверхностью крыла вихрей, играющих роль перегородок;
83
5) управление пограничным слоем (его турбулизация или
сдув), повышающее устойчивость к отрыву;
6) применение специальной механизации передней кромки
(предкрылков, отклоняемых носков).
Рис. 4.27. Меры борьбы с от*
рывом потока:
а — зуб; б — уступ; в — запил
§ 4.5. Особенности аэродинамических характеристик
крыльев сложной формы в плане
Основной отличительной особенностью крыльев сложной фор-
мы в плане является наличие наплыва — выступающей вперед
части, имеющей большую стреловидность и весьма малое удли-
нение по сравнению с остальным крылом. Поэтому такое крыло
гармонично сочетает в себе свойства как нестреловидных крыльев
умеренного удлинения, так и крыльев малого удлинения большой
стреловидности. Следствием этого является смешанный режим
обтекания передней кромки при М>1: на наплыве она обычно
дозвуковая, а на консольной части может быть сверхзвуковой.
Наличие консольной части малой стреловидности и умеренного
удлинения обеспечивает крылу сложной формы в плане сравни-
тельно высокие несущие свойства (значения коэффициента С“).
Как известно, при переходе от дозвуковых скоростей к сверх-
звуковым фокус крыла смещается назад, тем сильнее, чем боль-
ше удлинение и меньше стреловидность крыла. Наличие у крыла
сложной формы наплыва большой стреловидности и малого удли-
нения позволяет уменьшить смещение фокуса этого крыла при
переходе от М<1 к М>1 (рис. 4.28). Это объясняется тем, что
при переходе от дозвуковых скоростей к сверхзвуковым аэроди-
намические характеристики наплыва как крыла малого удлине-
ния большой стреловидности изменяются в меньшей степени, чем
84
характеристики консоли, в результате возрастает его роль в созда-
нии подъемной силы. Таким образом, наплыв играет стабилизи-
рующую роль в обеспечении необходимых аэродинамических ха-
рактеристик как на дозвуковых, так и на сверхзвуковых скоростях.
Этим также объясняется менее интенсивный рост волнового со-
противления у крыла сложной формы на трансзвуковых скоростях
(рис. 4.29).
Рис. 4.28. Влияние наплыва кры-
ла на смещение аэродинамиче-
ского фокуса
Рис. 4.29. Сравнение зависимо-
стей (М) для стреловидного
крыла и крыла сложной формы
в плане
Сложной формой в плане объясняется и необычный характер
распределения коэффициентов подъемной силы сечений Су по
размаху такого крыла. На наплыве закон изменения С'у по раз-
маху аналогичен крылу с большим сужением, например, треуголь-
ному, а на консоли — нестреловидному крылу большого удлине-
ния. В результате на крыле сложной формы в плане наибольшие
значения С’у имеют место обычно вблизи стыка консоли с на-
плывом (излома передней громки). Здесь же наблюдаются и наи-
большие положительные градиенты давления, вызывающие отрыв
потока с верхней поверхности крыла: при увеличении угла атаки
он обычно начинается на консоли вблизи излома. При увеличении
числа М полета в этих сечениях впервые появляются и местные
скачки уплотнения. Если консоль имеет значительную стреловид-
ность, то отрыв потока и местные скачки уплотнения вначале
возникают вблизи концов консолей (как на обычном стреловидном
крыле).
Местной отрыв потока на консоли, усиленный на больших до-
звуковых скоростях волновым срывом (влиянием местных скач-
ков), оказывает неблагоприятное влияние на зависимости коэф-
фициентов Су и mz от угла атаки а.
Влиянием наплыва объясняется и другая характерная особен-
ность обтекания крыла сложной формы в плане на больших углах
атаки. Вследствие большой стреловидности передней кромки на-
плыва на ней, как и на треугольном крыле (рис. 4.23), происходит
85
перетекание потока с нижней поверхности на верхнюю и образо-
вание двух вихревых жгутов (рис. 4.30). Поскольку при положи-
тельном угле атаки эти вихри проходят над верхней поверхностью
крыла, а внутри их имеется значительное разрежение потока, то
Рис. 4.30. Образование носовых вихрей на наплыве крыла
сложной формы в плане и их влияние на распределение аэ-
родинамической нагрузки по размаху
под их влиянием аэродинамические нагрузки тфыла возрастают,
увеличивается подъемная сила. Наблюдается положительный эф-
фект отрыва потока. Однако, как будет показано ниже, эти вихри
могут оказывать отрицательное влияние на обтекание горизон-
тального и вертикального оперений.
§ 4.6. Аэродинамические характеристики оперения
и рулевых органов
По своей геометрической форме горизонтальное оперение пред-
ставляет собой крыло, но меньших размеров, а вертикальное опе-
рение— полукрыло или крыло несимметричной формы при наличии
нижнего киля (гребня). Поэтому аэродинамические характери-
стики изолированных оперений аналогичны характеристикам
крыльев. На обтекание оперения, особенно хвостового, существен-
ное влияние могут оказывать крыло и фюзеляж. Это влияние, ко-
торое может быть как положительным, так и отрицательным, бу-
дет подробно рассмотрено в следующей главе.
Создание управляющих моментов осуществляется на самолете
путем отклонения рулевых органов (рулей высоты и направления,
элеронов, элевонов, управляемого, переставного и дифференци-
ально отклоняемого стабилизатора, интерцепторов). Рассмотрим
прежде всего рулевые органы, установленные в кормовых частях
86
крыла (оперения), а именно рули высоты, направления, элероны,
элевоны.
Принцип их действия рассмотрим на примере руля высоты
(рис. 4.31). При отклонении руля вниз на некоторый угол бв про
исходит изменение кривизны профиля горизонтального оперения,
Рис. 4.31. Принцип действия руля и влияние на его эффектив-
ность числа М
увеличивается разрежение на верхней поверхности оперения, воз-
растает давление на нижней поверхности, а аэродинамическая на-
грузка по хорде распределяется так, как показано на рис. 4.31, а.
Если суммарную подъемную силу оперения обозначить Уг. о, то
момент тангажа, создаваемый оперением относительно центра
масс самолета, будет:
214^= Уг.0^г. о»
где £г. о — плечо горизонтального оперения, равное расстоянию
между его фокусом и центром масс самолета.
Подъемную силу оперения выразим через ее коэффициент, ско-
ростной напор и площадь:
ру2 о
Кг. О ===: Су г. О^Г. О ^Г. О» Яг. О 2 *
Следовательно,
^2 = Су Г4 0<7г, 0^г, о^Г. О*
Перейдем к безразмерному коэффициенту т2, разделив момент
на скоростной напор невозмущенного потока q, площадь крыла S
и среднюю аэродинамическую хорду &а. Получим
=== Су г, о^г. о^г. о* (4.8)
где Дг. 0 — Sr. 0£r, — относительный статический момент пло-
щади горизонтального оперения, kr, o = qr. 0/q— коэффициент тор-
можения потока в области горизонтального оперения.
Поскольку при безотрывном обтекании коэффициент Су г,0 ли-
87
неино зависит от угла атаки горизонтального оперения аг.о и
угла отклонения руля высоты дв, то можно записать:
Су Г. О == Су г> 0«г. о + Су г. 0Вв.
Вынося за скобку С“г 0, получим:
Су г. о = С® г 0 (аГв 0 + ^в^в)’ (4*9)
где пв = С5уг О/С*г 0 — коэффициент относительной эффективности
руля высоты.
Коэффициент пв показывает, какому изменению угла атаки
горизонтального оперения эквивалентно с точки зрения изменения
подъемной силы отклонение руля высоты на один градус. Вели-
чина коэффициента эффективности руля высоты зависит от соот-
ношения площадей руля высоты SB и горизонтального оперения
Sr. о и числа М полета.
На дозвуковых скоростях полета (М<МКр) при отклонении
руля высоты происходит изменение аэродинамической нагрузки
не только на самом руле, но и на поверхности оперения, располо-
женной впереди руля (рис. 4.31,а). Коэффициент эффективности
руля высоты пв на этих режимах полета наибольший.
На трансзвуковых скоростях (Мкр<М<1) на оперении перед
рулем образуются местные скачки уплотнения, вследствие чего
при отклонении руля аэродинамическая нагрузка изменяется
только на руле и той части оперения, которая находится за скач-
ком уплотнения (рис. 4.31,6), так как возмущения через скачок
вперед не передаются. Эффективность руля высоты существенно
уменьшается.
И, наконец, при отклонении руля высоты на сверхзвуковых
скоростях полета нагрузка изменяется только на самом руле
(рис. 4.31,в), так как возмущения в сверхзвуковом потоке вперед
не распространяются, и коэффициент эффективности руля имеет
наименьшее значение пв = SB/Sr. 0.
Подставив значение коэффициента подъемной силы оперения
(4.9) в формулу (4.8), для коэффициента момента, создаваемого
горизонтальным оперением, получим
^Z = Су г. О Д'- О^Г. о (аг. о ^Лв)‘ (4. Ю)
Продифференцируем выражение (4.10) по SB
== - Су г. О^г. О^г. (Л1* (4.1 1)
Зависимость коэффициента tn* от числа М показана на
рис. 4.32. Как видно, она определяется характером изменения
по числам М коэффициентов Cjr.o и
Из-за очень низкой эффективности на сверхзвуковых скоростях
полета на современных маневренных самолетах рули высоты за-
менены полностью управляемыми стабилизаторами или перестав-
88
ными стабилизаторами с рулем высоты. При отклонении или пе-
рестановке стабилизатора (пв=1) аэродинамическая нагрузка из-
меняется на всей его поверхности как на дозвуковых, так и на
сверхзвуковых скоростях полета, а эффективность стабилизатора
определяется по формуле
Рис. 4.32, Зависимость коэффициента т* от
числа М
(4.12)
Эффективность руля направления по аналогии с уравнением
(4.11) можно определить коэффициентом
^уН “ Cz В. о^в. (Лв. о^н» (4*13)
где Дв. o = Sb. о/в. ol(Sl)—относительный статический момент пло-
щади вертикального оперения; SB. о — площадь вертикального опе-
рения; /в. о — его плечо, равное расстоянию между фокусом верти-
кального оперения и центром масс; £в.о — #в. о/# —коэффициент
торможения потока в области вертикального оперения; ин =
==С^нв JCzb. ° — коэффициент относительной эффективности руля
направления.
Для коэффициента эффективности элеронов можно получить
выражение
Су кр^э^э» (4.14)
где #э~Су9кр/Су кр — коэффициент относительной эффективности
элеронов, z3 = 2z3ll —относительная координата точки прило-
жения силы Уэ на полукрыле при отклонении элеронов (зависит
от формы крыла и элеронов, их расположения и числа М).
Чем меньше удлинение и больше стреловидность крыла (опе-
рения), тем меньше эффективность рулей. Так, увеличение стре-
ловидности крыла существенно снижает эффективность элеронов
89
(рис. 4.33). Поэтому на некоторых маневренных самолетах вместо
элеронов или в дополнение к ним используют дифференциальное
отклонение («ножницы») управляемого стабилизатора. В этом
случае левая и правая половины стабилизатора отклоняются на
разные углы, создавая момент тирена Мх.
Однако в некоторых случаях «ножницы» стабилизатора ока-
зываются недостаточно эффективными. В частности, у самолетов
с крылом изменяемой в полете стреловидности при малой стрело-
Рис. 4.33. Влияние стре-
ловидности крыла на
эффективность элеро-
нов
Рис. 4.34. Принцип действия
интерцептора
видности консолей вместе с «ножницами» стабилизатора исполь-
зуются интерцепторы. Они представляют собой тонкие длинные
поверхности, устанавливаемые на верхней стороне крыла ближе
к задней кромке. При отклонении интерцептора на достаточно
большие углы происходит срыв потока с его кромки и повышение
давления перед ним вследствие торможения потока (рис. 4.34).
В результате на той половине крыла, на которой интерцептор от-
клонен, подъемная сила уменьшается, а из-за разности подъемных
сил левой и правой половин крыла возникает момент крена А4ХИнт.
При увеличении стреловидности крыла эффективность интерцеп-
торов, как и элеронов, снижается, а неблагоприятное влияние на
обтекание горизонтального оперения увеличивается, поэтому при
повороте консолей назад интерцепторы постепенно выключаются
из работы, а эффективность «ножниц» ^стабилизатора в этой кон-
фигурации оказывается достаточной.
Следует иметь в виду, что при отклонении элеронов, как и
«ножниц» стабилизатора, кроме момента крена возникает и мо-
мент рыскания, а отклонение руля направления сопровождается
возникновением не только момента рыскания, но и некоторого мо-
мента крена. Поэтому коэффициенты управляющих моментов при
отклонении рулевых органов определяются по формулам:
тх = //фз9 + т^он; (4.15)
Шу =* т8у»8н +• Wy’B9; (4.16)
тг = т^в. (4.17)
90
Если вместо элеронов используются интерцепторы и дифферен-
циальное отклонение стабилизатора, а вместо руля высоты —
управляемый стабилизатор, то:
(4.18)
тх = тх и + + п?»Ъя,
my = tnvw-\- mfo 4- /Пу»8и;
(4.19)
(4.20)
ОСЬ /
руль
6
'^"-Триммер
. nv. 4.35. Образование
шарнирного момента
руля и способы его
уменьшения:
а — осевая компенсация;
б — внутренняя компенса-
ция; в —триммер
Действующие на рулевые сфганы при их отклонении аэродина-
мические силы R создают относительно оси поворота шарнирный
момент Л4Ш, который приходится преодолевать при управлении са-
молетом. Как следует из рис. 4.35, а,
Мш == —
где а — плечо аэродинамической силы R.
Шарнирный момент характеризуется безразмерным коэффи-
циентом
_ __
1П
(4.21)
где 5Р и Ьр — площадь и хорда руля.
Коэффициент шарнирного момента, например руля высоты, за-
висит от угла атаки горизонтального оперения аг. о и угла откло-
нения руля, поэтому его можно записать в виде
= тща + т^- ° «г. 0 + 8В. (4.22)
Коэффициенты тш0, та^-» — дтт/да и = дтш1дЪв
зависят от формы руля и оперения, расположения оси руля, чис-
ла М. При увеличении числа М аэродинамический фокус руля,
91
как и тфыла, смещается назад, вследствие чего шарнирные мо-
менты сильно возрастают. Поэтому для их уменьшения применяют
специальные устройства — аэродинамические компенсаторы. Наи*
более часто применяются осевая и внутренняя компенсации.
Сущность осевой компенсации состоит в том, что ось враще-
ния руля смещается назад и уменьшается плечо а (рис. 4.35, а).
Внутренняя компенсация достигается тем, что руль и крыло со-
единяются гибкой мембраной (рис. 4.35,6). При отклонении руля
на мембрану действует разность давлений, которая уменьшает
шарнирный момент.
На дозвуковых самолетах для управления величиной шарнир-
ного момента применяется триммер, представляющий собой не-
большой дополнительный руль, установленный в кормовой части
основного руля (рис. 4.35, в). Отклоняя триммер в сторону, про-
тивоположную отклонению руля, можно обеспечить тш = 0.
При наличии триммера коэффициент шарнирного момента руля
высоты можно представить в виде:
тш = тш0 + о«г. 0 4- т** 8В + /^р8тр;
<тр===4£-- (4.23)
Чтобы уменьшить шарнирные моменты при применении управ-
ляемых стабилизаторов, их ось вращения обычно располагается
между дозвуковым и сверхзвуковым фокусами. В этом случае при
переходе от сверхзвуковых скоростей к дозвуковым шарнирный
момент меняет знак, наступает перекомпенсация руля. Управле-
ние самолетом в этом случае возможно только с помощью руле-
вых приводов. При применении управляемого стабилизатора ко-
эффициент шарнирного момента определяется по формуле
= ^ШО + °аг. о- (4.24)
§ 4.7. Аэродинамические характеристики фюзеляжа
Фюзеляжи маневренных самолетов по форме могут быть как
близкими к телам вращения, так и отличными от них. Рассмотрим
фюзеляж в виде тела вращения (рис. 4.36). По длине его можно
разделить на три части: головную £г, цилиндрическую Ац и кор-
мовую Ак. Цилиндрическая часть имеет наибольшую площадь се-
чения SM, которое называется миделевым сечением.
Основной геометрической характеристикой фюзеляжа является
его удлинение k$ = L$/dM, где £ф — длина фюзеляжа, rfM = 2rM —
диаметр миделева сечения. Каждая часть фюзеляжа характери-
зуется своим удлинением. Кроме того, кормовая часть дополни-
тельно определяется относительной площадью донного среза
5д=5д/5м, где 5Д — площадь донного среза. У заостренной
головной части дополнительным параметром является угол полу-
92
раствора носка сог, а_у затупленной — относительный радиус за-
тупления носка ^*зат == ^зат/^м» где /*зат радиус вписанной в
носок сферы. При установке двигателя в фюзеляже последний
может быть выполнен с протоком.
Рис. 4.36. Фюзеляж в виде тела вращения и действу-
ющие на него распределенные аэродинамические силы
с
(4.25)
При обтекании фюзеляжа потоком воздуха на поверхность фю-
зеляжа действуют нормальные силы давления р и касательные
силы трения т (рис. 4.36). Введем аэродинамические коэффици-
енты сил и момента для фюзеляжа по формулам:
qSM ’ qS^ ’ ^мЛф’
При отсутствии подъемной силы на фюзеляж действует осевая
сила, которая складывается из силы трения и силы сопротивления
давления. Коэффициент сопротивления трения фюзеляжа, как и
крыла, зависит от чисел Re и М. Кроме того, он зависит от удли-
нения фюзеляжа Хф.
Сопротивление сил давления складывается из волнового и дон-
ного сопротивления, поэтому
= +СХД. (4.26)
Л ДаВЛ л 1 Л Д \ /
Волновым сопротивлением фюзеляжа называется сила, обуслов-
ленная действием давления на головную и кормовую части (ци-
линдрическая часть не создает осевой силы). Следовательно:
Сх = С 4- С . (4.27)
Х Во X В0Г 1 X В0К V /
При дозвуковых скоростях сила сопротивления сил давления
на головную и кормовую части невелика и ею можно пренебречь
(Схво^ 0). В этом случае
сх=сх^ + сх„ (4.28)
При обтекании фюзеляжа сверхзвуковым потоком образуется
головной скачок уплотнения (присоединенный или отошедший),
давление на головной части повышается. Это и является причиной
волнового сопротивления головной части.
93
При обтекании сужающейся кормовой части на ее поверхности
устанавливается пониженное давление (разрежение). На дозву-
ковых скоростях оно вызывается отрывом потока и появлением
вихревого движения (рис. 4.37,а), а при сверхзвуковых — расши-
рением потока при обтекании выпуклого угла (рис. 4.37,6). На-
Рис. 4.37. Обтекание сужающейся кормовой ча-
сти:
а — при дозвуковых скоростях; б — при сверхзвуковых
скоростях
личие разрежения на сужающейся кормовой части создает осе-
вую силу, направленную назад (волновое сопротивление кормо-
вой части).
Рис. 4.38. Образование донного сопротивления
фюзеляжа при дозвуковых скоростях
Донное сопротивление фюзеляжа вызывается разрежением за
дном. При обтекании фюзеляжа у его донного среза поток отры-
вается, образуя за дном область интенсивного вихревого движе-
ния с пониженным давлением (рис. 4.38). Кроме того, сорвав-
шийся с фюзеляжа поток эжектирует воздух из застойной зоны за
дном и способствует дополнительному разрежению потока.
94
При транс- и сверхзвуковых скоростях вблизи донного среза
появляются волны разрежения (характеристики), а за фюзеля-
жем— скачки уплотнения (рис. 4.39). Расширение сверхзвуко-
вого потока на веере характеристик увеличивает донный вакуум,
а наличие замыкающего скачка за донным срезом уменьшает его.
При увеличении числа М на сверхзвуковых скоростях коэффици-
ент Сх д уменьшается.
Волны расширения
Рис. 4.39. Образование донного сопротивления
фюзеляжа при транс- и сверхзвуковых скоро-
стях
При наличии угла атаки (а#0) происходит перераспределение
давления по поверхности фюзеляжа. В головной его части возра-
стает давление снизу и уменьшается сверху, а в кормовой, наобо-
рот, уменьшается разрежение сверху и увеличивается снизу. В ре-
зультате при положительном угле атаки на головной части обра-
зуется положительная подъемная сила, а на кормовой — отрица-
тельная. Кроме того, положительная подъемная сила создается
и на цилиндрической части фюзеляжа. Поскольку основную роль
в создании подъемной силы на фюзеляже играют передние его
части, то фокус фюзеляжа обычно расположен в районе головной
части.
При больших углах атаки на поверхности изолированного фю-
зеляжа может возникнуть срыв потока. Обычно он начинается
в кормовой части и по мере увеличения угла атаки распростра-
няется на цилиндрическую часть. Срыв потока сопровождается
интенсивным вихреобразованием и понижением давления на верх-
ней поверхности фюзеляжа; в результате возрастает подъемная
сила, а фокус смещается назад. Установка на фюзеляж крыла
препятствует отрыву потока, и он обычно не наблюдается. При
наличии у фюзеляжа удлиненной головной части на ней при
больших углах атаки или скольжения может возникнуть отрыв
потока, ’ аналогичный отрыву с передних кромок треугольных
крыльев, с образованием двух вихревых жгутов (рис. 4.40). При
малых углах атаки эти вихри являются симметричными
(рис. 4.40,а), а при больших симметрия может нарушаться
95
(рис. 4.40,б), при этом разрежения на левой и правой сторонах
фюзеляжа оказываются различными и даже при отсутствии сколь-
жения появляются значительные моменты рыскания.
Рассмотрим влияние формы фюзеляжа (его удлинения Хф) и
числа М на аэродинамические характеристики. Коэффициент со-
противления трения Схтр с увеличением удлинения возрастает, так
как при этом увеличивается от-
Рис. 4.40. Образование симметрич-
ных (а) и несимметричных (6) вих-
рей на носовой части фюзеляжа
носительная смачиваемая поверх-
ность (5ПОв/5м). Коэффициент
волнового сопротивления СХв ,
наоборот, при увеличении Хф
уменьшается вследствие уменьше-
ния кривизны поверхности фюзе-
ляжа (его относительной толщи-
ны ~~). На коэффициент дон-
ьФ /
ного сопротивления Схд удлине-
ние фюзеляжа влияет слабо. Сле-
довательно, для каждого числа
М имеется оптимальное удлине-
ние, при котором коэффициент
СХо минимален. При дозвуковых
скоростях основную долю со-
ставляет сопротивление трения
и минимум коэффициента СХо
смещается в сторону малых удлинений (ХОпт:=44-6). При транс-
и сверхзвуковых скоростях существенную роль играет волновое
сопротивление и минимум С смещается в сторону больших
удлинений (Хопт = 94-11).
Увеличение удлинения фюзеляжа приводит к увеличению
коэффициента С* и к смещению фокуса назад, так как воз-
растает доля подъемной силы, создаваемой цилиндрической
частью.
Рассмотрим изменение аэродинамических характеристик фюзе-
ляжа заданой формы при увеличении числа М. С ростом числа М
коэффициент Сх тр несколько уменьшается вследствие влияния
сжимаемости (роста температуры и уменьшения плотности в по-
граничном слое). Коэффициент донного сопротивления при
М<Мкр изменяется слабо, сильно возрастает на трансзвуковых
скоростях вследствие дополнительного расширения потока в кор-
мовой части, а на сверхзвуковых скоростях уменьшается. Коэф-
фициент волнового сопротивления фюзеляжа изменяется по чис-
лам М как и на крыле. В результате зависимость Сх* от М для
фюзеляжа, как и для крыла, на трансзвуковых скоростях имеет
максимум (рис. 4.41).
При увеличении числа М возрастает доля подъемной силы,
образующейся на цилиндрической части, так как на ее верхней
96
CTQpoHe создаются условия для дополнительного расширения по-
Рис. 4.41. Влияние числа М на коэффициент СХй и его составляю*
щие для фюзеляжа
Рис. 4.42. Влияние числа М на коэффициент С*
и безразмерную координату фокуса фюзеляжа
возрастает коэффициент С? фюзеляжа, а его фокус смещается
назад (рис, 4.42).
4-21
97
Раздел II
АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
МАНЕВРЕННЫХ САМОЛЕТОВ И ОСОБЕННОСТИ
ИХ СИЛОВЫХ УСТАНОВОК
Глава 5
АЭРОДИНАМИЧЕСКАЯ КОМПОНОВКА МАНЕВРЕННЫХ
САМОЛЕТОВ И ИХ ХАРАКТЕРИСТИКИ
§ 5.L Взаимное влияние частей самолета
В главе 4 были рассмотрены аэродинамические характеристи-
ки отдельных (изолированных) частей самолета: крыла, фюзе-
ляжа, оперения. Если эти элементы объединить в летательный
аппарат, то каждый из них изменит свои аэродинамические ха-
рактеристики вследствие влияния других элементов. Это взаимное
влияние частей самолета называется интерференцией.
Вследствие интерференции характеристики самолета нельзя по-
лучить простым сложением аэродинамических характеристик его
частей. Приходится либо вносить поправки на интерференцию,
либо определять аэродинамические характеристики самолета в
целом. В настоящее время используется как первый подход, осно-
ванный на определении коэффициентов интерференции, так и вто-
рой, который все шире опирается на численные расчеты с по-
мощью ЭВМ.
Интерференция частей самолета проявляется в изменении подъ-
емной силы, силы лобового сопротивления, действующих на само-
лет моментов. Интерференция может быть положительной (полез-
ной) и отрицательной (вредной). Если в результате' взаимного
влияния аэродинамические характеристики самолета улучшаются,
например возрастает аэродинамическое качество, то такая интер-
ференция считается положительной, и наоборот.
При определении сил и моментов, действующих на самолет,
обычно учитывают следующие виды интерференции:
— между крылом и фюзеляжем;
— между фюзеляжем и оперением;
98
Рис. 5.1. Влияние фюзе-
ляжа на крыло и крыла
на фюзеляж
— между крылом и оперением;
— между надстройками, воздухозаборниками, подвесками и
крылом' или фюзеляжем;
— между самолетом и земной или водной поверхностью при
взлете и посадке и др.
Физические причины, приводящие к изменению аэродинамиче-
ских характеристик частей самолета вследствие их интерферен-
ции, различны. Рассмотрим взаимное влияние крыла и фюзеляжа.
При обтекании фюзеляжа под углом
атаки вблизи его поверхности вертикальные
скорости возрастают, что приводит к уве-
личению местных углов атаки на крыле,
пристыкованном к фюзеляжу. Увеличива-
ются вследствие этого коэффициенты подъ-
емной силы сечений крыла (рис. 5.1) и
всего крыла в целом.
С другой стороны, разрежение над верх-
ней поверхностью крыла и повышенное дав-
ление под ним передаются соответственно
на верхнюю и нижнюю стороны фюзеляжа
(рис. 5.1). В результате появляется дополнительная подъемная
сила на фюзеляже, вызванная влиянием крыла.
Взаимное влияние крыла и фюзеляжа вызывает увеличение со-
противления самолета. В месте соединения крыла с фюзеляжем
пограничные слои крыла и фюзеляжа накладываются, происходит
утолщение пограничного слоя и его преждевременный отрыв.
Кроме того, происходит дополнительное поджатие струек в перед-
ней части крыла и их расширение на кормовой части. Это при-
водит к так называемому диффузорному эффекту, т. е. повыше-
нию положительного градиента давления в месте стыка >
>0), вызывает более ранний отрыв потока в этом месте и уве-
личение сопротивления давления. Этому способствует также рас-
смотренное выше увеличение углов атаки сечений крыла, приле-
жащих к фюзеляжу. Увеличение местных углов атаки влечет за
собой уменьшение критических чисел М и появление дополнитель-
ного волнового сопротивления.
Физическая сущность взаимного влияния фюзеляжа и опере-
ния, различных подвесок и крыла аналогична интерференции
крыла и фюзеляжа.
Рассмотрим взаимное влияние крыла и горизонтального опе-
рения. Если крыло обтекается под-углом атаки, то создание на
нем подъемной силы сопровождается, во-первых, отбрасыванием
некоторой массы воздуха вниз (в соответствии с третьим законом
Ньютона), во-вторых, вихреобразованием вследствие перетекания
воздуха с нижней поверхности на верхнюю, в-третьих, торможе-
нием потока. В результате за крылом поток имеет меньшую ско-
рость, некоторую вертикальную скорость Vy и оказывается ско-
4* 9!>
шенным вниз (рис. 5.2) на некоторый угол е, а на расположенном
сзади горизонтальном оперении углы атаки и подъемная сила
уменьшаются (отрицательная интерференция). Аналогично влияет
на крыло скос потока от впереди расположенного горизонтального
Рис. 5.2. Влияние крыла на горизонтальное
оперение и определение его угла атаки
оперения в схеме «утка».
Кроме того, впереди
крыла поток получает
дополнительную скорость,
направленную вверх, при
этом углы атаки и подъем-
ная сила впереди распо-
ложенного горизонталь-
ного оперения возрастают
(положительная интерфе-
ренция).
Углы скоса потока в
районе горизонтального
оперения зависят от ве-
личины подъемной силы
крыла, закона ее распре-
деления по размаху, от
удлинения крыла, от взаимного расположения крыла и оперения
й числа М.
Повышение несущих свойств крыла (коэффициента С“) спо-
собствует увеличению скоса потока. При уменьшении удлинения
крыла коэффициент С® уменьшается, однако, как было показано
в главе 4, возрастает роль вихреобразований, вызванных перете-
канием воздуха с нижней поверхности крыла на верхнюю, и скос
потока у горизонтального оперения возрастает. Увеличение чис-
ла М на дозвуковых скоростях (Л4<1) приводит к росту несущих
свойств крыла и коэффициента С“, в результате скос потока воз-
растает. На сверхзвуковых скоростях (М>1) увеличение числа М
Сопровождается уменьшением коэффициента и скоса потока.
Рассмотрим хвостовую часть самолета с поворотным стабили-
затором (рис. 5.2). Пусть угол атаки самолета есть а, угол по-
ворота стабилизатора ср, а угол скоса потока е. Тогда угол атаки
горизонтального оперения будет
«г. о = а + ? —
(5.1)
§ 5.2. Общие принципы аэродинамической компоновки
маневренного самолета и требования, предъявляемые к ней
Выбор аэродинамической компоновки маневренного самолета
является весьма сложной и во многом противоречивой задачей.
Наряду с требованиями аэродинамики конструктор должен удов-
летворить другим не менее важным, а зачастую решающим тре-
бованиям, вытекающим из условий размещения вооружения, обо-
100
рудования, двигателей, топлива, экипажа, из условий обеспечения
необходимой прочности, жесткости, надежности конструкции, из
условий эксплуатации и боевого применения и др. Многие из
этих требований противоречат требованиям аэродинамики. В част-
ности, для уменьшения волнового сопротивления на транс- и
сверхзвуковых скоростях необходимо уменьшать толщину крыла,
а это вызывает снижение его прочности и жесткости. Более того,
сами аэродинамические требования иногда противоречивы. На-
пример, для увеличения подъемной силы на взлете и посадке це-
лесообразно иметь нестреловидное крыло большого удлинения, но
такое крыло невыгодно для полета на транс- и сверхзвуковых
скоростях. Поэтому удовлетворить всем требованиям в конструк-
ции одного самолета практически невозможно и при разработке
аэродинамической компоновки конструктор принимает обычно
компромиссное решение. Однако для маневренных самолетов, ле-
тающих в плотных слоях атмосферы и использующих аэродина-
мические силы в широком диапазоне их изменения, требования
аэродинамики при выборе компоновки являются решающими. Эти
требования весьма обширны и разнообразны. Основными из них
являются следующие.
1. Уменьшение коэффициента лобового сопротивления Сх* при
нулевой подъемной силе. Это важно с точки зрения достижения
больших скоростей полета, так как в этом случае полет самолета
происходит на небольших углах атаки и в соответствии с форму-
лой (3.11) коэффициент лобового сопротивления самолета Сх
близок к Сх.
2. Уменьшение коэффициента А и коэффициента индуктив-
ного сопротивления Сх< в целях уменьшения сопротивления само-
лета при маневрировании (при больших значениях коэффициен-
та Су).
3. Обеспечение высоких несущих свойств и увеличение коэф-
фициентов подъемной силы Су. Это необходимо для получения
требуемых маневренных характеристик, улучшения взлетно-поса-
дочных характеристик.
4. Увеличение максимального аэродинамического качества
/Стах и качества К самолета на различных режимах полета. Это
выгодно с точки зрения улучшения маневренных характеристик и
увеличения дальности и продолжительности полета.
5. Обеспечение устойчивости и управляемости самолета на всех
режимах полета в широком диапазоне высот и скоростей.
6. Исключение опасных аэроупругих явлений (флаттер, дивер-
генция, реверс), т. е. таких упругих деформаций, которые могут
привести к нарушению безопасности полета.
7. Обеспечение защиты конструкции самолета, вооружения,
оборудования, экипажа от аэродинамического нагрева при дли-
тельном полете на больших сверхзвуковых числах М и др.
Ниже будут подробно рассмотрены способы получения задан-
ных аэродинамических характеристик в процессе разработки аэро*
101
динамической компоновки маневренного самолета. Здесь же оста-
новимся лишь на некоторых общих принципах решения этой про-
тиворечивой задачи. Чтобы правильно выбрать форму и геометри-
ческие параметры самолета и его частей, надо знать, как они
влияют на аэродинамические характеристики самолета. Для этого
используется накопленный аэродинамикой теоретический и экс-
периментальный материал. Например, известно, что для увеличения
коэффициента подъемной силы необходимо увеличивать удли-
нение крыла, уменьшать его стреловидность и т. п. Кроме того,
при разработке новой компоновки проводятся экспериментальные
исследования на моделях в аэродинамических трубах и расчеты
на ЭВМ, позволяющие с высокой точностью оценить аэродинами-
ческие характеристики проектируемого самолета.
При выборе формы и размеров частей самолета следует иметь
в виду, что их форма может изменяться вследствие упругих де-
формаций конструкции в полете под действием внешних нагрузок.
Поэтому выбор аэродинамической компоновки самолета должен
опираться не только на законы аэродинамики, но и на упругие
свойства конструкции, т. е. компоновка должна выбираться с уче-
том ее упругости. Кроме того, в последнее время все большую
роль в обеспечении заданных аэродинамических свойств, харак-
теристик устойчивости и управляемости начинает играть авто-
матика. Следовательно, получение заданных аэродинамических
характеристик самолета в этом случае опирается на законы аэро-
динамики, автоматики и упругости, а решаемая таким образом
комплексная проблема выбора аэродинамической компоновки по-
лучила название аэроавтоупругости.
В настоящее время для улучшения аэродинамических харак-
теристик маневренных самолетов начинают все шире применяться
различные энергетические способы, такие, как отклонение вектора
тяги, выдув струй газа на поверхности самолета, сдув и отсос по-
граничного слоя и др. Энергетическими способами можно сущест-
венно улучшить маневренные и взлетно-посадочные характери-
стики самолета, повысить его аэродинамическое качество.
§ 5.3. Способы уменьшения лобового сопротивления самолета
при нулевой подъемной силе
Лобовое сопротивление самолета создается всеми его частями.
Обычно лобовое сопротивление самолета больше суммы лобовых
сопротивлений его частей вследствие интерференции. В главе 4
подробно рассмотрено влияние различных факторов на лобовое
сопротивление изолированных частей самолета (крыла, оперения,
фюзеляжа). Здесь же остановимся на способах уменьшения ло-
бового сопротивления, вызванного интерференцией.
Как известно, сопротивление при нулевой подъемной силе скла-
дывается из сопротивления трения и сопротивления сил давления.
При М<Мкр коэффициент сопротивления давления намного мень-
ше коэффициента сопротивления трения (Сх давл<^СХтр). Поэтому
102
основным способом уменьшения лобового сопротивления самолета
на таких режимах является борьба с сопротивлением трения (обес-
печение гладкой поверхности самолета, ламинаризация погранич-
ного слоя, его сдув и отсос и т. п.).
Вследствие интерференции, например, крыла и фюзеляжа, опе-
рения и фюзеляжа, как уже отмечалось, может возрасти сопро-
тивление давления из-за влияния диффузорного эффекта. Наи-
меньший диффузорный эффект создает схема верхнеплан из-за
меньшего поджатия струй на верхней поверхности крыла. Поэтому
эта схема выгодна с точки зрения уменьшения сопротивления. Для
уменьшения сопротивления давления в местах стыков, неплавных
переходов устанавливают специальные зализы, обтекатели и т. п.
При М>Мкр коэффициент сопротивления давления резко воз-
растает из-за появления волнового сопротивления и может стать
больше коэффициента сопротивления трения (Схдавл>СА:тр). По-
этому здесь основные мероприятия аэродинамической компоновки,
направленные на уменьшение коэффициента Сх^ связаны с
уменьшением коэффициента СХДавл.
Значительное влияние на лобовое сопротивление самолета, и
прежде всего на коэффициент С^, оказывают внешние подвески
(вооружение, топливные баки и т. п.). При этом аэродинамическое
качество самолета уменьшается.
Для уменьшения волнового сопротивления самолета на транс-
и сверхзвуковых скоростях применяются так называемые правила
площадей. Различают трансзвуковое, сверхзвуковое и дифферен-
циальное правила площадей.
Эксперименты и расчеты показывают, что самолет обладает
на трансзвуковых скоростях наименьшим сопротивлением, если
площади поперечных сечений по длине самолета изменяются по
тому же плавному закону, что и у тела наименьшего сопротивле-
ния. В месте присоединения крыла к фюзеляжу в этом случае
делают «талию», т. е. уменьшают площади поперечных сечений
(рис. 5.3). При этом коэффициент Сх* на трансзвуковых скоростях
существенно уменьшается.
В последнее время на маневренных самолетах начало приме-
няться дифференциальное правило площадей. Оно заключается в
неравномерном распределении площади поперечных сечений фю-
зеляжа по высоте (рис. 5.4): нижняя часть утолщается, а верхняя
делается утоньшенной. При этом на умеренных сверхзвуковых
скоростях (М ^1,2) на больших углах атаки (например, при ма-
неврировании с большими значениями Су) сопротивление умень-
шается в большей степени, чем при применении обычного пра-
вила площадей. Это объясняется ослаблением диффузорного эф-
фекта в месте стыка крыла с фюзеляжем.
Заметного уменьшения лобового сопротивления можно достиг-
нуть, используя концепцию объединения крыла и фюзеляжа (ин-
тегральную схему). Это достигается плавным переходом крыла
в фюзеляж. В этом случае обеспечиваются более плавные кон-
103
туры самолета и уменьшается волновое сопротивление. Кроме
того, уменьшается обтекаемая («смачиваемая») поверхность,
а следовательно, и сопротивление трения.
Рис. 5.3. Самолет, выполнен-
ный по трансзвуковому пра-
вилу площадей
Рис. 5.4. Самолет, выполненный по
дифференциальному правилу площа-
дей
Зависимость коэффициента Сх° самолета от числа М качест-
венно такая же, как и для крыла.
§ 5.4. Обеспечение высоких несущих свойств.
Взлетно-посадочная механизация
Несущие свойства самолета создаются в основном его кры-
лом — в этом состоит его главное предназначение.
Стремление увеличить максимальную скорость полета привело
к применению на современных маневренных самолетах тонких
крыльев малого удлинения и большой стреловидности, имеющих
сравнительно малые значения коэффициентов С“. Это снижает
маневренные свойства самолетов. Поскольку маневренные само-
леты имеют длинные фюзеляжи, то это ограничивает значения
взлетно-посадочных углов атаки — увеличение этих углов требует
увеличения размеров и массы шасси самолета. Кроме того,
у крыльев современных самолетов большие критические углы
атаки. В результате взлетно-посадочные углы атаки у современ-
ных самолетов много меньше критических (аПос<СаКр). Следова-
тельно, самолеты имеют на взлете и посадке малые значения ко*
104
эффициента подъемной силы Су 0Тр и Су пос и большие скорости
отрыва и посадки.
Для улучшения маневренных свойств самолета и уменьшения
скоростей взлета и посадки необходимо увеличивать несущие свой-
ства крыла на эксплуатационных углах атаки. Это может быть
достигнуто применением на самолетах различной механизации на
передней и задней кромках крыла. К механизации задней кромки
Рис. 5.5. Влияние отклонения закрылка и
предкрылка на зависимость Cv(a)
Рис. 5.6. Влияние угла отклоне-
ния Зз на эффективность простого
и щелевого закрылков
относятся закрылки (простые, щелевые, многозвенные, выдвиж-
ные). В качестве механизации передней кромки используются
предкрылки, отклоняемые носки. Кроме того, как на задней, так
и на передней кромках может применяться струйная механи-
зация.
Принцип работы простого закрылка (рис. 1.9, а) аналогичен
принципу действия руля. При отклонении закрылка на угол д3
увеличивается кривизна крыла, поток под крылом тормозится,
над крылом разгоняется. В результате возрастает аэродинамиче-
ская нагрузка на закрылке и впереди расположенной части крыла,
увеличивается коэффициент подъемной силы самолета (рис. 5.5).
Увеличение угла отклонения закрылка 63 приводит к росту
положительного градиента давления на верхней поверхности за-
крылка, развивается срыв потока и рост коэффициента Су замед-
ляется. Чтобы затянуть срыв потока на большие углы б3, приме-
няют щелевые закрылки (рис. 1.9,6). Воздух, проходя через про-
филированную щель с нижней поверхности на верхнюю, увеличи-
вает скорость в пограничном слое и повышает его устойчивость
к обрыву. В результате увеличивается прирост коэффициента подъ-
емной силы &Суз (рис. 5.6).
105
Для повышения эффективности закрылков их иногда делают
многозвенными, многощелевыми (рис. 1.9, г). Кроме положитель-
ного влияния щелей здесь достигается также более плавное изме-
нение кривизны, что уменьшает положительные градиенты давле-
ния на закрылке, позволяет увеличить суммарный угол отклоне-
ния и прирост ДС^ з.
Рис. 5.7. Сдув пограничного слоя с закрылка
Выдвижной закрылок, в отличие от простого, одновременно с
отклонением вниз выдвигается назад (рис. 1.9,в). При этом уве-
личивается площадь крыла и число Re, уменьшается удлинение
крыла и положительные градиенты давления, в результате замет-
но возрастает коэффициент Су.
Как указывалось выше, при больших углах отклонения за-
крылка на его верхней поверхности начинается срыв потока и
рост коэффициента Су замедляется. Эффективным способом борь-
бы со срывом потока на закрылке является управление погранич-
ным слоем — УПС (сдув и отсос пограничного слоя).
Принцип управления пограничным слоем состоит в принуди-
тельном увеличении скорости частиц воздуха в пограничном слое
путем его сдува или отсоса. При сдуве струя газа, отбираемого
от двигателя, ч^рез узкую щель выдувается на верхнюю поверх-
ность закрылка (рис. 5.7). При этом коэффициент Су возрастает
по следующим причинам.
Во-первых, сдув увеличивает скорость течения в пограничном
слое, затягивает срыв потока и позволяет увеличить углы откло-
нения закрылка б3.
Во-вторых, газовая струя эжектирует воздух с верхней поверх-
ности крыла и увеличивает на ней разрежение, а также тормозит
поток и увеличивает давление на нижней поверхности (струя яв-
ляется как бы продолжением закрылка). И, наконец, газовая
струя создает реактивную силу /?, проекция которой увеличивает
подъемную силу (рис. 5.7).
При отсосе из потока удаляется заторможенная часть погра-
ничного слоя и скорости на верхней поверхности возрастают.
При применении струйного закрылка в узкую щель, располо-
женную вдоль задней кромки крыла, выдувается струя газа под
106
некоторым углом к хорде крыла. За счет эжектирующего дейст-
вия струи возрастает скорость и разрежение на верхней поверх-
ности крыла. В то же время струя тормозит поток под крылом
и увеличивает давление на нижней поверхности. В результате
подъемная сила возрастает. Кроме того, при наличии струи газа
появляется реактивная сила, проекция которой также увеличи-
вает подъемную силу.
Рис. 5.8. Взаимодействие вихрей треугольных крыльев в схеме
«утка»
Рассмотрим механизацию передней кромки.
При открытии (выдвижении) предкрылка (рис. 1.10) между
ним и крылом образуется профилированная щель. Воздух, пере-
текающий через нее с нижней поверхности на верхнюю, увеличи-
вает скорости в пограничном слое и повышает его устойчивость
к отрыву. В результате увеличивается критический угол атаки акр
и коэффициент Сутах (рис. 5.5).
Прй отклонении носков крыла (рис. 1.11) изменяется кривизна
крыла вблизи передней громки, в результате увеличивается кри-
тический угол атаки аКр и коэффициент Су тах.
Для повышения несущих свойств самолетов на взлете и по-
садке целесообразно по возможности увеличивать размеры ме-
ханизации. С этой целью на некоторых самолетах, в частности
на самолетах с крылом изменяемой в полете , стреловидности,
вместо элеронов используют дифференциальное отклонение поло-
вин стабилизатора и интерцепторы, а закрылки размещают прак-
тически по всему размаху крыла. При наличии крыла изменяемой
в полете стреловидности на взлете и посадке для увеличения не-
сущих свойств крыло устанавливается в положение минимальной
стреловидности, при этом возрастает коэффициент С“ вследствие
уменьшения стреловидности и одновременного увеличения удли-
нения крыла.
107
В настоящее время для увеличения несущих свойств манев-
ренных самолетов широко используется концепция полезного от-
рыва, рассмотренная в главе 4. На рис. 5.8 в качестве примера
приведена компоновка истребителя с треугольными крылом и пе-
редним горизонтальным оперением. Вихри, образующиеся при
отрыве потока с передних кромок крыла и оперения, сущест-
венно увеличивают подъемную силу крыла.
§ 5.5. Обеспечение высокого аэродинамического
качества самолета
Аэродинамическое качество самолета К=СУ/СХ изменяется в
широких пределах в зависимости от режима полета. От его вели-
чины зависят маневренные характеристики самолета, его даль-
ность и продолжительность полета, полезная нагрузка. На наи-
выгоднейшем угле атаки анаИв реализуется максимальное аэроди-
намическое качество Лтах. Если уравнение поляры самолета опи-
сывается выражением (3.11), то величина Хтах определяется фор-
мулой (3.16), в которой коэффициенты Сх и А могут быть най-
дены из выражений (3.8) и (3.10).
Из анализа перечисленных выше соотношений следует, что для
увеличения /Сщах необходимо уменьшать коэффициенты Сх° и А
т. е. уменьшать сопротивления трения и давления, увеличивать
несущие свойства самолета (коэффициент С®), обеспечивать по
возможности полную реализацию подсасывающей силы (увеличи-
вать коэффициент Ст). Пути уменьшения коэффициента Сх и
повышения несущих свойств (коэффициента С®) рассмотрены
выше.
Рассмотрим мероприятия, направленные на увеличение аэро-
динамического качества.
Величина коэффициента подсасывающей силы зависит от фор-
мы в плане несущих поверхностей (крыла, оперения), формы их
профилей, числа М полета, угла атаки и других факторов. На
профиле с острым носком подсасывающая сила не реализуется
(Ст = 0). Если передняя кромка закругленная и дозвуковая, то
на ней реализуется подсасывающая сила (Сг>0). Степень реа-
лизации подсасывающей силы зависит от формы в плане, числа
М, угла атаки. На дозвуковых скоростях наибольшая подсасы-
вающая сила реализуется на нестреловидных крыльях большого
удлинения. Придание крылу стреловидности и сужения, умень-
шение его удлинения снижают подсасывающую силу. Как отме-
чалось в главе 4, на сверхзвуковых скоростях подсасывающая
сила реализуется только на дозвуковой передней кромке, т. е.
при M<l/cosx (/ — угол стреловидности передней кромки). При
M^l/cosx подсасывающая сила не реализуется.
При отрыве потока с передней громки на больших углах атаки
или при большой стреловидности передней кромки подсасываю*
щая сила резко падает или исчезает вообще.
108
Величину коэффициента А можно уменьшить, применяя крут-
ку (рис. 5.9) или деформируя крыло в полете. Это достигается
посекционным отклонением закрылков, носков, предкрылков и
т. п. В этом случае обеспечиваются более плавное обтекание
Рис. 5.9. Влияние крутки крыла
на его поляру
Рис. 5.10. Положительная интер-
ференция при подвеске ракет
носка и более оптимальный (с точки зрения сопротивления) за-
кон распределения подъемной силы по размаху крыла. Этот спо-
соб оказывается наиболее эффективным для маневренных само-
летов при выполнении полета с
большими значениями коэффициен-
та Су (на больших углах атаки).
Определенного увеличения аэро-
динамического качества можно до-
стигнуть, используя полезную ин-
терференцию на сверхзвуковых ско-
ростях. В частности, в случае, по-
казанном на рис. 5.10, за счет по-
вышения давления за скачком на
подвеске не только уменьшается со-
j k АУшпп
Скачки уплотнения
Рис. 5.11. Положительная интер-
ференция на входе в воздухоза-
борник
противление, но и увеличивается
подъемная сила самолета, а следо-
вательно, и его качество по сравне-
нию с тем, которое было бы при от-
сутствии полезной интерференции. Для этих же целей могут ис-
пользоваться воздухозаборники и клиновидные обтекатели, уста-
навливаемые на нижних поверхностях самолета, а также клинья
воздухозаборников (рис. 5.11). В последнем случае на верхнем
клине, который выступает по сравнению с нижним клином вперед,
образуется дополнительная подъемная сила ДУ, которая возра-
стает на нерасчетном режиме работы двигателя, когда часть воз-
духа отбрасывается вниз.
109
Для увеличения коэффициента Су самолета применяют инте-
гральную схему, в которой значительную часть подъемной силы
(до 40% на сверхзвуковых скоростях) может создать фюзеляж.
Коэффициенты А и /Стах для самолета зависят от числа М.
качественно так же, как и для крыла (рис. 4.15 и 4.16).
§ 5.6. Обеспечение заданных продольных моментных
характеристик самолета во всем летном диапазоне чисел М
В общем случае прямолинейного движения, когда отклонены
органы управления, коэффициенты моментов, действующих на са-
молет, можно записать в виде:
тх = тхр + тхи + тМэ + mfy + т^8н; (5.2)
ту = т^ + туи + /п*н8н + (5.3)
т2 = mZs + mczyCy + ml<f. (5.4)
Моментные характеристики самолета определяют его устой-
чивость и управляемость. Их можно разделить на продольные и
боковые. К продольным моментным характеристикам можно
отнести зависимости коэффициентов mz, т*, тсгУ. ml (тя*в), mz
от параметров, характеризующих движение и обтекание само-
лета, а к б о ко в ы м— зависимости тх, т?х, яг/, ягу„ т^ т"
и др. от аналогичных параметров.
Продольные моментные характеристики формируются крылом,
горизонтальным оперением и в некоторой степени фюзеляжем са-
молета, а боковые — крылом, вертикальным оперением и в зна-
чительной степени фюзеляжем и горизонтальным оперением. Опе-
рение самолета, расположенное сзади центра масс, смещает фокус
самолета по углу атаки и по углу скольжения назад, а фюзеляж,
у которого подъемная и боковая силы создаются в основном на
головной части, смещает их вперед.
Для продольных моментных характеристик маневренных са-
молетов характерны следующие особенности.
1. Смещение фокуса вперед и появление «ложки» или «выпо-
лаживание» в зависимости коэффициента mz от угла атаки а
(рис. 3.10), связанные с отрывами потока с крыла или горизон-
тального оперения.
2. Резкое и значительное смещение фокуса назад при пере-
ходе от дозвуковых скоростей к сверхзвуковым, вызванное пере-
распределением нагрузки на несущих поверхностях (рис. 4.12)
и относительным увеличением эффективности щризонтального
оперения из-за уменьшения скоса потока при М>1. .
3. Изменение скоса потока от крыла в районе горизонтального
оперения при изменении угла атаки, различное при расположе-
нии горизонтального оперения выше или ниже плоскости крыла
(рис. 5.12).
ПО
Если горизонтальное оперение расположено выше плоскости
крыла, то при увеличении угла атаки оно приближается к зоне
максимальных скосов от крыла, и наоборот, если оно располо-
жено ниже плоскости крыла, то при увеличении угла атаки оно
Рис. 5.12. Влияние расположения горизонтального оперения по вы-
соте на зависимость угла скоса потока от угла атаки
удаляется от зоны максимальных скосов. Неблагоприятное влия-
ние на верхнерасположенное горизонтальное оперение могут ока-
зать вихри, образующиеся на наплыве крыла сложной формы
или изменяемой в полете стрело-
видности (рис. 4.30).
При увеличении угла атаки
возможно неблагоприятное изме-
нение коэффициента тг (рис.
5.13).
4. Значительное снижение эф-
фективности рулевых поверхно-
стей при переходе от дозвуковых
скоростей к сверхзвуковым, при-
чины которого подробно рас-
смотрены в гл. 4.
Поэтому основные мероприя-
тия аэродинамической компонов-
ки, связанные с улучшением про-
дольных моментных характери-
стик, направлены на стабилиза-
цию положения фокуса самолета
при изменении режима полета
(угла атаки и числа М) и стре-
Рис. 5.13. Влияние расположения
горизонтального оперения по вы-
соте на зависимость /п2(а)
ловидности крыла в полете,
а также на обеспечение достаточной эффективности органов про-
дольного управления. Меры борьбы с неблагоприятными послед-
ствиями отрыва потока и пути повышения эффективности рулей
были подробно рассмотрены в гл. 4. Здесь остановимся на основ-
ных мероприятиях по стабилизации положения фокуса при изме-
111
нении числа М и стреловидности крыла в полете. К ним относятся
следующие.
1. Переход к крылу малого удлинения и большой стреловид-
ности, у которого относительное смещение фокуса назад при пе-
реходе от дозвуковых скоростей к сверхзвуковым значительно
меньше, чем у крыльев большого удлинения и малой стреловид-
ности (рис. 5.14).
Рис. 5.14. Влияние удлинения и
стреловидности крыла на смеще-
ние фокуса назад при переходе
от дозвуковых скоростей к сверх-
звуковым
Рис. 5.15. Влияние неподвижной
части крыла изменяемой в поле-
те стреловидности на перемеще-
ние фокуса при изменении стре-
ловидности
2. Использование гибридного крыла (крыла с наплывом,
рис. 4.28). Наличие у таких крыльев наплыва малого удлинения
большой стреловидности, как показано в § 4.5, позволяет умень*
шить смещение фокуса при переходе от дозвуковых к сверхзву-
ковым скоростям.
3. Применение дестабилизаторов, т. е. небольших поверхно-
стей, расположенных впереди центра масс. Эти поверхности вы-
пускаются в поток при М>1 и препятствуют значительному смё-
щению фокуса назад. На дозвуковых скоростях они убираются
или выполняются «плавающими», т. е. работающими как флю-
гер, и не создающими нагрузки.
4. Использование неподвижной части (наплыва) у крыла из-
меняемой в полете стреловидности. На рис. 5.15 показан харак-
тер смещения фокуса при увеличении стреловидности для само-*
летов, имеющих цельноповоротное крыло (кривая 1) и крыло с
наплывом и поворотной частью (кривая 2). Наплыв у крыла из-
меняемой в полете стреловидности играет такую же стабилизи-
рующую роль, как и у крыла сложной формы.
Для продольной балансировки самолета существенное значе-
ние имеет коэффициент Он определяется несимметрией са-
молета относительно горизонтальной плоскости (формой фюзе-
ляжа и установочными углами крыла и горизонтального опере-
ния) и зависит от числа М.
112
Некоторое влияние на коэффициент продольного момента ока-
зывают внешние подвески (вооружение, баки). Подвески обычно
смещают фокус самолета вперед, так как они подвешивают-
ся под центром масс, а подъемную силу создают в основном
головные части подвесок, расположенные впереди центра
масс.
§ 5.7. Обеспечение заданных боковых моментных
характеристик самолета во всем летном диапазоне чисел М
Боковые моментные характеристики делятся на характеристи-
ки крена (тх, т*, nfy) и рыскания (ту, ^н). Как будет
показано в третьем разделе, для устойчивого в боковом движении
самолета необходимо не только и (чтобы воз-
никающие при скольжении моменты стремились устранить сколь-
жение), но и определенное соотношение между абсолютными ве-
личинами этих коэффициентов. Обеспечить это на всех режимах
полета непросто, так как для характеристик крена и рыскания
маневренных самолетов характерно следующее.
1. Коэффициенты nfix и неодинаковым образом зависят
от угла атаки: при увеличении а коэффициент п$х обычно уве-
личивается по абсолютной величине вследствие роста подъемной
силы половин крыла, а т?у —уменьшается из-за увеличения эф-
фективной стреловидности вертикального оперения по отношению
к набегающему потоку, затенения фюзеляжем и других причин,
которые будут рассмотрены ниже.
При движении самолета со скольжением эффективные углы
стреловидности правой и левой половин крыла будут разными
(рис. 5.16): на правой половине хп = х—Р, на левой Хл = х+Р- Если
{3>0, то Хп<Хл-
Но с изменением угла стреловидности изменяется коэффициент
у правой половины крыла он будет больше, чем у левой
(Суп>С* л). Следовательно, разными будут зависимости Су (а)
для правой и левой половин (рис. 5.17). При одном и том же
угле атаки на правой половине будет большая подъемная сила,
чем на левой (Ct/n>C^), в результате возникает момент крена
Мх. Чем больше угол атаки, тем больше разность коэффициентов
подъемных сил ДС^, тем больше момент крена (рис. 5.18).
Аналогичная картина наблюдается на вертикальном оперении
при изменении угла атаки. С ростом угла атаки увеличивается
эффективный угол стреловидности (хэф = х + а), а коэффициент
боковой силы Сгв, 0 и создаваемый вертикальным оперением мо-
мент рыскания уменьшаются.
2. На некоторых самолетах наблюдается значительное изме-
нение коэффициента т?х на трансзвуковых скоростях, вызванное
113
Рис. 5.16. Влияние скольжения на эффективные
углы стреловидности консолей крыла
Рис. 5.17. Возникновение
момента крена при
скольжении стреловид-
ного крыла
Рис. 5.18. Влияние угла ата
ки на зависимость mx(g)
114
развитием волнового кризиса (рис. 5.19). При скольжении у поло-
вины крыла, выдвинутой вперед, эффективный угол стреловидно-
сти и критическое число М уменьшаются, коэффициент подъем-
ной силы изменяется более интенсивно. На отстающей половине
вследствие увеличения эффективного угла стреловидности волно-
Рис. 5.19. Изменение коэффициента т)х на
трансзвуковых скоростях
вой кризис начинается при большем числе М, а коэффициент
подъемной силы изменяется в меньшей степени. В результате ко-
эффициент п$х, определяемый разностью коэффициентов подъем-
ных сил, в некотором диапазоне чисел М по абсолютной величине
уменьшается и даже может по-
менять знак.
3. При увеличении числа М
на сверхзвуковых скоростях ко-
эффициенты п$х и по абсо-
лютной величине падают, причем
сильнее, чем п$х (рис. 5.20).
Это объясняется уменьшением
Рис. 5.20. Зависимости коэффициен-
тов и от числа М
л у
несущих свойств крыла и опере-
ния при М>1 и некоторым увеличением несущих свойств фюзе-
ляжа (рис. 4.42).
4. Эффективность руля направления и элеронов (интерцепто-
ров, «ножниц» стабилизатора) снижается при переходе от до-
звуковых скоростей к сверхзвуковым (рис. 4.32).
Наибольшее влияние на боковые моментные характеристики
оказывают следующие мероприятия аэродинамической компо-
новки.
1. Чем больше стреловидность крыла, тем сильнее ее измене-
ние влияет на коэффициент подъемной силы (рис. 4.8), тем боль-
ше коэффициент тх при скольжении (рис. 5.21). Современные
маневренные самолеты со стреловидными крыльями имеют по-
115
вишенные значения коэффициентов т?х (по абсолютной величи-
не), и приходится принимать меры по их уменьшению.
2. Увеличение площади киля приводит к увеличению как ко-
эффициента так и т?х (боковая сила приложена выше оси
самолета), что не всегда желательно. Поэтому в некоторых слу-
Рис. 5.21. Влияние угла стреловид-
ности крыла на коэффициент момен-
та крена при скольжении
чаях увеличение площади вертикального оперения достигается
постановкой нижних килей (гребней) или двух килей вместо од*
ного (рис. 5.22).
Рис. 5.22. Влияние установки нижнего киля или двух
килей на коэффициенты боковых моментов при сколь-
жении
3. Изменение удлинения крыла приводит к изменению несу-
щих свойств крыла, в результате при уменьшении удлинения ко-
эффициент п$х существенно уменьшается. Поэтому у современ-
ных маневренных самолетов, имеющих крылья малого удлинения,
116
важную роль в создании момента крена играет вертикальное и
горизонтальное оперение.
4. Угол поперечного V крыла наиболее сильно влияет на ко-
эффициент самолета. У самолетов со стреловидными крыльям»
для уменьшения обычно применяется отрицательное попереч*
ное V (ф<0) (рис. 5.23). В этом случае при скольжении (Р>0)
Рис. 5.23. Влияние поперечного V крыла на момент
крена при скольжении
за счет поперечного V на правом полукрыле угол атаки и подъ-
емная сила уменьшаются, на левом — возрастают, в результате
уменьшается по абсолютной величине момент Мх. При положи-
тельном поперечном V (ф>0) наблюдается его увеличение.
5. Расположение крыла по высоте фюзеляжа влияет на коэф-
фициент /п£, увеличивая его по абсолютной величине в схеме
верхнеплан. В этом случае при скольжении (Р>0) за счет тор-
можения потока фюзеляжем давление под правой половиной
крыла увеличивается, а под левой из-за затенения фюзеляжем —
уменьшается. В результате появляется AAfx<0. В схеме низко-
план наблюдается обратная картина (AMx>0).
6. Фюзеляж самолета, особенно его носовая часть, сильно
влияет на момент рыскания. Поскольку боковая сила корпуса
приложена впереди центра масс, то она создает дестабилизирую-
щий момент рыскания (/^ф>0). Роль фюзеляжа в создании
117
дестабилизирующего момента рыскания возрастает по мере уве-
личения числа М и угла атаки, так как увеличивается доля бо-
ковой силы, создаваемой его носовой частью.
7. Внешние подвески, располагаясь вблизи центра масс само-
лета, уменьшают по абсолютной величине коэффициент за
счет обтекания головных частей при скольжении. Коэффициент т%.
при этом обычно возрастает по абсолютной величине вследствие
«высокопланного эффекта» — при скольжении возрастает давле-
ние под крылом из-за дополнительного торможения потока под-
веской, которая подвешивается снизу.
§ 5.8. Дополнительные аэродинамические моменты
при криволинейном и неустановившемся движении
При криволинейном и неустановившемся движении самолета,
например при его вращении или колебаниях, на самолет действуют
дополнительные аэродинамические моменты: демпфирующие и
Рис. 5.24. Вращение самолета вокруг поперечной оси
v9
Да
V
спиральные. Рассмотрим физическую сущность их образования.
При вращении самолета вокруг центра масс его элементы (крыло,
оперение, фюзеляж) получают дополнительные скорости Vx,
и при этом изменяются местные углы атаки и скольжения,
скорости обтекания сечений крыла, оперения и фюзеляжа, а сле-
довательно, и распределенные по самолету аэродинамические
силы. На рис. 5.24—5.26 показаны проекции самолета, вращаю-
щегося относительно осей Охь Оух и Oz\. Там же приведены
эпюры дополнительных скоростей Vx, Vy и VZi вызванных вра-
щением самолета, и построены треугольники скоростей, показы-
вающие изменения углов атаки и скольжения. По мере удаления
от осей вращения дополнительные сксфости возрастают, следова-
тельно в большей степени изменяются углы атаки и скольжения,
а также скорости обтекания сечений крыла и оперения. Чем
больше несущие поверхности и чем дальше они отнесены от центра
масс, тем больше дополнительные силы и моменты.
Другой причиной образования дополнительных сил и моментов
при неустановившемся движении является изменение углов атаки
и скольжения и скоростей обтекания за счет влияния вихрей,
сбегающих с несущих поверхностей. Например, при колебаниях
118
крыла периодически изменяется его угол атаки, а следовательно,,
подъемная сила. В соответствии с теоремой Н. Е. Жуковского
периодически изменяется циркуляция крыла, что согласно теоре-
ме Стокса эквивалентно изменению напряжения присоединенных
Рис. 5.25. Вращение самолета вокруг нормальной оси
вихрей. В результате при колебаниях крыла с него периодически
сбегают свободные вихри, которые уносятся потоком. Перемеще-
ние этих вихрей по крылу или вблизи расположенного за ним
Рис. 5.26. Вращение самолета вокруг продольной оси
оперения вызывает появление дополнительных нестационарных
скоростей Vx, Vy и Vz, а следовательно, дополнительных неста-
ционарных сил и моментов.
В общем случае неустановившегося движения самолета дей-
ствующие на него силы и моменты зависят от углов атаки а и
скольжения р, угловых скоростей сох, Ыу, &z, углов отклонения
рулей др и скорости изменения этих параметров во времени, т. е.
от производных da.[dt, d^dt, duxfdt, d^yldt. d^dt, d\fdi. По-
скольку угловые скорости вращения самолета и указанные выше
производные являются размерными величинами, то удобно пе-
119
рейти к безразмерным величинам, введя следующие обозначе-
ния:
• &А a I - /
a===~dF~V~' = u)x = u)x-2y- >
— I — bA— db)x /I \2
= COy"2V; а)^==^~’ a)^==“5r(w) ’
t =^L/_L_y. 8
У dt ( 2V / ’ z dt I V ) ’ °P“" dt V
(5.5)
где bA и I — средняя аэродинамическая хорда и размах крыла
соответственно, V — скорость полета.
Обычно при неустановившемся движении углы атаки и сколь-
жения, угловые скорости и углы отклонения рулей изменяются не
слишком сильно, поэтому параметры а, а, р,... являются малыми
величинами. Опыт показывает, что при малых значениях указан-
ных параметров коэффициент аэродинамического момента ли-
нейно зависит от них, поэтому его можно представить в виде:
tn = itIq *4~ tn tn л p -J~ tn x^x
4- Лр + zn’₽8p). (5.6)
Под демпфированием понимается сопротивляемость самолета
вращению относительно центра масс в полете. Рассмотрим соб-
ственное аэродинамическое демпфирование вследствие появления
демпфирующих моментов при вращении самолета вокруг центра
масс. К таким моментам относятся момент демпфирования крена
Мх демпф при вращении вокруг ОСИ OXi с угловой скоростью 0)х,
момент демпфирования рыскания Му деМпф при вращении вокруг
оси Оу\ с угловой скоростью сог/ и момент демпфирования тан-
гажа Mz демпф при вращении вокруг ОСИ Oz\ с угловой скоростью
<ог. Поскольку при вращении самолета происходит изменение углов
атаки и скольжения, картины обтекания и действующих на са-
молет сил, то демпфирующие моменты по своей природе в общем
случае неустановившегося движения самолета являются неста-
ционарными. В некоторых частных случаях, например при уста-
новившемся вращении самолета, демпфирующие моменты могут
быть стационарными.
В общем случае колебаний и вращения самолета его демпфи-
рование определяется следующими коэффициентами:
тх демпф = mxxwx + пътхх^х,
ту демпф = ту Р + + туу шу;
тг демпф = т*а +
(5.7)
где коэффициенты Шхх, туу, tn^z связаны с появлением
дополнительных скоростей при вращении самолета, а коэффи-
120
циенты Шхх, ту, т,уу, т* , т*х —с образованием и пере-
мещением вихрей.
В выражениях (5.7) коэффициенты т,хх9 Шуу9 т*г явля-
ются весьма малыми по сравнению с другими и ими можно
пренебречь.
Определим в качестве примера приближенное значение коэф-
фициента демпфирования m^^Q (за счет горизонтального опере-
ния).
Рассмотрим вращение самолета с угловой скоростью со2>0
(рис. 5.26). При вращении самолета фокус оперения получает до-
полнительную вертикальную скорость
Vу = °\гЛг. о»
где Lr. о — расстояние от фокуса оперения до центра масс само-
лета.
При этом изменяется угол атаки оперения
А ____ ________ Чг^г. о
аяг. о---у у
и на нем появляется дополнительная подъемная сила
ДГГ. о = С«у г< 0Д«г. о *7 г. 05г. о = с; г. 0 qt. л. 0. (5.8)
Эта сила на плече £г. о создает демпфирующий момент
г. 0=- д гг. 0£г. 0=- с; г. 0 0.
Учитывая, что —й, для демпфирующего момента
°л
горизонтального оперения имеем
£2
г. о “ г. о^г ~Ь~д О* (5*9)
Этот момент можно выразить через безразмерный коэффи-
циент
Т.0—тг г. oqSbA = ШггТ, ^zqSbA. (5.10)
Сравнивая (5.9) и (5.10), окончательно получим
«С. о = - С; г. 0 (^-)2 -%*- Лг. 0. (5.11)
Аналогичным образом можно определить приближенное зна-
чение коэффициента демпфирования вертикального оперения
<5Л2>
121
Заметим, что полученные коэффициенты демпфирования хотя
и не учитывают демпфирование крыла и фюзеляжа, а также демп-
фирование за счет нестационарного обтекания, определяемого па-
раметрами с точками (а, 0, ых,...), однако дают основную долю
суммарных коэффициентов демпфирования. Коэффициент демп-
фирования крена определяется по более сложным формулам.
Рис. 5.27. Зависимости коэффициентов продольного демпфи-
рования от числа М
Коэффициенты демпфирования самолета изменяются по чис-
лам М качественно так же, как и коэффициенты аэродинамиче-
ских сил (рис. 5.27 и 5.28). Как видно, на сверхзвуковых скоро-
стях демпфирование самолета резко ухудшается.
Рис. 5.28. Зависимости коэффициентов бокового демп-
фирования от числа М
Коэффициенты тху и тух называются производными от ко-
эффициентов спиральных моментов крена и рыскания. Основной
причиной образования спиральных моментов является вертикаль-
ное оперение. Нетрудно видеть (рис. 5.25), что при вращении
самолета с угловой скоростью шу появляется момент Мх, при
вращении вокруг оси Ох—Му.
Дополнительные спиральные моменты образуются также при
вращении самолета за счет обтекания крыла. Так, при вращении
самолета с угловой скоростью <од на опускающейся половине
122
крыла углы атаки, нормальная и продольная силы возрастают,,
а на поднимающейся —наоборот. В результате появляется мо-
мент рыскания Му. При вращении с угловой' скоростью ско-
рости обтекания идущей вперед половины крыла и ее нормаль-
ная сила возрастают, а половины, идущей назад, — наоборот.
В результате возникает момент крена Мх. Коэффициенты спи-
ральных моментов зависят от числа М. так же, как и коэффици-
енты демпфирования.
§ 5.9. Влияние близости земли на аэродинамические
характеристики самолета
При приближении самолета к поверхности земли (или воды)
существенно изменяются аэродинамические характеристики само-
лета и эффективность его механизации. Характер этого влияния
оказывается весьма сложным и не является однозначным. Физи-
ческая сущность влияния близости земли на аэродинамические
характеристики самолета состоит в следующем.
При приближении самолета к поверхности земли поток между
крылом и поверхностью земли тормозится и давление на нижней
поверхности повышается. Это вызывает дополнительное перете-
кание воздуха ч^рез переднюю кромку на верхнюю поверхность,
и, с одной стороны, на ней поток также тормозится, а разреже-
ние уменьшается, с другой стороны, увеличение объема воздуха,
протекающего над верхней поверхностью, способствует увеличе-
нию на ней скорости и разрежения. При не очень больших углах
атаки преобладает второй фактор и влияние близости земли на
подъемную силу оказывается положительным, а цри больших
углах атаки может преобладать первый фактор и влияние бли-
зости земли может стать отрицательным. Кроме того, поверх-
ность земли препятствует отбрасыванию воздуха вниз и припод-
нимает вверх спутный след самолета, уменьшая скос потока за
крылом.
Близость поверхности земли влияет также на перетекание воз-
духа через концы крыла и на формирование боковых вихревых
жгутов. При этом у крыльев малых удлинений эти жгуты под
влиянием близости земли расходятся в стороны, как бы увеличи-
вая их удлинение, а у крыльев больших удлинений приподни-
маются ввзрх и их влияние на обтекание крыльев уменьшается.
Поэтому имеется диапазон удлинений крыла, в котором влияние
близости земли на аэродинамические характеристики самолета
оказывается наиболее благоприятным.
Как показывают теоретические и экспериментальные исследо-
вания, приближение к поверхности земли современных маневрен-
ных самолетов способствует увеличению их подъемной силы. На
рис. 5.29 показана зависимость отношения коэффициентов подъ-
емной силыСу/С вблизи и вдали от земли для самолета с тре*
у
угольным крылом от безразмерного параметра /7 =-у, харак-
теризующего близость земли (Н— расстояние от центра масс
123
самолета до поверхности земли, I — размах крыла самолета).
Видно, что заметно влияет близость земли на подъемную силу
самолета при #<0,5.
Наиболее сильное влияние оказывает близость земли на со-
противление самолета, обусловленное подъемной силой, особенно
на крыльях с закругленной передней кромкой. Это объясняется
Рис. 5.29. Влияние близости земли на коэффици-
енты подъемной силы и индуктивного сопротив-
ления и на максимальное аэродинамическое ка-
чество самолета
двумя обстоятельствами. Во-первых, при приближении к земле
затрудняется перетекание воздуха через боковые кромки и сни-
жаются затраты энергии на создание вихревого движения. Во-
вторых, усиливается перетекание воздуха через переднюю кромку
и возрастает подсасывающая сила на ней. На рис. 5.29 показана
зависимость отношения коэффициентов индуктивного сопротивле-
ния CXi/CXioo вблизи и вдали от земли от параметра Н.
Одновременное увеличение подъемной силы и уменьшение ин«
дуктивного сопротивления самолета вблизи земли вызывает за-
метное повышение аэродинамического качества (рис. 5.29). Этот
положительный эффект используется при создании экранопланов
(экранолетов), т. е. летательных аппаратов, предназначенных для
движения вблизи поверхности земли или воды.
Приближение к поверхности земли вызывает смещение фокуса
самолета назад (рис. 5.30). Это объясняется следующими обстоя-
тельствами. Во-первых, под влиянием близости земли происходит
перераспределение аэродинамической нагрузки Др по хорде кры-
ла— увеличивается нагрузка в кормовой части сечений. Во-вто-
124
рых, увеличивается эффективность горизонтального оперения из-за
влияния близости земли (при наличии угла атаки оно может ока-
заться ближе к поверхности земли, чем крыло) и из-за уменьше-
ния скосов потока от крыла в районе горизонтального опере-
ния.
Рис. 5.30. Зависимость безразмерной координа-
ты фокуса самолета от относительного расстоя-
ния до земли
Близость земли оказывает заметное влияние на эффективность
механизации: при приближении к поверхности земли эффектив-
ность механизации повышается.
§ 5.10. Особенности аэродинамических характеристик
маневренного самолета на больших углах атаки
Большими принято называть такие углы, при которых на от-
дельных частях самолета начинают образовываться зоны отрыва
потока, приводящие к качественному изменению характера обте^
кания и аэродинамических характеристик самолета.
Современные сверхзвуковые самолеты с крыльями малого
удлинения имеют большие критические углы атаки, чем дозвуко-
вые. В то же время влияние угла атаки на моментные характе-
ристики у сверхзвуковых самолетов проявляется сильнее, чем
у дозвуковых. В частности, в характеристике шг(а) появляется
характерная «ложка» или «выполаживание» (рис. 3.10), вызван-
ные смещением фокуса самолета вперед. Это смещение фокуса
объясняется, во-первых, влиянием концевого срыва потока на
крыле; во-вторых, изменениегл скоса потока в районе горизонталь-
ного оперения; в-третьих, возрастанием дестабилизирующего мо-
мента от фюзеляжа и подвесок при увеличении угла атаки;
в-четвертых, созданием дестабилизирующего момента воздухоза-
борником работающего двигателя.
На самолетах с крылом изменяемой в полете стреловидности
при увеличении угла атаки возрастает подъемная сила на на-
плыве вследствие подсасывающего действия образующихся на
передних кромках наплыва вихрей (рис. 4.30). В результате фо-
кус самолетов смещается вперед.
125
Выход самолета на большие углы атаки сопровождается зна-
чительным изменением боковых моментных характеристик
(рис. 5.31). На больших углах атаки резко уменьшается по абсо-
лютной величине сначала коэффициент а затем п$х.
Причинами, вызывающими
уменьшение коэффициента
на больших углах атаки, яв-
ляются:
— увеличение эффективной
стреловидности вертикального
оперения при увеличении угла
атаки;
— затенение вертикального
оперения впереди расположен-
ным фюзеляжем и крылом;
— неблагоприятное влия-
ние вихревых потоков, образу-
ющихся на передних кромках
Рис. 5.32. Попадание вертикального
оперения в зону одного из вихрей
наплыва крыла при скольжении
наплывов большой стреловидности, а также носовых вихрей фюзе-
ляжа на обтекание вертикального оперения при скольжении
(рис. 5.32).
В этом случае киль попадает в зону одного из вихрей
(рис. 5.33), на нижней части киля создаются скосы и боковая
сила AZ, не препятствующие, а способствующие скольжению. При
этом коэффициент т* не только уменьшается по абсолютной ве-
личине, но и может поменять знак. Уменьшается по абсолютной
величине и коэффициент т?х.
Эффективным средством улучшения боковых моментных ха-
рактеристик в этом случае является применение двухкилевого
126
оперения. Действительно, при скольжении (рис. 5.34) один из
килей входит в зону вихревых потоков и на нем неблагоприятные
боковые скосы увеличиваются, а второй выходит из нее и рабо-
чие. 5.33. Влияние вихрей наплыва крыла на обтекание вертикального
оперения при скольжении
тает в условиях нормального обтекания. В результате моментная
характеристика улучшается.
Рис. 5.34. Влияние вихрей наплыва крыла на эффективность двух килей при
скольжении
Полет самолета на больших углах атаки сопровождается рез-
ким падением эффективности рулей высоты и направления, эле-
ронов (рис. 5.35)?
Рис. 5.35. Влияние угла атаки на эффективность элеронов
127
Одной из характерных особенностей поведения самолета на
больших углах атаки является аэродинамическая тряска, которая
вызывается колебаниями конструкции под действием нестацио-
нарных нафузок при отрывном обтекании. Коэффициент подъем*
ной силы самолета, соответствующий началу тряски, обозначают
Cr/тр. У современных маневренных самолетов Су тр Су max
(рис. 5.36), т. е. тряска имеет место в широком диапазоне эксплуа-
Рис. 5.36. Влияние числа М на коэф-
фициенты Су max И Су тр
тационных углов атаки. На боль-
ших дозвуковых скоростях она
усиливается за счет волнового
отрыва, а на самолетах с интер-
цепторным управлением — и от-
рывом потока с интерцепторов.
Нет общей закономерности в
проявлении тряски при увеличе-
нии угла атаки: у одних само-
летов она несколько усиливается,
у других практически не изменя-
ется. Поэтому у летчика нет до-
статочной естественной сигнали-
ским углам атаки. Особенно
лом изменяемой в полете
ную жесткость. Поэтому на
зации о приближении к критиче-
это характерно для самолетов с кры-
стреловидности, имеющим понижен-
современных маневренных самолетах
устанавливают датчики и указатели углов атаки, а также систе-
мы предупреждения.
На аэродинамические характеристики самолетов на больших
углах атаки некоторое влияние оказывают внешние подвески.
Хотя на несущие свойства они влияют незначительно, однако
наличие подвесок может уменьшить критический угол атаки и
вызвать более ранний срыв потока. Дело в том, что стеснение
потока подвесками под крылом приводит к его перетеканию через
переднюю кромку на верхнюю поверхность, к увеличению скоро-
стей и разрежений на верхней поверхности, к увеличению на ней
положительного фадиента давления и к более раннему срыву
потока. Особенно сильно этот эффект проявляется при скольже-
нии самолета.
§ 5.11. Влияние изменения стреловидности крыла в полете
на аэродинамические характеристики самолета
При noBQpoTe концевой части крыла изменяемой стреловидно-
сти назад (н-а увеличение угла стреловидности) происходит, как
известно, уменьшение удлинения крыла, его относительной тол-
щины и кривизны (по потоку) и некоторое изменение площади
крыла (рис. 1.8). Одновременное изменение этих параметров и
определяет изменение аэродинамических характеристик самолета
при изменении стреловидности крыла. При этом сильно падают
128
несущие свойства (коэффициент С“), особенно на дозвуковых
скоростях (рис. 5.37).
Коэффициент Сл* (рис. 5.38) при М<МКр практически оста-
ется неизменным, несколько уменьшаясь из-за увеличения числа
ГЛ V Ь
^е==__э так как ПрИ повороте консолей крыла назад увеличи-
Рис. 5.37. Влияние угла стрело-
видности Х2 поворотной части на
коэффициент С*
Рис. 5.38. Влияние угла стре-
ловидности поворотной части
на коэффициент СХо
ваются хорды. При М>Мкр и особенно при М>1 коэффициент
Сл* с увеличением %2 сильно падает, так как уменьшается вол-
новое сопротивление из-за уменьшения относительной толщины с
Рис. 5.39. Влияние угла стрело-
видности поворотной части на
коэффициент А
Рис. 5.40. Влияние угла стреловид-
ности поворотной части на макси-
мальное аэродинамическое качество
(рис. 5.38). Коэффициент А при увеличении yv2 возрастает, осо-
бенно интенсивно на дозвуковых скоростях (рис. 5.39), вследст-
вие падения несущих свойств (Cj) и уменьшения подсасываю-
щей силы (Ст). В результате указанного изменения коэффициент
тов СХв и А максимальное аэродинамическое качество на
дозвуковых скоростях при увеличении /2 сильно падает, а на
сверхзвуковых — несколько возрастает (рис. 5.40).
5—21
12»
Изменение координаты фокуса xF при увеличении %2 зависит
от соотношения поворотной и неподвижной частей крыла и от
числа М. При значительном размахе поворотной части фокус на
дозвуковых скоростях (рис. 5.15) сначала смещается назад (за
счет увеличения стреловидности), а затем несколько возвращается
вперед (вследствие резкого уменьшения удлинения). При малом
размахе поворотной части и при М>1 фокус, как правило, при
увеличении /2 смещается назад вследствие слабого влияния удли-
нения и более сильного влияния стреловидности (рис. 5.15).
Увеличение стреловидности при повороте концевой части кры-
ла назад приводит к заметному росту по абсолютной величине
коэффициента т?х и снижению эффективности интерцепторов,
поэтому по мере увеличения стреловидности они постепенно вы-
ключаются из работы.
Увеличение стреловидности крыла способствует более раннему
концевому срыву потока, поэтому при повороте концевой части
крыла назад уменьшается максимальный коэффициент подъем-
ной силы Сутах.
§ 5.12. Влияние упругости конструкции самолета на его
аэродинамические характеристики
В полете все элементы конструкции самолета, воспринимаю-
щие внешние аэродинамические нагрузки, деформируются, изме-
няя свою форму и размеры. Деформации в свою очередь вызьь
вают изменение аэродинамических сил и моментов.
Рис. 5.41. Упругое закручивание крыла
под действием аэродинамических нагру-
зок
Величина упругих деформаций зависит, как известно, от меха-
нических свойств (упругости) самой конструкции, а также от
приложенных к ней сил и моментов. Однако для конкретного
самолета при заданных углах атаки и скольжения, если влиянием
аэродинамического нагрева можно пренебречь, эффект упругих
деформаций конструкции связан непосредственно и только со
скоростным напором q. Покажем это.
Рассмотрим сечение крыла (рис. 5.41), находящееся под углом
атаки а. Пусть под действием аэродинамического момента это
сечение получило упругое изменение угла атаки Аа (повернулось
130
относительно оси жесткости на угол Да). Тогда действующий на
сечение аэродинамический момент можно представить в виде
ээр == tnaz ж (а + Да) qSb, (5.13)
где S и Ъ — характерные площадь и линейный размер (хорда се-
чения), — коэффициент момента тангажа относительно оси
жесткости.
С другой стороны, при
закручивании сечения на
него действует момент упру-
гих СИЛ Мгупр, который
пропорционален углу пово-
рота сечения, т. е.
Чупр = ^ (5.14)
где k — коэффициент про-
порциональности, характе-
ризующий жесткость крыла
на кручение.
При статической дефор-
мации действующие на се-
чение моменты уравнове-
шены:
^z аэр “ М, упр. (5.15)
Рис. 5.42. Упругие деформации стреловид-
ного крыла в полете
Подставив в уравнение (5.15) значения моментов из формул
'(5.13) и (5.14), для угла поворота сечения получим
Да
т* жад5Ь
k—m**qSb
(5.16)
Отсюда видно, что приращение угла атаки Да, а следователь-
но, и аэродинамические характеристики крыла зависят от ско-
ростного напора q. Поэтому в качестве определяющего фактора
при оценке эффекта упругих деформаций самолета обычно при-
нимается скоростной напор.
Увеличение скоростей и уменьшение высот полета заметно
усилило влияние упругих деформаций конструкции на аэродина-
мические характеристики современных маневренных самолетов,
поскольку скоростной напор возрастает, а конструкции становятся
все более тонкими и гибкими. На аэродинамические характери-
стики самолетов решающее влияние оказывают деформации кры-
ла, фюзеляжа, оперения и проводки управления. При этом ха-
рактер этого влияния неоднозначен и неодинаков для различных
самолетов.
Рассмотрим упругие деформации крыла (рис. 5.42). В полете
под действием аэродинамических сил крыло изгибается и закрут
5* 131
чивается, изменяя свою исходную геометрическую форму и ха-
рактер распределения по размаху углов атаки.
У самолетов со стреловидными крыльями при деформации
крыла угол атаки изменяется не только за счет кручения, но и
за счет изгиба крыла:
Дакр+ Даизг. (5.17)
Действительно, рассмотрим два сечения 1—2 и 3—4, парал-
лельные скорости набегающего потока V (рис. 5.42). Изгиб крыла
происходит относительно некоторой оси I—/. Нетрудно видеть,
что точки 2 и 4 (задние кромки) рассматриваемых сечений нахо-
дятся на большем расстоянии от оси I—I, чем точки 1 и 3 (перед-
ние кромки). Поэтому при изгибе крыла точки 2 и 4 имеют
большие вертикальные перемещения, чем соответственно точки I
и 3. В этом легко убедиться, сравнив положения точек Г, 2', 3'
и 4' на деформированной оси жесткости крыла. Следовательно,
при изгибе стреловидного крыла происходит закрутка его сечений
на уменьшение углов атаки, тем большая, чем ближе к концу
крыла расположено рассматриваемое сечение. При этом умень-
шаются коэффициенты подъемной силы сечений С',, особенно
в концевых сечениях (рис. 5.42).
Деформации кручения, в зависимости от взаимного располо-
жения центра жесткости и центра давления, могут как умень-
шать, так и увеличивать углы атаки сечений. У современных стре-
ловидных крыльев с углом стреловидности х>40° деформации
изгиба превалируют над деформациями кручения, поэтому угол
атаки уменьшается, а угол поперечного V возрастает.
Упругие деформации крыльев современных маневренных само-
летов обычно приводят к уменьшению углов атаки сечений и
коэффициента подъемной силы, увеличению коэффициента лобо-
вого сопротивления, смещению фокуса вперед вследствие умень-
шения подъемной силы концевых сечений, увеличению моментов
крена при скольжении из-за увеличения угла поперечного V кры-
ла. Следует заметить, что значительные деформации испытывают
в полете крылья изменяемой стреловидности вследствие наличия
узла поворота консоли.
Основной формой упругой деформации фюзеляжа является
его изгиб, который увеличивается с увеличением длины фюзеляжа
и скоростного напора. При постоянной скорости полета изгиб
фюзеляжа уменьшает восстанавливающие и демпфирующие мо-
менты горизонтального и вертикального оперений, а также сни-
жает эффективность органов управления (рис. 5.43).
Действующие на оперение аэродинамические силы и моменты
деформируют не только фюзеляж, но и само оперение, вызывая
его кручение и изгиб, что приводит к дополнительному изменению
угла атаки горизонтального оперения и угла скольжения верти-
кального оперения. При этом качественно оперение деформируется
так же, как и крыло.
Упругие деформации проводки управления вызывают:
132
— нарушение однозначной связи между положением команд-
ных рычагов и органов управления (рулей);
— самопроизвольное отклонение органов управления.
Конкретные данные по влиянию упругих деформаций самоле-
тов на. их аэродинамические характеристики обычно содержатся
в технических описаниях самолетов.
Рис. 5.43. Влияние упругости конструкции на
эффективность управляемого стабилизатора
§ 5.13. Аэродинамическая сущность валежки, реверса
элеронов, дивергенции, флаттера
Явления, сопутствующие взаимосвязи аэродинамических нагру-
зок и деформаций конструкции, называются аэроупру-
гостью. Различают статическую (взаимодействие аэродинами-
ческих и упругих сил) и динамическую (взаимодействие аэроди-
намических, упругих и инерционных сил) аэроупругость.
К явлениям статической аэроупругости относятся дивер-
генция, реверс элеронов, валежка; к явлениям динамической
аэроупругости — различные формы флаттера. Рассмотрим физи-
ческую сущность этих опасных аэроупругих явлений.
1. Дивергенция. Поскольку линия фокусов (центров давления)
обычно не совпадает с линией центров жесткости, то под воздей-
ствием аэродинамической нагрузки крыло (оперение) не только
изгибается, но и закручивается (рис. 5.42). Угол упругой закрутки
Да увеличивается с увеличением скоростного напора, при этом
аэродинамические моменты возрастают быстрее упругих. При
превышении некоторой скорости УДИв, называемой критической
скоростью дивергенции, аэродинамические моменты стано-
вятся больше упругих и происходит закручивание крыла вплоть
до разрушения. Явление беспредельного закручивания крыла под
действием аэродинамических нагрузок и получило название ди-
вергенции.
2. Реверс элеронов. При отклонении элерона вниз на крыле
возникает дополнительная подъемная сила ДУЭ (рис. 5.44). По-
скольку точка приложения этой силы обычно не совпадает с цен-
тром жесткости крыла, то она создает крутящий момент, который
уменьшает угол атаки на некоторую величину Да и подъемную
силу крыла на величину ДКа. Аналогичная картина наблюдается
133
и при отклонении элерона вверх. В результате эффективность
элерона уменьшается. При увеличении скорости сила ДУ рас-
тет быстрее, чем ДУЭ, и при некоторой скорости VpeB отклонение
элерона полностью компенсируется закручиванием крыла. На-
ступает полная потеря эффективности элерона, а соответствующая
скорость называется критической скоростью реверса
Рис. 5.44. Реверс элеронов
элеронов. При скорости, большей критической, имеет место
обратное действие элеронов — реверс (создаваемый при откло-
нении элеронов момент крена меняет знак).
3. Валежка. Валежкой называется самопроизвольное кре-
нение самолета на больших скоростях полета. Валежка обычно
вызывается двумя причинами. Первая связана с начальной гео-
метрической несимметрией, например с неодинаковыми углами
установки левой и правой половин крыла. В этом случае при уве-
личении скорости увеличивается геометрическая несимметрия
из-за упругих дeфqpмaций, растет разность подъемных сил кон-
солей и появляется значительный момент крена. Вторая причина
связана с упругой несимметрией, когда при увеличении скорости
полета одна консоль закручивается сильнее, чем вторая, при этом
с ростом скорости также увеличивается геометрическая несим-
метрия и может появиться недопустимый момент крена.
4. Флаттер. Флаттером называются самовозбуждающиеся
колебания частей самолета (крыла, оперения) под действием
аэродинамических сил. Флаттер возникает вследствие взаимодей-
ствия аэродинамических, упругих и инерционных сил. Флаттер
может быть различных видов (изгибно-крутильный, изгибно-эле-
ронный и др.). В качестве примера рассмотрим механизм воз-
никновения изгибно-крутильного флаттера.
Пусть под воздействием случайного возмущения крыло изогну-
лось вверх (рис. 5.45, положение 1). Тогда под действием упругой
силы Рупр, приложенной в центре жесткости, оно начнет двигаться
вниз. Этому движению будут препятствовать инерционная сила
Рин, приложенная в центре масс (положение 2), и сила аэроди-
намического демпфирования ДУдемпф, вызванная увеличением угла
атаки за счет движения крыла вниз. Если центр масс располо-
жен сзади центра жесткости, как показано на рис. 5.45, то под
действием сил Рин и Рупр крыло закручивается при движении вниз
134
на уменьшение угла атаки; так что дополнительная аэродинами-
ческая сила ДКа способствует движению крыла вниз (положе-
ния 2 и 3). В положении 3 крыло возвращается в нейтральное
положение, силы Рупр и РНн исчезают, но под действием силы ЛУ,
крыло продолжает движение вниз и появляются силы Руп₽ и Рнн
Рис. 5.45. Флаттер крыла
другого знака (положение 4). При движении крыла вверх кар-
тину аналогичная (положения 5—8). Характер колебаний зави-
сит от соотношения работ возбуждающих и демпфирующих сил.
На малых скоростях работа демпфирующих дил (аэродинамиче-
ских и упругих) Дд больше, чем возбуждающих (аэродинамиче-
ских) Ав, и колебания затухают (флаттер не возникает). При
увеличении скорости работа возбуждающих сил растет быстрее,
чем демпфирующих, и при некоторой скорости УфЛ, которая на-
зывается критической скоростью флаттера, колеба-
ния не затухают. При дальнейшем увеличении скорости проис-
ходит быстрое нарастание амплитуды колебаний и может про-
изойти разрушение крыла (оперения).
На самолетах максимальные скорости полета ограничиваются
таким образом, чтобы они были заведомо меньше рассмотренных
выше критических скоростей, а также принимаются специальные
меры по увеличению этих критических скоростей.
Глава 6
ОСОБЕННОСТИ СИЛОВЫХ УСТАНОВОК МАНЕВРЕННЫХ
САМОЛЕТОВ
§ 6.1. Схемы и основные параметры двигателей
На современных маневренных сверхзвуковых самолетах при-
меняются два основных типа газотурбинных двигателей — одно-
контурные и двухконтурные, как правило имеющие форсажные
135
,я камеры. Одноконтурные
| турбореактивные двига-
g тели с форсажными каме-
* рами сокращенно будем
з называть ТРДФ, а двух-
§ контурные — ДТРДФ.
К
о ТРДФ выполняются
g одно- и двухвальными,
° Одновальные ТРДФ име-
§ ют регулируемый комп-
| рессор. Регулирование
S компрессора у них обыч-
но но осуществляется пово-
° ротом лопаток направля-
® ющих аппаратов группы
‘о первых и группы послед-
g них ступеней. Двухваль-
g ные ТРДФ не нуждают-
ед ся в специальном регули-
S ровании каскадов комп-
§ рессора, так как необхо-
§« димые характеристики
устойчивости обеспечива*
° ются у них за счет изме*
§ нения скольжения рото*
Й Р°в-
S ДТРДФ обычно вы*
* полняются двух-или трех*
2 вальными. Схема двух-
§ вального ДТРДФ привс-
| дена на рис. 6.1. Он имеет
S компрессор низкого дав*
& ления (КНД), работаю-
£ щий на оба контура, и
н компрессор высокого дав-
2 ления (КВД), имеющий
® группу регулируемых
направляющих аппаратов
§ (НА) первых ступеней.
£ Через КНД проходит
§ весь воздух, входящий в
а двигатель GB. За КНД
В воздушный поток разде-
о ляется на два. Одна часть
4 воздуха, имеющая рас-
® ход Gbi, поступает в пер-
У вый (внутренний) кон-
а тур и далее проходит
136
через КВД, камеру сгорания и двухкаскадную турбину.
Вторая часть воздуха в количестве GBu подается во второй кон-
тур.
Степенью двухконтурности называют отношение рас-
ходов воздуха
w = (6-1)
ав[
Обычно у ДТРДФ т = 0,4—2.
Потоки вновь смешиваются на выходе из турбины, где уста-
навливается камера смешения, переходящая в общую форсаж-
ную камеру.
Во всех случаях истечение газового потока из двигателя осу-
ществляется через регулируемое сверхзвуковое реактивное сопло,
а предварительное сжатие воздуха в условиях полета, перед по-
ступлением его в двигатель, происходит в воздухозаборнике, где
энергия скоростного напора используется для повышения давле-
ния воздуха.
Тяга двигателя указанных схем определяется по форму-
ле Б. С. Стечкина:
О,(сс - И) = тв (ес - V), (6.2)
О
где GB— суммарный весовой расход воздуха (GB = GBl + GBn);
— массовый расход воздуха; сс — скорость истечения газа из
сопла; V — скорость полета.
Как видно из формулы (6.2), тяга двигателя тем выше, чем
больше расход воздуха и чем выше разность скоростей сс—V,
т. е. чем значительнее ускоряется газовый поток при его про-
хождении через тракт силовой установки. Величина сс—V (тяга,
получаемая от 1 кг воздуха) называется удельной тягой:
Рул = с^У. (6.3)
Соответственно
Р=/пвРуд. (6.4)
Чем выше Руд, тем меньше при заданной величине тяги по-
требный расход воздуха ч^рез двигатель, а следовательно, его
лобовые размеры и масса. С этой точки зрения выгодно иметь
высокие значения Руд. Наиболее эффективным средством повы-
шения Руд служит увеличение температуры 7* газа перед тур-
биной и температуры 7* в форсажной камере в сочетании с вы-
сокими значениями степени повышения давления воздуха в дви-
гателе, так как указанные факторы приводят к увеличению сс.
Для оценки экономичности силовой установки пользуются
удельным расходом топлива
Суд = от,час/Р. (6.5)
137
который равен отношению часового расхода топлива GT. час к тяге
двигателя. Если размерность расхода топлива — кг/ч, а тяги —
кгс, то единицей измерения для Суд является^кг/кгс • ч (в системе
СИ кг/Н • ч).
Чем ниже Суд, тем больше при заданной скорости дальность
и продолжительность полета самолета. Наиболее эффективным
средством снижения Суд у современных газотурбинных двигателей
является увеличение степени повышения давления воздуха в дви-
гателе. При этом двухконтурные двигатели обеспечивают лучшую
экономичность на бесфорсажных режимах, чем ТРДФ, в чем со-
стоит их основное преимущество.
Суммарной степенью повышения давления в
компрессоре называют отношение давления воздуха за комп-
рессором (на входе в камеру сгорания) к давлению воздуха на
входе в компрессор. Эта величина у ТРДФ равна 13—15, а у ДТРДФ
достигает 20—25 и более.
Тяга двигателя регулируется рычагом управления двигателем
(РУД), при перемещении которого система автоматического уп-
равления обеспечивает изменение подачи топлива в основную и
форсажную камеры сгорания. При увеличении GT возрастают
частоты вращения роторов низкого и высокого давлений, обозна-
чаемые соответственно для РИД — пи и для РВД — пв. При этом
увеличиваются GB и сс и повышается тяга двигателя Р. Наиболь-
шая бесфорсажная тяга достигается на максимальном режиме.
При включении форсажа тяга дополнительно увеличивается. Этот
прирост тяги принято оценивать степенью форсирования
Рф=-^. (6.6)
где Рф — тяга на форсаже, а Р — тяга на исходном бесфорсажном
режиме.
На бесфорсажных режимах двухконтурные двигатели, обладая
существенно лучшей экономичностью, имеют более низкую удель-
ную тягу, чем ТРДФ, что объясняется меньшими скоростями ис-
течения газа из сопла у этих двигателей вследствие отсутствия
подогрева воздуха, проходящего через второй контур. На фор-
сажных режимах у ДТРДФ со смешением потоков весь газовый
поток перед соплом подогревается до температуры Г* и вслед-
ствие этого удельная тяга у них получается столь же высокой»
как и у ТРДФ, поэтому они имеют более высокие степени фор-
сирования. Исходя из этого можно объяснить выгодность приме-
нения ДТРДФ на современных маневренных самолетах. Они
имеют более высокие степени форсирования и дают возможность
получать большие тяги на форсажных режимах, необходимые в
сверхзвуковом полете. Вместе с тем они обеспечивают лучшую,
чем ТРДФ, экономичность на бесфорсажных режимах, используе-
мых при дозвуковых скоростях полета.
138
§ 6.2. Особенности характеристик элементов
двигателя и причины их неустойчивой работы
Воздухозаборник. На сверхзвуковых маневренных самолетах
наиболее часто применяются плоские боковые регулируемые воз-
духозаборники с вертикальным или горизонтальным расположе-
нием клина или осесимметричные воздухозаборники.
Рнс. 6.2. Схемы течения газового потока в
сверхзвуковом воздухозаборнике:
•а — при расчетном М; б — при числе М полета, мень-
шем расчетного
Схема воздухозаборника дана на рис. 6.2. Торможение сверх-
звукового потока осуществляется в системе косых скачков и за-
мыкающем прямом скачке, которые образуются при обтекании
ступенчатой поверхности 1—2—3—4. Углы ступенчатого клина
(конуса) р(- и размеры панелей выбираются так, чтобы при рас-
четном числе М полета косые скачки фокусировались в точке А
передней кромки обечайки. В таком случае площадь входа в воз-
духозаборник FBx равна площади FH струи входящего в него по-
тока воздуха. Отношение <p = FH/FBx называют коэффициен-
том расхода воздухозаборника. На расчетном режиме <р=1.
Пройдя через систему скачков уплотнения, поток затормажи-
вается и уже, будучи дозвуковым, входит во внутренний канал
воздухозаборника. Его минимальное сечение FT называют пло-
щадью горла.
Торможение потока в скачках уплотнения сопровождается по-
терями, приводящими к снижению давления воздуха при его сжа-
тии. Потери, кроме того, возникают от попадания пограничного
слоя, образующегося на прилегающих к входному устройству по-
верхностях самолета, внутрь воздухозаборника. Они создаются
также при течении воздушного потока внутри канала воздухоза-
139
борника вследствие образования пограничного слоя на стенках
канала и наличия зон отрыва. Эти потери оценивают по величине
коэффициента сохранения полного давления
*
= (6.7)
Рн
где р*н и /?* —давления заторможенного потока воздуха соот-
ветственно перед воздухозаборником (в набегающем потоке) и
перед входом в двигатель.
Чем выше сгВх, тем больше при заданном числе М полета сте-
пень повышения давления воздуха во входном устройстве лВх>
так как
* *
~ = °»х = °вХ (1 + 0,2М2)3,5- (6.8)
Рн Рн
Хотя величина аВх с ростом числа М полета уменьшается, но
Лвх увеличивается и при М = 2,0-4-2,5 обычно тсВх = 8~-12, т. е. на
сверхзвуковых скоростях полета воздух перед поступлением в
двигатель претерпевает существенное сжатие от скоростного на-
пора.
Для снижения потерь полного давления воздуха в воздухоза-
борнике и повышения устойчивости течения газового потока в нем
осуществляется управление пограничным слоем. Для этого между
боковой поверхностью летательного аппарата и воздухозаборни-
ком выполняются щели для слива пограничного слоя, накопив-
шегося на прилегающих поверхностях перед воздухозаборником,
а на панелях клина выполняют перфорацию для удаления по-
граничного слоя, образующегося при обтекании поверхности тор-
можения.
Описанная схема течения воздуха (рис. 6.2, а) относится к рас-
четному (максимальному) числу М полета самолета. На мане-
вренных самолетах воздухозаборники работают в широком диа-
пазоне нерасчетных режимов. Изменяются число М полета, ре-
жим двигателя и направление набегающего потока. Это приводит
к изменению газодинамической картины течения воздуха в воз-
духозаборнике, что влияет на параметры и запас устойчиво-
сти воздухозаборника. Последний оценивают коэффици-
ентом Д/G/bx, характеризующим удаление рабочего режима воз-
духозаборника от границы его устойчивой работы (помпажа).
При числах М, меньших расчетного, углы наклона косых скач-
ков возрастают. Они располагаются круче. Это, как видно из
рис. 6.2,6, приводит к уменьшению пло'щади FH струи воздуха,
входящей в воздухозаборник. Коэффициент расхода <р становится
меньше 1. Пропускная способность системы скачков резко сни-
жается и значительно повышается внешнее сопротивление возду-
хозаборника. Одновременно уменьшается пропускная способность
горла. Это объясняется резким снижением плотности воздуха в
горле из-за уменьшения скоростного напора потока.
140
Снижение пропускной способности системы скачков и горла
нерегулируемого воздухозаборника при уменьшении М приводит
к тому, что он оказывается не в состоянии пропустить то количе-
ство воздуха, которое требуется для работы двигателя. В целях
согласования работы воздухозаборника и двигателя приходится
осуществлять его регулирование. У плоских воздухозаборников
регулирование достигается таким изменением расположения ре-
гулируемых панелей, при котором увеличивается Fr и умень-
шаются углы наклона косых скачков при уменьшении М. Это
обеспечивается специальным панельно-шарнирным устройством
(рис. 6.3), уборкой которого достигается желаемый эффект.
У осесимметричных воздухозаборников та же цель достигается
уборкой ступенчатого клина внутрь обечайки. При этом углы на-
клона косых скачков не уменьшаются, но они отодвигаются от
плоскости входа.
Регулирование воздухозаборников требуется также при изме-
нении расхода воздуха через двигатель, вызываемого изменением
частоты вращения (при перемещении РУД) или изменением тем-
пературы наружного воздуха Тн (влияние климатических усло-
вий). При перемещении РУД на уменьшение частоты вращения
и, следовательно, при снижении GB нужно уменьшать производи-
тельность воздухозаборника (выдвигать клин). Снижение Тн при-
водит к возрастанию плотности воздуха и, следовательно, увели-
чению <7в, что требует увеличения производительности воздухоза-
борника (уборки клина).
Для обеспечения оптимального согласования воздухозаборника
и двигателя в широком диапазоне режимов может оказаться це-
лесообразным иметь в системе регулирования воздухозаборников
еще и створки перепуска 8 воздуха в канале за горлом (рис. 6.3).
При их открытии часть воздуха перепускается во внешний поток,
чем повышается &КУвх. Их называют поэтому противопом-
п а ж н ы м и.
На взлете и при малых М дополнительное повышение пропуск*
ной способности воздухозаборника достигается применением
впускных створок 9 (рис. 6.3), открывающихся внутрь канала
под действием перепада давлений на створках, когда давление
перед двигателем становится меньшим атмосферного.
Если воздухозаборник перестает регулироваться или наруша-
ется правильное согласование его работы с двигателем, проис-
ходит ухудшение данных воздухозаборника и может возникать
неустойчивая работа — помпаж или зуд.
Помпаж воздухозаборника возможен при М>1,5-г-
4-1,6 в том случае, когда в воздухозаборник поступает больше
воздуха, чем требуется для двигателя. Воздухозаборник перепол-
няется воздухом высокого давления и возникает его выброс из
входного канала в атмосферу. После этого давление в канале
падает, затем происходит наполнение воздухозаборника сжатым
воздухом и повторный его выброс. В результате возникают ко-
лебания давлений малой частоты (6—12 Гц) и большой ампли-
141
Рис. 6.3. Схема плоского регулируемого воздухозаборника:
J — неподвижная панель; 2, 3, 4, ^—подвижные панели; 6 — шарнирные соединения; Z — перфорация; <3 — створки перепу-
ска; 9 — впускание створки; 10 — турбулизаторы
туды. Внешними признаками помпажа воздухозаборника на са-
молете являются хлопки, «бубнение» в канале и воспринимаемые
в виде толчков или ударов периодические продольные перегрузки,
появляющиеся из-за колебания тяги двигателя.
Помпаж воздухозаборника недопустим, так как он обычно
вызывает помпаж компрессора и, как следствие, недопустимое
повышение Г* или самовыключение двигателя. Возникновению
помпажа воздухозаборника способствуют все факторы, приводя-
щие к переполнению воздухом входного канала двигателя. Этими
факторами могут быть:
— прекращение выдвижения клина при разгоне самолета из-за
отказов системы управления воздухозаборником двигателя (УВД);
— недозволенно глубокое дросселирование двигателя при боль-
ших числах М полета;
— резкое маневрирование самолета при М> 1,54-1,6, приво-
дящее к недопустимому увеличению углов атаки (скольжения).
Для устранения помпажа воздухозаборника эффективными
средствами являются: снижение скорости полета самолета за
счет выключения форсажа, выдвижение клина, открытие проти-
вопомпажных створок. Дросселирование двигателя приводит к усу-
гублению помпажа.
Зуд воздухозаборника возникает в тех случаях, когда
пропускная способность воздухозаборника оказывается меньшей,
чем двигателя. В этом случае падает давление на входе в двига-
тель, что приводит к разгону потока в канале за горлом до М>1
и образованию (в процессе последующего торможения воздуха)
скачка уплотнения. Этот скачок, взаимодействуя с пристеночным
пограничным слоем, вызывает высокочастотные пульсации дав-
ления на входе в двигатель. Зуд оказывает неприятное воздейст-
вие на летчика (зудящее ощущение в теле). Пульсация потока
при зуде снижает запас устойчивости компрессора. Но зуд менее
опасен, чем помпаж.
Чтобы не допускать снижения ДК^вх при полете с большими
углами атаки, применяются специальные конструктивные меры
(например, установка горизонтальных перегородок в канале воз-
духозаборника с вертикальным расположением клина), а также
специальное регулирование (например, дополнительное выдвиже-
ние клина).
Управление воздухозаборником осуществляется автоматиче-
ской системой УВД. Перемещение клина (конуса) производится
автоматически в зависимости от ппР (или степени повышения дав-
ления в компрессоре Это объясняется тем, что влияние
параметров М, n, V, Н и Тн на потребную подачу воздуха в дви-
гатель наиболее полно учитывается величиной GB, ПР, но последняя
обычно связана однозначно с ипР, а также с п*.
Типичная программа управления воздухозаборника показана
на рис. 6.4. Здесь дано относительное выдвижение клина (в про-
центах) от гс*. Величина ГКл =100%, соответствующая полностью
143
выдвинутому клину, достигается при Мтах, когда тс* имеют наи-
меньшее значение. На взлете и при малых М, которым соответ-
ствуют наибольшие тс*, клин полностью убирается, a Fr макси-
мально увеличивается. Здесь же показано взаимное расположение
границ помпажа и зуда при фиксированном значении числа М
полета.
Рис. 6.4. Программа регулирования
сверхзвукового воздухозаборника
Компрессор. На современных ГТД применяются компрессоры
сложных схем. Обычно они выполняются по двухконтурной двух-
вальной схеме. Основными параметрами каждого каскада компрес-
сора являются: расход воздуха ОВг, частота вращения степень
повышения давления тс*., к.п.д. 7)*z и запас устойчивости &Kyi,
где индекс «I»‘обозначает наименование каскада компрессора. На
расчетном режиме каскады компрессора рассчитываются на вполне
определенные значения этих параметров. Высокоэффективная и
устойчивая работа каждого каскада достигается соответствующим
профилированием его проточной части. На расчетном режиме это
профилирование обеспечивает обтекание всех лопаточных венцов
без срыва с малыми гидравлическими потерями и с закруткой
воздуха, достаточной для получения высокого напора сту-
пеней.
При работе на нерасчетных режимах течение воздуха в отдель-
ных ступенях каскадов компрессора существенно меняется, что
приводит к изменению всех параметров компрессора. Как пока-
зывается в теории, совокупность изменения ряда эксплуатацион-
ных факторов (V, 7/, рн, Тн, п) воздействует на компрессор бла-
годаря изменению только двух приведенных параметров, которые
принято называть критериями подобия. Этими параметрами яв-
144
ляются приведенная частота вращения ппр и приведенный расход
воздуха GB. пр:
/ 288 . п 10330 1 Г Т*в
у,* > ^в. пр — GB » I/ 288 ’ (6-9)
1 В Ръ
где р*в и Т* — заторможенные параметры воздуха на входе а
компрессор.
Рис. 6.5. Расположение рабочей линии а б на характери-
стике компрессора (а), и зависимость запаса устойчивости
компрессора (б) от приведенной частоты вращения ро-
тора НПр
Указанные параметры являются критериями подобия по той
причине, что они однозначно определяют число М по относитель-
ной скорости воздуха на входе в компрессор. При этом параметр
пПр определяет число М по окружной скорости колеса компрес-
сора, а параметр GB. пр — число М по осевой скорости воздуха на
входе в компрессор. В частности, с ростом скорости полета при
постоянстве физической частоты вращения п величина яПр умень-
шается, снижается при этом и величина GB. Пр. Это обусловлено
возрастанием скорости звука на входе в компрессор вследствие
повышения температуры воздуха при его сжатии и снижением
чисел М по окружной скорости Ми = ^к/^в и по осевой скорости
Ма = £в/ав, где ик — окружная скорость колеса, а ав — скорость
звука в сечении В—В (рис. 6.1), св — осевая скорость воздуха на
входе в компрессор.
Об изменении режима работы и основных параметров компрес-
сора (каскада) судят по его характеристике. На рис. 6.5, а пред-
ставлена типичная характеристика компрессора (каскада) в виде
зависимости тс* от GB. пр и пПр. На эту характеристику нанесена,
рабочая линия а—р—б, где р — расчетный режим компрессора.
Взаимное расположение рабочей линии и границы помпажа позво-
ляет судить о запасах устойчивости компрессора. Величина Д/^
при каждом г?Пр как раз и характеризует относительное удаление
рабочей точки от границы помпажа компрессора. Как видно
145
(|рис. 6.5,6), Д/С/ снижается при ппр>Япр.р. В точке б, где ДЛ^ = 0,
возникает помпаж компрессора, вызываемый срывом потока на
последних ступенях. При пПр<^Пр. р у компрессоров, регулируе-
мых поворотом лопаток направляющих аппаратов (НА) ряда
ступеней, \КУ обычно увеличивается и компрессор работает устой-
чиво (рис. 6.5), а у нерегулируемых компрессоров (штриховые
линии на рис. 6.5) снижается, причем помпаж в этом
случае обусловлен срывом потока на первых ступенях компрес-
сора.
Рассмотрим физическую сущность явлений срыва потока и
помпажа компрессора. Заметим, что первопричиной этих явлений
служит такое рассогласование условий работы отдельных ступе-
ней, при котором на некоторых лопатках достигаются сверхкри-
тические углы атаки.
При значительном снижении ггпр происходит уменьшение тс* .
Следовательно, понижается плотность воздуха на последних сту-
пенях. Но проходные сечения межлопаточных каналов последних
ступеней выполнены значительно меньшими, чем первых (с учетом
расчетного повышения плотности воздуха в компрессоре). Тогда
в рассматриваемых нерасчетных условиях проходные сечения на
последних ступенях оказываются недостаточными, чтобы пропу-
стить менее плотный воздух. Но поскольку все ступени должны
пропускать одинаковое количество воздуха, осевые скорости его
на последних ступенях значительно возрастают, а вследствие дрос-
селирующего влияния последних ступеней осевые скорости на пер-
вых ступенях резко снижаются. Углы аргаки на первых ступенях
увеличиваются по сравнению с расчетными, а на последних — сни-
жаются. На первых ступенях при этом резко снижаются запасы
устойчивости, а на последних — падают к.п.д. Треугольники ско-
ростей для указанных ступеней (при /2 = const) показаны на
рис. 6.6: сплошными линиями при тс*<тс* , а штриховыми —
для гс* = тс* о. Чрезмерное увеличение углов атаки на первых
ступенях может привести к срыву потока на этих ступенях. В по-
летных условиях такие случаи (когда тс* О*. р) возможны либо
при значительном дросселировании двигателя, либо на режимах
с Птах, но при высоких Г*, что соответствует полету с большим М,
особенно в жаркое время года.
Срыв потока на последних ступенях компрессора (каскада)
возможен, когда ппр>ппр. р. В таком случае плотность воздуха на
последних ступенях (из-за тс*>тс*. ) превышает расчетную, что
приводит к относительному уменьшению осевых скоростей и уве-
личению углов атаки уже на последних ступенях. Этот случай
соответствует работе двигателя с nmax и при низких Тн и малых V,
когда температура 7* минимальна, а пПр — максимальна.
Как показали исследования, срыв потока в ступенях возникает
не на всех лопатках одновременно, а образует одну или несколько
срывных зон, охватывающих часть лопаток. Эти зоны не остаются
146
связанными с одними и теми же лопатками, а вращаются относи-
тельно корпуса компрессора в сторону вращения ротора.
Если вращающаяся срывная зона возникает
на последних ступенях, она оказывает дросселирующее
действие на впереди стоящие ступени, и срыв распространяется
на весь компрессор. Через срывную зону воздух из-за компрес-
Рис. 6.6. При 7?пр < ппр. р углы атаки а при об-
текании лопаток первых ступеней увеличивают-
ся (а), а последних — уменьшаются (б)
сора перетекает на вход. В момент прорыва воздуха через срыв*
ную зону возникает характерный хлопок, и давление за компрес-
сором падает. После кратковременного восстановления режима
срыв и хлопок могут повториться. При определенных условиях
это явление повторяется периодически в виде серии хлопков и
низкочастотных колебаний давления большой амплитуды, и в
таком проявлении оно именуется помпажом компрессора.
Характерным признаком помпажа компрессора в ГТД
кроме хлопков является резкое повышение температу-
ры газа 7* за турбиной и снижение частоты вра-
щения п.
Если срыв возникает на первых ступенях, где
лопатки более длинные, он вначале охватывает только небольшую
периферийную часть лопаток. Вращающаяся срывная зона в этом
случае развивается постепенно, и она может не сразу распростра-
ниться на весь компрессор. Но вращающийся срыв может вызвать
опасные вибрации лопаток. Если эта форма срыва переходит в
помпаж (в этом случае хлопки могут отсутствовать или быть
очень слабыми), его обнаруживают датчиками помпажа или по
147
повышению температуры газа за турбиной. В любом случае пом-
паж компрессора должен быть немедленно устранен.
Для расширения диапазона устойчивой работы компрессоров
применяют их регулирование. Принцип регулирования компрес-
соров поворотом лопаток направляющих аппаратов (НА) состоит
на лопатках регулируемых
ступеней вблизи расчетного
значения. Если, например,
на первых ступенях углы
атаки возрастают, а на по-
следних уменьшаются, это
несоответствие устраняют по-
воротом регулируемых НА:
в группе первых ступеней —
на прикрытие, а в группе
последних — на открытие.
В наибольшей степени нуж-
даются в регулировании
первые ступени высокона-
порных каскадов, в меньшей
степени — последние, и сов-
сем не требуют регулирова-
ния средние ступени.
Поворот лопаток НА
осуществляется системой ав-
томатического управления
двигателя. Углы поворота
лопаток 0 задаются в зави-
в поддержании углов атаки потока
Рис. 6.7. Типовая программа регулирова-
ния НА группы первых 1 и группы по-
следних 2 ступеней компрессора
симости от ппр и контролируются по положению первой и послед-
ней (z-й) ступени. Характер изменения 0i ст и 0ZCt от ггпр показан
на рис. 6.7. При м, близких к малому газу, перестановка НА z-й
ступени на 9 = 0 производится в целях уменьшения GB и облегче-
ния запуска двигателя. Величины углов 0 других регулируемых
ступеней определяются передаточным соотношением механизма
привода.
Применение двигателей двухвальной и двухконтурной схем
также способствует повышению устойчивой работы компрессора
в целом и его отдельных каскадов. Указанное ранее рассогласо-
вание первых (в КНД) и последних ступеней, например при
Р» приводит к тому, что ротор КНД со ступенями, рабо-
тающими с повышенными углами атаки, затяжеляется и умень-
шается мн этого ротора. Напротив, ротор КВД облегчается и уве-
личивается ив. В результате возрастает скольжение 5 = мв/ин, что
приводит к повышению запасов устойчивости и к.п.д. компрессора
в целом (вследствие снижения углов атаки на КНД и их увели-
чения на КВД). С ростом М, кроме того, повышается степень
двухконтурности, что приводит к относительному увеличению
осевых скоростей воздуха в КНД и предотвращает чрезмерный
рост углов атаки на лопатках его первых ступеней. Таким обра-
148
Рис. 6.8. Изменение коэффициента-
избытка воздуха а на установив-
шихся режимах (/), в процессе*
приемистости (2) и сброса газа (5)
и при чрезмерных избытках топли-
ва (4)
зом, каскады компрессора обладают в известной мере свойством
саморегулирования. Но, учитывая, что КВД имеют высокие зна-
чения лк. в, все же требуется и у них регулировать НА нескольких
первых ступеней КВД (рис. 6.1).
К средствам регулирования компрессора относится также пе-
репуск воздуха из его средних ступеней в атмосферу (или во
второй контур). У двухвальных двигателей перепуск воздуха мо-
жет осуществляться из-за КНД.
Перепуск иногда используется -
для увеличения запаса устойчи-
вости компрессора при запуске
двигателя. Он может применять-
ся для кратковременного повы-
шения при пусках ракет.
Камеры сгорания. Надеж-
ность работы силовой установки
в значительной степени опреде-
ляется устойчивостью процесса в
камерах сгорания — основной и
форсажной — на всех режимах
работы двигателя.
Процесс горения топлива в
камере сгорания зависит от мно-
гих факторов. Важное значение
имеет качество распыливания, ис-
парения и воспламенения топли-
вовоздушной смеси, надежность
стабилизации факела пламени и
другие условия, обеспечиваемые
рядом конструктивных мер, в частности, созданием постоянных
очагов пламени в зонах обратных токов. Но устойчивость про-
цесса горения зависит и от условий эксплуатации двигателя на
самолете. Среди них важнейшее значение имеет состав топливо-
воздушной смеси, характеризуемый коэффициентом избытка воз-
духа а, а также параметры воздуха и газов (температура Тк,
давление рк и скорость ск) на входе в камеру сгорания.
На установившихся режимах работы основной камеры сгора-
ния коэффициент а изменяется в небольших пределах, как пока-
зано линией 1 на рис. 6.8. Но при резком перемещении РУД на^
увеличение подачи топлива (линия 2) или на ее уменьшение (ли-
ния 3) коэффициент а, как видно, изменяется в широких преде-
лах. При увеличении GT на режимах приемистости а уменьшается,
а при снижении GT на режимах сброса газа а резко увеличивается.
Значительное обогащение или обеднение смеси приводит к нару-
шению правильности рабочего процесса основной камеры, что
вызывает первоначально снижение полноты сгорания топлива,
а затем при некоторых атщ и а max прекращение горения. При зна-
чительном снижении а происходит переобогащение зоны горения
топливом. Снижается температура и ухудшается поджигательная
149*
способность зон обратных токов — наступает «богатый» срыв пла-
мени (рис. 6.8). При увеличении а значительно снижается тем-
пература в зоне горения и падает скорость горения. В результате
часть топливовоздушной смеси не успевает сгореть полностью в
основной камере — наступает «бедный» срыв пламени.
Параметры на входе в основную камеру изменяются небла-
гоприятно в полете на больших высотах Н и при малых скоростях
полета Уприб. В этих условиях снижаются рк и Тк. Снижение рк
приводит к уменьшению степени турбулентности потока воздуха
и к замедлению интенсивности процессов смешения, воспламене-
ния и горения. Уменьшение Тк заметно ухудшает испарение топ-
лива. Наконец, уменьшение GB в этих условиях требует сниже-
ния GT. Это достигается уменьшением давления топлива перед
форсунками и приводит к ухудшению качества распыла топлива.
В результате диапазон устойчивой работы камеры сгорания между
«max и «пип существенно сужается, что приводит к необходимости
введения ограничений по темпу перемещения РУД на больших
высотах полета.
Отметим некоторые особенности процесса запуска (розжига)
основной камеры сгорания. Воспламенение топлива в основной
камере при запуске осуществляется пусковым блоком, состоящим
из пусковой форсунки и запальной электрической свечи. Процесс
воспламенения поступающего в основную камеру топлива осуще-
ствляется следующим образом. Вначале обеспечивается воспла-
менение топлива в пусковом блоке и создание пускового факела.
От этого факела происходит поджигание основного топлива у той
торелки, около которой установлен пусковой блок, и уже после
этого распространение (переброска) пламени на остальные го-
релки.
Обычно трубчато-кольцевые камеры сгорания состоят из не-
скольких жаровых труб, а пусковые блоки имеются не на всех
трубах. Для обеспечения запуска всей камеры между жаровыми
"трубами устанавливаются пламеперебрасывающие патрубки. Наи-
тгучшие условия для переброски пламени — в кольцевых камерах
сгорания, что является их важным преимуществом.
Понижение рк и Тк воздуха, поступающего в основную каме-
ру, резко сужает пределы воспламеняемости топливовоздушной
смеси. Поэтому розжиг основной камеры при запуске двигателя
на больших высотах затрудняется, что является причиной вве-
дения ограничений по максимальной высоте надежного запуска.
Подпитка пусковых блоков кислородом, существенно расширяя
пределы воспламеняемости смеси и повышая мощность пускового
факела, является эффективным средством увеличения максималь-
ной высоты надежного запуска двигателя в полете.
Главными факторами, влияющими на срыв пламени в форсаж-
ной камере, являются суммарный коэффициент избытка воздуха
(определяемый по суммарному расходу основного и форсаж-
ного топлива) и давление в форсажной камере р$. При уменьше-
но
нии в форсажной камере появляются зоны, переобогащенные
топливом, что приводит к неполному сгоранию топлива и сниже-
нию температуры газа в зонах обратных токов. При а= 1,14-1,2
может наступить «богатый» срыв. При увеличении происхо-
дит уменьшение скорости распространения пламени из-за обед*
Рис. 6.9. Области неустойчивых и срывных ре-
жимов работы форсажной камеры
нения смеси. Кроме того, часть топлива еще до подхода к фронту
пламени успевает испариться и перемешаться с выходящими из
турбины газами, образуя смесь негорючей концентрации. Это
также ухудшает работу форсажной камеры, может возникнуть
«бедный» срыв.
Уменьшение давления рф, с одной стороны, приводит к сни-
жению скорости горения и полноты сгорания топлива. С другой
стороны, с уменьшением рф снижается Ов, а следовательно, и по-
требный расход топлива. Это приводит к снижению давления фор-
сажного топлива и к ухудшению качества его распыла. Именно-
по этой причине при снижении давления рф сокращается диапа-
зон устойчивых режимов работы форсажной камеры. На рис. 6.9
приведена срывная характеристика форсажной камеры, представ-
ляющая собой зависимость диапазона ее устойчивой работы по
от давления рф. Как видно, при понижении рф диапазон устойчи-
вой работы форсажной камеры сужается (в основном за счет
смещения границы «бедного» срыва), а при давлении, меньшем
Рф min, устойчивая ее работа уже не обеспечивается при любом
Следовательно, в условиях полета на очень больших высотах и
малых скоростях полета, когда давление рф может значительно
снизиться, устойчивая работа форсажной камеры может быть
обеспечена лишь в узком диапазоне режимов работы двигателя
(например, только на режиме полного форсажа), а в случае ее
выключения повторный розжиг может оказаться возможным толь-
ко после уменьшения высоты полета (увеличения давления рф)>
151
«Бедному» срыву в форсажной камере обычно предшествует
неустойчивая работа, получившая название пульсационного
горения. Она может возникнуть на больших высотах при дрос-
селировании форсажа, т. е. при сильном обеднении смеси. В этом
случае пламя то погаснет, то вновь вспыхивает. Летчик ощущает
это явление по продольным толчкам самолета и колебаниям час-
тоты вращения роторов двигателя. Устранить это явление можно
снижением высоты и увеличением степени форсирования двига-
теля.
Одной из серьезных трудностей, которую приходится преодо-
левать при создании форсажных камер, является возникновение
особой неустойчивости в их работе, называемой вибрацион-
ным горением. Вибрационное горение проявляется в виде вы-
сокочастотных колебаний давления, сопровождаемых резким зву-
ком высокого тона. Возникшие колебания вызывают вибрации
элементов конструкции камеры, а также ведут к повышению тем-
пературы ее деталей. Суммарное воздействие этих факторов мо-
жет быть причиной разрушения камеры.
Вибрационное горение обычно возникает на таких режимах
работы двигателя, при которых становится ниже 1,1 —1,2,
а давление в камере велико (рис. 6.9). Как установлено, вибра-
ционное горение является автоколебательным процессом, проте-
кающим в газе, находящемся в форсажной камере.
Наиболее опасным с точки зрения вибрационного горения яв-
ляются режимы полета у земли с максимальной скоростью, когда
давление в форсажной камере достигает наиболее высоких зна-
чений. Основным способом предотвращения вибрационного горе-
ния в форсажной камере является установка антивибрационного
экрана с перфорированными стенками в районе, где фронт пла-
мени приближается к стенкам камеры. Такой экран, помимо аку-
стического демпфирования, осуществляет гашение колебаний
вследствие поглощения энергии колебательного движения потока
при его перетекании через отверстия перфорации.
Область возможного вибрационного горения в форсажной ка-
мере, как показано на рис. 6.9, примыкает к области «богатого»
срыва в ее верхней части, соответствующей высоким значениям
давления рф.
Наиболее эффективными средствами предотвращения вибра-
ционного горения летчиком, если оно возникло в условиях полета,
являются снижение степени форсирования двигателя — для повы-
шения и уменьшение скорости полета самолета — для сниже-
ния давления р$.
§ 6.3. Высотно-скоростные и дроссельные характеристики
Характеристиками авиационных силовых установок (СУ) на-
зывают зависимости Р и Суд от А4, Н и режима двигателя, зада-
ваемого положением РУД. В соответствии с этим различают ско-
ростные, высотные и дроссельные характеристики.
152
Основными режимами работы ТРД, задаваемыми положением
РУД, являются: земной малый газ (ЗМГ), полетный малый газ
(ПМГ), крейсерский режим (Кр), номинальный режим (Н) и
максимальный режим (М). У ТРДФ и ДТРДФ помимо указанных
установлены еще режимы минимального форсажа (МФ), частич-
ного форсажа (ЧФ) и полного форсажа (ПФ).
Режимы работы двигателя устанавливаются в соответствии с
требуемыми режимами полета. При этом для правильного расхо-
дования ресурса двигателя обычно нормируется суммарная нара-
ботка двигателя в полете на максимальном и форсажных режи-
мах, как наиболее напряженных режимах работы двигателя. Это
время указывается в инструкции по эксплуатации и составляет
не более 30—35% общего ресурса двигателя. Его учет необходимо
вести по записям в формуляре самолета.
Иногда ограничивается допустимое время непрерывной работы
двигателя на отдельных наиболее напряженных режимах. На-
пример, на земле допускается работа на режиме «ЗМГ» обычно
не более 10 мин, так как на этом режиме охлаждение двигателя
становится недостаточно эффективным. По этим же причинам
включение форсажа при опробовании двигателя на земле обычно
ограничено временем не более 15—20 с. У некоторых двигателей
имеются ограничения по длительности непрерывного использования
режимов «ПФ» и «М» либо во всех условиях полета (не более
20—30 мин), либо только при полете на больших скоростях и на
малых высотах.
Летчик должен твердо знать, что использование без особой на-
добности повышенных режимов работы двигателя отрицательно
сказывается на надежности его работы и может отразиться на
безопасности полетов.
Основные показатели силовой установки — тяга и удельный
расход топлива — в условиях полета при заданном режиме дви-
гателя, устанавливаемом с помощью РУД, существенно зависят
от принятого закона его управления.
Управление двигателем осуществляется системой автоматиче-
ского управления, которая реализует определенную (заранее вы-
бранную) программу управления двигателем. Управление двига-
телем осуществляется для изменения его режима и установления
таких значений управляющих параметров, при которых обеспе-
чивается наивыгоднейшее протекание характеристик СУ и ее
устойчивая и надежная работа. Наиболее эффективными средст-
вами воздействия на процесс работы двигателя являются изме-
нение у него трех управляющих параметров — частоты вращения
одного из роторов (это либо пн, либо Пв, т. е. в общем случае И/),,
а также температур Т* и Гф. Для управления этими параметра-
ми служат три управляющих фактора — расход топлива основной
камеры GT и форсажной камеры GT. ф и площадь критического»
сечения сопла FKp. Обычно О* воздействует на 6Т. ф — на Гф
и /\р — на
153.
Закон изменения управляющих параметров в зависимости от
внешних возмущающих воздействий и положения РУД называют
программой управления двигателя (ПУД). К внеш-
ним возмущающим воздействиям относят скорость полета V, вы-
соту полета Н и внешние атмосферные условия ри и Тн< Доказано,
что их изменение может оказывать влияние на управляющие па-
раметры только через изменение температуры Г* на входе в дви-
гатель. По указанной причине ПУД представляет собой зависи-
мости Т* и Г* от 7* и положения РУД.
На режимах «М» и «ПФ» задача ПУД — обеспечить мак-
симально возможную тягу двигателя. Теоретически для этой цели
нужно поддерживать в условиях полета максимальные значения
управляемых параметров, т. е. осуществлять ПУД:
= const; т; = = const; Гф = Г; const, (6.10)
.за счет соответствующего управления величинами GT, Gt. ф и Гкр.
Но реализация этой программы требует непосредственного изме-
рения температур Т* и Гф, что весьма сложно. Более простой
в' реализации является ПУД по температуре Г* за турбиной
я с косвенным регулированием температуры форсажа:
nt = const; Г* = const; -~-g* =const, (6.11)
Рк
где величина Г* на 250—300° меньше, чем 7^, причем условие
Т* — const приводит к 7* ~ const. Условие GT. ф/р* = const
обеспечивает ss const.
Практически, однако, приходится вводить ряд ограничений и
учитывать особенности двухвальной схемы двигателя, т. е. ука-
занные управляющие параметры нужно поддерживать не посто-
янными, а задавать закон их изменения по температуре Т*.
На рис. 6.10 представлена типичная ПУД двухвального ТРДФ.
Показан закон изменения параметров пн, Т* и От,ф/р* от Г*.
Здесь же дано соответствующее этой ПУД изменение Тф и сте-
пени понижения давления в турбине тс*. Заметим, что на бес-
форсажных режимах величины FKp и тс* изменяются по одному
закону (ГКр пропорционально тс*). При Т* < 288 К здесь тс* =
= const (FKp=const) и поддерживается только nH = const, поэтому
пв и Т* растут с увеличением Т*. В диапазоне от 288 до 330 К
выполняется ПУД, формула (6.11), что уже требует повышения
тс* (за счет увеличения FKp). При Т* =330 К осуществляется рас-
крутка РИД на 3% при 7’* = const, что делается из условия
увеличения тяги двигателя в области трансзвуковых и сверхзву-
ковых скоростей полета. В диапазоне от 330 до 400 К повторяется
ПУД предыдущего интервала по 7*. При Т* >400 К осущест-
вляется снижение Т* (а следовательно, и 7*) с увеличением 7*,
154
что замедляет интенсивность роста пв с увеличением 7*. Это
снижение Т* диктуется условиями охлаждения турбины — она
охлаждается воздухом из-за компрессора, а его температура рас-
Рис. 6.10. Программа управления
двухвального ТРДФ и изменение
его основных параметров по Тв
Рис. 6.11. Скоростные характеристи-
ки ТРДФ для высоты 11 км на ре-
жимах «Максимал» (/) и «Полный
форсаж» (2)
тет с ростом 7*. При Г* =470 К достигается максимально допу*
стимая по прочности величина пв, и при Т* >470 К осуществляв
ется ПУД /гв = const; 7* = /(7*) и С?т.ф/р* = const. В данной
ПУД еще характерным является ступенчатое увеличение 0т.ф/7^
при 7* = 360 К, что вызвано необходимостью поддержания 7*,
близкой к максимально допустимой, так как при От, ф/р* == const
фактически 7* снижается при увеличении 7* (рис. 6.10).
Скоростные характеристики ТРДФ для указанной
ПУД представлены на рис. 6.11. Они дают изменение Р и Сул
153
по М для режимов «М» и «ПФ» (штриховые линии) на Я=11 км.
Как видно из рисунка, на режиме «М» тяга вначале несколько
снижается (до М = 0,34-0,5), затем начинает возрастать, дости-
гает наибольших величин при М = 2, после чего интенсивно умень-
шается. Суд с увеличением М непрерывно возрастает и стремится
к бесконечности на М, при которых тяга обращается в нуль.
Такой характер зависимостей Р и Суд от М объясняется следую-
щим.
С увеличением М увеличивается лвх. Хотя тс* при этом сни-
жается (вследствие повышения температуры воздуха на входе
в компрессор), тем не менее общая степень повышения давления
воздуха в двигателе при увеличении М возрастает. Это приводит
к повышению давления р* за компрессором, а следовательно, и
давления р* перед турбиной. Но в этом случае возрастает и
давление /?* за турбиной, так как степень расширения в турбине
тс* изменяется не очень значительно. Из-за повышения /?* уве-
личиваются степень расширения газа в сопле и скорость истече-»
ния из сопла сс. Однако скорость сс увеличивается медленнее,
чем скорость полета, благодаря чему Руд = сс—V с увеличением М
уменьшается.
С увеличением М величина GB, напротив, все время возрастает,
что объясняется повышением плотности воздуха в газовоздушном
тракте двигателя вследствие повышения давления воздуха на
входе в двигатель от скоростного напора. Вначале с увеличением
скорости полета GB возрастает медленно, а затем все более ин-
тенсивно, что связано с законом изменения скоростного напора
по числу М полета.
Тяга двигателя, как произведение величины GB и Руд, сначала
(пока GB растет медленнее, чем падает Руд) несколько снижается,
затем (при резком увеличении GB) увеличивается. Падение Р при
дальнейшем увеличении М (М>24-2,5) объясняется значитель-
ным уменьшением Руд вследствие уменьшения разности скорости
истечения и скорости полета.
Удельный расход топлива с увеличением М увеличивается,
так как уменьшается Руд. Но это не значит, что экономичность
двигателя ухудшается. Если проследить, как изменяется расход
топлива не на единицу тяги, а на единицу мощности, то станет
ясно, что экономичность двигателя улучшается при увеличе-
нии М.
Рассмотрим теперь скоростные характеристики того же дви-
гателя на режиме «ПФ» (штриховые линии на рис. 6.11). Как
видно, при включении форсажа возрастает тяга, но и увеличи-
вается удельный расход топлива (ухудшается экономичность).
Это объясняется тем, что в форсажной камере, расположенной
за турбиной, давление ниже, чем в основных камерах, поэтому
и тепло в ней используется хуже. Но с увеличением М давление
в форсажной камере повышается, что способствует лучшему ис-
пользованию тепла. Поэтому с ростом М прирост тяги на фор-
156
саже увеличивается, а экономичность существенно улучшается.
На очень больших М, когда тяга нефорсированного двигателя
начинает быстро падать, форсированный двигатель обеспечивает
дальнейший рост тяги, а его удельный расход топлива может
стать даже меньше удель-
ного расхода нефорсирован-
ного двигателя. На рис. 6.11
«ступеньки» в кривых при
М=1,5 вызваны раскрут-
кой роторов, а при М =
= 1,9 — ступенчатым повы-
шением GT. ф.
Программы управления
и протекание скоростных
характеристик ДТРДФ со
смешением потоков газа за
турбиной в принципе не от-
личаются от рассмотренных
для ТРДФ, хотя они имеют
некоторые особенности. У
них обычно имеются три
характерных области изме-
нения управляемых пара-
метров по Г*. При низких
значениях Г* управление
двигателем осуществляется
ПО Мн. пр= Const При Ркр"~~
= const, что на бесфорсаж-
пых режимах обеспечивает
неизменность мв.пр и ят
и является причиной рез-
кого повышения мн, и
Т* с увеличением Г*
(рис. 6.12). На втором
участке в данном при-
мере (в диапазоне Т*
от 270 до 330 К на
рис. 6.12) принимается nH=const (или увеличение па по т. е.
постепенная раскрутка ротора), что дает снижение п* с ростом
Тд. Такой закон управления обеспечивает заданное благоприят-
ное расположение рабочей линии на характеристике КНД, необ-
ходимое для обеспечения устойчивой работы двигателя, но пара-
метры пв и Т* при этом увеличиваются. На третьем участке
(рис. 6.12, при Г* >330 К) обеспечивается ограничение по Т*тел
(тогда пн и пв падают). Степень двухконтурности двигателя с
увеличением Мя (с уменьшением ппр) у ДТРДФ возрастает.
157
У ДТРДФ переход на режимы «ПФ» и «ЧФ» обычно произ-
водится при той же ПУД, которая принята для режима «М», но
с добавлением условия =/(?'*), причем закон изме-
нения от параметров воздуха на входе в двигатель вы-
бирается таким, чтобы обеспечивалось поддержание требуемого
закона изменения Тф от Т* (в частности, 7’* = const). Необ-
ходимость коррекции О* ф/р* по Г* объясняется ростом степени
двухконтурности с увеличением Т*, что при условии Ох,ф/р* =
— const привело бы к значительному снижению 7"^ по числу М по-
лета.
Высотно-скоростные характеристики позволяют
судить о влиянии не только М, но и высоты полета на Р и Суд.
На рис. 6.13 они даны применительно к режиму «ПФ». Как вид-
но, тяга существенно снижается с ростом Н при М=const. При-
чиной этого является уменьшение GB вследствие значительного
158
снижения плотности воздуха с высотой. Удельная тяга с увели-
чением Н до 11 км несколько повышается (из-за увеличения \
вследствие уменьшения Тн), поэтому до высот 11 км тяга дви-
гателя падает медленнее, чем плотность воздуха. При /7=11 км
принимают, что P=constpw, т. е. здесь тяга двигателя уменьшается
пропорционально плотности воздуха в окружающей атмосфере.
Суд с ростом Я до 11 км при M=const снижается, что объясняется
увеличением я* и улучшением вследствие этого эффективности
использования тепла. При Я>11 км можно считать Cye=const
при M=const.
Дроссельные характеристики строят при M=const
и /7 = const в виде зависимостей Р и Суд от п или Суд от Р для
ряда режимов, задаваемых положением РУД. Эти режимы отме-
чены на указанных характеристиках (рис. 6.14). Как видно, фор-
сажным режимам при больших тягах свойственны и очень высокие
Суд. Это приводит к высоким часовым и километровым расходам
топлива, которые на «ПФ» в 3—4 раза выше, чем на крейсерских
(«Кр») режимах. Это требует от летчика внимательного отноше-
ния к использованию форсажных режимов, так как на них за
короткое время может быть израсходован весь запас топлива.
При переходе на режимы частичного форсажа Суд сильно сни-
жается. Это объясняется уменьшением относительной доли топ-
лива, подаваемого в форсажную камеру, где использование тепла
существенно хуже, чем в основной камере. При переходе с режима
«МФ» на режим «М» тяга и удельный расход топлива обычно
падают скачком, а не непрерывно. Это объясняется трудностью
обеспечения устойчивого процесса горения в форсажной камере
при очень малой подаче форсажного топлива. Большой скачок
в тяге при включении форсажа затрудняет пилотирование само-
лета. Например, в связи с этим не обеспечивается установившийся
полет (с V'npM6=const) в определенном (обычно трансзвуковом)
диапазоне скоростей.
При переводе РУД двигателя ниже режима «М» Суд продол-
жает уменьшаться и достигает наименьшей величины на крейсер-
ских режимах, где обеспечивается высокий к.п.д. компрессора,
а температура значительно меньше, чем 77тах. что более выгодно
с точки зрения использования тепла. Дальнейшее снижение ре-
жима от «Кр» до «МГ» сопровождается интенсивным снижением
тяги и значительным ростом Суд, что связано с уменьшением
и, следовательно, с ухудшением эффективности использования
тепла в двигателе.
Современные ГТД имеют систему охлаждения сопловых и
рабочих лопаток турбины воздухом, отбираемым от компрессора.
Этим обеспечивается надежная работа турбины при высоких тем-
пературах газа Т*. Но на режимах ниже максимального темпе-
ратура Т* уже в значительной степени снижается и надобность
в охлаждении конструктивных элементов турбины отпадает.
159
о
о Р, КГС
г кг
ь№кгс-ч
Н~0\ М=0
ПФ ?
а
5
Рис. 6.14. Способы представления дроссельных характеристик:
с — по частоте вращения; б — в виде зависимостей С от Р
у**
Охлаждающий воздух, отбираемый из-за компрессора и выпу-
скаемый через каналы системы охлаждения из лопаток за ступени
турбины, теряет работоспособность, что снижает экономичность и
тягу двигателя. Поэтому на этих режимах происходит автомати-
ческое отключение системы охлаждения турбины обычно по сиг-
налу от частоты вращения. Перекрытие подачи охлаждающего
воздуха приводит к снижению удельного расхода топлива
(рис. 6.14), поэтому полет на крейсерских режимах работы дви-
гателя целесообразнее выполнять с выключенным охлаждением.
Летчик должен при полетах на крейсерских режимах следить за
выключением охлаждения турбины по имеющейся сигнализации
в целях экономии горючего. Если сигнализация указывает на то,
что охлаждение не выключено, нужно немного снизить частоту
вращения двигателя.
В процессе эксплуатации СУ необходимо учитывать влияние
на Р и Суд температуры окружающего воздуха. При снижении тем-
пературы Тн всегда наблюдается увеличение тяги и небольшое
снижение Суд. Возрастание тяги объясняется увеличением GB
через двигатель (в основном из-за роста его плотности), а также
повышением Руд (из-за роста п* при n = const). Возрастание к*
и вызванное этим увеличение Руд является причиной снижения
Суд. Поскольку при увеличении температуры наружного воздуха
тяга двигателя уменьшается, в жаркую погоду увеличивается дли-
на разбега самолета при взлете, возрастает время разгона, ухуд-
шаются маневренные характеристики и может уменьшаться по-
толок самолета. Заметим, что степень влияния температуры на
данные силовой установки зависит от типа двигателя и принятой
ПУД.
§ 6.4. Переходные режимы работы ТРДФ и ДТРДФ
Эти режимы реализуются при приемистости, сбросе газа, а так-
же включении и выключении форсажа и запуске двигателя.
В процессе приемистости ускорение роторов достигается пода-
чей избыточного топлива в основную камеру. Это приводит к по-
вышению Г* и возрастанию мощности турбины. Избытки топлива
регулируются топливной аппаратурой с учетом ряда ограничений.
Это прежде всего защита турбины от перегрева, что требует огра-
ничения Г* max’ причем с учетом кратковременности воздействия
Г*тах может на 50—70°С превышать максимальную величину Г*
на режимах «М» и «ПФ». Типичное изменение От и Т* по пв по-
казано на рис. 6.15, а. На рис. 6.15,6 показано протекание рабо-
чих кривых на характеристиках компрессора одновального дви-
гателя или КВД двухвального двигателя. Здесь кривые 1 соответ-
ствуют установившимся режимам, 2 — режимам разгона (при-
емистости), 3 — режимам сброса газа (дросселирования).
6—21
161
При выборе закона подачи топлива в основную камеру учиты-
вается также влияние заброса топлива на запас устойчивости
компрессора. Как видно из рис. 6.15,6, в процессе приемистости
он резко снижается. При чрезмерном увеличении GT может быть
нарушена устойчивость компрессора (кривая 4), что недопустимо
из-за возможности возникновения помпажа. Поэтому в процессе
разгона обеспечивают AJG/min не менее 5—7%. При сбросе газа
Рис. 6.15. Изменение расхода топлива От, температуры Гг
и расположения рабочей линии на характеристике КВД на
установившихся режимах 1, при приемистости 2 и сбросе
газа 3
у двухвальных двигателей рабочая кривая на характеристике
КВД (как и у одновального двигателя) удаляется от границы
устойчивой работы, но рабочая кривая на КНД, наоборот, при-
ближается к границе помпажа. Это объясняется тем, что из-за
малого момента инерции ротора высокого давления скольжение
на режимах сброса уменьшается, а это приводит к торможению
потока воздуха в КНД со стороны КВД, частота вращения кото-
рого уменьшается быстрее, чем КНД. Указанные явления приво-
дят к необходимости ограничивать как темп увеличения, так и
темп уменьшения GT в двухвальных ГТД.
Наконец, учитывается и то, что изменение GT в процессах
приемистости и сброса изменяет а, как было показано на рис. 6.8.
В процессе приемистости режим основной камеры приближается
к границе «богатого», а в процессе сброса — «бедного» срыва.
При чрезмерных избытках топлива (кривая 4) возможно погаса-
ние камеры, что практически бывает на больших высотах. На
малых и средних Н раньше наступают ограничения по АЛ^тш
или г;тах.
Если при каждом значении частоты вращения ротора двига-
теля подача топлива поддерживается на максимальном уровне,
допускаемом указанными ограничениями, время переходного ре-
жима является минимальным. Такая приемистость является опти-
мальной.
162
Летчик обеспечивает приемистость двигателя перемещением
РУД, но темп подачи топлива при этом регулируется системой
управления двигателя из условия получения оптимальной при^
емистости. Тем не менее на некоторых режимах полета предус-
матриваются дополнительные ограничения по темпу перемещения
РУД или вообще запрещается пользоваться приемистостью.
Время от начала передвижения РУД двигателя до достижения
двигателем заданного режима повышенной тяги называется вре-
менем приемистости. Его обычно нормируют и контроли-
руют в процессе перехода от режима «ПМГ» до режима «М», от
режима «М» до режима «ПФ» и от режима «ПМГ» (или «ЗМГ»)
до режима «ПФ». Сокращение времени приемистости для быст-
рого достижения двигателем каждого режима имеет важное зна-
чение для улучшения маневренных свойств самолета.
Время приемистости от режима «ПМГ» до режима «М» обыч-
но увеличивается на больших высотах й малых 1/Приб. Это объяс-
няется уменьшением избыточной мощности турбины в связи с
уменьшением расхода воздуха через двигатель в этих условиях
и снижением допустимых избытков топлива в процессе приеми-
стости по условиям устойчивого горения. На малых высотах более
интенсивной подачей топлива можно сократить время приемисто-
сти, что осуществляется на ряде двигателей. Перестройка темпа
подачи топлива производится обычно автоматически по сигналу
от датчика высоты.
Основным фактором, ограничивающим допустимое снижение
подачи топлива при сбросе газа, помимо устойчивости КНД яв-
ляется предел устойчивой работы камеры сгорания на бедных
смесях. Срыв пламени в камере сгорания на этих режимах может
быть связан не только с чрезмерным обеднением смеси, но, и с
резким ухудшением качества распыла топлива, вызванным силь-
ным снижением перепада давлений на форсунках при малых его
расходах. Поэтому обычно в системе регулирования двигателя
предусматривается не только регламентирование темпа сброса
топлива, но и ограничение минимального расхода топлива через
форсунки (минимального давления топлива).
Если приемистость начинается сразу же после незакончивше-
гося процесса сброса газа (уменьшения частоты вращения), она
называется встречной. На больших высотах и при малых Гприб
встречная приемистость может вызвать самовыключение двига-
теля, и в таких случаях она запрещается.
Включение форсажа у ТРДФ и ДТРДФ обычно производится
на максимальном режиме двигателя. При этом исходят из недо-
пустимости значительного повышения давления газа в форсажной
камере в процессе включения форсажа, которое привело бы к
росту температуры Г* и снижению &КУ у КВД (из-за уменьшения
пт)» а У ДТРДФ также к торможению потока (и снижению ДК^)
в КНД. С этой целью предусматривается опережение раскрытия
створок сопла (увеличение FCtb) по отношению к подаче и вос-
6*
163
пламенению топлива в форсажной камере. В результате вклю-
чение форсажной камеры сопровождается временным нарушением
режима работы турбокомпрессора и «провалом» тяги. Изменение
параметров двигателя по времени при включении форсажа зави-
сит от его схемы и особенностей САУ.
tt tj t4 —Время t
Рис. 6.16. Осциллограмма процесса включения форсажа
двухвального ТРДФ
На рис. 6.16 приведена осциллограмма изменения параметров
двухвального ГТД, снабженного регулятором nH = const, по вре-
мени. В момент времени начинается раскрытие створок сопла,
что приводит к падению давления /?* за турбиной, и, следова-
тельно, к увеличению и повышению ггн. Регулятор парирует
увеличение ггн снижением подачи топлива GT в основную камеру,
что приводит к уменьшению Г* (Г*) и п3 (рис. 6.16). Снижение
/?* и Г* перед розжигом форсажной камеры приводит к времен-
ному «провалу» тяги. В момент времени t2 начинается подача
форсажного топлива, а в момент /3 происходит его воспламенение.
Это вызывает повышение р* и снижение величины пн. Регуля-
тор, парируя это снижение, увеличивает GT. При этом пй и Г*
восстанавливаются до значений, определяемых настройкой регу-
ляторов и те*. Тяга при этом увеличивается до значения, соот-
ветствующего заданному форсажному режиму.
Изменение пн и п3 в интервале времени от до /3 вызывает
кратковременное снижение скольжения роторов s = nQ/nH (рост
пн при падении ггв), что связано с торможением потока и сниже-
нием \КУ в КНД. Увеличение Т* и пв в интервале от /3 до
в темпе приемистости приводит к забросу Г* и снижению \КУ,
у КВД. При определенных условиях это может вызвать неустой-
чивую работу двигателя.
164
Заметим, что снижение («провал») температуры за турбиной
ДГ* на 50—100° (в зависимости от типа ГТД) при включении
форсажной камеры является нормальным явлением и указывает
на наличие требуемого упреждения в открытии створок сопла по
отношению к подаче форсажного топлива. Об отклонении ДГ*
от нормы, установленной для данного двигателя, летчик должен
информировать инженерно-технический состав, поскольку это го-
ворит о неисправности системы включения форсажа.
В тех случаях, когда управление FCT3 осуществляется от регу-
лятора Т*, ограничение величины Г*П1ах должно производиться
автоматически. Однако и в этом случае может иметь место опас-
ный заброс Г* (как следствие заброса 71*) в момент воспламе-
нения форсажного топлива, когда резкий рост /?* не может быть
парирован столь же быстрым увеличением Fcl3 из-за малого быст-
родействия системы управления створками. Для устранения за-
броса Г* применяется блокировка (кратковременное выключение
из работы) регулятора nH = const до тех пор, пока успеют рас-
крыться створки сопла (перейти в положение, обеспечивающее
заданное значение к*). При этом наблюдается лишь кратковре-
менное незначительное уменьшение пн без значительного сниже-
ния 71* и п3, а следовательно, без заметного «провала» тяги дви-
гателя.
Выключение форсажа также сопровождается «провалом» тяги
и колебаниями Г* и п из-за запаздывания закрытия створок соп-
ла по отношению к прекращению подачи форсажного топлива.
Характерным для двухвальных ГТД является снижение &КУ КНД
из-за уменьшения скольжения s = n3/nH в момент прекращения
подачи форсажного топлива при еще открытых створках сопла,
так как при этом происходит увеличение пи при одновремен-
ном снижении подачи топлива в основную камеру и уменьше-
нии п3.
Нерозжиг форсажа является опасным отказом двигателя. В
этом случае вследствие раскрытия сопла снижается давление за
турбиной и растет к*; возникает тенденция к увеличению частоты
вращения роторов. Система автоматического управления в целях
сохранения, например, nH = const уменьшает GT, что приводит
к падению Г*, п3 и соответственно к снижению тяги до величины,
меньшей, чем на режиме «М». Снижение s приводит к уменьше-
нию &КУ у КНД, что может привести к неустойчивой работе дви-
гателя. Поэтому при нерозжиге форсажа необходимо возвратить
РУД в положение «М», чтобы предотвратить чрезмерное расхо-
дование топлива через форсажный контур и восстановить режим
работы турбокомпрессора. Если при этом сопло не закроется
(о чем можно судить по падению Г* и S или по сигнализации),
то летчику рекомендуется избегать резких перемещений РУД и
пилотировать самолет, не выходя на большие углы атаки и сколь-
165
жения. Аналогичные явления происходят и при самовыключении
форсажа.
Необходимо обратить внимание на тот факт, что процессы
включения и выключения форсажа в ДТРДФ с общей форсажной
камерой (рис. 6.1) обладают следующей отличительной особен-
ностью. У них форсажная камера сообщается не только с затур-
бинным пространством, но через канал второго контура также
с КНД (вентилятором). По этой причине резкие колебания дав-
ления в форсажной камере не только влияют на изменение к*
турбины низкого давления, но и непосредственно на запас устой-
чивости КНД. Изменение я*, как указывалось, оказывает влияние
на режимы работы КНД и КВД за счет изменения скольжения
роторов S. Внезапные всплески давления в форсажной камере (за
счет подачи в нее избытков форсажного топлива) оказывают тор-
мозящее воздействие на поток воздуха, протекающего через КНД.
В результате этого уменьшаются осевые скорости воздуха в КНД
и увеличиваются углы атаки на его лопаточных венцах, что до-
полнительно снижает запас устойчивости КНД и может вызвать
его неустойчивую работу. Это предъявляет жесткие требования
к плавности подачи форсажного топлива как при включении фор-
сажа, так и при увеличении степени форсирования двигателя.
Конструктивно это требование реализуется применением несколь-
ких последовательно включающихся коллекторов для подачи фор-
сажного топлива к соответствующим группам форсунок. От лет-
ного состава требуется повышенное внимание к контролю за ра-
ботой двигателя при включении форсажа и выполнение ограниче-
ний по приемистости, дросселированию и выключению форсажа
на больших высотах.
Запуск двигателя на земле принято условно разделять на три
этапа: 1) раскрутку ротора стартером, 2) воспламенение топлива
в камере сгорания и дальнейшую раскрутку ротора за счет сов-
местной работы стартера и турбины, 3) отключение стартера (при
достижении достаточных избытков мощности на валу турбины) и
самостоятельную раскрутку ротора только от турбины до режима
«МГ», характеризуемого определенной частотой вращения пм, г.
Выполнение такой программы запуска осуществляется системой
автоматического управления двигателем, которая обеспечивает
переход от одного этапа к другому по времени или по сигналу
датчика частоты вращения.
В процессе запуска изменяется режим работы компрессора
(рис. 6.17). На первом этапе запуска, т. е. при прокрутке двига-
теля стартером, температура перед турбиной близка к атмосфер-
ной и рабочая линия на характеристике компрессора соответст-
вует кривой 1—2. На втором этапе — при воспламенении топлива
и увеличении Т* — за счет теплового дросселирования компрес-
сора рабочая линия смещается к границе устойчивости (кривая
2—3). В дальнейшем (на втором и в начале третьего этапа) тем-
пература Г* поддерживается на максимально допустимом уровне
166
(кривая 3—4). Значения Г*тах при запуске ограничиваются либо
запасом устойчивости компрессора, либо прочностью турбины.
При неправильной дозировке подачи топлива в камеру сгорания
рабочая линия на участке 3—4 может пересечь границу устойчи-
вых режимов. Это приведет к срыву потока в компрессоре и вы-
зовет так называемое «горячее зависание оборотов», когда не-
смотря на рост Т* частота вращения перестает увеличиваться.
Рис. 6.17. Желательное расположение рабочей
линии на характеристике компрессора в про-
цессе запуска
При недостаточной подаче топлива в камеру сгорания из-за малой
избыточной мощности турбины раскрутка ротора в процессе за-
пуска становится вялой и может произойти «холодное зависание
оборотов», т. е. прекращение раскрутки ротора. В конце третьего
этапа, когда п становится близкой к лм. г, подача топлива дози-
руется из условия снижения Т* до ее значения на режиме «МГ»
(кривая 4—5). Цифрой 6 на рис. 6.17 показано протекание рабо-
чей линии установившихся режимов двигателя. Как видно, от ав-
томатики требуется точная дозировка подачи топлива на всех
этапах запуска.
При запуске на земле двухвальных двигателей стартер обычно
раскручивает только РВД. Так как момент инерции РВД на-
много меньше суммарного момента инерции обоих роторов и
меньше момента инерции РИД, то потребная мощность пускового
стартера у них снижается. Но поскольку РНД раскручивается
без помощи стартера, то рост пк значительно отстает от роста пв,
в результате чего существенно возрастает скольжение роторов
(особенно на двух первых этапах запуска). При этом КНД ока-
зывает сильное дросселирующее воздействие на КВД, что может
привести к срыву потока в КВД даже при незначительном пре-
вышении GT и Г* по сравнению с допустимым. Для увеличения
КВД при запуске обычно осуществляется перепуск части воз-
духа из-за КВД в атмосферу (во второй контур), а также может
использоваться прикрытие НА регулируемой группы ступеней
167
КВД и раскрытие створок сопла (для повышения избыточной
мощности турбины низкого давления).
Запуск двигателя в полете имеет ряд особенностей. Его роторы
при отсутствии подачи топлива авторотируют, т. е. вращаются под
воздействием встречного потока воздуха, поэтому надобность в
раскрутке ротора стартером отпадает. Для запуска достаточно
обеспечить надежное воспламенение и устойчивое горение топли-
ва и его правильную дозировку в зависимости от частоты враще-
ния и внешних атмосферных условий. Выполнить эти условия тем
труднее, чем больше высота полета. Помимо этого надежный за-
пуск в воздухе обеспечивается лишь в определенном диапазоне
приборных скоростей, о чем упоминалось выше.
При самопроизвольном или принудительном выключении дви-
гателя ускорение процесса запуска и расширение диапазона ре-
жимов полета надежного запуска двигателя может быть достиг-
нуто, если, не дожидаясь снижения частоты вращения ротора до п
авторотации, включить зажигание и обеспечить подачу топлива
в основную камеру сгорания. Такой процесс получил название
встречного запуска. Он широко используется в автома-
тических системах ликвидации помпажа.
§ 6.5. Эксплуатационные ограничения режимов работы
ТРДФ и ДТРДФ
Требование получения высоких удельных параметров силовой
установки и связанное с этим все более сильное форсирование
рабочего процесса двигателей усложняют решение задачи обеспе-
ний режимов работы авиационной силовой установки с
ТРДФ и ДТРДФ
168
чения их надежной и устойчивой работы. Поэтому не удается из-
бежать ряда ограничений, которые ухудшают данные двигателя
и самолета, но диктуются обычно обеспечением безопасности по-
летов. Большинство ограничений осуществляется с помощью ав-
томатики двигателя, но некоторые предусмотрены инструкцией
летчику. Невыполнение ограничений возможно при отказах ав-
томатики или нарушениях инструкции. Летчик четко должен знать
существо и физические причины имеющихся ограничений и по-
следствия их нарушения. Области возможных ограничений даны
на рис. 6.18.
Большинство ограничений обусловлено либо неустойчивой ра-
ботой элементов силовой установки, либо недопустимостью нару-
шений условий прочности ответственных конструктивных узлов.
Ограничения по устойчивой работе
элементов силовой установки \
Ограничения по устойчивой работе компрессора обычно вво-
дятся для тех . режимов, где Д/Q < Д/<у доп. Рассмотрим их.
1. Характерным для высоконапорных компрессоров является,
как указывалось, приближение рабочей линии к границе помпажа
при высоких значениях яПр —288/Гв. В таком случае устанавли-
вают допустимую величину /гпр тах из условия, что Д^>7-?10%,
и с помощью автоматики двигателя обеспечивают во всех усло-
виях полета япр<япр тах. Рассматриваемое ограничение дости-
гается в условиях низких значений температур Г* на входе в дви-
гатель, т. е. при больших высотах полета и малых М (рис. 6.5 и
линия /—/ на рис. 6.18) и осуществляется уменьшением п (по
сравнению с /гтах) за счет снижения подачи топлива в основную
камеру двигателя. Это приводит к уменьшению температуры Г*
и снижению тяги двигателя в области ограничения (левее линии
1—1 на рис. 6.18). При отказах автоматики в данном случае воз-
можно возникновение помпажа компрессора из-за срыва потока
на его последних ступенях.
2. Неустойчивая работа компрессора может возникать при
пуске ракет из-за попадания на вход в двигатель горячих поро-
ховых газов от ракетных двигателей.
Степень влияния пуска ракет на устойчивость двигателя зави-
сит от многих факторов: мощности ракет, их расположения по
отношению к воздухозаборникам, начальной траектории полета
ракеты, а также режима полета самолета и работы двигателя.
В целях снижения этого влияния предусматриваются меры пре-
дупреждения неустойчивой работы при пусках ракет и автомати-
ческой ликвидации помпажа, если он все же произошел (см.
§ 6.6).
В зависимости от типа применяемых ракет может ограничи-
ваться диапазон Упр и Н для их безопасного пуска. При этом
следует иметь в виду, что при М>1,5 первопричиной неустойчи-
169
вой работы двигателя при пуске ракет может быть помпаж воз-
духозаборника, затем вызывающий помпаж компрессора.
3. К числу ограничений по устойчивости компрессора отно-
сится также запрещение вывода двигателя на максимальный ре-
жим без прогрева на взлете. Снижение на режиме «М» в
этом случае объясняется увеличением радиальных зазоров на по-
следних ступенях компрессора (тонкий его корпус прогревается
быстрее, чем ротор), а также и тем, что поток воздуха, интен-
сивно отдавая тепло элементам проточной части непрогретого
двигателя, сам охлаждается. Это приводит к увеличению плотно-
сти, снижению осевой скорости воздуха и увеличению углов атаки
на последних ступенях.
При появлении признаков помпажа компрес-
сора (хлопки, рост Т*, снижение л) независимо от его вызвав-
ших причин во избежание перегрева турбины и механических по-
вреждений лопаток компрессора инструкцией летчику
обычно предусмотрена установка РУД в положе-
ние СТОП, т. е. выключение двигателя, а затем его за-
пуск в воздухе (с учетом разрешенного для запуска диапазона Н
и Уприб). Выключение двигателя связано с уменьшением Т*, что
приводит к снижению сопротивления закомпрессорного тракта и
к росту осевых скоростей воздуха в компрессоре, а следовательно,
к уменьшению углов атаки и прекращению срыва потока на ло-
патках компрессора. Перевод РУД в положение ПМГ (без пол-
ного выключения двигателя) не всегда обеспечивает ликвидацию
помпажа.
Помпаж компрессора может приводить к самовыключению дви-
гателя. Это происходит вследствие того, что в следе зоны вра-
щающегося срыва из-за уменьшения расхода воздуха создается
переобогащение смеси, приводящее к погасанию пламени в ка-
мере сгорания. После прохождения зоны срыва горение обычно
восстанавливается. Но при больших Н и малых Упр в некоторых
типах камер сгорания (например, трубчато-кольцевых) скорость
переброски пламени из одной жаровой трубы в другую может
оказаться меньше скорости вращения срывной зоны. Тогда после
первого хлопка камера сгорания гаснет — происходит заглохание
двигателя (падение Т* и п, снижение тяги, отсутствие реакции
двигателя на перемещение РУД). Для восстановления исходного
режима в таком случае достаточно произвести запуск двигателя
в воздухе.
Ограничения по устойчивой работе воздухозаборника. Вводят-
ся эти ограничения только на сверхзвуковых скоростях полета,
когда возможен помпаж воздухозаборника.
1. Наиболее распространенным является ограничение по убор-
ке РУД (точнее, по снижению режима двигателя) ниже режима
«Максимал» обычно при М>1,5 (линия 2—2 на рис. 6.18). Это
ограничение обусловлено тем, что при уборке РУД снижается
пропускная способность компрессора, что требует снижения про-
170
пускной способности воздухозаборника соответствующим его ре-
гулированием (например, выдвижением клина), но при больших
М органы управления воздухозаборника находятся вблизи поло-
жения предельно малой подачи и дальнейшее ее снижение часто
оказывается конструктивно невозможным. Влияет в этом случае
также возрастающая при выдвижении клина неравномерность по-
тока на входе в компрессор, что может приводить к помпажу
компрессора. Чтобы этого не случилось, предусматривается авто-
матическое поддержание режима двигателя в указанной области
ограничения независимо от перемещения РУД, или стопорение
РУД. Это ограничение, регламентируя возможность сброса тяги
двигателя после выключения форсажа, ухудшает маневренные ха-
рактеристики самолета (увеличивается время торможения само-
лета).
2. К числу ограничений по помпажу воздухозаборника или
компрессора относится запрещение выключать форсаж на боль-
ших М и Н. Это связано с указанной особенностью переходного
процесса в двигателе при выключении форсажа. Прекращение
подачи форсажного топлива, как отмечалось выше, производится
в условиях, когда створки реактивного сопла еще продолжают
закрываться. Происходящий при этом «заброс» частоты вращения
ротора (связанного с регулятором) и вызванное этим снижение
GT и провал Т* сменяется затем увеличением подачи топлива в
основную камеру в темпе приемистости. Такое резкое изменение
Gt и п в условиях больших М и Н может вызвать помпаж комп-
рессора, а кратковременное рассогласование расходов компрессора
и воздухозаборника может привести к помпажу воздухозабор-
ника.
3. Имеются случаи ограничений по допустимым нормальным
перегрузкам самолета пу при маневрировании на больших числах
М полета, связанные с уменьшением запасов устойчивости возду-
хозаборника и компрессора при значительном изменении углов
атаки.
При заданном числе М полета запас по помпажу воздухоза-
борника на практике принято оценивать по величине перемеще-
ния клина Д£кл от его положения, заданного программой, до на-
ступления помпажа или зуда. Уборка клина будет приводить к
помпажу, а его выдвижение к зуду. На рис. 6.19 дана зависимость
запасов по ходу клина от углов атаки а при M = const. Выдвиже-
ние клина при больших углах а может приводить к помпажу
компрессора, вызываемому колебаниями давления от зуда воз-
духозаборника и создаваемой выдвижением клина неравномер-
ностью на входе в компрессор. Как видим, при больших а возмо-
жен помпаж как воздухозаборника, так и компрессора.
Ограничения по пилотированию самолета на больших а могут
быть связаны также и с тем, что коррекция программы управле-
ния воздухозаборником дополнительным выдвижением клина
обычно осуществляется по углу отклонения стабилизатора фСт. Но
1Л1
между углами а и <рСт нет однозначной связи. При изменении
центровки самолета (например, при сбросе ракет) одним и тем же
Фет соответствуют различные а. Это может приводить к уменьше-
нию кКувх. При полетах вблизи динамического потолка самолета
с управляемым стабилизатором проявляется его инерционность
по отношению к действию руля высоты, что также вызывает вре-
Рис. 6.19. Влияние угла атаки на границы ус-
тойчивой работы воздухозаборника и компрес-
сора
менное несоответствие указанных углов. В таких случаях из-за
запаздывания в срабатывании коррекции возможно возникнове-
ние помпажа. Ограничение пилотирования вблизи потолка сво-
дится к требованию плавности управления самолетом.
При помпаже воздухозаборника, не вызывающем
роста 7*, рекомендуется выключить форсаж и
обеспечить этим быстрое уменьшение скорости
полета самолета. Если в процессе торможения самолета
помпаж воздухозаборника прекратится и Т* не выйдет из нормы,
выключение двигателя производить необязательно. Тогда нужно
в процессе дальнейшего уменьшения скорости проконтролировать
уборку клина системой УВД или при отказе УВД перейти на руч-
ную (аварийную) систему управления воздухозаборником в соот-
ветствии с инструкцией.
Ограничения по устойчивости горения
/
Эти ограничения обычно сводятся к указанию диапазонов Vnp
и Н, в пределах которых: 1) запрещается быстрый (в темпе при-
емистости) переход на повышенные режимы двигателя либо рез-
кое его дросселирование; 2) не разрешается включение или дрос-
172
селирование форсажа; 3) не обеспечивается надежный запуск
двигателя. Рассмотрим их.
1. На ряде двигателей в условиях высотного полета, т. е. при
сильном снижении давления /?* (на входе в основную камеру),
система управления двигателя исключает возможность его дрос-
селирования ниже определенного режима (близкого к «М») либо
дросселирование двигателя в этих условиях запрещается инструк-
цией. Это ограничение, как указывалось, вводится из-за ухудшения
процесса сгорания в основной камере при низких значениях дав-
ления /?*. При нарушении устойчивости процесса горения в основ-
ной камере может вводиться ограничение по использованию встреч-
ной приемистости в полете на больших Н и малых VnP.
2. Возможно ограничение по дросселированию форсажа на
больших высотах и малых VnP (при низких значениях давления
на входе в форсажную камеру), что также связано с ухудше-
нием распыливания и сгорания топлива. Ограничение может на-
кладываться на допустимые режимы полета, где гарантируется
надежное включение форсажа. На рис. 6.18 штрихпунктирной ли-
нией показано расположение границы устойчивой работы фор-
сажной камеры (по ^min)» а линией 3—3 показана обычно уста-
навливаемая инструкцией граница по разрешенным значениям Н
и Vnp включения форсажа. Левее и выше этой линии (в заштри-
хованной области) надежное включение форсажа не обеспечи-
вается.
Включение форсажа запрещается во время разбега самолета
на взлете и сразу же после взлета на малых высотах, что связано
с наличием провала тяги по времени в процессе розжига форсаж-
ной камеры вследствие задержки подачи форсажного топлива по
отношению к открытию створок сопла.
3. Область надежного запуска двигателя в воздухе обычно
указывается в инструкции величинами Упр min; Упр тах и Ятах
(рис. 6.18). Нижний предел VnP обусловлен низким скоростным
напором и малыми скоростями воздуха в камере сгорания, при
которых не обеспечивается надежное поджигание и устойчивое
горение топливовоздушной смеси. При слишком больших УПР в
условиях высоких скоростей авторотации также может не обеспе-
чиваться надежный розжиг камеры. Высота надежного запуска
лимитируется величиной давления воздуха на входе в камеру
сгорания, но может быть увеличена применением кислородной
подпитки.
Ограничения по условиям прочности
Их введение вызвано тем, что при изменении условий полета
и режима двигателя сильно изменяются механические, аэродина-
мические, температурные и вибрационные нагрузки на элементы
силовой установки. Прочностные ограничения приходится вводить
для сохранения допустимых значений запасов прочности в ответ-
ственных элементах конструкции.
17i
1. Наиболее характерными прочностными ограничениями, осу-
ществляемыми автоматикой и контролируемыми летчиком, явля-
ются ограничения частот вращения роторов и температуры газа
7*. Последняя, как правило, контролируется летчиком по указа-
телю температуры газа за турбиной. Допускаются кратковремен-
ные забросы этих величин в процессах приемистости, включения
и выключения форсажа (по п до 4—6% и по 7* до 50—70°С).
Учитывая опасные последствия даже кратковременного превы-
шения допустимых значений указанных параметров (возможных
в случае неисправностей двигателя и систем его управления), они
должны постоянно контролироваться экипажем в полете и на
земле.
2. При полетах на больших Vnp, близких к максимально допу-
стимым, высокие скоростные напоры приводят к увеличению рас-
хода и давления воздуха и газа по тракту двигателя. Это увели-
чивает аэродинамические и вибрационные нагрузки на лопатках
компрессора и турбины, а также крутящие моменты на валах
роторов. Высокое избыточное давление в газовоздушном тракте
увеличивает также напряжения в корпусах двигателя. Для пре-
дотвращения перегрузки указанных узлов двигателя вводят огра-
ничение по максимально допустимому давлению воздуха за комп-
рессором/?* тах. Оно обеспечивается автоматикой двигателя за счет
снижения подачи топлива в камеру сгорания и приводит к рез-
кому уменьшению тяги двигателя в области ограничения. Обычно
ограничение по реализуется в диапазоне приборных скоро-
стей, превышающих Упр max самолета, и в таком случае они мало
сказываются на его летных характеристиках.
3. К числу прочностных относятся ограничения по максималь-
но допустимой температуре воздуха на входе в двигатель 7*тах
и по максимальному скоростному напору q = рнlZ2/2. Рост М со-
провождается увеличением 7* и температуры воздуха в тракте
компрессора. Это4 влияет на прочность элементов компрессора,
а также других элементов двигателя, охлаждаемых воздухом
из-за компрессора, в том числе и турбины. Ухудшаются условия
работы маслосистемы. При #>11 км это ограничение обычно
совпадает с М = Мтах, а при #<11 км не достигается в области
разрешенных для данного самолета М и Н (см. линию 4—4 на
рис. 6.18). Ограничение по //max может быть связано с прочностью
воздухозаборника. Ограничения по Мтах и ^тах обычно относятся
не только к двигателю, а ко всему самолету. Они указываются в
инструкции и контролируются экипажем (по указателям Vnp
и М).
§ 6.6. Помпаж и самовыключение двигателей при пуске ракет
Одним из наиболее серьезных недостатков ГТД является по-
теря газодинамической устойчивости силовой установки при попа-
дании на вход в двигатель выхлопных газов от ракет или реак-
174
тивных снарядов. Основным воздействующим фактором в этом
случае является быстрое нарастание по времени температуры воз-
духа Г* на входе в компрессор по всему его тракту при значи-
тельной неравномерности температурного поля. Другие сопутст-
вующие факторы, такие, как химическое воздействие (попадание
Рис. 6.20. Влияние попадания горячих вы-
хлопных газов от ракеты на вход в дви-
гатель на параметры его работы
в двигатель продуктов сгорания ракетного топлива), газодинами-
ческое воздействие (пульсации и неравномерности давления в по-
токе на входе в двигатель), не являются определяющими.
На рис. 6.20 показан качественный характер изменения темпе-
ратуры Т* и параметров двигателя при пуске ракеты. Момент
времени t\ соответствует началу теплового возмущения, а момент
ti — его окончанию. Время воздействия может составить десятые
доли секунды, температура Г* достигает 100°С, а скорость нара-
стания температуры по времени — 2000—3000°/с и более. Нали-
чие неравномерного температурного поля из-за несимметричности
условий полета ракеты относительно воздухозаборников приводит
к дополнительному усилению температурного воздействия на ус-
тойчивость работы двигателя.
Тепловое воздействие приводит к изменению параметров комп-
рессора и режима его работы. В начальный период времени (в ин-
175
растает скорость звука а — у
поэтому величины ггпр и GB. пр,
fynp
Рис. 6.21. Предупреждение неустой-
чивой работы компрессора при теп-
ловом воздействии методом предва-
рительного сброса топлива и после-
дующего встречного запуска
Характерными признаками
тервале от t\ до /2, рис 8.20) частота вращения и расход топлива
в силу инерционности системы регулирования остаются практиче-
ски неизменными, но претерпевают значительное снижение вели-
чины /гпр и GB. пр. Это объясняется тем, что с увеличением Тв воз-
kRTB на входе в компрессор и
соответственно пропорциональные
uJaB (числу М по окружной ско-
рости ротора) и СвМв (числу М
по осевой скорости воздуха на
входе), уменьшаются. При этом
давление за компрессором /?*,
а соответственно и л*, несколько
падает, но тем в меньшей сте-
пени, чем быстрее нарастает тем-
пература воздуха Т* на входе
в компрессор. Рабочая точка
на характеристике компрессора
(рис. 6.21) в таком случае бы-
стро перемещается к границе
устойчивой работы компрессора
(по линии 1—1), и в момент
времени /2 возникает его неус-
тойчивая работа, что вызывает
помпаж двигателя.
помпажа, как указывалось, явля-
ются хлопки, рост температуры газа за турбиной Г* и снижение
частоты вращения роторов. Летчик должен внимательно следить
за изменением 7* и п при пуске ракет. Давление /?* при пом-
паже резко падает и возникают его колебания, а давление /?* мо-
жет даже немного увеличиться, что объясняется выбросом части
сжатого воздуха из-за компрессора на вход через вращающуюся
срывную зону.
В момент времени t$ во избежание перегрева и разрушения
двигателя летчик должен в соответствии с инструкцией выклю-
чить двигатель переводом РУД в положение СТОП, если на дви-
гателе не предусмотрена автоматическая система ликвидации пом-
пажа. Повторный запуск двигателя после его выключения осуще-
ствляется в области дозволенных высот и скоростей полета
(рис. 6.18).
Эффективным средством предупреждения помпажа при пуске
ракет, как указывалось, является использование системы, сброса
подачи топлива и последующего встречного запуска. Сброс по-
дачи топлива приводит к уменьшению температуры 7* газа перед
турбиной, что вызывает уменьшение давления воздуха за комп-
рессором при очень малом изменении п вследствие инерционности
ротора. При этом осевые скорости воздуха в тракте компрессора
увеличиваются, а-углы атаки уменьшаются. Рабочая точка в поле
176
характеристик компрессора перемещается вниз (по линии, близ-
кой к nnp = const), т. е. удаляется от границы устойчивой работы»
чю и свидетельствует об увеличении запаса устойчивости комп-
рессора.
При этом, как показано на рис. 6.21, темп сброса топлива
выбирается таким, чтобы момент начала теплового воздействия
(точка 2 на рис. 6.21) соответствовал наибольшему удалению ра-
бочей точки от границы устойчивой работы. Тогда за весь период
теплового воздействия (участок 2—3—4) рабочая точка не вы-
ходит за пределы области устойчивых режимов. Последующее
восстановление режима двигателя (встречный запуск) осуще-
ствляется по линии 4—1. При этом надо иметь в виду, что сброс
топлива сопровождается кратковременным снижением тяги дви-
гателя и требует применения соответствующей техники пилотиро-
вания после пуска ракет.
Помимо сброса топлива для предотвращения помпажа двига-
теля при пуске ракет могут быть использованы средства регули-
рования компрессора и воздухозаборника. Однако их использо-
вание непосредственно в процессе действия тепловых возмущений
оказывается невозможным из-за быстротечности процесса. По-
этому регулирование этих элементов на повышение запасов устой-
чивости должно осуществляться с упреждением по отношению
к действию теплового возмущения. К числу управляющих воз-
действий, используемых в системах предупреждения помпажа, по-
мимо сброса подачи топлива относятся:
— перепуск воздуха из-за КНД в атмосферу или во второй
контур;
— поворот НА групп регулируемых ступеней компрессора на
уменьшение углов атаки;
— кратковременное выдвижение клина (конуса) воздухозабор-
ника на больших числах М полета.
Указанные меры основаны на кратковременном повышении
каскадов компрессора или Л/Сувх воздухозаборника по предвари-
тельному сигналу, например от нажатия пусковой кнопки. При
этом происходит уменьшение тяги и требуется быстрое восстанов-
ление исходного режима двигателя.
Если при действии возмущения возник помпаж, система управ-
ления двигателя должна обеспечить его ликвидацию. Наличие пом-
пажа обнаруживается специальными датчиками, обычно регистри-
рующими появление обратных токов в компрессоре и повышение
Т*. Эти сигналы поступают в блок системы, которая на определен-
ное время снижает режим двигателя, а затем осуществляет его
восстановление или автоматический запуск. При отсутствии си-
стемы ликвидации помпажа эти действия летчик выполняет вруч-
ную в соответствии с инструкцией.
Степень воздействия бортового оружия на работу силовой уста-
новки зависит от режима полета. Наиболее опасны с точки' зре-
ния заглохания двигателя при пуске ракет большие высоты при
177
малых значениях УПриб. Расход воздуха через двигатель в этой
области режимов полета существенно снижается, тогда как коли-
чество газов в струе за ракетой с высотой сохраняется неизмен-
ным, а конус раствора струи газов, вытекающих из сопла ракет-
ного двигателя, даже увеличивается. Это приводит к относитель-
ному увеличению доли горячих газов, попадающих на вход
в двигатель. При сверхзвуковых скоростях полета первопричиной
помпажа при пуске ракет может являться неустойчивая работа
воздухозаборника, вызывающая затем неустойчивую работу ком-
прессора.
Часть вторая
ДИНАМИКА ПОЛЕТА
ВВЕДЕНИЕ
Традиционно динамику полета делят на два основных раздела:
динамику точки и динамику системы. В первом разделе рас-
сматривается динамика движения центра масс самолета. В нем
изучаются такие летно-технические характеристики, как диапазон
скоростей и высот полета, маневренность, взлетно-посадочные ха-
рактеристики, дальность и продолжительность полета. Во второ м
разделе рассматривается движение самолета вокруг центра масс.
В нем изучаются устойчивость и управляемость самолета, его ста-
тические и динамические характеристики, а также критические
режимы полета.
В курсах теоретической механики изучению динамики системы
предшествует изучению динамики точки. Однако из методических
соображений при обучении летного состава для лучшей увязки
динамики движения самолета с техникой пилотирования целесо-
образно перед изучением летно-технических свойств рассмотреть
балансировку, устойчивость и управляемость самолета.
Общие сведения об устойчивости
и управляемости, требования к их
характеристикам
Полет самолета осуществляется под воздействием сил и мо-
ментов, действующих на него. В зависимости от воздействия мо-
ментов на самолет их разделяют на управляющие и возмущающие,
стабилизирующие и дестабилизирующие. Управляющие мо-
менты появляются в результате отклонения органов управления
летчиком (или автопилотом), в то время как возмущающие
моменты являются следствием воздействия различного рода воз-
мущений (неспокойной атмосферы, стрельбы, пуска ракет и т. д.).
Моменты, возникающие при нарушении равновесия и стремящиеся
возвратить его к исходному положению равновесия, называют ста-
билизирующими (восстанавливающими), если они уводят от
исходного режима равновесия — дестабилизирующими.
При выполнении той или иной задачи движение самолета на
различных этапах полета может быть установившимся и неуста-
179
повившимся. Под установившимся движением обычно понимают
такое движение, в процессе которого его параметры остаются не-
изменными. Установившийся режим полета характеризуется вполне
определенными значениями скорости, угла атаки (перегрузки),
высоты полета или вертикальной скорости, режима работы сило-
вой установки.
Отклоняя органы управления, летчик может регулировать ве-
личину и направление сил и моментов и соответственно изменять
параметры движения самолета в желаемую сторону. Равновесие,
созданное летчиком, может быть нарушено воздействием какого-
либо внешнего возмущения. Поэтому, когда режим полета уста-
новлен и самолет движется прямолинейно и равномерно, необхо-
димо обеспечить устойчивость этого движения.
Под устойчивостью самолета понимается его способ-
ность возвращаться к исходным значениям параметров движения
после того, как исчезнут причины, вызвавшие их изменение (от-
клонение). Если самолет устойчив по всем параметрам, то одно-
временно он возвратится и к исходному положению равновесия.
Для того чтобы исследовать устойчивость самолета, необходимо
рассмотреть его движение после воздействия возмущения, что тре-
бует решения дифференциальных уравнений возмущенного дви-
жения. Характер этого движения зависит от начальной тенденции
в поведении самолета, определяемой изменением сил и моментов
при воздействии возмущения. Поэтому некоторое суждение об
устойчивости самолета можно вынести из рассмотрения начальной
тенденции в поведении самолета без анализа дифференциальных
уравнений движения. Такое «статическое» рассмотрение устойчи-
вости породило широко применяемое понятие статической устой-
чивости.
Если под воздействием возмущающих причин силы и моменты
изменяются так, что стремятся возвратить самолет к заданному
летчиком режиму полета, то такой самолет считается статиче-
ски устойчивым. Чем большие возникают восстанавливающие
силы и моменты, тем с большим ускорением самолет будет воз-
вращаться к исходному положению равновесия. Таким образом,
под устойчивостью самолета понимается его реакция на отклоне-
ние параметров движения от исходного положения равновесия.
За характеристику (показатель) устойчивости принимается соот-
ношение между реакцией (ускорением) самолета на возмущаю-
щее воздействие и величиной этого возмущения:
Величина ускорения, характеризую-
щего реакцию самолета на внешнее
возмущение
Показатель устойчивости = --------------------------------
Величина изменения параметра,
характеризующего воздействие
возмущения
При упрощенном рассмотрении статической устойчивости за
показатель устойчивости принимается отношение величины изме-
180
нения коэффициента момента (силы), вызванной изменением па-
раметра при действии возмущения, к величине этого изменения
параметра.
Как будет показано ниже, наличие восстанавливающих сил и
моментов (т. е. наличие статической устойчивости) не всегда яв-
ляется необходимым и достаточным условием возвращения само-
лета к исходному режиму полета. Чем меньше параметры движе-
ния отклоняются под воздействием возмущающих причин от за-
данных значений и быстрее к ним возвращаются, тем лучшими
характеристиками устойчивости обладает самолет. Таким образом,,
под устойчивостью самолета фактически понимается его способ-
ность сохранять заданный режим полета.
Поскольку устойчивость есть характеристика равновесия, та
для исследования ее проявления необходимо предварительно-
создать равновесие. Кроме того, необходимо условиться о дей-
ствиях летчика. Обычно предполагается, что при нарушении рав-
новесия летчик не отклоняет органы управления. Вместе с тем
хорошо известно, что в реальном полете это условие не выдержи-
вается: летчик время от времени отклоняет органы управления
самолетом и вносит поправки.
Может возникнуть вопрос: есть ли смысл заниматься изуче-
нием устойчивости самолета, непилотируемого летчиком? Оказы-
вается есть. Дело в том, что если при нарушении равновесия са-
молет стремится сам (без вмешательства летчика) возвратиться
к исходному режиму полета, то с помощью летчика он еще быст-
рее возвратится к этому режиму. Параметры движения при этом
будут мало отклоняться от своих исходных значений. Если же
самолет неустойчив и сам к исходному режиму не приходит, то
соответствующим отклонением органов управления летчик может
возвратить его к этому режиму, но достаточно небольшой внеш-
ней причины, чтобы опять вывести самолет из равновесия. Иначе
говоря, на неустойчивом самолете летчик должен непрерывно
управлять, вносить коррективы. Это усложняет пилотирование,,
держит летчика в постоянном напряжении и отвлекает его от
выполнения основной задачи.
Поэтому анализ устойчивости самолета, не пилотируемого лет-
чиком,- рассмотрение его собственных свойств является важной
практической задачей.
Другой важнейшей характеристикой самолета является управ-
ляемость. Под управляемостью самолета понимают его
способность реагировать изменением параметров движения на
управляющее воздействие летчика. В качестве управляющего воз-
действия принимается действие летчика (усилие, прикладываемое
к рычагам управления, и их перемещение) в целях изменения па-
раметров движения самолета.
Управляемость самолета характеризуется соотношением между
управляющим воздействием летчика и вызванным им изменением
параметров движения самолета. Эти соотношения принято назы-
вать показателями управляемости:
181
Величина параметра, характеризую-
щего управляющее воздействие
летчика
Показатель управляемости = ---------------------------------
Величина изменения параметра, ха-
рактеризующего реакцию самолета
на это воздействие
О хорошо управляемом самолете летчики говорят, что он «по-
слушен в управлении», хорошо «ходит за ручкой». Это означает,
нто для выполнения маневров летчику необходимо совершать про-
стые по характеру отклонения рычагов и прилагать к ним неболь-
шие по величине, но четко ощутимые усилия, на которые самолет
отвечает соответствующим изменением положения в пространстве
не резко, но и без излишнего запаздывания. Управляемость —
важнейшая характеристика самолета, определяющая возможность
полета; на неуправляемом самолете летать невозможно.
Сопоставляя понятия устойчивости и управляемости самолета,
может показаться, что они противоположны друг другу. Дей-
ствительно, устойчивость есть способность самолета сохранять за-
данный режим полета, а управляемость — способность самолета
изменять его. С повышением устойчивости самолета увеличиваются
углы отклонения рулей, необходимые для изменения режима по-
лета. В соответствии с этим следует рычаги управления переме-
щать на большую величину и большие усилия прикладывать к
ним. При больших потребных отклонениях рулей могут быть огра-
ничены маневренные возможности самолета. При больших уси-
лиях на рычагах управления летчик быстро утомляется при вы-
полнении маневров'. О таком самолете говорят, что он «тяжел в
управлении».
Но самолетом трудно управлять и тогда, когда отклонения ру-
лей и усилия, потребные для их отклонения, слишком малы.
В этом случае самолет весьма чувствителен к изменению усилий
на ручке, реагирует на малое, иногда даже непроизвольное пере-
мещение ручки, требуя от летчика большого внимания, точного и
плавного управления. О таком самолете говорят, что он «строг
в управлении».
Очевидно, что при повышении устойчивости самолета, «строгого
в управлении», улучшится и его управляемость, так как увели-
чатся слишком малые потребные отклонения рулей и усилий,
л значит, упростится управление. Отсюда можно прийти к выводу,
что между устойчивостью и управляемостью никакой противопо-
ложности нет. Существующая между ними тесная связь показы-
вает, что хорошая управляемость самолета может быть обеспече-
на только при достаточной устойчивости.
Успешное выполнение задания и обеспечение безопасности по-
лета предъявляют целый ряд требований к характеристикам ус-
тойчивости и управляемости самолета. Так, например, устойчи-
вость и управляемость военного самолета должны обеспечивать!
— наиболее полное использование летных свойств самолета,
182
определяемых его конструкцией, энерговооруженностью и аэроди-
намикой;
— возможность эффективного выполнения боевой задачи, свя-
занной с точным пилотированием (прицеливанием, выдержива-
нием заданного режима и др.);
— простоту управления самолетом, минимально утомляю-
щего летчика, в том числе при полете в сложных метеоусловиях;
— максимальное ослабление воздействия внешних возмущений,
включая атмосферную турбулентность;
— предотвращение попадания самолета в опасные положения
(сваливание и вход в штопор, непроизвольный выход на большие
перегрузки и др.);
— информативность о режиме полета по невизуальным кана-
лам информации (по кинестетическим, тактильным, акселерацион-
ным и другим ощущениям);
— преемственность приобретенных навыков пилотирования при
переучивании с одного самолета на другой.
На основе летной практики и теоретических исследований было>
установлено, какими должны быть характеристики устойчивости
и управляемости самолета, чтобы удовлетворить этим требова-
ниям. В зависимости от выполняемых задач предъявляются раз*
личные требования к этим характеристикам.
Современные маневренные самолеты обладают большим диа-
пазоном скоростей и высот полета, изменяют параметры движения
(угол атаки, число М и др.) в широких пределах, вследствие чего
устойчивость и управляемость может претерпевать значительные
изменения. Для обеспечения высокой эффективности применения
самолета необходимо, чтобы в основной области, определяе-
мой режимами полета, на которых выполняются главные задачи*
самолет обладал наилучшими характеристиками устойчивости и
управляемости, обеспечивающими высокую точность пилотирова-
ния. В эксплуатационной области к характеристикам
устойчивости и управляемости предъявляются менее жесткие тре-
бования и определяются они главным образом, безопасностью по-
лета (простотой управления и уменьшением психофизиологической
нагрузки летчика). Еще менее жесткие требования к характери-
стикам устойчивости и управляемости предъявляются в так назы-
ваемой предельной области, характеризуемой режимами
полета, связанными с особыми случаями, и режимами, выход на
которые не разрешен по безопасности полета.
Уравнения движения самолета.
Разделение движения на продольное и боковое
В процессе полета самолет, перемещаясь, изменяет свое поло-
жение в пространстве. Для определения этого положения необхо-
димо, во-первых, выбрать тело, по отношению к которому рас-
сматривается движение самолета; во-вторых, надо выбрать систе-
му координат, с помощью которой можно определить положение
183
самолета в пространстве. В качестве «неподвижного тела», отно-
сительно которого изучается движение самолета, обычно выбира-
ется земля.
При рассмотрении траекторных задач динамики полета обычно
пользуются нормальной земной (OoXgf/gZg) и траекторной
(О^ь-Укгк) системами координат. Начало координат земной систе-
Рис. 0.1. Нормальная OQxgygzg и траекторная OxKyKzK системы
координат
мы находится на поверхности земли, ось OQyg направлена вверх
по местной вертикали. Оси OqXs и Oozg лежат в горизонтальной
плоскости, образуя с осью OQys правую систему координат
(рис. 0.1).
Начало координат траекторной системы координат О совме-
щено с центром масс самолета. Ось Охк направлена по вектору
скорости V самолета (рис. 0.1), ось OzK независимо от углового
положения самолета всегда находится в горизонтальной плоско-
сти. Следовательно, оси Охк и Оук лежат в вертикальной плос-
кости.
Положение траекторной системы координат Охиукгк относи-
тельно нормальной системы координат, перенесенной в центр масс
184
самолета (Охдудгд на рис. 0.1), определяется двумя углами Т и 0.
Угол между осями Огд и OzK (что то же между проекцией
вектора скорости полета на плоскость местного горизонта и
осью Охд) называется углом разворота*. Угол 6 между ско-
ростью самолета (осью Охк) и местной горизонтальной плос-
костью называется углом наклона траектории.
Рис. 0.2. Взаимное положение связанной Ox\yiZ\
и нормальной OxgygZg систем координат
При рассмотрении устойчивости и управляемости самолета
удобно пользоваться связанной системой координат Ох^г^ (см.
§ 1.3). Положение связанной системы координат Oxxy{zx относи-
тельно нормальной системы Oxgygzg (рис. 0.2) определяется тремя
углами: рыскания (курса), тангажа и крена. Углом рыскания
(курса) будем называть угол ф, заключенный между осью Oxg
и проекцией связанной оси Охг на горизонтальную плоскость (ли-
ния ОС на рис. 0.2). Он получается в результате поворота само-
лета вокруг оси Oyg. Углом тангажа будем называть угол &
между связанной осью Oxi и горизонтальной плоскостью. Его по-
явление связано с поворотом самолета вокруг оси О В. Углом
крена будем называть угол у, заключенный между вертикальной
плоскостью, проходящей через ось Ох{ и связанной осью Оу^. Он
возникает при вращении самолета вокруг оси Ох}. На рис. 0.2
показаны положительные направления осей координат, углов рыс-
кания ф, тангажа 0, крена у и угловых скоростей dtyldt\ d^fdt и
d^/dt.
* В отечественной литературе этот угол иногда называют углом пути. He-
следует его смешивать с навигационным путевым углом.
185^
При рассмотрении некоторых задач иногда удобно пользовать-
ся скоростной системой координат Oxyz (см. § 1.3). На рис. 0.3
показано взаимное положение связанной и скоростной систем ко-
•ординат. Из этого рисунка очевидны следующие связи между ско-
ростью полета и ее проекциями на связанные оси координат:
Vx — V cos a cos Р;
Vy = — И sin a cos Р; (0.1)
Иг = И sin р.
Рис. 0.3. Проекции вектора скорости на связанную
систему координат OxiytZt
Если углы а у Р невелики, то эти связи в первом приближении
ложно записать в следующем виде:
Vy
^®ир,
(0.1')
где углы аир выражены в радианах.
В процессе полета масса самолета изменяется. Однако скорость
ее изменения, связанная с выработкой топлива ТРД, настолько
мала, что позволяет в каждый данный момент времени массу са-
молета считать неизменной. Поскольку скорости и высоты дви-
жения современных самолетов существенно меньше, чем у косми-
ческих летательных аппаратов, то представляется возможным
поверхность земли считать плоскостью, а поле силы тяжести од-
нородным с постоянным земным ускорением.
Если рассматривать самолет как абсолютно твердое тело, то
юн имеет шесть степеней свободы. Это значит, что его положение
в пространстве определяется шестью параметрами: тремя коор-
динатами положения центра масс (xgt ygt zg) и тремя углами,
определяющими положение подвижной системы координат
186
\Ox\y\Z\), связанной с самолетом, относительно неподвижной си*
стемы координат (Oox8y8z8), связанной с землей.
Так как связанная система координат обычно близка к глав-
ным осям инерции, то динамические уравнения движения самолета
могут быть записаны в следующем виде *:
т (^Г- + J +°»
/ dVv \
Ш |- ^хСгу ~ “Ь
т (- “уКх) = + Oz>
1х-^ + (1г-/у)«>у<*г = Мх, (Q'2>
/у 4“ (1Х /г) === Му,
+(/у-/х)®х«>у = Я.
где УЛ, Vy, Уя, —соответственно проекции скорости по*
лета и угловой скорости на связанные оси координат OxiZ/iZi;
Л, ly, h — главные центральные моменты инерции; Ry, R**
Gx, Gy, G* — соответственно проекции поверхностных сил (аэро-
динамических и сил тяги) и сил тяжести на связанные оси коор-
динат Оххух2\\ Мх, Му, Mz — проекции моментов, действующих на
самолет, на эти же оси.
Если известны проекции сил и моментов на оси связанной си-
стемы координат, то решение дифференциальных уравнений (0.2)
позволяет найти проекции угловой скорости сох, ®у, coz и скорости
Vx, Vy, Vz на оси связанной системы координат и соответственно
определить углы атаки и скольжения (рис. 0.3):
а = — arctg ; р = arcsin = arcsin . (0.3)
В соответствии с рис. 0.2 проекции сил на оси связанной си-
стемы координат определяются выражениями:
Рх + Gx = Р — Хх — G sin Я;
Ру + Gy = Yr — G cos ft cos у; (0.4)
Pz 4- Gz = Zx + G cos ft sin y.
Таким образом, для вычисления проекций сил необходимо знать
пространственное положение самолета, определяемое углами ft,
ф. С этой целью воспользуемся кинематическими уравнениями Эй-
лера, устанавливающими связь между угловыми скоростями cox>
<*>!/, и углами тангажа, рыскания и крена. Для получения этих
уравнений воспользуемся рис. 0.2, на котором показаны положи*
• См. курс теоретической механики.
187
тельные направления проекций вектора угловой скорости враще-
ния (Ох, шу и (ог на связанную систему координат Oxxyxz\. На этом
же рисунке показаны положительные направления скорости изме-
нения углов тангажа dtydt, рыскания dty/dt и крена d^/dt, кото-
рые представляют собой проекции того же результирующего век-
тора угловой скорости, но только на систему координат ОххуёВ.
Проектируя составляющие вектора угловой скорости на ось ОВ,
получим следующую связь dtydt с углом крена и угловыми ско-
ростями Шу И Шг>
= <0г COS 7 + <0у sin у. (0.5)
Для определения угловой скорости вращения dty/dt спроекти-
руем составляющие шу, шг и d$ldt, dtyldt, d^dt на ось О А.
В результате получим:
dty а
COS v = (Dy COS Т — шг sin у,
решение которого относительно dfy/dt дает:
dty ___ ^у cos 7 — U)X sin 7
dt cos а ’ • v • /
Аналогично проектируя составляющие вектора угловой скоро-
сти на связанную ось Охх, получим:
Разрешая это уравнение относительно угловой скорости крена
d^/dt и подставляя значение dty/dt из выражения (0.6), находим
следующее значение d^ldt\
— tg »(<•>, cosy — <М1пт). (0.7)
Для отыскания координат центра масс самолета xs, уе, zg не-
обходимо решить сложную систему дифференциальных уравнений
(0.2, 0.5, 0.6, 0.7), устанавливающих связь между проекциями Vx,
Vy, V'z и углами &, ф, у. Если известны зависимости изменения ско-
рости, углов 0 и ¥ в функции времени, то координаты центра
масс самолета в нормальной системе координат определяются ин-
тегрированием следующих уравнений (рис. 0.1):
= V cos 6 cos 47, I
dt I
T-T = l/Sln’; <°-8>
= — V cos 0 sin Ф. I
188
Если при выполнении пространственного маневра закон управ-
ления (закон изменения углов атаки, скольжения и крена, поло-
жение рычага управления двигателем) известен, то траектория
движения самолета определяется первыми тремя уравнениями си-
стемы (0.2) (уравнениями сил). В этом случае удобно воспользо-
ваться траекторной системой координат, ось Охк которой совме-
Рис. 0.4. Проекции сил, действующих на самолет, на
стему координат OxKyKzK
траекторную си-
щена с вектором скорости, вследствие чего в уравнениях (0.2)
можно положить
l/, = V; V,~V, = 0; (0.9)
Предполагая, что тяга двигателя направлена вдоль продольной
оси самолета, а угол скольжения мал и его влиянием на аэроди-
намические силы можно пренебречь, первые три уравнения си-
стемы (0.2) можно записать в следующем виде (см. рис. 0.4):
т^- = Pcos а — X — Osin 6:
dt
tnV<&Zv. = К cos у -f-Psin a —О cos 6;
—/тг <nyKIZ = Y sin y.
Здесь угловые скорости равны:
V
= —тг = —:
dt ry *
dW „ А V cos2 0
“ук = ^гсоз9 = —
(0.Ю)
(0.И)
где гу и гг — радиусы кривизны траектории соответственно в вер-
тикальной и горизонтальной плоскостях.
В ряде случаев уравнения движения центра масс записываются
с использованием понятия перегрузки, которая характеризует на-
груженность конструкции самолета. Для уяснения этого понятия
вспомним, что все силы, действующие на самолет, по своей физи-
189
ческой сущности можно разделить на два основные класса: силы,
возникающие только при непосредственном соприкосновении тел,
называемые поверхностными или контактными, и силы, которые
Рис. 0.5. Проекции вектора перегрузки
скоростную систему координат Oxyz
на
ношение вектора равнодействующей
личине силы тяжести:
могут действовать в отсутст-
вии непосредственного кон-
такта между телами. К п е р-
вому классу сил относятся
аэродинамические силы и
сила тяги силовой установ-
ки, ко второму — силы
тяжести, обусловленные
гравитационным полем.
Если поверхностные си-
лы нагружают конструк-
цию самолета, создавая в
ней напряжения, то силы
тяжести взаимно не пере-
даются. Именно поэтому и
принято характеризовать
нагруженность конструкции
самолета так называемым
коэффициентом перегрузки
или просто перегрузкой,
представляющей собой от-
всех поверхностных сил к вё-
П = ~С •
Перегрузка показывает, во сколько раз конструкция самолета
в данном полете нагружена больше по сравнению с прямолиней-
ным установившимся полетом, в котором R=G и, следовательно,
я=1. Как и всякий вектор, перегрузка характеризуется величиной
и направлением. Для удобства анализа ее обычно представляют
в виде трех составляющих — по осям связанной или скоростной
системы координат.
Составляющие перегрузки по осям скоростной системы коор-
динат называются касательной (тангенциальной) nXi нормальной
пу и боковой nz перегрузками и в соответствии с проекциями на
эти оси всех поверхностных сил, действующих на самолет, опре-
деляются формулами:
Pcosa — X ।
— -Q-' — Q ;
Ry Y + Psin a
nv“ ~G~ ~ G ’
n*~ g ~ a •
(0.12)
Перегрузки nx, ny, nx положительны, если действуют в поло-
жительном направлении осей Ох, Оу, Oz (рис. 0.5).
190
Разделив правые и левые части уравнений (0.10) на т= —
и учитывая связи (0.12), получим уравнения движения центра масс
в перегрузках:
(0.13)
Рис. 0.6. Силы и моменты, определяющие продольное дви-
жение самолета
В полете в результате воздействия управляющих или возму-
щающих причин могут возникать и изменяться моменты одновре-
менно относительно нескольких осей координат. При этом появ-
ление моментов относительно одной оси может вызвать возникно-
вение их и относительно других осей. Так, например, моменты
крена Мх и рыскания а следовательно, и движения относитель-
но осей О и тесно связаны между собой и рассматривать их
изолированно можно только условно.
Вместе с тем при небольших отклонениях от исходного режима
появление продольного момента Mz не сопровождается появлением
поперечного Мх и путевого Mv моментов и, наоборот, возникнове-
ние моментов Мх и Му не сопровождается появлением момента М*.
Это объясняется наличием у самолета плоскости симметрии Ох^.
Именно потому, что самолет имеет плоскость симметрии, силы и
моменты, действующие на него, а соответственно устойчивость и
управляемость самолета делят на две группы.
В одну из этих групп включают силы, лежащие в плоскости
симметрии, и моменты этих сил относительно поперечной оси
Такими силами являются: подъемная сила У, сила лобового со-
противления X, сила тяги Р и сила тяжести G или ее составляю-
щие Gx и Gy (рис. 0.6). Движение самолета под действием этих
191
сил и продольного момента Мг называют продольным дви-
жением. Соответственно равновесие, устойчивость и управляе-
мость самолета в этом движении называют продольным рав-
новесием, продольной устойчи-
' востью и продольной управляе-
! 7 м о с ть ю.
I / Вдругую группу входят: составляю-
щая сила тяжести (рис. 0.7), боковая
аэродинамическая сила Z, возникающая
при несимметричном обтекании самолета,
%* и моменты Мх и Му относительно осей Oxi
и Оу\. Равновесие боковых сил, моментов
крена и рыскания принято называть бо-
ковым равновесием, а устойчивость
л У и управляемость самолета — боковой
III устойчивостью и боковой управ-
1 у л яемостью.
При рассмотрении изолированного про-
I дольного движения параметры бокового
д/ движения (р, у, ф, o)Xt (йу) обычно прини-
/|у маются равными нулю, и при изучении
III и, бокового движения параметры продольного
у движения а, 0, V (М) считаются постоян-
/ I \ ными, а угловая скорость о)2 = 0. При этих
J допущениях уравнения, описывающие изо-
’ лированные продольное (0.14) и боковое
г (0.15) движения, в связанной системе ко-
\ 7 ординат соответственно запишутся в сле-
дующем виде:
рн4 ______________________________________________
Рис. 0.7. Силы и моменты, определяющие боковое
движение самолета
=P-Xi-(7sin»;
т = Л — G e°s »;
4? = Hsin6;
at
(0.14)
0 = a 4- 0;
192
т ( “>^у — шу^) = + (7 cos & sin у;
7^ = 2J^
/,-^ = 2^
dty cos 7
dt cos ’
-jr=‘°x — ")y tg&COSf.
(0.15)
При изучении продольного движения уравнения сил удобно за-
писывать в скоростной системе координат. Учитывая связи (0.9),
систему уравнений (0.14) можно записать в следующем виде:
т-^г- = Pcosa — X — G sin 6;
dt
mV = sin a — G cos в:
,«=уЛ1.
‘1 ^{2 -
^- = l/sin9:
dt
& = a + 0.
(0.16)
Разделение общего движения самолета на продольное и боко-
вое и изолированное их рассмотрение существенно облегчают ис-
следование устойчивости и управляемости. Однако в некоторых
случаях (например, при выходе на большие углы атаки, при энер-
гичном вращении самолета вокруг продольной оси) продольное
и боковое движения оказываются настолько связанными между
собой, что изолированное их рассмотрение может привести к ка-
чественно неверным результатам. В этих случаях требуется сов-
местное рассмотрение продольного и бокового движений.
7—21
Раздел III
УСТОЙЧИВОСТЬ И УПРАВЛЯЕМОСТЬ
САМОЛЕТА. КРИТИЧЕСКИЕ РЕЖИМЫ
Глава 7
ПРОДОЛЬНАЯ БАЛАНСИРОВКА, СТАТИЧЕСКИЕ
ХАРАКТЕРИСТИКИ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ
§ 7.1. Продольное равновесие, балансировка самолета
Для прямолинейного равномерного полета необходимо, чтобы
силы и моменты, действующие на самолет, находились в равнове-
сии. Равновесие сил и моментов в продольном движении принято
называть продольным равновесием.
Обеспечение продольного равновесия требует выполнения сле-
дующих условий (см. 0.16):
Pcosa — X — Osin 0 = 0;
Y + Psina — Geos 0 = 0;
SAf, = 0.
(7.1)
Равновесие сил по касательной к траектории (первое условие
системы 7.1) летчик обеспечивает правильным подбором режима
работы двигателя, а равенство нулю сил по нормали к траектории
(второе условие системы 7.1) —установлением необходимого угла
атаки. Управление углом атаки и сохранение его неизменным
(обеспечение третьего условия системы 7.1) летчик осуществляет
соответствующим отклонением стабилизатора (руля высоты). Вы-
полнение первых двух условий системы (7.1) на различных эта-
пах полета будет подробно рассмотрено в IV разделе учебника.
Здесь же мы ограничимся рассмотрением только равновесия (ба-
лансировки) моментов на заданном угле атаки.
Предварительно рассмотрим моментную диаграмму, показыва-
ющую зависимость коэффициента момента тг от коэффициента
194
подъемной силы при прямолинейном движении самолета. Если
полет осуществляется с задросселированным двигателем, то, как
это было показано выше, коэффициент аэродинамического момен-
та, действующего на самолет, может быть записан по форму-
ле (5.4):
П1г — тг. + (я? — Хр) Су +
Если бы аэродинамические характеристики тг,, Хр и ml не
зависели от режима полета, то в пределах плавного обтекания при
данном положении центра тяжести хТ и неизменном положении
стабилизатора была бы линейная зависимость тг=[(Су). При
расположении центра тяжести впереди фокуса моментная диа-
грамма имеет отрицательный наклон. В этом случае при умень-
шении коэффициента Су появляется прирост кабрирующего мо-
мента.
В прямолинейном полете коэффициент Су и число М полета
связаны соотношением, которое можно получить из второго урав-
нения системы (7.1):
р ___ G cos 0 _ О cos 0 д.
qS ~ 0,7/>M«S *
Это значит, при увеличении числа М полета для обеспечения
прямолинейности движения необходимо уменьшать угол атаки.
Когда число М становится более 0,85—0,95, фокус начинает пере-
мещаться назад, что сопровождается заметным приростом пики-
рующего момента. Однако при дальнейшем увеличении числа М
(уменьшении Су) положение фокуса стабилизируется, прекраща-
ется прирост пикирующего момента и появляется значительный
кабрируюший момент (рис. 7.1).
Рис. 7.1. Зависимость коэффи-
циента продольного момента
от коэффициента Су в пря*
молинейном полете (жирная
линия — при планировании,
штриховая при работаю-
щем двигателе)
Выше мы рассмотрели моментную диаграмму при планирова-
нии (задросселированном двигателе). В зависимости от режима
работы двигателя и компоновки самолета силовая установка мо-
жет оказать значительное влияние на моментные характеристики
и поведение самолета. Практика показывает, что у самолета целе-
сообразно так располагать силовую установку, чтобы перемена
режима работы двигателя не изменяла продольный момент. Од-
нако это не всегда удается.
7* 195
В качестве примера рассмотрим момент, создаваемый турбо-
реактивным двигателем, установленным в фюзеляже (рис. 7.2).
Если ось двигателя не проходит через центр тяжести самолета,
то сила тяги Р создает момент, равный:
~ РУр-
Однако кроме этого прямого («тягового») эффекта турбореак-
тивная силовая установка создает косвенный эффект, природа ко-
торого состоит в следующем.
Рис. 7.2. Момент, создаваемый турбореактивным двигателем
Во-первых, при полете с некоторым углом атаки на входе в
воздухозаборник появляется нормальная сила Ур, создающая мо-
мент относительно центра тяжести. Возникновение этой силы свя-
зано с поворотом вектора скорости невозмущенного потока на
входе в воздухозаборник на угол а. Нормальная сила YP равна
секундному изменению количества движения mBVsina, где тв—
секундная масса воздуха, проходящая через двигатель. Таким
образом:
Yp = m3V sin a. (7.3)
Так как сила тяги, развиваемая ТРД, определяется выраже-
нием (6.2), то, разрешая его относительно тй и подставляя резуль-
тат в формулу (7.3), получим:
Гр =-----—sin а. (7.3')
—с- — 1
V 1
Зная нормальную силу, не представляет труда определить ее
момент относительно центра тяжести самолета по формуле:
^грг “ YpXp.
Во-вторых, реактивная струя, выходящая из двигателя, воздей-
ствуя на обтекание других частей самолета (например, горизон-
тального оперения), может вызвать заметное изменение продоль-
ного момента. Это воздействие связано с тем, что расширяющаяся
газовая струя, подсасывая воздух из окружающей среды, изменяет
направление его движения. Расчет взаимодействия газовой струи
с частями самолета чрезвычайно сложен и надежно Выявляется
только в летном эксперименте. Допустим, что при эксперименте
было определено, что газовая струя создает дополнительный про-
196
дольный момент ДЛ/^. Относя этот момент к тяге Р, можно свести
эффект действия газовой струи к смещению оси двигателя на ве-
личину Д//р. Тогда выражение продольного момента, создаваемого
турбореактивной силовой установкой, можно записать в следую-
щем виде:
рх
Мг = РУр+ ~ё Р-Sin
Р Сс I
V
где ур = Ур + ДуР.
Переходя к безразмерному коэффициенту продольного момен-
та и учитывая, что на малых углах атаки sina~a, выраженному
в радианах, получим:
М, - СрХр
"%—Tsr = *’ <7-4>
V
гле Cp = PfqS — коэффициент силы тяги; у' = уР/£; Xp — Xpfb.
Первый член в выражении (7.4) определяет величину измене-
ния момента относительно фокуса Д/пго, вызванного работой си-
ловой установки, второй член — изменение положения аэродина-
мического фокуса самолета. Величину смещения фокуса &хРр мож-
но оценить по формуле:
Отсюда следует, что при расположении входного устройства
впереди центра тяжести (л>>0) силовая установка смещает аэро-
динамический фокус вперед и тем на_ большую величину, чем
больше сила тяги (Cp = P/qS), плечо хР и меньше скорость (чис-
ло М.) полета. На рис. 7.1 штриховой линией показан характер из-
менения моментной диаграммы, вызванного силовой установкой.
Продольное равновесие самолета при данном отклонении ста-
билизатора возможно только на тех коэффициентах подъемной
силы Су, на которых моментная диаграмма пересекает ось Су
(пг2 = 0). Отклонение стабилизатора, необходимое для обеспече-
ния продольного равновесия самолета, называется балансиро-
вочным, а кривая, показывающая зависимость балансировочных
отклонений стабилизатора от скорости (числа М) или коэффици-
ента Су, называется балансировочной диаграммой по
отклонению стабилизатора.
Балансировочные отклонения стабилизатора в прямолинейном
полете можно определить, если приравнять нулю коэффициент
продольного момента:
тг, + (*» ~ •*>) = °-
197
Разрешая это уравнение относительно ф, получаем следующее
выражение, позволяющее рассчитать балансировочные отклонения
стабилизатора и построить балансировочную диаграмму:
ф = — --*> + ^.~х^Су . (7.5)
тг *
Обращаем внимание на то, что числитель в формуле (7.5)
представляет собой коэффициент момента при неотклоненном ста-
билизаторе. Именно поэтому балансировочная диаграмма повто-
ряет в некотором масштабе моментную диаграмму (рис. 7.1).
Подставляя значение Су из формулы (7.2) в формулу (7.5),
можно получить следующую зависимость балансировочных откло-
нений стабилизатора от веса самолета (удельной нагрузки на
крыло -y-J и режима полета: числа М и высоты полета, характе-
ризуемой давлением р:
т~ 1 г*
Т inf inf 0,7pM2S ~Xf(7*5
§ 7.2. Статические характеристики продольной
управляемости
7.2.1. Связь между балансировочными
отклонениями стабилизатора, ручки управления
и усилиями на ней
При отклонении стабилизатора (руля высоты) для балансиров-
ки самолета изменяется распределенная аэродинамическая на-
грузка, действующая на него, а соответственно и шарнирный мо-
мент. Если бы управление стабилизатором осуществлялось непо-
средственно летчиком, без рулевых приводов, то для отклонения
стабилизатора на величину <р летчик должен отклонить ручку
на величину хв, приложив к ней усилие Рв:
_ 1 ]
Хв~ kB . (7.6)
Ря = — I
где kB = dcp/dxB — передаточное отношение от стабилизатора к руч-
ке управления.
Величина шарнирного момента, как известно, определяется вы*
сражением:
Мш = тш43в6в,
где коэффициент шарнирного момента в общем случае зависит от
угла атаки горизонтального оперения аг. о, отклонений руля высо-
ты 5В и триммера &тр,
тш = т^- °аг. 0 4-/пЧв 4- т'шт₽§тр.
198
У самолета с управляемым стабилизатором бв=0 и бтр=О.
В этом случае коэффициент шарнирного момента определяется
углом атаки горизонтального оперения по формуле (5.1)
«г. о — а — 8 4- ?•
При перемене режима полета изменяется угол атаки а и скос
потока е в области горизонтального оперения. Для балансировки
самолета по моменту требуется изменять и угол отклонения ста-
билизатора <р. Это значит, что перемена режима полета сопровож-
дается изменением коэффициента тш, а соответственно и величины
шарнирного момента.
Рост скоростей полета сопровождается увеличением шарнир-
ных моментов, что требует для отклонения рулей значительных
усилий на ручке управления Рв. Особенно сильное изменение шар-
нирных моментов наблюдается на трансзвуковых скоростях по-
лета, на которых при перестройке обтекания от дозвукового к
сверхзвуковому шарнирный момент изменяется не только по вели-
чине, но и по направлению действия.
Практика самолетостроения показывает, что с помощью только
аэродинамических средств (различного рода компенсаций, трим-
меров и др.) не представляется возможным обеспечить приемле-
мые усилия на рычагах управления и тем более получить желае-
мый характер их изменения во всем летном диапазоне скоростей
и высот полета. Это побудило конструкторов искать другие пути
уменьшения усилий на рычагах управления.
Широкое применение получили рулевые приводы (гидроусили-
тели), устанавливаемые в системе управления и позволяющие во
много раз увеличить усилие, производимое летчиком. Поскольку
6, данном случае летчик отклоняет рули не непосредственно,
а с помощью рулевого привода, то такое управление принято на-
зывать управлением непрямого действия.
Рулевой привод не оказывает влияния на шарнирный момент,
он только уменьшает потребные усилия на рычагах управления,
воспринимая частично или полностью шарнирный момент. В пер-
вом случае рулевой привод включается по обратимой схеме (часть
шарнирного момента передается на рычаги управления и воспри-
нимается летчиком), во втором — по необратимой схеме.
На современных самолетах рулевые приводы включаются, как
правило, по необратимой схеме. В этом случае для перемещения,
например, ручки управления летчику требуется приложить усилие,
необходимое только для преодоления сил трения в проводке
управления и золотнике рулевого привода. Но управлять само-
летом, не ощущая усилий на ручке, ориентируясь только по поло-
жению ручки и ее перемещению, чрезвычайно трудно.
Усилие на ручке управления является важнейшей комплексной
характеристикой, позволяющей летчику правильно соразмерить
отклонения руля и ручки. Поэтому при установке рулевого при-
вода по необратимой схеме конструктор вынужден применять раз-
199
ного рода загрузочные механизмы, искусственно создающие (ими-
тирующие) усилие на ручке.
Наиболее простым и надежным, получившим вследствие этого
наибольшее распространение, является пружинный загружатель,
схема которого приведена на рис. 7.3. При отклонении ручки в ту
или другую сторону летчик с помощью упоров 4 и шайб 3 ежи-
Рис. 7.3. Схема простейшего загрузочного механизма
мает пружину 2 в цилиндре 1 и, таким образом, «ощущает» уси-
лие на ручке, величина которого тем больше, чем больше жест-
кость пружины и на большую величину она деформируется (пере-
мещается ручка).
В этом случае усилие на ручке управления определяется выра-
жением
= Св (*^в -*в0)’ (7-7)
гдеСв = Р*в —коэффициент, характеризующий жесткость загру-
зочного механизма, численно равный изменению усилия на ручке
управления при ее перемещении на единицу; л:Вв — положение
ручки, соответствующее нулевому усилию на ручке.
Включая электромотор 5 и изменяя положение точки Л, мож-
но менять положение ручки соответствующее нулевому уси-
лию на ней, и тем самым создавать триммерный эффект. Устрой-
ства, позволяющие изменять усилие на ручке при неизменном ее
положении, называются механизмами триммерного эф-
фекта.
Подставляя в формулу (7.7) хв= -Л-, получим следующее
лв
значение балансировочного отклонения усилия на ручке управ-
ления:
^. = -Сл. + -^т. (7.8)
200
Подставив в эту формулу значение <р из уравнения (7.5'), по-
лучим следующее выражение балансировочных усилий на ручке
управления:
где
Л>.-----^8 ( Л'в.
Рв = Р + ДРВ,
в Во ’ В»
1 \ . д Q Св Хт Хр
k* ] в fcu
(7.9)
G
0,lpWS
Первый член Рв выражения (7.9) мало зависит от режима
полета. Его величину летчик имеет возможность регулировать с
помощью механизма триммерного эффекта, изменяющего
Рис. 7.4. Балансировочная диаграмма по усили-
ям на ручке управления в горизонтальном по-
лете
Второй член ДРВ характеризует переменную составляющую, умень-
шающуюся с ростом числа М и давления р (уменьшением высоты
полета).Если бы аэродинамические характеристики самолета mz f
тУ, хР не зависели от числа М полета, то балансировочная диа-
грамма усилий на ручке управления в горизонтальном полете
имела вид, показанный тонкой линией на рис. J7.4. Однако на око-
лозвуковых скоростях полета фокус самолета xF интенсивно пере-
мещается назад, изменяются при этом mz* и гпу . Вследствие
этого балансировочная диаграмма по усилиям изменяется так, как
показано на рис. 7.4 жирной линией. Изменяя механизмом трим-
мерного эффекта Рв, можно регулировать скорость (число Мо),
на которой усилие на ручке равно нулю. В качестве примера на
рис. 7.4 штрихпунктирной линией показано изменение усилия на
ручке при нейтральном положении механизма триммерного эф-
фекта.
7.2.2. Б а л а н с и р о в о ч н ы е диаграммы и влияние
на них эксплуатационных факторов
Из рассмотрения уравнений (7.6) и (7.8) видно, что баланси-
ровочные отклонения ручки и усилия на ней при заданных значе-
ниях передаточного отношения kB и жесткости загрузочного меха-
201
низма определяются балансировочными отклонениями стабилиза-
тора.
Рассчитав по формуле (7.5х) балансировочные отклонения ста-
билизатора для различных чисел М на постоянной высоте полета,
можно определить балансировочные отклонения ручки и усилия
на ней и построить балан-
сировочные диаграммы
(рис 7;5). Более надежно
такие диаграммы строятся
по данным летных испыта-
ний, в которых осуществляв
ется запись отклонений ста*
билизатора и ручки управ-
ления, иногда и усилий на
ней. При анализе баланси-
ровочных диаграмм обраща-
ется внимание на достаточ-
ность отклонений стабили-
затора для обеспечения рав-
новесия самолета на всех
режимах полета, на потреб-
ные минимальные и макси-
мальные отклонения ручки и
усилия на ней, а также на
характер их изменения при
/---------Передняя центровка
/ ------задняя центровка
777777^77777777^ Предельное отклонение
\////////////////7 hQ K^pupobQHUQ
Рис. 7.5. Балансировочные диаграммы от-
клонений стабилизатора ср, ручки управ-
ления хв и усилий на ней Рв при разных
центровках
перемене режима полета.
Изменение балансировоч-
ных усилий на ручке управ-
ления и ее перемещения
должны позволять летчику
судить об изменении режи-
ма полета. Поэтому усилия
на ручке не должны быть
чрезмерно малыми или
слишком большими. Так,
например, для маневрен-
ного самолета давящие (от
себя) балансировочные уси-
лия на ручке управления я
горизонтальном полете нё
должны быть больше 10кг$
(100 Н), а тянущие (на
себя) не превышать 3 кгс (30 Н). Для сохранения усилий в этих
пределах служит механизм триммерного эффекта.
Потребные отклонения стабилизатора в горизонтальном полете
не только не должны превышать его предельные значения, опре-
деляемые конструкцией, но всегда должен оставаться запас в его
отклонениях, необходимый для выполнения маневра, парирования
возмущений, корректировки неточных отклонений летчиком ручки»
202
Из выражения (7.5') следует, что величина балансировочных от-
клонений стабилизатора, а соответственно ручки и усилий на ней,,
зависит не только_от числа М (рис. 7.5), но также от положения
центра тяжести (хт), веса самолета G и высоты полета (давле-
ния р).
При перемещении центра тя-
жести вперед возрастает расстоя-
ние между фокусом и центром
тяжести, что требует для балан-
сировки самолета увеличивать
отклонение ручки на себя, при-
кладывая к ней дополнительное
тянущее усилие. На рис. 7.5 штри-
ховыми и штрихпунктирными ли-
ниями показано изменение ба-
лансировочных диаграмм при пе-
ремещении центра тяжести соот-
ветственно вперед и назад. Наи-
большие отклонения ручки на
себя и стабилизатора на кабри-
рование требуются при передней
центровке. Следует при этом
прикладывать к ручке и наи-
большие тянущие усилия.
Из рассмотрения выражения
(7.5') следует, что при увеличе-
нии высоты полета (уменьшении
давления р) также необходимо
увеличивать отклонение стабили-
затора на кабрирование, а ручку
управления на себя (см. рис. 7.6).
Качественно такое же влияние
на балансировочные диаграммы
лизатора, ручки управления и уси-
лий на ней
оказывает и увеличение веса са-
молета G. Однако если последний у маневренных самолетов мо-
жет изменяться в полете максимально на 30—40%, то давление
при увеличении высоты до 15—20 км — в 10—20 раз.
Наибольшие потребные отклонения стабилизатора требуются в
горизонтальном полете с передней центровкой на больших высо-
тах и сверхзвуковых скоростях, когда фокус самолета максималь-
но смещается назад, а эффективность стабилизатора начи-
нает уменьшаться. Малые запасы в отклонении ручки и стабили-
затора на таких режимах полета могут явиться причиной ограни-
чения маневренных возможностей самолета. Небольшие запасы
в отклонении ручки и стабилизатора имеет самолет с передней
центровкой при выполнении посадки с выпущенной механизацией
вблизи земли, влияние которой сопровождается смещением фокуса
самолета назад. Вследствие этого на некоторых самолетах вво-
203
дится ограничение предельно передней центровки из условия до-
статочности стабилизатора для выполнения нормальной посадки.
При изменении угла стреловидности крыла в полете меняется
положение фокуса и центра тяжести самолета. Как было показано
в § 5.11, при увеличении угла стреловидности крыла фокус само-
лета сначала перемещается
назад, достигает максимума, а затем
Рис. 7.7. Влияние стреловид-
ности поворотной части кры-
ла на положение фокуса,
центра тяжести и баланси-
ровку самолета
начинает несколько смещаться вперед.
Центр тяжести самолета при этом
непрерывно смещается назад. Вслед-
ствие этого взаимное положение фо-
куса и центра тяжести xf—хт обычно
изменяется так, как показано на
рис. 7.7. Такое изменение xF—хт при
перемене угла стреловидности крыла
сопровождается нарушением продоль-
ного равновесия, требуя для обеспече-
ния балансировки самолета отклоне-
ния ручки (стабилизатора) при увели-
чении угла стреловидности до х = 40->
4-50° на себя, а при х>40ч-50°— от
себя (см. штриховую линию на
рис. 7.7).
При анализе балансировочных диа-
грамм выявляется правильность изме-
нения балансировочных отклонений
ручки управления и усилий на ней на
различных режимах полета. Необхо-
димо, чтобы при увеличении скорости или числа М (ДУ>0) для
балансировки самолета в прямолинейном движении требовалось
отклонять ручку управления от себя Дхв>0, прикладывая к ней
давящее усилие ДРв>0; при уменьшении скорости (ДУ<0), на-
оборот,— ручку выбирать на себя (Дхв<0), прикладывая к ней
тянущее усилие ДРв<0. Такой характер отклонений ручки и уси-
лий на ней является естественным для летчика при переходе с од-
ного режима полета на другой. Таким образом, при правильном
течении балансировочных диаграмм должны выполняться условия:
dxB 0, dPB q
dV dV '
(7.Ю)
Для выполнения условий (7.10) достаточно, чтобы выполня-
лось условие (7.11)
-^->0 или (-£?-) <0. (7.11)
Дифференцируя выражение (7.5) по С^, получим следующее
условие правильности течения балансировочной диаграммы от-
клонений стабилизатора:
/ \ __ _ -Гт ~
\dCy/п -1 т%
204
Из анализа балансировочной диаграммы, приведенной на
рис. 7.5, видно, что во всем диапазоне чисел М стабилизатора
вполне достаточно для балансировки самолета в прямолинейном
полете. Почти во всем летном диапазоне сохраняется качественно
правильный характер изменения всех балансировочных диаграмм.
Однако в диапазоне чисел требуются для баланси-
ровки самолета обратные отклонения ручки (стабилизатора):
с увеличением скорости необходимо ручку выбирать на себя, уве-
личивая тянущее усилие. Такое изменение балансировочных диа-
грамм называют «ложкой».
Обращаем внимание на то, что эффект действия стабилизатора
при этом не меняется: при положительном его отклонении (ручка
от себя) появляется прирост пикирующего момента, при отрица-
тельном (ручка на себя)—прирост кабрирующего момента. По-
явление «ложки» в балансировочных диаграммах отклонений руч-
ки и усилий на ней (заштрихованная область на рис. 7.5) является
нежелательным, так как это усложняет пилотирование. Тем не
менее это явление имеет место у всех современных самолетов на
трансзвуковых скоростях полета. Причиной неблагоприятного из-
менения балансировочной диаграммы в этом диапазоне чисел М
в_основном является интенсивное перемещение фокуса самолета
(xf) назад и неблагоприятное изменение момента относительно
фокуса (znzJ.
При соответствующей тренировке летного состава область об-
ратных отклонений ручки управления и усилий на ней при управ-
лении самолетом в прямолинейном движении особых трудностей
не вызывает.
§ 7.3. Устойчивость по перегрузке
7.3.1. Условие статической устойчивости
п о перегрузке
Прежде чем приступить к рассмотрению статических характе-
ристик продольной устойчивости самолета, обратим внимание на
одно важное свойство самолета, связанное с законом изменения
аэродинамических сил и моментов, действующих на него.
Как известно, эти силы и моменты пропорциональны их коэф-
фициентам и скоростному напору. Так, например, подъемная сила
Y = CySpV2/2 пропорциональна коэффициенту Су. Величина этого
коэффициента определяется главным образом значением угла
атаки. Величина же скоростного напора pV2/2 на данной высоте
полета зависит только от скорости полета. Поэтому для суждения
об изменении аэродинамических сил и моментов при нарушении
равновесия необходимо знать, как изменяются а и V.
Самолеты способны сравнительно быстро изменять угол атаки
и медленно — скорость. Это свойство самолета явилось обоснова-
нием разделения продольной статической устойчивости на два
205
вида: на устойчивость при постоянной скорости, называемой
устойчивостью по перегрузке, и устойчивость при изме-
няющейся скорости, называемую устойчивостью по скоро-
сти. Устойчивость по перегрузке является важнейшей характери-
стикой, определяющей пилотажные свойства самолета.
Самолет называется устойчивым по перегрузке, если самостоя-
тельно (без вмешательства летчика) стремится сохранить пере-
грузку исходного режима полета. Такое название этому виду ус-
Рис. 7.8. Возникновение стабилизирующего и дестабилизирующего
моментов при попадании в восходящий поток у устойчивого (а)
и неустойчивого (б) по перегрузке самолета
тойчивости дано потому, что при постоянной скорости увеличение
или уменьшение угла атаки сопровождается изменением подъем-
ной силы, а следовательно, и перегрузки ny=Y[G. Для лучшего
понимания устойчивости по перегрузке рассмотрим, как она про-
является.
Предположим, что в результате воздействия какой-либо воз-
мущающей причины (например, входа в восходящий поток) у са-
молета, летящего прямолинейно, увеличился угол атаки на вели-
чину Да. Это приведет к увеличению подъемной силы, а значит,
и перегрузки на величину &ny = &Y /G.
В общем случае фокус не совпадает с центром тяжести, поэто-
му прирост подъемной силы, приложенной в фокусе, вызовет по-
явление продольного момента относительно центра тяжести.
В случае когда фокус расположен позади центра тяжести
(рис. 7.8,а), появится пикирующий (восстанавливающий) момент,
впереди центра тяжести (рис. 7.8, б) — кабрирующий (дестабили-
зирующий) момент. В первом случае самолет будет стремиться
возвратиться к исходному углу атаки, «сбросить» появившийся
прирост перегрузки, во втором — продолжать отклоняться от ис-
ходного угла атаки и перегрузки.
Таким образом, статическая устойчивость самолета по пере-
грузке, характеризующая начальное его поведение при нарушении
равновесия, определяется взаимным расположением центра тяже-
сти и фокуса самолета. Для того чтобы самолет был устойчив по
перегрузке, необходимо, чтобы центр тяжести находился впереди
фокуса, т. е. необходимо, чтобы выполнялось условие: xF—хт>0.
206
Об устойчивости по перегрузке можно судить по моментной
диаграмме при постоянном числе М. С этой целью воспользуемся
выражением коэффициента продольного момента (5.4). Так как
при рассмотрении устойчивости по перегрузке скорость (число М)
считается постоянной, то, вычисляя частную производную коэффи-
циента момента по Су, получим:
тсг у = хт — хР.
Отсюда следует, что, для того чтобы самолет был статически
устойчив по перегрузке, достаточно * выполнить условие
/nS = хт — л><0, (7.12>
для чего необходимо, чтобы тангенс угла наклона моментной диа-
граммы при постоянном числе М был отрицателен.
При перемещении центра тяжести назад (или фокуса вперед)
устойчивость по перегрузке уменьшается.
7.3.2. Влияние эксплуатационных факторов
на устойчивость по перегрузке
Выше было показано, что устойчивость по перегрузке может
изменяться при изменении положения центра тяжести или фокуса
самолета.
Изменение положения центра тяжести в полете связано с вы-
работкой топлива, расходованием боекомплекта, сбрасыванием
грузов, изменением угла стреловидности крыла и т. п. и обычно
определяется центровочным графиком.
Чем меньше изменяется центровка самолета, тем меньшие из-
менения при данном положении фокуса претерпевают устойчивость
по перегрузке и характеристики управляемости. Поэтому для
уменьшения изменения устойчивости по перегрузке сбрасываемые
в полете грузы _располагают вблизи центра тяжести, топливные
баки размещают как впереди, так и позади центра тяжести и со-
ответствующей программой выработки топлива обеспечивают ми-
нимум изменения центровки (минимум изменения устойчивости по
перегрузке).
Положение фокуса самолета зависит от его аэродинамической
компоновки и режима полета. Влияние компоновки на положение
фокуса проявляется в первую очередь через угол стреловидности
крыла, взаимное расположение крыла и оперения, форму и распо-
ложение подвесок. Влияние последних может приводить не только
к изменению фокуса, но и центра тяжести.
При данной компоновке положение фокуса зависит от числа М,
угла атаки айв некоторой степени от скоростного напора.
♦ Как будет показано в § 8.2, условие (7.12) устойчивости по перегрузке
достаточно, но не необходимо.
207
Как было показано в главе 4, влияние числа М полета прояв-
ляется наиболее сильно при переходе через скорость, равную ско-
рости звука, вызывая при перестройке обтекания от дозвукового
к сверхзвуковому интенсивное перемещение фокуса назад. Вслед-
ствие этого на сверхзвуковых скоростях полета критерий устойчи-
вости по перегрузке (7.12) может быть в 3—6 раз больше, чем
на дозвуковых скоростях.
Влияние изменения угла атаки на положение фокуса и устой-
чивость по перегрузке проявляется только на больших углах атаки,
когда возникает срывное обтекание, и в сильной степени зависит
от аэродинамической компоновки самолета (см. § 5.10 и 8.4).
§ 7.4. Устойчивость по скорости и влияние на нее
эксплуатационных факторов
•Самолет считается устойчивым по скорости, если самостоятель-
но, без вмешательства летчика, стремится сохранить скорость ис-
ходного режима полета.
Рис. 7.9. Проявление устойчивости по скорости
Рассмотрим проявление устойчивости по скорости при наруше-
нии равновесия. Предположим, что в результате воздействия ка-
кой-либо возмущающей причины (например, изменения угла на-
клона траектории) скорость самолета возросла на величину АИ
(точка 1 на рис. 7.9). При изменении скорости нарушится равно-
весие сил как по касательной к траектории, так и по нормали.
Кроме того, может нарушиться и равновесие продольных момен-
тов, что приведет к сравнительно быстрому изменению угла
атаки.
Допустим, что при увеличении скорости лобовое сопротивление'
станет больше тяги двигателя, а подъемная сила больше силы тя-
жести самолета. В этом случае (точка 2) самолет начнет терять
скорость как вследствие увеличения лобового сопротивления, так
и искривления траектории и перехода самолета в набор высоты,
вызванного избытком подъемной силы. Очевидно, что в рассмат-
риваемом случае самолет будет обладать тенденцией вернуться
к исходной скорости.
208
Приведенные рассуждения позволяют прийти к выводу, что
проявление устойчивости по скорости зависит от характера изме-
нения сил по касательной к траектории Р—X и по нормали
У—G cos 0. В случае, рассмотренном выше, изменение этих сил
способствует восстановлению исходной скорости полета. Однако
роль тех и других сил в обеспечении устойчивости по скорости
различна. Как показывают исследования, изменение касательных
сил Р—X выполняет не столько роль восстанавливающих, сколько
демпфирующих сил, вызывающих затухание колебаний, появляю-
щихся при нарушении равновесия. Вследствие этого начальная
тенденция возвращения самолета к исходной скорости в основном
определяется характером изменения подъемной силы при пере-
мене скорости.
Если увеличение скорости сопровождается возрастанием подъ-
емной силы, а уменьшение скорости ее падением, то искривление
траектории движения будет обусловливать начальную тенденцию
возвращения самолета к исходной скорости за счет преобразова-
ния кинетической энергии в потенциальную, и наоборот.
Таким образом, условие статической устойчивости по скорости
математически можно записать в следующем виде:
44 > °- (7.13)
Так как изменение скорости может сопровождаться и некото-
рым изменением угла атаки, то под устойчивостью по скорости
фактически подразумевается устойчивость режима, т. е. стремление
самолета возвратиться не только к скорости, но и к углу атаки
исходного режима. Поскольку подъемная сила пропорциональна
квадрату скорости У = Cr/pV2/2S, то может показаться, что при уве-
личении скорости будет возрастать подъемная сила и самолет
всегда будет устойчив по скорости. Однако это не так.
Предположим, что увеличение скорости сопровождается при-
ростом пикирующего момента. Это может быть связано с разви-
тием волнового кризиса, упругими деформациями частей самолета
и др. Образовавшийся пикирующий момент может настолько
уменьшить угол атаки, что подъемная сила несмотря на увеличе-
ние скорости не только не увеличится, но даже уменьшится, вслед-
ствие чего траектория отклонится вниз, скорость еще больше уве-
личится и самолет будет все дальше уходить от исходного режи-
ма. Если летчик не вмешается в управление, то самолет будет
входить во все более крутое пикирование. Это явление называют
затягиванием в пикирование. Такое поведение самолета характе-
ризует неустойчивость по скорости.
На устойчивость по скорости заметное влияние оказывают из-
менение режима полета (числа М, приборной скорости), конфи-
гурации самолета и режима работы силовой установки.
Если на докритических числах М современные маневренные
самолеты, как правило, устойчивы по скорости, то в заштрихован-
ной области балансировочной диаграммы, приведенной на рис. 7.5,
209
такой устойчивостью не обладают. Потеря устойчивости по скоро-
сти при превышении числа Mi связана с приростом пикирующего*
момента при увеличении скорости, обусловленного развитием вол-
нового кризиса (перемещением фокуса назад и изменением тг ) .
При достижении числа М = М2 (рис. 7.5) положение фокуса ста-
билизируется, неустойчивость по скорости сначала исчезает, а за-
тем существенно возрастает устойчивость по скорости. Отсюда
можно сделать вывод, что устойчивость по скорости тесно связана
с изменением устойчивости по перегрузке.
Неблагоприятное влияние на устойчивость по скорости могут
оказать упругие деформации частей самолета, которые проявля-
ются на больших приборных скоростях (см. § 5.12). Проблема
снижения влияния упругих деформаций на характеристики устой-
чивости и управляемости особенно остро стоит у самолетов изме-
няемой в полете стреловидности, крылья которых обладают мень-
шей жесткостью.
Если упругие деформации оказывают сильное влияние на ус-
тойчивость по скорости на больших приборных скоростях, то из-
менение режима работы силовой установки, наоборот, на малых
скоростях.
Можно показать, что условие устойчивости по скорости (7.13)
эквивалентно условию
Удобство пользования критерием устойчивости (7.14) состоит
в том, что он позволяет оценить устойчивость по скорости по мо-
ментной диаграмме для прямолинейного полета (рис. 7.1). Так,
например, оценим устойчивость по скорости в трех точках рис. 7.1
Я, В и С, в которых продольный момент, действующий на само-
лет, равен нулю. Если в точках Л и С выполняется условие
dmz/dCy<.Q (самолет устойчив по скорости), то в точке В само-
лет устойчивостью по скорости не обладает dmz/dCy^-Q.
§ 7.5. Связь продольной управляемости с устойчивостью
по скорости
Выше было показано, что важными статическими характери-
стиками продольной управляемости являются показатели dxz/dV
и dPe/dV, которые непосредственно связаны с характеристикой
d^/dV или dq/dCy, позволяющей судить о правильности изменения
балансировочных отклонений стабилизатора. Можно показать, что
характеристика dq/dCy связана с устойчивостью по скорости в
прямолинейном движении следующим выражением:
(_dy__ \ _____dmz 1 /у 1
dCy т? • v-l°>
Из формулы (7.15) видно, что чем больше устойчивость по
скорости dmzIdCy, тем для перехода самолета с одной скорости на
210
другую, требующего для сохранения прямолинейного движения
изменить коэффициент подъемной силы на &СУ, необходимо боль-
ше отклонять стабилизатор.
Обычно летчик оценивает управляемость самолета не по вели-
чине отклонения рулей, а по перемещениям ручки управления и
усилиям, которые он прикладывает к ней для отклонения рулей.
При больших перемещениях ручки и усилиях на ней летчик быстро
утомляется; при малых —
требуется повышенное вни-
мание и четкость в управ-
лении.
Еще сложнее управлять
самолетом, если он неустой-
чив по скорости. В этом
случае для перехода с од-
ной скорости на другую без
изменения режима работы
двигателя летчик должен
совершать двойные движе-
Рис. 7.10. Суждение об устойчивости по
скорости по балансировочной диаграмме
ния ручкой: сначала для изменения угла атаки и угла наклона
траектории в желаемую сторону, а затем для балансировки са-
молета на новой скорости перемещать ручку в противоположную
сторону за исходное положение.
Рассмотрение балансировочных диаграмм по перемещению
ручки и усилиям на ней в прямолинейном полете позволяет вы-
нести суждение об устойчивости по скорости. Предположим, что
выполняя полет на скорости Vo, при которой балансировочное
усилие на ручке равно нулю (рис. 7.10), летчик желает увеличить
скорость на величину AV. Если самолет устойчив по скорости, то
при увеличении скорости появится прирост подъемной силы, кото-
рая будет стремиться искривить траекторию движения вверх и по-
гасить скорость. Для того чтобы устойчивый самолет при увеличе-
нии скорости не переходил в набор высоты, а совершал прямоли-
нейный полет, летчик должен отклонить ручку управления от себя,
прикладывая к ней давящее усилие ДРВ. При уменьшении скоро-
сти устойчивого самолета, очевидно, потребуется приложить к руч-
ке некоторое тянущее усилие. Таким образом, при полете на ско-
рости V=Vo (рис. 7.10) самолет оказывается устойчивым по ско-
рости.
Аналогичными рассуждениями можно показать, что в диапазо-
не скоростей Vi<V<V2 (рис. 7.10) самолет не обладает устой-
чивостью по скорости. Из приведенного рассмотрения можно сде-
лать вывод, что характеристика управляемости самолета dP^/dV^
определенная при Рв = 0, характеризует устойчивость самолета по
скорости.
У устойчивого по скорости самолета выполняется условие (7.10)
dPB/dV>0, у неустойчивого rfPB/dV<;0.
Заметим, что в отличие от неустойчивости по перегрузке не-
большая неустойчивость по скорости, вызывая ряд особенностей
211
в продольном управлении, обычно при соответствующей трени-
ровке не создает для летчика больших трудностей в пилотирова-
нии. Это объясняется довольно медленным изменением скорости
полета, вследствие чего летчик успевает заметить это изменение
и своевременно устранить его. Вместе с тем неустойчивость по
скорости нежелательна, а в ряде случаев и опасна. Именно по-
этому области неустойчивости по скорости, которые у современ-
ных самолетов могут встретиться на малых скоростях («вторые
режимы» полета, см. § 13.5) и околозвуковых скоростях полета
(область'Mi—М2 на рис. 7.5), используются только как проход-
ные.
Серьезные трудности в управлении самолетом могут возник-
нуть при сильной неустойчивости по скорости, сопровождающейся
затягиванием в пикирование, или когда резкое уменьшение устой-
чивости по скорости приводит к непроизвольному увеличению пе-
регрузки (скоростной «подхват», см. § 8.4).
Кроме рассмотренных выше статических характеристик про-
дольной управляемости самолета иногда применяется градиент
dPb/dxv, численно равный величине изменения усилия на ручке,
необходимого для балансировки самолета при изменении поло-
жения центра тяжести на единицу.
Градиент dPb/dx^ можно определить, если продифференциро-
вать выражение (7.9) по хт. В результате получим:
dPв_____С в 1 Q
dx. “ кв '0,7p№S •
Поскольку /nJ < 0, то при перемещении центра тяжести на-
зад для балансировки самолета в горизонтальном полете тре-
буется прикладывать к ручке управления давящее усилие и тем
большее, чем меньше скорость (число М), больше высота полета
и масса самолета. На рис. 7.10 штриховой линией показано изме-
нение усилия на ручке (dPB/dxT) Дхт при перемещении центра тя-
жести назад на Алт = хт* — azTj.
Глава 8
ДИНАМИЧЕСКИЕ СВОЙСТВА САМОЛЕТА В ПРОДОЛЬНОМ
ДВИЖЕНИИ
§ 8.1. Физическая природа развития продольного движения.
Разделение движения на малое и большое
Прежде чем приступить к исследованию динамических свойств
самолета в продольном движении, рассмотрим физическую приро-
ду развития и характер изменения основных параметров этого дви-
жения.
212
Управляя продольным движением, летчик отклоняет ручку
управления (стабилизатор) и меняет положение рычага управле-
ния двигателем (РУД). Для того чтобы понять, в какой последо-
вательности и почему летчик воздействует на органы управления»,
рассмотрим качественно поведение самолета и развитие продоль-
ного движения отдельно при отклонении либо ручки управления»,
либо рычага управления двигателем.
Рис. 8.1. Изменение параметров движения при отклонении
стабилизатора
Пусть в установившемся горизонтальном полете летчик энер-
гичным взятием ручки на себя отклонил стабилизатор на неко-
торую величину Дер (точка О на рис. 8.1) и удерживает его в этом
положении. Возникший кабрирующий момент вызовет уско-
ренное вращение самолета вокруг поперечной оси Ох и самолет
начнет увеличивать угол атаки и тангажа. При увеличении угла
атаки возникнет восстанавливающий момент, обусловленный
устойчивостью по перегрузке и равный вследствие чего
угловое ускорение начнет уменьшаться. При возникновении вра-
щения, кроме того, появится демпфирующий момент пре-
пятствующий вращению. В некоторый момент времени сумма мо-
ментов Л1“Да + станет равной управляющему моменту
и ускорение обратится в нуль, а угловая скорость достигнет мак-
симального значения. При дальнейшем увеличении угла атаки
сумма восстанавливающего и демпфирующего моментов станет
больше управляющего момента, что приведет сначала к уменьше-
нию угловой скорости, а затем к появлению вращения в противо-
положную сторону. Спустя некоторое время самолет приобретает
некоторое установившееся значение угла атаки ауСт, соответствую-
щее новому положению стабилизатора. Это приведет к росту подъ-
емной силы, которая станет больше силы тяжести G на величину
ДУ. В результате этого самолет, искривляя траекторию вверх
(d0/d/>O), перейдет в набор высоты. Поскольку в продольном
движении угол тангажа 9 равен сумме углов наклона траектории Э
213
и атаки а (0.14), то угол тангажа будет изменяться быстрее, чем
угол атаки.
Если положение РУД остается без изменения, то по мере уве-
личения высоты скорость полета будет уменьшаться, что в соче-
тании с падением плотности воздуха приведет к уменьшению подъ-
емной силы. На некоторой высоте (точка 2 на рис. 8.1) положи-
тельный прирост подъемной силы ДУ станет равным нулю. Углы
тангажа и наклона траектории в этой точке будут максимальны-
ми. Вследствие наличия вертикальной скорости в этой точке само-
лет будет продолжать набирать высоту и уменьшать скорость. При
неизменном положении стабилизатора (угла атаки) это приведет
к появлению отрицательного прироста подъемной силы ДУ, на-
правленного сверху вниз (точка <?). Начнется искривление траек-
тории вниз, благодаря чему самолет сначала прекратит набирать
высоту (точка 4), а затем перейдет на снижение (Д9<0), в про-
цессе которого скорость движения и плотность воздуха будут воз-
растать. Это приведет к увеличению и подъемной силы. В точке 5
(рис. 8.1) отрицательный прирост подъемной силы ДУ станет рав-
ным нулю, а углы наклона траектории и тангажа достигнут наи-
меньшего значения.
В дальнейшем при снижении подъемная сила станет больше
силы тяжести, что приведет к искривлению траектории вверх, уве-
личению углов тангажа и наклона траектории (уменьшению их
отрицательных значений). В точке 6 угол наклона траектории ста-
нет равным нулю, а скорость достигнет максимального значения
и далее процесс начнет повторяться.
Из рассмотрения изменения параметров движения самолета
при ступенчатом отклонении стабилизатора можно сделать вывод,
что продольное возмущенное движение можно разделить на два
этапа. На первом этапе, занимающем первые несколько секунд,
изменяется главным образом угол атаки и, как следствие, углы
тангажа и наклона траектории; скорость и высота полета на этом
этапе практически не успевают изменяться и их можно считать
постоянными. На втором этапе изменяются главным образом ско-
рость и, как следствие, углы наклона траектории, тангажа и вы-
сота полета; угол же атаки на этом этапе изменяется незначитель-
но и его в первом приближении можно считать постоянным.
Поскольку первый этап кратковременен, сопровождается сла-
бым изменением траектории движения, то его иногда называют
малым или короткопериодическим движением.
В процессе второго этапа, длительность которого на два-три по-
рядка больше, чем первого этапа, наблюдаются значительные из-
менения траектории (высоты, угла наклона траектории и скоро-
сти) и слабое затухание колебаний. Этот этап называют боль-
шим или длиннопериодическим движением. В дей-
ствительности малое и большое движения развиваются одновре-
менно и представляют единое продольное движение самолета.
Однако в начале возмущенного движения большое движение не
успевает сколько-нибудь заметно проявиться, а угол атаки успе-
214
вает приобрести установившееся значение и в процессе большого-
движения практически остается без изменения.
Совершив слабо затухающие колебания углов наклона траек-
тории и тангажа, высоты и скорости полета, самолет в процессе
большого продольного движения сбалансируется на некотором
установившемся значении Д9уСт>0, ДУуст<0, ДЯуСт>0. Интен-
сивность затухания колебаний параметров большого движения за-
Рис. 8.2. Изменение параметров движения при
увеличении тяги двигателя
висит в первую очередь от характера изменения лобового сопро-
тивления и тяги двигателя при изменении скорости. Если с ростом
скорости при неизменном угле атаки лобовое сопротивление X
увеличивается сильнее тяги двигателя Р, то колебания параметров
в большом продольном движении будут затухать. В самом делег
при таком изменении X и Р на нижней полуволне (точки 5, 6, 7f
рис. 8.1), где больше скорость, лобовое сопротивление больше тяги,,
а на верхней полуволне (точки 2, 4, 5) —наоборот. Такое измене-
ние X и Р при изменении скорости приводит к тому, что избыток
лобового сопротивления на нижней полуволне препятствует уве-
личению скорости, а соответственно и подъемной силы, на верхней
полуволне избыток тяги будет препятствовать падению скорости
и подъемной силы. Отмеченное влияние X и Р на изменение ско-
рости и подъемной силы и обусловливает затухание колебаний па-
раметров в большом продольном движении. Обычно демпфирова-
ние большого продольного движения слабое, поэтому время зату-
хания колебания в этом движении достаточно велико.
Частота и период колебаний большого продольного движения
в основном определяются устойчивостью по скорости (dY/dV).
Чем больше устойчивость по скорости, тем больше частота, а со-
ответственно меньше период колебаний Г, который значительна
(в 50—200 раз) больше периода малых продольных движений.
Именно поэтому большие продольные движения иногда называют
длиннопериодическими или фугоидными.
Рассмотрим теперь поведение самолета при изменении поло-
жения РУД и неизменном положении стабилизатора. Для просто-
ты предположим, что изменение тяги двигателя не сопровождается
нарушением равновесия продольных моментов. Тогда характер из-
менения параметров продольного движения при увеличении тяги
двигателя будет иметь вид, показанный на рис. 8.2. Видно, что в
215
переходном процессе практически отсутствует малое (короткопе-
риодическое) движение, связанное с изменением угла атаки. При
увеличении тяги в рассматриваемом случае переходный процесс
фактически начинается с роста скорости, что влечет за собой уве-
личение подъемной силы, вызывающее искривление траектории
вверх и переход самолета в набор высоты. Это сопровождается
соответствующим увеличением и угла тангажа. В процессе боль-
ших продольных движений самолет совершает длиннопериодиче-
ские колебания скорости, высоты, углов наклона траектории и
тангажа. По прекращении длиннопериодических колебаний, вы-
званных увеличением тяги двигателя при неизменном положении
стабилизатора, самолет балансируется на новых (больших) ско-
рости и высоте при практически неизменных углах атаки и тан-
гажа.
Выше мы рассмотрели поведение самолета, когда в процессе
возмущенного движения отклонение стабилизатора не меняется.
Если в процессе продольных движений летчик отклоняет стабили-
затор, например для сохранения постоянства высоты или угла
тангажа, то демпфирование большого движения настолько воз-
растает, что движение становится апериодическим, без колебаний.
Именно поэтому многие даже опытные летчики, осуществляющие
управление самолетом по естественному горизонту или показа-
ниям авиагоризонта, не знают и не подозревают о существовании
колебаний в большом продольном движении.
Летная практика показывает, что пилотажные свойства само-
лета в значительной степени определяются его динамическими
свойствами в малом продольном движении. Поэтому рассмотрим
-более глубоко эти свойства.
§ 8.2. Динамические свойства самолета в малом
(короткопериодическом) продольном движении
8.2.1. У р а в н е н и я движения и их линеаризация
В процессе малого продольного движения в первом приближе-
нии можно считать скорость и высоту полета неизменными. В этом
случае уравнение, описывающее закон изменения скорости, можно
спустить из рассмотрения. Тогда систему (0.14), описывающую
продольное движение, можно записать в следующем виде:
/пИ= Y + Psin а —• Geos 0;
I = <8Л)
dt* z'
= 0 -|- а,
где У является функцией угла атаки а, а продольный момент
ЛЬ — функцией а, а, со2, ср. В дальнейшем для упрощения записи
уравнений движения будем предполагать, что исходный полет яв-
216
ляется горизонтальным (во = О), а угол атаки мал. Тогда в систе-
ме (8.1) можно положить cos8 = 1; sina~a.
Полученная система даже при принятых допущениях является^
системой нелинейных дифференциальных уравнений, которая в об-
щем виде аналитически не решается. Это вынуждает прибегать к
использованию быстродействующих электронных вычислительных
машин (ЭВМ), на базе которых, например, создаются современ-
ные тренажеры. Несмотря на большое значение ЭВМ в исследо-
вании динамических свойств самолетов они не только не исклю-
чают, но даже требуют развития приближенных аналитических
методов решения дифференциальных уравнений. Последние в каж-
дом конкретном случае дают результаты менее точные, чем ин-
тегрирование на указанных ЭВМ, но позволяют установить общие
закономерности, справедливые для данного класса движений.
Одним из наиболее распространенных методов, применяемых
при исследовании динамических свойств самолета, является метод
малых возмущений. Применение этого метода, позволяет нелиней-
ную систему дифференциальных уравнений привести к линейной
системе, методы решения которой хорошо разработаны.
Пусть исходное невозмущенное малое продольное движение са-
молета определяется следующими параметрами Vo, (а) о, Оо>
0о^О, Яо(р)о- В соответствии с методом малых возмущений бу-
дем предполагать, что в процессе возмущенного движения углы
атаки, тангажа и наклона траектории получают небольшие при-
ращения Да, ДО, Д0 (скорость и высота в процессе малого дви-
жения предполагаются неизменными). Тогда каждый из изменяе-
мых параметров движения, подъемную силу и продольный момент
можно представить как сумму двух слагаемых:
аз=(а)о+Да» 1
О = 0о4- ДО; 0 = 0ОД0: Мг = Мгв + ЬМХ. /
Поскольку исходный полет установившийся, то
d% __ d&Q _ d$c _q
dt ~ dt ~~u
и, следовательно,
da __ d(Aa) , d§ _ d<№) _ . de _ d(A0) Qv
dt ~ dt ’ dt ~ dt dt dt ’
Так как приращения Да, ДО, ДУ и ДЛ12 малые величины, та
представим приращения подъемной силы и продольного момента
в следующем виде:
ДУ=УвДа;
ДАТ* = 2И«Да 4- Л4® a 4- М 4- МJД<р. (8.4)
Здесь через Кв, Л4®, Л4*, М* обозначены частные про-
изводные подъемной силы и продольного момента по параметру,.
217
который занимает место показателя степени. Подставляя уравне-
ния (8.2), (8.3) и (8.4) в систему (8.1) и учитывая, что в исход-
ном установившемся движении
Уо + Р «о — G — 0;
Af, = O,
получим следующую систему линейных дифференциальных урав-
нений:
= Г Да + РДа + G;
/. + Ч-. + м, <8'5)
В системе (8.5) двух дифференциальных уравнений отклонение
стабилизатора Д<р является управляющей функцией; искомыми па-
раметрами являются Да, Д0 и ДО. Для однозначности решения
задачи воспользуемся уравнением связи Д9=Д0 + Да и исключим
из системы (8.5) одну из переменных. Так, подставим в первое
уравнение системы Д0=ДО—Да, одновременно разделим это урав-
нение на mVo, а второе — на 1г. В результате систему (8.5) мож-
но привести к следующему виду:
d(M) d(Aa) , Г О Л_.
dt ~ dt ** miz0
d2(A3) Л1* dtfia) _ Ml
dt2 lz aat~ Iz dt 1г dt ~ 1г
где n=r + p.
Исключая переменную Д9 подстановкой из первого уравнения
dt
альное
(8.6)
во второе уравнение, получим следующее дифференци-
уравнение, определяющее закон изменения угла атаки:
+ч т<8-7)
М*
где п , а характеристика затухания пл и частота собствен-
? *2
ных колебаний 2в определяются следующими выражениями;
1 ( Mi+M^
~ 2 \ mV а 1г
мг м”> Гй
“ 1г 1г mV0 *
Как видно из выражения (8.8), коэффициент пх определяется
не только производными момента Л/“г и М*, характеризующими
вращение самолета вокруг оси Ozi, но и производной Kj, увели-
218
(8.8)
чивающей демпфирование колебаний самолета при искривлении
траектории.
Подставим в выражение, определяющее частоту собственных
колебаний ££, (8.8) значения:
У« = С;<75; Л1“ = Л1^уС; = тгсуГ^; М** = m^qSb.
В результате получим:
Учитывая, что
m“*V/b = /п“г,
и вводя обозначение
2m
tSb ~ ***
где jx — относительная массовая плотность самолета, получим сле-
дующее значение квадрата частоты собственных колебаний:
(8-9)
Таким образом, частота собственных колебаний определяется
не только статической характеристикой устойчивости по перегруз-
ке т^у, но и дополнительным членом обусловленным ди-
намикой движения самолета. Сумма
z-< /72- 2
+ = (8.10)
называется запасом устойчивости по перегрузке.
Уравнение (8.7) является линейным неоднородным дифферен-
циальным уравнением второго порядка, общее решение которого
является суммой, составленной из решения (Деи), соответствую-
щего однородному уравнению (без правой части) и какого-либо
частного решения (Даг) неоднородного уравнения. Таким образом,
общее решение уравнения (8.7) можно записать в следующем
виде:
Да = Aaj-J-Да2. (8.11)
8.2.2. Собственные динамические свойства
в малом продольном движении
Рассмотрим сначала решение однородного уравнения, опреде-
ляющего собственные динамические свойства самолета. Посколь-
ку решение линейного однородного уравнения всегда имеет вид
219
показательной функции, то будем искать рещение уравнения вто-
рого порядка (8.7) без правой части в следующем виде:
Да, = Atep'‘ + А2ер,‘. (8.12)
Здесь Ai и А2 постоянные коэффициенты, определяемые по на-
чальным исходным данным, а р\ и р2 корни характеристического
уравнения
Рг + Zaj) + 22 = 0.
Решение этого уравнения дает следующие значения корней
Л.2==-« ±К^Г=^. (8.13)
Вынося из-под корня частоту собственных колебаний и
вводя обозначения относительного коэффициента затухания £=*
— nJQ* и постоянной времени Г0 = 1/2а, выражение корней 2
можно записать в следующем виде:
A,2=-7-(£±l/^). (8.13')
Если частота собственных колебаний характеризует быстроту
•изменения параметров движения, то постоянная времени То —
инерционность самолета в малом продольном движении. Относи-
тельный коэффициент затухания является важнейшей характери-
стикой движения, определяющей корни характеристического урав-
нения, а следовательно, и характер движения. Если $>1, то из
формулы (8.13) следует, что корни р\ и р2 будут действительными,
а угол атаки будет определяться как сумма двух экспонент (двух
апериодических движений).
Для многих современных самолетов характерно значение ко-
эффициента затухания £<1. В этом случае мы получаем комплекс-
ные сопряженные корни (8.13), которые определяют изменение
угла атаки по следующему периодическому закону:
Да, = ft?-"»'Sin (wt 4- <ра),
где постоянные В и <?а находятся по начальным данным, а
вая частота % и соответствующий ей период колебаний
деляются выражениями:
% = |/ 2^2.
7\ = —.
Проанализируем полученные результаты. Прежде всего
ним влияние коэффициента устойчивости по перегрузке оя, опре-
деляющего частоту собственных колебаний 2а, на динамические
свойства самолета. Чем больше коэффициент устойчивости по пе-
регрузке On, тем при отклонении угла атаки от исходного значе-
220
(8.14)
круго-
опре-
(8.15)
выяс-
ния появляется больший восстанавливающий момент, который
при прочих равных условиях обусловливает большую круговую
частоту соа и соответственно меньший период колебаний. У само-
летов, устойчивых по перегрузке, период малых продольных дви-
жений обычно невелик (Та == 1-ч-4 с). Именно поэтому этот вид
движения часто называют короткопериодическим.
Рис. 8.3. Влияние коэффициента затухания $
на изменение угла атаки в процессе возмущен-
ного движения
Для того чтобы в процессе возмущенного движения амплитуда
колебаний угла атаки уменьшалась, а колебания быстро затухали,
необходимо, чтобы самолет обладал приемлемыми демпфирую-
щими свойствами.
Если бы демпфирование вообще отсутствовало (ла=0 и со-
ответственно £==0), то при наличии устойчивости по перегрузке
(оп<0) нарушение равновесия сопровождалось бы появлением
незатухающих колебаний (рис. 8.3) с круговой частотой а>а = 2
По мере увеличения демпфирующих свойств (увеличения g) уси-
ливается затухание колебаний и уменьшается частота колебаний
(возрастает период колебаний по формуле (8.15). Когда коэффи-
циент Н достигает единицы, круговая частота % становится рав-
ной нулю, а период—бесконечности. Это значит, что движение
из периодического переходит в апериодическое (рис. 8.3).
За характеристику затухания колебаний иногда принимают
число колебаний пзат до практически полного затухания. Под прак-
тически полным затуханием обычно понимают уменьшение началь-
ной амплитуды в 20 раз. Время ^зат, за которое происходит прак-
тически полное затухание, определяется из следующего соотноше-
ния:
ое 20 .
221
Сокращение на В и затем логарифмирование дают:
, _ /л20 __ 3
яат— я« ~ п« '
(8.16)
Зная /зат и период колебаний 7'а, определяемый формулой
(8.15), находим число колебаний до практически полного зату-
хания
Рис. 8.4. Определение положения нейтральной цент-
ровки
(8Л7)
Периодический закон изменения угла атаки будет иметь место
только при 2д>0, для чего необходимо, чтобы самолет был
устойчив по перегрузке (оя<0). Это условие может выполняться
и тогда, когда самолет статически нейтрален или даже имеет ста-
тическую неустойчивость по перегрузке (wfy 0), лишь бы до-
полнительный член, обусловленный вращением, из фор-
мулы (8.10) обеспечивал оя<0. Положение центра тяжести, при
котором самолет теряет устойчивость по перегрузке (<тя=0), на-
зывается нейтральной центровкой (хт.в). Для определе-
ния нейтральной центровки воспользуемся выражением (8.10).
Подставляя значение у = хТ. я — хР и приравнивая ая=0, по-
лучим
— — /и”*
jct. н = Хр —. (8.18)
Так как лг“*<0, то влияние динамики движения эквивалент-,
но смещению фокуса самолета назад (рис. 8.4) на величину
_ mmz
LX,, =------
J® I*
Как известно, демпфирующий момент, препятствуя вращению
самолета как при отклонении угла атаки от исходного значения,
222
-гак и при возвращении к исходному положению, вызывает зату-
хание возникающих колебаний. Поэтому на первый взгляд может
показаться странным, что с ростом демпфирующего момента уве-
личивается устойчивость по перегрузке. Чтобы в этом убедиться,
рассмотрим динамику движения самолета.
Допустим, что в процессе движения, обусловленного, например,
попаданием самолета в вертикальный поток, самолет начнет ис-
кривлять траекторию движения. Если бы при искривлении траек-
Рис. 8.5. Изменение угла атаки при искривлении тра-
ектории
тории направление продольной оси самолета оставалось неизмен-
ным (что может быть у устойчивого по перегрузке самолета
только при неограниченно большом демпфировании), то при от-
клонении траектории вверх угол атаки стал бы уменьшаться на
величину Да (рис. 8.5), а при отклонении вниз — увеличиваться.
Это значит, что само искривление траектории способствует воз-
вращению самолета к исходному углу атаки, т. е. приводит к по-
вышению устойчивости по перегрузке. Чем больше демпфирующий
момент, тем меньше при искривлении траектории движения будет
поворачиваться продольная ось самолета, а следовательно,
тем большей устойчивостью по перегрузке обладает самолет.
Отмеченное изменение угла атаки при искривлении траектории
движения вызывает стабилизирующее изменение подъемной силы:
при искривлении траектории вверх появляется отрицательный при-
рост подъемной силы, а при искривлении траектории вниз — по-
ложительный. Такое изменение угла атаки и подъемной силы при
искривлении траектории повышает и демпфирование колебаний
самолета, что отражено в характеристике /га (8.8) дополнитель-
ным членом Y*/mV.
Влияние динамики движения самолета на демпфирование ко-
лебаний и устойчивость по перегрузке уменьшается с увеличением
высоты полета (возрастает относительная массовая плотность ц).
Для обеспечения минимального запаса центровки (оЛ), кото-
рый у маневренных самолетов не должен быть менее 3% САХ,
устанавливается предельно задняя центровка, за которую центр
тяжести в ‘эксплуатации не должен переходить. При расположе-
нии центра тяжести между нейтральной и предельно задней цен-
тровками самолет будет вяло реагировать на изменение угла атаки
223
и перегрузки. О таком самолете говорят, что он мало устойчив по
перегрузке. Если центр тяжести будет совпадать с нейтральной
центровкой (аЛ = 0), то при изменении угла атаки или перегрузки
у самолета не будет появляться стабилизирующих сил и момен-
тов. Такое состояние самолета принято называть нейтральным или
безразличным.
При дальнейшем перемещении центра тяжести назад (или фо-
куса вперед) самолет становится неустойчивым по перегрузке
(сгл>0), а характеристика 2^, определяемая по формуле (8.9),
Рис. 8.6. Изменение угла атаки и его со-
ставляющих у неустойчивого по перегруз-
ке самолета (оп>0)
становится отрицательной. В этом случае получаем по формуле
(8.13) два действительных корня, один из которых будет отрица-
тельным, второй — положительным. Первый будет большим по
абсолютной величине, обусловливая быстрое уменьшение одной
составляющей движения A{ep'f выражения (8.12). Второй будет
малым положительным корнем, вызывающим апериодическое уве-
личение угла атаки (А^^), что с течением времени приведет
к уводу самолета от исходного угла атаки (рис. 8.6).
§ 8.3. Динамика переходного процесса и характеристики
управляемости продольного движения
Для изучения реакции самолета на отклонение стабилизатора
найдем общее решение неоднородного уравнения (8.7), определя-
ющее закон изменения угла атаки. Выше было показано в фор-
муле (8.11), что такое решение является суммой, составленной из
общего решения однородного уравнения и частного решения неод-
нородного уравнения. Первое, определяя переходную составляю-
щую движения, характеризует собственные свойства самолета и
было получено выше (выражение 8.14). Второе, определяя уста-
новившееся значение угла атаки, характеризует вынужденное дви-
жение. Заметим, что при рассмотрении вынужденного движения
обычно предполагается, что летчик мгновенно («ступенчато») от-
224
клоняет стабилизатор. В реальных условиях мгновенно отклонить
стабилизатор невозможно. Скорость его отклонения лимитируется
возможностью летчика быстро отклонять ручку управления и
быстродействием рулевого привода. Однако такое допущение
позволит наиболее просто исследовать вынужденное движение са-
молета.
Частное решение Даг ищется в виде, соответствующем правой
части уравнения (8.7). Так, например, за частное решение можно
принять-новое (установившееся) значение угла атаки Дауст, кото-
рое приобретает самолет после окончания переходного процесса,
вызванного отклонением стабилизатора. Выражение для Дауст по-
лучим, если в уравнении (8.7) положим d(Aa)/dt = Q и d2(&a) /dt2 =
= 0. В результате получаем следующее установившееся значение
угла атаки при ступенчатом отклонении стабилизатора на вели-
чину Дф
д“уст =-&-*?• (8.19)
Из полученного выражения следует, что при данном отклонении
стабилизатора установившееся значение угла атаки будет тем
меньше, чем больше частота собственных колебаний Sa, опреде-
ляемая запасом устойчивости по перегрузке
Таким образом, при периодическом изменении угла атаки
(£<1) общее решение неоднородного уравнения (8.7) получим,
подставив в формулу (8.11) значение выражения Дои и Да2 = ДауСт,
получим
Да = Ве~Пл*sin + сра) Н—Дер, (8.20)
где постоянные В и <ра определяются по начальным данным. Так
как при / = 0 в установившемся исходном движении Да = 0 и
d(Aa)/d/ = 0, то для определения В и <ра приравняем нулю Да
(формула 8.20) и ее первую производную, продифференцировав
предварительно выражение (8.20). Тогда, приняв ?=0, получаем
следующие два уравнения:
О = 5 sin Дер;
0 — — п В sin ® 4- Bw cos ср.
a i a 1 u i a
Из первого уравнения получаем
sin <pe *
8—21
225
Из второго уравнения находим
откуда
<P, = arctg-J£-. (8.21)
Рис. 8.7. Влияние относительного коэффи-
циента затухания на переходный процесс
Для определения значения sin <рв воспользуемся формулой
sin Ф — -iy------------------— .
а Ич-tg2^
Подставляя значение tg <ра = <»Jna, получаем sin <ри == o>a/Q2 и соот-
ветственно
В=--^Дф,
Таким образом, закон изменения угла атаки (8.20) при сту-
пенчатом отклонении стабилизатора принимает следующий вид:
Да = Дауст f 1 — -5-е sin (<о/ + <ра)
I ^ос
(8.22)
где ДаУст определяется выражением (8.19). На рис. 8.7 показана
переходная функция изменения угла атаки при ступенчатом от-
клонении стабилизатора для некоторого значения коэффициента
затухания £<1. Как видим, в процессе перехода самолета с од-
ного угла атаки на другой он совершает затухающее колебатель-
ное движение, отклоняясь от нового установившегося значения
ДаУст то в одну, то в другую сторону.
При рассмотрении продольного движения важно знать не
только величину и изменение угла атаки, но и нормальной пере-
226
грузки Пу. Если известен закон изменения угла атаки Да, то закон
изменения перегрузки определится выражением
сй
= Да, (8.23)
суг.п
где Су г. п — коэффициент подъемной силы в горизонтальном по-
лете.
Важными характеристиками переходного процесса являются:
время срабатывания, заброс угла атаки и время регулирования
(затухания). Под временем срабатывания /Ср понимается
время, в течение которого угол атаки после отклонения стабили-
затора первый раз достигает 95% установившегося значения Дауст.
Это время характеризует быстроту реакции самолета на ступен-
чатое отклонение стабилизатора, его быстродействие. Поскольку
/ср^Га/4, то о быстродействии самолета можно судить по вели-
чине периода колебания Та =2тт/о)а, определяемого круговой час-
тотой %. Из формулы (8.15) следует, что чем больше частота
собственных колебаний (больше запас устойчивости по пере-
грузке ап) и меньше характеристика затухания колебаний тем
больше круговая частота и соответственно лучше быстродействие.
Однако при уменьшении яа и увеличении 2а уменьшается
относительный коэффициент затухания £~/га/Йа, что сопровож-
дается все большими забросами (выбросами) угла атаки и коле-
бания медленнее затухают. Под забросом Да3аб понимается мак-
симальная динамическая ошибка, определяемая как разность
между текущим значением угла атаки и его новым установив-
шимся значением. При затухающих переходных процессах первый
выброс (заброс) является максимальным_Датах. Можно показать,
что относительный заброс угла атаки Дазаб = (^атах — Дауст)/Дауст
зависит только от коэффициента g:
—«——
^азаб в .
Переходные процессы, сопровождающиеся большими выброса-
ми, нежелательны. Кроме того, такие процессы, как правило,
имеют большое время регулирования (затухания). Под време-
нем регулирования /рег понимается время, в течение кото-
рого значение динамической ошибки уменьшается до 5%
(рис. 8.7). Поскольку время регулирования равно времени затуха-
ния колебаний Лат, то /рег — 3/ла.
Для уменьшения забросов угла атаки и времени регулирования
необходимо увеличивать демпфирование (характеристику пл). При
5^1 можно вообще получить монотонный (апериодический) про-
цесс. Однако при таких процессах существенно возрастает время
срабатывания ЛР, а следовательно, уменьшается быстродействие,
8* 227
что тоже нежелательно. На рис. 8.8 показан пример изменения
параметров малого продольного движения при ступенчатом откло-
нении стабилизатора при относительном коэффициенте затуха-
ния g, близком к 1.
Рис. 8.8. Изменение параметров малого
продольного движения при ступенчатом
отклонении стабилизатора
Важными характеристиками продольной управляемости само-
лета в установившемся криволинейном движении являются гра-
диенты усилия на ручке (Р*у) и ее перемещения (х"у) по
перегрузке. Градиент Р*у показывает, какое необходимо прило-
жить усилие к ручке управления для того, чтобы изменить пере-
грузку на единицу, а градиент х^у — на какую величину при этом
необходимо отклонять ручку.
При управлении самолетом без применения автоматических
устройств эти два градиента теснейшим образом связаны с гра-
диентом упу, показывающим, на какую величину необходимо от-
клонить стабилизатор для увеличения перегрузки на единицу.
Продифференцировав выражения (7.6) и (7.8) по пу, получим:
<y==-£vy;
(8.24)
228
Из выражений (8.24) видно, что чем больше градиент <рЛу,
тем при данных характеристиках системы управления (Св и йв)
требуется на большую величину перемещать ручку управления и
большее усилие прикладывать к ней для изменения перегрузки.
Выясним, от каких факторов зависит градиент С этой целью
представим установившийся прирост перегрузки в виде выраже-
ния (8.23)
Су
А^у уст === £ п ^ауст*
В соответствии с формулой (8.19) Дауст=== (л^/Й^Дср. Подставляя
в уравнение (8,23) значения Дауст, п и выражение (8.9), полу-
чим
mz
Д/Zy уст = -Q - Дер. (8.25)
Из (8.25) находим выражение градиента ^пу = Дср/Дпу
« — — С 0/2
уг-п «г
(8.26)
Таким образом, градиент <pny> а при неизменных характери-
стиках системы управления и градиенты л"у и тем больше,
чем больше устойчивость по перегрузке (оп), меньше эффектив-
ность стабилизатора (т%) и больше коэффициент подъемной
силы требуется для горизонтального полета (% = !) на данном
числе М. и высоте полета.
Если известны отклонения <р, хв и усилия на ручке Рв, необ-
ходимые для балансировки самолета в горизонтальном полете
(% = 1), а также градиенты <?"у, х"у и Р"у, то можно опреде-
лить балансировочные отклонения стабилизатора, ручки управле-
ния и усилия на ней в установившемся криволинейном движении
с перегрузкой пу по следующим формулам:
•^В — -^В(пу=1) + 1)>
+ ₽>,-!)•
(8.27)
§ 8.4. Влияние эксплуатационных факторов на динамические
свойства самолета в малом продольном движении
8.4.1. Влияние режима полета
На характеристики малого продольного движения существен-
ное влияние может оказать изменение режима полета, характери-
зуемого скоростью, высотой и величиной угла атаки. Рассмотрим
229
сначала влияние скорости на динамические свойства само-
лета.
Так как при переходе через скорость, равную скорости звука,
наблюдается не только количественное, но и качественное изме-
нение аэродинамических характеристик, то влияние изменения ско-
рости на динамические свойства самолета удобно рассмотреть раз-
дельно на дозвуковых и сверхзвуковых скоростях полета.
Рис. 8.9. Влияние числа М полета на характе-
ристики малого продольного движения
На дозвуковых режимах полета характеристика демпфирова-
ния и частота собственных колебаний 2а при неизменной
устойчивости по перегрузке изменяются примерно пропорцио-
нально скорости полета. Вследствие этого относительный коэффи-
циент затухания £ == яа/2а при изменении скорости практически
остается без изменения. В этом случае при увеличении скорости
полета уменьшается период колебаний Га, а соответственно вре-
мя срабатывания ^ср и время регулирования /рег при почти не-
изменных количестве колебаний до практически полного затуха-
ния Плат и относительном забросе перегрузки Дгг^ заб.
На трансзвуковых скоростях полета наблюдается интенсивный
рост устойчивости по перегрузке, что при незначительном увели-
чении числа М сопровождается интенсивным увеличением частоты
собственных колебаний 2а и соответственно уменьшением периода
колебаний и коэффициента g. На сверхзвуковых скоростях полета
характеристику затухания /га приближенно можно считать незави-
симой от скорости (числа М), в то время как частота собствен-
ных колебаний увеличивается примерно пропорционально VV •
На таких режимах рост скорости полета будет приводить к умень-
шению периода колебаний Тл и коэффициента £, увеличению ко-
личества колебаний /гзат при практически неизменном времени ре-
гулирования. На рис. 8.9 показан примерный характер изменения
в функции числа М полета коэффициента устойчивости по пере-
грузке On и относительного коэффициента затухания g (а), пе-
риода колебаний 7\ и количества колебаний /гзат до практически
полного затухания (б).
Это изменение динамических свойств самолета летчик должен
отчетливо представлять и правильно учитывать при управлении
230
самолетом. Так, например, на малых дозвуковых приборных ско-
ростях полета из-за малого быстродействия (большого времени
срабатывания) самолет вяло (со значительным запаздыванием)
реагирует на отклонение стабилизатора. Кроме того, на таких ско-
ростях полета требуются и повышенные расходы ручки (стабили-
затора). Поэтому на малых скоростях полета летчик должен для
получения желаемого эффекта действовать с некоторым упрежде-
нием или увеличивать отклонение стабилизатора с последующим
возвращением его в балансировочное положение.
На больших дозвуковых приборных скоростях полета КПр =
= 950-4-1100 км/ч увеличиваются быстродействие (уменьшаются
период колебаний и время срабатывания) и количество колебаний
до практически полного затухания. При этом повышается чувст-
вительность самолета на отклонение ручки (стабилизатора).
На таких режимах полета летчику трудно соразмерить откло-
нение ручки с положением самолета в пространстве, что может
иногда потребовать для корректировки отклонений ручки то в
одну, то в другую сторону. При малом периоде колебаний и есте-
ственном запаздывании летчика это может привести к непроиз-
вольной раскачке. В тех случаях,. когда возможна раскачка, от
летчика требуется особо точное пилотирование. Для прекращения
непроизвольно возникшей раскачки необходимо ручку управления
зафиксировать в положении, близком к балансировочному: рас-
качка быстро прекращается.
У самолетов с изменяемой в полете стреловидностью при пере-
кладке крыла с одного угла стреловидности на другой на каком-
либо числе М, с одной стороны, несколько изменяется устойчивость
по перегрузке, с другой, изменятся момент инерции 1г и демпфи-
рующий момент Это приводит к некоторому наруше-
нию балансировки и изменению динамических свойств самолета
в малом продольном движении.
Большое влияние на характеристики малого продольного дви-
жения оказывает высота исходного режима полета. Чем больше
высота полета (меньше плотность воздуха), тем при прочих рав-
ных условиях меньше изменяются аэродинамические силы и мо-
менты. Это вносит ряд особенностей в управление самолетом на
таких высотах.
Падение демпфирующих моментов на больших высотах полета
(при М = const) сопровождается значительным ухудшением зату-
хания колебаний, в результате чего время затухания и количество
колебаний до практически полного затухания сильно возрастают.
Так, например, на таких высотах количество колебаний /гзат мо-
жет возрасти до 10—15 и более. На первый взгляд может пока-
заться, что уменьшение демпфирующих моментов, препятствующих
вращению, будет облегчать управление самолетом. В действитель-
ности это не так. Оказывается, что пилотирование самолета при
отсутствии демпфирования, обусловливающего затухание колеба-
ний,.чрезвычайно затруднено. Это объясняется тем, что в рассмат-
231
риваемом случае колебания самолета, возникающие при отклоне-
нии стабилизатора, сами собой не исчезают. Для их прекращения
требуется отклонять стабилизатор против вращения самолета.
С ростом высоты полета из-за падения плотности воздуха, с
одной стороны, уменьшается частота собственных колебаний 2а
и, как следствие, увеличивается время срабатывания (растет пе-
риод колебаний), с другой — ухудшается реакция самолета на одно
и то же отклонение стабилизатора. Вялое (появившееся с запаз-
дыванием) вращение самолета создает у летчика впечатление
о значительном падении эффективности стабилизатора.
Стремление повысить быстродействие побуждает летчика на
больших высотах управлять с «перерегулированием» — отклонять
ручку управления на величину, большую, чем это требуется на
новом режиме. В процессе же перехода на этот режим — возвра-
щать ручку в балансировочное положение.
Уменьшение демпфирующих моментов, а соответственно и ухуд-
шение затухания колебаний в сочетании с повышенной инерт-
ностью самолета и вялой его реакцией на отклонение стабилиза-
тора требуют от летчика при полете на больших высотах с вы-
ключенным автоматом демпфирования повышенного внимания,
более точных, а иногда и двойных движений ручки.
8.4.2. Особенности управления малоустойчивым
самолетом
Из рассмотрения динамических свойств самолета следует, что
чем большей устойчивостью по перегрузке ап (а соответственно
и частотой собственных колебаний 2J обладает самолет, тем
лучше его реакция на отклонение стабилизатора. Однако излишне
большой запас устойчивости по перегрузке нежелателен из-за
ухудшения маневренных свойств и увеличения потерь на баланси-
ровку.
Чем большей «естественной» устойчивостью по перегрузке
обладает самолет, т. е. чем больше расстояние между фокусом и
центром тяжести, тем для обеспечения продольного равновесия
требуется создавать большую отрицательную подъемную силу на
горизонтальном оперении, тем больше будут потери на балан-
сировку.
Потери на балансировку можно существенно уменьшить, если
конструктивными мероприятиями (выбором формы крыла в плане,
применением дестабилизаторов, перемещающих фокус самолета
вперед, регулированием центровки перекачкой топлива и т. д.)
удается создать на дозвуковых и сверхзвуковых скоростях полета
примерно постоянный приемлемый по величине запас устойчивости
по перегрузке. Однако при практической реализации этих меро-
приятий возникает ряд трудностей, которые не всегда удается
успешно преодолеть. Поэтому у маневренных самолетов конструк-
торы чаще предпочитают требуемые характеристики устойчивости
232
и управляемости обеспечивать на сверхзвуковых скоростях полета
выбором более задней центровки, а на дозвуковых скоростях —
применением автоматических устройств (автоматов устойчивости
и демпфирования). Неиспользование таких устройств или их от-
каз в полете может привести к недостаточной устойчивости по
перегрузке на дозвуковых скоростях полета. Уменьшение устой-
чивости по перегрузке может наблюдаться при некоторых под-
весках, смещающих центр тяжести назад или фокус вперед, а так-
же при выходе самолета на большие углы атаки. Управление са-
молетом, обладающим недостаточной устойчивостью по перегруз-
ке, имеет ряд особенностей.
Во-первых, из-за высокой чувствительности самолета к откло-
нению стабилизатора на больших дозвуковых скоростях полета
самолет становится строгим в управлении, требуя от летчика по-
вышенного внимания и четкости в правильном дозировании вели-
чины усилия на ручке и ее отклонения. Трудность соразмерения
величины и темпа отклонения ручки на необходимую величину
вынуждает иногда летчика отклонять ручку несколько раз то в
одну, то в другую сторону.
Во-вторых, если летчику удается отклонить стабилизатор на
величину, необходимую для перевода самолета на новый режим
полета, то при малой устойчивости по перегрузке из-за большого
времени срабатывания самолет реагирует на это отклонение вяло,
не сразу, а через некоторое время.
Допустим, что для балансировки самолета с перегрузкой
требуется удерживать стабилизатор в положении <р0 (рис. 8.10).
Пусть летчик, решив выполнить маневр с перегрузкой nyt в мо-
мент времени прикладывает к ручке усилие и отклоняет стаби-
лизатор в положение epi, соответствующее балансировке самолета
на перегрузке пу, Тогда у малоустойчивого самолета перегрузка
будет изменяться так, как показано на рис. 8.10 сплошной ли-
нией.
Стремясь ускорить переход самолета с одной перегрузки на
другую летчик вынужден будет перемещать ручку и отклонять
стабилизатор на величину <р2, большую, чем это требуется для
балансировки на перегрузке пу . Если бы стабилизатор удержи-
вался в этом положении, перегрузка изменялась бы так, как по-
казано на рис. 8.10 штрихпунктирной линией. Видно, что по исте-
чении времени t2 самолет превысит заданное значение перегрузки
яУ1 и будет продолжать ее увеличивать до тех пор, пока не выйдет
на перегрузку, соответствующую балансировке при <р2. Чтобы са-
молет не превысил требуемое значение перегрузки пу > необходи-
мо в некоторый момент времени t\ возвратить стабилизатор в ба-
лансировочное положение epi, что приведет к изменению перегруз-
ки, как показано на рис. 8.11 штриховой линией.
Как видим, ускорение перехода самолета с перегрузки пу* на
сопровождается увеличением заброса перегрузки Д/гузаб. Па-
233
рирование этого заброса перегрузки требует дополнительного от-
клонения стабилизатора для погашения угловой скорости враще-
ния самолета с последующим возвращением его в балансировоч-
ное положение <рь
Следовательно, при небольшом запасе устойчивости по пере-
грузке трудность точной дозировки малых потребных перемещений
ручки с небольшими усилиями на ней и желание ускорить пере-
ход с одной перегрузки на другую вынуждает летчика отклонять
ручку то в одну, то в другую сторону. При этом создаются усло-
вия для непроизвольной раскачки самолета, которая является од-
ним из характерных признаков малой его устойчивости.
Наиболее благоприятные условия для раскачки у такого са-
молета будут возникать при точном пилотировании (например, при
прицеливании). Чем меньшей устойчивостью по перегрузке обла-
дает самолет, тем более точными и плавными должны быть пере-
мещения ручки управления для предотвращения раскачки.
Управление самолетом существенно усложняется, если по ка-
кой-либо причине самолет станет неустойчивым по перегрузке.
У устойчивого по перегрузке самолета с ростом угла атаки (пере-
грузки) увеличивается и пикирующий (стабилизирующий) мо-
мент, препятствующий увеличению угла атаки. Вследствие этого
при отклонении стабилизатора самолет как бы сам находит но-
вое балансировочное значение угла атаки, соответствующее этому
отклонению стабилизатора. Совсем по-иному ведет себя неустой-
чивый по перегрузке самолет. По мере роста угла атаки и подъ-
емной силы у него растет кабрирующий (дестабилизирующий)
234
момент, который продолжает увеличивать угол атаки и пере-
грузку.
Поэтому при управлении неустойчивым по перегрузке самоле-
том летчик как минимум один раз делает.двойное движение руч-
кой: сначала отклоняет ее в направлении желаемого изменения
угла атаки (для увеличения угла атаки — на себя,' для уменьше-
ния— от себя), а затем по мере приближения угла атаки к задан-
ному значению не только возвращает ручку в исходное положение,
но для балансировки самолета отклоняет ее в противоположную
сторону.
Неустойчивый по перегрузке самолет будет иметь одно важ-
ное преимущество перед устойчивым: для его балансировки тре-
буется на горизонтальном оперении создавать подъемную силу
ДУГ. о, направленную в ту же сторону, что и подъемная сила кры-
ла. Вследствие этого продольная балансировка будет приводить к
увеличению подъемной силы самолета.
Меньшее падение несущих свойств и, как следствие, уменьше-
ние потерь н'а балансировку привлекает внимание конструктора
к самолетам с малыми запасами устойчивости либо вообще не-
устойчивым по перегрузке. Чтобы управление самолетом с недо-
статочной устойчивостью по перегрузке было приемлемо для лет-
чиков, конструкторы вынуждены применять различного рода ав-
томатические устройства (автоматы демпфирования и устойчиво-
сти и др.), обеспечивающие необходимые динамические свойства
самолета и соответственно его хорошую управляемость.
8.4.3. Срыв ной «подхват»
Особенно нежелательно, а в ряде случаев и опасно неожидан-
ное для летчика уменьшение устойчивости по перегрузке в про-
цессе увеличения угла атаки и перегрузки при выполнении ма-
невра. Такое явление (см. § 5.10) может иметь место у некоторых
самолетов со стреловидным крылом. Связано оно с возникнове-
нием срывного обтекания на больших углах атаки, которое со-
провождается перемещением фокуса самолета вперед и соответ-
ственно уменьшением устойчивости по перегрузке.
Отмеченное проявляется в изменении зависимости продольного
момента от коэффициента Су, а следовательно, и в балансировоч-
ных отклонениях ручки и стабилизатора (рис. 8.11). Видно, что
в области малых углов атаки балансировочные отклонения стаби-
лизатора на постоянном числе М полета линейно зависят от ко-
эффициента Су. При дальнейшем увеличении коэффициента Су
балансировочная диаграмма сначала выполаживается, а затем
меняет наклон (характеристика <?су становится больше нуля),
образуется так называемая «ложка».
Если самолет имеет балансировочную диаграмму подобного
вида, то, начиная с коэффициента Су, равного коэффициенту Суп
начала неустойчивости по перегрузке, самолет будет самопроиз-
235
вольно увеличивать угол атаки и перегрузку — наступает срывной
«подхват». Если своевременно не отдать ручку управления от себя,
могут быть достигнуты перегрузка, превышающая допустимое зна-
чение, либо угол атаки аСв, соответствующий сваливанию само-
лета.
Заметим, что при дальнейшем увеличении коэффициента подъ-
емной силы Су^>Су (рис. 8.11) самолет снова становится устой-
чивым по перегрузке. Последнее объясняется тем, что срывное
обтекание, распространяясь от
концевых к корневым сечениям
стреловидного крыла в процессе
увеличения угла атаки, приводит
к выравниванию аэродинамиче-
ской нагрузки вдоль размаха
крыла. Это сопровождается сна-
чала прекращением перемещения
фокуса самолета вперед, затем он
начинает интенсивно перемещать-
ся назад, что приводит к восста-
новлению устойчивости по пере-
грузке. Диапазон и степень не-
устойчивости, а соответственно и
Рис. 8.11. Балансировочная диаграм-
ма отклонений стабилизатора с об-
ластью А неустойчивости по пере-
грузке
темп нарастания перегрузки при «подхвате» зависят от аэроди-
намической компоновки самолета (угла стреловидности крыла и
взаимного расположения крыла и горизонтального оперения),
числа М полета, центровки и приборной скорости (скоростного
напора).
У самолетов изменяемой стреловидности проявление неустой-
чивости по перегрузке при малых углах стреловидности обычно
начинается на меньших углах атаки. При средних углах стрело-
видности крыла неустойчивость по перегрузке наиболее интенсив-
но проявляется при маневрах со значительными перегрузками на
числах М = 0,74-0,9. Во всех случаях при задних центровках и
больших приборных скоростях (скоростных напорах) «подхват»
возникает на меньших углах атаки и развивается более резко.
Маневр, как правило, начинается на малых углах атаки, на
которых самолет устойчив по перегрузке. Это требует для увели-
чения угла атаки отклонять ручку управления на себя, прикла-
дывая к ней тянущее усилие. Однако в процессе увеличения угла
атаки (перегрузки) самолет неожиданно для летчика теряет ус-
тойчивость по перегрузке и начинает самопроизвольно увеличивать
перегрузку. В качестве примера на рис. 8.12 показано изменение
параметров движения самолета при выходе на срывной «подхват»
в процессе вывода из пикирования. Как видим, при фиксирован-
ной ручке управления самолет за 1 с увеличил перегрузку пу
с 5,6 до 10,1. Величина и скорость нарастания перегрузки в про-
цессе «подхвата» тем больше, чем на большую величину и с боль-
шим темпом отклоняется ручка управления.
236
Основная трудность в парировании «подхвата» в процессе вы-
полнения маневра состоит в неожиданном для летчика его прояв-
лении. Главной причиной «подхвата» является аэродинамическое
несовершенство самолета. Однако если летчик хорошо знает осо-
бенности поведения самолета и умеет приспособиться к управле-
нию им на больших углах атаки, то выход на «подхват» будет
практически исключен.
( Ипр ~1000 км/ч; If*-? °/с)
300 -100Q
— 800
200-000
в, рад М
0-0,9
-0,2-0,85
-ОА — О,8О
-0,6—0,75
--?х.
_!?
В--0.6
В—0,4 К
4—0,2
2—0,
О t,c
Рис. 8.12. Изменение параметров движения самолета
при выходе на срывной «подхват» в процессе выхода
из пикирования
Необходимо иметь в виду, что приближение к области неустой-
чивости по перегрузке летчик может ощущать по повышению ре-
акции самолета на отклонение ручки управления. Предупрежде-
нием о подходе к области начала неустойчивости по перегрузке на
некоторых самолетах служит предупредительная аэродинамиче-
ская тряска. При повышении реакции самолета на отклонение руч-
ки или появлении аэродинамической тряски летчик должен перейти
на плавное и особенно точное пилотирование, быть готовым к па-
рированию непроизвольного нарастания перегрузки. Практика
показывает, что основной ошибкой летчика, приводящей к выходу
на «подхват», является излишне большой темп отклонения ручки.
237
8.4.4. Скоростной «подхват»
Явление скоростного «подхвата» может наблюдаться при вы-
полнении криволинейного маневра с торможением от сверхзвуко-
вых к дозвуковым скоростям полета, когда самолет неустойчив
Рис. 8.13. Зависимость балансировочных откло-
нений ручки от числа М полета и перегрузки
Если при торможении устойчивого по скорости самолета для
поддержания заданной перегрузки необходимо увеличивать от-
клонение стабилизатора (ручку отклонять на себя), то у неустой-
чивого по скорости самолета при таком изменении скорости появ-
ляется прирост кабрирующего момента, требующий для его ба-
лансировки уменьшения отклонения стабилизатора (ручку откло-
нять от себя). Чем на большей перегрузке выполняется маневр,
тем для ликвидации перебалансировки самолета требуются боль-
шие отклонения ручки, тем более глубокую «ложку» имеет балан-
сировочная диаграмма (рис. 8.13).
Если бы при торможении ручка оставалась в неизменном по-
ложении, то при уменьшении числа М от М2 до Mi и соответст-
венно при потере устойчивости'по скорости отклонение ручки на
себя оказалось бы излишне большим, вследствие чего появивший-
ся прирост кабрирующего момента вызвал бы увеличение угла
атаки и перегрузки. Так, например, при выполнении маневра с
пу = 3 и фиксированном положении ручки хв (рис. 8.13) только
балансировочное значение перегрузки увеличится с 3 до 5. В дей-
ствительности это изменение может быть существенно большим.
Самопроизвольное увеличение перегрузки, наблюдающееся при
проявлении скоростного «подхвата», воспринимается летчиками как
238
потеря устойчивости по перегрузке. В действительности на около-
звуковых скоростях полета самолет обычно сохраняет устойчи-
вость по перегрузке, хотя при уменьшении числа М полета от М2
до М] она значительно уменьшается. Положение может существен-
но осложниться, если в процессе торможения скоростной «под-
Рис. 8.14. Изменение параметров движения са-
молета в процессе развития скоростного «под-
хвата»
хват», обусловленный неустойчивостью по скорости, перейдет в
срывной «подхват» из-за потери устойчивости по перегрузке вслед-
ствие выхода на Су>Суп.
Характер изменения перегрузки и других параметров движения
при торможении в рассматриваемом диапазоне чисел М зависит от
величины перегрузки, с которой выполняется маневр, высоты по-
лета, характера маневра, центровки самолета, режима работы дви-
гателя и положения тормозных щитков. Чем больше перегрузка,
более сильно изменяется устойчивость по перегрузке (а соответ-
ственно и по скорости), что имеет место при задней центровке,
и более интенсивно осуществляется торможение, тем больше гра-
диент изменения перегрузки и, следовательно, на большую пере-
грузку может выйти самолет в процессе скоростного «подхвата».
В качестве примера на рис. 8.14 показано изменение перегрузки
и числа М полета в процессе скоростного «подхвата» самолета
со стреловидным крылом при зажатой (зафиксированной) ручке,
выпущенных тормозных щитках, задней центровке и высоте полета
Н = 5000 м.
В рассматриваемом случае изменение параметров движения в
Процессе торможения можно разделить на два этапа. На первом
239
этапе проявляется чистый скоростной «подхват», приводящий к
увеличению перегрузки с ^ = 4 до лггу~6,5 и коэффициента подъ-
емной силы с Ct/ = 0,24 до Су~0,6. У рассматриваемого самолета
на таких коэффициентах Су возникает срывное обтекание, сопро-
вождающееся полной потерей устойчивости по перегрузке. По-
этому, начиная примерно с / = 3,5 с (рис. 8.14), скоростной «под-
хват» переходит в срывной «подхват», что сопровождается интен-
сивным увеличением коэффициента Су до 1,1 и перегрузки пу
до 8,5. Если бы при выходе на большие углы атаки рассматривае-
мый самолет не терял устойчивости по перегрузке, то перегрузка
при />3,5 с изменялась бы так, как показано на рис. 8.14 штри-
ховой линией.
Чтобы предотвратить самопроизвольное увеличение перегрузки,
летчик должен своевременным отклонением ручки парировать ско-
ростной «подхват». Практика показывает, что в прямолинейном и
криволинейном полетах с небольшими перегрузками летчик срав-
нительно легко парирует непроизвольное увеличение перегрузки,
которое обычно не превышает 0,5. Задача существенно услож-
няется, когда на скоростной «подхват» самолет выходит при ма-
неврировании со значительными перегрузками. В практике, на-
пример, имели место случаи, когда в процессе маневрирования с
торможением в трансзвуковой области перегрузка при непроиз-
вольном увеличении достигала 9—10. Поэтому следует избегать
энергичного маневрирования на числах М, равных или немного
превышающих единицу. В тех случаях, когда боевая обстановка
вынуждает к этому, летчик должен следить за указателем чис-
ла М и по мере уменьшения числа М (начиная с М= 1,14-1) быть
готовым к своевременному отклонению ручки для парирования
«подхвата». Точное пилотирование (например, прицеливание) на
околозвуковых скоростях полета затруднено и может привести
при выключенном автомате демпфирования к непроизвольной рас-
качке самолета летчиком.
С явлением скоростного «подхвата» летчик может встретиться
и на больших дозвуковых скоростях полета, на которых самолет
неустойчив по скорости. Так, например, при выполнении восходя-
щих маневров, начинающихся на больших приборных скоростях,
соответствующих числам М = 0,954-0,98, может наблюдаться при
энергичном пилотировании непроизвольное увеличение перегрузки
на 1—2. Это связано с уменьшением устойчивости по перегрузке
при торможении, что при неподвижной ручке сопровождается по-
явлением значительных кабрирующих моментов. Для предотвра-
щения непроизвольного увеличения перегрузки летчик должен
соразмерно отклонить ручку управления от себя.
§ 8.5. Требования к динамическим свойствам
и характеристикам продольной управляемости
Летная практика показывает, что в зависимости от выполняе-
мых задач к динамическим свойствам самолета в малом продоль-
ном движении могут предъявляться различные требования.
240
Кроме рассмотренных выше динамических характеристик важ-
ными характеристиками являются взаимные соотношения между
переходными процессами по углу атаки (перегрузке) и угловому
ускорению тангажа сог, по углу атаки и угловой скорости пово-
рота вектора скорости (наклона траектории) и отношение вели-
чины отклонения стабилизатора к вызванному им изменению угло-
вого ускорения тангажа. Рассмотрим эти характеристики.
Л = Да)гпах/Д/гу уст —максимальное угловое ускорение, со-
ответствующее единичному изменению перегрузки. Эта величина
характеризует угловое ускорение, возникающее у самолета в от-
вет на изменение угла атаки (перегрузки) при воздействии внеш-
него возмущения, например при попадании в вертикальный порыв
ветра. Можно показать, что эта характеристика также зависит от
собственных свойств самолета и определяется выражением:
(8.28)
где п* = dtiylda = CyjCy г. п (частная производная от перегрузки
по углу атаки).
Знак минус в выражении (8.28) показывает, что на возмуще-
ние, вызвавшее положительное изменение перегрузки &пу, устой-
чивый по перегрузке самолет ответит отрицательным угловым
ускорением тангажа, направленным на уменьшение угла атаки.
0а = Д0/Да— изменение угловой скорости поворота угла на-
клона траектории при изменении угла атаки на единицу. Эта ха-
рактеристика зависит от скорости полета и показателя
= (8.29)
(р°г= Д(р/Д(1)2—отклонение стабилизатора, Потребное для из-
менения углового ускорения тангажа на единицу. Эта характери-
стика изменяется в зависимости от режима полета, коэффициента
эффективности стабилизатора, инерционных и геометрических па-
раметров самолета:
ср“г= ______
Г mlqSb '
(8.30)
Характеристики переходного процесса взаимно однозначно свя-
заны с собственными свойствами самолета и полностью их опре-
деляют. Все они в значительной степени влияют на управляемость
самолета. Действительно, при излишне большом времени срабаты-
вания (для маневренных самолетов более 3 с) самолет кажется
летчику вялым, плохо слушающимся рулей, при очень малом
*ср — резким. Если относительные забросы по углу атаки или
перегрузке >0,2—0,3 и мала интенсивность затухания колебаний
(я3ат>4±5)> точное пилотирование весьма затруднительно, при-
241
целиваться плохо, рассеивание снарядов при стрельбе — большое.
Такой самолет также не получит хорошую оценку у летчика.
Когда малы (®пгУ <0,1), самолет недостаточно устойчив.
Точное пилотирование (особенно выдерживание высоты) весьма
затруднительно. Самолет на малые изменения угла тангажа отве-
чает большими отклонениями вертикальной скорости. Полет в
строю труден и опасен, точное прицеливание невозможно. Поэтому
ыпгУ является очень важной характеристикой.
От величины 0а зависит «поворотливость» самолета, его спо-
собность быстро изменять направление полета в плоскости сим-
метрии самолета. Эта характеристика увеличивается с увеличе-
нием скорости и уменьшением высоты, что видно, если записать
выражение для нее в следующем виде:
Изменение 0“ в основном зависит от режима полета, в связи
с этим выдерживание ее в каких-либо выгодных для пилотирова-
ния пределах практически невозможно. Поэтому эта характери-
стика не нормируется, но она влияет на управляемость самолета
и это надо знать. Не нормируется по этой же причине и характе-
ристика хотя она также оказывает существенное влияние на
управляемость, что будет показано ниже.
Требования предъявляются обычно к следующим характеристи-
кам переходного процесса: /сР, Д/гузаб, ^зат- Переходный
процесс — это характеристика реакции самолета. Он не может
определить полностью управляемость самолета. Летчику небез-
различно, какое усилие он должен приложить к ручке управле-
ния, чтобы на необходимую величину изменить тот или иной пара-
метр движения самолета. Не все равно летчику, какое при этом
требуется и перемещение ручки. Свойства человека таковы, что
он не может точно дозировать слишком малые усилия и переме-
щения ручки. Существует так называемый абсолютный порог чув-
ствительности. Если требуемое изменение усилия или перемещения
ниже порогового значения, дозирование управляющего воздейст-
вия практически невозможно. Излишне большие потребные усилия
и перемещения также не могут точно дозироваться. Поэтому реак-
ция самолета должна быть увязана с управляющим воздействием.
Только в этом случае можно оценивать управляемость самолета
в полной мере. В качестве таких связующих показателей управ-
ляемости принимаются обычно градиент усилия по перегрузке
рпу —
ДЛу
и градиент отклонения ручки управления по перегрузке
•V длу •
242
К этим показателям управляемости предъявляются определен'
иые требования. Так, для маневренных самолетов должно
иметь значение в диапазоне —1,5ч----3,5 кгс (~—15ч-----35 Н)
на единицу перегрузки, a xnQy должно быть больше 12 мм на еди-
ницу пу. Таким образом, для обеспечения хорошей управляемости
Рис. 8.15. Области показателей собственных свойств
самолета йа и £ обеспечивающие хорошее качество
переходного процесса
самолета необходимо значения характеристик переходного про-
цесса /ср, ^зат и показателей управляемости Р”у, х”у
иметь в рекомендуемых пределах. Эти пределы выбраны в резуль-
тате многолетней эксплуатации самолетов и зависят только от
психофизиологических свойств человека — летчика. Задача управ-
ления может оказывать влияние на эти пределы. Так, например,
потребные значения /сР, Дпузаб и Л для выполнения задач, свя-
занных с прицеливанием,— одни, а для набора высоты с заданной
вертикальной скоростью — другие. Из приведенных выше выраже-
ний видно, что все характеристики переходного процесса опреде-
ляются собственными свойствами самолета. В связи с этим можно
предъявлять требования и к характеристикам собственных свойств
с таким же правом, как и к характеристикам переходного про-
цесса: 2а, nJ.
Ограничивая какими-то пределами значения /ср, Дпузаб, /у,
тем самым предъявляем требования к 2а, nJ. На рис. 8.15
в координатах 2а и $ показана штрихпунктирной линией область,
243
в которой самолет хорошо ходит за ручкой при условии, что
остальные показатели /г*, Р”у и х”у выбраны в рекомендуемых
пределах. Аналогичные области существуют для всех показате-
лей устойчивости и управляемости. На этом же графике показаны
регламентируемые значения Дп!/заб:=0,2 и /Ср=1,5 с, а также ха-
рактер реакции самолета при управлении вне области хороших
характеристик.
С точки зрения управляемости самолета важно знать, как ха-
рактеристики переходного процесса или собственных свойств само-
лета обеспечивают движение самолета в ответ на изменение уси-
лия на ручке управления и на перемещение ее. Для достаточно
полной оценки продольной управляемости необходимо знать реак-
цию самолета не только по изменению угла атаки а или пере-
грузки пу, но и по скорости изменения перегрузки пу и даже по
второй производной от нее пу, а также реакцию самолета по из-
менению углового ускорения тангажа со2 и угловой скорости изме-
нения угла наклона траектории 0. Особую роль играет соотноше-
ние между усилием, прикладываемым к ручке управления, и соот-
ветствующим перемещением ее, т. е. градиент Р** == ДРв/Дхв.
Обычно этот градиент обозначают Св и он характеризует жест-
кость пружинного загружателя.
Продольная управляемость самолета определяется следующей
совокупностью показателей управляемости:
рпу__р пу— - р пу — •
в Д<’ д„у ’ в Диу ’
Р^ = ♦ РQ =
в ’ в дё в Дхв
Определяют ли рассмотренные выше характеристики собствен-
ных свойств самолета и показатели управляемости значения по-
казателей данной совокупности? Оказывается, полностью опреде-
ляют. Это видно из выражений, показывающих связь между
ними:
р "у = Р "z-
В В ’
Q2
p"y = —Ршг- рпу
* В Па в ’ в
"у
р о = _3l р
в £ П* В ’
Р*в
в
«У
p<“z-
в ’
рпву
(8.32)
При внимательном рассмотрении этих выражений нетрудно
увидеть, что характеристики собственных динамических свойств
самолета Qa, Е, п*, показатели управляемости Рву и х”у пол-
ностью определяют значения пяти показателей из данной сово-
купности. Только показатель Р/ определяется еще и скоростью
244
полета. Отсюда нетрудно прийти к выводу, что при нормировании
характеристик переходного процесса и двух показателей управ-
ляемости ~ /ср, Д#узаб> Р'^ х”у фактически осущест-
вляется нормирование совокупности показателей управляемости:
Рпу, Р\ Р\ P*z и Рх*
Практикой летчиков рожден термин «хождение самолета за
ручкой». Он имеет интегральный, т. е. обобщающий характер.
Обеспечение величин показателей управляемости в необходимых
пределах позволит самолету обладать свойствами хорошего «хож-
дения за ручкой». Это свойство в значительной степени определяет
хорошую управляемость самолета. Изменение собственных свойств
в широких пределах, связанных с большим диапазоном высот и
скоростей полета современных самолетов, вынуждает конструкто-
ров применять различные автоматы для улучшения характеристик
управляемости самолета. Рассматривая систему зависимостей
(8.32), легко увидеть, что практически все показатели можно ре-
гулировать с помощью различных автоматов, например:
Рвв = Св —с помощью АРЗ или АРУ (см. § 8.6);
Р*г —посредством АРУ, регулируя передаточное отношение
= Д<р/Дхв;
Р'[у — автоматом устойчивости по перегрузке можно регули-
ровать величину 22/^* (см. § 8.7);
Рв"у — автоматом, непосредственно управляющим подъемной
силой самолета, т. е. путем изменения
РB"v —автоматом демпфирования.
Не представляется возможным изменять градиент усилия по
угловой скорости угла наклона траектории Pf, если остальные
показатели регулировались в необходимых пределах. Аналогична
роль совокупности показателей управляемости по отклонениям
ручки управления лв>\ лву, x^z, Нетрудно ви-
деть, что эти показатели полностью определены, если заданы
значения рассматриваемой совокупности показателей по усилиям.
§ 8.6. Обеспечение продольной управляемости путем
регулирования систем управления
У современных маневренных самолетов управление стабили-
затором осуществляется с помощью рулевых приводов, а усилия
на ручке управления имитируются загрузочным механизмом.
В этом случае градиент усилия по перегрузке определяется выра-
жением (8.24)
Р> = Свх> = -^<рЧ
245
где градиент связан с запасом устойчивости по перегрузке вп
и коэффициентом подъемной силы в горизонтальном полете Су г. п,
характеризующим режим полета:
Если бы жесткость загрузки Св и передаточный коэффициент
не изменялись, то на больших дозвуковых приборных скоростях,
где требуются для горизонтального полета малые значения <СУ г. п,
на малую величину отклонялась бы ручка и слишком малые уси-
лия требовалось бы прилагать к ней. Управление было бы слиш-
ком легким, создавая опасность непроизвольной раскачки самоле-
та либо превышения допустимого значения перегрузки. Для устра-
нения этого недостатка на некоторых самолетах стали применять
загрузочные механизмы с «изломом» характеристики (штриховая
линия на рис. 8.16), облегчающие продольное управление на ма-
лых скоростях (при больших отклонениях ручки хв) и затяже-
ляющие его на больших околозвуковых скоростях (малых откло-
нениях ручки). В некоторых случаях в систему управления вклю-
чаются два загрузочных механизма: взлетно-посадочный и полет-
ный.
Однако такого типа загрузочные механизмы позволяют полу-
чить более или менее приемлемые усилия на рычагах управления
только элеронами и рулем направления. Применение таких загру-
жателей в продольном канале не исключает возможность непро-
извольного превышения допустимого значения перегрузки, напри-
мер при переходе с крутой характеристики на пологую. Невозмож-
ность обеспечить требуемый характер изменения усилия на ручке
управления стабилизатором во всем летном диапазоне скоростей
и высот полета с помощью простейших загрузочных механизмов
вынудила конструкторов устанавливать специальные автоматы, ре-
гулирующие загрузку ручки (Св) и передаточное число (£в),
Выясним, по какому закону при перемене режима полета не-
обходимо изменять жесткость загрузки Св и передаточное число
£в, чтобы обеспечить желаемые значения градиента Р’^.
Если бы жесткость загрузки Св и передаточное число йв не
регулировались, то градиент усилия по перегрузке (формула 8.24)
изменялся бы так же, как и градиент На рис. 8.17 (внизу)
показано характерное изменение градиента отклонения стабилиза-
тора по перегрузке у>пу в зависимости от приборной скорости и
высоты полета. Как видно, градиент^, а в рассматриваемом слу-
чае и градиент Р”у, могут изменяться в широких пределах. Ста-
тистика же показывает, что относительная ошибка управления,
допускаемая летчиком при управлении маневренным самолетом,
изменяется так, как показано на рис. 8.18. Видно, что наибольшая
точность управления обеспечивается при Р”у = — (2—2,5) кгс
246
(~—204—25 Н). Как при увеличении, так особенно при уменьше-
нии градиента усилия по перегрузке ошибка управления возра-
Рис. 8.16. Характеристика про-
стейшего загрузочного меха-
низма
Рис. 8.17. Характер изменения отно-
шения Съ!Кь, необходимого для
обеспечения значения градиента Рву
стает. Именно поэтому для маневренных самолетов регламентиро-
вано изменение градиента Р”у в пределах —-3,5< Р”у <;—1,5.
Рис. 8.18. Зависимость относительной ошибки,
допускаемой летчиком, от градиента усилий по
перегрузке
Зададимся постоянным (оптимальным) значением градиента
(например, Р”у = —2 кгс). Тогда, разрешив уравнение (8.24) от-
носительно Св//гв, получим желаемый закон изменения
г РПу
Св __ В
/у
На рис. 8.17 (вверху) показано изменение отношения Св/&в>
необходимое для обеспечения постоянного значения градиента
247
усилия по перегрузке. На современных маневренных самолетах
эта проблема решается применением автоматов регулирования за-
грузки (АРЗ) в сочетании с нелинейным механизмом и АРЗ в
регулирования передаточного отношения
сочетании с автоматом
Рис. 8.19. Схема автомата регу-
лирования загрузки (АРЗ)
(АРП).
АРЗ, схема которого приведена
на рис. 8.19, регулирует жесткость
загрузки ручки Св, затяжеляя
ее при увеличении скорости и
уменьшении высоты полета. Ав-
томат регулирования загрузки
Рис. 8.20. Характерная зависимость пере-
даточного отношения Дв и отклонения
стабилизатора от перемещения ручки,
обеспечиваемая нелинейным механизмом
состоит из телескопического кронштейна 1, на котором устанавли-
вается электромеханизм 2, загрузочного механизма 5, качалки 4
и электромеханизма триммерного эффекта 5. При изменении при-
борной скорости и высоты полета электромеханизм 2 исполнитель-
ного устройства меняет плечо 13 и тем самым изменяет загрузку
ручки.
Механизм нелинейной передачи от ручки к стабилизатору
уменьшает передаточное число kB при малых отклонениях ручки
(больших скоростях полета) и увеличивает при больших ее от-
клонениях, что требуется при полете на малых скоростях полета.
В качестве примера на рис. 8.20 показана типичная нелинейная
зависимость передаточного отношения kB и отклонения стабилиза-
тора от перемещения ручки, обеспечивающая при одном и том же
перемещении ручки Дхв малое отклонение стабилизатора вблизи
нейтрального положения ручки и большое отклонение в крайних
ее положениях.
АРЗ в сочетании с нелинейным механизмом работают надежно
и сохраняют полный диапазон отклонения стабилизатора на всех
режимах полета. Основным их недостатков является изменение
24-8
передаточного числа в зависимости от положения ручки, а не от
режима полета, благодаря чему удается получить оптимальные ха-
рактеристики управляемости только для определенного диапазона
высот полета.
Рис. 8.21. Схема автомата регулирования управления
(АРУ-ЗВ)
АРЗ в сочетании с автоматом передаточного отношения (АРП)
имеет большие возможности и принципиально позволяет получить
желаемые характеристики управляемости х”у) на всех ре-
жимах полета. На некоторых самолетах АРЗ и АРП конструктив-
но выполняются в виде единого агрегата-автомата регулирования
управления (АРУ). В качестве примера на рис. 8.21 показана
схема АРУ-ЗВ. В точке В штока исполнительного механизма АРУ
крепится тяга управления, идущая к рулевому приводу, в точ
ке А — загрузочный механизм. При перемещении штока вверх
уменьшается передаточное отношение k3 (исполнительный меха-
низм переходит с большого плеча /б на малое) и одновременно
увеличивается плечо /3 загрузочного механизма, что эквивалент-
но увеличению жесткости загрузки ручки. На рис. 8.22 показаны
законы изменения плеч и 13 в функции приборной скорости и
высоты полета, реализуемые в АРУ-ЗВ.
Из рисунка видно, что на малых скоростях полета, когда зна-
чения градиента упу достаточно велики, целесообразно иметь мак-
симальное значение коэффициента kB (участок а—б, рис. 8.22).
В этом случае АРУ работает на большом плече БВ (рис. 8.21).
249
Увеличение скорости на малых высотах приводит к уменьшению
градиента <р'Ч что при постоянном значении коэффициента k3 со-
провождалось бы уменьшением и потребных отклонений ручки
и усилий на ней Р”у. Для поддержания градиентов х”у и
Р!>у в желаемых пределах необходимо с ростом скорости умень-
Рис. 8.22. Законы изменения плеч /3 и /б в функции
приборной скорости и высоты полета, обеспечиваемые
АРУ-ЗВ
шать плечо Б В (участок б—в—г на рис. 8.22). При приборной ско-
рости, соответствующей началу развития волнового кризиса, когда
увеличивается запас устойчивости по перегрузке ол, начинает
увеличиваться градиент На таких скоростях полета целесо-
образно снова увеличивать плечо БВ, однако в рассматриваемой
на рис. 8.22 системе оно остается постоянным (участок г—д для
Н = 0-г-4,5 км).
Автоматы АРП, регулируя передаточное число £в от ручки
к стабилизатору, одновременно изменяют диапазон отклонений
стабилизатора. Так, например, при больших скоростях полета
полному отклонению ручки управления (рис. 8.22) будет соответ-
ствовать в два раза меньшее отклонение стабилизатора, чем на
малых скоростях полета. Так как при переходе на сверхзвуковые
скорости полета из-за увеличения запаса устойчивости по пере-
грузке Оп и некоторого уменьшения эффективности стабилизатора
/nJ интенсивно возрастают отклонения стабилизатора, необходи-
мые для увеличения перегрузки на единицу (градиент то
250
ограничение диапазона отклонения стабилизатора автоматом
АРУ-ЗВ может привести к существенному ограничению маневрен-
ных возможностей самолета. Поэтому для обеспечения высокой
маневренности целесообразно с переходом на сверхзвуковые ско-
рости полета увеличивать передаточное отношение £в, для чего на
таких режимах необходимо изменять плечи /б и /3 так, как пока-
зано на рис. 8.22 штрихпунктирной линией г—е.
Задача формирования усилий на рычагах управления сущест-
венно упрощается в системах электродистанционного управления,
которые начинают находить применение на некоторых современ-
ных самолетах. В таких системах управления между рычагами
управления и рулевым приводом нет механической проводки
управления. Отклонение рычагов управления передается сельси-
нам-датчикам, которые вырабатывают электрический сигнал. Этот
сигнал после обработки и усиления подается на электрогидроуси-
литель, непосредственно отклоняющий органы управления.
§ 8.7. Обеспечение продольной управляемости путем
регулирования динамических характеристик
самолета
8.7.1. Автоматы демпфирования
Одним из наиболее распространенных автоматических уст-
ройств, позволяющих улучшить динамические свойства самолета,
а соответственно и характеристики управляемости, являются ав-
томаты демпфирования. В первую очередь необходимо повысить
демпфирование колебаний большой частоты (малых продольных
и боковых движений), на которые летчик не в состоянии оказать
влияние. Поскольку демпфирующие моменты пропорциональны
угловым скоростям вращения, то для искусственного повышения
демпфирования можно использовать обычные органы управления,
отклоняя их пропорционально угловой скорости так, чтобы руле-
вые поверхности создавали моменты, препятствующие враще-
нию.
Автомат демпфирования колебаний самолета вокруг центра
масс представляет собой автоматическое устройство, состоящее из
датчика угловой скорости (ДУС), усилителя (У) и рулевого агре-
гата управления (РАУ), представляющего собой раздвижную тягу
винтового типа. Функциональная схема демпфера тангажа пока-
зана на рис. 8.23.
При вращении самолета датчик угловой скорости вырабаты-
вает электрический сигнал, пропорциональный угловой скорости
тангажа к и подает его на усилитель. Из усилителя сигнал
Z
поступает на электродвигатель РАУ, вызывая его вращение. С по-
мощью редуктора-преобразователя вращательное движение рото-
ра двигателя преобразуется в поступательное движение штока раз-
движной тяги. Перемещение штока РАУ на величину Дх пере-
251
дается на золотник рулевого привода, который и отклоняет ста-
билизатор на угол Дф для парирования возникшей угловой ско-
рости вращения. Чтобы стабилизатор отклонялся пропорциональ-
но угловой скорости вращения, в контур демпфера тангажа уста-
навливается обратная связь. В этом случае при перемещении
шток РАУ одновременно смещает щетку потенциометра обратной
Рис. 8.23. Функциональная схема автомата демпфиро-
вания
связи, благодаря чему на вход усилителя подается сигнал обрат-
ной связи Хо. с, пропорциональной Дх. Этот сигнал, суммируясь
с сигналом датчика угловой скорости Х.й , своевременно прекра-
щает движение штока.
При идеальной работе автомата демпфирования стабилизатор
отклоняется по следующему закону
= (8.33)
где — передаточное число (коэффициент усиления) демпфера
тангажа от угловой скорости к стабилизатору.
Передаточное число численно равно отклонению стабили-
затора в градусах при изменении угловой скорости тангажа на
1°/с.
Для исследования динамических свойств самолета с включен-
ным автоматом демпфирования необходимо во второе уравнение
системы (8.6) подставить
Дер — Дсрл 4- Дсрд = Д'рл 4- k^z, (8.34)
где Дфл — отклонение стабилизатора, вызванное летчиком; аг —
= d(M)/dt.
Тогда после исключения переменной Д8 подстановкой из пер-
вого уравнения d(№)/dt во второе уравнение системы (8.6), по-
лучим следующее дифференциальное уравнение, определяющее
закон изменения угла атаки самолета с включенным автоматом
демпфирования:
д« - <8-35)
Z Z
252
где характеристики затухания п
и частота собственных коле-
баний определяются следующими выражениями:
Рис. 8.24. Влияние автомата демпфирования
на переходный процесс изменения угловой
скорости тангажа
Так как то при увеличении передаточного коэффи-
циента демпфера тангажа k”* одновременно увеличивается как
затухание колебаний , так и частота колебаний (2а j .
Однако па возрастает быстрее, чем 2а . Вследствие этого
коэффициент затухания $ = /2а с ростом передаточного
коэффициента k** увеличивается, благодаря чему у самолета,
имеющего слабое естественное демпфирование, улучшаются дина-
мические свойства.
На рис. 8.24 показано влияние автомата демпфирования на пе-
реходный процесс изменения угловой скорости тангажа при от-
клонении летчиком ручки на себя на величину Дхв. Если бы авто-
мат демпфирования не был включен, то этому положению ручки
соответствовало бы отклонение стабилизатора на величину ДфЛ.
Переходный процесс имел бы вид, показанный на рис. 8.24 при
k*z = Q, Однако при возникновении угловой скорости со2 автомат
демпфирования отклоняет стабилизатор против вращения на ве-
личину Дфд, пропорциональную угловой скорости. В результате
этого переходный процесс изменится так, как показано на рис. 8.24
при £^>0. Как видно, без демпфера тангажа (^==0) вы-
ход самолета на новое установившееся значение угловой скорости,
253
а соответственно угла атаки и перегрузки сопровождается сильным
забросом и слабым затуханием колебаний параметров малого дви-
жения. При включении автомата демпфирования существенно
уменьшается заброс параметров движения, усиливается затухание
колебаний и несколько увеличивается период колебаний.
Выбором передаточного числа демпфера можно искусственно
обеспечить приемлемое демпфирование, а значит, и удовлетвори-
тельный переходный процесс. Поскольку при изменении высоты
и скорости полета естественное демпфирование претерпевает зна-
чительное изменение, то при постоянном передаточном числе
невозможно получить удовлетворительные переходные процессы
на всех режимах полета. При данном передаточном числе демп-
фер будет излишне увеличивать демпфирование на малых высо-
тах и недостаточно на больших. Отсюда следует, что заданное
качество переходного процесса можно обеспечить только с по-
мощью автоматов демпфирования, регулирующих в зависимости
от режима полета передаточные числа демпфера.
Из рис. 8.24 ясно, что с увеличением передаточного числа
демпфера тангажа уменьшается установившееся значение угловой
скорости, а соответственно угла атаки и перегрузки.
Физическое объяснение отмеченного состоит в том, что демп-
фер, парируя угловую скорость, уменьшает отклонение стабилиза-
тора на величину Дфд. Однако полученный результат можно ин-
терпретировать увеличением частоты собственных колебаний (см.
формулу 8.36), что эквивалентно смещению фокуса назад и уве-
личению устойчивости по перегрузке. Эту величину смещения аэро-
динамического фокуса назад (нейтральной центровки) можно оце-
нить по следующей формуле
= (8.37)
При вращении самолета автомат демпфирования отклоняет
руль, препятствуя вращению. Это значит, что при включенном
автомате демпфирования для выполнения маневров с заданной
угловой скоростью coz летчик должен дополнительно отклонять
ручку управления, компенсируя отклонение стабилизатора, вы-
званное демпфером. Отсюда следует, что выполнение маневра с
включенным автоматом демпфирования всегда будет требовать
больших «расходов» ручки и усилий, прикладываемых к ней. От-
меченное оказывается полезным для самолетов, у которых значе-
ния градиентов хпьу и Рпьу находятся ниже нормы. Однако та-
кой автомат демпфирования имеет и ряд недостатков.
Во-первых, при его работе полному отклонению ручки будет
соответствовать неполное отклонение руля, что в некоторых слу-
чаях может ограничить маневренные возможности самолета. По-
следнее особенно нежелательно на сверхзвуковых скоростях по-
лета, на которых из-за излишне большой устойчивости по пере-
254
грузке и пониженной эффективности стабилизатора и без того
требуются большие «расходы» ручки.
Во-вторых, в процессе выполнения всего маневра летчик дол-
жен прикладывать дополнительное усилие, которое при длитель-
ном маневрировании утомляет его.
Для того чтобы исключить нежелательное («паразитное») от-
клонение руля при выполнении маневров, в схему автомата демп-
фирования иногда включают специальный фильтр высоких частот,
который пропускает на усилитель только сигналы изменения угло-
вой скорости высокой частоты и не пропускает ее постоянную со-
ставляющую.
В этом случае при выполнении энергичных маневров при от-
клонении ручки управления автомат демпфирования сначала
уменьшает угол отклонения стабилизатора, препятствуя увеличе-
нию угловой скорости, затем в процессе установления угловой
скорости угол отклонения стабилизатора устанавливается соот-
ветственно положению ручки.
Особенность работы демпфера с фильтром высокой частоты
(изодромом) летчик должен учитывать, чтобы исключить непро-
извольный выход самолета за ограничение по перегрузке за счет
увеличения угла отклонения стабилизатора изодромом при фик-
сировании положения ручки.
8.7.2. Автомат устойчивости
Идея искусственного повышения устойчивости с помощью ав-
томатических устройств сводится к введению в управляющий сиг-
нал дополнительной составляющей, пропорциональной параметру,
Рис. 8.25. Функциональная схема автомата устойчивости
по которому необходимо улучшить устойчивость. Так, например,
для повышения устойчивости по перегрузке в отклонение стаби-
лизатора вводится сигнал по нормальной перегрузке (углу атаки).
На рис. 8.25 приведена функциональная схема такого автомата
устойчивости. В качестве датчика перегрузки используется датчик
вертикального ускорения. Вместо датчика перегрузки иногда ис-
пользуется датчик углов атаки и скольжения (ДУАС). При изме-
255
пении перегрузки (угла атаки) датчик перегрузки вырабатывает
электрический сигнал Хп . После прохождения усилителя (У)
этот сигнал подается на рулевой агрегат управления (РАУ), ко-
торый, вызывая поступательное перемещение штока на величи-
ну Ах, воздействует на золотник рулевого привода и отклоняет
стабилизатор для парирования изменения перегрузки. Стабилиза-
Рис. 8.26. Влияние автомата устой-
чивости на переходный процесс из-
менения угла атаки
тор отклоняется до тех пор, пока сигнал обратной связи Хо. с не
уравновесит управляющий сигнал Хп . При идеальной работе ав-
томата устойчивости стабилизатор отклоняется по одному из сле-
дующих законов:
Дсру = ^"уД/гу или Дсру = £*Да, (8.38)
где knBy. k? — передаточные числа (коэффициенты усиления) от
перегрузки и угла атаки к стабилизатору.
Для исследования динамических свойств самолета с включен-
ным автоматом устойчивости можно поступить так же, как при
изучении влияния автомата демпфирования: в систему уравнений
(8.6) подставить
Дер == Дсрл 4- Дсру = д<рл + А«Да.
Решение полученной системы уравнений показывает, что авто*
мат устойчивости, повышая устойчивость, а соответственно и час-
тоту колебаний, практически не оказывает влияния на демпфиро-
вание колебаний. Поэтому по мере роста частоты колебаний умень-
шается относительный коэффициент затухания £ = яа/2а и уси-
ливается колебательность процесса (рис. 8.26). В этом основной
недостаток автоматов устойчивости. Для устранения недостатка
приходится вместе с автоматом устойчивости устанавливать и ав-
томат демпфирования.
256
§ 8.8. Особенности управления самолетом при отказах
систем, улучшающих характеристики устойчивости
и управляемости
8.8.1. Особенности управления при отказах
автомата регулирования управления
При отказе АРУ показатели управляемости Р"у и х”у будут
изменяться пропорционально градиенту отклонения стабилизатора,
потребному для изменения перегрузки на единицу:
Пусть на самолете установлен АРУ, схема которого приведена
на рис. 8.21. В соответствии с законом регулирования плеч /б и 13
(рис. 8.22) все эксплуатационные
режимы полета могут быть раз-
биты на ряд областей. На рис.
8.27 приведены области полета,
соответствующие этому закону
регулирования. Если полет осу-
ществляется в области А (авто-
матика АРУ на большом плече),
перемещению ручки управления
на 1 мм соответствует отклонение
стабилизатора большее, чем при
полете во всех других областях.
Минимальное отклонение стаби-
лизатора при перемещении руч-
ки управления будет наблюдать-
ся в области В — полет на малом
плече. В областях Б и Г плечо
может иметь различные проме-
рив. 8.27. Области полета, соответ-
ствующие различному характеру
изменения ^в при законе регулиро-
вания, показанном на рис. 8.22
жуточные значения.
Поэтому при заедании штока исполнительного механизма АРУ
(раздвижной тяги) появляются особенности в управлении самоле-
том, которые зависят от того, на каком плече (малом или боль-
шом) зафиксирован механизм. Эти особенности наиболее сущест-
венно проявляются при переходе в другую область. Если заедание
штока произошло в области Б (рис. 8.27), изменение управляемо-
сти наблюдается только при наборе высоты и снижении. Причем
в первом случае управление будет затяжеляться по сравнению с
полетом без отказа АРУ, а во втором — облегчаться. Изменение
скорости не будет сказываться на управляемости до перехода в
область Г.
При заедании штока исполнительного механизма в области Г
как изменение скорости, так и изменение высоты будут влиять на
управляемость. Уменьшение скорости приведет к затяжелению
управляемости, а увеличение — к облегчению.
9—21
257
Только при отказе в области А (большое плечо АРУ) возмо-
жен полет без перехода в другие области вплоть до посадки.
В этом случае появляется опасность непроизвольной раскачки са-
молета на больших дозвуковых приборных скоростях (Упр^750-4-
4-800 км/ч), на малых и средних высотах. Раскачка особенно
опасна, если отказ своевременно не был обнаружен летчиком.
Раскачка вызывается уменьшением л”у и Р“у и происходит
из-за того, что, ощутив повышенную реакцию самолета на откло-
нение ручки управления, летчик инстинктивно чрезмерно отклоняет
ее в противоположную сторону, например на себя. Самолет интен-
сивно увеличивает угол тангажа, и летчик снова инстинктивно и
чрезмерно отдает ручку от себя, причем вследствие естественного
запаздывания собственной реакции, свойств самолета и системы
управления делает это со сдвигом по фазе по отношению к коле-
баниям самолета'. Амплитуда колебаний при этом все время уве-
личивается, и самолет может выйти на недопустимую перегрузку.
Пытаться парировать раскачку отклонением ручки ни в коем слу-
чае не следует. При появлении первых признаков раскачки само-
лета летчик должен немедленно зафиксировать ручку в положении,
близком к балансировочному, колебания сразу же прекратятся.
После прекращения колебаний необходимо уменьшить скорость
полета. С этой целью надо плавно уменьшить обороты двигателя
и при необходимости очень плавным отклонением ручки перевести
самолет в набор высоты. При этом не рекомендуется выпускать
тормозные щитки и резко убирать РУД, так как это приведет
к появлению дополнительных моментов, которые могут вызвать
непроизвольное резкое отклонение ручки летчиком и последующую
раскачку.
При отказе АРУ в области В или вблизи нее шток зафикси-
руется на малом плече или в положении, близком к нему. В этом
случае по мере уменьшения скорости полета управление самоле-
том становится более тяжелым по сравнению с обычным. Перейдя
на ручное управление плечом исполнительного механизма, если
оно конструктивно предусмотрено, летчик может регулировать пле-
чо АРУ в соответствии со скоростью и высотой полета.
Когда перевод плеча АРУ вручную конструктивно не предус-
мотрен или вследствие отказа невозможен, период пилотирования
с «затяжеленным» управлением может быть сокращен, если выход
из области В (т. е. торможение до скорости, необходимой для за-
хода на посадку) будет осуществляться непосредственно перед
приходом в район аэродрома.,
Посадка при этом имеет ряд особенностей. Для уменьшения
потребных отклонений стабилизатора необходимо скорость полета
несколько увеличить по сравнению с обычной. Вследствие того
что диапазон отклонения стабилизатора на малом плече АРУ
ограничен, при крутом планировании может оказаться невозмож-
ным выравнивание самолета. Поэтому планировать следует по
пологой глиссаде и выравнивание выполнять плавно, начиная его
258
с большей, чем обычно, высоты. Из-за уменьшения диапазона от-
клонения стабилизатора может оказаться невозможным создание
нормального- посадочного угла тангажа, вследствие чего призем-
ление будет выполняться на повышенной скорости и сопровож-
даться увеличением длины пробега.
При нарушении герметизации шлангов системы подвода дав-
ления к управляющему блоку автоматики АРУ возможно неожи-
данное изменение плеча исполнительного механизма, сопровож-
дающееся изменением перегрузки. Своевременно парировав воз-
никший момент, летчик может удержать самолет и затем пилоти-
ровать его, используя ручное управление АРУ.
Изменение плеча АРУ, не соответствующее заданному закону,
может произойти также при закупорке статической проводки от
ПВД, например при замерзании конденсата в системе на боль-
шой высоте полета.
Чтобы своевременно обнаружить неисправность автоматики
АРУ и предотвратить нежелательные последствия, летчик должен
периодически контролировать работу автомата по соответствую-
щему индикатору. Это особенно важно при разгоне самолета на
малых и средних высотах.
Отказ АРЗ, связанный с прекращением его функционирования,
существенного затруднения в пилотирование не вносит. Если от-
каз произошел на малом плече АРЗ (облегченное управление,
малые значения Св), возможна раскачка самолета только на ма-
лой высоте и большой скорости.
При затяжеленном управлении (отказ на большом плече) наи-
большие неудобства могут возникнуть при доборе ручки на по-
садке. В обоих случаях точное управление затруднено, но безопас-
ное пилотирование обеспечивается при повышенном внимании лет-
чика.
8.8.2. П о в е д е н и е самолета и управление им
при отказах автоматов демпфирования
и устойчивости
Особенности компоновки современных самолетов, а также ши-
рокий диапазон изменения режимов полета привели к необходи-
мости включения в систему управления ряда автоматических
устройств.
Как и всякое автоматическое устройство, демпферы обладают
определенной степенью надежности и в полете могут отказывать
в работе. Характерными являются отказы, приводящие к колеба-
ниям руля, либо к его одностороннему отклонению. Механизмы
демпферов тангажа при полном ходе перемещают рулевые поверх-
ности сравнительно на небольшую величину (не более 1—2°), по-
этому при их отказе управление самолетом сохраняется. Однаксн
при отказе демпфера тангажа, приводящем к уводу руля, неожи-
данно создается момент, приводящий к непроизвольному измене-
нию перегрузки. Отказ демпфера крена, обычно имеющего боль-
259
ший диапазон отклонения рулей, вызывает накренение самолета.
При уводе руля направления отказавшим демпфером рыскания
возникает неожиданное скольжение, а также накренение само-
лета.
При маневрировании с перегрузками или углами атаки, близ-
кими к максимально допустимым, неожиданный отказ демпфера
может привести к их превышению. Реакция самолета на отклоне-
ние руля при отказе демпфера зависит в значительной степени от
эффективности соответствующего руля на данном режиме полета.
Следует отметить, что на возникающее вследствие отказа демп-
фера вращение самолета летчик реагирует инстинктивно, с не-
большим запаздыванием, поэтому забросы перегрузки и изменения
углового положения самолета обычно бывают небольшими. Одна-
ко последующее пилотирование самолета может быть усложнено,
особенно при неправильных действиях.
Если самолет на данном режиме имеет недостаточный запас
устойчивости и недостаточное аэродинамическое демпфирование,
то стремление вернуть самолет к исходному режиму может сопро-
вождаться его колебаниями, а в некоторых случаях появляется
возможность раскачки. Из-за остановки штока в крайнем поло-
жении меняется балансировочное положение ручки или педалей,
поэтому для выдерживания режима летчику приходится прикла-
дывать усилия.
Иногда при этом летчик допускает ошибку. Правильно восста-
новив исходный режим полета, летчик снимает триммером воз-
никшие вследствие перебалансировки усилия с органа управления
и лишь затем выключает отказавший демпфер. В этом случае раз-
движная тяга демпфера становится в нейтральное положение и
отклонение рулей резко изменяется на величину, соответствующую
половине хода тяги демпфера, вследствие чего самолет снова по-
лучает импульс на вращение.
Таким образом, при отказе демпфера летчик после парирова-
ния рывка должен распознать отказ, выключить демпфер, снять
усилия с органов управления, уйти с режима пониженной устой-
чивости и при дальнейшем пилотировании учитывать отсутствие
демпфера.
Другой вид отказа демпфера может вызвать колебания соот-
ветствующего руля. Такое явление возникает при обрыве обрат-
ной связи. При исправной работе демпфера в случае воздействия
какого-либо возмущения изменение угловой скорости и отклонение
соответствующего руля будут происходить так, как показано на
рис. 8.28 сплошными линиями. Нормально работающая цепь об-
ратной связи обусловливает пропорциональность между величиной
угловой скорости и отклонением руля. При обрыве обратной связи
нарушается эта пропорциональность: руль будет отклоняться на
всю величину, контролируемую демпфером, независимо от вели-
чины угловой скорости и удерживаться в этом положении до тех
пор, пока угловая скорость в процессе колебаний не станет равной
нулю. При перемене знака угловой скорости в процессе колебаний
260
произойдет резкая перекладка руля в пределах хода демпфера
в противоположную сторону (штриховая линия на рис. 8.28).
Вследствие этого увеличивается частота колебаний и ухудшается
затухание колебаний, а при близости собственных частот колеба-
ний самолета и демпфера могут возникнуть незатухающие коле-
бания.
Как было указано выше,
отказы демпферов колеба-
ний опасны при полете на
малой высоте с большой до-
звуковой скоростью вслед-
ствие большой эффективно-
сти рулей на этих режимах,
особенно в случаях, когда
самолет при неработающем
демпфере обладает недоста-
точной устойчивостью.
Поскольку автоматы ус-
тойчивости устроены по то-
му же принципу, что и демп-
феры, последствия отказов
у них аналогичны. Особым
является случай, когда от-
каз автомата устойчивости
Рис. 8.28. Изменение угловой скорости
самолета и отклонения стабилизатора при
обрыве цепи обратной связи демпфера
приводит к значительной или полной
потере устойчивости самолетом.
Такой отказ автомата устойчивости в продольном канале мо-
жет привести к раскачке самолета летчиком, к превышению допу-
стимых значений перегрузки и угла атаки. Своевременное обна-
ружение отказа и соответствующее изменение манеры пилотиро-
вания: плавные, небольшие, соразмерные движения ручкой управ-
ления и повышенное внимание позволят благополучно завершить
задание и выполнить посадку.
Глава 9
БОКОВАЯ БАЛАНСИРОВКА, СТАТИЧЕСКИЕ
ХАРАКТЕРИСТИКИ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ
§ 9.L Боковое равновесие, балансировка самолета
В общем случае боковое движение описывается системой урав-
нений (0.15). Для равновесия самолета в прямолинейном боковом
движении необходимо, чтобы сумма проекций сил на ось О-ггц
и сумма моментов относительно осей Oxi и Оу\ были равны
нулю;
Zi + G cos & sin y = 0;
2^=0.
(9.1)
261
Боковая аэродинамическая сила Zi в пределах плавного обте-
кания линейно зависит от угла скольжения 0 и отклонения руля
направления
z
Z7cos3cosy
Рис. 9.1, Проекции силы тяжести G на оси связанной системы коор-
динат
Подставим Geos & sin 7 = О cos &cos у tg 7 в первое уравнение си-
стемы (9.1). Тогда, учитывая (рис. 9.1), что G cos & cos 7 = Y1=s
= CySq, первое уравнение системы (9.1) в коэффициентах мож-
но записать в следующем виде:
C₽p + C>8H + CyjtgT = O.
В прямолинейном полете моменты крена и рыскания опреде-
ляются выражениями:
2 < = МХа + Лф + Ж >8Э + ЖМН;
2МУА +
Моменты ЛГ и Му° обусловлены геометрической или аэроди-
намической несимметрией, несимметрией тяг правого и левого
двигателей и др.
Тогда уравнения (9.1), выраженные в коэффициентах, можно
записать в следующем виде:
C18 + C^H + Cy,tg-r = O;
+ /»!₽ + + тА = 0;
тУс + + дауН8н + Ч’8’ = 0-
(9.2)
Если самолет обладает геометрической и аэродинамической
симметрией (тх-=тУа = 0), то для обеспечения бокового рав-
новесия самолета в прямолинейном полете без скольжения и кре-
262
на net необходимости отклонять органы управления: боковая ба-
лансировка самолета получается сама собой. Иная картина по-
лучается, если полет осуществляется со скольжением, при не-
симметричной тяге или несимметричных подвесках.
Рис. 9.2. Аэродинамические силы и моменты, действу-
ющие на самолет при полете со скольжением
Наибольший интерес представляет рассмотрение бокового рав-
новесия самолета при прямолинейном полете со скольжением. Та-
кой полет иногда применяется, например, при выполнении посадки
с боковым ветром.
Выясним, какие требуются отклонения руля направления и
элеронов для обеспечения прямолинейного движения со скольже-
нием р. При скольжении, как известно, появится боковая аэроди-
намическая сила Zp, приложенная в боковом фокусе, с коорди-
натами и (рис. 9.2). Вследствие этого возникнут моменты
крена и рыскания Первый при будет стре-
миться накренить самолет в сторону отстающего полукрыла; для
его уравновешивания потребуется отклонить элероны и создать
момент Момент рыскания при /п^<0 будет стре-
миться устранить возникшее скольжение. Для того чтобы сохра-
нить заданный угол скольжения, необходимо отклонением руля
направления создать момент Л1унЗн, равный по величине моменту
но противоположного знака.
Значения балансировочных отклонений руля направления и
элеронов определяются из решения системы уравнений (9.2). Так,
например, пренебрегая в первом приближении моментом рыска-
ния, создаваемым отклонением элеронов, из-за его малости на лет-
ных углах атаки, и полагая тХй и ту9 равными нулю, получим
263
из третьего уравнения (9.2) следующее значение отклонения руля
направления, необходимое для балансировки моментов рыскания:
Рис. 9.3. Балансировочные отклонения рулей при прямолиней-
ном полете со скольжением
Подставляя это значение 6Н во второе уравнение системы (9.2) f
находим балансировочное отклонение элеронов, обеспечивающее
равновесие моментов крена:
/ 8Н \
8Э=-----+ Чи8н) =------------Г" <9-4)
Ш/ тх \ '
Из уравнений (9.3) и (9.4) видно, что балансировочные откло-
нения элеронов и руля направления требуются тем большие, чем
с большим углом скольжения выполняется полет. На рис. 9.3, а
показана характерная диаграмма отклонений 6Н и 6Э, необходимых
для уравновешивания моментов крена и рыскания при полете со
скольжением. Напомним, что положительными считаются отклоне-
ния руля направления вправо (правая педаль вперед) и правого
элерона вниз (ручка влево).
Отклонениями руля направления и элеронов моменты балан-
сируются. Но этого еще недостаточно для обеспечения прямоли-
нейного движения. Нужно уравновесить еще боковую аэродинами-
ческую силу Zi = Z₽|3 + Zs»SH. Если летчик этого не сделает, са-
молет начнет искривлять траекторию (выполнять плоский разво-
рот) в сторону отстающего полукрыла. Уравновешивание боковых
сил достигается накренением самолета в сторону полукрыла, на
которое осуществляется скольжение, так, чтобы составляющая
силы тяжести G cos & sin у уравновешивала боковую аэродинами-
ческую силу Zi (рис. 9.1).
264
Балансировочное значение угла крена определим из первого
уравнения системы (9.2), предварительно подставив балан-
сировочное значение отклонения 6Н из уравнения (9.3). В резуль-
тате получаем следующее балансировочное значение угла крена:
1 / \
'ет=Т7 С>Ч-“С’ <9-5)
У у J
Отсюда видно, что балансировочный угол крена тем больше,
чем больше угол скольжения 0 и меньше коэффициент подъемной
силы Су. Полученный результат можно объяснить следующим.
При увеличении угла скольжения растет боковая аэродинамиче-
ская сила Z₽|3. Для ее уравновешивания с ростом угла скольже-
ния следует увеличивать составляющую силы тяжести Geos 8 sin у,
что достигается увеличением угла крена. Поскольку при постоян-
ном угле скольжения сила пропорциональна скоростному на-
пору, для ее уравновешивания на больших скоростях полета не-
обходимо увеличивать и угол крена. На рис. 9.3, а штриховыми
линиями показаны значения балансировочных углов крена для
двух скоростей полета Vi = 400 км/ч и V2= 600 км/ч.
Таким образом, для осуществления прямолинейного полета со
скольжением надо отклонять элероны, руль направления и созда-
вать крен. При практическом выполнении такого полета летчик
обычно создает крен, а затем скольжение. Прямолинейность по-
лета регулируется величиной угла крена.
При летных испытаниях балансировочные диаграммы откло-
нений руля направления и элеронов обычно строят не по углу
скольжения 0, а по балансировочному углу крена у. Это объяс-
няется тем, что в полете угол крена можно измерить проще и
точнее, чем угол скольжения. Кроме того, летчику его легче кон-
тролировать. В качестве примера на рис. 9.3,6 показана баланси-
ровочная диаграмма отклонений элеронов и руля направления в
зависимости от угла крена при прямолинейном полете со сколь-
жением.
При анализе балансировочных отклонений рулей следует об-
ращать внимание на то, хватит ли (достаточно ли) величины от-
клонений элеронов и руля направления для балансировки и пра-
вилен ли характер их изменения. Расчетным случаем достаточ-
ности рулей является обеспечение посадки с боковым ветром,
когда борьбу со сносом летчик осуществляет не курсом,
а скольжением. Чем меньше скорость полета, тем больший угол
скольжения (0=^/V) будет требоваться при одном и том же
боковом ветре и соответственно большие отклонения элеронов и
руля направления необходимы для балансировки. Эффективность
органов управления определяет максимально допустимый боковой
ветер, при котором возможна посадка без изменения курса для
устранения сноса. У современных маневренных самолетов с крыль-
ями малого удлинения величина максимально допустимого боко-
вого ветра, как правило, определяется эффективностью элеронов.
265
Изменение балансировочных отклонений элеронов и руля на-
правления, показанное на рис. 9.3, привычно для летчика: при
скольжении, например на правое полукрыло, нужно отклонить
ручку вправо и давить на левую педаль. При правильном характе-
ре изменения отклонений элеронов и руля направления, потреб-
Рис. 9.4. Балансировочные уси-
лия на рычагах управления
при прямолинейном полете со
скольжением
ных для балансировки самолета в пря-
молинейном полете со скольжением,
положительному углу скольжения 0
(положительному балансировочному
углу крена у) соответствуют отрица-
тельные отклонения элеронов (ручка
вправо) и руля направления (дана ле-
вая педаль), т. е. выполняются сле-
дующие условия:
Авн q. Авэ /л
др ^U’ др
(9.6)
или
л.
Д7 и’ Д7
Для отклонения органов управле-
ния в балансировочное положение лет-
чик должен приложить к педалям и
ручке управления элеронами некото-
рые усилия Рн и Рэ. Чем больше ба-
органов управления, тем большие уси-
(9.6')
лансировочные отклонения
лия требуется прикладывать к рычагам управления. Следователь-
но, балансировочные диаграммы усилий (рис. 9.4) будут иметь
такой же вид, как и диаграммы балансировочных отклонений эле-
ронов и руля направления. Напомним, что усилия Рн и Р3 счи-
таются положительными, если летчик давит на правую педаль и
на ручку влево. При правильном характере изменения усилий на
ручке и педалях в прямолинейном полете со скольжением, напри- -
мер на правое полукрыло (Д0>О), требуется давить на левую
педаль (ДРн<0) и на ручку вправо (ДРэ<0), т. е. выполняются
следующие условия:
др
ДА
Др
(9.7)
ИЛИ
(9.?)
Градиенты Дби/Ду, Дбэ/Ду, ДРн/Ду и ДРэ/Ду численно равны
отклонениям руля направления и элеронов и изменениям усилий
на педалях и на ручке, необходимым для изменения в прямоли-
нейном полете со скольжением угла крена на 1°. Летная прак-
тика показывает, что приемлемые значения градиентов усилий по
266
углу крена для маневренных самолетов находятся в пределах от
1 до 4 кгс (~10—40 Н) по рулю направления и от 0,1 до 1 кгс
(1—10 Н) по элеронам. Это значит, что для балансировки само-
лета в прямолинейном полете со скольжением усилия на педалях
должны быть примерно в 4—10 раз больше, чем на ручке управ-
ления.
Если в систему путевого управления не установлен рулевой
привод, то наблюдающаяся у некоторых самолетов перекомпенса-
ция руля направления при больших его отклонениях может суще-
ственно изменить характер протекания балансировочных усилий
на педалях. В этом случае летчик должен для предотвращения
самопроизвольного увеличения отклонения руля изменять усилия
на педалях Рн так, как показано штриховой линией на рис. 9.4.
Нелинейная зависимость усилий на педалях от угла крена (сколь-
жения) может наблюдаться также у самолетов с рулевыми при-
водами, когда характеристика указанного механизма нелинейна
(например, имеет «излом», см. рис. 8.16). Отмеченные особенности,
естественно, усложняют управление, требуют от летчика повышен-
ного внимания и поэтому являются нежелательными.
§ 9.2. Путевая и поперечная устойчивость, их связь
с характеристиками управляемости
Боковое равновесие самолета при неизменном отклонении ор-
ганов управления может быть нарушено двумя факторами, орга-
нически связанными между собой: скольжением и креном. Так,
если первопричиной нарушения равновесия явилось изменение угла
скольжения, то появившийся прирост боковой аэродинамической
силы Zp (рис. 9.2), приложенный в боковом фокусе, обусловит
появление моментов рыскания и крена. Последний вызовет изме-
нение и угла крена. При нарушении бокового равновесия изме-
нением угла крена, как будет показано ниже, образуется сколь-
жение р на опущенное полукрыло.
Таким образом, скольжение и крен взаимосвязаны и практи-
чески изменяются одновременно. Это значит, что движения рыска-
ния и крена, а соответственно проявление путевой и поперечной
устойчивости взаимосвязаны. Однако статическое рассмотрение
совместного движения рыскания и крена не представляется воз-
можным. Поэтому здесь ограничимся изучением только изолиро-
ванных путевой и поперечной устойчивостей.
Под путевой (флюгерной) устойчивостью понимается
способность самолета самостоятельно, без вмешательства летчика,
противодействовать изменению угла скольжения. Если в исходном
режиме полета угол скольжения был равен нулю, то флюгерно
устойчивый самолет будет стремиться устранить появившееся
скольжение, т. е. вести себя подобно флюгеру, устанавливающе-
муся всегда по потоку. Отсюда и вытекает название этого вида
устойчивости.
267
Для обеспечения флюгерной устойчивости необходимо, чтобы
боковой фокус находился позади центра тяжести (^>0, рис. 9.5).
В этом случае при возникновении скольжения появится момент
рыскания Му = который, разворачивая самолет по
Рис. 9.5. Моментная диаграмма флюгерно устойчивого
(сплошная линия) и неустойчивого (штриховая линия) само-
лета
(9.8)
потоку, будет устранять скольжение. У флюгерно устойчивого са-
молета при возникновении положительного скольжения (Д|3>0)
появится отрицательный путевой момент (Дт^-СО), а при отрица-
тельном скольжении (Др<0)—положительный путевой момент
(Дт^Х)), т. е. выполняется условие:
др
Самолет, имеющий моментную диаграмму, показанную на
рис. 9.5 сплошной линией, в путевом отношении устойчив, у него
выполняется условие (9.8). Если бы боковой фокус находился
впереди центра тяжести самолет путевой устойчивостью
не обладал бы (см. штриховую линию на рис. 9.5). В этом случае
при возникновении скольжения появляется момент рыскания, ко-
торый стремится увеличивать угол скольжения.
Следует обратить внимание на условность термина «путевая
устойчивость». Самолет, обладающий путевой устойчивостью,
стремится устранить возникший угол скольжения, а не сохранить
268
направление полета. Как будет показано ниже, для выдерживания
заданного направления полета требуется вмешательство летчика
или работа курсового автопилота.
Под поперечной устойчиво-
стью понимается способность самолета
устранять возникший угол крена. Для луч-
шего понимания этого вида устойчивости
рассмотрим, как ведет себя самолет при
накренении, например на правое полукры-
ло (рис. 9.6).
Само по себе изменение угла крена еще
не вызывает изменения величин сил и
моментов, действующих на самолет. Одна-
ко при накренении самолета изменяет на-
правление действия подъемная сила, вслед-
ствие чего нарушается равновесие сил и
подъемная сила У уже не будет уравнове-
шивать силу тяжестИ—Самолета G. Их рав-
нодействующая Y + G начнет искривлять
траекторию движения в сторону опущен-
ного полукрыла. При искривлении траек-
тории самолет в первый момент не будет
поворачиваться вокруг оси Оу{, так как для
такого поворота требуется изменить момент
рыскания, а накренение самолета не при-
водит к нарушению равновесия моментов
Му. Но если траектория движения искрив-
ляется, а самолет продолжает двигаться
поступательно, то у него образуется сколь-
жение р на опущенное полукрыло (рис.
9.6). Самостоятельно устранить возникший
угол крена самолет может только тогда,
когда при накренении и возникновении
скольжения появится момент крена, вызы- Рис. 9.6. Возникнове-
вающий вращение в сторону отстающего ние скольжения на опу-
(в нашем случае поднятого) полукрыла. За- щенное полукрыло при
метим, что на величину моментов сам по крене
себе крен непосредственно не влияет. Его
влияние сказывается через скольжение: угол крена вызывает угол
скольжения, а последний уже обусловливает появление моментов
крена.
Таким образом, под поперечной устойчивостью самолета пони-
мается его способность крениться в сторону, обратную скольже-
нию. Для этого боковой фокус должен находиться выше центра
тяжести (Ур>0, рис. 9.7). В этом случае при скольжении воз-
никает момент крена Мх = вращающий самолет на
отстающее (поднятое) полукрыло. Заметим, что у поперечно устой-
чивого самолета при положительном (на правое полукрыло)
269
скольжении (Др>0) возникает отрицательный момент (Дтх<0),
а при отрицательном скольжении (Др<0) — положительный мо-
мент (Д/пх>-0), т. е. выполняется условие:
-^ = ^<0. (9.9)
Рис. 9.7. Моментная диаграмма поперечно устойчиво-
го (сплошная линия) и неустойчивого (штриховая ли-
ния) самолета
Если самолет имеет моментную диаграмму, показанную на
рис. 9.7, он поперечно устойчив, в этом случае условие (9.9) вы-
полняется. Если бы боковой фокус находился ниже центра тяже-
сти (ур<0), самолет поперечной устойчивостью не обладал бы
(см. штриховую линию на рис. 9.7).
Путевая и поперечная устойчивости тесно связаны с характе-
ристиками боковой управляемости самолета. Так, например, из
выражений (9.3) и (9.4) видно, что отклонения руля направления
и элеронов, необходимые для балансировки самолета в прямоли-
нейном полете с углом скольжения р, требуются тем большие,
чем большими путевой (т$) и поперечной (яг£) устойчивостями
обладает самолет.
Поскольку характеристики эффективности руля направления
(/Пун) и элеронов (яф) отрицательные числа, то для правиль-
ности характера изменения балансировочных отклонений бн и бэ
(рис. 9.3) при прямолинейном полете со скольжейием необходимо,
чтобы выполнялись условия:
mJ<0;
гп«
— ,-<0
* * rfy
(9.10)
270
ВиЗА
Рис. 9.8. Силы и моменты,
возникающие при отклонении
руля направления
Если для правильного изменения балансировочных отклонений
руля направления необходимо, чтобы самолет обладал путевой
устойчивостью, то, как видно из системы (9.10), для правильного
изменения балансировочных отклонений элеронов еще недостаточ-
но наличие только поперечной устойчивости <0). Необходи-
мо, чтобы момент крена при скольже-
нии был больше момента крена, вы-
званного отклонением руля направле-
ния для создания скольжения. Физи-
ческий смысл отмеченного состоит в
следующем. При отклонении руля на-
правления возникает не только момент
рыскания Л1ун8н» создающий сколь-
жение р, но и момент крена
(рис. 9.8). При несимметричном рас-
положении вертикального оперения
(только сверху) этот момент противо-
положно направлен моменту
Путевая и поперечная устойчиво-
сти определяются аэродинамической
компоновкой самолета и в зависимости
от режима полета могут изменяться
в широких пределах.
Путевая устойчивость является
важнейшей характеристикой самолета,
определяющей его динамические свой-
ства в боковом движении. Поэтому
потеря путевой устойчивости самоле-
том в полете недопустима. Как было
показано в главе 5, производная
характеризующая путевую устойчивость самолета, определяется
главным образом величиной площади и расположением (плечом)
вертикального оперения. С увеличением угла атаки и числа М.
полета на сверхзвуковых скоростях путевая устойчивость сущест-
венно уменьшается. Для предотвращения потери путевой устойчи-
вости у некоторых самолетов вынуждены вводить ограничение по
числу М полета.
При выходе на допустимое число М полета, определяемое пу-
тевой устойчивостью, у самолета сохраняется некоторый запас
путевой устойчивости не только в прямолинейном полете, но и при
всех возможных эволюциях в процессе маневрирования. Непро-
извольное превышение допустимого числа М полета еще не озна-
чает, что самолет сразу потеряет путевую устойчивость. В прямо-
линейном полете (на малых углах атаки) у самолета обычно со-
храняется путевая устойчивость при значительном превышении до-
пустимого числа М. Однако при маневрировании с выходом на
большие угды атаки на числах М, больших допустимых, самолет
может потерять путевую устойчивость. В этом случае он имеет
тенденцию самопроизвольно увеличивать скольжение. Если лет-
чик допустит значительное увеличение скольжения и поздно нач-
нет парировать его, то отклонения руля направления может не
хватить для предотвращения дальнейшего увеличения скольжения.
Поэтому при непроизвольном превышении допустимого числа М
летчик должен принять меры к уменьшению числа М полета (вы-
пустить тормозные щитки, уменьшить тягу двигателя), не выпол-
нять энергичных маневров и осуществлять координированное
управление, не допуская самопроизвольного увеличения скольже-
ния.
Поперечная устойчивость самолета в основном зависит от
формы и расположения крыла, высоты вертикального оперения,
наличия и вида подвесок и при перемене режима полета изменя-
ется в широких пределах. К поперечной устойчивости не предъяв-
ляются такие жесткие требования, как к путевой устойчивости.
Больше того, у некоторых маневренных самолетов на околозвуко-
вых скоростях полета может наблюдаться даже поперечная неус-
тойчивость (^>*0). Появление указанной неустойчивости может
быть связано с рядом причин.
Во-первых, это может быть вызвано несимметричным разви-
тием волнового кризиса на левом и правом полукрыльях при
скольжении на околозвуковых скоростях полета. Во-вторых, появ-
ление поперечной неустойчивости может быть связано с установ-
кой крыла с большим отрицательным поперечным углом ф для
уменьшения излишне большой поперечной устойчивости на боль-
ших углах атаки. Однако в этом случае самолет может стать по-
перечно неустойчив (шР>0) на малых углах атаки (больших
скоростях полета).
При отклонении руля направления, например влево, самолет
разворачивается влево и образует скольжение на правое полу-
крыло. У поперечно устойчивого самолета при этом появится мо-
мент, накреняющий его на левое полукрыло. Такое реагирование
самолета на отклонение руля направления принято называть нор-
м а л ь н о й или п р я м о й реакцией по крену на откло-
нение руля направления. Если самолет поперечно не-
устойчив, то при скольжении на правое полукрыло появился бы
момент Мх, накреняющий его на правое полукрыло. Такое поведе-
ние самолета при отклонении руля направления называют обрат-
ной реакцией по крену на отклонение руля на-
правления.
Потеря поперечной устойчивости и появление обратной реак-
ции по крену на отклонение руля направления требуют повышен-
ного внимания летчика и точных знаний, на каких режимах полета
это может наблюдаться. У современных маневренных самолетов
явление обратной реакции по крену на отклонение руля направле-
ния встречается сравнительно редко. Наблюдающееся уменьшение
поперечной устойчивости до нейтральности не вызывает у летного
27?
состава каких-либо затруднений в управлении таким са-
молетом.
Поскольку боковым движением летчик управляет, одновремен-
но отклоняя руль направления и элероны, то характеристики пу-
тевого и поперечного управления должны быть определенным об-
разом связаны. Одной из таких характеристик, связывающих дви-
Рис. 9.9. Зависимость характеристикиd§3/d§n от чис-
ла М. полета
жение крена и рыскания, является отношение 6э/6н (точнее Л)э/Л)н
или йхэ/^н), показывающее, насколько больше нужно отклонять
элероны (ручку хэ) при прямолинейном полете со скольжением,
чем руль направления (педаль хн). В качестве примера на рис. 9.9
показана сплошной линией зависимость производной d63/ddH в
функции числа М полета, характерная для некоторых самолетов
со стреловидным крылом умеренной стреловидности. Перемена
знака б/бэ/бЙн в диапазоне чисел объясняется потерей
поперечной устойчивости в этом диапазоне чисел М и появлением
обратной реакции по крену на отклонение руля направления.
На рис. 9.9. показано, как изменяется характеристика d63/rfdB
при уменьшении отрицательного поперечного ф (штриховая ли-
ния) и переходе к треугольному крылу малого удлинения (штрих-
пунктирная линия). Летная практика показывает, что управление
маневренным самолетом не вызывает затруднений, если характе-
ристика t/бэ/^бн режима полета находится в пределах: 0,1 <
§ 9.3. Особенности боковой управляемости
сверхзвуковых самолетов
Современные маневренные самолеты, как правило, обладают
хорошими характеристиками боковой управляемости во всем раз-
решаемом летном диапазоне скоростей и высот полета. Вместе
273
с тем на некоторых режимах полета характеристики боковой
управляемости могут иметь ряд особенностей, которые связаны
главным образом с падением эффективности органов управления
и зависят от изменения устойчивости самолета и характеристик
системы управления. Последние определяют загрузку рычагов
управления и передаточные отношения от ручки к элеронам
(db3/dxz) и от'педалей к рулю направления (d6H/dxH).
Управление боковым движением при маневрировании в основ-
ном осуществляется с помощью органов поперечного управления,
создающих моменты для изменения угла крена.
Руль- направления при маневрировании используется главным
образом для координированного управления, т. е. устранения не-
произвольно возникающего скольжения или создания небольшого
угла скольжения при выполнении некоторых пространственных
маневров, а также при посадке с боковым ветром или при полете
с несимметричными тягой или подвесках.
Изменение характеристик поперечной управляемости наиболее
заметно может проявиться на граничных условиях: на малых или
больших скоростях полета. Так, например, эффективность попереч-
ного управления может существенно изменяться как на больших
углах атаки, так и на больших числах М и приборных скоростях
полета.
9.3.1. Особенности поперечной управляемости
на больших скоростях
Как было показано выше, заметное снижение эффективности
элеронов может наблюдаться при полете на больших скоростях
полета. Это снижение обусловлено влиянием, с одной стороны,
образующегося на крыле сверхзвукового течения, с другой — упру-
гими деформациями крыла. Первое связано с увеличением числаМ
полета, второе — с увеличением приборной скорости (скоростного
напора).
Упругие деформации крыла оказывают существенное влияние
на эффективность элеронов и при достижении критической скоро-
сти реверса элеронов могут привести к полной ее потере. Полет
на скорости, превышающей критическую скорость реверса элеро-
нов, недопустим, так как на таких скоростях при отклонении эле-
ронов возникает момент, кренящий самолет в сторону, противо-
положную действию элеронов. Чем меньше критическая скорость
реверса элеронов, тем на меньшей приборной скорости полета на-
чинает снижаться их эффективность. Обеспечение необходимой
эффективности элеронов, установленных на стреловидном крыле,
при больших приборных скоростях довольно сложная задача. Это
объясняется тем, что у стреловидного крыла при его деформациях
угол атаки изменяется не только в результате кручения, но и в
результате изгиба, что вызывает дополнительное уменьшение эф-
фективности элеронов. Данная проблема остро стоит у самолетов
с крыльями изменяемой в полете стреловидности, обладающих не-
274
сколько меньшей жесткостью крыла. Стремление уменьшить про-
гиб и кручение крыла и, следовательно, повысить эффективность
поперечного управления у таких самолетов вынуждает конструк-
торов повышать жесткость конструкции крыла, что связано с уве-
личением его массы, смещать элероны ближе к фюзеляжу или
вместо них применять интерцепторы и осуществлять управление
с помощью дифференциального отклонения стабилизатора («нож-
ниц»).
Рис. 9.10. Схема появления крутящих моментов при попереч-
ной балансировке самолета, увеличивающих начальную не-
симметрию крыла
При полете с большими приборными скоростями на малых
высотах, а также на больших высотах при высоких значениях
чисел М у некоторых самолетов при нейтральном положении эле-
ронов может наблюдаться самопроизвольное накренение самолета.
Это явление получило название «валежки» самолета на крыло.
Интенсивность и направление накренения у различных само-
летов, обладающих таким свойством, могут быть различными. Не-
которые самолеты могут крениться на правое полукрыло, другие —
на левое. У одних самолетов эта тенденция выражена сильно,
у других — слабо. Для противодействия самопроизвольному на-
кренению самолета требуется отклонить элероны, приложить не-
которое усилие к ручке управления.
Причиной «валежки» является геометрическая или аэродина-
мическая несимметрия крыла. Появление «валежки» на малых
высотах (больших приборных скоростях) связано с уменьшением
эффективности элеронов, вызванным нежесткостью конструкции
крыла, а на больших высотах — с уменьшением эффективности
элеронов на больших числах М.
Предположим, что в процессе производства и сборки само-
лета средний угол атаки у правого крыла оказался больше, чем
у левого, на величину Дао. Несимметрия в углах атаки обусловит
появление в полете некоторого кренящего момента, для противо-
действия которому потребуется несколько переместить ручку впра-
во, отклонив немного левый элерон вниз, а правый вверх. При
отклонении элеронов появятся крутящие ДМКР моменты (рис. 9.10) f
275
направленные на левом крыле на уменьшение угла атаки, а на
правом — на увеличение угла атаки. По мере увеличения скорости
полета при неизменном угле отклонения элеронов крутящие мо-
менты ДЛ1кр будут расти пропорционально квадрату скорости.
Рост моментов АМкр приведет вследствие нежесткости крыла к
увеличению несимметрии крыла Да и, следовательно, кренящего
момента, для парирования которого требуется больше отклонить
элероны. Это еще больше увеличит скручивающие моменты, что
в свою очередь приведет к увеличению балансировочных отклоне-
ний элеронов и усилий на ручке.
Следовательно, при увеличении скорости полета упругая де-
формация крыла приводит к увеличению начальной его несиммет-
рии, требуя от летчика всевозрастающих отклонений элеронов для
парирования кренящих моментов в горизонтальном полете без
крена.
Затягивание самолета в крен может явиться одной из причин,
ограничивающей летные возможности самолета. Так, например,
если балансировка самолета в прямолинейном полете без крена
требует отклонения ручки поперечного управления более 1/3 ее
хода, то дальнейшее увеличение скорости не рекомендуется. При
высокой культуре производства современных самолетов «валежка»
может встретиться только в результате боевых повреждений, нека-
чественного ремонта, несимметричности подвесок либо использо-
вания самолета на режимах, которые не предусмотрены инструк-
цией. Так, например, попытка выполнения пилотажа на мини-
мальном угле стреловидности крыла самолета (изменяемой в по-
лете стреловидности) может привести в некоторых случаях к ин-
тенсивному затягиванию самолета в крен.
При полете на больших скоростях «валежка» проявляется бо-
лее интенсивно. Однако отсюда, конечно, не следует, что при пер-
вой тенденции к затягиванию в крен летчик должен немедленно
уменьшить скорость полета. Если кренение обусловлено несиммет-
ричностью подвесок, то уменьшение скорости потребует увеличе-
ния отклонения элеронов для парирования кренения. При начале
непроизвольного затягивания в крен летчик должен принять меры
для предотвращения накренения самолета. При этом противодей-
ствие кренению должно производиться в первую очередь органами
поперечного управления.
У самолетов, имеющих обратную реакцию по крену на откло-
нение руля направления, следует избегать пользоваться рулем
направления для парирования непроизвольного кренения, исполь-
зуя это средство лишь в исключительных случаях; при этом лет-
чик должен твердо помнить, что парирование «валежки» в та-
ких случаях необходимо производить плавным отклонением педали
в сторону образования крена.
Поскольку увеличение перегрузки пу может не только усилить
кренение, но и вызвать его проявление на меньших скоростях по-
лета, то при появлении самопроизвольного кренения не следует
гасить скорость путем увеличения перегрузки. Необходимо пред-
276
варительно погасить скорость, уменьшив тягу и выпустив тормоз-
ные щитки, и только тогда уже переводить самолет в набор вы-
соты.
9.3.2. Особенности поперечной управляемости
на больших углах атаки.
Применение АПС
Выше было показано, что на больших углах атаки эффектив-
ность элеронов из-за срывного обтекания резко падает. Уменьше-
ние эффективности элеронов на таких режимах полета усугубля-
ется еще тем, что при накренении самолета, вызванном отклоне-
нием элеронов, образуется скольжение на опускающееся полу-
крыло. Причина этого явления объясняется рядом причин.
Во-первых, между углами атаки и скольжения существует ки-
нематическая взаимосвязь, вследствие чего изменение угла атаки
при вращении самолета сопровождается изменением угла сколь-
жения, и наоборот (см. § 11.1).
Во-вторых, отклонение элеронов на больших углах атаки в
отличие от малых углов не столько изменяет подъемные силы ле-
вой и правой половин крыла, сколько их силы лобового сопротив-
ления. При этом лобовое сопротивление увеличивается у подни-
мающегося полукрыла с опущенным элероном и уменьшается у
полукрыла с поднятым элероном. Последнее приводит к возник-
новению момента рыскания, обусловливающего возникновение
скольжения на полукрыло с поднятым элероном.
Как первая, так и вторая причины приводят к появлению
скольжения на опускающееся полукрыло. По мере увеличения угла
крена этот эффект усиливается из-за влияния составляющей силы
тяжести (G cos 0 sin у). В результате этого у поперечно устойчи-
вого самолета появляется момент крена AfjP, направленный
противоположно моменту, создаваемому элеронами. Именно по-
этому такое непроизвольно возникшее скольжение называют не-
благоприятным.
Современные самолеты со стреловидными и треугольными
крыльями на больших углах атаки обладают излишне большой
поперечной устойчивостью и сравнительно малой путевой устой-
чивостью. Особенно сильно уменьшается путевая устойчивость на
больших углах атаки у самолетов с крыльями переменной по раз-
маху стреловидностью и имеющих широкие фюзеляжи и большие
углы стреловидности вертикального оперения. Вследствие этого
момент рыскания, обусловленный путевой устойчивостью, на боль-
ших углах атаки слабо противодействует изменению угла сколь-
жения, в то время как большая поперечная устойчивость вызы-
вает значительный момент крена, препятствующий вращению.
В некоторых случаях возникновение неблагоприятного скольжения
при вводе самолета в крен отклонением только элеронов может
дать обратный эффект — прекращение вращения в сторону откло-
277
нения ручки (элеронов) и энергичного кренения в противополож-
ную сторону, которое иногда воспринимается летчиками как сва-
ливание. Отмеченное характерно не только при поперечном управ-
лении, осуществляемом с помощью элеронов, но в той или иной
степени имеет место при использовании интерцепторов и диффе-
ренциального отклонения стабилизатора.
Таким образом, поперечная управляемость самолета на боль-
ших углах атаки ухудшается как из-за падения эффективности
элеронов, так и из-за возникновения неблагоприятного скольже-
ния, эффект которого тем больше, чем меньше путевая устойчи-
вость и больше поперечная устойчивость. Если бы летчик точно
осуществлял координированное управление и не допускал сколь-
жения, то, несмотря на уменьшение эффективности элеронов на
больших углах атаки, поперечная управляемость самолета прак-
тически всегда сохранялась бы в допустимых пределах. Слож-
ность координированного пилотирования на больших углах атаки
усугубляется снижением точности показаний указателя скольже-
ния, шарик которого при данном угле скольжения отклоняется
тем меньше, чем больше угол атаки (меньше скорость).
Стремление повысить эффективность поперечного управления
самолета вынуждает иногда летчика совместно с перемещением
ручки, например влево, отклонять и левую педаль для создания
благоприятного скольжения. Однако на больших углах атаки это
опасно, так как несоразмерно большое скольжение может спро-
воцировать преждевременный срыв потока и сваливание само-
лета на крыло. Поэтому благоприятное скольжение на таких углах
атаки можно использовать только для устранения крена, когда
для этого по какой-либо причине не хватает эффективности эле-
ронов. Недостаточная эффективность поперечного управления на
больших углах атаки у некоторых самолетов может быть даже
причиной ограничения минимальной скорости полета или допусти-
мого угла атаки.
Поскольку автомат демпфирования колебаний крена препятст-
вует вращению самолета по крену, то у некоторых самолетов в
целях повышения эффективности поперечного управления может
быть предусмотрено отключение демпфера крена при маневриро-
вании.
Необходимость повышения эффективности поперечного управ-
ления на больших углах атаки и трудность летчику правильно со-
размерить величину отклонения педалей для выполнения коорди-
нированных разворотов вынудили конструкторов разработать и
применить на некоторых самолетах автоматы перекрестных связей
(АПС). Такой автомат обеспечивает соразмерное отклонение руля
направления при перемещении летчиком ручки по крену. Величина
отклонения руля регулируется в зависимости от угла атаки.
В простейшем случае АПС работает по закону;
Д8Й — —
(9.11)
278
где kx^—передаточный коэффициент, показывающий, на какую
величину отклоняется руль направления в градусах при отклоне-
нии ручки х3 на 1 см.
В целях обеспечения безопасности полета при возможных от-
казах в системе управления величина отклонения руля направле-
ния автоматом обычно ограничивается значением 3—5°. Автомат
обычно подключается на углах атаки, на которых наблюдается
заметное ухудшение поперечной управляемости.
В результате применения автомата перекрестной связи удается
обеспечить эффективность поперечного управления до существен-
но больших углов атаки. На больших углах атаки наблюдается
значительное уменьшение путевой устойчивости, что у некоторых
самолетов может явиться причиной преждевременного сваливания
самолета (см. § 11.6), поэтому иногда в закон отклонения руля на-
правления АПС может вводиться сигнал боковой перегрузки nz
или угла скольжения р. В этом случае АПС работает по следую-
щему закону:
Д8н=^эхэ~йХ. (9.1Г)
Для повышения7 поперечной управляемости самолета на боль-
ших углах атаки может вводиться иногда связь между величиной
дифференциального отклонения стабилизатора (на создание кре-
на) и углом атаки самолета. В этом случае момент крена на
больших углах атаки увеличивается вследствие большего откло-
нения стабилизатора («ножниц») по крену при одинаковом пере-
мещении ручки хэ. На некоторых самолетах повышение попереч-
ной управляемости достигается одновременным применением
«ножниц» стабилизатора и элеронов.
§ 9.4. Особенности балансировки самолета
при несимметричных тяге и подвесках
9.4.1. Бал ансировка при несимметричной тяге
Предположим, что в полете произошел отказ двигателя, рас-
положенного не в плоскости симметрии самолета (рис. 9.11). В ре-
Рис. 9.11. Возникнове-
ние момента рыскания
при отказе бокового дви-
гателя
зультате этого возникнет разворачивающий момент вели-
чина которого определяется выражением:
Л1уР=(Р+А*дв) £дв>
(9.12)
279
где Р — тяга работающего двигателя; ДХдв— дополнительное со-
противление, создаваемое остановившимся двигателем; гдв— рас-
стояние между осью двигателя и плоскостью симметрии самолета.
Под действием этого момента самолет начнет разворачиваться
в сторону отказавшего двигателя, что обусловит возникновение
скольжения на полукрыло с работающим двигателем. Если само-
лет устойчив в путевом и поперечном отношении, то появление
угла скольжения |3 вызовет момент рыскания 7Иу(3, препятствую-
щий увеличению угла скольжения, и момент крена Мх^ создаю-
щий крен в сторону отказавшего двигателя. Чем больше попереч-
ная устойчивость самолета, меньше скорость полета и на более
высоком режиме работали двигатели, тем большее скольжение
возникнет при отказе двигателя и на больший угол успевает на-
крениться самолет до вмешательства летчика.
Поэтому при отказе двигателя в полете сначала следует с по-
мощью элеронов и руля направления устранить кренение и раз-
ворот самолета в сторону этого двигателя. На малых скоростях,
когда эффективность руля направления может оказаться недоста-
точной, целесообразно уменьшить тягу работающего двигателя.
При этом нужно принять меры, исключающие опасную потерю
скорости, уменьшив угол тангажа (наклона траектории). После
этого следует сбалансировать самолет в прямолинейном полете.
Прямолинейный полет с несимметричной тягой можно выполнять
с различными углами скольжения. При этом в зависимости от
величины и знака угла скольжения будут требоваться и различ-
ные балансировочные отклонения руля направления, элеронов и
крен. Величина балансировочных их отклонений определяется
уравнениями (9.2). Если пренебречь моментом рыскания, появляю-
щимся при отклонении элеронов, и считать в первом приближении
тх = 0, то балансировочные отклонения руля направления, эле-
ронов и угол крена определяются следующими выражениями:
tgT =
8Н =----------г-
** в
/Пун
т гпа
Уо X .
8 8 ’
/И//ПуН
(9.13)
1 {п CSH
м - ч7
С’н ту
/Пун ’
где
т — Му*
Уо qSl
(9.14)
Из полученных выражений видно, что балансировка самолета
с несимметричной тягой требует отклонения рулей и создания
крена даже при прямолинейном полете без скольжения. На
280
рис. 9.12 в качестве примера показаны отклонения руля направ-
ления, элеронов и угла крена, необходимые для балансировки са-
молета в прямолинейном полете при отказе левого двигателя. При
рассмотрении этой балансировочной диаграммы можно выделить
три наиболее характерных режима с от-
казавшим двигателем.
Полет без крена (положение 1
на рис. 9.12). Силы, действующие на
самолет при полете без крена, показаны
на рис. 9.13. В этом случае полет осу-
ществляется со скольжением на крыло
с отказавшим двигателем. Боковая аэро-
динамическая сила Z₽, обусловленная
скольжением, уравновешивается силой
ZH, создаваемой отклонением руля на-
правления. Поэтому шарик указателя
скольжения находится в центре, хотя
полет осуществляется со скольже-
Рис. 9.13. Силы,
действующие на
самолет при пря-
молинейном поле-
те без крена с от-
казавшим (ле-
вым) двигателем
Рис. 9.12. Балансировочная диаграм-
ма при прямолинейном полете с от-
казавшим (левым) двигателем
нием. Такой способ балансировки целесообразен при полете
в сложных метеоусловиях. Однако в этом случае требуются
весьма большие отклонения руля направления, необходимые не
только для балансировки момента, создаваемого несимметричной
тягой Л4уР, но и момента стремящегося устранить скольже-
ние. Кроме того, скольжение приводит к увеличению лобового со-
противления и, как следствие, повышенному расходу топ-
лива.
Полет без скольжения (положение II на рис. 9.12),
Силы и моменты, действующие на самолет при полете без сколь-
281
жения, показаны на рис. 9.14. В этом случае для балансировки
самолета требуются отклонения руля направления только для
уравновешивания момента от несимметричной тяги. Сила ZH, вы-
званная отклонением руля направления, приложена выше центра
Рис. 9.14. Силы, дейст-
вующие на самолет при
прямолинейном полете
без скольжения с отка-
завшим (левым) двига-
телем
Рис. 9.15. Силы, дейст-
вующие на самолет при
прямолинейном полете с
креном и скольжением
в сторону работающего
двигателя
тяжести и поэтому создает некоторый момент крена на полукры-
ло с отказавшим двигателем. Для его балансировки необходимо
незначительно отклонить элероны (в рассматриваемом случае от-
клонить ручку вправо). Для уравновешивания боковой аэродина-
мической силы ZH, создаваемой рулем направления, требуется
создать небольшой угол крена на крыло с работающим двигате-
лем. В эту же сторону отклонен шарик указателя скольжения, не-
смотря на то что скольжение отсутствует. Поскольку при рассмат-
риваемом способе балансировки обеспечивается минимальное ло-
бовое сопротивление, то он наиболее приемлем при полете с огра-
ниченным запасом топлива в простых метеоусловиях или при не-
достаточной тяге работающего двигателя,
282
Полет с неотклоненным рулем направления
(положение III на рис. 9.12). Силы и моменты, действующие на
самолет в рассматриваемом случае, показаны на рис. 9.15. Полет
осуществляется с креном и скольжением в сторону работающего
двигателя. Крен необходим для балансировки боковой аэродина-
мической силы возникающей при скольжении. Момент рыска-
ния А4^р, создаваемый несимметричной тягой, уравновешивается
моментом обусловленным путевой устойчивостью. Большие
потребные углы скольжения7 и крена при таком способе баланси-
ровки неудобны в прямолинейном полете и практически не при-
меняются. Вместе с тем при недостаточной эффективности руля
направления (например, при подтягивании во время захода на
посадку) часто применяется прямолинейный полет с креном и не-
большим скольжением в сторону работающего двигателя (режим
полета средний между положениями II и III).
Следует иметь в виду, что при прямолинейном полете с не-
симметричной тягой указатель скольжения дает неправильные по-
казания. Это объясняется тем, что указатель скольжения по прин-
ципу своей работы реагирует не на скольжение, а на боковую
силу. В обычном полете появление боковой силы является след-
ствием возникновения скольжения. Другое дело при полете с не-
симметричной тягой. В этом случае возникновение боковой силы
связано не только со скольжением, но и с отклонением руля на-
правления, необходимым для уравновешивания момента Мур.
9.4.2. Балансировка при несимметричных
подвесках
При прямолинейном полете с несимметричными подвесками
(например, после пуска ракет только с левого полукрыла) необ-
ходимо сбалансировать моменты крена (Mxn) и рыскания (Myn),
обусловленные весовой и аэродинамической несимметрией. По-
требные для балансировки отклонения руля направления, элеро-
нов и угла крена в рассматриваемом случае можно определить
из решения системы уравнений (9.2). Если пренебречь моментом
рыскания, появляющимся при отклонении элеронов, то баланси-
ровочные значения йн, бэ и у определяются следующими выраже-
ниями:
в9=
«у«
-Т- ( ~~Т~
m » \ /и н
tgf =
ту п
туЯ
' (с₽-с>-4
Cv. \ т8ун
У.
П19ти
у
CSH
3 + -^—г-
иу. т»
(9.15)
ту п
ГДС п — ttly п nfqSl.
283
Момент рыскания при несимметричных подвесках обычно мал
и его балансировка затруднений не вызывает. Поэтому рассмот-
рим только потребные отклонения элеронов, необходимые для ба-
лансировки момента крена'Мхп. Если балансировка самолета осу-
ществляется без крена и скольжения, то, пренебрегая в первом
приближении ту п, получим потребное отклонение элеронов в сле-
дующем виде:
= = —(9Л6)
тх тх$1 Ц
что момент крена определяется главным образом
весовой несимметрией и не зависит от режима полета. Тогда, как
это видно из выражения (9.16), чем меньше скоростной напор q
(приборная скорость) и ниже эффективность элеронов /ft/, тем
большее требуется отклонение элеронов, необходимое для балан-
сировки самолета. В некоторых случаях недостаточность эффек-
тивности элеронов на больших углах атаки (малых скоростях)
может вообще не позволить осуществить посадку самолета с не-
симметричными подвесками.
Глава 10
ДИНАМИЧЕСКИЕ СВОЙСТВА САМОЛЕТА В БОКОВОМ
ДВИЖЕНИИ
§ ЮЛ. Физическая природа развития бокового движения
Нарушение бокового равновесия самолета сопровождается воз-
никновением момента крена Мх и рыскания Му, что вызывает
вращение самолета одновременно вокруг осей Ох\ и Oyi. В этом
заключается особенность и сложность изучения динамических
свойств самолета в боковом движении, его устойчивости и управ-
ляемости. Собственно говоря, совместное проявление путевой и по-
перечной устойчивости и характеризует боковую устойчивость са-
молета.
Для того, чтобы лучше понять природу бокового движения,
рассмотрим развитие этого движения без управления летчиком
на примере воздействия бокового ветра (порыва).
Предположим, что устойчивый в путевом и поперечном отно-
шении самолет, выполняющий прямолинейный полет, попадает в
установившийся боковой поток, имеющйй скорость WZi в резуль-
тате чего возникает скольжение на правое крыло (поло-
жение I на рис. 10.1). Это приведет к появлению моментов крена
и рыскания. Под действием момента рыскания Му самолет будет
стремиться устранить скольжение, поворачиваясь навстречу на-
бегающему потоку (в нашем примере — вправо), а под действием
момента крена Мх начнет крениться в сторону, обратную сколь-
жению (в нашем примере на левое полукрыло).
284
ю
со
Рис. 10.1. Развитие малого бокового движения при воздействии бокового потока
Вращению самолета вокруг осей Охх и Оу\ препятствуют демп-
фирующие моменты крена и рыскания Когда
угол скольжения р станет равным нулю (положение //), крен до-
стигнет значительной величины. Обладая в этом положении неко-
торой угловой скоростью «г/, самолет будет продолжать вращаться
вправо, что приведет к возникновению скольжения на левое (опу-
Рис. 10.2. Изменение углов скольжения и крена
при малом боковом движении
щенное) полукрыло. В результате этого скольжения (положение
III на рис. 10.1) появятся моменты крена и рыскания другого зна-
ка. Первый момент начнет уменьшать угол крена, второй, погасив
сначала вращение самолета вправо, вызовет вращение его влево.
Затем весь процесс будет повторяться в обратном направлении до
тех пор, пока колебания не затухнут.
Когда колебания прекратятся, самолет развернется вправо
навстречу потоку на угол ф=р и сохранит некоторый остаточный
угол крена у0Ст. Начальное скольжение на правое полукрыло обус-
ловливает остаточный крен на левое полукрыло. Величина этого
угла крена будет тем больше, чем быстрее затухают колебания
рыскания и большей поперечной устойчивостью обладает самолет.
Период возникающих боковых колебаний сравнительно невелик
= 1-4-4 с), поэтому подобное движение иногда называют ко-
роткопериодическим или малым боковым движением. На рис. 10.2
показан характер изменения углов скольжения р и крена у в про-
цессе этого движения.
Из рассмотрения физической природы развития возмущенного
движения можно сделать вывод, что характер малого бокового
движения в основном определяется законом изменения угла сколь-
жения (движения рыскания). Величина и знак угла скольжения
определяют величину и знак моментов как рыскания так
и крена ЛГ₽р. Демпфирующие же моменты только препятствуют
вращению, обусловливая затухание возникающих колебаний. Та-
ким образом, колебания крена (движение крена) сопутствуют ко-
лебаниям рыскания и являются их следствием.
Рассмотрим дальнейшее поведение самолета после прекращения
малых боковых колебаний. Появление остаточного угла крена
286
Рис. 10.3. Развитие большого
бокового движения
после прекращения боковых колебаний самолета приведет к на-
рушению равновесия сил и подъемная сила уже не будет уравнен
вешивать силу тяжести. Появившаяся равнодействующая У-hG
(рис. 10.3) начнет искривлять траек-
торию в сторону опущенного полукры-
ла, что приведет к возникновению
скольжения на это полукрыло и, как
следствие, появлению моментов рыс-
кания и крена У устойчи-
вого самолета момент крена будет
стремиться устранить крен, а момент
рыскания — развернуть самолет и
устранить скольжение. Но как только
появится вращение вокруг оси Оух
(рыскание), возникнут демпфирующий
момент Адуеву, препятствующий вра-
щению, и спиральный момент крена
противоположно направлен-
ный восстанавливающему моменту
и, следовательно, стремящийся
увеличить угол крена. Если
> Л4"у(Ву*,го самолет, устраняя воз-
никшее скольжение, будет развора-
чиваться влево (в нашем примере) и
уменьшать угол крена. Когда крен и
угол скольжения будут устранены,
самолет успеет развернуться влево на
угол ф, совместив продолную ось са-
молета с исходным направлением дви-
жения (рис. 10.4).
Таким образом, по прекращении
бокового возмущенного движения, вы-
званного попаданием в боковой поток,
самолет, приобретая скорость по-
тока, совершает полет с углом сноса
(путевым углом) Т, равным по ве-
личине начальному углу скольжения
P = №z/V, но обратного знака. Из рассмотрения изменения траек-
тории и параметров движения в процессе бокового движения мож-
но прийти к выводу, что так же, как и продольное, боковое дви-
жение состоит из малого и большого движений (рис. 10.4). Малое
движение, развивающееся в первые несколько секунд после нару-
шения бокового равновесия, сопровождается сравнительно быстро
затухающими колебаниями углов скольжения, крена и угловых
* Точнее, если выполняется условие > МуМ^У, •
287
скоростей рыскания со у и крена со*. Слабое боковое перемещение
(вдоль оси Oz{) позволяет это движение в первом приближении
считать прямолинейным. Большое боковое движение, проявляю-
щееся в дальнейшем развитии возмущенного движения, приводит
с течением времени к значительному боковому перемещению цен-
Рис. 10.4. Развитие бокового движения при воз-
действии бокового потока
тра тяжести самолета. Строго говоря, большое и малое движения
развиваются одновременно. Однако за время, в течение которого
малые движения прекращаются, большие движения обычно не
успевают сколько-нибудь заметно проявиться.
Следует обратить внимание на то, что самолет, обладающий
путевой (яг₽<0) и поперечной (яг^ <0) устойчивостью, сам не
сохраняет направления движения. Больше того, если в процессе
развития больших боковых движений восстанавливающий момент
крена AfJ’p окажется меньше спирального момента крена
то самолет, предоставленный самому себе, будет увеличивать угол
крена и входить во все более глубокую спираль (штриховые ли-
нии на рис. 10.4). Такое поведение самолета называется спи-
ральной неустойчивостью. Так как спиральная неустой-
чивость приводит к сравнительно медленному увеличению угла
крена и кривизны траектории, то летчик или автопилот, осущест-
вляя управление, всегда может предотвратить вход самолета в
спираль и обеспечить прямолинейное движение. С этой точки зре-
ния спиральная неустойчивость опасности не представляет. Она
проявляется настолько медленно, что летчик часто ее вообще не
замечает.
Из сказанного следует, что управление самолетом в боковом
движении практически определяется только динамическими свой-
ствами самолета в малом боковом движении. Рассмотрим эти
свойства более подробно.
288
§ 10.2. Динамические свойства самолета в малом
боковом движении
Для исследования динамических свойств самолета в боковом
движении воспользуемся системой уравнений (0.15), которая с уче-
том связей (0.1) может быть записана в следующем виде:
mV == Z + G cos Н sin 7;
Jx~dt~ = ^ } (Ю.1)
j
у dt У’
где аэродинамические силы и моменты в пределах плавного обте-
кания являются следующими функциями параметров движения и
отклонения органов управления:
Z=Zpp +ZMH;
Мх = 4- + M*wy + Л1>8Э;
Му = МРр + 7И>Х 4- М^у 4- М^ЪЯ.
Для лучшего понимания динамических свойств самолета в ма-
лом боковом движении рассмотрим предварительно изолирован-
ные движения рыскания и крена.
При изолированном движении рыскания предполагается, что
угол крена у, угловая скорость cox и угловое ускорение крена
dtox/dt равны нулю. При этих допущениях первое и третье урав-
нения системы (10.1), описывающие движения рыскания, решаются
независимо от второго уравнения, описывающего движения крена.
Для упрощения решения задачи, кроме того, будем полагать,
что в процессе малых боковых движений самолет продолжает
двигаться прямолинейно. При таком движении My = d$/dt, первое
уравнение становится алгебраическим и его можно опустить из
рассмотрения. Тогда после деления третьего уравнения на Jy по-
лучим следующее дифференциальное уравнение, описывающее
изолированное движение рыскания:
+ + (Ю.2)
где
2*-,
Уравнение (10.2) имеет тот же вид, что и уравнение (8.7),
описывающее малое продольное движение. Поскольку для малого
бокового движения характерно £ = то по аналогии
с решением уравнения (8.22) для угла атаки получаем следующий
10-21 289
закон изменения угла скольжения при ступенчатом отклонении
руля направления:
3 = 0
г густ
1 - "₽'sin(a>/ + T₽) ,
(Ю.4)
Л п н *
где установившееся значение угла скольжения руст =—г°н
круговая частота = V Qj — nj; сдвиг фаз = arctg
Рис. 10.5. Переходный процесс изменения
угла скольжения при отклонении руля на-
правления
На рис. 10.5 показан типичный переходный процесс изменения
угла скольжения при ступенчатом отклонении руля направления,
из которого видно, что для изменения угла скольжения в движе-
нии рыскания (а соответственно и в малом боковом движении)
характерен периодический (колебательный) закон. Затухание ко-
лебаний (/гр) определяется путевым демпфирующим моментом
(ЛГ^у), а частота собственных колебаний (Йр) —путевой устой-
чивостью самолета. Поскольку естественное демпфирование коле-
баний рыскания меньше демпфирования колебаний малых про-
дольных движений, то заброс угла скольжения и время регулиро-
вания (затухание колебаний) обычно достигают значительных ве-
личин.
Зная круговую частоту оу можно найти период колебаний
угла скольжения Гр = 2т:/а)р и время срабатывания tcp^T^/4.
Рассмотрим теперь изолированное движение крена. При таком
движении предполагается, что угол скольжения и угловая скорость
рыскания не изменяются (например, равны нулю). Допустим, что
летчик отклонил элероны на величину 6Э. В результате появится
момент крена и самолет начнет ускоренно вращаться,
увеличивая угловую скорость и угол крена. По мере роста
будет. увеличиваться демпфирующий момент, препятствующий
вращению. Вследствие этого рост угловой скорости замедляется.
290
Когда демпфирующий момент станет равным моменту, создавае-
мому элеронами, угловая скорость достигнет максимального (уста-
новившегося) значения. Для аналитического исследования изоли-
рованного движения крена воспользуемся вторым уравнением си-
стемы (10.1), которое при сделанных допущениях запишется в сле-
дующем виде:
= (10.5)
где
. .0) ч
Мх*
Уравнение (10.5) представляет собой линейное неоднородное
дифференциальное уравнение первого порядка. Общее его решение,
как известно, является суммой, составленной из решения одно-
родного уравнения и какого-либо частного решения ш неодно-
родного уравнения:
= + %• <10-7)
Решение однородного уравнения ищем в следующем виде:
юх = ce,pi •
После подстановки этого решения в формулу (10.5) получаем:
рсер1 пш cept = 0.
Отсюда после сокращения на cept находим р = —па. .
X
В качестве частного решения неоднородного уравнения прини-
маем установившееся значение угловой скорости при ступенчатом
отклонении элеронов
«г
= ' (10'8)
Таким образом, общее решение (10.7) неоднородного уравне-
ния (10.5) запишется в следующем виде:
= (Ю.8')
Постоянную интегрирования с находим по начальным усло-
виям: при / = 0; сол = 0. После подстановки начальных условий в
(10.8') получаем
п*
о = с 4-S9,
ю*
291
откуда
л5
с =----------
ntn 3
Тогда закон изменения угловой скорости крена при ступенча-
том отклонении элеронов можно записать в следующем виде:
“х = ^Уст(1 (10.9)
Рис. 10.6. Изменение угловой скорости
и угла крена при отклонении элеронов
Поскольку М** < 0, а = >0, то с течением
"(D
времени е х уменьшается, а соответственно угловая скорость сох
увеличивается. При дальнейшем увеличении времени t угловая
скорость со>; стремится к
установившемуся значению
сох уст. На рис. 10.6 показан
сплошной линией переход-
ный процесс изменения уг-
ловой скорости крена при
ступенчатом отклонении
элеронов. Для определения
времени регулирования, в
течение которого угловая
скорость крена достигнет
0,95 co* уст, воспользуемся
формулой (8.16)
t
рег ~ ’
х
Если бы летчик продол-
жал удерживать элероны
в отклоненном положении,
то самолет, вращаясь с угловой скоростью шхуст, продолжал бы
неограниченно увеличивать угол крена (рис. 10.6). Поэтому
для накренения самолёта на заданный угол у3 летчик
должен своевременно возвратить элероны в нейтральное положе-
ние. В этом случае демпфирующий момент, препятствуя враще-
нию, сравнительно быстро погасит угловую скорость; угол же
крена будет продолжать расти до тех пор, пока угловая скорость
не станет равной нулю. На рис. 10.6 показано штриховой линией
изменение угловой скорости и угла крена при возвращении элеро-
нов в нейтральное положение в момент времени
Полагая при изолированном движении крена & = 0, получим из
(0.7) (/у/Л = (о%. Поэтому при известном законе изменения угло-
вой скорости крена угол крена определится
t
292
Этот интеграл численно равен площади, заштрихованной на
рис. 10.6. Ранее мы рассмотрели изолированные движения рыска-
ния и крена. В действительности эти движения взаимосвязаны и
проявляются одновременно. Связывающим параметром является
угол скольжения, который определяет величину и направление
мх
Рис. 10.7. Реакция поперечно устойчивого само-
лета на отклонение руля направления:
а — появление моментов рыскания и крена при откло-
нении руля направления; б — изменение угла крена
при отклонении руля направления
моментов рыскания и крена. Поэтому изменения угла скольжения
в процессе движения рыскания, как правило, сопровождаются и
движением крена. Больше того, у самолетов с высоким располо-
жением вертикального оперения при отклонении руля направления
сначала может начать развиваться движение крена, а затем уже
движение рыскания. Последнее объясняется тем, что при отклоне-
нии руля направления появляется не только момент рыскания, но
и крена (рис. 9.8), вследствие чего при моментах инерции Л, су-
щественно меньших моментов 1У, самолет сначала начинает кре-
ниться в сторону, противоположную отклонению руля направле-
ния (рис. 10.7), а затем уже после развития движения рыскания,
движение крена будет определяться изменением угла скольже-
ния,
293
Изолированное же движение крена практически можно реали-
зовать лишь на углах атаки, близких к нулю, и малых углах крена.
На углах атаки, отличных от нуля, вращение самолета с угловой
скоростью сох, как это было показано в § 9.2, приводит к возник-
новению скольжения на опускающееся полукрыло, а следовательно,
и к развитию движения рыска-
ния.
Отсюда следует, что малое
боковое движение представляет
собой совместное проявление дви-
жений рыскания и крена, для ис-
следования которого, строго гово-
ря, необходимо использовать пол-
ную систему уравнений (10.1).
Поскольку закон изменения
угла скольжения формируется в
движении рыскания, то и харак-
тер собственного малого бокового
движения в основном определя-
ется движением рыскания. Од-
нако отсюда не следует, что ко-
лебания крена не имеют значе-
ния. Если поперечная устойчи-
вость велика, то движение рыска-
ния будет сопровождаться силь-
ным изменением угла крена, что
существенно затрудняет пилоти-
рование самолета, например при
боковых порывах ветра, отказах
бокового двигателя.
10.8 показано штриховыми линия-
Рис. 10.8. Изменение углов сколь-
жения и крена при отказе левого
двигателя
В качестве примера на рис.
ми совместное проявление движения рыскания и крена при отказе
левого двигателя, расположенного на крыле, в установившемся
горизонтальном полете на высоте 5000 м и скорости 700 км/ч.
Как видно из рассмотрения этих кривых, в течение первой се-
кунды самолет накреняется на левое полукрыло на 13°, что не
представляет большой опасности. Однако положение существенно
ухудшается, если отказ двигателя произойдет в режиме разгона
или набора высоты, когда тяга максимальна, а скорость сравни-
тельно мала. На рис. 10.8 сплошными линиями показаны измене-
ния углов крена и скольжения при отказе двигателя на той же
высоте и скорости полета, но при форсажном режиме работы
двигателей в процессе разгона самолета. В этом случае к первой
секунде угол крена увеличивается до 40°, что уже представляет
серьезную опасность. Еще хуже было бы положение, если бы
отказ двигателя, работающего на форсажном режиме, произошел
на малой скорости, например на взлете. Опасное изменение пара-
метров движения при отказе одного двигателя у самолета с раз-
несенными по крылу двигателями иногда может явиться причиной
294
ограничения использования форсажного режима двигателей на
взлете.
Важным параметром, характеризующим одновременное прояв-
ление движений рыскания и крена в процессе малых боковых дви-
жений, является отношение угловой скорости крена к угловой
скорости рыскания со^.
Рис. 10.9. Ось вращения самолета в процессе малых боковых дви-
жений
Можно показать, что в процессе малого бокового движения
самолет вращается вокруг оси ДЛ, показанной на рис. 10.9. Зна-
чения координат Хо и уо, определяющих положение оси АА отно-
сительно центра масс самолета, можно вычислить по формулам:
xQ = ——; Уо =----—»
и тх^ z ту$
где и ур — координаты бокового фокуса.
Из рис. 10.9 находим отношение угловых скоростей крена и
рыскания:
шх
Уо *
Подставляя значения х0 и у0 и учитывая, что = zn^/zz^,
получаем следующее отношение угловых скоростей:
I
СОХ ___ тХ 2У
wy lx
(10.10)
Тактико-техническими требованиями, предъявляемыми к само-
летам, регламентируется не мгновенное отношение угловых ско-
ростей крена и рыскания, а их амплитуд (сох) шах/(сортах, обозна-
295
чаемое параметром х «каппа». Как показывают исследования, па-
раметр х пропорционален отношению их/ыу (10.10):
( мх) щах
(0Jy)max
тх Jy_
Му 4
(10.11)
С развитием авиационной техники, с ростом скоростей и вы-
сот полета маневренные самолеты приобретают все более вытяну-
тые формы с крыльями относительно малого размаха. Вследствие
этого соотношение моментов 1У/1Х все более увеличивается и мо-
жет достигать 10—15. Увеличивается при этом и параметр х. При
изменении режима полета претерпевают значительные изменения
характеристики поперечной и путевой устойчивости. Поэтому, как
показывает летная практика, у современных самолетов параметр х
может изменяться в широких пределах.
Если собственные динамические свойства в малом боковом дви-
жении определяются движением рыскания и параметром х, то
управление боковым движением при маневрировании в основном
осуществляется с помощью органов поперечного управления, созда-
ющих моменты для изменения угла крена.
Необходимость получения хороших маневренных свойств са-
молета предъявляет повышенные требования к эффективности по-
перечного управления и быстродействию движения крена. Харак-
теристикой быстродействия крена является максимальная угловая
скорость крена (сох)тах, создаваемая отклонением органов попе-
речного управления. Если предположить, что при отклонении орга-
нов поперечного управления (например, элеронов) самолет со-
вершает изолированное движение крена, то в соответствии с урав-
нением (10.8) максимальная угловая скорость крена определялась
бы выражением:
б
т »
=------8
' л/max со э max'
тх
Однако такие угловые скорости реально могут быть достигнуты
только на сравнительно малых углах атаки. Появление неблаго-
приятного скольжения при вращении самолета вокруг продольной
оси на больших углах атаки (рис. 9.12) сопровождается значитель-
ным снижением эффективности поперечного управления.
Важной характеристикой эффективности поперечного управле-
ния в криволинейном движении самолета является градиент
dcox/^бэ, показывающий, какую угловую скорость крена приобре-
тает самолет при отклонении элеронов на один градус. Производ-
ная dax/db3 определяется из выражения (10.8)
d^x
d*9
mJ?
(10.12)
296
Чем больше производная dcox/dd3, тем выше эффективность
элеронов. Об изменении эффективности поперечного управления с
изменением числа М полета можно судить по кривой, приведенной
на рис. 10.10. С увеличением скорости полета, с одной стороны,
уменьшается угол атаки и, как следствие, уменьшается неблаго-
Рис. 10.10. Зависимость характери-
стики от числа М полета
приятное скольжение, препятст-
вующее вращению; с другой сто-
роны, уменьшается величина, ха-
рактеризующая демпфирующий
момент крена Если бы ха-
рактеристика эффективности эле-
ронов tn* оставалась неизмен-
ной, производная d^x/db3 с рос-
том скорости (числа М) полета
увеличилась бы. Однако на боль-
ших околозвуковых скоростях,
особенно сверхзвуковых скоро-
стях полета, эффективность элеронов иг* существенно уменьшает-
ся, что и объясняет изменение производной dw>x/db3, показанное
на рис. 10.10.
Иногда в качестве характеристики поперечной управляемости ,
применяется величина, обратная d(ox/d63:
(О
тхх
т э
(10.13)
Она называется градиентом отклонения элеронов по угловой ско-
рости крена. Градиент db3/dax численно равен отклонению элеро-
нов, необходимому для получения угловой скорости крена 1 рад/с.
Важной характеристикой управляемости самолетом в криво-
линейном движении является градиент усилия по угловой скорости
крена Р"х = dP3/d®x. Он численно равен усилию на ручке управ-
ления элеронами, необходимому для получения установившейся
угловой скорости крена, равной 1 рад/с. Градиент усилия по угло-
вой скорости крена прямо пропорционален производной и
зависит от передаточного отношения от ручки к элеронам и жест-
кости загрузочного механизма.
§ 10.3. Влияние эксплуатационных факторов на динамические
свойства в малом боковом движении.
Требования, предъявляемые к ним
Выше выяснили, что собственные динамические свойства само-
лета в боковом движении определяются аэродинамической ком-
поновкой и зависят от характеристик tn?., т^х и соот-
ношения моментов инерции 1У : 1Х. Изменение аэродинамических
характеристик при данной компоновке самолета в основном зави-
297
сит от режима полета, а моментов инерции — от распределения
масс по длине фюзеляжа и размаху крыла.
Поскольку аэродинамические и инерционные характеристики
зависят от угла стреловидности крыла, то при изменении угла
стреловидности крыла в полете динамические свойства самолета
в боковом движении могут претерпевать значительные изменения.
Качество переходного процесса в малом боковом движении
оказывает большое влияние на условия пилотирования. Если слу-
чайно возникшее скольжение вызывает слабозатухающие и с боль-
шой амплитудой колебания самолета по крену, точное пилотиро-
вание, особенно при прицеливании и стрельбе, становится невоз-
можным. Поэтому к качеству переходного процесса в малом бо-
ковом движении предъявляются вполне определенные требования:
боковые колебания самолета должны быть быстрозатухающими
и небольшими по амплитуде.
Эти требования выражаются в нормировании основных харак-
теристик переходного процесса:
— времени затухания боковых колебаний (до 5% от началь-
ной амплитуды) /зат’,
— уменьшения амплитуды колебаний за один период тзат;
— соотношения амплитуд колебательных составляющих угло-
вых скоростей Крена И рыскания Х = ((tf х) max/(сортах.
Затухание колебаний считается приемлемым, если /3ат^б4-8 с,
а тзат^2ч-3. Эти характеристики в основном определяются путе-
вым демпфирующим моментом (^у) и путевой устойчивостью
«)•
Особую роль играет параметр х. Если величина х превышает
2,5—4, самолет в ответ на небольшие изменения угла скольжения
отвечает существенным накренением. Это затрудняет пилотирова-
ние и требует дополнительного внимания летчика. Как было по-
казано выше в формуле (10.11), параметр х зависит от соотно-
шения коэффициентов поперечной и путевой устой-
чивости и моментов инерции относительно нормальной (1У) и про-
дольной (Л) осей.
Малые значения х (вплоть до нуля) не вызывают каких-либо
ухудшений пилотирования, т. е. самолеты, обладающие малой
поперечной, но большой путевой устойчивостью всегда получают
хорошую оценку летчиков. Появившийся случайно угол скольже-
ния такой самолет устраняет непосредственно за счет момента
рыскания практически без крена. Летчик может и не заметить та-
кую реакцию самолета на скольжение.
Изменение режима полета влияет на величину параметра х.
Так, увеличение угла атаки приводит к росту поперечной устойчи-
вости, к уменьшению путевой и, следовательно, к увеличению па-
раметра х. На больших сверхзвуковых скоростях параметр х уве-
личивается вследствие уменьшения путевой устойчивости.
На величину этой характеристики, причем, как правило, на
ее возрастание, оказывают влияние и некоторые эксплуатацией*
298
ные факторы. На режимах полета, на которых путевая устойчи-
вость при обычной центровке мала, смещение центра тяжести са-
молета назад может заметно ее уменьшить. Это приведет к уве-
личению х.
Существенное влияние на характер переходного процесса в
боковом движении могут оказать подвески. Путевая устойчивость
у самолета с подвесками обычно уменьшается. Подвески ста-
раются размещать вблизи центра тяжести самолета. Но боковой
фокус самой подвески обычно располагается впереди ее центра
тяжести. Это приводит к смещению бокового фокуса вперед у
всего самолета и соответственно к уменьшению его путевой устой-
чивости.
В ряде случаев максимальная скорость (число М) самолета
с подвесками ограничивается вследствие уменьшения путевой
устойчивости. Подвески оказывают влияние и на поперечную устой-
чивость самолета.
С одной стороны, они препятствуют перетеканию потока под
фюзеляжем, что приводит к дополнительному повышению давле-
ния под крылом и соответственно к увеличению поперечной устой-
чивости самолета.
С другой стороны, это повышение давления приводит к воз-
никновению дополнительной боковой силы Z на подвеске. Момент
этой силы направлен в противоположную сторону и вызывает умень-
шение поперечной устойчивости самолета. Суммарный эффект за-
висит от конкретной компоновки самолета. В большинстве слу-
чаев т?х из-за влияния подвесок увеличивается.
Несимметричный сброс подвесок приводит к нарушению как
поперечного, так и путевого равновесия из-за весовой несиммет-
рии и несимметрии лобового сопротивления. Последнее обусловли-
вает появление скольжения на полукрыло со сброшенной подвес-
кой, в результате которого возникает кренящий момент у устой-
чивого в поперечном отношении самолета. Момент крена увели-
чивается за счет весовой несимметрии. На рис. 10.11 показано в
качестве примера изменение угловых скоростей и и углов
крена, скольжения и рыскания при несимметричном сбросе под-
весок (с левого полукрыла) на большой высоте. Предполагается,
что летчик при несимметричном сбросе подвески не вмешивается
в управление. Появившиеся моменты рыскания и крена развора-
чивают и кренят самолет в сторону правого полукрыла. Момент
рыскания обусловливает появление слабозатухающих колебаний
угла скольжения, которые несимметричны из-за увеличения угла
крена и связанного с ним возникновения скольжения на опускаю-
щееся полукрыло. К 2,5 с самолет успевает накрениться на 40°.
Накренение подъемной силы приводит к развороту самолета в го-
ризонтальной плоскости на угол ф.
Несвоевременное парирование возникающих моментов или не-
достаточная эффективность элеронов может в некоторых случаях
привести к перевороту самолета на спину. На сверхзвуковой ско-
299
роста вследстЁие увеличения лобового сопротивления подвесок и
уменьшения путевой устойчивости самолета эффект от несиммет-
ричного сброса подвесок усиливается.
У самолетов с изменяемой в полете стреловидностью крыла
характеристика х в сильной степени зависит от угла стреловидно-
сти. Увеличение угла стреловидности % вызывает увеличение попе-
Рис. 10.11. Изменение параметров боково-
го движения при несимметричном (с ле-
вого полукрыла) сбросе подвесок
речной устойчивости и незначительно влияет на путевую устойчи-
вость. Одновременно уменьшается момент инерции относительно
продольной оси /х. Это приводит к росту х (формула ЮЛЬ) и
соответствующему ухудшению характеристик боковых динамиче-
ских свойств самолета. Напротив, уменьшение параметра х при
уменьшении стреловидности оказывает благоприятное влияние на
управление при взлетно-посадочных режимах. Заметим, что уве-
личение параметра х до 2,5—4 не очень усложняет пилотирование.
Однако дальнейшее увеличение х допустимо лишь в том случае,
когда средствами автоматики представляется возможным сущест-
венно уменьшить время затухания боковых колебаний.
Обеспечение хороших маневренных свойств самолета предъяв-
ляет определенные требования к характеристикам поперечной
управляемости.
Во-первых, необходимо, чтобы при полном отклонении элеро-
нов самолет приобретал достаточно большую угловую скорость
крена. На рис. 10.12 показаны оценки эффективности поперечного
управления самолета, даваемые летным составом, в функции ско-
рости полета (в долях скорости сваливания в горизонтальном по-
лете). Как видим, хорошая оценка летным составом при
300
V/Vcb. г. n=2-r-3 500—750 км/ч) дается тогда, когда при пол-
ном отклонении элеронов самолет приобретает угловую скорость
крена ~2 рад/с. Это значит, что при такой эффективности элеро-
нов маневренный самолет за 1 с накреняется на угол не менее
90—100°.
Во-вторых, для создания угловой скорости крена летчик не
должен прикладывать как излишне большие, так и чрезмерно
малые усилия. Летная практика показывает, что для создания
Рис. 10.12. Летная оценка эффективности
поперечного управления
угловой скорости, равной 1 рад/с, летчик должен прикладывать
усилие (Р“х) не более 8—10 кгс (~80—100 Н) и не менее
2—3 кгс. При этом на различных режимах полета градиент
не должен изменяться более чем в 2—3 раза.
Глава 11
ВЗАИМОДЕЙСТВИЕ ПРОДОЛЬНОГО И БОКОВОГО
ДВИЖЕНИЙ
§ 11.1. Аэродинамические, кинематические и инерционные
перекрестные связи
Значительное изменение аэродинамических форм и компонов-
ки современных самолетов привело к существенному усилению
взаимодействия продольного и бокового движений. В результате
этого взаимодействия на некоторых режимах полета может на-
блюдаться необычная, на первый взгляд противоестественная, ре-
акция самолета на отклонение органов управления.
301
Причиной взаимодействия продольного и бокового движений
является наличие аэродинамических, кинематических и инерцион-
ных перекрестных связей.
Аэродинамические перекрестные связи. Под
аэродинамическими перекрестными связями понимают зависимость
аэродинамических сил и моментов продольного движения от па-
раметров бокового движения, и наоборот: зависимость аэродина-
мических сил и моментов бокового движения от параметров про-
дольного движения.
Примером возникновения аэродинамической перекрестной свя-
зи может служить зависимость характеристики поперечной устой-
чивости от угла атаки а и числа М полета. Физические при-
чины этой зависимости у самолетов со стреловидными и треуголь-
ными крыльями были рассмотрены в гл. 3. При уменьшении угла
атаки поперечная устойчивость у таких самолетов существенно
уменьшается. В результате этого при некотором небольшом поло-
жительном или отрицательном угле атаки самолет может потерять
поперечную устойчивость. При дальнейшем уменьшении угла атаки
он становится неустойчивым в поперечном отношении. Это значит,
что в зависимости от исходного угла атаки создание одного и того
же скольжения может вызвать не только изменение момента крена
по величине, но и по знаку, изменяя прямую реакцию по крену
на отклонение руля направления на обратную, и наоборот. Если
при положительном угле атаки возникло скольжение, а затем
летчик уменьшает угол атаки при сохранившемся скольжении, то
момент крена, обусловленный поперечной устойчивостью, сначала
уменьшается по величине, а начиная с некоторого угла атаки даже
меняет знак.
Некоторое влияние на изменение момента крена при скольже-
нии оказывает и несимметричное обтекание левой и правой поло-
вин стабилизатора. Так, например, при скольжении на правое по-
лукрыло отклонение ручки управления стабилизатором приводит
к большему изменению подъемной силы на правой половине ста-
билизатора (левая половина затенена фюзеляжем и килем), а при
скольжении на левое полукрыло — на левой половине стабилиза-
тора. Вследствие несимметричного изменения подъемных сил по-
ловин стабилизатора при скольжении отклонение ручки управле-
ния по тангажу сопровождается изменением момента крена: при
скольжении на правое полукрыло отклонение ручки от себя создает
момент крена влево, а отклонение ручки на себя—момент крена
вправо.
Другим примером возникновения аэродинамической перекрест-
ной связи, оказывающей большое влияние на проявление взаимо-
связи продольного и бокового движений, может служить зависи-
мость путевой устойчивости т?у, а соответственно и момента рыс-
кания от угла атаки и числа М полета. Эта зависимость прояв-
ляется наиболее сильно на больших углах атаки и дозвуковых
скоростях полета, она также имеет место и на больших сверхзву-
302
ковых скоростях полета. Потеря путевой устойчивости при выходе
на большие углы атаки на дозвуковых режимах полета может
явиться причиной преждевременного сваливания и входа самолета
в штопор (см. § 11.5).
Особенно сильная аэродинамическая взаимосвязь продольного
и бокового движений может наблюдаться на больших углах атаки,
на которых возможно возникновение срыва потока.
Рис. 11.1. Изменение углов атаки и скольжения при вращении самолета
вокруг продольной оси
Кинематические перекрестные связи. Эти связи
возникают при вращении самолета, которое сопровождается пе-
риодическим изменением углов атаки и скольжения, от величины
которых зависят силы и моменты в продольном и боковом движе-
ниях. При рассмотрении эффективности элеронов на больших уг-
лах атаки (глава 9) уже обращалось внимание на существование
кинематической перекрестной связи между углом атаки и сколь-
жения. Рассмотрим более подробно проявление этой связи в наи-
более характерном случае.
Предположим, что самолет выполняет полет с некоторым по-
ложительным углом атаки а при угле скольжения р = 0
(рис. 11.1,а). Пусть летчик отклонением ручки управления вправо
создал вращение самолета вокруг продольной оси с некоторой
угловой скоростью (ох. Легко усмотреть, что такое вращение бу-
дет сопровождаться периодическим изменением угла атаки и сколь-
жения. В самом деле при накренении самолета угол атаки начнет
уменьшаться, но появится скольжение на опущенное крыло. Если
самолет не будет препятствовать изменению углов атаки и сколь-
жения и вращение будет происходить строго вокруг продольной
оси О%1, то при накренении на 90° угол атаки станет равным нулю,
а скольжение на опущенное правое полукрыло достигнет угла р,
равного по величине исходному значению угла атаки (рис. 11.1,6).
Дальнейшее вращение самолета приведет к уменьшению угла
скольжения и появлению отрицательного угла атаки (рис. 11.1,в),
затем исчезновению угла атаки и возникновению скольжения на
левое полукрыло и т. д.
В соответствии с изменением углов атаки и скольжения будет
меняться поперечный момент, который при одном и том же откло-
нении элеронов будет либо увеличивать, либо уменьшать скорость
вращения самолета. Таким образом, меняя угол атаки, летчик при
неизменном положении элеронов изменяет в широких пределах
угловую скорость крена. Эту особенность необходимо учитывать
303
при пилотировании, чтобы значительное уменьшение угловой ско-
рости на больших углах атаки или выход на чрезмерно большие
угловые скорости крена при малых положительных или отрица-
тельных углах атаки не были для летчика неожиданностью.
При рассмотрении реакции самолета на отклонение элеронов
предполагали, что его вращение происходит строго вокруг про-
дольной оси Охр Чем меньше продольная и путевая устойчивость
Рис. 11.2. Ось вращения самолета при отклонении элеронов
самолета и больше угловая скорость крена, тем ближе к продоль-
ной оси его действительная ось вращения. Наличие устойчивости
по перегрузке и путевой устойчивости обусловливают при измене-
нии углов атаки и скольжения появление восстанавливающих про-
дольных и путевых моментов, которые препятствуют изменению
углов атаки и скольжения при вращении самолета. Так, например,
уменьшение угла атаки и появление скольжения на опускающееся
полукрыло при вращении самолета сопровождается возникнове-
нием кабрирующего момента, стремящегося восстановить исход-
ный угол атаки, и появлением момента рыскания, стремящегося
опустить нос самолета и устранить возникшее скольжение.
Если угловая скорость вращения самолета велика, а запасы
устойчивости по перегрузке и путевой устойчивости малы, то вос-
станавливающие моменты Mty и не успевают сколько-нибудь
значительно отклонить продольную ось самолета и она практиче-
ски совпадает со связанной продольной осью Охх (рис. 11.1). Дру-
гая картина происходит при малой угловой скорости вращения
и больших запасах устойчивости по перегрузке и путевой устойчи-
вости. В этом случае самолет успевает восстановить исходные
значения углов атаки и скольжения, практически вращаясь вокруг
вектора скорости. При таком движении носовая часть фюзеляжа
описывает в пространстве некоторый-конус, осью которого яв-
ляется вектор скорости. Углы атаки и скольжения при этом прак-
тически остаются неизменными. Обычно действительная ось вра-
щения самолета при отклонении элеронов располагается между
вектором скорости и продольной связанной осью Охх (рис. 11.2).
Инерционные перекрестные связи. Одной из при-
чин возникновения инерционных перекрестных связей является ги-
роскопический момент ротора двигателя, появляющийся при вра-
304
щении самолета вокруг оси, не совпадающей с собственной осью
вращения ротора двигателя.
Происхождение этих моментов можно показать на следующем
простом примере. Пусть две массы mb т2, соединенные стержнем,
вращаются вокруг оси Ох с некоторой угловой скоростью сох
(рис. 11.3,а). Попытаемся изменить положение оси вращения,
создав в момент прохождения стержнем горизонтального положе-
Рис. 11.3. Возникновение гироскопического момента
ния кратковременным импульсом угловую скорость о^. В резуль-
тате этого масса т\ приобретет дополнительную скорость AVb
направленную вперед, а масса т2 — скорость ДУ2, направленную
назад. При дальнейшем вращении системы с угловой скоростью со*
массы т} и т2, стремясь по инерции сохранить приобретенные ско-
рости, создадут гироскопический момент Л4гГир, который при пере-
ходе из положения а в положение б (рис. 11.3) будет стремиться
повернуть ось Ох вокруг оси Oz. Таким образом, гироскопический
момент появляется при вращении тела вокруг двух осей и дей-
ствует относительно третьей, им перпендикулярной, аналогично
тому, как это имеет место у гироскопа.
Вращающийся ротор компрессора и газовая турбина реактив-
ного двигателя представляют собой большие гироскопы. Такой
гироскоп, укрепленный на самолете, имеет три степени свободы.
Во-первых, он может вращаться вокруг собственной оси, которую
обычно считают совпадающей со связанной осью Охх, Во-вторых,
гироскоп может вращаться вместе с самолетом вокруг взаимно
перпендикулярных осей Оу\ и Ozb Величина продольного гиро-
скопического момента ротора двигателя, как известно, определя-
ется по формуле
^гир ===
где 7Р — момент инерции ротора двигателя; сор и со — соответст-
венно угловые скорости вращения собственно ротора двигателя и
305
вращения самолета вокруг оси, не совпадающей с осью вращения
ротора двигателя.
Направление действия гироскопического момента удобно опре-
делить, воспользовавшись следующим мнемоническим правилом.
Представьте себя сидящим в кабине самолета. Плоскость враще-
ния ротора двигателя изобразим окружностью, а направление вра-
щения ротора стрелками по окружности (рис. 11.4). Если из
Рис. 11.4. Определение направления действия гироско-
пического момента ротора двигателя
центра окружности провести одну стрелку 1 в направлении дви-
жения носа самолета при вращении с угловой скоростью соу,
а другую 2— по касательной к окружности в направлении враще-
ния ротора двигателя, то эта стрелка 2 покажет направление до-
полнительного (прецессионного) движения носа самолета, вызван-
ного действием гироскопического момента ТРД. Так, например,
при левом вращении ротора двигателя и принудительном разво-
роте носа самолета влево появится гироскопический (пикирующий)
момент, который будет стремиться опустить нос самолета
(рис. 11.4).
Самолет, вращающийся с некоторой угловой скоростью^ отно-
сительно одной из осей координат, также можно рассматривать
как некоторый гироскоп, который, сопротивляясь изменению по-
ложения оси вращения, создает гироскопический (инерционный)
момент. В самом деле, представим распределение масс в самолете
схематически в виде двух сосредоточенных масс, разнесенных
вдоль фюзеляжа (рис. 11.5). Предположим, что у самолета, вра-
щающегося вокруг оси Ох! с угловой скоростью сох, летчик откло-
нением руля направления создал вращение самолета вокруг оси
Ог/1 С УГЛОВОЙ СКОрОСТЬЮ (Dt/.
Одновременное вращение самолета с угловыми скоростями сох
и (Ог/ эквивалентно вращению самолета вокруг некоторой оси а—а
с угловой скоростью (о. Так как сосредоточенные массы т\ и т2
расположены не на этой оси вращения, то появятся центробежные
306
силы Fi и F2. Они создадут относительно центра тяжести само-
лета инерционный (гироскопический) момент вокруг оси ко-
торый, как это видно из рис. 11.5, стремится поднять нос самолета
и увеличить угол атаки. Величина этого момента М2Ин опреде-
ляется вторым слагаемым левой части уравнения моментов (0.2).
Если перенести это слагаемое в правую часть и рассматривать его
Рис. 11.5. Появление продольного инерционного момента
как действующий на самолет момент, то продольный инерцион-
ный момент определится выражением
ин = Ux — /у) "х^у- (11.2)
При вращении самолета вокруг оси, не совпадающей с одной
из связанных осей, кроме продольного инерционного момента воз-
никают инерционные моменты рыскания и крена:
^у ин = (Аг h) (11.3)
Мх ин “ (/у 4) шу®г- (11.4)
Как видим, инерционные моменты пропорциональны произведе-
нию угловых скоростей на разность моментов инерции 1Х—Iyt
lz—lx и 1У—Iz, В отличие от восстанавливающих (стабилизирую-
щих) моментов, обеспечивающих возвращение самолета к исход-
ному режиму полета, инерционные моменты являются дестабили-
зирующими, стремящимися увести самолет от заданного режима
полета.
§ 11.2. Критические скорости вращения.
Аэроинерционное вращение
При небольших скоростях вращения инерционные моменты
малы и без управляющих действий летчика уравновешиваются на
устойчивом по перегрузке и в путевом отношении самолете стаби-
лизирующими моментами при незначительном увеличении углов
атаки и скольжения. С ростом скорости вращения вокруг оси, не
совпадающей с одной из связанных осей, инерционные моменты
увеличиваются пропорционально квадрату угловой скорости. По-
этому для их балансировки требуются большие стабилизирующие
аэродинамические моменты, а следовательно, значительное изме-
нение углов атаки и скольжения. При некоторой большой скорости
307
йрйщения аэродинамические моменты уже не в состояний урав-
новесить инерционные моменты, и самолет теряет либо путевую,
либо продольную устойчивость.
Изменение аэродинамической компоновки современных само-
летов, связанное с применением тонких крыльев малого удлине-
ния, привело к тому, что масса самолета располагается в основ-
ном вдоль фюзеляжа. Поэтому моменты инерции самолета 1У и 1г
возросли во много раз по сравнению с моментом инерции 1Х.
В результате такого изменения инерционных характеристик само-
летов увеличиваются разности 1У—1Х и 1г—Л, что сопровождается
ростом инерционных моментов Л42ин и Му ин (формулы 11.2 и
11.3) и, как следствие, уменьшением критических угловых скоро-
стей крена, при которых наблюдается потеря путевой или про-
дольной устойчивости.
Критические угловые скорости крена можно определить по
следующим приближенным выражениям:
(П.5)
где ^кра и шкр₽ —критические угловые скорости, при которых
теряются соответственно продольная и путевая устойчивость. Так
как
/И” = т«р ~ Sb-,
ЛЦ = т?р¥-31,
то критические скорости вращения самолета тем больше, чем боль-
ше продольная и путевая устойчивости и на боль-
шей приборной скорости осуществляется полет. При изменении
режима полета меняются характеристики т* и приборная
скорость, а следовательно, и критические скорости вращения.
На рис. 11.6 показана сплошными линиями характерная зави-
симость критических скоростей вращения современного самолета
от числа М полета. Как видим, критические скорости «>кра и <окрР
могут существенно отличаться одна от другой. При этом если
на дозвуковых скоростях полета наименьшее значение критиче-
ской скорости вращения обычно определяется продольной устой-
чивостью, то на больших сверхзвуковых скоростях — путевой
устойчивостью.
Предположим, что при вращении вокруг продольной оси само-
лет превысил наименьшую критическую скорость, определяемую,
например, устойчивостью по перегрузке. На первый взгляд может
показаться, что в этом случае самолет, неограниченно увеличивая
308
угол атаки, под действием разности инерционного й аэродинами-
ческого моментов будет устанавливаться перпендикулярно к векто-
ру скорости. В действительности этого не получается. В рассматри-
ваемом случае при превышении наименьшей критической скорости
самолет, теряя продольную устойчивость, увеличивает угол атаки,
стремясь отклонить продольную ось самолета от его оси вращения.
Рис. 11.6. Зависимость критических угловых скоростей
вращения от числа М полета
Но, сохраняя путевую устойчивость, будет стремиться уменьшить
угол скольжения, а следовательно, и угол атаки, совмещая про-
дольную ось самолета с его осью вращения. Аналогичная картина
имела бы место и при потере путевой, но сохранении продольной
устойчивости. Таким образом, проявление взаимосвязи продоль-
ного и бокового движений, обуславливая при вращении потерю
устойчивости, в рассматриваемом случае не приводит к неограни-
ченному увеличению углов атаки и скольжения.
Таким образом, при превышении одной из критических скоро-
стей самолет будет совершать неустойчивое вращение, сопровож-
дающееся колебаниями углов атаки и скольжения. Так как враще-
ние самолета с угловой скоростью, превышающей наименьшее зна-
чение критической скорости, связано с большим влиянием инер-
ционных моментов, то такое движение называют аэроинер-
ционным вращением. Такое наименование этому вращению
дано потому, что инерционные моменты обусловливают возникно-
вение скольжения, а при скольжении возникают мощные аэроди-
намические моменты крена, которые в состоянии вращать самолет
даже против отклоненных элеронов. Поскольку причиной аэро-
инерционного вращения является скольжение, то для его предот-
вращения необходимо устранить скольжение «дачей ноги» против
вращения (против действия инерционного момента Му Ин).
На рис. 11.6 штриховой и штрихпунктирной линиями показаны
также установившиеся угловые скорости крена, соответствующие
максимальному отклонению элеронов разной эффективности. Как
видно из рисунка, в диапазоне чисел М2<М<Мз при полном от-
клонении элеронов малой эффективности (штрихпунктирная ли-
309
йия) невозможно вообще достичь наименьшей критической скоро-
сти крена. Кроме того, следует иметь в виду, что если самолет
достиг критической скорости, то это еще не означает, что он сразу
начнет неустойчивое вращение. Оно станет возможным только
тогда, когда в процессе вращения самолет приобретает вполне
определенные значения углов атаки и скольжения, но для этого
требуется некоторое время, зависящее от соотношения моментов
инерции 1У/1Х и lz/lx.
§ 11.3. Особенности проявления взаимосвязи продольного
и бокового движения при выполнении маневров
Совместное проявление аэродинамических, кинематических и
инерционных перекрестных связей характеризует взаимосвязь про-
дольного и бокового движения. При этом даже в тех случаях,
когда самолет не теряет устойчивости и сохраняет нормальную
реакцию на отклонение органов управления, перекрестные связи
могут привести к значительному забросу боковой пг и нормаль-
ной пу перегрузок, не соответствующих отклонению руля направ-
ления и стабилизатора. Необычное изменение параметров движе-
ния может быть при выполнении сложных и энергичных маневров,
связанных с одновременным вращением самолета вокруг двух
осей. К таким маневрам можно отнести, например, выход из пи-
кирования или ввод в горку с одновременным разворотом (вра-
щением вокруг продольной оси), резкое перекладывание самолета
из правого виража в левый, т. е. в тех случаях, когда при вы-
полнении энергичных маневров летчик резко отклоняет ручку по
диагонали.
В качестве примера на рис. 11.7 показано изменение парамет-
ров движения самолета при выполнении подобного маневра. Лет-
чик выполнял горизонтальный полет (пу^\) на высоте /7=11 700м
и скорости, соответствующей числу М^0,8, без скольжения (л2 = 0).
Затем в момент времени /=14 с перемещением ручки управления
вправо и на себя (ср и 6Э) летчик начал энергично вводить самолет
в правый разворот с набором высоты.
Если бы были отклонены только одни элероны, то при враще-
нии самолета вокруг продольной оси из-за кинематической связи
углов атаки и скольжения начал бы уменьшаться угол атаки и
появилось бы скольжение на правое крыло. Отклонение же стаби-
лизатора (ручка на себя) вызывает вращение самолета на кабри-
рование с угловой скоростью (о2. В результате одновременного
отклонения элеронов и стабилизатора при накренении самолета
угол атаки и перегрузка пу не уменьшаются, а увеличиваются.
Это приводит при вращении к более интенсивному росту угла
скольжения на опускающееся (правое) полукрыло даже при не-
отклоненном руле направления.
Однако в рассматриваемом примере летчик недостаточно точно
фиксирует руль направления и сразу после дачи элеронов и воз-
никновения вращения допускает увод руля направления влево.
310
Рис. 11.7. Проявление взаимосвязи продольного
и бокового движений при одновременном откло-
нении элеронов и стабилизатора
311
Такое отклонение руля направления также способствует увеличе-
нию угла скольжения на правое крыло.
Следует подчеркнуть, что в данном случае отклонение руля
направления есть следствие скольжения, а не его причина. По-
следнее подтверждается тем, что отклонение руля направления
происходит при практически нулевых усилиях на педалях (Рн~0),
Рис. 11.8. Изменение момента рыскания вслед-
ствие самопроизвольного отклонения освобож-
денного руля направления при скольжении
Самопроизвольное отклонение руля направления возможно у
самолетов, в системе путевого управления которых не установлен
рулевой привод (гидроусилитель). Причиной самопроизвольного
отклонения руля направления является шарнирный момент, появ-
ляющийся при скольжении. Так, например, при скольжении на пра-
вое полукрыло с углом р (рис. 11.8) на руль направления дейст-
вует боковая аэродинамическая сила ZH, которая относительно оси
вращения создает шарнирный момент Л1Ш. Если педали освобож-
дены (не зафиксированы усилием), то под действием этого мо-
мента руль направления будет стремиться стать по потоку (точ-
нее— занять положение, при котором шарнирный момент станет
равным нулю). Отклонение же руля направления на величину бн
вызовет изменение боковой аэродинамической силы вертикального
оперения на некоторую величину AZB. о (рис. 11.8). Это обусловит
появление момента рыскания \МУ, который будет стремиться раз-
вернуть самолет влево и увеличить скольжение на правое полу-
крыло. Отсюда следует, что самолет без рулевого привода в си-
стеме путевого управления с освобожденными педалями имеет
меньшую путевую устойчивость, чем с зажатыми педалями.
Таким образом, отклонение элеронов и стабилизатора в рас-
сматриваемом на рис. 11.7 случае сопровождается вращением са-
молета вокруг трех осей с угловыми скоростями сох, и>у и со2. Одно-
временное вращение самолета с угловыми скоростями сох и со2
эквивалентно его вращению вокруг оси а—а с угловой скоростью
(01 (рис. 11.9, а). При таком вращении появляется инерционный
момент рыскания
^у ин (Jz х)
3J2
который при положительных угловых скоростях СОх и сог стремится
развернуть самолет влево и увеличить скольжение на правое полу-
крыло.
Одновременное же вращение самолета с угловыми скоростями
(ох и (оу эквивалентно его вращению вокруг оси б—б с угловой
скоростью й)2 (рис. 11.9,6). При таком вращении возникает про-
Рис. 11.9. Появление инерционных моментов ры-
скания (а) и тангажа (б) при одновременном
вращении самолета с угловыми скоростями
Шу И COz
дольный инерционный момент, величина которого определяется
формулой (11.2)
ин ~ Цх /у) ^хфу
Поскольку 1у>1х, то при угловых скоростях Их и одинако-
вого знака появляется пикирующий инерционный момент, а при
противоположных знаках сох и — кабрирующий момент.
В результате действия момента рыскания Муии происходит
резкий заброс боковой перегрузки до пг— —1,4 (рис. 11.7). Сколь-
жение на правое полукрыло обусловливает появление большого
момента крена, который, несмотря на то что элероны отклонены
на величину 6Э = —17° (ручка вправо), прекращает вращение са-
молета вправо и с момента /=15,3 с вызывает вращение в проти-
воположную сторону с большой угловой скоростью крена сох=
= — (2-г-З) рад/с« — (1154-170) °/с. В результате такого враще-
ния появляется скольжение на левое полукрыло и соответственно
возникает заброс боковой перегрузки другого знака (пг= + 1,6).
Изменение знака при /=15,3 с приводит к появлению кабри-
313
руЮщего инерционного момента Мгин, в результате чего самолёт
при неизменном отклонении стабилизатора увеличивает перегрузку
пу с 1,5 до 3,4 (рис. 11.7 при / = 15-Ь 17 с).
Из рассмотренного примера вытекает, что совместное отклоне-
ние элеронов и стабилизатора при энергичном выполнении манев-
ров в отличие от их раздельного отклонения вносит следующие
необычные изменения параметров движения:
— сильный заброс боковой перегрузки до п2 =—1,5-ь +1,6,
тогда как даже полное отклонение руля направления у этого са-
молета на той же высоте и скорости, но без вращения вокруг про-
дольной оси не позволяет превысить пг — ±0,8;
Рис. 11.10. Влияние угловой скорости крена на
балансировочные отклонения стабилизатора
— вращение самолета с большой угловой скоростью крена в
сторону, противоположную отклонению элеронов;
— увеличение нормальной перегрузки пу при неизменном по-
ложении стабилизатора.
Если на больших углах атаки самолет может из-за потери
устойчивости по перегрузке выйти на «подхват», то благодаря
инерционным перекрестным связям при вращении самолета вокруг
продольной оси чэто может произойти на меньших углах атаки.
Отмеченное можно проследить по изменению балансировочных
отклонений стабилизатора (рис. 11.10).
Как видно из рис. 11.7, при постановке элеронов и руля на-
правления примерно в нейтральное положение, а стабилизатора
в положение, соответствующее балансировке при ny=lt самолет
практически без запаздывания прекращает вращение. На основе
рассмотренного примера можно сделать и практические рекомен-
дации по технике пилотирования. Чтобы избежать необычных за-
бросов нормальной и боковой перегрузок и вращения самолета
против отклоненных элеронов, не следует допускать резкого от-
клонения ручки по диагонали. Кроме того, если в системе путе-
вого управления не установлен гидроусилитель, то при вращении
самолета летчик должен не допускать самопроизвольного откло-
нения руля направления.
314
§ 11.4. Поведение самолета и управление им
на больших углах атаки
Поток воздуха плавно обтекает крыло лишь при сравнительно
небольших углах атаки. При дальнейшем увеличении угла атаки
возникает срыв потока.
При несимметричном возникновении и распространении зоны
срыва по крылу нарушается равновесие моментов относительно
продольной оси самолета и появляется кренящий момент, который
является причиной сваливания самолета на крыло. Величина кре-
нящего момента зависит от места возникновения срыва потока,
степени неравномерности его развития на левом и правом полу-
крыльях, скорости распространения, а также от режима полета.
На прямом крыле начальная зона срыва потока расположена,
как правило, в средней (центральной) части крыла, далее срыв
потока при небольшом увеличении угла атаки распространяется по
всему крылу. Поэтому у самолетов с прямым крылом сваливание
происходит на угле атаки, близком к критическому аКр (соответ-
ствующему максимальному коэффициенту подъемной силы Суп1ах).
Иной характер распространения срыва на стреловидном или тре-
угольном крыле. Начальная зона срыва потока, возникнув на кон-
цах при сравнительно небольшом угле атаки, при дальнейшем уве-
личении распространяется по крылу постепенно. В связи с этим
сваливание самолета с таким крылом происходит, как правило,
при угле атаки, существенно меньшем, чем акр. В данном случае
коэффициент подъемной силы, соответствующий сваливанию само-
лета, Су св меньше, чем Сутах, и путать их ни в коем случае не
следует. Таким образом, Сутах, соответствующий акр, может быть
достигнут в полете на самолетах со стреловидным или треуголь-
ным крылом лишь в процессе сваливания.
При несимметричном возникновении и распространении зоны
срыва по крылу может иметь место непроизвольное движение са-
молета вокруг поперечной оси (опускание носа, непроизвольное
кабрирование — «подхват»). Непроизвольное кабрирование бывает
у самолетов со стреловидным крылом вследствие сдвига фокуса
вперед при развитии срыва потока на концах крыла (уменьшение
и потеря устойчивости по перегрузке).
Начало возникновения срыва потока на крыле и поведение са-
молета при распространении срыва ограничивают область экс-
плуатационных углов атаки.
Углы атаки, соответствующие сваливанию — асв, удается реа-
лизовать, как правило, только на дозвуковых скоростях полета.
На сверхзвуковых скоростях вследствие большой устойчивости по
перегрузке и сравнительно небольшой эффективности стабилиза-
тора обычно не представляется возможным выйти на режим сва-
ливания. На больших дозвуковых скоростях и малых высотах по-
лета вследствие больших скоростных напоров увеличение угла
атаки ограничено по прочности, т. е. по допустимой перегрузке
п*
Утах*
315
Таким образом, в зависимости от скорости и высоты полета
значения эксплуатационных углов атаки могут ограничиваться
приближением к сваливанию, эффективностью стабилизатора, до-
стижением максимальной эксплуатационной перегрузки.
Предупреждающим признаком достижения углов атаки, близ-
ких к допустимому аДоп, часто является начало аэродинамической
тряски, возникающей при появлении зон срыва потока на крыле.
Однако на многих современных самолетах тряска возникает на
сравнительно небольших углах атаки, задолго до достижения аДОц.
Ограничение по началу тряски в этих случаях привело бы к су-
щественному недоиспользованию маневренных возможностей са-
молета, поэтому на таких самолетах сигналом о выходе на допу-
стимый угол атаки являются искусственные предупреждающие
признаки или начало возникновения покачиваний самолета с кры*
ла на крыло.
В последнее время широкое распространение получил указа-
тель угла атаки, используемый на многих этапах полета в каче-
стве вспомогательного пилотажного прибора, но главным образом
для контроля пилотирования на больших углах атаки. С этим
прибором имеет связь специальная сигнализация достижения до-
пустимого угла атаки — световая, звуковая или тактильная (по
ощущениям на ручке управления или педалях) или активная си-
стема (ограничения или отталкивания ручки управления).
Однако тряска самолета, другие признаки приближения к сва-
ливанию и указатель угла атаки могут сыграть свою роль лишь
при ограниченной скорости изменения перегрузки (угла атакц).
При энергичном увеличении угла атаки прекращение взятия ручки
на себя или даже отдача ее от себя могут не предотвратить пре-
вышение допустимого значения адоп, так как изменение угла атаки
запаздывает по отношению к отклонению стабилизатора. Поэтому
при ведении воздушного боя пилотировать надо энергично, но не
резко, не забывая о рекомендуемой скорости создания перегрузки.
Увеличивать перегрузку необходимо так, чтобы она достигла за-
данного значения без существенного заброса.
Сигнализация допустимого угла атаки обычно учитывает темп
увеличения угла атаки и при большой скорости нарастания сраба-
тывает раньше, т. е. на меньших углах атаки.
Летчик должен четко представлять, что причиной образования
срывов на крыле и сваливания самолета является выход на боль-
шой угол атаки (только угол атаки). Выражение «сваливание
из-за потери скорости» является неточным. Известно, что можно
уменьшить скорость до нуля и даже лететь хвостом вперед, напри-
мер при выполнении падения на хвост, и не сваливаться на крыло.
И, наоборот, выполняя вираж на сравнительно большой скорости
по прибору, можно, перетянув ручку (т. е. превысив асв), свалить-
ся в штопор.
Таким образом, важнейшей информацией для летчика при ма-
неврировании является информация об угле атаки. Об использо-
вании указателя угла атаки при маневрировании будет подробнее
316
сказано ниже. Однако в воздушном бою невозможно постоянно
следить за показаниями приборов. Здесь приобретает исключитель-
ную роль информация, поступающая от органов чувств летчика,
о движении и положении руки, об усилиях на рычагах управления
и о реакции самолета на управляющие воздействия. Сигналы от
этих органов чувств формируют обратную связь, возникающую при
выполнении действий органами управления. Развитие навыков
летного мастерства заключается в том числе и в использовании
указанных органов чувств. Это и позволяет опытному летчику, вы-
полняющему маневренный бой, практически не смотреть на при-
боры.
Однако на современных самолетах с необратимыми гидроуси-
лителями такое пилотирование не обеспечивает достаточную точ-
ность и безопасность полета. Когда требуется «выжать» максимум
маневренных возможностей самолета, приходится пилотировать
с минимальными «запасами» угла атаки и контролировать его по
указателю. Задача несколько облегчается при наличии на само-
лете световой, тактильной или звуковой сигнализации, и особенно
активных систем ограничения угла атаки и перегрузки.
Влияние особенностей боковой управляемости на пилотирова-
ние при больших углах атаки было рассмотрено в § 9.3.
§ 11.5. Особенности сваливания маневренных самолетов
и действия летчика по предотвращению входа в штопор
Сваливанием называется непроизвольное апериодическое
или колебательное с возрастающей амплитудой движение само-
лета на больших углах атаки, не парируемое полностью органами
управления без уменьшения угла атаки. Это движение происходит
с достаточно большими, заметными для летчика угловыми скоро-
стями относительно одной или более осей самолета.
Характер сваливания, как правило, зависит от срыва потока
на крылехи вызванных им изменений обтекания горизонтального
оперения и фюзеляжа. Срыв вызывает возникновение несбалан-
сированных аэродинамических моментов, которые в конечном сче-
те приводят к вращению самолета и сваливанию.
Вид сваливания зависит от места зарождения срыва потока,
характера его распространения и, естественно, от аэродинамиче-
ской компоновки самолета и режима полета. Наиболее благопри-
ятным видом сваливания является сваливание на нос. Оно наблю-
дается при симметричном развитии срывов на левом и правом
полукрыльях, сопровождающихся смещением фокуса самолета на-
зад. Сваливание на крыло наблюдается при несимметричном сры-
ве потока. Особый вид сваливания связан с потерей путевой устой-
чивости на больших углах атаки, что может наблюдаться у неко-
торых современных самолетов. Вследствие этого при непроизволь-
но возникшем скольжении на таких углах атаки из-за потери
путевой устойчивости появляется дестабилизирующий момент рыс-
кания, стремящийся увеличить угол скольжения. Сохранение на
317
больших углах атаки поперечной устойчивости обусловит при
скольжении возникновение момента крена, накреняющего самолет
на отстающее полукрыло. Скольжение, кроме того, может спрово-
цировать срыв потока на отстающем полукрыле, что приведет к
энергичному сваливанию самолета на это полукрыло. Поскольку
эффективность элеронов на таких углах атаки сильно уменьшается,
Рис. 11.11. Влияние угла скольжения на Су начала
сваливания
то отклонение элеронов для парирования кренения (без устране-
ния скольжения отклонением руля направления) может усилить
кренение. Последнее объясняется тем, что на больших углах атаки
отклонение элеронов сопровождается возникновением момента
рыскания, также направленного на увеличение скольжения.
Иногда за сваливание принимается «выбрасывание» самолета
из крена на сравнительно умеренных углах атаки, вызываемое
внутренним скольжением на самолетах с излишне большой попе-
речной устойчивостью. Такие «выбросы» могут парироваться лет-
чиком при своевременном вмешательстве без уменьшения угла
атаки, поэтому не относятся к сваливанию.
При создании угловой скорости крена на углах атаки, боль-
ших допустимого, срыв потока может наступить на опускающемся
полукрыле раньше достижения самолетом угла атаки сваливания
аСв. Это связано с тем, что местные углы атаки на этом полукрыле
увеличиваются за счет вращения самолета.
Сваливание различается также по знаку угла атаки, на кото-
ром оно произошло. Сваливание на положительном угле атаки
называется нормальным, на отрицательном — переверну-
тым. Так, сваливание в верхней точке петли из-за перетягивания
ручки управления может привести к нормальному сваливанию,
а связанные с недобором ручки и «зависанием» самолета — к пе-
ревернутому.
Значительное влияние на начало и характер сваливания ока-
зывает скольжение самолета. Скольжение приводит к более ран-
нему зарождению срыва на затененном (отстающем) полукрыле
и несимметричному его развитию. На рис. 11.11 показано пример-
318
Рис. 11.12. Пример правильных действий летчика при выво-
де самолета из сваливания
особенно важно выполнять маневры координированно, не допуская
скольжения.
На возможность сваливания оказывает влияние резкость пило-
тирования. При очень энергичном пилотировании выход на аСв
319
более вероятен, чем при пилотировании плавном. При выпущенной
механизации крыла сваливание, как правило, происходит значи-
тельно резче. Такое же влияние оказывают наружные подвески.
Основные действия летчика, направленные на предотвращение
входа в штопор при пилотировании на больших углах атаки, сво-
дятся к следующему:
— не допускать превышения аДОп;
— пилотировать координированно, не допуская скольжения;
— в случае превышения адоп уменьшить угол атаки;
— при первых признаках сваливания немедленно отдать ручку
от себя и педаль против вращения;
— если все же самолет вошел в штопор, немедленно вывести
его из этого режима, используя соответствующий метод вывода.
На рис. 11.12 в качестве примера показаны правильные дей-
ствия летчика при выводе самолета из сваливания.
§ 11.6. Штопор самолета
Штопором называется движение самолета по спиральной
траектории малого радиуса с одновременным вращением относи-
тельно всех трех осей на закритических углах атаки, сопровожда-
ющееся частичной или полной потерей управляемости.
Штопор является одним из самых сложных и в ряде случаев
весьма опасных движений самолета. Причины штопора и методы
вывода из него на заре авиации длительное время не были из-
вестны. Летчики, не располагая достаточными теоретическими ис-
следованиями, вынуждены были сами искать способы вывода са-
молета из штопора. Эти поиски увенчались успехом. 26 сентября
1916 г. русский военный летчик К. К. Арцеулов впервые в мире
произвел преднамеренный ввод самолета в штопор и вывод из
штопора. Эта была первая практическая попытка найти решение
проблемы штопора. Правда, она не давала ответа на многие во-
просы, связанные со штопором. Тем не менее найденный способ
вывода самолета из штопора был большим достижением летной
практики и как элемент летной подготовки вошел в программу
обучения в авиационных школах и училищах.
Большой вклад в экспериментальное исследование штопора
внесли выдающиеся летчики М. М. Громов, В. А. Степанчонок,
В. П. Чкалов, Г. Т. Береговой, А. А. Щербаков и др. Теоретиче-
ское исследование штопора, позволившее выявить его причины,
дать метод его расчета и разработать рациональный способ вы-
вода самолета из штопора, было впервые проведено профессором
В. С. Пышновым в 1927—1929 гг.
Во всех случаях штопору предшествует сваливание самолета.
Вход самолета в штопор возможен при резком несимметричном
срыве потока, который может быть вызван скольжением на углах
атаки, близких к асв (отклонением руля направления). В этом
случае появляется настолько мощный момент крена и такая боль-
шая угловая скорость крена, что, несмотря на изменение угла
320
скольжения при накренении, самолет, уменьшая угловую скорость
вращения, продолжает вращаться в прежнем направлении. При
повороте самолета вокруг продольной оси на угол у >90° от на-
чального положения, например влево, сначала начнет уменьшаться
внутреннее скольжение (на левое полукрыло), а с у>180° начнет
развиваться внешнее скольжение (на правое полукрыло). Вслед-
ствие этого появится момент крена, который будет увеличивать
угловую скорость вращения.
Рис. 11.13. Траектория движения самолета при входе
в штопор
Таким образом, даже при преднамеренном вводе современного
самолета в штопор, например отклонением руля направления на
минимальной или близкой к ней скорости в горизонтальном^ по-
лете, вращение самолета носит неравномерный, а в некоторых
случаях даже колебательный характер. Неравномерность движе-
ния проявляется в изменении угловых скоростей, углов атаки и
скольжения, в результате чего изменяются нормальная и боковая
перегрузки. При вводе самолета в штопор с горизонтального по-
лета угол тангажа в начале штопорного движения изменяется на-
столько сильно (от плюс 20—30° до минус 60—80°), что нос са-
молета переменно оказывается то выше, то ниже горизонта
(рис. 11.13).
В процессе штопора осевая линия, вокруг которой самолет со-
вершает спиралевидное движение, непрерывно отклоняется вниз.
По мере увеличения угла наклона траектории периодическое из-
менение угла скольжения и атаки уменьшается и вращение стано-
вится более равномерным. Этому способствует также увеличение
демпфирующих моментов с уменьшением высоты полета. При
входе в штопор на больших высотах, а следовательно, на больших
истинных скоростях переход от горизонтального полета к верти-
кальному штопору (и затем к установившемуся) очень длительный.
Некоторые самолеты с треугольным крылом, например МиГ-21,
выполняют более или менее устойчивый штопор только при пол-
ностью отклоненной педали и взятой на себя ручке. При освобож-
дении рулей они сами выходят из штопора.
11—21 321
Несмотря на многообразие как нормальных (на положитель-
ных углах атаки), так и перевернутых (на отрицательных углах
атаки) режимов штопора современных самолетов, штопоры мож-
но условно разделить на два вида: неустойчивый и устойчивый.
Под неустойчивым штопором понимается штопор, в
процессе которого угловые скорости вращения могут изменяться
не только по величине, но и по знаку. Неравномерность вращения
в таком штопоре может привести к остановкам вращения и изме-
нениям направления вращения. В результате действия гироскопи-
ческого момента ротора двигателя правый штопор может отли-
чаться от левого неравномерностью, особенно в первые 8—12 с.
Под устойчивым штопором понимается штопор, в про-
цессе которого самолет не изменяет направления вращения. При
этом параметры могут изменяться, но значительно меньше, чем
при неустойчивом штопоре. Если в процессе штопора амплитуда
колебаний параметров движения самолета мала, такой штопор
иногда называют устойчивым равномерным.
Нормальный штопор может быть устойчивым и неустойчивым.
Перевернутый штопор в отличие от нормального всегда характе-
ризуется более равномерным и устойчивым вращением. Влияние
отклонения элеронов на характеристики штопора у различных са-
молетов неодинаково. У некоторых самолетов изменяя отклонение
элеронов, можно значительно менять характер штопора: из устой-
чивого делать неустойчивый, и наоборот.
На сверхзвуковых скоростях самолеты, как правило, в штопор
не входят. При полностью отклоненной на себя ручке и отклонен-
ном руле направления (при нейтральных элеронах) самолет вы-
полняет сравнительно медленные «бочки» с потерей скорости. При
переходе на дозвуковые скорости из-за изменения поперечной ус-
тойчивости могут наблюдаться резкие колебания по крену. При
постановке рулей в нейтральное положение вращение самолета
прекращается, и он переходит в пикирование.
Угол атаки, при котором балансируется самолет при штопоре,
определяется из условия равенства аэродинамического продоль-
ного момента М2а продольному инерционному моменту по фор-
муле (11.2)
Мг ин = (Jx Iу) ^у^х*
При установившемся вертикальном штопоре (рис. 11.14) угло-
вые скорости крена сох и рыскания (&у выражаются через угловую
скорость штопора со: сох = —со cos a; соу==со sin а, поэтому формулу
для определения продольного инерционного момента Мгин можно
записать так:
2
ин = (^у Л) “2“ 2a.
Если бы угловая скорость вращения не зависела от угла атаки,
этот момент был бы равен нулю при а = 0 и а = 90° и достигал бы
максимума при а = 45°. Однако при отсутствии скольжения на
322
а<асв <Ох = 0 и инерционный момент Мг ин изменяется так, как
показано на рис. 11.15. На этом рисунке показана также зависи-
Рис. 11.14. Проекция вектора угло-
вой скорости вращения самолета в
процессе вертикального штопора
мость аэродинамического момента Мг^ от угла атаки при откло-
ненном на кабрирование стабилизаторе (<р<0).
Рис. 11.15. Зависимость аэродинамического и
инерционного моментов от угла атаки
Поскольку установившийся штопор возможен только в том слу-
чае, когда аэродинамический момент MZSL равен инерционному
11* 323
Рис. 11.16. Сохранение устойчивого
равновесия самолета в процессе
штопора
Mzw, для определения режимов установившегося штопора удобно
нанести на график зеркальное отображение графика М2а (штри-
ховая линия на рис. 11.15). Точки А и В пересечения кривых со-
ответствуют режимам установив-
шегося штопора. Из этого рисун-
ка видно, что при одном и том
же положении стабилизатора
самолет может выполнять што-
пор на двух режимах: на малом
угле атаки — в точке А (крутой
штопор) и на большом угле
атаки — в точке В (плоский што-
пор).
Инерционный момент являет-
ся дестабилизирующим, он стре-
мится увеличить угол атаки.
Ему препятствует аэродинамиче-
ский момент (рис. 11.16). Чем
больше инерционный момент и
более задняя центровка, тем на
большем угле атаки наступит равновесие, и, следовательно, более
пологим будет штопор.
§ 1L7. Вывод самолета из штопора
Трудности, возникающие при выводе самолета из штопора, свя-
заны со сравнительно большой устойчивостью вращательного дви-
жения самолета, как и всякого твердого тела. Такая устойчивость
Рис. 11.17. Сохранение устойчивости направления оси вра-
щения тела
вращательного движения легко объясняется следующим простым
примером. Пусть два груза 1 и 2 (рис. 11.17), соединенные стерж-
нем, вращаются относительно оси 00. Если с помощью кратковре-
менного импульса (например, в положении а создать угловую
скорость (Or/) попытаться изменить положение оси вращения, гру-
324
зы приобретают некоторую скорость AV. Но после поворота гру-
зов на 180° скорости их будут направлены против действия им-
пульсов (рис. 11.17,6), что приведет к восстановлению первона-
чального положения оси, т. е. система стремится сохранить поло-
жение оси вращения.
Рис. ПЛ8. Влияние отклонения руля направления на инер*
ционный момент
Поскольку основной причиной штопора является полет на боль-
ших углах атаки, для вывода самолета из штопора необходимо
уменьшить угол атаки, а следовательно, и угол между продольной
осью самолета и осью вращения. В этом и состоит основная за-
дача вывода самолета из штопора.
Для уменьшения угла атаки ручка управления отклоняется от
себя. Однако на штопорных режимах стабилизатор имеет пони-
женную эффективность и «дача» только ручки управления от себя,
как правило, не приводит к прекращению вращения самолета.
Поэтому для вывода самолета из штопора следует предваритель-
но уменьшить угловую скорость вращения (o)x и а)^). С этой целью
руль направления отклоняется против штопора. В результате по-
является внутреннее скольжение, уменьшается угловая скорость
вращения, а следовательно, и инерционный момент (рис. 11.18).
После этого отклоняется ручка управления от себя. С учетом этих
особенностей в свое время устанавливалась следующая стандарт-
ная методика вывода самолета из штопора:
— энергично и полностью отклонить руль направления против
штопора для уменьшения угловой скорости вращения, а соответ-
ственно и инерционных моментов;
— через 1/4—1/2 витка отклонить ручку управления от себя;
— по прекращению вращения поставить педали нейтрально и
после увеличения скорости полета вывести самолет из пикирова-
ния.
325
Своеобразие режимов штопора современных самолетов со стре-
ловидными и треугольными крыльями вносит ряд изменений в вы-
вод из штопора.
Применение так называемого стандартного метода вывода из
штопора таких самолетов с учетом возможных ошибок иногда мо-
жет привести к нежелательным и даже опасным последствиям.
Одной из причин этого является сильная реакция самолета со
О
2-й метод йыйода
Штопор
Вы йод из штопора
Протий штопора
1-й метод йыйода
Штопор
Выйод из штопора
Нейтрально
По штопору I 5
По штопору___) ,
Элероны нейтрально
3-й метод йыйода
5н-
Элероны нейтрально
По штопору
; Штопор
13| Выйод из штопора
* Протий штопора
По штопору_____8
<5, 4-й метод йыйода
ШтопорЧ\§. Выйод из штопора
rjug Протий штопора
Протий штопора
Элероны нейтрально
По штопору
5Н'( Протий штопора
Элероны на ^ыйод1^
Элероны
нейтрально
По штопору
tja
По ujmonopy_ ___
По штопору ________J
Рис. 11.19. Четыре основных метода вывода современных
самолетов из левого нормального штопора
стреловидными и треугольными крыльями на скольжение. Несвое-
временная постановка руля направления в нейтральное положе-
ние может вызвать переход таких самолетов в штопор противо-
положного направления. Кроме того, резкое и полное отклонение
ручки управления от себя приводит к переходу в более крутое
пикирование, для вывода из ’которого требуется большая потеря
высоты, а на некоторых самолетах (например, УТИ МиГ-15) это
может явиться причиной перехода самолета в перевернутый што-
пор.
Чтобы исключить эти нежелательные явления и учесть особен-
ности штопора, для современных самолетов рекомендуются четыре
метода вывода из нормального штопора (рис. 11.19) и три метода
из перевернутого (рис. 11.20). Все эти методы отличаются один от
другого постепенным увеличением эффективности действия рулями
для вывода самолета из штопора.
Определив направление вращения и установив предварительно
ручку управления полностью на себя, а педали (это делается для
увеличения хода рулей при выводе) по штопору, летчик должен
326
вывести самолет из штопора, применяя тот или иной метод в за-
висимости от характера штопора. Для вывода самолета из нор-
мального штопора наиболее часто применяют первый и второй
методы (рис. 11.19). Первый метод применяется при выводе из
неустойчивого штопора. При этом руль высоты и руль направления
одновременно устанавливаются в нейтральное положение. Это це-
лесообразно выполнить в момент прекращения или замедления
вращения.
Если штопор колебательный, применяется второй метод: сна-
чала отклоняется руль направления против штопора, а через 2—
4 с ставится в нейтральное положение стабилизатор (руль высо-
ты). В обоих методах элероны удерживаются в нейтральном по-
ложении.
Если самолет попадает в режим устойчивого штопора с боль-
шой угловой скоростью вращения, необходимы более эффективные
методы. При выводе из устойчивого равномерного штопора при-
меняется третий метод (рис. 11.19): руль направления полностью
отклоняется против штопора, а через 3—6 с полностью отклоня-
ется на пикирование стабилизатор, при этом элероны удержи-
ваются в нейтральном положении. Четвертый метод (использова-
ние элеронов для вывода из штопора) рекомендуется только в ис-
ключительных случаях, например при выводе из очень устойчи-
вого пологого (плоского) штопора или в случае, когда с помощью
третьего метода из штопора самолет не выходит. При этом нужно
помнить, что рули даются «накрест» — педаль влево — ручка впра-
во, и наоборот.
Необходимо отметить, что выбор метода вывода конкретного
самолета из штопора определяется только характером режима
штопора. В инструкции летчику обычно указывается наиболее
предпочтительный метод вывода из штопора конкретного типа са-
молета, т. е. с какого метода следует начинать попытки вывода.
Если после применения рекомендованного метода самолет из што-
пора не выходит, летчик, если высота позволяет, должен прове-
рить, правильно ли он определил направление вращения, затем
поставить органы управления снова по вращению, выждать неко-
торое время и в зависимости от характера штопора применить
более эффективный метод вывода. Так как при медленном откло-
нении органов управления эффект их действия ослабевает, во всех
случаях отклонения рулей при выводе из штопора должны быть
энергичными.
В некоторых случаях, например, при неправильном выполнении
отдельных фигур пилотажа (перевернутый полет, выход из полу-
петли и др.) или при более эффективном методе для выхода из
штопора, чем рекомендуемый, самолет может перейти на большие
отрицательные углы атаки, а затем, если руль направления остает-
ся отклоненным, и в перевернутый штопор. Вывод самолета из
перевернутого штопора при правильных действиях летчика
(рис. 11.20) надежнее, чем из нормального штопора. Это объяс-
няется большей эффективностью руля направления, потому что
327
в этом случае вертикальное оперение меньше затеняется спутной
струей крыла, фюзеляжа и горизонтального оперения. Кроме того,
в перевернутом штопоре эффективность руля направления, уста-
новленного на стреловидном вертикальнОхМ оперении, значительно
больше, чем в нормальном штопоре.
1-й метод
2-й метод
Штопор
+^6 max
с Выбод
из штопора
Штопор
+ max
5.-0
5,-0
53-О
3-й метод
Штопор
+ ^6 max.
ЬуО
- max
Выбод из штопора
5,-0
S'
с
Вы бод из штопора
"2 *&нтах
-6g max
б
' • + mai
а
Рис. 11.20. Три основных метода вывода современных само-
летов из левого перевернутого штопора
Трудности вывода самолета из перевернутого штопора связа-
ны с неблагоприятным воздействием на летчика отрицательных
перегрузок, с трудностью ориентировки и правильного определе-
ния направления вращения. Поэтому для вывода из перевернутого
штопора обычно рекомендуется одновременная установка всех ор-
ганов управления в нейтральное положение (первый метод на
рис. 11.20).
После прекращения вращения и перехода самолета в пикиро-
вание необходимо удерживать рули в нейтральном положении до
достижения скорости, рекомендуемой в инструкции летчику кон-
кретного типа самолета. По достижении этой скорости следует вы-
вести самолет из пикирования.
§ 11.8. Особенности поведения самолета и управления им
при попадании в спутный след
Летящий самолет оставляет за собой возмущенную область
атмосферы, называемую спутным следом. Этот след образуется:
— реактивной струей двигателя;
— турбулентным пограничным слоем, сбегающим с поверхно-
сти самолета;
— концевыми вихрями крыла, связанными с образованием
подъемной силы.
328
Самолет может попасть в спутный след от впереди летящего
самолета при атаке цели из задней полусферы, полете в сомкну-
тых боевых порядках, дозаправке топливом в воздухе, заходе на
посадку и взлете с малым интервалом по времени.
Струя реактивного двигателя обладает значительной энергией,
особенно при работе двигателя на форсажном режиме. Она пред-
ставляет собой узкий поток газов, выходящих из реактивного соп-
Рис. 11,21. Модель спутного следа
ла с большой скоростью и высокой температурой. Однако темпе-
ратура и скорость потока по мере удаления от двигателей быстро
уменьшается. На расстоянии 50—80 м от самолета относительная
скорость струи от двигателя равна примерно 3—5 м/с. После вы-
хода из двигателя струя расширяется под углом 3—4°. По мере
увеличения высоты полета этот угол несколько возрастает. Однако
размыв струи замедляется, так как плотность воздуха уменьша-
ется. Попадание самолета в струю от ТРД на близком расстоя-
нии может вызвать помпаж двигателя и его самовыключение.
Возмущение, вносимое в спутный след пограничным слоем,
сравнительно невелико. Воздействуя на самолет, оно вызывает
тряску, однако на расстоянии 100—150 м практически полностью
размывается.
Наиболее сильное воздействие на самолет оказывают концевые
вихри, образованные крылом. Модель спутного следа за крылом
изображена на рис. 11.21.
В результате перетекания потока воздуха из области повышен-
ного давления на нижней поверхности крыла в область понижен-
ного давления на верхней поверхности крыла через его торцы
образуются вихри. Направление вращения вихрей таково, что воз-
дух между ними отбрасывается вниз, а с внешних сторон —
вверх. Соответствующие направления имеют и скосы потока за
крылом (рис. 11.21). Величина скоса потока, как известно, опре-
деляется подъемной силой. Чем больше подъемная сила, с кото-
рой воздушный поток воздействует па крыло, тем больше скос по-
329
тока за крылом и, следовательно, интенсивнее спутный след само-
лета. Интенсивность вихревых жгутов выражается
г _ у _ ПУ°
°~ PV£B ’
Влияние спутного следа может быть оценено средней верти-
кальной скоростью отбрасываемого вниз потока:
Рис. 11.22. Поведение самолета при попадании
в различные области спутного следа (струи)
Значит, интенсивность спутного следа больше у тяжелых само-
летов, а также у легких самолетов при маневрировании с боль-
шими перегрузками.
Для данной массы самолета интенсивность спутного следа из-
меняется с изменением высоты и скорости полета. Полет на боль-
шой высоте с малой скоростью сопровождается наиболее интен-
сивным вихреобразованием. Оно возрастает и при уменьшении
удлинения крыла. Таким образом, тяжелые самолеты с крылом
малого удлинения создают вихри с наиболее высокими окружны-
ми скоростями.
Вихри вызывают интенсивное вращение (особенно кренение)
сзади летящего самолета. Характер накренения самолета зависит
и от того, в какую область спутной струи попадает самолет. На
рис. 11.22 показано, какие поперечные моменты действуют на лег-
кий самолет в различных областях спутного следа от тяжелого
самолета. Входя в спутный след с внешней стороны, летчик лег-
кого самолета будет сначала ощущать предупредительную тряску,
затем возникает внешнее по отношению к впереди идущему само-
лету накренение. При попадании в область, соответствующую оси
вихря, появится наиболее интенсивное внутреннее накренение.
Воздействие вихря на сзади летящий самолет зависит также
от расстояния между самолетами. При попадании в струю на до-
статочно близком расстоянии возникает настолько большой кре-
330
нящий момент, что полного отклонения элеронов может не хва-
тить для парирования этого момента, вызванного вихрем, и само-
лет может перевернуться. Примерная зависимость такого расстоя-
ния от массы самолета, вызвавшего вихри, приведена на рис. 11.23.
При попадании в струю от самолета массой 300 т эффективность
поперечного управления может оказаться недостаточной даже на
расстоянии 16 км. Однако для истребителя это не является опас-
ным, за исключением полета на
предельно малой высоте или в
сомкнутых боевых порядках, так
как самолет сразу же выбрасы-
вается из струи и управляемость
восстанавливается.
За легким самолетом вихри
менее интенсивные, чем за тяже-
лым, однако при маневрирова-
нии с большими перегрузками
интенсивность их возрастает. Тем
не менее попадание в спутную
струю во время атаки истребите-
ля обычно не является опасным.
Атаки, как правило, не срыва-
ются, хотя точное прицеливание в
возможно.
Рис. 11.23. Зависимость расстояния,
при котором полного отклонения
элеронов может не хватить для па-
рирования кренящего момента, от
массы самолета, вызвавшего вихри
момент нахождения в струе не-
Время существования следа tz может определяться одной из
двух причин: у самолетов с малым размахом крыла — волновой
неустойчивостью, а за тяжелыми самолетами с большим размахом
крыла — размыванием следа. При небольшом расстоянии между
жгутами (малый размах крыла) они сильно взаимодействуют
между собой. Случайное внешнее возмущение вызывает началь-
ное искривление оси жгута, что приводит к прогрессирующему
росту амплитуды обоих жгутов, их соприкосновению и разруше-
нию. Этот тип разрушения наиболее характерен для маневренных
самолетов. Время до разрушения спутного следа в этом случае
можно определить по приближенной формуле
о 4
/с^8,5и-р-
А о
8,5крУ
tip G
Положение следа в пространстве определяется главным обра-
зом его опусканием и воздействием возмущенной атмосферы. С те-
чением времени скорость его опускания уменьшается. Поэтому
в спокойной атмосфере след опускается на Д//тах= 100—300 м
относительно самолета и зависает.
Основными мероприятиями по предотвращению попадания в
спутный след являются:
— правильное построение боевых порядков при полетах
строем;
331
— обоснованное задание временных интервалов при взлете и
посадке;
— повышение точности пилотирования в строю и т. п.
Глава 12
ПРИНЦИПЫ АВТОМАТИЧЕСКОГО И ДИРЕКТОРНОГО
УПРАВЛЕНИЯ
§ 12.1. Распределение функций между летчиком
и автоматическими устройствами
Значительное расширение диапазона скоростей и высот полета
приводит к существенным изменениям динамических свойств са-
молета, его характеристик устойчивости и управляемости. Прак-
тика самолетостроения показывает, что изменением только кон-
структивных форм самолета невозможно обеспечить приемлемые
его динамические свойства во всем диапазоне скоростей и высот
полета. Изменение же характеристик устойчивости и управляе-
мости самолета в процессе полета требует, чтобы летчик не только
четко знал характер этого изменения, но и приспосабливался к
управлению самолетом с учетом этого изменения.
Одновременно возросла и информационная нагрузка на лет-
чика, что связано с увеличением числа контролируемых парамет-
ров при решении более сложных задач, выполняемых современ-
ной авиацией. Все это приводит к увеличению психофизиологиче-
ской нагрузки летчика, изменению характера его деятельности,
вследствие чего возникает насущная необходимость освободить лет-
чика от ряда функций, которые могут выполнить различного рода
автоматические устройства.
Для правильного распределения функций между летчиком и
автоматическими устройствами необходимо знать свойства лет-
чика-оператора. Одним из замечательных свойств летчика является
удивительная его приспособляемость к изменившимся условиям —
«самонастраивание», чего только частично удается добиться с
помощью автоматических устройств. Летчика чрезвычайно трудно
заменить автоматическими средствами в тех случаях, когда реше-
ние должно быть принято при неполной или противоречивой ин-
формации, по опознанию и выделению цели и в ряде других слу-
чаев. Исследования показывают, что вмешательство летчика в
управление для парирования последствий отказов техники, оши-
бок других операторов, воздействия неблагоприятных внешних
условий существенно повышает безопасность полета.
Вместе с тем летчик-оператор обладает и рядом недостатков.
Ему трудно выполнять сложные вычислительные и логические опе-
рации. Ответная реакция летчика всегда запаздывает и тем силь-
нее, чем большее число параметров он должен контролировать,
332
Время запаздывания реакции летчика зависит от вида раздражи-
теля, его интенсивности, психофизиологического состояния летчика
и изменяется в широких пределах. Характерными раздражителями
являются: световые, звуковые, акселерационные и кинестетические.
При резком изменении параметров движения время вмешатель-
ства летчика в управление для парирования этого изменения свя-
летчика в управление от интенсивности раздра^
жителя
зано главным образом с акселерационными раздражителями. Та-
кими раздражителями являются угловые ускорения и скорость из-
менения перегрузки.
В качестве примера на рис. 12.1 показано время запаздывания
вмешательства летчика /вм в управление в зависимости от скоро-
сти изменения нормальной перегрузки пу (например, при отказе
техники, приводящем к увеличению перегрузки). Видно, что с уве-
личением интенсивности раздражителя летчик раньше замечает
изменение перегрузки и с меньшим запаздыванием его парирует.
При большой скоротечности процессов летчик из-за запазды-
вания своей реакции не может осуществлять точное пилотирова-
ние, а при некоторой частоте возмущающего воздействия, превы-
шающей частоту пропускания летчика (0,5—1 Гц — одно колеба-
ние за 2—1 с), вмешательство летчика в управление может при-
вести к раскачке самолета. В соответствии с этим действия, вы-
текающие из решения определенных логических или функциональ-
ных связей, автоматические устройства могут выполнять лучше
(точнее и быстрее), чем летчик. Особенно это относится к случаям,
когда для принятия решения требуется сопоставить большое коли-
чество параметров или когда ответная реакция должна выпол-
няться с частотой, превышающей его физические возможности.
Это объясняет причину широкого использования на современных
самолетах различного рода автоматических устройств, повышаю-
333
щих демпфирование (автоматы демпфирования) и устойчивость
(автоматы устойчивости), автоматов балансировки, ограничителей
перегрузки, командных (директорных) приборов и других
автоматических устройств, позволяющих существенно облег-
чить летчику управление самолетом на различных этапах по-
лета.
В зависимости от распределения функций между летчиком и
автоматическими устройствами процесс управления параметрами
движения самолета принято разделять на три вида управления:
неавтоматическое (ручное), автоматическое и полуавтоматическое
(смешанное). При ручном управлении всю информацию о те-
кущих и заданных параметрах движения воспринимает, анализи-
рует и перерабатывает летчик. Он же вырабатывает решение и
осуществляет его исполнение. При автоматическом управ-
лении все функции по управлению самолетом выполняют автома-
тические устройства. При полуавтоматическом управлении
часть функций выполняет летчик, часть — автоматические устрой-
ства. Характерным примером полуавтоматического управления яв-
ляется директорное управление.
Первые автоматы (автопилоты) обеспечивали только стабили-
зацию и управление угловым положением самолета. Как правило,
автопилоты имеют три канала управления: продольный (танга-
жа), поперечный (крена) и путевой (рыскания). Однако на некото-
рых самолетах применялись двухканальные автопилоты (крена и
тангажа). Дальнейшим развитием автопилотов являются системы
автоматического управления (САУ), которые помимо чисто авто-
пилотных функций обеспечивают автоматическое управление тра-
екторией на различных этапах полета.
По мере развития авиационной техники и усложнения выпол-
няемых ею задач происходило развитие и совершенствование си-
стемы управления, приведшее к появлению комплексных систем
управления или автоматических бортовых комплексов управления.
Повышая точность пилотирования, обеспечивая безопасность по-
летов и облегчая работу летчика (освобождая его от выполнения
ряда функций), комплексные системы управления позволяют бо-
лее полно и эффективно использовать возможности маневренных
самолетов.
Автоматические системы управления современными самолетами
достаточно сложны, поэтому изучение их работы в общем случае
связано с серьезными трудностями. Задача существенно упрощает-
ся, если удается многоконтурную систему управления разделить
на несколько более простых. Во-первых, во многих случаях пред-
ставляется возможным общее движение самолета разделить на
продольное и боковое и рассматривать их раздельно. Во-вторых,
поскольку малые движения, определяющие движение самолета
вокруг центра масс, протекают значительно быстрее больших,
определяющих движение центра масс (траекторию полета), то си-
стемы автоматического управления продольным и боковым дви-
334
жением в свою очередь можно разделить на системы управления
движением вокруг центра масс и системы управления траекторий
полета.
§ 12.2. Автоматическое управление движением
вокруг центра масс
Автоматическое управление креном. Одним из наиболее про-
стых случаев автоматического управления полетом самолета яв-
ляется управление креном, которое осуществляется регулирова-
нием моментов вокруг оси Охх.
Рис. 12.2. Функциональная схема автопилота, управ-
ляющего креном
На рис. 12.2 представлена функциональная схема автоматиче-
ского управления углом крена с помощью элеронов. Чувствитель-
ным элементом автопилота является гировертикаль (ГВ), которая
фиксирует фактическое значение угла крена у. Электрический
сигнал Х^ выходящий из гировертикали, поступает на суммирую-
щее устройство (СУ). Если фактическое значение угла крена у
отличается от заданного значения у3, то появляется сигнал рас-
согласования Xу — X , который после усиления в усилителе (У)
• *з
подается на электрогидравлический рулевой привод (РП). Руле-
вой привод отклоняет элероны пропорционально разности сигна-
лов X — X , а значит и разности у—у3. Пропорционально вели-
чине отклонения элеронов через обратную связь (ОС) подается
на суммирующее устройство сигнал X , направленный противо-
• с
положно сигналу X — Х„ . Отклонение элеронов происходит до
т «з
тех пор, пока сигнал обратной связи Х^ не уравновесит разность
•с
X — X . Это вызовет ускоренное вращение самолета в сторо-
* *3
ну уменьшения угла крена. В результате начнет расти угловая
скорость сох и возникнет демпфирующий момент препят-
ствующий вращению. По мере приближения угла крена у к за-
данному значению у3 будет уменьшаться разность сигналов чув-
335
ствительного элемента и задатчика X — X , что приведет к
7 тз
превышению сигнала обратной связи X над разностью Xу — X .
Тс т т3
В результате этого на входе в усилитель появится результирую-
щий сигнал обратного знака и отклонение элеронов начнет умень-
шаться. Таким образом, с
течением времени момент крена, созда-
Рис. 12.3. Изменение парамет-
ров движения самолета в про-
цессе устранения возникшего
угла крена у0 автопилотом
ваемый элеронами, уменьшается, а
демпфирующий момент — увеличива-
ется. Когда эти моменты станут рав-
ными по величине (/ = /1), то угловая
скорость крена достигнет максималь-
ного значения. В дальнейшем демп-
фирующий момент станет больше мо-
мента, создаваемого элеронами, и уг-
ловая скорость начнет уменьшаться.
При приближении самолета к исход-
ному положению элероны постепенно
возвратятся в первоначальное поло-
жение.
Если собственное демпфирование
движения крена значительно,
то изменение параметров движения
будет происходить так, как показано
на рис. 12.3. Если же собственное
демпфирование мало, как это бывает,
например, на больших высотах у са^
молетов с крыльями малого удлине-
ния, то при подходе самолета к исход-
ному положению равновесия он будет
иметь еще значительную угловую
скорость вращения. Вследствие это-
го самолет может пройти положение
равновесия и процесс устранения на-
чального угла крена у0 будет происходить с перерегулированием
(колебательно). Возникшие колебания вокруг исходного положе-
ния равновесия будут затухать после одного или нескольких коле-
баний.
Для устранения колебательности процесса можно уменьшить
передаточный коэффициент с крена на элероны в результате
чего' уменьшатся отклонение элеронов и восстанавливающий мо-
мент крена Благодаря этому возвращение к положению
равновесия замедлится и при некоторых значениях передаточного
коэффициента движение станет осуществляться без перерегу-
лирования. Но в этом случае значительно увеличится время пере-
ходного процесса.
Устранить колебательность процесса без увеличения времени
переходного процесса можно введением коррекции по угловой ско-
336
рости крена, т. е. добавлением на вход в автопилот сигнала ,
выдаваемого датчиком угловой скорости (ДУС) пропорционально
величине ои (включением верхней цепочки на рис. 12.2). В этом
случае отклонение элеронов будет осуществляться по следующему
закону:
8э=^(т — Тз) + Сх^>
(12.1)
где Q и k™* — передаточные коэффициенты соответственно с
крена и угловой скорости крена на
Изменяя значения передаточ-
ных коэффициентов k\ и
можно обеспечить требуемый пе-
реходный процесс.
Рассмотрим теперь процесс
автоматического управления уг-
лом крена. Допустим, что тре-
буется осуществить переход с од-
ного угла крена (например, у = 0)
на другой (накренить на правое
крыло на величину у3). Это
можно обеспечить, если на вход
автопилота подать некоторый
управляющий сигнал. Он может
быть задан в виде ступенчатой
функции или в виде некоторой
функции времени.
Для простоты рассуждений
предположим, на вход автопило-
та поступил ступенчатый управ-
ляющий сигнал АГ . У идеально-
тз
го автопилота (без запаздывания)
этот сигнал вызовет ступенчатое
элероны.
Рис. 12.4. Изменение параметров
движения самолета в процессе ав-
томатического управления углом
крена
отклонение элеронов 8Эо (рис. 12.4), в результате чего появится
управляющий момент крена и самолет начнет ускоренно
вращаться вокруг продольной оси. Это приведет, с одной стороны,
к возникновению демпфирующего момента препятствующе-
го вращению, с другой — к росту угла крена и уменьшению сиг-
нала рассогласования АГ —АГ и, как следствие, уменьшению
отклонения элеронов. Когда момент, создаваемый элеронами,
А^?8Э станет равным демпфирующему Мх^шх, угловая скорость
крена достигнет максимальной величины. Дальнейшее движение
будет сопровождаться уменьшением угловой скорости крена. При
приближении угла крена у к заданной величине у3 сигнал рассо-.
рласования АГ — АГУ настолько уменьшится, что сигнал X ,
♦ «3 х
337
выходящий из датчика угловой скорости (рис. 12.2), обусловит
отклонение элеронов против вращения. Благодаря этому при пра-
вильно выбранных передаточных коэффициентах &э и k™* угол
крена будет монотонно или со слабым перерегулированием стре-
миться к заданному значению. На рис. 12.4 показано изменение
отклонения элеронов, моментов крена и параметров движения са-
молета при автоматическом управлении углом крена.
Рис. 12.5. Функциональная схема автопилота, управ-
ляющего тангажом
Автоматическое управление углом тангажа осуществляется с
помощью продольного канала автопилота, воздействующего на
стабилизатор (руль высоты). На рис. 12.5 показана функциональ-
ная схема автопилота, управляющего углом тангажа. Чувствитель-
ными элементами этой части автопилота, так же как и автопи-
лота, управляющего углом крена, являются гировертикаль (ГВ)
и датчик угловой скорости (ДУС), которые выдают сигналы, про-
порциональные фактическим значениям угла тангажа 8 и угловой
скорости тангажа сох. Эти сигналы поступают на суммирующее
устройство (СУ). Если сумма этих сигналов не уравновешивает
сигнал А$з, соответствующий заданному значению угла тангажа,
то суммирующее устройство формирует сигнал, который после уси-
ления поступает на рулевой привод (РП), вызывающий отклоне-
ние стабилизатора.
Рассмотрим работу такого автопилота в режиме стабилизации
угла тангажа. Предположим сначала, что управление углом тан-
гажа осуществляется автопилотом, не имеющим коррекции по угло-
вой скорости тангажа (верхняя цепочка на рис. 12.5 разъединена).
Допустим, что угол тангажа отклонился от заданного значения
83, вследствие чего из суммирующего устройства выходит сигнал
пропорциональный разности фактического и задан-
ного углов тангажа 8—83. Под действием этого сигнала, усилен-
ного в усилителе, рулевая машина перемещает одновременно ста-
билизатор и датчик обратной связи (ОС) до тех пор, пока сигнал
обратной связи не уравновесит сигнал А^. В резуль-
тате отклонения стабилизатора возникнет продольный момент
338
он вызовет вращение самолета, в процессе которого угол
тангажа начнет приближаться к заданному значению.
Так как продольное демпфирование обычно существенно мень-
ше поперечного, то при рассматриваемом законе отклонения ста-
билизатора переходный процесс будет осуществляться со значи-
тельным перерегулированием, сопровождающимся особенно на
больших высотах и сверхзвуковых
скоростях полета слабо затухающими
колебаниями. Предотвращение про-
дольных колебаний можно обеспечить
искусственным повышением демпфи-
рования путем подачи на суммирую-
щее устройство сигнала, пропорцио-
нального угловой скорости тангажа,
который формируется датчиком угло-
вой скорости (ДУС). Для этого необ-
ходимо включить верхнюю цепочку
схемы (рис. 12.5).
В соответствии с этим автопилот,
управляющий углом тангажа, имеет
следующий закон отклонения стаби-
лизатора:
= + (12.2
Рис. 12.6. Изменение парамет-
ров движения самолета в про-
цессе устранения прироста уг-
ла тангажа автопилотом
где k® и — передаточные коэф-
фициенты соответственно с тангажа и
угловой скорости тангажа на стабили-
затор.
При таком законе управления автопилота, работающего в ре-
жиме стабилизации, характер изменения моментов и параметров
движения самолета при одновременном отклонении углов тангажа
О и атаки а от их исходных значений будет иметь вид, показанный
на рис. 12.6. Для упрощения знаки А на рис. 12.6 опущены.
В начальный момент времени на самолет действует восстанав-
ливающий момент УИ’Да, обусловленный наличием устойчивости,
по перегрузке, и момент УИ^Дср, вызванный отклонением стабили-
затора, пропорционального сигналу рассогласования 0—83. С те-
чением времени угол атаки возвратится к исходному значению со
сравнительно небольшим перерегулированием. Изменение же угла
тангажа Д& будет несколько отставать от изменения угла атаки Да,
так как в процессе возмущенного движения начнет изменяться
и угол наклона траектории Д0=Д8—Да. При увеличении угловой
скорости тангажа растет и демпфирующий момент
По мере уменьшения угла тангажа и возрастания угловой ско-
рости сигнал по угловой скорости сначала станет равным
по величине и обратным по знаку сигналу — &3), а затем
339
и для получения
углом
Рис. 12.7. Изменение параметров
движения самолета в процессе ав-
томатического управления
тангажа
превысит его и вызовет отклонение стабилизатора в противопо-
ложную сторону. Такое отклонение стабилизатора создает момент,
препятствующий вращению. Отсюда следует, что сигналы по углу
тангажа и по угловой скорости тангажа являются принципиально
качественных переходных процес-
сов.
Следует сказать о том, что
в автопилотах часто используется
режим коррекции высоты или
скорости (числа М), т. е. под-
держание их заданных постоян-
ных значений, но всегда это де-
лается путем управления углом
тангажа.
Для стабилизации скорости
одновременно с выдерживанием
определенной траектории (на-
пример, на предпосадочном пла-
нировании) используются отдель-
ные устройства — автоматы тяги.
Рассмотрим теперь процесс
автоматического управления уг-
лом тангажа. На рис. 12.7 пока-
зано изменение параметров движения в процессе перехода с од-
ного угла тангажа (& = 0) на другой (83).
Управляющий сигнал, пропорциональный разности 0—&3, вы-
зовет отклонение стабилизатора на величину Дер. Появившийся
продольный момент, например кабрирующий, начнет поднимать
нос самолета, вследствие чего будут увеличиваться как угол тан-
гажа, так и угол атаки, а следовательно, и подъемная сила. В ре-
зультате с течением времени» начнет искривляться траектория
вверх (поворачиваться вектор скорости) и увеличиваться угол на-
клона траектории. Вследствие этого угол тангажа изменяется силь-
нее, чем угол атаки (рис. 12.7).
При увеличении угла тангажа и угловой скорости уменьшается
сигнал рассогласования —^3) и увеличивается сигнал
Это приводит к уменьшению отклонения стабилизатора. В неко-
торый момент времени сигнал, пропорциональный угловой скоро-
сти, сначала уравновесит все уменьшающийся сигнал — &3),
а затем превысит его и отклонит стабилизатор в противоположную
сторону. Благодаря этому угловая скорость начнет уменьшаться,
угол тангажа при правильно выбранных передаточных коэффици-
ентах будет монотонно или со слабым перерегулированием стре-
миться к заданному значению. Стабилизатор и угол атаки будут
стремиться к исходным балансировочным значениям.
Изменение угла тангажа на величину Д8 = 8—Эо приведет по
окончании переходного процесса к изменению угла наклона траек-
тории на такую же величину. Вследствие этого нарушается равно-
340
весне сил по касательной к траектории,
что с течением времени приведет к изме-
нению скорости. Поэтому для сохране-
ния постоянства скорости в процессе пе-
рестройки угла тангажа необходимо воз-
действовать и на тягу двигателя. Это
у большинства маневренных самолетов
летчик делает вручную. На тяжелых са-
молетах для этой цели используется ав-
томат тяги.
Автоматическое управление курсом.
Управление курсовым углом самолета
можно осуществлять рулем направления,
элеронами либо одновременно рулем
направления и элеронами.
Поскольку боковая аэродинамическая
сила Z значительно меньше подъемной
аэродинамической силы У, то при
управлении курсовым углом с помощью
руля направления курс изменяется мед-
ленно. Поэтому управление курсом с
помощью руля направления осущест-
вляется только в тех случаях, когда по
условиям боевого применения самолета
крен нежелателен (например, при вы-
полнении фоторазведки, довороте само-
лета на наземную цель). Более эффек-
тивно управление разворотом самолета
с помощью элеронов. В этом случае
управление курсом осуществляется кре-
нением самолета и поворотом вектора
скорости в горизонтальной плоскости под
действием . горизонтальной проекции
подъемной силы У sin у. На рис. 12.8 по-
казана стабилизация курсового угла с
помощью элеронов. Для этого на вход
в автопилот подается сигнал курсового
гироскопа, пропорциональный отклоне-
нию угла рыскания (курса) ф от задан-
ного. Автопилот отклоняет элероны про-
порционально разности ф—ф3 и самолет
начинает накреняться.
Для улучшения качества переходного
процесса на суммирующее устройство
автопилота одновременно с сигналом
курсового гироскопа подаются сигналы
стабилизации крена: сигнал угла кре-
на и сигнал угловой скорости крена.
Таким образом, закон управления кур-
ВидА
\ А
Рис. 12.8. Управление кур-
совым углом посредством
накренения самолета
341
совым углом с помощью элеронов имеет следующий
вид:
(ф - ф3) + ^ЭТ + (12.3)
Рис. 12.9. Изменение пара-
метров движения самолета
в процессе устранения воз-
никшего угла рыскания ав-
топилотом
Знак минус перед передаточным коэффициентом поставлен
потому, что для устранения положительного изменения угла ф
(нос самолета повернут влево) требуется отрицательное отклоне-
ние элеронов (правый элерон — вверх).
При накренении самолета появится
горизонтальная составляющая подъем-
ной силы Y sin у, которая начнет искрив-
лять траекторию, поворачивая вектор
скорости самолета к заданному курсу
с угловой скоростью, пропорциональной
углу крена. Так как после накренения
самолета момент рыскания не появляет-
ся, то в начальный момент при искрив-
лении траектории самолет будет дви-
гаться поступательно, в результате чего
продольная ось самолета начнет отста-
вать от поворота вектора скорости. Это
приведет к возникновению некоторого
угла скольжения 0 (в нашем случае на
правое полукрыло, рис. 12.8). Если са-
молет в путевом отношении устойчив, то при возникновении сколь-
жения появится момент рыскания, который вызовет вращение
продольной оси самолета вправо, стремясь совместить ее с векто-
ром скорости.
По мере разворота самолета будет уменьшаться сигнал курса
Фз), в результате чего сигнал угла крена превысит
его, что обусловит отклонение элеронов против крена и угол
крена начнет уменьшаться. Когда угол рыскания ф вернется к ис-
ходному значению, то вернутся к исходным значениям углы кре-
на у и скольжения 0. Характер изменения параметров движения
в рассмотренном переходном процессе показан на рис. 12.9. Здесь
путевой угол определяет угол поворота траектории самолета
(вектора скорости) в горизонтальной плоскости, а угол ф — пово-
рот продольной оси самолета. Разность ф—Ч7 определяет
угол скольжения 0. Заметим, что, стабилизируя курсовой угол ф,
автопилот, имеющий закон управления (12.3), не обеспечивает
полета по заданной линии пути (х0 на рис. 12.8): в процессе ста-
билизации курса самолет будет отклоняться от заданной линии
пути.
Заметим, что при больших значениях разности углов ф—ф3
управляющий сигнал ^(ф—ф3) (см. формулу 12.3) может при-
вести к накренению самолета более 90°, это недопустимо. Для
предотвращения этого сигнал № (ф — ф3) имеет ограничение,
342
предотвращающее чрезмерное накренение самолета автоматом
(обычно не более 40°).
При управлении курсовым углом только с помощью элеронов
продольная ось самолета поворачивается вследствие возникнове-
ния момента рыскания, обусловленного скольжением из-за несов-
падения вектора скорости с плоскостью симметрии самолета. При
малой путевой устойчивости углы скольжения могут достигать зна-
чительных величин, что нежелательно, а при полете на малых
скоростях (больших углах атаки) опасно из-за возможности воз-
никновения преждевременного срыва потока. Поэтому иногда при-
меняют координированную систему управления курсом. В этом
случае сигнал отклонения курса подается одновременно в канал
элеронов и канал руля направления. Первый вызывает накренение
самолета и вращение вектора скорости в горизонтальной плоско-
сти, второй — вращение продольной оси самолета в этой же плос-
кости.
§ 12.3. Автоматическое управление траекторией полета
Управление движением самолета в вертикальной плоскости
осуществляется с помощью двух органов управления: стабилиза-
тора и рычага управления двигателем. Меняя положение стабили-
затора и величину тяги двигателя, можно управлять высотой и
скоростью полета. При этом в общем случае управление высотой
и скоростью полета оказывается связанным, требуя координиро-
ванного изменения тяги двигателя и отклонения стабилизатора.
Однако для удобства управления самолетом целесообразно
осуществлять управление высотой и скоростью независимо друг
от друга (автономно). При этом, как правило, у маневренных са-
молетов автоматическое управление осуществляется только высо-
той полета; тягой двигателя и скоростью летчик обычно управ-
ляет вручную. Поэтому ограничимся рассмотрением автоматиче-
ского управления только высотой полета, предполагая, что задан-
ный закон изменения скорости обеспечивается летчиком (или ав-
томатом скорости).
Для автоматического управления высотой полета в канал ста-
билизатора подаются сигналы, пропорциональные высоте полета,
углу тангажа и угловой скорости тангажа. Таким образом, закон
отклонения стабилизатора при управлении высотой полета имеет
вид:
Д? = ^(//-Я3) + ^(»-»з)4-^. (124)
На рис. 12.10 показана функциональная схема автомата, со-
ответствующая этому закону. В качестве датчика высоты полета
используется высотомер (В), определяющий высоту по давлению.
Поэтому в рассматриваемом случае управление осуществляется
не геометрической, а барометрической высотой.
343
Рассмотрим работу автопилота, стабилизирующего высоту по-
лета (режим коррекции высоты). Допустим, что в процессе полета
высота стала меньше заданной на величину ДЯ = Я—Н3. Сигнал
с датчика барометрического высотомера Хн подается на сумми-
Рис. 12.10. Функциональная схема автоматиче-
ского управления высотой полета
рующее устройство канала стабилизатора, которое сличает его
с заданным сигналом ХНз и вырабатывает сигнал рассогласова-
ния Хн — ХНз. Последний после усиления подается на рулевой
привод, который отклоняет стабилизатор на величину Дер. Откло-
Рис. 12.11. Траектория движения самолета в процессе устранения
возникшего отклонения высоты при работе автопилота в режиме
стабилизации
нение стабилизатора происходит до тех пор, пока сигнал обратной
связи ХНс не уравновесит сигнал рассогласования Хн — ХНз.
Возникший в результате отклонения стабилизатора момент
(точка 1 на рис. 12.11) вызовет поворот продольной оси самолета,
что сопровождается увеличением углов атаки и тангажа.
344
Появившийся прирост подъемной силы (точка 2) искривляет
траекторию движения и переводит самолет в набор высоты. По
мере увеличения угла тангажа с гировертикали (ГВ) на вход
автопилота будет поступать сигнал Хн^ противоположный по зна-
ку сигналу рассогласования Хн— ХНз. Последний с ростом вы-
соты полета уменьшается. В результате сумма сигналов XHq
станет больше сигнала Хн — ХНз и отклонение стабилизатора
начнет уменьшаться, уменьшается при этом и угол атаки. В точ-
ке 3 стабилизатор и угол атаки возвратятся к исходным значениям.
При дальнейшем движении сигнал рассогласования Хн — ХНз про-
должает уменьшаться, что приведет к отклонению стабилизатора
в противоположную сторону. Это сопровождается уменьшением
угла атаки и подъемной силы, благодаря чему траектория движе-
ния начинает отклоняться вниз (точка 4 на рис. 12.11). В точке 5
самолет выходит в горизонтальный полет на заданной высоте, сиг-
нал рассогласования Хн — ХНз равен нулю, а стабилизатор будет
находиться в исходном (балансировочном) положении.
Из физического рассмотрения работы автопилота, управляю-
щего высотой полета, можно прийти к выводу, что для стабили-
зации высоты полета необходимыми являются только два сигнала:
сигнал отклонения от заданной высоты и сигнал отклонения от
заданного угла тангажа. Отсутствие сигнала по тангажу привело
бы к тому, что в течение всего времени приведения высоты к за-
данной стабилизатор был бы отклонен на кабрирование, угол
атаки был бы больше исходного. Вследствие этого при подходе
к заданной высоте самолет, имея большую вертикальную скорость,
проскочил бы заданную высоту и процесс восстановления высоты
был бы колебательным (штриховая линия на рис. 12.11). Таким
образом, сигнал тангажа при управлении высотой полета является
своего рода сигналом демпфирования колебаний высоты. Сигнал
же по угловой скорости тангажа для стабилизации высоты полета
принципиального значения не имеет и применяется только для
предотвращения угловых колебаний самолета по тангажу.
На некоторых самолетах с помощью стабилизатора (руля вы-
соты) при неизменном режиме работы двигателя осуществляется
стабилизация (автоматическое управление) числа М, например
при наборе высоты полета. В этом случае в законе управления
стабилизатором (12.4) вместо сигнала отклонения от заданной вы-
соты подается сигнал отклонения от заданного числа М. При та-
ком законе управления автопилот, работая в режиме стабилиза-
ции числа М и угла тангажа, будет обеспечивать полет самолета
с постоянным углом атаки. Вследствие этого по мере выработки
топлива и уменьшения массы самолет будет набирать высоту про-
порционально изменению массы, т. е. осуществлять полет «по по-
толкам».
Выше было рассмотрено управление барометрической высотой
полета. Такой принцип управления не представляется возможным
345
безопасно реализовать на малых и предельно малых высотах.
Для предотвращения столкновения самолета с пересеченным рель-
ефом местности на таких высотах необходимо осуществлять управ-
ление (стабилизацию) геометрической высотой относительно зем-
ной поверхности.
Сохранение постоянной относительной высоты ЯОт, измеряемой
радиовысотомером (или лазерным высотомером), требует облета
рельефа местности в вертикальной или горизонтальной плоскости.
Рис. 12.12. Управление по упрежденной высоте полета
Для облета рельефа местности необходимо отклонением стабили-
затора изменять подъемную силу (перегрузку) самолета и тем
сильнее, чем меньше высота полета и большую пересеченность
имеет местность. Поскольку величина изменения перегрузки огра-
ничена, то облет рельефа местности по информации текущей от-
носительной высоты полета может безопасно осуществляться
только над слабо пересеченной местностью.
Для обеспечения полета на меньших высотах либо над силь-
но пересеченной местностью необходимо осуществлять управление
по наклонной дальности или упрежденной высоте полета. Под
наклонной или упрежденной дальностью рупр (рис. 12.12) пони-
мается расстояние от самолета до элемента впереди лежащего
рельефа, измеряемое вдоль луча, образующего некоторый угол р
с продольной осью самолета или вектором скорости полета. В ка-
честве датчика наклонной дальности используется радиодально-
мер [19].
В случае отказа системы облета рельефа местности либо по
другим соображениям (например, при полете на высотах, мень-
ших разрешаемых) летчик в визуальном полете для выдержива-
ния предельно малой высоты над пересеченной местностью может
реализовать принцип управления наклонной дальностью, исполь-
зуя центральную марку прицела. При этом учитывается то обстоя-
346
тельство, что при полете с постоянной скоростью угол р между
вектором скорости и направлением взгляда летчика через опреде-
ленную точку на сетке прицела не изменяется. Для удобства ис-
пользуется центральная марка, отклоненная на определенный угол
Ц “ Нот/£\пр-
Выдерживая глазомерно на постоянной дальности £>упр впе-
реди самолета скользящую по поверхности точку пересечения
линии визирования через центральную марку с поверхностью зем-
ли (рис. 12.12) или препятствием, летчик сохраняет относительную
высоту полета практически постоянной. При появлении препятст-
вия на дальности £>упр летчик, поднимая линию визирования над
препятствием, обеспечивает безопасный пролет над ним. Наиболее
удобные для выдерживания высоты полета значения дальности
находятся в пределах от 1 до 5 км. Для выдерживания высоты
100 м выбирается дальность 5 км: ц= 100/5000 = 0,02 (или 20 тыс.
долей дальности).
Центральная марка прицела выставляется из условия обеспе-
чения этого соотношения. Для выдерживания меньшей высоты
следует пропорционально уменьшить дальность до земли по линии
визирования через центральную марку. Ошибка летчика в выдер-
живании наклонной дальности в 1 км дает ошибку в 20 м вы-
соты.
При полете на малых высотах с облетом препятствий в верти-
кальной или горизонтальной плоскости могут использоваться
РЛС обзора земной поверхности, а также заложенный в память
ЭВМ рельеф местности.
Управление движением самолета в горизонтальной плоскости.
Движение центра масс самолета в горизонтальной плоскости в
общем случае связано с одновременным проявлением продольного
и бокового движений. Для управления таким движением требуется
воздействовать на все четыре органа управления: элероны, руль
направления, стабилизатор и рычаг управления тягой двигателя.
Стабилизатор необходимо отклонять, для того чтобы обеспечить
движение самолета в горизонтальной плоскости при его накрене-
нии путем регулирования подъемной силы. Но при изменении подъ-
емной силы меняется и сила лобового сопротивления, поэтому для
сохранения постоянства скорости необходимо воздействовать на
тягу двигателя. Строго говоря, отмеченное должно осуществляться
и при управлении курсом. Однако для простоты рассуждений при
осуществлении управления движением самолета в горизонтальной
плоскости ограничимся рассмотрением только его бокового дви-
жения, полагая, что автопилот обеспечивает в процессе разворота
самолета полет на заданной высоте с постоянной скоростью.
В этом случае управлять движением центра масс в горизонталь-
ной плоскости можно только отклонением элеронов и руля направ-
ления. Это значит, что управление движением центра масс напо-
минает управление курсом. Действительно, направление полета
(курс) изменяется благодаря искривлению траектории в горизон-
тальной плоскости. Таким образом, изменение углового положения
347
самолета связано с управлением движением центра масс. Однако
при автоматическом управлении курсом боковое перемещение са-
молета является не самоцелью, а средством изменения курса.
В некоторых случаях (например, при заходе на посадку, при
выходе в заданную точку пространства и др.) возникает необхо-
димость управлять боковым перемещением самолета (координа-
Рис. 12.13. Траектория и изменение параметров дви-
жения самолета в процессе возникшего бокового от-
клонения при работе автопилота в режиме стабилиза-
ции
той Z). С этой целью в автопилот вводится сигнал, пропорцио-
нальный боковому отклонению самолета от заданной траектории Z.
Этот сигнал подается в тот канал автопилота, который обеспечи-
вает управление курсом. Поскольку управление курсом можно бо-
лее эффективно осуществлять с помощью элеронов, то сигнал от-
клонения самолета от заданной траектории обычно подается в ка-
нал элеронов. Добавляя к закону (12.3) сигнал бокового откло-
нения, получим следующий закон управления элеронами:
8э = ~ (Ф - Фз) + + k^x + k*3Z. (12.5)
При отклонении самолета от заданной траектории на величи-
ну Z автопилот отклоняет элероны пропорционально Z, вследствие
чего появляется момент крена и самолет накреняется в сторону
заданной траектории. По мере увеличения угла крена к автопи-
лоту поступает сигнал пропорциональный изменению угла
крена и противоположно направленный сигналу бокового откло-
348
нения что приводит к уменьшению отклонения элеронов.
Накренение самолета производится до тех пор, пока сигнал от-
клонения от заданной траектории не уравновесится сигналом
крена и элероны не будут возвращены в исходное положение (точ-
ка 1 на рис. 12.13). При накренении самолета появляется горизон-
тальная составляющая подъемной силы, искривляющая траекто-
рию движения самолета в сторону заданной траектории полета.
В процессе разворота и приближения самолета к заданной траек-
тории сигнал бокового отклонения будет уменьшаться, а сигнал
угла ф увеличиваться. Это приводит к отклонению элеронов в
противоположную сторону, и угол крена начинает уменьшаться.
С течением времени угол крена становится равным нулю (точ-
ка 2 на рис. 12.13), а затем самолет накреняется в противополож-
ную сторону (точка 3). Изменяя кривизну траектории полета, са-
молет монотонно приближается к заданной траектории. Когда Z
станет равна нулю, курсовой угол ф и угол крена возвратятся к
исходным значениям (см. изменение параметров движения на
рис. 12.13).
Из физического рассмотрения работы такого автопилота сле-
дует, что демпфирование движения центра масс самолета обеспечи-
вается введением коррекции по углу ф в закон отклонения элеро-
нов. Отсутствие сигнала по курсовому углу привело бы к тому,
что в течение всего времени приближения самолета к заданной
траектории угол крена не изменял бы знака. В результате само-
лет, имея большой угол ф, проскочил бы заданную траекторию и
процесс стабилизации был бы колебательным (см. штриховую ли-
нию на рис. 12.13).
§ 12.4. Комплексные системы автоматического управления
современных самолетов
Непрерывное расширение функций, выполняемых автоматиче-
скими устройствами, сопровождается увеличением еостава авто-
матического оборудования, устанавливаемого на современном са-
молете. Отсутствие единой идеи в проектировании систем авто-
матического управления не позволяет обеспечить необходимую на-
дежность таких систем управления и сопровождается установкой
неоправданно большого количества различного рода датчиков,
преобразователей, вычислителей, исполнительных устройств и дру-
гих элементов автоматического оборудования. Поэтому возникла
насущная "необходимость объединения всех бортовых автоматиче-
ских устройств в единую систему автоматического управления
(САУ).
Совокупность бортовых автоматических устройств и сложных
наземных радиотехнических устройств образует комплексную си-
стему автоматического управления. Такие системы предназначены
для расширения задач, выполняемых самолетом, повышения эф-
фективности его действия, обеспечения безопасности полета и мак-
симального облегчения работы летчика. Для каждого , типа са-
349
молета разрабатывается САУ со своим целевым назначением.
Так, например, на ряде современных самолетов пилотажно-нави-
гационные и прицельные системы, объединенные в единый комп-
лекс, образуют пилотажно-навигационный комплекс (ПНК) и т. д.
Однако в системах управления различных типов самолетов имеется
много общего.
Рис. 12.14. Функциональная схема комплексной системы автоматического
управления
На рис. 12.14 показана одна из возможных (упрощенных)
функциональных схем комплексной бортовой системы управления.
Такая система управления позволяет осуществить неавтоматиче-
ское (ручное), автоматическое управление и полуавтоматическое
директорное.
Неавтоматическое управление осуществляется летчиком,
воздействующим на рычаги управления, с помощью рулевых при-
водов. Для обеспечения обратной связи по усилиям к проводке
управления подключены загрузочные механизмы (ЗМ) с механиз-
мами триммерного эффекта (МТ). В продольный канал рассмат-
риваемой системы включен автомат регулирования управления
(АРУ).
Автоматическое управление в соответствии со схемой, по-
казанной на рис. 12.14, осуществляется с помощью двух испол-
нительных устройств: рулевых агрегатов управления (РАУ) и ме-
ханизмов триммерного эффекта (МТ), на которые подаются
управляющие сигналы, вырабатываемые вычислителем (В).
Рулевые агрегаты управления (РАУ), представляющие собой
управляемые «раздвижные тяги», включены в проводку между ры-
чагами управления и рулевыми приводами. Они могут работать
350
как В автоматическом, так и неавтоматическом режимах полета.
В последнем случае они предназначены для улучшения динамиче-
ских свойств самолета, обеспечивая с помощью автоматов устой-
чивости и демпфирования необходимые характеристики устойчи-
вости и управляемости самолета. Обладающим сравнительно боль-
шим быстродействием перекладки рулевых поверхностей (20—
40 °/с), РАУ в целях безопасности полета доверяется сравнитель-
но небольшой диапазон отклонений рулей. В случае отказа РАУ,
сопровождающегося уводом его штока в одно из крайних положе-
ний, возникает сравнительно небольшой возмущающий момент.
Благодаря этому при неуправляемом изменении параметров дви-
жения, вызванном отказом РАУ, летчик имеет возможность свое-
временно вмешаться в управление и парировать последствия этого
отказа. Кроме того, при отказе РАУ, сопровождающемся уводом
его штока в крайнее положение, остается достаточный запас от-
клонения руля для безопасного завершения полета.
Механизмы триммерного эффекта (МТ), включенные парал-
лельно в проводку управления, при сравнительно небольшом быст-
родействии (2—4 °/с) позволяют использовать практически весь
диапазон отклонения рулевых поверхностей. МТ в автоматическом
режиме управления могут быть включены в работу только при
снятии усилий с рычагов управления. Поэтому если при работе
САУ в автоматическом режиме летчик прикладывает некоторое
усилие к рычагам управления, то МТ автоматически отключаются,
а РАУ начинают выполнять функции автоматов демпфирования,
в некоторых случаях и автоматов устойчивости. С этой целью на
ручке и педалях или в проводке управления устанавливаются спе-
циальные концевые выключатели, которые срабатывают при при-
ложении усилий к рычагам управления. Этим достигается наибо-
лее быстрое отключение САУ.
Такая система управления позволяет обеспечить совмещенное
управление самолетом. При отсутствии усилий на ручке управле-
ния работает САУ. Если же требуется изменить положение само-
лета в пространстве, то летчик, как и при ручном управлении,
прикладывает усилия к рычагам управления, отключает автома-
тическое управление и осуществляет потребное отклонение рулей.
Когда желаемое угловое положение самолета создано, летчик
ослабляет усилие на рычагах управления и САУ снова подклю-
чается, стабилизируя новые, заданные летчиком углы тангажа и
крена.
Для аварийного отключения автоматического режима управле-
ния может быть использована специальная гашетка, устанавли-
ваемая на ручке управления всех современных самолетов.
На вычислитель (В) поступают сигналы от датчиков парамет-
ров движения и положения самолета (ДДПС), а также (в зависи-
мости от назначения самолета) сигналы от системы ближней
навигации и посадки (СНП), автономной системы дальней нави-
гации (АСДН), системы поиска наземной цели (СПНЦ), системы
огибания рельефа местности, системы дальнего (СДН) и
351
ближнего (СБН) наведения, системы вооружения (СВ) и др.
системы. На рис. 12.14 для простоты показаны только системы
наведения (СН) и системы навигации и посадки (СНП). Вычи-
слитель в соответствии с заданным режимом работы САУ выра-
батывает управляющие сигналы, которые подаются на исполни-
тельные устройства. Между вычислителем и исполнительными
устройствами устанавливается система обеспечения безопасности
(СОБ), которая пропускает на исполнительные устройства только
такие по величине сигналы, которые не могут вывести самолет за
существующие ограничения. При неавтоматическом (ручном)
управлении системы обеспечения безопасности могут также фор-
мировать управляющие сигналы для предупреждения и предот-
вращения выхода самолета на критические режимы [19].
Современные САУ создают большие возможности по расшире-
нию задач, выполняемых самолетом, позволяют надежно и с боль-
шой точностью выполнять режимы, задаваемые летчиком, разгру-
жают внимание летчика и повышают безопасность полета. Однако
было бы неправильно полагать, что при использовании САУ функ-
ции летчика сводятся только к выбору режима работы САУ, на-
блюдению и контролю за его работой. Летчик, отвечая за выпол-
нение задания и успешное завершение полета, является своего
рода резервом системы автоматического управления, он должен
быть всегда готовым к взятию управления на себя. Однако в ав-
томатическом режиме управления его возможности резервирова-
ния САУ при разрушении привычного стереотипа по ручному
управлению существенно снижаются. «Отчужденность» летчика
от управления понижает его бдительность, готовность к внезап-
ному взятию управления на себя. С этой точки зрения представ-
ляет большой интерес полуавтоматическое (директорное)
управление, при котором летчик более активно участвует в управ-
лении самолетом.
§ 12.5. Директорное управление. Особенности пилотирования
по КПП
При директорном (полуавтоматическом) управлении часть
функций выполняет САУ, часть — летчцк. Обобщение показаний
пилотажно-навигационных приборов и сложные математико-логи-
ческие операции выполняет вычислитель системы автоматического
управления, который выдает командные сигналы не на автопилот,
а на стрелки директорного (командного) прибора, в соответствии
с которым летчик отклоняет органы управления.
Смысл директорного управления заключается в том, что лет-
чику выдаются сигналы управления, а не сигналы отклонения от
заданной траектории или каких-то заданных параметров. При
исполнении летчиком команд, выдаваемых директорным прибором
(командно-пилотажным прибором — КПП), самолет будет дви-
гаться по оптимальной траектории, не превышая допустимых уг-
лов крена и перегрузки. В случае отклонения от заданной траек-
352
торий стрелки КПП отклоняются, показывая, как летчику надо
отклонить органы управления.
Практика показывает, что для выполнения горизонтального ма-
невра удобна команда на изменение угла крена, а для вертикаль-
ного маневра — команда на изменение угла тангажа. В соответ-
ствии с этим командно-пилотажный прибор, общий вид которого
показан на рис. 12.15, имеет в центре за силуэтом самолета две
командные стрелки: вертикаль-
ную /, предназначенную для
управления креном, и горизон-
тальную 3 — для управления
тангажом. Вертикальная стрел-
ка накреняется влево—вправо
относительно нижней точки
крепления, а горизонтальная
перемещается относительно
шкалы угла тангажа вверх—
вниз.
Поскольку изменение углов
крена и тангажа следует за
отклонением элеронов и ста-
билизатора с малым запазды-
ванием, то стрелки КПП
очень подвижны, почти мгно-
Рис. 12.15. Командно-пилотажный
прибор
венно реагируют на откло-
нение рулей. Если летчик не понимает сущности управления
по КПП, он иногда воспринимает большое отклонение командной
стрелки, как значительное отклонение самолета от заданной тра-
ектории, и соответственно этому перекладывает рули, стремясь
скорее выйти на заданную траекторию. Стрелки КПП при этом
перебрасываются в обратную сторону, что свидетельствует о чрез-
мерно большом отклонении рулей. При таком управлении летчик
может раскачать самолет. Для правильного пилотирования по
КПП следует плавно, не спеша совместить стрелки примерно
с центром прибора 7, помня, что их большое расхождение в отли-
чие, например, от планок положения или нуль-индикаторов еще
не означает, что самолет намного отклонился от заданной линии
пути. Это расхождение означает только, что отклонение рулей не
соответствует полету по заданной траектории. Если после совме-
щения директорных стрелок с центром прибора планки положе-
ния не приближаются к нулю, вот тогда отклонение самолета от
заданной траектории чрезмерно велико. Это может иметь место,
например, если, оказавшись в стороне от створа ВПП на слишком
малом удалении от аэродрома, пытаться выйти на посадочный
курс по директорным стрелкам КПП.
Выдерживание заданных углов крена и тангажа производится
по авиагоризонту, размещенному в центре прибора (силуэт само-
лета в, шкалы углов крена 9 и тангажа 10) и непосредственно по-
казывающему положение самолета относительно горизонта.
х 12—21
353
При пилотировании по КПП необходимо периодически контро-
лировать правильность движения самолета по планкам (стрелкам)
положения на этом приборе. В левой части прибора располагается
вертикальная шкала со стрелкой 2, которая показывает положе-
ние заданной высоты полета относительно самолета, а при заходе
на посадку — положение глиссады снижения. В верхней части
прибора размещена горизонтальная шкала со стрелкой 5, которая
показывает летчику положение равносигнальной зоны курсового
маяка относительно самолета при заходе на посадку. Однако ру-
ководствоваться надо только директорными стрелками, пока чрез-
мерное их расхождение или длительное расхождение по знаку от-
клонения с планками положения не сделают очевидной неправиль-
ную работу директорной системы.
В режиме автоматического управления управляющие сигналы
из вычислителя подаются не только на автопилот, но и на КПП.
Это позволяет летчику по положению командных стрелок КПП
контролировать правильность работы автопилота, а также (в слу-
чае необходимости) быстро переходить от автоматического управ-
ления к директорному.
354
Раздел IV
ЛЕТНО-ТЕХНИЧЕСКИЕ И МАНЕВРЕННЫЕ
СВОЙСТВА САМОЛЕТОВ
Глава 13
ГОРИЗОНТАЛЬНЫЙ ПОЛЕТ
§ 13.1. Силы, действующие на самолет
Для того чтобы изучить основные летно-технические и манев-
ренные свойства самолета и вскрыть их физическую сущность
сравнительно простыми средствами, будем рассматривать движе-
ние самолета только под действием сил, предполагая, что за все
время движения моменты, действующие на самолет, уравновеше-
ны соответствующим отклонением органов управления. Это озна-
чает, что в любой момент времени все силы, действующие на са-
молет, можно считать приложенными в его центре масс.
В зависимости от соотношения всех сил, действующих на са-
молет, его движение может быть криволинейным или прямолиней-
ным, установившимся или неустановившимся. Если сумма всех
нормальных сил равна нулю, т. е. они взаимно уравновешены,
причина искривления траектории отсутствует и движение само-
лета будет строго прямолинейным. Если же суммарная нор-
мальная сила не равна нулю, то под ее воздействием направление
движения самолета будет изменяться, траектория полета будет
искривляться в направлении действия этой силы. Движение са-
молета будет криволинейным.
При сумме всех сил, направленных по касательной к траекто-
рии, равной нулю, скорость будет сохраняться постоянной. Такое
движение самолета называют равномерным или установив-
шимся. Если же сумма касательных сил не равна нулю, то воз-
никает касательное ускорение в сторону действия суммарной силы.
Движение самолета будет происходить с разгоном или торможе-
нием, т.' е. скорость будет увеличиваться или уменьшаться. Такое
движение самолета называют неравномерным или неуста-
новившимся.
12*
355
Из всех сил, действующих на самолет, наиболее сложными в
смысле зависимости от многих параметров являются тяга двига-
теля Р и лобовое сопротивление X.
В главе 6 были рассмотрены высотно-скоростные и дроссель-
ные характеристики турбореактивного двигателя (рис. 6.13 и 6.14).
Из этих графиков следует, что сила тяги двигателя зависит от
высоты Н, скорости V и степени дросселирования. Последняя мо-
жет выражаться как в относительных величинах тяги Р = Р/Ртах,
так и в относительных или абсолютных величинах частоты враще-
ния ротора двигателя. Относительная величина частоты вращения
обычно выражается в процентах от ее величины при максималь-
ном режиме работы двигателя.
Сила лобового сопротивления X, как показано в главе 4, мо-
жет быть представлена как сумма двух слагаемых Xq и Xi. Пер-
вое из них не зависит, а второе зависит от угла атаки (подъем-
ной силы):
X=Xo + Xt\ (13.1)
хо = С S = O.lpM'C S\ (13.2)
Xt = ДС2 р-~ S = Q,7pM^AC}S. (13.3)
При анализе маневренных свойств самолета индуктивное со-
противление Xi удобнее представлять в виде зависимости не от ко-
эффициента Су, а от нормальной перегрузки пу. Для этого в фор-
мулу (13.3) подставим
Г Y —°Пу
qS ~~ qS •
Тогда получим
Х1 = р-у2~ ПУ = Х1 ГПу' (13.4)
~S
где Xi г— индуктивное сопротивление при перегрузке %=1.
у ___ А^ _ А&
Л^ — ?у2 0t7pM2S • (13.5)
2 5
На рис. 13.1 и 13.2 в качестве примера показаны графики XQ и
Х/г, рассчитанные по формулам (13.2) и (13.5) для различных вы-
сот. Как видно из этих графиков, Хо уменьшается с высотой и воз-
растает с увеличением числа М, а Х/г, наоборот, возрастает с вы-
сотой ц уменьшается при увеличении скорости (числа М). Наклон
кривых Хо с увеличением высоты уменьшается за счет уменьшения
плотности воздуха р (давления р). При больших скоростях Х/г во
много раз меньше, чем Хо, но это только при перегрузке ffy = l,
например в горизонтальном прямолинейном полете. В полете же
356
Хо>кгс
Рис. 13.1. Лобовое сопротивление при нулевой
подъемной силе
Рис. 13.2. Индуктивное сопротивление при пе-
регрузке nv = l
357
с большими перегрузками индуктивное сопротивление, пропорцио-
нальное квадрату перегрузки, весьма сильно возрастает и может
превысить Хо.
На рис. 13.3 в качестве примера показана зависимость сум-
марного лобового сопротивления от числа М для высоты 11 км
при различных постоянных перегрузках, построенная по форму-
Рис. 13.3. Зависимость лобового сопротивления
от числа М полета и перегрузки
лам (13.1) — (13.5). Здесь же штриховой линией показана тяга
двигателя на полном форсаже. Из графика видно, что уже при
/2^ = 4 лобовое сопротивление почти при всех числах М превышает
тягу двигателя.
§ 13.2. Минимальная скорость полета
Рассмотрим прямолинейный горизонтальный полет самолета
без скольжения. Очевидно, что при этом угол наклона траекто-
рии 0 = 0, высота Н остается все время постоянной, боковая сила
Z = 0 и боковая перегрузка пг = 0. Схема сил, действующих на са-
молет в таком полете, приведена на рис. 13.4.
Для сохранения прямолинейности траектории необходимо, что-
бы суммы проекций сил на нормальные оси Оук и OzK были рав-
ны нулю. Следовательно, проекции ускорения на эти оси тоже
будут равны нулю. Поэтому уравнения движения самолета в про-
екциях на оси траекторной системы координат запишутся в виде:
dV п „
т -тг- = Pcos а — X,
at
О = У Р sin а — О;
O=Ksiny или у = 0.
358.
Последние два уравнения представляют собой математическую
запись условий прямолинейности горизонтального полета. Ввиду
малости угла атаки а для упрощения анализа примем, что cosa==
₽1, sina = 0, и запишем уравнения движения в виде:
т^=Р-Х-, (13.6)
Y=Cy^-S=Q или лу = 1; (13.7)
1 = 0. (13.8)
Рис. 13.4. Силы, действующие на самолет в прямолинейном
горизонтальном полете
Иначе говоря, для сохранения прямолинейности горизонталь-
ного полета необходимо, чтобы подъемная сила была равна силе
тяжести и крен был равен нулю. При этом коэффициент Су и
скорость прямолинейного горизонтального полета Vr связаны за-
висимостью:
Vr= УC^pS’’ Cyr==~pV^S' (13'9)
Поскольку коэффициент Су зависит от угла атаки;
Су = С“ (« — а0),
то для сохранения условия прямолинейности (формула 13.7) при
уменьшении скорости необходимо соответственно увеличивать угол
атаки а.
Так как из условия обеспечения безопасности полета увеличи-
вать Су и а можно только до их допустимых значений СуЛоа и
аДоп, то и минимальная скорость прямолинейного горизонтального
359
полета должна быть ограничена. Одной из грубых ошибок в тех-
нике пилотирования является уменьшение скорости ниже мини-
мально допустимой. Уменьшение подъемной силы вследствие
уменьшения скорости приводит прежде всего к искривлению тра-
ектории вниз (рис. 13.5). При этом если летчик будет выдержи-
Рис. 13.5. Увеличение угла атаки вследствие потери скорости
вать угол тангажа неизменным, то угол атаки, увеличиваясь
вследствие искривления траектории, может превысить предельно
допустимое значение.
Таким образом, главная опасность состоит не в уменьшении
скорости самой по себе, а в неконтролируемом увеличении угла
атаки. Именно этим и диктуется необходимость ограничения ми-
нимальной скорости горизонтального полета.
Минимально допустимая скорость горизонтального полета и
скорость сваливания определяются из условия (формула 13.9):
Из формул (13,10) видно, что истинные скорости — минималь-
но допустимая Vmin доп и скорость сваливания Усв — увеличиваются
с высотой из-за уменьшения плотности. Минимальная приборная
скорость Vnpmin практически постоянна (рис. 13.6). Она незначи-
тельно увеличивается лишь вследствие уменьшения Су доп с ростом
числа М полета. Очевидно, что число iWmin = Vmm/я, соответствую-
щее истинной минимальной скорости, увеличивается с высотой,
так как минимальная скорость увеличивается, а скорость звука —
уменьшается. Поэтому на больших высотах число Mmin может
360
быть больше единицы, т. е. минимальная скорость может ока-
заться сверхзвуковой. В этом случае она определяется из условия
балансировки по предельно достижимой величине СУбал = Су?
при максимальном угле отклонения стабилизатора:
Рис. 13.6. Минимальные ско-
рости горизонтального полета
/ — приборная; 2 — истинная
Рис. 13.7. Лобовое сопротивление в пря-
молинейном горизонтальном полете
§ 13.3. Лобовое сопротивление самолета в прямолинейном
горизонтальном полете
В прямолинейном горизонтальном полете перегрузка пу = 1.
Поэтому лобовое сопротивление Хг состоит из двух слагаемых
(рис. 13.7), определяемых по формулам (13.2) и (13.3):
XT = Xo + XlI = Cx^S+^-. (13.11)
Так как Хо возрастает, a XiT уменьшается по скорости, то их
сумма Хг при некоторой скорости имеет минимум.
Скорость, при которой лобовое сопротивление в прямолиней-
ном горизонтальном полете минимально, называется наивыгод-
нейшей* скоростью Унв. Соответствующие значения Су и а на-
зываются тоже наивыгоднейшими Су Нв и «Нв.
* На первый взгляд кажется, что полет с минимальным лобовым сопротив-
лением всегда выгоден. Отсюда и произошло название .этой скорости. Однако
все зависит от цели, которая преследуется в конкретном полете. Например,
максимальная дальность горизонтального полета у земли достигается при ско-
рости, значительно большей, чем «наивыгоднейшая» (см. главу 20).
361
Рис. 13.8. Определение максимальной скорости
полета по кривым тяги и лобового сопротивле*
ния
362
Как было показано в главе 3, на наивыгоднейшем угле атаки
Сх = 2СХо, откуда следует, что Сх =Сх1 и Xti — XlT. Значения
Су нв и аэродинамического качества Кг на этом угле атаки опреде-
ляются выражениями (3.14) и (3.15):
Кг =
Y О
* “ *mln
1
Наивыгоднейшая скорость горизонтального полета может быть
вычислена по формуле:
Инв=/
2G
pSCy нв
(13.12)
На рис. 13.8 приведены графики ХГ(М) для различных высот.
Из формулы (13.12) видно, что наивыгоднейшая скорость, соот-
ветствующая Хг min, с увеличением высоты возрастает пропорцио-
нально l/k Д. Поэтому кривые Хг по мере увеличения высоты сме-
щаются на большие скорости, а их наклон уменьшается, как и
у кривых Хо (рис. 13.1), составляющих на больших скоростях ос-
новную долю Хг.
Минимальное лобовое сопротивление на дозвуковых скоростях
остается постоянным для всех высот, так как
*т1п = а ^max = = const
На скоростях, близких К скорости звука И больших ее, /Стах
уменьшается, a Xmin увеличивается за счет роста СХо и А.
§ 13.4. Максимальная скорость и ее зависимость
от высоты
Максимальной скоростью называется установившаяся
скорость прямолинейного полета на максимальном режиме рабо-
ты двигателя или на полном форсаже. В зависимости от режима
работы двигателя, угла наклона траектории и высоты полета мак-
симальная скорость может иметь различные значения. Важной
характеристикой летных свойств самолета является максимальная
скорость горизонтального полета.
Уравнение (13.6), характеризующее изменение скорости гори-
зонтального полета, показывает, что если тяга будет больше ло-
бового сопротивления, то скорость будет возрастать. Разгон само-
лета будет продолжаться до тех пор, пока лобовое сопротивление
не уравновесит силу тяги двигателя. Соответствующая скорость,
363
при которой Р=ХГ, и будет максимальной скоростью горизонталь-
ного полета.
Для определения максимальной скорости кривые силы тяги и
лобового сопротивления для каждой высоты наносятся на график
условно с одинаковым знаком. Точки пересечения кривых опреде-
ляют максимальные скорости. На рис. 13.8 показан пример гра-
фического определения максимальных скоростей сверхзвукового
самолета для различных высот полета. Для такого самолета ха-
рактерно интенсивное возрастание Vmax от малых до средних вы-
сот. Наибольшая максимальная скорость (Vmax)max лежит на вы-
соте не более И км. При дальнейшем увеличении высоты V^ax
обязательно уменьшается.
Такой характер изменения Vmax по высотам можно объяснить
с помощью формулы для Vmax, полученной из условия постоян-
ства скорости горизонтального полета при максимальном (фор-
сажном) режиме работы силовой установки
рУ2
р^= Xr = Cx--~-S.
Отсюда получим:
где
С,= С,- + А&„.
На высотах, больших И км, тяга уменьшается с высотой про-
порционально плотности. Следовательно, отношение Р/р остается
постоянным. Так как в горизонтальном прямолинейном полете
г — 20
ру2$ »
то для сохранения прямолинейности полета на заданной истинной
скорости по мере увеличения высоты необходимо увеличивать Суг.
Следовательно, в формуле (13.13) сомножитель в скобке (С +
4-ДС2) обязательно увеличивается и соответственно Vmax умень-
шается.
На рис. 13.8 (внизу) штриховыми линиями 1 и 2 показаны за-
коны изменения максимальных скоростей соответственно для до-
звуковых и околозвуковых самолетов. Такой характер изменения
максимальной скорости от высоты полета может иметь и сверх-
звуковой самолет при неполной тяге двигателя.
На максимальной тяге двигателя возможны две точки пересе-
чения кривых Р и Хг (рис. 13.9): правая точка пересечения —- мак-
симальная скорость, левая — минимальная скорость прямолиней-
ного горизонтального установившегося полета Vrrnn уст- Интервал
скоростей между ними называется диапазоном скоростей
горизонтального полета.
364
Для того чтобы установись постоянной любую из скоростей
горизонтального полета, нужно задросселировать двигатель на-
столько, чтобы его тяга стала равной лоборому сопротивлению.
Например, скорость Vi на рис. 13.9, при которой Рдр = Хт.
Рис. 13.9. Определение установившейся скоро-
сти при дросселировании двигателя и снижении
§ 13.5. Первые и вторые режимы полета
Понятие «режимы полета» обычно относится к установившимся
движениям самолета, при которых силы, действующие на самолет
по касательной к траектории, взаимно уравновешены. Режимы по-
лета, при которых равно-
весие этих сил устойчиво,
называются первы-
ми режимами поле-
т а. Режимы полета, при
которых равновесие сил,
действующих на самолет
по касательной к траек-
тории, неустойчиво, на-
зываются втор ым и ре-
жимами полета..
На рис. 13.10 приведе-
ны графики силы тяги Р
Рис. 13.10. Первый (/) и второй (2) ре-
жимы горизонтального полета на кривых
сил тяги и лобового сопротивления
для некоторого постоян-
ного режима работы дви-
гателя и лобового сопро-
тивления Хг для прямоли-
нейного горизонтального полета. В точках 1 и 2 силы Р и Хг рав-
ны по величине. Следовательно, горизонтальный прямолинейный
полет со скоростями и V2 будет установившимся.
Если по какой-либо причине режим полета в точке 1
рушен, например, в сторону уменьшения скорости на
будет на-
величину
365
AVi, to при этом окажется, что лобовое сопротивление при
сохранении условия прямолинейности Y=G станет меньше силы
тяги Р, начнется разгон. Скорость будет возрастать до тех пор,
пока в точке 1 снова не наступит равновесие сил Р и Хг. Следо-
вательно, равновесие этих сил устойчиво. Режим полета, соответ-
ствующий точке /, является первым режимом полета.
Другой характер равновесия сил наблюдается в точке 2. При
уменьшении скорости на величину ДГ2 лобовое сопротивление
станет больше тяги двигателя. Следовательно, не только не про-
изойдет восстановление скорости Г2 и равновесия сил Р и Хг,
а, наоборот, (при сохранении летчиком условия прямолинейности)
будет происходить дальнейшее торможение и удаление от положе-
ния равновесия. Таким образом, равновесие сил Р и Хг неустой-
чиво. Режим полета, соответствующий точке 2, относится ко вто-
рым режимам полета.
Для сохранения первого режима полета летчик не должен пред-
принимать каких-либо мер, кроме сохранения прямолинейности
полета, для чего достаточно управлять самолетом только ручкой.
Для сохранения второго режима полета летчику необходимо еще
и изменять тягу двигателя, а если запаса тяги нет, то перейти на
снижение и получить добавочную силу в виде составляющей силы
тяжести GsinO (рис. 13.9), чтобы прекратить начавшееся тормо-
жение.
Таким образом, вторые режимы полета прежде всего требуют
большего внимания летчика. Но это не так уж существенно по
сравнению с их возможной опасностью в тех случаях, когда мала
высота и нет запаса тяги. К таким случаям относится взлет на
полной тяге и предпосадочное планирование. Несмотря на боль-
шие запасы тяги при взлете современных самолетов в случае
преждевременного отрыва и создания чрезмерно больших углов
атаки, особенно при высокой температуре воздуха, вполне возмож-
но попадание на вторые режимы полета. Необходимо помнить, что
в случае недостаточной тяги выйти из второго режима полета на
малой высоте можно уменьшением лобового сопротивления, на-
пример сбросив подвески или убрав шасси.
Границей между первыми и вторыми режимами полета яв-
ляется скорость, при которой разность между тягой и лобовым
сопротивлением (избыток тяги) максимальна (скорость V3 на
рис. 13.10). Эта скорость близка к наивыгоднейшей, т. е. к скоро-
сти, при которой лобовое сопротивление Хг минимально.
Вторые режимы существуют и на сверхзвуковых скоростях по-
лета на больших высотах (рис. 13.11, диапазон М^Мг, где тяга
по скорости увеличивается быстрее, чем сопротивление), но опас-
ности не представляют ввиду большого запаса высоты и скорости.
Однако они могут привести к вынужденной потере высоты и к
ухудшению условий выполнения боевой задачи, например, при
перехвате.
Иногда вводят понятие «вторые режимы» при маневре, анало-
гичное понятию вторых режимов в прямолинейном полете. Извест-
366
но, что в полете с большой перегрузкой лобовое сопротивление
значительно увеличивается из-за больших углов атаки (рис. 13.3).
При этом скорость минимального сопротивления возрастает по
сравнению с наивыгоднейшей скоростью в прямолинейном полете.
Рис. 13.11. Вторые режимы на сверхзвуковой
скорости
13.12. Диапазон скоростей и
высот полета
Область дозвуковых вторых режимов при маневре смещается на
большие скорости (примерно от IZmin гУ7гу до ИнвгИп^)’ а темп
потери скорости будет выше из-за большого лобового сопротив-
ления. Однако не следует преувеличивать опасность так называе-
мых вторых режимов при манев-
ре с большой перегрузкой. Вы- //
вод из них не представляет ника-
кой сложности даже на предель-
но малых высотах (кроме слу-
чаев низкого вывода из пикиро-
вания). Достаточно лишь умень-
шить перегрузку, как появится
избыток тяги над лобовым со-
противлением.
§ 13.6. Статические потолки
Верхней границей возможных
высот прямолинейного горизон-
тального установившегося полета
является так называемая линия
потолков режимов, т. е. наибольших высот прямолинейного гори-
зонтального полета на данной постоянной истинной скорости
(рис. 13.12). Линия потолков является продолжением линии мак-
симальных скоростей, так как определяется теми же условиями,
что и линия максимальных скоростей: условием прямолинейности
367
горизонтального полета У—G (^=1) и условием постоянства
скорости Р = ХГ, т. е. точками пересечения кривых Р и Хг для
различных высот (рис. 13.8).
Потолок (статический потолок)—это наибольшая высота,
на которой еще возможен установившийся горизонтальный полет
(точка / на линии потолков режимов, рис. 13.12).
Расчет линии потолков наиболее просто выполняется по ме-
тоду профессора Б. Т. Горощенко, основанном на том, что при
данной постоянной истинной скорости (числе М) выше 11 км тяга
двигателя Р и лобовое сопротивление при нулевой подъемной
силе %о пропорциональны атмосферному давлению р, а индуктив-
ное сопротивление Xir обратно пропорционально давлению:
р=р"^- х'=х-^ х“
Xj г 11
Рн!рп
Из условия постоянства скорости Р = ХГ найдем:
п РН __ V РН I Xt г и
—-Аоп—
Отсюда:
рн ___ 1 f Xj г и
р\\ ' Ри — х011 *
Так как для стандартной атмосферы на Н> 11 000 м
нооо - н
Рн_=е 6300 ,
то, логарифмируя формулу (13.14), найдем:
11000— Н 1 1/ 4ги '
6300 г Pil—Хои*
Учитывая, что
In lA/'ry...- = - In .
Г "11 —Аои Г Л[ г И
окончательно получим:
Нпот = 11000 + 6300 In 1/.
г А/г И
(13.14)
(13.15)
В формуле (13.15) Рц( Хон» Х/Гц— тяга двигателя и состав-
ляющие лобового сопротивления для высоты 11 км и того числа М,
при котором рассчитывается потолок режима.
Для расчета линии потолков достаточно задаться рядом чи-
сел М и для каждого из них найти Рн (из характеристик двига-
теля), Хоп и Х/гп (из заранее рассчитанных кривых рис. 13.1 и
13.2), затем по формуле (13.15) найти потолки режимов и по-
строить из них кривую по числам М.
303
Установить точно режим горизонтального полета с постоянной
скоростью довольно трудно. Однако это вполне возможно и прак-
тически выполняется, если есть некоторый запас тяги, т. е. если
полет выполняется ниже потолка.
Значительно труднее длительно удерживать современный сверх-
звуковой самолет на потолке или на линии потолков при задан-
ной скорости, так как при этом избыток тяги равен нулю. При
недостаточно точном и тщательном пилотировании небольшое от-
клонение в сторону кабрирования приводит к набору высоты боль-
ше потолка с одновременным торможением. При незначительной
отдаче ручки от себя начинается заметное снижение с некоторым
разгоном. Если после этого летчик попытается вернуть самолет
на высоту потолка, то он убедится в том, что скорость самолета
стала меньше, чем до снижения или подъема. Потеря скорости
происходит вследствие заметного возрастания лобового сопротив-
ления при увеличении угла атаки, так как индуктивное сопротив-
ление на потолке значительно по величине. Оно примерно равно
сопротивлению при нулевой подъемной силе X/r«X0.
Таким образом, линию потолков, а тем более потолок, практи-
чески не удается использовать для длительного горизонтального
полета *. Приходится летать несколько ниже потолка, чтобы иметь
некоторый запас тяги, обеспечивающий возможность исправления
ошибок пилотирования. Поэтому иногда и вводится понятие прак-
тический потолок — высота, на которой при установившемся
наборе Vr/ = 3 м/с.
Для повышения точности пилотирования вблизи потолка реко-
мендуется сохранять заданный режим полета по истинной скоро-
сти (по тонкой стрелке указателя скорости).
§ 13.7. Диапазон скоростей и высот полета
Вся область скоростей и высот, на которых возможен горизон-
тальный полет с постоянной скоростью, ограниченная слева линией
минимальных скоростей (рис. 13.12), сверху — линией потолков и
справа — линией максимальных или максимально допустимых ско-
ростей, называется диапазоном скоростей и высот
прямолинейного горизонтального установивше-
гося полета.
Внутри этого диапазона возможен прямолинейный горизонталь-
ный полет с торможением, с разгоном или с постоянной скоростью
(длительный полет). На верхней и правой границах еще возможен
полет с постоянной скоростью, но невозможен горизонтальный
разгон. Выше потолков и правее линии максимальных скоростей
горизонтальный полет в пределах допустимых скоростей возможен,
но только с торможением (кратковременный полет). Левее грани-
* Кратковременный горизонтальный полет возможен и на высотах, боль-
ших потолка, о чем будет сказано ниже.
359
ЦЫ Vminr.n, т. е. со скоростями, меныпими IZmin доп, При Су > Су доп
горизонтальный полет не разрешается по условиям безопасности,
но принципиально возможен в интервале от Су доп до Сусз при
повышенной опасности сваливания.
Диапазон скоростей и высот прямолинейного горизонтального
полета является одной из важнейших летных характеристик, пока-
зывающих возможности выполнения на данном самолете длитель-
ного прямолинейного горизонтального полета. Очевидно, что чем
выше потолки и чем шире диапазон скоростей, тем большими
боевыми возможностями обладает самолет. Причем важно, чтобы
диапазон скоростей был шире как в сторону максимальных, так
и в сторону минимальных скоростей.
Не менее важной летной характеристикой самолета является
возможность выполнять длительный криволинейный полет, напри-
мер вираж с постоянными скоростью и перегрузкой.
Условие постоянства скорости горизонтального криволинейного
полета имеет тот же вид, что и для прямолинейного полета
(Р = Х), только лобовое сопротивление X теперь уже не будет
равно Хг (как при пу=1), а будет зависеть от перегрузки согласно
формулам (13.2) — (13.4):
Х=Х0 + Х1гп*. (13.16)
На рисунке 13.3 в качестве примера показаны кривые лобового
сопротивления при различных перегрузках и кривая силы тяги
двигателя на максимальном форсаже для высоты 11 км. Точки
пересечения кривых Р и X при перегрузках пу>\ определяет мак-
симальные скорости установившегося криволинейного поле-
та с различными перегрузками на высоте 11 км.
Если найти аналогичные точки пересечения на всех высотах, то
можно получить линии потолков и максимальных скоростей кри-
волинейного горизонтального полета с постоянными скоростями и
перегрузками, аналогичные линиям потолков и максимальных ско-
ростей прямолинейного горизонтального полета. Минимальная ско-
рость горизонтального криволинейного полета определяется из
условия
r=Gny==CyflOn^2-S,
т. е.
Таким образом, можно построить границы диапазона скоростей
и высот горизонтального установившегося полета с различными
постоянными перегрузками, что и показано в качестве примера на
37Q
рис. 13.13. Как видно из этих графиков, по мере возрастания пере-
грузки диапазон скоростей и высот установившегося горизонталь-
ного полета резко сужается за счет перемещения всех его границ.
Рис. 13.13. Диапазон скоростей и высот установившегося криволинейного по-
лета
§ 13.8. Влияние эксплуатационных факторов на диапазон
скоростей и высот полета
13.8.1. Метод дифференциальных поправок
Все летные характеристики, в том числе и диапазон скоростей
и высот полета, в технических описаниях самолетов приводятся
для стандартных атмосферных условий. Фактические условия по-
лета могут значительно отличаться от стандартных. Например,
температура воздуха у земли может отличаться от стандартной,
равной 15°, на 40—50° в сторону уменьшения и на 15—20° в сто-
рону увеличения.
Масса современных самолетов тоже изменяется в довольно ши-
роких пределах из-за выработки топлива, расходования боеприпа-
сов, сброса различных грузов и т. п. В зависимости от условий
полета и конфигурации самолета значительно изменяются тяга
двигателя и лобовое сопротивление самолета.
Все эти факторы вызывают существенное изменение летных ха-
рактеристик. Ниже рассмотрим влияние на диапазон скоростей
и высот полета наиболее важных из них: изменений массы, лобо-
вого сопротивления, тяги двигателя, температуры воздуха и стре-
ловидности крыла. Это влияние проявляется через изменение гра-
ниц диапазона скоростей и высот полета: кривых минимальной и
максимальной скоростей полета и линии потолков.
371
Обычно влияние эксплуатационных факторов на летные харак-
теристики самолета рассчитывается с помощью номограмм, т. е.
вычислительных графиков, которые строятся предварительно по
известным формулам для каждого конкретного типа самолета.
Использование номограмм сводит к минимуму затраты време-
ни на определение летных характеристик для конкретных условий
полета: высоты, скорости, температуры, массы и т. п., однако не
позволяет наглядно проанализировать и дать сравнительную оцен-
ку влияния различных факторов на летные характеристики.
Наиболее просто влияние эксплуатационных факторов на лет-
ные характеристики можно проанализировать с помощью метода
дифференциальных поправок. Сущность этого метода состоит в
следующем.
Как известно из математики, дифференциалом функции назы-
вается линейная часть приращения функции, которое получается
вследствие приращения аргумента. В математическом анализе эти
приращения считаются бесконечно малыми, т. е. стремящимися
к нулю. Однако оказывается, что соотношения между ними остают-
ся приблизительно верными с достаточной для практики точностью
и в том случае, когда эти приращения конечны и вполне ощутимы
(до 15-20%).
Метод дифференциальных поправок в том и состоит, что сна-
чала получаются дифференциальные соотношения между функ-
цией и ее аргументами, а затем дифференциалы заменяются ко-
нечными приращениями. Для того чтобы получить относительные
поправки (например, в процентах), интересующая нас зависи-
мость предварительно логарифмируется. Например, для исследо-
вания зависимости минимально допустимой скорости горизонталь-
ного полета от эксплуатационных факторов прологарифмируем и
затем продифференцируем формулу (13.10):
1° доп = ~Т <|П 2 + 1П G ~ 10 Р ~ |П Д°" “ 1П
доп________ 1 / dG
^min доп \ G
Заменяя дифференциалы
A^min доп 1 / &G
^min доп 2 \ G
rfp dCy доп dS
Р Gy доп S
конечными приращениями, найдем:
Др &Су доп AS
Р Gy доп S
(13.18)
13.8.2. Влияние изменений веса
Минимальная скорость. Из формулы (13.18) получим!
^£- = 0,5-^-.
Vmin °
Это значит, что каждые 10% изменения веса ^-^Я-=0,1) вы-
зывают изменение минимальной скорости на 5% в ту же сторону.
372
Потолок. Так как линия потолков современных самолетов ле-
жит выше 11 км, то исследовать влияние веса на высоту потолка
можно с помощью формулы (13.15)
/упот =11000+ 6300 in 1/ ,
где
г 11 = 0,7pnM2S ‘
После подстановки значения Xirii, логарифмирования радика-
ла, дифференцирования и перехода к конечным приращениям по-
лучим
ДНП0Т= - 6300 .
Иначе говоря, если при изменении веса самолета его конфигу-
рация остается прежней, то уменьшение веса на 10% вызывает
увеличение потолка на 630 м, и наоборот. По этой формуле можно
оценить изменение высоты потолка режима в любой точке линии
потолков, т. е. при любом заданном числе М.
Максимальная скорость. Изменение веса самолета при неиз-
менной его конфигурации влияет на максимальную скорость толь-
ко через индуктивное сопротивление, которое в прямолинейном по-
лете на максимальной скорости очень мало. Поэтому влияние из-
менения веса на максимальную скорость несущественно, за исклю-
чением высот, близких к потолку.
13.8.3. Влияние изменения тяги
и лобового сопротивления
Минимальная скорость. Изменение тяги и лобового сопротив-
ления практически не влияет на минимальную скорость горизон-
тального полета, если величины коэффициента Су и площадь кры-
ла остаются неизменными (без учета нормальной составляющей
силы тяги Psina). Заметим лишь, что время достижения
минимальной скорости при торможении существенно за-
висит от тяги и лобового сопротивления: чем больше превышение
лобового сопротивления над тягой двигателя, тем интенсивнее
будет торможение и тем быстрее самолет выйдет на минимальную
скорость.
Потолок. Влияние изменения индуктивного сопротивления
вследствие изменения веса уже рассмотрели в предыдущем пункте.
Влияние изменений Р и Xq оценивается по формуле, аналогично
получаемой из формулы (13.15)
Д/7П01 = 3150 • (13-19)
373
Если разность Рц—Хоп изменяется на 10%, то потолок из-
менится на 315 м в ту же сторону. Если одновременно с измене-
нием лобового сопротивления изменяется и вес самолета, напри-
мер при подвеске бомб, баков и других грузов, то необходимо
учитывать влияние обоих факторов:
ДЯ,.,= 3150[ -2-^].
Рис. 13.14. Влияние изменения тяги двигателя на максимальную скорость
полета
Максимальная скорость. Влияние изменений тяги двигателя и
лобового сопротивления самолета на максимальную скорость за-
висит от характера изменения разности этих сил по скорости, опре-
деляемого производными по скорости Pv —
На рис. 13.14 показаны два вида кривых Р и Хт. В случае
когда вблизи максимальной скорости наклоны кривых Р и Хг
резко различны (характерно для дозвукового самолета), при из-
менении тяги или лобового сопротивления максимальная скорость
изменяется мало (рис. 13.14, а). При таком же изменении тяги
максимальная скорость изменяется весьма существенно, если на-
клоны кривых тяги и лобового сопротивления мало отличаются по
величине, что характерно для околозвукового самолета
(рис. 13.14, б). Для иллюстрации этой зависимости можно исполь-
зовать формулу
- (13'20>
которая получается путем простого геометрического анализа гра-
фика Р—XT=f(V).
13.8.4. Влияние изменения температуры
Минимальная скорость. Изменение температуры воздуха при
постоянном давлении, т. е. на данной барометрической высоте,
приводит к изменению плотности обратно пропорционально абсо-
лютной температуре.
374
Учитывая эту зависимость, из формулы (13.18) получим
ЛУт!п п с ДГ
-=0,5-^.
v min л
Иначе говоря, изменение абсолютной температуры на 10% вы-
зывает изменение минимальной скорости на 5% в ту же сторону.
Потолок. Как было показано в главе 6, для современных ТРД
температура воздуха сильно влияет на тягу двигателя, что при-
близительно выражается зависимостью
= -(2,0ч- 2,5) (13.21)
Изменение высоты потолка при этом оценим с помощью фор-
мулы (13.19) сначала для чисел М, при которых на потолке К =
= Ктах, Т. е. Xo = y^ir*
Так как XQ = рЪК-С S и при постоянных р и М от тем-
пературы не зависит, то Д(Рц—Хоп)=ДРц и из формулы (13.19)
получаем
Д^пот = 3150 ~ .
Рн
Так как 11 = 4--, а на потолке Р = Хг=2Х0, то ХОц/Рц =
*11 гпот
5=1/2 и, следовательно:
ДЯПОТ= 3150-2^.
Тогда с учетом зависимости (13.21) найдем
д/7пот =-12600-^,
т. е. уменьшение абсолютной температуры на 10% (примерно на
22°) вызывает увеличение высоты потолка примерно на 1260 м,
и наоборот. На больших числах М влияние температуры на высоту
потолка будет сильнее, а на меньших — несколько слабее, чем при
М = M#max, но все же остается значительным.
При наборе сверхзвукового потолка в условиях повышенной
температуры уменьшение избытка тяги приводит к увеличению
времени разгона до заданного числа М. При этом расход топлива
может возрасти настолько, что окажется невозможным достичь
потолка из-за недостатка топлива.
Максимальная скорость. Влияние изменения температуры на
максимальную скорость проявляется через изменение тяги. Она
будет тем сильнее, чем меньше изменяется избыточная тяга по
скорости в окрестности Vmax (рис. 13.14).
375
Для иллюстрации этой зависимости можно использовать фор-
мулу
iVmax _ „ Р 1 АГ
V z V рУ уУ Т '
r max v max г — Л •*
которая получается из формул (13.20) и (13.21) с учетом того, что
при изменении температуры Д(Р—ХГ)=&Р,
13.8.5. Влияние изменения стреловидности
крыла
Минимальная скорость. Изменение стреловидности крыла при-
водит к изменению допустимого коэффициента Су доп. При этом не-
сколько изменяется также и площадь крыла. Из-за суммарного
влияния этих факторов минимальная скорость полета при мини-
мальной стреловидности обычно бывает на 50—100 км/ч меньше,
чем при максимальной стреловидности крыла.
Потолок. Увеличение стреловидности крыла вызывает уменьше-
ние Хо и увеличение Х/г вследствие уменьшения удлинения крыла
и некоторого уменьшения его площади. Поэтому при одном и том
же числе М суммарное влияние изменения стреловидности крыла
на потолок самолета невелико и по знаку зависит от конкретного
режима полета и от исходного угла стреловидности крыла. Дело
в том, что для каждого режима полета, определяемого числом М
и коэффициентом СУ) существует свой оптимальный угол стрело-
видности крыла, при котором высота потолка будет наибольшей.
При изменении стреловидности крыла в любую сторону от опти-
мального значения высота потолка будет уменьшаться.
Максимальная скорость. Величина XQ в прямолинейном горизон-
тальном полете на больших скоростях во много раз больше, чем
Х/г. Поэтому при увеличении стреловидности крыла суммарное ло-
бовое сопротивление Хг в полете на максимальной скорости сильно
уменьшается, вследствие чего Vmax возрастает и особенно интен-
сивно на средних и больших высотах, где избыточная тяга по ско-
рости изменяется слабо.
Глава 14
ДОПУСТИМЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ САМОЛЕТОВ.
ФИЗИЧЕСКАЯ СУЩНОСТЬ ОГРАНИЧЕНИЙ
§ 14.1. Классификация опасных режимов полета
Особые ситуации, создавшиеся в полете в результате воздей-
ствия неблагоприятных факторов, по степени опасности делятся на
следующие виды:
— усложнение условий полета;
376
— опасная ситуация;
— аварийная ситуация;
— катастрофическая ситуация.
Усложнение условий полета характеризуется тем, что летные
характеристики и поведение самолета изменяются незначительно,
требуется лишь повышенное внимание экипажа к источнику воз-
никновения особой ситуации и к управлению самолетом и его
системами. Полет продолжается и может быть успешно завер-
шен
Область
эксплуатационных режимоб
7 Область
предельных
4 режимоб
уу Область
критических режимоб
Оснобная
эксплуатационная
область
Усложнение 6 Опасная
условий у ситуация
полета х
Марийная и катост-
/ рабическая ситуации
Ярек
%-
^8оп
z
Рис. 14.1, Схема связи опасных ситуаций с величиной определяющего
параметра
Опасная ситуация характеризуется тем, что для предотвраще-
ния перехода ее в аварийную или катастрофическую требуются
своевременные и правильные действия экипажа, изменение режи-
ма полета. Рабочая нагрузка членов экипажа значительно увели-
чивается.
Аварийная ситуация характеризуется тем, что требуется не-
медленная посадка. Для предотвращения перехода ее в катастро-
фическую требуется чрезвычайное увеличение рабочей нагрузки
членов экипажа.
Катастрофическая ситуация характеризуется тем, что предот-
вращение потери самолета или гибели людей практически невоз-
можно, необходимо немедленное покидание самолета.
Степень опасности ситуаций связана с параметрами движения
летательного аппарата, от которых зависит безопасность полета,
так называемыми определяющими параметрами, например таки-
ми, как перегрузка пу, углы атаки а и скольжения 0, высота по-
лета /7, скоростной напор q, угловая скорость крена со* и т. п.
По величине этих параметров назначаются эксплуатационные
ограничения и выделяются области допустимых и недопустимых
по условиям безопасности режимов полета. Некоторые из опреде-
ляющих параметров могут иметь ограничения как наибольшего,
так и наименьшего экстремального значения параметра, необхо-
димого для выполнения маневра.
На рис. 14.1 для простоты представлена схема связи особых
ситуаций с величиной только наибольшего значения определяю-
377
щего параметра, показаны возможные области режимов полета,
которые разделяются характерными значениями определяющих
параметров. Область, лежащая левее наибольшего допустимого по
безопасности полета значения параметра Хдоп («доп, пу доп и т. п.),
определяет эксплуатационные режимы полета, которые могут быть
использованы в учебно-боевой подготовке. Однако для наиболее
простого и безопасного выполнения маневра инструкцией рекомен-
дуется определенное значение параметра хрек. Область между
хРеК и %доп хотя и безопасна, но требует повышенного внимания,
усложняя условия полета.
Критическим значением параметра полета называют
такое ‘значение, при превышении которого возможны необратимые
изменения в характеристиках самолета или в динамике его по-
лета. Область режимов полета, характеризуемая значениями па-
раметров полета, заключенными между хдоп и хкР, называется
.областью предельных режимов полета. Выход в эту
область допустим только в исключительных случаях боевого при-
менения самолета или для парирования летчиком последствий до-
пущенной ошибки (например, предотвращение столкновения с зем-
лей при выводе самолета из пикирования).
Режимы полета, при которых хотя бы один из определяющих
параметров превышает свое критическое значение, называются
критическими режимами полета. Они являются заве-
домо опасными и требуют от летчика для выхода из них, как
правило, необычных приемов пилотирования. Основные критиче-
ские и предельные режимы и соответствующие им ограничения
углов атаки и скольжения, угловых скоростей и чисел М рассмот-
рены в главах 5, 7, 11 и 13. Кроме того, в главах 5 и 6 рассмотре-
ны предельные режимы и соответствующие им ограничения по
устойчивости работы силовой установки и по температуре аэро-
динамического нагрева. В следующих параграфах настоящей гла-
вы мы рассмотрим лишь ограничения скорости и перегрузки и их
физическую сущность:
§ 14.2. Ограничения минимальной скорости полета.
Действия летчика при попадании в область недопустимо
малых скоростей
Предельно допустимый угол атаки, соответственно которому
вводится ограничение минимально допустимой скорости полета,
может назначаться по различным физическим причинам: по воз-
можности сваливания, по началу неустойчивости по перегрузке и
возможности выхода на «подхват», по ухудшению, поперечной
управляемости на больших углах атаки, по устойчивости работы
силовой установки, по возможности выхода на вторые режимы по-
лета. Кроме того, при маневрировании используется еще один
вид ограничения минимальной скорости (так называемая эволю-
тивная скорость).
378
Эволютивной скоростью называется наименьшая ско-
рость в процессе выполнения маневра, при которой управляемость
самолета еще обеспечивает его безопасное завершение. Для
каждого вида маневра существует своя эволютивная скорость.
Однако для удобства запоминания обычно назначается та, при
которой обеспечивается выполнение простейших маневров в гори-
зонтальном полете (развороты с креном 30—40° или с перегрузкой
пу= 1,5 с выходом на адоп). Для современных сверхзвуковых само-
летов эта скорость обычно равна 350—450 км/ч по прибору.
В случае полета с перегрузкой, меньшей 1, она может быть мень-
ше, чем в горизонтальном полете, так как потребные углы атаки
будут меньше.
Из,всех рассмотренных выше видов ограничений в инструкцию
по технике пилотирования конкретного типа самолета записывается
то ограничение, которое раньше всего наступает. Иначе говоря,
в качестве ограничения минимальной скорости назначается наи-
большая из минимально допустимых скоростей.
Характер действий летчика при выходе самолета на недопу-
стимо малые скорости зависит от поведения самолета при нару-
шении конкретного вида ограничения и от условий, в которых это
нарушение произошло. Прежде всего, если позволяет высота или
имеется запас тяги двигателя, необходимо принять все меры к тому,
чтобы увеличить скорость и перевести самолет в область допусти-
мых скоростей путем снижения самолета или увеличения тяги дви-
гателя.
Если причиной установления ограничения является возмож-
ность сваливания или плохая поперечная управляемость на боль-
ших углах атаки, то необходимо прежде всего стремиться устра-
нить именно эту первопричину опасности — большие углы атаки.
При этом часто оказывается, что, несмотря на психологические
трудности принятия решения об отдаче ручки от себя, например
на малых высотах, для выхода из создавшегося положения при
своевременных действиях требуется весьма мало времени и не-
значительная потеря высоты. Это объясняется известной способ-
ностью самолета быстро вращаться относительно центра масс,
в частности относительно поперечной оси, и в доли секунды из-
менять угол атаки.
§ 14.3. Ограничения максимальной скорости полета.
Допустимые области скоростей и высот полета
Ограничения максимальных скоростей бывают в основном трех
видов: по максимально допустимому скоростному напору, по мак-
симально допустимому числу М и по максимально допустимой
температуре аэродинамического нагрева элементов конструкции.
Рассмотрим причины и физическую сущность этих ограничений.
Аэродинамические силы, действующие на самолет, распределе-
ны по его поверхности неравномерно. Например, на лобовых час-
тях поверхности самолета -давление, как правило, больше атмо-
379
сферного. На всех других поверхностях, особенно на верхней по-
верхности крыла и фюзеляжа, давление пониженное по сравнению
с атмосферным. Чем больше скоростной напор, тем больше будет
нагружена обшивка самолета, и в первую очередь обшивка кры-
ла, разностью давлений на ее наружной и внутренней поверхно-
стях. Следовательно, обшивка самолета и каркас, к которому она
крепится/ должны быть рассчитаны на прочность при заданном
максимально допустимом скоростном напоре.
Этим обеспечивается так называемая местная прочность само-
лета.
Вторая причина ограничений скоростного напора связана с не-
достаточной жесткостью конструкции самолета, вследствие чего
ухудшается эффективность органов управления либо возникают
нарастающие изгибно-крутильные колебания (флаттер), приводя-
щие, как правило, к разрушению самолета. Для обеспечения на-
дежной поперечной управляемости предельно допустимая скорость
назначается меньшей критической скорости реверса элеронов не
менее чем на 100 км/ч.
Для предотвращения флаттера устанавливается максимально
допустимая скорость, меньшая критической скорости флаттера на
25—30%.
Следствием недостаточной жесткости крыла, несимметрии его
упругих деформаций и развития волнового кризиса является так
называемая «валежка» — явление непроизвольного кренения само-
лета при больших скоростных напорах на околозвуковых скоро-
стях полета. Как и реверс элеронов, это явление требует ограни-
чения скоростного напора, которое обычно устанавливается экспе-
риментально при испытаниях данного типа самолета.
Скоростной напор иногда ограничивается также по прочности
элементов конструкции самолета (узлов крепления подвесок, за-
крылков и др.), двигателя, по мощности рулевых приводов (гид-
роусилителей) и т. п.
Ограничение скорости по числу М полета свя-
зано с обеспечением устойчивости и управляемости самолета,
а также надежной работы силовой установки. В некоторых слу-
чаях ограничение числа М устанавливается и по флаттеру.
Путевая устойчивость на сверхзвуковых скоростях с ростом
чисел М значительно ухудшается, особенно на больших углах
атаки. Следовательно, числа М должны быть ограничены той ве-
личиной, при которой путевая устойчивость еще достаточна. Под-
веска под самолет баков, бомб, блоков, ракет и т. п. часто ухуд-
шает путевую устойчивость самолета. Поэтому при наличии внеш-
них подвесок предельно допустимое число М, как правило, умень-
шается.
Максимально допустимое число М может быть ограничено по
надежности работы силовой установки (по устойчивости работы
входного устройства, компрессора, камеры сгорания, по допусти-
мой температуре на входе в двигатель, по работоспособности
маслосистемы или системы охлаждения двигателя и т. п.).
380
Увеличение скорости полета сопровождается нагреванием кон-
струкции самолета и, как следствие, снижением прочности. Тем-
пература в точке полного торможения потока при cp/ci/ = l?4
определяется по формуле (2.40)
Г* = Г(1 +-0,2М2),
где Т — абсолютная температура воздуха на данной высоте.
Рис. 14.2. Допустимые области скоростей и вы-
сот полета
Чем выше 71*, тем на большую температуру нагреваются об-
шивка и каркас самолета. Однако с увеличением высоты полета
нагрев конструкции при данной Т* уменьшается из-за уменьшения
плотности воздуха (рис. 6.18). Поэтому для предотвращения пе-
регрева конструкции п р и снижении на скоростях, близ-
ких к ограничению по температуре, необходимо соот-
ветственно уменьшать число М полета.
Для обеспечения прочности силовые элементы конструкции со-
временных самолетов, рассчитанных на числа М>2,5, изготов-
ляются из термостойких сталей или из титана. Кроме того, при-
нимаются специальные меры для снижения температуры наиболее
нагреваемых участков конструкции самолета (повышение тепло-
емкости, устройство специальных систем отвода тепла и т. п.).
Из всех видов ограничений максимальной скорости полета на
определенной высоте в инструкцию летчику записывается одно,
наименьшее из всех. При этом, как правило, на малых и сред-
них высотах наименьшей максимально допустимой скоростью ока-
зывается ограничение по скоростному напору (по приборной ско-
рости), а на больших высотах, как правило, — ограничение по чис-
лу М полета. На графике (рис. 14.2) диапазона скоростей и высот
полета нанесены ограничения скорости по различным причинам.
Для современных сверхзвуковых самолетов максимальные скоро-
381
сти обычно больше максимально допустимых скоростей, а мини-
мально возможные скорости — меньШе минимально допустимых.
Таким образом, до п ус т и м а я область скоростей и вы-
сот полета оказывается более узкой, чем весь диапазон воз-
можных для данного типа самолета скоростей и высот полета.
Следует заметить, что форсажные режимы работы двигателей,
на которых достигается широкий диапазон сверхзвуковых скоро-
стей полета современных самолетов, не везде реализуются с оди-
наковой надежностью. На малых приборных скоростях и на боль-
ших высотах существует ограничение по устойчивости работы фор-
сажной камеры, показанное на рис. 6.18 сплошной линией 3. Левее
и выше этой линии может быть запрещено включение частичного
или полного форсажа, но полет с форсажем разрешается при
условии включения форсажа на меньших высотах.
Наконец, существует область, где разрешается производить за-
пуск двигателя в полете (рис. 6.18). Вне этой области не обеспе-
чивается надежный розжиг камер сгорания из-за слабой турбули-
зации потока воздуха на малых приборных скоростях или из-за
слишком большой скорости воздуха в камере сгорания на больших
приборных скоростях. В случае заглохания двигателя по тем или
иным причинам для осуществления надежного запуска двигателя
в воздухе необходимо предварительно выйти в указанную область
скоростей и высот полета.
§ 14.4, Действия летчика при превышении максимально
допустимой скорости полета
Если в обычных полетах превышение максимально допустимой
скорости запрещается и, как правило, это требование выполняется,
то в боевой обстановке нарушение ограничений становится более
вероятным, а иногда может стать и необходимым. Поэтому летчик
должен знать, по какой причине на его самолете установлено огра-
ничение скорости полета, к а к поведет себя самолет при
нарушении этого ограничения, и должен быть готовым
к четким действиям по выводу самолета из опасной ситуации. Во
всех случаях превышения ограничений скорости необходимо умень-
шить ее до допустимой величины, выпустив тормозные щитки и
задросселировав двигатель. В некоторых случаях можно ускорить
торможение переводом самолета в набор высоты. Однако для
искривления траектории полета требуется увеличить угол атаки,
что иногда может усугубить положение.
В случае превышения ограничений скорости по местной проч-
ности возможны остаточные деформации и даже разрушение соот-
ветствующих элементов конструкции, причем, как правило, асим-
метричное, например вспучивание обшивки, отрыв одной из под-
весок и т. п. В результате аэродинамическая симметрия самолета
нарушается, возникают боковые моменты рыскания и крена. Если
нарушение аэродинамической симметрии таково, что удается сба-
382
лансировать самолет и уменьшить скорость до допустимого зна-
чения, необходимо оценить степень опасности продолжения полета.
Как правило, дальнейшее выполнение задания прекращается и
принимается решение о посадке на свой или ближайший аэро-
дром или о покидании самолета, если продолжение полета и по-
садка невозможны.
Нарушение ограничений по реверсу элеронов или по «валеж-
ке» опасно (прежде всего на малых высотах) из-за частичной по-
тери управляемости. В случае психологической неподготовленно-
сти к этим явлениям у летчика складывается впечатление о пол-
ной потере управляемости и невозможности вывода самолета в
нормальный полет, что не соответствует объективному положению.
Достаточно уменьшить скорость, как управляемость восстанавли-
вается, как правило, без каких-либо вредных последствий. Если
при этом балансировка не нарушилась, что свидетельствует о со-
хранении аэродинамической симметрии самолета, то выполнение
задания может быть продолжено.
Чрезвычайно опасно достижение критической скорости флатте-
ра, возникновение которого приводит к быстрому разрушению са-
молета. Только в единичных случаях испытательных полетов уда-
валось вплотную приблизиться к началу флаттера и успеть умень-
шить скорость до разрушения самолета. При этом самолет полу-
чал такие деформации, что к дальнейшей эксплуатации был не-
пригоден. Ввиду чрезвычайно быстрого развития колебаний кры-
ла, приводящих к разрушению самолета, достижение критической
скорости флаттера недопустимо в любой ситуации.
Нарушение ограничений числа М полета по путевой устойчи-
вости самолета приводит к возникновению колебаний рыскания и
крена с большой амплитудой и со значительными боковыми пере-
грузками. Для прекращения этих колебаний следует зафиксиро-
вать педали в нейтральном положении (особенно при отсутствии
бустеров в системе путевого управления) и уменьшить скорость
выпуском тормозных щитков и дросселированием двигателя.
Фиксация педалей существенно повышает путевую устойчивость
по сравнению с тем случаем, когда они освобождены, и руль на-
правления становится по потоку. Уменьшать скорость переводом
самолета в набор высоты в данном случае нельзя, так как уве-
личение угла атаки приведет к дальнейшему уменьшению путевой
устойчивости и к возрастанию амплитуды колебаний. После умень-
шения скорости до допустимой следует убедиться в безопасности
продолжения полета и принять решение о возвращении на свой
аэродром или о продолжении выполнения задания.
Нарушение ограничений по устойчивости работы силовой уста-
новки может привести к помпажу и самовыключению двигателя.
При этом на самолетах с боковыми воздухозаборниками возмож-
но нарушение боковой балансировки из-за одностороннего пом-
пажа воздухозаборника. После уменьшения скорости, восстанов-
ления балансировки самолета и создания необходимых условий
для запуска двигателя нужно произвести запуск двигателя в воз-
383
духе и, убедившись в нормальной его работе, продолжить выпол-
нение задания.
Превышение ограничений скорости по нагреву элементов кон-
струкции дает эффект не .мгновенно, а через некоторое время,
когда конструкция успеет прогреться до недопустимо высокой тем-
пературы, и потеря прочности приведет к остаточным деформа-
циям. Время с момента превышения ограничения до достижения
опасных температур зависит от конкретной компоновки, наличия
систем охлаждения конструкции и от величины превышения чис-
ла М. Оно должно определяться в специальных испытаниях само-
лета с замером температуры наиболее нагреваемых элементов кон-
струкции.
§ 14.5. Минимально допустимые высоты полета.
Безопасность полетов на малых высотах
Полет на предельно малых высотах с большими скоростями
широко используется для достижения внезапности атаки назем-
ного противника и для уменьшения вероятности поражения своего
самолета зенитно-ракетными средствами противника. Известно,
что дальность обнаружения радиолокационными средствами само-
лета на малых высотах существенно снижается. Соответственно
сокращается и время воздействия на самолет зенитно-ракетных
средств, особенно на больших скоростях полета. Однако полет на
малых высотах с большими скоростями имеет целый ряд сущест-
венных особенностей, требующих от летчика повышенного внима-
ния и более точного управления самолетом. К ним относятся:
— возрастание опасности последствий отказов техники и оши-
бок в выдерживании режима полета и, как следствие, значитель-
ное повышение эмоциональной напряженности летчика, усиление
его реакции на отклонения самолета от заданного режима, повы-
шенная утомляемость;
— ограничение видимости наземных ориентиров и времени на-
блюдения за ними, а следовательно, значительные затруднения в
детальной ориентировке на местности, поиске и распознавании на-
земных целей;
— возрастание доли внимания летчика, уделяемого отслежи-
ванию рельефа местности и визуальному пилотированию, резкое
сокращение времени наблюдения за приборами, количества и точ-
ности воспринимаемой приборной информации. Полет на предель-
но малых высотах при ручном пилотировании возможен только
при достаточно хорошей видимости препятствий на местности (не-
ровностей рельефа, высоких строений, мачт, линий электропере-
дач и т. п.);
— существенное повышение чувствительности самолета к уп-
равляющим воздействиям (на больших приборных скоростях),
что в сочетании с повышенной эмоциональной напряженностью
летчика может привести к раскачке самолета летчиком, особенно
при отсутствии в системе управления автомата регулирования
384
АРУ, АРП, МПЧС и т. п. При появлении тенденции к раскачке
необходимо зафиксировать ручку, и колебания самолета быстро
прекратятся, так как естественное демпфирование на малых вы-
сотах весьма эффективно; .
— значительное сокращение дальности и продолжительности
полета; километровый расход топлива у земли примерно в 1,5 раза
выше, чем на высоте 5 км;
— резкое уменьшение дальности УКВ радиосвязи;
— повышенная вероятность столкновения самолета с птицами,
так как 73% перелетов птиц происходит на высотах до 300 м;
— сильная турбулентность атмосферы (болтанка), повышен-
ные вероятности превышения: аДОп на малых скоростях полета;
Пу max, повышенный темп расходования усталостного ресурса и
утомляемость экипажа на больших скоростях. Для уменьшения
чувствительности самолета к атмосферной турбулентности реко-
мендуется устанавливать максимальную стреловидность крыла и
некоторую среднюю скорость полета, при которой имеет место
максимальный уровень безопасности полетов.
Выбор минимально допустимой высоты из условий безопасно-
сти полетов производится с учетом всех перечисленных выше фак-
торов, а также с учетом натренированности летчика и интенсив-
ности бездействия на самолет средств ПВО противника. Для
уменьшения опасности отказов техники необходимо выбирать вы-
соту полета, гарантирующую своевременное парирование опасных
последствий отказов. Например, в инструкции летчику указы-
вается минимальная высота использования САУ, определяемая
в специальных исследованиях из условий обеспечения безопасно-
сти полетов при возможных отказах САУ.
Для повышения безопасности полетов на малых высотах важ-
ную роль играет автоматизация полета при достаточно высокой
надежности автоматических средств (например, автоматический
режим облета препятствий, автоматическое парирование воздей-
ствия на самолет атмосферной турбулентности и т. п.) и устрой-
ство системы индикации приборной информации на лобовом стек-
ле. Эти средства позволяют значительно снизить напряженность
летчика, уменьшить вероятность его ошибок, высвободить время
на своевременный поиск и распознавание целей и в конечном
счете повысить эффективность боевого применения авиации на
малых высотах.
§ 14.6. Располагаемые и допустимые перегрузки
Из всех сил, искривляющих траекторию полета, наибольшей ве-
личины достигает подъемная сила. Поэтому нормальная перегруз-
ка пу является важнейшей характеристикой м.аневренных воз-
можностей самолета: чем больше перегрузка (подъемная сила),
тем сильнее можно с ее помощью искривлять траекторию полета
и, следовательно, тем лучше маневренные свойства самолета.
13—21 385
Располагаемой перегрузкой называется наибольшая
перегрузка, которую можно получить в полете. Она определяется
по формуле
П ______ ^нб
""У Нб Q
С S
ьунб 2 °
G
(И.1)
На любых заданных высоте и скорости полета наибольшая пе-
регрузка достигается при предельно возможном коэффициенте
подъемной силы.
Рис. 14.3. Располагаемые и допустимые нор-
мальные перегрузки
В полете на дозвуковых скоростях могут быть достигнуты та-
кие углы атаки, при которых происходит сваливание самолета
(Су = Су Св). Поэтому по условиям безопасности полета обычно на-
значают предельно допустимую величину Су ДОп, которая меньше
Су св. На сверхзвуковых скоростях вследствие повышения устой-
чивости по перегрузке и снижения эффективности стабилизатора,
как правило, не удается достичь углов атаки, при которых проис-
ходит сваливание самолета. При полном отклонении ручки управ-
ления на себя (без скольжения) достигается лишь CV(p, меньший
Су СВ«
На рис. 14.3 в качестве примера показана зависимость допу-
стимых и располагаемых перегрузок пу доп и /г?(р от скорости и
высоты полета, рассчитанных по формуле (14.1), а также ограни-
чение перегрузки по прочности самолета — максимальная эксплу-
атационная перегрузка ^тах = 8. Из этих графиков видно, что на
высотах, меньших 5 км, и при числах М, больших 0,7—0,95, на
данном самолете имеется возможность создать перегрузку более
восьми. Предельно допустимая по прочности перегрузка ^утах
принимается меньше разрушающей в полтора раза. Однако пре-
вышать ограничение перегрузки по прочности л^тах нельзя во
386
избежание возможных остаточных или больших упругих дефор-
маций в силовых элементах конструкции.
Величина л* гпах для маневренных самолетов назначается в
пределах 5—8 при нормальном взлетном весе. Отсюда можно по-
лучить величину максимально допустимой подъемной силы, кото-
рая является постоянной для каждой конфигурации данного типа
самолета:
Гтах = ^тахО = СОПЗк
Из этого соотношения следует, что допустимая по прочности
планера самолета перегрузка обратно пропорциональна весу са-
молета:
Y3
пэ ____ тах
'^у max Q •
Например, если при нормальном взлетном весе Овзл==10 тс,
n{/max = 7, максимально допустимая подъемная сила Утах =
= 10-7 = 70 тс, то при перегрузочном варианте 6ВЗл. пер==12 тс по-
лучим следующую допустимую перегрузку:
э /max___70_ _ -
'Ъ max Q — 12 —
а при среднем полетном весе ОСР = 8 тс
— ^шах __ 70 _07г
'S max Q 3 —О,/О.
Предельно допустимая по прочности перегрузка зависит также
от прочности подвесок,^ креплений различных агрегатов, от конфи-
гурации самолета (угла стреловидности крыла, положения шасси
и посадочной механизации), так как при этом изменяются усло-
вия нагружения как отдельных частей самолета, так и основных
силовых элементов.
Если на самолете нет указателя угла атаки, то ограничение
угла атаки по сваливанию или по «подхвату» вводится ограниче-
нием перегрузки, так как при заданной приборной скорости пере-
грузка пропорциональна углу атаки (формула 14.1). Однако такой
способ ограничения угла атаки неудобен тем, что для каждой ско-
рости по прибору нужно запоминать свое предельно допустимое
значение перегрузки.
Как было показано в главе 8, возможность выхода самолета
на «подхват» зависит от темпа увеличения перегрузки: чем быст-
рее увеличивается перегрузка, тем больше вероятность выхода на
«подхват». Поэтому иногда вводится ограничение не только по
величине перегрузки, но и по темпу, ее изменения.
13*
387
Глава 15
НАБОР ВЫСОТЫ И СНИЖЕНИЕ
§ 15.1. Прямолинейный набор высоты. Первые и
вторые режимы наклонного полета
Движение самолета при наборе высоты и разгоне можно счи-
тать практически прямолинейным. Схема сил, действующих на
самолет в прямолинейном движении под углом к горизонту, пока-
зана на рис. 15.1.
Рис. 15.1. Схема сил, действующих на самолет при прямолинейном на-
боре высоты
Проектируя силы и ускорения на оси скоростной (траектор-
ной) системы координат, получим следующие уравнения движе-
ния:
т = Р cos а — X — G sin 0;
at
0= Y + Р sin a — Geos 9;
О = Ksin 7; у = 0.
В большинстве случаев для упрощения анализа прямолиней-
ного движения самолета можно принять, что cosa«l и пренебречь
нормальной составляющей силы тяги Psina«0, так как она при
малых углах атаки много меньше подъемной силы. Тогда урав-
нения можно записать в следующем упрощенном виде:
m^L = P — Хг — GsinO; (15.1)
Y— Geos 0=0; (15.2)
7 = 0. (15.3)
Уравнения (15.2) и (15.3) представляют собой условия прямо-
линейности полета под углом к горизонту. Из условия (15.2) сле-
дует, что перегрузка при наборе высоты (и снижении) na=cos0.
388
До углов 0=20-5-30° она мало отличается от единицы. Поэтому
лобовое сопротивление будет практически равно Хг.
Изменение скорости зависит от соотношения ,сил, направлен-
ных по касательной к траектории. Из схемы сил (рис. 15.1) и
уравнения (15.1) следует, что если P>Xr+Gsin0, то при наборе
высоты одновременно происходит разгон самолета; если Р=ХГ+
+ Gsin0, то полет происходит с постоянной скоростью; если Р<
<ZXr+G sin 0, то набор высоты осуществляется с торможением.
Рис. 15.2. Зависимость сил, действующих на самолет,
от скорости и угла наклона траектории
На рис. 15.2 для некоторой заданной высоты показаны графи-
ки зависимости касательных сил, действующих на самолет, от
скорости и угла наклона траектории. Так как составляющая силы
тяжести GsinG не зависит от скорости, кривые Xr+Gsin0 для
различных значений углов 0 эквидистантно смещены вверх и вниз.
Точки пересечения кривых Лг+GsinG с кривой Р определяют мак-
симальные скорости наклонного полета. Из графиков видно, что
с увеличением угла 0 максимальная скорость и диапазон скоро-
стей наклонного полета уменьшаются.
Вертикальная скорость набора высоты определяется как про-
екция. вектора скорости на вертикаль (рис. 15.3):
^- = ^y = HsinO. (15.4)
Для иллюстрации зависимости вертикальной скорости Vy и
максимальной скорости Vmax наклонного полета от угла 0 построим
следующий график. Из одной и той же точки О (рис. 15.3) для
каждого угла 0 проведем соответствующие векторы максимальных
скоростей наклонного полета, величины которых снимем с графика
389
(рис. 15.2). Затем концы векторов соединим плавной кривой, ко-
торая называется полярной диаграммой скоростей на-
клонного полета. Точка М на этом графике укажет угол 0
и скорость, при которых достигается максимальная вертикальная
скорость установившегося набора высоты, точка А — максималь-
Рис. 15.3. Полярная диаграмма скоростей наклонного
полета
ный угол наклона траектории 0тахуст. Эта точка является грани-
цей первых и вторых режимов наклонного полета: справа от нее
лежат первые режимы полета /, слева — вторые //.
Из самого способа построения кривой следует, что область,
расположенная ниже кривой, соответствует полету с разгоном.
Все точки на самой кривой означают полет с постоянными скоро-
стями. Область, расположенная выше кривой, характеризует по-
лет с торможением.
Если, например, из точки С установившегося набора высоты
с углом 0, равным 5°, отклонением ручки на себя перейти на по-
лет с углом 10°, то в первый момент скорость полета по величине
не изменится. Но так как точка D, соответствующая новому ре-
жиму полета, находится в области торможений, то скорость будет
уменьшаться до точки £, в которой установится режим полета с
постоянной скоростью. Таким образом, управление траекторией
при наборе высоты на первых режимах может в принципе осуще-
ствляться одним движением ручки управления.
Сложнее обстоит дело в области вторых режимов полета. Если,
например, из точки В отклонением ручки на себя попытаться уве-
личить угол наклона траектории от 15 до 17° (точка F), то нач-
нется торможение, и самолет вместо перехода в точку А потеряет
скорость и свалится. Чтобы этого не произошло, необходимо сна-
чала движением ручки от себя перевести самолет в область раз-
гонов, затем выполнить разгон до скорости, соответствующей точ-
390
ке А или несколько большей, и только после этого движением руч-
ки на себя перейти на более крутую траекторию — в точку А.
Таким образом, если полет на втором режиме происходит на
полной тяге двигателя, то, во-первых, управление траекторией
становится сложнее, так как его в принципе невозможно осуще-
ствить одним движением ручки управления; во-вторых, выход из
второго режима без перехода на траекторию полета с меньшим
углом невозможен, что, как уже отмечалось ранее, особенно опасно
на малой высоте.
Из уравнения (15.1) для установившегося набора высоты по-
лучим Р—Хг— Osin0 = 0, откуда
sin $VCT q ttx.
Следовательно, граница между первыми и вторыми режимами
наклонного полета 6тах будет, как и в горизонтальном полете на
скорости, где разность Р—Хг и, следовательно, продольная пере-
грузка пх максимальны (рис. 15.2).
§ 15.2. Скороподъемность. Энергетические характеристики самолета
Полная механическая энергия самолета Е состоит из кинетиче-
ской и потенциальной энергии
E = ^- + GH.
Важной характеристикой энергетических свойств самолета яв-
ляется энергия, приходящаяся на каждый килограмм веса само-
лета, так называемая удельная механическая энергия
Поскольку ее размерность дается в метрах, то величину Н3,
характеризующую уровень энергии, иногда называют энер-
гетической высотой.
Современные сверхзвуковые самолеты обладают большими за-
пасами механической энергии, в которых резко возросла доля
кинетической энергии. Например, дозвуковой самолет, летящий с
истинной скоростью 900 км/ч (250 м/с) на высоте 11 км, имеет
уровень энергии
На = -g- + Н = + 11 000 = 14 200 м,
в котором кинетическая энергия составляет 22,5%. У современного
сверхзвукового самолета, имеющего скорость 900 м/с (М~3) на
высоте 20 км, уровень энергии будет
7/, = -^- +20000 = 61 300 м,
а кинетическая энергия составляет уже 67,5%.
391
Если раньше для дозвуковых, и особенно для малоскоростных
самолетов, основными энергетическими характеристиками были
высота, вертикальная скорость и время набора высоты, то теперь
такие характеристики уже явно недостаточны, так как они харак-
теризуют лишь меньшую долю энергии — потенциальную энергию.
Теперь кроме уровня энергии Нэ необходимо знать еще и как
быстро накапливается энергия. Например, если два самолета, ве-
дущих бой, имеют одинаковые уровни энергии, а один из них мо-
жет накапливать энергию быстрее, чем другой, то через некоторое
время преимущество будет на стороне первого самолета..
Таким образом, скорость накопления полной механической
энергии или так называемая энергетическая скороподъ-
емность dH3/dt является также очень важной характеристикой
боевых возможностей самолета. По аналогии с вертикальной ско-
ростью Vyt характеризующей скороподъемность, обозначим энер-
гетическую скороподъемность через И* и найдем ее выражение
dH3 d / V* тЛ V dV . dH Z1 с-
Подставив выражение dV/dt и dH/dt из уравнений (15.1) и
(15.4), найдем
{Р~ х~ Osin 0) +1/810 9 = Vn*’ (157)
Накапливаемая механическая энергия в зависимости от вели-
чины угла 0 может распределяться в различных соотношениях по
двум каналам: на увеличение высоты (потенциальной энергии) и
на увеличение скорости (кинетической энергии). Если 0 = 0, то и
Vy = 0, тогда вся энергия идет на разгон. Если sin0 = nx, то dV/dt —
= 0, полет происходит с постоянной скоростью, и вся энергия идет
на набор высоты. В промежуточных случаях на подъем затрачи-
вается тем больше энергии, чем больше угол 0. Учитывая уравне-
ние (15.7), запишем формулу (15.6) в виде
V dV
g dt •
В крутом наборе высоты, когда ускорение dV/dt<ZO, за счет
перехода кинетической энергии в потенциальную можно получить
вертикальную скорость, большую по величине, чем энергетическая
скороподъемность.
Имея характеристики двигателя и кривые лобового сопротив-
ления Хг для различных высот, нетрудно построить графики И* =
= (рис. 15.4), характеризующие возможности накопления
энергии во всем диапазоне скоростей и высот полета при пере-
грузке, близкой к единице. Такие кривые определяются в летных
испытаниях, обязательно приводятся в техническом описании са*
молета,
392
Программа набора высоты обычно задается законом изменения
скорости по высоте V(H). В этом случае из графиков (рис. 15.4)
легко найти для каждой пары значений V и Н величину V* = V пх
и по формуле (15.5) рассчитать /7Э, т. е. получить функцию У* (/7Э),
а затем рассчитать время набора энергетической высоты интегри-
рованием уравнения (15.6)
Рис. 15.4. Зависимость энергетической скороподъемно-
сти от высоты и числа М полета
В конкретной тактической ситуации нередко требуется наби-
рать высоту на режиме максимальной энергетической скороподъ-
емности, что обеспечивает наиболее быстрое накопление энергии,
т. е. минимальное время выхода на заданную высоту и скорость.
В воздушном бою при выполнении маневров с большой пере-
грузкой величина 7* может резко уменьшиться и даже стать
отрицательной, когда лобовое сопротивление, резко увеличившись
при большой перегрузке, станет больше тяги двигателя. Тогда
вместо накопления механическая энергия будет уменьшаться. По-
теря преимущества над противником в уровне энергии является
тактически невыгодной. Поэтому без особой необходимости не
следует выполнять маневры с большой перегрузкой.
§ 15«3« Оптимальные режимы набора высоты и скорости
Выполнить маневр между заданными, начальными и конечными
условиями можно многочисленными способами. Пусть, например,
требуется с высоты Я=1 км и скорости 7=500 км/ч произвести
набор высоты Я=15 км с разгоном до скорости 7=2500 км/ч. Как
393
показано на рис. 15.5, такой маневр можно выполнить способом
/, 2 или 3. Таких вариантов может быть сколько угодно. Каждый
из возможных вариантов маневра имеет вполне определенные ха-
рактеристики: время маневра, расход топлива на маневр, горизон-
тальную дальность и т. п. Используя свободу выполнения маневра,
можем выбрать его наивыгоднейшим по какому-либо критерию.
Рис. 15.5. Примеры возможных режимов набора
высоты и разгона
Например, в случае набора высоты и скорости от Vi до Н2,
V2 можем установить такой режим полета, чтобы время маневра
было минимальным.
Рассмотрим упрощенный способ отыскания такого режима,
основанный на принятых допущениях, что траекторию можно счи-
тать практически прямолинейной, а перегрузку %, близкой к еди-
нице. Будем сначала считать режим работы двигателя заданным,
например «Полный форсаж». Поскольку нас интересует время пе-
рехода с одного уровня энергии (Нэ\) на другой (Нэ2)> то для
описания задачи вполне подходит уравнение (15.7)
= (15.7')
В правую часть этого уравнения кроме скорости входят тяга
двигателя и лобовое сопротивление, которые при заданном режи-
ме работы двигателя и известной перегрузке пу зависят только От
высоты и скорости. Заменив скорость с помощью выражения (15.5)
V = y2g{H3-H), (15.8)
можем представить Vnx как функцию Н и Яэ. Таким образом, одно
дифференциальное уравнение (15.7Z) включает в себя две неиз-
вестные функции Н(/) и Следовательно, оно имеет беско-
нечное множество решений, что и соответствует реальному факту
свободы выбора маневра, в данном случае — набора высоты и раз-
гона.
394
Разрешим уравнение (15.7') относительно интересующего нас
времени
^Э2 Н&2
t = f "Лг dH* = \F(H’ Нэ) dH" (15-9)
"а. Х
где Нл = Нх + V\l2g- Нэ2 = Нг + 1/22/2^.
Всякий раз, как только зададим какой-нибудь режим полета
в виде зависимости Н(НЭ) или (что то же самое) в виде V(H)t
появляется возможность проинтегрировать выражение (15.9) и по-
лучить строго определенное время полета t между НэХ и Нз2. За-
дача состоит в том, чтобы найти такой режим движения, который
при интегрировании обеспечил бы время движения наименьшее из
всех возможных вариантов, минимальное.
Заметим, что функциональная зависимость типа (15.9) носит
необычный, качественно новый характер. Если в обычных функ-
циональных зависимостях типа у=/(х) наблюдается однозначное
соответствие функции у аргументу х, т. е. числа — числу, то
в зависимостях типа (15.9) имеет место однозначное соответствие
числа t — функции Н(НЭ): каждому новому виду функции
Н[(НЭ), Н2(Нэ), Нз(Н3) и т. д. соответствуют строго определен-
ные числа Л, t2) t3 и т. д.
Такие зависимости в математике называются функционал а-
м и. Специальная отрасль математики, занимающаяся решением
задач на отыскание экстремумов (максимумов и минимумов)
функционалов, называется вариационным исчислением,
которое является чрезвычайно актуальной инженерной наукой.
Все задачи о наивыгоднейших маневрах летательных аппаратов
представляют собой задачи на отыскание экстремумов функцио-
налов (минимум времени, расхода топлива; максимумы дальности,
скорости, высоты, рубежа перехвата, вероятности перехвата и
т. п.) и называются вариационными задачами динами-
ки полета.
Принятые допущения настолько упростили нашу задачу, что ее
оказывается возможно решить без специальных математических
методов путем простых физических рассуждений. Для этого нуж-
но построить подынтегральную функцию выражения (15.9), исполь-
зуя данные, приведенные на рис. 15.4. Это удобно выполнить с по-
мощью расчетной табл. 15.1.
Пример такой зависимости показан на рис. 15.6. Любая ли-
ния на этом графике (в пределах возможных) представляет собой
вполне определенный режим движения, а площадь под ней в соот-
ветствии с выражением (15.9) — время движения. Например, кри-
вая Л1В1 на графике 15.6 соответствует режиму движения, изобра-
женному на графике 15.5 в виде кривой АВ.
395
Таблица 15.1
бора высоты и разгона, обеспечивающий минимальное время этого
маневра, определяется проведением огибающей (штриховая ли-
Рис. 15.6. Решение задачи набора высоты н разгона за ми-
нимальное время
ния) к семейству кривых (рис. 15.6), так как в этом случае пло-
щадь под кривой — величина интеграла (15.9)—будет мини-
мальна. Теперь надо только для каждой высоты в точке касания
кривой l/Vnx = F(H, Н3) с огибающей снять с графика 15.6 зна-
чение Нз и по формуле (15.8) вычислить скорость. Полученный
396
закон изменения скорости по высоте V(H) и будет искомым опти-
мальным режимом набора высоты и разгона.
Подсчитав площадь под огибающей графика на рис. 15.6, по-
лучим зависимость или, что то же самое, пэ тах (/), кото-
рая позволит построить кривые ^утах(0 и H(J), а по формуле
Рис. 15.7. Характеристики скороподъемно-
сти самолета
(15.4)—и кривую Vy(t). Эти кривые имеют вид, показанный на
графике 15.7, и являются важнейшими характеристиками скоро-
подъемности самолета.
Аналогичным способом решается задача о минимуме расхода
топлива на подъем и разгон. Только в этом случае нужно учесть
выражение для секундного расхода топлива
dQ, СуаР (15.10)
dt 3600 °5 кг/с' ' '
Поделив выражение (15.7') на (15.10), найдем
dQt С s
dH, “ Vnx’
откуда
Яэ, „ Нэ,
GT = [ ~^--dHt — Ha)dHe.
397
В остальном метод решения задачи не отличается от вышеопи-
санного.
На рис. 15.8 показаны примеры оптимальных режимов набора
высоты и разгона для одного из самолетов: кривая 1 — режим
GT min, кривая 2 — режим /min. Практически можно использовать
некоторый упрощенный режим набора высоты и разгона (штрихо-
Рис. 15.8. Наивыгоднейшие режимы набора высоты и раз-
гона:
/ — режим минимального расхода топлива; 2 — режим минималь-
ного времени; 3 — упрощенный универсальный режим
вая линия), который лежит достаточно близко к обоим оптималь-
ным режимам, состоит из участков с постоянными М или Н и легко
реализуем при ручном пилотировании.
Вопрос о наивыгоднейшем режиме работы двигателя в задаче
о минимуме времени на подъем и разгон самолета решается весь-
ма просто, если расход топлива не является существенным (не
ограничивается). Из существа задачи следует, что чем больше
будет тяга, тем быстрее произойдет подъем и разгон. Следова-
тельно, наивыгоднейшим режимом работы двигателя в данном
случае будет полный форсаж.
Более сложным является выбор наивыгоднейшего режима ра-
боты двигателя с точки зрения минимума расхода топлива. Из-
вестно, что при включении форсажа расход топлива резко увели-
чивается. Поэтому, несмотря на увеличение скороподъемности, на
малых высотах производная с№т/(1Нэ (затрата топлива на еди-
ницу прироста энергии) на форсажном режиме существенно боль-
ше, чем на бесфорсажном. С другой стороны, если не включать
398
форсаж, то даже при израсходовании всего запаса топлива вооб-
ще нельзя набрать той скорости и высоты (энергии), которую
можно достичь на форсажном режиме, израсходовав приемлемое
количество топлива.
Отсюда ясно, что существует вполне определенный наивыгод-
нейший режим работы двигателя, обеспечивающий минимум рас-
хода топлива на подъем и разгон. Если форсаж нерегулируемый
Рис. 15.9. Определение наивыгоднейшей высоты включения
форсажа при подъеме и разгоне
(включается сразу полный форсаж), то выбор оптимального ре-
жима работы двигателя сводится к определению наивыгоднейшего
момента включения форсажа (наивыгоднейшей высоты).
Эту задачу с достаточной для практики точностью можно ре-
шить следующим образом. Сначала нужно найти наивыгоднейшие
режимы подъема и разгона для максимального бесфорсажного и
для форсажного режимов работы двигателя и построить кривые
GT, t и Н в функции Нэ для обоих случаев на одном графике, как
показано на рис. 15.9, где кривые /, GT и Н соответствуют макси-
мальному бесфорсажному режиму, а кривые/ф, <7Т<Ф и /7Ф — фор-
сажному режиму подъема и разгона.
Из графика видно, что производная dGT/dH3 (наклон кривой
Gr к оси Нэ) на бесфорсажном режиме до некоторой высоты мень-
ше, чем на форсаже. Та высота, на которой dG^/dH3 = dG'l,^/dH3l
и будет определять момент включения форсажа. Ее легко найти,
переместив кривую GT. ф влево эквидистантно по горизонтали, на-
пример с помощью кальки так, чтобы она касалась кривой GT
(штриховая линия). Точка касания определит момент включения
форсажа, соответствующий минимальному расходу топлива на
399
подъем и разгон. Проведя из этой точки горизонтальную прямую
до пересечения с кривой Н$, найдем наивыгоднейшую высоту
включения форсажа НВкл. Переместив эквидистантно по горизон-
тали кривую /ф вправо до точки пересечения горизонтальной пря-
мой с кривой t, получим кривую суммарного времени разгона и
подъема (штриховая линия). Заданные высота Нзвл и уровень
энергии Н3. зад, которые требуется набрать, определят минималь-
ный расход топлива GTmin и суммарную затрату времени /min для
набора Нзаа и Нэ. зад. На рис. 15.9 на оси абсцисс через Ot, Ост и
О» обозначено начало отсчета t, GT и Н.
Практически выгодно включать форсаж на высоте, несколько
меньшей, чем Явкл, так как перерасход топлива 20—30 кг значе-
ния не имеет, а выигрыш времени будет существенным.
Для случая регулируемого форсажа частичное форсирование
двигателя можно начинать на 5—6 км ниже Нвкл с тем, чтобы
к моменту набора Нвкл постепенно довести режим работы двига-
теля до полного форсажа. Более точное решение задачи о наивы-
годнейшем режиме работы двигателя требует применения более
сложных методов вариационного исчисления.
§ 15.4. Динамический потолок. Особенности поведения
самолета на динамических высотах
Как известно, на верхней границе диапазона скоростей и высот
полета (линии потолков) выполняются условия постоянства ско-
рости Р=Хг и прямолинейности горизонтального полета Y=G.
Выше линии потолков в горизонтальном полете невозможно со-
хранить скорость постоянной, так как тяга двигателя будет мень-
ше лобового сопротивления. Однако прямолинейный полет все же
возможен в некотором диапазоне скоростей и высот, так как ра-
венство Y—G удается сохранить за счет увеличения угла
атаки.
Область скоростей и высот, расположенная выше линии по-
толков, в которой возможен прямолинейный горизонтальный по-
лет, называется о б л а с т ь ю динамических высот (ОДВ).
Левой границей этой области является линия минимальной ско-
рости горизонтального полета, продолженная на высоты, большие
потолка (рис. 15.10). Правую границу ОДВ можно приближенно
найти из условия постоянства максимального уровня полной ме-
ханической энергии самолета.
Максимум уровня энергии обычно имеет место в точке пересе-
чения линии потолков с линией ограничения максимальной скоро-
сти ПО числу М (рис. 15.10). Если ИЗ ТОЧКИ НЭтах выполнить ма-
невр с набором высоты при условии постоянства механической
энергии
Нэ max = + Н = C°nSt.
400
то по мере увеличения высоты скорость будет уменьшаться по за-
кону
И = /2^(/7эшах-//)
(кривая 1 на рис. 15.10). Но для этого необходимо, чтобы тяга
двигателя все время была равна лобовому сопротивлению,
Рис. 15.10. Область динамических высот полета
(Д — динамический потолок)
В действительности при наборе высоты с переходом через ли-
нию потолков механическая энергия самолета не сохраняется по-
стоянной, а несколько уменьшается. Это происходит, во-первых,
потому, что выше линии потолков тяга двигателя всегда меньше,
чем лобовое сопротивление Хг; во-вторых, потому, что при вводе
самолета в маневр с набором высоты необходимо создать пере-
грузку больше единицы, что вблизи потолка приводит к сущест-
венному росту индуктивного сопротивления, пропорционального
квадрату перегрузки. Кроме того, достичь точки Нэтах без нару-
шения ограничения скорости по Мпред нельзя. Можно только по-
дойти к ней сравнительно близко.
По указанным причинам правая граница области динамических
высот лежит несколько левее линии Нэ max = const и имеет не-
сколько меньший наклон (кривая 2 на рис. 15.12). Точку пере-
сечения правой и левой границ области динамических высот (точ-
ка Д) принято называть динамическим потолком.
Решение вариационной задачи о максимуме высоты и летные
исследования показали, что маневр выхода на динамические вы-
соты целесообразно начинать на 2—3 км ниже линии потолков,
где имеется достаточный избыток тяги для создания перегрузки
без потери энергии
Горизонтальный полет на динамических высотах возможен
только с торможением, так как Р<.ХГ. Продолжительность гори-
401
зонтального полета определяется временем торможения до мини-
мальной скорости. Для современных самолетов на высотах, боль-
ших потолка на 1—2 км, оно достигает 3—4 мин. Характерными
особенностями поведения самолета на динамических высотах яв-
ляются, во-первых, вялость реакции на отклонение рулей, инерт-
ность в угловых движениях, необходимость больших перемещений
рычагов управления; во-вторых, трудность сохранения заданной
высоты полета.
Использованию области динамических высот часто мешают
ограничения высоты и скорости по устойчивости работы силовой
установки. Возможности для выполнения маневров здесь весьма
ограничены еще и потому, что при создании перегрузки торможе-
ние в результате роста индуктивного сопротивления становится
настолько интенсивным, что до достижения минимальной скорости
самолет успевает развернуться не более чем на 30—50°. С боль-
шим успехом область динамических высот можно использовать
для выполнения пологих горок, выход из которых осуществляется
отдачей ручки от себя, т. е. с ^<1, что обеспечивает запас по
Су до Су св и уменьшение лобового сопротивления Х<ХГ.
При дальнейшем увеличении скоростей полета самолетов мак-
симальный уровень их энергии будет возрастать. Следовательно,
область динамических высот будет расширяться и ее роль станет
более значительной.
§ 15.5. Влияние эксплуатационных факторов
на скороподъемность самолета
Для анализа влияния эксплуатационных факторов на скоро-
подъемность самолета представим формулу для И* в следующем
развернутом виде:
= = 20J/7m^=^, (15.11)
где
ЛО2л2
X=O,7M4.S+o^JPs- (15.12)
Из этих формул видно, что на энергетическую скороподъем-
ность существенно влияют изменение веса, сил тяги, лобового со-
противления и атмосферных условий.
Из формулы (15.11) видно, что увеличение веса умень-
шает И* как непосредственно, так и через возрастание индуктив-
ного сопротивления. Последнее сильнее проявляется в полете с
перегрузкой, большей единицы, особенно на больших высотах.
Изменение сил тяги и лобового сопротивления оказывает влия-
ние на Й* пропорционально изменению их разности
и; Р—Х •
(15.12')
402
Следовательно, влияние обоих этих факторов будет тем силь-
нее, чем разность Р—X меньше.
Влияние изменения температуры наружного воздуха проявля-
ется прежде всего через изменение тяги двигателя Р.
Логарифмируя и дифференцируя выражение (15.11) при по-
стоянных М и G, найдем
dVy d(P-X) , dT
- p_x + u.a-p-•
Как видно из формулы (15.12), при постоянных М, G, давле-
нии р и Пу 1 лобовое сопротивление будет тоже постоянным. По-
этому d(P—X) =dP
и
dVy _ dP , Л Г dT P dP , dT
IZ* P —T ~~ P — X P + T •
У
Принимая в соответствии с формулой (13.21)
dP __ 9dT
Р ~ 2 Т ’
получим
dV* _ р dT n 5 dT _ /л 2 \ dT
у* — 2Р — Х г +0,0 г — lU.u ] т .
У \ ’“тН
Таким образом, увеличение температуры всегда понижает энер-
гетическую скороподъемность и тем сильнее, чем меньше разность
Р—X. Например, если Х=0,8Р, то
2 } dT q^^L
V* —VU,b 1—0,8 у Т ~ У’5 т ’
У '
т. е. увеличение температуры на 5° (для больших высот—на 2,3%)
уменьшает И* на 22%. В лучшем случае, когда
dT
—Ь5Т-
Влияние изменения стреловидности крыла на энергетическую
скороподъемность, как и на все другие летные характеристики,
зависит от режима полета, определяемого числом М и Су. Как
уже говорилось в главе 13, для каждой пары значений М и Су
существует своя оптимальная стреловидность крыла, при которой
1 Здесь рассматривается влияние изменения только одной температуры Т
при прочих постоянных параметрах.
403
энергетическая скороподъемность максимальна. На рис. 15.11 при-
веден пример такой зависимости для одного из самолетов с изме-
няемой стреловидностью крыла.
Из формулы (15.7) следует, что вертикальная скорость про-
порциональна энергетической скороподъемности. Поэтому влияние
Рис. 15.11. Зависимость оптимальной стреловид-
ности крыла от режимов полета
всех перечисленных эксплуатационных факторов на вертикальную
скорость аналогично влиянию их на энергетическую скороподъем-
ность.
§ 15.6. Снижение. Оптимальные режимы снижения
Траекторию полета самолета при снижении можно считать
практически прямолинейной. На рис. 15.12 показана схема сил,
действующих на самолет при прямолинейном снижении. Тяга дви-
гателя в этом режиме полета, как правило, бывает меньше лобо-
вого сопротивления, а при планировании с выключенным двига-
телем — отсутствует.
Уравнения движения, описывающие прямолинейное снижение
в траекторной системе координат, ничем не отличаются от урав-
нений движения при наборе высоты:
/n-~ = P-A'r-Gsin0; (15.13)
0==У —Gcos0; (15.14)
О—У sin у; (15.15)
404
_gLe^sine = lZ;
^ = I7cos0 = ^.
(15.16)
(15.17)
В случае установившегося снижения ускорение dV]dt равно
нулю, и первое уравнение будет представлять собой условие по-
стоянства скорости
P-Xv- Osin 0 = 0. (15.18)
Рис, 15.12. Схема сил, действующих на самолет при прямолиней-
ном снижении
Уравнения (15.14) и (15.15) являются условиями прямолиней-
ности движения. При этом, как и при наборе высоты, n?=cos0.
Уравнения (15.16) и (15.17) называются кинематически-
ми связями. Они представляют собой проекции вектора ско-
рости на оси неподвижной земной системы координат и исполь-
зуются для расчета высоты и горизонтальной дальности полета L.
Для расчета дальности снижения с уменьшением скорости,
т. е. с использованием запаса кинетической энергии для увеличе-
ния дальности полета, удобно использовать уравнения (15.17) и
(15.13), преобразованные ранее к энергетической форме в форму-
ле (15,7') з
Лт- = Исоз 0;
at
dH9
dt
Поделив их почленно, получим
dL ____ cos в
dfi» пх
(15.19)
405
Так как при снижении тяга двигателя обычно мала, то при-
ближенно можно принять, что
Тогда с учетом условия прямолинейности (15.14) найдем
dL _______________ G cos 0 Y „
dH~3 ~ X
Отсюда дальность планирования с уменьшением скорости (тор-
можением)
^9, КОН
La = - J /^//э«/<ср(//э.нач-/7э.К0„) = /<срД^. (15.20)
9. нач
Если снижение (планирование) происходит с постоянной ис-
тинной скоростью, то
нач кон ==: ^нач ^кон
и тогда из формулы (15.20) как частный случай получим
= Л'ср (#нач ~ ^кон) = KZ^H.
Чтобы достичь максимальной дальности снижения следует
планировать с максимальным качеством. Для этого удобно ис-
пользовать указатель угла атаки, если заранее определить для
различных чисел М приборные значения наивыгоднейшего угла
атаки аНв, на которых реализуется максимальное качество.
Так как в горизонтальном полете с большой скоростью углы
атаки меньше наивыгоднейшего, то при увеличении а до анв са-
молет вместо снижения перейдет сначала в набор высоты. По
мере уменьшения скорости при сохранении а = анв самолет будет
постепенно переходить к горизонтальному полету и к снижению.
Таким образом, при сохранении максимального качества профиль
снижения будет криволинейным, выполнимым с помощью указа-
теля угла атаки. Проще (вернее, привычнее) осуществлять умень-
шение скорости в горизонтальном полете с постепенным увеличе-
нием угла атаки до а = анв, а затем перейти на снижение. Однако
в этом случае дальность снижения будет несколько меньше.
На самолетах с изменяемой стреловидностью крыла для дости-
жения максимальной дальности снижения с уменьшением скоро-
сти следует постепенно уменьшать стреловидность крыла в соот-
ветствии с ее оптимальными значениями, показанными в качестве
примера на рис. 15.11.
§ 15.7. Предпосадочное снижение. Опасность вторых режимов
Вертикальная скорость предпосадочного снижения (15.16) не
должна быть больше 104-12 м/с. При приближении к земле она
уменьшается до 5—6 м/с. В противном случае трудно осуществить
выравнивание с достаточной точностью.
406
Скорости на предпосадочном снижении современных самолетов
составляют 80—100 м/с (290—360 км/ч). Следовательно, для
обеспечения достаточно малой вертикальной скорости необходимо
осуществлять снижение с углом наклона траектории, определяе-
мым из соотношения (15.16):
sin 0 = ~ _ _5_ = _ (0,063 4- 0,050),
откуда 0 = — (3,64-2,9°).
При меньших углах 0 плохо просматривается ВПП. Поэтому
угол снижения в сложных метеоусловиях 0 = —3° можно считать
оптимальным. В современных радиотехнических системах, обеспе-
чивающих заход на посадку по приборам, угол наклона глиссады
предпосадочного снижения выбирается примерно 3—4°, т. е. близ-
ким к оптимальному по условиям визуального выполнения по-
садки.
Для контроля режима предпосадочного снижения с углом 3°
можно использовать простое практическое правило: высота полета
в сотнях метров должна быть равна половине дальности до на-
чала ВПП в километрах. Например, при дальности 4 км высота
должна быть 200 м.
При малых углах снижения и малом качестве современных
сверхзвуковых самолетов составляющая сила тяжести G sin 0, на-
правленная вперед (рис. 15.12), оказывается недостаточной для
уравновешивания лобового сопротивления. Поэтому предпосадоч-
ное снижение выполняется с некоторой тягой двигателя.
Учитывая условия прямолинейности (15.14) и постоянства ско-
рости (15.18)
Г=Осо8 0; Р-Х —Gsin0 = O
и что
Y __ ”._ С? cos 0 . X _ cos 0
т “ х ; 7Г — ~К ’
из равенства (15.18) найдем
В табл. 15.2, рассчитанной по формуле (15.21), приведена тя-
говооруженность, необходимая для обеспечения постоянной ско-
рости при снижении с углом 0 = —3° (sin 0 = —0,05) при различ-
ных величинах аэродинамического качества. Например, при каче-
стве, равном 5, и весе самолета 12 000 кгс (120 000 Н) требуется
тяга Р = 12 000*0,15=1800 кгс (18 000 //); поскольку тяга двига-
теля не измеряется в полете, то летчик должен знать соответ-
407
Выпуск закрылков вызывает уменьшение аэродинамического
качества. Если частоту вращения при этом не изменить, то нач-
нется торможение. Потребная скорость планирования при выпу-
щенных закрылках будет меньше, так как увеличивается Су.
Однако из-за уменьшения качества приходится увеличивать тягу
двигателя.
В процессе предпосадочного снижения весьма опасно попада-
ние самолета на вторые режимы. Это может, в частности, произой-
ти, если летчик, желая несколько уменьшить скорость, чрезмер-
но уменьшит тягу двигателя и затем упустит контроль. за ско-
ростью и частотой вращения вала двигателя.
Если скорость продолжает уменьшаться, несмотря на обычное
корректирующее увеличение частоты вращения летчиком, что сви-
детельствует о нахождении самолета на втором режиме, необхо-
димо немедленно увеличить частоту вращения вплоть до макси-
мальной, пока скорость не начнет возрастать. Ввиду большого
времени приемистости и медленного разгона самолета можно, если
позволяет высота, увеличить угол снижения до набора необходи-
мой скорости. При этом следует учитывать, что на современных
самолетах увеличение скорости за счет снижения приводит к зна-
чительно большей потере высоты, чем на дозвуковых самолетах
с большим аэродинамическим качеством и меньшей скоростью по-
лета, a Vy легко увеличить, но трудно уменьшить. Поэтому в обыч-
ных (не в особых) ситуациях не рекомендуется увеличивать ско-
рость за счет увеличения угла снижения.
Выходить из второго режима при полете на малой высоте
включением форсажа не рекомендуется, так как из-за раскрытия
створок во время розжига форсажа тяга падает. Попадание на
второй режим может произойти и при неправильном уходе на
второй круг, когда летчик пытается уменьшить угол снижения,
не дождавшись выхода двигателя на максимальный режим.
При уходе на второй круг нужно перевести РУД в положение
МАКСИМАЛ и продолжать снижение, пока скорость не будет до-
статочной для перехода в набор высоты. Если высота мала, то
нужно продолжать снижение и выполнение посадки вплоть до
касания ВПП с последующим взлетом, когда скорость станет до-
статочной для отрыва.
Глава 16
МАНЕВРИРОВАНИЕ В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
§ 16.1. Разгон и торможение самолета в горизонтальном
полете. Влияние эксплуатационных факторов
на характеристики разгона и торможения
16.1.1. Разгон самолета
Горизонтальные разгон и торможение самолета представляют
собой прямолинейный полет с изменением величины скорости. За-
кон изменения скорости в рассматриваемом случае определяется
408
уравнением (13.6), разрешив которое относительно ускорения, по-
лучаем
dV = Р — Хг =
dt т
gnx.
(16.1)
Величина продольного ускорения определяется отношением из-
бытка тяги (Р—Лг) к силе тяжести самолета (О), т, е. величиной
продольной перегрузки пх.
Рис. 16.1. Зависимость продольной перегрузки
от числа М и высоты полета на форсажном ре-
жиме работы двигателя
Из всех режимов работы двигателя наибольшее ускорение,
естественно, обеспечивает полный форсаж. С увеличением высоты
полета уменьшение тяги двигателя обусловливает снижение уско-
рения разгона.
Изменение ускорения разгона самолета в эксплуатационном
диапазоне скоростей и высот полета на режиме полного форсажа
можно проследить по графику продольной перегрузки пх
(рис. 16.1). В дозвуковом диапазоне скоростей на малых высотах
при разгоне на полном форсаже продольная перегрузка у совре-
менных маневренных самолетов достигает пх=0,64-0,8, что обес-
печивает увеличение скорости на 20—25 км/ч за одну секунду.
С началом развития волнового кризиса при превышении
Мкр=0,94-0,95 наблюдается интенсивное уменьшение пх, что свя-
зано с ростом волнового сопротивления самолета. На максималь-
ном режиме работы двигателя разгон возможен обычно только до
чисел М=0,954-1,05.
На величину продольной перегрузки пх горизонтального раз-
гона кроме режима работы двигателя, скорости и высоты полета
409
существенно влияют также полетная масса самолета, его конфи-
гурация, габариты и масса подвесок вооружения и топливных ба-
ков, температура наружного воздуха. Степень влияния этих фак-
торов зависит от величины пх. С уменьшением величины пх их
влияние усиливается.
Рис. 16.2. Зависимость лобового сопротивления
самолета в горизонтальном полете от угла стре-
ловидности крыла
Влияние увеличения полетной массы самолета выражается в
увеличении лобового сопротивления за счет его индуктивной со-
ставляющей. При наличии подвесок вооружения или топливных
баков уменьшение пх происходит как за счет увеличения полетной
массы самолета, так и за счет дополнительного сопротивления.
Крупные подвески вооружения и топливные баки при переходе
на околозвуковые скорости настолько сильно ухудшают харак-
теристики разгона, что превышение числа М>0,9 становится прак-
тически невозможным.
Отклонение температуры наружного воздуха от стандартной
влияет на величину пх горизонтального разгона через измене-
ние тяги двигателя и может быть рассчитано аналогично
влиянию температуры на !/* (§ 15.5). Если при разгоне на
малых высотах в дозвуковом диапазоне скоростей на полном фор-
саже увеличение температуры наружного воздуха от стандартной
на 10° вызывает уменьшение пх на 5—6%, то в околозвуковом и
сверхзвуковом диапазоне скоростей на больших высотах — на
20—30%.
У самолетов с изменяемой геометрией крыла лобовое сопро-
тивление, а следовательно, и продольная перегрузка зависят от
угла стреловидности крыла (рис. 16.2). На малых дозвуковых ско-
ростях наибольшее значение пх соответствует минимальной стре-
410
ловидности (рис. 16.3), так как на этих режимах значительную
роль играет X/, величина которого наименьшая при минималь-
ной стреловидности. С увеличением скорости горизонтального по-
лета усиливается влияние безындуктивной составляющей лобо-
вого сопротивления, величина которой оказывается наименьшей
Рис. 16.3. Влияние стреловидности крыла на
продольную перегрузку самолета
у крыла наибольшей стреловидности. С учетом этого в процессе
дозвукового разгона самолета предусмотрена перекладка крыла
на увеличение стреловидности с таким расчетом, чтобы на числе
М = 0,84-0,9 она была максимальной, так как наибольшие уско-
рения разгона на числах М>0,9 получаются на максимальной
стреловидности крыла.
Важными характеристиками разгона являются время разгона,
путь, пролетаемый в процессе разгона, и расход топлива, необходи-
мый для разгона. Время разгона /р от скорости УНач до скорости
Укон определяется интегрированием уравнения (16.1)
и
кон
<16-2)
V
нач
Если в диапазоне скоростей Унач—Укон продольная перегрузка
изменяется незначительно, то, полагая пх=пх СР=const, получим
в результате интегрирования следующее приближенное выражение
для определения времени разгона:
j ^кон ‘— Vнач
₽ gnx ср ’
(16.2')
Для определения пути L, пролетаемого самолетом в процессе
разгона от скорости Унач до Укон, воспользуемся следующим оче-
видным соотношением:
V
_ dL dV _ dL
~~ dt dV ~ dV Sflx‘
411
Отсюда получаем уравнение
dt __ V
dV gnx ’
интегрирование которого дает
V
кои
Г VdV ^кон ^нач
J &пх
V
нач
(16.3)
Рис. 16.4. Время горизонтального разгона само*
лета на полном форсаже
Зная время разгона и средний часовой расход топлива Слср»
можно приближенно определить расход топлива GT. р в процессе
разгона по формуле
GT. р —
ср^р
3600 ’
(16.4)
Характеристики разгона конкретного типа самолета обычно
рассчитываются с помощью номограмм, позволяющих учитывать
изменение основных эксплуатационных факторов: режима работы
двигателя, высоты разгона, полетной массы самолета, вида под-
весок вооружения и топливных баков, стреловидности крыла и
температуры наружного воздуха.
Время разгона, путь и расход топлива могут быть представ-
лены и в виде графиков. Пример графика времени горизонталь-
ного разгона маневренного самолета на полном форсаже для
ряда высот и определенной полетной массы в стандартных атмо-
412
сферных условиях показан на рис. 16.4. Как видно из графика,
с увеличением высоты время разгона растет соответственно умень-
шению Пх (рис. 16.1). Наиболее интенсивное увеличение времени
разгона, пути и расхода топлива происходит на околозвуковых и
сверхзвуковых скоростях при малых пх. У современных маневрен-
ных самолетов при горизонтальном разгоне от М=0,9 до М = 2
на высоте 77=11000 м время разгона составляет 250—300 с, про-
летаемый путь— 180—200 км.
Техника выполнения горизонтального разгона требует учета не-
которых аэродинамических особенностей конкретного самолета.
Для разгона до сверхзвуковых скоростей режим работы двигателя
увеличивается до полного форсажа, крыло устанавливается в по-
ложение максимальной стреловидности (на самолетах изменяемой
геометрии крыла). При разгоне до заданной скорости в дозвуко-
вом диапазоне положение крыла согласуется с ее величиной и
характером последующего маневра.
В процессе горизонтального разгона по мере увеличения ско-
рости для сохранения постоянной высоты угол атаки должен по-
степенно уменьшаться отдачей ручки управления от себя. При этом
в дозвуковом и сверхзвуковом диапазонах скоростей, где само-
леты устойчивы по скорости, давящие усилия на ручке управле-
ния возрастают и при необходимости их следует уменьшать ме-
ханизмом триммерного эффекта.
При разгоне в околозвуковом диапазоне скоростей, где прояв-
ляется неустойчивость по скорости, ручку управления приходится
несколько брать на себя и прикладывать к ней тянущие усилия,
если перед входом в этот диапазон самолет был сбалансирован
при нулевых усилиях на ручке управления. Для улучшения ха-
рактеристик устойчивости и управляемости разгон рекомендуется
выполнять с включенным автоматом демпфирования. По мере на-
растания скорости контролировать работу АРУ.
При подходе к максимально допустимой скорости необходимо
контролировать ее величину по прибору и принимать своевремен-
ные действия для предотвращения ее дальнейшего роста: умень-
шить тягу, выпустить воздушные тормоза, перевести самолет в на-
бор высоты. Запаздывание с выключением форсажа при разгоне
на малых и средних высотах на самолетах с большой тяговоору-
женностью может привести к опасному превышению максимально
допустимой скорости. При разгоне на малых высотах рекомен-
дуется в целях обеспечения безопасности полета включать систе-
му увода самолета с опасной высоты.
Уменьшение продольной перегрузки в трансзвуковом диапа-
зоне скоростей (особенно при высоких температурах) вынуждает
иногда в интересах сокращения времени и расхода топлива раз-
гон на этом участке осуществлять со снижением, а при необходи-
мости также сбрасывать топливные баки перед началом разгона.
В этих условиях нецелесообразно совмещение разгона с разворо-
том, так как при %>! разгон может оказаться невозможным
даже на полном форсаже двигателя.
413
16.1.2. Торможение самолета
Торможение самолета в горизонтальном полете происходит
при отрицательных значениях продольной перегрузки. Величина
перегрузки и ускорения торможения зависит от скорости и высоты
полета, режима работы двигателя и выпуска воздушных тормозов
(рис. 16.5). Особенно интенсивное торможение наблюдается в око-
Рис. 16.5. Продольная перегрузка самолета и ее при-
рост при выпуске тормозных щитков
лозвуковом и сверхзвуковом диапазоне скоростей полета на малых
высотах. На таких режимах полета одно только выключение фор-
сажа приводит к быстрому падению скорости, а дросселирование
двигателя до малого газа приводит к увеличению ускорения тор-
можения до 8—10 м/с2. В этих условиях обычно отпадает необ-
ходимость в использовании тормозных щитков.
Выпуск тормозных щитков на маневренных самолетах приво-
дит к возрастанию безындуктивной составляющей лобового со-
противления почти в два раза и соответственно резко повышает
ускорение торможения, особенно на больших приборных скоростях.
Использование тормозных щитков для торможения самолета да-
леко не всегда целесообразно, так как приводит к бесполезному
расходу энергии. Такой же темп гашения скорости может быть
достигнут за счет перевода самолета в набор без потери энергии
или за счет выполнения криволинейного маневра, что может ока-
заться тактически более выгодным. На современных маневренных
самолетах выпуск тормозных щитков обычно применяется для пре-
дотвращения чрезмерного роста скорости при выполнении нисхо-
дящих маневров, а также для выхода из-под удара, если скорость
велика, с одновременным созданием пу доп.
414
Основными характеристиками торможения самолета в гори-
зонтальном полете является время (/т) и путь (Лт), которые мож-
но рассчитать по формулам (16.2) и (16.3). Характеристики тор-
можения самолета зависят от условий его выполнения, диапазона
скоростей, высоты, режима работы двигателя, положения тормоз-
ных щитков, наличия подвесок вооружения и топливных баков,
массы самолета и стреловидности крыла. Время и путь горизон-
тального торможения современных маневренных самолетов в до-
звуковом диапазоне скоростей от 1/пр=1000 км/ч до эволютивной
на малых высотах составляют соответственно 100—120 с и 20—
24 км с убранными тормозными щитками, 50—60 с и 10—11 км —
с выпущенными. С увеличением высоты полета время и путь тор-
можения возрастают.
Усилия на ручке при торможении изменяются в обратном по-
рядке по сравнению с разгоном. На сверхзвуковых и дозвуковых
скоростях давящие усилия уменьшаются и переходят в тянущие.
На трансзвуковых скоростях появляется стремление самолета к
кабрированию (скоростной подхват). У современных маневренных
самолетов в горизонтальном прямолинейном полете эта тенденция
к подхвату обычно невелика и требует небольшого парирующего
отклонения ручки управления и увеличения давящего усилия.
При торможении в сверхзвуковОхМ диапазоне скоростей дроссе-
лирование двигателя до малого газа может быть ограничено по
устойчивости работы силовой установки. В этом случае до опре-
деленного числа М полета торможение осуществляется на режиме
максимала (только за счет выключения форсажа), а далее (обыч-
но с М=1,6) режим работы двигателя допускается снижать до
малого газа, что часто обеспечивается автоматическими устрой-
ствами.
На самолете изменяемой геометрии по мере гашения скорости
производится перестановка крыла на уменьшение стреловидности
с учетом установленных для различных х максимально допусти-
мых скоростей. При этом из-за изменения устойчивости по пере-
грузке может нарушаться продольное равновесие самолета.
В процессе торможения необходимо контролировать приборную
скорость полета, чтобы не допускать ее уменьшения менее эволю-
тивной и тем более до ее опасных значений по сваливанию. По-
терю скорости ниже эволютивной нетрудно предотвратить свое-
временным увеличением режима работы двигателя или переходом
на снижение при наличии запаса высоты.
§ 16.2. Вираж (разворот), условия его выполнения.
Влияние эксплуатационных факторов на характеристики
виража (разворота)
Разворотом называется горизонтальный маневр самолета|
предназначенный для изменения направления полета. Вираж —
это разворот на 360°. Вираж, выполняемый с постоянными ско-
ростью и креном без скольжения, называется правильным.
415
Вираж с креном менее 45° принято считать мелким, а с креном
45° и более — глубоким.
На рис. 16.6 показана схема сил, действующих на самолет при
криволинейном движении в горизонтальной плоскости (0 = 0) без
скольжения. Проектируя эти силы на траекторную систему коор-
динат, получим следующую си-
стему уравнений, описывающую
такое движение:
Рис. 16.6. Схема сил, действующих
на самолет при выполнении виража
0 = Y cos 7 — G;
V2 v •
/п-у- — Y sin 7.
(16.5)
Первое уравнение системы
(16.5) позволяет определить за-
кон изменения скорости в процес-
се выполнения виража. Если тяга
Р равна силе лобового сопротив-
ления А', то ускорение =0 и
вираж выполняется на постоян-
ной скорости (установившийся
вираж). Второе уравнение систе-
мы (16,5) выражает условие вы-
полнения виража на постоянной
высоте — равновесие вертикаль-
ных сил. Разделив это уравнение
на силу тяжести G, получим пе-
регрузку пу, потребную для вы-
полнения виража в горизонталь-
ной плоскости:
= —. (16.6)
У cos f ' ’
На рис. 16.7 показан график за-
висимости потребной перегрузки
от угла крена. Нарушение этого
соотношения при выполнении ви-
ража приводит к искривлению траектории полета в вертикальной
плоскости: при %<1/созу — вниз, а при nff>l/cosY — вверх.
На участках ввода в вираж и вывода из него происходит изме-
нение крена, что требует для сохранения условия горизонтально-
сти соответствующего изменения перегрузки тем большего, чем
больше крен. Если для угла крена 45° перегрузка должна быть
увеличена до 1,41, то для угла крена 80° — до 5,76.
Характерно, что даже небольшое изменение крена при его зна-
чениях 70—80° требует большого изменения перегрузки (рис, 16.7),
416
Искривление траектории разворота происходит с помощью со-
ставляющей подъемной силы У sin у, направленной по нормали к
траектории в горизонтальной плоскости (рис. 16.6). Из третьего
уравнения системы (16.5) получаем радиус кривизны траектории
mV- у»
Fsin-y
Рис. 16.7. Потребная перегрузка пу для
выполнения виража в горизонтальной пло-
скости
Если строго выполняется условие горизонтальности Y cos у» Gt
то перегрузка и крен однозначно связаны выражением (16.6).
Тогда в формуле (16.7) можно исключить либо перегрузку, либо
угол крена.
Так, подставляя пи=1 /cosу в (16.7), получаем
1/2
Подставим в формулу (16.7) значение sin у, выраженное через
перегрузку:
sin т = И1 — cos2 7= \f 1--------= ——---------.
' ' V п‘ «у
В результате получаем
. =_EL_
гКлу—i’
(16.8')
14-21
417
Кроме радиуса кривизны траектории важными характеристи-
ками виража являются угловая скорость разворота сив, время вы-
полнения виража и расход топлива в процессе выполнения ви-
ража GT .в.
Так как 1/ = шв/'в, то угловая скорость разворота определяется:
у g — 1
(16.9)
Тогда время выполнения установившегося виража и расход
топлива могут быть рассчитаны по формулам:
2к
сов
= 0,64
V
У^
От. в
__£л£в
3600*
(16.10)
(16.11)
Увеличение перегрузки (угла атаки) приводит к увеличению
лобового сопротивления самолета. На рис. 13.3 показаны кривые
лобового сопротивления при перегрузках пу, равных 1, 2, 3, 4, 5,
соответствующие горизонтальному полету с углами крена 0; 60;
70; 75,5 и 78°.
Максимальная перегрузка, при которой лобовое сопротивление
становится равным полной тяге двигателя, принято называть пре-
дельной по тяге (пу пред), а вираж — п р е дел ь н ы м по
тяге установившимся виражом.
При увеличении крена и перегрузки более предельных по тяге
лобовое сопротивление становится больше тяги двигателя, вслед-
ствие чего скорость в процессе выполнения виража начнет умень-
шаться; будет уменьшаться при этом и радиус виража. Такой
вираж принято называть неустановившимся, а при пу. близкой
к пу доп, — форсированным. Форсированный вираж выполняется в
целях уменьшения времени виража (разворота).
Изменение скорости и время выполнения форсированного ви*
ража при известном законе изменения перегрузки по скорости
определяются численным или графическим интегрированием пер-
вого и третьего уравнений системы (16.5). При графическом ин-
тегрировании систему (16.5) удобно представить в виде:
dV
-dF-S^
dw 1
dt ~~ V
(16.12)
Построение траектории форсированного виража (разворота)
удобно выполнять графоаналитическим методом, вычисляя радиус
кривизны по формуле (16.8') и вычерчивая траекторию по малым
интервалам угла разворота ДТ (10—15°). При этом изменение
418
скорости и время разворота на малый угол ДЧ1* рассчитывают по
формулам:
} I 1 V. IUI
Ы = 'L_______ ДФ, I
g V п2у — 1 I
полученным из системы (16.12) переходом от дифференциалов к
конечным приращениям.
Расход топлива на форсированный вираж (разворот) можно
приближенно определить по среднему значению Сн, пользуясь той
же формулой (16.11), что и для установившегося виража.
Приведенные выше зависимости (16.8'), (16.9) и (16.10) пока-
зывают, что характеристики виража зависят только от скорости
и перегрузки при его выполнении: чем больше скорость и меньше
перегрузка, тем больше гв и меньше сов. Заметим, что влияние
скорости на гв сильнее, чем на coB, так как гв пропорционален ско-
рости в квадрате, а о)в — скорости в первой степени.
Наименьший радиус и наибольшая угловая скорость при вы-
полнении установившегося виража на заданной скорости дости-
гаются выдерживанием пу = пу пред, а при выполнении форсирован-
ного виража — при ny — ny^n. Заметим, что у маневренных само-
летов, как правило, пу доп>% пред- Однако существуют и такие
условия выполнения виража, при которых предельные по тяге
перегрузки могут быть больше максимально допустимых. Величи-
ны Пг/пред и пу доп зависят не только от скорости и высоты полета,
но и от полетной массы самолета, вида подвесок, стреловидности
крыла, режима работы двигателя и температуры наружного воз-
духа. Характер зависимости гг^пред от приборной скорости полета
на форсаже (сплошные линии) и максимале (штрихпунктирная
линия) и пу доп (штриховая линия) маневренного самолета в ка-
честве примера показан на рис. 16.8.
На рис. 16.9 показана зависимость от скорости и высоты по-
лета радиусов виражей (а) и угловых скоростей (б) предельных
по тяге (сплошные линии) и форсированных виражей (штриховые
линии), рассчитанных по формулам (16.8) и (16.9) для п^пред и
пу доп, показанных на рис. 16.8. Приведенная зависимость радиусов
виражей от скорости и высоты полета называется границей ви-
ра ж ей-по тяге, адоп и п3у тах.
Из графиков видно, что радиус виража увеличивается,
а угловая скорость уменьшается с ростом высоты Полета, что со-
провождается ухудшением маневренных свойств самолета, увели-
чением времени разворота и расхода топлива на маневр, особенно
на форсажных режимах работы двигателя. Отсюда вытекают прак-
тические рекомендации по экономии топлива: без тактической не-
обходимости не следует выполнять развороты на форсажных ре-
жимах и больших скоростях. При необходимости же выполнения
Ц* 419
Рис. 16.8. Зависимость предельной по тяге и
допустимой перегрузок от скорости и высоты
полета
Рис. 16.9В Влияние высоты и скорости полета на угловую скорость (б) и ра-
диус (а) предельного и форсированного виражей
420
разворотов на таких режимах следует придерживаться рекоменда-
ций инструкции летчику конкретного типа самолета по оптималь-
ным режимам разворотов, обеспечивающим минимальный расход
топлива.
Существуют так же и оптимальные режимы изменения стрело-
видности крыла, обеспечивающие минимальное время маневра и
минимальный расход топлива на маневр. Общим практическим
правилом выбора оптимальной стреловидности крыла является
следующее: стреловидность крыла должна быть тем больше, чем
больше скорость и меньше Су (рис. 15.11). Влияние стреловидно-
сти крыла на характеристики форсированного виража связано так-
же и с изменением максимально допустимых перегрузок по углу
атаки и по прочности конструкции. С увеличением стреловидности
крыла растут ^утах и лудоп, что позволяет за счет перестановки
крыла на увеличение стреловидности уменьшить гв и увеличить сов
форсированного виража. .
На современных самолетах изменяемой геометрии крыла и вы-
сокой тяговооруженности существуют режимы выполнения вира-
жа, на которых пу пред больше пу доп. Это характерно для малых
высот выполнения виража на полном форсаже с минимальной и
средней стреловидностью крыла без подвесок. Преимущество в
маневренности одного типа самолета перед другим определяется
его превосходством в величине пу пред и пу доп.
§ 16.3. Техника пилотирования, возможные отклонения
и ошибки на вираже и способы их исправления
Сложность выполнения виража (разворота) зависит от вели-
чины крена. Выдерживание высоты и заданных параметров манев-
ра с малым креном затруднений не вызывает. Выполнение вира-
жей (разворотов) с максимальным креном требует точных коор-
динированных отклонений ручки управления по тангажу и крену,
педалей и рычага управления двигателем *.
Перед вводом в вираж в прямолинейном горизонтальном по-
лете самолет должен быть сбалансирован на заданной скорости и
высоте при усилиях на ручке и педалях, близких к нулевым. Не-
обходимо убедиться по указателю в отсутствии скольжения.
Для ввода в вираж (разворот) сначала отклонением ручки
управления по крену, а затем с одновременным возрастающим от-
клонением ручки на себя создать крен и перегрузку. Для предот-
вращения возникновения скольжения необходимо отклонять пе-
дали по крену и тем больше, чем меньше скорость полета и энер-
гичнее ввод. Фиксирование заданного крена осуществляется дви-
жением ручки управления против вращения и возвращением ее
в положение, близкое к нейтральному. Педали в конце ввода так-
же возвращаются в положение, близкое к нейтральному, и не-
* Последнее делается только при выполнении тренировочных виражей, а
не в бою,
421
большим усилием на внешнюю педаль самолет удерживается от
опускания носа. При правильном соотношении в отклонениях руч-
ки по крену и тангажу угол тангажа и высота полета сохраняются
постоянными.
Продолжительность ввода в вираж во многом определяет ка-
чество его выполнения и влияет на характеристики маневра. При
отработке техники выполнения предельных виражей рекомендует-
ся ввод производить за время 3—5 с с угловой скоростью крена
15—25°/с. При этом удается более точно подбирать перегрузку
в соответствии с величиной крена и обеспечить горизонтальность
маневра без скольжения.
В процессе ввода в вираж возрастание лобового сопротивле’
ния по мере создания перегрузки требует увеличения тяги для
сохранения заданной скорости. При выполнении виража на фор-
саже перед вводом обычно устанавливается скорость на 40—
50 км/ч меньше заданной и включается форсаж. При этом в
процессе ввода скорость увеличивается до заданной.
В процессе установившегося виража основное внимание летчи-
ка должно быть направлено на выдерживание горизонтальности
траектории маневра по положению видимых частей кабины отно-
сительно линии естественного горизонта (или по авиагоризонту и
вариометру с периодическим контролем крена, скорости и сколь-
жения по приборам). Движения ручки управления по крену дол-
жны быть небольшими и согласовываться с изменением высоты
по вариометру и высотомеру. Отклонение скорости виража от за-
данной при полной тяге должно исправляться согласованным из-
менением крена и перегрузки. При нарастании скорости необхо-
димо приложением небольшого дополнительного тянущего усилия
увеличить перегрузку, а при начавшемся увеличении высоты од-
новременно несколько увеличить крен.
В процессе выполнения виража с у = 70~-80° и пу = 5-г-б необ-
ходимо помнить, что небольшое изменение крена требует значи-
тельного изменения перегрузки, для того чтобы не допускать из-
менения высоты. Чувствительность шарика указателя скольжения
при больших положительных перегрузках значительно ниже, чем
при пу=1. Поэтому даже малозаметное перемещение шарика со-
провождается действием боковой перегрузки nz и ощущением ее
действия.
Наиболее жесткие требования по согласованному выдержива-
нию крена и перегрузки должны быть при выполнении виража на
малых высотах. В этих условиях увеличение крена без согласо-
ванного увеличения перегрузки может вызвать опасное снижение.
На малых высотах в условиях неспокойной атмосферы ее возму-
щения способствуют отклонению параметров маневра от заданных.
Поэтому при выполнении виража на малых высотах корректирую-
щие отклонения ручки управления по крену и тангажу должны
исключить переход самолета на снижение. Для этого сначала уве-
личивают перегрузку, а затем крен, в случае возникновения сни-
жения уменьшают крен без уменьшения перегрузки.
422
Вывод из виража должен начинаться за 20—30° до намечен-
ного ориентира или курса по прибору. Он осуществляется согла-
сованным уменьшением крена и перегрузки без скольжения. Для
этого ручка управления отклоняется в сторону, обратную крену
с опережающим уменьшением тянущего усилия по тангажу и од-
новременным нажатием на обратную педаль для предотвращения
скольжения с таким расчетом, чтобы траектория маневра на
участке вывода сохранялась горизонтальной. Как и на участке
ввода нос самолета и положение видимых частей кабины сохра-
няются постоянными относительно линии естественного горизонта
и сохраняется неизменным положение шкалы тангажа авиагори-
зонта. По мере уменьшения крена и перегрузки необходимо умень-
шать тягу выключением форсажа и дросселированием режима
работы двигателя, чтобы заданная скорость на участке вывода
сохранялась постоянной. При выполнении виража на форсаже его
выключают при уменьшении крена до 50—40° и к моменту нуле-
вого крена режим работы двигателя должен быть равен потреб-
ному в горизонтальном полете.
При комплексном выполнении фигур, когда вывод из виража
сопрягается с вводом в предельный вираж другого направления
или в восходящий маневр, форсаж может не выключаться, но сле-
дует помнить, что в процессе вывода неизбежен рост скорости,
величина которого тем больше, чем медленнее осуществляется пе-
реход от одного маневра к другому. Резкий вывод из виража
обычно сопровождается изменением высоты из-за несогласованно-
го изменения крепа и перегрузки, отклонением направления вы-
вода от намеченного ориентира и курса.
Выполнение форсированного виража имеет ряд особенностей.
В отличие от установившегося предельного виража в процессе
ввода в форсированный вираж перегрузка увеличивается до мак-
симально допустимого значения, величина которой больше пре-
дельной по тяге. Поэтому в процессе его выполнения скорость
постепенно уменьшается. Интенсивность падения скорости зависит
от jorp, насколько пу маневра превышает гг^пред. Наиболее интен-
сивно скорость падает в сверхзвуковом диапазоне скоростей и на
больших высотах, где максимальные перегрузки при полном от-
клонении стабилизатора >яупред и в околозвуковом диа-
пазоне, где п* тах > пу пред.
После ввода в форсированный вираж, выдерживая максимально
допустимую перегрузку пу и соответствующий ей крен, необходи-
мо периодически контролировать постоянство высоты, изменение
угла атаки и скорости. При изменении скорости от максимальной
До УПр = 750~800 км/ч выдерживается постоянная лугаах. При этом
по мере падения скорости угол атаки растет до максимально до-
пустимого. В процессе дальнейшего разворота выдерживается по-
стоянным аДоп, а крен и перегрузка согласованно уменьшаются.
Выполнение виражей на больших высотах и сверхзвуковых ско-
ростях имеет ряд особенностей. Во-первых, вираж можно выпол-
423
йять с йолйостьй выбранной ручкой управления на себя, так кай
углы атаки при этом остаются меньше максимально допустимых,
а на числах М>1,24-1,3— меньше углов атаки начала тряски.
Во-вторых, переход от сверхзвуковых скоростей к дозвуковым в
процессе выполнения виража с фиксированным положением ручки
управления сопровождается ростом нормальной перегрузки (ско-
ростным подхватом) с увеличением угловой скорости разворота
и уменьшением радиуса.
Рис. 16.10. Изменение перегрузки при ско
ростном подхвате (пример)
Подхват выражен тем силь-
нее, чем быстрее падает ско-
рость, чем больше перегруз-
ка маневра и сильнее изме-
няется устойчивость по пере-
грузке в трансзвуковой об-
ласти. В качестве примера
на рис. 16.10 показано уве-
личение перегрузки в процес-
се торможения с фиксиро-
ванной ручкой для двух цен-
тровок. Видим, что при бо-
лее задней центровке хт2пе-
регрузка растет интенсивнее.
Для того чтобы выдержать заданную перегрузку маневра, близ-
кую к ^утах, и не допустить ее самопроизвольного возрастания
более допустимой, необходимо по мере падения скорости в этом
диапазоне быть готовым уменьшить отклонение ручки управления
по тангажу, сохраняя постоянным крен соответственно значению
постоянной перегрузки. Обычно летчик делает это рефлекторно,
ощущая тенденцию к росту перегрузки. Заметим, что на некото-
рых маневренных самолетах ограничение л^тах наложено сту-
пенчатым ее изменением при числе М = 0,8, что требует соот-
ветствующего изменения крена и перегрузки. Высокая эффектив-
ность управляемого стабилизатора позволяет осуществлять вы-
держивание заданных перегрузок без их увеличения в условиях
проявления скоростного подхвата небольшим предупредительным
уменьшением тянущего усилия на ручке управления.
Наиболее характерные отклонения при выполнении виража
обусловлены несогласованными движениями ручки управления по
крену, тангажу и педалей. Их исправление на вираже следует на-
чинать с уточнения величины крена. Развитие опасной ситуации
при выполнении виража с максимальным креном обусловливает
следующие возможные отклонения траектории и параметров ма-
невра от заданных.
Переход самолета в глубокую спираль. Такое изменение тра-
ектории маневра возможно как на участке ввода в вираж с мак-
симальным креном, так и на участке установившегося виража.
Если по мере увеличения крена перегрузка создается с запазды-
ванием, самолет переходит в нисходящую спираль с возрастанием
424
вертикальной скорости снижения. Летчик, не уменьшая крен, пы-
тается исправить ошибку отклонением ручки управления на себя
для увеличения перегрузки пу. При крене более 70° увеличение
перегрузки пу до максимально допустимой не обеспечивает умень-
шение угла наклона траектории, а увеличивает угловую скорость
, разворота и вертикальную скорость снижения. Исправить ошибку
и вывести из нисходящей спирали можно только, если уменьшить
крен, тогда даже небольшой положительной перегрузки будет
достаточно для вывода в горизонтальный полет.
Если в процессе вывода самолет за счет чрезмерного отклоне-
ния ручки по тангажу вышел на большие углы атаки, падение
эффективности органов управления может не позволить умень-
шить крен при отклонении ручки управления на вывод. В этом
случае необходимо уменьшить угол атаки (уменьшая тянущее
усилие на ручке) для восстановления поперечной управляемости
и лишь прсле этого отклонением ручки управления . в сторону,
обратную крену, уменьшить его, а затем увеличением перегрузки
вывести из снижения.
Величина отклонения траектории и параметров полета во мно-
гом зависит от запаздывания с исправлением. Поэтому, если при
выполнении виража с максимальным креном на Вводе или в про-
цессе его произошло увеличение вертикальной скорости снижения
более 15—20 м/с, необходимо вывести самолет из виража, для
чего, не допуская чрезмерного увеличения перегрузки, отклоне-
нием ручки управления устранить крен, а затем увеличением пу
вывести в горизонтальный полет.
Как правило, развитие особой ситуации с переходом в глубо-
кую спираль при непонимании происходящего и неправильных дей-
ствиях влечет за собой ошибки и такие последствия, как выход
самолета на опасные углы атаки по сваливанию, увеличение пере*
грузок выше максимально допустимых по прочности, снижение до
опасно малой высоты и т.д.
Чрезмерное увеличение перегрузки и угла атаки в процессе
выполнения установившегося предельного по тяге и особенно фор-
сированного виражей. Отсутствие достаточного навыка в регули-
ровании угла крена и в согласовании с ним перегрузки нередко
приводит к большим колебаниям скорости. Если летчик допускает
резкие и большие движения ручкой для уточнения величины кре-
на и перегрузки, то возможен выход за максимально допустимые
значения. Резкие, чрезмерно большие отклонения ручки управ-
ления по тангажу в процессе выполнения предельного установив-
шегося виража на приборных скоростях более 700—750 км/ч
особенно на малых высотах приводят к превышению п* тах и со-
провождаются падением скорости и большим отклонением высо-
ты маневра. На скоростях, менее указанных, несоразмерное пере-
мещение ручки управления по тангажу создает опасность превы-
шения аДоп. Это требует контроля угла атаки во время торможе-
ния при маневре. При этом необходимо иметь в виду, что прибор-
425
ная скорость, при которой происходит сваливание на маневре,
(Vnp. св) ман существенно больше приборной скорости сваливания
в горизонтальном полете (VnP. св)г. п:
(Упр. св)ман — Упр. св)г,п • (16.14)
Так, например, если в горизонтальном полете сваливание про-
исходит при 1/пР = 250 км/ч, то при маневре с перегрузкой пу = 7
сваливание произойдет при 1/пр = 250 К 7 =660 км/ч.
Снижение самолета на опасно малую высоту характерно при
выполнении виражей (разворотов) с максимальным креном на
малых высотах. Как правило, это происходит тогда, когда летчик
увеличивает крен резким отклонением ручки с запаздыванием в
увеличении перегрузки и без отклонения педалей. В этом случае
исправить ошибку при малом запасе высоты можно за счет энер-
гичного уменьшения крена при сохранении перегрузки в допусти-
мых пределах. С учетом сложности техники пилотирования и
вероятных отклонений выполнение виражей (разворотов) с мак-
симальным креном с учебной целью разрешается на высоте не
менее 1000 м над поверхностью земли. Высота выполнения пре-
дельных виражей (разворотов) при боевом маневрировании не
должна быть менее 200 м. Ниже 200 м в целях обеспечения безо-
пасности полета следует выполнять мелкие виражи: ниже 150 м —
на угол разворота не более 180°, а ниже 100 м — с набором высо-
ты. Ниже высоты 50 м выполнение виражей (разворотов) при
учебно-боевом маневрировании не рекомендуется.
Потери скорости менее эволютивной при выполнении форсиро-
ванного виража обычно возникают при недостаточном контроле
скорости по прибору. Быстрое падение скорости является резуль-
татом превышения максимально допустимых углов атаки и пере-
грузок или из-за стремления выполнить разворот на 360° и вы-
вести на ориентир без учета интенсивности падения скорости.
Глава 17
МАНЕВРИРОВАНИЕ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
§ 17.1. Условие криволинейного движения и особенности
выполнения маневров в вертикальной плоскости
Характерными маневрами в вертикальной плоскости являются
пикирование, горка, переворот, петля Нестерова и полупетля. Все
эти маневры, исключая прямолинейные участки пикирования и
горки, являются криволинейным движением. Для того чтобы дви-
жение происходило строго в вертикальной плоскости, необходимо,
чтобы угол разворота в процессе маневра не изменялся. Если
маневрирование осуществляется без скольжения, то угловая ско-
рость dW/dt будет равна нулю либо при у = 0, либо при у=180°
426
(перевернутый полет), так как при этом горизонтальная состав-
ляющая подъемной силы У sin у = 0 и искривление траектории в
горизонтальной плоскости не происходит.
Движение самолета в вертикальной плоскости описывается сле-
дующей системой уравнений в траекторной системе координат:
m~=P-X-Gsin 0;
at
у2 (17.1)
tn -у = У — Geos 0.
Первое уравнение этой системы определяет закон изменения
скорости в процессе маневрирования, второе — искривление траек-
тории и ее радиус кривизны в вертикальной плоскости. Характер
искривления траектории определяется при прочих равных усло-
виях величиной и направлением действия искривляющей силы, на-
правленной по нормали к траектории в вертикальной плоскости.
В создании искривляющей силы участвуют: подъемная сила и
проекция силы тяжести на нормаль к траектории. Для обычных
компоновок проекция силы тяги двигателя на нормаль к траек-
тории невелика и в большинстве случаев ею можно пренебречь.
Проанализируем роль подъемной силы и составляющей силы
тяжести в искривлении траектории. Прежде всего необходимо от-
метить, что, несмотря на то, что обе эти силы влияют на искрив-
ление траектории, между ними есть принципиальное различие.
Подъемной силой летчик может управлять, составляющей же силы
тяжести непосредственно управлять нельзя.
Искривление траектории происходит в ту сторону, в которую
действует суммарная искривляющая сила F=Y—G cos ©. При этом,
чем больше ее величина, тем меньше при данной скорости радиус
кривизны траектории, определяемый из второго уравнения (17.1):
У — G cos 0 g (пу — cos О) * ' ’ 7
На рис. 17.1, а, д показаны силы, действующие на самолет при
вертикальном маневре для случая, когда траектория искривляется
вверх. Для такого искривления траектории необходимо, чтобы аб-
солютное значение подъемной силы У было больше составляющей
силы тяжести Geos0, так как эти силы направлены в противопо-
ложные стороны. Чем больше подъемная сила, а следовательно,
и нормальная перегрузка пу, тем значительнее искривляющая сила
У—GcosG и меньше радиус кривизны траектории.
Участки вертикальных маневров, на которых траектория ис-
кривляется вниз, могут выполняться одним из способов, показан-
ных на рис. 17.1,6, в, г. При нормальном положении самолета
(рис. 17.1, в) кривизна траектории обеспечивается превышением
составляющей силы тяжести GcosG над подъемной силой У. Ис-
кривляющая сила GcosG—У здесь сравнительно невелика, она не
может быть больше силы тяжести.
427
Увеличить искривляющую силу при нормальном положении са-
молета можно созданием отрицательной перегрузки (рис. 17.1,г).
Здесь подъемная сила У и составляющая сила тяжести Geos 9
направлены в одну сторону, вследствие чего искривляющая сила
равна сумме этих сил.
Рис. 17.1. Условия криволинейного движения в вертикальной пло*
скости
Увеличение искривляющей силы приведет к уменьшению ра-
диуса кривизны траектории по сравнению со схемой сил, показан-
ной на рис. 17.1, в. Однако создание отрицательных перегрузок
ограничено по величине и по времени, особенно при работе дви-
гателя на режиме полного форсажа, поэтому вертикальные ма-
невры с отрицательными перегрузками выполняются сравнительно
редко.
Значительной величины центростремительная сила достигает,
если самолет находится в перевернутом положении (рис. 17.1, б).
Здесь при положительной перегрузке пу подъемная сила Y и со-
ставляющая силы тяжести GcosG направлены в одну сторону и
искривляющая сила У—GcosG равна их сумме (cosG<0). При
этом подъемную силу, а следовательно, и перегрузку можно уве-
личивать до больших значений.
Угловая скорость поворота траектории в вертикальной плос-
кости, характеризуемая изменением угла наклона траектории в
единицу времени, определяется следующим выражением:
(”-3)
Величина, стоящая в круглых скобках, как и при определении
радиуса кривизны траектории, будет представлять собой разность
или сумму пу и cos 0 в зависимости от их знаков.
428
Остановимся на некоторых особенностях, имеющих существен-
ное значение при выполнении вертикальных маневров. На восхо-
дящих маневрах обычно уменьшается скорость. В определенных
ситуациях (при ошибках, а также в боевых условиях) возможно
падение приборной скорости до значений, меньших эволютивной,
что отождествляется с опасностью сваливания, однако нужно
помнить, что причиной сваливания является не малая скорость,
а большие углы атаки. Поэтому сваливание принципиально может
произойти на любой скорости. Для этого достаточно лишь создать
угол атаки а^асв.
Скорость и перегрузка при а = асв будут связаны соотношением
(16.14), из которого следует, что приборная скорость сваливания
зависит от перегрузки пу. Например, если в прямолинейном гори-
зонтальном полете (%=1) сваливание происходит при скорости
250 км/ч, то при перегрузке ^ = 0,25 сваливание произойдет при
Vnp = 250 V 0,25 =125 км/ч, а при пу = 4— при УПр = 500 км/ч.
Из этого следует два важных практических вывода. Во-первых,
при перегрузке, меньшей единицы и близкой к нулю, скорость мо-
жет быть уменьшена без опасности сваливания до очень малых
величин. Во-вторых, при непроизвольной потере скорости летчик
должен прежде всего обеспечить сохранение угла атаки в допусти-
мых пределах, не допуская скольжения и неконтролируемого от-
клонения рулей. Самолет в этом случае сам перейдет на нисходя-
щую траекторию и начнет увеличивать скорость.
На нисходящих маневрах скорость, как правило, возрастает,
что при неизменной перегрузке сопровождается увеличением ра-
диуса кривизны траектории по формуле (17.2) и, как следствие,
увеличением потери высоты, необходимой для вывода из нисхо-
дящих маневров. Уменьшить потерю высоты можно предотвраще-
нием роста скорости путем увеличения перегрузки либо, в край-
нем случае, выпуском тормозных щитков и дросселированием дви-
гателя. При этом необходимо иметь в виду, что если маневр
выполняется с большими перегрузками, то из-за значительного уве-
личения лобового сопротивления даже при повышенных режимах
работы двигателя при малых углах наклона траектории скорость
может интенсивно уменьшаться. Для исключения нежелательной
потери скорости при выполнении нисходящих маневров летчик
должен правильно управлять тягой двигателя и пользоваться тор-
мозными щитками. Выпуск тормозных щитков на нисходящих ма-
неврах производится главным образом для предотвращения чрез-
мерного увеличения скорости и опасности превышения ограниче-
ний по скорости.
Для выполнения некоторых фигур необходимо в процессе ма-
невра осуществлять поворот вокруг продольной оси на 180° (вы-
полнять полубочку). Если при этом мала приборная скорость и
большие углы атаки, то необходимо учитывать снижение эффек-
тивности поперечного управления и увеличение поперечной устой-
чивости. Необходимо отметить, что при большой поперечной
429
устойчивости даже небольшое скольжение приводит к заметным
поперечным моментам, которые при маневрах могут вызвать не-
преднамеренное изменение угла крена^ Причиной появления сколь-
жения (увода шарика) может явиться гироскопический момент,
появляющийся при энергичном выполнении маневров в вертикаль-
ной плоскости.
В процессе выполнения вертикальных маневров скорость мо-
жет изменяться в широких пределах, как увеличиваться, так и
уменьшаться. При этом торможение от сверхзвуковой скорости
или околозвуковой до дозвуковой при фиксированной ручке управ-
ления может привести к появлению скоростного подхвата и не-
произвольному увеличению перегрузки.
При выполнении нисходящих маневров на больших дозвуковых
скоростях с увеличением скорости до М>0,9-?0,92 значительно
изменяется балансировка, что при неизменном положении стаби-
лизатора приводит к существенному уменьшению перегрузки, уве-
личению скорости и значительному увеличению радиуса кривизны
траектории. Кроме того, на некоторых самолетах при этих чис-
лах М уменьшается величина угла максимального отклонения
стабилизатора.
§ 17.2. Пикирование
Пикирование — фигура пилотажа, предназначенная для
атаки наземной цели или быстрого увеличения скорости за счет
преобразования потенциальной энергии в кинетическую. Пикиро-
Рис. 17.2. Траектория и соотношение нормальных сил
на участках пикирования
вание состоит из трех участков: ввода, прямолинейного участка и
вывода (рис. 17.2).
Ввод в пикирование осуществляется одним из следую-
щих способов: ввод с прямой при крене, равном нулю; ввод с раз-
ворота — созданием крена, не превышающего 90°; ввод полупере-
430
воротом — созданием крена 90°<т<180°; ввод переворотом (дву-
мя полубочками) —созданием крена, равного 180°.
При вводе с прямой не представляется возможным получить
большую искривляющую силу, так как создание длительных око-
лонулевых перегрузок запрещено по условиям нормальной рабо-
ты двигателя, а отрицательные перегрузки неблагоприятно влия-
ют на летчика и ухудшают точность пилотирования. Поэтому при
Рис. 17.3. Определение потери высоты на участках пи-
кирования
вводе с прямой перегрузка обычно находится в пределах 0,4 <
<«г/<0,7. Вследствие этого небольшая искривляющая сила обус-
ловливает вялый вход в пикирование, требует много времени и
сопровождается значительным ростом скорости.
При входе в пикирование переворотом летчик, выйдя в рас-
четную точку, координированным отклонением ручки и педалей
переворачивает самолет «на спину» до совмещения его плоскости
симметрии с целью. После этого создает перегрузку пу>\. Для
уменьшения потери высоты в процессе ввода перегрузка может
быть увеличена до максимально допустимой, обычно ограничивае-
мой на вводе по Су&оп. Ввод в пикирование для атаки наземной
цели чаще выполняется разворотом или полупереворотом, так как
при этих методах облегчается поиск и выбор цели.
В процессе ввода в пикирование скорость, как правило, воз-
растает. Однако если в первом приближении считать ее постоян*
ной, равной некоторому среднему значению Vcp, то потерю высоты
при вводе Д/Ybb можно определить по формуле (рис. 17.3)
A//BB = rBB(l-cos0), (17.4)
где радиус кривизны траектории при вводе с разворота опреде-
ляется выражением (см. гл. 18)
Гвв ~ср cos 7ср — cos 0ср) ’ (17.5)
еср=0/2 — среднее значение угла наклона траектории на вводе;
0 — угол пикирования.
431
Изменение скорости в процессе ввода можно определить инте-
грированием первого уравнения системы (17.1). Однако для при-
ближенных расчетов можно предположить, что полная механиче-
ская энергия самолета в процессе ввода не изменяется. Тогда,
приравняв удельные энергии в начале и конце ввода в пикирова-
ние, получим
Отсюда находим
\V^Vl-Vl = 2g(Ha-HK)
и, следовательно:
ДУ = Г2^Д//ВВ .
Тогда
Vcp = Ин + (17.6)
Время ввода в пикирование можно определить по среднему
значению угловой скорости в вертикальной плоскости:
^ = ^Г- = -7-----------------©Г* <17-7)
,ср g^nycos кср — cos-^J
В процессе ввода с разворотом самолет развернется в горизон-
тальной плоскости на угол ДЧ^в, величину которого можно оце-
нить по формуле
. nv sin ч
ДТва = "Лв = £ ——k 4в. (17.8)
V cos —
Если задан угол разворота Т, то при выбранной перегрузке
можно найти потребный угол крена в процессе ввода с разво-
ротом. .
На прямолинейном участке пикирования перегрузка
пу = cos 0. Продолжительность этого участка, потеря высоты и при-
рост скорости в процессе пикирования зависят от скорости, высо-
ты и способа ввода, угла пикирования и режима работы двига-
теля. При вялом вводе скорость начала прямолинейного движения
оказывается большой и быстро достигает установившегося значе-
ния. Время пикирования tn мало. При энергичном способе ввода
протяженность и время прямолинейного участка возрастают.
С увеличением угла наклона траектории время пикирования умень-
шается, что усложняет прицеливание и атаку наземной цели. При
крутом пикировании для предотвращения чрезмерного увеличения
скорости необходимо уменьшить тягу двигателя, а в ряде случаев
выпускать тормозные щитки. При пикировании в целях быстрей-
шего разгона самолета увеличиваются угол наклона траектории
и обороты двигателя, а при необходимости включается форсаж.
432
Потерю высоты на прямолинейном участке приближенно мож-
но определить по формуле
Щф = Vy ср /ПР = sin Q4p (17 9)
На рис. 17.4 показано изменение параметров движения само-
лета в процессе ввода, прямолинейного участка и вывода из пи-
кирования.
Рис. 17.4. Изменение параметров движения самолета в процессе ввода,
на прямолинейном участке и выводе из пикирования
Вывод из пикирования является самым ответственным
этапом пикирования. Определив момент начала вывода, летчик
плавным движением ручки управления на себя увеличивает пере-
грузку пу до 3—5, не допуская значительных забросов угла атаки
и перегрузки. Чем больше перегрузка пу и меньше скорость, тем
меньше потеря высоты при выходе из пикирования. Не следует
допускать крена, так как это приводит к увеличению потери вы-
соты на выводе. Приближенно потерю высоты при выводе из
пикирования можно оценить по формуле (рис. 17.3)
Д^выв==',выв(1 — COS0), (17.10)
где радиус кривизны траектории при выходе определяется
V2
^ = -7-------выв ёТ.- (17.11)
g 1 Пу — cos -%-)
При увеличении угла пикирования и скорости потеря высоты
энергично возрастает.
Среди части летного состава бытует понятие «просадки» са-
молета при выводе из пикирования. Фактически никакой просадки
не существует. Самолет всегда движется строго по законам меха-
ники, по траектории, определяемой величиной и направлением сил.
433
Появление понятия о «просадке» связано с ошибочным определе-
нием летчиками конца вывода из пикирования (и вообще из лю-
бой нисходящей фигуры — переворота, петли и т. п.). Вывод из
пикирования осуществляется с положительными углами атаки,
достигающими 6—10° и более. В определенный момент в процессе
вывода (положение а на рис. 17.5) самолет занимает горизон-
тальное положение. В этот
Рис. 17.5. Выход из пикирования, «про-
садка»
момент угол тангажа ра-
вен нулю, а вектор скорости
отклонен вниз на величину
угла атаки, самолет про-
должает снижение с вер-
тикальной скоростью Vy~
= — V sin а.
Для окончательного вы-
вода самолета в горизон-
тальный полет летчик дол-
жен продолжать удержи-
вать перегрузку до положи-
тельного угла тангажа, рав-
ного углу атаки (положение б на рис. 17.5). При этом высота
уменьшается на ДЯЛр, равную 100—150 м. Если же летчик оши-
бочно примет горизонтальное положение самолета (положение а
на рис? 17.5) за конец вывода из пикирования и преждевременно
уменьшит перегрузку, то потеря высоты ДЯПР, называемая «про-
садкой», может возрасти в два и более раз.
§ 17.3. Горка
Горка — фигура пилотажа, при выполнении которой самолет
набирает высоту по прямолинейной траектории, как правило, с по-
терей скорости. Горка применяется для быстрого набора высоты
с сохранением общего направления полета или для выполнения
атаки высоколетящей цели. В процессе выполнения фигуры с по-
терей скорости происходит превращение кинетической энергии в
потенциальную. Вывод должен быть закончен на скорости, не
менее эволютивной. Поэтому ввод в крутую горку производится
на достаточно большой скорости.
Горка с углом наклона до 30° называется пологой, с углом
более 30° — к р у т о й. ,
Горка состоит из трех участков: ввода, прямолинейного уча-
стка и вывода (рис. 17.6). На вводе происходит искривление тра-
ектории вверх. Это достигается плавным увеличением перегрузки
до Пу —24-3. Радиус кривизны траектории в вертикальной плоско-
сти на вводе определяется выражением (17.2). В процессе ввода
в горку самолет набирает высоту, определяемую по форму-
ле (17.10):
*Hn = rBB(l —- cos 0).
434
Конец ввода определяется по достижении заданного угла на-
клона траектории. Поскольку угол атаки на больших скоростях
невелик, то обычно считают 0 = 0 и отсчитывают последний по
авиагоризонту. Можно также в учебных полетах рекомендовать
для приближенного учета различия 8 и 0, т. е. угла атаки, перед
выводом в горку установить кремальерой авиагоризонта & = 0 при
0 = 0.
Рис. 17.6. Траектория и соотношение нормальных сил
на горке
На прямолинейном участке для сохранения постоянства угла
наклона траектории необходимо равновесие нормальных сил:
У = б cos 0 или пу — cos 0.
Таким образом, в конце ввода нормальная перегрузка должна
уменьшаться от 2—3 до значения, меньшего единицы. Закон из-
менения скорости на прямолинейном участке определяется инте-
грированием первого уравнения (17.1). В процессе набора высоты
уменьшается скорость и плотность воздуха, что требует для вы-
держивания прямолинейного движения увеличения угла атаки не-
большим движением ручки на себя. Набор высоты при этом
можно приближенно оценить
Д//г = Vy ср tT = sin 0r
где tr — время выполнения прямолинейного участка горки.
Вывод из горки начинается по достижении скорости начала
вывода. В процессе вывода из горки происходит уменьшение угла
наклона траектории до нуля. Это достигается уменьшением верти-
кальной составляющей подъемной силы, чаще всего за счет созда-
ния крена и уменьшения угла атаки так, чтобы Y cos y<G cos 0.
В конце вывода из горки самолет должен находиться в горизон-
тальном прямолинейном полете, т. е. при у = 0, пу=\. На рис. 17.7
показано характерное изменение основных параметров движения
' 435
й отклбйенйя органов упраблеция 6 процессе выполнения
горки.
Основными характеристиками горки являются: общий набор
высоты в процессе выполнения горки, продолжительность прямо-
линейного участка и горки в целом, потеря скорости за время
вывода. Последняя характеристика необходима для определения
скорости начала вывода из горки.
Рис. 17.7. Изменение параметров движения в процессе
выполнения горки
Время выполнения горки зависит от угла наклона тра-
ектории, продольной перегрузки пх и допустимого изменения ско-
рости AV:
/г = -^- = , &V . nv (17.12)
г /хер sin0) v 7
Чем больше угол 0, тем быстрее падает скорость (при прочих
неизменных факторах) и тем меньше /г. Время горки увеличи-
вается с ростом тяговооруженности самолета и разности скоростей
ввода и вывода.
Продолжительность прямолинейного участка горки при задан-
ных скоростях ввода и вывода, угле 0 будет зависеть от характера
ввода в фигуру. При вялом вводе большая часть кинетической
энергии перейдет в потенциальную еще в процессе криволинейного
движения и прямолинейный участок будет коротким. При больших
углах горки его вообще может не быть. При энергичном вводе
протяженность и время прямолинейного участка увеличи-
ваются.
Набор высоты за горку зависит в основном от разности
скоростей ввода и вывода, а также от времени выполнения фигу-
ры. Поскольку на прямолинейном участке и выводе тангенциаль-
ная перегрузка, как правило, больше нуля, то чем продолжитель-
нее будет горка, тем на большую величину возрастет энергия са-
молета и общий набор высоты за фигуру. Таким образом, набор
436
высоты на горке при неизменных Начальных и конечных скоростях
будет возрастать по мере уменьшения ее угла (рис. 17.8).
Потеря скорости за вывод определяется в основном
набираемой на этом участке высотой: чем она больше, тем больше
потеря скорости. Набор высоты за вывод зависит от угла горки
и способа вывода из нее. Способы вывода из горки такие же, как
и для ввода в пикирование. При малых углах горки (до 20°) вы-
Рис. 17.8. Влияние угла горки на ее параметры
вод из нее можно осуществлять с прямой или небольшим (до 45°)
креном. При средних углах (30—40°) вывод должен осуществлять-
ся разворотом с креном до 70—90°, а при больших — с созданием
крена более 90° или двумя полубочками.
§ 17.4. Переворот
17.4.1. Основные характеристики и варианты
выполнения переворота
Переворот — фигура пилотажа, при выполнении которой
самолет поворачивается относительно продольной оси на 180° с
последующим движением по нисходящей траектории в вертикаль-
ной плоскости и выводом в горизонтальный полет в направлении,
обратном вводу. Целью переворота является быстрое изменение
направления полета на 180° с одновременным уменьшением высо-
ты. В процессе переворота происходит превращение потенциаль-
ной энергии в кинетическую и самолет заканчивает фигуру, как
правило, на большой скорости.
Переворот применяется для атаки воздушной цели, летящей
ниже и на встречном курсе, ухода от атак истребителей против-
ника, быстрого увеличения скорости и последующего выполнения
восходящих маневров и т. д.
437
Рассмотрим движение самолета после выполнения полубочки.
Угол наклона траектории 0 на перевороте возрастает от —180*
до —90° и затем возрастает снова до нуля (рис. 17.9). Поскольку
авиагоризонт показывает угол тангажа *>АГД лишь в пределах от
—90 до +90°, то в процессе выполнения переворота 0 сначала
уменьшается от 0 (при 0 = —180°) до —90° (при 0 = —90°), а за-
тем увеличивается до 0 (при 0 = 0). Угол крена в первой половине
нисходящей части фигуры равен 180°, во второй — нулю (при
угле тангажа В=±90±5с авиагоризонт изменяет показания крена
на 180°).
С учетом указанных кинематических условий характер действия
сил на перевороте будет следующий. Нормальная составляющая
силы тяжести Geos© в первой половине переворота способствует
искривлению траектории, во второй — препятствует. Подъемная
сила и нормальная перегрузка должны постепенно возрастать от
минимального значения в верхней точке до максимального к кон-
цу фигуры.
Тангенциальная составляющая силы тяжести Gsin0 на про-
тяжении всей траектории фигуры направлена по вектору скорости
и способствует разгону самолета. В отвесном положении скорость
за счет действия силы тяжести может изменяться на 35 км/ч
в секунду. При малых углах наклона траектории, т. е. в начале
и конце фигуры, это ускорение невелико.
* Можно также считать, что после полубочки 8=180° и в дальнейшем
возрастает до 360°, как во второй части петли. Оба эти предположения не про®
тиворечат правилу знаков d&[dt = g[V (nv — cos 0) >0; и поэтому 6 возра-
стает.
438
На рис. 17.10 показано характерное изменение основных пара-
метров движения самолета и отклонения органов управления в
процессе выполнения переворота.
Основными характеристиками переворота являются: потеря вы-
соты (Д//пер), прирост скорости (AV), средняя угловая скорость
(соср) и время выполнения фигуры (/Пер).
Рис. 17.10. Изменение параметров движения самолета в процессе выполнения
переворота
Потеря высоты за переворот является важной характери-
стикой особенно с точки зрения безопасности полета. Приближен-
но ее значение можно определить по среднему радиусу кривизны
в вертикальной плоскости:
^^пер === /*ср.
Из формулы (17.2) имеем
Так как при перевороте пу Cp^>cos 0ср> то приближенно можно
принять cos 0ср~0. Тогда получим
2И2
ДЯп.рв-^-. (17.13)
ь ну ср
Таким образом, потеря высоты за переворот будет зависеть от
отношения квадрата скорости к нормальной перегрузке. На пер-
вый взгляд может показаться, что наименьшая потеря высоты
будет иметь место при выполнении переворота на возможно мень-
шей скорости. Однако с уменьшением скорости уменьшается и
значение максимальной (допустимой) перегрузки.
439
Если в формулу (17.13) подставить выражение нормальной пе-
регрузки, то она примет вид
Д^пер == gS?fJCy ’
где управляемым параметром является коэффициент подъемней
силы. Следовательно, от его значения, главным образом, и будет
зависеть потеря высоты: чем больше Су, тем меньше Д/7Пер-
При выполнении переворота с (?!/ = const по мере увеличения
скорости будет возрастать нормальная перегрузка (пропорцио-
нально квадрату последней), значение же среднего радиуса и со-
ответственно потери высоты останутся практически неизменными.
Это будет справедливо до скорости, на которой нормальная пере-
грузка достигнет своего максимума из условия ограничения по
прочности. Величину этой скорости можно определить из усло-
вия
Э ____Р С
^у max 2 0 ’
откуда
1/ _ 1 / °ПУ шах
V2~V cySpH '
При дальнейшем увеличении скорости потеря высоты будет воз-
растать пропорционально квадрату скорости, поскольку пере-
грузка остается постоянной, равной п3 тах, а Су уменьшается. Наи-
меньшая потеря высоты достигается при выполнении переворота
на Су доп (адоп) При Vnep<^1^2*
Угловая скорость на перевороте (со) является важной
характеристикой, поскольку ее величина определяет время выпол-
нения фигуры.
Величина средней угловой скорости на перевороте при
COS 0ср = О
Sny ср
Шср — V п •
у ср
Раскрыв выражение нормальной перегрузки, получаем
шср = 4,9 Су рсР 1/ср -g-.
Как видим, и здесь основную роль играет значение коэффици-
ента подъемной силы: чем он больше, тем больше перегрузка и
тем быстрее поворачивается самолет. Однако в отличие от потери
высоты, где величина скорости до V2 не имела существенного зна-
чения, угловая скорость пропорциональна последней. Поэтому при
выполнении переворота с Су = const по мере увеличения скорости
угловая скорость будет возрастать (с одновременным энергичным
ростом перегрузки). Наибольшее ее значение будет достигнуто
при выполнении переворота на Cy^Qn с перегрузкой, близкой к
44Q
максимально допустимой, т. е. на достаточно большой скорости.
Значение последней можно приближенно определить:
(^пер)(отйх ^min доп '^у Д°п ’
где ^min доп —минимально допустимая скорость горизонтального
полета.
Время выполнения переворота определяется по величине
средней угловой скорости
/ = —
Пер <оср •
Увеличение скорости за переворот зависит от времени выпол-
нения фигуры и значения тангенциальной перегрузки:
А!/ =УХ ср /Пер = я fax 0)]ср.
В целях уменьшения разгона самолета переворот целесообраз-
но выполнять при возможно большей перегрузке. С одной сторо-
ны это сокращает время выполнения фигуры, с другой — увели-
чивает лобовое сопротивление. Так, на самолете типа МиГ-21 на
приборных скоростях 500—700 км/ч и перегрузках 4—6 лобовое
сопротивление в 1,5—2 раза больше силы тяжести. При задроссе-
лированном двигателе переворот может быть выполнен с потерей
скорости.
С увеличением скорости ввода и сохранении уровня перегру-
зок увеличивается время выполнения фигуры, существенно возра-
стает прирост скорости за фигуру. При определенном значении
начальной скорости возможен выход на ограничение по прибор-
ной скорости.
Анализируя характеристики переворота, можно установить не-
сколько вариантов выполнения этой фигуры, в том числе два
экстремальных.
Переворот с минимальной потерей высоты должен выполняться
при максимально допустимом значении коэффициента подъемной
силы (угла атаки). При этом, с одной стороны, скорость не дол-
жна превышать величины, при которой перегрузка достигает
своего максимально допустимого значения по прочности. Для
большинства самолетов это соответствует приборной скорости
700—800 км/ч. С другой стороны, она не должна быть меньше
эволютивной. Так как в этих пределах скорость на потерю высоты
существенного влияния не оказывает, ее значение целесообразно
выбирать из условия приемлемого уровня перегрузок по физиче-
ской выносливости летчика. При пу = 4-4-5 это будет соответство-
вать 1/Пр = 500-4-600 км/ч.
Переворот за минимальное время должен также выполняться
при максимально допустимом значении коэффициента подъемной
силы, но на возможно большей скорости, т. е. на скорости, при
которой ду = л*тах. Таким образом, в этом варианте летчик дол-
441
жен выдерживать не только аДОп (по указателю или тряске), но
и Пу доп (по указателю).
Выполнение указанных переворотов требует xojpoinnx навыков
в технике пилотирования и может применяться при отработке эле-
ментов боевого маневрирования. В учебных полетах (особенно
при обучении курсантов) на предельных режимах фигуры не вы-
полняются. Принято считать, что запас на ошибку должен со-
Рис. 17.11. Варианты выполнения переворота:
1 — с минимальной потерей высоты; 2 — с постоянной
угловой скоростью <и; 3 —- наиболее безопасный
ставлять не менее 10—20%. Обычно переворот осуществляется
с достаточно энергичным искривлением траектории на основной
части и уменьшением угловой скорости в вертикальной плоскости
на выводе (вариант 3 на рис. 17.11). Иными словами, основная
часть переворота выполняется в варианте, близком к варианту
с минимальной потерей высоты, а после того, как летчик оконча-
тельно убедился в возможности вывода на безопасной высоте,
осуществляется разгон самолета до заданной скорости при доста-
точно слабом искривлении траектории, обеспечивающем точную
подгонку параметров вывода.
17.4.2. Техника и область выполнения
переворота
Основными задачами летчика на вводе в переворот являются
правильное выполнение полубочки и создание необходимого темпа
искривления траектории. Полубочка считается правильной, если
в процессе ее выполнения сохраняется направление полета, а са-
молет после полубочки фиксируется в перевернутом положении
(крен точно 180°).
В процессе выполнения полубочки угол тангажа уменьшается
из-за искривления траектории вниз на величину ДО и за счет
442
сохранения угла атаки в процессе выполнения полубочки на ве-
личину 2а, т. е. Л8 = Д0 + 2а (рис. 17.12). Поэтому, для того чтобы
закончить полубочку при 0 = 0, летчик должен перед ее выполне-
нием плавным движением ручки управления на себя с ^ = 1,54-2
увеличить угол тангажа до 10—15е. Затем (для уменьшения ис-
кривления траектории в горизонтальной плоскости при наклоне
нии подъемной силы) движением ручки управления от себя лет-
Рис. 17.12. Изменение угла тангажа при выполнении полубочки
чик уменьшает перегрузку до 0,8—1. После этого координирован-
ным движением ручки и педали летчик выполняет полубочку с
угловой скоростью ~60°/с и фиксирует самолет в перевернутом
положении без крена.
Далее необходимо плавным взятием ручки управления на себя
в течение 3—4 с вывести самолет на Су~ (0,84-0,9) G,доп, контро-
лируя соответствующее ему значение угла атаки по УУА. На са-
молетах, имеющих вблизи Су достаточно выраженную аэроди-
намическую тряску, можно использовать ее в качестве информа-
ции о величине Су. В этом случае пилотирование упрощается: лет-
чик не переносит взгляд на приборы (продолжает смотреть на
горизонт и землю), а достаточность отклонения ручки оценивает
по наличию и интенсивности аэродинамической тряски.
Если же на самолете нет указателя углов атаки и отсутствуют
предупредительные признаки выхода на большие а, контроль по-
следнего необходимо осуществлять по взаимно соответствующим
значениям перегрузки (по акселерометру) и приборной скорости,
которые можно рассчитать по формуле
„ Po-Si/2 Г м 1 Су доп ,п Г км 1
"Удоп —^удоп20 ипр[_ с J ~207,4О/S пр L ч J*
Например, при СудОп=0,85 и 6/5 = 400 кге/м2 получим
"удод — \ 312,5 / •
443
По этой формуле в качестве примера рассчитаны пары значе-
ний VnP и пу доп, приведенные в табл. 17.1.
Таблица 17.1
vnp. км/ч 400 500 600 700 800
пу доп 1.6 2,6 3,7 5,0 6,6
Обязательный контроль перегрузки осуществляется и в том слу-
чае, если ввод выполняется на достаточно большой скорости
(Vnp>6504-700 км/ч).
На первой половине переворота главной задачей летчика яв-
ляется выполнение этой части фигуры с возможно меньшей поте-
рей высоты, что обеспечивается поддержанием созданного на
вводе темпа искривления траектории в строго вертикальной плос-
кости.
При подходе к отвесному положению летчик контролирует ве-
личину приборной скорости. Если она больше расчетной, то не-
обходимо увеличить перегрузку и тем самым усилить искривление
траектории и уменьшить рост скорости. 'Степень увеличения пере-
грузки зависит от величины отклонения скорости и должна быть
рассчитана заранее. Например, при увеличении скорости на каж-
дые 30—50 км/ч перегрузка увеличивается на единицу. В момент
увеличения перегрузки летчик контролирует ее величину по аксе-
лерометру с тем, чтобы не превысить допустимого значения.
Если же скорость окажется меньше заданной, то в первую оче-
редь необходимо проверить величину угла атаки — не превышает
ли она допустимого значения. При необходимости ослаблением
тянущих усилий уменьшить его.
Основной задачей летчика на второй половине переворота яв-
ляется обеспечение вывода самолета в горизонтальный полет на
заданных высоте, скорости и режиме работы двигателя.
Область выполнимости переворота определяется из условий
вывода в горизонтальный полет на высоте, не менее безопасной,
и скорости, не более максимально допустимой. Рассмотрим для
примера диапазон скоростей и высот разрешенного ввода в пере-
ворот (рис. 17.13).
Наиболее широкий диапазон высот и скоростей ввода в пере-
ворот при его выполнении на режиме малого газа — с выпущен-
ными тормозными щитками. На высотах 6—8 км можно вводить
в переворот даже на максимально допустимой скорости. На этих
высотах при увеличении нормальной перегрузки до пу лобовое
сопротивление самолета достаточно велико, что позволяет выпол,-
пить переворот без увеличения скорости. При возрастании высоты
ввода более 8 км максимально допустимая приборная скорость
ввода уменьшается при постоянном максимальном числе М ввода
444
в переворот. Выход за пределы установленного числа М приведет
к превышению максимально допустимой скорости полета.
Невыпуск тормозных щитков, а также увеличение тяги двига-
теля приводит к более интенсивному разгону самолета, поэтому
ввод в переворот в этих случаях выполняется на меньших скоро-
стях.
Рис. 17.13. Области выполнимости разворота:
1 — на ПМГ с выпущенными тормозными щитками;
2 — на ПМГ с убранными тормозными щитками; 3 —
на максимале с убранными тормозными щитками
Наличие внешних подвесок может сузить диапазон выполни-
мости переворота. Например, подвеска авиабомб уменьшает мак-
симально допустимое число М полета до 1,3, а максимально до-
пустимую приборную скорость до 1000 км/ч.
Левой границей области выполнимости переворота является
минимально допустимая скорость ввода в переворот. Она выби-
рается из расчета достаточного запаса нормальной перегрузки до
сваливания самолета и на 50 км/ч больше эволютивной.
§ 17.5. Петля Нестерова
17.5.1. Общая характеристика, условия
выполнения петли
Петля Нестерова — фигура пилотажа, при выполнении
которой самолет описывает в вертикальной плоскости замкнутую
кривую, расположенную выше точки ввода (рис. 17.14). Траекто-
рия петли вытянута по вертикали тем больше, чем больше раз-
ность скоростей на вводе и в верхней точке.
445
Возможность движения самолета по петлеобразным траекто-
риям была предсказана Н. Е. Жуковским в работе «О парении
птиц» (1891 г.). Впервые петля была выполнена русским летчиком
П. Н. Нестеровым в 1913 г. Это послужило началом «фигурного
летания» и привело впослед-
ствии к созданию целого
ряда фигур простого, слож-
ного и высшего пилотажа.
Петля Нестерова счита-
ется правильной, если ее
траектория лежит в верти-
кальной плоскости, скорость
в верхней точке не менее
заданной, а нормальная
перегрузка на протяжении
всей фигуры положитель-
ная и не превышает допу-
стимую. Петля, как прави-
ло, начинается с горизон-
тального полета при крене,
равном нулю. В первой чет-
верти угол наклона траек-
тории возрастает до 90°, во
второй четверти — до 180°,
затем, после прохода верх-
ней точки — до 270° в от-
весном положении, в по-
следней, четвертой четвер-
ти — до 360°.
Тангенциальная состав-
ляющая силы тяжести Gsin© (рис. 17.14) в первой половине пет-
ли вызывает торможение самолета, а во второй — разгон.
Нормальная составляющая силы тяжести G cos © в первой и
четвертой четвертях препятствует искривлению траектории, что
при больших значениях скорости движения в этих частях петли
требует значительного увеличения перегрузки (до ^ = 4,54-5,5).
Во второй и третьей четвертях петли составляющая силы тяжести
способствует искривлению траектории движения. Поэтому, не-
смотря на малые плотность воздуха и скорость, а следовательно
и сравнительно небольшие возможные перегрузки (^ = 24-3), ра-
диус кривизны траектории в верхней точке петли минимален.
На рис. 17.15 показано характерное изменение основных пара-
метров движения самолета в процессе выполнения петли Несте-
рова.
Для того чтобы выйти в верхнюю точку на скорости, не менее
заданной, самолет на вводе должен обладать определенным за-
пасом скорости AV. Его величину можно определить следующим
образом.
Потеря скорости за первую половину фигуры будет зависеть
446
от величины среднего ускорения торможения и времени выхода
в верхнюю точку;
= ИВВ-ИВ Т = /ЖСРДЛ
Полагая в первом приближении пх = 0* и (sin Э)Ср = 2/т:, по-
лучим
2 р-
Jx ср ~ S (?гх sin Ь)ср •
Рис. 17.15. Изменение
параметров движения самолета в процессе выпол-
нения петли Нестерова
Время разворота в вертикальной плоскости на 0—180° при-
ближенно определим через среднюю угловую скорость, полагая' ее
постоянной и равной
S (Пу вв О
<о = — *,
v вв
Тогда окончательно
Ивв ~ К
\/ = _5_ —_____________
Wcp S (Пу вв “ 1)
- 2УВВ
В* Т пу ВВ 1
Из этого приближенного выражения можно найти потребное
отношение скоростей ввода и в верхней точке для выбранного зна-
чения перегрузки на вводе. Поделив обе части равенства на VB. »
и разрешив его относительно VBB/VB. т, найдем
Увв _ ^у вв 1
VB. т Пу ВВ “ 3
(17.15)
Физический смысл данной зависимости заключается в том, что
потеря скорости на восходящей части петли будет тем меньше,
* При достаточно большой перегрузке пи = 4—5 индуктивное сопротивле-
ние, пропорциональное квадрату перегрузки, велико и при максимальном и
даже форсажном режиме работы двигателя в первом приближении можно счи-
тать, ЧТО РСр« Яср.
447
чем энергичнее (с большей перегрузкой и меньшим радиусом)
она выполняется, т. е. чем меньше самолет наберет высоты, тем
меньше он -потеряет кинетической энергии. При получении зави-
симости (17.15) не учитывалась зависимость лобового сопротивле-
ния от перегрузки. В действительности при увеличении перегрузки
больше определенной величины, несмотря на уменьшение набора
высоты, интенсивный рост лобового сопротивления может привести
к уменьшению скорости в верхней точке петли. Поэтому для каж-
дого типа самолета и соответствующих условий ввода существует
некоторый оптимальный закон изменения перегрузки, при котором
самолет выйдет в верхнюю точку на наибольшей скорости.
17.5.2. Т ех н и к а и область выполнения петли
Ввод в петлю осуществляется плавным увеличением перегруз-
ки до ^==54-5,5 за 3—4 с. За это время угол наклона траектории
возрастет до 20—30°, угол атаки — до 8—12°. Следовательно, угол
тангажа при достижении расчетной перегрузки составит 30—40°.
При вводе на числах М>0,9 в процессе торможения может про-
явиться скоростной подхват. Поэтому на таких режимах ввода
летчик должен быть готовым к парированию заброса перегрузки.
На восходящем участке петли целью пилотирования является
поддержание заданного темпа искривления траектории строго в
вертикальной плоскости. На этом участке созданная перегрузка
поддерживается по мере падения скорости увеличением угла атаки,
требуя соразмерного подтягивания ручки управления на себя. При
достижении угла атаки а«(0,74-0,9) аАОП начинает выдерживаться
постоянным угол атаки вплоть до верхней точки петли. Вследст-
вие этого перегрузка уменьшается, достигая у верхней точки ми-
нимального значения (% = 1,54-2).
На самолетах, не оборудованных указателем углов атаки,
созданная перегрузка на вводе удерживается постоянной до тех
пор, пока угловая скорость в вертикальной плоскости не достигнет
рекомендуемого значения. Далее выдерживается сэ2 =const.
Если в верхней точке скорость и высота находятся в заданных
пределах, летчик продолжает нормальное выполнение петли. Для
этого он производит ввод в нисходящий участок петли: определяет
момент выключения форсажа, выключает его, устанавливает за-
данную частоту вращения ротора двигателя и сохраняет потреб-
ный темп искривления траектории. На самолетах, оборудованных
УУА, угол атаки несколько увеличивается до (0,84-0,9) адоп. На
самолетах без УУА летчик выдерживает имеющуюся угловую
скорость постоянной, для чего в начале нисходящего участка не-
сколько увеличивается угол атаки незначительным отклонением
ручки управления на себя. Достаточность отклонения ручки опре-
деляется как по постоянству сог> так и проявлению начала аэро-
динамической тряски.
Если скорость в верхней точке окажется меньше допустимой,
летчик принимает меры по предупреждению сваливания: прекра-
448
щает увеличение угла атаки, не уменьшая режима работы двига-
теля и не допуская скольжения. Самолет, продолжая искривление
траектории, разгоняется до приборной скорости на 50—100 км/ч
больше эволютивной. При достаточной высоте и уверенности в
успешном завершении фигуры выполняет нисходящую часть петли.
Рис. 17.16. Безопасный диапазон высот и скоро-
стей ввода в петлю Нестерова (пример)
В том случае, когда высота в верхней точке окажется меньше
заданной или минимально допустимой (2500—3500 м в зависимо-
сти от типа самолета) или скорость будет значительно больше
расчетной, вывод из петли может произойти на высоте, менее
безопасной. Поэтому ввод в нисходящую часть петли не произво-
дить, а выполнить полубочку, выключить форсаж и вывести само-
лет в горизонтальный полет, т. е. закончить фигуру полупетлей.
Диапазон высот и скоростей разрешенного ввода в петлю
определяется из условия выхода в верхнюю точку на скорости, не
менее заданной. Левой границей разрешенного диапазона явля-
ется минимальная скорость ввода. Ее величина зависит от режима
работы двигателя, высоты, уровня перегрузок по траектории и
конфигурации самолета.
При большой тяговооруженности самолета (P/G = 1,24-1,4)
ввод в петлю принципиально возможен на эволютивной скорости.
С увеличением высоты тяга двигателя уменьшается и возрастают
потери энергии самолета (или уменьшается ее прирост). Соответ-
ственно для ввода потребуется большой запас кинетической энер-
гии, скорость ввода увеличивается. На некоторой высоте мини-
мальная скорость ввода становится равной максимально допусти-
мой. Эта точка определяет наибольшую высоту ввода.
Существенное влияние на диапазон разрешенного ввода ока-
зывает и закон изменения перегрузки по траектории. На рис. 17.16
15—21 449
ой указан для оптимальной по потере скорости перегрузки. В том
случае, когда перегрузка чрезмерно велика (петля выполняется
на пу доп), резко возрастают энергетические потери и скорость
ввода увеличивается.
На самолете с крылом изменяемой стреловидности диапазоны
разрешенного ввода при различных стреловидностях крыла опре-
деляются не только из энергетических соображений, но и с учетом
ограничений самолета. Так, при минимальной стреловидности ввод
на большой скорости невозможен из-за жестких ограничений по
скоростному напору и числу М. При максимальной стреловидности
крыла вследствие существенного увеличения индуктивного сопро-
тивления возрастают потери энергии самолета, в результате уве-
личивается минимальная скорость и уменьшается максимальная
высота ввода.
§ 17.6. Полупетля
П о л у п ет л я — фигура пилотажа, при выполнении которой
самолет описывает восходящую часть петли Нестерова с после-
дующим поворотом относительно продольной оси на 180° и выво-
Рис. 17.17. Траектория и схема сил
на полупетле
дом в горизонтальный полет в
направлении, обратном вводу.
Полупетля применяется для быс-
трого набора высоты с измене-
нием направления полета на 180°.
По характеру движения полу-
петля представляет собой сочета-
ние первой половины петли и по-
лубочки (рис. 17.17). Поскольку
движение на восходящей части
петли достаточно подробно рас-
смотрено выше, остановимся
лишь на особенностях фигуры в
заключительной ее части.
При выполнении полубочки
самолет под действием сил, лежа-
щих в вертикальной плоскости
(Y cos у—G cos 0), хотя и с замед-
лением, но продолжает искрив-
лять траекторию книзу. Следова-
тельно, для выхода из полубочки в горизонтальный полет необ-
ходимо начать ее при положительном угле наклона траектории,
равном 0 (рис. 17.18). Для большинства самолетов при времени
полубочки 3—4 с он составляет около 10°.
Далее, поскольку вывод должен быть закончен в прямолиней-
ном горизонтальном полете, то перегрузка в конце полубочки дол-
жна быть равна единице, а при подходе к верхней точке она
обычно больше единицы. Следовательно, ее необходимо умень-
шить либо перед полубочкой, либо в процессе ее выполнения.
450
Кроме того, за счет наклона подъемной силы самолет разворачи-
вается в горизонтальной плоскости на угол ДТ, который тем боль-
ше, чем больше перегрузка и время полубочки. В целях его умень-
шения перегрузку целесообразно уменьшать перед выполнением
полубочки. При работе двигателя на максимальном режиме, а тем
более форсаже скорость в процессе полубочки увеличивается, так
как пу невелика.
Рис. 17.18. Силы, действующие на самолет, и его траектория в процессе
вывода из полупетли
С учетом этого техника вывода из полупетли может быть сле-
дующей. При подходе к верхней точке летчик оценивает величину
приборной скорости и, если она не менее заданной (обычно боль-
ше эволютивной на 50—100 км/ч), приступает к выводу. Для
этого при угле тангажа, близком к нулю, ослаблением тянущих
усилий на ручке управления уменьшает перегрузку примерно до
единицы, ориентируясь по ее ощущению и уменьшению угловой
скорости (ог. Затем координированным движением ручки и педа-
лей создает вращение вокруг продольной оси с таким темпом,
чтобы полубочка была выполнена за 3—4 с, контролируя вели-
чину угла тангажа, угловой скорости <вх и крена. При подходе
к т=0 отклонением ручки управления против вращения прекра-
щает его.
Другим вариантом выполнения вывода из полупетли является
начало полубочки без предварительного уменьшения перегрузки,
но с отклонением ручки управления по диагонали от себя; умень-
шение перегрузки происходит в процессе выполнения полубочки.
Это сокращает время вывода, но усложняет технику пилотирова-
ния, снижает ее чистоту.
В том случае, когда скорость в верхней точке будет меньше
заданной, летчик должен продолжать движение в перевернутом
положении, и, зафиксировав ручку, дать возможность самолету
15* 451
перейти на снижение, увеличить скорость до необходимой вели-
чины и только после этого выполнить полубочку. При затруднении
в определении крена по естественному горизонту использовать
авиагоризонт. После полубочки на установленной скорости вы-
ключить форсаж и вывести самолет в горизонтальный полет.
В случае необходимости выполнения полубочки на V<.V3Q де-
лать ее плавно с несколько большей отдачей ручки от себя, чтобы
пу была меньше единицы.
§ 17.7. Характерные отклонения при выполнении
вертикальных фигур и их исправление.
Меры безопасности
Отклонениями называются отличия фактических парамет-
ров от заданных или расчетных. Отклонения возникают вследст-
вие ошибок, допускаемых летчиком. Мерами безопасности при пи-
лотировании являются действия летчика, предупреждающие, ис-
ключающие выход самолета за ограничения и на критические ре-
жимы полета. Для удобства анализа отклонений, допускаемых
при выполнении маневров (фигур пилотажа) в вертикальной плос-
кости, целесообразно разделить их на восходящие (горка, полу-
петля, восходящая часть петли) и нисходящие (пикирование, пе-
реворот, нисходящая часть петли).
Восходящие маневры выполняются с уменьшением скорости,
поэтому наиболее характерным отклонением является потеря ско-
рости менее заданной. Основными причинами этого отклонения
являются:
— ввод в фигуру за пределами области выполнимости (на ско-
рости менее или высоте более разрешенных, на пониженном ре-
жиме работы двигателя, в конфигурации или с подвесками, не
предусмотренными для такого маневра);
— вялая манера пилотирования на криволинейных участках
фигуры (малые значения пу, <о2);
— большие значения угла горки или продолжительности ее
прямолинейного участка.
В первом случае запаса кинетической энергии недостаточно
или он расходуется слишком быстро для того, чтобы закончить
маневр на заданной скорости. Во втором и третьем — самолет на-
бирает больше высоты и соответственно больше расходуется на
это кинетической энергии.
Для исправления этого отклонения необходимо дать возмож-
ность самолету увеличить скорость до эволютивной (или больше
на 50 км/ч) как за счет снижения, так и за счет тяги двигателя,
а именно:
— уменьшить перегрузку (угол атаки) до величины, близкой
к нулю, поставить элероны и руль направления нейтрально — са-
молет сам перейдет на снижение и наберет скорость;
— увеличить тягу двигателя до максимальной, а при включен-
ном форсаже — не выключать его;
452
— после набора скорости убрать крен и вывести самолет в го-
ризонтальный полет.
Для предупреждения потери скорости необходимо:
— твердо знать границы области разрешенного ввода в вос-
ходящие фигуры для различной конфигурации, режима работы
двигателя и уровня перегрузок;
— в процессе выполнения всех фигур не допускать превыше-
ния допустимого угла атаки и перегрузки.
Потеря скорости при а<адоп при достаточном запасе высоты
неопасна. Лучше допустить меньшую скорость в верхней точке
фигуры, чем увеличивать угол атаки до а^адоп*
Основная опасность при потере скорости на восходящем ма-
невре состоит в возможности непроизвольного выхода самолета на
большие углы атаки, на которых существенно ухудшаются харак-
теристики устойчивости, управляемости современных самолетов и
появляется возможность сваливания. Поэтому одной из наиболее
грубых ошибок при потере скорости является попытка увеличе-
нием угла атаки энергичнее выполнить заключительную часть вос-
ходящей фигуры.
К этому же может привести незнание или неучет особенностей
продольной управляемости самолета, обусловленных выполажива-
нием моментной диаграммы в некоторых интервалах углов атаки,
расположенных в диапазоне 10—20°, или резким уменьшением
градиента Р^у при переходе с жесткой на мягкую пружину за-
грузочного механизма. При равномерном по усилиям выборе руч-
ки управления на себя угол атаки в этих случаях увеличивается
неравномерно — с ускорением в указанных условиях.
Вывод самолета на а^адоп летчик обнаруживает по показа-
ниям УУА, срабатыванию САУ или СОУА; на самолетах, не обо-
рудованных указателями, по характерным признакам для данного
самолета (аэродинамическая тряска, покачивание, ухудшение ха-
рактеристик устойчивости и управляемости). В перевернутом по-
ложении при перетягивании ручки самолет может выполнить
полубочку, или, как говорят летчики, «вывернуться из фи-
гуры».
При обнаружении превышения допустимого угла атаки летчик
должен немедленно ослабить тянущие усилия на ручке при ней-
тральном положении ее по органам поперечного управления и пе-
далей, обеспечив переход самолета на а<аДОп. На самолетах, не
оборудованных УУА, уменьшить перегрузку до пу<Л и удержи-
вать ее до исчезновения признаков полета на больших углах
атаки. После этого проконтролировать значение скорости. Вывод
самолета в горизонтальный полет начинать на У=Йэв + 50 км/ч.
Для предотвращения выхода самолета на а^адоп увеличение
перегрузки на приборных скоростях менее 750 км/ч осуществлять
с обязательным контролем угла4 атаки по УУА, а при его отсут-
ствии уметь определять дриближение к адоп по поведению само-
лета и взаимным значениям перегрузки и приборной скорости.
453
Вблизи адоп движения ручкой управления должны быть мелкими,
плавными, не допускать возникновения скольжения.
Нередким отклонением на вводе в восходящий маневр является
превышение расчетной или допустимой перегрузки. Его причинами
является резкое, энергичное увеличение перегрузки или неучет
особенностей поведения самолета при уменьшении скорости в
трансзвуковом диапазоне скоростей (скоростного подхвата).
Для предупреждения выхода самолета на Лутах необходимо
прежде всего не превышать рекомендуемого темпа увеличения пе-
регрузки (driy/dt). Чем выше темп создания перегрузки, тем боль-
ше заброс перегрузки и угла атаки, а соответственно, с тем боль-
шей вероятностью могут быть превышены «доп и п*п1ах. С учетом
свойств современных самолетов темп увеличения перегрузки не
должен превышать 1—1,5 ед./с. Вблизи ограничения параметра
увеличивать его нужно с постепенным уменьшением темпа или
в несколько приемов с соответствующим упреждением в дей-
ствиях.
Во избежание заброса перегрузки вследствие скоростного под-
хвата необходимо четко знать диапазон чисел М, в котором он
проявляется, перед вводом контролировать число М по указателю.
Если самолет находится в трансзвуковом диапазоне скоростей, то
перегрузку создавать в расчете на ее последующее непроизволь-
ное увеличение примерно на 1Ч-1,5. При появлении признаков ско-
ростного подхвата своевременной отдачей ручки управления от
себя удерживать значения перегрузки и угловой скорости со* в за-
данных пределах.
Наиболее опасным отклонением на нисходящих маневрах яв-
ляется большая потеря высоты. Основными причинами этого от-
клонения являются: ввод на высоте менее или скорости более раз-
решенных, на повышенном режиме работы двигателя; вялая ма-
нера пилотирования, особенно в начальной стадии нисходящих
фигур. Во всех случаях (кроме случая ввода на малой высоте)
происходит энергичный рост скорости, в результате которого уве-
личивается радиус кривизны траектории в вертикальной плоско-
сти и соответственно потеря высоты.
Для предупреждения чрезмерного разгона самолета необхо-
димо своевременно и решительно принимать меры для уменьше-
ния ускорения: увеличением перегрузки, уменьшением тяги дви-
гателя, а при необходимости и выпуском тормозных щитков. При
этом необходимо помнить, что увеличение перегрузки дает наи-
больший эффект торможения на малых и средних скоростях, вы-
пуск тормозных щитков — наибольший эффект торможения на
больших скоростях, наименьшая потеря высоты достигается на
приборных скоростях не более 750—800 км/ч.
Фактор приближения к земле обусловливает естественное
стремление летчика быстрее выйти в горизонтальный полет за
счет энергичного искривления траектории. В начальной стадии
нисходящих маневров (в начале переворота, после прохода верх-
454
ней точки петли, при вводе в пикирование переворотом и полу-
переворотом) на малой скорости при резких и длинных движениях
ручкой управления может произойти превышение допустимого
угла атаки,
В средней и заключительной частях фигуры может произойти
превышение допустимой перегрузки как вследствие неконтроли-
руемого ее увеличения, так и при неучеге особенностей поведения
самолета в трансзвуковом диапазоне скоростей (скоростной под-
хват).
Вне трансзвукового диапазона скоростей у некоторых самоле-
тов заброс перегрузки может произойти при выпуске тормозных
щитков за счет появления кабрирующего момента. Поэтому для
энергичного торможения желательно одновременно использовать
только два фактора: уменьшение тяги и увеличение перегрузки
или уменьшение тяги и выпуск тормозных щитков. Перегрузку
можно увеличивать только после полного выпуска тормозных
щитков.
Техника выполнения нисходящих фигур на самолете с подвес-
ками усложняется вследствие иногда вводимых более жестких
ограничений, как по скорости, так и по перегрузке. В этом случае
от летчика требуется особенно точное пилотирование. С одной
стороны, нельзя энергично искривлять траекторию из-за возмож-
ности превышения /Хутах> но, с другой стороны, вялая манера пи-
лотирования ведет к энергичному росту скорости и возможности
превышения Это приводит к необходимости дросселиро-
вания двигателя и более точного выдерживания параметров фи-
гуры. Вывод из нее производится на уменьшенной (но не малой!)
скорости с последующим прямолинейным разгоном.
Особую группу составляют отклонения, вызванные вращением
самолета по крену. Причинами этого отклонения могут быть: на-
личие скольжения (особенно на самолетах с большой поперечной
устойчивостью), непроизвольное отклонение ручки в поперечном
отношении при ее продольном движении, неточная пространствен-
ная ориентировка летчика. Во всех случаях наличие крена при-
водит к замедлению искривления траектории в вертикальной плос-
кости.
При выполнении петли наличие угловой скорости со* в первой
ее четверти может привести к выходу в верхнюю точку на мень-
шей высоте и большей скорости (рис. 17.19). Обнаружив это, лет-
чик должен выполнить полубочку и перевести самолет в горизон-
тальный полет. В противном случае нисходящая часть петли мо-
жет быть закончена на недопустимо малой высоте.
При наличии (ох во второй четверти петли самолет будет ин-
тенсивно терять скорость при медленном уменьшении угла на-
клона траектории. Необходимо убрать крен и обеспечить себя
скоростью.
При наличии крена или сох в заключительной (четвертой) час-
ти петли или переворота увеличивается потеря высоты за вывод.
455
Необходимо оценить действительное значение крена (по авиа- или
естественному горизонту), убрать его и выводить самолет в гори-
зонтальный полет в том направлении, в котором он оказался.
Рис. 17.19. Отклонения, возникающие при вращении самоле»
та по крену:
a-в I четверти; б — во II четверти
Глава 18
МАНЕВРИРОВАНИЕ ПО ПРОСТРАНСТВЕННЫМ
ТРАЕКТОРИЯМ
§ 18.1. Особенности пространственных маневров и условий
их выполнения
Пространственными маневрами называются такие
маневры, при выполнении которых изменяются все три координаты
центра масс самолета, т. е. одновременно происходит искривление
горизонтальной проекции траектории и изменение высоты полета.
Для этого должно быть установлено соответствующее соотноше-
ние сил, действующих по нормалям (перпендикулярам) к траек-
тории, лежащим в вертикальной и горизонтальной плоскостях.
На рис. 0.4 представлена схема сил, действующих на самолет
при выполнении пространственного маневра без скольжения. Дви-
жение самолета описывается системами уравнений (0.10) или (0.13).
Сумма проекций сил на нормаль к траектории OyKi лежащую
в вертикальной плоскости, покажет направление искривления тра-
ектории в вертикальной плоскости. Если в первом приближении
тягу двигателя считать направленной по оси OxKl то при Усозу>>
456
>Gcos0 (ny>cos 0/cos у) искривление траектории будет происхо-
дить вверх, точнее — в положительном направлении оси Оук. Если
Yeosy<Gcos0 (n»<cos0/cosу), то траектория будет искрив-
ляться в противоположную сторону (вниз).
Проекция сил на нормаль к траектории OzK, направленную по
горизонтали, покажет направление искривления траектории в го-
ризонтальной плоскости. Так как все другие силы, кроме подъем-
а.<0; ^<эо"
Рис. 18.1. Два способа искривления траектории вниз
ной У, расположены в вертикальной плоскости хкОук, то они не
дадут проекции на ось Огк. Проекция подъемной силы У sin у при
принятых допущениях является единственной причиной искривле-
ния траектории в горизонтальной плоскости. Ее направление и
определяет, куда будет искривляться траектория: при правом
крене и положительном угле атаки сила У sin у будет направ-
лена вправо и, следовательно, траектория будет искривляться
вправо. При левом крене траектория будет искривляться
влево.
Очевидно, что, чем больше будет нормальная сила, искривляю-
щая траекторию, тем больше будет кривизна траектории, т. е.
энергичнее маневр. Искривляющую силу в горизонтальной плос-
кости У sin у можно увеличить двумя способами: увеличением угла
атаки, а следовательно, и подъемной силы У, и увеличением угла
крена у.
Искривляющая сила в вертикальной плоскости У cos у— G cos 0
зависит от углов атаки, крена и наклона траектории 0. Для более
интенсивного искривления траектории вверх нужно увеличить
угол атаки (подъемную силу) и уменьшить угол крена у, вниз —
направить вниз составляющую подъемной силы У cos у. Это можно
сделать двумя способами: во-первых, путем отдачи ручки управ-
ления от себя уменьшить угол атаки до допустимого отрицатель-
ного значения и тем самым (при крене, меньшем 90°) направить
подъемную силу вниз (рис. 18.1,а), во-вторых создать креп боль-
ше 90° и увеличить угол атаки.
457
Первый способ неудобен и значительно менее эффективен,
так как создать отрицательную перегрузку можно значительно
меньшую по величине, чем положительную. Неудобство этого спо-
соба состоит не только в том, что отрицательную перегрузку пло-
хо переносит человек, но и в том, что при правом крене раз-
ворот будет происходить влево, а при левом крене — впра-
во. Второй способ значительно более эффективен и удобен,
так как положительную перегрузку можно создать в несколько
раз большую, чем отрицательную, и направление разворота будет
совпадать с направлением крена (рис. 18.1, б).
Выполнение пространственных маневров имеет ряд особен-
ностей в пилотировании самолета по сравнению с выпол-
нением горизонтальных и вертикальных маневров. Во-первых, оно
требует вполне определенного и, как правило, переменного соот-
ношения между перегрузкой и креном. Например, для искривле-
ния траектории вверх при крене, меньшем 90°, требуется выпол-
нять соотношение ©/cos у, а для искривления траектории
вниз — пу <cos 0/cos у. Во-вторых, в процессе , выполнения про-
странственных маневров значительно сложнее вести пространст-
венную ориентировку, т. е. определять положение самолета на
траектории маневра и угловое положение в пространстве, так как
происходит не только непрерывное изменение всех трех координат
самолета, но и непрерывное вращение его относительно всех трех
осей. При таком движении летчику трудно обеспечить выполнение
маневра без непроизвольного возникновения скольжения. В-треть-
их, при выполнении восходящих маневров с предельной перегруз-
кой происходит более интенсивное уменьшение скорости, чем при
выполнении аналогичных горизонтальных маневров, так как к тор-
мозящей силе — лобовому сопротивлению — добавляется состав-
ляющая силы тяжести G sin 0. Это обстоятельство требует более
строгого слежения за скоростью, и особенно за углами атаки и
скольжения, так как чрезмерное уменьшение скорости может при-
вести к неожиданному превышению допустимых значений угла
атаки.
Перечисленные особенности пространственных маневров при-
водят к тому, что выполнение их заметно сложнее, чем вертикаль-
ных и горизонтальных, требует большего внимания, большей точ-
ности пилотирования и натренированности летчика.
§ 18.2. Спираль
Спираль—-фигура пилотажа, при выполнении которой са-
молет, двигаясь с постоянным углом наклона траектории, разво-
рачивается в горизонтальной плоскости. Если угол наклона траек-
тории больше нуля, то происходит набор высоты и спираль на-
зывается в осходящей. При 0<О происходит снижение и спи-
раль называется нисходящей. Вираж можно рассматривать
как частный случай спирали с 0 = 0.
Спираль с креном до 45° называется мелкой, а с креном бо-
лее 45° — глубокой.
458
18.2.1. Восходящая спираль
В чистом виде восходящая спираль применяется для набора
высоты в ограниченном районе (пилотажной зоне, над приводной
радиостанцией и т. д.). Но в большинстве случаев летной прак-
тики используется ее часть — разворот в режиме подъема (при
наборе высоты по большому кругу, по маршруту, при боевом при-
менении и т. д.).
Траектория спирали представляет собой винтовую линию, на-
вернутую на вертикальный цилиндр. Если поверхность цилиндра
развернуть в плоскость, то траектория спирали превратится в на-
клонную прямую. Таким образом, восходящая спираль представ-
ляет собой сочетание режимов прямолинейного набора высоты и
разворота в горизонтальной плоскости. Установившаяся спираль
выполняется с постоянными значениями скорости и угла наклона
траектории: V — const; Q — const..
Уравнения движения с учетом этих условий будут:
Р — X — Gsin 0 — 0;
Y cos 7 — Geos 0 = 0; (18 1)
Y sin 7 -Ь -j- V cos 0 e>cn = 0.
Для сохранения постоянства скорости сила тяги должна урав-
новешивать сумму сил лобового сопротивления и продольной со-
ставляющей силы тяжести G sin 0, т. е. потребная тяга для вос-
ходящей спирали будет больше, чем на вираже, на величину
G sin 0.
Для обеспечения постоянства угла наклона траектория верти-
кальная составляющая подъемной силы У cos у должна уравнове-
шивать не полную силу тяжести, как на вираже, а только ее нор-
мальную составляющую. Следовательно, потребная нормальная
перегрузка на спирали для заданного крена будет несколько мень-
ше, чем на вираже, и определяется из второго уравнения систе-
мы (18.1):
Однако при небольших углах наклона траектории (до 15°) это
различие невелико (не более 4%) и можно считать, что потребная
перегрузка на спирали примерно такая же, как и на вираже.
Основными характеристиками спирали являются: угол подъ-
ема, угловая скорость или время витка, радиус и шаг спирали.
Восходящая спираль выполняется, как правило, на максимальном
или номинальном режиме работы двигателя. При этом распола-
гаемый угол подъема определяется из первого уравнения дви-
жения системы (18.1):
sin 0СП = тт в пх,
459
так как
У On?
К ~ К ’
то
. п Р пУ СП
sin 0сп — q К. *
На данной высоте полета угол подъема уменьшается по мере
увеличения перегрузки (крена) спирали. Это объясняется тем, что
с увеличением нормальной перегрузки возрастает лобовое сопро-
тивление и для сохранения равновесия сил по оси Охк при посто-
янном значении тяги необходимо уменьшить тангенциальную со-
ставляющую силы тяжести за счет уменьшения угла наклона тра-
ектории. При перегрузке, равной предельной по тяге, располагае-
мый угол подъема равен нулю, т. е. восходящая спираль превра-
тится в вираж.
Угловая скорость и время витка с п и р а л и опре-
деляются по соответствующим формулам виража:
Пу СП sin 1 tg 7 )
^сп— g ycos0 ~~ £ у ’ |
. _ I
сп~ wcn “ * J
Радиус спирали несколько меньше, чем виража с тем же кре-
ном:
(18.3)
__ V cos 0 __ У2 cos 0
Гсп — — £tg1
Но так как значение 0 обычно не превышает 10—15°, то это
отличие составляет не более 2—4%.
Шаг спирали — это высота, Tia6HpaeMaH (или теряемая) за
один виток. Величину шага можно определить из треугольника
на рис. 18.2:
(18.4)
(18.5)
Яв = 2кгсп tg 0,
или с учетом выражений (18.3) и (18.4):
Н, _ 0,64^
в tg 7 \ G К /
Из полученного выражения видно, что для набора возможно
большей высоты за один виток спираль необходимо выполнять
с небольшим креном.
Особенности техники выполнения восходящей спирали состоят
в следующем. Перед выполнением разворота в режиме подъема
для сохранения скорости необходимо уменьшить угол наклона
траектории отдачей ручки от себя или увеличить тягу и затем
ввести самолет в разворот таким же образом, как на вираже.
Иногда при разворотах с небольшим (до 30°) креном применяют
460
раздельный ввод: сначала создают крен без увеличения перегруз-
ки, в результате происходит уменьшение угла подъема, а затем
увеличивают перегрузку до заданной.
В процессе разворота ручка должна быть отклонена против
крена больше, чем на вираже. Это объясняется тем, что продоль-
ная ось самолета Охх наклонена к горизонтальной плоскости раз-
ворота не только из-за наличия угла атаки, но и угла наклона
Рис. 18.2. Траектория спирали и ее развертка. Схема сил, действующих на са-
молет
траектории. В результате угловая скорость вращения против
разворота, необходимая для сохранения крена, будет больше, со-
ответственно увеличивается поперечный демпфирующий момент
и потребное для его парирования отклонение ручки. Лет-
чики, не учитывающие этого, обычно допускают увеличение крена
в процессе восходящей спирали и, как следствие, уменьшение
угла подъема вплоть до перехода в горизонтальный полет. Посто-
янство скорости на спирали обеспечивается соответствующим под-
бором угла наклона.
18.2.2. Нисходящая спираль
Нисходящая спираль применяется для снижения в ограничен-
ном районе. Угол наклона траектории спирали будет отрицатель-
ным. Нисходящая спираль обычно выполняется с задросселиро-
ванным двигателем: Р«РМ. г»0.
Поэтому уравновешивание лобового сопротивления осущест-
вляется тангенциальной составляющей силы тяжести Gsin0, на-
правленной вперед. Соотношение нормальных сил (по оси Оук)
остается прежним и потребная нормальная перегрузка на нисхо-
дящей спирали такая же, как и на восходящей.
Угол снижения спирали определяется величиной лобового со-
противления, которое в свою очередь зависит от нормальной пере-
грузки: чем она больше, чем больше абсолютная величина угла
снижения
. пУ сп
sin 0 =-------j£-
461
Наименьшее значение угла снижения при выполнении спирали
с заданным креном достигается при полете на наивыгоднейшем
угле атаки (при Л"тах). При этом скорость полета по траектории
должна быть:
^сп °min ~ сп •
Величины угловой скорости, радиуса и времени витка опреде-
ляются теми же формулами, что и для восходящей спирали.
Шаг нисходящей спирали при Р = 0
= — 0,64
V2 cos 0
К sin 7
Как видим, величина потери высоты за виток спирали умень-
шается с увеличением крена и уменьшением скорости. Однако
следует помнить, что эти два фактора зависят друг от друга: по
мере уменьшения скорости полета уменьшается допустимое зна-
чение крена (перегрузки). Кроме того, для выполнения спирали
с большим креном требуется перевод самолета на снижение с
большим углом и вывод из него, что вызывает , дополнительную
потерю высоты. Поэтому увеличивать крен более 45—50° нецеле-
сообразно.
Перед выполнением нисходящей спирали в режиме прямоли-
нейного снижения необходимо дачей ручки от себя увеличить угол
снижения и затем ввести самолет в разворот. В процессе разво-
рота скорость выдерживается изменением угла снижения, при
увеличении скорости его нужно уменьшить, и наоборот. Ручка по
крену находится вблизи нейтрального положения. После вывода
из разворота для сохранения постоянной скорости угол снижения
необходимо уменьшить.
При ошибках в выдерживании крена спирали неизбежно воз-
никают отклонения в угле наклона траектории и скорости. На-
пример, крен увеличился и стал больше заданного. При этом
Feoscos0 и траектория начнет искривляться книзу. В ре-
зультате тангенциальная составляющая силы тяжести увеличится,
станет больше лобового сопротивления, что вызовет увеличение
скорости. Для исправления этого отклонения необходимо умень-
шить крен, установить заданный- угол снижения и снова ввести
самолет в разворот. Попытка предотвратить рост скорости про-
стым увеличением перегрузки может привести к входу самолета
в глубокую спираль.
При уменьшении крена самолет будет выходить из угла сни-
жения и терять скорость. В этом случае необходимо уменьшить
перегрузку, установить заданную скорость и угол снижения и за-
тем ввести самолет в разворот.
§ 18.3. Боевой разворот
Боевой разворот — фигура пилотажа, при выполнении ко-
торой самолет энергично набирает высоту с одновременным раз-
воротом на 180° (или на заданный угол). Он является одной из
462
самых распространенных фигур, используемых при боевом манев-
рировании. Боевой разворот применяется для занятия исходного
положения при атаке наземной цели с пикирования, для выхода
из нее и повторного захода, при атаке воздушной цели, следую-
щей на встречном курсе и большой высоте и т. д.
Рис. 18.3. Траектория боевого разворота и соотношение сил, дей-
ствующих на самолет
Быстрое увеличение высоты при выполнении фигуры происхо-
дит в основном за счет запаса кинетической энергии самолета,
поэтому ввод в боевой разворот начинается на достаточно боль-
шой скорости, а иногда близкой к максимальной.
По форме траектории боевой разворот представляет собой со-
четание горки и половины (части) виража, выполняемых одновре-
менно (рис. 18.3). Для искривления траектории в горизонтальной
плоскости (разворота самолета) используется горизонтальная со-
ставляющая подъемной силы У sin у, которая образуется при на-
кренении самолета в сторону разворота.
Для быстрого набора высоты траектория сначала искривляется
вверх, а затем (для выхода в горизонтальный полет) — вниз. При
выполнении боевого разворота в учебных целях может иметь
место участок траектории с постоянным значением угла ее накло-
на. На этом участке нормальные силы, действующие на самолет
в вертикальной плоскости, должны быть уравновешены:
Feos 7 = Geos 0.
Нормальная перегрузка будет иметь такое же значение, как
на спирали;
__ cos 0
cos у *
463
На первом участке (вводе) для искривления траектории вверх
необходимо, чтобы YcosGeos©. Это достигается увеличением
перегрузки в большей степени, чем крена, т. е.
cos 0
nv >------.
У cos 7
На третьем участке (выводе) необходимо иметь искривляю-
щую силу, направленную вниз:
Y cos 7 — G cos © < 0.
При этом нормальная перегрузка должна быть меньше по-
требной для спирали:
что достигается либо увеличением крена при постоянной перегруз-
ке, либо уменьшением перегрузки при постоянном крене, либо
уменьшением перегрузки в опережающей степени, чем крена.
Основными характеристиками боевого разворота являются на-
бор высоты за фигуру Нб, р и время ее выполнения /б. р. Время
выполнения боевого разворота можно определить по величине
угловой скорости в горизонтальной плоскости:
б-р_^Гр-
При ДЧг=180°, учитывая формулу (18.3), найдем
____ и / V cos 0 \
б-Р“~'У пу sin 7 /ср.
(18.6)
При заданных значениях скоростей ввода и вывода время раз-
ворота зависит в основном от величины крена и нормальной пе-
регрузки: чем ближе крен к 90° и чем больше перегрузка, тем
меньше время. Из этого вытекает, что для выполнения боевого
разворота за минимальное время необходимо на заданной (мак-
симальной) скорости создать крен, близкий к 90°, и максимально
допустимую по прочности перегрузку и выдержать их до выхода
самолета на адоп. Затем (по мере падения скорости) уменьшить
перегрузку и крен, сохраняя аДОп=const до конца разворота. Оче-
видно, что при таком способе выполнения фигуры самолет набе-
рет очень мало высоты, так как большая часть кинетической энер-
гии израсходуется на преодоление силы лобового сопротивления.
Описанный вариант выполнения фигуры называют форсирован-
ным боевым разворотом.
Набор высоты за боевой разворот можно определить энергети-
ческим способом, но с обязательным учетом изменения уровня
энергии самолета:
т/2 _у2
Лжср^ср*б.р. (18.7)
484
или
^б. р ^СР g Н~ ^х ср А), р у •
При заданных значениях скоростей ввода и вывода различие
в наборе высоты будет определяться величиной продольной пере-
грузки и продолжительностью боевого разворота. Напомним, что
чем больше нормальная перегрузка, тем меньше продольная и тем
Рис. 18.4. Изменение параметров движения при боевом раз-
вороте
меньше будет набор высоты при прочих равных условиях, т. е.
для набора возможно большей высоты боевой разворот необхо-
димо выполнять с возможно меньшей нормальной перегрузкой.
Время выполнения боевого разворота на набор высоты влияет
двояко. Если средняя нормальная перегрузка будет больше пре-
дельной по тяге, когда ггх<0, то увеличение времени будет при-
водить к росту потери энергии и уменьшению набора высоты, так
как при этом Х>Р, и энергия будет затрачиваться на преодоле-
ние лобового сопротивления. Если же нормальная перегрузка бу-
дет меньше предельной по тяге, когда пх>0, то, чем продолжи-
тельнее будет боевой разворот, тем больше будет прирост энер-
гии самолета и соответственно набор высоты за счет превышения
тяги над лобовым сопротивлением.
Из вышесказанного ясно, что для максимального набора вы-
соты боевой разворот необходимо выполнять с малыми значения-
ми .крена, перегрузки и угловой скорости в горизонтальной плос-
кости, т. е. по типу полувитка восходящей неустановившейся
спирали.
Как видим, требования максимального набора высоты и мини-
мального времени являются противоречивыми, а описанные ва-
рианты выполнения фигуры — крайними. Практически выполняе-
мые боевые развороты по манере пилотирования являются ком-
промиссными, лежащими между этими двумя предельными слу-
чаями, В качестве примера на рис. 18.4 показано характерное
455
изменение параметров движения и отклонения стабилизатора в
процессе практического выполнения боевого разворота.
В летной практике боевые развороты, выполненные с малыми
углами наклона траектории и крена, называют плавными,
а с большими — энергичными.
Энергичные боевые развороты применяются в целях сокраще-
ния времени маневра. Ввод в такой боевой разворот должен про-
изводиться в короткое время, т, е. с достаточно большой пере-
Рис. 18.5. Изменение параметров при выполнении различных типов
боевых разворотов:
а — по типу восходящей спирали; б — без спирального участка; в — по
типу косой полупетли
грузкой, а вывод — более сильным способом, т. е. с созданием
крена более 90°. Это может вызвать определенные трудности в
технике пилотирования. Поэтому на практике энергичные боевые
развороты часто выполняют по типу косой полупетли, в процессе
которых используется кинематическое изменение углов крена и
тангажа.
Изменение некоторых параметров при выполнении различных
типов боевых разворотов показаны на рис. 18.5.
Характерными ошибками и отклонениями при выполнении бое-
вого разворота являются следующие.
1. Превышение заданной перегрузки в конце ввода (при за-
данных значениях 9иу). В результате искривляющая сила в вер-
тикальной плоскости не станет равной нулю, а будет направлена
вверх и самолет будет продолжать увеличивать угол наклона тра-
ектории, что приведет к более интенсивному падению скорости.
Самолет потеряет скорость при большом значении угла наклона
траектории, не развернувшись до 180°.
Для исправления этого отклонения в поздней стадии (в конце
фигуры) необходимо увеличить крен и, не допуская значительного
уменьшения скорости, вывести самолет в горизонтальный полет.
Оставшуюся часть разворота выполнить в установившемся режиме.
При обнаружении ошибки в ранней стадии в момент превыше-
ния заданного угла тангажа (более 30°) необходимо уменьшением
466
перегрузки и некоторым увеличением крена установить заданное
значение угла тангажа, а затем угла крена.
2. При заданном угле тангажа летчик выдерживает крен мень-
ше заданного или рано начинает уменьшать его. Угловая скорость
в горизонтальной плоскости будет незначительной, самолет
выйдет на заданную скорость и высоту, не успев развернуться
на 180°.
3. Позднее начало вывода, т. е. летчик начал уменьшение
угла наклона траектории при скорости меньше заданной. Для
предотвращения значительной . ее потери необходимо «уси-
лить» вывод, т. е. увеличить крен до такого значения, которое
обеспечивает выход из боевого разворота на скорости не менее
эволютивной.
§ 18.4. Бочка
Бочка — фигура пилотажа, при выполнении которой самолет
поворачивается относительно продольной оси на 360° с сохране-
нием общего направления полета. Различают следующие виды
бочек:
— по количеству полных оборотов — одинарные (Ду = 360°),
полубочки (180°), полуторные (540°), многократные (Ду^720° —
двойные, тройные и т. д.);
— по времени выполнения одного оборота — быстрые (4—6 с и
менее), замедленные (8—12 с и более);
— по технике выполнения — неуправляемые, координирован-
ные и управляемые.
При выполнении неуправляемой бочки положение рулей от кон-
ца ввода до начала вывода не меняется. В процессе выполнения
управляемой бочки производится корректировка движения само-
лета по траектории путем отклонения ручки и педалей. Коорди-
нированная бочка выполняется при фиксированной ручке, но без
скольжения, что обеспечивается соответствующим отклонением пе-
далей.
При маневрировании бочка или ее элементы чаще используют-
ся в качестве переходного звена от одного вида движения (ма-
невра) к другому. Как самостоятельная фигура бочка выполняется
в спортивно-тренировочных и учебных целях. Полубочки являются
частью таких фигур, как переворот, полупетля, переворот на гор-
ке и т. п.
Нередко траекторию самолета, выполняющего бочку, изобра-
жают в виде прямой горизонтальной линии. Техника выполнения
такой бочки чрезвычайно сложна: летчик должен отклонять руч-
ку и педали таким образом, чтобы равнодействующая подъемной
и боковой сил все время уравновешивала силу тяжести и имела
бы проекцию на горизонтальную плоскость, равную нулю. Быстро
выполнить такую бочку нельзя, и никаких тактических выгод она
не дает, однако требует весьма точного пилотирования и приме-
няется только для отработки техники пилотирования высококва-
4G7
лифицированных летчиков. В летной практике чаще всего выпол-
няют быстрые неуправляемые или координированные бочки.
Рассмотрим движение самолета при выполнении правой бочки
с постоянной перегрузкой, равной единице, начатой в горизонталь-
ном полете (рис. 18.6).
Рис. 18.6. Силы, действующие на
с Пу — \ и ее
самолет, при выполнении бочки
траектория
В вертикальной плоскости. В начальный момент подъемная сила
уравновешивает силу тяжести самолета. Но как только крен начи-
нает увеличиваться, вертикальная составляющая подъемной силы
будет уменьшаться и самолет под действием разности сил
У cosy—G начнет искривлять траекторию вниз. Максимальное ее
искривление будет иметь место в перевернутом полете (у=180°),
когда подъемная сила и сила тяжести действуют практически в
одном направлении. И лишь в конце бочки (при у = 0) равновесие
вертикальных сил восстановится. Таким образом, за время бочки
самолет в вертикальной плоскости искривит траекторию книзу на
величину Д0 и соответственно потеряет определенную высоту ДЯ.
В горизонтальной плоскости. С момента создания крена обра-
зуется горизонтальная составляющая подъемной силы У sin у, ко-
торая будет искривлять траекторию в сторону бочки. Максималь-
ное искривление будет иметь место при крене 90° (вся подъемная
сила лежит в горизонтальной плоскости). При дальнейшем уве-
личении крена искривление будет замедляться и при у=180° пре-
кратится совсем. За время первой половины бочки самолет раз-
вернется в сторону ее выполнения на угол ДТ. При выполнении
второй половины бочки горизонтальная составляющая подъемной
силы будет направлена уже в другую сторону, что вызовет ис-
468
кривление траектории в сторону, противоположную бочке, на ту
же величину ДгР. Таким образом, самолет в конце бочки будет
лететь в прежнем направлении, но сместится в сторону ее выпол-
нения на величину Д£2.
Описанный характер движения определяет и характеристики
бочки: угол наклона траектории Д0б, угол поворота полубочки
ДЧ^п.б, потеря высоты Д//б и боковое смещение ДЛ2.
Величину угла понижения траектории приближенно можно
определить по средней угловой скорости в вертикальной плоско-
сти:
Д0б = СР ^б’
где
<°г ср = V I <ЛУ C0S $ ср — cos еср].
Так как со5уср=0, а созвер51»!, то при постоянном значении
нормальной перегрузки
(18.8)
Перейдя от радиан к градусам и от м/с к км/ч, получим
дв«=200°-г!г|Г1’
где V — истинная скорость.
Для восходящих и нисходящих бочек это выражение нужно
умножить на cos 0.
Потеря высоты за бочку:
АЯ6 = И, cp/6^IZsin^ i6.
При малых углах (до 15—20°)
sin ^§6. Л-
ъш 2 2
и
^б_-4 = _5Ч. 08.9)
Угол поворота полубочки определяется также по средней угло-
вой скорости, но в горизонтальной плоскости;
ДЧ?п.б = ЧГср/п.б,
где
469
На правой полубочке (sin у)Ср = 2/тг, на левой — 2/те.
Тогда
ДПГ ___ % 8 ПУ j.
или
Боковое смещение:
MU'
AZ2 = V sin -у- /б,
или
A4 = f/^. (18.10)
Как видим, угол понижения траектории тем больше, чем мень-
ше скорость полета и больше время выполнения бочки. От вели-
чины перегрузки (если она постоянна) угол понижения не зависит,
хотя при пу> \ форма траектории будет меняться.
Потеря высоты за бочку зависит лишь от времени ее выпол-
нения. Угол поворота полубочки и боковое смещение зависят от
указанных факторов аналогичным образом, но, кроме того, и от
величины нормальной перегрузки — чем она больше, тем сильнее
искривляется траектория в горизонтальной плоскости.
При выполнении бочки на неизменной приборной скорости углы
понижения и поворота траектории будут больше на малых высо-
тах, чем на средних, за счет уменьшения истинной скорости.
Анализ движения самолета показывает, что выполнить неуправ-
ляемую бочку в строго горизонтальном полете невозможно. Можно
лишь поставить некоторые условия. Например:
— закончить бочку на высоте ввода;
— закончить вывод из бочки в горизонтальном полете.
Для выполнения бочки по первому варианту необходимо ввод
в нее осуществить на угле подъема, равном Д©б/2. При этом вы-
вод произойдет с углом снижения, равным —Д@б/2 (рис. 18.7, а).
По второму варианту бочка должна начинаться с углом подъ-
ема, равным Д0б (рис. 18.7,6). При этом самолет за бочку набе-
рет высоту, равную Д#б. В учебных целях чаще всего применяется
первый вариант.
К числу характерных ошибок и отклонений при выполнении
бочки относятся:
— ввод в фигуру с углом подъема меньше потребного;
— выполнение бочки с перегрузкой больше единицы.
При вводе самолета в бочку с углом подъема меньше задан-
ного, выход из фигуры произойдет в угле снижения больше обыч-
ного. Попытка исправить это отклонение в процессе самой бочки
470
(взятием ручки на себя в последней четверти фигуры) является
малоэффективной и может привести к выводу самолета на адоп.
Ввод в бочку с перегрузкой больше единицы может произойти
следующим образом. Для быстрого перевода самолета из гори-
Рис. 18.7. Варианты выполнения неуправляемых бочек
зонтального полета в режим подъема летчик создает перегрузку,
обычно 2—2,5. По достижении заданного угла тангажа перегрузку
необходимо уменьшить при-
мерно до единицы. Но иногда
летчик (курсант) торопится
создать вращение по крену и
отклоняет ручку в сторону, не
отдав ее от себя. При выпол-
нении бочки с увеличенной пе-
регрузкой происходит более
энергичное искривление траек-
тории как в горизонтальной,
так и в вертикальной плоско-
стях.
§ 18.5. Косая петля.
Полупереворот
Косой петлей называ- Рис. 18.8. Траектория косой петли
ется петля, траектория которой
расположена в плоскости, наклоненной под углом ф к горизонту
(рис. 18.8). На рис. 18.9 изображена траектория первой половины
косой петли (вид по стрелке А, рис. 18.8), Во всех трех положе-
471
ниях самолета 1, 2, 3 сила тяжести G направлена под одним
углом ф к плоскости петли. Ее составляющая Gcoscp, направлен-
ная по нормали к плоскости петли, стремится искривить траекто-
рию в направлении действия этой силы, т. е. сделать ее неплоской
Рис. 18.9. Неправильно выполненная пер-
вая половина косой петли
(штриховая линия). Именно такой неправильный вид будет иметь
траектория косой петли, если летчик попытается выполнять ее, как
показано на рис. 18.9, т. е. без вращения самолета относительно
продольной оси, стремясь все время сохранить подъемную силу
в плоскости предполагаемой петли.
Чтобы выполнить косую петлю правильно, т. е. так, чтобы ее
траектория лежала строго в одной заданной наклонной плоскости,
необходимо уравновесить составляющую силы тяжести Gcoscp
путем отклонения в противоположном ей направлении подъемной
силы Y на некоторый угол е (рис. 18.10). Величина этого угла
определяется из условия равновесия сил, направленных по нор-
мали к плоскости петли:
Г sin е = G cos <?,
(18,11)
472
откуда
cos Ф
sine ==-—-X-
Z2y
(18.12)
В верхней точке петли вследствие уменьшения скорости полета
и плотности воздуха подъемная сила (перегрузка) будет значи-
тельно меньше, чем в нижней. Следовательно, для уравновешива-
Рис. 18.10. Условия выполнения правильной ко-
сой петли
ния одной и той же силы Gcostp угол е отклонения подъемной
силы от плоскости петли потребуется больший. Таким образом,
в первой половине петли с момента ввода и до верхней точки нуж-
но вращать самолет по крену в сторону верхнего полукрыла, уда-
ляя подъемную силу от плоскости петли (увеличивать угол е),
а во второй половине петли — вращать самолет в сторону нижнего
полукрыла, приближая подъемную силу к плоскости петли (умень-
шать угол s). Изменение угла крена, а следовательно, и угла s
зависит от перегрузки при вводе в петлю и в ее верхней точке,
а также от угла <р наклона плоскости петли.
В табл. 18.1 приведены значения потребных углов крена у и в
в градусах при различных углах наклона плоскости петли и пере-
грузках, рассчитанные по формуле (18.12).
Как видно из таблицы 18.1, п р и больших углах <р разни-
ца в углах е невелика. Так при q> = 60° и при изменении перегрузки
от нижней точки до верхней от 6 до 2 угол е изменяется от 5 до
473
Таблица 18.1
Точки косой петли Перегрузка Угол наклона плоскости петли, °
30 45 60 75
е т е т Б т s т
Нижняя 5 10 50 8 37 6 24 3 12
6 8 52 7 38 5 25 2 13
Верхняя 2 26 94 21 114 14 136 7 158
3 17 103 14 121 10 МО 5 160
4 12 108 10 125 7 143 4 161
14°, т. е. всего на 9°. На такой же угол и нужно повернуть
самолет относительно продольной оси в сторону верхнего полу-
крыла.
При малых углах ср не должно быть большой разницы в пере-
грузках вследствие небольшого набора высоты. Например, при
угле ср = 30° и изменении перегрузки от 5 до 4 угол е изменяется
всего на 2° (с 10 до 12°).
Таким образом, основной особенностью выполнения косой пет-
ли по сравнению с обычной петлей в вертикальной плоскости яв-
ляется несовпадение плоскости симметрии самолета с плоскостью
петли и необходимость поворота самолета относительно продоль-
ной оси на несколько градусов на восходящем участке петли в
сторону верхнего полукрыла (во внешнюю сторону петли), на
нисходящем участке — в сторону нижнего полукрыла (во внут-
реннюю сторону петли). Следует учитывать также, что изменение
скорости в процессе выполнения косой петли будет менее интен-
сивным, чем при выполнении петли в вертикальной плоскости, осо-
бенно при малых углах ср, так как в точке 2 рис. 18.9 максималь-
ная величина составляющей силы тяжести, направленной по ка-
сательной к траектории, будет равна не всей силе тяжести G,
а лишь G sin ср.
Искривление траектории в плоскости петли в нижней ее части
происходит под действием разности сил Kcoss—G sin ср, в верх-
ней точке — суммой сил Y cos e+G sin ср, а при углах поворота
касательной к траектории в плоскости петли 90 и 270° —состав-
ляющей подъемной силы У sin у. Как и у обычной петли, мини-
мальный радиус кривизны траектории будет в верхней точке пет-
ли, так как скорость здесь минимальна.
Косую петлю можно рассматривать как более общий маневр,,
при изменении угла наклона плоскости которого косая петля пре-
вращается либо в петлю Нестерова (при <р = 90°), либо в вираж
(при <р=0).
Полупереворот представляет собой вторую половину ко-
474
сой петли. Ввод в полупереворот с горизонтального полета осу-
ществляется аналогично вводу в переворот, только угол крена
устанавливается меньше 180°. В зависимости от угла ср наклона
плоскости полупереворота и перегрузки крен должен быть равен
(рис. 18.10, верхнее положение
самолета):
7 = 90° + ср — 8,
где 8 — берется из табл. 18.1
или рассчитывается по форму-
ле (18.12).
В табл. 18.2 приведены по-
требные значения углов крена
при вводе самолета в полупере-
ворот при различных значениях
угла ср и перегрузки.
Таблица 18.2
”y Потребные значения угла крена (т, °) при углах наклона плоскости полу- переворота <р, °
30 45 60 15
2 94 114 136 158
3 103 121 140 160
4 108 125 143 161
При малых углах ф необхо-
димо учитывать, что скорость будет нарастать заметно медленнее,
чем при обычном перевороте.
§ 18.6. Методы расчета траекторий и параметров
пространственного движения самолета
Уравнения пространственного движения центра масс самолета
в траекторной системе координат записываются в следующем виде
(0.10)2
т ^- = Р-Х-Оз\п 0;
dt
mV == ^cos I— Geos 0;
mV cos 0 *= — Y sin 7.
Для расчета параметров движения удобнее использовать урав-
нения (0.13), в которых вместо сил используются перегрузки:
-^ = g(nx — sin©);
- = -Я- (nv cos т — cos 0);
V z
cW g
ST-----V^0^sinI’
(18.13)
где
P— x
Q ’
X = XQ-\-Xlrn$ =
475
Для расчета координат центра масс
ним траектории полета используем
ния (0.8):
самолета и построения по
кинематические уравне-
dH
dt
= V sin 0;
—- = V cos 0 cos W;
nt 7
(18.13')
1
-5^-= — 1/cos 0 sin Ф.
dt f
В тех случаях, когда в процессе движения самолета расхо-
дуется значительное количество топлива, необходимо учитывать
также и переменность массы самолета, для чего запишем уравне-
ние расхода массы самолета в следующем виде:
= (18.14)
где Cs = СУд Р/3600 кг/с (секундный расход топлива).
Полученные семь уравнений (18.13, 18.13' и 18.14), полностью
описывающие движение центра масс самолета, позволяют рассчи-
тать все характеристики его движения и их изменение по времени,
если задан режим работы двигателя, законы изменения пере-
грузки и угла крена по времени и начальные условия движения
Vo, ©о, Ч\), Яо, Хо и zo. В некоторых случаях дополнительное соот-
ношение между перегрузкой и углом крена (например, при выпол-
нении косой петли или спирали) позволяет вычислить все пара-
метры движения при задании кроме режима работы двигателя
лишь одного из этих параметров: или перегрузки, или крена.
Определить зависимость перегрузки и угла крена от времени
можно также и из условия оптимальности маневра по какому-
либо параметру. Например, как указывалось выше, наивыгодней-
шая спираль, дающая минимум потери высоты за один виток, осу-
ществляется при крене около 45°.
Расчет пространственных маневров производится, как правило,
путем численного интегрирования уравнений (18.13, 18.13', 18.14).
Однако ручной счет весьма трудоемок и длителен, поэтому рас-
четы пространственных маневров производятся на электронно-вы-
числительных машинах (ЭВМ),
Глава 19
ВЗЛЕТ И ПОСАДКА
§ 19.1. Особенности движения самолета по земле.
Руление. Этапы взлета
В процессе руления, взлета и посадки происходит движение са-
молета по земле, которое имеет ряд существенных особенностей
по сравнению с движением в воздухе. Кроме обычных сил и мо-
476
ментов на самолет действуют еще силы реакции земли — нормаль-
ная N, продольная (тангенциальная) F и боковая ZK и их моменты
относительно центра тяжести (рис. 19.1). Самолет не имеет сво-
боды вращения относительно продольной оси и перемещения вдоль
оси Oyit а при движении на трех опорах или на велосипедном
шасси — также и свободы вращения относительно оси Oz\.
Мугх
Рис. 19.Г. Силы, действующие на самолет при
его движении по земле со скольжением
При сравнительно малой скорости движения аэродинамические
силы малы и рули неэффективны. Движение при взлете и посадке
неустановившееся.
Все перечисленные особенности движения самолета по земле
накладывают существенный отпечаток на его устойчивость и
управляемость и требуют принятия специальных конструктивных
мер для их обеспечения и повышенного внимания летчика при
управлении самолетом.
Искривление траектории (разворот) самолета в процессе его
движения по земле происходит под действием боковых сил трения
колес ZK и аэродинамической Z, которые возникают при повороте
самолета вокруг вертикальной оси на угол скольжения р
(рис. 19.1).
При рулении аэродинамическая сила Z отсутствует. Управ-
ление поворотом самолета относительно центра тяжести осущест-
вляется с помощью переднего колеса или асимметричного тормо-
жения главных колес. Асимметричная тяга двигателей, разнесен-
ных по размаху, ввиду большого времени приемистости исполь-
477
зуется редко, главным образом при рулении по скользкому грун-
ту, когда тормоза и переднее колесо малоэффективны, а иногда
и при разворотах.
При рулении по скользкой поверхности (мокрый бетон, голо-
лед) следует проявлять особую осторожность, так как начавшееся
вращение самолета трудно парировать ввиду малых боковых сил
трения и создаваемых ими боковых моментов.
Рис. 19.2. Схема взлета с разбегом
Руление на повышенных скоростях допустимо только по пря-
мой и вдали от препятствий, так как развороты в этом случае воз-
можны только с большим радиусом из-за больших боковых на-
грузок на шасси.
Взлет —это процесс перехода самолета от неподвижного по-
ложения на линии старта к управляемому полету. Для определен-
ности характеристик взлета условились, что взлет заканчивается
по достижении некоторой безопасной скорости и высоты стандарт-
ного препятствия.
В зависимости от типа самолета взлет может осуществляться с
разбегом по земле до скорости отрыва V0Tp или с отрывом от
земли с места (вертикальный взлет, взлет с направляющих с по-
мощью ускорителей и т. п.). На рис. 19.2 показана схема взлета
с разбегом, наиболее распространенного в настоящее время.
Взлет с разбегом состоит из двух этапов: разбега и раз-
гона после отрыва. Расстояние, которое проходит самолет
на этих этапах, соответственно называются длиной разбега
£Рб и длиной разгона £рг, а их сумма — в з л ет н о й дис-
танцией £в. д. Величины Zp6, Иотр и LB, д являются важнейшими
характеристиками взлета.
§ 19.2. Разбег, Особенности устойчивости и управляемости
Первая часть разбега выполняется на трех опорах. Когда рули
становятся эффективными, угол тангажа самолета несколько уве-
личивается, вследствие чего передняя опора отделяется от земли
и дальнейший разбег до скорости УОтр выполняется на главных
колесах.
478
Чтобы с момента начала движения ускорение было наиболь-
шим, перед началом разбега колеса затормаживаются и двигатели
выводятся на максимальный (форсажный) режим, после чего тор-
моза отпускаются.
До скорости 100—НО км/ч самолет практически не реагирует
на отклонение руля направления. Поэтому в начале разбега на-
правление следует выдерживать управляемым передним колесом,
а при неуправляемом переднем колесе — асимметричным тормо-
Рис. 19.3. Схема сил, действующих на самолет при
увеличении угла атаки в процессе разбега
жением главных колес. Последнего по возможности следует избе-*
гать, так как .оно увеличивает длину разбега и может вызвать
колебания рыскания. При дальнейшем увеличении скорости руль
направления становится эффективным. Его потребные отклонения
(сначала большие) постепенно уменьшаются.
Путевая устойчивость движения самолета по земле зависит от
боковых сил трения главных колес Zr. к (рис. 19.1), переднего ко-
леса Zn. к, боковой аэродинамической силы Z и моментов этих сил-
относительно центра тяжести самолета.
На малых скоростях на путевую устойчивость влияют в основ-
ном боковые силы трения Zr. к и Zn. к.
Боковые силы трения главных колес приложены позади центра
тяжести и потому создают стабилизирующий момент Муг, к, стре-
мящийся устранить угол скольжения 0. Боковая сила трения пе-
реднего колеса создает дестабилизирующий момент Муп. к, стре-
мящийся увеличить угол скольжения. Именно поэтому переднее
колесо (если оно неуправляемое) и делается свободно ориенти-
рующимся, чтобы уменьшить силу Zn. к и ее момент Муп. к прак-
тически до нуля, повысив тем самым устойчивость движения са-
молета по земле.
Продольная устойчивость самолета при разбеге на главных
колесах несколько хуже, чем при движении в воздухе, особенно
в начале движения на главных колесах после подъема переднего
колеса. Объясняется это дестабилизирующим влиянием изменений
сил реакции земли при изменении угла атаки. Поясним это с по-
мощью рис. 19.3, на котором изображена схема сил, действующих
на самолет при разбеге на главных колесах.
479
Сила нормальной реакции N вместе с подъемной силой Y
уравновешивает силу тяжести самолета G (вертикальной составляю-
щей силы тяги P^ = Psina пока будем пренебрегать):
Отсюда величина силы W определяется как разность сил G
и У:
N=O — Y.
Сила трения F равна произведению коэффициента трения f на
величину силы N:
F=f(G-Y). (19.1)
Пусть, например, угол атаки самолета по какой-то случайной
причине увеличился на Да. При этом подъемная сила возрастет
на величину ДУ, а нормальная реакция уменьшится на ту же ве-
личину ДМ = —ДУ. Изменение нормальной реакции ДМ будет на-
правлено вниз и на плече а создаст дополнительный момент от-
носительно центра тяжести ДЛ12 = ДМа, направленный на кабриро-
вание, который будет способствовать дальнейшему увеличению
угла атаки, уменьшая тем самым продольную устойчивость.
Изменение силы трения Д^=/ДМ направлено в противополож-
ную по отношению к F сторону и точно также будет создавать
дополнительный дестабилизирующий момент ДЛ1г=Д/?&. Поэтому
в первые секунды после подъема переднего колеса продольная
устойчивость самолета понижена. По мере дальнейшего увеличе-
ния скорости силы реакции земли М и F быстро уменьшаются и
продольная устойчивость улучшается.
Подъем переднего колеса различных типов современных само-
летов осуществляется на скоростях 150—300 км/ч. При этом,'
во-первых, скорость должна быть достаточна для необходимой
эффективности стабилизатора, во-вторых, для достижения мини-
мальной длины разбега целесообразно установить некоторый опти-
мальный угол атаки, при котором ускорение разбега максимально.
При увеличении угла атаки лобовое сопротивление возрастает
и несколько уменьшается горизонтальная составляющая силы тяги
Pcosa. Но при этом вследствие увеличения подъемной силы и
вертикальной составляющей тяги Psina уменьшается сила реак-
ции земли W, а следовательно, и сила трения F.
С учетом всех этих факторов оптимальный угол атаки при раз-
беге по бетонной ВПП составляет 2—3°. Поэтому разбег для со-
кращения его длины выгодно выполнять на трех точках, а подни-
мать переднее колесо только перед самым отрывом, за 20—
30 км/ч До достижения скорости отрыва.
Такой способ разбега прост по выполнению, так как не требует
точного продольного управления. Он обеспечивает минимальную
длину разбега и хороший обзор вперед. Недостатком его является
большая нагрузка на колеса, особенно на переднее. Поэтому на
тех самолетах, у которых допустимая скорость для переднего ко-
480
леса ограничивает выполнение разбега на трех точках, переднее
колесо поднимается как только стабилизатор становится доста-
точно эффективным. При этом оно лишь немного отделяется от
земли и в таком положении выполняется разбег. По достижении
скорости, на 20—30 км/ч меньшей скорости отрыва, необходимо
плавно, но достаточно, быстро увеличить угол атаки до аОтр, следя
чтобы он не превысил предельного значения. В момент достиже
ния V=VOtp произойдет плавное
отделение самолета от земли. I
Силы, действующие на само-
лет при разбеге, показаны на
рис. 19.3, а их изменение в про-
цессе разбега — на рис. 19.4.
Отметим, что тяга двигателя
в несколько раз больше, чем сум-
ма сил Х+А, и изменяется мало.
Сила лобового сопротивления
возрастает, а сила трения колес
F уменьшается по мере увеличе-
ния скорости. Их сумма X + F
изменяется тоже очень мало. По-
этому движение самолета при
разбеге приближенно можно счи-
Изтр И
Рис. 19.4. Изменение сил, действую-
щих на самолет в процессе раз-
бега
тать равноускоренным.
Тогда длина и время разбега £Рб и /Рб в зависимости от ско-
рости отрыва определяются по формулам равноускоренного дви-
жения:
V2
г ____ Уотр .
рб~ 2/ср ’
(19.2)
Так как в момент отрыва подъемная сила равна силе тяже-
сти, то
<19-3>
Среднее ускорение /ср зависит от сил, направленных по каса-
тельной к траектории, и массы самолета. С учетом формулы (19.1)
получим
Подставляя значение /ср и У2тр в формулу (19.2), получим
£рб = gfCy отр 8 [Р - Л -/ (G -УЩГ * (19Л)
481
16-21
Так как при У=0, Х = 0 и У=0, а при V=VOtp
° + Д-
Х = Хг = -~ и Y—G, то Хср= — / —П.5 ;
^ХОТр z fXOTp
Y„=°-^ = -^4 |Р-лг-/(О-пи =
=р»-°‘5
Подставив полученное значение квадратной скобки в форму-
лу (19.4), найдем
£,»=---------=-------------ГТ|. (19.5)
g?Cy отр S |_Рср 0,5 О ^/ + у J
где
р ___Рв + PV 0Тр
^Ср = 2 •
В формулах (19.3), (19.4) и (19.5) Су Отр берется для взлетной
конфигурации самолета, т. е. с учетом положения крыла, выпу-
щенной механизации и влияния близости земли. Коэффициент
трения при разбеге по бетонной ВПП /=0,034-0,05; по грунту
/=0,104-0,12.
§ 19.3. Разбег с боковым ветром. Разгон после
отрыва
Разбег с боковым ветром значительно сложнее, чем разбег в
безветрие.
Боковой ветер, имеющий скорость W, создает несимметричное
обтекание самолета воздухом, т. е. скольжение на угол W/V
(рис. 19.5). Вследствие скольжения возникает кренящий момент
особенно большой у самолетов со стреловидным или тре-
угольным крылом на больших углах атаки. Этот момент уравно-
вешивается дополнительными реакциями главных колес ДУП и
ДУЛ, которые на плече с создают противодействующий момент.
Вследствие изменений сил нормальных реакций ДУЛ и &Na изме-
няются и силы трения на величины ДАЛ и ДКП, направленные в
противоположные стороны и создающие момент Му к, разворачи-
вающий самолет по ветру (в данном случае влево).
Вместе с тем боковая аэродинамическая сила Z, возникающая
вследствие скольжения и приложенная позади центра тяжести
самолета, создает аэродинамический путевой момент 7Иу₽, стре-
мящийся развернуть самолет носом против ветра (в данном слу-
чае вправо).
Какой из этих двух моментов будет больше — зависит от кон-
кретной компоновки самолета. У самолетов с большой поперечной
482
устойчивостью (со стреловидным или треугольным крылом, с
верхним расположением крыла) и относительно малой эффектив-
ностью вертикального оперения
Му к. Такой самолет при разбеге
развороту по ветру (например, са-
молет МиГ-21). У самолетов, об-
ладающих малой поперечной
устойчивостью (с прямым кры-
лом, нижним расположением
крыла) и относительно большой
эффективностью оперения, прева-
лирующим оказывается момент
УИур. Такой самолет при разбеге
будет проявлять тенденцию к раз-
вороту против ветра.
превалирующим будет момент
будет проявлять тенденцию к
Для борьбы с моментом Му*
необходимо прежде всего устра-
нить его причину, т. е. отклоне-
нием ручки управления против
ветра создать поперечный мо-
мент, уравновешивающий момент
крена от скольжения Мх^. При
этом тенденция самолета к раз-
вороту по ветру прекратится.
Для борьбы с моментом Л4у;3
прежде всего необходимо откло-
нить педали по ветру для непо-
средственного уравновешивания
момента УИу3 моментом от руля
направления. Практически полу-
чается, что у всех самолетов, но
в несколько разной степени при
взлете с боковым ветром необхо-
димо отклонять ручку управле-
ния против ветра. Педали в за-
висимости от конкретной компо-
Рис. 19.5. Силы и моменты, действу-
ющие на самолет при его движении
по земле с боковым ветром
новки самолета отклоняются по ветру или ставятся практически
нейтрально.
По мере увеличения скорости на разбеге эффективность рулей
возрастает и их отклонения постепенно уменьшаются.
Если боковой ветер слишком велик, то полного отклонения ру-
лей может оказаться недостаточно, и тогда прямолинейный раз-
бег становится невозможным. По этой причине вводится ограни-
чение возможности взлета по скорости боковой составляющей
ветра, что также зависит от конкретной компоновки самолета.
Для каждого типа самолета определена своя максимально допу-
стимая при взлете скорость бокового ветра.
16*
483
Разгон в первые секунды после отрыва происходит на сравни-
тельно больших углах атаки и малых скоростях, когда попереч-
ная управляемость обычно бывает пониженной. На самолетах со
стреловидным или треугольным крылом параметр х, характери-
зующий соотношение поперечной и путевой устойчивости, на болы
ших углах атаки и малых скоростях иногда бывает завышенным,
вследствие чего самолет легко входит в крен из-да небольшого
скольжения. На таких самолетах после отрыва необходимо уде-
лять особое внимание поперечному управлению, своевременно и
быстро устранять появляющийся крен, используя при необходи-
мости руль направления.
При взлете с боковым ветром после отрыва начинается снос
самолета. Для борьбы со сносом производится доворот против
ветра, чтобы ввести поправку в курс и обеспечить прямолиней-
ность полета в заданном направлении взлета. Если при этом бу-
дет допущено скольжение, то в первые секунды после отрыва,
когда углы атаки большие и поперечная управляемость ухудшена,
возможно заметное проявление взаимосвязи между продольным
и боковым движениями. В целом взлет не представляет каких-
либо затруднений и считается одним из несложных элементов
полета. Разгон после отрыва как этап взлета считается за-
конченным по достижении так называемой безопасной скорости,
которая не менее чем на 20% должна превышать скорость от-
рыва и не менее чем на 10% —эволютивную скорость взлета.
Для маневренных самолетов безопасная скорость взлета обычно
лежит в пределах (1,24-1,3) V0Tp.
В процессе разгона после отрыва происходит изменение высо-
ты и скорости. Поэтому длину разгона удобнее всего можно рас-
считать энергетическим методом. Для этого используем уравнение
(15.19) при допущении, что cos 0^1:
dL = 1
dH3 пх
(19.6)
Продольную перегрузку пх найдем в предположении, что при
пологом подъеме У—G;
_РГ—Х_ Р х _ Р 1
П*~• G ~ G Y ~ G К. *
Силу тяги Р и аэродинамическое качество К на рассматривае-
мом коротком участке разгона после отрыва можно считать по-
стоянными, Тогда, интегрируя уравнение (19.6), найдем
' z _
**РГ р J »
где
V2 V'2
л тт v КОН . ГТ ¥ отр
484
Как уже говорилось выше, взлетная дистанция равна сумме
длины разбега и длины разгона после отрыва и наряду с длиной
разбега является важной взлетной характеристикой.
§ 19.4. Поведение самолета и действия летчика
при отказе двигателя на взлете
При отказе двигателя на разбеге самолета с одним двигателем
летчик должен принять решение на дальнешие действия: исполь-
зовать все средства торможения и сохранить самолет или ката-
пультироваться.
Резерв Времени Оля принятия
решения и начала торможения
Рис. 19.6. Определение критической скорости разбега само-
лета с одним двигателем
В зависимости от режима работы двигателя, массы самолета,
длины полосы, температуры и давления можно определить крити-
ческую скорость Укр, до которой при прекращении взлета обеспе-
чивается торможение в пределах концевой полосы безопасности
(рис. 19.6). Если длины полосы безопасности окажется недоста-
точно для полной остановки самолета, то для предотвращения
столкновения с препятствием можно убрать шасси. На больших
скоростях, если система катапультирования обеспечивает спасе-
ние летчика и если после полосы безопасности имеются препят-
ствия, следует покинуть самолет.
Выполнение взлета на форсажных режимах позволяет иметь
большие дистанции на случай прекращения взлета.
При асимметричном отказе двигателей на самолете с двумя
двигателями кроме уменьшения ускорения появляется еще и раз-
ворачивающий момент в сторону отказавшего двигателя
(формула 9.12):
Му р = (₽+ Д-Уцв) 2дв‘
При высокой тяговооруженности самолета и большом удале-
нии двигателей от продольной оси самолета асимметричный от-
485
каз двигателя особенно опасен. Задача летчика — прежде всего
удержать самолет от разворота и сохранить прямолинейное дви-
жение вдоль оси ВПП.
Уравновесить разворачивающий момент можно с помощью не-
симметричного торможения колес, отклонением переднего управ-
ляемого колеса или отклонением руля направления. В некоторых
случаях может потребоваться использование всех этих средств
Рис. 19.7. Определение скорости безопасного продолжения
взлета при отказе одного двигателя
управления одновременно. При этом необходимо учитывать, что
эффективность руля направления по мере роста скорости увели-
чивается, а эффективность отклонения переднего колеса падает
ввиду уменьшения нормальной реакции, а следовательно и силы
трения, действующей на переднее колесо. Поэтому иногда может
оказаться целесообразным отдать ручку от себя для увеличения
нормальной силы, силы трения и управляющего момента, созда-
ваемого отклонением переднего колеса.
Парируя разворот самолета, летчик должен оценить ситуацию
и принять решение на продолжение или прекращение взлета.
В данном случае следует рассмотреть две скорости: критическую
скорость УКР, до которой при прекращении взлета обеспечивается
торможение в пределах полосы безопасности, и скорость безопас-
ного продолжения полета при отказавшем двигателе Убез.
Безопасная скорость продолжения взлета оценивается исходя
из достаточности тяговооруженности для получения скорости от-
рыва в пределах данной ВПП и минимальной вертикальной ско-
рости y^min, достаточности эффективности рулей для парирова-
ния разворачивающих и кренящих моментов от асимметричной
тяги.
На рис. 19.7 показан благоприятный случай, когда критиче-
ская скорость превышает скорость безопасного продолжения взле-
та при одном отказавшем двигателе. В диапазоне скоростей от
Убез до Укр летчик может выбрать прекращение взлета или его
продолжение. Практически, если длина ВПП ZBnn и полосы безо-
486
пасности £без позволяют прекратить взлет, то его необходимо пре-
кратить.
Скорость безопасного продолжения взлета может оказаться по
величине большей, чем критическая скорость прекращения взлета,
и большей, чем скорость отрыва самолета. Так, на самолетах
с сильно разнесенными двигателями скорость безопасного продол-
жения полета существенно превышает скорость отрыва самолета.
Рис.' 19.8. Неблагоприятный случай соотношения кри-
тической и безопасной скоростей при разбеге
До достижения этой скорости после отрыва эффективности рулей
недостаточно для удержания самолета от разворота и кренения.
На рис. 19.8 в зоне от УКр до Увез длины полосы безопасности
недостаточно для прекращения взлета, а эффективность рулей не
позволяет удержать самолет от разворота и кренения. При от-
казе двигателя в этом интервале скоростей необходимо покинуть
самолет катапультированием.
Это является большим недостатком конструкции и заставляет
ограничивать использование максимальной тяги на взлете (чтобы
уменьшить разворачивающий момент).
§ 19.5. Особенности взлета в различных условиях.
Влияние эксплуатационных факторов на характеристики
взлета
При взлете с мягкого грунта или с заснеженных по-
лос значительно увеличивается сила сопротивления (сила тре-
ния F), возникающая при деформации грунта колесами с образо-
ванием глубокой колеи и, следовательно, уменьшается ускорение
самолета. Для уменьшения силы трения необходимо как можно
раньше поднять переднее колесо и увеличить угол атаки до а0Тр
и выполнять весь разбег на этом угле атаки. При этом сила
F=f(G—Y) будет минимальной.
При взлете с переувлажненного г р у н т а в первой
половине разбега наблюдается тенденция самолета к рысканию,
487
боковым колебательным перемещениям, а после подъема перед-
него колеса — к продольным колебаниям, затрудняющим выдер-
живание заданного угла атаки.
При взлете со скользкой поверхности (гололед,
мокрый бетон) усложняется выдерживание направления в начале
разбега из-за уменьшения коэффициента трения.
Взлет самолета с велосипедным ш а с с и имеет ряд
существенных особенностей.
Передняя и задняя опоры велосипедного шасси расположены
примерно на одинаковом расстоянии от центра тяжести. Нагрузка
на переднюю опору составляет обычно около 45% веса самолета.
Поэтому аэродинамического момента, создаваемого отклонением
руля высоты, недостаточно для подъема переднего колеса вплоть
до скорости отрыва. Весь разбег до момента отрыва выполняется
без подъема переднего колеса, а высота опор шасси подбирается
такой, чтобы стояночный угол атаки самолета был равен углу
атаки при отрыве.
В процессе разбега летчик не может контролировать продоль-
ную балансировку самолета. Поэтому ручка управления и трим-
мер руля высоты (механизм триммерного эффекта) перед взлетом
должны быть установлены в положение, обеспечивающее продоль-
ную балансировку самолета в момент отрыва, чтобы сразу после
отрыва не появились моменты на кабрирование или пикирование,
которые могут сильно усложнить взлет.
Кроме того, для самолета с велосипедным шасси при взлете
с боковым ветром важно особо тщательно контролировать отсут-
ствие крена, чтобы не допускать перегруженности крыльевых опор,
рассчитанных на сравнительно небольшое «поддерживающее» уси-
лие.
Влияние эксплуатационных факторов на длину разбега и ско-
рость отрыва можно проанализировать с помощью формул (19.4
и 19.3), применяя к ним метод дифференциальных поправок, из-
ложенный в главе 13.
Влияние изменений веса на длину разбега, как видно
из формулы (19.4), проявляется как непосредственно, так и через
изменение силы трения колес. В целом для маневренных самоле-
тов с ТРД обычно получается следующая зависимость:
^=(2,14-2,3)^.
Для скорости отрыва из формулы (19.3) получим '
±^ = 0,5-4^.
V 0Тр G
Иначе говоря, при увеличении веса на 10% длина разбега уве-
личивается на 21-5-23%, а скорость отрыва — на 5%.
Влияние изменений сил тяги, лобового сопро-
тивления и трения колес оценивается путем учета изме-
488
нения суммарной ускоряющей силы, стоящей в квадратной скобке
знаменателя формулы (19.4):
FX==P —X—f (G — Y),
(19.7)
а именно:
д£рб _ &FX
^рб ?х
Влияние каждого слагаемого в отдельности зависит от тягово-
оруженности, точнее от того, какой процент составляет каждое
Рис. 19.9. Влияние ветра на скорость отрыва
слагаемое от всей ускоряющей силы. Так, например, влияние из-
менения тяги для самолетов с тяговооруженностью P/G = 0,94-0,6
оценивается выражением
-^ = (1,14-1,2)-^. (19.8)
ьрб г
Изменение температуры наружного воздуха
влияет на плотность воздуха и тягу двигателя, что приводит к
следующему изменению длины разбега
-^ = (3,2 4-3,4)-^.
**рб *
Например, повышение абсолютной температуры на 30°, т. е.
примерно на 10% по отношению к стандартной, вызывает увели-
чение длины разбега самолета с тяговооруженностью 0,9—0,6 на
32—34% по сравнению с длиной разбега в стандартных условиях
(примерно 1% на 1° изменения температуры /н.в). Скорость отры-
ва при этом увеличится на 10%.
Влияние ветра на длину разбега можно оценить,
пользуясь формулой зависимости путевой скорости отрыва от про-
дольной составляющей скорости ветра:
Wx = Г cose,
где е — угол между направлением взлета и вектором скорости
ветра (рис. 19.9),
489
Очевидно, что путевая скорость отрыва равна алгебраической
сумме воздушной скорости отрыва и продольной составляющей
скорости ветра:
Иотр.пут=^отр+^ = ^отр+^С°5е.
При встречно-боковом и встречном ветрах угол s>90° и
cose<0. Путевая скорость будет меньше воздушной на величи-
ну Wx.
В соответствии с формулой (19.2), считая, что ДУотр= по-
лучим приближенную зависимость
й£р6 ^2 Wx ,
^рб V ОТр
т. е. чем больше продольная составляющая скорости ветра и мень-
ше скорость отрыва, тем большее влияние оказывает ветер на
длину разбега.
Более точные расчеты дают результаты, приведенные в
табл. 19.1.
Таблица 19.1
Отношение величин Ветер
встречный попутный
ух V отр —0,15 —0,10 —0,05 0,05 0,10 0,15
А^-рб £рб —0,28 —0,19 -0,10 0,10 0,21 0,32
Влияние уклона ВПП на длину разбега можно оценить,
используя формулу (19.8), считая, что продольная составляющая
сила тяжеста G sin 0 увеличивает или уменьшает касательную
силу Fx. При этом можно считать, что sin0«0 в радианах. Тогда
Д£₽б — л 1 • 1 °® ~ и-^-1.2 © [°]
£₽б “U’ • ’ ’ Р ~ 57,3 "IT"*
Учитывая, что в формуле (19.8) коэффициенты 1,1 и 1,2 рас-
считаны для тяговооруженностей 0,9 и 0,6 соответственно, полу-
чим
= (0,021 ч- 0,035) 0 [°].
Ьрб
Таким образом, при тяговооруженности 0,9 каждый градус
уклона ВПП дает изменение длины.разбега на 2,1%, а при тяго-
вооруженности 0,6 — на 3,5%.
490
Влияние высоты аэродрома над уровнем моря
на длину разбега проявляется через зависимость плотности воз-
духа и тяги двигателя от высоты. Для малых высот, эту зависи-
мость можно представить в следующем виде:
-^ = — 0,1224/7 [км];
р 1 J
-^ = -0,071447/ [км].
Учитывая эти соотношения, из формул (19.4) и (19.8) найдем
^==-^-(1,1 4-1,2)-^-= (0,20 4-0,21) ДЯ [км].
Таким образом, на каждые 1000 м увеличения высоты аэро-
дрома длина разбега увеличивается на 20—21%.
Следует отметить, что приборная скорость отрыва не зависит
от высоты аэродрома, что можно легко установить с помощью
формулы (19.3), а именно:
Р^отр Q
На скорость отрыва и длину разбега существенно влияет от-
клонение угла тангажа, а следовательно, и угла атаки самолета
от их расчетных значений в момент отрыва. Из формулы (19.4)
с учетом, что коэффициент Су зависит от угла атаки а, получим
А£рб _ 4Су 0Тр ___ __ Д’отр ___ 1 Д’отр
£рб Су 0Тр “отр — а0 । Др аотр
аотр
Угол атаки при отрыве аОтр для различных типов самолетов
лежит в пределах 8—12°, а ао при выпущенных закрылках — в
пределах от —5° до —7°. Следовательно, уменьшение угла атаки
на Г приводит к возрастанию длины разбега на 20—30%. Ско-
рость отрыва увеличится на 10—15%.
Ошибка в сторону увеличения угла атаки приводит к прежде-
временному отрыву на повышенных углах атаки. Для некоторых
самолетов это означает попадание в область плохой поперечной
управляемости. Тяга двигателя становится недостаточной для
дальнейшего разгона, особенно при большой взлетной массе и
высокой температуре наружного воздуха. Возникшая очень опас-
ная ситуация может быть устранена, если позволяет длина ВПП:
можно плавно коснуться колесами земли и продолжать разбег до
нормального отрыва.
Таким образом, простота выполнения взлета является в неко-
торой мере обманчивой, так как при взлете необходимо точное
выдерживание заданного угла атаки при отрыве.
Влияние эксплуатационных факторов на скорость отрыва за-
метно меньше, чем на длину разбега. Однако неучет суммарного
491
влияния нескольких факторов, например таких, как увеличение
взлетной массы и попутной составляющей скорости ветра, может
привести к превышению предельно допустимой для колес путевой
скорости.
§ 19.6. Этапы посадки. Выравнивание и выдерживание
Посадка — это процесс перехода самолета от полета со сни-
жением на безопасной скорости к движению по земле с тормо-
жением до полной остановки на ВПП (практически до скорости
руления).
Рис. 19.10. Схема посадки и силы, действующие на самолет при
выравнивании
Посадка состоит из этапов снижения, выравнивания, выдержи-
вания и пробега (рис. 19.10).
Выравнивание начинается на высоте 7—10 м. Для определен-
ности посадочных характеристик началом посадки считается вы-
сота 15 м, от которой и отсчитывается посадочная дистанция, за-
канчивающаяся в конце пробега.
Целью выравнивания и выдерживания является приземление
самолета на посадочной скорости и с минимальной вертикальной
скоростью, близкой к нулевой.
Выравнивание — это грубый подвод самолета к земле на
высоту 0,5—1,0 м.
Выдерживание — это точный подвод к земле с одновре-
менным уменьшением скорости до посадочной. Запас скорости,
т. е. угла атаки (коэффициента Су) на планировании необходим
для создания дополнительной подъемной силы, искривляющей тра-
екторию в процессе выравнивания. Запас скорости в начале вы-
держивания позволяет точно подвести самолет к земле и плавно
увеличить угол атаки до посадочного. Для этого требуется опре-
деленное время (обычно 3—5 с).
Для искривления траектории при выравнивании необходимо не-
492
сколько увеличить подъемную силу, чтобы она стала больше со-
ставляющей силы тяжести Geos© (рис. 19.10).
Перегрузку, необходимую для выполнения выравнивания, мож-
но определить по формуле*
у2сн
ЯувыР = 2^Д//выр + 11 (19-9)
где V^ch — вертикальная скорость снижения перед началом вырав
нивания; Д//Выр — потеря высоты в процессе выравнивания.
При ^^ = 5 м/с, высоте начала выравнивания 7—10 м и конца
выравнивания 1 м (Д/7Выр = 6~9 м) найдем
п —________________— 12—114
Л4увыр— 2.9,8-(6-т-9)
К началу выравнивания на нормальной высоте и скорости тяга
двигателя практически не нужна, она только увеличивает поса-
дочную дистанцию. Поэтому перед началом или в процессе вы-
равнивания двигатель должен быть задросселирован.
При работе двигателя на минимальных оборотах его тяга мала
по сравнению с лобовым сопротивлением. Поэтому в процессе вы-
равнивания происходит непрерывное уменьшение скорости.
Траектория выдерживания практически горизонтальна. Для
сохранения условия горизонтальности C{/SpV2/2=G в процессе
уменьшения скорости необходимо постепенно увеличивать угол
атаки. Для этого летчик должен все время выбирать ручку на
себя, следя за тем, чтобы расстояние до земли не увеличивалось.
На многих современных самолетах выравнивание и выдержи-
вание практически сливаются в одно движение выравнивания с не-
сколько растянутым заключительным участком, в конце которого
и происходит приземление.
Посадочная скорость определяется по формуле, полученной из
условия горизонтальности полета Y = G;
(19ЛО)
где Су пос — берется с учетом выпущенной механизации и влияния
близости земли.
Из формулы (19.10), учитывая зависимость коэффициента Су
от угла атаки а, по методике, изложенной в § 13.7, получаем
АУпОС __ _ 0 5 ^“ПОС _________0’5 t Авпос
Vпос °пос “ “о | ао “пос
апос
Посадочный угол атаки обычно составляет 8—12°, а ао при
выпущенных закрылках — 5—7°. Поэтому уменьшение угла атаки
* Эта формула получена при допущениях, что траектория выравнивания —
окружность с радиусом 'y = V2/g(riv— 1) (рис, 19.10) и sin0/2 —0/2 (в ра-
дианах).
493
в момент приземления на Г вызывает увеличение посадочной ско-
рости примерно на 13%.
§ 19.7. Пробег
Торможение при пробеге может осуществляться не только си-
лой трения заторможенных колес и лобового сопротивления са-
Y
Рис. 19.11. Схема сил, действующих на самолет при пробеге
молета, но и аэродинамическим сопротивлением тормозных пара-
шютов, а также реверсом тяги
Рис. 19.12. Изменение сил,
действующих на самолет при
пробеге
двигателей.
Схема сил, действующих на са-
молет при пробеге, показана на
рис. 19.11.
Сила трения F определяется так
же, как и при разбеге:
F = fN = f(G — Г), (19.11)
только коэффициент трения f при
торможении будет значительно
больше. Сила трения увеличивает-
ся с уменьшением скорости и
подъемной силы (рис. 19.12). Си-
ла лобового сопротивления при
постоянном угле атаки уменьша-
ется пропорционально квадрату
скорости. Поэтому суммарную тормозящую, силу можно в первом
приближении считать постоянной. Тогда длину и время пробега
можно найти по формулам равнозамедленного движения:
•^пр----
Aip—
V2
у пос
2/ср
У пос
/ср
(19.12)
(19.13)
где среднее ускорение
. _ £(* + Пср
/ср— Q
(19.14)
494
Посадочная скорость УПос определяется по формуле (19.10).
Подставляя УПос и /ср в формулу (19.12), найдем
Ц, =----------------------г • (19.15)
ПОС*$ /(пос J
Лобовое сопротивление самолета при пробеге зависит от угла
атаки. Например, при посадочных углах атаки апос = 84-12° с вы-
пущенными шасси и закрылка-
ми Сх = 0,084-0,1. После опуска-
ния переднего колеса при а==0
Сх = 0,034-0,04.
При уменьшении скорости ло-
бовое сопротивление быстро
уменьшается. Поэтому оно может
быть использовано для торможе-
ния лишь в первой половине про-
бега путем удерживания само-
лета на больших углах атаки.
Тормозной парашют эффек-
тивен в основном в первой поло-
вине пробега. На рис. 19.13 по-
казано примерное соотношение
лобовых сопротивлений самолета
X и тормозного парашюта Xnap и
пробеге.
Рис. 19.13. Соотношение сил лобо-
вых сопротивлений самолета и тор-
мозного парашюта
их изменение по времени при
Время раскрытия и наполнения парашюта составляет 2—4 с.
Поэтому для повышения эффективности тормозной парашют це-
лесообразно выпускать за 2—3 с до приземления, если позволяет
прочность парашюта. Это обычно осуществляется с помощью ав-
томатических устройств.
Необходимо учитывать, что при боковом ветре сила сопротив-
ления парашюта не проходит через центр тяжести самолета и по-
тому создает боковой момент Му, поворачивающий самолет носом
против ветра. Поэтому при выпуске парашюта необходимо быть
готовым к парированию этого момента. При сильном боковом вет-
ре использовать тормозной парашют следует только в первой по-
ловине пробега, затем сбросить парашют, когда разворачивающий
момент увеличивается, а эффективность парашюта уменьшается,
или совсем его не выпускать.
Эффективным средством торможения является реверс тяги,
важной особенностью которого является независимость тормозя-
щей силы от скорости и от состояния поверхности ВПП (к сожа-
лению, маневренные самолеты редко оборудуются им из-за до-
полнительной массы). Необходимо учитывать, что при посадке
на пыльный грунт или на заснеженную ВПП использование ре-
верса тяги при малых скоростях ведет к образованию впереди
самолета пыльного или снежного облака, ухудшающего видимость.
495
Основным и наиболее часто применяемым и эффективным сред-
ством торможения при пробеге являются тормоза. Они поглощают
от 70 до 90% начального запаса энергии самолета при призем-
лении.
Максимальный коэффициент трения /тах заторможенных колес
равен 0,6—0,7 для сухого бетона, 0,36—0,40 — для мокрого бе-
тона и 0,15—0,20 — для обледеневшей ВПП. Фактически реали-
Рис. 19.14. Зависимость относительного коэффи-
циента трения заторможенного колеса от коэф-
фициента проскальзывания относительно поверх-
ности ВПП
зуется примерно половина этих значений. Дело в том, что сила
трения заторможенных колес зависит от проскальзывания их по
поверхности ВПП.
На рис. 19.14 показана зависимость относительного коэффици-
ента трения f=f/fmax от коэффициента проскальзывания
^св
% в
где со и сосв — угловые скорости заторможенного и незаторможен-
ного (свободного) колеса. _Если торможения нет, то со = 0, если
колесо не вращается (юз), со= 1.
Как видно из графика, коэффициент трения будет максималь-
ным при коэффициенте проскальзывания со = 0,14-0,2, что соот-
ветствует некоторому оптимальному затормаживанию колес.
При недостаточном затормаживании колес не полностью ис-
пользуются возможности тормозов. При слишком сильном затор-
маживании коэффициент трения уменьшается и одновременно
сильно увеличивается износ шин колес, особенно при юзе, когда,
как правило, полностью выходят из строя пневматики.
Сам летчик практически не в состоянии реализовать оптималь-
ный режим торможения. Поэтому в системе управления тормо-
зами устанавливаются автоматы торможения, позволяющие реа-
лизовать коэффициент трения, близкий к максимальному (за-
штрихованный участок на рис. 19.14) и уменьшить износ шин.
496
Использование автоматов торможения является эффективным
средством сокращения пробега, если энергоемкость колес доста-
точна и эффективное торможение не приводит к чрезмерному пе-
регреву колес.
Для повышения эффективности тормозов применяется также
увеличение силы нормальной реакции N = G—Y (формула 19.11)
путем уменьшения подъемной силы/. Это достигается опусканием
переднего колеса сразу после приземления, уборкой посадочной
механизации и на некоторых самолетах — симметричным выпус-
ком интерцепторов, уменьшающих подъемную силу на обоих полу-
крыльях одновременно.
§ 19.8. Влияние эксплуатационных факторов на посадочные
характеристики. Посадка при боковом ветре
Влияние изменения посадочной скорости и
угла атаки на длину пробега можно определить по фор-
муле
А^пР __ g А Иное ___А^пос ________1____А^пос
^пр У пос апос ао । go апос
апос
Иначе говоря, увеличение посадочной скорости на 10% вызывает
увеличение длины пробега на 20%. Уменьшение посадочного угла
атаки на 10% (примерно на Г) вызывает увеличение посадочной
скорости примерно на 13% (§ 19.6) и соответственно длины про-
бега на 25%.
Отсюда очевидна важность приземления точно на рекомендуе-
мом посадочном угле атаки. Преждевременное приземление са-
молета на малых углах атаки и на повышенной скорости ведет
к значительному увеличению длины пробега и к повышенному из-
носу протекторов колес.
Встречный или попутный ветер изменяет путевую
посадочную скорость, от которой зависит длина пробега (форму-
ла 19.12). Следовательно, влияние ветра на длину пробега мож-
но определить по формуле
Д^пр _о wx
“7— = z "V—’
ъпр vпос
где Wx — составляющая, скорости ветра вдоль направления по-
садки.
Пусть, например, УПос=300 км/ч (83 м/с) и скорость ветра
равна 5 м/с. Тогда
^ = 2-4=0,12,
т. е. длина пробега при попутном ветре увеличится, а при встреч-
ном уменьшится на 12%. Таким образом, при посадке современ-
497
ных самолетов нельзя пренебрегать влиянием на длину пробега
даже довольно слабого ветра.
Влияние изменения веса и плотности воздуха можно
определить по формулам (19.10) и (19.15):
Д^пос Д£ПР _ ДО .
V^noc О ’ £пр G
Д^пос _ _ Q 5 Др . AZ-nP ______Др
^пос Р ^пр Р
Изменение плотности воздуха в зависимости от температу-
ры и давления определяется по известному уравнению газо-
вого состояния, из которого следует, что
Др __ др дг
Т~ ~~~р т~9
Пусть, например, давление р = 720 мм рт. ст., а температура
равна +30°, т. е. на 15° выше стандартной. Тогда
т. е. в результате такого изменения температуры и давления дли-
на пробега увеличится на 10,5% по сравнению с длиной пробега
в стандартных условиях.
Влияние высоты аэродрома определяется изменением
плотности воздуха. До высоты. 5 км можно приближенно считать,
что на каждые 1000 м плотность уменьшается примерно на 12%.
Следовательно, и длина пробега на каждые 1000 м превышения
аэродрома увеличивается на 12%.
Состояние поверхности ВПП значительно влияет на
длину пробега, так как сила трения колес является основной тор-
мозящей силой при пробеге. Для оценки влияния изменения коэф-
фициента трения на длину пробега необходимо учитывать, на
сколько процентов изменится при этом суммарная тормозящая
сила, так как
сум Д/7 Д/7 F
Например, если принять, что при посадке на сухой бетон сила
трения составляет 70% (==0,7), а сила лобового сопротив-
ления самолета и тормозного парашюта — 30% суммарной тор-
мозящей силы, то при уменьшении силы тренця в два раза =
=—0,5 (например, при посадке на мокрый бетон) получим
• ХТЁ = 0>5 • о,7 = 0,35,
ьПр г Л 4- г
т. е. длина пробега увеличится на 35%,
498
Влияние угла наклона ВПП определяется через изме-
нение ускорения, вызываемого составляющей силы тяжести
G sin 0 — G0:
Тогда с учетом формулы (19.14) найдем
4Лпр Ду_______________*8|°1 = _ 0.0350 [°]
Лп₽ Ус₽ 57,3 + f
~ \ Л.ПОС / 'Хаос
Рис. 19.15. Борьба со сносом с помощью скольжения
Посадка при боковом ветре имеет ряд особенностей.
Прежде всего в процессе предпосадочного снижения необходимо
бороться со сносом скольжением или изменением курса.
Для борьбы со сносом, скольжением создается крен против
ветра и отклоняются педали по ветру. Скольжение подбирается
так, чтобы продольная ось самолета была направлена вдоль оси
ВПП и чтобы движение самолета происходило также строго вдоль
оси ВПП. Это означает, что угол скольжения р подобран равным
углу сноса <р (рис. 19.15) и вектор путевой скорости ЙПут направ-
лен строго вдоль оси ВПП.
Чем больше скорость бокового ветра, тем больше потребуется
угол скольжения и отклонения руля направления и элеронов для
балансировки моментов Му и Мх- При сильном боковом ветре пол-
ного отклонения руля направления может оказаться недостаточно
для создания угла скольжения р=<р. В этом случае оставшийся
499
снос следует устранить изменением курса против ветра. Тогда
после устранения сноса продольная ось самолета будет направ-
лена не вдоль оси ВПП, а под некоторым углом к ней.
В процессе выравнивания и выдерживания борьба со сносом
продолжается вплоть до момента приземления. Крен и курс кор-
ректируются так, чтобы не было сноса относительно полосы. Перед
приземлением крен нужно уменьшать так, чтобы приземление про-
изошло без крена, а продольную ось самолета установить строго
по направлению оси ВПП отклонением педали по ветру.
В процессе пробега самолет ведет себя примерно так же, как
и при разбеге с боковым ветром. Кренящий момент устраняется
отклонением ручки управления против ветра, разворачивающий
момент — соответствующим отклонением педалей.
§ 19.9. Посадка с отказавшим двигателем
Полет на однодвигательном самолете с отказавшим двигателем
возможен лишь с потерей полной энергии. Можно увеличить ско-
рость полета за счет более энергичного снижения либо увеличить
высоту за счет падения скорости. Однако в том и другом случае
полная энергия падает, поскольку работа силы полного сопротив-
ления совершается непрерывно и ничем не компенсируется. Тео-
ретически при отказе двигателя в зависимости от высоты, скоро-
сти и курса полета, а также от расстояния до аэродрома посадки
возможны следующие три ситуации:
— полная энергия самолета точно соответствует потребной для
выполнения посадки;
— полной энергии недостаточно;
— имеется избыток энергии относительно потребной для вы-
полнения посадки.
Первая ситуация практически невероятна. Во втором случае
летчик должен, приняв соответствующие меры, покинуть самолет.
И только при третьей ситуации возможен заход па посадку с ис-
пользованием избытка энергии. Решение этой задачи является
весьма сложным для летчика: необходимо выполнить такой ма-
невр, который позволил бы потерять вполне определенный для
данного случая избыток энергии, ни больше, ни меньше. Если
будет потеряно энергии больше, чем требуется, посадка возможна
лишь до аэродрома, если меньше — с перелетом. Существуют два
основных метода расчета на посадку с отказавшим двигателем:
— метод контрольных точек;
— метод контрольной высоты.
Первый метод основан на знании летчиком определенных ори-
ентиров (контрольных точек), над которыми необходимо выпол-
нять развороты, и потребных высот над ними. Он может быть при-
менен только в простых метеоусловиях.
Второй метод не требует знания летчиком контрольных точек,
поэтому позволяет выполнить посадку на любой ближайший аэро-
дром, оборудованный приводной радиостанцией. Сущность метода
500
заключается в следующем. При отказе двигателя летчик устанав-
ливает заданную для данного самолета скорость (обычно 450—
500 км/ч) и разворачивает самолет с креном 45—50° в сторону
дальней приводной радиостанции (ДПРС) аэродрома, на который
принято решение производить посадку. Если крыло самолета из-
меняемой стреловидности — перевести его в посадочное положе-
ние, при наличии предкрылков — выпустить их.
Подход к аэродрому нужно выполнять с таким расчетом, чтобы
выйти на ДПРС с курсом, равным или близким к посадочному,
на высоте не менее некоторой высоты, заданной для данного са-
молета. За момент пролета ДПРС считать отклонение стрелки ра-
диокомпаса на 30—40°. В этот момент летчик запоминает высоту
(назовем ее Ннач) и вводит самолет в разворот с креном 45—50°,
выдерживая скорость заданной.
В процессе разворота летчик должен подсчитать контрольную
высоту Нк по формуле
где &Н — вполне определенная величина для данного самолета.
Она несколько больше или равна половине потребной высоты над
ДПРС на предпосадочном планировании после 4-го разворота с
неработающим (авторотирующим) двигателем. Эта высота опре-
деляется при специальных летных испытаниях и обычно равна
1100—1200 м. Развернувшись на 180°, летчик выполняет планиро-
вание с курсом, обратным посадочному, до высоты, равной /7К,
а затем выполняет разворот на 90° с креном 45—50°. Четвертый
разворот необходимо выполнить с таким расчетом, чтобы напра-
вить самолет на ДПРС с посадочным курсом.
Шасси выпускаются в месте, указанном инструкцией, обычно
аварийно после того, как летчик убедится в правильности расчета.
Задержка с выпуском шасси может привести к перелету, прежде-
временный выпуск —к недолету. Однако в необходимых случаях
можно, изменяя момент выпуска шасси, уточнять расчет на по-
садку.
Для каждого типа самолета имеется свой потребный диапазон
высот над ДПРС на предпосадочном планировании, который
обеспечивает приземление в допустимых пределах ВПП.
Процесс посадки с неработающим двигателем имеет сущест-
венные особенности по сравнению с обычной посадкой.
Установившееся планирование (без тяги двигателя) современ-
ных самолетов происходит с большой вертикальной скоростью
(порядка 25—30 м/с), которая не позволяет выполнять обычное
выравнивание с необходимой точностью. Поэтому вертикальную
скорость снижения необходимо предварительно уменьшить путем
уменьшения угла планирования примерно до 3°. При этом состав-
ляющая силы тяжести Gsin© окажется значительно меньше ло-
бового сопротивления (рис. 19.10), вследствие чего скорость будет
501
уменьшаться, поэтому для обеспечения посадки необходимо иметь
соответствующий запас скорости.
Таким образом, процесс выравнивания должен осуществляться
в два этапа (рис. 19.16). Вначале на высоте 150—200 м выпол-
няется первое выравнивание (участок Д5) до угла плани-
рования, близкого к обычному при посадке с работающим двига-
телем. Затем на участке БВ
производится планирование
с малым углом и с тормо-
жением. При этом задан-
ный запас скорости обеспе-
чивает в точке В начала
обычного (второго) вырав-
нивания скорость, несколь-
ко большую, чем при обыч-
ной посадке для данного
Рис. 19.16. Схема посадки с двумя вырав- самолета.
киваниями при неработающем двигателе Если по уменьшению
скорости после первого вы-
равнивания видно, что к началу второго выравнивания она будет
недостаточна, то можно немного увеличить угол снижения. При
большой скорости уменьшать угол планирования не следует, так
как скорость может быть погашена при выдержива-
нии.
Запас скорости, необходимый в точке Л, можно рассчитать по
формуле
/ у% _у2 \
£пд = - дад₽ = l-A2g -B + ^МсР’
откуда
Va = (19.16)
где Hi — высота начала первого выравнивания; £Пл — дальность
планирования между первым и вторым выравниванием, опреде-
ляемая по формуле
т ___ Hi _Hl. — OCtFf
Ьпл— tg© ~ 0,05
Если условия начала второго выравнивания (в точке В) со-
блюдены, то посадка выполняется обычным способом.
В целом посадка с неработающим двигателем весьма сложна,
требует строгого выдерживания рекомендованных для конкрет-
ного самолета скоростей и ее могут выполнять только летчики,
прошедшие тренировку в заходах на посадку с имитацией отказа
двигателя.
502
§ 19.10. Возможные отклонения при взлете и посадке
и их исправление
Наиболее часто встречающимися отклонениями от нормального
режима взлета являются:
— невыдерживание направления при разбеге;
— невыдерживание заданной скорости (угла атаки) при от-
рыве;
— отделение самолета с креном;
— невыдерживание направления после отрыва, особенно при
боковом ветре.
Невыдерживание направления чаще всего происхо-
дит в начале разбега, когда мала эффективность руля направле-
ния, и особенно при сильном боковом ветре, под воздействием ко-
торого возникают путевые моменты.
Парирование разворотов должно быть своевременным и энер-
гичным. Успех парирующего воздействия существенно зависит от
силы сцепления колес с грунтом. При скользкой ВПП и сильном
боковом ветре может произойти значительное отклонение от на-
правления оси ВПП, грозящее выкатыванием за ее пределы.
Тогда взлет должен быть прекращен.
Наиболее опасным случаем невыдерживания заданной
скорости (угла атаки) при отрыве самолета является
преждевременный отрыв самолета («подрыв») с выхо-
дом на недопустимо большие углы атаки. Такая ошибка опасна воз-
можностью потери поперечной управляемости или выходом на
вторые режимы полета. Иногда она приводит к повторному гру-
бому касанию колесами ВПП, пока скорость не достигнет нор-
мальной величины. Резкие движения рулями в этом случае могут
лишь усугубить ситуацию. Поэтому рекомендуется зафиксировать
продольное управление вблизи положения, соответствующего аОтр.
Отрыв самолета на повышенной скорости (а<аОтр) приводит
к чрезмерной нагрузке на колеса из-за превышения их допустимой
частоты вращения и к возможности разрушения пневматиков.
Отделение самолета с креном чаще всего происхо-
дит при взлете с боковым ветром, когда летчик не соразмерил от-
клонение поперечного управления с возникшими поперечными мо-
ментами. Эта же ошибка приводит икневыдерживанию на-
правления разгона после отрыва. Оба эти вида оши-
бок легко устраняются летчиком.
Если при малой скорости эффективности поперечного управле-
ния недостаточно для устранения крена, то необходимо использо-
вать отклонение руля направления для создания момента крена
от скольжения.
Наиболее распространенными отклонениями на посадке яв-
ляются:
— высокое или низкое выравнивание;
— взмывание и «козел»;
— приземление с креном или со сносом;
503
— приземление на большой скорости;
— приземление под углом к ВПП;
— приземление с большой вертикальной скоростью.
Эти ошибки, как правило, являются следствием:
— неточности захода на посадку и условий к началу вырав-
нивания по скорости, высоте или курсу;
— неправильного определения расстояния до земли на вырав-
нивании и выдерживании;
— несоразмерного уменьшению скорости выбирания ручки на
выдерживании;
— резких движений ручки управления;
— перемещения ручки управления в момент касания;
— неучета направления и скорости ветра;
— неумения бороться со сносом в процессе посадки.
Для исправления высокого выравнивания рекомендуется за-
держать ручку, т. е. приостановить ее выбирание и по мере
дальнейшего снижения продолжать выбирание ручки до создания
обычного посадочного положения. При этом необходимо тщатель-
но устранять крен.
Для исправления взмывания плавным движением ручки пре-
кратить увеличение высоты и по мере начала дальнейшего сниже-
ния завершить посадку обычным способом, плавно подводя само-
лет к земле.
Отделение самолета от земли («козел») происходит, как пра-
вило, в том случае, если летчик берет ручку на себя в момент при-
земления. При отделении самолета на посадочной скорости ни в
коем случае не отдавать ручку от себя, а только задержать ее и
быть готовым к плавному взятию ее на себя по мере дальнейшего
снижения.
§ 19.11. Способы улучшения взлетно-посадочных
характеристик
Для удобства анализа перепишем формулы (19.2), (19.12),
(19.3) и (19.10) для длин разбега и пробега и для скоростей от-
рыва и посадочной в следующем виде:
у2 у2
Г __ v отр , г _________у пос ,
2jCp. рб ’ П₽ Уср. Пр
у — 1 / . у — У________Ж____
И°ТР- V pCyoTpS’ ”°С У pCynocS*
Как видно из этих формул, уменьшить длины разбега и про-
бега можно путем уменьшения удельной нагрузки на крыло и пу-
тем увеличения коэффициента Су и ускорения.
Чрезмерное уменьшение удельной нагрузки (увели-
чение площади крыла) ведет к увеличению силы тяжести самоле-
та и его лобового сопротивления, следовательно, к ухудшению лет-
ных харак1еристик. Поэтому прежде всего добиваются увеличения
коэффициента Су. Для этого широко применяется взлетно-поса-
504
дочная механизация крыла: закрылки, предкрылки, отгибаемый но-
сок крыла, струйно-аэродинамические закрылки, сдув и отсос по-
граничного слоя, о чем подробно было сказано в главе 5.
Применение сдува или отсоса пограничного
слоя обеспечивает существенное повышение коэффициента Су и
уменьшение скорости отрыва и посадочной скорости.
Воздух для системы управления пограничным слоем (УПС) от-
бирается от компрессора двигателя и система работает при не-
сколько повышенной (по сравнению с минимальной) частоте вра-
щения двигателя, для чего устанавливается специальный проме-
жуточный упор РУД.
Выравнивание и выдерживание выполняется на меньших ско-
ростях. Самолет становится заметно более «летучим». При вклю-
чениии системы УПС обычно возникает кабрирующий момент,
легко парируемый отклонением ручки управления.
Сопротивление самолета из-за большого отклонения закрылков
увеличивается. Поэтому необходимо увеличить обороты двигателя.
На планировании при малой скорости самолет более устойчив и
управляем, что иногда создает иллюзию повышенной скорости.
В конце выравнивания РУД убирается до промежуточного упо-
ра. В начале выдерживания обычно проявляется неустойчивость
по скорости, требующая небольшого отклонения ручки от себя,
а перед самым приземлением устойчивость резко повышается из-за
влияния земли. Ручка управления энергично берется на себя для
парирования уменьшения угла тангажа, и самолет сразу же при-
земляется. Эта особенность требует повышенного внимания, чтобы
избежать грубого приземления.
В настоящее время широкое распространение получили
крылья изменяемой в полете стреловидности. При
взлете и посадке крыло переводится на минимальную стреловид-
ность. Несущие свойства крыла резко улучшаются прежде всего
вследствие увеличения удлинения крыла. Прямое крыло при од-
них и тех же углах атаки создает большую подъемную силу, чем
стреловидное.
Наконец, при переводе крыла на минимальную стреловидность
несколько увеличивается его площадь и повышается эффект от
взлетно-посадочной механизации. В итоге коэффициент Су резко
повышается и соответственно улучшаются взлетно-посадочные ха-
рактеристикио
При посадке самолета с крылом изменяемой стреловидности
наблюдается повышенная «летучесть» самолета на выдерживании,
т. е. он дольше, чем самолет с малым удлинением крыла, теряет
скорость. Объясняется это увеличением аэродинамического каче-
ства.
Увеличение ускорения на взлете достигается глав-
ным образом путем увеличения тяги двигателя. Включение
форсажа, как известно, приводит к резкому повышению расхо-
да топлива и, следовательно, к снижению дальности полета и рас-
полагаемого запаса времени для боя. Однако использование фор-
505
сажа необходимо при максимальной взлетной массе самолета и
высоких температурах.
Весьма эффективным средством увеличения ускорения и умень-
шения длины разбега являются стартовые ускорители —
специальные подвесные ракетные двигатели, работающие на твер-
дом топливе. Они развивают значительную тягу при малых габа-
ритах и массе. Ускорители обычно работают 13—15 с и дают
Рис. 19.17. Силы, действующие на самолет при
вертикальном взлете
наибольший эффект при включении их во второй половине раз-
бега: длина разбега при этом будет заметно меньше, чем при
включении ускорителей в начале разбега.
При взлете с форсажем и особенно со стартовыми ускорителя-
ми характерным является быстрое увеличение скорости и в связи
с этим необходимость быстрого перехода от стояночного угла ата-
ки к подъему переднего колеса и увеличения угла атаки до аОтр.
Это может происходить настолько быстро, что практически сли-
вается в одно плавное движение вращения самолета относительно
оси Огь поэтому требует повышенной точности и своевременности
движения ручкой управления.
Радикальным способом уменьшения длины разбега и пробега
до нуля является создание самолетов вертикального
взлета и посадки (СВВП).
Для осуществления вертикального взлета тяговооруженность,
очевидно, должна быть больше единицы. Причем это необходимо
не только для уравновешивания силы тяжести и создания управ-
ляющих сил струйными рулями, но и для достаточно быстрого
разгона до эволютивной скорости с помощью горизонтальной со-
ставляющей силы тяги при условии, что вертикальная составляю-
щая остается в первые секунды разгона равной силе тяжести
(рис. 19.17). Запас тяги нужен также для обеспечения достаточ-
ной тяговооруженности при высоких температурах наружного воз-
духа, при значительной высоте точки взлета над уровнем моря.
506
В итоге получается, что для надежного обеспечения вертикального
взлета в реальных условиях необходима тяговооруженность в стан-
дартных условиях не менее 1,3—1,4.
Особенности взлета и посадки на таких самолетах связаны
главным образом с обеспечением управляемости на малых скоро-
стях и эксплуатацией на этих режимах силовой установки. От
мощной струи подъемных двигателей поверхность ВПП разру-
шается и ее частицы попадают во входное устройство двигателя.
Кроме того, на малых скоростях практически отсутствуют демп-
фирующие моменты, что не может не сказаться на управляемости
и устойчивости самолета. Характер проявления всех этих особен-
ностей в значительной мере индивидуален для каждого типа са-
молета. При перегрузочной массе, в высокогорных условиях или
при высокой температуре наружного воздуха может быть приме-
нен взлет с коротким разбегом.
Глава 20
ДАЛЬНОСТЬ И ПРОДОЛЖИТЕЛЬНОСТЬ ПОЛЕТА
§ 20.L Расход топлива, дальность и продолжительность полета
при наборе высоты и снижения
Под дальностью полета понимается длина проекции
траектории полета на земную поверхность,
Пролететь расстояние между двумя точками можно на различ-
ных высотах и скоростях, режимах работы двигателей и углах
стреловидности крыла. При этом в каждом варианте режима по-
лета будет затрачено различное время и различное количество топ-
лива. Для наиболее полной реализации боевых возможностей са-
молета часто бывает необходимым выбрать такой режим полета,
который обеспечивал бы минимальный расход топлива для полета
между двумя заданными точками или, что то же самое, при за-
данном запасе топлива позволил бы достичь максимальной даль-
ности полета.
В некоторых случаях требуется обеспечить максимальную
продолжительность полета, например при дежурстве в воз-
духе.
Для удобства анализа и выбора наивыгоднейшего режима по-
лета в смысле достижения максимальной дальности или продол-
жительности всю траекторию полета разбивают на характерные
участки, режимы полета которых резко отличаются один от дру-
гого. Например, при обычном перелете из одной точки в другую
таких участков получается всего три. Набор высоты, крейсерский
режим (горизонтальный полет или полет с постепенным набором
высоты за счет выработки топлива) и снижение (рис. 20.1,а).
В других случаях по тактическим соображениям профиль полета
507
может иметь другую, более сложную конфигурацию (рис. 20.1,6,
в). Однако во всех случаях будут иметь место три вида указанных
характерных участка, из которых может быть набран любой про-
филь полета. Далее проанализируем каждый из характерных уча-
стков, их взаимное влияние и роль каждого из них для достиже-
ния максимальной дальности полета.
У7777777777777777777777777Г77
а
Рис. 20.1. Варианты профилей полета
Обычно полет на максимальную дальность выполняется на до-
звуковых режимах. В этом случае при наборе высоты скорость из-
меняется сравнительно мало. Однако конкретная ситуация мо-
жет вызвать необходимость полета на максимальную дальность
с выходом на сверхзвуковые скорости полета, например при пере-
хвате или наборе высоты на сверхзвуке при дефиците времени.
Данный случай является наиболее общим. Поэтому основное вни-
мание в дальнейшем будет уделяться этому случаю,,
Характерным свойством участка набора высоты современных
маневренных самолетов является большой расход топлива, осо-
бенно при разгоне до сверхзвуковых скоростей и наборе высоты
на сверхзвуковой скорости. В этом случае расход топлива на на-
бор может составлять до 40—50% всего запаса топлива. Поэтому
от того, насколько экономно был выполнен участок подъема и
разгона, зависит и суммарная дальность полета.
Существуют специальные методы определения наивыгоднейшего
по расходу топлива режима набора высоты и разгона (см. § 15.3),
в том числе и режима работы двигателя. Полученные с помощью
этих методов оптимальные режимы проверяются в летных испы-
таниях и включаются в инструкцию летчику конкретного типа
самолета в виде законов изменения скорости и режима работы
двигателя по высоте. Соблюдение этих режимов очень важно для
полной реализации боевых возможностей самолета.
Расход топлива GT. н. р, дальность LH. р и продолжительность
/н.р полета на участке набора высоты и разгона самолета при из-
вестном законе изменения скорости и режима работы двигателя
508
по высоте можно приближенно определить по следующим фор-
мулам:
^т. Н. р = Vnx )ср кон ^э*Нач) £ V (х) 1 ср ^^э*’ (20.1)
Т ____ / COS 0 \ д т Г
^н. р — ( Пх )ср д#э‘. (20.2)
^н. р ~ 3 » (20.3)
у пх ср
где Cs — секундный расход топлива, V — истинная скорость, м/с,
Нэ нач И Н3. кон — начальный и конечный уровни энергии при на-
боре высоты и разгоне.
Из формулы (20.1) следует, что расход топлива на набор вы-
соты и разгон пропорционален силе тяжести самолета и заметно
зависит от лобового сопротивления, особенно при малых избыт-
ках тяги. Поэтому в специальную инструкцию по расчету дально-
сти и продолжительности полета включаются таблицы времени,
пути и расхода топлива на набор высоты для различных масс
самолета и различных подвесок. Расход топлива GT. н. р пропор-
ционален секундному расходу топлива, который при включении
форсажа возрастает в 3—4 раза. Поэтому момент включения фор-
сажа при наборе высоты и разгоне определяется специальными
методами, проверяется в испытаниях и рекомендуется в инструк-
циях летчику. Наконец, из той же формулы (20.1) очевидна и
причина большого расхода топлива на подъем и разгон: расход
топлива пропорционален приросту механической энергии ЛЯЭ =
=-=Яэ. кон—//э. нач, а уровни энергии современных самолетов весьма
высоки.
По этой же причине дальности снижения (планирования) со-
временных сверхзвуковых самолетов при большой начальной ис-
тинной скорости могут быть также очень большими.
Дальность снижения с уменьшением скорости, т. е. с исполь-
зованием запаса кинетической энергии для увеличения дальности,
можно рассчитать по формуле
ZCH ===
полученной в главе 15. Дальность снижения с постоянной ско-
ростью рассчитывается по той же формуле, где &НЭ=ЛН— потеря
высоты при снижении. Рекомендуемые оптимальные режимы сни-
жения приведены также в главе 15.
Продолжительность полета и расход топлива на участке сни-
жения приблизительно можно рассчитать аналогично участку на-
бора высоты:
^сн — Vn 9 ’ сн — ср^сн I ч-1 ’
у их ср
где Ch ср — средний часовой расход топлива на участке снижения;
t<M — время снижения, ч.
509
Отличие состоит лишь в том, что здесь пх<0 и энергия не уве-
личивается, а уменьшается (Л//э<0), так как Р<Х.
§ 20.2. Дальность и продолжительность горизонтального полета
Расход топлива, время и дальность горизонтального полета с
разгоном определяются по тем же формулам, что и в наборе вы-
соты с разгоном, так как основная доля энергии, заключенная в
топливе, в этом случае также расходуется на увеличение механи-
ческой энергии самолета.
Рассмотрим установившийся прямолинейный горизонтальный
полет, в котором энергия топлива расходуется только на преодо-
ление лобового сопротивления самолета. Дальность в километрах
и продолжительность в часах такого полета определяются по из-
вестным формулам:
г ___ г. П . J. бгт, г, п
^г.п— q , *г.п— Cfi •
где q — километровый расход топлива, кг/км.
Располагаемый запас топлива на горизонтальный полет GT. г. п
можно легко найти, если известны расходы на всех других этапах
движения самолета (они даются в инструкции по расчету дально-
сти и продолжительности):
^т. г. п = (GT, зем 4“ От. н. р + GT. сН + Сгт П0с 4-
4“ ОТв боя + От . гар 4“ От . нев)*
Гарантийный запас топлива GT. гар предусматривается на воз-
можное несоответствие расхода топлива указанному в инструкции,
ухудшение аэродинамики самолета в процессе эксплуатации и
устанавливается в количестве 5—7% всего запаса топлива.
Километровый расход q определяется делением часового рас-
хода топлива Ch (кг/ч) на истинную скорость полета (км/ч).
Учитывая, что
СА = СуаР
и что для установившегося полета Р=ХТ= , найдем
__________________ Ch СуЛР СуаХг СуЛС
Ч V у у — ^у •
где Суд — удельный расход топлива на данном режиме полета,
кг/ч/кгстяги.
Очевидно что, чем меньше километровый и часовой расходы
топлива, тем больше дальность и продолжительность горизонталь-
ного полета соответственно.
Для определения скоростей, при которых километровый и ча-
совой расходы топлива будут минимальными, проанализируем фор-
мулы (20.4) и (20.5),
510
(20.4)
(20.5)
Рис.
дальности и максимальной продол-
жительности горизонтального полета
20.2. Режимы максимальной
значительное дросселирование
Тяга двигателей, необходимая для установившегося полета,
может быть значительно меньше максимальной, особенно на ма-
лых высотах. Удельный расход топлива Суд, как было показано
в главе 6, существенно зависит от дросселирования двигателя: при
значительном дросселировании с уменьшением тяги до
(0,20,3) Ртах удельный расход возрастает в 2—1,5 раза (глава 6,
рис. 6.14) .
На средних и больших высо-
тах, где тяга находится в преде-
лах ОТ 0,5Ртах до Ртах, уДСЛЬНЫЙ
расход топлива при дросселирова-
нии изменяется сравнительно ма-
ло. Поэтому, учитывая, что Р = ХГ,
по формуле (20.4) находим, что
минимальный часовой расход топ-
лива, а следовательно, и макси-
мальная продолжительность го-
ризонтального полета будут на
той скорости, на которой Хг ми-
нимально, т. е. на наивыгодней-
шей СКОрОСТИ (рИС. 20.2): Vfmax =
= Vhb.
На малых высотах ввиду
больших избытков тяги требуется
двигателя, при котором Суд увеличивается, что невыгодно. По-
этому минимальный часовой расход топлива достигается при ско-
рости, несколько большей наивыгоднейшей, при которой требуется
меньшее дросселирование двигателя.
Из формулы (20.5) следует, что минимальный километровый
расход топлива, а следовательно, и максимальная дальность го-
ризонтального установившегося полета при Суд = const будут до-
стигаться на скорости, при которой отношение Xr/V минимально.
Такая скорость называется крейсерской (VKPC). Она опреде-
ляется проведением касательной к кривой Хг из начала координат
(рис. 20.2).
На малых высотах в связи с увеличением Суд при значитель*
ном дросселировании двигателя скорость минимального километ-
рового расхода топлива несколько увеличивается по сравнению
с крейсерской.
В инструкциях по расчету дальности и продолжительности по-
лета конкретных самолетов для каждой высоты приводятся ре-
жимы полета, на которых достигается максимальная дальность и
продолжительность полета.
На рис. 20.2 заштрихованы области скоростей горизонтального
полета, оптимальных по условиям максимальной продолжитель-
ности Vfmax и максимальной дальности Vi max*
С увеличением высоты уменьшаются избытки тяги над лобо-
вым сопротивлением и, следовательно, требуется все меньше и
511
Рис. 20.3. Зависимость километрово-
го расхода топлива от высоты поле-
та и приборной скорости
меньше дросселировать двигатель. При этом удельный расход топ-
лива до некоторой высоты, меньшей потолка на 2—3 км, умень-
шается, а далее несколько возрастает. Этим и определяется вы-
сота, на которой достигается максимальная продолжительность
горизонтального установившегося полета.
Километровый расход топлива с высотой уменьшается значи-
тельно сильнее, чем часовой, так как кроме уменьшения Суд здесь
большую роль играет увеличение крейсерской (истинной) скоро-
сти полета ввиду смещения кри-
вых лобового сопротивления Хг
па большие истинные скорости
(гл. 13, рис. 13.8).
На рис. 20.3 показан пример
изменения километрового расхо-
да топлива по приборной скоро-
сти для различных высот. Как
видно из этого графика, прибор-
ная скорость режима максималь-
ной дальности уменьшается с вы-
сотой (приближаясь к крейсер-
ской), а минимальный километ-
ровый расход при увеличении
высоты .от нуля до 10 км умень-
шается более, чем в два раза за счет роста истинной скорости,
уменьшения температуры воздуха и степени дросселирования дви-
гателя, влияющих на удельный расход топлива.
Наивыгоднейшая высота, на которой достигается минималь-
ный километровый расход топлива, располагается на 1—2 км
ниже дозвукового потолка.
При выгорании топлива масса самолета постепенно уменьша-
ется, что приводит к увеличению потолка, а вместе с этим и наи-
выгоднейшей высоты, на которой километровый расход топлива
минимален. Следовательно, для достижения максимальной даль-
ности нужно, постепенно увеличивая высоту соответственно изме-
нению массы самолета, все время лететь на наивыгоднейшей вы-
соте.
Набор высоты при этом происходит с очень малым углом на-
клона траектории, а для выдерживания такого режима на высо-
тах, больших 11 км, достаточно сохранять число М полета и ре-
жим работы двигателя постоянными, и самолет сам будет наби-
рать высоту по мере уменьшения массы. Такой режим полета на-
зывают п о л е т о м по потолкам.
Рассчитаем дальность полета по потолкам с учетом перемен-
ного веса.
Так как масса самолета непрерывно уменьшается, то уравне-
ние изменения массы по пролетаемому пути запишется в виде
512
Подставляя сюда выражения для километрового расхода (20.5),
найдем
dG __ Cyifi
“ КУ ’
откуда
Так как в процессе полета по потолкам скорость, угол атаки
и удельный расход постоянны, то полученное уравнение легко ин-
тегрируется
суд г суд ^кон
инач
В полученном выражении истинная скорость V, аэродинамиче-
ское качество К и удельный расход топлива Суд соответствуют ре-
жиму минимального километрового расхода и остаются постоян-
ными в течение всего полета по потолкам, а километровый расход
в соответствии с формулой (20.5) уменьшается пропорционально
массе.
В полете на сверхзвуковых скоростях, для достижения кото-
рых необходимо использование форсажа, часовой расход топлива
в 3—4 раза больше, а продолжительность меньше, чем в полете
на дозвуковых скоростях и бесфорсажных режимах. При включе-
нии форсажа удельный расход топлива возрастает в 2—2,5 раза.
Километровый расход топлива при этом возрастает в меньшей
степени, так как он обратно пропорционален скорости (форму-
ла 20.5). Для самолетов, которые будут летать на числах М^З,
возможно уменьшение километрового расхода топлива за счет ско-
рости настолько, что он станет меньше, чем на дозвуковых ско-
ростях на бесфорсажных режимах работы двигателя. Однако это
не означает,-что максимальная сумм-арная дальность полета будет
достигаться на сверхзвуковых скоростях с использованием фор-
сажных режимов. Дело в том, что потребуется много топлива для
достижения чисел М^З.
Расход топлива на маневр рассчитывается по известному ре-
жиму работы двигателя, часовому расходу топлива на этом ре-
жиме и продолжительности маневра:
^т. ман ==: (-'//ман*
Если в процессе маневра значительно изменялись высота и
скорость полета, например на полупетле, то приближенный расчет
расхода топлива на маневр может быть выполнен по той же фор*
муле с осреднением часового расхода:
От. ман == Сh ср^ман*
Для более точных расчетов требуется интегрирование уравне-
ний движения совместно с уравнением расхода теплива.
17—21
513
§ 20.3. Суммарная дальность и продолжительность
полета и влияние на нее эксплуатационных факторов
Различают три характеристики дальности полета: техническую,
практическую и тактическую.
Техническая дальность полета — это максимальное
расстояние, которое мог бы пролететь самолет в стандартных ат-
мосферных условиях и безветрии до полного израсходования топ-
лива от взлета до посадки.
Практическая дальность полета — это максималь-
ное расстояние, которое может пролететь самолет в реальных ме-
теоусловиях с учетом расхода топлива на запуск двигателей, ру-
ление перед взлетом и после посадки, возможный повторный за-
ход на посадку, а также с учетом навигационного и гарантийного
запасов и невырабатываемого остатка топлива.
Техническая и практическая дальности существенно зависят от
высоты полета и являются важными летными характеристиками,
по которым самолеты сравниваются между собой.
Тактическая дальность полета — это максимальное
расстояние, которое может пролететь самолет с заданными режи-
мом и профилем полета с выполнением поставленной боевой за-
дачи. В зависимости от характера задания и конкретной ситуации
тактическая дальность полета может изменяться в широких пре-
делах. Для выполнения боевой задачи могут потребоваться раз-
личные время пребывания над территорией противника и над
целью, время боя и дежурства в воздухе, профили полета и режи-
мы работы двигателя. Например, в полете на малых высотах,
особенно на форсажных режимах, тактическая дальность может
быть в несколько раз меньше, чем в полете на большой высоте,
обеспечивающей максимальную дальность.
Очевидно, что тактическая дальность должна определяться с
учетом конкретных особенностей полета.
В простейшем случае дальность полета складывается из даль-
ностей трех участков: набора высоты с разгоном, крейсерского
участка и снижения:
L = ^н. Р 4” «^Г. П 4” ^СН«
Рассмотрим влияние эксплуатационных факторов на суммар-
ную дальность полета.
Изменение массы самолета. Согласно формуле (20.5)
километровый расход топлива в горизонтальном установившемся
полете изменяется пропорционально массе. Но при увеличении
массы необходимо увеличить скорость полета и тягу двигателя,
что приведет к изменению удельного расхода топлива Суд.
Изменение режима полета на больших высотах незначительно
влияет на километровый расход топлива. Поэтому последний из-
меняется практически пропорционально массе. На малых высотах
с учетом изменения режима полета километровый расход топлива
зависит от массы самолета значительно меньше, чем на больших
514
расход топлива на участке
Рис. 20.4. Зависимость крейсер-
ской воздушной скорости от ско-
рости ветра
высотах, так как при увеличении массы и соответственно тяги дви-
гателя удельный расход уменьшается вследствие уменьшения сте-
пени дросселирования двигателя.
Необходимо учитывать, что расход топлива на набор высоты
и разгон примерно пропорционален массе (формула 20.1). По-
этому суммарная дальность полета на больших высотах сильнее
зависит от массы, чем километровый
горизонтального полета.
Увеличение лобового сопротив-
ления в равной мере увеличивает
километровый расход топлива в го-
ризонтальном полете и уменьшает
дальность планирования (формулы
20.5 и 20.2) и в меньшей степени
влияет на расход топлива при на-
боре высоты и разгоне. При наруж-
ных подвесках происходит одновре-
менное увеличение массы и лобового
сопротивления. Суммарное умень-
шение дальности полета в этом слу-
чае может достигать 15—30%.
Повышение температуры
на километровый расход топлива в горизонтальном полете. Это
можно установить с помощью формулы (20.5), если учесть, что
часовой расход Ch и истинная скорость при постоянном давлении
(постоянной высоте по барометрическому высотомеру) и постоян-
ном Су изменяются одинаково— пропорционально У Г.
При наборе высоты и разгоне повышение температуры на-
ружного воздуха несколько увеличивает расход топлива, особенно
при малых избытках тяги. В целом суммарная дальность полета,
как правило, уменьшается незначительно.
Влияние ветра на дальность полета существенно,
особенно на больших высотах, где скорость ветра может достигать
150—200 км/ч. Километровый расход топлива с учетом попутного
или встречного ветра определяется по формулам:
?поп = у + дет* <7встр = у •
наружного воздуха не влияет
Учитывая, что истинные крейсерские скорости современных
самолетов лежат в пределах 700—900 км/ч, приходим к выводу,
что на больших высотах ветер может изменить дальность гори-
зонтального полета на 15—25%.
Влияние ветра на участках набора высоты и снижения учи-
тывается путем введения поправки в дальность по формулам;
^н.р=^н.р^ —
Строго говоря, крейсерская скорость, а следовательно, и ско-
рость зависят от скорости ветра. Иллюстрация этой зависи-
мости приведена на рис. 20.4,
17*
515
В предыдущем параграфе анализ дальности горизонтального
полета с помощью кривой лобового сопротивления Хг приводился
в предположении безветрия. Для реальных условий такой анализ
нужно проводить с учетом ветра, т. е. график Хг должен быть по-
строен не по воздушной, а по путевой скорости.
При встречном ветре путевая скорость будет меньше воздуш-
ной на величину скорости ветра Wx. Поэтому для определения
крейсерской скорости по кривой Хг начало координат О нужно
сместить вправо (против ветра) на величину Wx—в точку О' и
касательную к кривой Хг проводить от точки О'.
Из графика видно, что при встречном ветре крейсерская ско-
рость увеличивается, а при попутном — уменьшается.
Для дозвуковых, и особенно для малоскоростных, самолетов
при сильном ветре эту поправку в режим максимальной дальности
необходимо учитывать. Для современных скоростных самолетов,
имеющих сравнительно большие крейсерские скорости, влияние
ветра на режим максимальной дальности до средних высот несу-
щественно, и полет практически выполняется со скоростью режима
максимальной дальности, рекомендованной в инструкции по рас-
чету дальности и продолжительности полета для безветрия. Необ-
ходимо лишь учитывать изменение километрового расхода топли-
ва по приведенным выше формулам.
§ 20.4. Способы увеличения дальности полета
На самолетах с двумя двигателями в полетах на малых и сред-
них высотах можно заметно увеличить дальность полета за счет
выключения одного двигателя. При этом тягу работаю-
щего двигателя нужно увеличить в два раза. Степень дросселиро-
вания, а следовательно, и удельный расход топлива уменьшатся.
Этот способ можно рекомендовать лишь для самолетов, у ко-
торых двигатели расположены близко к продольной оси, так что
выключение одного двигателя не вызывает возникновения боль-
ших моментов и самолет может быть легко сбалансирован. Если же
при выключении одного двигателя появляются большие боковые
моменты, которые трудно сбалансировать без применения сколь-
жения, эффект увеличения дальности от уменьшения Суд может
быть сведен к нулю повышением лобового сопротивления при
скольжении. Поэтому такой способ повышения дальности полета
на малых и средних высотах требует индивидуального подхода для
каждого типа самолета.
На высотах, больших 5000—7000 м, выключение одного двига-
теля ничего не дает, так как двигатели уже работают на режиме,
при котором удельный расход топлива близок к минимальному.
Изменяемая стреловидность крыла позволяет повы-
сить дальность полета за счет уменьшения километрового расхода
топлива в горизонтальном полете и некоторого уменьшения рас-
хода топлива на набор высоты и разгон путем выбора стреловид-
ности крыла,
516
Для каждого числа М и коэффициента Су существует опти-
мальный угол стреловидности крыла. Пример такой зависимости
показан на рис. 15.11.
Чем больше Су и меньше число М, тем меньше должен быть
угол стреловидности крыла. С увеличением высоты горизонталь-
ного полета коэффициент Су, при котором достигается максималь-
ная дальность полета, несколько увеличивается, приближаясь к
Су крс, а число М незначительно увеличивается, оставаясь меньше
0,9. В целом оптимальная стреловидность крыла, при которой до-
стигается максимальная дальность полета на дозвуковой скорости,
лежит в пределах 15—30° и для каждого конкретного типа само-
лета указывается в инструкции летчику. Часто в крейсерском по-
лете используется взлетное положение крыла (минимальная стре-
ловидность).
Ощутимый эффект крыло изменяемой стреловидности должно
давать для увеличения дальности сверхзвукового полета, так как
большая стреловидность крыла позволяет снизить лобовое сопро-
тивление самолета.
Для увеличения дальности полета широко применяются под-
весные баки, которые однако наряду с увеличением запаса
топлива одновременно увеличивают массу и лобовое сопротивле-
ние самолета. Последнее обстоятельство заметно снижает эффект
применения подвесных баков, особенно в том случае, когда они
не сбрасываются после выработки из них топлива.
Весьма эффективным средством увеличения дальности полета
является дозаправка самолета в воздухе. Дозаправка
может быть попутной, т. е. на маршруте к цели, или встречной,
т. е. при встрече самолетов заправщиками на обратном маршруте.
Особенно большой эффект дает дозаправка от тяжелых самоле-
тов-заправщиков, способных восполнить до 80% топлива заправ-
ляемого самолета. В зависимости от возможностей самолета-за-
правщика дозаправка может увеличить дальность полета в 1,5—
2 раза.
Глава 21
ОСОБЕННОСТИ ПОЛЕТА САМОЛЕТА В ГРУППЕ
Групповым полетом называется совместный полет двух и
более самолетов. Групповые полеты выполняются в боевых по-
рядках или строях. Боевые порядки подразделяются на сомкну-
тые, разомкнутые и рассредоточенные.
В сомкнутых боевых порядках полет группы выполняется
на расстояниях, обеспечивающих одновременное маневрирование
самолетов, как правило без перемены их взаимного расположения.
В разомкнутых боевых порядках экипажи производят полет
в пределах визуальной видимости на увеличенных расстояниях,
обеспечивающих взаимное маневрирование в интересах огневого
517
взаимодействия. Основой боевых порядков является пара само-
летов.
Строи также могут быть сомкнутыми и разомкнутыми*
Сомкнутый строй — расположение самолетов в полете, при ко-
тором расстояние между ними
не превышает двух размахов и
двух длин самолетов. В р а-
зомкнутом строю эти рас-
стояния превышают два раз-
маха и две длины самолетов,
но между ними обеспечивается
надежная зрительная связь.
Таким образом, полет в сомк-
нутом боевом порядке выпол-
няется на расстояниях,соответ-
ствующих разомкнутому строю.
Применяются следующие
основные формы строя: пеленг,
фронт, колонна, клин и ромб.
Рис. 21.1. Параметры строя
§ 21.1. Параметры строя,
их определение в полете
Параметры строя —
это координаты самолета ведо-
мого в системе отсчета, связан-
ной с самолетом ведущего (или,
наоборот, координаты самоле-
та ведущего в системе отсчета,
связанной с самолетом ведомо-
го). При этом может приме-
няться как прямоугольная, так
и полярная система координат,
удобна для расчета и анализа
Прямоугольная система
движения самолетов. Параметрами строя в этой системе являются
(рис. 21.1):
— дистанция £>(х);
— интервал И(г);
— принижение или превышение h(у).
В полярной системе координат, используемой летчиком в
полете, параметрами строя будут:
— поперечный (горизонтальный) угол визирования (<рг) — в
системе ведомого или ракурс (ег)—в системе ведущего;
— продольный (вертикальный) угол визирования (фв) или ра-
курс ев;
— дальность d.
В некоторых случаях вместо угла визирования <рв летчик ис-
пользует линейную координату h(y).
Оценку параметров строя в полете ведомый осуществляет либо
по месту своего самолета относительно самолета ведущего — в си-
518
стеме ведущего, либо по положению и размерам самолета веду-
щего относительно видимых частей своего самолета — в системе
ведомого.
При первом способе ведомый летчик может держать свое место
в строю только при небольших интервалах и дистанциях (в строях,
близких к сомкнутым) и при достаточно плавном пилотировании
ведущим.
Рис. 21.2. Определение параметров строя:
а — в системе ведущего; б •« в системе ведомого
При втором способе определения параметров строя (в системе
ведомого) ведомый летчик оценивает положение изображения са-
молета ведущего относительно видимых частей своего самолета
по двум углам визирования — горизонтальному <рг и вертикаль-
ному срв (рис. 21.2). Первый отсчитывается от плоскости симмет-
рии своего самолета до линии визирования на самолет ведущего,
второй — от плоскости (линии), проведенной через середину опти-
ческого прицела, параллельно полу кабины (перпендикулярно пер-
вой линии). Дальность определяется по угловым размерам само-
лета ведущего Тс. Система ведомого используется им на расстоя-
ниях порядка 200—400 м.
Точность выдерживания своего места в строю зависит от точ-
ности определения параметров строя летчиком и возможностями
самолета по их изменению. Степень изменения параметров строя
определяется их производными, т. е. скоростями относительного
перемещения:
2ЁЛ — 1/с. J^L — yc
dt х' dt dt у’
либо в полярной системе координат по изменению дальности
dd ту с
v
и углов визирования
519
§ 21.2. Прямолинейный полет в составе пары
21.2.1. Выдерживание параметров строя
Выдерживание дистанции. После занятия своего места в строю
сохранение заданной дистанции в прямолинейном полете обеспе-
чивается равенством скоростей ведомого и ведущего. В результате
даже при.незначительной разности скоростей дистанция начинает
Рис. 21.3. Обоснование действий летчика по сохранению ди-
станции при непреднамеренном ее увеличении (а) и умень-
шении (б)
изменяться. Заметив изменение дистанции, ведомый летчик дол-
жен без промедления исправить возникшее отклонение. Действия
его должны быть следующими.
При увеличении дистанции летчик должен увеличить тягу дви-
гателя (рис. 21.3, а) и вызвать разгон самолета до скорости, не-
сколько большей, чем у ведущего РВщ (участок /). После того как
началось сближение, тягу необходимо уменьшить, для того чтобы
скорость сближения не увеличивалась (участок 2). При подходе
к заданной дистанции тягу необходимо уменьшить для погашения
скорости сближения (участок 5). После того как дистанция пере-
станет изменяться, частоту вращения ротора двигателя необходи-
мо увеличить для поддержания скорости, равной скорости веду-
щего УвЩ (участок 4).
Действия РУД и изменения параметров строя при уменьшении
дистанции между самолетами показаны на рис. 21.3, б. Как видно,
изменение дистанции производится двойным изменением тяги раз-
ного знака, каждое из которых в свою очередь осуществляется
двойным движением РУД.
Потребные импульсы тяги будут зависеть от дальности — чем
она больше, тем больше колебания самолета по дистанции, ско-
520
рости сближения (отставания) и соответственно потребные уско-
рения.
При уменьшении заданной дистанции частота работы РУД воз-
растает, промежуточный участок 2 сокращается и на малых ди-
станциях (50 м и менее) может вообще отсутствовать: после им-
пульса на разгон частота вращения ротора двигателя сразу умень-
шается для торможения, и наоборот, т. е. летчик в большей сте-
пени ориентируется по изменению скорости. На больших дально-
стях для оценки скорости сближения можно использовать указа-
тель скорости (если известна скорость ведущего).
Выдерживание интервала. Допустим, что в результате непроиз-
вольного сближения самолетов уменьшился интервал между само-
летами. Заметив это, летчик создает крен в сторону от ведущего,
чем вызывает разворот своего самолета. Разворот следует про-
должать до тех пор, пока интервал не начнет увеличиваться. После
этого крен убирается и при значительном изменении интервала
самолет некоторое время движется с V*, удаляясь от ведущего.
При подходе к заданному интервалу летчик создает крен в проти-
воположную сторону и ставит свой самолет на курс, параллель-
ный ведущему.
При создании значительного крена от ведущего возможно его
закрытие своим самолетом. Поэтому при выполнении такого ма-
невра следует заранее обеспечить себе необходимое принижение.
Выдерживание принижения. При увеличении принижения лет-
чик кратковременным увеличением перегрузки искривляет траек-
торию вверх и создает вертикальную скорость сближения При
подходе к заданному значению принижения летчик движением
ручки управления от себя кратковременно уменьшает перегрузку,
после чего вновь продолжает полет с прежней перегрузкой.
21.2.2. Упр авляемость самолета в строю
Под управляемостью самолета в строю будем понимать его
способность изменять параметры строя за ограниченное время,
т. е. располагаемые относительные скорости Vcx, V%. Так как
ведомый летчик не использует максимальные значения этих ско-
ростей, то целесообразно рассматривать их значения, достигае-
мые за сравнительно короткое время, порядка нескольких секунд
(А/).
В прямолинейном установившемся горизонтальном полете рас-
полагаемые скорости определяются:
Способность ведомого самолета изменять скорость по дистан-
ции определяется значениями располагаемых тангенциальных пе-
регрузок как при увеличении частоты вращения ротора двигателя,
так и при ее уменьшении. Маневренность по интервалу зависит от
521
величины создаваемого крена, а по принижению — от изменения
нормальной перегрузки.
Наиболее управляемым (чувствительным) самолет является по
принижению, а наименее — по дистанции. Соответственно времени
регулирования параметров строя распределяется и внимание лет-
чика.
21.2.3. Влияние режима полета на выдерживание’
параметров строя
Скорость. Вблизи наивыгоднейшей скорости, с одной стороны,
имеется большой запас тяги, а с другой, из-за большой чувстви-
тельности самолета к изменению тяги требуется более точное ее
регулирование. Вследствие этого на таких скоростях полета по-
вышается возможность непроизвольной раскачки самолета по
дистанции. На скоростях полета, близких к максимальной (до-
звуковой), несмотря на уменьшение запаса тяги, а следовательно,
увеличение времени регулирования, точность выдерживания
дистанции повышается. Однако на таких скоростях полета из-за
сравнительно небольших градиентов и х”у повышается чув-
ствительность самолета к изменению усилия на ручке и ее пере-
мещению, что опасно возможностью раскачки самолета по высоте
полета (принижению).
Поэтому оптимальной скоростью для полета строя является
некоторая средняя скорость между наивыгоднейшей и максималь-
ной, на которой примерно одинаковы модули тангенциальных пе-
регрузок при разгоне и торможении.
Высота. С увеличением высоты полета при одинаковых пере-
мещениях РУД происходит меньшее изменение тяги. Кроме того,
при изменении истинной скорости с ростом высоты меньше изме-
няется лобовое сопротивление самолета. Вследствие этого само-
лет становится более инертным. Это несколько усложняет выдер-
живание параметров строя. Оптимальная приборная скорость по-
лета строем с увеличением высоты полета уменьшается.
Угол наклона траектории. При подъеме положительный избыток
тяги уменьшается, отрицательный увеличивается. Возможности ве-
домого по сокращению дистанции становятся значительно хуже,
чем по ее увеличению. Поэтому движение РУД на уменьшение
оборотов должны быть мелкими, дистанцию увеличивать лучше
в несколько приемов. При значительном отставании целесообразно
выполнить «волну вниз»: уменьшить угол наклона до величины,
меньшей чем у ведущего, разогнать самолет, при подходе к за-
данной дистанции выполнить пологую горку.
На снижении наблюдается обратная картина — возможности
по догону значительно превышают возможности по отставанию.
В этом случае предпочтителен строй на увеличенной дистанции.
522
Сокращение последней лучше выполнять в несколько приемов.
Для более энергичного торможения можно выпускать тормозные
щитки или выполнить змейку.
§ 21.3. Маневрирование для изменения параметров строя
Такими маневрами являются:
рестроение.
Пристраиванием называ-
ется маневр ведомого по сокра-
щению расстояния до самолета
ведущего в целях занятия задан-
ного места в строю. Порядок при-
страивания определяется требо-
ваниями обеспечения безопасно-
сти полета и управляемости само-
лета по параметрам строя. По-
скольку наибольшее время затра-
чивается на изменение дистанции,
то ее заданное значение и уста-
навливается в первую очередь.
Два других параметра в процес-
се установления дистанции вы-
держиваются увеличенными при-
мерно в два раза. После занятия
исходной дистанции и выравни-
вания скоростей последователь-
но сокращаются до заданных
сначала интервал, и в последнюю
очередь наиболее управляемый
параметр — принижение.
Размыканием называется
маневр ведомого в целях увели-
чения параметров строя. Размы-
кание производится в порядке,
обратном пристраиванию: снача-
ла увеличивается принижение,
затем интервал, в последнюю
Рис. 21.4. Порядок перестроения
очередь — дистанция.
Перестроением называется маневр ведомого, связанный с
изменением места в строю. В большинстве случаев это смена пе-
ленга. Такое перестроение выполняется следующим образом. Сна-
чала увеличивается принижение настолько, чтобы самолет ведо-
мого был ниже спутного следа от самолета ведущего с достаточ-
ным запасом. При полете в плотных строях (0^50 м) после этого
увеличивается дистанция. На больших расстояниях дистанция
обычно не изменяется. Затем создается крен в сторону ведущего
и начинается разворот (рис. 21.4). В момент прохода под траек-
торией ведущего крен изменяется на обратный, при этом выход
523
в противоположную сторону осуществляется на интервал больше
заданного на величину \И (также в целях безопасности). Это
достигается либо уменьшением крена, либо выполнением паузы.
Во втором случае ведомый в момент прохода створа ведущего
выводит самолет из крена и летит прямолинейно в течение Д/п:
. где V Ч = tg 7,
затем выполняет разворот на курс, параллельный ведущему, с та-
ким же креном, с каким он начинал перестроение. После уточне-
ния дистанции ведомый сокращает интервал и принижение до за-
данных.
При больших интервалах и кренах за счет существенного ис-
кривления траектории становится отрицательной и возможно
увеличение дистанции. Во избежание этого перед разворотом не-
обходимо несколько увеличить частоту вращения ротора двигателя
и соответственно скорость самолета.
На малых высотах перестроение производится с превышением.
Во избежание закрытия ведущего дистанция перед перестроением
увеличивается.
§ 21.4. Взлет пары (группы)
21.4.1. Взлет в паре
При взлете с ИВПП вследствие ее ограниченной ширины па-
раметры строя существенно уменьшаются: интервал до 20—30 м,
дистанция до 30—40 м, принижение равно нулю. Это накладывает
особенности на технику их выдерживания.
Перед взлетом необходимо занять соответствующий пеленг —
с наветренной стороны, с тем чтобы не попасть в спутный след
самолета ведущего. В процессе разбега интервал выдерживается
сохранением направления движения самолетов. При этом ведомый,
имея в поле зрения самолет ведущего, следит за перемещением
своего самолета относительно ВПП с тем, чтобы не допустить
сближения и не выкатиться за боковую границу полосы. Подъем
носового колеса при нормальной дистанции производится по веду-
щему.
При взлете на неизменном режиме работы двигателя (макси-
мал, полный форсаж) ведомый практически не может регулиро-
вать величину дистанции, поэтому здесь возможен как обгон, так
и отставание. Для предотвращения обгона пары обычно комплек-
туются таким образом, чтобы тяга самолета ведомого была не-
сколько меньше. Кроме того, ведомый в начале разбега может
частично использовать тормоза. Если все же обгон произошел, ве-
домый предупреждает об этом по радио ведущего и продолжает
выполнять взлет самостоятельно. Ведущий после этого следит за
ведомым и занимает свое место после взлета на безопасной вы-
524
соте. При отставании ведомый, удерживая в поле зрения самолет
ведущего, выполняет взлет как одиночно (подъем носового коле-
са— с контролем скорости!) и на определенной высоте пристраи-
вается к ведущему.
После взлета на установленной высоте ведомый производит
размыкание и занимает свое место в полетном строю (боевом по-
рядке).
21.4.2. Взлет по одному и сбор пары (группы)
Выполняется при невозможности взлета в паре из-за состояния
ВПП, при сборе звеньев и эскадрилий ведущими групп одновре-
менно взлетающих самолетов.
В этом случае ведомый начинает разбег после отрыва ведущего
через временной интервал Д/р. Вследствие этого после взлета, са-
молет ведущего уходит от ведомого на расстояние до 3—5 км,
Догон по прямой в этом случае займет слишком много времени.
Поэтому сбор группы осуществляют обычно в три этапа. Пер-
вый из них — этап предварительного сближения осуществляется
за счет слитно выполняемых одного-двух разворотов (на 180°),
которые ведомый должен начинать после ведущего через опреде-
ленное время /н. р:
аги.р— 2 ' 2У ’
где с?2 — расстояние между самолетами после разворота. Так, для
выхода на d2=l км при Д/р = 20 с и V = 720 км/ч Д^н. Р =12,5 с.
Второй этап — догон, выполняется по заранее рассчитанной
программе сближения. Его целью является выход ведомого в точ-
ку пространства, из которой возможно безопасное пристраивание.
Выйдя в расчетную точку на удвоенном интервале и приниже-
нии, ведомый выполняет третий заключительный этап сбора —
пристраивание.
§ 21.5. Выполнение разворотов, виражей, спиралей
Выполнение маневра с сохранением всех параметров строя, в
том числе и относительного принижения, называется маневром
«в одной плоскости». Если же сохраняется абсолютное приниже-
ние, то говорят, что маневр выполняется «на одной высоте».
.Рассмотрим движение внешнего ведомого при выполнении ви-
ража «в одной плоскости» (рис. 21.5). Для сохранения своего мес-
та в строю ведомый должен двигаться по дуге большего радиуса
с такой же угловой скоростью в горизонтальной плоскости, что
и ведущий. Если известна скорость УВщ и радиус гвщ ведущего, то
потребную скорость ведомого VBM можно определить из следую-
щего условия
О) — — ^вм
Гвщ гвм
525
Отсюда
17 _ ]/ г°м
И ВМ--- v вщ г
Г ВЩ
Гвщ + и COS 1 \
~г I — * вщ
' вщ /
+ AV,
где
ДУ = 0>И COS 7 = _£И£ЙЦ_ *
V ВЩ
Рис. 21.5. Изменение взаимного положения ведомого и ведущего при
вводе в вираж «в одной плоскости»
При интервалах порядка 50—100 м разность скоростей не пре-
вышает 10—15 км/ч, поэтому различие в частоте вращения рото-
ра двигателя ведомого и ведущего в процессе установившегося
разворота будет несущественным. Основные трудности возникают
в процессе ввода и вывода из виража. Во-первых, внешний ведо-
мый должен за время ввода /Вв обеспечить разгон своего само-
лета с ускорением
• _ Hsin*t
Jx ВМ - f S / •
*ВВ V ВЩ*ВВ
для чего потребуется избыток тяги
а И sin т
--ЗхылШ --- G V t '
v ВПСВВ
Во-вторых, для сохранения плоскости строя ведомый должен
набрать высоту AH—Hsiny, двигаясь в процессе ввода с углом
набора высоты 0Ср, определяемым выражением
sin 0сра .
V Вщ^вв
526
Для уравновешивания составляющей силы тяжести необходимо
дополнительно увеличить тя.гу на величину
AP2 = Gsin ©
v вщгвв
Таким образом, суммарное потребное увеличение тяги на вво-
де в разворот (вираж) по отношению к тяге ведущего составит
ДР=ДР! +AP2=2g4^P-. (21.1)
У вщгвв
Оно тем больше, чем больше интервал и меньше время ввода.
Кроме того, если вираж установившийся, тяга ведомого должна
возрастать и для уравновешивания возрастающего вследствие уве-
личения перегрузки лобового сопротивления.
На выводе из виража самолет внешнего ведомого должен
уменьшить высоту на Д// и скорость на ДУ, т. е. затормозиться на
снижении. Для этого необходимо уменьшить тягу на ДР по фор-
муле (21.1) или увеличить лобовое сопротивление выпуском тор-
мозных щитков. Так как при установившемся развороте угловые
скорости (й = ^1^у/УВщ ведущего и ведомого самолетов должны
быть равны, то у ведомого, имеющего большую скорость, должны
быть больше угол крена и перегрузка пу. Однако при сравнитель-
но больших скоростях полета (больших радиусах виража) и ма-
лых интервалах между самолетами потребные крены и перегрузки
самолетов строя различаются незначительно.
С учетом сказанного техника выполнения виража «в одной
плоскости» внешним ведомым должна быть следующей.
Для учета времени реакции летчика и приемистости двигателя
ведущий заранее предупреждает ведомого о предстоящем маневре.
Ведомый, получив команду, увеличивает частоту вращения ротора
двигателя. При создании крена ведущим ведомый вводит самолет
в разворот с одновременным увеличением угла наклона траектории
и дополнительным увеличением частоты вращения (рис. 21.6, а).
При подходе к заданному крену самолет переводится из набора
высоты в горизонтальный разворот кратковременным уменьше-
нием перегрузки с увеличением крена и одновременно тяга дви-
гателя уменьшается до потребной на вираже.
В процессе установившегося разворота ведомый регулирует ве-
личину интервала изменением крена: при его увеличении интер-
вал сокращается, при уменьшении — увеличивается. Дистанция и
принижение выдерживаются так же, как и в прямолинейном по-
лете.
В начале вывода из виража ведомый должен перевести само-
лет на снижение, т. е. опережающим должно быть движение руч-
ки управления «от себя» и затем — в сторону для уменьшения
крена. Одновременно уменьшается частота вращения ротора дви-
гателя в значительно большей степени, чем у ведущего. Во избе-
жание глубокого дросселирования двигателя или уменьшения вре-
527
мени вывода можно выпустить тормозные щитки. В конце вывода
тяга увеличивается до потребной в горизонтальном полете.
Задачей ведущего является обеспечение минимально необходи-
мого времени ввода и вывода, а также создание условий, облег-
чающих выдерживание места ведомым. Так при выводе с внеш-
ним и при вводе с внутренним ведомым можно кратковременно
увеличивать частоту вращения ротора двигателя.
Рис. 21.6. Потребная тяга на вираже:
а — внешний ведомый; б — внутренний ведомый
При выполнении виража внутренний ведомый в начале ввода
должен уменьшить тягу, в конце ввода довести ее до потребной
на вираже, при выводе — увеличить тягу для обеспечения разго-
на при подъеме, в конце вывода уменьшить до потребной в гори-
зонтальном полете (рис. 21.6,6).
Техника выполнения спирали парой имеет много общего с тех-
никой выполнения виража. Отличие заключается в том, что веду-
щий дросселирует двигатель и возможности ведомого по тормо-
жению существенно ухудшаются. Это может привести к сокраще-
нию дистанции при вводе в спираль внутренним ведомым и при
выводе — внешним. Во избежание этого ведомый может исполь-
зовать выпуск тормозных щитков, а ведущий — повышенную тягу
двигателя за счет более позднего уменьшения частоты вращения
ротора двигателя при вводе в спираль и предварительного ее уве-
личения перед выводом.
§ 21.6. Выполнение пикирования и горки
Так же как и в одиночном полете, ввод в пикирование может
осуществляться с прямой, разворота, полупереворота и перево-
рота.
528
Ввод с прямой целесообразно осуществлять при пилотировании
в системе ведомого, т. е. удерживая изображение самолета веду-
щего в определенной части фонаря кабины. В процессе ввода углы
пикирования у самолета ведущего будут несколько больше, чем
у ведомого, скорость нарастает быстрее и для сохранения дистан-
ции ведомый должен увеличивать тягу. В конце ввода ведущий
дросселирует двигатель с таким расчетом, чтобы оставить запас
тяги ведомому.
Ввод с разворота внутренним ведомым выполняется «в одной
плоскости», внешним — «на одной высоте». При сохранении от-
носительного принижения внешний ведомый в момент создания
крена должен перевести самолет в набор с разгоном, а затем пе-
реводить его на снижение с большей высоты и скорости, чем веду-
щий. Для реализации такого движения требуются большие избыт-
ки тяг и существенные приросты перегрузки, сначала положитель-
ные, затем отрицательные. При сохранении абсолютного приниже-
ния участок «взмывания» (набор и потеря Н) срезается, относи-
тельное изменение тяги и перегрузки уменьшается, маневр стано-
вится более простым и безопасным.
Ввод внутренним ведомым осуществляется с обязательным со-
хранением (или некоторым увеличением) относительного приниже-
ния. В этом случае ведомый уменьшает тягу с началом создания
крена. Если ведущий сделает то же самое сразу после создания
крена и начнет переводить самолет на снижение, действия ведо-
мого значительно упрощаются: его самолет будет продолжать
искривлять траекторию книзу, различие в скоростях будет сведено
к минимуму. В конце ввода ведомый может переходить к пило-
тированию «на одной высоте».
Вывод. В процессе пикирования ведомый, выдерживающий от-
носительное принижение, находится, как правило, выше ведущего
(рис. 21.7). При одновременном начале вывода с равной перегруз-
кой это приводит к выходу из пикирования с превышением (/).
При выдерживании фв = const ведомый будет двигаться по более
короткой траектории, что приведет к сближению самолетов (2).
Во избежание этого ведомый должен либо уменьшить тангенци-
альную перегрузку, либо начинать вывод с задержкой Д/ (5).
При выводе из пикирования с сохранением ведомым абсолют-
ного принижения векторы скоростей самолетов будут параллельны
и при равной тяге одинаковы. Это значительно упрощает технику
пилотирования, но неприменимо при выводе на малой высоте.
Ввод в пикирование с кренами более 90° выполняется только
в сторону ведущего. В противном случае самолет ведущего неиз-
бежно попадает в непросматриваемую зону.
При вводе переворотом и одновременном выполнении полубоч-
ки пеленг кинематически изменяется на противоположный, кроме
того, самолет ведомого оказывается с относительным превыше-
нием, которое по мере создания угла пикирования будет кинема-
тически увеличиваться, и возможно закрытие (потеря) ведущего.
Поэтому такой ввод выполняется с сохранением относительного
529
принижения. Для предотвращения кинематического уменьшения
принижения создание крена (полубочку) ведомый начинает с не-
которой задержкой, после того, как ведущий уменьшит высоту.
Ввод в горку. Относительное движение самолетов при вводе в
горку аналогично выводу из пикирования. Однако пилотирование
«на одной высоте» ограничено из-за существенного роста относи-
Рис. 21.7. Вывод из пикирования пары при сохранении ведомым:
а — относительного принижения; б — абсолютного принижения
тельного превышения и возможности закрытия самолета ведущего.
Данный способ можно применять при небольших дистанциях и
значительном интервале (фронте самолетов). В остальных слу-
чаях целесообразно выдерживать относительное принижение.
При выдерживании <pB=const возможно сближение самолетов,
поэтому ведомый должен либо уменьшать тягу (медленнее увели-
чивать), либо выполнить ввод с задержкой.
На прямолинейном участке самолет ведущего будет находить-
ся выше плоскости горизонта ведомого на sin 0 + Ao/cos 0.
Вследствие этого его скорость будет уменьшаться быстрее, дистан-
ция будет сокращаться. При больших значениях тяги ее сохране-
ние для ведомого не представляет особой сложности.
Вывод из горки осуществляется теми же способами, что и ввод
в пикирование.
§ 21.7. Обеспечение безопасности групповых полетов
Опыт групповых полетов показывает, что наибольшее количе-
ство летных происшествий и предпосылок к ним связано с опас-
ными сближениями самолетов.
530
Первой и основной причиной сближения самолетов является
потеря контроля ведомым за самолетом ведущего. При визуальном
наблюдении это происходит в результате попадания самолета ве-
дущего в непросматриваемую зону ведомого. Последняя опреде-
ляется конструктивными особенностями самолета, условиями об-
зора из кабины. Основная часть этой зоны приходится на нижнюю
полусферу. При отсутствии перископа условия обзора задней по-
лусферы значительно хуже, чем передней.
Рассмотрим влияние параметров строя на возможность потери
(закрытия) самолета ведущего. При нормальных значениях ин-
тервала и принижения ведомый может наблюдать за ведущим при
изменении дистанции довольно в широких пределах: в сторону
увеличения — практически неограниченно, в сторону уменьшения —
вплоть до выхода вперед на одну-две дистанции. Точно также из-
менение интервала в любую сторону и принижения в сторону
увеличения при сохранении дистанции практически не приводит
к потере ведущего.
При уменьшении принижения и переходе к превышению воз-
можно закрытие ведущего. Чем ближе ведомый находится к са-
молету ведущего и чем меньше горизонтальный угол визирования
на него, тем при меньшем превышении может произойти попада-
ние последнего в зону закрытия.
Большое влияние на величину зоны закрытия оказывает крен.
При накренении на ведущего зона закрытия уменьшается, прини-
жение увеличивается до значительных кренов (150—160°). При
накренении от ведущего самолет последнего попадает в зону за-
крытия тем раньше, чем меньше принижение и больше интервал.
Реальная возможность потери ведущего при накренениях воз-
никает при вводе в разворот у^внутреннего ведомого и при выво-
де— у внешнего. Поэтому на4 этих участках ведомый должен
прежде всего позаботиться о сохранении достаточного приниже-
ния, предварительно увеличив его, или начинать ввод (вывод)
с опережающим искривлением траектории за счет уменьшения
перегрузки. При малых углах визирования накренение с сохране-
нием прямолинейности полета не ведет к закрытию ведущего.
Второй причиной столкновений является сближение самолетов
на расстояния, с которых летчик не успевает выполнить маневр
отворота и прохода на безопасном удалении от самолета веду-
щего.
Минимально допустимое (безопасное) расстояние сближения
с ведущим приближенно можно оценить:
И —yzli J 1/ 2<бКЛ.
/Хо. с v х ^в у gtgl/
где /в — время запаздывания летчика, Гб — радиус безопасной зо-
ны, величина которого зависит от точности определения расстоя-
ния летчиком и допускаемых им отклонений в параметрах дви-
жения.
531
Как видим, дальность начала отворота тем больше, чем боль-
ше скорость сближения самолетов и их скорость полета.
При визуальном контроле за ведущим наибольшую скорость
сближения ведомый может допустить при постоянном угле визи-
рования. Следовательно догон или сокращение дистанции должно
осуществляться на параллельных курсах и достаточном интервале,
угол визирования при этом будет увеличиваться. При подходе к
Рис. 21.8. Зоны опасного сближения при полете парой (пример)
заданным параметрам строя своевременно уменьшать а при
опасном сближении — немедленно начинать отворот с одновре-
менным торможением самолета. Увеличение крена при этом позво-
ляет пройти на большом расстоянии от ведущего, однако необхо-
димо помнить о возможности потери его из виду. Пример зоны
опасного сближения показан на рис. 21.8.
К нарушению безопасности группового полета может привести
временная потеря управляемости самолета ведомого в результате
сваливания или попадания в спутный след. Для предотвращения
попадания в спутный след необходимо знать его размеры, интен-
сивность и протяженность. При маневрировании в строю обходить
его с принижением или с превышением. При выполнении взлета
и посадки за впереди летящим самолетом необходимо соблюдать
безопасные временные интервалы, в течение которых спутный след
смещается с линии пути или разрушается.
При попадании в спутный след на достаточной высоте не сле-
дует допускать резких движений рулями для парирования непро-
извольного движения самолета. После выхода из спутного следа
необходимо убрать крен, вывести самолет в горизонтальный полет
и проверить работу двигателя.
532
Сваливание ведомого может произойти при разворотах в его*
сторону на малых скоростях (например, вывод из горки с запаз-
дыванием) или в процессе энергичного отворота при опасном сбли-
жении. Во избежание этого ведомый должен прежде всего обеспе-
чить необходимое принижение, не допускать полного дросселиро-
вания двигателя и резких движений ручкой управления. Данная,
опасная ситуация может быть предотвращена грамотными дейст-
виями ведущего, который должен обеспечить ведомому необходи-
мый запас скорости, углов атаки и перегрузок.
§ 21.8. Летные характеристики группы самолетов
21.8.1. Располагаемая тяга в групповом полете
Располагаемая тяга в групповом полете — это наибольшая
тяга ведущего самолета, при которой ведомые имеют возможность
сохранять место в строю. Она меньше располагаемой тяги одиноч-
ного самолета на величину резерва тяги бР, который ведомый ис-
пользует для регулирования дистанции. Величина резерва тяги за-
висит от параметров строя, способа пилотирования, выполняемых
маневров, количества самолетов в группе, метеорологических усло-
вий и уровня натренированности летчиков.
Обычно считается, что первому ведомому достаточно иметь ре-
зерв до 3—4% частоты вращения ротора двигателя на дистан-
ции 50 м и 6—7% на дистанции 300 м. Резерв тяги звена дости-
гает 14%, эскадрильи — 20%. Следовательно, для увеличения рас-
полагаемой тяги группы самолетов целесообразно иметь более
плотные боевые порядки и малое количество самолетов в само-
стоятельных группах. .
Все это не означает того, что ведущий не может использовать
максимальную тягу двигателя. Пара может выполнять полет и
при отсутствии резерва тяги. Но в этом случае сохранение дистан-
ции обеспечивается совместными действиями ведомого и ведущего.
Так, в прямолинейном полете при отсутствии ведомого ведущий
может кратковременно выпускать тормозные щитки или выпол-
нить змейку, в то время как ведомый будет следовать по прямой.
При маневрировании ведомый сохраняет дистанцию за счет пере-
хода на траектории с меньшими радиусами кривизны, смещаясь
внутрь разворотов.
21.8.2. Д и а п а з о н скоростей полета
Максимальная скорость горизонтального полета группы за счет
уменьшения располагаемой тяги на 6Р будет меньше, чем одиноч-
ного самолета. Ее значение можно определить по кривым распо-
лагаемой тяги и лобового сопротивления (рис. 21.9, а) или при-
ближенно оценить по формуле (13.20).
533
Максимально допустимая скорость группы уменьшается. Это
•объясняется колебаниями скорости самолета ведомого, которые он
неизбежно допускает при сохранении дистанции. Следовательно,
ведущий должен выдерживать такую скорость, при которой ведо-
мый, допустив максимальное увеличение скорости при догоне, не
Рис. 21.9. Располагаемая тяга (а), диапазон вы-
сот и скоростей полета (б):
-------------------одиночного самолета;
—------------------группы самолетов
вышел бы за ее ограничение по скоростному напору или числу М.
Колебания скорости ведомого (И® ) в среднем составляют
ют 3 м/с на Р = 100 м до 7 м/с на £> = 300 м. Максимальные от-
клонения превышают их примерно в три раза и составляют от
30 до 70 км/ч. Кроме того, необходимо учитывать кинематическое
изменение скорости при маневрах (до 10—15 км/ч). Следователь-
но, максимально допустимая скорость пары должна быть на 50—
100 км/ч меньше, чем одиночного самолета.
Аналогичные причины вынуждают увеличивать минимально до-
пустимую (эволютивную) скорость. Таким образом, эксплуатаци-
онный диапазон скоростей полета группы самолетов сужается
(рис. 21.9,6).
534
21.8.3. Скороподъемность и потолок группы
самолетов
Необходимость иметь запас тяги снижает в групповом полете
скороподъемность и потолок самолета. Изменение максимальной
вертикальной скорости и потолка самолета можно оценить па
формулам (15.12' и 13.19). Практически можно считать, что
уменьшение тяги на 1% вызывает снижение дозвукового потолка
на 50—60 м, сверхзвукового — на 120—150 м.
Более существенное снижение сверхзвукового потолка объяс-
няется тем, что он достигается примерно при одном и том же
числе М, но с увеличением высоты полета уменьшается приборная
скорость и увеличивается аэродинамическое качество. Дозвуковой
же потолок достигается практически на постоянной приборной
скорости, близкой к наивыгоднейшей.
21.8.4. Р а сход топлива в групповом полете
При полете в группе расход топлива у ведомых увеличивается
вследствие ряда причин. Во-первых, за счет практически непре-
рывного изменения режима работы двигателя. Во-вторых, само-
лет ведомого, совершая колебания относительно траектории веду-
щего, проходит большее расстояние. В-третьих, выполняя эволюции
и особенно выпуская тормозные щитки, ведомый тем самым уве-
личивает лобовое сопротивление своего самолета. Наконец, для
сбора и роспуска боевых порядков (строя) самолеты могут вы-
полнять маневры, не являющиеся необходимыми для одиночного
самолета.
Увеличение расхода топлива зависит от типа самолетов (дви-
гателей), количества их в группе, выполняемых маневров. Так,
для большинства современных самолетов принято считать увели-
чение часового расхода топлива в паре и звене: при полете в
установившихся режимах — на 3—5%, при маневрировании — на
7—10%. Соответственно этому будут уменьшаться дальность и
продолжительность полета. Последняя может уменьшаться еще и
потому, что минимально допустимая скорость группы будет выше
скорости максимальной продолжительности полета.
21.8.5. Огр аничение углов атаки и перегрузок
Как было показано выше, при сохранении положения самолета
в группе (в прямолинейном полете и при выполнении маневра)
ведомый самолет совершает дополнительные эволюции, вследствие
чего его угол атаки и перегрузка отличаются от углов атаки и
перегрузки ведущего. Для обеспечения полетов и предотвращения
сваливания или превышения допустимого значения перегрузки ве-
дущий не может использовать разрешенные для одиночного само-
лета допустимые значения угла атаки и перегрузки. Запас угла
535-
атаки и перегрузки для дополнительных эволюций ведомого дол-
жны быть тем больше, чем больше число самолетов в группе.
Так, например, при допустимых значениях угла атаки аДОп и
перегрузки пу доп одиночного самолета ведущий в группе не дол-
жен превышать следующие значения перегрузки и угла атаки:
Пу ДОП в _ адоп
пу ДОП. Гр — j + ; «доп. Гр — 1 + »
где N — максимальное количество самолетов на одной линии,
£ = 0,2.
Для пары, например, получаем следующее допустимое значение
угла атаки:
________ адоп ____~ 7
адоп. гр— 1+04 '—'и,/адоп«
Уменьшение допустимого угла атаки накладывает ограничение
па минимальные эволютивные скорости группы самолетов, требует
увеличения скорости выполнения некоторых маневров.
536
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Жуковский Н. Е. О присоединенных вихрях. — В сб.: Труды отд»
физ. наук Общ. любителей естествознания. Вып. 2, 1906, т. 13, с. «12—25»
(Избр. соч.— М.— Л.: ОГИЗ, 1948, т. 2, с. 97—114).
2. Жуковский Н. Е. О парении птиц. — В сб.: Труды отд. физ. наук
Общ. любителей естествознания. Вып. 2, 1891, т. 4, с. 29—43. (Избр. соч.—
М —Л.: ОГИЗ, 1948, т. 2, с. 74—96).
3. Жуковский Н. Е. Динамика аэропланов в элементарном изложении
(статья 1-я). — В сб.: Труды отд. физ. наук Общ. любителей естествознания.
Вып. 2, 1913, т. 16, с. 33—50. (Избр. соч. — М — Л.: ОГИЗ, 1949, т. 2, с. 356—
379).
4. Жуковский Н .Е. Динамика аэропларов в элементарном изложении
(статья 2-я). Труды отд. физ. наук Общ. любителей естествознания. Вып. 1,
1916, т. 18, с. 40—67. (Избр. соч. —М —Л.: ОГИЗ, 1949, т. 2, с. 380—404).
5. Ветчинкин В. П. Динамика самолета. — М.: Грсмашметиздат, 1933».
400 с. (Избр. труды, т. 1, —М.: Изд-во АН СССР, 1956, с. 35—317).
6. А р х и п о в М. С., Жулев В. И., Иванов В. С. и др. Системы уп-
равления летательных аппаратов. — М.: изд. ВВИА им. проф. Н. Е. Жуков-
ского, 1978, 355 с.
7. Б е л о ц е р к о в с к и й С. хМ. Тонкая несущая поверхность в дозвуко*
вом потоке газа. — М.: Наука, 1965, с. 244.
8. Белоцерковский С. М., Скрипач Б. К., Табачников В. Г.
Крыло в нестационарном потоке газа. — М.: Наука, 1971, 768 с.
9. Белоцерковский С. М., Н и ш т М. И. Отрывное и безотрывное
обтекание тонких крыльев идеальной жидкостью. — М.: Наука, 1978, с. 352.
10. Бюшгенс Г. С., Студнев Р. В. Динамика продольного и боко-
вого движения. — М.: Машиностроение, 1979, 352 с.
11. В ед ров В. С. Динамическая устойчивость самолета. — М.: Оборон-
гиз, 1938, 236 с.
12. Вотяков В. Д. Аэродинамика летательных аппаратов и гидравлика-
их еистем. Часть 1. Аэродинамика. — М.: изд. ВВИА им проф. Н. Е. Жуков-
ского, 1972, 650 с.
13. Галлай М. Л. Полет самолета с неполной и несимметричной тягой.—
М.: Машиностроение, 1970, 191 с.
14. Горощенко Б. Т. Динамика полета, часть 1. Аэродинамический1
расчет самолета. — М.: изд. ВВИА им. проф. Н. Е. Жуковского, 1958, 304 с.
15. Доброленский Ю. П., Завалова Н. Л., Пономарен-
ко В. А., Т у в а е в В. А. Методы инженерно-психологических исследований
в авиации. — М.: Машиностроение, 1975, 280 с.
16. Калачев Г. С. Самолет, летчик и безопасность полета. — М.: Маши-
ностроение, 1979, 222 с.
W. Котик М. Г., Павлов А. В., Пашковский И. М. и др. Летные
испытания самолетов. — М.: Машиностроение, Г968, 424 с.
18. Котик M/Г., Филиппов В. В. Полет на предельных режимах.—
М.: Воениздат, 1977, 239 с.
19. К р а с о в с к и й А. А. Системы автоматического управления полетом и
их аналитическое конструирование. — М.: Наука, 1973, 560 с.
537
20. Л ы с е н к о Н. М. Динамика полета. — М.: изд. ВВИА им. проф.
Н. Е. Жуковского, 1967, 640 с.
21. Медников В. Н. Динамика полета и пилотирование самолетов.—
М.: изд. ВВА им. Ю. А. Гагарина, 1976, 547 с.
22. Н е ч а е в Ю. Н., Федоров Р. М. Теория авиационных газотурбин-
ных двигателей, часть I. — Мл Машиностроение, 1977, 306 с.
23. Нечаев Ю. Н., Федоров Р. М. Теория авиационных газотурбин-
ных двигателей, часть II. — Мл Машиностроение, 1978, 327 с.
24. Пашковский И. М. Устойчивость и управляемость самолета. — Мл
Машиностроение, 1975, 328 с<
25. П о н о м а р е в А. Н. Советские авиационные конструкторы. — Мл Во-
ениздат, 1977, 278 с.
26. Практическая аэродинамика маневренных самолетов/ Под общей ре-
дакцией Лысенко Н. М. — Мл Воениздат, 1977, 439 с.
27. Пышнов В. С. Аэродинамика самолета. — Мл Государственное
издательство оборонной промышленности, 1943, 439 с.
28. П ы ш н о в В. С. Динамические свойства самолета. — Мл Оборонгиз,
1959, 175 с.
29. П ы ш н о в В. С. Устойчивость и управляемость самолета. — Мл изд.
ВВИА им. проф. Н. Е. Жуковского, 1953, 2'11 с.
30. Радченко М. И. Научно-методические материалы по выбору харак-
теристик продольной устойчивости и управляемости пилотируемого военного
самолета. — Мл изд. ВВИА им. проф. Н. Е. Жуковского, 1978, 21 с.
31. Снешко Ю. И. Исследование в полете устойчивости и управляемо-
сти самолета. — Мл Машиностроение, 1971, 328 с.
32. Т а р а с е н к о в А. М., Брага В. Г., Тараненко В. Т. Динамика
полета и боевого маневрирования летательных аппаратов. Часть I. Траекто-
рия движения и летные характеристики. — Мл изд. ВВИА им. проф. Н. Е. Жу-
ковского, 1973, 313 с.
33. Т а р а с е н к о в А. М., Брага В. Г., Тараненко В. Т. Динамика
полета и боевого маневрирования летательных аппаратов. Часть II. Баланси-
ровка, устойчивость и управляемость. — Мл изд. ВВИА им. проф. Н. Е. Жу-
ковского, 1976, 335 с.
34. Цейтлин Г. М., С о л ь ц М. И., Попов В. М. Аэродинамика и ди-
намика полета самолета с ТРД. —-Мл Воениздат, 1973, 428 с,
538
Предисловие
СОДЕРЖАНИЕ
Стр.
з
Часть первая
Аэродинамика маневренного самолета
Введение г.т.’..............*......................................... 8
Раздел I
Основы аэродинамики маневренного самолета
Глава 1. Общие сведения о маневренных самолетах .! . •.................12
§1.1. Назначение маневренных самолетов ......................... —
§ 1.2. Основные части самолета и их назначение.................. 13
§ 1.3. Стандартные оси координат. Углы атаки и скольжения.
Угловые скорости вращения .гн . . . . . в) 15
§ 1.4. Крылья маневренных самолетов и их геометрические ха-
рактеристики . . . ...................-. . ... . .................15
§ 1.5. Особенности крыльев сложной формы в плане и крыльев
изменяемой в полете стреловидности . . . . ..................... 19
§ 1.6. Органы управления и механизации маневренных самолетов 20
§ 1.7. Схемы и компоновка маневренных самолетов ................ 22
Глава 2. Основные законы аэродинамики. . .........3 23
§ 2.1. Основные понятия аэродинамики. Общая картина обтека-
ния тела .......................... '........................... —
§ 2.2. Уравнение постоянства расхода . .^. .................-. 28
§ 2.3. Уравнение сохранения энергии и его различные формы. 29
§ 2.4. Распространение возмущений в воздухе. . . .'.........л 32
§ 2.5. Физическая природа скачков уплотнения. Течения расширения 34
§ 2.6. Изменение параметров воздуха на скачках уплотнения ... 38
§ 2.7. Пограничный слой и сопротивление трения ..... 40
§ 2.8. Аэродинамический нагрев . и.-. . . . . . .-....... 44
§ 2.9. Принципы измерения скорости и числа М............. 46
Глава 3. Аэродинамические силы и моменты.................... 50
§ 3.1. Картина распределения давления на крыле............ —
§ 3.2. Полная аэродинамическая сила и моменты и их состав-
ляющие. Аэродинамические коэффициенты............................ 52
§ 3.3. Зависимость коэффициентов аэродинамических сил от углов
атаки и скольжения . . . •..................................... 55
§ 3.4. Поляра и аэродинамическое качество....................... 57
§ 3.5. Зависимость коэффициентов аэродинамических моментов от
углов атаки и скольжения......................................... 60
§ 3.6. Центр давления и аэродинамический фокус. Средняя аэро-
динамическая хорда .............................................. 62
539
Стр,
Глава 4. Аэродинамика частей самолета..............................
§ 4.1. Теорема Н. Е. Жуковского о подъемной силе крыла . . .
§ 4.2. Влияние геометрических параметров крыла на его аэроди-
намические характеристики....................................
§ 4.3. Влияние чисел М и Re на аэродинамические характери-
стики крыла ......................................'..........
§ 4.4. Аэродинамические характеристики крыльев на больших
углах атаки .................................................
§ 4.5. Особенности аэродинамических характеристик крыльев слож-
ной формы в плане............................................
§ 4.6. Аэродинамические характеристики оперения и рулевых
органов .....................................................
§ 4.7. Аэродинамические характеристики фюзеляжа .......
65
67
72
79
84
86
92
Раздел II
Аэродинамические характеристики маневренных самолетов и особенности
их силовых установок
Глава 5. Аэродинамическая компоновка маневренных самолетов и
их характеристики................................................. . 93
§ 5.1. Взаимное влияние частей самолета.......................< __
§ 5.2. Общие принципы аэродинамической компоновки маневрен-
ного самолета и требования, предъявляемые к ней . . . юо
§ 5.3. Способы уменьшения лобового сопротивления самолета при
нулевой подъемной силе......................................... 102
§ 5.4. Обеспечение высоких несущих свойств. Взлетно-посадоч-
ная механизация................................................ Ю4
§ 5.5. Обеспечение высокого аэродинамического качества самолета юз
§ 5.6. Обеспечение заданных продольных моментных характери-
стик самолета во всем летном диапазоне чисел М . . . . цо
§ 5.7. Обеспечение заданных боковых моментных характеристик
самолета во всем летном диапазоне чисел М....................... цз
§ 5.8. Дополнительные аэродинамические моменты при криволи-
нейном и неустановившемся движении . ............................ цз
§ 5.9. Влияние близости земли на аэродинамические характери-
стики самолета ................................................ ]23
§ 5.10. Особенности аэродинамических характеристик маневрен-
ного самолета на больших углах атаки...................... . . 125
§ 5.11. Влияние изменения стреловидности крыла в полете на
аэродинамические характеристики самолета........................ 128
§ 5.12. Влияние упругости конструкции самолета на его аэроди-
намические характеристики....................................... 130
§ 5.13. Аэродинамическая сущность валежки, реверса элеронов,
дивергенции, флаттера........................................ 133
Глава 6. Особенности силовых установок маневренных самолетов . 135
§ 6.1. Схемы и основные параметры двигателей................. ......
§ 6.2. Особенности характеристик элементов двигателя и причи-
ны их неустойчивой работы. . . ......................... . . 139
§ 6.3. Высотно-скоростные и дроссельные характеристики......... 152
§ 6.4. Переходные режимы работы ТРДФ и ДТРДФ................... 161
§ 6.5. Эксплуатационные ограничения режимов работы ТРДФ
и ДТРДФ...................................................... 168
§ 6.6. Помпаж и самовыключение двигателей при пуске ракет . .. 174
540
Стр.
Введение
Часть вторая
Динамика полета
179
Раздел III
Устойчивость и управляемость самолета. Критические режимы
Глава 7. Продольная балансировка, статические характеристики ус-
тойчивости и управляемости......................................... 194
§ 7.1. Продольное равновесие, балансировка самолета............ ......
§ 7.2. Статические характеристики продольной управляемости . . jgg
§ 7.3. Устойчивость по перегрузке.............................., 205
§ 7.4. Устойчивость по скорости и влияние на нее эксплуатацион-
ных факторов ............................................... 208
§ 7.5. Связь продольной управляемости с устойчивостью по
скорости........................................................ 210
Глава 8. Динамические свойства самолета в продольном движении 212
§ 8.1. Физическая природа развития продольного движения. Раз-
деление движения на малое и большое................................__
§ 8.2. Динамические свойства самолета в малом (короткоперио-
дическом) продольном движении..............................-.’ни 216
§ 8.3. Динамика переходного процесса и характеристики управ-
ляемости продольного движения................................... 224
§ 8.4. Влияние эксплуатационных факторов на динамические свой-
ства самолета в малом продольном движении . . . .-. . . 229
§ 8.5. Требования к динамическим свойствам и характеристикам
продольной управляемости ........................................ 240
§ 8.6. Обеспечение продольной управляемости путем регулирова-
ния системы управления........................................... 245
§ 8.7. Обеспечение продольной управляемости путем регулирова-
ния динамических характеристик самолета.................. 251
§ 8.8. Особенности управления самолетом при отказах систем,
улучшающих характеристики устойчивости и управляемости 257
Глава 9. Боковая балансировка, статические характеристики устой-
чивости и управляемости............................................... 261
§ 9.2. Путевая и поперечная устойчивость, их связь с характе-
ристиками управляемости...........................................267
§ 9.3. Особенности боковой управляемости сверхзвуковых самолетов 273
§ 9.4. Особенности балансировки самолета при несимметричных
тяге и подвесках............................ •.................. 279
Глава 10. Динамические свойства самолета в боковом движении . . 034
§ 10.1. Физическая природа развития бокового движения .... __
§ 10.2. Динамические свойства самолета в малом боковом движении hqq
§ 10.3. Влияние эксплуатационных факторов на динамические
свойства в малом боковом движении. Требования, предъ-
являемые к ним .............................................. 297
541
Стр.
Глава 11. Взаимодействие продольного и бокового движений .... 301
§ 11.1. Аэродинамические, кинематические и инерционные пере-
крестные связи .................... . -........................ —
§ 11.2. Критические скорости вращения. Аэроинерционное вра-
щение . ......................................... .-л - .J..-. .] 307
§ 11.3. Особенности проявления взаимосвязи продольного и боко-
вого движений при выполнении маневров . . . .310
§ 11.4. Поведение самолета и управление им на больших углах атаки 315
§ 11.5. Особенности сваливания маневренных самолетов и действия
летчика по предотвращению входа в штопор ...................... 317
§ 11.6, Штопор самолета........................................ 320
§ 11.7. Вывод самолета из штопора............................. 324
§ 11.8. Особенности поведения самолета и управления им при по-
падании в спутный след ...................................: .3 <j 328
Глава 12. Принципы автоматического и директорного управления 332
§ 12.1. Распределение функций между летчиком и автоматиче-
скими устройствами . . . . . . и.'.*................—
§ 12.2. Автоматическое управление движением вокруг центра
масс . . . . ............. . . . . 335
§ 12.3. Автоматическое управление траекторией полета 343
§ 12.4. Комплексные системы автоматического управления со-
временных самолетов . ....'. ...7.1.’. . а 349
§ 12.5. Директорное управление. Особенности пилотирования
по КПП ................................................... 352
Раздел IV
Летно-технические и маневренные свойства самолетов
Глава 13. Горизонтальный полет ................•и 355
§ 13.1. Силы, действующие на самолет .......................... —
§ 13.2. Минимальная скорость полета ......................... 358
§ 13.3. Лобовое сопротивление самолета в прямолинейном гори-
зонтальном полете . < . .>.] . . .-. 361
§ 13.4. Максимальная скорость и ее зависимость от высоты . . . 363
§ 13.5. Первые и вторые режимы полета ....... .......... 365
§ 13.6. Статические потолки ................................. 367
§ 13.7. Диапазон скоростей и высот полета......................369
§ 13.8. Влияние эксплуатационных факторов на диапазон скоро-
стей и высот полета......................................... 371
Глава 14. Допустимые области применения самолетов. Физическая
сущность ограничений , . . ... ................................... 376
§ 14.1. Классификация опасных режимов полета.................... —
§ 14.2. Ограничения минимальной скорости полета. Действия лет-
чика при попадании в область недопустимо малых скоростей 378
§ 14.3. Ограничения максимальной скорости полета. Допустимые
области скоростей и высот полета .’. . . . . . 379
§ 14.4. Действия летчика при превышении максимально допусти-
мой скорости полета . . . . . . . < . ........... 382
§ 14.5. Минимально допустимые высоты полета. Безопасность
полетов на малых высотах.................................... 384
§ 14.6. Располагаемые и допустимые перегрузки................. 385
542
Стр.
Глава 15. Набор высоты и снижение................................. 333
§ 15.1. Прямолинейный набор высоты. Первые и вторые режимы
наклонного полета .......................................... ......
§ 15.2. Скороподъемность. Энергетические характеристики...... 39]
§ 15.3. Оптимальные режимы набора высоты и скорости.......... 393
§ 15.4. Динамический потолок. Особенности поведения самолета
на динамических высотах...................................... 400
§ 15.5. Влияние эксплуатационных факторов на скороподъем-
ность самолета ................ . . . .....................- 402
§ 15.6. Снижение. Оптимальные режимы снижения................. 404
§ 15.7. Предпосадочное снижение. Опасность вторых режимов и и 406
Глава 16. Маневрирование в горизонтальной плоскости 408
§ 16.1. Разгон и торможение самолета в горизонтальном полете.
Влияние эксплуатационных факторов на характеристики
§ 16.2. Вираж (разворот), условия его выполнения. Влияние экс-
плуатационных факторов на характеристики виража
(разворота) . . . .< .у.Тв1 л - . . ........ 415
§ 16.3. Техника пилотирования, возможные отклонения и ошибки
на вираже и способы их исправления........................• • • 421
Глава 17. Маневрирование в вертикальной плоскости .................... 426
§ 17.1. Условия криволинейного движения и особенности выпол-
нения маневров в вертикальной плоскости ....... ___
§ 17.2. Пикирование . .......................................... 430
§ 17.3. Горка . . .............................................. 434
§ 17.4. Переворот .............................................. 437
§ 17.5. Петля Нестерова ....................................... 445
§ 17.6. Полупетля ............................................. 450
§ 17.7. Характерные отклонения при выполнении вертикальных фи-
гур и их исправление. Меры безопасности ........................ 452
Глава 18. Маневрирование по пространственным траекториям 455
§ 18.1. Особенности пространственных маневров и условий их
выполнения ................................................... ......
§ 18.2. Спираль..........................................; . . 453
§ 18.3. Боевой разворот......................................... 462
§ 18.4. Бочка ................................................. 467
§ 18.5. Косая петля. Полупереворот............................. 471
§ 18.6. Методы расчета траекторий и параметров пространствен-
ного движения самолета....................................... 475
Глава 19. Взлет и посадка............................................ 476
§ 19.1. Особенности движения самолета по земле. Руление.
Этапы взлета ............................................ , —
§ 19.2. Разбег. Особенности устойчивости и управляемости .... 478
§ 19.3. Разбег с боковым ветром. Разгон после отрыва............ 482
§ 19.4. Поведение самолета и действия летчика при отказе
двигателя на взлете ........................................... 485
§ 19.5. Особенности взлета в различных условиях. Влияние экс-
плуатационных факторов на характеристики взлета .... 487
§ 19.6. Этапы посадки. Выравнивание и выдерживание.............. 492
§ 19.7. Пробег ................'................................ 494
§ 19.8. Влияние эксплуатационных факторов на посадочные ха-
рактеристики. Посадка при боковом ветре......................... 497
§ 19.9. Посадка с отказавшим двигателем ... .................... 500
543
Стр.
§ 19.10. Возможные отклонения при взлете и посадке и их ис-
правление ..................................................... 503
§ 19.11. Способы улучшения взлетно-посадочных характеристик . 504
Глава 20. Дальность и продолжительность полета . ................... 597
§ 20.1. Расход топлива, дальность и продолжительность полета
при наборе высоты и снижении ........................... . л ________
§ 20.2. Дальность и продолжительность горизонтального полета 5Ю
§ 20.3. Суммарная дальность и продолжительность полета и влия-
ние на нее эксплуатационных факторов............................ 514
§ 20.4. Способы увеличения дальности полета.................... 516
Глава 21. Особенности полета самолета в группе .................. 517
§ 21.1. Параметры строя, их определение в полете .............. 518
§ 21.2. Прямолинейный полет в составе пары . ... .............. 520
§ 21.3. Маневрирование для изменения параметров строя .... 523
§ 21.4. Взлет пары (группы).................................... 524
§ 21.5. Выполнение разворотов, виражей, спиралей............... 525
§ 21.6. Выполнение пикирования и горки . . л,-............... 528
§ 21.7. Обеспечение безопасности групповых полетов............. 530
§ 21.8. Летные характеристики группы самолетов................. 533
Использованная литература .......................................... 537
АЭРОДИНАМИКА И ДИНАМИКА ПОЛЕТА
МАНЕВРЕННЫХ САМОЛЕТОВ
Редактор Л. М, Фролов
Технический редактор А. А. Перескокова
Корректор С. И. Яворская
Сдано в набор 28.12.81. Подлисано в печать 07.07.83. Г-62780
Формат 60X90/16. Печ. л. 34. Усл. печ. л. 34. Усл. кр.-отт. 34. Учлизд. Л. 34,12
Изд. № 7/7730 Бесплатно Зак. 21
☆
«Для внутриведомственной продажи» цена 1 р. 60 к.
Воениздат, 103160, Москва, К-160
2-я типография Воениздата
191065, Ленинград, Д-65, Дворцовая пл., д. 10
542