Б. ЗЕЛЬДОВИЧ, А. Д. МЫШКИС
ЭЛЕМЕНТЫ
ПРИКЛАДНОЙ
МАТЕМАТИКИ
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 9 7 2

ОГЛАВЛЕНИЕ
Предисловие . 7
Глава 1. Некоторые численные методы 11
§ 1. Численное интегрирование , 12
§ 2 Вычисление сумм при помощи интегралов 17
§ 3. Численное решение уравнений 25
Ответы и решения 33
Глава 11. Математическая обработка результатов опыта 36
§ 1. Таблицы и разности 36
§ 2. Интегрирование и дифференцирование функций, заданных таблично 41
§ 3. Подбор формул по данным опыта по .методу наименьших квадратов 45
§ 4. Графический способ подбора формул 51
Ответы и решения 58
Глава III. Дополнительные сведения об интегралах и рядах 61
§ 1. Несобственные интегралы 61
§ 2. Интегрирование быстроменяющихся функций , 69
§ 3, Формула Стирлинга . . . • 77
§ 4. Интегрирование быстроколеблющихся функций 79
§ 5. Числовые ряды 82
§ 6 Интегралы, зависящие от параметра 93
Ответы и решения 97
Глава IV. Функции нескольких переменных 100
§ 1. Частные производные 100
§ 2. Геометрический смысл функции двух переменных 107
§ 3. Неявные функции 108
§ 4. Радмола1\1па 116
§ 5. Огибающая семейства линий 118
§ 6. Ряд Тейлора и задачи на экстремум 120
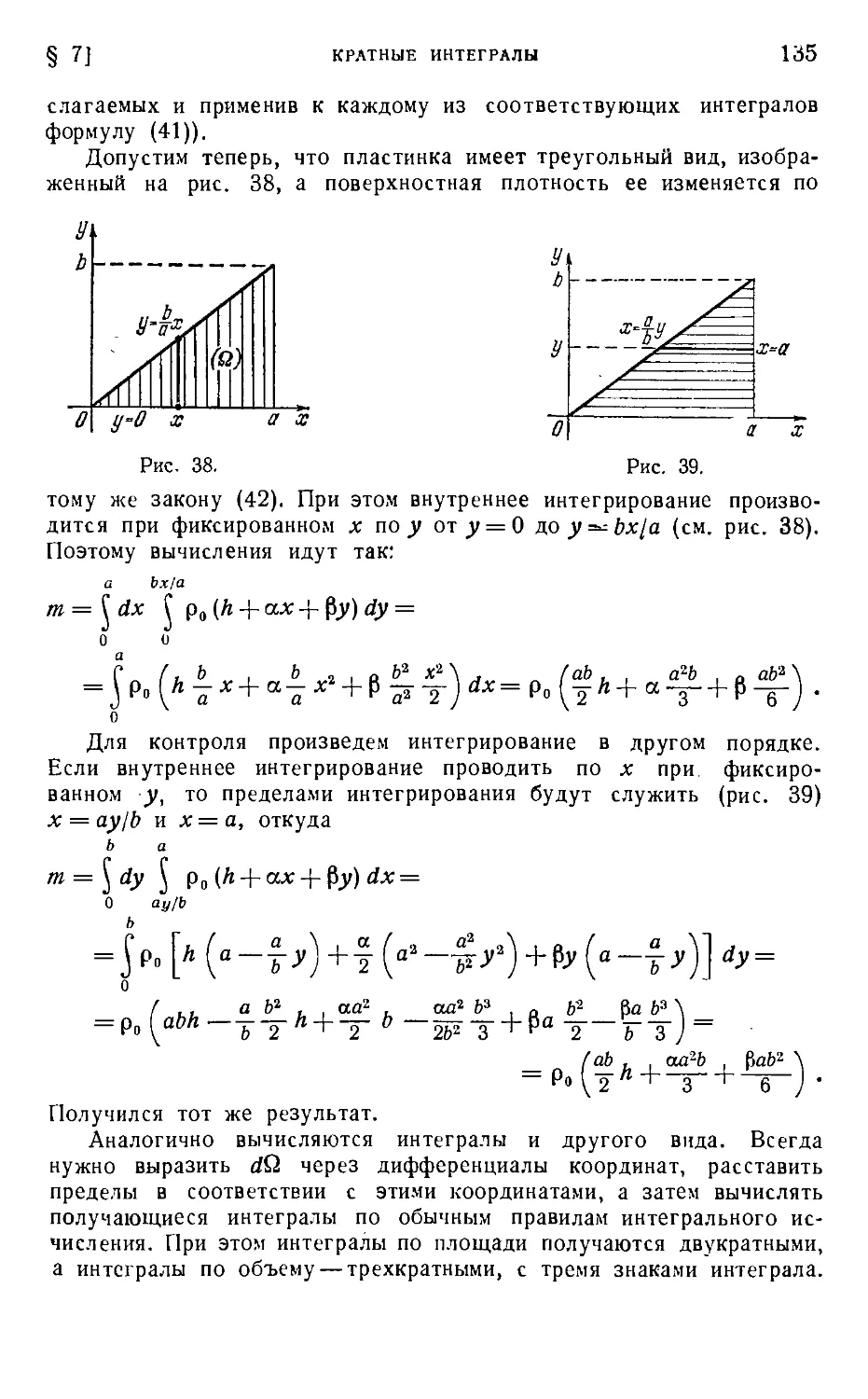
§ 7. Кратные интегралы 127
§ 8. iMiioroMepHoe пространство и число степеней свободы 137
Ответы и решения 141
Глава V. Функции комплексного переменного 144
§ 1. Простейшие свойства комплексных чисел 144
§ 2. Сопряженные комплексные числа 147
§ 3. Возведение в мнимую степень. Формула Эйлера 150
§ 4. Логарифмы и корни , 154
§ 5. Описание гармонических колебании с помощью показательной
функции от мнимого аргумента 157
§ 6. Производная функции комплексного переменного , 164
1*

4 ОГЛАВЛЕНИЕ
§ 7. Гармонические функции . 166
§ 8. Интеграл от функции комплексного переменного . 168
§ 9. Вычеты 172
■ Ответы и решения 180
Глава VI. Дельта-функция Дирака 183
§ 1. Дельта-функция Дирака 6(х) 183
§ 2. Функция Грина 188
§ 3. Функции, связанные с дельта-функцией 193
§ 4. Понятие об интеграле Стилтьеса 198
Ответы и решения 199
Глава VII. Дифференциальные уравнения 201
§ I. Геометрический смысл дифференциального уравнения первого
порядка 201
§ 2. Интегрируемые типы уравнений первого порядка 204
§ 3. Линейные однородные уравнения второго порядка с постоянными
коэффициентами 212
§ 4. Простейшее линейное неоднородное уравнение второго порядка 217
§ 5. Линейные неоднородные уравнения второго порядка с постоянными
коэффициентами 224
§ 6. Устойчивые и неустойчивые решения 230
Ответы и решения ." . . 235
Глава VIII. Дальнейшие сведения о дифференциальных уравнениях 237
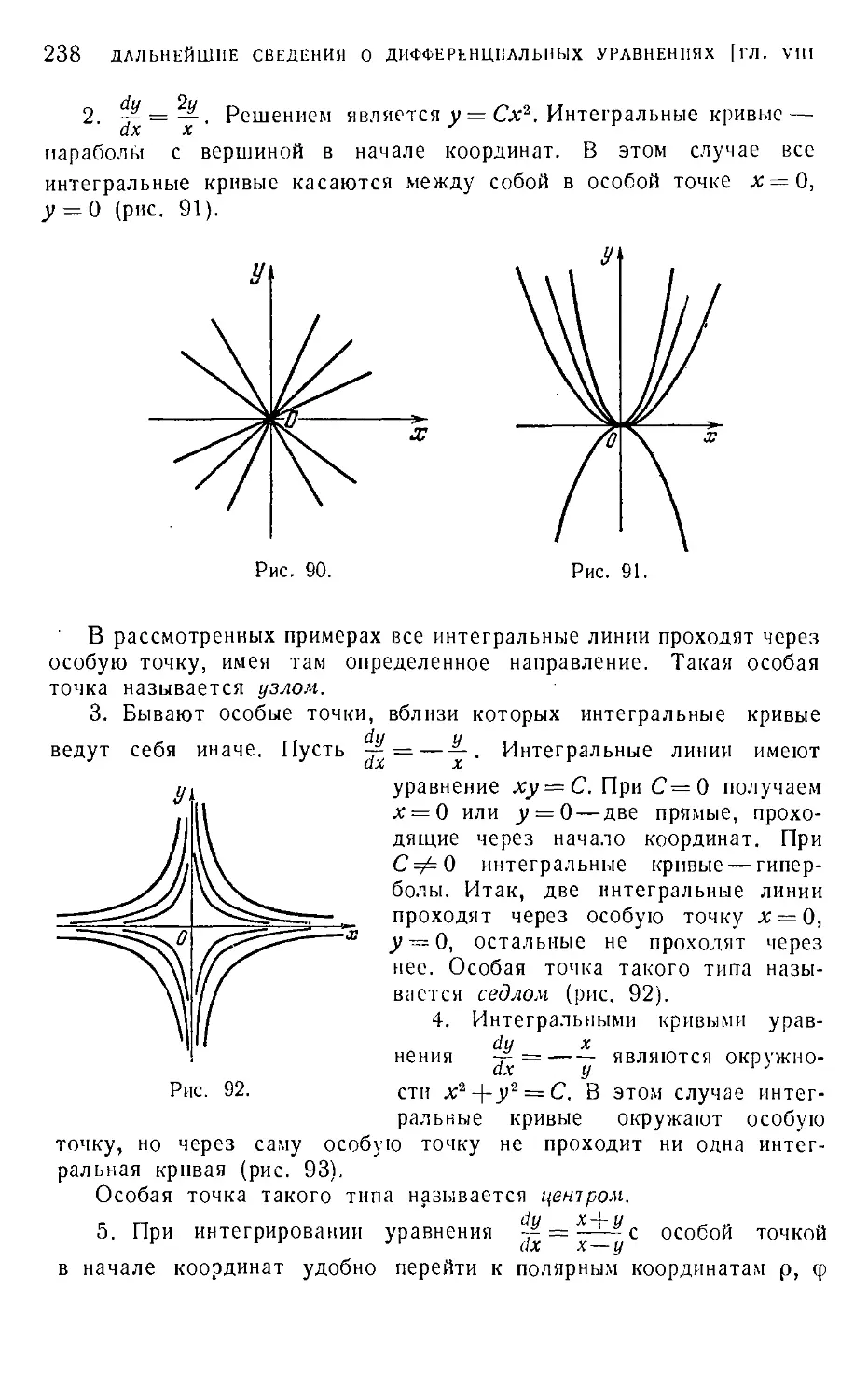
§ Ь Особые точки 237
§ 2. Системы дифференциальных уравнений 239
§ 3. Определители и решение линейных систем с постоянными коэффи-
коэффициентами 242
§ 4. Устойчивость по Ляпунову состояния равновесия 247
§ 5. Построение приближенных формул для решения 250
§ 6. Адиабатическое изменение решения 258
§ 7. Численное решение дифференциальных уравнений 261
§ 8. Краевые задачи 269
§ 9. Пограничный слой 275
§ 10. Подобие явлений 276
Ответы и решения 280
Глава IX. Векторы 282
§ 1. Линейные действия над векторами 283
§ 2. Скалярное произведение векторов 287
§ 3. Производная от вектора 289
§ 4. Движение материальной точки 291
§ 5. Понятие о тензорах 295
§ 6. Многомерное векторное пространство . 300
Ответы и решения 303
Глава X. Теория поля 306
§ 1. Введение 306
§ 2. Скалярное поле и градиент 307
§ 3. Потенциальная энергия и сила 311
§ 4. Поле скорости и поток 316
§ 5. Электростатическое поле, его потенциал и поток 320
§ 6. Примеры 323
§ 7. Общее векторное поле и его дивергенция 332
§ 8. Дивергенция поля скорости и уравнение неразрывности ..... 336

оглавление 5
. . ■ § 9. Дивергенция электрического поля и уравнение Пуассона , . . . 339
§ 10. Вектор площадки и давление 342
. Ответы и решения 346
.Глава XI. Векторное произведение и вращение 349
' } 1, Векторное произведение векторов 349
§ 2. Некоторые приложения к механике 353
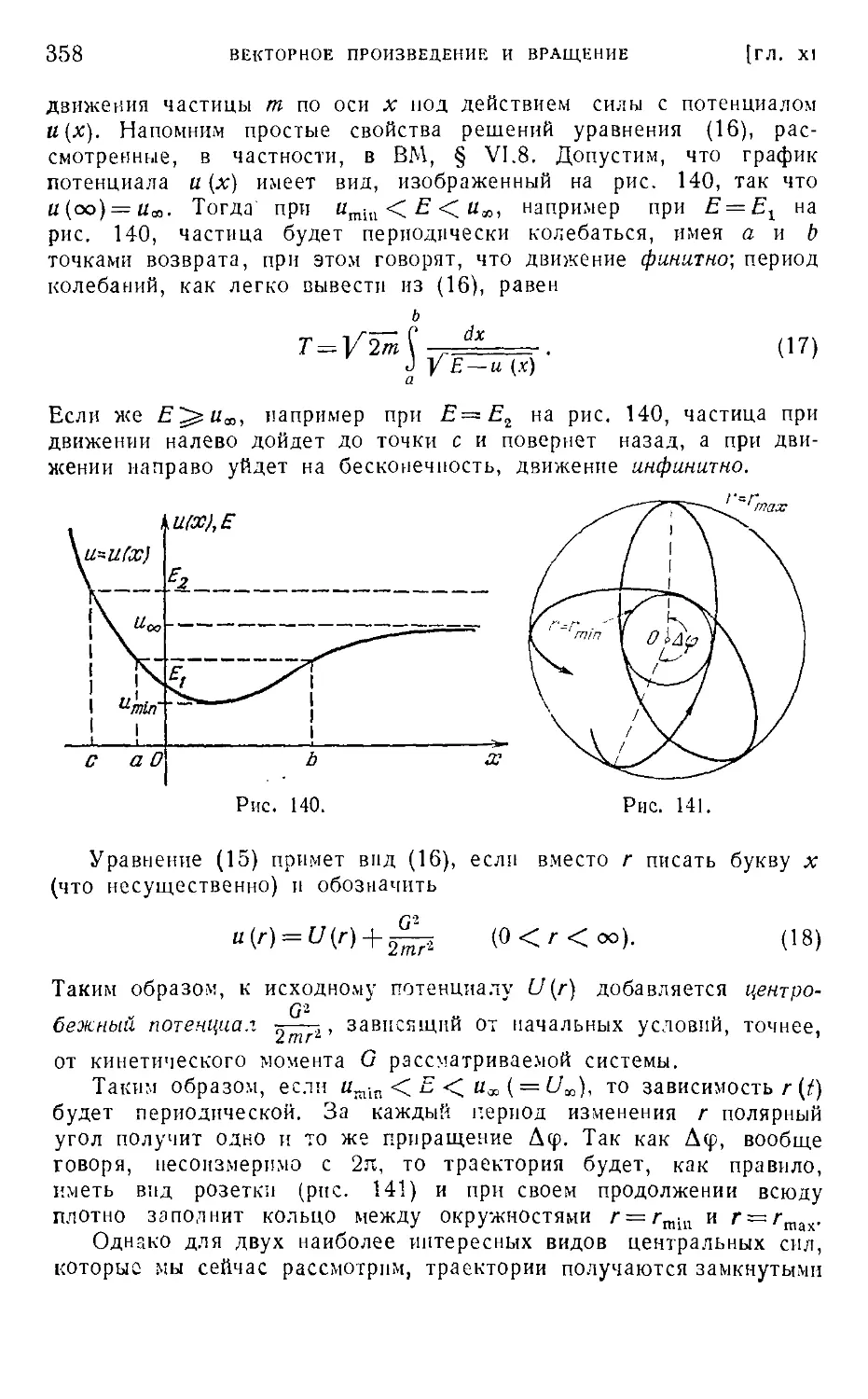
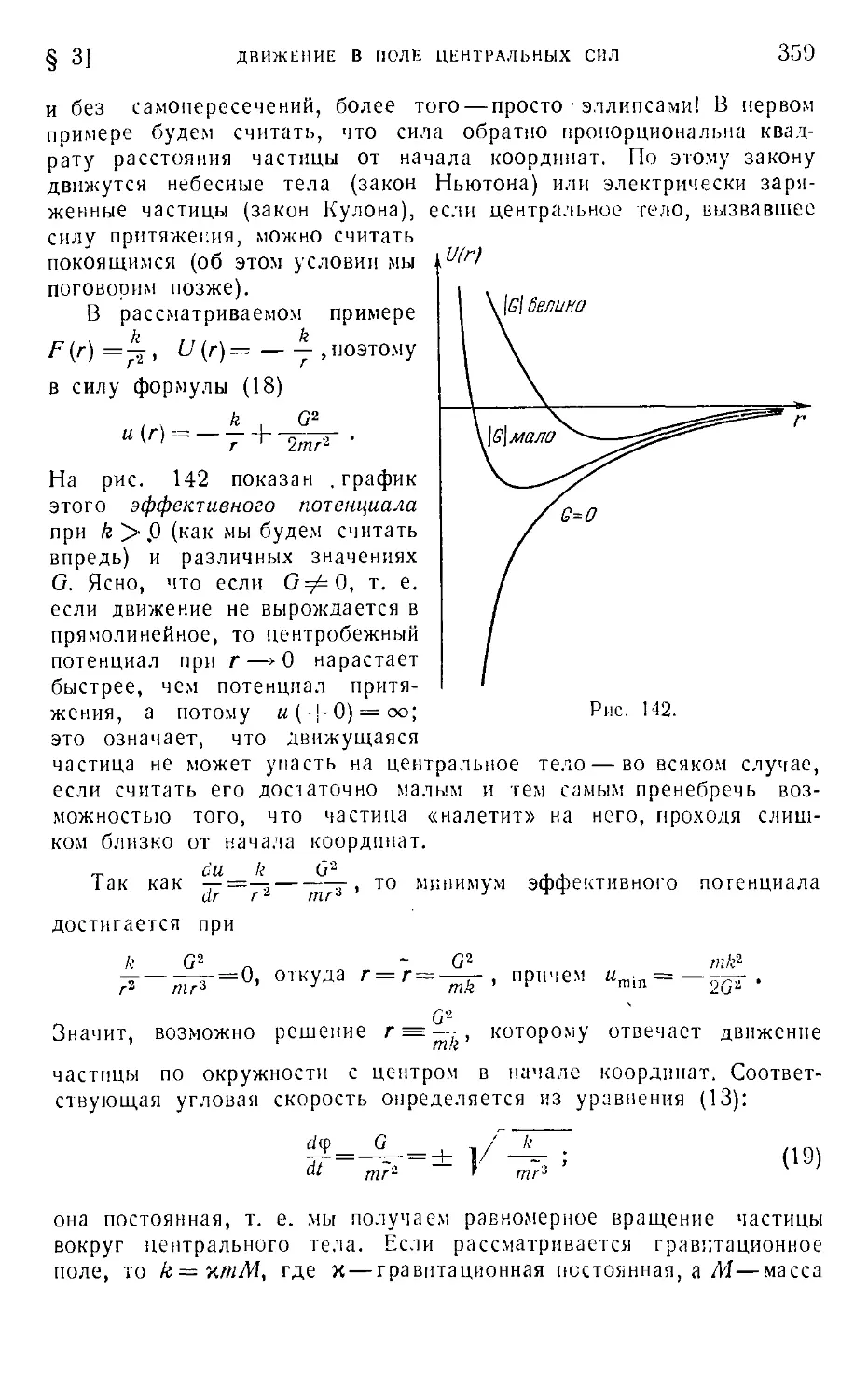
§ 3. Движение в поле центральных сил ■ . . . 356
§ 4. Вращение твердого тела 363
- ' § 5. Симметрические и антисимметрические тензоры 366
§ 6. Истинные векторы и псевдовекторы .371
§ 7. Ротор векторного поля 373
§ 8. Оператор Гамильтона «набла» ..-..■..-....•. 379
- § 9. Потенциальные поля 382
§ 10. Ротор поля скорости 386
§ 11. Магнитное поле и электрический ток 388
§ 12. Электромагнитное поле и уравнения Максвелла 392
' | 13. Потенциал в многосвязной области 396
Ответы и решения 398
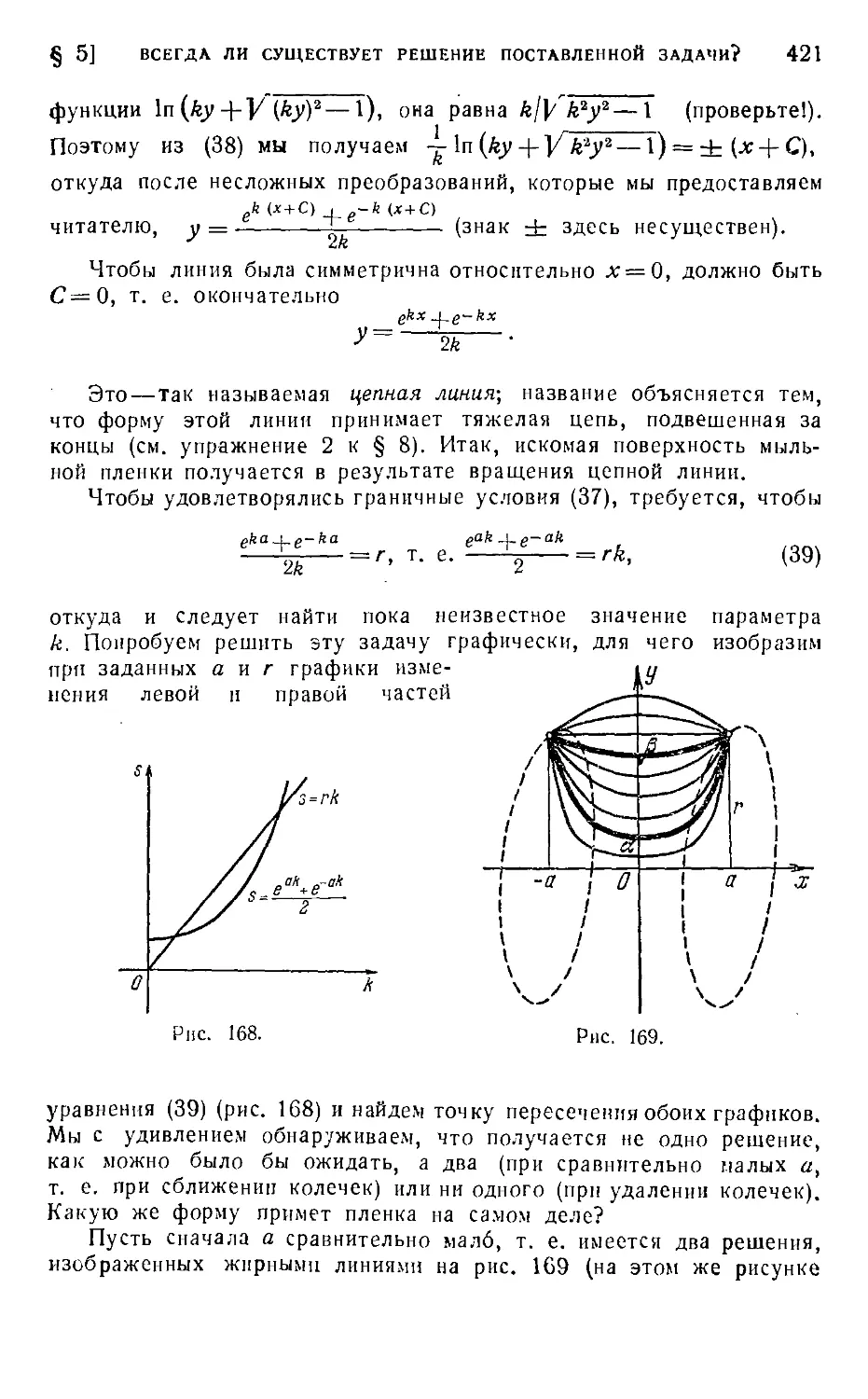
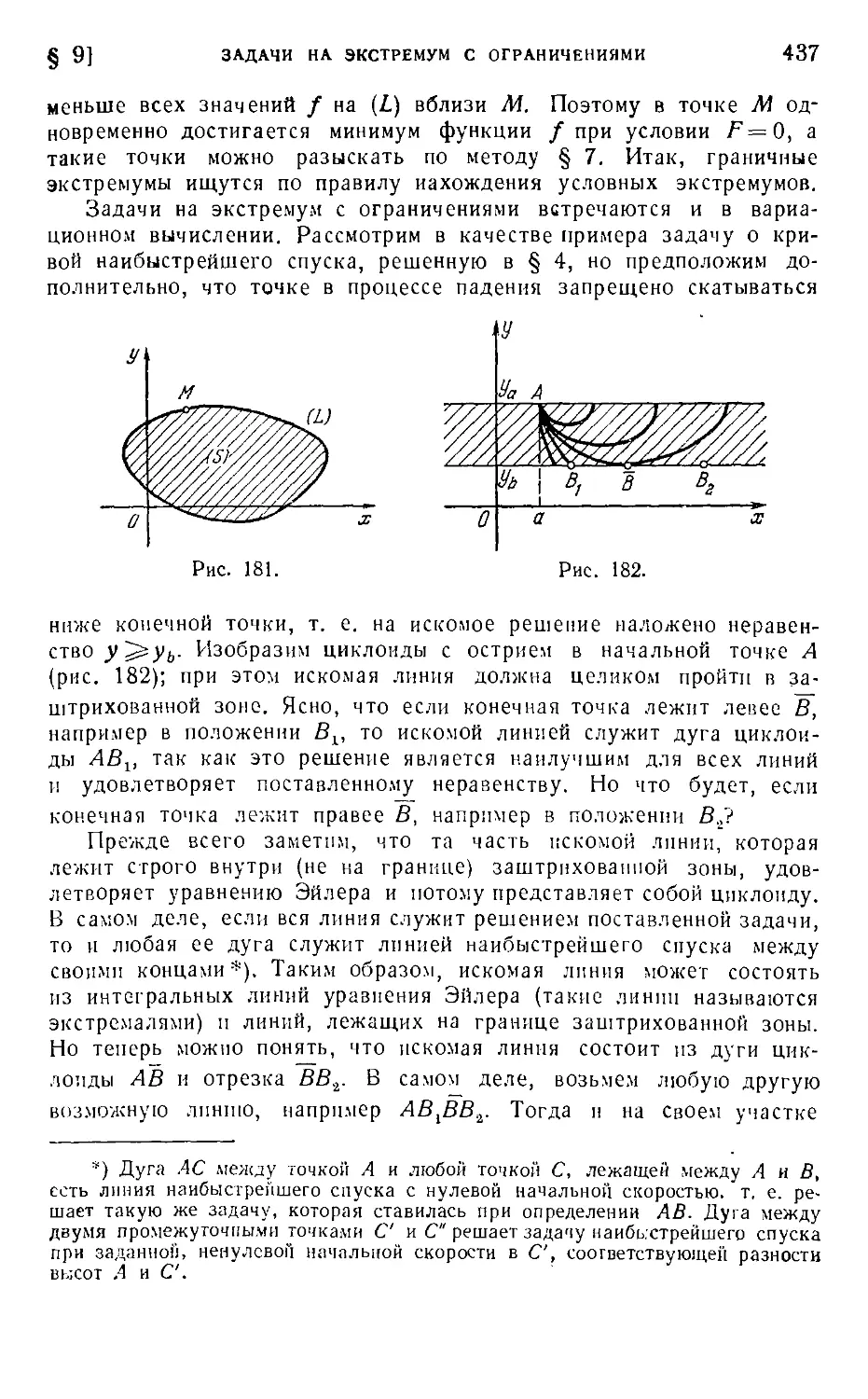
Глава XII. Вариационное исчисление 402
£ 1. Пример перехода от конечного числа степеней свободы к беско-
нечному 402
§ 2. Функционал 408
§ 3. Необходимое условие экстремума 411
>. § 4. Уравнение Эйлера 414
§ 5, Всегда ли существует решение поставленной задачи? 419
§ 6. Варианты основной задачи 423
§; 7. Условный экстремум для конечного числа степеней свободы . . . 425
8. Условный экстремум в вариационном исчислении 428
9. Задачи на экстремум с ограничениями ....'." 436
10. Вариационные принципы. Принцип Ферма в оптике 438
11. Принцип наименьшего действия 445
§ 12. Прямые методы ' 449
Ответы и решения 453
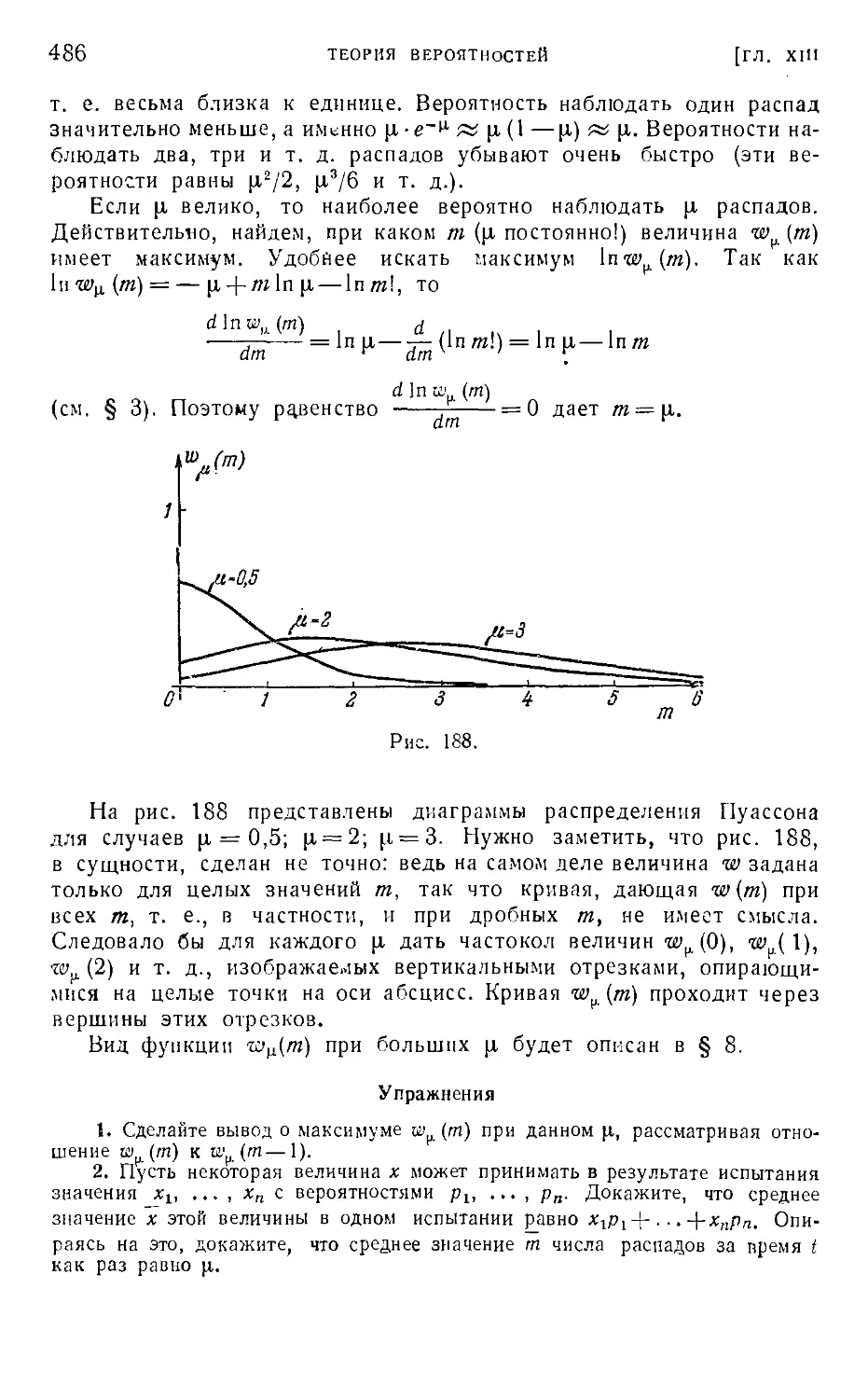
.Лава XIII. Теория вероятностей 459
!-■ § 1. Постановка вопроса 459
•- § 2. Умножение вероятностей 462
* ^ . . § 3. Анализ результатов многих испытаний 467
, ' ': § 4. Энтропия 478
;Ш'! ; ■ § 5. Радиоактивный распад. Формула Пуассона 483
§ 6. Другой вывод распределения Пуассона 487
, е . § 7. Непрерывно распределенные величины 488
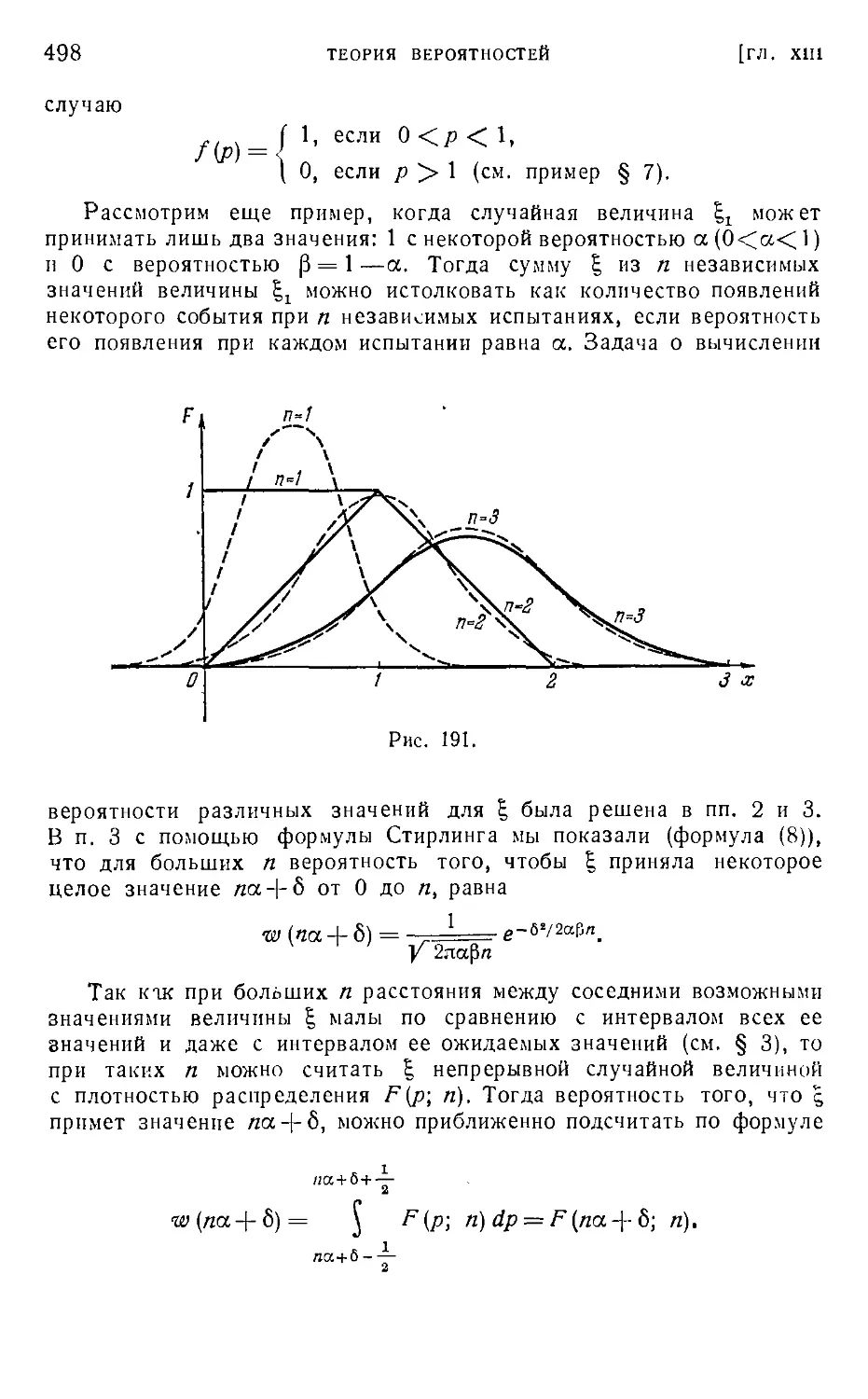
'А Z, § 8. Случай весьма большого числа испытаний 493
§ 9. Корреляционная зависимость 500
х- '■; "' §10. О распределении простых чисел 505
1 Ответы и решения 511
' 'Глава XIV. Преобразование Фурье , 516
?; § I. Введение 516
а "' § 2. Формулы преобразования Фурье 520
, :, • § 3. Причинность и дисперсионные соотношения 527
, ,.£. § 4. Свойства преобразования Фурье 531
§ 5. Преобразование колокола и принцип неопределенности 539
§ 6. Спектральный анализ периодической функции 544

6 ОГЛАВЛЕНИЕ
§ 7. Пространство Гильберта 548
§ 8. Модуль и фаза спектральной плотности ' ' 553
Ответы и решения 556
Глава XV. Электронные цифровые вычислительные машины 559
§ 1. Моделирующие вычислительные машины 560
§ 2. Цифровые вычислительные машины ' 561
§ 3. Запись чисел и команд в ЭЦВМ 563
§ 4. Программирование ! ! ! 568
§ 5. Пользуйтесь ЭЦВМ! [ 574
Ответы и решения 581
Предметный указатель 584

ПРЕДИСЛОВИЕ
Эта книга является не систематическим учебником, а скорее,
книгой для чтения. На простых примерах, взятых из физики, на
различных математических задачах мы старались ввести читателя
в круг идей и методов, широко распространенных сейчас в прило-
приложениях 1чатематики к физике, технике и некоторым другим областям.
Некоторые из этих идей и методов (такие, как применение дельта-
функции, принципа суперпозиции, получение асимптотических выра-
выражений и т. д.) еще недостаточно освещаются в распространенных
математических учебниках для нематематиков, так что здесь наша
книга может служить дополнением к этим учебникам. Нашей целью
было пояснить основные идеи математических методов и общие
закономерности рассматриваемых явлений. Напротив, формальные
доказательства, рассмотрение исключений и усложняющих факторов
по возможности опущены. Взамен этого мы в некоторых местах
старались входить более подробно в физическую картину рассма-
рассматриваемых процессов.
Предполагается, что читатель владеет основами дифференциаль-
дифференциального и интегрального исчисления для функций одной переменной,
включая разложение таких функций в степенные ряды, и может
применять эти разделы математики к решению физических задач.
Достаточно (но не необходимо!), например, знакомство с книгой
Я. Б. Зельдовича «Высшая математика для начинающих и ее приложе-
приложения к физике», на которую мы будем иногда ссылаться, обозначая ее
буквами ВМ (имеется в виду издание 5, «Наука», 1970). Более
того, настоящая книга в какой-то степени может рассматриваться
как продолжение ВМ. В немногих местах изложение близко книге
А. Д. Мышкиса «Лекции по высшей математике», издание 3 («Наука»,
1969). Тем не менее настоящая книга является совершенно само-
самостоятельной, поскольку от читателя никаких специальных познаний,
помимо только что указанных, не потребуется.
Содержание книги ясно из прилагаемого оглавления. Ее не
обязательно читать подряд: читатель может знакомиться с интере-
интересующими его разделами независимо от других разделов и только
в явно указываемых случаях из этих других разделов потребуются
отдельные сведения. Поэтому для удобства в начале отдельных глав
и параграфов указываются сведения из предыдущих глав, знакомство

8 ПРЕДИСЛОВИЕ
с которыми необходимо. Нумерация параграфов и формул
производится в каждой главе самостоятельно, а при ссылках в
пределах одной главы ее номер не указывается.
Книга может быть полезна студентам — инженерам, физикам и
представителям других специальностей (в том числе, заочникам),
начиная, примерно, с середины второго семестра 1-го курса в ка-
качестве пособия к изучаемому ими курсу математики. Она пригодна
и практику, если он захочет подробней ознакомиться с тем или
иным разделом математики, который может понадобиться ему в его
работе.
Несомненно, что разнородный материал трудно читать активно.
Целеустремленная проработка обычно подразумевает читателя, перед
которым жизнь поставила в данный момент одну определенную за-
задачу. Такой читатель склонен пропускать все, что не относится к
его задаче.
Возникает общий вопрос: целесообразно ли читать подобную
книгу «впрок», не будет ли такое чтение поверхностным, не окажутся
лн приведенные в ней советы забытыми вскоре после прочтения?
В ответ на это авторы могут высказать два аргумента.
Во-первых, мы везде старались давать не только практические
рецепты, но и те глубокие общие идеи, из которых эти рецепты
возникают. Такие идеи обогащают интеллект читателя, развивают
его научный кругозор, дают возможность по-иному взглянуть на
окружающий мир и потому задерживаются гораздо прочнее.
Второй аргумент относится к психологии памяти. Очень часто
бывает так, что хотя Вы не можете воспроизвести прочитанное все
подряд, в том порядке, в котором материал Вам преподносился, но
этот материал не изгладился из памяти! Отдельные его части могут
быть воспроизведены Вами при ассоциативном воспоминании, напри-
например, когда Вы сталкиваетесь с задачей, требующей того или иного
приема. Даже смутное воспоминание о том, где можно найти этот
материал, и то часто оказывается полезным*). Говоря грубо, имеются
вещи, понятия и связи, которые мы вспоминаем лишь тогда, когда
это нам очень нужно. Вспомните, что сказал по аналогичному поводу мо-
монах Варлаам: «Я давно не читывал и худо разбираю, а тут уж раз-
разберу, как дело до петли доходит».
Итак, читайте нашу книгу и изучайте ее. Но даже если нет воз-
возможности изучать ее глубоко, читайте, как детектив, и, может быть,
она поможет Вам найти решение трудных задач.
Пусть судьба хранит Вас от петли, но не от трудностей.
Только решая трудные задачи, человек полностью раскрывает
свой талант, свои возможности, только в трудных задачах он дает
максимальную отдачу.
*) Следуя 3. Фрейду, можно было бы сказать, что забытые теоремы на-
находятся в подсознании, где-то рядом с подавленными импульсами раннего
детства.

ПРЕДИСЛОВИЕ 9
Мы будем благодарны читателям за любые замечания по содер-
содержанию и изложению материала книги. Несомненно, что на отдельных
местах книги сказались различные навыки ее авторов, один из кото-
которых является физиком, а другой — математиком. Порой мы упорно
тянули в разные стороны. Теперь сюда приложит свои усилия еще
и читатель, так что все эти усилия будут складываться*). Подобный
случай был разобран еще в известной басне Крылова, однако мы
надеемся, что у нас результаты будут не столь плачевны.
Авторы выражают свою признательность К. А. Семендяеву,
который прочитал рукопись книги и сделал ряд ценных заме-
замечаний.
По истечении четырех лет оказалось необходимым новое, третье
издание книги. Этот факт авторы рассматривают как одобрение
основного замысла — вооружить читателя практически полезными мето-
методами и сведениями, предельно упрощая и облегчая формальные
определения и доказательства.
Вместе с тем, новое издание налагает и новую ответственность.
Поэтому книга была подвергнута тщательному пересмотру (з кото-
котором большое участие принял редактор А. А. Овчинников) и добав-
добавлены важные разделы.
В третьем издании значительно переработаны §§ IX.1, IX.2,
расширены §§ Х.9, XIV.4, X1V.7, добавлены §§ III.4, VIII.10, XI.3,
XI.5, XIV,8 и небольшая гл. XV. При этом были учтены замечания
А. Н. Тихонова, которому авторы выражают свою признательность.
Наиболее существенным добавлением является глава XV, посвя-
посвященная электронным цифровым .машинам. В ней изложены принципы
действия машин и программирования наиболее простых задач. Эта
глава не должна заменять специальные учебники для программистов,
однако она позволяет понять некоторые общие принципы и специ-
специфику численных расчетов.
В третьей главе подробнее рассмотрено интегрирование быстро-
колеблющихся функций. В главе VIII добавлен параграф о подобии
явлений, в котором с физической и математической сторон рас-
рассматриваются теория размерности, понятие подобия и автомодель-
ности.
В главах IX и XI более подробно и четко даны определения
вектора и тензора, связь этих понятий с линейными преобразова-
преобразованиями. Подробно рассмотрены симметрические и антисимметрнческие
тензоры; в частности, описано введение псевдовектора, эквивалент-
эквивалентного антисимметричному тензору в трехмерном пространстве. Добав-
Добавлены физические задачи о движении точки в поле центральных сил
и о вращении твердого тела. Эти задачи были и остаются класси-
классическими примерами приложения теории обыкновенных дифференци-
дифференциальных уравнений к физике.
*) Сложение сил по векторному закону изложено в гл. IX.

10 ПРЕДИСЛОВИЕ
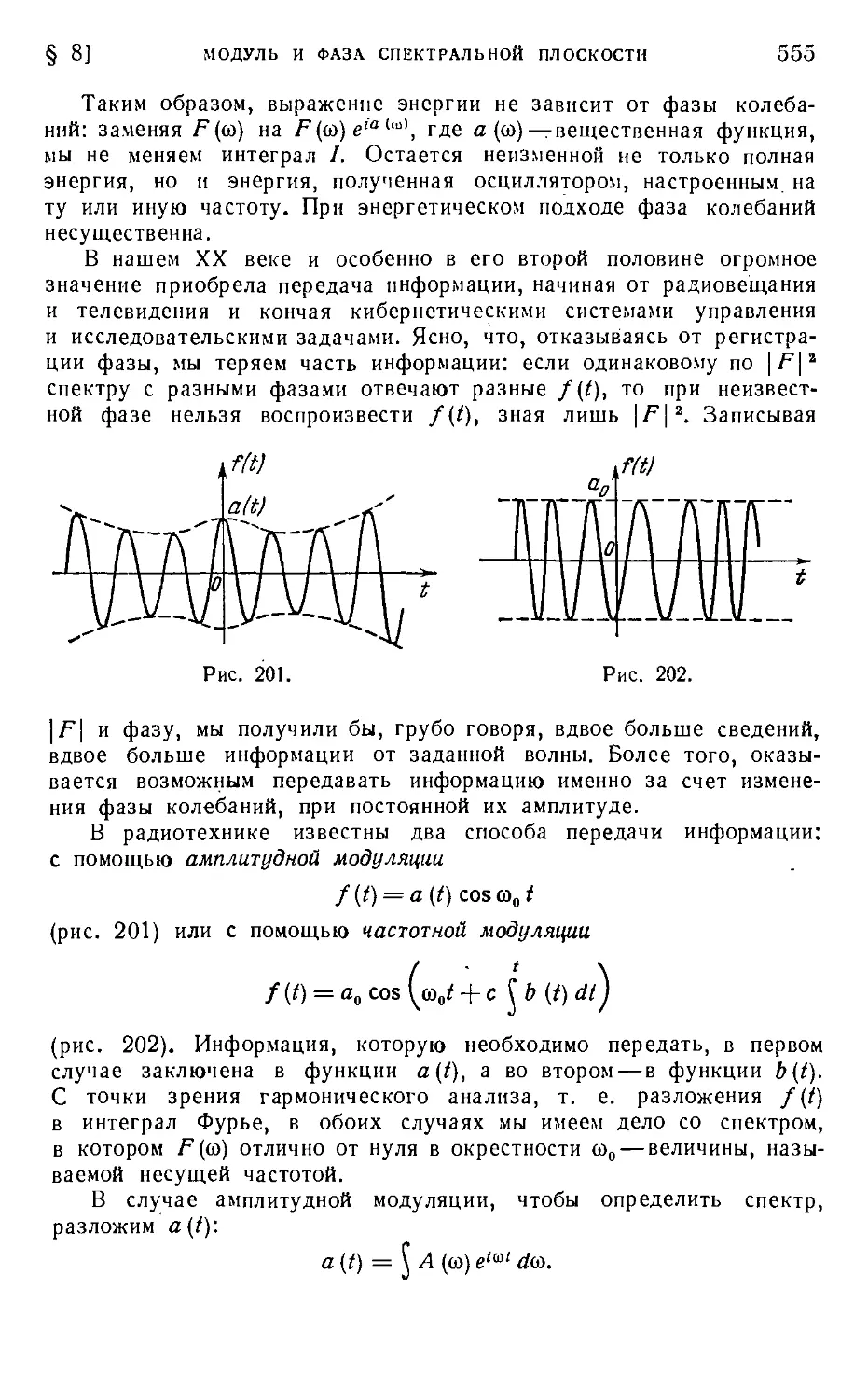
В связи с теорией спектрального разложения рассмотрен вопрос
о фазг Фурье-компонент; потеря информации при переходах к спек-
спектральной плотности стала привычной, полезно напомнить о том,
что, кроме квадрата модуля, колебания характеризуются также фазой.
В целом мы надеемся, что добавления, не меняя общей устрем-
устремленности и доступности изложения, делают книгу более физической
и несколько более современной.
Мы отдаем себе отчет в том, что название книги не вполне от-
отражает ее содержание; может быть, ее следовало бы назвать как-то
иначе. Однако для того, чтобы было ясно, что эта книга является
новым изданием предыдущей, основа которой осталась прежней, мы
были вынуждены название сохранить.
В заключение добавим, что в настоящее время авторы заканчи-
заканчивают работу над книгой «Среда из невзанлюдействующих частиц»,
которая непосредственно примыкает к настоящей книге и составля-
составляет первую часть курса математической физики,

ГЛАВА I
НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
Решение физической задачи, полученное в математических тер-
терминах, например в виде комбинации различных функций, производ-
производных, интегралов и т. п., нужно уметь «довести до числа», которое
чаще всего и служит окончательным ответом. Для этого в различ-
различных разделах математики выработаны разнообразные численные ме-
методы. В элементарной математике рассматриваются, как правило,
лишь методы точного решения поставленных задач — решения урав-
уравнений, геометрических построений и т. п. Это является ее слабой
стороной, так как такое решение возможно в очень редких случаях
(что приводит к резкому сокращению круга рассматриваемых задач),
а если и возможно, то часто получается чрезвычайно громоздким.
Даже такой сравнительно простой вопрос, как решение об./.их
(с произвольными коэффициентами) алгебраических уравнений л-й сте-
степени, оказался в рамках элементарной математики при л > 2 непо-
непомерно сложным и громоздким, а при л>4 и вовсе неразрешимым.
И только систематическое применение методов приближенных вычи-
вычислений на основе аппарата высшей математики дало возможность
доводить до конца, и притом единообразным способом, решение
широкого класса важных для приложений математических задач.
Более того, развитие численных методов высшей математики и внед-
внедрение современной вычислительной техники привели к тому, что если
какая-либо задача достаточно четко сформулирована математически,
то (за исключением уж особо сложных случаев) она обязательно
будет решена с достаточной для практики точностью. Таким обра-
образом, высшая математика дает не только идеи, лежащие в основе
анализа физических явлений, но и численные методы, позволяющие
довести решение конкретных задач физики и техники до конца.
Некоторые из этих методов указываются и в начальном курсе
дифференциального и интегрального исчислений: например, простей-
простейшие методы вычисления производных и интегралов, вычисление зна-
значений функции с помощью рядов и т. п. В этой и в последующих
главах (в частности, гл. 11, HI, VI11) мы остановимся на таких ме-
методах более подробно. Они не связаны непосредственно один с дру-
другим и потому с ними можно знакомиться независимо.

12 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
§ 1. Численное интегрирование
Когда та или иная практическая задача сведена к вычислению
определенного интеграла, то можно сказать, что самая трудная часть
дела уже позади. Если подынтегральная функция f{x) такова, что
можно выразить неопределенный интеграл F{x) при помощи конеч-
конечного числа элементарных функций, то величину определенного ин-
интеграла принципиально получить нетрудно, пользуясь формулой
ь
\f{x)dx = F(b)—F(a). При этом придется выполнять ряд арифме-
а
тических действий для того, чтобы найти значения величин F(b) и
F(a). На практике, однако, это может привести к существенным
затруднениям, так как для неопределенного интеграла F(x) может
получиться очень сложная формула.
Указанный способ может оказаться и вовсе непригодным, если
(а это случается нередко) не удается получить формулу для неоп-
неопределенного интеграла.
Иногда рассматриваемый интеграл выражается через неэлементар-
неэлементарные, но хорошо изученные функции, для которых составлены под-
подробные таблицы (см., в частности, книгу: Е. Янке, Ф. Эмде и Ф. Лет,
Специальные функции, «Наука», 1968). К таким функциям относятся,
например,
\e-x*dx, С — их, C^dx, \e-^dx, Csin^d*, Ccos^dx
и т. д. Эти интегралы, не выражающиеся через элементарные функ-
функции, даже имеют специальные наименования: интеграл ошибок (см.
гл. XIII), интегральный синус и т. д.
В других случаях интеграл удается вычислить, разлагая подын-
подынтегральную функцию в ряды того или иного вида. Например, для
интеграла
i
, С
=)
о
i
sin х
о
соответствующий неопределенный интеграл не выражается через эле-
элементарные функции. Тем не менее, воспользовавшись рядом Тейлора
для синуса
получаем
i
С I x2 x*

§ 1]
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
13
Вычисляя последовательно члены полученного ряда, мы останавли-
останавливаемся, когда достигаем выбранной разумной степени точности. На-
Например, при вычислении с точностью до 0,001 достаточно ограни-
ограничиться тремя первыми членами ряда, что даст значение /=0,946.
Некоторые определенные интегралы удается подсчитать точно
с помощью методов теории функций комплексного переменного. Так,
например, в § V.9 мы покажем, что
0)
Уо
х,
Рис. 1.
Ь-х„
хотя соответствующий неопределенный
интеграл не выражается через элементар-
элементарные функции.
Если и эти методы непригодны, то
величину определенного интеграла можно
подсчитать численно с помощью формул
численного интегрирования, к которым мы сейчас переходим.
Простой и вместе с тем хороший способ (который был уже осве-
освещен в ВМ, § I. 7) состоит в следующем: промежуток интегрирова-
интегрирования разбиваем на несколько малых равных частей. Интеграл по каж-
каждому малому промежутку приближенно считаем равным произведению
длины промежутка на среднее ариф-
jj_ метическое значений подынтеграль-
; J J ' ' ' *~~aL^i н°й Функции в начале и в конце
123 ' промежутка. Этот способ называет-
рис 2. ся способом, трапеций, потому что
получается такой результат, как если
бы в каждом малом промежутке дуга графика у=/{х) заменя-
заменялась на ее хорду, а площадь под этой дугой (величина интеграла)
заменялась площадью получающейся трапеции с вертикальными осно-
основаниями (рис, 1). Соответствующая формула имеет вид (проверьте!)
B)
где для краткости обозначено f(Xi)=y{.
Еще более эффективную формулу можно получить, если кривую
y=f(x) на малом интервале заменить параболой, т. е. графиком
квадратичной зависимости. Разобьем промежуток интегрирования от
х — а до х = Ь на четное число 2/и равных промежутков. Границы
промежутков пусть будут хо — а, хг, хг, . . ., хгт = Ь (рис. 2). Длину
одного промежутка обозначим через А, так что х1 = х0-\-h, хг =
h hк

14 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
Рассмотрим
\ \ f(x)dx,
т. е. вклад в исходный интеграл от первых двух промежутков. Кри«
вую_у=/(*) на промежутке от х = хй до х = х2 заменим параболой,
проходящей через точки (х0; у0), (х±; у,), (х2; у2); и площадь под
кривой приближенно заменим площадью под параболой. Уравнение
параболы имеет вид у = тх'2 -\-nx-\-l. Коэффициенты т, п, I опре-
определяются из условия, что парабола проходит через три данные точки:
У о = тх1 + пхо +1>
у1 = тх\-^пх1-^1,
уг = тх\-\- пх2-\-1.
Однако это приводит к довольно длинным выкладкам.
Проще поступить так. Будем искать уравнение параболы в виде
у = А (х-хв) (x—xJ + B (x—xB) (x-x2) + C(x—Xl) {x—xt). C)
Ясно, что справа в C) стоит многочлен второй степени, так что C)
действительно есть .уравнение параболы. Положим в C) л; = л;0, по-
получим _уо = С(*<) — ^iH-^o — хг)> или _у0 = С2Л2; полагая в C) х = хх —
= xo-\-h, получим _yl=- — Bh2; наконец, полагая в C) л; = л;2 = xB-\-2h,
получим y2—2Ah2. Отсюда
Площадь под параболой есть
+ C{x — xl) (x—x2)] dx = A~ hs — B i A»-|- C-| A».
(При выполнении интегрирования удобно сделать замену переменной
х — xl = s; при этом надо учесть, что хв~х1 — h, x2 = x1 -f-A.) По-
Поэтому
х2
/(.V) dx « A j hs—В 1 hs + С | h\
л-'о
*) Отметим, что совершенно аналогично решается следующая задача: найти
многочлен степени л, принимающий заданные значения для л + 1 значений х.
Эта интерполяционная задача встречается при подборе эмпирических формул
(см. § II. 4), при действиях с функциями, заданными таблично, и т. д.

§ 1] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 15
Пользуясь D), находим
Г h
E)
*4 Xim
Таким же способом можно подсчитать \jf{x)dx, ..., ^ f(x)dx.
т г
Для интеграла по всему промежутку от х = а до л: = 6 получим
ь
откуда
ь
,-i)]. F)
где h = ——. Эта формула называется формулой Симпсона.
Если переписать формулу E) в виде
1 "°\ flx\dx~ 2 v I Уо + Уг
то получим, что формула Симпсона основана на приближенной за-
замене среднего значения у функции у (х) на промежутке от хв до
ха-\- 1h на
j^l^ + fe. G)
Формула трапеций дала бы (проверьте!)
(8)
Для проверки вида формул можно положить у (х) = k = const, откуда
и_у = &; тогда обе формулы становятся точными. Из вывода фор-
формул следует, что обе формулы G) и (8) являются точными для линейных
функций (вида у—рх-]-п), а формула G) — также и для квадратичных
функций (вида у =рхг-{- пх-\-1). Интересно отметить, что формула G)
на самом деле является точной и для кубических функций (у=рхя~\-
+ * l k
При разбиении промежутка на то же самое число частей фор-
формула Симпсона, как правило, значительно точнее формулы трапеций.

16 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
Рассмотрим примеры.
1
1. Найтн/^J^.
о
Разобьем промежуток интегрирования на две части и подсчитаем
интеграл по формуле трапеций и по формуле Симпсона.
Находим необходимые значения подынтегральной функции
л: 0 0,5 1
у 1 0,6667 0,5
Формула трапеций дает
H^ +0,6667) = 0,7083.
Формула Симпсона дает
J_
6
/=1A+4. 0,6667 +Ю,5) = 0,6944.
Так как /=1пA
= 1п 2 = 0,6931 (с точностью до четырех
о
знаков), то формула Симпсона дала ошибку примерно 0,2%, а фор-
формула трапеций 2%.
1
2. Найти /= С ln1(V^2X) dx. (Заметим, что С *"* V^-Я dx не берется
о
в элементарных функциях.) Разбиваем промежуток так же, как и
в примере 1, и находим необходимые значения подынтегральной
функции
х 0 0,5 1
у 0 0,324 0,346
По формуле трапеций получаем /=—■(— |-0,324 ) = 0,248. По
формуле Симпсона / = -f @,324-4 + 0,346) = 0,274. Точное значение
(с тремя верными знаками) этого интеграла есть 0,272. Поэтому
ошибка при подсчете по формуле трапеций составила около 10%,
а по формуле Симпсона менее 1%.
Преимущество формулы Симпсона особенно сказывается при уве-
увеличении числа п интервалов разбиения. Можно показать, что при
этом ошибка формулы трапеций убывает обратно пропорционально
л2, а ошибка формулы Симпсона — обратно пропорционально л4 (в том
случае, если производная третьего порядка от интегрируемой функ-
функции остается на интервале интегрирования конечной).

§ 2] ВЫЧИСЛЕНИЕ СУММ ПРИ ПОМОЩИ ИНТЕГРАЛОВ 17
Приведенные примеры показывают, насколько быстро и просто
численные методы позволяют находить интегралы. Часто даже в тех
случаях, когда для интеграла можно получить точную формулу, его
быстрее и легче найти численным интегрированием.
После смерти великого итальянского физика Энрйко Ферми, по-
построившего первый урановый котел, были опубликованы странички,
из его рабочей тетради. По ходу расчетов надо было вычислить
интеграл. Ферми предпочел найти его численно, хотя интеграл можно
было выразить через логарифмы и арктангенс.
Упражнения
1. Найдите величины следующих интегралов по формуле Симпсона и по фор-
формуле трапеций, разбивая промежуток интегрирования на 4 части:
3 2 я
С dx (* 2 (* sin х ,
а) \ -— , б) \ е~х dx, в) \ ——- ах-
1 О О
Вычисления ведите в пределах точности логарифмической линейки. Значения
показательной функции можно взять, например, из справочника по математике
И. Н. Бронштейна и К. А. Семендяева *).
3
(* х dx
2. Найдите \ х , . по формуле Симпсона, разбивая промежуток интегриро-
о
вания на 4 части. Вычисления ведите с четырьмя знаками после запятой. Для
контроля найдите величину этого же интеграла, разбивая промежуток интегри^
рования на 6 частей.
3. Проверьте непосредственно, что формула (8) является точной для много-
многочленов первой степени, а формула G)—для многочленов второй степени.
Указание. Проверьте сначала точность этих формул для функции у = х,
а формулы G) —для функции у = хг.
§ 2. Вычисление сумм при помощи интегралов
Рассмотрим суммы нескольких чисел, образованные по опреде-
определенному закону, например,
или
S9e = V~5 + V'6 + /7 + ... + /99 + /Тбб,
или
Сумму обозначаем буквой S. Индекс, стоящий внизу у этой буквы,
указывает на число членов в сумме. Каждую такую сумму можно
*) И. Н. Бронштейн, К. А. Семендяев, Справочник по матема-
математике, «Наука», 1964.

18 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
записать более компактно, если удастся установить связь между
величиной отдельного слагаемого в сумме и его номером. Так в пер-
первой сумме слагаемое а„ просто равно номеру я, который меняется
от 1 до 6, а потому первая сумма равна
6 б
-s.= 2*» = 2 п.
Иногда бывает удобнее, чтобы номер начинался от нулевого; тогда
надо обозначить п — \=т, т. е. л = /»+1, что даст
5
= 2
0
впрочем, здесь вместо т можно вновь писать п или любую другую
букву, так как индекс суммирования является «немым», т. е. вели-
величина суммы не зависит от его обозначения. (В этом индекс сумми-
суммирования аналогичен переменной интегрирования в определенном ин-
интеграле; ср. ВМ, § 1,8). Обратите внимание на то, что в последней
сумме индекс меняется от 0 до 5, а число слагаемых в соответствии'
с этим равно шести.
Подобным образом, вторую из выписанных сумм можно записать
так:
юо _
Soe=2/P-
р=5
Однако лучше, чтобы индекс менялся от 1 или от 0; для этого надо
обозначить р — 4 = т или р — 5 = я, что даст
96 95
S96 = 2 Vm+4= 2 V
tn= 1 п=0
Третья сумма имеет вид
20
= 2-1
+0-, Ill'
Мы видим, что ее можно рассматривать как сумму значений функ-
функции f (х) = — , когда х принимает значения от х = 1 до х= 3 через 0,1
(этот подход полезен для дальнейшего). И в других случаях часто
бывает удобно рассматривать заданную сумму как сумму значений
некоторой функции f(x) для х, меняющегося от некоторого х = а
до х = Ь с постоянным интервалом Дл: = й.
Выписанные суммы не так трудно вычислить, однако, если сумма
состоит из большого числа членов, то ее вычисление становится
утомительным. К тому же часто приходится сравнивать суммы, со-
составленные по одному и тому же закону, но с разным числом чле-

§ 2] ВЫЧИСЛЕНИЕ СУММ ПРИ ПОМОЩИ ИНТЕГРАЛОВ W
нов. В этом случае желательно знать не только величину суммы
при некотором конкретном числе ее членов, но и зависимость вели-
величины суммы от числа ее членов.
Во многих случаях можно приближенно находить суммы при по-
помощи интегралов.
Вспомним, что изучение определенных интегралов начинают
с приближенного представления интеграла в виде суммы конечного
числа членов. Затем устанавливают, что точное интегрирование мно-
многих функций с помощью неопределенных интегралов не представляет
затруднений.
Воспользуемся этим для вычисления сумм.
Запишем формулу трапеций, дающую приближенное выражение
интеграла в виде суммы. Если промежуток интегрирования от х=а
до х = Ь разбит на п равных промежутков длиной = h каждый,
то
/(х) dx « h■ [1 /(а) + /(а + h) +
+ (л_1)А)+/(а + л
где a-}-nh = b.
Из этой формулы мы получаем следующее выражение для суммы:
<9>
Отбрасывая в правой части (9) слагаемое -п"/(#)+ -=-/(&), что
оправдано, если
ь
~ [ fiv\ rff^l f ln\ J
2
1/F),
a
т. е. если число членов суммы велико и функция f(x) меняется не
слишком быстро, мы получим более грубую формулу:
ь
f(a) +/(fl + h) +/(а + 2A) + ... +/(&) « 1 J/(*) dx A0)
a
Если величина Л мала, то можно воспользоваться приближенными
формулами
1
a b+—h
1 „ , 1
а - -тг ''

20 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
Тогда из (9) получаем
■4-*
f{x)dx+~
ИЛН
ь+т
a~'2
f(x)dx. A!)
При выводе формул A0) и A1) мы исходили из формулы (9), а она
получена из формулы трапеций, которая является приближенной.
Поэтому хотя (9) и A1) точнее формулы A0), они, однако, тоже
приближенные, а не точные формулы. При уменьшении величины h и
соответствующем увеличении числа членов суммы точность формул
возрастает.
Применим полученные формулы к вычислению сумм, приведенных
в начале параграфа.
Для суммы Se = 21, f(x) = x, A=l. По формуле A0) получаем
6
С
J
xdx =4- л;2!6 = 17,5.
J
Ошибка составляет 17%. По формуле (9) находим
l
Наконец, по формуле A1) находим
6.5
0,5
При применении формул (9) и A1) мы получили абсолютно точный
результат. Это связано с тем, что в рассматриваемом примере
функция f(x) линейная (см. упражнение 3).
Для следующей суммы 58в = |/ 5 -f Y 6 + ... + 1^100 получаем,
учитывая, что f(x) = \^x, h=\, по формуле A0)
100
2 ...
~
= -| A000 — 5 У) = 659,2.

К 2] ВЫЧИСЛЕНИЕ СУММ ПРИ ПОМОЩИ ИНТЕГРАЛОВ 21
По формуле (9) находим Su ж 665,3 и по формуле A1) находим
SM «665,3. Значение суммы See, вычисленное непосредственно
(с точностью до четырех значащих цифр), есть также 665,3.
Для последней суммы f(x) = — , h =0,1. Поэтому по формуле A0)
получаем
По формуле (9) находим S21« 11,66 и по формуле A1) получаем
SiXM 11,51. Значение суммы, вычисленное непосредственно, есть
Sai= 11,66 (с точностью до двух знаков после запятой).
В приведенных примерах формулы (9) и (!!) дают вполне удов-
удовлетворительную точность, так что ими и следует пользоваться на
практике. Грубая формула A0) может быть полезной для формули-
формулировки закона возрастания суммы при неограниченном увеличении
числа ее членов. Однако при всех численных расчетах с определен-
определенным числом членов суммы надо пользоваться формулой A1), кото-
которая не сложнее A0), но значительно точнее*).
Во всех рассмотренных нами примерах отдельные слагаемые,
входящие в состав суммы, имели одинаковые знаки.
Если слагаемые имеют разные знаки, то для вычисления суммы
при помощи интеграла надо было бы рассматривать интеграл от
функции, меняющей знак несколько раз на промежутке интегрирова-
интегрирования. Для таких интегралов формула трапеций дает очень плохие резуль-
результаты, Поэтому полученные нами формулы годятся только для сумм,
в которых все слагаемые имеют один знак, и неприменимы к сум-
суммам, у которых отдельные слагаемые имеют разные знаки. В част-
частности, полученные формулы неприменимы к суммам, в которых сла-
слагаемые меняют знак через один. Суммы такого рода называются
знакочередующимися. Примером знакочередующейся суммы может
служить
4 5 + 6 7~+~8 9+10 11 *
Как же находить такие суммы?
Если члены знакочередующейся суммы убывают (или возрастают)
по абсолютной величине, так что абсолютная величина каждого
последующего члена меньше (или больше) абсолютной величины пре-
предыдущего члена, то можно применить следующий прием.
*) Применение формулы A0) связано с очевидной систематической ошибкой,
получающейся из-за отбрасывания двух слагаемых при выводе этой формулы.
Если все слагаемые одинаковые, т. е. j (х) = А = const, a F—о)//г--=л, то
рассматриваемая сумма равна (п + l) А, тогда как формула A0) дает только л А
(а формула A1) дает в этом случае точное значение).

22 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. I
Объединим попарно соседние положительные и отрицательные
члены. После этого задача сводится к вычислению суммы, у кото-
которой знаки всех членов одинаковы.
Так, например,
£ _ 1_±4-±_±4-±—L+ '-l
0)8 ~Т 5 + 6 7 """ 8 * 9 +Т0 11
10 11 у 4-5 ' 6-7 ' 8-9 ' 10-11 '
Будем считать, что исходная знакочередующаяся сумма состоит
из четного числа членов. Тогда если она начинается с положитель-
положительного члена, то кончается отрицательным. Такую сумму можно за-
записать в виде
Sn+i = /(«)-/(« + h)+f(a + 2h)— f(a + 3h) + ...—/(&), A2)
где положено b=a-\-nh.
Разность между двумя соседними членами этой суммы можно
записать так:
-j\ h
Это равенство приближенное, однако оно тем точнее, чем меньше Л*).
Сумма A2) принимает вид
/■/ / I la \ I J ■£? { hi I /1 Ч\
Применим к правой части формулу A1). Заметим, что в формуле A1)
h представляет собой разность между соседними значениями неза-
независимой переменной. В формуле A3) эта разность равна a-\-(k + ут) А —
— а-\- Ik—^ ) А = 2А. Поэтому, применяя формулу A1), мы должны
*) Если обозначать a-\-kh = x и поменять знаки, то последнее равенство
можно переписать в виде f(x-{-h)— f (*)» hf [ х-\--к )• Легко оценить его
ф Тй
точность: в самом деле, по формуле Тейлора
)-f(x) = f'
Таким образом, разложения различаются, лишь начиная с членов третьего
порядка малости в сравнении с /г.

§ 2] ВЫЧИСЛЕНИЕ СУММ ПРИ ПОМОЩИ ИНТЕГРАЛОВ 23
вместо h взять 2/г; тогда получаем
b-\+h
~h-k f f'(x)dx=—\f(x)
e+4-й
м«-4)->
2
Применим эту формулу для вычисления суммы
8 4 5 + 6 7 + 8 9+10 11*
Здесь
= !, e = 4, ft=ll, A=l,
поэтому находим
Непосредственное суммирование дает ^8 = 0,0968 (ошибка менее 8%).
Если знакочередующаяся сумма имеет нечетное число членов, то,
начинаясь с члена /(а), она кончается членом f(b) того же знака,
что и /{а). В этом случае мы сперва по формуле A4) найдем сумму
без последнего члена f(b), а затем добавим этот член:
$„,=/(<>)—/(» + *)+/<а+2*)—...+/(»)»
Если h малб, то для вычисления fib+-~\ можно ограничиться
двумя первыми членами ряда Тейлора:
Полагая здесь х=Ь—-j , найдем fib — -^\cvf(b) — т? f (b), &no-
лагая л;= Ь-\--^ , найдем /( Ь-\- -^ ) »/(&) -\--к f (b). Поэтому

24 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. I
Окончательно сумма для случая нечетного числа членов равна
Эта формула не менее точна, чем A4), с помощью которой она по-
получена. Рассмотрим примрр:
~ _^ L , 1 Lj__! L j-1_1j- l
9~4 5 + 6 7 + 8 9+10 11+12"
По формуле A5) получаем S9 да -д- ( ^-г+пг^ ) — 0,1829, непосред-
ствемное суммирование дает ^9 = 0,1801. Ошибка составляет при-
примерно 1,5%. Отметим, что величина знакочередующейся суммы,
как это видно из формул A4) и A5), имеет тот же порядок, что
и отдельные слагаемые. Поэтому добавление одного члена сущест-
существенно меняет эту величину. Так, в рассмотренном примере S, почти
в два раза больше, чем S3.
Отметим существенное различие между знакочередующейся суммой
и суммой с членами одного знака. Будем увеличивать число членов
суммы так, что первый и последний члены не изменяются и не ме-
меняется закон образования суммы. Для этого будем уменьшать раз-
различие между соседними членами суммы, т. е. уменьшать величину h.
Таким способом можно из суммы l+V + 'T полУчить суммы 1-f-
1,11 1 111!1! I1
+ Т7Г + ГД + Пз+---+Т' или 1 + f7oT + TTo2i~--- + 3'
Если все члены суммы имеют одинаковый знак, то величина суммы
приблизительно пропорциональна числу членов. Это видно, например,
из формулы A0). Действительно, перед интегралом в правой части
A0) стоит множитель -г, а величина h обратно пропорциональна
числу членов суммы. Поэтому в описанном процессе величина суммы
неограниченно возрастает имеете с ростом числа членов суммы.
В случае знакочередующейся суммы с четным числом слагаемых
ее величина при описанном увеличении числа членов приближается
к определенному числу, не зависящему от количества членов суммы,
а именно, к
J^^b\ A6)
Это легко усмотреть из формулы A4), так как* при большом числе
члено» h будет близко к нулю и потому /(а—у) да/(а),
). Аналогично при нечетном числе слагаемых из

§ 3] ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 25
формулы A5) в пределе получаем другое значение, а именно:
S-lto+'M. A7)
Заметим, что при малом числе слагаемых, т. е. когда величина h
велика, упрощенные формулы A6) и A7) гораздо хуже формул A4)
и A5). Рассмотрим пример. Пусть S=\—2 + 3 — 4 =—2. По упро-
щенной формуле A6) получаем Sж—-^ (ошибка 25%), а формула
A4) дает
т. е. точный результат.
Выражения для сумм, которые были получены нами, являются
приближенными, причем их точность увеличивается, когда соседние
члены в сумме становятся более близкими друг к другу, т. е. когда
уменьшается величина h.
Упражнения
1. Найдите сумму 1 -f- r/^-f- f/'3-{-... -f- \/n, пользуясь формулой (II).
Сравните с величинами, найденными непосредственным суммированием для
п = 3; 4) 5.
2. Найдите величину суммы
3/3 0 /20'
3. Докажите, что формулы (9) и A1) абсолютно точны, если f (х) — линей-
линейная функция; при этом члены суммы образуют арифметическую прогрессию.
§ 3. Численное решение уравнений
В практических вычислениях довольно часто приходится сталки-
сталкиваться с численным решением уравнений вида
A8)
где /—заданная функция. Такие уравнения могут быть алгебраиче-
алгебраическими или трансцендентными (т. е. неалгебраическими, например
тригонометрическими и т. п.); как те, так и другие иногда называ-
называются конечными в отличие, например, от дифференциальных уравнений.
Сейчас имеется большое число методов решения различных классов
уравнений вида A8). Мы рассмотрим лишь три наиболее универсаль-
универсальных метода, широко применяемых и в других отделах математики.
Обычно начинают с нахождения грубого, совсем приближенного
решения, так называемого нулевого приближения. Если решается
физическая задача, то это грубое решение может быть известно из

26
НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. I
физического смысла задачи. Можно набросать график функции /(х)
и получить грубое решение, наметив точку пересечения этого гра-
графика с осью х.
Допустим, что такое грубое решение х0 нам известно. Обозначим
тогда точное решение, нам пока неизвестное, через х= xu-\-h. Поль-
Пользуясь формулой Тейлора, получим
Л I
fly I U\ fty \ I f {у \ _1 / 1 Q\
Но левая часть должна равняться нулю; отбрасывая многоточие, т. е.
члены высшего порядка малости, получаем
т. е.
X /■**/ An "
/(*о)
Если обозначить правую часть через хг, т. е.
B0)
то мы получаем «первое приближение» (таким образом, индекс равен
номеру приближения). С ним можно проделать то же самое; это
даст «второе приближение»
'!!'№
и т. д. Так как отбрасывание членов высшего порядка в формуле A9)
равносильно замене графика функции f(x) на касательную к нему
при jc = jc0, то геометрический смысл
рассматриваемого метода состоит в
последовательном построении каса-
касательных к графику и нахождении
точек пересечения этих касательных
с осью х (см. рис. 3). Очевидно, что
последовательные приближения бы-
быстро сходятся к искомому решению,
если только нулевое приближение
не лежало от него слишком далеко.
Этот метод называется методом
Ньютона (или методом касательных
рис з. в соответствии с его геометрическим
смыслом). Удобство этого метода
состоит в том, что при его применении приходится только вычис-
вычислять значения функции f{x) и ее производной и производить ариф-

§ 3] ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 27
метические действия, что для функции, заданной формулой, не
вызывает существенных затруднений.
Рассмотрим пример. Пусть надо решить уравнение
X3_3*_i=o. B1)
Так как левая часть равна —3 при х—\ и равна 1 при х=2, то
между х=\ и х = 2 имеется корень уравнения, причем естественно,
что этот корень ближе к 2, чем к 1. Поэтому примем хо = 2. Тогда
формула B0) даст
fe£iY =1,889.
Аналогично получаем, вычисляя с тремя знаками после запятой,
л:2= 1,879, х3 = 1,879.
Таким образом, с данной точностью решение л;= 1,879.
Интересно отметить, что в этом примере можно было написать
и точное решение уравнения. Уже в XVI веке итальянский матема-
математик Кардано опубликовал формулу для решения кубического урав-
уравнения
которая имеет вид
-1 / q М
= ]/ —Т+
Т+27 + У -^~У Т + 27-
Однако если в эту формулу подставить значения коэффициентов
уравнения B1), то мы обнаружим, что под знаком кубических корней
стоят мнимые числа 0,5 ± /\' 0,75 и лишь сумма этих корней веще-
вещественна. Таким образом, надо еще извлекать корни из мнимых чисел
(ср. § V.4), т. е. даже для приведенного простого примера метод
Ньютона оказывается гораздо проще применения «точной» формулы.
Что же тогда говорить об уравнениях четвертой степени, где точная
формула настолько громоздка, что ее не выписывают даже в спра-
справочниках! Или об уравнениях выше четвертой степени, а также
о подавляющем большинстве трансцендентных уравнений, где «точной»
формулы совсем не существует! Для таких уравнений преимущество
численных методов особенно очевидно.
Метод Ньютона принадлежит к числу итерационных методов
(иначе говоря, методов последовательных приближений), в которых
некоторый единообразный процесс последовательно повторяется («ите-
(«итерируется», от латинского «мтерацио» — повторение), в результате
*) Общее уравнение третьей степени ауъ-\-by2-\- су-{- d = 0 приводится к та-
такому виду с помощью подстановки (/ = *—^-.

28 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. I
чего получаются все более точные приближенные решения. В общем
виде в применении к уравнению A8) метод итераций выглядит так:
уравнение переписывается в равносильной форме
Затем выбирается некоторое значение х = х0 в качестве нулевого
приближения; последующие приближения вычисляются по формулам
х1 = <р(х„), xi = (f(xl), ..., вообще,
*„ + 1 = Ф (■*„)• B3)
При этом может быть два случая:
1) процесс может сходиться, т. е. последовательные приближения
стремятся к некоторому конечному пределу х; в этом случае, пере-
переходя в формуле B3) к пределу при п—>оо, видим, что х = х является
решением уравнения B2);
2) процесс может расходиться, т. е. конечного предела постро-
построенных «приближений» существовать не будет; из этого не следует,
что и решения уравнения B2) не существует, просто могло оказаться,
что процесс итераций выбран неудачно.
Поясним сказанное на простом примере уравнения, которое можно
решить без всякой «науки»,
*=4+1 B4)
с очевидным решением х — 2. Если положить хо = О и вычислять
с точностью до 0,001, то получим
.^=1; лга= 1,5; дг3=1,75; л;, = 1,875; д:5= 1,938;
хе= 1,969; jc,= 1,984; xs= 1,992; я, = 1,996;
л;10= 1,998; .vu= 1,999; д:12 = 2,000; x~ = 2,000,
т. е. процесс практически сошелся. Предел можно найти быстрее,
если заметить, что в данном случае разности между последователь-
последовательными приближениями образуют геометрическую прогрессию с первым
членом а = лг1—х0 и знаменателем ^ = -5 -. Поэтому сумма всей
прогрессии, т. е. х—х0, равна
а Х[—Xq \Х i -^о)
1 — q . хг—x-i
откуда
«1—*о—*а
В более сложных примерах последовательные разности лишь напо-
напоминают геометрическую прогрессию; в этих примерах формула B5)

§ 3] • ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 29
не дает точного решения, но дает возможность «перескочить» через
несколько приближений и получить приближенное значение решения,
от которого можно вновь начать итерации. (Это метод Эйткена.)
Если уравнение B4) разрешить относительно х, стоящего в пра-
правой части, т. е. переписать в равносильной форме
х = 2х — 2 B6)
и начать с ХО = О, то мы получим последовательно хг=—2;
л:2=—6; х3 = —14 и т. д., т. е. процесс сходиться не будет.
Это можно было предвидеть, заметив, что из B3) вытекает равенство
*н+1— *«= Ф (*,<)— Ф (*n-l).
т. е.
Стало быть, если значения функции ф (х) меняются медленнее, чем
значения ее аргумента, то расстояния между последовательиыми
приближениями будут все меньше и меньше, а если значения функ-
функции ф(лг) меняются быстрее, чем значения ее аргумента, то расстоя-
расстояния между последовательными приближениями будут все больше и
больше, и процесс разойдется. Так как скорость изменения значений
<р (х) по отношению к х равна ф' (х), то мы получаем, что если
|q>'(*)|<fc< 1, B7)
то процесс итераций сходится и притом тем быстрее, чем меньше k;
если же
то процесс расходится. Эти неравенства должны выполняться для
всех х либо, во всяком случае, вблизи искомого корня х уравне-
уравнения B2).
Мы видим, что уравнения B4) и B6) полностью равносильны,
но порождают различные итерационные процессы. (Чтобы пояснить
эту разницу, нет надобности даже переписывать уравнение B4)
в виде B6); достаточно заметить, что для получения последующего
приближения надо подставлять предыдущее приближение по первому
способу — в правую часть уравнения B4), а по второму способу —
в левую часть того же уравнения.) И в других случаях уравнение A8)
можно переписать в форме B2) многими способами, каждый из ко-
которых порождает свой итерационный метод, причем одни из них
могут оказаться быстро сходящимися и потому наиболее удобными,
другие — медленно сходящимися, а третьи — даже вовсе расходя-
расходящимися.

30 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. I
Приведенное выше решение уравнения B1) можно теперь понять
так: уравнение переписано в равносильной форме
хъ—Ъх—\
ХХ
после чего применен метод итераций, начиная с значения хо = 2.
В общем виде метод Ньютона для уравнения A8) сводится
к тому (см. B0) и далее), что это уравнение переписывается
в равносильной форме
после чего применяется метод итераций. Эта форма могла бы пока-
показаться несколько искусственной: хотя и легко показать равносиль-
равносильность уравнений A8) и B8), т. е. из A8) вывести B8) я- обратно,
но не сразу видно, чем помогает знаменатель /' (лг). Однако легко
проверить, что производная от правой части, т. е.
/У = 1 ff'-ft'^ff
Г ) ■ г- Г '
обращается в нуль при х = х, где х—решение уравнения A8).
Значит (см. рассуждения, связанные с оценкой B7)), чем ближе
последовательные приближения подходят к х, тем быстрее сходится
процесс.
Более того, так как при выполнении оценки B7) итерации схо-
сходятся не медленнее, чем прогрессия со знаменателем й, то мы
получаем, что метод Ньютона сходится быстрее геометрической
прогрессии с любым знаменателем!*)
Перейдем теперь к описанию метода малого параметра (он же
метод возмущений), который," как и метод итераций, представляет
собой один из наиболее универсальных методов в прикладной мате-
математике. Поясним этот метод на простом примере.
Пусть требуется найти решение трансцендентного уравнения
г*-1 = 2— х + а B9)
*) Скорость этой сходимости легко установить на следующем простом ти-
типичном примере. Пусть рассматриваются приближения по способу Ньютона
к нулевому корню уравнения х-\-хг = 0. Эти приближения связаны друг с дру-
другом соотношением
==
Хп'
1 + «и 1 г *хп
Допустим, что 0 < х0 < 1; тогда мы последовательно получим
х0, Х3 < xl < Хо, . . ., Хп
Можно показать, что и в общем случае скорость сходимости метода Нью-
Ньютона имеет порядок а2" @ < а < 1).

К 3j ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 31
при малых |ос|. Заметим для этого, что при а = 0 можно най-
найти простым подбором решение: х=\. Поэтому если решение
уравнения B9), зависящее от а, искать разложенным в ряд по сте-
степеням а,
х = х0 4- аа + Ьо? + сое3 + ...,
то, подставляя а=0, получим, что х0 должно равняться 1. Подста-
Подставим теперь разложение
х=1 + аа + Ьаг + са3 + ... C0)
в обе части уравнения B9) и воспользуемся известным разложением
показательной функции в ряд Тейлора; это даст
(аа-\-Ьа-+ са? + ,. .)а ,
+
,, i 2!
■ -+ ... =2 — A +aa + ba2 + са3
Раскрыв скобки и удерживая члени до а3, получим
\+аа + Ьаг + са3 + ~ а2 + aba3 + ^- а3 + ... =
= 1 —аа — Ьа2 — са3— ... 4- а.
Приравнивая в обеих частях коэффициенты при одинаковых степе-
цях а, получим соотношения
а = — а+1,
а"- ,
b
откуда последовательно найдем
а— 2 , о— 16, с—ig2, ..,
Подставляя эти значения в C0), получаем искомое решение урав-
ния B9) в виде ряда
х=^+~2 Тб ~^ТЭ2^~ * * *'
хорошо сходящегося при'небольших |а|.
В общем случае метод малого параметра применяется следующим
образом. Пусть формулировка некоторой задачи, помимо основных
неизвестных величин, содержит некоторый параметр а, причем эта
задача при а = 0 может быть более или менее легко решена (не-
(невозмущенное решение). Тогда решение задачи при а, близких к 0,

32 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 1
во многих случаях можно получить разложенным по степеням а с той
или иной степенью точности. При этом первый член разложения,
не содержащий а, получается при а = 0, т. е. дает невозмущенное
решение. Дальнейшие же члены дают поправки на «возмущение»
решения; эти поправки имеют первый, второй и т. д. порядки малости
по сравнению с а. Сами члены часто находятся по методу неопре-
неопределенных коэффициентов, т. е. коэффициенты при а, а2 и т. д.
обозначаются какими-то буквами, которые определяются затем из
условий задачи.
Метод малого параметра дает хороший результат только при
малых |а|; при больших |а| метод может привести к принципиаль-
принципиальным ошибкам, так как может получиться, что отбрасываемые (не вы-
выписываемые) члены более существенны, чем оставляемые.
Таким образом, метод малого параметра дает возможность,
исходя из решения некоторых «узловых» задач, получить решение
задач, формулировка которых близка к этим «узловым», если,
конечно, изменение формулировки не влечет за собой принципиаль-
принципиального, качественного изменения решения.
Во многих задачах уже вид члена первого порядка малости дает
возможность сделать полезные выводы о зависимости решения от
параметра при его малом изменении.
Метод малого параметра непосредственно связан с методом
итераций, что мы продемонстрируем на примере уравнения B9).
Прежде всего удобно, чтобы невозмущенное решение было нулевым;
это достигается с помощью подстановки х= 1 -\-у, откуда
еУ=\—у + а. C2)
Для проведения итераций заметим, что если искомый корень у
уравнения близок к 0, то уравнение удобно переписать в такой
форме у = <р(у), чтобы разложение cp(j) по степеням у не содер-
содержало первой степени, а содержало только свободный член, члены
с у2, у3 и т. д. В самом деле, тогда разложение ф' (у) не будет
содержать свободного члена и потому при у, близких к у, а значит
к 0, | ф' (у)| будет принимать малые значения, откуда вытекает схо-
сходимость метода итераций. Поэтому в исходном уравнении надо все
члены с у в первой степени перенести в левую часть, а все
остальные члены — в правую часть, после чего уже проводить
итерации.
В нашем примере, в уравнении C2), левая часть, т. е. су, в силу
формулы Тейлора
2 fl
содержит слагаемое у; значит, ее надо записать в пиле
еУ = У + (еу—у),
причем разложение скобки уже не содержит у в первой степени.

ОТВЕТЫ И РЕШЕНИЯ 33
Поэтому взамен C2) пишем
у + (еУ-у)=\-у+а,
откуда, объединяя члены с у (но не раскрывая скобок!), приходим
к уравнению
Это уравнение, равносильное C2), уже приспособлено к проведению
итераций. После разложения правой части по степеням у получим
,, « У2 У3
У = у—4~ "[г— •••
Теперь можно проводить итерации, начиная с ^0 = 0. Подставляя
это значение в правую часть C3), найдем
Подставляя у=уг в правую часть C3), получим
У* — ~2 16 96 •"■
Мы видим, что первое приближение C4) совпадает с точным реше-
решением C1) до членов первого порядка, второе приближение C5)—
с точностью до членов второго порядка. Для построения третьего
приближения можно подставить в правую часть C3) просто
тогда получится разложение, совпадающее с точным до членов
третьего порядка включительно, так что при вычислениях можно
учитывать только эти члены и т. д. Это дает возможность при вы-
вычислении каждой последующей итерации иметь дело лишь с конеч-
конечными суммами.
Упражнения
1. Примените метод Ньютона к уравнению B1), начиная от значения
*о = °"> *о = 1-
хз 1
2. Переписав уравнение B1) в форме х=—5—< примените к нему метод
о
итераций, начиная от значения *0 = 0; 1; 2.
3. Найдите решение уравнения х3-\-ах—1=0 при малых |а| по методу
малого параметра.
ОТВЕТЫ И РЕШЕНИЯ
§ 1
I. По способу трапеций
а) 1,12; б) 0,88; в) 1,84.
По способу Симпсона
а)'1,10; б) 0,88; в) 1,85.
2 Я. Б. Зельдович, А. Д. Мышкио

34 НЕКОТОРЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ.
3
2. Разбивая промежуток интегрирования на 4 части, находим \ ■
xdx
о
= 0,6275. Разбивая промежуток интегрирования на 6 частей, получаем также
3
Xdx =0,6275.
ех+1
о
3. Рассмотрим формулу (8) для функции у=х на промежутке от х0 до
2А. Здесь
тогда как '
Результаты совпадают, т. е, в данном случае формула является точной- Отсюда
вытекает точность формулы (8) и для функции у —ах (а = const), так как а
служит общим множителем во всех слагаемых. Записав точное равенство (8)
для у = ах и j/ = & (уже проверенное ранее) и сложив левые, а также правые
части, получим справедливость равенства (8) и для функции y = ax-\-k. Анало-
Аналогично рассматривается равенство G),
§2
1. В нашем случае / (х)*ар^х, А=1, а=1, Ь = п, По формуле A1)
получаем
л + 7а n + 7
^ f \/lcdx= f
или
д п = 3 формула дает S3 = 3,34, непосредственно находим S3 = 3,70.
Ошибка 11%.
Для п = 4 по формуле получаем S4 = 4,93, непосредственно находим
5^ = 5,29. Ошибка 7%. Для п = 5 по формуле S6 = 6,64, непосредственно на-
находим S5 = 7,00. Ошибка 5%.
2. По формуле A1) получаем S = 2,39.
3. Пусть / (x) = px-\-k, т. е. сумма имеет вид
где b = a-\-nh. Получилась арифметическая прогрессия с первым членом
+ k и разностью d = ph. Сумма такой прогрессии, как известно, равна

ОТВЕТЫ И РЕШЕНИЯ 35
Применим, например, формулу (9). По этой формуле получаем значение
ь
4- Upx + k)dx + \r(pa + k)+~(pb + k) =
Ъ—а( а + Ь , Л , Г а+Ь
что совпадает с точным значением для суммы.
§3
1. При хо = О получаем еще один корень * = —0,347 уравнения B1).
При хо=1 применение метода невозможно (знаменатель обращается в нуль).
2. При хо = О и *0=1 получаем сходимость к корню х из упражнения 1.
При *0 = 2 процесс итераций расходится.
3. Разложение решения имеет вид

ГЛАВА II
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
В практической работе часто бывает так, что зависимость между
переменными величинами — скажем х и у получается в результате
опыта, измерений. Обычно в таком случае эта зависимость оказы-
оказывается заданной при помощи таблицы, в которой для каждого зна-
значения х, при котором проводилось измерение, поставлено соответст-
соответствующее, найденное путем измерения значение у. Поэтому мы рас-
рассмотрим в этой главе сначала общие правила действий с таблицами,
а затем те новые моменты, которые возникают при обработке ре-
результатов опытов.
§ 1. Таблицы и разности
Нам очень часто приходится рассматривать функции, заданные
с помощью таблицы. Это могут быть математические таблицы, на-
например таблицы логарифмов, синусов, квадратов и т. п. Это могут
быть физические таблицы, взятые из каких-либо справочников,
например таблицы зависимости температуры кипения той или иной
жидкости от давления и т. п. Наконец, зависимость между перемен-
переменными величинами может получиться в виде не вполне обработанных
результатов опыта, измерений. Во всех этих случаях численные зна-
значения зависимой переменной задаются с помощью таблицы при опре-
определенных численных значениях независимой переменной. Функции,
заданные таким образом, могут входить в дальнейшие операции,
в частности, может потребоваться эти функции дифференцировать
или интегрировать. Могут понадобиться значения функции при про-
промежуточных, не выписанных в таблице, значениях независимой пере-
переменной (задача интерполяции) или при значениях независимой пере-
переменной, лежащих за пределами таблицы (задана экстраполяции) *).
Мы будем считать для простоты, что независимая переменная х
принимает значения, образующие арифметическую прогрессию, т. е.
х = х0, x = x1 = x0 + h, x = x2 = x0 + 2h, ..., x = xn = x0 + nh; эти
значения аргумента будем условно называть целыми, a h — назы-
*) Слова «интерполяция» и «экстраполяция» происходят от латинских
корней «интер» — внутри, «экстра»—снаружи, «полюс»—точка.

§ 1}
ТАБЛИЦЫ И РАЗНОСТИ
37
вать шагом таблицы. Соответствующие значения функции, помещен-
помещенные в таблице, обозначим через у0 =у (х0), у1 =у (xj, ...,yn=y (хп).
Приращения переменной х все одинаковые и равны п. Приращения
переменной у, вообще говоря, различные. Они называются первыми
разностями (более подробно разностями первого порядка) и обозна-
обозначаются через
так как их естественно сопоставлять полуцелым значениям х, т. е.
серединам между соседними «целыми» значениями аргумента:
От этих разностей можно опять брать разности, в результате чего
получатся вторые разности, определенные вновь для «целых» зна-
значений х:
б2у,=б^1 + ./, — 6>/„ 6^ = 6^2 + 7,-6^! + ./,, ..., 6а^п_1 =
(двойка сверху здесь означает порядок разности, а не показатель
степени) и т. д.
Приведем в качестве примера отрывок из таблицы десятичных
логарифмов с вычисленными разностями, которые умножены на 10й.
Таблица 1
ft
х
Ук
\0ЧУк
10ъ62ук
0
10,0
1,00000
ft
*k
Ук
10&бук
10562{/>
1/2
10,05
432
4
10,4
1,01703
—3
I
10,1
1,00432
—4
9/2
10,45
416
— 1
3/2
10,15
428
0
5
1
1,
0,5
32119
-4
2
10,2
1,00860
4
11/2
10,55
412
— 1
5/2
10,25
424
—1
6
10,6
1,02531
—о
3
10,3
1,01284
—5
13/2
10,65
407
7/2
10,35
419
2
7
10,7
1,02938
*) Иногда разность yk+i—Ук сопоставляется не значению jc = .v^ + i, , а зна-
значению х = хк. Тогда она обычно обозначается Аук, т. е. Аук = Ау | К=х ={/fc+i—ук.
При таком обозначении, как у нас, т. е. ук+1—Ун = ^Ук + '/Й=='^У\х=х1- + 1/ж' Раз*
ности называются центральными.

88
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
[ГЛ. II
У
Малость вторых разностей по сравнению с первыми и их почти
постоянство (третьи разности имеют уже порядок ошибок округле-
округления) в приведенном примере указывают на плавность хода изменения
функции, на отсутствие случайных «выпадов» из этого хода. Та-
Такая закономерность может проявляться в разностях более высокого
порядка и всегда свидетельствует о «правильности» хода измене-
изменения функции (ср. упражнение 2).
Конечно, если шаг не мал, а
также вблизи точек разрыва
и т. п., разности могут и не быть
малыми, но обычно в них прояв-
проявляется та или иная закономер-
закономерность.
Разности широко применяются
при интерполяции. Пусть требует-
требуется найти значение у при неко-
некотором значении х, заключенном
между табличными значениями xk
и xk + l. Самый простой способ —
Рис. 4. линейная интерполяция — состоит
в приближенной замене изучае-
изучаемой функции на линейную функцию, причем так, чтобы обе функции
О
совпадали при х = хк и при
АВ
= x
k+i
(рис. 4); геометрически это
означает замену дуги ^АВ неизвестного нам графика, показанного
на рис. 4 штрихами, на хорду АВ, соединяющую две его извест-
известные точки А и В. Обозначим х — xk — s. Так как линейная функция
выражается уравнением первой степени, то искомое значение у зависит
от 5 по формуле
y = a + bs, A)
где а и Ъ — некоторые коэффициенты. Из условий при xk и дсл + 1
получаем yk= a, yk+1 = a-\-bh, откуда
Выражая отсюда а и Ъ и подставляя в A), получаем окончательно
формулу для линейной интерполяции
■чЛ- B)
(Выведите эту формулу из подобия треугольников на рис. 4.) Фор-
Формулой B) можно пользоваться, если изучаемая функция на интер-
интервале от хк до xk+i мало отличается от линейной, т. е. если h до-
достаточно малб*). При k = 0 и 5<0 формула B) осуществляет
*) Из более точной формулы D) нетрудно вывести, что при малом h
ошибка при линейной интерполяции имеет порядок Л2, так как такой порядок
имеют вторые разности.

§ 1]
ТАБЛИЦЫ И РАЗНОСТИ 39
линейную экстраполяцию рассматриваемой функции в сторону х < лг0,
а при k — п— 1 и 5>Л —в сторону х > хп. Конечно, при экстра-
экстраполяции нельзя далеко уходить от табличных значений х, так как
принятый нами линейный закон изменения функции оправдывается
лишь на малом интервале изменения х.
Формулу линейной интерполяции B), как и последующие фор-
формулы, можно переписать в виде, не содержащем разностей. Под-
Подставляя в B) выражение бу i =Ук+1—Ук' получим равносильную
2
формулу
Хорошо видно, что при изменении s от 0 до Л коэффициент при
ук меняется от 1 до 0, а коэффициент при yk+1 — от 0 до 1; таким
образом, при s = 0 получается у =ук, а при s = h получается у =ук+1.
Ббльшую точность дает квадратичная интерполяция, при которой
изучаемая функция приближенно заменяется на квадратичную функ-
функцию, причем так, чтобы обе функции совпадали при х = хк, хк+1
и хк+2 (это в других обозначениях было проделано в § 1.1 при
выводе формулы Симпсона). Указанную квадратичную функцию удобно
искать в виде
y = a + bs + cs(s —h). C)
Согласно условию
откуда
2
Выражая отсюда с, Ь, с и подставляя в C), получаем формулу
Ньютона для квадратичной интерполяции
Как и выше, эту формулу можно использовать также для экстра-
экстраполяции. Формула D) не совсем симметрична: в ней использованы зна-
значения yk, yk+1 и ук+2, тогда как х расположен между xk и xk+1. Если
обратить направление оси х и подобным же образом использовать
значения yk+1, yk и ук_х, то взамен D) мы получим формулу
несимметричную уже в другую сторону. Взяв теперь полусумму

40
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
[ГЛ. II
правых частей формул D) и E), получим симметричную формулу
Бесселя
у=
1
обладающую высокой точностью. Мы предоставим читателю преоб-
преобразовать формулы Ньютона и Бесселя так, чтобы у оказался выра-
выраженным непосредственно через «узловые» значения ук, а не через
их разности.
Подобным образом можно было бы вывести интерполяционные
формулы еще более высокой степени. Однако, так как точность
экспериментальных данных ограничена, равно как и точность при-
применяемых таблиц функций, то обычно применение разностей слишком
высокого порядка не оправдано. В большинстве случаев (за исключе-
исключением измерений и вычислений, проводимых с особо высокой точностью)
бывает достаточно вторых или даже только первых разностей.
Если изучаемая функция разрывна, то интерполяцию можно про-
проводить только на интервалах, не содержащих точек разрыва; если
не обратить на это внимания, то интерполяция может дать совер-
совершенно неправильное представление о действительном поведении
функции. Так, на рис. 5 показана зависимость внутренней энергии,
£
'Скрытая
теплота
кипения
^j Скрытая
теплота плавления
100
Рис. 5.
Рис. 6.
которой обладает единица массы воды при нормальном давлении,
от температуры*). Эта зависимость имеет разрывы при температурах
фазовых переходов, т.е. при замерзании и при испарении воды. Там
же пунктиром показан результат квадратичной интерполяции в случае,
если выбранные «узловые» точки отвечают различным фазам; видно,
что эта интерполяция искажает реальную картину. Аналогичное
искажение получается при разрыве производной (т. е. при изломе
графика) у изучаемой функции. Так, на рис. 6 пунктиром показан
результат линейной интерполяции при наличии «острого» максимума;
хорошо видна ошибка, получающаяся вблизи этого максимума.
*) Чаще пользуются так называемой энтальпией {теплосодержанием)
H = E-{-pV, где р— давление, а V —объем. Теплоемкость при постоянном дав-
давлении равна как раз производной от Н по д.

!jg 2] ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ 41
Упражнения
1. Пусть i/o= 1.00; ух*= 1,25; уг = 1,65; t/3 = 2,34. Найдите у3/г по формулам
Г2). D)> E) и п0 Ф°РмУле Бесселя.
■ 2. Проверьте, что если таблица составлена для многочлена степени п, то
■ разности порядка п постоянны, а разности порядка п-\-\ равны нулю.
§ 2. Интегрирование и дифференцирование функций,
заданных таблично
Интегрирование функций, заданных таблично, ничем не замеча-
замечательно. Ведь и раньше при численном интегрировании функций,
заданных формулами, мы сперва составляли таблицу подынтеграль-
подынтегральной функции (см. § 1.1).
При вычислении производной функции, заданной таблицей, следует
иметь в виду, что лучший способ найти производную у' (х) по двум
значениям функции — это взять такие значения справа и слева на
равном расстоянии от того значения х, для которого мы хотим под-
подсчитать величину производной
У
Таким образом, если даны значения у для значений х, располо-
расположенных через равные промежутки (т. е. в арифметической прогрес-
прогрессии), то удобно вычислять производные в серединах промежутков.
Другими словами, если значения у были заданы для «целых» зна-
значений х (см. § 1), то значения у' будут подсчитаны для «полу-
«полуцелых» значений х. По значениям у' можно таким же способом
найти производную от у', т. е. у". При этом значения у" получатся
снова для целых значений х. Можно выразить j*" непосредственно
через у:
h ~
y(x + h)-y(x) yjx)-y(x-h)
h h _y(x+h)-2y(x
h ¥ •
Указанные сейчас формулы удобно записать в обозначениях § 1:
h k
ъ = :
это равенство и является обоснованием того, что разность ук+1—ук

42
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
мы относили значению х*=х г . Аналогично
Приведем пример (таблица 2)*).
Таблица 2
X
1,00
1,10
1,20
1,30
1,40
1,50
у
1,6487
1,7333
1,8221
1,9155
2,0138
2,1170
у'
0,846
0,888
0,934
0,983
1,032
и"
0,42
0,46
0,49
0,49
Если нужны значения у' для других х, то их можно получить
интерполяцией. В частности, для целых х получаем с помощью ин-
интерполяции
1
Ук+1 —
1—Ук\
h )
2h
Таким образом, можно сразу определять значения у' для целых х
по значениям у при целых х справа и слева (см. таблицу 3).
Таблица 3
X
1,00
1,10
1,20
1,30
1,40
1,50
У
1,6487
1,7333
1,8221
1,9155
2,0138
2,П70
У'
0,867
0,911
0,960
1,002
Однако при таком способе мы, во-первых, получим значений
производных на одно меньше, чем при первом способе, во-вторых,
*) В таблице не выписаны полуцелые значения аргумента.

§ 2]
ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ
43
мы получаем меньше сведений о поведении производной на концах
промежутка. Так, в таблице 2 мы знаем производную при л: = 1,05
(около начала промежутка х=\) и при л:=1,45 (около конца про-
промежутка лг= 1,5), а в таблице 3 лишь при л: = 1,1 и при лг= 1,4,
т. е. при значениях аргумента, более удаленных от концов проме-
промежутка. Наконец, при вычислении значений у' для нецелых (в част-
частности, для полуцелых) значений х с помощью интерполяции значе-
значения, полученные из таблицы 2, оказываются достовернее значений,
полученных из таблицы 3, так как наклон кривой более точно пе-
передают маленькие хорды, чем большие. Поэтому первый способ
предпочтителен.
Очень важные, принципиальные вопросы возникают в связи с
ограниченной точностью и ошибками, присущими каждому измерению.
При вычислении интеграла каждое отдельное измеренное значе-
значение у умножается на величину Ах. Поэтому при увеличении числа
отдельных измеренных значений функции у коэффициент, с которым
в выражение интеграла входит каждое отдельное значение, умень-
уменьшается обратно пропорционально числу промежутков Ах.
Следовательно, уменьшается и ошибка в интеграле, происходя-
происходящая за счет ошибок при каждом отдельном измерении величины у.
При вычислении производной разность двух значений у делится
на Ах. Чем меньше промежуток Ах, т. е. чем меньше знаменатель,
У
3
2
1
0
1
2
3
***^
4-
Рис. 7.
тем большую ошибку в величину производной вносит данная ошибка
в каждом измеренном значении у. Поэтому производная функции,
заданной экспериментальными значениями, оказывается известной
с меньшей точностью, чем сама эта функция.
Разницу между дифференцированием и интегрированием поясним
примером.
На рис. 7 изображены две кривые — одна нарисована сплошной лини-
линией, другая пунктиром. Сплошная кривая — это график функцииу—х—

44
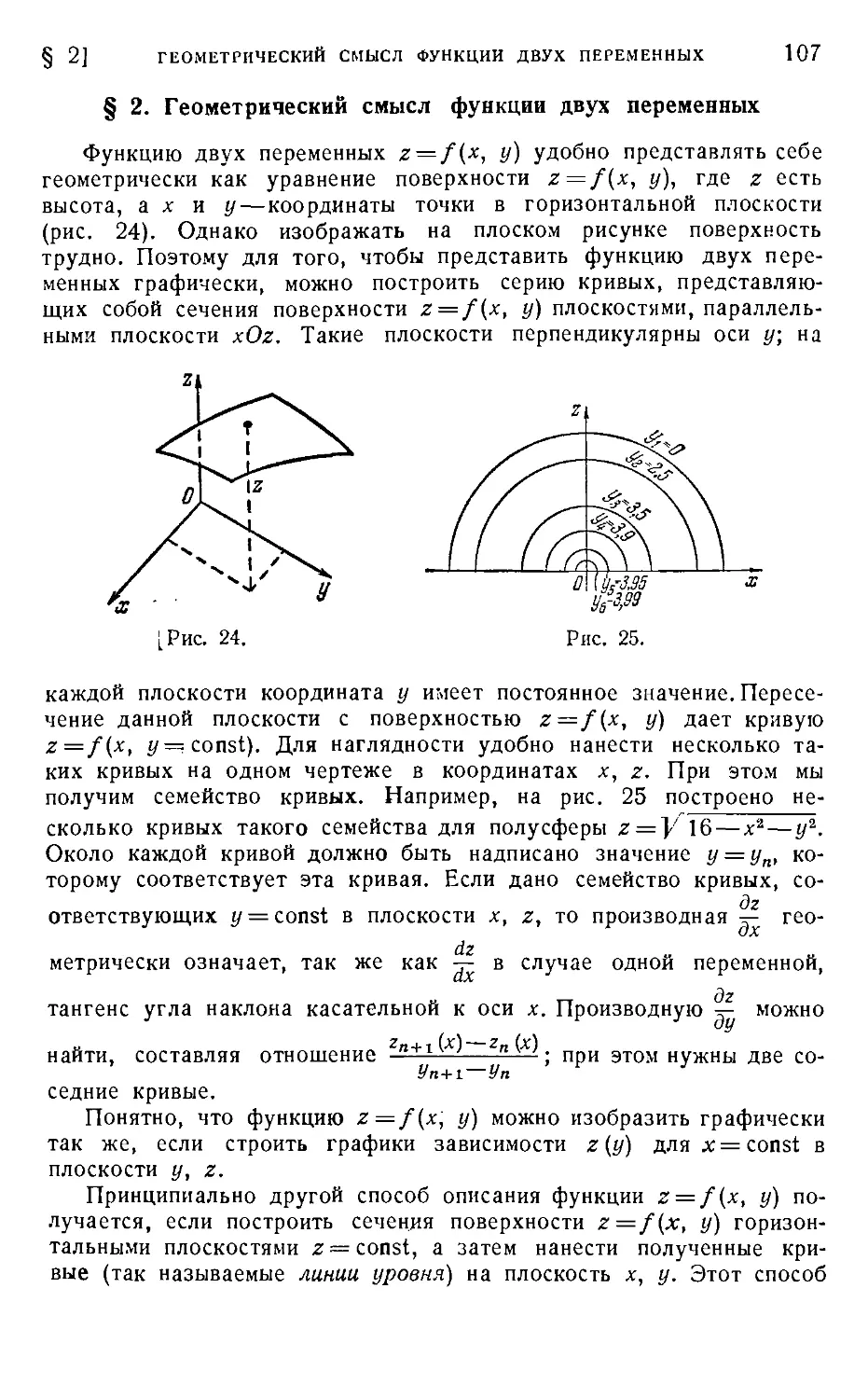
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
[ГЛ. II
— 0,1л:2, пунктирная — график функции yl = x— 0,1л:2+0,5е~8и-3J.
Из рисунка видно, что одна кривая заметно отличается от другой
лишь в небольшом промежутке изме-
изменения X.
На рис.
X
8
показаны
X
графики
i и I1(x)=\iy1dx{nynK-
0 0
тирная кривая). Мы видим, что отли-
отличие между кривыми у (х) и у1 (х) дает
небольшую добавку в интеграл /х (х),
заметную на графике лишь при х >
> 2,8. В целом кривые /(лг)и/г(л;)
отличаются мало.
На рис. 9 показаны графики про-
■ г изводных у' (х) и у[ (х). Мы видим, что
х небольшое изменение функции в малом
промежутке вызвало в этом промежутке
большие изменения производной. Еще
сильнее разнятся вторые производные. Их графики изображены на
рис. 10, где масштаб по оси у взят в два раза меньше, чем на
рис. 7—9.
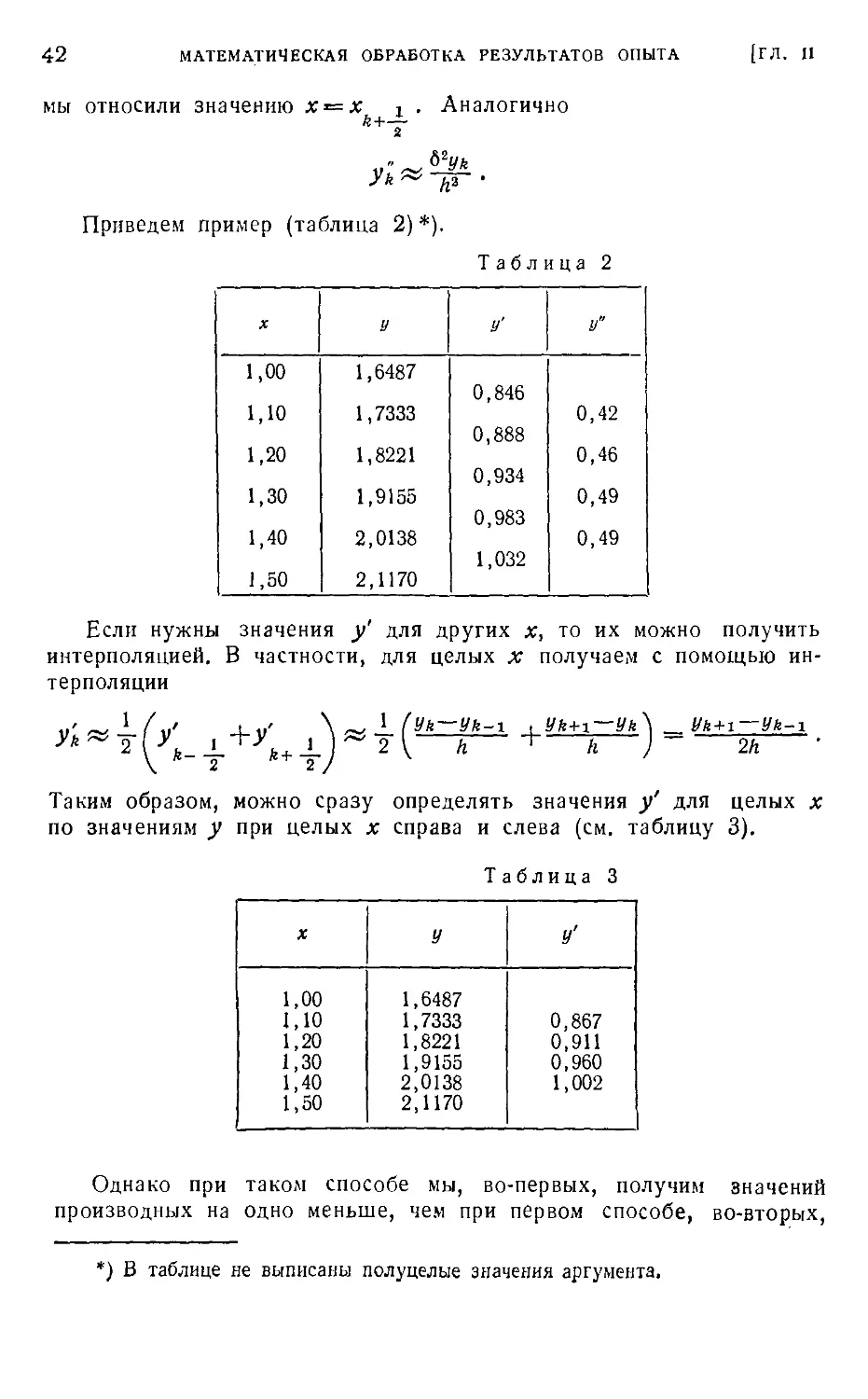
В случае, когда кривая получена из опыта, небольшое изменение
хода кривой на каком-либо промежутке может быть результатом
Рис. 8.
Рис. 9.
ошибки отдельного опыта. Из предыдущего примера видно, что на
величине интеграла такие отдельные ошибки сказываются незначи-
незначительно, а на величину производной (и особенно высших производных)
они влияют сильно.
Для того чтобы получить надежные значения производной, нужно
сперва подобрать формулу, хорошо описывающую опытные данные,
а затем находить производную, пользуясь этой формулой.

§ 3]
ПОДБОР ФОРМУЛ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
45
Так как формула строится с учетом всех опытных данных, то
значение производной при каждом значении х будет найдено по
формуле с учетом всех данных, а не только двух-трех ближайших.
О
-1
-г
-з
-4
-5
■•5
-7
-8
А
\ 4
I |
I
I i
1!
и
Рис. 10.
Поэтому естественно ожидать, что случайные ошибки в отдельных
измерениях меньше скажутся на величине производной.
Подбор формулы, описывающей результаты опыта, вообще яв-
является существенной частью обработки экспериментальных данных.
Задаче подбора формулы по данным опыта посвящены два следую-
следующих параграфа.
Упражнение
В условиях упражнения 2 к § 1 подсчитайте значения у' для полуцелых
значений х, приняв Дх=Л = 0,5. Проинтерполируйте результат линейно,
а также по формулам D) и E) на целые значения х.
§ 3. Подбор формул по данным опыта по методу
наименьших квадратов
Подбор формул по экспериментальным данным называют подбором
эмпирических формул. На самом деле, конечно, формула тем лучше,
чем больше теоретических представлений вложено в нее, чем в мень-
меньшей степени она является эмпирической. В действительности нужно
сперва задаться видом формулы, а затем, пользуясь результатами

46 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
опыта, определять значения различных постоянных величин, входя-
входящих в нее.
Перед тем как приступить к подбору формулы, полезно нанести
опытные данные на график, после чего на глаз, от руки провести
через полученные точки наиболее правдоподобную кривую. При этом
сразу выявляются те данные, в которых можно подозревать большие
ошибки. Очень важно при проведении кривой, кроме эксперименталь-
экспериментальных точек, использовать общие соображения о том, как должна
вести себя кривая при значениях аргумента, весьма близких к ну-
нулю, при больших значениях аргумента, проходит ли кривая через
начало координат, пересекает ли координатные оси, касается ли
их и т. п.
Итак, пусть эта предварительная работа проделана, выбран вид
формулы и нужно определить значения входящих в формулу по-
постоянных величин.
Как это сделать?
Рассмотрим наиболее простой пример.
Предположим, что у пропорционально х, т. е. ищем формулу
вида у = kx. Задача сводится к определению коэффициента А. Каж-
Каждый опыт дает определенное значение k, именно
"л == ~S~ >
хп
где хп, уп—значения величин х,у, полученные в п-м опыте. Индекс п
у величины k показывает, что это — значение, соответствующее л-му
опыту. Из значений kn можно образовать среднее, положив
где р — общее число опытов. Мы получаем формулу у — kx.
Отметим, что это — самый простой, но не самый лучший способ
выбора величины k. В самом деле, пусть х есть величина, характе-
характеризующая условия опыта, которую мы задаем точно, а у есть ре-
результат опыта, причем этот результат содержит в себе некоторую
ошибку измерения. Допустим, что и при малых и при больших
значениях у ошибка измерения А_у примерно одинакова. Тогда ошибка
в величине kn, равная —— , тем больше, чем меньше хп. Следова-
Следовали
тельно, определяя величину k, лучше ориентироваться на опыты
с большими хп.
Поставим задачу о нахождении того значения k, при котором
функция у = kx наилучшим образом соответствует опытным данным.
(Смысл нечеткого выражения «наилучшим образом» станет ясен из
дальнейшего.) За меру отклонения функции от экспериментальных
данных для п-го опыта выберем величину (уп — kxnJ. Почему берется

К 3] ПОДБОР ФОРМУЛ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ 47
именно величина (_у„— kxnf, а не уп— kxn? Ясно, что оба знака
уклонения kxn от уп нехороши: плохо, если k таково, что yn<kxn,
но также нехорошо, если k таково, что уп > kxn. Если бы за меру
отклонения мы взяли величину уп — kxn, а затем стали находить
сумму отклонений в нескольких опытах, то мы могли бы получить
весьма малую величину за счет взаимного уничтожения отдельных
слагаемых большой величины, но разных знаков. Это, однако, вовсе
не говорило бы о том, что взятая функция y = kx хороша. Если
же за меру отклонения взять (уп—kxnJ, то такого взаимного
уничтожения не произойдет, так как все величины (у„ — kxnJ по-
положительны. Отметим, что вместо {уп — kxnJ в принципе можно
было бы взять \уп — kxn\, (уп — kxnY и т. д. Однако при этом даль-
дальнейшие вычисления значительно усложнились бы.
В качестве меры общей ошибки S в описании опытных данных
функцией _у = kx возьмем сумму мер отклонений для всех опытов, т. е.
Уп-кхп)\ F)
я = 1
Метод определения констант, входящих и формулу, из требования,
чтобы общее отклонение S было наименьшим, называется методом
наименьших квадратов.
Заметим, что если одна величинауп—kxn=\0, т. е. при каком-то
одном х = хп формула дает ошибку в 10 единиц, то в величину 5
это внесет 100 единиц. С другой стороны, наличие 10 ошибок по
1 единице каждая внесет в S всего 10 единиц. Поэтому ясно, что
на величину S сильнее всего влияют самые большие ошибки,
а малые ошибки, даже если они встречаются часто, влияют мало.
Метод наименьших квадратов нацелен на уменьшение самых боль-
больших отклонений. _
Для того чтобы найти k = k, при котором S наименьшее, решим
уравнение -тт = 0. Пользуясь F), находим
откуда
что дает
/,
л
р
= ^S 0
п= I
2k £ л,1
/(=1
^ V 2
п= I
п= i
2 .
(-*„) = 0,
2 2
- Л^2 —|— . * * -j- Хп
G)

48 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
Если в каждом опыте получается точно yn = kxn, то из фор-
формулы G) получаем
Если для различных опытов величина kn = — различна, то, под-
ставляя в G) вместо уп его значение knxn, получим
= _
x\+xl + ...+4 W
Среди величин klt k2 kp, полученных в различных опытах,
есть наибольшая величина /гтах и наименьшая /гт{П. Если заменить
в правой части (8) все kn на /гтах, то дробь только возрастет и мы
получим
=7 , ^max*l + "тпах*2 + • • • + «тах*р ,
^ „2 _, „2 _, ~ГЗ —«max-
Xi+Xi+...+Хр
Совершенно аналогично доказывается, что k > kmin.
Таким образом, величина k, найденная из условия минимума S,
удовлетворяет неравенствам km\n < k < ктах, т. е. действительно
является средней из всех значений kv k2, ..., kp, однако это сред-
среднее составляется по более сложному правилу, нежели
p
В формуле (8) каждая величина kn входит в числитель с мно-
множителем х\. Этот множитель называют весом*).
Ясно, что чем больше вес х2п, тем сильнее влияет на величину k
измерение, соответствующее значению х = хп. Это подтверждает
высказанную ранее мысль о том, что измерения с большими хп
важнее для правильного определения k.
Если нет оснований предполагать, что_у = 0 при лг = О, то наи-
наиболее простой является формула у = kx-\-b. В зтом случае также
*) Название «вес» происходит от следующей механической аналогии. Пред-
Представим себе шкалу, на которой откладываются расстояния klt k% ft и
в соответствующих точках шкалы помещаются грузы. Если все эти грузы
одинаковые, то центр тяжести такой системы (весом самой шкалы пренебрегаем)
— k1 + ki + ...+kp
находится в точке шкалы к= ~. Если же в точку k1 поме-
поместить груз веса х\, в точку k2—груз веса х\ в точку kp—груз веса х\,
то положение центра тяжести дается формулой (8). Таким образом, эта фор-
формула соответствует представлению о разной значимости, разном весе различных
наблюдений.

§ 3] ПОДБОР ФОРМУЛ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ 49
можно применить метод наименьших квадратов. Величина 5 для
этого случая дается формулой
n-kxn-b)>. (9)
Надо выбрать числа k и b так, чтобы величина 5 была наименьшей.
Для этого поступим так. Если бы b было уже найдено, то
в правой части (9) можно было бы изменять только k, поэтому
должно было бы быть *)
р
д4
п=\
С другой стороны, если бы уже было найдено k, то должно было
бы быть
Эти два условия дают нам следующую систему уравнений для опре-
определения чисел k и Ь:
)
A0)
л=I п—I
р р
УП — *]£■*,, —Ьр =0.
п=\ п-\
Из системы уравнений A0) нетрудно найти числа k и Ь. С этой
целью обозначим для краткости
2 22j 2>«> ri= 21
л= I л= I л=1 п—
Тогда систему A0) можно переписать в виде
alk+pb = r0.
Решая ее, получим
к— —, и
, и — .
pai—a1 ро2 — а!
На описанный метод можно смотреть также с иной точки зрения.
*) При рассмотрении функции от нескольких переменных производная по
одной из этих переменных при зафиксированных остальных обозначается с по-
помощью буквы д, а не d (ср., например, ВМ, § П. 12). Подробнее об этом мы
поговорим в гл. IV.

50 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
Задавшись формой линейной зависимости
у = kx + Ь
между рассматриваемыми величинами хну, мы получаем два неиз-
неизвестных параметра k и Ь. В результате измерений мы приходим
к соотношениям между этими параметрами
т. е. к системе из р уравнений с двумя неизвестными. Такая система
при р > 2 является переопределенной, так как в принципе достаточно
двух уравнений, чтобы найти эти неизвестные. Однако учитывая, что
физические величины х ну замеряются с определенной погрешностью,
мы получаем, что в случае двух измерений (т. е. при р =• 2) на зна-
значения k и Ъ могут существенно влиять случайные ошибки измере-
измерений, так что при этом точность результата останется неясной.
Поэтому уменьшение чпсла уравнений, содержащих такие случайные
факторы, опасно. Напротив, чем больше измерений, т. е. чем в боль-
большей степени система переопределена, тем лучше, так как тогда
случайные ошибки отдельных измерений погашают друг друга, и
решение, найденное по методу наименьших квадратов, становится
более достоверным.
Не представляет труда обобщить метод наименьших квадратов
для случая более сложных зависимостей между величинами х и у.
Следует отметить, однако, что метод наименьших квадратов часто
приводит к довольно громоздким вычислениям. В случаях, когда
искомые параметры входят в участвующие зависимости нелинейно,
метод приводит к системе нелинейных уравнений, и вычислительные
трудности особенно возрастают. Поэтому в практической работе зачас-
зачастую более эффективными оказываются графические методы подбора
формул, которые мы рассмотрим в следующем параграфе.
Упражнения
1. Подберите формулу вида y = kx методом наименьших квадратов в слу-
случае следующих данных опыта:
а)
X
У
0,25
0,40
0,50
0,50
0,75
0,90
1,00
1,28
1,25
1,60
1,50
1,66
1,75
2,02
2,00
2,40

§ 4]
ГРАФИЧЕСКИЙ СПОСОБ ПОДБОРА ФОРМУЛ
51
б)
в)
X
У
X
У
0,
0,
о,
0,
25
16
4
69
0
0
0
1
,50
,18
,8
,44
0,75
0,80
1,2
2,08
1
0
1
2
,00
,60
,6
,74
1,25
1,08
2,0
3,52
Нанесите на график в каждом из трех случаев табличные точки и прямую,
полученную по методу наименьших квадратов. (Графики стройте на миллиметро-
миллиметровой бумаге.)
2, По данным следующей таблицы подберите числа k и Ь для формулы
y = kx-\-b методом наименьших квадратов:
X
У
—0
о,
,20
96
0
1
,20
,40
0
1
,40
,56
0
1
,60
,74
0
1
,70
,92
0
2
,80
,04
3. Пусть даны две точки (%; j/x) и (*21 уЛ Будем по этим данным подби-
подбирать числа knb для уравнения прямой у = kx-\-о методом наименьших квадратов.
Покажите, что при этом получим абсолютно точный результат, т. е. получится
уравнение прямой, проходящей через указанные две точки.
§ 4. Графический способ подбора формул
Напомним, что уравнение прямой линии имеет вид y = kx-\-b,
причем числа knb имеют простой геометрический смысл (см., на-
например, ВМ, § IV.4): Ъ есть величина отрезка, отсекаемого прямой
на оси у, а к есть тангенс угла а наклона прямой к оси х (рис.11).
Пусть предполагается, что величины у и х связаны линейно,
т. е. у = кх-\-Ь. Нанесем экспериментальные точки на график. На-
Наложив на график прозрачную линейку и передвигая ее, нетрудно по-
получить такую прямую, к которой экспериментальные точки лежат
ближе всего (рис. 12).
у
Проведя эту прямую, мы определяем из чертежа Ъ и&=-гг.
А
Большое преимущество графического способа связано с его
наглядностью. Если экспериментальные точки ложатся на прямую,
за исключением отдельных выпавших точек, то эти точки наглядно

52
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
[ГЛ. II
выделяются и видно, какие точки следует проверить. Если экспери-
экспериментальные точки в целом не лежат на прямой, то это также видно
из графика. В этом случае зависимость между величинами х,у имеет
более сложный вид, нежели y = kx-\-b. Кроме этого, при примене-
применении графического способа не нужны сравнительно длинные расчеты,
связанные с методом наименьших квадратов, в которые всегда может
вкрасться вычислительная ошибка.
Прямая линия занимает исклю- у
чительное положение в графиче-
графическом подборе формул. Никакая
х
Рис. 11.
Рис. 12.
другая линия не может быть так просто и вместе с тем так на-
надежно проведена по данным точкам. Всякий, кто в практике лабора-
лабораторной работы сравнивал определение чисел k и b в уравнении прямой
по графику с определением их по методу наименьших квадратов,
знает, что различие всегда весьма невелико.
Как же подобрать, пользуясь графиком, константы, входящие
в формулу, если эта формула имеет более сложный вид, нежели
у = kx + b?
Рассмотрим пример.
Пусть исследуется зависимость между температурой Тпроволоки
и силой i постоянного тока, текущего по этой проволоке. Ясно, что
изменение направления тока не меняет величины Т, т. е. Т(—/) =
= T(i). Поэтому зависимость вида T=ai + b не годится. Будем
искать формулу вида Т= ai2 -\-Ь. График функции T(i) есть пара-
парабола, а провести на глаз параболу трудно. Поэтому введем новую
переменную z = i2, тогда T=az-\-b, так что в координатах z, Tиско-
Tискомая зависимость изображается прямой линией. При этом значение
температуры Ь=Т0 при отсутствии тока можно считать известным,
так что остается определить коэффициент а при г2.
При большой силе тока, когда достигаются высокие температуры,
сопротивление проволоки нельзя считать постоянным. Поэтому теп-
тепловая мощность (количество тепла, выделяющееся в единицу времени),
равная W = Ri2, в действительности не просто пропорциональна г2,

§ 4] ГРАФИЧЕСКИЙ СПОСОБ ПОДБОРА ФОРМУЛ 53
так как меняется R. В уравнении теплового баланса
1 Т \
где а — коэффициент теплоотдачи, а 5 — поверхность проволоки, при
больших температурах коэффициент а также непостоянен. Однако
равенство температур для токов г и —i по-прежнему имеет место.
Поэтому естественно добавить в формулу Т=аР-\-Ь, которая теперь
может оказаться неточной, член сг4 (а не сР).
Итак, ищем формулу в виде Т= cil-\-ai2-\-b.
Заметим, что Т=Ь при г = 0, так что b не отличается от темпе-
температуры окружающей среды, а потому известно (см. выше). Перепи-
Перепишем формулу так:
—^~ = сР + а.
Вводя новые переменные л; = г2, у = —^—, получаем д^ = сх-\-а,
т. е. х и у связаны линейной зависимостью. Построив график в коор-
координатах х, у, легко определить числа сие.
Таким образом, общая идея графического метода состоит в том,
что надо ввести новые переменные так, чтобы в этих переменных
интересующая нас зависимость становилась линейной.
Приведем еще несколько примеров.
Часто встречается такая зависимость между х и у, когда заве-
заведомо известно, что при л;=0 должно быть ^ = 0, но опытные дан-
данные на графике не ложатся на прямую. В этом случае может
оказаться справедливой формула
Разделим все члены на х, получим — = а-\-Ьх. Положив — = 0, по-
получаем линейную зависимость z от х
Другая формула, которая может оказаться годной для этого
случая, это у = ахп. Как определить показатель степени л? Для
этого прологарифмируем обе части формулы:
Вводя новые переменные z = \gy, t=\gx, получим линейную зави-
зависимость
Закон радиоактивного распада описывается формулой n = nQe-u>t,
где п — число атомов, еще не распавшихся к моменту времени t, п0 —
общее число атомов, со — вероятность распада. Логарифмируя обе
части формулы, получим
= 1п п0 —со/.

54 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
Следовательно, мы получим прямую линию в координатах t, у = \пп.
(Подробнее о радиоактивном распаде см. ВМ, § V. 3.)
При исследовании зависимости какой-либо величины х от темпе-
температуры Т очень часто получается формула вида
А
х = Ве~кТ.
Такая формула получается в тех случаях*), когда дают вклад только
те молекулы (или электроны), энергия которых больше величины А;
величина k—постоянная Больцмана ( k— 1,4
д)
-^; | .
град)
А 1
Логарифмируя, получим 1пд; = 1п5 Tf * Зависимость стано-
становится линейной, если рассматривать величины _у = —и z = \nx, дей-
ствительно, z = \nB -т-у.
Во всех рассмотренных нами примерах мы после выбора вида
формулы вводили новые переменные так, чтобы зависимость между
этими новыми переменными была линейной. Может, однако, случиться,
что в новых переменных экспериментальные точки не будут ложиться
на прямую. Это означает, что вид формулы выбран неудачно, сле-
следует подбирать формулу другого вида.
Пусть проделан ряд опытов, в которых при значениях аргу-
аргумента хг, хг,...,хр получены значения функции уи у2,...,ур.
Пусть значения аргумента расположены в порядке возрастания
xi < Х2 < • • • <ХР- Определение ожидаемого из опыта значения у
при значении х, лежащем внутри исследованного промежутка изме-
изменения аргумента (хл < х < х), составляет задачу интерполяции (ср.
начало § 1).
Интерполяцию легко и просто произвести, если подобрана эмпи-
эмпирическая формула. При этом если формула подобрана хорошо, то
интерполяция обычно дает хорошие результаты, редко приводит
к большим ошибкам. Значительно труднее другая задача: найти,
какое значение у следует ожидать из опыта при некотором значе-
значении х, лежащем вне исследованного на опыте промежутка изменения
аргумента, например при х > хр. Определение такого значения по
данным опыта составляет задачу экстраполяции.
Решение задачи об экстраполяции в каждом конкретном случае
требует глубокого понимания существа изучаемого явления, такую
задачу нельзя решать формально, пользуясь подобранной формулой.
(Правильно высказалась по этому поводу Кретя Патачкувна в книге
«Пи»: «Очень трудно что-либо предвидеть, особенно на будущее».)
*) Несколько таких случаев рассмотрено в ВМ, гл. VII.

« 4] ГРАФИЧЕСКИЙ СПОСОБ ПОДБОРА ФОРМУЛ 55
Например, если по экспериментальным данным подобрана формула
вида у = а-\-Ьх-\- сх2-\-рх3, причем она очень хорошо описывает
результаты опыта, то, как правило, члены сх2, рх3 вводятся в фор-
формулу, чтобы описать отклонение экспериментальных точек от прямой
в том промежутке изменения х, где производились измерения. При
этом члены сх2 и рх3 обычно носят характер малых поправок к глав-
главному члену а-\-Ьх,
Если же, пользуясь такой формулой, мы будем производить
экстраполяцию у для больших, далеких от исследованных на опыте,
значений х, то члены схъ и рх3 начнут играть главную роль, что,
однако, может совершенно не соответствовать существу явления.
Положение вещей напоминает сказку Андерсена, в которой тень,
отделившись от человека, начинает жить самостоятельно, делает
карьеру и, наконец, заставляет самого человека служить себе.
Если при неограниченном возрастании х величина^ приближается
к определенному значению ух, то бывает полезно отыскать это зна-
значение. Такая задача называется экстраполяцией на бесконечность.
При ее решении часто оказывается целесообразным ввести новую
независимую переменную г, которая оставалась бы конечной при
х = оо, например z = — . После
такого перехода интервал (по z),
на который производится экстра-
экстраполяция, будет уже конечным.
Рассмотрим пример.
Пусть в длинном заряде взрыв-
взрывчатого вещества с одного конца
при помощи капсуля вызвана де-
детонация (взрыв), которая начинает
распространяться по длине заряда. Рис. 13.
Ясно, что при весьма большой
длине заряда действие его на какую-либо преграду перестает зави-
зависеть от длины заряда. Действительно, когда мы увеличиваем длину
достаточно длинного заряда, то мы увеличиваем количество взрыв-
взрывчатого вещества, находящегося далеко от преграды, а потому оказы-
оказывающего весьма малое действие. Пусть, например, через у обозна-
обозначена максимальная толщина стальной стенки, которую разрушает
заряд длины х. На графике рис. 13 нанесены опытные данные. Из
рисунка видно, что с ростом х величина^ приближается к определен-
определенному значению уа. Однако определить по графику это значение^»
нельзя.
Как же найти его? Предположим, что при больших х формула
имеет вид у =ух . Введя новую переменную z = — , получаем
У=У& — a-z. Теперь ух соответствует значению z = 0. Построив
У
0
C)
. 'B)
0)
A)
F)

56 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. II
данные опыта в координатах z, у*), мы можем на глаз определить
предполагаемое значение у при z — О (рис. 14).
Формула у=ух справедлива лишь для достаточно боль-
больших х. При х = — она дает у = 0, а если х < — , то получаем
даже у < 0, что совершенно бес-
„ смысленно. Поэтому на рис. 14
точки, полученные из опыта, ле-
лежат не на прямой, а на кривой,
однако в координатах z, у можно
..ft) эту кривую экстраполировать на
' 'z = 0, что соответствует л;=оо.
w . sj\ Из физического смысла задачи
B) • ясно еще, что должно быть у = 0
i 1 1— — при х = 0. Наиболее простая фор-
2 мула, отражающая оба известных
Рис. 14. нам свойства функции у(у = 0 при
х = 0 к у неограниченно прибли-
приближается к значению ул, если х неограниченно возрастает), имеет вид
Как определить, пользуясь экспериментальными данными, постоян-
постоянные ух и Ь?
Для этого перепишем формулу так:
У У**'
или
У Уф Усе' х '
Поэтому можно надеяться, что если мы будем строить на графике —
в зависимости от —, то получим прямую линию и определим
— и —. Даже если точки будут плохо ложиться на прямую, то
У л Уев
все равно экстраполяция по такому графику надежнее, чем по гра-
графику рис. 14, так как формула A1) построена с учетом двух (а не
одного, как раньше) свойств функции у (х).
*) На графиках рис. 13 и 14 точки, соответствующие друг другу, снабжены
одинаковыми номерами.

§ 4]
ГРАФИЧЕСКИЙ СПОСОБ ПОДБОРА ФОРМУЛ
Упражнения
1. По данным следующей таблицы подберите формулу вида
57
X
У
0,5
1,20
1,0
1,10
1,5
2,35
2,0
3,05
2,5
4,40
3,0
5,50
Решите задачу двумя способами:
а) методом наименьших квадратов,
б) графически.
2. Графическим способом подберите формулу вида
результаты опыта таковы:
= ax2-^-bx, если
X
У
0
0
0,5
1,7
1,0
3,1
1,5
3,8
2,0
3,9
2,5
3,8
3,0
3,0
3. По данным таблицы
X
У
1
0,5
2
1,4
3
2,5
4
4
подберите формулу вида у = Ахь. (Примените графический способ.)
4. Результаты измерений дали следующее:
X
У
.0,5
1,66
1,0
1,58
1,5
1,50
2,0
1,44
2,5
1,37
3,0
1,30
3,5
1,22
4,0
1,17
Кроме того, известно следующее:
а) при неограниченном увеличении х величина у приближается к нулю;
б) при х = 0 величина у имеет вполне определенное значение. Этим усло-
условиям удовлетворяют, например, такие простые формулы:
Акх
Подберите значения параметров, входящих в эти формулы. Пользуясь форму-
формулами, получите значения у при *=1,25; *=3,75; х — — 1; х=—2; х = — 3.
Сравните результаты.

58 МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА [ГЛ. 11
5. Результаты опыта дали следующее:
X
У
1,0
1,6
1,5
1,7
2,0
2,0
3,0
2,3
4,0
2,4
5,0
2,5
Известно, кроме того, что при неограниченном возрастании х величина у прибли-
приближается к некоторому значению ух. Найдите это предельное значение двумя
способами:
а) подбирая формулу вида у = А-\ ;
б) подбирая формулу вида у =
ах
ОТВЕТЫ И РЕШЕНИЯ
§ 1
1. По формуле B) г/3/г=1,45; по формуле D) г/3/ =1,41; по формуле E)
j =1,43; по наиболее точной формуле Бесселя уэ^ =1,42.
2. Если У[ — у\х-х. = х", а Дл: ==Л, то по формуле бинома Ньютона
Обозначив Xi-\-hj2=x'., получим
— h ( ' ^ А™^" ("'
""'t~ V1~~2J + 2
\)
" \xi 2
Раскрыв в правой части скобки, мы видим, что в этом примере разности
образуют последовательность значений многочлена степени п— 1. То же будет
для функции у=ахп (a = const), так как при образовании разностей коэффи-
коэффициент а служит общим множителем. Заметив, что при сложении функций их
разности также складываются, мы заключаем, что для любого многочлена
степени п разности образуют последовательность значений некоторого много-
многочлена степени п. — 1. Значит, вторые разности образуют последовательность
значений многочлена степени п—2 и т. д., а п-е разности —последователь-
—последовательность значений многочлена нулевой степени, т. е. константы. Поэтому разности
(гс-[~1)'г0 порядка в этом случае равны нулю.
§2
г/',, =0,50; г/3/2=0,80; у,^=1,38. По линейной интерполяции г/1= 0,65;
у'2=\,№. По формуле D) у[ = 0,62. По формуле E) ^=1,06.
§3
1. а) у=1,\8х\ б) у=0,78х; в) у=\,75х.
2. у= 1,03л;— 1,19.

ОТВЕТЫ И РЕШЕНИЯ 59
3. Уравнение прямой имеет вид y = kx-{-b. Числа k и 6 определяются из
условий у=У\ при х=хх и f/=j/2 при х=х2. Получаем систему уравнений
«2+6 = У2, /
кх.г
из которой находим
(. Ух — Уу. и ххУ 1 — Х'2У\ /io\
Х\ Х2 Хх Х.г
Покажем, что такие же значения k и 6 мы получим, применяя метод
наименьших квадратов.
В нашем случае
Поэтому
= —2 [B/i — kxx — 6) хх + (г/2 — fe*2 — 6).
5S
dk
dS_
db
6=пост
= — 2 [(г/1 — ft*i — 6) + (г/2 — кх.г — Ь)\.
Приравнивая эти производные нулю, получаем систему уравнений
.=0.1
ь=о. /
yt — kxx — Ъ-\-у2 — ft;
Решая систему, находим те же значения A2).
Впрочем, совпадение результатов можно вывести и из того простого сооб-
соображения, что через любые две точки можно провести одну прямую линию.
§4
1. Для применения метода наименьших квадратов составляем сумму.
6
S=2 iHk~ax\-bf.
k=l
Действуя дальше обычным способом, находим а = 0,48; 6=1,23, т. е. искомая
формула
у = 0,48л:2 + 1,23.
Для того чтобы решить задачу графически, вводим новую переменную
t=x2, тогда </ = а^ + 6. В координатах (t\ у) получаем прямую линию. Нанеся
точки (^ — х\\ уь) на график, находим а = 0,49; 6=1,35, т. е.
2. Полагаем — =z, тогда г = ах-\-Ь. Построив точки в координатах (х; г),
найдем а = — 1,02, 6 = 4, так что у = — 1,02л:2 + 4л:.
3. В этом случае по осям координат надо откладывать соответственно
Igjc н lgj/. Получим Л=0,5; 6=1,5; {/ = 0,5д:1.6.

60
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА
[ГЛ. И
4. Графическим способом находим у =. ___, . ._- ; i/= l,74e-°i1Jc. Значе-
Значения у, найденные по первой и по второй из этих формул при нескольких
указанных значениях, сведены в следующую таблицу:
X
1,25
3,75
— 1
—2
-3
Значение и
по первой
формуле
1,54
1,22
2,01
2,38
2,86
Значение у
по второй
формуле
1,54
1,20
2,00
2,12
2,35
Смысл последнего расчета состоит в следующем: интерполяция, как упо-
упоминалось в тексте, редко приводит к большим ошибкам, в нашем случае обе
формулы при л: = 1,25 и при * = 3,75 дают весьма близкие результаты; экстра-
экстраполяция, наоборот, мало надежна. Из таблицы видно, что чем дальше отстоит х
от табличных, тем сильнее разнятся значения у, полученные по разным фор-
формулам. Отметим еще, что при * = —8 первая формула вообще теряет смысл,
а при х < — 8 первая формула дает у < 0, а вторая у > 0.
5. а) ^=2,8; б) {/„ = 2,9.

ГЛАВА III
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ
И РЯДАХ
§ 1. Несобственные интегралы
При обычном определении интеграла (см., например, ВМ, § 1.8)
считается, что интервал интегрирования конечен и что подынтеграль-
подынтегральная функция на нем не обращается в бесконечность. Такие интегралы
называются интегралами в собственном смысле или, коротко, собст-
собственными. Если хотя бы одно из этих двух условий не выполнено,
то интеграл называется несобственным. Такие интегралы встречаются
уже в простых задачах интегрального исчисления (см., например,
ВМ, §§ 11.16, Ш.З, VI.2). Здесь мы рассмотрим эти интегралы более
подробно.
Рассмотрим сначала интеграл вида
00
I=\f(x)dx, A)
а
где нижний предел а и подынтегральная функция/(лг) при а^лг< оо
предполагаются конечными. Такой интеграл является несобственным
из-за того, что его верхний предел бесконечен; как говорят, он
имеет особенность на верхнем пределе.
Допустим, что интеграл A) получился при решении некоторой
физической задачи и переменная химеет непосредственный физический
смысл (длина, время и т. п.). Тогда реально х изменяется не до
бесконечности, а до какого-то очень большого, но конечного предела,
который мы обозначим через Л/, т. е. взамен A) надо рассмотреть
интеграл
N
IN=\f(x)dx. B)
а
Может оказаться, что интеграл B), хотя и зависит от N, но
при достаточно больших N практически не меняется. Тогда это зна-
значение принимается за значение интеграла A); более точно, тогда

62 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
принимается
да N
\f(x)dx= lim [f(x)dx,
a W->co a
а интеграл A) называется сходящимся. Из этого предела и равенства
00 jV 00
\f(x)dx= ^f(x)dx+ [f{x)dx
N
видно, что основной вклад в сходящийся интеграл дает его «конечная»
(«собственная») часть, тогда как вклад особенности при достаточно
большом ./V как угодно мал. Другими словами, в случае сходимости
интеграла A) можно «реальный» интеграл B) при большом ./V, ко-
которое часто бывает точно и не известно, заменять на «предельный»
интеграл A), который обычно проще в теоретических исследованиях.
Если значение интеграла A) с ростом Лг не «устанавливается»,
а стремится к бесконечности или колеблется, не имея определенного
предела, то интеграл A) называется расходящимся. В этом случае
значение интеграла B) при больших N существенно зависит от N
и заменить B) на A) нельзя. Тогда может возникнуть вопрос о более
детальной характеристике поведения интеграла B) при возрастании N,
т, е, о получении асимптотических формул для этого интеграла.
(Кстати, такой вопрос возникает и для сходящихся интегралов A),
так как установить лишь факт сходимости или расходимости и даже
найти численное значение в случае сходимости часто оказывается
недостаточным — может понадобиться еще сам закон сходимости.)
Из сказанного следует, что факт сходимости или расходимости
интеграла A) зависит только от поведения функции /(х) «в особен-
особенности интеграла», т. е. при х—>оо. Наиболее часто этот факт рас-
Q
познается при помощи сравнения f(x) со степенной функцией —р, от
которой интеграл легко берется. Рассмотрим интеграл
00
J=^dx (C= const), C)
где х0 — любое положительное число (если взять х0 отрицательным,
то интеграл будет иметь особенность также и при х = 0, где подын-
подынтегральная функция обращается в бесконечность). Этот интеграл
легко взять:
*0
Здесь приходится различать два случая. Именно, если р>1, то
р — 1 > 0, оо^ —оо и последний член в правой части D) равен

S 1] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 63
нулю. Значит, в этом случае интеграл C) сходится. Если же р<1,
то ооР'1 = —j—j = 0 и потому последний член в D) равен бесконеч-
бесконечности. Значит, в этом случае интеграл C) расходится к бесконеч-
бесконечности, т. е. соответствующий интеграл fN, взятый от х0 до N, стре-
стремится к бесконечности при возрастании N. Выражение для IN полу-
получится, если в правую часть D) подставить N вместо оо (и в других
случаях выражение для IN, если соответствующий неопределенный
интеграл берется, получается весьма просто). Хорошо видно, что
в этом выражении для больших N главным членом при р > 1 будет
первый, а при р <1—второй.
При р = 1 интеграл C) равен
— dx = С In x
x
=Clnoo — С1плг0=оо,
т. е. интеграл также расходится к бесконечности. Итак, интеграл C)
сходится при р>1 и расходится при р ^ 1.
На основе этого результата мы можем заключить, например, что
интеграл
СО
\—^=dx, E)
о у
имеющий особенность на верхнем пределе, расходится к бесконеч-
бесконечности, так как при больших л: подынтегральная функция
1
асимптотически равна
х
Напротив, интеграл
т. е. в данном случае р = -к
--dx G)
сходящийся, так как подынтегральная функция асимптотически, при
1 3
х—>-оо, равна , т. е. в данном случае Р = -^ > 1. Интеграл
'** dx (8)
также сходящийся, так как подынтегральная функция при х-—>оо
стремится к нулю быстрее любой степени х. Во всех этих примерах
соответствующие неопределенные интегралы не выражаются через

64 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ OB ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
элементарные функции, так что установить сходимость при помощи
вычисления неопределенного интеграла было бы затруднительно.
Нетрудно получить асимптотические выражения трех последних
интегралов, взятых от 0 до N, при увеличении N. Для расходяще-
расходящегося интеграла вида A) применяется следующий прием: подбирается
функция /, (дг), от которой интеграл берется просто, причем асимп-
асимптотически (при х—*оо) почти равная /(х); тогда в правой части
равенства
N N N
$/(*) <**=$/, (х) dx+ $ [/(*)-/, (х)] dx
а а а
первый интеграл (главный член) легко исследуется, а второй может
оказаться сходящимся при N—► оо или же к нему можно применить
тот же прием. Для интеграла E) естественно принять /((л:) = х~2/'3,
т. е. написать
(9)
a
N N
Здесь мы перешли от \ к J, где а — какое-либо положительное
О а
число (хотя это в данном примере необязательно), чтобы избежать
N
несобственного интеграла ^лг~2/3^лг, имеющего особенность на
о
нижнем пределе. Можно проверить, что последний интеграл в (9) при
N—> оо сходящийся и потому при больших N все выражение (9)
имеет асимптотическое представление 3 ^/77+С-)-бесконечно малая,
где С—некоторая постоянная. Чтобы найти значение постоянной С,
надо воспользоваться равенством
о v
для некоторого N, причем интеграл в правой части подсчитать по
одной из формул численного интегрирования.

§1] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 65
Аналогично исследуется асимптотическое поведение интегралов
G) и (8). Для сходящегося интеграла часто оказывается полезным
преобразование
N оо оо
J / (*) dx = J / (х) dx — J f(x) dx.
а а N
Для интеграла G) получаем
J
ЛГ
со со
С dx Г 1 , г. 2
« \ — \ —f=- dx= D—
J Vx3+ 1 J Vx»
0 N
где постоянную D, равную значению интеграла G), можно подсчи-
подсчитать, как С в предыдущем абзаце.
К интегралу (8) применяем интегрирование по частям:
N оо оо оо
-* dx= \ е~х dx—\ е~*^dx = E-\-
%J ■
N
Постоянная Е, т. е. значение интеграла (8), как мы увидим в § IV.7,
равна V л/2.
В качестве другого примера рассмотрим несобственный интеграл
^ A0)
о
В данном случае интеграл по конечному промежутку
N
siuxdx=—cosx0=l — cos N. A1)
о
При возрастании N значение cosN колеблется и не имеет опре-
определенного предела. Значит, интеграл A0) расходящийся, причем «ко-
«колебательным» способом.
Легко проверить, что введение под знак интеграла A0) затухаю-
затухающего множителя е~а*(а= const>0) приводит к сходящемуся интегралу
00
J e~aXsiux dx.
о
3 Я. Б. Зельдович, А. Д. Мышкио

66 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. Ш
Можно доказать, что сходится и интеграл более общего вида
00
\ f(x) sinxdx,
о
где /(х)—любая убывающая функция, стремящаяся к нулю при
х—>-оо.
Несобственные интегралы отличного от A) вида рассматриваются
аналогично A). Например, пусть дан интеграл
ь
A2)
\f{x)dx,
для которого пределы интегрирования конечны, но подынтегральная
функция при х—у а обращается в бесконечность, т. е. интеграл
имеет особенность при х = а. Тогда особенность «отрезают», т. е.
рассматривают взамен A2) интеграл
ь
\ f(x)dx, A3)
а+8
где е — малое положительное число. Если при достаточно малом е
интеграл A3) практически перестает зависеть от е, то интеграл A2)
называют сходящимся и полагают
ь
\f{x)dx
: lim \ f(x)dx.
E- 0/,4-P.
В этом случае от интеграла A3) (который часто появляется при
решении физической задачи, так как все физические величины ко-
конечны) можно перейти к более простому интегралу A2), т. е.вкладом
особенности в интеграл A2) можно пренебречь. Если же интеграл A3)
при малых е существенно зависит от е, т. е. при 8—>0 он не имеет
конечного предела, а стремится к бесконечности или колеблется, не
имея определенного предела, то интеграл A2) называется расходя-
расходящимся; в этом случае переходить от A3) к A2) нельзя.
Факт сходимости или расходимости несобственного интеграла
вида A2) обычно устанавливают, сравнивая подынтегральную функ-
Q
цию f(x) со степенной функцией -. ^, также равной бесконечно-
х-а)Р'
сти при х=а и легко интегрируемой. Мы предоставляем читателю
проверить, что несобственный интеграл
ь
^)Pdx (С-const) A4)
сходится при р<1 и расходится при

§ 1]
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
67
Рассмотрим для примера задачу об истечении жидкости из ци-
цилиндрического сосуда, в дне которого проделано отверстие площади а
(рис. 15). Высота h уровня жидкости зависит от времени t, т. е.
h—h{t). Если жидкость не вязкая и силами поверхностного натя-
натяжения можно пренебречь, то скорость v истечения жидкости из со-
сосуда с достаточной точностью описывается за-
законом Торричелли
~-dh
Поэтому объем, вытекший за время dt, равен
avdt — a V2ghdt.
С другой стороны, тот же объем равен — Sdh
(надо учесть, что h убывает и потому dh < 0).
Приравнивая оба выражения, получим, что
Рис.
т. е. dt= * ^й
Чтобы получить полное время истечения, надо произвести интегри-
интегрирование:
~~ " s
т S_ Г dh _ S hVi о __S ,/Я
~~ а Кгг \ К^ ~~ a Y%g l Н~ о V g '
J "о"
Реально истечение происходит не до h — 0, а до h = e, где е —
некоторая величина, сравнимая с шероховатостями дна или с тол-
толщиной смачивающей пленки, т. е. формулу A5) надо было бы пи-
писать в виде
Т=
——Г
н
dh
A6)
Однако так как несобственный интеграл A5) получился сходящимся
(это показали вычисления A5), да к тому же рассматриваемый ин-
теграл—это интеграл вида A4) при Р = -к ) , то интеграл A6) можно
заменить на A5). Как видим, в данном примере е нам не было точно
известно, но оно и несущественно, так как для сходящегося инте-
интеграла важно только знать, что е малб.
При численном интегрировании (ср. § 1.1) несобственные инте-
интегралы требуют особенного внимания. Часто заданный интеграл пред-
представляют в виде суммы собственного, полученного исключением
интервала около особенности из интервала интегрирования, и несоб-
несобственного, взятого по интервалу около особенности. Первый находят

68 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
численно, а во втором применяется разложение в какой-либо ряд
или просто подынтегральная функция приближенно заменяется на
какую-либо другую функцию (например, степенную), от которой
я
интеграл взять легко. В качестве примера вычислим I —F^=z. Здесь
J К sin*
о
подынтегральная функция неограниченно возрастает при приближе-
приближении л: к 0 и при приближении х к я. Разобьем промежуток инте-
интегрирования на три части: от 0 до -g-, от -g- до -^- и от -^- до я.
В первом промежутке можно считать, что siuxmx, так как х не-
невелико. Поэтому
я/6 я/6
/
J Vsinx
В третьем промежутке, т. е. при — < х < я, воспользуемся фор-
формулой sin;e = sin(:n; — х), и так как величина я—х мала, то
sin (я—х) « я—х. Окончательно в этом промежутке sin х л; я—х.
Получаем
г
) J
5л
0
dx
/ sin*
Г ^х 11/
" j y"n"-^* -\ л х
5я
6
я
5я
6
Интеграл по среднему промежутку подсчитаем по формуле Симпсона,
разбивая этот промежуток на две части. Получим
dx
^-[1,41+4.1 + 1,41] = 2,38.
6
*) Для большей точности здесь можно применить разложение в ряд
dx Г \ fs\nx\-W2 f I / х2 х1 \ -1 / 2
Однако прм применяемой степени точности вычислений поправка ничтожна (по-
(получится 1,46); полезным является только то, что мы узнаем о степевш досто-
достоверности полученного результата.

fi 2] ИНТЕГРИРОВАНИЕ БЫСТРОМЕНЯЮЩИХСЯ ФУНКЦИЙ 69
Следовательно,
f^==« 1,45 + 2,38 + 1,45 = 5,28.
J у sin х
о
Точное значение этого интеграла (с двумя десятичными знаками)
есть 5,25.
Упражнение
я/2
Г
/
Г dx
Вычислите интеграл I а,. , проводя вычисления в пределах точно-
J i/ sin*
о *
ста логарифмической линейки.
§ 2. Интегрирование быстроменяющихся функций
При численном интегрировании полезно уметь заранее оценить
порядок величины интеграла. Из геометрического смысла интеграла
ъ
l=\y{x)dx
а
сразу вытекает очевидная оценка
ъ
где Утя* — наибольшее значение подынтегральной функции у(х) на
промежутке интегрирования. Если эта функция положительна и мало
меняется на промежутке интегрирования, то можно принять у жутах,
«Ц>-а) A7)
(эта оценка уже встречалась в ВМ, § 11.16).
Отметим сразу же, что оценкой A7), как и дальнейшими оцен-
оценками этого параграфа, неудобно пользоваться для знакопеременных
функций у (х). В этом случае промежуток интегрирования можно
разбить на несколько частей так, чтобы внутри каждого из полу-
полученных промежутков у (х) сохраняла знак, после чего оценить ин-
интегралы по этим промежуткам. Однако суммарная оценка будет
удовлетворительной, только если вклад интегралов одного знака
существенно превосходит вклад интегралов противоположного знака.
Поэтому мы впредь в этом параграфе будем считать подынте-
подынтегральную функцию положительной на интервале интегрирования.
Если функция у (х) на промежутке интегрирования, оставаясь
положительной, очень быстро убывает, а Ъ сравнительно велико, то
оценка A7) может привести к большим ошибкам. В самом деле,

70
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
пользуясь оценкой A7), мы заменяем функцию ее максимальным
значением. Однако если функция изменяется быстро, то ее значения
близки к максимальному только в малой части области интегриро-
ь
вания. В качестве примера рассмотрим /= ^ е~х dx(b > 0). Макси-
о
мальное значение подынтегральная функция на промежутке интегри-
интегрирования получает при ;е=0; это максимальное значение равно 1.
Оценка A7) дает / яг Ь. Однако в данном примере для интеграла
легко получить точную формулу: 7=1—е~ь. Составим таблицу за-
зависимости точного значения величины / от Ь:
Ъ 0 0,1 0,2 0,5 1 2 3 5 10
/ 0 0,095 0,18 0,39 0,63 0,86 0,95 0,993 0,99996
Из таблицы видно, что пока Ъ малб (при этом функция в области
интегрирования изменяется мало), оценка A7) неплоха. Однако если b
велико, то приближение IжЪ становится очень плохим.
Пусть функция у(х) на всем промежутке интегрирования быстро
убывает. Тогда максимальное значение функции достигается на левом
конце промежутка, т. е. при л; = а.
(Отметим, что отсюда не следует равен-
равенства ^ =у'(а) = 0; см. рис. 16.)
их х—а
Так как для быстрозатухающей функ-
ь
ции у {х) интеграл /= \ ydx не может
а
существенно изменяться при увеличении
Ь, то грубая оценка интеграла / не
должна включать Ь, мы как бы пола-
полагаем Ь=оо. Естественно считать, что
в этом случае интеграл приближенно равен произведению ymayi =
=у(а) на некоторую не зависящую от b длину Дл: промежутка
интегрирования. Эта длина при заданном у(а) должна быть тем
меньше, чем быстрее убывает функция, т. е. чем больше |у'(а)|-
Величину Дл; такой же размерности, что и х, можно построить,
исходя из величин у (а) и |.у'(а)|, единственным способом
Ах=ТуЩ\т>
где т — безразлерный коэффициент пропорциональности. После этого
получаем
'Х=\„' (п\'\т- A8)
Если функция у (х) возрастает на промежутке интегрирования,
то она достигает максимума на правом конце промежутка, т. е. при

К 2] ИНТЕГРИРОВАНИЕ БЫСТРОМЕНЯЮЩИХСЯ ФУНКЦИЙ 71
х = £>. В этом случае формула A8) принимает вид
Типичным примером быстроменяющейся функции может служить
показательная функция у = Се~кх (С > 0; k > 0). Выберем значение т
в формуле A8) из- условия, чтобы формула A8) была абсолютно
точна для
Так как y = Ce~kx, y' = — kCe~kx, то y(a)=Ce~ka,
= kCe~ka, поэтому формула A8) дает
СЧ~-ка Се-ка т . ,
1=т — = т = _ у {а).
Точное значение рассматриваемого интеграла есть
= —y е~кх
Сравнивая результаты, получаем — y(a) = -j-y (а), откуда /и=1. По-
Поэтому формула A8) принимает вид
Эта формула в случае бесконечного промежутка для быстроменяю-
быстроменяющихся функций другого вида, а также в случае конечного проме-
промежутка, вообще говоря, не является точной, однако дает неплохие
результаты.
Для того чтобы выяснить наглядный геометрический смысл оцен-
оценки A9), поступим следующим образом. Проведем к кривой у—у{х)
касательную в точке А (рис. 16) и найдем длину отрезка AJSI.
Уравнение касательной есть у—у(а)=у'(а)(х — а); полагая в нем
д|=0, получим точку пересечения касательной с осью х. Это дает
х=а—^тт\, или, замечая, что у' (а) < 0, так как у (х) — убываю-
убывающая функция, получаем х =■ a -f-. , .. Поэтому
... , у (а) ц(а) .
А.М=а + . ,. ;.. — а= . у, ;. . = Длг.
1 \У (а)\ \У (а)\
Оценка интеграла по формуле A9) соответствует замене площади
под кривой у =у (лг) площадью прямоугольника, изображенного на
рис. 16.

72 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ OB ИНТЕГРАЛАХ И РЯДАХ [гЛ. Ш
Пример. Найдем по формуле A9) C^jj. Здесь у = \, у' =
= ~ТГ, поэтому
4
§■«4 = 0,125.
00
Точное значение этого интеграла есть /=Г —= L
J дсв 7х7
= 0,143. Ошибка составляет 13°/0.
Часто встречается другой вид интегралов, у которых подынте-
подынтегральная функция^ (х) достигает максимума при х = хт где-то внутри
у, промежутка интегрирования (рис. 17, а).
При этом в точке максимума у' (х) = 0.
Можно разбить интеграл на два интег-
интеграла от а до хт и от хт до Ъ. Тогда
в каждом из них подынтегральная
функция достигает максимума на краю
промежутка. Может показаться, что
задача сведена к предыдущей. В дей-
действительности это не так, разбиение
интеграла на два ничего не дает, так
как при х = хт все равно у'=0 и
оценка A9) неприменима. Значит, это
действительно новый случай и надо
по-другому выделять из всего проме-
промежутка интегрирования необходимую его часть Ах. Идея заключается в
том, что в этом случае величина Ах определяется значением / (хт), т. е.
определяется величиной кривизны в точке максимума. Из чертежа
ясно, что чем круче кривая, тем меньше следует брать A*. Раз-
Размерность второй производной совпадает с размерностью величины
—?. Поэтому величина той же размерности, что и Ллг, получается
6)
а 0 1 b
Рис. 17.
из величин у(хт) и у" (хт) так: Ax = l
*). (Мы пишем
*) К выражению такого вида для Ах мы можем прийти еще так: разложим
у{х) в ряд Тейлора вблизи максимума, т. е. по степеням х—хт< и возьмем
два первых члена, которые не обращаются в нуль. Получим у(х)=у(,хту\-
+ ~2 (Х—ХтJ-У"(хт). Найдем значение разности х—хт=Ах, при которой об-
обращается в нуль это приближенное выражение для у(х):

§ 2] ИНТЕГРИРОВАНИЕ БЫСТРОМЕНЯЮЩИХСЯ ФУНКЦИЙ 73
|/(*Л> а не У"(хт)> потому что/'(*,„)< 0, так как прн х = хт
функция у(х) имеет максимум.) Величина / есть безразмерный коэф-
коэффициент. Для интеграла получаем оценку
B0)
Значение коэффициента / определим из условия, чтобы формула B0)
была абсолютно точна для \ ydx, где
) = Се-кх\ А>0, C>0.
(График функции у = Се~кх2 для случая С=3, 6 = 0,5 изображен на
рис. 17, б.)
В этом случае хт = 0, у (хт) = С, у" (хт) = — 2Ck. По формуле B0)
находим
Чтобы найти точное значение интеграла \ Ce~kx dxy выполним
— со
в нем замену переменной по формуле z = xV k, dz = УЪ dx. По-
лучнм
„-г2
A J
— СО
e~zidz.
00
Величина интеграла \ e~z dz может быть найдена точно; в § IV.7
— со
мы покажем, что этот интеграл равен ]/л. Поэтому
Сравнивая эту формулу с B1), находим
откуда
т~ У У"{хт)" У \У"{хт)\
Соответственно приближенное значение для / получается равным

74 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [гЛ. III
откуда 1=\ 2л. Формула B0) принимает вид
Таким образом, для двух типов быстроменяющихся функций мы
получили две формулы A9) и B2), причем коэффициенты в этих
формулах подобраны так, что формулы точны для интегралов по
бесконечному промежутку от типичных функций: формула A9) точна
00 + СО
для \Ce-kxdx, а формула B2) — для \ Се~кх* dx. При другом вы-
а -оо
боре типичных функций формулы содержали бы другие коэффициенты.
Определим, например, значение коэффициента / из условия, чтобы
+ «)
формула B0) была точна для /= I ^ dx, С > 0, k > 0. [ Чи-
-00
татель легко убедится сам, что функция у = . ,, имеет максимум
1 ~~г~ RX"
, = 0.) Так кшу = г^л, f = 2Ck^rj^k, то B0) дает
^ 1С
2Ck~
Для того чтобы вычислить интеграл 'точно, положим Уkx = z,
dz—V kdx, тогда
С Г
+ 00
dz Cn
1С
Поэтому г__- = ^"_ , откуда / = л]/ 2. В этом случае мы получаем
формулу
/«„/да
У \У (Хт)\
Однако предпочтение отдается именно формулам A9) и B2).
Причина этого заключается в следующем. Оказывается, что если
получать быстроменяющиеся функции путем возведения в степень п
какой-либо данной функции / (х), для которой \/(х) \ < f(xm) при
х=£хт, то при достаточно больших п относительная погрешность
формул A9) и B2) становится как угодно малой.
Поясним сказанное двумя примерами.
1. Будем интегрировать последовательные степени функции
u = -rj— в пределах от лг = О до лг=оо. Для этого обозначим и„=
=и" = ■; это — быстроменяющиеся функции первого типа

§ 2] ИНТЕГРИРОВАНИЕ БЫСТРОМЕНЯЮЩИХСЯ ФУНКЦИЙ 75
с максимумом на краю, причем чем больше показатель степени л, тем
круче спадает функция ип при увеличении х от 0. Найдем /(п> =
X
J
о
\п ПРИ помощи формулы A9).
о
Так как Ыд = 1, то |и^@)| = я, а потому приближенное
значение этого интеграла есть
/(*> =1
прибл п •
Точное значение рассматриваемого интеграла есть
ее
dx 1 1
О га — 1 '
Отношение
/(п) .
прибл П—1
Так как дробь тем ближе к единице, чем больше л, то при
весьма больших л получаем
прибл
/(л)
точн
1,
что и утверждалось. При выборе в формуле A8) тф\ значение т
осталось бы в правой части последней формулы, т. е. при больших п
мы получили бы систематическую ошибку.
2.Пустьг = т——j, причем —оо<д:<оо. Образуем быстро-
меняющиеся функции zn = zn= .. а.п. Это функции второго типа,
с максимумом внутри области (в данном случае A:m = 0). Найдем
С dx
приближенно величину /<">= \ ___—_( пользуясь формулой B2).
— <ю
Получим /Прибл = 1/ — • Интеграл Iw можно вычислить точно, при
этом он оказывается равным
,(п) 1-3-5.. .Bга — 3) „..
■*) Докажите это, интегрируя равенство
х V 2га —3 2га—2

76 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. 111
Отношение
/пр)ибл = 2-4-6.,.Bгг-2)
4"чн /™ 1-3-5...Bл-3)*
Подсчитаем значения правой части B3) для нескольких значений л.
При л=2 получаем 0,797, При л = 4 получаем 0,904; при л = 6
получаем 0,938; при л = 8 получаем 0,962; наконец, при л = 10
получаем 0,978. Таким образом, при увеличении л значение правой
части в формуле B3) приближается к 1 *).
Перейдем к общему случаю. Рассмотрим у = [f(x)]n, где функция
f(x) > 0 имеет единственную точку максимума. Пусть \n/(x) — (f (х),
тогда f(x) = e? u>. Поэтому
у = e"f <*>. B4)
ь
Величина интеграла I=Kydx определяется главным образом
а
значениями подынтегральной функции в той области, где_у не слишком
сильно отличается от своего максимального значения.
Ясно, что у достигает максимума одновременно с ф (х), т, е, при
одном и том же значении х = хт. Для того чтобы у уменьшилось
в е раз по сравнению с утак, нужно, чтобы Лф(д;) было на единицу
меньше, чем пц>(хт), т, е, чтобы было Лф (х) = пц> (хт) — 1, откуда
ф (*) = ф (Xj— 1.
Чем больше л, тем меньше ф (л:) отличается от ф (хт). Поэтому
чем больше л, тем точнее замена ф (л:) первыми двумя не равными
нулю членами ее разложения в ряд Тейлора, Записав два члена
разложения, получим ц>(х) = ц>(хт)-\-(х—хт) ф' (хт) (для функции,
имеющей максимум на границе) либо ф (л:) = ф (хт) + у (х—хтJ ф" (хт)
(для функции, имеющей максимум внутри промежутка),
В первом случае, пользуясь формулой B4), находим
у = е«Ф (*m) + « (x-xm)<f' {хт)—-Де-Ь (лг-лгт))
где положено А = еп<о <*»•>, Ь = — лф' (хт) = п | ф' (хт)\.
Во втором случае получаем
где положено с = — -i-лф" (хт) = -^ л |ф" (хт)\.
Таким образом, функция у (х) может быть приближенно заменена
либо функцией, для которой абсолютно точна формула A9), либо
*) Более строго это можно доказать с помощью формулы Стирлинга
(см. упражнение к § 3).

§ 3] ФОРМУЛА СТИРЛИНГА 77
функцией, для которой абсолютно точна формула B2), притом эта
замена тем точнее, чем больше п.
Будем предполагать для простоты, что хт = 0. Тогда для
построения быстроменяющейся функции можно было бы от /(х)
перейти не к [/(х)]", а к /(пх). Однако при таком переходе обе
части формулы A9) или соответственно B2) просто делятся на я,
т. е. относительная ошибка обеих формул не меняется. Это связано
с тем, что при указанном переходе относительная доля вклада
в интеграл больших и малых значений функции /(х) сохраняется
неизменной (тогда как при переходе от /(х) к [/(л:)]" доля малых
значений с ростом п стремится к нулю).
В заключение упомянем о книге А. Б. Мигдала и Bj П. Край-
нова «Приближенные методы квантовой механики» (Физматгиз, 1966),
в которой приведен ряд методов оценок интегралов и других мате-
математических выражений.
Упражнения
00
1. Найдите величину интеграла /= \ х , разбив его на сумму двух ин-
0
3 00
С х dx С х dx
тегралов: ^=\-] -+ \ х. Первый интеграл вычислите по формуле
о з
Симпсона, а второй по формулам настоящего параграфа. Вычисления ведите
в пределах точности логарифмической линейки.
со
2. Найдите величину интеграла /= \ У xe~xd dx, разбив его на сумму двух
о
а оо
интегралов: /= \ Y~xe~xZ dx-\-[ У~ хе-х* dx, и находя первый интеграл по
О а
формулам § 1.1, а второй —по формулам § 2. Рассмотрите случаи а=1; 2.
Вычисления ведите с тремя знаками после запятой.
00
3. Оцените величину интеграла \e~*2dx, рассмотренного на стр. 65.
N
§ 3. Формула Стирлинга
В качестве интересного примера применения формул § 2 мы
сейчас получим удобную формулу для приближенного вычисления
величины п\—п(п — 1)(я — 2) ... 3-2-1 при больших значениях п.
Эта формула будет очень полезна при изучении теории вероятностей.
С помощью интегрирования по частям легко установить (см., например,

78
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
ВМ, § Ш.З), что при целом положительном л справедливо ра-
равенство
Оценим этот интеграл по способу предыдущего параграфа.
В нашем случае у = хпе~х, у' =(пхп~1 — х")е~х. Приравнивая
нулю первую производную, получим два значения: х = 0 и х-—п.
Нетрудно убедиться, что при лг = л функция у (х) имеет максимум,
Рис. 18.
а при лг=О она равна нулю. (На рис. 18 изображены графики
функции у = хпе~х для л = 3 и л = 4.) Итак, для вычисления интег
рала нужно рассматривать область максимума х — п функции, т. е«
пользоваться формулой B2).
Найдем /', получим у" = [л(л— \)хп~2 — 2/глг"-1 +хп] е~х. Сле-
Следовательно, у" (л) = — п"-1е~п — ( — ) . Поэтому
Итак,
(п) |
Эта формула называется формулой Стирлинга. Ее относительная
погрешность стремится к нулю с ростом л (это вытекает из рас-

§ 4]
ИНТЕГРИРОВАНИЕ БЫСТРОКОЛЕБЛЮЩИХСЯ ФУНКЦИЙ
79
суждений в § 2, если представить хпе~х как л" ( — е~ j J, однако
даже при малых л она дает очень хорошие результаты, например:
л=1; л! = 1, 1/л("гУ = 0,92, ошибка 8%;
» 4%;
» 2,7%;
л = 4; л! = 24, /bit f тУ = 23'5» » 2'1%:
» 1,7%.
л = 2; л!-2, /4л (у)'= 1,92,
л=:3; л! =6,
л = 5; л! = 120, /Юя f |-Y = 118,
Упражнение
Докажите, что отношение B3) при п -> оо стремится к 1.
Указание. Домножьте числитель и знаменатель дроби на ее числитель.
§ 4. Интегрирование быстроколеблющихся функций
При изучении быстро осциллирующих воздействий на физические
системы приходится рассматривать интегралы от быстроколеблющихся
функций, т. е. функций, которые на конечном интервале интегриро-
интегрирования много раз меняют знак.
Такие интегралы имеют свои спе-
специфические особенности.
Пусть надо вычислить ин-
интеграл
ь
F(x)dx, B5)
ас
где график функции F(x) имеет
вид, изображенный на рис. 19.
Будем сначала считать со — часто- Рис. 19.
ту колебаний — постоянной, а амп-
амплитуду меняющейся по закону y=f{x); другими словами, будем
считать, что интеграл B5) имеет вид
= \i/(x)sm(d)XJra)dx,
B6)
где со велико.
Из рис. 19 ясно, что при большом со интеграл B6) мал, так как
его положительная часть почти нейтрализуется отрицательной. Для

80 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. 111
более точной оценки произведем интегрирование по частям, что даст
ь
/= JL [/(a)cos((oa+a)—f(b)cos(ab+a)]+^/'(x)cos(ax + a)dx. B7)
а
Полученный интеграл имеет вид B6), а потому весь последний член
при большом а имеет порядок малости выше, чем 1/со. Отбрасывая
этот член, получаем приближенную формулу
/ж -^ [/(a) cos (aa +a) — /(b) cos (ab + a)]. B8)
Этот результат можно выразить и через подынтегральную функцию
F(x) исходного интеграла B5): так как
F' (х) = /' (х) sin (ах -f- а) -f- а/ (х) cos (ах -f- а) ж а/ (х) cos (ax -f- а),
то можно написать также
I^-L[F'(a)-F' (b)] = -±F' (х)^ B9)
Для дальнейшего уточнения можно в правой части B7) произ-
произвести еще одно интегрирование по частям; после отбрасывания полу-
полученного интеграла мы придем к приближенной формуле
/ « — [/(a) cos (аа-f-а) —f(b) cos (ab-\- a)] -f-
+ -^{Г (b)s\n(ab + a)—f (a)sm(aa + a)]. C0)
Здесь также можно написать формулу, аналогичную B9). Для этого
надо из выражений для F' (х) и F'" (х) вычислить f(x) cos (солг-|-а)
и —/' (х) sin (ax + а) с точностью до членов порядка —у и резуль-
результат подставить в C0). Пропуская выкладки, которые мы предостав-
предоставляем читателю, напишем окончательную формулу:
Эта формула, как и C0), верна с точностью до членов порядка —j-.
По описанной схеме можно производить и дальнейшее уточнение
асимптотических формул для /; однако получающиеся формулы будут
все более громоздкими и все менее удобными для практического
применения. На практике чаще всего пользуются формулами B8)
или B9). Интересно, что во всех этих формулах участвуют значе-
значения функций / или F и их производных только на концах интервала
интегрирования; впрочем, это находится в согласии с полученными
в § 1.2 приближенными формулами для знакочередующихся сумы.

§ 41
ИНТЕГРИРОВАНИЕ БЫСТРОКОЛЕБЛЮЩИХСЯ ФУНКЦИЙ
81
(Отметим, что в предыдущих формулах надо было считать, что
функция f(x) и ее производные рассматриваемых порядков внутри
интервала интегрирования непрерывны. Если /(х) имеет там конечный
скачок при х=с, то надо перейти к сумме интегралов от а до с
и от с до Ь, после чего к каждому из этих интегралов применить
указанные преобразования, в результате чего точка # = с даст свой
вклад в асимптотические формулы. Особенно существен этот вклад в
важном случае, когда а = —оо, b — оо и f(x) при лг=±оо обра-
обращается в нуль вместе со всеми своими производными, так как тогда
правые части формул B8) и C0) равны нулю. Более глубоко этот
вопрос будет освещен в § XIV.4.)
ъ
Рассмотрим в качестве примера интеграл /= \ е~х sin axdx. Его
точное значение равно
— t 8 (sin co6 -)- со cos co6).
Формула B8) дает приближенное значение
, = — A—e-bcosco6);
формула B9)—значение
/B9) = —г [со — е ~ ь (со cos (nb—sin соб)].
Обе приближенные формулы имеют погрешность порядка 1/со2.
Рассмотрим теперь случай, когда быстроколеблющаяся функция
F(x) под знаком интеграла
B5) имеет график, как на
рис. 20, т. е. меняет как свою
амплитуду, так и частоту. В
этом случае интеграл B5) ча-
часто бывает возможно записать
в виде
ь
sin (cocp (х) + a) dx,
C1)
Рис. 20.
гдеф(лг)—возрастающая (ноуже не с постоянной скоростью!) функция.
Интеграл C1) можно привести к виду B6) с помощью замены
переменной интегрирования ф(лг) = 5. Если обозначить через x — g(s)
обратную функцию, мы получим
/= \ f{g{s))g'{s) sin (as + a) ds.

Применение приближенной формулы B8) дает
82 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. Ill
иближенной формул
)) S' (s) cos (cos + a)] j j(a)
=-^[^cos^w+a>]|L C2)
(при этом мы воспользовались формулой g/ {s) — \/(f' (x) для произ-
производной обратной функции). Если q>(x)=sx, то формула C2) пере-
переходит в B8). Видоизмененная формула B9), которую мы предлагаем
вывести читателю, приобретает вид
. F'(x)
Упражнения
а
1. Примените формулы B8), B9) и C0) к интегралу \ - а rfx.
— а
2. Напишите аналог формулы C0) для интеграла C1).
2
Г* si п сих
3. Вычислите интеграл /= \ d*- при со = 1 и со= 10 по приближен-
приближенным формулам B8), B9) и C0). Сравните полученные значения с точными,
найденными по таблицам интегрального синуса.
§ 5. Числовые ряды
Числовым рядом называется «бесконечная сумма» чисел
аг + а2 + а3+...-гал + а„+1+ ...*). C3)
Конечно, это не совсем «настоящая» сумма, так как реально можно
сложить лишь конечное количество чисел, это — сумма «с особенно-
особенностью», аналогичной особенности для несобственных интегралов, рас-
рассмотренных в § 1. Поэтому и подход к понятию суммы ряда C3)
аналогичен тому, который был применен в § 1. Именно, сначала
особенность как бы отрезают, т. е. рассматривают частные суммы
ряда C3)
S1 = a1, Si = a1 + a2, S3 = a1-\-a.z + a3, ...,
Sn=a1 + al + a3+...+an. C4)
Если теперь увеличивать л, т. е. «исчерпывать особенность», и сле-
следить за поведением частной суммы C4), то могут представиться два
случая:
1) частная сумма может приближаться к определенному конеч-
конечному пределу б1, так что для больших п она практически просто
*) Такие ряды встречались в ВМ, начиная с § 11.17. Здесь мы рассмотрим
эти ряды более систематично. В этом параграфе используются результаты § 1.2.

§ 5] числовые ряды 83
равна S. В этом случае ряд C3) называется сходящимся, а сумма
его полагается равной б1. Таким образом, в случае сходимости
можно от частной суммы с большим номером переходить к полной
сумме ряда и обратно, т. е. вклад особенности в полную сумму
ряда не является существенным, он как угодно мал при большом я;
2) частная сумма может стремиться к бесконечности или может
колебаться, не имея определенного предела. В этом случае ряд C3)
называется расходящимся.
Простейший пример сходящегося ряда дает сумма бесконечной
убывающей геометрической прогрессии
?+...+cuF-1 + cur+...(\q\<l). C5)
В данном примере, как известно,
и так как при больших п степенью q" можно пренебречь, то в пре-
пределе получаем сумму ряда C5)
Ряд 1 + 1 + 1 + ... —это пример ряда, расходящегося к бесконеч-
бесконечности, а ряд 1 —1 + 1 —1 + 1 —1 + ...—это пример ряда, расхо-
расходящегося «колебательным образом», так как его частные суммы
последовательно равны 1, 0, 1, 0, 1, ... и не имеют определенного
предела.
Так как у сходящегося ряда частные суммы с большими номе-
номерами почти одинаковы, то его члены с большими номерами почти
равны нулю; более точно: если ряд C3) сходится, то его «общий
член» ап с возрастанием номера стремится к нулю. Однако и у рас-
расходящегося ряда общий член может стремиться к нулю: например,
так будет для расходящегося ряда
, 1 ^^ ,_J
1
То, что этот ряд расходится, можно показать так: £п =
+ +>++++ л
y уу7ТУ у
= ]/п s-oo.) Следовательно, только по этому признаку нельзя
установить сходимость ряда. Тем не менее, если зависимость
общего члена ап от номера п нам известна и имеет не очень слож-
сложный вид, то сходимость или расходимость ряда C3) обычно бывает
нетрудно установить на основании других признаков, которые мы
вскоре укажем. Если же такой простой зависимости установить не

84 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ ГЛ. III
удается, то просто вычисляют члены один за другим, и если они
выходят за пределы принятой точности вычисления, причем нет
основания ожидать, что дальнейшие члены дадут в сумму сущест-
существенный вклад, то все дальнейшие члены отбрасывают, ряд объявляют
сходящимся, а его сумму равной частной сумме вычисленных членов.
Первый признак сходимости ряда C3), так называемый признак
'Даламбера, основан на аналогии с суммой бесконечной геометриче-
геометрической прогрессии C5). Для «чистой» прогрессии C5) отношение каж-
каждого последующего члена к предыдущему есть величина постоянная
(равная знаменателю q прогрессии). Допустим теперь, что для ряда
C3) отношение
последующего члена к предыдущему уже не постоянно, но стремится
к некоторому пределу q с возрастанием номера. Тогда для больших
я это отношение приблизительно равно q и, как и ряд C5), ряд C3)
сходится, если | ^ j = lim -^±i <^\) рЯд C3) расходится, если
\q\ > 1. И только если |^|=1, то по признаку Даламбера нельзя
установить, сходится ли ряд C3), так что приходится применять
другие признаки.
Рассмотрим, например, ряд
— 4- — 4- — 4- 4-—4-
Применяя признак Даламбера, найдем
Таким образом, при |а|<1 ряд C6) сходится со скоростью гео-
геометрической прогрессии, а при |а|>1—расходится; при а — ±\
признак Даламбера к ряду C6) неприменим.
Рассмотрим теперь более сильный интегральный признак Коши,
применимый к ряду с положительными членами. Допустим, что
известно выражение общего члена ап ряда C3) в виде функции от
номера я, т. е. а„=/(я), причем функция /(я) положительна и
убывает с ростом я. Тогда в силу формулы A.9) в качестве при-
приближенного значения для частной суммы C4) можно принять
C7)

§ 5] числовые ряды 85
Таким образом, если интеграл
C8)
\f{x)dx
сходится, то правая часть C7) при п—>■ оо остается конечной, т. е.
ряд C3) сходится. Если же интеграл C8) расходится к бесконечно-
бесконечности, то и ряд C3) расходится.
Рассмотрим, например, ряд
Tr+i+h+---+h+-- C9)
который получается из ряда C6) при а—\, когда признак Далам-
бера не действует. Чтобы применить интегральный признак Коши,
надо рассмотреть интеграл
00
Cdx
J хР'
1
Этот интеграл был рассмотрен в § 1 (формула C)), где мы пока,
зали, что он сходится при р>1 и расходится при /?<!1. Значит,
и ряд C9) сходится при р>1 и расходится при р<!1. В част-
частности, при р = 1 получаем так называемый гармонический ряд
1+т+т+•••+£+• "в0°-
Что касается рядов с членами произвольного знака, то здесь ча-
часто применяется признак Лейбница, согласно которому ряд
al—a2 + a3—at + ai — ae+... D0)
(все а,- считаются положительными, так что знаки двух соседних
слагаемых противоположны) сходит-
сходится, если ^?
8
В самом деле, если на некоторой ;
вспомогательной оси изобразить Рис. 21.
(рис. 21) частные суммы ряда C2),
то из условия D1) вытекает, что переход от St к 52, от 52 к S3,
от S3 к St и т. д. имеет вид затухающих колебаний, т. е. эти част-
частные суммы стремятся к определенному пределу.
Таким образом, например, ряд
1 2p~^~ZP iJ5
сходится при любом р > 0.

86 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [гЛ. Ш
Если, как в предыдущем признаке, члены ряда D0) имеют вид
/(л), то приближенное значение его суммы можно подсчитать по
методам § 1.2. О способах уточнения этого значения будет сказано
ниже.
Сходящиеся ряды с членами произвольного знака (не обязательно
знакочередующиеся, как D0)), бывают двух типов:
1) может оказаться, что сходятся как «положительная часть»
исходного ряда (т. е. ряд, составленный из одних положительных
членов исходного ряда), так и его «отрицательная часть». Тогда
исходный ряд называется абсолютно сходящимся, так как сходится
и ряд, составленный из абсолютных величин его членов;
2) может оказаться, что и положительная и отрицательная части
исходного ряда расходятся к бесконечности, но сам ряд сходится
из-за компенсации этих бесконечностей. Такой ряд называется не-
неабсолютно сходящимся, так как ряд, составленный из абсолютных
величин его членов, расходится.
Например, вспоминая о ряде C9), мы заключаем, что ряд D2)
при р>1 абсолютно сходящийся, а при 0<р^1 неабсолютно
сходящийся.
Со сходящимися рядами можно производить такие же действия,
как и с конечными суммами, так как практически сумма сходящегося
ряда просто равна его частной сумме с достаточно большим номе-
номером. Не совсем очевидное осложнение возникает при перестановке
членов сходящегося ряда. Именно, на сумме абсолютно сходящегося
ряда такая перестановка не сказывается, но неабсолютно сходящийся
ряд может после перестановки членов изменить свою сумму или
даже стать расходящимся, так как такая перестановка может изме-
изменить или даже нарушить «компенсацию бесконечностей», о которой
было сказано выше. Рассмотрим, например, сходящийся ряд
1-У¥+7Т рТ+ТТ~ТТ+>" D3)
и переставим в нем члены так, чтобы за двумя положительными
следовал один отрицательный:
! г J! , J i J! , J4- -1 l—4-
Частная сумма S3n с номером Зя этого ряда состоит из группы по-
по3n
ложительных слагаемых
и группы отрицательных слагаемых
11!

§ 5] числовые ряды 87
Но первая сумма превосходит
~  -/—т I -./—77 Г ,/—~ Г • • •  -шГл —^ Г ,/--— >
V~2 ' /1 ' /6
и потому общая сумма
о . 1,1
1 ' * I * I I ' I ' ^
~ -./ :—~ \ • • • "Г -.Гп г ~Г~ ~г-рг- \ •
1^2
В силу оценки A.11) правая часть приближенно равна
► оо.
Итак, 'из двух рядов D3) и D4), различающихся лишь порядком
членов,- первый сходится, а второй расходится к бесконечности.
Если мы хотим, как это часто делают на практике, заменить
сумму ряда на частную сумму нескольких его первых членов, то
для этого ряд должен не просто сходиться, а быстро сходиться,
чтобы, взяв небольшое число членов, мы почти исчерпали полную
сумму, получив ее с хорошей точностью. Для медленно сходящихся
рядов (ими, в частности, обычно оказываются неабсолютно сходя-
сходящиеся ряды) приходится остаток ряда не отбрасывать, а оценивать
по методам § 1.2.
Как для сходящихся, так и для расходящихся рядов бывает су-
существенно найти асимптотический закон изменения частной суммы
в процессе увеличения ее номера. Это можно сделать с помощью
методов § 1.2, т. е. с помощью применения формул A.9), A.11),
A.14) или A.15), хотя при этом получается определенная ошибка.
Ограничимся для простоты рядами с положительными членами.
Обычно частная сумма ряда имеет вид
где число членов возрастает за счет увеличения п, а величина /:
остается неизменной. Так, например, из суммы S^I+y+T
получается сумма

88 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
ИЛИ
В таком случае, как правило, абсолютная величина ошибки не
уменьшается с увеличением числа членов суммы.
Рассмотрим примеры.
1. 5„ = 1 + 53 + оЗ+ • • • Ч—г • Согласно (Ml) получим
$п ~ \ ~^ — 2 г. По формуле A.9) находим
2
S ~ С —4- — 4- — — 1 5 -4--1 -— 1 5 2/t—1
Известно, что при неограниченном увеличении п значение Sn не-
неограниченно приближается к числу £ = -£-« 1,665. (Здесь мы не
доказываем этого факта.) Для весьма больших п формула A.11)
дает ^„ = 2 (ошибка 20%), формула A.9) дает 6^=1,5 (ошибка 10%).
Отметим, что в этом случае легко уточнить расчет. Причина
довольно значительной ошибки заключается в том, что первые члены
суммы изменяются быстро, следовательно, на промежутке интегри-
интегрирования, соответствующем расстоянию между двумя последователь-
последовательными членами суммы, функция f(x) изменяется слишком неравно-
неравномерно, а поэтому формула трапеций, на которой был основан вывод
формул A.9) и A.11), дает плохой результат.
Поэтому можно найти сумму нескольких первых членов непосред-
непосредственным сложением, а к оставшейся сумме применить приближенные
формулы. В нашем примере найдем сначала сумму первых трех
членов непосредственно:
1 ' ■ « «" • ~ -ц =1,361.
Пусть
По формуле A.11) находим 6^_3 « 0,286 г-, по формуле A.9)
находим S'n_3 & 0,281 ^т~ • Поэтому
6'„« 1,647 Ц-

§ 5] числовые ряды 89
по A.11) и
о 1 ело 2n —I
5„ да 1,642 53Г-
по A.9). При неограниченном увеличении п формула A.11) дает
5й 1,647, формула A.9.) дает 5^1,642. В каждом случае ошибка
меньше 2%.
2. Рассмотрим сумму убывающей геометрической прогрессии
S1+ + i++^
где z>l. Точная формула, как известно, такова:
1-4 — '
<> _ г" _ г"-1
откуда при неограниченном росте п находим 5 = -г. По фор-
формуле A.11) получаем
1 1
1 #- I •-
~~ 1пг
При неограниченном росте п находим 5«^~-. Из приведенной
ниже таблицы видно, что при z, близком к единице, обе формулы
дают близкие результаты:
г 1,2 1,5 2,0 3,0 6,0 20,0
—5-г 6,00 3,00 2,00 1,5 1,20 1,05
V-- 6,00 3,01 2,04 1,57 1,36 1,49
In z
Если же z^>\, то соседние члены прогрессии сильно отличаются
и поэтому приближенная формула дает плохие результаты.
В некоторых случаях сумма может неограниченно возрастать при
увеличении числа членов, несмотря на то, что члены суммы неогра-
неограниченно уменьшаются (это случаи расходимости соответствующих
бесконечных рядов).
Рассмотрим примеры.

90 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
По формуле A.11) получаем
1
2
V X
I
2
П 1
1
2
1
2
9 l/
— *• 1/
1
Л+ 2 '
/" 1
По формуле A.9) получаем
При больших п получаем из A.11)
~я—1,41,
а из A.9) 5n«2V л—1,50. (При этом мы отбрасываем член, про-
пропорциональный —==- . J
Более точная формула (она получается непосредственным сложе-
сложением нескольких первых членов) такова:
л- 1,466.
2. Во многих вопросах встречается сумма
При больших п, пользуясь формулой A.11), находим Snm\nn-\-
+ In 2 = In n + 0,69, а пользуясь A.9), находим Sn да In /; + 0,50.
Предел разности 5П — 1пл при неограниченном увеличении п обозна-
обозначается буквой С и называется постоянной Эйлера. Таким образом,
можно написать формулу 5'п = 1п п-\- С + а„, где ап —* 0 при л—»-оо.
Поэтому асимптотически точная формула имеет вид Sn та 1п п-{- С. Мы
получили весьма грубые приближенные значения для постоянной
Эйлера, однако при помощи формул A.9) и (Ы1) можно получить
более точное значение С, суммируя непосредственно несколько первых
членов. Оказывается, что С = 0,5772...
Теперь рассмотрим суммы, члены которых растут с увеличением п.
Величина такой суммы неограниченно возрастает с увеличением числа
членов, т. е. с ростом п. При увеличении п возможны два случая.
1. Ошибка приближенных формул A.9) и A.11) с увеличением п
уменьшается (по абсолютной величине) или хотя и увеличивается, но
медленнее, чем сама сумма, так что относительная ошибка умень-
уменьшается. Этот случай получается, если члены суммы возрастают мед-
медленнее геометрической прогрессии, например, как степени.

§ 5] числовые ряды 91
2. Относительная ошибка (а тем более и абсолютная) с увели-
увеличением п не уменьшается.
Второй случай получается тогда, когда члены суммы возрастают
в геометрической прогрессии, т. е. когда сумма имеет вид Sn = а -\-
-\-ау -\-ауг-{-ау3-{- . .. -j-qy", где |_у|>1, а также если члены
суммы растут быстрее прогрессии, например Sп=у-{-у*-{-ув-{-.. .+у"г.
В этом случае последний член составляет основную часть всей суммы.
Например, для случая суммы Sn =y +yi +у* + ... +уп* мы приводим
с
таблицу значений величины —^- при у = 2:
и 1 2 3 4 5
2п"~ 2 16 512 65 536 33 500 000
Sn 2 18 530 66 066 33 600 000
S>1 I 1,12 1,03 1,01 1,003
2"
Из таблицы видно, что при больших п величина всей суммы
практически определяется величиной одного последнего члена.
Аналогичная картина имеет место и для возрастающей геометри-
геометрической прогрессии.
Действительно, в формуле
Sn=\+z+...+z = (И>1)
пренебрежем единицей по сравнению с zn, тогда получим
Поэтому
"\ ж ——: г- = г- = const
гп-\ zn-1{z—l) г — 1
(при достаточно больших п). Значит, в этом случае доля вклада
последнего члена приближается к постоянному числу, а при больших
\z\ эта доля близка к 1, Ясно, что в этом случае нет надобности
в формулах суммирования. Действительно, для того чтобы получить
величину суммы с хорошей степенью точности, достаточно найти
сумму нескольких последних членов.
Формулы суммирования полезны тогда, когда отношение суммы
к последнему члену возрастает с увеличением п. Тогда формула
дает возможность сократить вычисления при больших п. При этом
всегда осуществляется случай 1, т.е. относительная ошибка формул
A.9) и A.11) обязательно уменьшается. Приведем пример.
Из элементарной алгебры известна формула
и3 , п1 , п

92 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. Ш
Применим к сумме Sn приближенную формулу A.11). Получим
_ и3 и2 п
""Т + Т + Т*
Абсолютная ошибка равна S'n—$п = ~\2 и» следовательно, растет
с увеличением п. Относительная ошибка
Sn-Sn _ п _ п 1
Она быстро уменьшается с увеличением л.
Рассмотрим сумму
(р> — 1).
Применив формулу A.10), мы получим
Таким образом, при больших п справедлива простая, хотя и грубая
формула
Упражнения
1. Уточните значение постоянной Эйлера С (см. стр. 90), найдя непосред-
непосредственно сумму пяти первых членов, десяти первых членов.
2. Пусть дана сумма
Sn = «i + «2+...+««
такая, что
0 < и1 < и2 < и3 < ... < ип.
Образуем сумму
Ясно, что члены этой суммы убывают. Как ведет себя с„ с увеличением п,
если Sn есть возрастающая сумма первого типа; второго типа?
*) В случае, когда р — целое положительное, элементарная алгебра позво-
позволяет написать точную формулу для Sjf* (в частности, мы пользовались такой
формулой для р = 2). Однако при больших р формулы становятся громоздкими,
поэтому приведенная грубая формула может оказаться полезной и для целых
положительных р.

§ 6] ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 93
§ 6. Интегралы, зависящие от параметра
Рассмотрим интеграл вида
ь
I=\f{x,X)dx, D5)
где под знак интеграла, помимо переменной интегрирования х, вхо-
входит параметр (произвольная постоянная) %, т.е. величина, которая
в процессе интегрирования считается постоянной, но вообще может
принимать различные значения. Тогда и результат интегрирования,
вообще говоря, зависит от X, т.е. 1=1 (к). Такие интегралы часто
встречаются в приложениях, когда интегрируемая функция включает
в себя какие-либо массы, размеры и т. п., которые в процессе интег-
интегрирования являются постоянными. Приведем простые примеры:
E> —1).
При рассмотрении собственных интегралов имеют место те же
свойства, что и при рассмотрении конечных сумм функций. Так, мы
знаем, что производная от суммы функций равна сумме производных.
Подобным образом производная от интеграла D5) по параметру равна
dl С df(x, X) .
интегралу от производной по этому параметру: -jr= \ \«—-ах;
а
здесь под знаком интеграла стоит производная от функции /(х, X),
по X, взятая при фиксированном х. Аналогичное правило выполняется
при интегрировании по параметру:
Р ь /Р \
$/(*,)<&=$( $/(*, X)dXjdx.
а а \а '
Для проверки этих простых правил надо было бы выписать их для
интегральных сумм, а затем перейти в пределе от сумм к интегра-
интегралам, однако мы не станем здесь этим подробно заниматься.
Для несобственных интегралов, зависящих от параметров, могут
возникнуть осложнения, связанные прежде всего с возможностью их
расходимости. Наиболее просто обстоят дела для «правильно
сходящихся» несобственных интегралов; так, интеграл вида
\)dx, D6)

94
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
где сама функция / конечна, называется правильно сходящимся,
если он мажорируется сходящимся интегралом, не зависящим от
параметра, т.е. если |/(лг, ^)
мер, интеграл
, где J F(x)dx < оо. Напри-
а
правильно сходящийся, так как
sin Хх
1 Г 1 ,
—г . \ —~-ах =
х2 ' J xJ
оо.
Свойства правильно сходящихся интегралов такие же, как собствен-
собственных интегралов*).
При изучении неправильно сходящихся, а также расходящихся
интегралов вида D0) часто поступают следующим образом: отрезают
особенность, т. е. переходят к собственному интегралу
N
после чего рассматривают асимптотическое поведение этого интеграла
при ./V—*■ оо. Этим бывает возможно оправдать действия над несоб-
несобственными и даже расходящимися интегралами.
Очень важно, что результат выполнения различных действий —
вычитания, дифференцирования по параметру и т.д.— над расходя-
расходящимися интегралами может оказаться конечной величиной, в част-
частности, может выражаться через сходящиеся интегралы (может слу-
случиться и обратное). Рассмотрим, например, расходящийся интеграл
После дифференцирования по параметру мы приходим к сходящемуся
интегралу
d/
a
I
*). Здесь требование правильной сходимости можно заменить на несколько
менее ограничительное требование равномерной сходимости, которое означает
что max
их
J
N
0.
JV->oo

§ 6]
ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
95
Чтобы разобраться в смысле полученного равенства, отрежем осо-
особенность, что даст
N
= \n(N+%)—\nX.
х=0
Дифференцируя, получим
dIN
dX '
x •
dIN
dX
— Y, т. е. мы при-
Если теперь N—уоо, то IN(k)—±oo, a
ходим к полученному выше результату. Аналогичный смысл (про-
(проверьте!) имеет равенство
о
Поясним еще на примере осложнение, которое может получиться
для неправильно сходящихся интегралов. Рассмотрим интеграл
sin Хх
dx.
Можно проверить (см. упражнение 2), что при 1=1 он сходится и
равен Y- Отсюда с помощью под-
подстановки Хлг = 5 при % > О сразу
следует, что
r\
jN(A), малое Н
Л
JH(A), большое N
2
Рис. 22.
В то же время при Х = 0 полу-
получается /=0, а при X, < 0, вынося
— 1 за знак интеграла, получаем,
что /= —я/2. Итак, в данном при-
примере I (к) при ?v = 0 имеет скачок. Это может показаться стран-
странным, так как при малом изменении % подынтегральная функция
меняется как угодно мало. Однако малое изменение подынтегральной
функции на бесконечном интервале может привести к немалому изме-
изменению интеграла! На рис. 22 показаны разрывный график /(%) и
*) Начиная с пятидесятых годов XX века физики, развивая квантовую
электродинамику, широко пользуются несовершенной теорией, которая содер-
содержит расходящиеся интегралы; при этом вычисляют величины типа производ-
производных и разностей этих интегралов. Такие величины оказываются конечными
и великолепно согласуются с опытом, который является высшим критерием
истины.

96 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. Ill
графики
° -'п Хх ,
—— dx
о
при различных N. Хотя эти последние и не имеют разрыва, но при
»г Я. Л
большом N переход от •—к к -^ совершается на малом интервале
X, причем чем больше ./V, тем этот интервал меньше. В пределе,
при N= со, этот переход осуществляется на бесконечно малом
интервале X, т. е. появляется разрыв.
К функциям
00 0D
sin Хх , д1 С , .
dx и -~г- — \ cos Xx dx
(в других обозначениях) мы еще вернемся в § VI.3 в связи с теорией
разрывных функций и в § XIV.2 в связи с преобразованием Фурье.
При рассмотрении рядов, члены которых зависят от параметра,
возникают в точности те же вопросы, что и при рассмотрении
несобственных интегралов, зависящих от параметра. Получающиеся
здесь свойства совершенно аналогичны, и потому мы не будем их
здесь приводить.
Упражнения
0D
1. Исходя из интеграла \ е~^ dx(k > 0), получите с помощью дифферен-
о
0D
цнрования по параметру при Я = 1 значение интеграла \xne~xdx (ср. § 3),
U
0D
\
а с помощъю интегрирования по параметру — значение интеграла \ dx
о
(отметим, что в последнем примере неопределенный иитеграл не выражается
через элементарные функции).
со
2. Исходя из интеграла V е~кх sin x dx(k > 0), интегрируя по параметру
(I
в пределах от а до р1, а затем полагая E—>.оо, получите формулу
re-«!iE£rf;t = JL_arctga (a > 0). D7)
J x 2
и
(Значение этого интеграла при <х = 0 упоминалось в тексте.)

ОТВЕТЫ И РЕШЕНИЯ
§ 1
Непосредственно применять способ трапеций или Симпсона нельзя, тпк как
подынтегральная функция обращается в бесконечность при х = 0. Поэтому
разобьем промежуток интегрирования на два: от х=0 до * = -V » от х — ~с~
до х = ^ . При 0<д:<-^- справедливо соотношение sin л х, поэтому
2
Г Л*
Интеграл /2= I - ,-——■. подсчитаем по формуле Симпсона. Разбив промежу-
л
6
ток на две части, получим /2 « 1,13. Отсюда
я
■z
\ dx и 0,98 + 1,13=2,11.
« ^/sin д:
§2.
1. Значение первого из этих интегралов было получено (см. задачу 2 упраж-
00
иеиий к § I. 1). Найдем \ ■ х,. • Подынтегральная функция есть j (х) =
з
i поэтому /' (х)=—. х, 11J* • Так как /' C) ф 0, то применяем фор-
фор= х ,, i поэтому / (х)=—. х, 11J
мулу A9). Получаем
^0,63+0,23 = 0,86.
з о
Отметим для сравнения, что точное значение искомого интеграла (с двумя зна-
знаками после запятой) есть 0,82.
2. 0,67; 0,59. (Точнее значение с тремя знаками после запятой есть 0,612.)
3. Здесь у = е~х2, у'=—2хе~х\ а = Л'; по формуле A9) получаем, что
как и было указано на стр. 65.
§3
Рассматривая дробь D после указанного преобразования равна
[2-4-6...Bя—2)]j {2"-1-l-2-3...(n—l)]i 22"~a [(« —I)!K
l/"Snl-2-3-4...Bn — 3)Bя — 2)= УшBп — 2)\ = l^Hn B/i —2I
4 Я. Б. Зельдович, Л. Д. Мышкпс

98 ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИНТЕГРАЛАХ И РЯДАХ [ГЛ. III
Применяя формулу Стирлиига, получаем при больших п
2Л Aп — 2) (
9\2л-2
1= ]
_ 22"-2 2я (га— 1) (п— IJ"-2 е-'2"-^
§4
2.
2sincoa . . 4a cos соя . . 4a cos сод
; У'+ 2 A+a2J' (so)~"'B8>~co2 A+a2K
\Ф (
3. При co=l точное значение / = si2co—si со = 0,66; приближенные значе-
значения: /B8)=0,75, /B9)=0,13, /C0) = l,36; как видим, точность совершенно не-
неудовлетворительная. При со= 10 точное значение / = — 0,110, приближенные
значения: /(гв) = — 0,104, /B9) =—0,115, /(зо>=—0,112, точность порядка
нескольких процентов.
§5
— — 1 1 1
1. Sn = S5 + Sn_3, rfleSn_5 = -g- + y+...+—. Примеияя формулу A.9),
п
получим Sn_6 « \ ——-р5 + 9~~ In « —In 6+0,083. Так как
6
S6 = l+y + | + | + y-2,283,
те
Sn« ln«—1п6+0,083 + 2,283=1п«+0,575,
откуда С = 0,575. Суммируя 10 первых членов, получим С=0,576.
2. В первом случае ап иеограиичеиио увеличивается при неограниченном
увеличении п, во втором случае а„ иеограиичеиио приближается к 1.
§6
1. Имеем
CD
fe-xxdx=eJ±L" =1 ^>в)- D8)
о
Этот интеграл правильно сходится иа любом промежутке а<А<Р, где
О < a < P < оо, так как иа таком промежутке е~кх <е~аХ, а \ е ах dx < оо.
о

ОТВЕТЫ И РЕШЕНИЯ 99
Дифференцируя по параметру X, получаем последовательно
— xf e~^ dx=(—l)(—2) l~3;...;
С (_ х)п е-\х dx=(—\)(—2)...(—«) K-
о
Полагая Х = 1 и сокращая на (—1)", получаем
x"e~x dx = n\.
о
Интегрируя формулу D8) по параметру от 1 до %, получаем
'■ dx = In X.
в \i
2. Интеграл
вычисляется элементарно, с помощью неопределенного интеграла. Как и в
задаче 1, интеграл правильно сходится на любом интервале ?P
(О < а < Р < оо). Интегрируя по X от а до р, получаем
I (e-ax_e-p*)iiH dx =
*) х
— arctg a.
Переходя к пределу при р—>. оо, получаем отсюда формулу D7). При а=0
эта формула дает
Следует отметить( что формула D7) выведена нами при а > 0 и справедливость
ее при <х = 0 требует специальиого обосиоваиия, иа котором мы здесь не будем
останавливаться.

ГЛАВА IV
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
До сих пор мы рассматривали только функции одной независимой
переменной; функции нескольких переменных встречались у нас
только эпизодически (см., например, ВМ, § 11,12). Теория функций,
зависящих от нескольких независимых переменных, содержит много
новых моментов. При этом почти все принципиально новые положе-
положения проявляются уже на примере функции двух переменных:
z=f(x,y).
Для простоты мы будем, как правило, рассматривать именно этот
случай.
Само понятие функции двух переменных достаточно просто: вели-
величина z задается какой-то формулой или таблицей так, что каждой
паре значений х и у соответствует определенное значение z.
§ 1. Частные производные
В случае функции одной переменной g—g(x) малое изменение dx
переменной х приводило к малому изменению функции g, причем
g (х + dx) — g (x) = g1 (x) dx.
В этой формуле, правая часть которой обозначается через dg, мы
пренебрегаем членами порядка (dx)*, так как dx есть весьма малая
величина. В случае функции двух переменных изменение функции
происходит в результате изменения обеих переменных х и у и равно
f(x + dx, y + dy)—f(x,y).
Покажем *), что это изменение состоит из двух частей, причем
одна часть пропорциональна dx, а другая пропорциональна dy, т. е.
f(x + dx, y + dy)—f(x,y) = adx + bdy. A)
При этом мы пренебрегаем членами порядка (dxJ, (dy)-, dx-dy, так
кмк dx и dy — весьма малые величины.
*) Здесь мы с некоторыми изменениями повторяем рассуждение § 11.12 ВМ.

§ 1]
ЧАСТНЫЕ ПРОИЗВОДНЫЕ
101
Запишем левую часть A) так:
f(x + dx, y + dy)—f(x,y) = f(
, y + dy) —
,y)+f(x+dx,y)—f(x,y).
Рассмотрим разность двух последних членов f(x-\-dx, у)—f(x, у).
При каждом конкретном, закрепленном у эта разность, с точностью
до членов порядка (dxJ, есть дифференциал функции, зависящей
только от х:
дх
dx,
где
, у)
обозначает производную функции f(x, у), вычислен-
«ую в предположении, что у постоянно. Такая производная назы-
называется частной производной функции f(x,y) no x при постоянном у;
ее можно обозначить и так: f'x(x,y). Аналогично, с точностью до
членов порядка (dyJ,
где
f(x + dx,
df(x+dx,y)
x+dx
dy,
dy
x+dx
есть частная производная по у при постоян-
постоянном первом аргументе, равном x-\-dx. Ясно, что величина
df(x + dx,y)
ду
x+dx
дЦх, у)
ду
L
тем меньше, чем меньше dx, точнее,
df(x+dx,y)
ду
x+dx
df(x,y)\ _
ду
-adx,
где величина а ограничена. Левая часть A) при указанных упроще-
упрощениях равна
df(x,y)
дх
df (x, у)
ду
-\-adx\ dy —
_df(x,y)
дх
Окончательно, учитывая, что членом adxdy можно пренебречь,
получаем, что с точностью до величин порядка (dxJ, (dyJ и dxdy
левая часть A) равна сумме, которая обозначается через df и назы-
называется полным дифференциалом функции /:
df=
df(x,y)
дх
df(x,y)
dy.
B)
Из сравнения с A) находим

102 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
Если по смыслу ясно, какая величина считается постоянной при
вычислении частной производной, то ее не указывают и вместо -^-
пишут короче: -~. Однако поскольку в задаче в целом перемен-
переменными являются и х и у, то производную пишем с круглыми д, чтобы
отличить ее от обычной производной*). Из сказанного следует, что
величину —- следует находить так, как будто бы у в выражении
df
f(x, у) не изменяется. Точно так же ^- находим, считая, что изме-
изменяется только у, а х остается постоянной. Например, если
C)
то
-J- = 2ху3 -\- еу, J- = Зх2у2 -\- хеУ.
ОХ иу
Чтобы представить формулу B) более наглядно, рассмотрим
«плоскость независимых переменных», т. е, плоскость х, у. Каждая
точка М на этой плоскости имеет
И
f df Sf . определенные координаты х, у и
дх^ду У потому этой точке отвечает оп-
определенное значение функции
f(x, у); можно считать, что функ-
функция в каждой точке плоскости
принимает определенное значе-
значение. Если мы дадим малое при-
приращение только переменной х,
или только у, или обеим сразу,
j то мы получим на плоскости х,
у точки малого прямоугольника
Рис, 23. MNPQ, изображенного в увели-
увеличенном размере иа рис. 23. Внут-
Внутри прямоугольника обозначены координаты его вершии, а вие его
выписаны значения функции (с отброшенными малыми второго по-
порядка) в соответствующих вершинах; под / понимается значение
f(*,y)-
Формула, аналогичная B), справедлива для любого числа неза-
независимых переменных, а ие только для двух, например df(x, у, z, и) =
= -^-dx-\- -j- dy-\--J- dz-\--l-du. При этом -J- вычисляется в предполо-
*) В формуле — (ekx) = kekx мы также, по существу, имеем дело с част-
частной производной, вычисленной при постоянном k. Однако здесь иет надобности
употреблять знак частной производной, потому что k оставалось постоянным
в ходе всего рассмотрения задачи.

§ 1] ЧАСТНЫЕ ПРОИЗВОДНЫЕ 103
df
жении, что у, z, и постоянные, -£- вычисляется в предположении,
что х, z, и постоянные, и т. д.
Покажем на примере, что величина частной производной сущест-
существенно зависит от того, как выбраны другие, закрепленные леремен-
Сср2 о2
ные. Из физики известно, что энергия конденсатора ^7=^~=='^">
где q=C(f, здесь С-—емкость конденсатора, ср — разность потен-
потенциалов на его обкладках и q — количество электричества, т. е.
dW
заряд. Рассматривая зависимость IF= и7(С, ср), получим -т-=г
ф2 \j7 gyp
— -^ =-т=г-. Рассматривая зависимость W= W(C, q), получим ^r—
92 W „ dW\ dW
= -2Ci = - —• П0ЭТ0МУ dcl = --d
До сих пор мы считали переменные хну изменяющимися со-
совершенно независимо одна от другой. Пусть теперь они сами зави-
зависят от некоторой переменной t, т. е.
x=x(t), y = y(t). D)
Эти равенства «параметрически» задают на плоскости х, у некото-
некоторую линию, причем параметром служит t (см., например, ВМ, § IV.8).
Параметр t может иметь различный физический смысл, однако удоб-
удобнее всего его рассматривать как время, т. е. считать, что рассмат-
рассматривается траектория точки, движущейся в плоскости х, у. Тогда
z=f(x, y)=f(x(t), y(t)), так что в действительности z есть функ-
функция одной переменной t, только заданная сложным образом. Найдем
ее производную -г (полную производную вдоль линии D)) *). Так как
из B) и D) получаем
. dz , . dz , дг dx ,, , dz dy ,, fdz dx . dz dy
dz = lTxdx + Tydy = ¥x*dt+d-yitdt=[rT + -7
TO
dz _dz dx , dz dy
Tt~~dxTt~T"dy~dl'
В частности, если z = f(x, у), где у = у(х), то ^ = ^ + ^^-
-г-
видим, что значение -г- полной производной вдоль линии при дан-
данных х, у зависит не только от вида функции /, но и от -~ , т. е.
от наклона линии в данной точке к оси х.
Обе последние формулы легко понять с помощью рис. 23. Если
точка за время dt перешла из положения М в Р вдоль пунктирной
*) Советуем читателю повторить вывод формулы для производной сложной
функции одной переменной (см., например, ВМ, § 11.3).

104 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
линии, то скорость изменения функции равна
dx + dy
df _fadx + dj}dy _dfdx , df dy
dt~ dt ~ dx dt ' dy dt '
Для получения второй формулы надо df относить не к dt, а к dx.
Рассмотрим для примера случай, когда некоторая величина и,
например давление или температура в потоке газа, определена в
каждый момент времени t в каждой точке (*; у; z) пространства.
Тогда эта величина и будет функцией четырех переменных х, у, z,
t, т. е. и = и(х, у, z, t). Пусть, далее, задан закон движения x = x(t),
y — y(t), z = z(t) некоторой частицы Ж. Если рассматривать значение
и в Ж по мере движения, то это значение будет представлять со-
собой сложную функцию времени:
u = u(x(t), y(t), z(t), t).
Скорость изменения этого значения и, т. е. скорость изменения
величины и «вдоль траектории», равна, в силу формулы для произ-
производной сложной функции,
du dudx.dudy.dudz.du ._.
Если величина и не зависит явно от t (тогда говорят, что «поле
и стационарное»), то ^- = 0, и справа остаются только первые три
слагаемых; таким образом, они дают скорость изменения и, полу-
полученную только за счет перехода точки М вдоль траектории от одних
значений и к другим (например, если и—температура, то за счет
перехода из менее нагретой части пространства в более нагретую
и т. п.). Эта скорость называется переносной (конвективной). Пос-
Последнее слагаемое дает скорость изменения поля в неподвижной
точке, полученную из-за нестационарности поля; эта скорость назы-
называется местной (локальной). В общем случае действуют оба указан-
указанных фактора, и скорость изменения поля вдоль траектории склады-
складывается из переносной и местной скоростей изменения поля.
Вернемся к случаю функции z — f(x, у) от двух независимых
переменных. Ясно, что частные производные ^- и -г- этой функции
сами зависят от х и у. Поэтому можно находить их частные произ-
производные. Эти частные производные называются частными производными
второго порядка, их частные производные — частными производными
третьего порядка и т. д. Можно образовать следующие частные про-
производные второго порядка:
d f dz\ d fdz\ d Idz\ d (dz\
dx \dx) ' Ъ~у \d~xj ' Tx \Ty) ' dy \dy) '

§ 1]
ЧАСТНЫЕ ПРОИЗВОДНЫЕ
105
или,
в
других
zxxz
обозначениях,
d4 „ d4
OX* OX Oy
zyx
d4
dydx '
zyy
d4
di/'-
„ д-z дЧ
Производные ^—г- и , . называются смешанными.
^ дхду дудх
Так, в примере C)
Ту
хеУ) =
хеУ) =
дЧ дЧ
Мы видим, что в этом примере ,,=,,, т. е. смешанные про-
производные не зависят от того, в каком порядке производится диффе-
дифференцирование.
Покажем, что и в общем случае смешанные производные равны.
Для этого заметим, что согласно определению производной (см. § II.2)
дЧ
дхду
х=хо~ ду\дх] \х=х„'
У=Уо У = Уо
dz
дх
dz
(с любой точностью), если только k достаточно мало*). Томно так'же
_f(xo + h, yo + k) — f(xo—h, ур + k)
dz
дх
dz_
дх
2А
_f(xo+h, yo—k)—f(xo—h, yo —
Подставляя эти выражения в формулу для смешанной производной,
получим
_f(xo + hl yo + k)—f(xo—h,
дхду
o — k)—f(xo—h, yo — k)
Ahk
F)
Теперь таким же образом получим, что
dz
~д~у
дЧ
дудх
д [dz
х-х0 дх \dyj \х=
x=xo
__ 11 = Уо
^1
dy\x=x0-h
У=Уо
2/г
У=Уо
*) Точная формулировка: производная есть предел, к которому стремятся
правая часть при к, стремящемся к нулю. Аналогичные формулировки отно-
относятся к следующим формулам.

106
где
dz
dz
ду
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ч
f(*0
x=xo+h
У=Уо
x-xa-h
У-Уо
Окончательно находим
ду дх
Ц=Уо
Ч + h, yo + k) — f(xo + h, y0
Ahk
Сравнивая F) и G), видим,
дЧ
дудх
_д
-ft)
ЧТО
х=ха
2k
o + k) — f(xu—
2k
f(xo — h, yo-f
дЧ
~~ дхду
x=x0 ,
h, yo—k)
f
•
k fix
Ahk
[r
h, yQ-k
У-Уа
У=Уо
а так как точка (х0; у0) совершенно произвольная, то эти производ-
производные равны при всех значениях х и у.
Подобным образом для производных любого порядка от функции
любого числа переменных существенно только то, сколько раз по
какой переменной производится дифференцирование, но не то, в ка-
каком порядке это делается.
Чтобы лучше уяснить смысл смешанной производной, найдите
в плоскости независимых переменных те четыре точки, к кото-
которым относятся значения функции, входящие в правые части фор-
формул F) и G). Сравните F) и G) с аналогичными выражениями
дЧ d2
ДЛЯ -5-7 И 3-5
дх1 Э(/2
1. z = *2
Упражнения
тт - dz , , dz
Найдите ^- при x=l, y= 1 и — при х = 2, у = 0,5.
Найдите частные производные следующих функций:
2. z = e~(-t2+Jf2). 3. z=xey-\-yex. 4. z—xs\n у. 5. z = sin (лу).
6. z = Yx* -f уа.
Найдите полные производные следующих функций:
9. z = a:3 + 3a:i/2, * = k у='е~К
10. Найдите *, если z = ln(.v+<^), i/=a;2.
11. Для всех функций задач 2—6 проверьте равенство
дх ду ду дх '

§ 2]
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
107
§ 2. Геометрический смысл функции двух переменных
Функцию двух переменных z = f(x, у) удобно представлять себе
геометрически как уравнение поверхности z = f(x, у), где г есть
высота, ахи у — координаты точки в горизонтальной плоскости
(рис. 24). Однако изображать на плоском рисунке поверхность
трудно. Поэтому для того, чтобы представить функцию двух пере-
переменных графически, можно построить серию кривых, представляю-
представляющих собой сечения поверхности £=/(х, у) плоскостями, параллель-
параллельными плоскости xOz. Такие плоскости перпендикулярны оси у; на
X
[Рис. 24.
Рис. 25.
каждой плоскости координата у имеет постоянное значение. Пересе-
Пересечение данной плоскости с поверхностью z=f(x, у) дает кривую
z=/(x, у— const). Для наглядности удобно нанести несколько та-
таких кривых на одном чертеже в координатах х, z. При этом мы
получим семейство кривых. Например, на рис. 25 построено не-
несколько кривых такого семейства для полусферы г = У 16—х2—у2.
Около каждой кривой должно быть надписано значение у = уп, ко-
которому соответствует эта кривая. Если дано семейство кривых, со-
дг
ответствующих у = const в плоскости х, z, то производная j- гео-
dz
метрически означает, так же как -т- в случае одной переменной,
dz
тангенс угла наклона касательной к оси х. Производную j- можно
найти, составляя отношение г"+1 '—г" w; при этом нужны две со-
Уп+1 — Уп
седние кривые.
Понятно, что функцию z=f(x, у) можно изобразить графически
так же, если строить графики зависимости г (у) для х= const в
плоскости у, z.
Принципиально другой способ описания функции z = /(x, у) по-
получается, если построить сечения поверхности z=/(x, у) горизон-
горизонтальными плоскостями z — const, а затем нанести полученные кри-
кривые (так называемые линии уровня) на плоскость х, у. Этот способ

108
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
применяется на географических картах для изображения рельефа
местности. На рис. 26 показан пример такого изображения для
функции z — x*" — у2. Каждая кривая соответствует определенному
постоянному значению z.
Рис. 26.
Рис. 27.
Как находить производные на графике такого типа? Часть гра-
графика показана в увеличенном масштабе на рис. 27. Ясно, что если
линии уровня проведены достаточно густо, то с любой точностью
dz _zn+1— zn dz _zn+l—zn
дх хь—ха ' ду Ус—Уа
Чем ближе одна к другой расположены линии с различными значе-
значениями z, тем больше частные производные. (Предполагается, что
эти линии проведены через равные промежутки по z.)
Упражнения
Постройте семейство кривых, соответствующих у = const, для следующих
функций:
1. z = xy. 2. z = x"-—yK 3. z= У ;
4. Постройте семейство кривых, соответствующих z = const, для функции
г=&— у1.
§ 3. Неявные функции
Применение понятий теории функций нескольких переменных
часто оказывается полезным и при исследовании функций одного
переменного. (Это применение было показано уже в ВМ, § 11.12,
однако сейчас мы остановимся на нем более подробно.) Такая
функция обычно задается с помощью «явной» формулы, например
у = ахг или у = Ьеах и т. п., в которой непосредственно указано,
как надо вычислять значение у, отвечающее данному х. Такие фор-
формулы наиболее приспособлены к выполнению математических действий.

§ 3]
НЕЯВНЫЕ ФУНКЦИИ
109
Другой возможный способ задания зависимости у от х—так на-
называемое неявное задание, при помощи зависимости
например
или
/(*, у) = 0,
с3 + ;/3 + Заху = 0
х + у)я — ЬЦх — у) = 0
(8)
(9)
A0)
и т. д.
В этом случае для нахождения у при данном х необходимо ре-
решить относительно у уравнение (8). Решение уравнения иногда имеет
вид гораздо более сложный, чем формула (8). Так, в приведенном
примере (9)
Часто решение вообще не может быть написано в виде формулы
и уравнение (8) можно решать только численно.
Тем не менее и здесь бывают случаи, когда для исследования
рассматриваемой функциональной зависимости достаточно привлекать
только функции одного переменного. Именно так будет в случае,
когда уравнение решено или легко решается относительно х, т. е.
когда его можно записать в виде
Х = Ч>(У), A1)
а также в случае, когда уравнение можно разрешить в «парамет-
«параметрической форме», о которой будет сказано немного позже. Так, в
примере (9) у выражается через х весьма сложно, но легко можно
найти
х = ■
Ъау
Тогда, задаваясь различными значениями у, легко найти соот-
соответствующие значения х. Результат можно записать в виде табли-
таблицы и изобразить на графике в координатах х, у. (Для случая а = 1,
Таблица 4
У
—4,0
-3,0
-2,0
-1.5
— 1,0
* 1
-5,08
—2,66
—0,83
—0,084
—0.67
1 -0,5
—0,25
0,25
0,5
1,0
X
1,91
3,98
—4,02
—2,02'
— 1,33
У
1,5
2,0
2,5
3,0
4,0
X
-1,42
-1,83.
—2,48'
—3,34
—5,58

по
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
с =1,44 см. таблицу 4 и график рис. 28.) Построив кривую, мы
можем найти у по заданному х. Для этого (рис. 28) проводим
вертикаль, соответствующую нужному х, и находим интересующее
нас значение у*). Если имеется таблица значений х для некото-
некоторых значений у, то величину у, со-
соответствующую значению х, не име-
имеющемуся в таблице, можно найти
хотя бы с помощью линейной интер-
интерполяции (ср. § II.1).
д\ 2 3 Для этого по таблице отыскива-
-3 -2 -1 \ : /^—J— л ем две пары чисел (г/х, xj и (у2, х,)
такие, что хх < х < х2. Будем счи-
считать, что при изменении х от xt
до хг график функции мало отли-
отличается от прямой линии y = kx-\-b.
Рис. 28. Числа k и Ъ легко определить, поль-
пользуясь тем, что у = уг при х — хх
и у = у2 при х = хг. Действительно, y1=^kx1-\-b, y2 = kx2-{-b. Отсю-
х. Уч—Ух и хгУ\—х\Уч. т-т
да k = ——— , Ъ = -^ — . Поэтому
Х — X Х — Х
1, —
Значения у для всех х, расположенных между х1 и хг, можно под-
подсчитать по полученной формуле. Эта формула для у тем точнее,
чем ближе числа хг и хг, а также уг и у2, т. е. чем ближе одна
к другой расположены точки в таблице.
Как в таком случае найти производную -^? Для этого нет на-
надобности решать уравнение и находить y = f(x). Если функция за-
задана в виде х = <р(у), то dx = -jdy, откуда
dy_ 1 _ 1
их dcp ф' (у)'
Единственный недостаток этого выражения заключается в том,
что производная получается заданной как функция у. Поэтому если
нужно найти -~ при данном х, то нам сперва придется находить у,
соответствующее данному х, а уже после этого подставлять
*) Из рис. 28 видно, что некоторым значениям х соответствует одно значе-
значение у, некоторым значениям х соответствуют три значения у, а одному значе-
значению х соответствуют два значения у. Это объясняется тем, что уравнение третьей
степени может иметь один, два или три вещественных различных корня (если
корней два, то одни из них двойной, он соответствует касанию прямой х=
= const и кривой).

§ 3] НЕЯВНЫЕ ФУНКЦИИ 111
найденное у в выражение
dy 1
dx ф' (у)'
На первый взгляд может показаться, что проще определять про-
производную численно, как в § II.2. Действительно, если мы умеем
определять у при данном х, то мы можем найти еще и у (х-\- Ьх),
соответствующее величине лг+Дл;, после чего приближенное зна-
значение производной определяем хотя бы по формуле
Ьх
В действительности такой способ гораздо хуже: в этом случае нам
пришлось бы находить у для двух различных значений х, т. е. два
раза решать уравнение A1). При этом величину у надо определять
с высокой степенью точности, потому что нам нужна разность близ-
близких значений у и малая ошибка в каждом из у дает большую от-
относительную ошибку в их разности. В выражении для производной
в знаменателе стоит малая величина Дл: и поэтому даже малая
ошибка в числителе может привести к большой ошибке в произ-
производной. Следовательно, лучше пользоваться формулой
dy_ 1
dx" ф'(у) '
Отметим, что формула для второй производной имеет более
сложный вид. Не следует думать, что
d?y _ 1 __ 1
dx'1 dbc_ й2ф *
It? 1ф
В самом деле, эта формула неправильна даже по размерности:
имеет размерность yjx2, а и
ная формула получается так:
имеет размерность yjx2, а и-з-у- имеет размерность у2[х. Правиль-
Правильd*x
_=_ _ _.= \_ 4>"(y) _
dx* dx \dx) dx dy \dxj ф' (у) dy Vф' (у)
<Py _ d (dy\ _dy d (dy\ _ 1 df I \_ Ф"(у) dy-
ь —" " a 1 4 I 4 alii ^^^™ ■>* ■ 1 "'41 ^^^^" Г f / \ 1 *> ^^^^^ '— "" "
)у [ф (y)lJ
Vdy\
Легко проверить размерность этого выражения: она такая же,
как размерность отношения ■л:г/ =-^, что и должно быть.
(х/у) х
При рассмотрении неявной функциональной зависимости (8) может
представиться более общий случай, когда обе переменные х и у
оказывается возможным выразить в виде функции одной и той же
вспомогательной переменной t, т. е.
c = x(t), \
f=y(t). J
Л" =
у

112 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
Так, если в примере A0) обозначить
x+y = t, A2)
то из A0) получаем х—у = Р/Ь2, откуда, привлекая A2), находим
л 2 * 2Ь°- '
Такой способ задания функции называется параметрическим,
а переменная t называется параметром. Этот способ может полу-
получиться и без связи с зависимостями вида (8); он рассматривается
в началах курса высшей математики (см., например, ВМ, §§ II.3,
IV.8, VI. 14). Там же показывается, как находить производную от
dx
такой функции: запишем dx в виде dx = -rr dt = x (t) dt, аналогично
Найдем вторую производную -т-|.
Для этого воспользуемся соотношением
dz__dz_ dt__dz_^Ji_
dx~ dt ' dx~ dt ' dx'
It
Поэтому
у' (t)'
dx* dx \dxj dx \ x' (t) J dt \x' (t) j dx '
откуда
d?y 1 d (y'(t)\_ y"(t) y'(t)x"(t)
dx* x'{t) dt\x'(t)J \x'{t)Y [x'@P '
где штрихи обозначают производные по t.
В общем случае неявного задания функция /(х, у) может быть
такой, что уравнение (8) не разрешимо ни в форме A1), ни в пара-
параметрической форме. Рассмотрим, например, зависимость у от х, за-
заданную при помощи формулы
УЧ-ху + х5 — 7 = 0. A3)
(Геометрически эта формула задает кривую в плоскости х, у.) По-
Получить отсюда выражение у=/(х) невозможно. Чтобы найти про-
производную -j-, приравняем производные от обеих частей равенства A3),
считая в нем у функцией от х, у = у(х), определенной из этого
равенства. При таком истолковании оно является тождеством и потому
допускает дифференцирование:

§ 3]
НЕЯВНЫЕ ФУНКЦИИ
113
Отсюда находим
у dx
Подчеркнем, что в правой части х и у не являются независимыми,
а связаны друг с другом соотношением A3), так что независимая
переменная только одна. Для того чтобы найти у' при данном х
н-адо, численно решая A3), найти у при данном х и подставить это
у в A4).
Перейдем теперь к общему случаю неявной функции нескольких,
например двух, переменных.
Если z задано как функция от х и у, то, решая уравнение
z=f(x,y) относительно х, можно получить зависимость х от у и z:
х = <р(у, z), а решая уравнение z=f(x, у) относительно^, можно
найти y = ty(x, z). Однако независимо от того, решили мы или нет
уравнение z = /(x, у) относительно х, это уравнение дает зависи-
зависимость величины х от величин у и z, т. е. определяет х как функ-
функцию у и z. Такое задание функции х называется неявным.
Производные ^- и ^- можно найти, и не выражая х в явном виде.
Покажем, как это сделать. Из соотношения z=/(x, у) находим
=idx+idy' откуда
dx=[lr) dz— -з-
\дх] \ду
dz
кдх] *
С другой стороны, если x = q>(y, z), то
A5)
Сравнивая выражения A5) и A6), находим
дх
дг
у
дх\
ду\г
1
dz
дх
>
и
dz
ду
dz
dx
A7)
A8)
Формула A7) представляется вполне естественной. В формуле
A8) есть удивительный знак минус. Убедимся в справедливости этой
формулы еще из геометрических соображений.
Рассмотрим рис. 26 и 27. На этих рисунках нанесены кривые
дх
z = const, так что у есть взятая обычным образом производная
-г- вдоль этих кривых. Поэтому
дх
dx
f,— хс
dy~ Уь—

114
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
Замечая, что yb=ya, xc = xa, находим
дх _хь—ха
ду г Уа — Ус'
Вспоминая значения -^ и ^ , находим, что
дг j дг Xf,—ха
I
j
ду I дх ~ ус—у а ~
Формулу A8) можно записать так:
- дг
Замечая, что -г-
дх
ду
дх
ду
1ду
дг
X
. dz
г дх
у
, получаем
дг
'ду
дх
X
г дг \х дх
^ •£ =-1. Послед-
няя формула, как и формула A8), показывает, что в отличие от слу-
случая сложной функции одного переменного здесь нельзя сокращать
дх, ду, dz в числителе и знаменателе. Дело заключается в том, что
три частные производные в этой формуле вычисляются в различных
условиях (при постоянном z первая, при постоянном х вторая и
при постоянном у третья).
BW
В § 1 мы видели, что значение частной производной ^тг зависит
С/О
от того, какой аргумент считается постоянным при ее вычислении.
Уже это показывает, что с dW и дС нельзя обращаться как с чис-
числами и сокращать их с dW и дС в других формулах, не глядя на
то, при каких условиях вычисляются соответствующие частные про-
производные.
Покажем вычисление производных от неявных функций на примере.
Пусть г = хг -\-px-\-y2 -\-qy-\- kxy.
Найдем производные ^- и ^-. Для того чтобы выразить х через у
и z, нужно решить квадратное уравнение. В этом нет принципиаль-
принципиальных трудностей, однако получится громоздкое выражение с корнями.
Так как -^ = 2x-\-p-\-ky, -^-=2y-\-q-\-kx, то по формулам A7) и
дх
A8) находим
ду
дх
дг'
дх
ду'
2y+q + kx
тт л дх дх
Для того чтобы определить значения ^- и ^- при конкретных дан-
данных у и z, надо знать численное значение х при этих у и z, но
можно не иметь аналитического выражения x = ty(y, z). Ясно, что
найти численно решение уравнения z = f(x, у) относительно х при
определенных значениях у и z гораздо проще, чем построить общую
формулу д; = я|)(_у, z). Кроме того, в случае уравнения выше чет-

§ 3] НЕЯВНЫЕ ФУНКЦИИ 115
вертой степени, а также в случае, когда в уравнение входят транс-
трансцендентные функции, построение общей формулы зачастую оказы-
оказывается невозможным.
Наиболее общим способом неявного задания функции двух пе-
переменных является задание ее с помощью соотношения вида
F(x, у, z) = 0. Мы представляем читателю, дифференцируя это
соотношение, получить выражения для частных производных ^, -^
и т. д. и применить результат к рассмотренному выше соотноше-
соотношению z=f(x, у), переписав его в виде z—f(x, y)=0.
Изложенные приемы удобно применять и в случае функции одного
переменного, заданной неявно, с помощью уравнения вида (8). Для
этого надо рассмотреть функцию двух переменных z = /(x, у), дру-
другими словами, рассмотреть соотношение (8) как уравнение нулевой,
т. е. отвечающей значению /=0, линии уровня функции z — f(x, у).
Тем самым задача о вычислении -~ сводится к только что разоб-
ил
ранной задаче о вычислении —■
ОХ г = const
обозначить
г = уъ -\-xy-\-x5.
Тогда по формуле A8)
. Так, в примере A3) надо
их дх
__dz\ jdz_ _ у+Бх*
т. е. мы еновь приходим к формуле A4).
Упражнения
1. Найти -j- и -т-| для следующих функций, заданных параметрически:
a) x—y(i У = Р + *; 6)x = 2sin3^, y = 2cos3t; в) x = cost + i slnt,
y=sin t — t cost.
2. x = s\ut, y = cos2t. Найти -f при *=-=-.
CtX £•
3. z = x3-\-y3-\-xy. HaiiTH -^- , ^- при у = 0, 2=1.
4. г = хь+хуг + уЬ. Найти ■£, щ.
5. x2 + y2 — 4x— 10г/=— 4. Найти ^.
6. х*у+ху*—х*у2—1=0. Найти ^|.

116
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
§ 4. Радиолампа
Интересным примером функции двух переменных является сила
тока у, проходящего через анод лампы с тремя электродами (рис. 29).
На поток электронов, попадающих на анод, влияют потенциал
сетки «с и потенциал самого анода (катод заземлен, так что его
потенциал равен нулю). Таким образом, мы имеем дело с функцией
двух переменных J=j(uc, иА). На графике принято изображать
семейство кривых в коорди-
натах Ис, ] с постоянными •" А
значениями Ид на каждой кри-
кривой. На рис. 30 приведен
пример такого семейства кри-
кривых для лампы 6С1Ж. Ток J
дан в миллиамперах, напря-
напряжения Ис и Ид —в вольтах.
-16 -12 -в
ик, вольты
-4-
Рис. 29.
Рис. 30.
Производная
с "а
пропорциональна тангенсу угла наклона каса-
касательных к кривым рис. 30. Фактически в довольно большом про-
промежутке изменения Ис эти кривые мало отличаются от прямых.
Наклон их в этом промежутке называется крутизной характери-
характеристики лампы и обозначается через S, так что «Ь*=о— . Вели-
Величину 5 выражают в миллиамперах на вольт.
Образуем -т^—
. Обратная ей величина, т. е.
1 диА
г> _
«с
«с
носит название внутреннего сопротивления лампы. Смысл этого
названия легко понять: если бы в схеме вместо лампы стояло

§ 4]
РАДИОЛАМПА
117
постоянное сопротивление Rv то по закону Ома/=-^-, откуда
dj _ 1
диА Rj, '
пли
1
диА
Когда ток выражен в миллиамперах, а потенциал — в вольтах, то R
получается в кнлоомах. Наконец, для характеристики лампы важ-
диА
нейшее значение имеет величина ^— . Это — безразмерная отрица-
отрицали,
тельная величина. Число ц = —5—
г диг
i
называется коэффициентом
усиления лампы. Согласно формуле A8)
(S
' диг
«А \ди1
"с/
Найдем соотношение между изменением потенциала на сетке и
изменением потенциала анода. Рассматривая Ид как функцию пере-
переменных uq и j, находим
ди
"с
ди.
duc, откуда
i
= Rdj—\iduc.
Если поддерживать все время анодный ток постоянным, то dj=O и,
следовательно, duA = —\iditc. Таким образом, изменение потенциала
на аноде в ц раз больше изменения потенциала на сетке. Поэтому
можно сказать, что лампа в (д, раз увеличивает, усиливает изменение
напряжения на сетке. Отсюда и название для ц — коэффициент
усиления.
Соотношение ■— = —ц относится к идеальному случаю, когда
ток J не изменяется. В действительности изменение цс, как прави-
правило, вызывает некоторое изменение тока; при этом изменение ид
оказывается меньше, чем в случае /= const. Рассмотрим схему
рис. 29, где в цепь анода последовательно включено сопротивление г
и подано постоянное напряжение и0. Тогда по закону Ома
^=J(u^' "с),
где в правой части стоит функция, рассмотренная в начале параг-
параграфа. Возьмем полный дифференциал от правой и от левой частей
этого равенства (считая и0, г постоянными)
1 , dj , , dj
dudUA +

118 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
ИЛИ
откуда
S-Rr ,
; dU с = —
Из этой формулы видно, что в схеме рис. 29 абсолютная величина
отношения —^- меньше ц, так как Г п < 1. Если r^> R, то ток j
почти постоянен и -т-^ весьма близко к и. Однако для того чтобы
аис ~
пропускать данный ток через большое сопротивление г, необходи-
необходимо высокое напряжение ис. При этом на сопротивлении г бесполезно
превращается в тепло значительная электрическая мощность. Ока-
Оказывается, что во всех случаях, кроме задачи усиления постоянного
или медленно меняющегося напряжения, выгоднее вместо сопротив-
сопротивления г ставить катушку индуктивности.
Факты, изложенные в этом параграфе, показывают, что точная
математическая формулировка законов работы лампы связана с функ-
функциями двух переменных, а основные величины, характеризующие
лампу, — это частные производные.
Упражнение
С помощью рис. 30 найти значения S, R и ц для лампы 6С1Ж.
§ 5. Огибающая семейства линии
В качестве другого приме-pa применения частных производных
рассмотрим задачу о разыскании огибающей однопараметрического
семейства линий. Разберем эту задачу на типичном примере.
Рассмотрим совокупность траекторий снарядов, выпущенных из
одной точки (из начала координат) с одной и той же начальной
скоростью v0, но под различными углами ср, которые могут прини-
принимать значения от 0 до 180" (рис. 31).
Каждая траектория представляет собой кривую в плоскости х,
у, т. е. характеризуется определенной зависимостью у (х). Выпи-
Выписав зависимости х = х(() и у =у (t), без учета сопротивления воз-
воздуха, и исключая из них t, легко найти (см., например, ВМ,
§ VI.14) зависимость у от х:
A9)
х\
2оо cos2 ф
При каждом конкретном значении ср получается определенная кривая.
Рассматривая различные значения параметра ср, мы получим семей-
семейство кривых. Мы можем считать, что высота траектории снаряда у

§ 5]
ОГИБАЮЩАЯ СЕМЕЙСТВА ЛИНИЙ
119
есть функция двух переменных: горизонтального расстояния х и угла
бросания ф, т. е. у=у(х, ф). Тогда отдельные траектории дают
зависимость у от х при постоянном ф. (Семейство траекторий изо-
изображено на рис. 31.) Рассматривая семейство траекторий, легко за-
заметить, что траектории заполняют одну часть плоскости х, у, а в
другую часть плоскости они не попадают. Таким образом, есть не-
поражаемая зона, в которую при данной начальной скорости снаря-
снаряда нельзя попасть ни при каком угле бросания.
s\
x
Рис. 31.
Постараемся определить границу зоны поражения. (Эта граница
нанесена пунктиром на рис. 31.) Каждая точка границы является
одновременно точкой на какой-то траектории, потому что иначе гра-
границы нельзя было бы достичь. Отметим, что на части границы, ко-
которая изображена на рис. 31, каждая точка является точкой траек-
траектории, соответствующей углу бросания ф ^ 45°. (Можно показать,
что при ф = 45° достигается наибольшая дальность бросания. Траек-
Траектории, которые соответствуют ф < 45°, соприкасаются,— как это бу-
будет видно из дальнейшего,— с границей зоны поражения ниже оси х.
Эта часть границы представляет практический интерес, если стрель-
стрельба ведется по цели, расположенной ниже орудия.) Вместе с тем
траектория не может пересекать границу, а должна касаться ее.
Если бы траектория пересекла границу, то она вышла бы за пре-
пределы границы, а это противоречит тому, что граница отделяет пора-
поражаемую зону от непоражаемой.
Граница области, заполненной семейством кривых, касающихся
этой границы, носит название огибающей семейства кривых. Найдем
уравнение огибающей семейства траекторий. Для этого проведем
вертикальную линию ААг и найдем ту точку В, в которой эта вер-
вертикальная линия пересекается огибающей. Проводя вертикальную
линию, мы взяли определенное значение х. Точка В соответствует
наибольшей высоте у, на которой может находиться снаряд, проле-
пролетая горизонтальное расстояние х при каком бы то ни было угле
бросания ф. Поэтому надо найти максимум у (ф) при данном

120 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
закрепленном х. Мы получаем условие
ду(х,
д<р
X
= 0. B0)
Условие B0) дает нам уравнение, связывающее между собой х
и ф. Для каждого значения х есть свое значение ср, определяемое
из уравнения B0), так что получаем ср = ср (х). Подставляя cp = cp(x)
в уравнение семейства A9), найдем уравнение огибающей.
Проделаем необходимые выкладки. Для удобства введем вместо
переменной ср переменную 6 = tgcp. Замечая, что по известной фор-
формуле тригонометрии —^— = tg3cp-f-1 = 62-f- 1, перепишем уравнение
A9) в виде
2
Наконец, вводя обозначение — = / (величина /, как будет видно из
B2), есть максимальная горизонтальная дальность стрельбы), получим
откуда
Условие B0)*) дает б = —. Подставляя это значение в B1), полу-
получим уравнение огибающей
y = i~£- B2)
Советуем читателю проделать весь вывод, не переходя к перемен-
переменной 9.
Упражнение
Снаряд вылетает из орудия со скоростью t>0=100 м/сек. Можно ли из
этого орудия поразить цель, находящуюся на горизонтальном удалении 500 м
от орудия на высоте 300 м; на высоте 500 л?
§ 6. Ряд Тейлора и задачи на экстремум
Степенной ряд Тейлора, хорошо известный для функций одного
переменного, оказывается полезным и для функций нескольких пе-
переменных. Напомним (см., например, ВМ, § 11.17), что для функций
*) При замене переменной по формуле ф = ф@) получаем ^д=^г ' ~^>
ду , ди „ ду п ду .
что, -и Ф -г- . Однако условие за = 0 совпадает с условием — = 0.
ОО Оф ОО Оф

§ 6] РЯД ТЕЙЛОРА И ЗАДАЧИ НА ЭКСТРЕМУМ 121
одного переменного этот ряд имеет вид
!^(x-a) + f-^(x-ar+f-^r(x-a)>+... B3)
Рассмотрим теперь функцию f(x, у) двух переменных. Пусть х
близок к постоянному значению а, а у— к постоянному значению Ь.
Тогда наиболее грубая приближенная формула, формула «нулевого
приближения», не учитывающая изменения х к у, имеет вид
f(x,y)=f(a, Ь).
Более точная формула «первого приближения», учитывающая члены
первого порядка малости, такова:
Дх,У)=/(<*, b) + A(x—a) + B{y—b), B4)
где А и В— некоторые числовые коэффициенты. Чтобы их найти,
возьмем частные производные от обеих частей равенства B4) по х:
/х(х,у) = А
(первое и третье слагаемые в правой части B4) не зависят от х,
и потому их частные производные по х равны нулю). Так как
коэффициент А должен быть постоянным, то отсюда получаем
A=f'x{a, Ь). Подобным образом, дифференцируя B4) по у, находим
В = /'у(а, Ь), т. е. B4) на самом деле имеет вид
x(a, b)(x—a)+f'y{a, b)(y-b). B5)
(Выведите эту формулу непосредственно из результатов § 1.)
Еще более точная формула «второго приближения», учитываю-
учитывающая также и члены второго порядка малости, имеет вид
f(x, у)=/(а, Ъ) + [А(х—а)
-bV],. B6)
где А, В, С, D, Е—некоторые числовые коэффициенты. Чтобы
их найти, вычислим частные производные первого и второго порядков:
f'y(x, y) = B
/;; (*, у) = 2с, /;.; (х, У) = /;; (х, у) = д г;у (х, у) = 2Е.
Полагая в этих равенствах дг = а, у=Ь, получим
А=/'х(а, Ь), В=/[,(а, Ь), С=±/'хх(а, b), D = f^(a, b),
E = \ru'y(a, b).
Подставляя эти значения в B6), получаем окончательно формулу

122
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ГЛ. IV.
\У
х
второго приближения
/(*, У)=/(а, Ь) + [/'х(а, b)(x—a)+f'y(a, b)(y—b)] +
+ ^[f'A(a, b)(x-ay + 2f'xy(a,b)(x—a)(y—b)+fyy(a,b)(y—by*].
B7)
Хотя мы выводили эту формулу независимо от B5), но мы видим,
что в правой части получилась та же линейная часть, что в B5),
и, кроме того, появились поправки второго порядка малости. Мы
предоставляем читателю вывести аналогичным образом формулу
третьего приближения (впрочем,эта
формула применяется редко); в ней
к правой части B7) добавятся еще
поправки третьего порядка малости.
(Для контроля примем, что
функция / не зависит от у; тогда
в правых частях B5) и B7) все
( ( sy/// частные производные, в которых
V ^/s// участвует дифференцирование по у,
отпадут, и мы получим частные сум-
суммы ряда B3) для функции одного
переменного.)
Как и для функций одного пе-
переменного, формулами B5) и B7)
наиболее удобно пользоваться, если \х—а\ и \у—b | очень малы;
если же эти разности велики, то формулы перестают быть справед-
справедливыми и могут привести к ошибочным выводам. Соответствующие
формулы для функций от более чем двух независимых переменных
имеют аналогичный вид, и мы не станем на них останавливаться.
Полученные формулы можно применить, в частности, для иссле-
исследования точек экстремума функции f(x, у). Допустим, что эта функ-
функция имеет экстремум (максимум или минимум) при х = а, у = Ь.
Примерное расположение линий уровня функции / в плоскости аргу-
аргументов вблизи точки М экстремума показано на рис. 32. Тогда
ясно, что если положить у=Ь, а изменять только х, то получаю-
получающаяся функция /{х, Ь) от одного переменного х имеет при х=а
экстремум. Геометрически это означает, что если следовать вдоль
прямой, изображенной на рис. 32 штрихами, то в точке М мы бу-
будем иметь экстремум. Но тогда, как известно из дифференциаль-
дифференциального исчисления функций одного переменного, производная в точке
экстремума должна равняться нулю
= 0.
■■а
Здесь в квадратных скобках стоит производная по х при зафикси-
зафиксированном значении у = Ь, т. е. это—частная производная по х.
Рис. 32.

§ 6]
РЯД ТЕЙЛОРА И ЗАДАЧИ НА ЭКСТРЕМУМ
123
Аналогично рассматривается случай зафиксированного х = а и из-
изменяющегося у. Мы приходим к необходимым условиям экстрему.ма
функции двух переменных:
/;(а, Ь) = 0, /у (а, Ь) = 0. B8)
(Аналогичным рассуждением мы пользовались в § II.3 при рассмот-
рассмотрении метода наименьших квадратов.)
Как известно, для функции f(x) одного переменного необходимое
условие /' (а) = О экстремума является «почти достаточным»: напри-
например, если /" (а) =£= О, то в точке х=а обязательно будет экстремум —
максимум при /" (а) < 0, минимум при /*(а)>0. Можно было бы
ожидать, что и для функции двух переменных при выполнении
условия B8) экстремум в точке (а; Ь) обязательно будет, если в
ней частные производные второго порядка отличны от нуля. Но это
не так: достаточное условие оказывается более сложным.
Рассмотрим сначала примеры. Пусть
z = f(x, у) =
Условие B8) дает 2.*: = О, 2у = 0, т. е. точкой, «подозреваемой» на
экстремум, служит начало координат. И в самом деле, здесь в на-
начале координат будет минимум, так как там z — О, а в остальных
точках z > 0. Что касается частных производных второго порядка,
то в данном примере они постоянны,
причем/;,=2, /;,=о, /;,=2. по-
добным образом легко проверить,
что функция
z = Ax2 + Суг B9)
имеет при Л>0, С>0 в начале
координат минимум, а при А < 0,
С < 0 — максимум.
Совершенно новая картина бу-
будет, если в выражении B9) А и С
разных знаков, например, если рас-
рассматривается функция
= x2—у2
Рис. 33.
Соответствующие линии уровня показаны на рис. 33, причем часть
плоскости, где z > 0, на рисунке заштрихована; маленькие стрелочки
указывают направление понижения уровня, т. е. для географической
карты — направление стока воды. При _у = 0 получаем z = x2, т. е. от
начала координат вдоль оси х функция в обе стороны возрастает,
а в самбм начале имеет минимум. Если же х — 0, то z=—у2, т. е.
вдоль оси у функция в обе стороны убывает, а в самбм начале имеет
максимум. Если рассмотреть другие прямые, проходящие через на-
начало координат, то вдоль одних из них функция имеет в начале

124 ' ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
максимум, а вдоль других — минимум. Такой случай называется ми-
нимакс, и здесь экстремума в начале координат не будет, хотя
необходимые условия B8) выполняются и частные производные вто-
второго порядка не все равны нулю. В география минимакс—это седло-
седловина, которая наблюдается, например, в точке перевала через гор-
горный хребет; другой пример—это просто седло. Так, на седло,
отвечающее рис. 33, можно сесть, свесив ноги вдоль оси у и глядя
вдоль оси х; при этом спереди и сзади, вдоль оси х, седло под-
поднимается.
Аналогичный минимакс имеет место для функции z = xy в начале
координат; соответствующая картина линий уровня изображена на
рис. 26. (Где на рис. 6 z > 0 и где z < О?)
Рассмотрим теперь общий случай. Если выполнены необходимые
условия B8), то формула B7) приобретает вид
fix, y)=f(a, b) + ±[/;x(a, b)(x-a)> +
a, b)(x-a){y-b)-\-fyB(a, b)(y-b)*]. C0)
Конечно, при выводе этой формулы мы пренебрегаем членами третьего
порядка малости, но при исследовании экстремума нужно находиться
вблизи значений х = а, у = Ь, а там эти члены менее существенны,
чем выписанные члены второго порядка малости. Обозначим для
краткости
/;х(а, Ь) = А, /;у(а, b)=B, fyy(a,b) = C,
х—а = 1, у—Ь=ц.
Тогда формула C0) показывает, что все зависит от поведения квад-
квадратичной формы, (т. е. однородного многочлена второй степени)
Р{%, ц) = А1?-\-2ВЪ>ц-\-Сц2, так как приближенно, вблизи значений
х = а, y = b, f(x, y)—f(a, Ь)-\--~Р(Ь„ ц). Если она положительна
при всех £, т] (например, имеет вид £2 + ту2), то f(x, у)>/(а, b)
вблизи точки (а; Ь) и тем самым в этой точке функция / имеет ми-
минимум. Если эта форма отрицательна, то функция / в точке (а; Ь)
имеет максимум. Если же эта форма может принимать значения
обоих знаков (например, имеет вид £2 — ту2), то в точке (а; Ь) будет
минимакс, т. е. экстремума не будет.
Как же узнать но коэффициентам А, В, С, какой из этих слу-
случаев имеет место? Для этого напишем
Р F, Ц) = rf [А (|J + 251 + С] = if (At* + 2Bt + С), C1)
где через t мы обозначили %/т]. Из элементарной математики известно,
что если дискриминант
В% — ЛС>0, C2)

§ 6]
РЯД ТЕЙЛОРА И ЗАДАЧИ НА ЭКСТРЕМУМ
125
то многочлен, стоящий в скобках имеет два вещественных нуля, при
переходе через которые он меняет знак. Значит, это — случай мини-
макса. Если же
В2 — АС<0, C3)
то указанный многочлен имеет мнимые нули и потому знака не ме-
меняет (многочлен может изменить знак, только пройдя через нуль).
Значит, это — случай экстремума. Чтобы узнать, какой именно знак
имеет правая часть C1),
положим ^ = 0. Мы видим,
что есл-и дополнительно
к C3) будет - С > 0, то
правая часть C1) поло-
положительна при всех t и
потому в силу предыду-
предыдущего абзаца функция /
имеет в точке {а; Ь) ми-
минимум. Если же допол-
дополнительно к C3) будет
С < 0, то функция /
имеет максимум. (Про-
(Проверьте выполнение всех
этих условий на разо-
разобранных выше примерах.)
Точки минимакса имеют большое значение при решении важного
класса задач, который мы продемонстрируем на наглядном примере.
Пусть в холмистой местности, линии уровня которой показаны на
рис. 34, расположены две деревни А и Б, и пусть требуется сое-
соединить их дорогой. Это можно сделать многими способами, и не-
несколько вариантов показано на рис. 34 пунктиром. (Там же в не-
нескольких точках указано направление стока воды, чтобы наглядней
представить рельеф.) Следуя по любой дороге (/) из А в В, нам
приходится сначала набирать высоту до точки, показанной на рис. 34,
после чего начинается спуск. Если такой набор высоты вызывает
трудности, то естественно потребовать, чтобы он был минимально
возможным. Для более точной формулировки этого требования обо-
обозначим через z (М) высоту местности в любой точке М плана. Тогда
упомянутый набор высоты вдоль линии (/) равен max z(M)— z (A),
М на (I)
где под max z (M) понимается наибольшее значение высоты z вдоль
М на @
линии (/). Но значение z (А) для всех сравниваемых линийЪдинаково;
таким образом, требуется среди всех линий (/), соединяющих А с В,
найти линию, вдоль которой max z (М) минимален, т. е. линию, реа~-
М на @
лизующую min max z(M). Ясно, что искомая линия должна пройти "че-
U> М на (.')
рез точку перевала С, которая как раз и является точкой минимакса

126 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ, IV
для функции z(M). Правда, имеется еще одна точка перевала D,
но она лежит выше и поэтому менее выгодна. (Проверьте, что
если линии уровня на рис. 34 проведены через 100 м, то проме-
промежуточный набор высоты вдоль изображенных дорог соответственно
равен 500, 600, 300, 200 и 400 м.)
На различии между случаями C2) и C3) основана классификация
точек произвольной поверхности в пространстве. Пусть задана не-
некоторая поверхность (S) и N—любая ее точка. Выберем систему
координат так, чтобы оси х и у были параллельны касательной пло-
плоскости (Р) к (S) в точке N. Тогда вблизи N поверхность (S) можно
представить уравнением z = f(x, у), причем в точке N в силу выбора
осей выполняются равенства B8), где a, b — значения координат х,
у.в точке N, так что N=(a; b; f(a, b)). При этом в зависимости
от того, выполняется ли неравенство C3) или C2), точка N назы-
называется эллиптической или гиперболической точкой поверхности (S).
В первом случае поверхность (S) вблизи N выпукла и расположена
по одну сторону от (Р). Во втором случае поверхность (S) вблизи
N имеет седлообразный характер и расположена по обе стороны
от (Р); касательная плоскость (Р) пересекает (S) по двум линиям,
пересекающимся в точке N.
Можно доказать, что условия C2) и C3) не нарушаются при
повороте осей координат в пространстве. Поэтому если уравнение
поверхности (S) задано в виде z=f(x, у), то для выяснения типа
какой-нибудь точки этой поверхности нет надобности выбирать новые
оси координат, чтобы удовлетворить условию B8), Надо просто
проверить выполнение условия C2) или C3) в исходной системе
координат х, у, z.
Бывают поверхности, например сфера, эллипсоид, параболоид
вращения и т. д., у которых все точки эллиптические; такие по-
поверхности выпуклы в целом. Бывают поверхности, например поверх-
поверхность с уравнением z = x*—у%, отвечающая рис. 33, у которых
все точки гиперболические. Однако бывают и поверхности, обладаю-
обладающие точками обоих типов; такой является, например, поверхность
тора, т. е. бублика идеальной формы. В этом случае куски, запол-
заполненные эллиптическими точками, от кусков, заполненных гиперболи-
гиперболическими точками, отделяются линиями, в точках которых В2 — ЛС = 0;
такие точки называются параболическими. На торе это точки, в ко-
которых касательная плоскость перпендикулярна оси тора, они запол-
заполняют две окружности. (Подумайте, где находятся линии параболи-
параболических точек на поверхности Вашего тела.) Впрочем бывают и
поверхности, например цилиндрические или конические, сплошь
заполненные параболическими точками.
Ясно, что тип точки поверхности не меняется при любом пере-
перемещении этой поверхности в пространстве, т. е. указанная класси-
классификация точек поверхности является геометрически инвариантной.
В отличие от этого понятие самой высокой и-ли самой низкой точки

§ 7] КРАТНЫЕ ИНТЕГРАЛЫ 127
поверхности, существенное при изучении экстремумов, не является
инвариантно связанным с самой поверхностью, так как при пово-
повороте поверхности ее самая высокая точка перестает быть таковой.
Аналогичным образом точки графика (Z) функции у = <р(х),
отвечающие ее экстремальным значения»», не связаны с линией
инвариантно (в отличие, например, от точек перегиба этой линии).
Не инвариантны в этом смысле также точки линии с уравнением
/(х, 3') = 0, в которых гг = 0 или -^=оо.
Наши рассмотрения можно применить к исследованию строения
линии (L) с уравнением f(x, у) = 0 на плоскости х, у в окрестности
некоторой точки N(а; Ь) этой линии. Для этого полезно рассмотреть
вспомогательную поверхность (S) с уравнением z=f(x, у), так что (L)
получается в результате пересечения (S) с плоскостью (P):z = 0.
При этом линия (L) оказывается включенной в семейство линий
с уравнением /(х, у) = С при различных значениях С, т. е. линий
уровня функции /, получающихся в результате пересечения (S)
плоскостями z = C, параллельными (Р). Если f'x(a, b)=/=0 или
f'y (a, b) =7^ 0 — тогда N называется обыкновенной точкой линии (L),—
то (Р) не касается (S) в точке (а; Ь; 0), а потому (L) вблизи N
имеет вид гладкой дуги. Если же fx{a, b)=fy(a, b) = 0, то N на-
называется особой точкой линии (L) и тогда (L) состоит из точек,
общих для поверхности (S) и плоскости (Р), касательной к (S). Из
предыдущего вытекает, что если выполнено неравенство C3), то N
является изолированной точкой линии (L), т. е. в некоторой окрест-
окрестности Л/ нет других точек линии (L). Если выполнено неравенство C2),
то N является точкой самопересечения линии (L), т. е. в некоторой
окрестности N линия (L) состоит из двух дуг, пересекающихся в N.
Если же В — ЛС=0, то строение линии (L) в окрестности N может
быть существенно сложнее. (В качестве примера постройте с по-
помощью перехода к полярным координатам линии х2—_у2 = {х*-\-у*)%
и х% -\-у% = (лг2+_у2J; чем является начало координат для каждой
из них?)
Упражнение
Исследуйте на экстремум функции:
а) Их, у) = х2—ху+у2 — 2х + Ау~ 1; б) /(*, у) = х°*+3ху—2у+2;
в) fix, у, г) =
§ 7. Кратные интегралы
Начнем с примера. Рассмотрим тело (Q), плотность р г/сл!3 ко-
которого известна, но неоднородна, т. е. в разных точках различна,
и предположим, что нам требуется подсчитать массу m этого тела.
Аналогичная задача для линейного распределения массы, как известно,
решается с помощью обычных интегралов: если масса распределена

128
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
вдоль отрезка a, b с линейной плотностью а г/см, то
ь
т = J а (х) dx.
а
Пространственный случай исследуется совершенно аналогично
линейному. Для этого разобьем мысленно (Q) на объеычики (AQJ,
(ДЙ2), . .., (ДЙ„) и выберем в каждом по одной точке, соответ-
соответственно Мх, М2, ..., М„ (рис. 35, где картину надо представлять
себе пространственной; нумерация объемчиков производится в произ-
произвольном порядке). Если объемчики достаточно малые, то в каждом
из них плотность можно считать по-
постоянной. Тогда массу т^о^ первого
объемчика можно подсчитать как произ-
произведение плотности на численное значение
объема, т. е. р(Мг)кпг, масса второго
объемчика находится аналогично и т. д.
В целом получаем
+ ... 4-
(Щ) Ло1
где под Дь2й понимается численное зна-
значение объема (AQft) (в см3).
Это равенство—приближенное, так
как плотность внутри объемчиков все же
не постоянная; однако оно тем точнее, чем мельче разбиение, и
в пределе, при безграничном измельчении рассматриваемого раз-
разбиения, получаем точное равенство
= lim 2 Р
C4)
Рассуждая аналогичным образом, можно заключить, что если
в теле (Q) распределен заряд с плотностью о, то сам заряд q мож-
можно подсчитать по формуле
2
k— I
C5)
при таком же смысле обозначений.
Единообразие формул C4) и C5) дает основание для общего
определения понятия объемного интеграла.
Пусть задана конечная часть пространства или, как говорят
иначе, конечная область (Q) и на ней (т. е. в каждой ее точке М)
задана функция u = f(M), принимающая конечные значения. (В на-
нашем первом примере областью служило тело (О), а функцией—его

§ 7] КРАТНЫЕ ИНТЕГРАЛЫ 129
плотность, которая в каждой точке принимает свое значение.) Тогда
для составления интегральной суммы область (Q) разбивается на
объемчики (AQi), (AQ2), ..., (AQJ и в каждом произвольно вы-
выбирается точка соответственно Mlt M2, ...,Мп. Затем составляется
сумма
C6)
где иод AQft понимается численное значение объемчика
Зта интегральная сумма обладает высокой степенью произвола: ее
значение зависит как от способа разбиения области (Q) на объем-
объемчики (АИ/;), так и от выбора точек Mk внутри каждого объемчика.
Однако при измельчении разбиения области (Q) произвол в состав-
составлении суммы почти не влияет на значение этой суммы и в пределе
совсем не сказывается. Предел интегральной суммы при бесконечном
измельчении разбиения области (Q) называется интегралом (объем-
(объемным) от функции / по области (Q):
\ udQ = ^ f(M) dQ = lim J} /(Щ AQft. C7)
B) B) 4=1
Таким образом, формулы C4) и C5) можно записать таю
/»<q)= ) pdQ, g(Q) = ) adQ.
B) B)
Произведение р dQ, отвечающее бесконечно малому объему
(«элементу объема») (dQ), называется элементом (дифференциалом)
массы и обозначается
dm=pdQ, C8)
где р — это плотность в какой-либо из точек (dQ). При составлении
этого выражения можно отбрасывать малые высшего порядка (полу-
(получающиеся из-за того, что плотность даже в малом объеме переменна),
так что оно оказывается прямо пропорциональным объему dQ. Сум-
Суммируя все элементы C8) по объему (Q), получаем полную массу
= \ dm= j p dQ.
B) B)
Основные свойства объемных интегралов аналогичны соответ-
соответствующим свойствам «простых» интегралов.
Интеграл от суммы равен сумме интегралов, т. е.
S (u1±u2)dQ= ^ u^Q± ^
B) B) B)
Я. Б. Зельдович, А. Д. Мышкио

130 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
Постоянный множитель можно выносить за знак интеграла, т. е.
$ CudQ = C $ udQ (C= const).
(Q) (О)
При любом разбиении области (Q) на части, скажем, (Qt) и (Q2),
будет
\ = \ и
(О) B,)
Интеграл от единицы равен объему области интегрирования, т. е.
dQ=Q.
(О)
Если рассматриваемые переменные размерны, то размерность
интеграла равна произведению размерности интегрируемой величины
на размерность объема:
L(Q)
где квадратными скобками обозначена размерность величины.
Пример: [р] =г-см~3; [J" p dQ] = г-см~3-см3 = г= [да].
Среднее значение («среднее интегральное», «среднее арифмети-
арифметическое») функции и(М) по области (Q) вводится как постоянная и,
интеграл от которой по области (Q) равен интегралу от функции и
по этой области. Таким образом,
(Q) (Q)
откуда
udQ =uQ и и =■
Как и для «простых» интегралов, выводится, что min ц ^ц ^тах и.
(Q) B)
В начале этого параграфа мы рассматривали понятие плотности
как непосредственно ясное и выразили через плотность массу с по-
помощью интегрирования. Обратно, можно исходить из массы и выра-
выразить через нее плотность. Для этого надо составить отношение
массы, отвечающей малой области (AQ), к объему этой области. Это
отношение есть средняя плотность в области (AQ); чтобы получить
плотность в некоторой точке М, надо заставить (AQ) безгранично

§ 7] КРАТНЫЕ ИНТЕГРАЛЫ 131
стягиваться к этой точке и взять предел указанного отношения
р (М) = lim 'А ) = -^ . C9)
(Дй) -> М ЛЬ2 "ir!
Этот процесс аналогичен дифференцированию.
Если учитывать дискретное, молекулярное строение вещества,
то в формуле C9) объем (AQ) нельзя даже мысленно безгранично
стягивать в точку. Взамен этой формулы надо написать
где (ДО)—«практически бесконечно малая область», содержащая
точку М, т. е. область, достаточно малая по сравнению с разме-
размерами макроскопических тел и в то же время достаточно большая
по сравнению с молекулярными размерами. Здесь мы как бы пере-
переходим от дискретной картины материального тела к его непрерывной
модели, плотность которой получается в результате осреднения,
т. е. вычисления средней плотности исходной картины по объемам
указанных «практически бесконечно малых» размеров.
Впредь при рассмотрении сплошной среды мы будем, отвлекаясь
от дискретного строения материи, считать, что такой переход к не-
непрерывной модели среды и ее плотности уже совершен.
Может оказаться, что одно из измерений части пространства,
занятой массой или зарядом, значительно меньше двух других изме-
измерений (например, толщина значительно меньше длины и ширины);
тогда можно принять, что масса или заряд распределены по повер-
поверхности. Аналогично, если два из измерений этой части значитель-
значительно меньше третьего, то можно принять, что масса или заряд рас-
распределены по линии. В этом случае формулы C4) и C5) остаются
в силе, если под плотностью понимать поверхностную (т. е. отне-
отнесенную к единице площади) или линейную (т. е. отнесенную к еди-
единице длины) плотность, а под AQft понимать соответственно площадь
или длину частички (AQj). В общем случае говорят, что Дйк есть
мера области (AQft), понимая под этим объем, площадь или длину
в зависимости от того, рассматриваются объемные, поверхностные
или линейные области.
Определение интеграла по поверхности (плоской или кривой),
а также интеграла по линии дается совершенно аналогично интег-
интегралу по объему, т. е. по формуле C7); конечно, при этом взамен
объема частички надо взять ее площадь или длину. Объемные и
поверхностные интегралы называются кратными по причинам, кото-
которые будут ясны позже, причем поверхностные интегралы называются
двойными, а объемные — тройными. Интеграл по линии называется
криволинейным интегралом. Свойства у всех этих интегралов также
совершенно аналогичные; они будут широко применяться в нашем
курсе при изложении теории векторного лоля £гл. X и XI).

132
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
Кратные интегралы вычисляются с помощью обычных интегралов.
Рассмотрим, например, двойной интеграл
/= J udQ,
B)
распространенный по области (Q) в плоскости. Чтобы перейти к обыч-
обычным интегралам, надо на этой плоскости ввести координаты, напри-
например декартовы координаты х, у
(рис. 36). Тогда функцию и мож-
можно рассматривать как функцию
от х, у, т. е. получим
/= [ и(х, y)dU.
B)
Так как при определении интег-
интеграла разбиение области (Q) можно
выбирать произвольно, то возь-
возьмем разбиение прямыми х = const
n_y = const, которое и отвечает
интегрированию в декартовых ко-
кобй
Рис. 36.
11 ■ »
ординатах. Тогда все частички (ДО) будут представлять собой пря-
прямоугольники со сторонами dx и dy, так что dQ =dxdy, т. е.
(Ь)
Здесь написаны два знака интеграла, так как суммирование естест-
естественно проводить в два этапа: например, сначала провести суммиро-
суммирование по всем прямоугольникам из какого-либо столбца, отвечаю-
отвечающего некоторому фиксированному х, а затем просуммировать резуль-
результаты по всем х. Первое суммирование даст
5 (
и(х, y)dxdy = l ] u(x,y)dy)dx,
где у~у1(х) и у=уг{х) (см. рис. 36) — координаты нижней и верх-
верхней точек области (Q) при данном х. После второго суммирования
получим окончательно
Ь ,Уг (X) \
и(х, y)dy)dx
или, как чаще пишут,
у, (х)
u(x, y)dy.
D0)

§ 7] КРАТНЫЕ ИНТЕГРАЛЫ 133
Итак, вычисление двойного интеграла сводится к двукратному
обычному интегрированию.
Сначала надо вычислить внутренний интеграл
J u(x, y)dy.
у, W
После интегрирования и подстановки пределов получится результат,
вообще говоря, зависящий от х (так как х в процессе этого интег-
интегрирования считается постоянным), т. е. получится некоторая функ-
функция /(х). Ее надо проинтегрировать по х, что даст окончательный
результат:
l=\/(x)dx.
Можно было производить интегрирование в другом порядке:
первое (внутреннее) по х, а второе (внешнее) по у. Результат полу-
получится тот же, хотя при практическом вычислении один способ может
оказаться более трудным, а другой—более легким.
Наиболее просто расставлять пределы интегрирования, если об-
область (Q) представляет собой прямоугольник со сторонами, парал-
параллельными осям координат: тогда не только пределы внешнего ин-
интеграла, но и пределы внутреннего интеграла будут постоянными.
Если же, кроме того, подынтегральная функция представляет собой
произведение функции, зависящей только от х, на функцию, зави-
зависящую только от у, то и весь двойной интеграл можно разложить
в произведение двух обычных («однократных») интегралов
ь d
\dx\[f{x)q{y)]dy =
id \ й Ь
(\)\\ D1)
Вычислим для примера массу плоской пластинки, изображен-
изображенной на рис. 37, поверхностная плотность которой изменяется по
закону
D2)
где а, Р — некоторые постоянные коэффициенты. Такой закон полу-
получится, если пластинка однородная, но снизу ограничена координат-
координатной плоскостью х, у, а сверху — другой плоскостью с уравнением
z~ h-\-ax-\- P_y, скошенной относительно первой. Тогда поверхност-
поверхностная плотность в любой точке (л;; у) получится в результате умно-
умножения плотности материала пластинки р0 на высоту z пластинки

134
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
в данной точке, т. е. мы приходим к формуле D2). (Заодно мы
видим, что массу, распределенную по плоскости, можно получить
просто в результате проектирования на эту плоскость массы, рас-
распределенной по объему.)
Согласно формуле D0) получим
т
adQ =
а Ь
, y)dxdy=\jdx\jpo(h + ax + $у) dy.
Внутреннее интегрирование производится по у при зафиксированных
х, т. е. вдоль параллельных отрезков, по-
казанных на рис. 37. Вычислим внутрен-
внутренний интеграл:
а х
Рис. 37.
= р0
Теперь остается этот результат, зависящий от х, проинтегрировать по х:
т
a a
У dx =
Физический смысл проведенных вычислений состоит в том, что мы
как бы проектируем пластинку на ось х, в результате чего полу-
получается масса, распределенная по линии, именно материальный отре-
отрезок с линейной плотностью
y)dy
(это — внутренний интеграл). При этом хорошо виден смысл линей-
линейной плотности: это—масса пластинки, приходящаяся на единицу
длины, так что на интервал от х до x-\-dx приходится масса пла-
пластинки dm = т (х) dx. Интегрируя этот результат по отрезку оси х,
получаем массу пластинки. (Проверьте найденное выражение для
массы, произведя интегрирование в противоположном порядке—сна-
порядке—сначала по х, затем по у, а также разложив выражение D2) на три

§ 7]
КРАТНЫЕ ИНТЕГРАЛЫ
135
слагаемых и применив к каждому из соответствующих интегралов
формулу D1)).
Допустим теперь, что пластинка имеет треугольный вид, изобра-
изображенный на рис. 38, а поверхностная плотность ее изменяется по
У
h
и
0
U'-x
yffflllJI
У=0 х
4
<т
II
а х
О
Рис. 38. Рис. 39.
тому же закону D2). При этом внутреннее интегрирование произво-
производится при фиксированном х по у от_у = 0 до у=^Ьх[а (см. рис. 38).
Поэтому вычисления идут так:
а Ьх/а
m=\jdx
Для контроля произведем интегрирование в другом порядке.
Если внутреннее интегрирование проводить по х при фиксиро-
фиксированном у, то пределами интегрирования будут служить (рис. 39)
х = ау/Ь и х = а, откуда
= \dy \
О ау/Ь
а б2
аа2 б3
Ва б3 \
ab
Получился тот же результат.
Аналогично вычисляются интегралы и другого вида. Всегда
нужно выразить dQ через дифференциалы координат, расставить
пределы в соответствии с этими координатами, а затем вычислять
получающиеся интегралы по обычным правилам интегрального ис-
исчисления. При этом интегралы по площади получаются двукратными,
а интегралы по объему — трехкратными, с тремя знаками интеграла.

136
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
Если после перехода к координатам подынтегральная функция
окажется не зависящей от одной из координат, то интегрирование
по этой координате выполняется тривиально, и мы сразу переходим
от двойного интеграла к однократному, а от тройного — к двойному
или даже к однократному. Например, площадь фигуры (Q), изобра-
изображенной на рис. 36, можно найти как двойной интеграл от единицы
(см. свойства интеграла):
Q= J dQ=\\dxdy.
Ш> Ш)
Для перехода к однократному интегралу расставим пределы
Ь у, (х) Ь
U = J dx \ dy=\\yi (х) —у, (х)] их.
а у, U) а
Мы пришли к формуле очевидной, если вспомнить геометрический
смысл определенного интеграла. Подобным образом при вычислении
объема мы можем от тройного интеграла немедленно перейти к двой-
двойному. Мы, в сущности, это и делали, когда вычисляли массу пластинки.
В качестве примера приложения двой-
двойных интегралов вычислим интеграл
«-S
Рис. 40.
о котором говорилось в § III.2. Для этого
надо рассмотреть вспомогательный инте-
интеграл
/=
где (Q) — полная плоскость х, у. Расставляя пределы в координатах
х, у, когда dQ=dxdy, получим, учитывая формулу D1),
/= $ dx■
— 00 —00
= I dx I е~х*е-Уг dy =
—00 ■*- QO
= \ е-*г dx
— OJ — 00
С другой стороны, тот же интеграл /можно вычислить с помощью
полярных координат р, ф. Тогда плоскость (Q) более естественно
разбивать на частички с помощью окружностей р = const и лучей
ф = const. Площадь полученных частичек (на рис. 40 изображена
одна из них) равна, как это видно из рис. 40, dQ. = p dtp dp. Так

§ .8] МНОГОМЕРНОЕ ПРОСТРАНСТВО И ЧИСЛО СТЕПЕНЕЙ СВОВОДЫ 137
как л:2 -\-у* "=* Р21 т0 получаем (продумайте расстановку пределов)
»л » 2л <ю
(Я) 0 0 0 0
:ф
2Л .-pJ
О
Приравнивая найденные результаты, получаем, что
2д • j = я.
т. е.
Упражнения
1. Вычислите интеграл от функции xs\nxy по прямоугольнику 0<*<;!,
О < у < п.
2. Вычислите среднее значение функции и = ехУ в квадрате
1
Указание. Для второго интегрирования проведите разложение подын-
подынтегральной функции в ряд Тейлора.
1 1
3. Вычислите интеграл / = \ dx \ еУг dy.
о х
Указание. Измените порядок интегрирования.
§ 8. Многомерное пространство и число степеней свободы
Подобно тому как для функции двух переменных мы в § 2 рас-
рассматривали «плоскость аргументов», так и для функции трех
переменных можно рассматривать «пространство аргументов». Эти
понятия очень наглядны, поэтому желательно сохранить представ-
представление о пространстве аргументов и для случая функций любого
числа независимых переменных, даже большего трех. Это делается
следующим образом. Пусть, например, рассматривается функция
четырех переменных u=f(x, у, z, t). Тогда условно говорят, что
каждый набор значений х, у, z, t определяет «точку» в «четырех-
«четырехмерном пространстве аргументов» х, у, z, t. Такой точке и такому
пространству не дается наглядного геометрического истолкования.
Строго говоря, точка — это не что иное, как набор значений х, у, z, t,
а пространство—совокупность всевозможных таких наборов. Так,
набор (—3; 0; 2; 1,3) — это одна такая точка, набор @; 0; 0; 0) —
другая точка («начало координат») и т. п. Теперь можно гово-
говорить, что функция / определена во всем четырехмерном простран-
пространстве х, у, z, t или в его части («области»).
Для функции z—f(x, у) двух переменных «пространство аргумен-
аргументов» представляет собой плоскость х, у, а пространство аргумен-
аргументов и функции, в котором расположен график функции, — обычное

138 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. IV
трехмерное пространство х, у, z; в этом случае графиком служит
двумерная поверхность в трехмерном пространстве. Подобно этому
«график» функции u=f(x, у, z, t) уже требует пятимерного про-
пространства аргументов и функции х, у, z, t, и: для нахождения то-
точек этого графика надо придавать х, у, z, t произвольные значения
и находить соответствующие значения и. Например, проверьте, что
график функции u = xz— 2уН проходит через точки A; 1; 2; 0; 2),
(—1; 2; 0; —2; 16) и т. д. Таким образом, зависимость
и=/(х, у, z, t) определяет четырехмерную поверхность в пятимер-
пятимерном пространстве.
С этой терминологией непосредственно связано понятие числа
степеней свободы. Известно, что положение точки в (обычном)
пространстве можно охарактеризовать декартовыми координатами
х, у, z. Имеются и другие системы координат, но для всех них
общим является то, что положение точки в пространстве опреде-
определяется тремя координатами (тогда как положение точки на пло-
плоскости определяется двумя координатами, а на линии — одной). Этот
факт выражают словами: при выборе точки в физическом простран-
пространстве или, что то же, при движении точки в пространстве имеется
три степени свободы. При выборе точки на плоскости, а также на
любой поверхности, имеется две степени свободы, а на линии — одна.
Другими словами, пространство трехмерно, тогда как поверхности
двумерны, а линии одномерны.
В общем случае понятие о числе степеней свободы вводится так.
Пусть имеется некоторая совокупность объектов (в предыдущем при-
примере— совокупность всех точек в пространстве), каждый из которых
может быть охарактеризован указанием численных значений некото-
некоторых непрерывных параметров (в предыдущем примере — координат).
Пусть эти параметры являются:
1) независимыми, т. е. могут принимать произвольные значения:
например, если зафиксировать все параметры, кроме одного, то этот
один можно еще произвольно менять, быть может, в некоторых
пределах;
2) существенными, т. е. при любом изменении параметров рас-
рассматриваемый объект фактически меняется. Тогда, если таких пара-
параметров k, то говорят, что при выборе объекта из рассматриваемой
совокупности имеется k степеней свободы, а сама совокупность
называется (обобщенным) k-мерным пространством или k-мерным
многообразием. Сами параметры называются (обобщенными) коорди-
координатами в этом пространстве; как и в случае обычных координат
в обычном пространстве, их можно выбирать различными способами,
как это окажется удобнее в том или ином исследовании. Таким
образом, многомерное пространство получает конкретное истолко-
истолкование.
Например, в физике систематически рассматривается совокупность
«событий», каждое из которых характеризуется ответами иа вопросы

§8] МНОГОМЕРНОЕ ПРОСТРАНСТВО И ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 139
«где»? и «когда»? На первый вопрос можно ответить указанием
декартовых координат х, у, z, а на второй—указанием момента
времени t. Эти параметры независимы (их можно произвольно ме-
менять) и существенны (при их изменении событие заменяется на дру-
другое событие). Таким образом, пространство событий—четырехмер-
событий—четырехмерное, и обобщенными координатами в нем могут служить л-, у, z, t.
В качестве другого примера рассмотрим последовательность
(систему) зубчатых колес, из которых каждое последующее зацеплено
с предыдущим. Здесь имеется всего лишь одна степень свободы,
причем за обобщенную координату можно принять угол поворота
первого колеса, так как задание этого угла полностью определяет
положение и остальных колес. (Сколько степеней свободы было бы,
если бы колеса не были зацеплены?)
Подсчитаем, сколько степеней свободы имеет отрезок данной
длины / при движении на плоскости. Каждый такой отрезок полно-
полностью определяется координатами (лг1; _yt) и (лг2; _у.2) его концов; эти
координаты можно принять за параметры, определяющие положение
отрезка. Эти параметры, очевидно, существенные, однако они не
являются независимыми, а связаны соотношением
(почему?). Таким образом, только три параметра можно считать
независимыми, а четвертый выражается через них из этого соотно-
соотношения. Значит, отрезок данной длины при движении на плоскости
имеет три степени свободы.
В общем случае, если параметров п и они существенные, но
связаны т независимыми уравнениями (т. е. такими уравнениями, из
которых ни одно не вытекает из остальных), то п — т параметров
можно принять за независимые, а остальные т будут через них
выражаться, т. е. будет п — т степеней свободы.
Подсчитаем, наконец, число степеней свободы при выборе беско-
бесконечной прямой на плоскости. Можно рассуждать так: выберем про-
произвольно две точки А и В на плоскости (каждая имеет по две
координаты) и проведем через них прямую Р, которая будет опре-
определяться, таким образом, четырьмя параметрами. Так как эти пара-
параметры независимые, то, казалось бы, получается четыре степени
свободы. Однако такое рассуждение неверно, так как при изменении
этих параметров (координат) точки А и В будут, правда, меняться,
но прямая Р может при этом оставаться неизменной; значит, требо-
требование существенности параметров не выполняется. Так как прямая Р
не меняется, если точка А скользит по ней (одна степень свободы)
или точка В скользит по ней (еще одна степень свободы), то при
нашем подсчете получилось две лишних степени свободы и на самом деле
число степеней свободы равно 4 — 2 = 2. За независимые и сущест-
существенные параметры можно взять, например, коэффициенты k и b
в уравнении y = kx-[-b; правда, прямые, параллельные оси у, не

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ, IV
описываются такими уравнениями, но эти особые случаи не могут
сказаться при подсчете числа степеней свободы.
Число степеней свободы бесконечной прямой в плоскости оказа-
оказалось равным числу степеней свободы точки на плоскости, Таким
образом, прямые на плоскости можно сопоставить точкам на этой
или другой плоскости. Наиболее удобно это сделать так: последнее
уравнение разделить на Ь и записать его в виде
ах -\- $у = 1, D3)
после чего прямой с этим уравнением сопоставить точку с коорди-
координатами (а; Р), При этом естественно рассмотреть две плоскости:
с координатами х, у и с координатами а, |3 (рис. 41), Так, прямой
Рис. 41.
A)у = 2*4-1, т. е. —2х-\-у=\, отвечает точка V плоскости а, |3
с координатами (— 2; 1). Эта же формула D3) сопоставляет точке
(х; у) первой плоскости прямую с уравнением D3) второй плоскости;
например, точке AfB; —1) отвечает прямая (т') с уравнением
2а—Р=1| точке N(\; 3) — прямая (п') с уравнением ос-|-3|3=1
(см. рис, 41). Нетрудно доказать и в общем виде, что если в пер-
первой плоскости некоторая прямая (/) проходит через какую-то точку N,
то во второй плоскости прямая (п'), соответствующая точке N,
пройдет через точку L', отвечающую прямой (/). Тем самым из любого
утверждения, относящегося к произвольной комбинации точек и пря-
прямых на плоскости, вытекает «двойственное» утверждение,, в котором
прямые заменены точками, а точки — прямыми. Имеется специальная
область геометрии — так называемая «проективная» геометрия, в ко-
которой детально изучаются подобные утверждения, а также и соот-
соотношение двойственности. Следует заметить, что уравнения прямых,
проходящих через начало координат, нельзя записать в виде D3),
т. е. таким прямым не соответствуют при указанном способе соот-
соответствия никакие точки, а самому началу координат не соответствует
никакая прямая. Поэтому в проективной геометрии вводятся «беско-

ОТбЕТЫ И РЕШЕНИЯ
141
нечно удаленные точки» и «бесконечно удаленная прямая» плоско-
плоскости, после чего указанное соответствие уже не имеет исключений.
Мы не будем здесь останавливаться на этом.
Упражнение
Сколько степеней свободы имеет при движении в пространстве;
а) отрезок данной длины?
б) треугольник с заданными сторонами, т, е, «жесткий» треугольник?
в) абсолютно твердое тело с закрепленной точкой?
г) свободное абсолютно твердое тело?
§ 1
дг о дг
^-=2х, поэтому
ОТВЕТЫ И РЕШЕНИЯ
= 1.
7 f*£_dz dx
' dt~dx ' dt ' ду
_ dx
Замечая, что -r,
dt
1. Семейство прямых, проходящих через начало координат.
2. г — хг—с2, семейство парабол (рис. 42).
3. Семейство гипербол, расположенных в верхней полуплоскости (рис. 43).
4. Семейство гипербол (рис. 33).
§3
_,, | о &У d (dy\_
аЧ^-Тх [TxJ-
dD/ + 2)
dx
it+ 2)
dt
1 dt
Л
dt
dr.

142
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. IV
Заметим, что -^=—, поэтому "г=2> так что -т-|=8-
dx
Рис. 42.
Рис. 43.
2. -р= — 4 sin/; значение /, соответствующее значению х = -^-, получается
1 ^~ я dw
из уравнения -2"=sin/. Отсюда '=-g-'. j-
= — 4 • -^-= — 2. Другое зна-
чение t = 2n — V Дает т- = 2.
6 djc
3. ^=
дг
1
. Полагая у = 0, г—\ в формуле </=л:3-{-
', получим *8=1, откуда *=1. Поэтому
1 дх
3 '
г=1
3 "
г=1
5л:
5л:4+ (/2
^■ду-
dx~ у— 5"
d(/ _ 2хуг — у* — 4xsy
dx~x*-\-4xy»—2x2y'
§4
S = 4,5 миллиампер/вольт; R = 6.7 килоол; [i = 30.
§5
2
Так как / = ——, то в интересующем нас случае / — 1020. Уравнение оги-
Сающей имеет вид у=510 —
и х—^№ м находим (/=390 м. Следова-
Следова9040"
тельно, цель на высоте 300 м поразить можно, а на высоте 500 м нельзя.

ОТВЕТЬ! И РЕШЕНИЯ
143
§6
Функция имеет: а) минимум в точке *=0, у=—2; б) минимакс в точке
2 4
=-г-, (/=—д-; в) минимакс в точке * = 0, (/=0, г=1.
§7
I л
0 0
1. \ dx \ л; sin *!/ dy = \ dx (— cos xy)
о
= \ A—
Отметим, что при интегрировании в другом порядке (сначала по х, потом по у)
пришлось бы применить интегрирование по частям.
2. Так как площадь квадрата равна 1, то
i i
о о
ехУ\
- J
у=0 0
х , л:2 , л:» , л:1
Т + Т + ^ + 24
+ + +
+
3. Во внутреннем интеграле интегрирование по у проводится от </=* до
{/=1; поэтому весь двойной интеграл распространен по треугольнику, пока-
показанному на рис. 44. Меняя порядок интегрирова-
интегрирования, получим фУ
I U
/= \ dy \ еУг dx-
о и
е11
2
=6—^-=0,859.
Рис. 44.
Интересно, что в данном примере интегрирование
в исходном порядке нельзя было выполнить с по-
помощью элементарных функций, а после перемены порядка интегрирование
совершенно элементарно.
§ 8
а) 5; б) 6; в) 3; г) 6.

ГЛАВА V
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
§ 1. Простейшие свойства комплексных чисел
В курсе алгебры вводится мнимая единица, которая обозначается
через /. Эта величина определяется условием /2 = —1.
Величины вида x-\-iy (где х и у вещественные числа) назы-
называются комплексными числами. Они получаются прежде всего при
решении алгебраических уравнений: уже сама мнимая единица, оче-
очевидно, есть корень квадратного уравнения хг ——1.
Если говорить только о вещественных корнях, то квадратное
уравнение в зависимости от его коэффициентов либо имеет два
корня, либо не имеет ни одного. Если же рассматривать все корни,
вещественные и мнимые, то квадратное уравнение имеет всегда два
корня. Точно так же уравнение третьей степени имеет всегда три
корня и т. д. Таким образом, рассмотрение комплексных чисел
позволяет установить общую теорему о числе корней алгебраического
уравнения. При этом мы производим алгебраические действия
с комплексными величинами. Рассматривая более сложные функции
комплексных величин (например, возведение в комплексную степень),
удается получить много важных и красивых результатов. Целый ряд
соотношений между вещественными величинами удобно получать,
используя по пути комплексные величины*). Именно поэтому комплекс-
комплексные величины так важны для физики и других естественных наук,
несмотря на то, что любое измерение, результат любого опыта вы-
выражаются вещественным числом.
Напомним некоторые свойства комплексных чисел, известные из
школьного курса алгебры.
Комплексное число z=x-^-iy можно изображать точкой на пло-
плоскости (рис. 45). При этом по оси абсцисс откладывают величину х
(т. е. вещественную часть), а по оси ординат — величину у (она на-
называется мнимой частью числа z\ иногда мнимой частью числа z
называют все произведение iy, что может показаться более естест-
естественным, однако оказывается, что удобнее придерживаться именно дан-
*) Выдающийся французский математик Ж. Адамар A865—1963) сказал:
«Наиболее короткий и наилучший путь между двумя истинами в вещественной
области часто проходит через мнимую область».

§ 1] ПРОСТЕЙШИЕ СВОЙСТВА КОМПЛЕКСНЫХ ЧИСЕЛ 145
ного выше определения.) Каждому z отвечает определенная точка
плоскости. Вместо того чтобы говорить о точке z, можно говорить о
векторе*) z, т. е. о направленном отрезке, начало которого совпадает
с началом координат, а конец—с точкой z. Положение точки на
плоскости можно характеризовать ее расстоянием от начала коорди-
координат г и углом ф между вектором z и осью х, т. е. можно говорить
о длине вектора z (она называется модулем комплексного числа и
обозначается \z\) и о направлении вектора z, которое характери-
характеризуется углом ф. Угол ф называется аргументом комплексного числа.
Он отсчитывается от положительной части оси х против часовой
стрелки. Для вещественного положитель-
положительного числа ф = 0, для чисто мнимого числа У
л . п.. Зя.
Ф = -*■ (например, для числа 2«) или ф = -у „
(например, для числа —2/).
Как видно из рис. 45, x = r cosq>,
y — rsinq>, так что можно выразить z через
г и ф:
X Я!
Запись z = r (cos ф -f- / sin ф) называется
тригонометрической формой комплексного числа. Отметим еще, что,
зная х и у, нетрудно (см. рис. 45) найти ли ф по формулам
Алгебраические действия с комплексными числами производятся
по обычным правилам алгебры с учетом соотношения /а= — 1. По-
Полезно остановиться на геометрической картине алгебраических дей-
действий. При сложении двух чисел z1 = xl-{-iyl и гг = х2-{-гуг:
•* = •*!-+- Z2 = (•*, -Н *г) + ' (Уг +Уг)-
Легко убедиться, что на плоскости число z изображается вектором,
который получается из векторов zl и z2 путем сложения по правилу
параллелограмма, т. е. так же, как получается, например, равно-
равнодействующая двух сил (рис. 46).
Произведение комплексного числа z на положительное вещест-
вещественное число k, Zy — kz, представляет собой вектор, направленный
туда же, куда направлен вектор z, но его модуль (длина) равен kr,
где г — модуль числа z. Если же k — отрицательное вещественное чи-
число, то вектор kz имеет модуль \k\r, но направлен противоположно
вектору z. Легко построить также произведение zy кодчплексного числа
z — x-\-iy на мнимую единицу /. Именно, zx = i(x-\-iy)=—y-\-ix.
*) Подробно теория векторов будет излагаться в гл. IX. Здесь нам доста-
достаточны простейшие сведения о них, известные из школьного курса физики.

146
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ. V
Из чертежа (рис. 47, где мы для наглядности вместо х, у употре-
употребили соответственно буквы а, Ь) легко убедиться, что вектор z
перпендикулярен вектору z. Он повернут относительно вектора z
на прямой угол в направлении против часовой стрелки. Модуль zy
равен модулю z.
-ь
о
<г
Рис. 46. рис. 47.
Произведение комплексных чисел находится по простой формуле
= (х^—у^) + i (х1Уг +ylxt).
В алгебре очень просто доказывают (проделайте это!), используя
формулы для синуса и косинуса суммы, что если
то
i = ri (cos «Pi + i sin ф^, гг = гг (cos ф2 + « sin ф2),
z = г,гг = г,гг [cos (ф1 + фз) + / sin (ф1 + ф2)],
так что при перемножении комплексных чисел их модули перемно-
перемножаются, а аргументы складываются. Мы получим этот результат
другим путем в § 3.
Отметим в заключение, что комплексные числа нельзя соединять
друг с другом знаком неравенства: одно комплексное число не может
быть больше или меньше другого. Могло бы показаться естествен-
естественным считать Zy > z2, если |Zj | > |гг |, т. е. сравнивать комплексные
числа по их модулям. Но тогда бы пришлось считать, например,
—3>—1, т. е. мы вступили бы в противоречие со сравнением
вещественных чисел.
Упражнение
Запишите в тригонометрической форме числа 1—i; 3-f-4i; _2i; _3; 1; О

§ 2] СОПРЯЖЕННЫЕ КОМПЛЕКСНЫЕ ЧИСЛА . 147
§ 2. Сопряженные комплексные числа
Два комплексных числа, отличающихся только знаком мнимой
части, называются сопряженными. Будем число, сопряженное к комп-
комплексному числу z, обозначать через z*. Тогда если z = x-\-iy, то
z* = x — iy. В частности, для вещественных чисел и только для них
справедливо соотношение А* —А, так как в этом случае мнимая
часть равна нулю. Для чисто мнимых чисел (т. е. чисел с равной
нулю вещественной частью) и только для них справедливо соотно-
соотношение А* = — А.
Пусть даны два комплексных числа z1=x1-\- iyx и z2 — x2 -\- iy2.
Сложив их, мы получим
Образуем теперь сумму сопряженных чисел
)—i (у1 +уг).
Мы получили комплексное число, являющееся сопряженным по от-
отношению к сумме г1-\-гг.
Таким образом, если zi-\-zi = w, то г\-\-z\=w*y т. е. если
слагаемые в сумме заменить на сопряженные, то и сумма заме-
заменится на сопряженную.
Покажем, что аналогичное свойство справедливо и для произ-
произведения комплексных чисел, т. е.
если zxz% = w, то z\z\ = w*. A)
Действительно,
Сравнивая два последних равенства, мы убеждаемся в справедли-
справедливости A).
Полагая в A) гг = гг, получим, что если z\ = w, то (z{J =w*,
т. е. при возведении в квадрат сопряженных чисел результаты также
получаются сопряженными. Ясно, что это справедливо для любых
целых положительных степеней. В самом деле, пусть, например,
z3 = w. Запишем это так: z%z = w. Согласно A) отсюда следует,
что (z2)*z* — w*, но (z2)*=(z*J, так что (z*K = w*. Итак, из равен-
равенства z3 — w следует (z*)a = w*.
*
Нетрудно установить, что если — = w, то ~-=w* (см. упраж-
г2 г2
нение 1). Объединяя все эти результаты, мы получаем следующее
общее положение.
Пусть над комплексными числами zlt z2, ..., zn произведено
некоторое число арифметических действий (сложений, умножений,
делений, возведений в целую степень), причем результат оказался

148 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
равным w. Тогда если эти же действия (и в этом же порядке) про-
произвести над числами z\, г\, .. ., г*, то результат будет равен w*.
Другими словами, если в равенстве, содержащем комплексные числа,
все комплексные числа заменить сопряженными, то опять получим
верно? равенство. Можно показать, что это правило остается спра-
справедливым и для неарифметических действий (извлечение корня, лога-
логарифмирование и т. д.). Отсюда следует, что любое соотношение
между комплексными числами остается справедливым, если мы всюду
в нем заменим / на —/, так как при этом мы просто переходим от
равенства комплексных чисел к равенству сопряженных комплексных
чисел. Таким образом, числа / и —/, по существу, неразличимы*).
(Впрочем, сказанное, конечно, не означает, что 2 + 3/ = 2— 3/1)
Рассмотрим квадратное уравнение с вещественными коэффици-
коэффициентами
+ c = 0. B)
Пусть zo = xo-\-iy0 — корень этого уравнения. Тогда
Заменяя в этом равенстве все числа на сопряженные и вспоминая,
что а*=а, b* = b, с* = с, так как а, Ь, с — вещественные числа,
получим
т. е. z* также есть корень этого квадратного уравнения. Следова-
Следовательно, если квадратное уравнение с вещественными коэффициен-
коэффициентами имеет мнимые (т. е. невещественные**)) корни, то эти корни —
сопряженные комплексные числа. Этот факт, впрочем, сразу же сле-
следует из формулы для корней квадратного уравнения. Уравнение B)
имеет корни
— Ь±
z
zi, % — 2а #
Корни получаются мнимые, если Ьг— 4ас < 0, причем
ь • УГ4ас—ь'2 ь ■ У*ас
Z + ' Z 1
Zt ~~ 2а+ ' 2а ' Z* ~ 2а 1 2а
т. е. это — сопряженные комплексные числа.
Ценность изложенного здесь приема состоит в том, что он
годится не только для квадратного уравнения, но и для уравнения
*) К этому результату можно придти прямо, если заметить, что (—/J =—1,
как и !2 =—1: отсюда и следует, что —i и / имеют одинаковые свойства.
**) Не следует путать понятия мнимый (т. е. невещественный) и чисто
мнимый (т. е. с равной нулю вещественной частью).

§ 2] . СОПРЯЖЕННЫЕ КОМПЛЕКСНЫЕ ЧИСЛА 149
любой степени. Действительно, пусть уравнение
1г + ап = 0 C)
с вещественными коэффициентами а0, аг, ..., ап имеет мнимый
корень z0 = х0 -\- iy0. Тогда
Заменяя в этом равенстве все числа на сопряженные и учиты-
учитывая, что а*0 = а0, aj = a,, ..., а"п = ап, получим
= 0* = 0.
Поэтому г*0 = х0— iy0 также есть корень уравнения C). Следова-
Следовательно, у вещественного многочлена (т. е. многочлена с вещест-
вещественными коэффициентами) мнимые корни могут встречаться только
сопряженными парами: если есть корень xo-^-iyo, то есть и корень
Из сказанного, в частности, вытекает, что вещественный мно-
многочлен может.иметь лишь четное число мнимых корней. В высшей
алгебре доказывается, что многочлен степени л имеет ровно п
корней. Поэтому вещественный многочлен нечетной степени обяза-
обязательно имеет хотя бы один вещественный корень. (Докажите это
иначе, рассмотрев поведение графика многочлена Р(х) нечетной
степени при больших \х\.) Многочлен четной степени может и не
иметь вещественных корней.
Из школьного курса алгебры известно, что если уравнение C)
им-еет корни гх, гг, ..., zn, то многочлен, стоящий слева в C),
разлагается на множители следующим образом:
aozn + alz"-1+ ...+an^lz-\-an = a0(z — zl)(z~zi)...(z — zn). D)
Поэтому если xo-\-iyo есть корень многочлена, то в разложение
этого многочлена на множители входит комплексный множитель
(z — х0 — iy0). Так как в этом случае многочлен также имеет корень
х0 — /у„, то в его разложение входит множитель (z — xo-\-iyo).
Чтобы в записи D) не иметь дела с мнимыми числами", эти два
множителя удобно объединить в один
(z — х0 - iy0) (z — xo + iy0) = z* — 2xoz + xl +yl
Вместо двух множителей с мнимыми коэффициентами мы получаем
один множитель с вещественными коэффициентами, но со второй
степенью переменного z. Таким образом, из основной теоремы
алгебры (правда, мы ее не доказали, а приняли на веру) следует,
что любой вещественный многочлен раскладывается на веществен-
вещественные множители, содержащие переменную z в первой и второй сте-
степенях— но не в более высокой степени.

ISO ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
Упражнения
1. Покажите, что если — = w, то -—= ш*.
г2 г2
2. Найдите все корни многочлена г*-— 6г3 + 11 г2 — 2г—10, если известно,
что один из его корней равен 2 — i.
3. Покажите, что г** = г.
4. Пусть z=x-\-iy. Найдите г-г*.
§ 3. Возведение в мнимую степень. Формула Эйлера
Перейдем к важнейшему вопросу о том, что означает возведение
в мнимую степень.
Как подойти к этому вопросу? Проследим, как в алгебре решался
более простой вопрос об отрицательных и дробных степенях. Не-
Непосредственно и наглядно дается только определение целых поло-
положительных степеней:
а1=а, a2 = fl-a, as = a-a-a, ..., а" = а-а ... а.
п раз
На примере целых положительных степеней устанавливаются пра-
правила:
— = ап~т (если я "> т), (ап\т = апт
ат \ у п \ /
Далее считают, что эти правила остаются справедливыми для
любых показателей степени, а не только для целых и положитель-
положительных. Отсюда следует определение того, что собой представ-
представляют дробные и отрицательные степени. Например, из формулы
n
ап ] =ап =аг=а следует, что а" есть число, которое, бу-
дучи возведено в степень л, дает а, т. е. ап есть у а. Точно так
же получается а° — 1, а~п = —.
Определить таким путем, что представляет собой а', не удается.
Попробуем это сделать с помощью того, что мы знаем о производ-
производной показательной функции, т. е. с помощью средств высшей мате-
математики. Наиболее просто и удобно, без лишних коэффициентов,
выглядят формулы дифференцирования для е', ekt:
If-6'
If-6' dt
Эти формулы и являются исходными для определения возведения
*) Именно условие, чтобы формулы имели такой простой вид, и опреде-
определяет число е (см.1 например, ВМ, § II.8).

§ 3]
ВОЗВЕДЕНИЕ В МНИМУЮ СТЕПЕНЬ. ФОРМУЛА ЭЙЛЕРА
151
в мнимую степень:
dt
dz
Положим en — z{t), тогда -r = iz. Соотношение между z и dz пока-
dt
зано на рис. 48. Так как dz = izdt, то, при вещественных t и dt,
dz перпендикулярно z. Значит, изменение z = elt при увеличении t
на величину dt геометрически сводится к повороту вектора z на
угол dcp. Из рисунка видно, что так как dz перпендикулярно z, то
У
х
Рис. 48.
X
dq> равно отношению длины отрезка dz (равной г dt) к длине
отрезка z (равной г). Поэтому dq> = dt. Конечно, при этом углы
(ф, dq> и т. д.) должны быть выражены в естественных единицах,
т. е. радианах, а не градусах.
При ^ = 0 будет еп \t=o = e° = \, т. е. z @) есть горизонтальный
вектор, длина которого равна единице. Поскольку изменению t на
dt соответствует поворот вектора z на dq> = dt, то изменению t от
0 до данного значения t1 соответствует поворот на угол ф = ^х.
Таким образом, 2 = e'? есть вектор, получающийся из г@) = 1
поворотом на угол ф. Положим z = e'f = x-\-iy. Из рис. 49 ясно,
что х= 1 • cos ф = cos ф, у = 1 -sin ф = sin ф. Поэтому
е'т= cos ф + г эшф. E)
Это — формула Эйлера. Легко проверить, что при этом — (е'ч) = ie'f.
Действительно,
d ■ d . d
— (e'f) = -г- (cos ш) + 1 т- (sin cp) = —sinm-t- i cos a> =
d<X> d<X> "^ аф * *
= it sin ф -\- i cos ф = i (cos ф + i sin ф) = ie'f.
Формула Эйлера была получена другим способом в ВМ, § 11.18,
на основе разложения ее левой и правой частей в ряд Тейлора.
Но само определение функций е'', ekt в ВМ было основано на выра-
выражении производной от экспоненциальной функции; значит в прин-
принципе оба доказательства имеют одну и ту же основу.

152 ■ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
С помощью формулы Эйлера произвольное комплексное число z
с модулем г и аргументом ф можно записать так:
z = г (cos ф +г sin ф) — re1?.
Запись г = ге"Р называется показательной формой комплексного числа.
При этом правило сложения аргументов при умножении комплексных
чисел становится простым следствием сложения показателей при
умножении степеней. В самом деле, пусть zi = r1eiv^ z2 = гге1<9г.
Тогда
z = z^z% = r^'fi • r^'f' = rtr3 • б''*' + <p«) = ге'ч,
где /- = /y2, ф = Ф! + ф2.
Из формулы Эйлера легко получить формулы для синуса и
косинуса суммы. Действительно, e'«P+1l') = cos (ф + i]>) + i sin
С другой стороны,
(cos if + i sin г|)) =
cosiJj — 51Пф sinifH-/ E1Пф cos г|)+ cos ф sin tj;).
Сравнивая вещественные и мнимые части в двух выражениях для
е'(<р+1|')) получаем
cos (ф + г|)) = cos ф cos г|)—sin ф sin ijj,
sin (ф -\- г|)) = sin ф cos г|) -\- sin ty cos ф.
Конечно, в этом простом случае мы получили хорошо известные
формулы, которые легко доказываются в тригонометрии без приме-
применения комплексных чисел. Однако если нужно выразить, например,
cos 5tp и вт5ф через соэф и втф, то применение формулы Эйлера
практически удобнее обычных тригонометрических преобразований.
Делается это так:
(е'ф N =■. e{t<f = cos 5ф + i sin 5ф.
С другой стороны,
e'f = cos ф + i sin ф,
поэтому
(e't)b = (cos ф + / sin фN =
= со5*ф + ^б cos* фэшф— 10 cos3 ф sin* ф — ПО cos2ф sin3 ф4-
-\- 5 cos ф sin4 ф -\- i sin5 ф *).
(Мы выполнили возведение в степень по формуле бинома Ньютона.)
*) Заменив в этом рассуждении показатель 5 на любое целое число п, мы
придем к тождеству (cos <p+i: sin (p)" = cos /г<р—[- i: sin /г<р, называемому фор-
формулой Муавра,

§ 3] ВОЗВЕДЕНИЕ В МНИМУЮ СТЕПЕНЬ. ФОРМУЛА ЭЙЛЕРА 153
Сравнивая вещественные и мнимые части, находим
СО5 5ф= СО55ф— 10 COS3 W Sin2 ф4-5 СОЭф 5Ш4ф,
sin 5ф —• sin° ф —10 sin3 ф cos2 ф + 5 sin ф cos* ф.
Приведем еще один пример применения формулы Эйлера. Пусть
требуется найти \ еах cos bx dx. Рассмотрим равенство
, F)
~- a + ib ' "'
где C = C1-\-iCi. Заметим, что по формуле Эйлера
Г e(e+ ib) х dx= [ eax cos bx dx-\-i [ eax sin bx dx.
Чтобы отделить в правой части F) вещественную часть от мнимой,
проделаем следующие преобразования:
е(а+ ib)x =, eaxeibx = gax (cos bx + ; sin bx)t
1 a—ib a . b
a -f ib (a -
Перемножая, получаем, что частное в правой части F) равно
-Хгтг (а cos bx-{-b sin bx) + i , ц (a sin bx — b cos bx).
Равенство F) принимает вид
V eax cos bx dx -f i \ eax sin &лс d# =
= '2 . ,a (acos bx-\-bsin&лс) + i .а , ..j (asinfac — & cos&лс) + С.
Сравнивая вещественные и мнимые части, находим
i sin bx) r
г w>
с—6 cos Ьд-) „
Упражнения
1. Запишите в показательной форме следующие числа:
a) l+i; b) I —i; в) —1; г) 3i.
2. Пользуясь формулой Эйлера, найдите:
а) A+0": б)
3. Выразите соэЗф, sin 4ф через sin ср и cos
4. Докажите формулы

154 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
§ 4. Логарифмы и корни
Замечательно, что при мнимых показателях показательная функ-
функция становится периодической. В самом деле, из формулы Эйлера
следует, что e2l"'=cos 2л+zsin 2л= 1, поэтому еш+м = епегк1'=еп,
т. е. функция z(t)=eli имеет период 2л.
Периодические свойства степени проступают уже на следующих
простых примерах:
1. (-1H=1; (—1I = —1; (—1)»=1;
(—1K = —1; ...; (
2. /°=1; i1 = i; г» = —
Из этих примеров мы заключаем, что (— 1)^ как функция g имеет
период 2, a is как функция 5 имеет период 4.
Покажем, что периодичность этих функций есть следствие перио-
периодичности функции e!t. Действительно, пользуясь формулой Эйлера,
запишем —1 в показательной форме; получим —1 = еп1. Поэтому
(—\)£=е'п£, где g—любое число. Определим период функции е'ж£
при вещественном g. Если G—ее период, то eh<L^+G)= el%%. Для
этого должно быть ei%G=\, откуда nG = 2n, G—-2. Аналогично
я га us
~2~ ~2" ~2~
i=e , поэтому is=e . Период функции е равен 4.
Периодичность показательной функции приводит к интересным
следствиям для логарифма. Логарифмом комплексного числа z на-
называется такое комплексное число w, что ew~-z.
Пусть z = re'f. Запишем число г в виде г — е*>, где р есть ло-
логарифм (натуральный) положительного числа г. Тогда г = ер+/?,
поэтому
w = In z = р -\- щ = 1п г -\- /ф.
Но мы уже знаем, что е2я*'=1, если k — целое число; поэтому мы
можем написать г=е*+'*+**к1, откуда In z = ]п/" + *'(ф + 2/гл).
Таким образом, логарифм комплексного числа имеет бесчислен-
бесчисленное множество значений. Это положение похоже на соотношение
между тригонометрическими и обратными тригонометрическими функ-
функциями. Например, так как tgcp имеет период, равный п, т. е.
tg (ф -\- кл) = tg ф, если k—целое, то Arctgjc имеет бесчисленное
множество значений. Действительно, если ф — arctg лс—одно из зна-
значений арктангенса, то и ц>-\-кл также есть значение арктангенса
(k — целое).
Периодичность показательной функции приводит к важным след-
следствиям и при извлечении корня, т. е. при возведении в дробную
степень.

§ 4] логарифмы и корни 155
Пусть z = rel'f; как мы видели, можно написать z = ге"*+ inkl.
Тогда
где через с обозначено rnelnt*. Если п целое, то ег**п'=1, поэтому
получается лишь одно значение гп, именно число с. Таким образом,
возведение в целую степень есть действие однозначное. Положение
меняется, если п дробное, п = — , где р и q > 0 — взаимно простые
(не имеющие общих делителей, кроме единицы) целые числа. Тогда
гг%и.т МОжет быть отличным от 1 и по формуле G) мы получаем
новые значения zn, отличные от с. При этом можно доказать, что
общее число различных значений zn равно q.
Рассмотрим пример. Найдем все значения I1/. = £/i. Так как
\=е2кк!, то 1'/, — е 3 . Положив в последнем равенстве /z = 0, по-
получим 11/» = 1, положив /z—1, получим
2Я1
1V _ ~Г _ 2л . . 2л 1_ у^З
1 ' — е — cos -у + г sm 3 — -^ -\-1 -^— ,
положив /г = 2, получим
4Ж
Т 4л ... 4л 1 .уз
= е = cos -g- +1 sin -g- =—-g- — г -^-g—
Таким образом, мы получили три значения j/ 1. (Проверьте с помощью
непосредственного возведения в степень, что ( —2"±i-^-j =1.)
Легко убедиться, что, полагая k = 3,4, ... или k = — 1, —2, ...,
мы не получим новых значений корня.
Если п — целое число, то корни уравнения х" = 1 суть п чисел
вида
, где /z = 0, 1, 2, ..., л — 1.
При этом, подставляя k — Q, получим ^O = cos0 + i sin 0 = 1, т. е.
общеизвестное значение. На плоскости числа xk изображаются
точками, расположенными в вершинах правильного л-угольника,
вписанного в круг радиуса 1. Действительно, модуль любого из
)/ , 2 fen , . ,2 fen ,
/ cos^ f-sin =1| аргумент числа х0
равен нулю, а при увеличении k на единицу аргумент увеличивается
на —.На рис. 50 показаны корни уравнения хъ = \.

156
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ.
На примере простейшего уравнения степени п(п — целое поле
жительное) хп=1 мы убедились, что общее число вещественны
и мнимых корней равно п. В действительности (здесь мы не сможе
дать доказательства этой теоремы) любое алгебраическое уравнена
степени п имеет п комплексных корней, причем некоторые из ни:
могут быть вещественными, так как всегда считается, что вещест!
венные числа — это частный случай комплексных. Число различны)
корней может оказаться меньшим п, так как корни могут совпадав
друг с другом («кратные корни»). На
пример, уравнение четвертой степей!
Рис. 50.
имеет трехкратный корень хг 3,э=1
и простой корень xt = —1, а всего
четыре корня.
В заключение этого параграфа про-
проследим, как в процессе усложнения ма-
математических действий развивается по-
понятие числа. Исходным является класс
(совокупность) целых положительных
(натуральных) чисел. Если пользовать-
пользоваться только такими числами, то всег-
всегда выполнимо сложение, так как ре-
результат сложения двух натуральных чисел есть снова натуральное
число, но н-е всегда выполнимо вычитание. Для того чтобы вы-
вычитание было всегда возможным, приходится рассматривать целые
отрицательные числа и нуль.
Рассмотрим следующую пару действий — умножение и деление.
Результат умножения двух целых чисел есть целое число, однако
действие деления целых чисел не всегда выполнимо в целых числах.
Для того чтобы всегда было выполнимо деление, нужно ввести но-
новые числа — дроби. Целые и дробные числа вместе составляют класс
рациональных чисел. Но хорошо известно, что пределом последо-
последовательности рациональных чисел может служить число не рациональ-
рациональное, т. е. иррациональное (они подразделяются на «алгебраические»
и «трансцендентные», на чем мы здесь не будем останавливаться).
Рациональные и иррациональные числа вместе образуют класс веще-
вещественных чисел, в котором операция предельного перехода всегда
выполнима. Однако в последнем классе не всегда выполнимы алге-
алгебраические действия: например, можно извлекать корни любой сте-
степени из положительных чисел, но нельзя извлекать корни четных
степеней (в частности, квадратные) из отрицательных чисел.
Извлечение квадратного корня из отрицательного числа стано-
становится возможным только с введением комплексных чисел. Замеча-
Замечательно, что введение комплексных чисел является последним
расширением числовой системы. Действительно, если мы располагаем

§ 5] ОПИСАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ 157
комплексными числами, то мы можем извлекать корни любой степени
не. только из отрицательных, но и из любых комплексных чисел.
Результатами являются некоторые комплексные числа. Однако
в математике имеются и другие действия, выполнить которые не-
невозможно, если ограничиваться лишь вещественными числами. Так,
при возведении положительного числа в любую вещественную сте-
степень получается всегда положительное число, так что нет логариф-
логарифмов отрицательных чисел. Еще одна невыполнимая операция — не
существует вещественного числа ф такого, например, что cos ф = 2.
Возникает вопрос: может быть, для того чтобы находить логарифмы
отрицательных чисел, потребуется введение какой-то новой «мнимой
единицы», отличной от i, которую мы ввели, чтобы иметь возмож-
возможность извлекать корни четной степени из отрицательных чисел?
Не потребуется ли для решения уравнения соэф = 2 еще какой-то,
третьей «мнимой единицы»? Оказывается, что это не так: с введе-
дением комплексных чисел мы получаем возможность находить ло-
логарифмы как отрицательных, так и комплексных чисел (см. выше),
решать уравнения вида соэф = 6, где k — любое число (см. ниже,
упражнение 4), и т. д. Таким образом, любые действия над комп-
комплексными числами выполнимы, в результате этих действий опять
получаются комплексные числа, так что введения каких-то новых
чисел больше не требуется.
Упражнения
1. Найдите логарифмы следующих чисел:
а) —1; б) I; в) — i; г) 1 + /.
2. Найдите все значения j/ —1. 3. Найдите все значения £/ 1.
В задачах 2 и 3 получите значения корней и в тригонометрической и в ал-
алгебраической формах. Проверьте найденные значения корней возведением
в Соответствующую степень по формуле бинома Ньютона.
4. Решите уравнение cosq> = 2. Укажите все решения.
5. Укажите все решения уравнения sinq> = 2.
Указание. В задачах 4—5 воспользуйтесь формулами, выражающими
синус и косинус через показательную функцию. (См. упражнение 4 к § 3.)
§ 5. Описание гармонических колебаний с помощью
показательной функции от мнимого аргумента
Зная, что показательная функция периодична для мнимых пока-
показателей, можно пользоваться ею при решении задач на колебания
из механики и теории электрических цепей.
Рассмотрим, например, гармонические колебания (т. е. колебания,
происходящие по синусоидальному закону) электрического тока
в цепи, при которых сила тока изменяется по закону
(8)

158
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ. V
здесь j0 — амплитуда колебаний (наибольшая сила тока), со—частота
и а—начальная фаза (значение фазы, т. е. u>t~\-a, при ^ = 0).
Оказывается удобным наряду с (8) ввести понятие комплексной си-
силы тока:
у=_/„«/«<■>+■>, (9)
для которой «настоящая» сила тока (8) служит мнимой частью, так
как в силу формулы Эйлера E)
(ш'+"> = /0 cos (at
a) + ij0 sin И + а).
Комплексная сила тока (9) изображается в комплексной плоскости
вектором (рис. 51) длины Jo, образующим с положительным направ-
направлением вещественной оси угол со^-|-а;
таким образом, этот вектор при t — 0
имеет наклон а, а при увеличении /
равномерно вращается с угловой ско-
скоростью со. Сила тока (8) получается
в результате проектирования конца век-
вектора J на мнимую ось. (Если бы сила
тока изменялась, взамен (8), по закону
J — Jo cos (M^ + a)i то она была бы веще-
вещественной частью комплексной силы то-
тока (9) и получалась в результате про-
проектирования J на вещественную ось.)
Выражение (9) представляет собой пример комплексной функции
от вещественной независимой переменной. В общем случае любую
такую функцию можно записать в форме
где g(t) и h (t) — обычные вещественные функции от вещественной
независимой переменной. Такие комплексные функции обладают
следующими очевидными свойствами:
если комплексные функции складываются, то их вещественные
и мнимые части также складываются;
если комплексная функция умножается на вещественную посто-
постоянную или вещественную функцию, то вещественная и мнимая части
получают тот же множитель;
если комплексную функцию продифференцировать или проинте-
проинтегрировать, то над ее вещественной и мнимой частями произведутся
те же действия.
Эти свойства дают возможность, вместо того чтобы производить
указанные действия над вещественной или мнимой частью, осущест-
осуществить эти действия над всей комплексной функцией, а от результата
взять вещественную или соответственно мнимую часть. Замечательно,
что такой переход к комплексным величинам с обратным переходом
к требуемым вещественным величинам может оказаться проще и на-

§ 5]
ОПИСАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
159
гляднее, чем непосредственные действия над вещественными вели-
величинами.
Рассмотрим, например, наложение колебаний, происходящих
с одинаковой частотой. Пусть надо сложить токи
j = j\ sin (со* -f ax) 4-Л sin (со* 4- а»)-
Мы видели, что соответствующие комплексные токи Jx и У2 изобра-
изображаются в плоскости комплексного переменного векторами, равно-
равномерно вращающимися с угловой ско-
скоростью со. А в § 1 мы показали, что
такие векторы складываются по правилу
параллелограмма. Значит, и суммарный
комплексный ток J будет равномерно
вращаться с угловой скоростью со, т. е.
его можно записать в виде (9), где _/„
и а легко получить геометрически. На
рис. 52 показано положение вращаю-
вращающегося параллелограмма в момент
* = 0, которое только и нужно для
определения _/0 и а. Эти параметры
можно получить с помощью геометри-
геометрического построения, как на рис. 52, но можно найти и аналитически.
Для нахождения /0 можно применить теорему косинусов к треуголь-
треугольнику ОАВ, что дает
Л = ОВг = АОг 4- АВг — 2АО ■ АВ cos (АоГаВ) =
Для нахождения а заметим, что проекции вектора У|*»| и« оси
координат равны соответственно
откуда
tga =
/, sin a,+/2 si
/i cos <
2 cos a2
Аналогичные результаты получаются при наложении любого
числа колебаний, происходящих с одинаковой частотой. В то же
время ясно, что при наложении колебаний, происходящих с разной
частотой, суммарный ток будет иметь сложный вид и уже не будет
изменяться по гармоническому закону.
Еще более наглядным является дифференцирование комплексного
тока. Из (9) получаем
^. = yoe'(<D'+«>to = /(a/. A0)
В силу § 1 такое умножение сводится к растяжению вектора J
в со раз и повороту его на 90° против часовой стрелки. Значит,

160
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ.
dJ
вектор -тг также равномерно вращается со скоростью со. Аналогичн
отбрасывая произвольную постоянную, получаем
J
16)
ш
A
т. е. этот вектор получается из J сжатием в со раз и поворот
его на 90° в отрицательном направлении. Положение этих векторо
в момент ^=0 показано на рис.
(на так называемой фазовой диа
грамме).
Эти результаты можно приме
нить к расчету колебаний в электри-
электрическом контуре, содержащем любые,
комбинации сопротивлений, индуктив1
——*" ностей и емкостей. При этом исполь-
используется показанная на рис. 54 связь
между падением напряжения на эле-
элементе цепи и силой тока в нем.
(Соответствующие формулы выводятся
в курсах теории электричества; см.
также ВМ, § VIH.1.) Кроме того,
применяются законы Кирхгофа, согласно которым алгебраическая
сумма всех токов, подходящих к любой точке цепи, равна нулю;
\
Рис. 53.
Сопротивление
Индуктибность
Емкость
R
Рис. 54.
алгебраическая сумма падений напряжений на любой последователь-
последовательности элементов, образующих замкнутую цепь, равна нулю. Об этих
законах приходится вспоминать для сложных разветвленных це-
цепей, так как для простых цепей они
ничего не дают сверх очевидных исход-
исходных соотношений.
Рассмотрим, например,/?, /.-цепь, по- ■'"
казанную на рис. 55, к которой подклю- ^ч^с
чеи источник напряжения, изменяющегося Т
по гармоническому закону | |
Ф = ф0 sin(co^-f- P). A2) Рис. 55.
При этом в цепи возникает ток, меняющийся по гармоническому
закону (8), однако у'о и а нам заранее не известны. Приравнивая ф
сумме падений напряжений на /? и L на основе формул рис. 54,

§ 5] ОПИСАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ 161
получаем (здесь мы в неявной форме пользуемся обоими законами
Кирхгофа)
3
Переходя к комплексному току (9) и комплексному напряжению
Ф = фое''(т'+Р>,
получаем
Ш+1^- = Ф A3)
или, пользуясь A0),
Q>, A4)
откуда
/ ф
Мы видим, что индуктивность L можно истолковать как некое со-
сопротивление, численно равное /со/.; это значение называется кажу-
кажущимся сопротивлением, или импедансом, элемента L. Теперь остается
от последнего выражения взять мнимую часть, чтобы получить
искомую силу тока. Однако еще проще записать коэффициент Д0**
ё показательной форме joe'at что сразу даст искомые значения /0 и а.
Отсюда видим, что
R + i
(здесь мы пользуемся тем, что аргумент arg комплексного числа не
меняется при умножении этого числа на вещественное положитель-
положительное число). Следовательно, фаза тока в R, /.-цепи запаздывает по
сравнению с фазой источника напряжения, что, конечно, объясняется
наличием индуктивности.
Искомую силу тока можно получить и с помощью геометричес-
геометрического построения, показанного на рис. 56. Допустим на минуту, что
нам был задан ток (8), тогда как напряжение A2) является искомым.
Тогда нетрудно построить вектор J\t = a=joe'a, а с ним и взаимно
перпендикулярные векторы RJ\t~0 и i(oLJ\i=a. Но в силу равен-
равенства A4) вектор ф |<=0 = <рое'Р служит диагональю прямоугольника,
построенного на двух последних векторах, т. е. и последний вектор
легко построить.
Вернемся теперь к исходной задаче об отыскании тока по напря-
напряжению. Изобразим вектор ф|<жо =;<рое'Э внешнего комплексного напря-
напряжения в момент ^ = 0 (его модуль ф0 и-аргумент р нам заданы).
6 Я. Б. Зельдович, А. Д. Мышкис

162
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ. V
Этот вектор должен служить диагональю прямоугольника, построен-
построенного на векторах RJ\t=0 и i(x>LJ\t-0, однако вектор J\t=a нам не
дан и является искомым. Но этот прямоугольник подобен прямоуголь-
прямоугольнику, построенному на векторах R и /coZ. (меньший прямоугольник
на рис. 56). Значит, нужно проделать следующее: построить этот
последний прямоугольник; затем подобно увеличить или уменьшить
его так, чтобы его диагональ стала равной ср0; затем повернуть его
Рис. 57.
так, чтобы его диагональ совпала с вектором Ф|<=0, тогда он при-
примет положение большого прямоугольника рис. 56; наконец, сторону
RJ\t~o разделить на R, что даст J\t=a.
Рассмотрим еще L, С-цепь, показанную на рис. 57. Здесь
взамен A3) получаем
откуда, пользуясь A0) и A1), находим, что
т. е.
j — .
Ф
\ wC
A5)
(Таким образом, кажущимся сопротивлением, или импедансом, емко-
емкости служит величина -^. J Здесь возможны различные случаи.
Если частота со внешнего источника напряжения достаточно велика,
более точно, если со2 >• ттч , то скобка, стоящая в знаменателе, по-
-1-2-
ложительна. Представив —i = e 8 , мы можем записать

£ 5] ОПИСАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ 163
Таким образом, в цепи устанавливается ток в амплитудой
/о 7 I
и фазой, запаздывающей на 90° по сравнению с источником напря-
напряжения. Если частота со мала, т. е. со2 < т^, то аналогично прове-
проверяется, что фаза устанавливающегося тока на 90° опережает фазу
внешнего напряжения. Особый интерес представляет промежуточный
случай, когда
т. в.
и решение A5) непригодно, так как в правой части появляется нуль
в знаменателе. В этом случае при любых /0 и а выражение (9) удов-
удовлетворяет соотношению
. J iL ( „ 1
т. е. в цепи без внешнего источника напряжений (накоротко замкну-
замкнутой) возможны незатухающие гармонические колебания по закону (8).
Такие колебания, происходящие при отсутствии внешнего воздейст*
вия, называются собственными, или свободными. Таким образом,
если частота внешнего напряжения удовлетворяет соотношению A6),
то она равна частоте собственных незатухающих колебаний в цепи.
Из физики известно, что при этих условиях возникает резонанс и
взамен периодических, гармонических колебаний, которые мы здесь
только и рассматриваем, возникают колебания с возрастающей ампли-
амплитудой. Случай резонанса будет разобран в гл. VII.
Следует отметить, что с помощью описанного метода можно
получить только ток, который устанавливается в цепи по прошествии
некоторого «переходного периода». Переходный процесс описывается
также по методам гл. VII.
Упражнения
1. Рассмотрите цепь, в которой последовательно включены сопротивле-
сопротивление R, индуктивность L и емкость С. Что будет в частном случае, когда
LC
2. Рассмотрите цепь, в которой сопротивление R, и индуктивность L вклю-
чены параллельно.

164 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРеМЕННОГО [ГЛ. V
§ 6. Производная функции комплексного переменного
Переменная то— f(z) называется функцией комплексного числа г,
если каждому значению z отвечает определенное значение f(z). Так
как z = x~\-iy, где х — вещественная часть, у— мни.мая часть, то
задание z означает задание двух вещественных чисел х и у. При
этом f{z) = u{x, y)-\- lv (х, у), где и(х,у) и v (x, у) — вещественные
функции. Каждому z соответствуют определенные х и у, а значит,
определенные и и v и, следовательно, определенная величина f(z).
Однако мы будем теперь рассматривать как функцию f (z) не всякое
выражение и [х, у)-\-iv(x, у), а лишь такую величину, которая зави-
зависит от z по таким формулам, как, например, f(z) = 1 -\-z2, f(z)=z,
f(z) = ez, /(z) — sinz и т.д. Эти формулы могут содержать алгеб-
алгебраические действия над z или неалгебраические, но такие, которые
можно выразить с помощью степенных рядов Тейлора от z, напри-
например, ez, sin z и т. д.
Таким образом, мы рассматриваем формулы, в которые входит
именно z, но не его вещественная или мнимая часть в отдельности.
(С этой точки зрения, например, z* — x — iy или \z не рассматри-
рассматриваются здесь как функции z, хотя, зная z, легко найти z* и \z\.)
При таком определении f{z) у всех функций f(z) есть одно общее
свойство: по обычным правилам дифференцирования функций можно
найти производную
Функция f(z), имеющая производную, называется аналитической
функцией, Мы, следовательно, рассматриваем только аналитические
функции.
Для функций, заданных простыми формулами, вычисление произ-
производных ничуть не сложнее, чем для функций от вещественного
переменного. Рассмотрим, например, функцию w = z2. Придавая z
приращение Az, получим приращение функции
Aw = (z+ АгJ — z2 = 2z Az + (Azf,
откуда, переходя к дифференциалам и отбрасывая малые высшего
порядка (по модулю), получаем
dw = 2zdz, % = 2z, т. е. ±g)
Как видим, при этих вычислениях несущественно, принимает незави-
независимая переменная комплексные или только вещественные значения.
Однако в общем случае комплексной переменной существование
производной совсем не так очевидно и просто, как в случае вещест-
вещественной переменной, В самом деле, z = x-\-ly n можно дать прираще-
приращение dz, меняя х и у одновременно; dz—dx-\-idy\ можно дать при-

Щ 6] ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 165
щ ращение dz, меняя только х; dz = dx; а можно, меняя только у:
$° {Jz=idy. Если производная f (z) существует, то это означает, что
- при различных способах изменения z соответствующие изменения /
-. таковы, что j- при этом одинаковы.
Запишем f(z) в виде /(z) = u (x, y)-\-iv(x, у). Пусть изменяется
только х, тогда dz = dx и
df дх ди , .dv
1 , , 1_ 1 ,
■<-" • dz ~~ dx ~~ дх дх'
"Если же изменяется только у, то dz=idy, поэтому
',..-,. df _d~ydy _\d~y + l dy)dy _ 1 ди dv _ . ди dv
'- ' dz i dy i dy i ду ду ду ду '
Приравнивая два выражения для производной, полученных раз-
"*'.. личными способами, находим
ди . dv _ . dtx . dv_
dx"j~ldx'~~ld~y~jrdy''
а значит,
ди _dv ди ди .._
Ш~ду' Ъ~х~~ду~- U '
Щ, Эти формулы называются условиями Коши — Римана. Итак, у анали-
J* тической функции f(z) вещественная и мнимая части связаны опре-
определенными соотношениями.
Рассмотрим пример. Пусть
,| / (z) = z2 = (х + iyf = х2 —у2 + i • 2ху.
Здесь и = хг—уг, v = 2xy,
V ■' dJL==fo==2x - = — — = 2v
дх ду ' дх ду *'
Таким образом, условия Коши — Римана A7) выполняются.
Рассмотрим пример противоположного характера. Пусть f(z) =
!;„ =z* = x—iy, где z=x~\-iy. Выше мы отмечали, что хотя такая /(г)
"У и может быть в каком-то смысле названа функцией от г (каждому z
отвечает вполне определенное z*), но это не аналитическая функ-
'■■ ция. Действительно, в этом случае и = х, v=—у, поэтому
■ *-1 ^-0- — = 0 --—1-
.- дх~'' дх~ ' ду ' ду~
первое из условий Коши — Римана не выполнено.
Упражнение
; Проверьте условие Коши —Римана для функции /(г)=г'.

1 66 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
§ 7. Гармонические функции
Вернемся к аналитическим функциям. Возьмем производные по х
от первого равенства A7) и по у от второго равенства A7). По-
Получим
дги __ дго дЪ _ dht_
Ш ~~ дхду ' дхду ~ ~ ду2 '
откуда
д*и д*и „
+ о
Аналогично, дифференцируя первое равенство A7) по у, а второе
по х, получим 7м + ут=0- ^Равнение 08) называется уравнением
Лапласа. Задаваясь различными f(z), можно получить различные
решен-ия этого уравнения, которые называются также гармонически-
гармоническими функциями.
Итак, в качестве вещественной и мнимой частей аналитической
функции могут быть взяты не какие угодно функции и(х, у) и
v(x, у), а только гармонические функции. Кроме того, эти функции
должны быть связаны друг с другом соотношениями A7); такие
функции называются сопряженными гармоническими функциями. Можно
проверить, что если одна из двух сопряженных функций уже выб-
выбрана, то в силу этих соотношений вторая определена полностью,
с точностью до произвольного постоянного слагаемого. В самом
деле, пусть функция v выбрана и соотношениям A7) удовлетворяют
, ~ ди, ди« „
две функции: и = и1 и и — и2. Тогда -~ = -^ . так как обе эти про-
изводные равны ^-. Поэтому *—^ = 0, т. е. и1 — иг не зависит
от х. Аналогично получаем, что ~ — 0> т' е' разность^—к,
не зависит и от у, а потому является постоянной.
Уравнение Лапласа имеет большое значение в математической
физике. Например, электростатический потенциал в пространстве
между длинными проводниками, вытянутыми перпендикулярно плос-
плоскости х, у, является функцией только х, у и удовлетворяет уравне-
уравнению A8). В тех точках плоскости х, у, где она протыкается провод-
проводниками, уравнение Лапласа для потенциала нарушается. В частности,
там, где плоскость пересекает проводник, сечение которого имеет
бесконечно малый диаметр, потенциал имеет особенность (обращается
в бесконечность). Таким образом, более точно надо сказать, что
потенциал является гармонической функцией в той части плоскости,
где нет зарядов. Подробнее об этом будет сказано в § Х.5.
Связь между и и v имеет простой геометрический смысл, Дейст-
Действительно, построим линию и (х, у) = const. Так как ^-dx-\- ■£■ dy = 0,
ох оу

§ 7]
ГАРМОНИЧЕСКИЕ ФУНКЦИИ
167
то тангенс угла наклона этой линии к оси х равен
U=const
ди jdu
dxl ду'
Подобным образом тангенс угла наклона линии v(x, у) = const к оси х
равен
dy dv I ду
& 2 ~ dx o=const ~~ dxldy'
Пользуясь условиями Коши — Римана, получаем
_ди \ди
tga2- ду1
A9)
Мы получили условие перпендикулярности касательных к линиям
и (х, у) = const и v (х, у) =
= const*).
Таким образом, взяв
любую аналитическую функ-
функцию f(z) = a(x,y)-\- iv(x,y),
мы получим два семейства
кривых, пересекающихся в
каждой точке под прямым
углом. Для приведенного
выше примера f(z) = z2 эти
кривые показаны на рис. 58.
Еслии— электростатиче-
электростатический потенциал, то а (х,у) =
const — это линии постоян-
постоянного потенциала, av(x,y) =
const — линии напряженно-
напряженности («силовые линии») поля;
в каждой точке линия на- _ _„
Рис. 58.
пряженности направлена по
нормали к линии и (х, у) = const, проходящей через эту точку.
Упражнения
1. Пусть / (г) = и (х, у) + iv (х, у). Зная, что и {х, у)=х-\-х'2—у'*, опреде-
определите v(x,y), если известно, что /@) = 0.
2. Известно, что v (х, у) = — 2ху, /@)=1. Определите и (х, у).
*) Для перпендикулярности должно быть а.2 = а1 ± 90°, т. е.
tga.i = tg(a1 ± 90°) = —ctga!=—t-^-.
Это и есть условие A9).

168
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[гл. v
§ 8. Интеграл от функции комплексного переменного
Дадим определение интеграла от комплексной функции f(z).
Возьмем две точки —начальную zm4 и конечную гкт — на плоскости
и соединим их какой-нибудь линией (/) (рис. 59). Разобьем эту линию
на р малых участков и граничные точки занумеруем так:
Составим сумму
B0)
где точка \j произвольно выбрана на участке линии"(/) между
2,-_i и Zj. Обращаем внимание читателя на то, что значения функ-
функции f(lj) и величины Zy—Zi-1 — это комплексные числа, поэтому
Рис. 59.
•кон.
У\
Рис. 60.
прн составлении суммы B0) мы производим действия с комплексными
числами, и результат, т. е. величина S,— также комплексное число.
Интегралом мы будем называть сумму 5 при условии, что ли-
линии (/) разбита на столь мелкие участки, что дальнейшее их раз-
размельчение практически не изменяет величину суммы 5(более точно,
предел суммы при бесконечном размельчении этой линии). Интеграл
будем обозначать так:
кон
/= $ f(z)dz.
Из определения следует, что интеграл множится на —1 при изме-
изменении направления интегрирования. Действительно, при перемене
направления все разности Zj — Z\—x, а потому и сумма B0) множатся
на —1.
Возникает следующий вопрос. Ясно, что точки zm4 и zKOfi можно
соединить различными способами (рис. 60). При этом, составляя
сумму B0) для различных линий, соединяющих точки г„ач и zKoa,
мы будем иметь дело с различными значениями /(£/) и Zj — £/_]..

ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
169
■'< Зависит ли интеграл / от выбора пути или он зависит только от
^начальной (гнач) и конечной (zKon) точек?
Оказывается, что если f(z) — аналитическая функция и если
..■ в области, ограниченной различными путями, f{z) нигде не обра-
.'.- щается в бесконечность, то интеграл не зависит от выбора пути*).
:" Для доказательства обозначим замкнутый контур zm4AzK0HBzH!t4
буквой (/,), а интеграл (pf(z)dz буквой / (символом ф обозначает-
обозначается интеграл по замкнутому контуру). Так как
- \ f{z)dz =
гнач кон
Az
f(z)dz- J f(z)dz,
г Вг
нач кон
П)
то достаточно проверить, что 1=0. Обратно, если интегралы от
f(z) no контурам zm4AzKm и zHa4BzKm равны, то 1=0. Значит, неза-
независимость интеграла аналитической функции
от пути интегрирования равносильна следую-
следующему утверждению, известному под наз-
названием теоремы Коши: интеграл, взятый по
замкнутому контуру от функции, аналитиче-
аналитической всюду внутри этого контура и на нем,
равен нулю.
Для доказательства теоремы Коши ра-
разобьем часть плоскости, ограниченную замк-
замкнутым контуром (L), на маленькие квадра-
тнкн с контурами (Lk) и будем каждый из
этих контуров проходить против стрелки часов, т. е. в том же
направлении, в котором обходится (L). (На рис. 61 показан один из
контуров.) Тогда
(L) к (L,;)
так как в правой части все интегралы, взятые по внутренним сто-
сторонам квадратиков, взаимно уничтожаются. Если внутри (Lk) выбрать
какую-либо точку zk, то на (Lk) будет
Рис. 61.
z~zk
то есть
=/'(*,
а,
*) Кроме условия, чтобы /(г) не обращалось в бесконечность, нужно еще,
чтобы f (г) была однозначной функцией, пли, во всяком случае, чтобы при
переходе от одного пути к другому мы все время пользовались одной ветвью
функции / (г) (см. конец этого параграфа).

170 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
где а — бесконечно малая, имеющая порядок длины h стороны
квадратика. Отсюда
§f{z)dz = § [f(zk)+f (zk)(z-zk) + a(z-zk)]dz.
(L,,) (Lk)
Интеграл от первых двух слагаемых берется легко и, так как инте-
интегрирование производится по замкнутому контуру, равен нулю. Зна-
Значит, остается лишь интеграл от третьего слагаемого, который имеет
порядок А3, так как длина контура интегрирования имеет порядок h
и множитель z — zk имеет тот же порядок. Но в правой части вы-
выражения B1) число слагаемых в сумме имеет порядок р-, и тем са-
самым вся сумма имеет порядок h. Значит, при бесконечном измель-
измельчении квадратиков, когда h —»- 0, правая часть стремится к нулю;
но она должна равняться постоянной левой части, т. е. эта посто-
постоянная равна нулю, что и требовалось доказать.
Позже мы сможем с помощью методов векторного анализа дать
другое доказательство этой важной теоремы (см. упражнение 2
к § XI.7).
г
Таким образом, величина \ f(z)dz при закрепленном zHa4 за-
нач
висит только от конечной точки z пути, т. е. является функцией
2
от г. Обозначим эту функцию через Ф (z), тогда \ f{z) dz =
г
нач
Найдем производную этой функции
z + dz г z+dz
\ j(z)dz- ^ j(z)dz ^ f(z)dz
Q>(z) гначгнач г
dz ~ dz ~~ dz dz
Рассмотрим \ f(z)dz. Так как числа z и z~\-dz весьма близки, а
2
/(г) — непрерывная функция, то при изменении z в этих пределах f(z)
z + dz
i:e успеваетзаметноизмениться. Поэтому j f(z)dz&f(z)(z + dz—z) —
z
=f(z)dz, причем это равенство можно сделать сколь угодно точ-
точным за счет уменьшения dz. Следовательно,
dO (г) _ / (г) dz
dz dz
■=/(г). B2)
Формула B2) показывает, что зависимость между подынтеграль-
подынтегральной функцией f{z) и интегралом Ф (z) остается такой же, как и в
случае функции вещественного переменного.

S 8] ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 171
Покажем еще, что сохраняется обычная формула для вычисления
интеграла
кон
* = <D (*«„,,)—Ф(*„.ч), B3)
где Ф (z)— любая функция, удовлетворяющая соотношению B2).
2
Действительно, теперь уже \ f(z) dz = Ф (z)JrC, где С—посто-
2
нач
янная. Полагая в этом равенстве 2 = гиач, получим 0 = Ф(,гнач) + С,
г
откуда С=—Ф(гнач). Поэтому $ f(z)dz=Q>(z)—<3>(zaa4).
нч
Положив здесь z = zK0H, мы получим B3). Формулы B2) и B3)
показывают, что все правила нахождения интегралов, известные
для обычных, вещественных интегралов (см., например, ВМ, гл. II),
применимы и к интегралам от комплексных функций.
В теории аналитических функций часто встречаются многознач-
многозначные функции. Рассмотрим, например, функцию w = Y~z. В § 4 мы
показали, что эта функция имеет два значения: если z = re"?, то
ф
,,— (—
= V re 2,
-/ ф \
—ч —+я |
re \ 2 J.
Если выбрать какое-либо одно значение, как говорят, одну ветвь
этой функции, то мы столкнемся со следующим интересным свой-
свойством. Пусть z обойдет точку z = 0 в положительном направлении*)
и подойдет к исходному положению. Тогда к ф прибавится 2л, а
потому значение w1 перейдет в
, ф+ 2Я
подобным образом w% перейдет при этом в
Уге\ г )=Уге *-е™' = Уге i-\=wv
Таким образом, две ветви функции чю=Уz при обходе точки
2 = 0 непрерывно переходят одна в другую, а если обойти точку
г = 0 два раза, то мы вернемся к исходной ветви.
Точка z = z0, при обходе которой одна ветвь многозначной функ-
функции сменяет другую, называется точкой ветвления. Таким образом,
, *) Мы считаем направление обхода положительным, если точка г = 0 при
°ходе все время остается слева.

172 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
для функции w — ]>^z точка 2 = 0 служит точкой ветвления второго
порядка (так как здесь имеются две ветви). Другой точкой ветвле-
ветвления для этой функции принято считать «бесконечную точку» 2=оо.
В точке ветвления могут чередоваться и более двух ветвей: например,
функция чй^^У z имеет л ветвей, которые непрерывно сменяют одна
другую в круговом порядке при обходе точки ветвления 2 = 0.
Другой важный пример многозначной функции дает функция
w = \nz. В § 4 мы видели, что эта функция имеет бесконечное число
значений: wk = In г-j- i (cp-J- 2Ал) (k — 0, ±1, ±2,...). Если точ-
точка z обходит начало координат и к ср прибавляется 2я, то зна-
значение w0 переходит в wlt значение w1 — в w2 н т. д. Если опять
обходить начало, то мы будем переходить к новым и новым ветвям
и никогда не вернемся к исходной ветви. Такая точка ветвления
называется точкой ветвления бесконечного порядка.
Чтобы можно было рассматривать одну ветвь независимо от дру-
другой, нужно каким-то способом запретить точке z обходить точки
ветвления рассматриваемой функции. Обычно для этого< в плоскости
проводятся одна или несколько линий, «разрезов», соединяющих
точки ветвления, и эти разрезы запрещается пересекать. Например,
при рассмотрении функции w=l^z можно провести разрез вдоль
вещественной положительной полуоси от точки 2 = 0 до бесконеч-
бесконечности. Если точка z меняется произвольно в плоскости вне .этого
разреза, то она не может обойти точку ветвления 2 = 0 и потому
одна ветвь не может сменить другую. После проведения такого раз-
разреза каждая ветвь может считаться однозначной аналитической
функцией (хотя вдоль разреза ветвь имеет разрыв, она на разных
«берегах» разреза принимает различные значения); в частности, к
такой ветви можно применить теорему Коши.
Впредь мы будем в качестве подынтегральных функций рассмат-
рассматривать только однозначные аналитические функции. Впрочем, в § 9
мы увидим, что это не спасет нас от необходимости рассматривать
неоднозначные функции, появляющиеся в результате интегрирования.
Упражнение
Найдите интегралы по верхней и нижней полуокружностям с центром в
точке 2 = 0, идущим из z = —1 в 2=1, от функций: а) г2; б) —, в) Y z
(для ветви, равной i при г= — 1). Объясните совпадение результатов в случае
а) и несовпадение в случаях б) и в).
§ 9. Вычеты
Итак, если интеграл не зависит от пути, то интеграл по замк-
замкнутому контуру равен пулю. Выше говорилось, что интеграл не
зависит от пути, если подынтегральная функция не обращается

§ 9]
ВЫЧЕТЫ
173
в бесконечность. Рассмотрим пример, в котором
функция обращается в бесконечность.
'dz
подынтегральная
Пусть /= ф—. Здесь f(z) = — обращается в бесконечность при
О Z Z
2 = 0. Вычислим интеграл по замкнутому пути, обходящему в поло-
положительном направлении (т. е. против хода стрелки часов) точку
2 — 0, например по окружности (С) радиуса г с центром в начале
координат (рис. 62). На такой окружности z = re'f, где г — радиус
окружности, а переменная ср изменяется от 0 до 2л. Тогда dz = re''H dq
Интеграл по замк-
©
нутому кругу оказался не равным нулю. " ^ '
Мы знаем, что \— = \пг. Неравенство
Xdz
нулю интеграла ф — по замкнутому конту-
контуру находится в замечательном соответствии
с неоднозначностью функции \nz. Рассмот-
2
рим пример /= \ — , Идя от z = 1 к z = 2
по кратчайшему пути (рис. 63, а), найдем
. /= 1п 2— In 1 = In 2 = 0,69. Выбрав более длинный путь: сначала
един круг вокруг начала координат, а потом к цели (рис. 63,6),
получим /1 = 2га"+ 0,69. Если сделать п оборотов вокруг начала
координат, то получим /п =2лг-л + 0,69.
х
Рис. 62.
Рис. 63.
В § 4 мы выяснили, что, действительно, величины 2л: -п + 0,69
при всех целых п служат логарифмами чи£,ла 2, так как егп('п=\.
Таким образом, неоднозначность логарифма есть результат возмож-
возможности разного выбора пути, с разным числом обходов вокруг точки
2 = 0, где — обращается в бесконечность.
Величина интеграла зависит от того, сколько раз и в каком
направлении мы сделали обход вокруг начала координат, но не

174
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[ГЛ. V
зависит от того, по какому пути производился этот обход. Докажем
последнее утверждение. Для этого постараемся найти /Л = Ф— по
какому-нибудь пути ABA (рис. 64, а). Рассмотрим интеграл/0=Ф—^
по пути, изображенному на рис. 64, б. Этот путь состоит из пути
ABA, двух близких прямых АС и СА и окружности радиуса ОС
Рис. 64.
с центром в начале координат. /0 = 0, так как это — интеграл по
замкнутому контуру, внутри которого — нигде не обращается в бес-
бесконечность.
Интеграл /0 слагается из /А, двух взаимно уничтожающихся
А С
интегралов \ — и \— и интеграла по окружности радиуса ОС. Так
С А
как по окружности интегрирование происходит в направлении, про-
противоположном направлению отсчета углов, то соответствующий ин-
интеграл равен —2ш. Поэтому /0 = 0 = /л—2ш или IA = 2ni, т. е.
величина 1А совпадает с величиной интеграла по окружности любого
радиуса.
Аналогичными способами удается сводить интегралы по неудоб-
неудобным для расчета линиям к интегралам по маленьким окружностям
вокруг точек, обращающих подынтегральную функцию в бесконеч-
бесконечность. При этом не следует думать, что интеграл обязательно ока-
окажется отличным от нуля. Например, у интеграла
§±'
(да = 2, 3,4, ...)
B4)
подынтегральная функция имеет особенность (обращается в беско-
бесконечность) при z = 0. Однако этот интеграл равен нулю по любому
замкнутому контуру, как не охватывающему, так и охватывающему
эту точку (но не проходящему через нее!). В самом деле, в данном
г - т +1
примере неопределенный интеграл равен —-j- С, т, е. представ-

§ 9] вычеты 175
^игет собой однозначную функцию; а приращение однозначной функ-
функции по замкнутому контуру равно нулю. (Почему?)
Интеграл B4) по окружности \z\=r при любом т можно под-
подсчитать также следующим образом. Положим г = ге'Ч", тогда после
простых преобразований интеграл примет вид
2Я
lrl~m С е<A-т)ф^ф
О
Непосредственное вычисление показывает, что он равен нулю при
любом целом т^ф\. Случай нецелого т мы исключили, так как
тогда подынтегральная функция неоднозначна.
Рассмотрим еще один пример. Пусть надо вычислить интеграл
§
cos г . ,пг-у
—^rdz B5)
по замкнутому контуру, обходящему в положительном направлении
начало координат z = 0, которое в этом примере является особой
точкой для подынтегральной функции, так как там эта функция
обращается в бесконечность.
Вспомнив разложение функции cosz вокруг точки г==0 в сте-
степенной ряд Тейлора,
cosz = 1_|l + £t_£i+..M
можем написать
cos г _ 1 1 г_ г3
~¥~~zs 2!г+41 6!+###
В этом примере при z-+0 подынтегральная функция стремится
к бесконечности со скоростью j—pj-; такая особая точка называется
полюсом третьего порядка.
Чтобы вычислить интеграл B5), произведем почленное интегри-
интегрирование ряда B6). Неопределенный интеграл от любого члена, кроме
второго, даст однозначную функцию (степень с целым показателем),
и потому соответствующий интеграл по замкнутому контуру равен
нулю. (В частности, равен нулю интеграл от первого, главного члена
разложения B6),) Что касается интеграла от второго члена, то в
силу предыдущего он равен
—7«—*
Значит, в этом примере и весь интеграл B5) равен —ш.
Рассмотрим теперь полюс общего вида. Если (однозначная!) функ-
функция/^) имеет в некоторой точке z = a полюс порядка п, то вокруг

176 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
этой точки она разлагается в так называемый ряд Лорана
+ Cl(z-a) + c2(z — a)*+... B7)
по целым положительным и отрицательным степеням z — а, начиная
с я-й степени. Пусть требуется вычислить интеграл
ff(z)dz
B8)
по контуру, обходящему точку z — a в положительном направлении
и не содержащему, кроме этой точки, внутри себя других особых
точек. Как было сказано, от заданного интеграла можно перейти
к интегралу по маленькой окружности с центром в точке а, а вблизи
этой точки можно пользоваться разложением B7). Аналогично по-
последнему примеру, после интегрирования по замкнутому контуру
интегралы от всех членов окажутся равными нулю, за исключением
Ф ■£=+- dz = '2nic_1. Этому значению равен и весь интеграл B8).
Коэффициент с_, при (— 1)-й степени z— а в разложении Лорана
имеет специальное название: вычет функции f(z) в точке с; таким
образом, интеграл B8) равен
2шВыч2=0/(г). B9)
Пусть теперь требуется вычислить ин-
интеграл вида B8) по некоторому контуру (Z.)
(рис. 65), причем подынтегральная функция
/(z)является однозначной и аналитической
всюду на контуре (L) и внутри него, за исклю-
' ~ чением некоторого числа особых точек. (На
Рис 65 рис. 65 имеются три такие точки: а,, а2
и а3.) Проведем вспомогательные линии
(на рис. 65 они показаны пунктиром) так, чтобы область, огра-
ограниченная контуром (L), разбилась на части, в каждой из кото-
которых расположено по одной особой точке. Обозначим контуры этих
частей, проходимые в положительном направлении, через B.Д (Z.2)
и (£3)- Тогда легко проверить, что
§f{z)dz+§f{z)dz,
Щ (L.) d2) <£,)
так как в правой части интегралы, взятые по вспомогательным ли-
линиям, взаимно уничтожаются. Каждый из контуров (Z.x), (Z.2), (L3)
содержит внутри себя только одну особую точку, поэтому каждый
из интегралов в правой части C0) вычисляется по формуле B9), и

§ 9]
вычеты
177
мы получаем
§ f{z) dz = 2гоВыч2=а,/B) + 2л/Вычг=а2/(г)
а)
= 2л/ [BH42=
а)
C1)
Итак, интеграл B8) равен произведению 2л/ на сумму вычетов
подынтегральной функции во всех особых точках, расположенных
внутри контура интегрирования.
Покажем, как вычисляется вычет для наиболее важного случая
полюса первого порядка. Такой полюс обычно получается, если
подынтегральная функция f(z) представляет собой отношение двух
конечных функций: f(z)=g(z)jfi(z), причем в некоторой точке z=a
числитель отличен от нуля, а знаменатель имеет нуль первого по-
порядка, т. е. разложение знаменателя по степеням z — а начинается
с члена первой степени. Записав разложение числителя и знаменателя
в ряд Тейлора вокруг точки z — a, получим
' (а) (г -а)
(г-ау-+
Вблизи точки z=a правую часть можно заменить на ■ ,, _ ч •
Поэтому вычет, т. е. коэффициент при (z — а), в данном случае
равен
Вычг=а/(г)=|^. C2)
Рассмотрим пример. Пусть требуется ' ^ч
вычислить интеграл
^ dz,
Рис 66
-Л
где (L) — окружность радиуса 2 с центром
в начале координат (рис. 66). В этом при-
примере неопределенный интеграл не выра-
выражается через элементарные функции; однако интеграл по замкнутому
контуру мы найдем без труда! Для этого заметим, что подынтеграль-
подынтегральная функция имеет особенности там, где ее знаменатель обращается
в нуль, т. е. при z—\ и z = kn (k— любое целое). Из этих точек,
изображенных на рис. 66, внутрь (L) попадают только две: z = Q
и z=\. Поэтому в силу формулы C1)
Так как в каждой из этих точек знаменатель имеет нуль первого
порядка, а числитель отличен от нуля, то мы имеем два полюса

178 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
первого порядка и вычеты в них можно подсчитать по формуле C2).
В данном примере
g(z)—-z-\-\, h(z) = (z—l)smz, h' (z) — sin z -f (z—ljcos.?,
откуда $$
Подставляя в C3), получаем
Теория вычетов применяется также при вычислении некоторых
вещественных интегралов с помощью искусственного сведения их к
комплексным. Рассмотрим, например, интеграл
00
Р
= j
COS (ИХ
Здесь неопределенный интеграл также не выражается через элемен-
элементарные функции, так что вычисление /t по стандартному методу
невозможно. Для вычисления /t заметим сначала, что
smwx
как интеграл от любой нечетной подынтегральной функции в сим-
симметричных относительно нуля пределах. Из C4) и C5) следует, что
00
Г
J т
00
<'"x j Г cos ax-\-i sin ax , . ,„г.
^* = 1 —r—dx = /i- C6)
Рассмотрим теперь вспомогательный интеграл
где контур (Z.^) состоит из полуокружности и ее диаметра, изобра-
изображенных на рис. 67. Так как подынтегральная функция имеет полю-
полюсы первого порядка в точках z=±t, из которых внутри {LR) со-
содержится только одна, то по формулам C1) и C2) получаем
IR = 2л/ Вычг=<-
1 +z2 2(
С другой стороны, интеграл C7) можно представить в виде суммы
интеграла по отрезку вещественной оси, равного
R
\ m*dx> C8)

§ 9]
ВЫЧЕТЫ
179
и интеграла по полуокружности, которую мы обозначим через (L'R).
Оценим этот последний интеграл. Из
определения интеграла легко вывести
оценку
\f{z)dz
; max \f(z) |-длину (L)\
I
-R
Рис. 67.
поэтому
\ ^-—r.dz <max i-^pfj-л/?. C9)
iLR) <L«>
Представив z = * + (y и заметив, что _y ^ 0 на (L'R), получим на
(L'R), что | е'И2| = |е<и<*+'</) | = \eiax \ \ е-аУ\ = е~аУ ^. 1. С другой сто-
стороны, на (L'R) имеем
(при больших R=\z\). Значит, правая, а с ней и левая части C9)
при R—>оо стремятся к нулю как -^ R = ^-.
Подводя итог, мы видим, что/л = ле~ш можно представить в виде
суммы интеграла C8) (который в пределе, при R—к», стремится
к C6), т. е. к /t) и интеграла по (L'R), стремящегося к нулю. Пе-
Переходя к пределу при R—>■ оо, получаем, что /j^^e", т. е.
1
COS (ОХ ,
-г—.—г, dx =
1 -\-х1
D0)
Последняя формула совершенно неочевидна, и ее получение без
привлечения комплексных чисел весьма затруднительно и требует боль-
большого искусства. При помощи свойств интегралов от комплексных функ-
функций удается находить многие интегралы такого рода от вещественных
функций стандартными приемами, требующими лишь аккуратности.
На практике рассмотренный интеграл получается в задаче о воз-
возбуждении колебаний в системе с собственной частотой и при дей-
действии силы, меняющейся со временем но закону /(/) = у-т—^ . Полу-
Полученный результат дает закон уменьшения амплитуды возбуждаемых
колебаний при увеличении собственной частоты о) системы (см. § VII.5).
На формулу D0) интересно взглянуть с точки зрения резуль-
результатов § III.4. Это как раз случай, когда функция f(x) = - j об-
обращается в нуль вместе со всеми производными на концах х=-^оо
интервала интегрирования. Так как все эти производные не имеют
разрывов, то из § III.4 следует, что интеграл /х(со) при со^оо
стремится к нулю быстрее любой отрицательной степени и; одна-
однако точную скорость этого стремления нам удалось получить, только

180 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
применяя теорию вычетов, Мерой негладкости функции f(x), опре-
определяющей эту скорость, здесь служит расстояние от полюса этой
функции, продолженной в комплексную плоскость, до мнимой оси.
Конечно, короткий параграф не мог, к сожалению, научить чи-
читателя пользоваться техникой интегрирования комплексных функ-
функций; но мы надеемся, что он все же помог читателю ощутить кра-
красоту теории функций комплексного переменного,
Упражнения
1. Вычислите интеграл ф -j—: по окружности (L) радиуса 4 с центром
в точке 3(.
00
2. Вычислите интеграл \ 6 .
— 00
ОТВЕТЫ И РЕШЕНИЯ
■isin-д-); 3 (cos л+('sin л); 1 (cosO+< sinO); 0(cos ф + i'sin ф) (ф—любое).
§2.
z
1. Если — =w. то гг = г4о), откуда z*l = (z2w)* = z*w*, т. е. ау*=—1.
2. Так как второй корень равен 2-j-t, то левая часть должна делиться иа
|г —B—(')] 1г — B+01 = г3—4г + 5. Произведя деление и решив остающееся
квадратное уравнение, находим z3i = l±}^3.
3. Если z = x-\-iy, то z*=x — iy=x-\-i(—y), а г** —x — i (—y) = x-j-iy=z.
4. zz* = *2 + #2 = | г Г2. Интересно, что вещественность произведения гг*
можно доказать и не переходя к вещественной и мнимой частям, на основании
свойств сопряженных чисел: (zz*)*=z*z** = z*z = zz*. а число, равное своему
сопряженному, обязательно вещественное.
(— _ -(— i
§3.
_ (— ■ _( _
1. a) l + ( = Vr2e 4 ; б) I — t = |А2е 4 = >^2е 4 ; в) — 1 =е'*; г) Ы = Ъе 2 .
2. а) Прежде всего запишем число 1-j-i в показательной форме, получим
1+ i = }^2 е'4, отсюда A+015 = 1^2е 4 J =(ул2I«.е4' =28.е'*к =
= 23 = 256; б) —1,
3. cos Зф = соз3 ф —3cos (psin3 ф; sin 4ф=4соз:| ф sin ф —4cos фзш3 ф.

ОТВЕТЫ И РЕШЕНИЯ 181
4. В формуле Эйлера e''? = cos ф + i sin ф заменим ф на —ф, получим
е-ip = cos ф — I sin ф. Складывая эти две формулы почленно, получим
^'т-(-е~'? = 2 cos ф, откуда cos ф = 0 —-. Почленным вычитанием получим
вторую формулу.
§ 4.
\ 2 у \ 2
г) 1 " ' " '
2. Так как —1 =cos л + £ sin и, то общий вид чисел х^ таких, что
х\ = — 1, есть
__ л + 2/гл . л + 2/гл.,_0 .
Поэтому
_ _л . . ^t __ j_ . vT _co
5л . . 5л 1 .1^3"
4. На основании упражнения 4 к § 3 приходим к уравнению -^ =2.
Отсюда после легких преобразований получаем ea'f — 4e£v-f-1=0.
Это—квадратное уравнение относительно e'f; решая его, находим е'ч> = 2± у^З
Отсюда 1ф = 1п B± \r3)-\-2kni (ft —любое целое). Деля на i и заметив, что
21^3" = и ПОТОМУ In B—1^3) =—In B+|^3), получаем оконча-
З
2—1^3 = y=
2+ УЗ _
тельный ответ: ф= ±1п B + у'З ) *' + 2£л = ± 1,ЗШ-\-2кк. Все эти решения
мнимые.
5. Аналогично находим ф= ±1п B+ У 3 ) / + -^- + 2£л.
§ 5.
1 J ^^*. Таким образом, получаются те же формулы
что для разобранного в тексте случая R,L-nenu, однако вместо coL надо под-
подставить coL ^. В частном случае, когда со2 = —-, будет o)L ^=0,
т. е. индуктивность и емкость как бы взаимно уничтожаются.
2- •/=(^ + -^:)фо^''иI-Отсюда /„= ]/^ + -q-8q0-e = P +
ГС
— -^ при том же смысле обозначений, что в тексте.

182 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [ГЛ. V
§6.
f(z) = (x + iyK = x3-\-i3x2y—Зхуг — iy3, откуда и=х3—Зху2, и = 3хгу—у3;
дх ду я дх ду "
§7- ^
1. Из условия и=х-{-х2—у2 находим -^-—\-\-2х.
Пользуясь первым из условий Коши—Римана, получаем -з-=1 +2*. Для
того, чтобы отсюда найти v, достаточно проинтегрировать это равенство по у,
считая х постоянным. Получим
( У)
Теперь находим -r-=2y-f-cp' (*). Но согласно второму из условий Коши—Римана
ОХ
-^=-—— Так как —= — 2у, то получаем 2у+ф' (х) = 2у, откуда ф'(*) = 0,
т. е. |р(л)зС, где С—постоянная. Следовательно, v(x, y)=y-\-2xy-\-C.
Для определения С воспользуемся условием /@)=0, оно означает, что
и=0, v = 0 при х = 0, у = 0. Итак, v = 0 при х=0, у = 0, поэтому С = 0,
( 2
( y) y + y
2. и(х, у) =
§8.
2 2 2 2
а) -, -; б) — м, ni; в) -5- A + 0> "о" (~'+0 (сначала пишется ре-
результат для верхней полуокружности, потом для нижней). В случае а) под-
подынтегральная функция аналитична всюду и потому интеграл не зависит от пути
интегрирования. В случае б) подынтегральная функция обращается при г = 0
в бесконечность, а в случае в) она имеет там точку ветвления.
§9.
1. Подынтегральная функция имеет внутри (L) два полюса первого поряд-
порядка: г1=0, г2 = 2ш. Поэтому интеграл равен
2п/
2. Подобно примеру C4), рассматриваемый интеграл равен интегралу от
функции / (г) == , 6 по контуру (L#) рис. 67 при большом R. Но f (г) имеет
i/~ 1 1^3~ 1
внутри (LR) три простых полюса: 2j =-£-+1 у , г2=/, г3= ^—'"'"г"'
Поэтому интеграл равен
В этом примере неопределенный интеграл выражается через элементарные
функции, однако приведенный способ вычисления гораздо проще.
*) Так как при интегрировании х постоянно, то роль постоянной интегри-
интегрирования может играть любая функция ф, зависящая только от одного пере-
переменного X.

ГЛАВА VI
ДЕЛЬТА-ФУНКЦИЯ ДИРАКА *)
§ 1. Дельта-функция Дирака 6 (jc)
Возьмем функцию у=Ф1(х) имеющую максимум при х = 0,
быстроубывающую в обе стороны от х — 0, и притом такую, что
j (х) dx=\.
Эти условия отнюдь не определяют вид функции Ф1 (х); можно
придумать много функций, удовлетворяющих всем поставленным
выше требованиям, например:
Ф1(*) = -7^е-"**). B)
Числовой множитель обеспечивает равенство интеграла единице.
Графики этих функций приведены на рис. 68. Произведем над линией
-2
у = Ф1 (х) следующее преобразование: увеличим ее высоту в т раз
и одновременно уменьшим ее ширину во столько же раз. Напомним
*) Эта глава, хотя и написана независимо, непосредственно перекликается
с Добавлением к ВМ.
+ 00
**) Можно доказать, что \ е~х2с1х=У~л, см. § IV.7,

184 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VI
(см., например, ВМ, § IV.7), что если увеличить высоту линии
у = Фх(х) в т раз, то ее уравнение приобретает вид у = тФ1(х),
а если уменьшить ширину в т раз, то уравнение станет таким:
у — Ф1 (тх). Значит, после обоих преобразований уравнение кривой
будет у = Фт(х) = тФ1(тх), Например, из A) получим фт(х) —
=—т—-.—р. Ясно, что площадь, заключенная между графиком и
осью х, при растяжении кверху увеличится в т раз, а при сжатии
с боков уменьшится во столько же раз, т. е. в конечном счете
останется без изменения. Впрочем, это легко доказать и с помощью
интегрирования после замены переменной интегрирования mx = s:
\фт(х)йх = \ тФ1(тх)с1х= [ Фх(тх) d(mx) =
— 00 — 00 — 00
00 00
х(*)й$ = \фх(х)йх.
Какой вид имеет преобразованная функция при очень больших т,
или, выражаясь точнее, в пределе, при неограниченном возрастании т?
При любом фиксированном х=£0 величина у = тФг(тх) будет
неограниченно приближаться к нулю при неограниченном росте т,
потому что уменьшение Фх {тх) при увеличении от происходит быстрее,
чем рост множителя т. Для этого надо, чтобы Ф, (х) при х —<- + ос
стремилась к нулю быстрее, чем — (это и означает, что функция
быстроубывающая *)). Так, например, в выражении фт(х) = —г—— -
при данном лг=^О и при достаточно большом т будет (mx)'z%>\
t 1
и, следовательно, Фт (х) да 2~г = г> т> е> неограниченно убы-
вает при возрастании т. Еще быстрее убывает при росте т вели-
величина Фт(х), полученная из формулы B). Действительно, в этом
случае Фт(х) ==- e~imx) , а известно, что показательная функция
у л
с отрицательным показателем убывает быстрее любой степени т
(см., например, ВМ, § 11.21).
Пусть теперь х = 0. Тогда Фг (тх) = Ф1 @) постоянна при любом т,
а поэтому Фт @) = тФг @) неограниченно увеличивается с ростом т.
Следовательно, неограниченно увеличивая т, мы получаем функ-
функцию со следующими свойствами:
1) функция равна нулю при всех х < 0 и при всех х > 0;
2) функция бесконечна при х—0;
*) Такая скорость убывания автоматически следует из сходимости ин-
интеграла (см. § III.1).

§ 1] ЛЕЛЬТА-ФУНКЦИЯ ДИРАКА б (X) 185
3) интеграл от этой функции, взятый в пределах от —с» до
-j-oo, равен 1.
Функция, обладающая этими свойствами, называется дельта-функ-
дельта-функцией Дирака и обозначается через 6 (#)*). Функция 6 (дг) необычайно
удобна и широко применяется сейчас в физике.
Мы пришли к понятию б(л'), рассматривая обычные хорошо
известные функции и преобразуя их определенным образом. Замеча-
Замечательно, однако, что для применения б (х) достаточно знать три ее
свойства, которые мы перечислили выше, и совершенно не требуется
/11 1 „2
знать, из какой именно функции (—=—т—^, или е~х , или еще
какой-нибудь) получена функция Ь(х). Грубо говоря, дельта-функ-
дельта-функция — это функция, принимающая на узком участке большие значе-
значения, причем эти значения согласованы с шириной участка так, что
выполняется условие 3). (Отсюда следует, в частности, что раз-
размерность [б (л:)] = 1/[л:].)
Из свойств б (х) следует основное соотношение
/= \b(x)f(x)dx=f{0). C)
В самом деле, b(x) = Q при всех х=£0, поэтому
+ оо +г
/= \b{x)f{x)dx= \b{x)f{x)dx,
- оо -е
где е — малая величина. В последнем интеграле промежуток интегри-
интегрирования мал (его длина равна 2е), поэтому на нем f(x) «/@),
следовательно,
/= J b(x)f(x)dx= J 6{x)f{0)dx = f{0) J b{x)dx =
-e - e -e
+ CD
= /@) J 6{x)dx=*f@).
— t»
Итак, формула (З) следует из трех свойств Ь(х). Справедливо и об-
обратное утверждение: если определить б (х) как функцию, для которой
выполняется соотношение C) при любой f(x), то отсюда следуют
все три свойства б (х). Не останавливаясь на детальном доказатель-
доказательстве этого факта, покажем, например, что из C) следует первое
свойство: б(л:) = 0 при х=£0.
*) Поль Адриан Морис Дирак, именем которого названа функция, круп-
крупнейший английский физик-теоретик, предсказавший в 1929 году существование
античастиц — позитрона, антипротона и других, которые позже были открыты
экспериментально.

186 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VJ
Действительно, из формулы C) ясно, что величина интеграла
не зависит от поведения функции f(x) при хфО, а зависит только
от /@). Это означает, что f(x) входит под знак интеграла с мно-
множителем, равным нулю при х=^=0, т.е. б(л;) = О при х=?*=0.
Заметим, что б (х — а) отлично от нуля (и притом бесконечно)
только при х—а. Рассуждая, как при выводе формулы C), получаем
формулу
+ «
J S(x-a)f(x)dx = f(a). D)
Отметим еще некоторые интересные формулы для дельта-функции.
Прежде всего
Ь(ах)=~б(х) (а = const фО).
В самом деле, функция | а | б (ах) удовлетворяет всем трем свойствам,
определяющим дельта-функцию. Чуть-чуть менее очевидное третье
свойство проверяется с помощью подстановки ax = xt так:
а>0; *\j\a\b(ax)dx = $ b(ax)adx =
~ 00 — 00 — 00
00 00
а < 0; \\а\Ь (ах) dx = — ^ б (ах) adx =
— 00 — 00
— 00 00
= - J 6^)^= J
Еще одно свойство:
если ф (х) обращается в нуль лишь при х = х0. Это свойство следует
из предыдущего, так как вблизи х = х0 с точностью до малых выс-
высшего порядка можно написать
ф (X) = ф (Хо) -f ф' (Хо) (Х—Хо) = ф' (Хо) (Х—Хо).
Наконец,
что сразу вытекает из равенства функции б (х—а) нулю при х=^=а.
С помощью б-функции чрезвычайно удобно записывать многие
физические соотношения. Рассмотрим, например, тонкий стержень,
на котором в нескольких отдельных местах помещены грузы. Пусть
размеры грузов весьма малы по сравнению с длиной стержня, а их
массы того же порядка, что и масса стержня. Тогда при решении
задач (определение полной массы, определение положения равновесия

§ 1] дельта-функция дирлка 8 (х) 187
и т. п.) приходится рассматривать и массы грузов (их называют
сосредоточенными массами) и массу стержня (распределенная масса).
Пусть плотность стержня есть рр (х) *). Тогда масса стержня, начало
которого помещено в начало координат, а конец в точку х-=1,
1
равна /»р= <\ipv(x)dx.
о
Пусть в точке х = а стержня находится груз та. Тогда полная
масса стержня и груза равна
С помощью б-функции можно представить сосредоточенную массу
как массу, распределенную с плотностью рс (х) = та8 (х — а). Дей-
Действительно, последняя формула означает, что плотность отлична от
нуля лишь в малой окрестности точки х = а, причем
5 рс (х) dx = та \ б (х—a) dx — та.
о о
Таким образом, введя функцию рс (х), мы можем сосредоточенную
массу записать в форме, которая по виду совпадает с формой
записи для распределенной массы.
Положим теперь
р (х) = рр (х) + рс (х) = рр (х) + таЬ (х—а).
Тогда полная масса равна
т — ^ р (х) dx.
о
Таким образом, полную массу можно не писать как сумму членов
разного вида; она записывается при помощи интеграла, т. е. так же,
как распределенная масса. Различный характер распределенной и
сосредоточенной масс сказывается лишь на виде функции р(х).
Благодаря этому мы можем единообразно записывать все те соотно-
соотношения, которые были нами получены раньше лишь для распределен-
распределенной массы.
Так, например, масса, находящаяся между точками х = Ь и х=с
с
стержня, равна \jp(x)dx. Никаких оговорок о том, что Ъ > а, или
ь
Ъ < а и т. п. не требуется: функция р (х) содержит б (х—а), а
*) Индексы «р» и «с» будут обозначать «распределенный» и «сосредото-
«сосредоточенный».

188 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VI
интегрирование функции б (х—а) автоматически добавит к массе стер-
стержня массу груза, если только груз расположен между точками х~ь
и х = с.
Точно так же положение центра тяжести стержня дается форму-
хр(х) dx
лой хс = ~ , независимо от того, имеется на стержне сосре-
\pMdx
о
доточенная масса или нет.
" Случай нескольких сосредоточенных масс рассматривается бук-
буквально так же.
Рассмотрим еще пример. В механике наряду с действием сил,
плавно изменяющихся с течением времени, приходится рассматривать
резкий удар, столкновение тел. При ударе на тело действует крат-
кратковременная, но очень большая сила. В большинстве случаев деталь-
детальное изучение зависимости силы от времени на протяжении короткого
момента, в течение которого длится удар, не представляет интереса
(см., например, ВМ, § VI.5). Достаточно знать импульс силы, т.е.
I =[Fdt. Тогда силу при ударе можно записать так: F(t) = Iyx
X б (t — ty), где ty — момент удара, /у — импульс удара. Эта запись
показывает, что сила отлична от нуля лишь в момент удара,
а импульс этой силы равен /у.
Отметим в заключение, что дельта-функция рассматривается лишь
для вещественных значений независимой переменной.
Упражнения
OD
1. Вычислите \ х2Ь(х—3) dx.
— OD
2. Упростите выражения:
а) (х2 + 3N(х + 5); б) 6Bх—8); в) Ь(хг+х—2).
§ 2. Функция Грина
Рассмотрим сначала пример. Пусть тонкая гибкая нить длины /
натянута вдоль оси х постоянной силой F. В системе, изображенной
на рис. 69, такое натяжение осуществляется при помощи блока и
груза. Пусть на нить действует перпендикулярно оси х сила, рас-
распределенная с плотностью /(х), т.е. на малый участок нити между
точками х и x-\-dx действует сила f(x)dx, а на всю нить действует
сила \/(x)dx. Найдем форму у (х), которую при этом примет нить;

§ 2]
ФУНКЦИЯ ГРИНА
189
здесь функция у (х)— это отклонение той точки нити, которая в пер-
первоначальном состоянии находилась в точке х оси х.
Мы будем считать, что натяжение F нити гораздо больше всей
силы, действующей на нить, так что отклонение нити мало. Тогда
можно пользоваться законом линейности, согласно которому при
наложении нескольких нагрузок соответствующие прогибы также
складываются.
Допустим сначала, что приложенная нагрузка имеет специальный
вид, а именно, представляет собой единичную сосредоточенную
If Ш
Рис. 69.
Рис. 70.
нагрузку, приложенную в некоторой точке воздействия % оси х, и
обозначим через y = G(x; £) соответствующий прогиб в любой точке
наблюдения х (рис. 70). Эта функция G(x; £) называется функцией
влияния или функцией Грина (по имени английского математика
Дж. Грина A793—1841)) рассматриваемой задачи. Мы сейчас покажем,
что если она известна, то легко найти прогиб и от воздействия
произвольной нагрузки с плотностью /(х).
В самом деле, рассмотрим нагрузку, приходящуюся на участок
оси от точки | до точки £,-\-dc,. Эта нагрузка равна f{^)d\\ поэтому
прогиб от нее в точке х равен G(x; £)/(£) d£, так как из закона
линейности вытекает, что если внешнюю нагрузку умножить на посто-
постоянный множитель, то и прогиб умножится на тот же множитель.
Складывая такие бесконечно малые прогибы от всех элементов
нагрузки от £ = 0 до £ = /, получаем суммарный прогиб (см. рис. 69)
E)
В рассматриваемом примере нетрудно выписать функцию G(x; £)
в явном виде. В самом деле, найдем составляющие сил натяжения
нити вдоль оси у. Слева от точки | она равна (см. рис. 70)
— /7sincc= —F -?■ ,
6
где z — отклонение точки |, нам заранее не заданное; отметим, что
при этом выводе мы воспользовались малостью отклонений и поэтому

190 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VI
при подсчете синуса заменили гипотенузу треугольника на его боль-
больший катет. Аналогично получаем составляющую силы натяжения
справа от g
Если под действием заданной силы нить находится в равновесии,
то это означает, что сумма всех сил, действующих на нить, т. е.
сумма сил натяжения и заданной силы, равна нулю. Поэтому равна
нулю и сумма составляющих этих сил по оси у. Так как в нашем
случае заданная сила равна 1 и действует вдоль оси у, то на
основании предыдущего получаем
f
откуда находим z = ■ . Если г известно, то отклонение любой
точки нити найти легко, пользуясь тем, что нить имеет форму лома-
ломаной. Получим
y(x)=Zj, если х<1,
y(x)=zjEj> если х>1,
Подставляя сюда найденное значение г и вспоминая, что форма
отклонения при единичной сосредоточенной нагрузке дает функцию
Грина, получаем в данной задаче
Г -jj-xil — t), если х<%,
G(x; Ъ)=\ 7
{ tt%v—x)> если х>1-
Найденное выражение для функции Грина можно подставить
в формулу E) для прогиба от произвольной нагрузки. Так как
G(x; I) при \<х и при | > х записывается с помощью различных
формул, то интеграл разбиваем на два:
1-х
Fl
Тот же результат можно получить, выписав дифференциальное
уравнение для функции у (х) и решив его. Однако замечательно,
что нам удалось найти решение задачи, даже не выписывая самого
дифференциального уравнения. Нам достаточно было знать, что дей-
действует закон линейности.

§ 2] ФУНКЦИЯ ГРИНА 191
Перейдем теперь к общей схеме построения функции влияния.
Пусть внешнее воздействие на какой-либо объект описывается функ-
функцией /(лг) (а ^ лг ^ Ь; в приведенном примере это и была функция
/(лг)), а результат этого воздействия — функцией F(x) (в приведен-
приведенном примере это была функция h{x)). Можно себе представить, что
каждой заданной функции/отвечает новая функция F, т. е. получается,
что каждая функция / по какому-то определенному закону преобра-
преобразуется в новую функцию F. Такой закон преобразования функций-
прообразов в функции-образы в математике называется оператором.
Например, хорошо известен оператор дифференцирования D, дейст-
действующий по закону D/=/', т. е. D (sin лг) = cos лг, D (лг3) = Злг2 и т. д.
Здесь s'mx — прообраз, который преобразуется оператором D в образ
соэлг и т. д. Понятие оператора аналогично понятию функции, но если
функция давала закон преобразования чисел (значений независимой
переменной) в числа (значения зависимой переменной), то оператор
преобразует функции в функции.
Обозначим оператор перехода от функции внешнего воздействия
/(лг) к функции-«отклику» F(х) через L, так что F=Lf. Мы пред-
предположим, что действует закон линейности или принцип суперпозии: при
сложении внешних воздействий их результаты также складываются;
этот закон часто выполняется с достаточной точностью, когда внеш-
внешние воздействия не слишком велики. Его можно записать в форме
F)
Оператор, обладающий таким свойством, называется линейным.
(Проверьте, что, например, оператор дифференцирования является
линейным.) Из этого свойства можно вывести, что при умножении
внешнего воздействия на константу его результат умножится на ту
же константу, т. е.
L(Cf) = CLf (C= const). G)
Мы не будем этого доказывать. (Попробуйте это обосновать, считая
сначала С целым положительным, затем полагая С = — (л=2, 3,
4, ...), далее полагая С = —, где m и п — целые положительные,
затем для С—0 и, наконец, считая С отрицательным.)
В примере, разобранном в начале этого параграфа, мы под
О (лг; £) понимали результат воздействия единичной силы, сосредо-
сосредоточенной в некоторой точке £, т. е., другими словами (см. § 1),
распределенной с плотностью б (лг—£). Так и в общем случае мы
обозначим через О(лг; £) результат внешнего воздействия, описы-
описываемого дельта-функцией с особенностью в некоторой фиксированной
точке £, т. е. функцией б (лг — £). Таким образом,

192
ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
[ГЛ. VI
Как же с помощью этой функции Грина О{х; £) выразить резуль-
результат преобразования любой заданной функции/(лг)? Для этого предста-
представим функцию / в виде суммы «столбчатых» функций (рис. 71), каждая
из которых сосредоточена лишь в одной точке \, а вне бесконечно
малой окрестности этой точки она
равна нулю. Поэтому такая столб-
столбчатая функция пропорциональна
дельта-функции б (лг—£), а так как
интеграл от столбчатой функции
равен f (%) d\, то она просто равна
[/(|) dl,\б (лг—£). Таким образом, мы
получаем представление
У-ffx)
А
mi
У
\~— b
fti)
Рис. 71.
Строго говоря, при бесконечно ма-
малых d\ здесь надо писать не знак
суммы, а знак интеграла, так что
это, по существу, формула D) в
другой записи; однако закон линей-
линейности для сумм в пределе перено-
переносится и на интегралы.
Каждая столбчатая функция в
силу свойства G) преобразуется в
41/F) <$] (*-£)] =
= \f(l)d\\L[b(x-l)]=f(%)G(x;l)dl.
Поэтому сумма таких функций в силу свойства F) преобразуется в
[2 If it) dl] б (лг- D] = ^ L
б (х-Щ =
О(лг;
При бесконечно малых dl, эта сумма является интегралом, т. е. окон-
окончательно
ъ
F(лг) = L [у (лг)] = j &(х; с,) f (б) dc, (8)
а
(сравните с формулой E)).
Функцию влияния можно в более простых случаях подсчитать
теоретически, как в разобранном выше примере, а в более сложных
задачах определить экспериментально, произведя необходимые замеры,
например измеряя деформацию системы под действием сосредото-
сосредоточенной силы. При этом возможность применения принципа суперпо-
суперпозиции или, как говорят, линейность рассматриваемой системы либо
следует из общетеоретических принципов, либо также может быть
проверена экспериментально. После того как функция Грина найдена
и линейность системы установлена, решение задами пишется по фор-
формуле (8) для любого внешнего воздействия /.

§ 3]
ФУНКЦИИ, СВЯЗАННЫЕ С ДЕЛЬТА-ФУНКЦИЕЙ
193
Таким образом,, иногда даже самые общие представления о свой-
свойствах физических систем указывают путь решения конкретных задач.
Отметим в заключение, что функции-образы Lf не обязаны быть
определенными на том же интервале, что функции-прообразы /;
более того, независимые переменные х и £ в формуле (8) могут иметь
разный физический смысл. Независимая переменная | может играть
роль времени; тогда функция влияния описывает результат воздей-
воздействия «единичного импульса», подействовавшего в момент |.
Упражнение
Напишите функцию влияния для операторов: a) Lf = 2f (х); б) Lf = s\n x-f (х);
в) Lf = f(x+l); г) Lf = f(x%
§ 3. Функции, связанные с дельта-функцией
При помощи б-функции легко записываются некоторые другие
функции, имеющие большое значение. Важным примером может слу-
служить единичная функция е(х) (другое обозначение Ф(х)):
е(лг)=
(9)
Ясно, что при х < 0 получаем е(лг) = О, а при х > 0 получаем
е(лг)=1. Таким образом, е (х)—это разрывная функция, испытываю-
испытывающая скачок при лг=О. Ее график («ступенька») изображен на рис. 72,
\У
/
Рис. 72.
О
Рис. 73.
она получается при внезапном подключении какого-либо постоянного
воздействия, например, напряжения в электрическую цепь (при этом
независимая переменная играет роль времени).
Равенство (9) можно получить также с помощью приближенных
представлений дельта-функции. В § 1 мы видели, что одним из таких
представлений служит функция — т-гт—г2 при большом т. Однако
л
С1
\ т , 1
- т-г-.—^ dx = — arctg mx
Я. Б. Зельдович, А. Д. Мышкио

194
ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
[ГЛ. VI
6)
График этого интеграла при те=1 и т = 5 показан на рис. 73.
В пределе, при т—► оо, из интеграла получаем е (х), т. е. приходим
к равенству (9).
Тот же результат можно получить с помощью столбчатой функ-
функции, график которой изображен на 'рис. 74, а (из нее также в пре-
пределе, при N—I- оо, получается
дельта-функция). График интеграла
от нее показан на рис. 74, б. В
пределе, при N—>-оо, и здесь по-
получаем равенство (9).
Равенство (9) можно продемон-
продемонстрировать на следующем физи-
физическом примере. Рассмотрим прямо-
' ' " *fc линейное движение массы т под
действием переменной силы F(t),
направленной вдоль этой же прямой.
Записав выражение второго закона
Ньютона и проведя интегрирование,
получим равенство (см., например,
~——~ ВМ, § VI.4)
1/N
i
А
Цв-Я
f/ff
Рис. 74.
v(t)
4J
dt
(мы приняли, что начальная ско-
скорость при t = —оо равна нулю).
Пусть сила имеет характер удара:
= Lb{t — ty) (см. конец § 1). Интегрируя, получим
т. е. скорость v равна нулю до удара и равна — после удара.
Вернемся к математике. Если продифференцировать равенство (9),
то получится, что
е'(х) = 6(х). A0)
Это равенство также можно показать на только что разобранных
примерах. Так, в качестве приближенного представления функции е (х)
можно взять функцию, изображенную на рис. 74, б, производная
которой показана на рис. 74, а; в пределе, при N—>■ оо, мы приходим
к равенству A0).
Мы в нашем изложении исходили из дельта-функции и пришли
к единичной функции с помощью интегрирования. Можно было пойти
и по обратному пути: исходить из функции е (х) и получить функцию
б (лг) с помощью дифференцирования. Таким образом, дельта-функция

ФУНКЦИИ, СВЯЗАННЫЕ С ДЕЛЬТА-ФУНКЦИЕЙ
195
ррлучается при дифференцировании разрывной функции е (лг). Подобно
'этому при дифференцировании любой разрывной функции появляются
дельта-слагаемые.
Рассмотрим, например, функцию/(лг), заданную двумя формулами:
г3, если 0<лг< 1,
га+2, если1<лг<оо.
Г
\
График этой функции, имеющий разрыв при лг=1, показан жирными
линиями на рис. 75. Было бы ошибоч-
ошибочно приравнять /'(х) просто функции ср(х),
полученной дифференцированием обеих
формул:
6х*, если 0 < лг < 1,
2лг, если 1 < лг < оо.
(И)
В самом деле, если мы проинтегрируем по-
последнюю функцию, например, от значения
х = 0, то мы получим
при 0 < лг < 1: ^ ф i
при х > 1: ] ф (х) dx = ^ Ф (х) dx -\-
Рис. 75.
!
: = ^ 3x2dx ■
о
2х dx =-- х3
Таким образом, получается не f(x), а непрерывная функция fx (x),
график которой при х > 1 показан на рис. 75 пунктиром. Чтобы из
fx (x) получить f(x), надо к первой функции прибавить «ступеньку»
с разрывом при х= 1, равным разрыву функции f(x), т. е. равным
/A+0)—/A— 0) = A3 + 2)— Р = 2*).
Таким образом, f{x)—f1(x)-\-2e{x—1), откуда окончательно
/' (*)=/; (*) + 2в' (х— 1) = Ф (х) 4- 26 (х— 1),
где ф (х) задана формулами A1).
С функцией е (х) тесно связана функция sign *■**), которую можно
определить так:
sign*=-nrf
*) Запись /A—0)—это условное, но удобное обозначение для предела
значения /A_е) При е—^0(е>0); аналогично расшифровывается запись
**) sign—первые буквы латинского слова signum (знак).

196
ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
[ГЛ. VI
Она раена —1 при х < О и -\-\ при х > 0; таким'образом, она-по-
она-показывает знак числа х. Легко убедиться в правильности соотношении
sign.xr= 2е [х) — 1.
Г(ри интегрировании функции е (х) получается уже непрерывная
функция, график которой изображен на рис. 76, так как
( х
х при х < 0 равен ^ 0 dx = 0,
_[e(x)dxl
^при лг>0 равен ^ 0 dx-\-] \ dx = x.
(Проверьте, что эта функция равна ■■- ' ' .
Дельта-функцию можно не только интегрировать, но и диффе-
дифференцировать; ее производная б' (лг) имеет еще более «острую» осо-
особенность, чем б (лг), причем при-
принимает значения обоих знаков. Так,
если исходить из приближенного
представления функции б (лг) в виде
Рис. 76.
-0,47т'
Рис. 77.
т
у^е <ш*)* ПРИ большом т (см. § 1), то мы получаем приближенное
представление б' (лг) в виде функции
график которой показан на рис. 77. Эта функция принимает экст-
экстремальные значения при х = ± —L- = ■+- ^-, равные по абсо-
/~2~
лютной величине у —те2 = 0,47те2. (Проверьте.) Эти значения про-
пропорциональны уже те2, а не т, как при представлении функции б (лг).
Можно исходить из приближенного представления функции б (лг)
в виде треугольника, показанного на рис. 78, а, при большом /И;

ФУНКЦИИ, СВЯЗАННЫЕ С ДЕЛЬТА-ФУНКЦИЕЙ
197
>гда функция б'(лг) будет приближенно представлена графиком, по-
поданным на рис. 78, б.
Если б-функция описывает плотность единичного заряда, распо-
расположенного в начале координат (ср. § 1), то б'(лг) описывает плот-
рость «диполя», расположенного там же. Такой диполь получается,
|»сли разместить заряды q и —q соответственно в точках лг = О и
i=l, а затем, оставляя p = ql (мо- ,,•,.
(цент диполя) без изменения, устре-
устремить / к нулю, a q к бесконечности
ак что в пределе получатся два рав-
равных бесконечно больших заряда про-
-4М*
Рис. 78.
тивоположного знака на бесконечно близком расстоянии. До пе-
перехода к пределу плотность заряда имеет вид
поэтому после перехода к пределу при / -*■ 0 плотность заряда
равна рЬ' (лг).
с Интегралы с участием б'(лг) вычисляются с помощью интегриро-
tвания по частям:
f{x)V{x—a)dx
A2)
Дельта-функцию можно рассматривать также на плоскости и в
престранстве. Например, в пространстве под функцией б (лг, у, z) надо
понимать функцию, равную нулю всюду вне начала координат @; 0; 0),
равную бесконечности в начале и притом такую, что интеграл от
нее по всему пространству равен единице. Легко проверить, что этим
уёлёвиям, в частности, удовлетворяет функция
> ., 6(лг, з', г) = Ь(х)Ь(у)Ь(г).

198 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VI
Таким образом, массу т, сосредоточенную в точке (а; Ь; с), мЪжмо
рассматривать как массу, распределенную в пространстве с плот-
плотностью
р(х, у, z) = m6(x—aN(y—-b)S(z — c).
Упражнения
1. Найдите \х\'; \х\".
2. Найдите |Д'+еТ/ J •
3. Убедитесь в справедливости формулы A2) непосредственно,, воспользо-
воспользовавшись разложением функции f (х) в ряд по степеням х—а и приближенным
представлением функции б' (х) в виде, показанном на рис. 78, б.
§ 4, Понятие об интеграле Стилтьеса
С дельта-функцией непосредственно связано одно полезное рас-
расширение понятия интеграла. Рассмотрим сначала пример. Пусть на
отрезке (/) оси х с концами a, b расположена некоторая масса т
и требуется определить силу, с которой эта масса притягивает еди-
единичную точечную массу т0, расположенную в точке х — с, левее (/),
той же оси. Ответ очень простой. Так как по закону Ньютона
масса dm, расположенная в точке х, притягивает т0 с силой
dF=xr-^—rj (здесь коэффициент пропорциональности к — так назы-
v* — с)
ваемая гравитационная постоянная), то общая сила равна
"г*». A3)
(х — с)> v '
(I) Ф
Если масса т распределена вдоль (/) так, что она в каждой
точке х имеет конечную плотность р = р(лг), то dm = p(x)dx и от
интеграла A3) можно перейти к обычному интегралу
кт \ ' dx.
0 J {x — су
а
Однако, как было указано в § 1, масса т может содержать
часть, сосредоточенную в отдельных точках. Тогда интеграл A3)
можно понимать как интеграл по мере т. Под этим понимается, что
каждой части (Д/) отрезка (/) (в том числе, и каждой точке этого
отрезка) отвечает его «мера» (в данном примере масса) т(А1), причем
выполняется закон сложения: мера целого равна сумме мер частей.
Интеграл по мере (он также называется интегралом Стилтьеса)
в общем .случае имеет вид
p A4)
(е)

ОТВЕТЫ И РЕШЕНИЯ 199
-равен, по определению, пределу
lim S/(*/)H СЧ)>
Доставленному ft точности по тому же правилу, как для обычного
^интеграла (см., например, ВМ, § 1.8), однако взамен длины частей
^Д/,-) основного интервала (/) берется их мера [л(Д/(). Если в ка-
качестве меры взять обычную длину, то мы приходим к обычному
определению интеграла, т. е. интеграл Стилтьеса является обобще-
обобщением этого обычного интеграла*).
■'Если заданная мера имеет конечную плотность р = --^, то от ин-
интеграла Стилтьеса A4) можно перейти к обычному интегралу
ь
' [f{x)d»=\f(x)p(x)dx. A5)
(О а
Если же имеются точки с отличной от нуля мерой, то, как мы ви-
видели в § 1, плотность р (л:) будет иметь дельтообразные слагаемые.
Допуская такие слагаемые, мы можем совершить переход A5) и в
атом случае.
Упражнение
Часто мера на оси х задается с помощью вспомогательной функции g (x) по
правилу: мера интервала <x<;cs£E равна g(|5 +0)— g{a — 0) (или просто
Ф)— £(<*)• если функция g (x) непрерывная). Тогда вместо интеграла A4)
пишут \ f(x)dg(x), а формула A5) приобретает вид \ / (х) dg (х) = \ / (x)g'(x)dx.
V) (О о
11 1
Найдите \ х3 d (x2); f s\nxde(x); С cosxde(x).
о -1 -о
ОТВЕТЫ И РЕШЕНИЯ
§ 1
1. 32 = 9.
2. а) [(-5J+3] б (х + 5) = 286 (х + 5); б) 6 Bх — 8) = 6 B (л:-4))=1 6(х-4);
в) многочлен Р(х)=х2-\-х—2 имеет нули xt=\, хг~—2, причем ^'(^^=3,
Р'(х2) = -3. Отсюда6(л:г+^-2) = 1б(^-1) + -1-б(^ + 2).
§ 2
а) 26 (х-!); 6)smx-6(;e-E):=sing-6(x-|); в) 6(х-£ + 1); г) 6(^-1) =
*) Чтобы отличать обычный интеграл от интеграла Стилтьеса, его иногда
называют интегралом Римина.

200 ДЕЛЬТА-ФУНКЦИЯ ДИРАКА [ГЛ. VI
§3
1. sign*; 26(х).
2. Vl+e;
l
oo a . 2M
3. С f(xN'(x—a)dxx { f(xLM*dx— { f(xLM2dxv
— oo 1 a
f „ a + T,
г г
J J
Переходя к пределу при М —>■ oo, получаем точное равенство A2).
§4

ГЛАВА VII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Простейшие дифференциальные уравнения, возникающие при рас-
рассмотрении различных физических процессов, например вытекания
воды из сосуда, радиоактивного распада, движения материальной
точки, решаются уже в основах интегрального исчисления (см., на-
например, ВМ, гл. V, VI и VII). Здесь мы познакомим читателя с не-
некоторыми общими понятиями, относящимися к дифференциальным
уравнениям, и рассмотрим отдельные классы уравнений, которые
нетрудно решить. Некоторые дальнейшие сведения о дифференциаль-
дифференциальных уравнениях содержатся в следующей главе.
Дифференциальные уравнения с одной независимой переменной
называются обыкновенными дифференциальными уравнениями. Если
независимых переменных две или больше, то в дифференциальное
уравнение входят частные производные по этим переменным. Такие
уравнения называются дифференциальными уравнениями с частными
производными.
В этой и следующей главах мы будем рассматривать только
обыкновенные дифференциальные уравнения. Нам потребуются ре-
результаты §§ VI. 1—2 и формула Эйлера из § V.3.
§ 1. Геометрический смысл дифференциального
уравнения первого порядка
Дифференциальным уравнением первого порядка называется соот-
соотношение вида
где у— неизвестная функция х. В дальнейшем мы будем считать
это уравнение разрешенным относительно производной, т. е. имею-
имеющим вид
%=/(*, у)- A)
Оказывается, что, даже не отыскивая решения у (х) аналитически,

202
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ.| VII
в виде формулы, можно составить представление об общей картине
этих решений на основе геометрического смысла уравнения A).
В этом параграфе мы рассмотрим, как это делается.
Вспомним геометрический смысл производной -j- . В плоскости х,
у для кривой у=у(х) величина ~ равна тангенсу угла наклона ка-
каУ\
Уа
0
V*
хп
сательной к кривой. Следовательно, зная
dy
зависимость -j- от переменных х, у, вы-
выраженную уравнением A), можно найти
направление касательной к кривой, яв-
являющейся графиком решения A), причем
это направление можно определить для
любой точки плоскости. Отметим, что
график решения дифференциального
уравнения называется интегральной ли-
Рис. 79.
х нией этого уравнения.
Направление касательной можно по-
показать на чертеже, проведя через лю-
любую данную точку (х; у) маленький отрезок прямой под углом t>,
удовлетворяющим условию tg-&—f(x, у)*).
Так, например, пусть jf = А+.У21 тогда f(x, y)=x2+y2.
Составим таблицу:
X
— 1
]
— 1
0
0
у
— 1
0
1
1
0
2
1
2
1
0
X
0
1
1
1
У
1
— 1
0
1
dx
1
2
1
2
На рис. 80 показаны направления касательных в каждой из де-
девяти точек, приведенных в таблице. Если на чертеже увеличивать
число точек, в которых проведено направление касательной, то на
глаз видно, как вырисовывается совокупность кривых, удовлетво-
удовлетворяющих дифференциальному уравнению. (См. рис. 81, соответствую-
*) При построении нет надобности находить угол ft и строить его. Гораздо
быстрее найти нужное направление, откладывая по оси х отрезок длины 1, а
по сси у отрезок длины -j(=(gu (рис. 79).

§1Г
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
203
щий уравнению -^=лг2+>'2-) Ясно, что уравнение имеет бесконеч-
бесконечное количество интегральных линий и через каждую точку (лг0; у0)
плоскости проходит одна такая линия. Таким образом, чтобы выде-
выделить из всех решений уравнения A) какое-то одно определенное
частное (т. е. конкретное) решение, надо задать дополнительное
условие:
при некотором лг = лг0 задано значение у=у0. B)
Это условие называется начальным условием, так как если незави-
независимой переменной служит время, то условие B) означает задание
искомой функции в начальный
момент времени.
У
'-1
1
I /
//
г
I
Рис. 80.
Рис. 81.
Хотя в начальном условии B) задаются два параметра х0 и у0,
но на самом деле при выборе частного решения уравнения A) имеется
лишь одна степень свободы. Действительно, точка (х0; у0) может
перемещаться вдоль определяемой ею интегральной линии, отчего
эта линия, конечно, не меняется. При таком перемещении имеется
одна степень свободы, которая, таким образом, для выбора инте-
интегральной линии является лишней, т. е. на самом деле при таком
выборе имеется 2—1 = 1 степень свободы (см. аналогичное рассуж-
рассуждение в § IV.8). Чтобы указать существенный параметр при этом
выборе, можно зафиксировать х0 и провести вертикальную прямую
х = х0, тогда различные интегральные кривые пересекут ее на раз-
различной высоте. Это означает, что различные кривые соответствуют
различным значениям у (хо)= у0.
Для того чтобы провести большое количество отрезков, дающих
направление касательной, удобно воспользоваться следующим при-
приемом. Построим на чертеже линии f(x, y) = C для нескольких зна-
значений постоянной С. В каждой точке такой линии, согласно A), ве-
величина tg 0 постоянна и равна С. Таким образом, все интересующие

204 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
нас отрезки, показывающие направление касательной*) в любой
точке линии f(x, у) = С, параллельны.
Линии f(x, y) = C называются изоклинами. В частности, линия
f(x, у) = 0 называется изоклиной нулей; в каждой точке этой линии
касательная к интегральным кривым уравнения A) горизонтальна.
Линия, в точках которой касательные вертикальны, называется изо-
изоклиной бесконечностей. Например, для уравнения -г = _ _ ■ изо-
изоклина бесконечностей есть прямая х—_у=1.
На рис. 81 наглядно видно, что интегральные кривые не пере-
пересекаются одна с другой, во всяком случае под ненулевым углом.
Действительно, уравнение A) показывает, что при данных х и у есть
только одно определенное значение величины -т- , т. е. через дан-
данную точку кривая может проходить только под одним определенным
наклоном. Более подробное исследование показывает, что различные
интегральные кривые не могут и соприкасаться друг с другом в ка-
какой-либо точке, если в ней правая часть уравнения A) и ее част-
частная производная по у принимают конечные значения. Таким обра-
образом, условие B) действительно определяет единственное решение
уравнения A).
Упражнения
1. Найдите изоклины уравнения ~ = х2 -\-у2.
2. Найдите уравнение геометрического места точек перегиба интегральных
кривых общего уравнения A); уравнения -¥=х2-\-у2.
§ 2. Интегрируемые типы уравнений первого порядка
Рассмотрим несколько видов дифференциальных уравнений, ре-
решения которых получить нетрудно.
I. Уравнения с разделяющимися переменными. Так называются
уравнения вида
f = <p (у).у (*)**). C)
В этом уравнении правая часть <р(у) -i|) (x) есть произведение двух
функций, одна из которых зависит только от у, а другая только от х.
*) Следует помнить, что речь идет о касательных к интегральным линиям
дифференциального уравнения -г=1 {х, у), а не о касательных к самой ли-
линии f(x, y) = C.
**) Уравнения такого вида встречаются, например, в задаче о радиоактивном
распаде и в задаче о вытекании воды из сосуда (см. ВМ, гл. V).

§ 2] ИНТЕГРИРУЕМЫЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА 205
Перепишем уравнение так:
■Н-: = гЬ (х) dx.
ф@ vv '
Проинтегрируем правую и левую части последнего равенства:
(мы пишем лишь одну произвольную постоянную, так как обе по-
постоянные, получающиеся при вычислении интегралов, можно объ-
объединить в одну). Из этого общего решения уравнения C) получаем
его частные решения, придавая С всевозможные значения. Мы ви-
видим, что в общем решении уравнения A) присутствует одна произ-
произвольная постоянная, что находится в соответствии с наличием одной
степени свободы при выборе частного решения (§ 1).
Если дополнительно задано начальное условие B), то легко найти С.
Для этого запишем для краткости формулу D) в виде
Полагая здесь лг = лг„, у = у0, получим
Ф0>.) =¥(*„) +С,
откуда
С = Ф(уо)-У(хо)
и окончательно
т. е.
Найденное частное решение можно также записать в виде
{jiL L{x)dx.
J ф (у) J Y
Уч х„
Непосредственно ясно, что это решение удовлетворяет условию B).
Выполнив фактически интегрирование, получим искомое решение.
II. Лииейиые однородные уравнения. Линейным однородным
уравнением первого порядка называется уравнение
! = /(*)>-. E)
Оно представляет собой частный случай уравнения C), но мы оста-
останавливаемся на нем особо из-за его большой важности. Проводя
в E) разделение переменных и интегрируя, получим
X
j=/(x)dx,

206' ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
в правой части мы записали произвольную постоянную в форме In С
для удобства дальнейших выкладок. Отсюда находим у
X
/ f (Jt) dx
У=Сеа , F)
где а — какое-либо фиксированное значение х. Формула F) дает
общее решение уравнения E).
Обозначим для краткости
X
/ ! (х) dx
у1 (х) = е« . G)
Так как эта функция получается из F) при С=\, то она пред-
представляет собой частное решение уравнения E). Формулу F) можно
записать в виде
У = Су,(х). (8)
Легко и непосредственно проверить, что если ух (х) представляет
собой какое-то частное решение уравнения E), то и функция (8)
при любом постоянном С также удовлетворяет уравнению E):
dx j \ > j\ j \ > J
dx dx dx
Таким образом, чтобы получить общее решение уравнения E),
надо взять какое-либо одно его частное решение и умножить это
частное решение на произвольную постоянную. Полагая, в частно-
частности, С=0, мы видим, что одно из частных решений уравнения E)
представляет собой тождественный нуль; конечно, это нулевое ре-
решение непригодно для построения общего решения.
111. Лииейиые неоднородные уравнения. Линейное неоднородное
уравнение первого порядка имеет вид
%=f{x)y + g(x)*). (9)
Будем искать то решение уравнения (9), которое обращается в нуль
при некотором значении лг = лг0. При зафиксированной функции f(x)
это решение у (х) определяется выбором функции g(x), т. е; g (x)
можно истолковывать как некое внешнее воздействие, а у(х) — как
*) Такое уравнение встречается, например, в задаче о радиоактивном се-
семействе (см. ВД1, гл. V). В этой задаче независимой переменной л: служит время,
а функцией у—количество данного радиоактивного вещества в системе, так что
искомое решение у (х) описывает закон изменения этого количества во времени.
Коэффициент f (х) равен отрицательной постоянной, абсолютная величина ко-
которой представляет собой вероятность распада данного вещества в единицу
времени, а свободный член g(x) равен скорости ввода этого вещества в рас-
рассматриваемую систему.

§ 2] ИНТЕГРИРУЕМЫЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА 207
его результат (другими словами, закон, по которому функции g(x)
сопоставляется решение у(х), является оператором, см. § VI.2),
Легко проверить, что при этом имеет место принцип суперпозиции,
т. е. если функции g(x) складываются, то и соответствующие ре-
решения складываются. В самом деле, если
причем у1(х0) = 0, у2(х0) = 0, то функция у—-ух (х) -\-уг (лт) удовлет-
удовлетворяет уравнению
и условию у(х0) = 0 (почему?).
На основании § VI.2 решение уравнения (9) можно получить
с помощью построения соответствующей функции влияния G(x; £),
которая служит решением уравнения
%=/(х)у + 8(х-1) A0)
при любом фиксированном \. Будем считать, что \ > х0; тогда при
•^о < х <С I уравнение A0) превращается в E), т. е. решение имеет
вид (8), но так как ищется решение, для которого у (х0) = 0, то
С—0, т. е. у (х) 53 0. Если, далее, проинтегрировать уравнение A0)
от х=\ — 0 до лг = | + О, то мы получим
1+0 1+0
У(Ъ + 0)—у&-0)= J f(x)ydx+ J
l-o
(так как решение у остается конечным, то интеграл от первого сла-
слагаемого в правой части A0) по бесконечно малому промежутку бе-
бесконечно мал и им можно пренебречь). Но согласно только что до-
доказанному у (^ — 0) = 0; отсюда
\. (И)
Однако при х > Ъ, уравнение A0) также превращается в E) и по-
потому имеет решение (8); условие A1) дает
т.е.
Итак, в данной задаче функция Грина имеет вид
С 0 (хо<х<1),
График функции G(x; .£) при фиксированном | показан на рис. 82
жирной линией, имеющей разрыв при * = £.

208 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ : [ГЛ. VII
Теперь можно написать искомое решение уравнения (9) при лю-
любой функции g{x) на основе соответствующим образом преобразо-
преобразованной общей формулы (VI.8):
; Ъ) g(t)d%+§ G(x; l
0
где функция yt (x) дается формулой G). Аналогично можно прове-
проверить, что та же окончательная формула A2) справедлива и при
х < х0. Отметим, что в се правой части можно вынести _у, (лг) (но не
ул (£)!) из-под знака интеграла.
У Особенно часто пользуются последней
формулой при лго = —оо, что физически
наиболее естественно. Тогда решение
A2) обладает тем' свойством, что если
функция g(x) тождественно равна нулю
до некоторого х, то и решение тождест-
£, х венно равно нулю до этого х. Таким обра-
образом, в этом случае формула A2) дает в
Рис 82. каком-то смысле «чистый» результат воз-
воздействия функции g(x).
Формула A2) дает частное решение уравнения (9) — именно то,
которое при лг = лг0 обращается в нуль. Чтобы получить общее ре-
решение уравнения (9), заметим, что разность двух любых решений
этого уравнения удовлетворяет соответствующему однородному урав-
уравнению E): если
то
(почему?). Значит, эта разность должна иметь вид (8), где С про-
произвольно. Итак, общее решение линейного неоднородного уравнения
представляет собой сумму какого-либо его частного решения и об-
общего решения соответствующего однородного уравнения. Выбирая
в качестве этого частного решения найденное нами решение A2),
получаем общее решение уравнения (9) в форме

2J» ИНТЕГРИРУЕМЫЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА 209
интересует частное решение, удовлетворяющее условию B),
к подставляя в A3) х = х0, находим
" * = <> + <:,, (*.), т. е. С =
"окончательно получаем искомое решение
К тем же результатам можно прийти другим путем, с помощью
лее быстрого, но искусственного способа «вариации произвольной
"стоянной». Выдающийся французский математик и механик Ла-
~анж предложил, исходя из формулы (8), искать решение уравне-
"Я (9) в форме
"-'•'■ У = и(х)у1(х), A4)
fce к (лг)— некоторая неизвестная функция, а ух(х) имеет прежний
5лысл G). Подставляя A4) в (9), получаем
,о так как у1 представляет собой решение однородного уравнения,
) первые слагаемые слева и справа взаимно уничтожаются, и мы
^лучаем
откуда «' =
. последнем интеграле мы заменили обозначение переменной инте-
рирования на |, чтобы отличить его от верхнего предела). Под-
.гавляя полученный результат в A4), приходим к формуле A3).
IV. Простые случаи линейных уравнений. Имеются случаи, когда
№шение линейного уравнения выглядит особенно просто. Так будет,
ч частности, если коэффициент /(лг) постоянный:
J f(x)?=p = const.
Тогда однородное уравнение E) имеет вид
и общее решение
у = СеР*, A5)
"то можно получить из формул G) и (8), приняв для простоты а = 0,
но легко получить и непосредственно с помощью разделения пере-
переменных или простой подстановкой.

210 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
Соответствующее неоднородное уравнение особенно просто ре-
решается, если свободный член, т. е. g(x), представляет собой по-
постоянную или экспоненту (показательную функцию). Рассмотрим
сначала уравнение
fx=py + A (Л-const). ■ A6)
Как мы знаем, для получения его общего решения надо найти ка-
какое-либо его частное решение, а затем сложить результат с общим
решением A5) соответствующего однородного уравнения. Однако
частное решение уравнения A6) легко разыскать вформе.у = 5 = const.
Подставляя в A6), получаем
, т. е. В = — — .
Итак, общее решение уравнения A6) имеет вид
Рассмотрим теперь уравнение
d£=py+Ae><x. A7)
Производная от показательной функции пропорциональна самой
функции; поэтому естественно искать частное решение уравнения A7)
в форме
у = Ве"х, A8)
так как тогда после подстановки в A7) все члены будут подобными,
и возникает надежда добиться равенства с помощью подбора В.
Проделаем это:
Bkekx —рВекх + Ае"х.
д
Отсюда легко находим 5 = г ■ Подставляя в A8), получаем част-
к — р
ное решение уравнения A7), а после добавления общего решения
соответствующего однородного уравнения — общее решение уравне-
уравнения A7):
y = re
* k — p
где С—произвольная постоянная.
Полученное решение, очевидно, непригодно, если k — p. В этом
особом случае решение уравнения A7) найдем с помощью общей
формулы A3), заметив, что в рассматриваемом случае частное ре-
решение _yt (лг) однородного уравнения равно е?х. Получим, приняв для

g,2]- ИНТЕГРИРУЕМЫЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА 211
простоты х0 = О,
• X X
. у= Гe—Aertdl + CePx = AePx {dl + CeP* = АхеРх+ СеР*. A9)
J eP- J
о о
Итак, для k=p в частном решении при экспоненте появляется до-
дополнительный множитель х.
Общее неоднородное уравнение
решается с помощью функции Грина, которая в данном случае
имеет особенно простой вид
( О (лг0 < х < £),
G(x; £)= еР1 = ери^) g
^ еРг-
Общее решение в силу формулы A3) имеет вид
Рассмотренными здесь уравнениями не исчерпываются типы урав-
уравнений, решения которых могут быть записаны в виде точных фор-
формул, содержащих элементарные функции и интегралы от них.
В курсах дифференциальных уравнений можно найти еще несколько
таких типов; наиболее полно они рассмотрены в книге Э. Камке
«Справочник по обыкновенным дифференциальным уравнениям»,
«Наука», 1971.
Упражнения
Найдите решения следующих дифференциальных уравнений, удовлетворяю-
удовлетворяющие указанным начальным данным.
\.-~=2ху, у—\ при х = 0.
2.^=У-, у=\ при *=1.
их х р
3. ^- = е-У, у=\ при х = 0.
dx
4. j- = — , у=\ при х = 0.
dx у
5- j-x=— У + ех, у = — при х=\.
6. ^=-2(/ + 4д;, у= — 2 при лг =
7. Jx + y = cosx, y = -£ при х = 0.

212 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. V[i
§ 3. Линейные однородные уравнения второго порядка
с постоянными коэффициентами
Дифференциальное уравнение второго порядка содержит вторую
производную от искомой функции; его общий вид таков:
dy dly\ n
х, v, -г , -Л =0.
' ' ' dx dx2 j
Если это уравнение зависит от искомой функции и ее производных
линейно (зависимость от х может быть любой), то оно называется
линейным. Таким образом, линейное уравнение второго порядки
имеет общий вид
Мы рассмотрим наиболее важный частный случай, когда коэф-
коэффициенты а, Ь, с при искомой функции и ее производных являются
постоянными. Такое уравнение встречается в задачах о механиче-
механических и электрических колебаниях (см., например, ВМ, гл. VI и VIII),
причем в этих задачах независимой переменной служит время t.
Мы остановимся на рассмотрении механических колебаний простей-
простейшего осциллятора; тогда уравнение имеет вид
*
mQ + hft+ky=f(t), B0)
где у— отклонение колеблющейся точки от положения равновесия,
ш — ее масса, h — коэффициент трения (считается, что сила трения
пропорциональна скорости), k—коэффициент упругости восстанав-
восстанавливающей силы (эта сила принимается пропорциональной отклонению)
и f{t) — внешняя сила*).
Рассмотрим сначала уравнение свободных колебаний; оно име-
имеет вид
и называется линейным однородным уравнением. Его свойства во
многом аналогичны свойствам линейного однородного уравнения
первого порядка, разобранным в § 2. Так, легко проверить, что
если у1(() — какое-либо частное решение уравнения B1), то и
Cy1{t), где С—любая постоянная, также служит решением того же
уравнения. В частности, при С=0 получаем тождественно нулевое
решение уравнения B1). Кроме того, легко проверить, что если
.У»-(О и Уг @ — Два частных решения уравнения B1), то их сумма
*) При этом нам придется частично повторить результаты из гл. VI ВМ,
однако здесь изложение будет более полным и будет проводиться с более
общих позиций.

3] ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 213
р = _у1 (/) -Н^а (/) также служит решением того же уравнения (про-
1ерьте, подставив эту сумму в B1)!).
Из сказанного следует, что если найдены два частных решения
~x(t) и у.г(() уравнения B1), то их линейная комбинация
t), ' B2)
j-де С, и С2 — произвольные постоянные, также служит решением
того же уравнения. Но общее решение дифференциального уравне-
уравнения второго порядка получается в результате двух интегрирований
■потому содержит в себе две произвольные постоянные. Значит,
выражение B2) служит общим решением уравнения B1). Конечно,
при этом yt (t) и уг (t) не должны быть пропорциональными, так как
■«ели yi(t) = kyl(t), то
СхУ, @ + СгУг @ = (Сх + Ctk)y, (/) = Су, (t),
[.т. е., по существу, здесь имеется только одна произвольная по-
постоянная (не выполнено условие существенности параметров, ср.
« IV.8).
;: Как же найти два «независимых» решения уравнения B1)? Эйлер,
основываясь на свойстве пропорциональности экспоненты своим про-
ь-изводным, предложил искать частные решения в виде
У=е", B3)
где р— некоторая постоянная, которую нужно определить. Так как
■йри таком выборе -^=ре"', ^=Р2ер11 то после подстановки в B1)
и сокращения на е>>' получаем для определения р квадратное урав-
уравнение (так называемое характеристическое уравнение)
'■-' mp* + hp-\~k=0. B4)
- Как известно из алгебры, при решении квадратного уравнения
могут представиться различные случаи в зависимости от знака
. дискриминанта
' Если трение велико, точнее, если А2 > 4mk, то уравнение B4)
- имеет вещественные корни
_ —h± Y¥—
Pi, 2— чт
Обозначим их pt =—а, р2=—Ь, так как они оба отрицательные.
Тогда на основе B2) и B3) получаем общее решение уравнения
B1) в виде
y = Cle-at + C,e-t>t, B5)
где С, и С2—некоторые постоянные. Таким образом, при большом

214 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. Vlj
трении отклонение точки от положения равновесия с возрастанием *
стремится к нулю по экспоненциальному закону, без колебаний.
Если трение мало, точнее, если А2 < Атк, то уравнение B4)
имеет мнимые сопряженные корни
h f k hl
где обозначено у — ~—, со= 1/ -г—5. Имея в виду B3), пол\-
чаем общее решение B2)
v — р p—yt+imt i /"> p-y<-iu>t р~т' 1С о'ш? _1- ^° «"'и') /Of?\
Множители etu>t и е~'1иЛ, как выяснено в § V.4, являются периоди
ческими функциями. Их период равен Т=—-. Поэтому со есть кру-
круговая частота колебаний. Множитель е~т* характеризует скорость
затухания колебаний. Выражение B6) будет решением уравнения
B1) при любых постоянных Сх и С2. Для того чтобы получить ве-
вещественное решение, возьмем любое C1=-^-retf и положим С2 =
= -1/•<;-'¥= С*. Тогда
y = e-it (^-ге^еш+^ге-^е-!шЛ =1.ге~^ [е1 ы+^ + е'1' {шг+^].
Воспользуемся формулой Эйлера. Получим
V =-»-ге~т* [cos (со^4" ф) 4- ^sl'n (ft>^4" ф) 4" cos (cot 4"ф) —
— / sin (cor 4- ф)] = re~il cos (cot 4~ Ф).
Решение у = re~f{ cos (со^+ф) — вещественное, оно содержит две
произвольные постоянные г и ср. Иногда его записывают в ином
виде, раскрыв косинус суммы:
у = re~f' (cosсо?1 cos cp — sin со/ sin ф) =
= (г cos ф) е~1* cos со/+ (— г sin<$) e~i' sin at —
= Cje~T; cosco/4-C2e~Tf sinco/,
где через Сх и С, обозначены соответствующие множители в скоб-
скобках (они не равны Сх и С2 в формуле B6)!). Здесь хорошо видны
вещественные независимые решения уравнения B1) (см. формулу B2)).
Обычно эк/г переход к вещественному решению проводят быст-
быстрее, исходя из следующих соображений. Если в левую часть урав-
уравнения B1) подставить комплексную функцию от вещественного
аргумента / и произвести все действия, то в силу указанных в § V.5
свойств таких функций те же действия пропзведутся над вещест-
вещественной, а также над мнимой частями этой функции. Поэтому если

§ 3] ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 215
после выполнения этих действий над комплексной функцией полу-
получится нуль, то и после выполнения действий над вещественной
частью этой функции получится нуль, то же и над мнимой. Таким
образом, если имеется комплексное решение B3) уравнения B1), то
вещественная и мнимая части решения также являются решениями
уравнения B1).
Отметим, что последнее утверждение справедливо для любого
линейного однородного уравнения (т. е. уравнения, в которое у и
его производные входят линейно, причем в уравнении нет члена, не
содержащего ни у, ни какой-нибудь его производной) с веществен-
вещественными коэффициентами. Если же у или его производные входят в
уравнение нелинейно, то это утверждение неверно. Поэтому, например,
если квадратное уравнение имеет два мнимых корня, то веществен-
вещественная и мнимая части корней не являются в отдельности корнями
этого уравнения.
Итак, когда трение мало, колебания затухают по экспоненциаль-
экспоненциальному закону. Особое значение имеет случай, когда трение отсутст-
отсутствует, т. е. А=-0. В этом случае характеристическое уравнение B4)
приобретает вид
откуда
Px,z = ±i У ~-
Решение дифференциального уравнения имеет вид
у = С1еш-\-Сге~ш = г cos (со/4-ф). где со •= 1/ ~ , B7)
т. е. в рассматриваемой системе происходят незатухающие гармони-
гармонические колебания с произвольными амплитудой и начальной фазой
и вполне определенной частотой со= 1/ —.
Интересно проследить за поведением полной энергии системы.
Нетрудно показать (см., например, ВМ, § VI. 10), что эта энергия
имеет выражение
+ [[) +* B8)
причем в npnnofi части первое слагаемое равно кинетической, а вто-
второе— поте-.;;:;; мной энергии осциллятора. Подставив сюда форму-
формулу B7) .■■ля решения, получим
Е = -н- пко-r'2 sin2 (со/ + ф) + у kr- cos2 (со/ + ср) == — kr2.
Таким образом, в случае /г = 0 полная энергия остается постоянной
и в процессе колебаний происходит только «перекачка» кинетиче-
кинетической энер!ни в потенциальную и обратно.

216 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
Если трение имеется, то полная энергия системы убывает, рас-
рассеивается (переходит в тепло, которое в дифференциальном урав-
уравнении не учитывается). Действительно, дифференцируя формулу B8>
и используя дифференциальное уравнение B1), найдем
производная отрицательна, следовательно, Е убывает.
В реальных задачах нас интересует не общее решение, а вполне
определенное частное решение. Так как в общем решении ■ диффе-
дифференциал ького уравнения второго порядка имеются две произвольные
постоянные (т. е. две степени свободы), то для выбора частного
решения требуется задать два дополнительных соотношения, с по-
помощью которых и находим значения этих произвольных постоян-
постоянных. Обычно в качестве таких дополнительных условий задаются
так называемые начальные условия, а именно, при некотором зна-
значении независимой переменной задаются значения искомой функции
и ее производной.
Для уравнения B1) начальные условия состоят в задании зна-
значений
:,о=»., B9)
т, е. начального отклонения и начальной скорости колеблющейся
точки. Из физических соображений ясно, что эти условия полностью
определяют процесс колебаний. Это легко доказать и .математи-
.математически. Рассмотрим, например, случай большого трения, когда общее
решение имеет вид B5). Дифференцируя это решение и подставляя
t — t0, на основании B9) получим
— Су ae~at°—C2be~bt° = v0,
откуда- находим для Су и Сг вполне определенные значения
Г c
Ч~ Ь-а е > Ч - a_b e ■
Подставив эти значения в B5), получим искомое частное решение,
удовлетворяющее условиям B9):
bye + v0 I t
s b—a ~
c
b—a a—b
be-a(.t-t0)_ae-b{t-ta) e-a(t-ta)—e-bif-ta)
Формула C0) дает возможность рассмотреть еще не разобранный
промежуточный случай, когда A2 = 4mk и потому характеристическое
уравнение B4) имеет совпадающие корни pli2=—а. Тогда реше-

§ 4] ПРОСТЕЙШЕЕ ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ 217
ние B5) не является общим, так как Сге~аг -\- C2e~at = (Cl-{-C2) e~ai~
= Ce~at, т. е. здесь, по существу, имеется лишь одна степень сво-
свободы, а не две, как требуется. Если в формуле C0) совершить
переход к пределу при b—>-а, то, воспользовавшись правилом Ло-
питаля (см., например, ВМ, § П.21), получим в пределе решение
=Уое-° «-Ui + {ayo+Vo) {t_to) е-а ,/-/„>. C1)
Мы видим, что здесь в решении появляется член вида te~at. При
возрастании t этот член стремится к нулю, так как показательная
функция стремится к нулю быстрее, чем любая степень t стремится
к бесконечности (см. там же). Таким образом, и в данном случае
происходит затухание без колебаний.
Если заметить, что начальные условия произвольны, и перегруп-
перегруппировать слагаемые в правой части C1), то можно записать общее
решение уравнения B1) в данном промежуточном случае в виде
Упражнения
Найдите решения следующих дифференциальных уравнений, удовлетворяю-
удовлетворяющие указанным начальным данным:
0, у = 0, у'=-2 при /=■£.
2. 4у"—8у' + 5у = 0, у = 0, y'=-j ПРИ '=
3.
4.
5.
6.
у"—у=о.
у"+4у' + 4у = 0.
У = 2,
У == 4
У = Ъ,
У'
у'
у'
у'
= 3
= —2
= й
=3
при
при
при
при
/ = 0.
/ = 0.
/ = 1.
/ = 0.
§ 4. Простейшее линейное неоднородное уравнение
второго порядка
Перейдем к рассмотрению уравнения вынужденных колебаний B0).
Прежде всего надо заметить, что рассуждения § 2 о связи решений
неоднородного уравнения с решениями соответствующего однород-
однородного уравнения остаются здесь в силе; поэтому общее решение
уравнения B0) имеет вид
y=Y (x) + €,у, (х) -f C,y., (х),
где Y(x) — некоторое его частное решение, а С1у1 (лг) + Сгуг (лг) —
общее решение соответствующего однородного уравнения B1).
Частное решение уравнения B0) можно подобно § 2 построить
с помощью функции Грина. Рассмотрим сначала самый простой слу-
случай, когда /г = А = О, т. е. когда уравнение B0) имеет вид
$ C2)

218 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
это означает, что тело движется под действием силы, зависимость
которой от времени задана. Найдем решение, удовлетворяющее ну-
нулевым начальным условиям:
-О, v-dt
/=/.
= 0*). C3)
Как и в § 2 (см. начало раздела III), убеждаемся, что решение
у (t) полностью определяется заданием функции f(t), причем имеет
место принцип суперпозиции. Значит, на основании общей методики
§ VI.2 можно построить функцию Грина, решив уравнение
m^ = b{t—x) C4)
при любом зафиксированном т и начальных условиях C3). Будем
считать для определенности, что t > t0. Тогда в промежутке от tg
до т правая часть уравнения C4) равна нулю, а потому при нуле-
нулевых условиях C3) и решение равно нулю. Проинтегрировав урав-
уравнение C4) от т—0 до т+О**), получим
dy
4
_dy
т+о dt
т-0
и du
Но в силу только что доказанного -^
т-0
1
1
=0, откуда
Ч, =-• C5)
dt т + О т
Мы видим, что при t = -z производная -~| имеет конечный разрыв
(конечный скачок); поэтому сама функция у (t) при t — j разрыва
не имеет, т. е.
.у|т+о=.Нт-о=О. C6)
d'}u
Однако при ^>т уравнение C4) имеет вид т~ = 0, т. е.
с-~ = 0, и нам нужно найти решение этого уравнения при началь-
начальных условиях C5) и C6). Нетрудно непосредственно проверить, что
всем этим требованиям удовлетворяет функция у = — (t—т). Итак,
мы получаем функцию Грина для рассматриваемой задами
{ 0 (to<t<T),
*) Здесь можно принять /0=—со, что во многих задачах наиболее фи-
физически естественно (ср. § 2). Мы, однако, оставляем произвольнее t0 для пе-
перехода к дальнейшемI, так как при /0 = — со неудобно задавать ненулевые
начальные условия.
**) См. это обозначение в сноске на стр. 195.

i
§ 4] ПРОСТЕЙШЕЕ ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ 219
(То, что эта непрерывная функция с «изломом»-при t — x удовлет-
удовлетворяет уравнению C4), вытекает также из рассмотрений § VI.3; см.
рис. 76, где изображена функция, вторая производная которой равна
8 (лг).) В силу общей формулы (VI.8), примененной к данному слу-
случаю, получаем искомое решение уравнения C2) при начальных усло-
условиях C3):
C8)
Вывод формулы для решения закончен, и желающие могут сразу
перейти к § 5, где разбирается общее уравнение вынужденных ко-
колебаний. Однако мы здесь сделаем еще несколько замечаний по по-
поводу разбираемого здесь частного случая.
Функцию Грина C7), а с ней и формулу C8) можно получить
и непосредственно из физических соображений. В самом деле, урав-
уравнение C4), определяющее функцию Грина, означает, что на тело,
которое в начальный момент находилось в начале координат и было
неподвижным, в момент т подействовала мгновенная сила с единич-
единичным импульсом (см. конец § VI.1). Но после действия кратковре-
кратковременной силы тело движется с постоянной скоростью, равной отно-
отношению импульса силы к массе тела (см., например, ВМ, § VI.5),
т. е. в данном случае ■—-. Поэтому y(t), т. е. пройденный путь,
выражается как раз по формулам C7).
Формулу C8) можно получить и без упоминания о функции
Грина, хотя, по существу, тем же методом. Для этого достаточно
мысленно представить силу / на промежутке от t0 до t как после-
последовательность кратковременных сил, каждая из которых действует
на некотором промежутке от т до т+Л и потому имеет импульс
f(x)dx. Если бы действовала только эта кратковременная сила, то
тело набрало бы скорость ——- и к моменту t прошло бы путь
^~r). C9)
Однако в силу линейности уравнения C2) имеет место принцип
суперпозиции, другими словами, принцип сложения движений, согласно
которому при наложении нескольких сил законы движения также
складываются. Поэтому результаты C9) надо сложить по всем т от
t0 до t, т. е. мы приходим к формуле C8).
Выведем теперь формулу C8) совсем иным путем, с помощью
двукратного интегрирования формулы C2). Первое интегрирование

220
дает
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[Г,Ч. V1J
или, с учетом второго условия C3),
' (t) = \f(t)dt.
ту' (t) =
В этой формуле переменная интегрирования обозначена той же бук-
буквой /, что и верхний предел. Обычно такие обозначения не приводят
к недоразумениям; однако сейчас нам
удобнее применить более аккуратное
обозначение
D0)
t
ч
0
'I
d
F)
\ и
I
I
t0 t t,
ny'(t) = \/(x)dx,
Рис. 83.
в котором строго различается переменная
интегрирования т от верхнего предела t:
скорость тела в момент времени t зависит
от значений силы во все предыдущие
моменты т, т. е. зависит.от /(т), где т
принимает все значения от t0 до t. (Такое
различение совершенно необходимо в формуле C8), где в подынтег-
подынтегральное выражение входит разность t—т.)
Вновь интегрируя формулу D0), получаем с учетом первого
условия C3)
ту (t) =
Получился двукратный интеграл (ср. § IV.7), в котором переменная
/j внешнего интегрирования меняется от /„ до t, а при каждом t1
переменная т внутреннего интегрирования меняется от т=/0 до
x=t1. Таким образом, интегрирование производится по треуголь-
треугольнику (а), показанному на рис. 83. Однако, как известно, двойной
интеграл можно вычислять и в противоположном порядке, сначала
по tv а затем по т. Тогда интегрирование по tl будет произво-
производиться при фиксированном т от t1—x до fx = t (см. рис. 83),
а внешнее интегрирование по т—от t0 до t\ в результате получаем
(О)
Но из-под знака внутреннего интеграла можно вынести /(т), не

§ 4] ПРОСТЕЙШЕЕ ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ 221
зависящее от переменной интегрирования tlt так что
t t t
ту (О- J dx/(x) J dt,= \ dx-/(x) (t—t),
и мы приходим к формуле C8).
Проверим, что формула C8) действительно дает решение постав-
поставленной задачи; это будет также полезным упражнением на диффе-
дифференцирование. Мы будем исходить из двух формул. Первая
J D1)
[f{s\ t) ds) = ^ Ft (s; t)ds (a, £ = const) D2)
(производная интеграла по верхнему пределу) хорошо известна из
интегрального исчисления, вторая формула
d_
dt
(производная интеграла по параметру) была указана в § Ш.6. Но
как найти производную от правой части C8), куда t входит и в качестве
предела интегрирования и в качестве параметра под знак интеграла?
Для этого надо взять сумму двух слагаемых, одно из которых
получается в результате дифференцирования интеграла C8) при
зафиксированном t под знаком интеграла, .а другое — при зафикси-
зафиксированном t в верхнем пределе (ср., например, ВМ, § П.4). Диффе-
Дифференцирование производится по формулам D1) и D2):
t t
dt
D3)
При вторичном дифференцировании пользуемся формулой D1), т. е.
dt* m J y '•
Отсюда вытекает, что уравнение C2) удовлетворяется. Справедли-
Справедливость условий C3) получится, если в формулах C8) и D3) поло-
положить t = t0.
В качестве примера найдем закон движения тела, на которое
действует сила, пропорциональная времени, протекшему с начала
движения. В этом случае f(t) = a(t — ^0), поэтому /(х) = а(т—10).
Получаем
/_/ \У — *«? а
»' 2 т 3 ~ 6т

222 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ' [ГЛ. VII
Мы решили задачу с нулевыми начальными данными. Это — самая
важная часть дела, так как если мы умеем решать задачу с нуле-
нулевыми начальными данными, то решение задачи с произвольными
начальными данными _у=_у0, г> = г>0 при t*=t0 не представляет труда.
Действительно, пусть
d2u
-^Г =/('), У=Уо, v = v0 при t=t0.
Тогда
где ya)(t) есть решение задачи с нулевыми начальными дан-
данными:
-о,
а _уB) (t) есть решение задачи без силы
(Читатель легко проверит, что _у = у1>-|-У2) является решением
поставленной задачи.) Функцию _у12) @ найти просто, yl2)(t) =
= г>о(*—*о)+Уо, поэтому
Исследуем решение C8), отвечающее нулевым начальным усло-
условиям, приняв для простоты t0 = —оо. Для этого запишем его так:
Так как t не есть переменная интегрирования, то ее можно вынести
за знак интеграла, поэтому
Эту формулу на основании D3) можно переписать так:
t

§ 4]
ПРОСТЕЙШЕЕ ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНР.НИР.
223
Вынесем v(t) за скобку, получим
y{t)=v{t)-{t—%
где положено
t t
xf (т) dx J т/ (т) с(т ;
-"■Г ,a,@ = 4-i/(x)dt.
т
v(t)
J / (т) Л
Записанные таким образом формулы особенно удобны, если сила по
прошествии некоторого промежутка времени перестает действо-
действовать. Для моментов времени t после
окончания действия силы интегралы <>\
t t
\т/(т) dx и \/(т) йт не зависят от t. Уве-
— да — со
личение t в этих интегралах приводит
только к увеличению той части области О
интегрирования, где подынтегральная функ- S"
ция равна нулю. После окончания действия
силы тело движется с постоянной скоростью
■» = г>кон, при этом величина 9 = 9КОН также
постоянна. Поэтому график y(t) после окончания действия силы
есть прямая линия
'km.
Рис. 84.
Величина 9КОН есть абсцисса точки пересечения этой прямой с осью t
(рис. 84). Физический смысл величины 0КОН таков: если тело начнет
движение в момент времени ^ =
со скоростью v—vK0W то оно
будет двигаться по тому же закону, по которому фактически дви-
движется тело после окончания действия силы.
Упражнения
Найдите решения следующих дифференциальных уравнений, удовлетворяю-
удовлетворяющие указанным начальным данным:
2. ^ = 1, *@) = -2.
3. i?l = sin/. *@) = 0,
) = 0.
4.
di*
(— эо) = 0,

224 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ГЛ. VII
§ 5. Линейные неоднородные уравнения второго порядка
с постоянными коэффициентами
Функцию Грина можно применить и к общему уравнению B0),
описывающему движение упруго закрепленного тела под действием
внешней силы, зависящей только от времени, при наличии трения,
пропорционального скорости.
Как и в § 4, будем искать решение при нулевых начальных
условиях C3). Для построения функции Грина нужно подобно § 4
(см. уравнение C4)) решить уравнение
m^ + h^ + ky^bit-T) D4)
при начальных условиях C3). Считая t > t0, получаем, что y(t)^sO
при t0 < t < т, а интегрируя D4) от t = -z — 0 до / = т+0, прихо-
приходим к тем же условиям C5) и C6), так как интегралы от конечных
второго и третьего слагаемых в D4) равны нулю. Таким образом,
при ^>т требуется найти решение однородного уравнения B1) при
начальных условиях C5) и C6). Исходя из общего решения уравне-
уравнения B1)
у = С^' + СгС'',
где рх и />2 — корни характеристического уравнения B4), и рассуж-
рассуждая подобно кониу § 3, получаем искомое решение
' m(Pi-Pi) т{Рг—Р\) ™ (Pi—/>■>)
это решение пригодно как для малого, так и для большого трения.
Итак, получаем функцию Грина
{ 0 \h<t< т),
G(t; т)= j _i TePllt-i)_ePtti-in (X < t < ос).
(Эта функция, как и в условиях § 4, непрерывна, но имеет при
t = j излом.) Отсюда подобно C8) получаем решение уравнения B0)
при нулевых начальных условиях C3)
*/т. D5)
,
р2) J
Как и в § 1 (раздел IV), при внешней нагрузке особенно про-
простого вида решение уравнения B0) можно найти без всякой функ-
функции Грина. Так будет, если f{t) = const, т. е. если рассматривается
уравнение
5^=л (=const)- D6)

§ 5] ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 225
Нетрудно разыскать частное решение вида у = В = const. Подстав-
Подставляя в D6), получим
0-\-0+kB = A, т. е. В = ~.
Учитывая замечание, сделанное в начале § 4, получаем общее ре-
решение уравнения D6)
.y = JJ-+C1eP.'+C9eP«', _ D7)
где Сг и С2—произвольные постоянные, определяемые из началь-
начальных условий. В § 3 мы видели, что решение однородного уравне-
уравнения B1) при возрастании t стремится к нулю, так как р1 и р,—
либо отрицательные вещественные, либо- мнимые с отрицательной
вещественной частью; таким образом, из D7) получаем при больших t
_у = 4- D8)
Этот результат ясен и физически. При постоянной внешней силе и
при наличии трения колебания затухают и по прошествии «пере-
«переходного процесса», определяемого начальными условиями, тело
остановится в положении-, где сила упругости ky (взятая с обратным
знаком) будет равна внешней силе А; отсюда н получаем D8). Это
стационарное положение уже не зависит от начальных условий.
Простым является и решение уравнения
т~Ж + к ~k + ky = Aeit. {щ
В этом случае легко найти частное решение вида у = Ве^. Под-
Подставляя, получаем mBq2e'>t-\-liBqe4t+kBe4t~Ae'>t, т. е. В=—г—у—— ,
tlXCf ' -у- flCj ~~|— к
откуда искомое частное решение имеет вид
E0)
Это решение непригодно, если q является корнем характеристиче-
характеристического уравнения B4), так как тогда знаменатель обращается в нуль.
Подобно § 2 можно, исходя из общей формулы D5), показать, что
в этом особом случае уравнение D9) имеет частное решение вида Btegt.
Рассмотрим, наконец, решение уравнения
W5+Alf +ky = Asinat. E1)
Здесь можно воспользоваться тем, что в силу формулы Эйлера пра-
правая часть является мнимой частью функции Ae!mt. Значит,
8 Я. Б. Зельдович, А: Д. Мышкно

226 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
достаточно решить уравнение
а у полученного решения взять мнимую часть (см. аналогичные
рассуждения в § V.5). На основании E0) получаем комплексное
решение
=3 е =
т (iw)~-\-hio)-{-k к—тсо'2-)- iha>
A\(k — ты1)— thai]
= T J
Отсюда легко выделить мнимую часть, т. е. частное решение урав-
уравнения E1)
у = —, ,., ,,.,., \{k — /wco2)sinuj^ — ha cos соЛ. E2)
Чтобы получить общее решение уравнения E1), надо к найденному
частному решению E2) добавить общее решение соответствующего
однородного уравнения. Но так как каждое из решений однород-
однородного уравнения при возрастании t стремится к нулю, то после
переходного процесса тело начинает колебаться по гармоническому
закону E2), не зависящему от начальных условий. Это стационар-
стационарное решение можно было найти и по методам § V.5.
Остановимся особо на случае, когда трение отсутствует, т. е.
уравнение B0) заменяется на
m^ + ky=f(t). E3)
В этом случае характеристическое уравнение имеет корни рь 2 =+гсо0,
где
й)»=
— частота свободных колебаний системы, т. е. колебаний без внеш-
внешней силы. Формула D5), преобразованная по формуле Эйлера, дает
решение при нулевых начальных условиях C3)
1
у =—J— Г \еш° <'~x> — е-"°° <'~х> ]/(x)dx =
J m-2i(o0 J l и \ i
I
(Проверьте с помощью дифференцирования, что правая часть дей-
действительно удовлетворяет уравнению E3) и начальным условиям C3).)

§ 5] ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 227
Пользуясь формулой
sin соо (t — т) = sin u>ot • cos <вот — sin со0х- cos coot,
перепишем решение в виде
i t
y(t)= — sin (o0t • J/(х) cos соо т dx — — cos су • ] /(т) sin con x dr.
h U
Если по истечении некоторого промежутка времени tx действие
силы f(t) прекращается, то интегралы в этой формуле перестают
зависеть от времени при t > tx и решение принимает вид
у (t) = acos(>Ht-\-bsinaj, если t > tlt
где
к
fi) cos
а = \ /(т) sin conxrfx, b= \ fix)
t U
Таким образом, если первоначально тело покоилось, затем в тече-
течение некоторого времени на него действовала внешняя сила f(t), то
но окончании действия силы тело будет совершать свободные коле-
колебания с частотой <в0 и амплитудой "j,/aa_j_^a_
Формулу E4) можно записать иначе, введя «комплексное откло-
отклонение от положения равновесия»
t t
w(t) = (VM<'-T>/(x)dx
o J
U U
для которого вещественное отклонение y(t) служит мнимой частью.
Если t0 — начальный момент действия силы, то формулу можно пе-
переписать в виде
w (t) = ■
так как при этом преобразовании к интегралу добавляется часть,
равная нулю. Если сила действует только до некоторого момента ti
времени, то, начиная с этого момента, можно написать
00
^ 1 //.1 т f / \ f 1/Л t / С Г" \
@0)
(этот интеграл фактически распространен по интервалу от t = t0
до t=f1). Получается гармоническое колебание с частотой соо и
амплитудой
8*

228 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
Подобные интегралы (так называемые «интегралы Фурье») мы будем
рассматривать в гл. XIV.
Ксли вынуждающая сила имеет вид f(t) = A sinco^, то можно
найти частное решение уравнения по формуле E2), которая при от-
отсутствии трения, т. е. при /г = 0, упрощается и приобретает вид
А А
у= sinco^ =——- — sin co^. E6)
k — ты2 т(щ—со )
На это колебание, происходящее с частотой со вынуждающей силы,
накладывается свободное колебание с собственной частотой соо, за-
зависящее от начальных условий и при отсутствии трения не зату-
затухающее.
Особо интересен случай, когда синусоидальная цнешняя сила
действует на осциллятор без трения при нулевых начальных усло-
условиях. Тогда решение находится по формуле E4) и, приняв для
простоты t0 =0, получим
i
• \ sin co0 (t — т) A sincoxrfx =
A P 1
= —] y[cos(coT—co0(^ —t)) — cos(cot + co0(^ —t))] dx =
0
A ["sin (cot — (oo (t — т)) sin((oT + coo(i—т))"|' _
[ co-{-(oo со —coo Jt=o
_ A fsincoi sinwt sin(—wot) , sina>ot 1 __
"~ 2mcoo [ш + Шо ш — шо Ш + Шо со —ш0 J ~
Sin ^"^ sin
Пусть частота со вынуждающей силы близка к собственной ча-
частоте со0 осциллятора. Преобразуя правую часть E7) по формуле
А А
;(sin °V — sincoOH ; rsincoj =
—teo)v ° '~ mcoo((o + (o0) °
,—; г;
((o + (oo)(co
2Л . coo —со
и заменяя приближенно а»0 + со на 2со0, получим
— А . со—соо , Л
sin s ^ cos с^ |
2
) — coo) 2 2тщ
Наиболее интересно первое, главное слагаемое. Его можно запи-
записать в виде
M(t) cos ojot, где M(t) =
—со0) 2

§ 5]
ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
229
и истолковать как гармоническое колебание с частотой соо и мед-
медленно изменяющейся амплитудой. Эта амплитуда меняется от 0 до
А
Мо = max | М (I) | =
тсо0 |со— (
E8)
с периодом
2я
со— со,,
Такие колебания называются биениями, их график изображен на
рис. 85. Они получаются в результате интерференции вынужденного
Рис. 85.
E6) и свободного колебаний из-за близости их по амплитуде и ча-
частоте (см. формулу E7)). Мы видим, что как время раскачки при
биениях, так и амплитуда биений обратно пропорциональны j со — соо|,
т. е. разности частот свободных колебаний и вынуждающей силы.
Если осциллятор обладает малым трением, то процесс колебаний
также начнется с биений, однако по прошествии достаточного
времени свободное колебание затухнет и останется только вынуж-
вынужденное колебание E2). Его амплитуда равна" при очень малом h
А
(k—тсо2J-ЬЛ2со2
А
А
A
\k — тоУ2
т | соо — со | (соо + со)
оо (со — соо)
Сравнивая с формулой E8), мы видим, что амплитуда вынужденных
колебаний равна половине амплитуды биений. Таким образом, гра-
график колебаний имеет вид, показанный на рис. 86. Интервал времени,
на котором биения переходят в чисто гармонические колебания,
является переходным периодом, а сам этот процесс — переходным
продессом.
Если осциллятор без трения, то в особом случае, когда <в = соо,
т. е. частота вынуждающей силы совпадает с собственной частотой,
формула E6) непригодна; напомним, что это тот самый случай, ко-
который был нами пропущен в конце § V.5. Воспользуемся общей

230
ДИФФЕРЕИЦИЛЛЬНЫЕ УРАВНЕНИЯ
(ГЛ. VII
формулой E4), приняв для простоты ^„ = 0:
у = — \ sin соо (/ — т)- A sincu0T<fr =
о
'-2т)
2т
— 2со„
— т cos
■п sin (£>J — 77- i cos со„
2mco0 ° 2m °
Первое из полученных слагаемых представляет собой свободное
гармоническое колебание и присутствует только из-за необходимости
удовлетворить нулевым граничным условиям. В отличие от этого
Рис. 86.
второе слагаемое представляет собой колебание, амплитуда которого
с течением времени стремится к бесконечности по линейному закону.
В этом и состоит очень важное явление резонанса, который полу-
получается, когда частота вынуждающей силы совпадает с собственной
частотой системы.
Упражнения
Найдите решения следующих дифференциальных уравнений, удовлетворяю-
удовлетворяющие указанным начальным данным:
1. у" — у=\, </ = 0, (/'=0 при / = 0.
2. y" + y = t, i/=i, i/' = 0 при / = 0.
§ 6. Устойчивые и неустойчивые решения
Начнем с самого простого уравнения
-£- = ау (а = const),
E9)
причем переменную t будем истолковывать как время. Его общее ре-
решение легко получить:
y = Ceat, F0)

§ 6] УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ РЕШЕНИИ 231
где С—произвольная постоянная, определяемая из начального
условия
У(*о)=Уо-
Подставляя в F0), находим
уо = Сеа'«, т. е. С=уое-°<°
и окончательно
у=уоеа«-'°К F1)
В частности, при у0 = 0 получаем нулевое решение у = 0.
Однако допустим теперь, что начальное значение у0, которое мы
считали равным нулю, на самом деле оказалось хотя и малым, но
отличным от нуля. Как будет вести себя тогда решение с течением
времени, т. е. с возрастанием О Будет ли такое возмущенное реше-
решение приближаться к невозмущенному нулевому решению или уда-
удаляться от него?
Ответ на эти вопросы существенно зависит от знака коэффи-
коэффициента а. Если а < 0, то формула F1) сразу показывает, что при
увеличении t решения безгранично приближаются к нулю, так что
при больших t они практически становятся просто равными нулю.
В такой ситуации невозмущенное решение называется асимптоти-
асимптотически устойчивым относительно изменения (возмущения) начального
условия или асимптотически устойчивым по Ляпунову по имени выдаю-
выдающегося русского математика и механика А. М. Ляпунова A857—
1918), который впервые начал систематически изучать понятие устой-
устойчивости процессов.
Совсем иная картина будет в случае а > 0. Здесь при уаф§
и при возрастании t решение по абсолютной величине безгранично
увеличивается, т. е. становится не малым, даже есл;. у0 было как
угодно малым. Здесь невозмущенное решение называется неустой-
неустойчивым. Уравнение E9) при а > 0 получается, например, при рассмот-
рассмотрении размножения бактерий в питательной среде, причем у означает
массу бактерий в единице объема, а а— это интенсивность размно-
размножения. Ясно, что если бактерий в начальный момент совершенно
не было, то и с течением времени они не появятся. Однако эта
картина неустойчива в том смысле, что сознательное или случайное
внесение в среду как угодно малого количества бактерий приводит
с течением времени к мощному загрязнению среды бактериями. «
Интересен промежуточный случай а — О. Здесь решения будут
просто постоянными и потому при малом начальном отклонении воз-
возмущенного решения от невозмущенного первое будет и при возра-
возрастании t близким ко второму, хотя и не будет к нему асимптоти-
асимптотически (при t—>- оо) приближаться. Такая картина называется не-
неасимптотической устойчивостью невозмущенного решения.
Рассмотрим теперь более общее уравнение

232
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. VII
Нетрудно найти все стационарные решения, т. е. решения вида
у = const. Для этого надо в F2) положить у=у = const, что даст
f(y) = 0. F3)
Таким образом, стационарные решения уравнения F2)—это пули
функции /(у), стоящей в правой части. Остановимся на одном та-
таком решении у=у и выясним, будет ли оно устойчивым.
Допустим сначала, что функция /(у) является убывающей, во
всяком случае, в некоторой близости значения у=у; тогда если у
переходит через значение у, то /(у) переходит от положительных
значений к отрицательным. В этом случае примерная картина поля
s /
У
У.
\
0
\
\
/
\ \
Лп\
t
*
/
0
/
—■—^
/ У
/
t
Рис. 87.
Рис. 88.
направлений, определенного уравнением F2) (ср. § 1), показана на
рис. 87; при построении этого поля надо учесть, что изоклины для
уравнения F2) имеют вид у = const (почему?), т. е. представляют
собой прямые, параллельные оси t (они также показаны на рис. 87).
На рис. 84 жирными линиями показаны интегральная прямая у=у,
изображающая невозмущенное стационарное решение, и несколько
других интегральных линий, получающихся при изменении началь-
начального условия. Ясно, что если у0 мало отличается от у (например,
в пределах рисунка), то возмущенное решение мало отличается от
невозмущенного и при возрастании t, а при t—»■ с» асимптотически
к нему приближается. Таким образом, в данном случае иевозмущен-
ное решение асимптотически устойчиво.
Пусть теперь /(у) возрастает от отрицательных значений к по-
положительным, когда у переходит через значение у. Соответствую-
Соответствующая картина показана на рис. 88. Ясно, что как бы ни было у0
близким к у (но не равным у]), соответствующее решение у (t)
с возрастанием t уйдет от невозмущенного решения на конечное,
не малое расстояние. Это значит, что в данном случае невозмущен-
невозмущенное стационарное решение неустойчиво. (Проверьте, что полученные
ранее признаки устойчивости и неустойчивости для уравнения E9)

« 61 устойчивые и неустойчивые решения 233
можно получить как следствие общих признаков, указанных дли
уравнения F2).)
Полученные сейчас признаки можно вывести иным способом, не
опираясь на геометрическую картину. Разложим правую часть F2)
в степенной ряд около значения у—у; тогда в силу условия F3)
постоянного члена в разложении не будет и мы получим
то есть
Щ^1 =/'Су)(у~У)+..., F4)
где многоточием обозначены члены высшего порядка малости. Под-
Подчеркнем, что при выяснении устойчивости по Ляпунову изучается
поведение возмущенных решений, мало отличающихся от невозму
щенного, т. е. рассматриваются лишь малые значения у—у. Поэтому
в правой части уравнения F4) основную роль играет выписанный,
линейный член. Отбрасывая члены высшего порядка малости, полу-
получаем уравнение вида E9), в котором а=/'(у). Применяя резуль-
результаты, полученные выше для уравнения E9), находим, что при
/'(^)<0 решение у—у = 0, т. е.у=у, асимптотически устойчиво;
если же f (у) > 0, то решение у—у неустойчиво. Однако в первом
случае функция /(у) убывает (во всяком случае, около значения
дг=_у), а во втором — возрастает, так что мы приходим к тем же
выводам, которые были получены из геометрических соображений.
В особом случае, когда /'{у)—а — 0, для уравнения E9) имеет
место неасимптотпческая устойчивость, т. е. решения, близкие к не-
невозмущенному, не стремятся к нему, но и не уходят от него; тогда
для полного уравнения 'F4) начинают играть существенную роль
члены высшего порядка малости, которые в одном примере могут
направить возмущенные решения к невозмущенному, а в другом —
увести их на значительное расстояние. Мы не будем разбирать этот
особый случай.
В качестве примера рассмотрим тепловой режим в некоторой
объеме, если в нем происходит химическая реакция, связанная с вы-
выделением тепла, и в то же время тепло отводится в окружающее
пространство. Так как скорость реакции зависит от температуры Т
в данном объеме (мы будем рассматривать среднюю температуру
в данный момент времени t), то и скорость Q выделения тепла при
реакции зависит от Т, Q = Q(T), Примем эту зависимость такой,
как показано на рис. 89. Кроме того, примем, что скорость отвода
тепла в окружающее пространство равна а(Т—То), где а — коэффи-
коэффициент пропорциональности, а То — температура окружающей среды.
Тогда при постоянной теплоемкости с рассматриваемого объема

234
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(ГЛ. VII
дифференциальное уравнение процесса приобретает вид
F5)
В силу сказанного выше стационарное состояние, при котором тем-
температура в процессе реакции остается постоянной, возможно при
тех Т, для которых правая часть обращается в нуль, т. е. график
Q(T) пересекается с графиком а (Т—То) (см. рис. 89). Мы видим,
что если окружающая температура Т„ достаточно велика (на рис. 89
при Т0=Т0), то стационарное состояние невозможно, подача тепла
будет все время больше его отвода,
и объем будет все время разогреваться.
Если же эта температура мала (на
рис. 89 при То = То) ,то мыслимы два
стационарных состояния, с темпера-
температурой 7\ или Т2. Вблизи значения 7\
правая частьF5) переходит от положи-
положительных значений к отрицательным,
т. е. убывает. Мы видели ранее, что
такое состояние является устойчивым.
Это видно и из рис. 89, так как если
температура Т опустится ниже 7,, то
выделяться при реакции будет больше
тепла, чем отводиться, т. е. объем будет
разогреваться, а если Т поднимется выше Тг, то тепла будет от-
отводиться больше, чем выделяться, и объем будет остывать. Анало-
Аналогично проверяем, что стационарная температура Т2 будет неустой-
неустойчивой. Таким образом, при То= Тд развитие процесса зависит от
начальной температуры следующим образом: если она была менее Т2,
то с течением времени температура стремится к стационарному зна-
значению 7\, если же начальная температура была более Т2, то тем-
температура будет катастрофически нарастать. Эти соображения были
положены в основу теории теплового взрыва лауреатом Нобелевской
премии Н. Н. Семеновым в 1927 г;
Перейдем теперь к уравнению свободных колебаний
Рис. 89.
= 0 (m, h, k >0)
с общим решением
у =
B1)
F6)
где pt и р2 — корни характеристического уравнения B4), а С, и С2—
произвольные постоянные, определяемые из начальных условий. Это
уравнение имеет стационарное решение _у = 0. В § 3 уы видели,
что все остальные решения при возрастании t стремятся к пулю
(колебательным или неколебательиым образом) и, таким образом,

ОТВЕТЫ И РЕШЕНИЯ 235
указанное стационарное решение является асимптотически устойчи-
устойчивым. При отсутствии трения, т. е. при /г = 0, мы видели, что решения
периодичны; поэтому при малых начальном отклонении и начальной
скорости решение будет малым и с возрастанием t, но не будет
стремиться к нулю. Значит, при отсутствии трения стационарное
решение будет устойчивым, но не асимптотически.
С помощью специально подобранных схем возможно построить
системы с одной степенью свободы, описываемые уравнением B1)
(где у представляет собой отклонение системы от стационар-
стационарного состояния), для которых h < О пли k < 0. Такие системы
можно истолковать как системы с отрицательным трением пли
с отрицательной упругостью. (См., например, описание работы тун-
туннельного диода в ВМ, § VIII.16, при которой систему можно ис-
истолковать как осциллятор с отрицательным трением.) Легко проверить,
что у всех таких систем стационарное решение _у = 0 неустойчиво.
Б самом деле, из алгебры известны свойства корней/^ ир2 квадрат-
квадратного уравнения B4):
h k
Из первого равенства видно, что если h < 0, то либо по крайней
мере один корень вещественный положительный, либо же корни
мнимые сопряженные с положительной вещественной частью. Из
второго равенства видно, что если k < 0, то корни разного знака
и потому среди них имеется один положительный. Таким образом,
во всех этих случаях среди корней имеется по крайней мере один
либо вещественный положительный, либо мнимый с положительной
вещественной частью. Пусть р1—этот корень. Тогда первое слагае-
слагаемое в правой части F6) имеет вид
С^"'' (р, > 0) либо Clea+l<0)f=Clen(cos<iit +
и потому при как угодно малом Сх (т. е. при как угодно малых
начальных данных) при возрастании t оно стремится к бесконечности.
Это и означает неустойчивость стационарного решения.
Упражнение
Найдите стационарные решения уравнения -ту = г/3 — 4г/ и выясните их
устойчивость.
ОТВЕТЫ И РЕШЕНИЯ
§ I
1. Окружности хг-\-у''-=С с центре* в начале координат.
2. В точках перегиба должно быть у" = 0. В силу уравнения (I) и фор-
формулы для производной сложной функции (§ IV. I) получаем y" — (f(x, i/))' =
= f'x(x, y) + f'y(x, у) у' = f'x + f'yl-Значит, искомое уравнение имеет вид/i-f-/^/=0.
Для уравнения ~- = х2-(~у'2 получаем х-{-у (х2-{-у2) — 0.

28() ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. VII
§ 2.
ех i е
2. у = х. 6. г/ = 2д;— 1— е~2х.
3. i/=ln (*+е). 7. i/ = e-*+-9-(i
4. (/= /1+а;2.
§ 3
1. i/ = 2cos/. 4. t/
2. i/=^-e4'sin2/. 5. y = (t— \)eK
3. y^&t + e*. 6. i/ = E/ + l)e-2f.
§4
1. * = —3(/ —2)+l=—3/ + 7. 2. ^ = ^--2.
3. x = 2t — sin/. 4. д^= f (/ —
§ 5
2. j/ = /-f-cos/ —sin/.
§6
j/ = ± 2 (неустойчивые), j/ = 0 (устойчивое).

ГЛАВА VIII
ДАЛЬНЕЙШИЕ СВЕДЕНИЯ
О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ
Эта глава является непосредственным продолжением предыдущей
и существенно на нее опирается.
§ 1. Особые точки
В § VIM мы установили, что интегральные линии уравнения
-г- = /(х, у) не пересекаются между собой. Однако из этого правила
есть важное исключение. Действительно, может оказаться, что при не-
некоторых значениях х и у функция f(x, у) не имеет определенного
значения. Например, /(х, у) = — не имеет определенного значения
при х = 0, у = 0. Точка плоскости, в которой /(х, у) теряет смысл,
называется особой точкой дифференциального уравнения -г-= f(x,y).
Через особую точку может проходить несколько интегральных кри-
кривых.
Если /(х, у) имеет вид отношения двух функций простого вида
(например, двух многочленов), f(x, у) =, , ' У\. то координаты
ц>(х, у)
особой точки находятся из системы уравнений
Ф (х, у) = 0, \
!( ) 0 /
Рассмотрим несколько примеров особых точек, принадлежащих к
наиболее часто встречающимся в приложениях типам.
1. -г- = — . Решением этого уравнения является функция у =Сл;
при любом постоянном С. Совокупность интегральных линий пред-
представляет собой все прямые линии, проходящие через начало коор-
координат (рис. 90). Таким образом, интегральные линии пересекаются
в особой точке х — 0, _у = 0.

238 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ ГЛ. VIII
2 — = —, Решением является у = Сх2. Интегральные кривые —
' dx х J
параболы с вершиной в начале координат. В этом случае все
интегральные кривые касаются между собой в особой точке х = 0,
у = 0 (рис. 91).
Рис. 90.
Рис. 91.
ведут
В рассмотренных примерах все интегральные линии проходят через
особую точку, имея там определенное направление. Такая особая
точка называется узлом.
3. Бывают особые точки, вблизи которых интегральные кривые
себя иначе. Пусть ~ =——. Интегральные линии имеют
уравнение х_у=С. При С=0 получаем
х = 0 или _у = 0 — две прямые, прохо-
проходящие через начало координат. При
С фО интегральные кривые — гипер-
гиперболы. Итак, две интегральные линии
проходят через особую точку х = 0,
у =0, остальные не проходят через
нее. Особая точка такого типа назы-
называется седлом (рис. 92).
4. Интегральными кривыми урав-
dy х
нения —- = являются окружно-
окружности х24-.У2 = С. В этом случае интег-
интегРис. 92.
ральные кривые окружают особую
точку, но через саму особую точку не проходит ни одна интег-
интегральная кривая (рис. 93),
Особая точка такого типа называется центром.
5. При интегрировании уравнения —- = ^ с особой точкой
их х—у
в начале координат удобно перейти к полярным координатам р, ср

§ 2]
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
239
по формулам x = pcoscp, _y = psincp, откуда
dx = cos ф • dp — р sin ф dcp, йу — sin ф • dp -f- p cos ф d<p.
После подстановки в уравнение и приведения подобных членов
получим (проверьте!) dp = pckp, откуда -£ = rfcp и р = Се'?. Прида-
Придавая С всевозможные значения, получим семейство спиралей, накру-
накручивающихся на начало координат (рис. 94). Особая точка такого
типа называется фокусом.
Рис. 93.
Рис. 94.
В приведенных примерах легко установить характер поведения
интегральных кривых вблизи особой точки, так как легко решить
дифференциальные уравнения. В более сложных случаях можно со-
составить примерное представление о характере особой точки, вычер-
вычерчивая изоклины. Более эффективные способы исследования особых
точек лежат за пределами нашей книги. Применение этих способов
показывает, в частности, что при выполнении условия (р'х^>y=^=(f'y\|з*
особая точка обязательно принадлежит к одному из разобранных
типов.
Упражнение
., dy
dy
Определите характер особой точки для уравнений -р=— ; -f- =
dx
dx~
dx'
§ 2. Системы дифференциальных уравнений
До сих пор мы считали, что нам дано одно дифференциальное
уравнение, из которого нужно найти одну искомую функцию. Бывает,
что неизвестных функций больше одной, например две: y(x)nz(x).
Тогда и дифференциальных уравнений должно быть два. Если это —
уравнения первого порядка (разрешенные относительно производных

240 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
от искомых функций), то они имеют общий вид
dz , ,
^ = ф (JC, у, Z)
т. е. мы получаем систему дифференциальных уравнений первого
порядка.
От одного уравнения второго порядка
с одной искомой функцией легко перейти к равносильной системе
из двух уравнений первого порядка с двумя искомыми функциями.
Для этого надо рассматривать ■— как дополнительную неизвестную
функцию. Обозначая ее через г, получим
йу _ йгу _ d /dy\ _dz
dlc~ Z' !x*~Tx [dxj ~dx '
Поэтому вместо уравнения B) можно написать равносильную систему
— = г (х, у, z).
Аналогично уравнение третьего порядка
'У' dx' Л?)
можно заменить равносильной системой трех уравнений первого
порядка. Для этого надо положить
dy _ d~zy dz
d
Тогда получаем систему
dx Z> dx* dx ~
dx
dz
Подобным образом от уравнения любого порядка и даже от си-
системы уравнений любого порядка легко перейти к системе первого
порядка. Обратно, можно проверить, что от системы п уравнений
первого порядка с п искомыми функциями можно перейти к одному

§ 2] систнмы диффцрннцилльных уравнений 241
уравнению порядка п с одной искомой функцией. Поэтому общее
решение такой системы получается в результате п интегрирова-
интегрирований и, таким образом, содержит п произвольных постоянных. Зада-
Задания п начальных условий (при некотором значении х задаются зна-
значения всех искомых функций) как раз достаточно, чтобы найти
значения этих постоянных и, таким образом, получить частное
решение.
Будем рассматривать для простоты систему из двух уравнений
первого порядка вида A). Иногда удается, даже не решив
систему, найти соотношение, связывающее компоненты (т. е.
у (х) и z (х)) любого ее частного решения. Такое соотношение име-
имеет вид
Н(х, у, г; С) = 0 C)
(причем С—постоянная, которая меняется от решения к решению)
и называется первым интегралом этой системы уравнений. Знание
первого интеграла дает возможность понизить число уравнений
в системе на единицу, т. е. перейти к одному уравнению первого
порядка с одной искомой функцией. Для этого можно из C) выра-
выразить z через все остальное и подставить результат в первое урав-
уравнение A); тогда получится одно уравнение первого порядка с одной
искомой функцией у(х). Если это уравнение проинтегрировать, т.е.
найти у (х), то z (х) можно будет найти без интегрирований из ра-
равенства C).
Аналогичным образом знание двух независимых первых интегра-
интегралов (т. е. таких, что ни один из них не является следствием другого)
Нх (х, у, z; Сх) = О, 1
Н2 (х, у, z; С2) = 0 /
дает общее решение системы A), записанное в неявной форме. Для
системы из п уравнений первого порядка общее решение получается
из п независимых первых интегралов.
В некоторых случаях первые интегралы подсказываются физи-
физическими соображениями, чаще всего теми или иными законами со-
сохранения. Например, запишем уравнение одномерных упругих ли-
линейных колебаний без трения (см. § VII.3)
(Рх
в форме системы первого порядка
dx dv
В § VII.3 мы уже упоминали о выражении для полной энергии ко-
колеблющейся точки
£ — 2 -+- 2 . (О)

242 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
При свободных колебаниях без трения энергия должна сохраняться.
И действительно, в силу D)
dE dv , , dx , . , „
dT= mvj-t + kXj-t=—kxv + kxv = O
(это—математическое доказательство закона сохранения энергии
в данном примере). Таким образом, £= const для любого решения
системы D), т. е. формула E), в которой Е играет роль произвольной
постоянной С, служит первым интегралом системы D).
Подчеркнем в заключение, что, как видно из предыдущего,
наиболее естественно рассматривать системы, в которых число урав-
уравнений равно числу неизвестных функций; такие системы принято
называть замкнутыми. Если уравнений меньше, чем искомых функций,
то система называется незамкнутой (недоопределенной); чаще всего
незамкнутость системы свидетельствует о том, что просто не все
необходимые соотношения выписаны. Если уравнений больше, чем
неизвестных функций, то система называется переопределенной;
переопределенность системы обычно свидетельствует либо о ее
зависимости (т. е. о том, что некоторые из уравнений являются
следствиями остальных и потому излишни), либо об ошибке при ее
составлении.
Упражнение
Рассмотрите систему уравнений
dz
Умножив первое уравнение на у и второе на г, а затем сложив результаты,
найдите первый интеграл системы. Какие можно сделать из него выводы
о поведении частных решений при х—у ±оо?
§ 3. Определители и решение линейных систем
с постоянными коэффициентами
Прежде чем п.ерейти к дальнейшему, рассмотрим понятие опре-
определителя, играющее большую роль при решении и исследовании
систем линейных уравнений различного вида. Начнем с системы
двух алгебраических уравнений первой степени с двумя неиз-
неизвестными
Решая ее (что мы предоставим сделать читателю), получим ответ
diV-M Ма~ Мг
a1b.1~b1a, ' y Mi —Ma '
Выражение a^b2 — 1\а^ называется определителем (детерминантом)

§ 3|
ОПРЕДЕЛИТЕЛИ И РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ
243
второго порядка и записывается в виде
a1b1
(8)
где вертикальные черточки — знак определителя. С помощью этого
обозначения формулы G) можно переписать в виде
х =
d.262
albl
а2 6.2
) У
о, dx
аг d2
а, 6,
о2 £>2
(9)
Покажем на примере вычисление определителя:
° ~\ =0-1-(-3).2 = 0 + 6 = 6
Аналогичное решение системы уравнений
c2z =
A0)
приводит к формулам
х =
d, 6, cj
d2 6 2 c2
з з ^"з
fl, 6, С!
flg Ь3 C3
1 У =
0] di
о» d2
a3 d3
o, 6,
o26.2
o3 63
c»
c2
c3
c,
c2
c3
5*
! *
°3
fl,
a 2
«3
6. d.
62 d2
63 d3
6,c,
62 c2
63 c3
где в числителях и знаменателях стоят определители третьего по-
порядка, вычисляемые по формуле
аг
A2)
Формулы A1) совершенно аналогичны формулам (9). В знамена-
знаменателе стоит один и тот же определитель, составленный из коэффи-
коэффициентов при неизвестных (так называемый определитель системы).
В числителе же для каждой из неизвестных стоит определитель,
полученный из определителя системы подстановкой столбца свобод-
свободных членов вместо столбца коэффициентов при данной неизвестной.
Определитель третьего порядка можно выразить через опреде-
определители второго порядка. Для этого надо преобразовать выражение

244 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VII (
A2) и воспользоваться обозначением (8):
a, ft, с,
, — сгЬ3) — bx (а.1с3 — сга3
Ьз сз
с, (аф3 — Ьга3) =
— а,
Ьг сг
-ь,
аг с2
аз с3
а3 Ь3
A3)
По этой формуле можно вычислять значение определителя. Например,
1
— 1
3
0
1
1
— 2
1
О
2
= 1
1
1
L

2
— 0
— 1
3
2
2
+ (-2)
— 1
3
1
1
= 1A.2-1.1)—2 (-1-1-1-3) =-3+8 = 9-1.
Оказывается, что формулы, аналогичные (9) и A1), справедливы
для систем, состоящих из любого числа уравнений первой степени,
если число неизвестных равно числу уравнений. При этом детерми-
детерминанты (определители) четвертого порядка определяются по анало-
аналогии с формулой A3):
аг
аз
at
bi
Ьг
Ьз
К
с2
сз
di
dt
d3
d,
_
b., c, d.,
" a Z
b °c a
4 4 4
1
nt c2 rf2
a" °c d
4 4 4
аг
at
bi
bs
bt
d2
d3
dt
— d,
аг b^ сг
a3 Ь-л c3
at b4 ct
(надо как следует продумать структуру выражения, стоящего в пра-
ной части). Определители пятого порядка выражаются через опре-
определители четвертого порядка и т. д.
В формулах (9) и A1) подразумевается, что определитель сис-
системы, стоящий в знаменателях, не равен нулю. В этом случае сама
система F) и соответственно A0) имеют вполне определенное един-
единственное решение; конечно, под решением такой системы понима-
понимается набор значений всех неизвестных. Иногда встречаются системы
с определителем, равным нулю; их свойства совсем иные.
Рассмотрим для простоты систему F). Если ее определитель
равен нулю,

§ 3] ОПРЕДЕЛИТЕЛИ И РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ 245
ТО
т. е. левые части системы пропорциональны. Например, система
может иметь вид
2х + 3y = du \
8x+\2y=--d2. j V '
Ясно, что при произвольном выборе правых частей система несов-
несовместна, противоречива (не имеет ни одного решения). И только если
правые части находятся в той же пропорции, что и левые (в дан-
данном примере rf2 = 4rf,), то одно из уравнений является следствием
другого и потому может быть отброшено. Но тогда останется одно
уравнение с двумя неизвестными вида
которое имеет бесконечное количество решений; например, можно
придать х любое значение и найти соответствующее у.
Оказывается, что рассмотренная картина является типичной. Именно,
если определитель системы равен нулю, то между левыми частями
системы имеется определенное соотношение. Если такое же соот-
соотношение справедливо для правых частей, то система имеет беско-
бесконечное количество решений; в противном случае нет ни одного
решения.
Важным частным случаем является система п линейных однород-
однородных (т. е. без свободных членов) уравнений с п неизвестными.
Например, в случае л=3 система имеет вид
-f- с„г = 0,
Такая система, конечно, имеет нулевое («тривиальное», т. е. неин-
неинтересное) решение x=y = z = 0. Часто бывает важно выяснить,
имеются ли другие (ненулевые) решения. На основании предыдуще-
предыдущего легко дать ответ на этот вопрос. Если определитель системы
не равен нулю, то имеется только одно решение, а значит, нену-
ненулевых решений нет. Если же он равен нулю, то система имеет бес-
бесконечное количество ненулевых решений, так как несовместной в
данном случае она быть не может. Чтобы найти эти решения,.одно
из уравнений системы отбрасывается, подобно тому как это было
сделано для системы A4).
Применим полученные результаты к решению системы линейных
однородных дифференциальных уравнений с постоянными коэффи-
коэффициентами.

246 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Рассмотрим, например, систему
-j- = a,y-\-b.z,
t L
(l5)
в которой все коэффициенты ал, blt a2> Ьг постоянны. Ее частные
решения ищут в виде
у = кеРх, z = \x,ePx, A6)
где К, ц, р— пока неизвестные постоянные. Подстановка в A5) дает
после сокращения на е?" и переноса всех членов в одну сторону
K '
Эти равенства можно рассматривать как систему из двух алгеб-
алгебраических однородных уравнений первой степени с двумя неизвест-
неизвестными К, \i. Чтобы она имела ненулевое решение, а только такое
решение в силу A6) нас интересует, необходимо и достаточно,
чтобы определитель системы был равен нулю:
al—p bl
а2 Ьг—р
= 0.
A8)
Это—характеристическое уравнение для системы A5), из которого
мы находим возможные значения для р. Его можно переписать,
«раскрыв» определитель, в виде
(проверьте!).
Мы видим, что уравнение A8) имеет вторую степень относительно
р; поэтому оно имеет два корня plt рг. Если эти корни различные, то
можно любой из них (pk) подставить в систему A7), найти какое-либо
ненулевое решение Kk, \ак и по формуле A6) получить соответст-
соответствующее решение у(х), z (x) системы A5). Так как величины Кк, цк
определены с точностью до произвольного общего множителя, то
умножим решение, отвечающее корню plt на произвольную постоян-
постоянную Cj, а решение, отвечающее корню рг, на С2 и сложим резуль-
результаты. Мы получим общее решение системы A5)
Здесь произвольные постоянные С1 и С2 можно найти, например,
даны дополнительно начальные условия, имеющие для системы
A5) вид:
при х — х0 заданы у ~уа и г — гй.

§ 4] устойчивость по Ляпунову состояния равновесия 247
Если корни уравнения A7) мнимые, то решение можно либо
оставить в форме A9), либо записать в вещественной форме, подобно
§ VII,3. Если р1=р2, то у и z получаются в виде комбинации функ-
функций еР'Х и хеР'Х (ср. § VII.3).
Упражнения
1. Исследуйте разрешимость системы алгебраических уравнений
при различных а, Ь.
2. Найдите общее решение системы — = Ах — у, -%-= — 6лг+ Зу.
at Ut
§ 4. Устойчивость по Ляпунову состояния равновесия
Понятие устойчивости как способности того или иного объекта,
состояния или процесса сопротивляться неучитываемым заранее
внешним воздействиям появилось еще в античной науке и сейчас
занимает одно из центральных мест в физике и технике. Сущест-
Существуют различные конкретные реализации этого общего понятия в за-
зависимости от типа рассматриваемого объекта, характера внешних
воздействий и т. д. Здесь мы рассмотрим понятие устойчивости по
Ляпунову, одно из наиболее важных, уже освещенное на простых
примерах в § VII.6.
Пусть состояние некоторого объекта описывается конечным числом
параметров, для простоты двумя параметрами х, у, так что измене-
изменение этого объекта во времени задается двумя функциями x = x(t),
y=-.y(t) (t — время). Пусть закон этого изменения имеет вид системы
дифференциальных уравнений
B0)
с заданными правыми частями, не содержащими явно независимой
переменной t. Последнее условие означает, что дифференциальный
закон развития процесса не меняется с течением времени; такие
процессы называются автономными. (Автономные системы появляются,
в частности, когда уравнения охватывают все тела, участвующие
в задаче, так как законы природы неизменны во времени.)
Пусть состояние равновесия рассматриваемого объекта (когда он
не меняется с течением времени) описывается постоянными значе-
значениями х — хй, у = у0; тогда эта система постоянных, рассматривае-
рассматриваемых как функции времени, также должна удовлетворять системе B0).
Из непосредственной подстановки в B0) следует, что для этого
необходимо и достаточно, чтобы одновременно
P(*v >'o) = O, Q(x0< yo) = O. B1)

248 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Пусть в некоторый момент tg объект под влиянием каких-то при-
причин вышел из состояния равновесия, т. е. параметры х, у стали
равными х — х0-j- Ахд, у = уо-\- Ау0. Тогда для выяснения дальней-
дальнейшего изменения рассматриваемого объекта надо решить систему
уравнений B0) при начальных условиях;
Исследуемое состояние равновесия называется устойчивым по
Ляпунову, если 'после малого отклонения от этого состояния объект
продолжает оставаться вблизи от него в продолжение всего даль-
дальнейшего времени. Другими словами, при малых Дл;0, Ау0 для реше-
решения системы B0) при начальных условиях B2) разности Ax = x(t)—х0,
Ay=y(t)—у0 должны быть малыми при всех t > t0.
Для выяснения того, будет ли иметь место устойчивость, под-
подставим в систему B0)
что даст
d (Ax)
— = Р ixo -\- Ах, у„-\- Ау) = (РхH Ах -\- (РуH Ау -\-
d(L) J" B3)
й-Ш = Q (х0 н- Д*. у0 + Ау) = (Qx\ Ах + (Q'yH Ay+...,
где обозначено (Р'хH = Рх(х0, у0) и т. п. Здесь при преобразовании
правых частей мы воспользовались формулой Тейлора (§ IV.6) и
формулами B1); многоточиями обозначень'1 члены выше первого
порядка малости.
Так как при выяснении устойчивости рассматриваются лишь ма-
малые Ах, Ау, то в правых частях системы B3) основную роль
играют выписанные, линейные члены (ср. аналогичное рассуждение
в § VII.6). Поэтому заменим систему B3) на укороченную систему
(систему первого приближения), отбросив члены высшего порядка
малости:
B4)
Система B4)—это линейная система с постоянными коэффициен-
коэффициентами, которая решается по методу § 3. Согласно формуле A9) (где,
правда, были применены иные обозначения) решение системы B4)
получается как комбинация функций вица е?г, где р удовлетворяет
характеристическому уравнению
(Р'х)о-Р (Р'уH
(Q'x)o (Q'yU-
= 0. B5)

§ 4] УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ СОСТОЯНИЯ РАВНОВЕСИЯ 249
При этом малым Ах0, Ау0 отвечают малые значения произволь-
произвольных постоянных С\, С; и поэтому все дело в поведении функции ept
при возрастании t. Так как р может быть и мнимым, p = r-\-is,
а тогда
ePf = ert (cos st + i sin st), B6)
то нарастание или затухание возмущения определяется знаком />,
если р вещественное, и знаком г, если р мнимое: если этот знак
плюс, то возмущение нарастает, а если минус, то затухает. Мы
приходим к следующим выводам. Если все корни характеристиче-
характеристического уравнения B5) имеют отрицательную вещественную часть
(в частности, они могут быть вещественными отрицательными), то
рассматриваемое состояние равновесия (л;0; уд) устойчиво по Ляпу-
Ляпунову. Кроме того, тогда при малых Ах0, Ду0 будет x(t) —>-хд,
у (t)—*у0 при t—i-oo; такая устойчивость, как мы указывали
в § VII.6, называется асимптотической. Если же среди корней урав-
уравнения B5) имеется по крайней мере один с положительной вещест-
вещественной частью, то рассматриваемое состояние равновесия неустой-
неустойчиво по Ляпунову.
Эти результаты мы вывели для системы B4), но согласно ска-
сказанному выше те же утверждения справедливы для полной системы
B3). Отметим, что наличие двойного корня у уравнения B5) не
нарушает наших утверждений, так как хотя тогда в решении
появляется t в качестве множителя, но экспонента ept при р < О
стремится к нулю быстрее, чем t к бесконечности.
Оба полученных вывода не охватывают случая, когда среди
корней уравнения B5) нет корней с положительной вещественной
частью, но имеется по крайней мере один с нулевой вещественной
частью. Тогда в общем решении системы B4) появляются функции
вида
eisl = cos st -f- i sin st, \ eist | = 1 или е°'=1,
т. е. получается, будто бы рассматриваемый объект колеблется (или
остается неподвижным) около состояния равновесия, не стремясь
к нему. Но тогда из-за неограниченности времени начинают влиять
отброшенные члены высшего порядка малости, которые могут нару-
нарушить устойчивость. Итак, в рассматриваемом особом случае по кор-
корням уравнения B5) нельзя заключить об устойчивости или неустой-
неустойчивости состояния равновесия; чтобы это сделать, надо привлечь
какие-либо дополнительные соображения, например привлечь даль-
дальнейшие члены разложений B3). Мы не будем проводить такое
исследование, отметим лишь, что малые возмущения здесь будут
нарастать или затухать значительно медленнее, так как время изме-
изменения такого возмущения' в заданное число (например, в г) раз
будет обратно пропорциональным этому возмущению или даже
иметь еще более высокий порядок.

250 ДЛЛ1.НЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Упражнение
Найдите состояния равновесия для системы
dx
и исследуйте их устойчивость
§ 5. Построение приближенных формул для решения
Методы построения приближенных формул для решения диффе-
дифференциального уравнения во многом аналогичны описанным в § 1.4
методам решения «конечных» уравнений. Мы будем для простоты
рассматривать уравнения первого порядка, хотя те же методы
естественно переносятся на уравнения любого порядка и на системы
уравнений.
Начнем с метода итераций. Пусть рассматривается дифферен-
дифференциальное уравнение первого порядка с заданным начальным условием
B7)
Если взять интегралы от обеих частей уравнения, получим
>, y(s))ds*),
Xq Xq
т. е.
X
у (х) =у0 -{- С / (s, у (s)) ds. B8)
Уравнение B8) равносильно сразу обоим равенствам B7), так
как после его дифференцирования получается первое равенство,
а после подстановки х = хд — второе. Уравнение B8) является
интегральным уравнением, так как в нем неизвестная функция стоит
под знаком интеграла. Поскольку оно включает в себя не только
первое, нб и второе равенства B7), то оно имеет лишь единствен-
*) Мы часто применяем обозначения вида \ ф (х) dx, однако в данном слу-
чае нужно применять более аккуратную запись, различая верхний предел и
переменную интегрирования (ср. ВМ, § 1.14).

§ 5] построение приближенных формул для решкния 251
ное решение, а не бесконечное количество, как дифференциальное
уравнение.
Вид уравнения B8) удобен для применения метода итераций
(сравните с уравнением A.22)), хотя сейчас неизвестной является не
число, а функция. Выбраз некоторую функцию уо(х) в качестве
нулевого приближения (желательно, чтобы она была по возможности
ближе к искомому решению; если о последнем ничего не известно,
то можно положить хотя бы у0 (х) =.у0), находим первое приближе-
приближение по формуле
Подставляя результат в правую часть B8), находим второе прибли-
приближение и т. д.; вообще
х
Подобно § 1.4, если процесс итераций сходится, т. е. если после-
последовательные приближения стремятся с ростом п к некоторой пре-
предельной функции, то она удовлетворяет уравнению B8).
Замечательно, что метод итераций для уравнения B8) сходится,
во всяком случае для всех х, достаточно близких к х0. Это свя-
связано с тем, что при вычислении последующих приближений надо
интегрировать предыдущие, а при последовательном интегрировании
функции в целом «сглаживаются» и всякие неточности, происходя-
происходящие из-за выбора нулевого приближения, погрешностей округления
и т. п., постепенно устраняются.
(В отличие от этого при последовательном дифференцировании
функции, как правило, ухудшаются, первоначальные неточности
разрастаются, и поэтому итерационный метод, основанный на последо-
последовательном дифференцировании, не дал бы сходимости. Ср. анало-
аналогичные соображения в § 11.2.)
Рассмотрим, например, задачу
_у@)= 1.
После интегрирования получим
Выберем в качестве нулевого приближения для искомого реше-
решения, о котором мы пока ничего не знаем, функцию _yu(.v)=l, так

252 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [1Л. V1I1
как она удовлетворяет хотя бы начальному условию. Тогда получим
(проверьте!), выписывая степени до х4 включительно,
Графики последовательных приближений показаны на рис. 95, где
пунктиром показано также точное решение. Мы видим, что для не-
небольших |л;| процесс сходится.
Вопрос о том, на каком приближении нужно остановится, на
практике обычно решается с помощью сравнения последующих
приближений с предыдущими.
Другой приближенный способ основан на том, что из данных B7)
можно с помощью дифференцирования найти значения у' (хд), у" (хд)
и т. д., после чего составить разложение решения в степенной ряд
Тейлора (см., например, ВМ, § 11.17). Необходимое количество чле-
членов определяется с помощью их последовательного вычисления и
сравнения с выбранной степенью точности.
Рассмотрим, например, задачу B9). Подстановкой в правую часть
уравнения находим, что у' @) = 03 + I3 = 1. Если продифференциро-
продифференцировать обе части уравнения, получим у" = 2х-\-2уу' и, подставив х = 0,
найдем у" @) = 2-0+ 2-1 • 1 = 2. Аналогично находим
/"(<>) = 8;
/v@) = 28
и т. д. Подставляя это в формулу Тейлора, получим
^^ j lx*+... C0)
Мы получили ту же формулу, что и по методу последователь-
последовательных приближений. Этой формулой можно пользоваться лишь для
небольших \х\; например, при х=\ ряд C0) (как и описанный
выше метод итераций) расходится. Можно показать, что это вызвано
существом рассматриваемой задачи. В самом деле, рассмот-
рассмотрим решение У1(х) уравнения ^г=У2 ПРИ начальном условии

§ 51
ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ФОРМУЛ ДЛЯ РЕШЕНИЯ
253
уг{0)=\. Так как хг+уг >yi, то поле направлений в плоскости
х, у, определяющее исходное решение у (х), расположено круче,
чем поле направлений, определяющее решение у1 (х). Но у @) =у1 @);
значит, при х > 0 линия у.= у(х) проходит выше, чем линия
Рис. 95.
у=у1(х). Решение у1 (х) легко найти с помощью разделения пере-
переменных, У1(х) = т~. Итак, y{x)>Y^-x (л:>0). При лг—И— О
правая часть стремится к бесконечности; значит, решение у (х) при
возрастании л: от 0 также обращается в бесконечность при некото-
некотором х = х1^1. Подсчет значения хх (которое зависит от начального
значения у @)) по методам § VIII.7 дает х1== 0,959. При х-+хх~0
будет х2<^(/3, и потому у (х)«1/ {хг—х).
С описанным методом тесно связан метод применения степенных
рядов с неопределенными коэффициентами. Он состоит в том,
что решение уравнения ищется в форме ряда с неизвестными коэф-
коэффициентами
у^= a + b (x-x0) + с (х-хй)* + d (х—хоу + ...,

254 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ, VII1
которые находятся с помощью подстановки в уравнение, последую-
последующего приравнивания коэффициентов при одинаковых степенях и
применения начального условия, если оно задано.
Применим метод неопределенных коэффициентов к рассмотренной
выше задаче B9). Так как хо = О, то пишем
у = а + Ъх + сх2 + dx3-+-ex* + ... C1)
Подставляя х = 0, получаем в силу начального условия, что а —1,
Перед подстановкой ряда C1) в уравнение B9) удобно правую часть
этого уравнения разложить по степеням у—1. (В общем случае
производится разложение правой части в ряд Тейлора по степеням
х—х0, у—у0 согласно формуле
/(*, У) =/о + (Л)» (* —*о) + Юо (У~Уо) +■■;
где нулевой индекс означает подстановку значений х = х0, у=у0-)
Получим
у'=& + [(у—\)+\]* = Х*+ 1+2 {у— 1) + (у—1)\
Подставляя ряд C1), получаем
dx3 + ехА + ...) +
Раскрывая в правой части скобки и приводя подобные члены, а
затем приравнивая коэффициенты при одинаковых степенях х, прихо-
приходим к соотношениям b = 1, 2с = 2Ь, 3d = 1 + 2с + b2, Ae = 2rf + 2ftc',...,
4 7
откуда последовательно находим b=\, c = l, d = -~-, е = -£-, ...
Подставляя эти значения в C1), мы вновь приходим к ряду C0).
При решении дифференциальных уравнений применнется также
метод малого параметра (см. § 1.4). Приведем примеры.
Задача
/ = ТТ№ *(°> = ° C2)
не содержит параметров. Однако можно рассмотреть более общую
задачу
У' = тт^у> ^°) = 0' C3)
из которой C2) получается при а = 0,1. Задача C3) легко решается
при а = 0: тогда получается У = -п- Поэтому ищем решение разло-
разложенным в ряд по степеням а, т. е.
y = ~ + au + alv + а3та + . .., C4)
где и = и{х), v = v(x) и т. д.— пока неизвестные функции х.

§ 5] ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ФОРМУЛ ДЛЯ РЕШЕНИЯ 255
Подстановка C4) в C3) дает после умножения на энаменатель
(х + аи'+ aV+aW + ...)(\ +f x3 + a?xu+a3xv+... \ = х; C5)
. . . = 0,
т. е.
и@)=0, viO) = O, w@)=0, ... C6)
Раскрывая скобки в C5) и приравнивая нулю коэффициенты при
степенях а, получим последовательно
в' + *1 0 v' + ^
х3
w' + -р- v' + хии' -f- x*-v = О и т, д,,
откуда с учетом равенств C6) найдем (проверьте!)
хъ 7 „ 71 ..
Поэтому формула C4) дает
*2 а 5 _i ^а2 в 71а3
В частности, для уравнения C2) получим
хг хъ 7х<* 71л:11
•^ ~ 2 ТОО + 16 000 "" 1 760 000 "г ' ' '
Этот ряд прекрасно сходится при |л;|^1 и неплохо — при
1</*|<2*).
Рассмотрим в качестве другого примера задачу
y' = sin(xy), y@) = a. C7)
В отличие от предыдущего примера здесь параметр входит в началь-
начальное условие. При а = 0 задача C7) имеет решение у = 0. Поэтому
при малых |а| ищем решение в форме
у = аи -\-a2v + oJ>"w + ... (и = и (х), v = v(x), . . .). C8)
Подстановка значения л; = 0 дает
и@)=1, v@) = 0, ra@) = 0. C9)
*) Замена s = —a.xy, v(s) = —a.v3, которую мы предоставляем читателю,
переводит C3) в уравнение, не содержащее параметра. При s=l происходит
катастрофа: \ay/dx\=co. Численное интегрирование по методам § VIII. 7 по-
показывает, что сA) = 1,087, Поэтому ряд C4) не может сходиться пои
з
х> ]/"l,087/a; при а = 0,1 правая часть равна 2,16.

256 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРЛВНННИЯХ [ГЛ. V111
С другой стороны, подставив C8) в дифференциальное уравне-
уравнение C7), получим, с учетом ряда Тейлора для синуса,
аи' -\- cPv' -f- aW -■)-...=
_ {ахи -)- of-xv -f a?xw -\- ., ,) {ахи-]-агх-о -\-a3xw-\-... f
J| gj h • • •
Приравнивание коэффициентов при одинаковых степенях а дает
, , . хъи?
и — хи, v = xv, w = xw —5Т~ > • • •
Интегрируя эти уже линейные уравнения с учетом начальных
условий C9), найдем (проверьте!)
Подстановка этих выражений в C8) дает разложение искомого реше-
решения, пригодное для небольших |а|. При этом, чем больше |л;|, тем
больше коэффициенты и потому тем меньше интервал значений а,
при которых ряд применим.
В более сложных случаях при применении метода малого пара-
параметра часто бывает полезно найти хотя бы первый содержащий
параметр член разложения, так как он дает представление о поведе-
поведении решения при небольшом изменении этого параметра.
Подчеркнем в заключение, что на практике, особенно при грубых,
прикидочных расчетах, широко применяется упрощение самого исход-
исходного уравнения путем отбрасывания сравнительно малых членов,
замены медленно меняющихся коэффициентов на постоянные и т. п.
После такого упрощения может получиться уравнение одного из
интегрируемых типов и, интегрируя, мы получим функцию, которая
может считаться приближенным решением исходного, полного урав-
уравнения; во всяком случае, она часто правильно передает характер
поведения точного решения. Найдя это «нулевое приближение»,
иногда удается с его помощью внести поправки, учитывающие упро-
упрощение, и тем самым найти «первое приближение» и т, д.
Если уравнение содержит параметры (например, массы, линейные
размеры исследуемых объектов и т. п.), то нужно иметь в виду, что
при одних значениях этих параметров относительно малыми могут
быть одни члены уравнения, а при других значениях — другие, так
что упрощение будет при разных значениях параметров производиться
по-разному. Кроме того, иногда приходится разбивать интервал изме-
изменения независимой переменной на части, на каждой из которых упро-
упрощение проводится по-своему.
Особенно полезно такое упрощение уравнения в случаях, когда
при самом выводе (написании) дифференциального уравнения дела-
делались существенные упрощающие предполбжения или когда точность,

§ 5] ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ФОРЛ1УЛ ДЛЯ РЕШЕНИЯ 257
с которой известны рассматриваемые величины, невелика. Например,
члены уравнения, меньшие допускаемой погрешности в других его
членах, надо безусловно отбросить.
Рассмотрим, например, задачу
/ + i^^.y+(W = 0, y@)=\, /@) = 0, 05g*<2. D0)
Так как коэффициент при у меняется медленно, то заменим его
на его среднее значение
k; * = 0, /е=1; х = 2, £ = -± = 0,83;
1+0,1
Кроме того, сравнительно малое третье слагаемое отбросим.
Получим уравнение
/' + 0,92^ = 0
с решением при данных начальных условиях
у = cos 0,96л;. D1)
Вид этого приближенного решения подтверждает правомерность
отбрасывания последнего слагаемого в уравнении, так как отноше-
отношение третьего члена ко второму получается порядка 0,2^2 < 0,2 и
потому сумма первых двух членов мала по сравнению со вторым, т. е.
первый член должен с ним «почти взаимно уничтожиться».
Внесем поправку на последнее слагаемое, для чего подставим
в него приближенное решение D1), оставив коэффициент осредненным:
у" + 0,92у = — 0,2 cos3 0,96л:.
Интегрирование этого уравнения по методу § VII.5 дает при задан-
заданных начальных условиях
у = 0,99 cos 0,96л: — 0,08л: sin 0,96л: + 0,01 cos 2,88л:.
Разница по сравнению с нулевым приближением D1) невелика,
так что вывод в значении отдельных слагаемых в уравнении D0)
остается в силе; в то же время третий член уравнения D0) внес
свой вклад в решение. (Для учета непостоянства коэффициента k
можно было бы второй член в уравнении D0) заменить на
[1,1+0,1 (х— \)\~1у = .±[1+0,91 (%—l)]-1^ « 0,9 lj>—0,08 (х— 1)Х
X cos 0,96.x;; однако и это не привело бы к существенной замене ре-
решения.)
Подобные рассуждения зачастую не блещут строгостью (и иногда
приводят к ошибкам), однако если они проводятся в соответствии
со здравым смыслом, то все же, и притом довольно часто, дают
решение, которым можно пользоваться на практике.
9 Я. Б. Зельдович, А. Д. Мышкио

258 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАЗНЕНИЯХ [ГЛ. VII!
Упражнения
1. Примените метод последовательных приближений к задаче -р=у,
0@)= 1.
2. С помощью вычисления производных найдите разложение по степеням х
решения задачи -~=ехУ, у @) = 0 с точностью до хъ.
8. Найдите первые два члена разложения решения задачи -р = у2-\-ах,
#@)=»1 в ряд по степеням а
§ 6. Адиабатическое изменение решения
Рассмотрим еще один важный метод приближенного решения
дифференциальных уравнений на примере линейного уравнения
х + оЛс = 0 (x = x(t), (й = ы(О), D2)
где точкой сверху обозначается производная по времени t, а зави-
зависимость ю(t) задана. Это уравнение колебаний осциллятора, пара-
параметры которого с течением времени меняются; например, это может
быть маятник, у которого меняется длина подвеса, и т. п.
В общем случае уравнение D2) не интегрируется в квадратурах,
и исследовиние его довольно сложно. Однако в важном частном
случае, именно, когда коэффициент ю (t) > 0 меняется медленно,
такое исследование можно провести. При этом понятие медленного
изменения уточняется следующим образом. Пусть сначала ю = const;
тогда в § VII.3 мы видели, что со служит частотой свободных коле-
колебаний осциллятора, а потому у нас имеется естественная мера вре-
времени, равная периоду — этих колебаний. Примем, что какая-либо
величина р {() меняется медленно, говорят также—адиабатически,
если ее относительное изменение за этот период малб, т. е. если
^IpI или> чт0 т0 же> IрI
Этим определением мы будем пользоваться п для случая со = со(/);
адиабатичность изменения со означает, что ]«j<^co2.
Если со = const, то общее решение уравнения D2) можно записать
в виде
х= Сх cos со/ -f- Ct sin о/ = A sin (<v;/ -}-cp0),
где А и cp0 — произвольные постоянь;ые. Короче,
A- = ^sin(p, D3)
где ф = оз^-|-а>о, и потому
% = »• D4)

§ 6] АДИАБАТИЧЕСКОЕ ИЗМЕНЕНИЕ РЕШЕНИЯ 259
Если теперь со зависит от t, но меняется медленно, то естест-
естественно считать, что в каждый небольшой промежуток времени коле-
колебания осциллятора являются почти гармоническими с частотой, рав-
равной текущему значению к», и примять, что решение уравнения D2)
все равно имеет вид D3) при условии D4), где, однако, уже Л = Л (/),
t
со = со(^). Из D4) получаем, что ф=Ссо(/)<^, причем постоянный
нижний предел этого интеграла несуществен.
Пусть не только со, но и со меняются медленно; тогда естественно
принять, что А и А также меняются медленно. Из D3) получаем
х = A sin ф + A cos ф • со,
х = A sin ф +2Л cos ф-со — A sin ф-со2 -\- A cos ф-со,
и подстановка в D0) дает
A sin ф + 2Л cos ф-со -|-/4 соэф-со = 0. D5)
Так как по предположению первый член имеет высший порядок
малости по сравнению со вторым, то второй и третий члены должны
взаимно уничтожаться. После сокращения на созф получаем
со = 0, т. е. 2-^-
и после интегрирования находим, что 2 \пА -fin со = 1п С, Л2со = С.
Итак, мы видим, что в наших предположениях амплитуда колебаний
меняется обратно пропорционально корню квадратному из текущего
значения собственной частоты.
Конечно, так как мы в уравнении D5) пренебрегли членом выс-
высшего порядка малости, то и выражение Л2со на самом деле не
постоянно. Оно меняется с течением времени, но относительная ско-
скорость его изменения имеет высший порядок малости по сравнению
с относительной скоростью изменения собственной частоты. Как
говорят, величина Ласо является адиабатическим инвариантом.
К аналогичному результату можно прийти из энергетических
соображений. Энергия осциллятора равна (см. формулу E))
„ mu2 , kx2 m . •„ . , ..
£ = ~ + ~ = ~2~(*+ Ю Х )'
откуда, дифференцируя и пользуясь уравнением D2), получаем при
m— const
Е = -j- Bхх + 2coco.v2 + 2а2хх) = тесосолЛ D6)
Если со и со изменяются медленно, то коэффициенты при х2 в пра-
правых частях на текущем периоде, т. е. на временнбм интервале

260 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [гл. VI11
длины ■—-, являются почти постоянными, и можно произвести осред-
нение по этому интервалу. Учитывая формулу sin2 (at -\- ср0) =: -^ —
— -g-cos2((D/-{-(p0), получаем, что дг2 = уЛ2 и аналогично хг =-^(агАг.
Поэтому после осреднения мы получаем
£ = -1«ю2Л2, £ = -1/исоюЛ2 D7)
(так как Е меняется медленно, мы заменили Е снова на Е) .Отсюда
-=- = — , In £ = In со -|-1п Сх, £= С^ю, т. е. энергия осциллятора прямо
пропорциональна мгновенному значению его собственном частоты.
Подставляя этот результат в первое равенство D7), получаем CjCO =
= -k тьJА'ъ, т. е. соЛ2 =—- = const, как и выше.
Интересно, что полученную пропорциональность Е<^>(а легко
понять с позиций квантовой механики. Дело в том, что энергия
одного кванта равна 2ллю, где я я$ 10~27—-%—постоянная Планка;
энергия осциллятора, находящегося на л-м уровне (п= 1, 2, 3,. . .),
равна 2лаып. Если частота ю меняется медленно, то осциллятор остает-
остается все время на одном и том же уровне, т. е. л= const, откуда и
вытекает пропорциональность Е<^а>. (См. по этому поводу заметку
П. Парадоксова «Как квантовая механика помогает понять выводы
классической механики», Успехи физ. наук, 89, № 4 A966),
стр. 707—70).)
Рассмотрим теперь другой важный частный случай, когда мед-
медленно меняется ю,. но не to, на примере уравнения D2) с (о=со0 +
-{-asinkt, где |а|<^а>0, а постоянная k имеет тот же порядок, что
и ю0. В этом случае при осреднении правой части D6) надо ее пред-
предварительно преобразовать по формуле
m<doak cos kt ■ А* -»-—к- cos2(to0^ + (p0) = -^ma^o.kA1 cos kt —
—-^ ma0akA2 cos [Bco0 + k) t + 2cp0] —
— -j m^^akA1 cos [B©0 — ft) t + 2cp0].
Теперь может быть два случая. Если £=^=2а>0, то среднее значение
правой части как среднее значение от суммы чистых гармоник равно
нулю, т. е. £=*0, Е представляет собой адиабатический инвариант.
Если же /г = 2со0, то последнее слагаемое в правой части иревра-

§ 7] ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ '261
щается в константу, откуда после осреднения получаем Е =
'=— ^-m(o0a2to0A2cosB(p0) = — a cos Bcp0) £, т. е. £=Ce-aC0S<2<f>°>-<.
Итак в рассматриваемом случае энергия осциллятора, а с ней и
амплитуда колебаний являются экспоненциально возрастающими или
затухающими во времени, в зависимости от знака cos 2ф0. Это явле-
явление, аналогичное резонансу (п. VII.5) и проистекающее из-за перио-
периодического изменения параметров осциллятора, называется параметри-
параметрическим резонансом (и между прочим, используется при раскачивании
качелей).
§ 7. Численное решение дифференциальных уравнений
Часто бывает, что ни точного, ни достаточно удовлетворитель-
удовлетворительного приближенного решения в виде формулы построить нельзя.
Тогда применяется численное решение, при котором искомое частное
решение (при конкретных значениях параметров, если ^ни входят
в постановку задачи) строится в табличном виде. Принцип числен-
численного решения дифференциального уравнения чрезвычайно прост и
прямо вытекает из смысла производной.
Пусть уравнение имеет вид j-=f{x,y) и дано начальное усло-
условие у=у0 при х — ха. Тогда, подставляя значения х0, у0 в функ-
функцию /(х, у), мы найдем величину производной в точке х0:
dy
dx
Отсюда, считая, что Ах — малая величина, получаем
Полагая для краткости записи f (x0, _У„)=/0, записываем этот
результат так:
У1=*Ув+/о-Ьх- D8)
Теперь, принимая точку (х^, yt) за исходную, можно точно таким
же методом получить у2=у(х.2), где хг = х1-{-Ах. Таким образом,
шаг за шагом, можно вычислять значения решения у для различных
значений х. Это—метод Эйлера.
Пользуясь таким методом, мы получаем, конечно, не точные, а
приближенные значения у. Действительно, ведь производная —■ не
останется постоянной на промежутке от х = х0 до x = xv Поэтому,
пользуясь формулой D8), мы допускаем ошибку в определении у,
притом тем большую, чем больше Ах.

262 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. Vlll
Более точно, так как правая часть D8) представляет собой сумму
двух перзых членов разложения у (хй-\-Ах) по степеням Ах, то
ошибка формулы D8) имеет порядок (АхJ, т. е. не превосходит
а(Ах)'г, где коэффициент а зависит от вида функции f(x,y).
Пусть необходимо, зная начальное условие у(хо)=уо, получить
значение решения при х = хо-{-1, причем / велико, так что при
пользовании формулой D8), полагая в ней Ах — 1, мы допустим огром-
огромную ошибку. Чтобы отыскать у{хо-\-1), разобьем промежуток от
х^х0 rox —хо-\-1 на п равных малых промежутков, тогда длина каж-
каждого из них есть Дл' = —. Для полученияу(хо-\-1) нам придется сде-
сделать п шагов, последовательно получая у [хо-\ ) , у [хо-\-2 —
...,у(хо + 1).
На каждом таком шаге ошибка порядка а [ — У, а на всех п
n
i I N2 all „
шагах ошибка порядка a I — I л = —. Следовательно, ошибка, воз-
никающал при применении способа Эйлера, обратно пропорциональна
числу шагов. Если задана точность е, то необходимое число шагов п
есть величина порядка —. Ясно, что чем больше шагов, тем меньше
ошибка, тем точнее найдем мы величину у{хо-\-1). Однако ошибка
убывает очень медленно при увеличении числа шагов. Поэтому для
достижения заданной точности иногда необходимо очень много
шагов.
Приближенное значение для у, даваемое формулой D8), будем
называть первым приближением (_у,), так что ух =>>„+/„ Ах. Для
получения более точного второго приближения будем брать среднее
арифметическое производной в начале и в конце промежутка, вычис-
вычисляя производную в конце промежутка при помощи первого прибли-
приближения ух. Таким образом,
'dy _l
х = х0 ' dx
"=.'/,
ИЛИ
У» =
=Уо + у [Л +/{х0 + Ах, у0 +/0 Ах)] Ах.
Можно показать, что величина уи имеет ошибку порядка Ь{АхK,
где 1> — постоянная, зависящая от вида f(x,y). Поэтому полная
— ) • п =
— , а число шагов л, необходимое для достижения заданной точ-

§ 7] ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 263
ности е, есть величина порядка I/ —.В этом случае ошибка об-
ратно пропорциональна квадрату числа шагов, т. е. с ростом числа
шагов убывает значительно быстрее, нежели при пользовании пер-
первым приближением уу
Отметим, однако, что при нахождении уп нужно на каждом шаге
вычислять f(x,y) два раза, в то время как при нахождении _у, на
одном шаге нужно вычислять лишь одно значение f(x,y). В самом
деле, действуя по способу Эйлера, мы, начиная расчет от точки
(*0; Уо)> находим ух (*i)=.yo+/o-A.v, затем вычисляем /(.v,, _у, (д^))
и переходим к следующему шагу.
Если же мы хотим отыскивать второе приближение, то схема
такова. Сперва находим _у, (xl)=ylt-\-f0- A.v, затем определяем
Я*1. У\ (*i)) и
/о = [/(*Q. Уо) + /(•*!. У\ (*l))]-
После этого мы находим уи (xl)=y0 +/о' ^х и> наконец,
f{xv уи{х1)). Только теперь все приготовлено для перехода к сле-
следующему шагу. Такую схему вычислений называют схемой с пере-
пересчетом, потому что величина f(x,y) на каждом шаге пересчиты-
вается, заменяется более надежной величиной f(x, у).
Вычисление значений /{х, у) является, как правило, наибо-
наиболее трудоемкой операцией (остальные операции—умножение на Ах,
сложение — делаются гораздо быстрее), так что затрата труда
на п шагов в схеме с пересчетом равносильна затрате труда на 2п
шагов в схеме для определения _у,. Однако, несмотря па это,
если требуется высокая точность, т. е. если е весьма мало, то
''"ьР al"^
схема с пересчетом выгоднее, так как 2 1/ —<с —, если е малб.
г 8 8
Схема с пересчетом имеет еще одно преимущество. В этой схеме
есть хороший контроль правильности вычислений и выбора вели-
величины Дд;, которую называют шагом: ясно, что расчет хорош лишь
до тех пор, пока значения f(x, у) и f(x,y) мало отличаются.
Рассмотрим пример. Пусть у есть решение уравнения _у'=л"а—_уа
с начальным условием у = 0 при х = — 1. Определим значение реше-
решения при х = 0. Воспользуемся схемой с пересчетом, взяв шаг
Дл: = 0,1.
Вычисления сведены в таблицу 5. Во втором и третьем столбцах
таблицы в скобках вписаны промежуточные результаты, а под ними —
результаты пересчета. В последнем столбце таблицы выписаны зна-
значения у, верные с точностью до четырех знаков после запятой.
Сравнивая их с теми, которые мы получили, видим, что во всег.
найденных значениях три знака после запятой верны.
Метод пересчета поддается дальнейшему уточнению, результатом
которого являются широко применяемые сейчас в вычислительной

264 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Таблица 5
X
—1,0
-0,9
—0,8
-0,7
-0,6
—0,5
-0,4
—0,3
—0,2
—0,1
0,0
у
0,0000
@,1000)
0,0900
@,1702)
0,1606
@,2220)
0,2133
@,2577)
0,2502
@,2799)
0,2736
@,2911)
0,2861
@,2939)
0,2902
@,2908)
0,2883
@,2840)
0,2826
@,2756)
0,2753
1,0000
@,8000)
0,8019
@,6110)
0,6142
@,4407)
0,4444
@,2936)
0,2974
@,1717)
0,1752
@,0753)
0,0782
@,0036)
0,0058
(_0,0446)
—0,0699
(—0,0706)
—0,0699
—0,0760)
—0,0758
f
0,9000
0,7064
0,5274
0,3690
0,2345
0,1252
0,0409
—0,0194
—0,0568
—0,0730
^точное
0,0000
0,0900
0,1607
0,2135
0,2504
0,2738
0,2862
0,2902
0,2882
0,2823
0,2749
практике методы Рунге-Кутта и Милна, которые можно найти в курсах
численных методов. Распространен также метод Адамса, основанный
на применении конечных разностей (§ II.1). Изложим этот метод
в несколько упрощенном варианте (обычно он доводится до третьих
разностей, но мы ограничимся вторыми). Мы исходим из формулы
Ньютона (II.5), примененной к производной *от искомого решения
у'(х), причем вместо k мы возьмем k—1
h т 2 h
s = х хк_1.
Интегрирование этого равенства от х = хк до х~.
= h до s = 2h, дает (проверьте!)
т. е. от
т. е.
Т2
fe-42'
D9)
Эта формула применяется следующим образом, Сначала каким-либо
способом (например, с помощью формулы Тейлора, § 5, пли с по-
помощью метода пересчета) находим значения yl=y(x0-\-h) н

§ 7] ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 265
yt=y (х0 -\-2h). Затем вычисляем соответствующие значения
с помощью которых находим
Sy'j_=/i— У„ &У'.±=У',—у[, 6*у[ = 6у' 1— S/j_.
2 2 21 2
Далее, полагая в формуле D9) k = 2, вычисляем у3, а с его помощью
Затем, полагая в формуле D9) £ = 3,
помощью y\=f{x4, У^ и т. д.
Особая осторожность при численном решении дифференциальных
уравнений нужна в том случае, когда искомая функция может не-
неограниченно возрастать. Пусть, например, нам дано уравнение
-т-=Уг и начальное условие у = 1 при х=\.
Для этого уравнения легко найти точное решение. В самом деле,
у х
^L=dx, откуда \-4-= \ их, или 1 ——=х — \, что дает у =,—- .
У о У v У бл
I 1
Ясно, что у неограниченно возрастает при приближении х к 2.
Если бы мы решали это уравнение численно, то, конечно, и при
лг = 2 получили бы вполне определенное, хотя, может бьпч , и очень
большое значение у.
Значение аргумента д; = 2, при приближении к которому решение
неограниченно возрастает, мы отыскали только благодаря тому, что
смогли написать искомое решение в явном виде. Однако многие
уравнения не имеют такого решения. Как же, решая уравнение
численно, найти то значение лг, при приближении к которому решение
неограниченно возрастает?
Как быть, например, с уравнением Риккати
% = <?{х)-у' + у{х), E0)
которое при произвольных ф(л;) и ty{x) точно решить нельзя?*)
Введем новую искомую функцию z = —-. Тогда при интересую-
интересующем нас значении х будет г = 0. Заметим, что -т— = — —5- -Д. Раз-
J ' dx yl dx
делим уравнение D4) на —у2, получим г^~ — Ф (х) — ^г' > или
()*$()
dll
*) Только что рассмотренное уравнение у-_ = j/2 получается из E0) при

266 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Решая численно последнее уравнение, мы найдем значение х,
при котором z = 0.
Изложенные способы численного решения дифференциальных
уравнений легко переносятся на случай системы двух или большего
числа уравнений. Покажем это на примере системы двух уравнений
'£=/{*, у,*), \
dz
dx
= y{x,y,z). J
Пусть даны начальные условия у = у„, z = zn прих — хп. Положим
f(xo,yo, 20) = /0, ф(л0, у0, zo) = (fo. Тогда первое приближение есть
У\ (* i) =У\ (*о + д'*) =Уо
Длс.
Для получения второго приближения находим, используя первое
приближение, значения производных в конце промежутка, т. е. при
.г, = хп -\- Ах; получаем
dx
Затем определяем средние величины
1
y. ф = у (ф 0 + 4>i)-
Второе приближение есть
Наконец, получив уи и г,,, мы пересчитаем значения производных
при jjc = jc0 —J— Дх:
Уравнение второго и более высоких порядков можно, как было
показано в § 2, свести к системе уравнений первого порядка.
Поэтому изложенные приемы численного решения применимы и для
уравнений выше первого порядка.
Отметим один частный случай. Пусть рассматривается уравнение
W = ¥(*.<)■ E1)

§ 7] ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2G7
В отличие от общего случая уравнения второго порядка здесь
dx *,
правая часть не содержит —г— *).
Уравнение E1) допускает решение в аналитическом виде в двух
следующих случаях.
1. Если правая часть ф (х, t) не зависит от х. Тогда D5) при-
принимает вид —f-=(p(Oi откуда -£- = \ ф (f) dt\ интегрируя еще раз,
найдем x(t).
2. Если правая часть не зависит от t, т. е. уравнение D5) имеет
(fix dx
вид -р- = ф(х). В этом случае положим v = -r-, тогда
d'zx dv dv dx dv Id (a3)
V
dt* dt dx dt dx 2 dx
Уравнение перепишется так: у ' 7 = ф(х), откуда
v2 = 2 \ ф (х) dx, v = -^-— у 2 ^ ф (х) dx.
Мы получили уравнение с разделяющимися переменными.
Однако в с'Лучае, когда правая часть зависит и от х и от t,
ни один из этих способов применить нельзя, так что приходится
„ dx
решать уравнение численно. Прежде всего, положив — =г», заменим
E1) системой уравнений первого порядка
dx _
E2)
Система E2) обладает следующей особенностью: правая часть
первого уравнения системы не содержит х, а правая часть второго
уравнения системы не содержит v. Благодаря этому можно предло-
предложить очень удобную схему вычислений.
dx
Пусть даны начальные условия х = х0, -— = v — vu при t = ta.
Выберем шаг Д^, т. е, будем находить значения решения при сле-
следующих значениях аргумента: tl = t0-JrAt, t2 = t0 + 2At, t3 =
= to + ZM п т.д.
Значения аргумента t0, tlt /,, ts, ... будем называть целыми,
а значения Л/г, t^/^, /2i,-2 ...—иолуцелыми. Будем вычислять зна-
значения v = -T-- для полуцелых значений аргумента, а значения х для
*) Такое уравнение описывает, например, движение тела под действием
силы, зависящей от положения тела и от времени, при отсутствии трепня.

2G8 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VII!
целых значений аргумента. Тогда последовательность действий такова.
Зная х0 и v0, мы находим vi/t по формуле гь/2 = г>0-)-ф0 ■ -^, где
= ф(я0, t0). Затем определяем xx — xu-\-vx^- S.t, фх =
и v^y2 = №/2 + ф1- Д/. Дальше процесс повторяется:
Вычисления удобно располагать в виде следующей таблицы.
Таблица 6
положено
= ф(д:1,
t
\
t
t
t
0
./.
l'/2
8
37,
л;
*i
X
х3
xt
Ф (*. 0
Фо
Ф1=ф(*1.
ср2 = ф (xit
Ф8
Ф4
'l)
'*)
"V,
11
21/2
/ 2
Таким образом, при переходе, например, от лг5 к х2 мы пользу-
пользуемся значением производной t^i/.,, соответствующим середине про-
промежутка. Благодаря этому точность способа такого же порядка, как
точность второго приближения в обычном способе. (Ошибка на
каждом шаге порядка (Да1K.) Поэтому при затраченной работе такой
же, как и при пользовании первым приближением, мы получаем
лучшую точность за счет разумного построения схемы вычислений.
Отметим еще раз, что такая схема возможна лишь благодаря
указанным нами особенностям системы E2).
Упражнения
1. Составьте таблицу значений функции у — е*, решая численно уравнение
у' = у с начальным условием j/=l при * = 0.
Получите значения ех при х = 0,1; 0,2; 0,3 и т. д. через 0,1 до х—1.
Вычисления велите по первому приближению с четырьмя знаками после запятой.
Затем возьмите шаг Лл; = 0,05 и пользуйтесь схемой с пересчетом. Результаты
сравните с табличными.
2. Пусть у (х) есть решение уравнения -т^=л;2 + {/2 с начальным условием
у =0,5 при * = 0. Найдите у @,5).
Решите задачу двумя способами:
а) считайте по первому приближению с шагом Лл; = 0,025;
б) считайте по второму приближению с шагом Л* = 0,05. Сравните резуль-
результаты *).
*) Дифференциальные уравнения задач 2 и 5 нельзя решить аналитически.

§ 8] КРАЕВЫЕ ЗАДАЧИ 269
3. Пусть тело массы т движется под действием силы f(t) = at(Q—t) и ис-
испытывает сопротивление среды, пропорциональное скорости (коэффициент про-
пропорциональности равен k).
Пусть в начальный момент времени скорость тела была равна 0. Составьте
дифференциальное уравнение и решите его численно для случая т = 10 г,
а = 5-—'— , 9 = 20 сек, k=l — . Определите скорость тела через 1,5сек после
начала движения.
Указание. Воспользуйтесь схемой с пересчетом, взяв М ==0,05. Вычис-
Вычисления ведите с тремя знаками после запятой.
4. Составьте таблицу значений функции у = sin лг, решая численно урав-
уравнение j/"-)-j/ = O с начальными условиями t/=0, -т^ = 1 при х = 0. Получите
значения при * = 0,1; 0,2; 0,3 и т. д. через 0,1 до х=\. Пользуйтесь схемой
с пересчетом, взяв шаг Дл; = 0,1. Сравните результаты с табличными. Вычис-
Вычисления ведите с тремя знаками после запятой.
5. Составьте таблицу значений решения уравнения -тр- = t + х- с началь-
dx
ными условиями х = 0, —?г — 1 ПРИ '=0. Таблицу составьте от ^ = 0 до< = 0,5.
Возьмите шаг Л^ =0,1 и считайте по схеме с полуцелыми значениями аргумента
с тремя знаками после запятой.
§ 8. Краевые задачи
Общее решение дифференциального уравнения п-го порядка
содержит п произвольных постоянных, т. е. обладает п степенями
свободы (см. § IV.8). Чтобы выделить из общего решения какое-
либо частное, мы до сих пор пользовались начальными условиями,
согласно которым искомая функция и ее производные задаются при
одном значении аргумента. Это особенно естественно, если незави-
независимой переменной служит время, т. е. если изучается развитие
некоторого процесса: тогда начальные условия просто служат мате-
математической записью начального состояния процесса. Именно поэтому
применяются наименования начальные условия, начальная задача
и в случае, если независимая переменная имеет другой физический
смысл. Однако бывают задачи с иной постановкой, например, такие,
в которых имеются два равноправных «узловых» значения независи-
независимой переменной, при которых задается искомая функция. Так, при
рассмотрении отклонения у (х) струны, закрепленной на концах х—а
и х — Ь, на искомую функцию у (х) накладываются условия у(а) = 0,
у(Ь) = 0. Имеются и другие способы выделения частного решения
из общего, которые встречаются в практических задачах. Все эти
способы объединяет то, что количество дополнительных равенсти,
накладываемых на искомое решение, должно равняться числу сте-
степеней свободы в общем решении рассматриваемого уравнения, т. е.
порядку этого уравнения.
В дальнейшем мы рассмотрим решение уравнения
у"+р(х)у' +q(x)y=f(x) (a<^x<^b) E3)

270 ДАЛЬНЕЙШИЕ СВЕДКНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
при дополнительных условиях
аг, E4)
хотя все полученные общие вывод!»! справедливы для линейных
дифференциальных уравнений любого порядка п при линейных до-
дополнительных условиях любого вида. Условия вида E4), наложенные
на концах интервала, на котором строится решение, называются
краевыми условиями, а задача о решении дифференциального урав-
уравнения при заданных краевых условиях называется краевой задачей.
В гл. VII (§§ 2, 3 н 5) мы видели, что общее решение линей-
линейного неоднородного уравнения E3) имеет следующую структуру:
у=У(х) + С1у1(х) + С,у2(х); E5)
здесь Y (х)— некоторое частное решение уравнения E3), ух и у2 —
два независимых решения соответствующего однородного уравнения,
а С\ и С,— произвольные постоянные. Подставляя формулу E5)
в условия E4), получим два соотношения для нахождения Сх и С2:
При решении этой системы двух алгебраических уравнений первой
степени с двумя неизвестными югут представиться два случая (см. § 3).
1. Основной случай: определитель системы отличен от нуля.
В этом случае система E6) имеет вполне определенное решение, и
потому уравнение E3) при условиях E4) имеет одно и только одно
решение при любом неоднородном члене f (х) и любых числах alt a2.
2. Особый случай: определитель системы равен нулю. В этом
случае система E6), как правило, противоречива, но при некоторых
правых частях она имеет бесконечное количество решений. Значит,
и уравнение E3) при условиях E4) при произвольном выборе функ-
функции f (х) и чисел alt а2, как правило, не имеет ни одного решения;
олнако при некоторых таких выборах задача имеет бесконечное
количество решений. Например, можно проверить, что если /(х)
и аг уже выбраны, то бесконечное количество решений получится
лишь при одном значении а2, а при остальных значениях задача
не будет иметь ни одного решения.
Подчеркнем, что то, какой именно случай имеет место, зависит
от вида левых частей уравнения E3) и условий E4),
Согласно § 3, для того чтобы имел место основной случай,
необходимо и достаточно, чтобы соответствующая оДйородная за-
задача (в которой положено /(*)£=(), а1 = а2 = 0) имела только нуле-
нулевое решение. В особом случае однородная задача имеет бесконеч-
бесконечное количество решений, а если неоднородная задача имеет хотя бы
одно решение, то общее решение получится, если к этому частному
решению прибавить общее решение соответствующей однородной
задачи.

$ 8] КРАЕВЫЕ ЗАДАЧИ 271
При решении начальной задачи (так называемой задачи Коиш,
т. е. задачи с начальными условиями) всегда имеет место основной
случай, так как такое решение всегда существует и единственно.
При решении краевой задачи может представиться и особый случай.
Например, рассмотрим задачу
у"+у = 0 (о<*<-?-}, jf(O)=ai, .у (-£)=«,.
В силу § VII.3 общее решение уравнения имеет вид
у = С\ cos х -(- Сг sin х, E7)
Подставляя граничные условия, получим
С1 = а1т С, = а4.
8начит, получаем при любых ах, а2 вполне определенное решение
у = ах cos х-\-аг sin *.
Это — основной случай.
Для задачи
у"+у = 0 @<*<я), y(O)=alt y(n)=at E8)
подстановка граничных условий в то же общее решение E7) даст
С1 = а1, —С1 = аг, т.е. С1 = — а2.
Таким образом, если а-^-ф — а.2. то задача E8) не имеет ни одного
решения. Если же а1 — — а2, то эта задача имеет решение
у = аг cos х -f С, sin л:,
р котором С2 совершенно произвольно, т. е. мы имеем бесконечное
Число решений. Это — особый случай
Рассмотрим, наконец, задачу с параметром Я =const
/ + \У =/(*) @ < х < /), у @) = а1г у (!) = а4, E9)
причем будем считать сначала, что к > 0. Тогда независимыми
решениями соответствующего однородного дифференциального урав-
уравнения служат функции ух {х) = cos]/~Tx, y.,(x) = sm\rXx и опреде-
определитель системы E6) равен
у1 @) у.г @)
1 0
sin
Приравнивая его нулю, получим значения
1'-(т)'. (¥)'• (т)' <«»
рри которых для задачи E9) имеет место особый случай, т. е. нару-
нарушается либо существование, либо единственность решения.

272 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VIII
Набор значений параметра, входящего в формулировку задачи,
при которых задача в том или ином смысле, вырождается (т. е.
теряет какие-либо весьма существенные свойства, приобретая качест-
качественно иные), называется спектром этой задачи. Мы предоставляем
читателю проверить, что при ^.^0 для задачи E9) всегда имеет
место основной случай, и тем самым набор значений F0) представ-
представляет собой весь ее спектр.
Спектр F0) задачи E9) можно получить также несколько иным,
по существу равносильным методом. Как было сказано, особый
случай для краевой задачи характеризуется тем, что соответствую-
соответствующая однородная задача
у" + Ху = 0, у@) = 0,
может иметь ненулевое решение. Общее решение этого дифферен-
дифференциального уравнения имеет вид
у = Сг cos V\x + С, sin У%х = C(D cos \/~Хх -f sin VXx),
где обозначено С—Сг, D = -tt-. Применение граничных условий дает
С (D cos l/To -f sin V%0) = 0, С (D cos VTl + sin VTl) = 0.
Мы видим, что постоянная С остается произвольной, тогда как для
нахождения двух постоянных D и К остается два уравнения
D cos ]/То + sin I/TO = 0, D cos V^l + sin V\ I = 0.
Отсюда получаем
D = 0, sinV/rU = 0, V\l=kn (k=\, 2, ...),
и мы приходим к тем же значениям F0) для X.
Полученный результат имеет интересное приложение к исследо-
исследованию устойчивости упругого стержня при его сжатии. Пусть одно-
д\ родный (одинаковый по всей длине) уп-
— ^ ругий стержень расположен вдоль оси х
и сжимается вдоль нее силой Я, причем
оба конца стержня удерживаются на оси
х, но могут свободно вращаться вокруг
точек закрепления (рис. 96, а). Тогда
при достижении силой некоторого крити-
рис 96. ческого значения Якр стержень изгибает-
изгибается, принимая положение, изображенное на
рис. 96, б. Если обозначить через у поперечное отклонение точки
стержня от ее исходного положения, то, как доказывается в курсах
сопротивления материалов, функция у(х) с достаточной точностью
удовлетворяет дифференциальному уравнению и краевым условиям:
/ + Е7.У = 0. У@)=УA) = 0: F1)

§ 8] КРАЕВЫЕ ЗАДАЧИ 273
здесь Е и J — так называемые «модуль Юнга» материала стержня
и «момент инерции» поперечного сечения стержня. Как вытекает
из F0), при
■ ш<(т) ™
для задачи F2) имеет место основной случай, т. е. она имеет
только нулевое решение; изгибания не происходит. Как только
с увеличением Р неравенство F2) переходит в равенство, то насту-
наступает особый случай, и задача F1) наряду с нулевым решением
имеет решение вида у — С sin -у- х, где С—произвольная постоян-
постоянная. Но тогда стержень ничем не удерживается в прямолинейном
состоянии и малые внешние воздействия*) могут привести к конеч-
конечным отклонениям от этого состояния; стержень теряет устойчивость.
Получающееся выражение для Ркр
было найдено Л. Эйлером в 1757 году. Могло бы показаться, что
при Р > Ркр стержень должен опять выпрямиться. Однако это не
так. Уравнение F1) описывает отклонение стержня точно лишь
в пределе при малых отклонениях, а анализ более точного уравне-
уравнения, справедливого при любых отклонениях (оно оказывается нели-
нелинейным), показывает, что при переходе Р через Ркр наряду с не-
неустойчивой прямолинейной возникает искривленная форма равнове-
равновесия, которая и является устойчивой. С ростом Р кривизна этой
формы быстро возрастает, и стержень разрушается.
К решению неоднородного уравнения при однородных краевых
условиях
«, = 0. ,№,_.. < <63>
в основном (неособом) случае можно применить функцию Грина
(§ VI.2), так как ясно, что при сложении правых частей решения
также складываются. В соответствии с § VI.2, если через G(x; |)
обозначить решение задачи F3), в которой вместо f(x) взята дельта-
функция б (х—|), то при произвольной функции f(x) решение
задачи F3) получится по формуле
b
y{x)=\f{l)G{x;l)dl. F4)
*) Подразумеваются такие внешние воздействия, которые стремятся откло-
отклонить стержень от прямопинейного состояния, например малая сила, направ-
направленная перпендикулярно стержню.

274 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VTrt
Приведем простой пример. Пусть рассматривается задача
/ = /(*) @ <*</), у@)=уA) = 0. @5)
Если взамен f(x) поставить б (х— |), то при 0^х<1 и при
\ < х ^ / получится просто у" = 0, т. е. решение
у = ах + Ь @ <*<&), _y = c* + rf (!<*</).
где а, fr, с, d— какие-то постоянные. Применение краевых условий по-
показывает, что 6 = 0 и cl + d = 0, т. с.
>=e* @ <*<<;),
F6)
Рис. 97.
Если равенство у" = Ь(х — \)
проинтегрировать от х = Ъ,— О
до х=Ь> + 0, то получится, что
у'A+0)—у'(% — 0) = I; кстати, для
левой части уравнения F3) полу-
получился бы такой же результат, так
как интегрирование конечной функ-
функции по отрезку нулевой длины
дает нуль. При вторичном интегрировании дельта-функции получается
уже непрерывная функция, так что у (Н — 0)=_у(|-}-0) и из F6)
получаем с — а — \, а\= с (£ — /), откуда
~ — Lzl _!
Подставляя в (G6), находим функцию Грина для задачи F5):
£
G (x; I) =f= •'
Эта функция изображена на рис. 97; нетрудно влдеть, что она лишь
постоянным множителем —F отличается от функции, построенной
в § VI.2. В силу формулы F4) получаем решение задачи F5) при
любой функции f(x):
; \) f (I)
G (х- l)f(\)dl =
Упражнения
1. Найдите спектр краевой задачи у"-\-'Ку = 0, г/@) = 0, г/'(/)
2, С помощью функции Грина постройте решение задачи y
) 0 B) 0

§ 9]
ПОГРАНИЧНЫЙ СЛОЙ
273
§ 9. Пограничный слой
Часто бывает, чю изучаемое дифференциальное уравнение или
система таких уравнений содержит один или несколько параметров,
которые могут принимать различные постоянные значения. Рассмот-
Рассмотрим для простоты уравнение первого порядка
?
dx
г
F7)
(где % — параметр) при определенных начальных условиях х — хй,
Будем считать, что точка (х0; у0) неособая (§ 1), т. е. при
заданных условиях существует единственное решение уравнения F7).
Тогда из геометрического смысла уравнения F7) (§ VII. 1) следует,
что если его правая часть зависит от X непрерывно, то при малом
изменении X поле направлений будет меняться мало, а потому и
решение у (х; ).) будет зависеть от к непрерывно.
Однако иногда параметр входит в дифференциальное уравнение
таким образом, что при некоторых значениях этого параметра урав-
уравнение понижает свой порядок, т. е. вырождается. При этом возни-
возникают новые обстоятельства, которые мы поясним на примере.
Рассмотрим задачу
= 0, у\х=0=1, F8)
с решением _у = е--т?-. При Я,= 0 получается вырождение (почему?).
Пусть решение рассматривается при х^О и К—*-}-0; это решение
показано на рис. 98. Уравнение F8) в
пределе переходит в равенство у—0, но
мы видим, что при малом X решение близко
к нулю не сразу отд;=0, а только от
некоторого х—к. Промежуток 0 < х < h,
называемый пограничным слоем, служит
для перехода от единичного начального
значения F8) к близкому к нулю зна-
значению. Ширина пограничного слоя ус-
условна, так как теоретически решение
нигде не становится точно равным нулю.
Если, например, принять за ширину
пограничного слоя значение x=h, при
котором решение уменьшается в е раз по сравнению с исходным
значением, то мы получим
Рис. 98.
т. е. для задачи F8) ширина пограничного слоя просто равна \,
Такого рода профиль имеет скорость жидкости при скользящем
движении пластинки в покоящейся жидкости. При этом х— это pat*

276 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VII]
стояние от пластинки, отсчитываемое по нормали к ней, по оси у
откладывается скорость жидкости, а параметр X пропорционален
вязкости жидкости. Оказывается, что для уравнений движения вязкой
жидкости (это система уравнений с частными производными) коэф-
коэффициент вязкости служит множителем при старшей производной,
т. е. для этих уравнений получается та же ситуация, что для мо-
модельной задачи F8). При наличии вязкости жидкость прилипает к
пластинке, причем слой жидкости, увлекаемый пластинкой, тем уже,
чем меньше вязкость; это, впрочем, ясно и из физических сообра-
соображений. В пределе, когда вязкость равна нулю (такая жидкость на-
называется идеальной), пластинка скользит, не увлекая за собо;"]
жидкость, и скорость жидкости равна нулю вплоть до самой по-
поверхности пластинки.
Если %—> — О, то получающееся решение, изображенное на
рис. 98 пунктиром, стремится к бесконечности при любом х > 0.
Этот случай представляет меньший интерес.
Упражнение
Рассмотрите поведение решения задачи Ху"—у=1, у (— 1) = г/A) = 0 при
? + 0
§ 10. Подобие явлений
Два или несколько явлений называются в физике (химии, тех-
технике, социологии и т. д.) подобными, если они различаются только
масштабами. Например, подобными будут процессы изменения тока
в цепи по законам, изображенным на рис. 99: в обоих случаях ток
в течение некоторого времени равномерно нарастает, начиная от
2
j, ампер
3
2
1
Z t,cex
Рис. 99.
j, ампер
t,cei<
нулевого значения, затем в течение такого же времени остается
постоянным, после чего скачком спадает до нуля. Таким образом,
если выбрать в качестве характерного времени tx (принимаемого
в данном процессе за эталон для сравнения) время нарастания тока,
в качестве характерного тока /х — максимальный ток, а отсчет

§ 10] ПОДОБИЕ ЯВЛЕНИЙ 277
времени производить от начала нарастания, после чего обозначить
где i и у— безразмерные время и сила тока, то закон зависимости / (/),
изображенный на рис. 100, для обоих процессов будет одинаковым.
Отметим, что графики рис. 99 в смысле элементарной геометрии,
конечно, подобными не будут, так как при переходе от одного гра-
графика к другому углы меняются и длины не пропорциональны. Однако
если по осям откладываются величины разной размерности, то нас
никогда не интересуют углы и длины отрезков, не параллельных
осям координат. Например, на рис. 99 расстояние некоторой точки
от начала координат по правилам аналитической геометрии равно
'Vti-\-ji, но это выражение бессмысленно ~
с точки зрения размерности и потому J"
никогда не может встретиться.
Если подобны зависимости j(t), то -
подобны и другие зависимости, такие,
t
например,как \ j(t)dt — зависимость ве- """
личины протекшего заряда от времени,
Ftp — зависимость мощности тока от вре- ИС- "^
мени и т. д. Однако представим себе, что
в цепи имеется устройство, которое включается, когда сила тока до-
достигает определенного значения у0; работа такого устройства описы-
описывается функцией е (у—у0), где е — единичная функция (§ VI.3).
Ясно, что по отношению к такому устройству подобия, вообще говоря,
не будет. Таким образом, необходимо говорить не вообще о подобии
явлений, а об их подобии по отношению к тем или иным их харак-
характеристикам.
Как узнать, подобны ли два явления? Если характеристики, по от-
отношению к которым рассматривается подобие, получаются из реше-
решения некоторых уравнений, то надо посмотреть, можно ли сделать
линейные преобразования величин, входящих в эти уравнения (т. е.
замены вида х—>ахх-\-Ьх, означающие изменение масштаба и на-
начала отсчета), так, чтобы уравнения для обоих случаев стали оди-
одинаковыми. Конечно, если речь идет о дифференциальных уравне-
уравнениях, то после преобразования должны совпасть и начальные усло-
условия, которые также нужны для определения решения. Равносильный
способ: если уравнения для двух явлений можно с помощью линей-
линейных преобразований привести к одному и тому же «эталонному»
виду, то явления подобны.
Приведем пример. Пусть рассматриваются вынужденные колеба-
колебания линейного осциллятора без трения (§ VII.5), определенные
уравнением
mW +kx = A sm<^ F9)

278 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VI11
и начальными услозпямм
В этой задаче пять параметров: т, k, Л, со, х0. Чтобы выяснить,
когда при различных комбинациях этих параметров колебания будут
подобными, примем 1 /со и х0 =fc 0 за характерные время и длину
и обозначим t = — t, х — хох. После перехода к безразмерным пере-
переменным t, х и простых преобразований мы получим дифферен-
дифференциальное уравнение и начальные условия в виде
d-x k - А ~ -| , dx
—= Н Д = ; Sin Г, X ~=о=>> ~^
dli мм2 хцтш2 ' ' ° dt
= 0. G1)
i
Таким образом, если у одного осциллятора значения
Л=-^, Л = -^-1 G2)
1 тел- " v. т (л^ ' * '
будут теми же, что у другого, то эталонные задачи G1) для них
будут одинаковыми, т. е. соответствующие колебания — подобными.
Нетрудно проверить, что величины f1 и /2 безразмерны. (Применив
результаты § VII.5, легко получить формулы/t = ooj/oo2, /.2 = *сво(;/*0,
где (в0—собственная частота осциллятора, а хсво6—амплитуда ко-
колебании свободной массы т под действием силы A sin co^,) Такие
безразмерные величины, совпадение которых обеспечивает подобие
явлений, принято называть критериями подобия. Итак, в рассматри-
рассматриваемой задаче имеется два критерия G2), из которых только 1У
определяется параметрами осциллятора, тогда как совпадение /2
можно обеспечить за счет подбора начальных условий, (В преды-
предыдущих рассуждениях был исключен случаи д;0 = 0. Мы предостав-
предоставляем читателю убедиться, что в этом случае единственным крите-
критерием подобия будет /г)
Решение эталонной задачи G1) имеет вид x = y(t; Iv /2), где
конкретный вид функции ср легко получить по методу § VII,5. Воз-
Возвращаясь к исходным переменным, получаем закон колебаний
Во многих случаях критерии подобия можно установить непосред-
непосредственно из соображений размерности, Так, в разобранной задаче
примем за основные размерности массы М, времени Т и длины L.
Тогда размерности параметров задачи будут равны [/и]=Ж,
[k]=MT-\ [А]=МТ-гЬ, [ш] = 7-1, [xo]=L (проверьте!). Из
этих параметров можно составить только одну безразмерную комби-
комбинацию, не содержащую начальных данных, а именно fl. (Конечно,

§ 10] ПОДОБИЕ ЯВЛЕНИЙ 279
величины 1\, У^'/2 и т. п. также будут безразмерными, но они не
дадут новых, независимых критериев подобия.) Другой безразмерной
комбинацией, содержащей начальные данные, г.вляется 1%. Нетрудно
проверить — это мы предоставляем читателю,— что любую безраз-
безразмерную комбинацию вида makbAc<iidx\ :;ожно представить следующим
образом: l\!i, т. е. в данной задаче критериев подобия, независимых
от /х и /2, нет.
Рассмотрим еще один пример. Пусть шарик массы т подвешен
на нити длины / и колеблется с частотой v и максимальным углом
а отклонения от вертикали; при этом сопротивлением воздуха,
массой нити и другими усложняющими факторами будем пренебре-
пренебрегать. Ясно, что между указанными параметрами и ускорением тяго-
тяготения g имеется одно соотношение: например, можно задать т, I,
g и а произвольно, тогда v определяется однозначно. Напишем
размерности всех параметров: [т\~М, [l\ = L, [v] = T~\ [a] = l,
[^]=1Т~2. Здесь полной системой безразмерных критериев будет
S — lx2g~l и а; а так как между ними должно быть соотношение,
то S должно зависеть только от а, откуда
S'/3 = /VJV£-V, =/(«), т. е. v= У f/(а). G3)
Функцию /(ос) можно получить либо численно, с помощью ин-
интегрирования соответствующего дифференциального уравнения, либо
экспериментально, с помощью измерения v при заданных значениях
остальных параметров. Так как S выражается через а, то а в дан-
данной задаче является единственным критерием подобия.
Как видим, простые соображения размерности дали возможность
получить важные сведения о колебаниях. Конечно, это только самые
простые примеры приложения теории подобия и размерности, кото-
которая сейчас широко применяется в различных разделах физики.
Упомянем несколько книг, содержащих изложение этой теории и ее
приложений: П. В. Бриджмен, Анализ размерностей, ОНТИ, 1934;
Л. И. Седов, Методы подобия и размерности в механике, «Наука»,
изд. 6, 1967; Д. А. Франк-Каменецкий, Диффузия и теплопередача в
химической кинетике, нзд. 2, «Наука», 1967. Начиная с некоторого
уровня, математическая теория тесно переплетается здесь с физикой
и развивается в различных областях физики по-разному.
На подобии явлений основано моделирование, при котором пове-
поведение какого-.тлбо объекта выясняется на его модели, подобной в
указанном выше смысле. Например, чтобы выяснить, с какой час-
частотой будет при заданном а качаться маятник на Луне, можно из-
измерить частоту при том же а в земных условиях, после чего про-
произвести пересчет по формуле
вытекающей из соотношения G3).

280 ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ [ГЛ. VU]
ОТВЕТЫ И РЕШЕНИЯ
§ 1
Седло; узел; центр.
§2
d (ii2-\-z2)
уу'-\-zz'—y'*-\-zi, —L [ ' 2 = 2dx, откуда у*-{-г2 = Се-х. Отсюда видно,
что при х—у оо все частные решения (кроме нулевого) уходят в бесконеч-
бесконечность, а при х—>—оо они стремятся к нулю.
§3
1. Если а Ф 6, система имеет ровно одно решение. При а = 6, b ф 9 си-
система несовместна. При а = 6, 6 = 9 система имеет бесконечное количество
2 £
решений: x = t, у — —-— (при любом t).
2. p1=l, Хх = 1, Hi=3; р.2 = 6, Х.2=1, |Л2=— 2; х^-С^
у
§4
Равновесие в точке @; 0) устойчивое; в точках A; —1) и (—1; 1) не-
неустойчивое.
§5
1. уа(х)=1; у1(х)=:1 + х; уг{х)=\+х+^ ; ys (дс)= 1 +х + ^ +^ ; ...
В пределе получаем точное решение у = ех, разложенное в ряд по степеням х.
++ -
§6
1. Приводим результаты вычислений по первому приближению, по второму
приближению и точные значения:
X Упо первому Упо второму Уточи.
0,0 1,0000 1.0Q00 1,0000
0,1 1,1000 1,1051 1,1052
0,2 1,2100 1,2212 1,2214
0,3 i,3310 1,3496 1,3499
0,4 1,4641 1,4915 1,4918
0,5 1,6105 1,6483 1,6487
0,6 1,7716 1,8216 1,8221
0,7 1,9488 2,0131 2,0138
0,8 2,1437 2,2248 2,2255
0,9 2,3581 2,4587 2,4596
1,0 2,5939 2,7172 2,7183
2. По первому способу у @,5) = 0,7081; по второму — 0,7161.
3. Дифференциальное уравнение имеет вид —=0,5^B0 — t) — 0,2i>. Ско-
Скорость через 1,5 сек после начала движения равна 9,682 ~ .

ОТВЕТЫ И РЕШЕНИЯ
4. Приводим результаты вычислений и точные значения
281
х 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
i/поийл 0,000 0,100 0,199 0,296 0,390 0,480 0,565 0,645 0,718 0,784 0,842
Уточн.' 0,000 0,100 0,199 0,296 0,389 0,479 0,565 0,644 0,717 0,783 0,842
б. Приводим таблицу значений решения
t 0,0 0,1 0,2 0,3 0,4 0,5
х 0,000 0,100 0,201 0,305 0,412 0,525
§7
1. Пусть к > 0. Тогда ух (х) = cos У К х, y.,(x)^=s}n У к х и определи-
определитель системы, аналогичной E6), равен
У,@) i/2 @)
Ух (I) Уг @
— У
"
1 О
, sin У~к1 yTcos У~к,
У' kl.
Отсюда спектр определяется из равенства cos У к / = 0, т. е. У к / = —jj- +
V~ х
= '• 2- ■ • •)• Если
т0
= е~
1
, определитель равен
-\-е~ ) < 0, т. е. в нуль не обращается. При к = (
будет У1=\, у2 = х, определитель равен
1 0
0 1
( —cos £ sin х @< х<£;),
2. В данной задаче G (х; |) = < . t /t л\ Отсюда ре-
' | —sin | cos x [ 6 — - -^ > r
шение задачи имеет вид
X
у= —cos х \ sin i
§8
Решение имеет вид
л
Т
dg-sin л; ^ cos
При к—«- + 0 оно стремится к решению вырожденного уравнения, т.е. к
У—— 1 для всех х между —1 и 1. Вблизи обоих концов возникает погранич-
пограничный слой, ширина которого асимптотически при к—*0 равна У к.

ГЛАВА IX
ВЕКТОРЫ
В физике мел часто встречаемся с векторами, т. е. с величинами,
которые характеризуются не только числовым значением, но и
направлением. Примерами таких величин могут служить отрезок,
соединяющий начало координат с данной точкой; скорость движе-
движения материальной точки; сила, действующая на тело.
Если тело движется по определенной линии, например по прямому
рельсовому пути, то положение тела можно определять расстоянием
от определенной точки данной линии, измеренным вдоль этой ли-
линии. Вдоль заданной линии движение возможно лишь в двух на-
направлениях, которые можно различать, приписывая одному направлению
знак плюс, а !1ротпвоположному— знак минус.
Если же нам известно, что тело движется по плоскости (или в
пространстве), то мы не сможем указать положение тела в данный
момент времени, если задано только расстояние тела от определен-
определенной точки; необходимо задать еще направление линии, соединяющей
тело с этой точкой (началом координат). Точно так же, задавая
скорость тела, надо указывать ее величину н направление. Вели-
Величины, имеющие направление, называются векторами. Мы будем обо-
обозначать их полужирным шрифтом или буквами со стрелкой наверху.
В отличие от векторов, величины, не имеющие направления и пол-
полностью определяющиеся своим числовым значением в выбранной
системе единиц, называют скалярами. Примерами скаляров служат
масса тела, его энергия, температура тела в какой-либо точке.
Пока мы не рассматривали векторов, специальное слово «скаляр»
можно было не вводить в употребление.
Векторы можно рассматривать в трехмерном пространстве, или на
плоскости (т. е. в «двумерном пространстве»).
Если отвлечься от направления векторной величины, то можно
пользоваться модулем этой величины. Модуль — это положительный
скаляр, имеющий размерность рассматриваемой величины. Например,
для вектора F силы вон, имеющего определенное направление,
модулем (он обозначается через \F\ или F) будет 5 и, \F\ = 5 н.
Два вектора считаются равными, если они имеют равные модули,
параллельны и направлены в одну и ту же сторону. Это значит, что
каждый вектор можно, не меняя его, перенести поступательно (па-

ЛИНЕЙНЫЕ ДЕЙСТВИЯ НАД ВИКТОРАМИ
28.3
раллельно самому себе) в любое место, т. е. начало этого вектора
может находиться где угодно. Таким образом, задать вектор — это
значит задать его модуль и направление.
Вектор геометрически изображают отрезком, направление кото-
которого отмечается стрелкой. Конечно, для этого надо условиться о
масштабе (например, указать, что сила в 1 я изображается отрезком
в 3 см и т. п.). Лишь векторную величину, имеющую размерность
длины, можно изобразить без этого условия, т. е. в масштабе 1:1.
Поэтому, например, о векторе перемещения можно сказать, что, от-
отложенный от точки А пространства, он достигнет точки В, тогда
как для вектора силы такое утверждение бессмысленно.
§ 1. Линейные действия над векторами
К линейным действиям над векторами относятся сложение (и
связанное с ним вычитание) и умножение вектора на скаляр. (Сло-
(Сложение вектора со скаляром так же нелепо, как сложение секунд
и сантиметров.) Величина может называться векторной, только если
эти действия осуществляются по описываемым ниже правилам.
Ь ^_ —
В
Рис. 102.
Сложение двух векторов выполняется по хорошо известному из
школьного курса физики и показанному на рис. 101 правилу парал-
параллелограмма. При этом, конечно, для нахождения суммы достаточно
построить только одни из показанных на рис. 101 треугольников.
Отсюда легко получить правило сложения нескольких векторов: на
рис. 102
(В трехмерном случае векторы a,b,c,d не обязаны лежать в од-
одной плоскости!) Таким образом, сумма нескольких векторов изобра-
изображается отрезком, замыкающим ломаную, звеньями которой служат
векторы-слагаемые; направление этого замыкающего вектора берегся
от начала первого слагаемого вектора к концу последнего.

284 векторы ■ [гл. ix
Изменив на рис. 102 направление вектора OD на противополож-
противоположное, мы приходим к следующему интересному выводу. Если векторы обра-
образуют замкнутый многоугольник, т. е. каждый следующий вектор прило-
приложен началом к концу предыдущего, а конец последнего совпадает с
началом первого, то сумма всех этих векторов равна нуль-вектору 0,
т. е. вектору, конец которого совпадает с его началом. Модуль
нуль-вектора равен нулю, а направление не определено.
Отметим, что векторы нельзя соединять друг с другом знаком
неравенства, в частности, не бывает положительных и отрицатель-
отрицательных векторов.
Умножение вектора на скаляр (в частности, на число) получается
в результате естественного обобщения сложения и вычитания век-
векторов. Так, под вектором 3F понимается
сумма F-\-F-\-F; из построения ясно, что
этот вектор направлен так же, как F, но в
три раза длиннее. Под вектором (—1)/7= —F
понимается вектор, который в сумме с Fда-
Fдает 0; ясно, что этот вектор направлен проти-
противоположно вектору F и имеет тот же модуль,
что F. Обобщая эти определения, под kF(rae
к— любой скаляр) понимают вектор, модуль
Рис. 103. которого равен | Л, 11 ^*|, причем ^парал-
^параллелен F и направлен в ту же сторону, что
F, если к > 0, ив противоположную, если к < 0. (При к<СО
иногда говорят, что векторы kF и F антипараллвльны.)
При линейных действиях над векторами выполняются все обыч-
обычные правила элементарной математики. Например, можно слагаемое
а в одной части равенства заменить на —а в другой, т. е. пере-
перенести слагаемое с изменением перед ним знака из одной части ра-
равенства в другую; обе части векторного равенства можно помно-
помножить или разделить на один и тот же скаляр по обычным правилам
и т. п.
Всякое выражение вида ka-\-kb-\- ... -\-\,d, где к, |А, ...
. . ., £—некоторые скаляры, называется линейной комбинацией векторов
а, Ь, . . . , d. Заданные векторы называются линейно зависимыми,
если какой-либо из этих векторов является линейной комбинацией
остальных; -в противном случае эти векторы называются линейно
независимыми (между собой).
Линейная зависимость для двух векторов означает их параллель-
параллельность (продумайте это!). Если взять на плоскости любые два
непараллельных вектора й и ft, то какой угодно третий вектор с в
этой же плоскости можно < разложить по векторам а и й», т. е.
представить в виде линейной комбинации (рис. 103).
с ~ka-\-)xb. A)
Поэтому на плоскости можно указать два линейно независимых

§ 1]
ЛИНЕЙНЫЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ
285
вектора, но всякие три вектора уже линейно зависимы. Разложе-
Разложение A) часто применяется в механике и других дисциплинах (раз-
(разложение силы по двум направлениям и т. п.), причем каждое из
слагаемых Ка и \\Ь называется составляющей (компонентой) век-
вектора с, а совокупность векторов а, Ъ называется базисом..
Подобным образом в пространстве можно указать уже три ли-
линейно независимых вектора (любые три вектора, не параллельные
одной плоскости). Их можно принять за базис, т. е. но ним можно
разложить какой угодно четвертый вектор, а потому в пространстве
любые четыре вектора линейно за-
зависимы. Различие с утверждениями
предыдущего абзаца связано с тем,
что плоскость двумерна, а простран-
пространство трехмерно. Если в л-мерном
пространстве (§ IV.8) ввести понятие
вектора, то там базис будет состоять
уже из п векторов (см. § 5).
Наиболее широко применяются
базисы, состоящие из единичных
(т. е. с безразмерным модулем, рав-
равным 1) взаимно перпендикулярных
векторов; такие базисы называются
декартовыми или евклидовыми. Век-
Векторы, образующие декартов базис, обычно обозначаются i, j (на
плоскости) и /, j, k (в пространстве); таким образом, аналогично
A) можно написать разложение любого вектора
рис Ю4.
на плоскости и
ay f-\-a2k
в пространстве, где ах, а , аг—коэффициенты разложения.
Легко выяснить геометрический смысл этих коэффициентов, на-
называемых декартовыми координатами вектора а; при этом будем
для определенности говорить о векторах на плоскости, так как в
пространстве получаются совершенно аналогичные результаты, Вы-
Выберем на плоскости произвольно точку О, которую назовем началом
координат, и проведем через нее оси параллельно векторам выбранного
базиса; эти оси обозначим соответственно буквами х и у (рис. 104).
Мы получим дека ртову систему координат, в которой положение каждой
точки Л на плоскости определяется координатами (хД;уА). Из рис. 104
мы видим, что для вектора а = АВ будет
ах = хв — хА, ау=ув—уд.
Разность хв — хА называется также проекцией вектора АВ на
ось х. Вообще, проекцией пргс вектора а = АВ на какую-либо ось /
(т. е. на прямую, для которой указано, какое из двух ее направлений

286
ВЕКТОРЫ
[ГЛ. IX
принято за положительное) называется модуль вектора А'В', опре-
определенного основаниями перпендикуляров (рис. 105), опущенных из
точек А и В на ось /; причем этот модуль берется со знаком «-f » или
«—» в зависимости от того, пройдет ли вектор А'В' в положитель-
положительном или отрицательном направлении оси /. Аналогично определяется
проекция одного вектора на другой; в этом случае перпендикуляры
опускаются на этот другой вектор или на его продолжение.
Рис. 105,
Рис. 106.
Таким образом, декартовы координаты вектора — это его проек-
проекции на базисные векторы:
= пр/ с,
az = прг а= прАс.
Подчеркнем, что проекция вектора — скаляр, Ее физическая раз-
размерность такая же, как размерность проектируемого вектора. Из
рис. 106 сразу следует простая формула для вычисления проекции:
npf а — | а | cos а = | а | cos (с, /).
B)
Отсюда вытекает, в частности, широко применяемая в математике
формула для декартова разложения единичного вектора е:
/ч /ч /ч
e=exi-\-eyj-\- ezk = cos (e, x) i + cos (e, y)j+ cos (e, z) k.
Применение декартовых проекций дает возможность вместо гео-
геометрических построений пользоваться формулами и вычислениями,
что обычно оказывается проще, Получим в качестве примера условие
параллельности двух векторов, заданных своими разложениями
Это условие можно записать в виде векторного равенства
где К — какой-то скаляр, или в проекциях на оси координат

§ 2] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 287
Выражая из каждого равенства к и приравнивая результаты, приходим
к требуемому условию
Это условие состоит из двух равенств, а так как вектор определяется
Тремя, то при выборе вектора, параллельного данному, остается еще
одна степень свободы — модуль. (Выведите эти равенства геометри-
геометрически, исходя из свойств подобия треугольников,)
В заключение подчеркнем, что вектор с полностью характеризуется
своими декартовыми проекциями ах, а аг, тоЛЬко если декартов
базис /, j, k зафиксирован. Если выбрать этот базис по-другому,
т. е. если повернуть оси координат, то тот же вектор будет иметь
другие проекции (координаты). Мы поговорим об этом подробнее в § 5.
Упражнения
1. Пусть ОА —а, ОВ = Ь. Найдите вектор ОС, гдеС — середина отрезка АВ.
2. В тех же условиях найдите вектор OD, где D делит отрезок АВ в отно-
отношении к; 1.
3. Начало вектора в точке А B; 3), конец его в точке В (— 1; 4). Разло-
Разложите этот вектор по единичным векторам координатных осей.
§ 2. Скалярное произведение векторов
Скалярным произведением двух векторов называется скаляр, равный
произведению модуля одного вектора на проекцию на него другого
вектора. Скалярное произведение векторов с и & обозначается так:
а-Ъ или (а, Ь). Таким образом, a-b=\a\npab, а если воспользо-
воспользоваться формулой B) для вычисления проекции, мы получим
а-Ь = \а\ пра6 = |с|]&| cos (с, Ъ). C)
Отсюда сразу видно, что скалярное произведение не зависит от
порядка сомножителей: a-b = b-a. Кроме того, видно, что для нену-
ненулевых векторов с и & скалярное произведение а-Ъ будет положи-
положительным, отрицательным или равным нулю в соответствии с тем,
будет ли угол между векторами с и & острым, тупым или прямым.
Особенно важно запомнить равенство
как необходимое и достаточное условие перпендикулярности векторов
а и Ь. Частным случаем является также скалярное произведение
вектора самого на себя [скалярный квадрат вектора):
а ■ а = | а \ \ а \ cos 0 = | а \2.
Важным примером скалярного произведения является работа,
которую совершает сила F на прямолинейном пути S. Если тело

288 векторы [гл. lx
движется по прямой и сила направлена по этой же прямой, работа
равна произведению силы на путь. Если же направление силы не
совпадает с направлением движения, то работа равна произведению
пути на величину составляющей силы, действующей вдоль направ-
направления движения, т. е.
где 9— угол между направлениями силы и перемещения. Таким
образом, работа равна скалярному произведению силы на путь.
Частный случай, когда сила действует вдоль направления движения,
охватывается этой формулой. При этом если направление силы сов-
совпадает с направлением движения, то 9 = 0, cos 9=1, ^ = |/r||S|,
работа положительна. Если же сила направлена противоположно
движению, то 9 = я, cos 9 = — 1, А = — | F\ | S\, работа отрицательна.
Отметим еще следующие свойства скалярного произведения:
(ка)-Ь = X (a-b), (a-\-b)-c = ac-\-bc.
Мы не станем останавливаться на простом доказательстве этих свойств;
желающие могут провести его самостоятельно, исходя из определения
скалярного произведения. Эти свойства дают возможность при дей-
действиях со скалярным произведением пользоваться обычными правилами
алгебры, помня, однако, что скалярно перемножать можно только
два вектора.
Применяются также следующие формулы, проверить которые
мы предоставляем читателю: если е, е', е" — единичные векторы, то
с-е = пр,,с, е'-е" = cos (e', е").
Выведем теперь важную формулу, позволяющую вычислить ска-
скалярное произведение, если известны проекции перемножаемых век-
векторов в некотором декартовом базисе i, j, k (§1):
а = aj + ayj +azk, b = bj + by j -f bzk. D)
Если-учесть, что
(почему?), то, подставляя вместо с и & их разложения D), получим
a-b = axbx-\-ayby-\-azbz E)
(проверьте!). Как мы уже отмечали в конце § 1, при повороте осей
координат проекции векторов с и & на оси координат, вообще говоря,
меняются; однако правая часть E) остается неизменной (инвариант-
(инвариантной), так как она равна левой, а определение скалярного произве-
произведения было дано независимо от расположения осей координат.
Если в формуле E) положить Ь = а, мы получим выражение для
квадрата модуля вектора через его декартовы координаты;

§ 3]
ПРОИЗВОДНАЯ ОТ ВЕКТОРА
289
Для вектора на плоскости получаем | а |
\-\-0y. Эта формула
равносильна теореме Пифагора, а предыдущая — аналогу теоремы
Пифагора для пространства (квадрат диагонали прямоугольного па-
параллелепипеда равен сумме квадратов трех его ребер).
Упражнения
1. Два вектора единичной длины образуют угол ф = 30°. Найдите их скаляр-
скалярное произведение.
2. Найдите скалярное произведение векторов, изображенных на рис. 107.
3. Вычислите угол 6 между векторами
4. Докажите, что векторы, имеющие начало в точке А (— 1; 1), а концы
в точках В A: 2) и С @; — 1) соответственно,
перпендикулярны.
5. Параллелограмм ABCD построен на век-
векторах AB = F и AD=G. Выразив диагонали
АС и DB через F и С и рассматривая АС-АС
и DB-DB, докажите теорему: сумма квадратов
диагоналей параллелограмма равна сумме квад-
квадратов всех его сторон.
6. В кубе со стороной а найдите длину
диагоналей (внутренних!); углы между диаго-
диагоналями; проекции сторон на диагонали,
7. Правильный тетраэдр со стороной а
расположен так, что одна из его вершин на-
находится в начале координат, другая — на поло-
положительной полуоси х, третья — в первой чет-
четверти плоскости ху. Найдите координаты всех вершин и центра тетраэдра;
угол между прямыми, идущими из центра к вершинам.
У
4
3
г
и
F/
1
I
~ i
i
/
'}
1\
i
1
i
I
I
2
IF
3
,
i
i
4 х
Рис. 107.
§ 3. Производная от вектора
Найдем производную от вектора, зависящего от некоторой пере-
переменной, например от времени t, по этой переменной.
Будем откладывать вектор А(() от некоторой определенной
точки О. Тогда конец вектора при изменении t начертит линию (L)
(рис. 108).
Возьмем весьма малое dt и составим отношение
A(t + dt)-A(t)
dt
Это отношение также есть вектор. (Вектор A(t-\-dt)—A (t) изобра-
изображается на рис. 108 отрезком A1yM2.) Оно является производной век-
dA
dt
dA__A(t + dt) — A(t)
dt" dt
тора A (t) по переменной t и потому обозначается через -г-, так что
F)
Я. Б, Зельдович, А. Д. Мышкис

290 векторы [гл. lx
(Более строго, в правой части надо поставить знак предельного
перехода при dt -*■ 0.)
Формулу F) можно переписать и так:
с точностью до малых высшего порядка. Как и в случае обычных
. функций, можно написать ряд Тейлора
Ясно, что при весьма малом dt точки М%
и Aft линии (Z.) весьма близки, так что век-
вектор -тт направлен по касательной к ней.
Если С — постоянный вектор, то C(t-\-dt) — С @=0, так что
в этом случае — = 0.
Пользуясь определением производной, легко доказать две сле-
следующие формулы:
1. ±[a1Ai(t) + atAt(t)]=a1^P + ai^P-, где av а2-
стоянные скаляры.
2. |
если вектор С — постоянный. Таким образом, мы видим, что произ-
производная от вектора вида f(t) С оказывается параллельной самому
этому вектору (тогда как из рис. 108 видно, что в общем случае
это не так).
Найдем производную от скалярного произведения. Пусть А и
В — два переменных вектора. Согласно определению производной
— (А В\ — АУ + Ш
Пользуясь формулой G), находим
ИЛИ
dt v" "' dt

Л 4] ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 291
Пренебрегая членом, содержащим dP, окончательно получаем
dt^ dt dt
Таким образом, формула имеет такой же вид, как формула для
производной от произведения двух скалярных функций.
Положив, в частности, в формуле (8) А = В, получим
Однако Л-.Д = |.Д|2 и потому -г- (Д-Д) = 2 | А |—i^- Приравнивая
эти результаты, получаем
\А\ИМ-АМ т е "Я[ А~
\Л ,, — Л ,, , 1. С.
dt -" dt ' • dt ~ \A\ '
Отсюда легко вывести, в частности, что если вектор A(t) имеет
постоянный модуль, а изменяется лишь его направление, то вектор
dA
-тт перпендикулярен вектору А. В самом деле, тогда |/l| = const,
d I A I dA
т. е. —^г~^=0' и в силу последней формулы Д--тт = 0, а равенство
нулю скалярного произведения означает, что А и -г- перпенди ;у-
лярны.
Упражнение
Найти угол, который составляет винтовая линия x = R cos со/, у = R sin co^8
z = vt с ее осью (осью г).
§ 4. Движение материальной точки
При движении материальной точки в пространстве зависимости
между положением точки, ее скоростью и ускорением являются со-
соотношениями между векторами. Пусть положение точки характери-
характеризуется вектором г, проведенным из начала координат в эту точку,
скорость — вектором и, ускорение — вектором а. Тогда из определения
производной немедленно вытекает
_dr_ _du_d*r
Запишем вектор г через единичные векторы координатных осей:
В этом равенстве х, у, z — это проекции, которые при движении
точки изменяются со временем, а векторы /, /, k — постоянные.
10*

292 векторы [гл. ix
Поэтому
dr d , . , . . ., dx . , dy . . dz .
Следовательно, проекции вектора скорости и на оси координат
равны производным от соответствующих проекций вектора г:
_dx __dy _ dz
u*~Tt' uy~Tt' u*'~~df
Точно так же для ускорения получаем
_dUx__cPx _duy_d*y d"z_ rf2z
a* ~ dt ~ d t*' ay'~~ dt ~ dt°-' а* ~ dt ^ It* '
В силу формулы A0) скорость изменения расстояния \г\ точки
от начала координат равна
d\r\ _ dt __ г и
dt ~ | г | ~ | г | •
С помощью последней формулы легко найти, в частности, усло-
чие, при котором расстояние точки от начала координат не нзм>
няется, т. с, | г j ^sb const. Именно, так будет в следующих двух
случаях. Во-первых, если и = 0 (в этом случае точка не движется),
и, во-вторых, если в каждый момент времени скорость и перпенди-
перпендикулярна вектору г (в этом случае тело движется по сфере радиуса
|г| с центром в начале координат).
Подобным образом, из (9) получается формула
d и
dt
= 2(а-и). (И)
Из формулы A1) следует, что величина скорости постоянна в двух
случаях: если равно нулю ускорение, либо если ускорение не равно
нулю, но направлено перпендикулярно скорости.
Уравнение движения материальной точки имеет вид ma = F,
где т — масса точки, F—сила, действующая на точку. (Второй
закон Ньютона.) Умножим обе части этого уравнения скалярно на
вектор скорости и. Получим
т {а-и) = Fu,
Пользуясь формулой A1), получим
1 d , ..,., „
млн
d
dt

Л 4] ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 293
Покажем, что величина F-u есть мощность силы F. В самом
деле, за время dt точка перемещается на dr, при этом производится
работа Fdr. Отношение этой работы ко времени dt, равное
H-dr r dr F
есть работа, производимая в единицу времени, т. е. мощность.
Если обозначить — |и|2=Г, то уравнение A2) принимает вид
-~Z_= F-u, откуда Г2 — T. = \F-udt (справа стоит работа силы F).
dt J
Таким образом, из второго закона Ньютона следует, что суще-
существует определенная величина Т, выражающаяся через массу и ско-
скорость движущейся точки и притом такая, что увеличение Т в
процессе движения как раз равно работе внешней силы F. Это и
• служит обоснованием того, что величину Т называют кинетической
энергией движущейся материальной точки.
Иногда в качестве параметра, определяющего положение дви-
движущейся точки вдоль траектории, берут длину s дуги, отсчитыва-
отсчитываемую вдоль траектории от некоторого начала отсчета, т. е. пола-
полагают r — r(s). Так как отношение длины бесконечно малой дуги к
стягивающей ее хорде стремится к единице (в силу того, что такая
дуга почти не успевает изменить свое направление, т. е. «искри-
«искривиться»), то при As—*0
As
1, т. е.
Аг
As
= 1. A3)
Поэтому производная dr/ds представляет собой единичный вектор,
направленный по касательной к траектории. Этот вектор принято
обозначать буквой т, откуда
dr dr ds
где обозначено и = \и\.
Из формулы A3) вытекает также выражение для дифференциала
дуги в декартовых координатах
ds = \ dr | = | d (xi + yj+ zk) | = | dxl + dyj+dzk \ = У dxi + dy* -f dz\
Так как | т (s) \ = 1 = const, то (см. § 3) -т-_|_т. Таким образом,
прямая рр (рис. 109), проведенная через некоторую текущую
точку М траектории (L) параллельно dr/ds, будет служить нор-
нормалью к (Z.), т. е. перпендикуляром к касательной // в точке М,
Чтобы отличить ее от остальных нормалей (а в каждой точке линии
в пространстве можно провести к ней бесконечное число нормалей,
которые заполняют «нормальную плоскость»), ее называют главной

294
ВЕКТОРЫ
[гл. ix
нормалью в точке М к линии (L). Длина вектора dx/ds называется
кривизной линии (Z.) в точке М и обозначается буквой k, т. е.
dx
где п — единичный вектор главной нормали (см. рис. 109).
Из рис. ПО виден геометрический смысл кривизны;
. ВС
Дт
~дТ
As
а
ПД^'
где а—угол между касательными к (L) в близких точках В и С;
в последнем переходе мы заменили отрезок ВС на дугу окружности
единичного радиуса. Таким образом, кривизна есть скорость пово-
поворота касательной в расчете на единицу длины пройденного пути.
А/
(О
Р
Рис. 109.
Рис. 110.
Отсюда видно, в частности, что во всех точках окружности радиуса
R кривизна k—\/R (об этом говорилось в ВМ, § III.5, при рас-
рассмотрении понятия кривизны плоской кривой). Заодно видно, что
вектор x's = -j- , а с ним и я направлены в ту сторону, куда кривая
Ct S
заворачивает.
Дифференцируя формулу A4) по t, получим
dtr du , dx du , dx ds du , ,, ,,_.
a = dT*=dtx + uTt='dtx + uTsTt==dix + lfikn' <15)
Эта формула широко применяется в физике, так как она дает раз-
разложение вектора ускорения на «тангенциальную» (т. е. направлен-
направленную по касательной) и нормальную составляющие; последняя, как
видим, направлена именно по главной нормали.
Таким образом, вектор а, будучи отложен от точки М, обяза-
обязательно лежит в плоскости, проходящей через касательную и глав-
главную нормаль, проведенные в этой точке; эта плоскость называется
соприкасающейся плоскостью к линии (Z.) в точке М. Можно дока-
доказать, что это не что иное, как плоскость, проходящая через три

R 5] ПОНЯТИЕ О ТЕНЗОРАХ 295
точки линии (L), расположенные в бесконечной близости от М.
(Подобно тому как касательная — это прямая, проведенная через две
бесконечно близкие точки линии.)
Из формулы A5) вытекают важные выводы о силах, действующих
на точку в процессе движения. Подставим в формулу второго за-
закона Ньютона F — ma выражение для а из A5). Мы видим, что
действующая сила имеет тангенциальную составляющую
F,= Ff = m£tT A6)
и нормальную составляющую
Fn = Fnn = mu*kn, A7)
направленную по главной нормали к траектории. Соприкасающаяся
плоскость к траектории в ее некоторой точке — это плоскость век-
векторов и и F в этой точке.
Из формулы A6) получаем
„ du d fmu2\ dT
U^=UmTt = d-t{—)=-aT>
откуда приращение кинетической энергии равно
Г2— Тл =
Мы видим, что работу производит лишь тангенциальная составля-
составляющая силы. Нормальная же составляющая (она называется также
центростремительной силой) не меняет скорости движения точки, но
порождает искривление траектории, причем кривизна согласно A7)
равна
ти*'
Напомним, что размерность кривизны (см*1) обратиа размерности
длины.
Упражнение
Найдите кривизну винтовой линии из упражнения к § 3.
§ 5. Понятие о тензорах
Мы уже подчеркивали в конце § 1, что если характеризовать
вектор тройкой его декартовых проекций, то надо иметь в виду,
что эта тройка существенно зависит от выбора декартова базиса.
Рассмотрим этот вопрос подробно. Будем обозначать векторы ба-
базиса буквами еи ег, е3, а проекции вектора а—символами ах, а2,

296 векторы [гл. ix
аа, так что
с = а1е1 + аге2 + а3е3. A8)
Допустим теперь, что выбран новый декартов базис е[, ёг, е'3,
выражающийся через старый по формулам
з
auej (i = l, 2, 3).
В тензорной алгебре принято писать более коротко:
e'i = aue/, A9)
при этом подразумевается, что по повторяющемуся индексу произ-
производится суммирование в соответствии с размерностью пространства—-
так, для трехмерного пространства у=1, 2, 3. Такой индекс яв-
является немым, т.е. может быть обозначен любой буквой: а,-;-е;-=
= alkek = awei' и т. д.
Умножив обе части A9) скалярно на е^ получим, что а,-;- =
= e'l-e/. Аналогично, из формул е( = Р(;е/, выражающих старый
базис через новый, получаем, что $^ = е('е). Но это значит, что
Р(-; = а;7, т. е. старый базис выражается через новый по формулам
е,. = а,,.е;. B0)
(Это равенство можно переписать в виде е;. = cci;-e(', так что полу-
получается, что в равенстве A9), связывающем декартовы базисы, можно
просто «переставить» множитель a(J из одной части в другую.)
Если подставить выражения B0) в A8) и обозначить через а\
проекции вектора а в базисе е\, мы получим
= S ai ei =
2 °/ 2 aHe'i = 2 a/iaie'h
i I i. i
Меняя обозначения /<->/', получим
a = 2 ai/a/e'i =
t. i
откуда
a; = a,/zy. B1)
Сравнивая с A9), мы видим, что проекции любого вектора преоб-
преобразуются по тем же формулам, что и базисные векторы.
Конечно, в предыдущих рассуждениях под а не обязательно
понимать «геометрический» вектор, т. е. направленный отрезок на
плоскости пли в пространстве. Это может быть вектор силы или
скорости и т. д.; во всех случаях его проекции преобразуются по
формулам B1). Нетрудно проверить, что и обратно, каждую тройку
величин, приобретающих определенные значения только после ука-
указания декартова базиса и преобразующихся по формулам B1) при
замене A9) этого базиса, можно истолковать как тройку координат

к 5] понятие о тензорах 297
некоторого вектора, т. е. считать, что такая тройка определяет не-
некоторый вектор. (В то же время вряд ли полезно истолковывать
любую тройку величин как вектор. Например, при изучении потока
газа можно рассматривать тройку величин—температуру Ф, давле-
давление р и плотность р, характеризующих состояние газа в некоторой
точке пространства. Однако истолковывать такую тройку как вектор
нецелесообразно, так как повороты базиса в пространстве не ска-
сказываются на значениях величин, составляющих тройку. Три скаляра
не составляют вектор.)
Бывают величины, преобразующиеся при замене A9) базиса по
более сложному закону, чем B1). Важный пример таких величин
получается при рассмотрении линейного отображения пространства
в себя. Говорят, что задано такое отображение Т, если каждому
вектору а поставлен в соответствие вектор Та (того же простран-
пространства), причем сумме прообразов соответствует сумма образов, т. е.
Т(а~\-Ь) = Та-\- Tb, ТСка) — кТа. Примерами линейных отображений
могут служить поворот пространства вокру! некоторой точки, рав-
равномерное сжатие его к некоторой плоскости, прямой или точке
и т. д. (продумайте это!).
Чтобы охарактеризовать такое отображение числами, выберем
в пространстве базис et и разложим каждый из векторов Tet по
этому базису:
Те{=рле, B2)
(обратите внимание на порядок индексов). Знание девяти коэффи-
коэффициентов Pij- позволяет найти образ 6= Та любого вектора A8).
В самом деле,
b = £ bfii = Т ф a fi() = ^aiPj!ej ==2 ajPliet,
откуда b;=p(j-aj.
Набор коэффициентов ptJ, зависящих от двух индексов, часто
записывают в виде матрицы, т. е. таблицы
Ргг Р1
(Pl/)=\Pzi Рг-г Ргъ
з1 Ръг Рзз/
Посмотрим теперь, как изменятся коэффициенты p;j при переходе
к новому базису е'{. Так как в силу B2) р,у = Геуе,., то, учитывая
формулы A9), получим
р'ц = Те) ■ е] = ап Tet • aikek = aik<xf[pkl, B3)
Отсюда, в частности, легко показать, что сумма рп при таком
переходе остается инвариантной, т. е. она представляет собой ска-
скаляр. В самом деле,
Ра = v-nPuPki =-■ Ъ ■ etfWkL = ек ■ [Фи) Ры = ек ■ etpkl - ри.

298 векторы [гл. ix
В рассмотренном примере величины р^ были безразмерными.
Можно проверить, что, и обратно, каждый набор безразмерных ве-
величин pip преобразующихся по формулам B3) при замене A9)
декартова базиса, можно истолковать как матрицу некоторого ли-
линейного отображения пространства в себя. В § XI.5 будут приве-
приведены примеры размерных величин, имеющих иной физический
смысл, но также преобразующихся по формулам B3) при замене
базиса.
Перепишем формулы B1) и B3), изменив обозначения индексов:
а], = anal, p'fj. = ai'iai'jP/j.
Мы еидим, что эти формулы имеют общую структуру. Обобщая, мы
приходим к закону преобразования величин д1,-/ ... i, зависящих от
т индексов г, j, ., . , /, каждый из которых принимает значения
1, 2, 3 (для трехмерного пространства) или 1, 2 (для плоскости):
qi'i'..J' = ai'iai'i- • >a-viqr,...i> B4)
Если величины q;j..,i принимают определенные значения только по-
после указания декартова базиса и преобразуются по формулам B4)
(в правой части стоит /и-кратная сумма!) при замене A9) этого
базиса, то говорят, что величины q~{j л образуют тензор ранга т.
Таким образом, набор проекций вектора образует тензор 1-го ранга,
набор коэффициентов линейного отображения — тензор 2-го ранга
(этот набор коэффициентов в каждом базисе свой, но определяет
одно и то же отображение, не зависящее от выбора базиса). Отме-
Отметим, что с точки зрения приведенного определения тензором ранга
О надо считать величину, принимающую в выбранных единицах
измерения числовое значение и инвариантную относительно замены
базиса, т. е. скаляр.
К понятию тензора возможен также следующий подход. Рассмот-
Рассмотрим для определенности тензор 2-го ранга, т. е. набор величин
Pij, преобразующихся при замене A9) базиса по формулам B3), и
сопоставим этому набору формальное выражение
з
^=2 PUeier B5)
При этом тензорное произведение е{е^ (не путать со скалярным
произведением е^-е/.) не сводится к какому-либо более простому
объекту — скаляру или вектору. Перестановка множителей в тензор-
тензорном произведении невозможна, т. е. е(еj^ ej-eh но в тензорном
произведении сумм можно раскрывать скобки по обычным правилам,
следя за порядком сомножителей, например:

§ 5] понятие о тензорах ' 299
В новом базисе е\ взамен B5) надо написать выражение
Однако с учетом формул B3) и B0) получим
2
i.l.k.i
к,i
I
Итак, выражение B5) — оно и называется тензором—инвариантно
относительно замены декартова базиса. Аналогично вводится понятие
тензора любого ранга, причем тензор 1-го ранга 2a/ei есть вектор.
i
Тензоры, тензорная алгебра и тензорный анализ (в котором изу-
изучаются правила дифференцирования тензоров) играют в современной
физике очень важную роль. В тензорных терминах формулируются
основные законы теории упругости, электродинамики и оптики ани-
анизотропной среды и т. д. Это дает возможность не связывать рас-
рассмотрение с какой-то одной, искусственно выбранной системой коор-
координат, не оправданной существом исследования. Отметим, что во
многих случаях оказывается недостаточным ограничиваться декарто-
декартовыми базисами; тогда приходится изменить определение тензора так,
чтобы он оставался инвариантным при переходе к любому, не обя-
обязательно декартову базису. Мы не будем рассматривать здесь это
измененное определение.
А. Эйнштейн применил тензорный анализ к электродинамике и
теории тяготения, чем привлек к тензорам широкое внимание физиков
и математиков. В его небольшой книге «Сущность теории относи-
относительности» содержится лучшее краткое изложение теории тензоров.
Упражнение
Напишите матрицы линейных отображений плоскости в себя, описан-
описанных на'рис. 111. Укажите, во что переходит квадрат при различном напра-
направлении его сторон.
V,
A/L
а)
Ф
сг
Л
г)
д)
X,
Рис. 111.

300 векторы [гл. ix
§ 6. Многомерное векторное пространство
В § IV,8 мы видели, что к понятию многомерного пространства
можно подойти двояко: либо исходя из числовой схемы, либо же
исходя из рассмотрения системы со многими степенями свободы.
Аналогичные подходы возможны к понятию многомерного векторного
пространства, которые выделяются из общих пространств возмож-
возможностью выполнения линейных действий. Рассмотрим сначала первый
подход, причем дли определенности будем говорить о четырехмер-
четырехмерном пространстве (общий случай рассматривается аналогично).
Как мы видели, точкой в четырехмерном пространстве можно
считать просто набор четырех чисел (xt; х2; х3; xt). Единичный
вектор е1 первой координатной оси (оси х,) надо представлять себе
как отрезок с началом в начале координат @; 0; 0; 0) и концом
в точке A; 0; 0; 0). Впрочем, исходя из возможности переносить
любой вектор параллельно самому себе, ех можно рассматривать как
отрезок с началом в любой точке {хг\ х2; х3; хА) и концом в точке
(xl-\-\; x2; x3; xt). Аналогично вводятся единичные векторы е2,
е3, е4 других трех координатных осей. Рассматривая линейную ком-
комбинацию этих четырех векторов
x = x1e1 + x.ze2 + x3e3 + xiei, B6)
мы получаем вектор, ведущий из начала координат в точку (лгг; хг;
хя; х4), т. е. радиус-вектор этой точки. Вектор х можно отклады-
откладывать не от начала координат, а от любой другой точки; во всяком
случае, коэффициенты хг, х2, х3, х4 в формуле B6) —это проекции
вектора х на оси координат.
Действия над четырехмерными векторами осуществляются по тем
же формальным правилам, что и над двумерными и трехмерными.
Наиболее просто рассматривать векторы разложенными по осям ко-
координат, т. е. представленными в виде B6). Если наряду с векто-
вектором Bо) мы имеем вектор y=ylel-\-y2e2 + y3e3-\-yiei, то
х + у = (хг +уг) ех + (х2 +уг) ег + (х3+у3) е3 + (xt + yt) eit
Xx = Xxlel + Xx2e.i + Xx3e3 + 'kxiei (X — скаляр),
x-y = xly1-\-x2y.i-\~x3y3-\-x,yi. B7)
Можно проверить, что все основные свойства, описанные выше для
двумерных и трехмерных векторов, сохраняют силу и для четырех-
четырехмерных векторов. Однако некоторого внимания требуют свойства,
связанные с понятием линейной зависимости (§ 1). Де.чо в том, что
в четырехмерном пространстве возможны плоскости двух «сортов»—
двумерные и трехмерные. Двумерная плоскость получается, если
взять два линейно независимых (т. е. непараллельных) вектора,
а затем их всевозможные линейные комбинации отложить от какой-
либо фиксированной точки, например от начала координат. Если это
проделать с тремя линейно независимыми векторами, то получится

К 6] МНОГОМЕРНОЕ ВЕКТОРНОЕ ПРОСТРАНСТВО 301
трехмерная плоскость (говорят также «трехмерная гиперплоскость»)
в четырехмерном пространстве. Если же взять четыре линейно неза-
независимых вектора (т. е. не параллельных одной трехмерной плоско-
плоскости), то их линейные комбинации заполнят все пространство, т. е.
по ним можно разложить любой пятый вектор. Таким образом,
в четырехмерном пространстве любые четыре линейно независимых
вектора можно принять за базис (ср. § 1).
Рассмотрим теперь другой подход к понятию многомерного век-
векторного пространства. Будем исходить из некоторой совокупности R
каких-то объектов, над которыми можно, оставаясь в рамках R,
производить линейные действия, т. е. складывать друг с другом
и умножать на скаляры (вещественные числа). Кроме того, требуется,
чтобы при этих действиях соблюдались те же свойства, которые
были указаны в § 1 для линейных действий над векторами на пло-
плоскости или в пространстве. В этом случае R называется линейным
(или векторным) пространством, а составляющие его объекты назы-
называются (обобщенными) векторами.
Основной числовой характеристикой заданного векторного прост'
ранства является максимально возможное число линейно независимых
векторов, называемое также размерностью этого пространства. Напри-
Например, если пространство R четырехмерно, то это означает, что в нем
можно указать такие четыре линейно независимых вектора аг, а2,
а3, а4, что любой другой вектор х из R можно представить в виде
* = Л,,а1 + М2 + Мз + М4- B8)
Таким образом, эти векторы а1У а2, а,, а4 можно в R принять за
базис. Так как для разных векторов х коэффициенты разложения
в B8) могут принимать всевозможные значения, то при выборе век-
вектора х в пространстве R имеется четыре степени свободы, т. е.
пространство R оказывается четырехмерным и в смысле § IV.8.
Может оказаться, что в рассматриваемом линейном пространстве
можно указать как угодно большое число линейно независимых
векторов. Такое пространство называется бесконечномерным; пример
бесконечномерного пространства мы рассмотрим в § XIV.7.
Если в конечномерном линейном пространстве введено понятие
скалярного произведения, удовлетворяющее описанным в § 2 свой-
свойствам обычного скалярного произведения, то это пространство на-
называется евклидовым. В евклидовом пространстве естественно вво-
вводятся понятия модуля векгора (по формуле | х | = У х-х), единичного
вектора, ортогональности векторов (если х-у = 0). В евклидовом
пространстве обычно выбирается не какой угодно базис, а ортого-
ортогональный базис, т. е., например, для четырехмерного случая сово-
совокупность четырех взаимно ортогональных вектороз ах, а2, а3, а4.
В этом случае коэффициенты разложения B8) любого вектора х
легко найти следующим образом: помножим обе части равенства B8)

302 векторы [гл. ix
скалярно на какой-то из векторов а;, что даст
x-aj = kj{aj-aj);
остальные слагаемые в правой части пропадают в силу условия
ортогональности. Отсюда
'V = ^(V=1, 2- 3'4)- B9)
Наличие скалярного произведения делает возможными повороты
в линейном пространстве, которое приобретает свойство изотропии
(равноправия направлений); при этом векторное пространство стано-
становится существенно более полноценным. Вернемся к упомянутой в § 5
характеристике состояния газа в точке с помощью величин 0, р, р.
Над приращениями этих величин можно производить линейные дей-
действия, т. е. тройки таких приращений образуют трехмерное линей-
линейное пространство. Однако в этом пространстве нет скалярного
произведения и поворотов, т. е. оно не является евклидовым, чем и
объясняется его неполноценность*).
Упомянем еще о псевдоевклидовых пространствах, в которых
квадрат модуля вектора (скалярное произведение его самого на себя)
может быть положительным, отрицательным или равным нулю. Именно
таким в силу теории относительности является четырехмерное про-
пространство х, у, z, t декартовых координат и вре.мени. В псевдоев-
псевдоевклидовом пространстве возможны повороты, хотя и не все направ-
направления в нем оказываются равноправными.
До сих пор мы считали, что скаляры—это произвольные веще-
вещественные числа; в этом случае линейное пространство называется
вещественным. Рассматриваются также комплексные линейные простран-
пространства, в которых в качестве скаляров можно брать произвольные
комплексные числа. Тогда при определении евклидова пространства
имеется новый момент: именно, требуется, чтобы
(у, х)=(х, у)*, C0)
т. е. чтобы при перестановке сомножителей в скалярном произведе-
произведении оно заменялось на комплексно сопряженное число. Однако если
в формуле C0) положить у = х, то мы получим, что скалярный
квадрат любого вектора представляет собой число вещественное
(и даже, как можно проверить, положительное, так что модуль век-
вектора можно находить по той же формуле, что и раньше, и этот
модуль оказывается положительным). Кроме того, при вынесении ска-
скалярного множителя за знак скалярного произведения пользуются
следующими формулами:
(Хх, у) = Х(х, у), (х, Ху) = Х*(х, у).
Простейший пример четырехмерного комплексного евклидова про-
*) Не надо п\тать эту «неевклидовость'» с так называемой неевклидовой
геометрией, которая к теории линейных пространств не имеет отношения.

ОТВЕТЫ И РЕШЕНИЯ 303
странства — это пространство, рассмотренное в начале этого пара-
параграфа, где, однако, числа xt, jc2, jc3, х4 надо считать комплексными,
а взамен формулы B7) надо воспользоваться формулой
ху =
Упражнения
1. Укажите формулу для длины вектора B6).
2. Проверьте, что радиусы-векторы точек A; 1; 1; —1), A; 1; —1; 1) и
@; 0; 1; 1) взаимно перпендикулярны; постройте четвертый (не нулевой) век-
вектор, перпендикулярный этим трем.
ОТВЕТЫ И РЕШЕНИЯ
§ 1
,. £+».2. £±**. 3. AB^-
2. 1 -f- А
§2
2. Из рисунка видно, что Fx—\, Fv — 3, Gx = 3, Gv=l. Поэтому /•"•(? = 6.
3. cos6=—V*. 6= 120°.
4. ~AB = 2i+j, AC = i—2j, поэтому AB-A~C = 2 —2 = 0.
5. ~AC — F+G, ~DB — F—G, откуда
= 2F- F+ 2G- G = A S3 -f- ВС- + CD2 -f- DA2.
6. Расположим оси координат, как на рис. 112. Тогда OA—ai, OB = aj,
OC—ak. Длины всех диагоналей одинаковы; например, OD=ai-{-aj-\-ak,
OD = У а2 + а'2 + az = У За = 1,73а. Углы между диагоналями также одинаковы;
например, угол между OD и CE=ai-{-aJ—ak вычисляется по формуле
т. е. О =
З 3
И проекции сторон на диагонали одинаковы; например, проекция стороны ОА
пг. Ъа ■~оЬ а2 а п со
на диагональ OD равна —7Т-— = ——-= —г= = 0,58а.
OD у2,а УЗ
7. Обозначим точки, упомянутые в формулировке задачи, как на рис. 113.
Ясно, что О имеет координаты @; 0; 0), а А (а; 0; 0). Пусть В имеет ко-
координаты (хя; ув; 0), а С (хс; ус; гс). Тогда OB —a, ~Ob15a =a-a-tos 60° =
а2 2 2, в2 а а Уз _
= -2", т.е. х%+у% = а2, хва = у, откуда ^a^-g". Уд = —^—• Далее,
ОС=а, 0С.О4 = J, 0С-Ш = ^, т. е.
„а а /3" а2 а а /
*с-2 +Ус-2—= -2-, откуда *с = _ , </с =^-р~ - гс= )/ j a.

304
ВЕКТОРЫ
[гл. ix
а точно
Приравнивая
Так как точка D, в силу соображений симметрии, расположена точно
fa a
пол. С, то обозначим ее координаты через I -~-; —^= ;
длины векторов DC и DO, получим
2/3
Л2?
Рис. 112.
Рис. ИЗ.
откуда го = —^=(=^4. Наконец, так как DC\\k, a DO = — 4-
2 у 6 V ** / ^
— / ft, то искомый угол можно найти по формуле
2 УТУ 2/6
а
cos a =
k-DO
\k\-DO~~
2/6
:=—— , откуда а=109°28',
i о
Радиус-вектор точки винтовой линии равен r = xi-\-yj-\-zk = R cos со/ / +
+ R sin со/ j+vtk. Отсюда
^-=— tfcosin со( /+£cocos co/y + uft. C1)
Так как этот вектор направлен по касательной, то остается найти его угол $
с вектором ft;
cos § = -
li
1*1
-fil* 1_ 7|2

ОТВЕТЫ И РЕШЕНИЯ 305
§4
В силу C1) ds = \ dr | = | — flcosfnco/* + /?<» cos ш/у+ь*| Л=
Поэтому
dr — У?со sin со/ i-+- Лео cos со/ /-f iA
T
Л ds
• §5
a> {О \)' 6> \Q k)' B)Uina cosaj ■ гЧо lj- д) (, 01
В примерах б), в) и д) каждый квадрат переходит снова в квадрат.
В примерах а) и г) из квадрата получится, вообще говоря, косоугольный
параллелограмм. Если стороны квадрата параллельны осям координат в слу-
случае а) или имеют угловой коэффициент у ± у _ -j_ i в случае г), то полу-
получится прямоугольник. Если кз указанного положения повернуть квадрат на
45°, то получится ромб.
§6
2. Перпендикулярность проверяется с помощью формулы B7), так как
скалярное произведение любой пары векторов оказывается равным нулю. Если
четвертый вектор имеет проекции хг, хг, х3, х4, то из условия перпендикуляр-
перпендикулярности получаем хг-\-хг-\-х3—.*4 = 0, x-l-\-xi — x3-\-xi = Qt x3 + xt = 0, откуда
легко выводится, что х3 = а'4 = 0, л^ + х^О. Таким образом, можно принять
проекции четвертого вектора равными 1, —1, 0, 0.

ГЛАВА X
ТЕОРИЯ ПОЛЯ*)
§ 1. Введение
Говорят, что в пространстве задано поле некоторой величины,
если в каждой точке пространства (или некоторой его области,
т. е. части) определено значение этой величины. Например, при
рассмотрении потока газа приходится исследовать температурное
поле (в каждой точке температура имеет определенное значение),
поле плотностей, поле давлений, поле скоростей и т. д. Поле может
быть скалярным или векторным в зависимости от характера иссле-
исследуемой величины: например, поля температур, давлений или плотно-
плотностей являются скалярными, а поля скоростей или сил — векторными.
Поле может быть стационарным (установившимся), если оно не ме-
меняется с течением времени в каждой точке пространства, или не-
нестационарным (неустановившимся), если такое изменение имеет место.
Обозначим рассматриваемую (для определенности, скалярную)
величину буквой и и введем в пространство декартову систему ко-
координат х, у, z. Заданием этих координат определяется точка в про-
пространстве и тем самым соответствующее значение и = и(х, у, z).
(Если поле нестационарное, то и = и(х, у, z, t), где t— время; од-
однако при этом мы рассматриваем время не как равноправную чет-
четвертую координату, а скорее как некоторый дополнительный пара-
параметр, так что дальнейшие построения будут относиться к любому,
но фиксированному моменту времени.) Таким образом, с формальной точ-
точки зрения стационарное поле—это просто функция трех переменных х,
у, z. Однако надо иметь в виду, что координаты в пространстве
можно ввести по-разному. При этом выражение и (х, у, z) будет из-
изменяться; но в любой данной точке М значение и, конечно, не за-
зависит от выбора системы координат. Поэтому часто говорят, что и
представляет собой функцию точки, и = и(М), так как задание точки М
полностью определяет соответствующее значение и, т. е. значение
*) Эта глава является непосредственным продолжением предыдущей н су-
существенно опирается на материал §§ IX. 1—2. Применяются также понятия
кратного интеграла (§ IV.7) и функции Грина (§ VI .2).

с 2] СКАЛЯРНОЕ ПОЛЕ II ГРАДИЕНТ 807
величины и в точке М. Функция точки при рассмотрении поля яв-
является первичной по отношению к функции координат, так как поле
имеет смысл и может быть исследовано без всяких систем координат.
Если исследуемая величина по своему смыслу задана в плоскости,
то соответствующее поле называется плоским; такие поля получа-
получаются, например, при исследовании тепловых процессов в пластинке,
толщиной которой мы пренебрегаем.
Если поле величины и пространственное, но в некоторой декар-
декартовой системе координат х, у, z эта величина оказывается не зави-
зависящей от z, то поле называется плоскопараллельным. В таком слу-
случае часто бывает возможным отвлечься от координаты z, рассматривая
поле в плоскости х, у (т. е. рассматривать вместо плоскопараллель-
плоскопараллельного поля — плоское) и помня о том, что во всех параллельных пло-
плоскостях поле имеет в точности тот же вид, т. е. на перпендикулярах
к этим плоскостям все величины, характеризующие поле, постоянны.
Упражнение
Пусть величина и имеет в некоторой декартовой системе координат выра-
выражение u = x2-(-i/2-(-2i/z + z2. Докажите, что эта величина образует плоскопа-
плоскопараллельное поле.
Указание. Поверните систему координат на 45° вокруг оси х.
§ 2. Скалярное поле и градиент
Будем для простоты считать, что в пространстве задана декар-
декартова система координат х, у, z, и рассмотрим стационарное скаляр-
скалярное поле и = и(х, у, z). Пусть, кроме того, в
пространстве дана некоторая точка М. Из нее
можно выходить по всевозможным направлениям;
на рис. 114 показано одно из таких направ-
направлений I. Производной от и по направлению /
называется скорость изменения поля в этом
направлении в расчете на единицу длины;
du u(N) — u(M) ,. Аи
-г,= I'm ..., —'= lim —
al pj _^ ,, MN As _y q As
Рассуждая так же, как при выводе формулы (IV.5), получим
du ди dx ди dy ^ ди dz
dl ~ dx dl dy dl ' dz dl '
Правую часть удобно представить в виде скалярного произведения
двух векторов (см. формулу (IX.5))
! . , ди . , ди .\ [dx . , dy , , dz

308
ТЕОРИЯ ПОЛЯ
[гл. х
Первый из ннх называется градиентом поля и и обозначается
ди .
gradu = -
ди . ди ,
"duJ^~Tzk''
0)
его физический смысл будет показан несколько позже. Второй вектор
dl
d(xi + yj+zk) dr
dl ~ dl"
— это единичный вектор направления I (см. § IX.4). Таким образом,
du
Tt~~
B)
Первый множитель в правой части, при заданном поле и, зависит
лишь от выбора точки М; второй множитель зависит лишь от на-
направления I.
Так как скалярное произведение какого-либо вектора на единич-
единичный вектор равно просто проекции первого вектора на второй, то
формулу B) можно переписать в виде
du __ _, t {3)
(это обозначение для проекции градиента на направление /).
Пусть заданы поле и и точка М; поставим вопрос: по какому
направлению / производная du/dl самая большая? Согласно форму-
формуле C) этот вопрос сводится к следующему: на какое направление
проекция вектора gradи самая большая?
Очевидно, что любой вектор при проектиро-
проектировании на различные направления дает самую
большую проекцию, равную его длине, при
проектировании на его собственное направ/
ленне. Таким образом, вектор grad к в точ-
точке М указывает в сторону намбыстрейшег^
возрастания поля и, причем эта наибыстрей-4
шая скорость, отнесенная к единице длины,
равна | grad и |; чем поле меняется быстрее,
тем grad к длиннее. На рис. 115 показаны
векторы градиента температуры в отдельных
точках проводника тепла, подогреваемого
изнутри (из заштрихованной зоны) и охлаждаемого снаружи. Гра-
Градиент температуры направлен «к печке».
Полученный физический смысл градиента показывает также, что
градиент инвариантно связан с рассматриваемым полем, т. е. остается
неизменным (инвариантным) при замене декартовых осей (этого не
было видно из его определения A), данного в «неннварнантной»
форме, «привязанной.--: к какой-то одной системе координат). Более
того, если задано по.ме и, то в каждой точке пространства можно
найти направление и скорость наибыстрейшего возрастания поля и;
Рис. 115.

ft 2] СКАЛЯРНОЕ ПОЛЕ И ГРАДИЕНТ 309
так можно найти вектор gradu, не прибегая к координатам и к за-
заданию и (х, у, г). Итак, градиент скалярного поля образует вполне
определенное векторное поле.
Аналогичное требование инвариантности ставится для всех основ-
основных понятий теории поля. Как мы говорили в § IX.5, при замене
осей декартовой системы координат хотя векторы и остаются неиз-
неизменными, инвариантными, но их проекции меняются. Таким образом,
если какое-либо понятие теории векторного поля сформулировано
с помощью координат и проекций этого ноля, то это понятие должно
удовлетворять требованию инвариантности относительно изменении
этих координат и проекций при по-
повороте осей координат. Так будет, в
частности, если формулировка вы-
выражена в терминах скаляров, векто-
векторов и тензоров (§ IX.5).
Отметим, что производные и'х, u'v
и и2 также являются производными
по направлению: например, и'х — это рис ug
производная по направлению оси х.
Градиент поля и (х, у, г) тесно связан с поверхностями уровня
этого поля, т. е. поверхностями, на которых поле имеет постоянное
значение, и (х, у, z) = const; в зависимости от физического смысла
поля они могут называться изотермическими, изобарическими и т. п.
.поверхностями. Именно, в каждой точке М градиент поля нормален
(т. е. перпендикулярен касательной плоскости) поверхности уровня,
проходящей через М. Действительно (рис. 116), если АС малб, то
вблизи М поверхности ц = С и ц== С+АС можно считать почти
плоскими и
du ДиДС
где А/ — расстояние между поверхностями по направлению /.
Но ясно, что А/ будет самым малым, а потому производная — самой
большой, если / направлено по нормали к поверхности. Отсюда и
следует наше утверждение.
Все понятия, введенные для пространственного поля, переносятся
с соответствующими упрощениями на плоские поля (см. § 1). Так,
градиент поля и(х,у), вычисляемый по формуле ^ ^
представляет собой вектор, лежащий в плоскости х, у. В каждой
точке градиент поля нормален линии уровня поля, т. с. линии
и(х, у) = const, проходящей через эгу точку (рис. 117). При этом
из формулы D) видно, что модуль градиента обратно пропорционален
расстоянию между линиями уровня. Там, где линии уровня сближа-

310
ТЕОРИЯ ПОЛЯ
[ГЛ. X
ются, градиент увеличивается (сравните, например, градиент поля
в точках А и В на рис. 117).
Вычислим в качестве примера градиент центрально-симметричного
поля и = /(/•), где r=V х1-{-уг-{-z2. В этом случае значение и
зависит только от расстояния точки до начала координат, а потому
поверхностями уровня служат сферы с центром в начале координат.
Если взять две сферы, радиусы которых отличаются на dr, то зна-
значения функции / на них будут отличаться
на df. Поэтому скорость изменения поля по-
поперек поверхностей уровня (т. е. вдоль ра-
диусов) равна -j , а потому
grader) =lf = f **
E)
Здесь г — радиус-вектор, проведенный из
начала координат в любую текущую точку
Рис 117 (х; у; z); r = \r\; r" =-j
вектор единич-
единичной длины, направленный вдоль г.
Получим формулу E) другим способом, опираясь на выражение
градиента в координатной форме A). Имеем
Аналогично
ди
дх
dfdr
dr dx~
df
dr
ди df у ди df Z
d[x_
dr r
Так как — J-—скаляр, то мы видим, что при ~ > 0 векторы
grad и всюду продолжают соответствующие векторы г (как колючки
у свернувшегося ежа), а если ^ < 0, то векторы grad и всюду об-
обращены к началу координат.
Упражнения
1. Найдите производную от поля и = ху — г2 в точке М B; 1; —3) по на-
направлению вектора a = f-f-3£.
2. Найдите градиент поля u = — H—- , где klt ft, = const, а гх, га — расстояния
ri гг
от некоторых фиксированных точек Afx, Мг.

£ 3] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ И СИЛА 311
§ 3. Потенциальная энергия и сила
Предположим, что на тело*), произвольно перемещающееся
в пространстве, действует сила F, зависящая лишь от положения
тела. Другими словами, в каждой точке М пространства определен
соответствующий вектор силы F=F(M), который образует, таким
образом, векторное силовое поле. При перемещении тела эта сила
производит работу, которая тратится на изменение кинетиче-
кинетической энергии тела или на преодоление сопротивления каких-то внеш-
внешних сил.
Легко подсчитать работу, которую производит сила F на задан-
заданном пути тела. В самом деле, при бесконечно малом перемещении dr
силу можно считать постоянной и потому соответствующая работа
равна (см. § IX.2) скалярному произведению
dA = F-dr.
Суммируя такие элементарные работы, получаем общую работу,
производимую силой F, когда тело проходит некоторый путь (L),
Л= J F-dr. F)
<£)
Такой интеграл, взятый вдоль линии (L), называется линейным.
Чтобы его вычислить, должны быть заданы не только поле F и
линия (L), но и направление, в котором эта линия проходит; как
говорят, линия (Z.) должна быть ориентирована. Если линия (L) разом-
разомкнута, то для ее ориентации можно просто указать, какая из двух
граничных точек считается ее началом, а какая — концом, т. е. ука-
указать пределы интегрирования. Эта ориентация существенна, так как
если в том же поле ту же линию проходить в противоположном
направлении, то dr заменится на —dr, в результате чего А заме-
заменится на —А, работа изменит знак.
Выражение F) линейного интеграла можно записать в других
полезных формах. Если вспомнить, что dr = x ds, где т — единичный
вектор касательной к (L), a ds — дифференциал длины дуги, то по-
получим
А= I F-xds= $ Fzds,
где Fx означает проекцию вектора F на т, т. е. «тангенциальную»
проекцию вектора F. С другой стороны, если написать в декартовых
координатах х, у, z
F=FJ + Fvj+Fzk, r = xi+yJ-'rzk,
*) Подразумевается, что размеры тела очень малы; такие тела иногда на-
называют материальными точками.

312 ТЕОРИЯ ПОЛЯ [ГЛ. X
откуда dr=*dxi-{-dyj-{-dzk, и вспомнить выражение (IX.5) для ска-
скалярного произведения в декартовых проекциях, получим
y Fzdz).
)
Работу силы можно выразить и как интеграл по времени; если
задано движение тела, т. е. задана функция r(t), то и сила, дей-
действующая на тело, оказывается сложной функцией времени
F = F(r) = F[r(t)]=F(t).
Работу силы за время dt можно выразить через скорость v, где
V=^jr', так как dr—-Vdt, из формулы F) получаем
к
А= \F(t)-v{t)dt,
где tH и tK — моменты начала и конца движения.
Таким образом, величина F-V—скалярное произведение силы
на скорость — равна работе, отнесенной к единице времени; как
известно, она носит специальное название «мощность».
Мы рассматриваем в этом параграфе силу, зависящую только
от положения тела. Зависимость силы, действующей на тело, от
времени является результатом перемещения тела. В этом случае
можно утверждать, что работа А при перемещении по данному пути
в действительности не зависит от скорости тела, не зависит от вида
функций V (t) и г (t), а зависит только от траектории, по которой
перемещается тело, несмотря на то, что v (t) в явном виде входит
множителем в подынтегральное выражение для А, Дело в том, что
при изменении функции v(t) меняется и г (t); следовательно, меняется
и вид F' (t) при данном F=F{r) = F (х, у, z); меняются и пределы
интегрирования tH и tK, отвечающие заданным начальной и конечной
точкам пути, Г(*„) = ГИ, r(tK) = rK.
Для целого ряда физических силовых колей F оказывается, что
если тело обходит замкнутый контур, то суммарная работа силы F
при этом равняется нулю; другими словами, если на одном участке
контура сила производит некоторую работу, то на остальной его
части тело движется против действия силы и возвращает накоплен-
накопленную энергию полю. Так ведут себя гравитационное иоле (поле тя-
тяготения), электростатическое и многие другие поля. Математически
зто означает, что
(f)F-(lr = 0 G)
для любой замкнутой линии (L), где под Ф понимается линейпыйинтеграл
по замкнутому контуру. Такой интеграл называется еще циркуля-

§ 3]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ И СИЛА 313
цией\ итак, мы предполагаем, что циркуляция силы F по любому
замкнутому контуру равна нулю.
Предположение G) можно равносильным образом сформулировать
так: работа F) силы F по любому разомкнутому контуру (L) зави-
зависит только от положения начала и конца этой линии, но не зависит
от вида самой линии. В самом деле, пусть условие G) выполнено,
а линии (LJ и A2) имеют общие начало М и конец /V, и пусть
работа силы F вдоль (Z.t) равна Alt а вдоль A2) равна А2. Обра-
Образуем замкнутый контур, пройдя от М к N по (Z1), а затем от N
к Ж по (£2). Тогда в силу сказанного выше работа силы F по та-
такому контуру равна А1 — Аг. С другой стороны, в силу условия G)
получаем А1—Л2 = 0, откуда А1 = А2. Мы предоставляем читателю
доказать аналогичным образом, что, обратно, из последнего равен-
равенства вытекает условие G).
В предположении G) можно ввести понятие потенциальной энер-
энергии тела, т. е. энергии, зависящей от положения тела (это понятие для
одномерного движениябыло подробно рассмотрено вВМ, гл. VI).Именно,
значение потенциальной энергии U в любой точке М, по определению,
равно работе, которую совершает сила F, когда тело перемещается
из точки М в некоторую фиксированную точку Мо. (В конкретных
задачах точка УИ0 часто выбирается на бесконечности, так что речь
идет о работе, совершаемой, когда тело удаляется на бесконечность;
для этого указанная работа должна быть конечной и не зависеть от
способа такого удаления.) Другими словами,
U(M)= J F-dr. (8)
При этом выбор конкретного пути, ведущего из М в Мо, несуще-
несущественен.
С помощью потенциальной энергии легко выразить работу, со-
совершаемую силой F, когда тело перемещается из любой точки Мх
в любую другую точку Мг. Именно, если при таком перемещении
пройти через Мо (что возможно, так как выбор пути не сказывается
на работе) и рассмотреть работу на этапах от Ж, до Мо и от Мв
до M.z, то мы получаем, что рассматриваемая работа равна U(MX)—
— U(M,). Итак, работа, совершаемая полем, равна уменьшению по-
потенциальной энергии тела.
При определении потенциальной энергии имеется некоторый
произвол в выборе точки Ма, т. е. точки, в которой потенциальная
энергия полагается равной нулю, Посмотрим, что получится, если
заменить Мо на какую-нибудь другую точку Мо. Так как работа
О(М), совершаемая при перемещении из М в Ма, равна работе U(M),
совершаемой при перемещении из М в Мо, плюс работа, совершаемая
при перемещении из Мо в Мо, то U(М) отличается от U(М) на
постоянное слагаемое. Итак, потенциальная энергия определена

314 ТЕОРИЯ ПОЛЯ [ГЛ. X
с точностью до постоянного слагаемого. Однако этот произвол не
сказывается на разности значений потенциальной энергии в двух
точках, т. е. он пропадает при подсчете работы, совершаемой при
перемещении из одной точки в другую.
Мы доказали существование потенциальной энергии в силовом
поле, т. е. потенциальность этого поля, исходя из условия G) ра-
равенства нулю работы по любому замкнутому контуру; Легко прове-
проверить, что и обратно, если потенциальная энергия существует, то
при подсчете работы, совершаемой полем при перемещении тела из
точки М в точку N, существенно только положение этих точек, но
сам путь, по которому перемещается тело, роли не играет, так как
эта работа равна U(M) — U{N). А мы видели, что это равносильно
условию G).
Формула (8) определяет потенциальную энергию, если задано
силовое поле. Получим обратную формулу, выражающую поле через
потенциальную энергию. Допустим, что тело совершило бесконечно
малое перемещение dr = dxi-\-dyj-\-dzk. Тогда сила F=Fxi-\-
+ Fyj + FJt совершит элементарную работу
dA = F-dr= Fxdx + Fydy -j- Fjdz.
С другой стороны, эта работа равна
dy + dz).
у ■" ' дг J
Сравнивая обе формулы, находим
__dU_ F __dU_ F <Ш
* ~ дх' У~~ ду ' z~~ дг'
откуда
F=FJ + Fyj+F,k = ~fxt-d-^j-d^k = -grauU (9)
(см. § 2).
Пусть частица массы т движется под действием заданного поля
сил F=—grad U. Тогда согласно § IX.4 приращение кинетической
энергии равно
Значит,
,2 2
~Т + U*= V" + ^i'
т. е. величина полной энергии частицы

§ 3]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ И СИЛА 815
в процессе движения остается постоянной. Как видим, полная энер-
энергия представляет собой сумму кинетической и потенциальной энер-
энергий (Для одномерного движения аналогичное рассмотрение при-
приведено в ВМ, § VI.8.)
Рассмотрим в качестве примера притяжение по закону Ньютона,
т. е. случаи, когда на тело действует сила, направленная к неко-
некоторой фиксированной точке О (за которую мы примем начало коор-
координат) и обратно пропорциональная квадрату расстояния от этой
точки. Так как вектор ■ направлен к началу координат и имеет
единичную длину, то рассматриваемое силовое поле имеет вид
г'- г
A0)
где k — коэффициент пропорциональности. В силу центральной сим-
симметрии силы легко убедиться*), что и потенциальная энергия имеет
вид U = f{r). Но тогда в силу формул (9) и E) получаем
f gradLT gf.
Сравнивая эту формулу с A0), получаем
Тг = -" °™Уда U=fH = ~-y (П)
с точностью до произвольного постоянного слагаемого. Таким обра-
образом, ньютоново силовое поле потенциально, и его потенциал опре-
определяется по формуле A1). Эта формула дает потенциал, нормиро-
нормированный (нормировкой называется выбор из равноправных объектов
какого-то одного) условием обращения в нуль на бесконечности.
Иногда возникает задача о построении векторных линий силового
поля F или, как говорят короче, силовых линий поля F. Так назы-
называются линии, идущие в каждой своей точке вдоль поля, т. е. ка-
касающиеся в каждой своей точке вектора поля F. Задача о построе-
построении таких линий легко сводится к задаче об интегрировании системы
дифференциальных уравнений: надо ввести в пространстве декар-
декартовы координаты х, у, г, после чего записать условие параллель-
параллельности векторов
dr = dxi + dyj+dzk
и
F=Fx(x, у, z)t + Fy(x, у, z)j+Fz(x, у, z)k
(см. конец § IX.1):
dx d>JdJ
Fx(x, у, г) Fy{x, у, г) Ft(x,y, г)'
*) Рассмотрите перемещение тела по сфере с центром в точке 0, когда
r=const. Работа силы при таком перемещении равна нулю.

316 ТЕОРИЯ ПОЛЯ [ГЛ. X
Здесь мы пользуемся тем, что вектор dr идет как раз по касатель-
касательной к линии (см. § IX, 4). Уравнения A2) образуют систему диф-
дифференциальных уравнений векторных линий поля F, записанную в
«симметричной форме», в которой все три координаты выступают
как равноправные. Отсюда легко выразить -у и -т- и перейти к си-
системе из двух дифференциальных уравнений относительно у (х) и
z(x), записанной в обычной форме (§ VIII. 2).
Как ясно из геометрического смысла (и подробно разбиралось
в теории дифференциальных уравнений), через каждую точку про-
проходит ровно одна силовая линия; таким образом, все пространство
(или часть его, в которой задано силовое поле) заполняется сило-
силовыми линиями.
Для ньютонова поля силовые линии суть лучи, выходящие из
центра притяжения, т. е. из точки О. Они не пересекаются нигде,
кроме самой точки О, которая является особой точкой системы диф-
дифференциальных уравнений (ср. конец § 2).
В § 2 мы видели, что в каждой точке вектор grad U нормален
к поверхности U= const, проходящей через эту точку. Поэтому из
формулы (9) следует, что силовые линии в каждой своей точке нор-
нормальны к эквипотенциальным поверхностям. Это, впрочем, ясно и из
того, что наибольшая работа на единицу длины пройденного пути
производится, если тело перемещается нормально к поверхностям
равного потенциала, а с другой стороны, так будет, если тело пе-
перемещается вдоль силовых линий.
Упражнение
Пусть плоское силовое поле имеет потенциал U = axy (сс=const). Найдите
само поле и его силовые линии.
§ 4. Поле скорости и поток
Пусть рассматривается стационарное течение газа или жидкости.
В любой точке М скорость частицы газа имеет вполне определен-
определенное значение v = v(M), т. е. мы имеем векторное поле скорости.
Рассмотрим траекторию {L) какой-либо частицы или, как говорят,
линию тока. Хорошо известно (см., например, § IX.4), что в каждой
точке (L) вектор скорости v касателен к (L). Значит, для поля
скорости векторными линиями (§ 3) служат линии тока. Дифферен-
Дифференциальные уравнения для них, аналогичные A2), легко получить не-
непосредственно, если из равенств
йк dy dz
Jt^vx, Jt=vy, Tt=vz
выразить dt и приравнять полученные результаты.
Перейдем теперь к очень важному для дальнейшего понятию
потока вектора через поверхность. Допустим, что в пространстве

§ 4]
ПОЛЕ СКОРОСТИ И ПОТОК
317
мысленно выбрана некоторая замкнутая или незамкнутая «ориенти-
«ориентированная» поверхность (сг). Поверхность называется ориентированной,
если указано, какая ее сторона считается наружной, а какая внут-
внутренней. Такую ориентацию можно осуществить двумя способами
(рис. 118).
Подсчитаем объем газа, проносимого через (а) за единицу вре-
времени изнутри наружу. Найдем сначала объем, проносимый за малое
время dt через элемент поверхности (do) (рис. 119). Это объем
Наружная
сторона
Внутренняя
сторона
Внутренняя
сторона
Наружная
'стирана
Рис. 118.
Рис. 119.
косого цилиндрика с основанием da и образующей vdt. Высота ци-
цилиндрика равна проекции образующей на перпендикуляр к основа-
основанию, т. е. равна vndt, где vn — проекция вектора скорости v на
единичный вектор п внешней (т. е. направленной во внешнюю сто-
сторону) нормали к поверхности. Таким образом, объем цилиндрика
равен vndt da.
Если за время dt через элемент поверхности (da) проходит объем
vndt da, то за единицу времени через тот же элемент пройдет
объем vnda. Суммируя эти объемы для всех элементов, получим,
что через всю поверхность (а) за единицу времени проходит объем
>= vnda
О
(О)
A3)
изнутри наружу. Такой интеграл от нормальной проекции называет-
называется потоком вектора v через поверхность (а) *).
В гидродинамике наряду с полем скорости V часто пользуются
полем «массовой скорости» pv, где р — плотность газа в данной
точке. Рассуждая в точности, как выше, легко доказать, что поток
pvn da
(о)
этого вектора через любую ориентированную поверхность (а) равен
*) Интеграл A3)—это частный случай интеграла по поверхности, о кото-
котором мы говорили и § IV.7.

318 ТЕОРИЯ ПОЛЯ [ГЛ. X
массе (а не объему, как раньше!) газа, проносимого за единицу
времени через (а) изнутри наружу.
Поток, очевидно, есть величина скалярная. Он существенно за-
зависит от ориентации поверхности (а): если изменить эту ориента-
ориентацию на противоположную, то в формуле A3) vn, а с ней и Q
поменяют знак. (Впрочем, это ясно и из указанного нами смысла
интеграла A3),) Если поверхность (а) расположена так, что линии
тока пересекают ее всюду изнутри наружу, то Q > О, а если
всюду снаружи внутрь, то Q < 0; если же линии тока частично
пересекают (а) изнутри наружу, а частично снаружи внутрь, то по-
поток равен сумме положительной и отрицательной величин (каких?)
и может оказаться положительным, отрицатель-
отрицательным или равным нулю. Всегда равен нулю по-
поток вектора скорости через поверхность, цели-
ком заполненнУЮ линиями тока (т. е. через
каждую точку которой проходит линия тока,
целиком лежащая на этой поверхности) *).
Поток A3) иногда записывают в другой
форме. Если дана ориентированная плоскаяпло-
рис 120. щадка (а), то ей принято ставить в соответ-
соответствие вектор а, направленный перпендикуляр-
перпендикулярно (а) от внутренней стороны к "наружной (рис. 120), причем мо-
модуль этого вектора берется равным площади (а). Так поступают в
случае, если существенны только площадь (а) и ее направление
в пространстве, но конкретная форма (а) (т. е. будет ли это круг,
или прямоугольник и т. д.) не играет роли. При таком обозначе-
обозначении вектор da пойдет по п (см. рис. 119) и можно написать
vnda = v-da (см. формулу (IX.3)). Таким образом,
yfo= С vda. A4)
(О) (О)
Поток вектора v через поверхность (а) иначе называется коли-
количеством векторных линий (т. е. линий тока), пересекающих (а) из-
изнутри наружу. Это название условное, так как указанное количе-
количество имеет размерность и, как правило, получается дробным, но
из-за своей наглядности широко применяется. Надо иметь в виду,
что это «количество» понимается в алгебраическом смысле, так что
если часть (а) пересекается линиями изнутри наружу, а другая
часть — снаружи внутрь, то оно может быть любого знака (и даже
равным нулю) в зависимости от того, какую часть пересекает боль-
больше линий.
Приведем простые примеры подсчета потока. Пусть сначала
поле v постоянное (однородное, одинаковое во всех точках), а
*) Говоря наглядно, это —поверхность, вдоль которой скользит газ при
своем движении.

о 4j поле скорости и поток 319
поверхность (а) плоская. Тогда из формулы A4) вытекает, что
Q = vne = v-e. A5)
Пусть поле v пропорционально радиусу-вектору г, т. е. V--kr
/fe коэффициент пропорциональности), а (а) — сфера с центром в
начале координат, ориентированная естественным образом (к началу
координат обращена ее внутренняя сторона). Тогда vn = vr = kr, и
так как r= const на (а), то
Q
С Г
(а) (а)
Рассмотрим, наконец, общее центрально-симметричное поле в
пространстве, определенное формулой
V =/(/") Г°
-f)-
A6)
где г — радиус-вектор текущей точки, а г — его длина, так что
г° — это единичный вектор, идущий по радиусу-вектору и указываю-
указывающий направление поля. Тогда поток поля через
сферу радиуса г с центром в начале коорди-
координат равен
l^(r)da^f(rLnr\ A7)
Из формулы A5) вытекает интересное
следствие. Рассмотрим некоторый замкнутый
многогранник (рис. 121); ориентируем его гра-
грани так, чтобы одна из граней (на рис. 121 (о))
была «замыкающей» для совокупности осталь-
остальных граней. Тогда ясно, что если этот многогранник мысленно по-
помещен в однородное поле скорости v, то поток через (а) равен
алгебраической сумме потоков через остальные грани: Q= Qi-\- Qa +
+ Q3. Отсюда
Рис. 121.
и в силу произвольности V
а = а1 + а1 + а,. A8)
Итак, вектор замыкающей площадки равен сумме векторов «состав-
«составляющих» площадок, т. е. площадки можно складывать, как векторы.
Мы существенно пользовались тем, что площадки изображаются
векторами именно так, как показано на рис. 120, что и является
одним из важных доводов в пользу разумности такого изображения.
К этому вопросу возможен иной подход. Ориентируем все грани
многогранника рис. 121 «естественным» образом, так, чтобы векторы
и а смотрели наружу. Тогда в формулу A8) вместо
а,- надо

320 теория поля jr/i. x
подставить—а,- и, перенеся все слагаемые в левую часть, получим
а1цгог->га3->га = 0. Это соотношение вполне аналогично хорошо
известному из векторной алгебры правилу о равенстве нулю суммы
векторов, образующих замкнутый многоугольник (см. § IX.1). Этим
также подтверждается закономерность изображения площадок век-
векторами.
В пределе из многоугольника можно получить любую замкнутую
линию (L), а из многогранника — любую замкнутую поверхность (а);
таким образом, мы приходим к равенствам фйг = 0, Ф do = 0 (первое
Ю (а)
очевидно), где кружок у знака интеграла (его выписывать необя-
необязательно) подчеркивает, что интеграл берется по замкнутой ли-
линии или поверхности.
Упражнение
Рассмотрите общее есесимметричное поле в пространстве, определенное фор-
формулой v = f (| р [, г) р° ( р° =-р-у ) , где р — вектор, идущий из точки @; 0; г)
в точку (х; у; г). Чему равен поток этого поля через поверхность прямого
кругового цилиндра радиуса | р [ с осью г? Чему равен этот поток в частном
случае плоскопараллельного поля?
§ 5. Электростатическое поле, его потенциал и поток
Хорошо известно, что заряд, помещенный в пространство, порож-
порождает электрическое поле, которое можно проанализировать на основе
закона Кулона. Мы будем для простоты считать пространство пустым
(вакуум) и рассмотрим сначала поле от заряда q, помещенного в на-
начале координат О. Для исследования поля можно в произвольную
точку М поместить пробный единичный заряд и посмотреть, с какой
силой поле на него действует; эта сила Е называется напряжен-
напряженностью электрического поля. Так как в разных точках М напря-
напряженность Е различная, то мы имеем векторное поле £= Е(М), пред-
представляющее собой, по существу, частный случай рассмотренного
в § 3 силового поля (если все время иметь в виду, что речь идет
о воздействии на пробный единичный заряд). Закон Кулона по мате-
математической формулировке аналогичен закону Ньютона, рассмотрен-
рассмотренному в § 3. Для точечного заряда q он имеет вид
r° = единичный вектор, идущий вдоль радиуса-вектора Ч
эта формула несколько отличается от A0), так как сила должна
быть прямо пропорциональна q и, кроме того, при q > 0 пробный
единичный положительный заряд не притягивается, а отталкивается.
Коэффициент k в последней формуле зависит от выбранной системы

§ 5] ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ, ЕГО ПОТЕНЦИАЛ И ПОТОК 321
единиц, и мы для простоты положим его равным единице*), т. с.
будем писать
В § 3 мы видели, что такое поле имеет потенциал
который связан с полем Е соотношением
Е= — gradcp B0)
и нормирован условием обращения .в нуль на бесконечности. В силу
однородности пространства такой же заряд q, помещенный в точку
М0{х0; у0; z0), порождает потенциал (будем писать ср (г) вместо
ф(М), считая г радиусом-вектором точки М)
где г0 —радиус-.вектор точки Мо **).
Пусть теперь в пространстве имеется система зарядов; тогда
электрические ноля Е, отвечающие этим зарядам, складываются
друг с другом. (Этот важный факт, означающий независимость
действия отдельных зарядов, установлен экспериментально.) Но из
формулы B0) легко проверить, что и соответствующие потенциалы
складываются друг с другом. В самом деле, если Е=Е1-\-Ег, где
то, складывая одноименные проекции, получаем
т. е. Ф=Ф! + Ф2 служит потенциалом поля Е.
Мы видим, что электрическое поле, образованное любой систе-
системой покоящихся зарядов, обладает потенциалом и, кроме того, при
изучении зависимости потенциала от поля имеет место принцип
суперпозиции (закон линейности, см. § VI.2). Это дает возможность
по общему методу построить потенциал электрического поля, полу-
получающегося, когда заряды распределены в пространстве с некоторой
переменной плотностью р. Если плотность имеет вид пространст-
пространственной дельта-функции (см. § VI.3), т. е. если
p(r) = 8(r-r0), B2)
то соответствующий заряд — это единичный заряд, сосредоточенный
в точке с радиусом-вектором г0. Поэтому потенциал, отвечающий
*). Это значит, что £ и о выражены в электростатической системе еди-
единиц CGSE.
**) Не следует путать радиус-вектор га с единичным вектором г°.
•• Я. Б. Зельдович, А. Д. Мышкио

322 теория поля [гл. х
плотности B2), — а он представляет собой функцию Грина в данной
задаче, — вычисляется по формуле B1) с q— 1, т. е.
Здесь г0 определяет точку воздействия, а г — точку наблюдения.
Зная функцию Грина, легко по общему методу § VI.2 получить
выражение для потенциала в случае произвольной плотности р (г):
Ф (г) = J О (г; г0) р (r0) rfQ0 = |
(ЗД (Qo)
где интегрирование производится по всей области (Яо), занятой
зарядом. В координатной форме то же можно написать так:
Ф (х, у, z) = С С С РС-^о- go. го> d ^ ^ B3)
Примеры вычисления потенциала будут рассмотрены ниже, в § 6.
Рассмотрим теперь поток вектора Е через замкнутую поверх-
поверхность (а), ориентированную «естественным» образом, т. е. так, что
ее внутренняя сторона смотрит в конечную область, ограниченную
(а), а внешняя сторона смотрит в бесконечность. В § 4 мы говорили,
что такой поток иначе называется количеством векторных линий
(т. е. для поля Е — «электрических силовых линий»), пересекающих (а)
изнутри наружу. Так как это количество понимается в алгебраи-
алгебраическом смысле, т. е. как разность между числом выходящих линий
и числом входящих, то его же можно понять как число линий, начи-
начинающихся внутри (а).
В самом простом случае, когда Е порождается точечным заря-
зарядом <7> расположенным в начале координат, а (а) представляет собой
сферу с центром в начале и радиусом R, поток найти совсем просто.
В самом деле, на (а)
так как на сфере г° совпадает с единичным вектором внешней нор-
нормали и. Но тогда на сфере Еп=~^= const и, по определению (ср.
формулу A3)), поток равен
^.do = -jL§ rfa = |j4л/?2 = 4m/. B4)
(а> (а)
Итак, рассматриваемый поток не зависит от радиуса R и прямо про-
пропорционален величине заряда.
Аналогично B4) доказывается, что поток вектора Е через часть
сферы с центром в точечном заряде (рис, 122) равен ад, где со —

§ 6]
примеры 323
соответствующий «телесный угол», т. е. соответствующая площадь
на сфер*е единичного радиуса. Но отсюда сразу следует, что для
поля порожденного точечным зарядом, электрические силовые линии
не могут начинаться или заканчиваться ни в каком объеме, не со-
содержащем этого заряда (т. е. они начинаются или заканчивается
только на этом заряде). В самом деле, выбрав малый объем (rffi),
как показано на рис. 122, легко убе-
убедиться, что через его сферические стенки
выходит столько же линий, сколько и вхо-
входит, а через коническую стенку линии
вообще не проходят.
Таким образом, для любой поверхно-
поверхности (а), содержащей точечный заряд q
внутри себя, количество силовых ли-
линий, начинающихся внутри (а) (т. е. по-
поток вектора Е через (а)), равно 4щ.
Другими словами, для рассматриваемого
поля силовые линии при q > О начинаются
на заряде (причем их количество пропорционально заряду) и уходят
на бесконечность. Если заряд отрицательный, то силовые линии
начинаются в бесконечности и заканчиваются на заряде.
Пусть теперь внутри замкнутой поверхности (а) содержится
несколько зарядов, например qv q2 и q3. Тогда соответствующие
поля, а потому и потоки складываются, т. е. суммарный поток
через (а) равен 4nql-{-4rtq2Jr4nq3 = 4n(ql + q2 + q3) = 4nq, где
Я ~ Я\ 4-Яг + Чз — суммарный заряд, расположенный внутри (а).
Итак, количество электрических силовых линий, начинающихся
в любом объеме пространства, пропорционально (с коэффициентом
пропорциональности 4л) общему заряду, заключенному в этом объеме.
Это утверждение называется теоремой Гаусса.
' § 6. Примеры
Поле, созданное точечным зарядом,— наиболее простое электри-
электрическое поле. В результате комбинации полей от точечных зарядов,
помещенных в различных точках, получаются и другие, более слож-
сложные поля.
Во многих важных случаях поле можно построить с помощью
непосредственного применения теоремы Гаусса (см. конец § 5).
Рассмотрим, например, поле, созданное шаром радиуса Ro, заряженным
с постоянной объемной плотностью р. Если принять центр шара за
начало координат, то в силу сферической симметрии задачи ясно,
что напряженность Е поля имеет вид
E = F{,)r\ B5)
11*

324 теория поля [гл. х
где F(r) — некоторая скалярная функция. Приравнивая- по теорем-й
Гаусса поток вектора Е через сферу радиуса г, вычисленный но
формуле A7), заряду внутри этой сферы, умноженному на 4л, по-
получим
1
(r>'R0),
где q — общий заряд шара. Отсюда, находя F{r) и подставляя
в B5), получаем
*|Е|
о 4
4л i- rr0 = -v лрг (внутри шара),
О О
4- г" (вне шара).
В частности (ср. формулу A9)), вне
„ „ — шара напряженность поля в точности
' ° г такова, как если бы весь заряд бил
р„с !2з. сосредоточен в центре шара. График-
модуля вектора Е в зависимости от
радиуса показан на рис. 123 сплошной линией.
Соответствующий потенциал в силу соображений симметрии имеет
вид U— U{г). Вспомнив формулу E), получаем, что
Отсюда
(О </■</?„),
где Cj, Сг — некоторые постоянные. Нормируя потенциал условием
£/(оо) = 0, получаем, что Са = 0; а чтобы U(r) было непрерывно
при r=-R0, должно быть
— -тг-npRl + C^-l- , т. е. Сх =-J-+ "?■
Итак, окончательно

§6]
ПРИМЕРЫ
325
Рассмотрим теперь поле от заряда, распределенного с постоян-
-ной плотностью а между двумя концентрическими сферами радиусов
R и /?0. В силу принципа суперпозиции это поле можно получить
как разность полей, полученных при распределении заряда плот-
плотности р в шаре радиуса Ro и в шаре радиуса Rv Графики обоих
полей показаны на рис. 123. Мы видим, что внутри полости (т. е.
внутри сферы радиуса /?х) разность равна нулю, т. е. электриче-
электрического поля нет; другими словами, там потенциал постоянный.. Вне
сферы радиуса Ro поле имеет вид
Лтт^2 Лт^*2 4тТ^ 4тт ^
т. е. и в этом случае поле таково, как если бы весь заряд был сосре-
сосредоточен в центре. График поля для полого шара показан на рис. 124.
Эти же выводы справедливы для
бесконечно близких /?х н Ro, т. е.
при равномерном распределении за- >,
ряда на сфере.
Рис. 124.
Рассмотрим в качестве следующего примера заряд, распреде-
распределенный с постоянной линейной плотностью ц вдоль бесконечной
прямолинейной нити, за которую мы примем ось г. Это поле —
плоскопараллельное (§ 1), и его можно получить в результате сум-
суммирования (интегрирования) полей от малых зарядов, расположенных
вдоль нити. Но проще использовать теорему Гаусса. Заметим, что
в силу осевой симметрии задачи, поле должно иметь вид
где р — это вектор, перпендикулярный нити и направленный от нее
в текущую точку (если нить идет по оси г, то p = xi-\-yj); р° = г^-,—
единичный вектор (не следует путать вектор р с объемной плот-
плотностью заряда); <р (| р |) — некоторая скалярная функция. Применяя
теорему Гаусса к цилиндру высоты h и радиуса |р |, изображен-
изображенному на рис. 125, получим
Ф (| р |) 2я | р | h =

326 ТЕОРИЯ ПОЛЯ [ГЛ. X
(при этом надо учесть, что поток вектора Е через основания цилиндра
равен нулю, так как электрические силовые линии идут вдоль этих
оснований). Отсюда имеем <р (| р |) = р*-:, т. е.
На рис. 125 показаны соответствующие силовые линии; они начи-
начинаются (в случае \х > 0) на заряженной нити и расходятся на бес-
бесконечность.
Интересная трудность возникает при вычислении потенциала
рассматриваемого поля. Можно было бы попытаться просуммировать
потенциалы от элементарных зарядов нити. В силу формулы B1)
это дало бы в некоторой точке М (х; у; z)
= г ме = г
Но знаменатель при больших |£| ведет себя, как К£а = | £ |. и п0'
тому интеграл B7) расходится к бесконечности (см. § III.1), т. е.
имеет бесконечное значение! Ясно, что так найти потенциал нельзя.
Однако вспомним о том, что нас всегда интересует не само
значение потенциала, а производные от него (для нахождения поля Е)
или разность его значений для двух точек. Поэтому ситуация как
раз такова, как описано в § III.5 при рассмотрении расходящегося
интеграла, зависящего от параметра (в данном случае имеется три
параметра: х, у, z). Учтем к тому же, что реально нить всегда
конечна, т. е. взамен B6) надо рассмотреть интеграл
N
'~ J
при очень большом N. Этот интеграл удобно разбить на два:
2 N
\ -\- \—и в первом заменить £ — z на £, а во втором z—£ на г\,
-N z
после чего получится (проверьте!)
qV= —[г In (*»+/) + [i In [N—z + Vx* + /- + (N — гI] +
= —|iln (*»+/)+/V(*. y, z), B8)
где через PN обозначена сумма «длинных логарифмов». Следова-
Следовательно, потенциал в фиксированной точке Q(x; у; z), зависящий от
длины нити, обращается в бесконечность, когда длина нити стре-
стремится к бесконечности. В природе мы никогда не имеем дела с

§ 6]
примеры 327
нитями бесконечной длины с постоянной плотностью заряда на них;
для вычисления потенциала существенно, что когда длина нити
конечна, величина N, характеризующая длину, входит в ответ,
в-частности, и при N->оо.
Замечательно, что, несмотря на это, поле Е вблизи нити не за-
зависит от длины нити *).
Точный способ действий заключается в следующем: зафиксируем
какое-то большое, но конечное N и найдем поле по общему пра-
правилу B0):
(N — г -\- Ух'1 -\-yi-\-(N —гJ) Уx1-\-ylJr(N — г)'2
+ аналогичный член с N-{-z;
выражение Еу получается заменой х на у;
у
Е, — —г— = , - + янплпгичиый член с N4-z.
Теперь, после дифференцирования, устремим N к бесконечности;
ЗЯд, dPN дР„
при этом члены —з—, —5—, -= * 0, и мы получим простой, не
зависящий от N ответ
Подробная процедура с,получением выражения tp для конечного N,
нахождением Е и последующим переходом к пределу при /V-+oo
не необходима. Откажемся от нормировки потенциала ср условием
ср = О на бесконечности. Примем за нуль, например, потенциал в точке
лг=1, у=0, 2 = 0 и обозначим через Ф нормированный так потен-
потенциал. Он получится добавлением к B8) константы C = CN;
Ф = - ц 1 п (*» + /) + PN {х, у, z) -|- С,
откуда
С= — Ру(\, 0, 0) = — 2\i\n(N+[/'\+Ni).
Легко убедиться, что в пределе при N-у оо
У, z) + C=--PN(x, у, г)—Рк{\, 0, 0)-*0,
*) Для того чтобы это утверждение было правильно, нужно выполнение нера-
неравенств —J , -4г , Цг"^1' Проверьте, что если хотя бы одна из этих величин
удовлетворяет обратному неравенству, т. е. Щ^>1, или Цг^>1. или^^>1,
то потенциал и поле близки к полю конечного заряда, равного 2|.wV и находя-
находящегося в начале координат.

328 ТЕОРИЯ nQ/IH [ГЛ. X
откуда
ф = — ii \п(х2 -\-у'2).
Вычисляя Е = — grad Ф, получим предыдущий результат. Этот
результат совпадает с тем, что был получен с применением теоремы
Гаусса (ср. формулу B6)). В отличие от потенциала при вычисле-
вычислении поля по теореме Гаусса можно (и нужно!) сразу рассматривать
бесконечную нить.
Поле можно найти также интегрированием — сложением элементар-
элементарных нолей dE зарядов dq = \id£,, расположенных на элементе нити.
Так как Е есть вектор, то нужно отдельно складывать компоненты
dE = VydZ dE = и (г — j)dl
у [*- + ;]3/2' * [*°1у
Соответствующие интегралы сходятся, так как при больших £ по-
подынтегральная функция убывает как |£|~3 пли |£j~2. Поэтому
можно сразу брать интегралы в преде-
пределах от £= — оо до £=оо (см. упраж-
упражнение 1),
j Рассмотрим, наконец, поле, порож-
'"/} денное зарядом, равномерно распреде-
^jS ленным по плоскости, за которую мы
' примем плоскость yOz, с постоянной по-
0 X ^^-/ верхностной плотностью v. Здесь опять
у удобно применить теорему Гаусса, Заме-
Заметим, что в силу соображений симметрии
'Е силовые линии должны идти параллель-
рис J26 но оси А'' Возьмем (рис. 126) тонкий
цилиндр, расположенный симметрично от-
относительно плоскости yOz. Поток через его боковую поверхность равен
нулю, а через основания, из тех же соображений симметрии, равен 2Eds.
С другой стороны, этот поток, по теореме Гаусса, равен произведе-
произведению in на заряд, заключенный внутри цилиндра, т. е. на vds, При-
Приравнивая результаты, получаем 2Eds = Anv ds, откуда £=2jtv. Таким
образом, в данном примере
E=2nvi (*>0), E=—2n\i (.*< 0). B9)
Мы видим, что напряженность по обе стороны от заряженной плос-
плоскости постоянная, а при переходе через эту плоскость испытывает
скачок invi,
Что же будет, если заряжена не бесконечная плоскость, а, как
всегда на практике, конечный ее кусок? Тогда вблизи этого кускм
(причем не у границы, а у внутренней части) конечность куска ска-
сказывается слабо и мы имеем почти однородное поле, вычисляемое

§ 6] примеры 329
по формулам B9). Вблизи границы куска, а также при удалении от
него однородность поля существенно нарушается. На достаточ-
достаточном расстоянии от куска (как и от любой конечной системы заря-
зарядов) его можно просто заменить на поле точечного заряда, равного
суммарному заряду на указанном куске, т. е. можно пользоваться
формулой A9).
Важный случай представляет собой схематически изображенный на
рис. 127 плоский конденсатор, т. е. две параллельные пластины
с равными и противоположными по знаку зарядами на
ннх (v единиц на 1 си2 одной и — v единиц на 1 см-
другой пластины). Проверьте, что слева от А и спрана
от В поля двух пластин направлены в противополож-
противоположные стороны и в сумме равны нулю. Внутри конден-
конденсатора, между Л и В, поле равно £=4я\> и направ-
направлено от положительной пластины к отрицательной.
Однако нужно помнить, что это поле наполовину обу-
обусловлено зарядами пластины А и наполовину — зарядами
пластины В. В частности, сила, действующая на пла-
пластину А, равна 2jtSv2 = -^дЕ,так как на пластину А
действует только поле зарядов В (ср. ВМ, § VIII.4). р"с- 127-
Иначе можно коэффициент -~- получить так: заряды па А рас-
ноложены на границе между областью, где £ = 0 (слева от А), и
областью, где £'=4лv (справа от А); поэтому среднее поле равно
■^-(•titv-j-O) = 2nv. Но это усреднение и есть способ рассмотреть
только ту часть поля, которая создана Б-зарядами и одинакова
слева и справа от А. Поле самих зарядов А имеет слева и -права
от А противоположный знак и при усреднении пропадает.
Перейдем теперь к случаям, когда поле получается с помощыо
.непосредственного наложения полей от точечных зарядов.
Рассмотрим комбинацию двух зарядов, +<? и —q, в точках
(-к-; 0; 0) и (—-сг; 0; 0 ). .Обозначая через г+и г_ радиусы-векторы
\г ) \ * I
этих точек, получим в силу формулы B1) суммарный потенциал
VV> \г-г+\ |г-г_| .
' ' V C0)
Так как поле симметрично относительно оси х, то достаточно пред-
представить его картину в какой-либо плоскости, проходящей че-
через эту ось, например в плоскости xOz. На рис. 128 изображены
сплошными линиями следы пересечения плоскостью xOz эквипо-
эквипотенциальных поверхностей, которые получаются, если приравнять

330
ТЕОРИЯ ПОЛЯ
[гл. х
правую часть C0) постоянной (это — замкнутые овальные поверхно-
поверхности восьмого порядка). Пунктиром изображены силовые линии; они
начинаются на положительном заряде (это—«источник» силовых линий,
I
Рис. 128.
имеющий «обильность» 4nq) и заканчиваются на отрицательном (это —
«сток»), В силу соотношения B0) эти линии нормальны к эквипо-
эквипотенциальным поверхностям (пересекают их
под прямым углом).
Если h бесконечно малб, т. е. источник
и сток расположены в бесконечной близости
друг от друга, то система зарядов называет-
называется диполем. Однако если при этом сами
заряды остаются конечными, то их поля про-
просто взаимно уничтожаются, так что в сумме
получается нулевое поле. Поэтому интерес
представляет только случай, когда заряды
бесконечно большие, причем такие, чтобы
произведение m=qk (это произведение
называется моментом диполя) оставалось конечным. Диполь в про-
пространстве характеризуется не только местом расположения и моментом,
но и направлением, для получения которого нужно провести ось
через заряды в направлении от отрицательною к положительному.
Для вывода поля от диполя рассмотрим рис. 129, где /—ось
диполя. При достаточно малом h в любой точке М будет
£х г_
о _ ч _ .,. г? гЪ . Л '
129.
h
К

§ 6]
ПРИМЕРЫ
33!
где _~. означает производную, полученную при изменении поло-
положения заряда (она отличается от производной, полученной при
изменении положения точки наблюдения М, множителем—^.Упро-
множителем—^.Упрощая правую часть C1), получим (проверьте!)
_ ( 1 dr 3rdr\ m (Ъг ,„
Е=т —.-г. г— =т — cos a — 1°
\г> d! л1 di I г3 \ г
где /°— единичный вектор, идущий по оси /, а а — угол между
векторами /° и Г.
Рис. 130.
Аналогичное рассмотрение потенциала диполя дает выражение
d ( 1 \ cos a
т dl \ г ) г'-
Если принять ось диполя совпадающей с осью х и,' подобно рис. 128,
рассмотреть картину в плоскости xOz, то мы получим cosa = x/r,
т. е. ц> = т^= т ■■■_., ., t . На рис. 130 показаны следы эквипо-
эквипотенциальных поверхностей (это овальные поверхности шестого по-
порядка) и электрические силовые линии, которые, как- видим, начина-
начинаются на диполе и на нем же заканчиваются. (Подумайте, как полу-
получить рис. 130 из рис. 128.)

332 тьотя поля [гл. х
Упражнения
1. Вычислите поле от бесконечной однородной заряженной прямолиней-
прямолинейной нити с помощью интегрирования.
2. Вычислите поле от бесконечной однородной заряженной плоскости с по-
М1.,щью интегрирования.
3. Вычислите поле и потенциал от «плоского диполя», представляющего
ее Сом результат наложения двух противоположно заряженных однородных пря-
прямолинейных бесконечно близких нитей.
§ 7. Общее векторное поле и его дивергенция
Теперь легко сформулировать введенные понятия в общем виде,
для некоторого стационарного векторного поля А= А (М), независимо
от его физического смысла. Естественно обобщается понятие век-
векторных линий как линий, идущих в каждой .своей точке вдоль поля.
Как и в § 4, вводится понятие потока вектора А через ориентиро-
ориентированную поверхность (а) по формуле Q= ^ Ando= ^ A-da. Этот no-
fa) (о)
ток иначе называется количеством векторных линий, пересекающих
(а)' изнутри наружу.
Как и в § 5, можно рассматривать поток вектора А через замк-
г.утую поверхность (а),
Q = §Ada C2)
(О)
(кружок у знака интеграла выписывать не обязательно; он подчер-
подчеркивает, что интеграл берется по замкнутой поверхности). Такой по-
поток обладает следующим простым свой-
свойством: если некоторое тело (Й) с по-
помощью каких-то поверхностей разбито
на части (Йх), (Й2), . . . , то поток поля
через поверхность тела (Й) изнутри
наружу равен сумме аналогичных но-
(бг) токов, взятых для каждого из тел (Йх),
(й2), ... Например, на рис. 131 пока-
показано разбиение (й) на две части, (Q,)
Рис 131. !1 (-г)- Поток вектора А через по-
поверхность тела (Й,) можно предста-
представить в виде суммы двух интегралов, но (а,) и по (а3); моток же
через поверхность тела (Q2) равен сумме интегралов по (а2) и но (а3).
Если сложить эти потоки, то интегралы по (а3) взаимно уничтожатся
(почему?), а интегралы но (ах) и по (а2) в сумме дадут поток век-
вектора А через поверхность тела (Й).
Доказанное свойство дает возможность истолковать интеграл C2)
как количество векторных линий, начинающихся внутри объема (Q),

Л 7] ОБЩЕЕ ВЕКТОРНОЕ ПОЛЕ И ЕГО ДИВЕРГЕНЦИЯ 333
ограниченного поверхностью (а). Если Q > О, то говорят, что в (Q)
имеется источник векторных линий, a Q называется обильностью этого
источника. Если Q < О, то говорят, что в (Q) имеется сток или, что
то же, источник отрицательной обильности; для простоты мы будем
всегда считать сток частным случаем источника. Если Q = 0, то
либо в (Q) нет ни источников, ни стоков, либо же они взаимно ком-
компенсируются; впрочем, и при Q=5^=0 в (Q) .могут быть как источники,
так и стоки, которые, однако, в этом случае компенсируются на
полностью.
Пусть векторные линии возникают по всему пространству. Мож-
Можно говорить о средней плотности источника Q/Q в любом объеме (Q)
(под Q понимается численное значение объема (Q)) и о плотности
источника в любой точке Л'1 пространства; эта плотность равна
Ada
lim Ш= lim <k> C3)
где под (ДЙ) понимается малый объем, содержащий точку М, а иод
(До)— его поверхность. Эта плотность источника называется также
дивергенцией (по-русски расходимостью) векторного поля А и обо-
обозначается через div А. Таким образом, можно сказать, что дивер-
дивергенция векторного поля—это количество векторных линяй, начина-
начинающихся в бесконечно малом объеме (или, что то же, поток поля А
через поверхность этого объема), отнесенное к единице этого объема.
Отметим, что дивергенция векторного поля есть величина скалярная
или, точнее, образует скалярное поле, так как она принимает в каж-
каждой точке пространства свое значение.
Формулу C3) можно переписать в виде
divA = ^|,T. e. dQ = d\\'AdQ. C4)
Получилось выражение для количества векторных линий, начина-
начинающихся в элементарном объеме (dQ). Производя суммирование (§ IV. 7),
получаем выражение для количества векторных линий, начинающихся
в конечном объеме (Q), т. в. для потока вектора А,
f^dQ, C5)
(о) (й)
где (Q) — конечный объем, а (а) — его поверхность. Эта важная фор-
формула называется формулой Остроградского.
Иногда оказывается удобным подсчитать дивергенцию непосред-
непосредственно на основе ее определения C3). Рассмотрим, например,
центрально-симметричное поле в пространстве, определенное формулой
А=/(г)г°. C6)
Как было показано в § 4 (формулы A6) — A7)), поток поля через сферу

334
ТЕОРИЯ ПОЛЯ
[гл. х
радиуса г с центром в начале координат равен Q(r) = 4лл2/(г), а по-
потому количество векторных линий, начинающихся в тонком слое
между двумя такими сферами, равно dQ*= 4nd [г2/(г) ] = 4л [2rf(r) -f-
Значит, на единицу объема этого слоя приходится
л:„ л_ dQ 2,
C7)
В частности, центрально-симметричное поле без источников вне
начала координат характеризуется тем, что
у/(г)+/'(г)^0, откуда f(r) = y2 (С = const).
Мы пришли к закону Ньютона A0). В силу формулы A7) в самом
начале координат в данном случае начинается Сг~2-4я/2 = 4лС век-
векторных линий. Но точечный источник обильности 4лС в начале
координат имеет плотность 4лСб (г). Таким образом, в силу C6)
С
div (^-г°)=4яСб(г), т. е.
div '-,) =
C8)
/
f,
dz dy
У
/
/
/п„
У
В этом важном примере забвение дельта-функции привело бы к гру-
грубой ошибке! Здесь фигурирует трехмерная б-функция (см, § VI,3):
б (г) = б (х) б (у) б (г). Пользование дель-
дельта-функцией гораздо удобнее длинных
словесных формулировок: «дивергенция
равна нулю везде, кроме особой точки
поля, где она бесконечна» и т. п. Начало
координат является особой точкой, так
как скорость в этой точке бесконечна
и не имеет определенного направления.
В этом примере все векторные линии
уходят в бесконечность. Подумайте, где
начинаются и где заканчиваются (или
куда уходят) векторные линии, если f(r)
при г—^0 возрастает.медленнее или бы-
быстрее, чем г~г.
Определение дивергенции C3) было дано в инвариантной форме,
не зависящей от выбора системы координат. Представляет интерес
также вывести формулу для вычисления дивергенции с помощью
декартовой системы координат х, у, z. Для этого воспользуемся
тем, что в формуле C4) форма элементарного объема (dQ) несу-
несущественна, и выберем в качестве этого объема бесконечно малый
прямоугольный параллелепипед с ребрами, параллельными осям ко-
координат (рис. 132). Тогда поток dQ вектора А через поверхность
параллелепипеда (т. е. числитель дроби, стоящий в первой фор-
формуле C4)) можно представить в виде суммы шести слагаемых,
отвечающих шести граням параллелепипеда. Рассмотрим сумму двух
Рис. 132.

§ 7] ОБЩЕЕ ВЕКТОРНОЕ ПОЛЕ И ЕГО ДИВЕРГЕНЦИЯ 33"»
из этих слагаемых, отвечающих задней и передней граням, которые
мы обозначим соответственно цифрами I и II, Тогда И„)ц = (Ax')\v
(Лп),= —(Ах)\ (почему?), и потому указанную сумму можно записать
в виде
(S A«do),+(SA" da)n=- 5 ^*>. do+ S ^л rfa=
Подынтегральная функция с точностью до малых высшего порядка
дА
равна дхАх = -~ dx; это «частный дифференциал» от Ах по х, по-
получающийся из-за того, что точки передней грани отличаются от
соответствующих точек задней грани значением координаты х. По-
Поэтому весь интеграл, с точностью до членов высшего порядка
малости, равен
дАх , С 1 дАх , , ,
-~-* dx \ do = ~ dx dy dz.
дх , дх '
Проводя аналогичные вычисления для двух других пар граней, по-
получим весь элементарный поток
dAv дА
Но так как dV= dxdy dz, то в силу первой формулы C4) получаем
окончательно
дАх dAv дА,
div А = ~ + -/ + -^ . C9)
дх ' ду ' дг v '
В заключение обратим внимание на следующее обстоятельство.
Из формулы C3) хорошо видно, что поток вектора через малую
замкнутую поверхность имеет порядок не площади этой поверхности
(как можно былб бы ожидать от интеграла по поверхности), а
ограниченного ею объема, т. е, по сравнению с линейными разме-
размерами имеет не второй, а третий порядок малости. Это можно
объяснить следующим образом. Поток вектора через разомкнутую
поверхность, действительно, имеет второй порядок малости. Однако
поток постоянного вектора через замкнутую поверхность всегда
равен нулю! (Это свойство легко вытекает из предыдущего мате-
материала; докажите его, например, с тмощью последней формулы § 4
или формулы C5).) Поэтому если внутри малой замкнутой поверх-
поверхности разложить по.че по формуле Тейлора (§ VI.6), то интеграл от
первого, постоянного члена даст нуль, а интеграл от членов пер-
первого порядка малости будет иметь третий порядок малости.
Сделанное замечание не относится к случаю, когда внутри замк-
замкнутой поверхности находятся особенности поля, в которых объемная

336 ТЕОРИЯ ПОЛЯ [ГЛ. X
плотность источника обращается в бесконечность. Если впу'рн
поверхности имеется источник векторных линий, распределенный по
площади, то поток имеет второй порядок малости; если источник
распределен по линии, то поток имеет первый порядок малости
(пропорционален длине линии); наконец, поток через поверхность,
внутри которой имеется точечный источник (т. е. дивергенция имеет
характер дельта-функции), вообще не является малым. Именно с
таким случаем мы столкнулись выше в весьма важном случае ку-
лоновского г.оля (см. формулу C8)).
Упражнения
1. Пользуясь формулой Остроградского, найдите поток через сферу
х--\-уг-\-z1 — R'1 изнутри наружу полей А = Ixl -f-yk; P = y'2i— г2/.
2. Получите формулу C7) с помощью формулы (.;9).
3. Найдите дивергенцию плоскопараллельного ссесимметричиого поля
Л = /(|р[)р°. В каком случае это поле не имеет источников вне оси г?
§ 8. Дивергенция поля скорости и уравнение неразрывности
Вернемся теперь к рассмотрению стационарного течения газа
(см, § 4) и будем считать, что в процессе течения масса газа не
меняется, В § 4 мы установили, что поток вектора скорости г» чепе:?
ориентированную поверхность (о) равен объему газа, проносимому
через (а) в единицу времени изнутри наружу. Значит, если поверх-
поверхность (а) замкнутая, то этот поток равен разности между объемом,
выходящим за единицу времени из (а) по той части поверхности,
где v направлено наружу, и объемом, входящим внутрь (а) по той
части поверхности, где v направлено внутрь.
Почему поток вектора v через замкнутую поверхность может
быть отличным от нуля? Если газ считается несжимаемым в процессе
течения (так будет при рассмотрении скоростей течения, значительно
меньших скорости звука, а также при рассмотрении жидкостей), то
втекающий объем ранен вытекающему и потому указанный поток
равен нулю, Однако, если (а) находится в зоне, где газ по мере
течения расширяется, то вытекающий объем будет больше втека-
втекающего и потому суммарный поток будет положительным; аналогично
в зоне сжатия суммарный поток отрицателен,
Теперь ясно, что такое дивергенция вектора скорости. В силу
§ 7, чтобы получить div v, надо разделить ноток вектора v через
поверхность бесконечно малого объема (rfQ) на численное значение
(Зп этого объема. Таким образом, получается отношение объема,
«рождающегося» в (dQ) за единицу времени, к объему dQ; это
отношение естественно назвать «скоростью относительного увеличе-
увеличения объема». Отсюда ясно, что равенство divt>=0 — это условие
несжимаемости газа, а соотношения divi»>0 и divz»<0 выполня-
выполняются соответственно в зоне расширения и в зоне сжатия,

§ 8] дивеггенция поля скорости и уравнение нерлзрывности 33 7
Рассмотрим ноле «массовой скорости» pv. В § 4 мы показали,
что поток такого вектора через ориентированную поверхность (а)
равен массе газа, проносимого за единицу времени через (а) изнутри
наружу. Но так как масса газа остается неизменной, то полный
поток вектора pv через любую замкнутую поверхность обязательно
равен пулю, так как внутрь такой поверхности втекает такая же
масса, как и вытекает из нее, Так будет и для бесконечно малого
объема, и потому в силу § 7 мы приходим к равенству
div(pi») = 0 D0)
для стационарного течения, при котором внутри каждого элемента
объема масса газа с течением времени не меняется. Это уравнение
неразрывности — одно из основных соотношений гидродинамики, вы-
выражающее закон сохранения массы.
Распишем это выражение в координатах. Вектор pv имеет, оче-
очевидно, компоненты pvx, pv , pvz. Поэтому
diV (P*) = дх №х) "I" g-y (Pvy) + д~г (fWz) =
dvx- dvv dvz\ dp dp dp
dy l dz J * x dx ' У dy~ * dz r
(иным путем это будет выведено в § XI.8), Следовательно, условие
сохранения массы приводит к соотношению
div v = v ■ grad p,
Для несжимаемой жидкости р = const, gradp = O, div v = 0, Что
такое величина i»'gradp в стационарном потоке сжимаемой жидкости
(именно такой поток мы рассматриваем, для пего div (pv) = 0)?
Найдем изменение плотности частицы. В стационарном потоке
р=р(лг, у, z), плотность в данной точке не зависит от t, т.е.
dp/dt = Q. Но когда мы переходим к рассмотрению данной час-
частицы, то нужно учесть, что ее координаты зависят от г.ремени.
Скорость v как раз и характеризует эту зависимость:
dx__r_ dy _ dz __
По общему правилу (ср. формулу (IV.5)), рассматривая р=р[лг(/),
y(t), z(t)] = p(t), найдем
dp^dpdx , d£dy±<>Pdz^v.SIV
dt dxdt^dydt ' dz dt
Итак,
,. 1 dp
divi»= —■"- ~r4 .
p dt
Это и есть количественное выражение сделанных выше высказываний

338 ТЕОРИЯ ПОЛЯ [ГЛ. х
о divf в области, где газ сжимается (dp/dt >0) или расши-
расширяется (dp/dt <C 0) при j? = 0.
Рассмотрим теперь нестационарное течение газа, когда поле
скоростей и другие рассматриваемые здесь поля меняются с тече-
течением времени. Тогда все введенные ранее понятия'нужно (как и r
случае нестационарного поля с любым физическим смыслом) рас-
рассматривать для любого фиксированного момента времени. При этом
линии тока (т. е. линии, которые строятся в любой фиксированный
момент времени и в этот момент в каждой точке идут вдоль вектора
скорости) уже не совпадают с траекториями частиц жидкости
(подумайте, почему!).
Если в нестационарном случае рассмотреть некоторый объем (dQ),
то здесь поток вектора г>г» через поверхность, равный в силу фор-
формулы C4) div (pv) dQ, дает скорость уменьшения массы газа в этом
объеме, т. е. массу газа, выходящего из этого объема за единицу
времени. Однако масса газа, содержащегося в бесконечно малом
объеме (dQ), равна р dQ и потому увеличивается*) со скоростью
Таким образом, получаем
div (pv) dQ = —^ i
откуда
Это и есть уравнение неразрывности, которое и для нестационар-
нестационарного случая означает, что в процессе движения газа он не по-
порождается и не исчезает. В стационарном случае уравнение D1),
очевидно, переходит в уравнение D0).
В нестационарном случае скорость -— изменения плотности в
( Ф ж
частице (в отличие от скорости —■ изменения плотности в фикси-
фиксированной точке] равна
d д
Отсюда найдем, что в нестационарном случае формула
1 rfp
р dt
остается без изменения.
.*) Слово «увеличивается» надо понимать в алгебраическом смысле: если
dpldl > 0, то масса внутри dQ увеличивается, а если dp/dt < 0, то масса
уменьшается.

§ 9] ДИВЕРГЕНЦИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И УРАВНЕНИЕ ПУАССОНА 339
Упражнение
Пусть рассматривается поток «нейтронного газа» в реакторе, причем нейт-
нейтроны поступают в поток по всему объему за счет реакции деления ядер
урана, происходящей в данном объеме. Как изменится уравнение неразрыв-
неразрывности?
§ 9. Дивергенция электрического поля и уравнение Пуассона
Пусть в пространстве распределен заряде некоторой плотностью р,
и им порождается электрическое ноле Е. В § 5 мы внделм, что
поток Q вектора Е через поверхность любого объема (Q), т. е. ко-
количество электрических силовых линий, начинающихся в (Q), рав-
равняется произведению 4л на заряд q, содержащийся в (Q). Отсюда,
если объем бесконечно мал, получаем
т. е. окончательно
div£=4np. D2)
Итак, дивергенция напряженности электрического поля, т. е. плот-
плотность возникновения электрических силовых линий, прямо пропор-
пропорциональна плотности распределенных зарядов.
В § 5 мы видели, что электрическое поле имеет потенциал ф,
связанный с вектором Е соотношением B0). Подставляя B0) в D2),
получаем уравнение для потенциала
div grad cp= —4яр.
Комбинация div grad называется оператором Лапласа и обозначается
буквой Д; поэтому уравнение для потенциала можно переписать
в виде
Дф=— 4лр. D3)
Это уравнение называется уравнением Пуассона; его решение B3),
равное нулю на бесконечности, было найдено ранее. В части прост-
пространства, свободной от зарядов, уравнение D3) приобретает вид
Дср = О D4)
и называется уравнением Лапласа.
Легко получить выражение для оператора Лапласа в декартовых
координатах. Из формул A) и C9) получаем
d.vgrad *= div (§
дх\дх )~т~ду{ду )~r дг\дг

340 ТЕОРИЯ ПОЛЯ [ГЛ. X
Таким образом, урааиение D4)'—это то самое уравнение Лапласа,
которое уже встречалось нам в § V.7, но записанное для трехмер-
трехмерного случая.
Иногда удобнее вычислять оператор Лапласа в других системах
координат. Например, для центрально-симметричного поля ср(г) в
силу формул E) и C6)—C7) получаем
Лф (г) = div grad ср (г) =
!*± L\—l ( !*l\ л. (iaX—^JLl. ^L
dr r j~~ r WW V dr )r~~ df^ r dr '
Оперптор Лапласа связан простой формулой со средним значе-
значением функции на малой сфере. Для вывода этой связи положим в
формуле Остроградского C5) A = gradcp; получим
<^gradnq> da = Г div grad ф^й, т. е, §j~da = § Дер dQ.
@1 (Ь) (G> (Н)
Допустим, что {а) = {а)г — сфера радиуса г с центром в некоторой
точке 0; тогда dff=r2dco, где dco— элемент телесного угла с вер-
вершимой 0 (§ 5), откуда
jj ^rr* dco= & AqdQ, т. е. £ (f q, d<a =-^ С AcpdQ.
(К интегрированию по со мы перешли, чтобы область интегрирова-
интегрирования не зависела от параметра г и потому можно было применить
правило § 111.6 дифференцирования интеграла по параметру.) Инте-
Интегрируя последнее равенство по г, начиная от г = 0, получим
г
—if ср dco! _о =И j| \ ДфdQ.
О (И),
Однако ф | г=0 = ф (О) = const, ffl dco = 4n (почему?), откуда, поделив
на 4п, получаем
^ I ф D5)
(О) г
Из этой формулы мы выведем некоторые следствия. Прежде
всего, допустим, что Лф==0 в некоторой области, включающей
шар (Q)f; тогда функция ср называется гармонической (ср. § V.7) и
в силу формулы D4)
У D6)
(О) г
Таким образом, значение гармонической функции в центре сферы
равно среднему значению этой функции на сфере.

§ 9] ДИВЕРГЕНЦИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И УРАВНЕНИЕ ПУАССОНА 341
Отсюда вытекает, в частности, что гармоническая функция не
может иметь внутри области своего определения максимумов пли
минимумов. В самом деле, если, например, в точке 0 будет минимум,
а г достаточно мало, то среднее значение функции ср на (о) будет
больше ср @) (почему?), а это противоречит формуле D6). По-дру-
По-другому это свойство было доказано в ВМ, § VI,3, где было отмечено
и следствие из него: заряд в электростатическом поле в области,
свободной от других зарядов, не может иметь положений устойчи-
устойчивого равновесия.
Другое следствие из формулы D5) для произвольной функции ср
получится, если считать г малым, Тогда (Дф)(ц), ~ Дер |о, откуда
■■» ] = ~ л2
Поэтому, с точностью до величин, малых при малом г,
6 Г 1 С . ; _  „ф(|7)'-ф@
D7)
@)r
где под ф(а'г понимается среднее но сфере (с\, Отсюда видно, в
частности, что если ф(а>г = ф @), т.е. выполняется описанное выше
свойство среднего по сферам, то Дф=0, т.е. функция ф
гармоническая.
Формула D7) весьма напоминает формулу
(* + А)-:-ф(х—Л)
2 ^~(Г
которую при малом Л для функции ф (х) одного переменного легко
проверить с помощью формулы Тейлора (проделайте это!). Во мно-
многих случаях формула D7) дает возможность глубже понять смысл
соотношений, в которые входит оператор Лапласа. Например, в тео-
рии теплопроводности выводится уравнение ^- = const- Av распростра-
распространения тепла в однородной среде, где v—температура. В силу фор-
формулы D7) это означает, что если вокруг точки О температура
в среднем выше, чем в О, то температура в О должна повышаться.
Упражнения
1. Чему равно Дф (| р |), где р — xl -f- yj (§ 6)?
2. Докажите, что значение гармонической функции в центре шара любого
радиуса равно среднему значению этой функции на шаре.1
3. Докажите формулу D7) с помощью разложения функции ф в ряд
Тейлора.

842 теория поля [гл. х
§ 10. Вектор площадки и давление
В § 4 мы говорили о том, что ориентированную плоскую пло-
площадку примято изображать вектором. Особенно естественен такой под-
подход при исследовании сил давления в жидкости или газе. В самом
деле, пусть в некоторой точке давление равно р; это, конечно, вели-
величина скалярная *). Пусть в этой точке расположен ориентированный
элемент поверхности (do) (см. рис. 120). Тогда сила, с которой
жидкость, расположенная по внутреннюю сторону поверхности, давит
на этот элемент, направлена по нормали к (do) во внешнюю сторону
и численно равна р do; таким образом, эта сила равна
dF = pda. D8)
Вектор площадки получает непосредственное истолкование.
Теперь легко подсчитать суммарную силу, с которой жидкость
давит па некоторый мысленно выделенный в ней объем (Q) с поверх-
поверхностью (а). Для этого надо просуммировать элементарные силы D8),
поменяв, однако, в правой части знак, так как поверхность (а) мы
будем, как и в предыдущих параграфах, считать ориентированной
внутренней стороной к (Q), а не к давящей жидкости. Тогда мы по-
получим
F = — \pda. D9)
(О)
При вычислении интеграла D9) часто бывает удобно перейти
к интегрированию по (Q). Для этого заметим, что
/\ /\ /х
pda — pn do — p [cos (я, x)t + cos(n, y)J+ cos (я, z)k]do E0)
(см. конец § IX. 1). С другой стороны, pcos(n, x) = (pi)n, где знач-
значком п обозначена проекция на внешнюю нормаль. Поэтому в силу
формулы Остроградского C5) и формулы C9) для вычисления дивер-
дивергенции получаем
(fjpcos(n, x)d6=(j) (pi)ndo= \d\v(pi)dQ=
(<J) (a) (Q) (Й)
и интеграл от первого слагаемого в правой части E0) оказывается
равным i \ ~dQ. Аналогично преобразуются интегралы от двух дру-
(й)
гих слагаемых, и в результате мы получаем
«Л (й) (£>)
*) Жидкость или газ подчиняются закону Паскаля; мы не рассматриваем
ни прочности, ни вязкости, которые приводят к различию сил, действующих
па площадки, по-разному направленные.

§ 10] ВЕКТОР ПЛОЩАДКИ И ДАВЛЕНИЕ 343
(см- формулу A))- Итак, сила давления равна
radp)dQ, E2)
Рассмотрим примеры. Пусть сначала давление постоянно, р — const.
Тогда grad р = 0, и формула E2) показывает, что и /г = 0.
Мы приходим к выводу, что постоянное давление, приложенное со
всех сторон к телу как угодно сложной формы, дает нулевую
результирующую си.чу. Именно поэтому нас не выталкивает атмо-
атмосферное давление, которое интенсивно, но с постоянной силой давит
на сложную поверхность нашего тела. По существу, данный пример
уже был рассмотрен в конце § 4; в частности, мы видим, что
если в жидкость помещен многогранник, показанный на рис. 121, то
Р(-°)+Р (<М +Р К) +Р (ot) = 0.
Сокращая на р, мы вновь приходим к формуле A8).
В качестве другого примера рассмотрим давление в жидкости,
находящейся в поле тяготения. Если направить ось z от свободной
поверхности вверх, то, как хорошо известно, давление в жидкости
зависит от z следующим образом:
Р=Ро~ SPZ>
где рп — давление на свободной поверхности*), р — плотность жид-
жидкости и g—ускорение земного тяготения. Отсюда в силу E2) по-
получаем выталкивающую силу
F= ^gpkdQ^-gpQk.
Так как произведение gpQ равно весу жидкости в объеме (Q), то
мы приходим к известному закону Архимеда.
Вернемся к общему случаю и найдем результирующую сил дав-
давления, приложенных к бесконечно малому объему (dQ). Так как
в случае постоянного давления эта результирующая, как мы только
что показали, равна нулю, то, рассуждая, как в конце § 7, можно
вывести, что хотя силы давления приложены к поверхности,
но результирующая пропорциональна не площади, а объему. Это
видно и из формулы E2), откуда следует, что для бесконечно
малого объема интегрирования
dF— —(gradp) dQ. E3)
К объему (dQ) могут быть приложены некоторые объемные силы
(например, силы тяготения, центробежные силы и т. д,), распределенные
*) Обратите внимание на то, что в жидкое;и. очевидно, г < 0, так что
давление р по формуле больше р0, как и должно бьнъ.

344 теория поля [гл. х
с плотностью /. Результирующая таких сил равна
Обе.эти силы придают массе pdQ. ускорение —, т. е.
о du d~ = —(grad P)du +/<Ж,
откуда, сокращая на o'Q, получаем уравнение движения
p^=-gradp+/. E4)
В левой части здесь стоит скорость изменения вектора V вдоль
траектория частицы. Эта скорость записывается подобно тому, как
это было сделано я § IV. 1 для случая скалярного поля (т. е. она
состоит из локальной и конвективной скоростей); ее координатное
выражение ми получим в § XI.8.
Рассмотрим, в частности, стационарное течение несжимаемой (т. е.
при р = const) жидкости в поле тяготения. В этом случае, направив
ось z вертикально вверх, получим, что /, т. е. сила, действующая
на единицу объема, равна—pgk. Умножив обе части уравнения E4)
скалярно на dr — vdt, получим в левой части
pdv-V = ~d[v-v) = ^-d(vi) (здесь г/ = |г>|).
В правой части первое слагаемое после умножения дает
а второе — pgkdr = —pgdz. Итак,
^■d(v-)= —dp —pgdz.
Подчеркнем, что это соотношение выполняется вдоль линии тока:
мы пользовались этим, когда писали dr = vdt, так как такое равен-
равенство определяет смещение движущейся частицы вдоль траектории
(см. § IX.4). Интегрируя вдоль такой линии, получаем соотношение
?Y+P + Pgz= const, E5)
которое должно выполняться в стационарном потоке вдоль каждой
линии тока. При этом постоянная интегрирования, стоящая в правой
части, принимает на различных линиях тока, вообще говоря, раз-
различные значения. Соотношение E5), называемое интегралом Бер-
нулли, выражает закон сохранения энергии при движении частицы
жидкости. Это особенно ясно, если помножить обе части на rfQ,
а затем взять приращение Д (не путать с оператором Лапласа!)

R 10] ВЕКТОР ПЛОЩАДКИ И ДАВЛЕНИЕ 845
обеих частей равенства вдоль некоторого участка линии тока. Мы
получим
Д Щ- dQ -f Др dQ + Д pgz dQ = 0,
т. е.
Д —s— + dm-gz ) = —Ар-dQ.
Так как в скобках стоит сумма кинетической и потенциальной энергий
движущейся частицы, то левая часть равна приращению полной энер-
энергии этой частицы. Правую часть можно представить в виде интеграла
вдоль линии тока
- J -jj ds • dQ = — у (grad p).ds ■ dQ. = J F.ds
(см. формулу E3)). Значит, эта правая часть равна работе сил дав-
давления при движении частицы. Итак, формула E5) означает, что
прир"ащение полной энергии части- _--—-л О
цы равно работе действующих на ^-^^^Турбина
нее сил.
В стационарном потоке закон
сохранения энергии можно приме-
применить еще и другим способом. Рас-
Рассмотрим «трубку тока», т. е. трубку, Рис' '33.
через боковую поверхность которой
линии тока не выходят и не входят; схематически эта трубка изобра-
изображена на рис. 133. При этом стенки могут быть твердыми, так как
на стенках работа не совершается и жидкость через них не прохо-
проходит. Сравним мощность насоса (т". е. энергию за единицу времени),
затрачиваемую на подачу жидкости в трубку, с мощностью турбины
на выходе из трубки; если пренебрегать потерями на трение, то эти
мощности должны быть равными. Через входное отверстие в трубку в
единицу времени поступает "OXSX единиц объема жидкости, где
S — площадь поперечного сечения трубки, а индекс 1 указывает па
то, что рассматриваемые величины относятся ко входу. Эта жидкость
обладает кинетической энергией
Кроме того, на создание давления pt в объеме vlS1 тратится мощ-
мощность насоса р^^^ а на поднятие на высоту zl (от некоторой
стандартной высоты z = 0) — мощность pvlSlgzl. Составляя аналогич-
аналогичные выражения для выходного сечения и приравнивая суммы, по-
получим запись закона сохранения энергии
^ I С* I г\т С* rr i tZ.Ci.\

34 6 ТЕОРИЯ ПОЛЯ [ГЛ. X
Однако в силу сохранения массы и несжимаемости жидкости имеем
vxSx =v,iSi. Сокращая E5) на эту величину, получим
2 2
^ ^
Это равенство равносильно интегралу Бсрнулли E5).
Из интеграла Бернулли хорошо видно, что при постоянной или
мало изменяющейся высоте давление в струе существенно зависит
от скорости течения: чем больше скорость, тем меньше давление.
Это и естественно: если частица переходит из области с меньшим
.давлением в область с большим давлением, то равнодействующая
сил давления на нее направлена против скорости, т. е. движение
тормозится. Если же по мере движения давление падает, то давле-
давление «в спину» частицы больше, чем давление ей «в грудь», и
частица разгоняется. При достижении определенной скорости в силу
E5) давление должно было бы стать отрицательным; на самом
дгле этого не происходит, жидкость теряет сплошность—в ней
возникают полости (возникает так называемая «кавитация»).
Упражнение
Выведите с помощью формулы E1) инвариантное, не связанное с выбором
системы координат, определение градиента, аналогичное определению C3)
дивергенции.
ОТВЕТЫ И РЕШЕНИЯ
§ 1
Легко проверить, что связь старых координат х, у, z с новыми х', у', г'
, у'—г' (/'+г' _
такова: х = х; у—-—у=-; z = "—у^-• Подставляя эти формулы в выражение
для и, полечим и = д'2 + 2{/'2. Так как г' не входит, то поле плоскопараллелыюе.
§ 2
1. Так как prp.d и = yi-\-xj— 2zk, то (grad и)л1 = ii-Я/+ &*• Искомая про-
а 19 ,п
пзводпая равна gnid и -=—г=г=£,0.
|я| У 10
§ з
F = —grad U =—ayi — axj. Силовые линии определяются уравнением
dx di/ , , о .
— ' , откуда хах=-уау, xi = y--\-C, сто — гиперболы с центром
—at/ —ах
в начале координат (рис. 33).
Q —2л | р | \ / (| р | , г) dz, где г = а и z = b—
плоскости оснований цилиндра.
а
В случае плоскопараллелыюго поля / не завист ог г и Q —2я | р | / (| р |) Л,
где к— высота цилиндра.

ОТВЕТЫ И РЕШЕНИЯ 347
§6
1. Интегрируя выражение для dEx, указанное в тексте, получаем (с по-
помощью подстановки £ — z — V xi + yi tg a)
'.-J
их dt,
— со
■ cos'g_ Ц* V _ ,„_ 2ц*
4
cos3 a
. 2ии _ 2ид; , , 2ui/
Аналогично находим £u~ , g , , £, = 0. Отсюда Е—^—г1—? <+ о . » У=
= . | а= | . р°. Результат совпадает с B6).
2, Приняв заряженную плоскость за плоскость уОг, получим в точке
0) 0 £у=£г = 0,
{х; 0; 0) при ж > 0 £у=£г = 0, тогда как
ее со
'.- f f
J И Т '1 Т ii )
— со -со
Переходя к полярным координатам р, ср в плоскости т), t,, как в конце § IV.7,
получим
2Л со - со
С С vx p dp С р dp — 1 со
Ех= \ dtp \ ■ —Lj7~ = "JIVJC I —— »/ =2nv.v ;— =2nv,
J J (*2 + P2) J (^ + P2) (*2+P2) p=o
0 0 0
Отсюда £ = 2nv/, что совпадает с B9).
3. Рассуждая, как в конце § 6, получаем при естественном смысле букв
о d , COS ОС
ф= m dT(~In|pl)= TpT "
Можно проверить, что следы цилиндрических эквипотенциальных поверхностен,
а также электрические силовые линии расположены, как на рис. 130, но
теперь и те и другие будут окружностями.
§7
1. По формуле C9) div4=2, divfi=0. Поэтому по формуле Остроград-
Остроградского искомый поток равен
Cdi
J
(У)

348 теория поля [гл. х
2. Так как А = / (г) г° = —^ г, то Ах~—^—,
дА х_
<ЗЛ,, дА,
Аналогично находим —;— , -т— . Отсюда
иу ог
3. Рассуждая, как при выводе формулы C7), получим
при этом di\'/4 = 0, если /(|(jj)=-—- . Это — поле B6), рассмотренное в § 6.
§8
1. —j- + di v (р») = /, где } = 1(х, у, г, /)=- ' , a d.M—масса нейтро-
lioa, поступающих в поток в объеме (dQ) за время dt.
2. Разобьем шар (Q)r на бесконечно тонкие «пузыри» радиуса s и тол-
толщины ds @ <s <;/•). Тогда в силу формулы D6)
Г г
Г С / С ^ С 4
\ q,dQ=W \ <p da Us= \ 4.us2(p (О) ds = ^r nr\(O),
t) и \ к) } О &
(Н)г о \(o)j / о
откуда и вытекает требуемое утверждение.
3. Пусть О — начало координат. Из соображении симметрии
\ х do = \ у d<3 = \ г da == \ ху do = \ д-г da = \ i/z da = 0
Г ^ Г*
(все интегралы берутся по (о)г); кроме того, \ хг do= \ у1 do= \ z'1 do, откуда
*) J J
\ *2da = -g" \ U2 + (/2 + 2'2) da = y r*-inr'2 = — л/-4. Применяя разложение вида
(IV.27) с о = 6 = 0, получим, с точностью до малых пятого порядка,
(О);
откуда легко вытекает формула D7).
§8
4'<lPD + -[fj
§ 10
& pdo & pdo
Отметим, что эта формула справедлива для любого скалярного поля, а не
только для поля давлений.

ГЛАВА XI
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ*)
§ 1. Векторное произведение векторов
В векторной алгебре наряду с умножением вектора на скаляр
(§ IX.1) и скалярным произведением двух векторов (§ IX.2) опре-
определяется также векторное произведение двух векторов, к описанию
которого мы переходим.
Напомним (§ Х.4), что поверхность в пространстве ориентирована,
если указано, какая ее сторона считается внешней, а какая—внут-
какая—внутренней. Принято считать, что если эта поверхность незамкнутая
(т.е. с краем), то ориентация поверхности порождает также ориен-
Наружная
сторона
Правый
Винт
Наружная
сторона
Левый
бинт
Направление
обхода контура
Направление
обхода корпуса
Рис. 134.
тацшо ее контура, т. е. направление его обхода. Обратно, если
указывается направление обхода контура, это приводит к ориента-
ориентации самой поверхности. Связь между ориентацией поверхности
и ориентацией ее контура указана на рис. 134: если за основу
системы координат взята правая тройка векторов I, j, k (т. е. такая
тройка, что, смотря с конца третьего вектора, мы видим кратчай-
кратчайший поворот от первого ко второму против часовой стрелки), то
применяется правило правого винта, в противном случае — правило
левого винта. Например, правило правого винта можно сформули-
сформулировать так: если правый винт (который обычно применяется н
*) Эта глава является непосредственным продолжением двух предыдущих
и существенно опирается на материал §§ IX. 1—2 и Х.1—4, 7. Кроме "того,
используются понятия кратного интеграла (§ IV.7), определителя (§ VIII.3) и
б-фупкции (§ VI.1). В § 12 используется также материал §§ Х.,.5—9.

350
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
технике и обыденной жизни) вращать в направлении обхода контура,
то винт должен пойти от внутренней стороны поверхности к наруж-
наружной. Или, другими словами: если маленький человечек обходит по
наружной стороне поверхности ее контур по указанному направле-
направлению обхода (см. рис. 134), то сама поверхность должна быть у него
по левую руку *).
Переходим к понятию векторного произведения. Векторное произ-
произведение двух векторов а и I), по определению, представляет собой
вектор S площадки (S) (см. § Х.4),
которая получится, если а и Ь отнести
к одному началу, затем построить на
этих векторах параллелограмм и обхо-
обходить его контур, начиная с первого
вектора (т. е. а; см. рис. 135, Где
принято правило правого винта, ко-
которым мы всегда будем пользоваться,
если не оговорено противное).
.Таким образом, векторное произве-
произведение двух векторов а и Ь—это век-
вектор, направленный перпендикулярно
обоим векторам, по модулю равный
построенного на а и б, и образующий
такого же смысла (т. е. правую или
левую), как векторы I, j, k. Обозначается векторное произведение
косым крестом а X Ь или квадратными скобками [а, Ь\.
Отметим наиболее важные свойства векторного произведения.
Так, векторное произведение двух непулевых векторов равко нуль-
вектору в том и только том случае, если векторы параллельны:
а X 6 = 0 равносильно а\\Ь,
так как параллельность векторов означает вырождение параллело-
параллелограмма в отрезок, площадь которого равна нулю. В частности,
всегда а ха = 0.
Векторное произведение «антикоммутативно» **)
Ь х а = — (а х Ь).
Действительно, при перемене порядка множителей параллелограмм
не изменится, но контур его будет проходиться в противоположном
площади
с этими
Рис. 135.
параллелограмма,
векторами тройку
*) Первые три картинки рис. 134 откосятся к правой системе коорди-
координат. Как видно из рисунка, если вертеть правый винт от i к j, т. е. вывин-
вывинчивать его из пластинки, то винт в целом перемещается в направлении k.
Обход контура в эту сторону соответствует тому, что нижняя сторона поверх-
поверхности (о)—внутренняя, верхняя—наружная, вектор а направлен по k.
**) Коммутативность означает переместительность. Например, умножение
обычных чисел пли скалярное умножение векторов коммутативны. Вообще
некоторая операция над какими-либо объектами называется коммутативной,
если она не зависит от порядка, в котором берутся эти объекты.

§ 1]
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
351
направлении и потому вектор площадки заменится на противопо-
противоположный.
Можно проверить, что скалярный множитель можно выносить за
знак векторного произведения:
(la) xb = ax (Щ =l(axb)
и что справедлив распределительный закон:
(а + b) х с = а х с + Ь х с; с х (а + Ь) = с х а 4- с х Ь.
Раскрывая скобки в выражениях, включающих векторное произ-
произведение, надо тщательно следить за порядком множителей. Приве-
Приведем пример:
(а + Щ X Bа — 36) = 2аха — За X b + 4b х a—
Пусть векторы а и b даны своими разложениями в декартовых
проекциях
а = aj 4- ayj + azk, Ь = bj + byj+ bzk.
Тогда, если воспользоваться равенствами (проверьте их!)
iXJ=k; jxi = — k; Jxk = i; kxj= — i\
kxi=j; ixk = —j, (I)
получим
a X b = (aj + ayj+ azk) X (bj + byj+ b2k) =
B)
z — azby)-\-j{azbx-axbz) + k (axby —
(продумайте структуру последнего выражения!).
Этот результат очень просто запомнить, если записать его в
виде определителя (см. формулу (VIII.13)):
« J
ar a,,
C)
Пусть, например, надо вычислить площадь 5 параллелограмма,
построенного на векторах а = Ы — 2j-\-k и b=—2i-\-j-\-4к. Так
как S = \axb\, то вычисляем
j
I
3
—2
(—2—1
C — 4)=— 9t— Uj— k;
\ = \ "9г -г 1~4- ■]- У1 -=- 16,7 .

352
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
Так как в этом примере векторы а, Ъ безразмерные, то и пло-
площадь 5 получается, соответственно, безразмерной.
Иногда применяется также векторно-скалярное или, иначе, сме-
смешанное произведение трех векторов а, Ь, с, которое, по определе-
определению, равно скалярной величине [ахЬ)-с. Ее геометрический смысл
виден из рис. 136:
т. е. смешанное произведение трех векторов равно объему парал-
параллелепипеда, построенного на этих векторах. На рис. 138 векторы
а, Ь, с образуют правую тройку, и
получился объем со знаком плюс. Для
левой тройки угол между cud был
бы тупой; в этом случае (ахб)-£ =
= —V. (Предполагается, что за основу
принято правило правого винта.) Век-
Векторно-скалярное произведение равно
нулю тогда и только тогда, когда все
три вектора параллельны одной плос-
плоскости, так как такая параллельность
означает, что параллелограмм вырож-
вырождается в часть плоскости, т. е. имеет нулевой объем.
Легко получить выражение для смешанного призведения в случае,
если даны разложения сомножителей в декартовой системе коорди-
|:ат. Для этого нужно правую часть B) помножить обычным спосо-
Гом скалярно (по формуле (IX.5)) на вектор с= cxi-\- cyj-\- czft. Это
даст после перегруппировки слагаемых
(axb)-c= (ayb2 — агЬу) сх-f (azbx — ахЬг) cy + (axby — aybx) сг =
г—Ь£с) — a {bxcz — Ьгсх) + аг (Ьхс — b cx) =
Нам понадобится еще формула для векторно-векторного произ-
произведения аХ (Ьхс) трех векторов. Для ее вывода представим себе,
что мы вкбрали оси координат так, что ось х пошла по вектору Ь,
а ось у лежит в плоскости векторов b и с. Тогда вектор b будет
иметь проекцию только на ось х, т. е. b = bj; аналогично с~ cxi-\-
4- cyJ, a= axi-\-ayj-\-azk. Пользуясь формулой C), получаем
i
bx
cx
j
0
k
0
0
= bxcvk;
i j k
ax ay az
0 0 bxcy

§ 2]
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К МЕХАНИКЕ
353
Этот результат неудобен тем, что «привязан» к специальному
выбору осей координат. Поэтому преобразуем его (проверьте!);
j — axbx(cxi+cyj)^
)~ c(a-b). D)
Эта формула уже не содержит координатных проекций, а потому
не зависит от специального выбора системы координат. Для запо-
запоминания этой формулы студенты пользуются, фразой; «абц равно
бац минус цабу>.
Упражнения
1. Найдите площадь треугольника с вершинами Л A; 0; —2), В(—1; 1; 2),
С A; 3; 3).
2. Какую тройку образуют векторы a=2i—j, ft=3i-}-2ft, c=—i—j+k?
3. Вычислив (ixi)Xj и ix(ixj), покажите, что векторное произведение
не обладает свойством ассоциативности.
§ 2. Некоторые приложения к механике
Векторное произведение особенно удобно при описании враща-
вращательного движения и связанных с ним понятий. Рассмотрим враще-
вращение твердого тела вокруг некоторой оси (рис. 137) с угловой
скоростью со. Такое вращение принято изображать
вектором угловой скорости се, который распо-
расположен по оси вращения и направлен в соответ-
соответствии с направлением вращения согласно выбран-
выбранному правилу винта; например, на рис. 137 на-
направление (о выбрано по правилу правого винта,
как мы всегда будем делать. Где именно на
оси берется вектор (о — безразличию; такой век-
вектор, который можно произвольно перемещать
вдоль некоторой оси, но не в сторону от этой
оси, называется скользящим*).
Будем ' считать, что начало координат О вы-
выбрано в любой точке оси вращения, и найдем ли-
линейную скорость v произвольной точки М с ра-
радиусом-вектором г (рис. 137). Очевидно, что век-
вектор v перпендикулярен обоим векторам г н to,
а потому перпендикулярен и всему параллелограмму (S), построен-
построенному на последних векторах. Численное значение v равно произве-
произведению со на кратчайшее расстояние точки .VI до оси вращения, т. е.
как раз площади указанного параллелограмма. Но этим условиям,
сформулированным для вектора v, удовлетворяет векторное произ-
произведение (охГ. Таким образом,
E)
Рис. 137.
*) Напомним, что раньше точка приложения вектора ие фиксировалась,
считался возможным параллельный перенос вектора в любую точку.
12 я. Б Зельдович! А. Д. Мышнис

354
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
(проверьте, что векторное произведение надо брать именно в выпи-
выписанном порядке и что правая часть E) не зависит от конкретного
выбора точки О на оси вращения).
Удобство вектора угловой скорости видно, в частности, из сле-
следующего. Допустим, что тело испытывает одновременно два вра-
вращения с (вообще говоря, непараллельными) векторами угловой ско-
скорости (Oj и ш2, причем оси вращения пересекаются в точке О. Тогда
в силу формулы E) линейная скорость любой точки М равна
где обозначено ш = (аг -\-а>%. Значит, тело вращается с угловой
скоростью (о, и мы приходим к выводу, что при сложении вращений
векторы угловой скорости складываются по правилу параллелограм-
параллелограмма. Именно поэтому и можно называть угловую скорость вектором!
С помощью векторного произведения вводится такое важное
понятие, как момент произвольного вектора b с началом в точке М
относительно любой точки О: по определению, этот момент равен rxb,
где г = ОМ. В механике наиболее часто рассматривают момент
силы F, т. е. величину rxF, и момент количества движения mv,
т. е. величину mrxv-
При вычислении момента вектора этот вектор можно считать
скользящим. В самом деле, если вектор b скользит сам по себе,
то это значит, что к г прибавляется Kb,
где К — какой-то скаляр. Однако
(r + Kb)xb = rxb + (Kb) x b =
SO
т. е. от такого скольжения момент вектора
не меняется (рис. 138). Если же вектор от-
относить в сторону относительно его направ-
направления, то момент изменяется.
Рассмотрим систему как-то связанных
между собой материальных частиц, каждая
из которых имеет постоянную массу /я,- и
(вообще говоря, переменный) радиус-вектор
ri = ri(t). Пусть на каждую из этих точек
действуют различные силы; обозначим равнодействующую всех
«внутренних» сил (т. е. сил взаимодействия между точками си-
системы), приложенных к £-й точке, через F\n, а равнодействующую
всех «внешних» сил—через Ff*). Характерная особенность внут-
внутренних сил состоит в том, что на основе третьего закона Ньютона
(«действие равно противодействию») для каждой внутренней силы
имеется противоположная ей внутренняя сила, причем, что очень
важно, расположенная на продолжении первой. Поэтому сумма всех
*) Индексы происходят от латинского «intra» — внутри и «extra»—вне.

§ 2] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К МЕХАНИКЕ 355
внутренних сил, а также сумма их моментов относительно любой
точки равны нулю.
Основные уравнения движения системы частиц получаются, если
записать второй закон Ньютона («сила равна произведению массы
на ускорение»):
mq$ = FT + F'C. F)
Если просуммировать эти равенства по всем частицам, получим
так как сумма всех внутренних сил, как было сказано выше, равна
пулю. Удобно ввести точку С с радиусом-вектором
где 'и =
— общая масса системы; эта точка называется «центром масс»
рассматриваемой системы. При таком обозначении уравнение G)
можно переписать в виде
*-
i ( 1
Итак, центр масс движется так, как будто он обладает полной
массой системы и на него действует сила, равная сумме всех внеш-
внешних сил. В частности, если внешние силы отсутствуют, то центр
масс системы движется прямолинейно и равномерно, rc=at-\-b.
Перейдем к моментам. Если обе части равенства F) умножить
слева векторно на г,-, мы получим
mtrt X 5г=г,.х/=? + r,xF'f. (8)
Воспользуемся равенством
которое вытекает из общей формулы производной векторного про-
произведения; эта формула ^DxB)=rXB+/lX-v выводится
совершенно так же, как аналогичная формула (IX.8) для скалярного
произведения. Отсюда равенство (8) можно переписать так
± (Г. х ntiVi) = г; х Fix + г, X Ff.
Суммируя эти равенства по всем /, получим
12*
Л2- (гiXmtv,) = 2-»",■ X/=7 + 2- г«XF\n = 2^rtXF\\ (9)
i iii

356 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
так как сумма моментов всех внутренних сил равна нулю. Сумма
tXtnpi A0)
моментов количества движения всех частиц, составляющих систему,
называется кинетическим моментом (моментом вращения) этой системы
относительно той же точки О, по отношению к которой берутся
все моменты. Сумма
моментов всех внешних сил, действующих на систему, называется
полным [главным) моментом внешних сил. Таким образом, формулу
(9) можно переписать
—-L A1)
т. е. скорость изменения кинетического момента системы равна
полному моменту внешних сил, действующих на эту систему.
В частном случае, если внешние силы отсутствуют или если их полный
момент равен нулю, получаем, что кинетический момент системы
остается постоянным.
Упражнение
Когда момент вектора Ь относительно точки О равен нулю?
§ 3. Движение в поле центральных сил
Пусть при движении материальной частицы на нее действует
сила, изменяющаяся по произвольному закону, но направленная все
время точно к началу координат О (или от него); такое поле сил
называется центральным. Если в начальный момент
времени провести через начало координат и век-
вектор скорости плоскость (Р), то точка в процессе
движения не может ее покинуть, так как нет
сил, которые могли бы вывести точку из (Р).
(Плоскость (Р) совпадает с плоскостью рис. 139.)
Так как внешняя сила направлена вдоль радиу-
радиуса-вектора, то ее момент равен нулю, и потому
кинетический момент точки, т. е. ее момент ко-
dr
Pitc 139. личества движения, гхи-^ остается все время
постоянным. Однако модуль вектора гXdr равен
удвоенной площади треугольника (dS), изображенного на рис. 139
(почему?). Поэтому в процессе движения точки производная dS;dt
остается постоянной, т. е. 5 в зависимости от времени меняется
по линейному закону. Таким образом, мы приходим ко второму за-
закону Кеплера: при центральной силе площади секторов, заметаемых

§ 3] ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНЫХ СИЛ 357
радиусом-вектором за равные промежутки времени, равны. Прочие
законы Кеплера, о которых мы скажем позже, существенно исполь-
используют конкретный вид зависимости силы от длины радиуса-вектора *).
Пусть F— — F(r)r°. В силу § Х.2 такое поле имеет потен-
потенциал U{г), где функция £/(/•) —первообразная кР(г), т. е. -г— = F(r).
Введем в плоскости (Р) полярные координаты г, ср; тогда закон
движения частицы определяется зависимостями /■ = /■(/), ср = гр (t).
Чтобы найти эти зависимости, воспользуемся двумя законами
сохранения — кинетического момента (§ 2) и полной энергии (§ Х.З).
Для этого обозначим через s° вектор, полученный из г° поворотом
на 90° в положительном направлении. Тогда
dt dt
(Эта довольно очевидная формула является частным случаем фор-
формулы (IX.14) и, по существу, совпадает с формулой (V.10).) Отсюда
dr d , п„ dr n , dw n dr , dw
Так как вектор г°Х5° = Я|) перпендикулярен плоскости (Р)
и имеет постоянный модуль, равный 1, то закон сохранения кине-
кинетического момента можно записать в виде
m/-*^=O( = const). A3)
Закон сохранения полной энергии в силу A2) приобретает вид
«*<= const). A4)
При этом постоянные G и Е определяются начальными' условиями.
Выразим из соотношения A3) -~ и подставим в A4). Мы по-
получим дифференциальное уравнение 1-го порядку
для г (t); найдя r(t), мы можем получить (р (t) из уравнения A3).
Уравнение A5) совершенно аналогично уравнению
— — 4- и 1х\ = £
*) Кеплер нашел свои законы эмпирически, исследуя движение планет
солнечной системы. Только Ньютон показал, что эти законы являются след-
следствием определенного вида силы тяготения, с которой центральное тело —
Солнце-действует на планеты.

358
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
движения частицы т по оси х под действием силы с потенциалом
и(х). Напомним простые свойства решений уравнения A6), рас-
рассмотренные, в частности, в ВМ, § VI.8. Допустим, что график
потенциала и (х) имеет вид, изображенный на рис. 140, так что
и(оо) = из,. Тогда при «mhl <£<«*,, например при £ = £1 на
рис. 140, частица будет периодически колебаться, имея а и b
точками возврата, при этом говорят, что движение финитно; период
колебаний, как легко вывести из A6), равен
ь
=
-u. (x)
A7)
Если же
х, например при Е=Е2 на рис. 140, частица при
движении налево дойдет до точки с и повернет назад, а при дви-
движении направо уйдет на бесконечность, движение инфинитно.
Рис. 141.
Уравнение A5) примет вид A6), если вместо г писать букву х
(что несущественно) и обозначить
G2
@ < г < оо).
A8)
Таким образом, к исходному потенциалу U(r) добавляется центро-
QI
бежный потенциал
зависящий от начальных условий, точнее,
■*—i,
от кинетического момента G рассматриваемой системы.
Таким образом, если umin < Е < «л ( = Ux), то зависимость г (t)
будет периодической. За каждый период изменения г полярный
угол получит одно и то же приращение А(р. Так как А(р, вообще
говоря, несоизмеримо с 2л, то траектория будет, как правило,
иметь вид розетки (рис. 141) и при своем продолжении всюду
плотно заполнит кольцо между окружностями r = rm-ia и r = /"max.
Однако для двух наиболее интересных видов центральных сил,
которые мы сейчас рассмотрим, траектории получаются замкнутыми

§ 3]
ДВИЖЕНИЕ В ПОЛЕ ЦЕНТРАЛЬНЫХ СИЛ
359
и без самопересечений, более того — просто • эллипсами! В первом
примере будем считать, что сила обратно пропорциональна квад-
квадрату расстояния частицы от начала координат. По этому закону
движутся небесные тела (закон Ньютона) или электрически зари-
женные частицы (закон Кулона), если центральное тело, вызвавшее
силу притяжения, можно считать
покоящимся (об этом условии мы
поговорим позже).
В рассматриваемом примере
„, . k ... , k
F(r)=—, U(r)— .поэтому
в силу формулы A8)
/г G2
На рис. 142 показан .график
этого эффективного потенциала
при k > „О (как мы будем считать
впредь) и различных значениях
G. Ясно, что если 0=^=0, т. е.
если движение не вырождается в
прямолинейное, то центробежный
потенциал при г—> 0 нарастает
быстрее, чем потенциал притя-
притяжения, а потому и( + 0) = оо;
это означает, что движущаяся
частица не может упасть на центральное тело—во всяком случае,
если считать его достаточно малым и тем самым пренебречь воз-
возможностью того, что частица «налетит» на него, проходя слиш-
слишком близко от начала координат.
~ du к G2 , ,
Гак как -г=—, г, то минимум эффективного потенциала
dr г1 шг3 J ^~
достигается при
Рис. 142.
к G2 - G2
— г = 0, откуда л=л = —т-
G2
причем
ш/г2
Значит, возможно решение г = —, которому отвечает движение
частицы по окружности с центром в начале координат. Соответ-
Соответствующая угловая скорость определяется из уравнения A3):
df
A9)
она постоянная, т. е. мы получаем равномерное вращение частицы
вокруг центрального тела. Если рассматривается гравитационное
поле, то k=xmM, где х — гравитационная постоянная, а М—масса

360 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
центрального тела. Отсюда в силу A9) получаем период обращении-.
Мы пришли к третьему закону Кеплера: квадраты периодов обра-
обращения планет пропорциональны кубам их расстояний от Солнца.
Здесь он доказан только для круговых орбит, но при соответствую-
соответствующем уточнении формулировки он оказывается справедливым дли
любых орбит (см. упражнение 1).
Чтобы выяснить вид некруговых траекторий при О=^0, подста-
подставим в уравнение A5) U(г) = — kjr и произведем дополнение до
полного квадоата; мы получим (проверьте!)
(dry , (k а у_„, B0)
где для краткости обозначено q = —\Е~*г~о7ч) ] • ^Ри э™ МЬ|
ink2
учитываем неравенство Е > — ^^ (откуда оно вытеи'ает?). В силу B0)
можно обозначить
k G . dr . , ,r,
-~ =<7 cos \b, -тт = <? sin ib, где \b=\b(^). B1)
Дифференцируя первое равенство B1), получим (О/иг2)-ту =
= — q sin ■ф-jT') откуда, учитывая второе равенство B1), а так-
., „. df Jib
же равенство A3), получаем, что ~гг— ~т^> т> е- ^ = ^ — ф^
где а= const определяется начальными условиями. Из первого ра-
равенства B1) получаем
G2 Г Gq I -1 , i_
где обозначено
G2 _Gq
km ' k
Из уравнения B2) сразу видно, что при е < 1 траектория будет
замкнутой (рис. 143), тогда как при е^1 она уходит на беско-
бесконечность. Нетрудно проверить, что условие е < 1 равносильно не-
неравенству Е < 0; таким образом, траекториями ограниченных дви-
движений (см. рис. 142) служат замкнутые линии. Более точно,
уравнение B2) при е < 1 определяет эллипс с фокусом в начале
координат и большой осью, наклоненной под углом а к полярной
оси. (Для доказательства этого утверждения, которое мы предоста-
предоставим читателю, можно перейти к декартовым координатам по фор-
формулам х' — р cos (ф—а), у = рзт(ф — а),) Таким образом, траекто-

§ 3]
ДВИЖЕНИЙ В ПОЛГ. ЦЕНТРАЛЬНЫХ СИЛ
361
риямиограниченных движений служат эллипсы с одним из фокусов
в центральном теле; в этом состоит первый закон Кеплера. Аналогично
проверяется, что при е > 1 движение происходит по гиперболе,
а в пограничном случае, при е—1,— по параболе.
Можно доказать, что, и обратно, из законов Кеплера вытекает
закон притяжения F(г) = /г/л2; поэтому движения по такому закону
называются кеплеровы.чи.
До сих пор мы считали центральное тело как бы «приклепанным»
к началу координат. Движением центрального тела можно прене-
пренебречь, если его масса М существенно больше движущейся массы т,
Рис. ИЗ.
iJnc. 141.
. Оказывается — мы не будем здесь это доказывать,—что
случай сравнимых масс Мит приводится к разобранному, однако
кривые второго порядка, по которым движутся обе массы, будут
тогда иметь фокус в центре масс всей системы. Интересно, что
при этом распределение между обоими телами как значений кине-
кинетической энергии, так п моментов количества движения относительно
центра масс получается обратно пропорциональным мас-
массам этих тел. В самом деле, ограничимся для простоты случаем,
когда тела движутся по окружностям с центром в центре масс О
с постоянной угловой скоростью со, и обозначим через d (постоян-
(постоянное) расстояние между телами (рис. 144). Тогда кинетическая
энергия и момент количества движения .массы М равны соответег-
М ( Bmii \2 md Matmd
Вен НО *7Г" ( Т1—I ) И ~rz ; j ~jTi ; , Т
2 \M-\-m J М-\-а М-+-т
т ( d)Md V2 Md тМ/Ш
личины равны --■——) и хг—-хг__., откуда
М -J- in
массы т эти ве-
и вытекает
2 \ .vi -j- m
обратная пропорциональность.
Случай отталкивания по закону Кулона, т. е. k < 0, мы предо-
предоставляем рассмотреть читателю; отметим только, что при G=^=0
траектории предста'вляют собой гиперболы.
В качестве другого примера центральной силы рассмотрим силу
.F——Аг(А>0), пропорциональную расстоянию частицы ог

362
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 11 ВРАЩЕНИЕ
[ГЛ. XI
начала координат. Здесь потенциал U(r) =-^-гг. В декартовых ко-
координатах рассматриваемый потенциал можно записать в виде
В силу § IV.6 такой вид имеет главная (квадратичная) часть раз-
ложения потенциала U по
его минимума в изотропном
степеням х, у, z а окрестности точки
случае, т. е. когда эквипотенциальные
поверхности представляют собой, с
точностью до малых высшего поряд-
порядка, не эллипсоиды, а сферы. Поэтому
рассматриваемый потенциал описывает
i\ia.r!bie колебания частицы вблизи про-
произвольного положения ее устойчивого
равновесия (без особенности у потеи-
цнала) в изотропном случае. Такой
случай реализуется, например, для схе-
схемы рис. 145, если все пружины имеют
одинаковую жесткость. Из § Х.6 вы-
вытекает, что такой потенциал возни-
возникает также внутри однородного притя-
притягивающего шара; можно представить,
что частица движется внутри канала, просверленного в соответствии
с рассчитанной траекторией в этим шаре, настолько тонкого, что
влиянием его на гравитационное поле можно пренебречь.
Если принять плоскость, в которой движется частица, за пло-
плоскость х, у, то в рассматриваемом примере дифференциальное
уравнение движения можно записать в виде
т ^ (xi + yj) = — krr° = — kr = — k (xi
или, в проекциях,
Таким образом, в декартовых координатах переменные разделились,
т. е. колебания по обеим осям происходят независимо друг от друга.
I3
Закон движения в силу § VII.3
х= rl cos (со/ -j-
имеет вид
у = гг cos (со/
Ф»),
где о)= Vk/m,
а постоянные rL, ц\, г2, ср_ определяются
B3)
начальными
условиями. Мы предоставляем читателю убедиться в том, что урав-
уравнения B3) определяют в качестве траектории частицы эллипс с
центром в начале координат.
Таким образом, для силы F(r) = kr все траектории также ока-
оказываются замкнутыми, причем период 2л/со = 2л У m[k колебаний

§ 4) ВРАЩЕНИЕ ТВЕРДОГО ТКЛЛ 363
частицы не зависит от начальных условий. Отсюда вытекает, на-
например, что если прорыть через центр Земли колодец и выкачать
из него воздух, то период колебаний камня, брошенного в этот
колодец, не будет зависеть от амплитуды и окажется равным вре-
времени обращения спутников на уровне земной поверхности (без со-
сопротивления воздуха).
Конечно,, во втором из разобранных примеров замкнутость траек-
траекторий получилась из-за того, что в декартовых осях переменные
разделились, а колебания по обеим осям имели одинаковый период.
Но удивительно п замечательно то, что и в первом примере, где
переменные не разделяются, траектории тоже оказались замкнутыми!
Это похоже на некое математическое чудо. В самом деле, форма
закона F = k/r2 была в § Х.7 получена непосредственно из условия
u\vF(r)=0 (r^=0), естественного с точки зрения физики. В отли-
отличие от этого, замкнутость траекторий при таком законе притяжения
отнюдь не очевидна и доказана с помощью искусственных матема-
математических выкладок. Это «чудо» значительно облегчило измерение
и тем самым упростило анализ сравнительно малых отклонений
реальных траекторий от эллиптической формы (например, движение
перигелия Меркурия; как известно, объяснение этого движения,
вытекающее из общей теории относительности, послужило одним из
первых решающих подтверждений этой теории).
Упражнения
1. Найдите период колебаний частицы по эллипсу B2) и установите связь
этого периода с большой полуосью эллипса.
2. Найдите период изменения радиуса частицы для закона притяжения
F= —kr с помощью формулы A7) и объясните расхождение ответа с резуль-
результатом, полученным в этом параграфе.
§ 4. Вращение твердого тела
Рассмотрим вращение твердого тела (Q) вокруг фиксированной
оси, за которую мы примем ось г. Кинетический момент G этого
тела относительно какой-либо точки О на оси вращения легко свя-
связать с угловой скоростью (o = G)ft вращения, пользуясь формулой E):
G =\jrxvdm~ ]rx(coftxr) р dQ = а ^ prx(ftXr)dQ,
где через р мы обозначили (вообще говоря, непостоянную) плот-
плотность тела. Вспомнив, что r = xi-{-yj-\-zk, найдем по формуле D)
г X (ft X г) = (г ■ г) ft — (г ■ ft) г = (л-а +У2 + г2) k — z(xi +у/ + zft) =
= —xzi — yzj+ (x* -fy*) ft,

364 ВККТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
откуда
Gx = — со \ pxz du, Gy =. — (о \ руг Л1,
Gx = lo \ p(.v2-f/)
В частности, последний интеграл
1г= { р (х2-гу2) iiQ B4)
называется моментом инерции тела (Я.) относительно осп z, так что
Допустим, что на тело (Q) действуют некоторые заданные силы
F'lx и силы F°n реакции в опорах, заранее не заданные. Если эти
последние силы приложены к осп вращения, то их момент r°nxF°n =
~zonkx^Fcjn перпендикулярен осп z. Чтобы не рассматривать эти
неизвестные силы, спроектируем равенство A1) на ось z, что даст
dt dt -*'
причем при образовании правой части, т. е. проекции полного мо-
момента внешних сил на ось вращения, надо учитывать только задан-
заданные силы Fjx. Таким образом, от векторного равенства A1) мы
перешли к скалярному равенству B5).
Рассмотрим, в частности, случай, когда внешние силы Ffx отсут-
отсутствуют или направлены параллельно оси вращения. Тогда £г = 0 и
из B5) получаем со/г = const. Если при этом тело не меняется, то
/г= const, а потому и со = const, т. е. угловая скорость вращения
не меняется. (При этом мы пренебрегаем трением в опорах, которое
приводит к дополнительному слагаемому в правой части B5) и, как
следствие, к затуханию скорости вращения.) Если же 1г меняется,
то со изменяется обратно пропорционально Iz. Зтпм свойством поль-
пользуется танцовщица, когда она вращается («делает туры») на одной
ноге. Начав вращение с расставленными руками, она быстро сводит их
(обычно книзу, переводя их в «подготовительное положение»). При
этом в силу формулы B4) получается, что она уменьшает 12 своего
тела (причем довольно сильно, так как расставленные руки дают
в 1г значительный вклад) и соответственно увеличивает со. (Как
сказано в «Основах классического танца» А. Я. Вагановой, «этим
движением рук и берется нужный для тура форс».) Одновременно
она приподнимается на носок (на «полупальцы» или на пальцы) для
уменьшения трения. После нескольких оборотов она вновь разво-
разводит руки, уменьшая со, и становится на обе ступни, что приводит
к полной остановке.

§ 4] ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА 365
Рассмотрим теперь гироскоп (волчок), т. е. твердое тело, вра-
вращающееся вокруг неподвижной точки, которую мы примем за начало
координат. Принимается, что гироскоп имеет ось симметрии; прохо-
проходящую через точку закрепления, и быстро вращается вокруг этой
оси, а силы трепня пренебрежимо малы.
Заметим, что если твердое тело вращается вокруг оси симмет-
симметрии, проходящей через начало координат, то кинетический момент
этого тела направлен по оси вращения и пропорционален угловой
скорости вращения. В самом деле, первое вытекает хотя бы из сообра-
соображений симметрии, а второе — непосредственно из определения A0).
С другой стороны, в механике выводится,
что силы тяжести можно заменить равно-
равнодействующей, проходящей через центр
тяжести тела, который, очевидно, лежит
на оси симметрии. Поэтому если гироскоп
закреплен в центре тяжести или если он
запущен в вертикальном положении
(в обоих этих случаях момент силы тяже-
тяжести равен нулю), то из равенства A1) вы-
вытекает, что кинетический момент,а с ним
и ось вращения остаются постоянными.
При кратковременных толчках правая
часть A1) может на короткое время становиться отличной от
нуля. При этом G получит некоторое приращение, однако чем
больше угловая скорость, т. е. чем больше | G |, тем меньше от-
относительное значение этого приращения, т, е. тем устойчи-
устойчивее гироскоп. На этом свойстве основано применение гироскопа в
технике.
Рассмотрим теперь, что произойдет, если центр тяжести распо-
расположен выше точки закрепления (как это будет, в част .ости, дш
детского волчка), а ось вращения расположена невертнкально.
В этом случае сила тяжести Р, приложенная к центру тяжести С,
создает опрокидывающий момент гс>:Р (рис. 146). И силу уравне-
уравнения A!) кинетический момент G за зремя dt получ::т бесконечно
малое приращение dG= (rcxP) dt. Так как этот бесконечно малый
вектор горизонтален и перпендикулярен вектору G, то вектор G-ftfS
получается из G поворотом на бесконечно малый угол вокруг вер-
вертикальной оси. Это значит, что численное значение углозой скоро-
скорости не изменится, но ось вращения гироскопа повернется вокруг
вертикальной оси. К новому положению можно применить то же
рассуждение, и мы видим, таким образом, что под действием силы
тяжести ось симметрии гироскопа получает дополнительное разно-
разномерное вращательное движение (так называемое пргцгесионноа дви-
движение) вокруг вертикальной осп. Скорость прецессии тем меньше,
чем больше и, так как при большом G то же самое dG влечет за
собой меньший поворот.

366 ВЕКТОРНОЕ ПРОИЗВКДКНИЕ И ВРАЩЕНИЕ [ГЛ. XI
Сделанные выше выводы не являются вполне точными, так как
из-за прецессии кинетический момент идет не точно по оси гиро-
гироскопа, а отклоняется от нее. Поэтому в действительности движение
гироскопа является более сложным, чем описано выше. Однако пока
угловая скорость w велика, эта поправка незначительна. Если гиро-
гироскоп не подкручивается и из-за неизбежного постоянно действую-
действующего трения угловая скорость уменьшается, то скорость прецессии
увеличивается, а когда эти скорости» становятся сравнимыми, харак-
характер движения существенно изменяется и, в конце концов, волчок
падает.
Упражнение
Вычислите Jг для однородного: а) цилиндра радиуса R массы М с осью
вращения Ог; б) прямолинейного стержня длины L массы т, если ось Ог слу-
служит перпендикуляром к середине стержня.
§ 5. Симметрические и антисимметрические тензоры
Рассмотрение кинетического момента твердого тела служит хо-
хорошей областью приложения понятия тензора (§ IX.5). Будем поль-
пользоваться тензорными обозначениями, примененными в § IX.5. Пусть
начало координат О зафиксировано, но оси координат могут выби-
выбираться по-разному. Из § 4 видно, что при рассмотрении кинетиче-
кинетического момента тела Q существенную роль играют интегралы
— \pxlXjdQ (i¥=j),
hj = \ г ., , jr> ,, ,ч B6)
Нетрудно проверить, что при замене координатного базиса ве-
величины B6) преобразуются по тензорному правилу (IX.23) л потому
образуют тензор 2-го ранга
/=/1-ув/в/1 B7)
называемый тензором инерции тела (Q) относительно точки О. Для
доказательства запишем величины /,-у едикой формулой:
hj=
(
где символ Кронекера b;j- при любом выборе базиса определен ра-
равенствами
°
Мы предоставляем читателю убедиться в том, что величины 8£

§ 5]
СИММЕТРИЧЕСКИе И АНТИСИММЕТРИЧЕСКИб ТЕНЗОРЫ
867
образуют тензор 2-го ранга (он называется единичным тензором).
Если теперь баз::с заменен по формулам (IX.19), то величины х;,
как проекции вектора г, преобразуются по формулам л;/= ос^у-Ху,
откуда, применяя равенство x'kx'k' — xkxk (откуда оно следует?),
получаем
i'il = \ Р Ф'цЧх'к — x'tx'j) dQ = J p {airajfirlxkxk — a;rajlxrxl) dQ =
Ш) (Q)
E2)
что и требовалась доказать.
Пусть теперь тело (Q) вращается с угловой скоростью (о вокруг
оси, проходящей через начало координат О; покажем, как выра-
выражается соответствующий кинетический момент О относительно О.
Рассуждая, как в § 4, и пользуясь формулой D), получаем
G= [prx(<oxr)dQ = [p [(г-г) (о — (г-ы)г] dQ =
(Н)
= )Р\
E2)
B8)
Чтобы вынести под знаком интеграла за скобки coy и е,-, запишем
со; = 6,-уСОу (продумайте эту формулу!); это даст
О = ^ р ^ijxkxk—,xixj) соув,- dQ=/i/a>/ei,
другими словами,
G,.=
B9)
О
Рис. 147.
(Можно написать также G = I-<a, где скалярное
произведение тензора 2-го ранга на вектор опре-
определяется с помощью формул (ab)c = a{bc) = (bc) а, откуда
/■<о = (/,.уе,.еу) -cufteft = /,vcofte,- (e,-eft) = /,/ufte,-6yft = /,-уСйув, = G.)
Формула B9), по существу, совпадает с формулами § 4, однако
не связана, как это было в § 4, со специальным выбором декарто-
декартовых осей. Она показывает, в частности, что, за исключением сфе-
сферически симметричного случая (когда 1^ = 1Ь^), направления векто-
векторов (о и G, вообще говоря, различны. Например, если для тела,
изображенного на рис. 147, массы втулки и стержня пренебрежимо
малы по сравнению с т, то момент вращения согласно формуле D)
равен
G = рг х ((о X г) = рг-(о — (со пр1Ог) г,
т. е. вектор G вращается с угловой скоростью (а. Это изменение

ft;8 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
момента вращения в силу формулы A1) компенсируется моментом,
передаваемым втулкой на ось вращения.
Выведем еще формулу для кинетической энергии Т вращающе-
вращающегося тела (Q). Для этого' заметим сначала, что для любых двух
векторов я, b '.'а основании известной формулы для площади парал-
паралич
лелограм.ма будет | axb | = ab sin (а, Ь), С другой стороны, а-Ъ =
— ah cos (а?ft). Отсюда
axb\1-(a-b}i = a2b- [sin2 (аГ&)-f cos2 (a,'b)] = alb*. C0)
Умножим равенство B8) скалярно на (о и воспользуемся форму-
формулой C0); .мы получим
С-<о= [ р {{г-г) (со-со) — (г-ы)(г-<й)]Aп= \ р |гх(о |2 (/Q = 27.
A2) (")
Отсюда в силу B9)
7=iG-(o=^/,7w,to/. ' C1)
Тензор B7) обладает важным свойством симметричности:
'//= '//. C2)
что сразу вытекает из его определения B6). Вообще, тензор 2-го
ранга, обладающий таким свойством, называется симметрическим.
При этом нетрудно проверить, что если свойство C2) выполняется
при каком-то одном выборе базиса, то оно выполняется и при любом
другом выборе базиса. ,
Основным свойством симметрического тензора (IX,25) является
возможность приведения его к диагональному виду, т. е, возможность
такого выбора базиса е{, для которого все величины p;j при i=^=j
обращаются в нуль. Мы не будем здесь доказывать это общее утвержде-
утверждение (справедливое для симметрических тензоров в пространстве любого
числа измерений), а сделаем только два замечания по этому поводу.
Прежде всего, так как диагональный тензор обладает свойством
симметричности, а это свойство сохраняется при замене базиса, то к
диагональному виду можно приводить только симметрические тензо-
тензоры. Во-вторых, так как при выборе евклидова базиса в трехмерном про-
пространстве имеется три степени свободы (почему?), а для приведения
тензора к диагональному виду надо удовлетворить трем равенствам
/>,., =/>1з =^.-з = 0, то степеней свободы оказывается как раз столько,
сколько нужно.
В осях Xj, в которых тензор инерции имеет диагональный вид
(они называются главными осями этого тензора), выражения B9) для
проекций кинетического момента и C1) для кинетической энергии

§ 5] СИММЕТРИЧЕСКИЕ И ЛНТИСИММЕТРИЧЕСКИЕ ТЕНЗОРЫ 369
приобретают вид
, = 7„2со2,
TL50- C3)
Чтобы нагляднее представить себе зависимость кинетической
энергии Т от направления момента вращения G, изобразим па сфере
|G| = const, жестко связанной с телом (й), линии, которым отвечают
равные значения Т; другими словами, это линии с уравнением C3)
-F,
Рис. 148.
Рис. 149.
при различных значениях Т (рис. 148). Допустим для определенно-
определенности, что Уп < /22 < /33. Тогда при заданном \G\
чение Т, равное
2/,
|О|
получится, когда
G2=G3 =
наибольшее зна-
знание. 148);
при G1=G2 = 0 будет наименьшее значение Т, тогда как при
Gj = G3 = 0 T будет иметь миннмакс. При свободном вращении G
и Т постоянны, но (о меняется как ко направлению, так и г;о моду-
модулю (за исключением вращения вокруг одной из осей xh когда
( Q
| G
ру h
. Тело (Q) поворачивается так, что вектор G все время
проходит через одну из изображенных лиши"! (на рис. 148 показано
перемещение С относительно (О.)).
В качестве другого важного примера симметрического тензора
упомянем о тензоре упругих напряжений. Пусть рассматривается
напряженное состояние твердого тел.а, вызванное приложенными к
нему силами. Выделим мысленно в изучаемой среде кубик со сто-
стороной h и с ребрами, параллельными осям координат. Тогда упру-
упругое воздействие окружающей среды на каждую из граней этого
кубика можно заменить силой (рис. 149), которая при малом h будет
пропорциональна /г2:

370 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
Величины а,у- зависят от выбора направления осей координат. Можно
показать, что при замене базиса они преобразуются но тензорному
правилу (IX.23) и потому образуют тензор 2-го ранга, который на-
называется тензором упругих напряжений и характеризует напряжен-
напряженное состояние среды в рассматриваемой точке. Диагональные члены
этого тензора определяют напряжения сжатия или растяжения,
а внеднагональные — сдвиговые напряжения.
Нетрудно проверить, что тензор упругих напряжений симметри-
симметрический. В самом деле, полный момент внешних сил, действующих
на кубик, относительно его центра с точностью до малых высшего
порядка равен ^ 2 • у hetxF) = ^ /г3а;уе;-X еу-. Если какое-либо
i с /
ст(.у-=^= ау-;', то этот момент был бы отличен от нуля, что невозможно,
так как момент инерции кубика порядка Ь? и получилось бы бес-
бесконечное угловое ускорение.
Применяются также антисичметрические тензоры (р,-у), для которых
?U=-Pji\ C4)
диагональные члены такого тензора по необходимости равны нулю.
Нетрудно проверить, что если свойство антисимметрии C4) выпол-
выполнено при каком-то одном выборе базиса, то оно выполняется и при
любом другом выборе базиса.
Антисимметрпческий тензор в трехмерном пространстве непосред-
непосредственно связан с векторным произведением. Именно, пусть дано
линейное отображение пространства в себя с антисимметричной
матрицей коэффициентов рц (см. § IX.5; мы упоминали там, что
любой тензор 2-го ранга можно с точностью до размерности истол-
истолковать как матрицу некоторого линейного отображения простран-
пространства в себя). Тогда любой вектор r=xiei отображается по формуле
Тг =puxj-ei=pl2xiel +р13х3е1—р1гх1е2 ^pi3x3e.,~plsxle;i — pi3x.ie3.
Но тот же результат получится (проверьте!), если векторно помно-
помножить вектор р=— (Pi1e3-'rPi3elJrPslei) на г; итак, Тг =рхг. Из
последнего равенства видно, что вектор р определен отображением
Т, а потому и тензором рц инвариантно, т. е, независимо от выбора
декартова базиса.
Рассмотрим в заключение тензор линейного отображения, близ-
близкого к тождественному. Он имеет вид Ьц-\- ч\ц, где 5,-у— единичный
тензор, а г)(-у-—малые коэффициенты; такой тензор получается,
в частности, при рассмотрении малых деформаций упругого тела.
Представим тензор т](-у в виде суммы симметрического тензора
р/;- и антисимметрического тензора у!;-, где
Р*7=-2-(т1<7 + 11//). 7// = -2"(т1гу—'Чу/)- C5)

§ 6] ИСТИННЫЕ ВЕКТОГЫ И ПСЕВДОВККТОГЫ 371
Тогда тензор C,-у в некоторых осях xt принимает диагональный вид
и потому определяет комбинацию малых равномерных растяжений
вдоль этих осей: вдоль оси хх в 1-]-Рп раз (конечно, если рп < О,
то на самом деле получится сжатие) н т. д. При этом объем уве-
увеличится в A+PU) A-ЬРга) A+Р:K) или> с точностью до малых
высшего порядка, в 1 + Ри + Р22- Р33= 1 + Р;,- раз. Но Р;,= Р,7
(см. § IX,5), а петому в силу C5) р// = т},-,-.
Что касается тензора ytj, то он определяет малый поворот.
В самом деле, при таком повороте вокруг вектора р° на малый
угол г|з каждый вектор г, с точностью до малых высшего порядка,
переходит в вектор г -\--\ppvXr, а мы показали выше, как по анти-
антисимметрическому тензору 7;/ можно подобрать соответствующий
вектор р = \рр".
Итак, линейное отображение, близкое к тождественному, сво-
сводится к комбинации равномерных растяжений вдоль взаимно пер-
перпендикулярных осей и поворота. Так как при повороте объем не
меняется, то сумма ii;7 (она называется следом тензора rj;y) пред-
представляет собой коэффициент приращения объема, т. е. при рас-
рассматриваемом отображении объем увеличится в l-j-т),-,- раз.
Подчеркнем, что наложение деформаций приводит к сложению
соответствующих тензоров только для малых деформаций; по
существу, это получается в результате применения формулы
A+а) A+Р) « 1+(а+Р) при малых а, р. Большие деформации
(например, повороты на конечный угол) накладываются по совсем
иному, вообще говоря, некоммутативному закону, который мы здесь
не будем рассматривать.
Упражнения
1. Докажите теорему о возможности приведения симметрического тензора
к диагональному виду для двумерного случая.
2. Разложите малый сдвиг (рис. 111, г) на растяжения и поворот.
§ 6. Истинные векторы и псевдовекторы
Между вектором линейной скорости и вектором угловой скорос-
скорости имеется следующее принципиальное различие. Куда именно на-
направлен вектор линейной скорости, не вызывает никаких сомнений.
В отличие от этого согласно § 2 вектор угловой скорости отклады-
откладывается по оси вращения; но в какую именно сторону? В § 2 мы вы-
выбрали эту сторону в соответствии с правилом правого винта. Но с
таким же основанием можно условиться опираться на правило левого
винта, и тогда на рис. 137 вектор со был бы направлен вниз. Таким
образом, выбор направления вектора угловой скорости по оси враще-
вращения является условным и зависит от выбранного правила винта, так

372 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
что при перемене этого правила на противоположное этот вектор
заменяется на противоположный. Векторы, обладающие таким свойст-
свойством, называются псевдовекторами в отличие от истинных векторов,
не зависящих от выбора правила винта. Итак, вектор линейной ско-
скорости— это истинный вектор (такими же являются векторы силы,
ускорения, электрической напряженности и т. д.), а вектор угловой
скорости — это псевдовектор. Принята также другая терминология,
истинные векторы называют полярными (от слова «полюс»), а псевдо-
псевдовекторы— аксиальными (от латинского названия оси)*).
Из определения векторного произведения ясно, что векторное
произведение двух истинных векторов представляет собой псевдовек-
псевдовектор, так как при перемене правила винта бывшая наружная сторона
параллелограмма, построенного на перемножаемых векторах, станет
внутренней (см. рис. 134 и 135). Таких! образом, момент силы и ки-
кинетический момент (§2) — это псевдовекторы. Аналогичным образом
легко проверить, что векторное произведение истинного вектора на
псевдовектор представляет собой истинный вектор (см., например,
формулу E)), а двух псевдовекторов — также псевдовектор.
Вопрос об эквивалентности правой и левой систем координат
совсем не так прост, как это может показаться с первого взгляда.
Эта эквивалентность означает, что для любого явления теоретичес-
теоретически возможно зеркально отраженное явление, при котором все гео-
метричгские формы язляются как бы зеркальными отражениями соот-
соответствующих форм для первого явления, подобно тому как правая
перчатка является зеркальным отражением левой. (Так называемый
«закон сохранения четности».) Недавно обнаружено, что этот закон
не имеет универсальной силы, и в связи с этим крупнейший совет-
советский фпзик-теоретг.к лауреат Ленинской и Нобелевской премий
Л. Д. Ландау A908—1968) предложил «принцип комбинированно!!
четкости», согласно которому все физические явления допускают зер-
зеркальное отражение только при замене всех частиц античастицами**).
Отмстим в заключение, что векторное умножение двух векторов,
при котором проекции вектора-произведения выражаются через проек-
проекции векторов-сомножителей (но в то же время произведение инвари-
инвариантно относительно выбора осей координат) и выполняются естест-
естественные правила умножения, — это операция, характерная для трех-
трехмерного пространства. Грубо говоря, дело здесь заключается в том,
что в трехмерном пространстве можно условиться каждым двум раз-
разным ортам, например i и j (по осям х и у), ставить в соот-
соответствие третий недостающий до комплекта орт k (по оси г). Так
*) При рассмотрении процессов, происходящих во времени, возникает еще
классификация вектороа по их поведению при изменении знака t (сравните,
например, векторы скорости и перемещения).
**) В конце 1964 г. появились новые экспериментальные данные, согласно
которым принцип комбинированной четности также нарушается и не является
точным

§ 7] ротор векторного поля 873
можно прийти, производя циклические (круговые) перестановки, к
формулам A) векторного умножения ортов. (В самом деле, если
ixj=.-k, то обязательно jxk = i, так как вектор k расположен
относительно векторов i,js точности так же, как вектор ( относительно
векторов j, k.) Из последних получатся формулы векторного умно-
умножения любых векторов. В л-мермом векторном пространстве (§ IX.6)
нужно взять л—1 ортов, чтобы определить и-й недостающий. По-
Поэтому аналогом векторного произведения в /2-мерном пропранстве
является вектор, определенным образом построенный из п—1 век-
векторов*). Таким образом, векторное произведение двух лекторов спе-
специфично для трехмерного пространства. Понятно, что мы не пере-
перечислили всех условий, необходимых для определения векторного
произведения. Все же хотелось отметить разницу между векторным
произведением и скалярным произведением, которое определяется
совершенно одинаково в пространстве любого числа измерений.
Упражнения
1. Справедливы ли формулы A) и C) в левой системе координат?
2. Постройте разумное определение векторного произведения в четырехмер-
четырехмерном пространстве.
§ 7. Ротор векторного поля
В § Х.З при вычислении работы силового поля мы уже пришли
к понятию линейного интеграла. Сейчас мы рассмотрим это понятие
в общем виде.
Пусть в пространстве, в котором задано ноле вектора А, выбра-
выбрана ориентированная линия (L). Тогда линейным интегралом вектор;]
А по линии (L) называется интеграл
!=
где А. — проекция вектора А на касательную к (L), проведенную в
направлении обхода (рис. 150). Так как вектор dr идет вдоль по т,
a \dr\ = dL (§ IX.4), то выражение для линейного интеграла можно
переписать так:
\ ^-dr^- JJ (Ax dx + Ay dy + A2dz).
(L) (L) (L)
*) Аналог смешанного произведения (стр. 352) составляется для п векто-
векторов; это произведение равно я-объему «параллелепипеда», натянутого н<т
эти векторы. В частности, для плоскости, т. е. при я = 2, получаем площадь,
которая является скаляром пли, точнее,— псевдоскаляром. Слово <нсевдо» зна-
значит «почт»»; в данном случае имеется в виду, что величина не меняется при
поворотах системы координат, но множится на — 1 при перестановке осей А' п
у. Примербм псевдоскаляра в трехмерном пространстве была величина смешан-
смешанного произведения трех истинных векторов, рапная объему: знак этой величины
при данных трех векторах зависит от выбора правой или левой системьь

374
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[гл. XI
Линейный интеграл есть величина скалярная и обладает обыч-
обычными свойствами интегралов. При перемене ориентации линии (/.)
он меняет только знак. Если угол а (см. рис. 150) во всех точках
линии (L) острый, то / > 0, а если он тупой, то /<0. Равенство /=0
получается, если угол а все время прямой или (что бывает чаще)
если интегралы по частям (L), где а острый и а тупой, взаимно
уничтожаются.
Внешняя сторона
Рис. 150.
Рис. 151.
Если линия (L) замкнутая, то линейный интеграл
Г= § A-dr =
а)
C7)
называется циркуляцией вектора А по линии (L). Циркуляция обла-
обладает следующим важным свойством аддитивности (сложения). Допус-
Допустим, что некоторая ориентированная незамкнутая поверхность (S)
разбита на несколько частей, например на три части (Sj), (St) и (S3),
как на рис. 151. Обозначим контуры (S) и этих частей, в соответст-
соответствии с ориентацией (S), через (L), (Z.j), (Z.2) и (L3), а соответствую-
соответствующие циркуляции — через Г, Гц Гг и Г3. Тогда
В самом деле, если п правой части все циркуляции представить
в виде суммы линейных интегралов по отдельным дугам, изобра-
изображенным на рис. 151, то интегралы по внутренним к (S) дугам все
взаимно уничтожаются (так как каждая такая дуга проходится
дважды в противоположных направлениях), а интегралы по контур-
контурным к (S) дугам сложатся и дадут циркуляцию, стоящую в левой
части.
Доказанное свойство аддитивности дает возможность говорить
о том, что циркуляция C7) «порождается» на поверхности (S),
а тем самым и о «плотности порождения циркуляции», т. е. о цир-
циркуляции, порождаемой бесконечно малым куском поверхности и от-
отнесенной к единице площади этого куска. К целесообразности

§ 7]
РОТОР ВЕКТОРНОГО ПОЛЯ
375
рассмотрения такой плотности приводит также следующее соображе-
соображение. Легко проверить, что циркуляция постоянного вектора всегда
равна нулю;
§ (С, dx + С, dy + С3 dz) = (С,х + Сгу + С3г)
(L.) (А)
где последний значок говорит о том, что нужно взять приращение
результата интегрирования, когда точка обходит контур (L). Однако
после такого обхода последнее выражение, стоящее в скобках,
возвращается к своему исходному
значению, и потому приращение
равно пулю. Но теперь можно
рассуждать подобно тому, как это
было сделано в конце § Х.7.
Именно, в силу формулы Тей-
Тейлора внутри бесконечно малого
контура вектор А можно пред-
представить в виде суммы постоян-
постоянного вектора и членов первого
порядка малости. При этом про-
происходит почти полная компен-
компенсация: интеграл от постоянного
вектора равен нулю, а интеграл от членов первого порядка ,чало-
сти даст величину второго порядка малости. Таким образом, цир-
циркуляция по бесконечно малому контуру пропорциональна не длине
контура, а площади, охватываемой этим контуром.
Чтобы подсчитать указанную плотность порождения циркуляции,
вычислим циркуляцию вектора А по бесконечно малому контуру.
Сначала допустим, что этот контур лежит в плоскости z= const.
Кроме того, так как при подсчете плотности форма контура несу-
несущественна, то возьмем за этот контур прямоугольник со сторонами,
параллельными осям координат (см. рис. 152, где размер этого
прямоугольника несколько преувеличен). По формуле C7) соответ-
соответствующая циркуляция равна
у
О
Рис. 152.
dT= J Axdx+ ^
A) B)
Asdx
C)
Aydy
C8)
D)
(цифрами обозначены последовательные стороны прямоугольника,
см. рис. 152), так как на каждой стороне изменяется только одна
переменная, а остальные дифференциалы р;'.:;ны нулю. Учитывая
направление обхода указанных сторон, получим из C8)
dT = (Ах), ах + (АуJ dy—(AxK dx—(Ay)t dy =
= [(Ау)-г-(Ауи] dy - [U1J, -
),] dx, C9)

376
ВЕКТОРМОК ПРОИЗВЕДЕН!!!-: И ВРАЩЕНИЕ
[ГЛ. XI
где цифровой индекс указывает, на какой стороне берется соответст-
соответствующая проекция. Однако с точностью до малых высшего порядка
0Av дАх
и потому формула C0) дает
dAv дАх /dAv 0Ах\
dl = —,-'- dx dv =г— dv dx = ~ — dS.
Ox J ду \ дх ду
Итак, для бесконечно малою замкнутого контура
ИГ Я Л г) А
Ul xy Urty ""I
d S г „ OX
D0)
(индексы в левой части указывают на то, что контур параллелен
плоскости х, у). При этом имеется в виду, что контур обходится
в положительном направлении; в противном случае надо поменять
знак пли, что то же, считать dSxv < 0.
Декартовы координаты в пространстве полностью равноправны,
и потому из любой формулы, содержащей эти координаты, можно
получить другую верную формулу, заменив х, у, z соответственно
на у, z, х или на z, x, у. (Такая пере-
перестановка, упоминавшаяся в § 6, назы-
называется циклической пли круговой; при
ней правая система координат остается
правой.) Поэтому из D0) вытекает
dSv
0Аг
~'^У
дАу
"ЬТ
дг
dAz
"Ъ~х~
У
Рис. 153.
D1)
Рассмотрим теперь бесконечно ма-
малую ориентированную площадку (dS),
произвольно наклоненную относитель-
относительно осей координат. Для подсчета циркуляции эту площадку удобнее
всего влить в форме треугольника, как на рис. 153. Построим на
этом треугольнике тетраэдр с гранями, параллельными координат-
координатным плоскостям, и обозначим вершины этого тетраэдра цифрами, как
па рис. 153. Тогда легко проверить, что
так как' в правой части интегралы по отрезкам 41,42 и 43 взаимно
уничтожаются. Но полную часть можно подсчитать по формулам D0)
и D1)
\у дАЛ , /dAt дАу
х ду ] lii l \ ду дг
где цифровые индексы показывают, о каких площадях идет речь.

S 7) ротор векторного поля 377
Полученный результат становится более обозримым, если ввести
вектор, называемый ротором [вихрем, или вихревым вектором) поля А
и обозначаемый буквами rot Л, по формуле
дА, ЗАЛ /дАх дЛЛ /dAv дАЛ
~ ^_ / — - / ' - - k D3)
ду dz J ' \ дг дх J \ дх ду J '
Если заметить дополнительно, что в силу формулы (Х.18)
dS.,aii -\--dS l3J-\- dSl2ik = dSiril-r dSi3l + dSU4 = dS = n dS,
и поделить на dS, то формулу D2) можно переписать в более
простоя виде:
t)-n = rotr,A; D4)
в последнем выражении индекс п указывает на то, что берется
проекция ротора на нормаль п. Эта формула дает циркуляцию по
бесконечно малому контуру, отнесенную к единице площади, охва-
охватываемой этим контуром*).
Таким образом, проекция ротора поля на любое направление п
равна отношению циркуляции поля по бесконечно малому контуру,
перпендикулярному п, к площади, охватываемой этим контуром.
Отсюда, в частности, видно, что ротор, определение D3) которого
привязано к выбранной системе координат, на самом деле связан
с полем инвариантно (образует нозое векторное иоле, так как имеет
в каждой точке пространства, вообще говоря, свое значение): он
не зависит от выбора системы координат, так как левая часть фор-
формулы D4) не зависит от этого выбора, а знание проекции вектора
на каждое направление определяет этот вектор однозначно. Вместе
с тем ротор истинного вектора является псевдовектором (см. § 6),
так как при смене правила винта при той же ориентации пло-
площадки (dS), т. е. при том же векторе ге, обход ее контура сме-
сменяется на противоположный, а потому циркуляция сменяет знак.
Отметим, кстати, что получение нового векторного поля путем
определения ротора (вихря) другого векторного ноля является спе-
специфичным для трехмерного пространства, Между тем получение
векторного поля как градиента скалярного поля в пространстве
любого числа измерений происходит одинаково. Соотношение здесь
такое же, как между векторным п скалярным произведениями (см.
ком с и § 0).
") Отсюда следует, что направление вектора rot А в пространстве опреде-
определяется как направление нормали к такой площадке, для которой — макси-
мально. Это определение сходно с определением направления градиента ска-
скаляра ф как направления линии (/), в котором достигает максимума — .

378
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
Пусть теперь в пространстве задана уже не бесконечно малая
а конечная ориентированная поверхность (S) с контуром (/.). Мы
видели выше, что циркуляции, отвечающие отдельным участкам
этой поверхности, складываются, т. е. общая циркуляция
Из формул C7) и D4) поэтому вытекает
§A-dr= \ (xoinA)dS = \ xoiA-dS,
(S)
(S)
D5)
т. е. циркуляция поля по замкнутому контуру равна потоку (см.
§ Х.7) ротора этого поля через поверхность, ограниченную указан-
указанным контуром. Эта важная формула называется формулой Стокса.
Имеется еще одна полезная интегральная формула, включаю-
включающая ротор, которая преобразует интеграл
по замкнутой поверхности (S) (ориентированной естественным обра-
образом, т. е. наружной стороной к бесконечности) в интеграл по
объему (Q), ограниченному (S). Для ее вывода заметим, что
/=/./= ф (А х dS)-i= ф (i х A)-dS;
(i)
(S)
здесь мы пользуемся тем, что в силу геометрического смысла век-
торно-скалярного произведения оно при «круговой» перестановке
сомножителей не меняется. Однако
i j k
i x A = | 1 0 0
Ax Ay Az
= -AJ+Ayk,
т. e.
(S)
Преобразуя этот интеграл по формуле Остроградского (§ Х.7\
получим
(И)
Аналогично находим
у - Г (д± + д±
'У~~ J \ дг ^ дх
(й)
= (
dAv дАх\
дх ду J '

§ 8] Оператор гамильтона «набла» 379
откуда
(И)
dAv ЗА
(S) <Q)
С
Упражнения
1. Получите с помощью последней формулы инвариантное, не связанное
с выбором системы координат определение ротора, аналогичное определе-
определениям (Х.ЗЗ) дивергенции и (X.57)'градиента.
2. Докажите с помощью формулы Стокса теорему Коши об интеграле от
аналитической функции (§ V.8).
Указание. Перейдите к вещественным интегралам и воспользуйтесь
условиями Коши—Римана (V.17).
§ 8. Оператор Гамильтона «набла»
Выпишем оснозные дифференциальные операции (действия), ко-
которые можно производить над скалярным полем и и векторным по-
полем A = Axi-\-Ayj-{-Azk:
ди .
дх
дАх
~дх~~
. ди .
+ dyJ
дАу
"*~ ~ду~~
, ди
+ дг'
дАг
ЗА
Английский математик У. Гамильтон заметил, что эти три опе-
операции можно более просто записать, если ввести символ
'
называемый набла. Отдельно взятый, этот символ представляет со-
собой знак действия, т. е. «оператор», причем векторно-дифференциаль-
ный, сохраняющий при своем применении как черты вектора, так и
черты оператора дифференцирования. (Общее понятие оператора
см. в § VI.2.)
«Умножение» (т. е. действие) оператора Гамильтона на скаляр
(точнее, на скалярное поле) и и на вектор А производится по

380
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. X!
следующим естественным правилам:
ди .
die"
+j
. ди .
~ J ■=;—f~ »
•'dy '
—
, du
г^г = gi
г Ф '
'ad u,
dAz
1
иг
= div
A,
V X А =
i
д
дх
j
д_
ду
A..
k
д_
дг
дА,
ду
0А
-^
иг
= i[^z+-^ ) + и т. fl.= rot A.
\ ду иг I '
Набла как дифференциальный оператор действует только на
множитель, который стоит непосредственно за ним: например,
(Vm) v = (grad u)v — v grad и, V (uv) = grad (uv).
Поэтому если в каком-либо выражении за наблой нет множителей,
то оно представляет собой оператор: например,
'li+'i + iiU/l — Л-А — 'А —
' дх * ду дг) х дх ' У ду~^ z дг
— это скалярный дифференциальный оператор, который может дей-
действовать на скалярное или векторное поле. Он применяется, в част-
частности, в формуле для скорости изменения поля вдоль траектории
(§ 1V.1)
du flu , ди . ди , ди , _. , ди
Повторив вывод этой формулы, легко проверить, что и для скорости
изменения векторного поля вдоль траектории имеет место аналогич-
аналогичная формула
dA__ . , дА
lr-(V-V)A , ж,
отдельные слагаемые в которой имеют тот же смысл, что в D6).
Это дает, в частности, возможность переписать уравнение (Х.54)
движения жидкости в форме
р (v- V) v + р ^-= — gradp -)-/,
от которой уже легко перейти к координатной форме.
При действиях с оператором набла надо пользоваться пра-
правилами векторной алгебры и правилами дифференцирования. На-
Например,
rot (А -{- В) = V X (A-\-B)=V X А + V X В = rot A + rot В,
d\\(XA)=-4-(XA) = XD-A) = Xd\vA (X = const), D7)

§ 8] ОПЕРАТОР ГАМИЛЬТОНА «НАБЛА» 381
так как и умножение на вектор, и дифференцирование обладают
этими свойствами линейности. В то же время в формуле D7) нельзя
было бы считать X, зависящим от точки пространства (т. е. скаляр-
скалярным полем), таи как тогда получилось бы, что мы вынесли пере-
переменную величину за знак дифференцирования. Чтобы охватить этот
случай, заметим, что в обычной формуле для производной произ-
произведения
(uv)' = u'v 4- uv' D8)
первое слагаемое получается, если в процессе дифференцировании
считать v постоянным, а второе — если в этом процессе считать и
постоянным; поэтому дифференцирование D8) можно выполнить так:
(uv)' = (ucv)' -I- (uvc)' = ucv + u'vc — uv' -1- u'v,
где индекс с указывает, что при дифференцировании к- данной ве-
величине надо относиться, как к постоянной (конечно, если величина
стоит вне знака дифференцирования, то индекс с с нее можно
снять). Таким образом,
"div (uA) = V • (иА) = V • (исА) -j- V • (uAc) =
= « (V -A) -i- (V«) -А —и div A -\-gradii'A
(эта формула иным путем была выпедена в Х.8).
После применения дифференциальной операции к полю полу-
получается новое поле, к- которому можно вновь применять эти опера-
операции. Рассмотрим, например, «составную» операцию rotgradu. Ее
можно записать в виде V X (Vu). Но для «обычного» вектора а н
«обычного» скаляра и всегда
а х (аи) = 0 D9)
(почему?). Значит, если вместо а в левую часть подставить его
разложение по декартовым осям и произвести вычисления по фор-
формальным правилам векторной алгебры, то мы получим нуль. Но
вычисление комбинации V X (Vu) производится по тем же формаль-
формальным правилам, что и D9), только вместо а., av, a2 надо взять
а д д „
у, s-, -=г. Значит, и здесь получится нуль, т. е. всегда
дх ду' дг J J
rotgrad«-=0. E0)
Аналогично получаем (проверьте!), что всегда
div rot Л = 0. E1)
Это простое своПстзо имеет важное следствие, Именно, для любого
поля А можно наряду с векторными линиями (§ Х.7) рассматривать
вихрезыг линии, т. е. векторные линии поля rot А, Формула E1)
говорит, что вихревые линии не могут иметь ни источников, h;i
стоков, т. е. они не могут ни начинаться, ни кончаться.

382 bf.ktopiiok произведение и вращение [гл. xi
Наконец, комбинация
д2 д2 д%
V-V=V2 = ^ + ^ + ^
(оператор Лапласа Д) была рассмотрена в § Х.9.
Упражнения
1. Выведите формулы для rot (nA)\ divD X В).
2. На основе формул (Х.ЗЗ), (Х.57) и решения упражнения 1 § 7 напи-
напишите символическое выражение v в виде интеграла.
§ 9. Потенциальные поля
В § Х.З мы рассмотрели вопрос о существовании потенциала
(потенциальной энергии) у силового поля. Сейчас мы рассмотрим
этот вопрос в общем виде. Векторное поле А называется потенци-
потенциальным, если оно является градиентом некоторого скалярного моля;
если обозначить это поле через —ср, то
Л = — gradcp E2)
(ср. формулу (Х.9)). При этом поле ср называется потенциалом
поля А.
Так как градиент постоянного скалярного поля равен нулю, то
потенциал любого поля А, если он имеется, определен с точностью
до произвольного постоянного слагаемого. Подбирая это слагаемое,
можно сделать значение потенциала равным нулю в любой' заданной
точке; чаще всего принимается равным нулю значение потенциала
на бесконечности. Разность значений потенциала в двух точках
уже не зависит от этого небольшого произвола в выборе потен-
потенциала, так как постоянные слагаемые в такой разности взаимно
уничтожаются.
Далеко не всякое поле является потенциальным. Именно, из E2)
сразу следует, что
rot А = —rotgradcp = 0 E3)
(см. формулу E0)), т. е. потенциальное поле обязательно является
безвихревым. Учитывая выражение D3) для ротора, условие E3)
можно переписать в виде
oA2_0Av оАх_дА^ ГАу__САх
иу Ог ' дг дх ' ох <)у '
Условия E4) можно вывести и другим способом. Равенство E2)
в координатной форме имеет вид

§ 9] потенциальные поля 383
откуда следует, что
А =_^ А -_*Е. А ---_*£.
* 5а: ' ^"" cty ' г" ' дг '
Но тогда
дАг 5'2ф 5Лу 5'2ф
дг/ дг ду ' дг ду ог '
и из равенства смешанных частных производных (§ IV. 1) получаем
первое соотношение E4). Аналогично выводятся и остальные.
Обратно, пусть поле, заданное во всем пространстве, является
безвихревым*). Тогда это поле обязательно является бесциркуля-
бесциркуляционным, т. е.
§
A-dr =
для любого замкнутого контура (L), В самом деле, «натянем» па
контур (L) поверхность (S), Применяя к ней формулу Стокса A8),
получим, если rot A = О,
(f
Adr = ] rotA-dS = 0.
Иначе говоря, для безвихревого поля циркуляция по любому бес-
бесконечно малому контуру равна нулю, а потому и циркуляция по
любому конечному контуру равна нулю.
В § Х,3 мы показали, что бесциркуляционное поле обязательно
имеет потенциал, который строится по формуле (см. формулу (Х.8))
Ф(М)= ^ Adr' E5)
где Мо — какая угодно фиксированная точка, а выбор конкретного
пути интегрирования несуществен, гак как в бесциркуляционно-м
поле линейный интеграл зависит только от положения начала н конца
пути интегрирования. Правда, в § Х.З мы говорили о силовом поле
и истолковывали потенциал как работу, но с математической точки
зрения такое конкретное истолкование несущественно, можно гово-
говорить о любом векторном поле и о его потенциале.
Итак, при рассмотрении векторного поля во всем пространстве
требования, чтобы это поле было потенциальным, безвихревым или
бесциркуляционным, полностью равносильны, так что из выполнения
одного этого требования вытекает выполнение остальных. Из фор-
формулы E5) в силу произвольности точки Мо еще раз вытекает,
что потенциал определен с точностью до постоянного слагаемого.
*) Если поле рассматривается не во всем пространстве, а в некоторой его
части, то в этом пункте могут быть осложнения, которые будут освещены в § 13.

384 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
Если векторное поле А яв.мяется не только безвихревым, но и
не имеет источников векторных линий (см. § Х.7), т. е. если
rot Л = 0 и div А — 0,
го и;) ncpisoro следует, что А = — gradcp, а пз второго — что
divgradcp = — div А ~ 0, т.е. у'2'р = 0.
Таким образом, в этом случае потенциал ноля должен удовлетворят:,
уравнению Лапласа (которое уже встречалось нам в § Х.9) или,
как выражают это другими словами, быть гармонической функцией.
Если у безвихревого поля, рассматриваемого во всем простран-
пространстве, нет'источников не только на конечном расстоянии, но и на
бесконечности, то вектор такого поля просто тождественно равен
пулю, т. е., но существу, поля нет. Этому соответствует следующю
свойство гармонических функции: функция, гармоническая во всеч
пространстве п равная нулю на бесконечности, тождественно равна
нулю. Можно доказать (мы не будем этого делать) более общий
факт: функция, гармоническая во всем пространстве и ограниченная
на бесконечности, тождественно равна постоянной, т. е. такому
потенциалу также отвечает нулевое поле. Таким образом, чтобы
теория стала содержательной, нужно либо допустить источники поля
на бесконечности, т. е. неограниченность потенциала на бесконеч-
бесконечности, либо допустить источники на конечном расстоянии, т. е. считать
потенциал гармоническим не во всем пространстве. Например, полю
А = const отвечает потенциал ср = — А-т (проверьте!), неограничен-
неограниченный на бесконечности, а ньютонову полю (§ Х.З) отвечает потен-
потенциал, гармонический всюду, кроме одной точки4').
Вернемся к рассмотрению силового поля F, а буквой А будем,
как и в § Х.З, обозначать работу. Эта сила может обладать потен-
потенциалом, но может и не соответствовать никакому потенциалу. Пг-
следнее можно выяснить двумя " способами: либо проверить, что
rot Z7^= 0, т. е. что хотя бы одно пз условий
dFz dFv dFx uFz dFy dFx
dy ~~ dz ' dz ~ дх ' дх ~~~ dy
(см. условия E4)) не выполнено, либо же проверить, что поле
не является бесциркуляционным, т. е. что хотя бы для одного зам-
замкнутого контура работа силы F отлична от нуля.
Рассмотрим пример. Пусть сила F лежит в плоскости х, у,
т. е. образует плоское поле, и в каждой точке перпендикулярна
прямой, соединяющей эту точку с началом координат (перпендику-
(перпендикулярна радиусу-вектору), причем направлена против стрелки часов.
*) Б этой точке Дф бесконечен, пропорционален дельта-функции, так что
sr-тя течка «мала» по сравнению с бесконечным объемом, забывать об этой
ТОЧКС hWlliJil.

§ 9]
ПОТЕНЦИАЛЬНЫЕ ПОЛЯ
385
Пусть при этом величина силы пропорциональна расстоянию г от
точки до начала координат, т. е. \F\ = ar, где а — постоянный ко-
коэффициент пропорциональности. (Для нескольких точек плоскости та-
такая сила изображена на рис. 154.) Пусть под действием такой силы
тело движется по окружности
Ук радиуса R (рис. 155). Весьма
* малый путь от точки М до
\ч точки N (он соответствует
/ Г
Рис. 154.
Рнс. 155.
повороту на угол d<$) можно приближенно считать прямолинейным.
Он равен Rd<p, как длина дуги окружности, соответствующая
центральному углу d(p. Сила направлена вдоль пути, поэтому работа
на участке MN есть
dA = R dtp • | F | = R d(p ■ aR = aR2 dq>.
Следовательно, работа при обходе точкой всей окружности есть
2я 2л
А = J aR2d(p = aR2 Л d(p = я/?2 • 2а.
о о
Работа пропорциональна площади круга и отнюдь не равна нулю.
(Можно доказать, что для рассматриваемой силы работа, совершен-
совершенная при обходе замкнутой линии, пропорциональна площади,
ограниченной линией движения, при любой форме этой линии.)
Ясно, что такая сила не может соответствовать никакому по-
потенциалу.
Последний вывод можно сделать и с помощью формального под-
подсчета ротора. Так как поле сил получается в данном примере таким
же, как поле линейных скоростей при вращении вокруг сен z с уг-
угловой скоростью а, то можно воспользоваться формулой E), что даст
F=(ak)xr =
i
0
X
j
0
У
k
а
0
= — ayi -f axj
E6)
13 Я. Б. Зельдович, А. Д. Мышкно

386
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
(это легко получить и непосредственно из рис. 154). Отсюда
i j k
v дх ду дг
— ау ах О
Итак, ротор не равен нулю, и потому поле не потенциальное.
Упражнение
Докажите, что поле
потенциальное, и постройте его потенциал.
§ 10. Ротор поля скорости
Понятие ротора особенно наглядно при рассмотрении поля ли-
линейных скоростей v частиц сплошной среды. Рассмотрим несколько
примеров.
Пусть среда движется поступательно, как твердое тело. Тогда
<о = const, и так как ротор выражается с помощью операций диффе-
дифференцирования, то rotp = 0. В данном случае циркуляция скорости
отсутствует.
Пусть среда вращается вокруг некоторой оси с угловой ско-
скоростью со, как твердое тело. Воспользуемся тем, что ротор связан
с полем инвариантно и, стало быть, при его вычислении мы можем
располагать оси координат по своему усмотрению, как нам удобнее;
поэтому направим ось z по оси вращения. Тогда вычисления, ана-
аналогичные проведенным в конце § 9, дают
v = — ayi -f- «л:,/,
rot г» = 2toft = 2со.
Итак, в данном случае ротор постоянный во всем пространстве
и равен удвоенному вектору угловой скорости. Поэтому циркуляции
линейной скорости по малому контуру максимальна, если этот контур
расположен перпендикулярно оси вращения (тогда ротор проекти-
проектируется на нормаль к соответствующей малой площадке своей полной
длиной), а если плоскость контура параллельна оси вращения, то
циркуляция равна нулю.
Можно доказать, что любое движенце твердого тела в каждый
момент времени получается в результате наложения поступательного
и вращательного движений. В силу двух предыдущих абзацев ротор
линейной скорости твердого тела в каждый момент времени одинаков
во всех точках тела и равен удвоенному мгновенному вектору угловой
скорости.

РОТОР ПОЛЯ СКОРОСТИ
387
Перейдем к движению среды, при которых расстояния между ее
точками изменяются. Пусть рассматривается «чистое» сжатие газа
поршнем вдоль оси х к плоскости х — 0; тогда поле скоростей
имеет вид
v= — %xi,
где % — коэффициент пропорциональности. Подсчитывая ротор, по-
получаем
rot
I
д
дх
— Хх
J
д
ду
0
k
д
dz
0
= 0.
о
Коши доказал, что любое движение малого объема деформи-
деформируемой сплошной среды (газа, жидкости или деформируемого твер-
твердого тела) в любой момент времени получается в результате нало-
наложения поступательного и вращательного движений, а также «чистых»
сжатий и растяжений. (Отметим, что и малые порции несжимаемой
жидкости могут испытывать одно-
одновременно «чистые» сжатия и рас-
растяжения по различным направле-
направлениям.) Так как ненулевой ротор
получается лишь для вращательно-
вращательного движения, то мы видим, что при
произвольном движении среды ротор
поля линейной скорости v частиц
равен в каждой точке удвоенному
вектору угловой скорости соответ-
соответствующей частицы. Конечно, в об-
общем случае ротор получается в
различных точках различным. Таким
образом, при течении жидкости или газа отличие ротора поля ли-
линейной скорости от нуля указывает на наличие завихренности, вра-
вращения, чем и объясняется название ротор.
Рассмотрим в качестве следующего примера «сдвиговое» течение,
изображенное стрелками на рис. 156. Такая картина получается при
течении вязкой жидкости вдоль твердой стенки. В этом случае
V — ayi, где а — коэффициент пропорциональности, откуда rot v = — ak
(проверьте!). Итак, это течение завихренное, каждая частица жид-
жидкости вращается с угловой скоростью а/2 по часовой стрелке.
Рассмотрим, наконец, простейшую «вихревую линию», т. е.
плоскопараллельное поле, определенное в плоскости х, у ра-
равенством
W///M////////////////////////////'*
Рис. 156.
13*

388
ВЕКТОГНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
Это поле, показанное иа рис. 157, несколько напоминает ноле
рис. 154, но в данном случае модуль вектора поля не прямо про-
пропорционален, а обратно пропорционален расстоянию от начала
координат. Осью вихревой линии в данном случае служит ось z.
Подобно E6), найдем выражение скорости в координатной форме:
•0=
РУ
px
а:
Ркс. 157.
откуда легко с помощью непосред-
непосредственного вычисления подсчитать,
что вне оси z будет rotf = 0 (про-
(проверьте!). Таким образом, част::цы
жидкости обходят вихревую линию,
деформируясь, но не совершая вра-
вращательного движения относительно
собственной оси. В то же время,
так как циркуляция вектора v по
любой окружности с центром в на-
начале координат равна
^ ■ 2пг =
то в начале координат имеется «источник циркуляции», плотность
которого на плоскости х, у равна
-gr = 2прЬ (г)
(где б — дельта-функция *), см. § VI.3). Так как ротор плоскопарал-
плоскопараллельного поля перпендикулярен плоскости поля, то мы получаем
в данном примере
rot v = 2л/;б (xi +yj) k = 2прд (х) б (у) k E8)
(по поводу последнего представления см. § VI.3).
Упражнение
Найдите направления в частице вихревой линии, остающиеся инвариантны-
инвариантными при бесконечно малом перемещении.
Указание. Исходите из того, что вектор dr не должен повернуться.
§ 11. Магнитное поле и электрический ток
Понятия векторного произведения и ротора широко применяются
при рассмотрении магнитных полей. Мы ограничимся для простоты
рассмотрением полей в вакууме.
*) В данном случае имеется в виду двумерная дельта-функция: б (г) =
= б (х) б (у), поскольку интегрирование ведется по плоскости, Г= \ rot AdS.

R И] МАГНИТНОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК 389
Магнитное поле в каждой точке пространства полностью харак-
характеризуется вектором Н «напряженности магнитного поля». Этот
вектор во многом аналогичен вектору Е напряженности электри-
электрического поля (§§ Х.5 и Х.9), но проявляется своим действием не
на неподвижные заряды, как Е, а на постоянные магниты или (что,
как мы сейчас увидим, равносильно) на движущиеся заряды. Созда-
Создается магнитное поле также постоянными магнитами или движущи-
движущимися зарядами.
Рассмотрим сначала самую простую схему. Пусть магнитное поле
создается током J, текущим вдоль бесконечно длинного (практи-
(практически весьма длинного) прямолинейного
проводника, который мы предположим '
совпадающим с осью z. Ясно, что при этом
получается плоскопараллельное поле, ко-
которое достаточно, таким образом, рас-
рассматривать только в плоскости х, у. Из
эксперимента известно, что при этом век-
вектор Н получается, как на рис. 158: он "
лежит в плоскости х, у и перпендику-
перпендикулярен радиусу-вектору г, причем направ-
направление Н определяется по правилу право- х
ко винта. Величина напряженности прямо
пропорциональна силе тока и обратно Рис. 158.
пропорциональна расстоянию точки от
проводника, т. е. Н—а —, где а — некоторый коэффициент про-
пропорциональности; при определенном выборе единиц Я и У он оказы-
вается равным 2/с, где с — скорость света, так что // = —-.
Рассматриваемое нами поле И имеет в томности вид, изобра-
изображенный на рис. 157, т. е. имеет формулу E7), где взамен р надо
1J
поставить . Отсюда по формуле E8)
С другой стороны, произведение Уб (дг) б (у) k представляет собой
плотность тока, показанного на рис. 158. Мы будем плотность тока
обозначать через j (не путать с единичным вектором оси у\)\ таким
образом, в данном примере
rot H=^J. E9)
По этой формуле j выражается через Н. Можно получить и об-
обратную формулу, по которой И выражается через j. Для этого
введем «векторный потенциал» А поля И, аналогичный скалярному

390
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[гл.
XI
потенциалу электрического поля (см. § Х.5),
F0)
В рассматриваемом примере этот потенциал равен
со со
Jkd'C,
= = - f =
\i С \ Yvl.
I и г л
■ft.
Хотя последний интеграл расходится, но мы можем его дифферен-
дифференцировать по параметрам (ср. § Х.6); отсюда, в частности,
I j k
JL i. A
дх ду дг
j p
._д_
J_( д_ С d
Этот интеграл легко взять с помощью подстановки £—2 =
= у х1 -j-_y2 tg s, и мы получаем (проверьте!)
2J
Мы опять пришли к формуле E7) ч р — —, т. е. к Н:
tf=rot Л =
rot
Г ./(Гр)
J |r-ro|
(Gl)
При рассмотрении системы бесконечных прямолинейных провод-
проводников их магнитные поля И, а также плотности токов складываются,
т. е. формулы E9) и F1) все равно остаются справедливыми. Мы
примем, что они справедливы и при любом стационарном, не обяза-
обязательно прямолинейном распределении токов в пространстве. (Для
формулы E9) это довольно ясно, так как она связывает значения
И я J в одной и той же точке, а формулу F1) можно вывести
из E9), на чем мы не будем останавливаться.) Это допущение обосно-
обосновывается тем, что получающиеся из него следствия согласуются
друг с другом и подтверждаются экспериментами.
Из формулы E9) вытекает важное следствие. Для его получения
применим к вычислению циркуляции вектора //по любому замкнутому

§ 11] МАГНИТНОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК 391
контуру "(I), ограничивающему поверхность (а), формулу Стокса:
-dr = ^ (rot //)„ da = f j jn da. F2)
Интеграл в правой части имеет простой физический смысл (ср. § Х.4):
это количество электричества, проходящее через (а) за единицу
времени с внутренней стороны к наружной, т. е. полный ток J
-через (а). Таким образом, циркуляция вектора И по любому замкну-
замкнутому контуру пропорциональна полному току через поверхность,
ограничиваемую этим контуром.
Другое важное следствие получится, если взять дивергенцию
обеих частей формулы E9). Мы получим
divy'=x- div rot Я= О
(см.E1)). Этот «закон сохранения электричества» в стационарном
случае можно было вывести независимо от формулы E9): он означает,
что в любой объем за единицу времени втекает столько же электри-
электричества, сколько вытекает, т. е. полный поток вектора j через лю-
любую замкнутую поверхность равен пулю (ср. аналогичные рассужде-
рассуждения в § Х.8).
Если взять дивергенцию обеих частей равенства F1), то мы
увидим, что
div И= div rot A = 0. F3)
Таким образом (см. § Х.7), магнитное поле в отличие от электри-
электрического не имеет источников векторных линий, т. е. магнитные
силовые линии не могут ни начинаться, ни заканчиваться. (Так как
при этом мы опирались только на формулу E1), то и в общем случае
векторное поле может быть ротором некоторого «векторного потен-
потенциала», только если дивергенция этого поля равна нулю, т. е. оно
не имеет источников векторных линий; такие поля принято называть
соленоидальными.)
Вычислим в качестве примера магнитное поле от бесконечной
цилиндрической катушки с обмоткой в п витков на единицу длины,
по которой течет ток J. Толщиной обмотки будем пренебрегать
(в дальнейшем мы увидим, что она несущественна) и будем для
простоты считать обмотку не винтовой, а кольцевой. Из формулы F0)
мы видим, что в данном примере векторный потенциал А параллелен
плоскости витков и по смыслу задачи образует плоскопараллельное
поле. Но тогда из формулы F1) и определения D3) ротора сразу
следует, что поле Н всюду параллельно оси катушки и не меняется
вдоль катушки, т. е. также является плоскопараллельиым. Применим
теперь формулу F2) к прямоугольному контуру ABCD, показанному
на рис. 159. Так как интегралы ио отрезкам ВС и DA равны нулю

392
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ.
XI
и так как через поверхность, ограниченную этим контуром, ток по
проходит, то получаем
Aг—высота прямоугольника), откуда НХ = Н^. Итак, магнитное поле
внутри соленоида (катушки) постоянно не только по высоте, но и и
поперечном сечении. Аналогично получаем, что поле и вне катуш^-ц
постоянно, а так как в бесконечном удалении от катушки оно равно
нулю, то оно равно нулю всюду вне катушки. Применив в заключе-
заключение формулу F2) к прямоугольному контуру EKGh\
— — Jnh,
С
мы получим t!h — — Jnli, откуда находим папря-
С
женность магнитного поля внутри катушки
Мы видим, что она не зависит от радиуса ка-
катушки, а только от числа «ампервитков» на еди-
единицу длины. Отсюда, в частности, вытекает упо-
упомянутая ранее независимость поля от толщины
обмотки. Предоставляем читателю получить выра-
жение для потенциала А = у геч (/"<г0), А~
где r — xi-\-yj, r — \r\, еф = ft x г, /■„ —радиус
~ 2л "'
катушки.
К задаче о построении магнитного поля от заданной системы
токов возможен иной подход. Именно, допускается, что магнитно-
голе в любой точке М создается каждым «элементом тока» dJ — jdii
и соответствии с законом Био — Савара
где Мо — точка, в которой расположен элемент тока. Полный вектор И
в точке М находится с помощью интегрирования по всем элементам
тока. То, что формула для dH пишется именно в таком виде, обосно-
обосновывается согласованностью следствий из этой формулы с экспери-
экспериментом. Этот подход полностью равносилен разобранному нами выше,
из закона Био — Савара можно вывести формулы E9) и F1), и
обратно.
Упражнение
Получите из закона Био — Савара напряженность магнитного поля: a) oi
прямолинейного бесконечно длинного проводника; б) на оси соленоида ог
одного его витка.
§ 12. Электромагнитное поле и уравнения Максвелла
На самом деле в общем случае в одной и той же области про-
пространства существуют и электрическое и магнитное поля; при этом
получается электромагнитное поле, которое в каждой точке про-

§ 12]
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ И УРАВНЕНИЯ МАКСВЕЛЛА
393
странства (во всяком случае, в вакууме, что мы будем предполагать)
характеризуется двумя векторами: электрическим Е и магнитным
//. Дифференциальные уравнения, связывающие эти векторы, назы-
называются уравнениями Максвелла и имеют очень большое значение в
физике.
Для стационарного электромагнитного поля соответствующие
уравнения были, по существу, уже нами выписаны. Это прежде
всего уравнения
rot£=0, div£
из которых первое вытекает из потенциальности стационарного
электрического поля (§§ Х.5 и XI.9), а второе — это уравнение (Х.42).
Кроме того, это уравнения
rot H = ~J, divtf=0
(см. E9) и F3)).
Для стационарного случая взаимосвязь электрического и магнит-
магнитного полей еще не сказывается. Не то будет в нестационарном
случае, к которому мы сейчас пере-
переходим. Оказывается, что всякое изме-
изменение электрического поля влияет на
магнитное поле, а всякое изменение
магнитного поля воздействует на элект-
электрическое поле, так что эти поля рас-
рассматривать порознь уже нельзя.
При рассмотрении первого воздей-
воздействия чрезвычайно полезно представле-
представление о «токах смещения». Для вывода
соответствующих формул рассмотрим
сначала конденсатор (рис. 160), об-
обкладки которого заряжены с поверхно-
поверхностной плотностью -j~v левая и —v правая. Каждая из этих обкладок
порождает в пространстве между ними электрическое поле, которое
можно подсчитать по формулам (Х.29), так что суммарное поле
£ = 4яу/. F4)
Если v увеличивается, то к левой обкладке подходят извне поло-
жительные заряды и оседают на ней со скоростью У= —^^ , где
5 — площадь одной обкладки, а на правой обкладке оседают отри-
отрицательные заряды с той же скоростью. Если на минуту представить
себе, что точки А и В соединены проводником, на котором заряды
не оседают, то в силу закона сохранения электричества через любое
сечение между А и В должен проходить один и тот же ток J.
На самом же деле заряды между обкладками конденсатора не пере-
переносятся; однако закон постоянства токов можно сохранить, если
■ввести понятие тока смещения силы J, который «как будто» течет
|и
"f
4.
*
> ->
>
~ E
■z-°5
—
Рис. 160.

394 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [ГЛ. XI
от А к В. Плотность этого тока смещения в силу формулы F4) равна
Лм — s * — dt l — 4я at g
Оказывается, что и в формулах, связывающих магнитный вектор Н
с током J, изменение электрического поля нужно заменить током
смещения, плотность которого вычисляется но той же формуле,
1 Л/**
/=__-__ Поэтому для нестационарного'электрического поля вза-
4л ut
мен E9) надо написать уравнение
... 4я ..... 4я . . 1 дЕ „
rotH=-T(J+JcJ=TJ + TW. F5)
Подобным образом, и в формуле F1) для построения Н взамен j
надо поставить j + усм. Но отсюда, рассуждая, как в § 11, мы можем
вывести соотношение
div#=0 F6)
(см. F3)).
Обратимся к переменному магнитному нолю. Опыт показывает
(Фарадей), что изменение магнитного поля возбуждает (индуцирует)
электрическое поле, которое в отличие от ноля, порожденного
зарядами, является вихревым. Мы сейчас покажем, что соответст-
соответствующий закон индукции имеет вид
rot£=-lf. F7)
В силу § 9 в этом случае электрическое поле не имеет потенциала,
т. е. нельзя говорить о разности потенциалов в поле, а работа,
совершаемая полем, зависит не только от начала и конца пути, но
и от всей трассы.
Для вывода формулы F7) поместим мысленно в поле замкнутый
проводник (Z.), ограничивающий поверхность (а). Согласно результатам
опытов Фарадея изменение магнитного потока \ H-da влечет за
(о)
собой появление ЭДС в контуре (Z.), пропорциональной скорости
изменения потока. Однако указанная ЭДС равна сумме элементарных
ЭДС в малых участках контура, а эти малые ЭДС, как легко понять,
равны Е-dr. Итак,
{L) {о) (а)
здесь знак минус взят по правилу Ленца, согласно которому возни-
возникающая ЭДС стремится воспрепятствовать изменению потока; k —
коэффициент пропорциональности, который, как можно показать,
равен — ; дифференцирование но t внесено под знак интеграла как

§ 12J- ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ И УРАВНЕНИЯ МАКСВКЛЛА 39 О
дифференцирование по параметру (§ III.6). Преобразуя левую часть
по формуле Стокса, получим
\ rot£.aa= \ -^-aa.
(oi (a)
Отсюда п силу произвольности (а) и вытекает F7).
Случай силы, не соответствующей потенциалу, осуществляется
в трансформаторе. Первичная обмотка, когда по ней течет ток, соз-
создает магнитное поле. Если ток в первичной обмотке с течением
времени изменяется, то создается переменное магнитное поле, кото-
которое сопровождается появлением электрического поля как раз такого
типа (так называемое вихревое поле), как показано на рис. 154.
Значит сила, действующая на заряженное тело, например на электрон,
находящийся внутри вторичной обмотки, не соответствует никакому
потенциалу.
Двигаясь по кругу, электрон может набирать все большую
и большую энергию. Это, конечно, не означает нарушения закона
сохранения энергии, так как ускоренное движение электрона в свою
очередь влияет на первичную обмотку, вызывая дополнительный
расход энергии в питающих ее источниках тока. Но для отдельного
электрона закон «сумма кинетической и потенциальной энергии элек-
электрона постоянна» не выполняется, так как сила, действующая на
электрон, не соответствует никакой потенциальной энергии. Такой
принцип ускорения электронов успешно применяется в машине, на-
называемой бетатроном. При этом электрическое поле ускоряет элек-
электроны, а магнитное поле надлежащим образом искривляет их путь,
обеспечивая движение по окружности.
Так как вихревое электрическое поле появляется только в про-
процессе изменения магнитного поля, то такое электрическое поле не бу-
будет постоянным в течение длительного времени: когда магнитное поле
достигнет максимума, скорость его изменения станет равной нулю,
после чего электрическое поле также исчезнет.
Вследствие малой длительности электрического поля в бетатроне
тяжелые частицы, например протоны, не успевают набирать большую
энергию. Хорошо набирают энергию легкие электроны. Существуют
бетатроны, в которых электроны набирают энергию в десятки мил-
миллионов электрон-вольт, т. е. такую же, как если бы они прошли
разность потенциалов в десятки миллионов вольт. Быстрые электроны,
испускаемые при радиоактивных превращениях, были названы бета-
лучами в начале исследования радиоактивности, когда физическая
природа этих лучей еще не была ясна. Отсюда и происходит назва-
название «бетатрон» для прибора, в котором быстрые электроны полу-
получаются путем ускорения медленных, без участия явления радиоак-
радиоактивности.
Уравнение
div E — 4л.р, @8)

306 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [гл. XI
связывающее электрическое поле и заряды (см. (Х.42)), сохраняет
силу и в нестационарном случае. Все четыре указанных уравнения
F5)—F8) и образуют систему уравнений Максвелла. К ним можно
добавить уравнение неразрывности
±
F9)
которое выводится в точности как аналогичное уравнение (Х.4Г,1
в гидродинамике, а также то или иное соотношение, связывающее
у с £ (обобщенный закон Ома, имеющий в простейших случаях вид
]=кЕ, где \ — коэффициент электропроводности) и включающее а
себя в общем случае действие внешних сил.
Упражнение
Выведите уравнение F9) из уравнений F5) и F8).
§ 13. Потенциал в многосвязиой области
Рассмотрим поле силы F. Из обоих условий существования по-
потенциала— условия rot /*■= 0 (§ 9) и условия равенства нулю работы
при обходе замкнутой линии (§ Х.З) — видно, что возможность на-
нарушения этих условий, т. е. возможность существования сил непо-
непотенциального типа, связана с рассмотрением функции не одной,
а двух или трех переменных. В самом деле, в случае одной пере-
переменной (движение по прямой) вернуться в точку, из которой вышел,
можно лишь при таком движении, когда каждый отрезок пути про-
проходится дважды: один раз в одном направлении, другой раз — в про-
противоположном. Поэтому (если только сила не зависит от времени
или от скорости движения, а зависит только о г положения тела) при
движении вдоль одной прямой работа силы равна нулю, если
только путь заканчивается возвращением в исходную точку.
При произвольном движении на плоскости или в пространстве
можно, выйдя из начальной точки, пройти по некоторой линии в
конечную точку, а затем вернуться в начальную точку по совер-
совершенно другой линии. При этом может оказаться, что работа i;e
равна нулю. В этом и заключается различие между движением по
одной прямой, когда любой силе F (х) соответствует потенциальная
энергия U(x), и движением в плоскости или в пространстве, когд;!
потенциальной энергии может вовсе и не быть.
Рассмотрим теперь движение тела на плоскости или в простран-
пространстве. Если заставить тело двигаться только по одной определенной
и притом незамкнутой линии, то мы вернемся к тому же положению,
которое имеет место при движении вдоль прямой. Действительно,
в этом случае будем характеризовать положение тела на линии ве-
величиной пути, пройденного телом вдоль линии (путь отсчитываем

§
ПОТЕНЦИАЛ В ММ0Г0СВЯЗН0Й ОБЛАСТИ
397
Рис
е. поле F должно
от какой-нибудь выбранной точки на линии). Тогда фактически мы
имеем дело с одной переменной — величиной пути вдоль линии.
Поэтому, рассматривая незамкнутую вторичную обмотку трансфор-
трансформатора, можно говорить о разности потенциалов (или лучше об
электродзижущей силе) на ее концах. Однако если внутри первичной
обмотки поместить замкнутое кольцо, то в нем нет определенной
разности потенциалов между двумя его точками А и В (рис. 161).
работа по перемещению заряда из точки А в
точку В зависит от того, вдоль какой линии,
ADB или АСВ, происходит движение.
Пусть теперь тело не обязано двигаться
вдоль фиксированной линии, а может сдви-
сдвигаться н в стороны. Тогда для существования
потенциала прежде всего требуется, чтобы
работа силы при перемещении тела по любому
бесконечно малому замкнутому контуру была
бы равна нулю. Это в силу § 7 равносильно
условию rotF=Q (так как такая работа равна
циркуляции вектора F по указанному контуру), т.
быть безвихревым.
Но пусть rot F=0 не во всем пространстве, а только в некоторой
его области (части) (G). Тогда работа по конечному замкнутому
контуру (L), лежащему в (G), не обязана рав-
равняться нулю! Можно только утверждать, что при
бесконечно малой деформации замкнутого контура
работа не изменится, так как работа по контуру
ABXCDA (рис. 162) отличается от работы по кон-
контуру AB2CDA на работу по контуру ABtCBtA,
равную нулю. Совершая такие деформации, можно
получить контур, лежащий в (О) и существенно
отличающийся от исходного, однако
F по этим контурам одинакова.
Отсюда ясно, что если контур
пределах (G) путем непрерывной деформации
«стянуть в точку», то работа силы по (L) равна нулю. В самом деле,
после такого стягивания работа уже, очевидно, равна нулю (так
как перемещение отсутствует). По так как при деформации контура
работа не меняется, то она равнялась нулю и для исходного контура.
Область (G) может обладать свойством односвязности: это значит,
что в ней можно любой замкнутый контур путем непрерывной де-
деформации стянуть в точку, не касаясь границ области. Например,
внутренность кругового цилиндра, внутренность или внешность
сферы — это односвязные области; все пространство или вся плоскость
также причисляются к односвязным областям. В отличие от этого
внешность бесконечного кругового цилиндра, внутренность или
внешность «тора» (поверхности бублика)—это неодносвязные области.
Рис. 162.
работа силы
(Z.) можно в

398
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ
[ГЛ. XI
(D
Если область (G) односвязная, то из сказанного выше вытекает,
что в этом случае работа силы по конечному замкнутому контуру;
лежащему в (G), обязательно равна нулю. Если отвлечься от кон-
конкретного физического истолкования поля, то можно сделать следую-
следующий общий математический вывод (ср. § 9): в односвязной области
безвихревое поле обязательно является потенциальным, т. е. бес-
бесциркуляционным,,
В отличие от этого, если область неодпосвязная, то циркуляция
безвихревого поля 1\:ожет быть отличной от нуля (если рассматри-
рассматриваемый контур нельзя путем непре-
непрерывной деформации стянуть в точку,
оставаясь в пределах области), т, е,
безвихревое поле может быть цир-
циркуляционным. Такими будут, на-
например, магнитное поле внутри
торовидной катушки (с плоскостями
витков, проходящими через ось вра-
вращения), по которой проходит по-
постоянный ток; поле скоростей при
безвихревом течении жидкости, об-
обтекающей замкнутый канал, и т. д.
Если при этом строить потенциал
по формуле E5), то он получится неоднозначным: если обойти зам-
замкнутый контур, то из потенциала вычтется циркуляция поля по
этому контуру. Когда мы говорим о потенциальном поле, мы имеем
в виду только однозначный потенциал; таким образом, безвихревое
ноле в неодносвязной области не обязано быть потенциальным.
Большой интерес представляет торовидный трансформатор с же-
железным кольцевым сердечником. При пропускании через обмотку
переменного тока во внешней части пространства образуется без-
безвихревое электрическое поле, которое, однако, имеет отличную ос
нуля циркуляцию по контуру (L), зацепленному за тор (рис. 163).
Рис. 163.
"Упражнение
Докажите, что плоское поле, определенное формулой E7) вне окружности (Z.)
с центром в начале координат, является безвихревым. Что получится, если
строить потенциал этого поля по формуле E5)?
§
ОТВЕТЫ И РЕШЕНИЯ
1. АВ=— 2/+/ + 4ft; /4С = 3/ +5ft; АВхАС=
—2 1 4
0 3 5
=-7*+ 10/—6ft;

ОТВЕТЫ И РЕШЕНИЯ 399
2. Так как (аХЬ)-с =
2—10
3 0 2
= 9>0, то тройка правая.
-1 -1 1
3. («XI) ХУ=0, i X (« X j)=—j, т. е. (i X i)Xj Ф1Х (i X j).
§2
Если 1) ft = 0, или 2) b приложен к точке О, или 3) b направлен точно
на О или от О, так что прямая, на которой лежит вектор Ь, проходит через О
При этом третий случай охватывает первые два.
§3
1. Г= \ dt = \ ; подстановка — из уравнения A5) приводит к ин-
тегралу Т = 2 I 1/ -=-'(£-| - - dr; вычисление при —;
' г ^ Y Г 2. ttXT'" J
mln
дает T = nk 1/ —оТ^з ■ Большая полуось эллипса а равна -^- ( —!- hr-^—).
k 2л
или, после преобразований, — —. При k = xmM получаем, что Г= а*/г;
вто формулировка третьего закона Кеплера в общем случае.
2. Применение формулы A7) дает в качестве периода изменения радиуса
max
,/-=— ('/„£„ G2 \-/i, _ / ra
значение V 2m \ £ л2—^ ? dr = ni/ —-. Различие ооъ-
J V 2 2га/-3 J V k
rmin
ясняется тем, что в рассматриваемом виде движения период изменения радиуса
г (t) в два раза меньше периода обращения частицы.
§4
а) Переходя к полярным координатам (а, ф) (см. конец § IV.7), получим
h in
R
)u = \ dz \ dtp \ ра% da = 2лр -j- h =
ооо
ооо
б) Обозначим через \ линейную плотность стержня; тогда
L/1
1 V mV-
12 '
о
Эти два результата, между прочим, дают возможность более точно проанали-
проанализировать вращение танцовщицы.
§5
1. В двумерном случае, если базис е\ получгн из базиса е,- поворотом на
угол ф, то an = a.22 = cos ф, а12 = — а21 = sin ф. Если тензор р-^ симметриче-
симметрический, то
Pia = alfea2,pft, = (p2, — pn) sin ср cos ф + р12 (cos2 ф —sin2 ф) =
= ~2 (Рм — Ри) sin 2ф + р1гсоз 2ф.
Выбирая tg 2ф = 2р12/(лп —р22), получим Pl; = O, чго и требуется,

4 00 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ И ВРАЩЕНИЕ [Гл.
XI
2. Здесь Ti12 = fe (малое), прочие т)^ = 0; поэтому pla = psl = Y12=—V2i=*/2,
прочие p,-y=Yi7 = 0- Применяя решение задачи 1, получаем, что тензору р;.
, , k
отвечает растяжение вдоль прямом жг = л:2 в ' +~?т Раз и сжатие вдоль пря-
мои *!=—*а в 1—=- раз; тензору ум в силу решения третьего упражнения
§ IX.5 отвечает поворот на угол а=—у, Всю картину можно рассматри-
рассматривать как плоскую (в плоскости xv дс2) либо как плоскопараллельную.
§6
1. Да.
2. Основная формула: [еи е2, е3] = е4. Из нее вытекают три другие фор-
формулы с помощью круговых перестановок. При перестановке двух множителем
результат множится на —1. Формула для произведения трех любых вектогог.
аналогична C), но определитель в ней имеет четвертый порядок. (Можно про-
проверить, что векторное произведение перпендикулярно всем перемножаемы-.!
векторам, по модулю равно объему построенного на них параллелепипед,!
и образует с ними четверку «того же смысла», что четверка ег, е2, е3, t, ';
£ AxdS (f) AxdS
=_ lim
= m ^.
dQ (дп) -»м AQ
2. £ f(z)dz = £ (u + iv) (dx + i dy) = £ (udx—vdy)-^
(L) (L) (L)
-\-i Ф (v dx-y-u dy). Если рассмотреть поле A = ui—vj, то интеграл
(и 6.x — v dy) равен циркуляции этого поля но (L), и потому по формуле
U)
Стокса ф (u dx—vdy)= \ rot A-dS. Но А — Ах(х, y)i-\-Ay(x, y)j, т. е. по
(Ц (S)
формуле D3)
(дАу ЗАЛ ( dv ди\
rot А=[ -~ j— I k=[ -3 -г- I ft = 0,
\ дх ду / \ ах ду /
в силу второй формулы (V. 17). Значит, последний интеграл равен нулю.
Аналогично исследуется интеграл m (v dx-\-u dy).
(i.)
§8
1. urot Л + grad uxA; B-rol A — A-rotB.
2. v = (dQ)~l £ -da.
rot A =
(do)
i J k
= 0. Применяя формулу E5), выберем Afo = @; 0; 0).
дх ду dz
2xz у2 х2
а путь ММ0 — состоящим из отрезков, соединяющих точки (х; у; г) с @; у; :),

ОТВЕТЫ И РЕШЕНИЯ 401
@; у, г) с @; 0; г) и @; 0; г) с @; 0; 0). Отсюда
0 0 0
х, у, г)=
х=о
dz=—x2z — ~,
3
Так как за время dt вектор dr переидет в вектор dr + dvdt, то условие
инвариантности направления dr имеет вид dv\\dr. Так как v = (pk)X—2,
то dv = {pit)X f — — r J и из dv\\dr получаем —^ j—f\_dr, т. е.
(г4 dr—2 (r-dr) r) ■ dr = 0. Поэтому Н (drK — 2 (г-drJ = 0, cos (rTdr)=
-=± —тг-. т. е. dr должен с г образовывать угол ± 45°.
§ 11
а) Пусть ток 1 течет по оси г, и мы подсчитываем вектор Н в точке
плоскости хОу с радиусом-вектором г. Тогда
<М- ,.. .'„(■/ dtkx(r-W) =—-^
л/2
-л/2
(здесь мы положили £ = rtgs). Мы пришли к уже рассмотренному закону,
б) Пусть ток ./ течет по окружности радиуса R с центром в начале коор-
координат, расположенной в плоскости хОу, и мы подсчитываем напряженность
в точке @; 0; г). Тогда, представив окружность в параметрическом виде
* = .ftcostp, y = /?sincp, получим
2Л
j
(( —«sin ф£+^ cos фу)йф (zk — R cos q> / — R sin <fj)) =
о
2л
Отсюда, между прочим, легко вывести формулу для магнитного поля от бес-
бесконечного соленоида.
§ «2
Надо взять дивергенцию от обеих частей равенсхва F5).
§ 13
Равенство roti) = 0 проверяется по формуле D3). Так как левая часть E7)
равна grad(parctg {у/х)), то по формуле E5) получаем ф (х, у) =
= —parctg (y/x) ^-const.STOT «потенциал» многозначен, при обходе окружно-
окружности (L) он получает приращение — 2лр, т. е. исходное безвихревое поле не
является потенциальным.

ГЛАВА XII
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
В началах математического анализа (см., например, ВМ, § 1.6)
изучается вопрос об отыскании экстремумов функции одной пере-
переменной, а в § IV.6 мы рассмотрели вопрос о разыскании экстрему-
экстремумов для функции нескольких переменных, другими словами, для
задачи с конечным числом степеней свободы. Основная цель вариа-
вариационного исчисления — получить общие методы разыскания экстрему-
экстремумов для задач с бесконечным числом степеней свободы. В этой
главе нам понадобятся сведения из теории функций нескольких
переменных (в основном §§ IV.1 и 6).
§ 1. Пример перехода от конечного числа степеней
свободы к бесконечному
Рассмотрим натянутую между двумя неподвижными точками це-
цепочку из материальных частиц, последовательно связанных друг
с другом одинаковыми пружинками. Пусть на частицы дейстиу.'от
малые поперечные силы, вызываю-
вызывающие отклонение цепочки от непо-
непогруженного состояния равновесия
(рис. 164), причем для простоты
будем считать, что перемещения
частиц перпендикулярны линии нс-
нагруженного состояния, т. е. ^си
х. Найдем нагруженное состояние
равновесия, которое характеризует-
характеризуется отклонениями yv _y2, ..,, у„-\
частиц от оси л;.
Для этого определим потеншмль-
Рис. 164. ную энергию U цепочки в люл nl
(необязательно равновесном) откло-
отклоненном состоянии, отсчитывая U от ненагруженного, но уже натк-
наткнутого состояния цепочки. Эта энергия складывается из двух час;~-м:
У,
0
h
1
У,
h
F'
Уг
h
FB
1

с i] пример 403
первая представляет собой работу, затраченную на преодоление
упругости пружинок, а вторая — на преодоление внешних сил. Первая
пропорциональна удлинению Д/ цепочки
Uw = PM, B)
где Р—сила натяжения цепочки; мы будем считать, что эта сила
при отклонениях остается постоянной. Удлинение пружинки, соеди-
соединяющей частицы М; и М[+1, равно (см. рис. 164)
-hi
i l
2 К1 ~ 2/j
здесь мы воспользовались приближенной формулой ]/1 -f-cx= I -f--^ ее,
справедливой при малых |а|, т. е. в нашем случае мри малых
(-^£. В силу формулы B)
11 у
i
Еще проще находится
внешн 2
Таким образом, в силу A)
В положении равновесия потенциальная энергия должна иметь
«стационарное» значение, т. е. бесконечно малые изменения коор-
координат должны приводить к изменениям высшего порядка малости
в потенциальной энергии; другими словами, производные от потен-
потенциальной энергии по координатам в положении равновесия должны
равняться нулю. В самом деле, легко проверить, что производная
^— равна, с противоположным знаком, общей силе, действующей
на г-ю частицу; таким образом, отличие производной от нуля сви-
свидетельствовало бы о неско.миенснрованной силе, что невозможно при
равновесии. В устойчивом же положении равновесия потенциальная
энергия должна иметь минимум. Это необходимо для того, чтобы
сдвиг из положения равновесия порождал компенсирующую силу,
возвращающую систему в положение равновесия, другими словами,
чтобы для такого сдвига обязательно требовалось затратить поло-
положительную работу.

404 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [гл_ Х|1
Так как в правую часть C) координата у; нходчт в три чл::ца
21г 10% У'-х> тМЛ + i У0 J ,У„
то
и условие стационарности дает
р
-j- (У1 + 1— 2У1+У1-х) + F;=0 (i—\, 2, ..., п— 1). D)
Получается система из п—1 алгебраических уравнений норной
степени с п—1 неизвестными координатами ylt _y2, . ..,>*„_,. Отме-
Отметим, что при (=1 в уравнение D) входит у0, которое надо положить
равным нулю (это закрепленная точка), а при i = n—1 входит >.'„,
которое также надо положить равным нулю. Решив систему D),
найдем искомое положение равновесия.
Рассмотрим пример. Пусть все силы F(=F одинаковы. Перепишем
систему D) в виде
— - — — 4-
- _^1
~ ~ Р '
I — 2Уа+У*=— ¥•
Складывая первое и второе равенства, первое, второе и третье
и т. д., получим (проверьте!)
У*—У1 = —р- + У1'
о h'F ,
У»—У*=—2-р+У»
ohF ,
у*—у*= — 3-р+Ук
Перенеся в первом равенстве ух из левой части в правую, а затем
проведя ту же процедуру сложения, получим, применяя легко про-
проверяемое равенство 1 + 2 + .. . + k = —= ,
У
2-3/г/7
У* 2 Р

- jj пример 405
и общем виде
(i-l)ihF
Так как уп должно получиться равным нулю, то
(n-l)nhF , . (n—\)hF
— 2 -р- + /zyt = 0, откуда Л-—2fT—
Подставляя в E), находим окончательно
_ A-1I Af (n-l)/if _ i(n-i)hF ,
У/ 2 T+l 2Р ~' 2Р W
A=1, 2, ..., л—1);
формула верна и при г = 0 и при t — n.
Рассмотренная система определяется отклонениями п—1 ее ча-
частиц, т. е. имеет п—1 степеней свободы. Увеличивая п при задан-
заданной длине I цепочки, мы одновременно бесконечно увеличиваем число
степеней свободы, и в пределе получаем из цепочки непрерывную
струну, которая представляет собой систему с бесконечным числом
степеней свободы (так как при рассмотрении струны можно произ-
произвольно задавать отклонения как угодно большого числа ее" точек).
Итак, из дискретной, точечной системы частиц мы получаем в пределе
сплошную среду с непрерывно распределенной массой.
Посмотрим, как преобразуются в пределе выражение для потен-
потенциальной энергии и условие статического равновесия. Будем считать,
что внешняя поперечная сила распределена по струне с некоторой
плотностью /(х), так что на малую длину h струны приходится
сила f(x)h. Перепишем выражение C) для потенциальной энергии
в виде
При больших п, т. е. малых h, можно заменить ^-ii—— на у'{- и по-
потенциал принимает вид
так как h — kx. Но это — интегральная сумма, и в пределе при
h—► 0 она переходит в интеграл
LT=J [-^-(/)*-/(*) .у] d*. G)
Это и есть выражение для потенциальной энергии в случае не-
непрерывной струны. Таким образом, задачу об отыскании формы
равновесия натянутой нагруженной струны математически можно

406 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [гл.
XII
сформулировать так: найти функцию у (х) (описывающую форму
струны), удовлетворяющую условиям закрепления
и придающую интегралу G) минимально возможное значение. Так
как при выборе такой функции имеется бесконечное число степеней
свободы, то эта задача относится уже не к теории функций несколь-
нескольких переменных, а к вариационному исчислению.
Посмотрим теперь, во что в пределе перейдет условие D) ста-
статического равновесия, которое теперь надо переписать в виде
(9)
Для этого напомним (§ II.2), что отношение
к*
— так называемая вторая разделенная разность, — при малых h близко
к значению второй производной у". Таким образом, в пределе, при
h—>-0, из (9) мы получаем
РУ"+/(*) = 0, т. е. у'=—1./(х), A0)
и нам нужно найти решение у (х) этого уравнения, удовлетворяющее
условиям (8). Эта задача была нами решена в § VIII.8.
Итак,' вариационная задача о разыскании минимума интеграла
при условиях (8) свелась к решению дифференциального уравнения
A0) при тех же условиях. Подчеркнем, что при выводе уравнения A0)
мы, по существу, не пользовались тем, что разыскивается именно
минимум интеграла G), так как при выводе условий D) мы пользо-
пользовались только условием стационарности выражения C). Таким обра-
образом, уравнение A0)—это условие статического равновесия в рас-
рассматриваемой задаче. Однако легко проверить, что в данном примере
равновесие устойчивое, и тем самым потенциальная энергия G) при-
принимает для найденного решения не просто стационарное, но мини-
минимальное значение. В самом деле, из физических соображений ясно,
что какое-то положение струны, отвечающее минимуму потенциальной
энергии, имеется. Но в § VIII.8 мы видели, что уравнение A0) при
условиях (8) имеет лишь единственное решение. Значит, это реше-
решение и доставляет интегралу G) минимум.
Рассмотрим пример. Пусть f (x) =/0= const. Тогда уравнение A0)
легко интегрируется:
v' —.JjLyj г у ULz I г х А- С
У — р х т W> У— р 2 т uix 1 и2-

с i] пример 407
0з условий (8) получаем
(
откуда окончательно
1 = 0 С = — —
Р 2 ' р 9 9Р *
[Получите это же выражение из решения F) для дискретного слу-
случая, положив F = foh, n = -^, 1 = -^.\
Упомянем в заключение о более общем случае, когда на ча-
частицы Ж; (а в пределе на точки струны) действует ещё и упругая
сила, стремящаяся вернуть их в ненагруженное состояние равно-
равновесия, с коэффициентом упругости К (упругая подкладка). В этом
случае на преодоление упругости подкладки затрачивается работа
У1
и потому выражение для потенциальной энергии, взамен C), приоб-
приобретает вид
Условие стационарности, т. е. статического равновесия, дает
При переходе к непрерывной струне естественно ввести понятие
«линейной плотности коэффициента упругости» k, так что сила
упругости, приходящаяся на длину к струны, равна khy. Тогда
взамен G) и A0) мы получаем соотношения
0. A2)
Таким образом, решение вариационной задачи и здесь свелось
к решению краевой задачи для дифференциального уравнения.
Упражнение
Найдите решение системы D) при условиях (8) в общем случае. Получите
при п—>■ оо решение для сплошной струны.

408
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ.
XII
§ 2. Функционал
Следующая вариационная задача, возникшая в конце XVII века
и решенная Лейбницем, Лопиталем и Ньютоном независимо д:>уГ
от друга, показала силу создаваемого в то время математического
анализа.
Пусть материальная частица ■ М под действием силы тяжчч-щ
скатывается без трения с нулевой начальной скоростью от точки .4
до точки В но линии (L) (рис. 165); i ак
выбрать эту линию, чтобы падение про-
произошло в минимальное время? Для ана-
аналитической формулировки задачи обо-
обозначим неизвестное уравнение линии через
у=у{х)\ тогда функция у (х) прежде
всего должна удовлетворять условиям:
У(а)=Уа, УФ)=УЬ, A3)
Рис JQ5. гДе Уа и Уь — ординаты заданных точек
А к В. Скорость движения частицы М в
любой текущий момент легко определить, исходя из закона сохра-
сохранения энергии:
^-=mg(ya—y), откуда v = Vig{ya—y).
1
Горизонтальная составляющая скорости равна
dx dx ds dx dx ,
dx ds dx
4F~4sdl = V~ds~VY
Выражая отсюда dt и интегрируя, получим полное время падения
Ч-
■dx.
A4)
Таким образом, требуется изо всех функций, удовлетворяющих
условиям A3), выбрать такую, для которой интеграл A4) принимает
наименьшее возможное значение.
Разобранная задача, как и задачи, поставленные в § 1 дчи
непрерывной струны, являются типичными задачами вариационно! о
исчисления. Для таких задач характерны два обстоятельства.
Прежде всего это — задачи на экстремум (максимум или минимум),
т. е. задачи, в которых требуется придать экстремальное значение
некоторому числовому параметру (U в задачах § 1, Т в задаче о ли-
линии наибыстрейшего спуска). Задачи на экстремум мы уже решали,
причем для функций одной переменной искомым являлось некоторое
число, а именно значение независимой переменной, а для функций
нескольких переменных искомым являлся набор чисел. В отличие

§ 21 функционал 409
от этого в разобранных задачах этой главы искомой является не
число или набор чисел, а функция у (х), через все значения ко-
которой выражается указанный числовой параметр (по формулам G)
или A1) в § 1 и A4) в последней задаче).
Имеется много других задач на экстремум, в которых ищется
функция (геометрически — линия или поверхность) или набор функ-
функций. Все такие задачи и составляют предмет вариационного исчи-
исчисления.
На задачи вариационного нечисления можно взглянуть также со
следующей точки зрения. При подборе значения независимой перемен-
переменной имеется одна степень свободы. Если ищется набор п значений
таких переменных (как в гл. IV), то имеется п степеней свободы.
Если же произвольно меняется функциональная Зависимость, то
имеется бесконечное число степеней свободы: в самом деле, можно
произвольно задавать Значения функции для как угодно большого
числа значений независимой переменной. Значит, задачи вариацион-
вариационного исчисления—это задачи на экстремум для случая бесконеч-
бесконечного числа степеней свободы в выборе искомого объекта.
Итак, для задач вариационного исчисления характерна следую-
следующая схема. Имеется некоторый скалярный параметр / (это U в § 1
и Т в последней задаче), выражающийся по определенной формуле
(G), A1) или A4)) через неизвестную функцию у (х) (мы пока огра-
ограничимся функциями одного переменного), которую нужно подобрать.
Эта функция является более или менее произвольной, хотя и удо-
удовлетворяет тем или иным условиям: например, условиям (8) в § 1 и
A3) в задаче этого параграфа, а также требованию непрерывности.
Такой закон, согласно которому каждой функции из определен-
определенного класса функций соответствует значение некоторого скалярного
параметра, называется функционалом. Таким образом, основная
задача вариационного исчисления—это задача о нахождении экст-
экстремума заданного функционала.
Чтобы пояснить понятие функционала, вспомним еще раз поня-
понятие функции. Рассмотрим, например, формулу у=^х2. В силу этой
формулы каждому значению х отвечает некоторое значение у:
например, при х = 2 получается у — 4, при л; = г- получается
У~~к и т. д. Таким образом, мы имеем закон, согласно которому
числам х отвечают числа у. Формула у = х3 определяет другой
закон зависимости, т. е. другую функцию, формула _y = sin;e —
третью и т. д.
Простейшим примером функционала является определенный ин-
интеграл. Рассмотрим, например, формулу
A5)

410 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [гл Х[1
Если вместо у (х) подставлять различные конкретные функции то
будут получаться конкретные числовые значения /. Например, выбрав
у = лг2, получим
i
/ =
6
выбрав у = х3, получим /=-=-=0,143; Еыбрав y = s\nx, получим
/= т = 0,273 и т. д. Таким образом, формула A5) задает
закон, согласно которому каждой функции у (х) соответствует зна-
значение /, т. е. формула A5) определяет функционал. Формула
i
/ = J xy' dx (y = y (х); у' = dy/dx) A6)
о
определяет другой функционал; формула
з
/= \y"-dx (y=y(x))
-I
—третий (обратите внимание на пределы интегрирования) и т. д.
Итак, если числам ставятся в соответствие числа, то ми гово-
говорим, что задана функция. Если функциям ставятся в соответствие
числа, то задан функционал. Напомним, кстати (§ VI.2), что если
функциям ставятся в соответствие функции, то говорят, что задан
оператор.
Функционал A6)—линейный; это значит, что при сложении
функций у (х) значения функционала / также складываются:
i i i
\ х (Л + У*У с1х = \ хУх dx + S
0 0 0
Функционал A5)—нелинейный (квадратичный).
При исследовании функционала бывает важно выяснить, как
меняется его значение при малом изменении функции, от которой
он зависит. Рассмотрим этот вопрос на примере функционала A5).
Пусть в правую часть была сначала подставлена некоторая функ-
функция у(х), а затем некоторая новая функция у (х) -\- Ьу (х), где
Ьу [х) — вариация у — произвольная функция, принимающая малые
значения. (Например, могло быть сначала у = .v2, а затем у = х2-{-ах3.
где постоянная а мала.) Тогда и значение функционала немного
изменится и станет равным

S 3] НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА 411
Таким образом, приращение этого значения равно
i i
AI=2<\jy6ydx+<\j FyJrfx A7)
Если временно зафиксировать функцию у (х) и менять ее вариа-
вариацию, то мы видим, что в правой части A7) в зависимости от Ьу
первый член — линейный, тогда как второй — квадратичный (в общем
случае присутствуют также и члены более высоких степеней). Так
как значения бу малы, то главную роль в правой части играет
линейный член, а квадратичный имеет высший порядок малости.
Этот линейный член в приращении функционала называется ва-
вариацией функционала и обозначается б/, т. е. для примера A5)
i
*. A8)
Таким образом, с точностью до членов высшего порядка малости
Д/«6/. A9)
В тех случаях, когда членами второго и следующих порядков ма-
малости можно пренебречь, говорят просто, что вариация функцио-
функционала— это его бесконечно малое приращение, полученное за счет
бесконечно малого изменения («варьирования») функции, от которой
зависит значение функционала. (Однако при немалых 8у, конечно,
Д/=^=6Л) Если вспомнить основы дифференциального исчисления,
то можно усмотреть полную аналогию между понятиями дифферен-
дифференциала функции и вариации функционала.
Упражнения
1 1
1. Найдите вариацию функционалов /= \ —- dx; i/2@)+ \ (ху +yri) dx.
о о
I
2. Для функционала /= \ ф dx положите у = 2х, 6у = ах2 и сравните б/
о
с Ад при а=1; —0,1; 0,01.
§ 3. Необходимое условие экстремума
Пусть функция у (х) реализует экстремум функционала /; дру-
другими словами, значение функционала для функции у (х) больше
(в случае максимума) или меньше (з случае минимума) значений
этого функционала для всех функций, достаточно близких к у(х).
(Последняя оговорка связана с тем, что функционал, вообще говоря,
может иметь несколько экстремумов, подобно тому как функция может

412 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XI!
иметь несколько точек экстремума.) При этом А/ будет отрицательным
в случае максимума и положительным в случае минимума для всех
указанных функций, т. е. в обоих случаях не меняет знака. Но
отсюда следует, что
о/=0. B0)
В самом деле, из формулы A9) вытек-ает, что если 6/=£0, то А/
и б/ имеют одинаковый знак; но в силу линейной зависимости б/
от б_у при перемене знака у 6у и б/ изменит знак (см., например,
формулу A8)), что противоречит предыдущему.
Итак, условие B0) и является необходимым условием экстре-
экстремума; кстати сказать, оно совершенно аналогично необходимому
условию экстремума функции, известному в дифференциальном
исчислении. Если функция у(х) осуществляет экстремум по срав-
сравнению со всеми близкими функциями, то б_у в левой части B0)
может быть произвольной (даже не требуется малость этой функ-
функции, так как из-за линейности б/, если б/=0 для малых 6у, то
это же верно и для любых б_у). Если же экстремум осуществляется
по сравнению с функциями некоторого класса (см., например, усло-
условия (8) и A3)), то б_у должна быть такой, чтобы у-\-Ьу принадле-
принадлежала этому классу.
Условие B0) — это условие стационарности функционала / при
изменении вида функции у(х), от которой этот функционал зави-
зависит. Во многих задачах нас могут интересовать все стационарные,
а не только экстремальные значения функционала. Так, на приме-
примерах задач § 1 мы видели, что если в качестве функционала рас-
рассматривается потенциальная энергия сплошной среды, то каждому
стационарному значению отвечает статическое положение равнове-
равновесия, тогда как минимальным значениям функционала отвечают устой-
устойчивые состояния равновесия.
Покажем применение условия B0) на простейшей задаче об
отыскании экстремума функционала вида
I=\F(x,y)dx, B1)
а
где в качестве у подставляется любая функция х. Чтобы найти б/,
подставим у-\-&у вместо у и разложим результат по формуле
Тейлора:
/+ А/= $ F (х, у + 6у) dx =

S 3] НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА 413
Вариация функционала, т. е. линейная часть приращения, равна
ь
Ы= ^ F'.(x,yNydx.
Отсюда в силу произвола в выборе Ьу (х) вытекает, что
Р'у (*, У) = 0. B2)
В самом деле, если положить by=^a.F'y (x, у (х)) (а малое), то
последний интеграл будет равен
a\(F'yy-dx.
Но он должен равняться нулю, откуда и следует наше утвержде-
утверждение. (Если непрерывная функция не принимает отрицательных зна-
значений, а интеграл от нее равен нулю, то функция тождественно
равна нулю.)
К условию B2) можно прийти иначе. Если интеграл B1) должен
иметь экстремальное, например минимальное, значение, то и подын-
подынтегральная функция должна быть минимально возможной. Другими
словами, если мы складываем не зависящие друг от друга слагае-
слагаемые, то для минимальности суммы каждое слагаемое должно быть
минимально возможным. Таким образом, при каждом х значение у
надо подобрать из условия минимальности функции F, что немед-
немедленно приводит к B2). Итак, в этом случае по сравнению с зада-
задачами, разбираемыми в основах дифференциального исчисления, не
возникает ничего принципиально нового.
К функционалу вида B1) мы приходим, в частности, если в рас-
рассмотрениях § 1 положим, что точки струны не обладают упругой
связью друг с другом, а подвержены только действию внешней
силы и упругости подкладки. Ясно, что при этом каждая точка
струны расположится независимо от положения остальных точек,
так что принципиально нового по сравнению со статикой точки здесь
ничего нет. Функционал в этом примере имеет вид
(т.е. A1) при Р~0), а условие равновесия B2) дает
ку—/{х) = 0, т.е. _у = 1/»;
тот же результат получается из A2) при Р = 0. Интересно, что это
решение получается, вообще говоря, разрывным, как из-за возмож-
возможных разрывов у функции /(х) (так будет, например, если внешняя

414 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ, XII
нагрузка приложена лишь к части струны), так и из-за граничных
условий (8). Конечно, так и должно быть, если точки струны друг
с другом ничем не связаны; собственно говоря, о «струне» в такой
ситуации можно говорить с очень большой натяжкой.
Упражнение
Найти функции у(х), придающие минимальное значение функционалу:
12
о о
§ 4. Уравнение Эйлера
Вернемся к рассмотренной в § 1 задаче о равновесии упругой
струны под действием внешней силы. Мы видели, что эта задачи
сводится к нахождению экстремума (или даже просто стационарного
значения) функционала в классе функций, удовлетворяющих гранич-
граничным условиям (8). Попробуем найти решение с помощью условия B0),
для чего сначала подсчитаем bU. Пусть у получит приращение by,
тогда у' получит приращение б(У). Однако нетрудно проверить, что
6 (У) = (б_у)': в самом деле, если by=Y(x)—у(х), то б (у') =-
= V {x)—yf (x) = [Y(x)—y(x)]'=(8y)'. Отсюда
0>х-
Отбрасывая член второго порядка малости, получаем
i
6G= J [ру'Ьу'-/(х) by] dx.
о
Необходимое условие B0) дает
i i
p\y'by'dx—\f[x)bydx = O, B3)
о о
причем это равенство должно выполняться для любой вариации by,
удовлетворяющей условиям
6у@)=0, бу (/) = 0, B4)
которые нужны для того, чтобы у-\-Ьу удовлетворяла тем же усло-
условиям (8), что и у.

§ 4] УРАВНЕНИЕ ЭЙЛЕРА 415
Новым в условии B3) является то, что в него наряду с б_у вхо-
входит и б_у', а эти две величины нельзя считать независимыми. По-
Поэтому проинтегрируем первый член по частям, применяя равенства
B4):
; i i
О = Ру'Ьу |'.=о—Р I у"Ьу dx-\f (х) bydx = — \ [Py"-\f (x)]by dx.
0 0 О
Воспользовавшись теперь произвольностью в выборе б_у и рассуждая,
как в § 3, получим отсюда
Р/+/(*)= О,
т. е. уравнение A0).
Таким образом, наличие у' в выражении функционала связывает
соседние значения у (ср. пример с пружинками, разобранный в § 1).
В этом случае нельзя подбирать каждое значение у независимо от
соседних, как для функционала B1), и мы получаем не конечное
уравнение, как в § 3, а дифференциальное.
Выведем теперь аналогичное дифференциальное уравнение для
функционала более общего вида:
ь
I=\F{x, у, y')dx <y=y(x), y' = dy/dx), B5)
а
где F—заданная функция, а а и Ь — заданные пределы интегриро-
интегрирования. Пусть ищется экстремум этого функционала при заданных
краевых условиях
У(а)=Уа, УФ)=УЬ. BG)
Рассуждая,'как в только что разобранном примере, и пользуясь
общей формулой (IV.2), в которой роль х, dx, у, dy играют соот-
соответственно у, Ьу, у', 6_у', получим вариацию функционала B5)
ь
б/= \ [F'y(x, у, y')by + F-y, (х, у, у') 6/] dx.
а
(По этому образцу составляется вариация и функционалов иной фо-
формы). Если теперь некоторая функция у (х), удовлетворяющая усло-
условиям B6), реализует экстремум функционала B5) по сравнению со
всеми близкими функциями, удовлетворяющими тем же условиям, то
по признаку B0) должно быть
ь
UF'y(x> У> y')by + F'y(x, У, y')by']dx = 0. B7)
а
Это равенство должно выполняться для любой вариации бу, удов-
удовлетворяющей соотношениям
6у(а)=0, бу{Ь)=О, B8)

416 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
которые нужны для того, чтобы y-f-бу удовлетворяла тем же усло-
условиям B6), что и у.
Можно ли удовлетворить уравнению B7), положив Fy = 0, F'y, = 0?
Мы при этом получим два уравнения для одной искомой функции
у (лг) (напомним, что выражение F (х, у, у') задано). В общем случае
два уравнения с одной искомой функцией общего решения не имеют.
Решение нашей задачи, однако, существует по той причине, что <3у
и бу' не являются величинами независимыми друг от друга. Можно
найти такое у (лг) или, лучше сказать, такое одно уравнение для
у (лг), чтобы при любом бу и соответствующем ему бу' один член,
т. е. \ F'y by dx, в точности компенсировался бы другим членом,
\ F'y, by' dx, хотя в отдельности они и не равны нулю. Покажем,
как это сделать.
Интегрируя по частям второе слагаемое B7) i; прнменяя'соотно-
шения B8), получим
ь ь ь
Отсюда в силу произвола в выборе бу вытекает, что последняя
квадратная скобка тождественно равна нулю. В самом деле, если
взять бу равной этой скобке и лишь вблизи точек а и b заставить
быстро спадать до нуля (это нужно, чтобы удовлетворить соотно-
соотношениям B8)), то последний интеграл будет приближенно равен
ь
\ \F'y — — F'b,\ dx. Но он должен равняться 0, откуда и следует
а
утверждение.
Итак, мы пришли к так называемому уравнению Эйлера
F'y{x, y,y')-^F;,(x, у, Я = 0. B9)
Отметим, что в нем при дифференцировании -г величина у рассмат-
рассматривается как функция лг; более подробно, по правилу дифференци-
дифференцирования сложной функции, уравнение Эйлера можно переписать
в виде
Fy(x, У, У')-Гму (х, у, y') — FmBu.(x, у, У')У'-
-Г;,,,(х, у,у')у"=0. C0)
Здесь частные производные от ^(лг, у, у') берутся уже без учета
зависимости у и у' от лг. Видно, что это — дифференциальное урав-
уравнение второго порядка, и потому его общее решение содержит две
произвольные постоянные, которые определяются с ломощью краевых

§ 4] УРАВНЕНИЕ ЭЙЛЕРА 417
условий B6). Уравнение Эйлера обобщает уравнения статического
равновесия A0) и A2), разобранные в § 1.
Приведем еще один вывод уравнения Эйлера B9), не исполь-
использующий формальный прием интегрирования по частям. Для этого
разобьем интервал а^лг^ГЬ с помощью точек лг0 = a<JC1<JC2<. ..
...<.*:„ = £> на маленькие участки равной длины h и запишем при-
приближенно интегралы от каждого из слагаемых в левой части B7) а
виде интегральных сумм, причем первую сумму возьмем по «целым»,
а вторую—по «полуцелым» точкам деления (§ П.1 — 2). Если затем
заменить производную на разностное отношение, то взамен B7) мы
получим условие
X^b6^ + V(/-;,),+I/2^^-6y^o. C1)
На первый взгляд может показаться, что коэффициент при Ьук во
второй сумме существенно превосходит соответствующий коэффици-
коэффициент в первой сумме, так как при малом h \(F'y)k+\i2\lh^>\(F'u)k\.
Но надо учесть, что во второй сумме Ьук участвует в двух соседних
слагаемых: с (/7'у')д+1/2. и (F'b.,)^~i) + \/2'> поэтому общий коэффициент
при Ьук в левой части C1) равен
[i ] C2)
Итак, h сократилось, т. е. оба члена в правой части C2) имеют
одинаковый порядок.
В силу произвольности byk из условия C1) получаем, что этот
коэффициент должен равняться нулю, т. е. приходим к B9).
Рассмотрим в качестве примера задачу § 2 о линии наибыстрей-
наибыстрейшего спуска. В этом случае (см. A4)) надо положить
F= /'+?'* C3)
V2g{ya-y)
Так как в правую часть не входит непосредственно х, то в левой
части C0) отсутствует второе слагаемое, и после умножения обеих
частей C0) на у' его можно переписать в виде (F—F'y,y')' = 0.
Отсюда, интегрируя, получаем
/=■-/>/ =С1( C4)
что для конкретного примера C3) даст
У'
т ё.
' =? = CV
1'1 Я. Б. Зельдович. А. Д. Мышкио

418 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
Для интегрирования этого уравнения введем искусственный пара-
параметр t по формуле
ya—y — r(\—zost), где r =
Тогда, преобразуя, получим
' — cos
1+cos/ sin2/
1—cos/ A—cos/J'
Это выражение вместе с предыдущим выражением для у дают пара-
параметрические уравнения так называемой циклоиды (см., например,
ВМ, § IV.8), т. е. линии, которую
описывает точка окружности ра-
радиуса г, катящейся снизу без сколь-
скольжения по горизонтальной прямой,
проведенной через А. Таким обра-
образом, линией наибыстрейшего спуска
служит циклоида с острием в точ-
точке А; радиус г при этом должен
быть подобран так, чтобы первая
^ ^** л арка циклоиды прошла через конеч-
рис jgg ную точку. На рис. 166 показано
несколько таких арок, из которых
через конечную точку проходит четвертая; интересно отметить,
что эта арка частично проходит ниже конечной точки, чего мож-
можно было заранее не предвидеть. Впрочем, глядя на ответ, это лег-
легко понять; чтобы пройти большой путь по горизонтали, выгодно
опуститься пониже, набрать большую скорость, а уже под конец
пути подняться к месту назначения. Точка В должна быть ниже
точки А, иначе, естественно, решения вообще не существует.
Вернемся к общему функционалу B5) при граничных условиях
B6). Пусть, зафиксировав эти условия, мы получили какое-то решение
у (х) задачи на экстремум. Представим теперь, что эти условия
могут изменяться. Тогда экстремальное значение функционала / будет
зависеть от этих условий
1=1 (а, Ь,уа> уь). C5)
При этом мы в / подставляем только функции, придающие ему
экстремальное значение для фиксированных граничных условий; если
бы это не было сделано, то / зависело бы, помимо граничных
условий, еще от произвольной функции у (х).

§ 5] ВСЕГДА ЛИ СУЩЕСТВУЕТ РЕШЕНИЕ ПОСТАВЛЕННОЙ ЗАДАЧИ? 419
. Может оказаться необходимым изучить функциональную зависи-
зависимость C5) значения / при изменении граничных условий у (а) =уа,
y(b)=yb. Так как функция C5) зависит уже от конечного числа
независимых переменных, то эта задача решается средствами обычно-
обычного анализа, с помощью вычисления производных. Покажем, например,
как вычисляется производная-^—. Если зафиксировать а, Ь,уь и из-
изменять уа, то решение у (х) задачи на экстремум изменится, получит
приращение Ьу (х). При этом, с точностью до малых высшего порядка,
ъ ъ
А/ = J (F'yby + F'y,by') d* = /y6y|* + J [гу--± (/у)] 6у их.
а а
Но так как у (х) была решением задачи на экстремум, то она удов-
удовлетворяет уравнению Эйлера, и потому последний интеграл обра-
обращается в нуль. Кроме того, 8у(Ь) = О (так как уь не меняется), и мы
получаем
Аналогично вычисляются остальные производные функции C5).
Упражнения
1
1. Найдите решение задач: a) / = min \ {у2-{-у) dx, j/@) = 0, j/(l) —1;
б) I =
о
2. В последней задаче найдите —— непосредственно и по формуле, выве-
выведенной в тексте.
3. Выведите с помощью вариационного исчисления уравнение прямой как
кратчайшей линии, соединяющей две заданные точки.
§ 5. Всегда ли существует решение поставленной задачи?
Условие B0) является только необходимым для экстремума.
Достаточные условия довольно сложны, однако в большинстве прак-
практических задач они не требуются. Например, в задаче, разобранной
в § 4, мы не проверяли, что для построенной арки циклоиды осу-
осуществляется именно минимальное время падения. Однако из физи-
физических соображений ясно, что какое-то решение задачи о минимуме
при уа~>уь имеется и его только надо накти. А так как с помощью
применения необходимого условия (уравнения Эйлера) получилось
лишь одно решение, то оно и является искомым. Конечно, не вду-
вдумавшись в смысл задачи, мы могли поставить вопрос об отыскании
14*

420
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
линии с максимальным временем падения и прийти к тому же урав-
уравнению Эклера и к тому же решению. Но этот ответ был бы оши-
ошибочным, так как мы видим теперь, что построенное решение (кото-
(которое является единственным) даст именно минимум времени падения.
Что касается соответствующей задачи
на максимум, то она вовсе не имеет
решения и легко построить линии с как
угодно большим временем падения.
Таким образом, задача на экстре-
экстремум может не иметь решения; в не-
некоторых случаях это более или менее
х сразу ясно из формулировки задачи
(как в предыдущем примере при рас-
рассмотрении задачи на максимум), тогда
как в других случаях вытекает из ре-
результатов вычислений. Покажем это на
примере.
Пусть требуется найти форму плен-
пленки минимальной площади, если, эта
пленка натянута па два равных колечка, расположенных перпен-
перпендикулярно их линии центров. Такую форму принимает мыльная пленка,
натянутая на эти колечки (рис. 167, где жирными линиями изображе-
изображено осевое сечение пленки). Так как из соображений симметрии ясно,
что искомая поверхность будет поверхностью вращения, а площад.',
поверхности вращения, как известно (см., например, ВМ, § III.7),
равна
Рис. 167.
= 2л \
C6)
то дело сводится к отысканию функции у (х), реализующей минимум
интеграла C6) при граничных условиях:
у( — а) = г, у(а) = г. C7)
И здесь х под знак интеграла не входит непосредственно, так что
можно воспользоваться промежуточным интегралом C4), что даст
2лу у 1 + V У = С\, т- е- -= тг ■
у 1 +</'2 у \ +г/'2 ^л
Обозначив правую часть через -г- и проводя преобразования, по-
получим
J/ ' &у* =
dy . wv
dx) ' dx
- dy
C8)
Последний интеграл при £— 1 приведен в ВМ, стр. 167 (№ 31).
он равен 1п\у -\-уу2 — 0- Попробуем вычислить производную от

§ 5] ВСЕГДА ЛИ СУЩЕСТВУЕТ РЕШЕНИЕ ПОСТАВЛЕННОЙ ЗАДАЧИ? 421
функции \n(ky-\-У {kyJ—1)> "на равна k\\ k2y2—1 (проверьте!).
Поэтому из C8) мы получаем -^ In (ky + Vk2y2 —1) = ±
откуда после несложных преобразований, которые мы предоставляем
читателю, у =
gk (х + С) , g-k (х+С)
2k
(знак ± здесь несуществен).
Чтобы линия была симметрична относительно х=0, должно быть
С—0, т. е. окончательно
2k
Это—так называемая цепная линия; название объясняется тем,
что форму этой линии принимает тяжелая цепь, подвешенная за
концы (см. упражнение 2 к § 8). Итак, искомая поверхность мыль-
мыльной пленки получается в результате вращения цепной линии.
Чтобы удовлетворялись граничные условия C7), требуется, чтобы
ека
е-ка
C9)
откуда и следует найти пока неизвестное значение параметра
к. Попробуем решить зту задачу графически, для чего изобраз---
при заданных а и г графики изме-
изменения левой и правой частей
им
Рис. 168.
Рис. 169.
уравнения C9) (рис. 168) и найдем точку пересечения обоих графиков.
Мы с удивлением обнаруживаем, что получается не одно решение,
как можно было бы ожидать, а два (при сравнительно палых а,
т. е. при сближении колечек) или ни одного (при удалении колечек).
Какую же форму примет пленка на самом деле?
Пусть сначала а сравнительно малб, т. е. имеется два решения,
изображенных жирными линиями на рис. 169 (на этом же рисунке

422
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. Х||
пунктиром обозначены колечки). Если мысленно представить себе
другие формы пленки, изображенные на рис. 169 тонкими линиями,
то площади соответствующих поверхностей вращения будут иметь
значения, изображенные графически на рис. 170. Мы видим, что
из двух решений именно для верхнего реализуется минимум пло-
площади, а для нижнего — максимум. Поэтому верхнее решение дает
устойчивую форму равновесия пленки, а нижнее — неустойчивую.
Рис. 170.
Рис. 171.
Если теперь а увеличивать (при данном г), т. е. отодвигать ко-
колечки друг от друга, то точки экстремума ос и C сближаются и для
достаточно больших а график площадей принимает вид, изображен-
изображенный на рис. 171. Таким образом, в этом случае пленка, стремясь
уменьшить свою площадь, стягивается к линии центров, расцепляется
и приобретает вид двух отдельных кружков, каждый из которых
натянут на свое колечко. (Кстати, так же ведет себя пленка при
малых а, если она начинает деформироваться, имея слишком тонкий
перешеек.) Итак, в этом случае единой поверхности действительно
не будет. Вид графиков на рис. 170 и 171 подтверждается тем,
что при у = 0 будет S=2iir2, а при у = г будет S=bnra, так что
при малых а последнее значение меньше S\y=a, а при больших
а — больше. При больших а форму, состоящую из двух отдельных
кружков, можно считать обобщенным решением нашей задачи. Это
решение имеет характер «концевого», «острого» минимума, для него
уравнение Эйлера не выполняется (ср. § 9).
Мы видим, что в результате вычислений мы приходим к выводам,
которые заранее можно было и не предвидеть.
Легко подсчитать, какое значение — является критическим в том
смысле, что при меньших значениях равновесие возможно, а при
больших — невозможно. Это будет, когда на рис. 168 оба графика
касаются друг друга, т. е. производные от обеих функций по k равны
аеак— ае~ак
К = Г.
Комбинируя это равенство с C9) и
обозначая —= К
г
(это и есть

§ 6] ВАРИАНТЫ ОСНОВНОЙ ЗАДАЧИ 423
критическое значение), получим
и
— е-ак 1
rX
; e
1 л
V\
«ft fh l_
- rfi \-
a
1
к '
)-
е-ак
—e~V
2
rh
1
1
A, '
1
X ш
Итак, X находится из последнего уравнения. Грубый численный
расчет дает приближенное значение Х = 0,7.
Интересно отметить, что если верхнее решение на рис. 169 реа-
реализует абсолютный минимум площади поверхности вращения, то
нижнее решение реализует максимум только в изображенном семей-
семействе поверхностей. Если выйти за рамки этого семейства, то нижнее
решение будет стационарным, так как оно удовлетворяет уравнению
Эйлера, но отнюдь не максимальным, а имеет характер минимакса
(ср. § IV.6). Если выбрать на нижнем решении любые две доста-
достаточно близкие точки и рассматривать их как граничные условия,
то дуга, заключенная между ними, является устойчивой, т. е. реализует
решение задачи на минимум. Значит, при любом изменении нижнего
решения на достаточно малом интервале площадь будет возрастать.
Задача на максимум поверхности вращения решения не имеет. (Это
ясно также из возможности «гофрировать» любую поверхность.)
То соображение, что малый участок стационарного решения
является не только стационарным, но и экстремальным, оказывается
полезным во многих задачах.
Упражнение
а
Рассмотрите задачу на минимум функционала /=\((/'2—у2) dx (а > 0)
о
при граничных условиях у @) = (/ (я) = 0. Этим условиям удовлетворяют, в
частности, функции у = Сх(а—х) и у = С sin'—. Какой отсюда можно сделать
вывод о существовании решения задачи?
§ 6. Варианты основной задачи
Имеется большое число других типов вариационных задач, ко-
которые разбираются в курсах вариационного исчисления. Некото-
Некоторые кз этих задач исследуются подобно тому, как мы рассмот-
рассмотрели в § 4 задачу об экстремуме функционала B5) при усло-
условии B6). Например, под знак интеграла могут входить производ-
производные более высокого, чем первого, порядка от искомой функции;
тогда и уравнение Эйлера имеет более высокий порядок, чем второй

424 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ, XII
(а именно, в два раза более высокий, чем наивысший порядок про-
производных, входящих в функционал), Под знак интеграла может вхо-
входить несколько неизвестных функций; тогда для их отыскания полу-
получается система дифференциальных уравнении Эйлера, причем число
уравнений в системе равно числу искомых функций, так как надо
приравнять нулю вариации функционала, полученные в результате
варьирования каждой из этих функций. Так получится, в частности,
при разыскании линии в пространстве, потому что такая линия опре-
определяется двумя функциями, например у (х) и z(x).
Рассмотрим теперь вариационную задачу для функции несколь-
нескольких, для определенности двух, независимых переменных. Пусть ищется
функция z (х, у), придающая экстремальное значение интегралу
IJ
F (х, у, z, z'x, z'y) dx dy, D0)
(О)
где (сг) — некоторая заданная область с границей (Z.), при условии
на границе
г\ш = Ч (задано). D1)
Рассуждения, аналогичные проведенным в § 4, приводят к уравне-
уравнению Эйлера, которое в данном случае имеет вид
г'-^-^Г0; D2)
д д
при этом надо иметь в виду, что при вычислении у- и у- здесь z
рассматривается как функция переменных хну. Таким образом,
для нахождения решения получается дифференциальное уравнение
второго порядка D2) с частными производными при граничном усло-
условии D1). Решение таких уравнений выходит за рамки этой книги,
однако один физически важный пример будет нами разобран (дру-
(другой см. в § 12).
Найдем уравнение для формы равновесия мембраны, натянутой
на жесткий контур. Будем считать мембрану однородной (одинако-
(одинаковой во всех точках), изотропной (одинаковой во всех направлениях)
и натянутой с силой Т на единицу длины. Потенциальная энергия
мембраны, получающаяся при натяжении ее на контур, возникает
из-за увеличения ее площади по сравнению с горизонтальным поло-
положением. В интегральном исчислении доказывается, что площадь
Q поверхности, описываемой уравнением z = z(x, у), равна
J S
(О)
так что увеличение AQ площади мембраны равно
-a=\\ [V~\ + (г'х)*-f {г'в)г — l\dxdy.

§ 7) условный экстремум 425
Считая отклонение малым (для этого нужно, чтобы заданный кон-
контур мембраны мало отклонялся от плоскости z = 0), а потому и ве-
величины z'x и z'y малыми, разложим подынтегральную функцию в
ряд и отбросим члены высшего порядка малости:
^[\!/]чя. высш. пор.
(а)
малости] y ^
(а)
сти] —\\dxdy = — ^ [(z'x)* + {z'yJ\ dxdy.
()
Приняв, что в процессе растяжения мембраны ее натяжение остается
неизменным, получим, что в этом процессе совершается работа
D3)
(О)
Значит, такой будет и накопленная потенциальная энергия.
Однако из физики известно, что из всех возможных форм рав-
равновесия мембрана выбирает такую, для которой потенциальная энер-
энергия минимальна. Таким образом, получается задача о минимуме
интеграла D3)., В силу общего уравнения Эйлера D2) получаем
~T\Y 2z'x)~dy\~2 2z'v)—Q> т- е- после сокращения
Итак, форма равновесия мембраны описывается функцией z = z (х, у),
удовлетворяющей уравнению Лапласа (см. § V.7). Для нахождения
этой формы в конкретном случае надо найти решение уравнения D4)
при граничном условии D1).
Упражнения
ь
1. Выведите уравнение Эйлера для функционала /=\ F (х, у, у', у") dx
а
при граничных условиях у(а) = уа. у' (а) = уа, У(Ь) — уь, у'ф)=у'ь.
2. Запишите уравнение D2) в развернутом виде, наподобие C0).
§ 7. Условный экстремум для конечного числа
степеней свободы
Вернемся к задачам на экстремум для систем с конечным числом
степеней свободы. В задачах, рассмотренных в § IV.6, независимые
переменные не были связаны между собой никакими соотношениями;
такой экстремум называется безусловным. Встречаются также за-
задачи на условный экстремум, в которых независимые переменные
связаны между собой определенными равенствами. Начнем с функций
от двух переменных.

426
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
Пусть ищется максимум или минимум функции z — /(x, у) при
условии, что переменные х и у не являются независимыми, а свя-
связаны соотношением
F(x, y) = h. D5)
Это означает, что значения функции / рассматриваются и сравни-
сравниваются только для точек (в плоскости аргументов), лежащих на
линии с уравнением D5). Например, на рис. 172 изображены линии
уровня некоторой функции /(х, у), имеющей безусловный максимум
к точке К] там же изображена жирно
линия (!) с уравнением D3). Следуя
вдоль (Z.), мы в точке А подходим к
линии уровня с наивысшей отметкой
и сразу же затем отходим в область
с более низкими отметками, т. е. в
область меньших высот. Значит,в точ-
точке А функция / имеет условный мак-
максимум; он не является безусловным,
так как, уйдя с (L) в сторону К, мы
могли бы вблизи А найти еще более
высокие значения /. Аналогично про-
проверяем, что в точке В будет условный
минимум, а в точке С—другой услов-
условный максимум, т. е. здесь имеется три условных экстремума. Итак,
безусловный максимум — это как бы вершина горы, а условный —
это самая высокая точка заданной горной тропы (проекция этой
тропы на плоскость х, у имеет уравнение D5)).
Если из «уравнения связи» D5) можно выразить у через х, то
этот результат можно подставить в выражение для z,
У х
Рис. 172,
z=/[x,
D6)
и получить, таким образом, z как функцию одного независимого
переменного. Так как условия больше нет (оно учтено подстановкой
у— у(х)), то задача об отыскании экстремума z становится задачей
на безусловный экстремум. Аналогичный результат получится, если
уравнение D5) можно разрешить относительно х или если уравнение
линии D5) можно представить в параметрическом виде.
Однако такое разрешение уравнения D5) не всегда возможно
и целесообразно. Тогда можно рассуждать так. Уравнение связи D5)
определяет принципиально некоторую зависимость у = у (х), хотя бы
нам явно и не известную. Таким образом, z является сложной
функцией D6) независимого переменного х, и необходимое условие
акстремума дает по формуле производной сложной функции
dx
D7)

§ 7] условный экстремум 427
Здесь dyldx означает производную неявной функции у (х), определен-
определенной из условия D5). По правилам § IV.3'получаем, что F'x-\-F'y j-= О,
т. е. -j- =—F'xIF'y. Подставляя это выражение в D7), видим, что
в точке условного экстремума
/;—-^-/;=о, т. е.—-Ц-=— -4, или К=К.
Jx F/y ' Fy fy' Fx F'u
(Среднее равенство, в силу § IV.3, означает, что линия D5) в точ-
точке условного экстремума касается линии уровня функции /, ср.
рис. 172.) Обозначим величину последнего отношения в рассматри-
рассматриваемой точке буквой к. Тогда получим в точке условного экстремума
M-=*-k- = K D8)
т. е.
f'x-kF'x = 0, Ги-Щ^0. D9)
Обозначим
/•(*, у; *)=/(*, у)—№(*, у), E0)
где к— неизвестный параметр, который называется множителем
Лагранжа. Тогда уравнения D9) можно записать так:
Таким образом, получаются те же уравнения, как и в случае без-
безусловного экстремума (см. (IV.28)), однако они составляются не для
самой функции /, а для измененной функции /*, определенной но
формуле E0). Уравнения E1) вместе с уравнением связи D5) обра-
образуют систему трех уравнений с тремя неизвестными х, у, к; из этих
уравнений и находятся точки условного экстремума.
Множитель Лагранжа к имеет простой смысл. Для выяснения
его обозначим координаты точки условного экстремума и само
экстремальное значение соответственно через х, у и z. До сих пор
мы считали h зафиксированным, но если менять А, то эти три
величины будут зависеть от Н. Вычислим, с какой скоростью
меняется экстремальное значение z пртг изменении А. Так как z (h) =
= /(x(h),y(h)), то
EL-f Ё1 j-f d'y
dh -/xdk ' J^dh-
С другой стороны, в силу D5)
, dx F, d~y

428 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
Из E2), D8) и E3) получим
di , F, dx *F, d~y _. f , die
Итак, множитель к равен скорости изменения экстремального зна-
значения при изменении параметра h в условии. Метод Лагранжа за-
замечателен тем, что производную dzjdh удается найти, не выписывая
в явном виде функцию z (А), которая может быть очень сложной.
Постановка задачи на .условный экстремум типична для эконо-
экономики: ищем максимум количества z продукта при заданных затра-
затратах А; известна зависимость г и А от способа действий, характери-
характеризуемого переменными х, у. При наилучшем способе действий
каждому h соответствует одно определенное z. Производная dhjdz
есть себестоимость (добавочного) продукта в идеально налаженном
хозяйстве, где уже сделаны затраты h и произведено z, а теперь
потребовалось увеличить производство.
Для функций любого числа переменных и для любого числа
связей исследование условного экстремума проводится аналогично.
Например, если ищется экстремум функции f(x, у, г, и, v) при
условиях
F1(x, у, z, и, v) = 0, F2(x, у, z, и, v) = 0,
Fa (х, у, z, и, v) = 0, I04'
то надо поступать так, как если бы мы искали безусловный экстре-
экстремум для функции /* = /—X1F1—А,2/\, — h3F3, где к\, кг, к3 — неиз-
неизвестные множители Лагранжа. Необходимое условие экстремума для
/* дает /Г = 0, /;' = 0, /*'=0, /*' = 0, ft'= 0, что вместе с E4)
дает 5 + 3 уравнений с 5 + 3 неизвестными х, у, г, и, v, кх, к2, к3.
Упражнение
Найдите условным экстремум функции и (х, у, г)=х- — </2 + г2— 2х: а) при
условии х-\-2у—г = 3; б) при условиях х-\-у — г = 0, л: + 2у=1.
§ 8. Условный экстремум в вариационном исчислении
Задачи на условный экстремум в вариационном исчислении ста-
ставятся и решаются аналогично тому, как это было сделано в § 7
л."м задач с конечным числом степеней свободы. Рассмотрим, напри-
например, задачу о нахождении экстремума функционала B5) при гра-
граничных условиях B6) и дополнительном интегральном условии
ь
\ G(x, у, y')dx = K, E5)

§ 8] УСЛОВНЫЙ ЭКСТРЕМУМ В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ 429
где О—заданная функция, а К—заданное число. Если разбить
интервал интегрирования на большое количество мелких частей и
заменить интегралы B5) и E5) на суммы, зависящие от значений уг
искомой функции в точках деления (т. е. совершить как бы переход,
обратный сделанному в § 1), то мы приходим к задаче на условный
экстремум функции от конечного числа переменных у{. В силу ре-
результатов § 7 эта задача равносильна задаче о безусловном экстре-
экстремуме выражения
ь ь ь
\F{x, у, y')dx—k^G(x, у, y')dx=\{F—kG)dx
а а а
(мы от сумм опять перешли к интегралам), где к— неизвестный
заранее постоянный множитель Лагранжа. Таким образом, взамен
уравнения B9) надо написать аналогичное уравнение Эйлера для
функции /7*=/7—kG; после решения этого уравнения две посто-
постоянные интегрирования и постоянную к находим из трех условий
B6) и E5). При этом в силу § 7 величина к имеет важное значе-
значение, так как она равна
Это равенство дает возможность выяснить характер зависимости
экстремального (в общем случае стационарного) значения /экстр
функционала в том случае, если параметр К в' условии E5) может
изменяться (тогда, конечно, это значение /экстр зависит от К).
Рассмотрим в качестве примера знаменитую задачу Дидб. Легенда
рассказывает, что в древности жила финикийская царица Дидд.
Преследуемая властителем соседнего государства, она бежала в
Северную Африку и обратилась к местному племени с просьбой
приютить ее, выделив для этого столько земли, сколько можно
охватить шкурой вола. Когда эта просьба была удовлетворена, Дпдо
разрезала шкуру на тончайшие ремешки и, связав их последова-
последовательно один с другим, получила длиннейшую нить. Охватив на
глазах у изумленной публики этой нитью изрядный по тем временам
участок земли, Дидо развернула там строительство и основала зна-
знаменитый город Карфаген.
Уже античная наука заинтересовалась задачей: как следовало
Дидо расположить свою нить, чтобы охватить наибольшую площадь,
другими словами, как выбрать из всех линий заданной длины
ту, которая охватывает наибольшую площадь. Оказалось, что
решением этой изопериметрической задачи служит окружность (если
линия берется замкнутой) или дуга окружности (если линия бе-
берется незамкнутой, например, если Дидо расположила свою нить кон-
концами у моря, см. рис. 173). Однако доказать это строго совсем
не просто.

430
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
Посмотрим, как сформулировать задачу Дидо аналитически. Для
этого допустим для простоты, что берег прямой, и расположим
оси координат, как на рис. 173. Рассмотрим вариант, в котором за-
зафиксировано положение концов нити. Тогда форма нити задается урав-
уравнением у = у(х), причем функция у (х) заранее не известна, однако
должна удовлетворять условиям
у(а) = 0, у(Ь) = О. E7)
Kpof.se того, задана длина линии
ь
"У
* 0
I
*
b
ч ч
Земля ч-
*/ Город
шш.
Ь ч-
■ч- «
\ -
///////
ш
J К' 1 + /2 dx=L
E8)
Рис. 173.
(формула для длины линии выводит-
выводится в интегральном исчислении, см., на-
например, ВМ, § III.5). При этом требует-
требуется, чтобы площадь, т. е.
S=\ydx, E9)
была максимальной. Итак, получается следующая задача: среди всех
функций у = у(х), удовлетворяющих условиям E7) и E8), надо
выбрать такую, для которой интеграл E9) имеет наибольшее воз-
возможное значение.
Задача Дидо была впервые решена геометрическими методами,
с привлечением очень остроумных, но не очевидных соображений.
На основе аппарата вариационного исчисления она решается совер-
совершенно стандартно. В силу сказанного в начале этого параграфа
просто требуется решить уравнение Эйлера для функции
Пользуясь промежуточным интегралом C4), находим
F0)
Преобразуя, получим
dy
i-j'); у =ir~,
= ax;
-Cy = W. F1)

§ 8]
УСЛОВНЫЙ ЭКСТРЕМУМ В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ
431
Итак, получилось уравнение окружности, т. е. решением задачи
Дидо служит дуга окружности, как и было уже указано. Поскольку
длина L дуги окружности и ее концы заданы, то не представляет
труда найти центр окружности и изобразить саму дугу.
Задача Дидо имеет варианты. Так, если длина L задана, но
концы a, b дуги не заданы, то из всех дуг данной длины надо
выбрать такую, которая ограничивает наибольшую площадь. Можно
проверить, что искомая дуга окружности должна подходить к бе-
берегу перпендикулярно; в частности, если берег прямой, то надо
взять полуокружность. Если же моря нет, и линия берется замкну-
замкнутой, то как было сказано выше, получается окружность. Проверим
в этом случае соотношение E6). Здесь /экстр = я/?г, K=L
(R—радиус окружности), откуда
dl
dK
= R.
Это как раз соответствует формуле F1), из которой видно, что
радиус окружности равен \к\ (ниже мы увидим, что X = R, так что
и знаки в формуле E6) согласуются).
Задача Дидо имеет простое физическое истолкование. Предста-
Представим себе горизонтальную жесткую рамку, на которую натянута
мыльная пленка, и пусть на этой пленке плавает тонкая нить, при-
прикрепленная концами к рамке (рис. 174, а) в точках а и Ь. Если
а)
Рис. 174.
проколоть иглой пленку внутри нити, то в силу поверхностного
натяжения пленки она натянется так (рис. 174,6), чтобы ее пло-
площадь была по возможности меньшей, а значит, чтобы свободная от
пленки площадь была по возможности большей. Мы приходим как
раз к задаче Дидо.
Такая физическая картина дает возможность истолковать урав-
уравнение Эйлера, подобно § 1, как уравнение статического равновесия.
Если длина L нити задана, то потенциальная энергия U системы
пропорциональна поверхности пленки, т. е.
U = 2a(Se-S),

432
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
где а—«коэффициент поверхностного натяжения» (множитель 2 свя-
связан с тем, что пленка имеет две стороны), a So — площадь, охва-
охваченная рамкой, так что So — 5 есть площадь пленки. Условие ста-
статического равновесия, как мы видели, сводится к стационарности
потенциальной энергии U, что равносильно стационарности величи-
величины 5 (причем максимальность 5 означает минимальность U, т. е.
устойчивость равновесия). Таким
образом, мы приходим к уравнению
Эйлера для функции F*.
Найденное нами решение также
можно получить из физических 'со-
'соображений. Рассмотрим (рис. 175)
элемент (dL) нити, на который дей-
действует сила 2а dL поверхностного
натяжения и силы натяжения нити Р и P-\-dP, приложенные к его
концам. Проектируя эти силы на касательную к элементу и отбра-
отбрасывая члены выше первого порядка малости, получим
\2№
Рис. 175.
>=*=<
(при этом надо учесть, что косинус малого угла отличается от еди-
единицы на величину второго порядка малости). Отсюда dP = 0, т. е.
вдоль нити Р= const. Проектируя силы на __„_„„^_
нормаль, получим
2Рsin da=2P da = 2аdL, F2)
откуда
2da 2o
_ = т= const.
Отношение -тт- представляет собой кри-
кривизну k нити (§ IX.4). Таким образом,
нить в положении равновесия имеет по- Рис. 176.
стоянную кривизну, т. е. представляет
1 Р
собой дугу окружности радиуса /? = — =_ . (Впрочем, по-
постоянство Р можно получить и из формулы F2), которую можно пере-
переписать в виде P—2(sR, исходя из найденного решения F1) задачи на
условный экстремум, причем R — X, т. е. Р=2ак.)
К решению задачи о мыльной пленке можно подойти иначе.
Именно, будем считать натяжение Р нити заданным, а ее длину L
не заданной, т. е. рассмотрим схему, изображенную на рис. 176. В
этом случае потенциальная энергия системы равна
£7= const —
= const — 2a f.S— ~L

§ 8]
УСЛОВНЫЙ ЭКСТРЕМУМ В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ
433
так как при увеличении L на AZ. груз поднимается на AI, т. е. U
возрастет на PAL. Таким образом, мы приходим к задаче на без-
безусловный экстремум функционала
Для этого надо составить уравнение Эйлера для функции F0) с
р
h =«—; как мы видели, решением уравнения служит линия с урав-
уравнением F1), т. е. дуга окружности радиуса
Я=|Х|=--£. F3)
Итак, решение задачи на условный экстремум при новом истолко-
истолковании можно рассматривать как решение задачи на безусловный экс-
экстремум, причем этот переход имеет
физический, а не только формаль-
формальный смысл.
Рис. 177.
Рис. 178.
Интересно, что при второй трактовке задача имеет два реше-
решения: из F3) мы получаем значение радиуса искривленной нити, но
ведь имеется два возможных положения нити с заданным радиусом
(рис. 177)! Если рассмотреть* семейство окружностей, проходящих
через точки а и Ь, то график зависимости О от h имеет вид, изо-
изображенный на рис. 178. Таким образом, из двух возможных поло-
положений груза более низкое является устойчивым, а более высокое —
неустойчивым. При этом, как и в конце § 5, минимум имеет абсо-
абсолютный характер, а максимум экстремален только среди дуг окруж-
окружностей; в действительности для более высокого положения энергия
имеет минпмакс.
Можно обобщить задачу Дндо, предположив, что требуется ох-
охватить наиболее ценный участок, причем стоимость единицы пло-
площади не постоянна, а зависит, например, от расстояния до моря.
Элементарно решить такую обобщенную задачу уже нельзя. Одна-
Однако ее можно решить с помощью уравнения Эйлера, заметив, что

434 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. Хм
ь
вместо E9) в данном случае надо максимизировать интеграл j F(y) dx,
у а
где F {у) = \ф (r|) dx\, а ф (г|)— стоимость единицы площади на рас-
о
стоянии т] от моря. (Если ф(г|)=1, то мы возвращаемся к E9).)
Рассмотрим еще одну задачу иа условный экстремум, именно за-
задачу о распределении зарядов в проводнике. Представим себе уеди-
уединенный проводник (Q) любой формы, на который помещено количе-
количество электричества q. Это количество разместится на проводнике с
плотностью р, которую и нужно найти.
Для решения этой задачи вспомним формулу (Х.23) для потен-
потенциала, порожденного распределенным зарядом, которую перепишем
в виде
1гЬ
(Q)
Поэтому полная потенциальная энергия заряда равна
,,j 'Г / \ / ч ^п 'Г f p(ro)p(r)dQdQo
(Q) <Н> (Й) (Й)
Согласно общему принципу статического равновесия этот интег-
интеграл должен принимать минимальное (или, во всяком случае, стаци-
стационарное) значение при условии
(Q)
так как заряды могут только перераспределяться, но не порождаться
или исчезать. Таким образом, получилась задача на условный экст-
экстремум. Чтобы ее решить, надо приравнять нулю вариацию б (U—%q),
где к — множитель Лагранжа.
Однако по формуле дифференциала произведения
ьи
6p(r0)-p(r)dQdQ0 .Iff p(roNp(r)dQdQo
_1 Г f flp(r0)-p(f)rfQrfQ0 1 f f
2 J J \r-ro\ ^ 2 J J
. . \r—r0
(Й)(Й) (Й) (Q)
Если в первом интеграле обозначить г через г0, а г0 — через г, то
мы видим, что он равен второму, откуда
0 = 6 (U— kq) =
(Й) (Q) (Q) (Й)
В силу произвольности бр (г) отсюда получаем ф (г) — К = 0, т. е.
ф(г) = % = const.
Итак, мы видим, что свободный заряд в проводнике располагается
так, что потенциал ф0 во всех точках проводника одинаков; при этом

§ 8]
УСЛОВНЫЙ ЭКСТРЕМУМ В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ
435
Прободник
О
Внешняя
д
Рис. 179.
видно также, что множитель Лагранжа в этой задаче равен ф0 (выведите
последний результат из формулы E6)). К выводу о постоянстве
потенциала можно было прийти и из физических соображений: если
бы потенциал был в разных точках различным, то заряды, свободно
перемещающиеся в проводнике, перетекали бы от областей с ббль-
шим потенциалом в области с меньшим потенциалом, так что ста-
статическое равновесие при таких усло-
условиях невозможно.
Так как потенциал связан с за-
зарядами известным уравнением Пуассо-
Пуассона (Х.43), то из постоянства потен-
потенциала можно сделать вывод, что внут-
внутри проводника р = 0, т. е. весь заряд
располагается на поверхности провод-
проводника. Впрочем, и к этому выводу можно
прийти из физических соображений.
При переходе через поверхность
проводника потенциал имеет «излом»
(рис. 179), т. е. разрыв в первой про-
производной. Если выбрать оси координат
так, чтобы начало координат нахо-
находилось в некоторой точке проводника,
а ось z пошла в направлении внешней
нормали к поверхности проводника, то производная -~ будет иметь
скачок — tg ос. Поэтому -т-|, а с ней и Дф будет иметь дельтообразную
особенность вида —tgaS(e). С другой стороны, если заряд распо-
расположен на поверхности с плотностью а, то вблизи рассматриваемой
точки будет р = об(г). Поэтому уравнение (Х.43) дает —tgcc6(z) =
= —4лаб (г), т. е. tga = 4na.
В заключение отметим, что решение задачи на условный экстремум
всегда одновременно является решением некоторой «сопряженной»
задачи на условный экстремум. Например, в задаче Дидо тот же
ответ получится, если искать минимальную длину шнура, охваты-
охватывающего заданную площадь. В самом деле, если бы некруговой
контур (Z.j) охватывал ту же площадь, что и круг (L), причем
Z.J < L, то, подобно увеличивая контур (Z.x), мы могли бы получить
контур (L2), L2 — L, охватывающий ббльшую площадь, чем (L), а
это противоречит решению задачи Дидо. Аналогично в задаче на
потенциал можно было искать максимальный заряд, который уме-
умещается на проводнике при заданном значении потенциальной энер-
энергии. В общем случае оказывается, что задача о стационарном зна-
значении величины А при условии постоянства величины В и задача
о стационарном значении величины В при условии постоянства
величины А приводят к одним и тем же решениям. В самом деле,

436 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. X;i
они сводятся к задачам о стационарности величины A-j-XB и.»ц
В-j-\iA = \i(A-\-XlB) (Я,1 = 1/[х), т. е., в силу постоянства \х, вели-
величины А -)- Х^; значит, обе задачи равносильны.
Упражнении
1. Найдите тело вращения наибольшего объема, имеющее заданную площад',
поверхности.
2. Найдите <}орму равновесия однородной тяжелой нити, подвешенной 3i
концы.
Указание. Нить должна расположиться так, чтобы ее центр тяжести
был по возможности ниже.
3. В обеих задачах укажите смысл множителя Лаграпжа.
§ 9. Задачи на экстремум с ограничениями
Остановимся еще па одном классе задач на экстремум, получив-
получивших широкое распространение в последние годы. Речь идет о зада-
задачах, в которых па искомые величины или на искомую функцию нало-
наложены дополнительные ограничения, имеющие вид неравенств.
Начнем с самого простого случая. Пусть ищется экстремум функ-
функции у = /(х), причем изменение независимой п.еременной х ограничено
неравенствами а^х^.Ь (рис. 180).
У t Тогда возможны как внутренние экст-
экстремумы (на рис. 180 максимум при
х — с и минимум при x = d), так и
концевые экстремумы (на рис. 180 кон-
концевой минимум при х=а и концевом
■максимум при х = Ь). При нахождении
внутренних экстремумов можно вос-
воспользоваться условием стационарности
у'~ 0, тогда как для концевых экстре-
Рис. 180 мумов это условие не действует, т. е.
эти последние имеют характер «ост-
«острых» экстремумов (ср., например, ВМ, § III.2).
Пусть теперь ищется экстремум функции двух переменных
z=f(x, у), причем независимые переменные связаны ограничением
F(xt У) г^ 0; мы предположим, что это неравенство определяет в
плоскости аргументов х, у некоторую конечную область (S) с гра-
границей (L) (рис. 181), на которой Fs=Q. Функция / может иметь
как внутренние экстремумы, достигающиеся внутри (S), так и гра-
граничные экстремумы, достигающиеся на (L). Для нахождения первых
можно воспользоваться условиями стационарности, разобранными п
§ IV.6, Однако, как и в одномерном случае, для граничных экстре-
экстремумов эти условия не действуют, Для нахождения граничных экст-
экстремумов можно заметить, что если в некоторой точке М (рис, 181')
функция / имеет экстремум, например минимум, то значение /(/И)
О
х

§ 9]
ЗАДАЧИ НА ЭКСТРЕМУМ С ОГРАНИЧЕНИЯМИ
437
меньше всех значений / на (I) вблизи М. Поэтому в точке М од-
одновременно достигается минимум функции /при условии /7=0, а
такие точки можно разыскать по методу § 7. Итак, граничные
экстремумы ищутся по правилу нахождения условных экстремумов.
Задачи на экстремум с ограничениями встречаются и в вариа-
вариационном вычислении. Рассмотрим в качестве примера задачу о кри-
кривой наибыстрейшего спуска, решенную в § 4, но предположим до-
дополнительно, что точке в процессе падения запрещено скатываться
Рис. 181.
Рис. 182.
ниже конечной точки, т. е. на искомое решение наложено неравен-
неравенство у^уь. Изобразим циклоиды с острием в начальной точке А
(рис. 182); при этом искомая линия должна целиком пройти r за-
заштрихованной зоне. Ясно, что если конечная точка лежит левее В,
например в положении Вх, то искомой линией служит дуга циклои-
циклоиды ABV так как это решение является наилучшим для всех линий
и удовлетворяет поставленному неравенству. Но что будет, если
конечная точка лежит правее В, например в положении В„?
Прежде всего заметим, что та часть искомой линии, которая
лежит строго внутри (не на границе) заштрихованной зоны, удов-
удовлетворяет уравнению Эйлера и потому представляет собой циклоиду.
В самом деле, если вся линия служит решением поставленной задачи,
то и любая ее дуга служит линией наибыстрейшего спуска между
своими концами*). Таким образом, искомая линия может состоять
из интегральных линий уравнения Эйлера (такие линии называются
экстремалями) и линий, лежащих на границе заштрихованной зоны.
Но теперь можно понять, что искомая линия состоит из дуги цик-
циклоиды АЪ и отрезка ВВ2. В самом деле, возьмем любую другую
возможную линию, например АВ{ВВ2. Тогда и на своем участке
*) Дуга АС между точкой А и любой точкой С, лежащей между А и В,
есть линия наибыстрейшего спуска с нулевой начальной скоростью, т. е. ре-
решает такую же задачу, которая ставилась при определении АВ. Дуга между
двумя промежуточными точками С и С" решает задачу наибыстрейшего спуска
при заданной, ненулевой начальной скорости в С", соответствующей разности
высот А и С.

438 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XI]
АВ1В она должна быть решением задачи на минимум, что неспра-
несправедливо, так как дуга циклоиды АВ дает меньшее время падения.
Легко убедиться, что нужно взять дугу именно той циклоиды, для
которой В наиболее сдвинуто вправо, т. е. циклоиды, касающейся
нижней прямой.
Таким образом, решение вариационной задачи с ограничениями
может лишь частично или совсем не удовлетворять условию стаци-
стационарности (уравнению Эйлера); это решение, как и для функций
одного переменного, имеет характер острого экстремума.
Задачи на экстремум с ограничениями могут возникать в про-
процессах управления. Например, при управлении движением какого-
либо объекта может быть поставлена задача так поворачивать рули,
чтобы за кратчайшее время вывести его на заданную траекторию.
Так как искомым является закон поворота рулей во времени, то
получается вариационная задача. При этом если рули имеют огра-
ограничители поворота (предназначенные, например, для ограничения
центробежных сил), то получается задача с ограничениями. При оп-
оптимальном процессе управления, полученном в результате решения
вариационной задачи, имеются интервалы времени, когда рули ле-
лежат на ограничителях, т. е. решение проходит по границе области,
в которой оно может находиться. При подходе к этой границе ре-
решение должно удовлетворять определенным условиям, которые мы
здесь не рассматриваем.
Упражнения
1. Найдите наибольшее и наименьшее значения функции г = х2—уг—x+t/
в треугольнике, ограниченном прямыми х — 0, у —О, х-\-у = 2.
2. Найдите положение однородной тяжелой нити длины L > 2, подвешенной
в точках (—1; 1) и A; 1), если эта нить расположена в верхней полупло-
полуплоскости О
§ 10. Вариационные принципы. Принцип Ферма в оптике
Помимо отдельных задач вариационного характера, примеры ко-
которых были разобраны в предыдущих параграфах, имеются вариа-
вариационные принципы, каждый из которых применим к анализу широ-
широкого класса явлений. Каждый из этих принципов обычно утверждает,
что из всех состояний, процессов и т. п., которые допустимы при
имеющихся связях, ограничениях в рассматриваемой физической
системе, на самом деле реализуется такое состояние, такой процесс
и т. п., для которых некоторый (вполне определенный для данного
принципа) функционал принимает стационарное значение. Каждый
из этих принципов дает возможность единообразного рассмотрения
многих задач, включения их в единую теорию и поэтому часто яв-
является значительным научным достижением.
Один из наиболее важных и общих принципов физики был уже
продемонстрирован нами на большом числе примеров. Он состоит

§ 10] ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ПРИНЦИП ФЕРМА В ОПТИКЕ 439
в том, что из всех возможных положений физической системы,
допустимых при заданных связях, равновесным является такое, при
котором потенциальная энергия рассматриваемой системы имеет ста-
стационарное значение (а при устойчивом равновесии системы имеет
минимальное значение). Если система имеет конечное число степе-
степеней свободы, то потенциальную энергию можно выразить в виде
функции конечного числа обобщенных координат (см. § IV.8), так
что применение указанного принципа сводится к нахождению мини-
минимума функции нескольких переменных (см. § IV.6). Если же рас-
сматравается сплошная среда, состояние которой описывается неко-
некоторой функцией координат (или системой таких функций), то
потенциальная энергия является функционалом, и применение этого
принципа производится на основе методов вариационного исчисления,
подобно тому как это было сделано ранее.
Одним из первых в истории науки был вариационный принцип
Ферма в оптике, который утверждает, что из всех мыслимых путей,
соединяющих две заданные точки, луч света избирает такой, кото-
который он проходит за минимальное время. Чтобы записать принцип
Ферма математически, напомним, что скорость света с в пустоте
имеет вполне определенное значение,
тогда как в прозрачной среде эта ско-
с
рость равна —, где я > 1—«показа-
1—«показатель преломления» среды, зависящий, рис. ig3.
вообще говоря, не только от среды, но и
от длины световой волны. Мы будем для простоты рассматривать
случай, когда п не зависит от длины волны и потому в каждой
среде будет иметь вполне определенное значение. Так как путь dL
проходится светом за время dt = dL: — = — dL, то время t прохож-
дения данного пути (L) вычисляется по формуле
t = -1 С п dL. F4)
с\
Таким образом, мы имеем функционал, зависящий от выбора пути,
соединяющего две точки, так что задача о нахождении формы све-
светового луча является вариационной задачей.
Из принципа Ферма можно вывести основные законы распростра-
распространения света.
Например, в случае распространения света в среде с постоян-
постоянной оптической плотностью, т. е. постоянной скоростью света,
принцип Ферма приводит к выводу, что свет распространяется по
примой линии (рис. 183, где через И обозначен источник света, а
через А—точка наблюдения), так как прямая ИА короче любой
другой линии, соединяющей точки И и А.

440
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
Рис. 184.
Отсюда в свою очередь вытекает, что если путь света состоит
из нескольких участков (например, между последовательными отра-
отражениями, преломлениями и т. д.), каждый из которых проходит н
среде постоянной оптической плотности, то каждый из этих участ-
участков представляет собой отрезок прямой, а весь путь — ломаную
линию. Для определения этого пути требуется найти координаты
вершин ломаной, т. е. здесь имеется лишь конечное число степеней
свободы. Поэтому такие задачи решаются средствами дифференци-
дифференциального исчисления. В частности, таким способом, при помощи
решения задачи на минимум, легко вывести законы отражения света
от плоской поверхности и преломления его при переходе через
плоскую поверхность раздела двух сред
(см., например, ВМ, § III.1).
Таким образом, действительно,
принцип Ферма приводит к правиль-
правильным, согласующимся с опытом выводам
для отражения и преломления света.
Рассмотрим теперь отражение света
от искривленной поверхности, касаю-
касающейся плоскости в той точке О, в ко-
которой происходило бы отражение в случае плоскости (рис. 184). На
рисунке показаны два примера' таких поверхностей, изогнутых в
противоположные стороны: IOI, касающаяся снизу, и ПОП, касаю-
касающаяся сверху оси абсцисс. (Мы рассматриваем цилиндрические по-
поверхности с образующими, перпендикулярными плоскости чертежа.)
Можно показать, что при этом достаточно рассматривать лучи,
лежащие в плоскости рисунка, и сечения отражающих поверхностей
плоскостью чертежа. Поэтому в дальнейшем будем говорить не об
отражающей плоскости, а об отражающей прямой, не об отражаю-
отражающих кривых поверхностях, а об отражающих кривых линиях IOI и
ПОИ в плоскости рис. 184.
Для рассмотрения задачи не надо конкретных вычислений. Из-
Известно (см., например, ВМ, § 11.17), что расстояние между кривой
и касательной пропорционально (л: — х0J, где х0 обозначает абсциссу
точки касания О.
Рассмотрим длины ломаных Ln {ИОПА), L] {ИО{А) и Lu (ИОиА).
Сами эти ломаные на рис. 184 не показаны, чтобы не затенять
чертеж, точки Оп, О,, Ои, как видно на рисунке, лежат правее
точки касания О, при одном и том же значении х; при этом Оп
лежит на прямой, О, — на нижней линии /, Ои— на верхней линии
//. Видк на рисунке точки И, A, On, Ор On, нетрудно представить
себе и ломаные линии.
Абсциссы Оп, О,, О,, одинаковы. Ординаты On, Oj и Ои отли-
отличаются на величину, пропорциональную (х—х0J. Следовательно,
и длины Ln, Lv Lu отличаются только на величину, пропорциональ-
пропорциональную (х — XqY- Запишем разложения Ln, Lt и Ln в ряд Тсйлира по

§ 10] ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ПРИНЦИП ФЕРМА В ОПТИКЕ 441
степеням (х—х0):
Ln (х) = Ln (х0) + (х- х0) Ln (х0) + (х~Хв)* Ln (*0) +...,
L{ (х) = L{ (х0) + (х — х0) L\ (х0) + (*~*о)* Ц (х„) +...,
Ln (х) = Lu (х0) + (х — х0) Lu (*,)+ {x~£o)t Lu (x(i) + . . . .
Раз La, L{ и Z,|, отличаются только на величину порядка (х — х0)'1,
значит,
Ln(x0) = Ll(x0) = Lu{xa), F5)
Ln (х0) = Ц {х0) = Lu (x0) (= 0), F6)
\ "(xo). F7)
Первые из этих равенств, F5), суть очевидные следствия того,
что все три линии — прямая П, кривая / и кривая //—проходят
через одну точку О, х = х0.
Вторые равенства, F6), получились благодаря тому, что в точке О
указанные три линии касаются друг друга, а угол падения луча
равен углу его отражения.
Мы знаем, что равенство нулю производной означает, что Ln, /,,
и Lu как функции д; могут иметь при х = ха минимум или макси-
максимум. Будет ли это именно минимум, а не максимум, определяется
знаком второй производной.
Для прямой мы имеем минимум, Ln > 0. Однако, мы видим из
F7), что отсюда нельзя сделать вывод для кривых линий / и //.
В частности, для линии // при достаточной кривизне ее длина /,,,
имеет в точке О, при х = х0, именно максимум, а не минимум. Бла-
Благодаря подъему кривой // слева и справа от О путь ИОиА короче
ИОА, путь ИОА является наиболее длинным из всех соседних путей
из точки И в какую-либо точку линии // и оттуда в точку А.
Опыт показывает, что и в случае кривой // отражение проис-
происходит в точке О, т. е. в той точке, где длина пути имеет максимум;
очевидно, в этой точке по-прежнему угол падения равен углу от-
отражения.
Тот факт, что длина пути может быть не минимумом, а макси-
максимумом, очень важен для понимания смысла и происхождения принципа
Ферма. Очевидно, что этот принцип не есть следствие какого-то
«стремлении» света выбирать кратчайшие пути: в случае такою
«стремления» свету было бы небезразлично, имеем ли мы дело с ми-
минимумом или с максимумом.
На самом деле принцип Ферма есть следствие того, что распро-
распространение света есть распространение волн, в которых электрическое
и магнитное поли очень быстро A015 раз в секунду в случае види-
видимого света) меняют свой знак. Соответственно очень мала и длина

442 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
волны света. В данный момент в точках, находящихся на расстоянии
половины длины волны друг от друга, знак поля противоположный.
Пусть в определенный момент в точке И (источнике света) поле имело
отрицательный знак. Знак поля в точке А зависит от того, сколько
раз успевает измениться знак на пути от //до А. Если мы рассмот-
рассмотрим два соседних пути от И до А, то при одинаковой длине путей
те поля, которые придут в точку А из И по этим путям, будут
иметь одинаковый знак; они сложатся, усиливая друг друга.
Если длины путей разные, то поля могут оказаться с одинаковым
знаком, а могут оказаться с разным знаком и в среднем взаимно
уничтожатся. В этом причина того, что для распространения света
играют роль пучки лучей одинаковой длины, с одинаковым временем
распространения.
Равенство нулю производной длины пути по координате точки
отражения означает, что по крайней мере с точностью до членов
порядка (х—х0)' длины путей одинаковы, волны, прошедшие через
точку О и ближайшие, соседние к ней, взаимно усиливаются. С этой
точки зрения, очевидно, безразлично, имеем мы дело с минимумом
или максимумом, L" > 0 или L" < 0. Более того, очевидно, что
наилучшие условия отражения получаются, когда длина пути на
возможно большем участке отражающей поверхности одинакова.
Значит, желательно, чтобы было L" = 0; тогда зависимость L от х,
при малых х, еще слабее — только в членах (х — л:0K и более
высоких. Физически £"= 0 соответствует такой кривизне отражающей
линии, при которой зеркало собирает, фокусирует в точке А лучи,
вышедшие из И.
В геометрической оптике лучи рассматриваются как геометри-
геометрические линии. На примере отражения мы только что видели, что
законы геометрической оптики являются следствием волновой при-
природы света. При этом рассматривался не один луч, а пучок сосед-
соседних лучей.
Можно дать оценку толщины этого пучка. Складываются между
собой амплитуды тех волн, у которых длина пути от И до А от-
отличается меньше, чем на половину длины волны. Составим условие
L(x) — L (х0) | = -н-. Вблизи точки отражения L' (лс0) = 0, | L (х)—
— L(xo)\ = -±—j^—\L"{xo)\, откуда \х — ха\= у [ ^ ( „ . Таким
образом, в действительности свет отражается не в одной точке
зеркала, а на пятнышке, размеры которого, как видно из формулы,
только стремятся к нулю при стремлении к нулю длины, волны.
На основании принципа Ферма можно рассмотреть и более слож-
сложную задачу о форме луча света в среде с постепенно меняющейся
оптической плотностью, например луча света, идущего от-звезды
к наблюдателю, если учитывать постепенное изменение плотности
атмосферы. Форма луча в этом случае будет криволинейная и оп-

§ 10] ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ПРИНЦИП ФЕРМА В ОПТИКЕ 443
ределится из условия стационарного значения (обычно минимума)
интеграла F4). В некоторых случаях интегрирование соответствую-
соответствующего уравнения Эйлерл можно довести до квадратур. Рассмотрим,
например, распространение света в плоскости х, у, если скорость
света зависит только от высоты у, т. е. п = п(у). Переписав F4)
в виде
ct =
можно воспользоваться промежуточным интегралом C4) уравнения
Эйлера, что даст
Отсюда легко находим
dy_V[n(y)Y--C\ Cx dy _
Если последний интеграл при том или ином специальном виде функ-
функции п (у) удастся взять, то мы получим уравнение луча в конечном
виде; в противном случае интеграл можно вычислить приближенно
(гл. I). Интересно, что при п. = " получается задача, решен-
УУи—У
ная в § 4, т. е. свет распространяется по циклоидам, а при п —поу
получается задача, решенная в § 5, т. е. свет распространяется но
цепным линиям.
Заметим, что в общем случае, когда показатель преломления
зависит от частоты света, необходимо различать так называемые
групповую и фазовую скорости света в среде.
Фазовая скорость света Сф дает соотношение между длиной волны
и периодом колебаний
При этом все поля зависят от х и t гармонически
Н, Е со cos (-= ^- J = cos \-j- {c^t — х)
(оо знак пропорциональности). Величина, стоящая под знаком коси-
косинуса, может быть названа фазой. Отсюда и происходит название
«фазовая скорость». Показатель преломления непосредственно харак-
характеризует именно фазовую скорость Сф = — , где с — скорость света
в пустоте.

444 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [гл. XII
От Сф надо отличать так называемую групповую скорость света с
Групповая скорость входит в ответ на такой вопрос: через какое
время после открытия заслонки в точке 1 свет придет в точку 2
распространяясь в однородной среде? Ответ гласит t = r1jcc, а ве-
величина сг выражается через показатель преломления так:
с„ =
, dn
Следовательно, выражение сг равно сф лишь в том частном случае,
когда п не зависит от со, сг=с^; в общем случае они различны.
Например, для рентгеновых лучей в среде л= 1 ^-, показатель
преломления меньше 1. Значит, Сф > с. Но это не значит, что сиг-
сигнал может распространяться со скоростью больше скорости света!
В самом деле, легко найдем
, dn , а . 1а , , а
1 da со2 ' «•* ' со3 '
так что сг < с.
Опыт показывает, что в принцип Ферма входят именно п и сф;
тем самым еще раз видно, что принцип Ферма не есть результат
стремления света поскорей дойти из одной точки в другую. Дело
именно в условии сложения волн, зависящем от фазы волны.
Разницу между минимальностью и стационарностью значения
функционала в реальном процессе можно понять также на следую-
следующем простом примере, взятом из статьи «Принцип наименьшего дей-
действия» знаменитого немецкого физика-теоретика Макса Планка
A858—1947). Путь свободной материальной точки, движущейся по
поверхности без воздействия внешних сил, представляет собой крат-
кратчайшую линию, соединяющую начальную и конечную точки пути.
В частности, на сфере такой линией служит дуга большого круга.
Но если путь длиннее, чем половина окружности большого круга,
то значение его длины будет, хотя и стационарным, но уже, как-
легко понять, не минимальным по сравнению с длинами соседних
путей. Это значение не будет и максимальным, так как с помощью
внесения извилин всегда можно, оставив начало и конец пути бе!
изменения, увеличить его длину. Это значение имеет характер ми-
нимакса (см. § IV.6). Вспомнив высказывающуюся одно время идею,
что в природе господствует божественный промысел и что в основе
всякого явления природы лежит сознательное намерение, направ-
направленное к определенной цели, причем эта цель достигается крат-
кратчайшим путем и наилучшими средствами, Планк по этому поводу
не без ехидства замечает: «Значит, за пределами полуокружности
божественное провидение уже не действует».

§ 11]
ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
445
Упражнения
1. Как известно, уравнение эллипса выводится из условия, что сумма
расстояний любой его точки К от двух точек F1(x1 = —с, (/ = 0) и /г2(д:,2 = с,
у — О), т. е, сумма /'\К + F2К = L, одинакова для всех точек (рис. 185). Най-
Найдите касательную и нормаль к эллипсу в произвольной его точке К- Найдите
углы между линиями F1K, F.LK и нормалью в точке К. Покажите, что все
лучи, вышедшие из Flt проходят после отражения через F2, а следовательно,
фокусируются в F2-
У
I
Рис. 185.
0\
Рис. 186.
2. Рассмотрите отражение от параболы у = хг параллельного пучка света,
идущего вниз по оси ординат (рис. 186). Считая, что свет идет из точки Л,
л:д = 0, (/д = У, и считая Y большим, замените на Y—уц расстояние Л/С,
равное У Xpr-\-(Y — Ук)г- Найдите длину L=AKN и найдите точку N, для
которой ——' = 0. Найдите касательную и нормаль к параболе в точке К "
убедитесь в том, что для точки N удовлетворяется условие равенства угла
падения углу отражения.
3. Точки И и А находятся на высоте 1 см над зеркалом и на расстоя-
расстоянии 2 см друг от друга. Найдите L" (х0) и при Л, = 5• 10—5 см найдите размеры
отражающей области.
§ 11. Принцип наименьшего действия
Успех универсального принципа минимума потенциальной энергии,
с помощью которого определяются положения равновесия системы,
побудил к поискам аналогичного универсального принципа, с помощью
которого можно было бы определять возможные движения системы.
Это привело к открытию «принципа наименьшего действия».
Рассмотрим сначала частный пример. Пусть частица массы т
движется по оси X под действием силы с потенциалом U(x).
Как известно (см., например, ВМ, § VI.8), уравнение движения при
этом имеет вид
"dfi
т. е.
= 0.
F8)
Нетрудно подобрать функционал, для которого последнее уравнение

446 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
было бы как раз уравнением Эйлера (§ 4). Обозначив ~ = х, пере-
перепишем F8) в форме
= 0. F9)
Последнее уравнение по форме напоминает уравнение Эйлера, кото-
которое в случае искомой функции х {t) должно иметь вид (ср. B9))
G0)
Однако в уравнении G0) в обоих членах дифференцируется однл
и та же функция, тогда как в уравнении F9) это не так. Поэтому
«подгоним» уравнение F9) иод вид G0), добавив под знаками про-
производных слагаемые, производная которых равна нулю:
д_
дх
Мы видим (ср. формулы B5) и B9)), что искомым функционалом
является
Заметим, что член -к- как раз равен кинетической энергии Т дви-
движущейся частицы, и обозначим подынтегральную функцию
L=T—U; G1)
это так называемая функция Лагранжа. Тогда вариационная задача
состоит в отыскании стационарного значения интеграла
G2)
который называется действием. Здесь tx и t%—начальный и конеч-
конечный моменты движения, а сравниваются между собой все мыслимые
виды движений с одинаковыми начальными условиями, а также с
одинаковыми конечными условиями. Можно проверить, что в целом
ряде случаев, например, если промежуток времени t2—^достаточно
мал, интеграл G2) имеет для реального движения не просто ста-
стационарное, а минимальное значение. Поэтому возможность отыскать
это движение, исходя из вариационной задачи для интеграла G2),
называется принципом наименьшего действия.
Оказывается, что вариационный принцип наименьшего действия
имеет универсальный характер и выполняется для любых замкнутых
систем без диссипации энергии (т. е. рассеяния, потери энергии —
например, из-за наличия трения; впрочем, систему с диссипацией

§ 11] ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ 447
можно в определенном смысле считать незамкнутой). Согласно
этому принципу из всех мыслимых (при данных связях) способов
перехода из некоторого состояния в момент /, в некоторое дру-
другое состояние в момент t.z система выбирает такой способ, для
которого действие, т. е. интеграл G2), принимает стационарное (как
правило, минимальное) значение. При этом функция Лагранжа L
представляет собой разность G1) между кинетической и потенциаль-
потенциальной энергиями системы, а каждая из этих энергий выражается через
обобщенные координаты системы (см. § IV.8) и производные от них
по времени. Принцип наименьшего действия применим как к систе-
системам с конечным числом степеней свободы, так и к сплошным средам,
причем не только к механическим, но и к электромагнитным и иным
явлениям.
Применим принцип наименьшего действия к вызоду уравнения
поперечных малых колебаний натянутой мембраны, рассмотренной
в конце § 6. Так как кинетическая энергия элемента (da) мембраны
равна
дг
где р — поверхностная плотность мембраны, то общая кинетическая
энергия мембраны равна
11
(а)
Пользуясь выражением D3) для потенциальной энергии, получаем
функцию Лагранжа и действие
«Л
I, (а)
Применяя уравнение Эйлера по трем независимым переменным
(ср. § 6), получаем уравнение колебаний мембраны
_д_
т. е.
d"-z Т [дЧ . дЧ\ ,{d-z . dh\ ( , f~T
at* p \dxz ay1) \oxL ay-) \ } p
На первый взгляд выражение G1) для функции Лагранжа пред-
представляется формальным, неестественным, так как непонятно, какой
смысл может иметь разность энергий. Положение проясняется на
следующем простом примере. При движении частицы с заданной

448 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
энергией Е в заданном стационарном потенциальном поле U траек-
траектория определяется условием минимума \p'dr вдоль пути, где
p — mv—импульс, а г — радиус-вектор. В самом деле,
T—U= 2Т—(Т + U)=r-2T—E.
Значит,
1г I, 1г 'г
$ Ldt =^ 2Tdt—'\jEdt=t\i2Tdt — E{t2 — 1l),
U '• 'г '■
где член Е(гг — tx) постоянен. Запишем 27 = 2 'Щ- = mv-v, vdt = dr
и отсюда получим, что условие экстремума \ L dt совпадает с усло-
вием экстремума [p-dr при заданных начале и конце пути и за-
заданной энергии. При этом рг = 2т(Е—U).
В то же время условие стационарности \p-dr полностью
аналогично принципу Ферма. Дело в том, что в квантовой механике
длина волны, связанная с движением тела, равна К—2я%/р, где
% — постоянная Планка, %=\0~'" . При этом вероятность найти
частицу в данной точке пропорциональна квадрату амплитуды волны,
а вблны, прошедшие по разным путям, складываются. Условие ста-
стационарности \p-dr вдоль траектории, вычисленной в классической
механике, как раз и представляет собой условие сложения с одина-
одинаковой фазой волн, прошедших по путям, близким к траектории.
Аналогия между механическими принципами наименьшего дейст-
действия и принципом Ферма сыграла большую роль в становлении кван-
квантовой механики.
Известен целый ряд других вариационных принципов в различных
областях, в том числе даже столь далеких от физики, как, например,
экономика. При решении экономической задачи мы обычно распола-
располагаем теми или иными ресурсами (деньгами, материалами и т. д.),
которые должны использовать так, чтобы в том или ином смысле
получить максимальную пользу. Таким образом, получается задача
на максимум, в которой искомым является оптимальный план исполь-
использования ресурсов, а максимизируется польза. В зависимости от ха-
характера задачи при выборе плана может быть либо конечное число
степеней свободы, т. е. искомым является набор параметров, опре-
определяющих план, либо же может быть бесконечное число степеней
свободы, так что искомой является некоторая функция. В первом
случае задача иногда решается средствами дифференциального
исчисления (§ IV.6 и § 7), а иногда, если число искомых величии
и наложенных на них ограничений велико,— средствами новой мате-

§ 12] прямые методы 449
матической дисциплины, которая называется «теорией математиче-
математического программирования». Во втором случае задача принадлежит
вариационному исчислению. Аналогичные экстремальные принципы
мы постоянно применяем и в своем поведении, хотя не всегда это
четко осознаем и не всегда применяем их наилучшим образом.
Упражнение
Исходя из выражения A1) для потенциальной энергии однородной струны
на упругой подкладке, выведите уравнение движения такой струны, не учи-
учитывая кинетической энергии подкладки.
§ 12. Прямые методы
Долгое время почти единственным путем решения вариационных
задач считался переход к дифференциальным уравнениям Эйлера.
Однако решение получающихся краевых задач для дифференциаль-
дифференциальных уравнений оказывается очень часто довольно сложным делом;
явное решение в квадратурах удается получить редко, и приходится
пользоваться приближенными методами. Еще реже получается явной
решение уравнений Эйлера для вариационных задач с несколькими
независимыми переменными.
Поэтому в последнее время часто применяется ^яд эффективных
приближенных методов непосредственного решения вариационных
задач, не связанных с переходом к дифференциальным уравнениям;
эти методы получили наименование прямых методов вариационного
исчисления. Большинство из них основано на переходе к задачам
на экстремум функции нескольких переменных, т. е. к задачам с
конечным числом степеней свободы. Мы рассмотрим здесь два таких
метода.
Первый метод основан на процессе, противоположном тому, ко-
который был описан в § 1. Там мы перешли от задачи с конечным
числом степеней свободы к вариационной задаче с помощью измель-
измельчения разбиения интервала, в результате чего сумма C) перешла
в интеграл G). С помощью обратного процесса можно перейти от
интеграла к сумме и тем самым свести задачу об экстремуме функ-
функционала к задаче об экстремуме функции нескольких переменных.
Пусть, например, рассматривается экстремум функционала B5)
при краевых условиях B6). Разбив интервал интегрирования на п
равных частей с помощью точек деления хо = а, хи х.г, ..., хп —
и обозначив у(х() =у;, заменим приближенно y'i = ^-^l
b л- I л-1
F (x, у, у') dx&^F (xh yh y't)h^h^F[ xt, yh «ШрЦ ). G3)
1=0 i=0
a
15 Я. Б. Зельдович, Л. Д. Мышкис

450 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XI!
(Как и в §§ 1.1 и П.2, можно было бы воспользоваться более точ-
точными формулами численного дифференцирования и интегрирования,
но цы здесь не будем на этом останавливаться.) Так как значения
уо=уа и уп=Уъ заданы, то задача сводится к отысканию экстре^
мума функции п—1 переменных^, _у2, ...,ytt-lt стоящей в правой
части G3). Как было показано в § 1, эту задачу иногда бывает не-
нетрудно дозести до конца.
Одним из наиболее распространенных прямых методов вариацион-
вариационного исчисления является сейчас так называемый метод Ритца*),
состоящий в том, что искомая функция ищется в виде, включаю-
включающем несколько произвольных постоянных (параметров); например, в
случае одного независимого переменного в виде
у = <р(х; С1; С„ .... С„). G4)
При этом правая часть выбирается так, чтобы для любых значений
этих параметров удовлетворялись поставленные граничные условия.
Подставляя G4) в выражение для заданного функционала, получаем,
что значение функционала оказывается зависящим от С1; С2, . .., Сп.
Тем самым задача об экстремуме функционала сводится к задаче
об экстремуме функции от п независимых параметров Сг, С2, ..., Сп,
последняя же задача решается по методам гл. IV. Конечно, полу-
получающееся при этом решение является лишь приближенным решением
исходной задачи, так как в виде G4) можно представить далеко не
любую функцию. Чем больше введено параметров С,-, тем более
«Гибкой» является формула G4), т. е. тем точнее можно предста-
представить этой формулой искомое решение, но тем сложнее получаются
вычисления. Поэтому на практике число этих параметров берется
небольшим, иногда бывает достаточно даже принять п = 1.
Приведем примеры. Пусть ищется минимум функционала
\dx G5)
о
при краевых условиях
0,уA) = \. G6)
Будем искать приближенное решение в виде
у = х + Сх(\—х). G7)
(Первое из этих слагаемых удовлетворяет условиям G6), а второе —
*) Этот метод был предложен в 1908 г. немецким физиком и математиком
Ф. Ритцем. В 1915 г. русский механик Б. Г. Галеркин A871 — 1945) применил
более общий метод, пригодный для краевых задач не обязательно вариацион-
вариационного происхождения; поэтому описанный метод иногда называют методом
Ритца-Галеркина.

§ 12] ПРЯМЫЕ МЕТОДЫ 451
соответствующим однородным условиям, не нарушающимся при
умножении на произвольную постоянную, так что вся сумма также
удовлетворяет условиям G6); по такому образцу часто составляется
функция G4) и в других примерах.) Подстановка G7) в G5) дает
после вычислений
Чтобы найти минимум этой функции от С, приравняем нулю произ-
производную:
откуда найдем С=^= — 0,227, т. е. приближенное решение G7)
имеет вид
ух = л:—0,227л: A —х) = 0,773* + 0,227л:2.
Более точный результат получится, если искать приближенное
решение в виде у = х-\-С1х(\—л:) + С2л:гA—х), включающем два
параметра. Подстановка в G5) и приравнивание нулю производных
по С1 и С2 приводят (соответствующие вычисления мы предоставляем
читателю) к значениям Сх = — 0,146, С2 =—0,163, т. е. к прибли-
приближенному решению
уи=х— 0,146л-A— х) — 0,163л:2 A— х) =
= 0,854л:—0,01 7л:2+ 0,1 63л:3.
В разобранном примере легко получить точное решение. В самом
деле, уравнение Эйлера для функционала G5) имеет вид
2у—&<??) = °> т-е- у"-у=°>
и обладает общим решением (§ VII.3)
где А и В—произвольные постоянные. При условиях G6) получаем
gX g-X
У = 1=^г-
15*

452
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XII
Это точное лишение легко сравнить с обоими приближенными ре-
решениями (см. таблицу).
X
0,0
0,1
0,2
0,3
0,4
0,5
0,000
0,080
0,164
0,252
0,346
0,443
0
0
0
0
0
0
,000
,085
,171
,259
,349
,443
уточн
0,000
0,085
0,171
0,259
0,350
0,444
X
0,
о,
о,
о,
1,
6
7
8
9
0
0
0
0
0
1
,546
,652
,764
,880
,000
0
0
0
0
1
"И
,541
,645
,756
,874
,000
. У
0
0
0
0
1
ТОЧИ
542
645
754
873
000
Таким образом, даже в простейшем варианте метод Ритца дает
в данном примере очень хорошую точность.
Еще лучшую точность дает метод Ритца, если требуется найти
не функцию, реализующую экстремум, а само экстремальное значе-
значение функционала. В самом деле, малая вариация функции вблизи
стационарного значения функционала приводит к еще меньшему
изменению значения функционала. (Сравните изменения независимого
и зависимого переменных вблизи стационарного значения функции,
например изменения х и у вблизи значения х = с на рис. 180.)
Поэтому погрешность в значении функционала будет высшего по-
порядка малости по сравнению с погрешностью в функции, которая
реализует экстремум. Так, в разобранном только что примере при
подстановке функции _у, (л:) функционал G5) дает приближенное ми-
минимальное значение 1,314, тогда как точное значение равно 1,313.
Ошибка составляет 0,1%. А чтобы уловить ошибку при подста-
подстановке уп (х), потребовались бы вычисления с значительно большей
точностью.
Если проделать аналогичные вычисления для функционала
xy2)dx,
G8)
что мы предоставим сделать читателю, то почти при том же объеме
вычислений мы также получим приближенное решение с хорошей
точностью, хотя в данном случае точное решение уже не выра-
выражается через элементарные функции. Для прямых методов это
обстоятельство не является препятствием.
Приведем еще пример на экстремальную задачу для функции
двух переменных. Пусть ищется экстремум функционала
г
диу (да
dx dy
G9)

ОТВЕТЫ И РЕШЕНИЯ 453
среди функций, обращающихся в нуль на границе квадрата, огра-
ограниченного прямыми Л"=+1, J>=±1. В этом случае уравнение
Эйлера не решается точно с помощью элементарных функций. При-
Приближенное решение по методу Ритца ищем в виде
и = СA— л:2) A— у2).
Подстановка в G9) дает
i i
/= J J {[ —2С* A—/)]■+[ —2СуA—**)]»->
-I -I
+ 2С A — х4-) A — у2)} dx dy =
Приравнивание производной нулю дает минимум при С= ■—jg.
Значит, решение задачи о минимуме функционала G9) при задан-
заданных граничных условиях приближенно имеет вид
Сравнение с точной формулой (имеющей вид бесконечного ряда)
показывает, что погрешность этого приближенного решения в среднем
равна 1,5%; погрешность в значении функционала / около 0,2%.
Упражнения
1. Найдите приближенное решение задачи о минимуме функционала G5)
при условиях G6), выбрав приближенное решение в форме у=х-\-С sin пх.
Сравните полученные значения / и у @,5) с точными.
2. Найдите приближенное решение задачи о минимуме функционала G8)
при условиях G6), выбрав приближенное решение в виде G7).
3. Найдите приближенное решение разобранной в основном тексте задачи
о минимуме функционала G9), выбрав приближенное решение в виде
u = Ccos ^cos'-jj-. Сравните полученные значения / и ы@, 0) с найденными
в основном тексте.
ОТВЕТЫ И РЕШЕНИЯ
§ 1
Рассуждая, как в тексте, находим
yl=-~[(i-l)Fl + (i-2)F2+...+F;.1] + ii,l]

454 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
откуда
д/
1,2
—0,098
0,01002
0
б/
1
-0,1
0,01
0
относительная ошибка
—2%
-0,2%
+—
Полагая л=—, '=-т*> F,- = f(xi)h, h—>■ 0, получим в пределе
С-9/ЙL (ср- § VI.2).
6 X
§2
I I
1. б/ = — Г ^ йа;; 2</ @) б</ @) + Г (хоу + 2</'6</') d*.
J У J
о о
Sf ее2
Bл: + ах2J йл; — \ Bл;J йл;= а + -g-; о/ = а.
J о
Результаты подсчета:
а
-0,1
0,01
§3
Уравнение B2) в обоих случаях имеет вид A—хJ(у—2л;) —0, откуда
у = 2х. Это решение придает функционалу стационарное значение / = 0, кото-
которое лишь в случае а) является минимальным. В случае б) решение имеет
характер мииимакса (ср. § 1V.6), а задача па минимум решения не имеет.
§4
1. а) Уравнение Эйлера имеет вид 2у—-г- Bу') = 0, т. е. у"—у = 0, откуда
у = С1ех-\-Сге~х (см. § VII.3). Из граничных условий получаем 0 = С1-\-С2,
l=Cie+C2e-1» откуда С1= _ у , С2 = ^_ -_j и окончательно
б) по формуле C4) уу'* — 2уу'-у' = С, уу'*=—С, V"ydy= ± У^С dx,
О
у3/'=± — У—Cx-\-C2 = Clx-}-C2. Из граничных условий р'/г = С2,
q'/s =C1JrC2, откуда у'/г ■= {д'/г—р'/г) х-\-р'/г и окончательно у =
2. Подстановка последнего решения в / дает после вычислений значе-
значение -_- {q3/' — ps/'J; отсюда ^-= о" Р>/г (ч"/г —Р /z)- По формуле, выведенной
dl
в тексте, т—=—■
'dp
= —g р'/2{д3/г~-р'/г), т. е. то же.

ОТВЕТЫ И РЕШЕНИЯ 455
ь
3. Так как длина графика у = }(х) (а<л;<6) равна \ Y~\ -\-y'2dx, то за-
а
дача сводится к определению линии, придающей этому функционалу минимальное
значение при условиях B6). Из C4) получаем V^l+y'2 jJUL=r=C, от-
откуда y' = Clt i/ = C1a; + C2. Это—уравнение прямых.
§5
Из уравнения Эйлера получается, что при а Ф л, 2я, Зя, ... единствен-
единственной функцией, удовлетворяющей граничным условиям и придающей функцио-
функционалу стационарное значение, служит г/эаО. Подставляя у = Сх(а—х), полу-
дЗ
чим / = С2~„A0— а2), откуда видим, что при а > у 10 задача на минимум
пх С2
решения не имеет. Подставляя у = С sin—, получаем / = т—(я3—а2), откуда
видим, что при а > л задача на минимум решения не имеет. Можно доказать,
что так будет и при а^=2л, Зя, ..., а при а < л функция </ = 0 служит ре-
решением задачи на минимум.
§в
ь
1. Аналогично B7) приходим к равенству \ (F'yby-\-Fy'by' + F'ynby°) dx = 0.
j
а
Интегрируя по частям второе слагаемое один раз, а третье—два раза, по-
получим
Ь
■j ('J-5';•+!?
a
откуда приходим к искомому уравнению
у dx v dx'1 y
2. Обозначим для краткости г'х = р, г'=д; получим уравнение
F'—F" —F" —-F" ~—2F" ^- — f -F" —-.F" d2z— 0
§7
а)и*=х2—j/2 + z2—2х—\ (х-\-2у— г); отсюда условия стационарности
дают
2х— 2—1 = 0, — 2у— 2Х = 0, 2г + Х = 0.
Выражая отсюда х, у, г через \ и подставляя в уравнение связи, получаем
Х=—2, откуда координаты точки условного экстремума х = 0, у = 2, г=1;
б) и* =x2—y2+z2 — 2x—'ki (х-}-у—г) — Х2 (х + 2у). Отсюда 2х—2— %г — Х^ = 0,
—2у—Xj — 2Х2 = 0, 2г + Х1 = 0. Привлекая уравнения связи, получаем *=-к->
1 3

456 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XU
§8
1. Пусть Ох—ось вращения, а у = у(х)^гО (а<л;<Ь)—уравнение кон-
контура осевого сечения; тогда объем и поверхность тела вращения выражаются
ь ь
но формулам (см. например, ВМ, § III.7) V = n \ у2 dx, S = 2n \ у Y~\-\-y'-dx.
а а
Промежуточный интеграл C4) для функции л {у4- — 2\у У~1+у'2) имеет вид
т. е.
2К
как у может равняться нулю, то С1=0, и мы получаем у— =0,
V 1+J/'2
откуда, интегрируя, находим (* + CJ + </2 = 4A.2. Искомым телом является шар.
2. Так как длина L подвешенной нити (L) с уравнением у = у(х) задана,
а высота центра тяжести, как вытекает из § XI.2, определяется формулой
Уи.. т.= ~г~ \ У dLt то задача сводится к минимизации интеграла В= \ у AL =
(М (L)
= \ у У~\ + у'~* dx при заданном L= \ |/"l -\-у"г dx. Уравнение Эйлера надо
(L) (Ц
писать для функции у V~l-\-y'2 — A. Vl+y*=(y—к) Vi+y, которая после
подстановки у—Ъ = у переходит в функцию, исследованную в примере § 5.
Решением задачи служит цепная линия с уравнением У — щ 1е>с
_j_ e-k u+C)j_j_^( где ^) Qt ^—произвольные постоянные.
3. В первом примере ^. = „-5-, где R — радиус шара. Во втором при-
мере А. равно разности между ординатой крайней нижней точки цепной линии
и радиусом кривизны в этой точке.
§ 9
1. Функция г имеет стационарное значение г = 0 в точке \-п\ "о"
катетах имеется по одному условному стационарному значению z=-j-
в точке ( 0; -=-1 и г -— -г в точке (-=-; 0).В вершинах значения равны 0,
—2 и 2. Значит, гтах = 2 достигается в точке B; 0), zmjn = — 2 достигается
в точке @; 2).
2. В упражнении 2 § 8 мы получили уравнение висящих участков нити.
Здесь возможны доа случая. Если нить достаточно коротка, L < Lo. так что
gfeX _L g— kX
она не достает до «пола», т. е. прямой г/ = 0, получаем г/= ^
gk e~k
j\-l. При этом L = , так что при заданном L можно чис-
2 J-2ft—ек е~к
ленно найти ft. Так как j/min = —' =1 • то ^о определяется потому k > 0,
для которого 2 + 2ft = es + e-*. При L > Lo линия состоит из двух провисаю-
провисающих участков и одного, лежащего на полу. Правый провисающий участок
gfcU-C) e-h's-C) 1 gk (l-C) 1 e-k (l-C)
имеет уравнение г/ = —^ 1 ^ — , причем ^

ОТВЕТЫ И РЕШЕНИЯ 457
■—т- = 1, откуда можно выразить С через к. Длина всей линии равна L =
рк A-С) р-к A-С)
§ Ю
1. Уравнение эллипса У~(Х+СУ2+У2 + Y'(x—cyi-}-yi — L, после преобра-
преобразований 4 (L2 — 4с2) x2+4Laj/a = L2 (La—4с2). Уравнения касательной и нор-
нормали в произвольной точке (х0; у0) соответственно
-x°] и у-у°=
Искомые углы находятся по формуле tg ф — а) = уцК 1—о • Для первого
угла надо положить tgcc = —Щ— , tgP = -T-r—j^r—, откуда находим после
Xq-j-C (L 4c j Xo
преобразований tg (P—а) = ' . Тому же оказывается равным тангенс
второго угла, откуда и вытекает последнее утверждение упражнения 1.
2. Если точка N имеет координаты @; г/дг), то
тг dL „ 1 ,,
Из условия —г— =0 находим, что Удг = -т ■ Уравнения касательной и нор-
мали в точке К имеют соответственно вид
у—х\=2хк{х—хк) и у—х\=— к--(х—хк),
ХК J
а уравнение прямой NK имеет вид у—х% = (•*—хк)- Равенство тре-
ХК
буемых углов доказываем подобно упражнению 1.
3. Пусть точки И и А имеют координаты (—1; 1) и A; 1). Тогда
L = У(х + 1 )J + 1 + V(x — 1 У1 + 1, *0 = 0, L" (х0) — —— см, откуда отражаю-
;~Ъ-10~5
щая область имеет диаметр 2 1/ ■ —— = 1,7• 10~2 см =0,1/ мм,
t 1/^2
§ П
В данном примере
Выписывая интеграл действия, а затем применяя уравнение Эйлера из § 6,
получим искомое уравнение в виде —ky-\-f (х) — -=-, ( р -jr. J + j- ( f ч^ ) =0,
а-!/ Р 52j/ ft 1 £ , ,

458 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XII
§ 12
4 2 л2+1
1. Подставляя д = х + С sin гтх в G5), получаем / = -к-Н—СЧ ~— С2.
Из условия -7тт = 0 находим С= ,Т, ,. =—0,0588. Значения/ и г/ @,5)
аС л (n'-f-1)
получаются равными 1,315 (ошибка 0,2%) и 0,441 (ошибка 0,7%).
5 С 1С1
2. Подставляя, получаем / = -j- + ^ + -^- . Из условия минимальности
3. Подставляя, получаем /=—=—] j-. Из условия минимальности
32
С= j=—0,331. Значения / и и @, 0) получаются равными ^0,537 и
1—0,331 вместо —0,556 и —0,312.

ГЛАВА XIII
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
§ 1. Постановка вопроса
В природе и в технике часто встречаются явления, изучение
которых требует знания особой отрасли математики, так называе-
называемой теории вероятностей.
Простейший пример, который всегда приводится по этому поводу,
состоит в следующем. Будем подбрасывать монету. При падении
она ложится на стол либо вверх гербом, либо вверх стороной, на
которой обозначена стоимость (решкой). Если бросить монету так,
чтобы она сделала в воздухе много оборотов, то в среднем монета
будет падать одинаково часто вверх гербом и вверх решкой. Если
произвести большое число N подбрасываний, то получим прибли-
приблизительно \y)N pa3 герб и \y)n Раз РешкУ- Множители при
N одинаковые и равны у как для случая выпадания герба, так и
для случая выпадания решки. Их в данном случае называют вероят-
вероятностями. Таким образом, говорят, что при отдельном бросании
вероятность wt получить герб равна у, вероятность wv получить
1
решку также равна -н-.
Возьмем еще пример. Рассмотрим кубик, одна грань которого
выкрашена в белый цвет, а остальные пять сторон — в черный.
При бросании такого кубика большое число N раз мы получим
приблизительно (-g-)N раз сверху белую сторону и (-g-)A/ раз —
черную*). Поэтому говорят, что вероятность появления наверху
белой грани w6=-zr, а вероятность появления наверху черной грани
w4—-r. Ясно, что если есть два взаимно исключающих нехода
отдельного испытания (герб пли решка в первом примере, белая
*) Мы предполагаем, что кубик изготовлен из однородного материала.

460 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
или черная грань во втором примере), то сумма их вероятностей
равна 1.
Следующий пример связан с вопросом о радиоактивном распаде.
(Подробно радиоактивный распад был рассмотрен в ВМ, гл. V.)
Будем наблюдать за отдельным атомом радиоактивного вещества.
Вероятность того, что за малое время т, прошедшее после того, как
мы начали наблюдать за этим атомом, он распадается, равна wx,
где w—постоянная величина, т. е. эта вероятность пропорциональна
продолжительности промежутка времени т. Вероятность того, что
за это время радиоактивного распада не произойдет, равна, следо-
следовательно, 1—wx. Постоянная w характеризует данное радиоактив-
радиоактивное вещество. Она имеет размерность — и связана со средним вре-
менем жизни Т данного элемента соотношением да = ^г.
Ясно, что вероятность распада может быть равна wx лишь для
весьма малых промежутков времени т. Действительно, для больших
х мы можем получить, например, тут>1, что явно бессмысленно.
Поэтому мы должны рассматривать весьма малый промежуток вре-
времени dt. При этом мы будем иметь дело с весьма малой вероят-
вероятностью распада w-dt и с весьма близкой к единице A—w dt)
вероятностью атома не испытать распада. Отсюда в § 5 получится
вероятность а не распасться за конечное время t, а=(\—wdt)l/dt =
= e~wt, и вероятность Ь распада за это время, Ь=1—а=\—е~ш.
Бывает так, что возможно несколько (больше двух) исходов
отдельного испытания. Так, например, при бросании обычной играль-
игральной кости (кубика с различными цифрами от 1 до 6 на его гранях)
возможны шесть различных исходов: может выпасть грань с циф-
цифрой 1, может грань с цифрой 2 и т. д. до цифры 6. Вероятность
каждого исхода равна -^.
Наконец, результат отдельного испытания может характеризо-
характеризоваться величиной, которая принимает непрерывный ряд значений.
Таков, например, при ловле рыбы удочкой вес р отдельной вылов-
выловленной рыбы. Грубо можно подразделить рыб, например, на маль-
мальков весом до 100 г*), средних, весом от 100 г до 1 кг, и боль-
больших, весом больше 1 кг. Тогда возможный исход вытаскивания из
пруда одной рыбы будет характеризоваться тремя числами: вероят-
вероятностью вытащить малька wM, вероятностью вытащить среднюю рыбу
wc и вероятностью вытащить большую рыбу w6. При этом
Однако такое описание рыбной ловли является очень грубым. Так,
например, ответ «поймана большая рыба» может означать, что
выловлена рыба в 1,1 кг, а может означать, что выловлена рыба в 20 кг.
*) Мы сознаем, что такое определение малька является довольно спор-
спорным с точки зрения профессионального рыболова.

§ 1] ПОСТАНОВКА ВОПРОСА 461
Вероятность вытащить рыбу, вес которой лежит в пределах от
р до p-\-dp, где dp — весьма малое приращение веса, будем обозна-
обозначать через dw. Естественно, эта вероятность пропорциональна dp.
Кроме того, dw зависит и от р.
В самом деле, нет никаких оснований считать, что вероятность
поймать рыбу, вес которой заключен в пределах от 100 до НО г,
такова же, как вероятность поймать рыбу, вес которой лежит в пре-
пределах от 1000 до 1010 г. Положим поэтому
dw = F (p) dp.
Входящая сюда функция F (р) называется функцией распределения
вероятностей.
Мы знаем, что сумма всех вероятностей выловить ту или иную
рыбу равна 1, это дает
со
nF(p)dp=\.
Можно несколько видоизменить задачу и рассматривать не вылав-
вылавливание какой-либо рыбы, а в качестве отдельного испытания рас-
рассматривать забрасывание крючка. Это забрасывание крючка иногда
сопровождается вылавливанием рыбы, а иногда (к сожалению, не-
нередко) и не приводит к вылавливанию рыбы. Можно ввести вероят-
вероятность вытаскивания пустого крючка k и вероятность вытаскивания
рыбы (любого веса), равную 1—k, а затем уже подразделять слу-
случаи вытаскивания той или иной рыбы в соответствии с функцией
F (р). Можно пойти по другому пути. Вытаскивание пустого крючка
можно назвать «вылавливанием рыбы, вес которой равен• нулю».
Тогда не надо будет явно упоминать о таком печальном случае,
как вытаскивание пустого крючка. При этом получится новая
функция распределения вероятностей /(р). Это будет функция, для
со
которой нуль является особой точкой. Интеграл \f(p)dp=\, но
о
в этот интеграл точка р = 0 дает конечный вклад; это значит, что
/ (р) содержит член вида Лб (р) (см. о понятии дельта-функции
в гл. VI). Новая функция f(p), относящаяся к одному забрасыва-
забрасыванию крючка, связана со старой функцией F(р) (которая относилась
к одной настоящей, с р > 0', выловленной рыбе) соотношением
На нескольких примерах мы обрисовали тот материал, с кото-
которым имеет дело теория вероятностей. Ниже будет рассматриваться
ряд вопросов, возникающих при этом.
Например, пусть монета брошена пять раз. Какова вероятность
того, что во всех пяти бросаниях выпадает герб? Какова вероят-
вероятность того, что в четырех случаях будет герб, а в одном — решка

462 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
(причем безразлично, в каком именно по порядку бросания появи-
появилась решка — в первом, втором н т. д. или в последнем)? При этом
мы считаем, что вероятность- получить герб в одном бросании
равна -я-. Решение такого рода задач требует известной алгебраи-
алгебраической сноровки, а при очень больших числах бросания приходится
применять методы высшей математики, так как иначе расчеты ста-
становятся практически невыполнимыми. Следующий круг вопросов —
явление радиоактивного распада. Основываясь на вероятности распада
за время dt, требуется найти вероятность распада за время t, которое
может быть каким угодно, а вовсе не обязательно малым. При реше-
решении этого вопроса нам потребуется аппарат высшей математики,
(Мы получим, в -частности, ряд результатов ВМ, гл. V, применяя,
однако, несколько иной ход рассуждений.)
В главе V ВМ рассматривалось большое число атомов N и полу-
получился закон изменения N со временем. По существу, там рассмат-
рассматривались только средние величины. Новый подход позволит решить
гораздо более тонкие вопросы, например: какова вероятность наблю-
наблюдать в некотором приборе то или иное число распадов, отличаю-
отличающееся от среднего?
В задаче о рыбной ловле можно ставить вопрос о вероятности
получить тот или иной улов в результате вылавливания 2, 3, ..., п
рыб или в результате забрасывания крючка 2, 3, ..., п раз. По-
Последняя задача требует довольно высокой математической техники.
При выводе законов теории вероятностей нам понадобится фор-
мула Стирлинга (§ III.3), а также формула \ е~*2 ^дг = ]/я, выведен-
ная в § IV.7.
Упражнение
При игре в «подкидного дурака» пользуются колодой из 36 карт, распре-
распределенных по четырем мастям. Какова вероятность того, что первой сданной
картой будет карта пиковой масти? дама? дама пик? козырь (козырной слу-
служит масть первой карты, оставшейся после сдачи)?
§ 2. Умножение вероятностей
Основой решения задач, поставленных в § 1, является правило
умножения вероятностей независимых событий.
Поясним это правило на простом примере. Пусть один кубик
имеет одну белую и пять черных граней, так что вероятность
появления белой грани w6 = —, а вероятность появления черной
грани w4=-g-. Пусть имеется еще один кубик, у которого
две грани окрашены в зеленый цвет, а четыре — в красный. Для
этого кубика вероятности появления зеленой и красной граней

§ 2] УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 463
соответственно равны
2
Положим оба кубика в один стакан, потрясем его и бросим кубики
на стол. Возможны четыре различных исхода опыта, а именно, на
одном кубике белая грань, на другом— зеленая; на одном кубике
белая грань, на другом — красная; на одном кубике черная грань,
на другом—зеленая, и, наконец, на одном кубике черная грань,
на другом — красная. Будем эти исходы обозначать коротко так:
бз, бк, мз, чк. Число случаев, в которых осуществляются эти
исходы, обозначаем через N63, N6li, N43, N4K, а соответствующие
вероятности через w&3, w6li, w43, w4K. Поставим задачу определить
эти вероятности.
Пусть мы проделали очень большое число опытов N, Разделим
все опыты на две группы: те, в которых на первом кубике появи-
появилась белая грань (б) (независимо от цвета грани на втором кубике),
и те, в которых на первом кубике появилась черная грань (ч)
(независимо от цвета грани на втором кубике). Таким образом,
N' 1
N=N6-\-N4. Так как w6 = -rp , то N6 = w6• N = -^N. Точно так же
N4 = w4-N=~N.
С другой стороны, ясно, что N6 = N63-\- N6li. Дальше нам необ-
необходимо воспользоваться понятием независимости событий. Мы пред-
предполагаем, что тот факт, что на первом кубике выпала именно белая
грань, не влияет на вероятность появления зеленой или красной
грани на втором кубике. Иначе говоря, мы считаем, что два собы-
события— появление грани определенного цвета на первом кубике и
появление грани определенного цвета на втором кубике—незави-
кубике—независимы. Исход одного из этих событий никак не влияет на исход
другого. Ввиду этого вероятность появления на втором кубике зеле-
зеленой грани да3 = -др-, а вероятность появления на втором кубике
красной грани wK—-j^-. Отсюда находим N63 = w3'N6 = w3-w6-N.
С другой стороны, дабз = -гг, поэтому
w63 = w6-w3.
Таким образом, вероятность сложного события (появление на
одном кубике белой, а на другом зеленой граней) равна произве-
произведению вероятностей простых независимых событий.
Теперь ясно, что
w6k = W6-Wxv W43 = W4-W3, ™ЧК=те'ч-'а;к'
Мы уже отмечали, что при одновременном бросании двух куби-
кубиков, о которых идет речь, возможны лишь четыре следующих ис-
исхода; бз, бк, чз, чк.

464 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Поэтому должно быть
^бз + ^бк + ^чз + ^ч^1-
Нетрудно убедиться, что это действительно так. В самом деле,
= W6 • (W3 + WK) + W4 ■ {W3 + WK) = (W3 + WK) (W6 + W4).
В каждой из последних двух скобок написана сумма вероятнос-
вероятностей двух простых событий, каждое из которых исключает другое
и какое-то одно из которых обязательно произойдет. (Если выпадет
белая грань, то не выпадет черная, и наоборот. Либо черная, либо
белая грань появятся обязательно). Ясно, что такая сумма вероят-
вероятностей равна единице:
w6 + w4 = 1, + 1
откуда и следует, что
Перейдем к следующему примеру. Пусть имеется кубик с неко-
некоторым (неважно, каким именно) количеством белых и некоторым
количеством черных граней. Обозначим вероятности появления белой
и черной граней при одном бросании кубика через а и |i соответ-
соответственно. Пусть опыт состоит в трехкратном бросании такого кубика.
Так как в каждом бросании возможны два исхода, то в результате
нашего опыта возможно 23 = 8 различных исходов*).
Перечислим их в следующей схеме:
Первое
бросание
Второе
бросание
Третье
бросание
у б
Исход трех
бросаний
16; 26; 36
Вероятность
исхода
а3
16; 26; Зч
. у б
"ч
^^_—-+6
У Ц
~~ * ч
16; 2ч; 36
16; 2ч; Зч
1ч; 26; 36
1ч; 26; Зч
1ч; 2ч; 36
1ч; ч; Зч
а?р
ар3
я2р
а|-
арз
*) Если опыт состоит в бросании кубика п раз, то возможны 2" различ-
различных исходов.

§ 2] УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 465
Проследив за каждой стрелкой схемы, мы видим все восемь воз-
возможных исходов. В предпоследнем столбце схемы эти исходы запи-
записаны кратко: цифра означает номер бросания, а буква — исход этого
бросания. Так, например, запись 1ч; 26; Зч означает, что в первом
бросании появилась черная грань, во втором бросании—белая, в
третьем—опять черная. В последнем столбце выписаны вероятности
каждого из этих восьми исходов. Эти вероятности легко подсчиты-
ваются по правилу умножения вероятностей.
В составленной выше таблице мы различаем, например, случаи
16, 26, Зч и 1ч, 26, 36; в обоих этих случаях один раз выпала
черная грань и два раза белая, только в первом случае черная
грань появилась при третьем бросании, а во втором случае — при
первом. Обычно в конкретных задачах такого типа нас интересует
только общее количество появлений белой грани и общее количе-
количество появлений черной грани, а порядок появлений безразличен.
С этой точки зрения восемь рассмотренных случаев разбиваются
на четыре группы:
6 = 3, ч = 0; 6 = 2, ч=1; 6=1, ч = 2; 6 = 0, ч = 3*).
Эти обозначения понятны: б = 2, ч= 1 означает группу, состоящую
из всех случаев, в которых два раза выпала белая грань и один
раз черная. (Порядок выпадения безразличен.) Составим таблицу,
в которой выписаны все эти группы, все случаи, на которые рас-
распадается каждая группа, вероятности каждого случая и вероятности
каждой группы.
Для того чтобы подсчитать вероятность группы, заметим сле-
следующее.
Если какая-нибудь группа событий объединяет несколько несов-ч
местных случаев, то вероятность группы, т. е. вероятность того,
что произойдет какой-либо один из этих случаев, равна сумме вероят-
вероятностей независимых случаев, составляющих группу. Поясним сказан-
сказанное примером. Пусть мы бросаем кубик, у которого есть белые,
черные и красные грани, причем вероятности появления граней этих
цветов соответственно равны
"Wtr fWu *W (t^(< ~]*~ *№ ~^~ *№ ^-^ 1).
Рассмотрим группу событий, состоящую в том, что появилась либо
белая, либо черная грань. Вероятность этой группы обозначим через
w6+4. Найдем w6+4.
Так как w6='-£, w4 = '-~, то N6 = w6-N, N4 = w4-N, где Л; —
общее число бросаний кубика. Ясно, что таб+ч = ■'■■f' * ' ч = Шб'''Т"'4 =
= таб + и;ч. Итак, w6 + 4==wf)-\-w4.
*) Если опыт состоит в бросании кубика п раз, то 2" случаев разби-
разбиваются на п+1 группу
б = п, ч = 0; б = п—1, ч=1; б = я—2, ч = 2; ...; 6 = 0, ч = п.

466 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Теперь приводим таблицу, о которой шла речь выше.
[гл. хщ
Группа
0 = 3, 4 = 0
6 = 2, 4=1
6=1, 4 = 2
6 = 0, 4 = 3
Случаи
16; 26; 36
16; 26; 34
16; 2ч; 36
1ч; 26; 36
16; 2ч; Зч
14; 26; Зч
1ч; 24; 36
1ч; 2ч; 34
Вероятность
случаи
а3
CCrft
a2f5
сф3
ар2
Р3
Вероятность
группы
а3
3a2P
Зсф2
Нетрудно убедиться, что при я-кратном бросании кубика вероят-
вероятность появления т белых и k черных граней (/»-|-& = я) при задан-
заданном законе чередования белых и черных граней равна am|ift. Группа
б = т, ч = k включает в себя все случаи, в которых выпало т белых
и k черных граней с различным порядком чередования белых и чер-
черных граней.
Вероятность группы б — гп, ч = й равна тому члену разложения
бинома Ньютона
который содержит множитель am|ift, т. е. равна -^~г-.а.т§к.
В самом деле, что представляет собой коэффициент при am|ift
в разложении (сх —j— fi)" по формуле бинома Ньютона? Это число спо-
способов, которыми можно набрать тп множителей а и k множителей |i,
раскрывая скобки в произведении
... (a+fth
п раз
Точно так же число случаев в группе есть число способов, кото-
которыми можно осуществить m белых граней и k черных граней, чере-
чередуя в различном порядке белые и черные грани. Следовательно,
коэффициент при a'"|Jft в разложении (a-|-|J)n по биному Ньютона
равен числу случаев в группе. Вероятность каждого определенного
случая б = rn, 4 = fe равна согласно правилу умножения вероятно-
вероятностей am|ift. Поэтому вероятность группы равна соответствующему
члену разложения по биному Ньютона.
Ясно, что сумма вероятностей всех групп должна быть равна 1,
так как все группы охватывают все возможные случаи. Проверим это.

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 467
Так как ос + |}=1, то (oc-f |i)"= 1. С другой сторонь^
= wF = n, ч = 0) -\-w F = п— 1, ч=1) +
JrwF = n — 2, ч = 2) + ...+та F = 0, ч = л)*).
Таким образом,
■к>(б=я, ч = 0)+да (б = л—1, ч = 1)+ ... + да F = 0, ч = л) = 1.
Упражнения
1. Какова вероятность, что при двукратном бросании монеты она оба
раза ляжет гербом вверх.
2. Монета брошена три раза. Какова вероятность, что все три раза монета
ляжет гербом вверх; два раза вверх гербом и один раз вверх решкой?
3. Четыре грани кубика окрашены в черный цвет, а две — в белый. Какова
вероятность, что при двукратном бросании выпадут оба раза белые грани;
оба раза черные грани; один раз белая, другой раз черная грань?
4. Кубик предыдущей задачи бросают три раза. Какова вероятность того,
что два раза появится белая грань и один раз черная; два раза черная и
один раз белая?
5. Производится стрельба по мишени. При каждом выстреле вероятность
попасть равна 0,1, а вероятность промахнуться равна 0,9. Произведено два
выстрела. Какова вероятность того, что будет одно попадание и один промах?
6. В условиях упражнения 5 произведено три выстрела. Какова вероят-
вероятность того, что среди них одно попадание и два промаха; два попадания и
один промах?
7. Производится стрельба, описанная в упражнении 5. Какова вероят-
вероятность попасть в мишень один раз, если сделано четыре выстрела; если сде-
сделано пять выстрелов?
§ 3. Анализ результатов многих испытаний
В предыдущем параграфе получены общие формулы для случая п
одинаковых испытаний, в каждом из которых возможны два различ-
различных исхода с вероятностями а и |i соответственно.
При небольших значениях числа испытаний п эти формулы до-
достаточно просты и наглядны.
Однако если п велико, то формулы перестают быть наглядными.
Поэтому необходимо проделать дополнительную работу для того,
чтобы записать эти формулы в удобном и наглядном виде. Только
после такой работы, "подобной извлечению драгоценного камня из
породы **) и шлифовке его, результаты станут яркими, запоминаю-
запоминающимися, зовущими к дальнейшим обобщениям.
*) Запись wF=m, ч — k) означает вероятность той группы, в которой
белая грань появляется т раз, а черная k раз.
**) «Наука та же добыча радия — в грамм добыча, в год труды, изводишь
единой формулы ради тысячу тонн словесной руды», мог бы сказать Мая-
Маяковский.

468 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Рассмотрим сначала простейший случай а= |} = 1/2, соответствую-
соответствующий, например, бросанию монеты или бросанию кубика с тремя
белыми и тремя черными гранями.
Возьмем, например, я=100. Ясно, что вероятность получить при
ста бросаниях монеты вес 100 раз герб (или все 100 раз решку)
весьма мала. Согласно результатам § 2 она равна (-к-) — ш>~
~ Tmo ■ Если машина производит 100 бросаний монеты в секунду,
то потребуется в среднем 1028 сек« 3-1030 лет, чтобы получить
один такой случай, когда 100 раз подряд выпадет герб. Ясно, что
в подавляющем большинстве случаев в результате ста бросаний
выпадет примерно 50 раз герб и 50 раз решка. Но совершенно не
очевидно, какова вероятность того, что в ста бросаниях получится
точно 50 раз герб и точно 50 раз решка. Неясно, какова вероят-
вероятность исхода, отличного от среднего. Например, какова вероятность,
что выпадет 55 гербов и 45 решек или 60 гербов и 40 решек? .
Постараемся ответить на поставленные вопросы.
Прежде всего заметим, что вероятность каждого определенного
случая появления 50 решек и 50 гербов, например, когда в первом
бросании появляется герб, во втором — решка, затем опять герб,
потом опять решка и т. д. (герб и решка появляются по оче-
очереди), равна -moo" ^ Tmo • как было установлено в § 2, т.- е. эта
вероятность равна вероятности появления герба 100 раз подряд.
Значительно большая вероятность появления 50 гербов и 50 решек
(в любом порядке) происходит за счет того, что это событие, эта
«группа», как мы говорили в § 2, состоит из очень большого числа
различных случаев разного чередования гербов и решек,
В § 2 мы выяснили, что эта вероятность равна
m\k\ ' '
где а — вероятность герба, |i—вероятность решки, п — число броса-
бросаний, m — число появлений герба, k—число появлений решки
(m-\-k — п). Будем рассматривать четное п (в нашем конкретном при-
примере п = 100). Тогда нас интересует появление -*- решек и -р- гербов.
Поэтому
п\ _ ■ п\
т\ k\'
а вероятность интересующего пас события есть
п п \ п\
' ~2

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 469
При больших п это выражение крайне неудобно для вычисле-
вычислений. Упростим его, используя приближенную формулу Стирлинга для
выражения п\ (см. § III.3).
По формуле Стирлинга я! = |/яя ( — ) , (-^ )! =]/ял (•£■
поэтому получаем
В частности, для л =100 находим w= у -^0,08. Вероят-
Вероятность появления 50 гербов и 50 решек в определенном порядке
равна приблизительно 10~30. Поэтому число различных случаев, в ко-
которых в различном порядке осуществляется одинаковый результат,
равно
Теперь постараемся научиться определять вероятность исхода
испытания, мало отличающегося от наиболее вероятного. (В рас-
рассматриваемом примере наиболее вероятный исход — 50 решек и
50 гербов.) Обозначим через 6 отклонение исхода от наиболее ве-
вероятного, 6 = т—п~. Так, например, 6 = 5 соответствуют 55 гербов,
45 решек, 6 = — 5 соответствуют 45 гербов, 55 решек, 6 = 3 соот-
соответствуют 53 герба, 47 решек и т. д. Вероятность соответствующего
исхода испытания обозначим через w(8). Наиболее вероятному
результату соответствует 6 = 0, так что
w@)= 1/ — . A)
к ' У пп w
Подсчитаем вероятность w F). Эта вероятность появления т =
= — + 6 гербов и & = -н- — 6 решек, поэтому она равна
Следовательно,
Увеличим теперь 6 на единицу, т. е. подсчитаем w F+ 1), получим
wFjl)

470
Поэтому
Заметим, что
так что
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. XIII
Ц)(б + 1)_
а-F)
-^- + 6+1
1F+1) '
Логарифмируя правую и левую части, находим
- B)
Мы рассматриваем большое число опытов п и предполагаем, кроме
того, что величина о<^.-^-> т- е> мы изучаем малые уклонения от
, п 26 2F+1)
наиболее вероятного результата. Поэтому величины — и —i—!—'
малые и, следовательно, логарифмы, стоящие справа в B), можно
разложить в ряд. Выполним это разложение, ограничиваясь первыми
членами ряда. Получим
Формула B) принимает вид
In w F + 1) — In w F) =
Заметим, что In w F+1) — In w F) можно приближенно заменить
на значение производной функции \i\w(z), вычисленной в середине
промежутка, т. е. прл значении аргумента, равном 6 + -^, так что
^ Unw
Конечно, wF+-^-J—это уже не вероятность того, что откло-
отклонение числа гербов от наиболее вероятного станет равным 6 + -^-,
так как это отклонение обязательно целое; это результат интер-

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 471
полиции (§ II.1) функции w F) с целых значений аргумента на
полуцелые. Итак,
1
Положим здесь o-\--^=z, тогда d& = dz, получим
d 4г
-г- In W (z) = .
dz n
Проинтегрируем это соотношение от z = 0 до z = 6, получим
2§2
In да F) — In да @) = , или, потенцируя,
w F) = да @) е~~.
Используя A), находим окончательно
г— _^
Легко убедиться, что результат согласуется с требованием
w(8)d&=\. D)
Зная вид зависимости да с\э е~2й"~/п, можно было определить да@),
не пользуясь формулой Стирлинга, из условия D). В действитель-
действительности 6 является целым числом и меняется лишь в пределах
! -=-, но да F) при большом п меняется столь медленно
и на краях так мало, что мы не вносим заметной ошибки, заменяя
сумму интегралом и интегрируя от —оо до -|-оо.
График зависимости w от 6 — это график как раз такого типа,
который был рассмотрен в § VI, 1 в связи с определением дельта-
функции. При п=2 получается график у(г)(х), показанный на
рис. 68, а при других п график _уB) (аг) надо сжать в у -к Раз
к оси абсцисс и растянуть в 1/ -„- раз от оси ординат. Кривая,
соответствующая формуле C), называется кривой распределения
вероятностей. Она имеет характерный колоколообразный вид. Из
формулы C) видно, что w (—6) = даF). Этого следовало ожидать:
вероятность появления 55 гербов и 45 решек F = 5) равна вероят-
вероятности появления 45 гербов и 55 решек.
*) С помощью аналогичных рассуждений, обозначив / (п) = In (n 1) и исходя
из равенства }(п-\-\) — / (rc) = ln (rc-j- 1), можно вывести саму формулу Стир-
Стирлинга, с точностью до постоянного множителя. (Проделайте это!)

472
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. XIII
Пользуясь формулой C), находим для случая л =100, когда,
как мы знаем, та @) = 0,08:
та A) = та @) • е-0-02 = 0,98та @),
та B) = та @) • е-0'08 = 0,92та @),
та E) =та @) • е-0'5 = 0,61та @),
таA0)=та@)-е-2 = 0,14та@),
та B0) = та @) • е~8 = 0,00034та @).
Условимся называть ожидаемыми такие исходы испытания, для
которых —та @) ^ та F) ^ та @). Случаи с меньшей вероятностью
будут осуществляться редко. Таким образом, ожидаемыми являются
события, для которых —ej^e^e^ где 62 определяется из усло-
26?
вия w FХ) = —та @) (рис. 187). Последнее дает та @)-е " — — w{Q),
ю
2б| ,
или —= 1, откуда
окончательно
Следовательно, ожи-
ожидаемы такие исходы, в которых
В нашем примере наиболее ве-
вероятен исход, соответствующий
Рис- 187- 6 = 0 E0 гербов и 50 решек).
Однако вероятность его невелика,
она равна 0,08 и ненамного больше вероятности близких исходов.
Например, вероятность получить 51 герб и 49 решек (или 49 гер-
гербов и 51 решку) почти такая же, а именно 0,98-0,08 = 0,078.
Значительно меньше вероятность получить 57 гербов и 43 решки
(или 43 герба и 57 решек)'. Эта вероятность равна —— = 0,029.
Поэтому можно считать ожидаемым получение результата с числом
гербов в пределах от 43 до 57, т.е. 50 + 6, где 0^6<^6х = 7.
Величина 6j пропорциональна \ п, поэтому чем больше п, тем
шире границы для ожидаемого исхода. Так, например, для п— 10 000
получаем 6, =■•
У 20 000
70, так что следует ожидать результата
с числом гербов от 4930 до 5070. Однако доля числа бх по отно-
, б,
шению к числу опытов п убывает с ростом п, так как величина —
1
пропорциональна —^=, т. е. тем меньше, чем больше п.
У п.

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 473
Пусть мы хотим, бросая монету, установить опытным путем
вероятность появления герба. При этом мы заранее не знаем, не яв-
является ли монета погнутой, ввиду чего одна ее сторона выпадает
чаще, чем другая. Пусть на самом деле монета ровная, и вероятность
появления герба wr = 0,5.
Проделав 100 бросаний, мы скорее всего получим от 43 до 57
гербов, т.е. получим 0,43 ^wr ^ 0,57. Ошибка в определении
вероятности будет не более 0,07 в ту или другую сторону. Значит,
получив, например, из ста бросаний 44 решки и 56 гербов, не сле-
следует делать заключения о большей вероятности герба, — для этого
недостаточно точен опыт, отклонение от 50 лежит, как говорят,
в пределах статистической ошибки. Можно сказать лишь, что веро-
вероятность выпадания герба лежит в пределах w = 0,56 ± 0,07, т. е.
между 0,49 и 0,63; 0,49 ^ w ^ 0,63; w = 0,50 отнюдь не исключено.
Для уточнения нужно увеличить число бросаний. Проделав 10 000
бросаний, мы скорее всего получим от 4930 до 5070 гербов, т. е.
получим 0,4930 ^та2 ^ 0,5070. В этом случае ошибка в определении
вероятности будет не более 0,007 в ту или другую сторону. Ясно,
б, 1
что ошибка — в определении вероятности пропорциональна —р= .
п у п
Поэтому для того, чтобы уменьшить в 10 раз ошибку в определении
вероятности, надо в 100 раз увеличить число опытов.
Формула C) получена в предположении, что б мало. Поэтому
можно ожидать, что при больших б эта формула дает значительные
ошибки. Подсчитаем, например, для случая п = 100 вероятностью E0),
т. е. вероятность того, что все 100 раз получится герб и ни одного
раза не выпадет решка. По формуле C) находим
2-50г
та@)е~~ш~ = 0,08-е-50 « 10~23.
С другой стороны, мы уже вычисляли эту вероятность по точной
формуле и нашли, что она равна 10~30. Таким образом, приближен-
приближенная формула C) действительно при больших б дает значительные
ошибки. Однако ошибки эти маловажны, так как при больших б
сами значения вероятностей ничтожны.
Какова вероятность wom получить какой-нибудь из ожидаемых
результатов, т. е. такой результат, для которого б заключена в
пределах от —Ьх до +бх? Очевидно, что эта вероятность равна
\
-б,
или, пользуясь C),
+- У~п
2
г— Г _£*!

474 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
В последнем интеграле выполним замену переменной по формуле
26
тогда df> = У п di. Интеграл будет в пределах от —^ до -\-tx, где
Поэтому
V?
2 J e ^~У7Г J
2 Г -—
Для функции Ф (х) = г : 1 е 2 dt (она называется интегралом ее-
У In J
о
роятностей) составлены таблицы. Таблица приведена в конце главы.
Пользуясь таблицей, находим
= ФA,414) = 0,842.
Следовательно, те случаи, которые мы назвали ожидаемыми*), со-
составляют 84% всевозможных исходов испытания, а на долю всех
остальных случаев приходится лишь 16%.
В некоторых задачах представляет интерес вероятность получить
результат, для которого величина б не превосходит данного б0. Эта
б„ 2б!
вероятность ге>= 1/ — \ е п db>.
— 00
Выполнив замену переменной, такую же, как в предыдущем
случае, получим
to (t 'о (J
/2n J 2 /2я J ° Yn
так что
где Ф см. в таблице.
Рассмотрим теперь случай а^=р. Если производится п бросаний
кубика, причем вероятность появления в отдельном бросании белой
*) Ясно, что выражение «ожидаемое» применяется здесь в условном смысле,
поскольку вероятность получить не «ожндаемый» результат (вряд ли его можно
назвать «неожиданным») не так мала, равна 16% при принятом определении.

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 475
грани равна а, а черной В, то вероятность появления т белых и k
черных граней (m-\-k = n) согласно § 2 есть ги = -^-га"В*.
m\k\
Найдем максимум то в зависимости от т. Нам удобнее искать
не максимум w, а максимум In то. (Ясно, что то и In то достигают
максимума при одном и том же значении т.) Имеем 1пто = 1пя1 —
— 1п/и! — In k\ -\-m\na-\-k In В, или, вспоминая, что /г = я — т, полу-
получаем
1пта/ = 1п п\ — 1п т\ —1п (п—т) 1 -\- т In а -+- (п—т) 1п В.
Будем считать, что число бросаний п фиксировано, а потому Into
зависит только от т. Найдем производную —-—•, не смущаясь тем,
что по смыслу задачи величина т принимает лишь целые значения.
Получим
din и; d In т 1 d\n(n — m)\ , , , о
—j—= -, ^ ^- + ln а — In В.
dm dm dm '
Первое слагаемое в правой части вычислим так:
dlnml ln(m-M)l — 1п т 1 , , , ., , , , (, , 1
—з = —\ , ,. = 1п (т+ 1) = 1п /и+1п 1 -\—
dm (m-\-[)—m v i / i \ ' m
Так как при большом числе опытов л число т чаще всего также
будет большим, то величиной In I 1 -j—j » —пренебрегаем по срав-
сравнению с 1п/и. Следовательно,
d In ml
dm
Поэтому
— 1П
E)
Условие максимума — равенство нулю производной дает
, а(л — т) п а л — т .
1п —i—з—^ = 0, или -з =1,
наконец,
/я
Последний результат легко понять: наиболее вероятен такой исход
опыта, при котором число белых (т) так относится к числу чер-
черных (п — /и), как вероятность получения в одном отдельном опыте
белого (а) относится к вероятности получения в одном отдельном
опыте черного (В).
Из последнего соотношения находим «В=а(л—/и), откуда
т (а + 3) = an. Так как а -\- В = 1, то отсюда т — an. Следовательно,

476 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
k = n — т=п{\—а) = /ф. Итак, наиболее вероятен исход, при ко-
котором an раз выпадет белая грань и |3я раз — черная*).
Обозначим вероятность этого исхода через zu(na). Тогда
w (па) -= . " ' а"" ■ В"? F1
w кпа>' (ал) 1 фп)! а р • w
По формуле Стирлинга получаем
поэтому
л!
(ал) ! (рл) I ]А2ллаР а Р"Э"
Пользуясь формулой F), находим
(ла) = . . G)
1/2ллар
Поставим задачу — определить вероятность исхода, мало откло-
отклоняющегося от наиболее вероятного. Более точно, найдем вероятность
того, что число белых граней будет равно /и = ла + 6, где б невелико
по сравнению с п.
Будем исходить из формулы E), в которой полагаем т = па-\-Ь1
dm — db. Тогда E) принимает вид
й 1п к>(яа + б) _ , у фп — б)
db ~ (а« + б)Р '
Преобразуем правую часть следующим образом:
In . ' ... ' = In т^ ^-i- = \n 1 — -г 1— п N •
(a« + S)P /! V «РУ V ^ па)
Так как величины -^ и — малы по сравнению с единицей, то можно
лр ла
положить
1П 1 5 = !Т , In 1 Н =—'.
V лру лр' V па/ па
откуда получаем
d\nw(na-\-6) б б б
d6 ~ лВ па~ лаб'
*) Заметим, что числа ал и рл могут оказаться нецелыми. Тогда наиболее
вероятное число появлений белой грани принимаем равным целому числу,
ближайшему к ал.

§ 3] АНАЛИЗ РЕЗУЛЬТАТОВ МНОГИХ ИСПЫТАНИЙ 477
Итак,
d In w(na-{-6) _ б
db ~ ~ поф "
Интегрируя последнее равенство от 0 до б, находим
In w{na + 6) — \nw {па) = —
-~ ,
откуда
w [па + б) = w {па) е 2яаЗ.
Вспоминая, что w {па) = —г==-, получаем окончательно
У 2ла|3я
1
w {na + б) = .. е 2аР". ■ (8)
/2ларя
Это и есть вероятность исхода, в котором число белых граней отли-
отличается на б от наиболее вероятного.
Будем снова условно называть ожидаемыми такие исходы, для
которых — w{na)^.w {па-\-Ь)-^.хи){па), т. е. для которых — б1^б^б1,
где 6Х определяется из условия w {па-{- бх) = — w {па). Пользуясь
G) и (8), получаем
б2
улофл ~~ еу^гларя ' ' " 2аря ~ '
окончательно 81 = |/2оф/г.
Пользуясь (8), легко проверить, что j w {па -f б) d6 = 1. Легко
проверить также, что при а=р=1/2 мы получаем формулы, выве-
выведенные в начале этого параграфа.
Упражнения
1. Монета брошена 1000 раз. Какова вероятность получить ровно 500 раз
герб; ровно 510 раз герб?
2. Монета брошена 1000 раз. Какова вероятность получить при этом не
менее 500 гербов; не менее 510 гербов?
3. Произведено 100 выстрелов, причем вероятность попадания равна 0,1,
а вероятность промаха равна 0,9, Какова вероятность того, что цель будет
поражена ровно 10 раз; ровно 8 раз?
4. Какова в условиях упражнения 3 вероятность того, что цель будет
поражена не менее 8 раз; не менее 10 раз; не менее 12 раз?
5. По цели выпущено 1000 снарядов, причем вероятность попадания равна
0,01. Какова вероятность того, что хотя бы 8 снарядов поразили цель; 11 сна-
снарядов поразили цель?

478 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
§ 4. Энтропия
Итак, мы видели, что диапазон ожидаемых исходов пропорцио-
пропорционален 'У п, тогда как диапазон всех мыслимых исходов равен п.
При нашем определении ожидаемых исходов, когда требовалось,
чтобы их вероятность была больше — от максимальной, они состав-
6
ляют при большом числе испытаний 84% от всех исходов. Можно
было бы задаться другим определением ожидаемых исходов, например,
заменив коэффициент — на 0,001; тогда бы мы получили, что бх всё
равно пропорционально ~У п (z другим коэффициентом пропорцио-
пропорциональности), а ожидаемые исходы составляют уже около 99,98% от
всех и т. д. В то же время интервал ожидаемых исходов при очень
больших п составляет лишь ничтожную часть интервала всех мысли-
мыслимых исходов, так как
————»- 0 при п—>-оо.
Этот закон, согласно которому значения случайной величины
(в данном примере число появлений белой грани) при достаточно
большом числе испытаний с как угодно высокой относительной
точностью группируются вокруг ее наиболее вероятного среднего
значения, имеет многие важные приложения в физике. При этом
обычно пользуются принципом, согласно которому взамен большого
числа испытаний над единичным объектом можно провести одно
испытание над статистическим массивом, т. е. системой из большого
числа одинаковых объектов. Например, вместо многократного бро-
бросания одного кубика можно рассматривать одновременное бросание
многих кубиков, при этом число выпавших белых граней будет
подчиняться тому же закону, т. е. так же концентрироваться вокруг
наиболее вероятного значения.
Рассмотрим сначала простой мысленный пример. Пусть имеется
колода из огромного количества N (например, М= 1012) карт, среди
которых аМ красных и (W черных (a-f|3=l). Карты одного
цвета мы не будем различать друг от друга. Если считать состоя-
состоянием колоды порядок расположения в ней красных и черных карт,
то легко понять, что общее число Q=Q{N, а) возможных состояний
равно числу сочетаний из N элементов по aN, т. е.
= («Л')! (p/V) I #
Воспользовавшись формулой Стирлинга, получим (см. вычисления
на стр. 476)
п — ' 1 '

§ 4] энтропия 479
Мы видели, что далеко не все эти состояния равновероятны,
Например, легко подсчитать вероятность того, тго при N = 10й,
а=0,5 средняя плотность красных карт в первых 1010 картах больше
чем на 1% превысит (при добросовестном тасовании) среднюю плот-
плотность их во всей колоде, равную 0,5. Так как 1010 составляет лишь
небольшую часть от 1012, то можно принять, что несколько повы-
повышенная частота появления красных карт в этой первой части колоды
не меняет вероятности 0,5 каждой следующей карте оказаться
красной, Значит, искомая вероятность равна рассмотренной в § 3
вероятности того, что при 1010-кратном бросании монеты герб вы-
выпадет > 1,01 -0,5-1010 =@,5-1010 +0,5-108) раз. В силу формулы
C) искомая вероятность равна
СО
= f ' в-
» У
1
0,5'Ю» 10» У
(Здесь мы положили 2-10~6б = ^.)
Для таких больших значений аргумента значения интеграла
вероятностей в нашей таблице отсутствуют, но с помощью метода,
описанного на стр. 65, легко получить, что при больших, х
ОО
_ф (х) = -Д=- Г e-'V» Лда ^J=
/2я J ^2я*
Поэтому искомая вероятность равна —~=r 10~3е~108/2да 10~2l1°s. Это
число невообразимо мало. Можно быть уверенным, что если колода
тасуется и проверяется миллиарды раз в секунду в течение всего
времени существования солнечной системы, то описанное повышение
средней плотности красных карт в первой части колоды ни разу не
представится. Состояние колоды должно быть таким, что любой ее
участок, состоящий из весьма большого числа п карт, содержит
примерно an красных и |3я черных карт с диапазоном ошибки по-
порядка У п. Конечно, при небольшом п, например п= 10 или 100,
средняя плотность красных карт в таком участке может оказаться
существенно отличной от а, т. е. эта плотность может иметь ло-
локальные флуктуации.
Назовем энтропией рассматриваемой колоды число S = lnQ, т. е.
логарифм числа ее возможных состояний. Из предыдущего мы по-
получаем
S да аЛПп - + |ЗЛПп 4—41п BлсфЛ0 да ЛГ (а 1п - + |5 In -j/
причем в правой части мы пренебрегли членом порядка ^
Энтропия'в расчете на отдельную карту равна -тт = а 1п—|-(Нп-о-.

480 теория нкроятностей [гл. хш
Представим себе теперь две колоды с характеристиками Л^, ах
и *V2, а.г соответственно, причем между этими колодами обмен кар-
картами невозможен. Такая система имеет Q = QjQ,, возможных состоя-
состояний (любое состояние первой колоды комбинируется с любым состоя-
состоянием второй колоды), откуда соответствующая энтропия
S = In Q = In Q, + In Q2 = S1 + S2,
т. е. энтропия системы из нескольких невзаимодействующих компо-
компонент равна сумме энтропии этих компонент. Если же эти две колоды
перетасовываются совместно, то они составляют одну общую колоду
с числом карт N=Nl-{-Ni, из них красных alN^-raiNi = aN, где
сс= —— ' —-. Соответствующая энтропия равна
= («Ai +С(Д) In ^дГ-Т^-дГ+ (РА, + РАг) 1п а д/ 1й /у •
Легко проверить, что при а2 = а, (и, следовательно, р2 = Рх) будет
S = S; это ясно и из того, что при a.2 = a, взаимодействие между
колодами, т. е. их совместное перетасовывание ничего нового не дает.
Если же агфаи то, как мы сейчас проверим, обязательно S>S.
В самом деле,
5 — 5= (оД. +«Д) In- ' '" " ' " "'х '
Если считать yVx, yV2 и а, заданными, а a2 переменным и учесть,
что Р2=1—а2, то легко непосредственно подсчитать, что
d{S-S)_ , (Mj + Wb,
a.,/V2)
При ai = al получается S — S — Q,—-, = 0, а так как из выра-
жсния второй производной вытекает, что она положительна при нсех а2)
а потому график зависимости S — S от аг выпуклый книзу, то при
а^Фа1 будет 5 — S > 0, т. е. 5 > S, что и утверждалось.
Если представить себе, что две колоды с характеристиками Nlt
ах и yV2, a2 приложены друг к другу, но из-за их большого объема
производится лишь «локальное перетасовывание» сравнительно
небольших участков объединенной колоды, то при а.г > а, по мере
такого перетасовывания будет происходить постепенное «днффунди-

§ 4] энтропия 481
рование» красных карт из второй колоды в первую, средняя плотность
красных карт будет постепенно выравниваться. Поставив в любой
момент этого процесса перегородку между первыми Л^ и последними .V3
картами, мы можем остановить диффузию и подсчитать энтропию
в промежуточном состоянии после такого разделения. По мере вырав-
выравнивания средней плотности красных карт эта энтропия возрастает.
После выравнивания энтропия остается практически постоянной.
Конечно, из-за постоянного перемешивания можно представить себе,
что в одной части колоды средняя плотность красных карт станет
существенно больше, чем во второй. Однако выше мы показали,
что при большом числе карт вероятность такого события невообра-
невообразимо мала. Таким образом, процесс возрастания энтропии является
необратимым.
Рассмотренная колода является простейшей моделью статисти-
статистической физической системы. Эта модель одномерна (карты располо-
расположены в ряд), а каждая карта могла быть всего в двух состояниях—быть
красной или черной. (Для объекта, который может быть в несколь-
нескольких состояниях с вероятностями/);, энтропия в расчете на один экземп-
экземпляр получается равной J^Pi^ — Л Аналогичные свойства имеют
более сложные реальные статистические системы, например система
молекул газа, содержащегося в определенном объеме.
Согласно квантовой механике, каждому значению энергии Е от-
отвечает определенное, весьма большое число Q квантовых состояний
рассматриваемой системы, внутренняя энергия которой не превосхо-
превосходит Е, Чтобы представить себе порядок этого числа, воспользуемся
доказываемой в квантовой механике приближенной оценкой числа Ql
состояний отдельной молекулы в объеме V, импульс которой не пре-
превосходит некоторого значения р: fit =p3V/6n2^3 (ft та 10~2? эрг-сек —
постоянная Планка). Средний импульс одной молекулы связан с тем-
температурой т газа формулой р =]/ 3/гдат, где k= 1,38-10~16 эрг/град —
постоянная Больцмана, a m — масса молекулы, равная -ту-, где
(д,— молекулярный вес, a No = 6,02- К)-3 (число Авогадро) — число
молекул в грамм-молекуле газа. Для кислорода (|д, = 32) в
1 л=103 еж3 при т = 0°С = 273°К получаем
Однако в 1 л газа при нормальных условиях содержится около
Л/ = 3-Ю" молекул. Поэтому за общее число всех квантовых со-
стоинг.к такой порции кислорода можно приближенно принять
16 Я. Б. Зельдович, А. Д. Мышкис

482 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Это число невообразимо велико. Впрочем, как будет видно из даль-
дальнейшего, реально в расчеты входит не само оно, а его логарифм
(который тоже очень велик) и даже, более того, разность значений
этого логарифма для системы в различных условиях.
Величина S = k\nQ называется энтропией системы; здесь k —
принципиально несущественный коэффициент пропорциональности,
равный постоянной Больцмана. Появление этого коэффициента
объясняется тем, что понятие энтропии было первоначально введено
из других соображений, в связи с изучением тепловых процессов.
Поэтому единица измерения энтропии выбирается такой, чтобы она
сохраняла то же значение, что и в термодинамике. Другими сло-
словами, коэффициент k дает возможность получать температуру не в
эргах, а в градусах.
При изменении Е меняется и Q, а потому и S, причем в случае
dE
неизменного объема газа отношение -т?.= т называется его темпе-
dS
ратурой. При совместном рассмотрении двух систем а и Ь, пока они
не взаимодействуют, для общей системы будет Q = QaQb, а потому
S = Sa-\- Sb. Если системы могут обмениваться энергией, но в ос-
остальном независимы (порции газа разделены тонкой перегородкой),
ю сохраняются те же соотношения, но участвующие величины
будут меняться с течением времени. Если система в целом изоли-
ровама от окружающей среды, то энергия сохраняется, Е= Еа-\- Еь =
= const, откуда Еа-\-Еь = 0, где точкой обозначена производная по
времени. Отсюда
Значит, при та = ть будет £=0, при равных температурах взаимо-
взаимодействующих порций газа энтропия не меняется. Если же темпера-
температура системы а меньше температуры системы Ь, тй<ть, то Еа^>0
и 5 > 0, т. е. система а приобретает энергию от системы Ь, энт-
энтропия общей системы возрастает. Аналогичное возрастание энтропии
будет и з случае ха > ть. Этот процесс перекачки энергии и воз-
возрастания энтропии продолжается до выравнивания температур. После
этого энтропия практически остается постоянной. Логически возмо-
возможен случай, когда из-за обмена энергиями в какой-то момент тем-
температура одной части системы снова станет выше температуры другой
ее части, однако это еще неизмеримо менее вероятно, чем разо-
разобранное выше изменение плотности красных карт. Впрочем, в весьма
малых порциях газа возможны флуктуации температур и связанных
с ними скоростей частиц: эти флуктуации можно наблюдать на из-
известном явлении броуновского движения.
Так как энтропия статистической системы может лишь возрас-
возрастать или оставаться постоянной, то процессы, при которых энтро-
энтропия возрастает, являются необратимыми, Эти процессы становятся

§ 5] РАДИОАКТИВНЫЙ РАСПАД. ФОРМУЛА ПУАССОНА 483
невозможными, если, засняв их на кинопленку, прокручивать ленту
в обратном направлении. (Такой способ обращения необратимого
процесса был применен при съемке фильма «Веселые ребята» для
показа стада коров, выстраивающихся по команде пастуха — Леонида
Утесова: коров выстроили в шеренгу, сняли, как они разбежались,
а затем заснятую пленку вклеили в обратном направлении.) Мате-
Математически обращение процесса сводится к замене времени t на —t.
Таким образом, если закон развития процесса записан в виде ли-
линейного дифференциального уравнения, не содержащего явно
времени t, то условие обратимости заключается в наличии в этом
уравнении производных по t только четного порядка. Это можно
проиллюстрировать на примере линейного осциллятора, рассмотрен-
рассмотренного в § VII.3: в уравнении (VII.21) член h -j- отвечал силе трения
в системе, а наличие трения приводит к диссипации энергии и тем
самым к необратимости процесса.
В заключение отметим, что закон неубывания энтропии — так
называемый второй закон термодинамики — имеет вероятностный
характер и в конечном счете связан с тем, что каждое состояние
встречается в природе тем чаще, чем оно вероятнее. Другими сло-
словами, процессы, связанные с убыванием энтропии, реально не на-
наблюдаются не из-за их логической, формальной противоречивости,
а из-за их крайне малой вероятности.
§ 5. Радиоактивный распад. Формула Пуассона
Рассмотрим явление радиоактивного распада. Как известно (см.,
например, ВМ, § V.3), вероятность того, что один отдельный
атом распадается на весьма малое время tx, равна wtx; вероятность
того, что за это время распада не произойдет, равна 1—wtv (Здесь
w — постоянная, характеризующая данное радиоактивное вещество.)
Рассмотрим большой промежуток времени t. Найдем вероятность
w (t) того, что в течение этого промежутка времени распада нэ
произойдет. Для этого разобьем весь промежуток t на малые про-
промежутки длительности tlt t2, ..., tn. Вероятность того, что распад
не произошел за промежуток tlt равна
Вероятность w (t) равна произведению вероятностей того, что рас-
распад не произошел ни за один из промежутков времени tlt t%,...,tn%
Поэтому
w {t) = {\-wtj)■ A —wt2)...A —win).
Рассмотрим \nw(t). Ясно, что
In w (t) = In A —wt^ + In A —wt2) + ... + In A —wtn).
16s

48 J- ТЕОРИЯ вероятностен [ГЛ. XIII
Так как величины wflt wtit ..., wtn малы по сравнению с 1, то
логарифмы, стоящие справа, можно разложить в ряд. Ограничиваясь
первым членом разложения, находим
In w (Л = — wt, —iyt.i— . • . —'wi i= ~— ti)t.
Потенцируя, получаем
Таким образом, мы получили хорошо известный результат: отно-
отношение числа атомов, не распавшихся за время t, к первоначальному
числу атомов есть e~wi.
Вероятность того, что атом не распадается за время t, обозначим
через р, тогда р = е~ш'. Вероятность а того, что за время t атом
распадается, есть а—\—e~wt.
Если имеется п атомов, то вероятность w (m; п) того, что т из
них распадется, a k=n — т не распадется, выражается формулой
w{m; п) = -^а^к, (9)
где а=1— e~wt, $ = e-wl (см. §2)..
Рассмотрим важный частный случай: пусть общее число радио-
радиоактивных атомов п весьма велико, а вероятность распада за время t
весьма мала, так что наиболее вероятное число распадов за проме-
промежуток времени t — конечное число. Обозначим его через (д,, тогда
\i = an, как было установлено в § 3.
Итак, нас интересует, какой вид примет формула (9), если п
неограниченно увеличивается, а неограниченно приближается к нулю,
а их произведение ося=|л (как и т) остается конечным числом.
_ л! а п\ат
Рассмотрим множитель —— = -. г-г; запишем его так:
= {па) (па—а) (па — 2а). . . [па— (т— 1) а] =
= jo, Du —а) (|Л — 2а).. . [|д—(т — 1) а].
Поэтому для весьма больших п при зафиксированном т будет
п\ат ^ т
п — т)\ "
Теперь рассмотрим величину pft=P"~m=(l—а)"~т. Так как а —
весьма малая величина, то (J близка к единице. Однако показатель
степени п — т велик, поэтому, заменив р"~т н"а 1, мы можем до-
допустить значительную ошибку.
Поступим следующим образом:

§ 5] РАДИОАКТИВНЫЙ РАСПАД. ФОРМУЛА ПУАССОНА 485
так как величина A—а)т близка к 1. Вспоминая, что па=|л, на-
находим
так как величина A — — ) тем ближе> к е, чем больше п.
Окончательно из (9) при п—*■ оо находим
w(m; n) = Wri(m; n)—>-wu(m) = ^~. e~^. A0)
1711
Новое обозначение w^ (m) означает вероятность наблюдать т рас-
распадов, если наиболее вероятное число распадов есть (д,, а число
атомов п весьма велико, так что число распадов составляет малую
долю числа атомов.
Закон, выражаемый формулой A0), называется распределением
Пуассона.
Убедимся, что сумма вероятностей w^(m) для всех значений т
равна 1, т. е. что
В самом деле,
Распределение Пуассона показывает, какова вероятность наблю-
наблюдать т распадов, если наиболее вероятное число распадов есть [X,
причем отдельные распады независимы, т. е. тот факт, что уже
получено некоторое число распадов, не меняет вероятности получить
еще распад (для этого мы оговорили, что общее число радиоактив-
радиоактивных атомов п. велико, так что |А<^л, т<^.п).
В отличие от задач предыдущих параграфов, здесь общее число
-распадов никак не ограничено. В предыдущих параграфах мы рас-
рассматривали случаи, когда проделывается определенное, хотя, может
быть, и очень большое, число опытов п. Это число п мы задавали,
и оно входило в окончательные результаты. В этом параграфе п
(число агомов или, что то же самое, число опытов, причем опыт
состоит в испытании — распадется атом или нет) предполагается
неограниченным. Следовательно, неограниченно и число актов рас-
распада. В принципе возможно, хотя и маловероятно, наблюдать любое,
сколь угодно большое число распадов при одном п том же наибо-
наиболее вероятном числе распадов |д,.
Если |.1 Maio, а именно |.i<^: 1, то, пользуясь 00), находим, что
вероятность не наблюдать ни одного распада равна е~^ да 1 — |х,

486
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[гл. хш
т. е. весьма близка к единице. Вероятность наблюдать один распад
значительно меньше, а именно |д ■ е~^ да |д A —|д) « |Д. Вероятности на-
наблюдать два, три и т. д. распадов убывают очень быстро (эти ве-
вероятности равны (д.2/2, (Д3/6 и т. д.).
Если (Д. велико, то наиболее вероятно наблюдать |д распадов.
Действительно, найдем, при каком т (|Д постоянно!) величина w^(m)
имеет максимум. Удобнее искать максимум \nw^(m). Так как
1идац(/и) = — \i-\-m\n\i — 1пот!, то
d\nw(m) d
= In |д— -т— (In от ) = In li—1пот
r dmv ' "
dm
(cm. § 3). Поэтому равенство
1 ■
dm
d\nu.'v (m)
dm
= 0 дает от = |д.
На рис. 188 представлены диаграммы распределения Пуассона
для случаев \х = 0,5; (д. = 2; [.1 = 3. Нужно заметить, что рис. 188,
в сущности, сделан не точно: ведь на самом деле величина w задана
только для целых значений т, так что кривая, дающая w (m) при
всех т, т. е., в частности, и при дробных т, не имеет смысла.
Следовало бы для каждого (Д. дать частокол величин те>^@), w (\),
•0^B) и т. д., изображаемых вертикальными отрезками, опирающи-
опирающимися на целые точки на оси абсцисс. Кривая Wv (m) проходит через
вершины этих отрезков.
Вид функции w^m) при больших (д будет описан в § 8.
Упражнения
рассматривая отно-
отно1. Сделайте вывод о максимуме wy(m) при данном
шение w (т) к wy,(m—1).
2. Пусть некоторая величина х может принимать в результате испытания
значения xlt ... , хп с вероятностями plt ... , р„. Докажите, что среднее
значение х этой величины в одном испытании равно *iPi+ . •. +хпрп. Опи-
Опираясь на это, докажите, что среднее значение т числа распадов за премя t
как раз равно |г.

§ 6] ДРУГОЙ ВЫВОД РАСПРЕДЕЛЕНИЯ ПУАССОНА 487
§ 6. Другой вывод распределения Пуассона
Дадим теперь другой вывод распределения Пуассона, исходя m
соображений, отличных от тех, которыми мы пользовались в § 5.
Представим себе большое число приборов (счетчиков), каждый из
которых регистрирует распады в одинаковых образцах, содержащих
долгоживущее радиоактивное вещество.
Для удобства вычислений будем считать, что в среднем в еди-
единицу времени в каждом образце происходит один распад. Тогда за
время t в среднем в каждом образце произошло t распадов. Обо-
Обозначим через л:0 число счетчиков, которые не зарегистрировали ни
одного распада (от = 0), через хх— число счетчиков, которые заре-
зарегистрировали по одному распаду (от = 1), через х„_— число счетчиков,
которые зарегистрировали по два распада (т=2), и т. д. Ясно, что
величины хй, хх, хг ... зависят от времени, прошедшего с начала
опыта. Пусть в определенный момент времени t известны величины
xo(t), xl{t), x2{t), ... , т. е. известно количество счетчиков, заре-
зарегистрировавших 0, 1, 2, ... распадов.
Как изменятся эти количества счетчиков, когда пройдет малый
промежуток времени dt?
В любой группе из п счетчиков за единицу времени произойдет
п распадов, а за время dt произойдет ndt распадов. Значит, в этой
Труппе ndt счетчиков зарегистрируют по одному распаду.
Рассмотрим группу счетчиков, не зарегистрировавших ни одного
распада. В л:0 (t) dt из этих счетчиков произойдет по одному рас-
распаду, и эти счетчики перейдут в другую группу, а именно в груп-
группу хх. Поэтому число счетчиков, не зарегистрлровавших ни одного
распада по истечении промежутка времени ^ + ^,.есть
xo(t + dt)=xo(t) — xo(t)dt.
Отсюда
xo{t + dt) — xo{t)=-xo(t)dt, или ^=-*„.
Рассмотрим группу Xl ((). Аналогично предыдущему, Хх (t) dt из
этих сметчиков перейдут в группу хг, однако в рассматриваемую
группу перейдут л:и (t) dt счетчиков из группы л:0. Поэтому
Xl (t + dt) = х, (t) —Xl (t) dt + x0 (t) dt,
откуда
dt ~x° Xv
Продолжая эти рассуждения, мы приходим к цепочке дифферен-
дифференциальных уравнений
dxo _ г
dt ~ 01
*Ь-Х-Х
dt — °

488 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Ясно, что в начальный момент времени ^ = 0 будет л:0 = Л/, где
yV—полное число счетчиков, xY = х.2 = х3 = . . . =0. Уравнения A1)
легко решаются одно за другим (см. § VII.2). Получаем
Пусть прошло (д, единиц времени после начала процесса. За это
время в каждом образце в среднем произошло [I распадов, а в каж-
дом счетчике группы т, численность которой равна хт (\i) = N^—j e~^,
произошло по т распадов. Поэтому вероятность того, что в наудачу
взятом счетчике наблюдалось т распадов, равна отношению числа
счетчиков группы хт (|х) к общему числу счетчиков, т. е.
Мы получили тот же результат, что и в § 5.
Упражнение
Рассмотрите следующее обобщение разобранной задачи. Пусть некоторый
объект может быть в состояниях ..., С_2, С_1т Со, Сх, С,, ..., причем в мо-
момент t = 0 он находился в состоянии Со, а за время dt он переходит с вероят-
вероятностью со dt в следующее состояние и с вероятностью adt — в предыдущее.
Укажите систему уравнений, которой удовлетворяют вероятности p;(t) нахо-
находиться в момент t в состоянии С/, найдите приближенные выражения для
Pi (i) по методу последовательных приближений, найдите среднее значение
номера состояния в момент t. При каких значениях а и со получается разо-
разобранная d основном тексте задача?
§ 7. Непрерывно распределенные величины
Обратимся к задаче о рыбной ловле, которая была поставлена
в § 1.
Пусть вероятность вытащить рыбу, вес которой заключен в пре-
пределах от р до p-\-dp, равна f(p)dp*). Функция f (р) называется
функцией распределения вероятностей. Она удовлетворяет условию
+ ее
\f(p)dp=\, так как этот интеграл есть сумма вероятностей всех
о
могущих произойти событий.
*) Мы считаем, что вытаскивание пустого крючка—это вылавливание
рыбы весом р = 0; см, грустные шутки по этому поводу на стр. 461.

§ 7] НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫЕ ВЕЛИЧИНЫ 489
Заметим, что на самом деле в любом водоеме нет рыб, нес
которых больше некоторого числа Р. Однако мы ставим верхний
предел интегрирования не Р, a -j- cx>. Это можно делать, взяз
функцию f(p) равной 0 при /? > Р или, во всяком случае, быстро убы-
убывающей при возрастании р и со столь малыми значениями при /r> P,
что на величину интеграла эти значения практически не влияют*).
Важно отметить следующее. Ми считаем, что в процессе ловли
вылавливается лишь весьма малая часть всей рыбы, имеющейся в
водоеме. Поэтому вероятность выловить рыбу, вес которой заключен
в пределах от р до p-\-dp, не зависит от того, сколько рыб и ка-
какого песа уже поймано. Говоря другими словами, функция /(/;) не
зависит от того, какие рыбы были уже пойманы. Эта функция ха-
характеризует данный достаточно большой водоем.
Поставим прежде всего следующую задачу. Пусть было вылов-
выловлено большое число п рыб (точнее, крючок вынут п раз). Каков будет
средний вес одной выловленной рыбы? Вероятность поймать рыбу,
вес которой лежит в пределах от р до p-\-dp, где dp малое, равна
f(p)dp. Поэтому из общего числа п в n-f(p)dp случаях будет
поймана рыба веса /?**). Вес всех таких рыб равен p-nf (p) dp.
Интегрируя последнее выражение по всем р, т. е. от р = О до
f>=-|-oo, мы получим общий вес улова после п забросов крючка
= n\pf(p)dp.
Разделив общий вес улова Рп на число п забросов крючка, мы
получим средний вес рыбы в расчете на один заброс крючка
р. A2)
Теперь поставим более сложную задачу. Пусть выловлено п рыб.
Вероятность, что при этом общий вес улова будет заключен в гра-
границах от р до p-\-dp, есть Fn{p)dp. Функция Fn(p) является функ-
функцией распределения по весу улова, состоящего из п рыб. Поставим
*) В других задачах рассматриваемая величина (в данном случае это вес
рыбы) может принимать и отрицательные значения. В этом случае / (р)
+ 00
удовлетворяет условию \ /(p)dp=l.
— :о
**) Точнее говоря, рыба, вес которой весьма близок к р, а именно нахо-
находится в интервале dp около р. Заметьте, что для величины, меняющейся не-
непрерывно, которая не обязана принимать определенные целые (в общем слу-
случае— дискретные) значения, бессмысленно спрашивать, какова вероятность
того, что величина примет точно определенное значение; эта вероятность,
очевидно, равна нулю. Имеет смысл только вероятность попасть в определен-
определенный интервал—и эга вероятность пропорциональна длине интервала, когда
интервал мал.

490 теория вероятностей [гл. хш
задачу найти эту функцию. Для этого прежде всего составим урав-
уравнение, связывающее величины Fn+1(p) и Fn(p).
Пусть после п вытаскиваний получилось распределение Fn (р).
Каким образом после п-\-\ вытаскиваний может получиться общий
вес улова, лежаТций в пределах от р до p-\-dpl
Если вес последней (n-}-\)-Pi рыбы лежит в пределах от ц до
\х-}-с1ц, где flfjx гораздо меньше, чем dp, то для того, чтобы сумма
весов п рыб и (л-(-1)-й рыбы попала в заданные границы от р до
p-\-dp, нужно, чтобы вес п рыб лежал в пределах от р — \i до
p-\-dp—ц (при этом мы пренебрегаем малой величиной d\i).
Вероятность выловить (п-\- 1)-ю рыбу весом от ц до \i-\-d\\, равна,
как мы знаем, /(ц) d\i. Вероятность того, что вес п первых рыб
лежит в пределах от р — ц до р— \i-\-dp, равна Fn (р — \i)dp.
Вероятность события, состоящего в том, что вес первых п рыб
оказался в указанных пределах и вес (п-(- 1)-й рыбы оказался также
в указанных пределах, равна произведению вероятностей этих от-
отдельных событий и, следовательно, равна
f(\>)dvFa(p — )).)dp. A3)
Заметим, что получить окончательно вес всех выловленных рыб,
лежащий в указанных пределах, можно множеством способов, так
как вес ц последней рыбы может иметь всевозможные значения от
0 до -(-то- Поэтому общая вероятность того, что вес всех вылов-
выловленных рыб лежит в указанных пределах, равна сумме выражений
A3), записанных для различных значений ц. При этом так как ц
принимает всевозможные значения, то вместо суммы появляется
интеграл. Таким образом, эта вероятность есть
—ц) dp = dplf(n)Fn(p — n)dyL. A4)
Но, согласно определению, вероятность того, что общий вес
п-\-\ рыб лежит в пределах от р до p-\-dp, равна Fn+I(p)dp. При-
Приравнивая последнее выражение правой части A4) и сокращая на dp,
получим
A5)
о
Формула A5) дает возможность, зная функцию F1 (ц) =/([.i) (так
как Fl (p) относится к случаю улова, состоящего из одной рыбы)
и зная Fn, находить Fn+1 (p), т. е. переходить последовательно от
индекса п к индексу п-\-\*).
*) Фактически в формуле A5) выполняется интегрирование от 0 до р, так
как Fn(p — ц) при \i > р равна нулю, и потому (i может принимать значения
только от 0 до р. Если взамен веса рыбы рассматривается величина, кото-
которая может принимать значения обоих знаков, то в формуле A5) интегрирова-
интегрирование проводится от —оо до +00'

§ 7] НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫЕ ВЕЛИЧИНЫ 491
Рассмотрим простейший пример,
Пусть f(p) = —, если 0<р<<7 и/(р) = 0 при всех остальных
значениях р. Это означает, что в водоеме нет рыб, вес которых
больше <7, а вероятность выловить любую рыбу, вес которой мень-
меньше д, одинакова; поэтому нет и «нулевых» рыб (в /(/?) нет б-сла-
гаемого). Средний вес выловленной рыбы равен
о
0
Ясно, что условие \>f(p)dp=\ выполняется. Действительно,
dP ql
о
q
0 0 0
Как было указано выше, F1(p)=f{p). Найдем Рг(р). Пользуясь
A5), получаем
Так как /(ц) отлична от нуля и при этом равна — только при
q
О < \i < <7, то /\, (р) = \—f(p — \i)d\i. В последнем интеграле по-
0
ложим р — ц = t, тогда dt=—d\i; получим
p-q p
p p-q
Теперь рассмотрим отдельно случай 0<р<<7 и случай q <^p < 2^.
Если 0<Cp <<7, то р—q < 0. Учитывая, что функция f(t) отлична
от нуля (и при этом равна 1/<7) лишь при 0 < t < q, получаем
р
F2(p)=— \—dt = —2. Если же q<p<2q, то интегрируем от
о
q
р — q до q. Поэтому в этом случае F2(p)=— \ — dt = -q~P. Та-
p-q
ккм образом,
-£г, если 0</р <q,
Ъ(Р) = \ l-i
, если q<p <2q.
Отметим еще, что F%(p) = 0, если р<0 и если р > 2<7, так как

492
теория вероятностей
[гл. хш
вес улова не может быть отрицательным и вес улова, состоящего
из двух рыб, не может быть больше 2q, потому что в водоеме нет
рыб, вес которых больше q. График функции F2 (р) изображен на
рис. 189. Предлагаем читателю
получить" функцию F3 (р) и по-
построить ее график. (См. упраж-
упражнение.)
Сообщим два простейших
свойства функций Fn(p),
р
Рис. 189.
= \ (при лю-
бом п). Это свойство очевидно,
исходя из того, что Fn(p) есть функция распределения вероятно-
вероятностей. Читатель легко проверит, что это соотношение справедливо
для функций F2(p), Fa(p) предыдущего примера.
2. Обозначим через рп+1 средний вес улова, состоящего из
Gz-f-l) рыб. Это надо понимать .так. Пусть мы многократно произ-
производили забрасывание крючка (п-+-1) раз подряд, а затем подсчитали
средний вес улова, состоящего из (л+1) рыб. Тогда pn+1=Pn+p1,
т. е. средний вес улова из (/z-f-1) рыб равен сумме среднего веса
улова из п рыб и среднего веса улова, состоящего из одной рыбы.
Поэтому P2=p1+P1 = 2p1; P3=P2+P1 = Sp1 и т. д., т. е.
Р„ = лр1. A6)
Отметим в заключение несколько общих свойств случайных ве-
величин, т. е. величин, которые принимают определенные значения в
результате «испытания». (Например, случайной величиной является
вес рыбы, пойманной при испытании — вытягивании крючка.) Пусть
имеются две случайные величины \ и ц; обозначим через р и соот-
соответственно q возможные значения этих величин, а через /(/?) и
ф (q)— соответствующие функции распределения. Как мы видели,
среднее значение \ (можно писать также р) величины £ можно вн-
внес
числить по формуле £= \pf(p)dp, аналогично выражается it. Легко
— 00
доказать, что всегда
|+^=1 +л- cl=Cl (C=const). A7)
В самом деле, если обозначить через р- и qt значения величин £ и
1] в г'-м испытании, то при весьма большом числе N испытаний
можно написать
! N j N х N
1+п="й" И(/р'+^ = ~ !/'■+ж Z ^=^+t]-
1=1 1=1 /=|
Аналогично проверяется второе равенство A7).

§ 8] СЛУЧАЙ ВЕСЬМА БОЛЬШОГО ЧИСЛА ИСПЫТАНИЙ 493
Если величины £ и г| независимы, то можно доказать также, что
|rj=l-Ti. В самом деле, вероятность того, что £ примет значение
между р и p~\-dp, а г| — значение между q и q-\-dq, в силу усло-
условия независимости, равна / (р) dp cp (q) dq; соответствующее же зна-
значение £г| равно pq. Поэтому среднее значение £г| получается по
формуле
£п = $ \ РЧ [f(P) dP Ф (Ч) dq] = I pf{p) dp- $ qq> (q) dq =1-\
— Я — 00 — X — CO
что и требовалось доказать.
Рассеяние величины £ вокруг ее среднего значения характерн-
характернее
зуется средним квадратом разности А| = (£—1J= \ (р—\)*f{p)dp,
который называется дисперсией величины |. (Заметим, что последний
интеграл действительно есть положительное число, так как подын-
подынтегральная функция положительна.) Легко проверить, что дисперсия
суммы независимых величин равна сумме их дисперсий:
|-м)=[(£ + Л) —(Е + т))]а = [(£—£) +(Л —Л)]8 =
= (I—IJ + 2 (|—1) (п —Л) + (Т1—ПJ = Д| + 2• О-
так как \—1 = £ — £=£ —1=0. Это свойство немедленно распрост-
распространяется на сумму любого числа независимых случайных величин.
Отсюда, в частности, вытекает, что для суммы с, из п независи-
независимых значений величины £х дисперсия Д^ будет равна A£ = /zAf.
Упражнение
Найдите функцию F3 (p) для случая
{
v 0, если р < 0 или р > q.
Постройте график этой функции.
§ 8. Случай весьма большого числа испытаний
В этом параграфе мы рассмотрим вопрос о поведении функции
Fn(p), введенной в § 7, при весьма больших значениях п. При этом
мы будем для простоты сначала взамен веса рыбы рассматривать
какую-то величину £t, среднее значение которой равно нулю; конечно,
такая величина может принимать значения обоих знаков. Fn(p)—
это функция распределения суммы п независимых значений вели-
величины £х.

494 теория вероятностей [гл. хш
Будем исходить из полученной в § 7 формулы A5); однако, как
было сказано в сноске на стр. 490, интеграл в этой формуле надо
брать в пределах от —оо до оо. Разложим Fn(p— (i) в ряд по
степеням ц, ограничивагсь членом, содержащим (J,2. Получим
Пользуясь этим разложением, из A5) находим
со
Заметим, что \ / (\л) d\i = \, так как f(p) — функция распреде-
— со
да
ления вероятностей. Кроме того, \ / (\х) \х d[i = 0, так как в силу
— СО
§ 7 этот интеграл равен среднему значению величины £х. Наконец,
введем дисперсию AJ= J ^/(Ю d\i величины g1§
— со
Теперь формула A9) дает
Fn+1(p) = Fn(P)+i^d^T1- B0)
Будем теперь рассматривать Fn (p) как функцию двух переменных
р и п и записывать Fn(p) = F(р; п). При этом мы будем пользо-
пользоваться частными производными как по р, так и по п, не смущаясь
тем, что п принимает только целые значения, так как при больших
п изменение п на одну единицу можно считать весьма малым по
сравнению с п. Формулу B0) перепишем так:
F(p; n+\)=F(p; л)+|д^. B1)
Разложим теперь левую часть по формуле Тейлора, ограничи-
ограничиваясь двумя первыми членами, это даст
F(p; n+\) = F{p; n) + ~.\. B2)
Приравнивая правые части B1) и B2), а затем отбрасывая слагаемое
F(р; п), приходим к основному уравнению для функции F;
дп — 2 Й1 dpi ' ■

§ 8] СЛУЧАЙ ВЕСЬМА БОЛЬШОГО ЧИСЛА ИСПЫТАНИЙ 495
Прежде чем указать решение этого уравнения, проведем допол-
дополнительное исследование функции F(p; n), которое внесет большую
ясность в применение формулы Тейлора. Рассмотрим график функции
F(p\ n) = Fn{p), которая является функцией распределения случайной
величины £. Так как £ = л£1 = О, то центр тяжести графика при всех
п расположен в начале координат. За ширину графика можно принять
среднее квадратичное уклонение А„=у А%, имеющее ту же размер-
размерность, что £. Однако в конце § 7 мы показали, что АЪ, = пА1, т. е.
А„ = }/*лД1; ширина графика имеет порядок ]/ п. Но тогда из условия
нормировки \ Fdp=\ вытекает, что Fоо п~{/2. Отсюда -у-оол~3/2,
-y-j-oo Л/2 и т.д. А из оценки ширины графика вытекает, что
dF ,,0 1/— , d2F , -,/— о,,
-—оол -ч2: у п = п'1, -^—rcon~1:yn = n~i'2 и т.д.
ар др1
Значит, разложения B1) и B2) доведены до членов одного асимп-
асимптотического порядка, а потому уравнение B3) является асимптоти-
асимптотически точным.
Любопытно, ч-то асимптотический порядок ширины графика Fn
можно было бы получить непосредственно из уравнения B3) с по-
помощью дифференцирования по параметру под знаком интеграла
(§ Ш.6) и интегрирования по частям: .
dn
(При этом мы принимаем, что F—»• 0 достаточно быстро при
/?—<-±оо.) Отсюда А^оолА^.
Не надо жалеть времени, потраченного на такой анализ. С одной
стороны, попутно было получено еще без решения важное общее
свойство F, а именно выражение V п Ах ширины. Кроме того,— и
это немаловажно,— повысилась Ваша бдительность. Вы лучше усво-
усвоили общее правило: чтобы вводить приближения (оставлять одни
члены и отбрасывать другие в ряде Тейлора), нужно узнать о функ-
функции все, что возможно.
Обратимся к решению уравнения B3). Можно показать, что
асимптотически при больших п решением уравнения B3) является
функция F(p; п) =А ——■ е~ рг*'2п^\, где А—любая постоянная. Мы
У п
сообщаем это без вывода. Тот факт, что указанная функция удов-
удовлетворяет B3), нетрудно проверить, составляя dF/дп, d'2F/dp2 и под-
подставляя полученные выражения в B3). Значение постоянной А выберем

496 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. Х1П
из условия, чтобы выполнялось требование \Fdp=\:
-p2l*nh4p=\. ■ B4)
4=
V п
— СО
Выполним замену переменной p/A1]/'2n = t1 dpfA1}/r2n = dt. Тогда
А
= A. Лг|/~2. Кя=1.
edp
М J
— 00 —СО
Итак, АА1У2п=\, откуда /1= 1/Да |/я, и окончательно:
F(p; п)= ' а-Р'/2Яд|. B5)
Д ]/ 2ля
Рассмотрим теперь случай, когда среднее значение |х не обяза-
обязательно равно нулю. Тогда обозначим |х— ^>1 = Ь1[, откуда £1 = £1-f-£i,
где |i = 0. Поэтому сумма £ из п независимых значений величины
|j равна результату сложения постоянной л^ с суммой £' из п неза-
независимых значений величины ^. При большом л сумма £' имеет закон
распределения B5). Но если к случайной величине прибавить посто-
постоянную, то соответствующая функция распределения просто сдвинется
на эту постоянную, т. е, в результате мы получим функцию распре-
распределения
F(p; n)= 1=^е-(Р-"Р1J/2пд21) B6)
А, у 2пп
где мы вернулись к обозначению § 7: рг вместо |х.
Можно было бы получить решение B6) непосредственно, минуя
частный случай B5). Для этого нужно с помощью разложений A9)
и B2) получить уравнение для функции F, уже не предполагая,
что р1 — 0. Это уравнение имеет вид
&F ~ dF , I a» &F
Ж=-~Р^+~2А~^ B7)
(при рг = 0 оно переходит в уравнение B3)). После этого уже
нетрудно проверить непосредственной подстановкой, что функция
B6) удовлетворяет уравнению B7).
На рис. 190 дан график F(p; п) для случая л = 4, Д1 = 1,
pl=\; для наглядности на осях выбраны разные масштабы.
Функция F (р; п) при каждом конкретном п представляет собой
колоколообразную кривую, симметричную относительно вертикальной
прямой, проходящей через точку максимума. Максимум получается,
как видно из B6), при р = прг, что совпадает с найденным в § 7

§ 8]
СЛУЧАЙ ВЕСЬМА БОЛЬШОГО ЧИСЛА ИСПЫТАНИЙ
497
средним значением /?„. Высота максимума есть \/А1у2пп, т.е.
пропорциональна \/уп, как было сказано выше. Таким образом,
при увеличении п максимум смещается вправо.
6 p
Рис. 190.
Определим ширину кривой, т. е. узнаем, насколько следует
отступить от ртах = лр1, чтобы высота кривой уменьшилась в.е раз
по сравнению с максимальной. Для этого надо определить р из
условия
(Р-/7Р,)'
1
znn
откуда
——
=1, или/? — прг =
Таким образом,/?—/?max= ±Aj V 2л, т.е. ширина кривой про-
пропорциональна V л, как указывалось выше. Естественно, что высота
максимума обратно пропорциональна ширине кривой, как и должно
быть при сохранении площади под кривой.
Отметим, что даже если по своему смыслу изучаемая величина
принимает лишь положительные значения, то функция B6) дает
отличные от нуля значения при /?<0, что, конечно, не соответствует
действительности. Однако F(/?; п) при /? < 0 настолько мало при
сколько-нибудь больших п, что этот недостаток не имеет практи-
практического значения.
На рис. 191 показано, как точные кривые F(/?; п), полученные
по формуле A5) и показанные сплошными линиями, сближаются
с приближенными кривыми, полученными из формулы B6) при п = 1,
/1 = 2, п=3 и показанными пунктиром *). Эти рисунки соответствуют
*■) На рис. 191 было трудно показать, что F (р; 1) — функция разрывная —
изображается ступенькой с вертикальным падением при р=\. Функция
F (р; 2) изображается прямоугольным треугольником, лежащим на шпотенузе.
Точки р=1, ^=1 у F (p; l) и F (р; 2) совпадают.

498
случаю
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. X1I1
\ О, если р > 1 (см. пример § 7).
Рассмотрим еще пример, когда случайная величина |х может
принимать лишь два значения: 1 с некоторой вероятностью а @<а< 1)
и 0 с вероятностью Р = 1—а. Тогда сумму | из л независимых
значений величины |х можно истолковать как количество появлений
некоторого события при п независимых испытаниях, если вероятность
его появления при каждом испытании равна а. Задача о вычислении
Рис. 191.
вероятности различных значений для | была решена в пп. 2 и 3.
В п. 3 с помощью формулы Стирлинга мы показали (формула (8)),
что для больших л вероятность того, чтобы \ приняла некоторое
целое значение ла + б от 0 до л, равна
W {Па + б) = .. е-б'/2арл
У^лсфя
Так кяк при больших л расстояния между соседними возможными
значениями величины | малы по сравнению с интервалом всех ее
значений и даже с интервалом ее ожидаемых значений (см. § 3), то
при таких п можно считать | непрерывной случайной величиной
с плотностью распределения F(p; n). Тогда вероятность того, что с,
примет значение ла + б, можно приближенно подсчитать по формуле
w{na-\-b)=
F(p;
= F(na-{-b; n).
ла+б- —

§ 8] СЛУЧАЙ ВЕСЬМА БОЛЬШОГО ЧИСЛА ИСПЫТАНИЙ 499
Сравнивая две последние формулы и обозначая па-\-Ь=р, получаем
F(p- П)=: }
Однако для рассматриваемой случайной величины будет
A^fo-fj2 = A -с.Jа + @-аJр = ар.
Заменяя в последнем выражении для F(p; п) а$ на Af, а па на прг,
мы вновь приходим к формуле B6), полностью доказав ее, таким
образом, для случайных величин рассматриваемого специального вида.
Пусть величины £и ^2, . .., \п независимо принимают случайные
значения из промежутка —оо, оо, причем каждая из этих величин
имеет свое распределение вероятностей
Л (*),/„(*). ...,/„(*).
Их сумма ! = £i + £a+ • • • +1„ также будет принимать те или иные
случайные значения. Пусть ее распределение вероятности есть F{x),
В теории вероятностей доказывается, что в этом случае, если п
велико, то
, (*-*)'
e~~' B8)
Такой закон распределения вероятностей носит название нормального
закона. Для того чтобы задать формулу B8), нужно указать две
величины: х и А. [хЪ2
Множитель, стоящий перед е 2дг , определяется из условия
+ с0 (л -*)'
\ F(x) dx = 1. Действительно, пусть F(x) = Ae 2дг , тогда
— 00
+ СО
\F(x)dx = A ^ e 2дг dx. Найдем последний интеграл. Полагая
— 00 — 00
x __ =t, dx=AV 2dt, получим \ e A* dx = A]/A2 \ e~pdt =
Д/2 J J
= А Y 2я. Из условия ] /7(л;)йл;=1 находим Л-А ]/2я=1, откуда
— 00
Л_ '
Д
Предлагаем читателю проверить (см. упражнения), что для
определенной формулой B8), справедливы соотношения
+ 00 +00
VР ( v\ fi ¥ — у \ ( у* _^_ V* \ 2 р I у«\ А у* — Л 2
) — 00

500 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. Х111
т. е. х и Д2 представляют собой среднее значение и дисперсию
случайной величины £.
Выше все эти соотношения были выведены для частного случая
суммы п величин с одинаковым распределением вероятностей /(/;).
Упражнения
+ 00 + СО
1. Найдите \ xF (х) dx и \ (х—x)'z F (x) dx, где F (х) дается форму-
— со — со
лой B8).
2. }{p)Jj
I 0,
если р > q и если р < 0.
Найдите по формуле B6) распределение вероятностей F (р\ п) для слу-
случая п = 10; « = 20.
Указание. Предварительно найдите величины рг и Д^.
3. Рыболов ловит рыбу в пруду, где имеются рыбы весом не более 2 кг.
Пусть при каждом забрасывании крючка равновероятно поймать любую рыбу
весом от 0 до 2 кг.
а) Каков средний вес улова, состоящего в забрасывании крючка 20 раз
подряд?
б) Какова вероятность того, что при 20 забрасываниях крючка вес улова
будет не больше 20 кг; 22 кг; 25 кг}
§ 9. Корреляционная зависимость
Теория вероятностей имеет важные приложения к изучению за-
зависимостей величин друг от друга. До сих пор мы рассматривали
только функциональные зависимости, т. е. такие, при которых, за-
задав значения одних величин, мы полностью, точно получали значе-
значения других. Однако рассмотрим, например, такие величины, как дли-
длина / и вес р выловленной рыбы. Естественно ожидать, что чем
больше /, тем больше и р, т. е. какая-то зависимость здесь имеет-
имеется. Однако эта зависимость осуществляется лишь «в среднем», так
как длина / рыбы не определяет ее вес р однозначно — рыбы оди-
одинаковой длины могут иметь разный вес, длинная рыба может ока-
оказаться настолько тощей, что ее вес будет меньше веса короткой,
II Т. Д.
Такая «мягкая» зависимость между величинами, которая осу-
осуществляется лишь в среднем, называется корреляционной, в отличие
or «жесткой», функциональной. Корреляционными являются зависимо-
зависимости между возрастом человека и его ростом, между знаниями студента
и его оценкой па экзамене и т. д.; утверждают также, что имеется кор-
корреляционная зависимость между успехами в картах и в любви.
Корреляционная зависимость получается в случае, когда сказы-
сказывается влияние факторов, которые почему-либо не учитываются,
например из-за сложного характера этого влияния. Однако такая

§ 9] КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ 501
зависимость может получиться и по необходимости, независимо от
сложности этих факторов. Дело в том, что если, скажем, две ве-
величины х и у функционально зависят от одного параметра: x = x(t),
y=y(t), то эти два соотношения определяют жесткую функциональ-
функциональную зависимость между хну (см. стр. 111). Но если таких пара-
параметров два или более, т. е.
x = x(tlt t2, ..., У, y=y(tlt t2, ..., ta),
то эти соотношения в принципе уже не определяют функцио-
функциональной зависимости между х и у. И только если учитывать частоту
реализаций различных комбинаций значений параметров tlt t2, . . .,tn,
то можно говорить о зависимости между х и у, которая, однако,
будет лишь корреляционной. Именно такова ситуация для величин
/ и р, указанных выше, где, впрочем, полный набор существенных
параметров было бы трудно указать.
Важный пример корреляционной зависимости получается при
подборе эмпирических формул (§ II.3—4). Даже если истинная
зависимость у=/(х) между физическими величинами х и у явля-
является функциональной, зависимость между измеренными значениями
х и у при наличии ошибок измерения оказывается лишь корреля-
корреляционной.
Рассмотрим общий случай. Пусть имеются две случайные вели-
величины | и г), как-то связанные между собой. Как мы доказали выше,
если эти величины независимы, то £г) = |г), т. е. \х\ — fti = O. По-
Поэтому последнюю разность можно принять за самую грубую меру
зависимости между \ и г). Однако чаще переходят к безразмерному
коэффициенту корреляции
где в знаменателе стоят средние квадратичные уклонения величин \ и т].
В силу сказанного выше, для независимых величин этот коэф-
коэффициент равен нулю. (Обратное, вообще говоря, неверно.) Рассмот-
Рассмотрим теперь другой крайний случай, когда между \ и т) имеется
функциональная и притом линейная зависимость, т. е. х\ = 0%^-Ь,
где а и Ъ—постоянные. Тогда легко проверить, что Д,г1=а2Д|, т. е.
Д, = |«|д» из равенства Д2Е= (£ —|)» =р —2&I + I" =F2-? выте-
вытекает, что
-<&, -Ь\
^ I ДЕ | а | д| | а | '
т. с. г (|, т)) = 1, если а > 0, и г (|, п) = — 1, если а < 0.
Можно доказать (мы не будем этого делать), что во всех слу-
случаях, кроме линейной функциональной зависимости, коэффициент
корреляции заключен строго между —1 и 1, —!</■(!, ц) < 1.

502 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Этот коэффициент характеризует степень отклонения зависимости
между | и г) от линейной функциональной.
Рассмотрим пример. Пусть физические величины х и у связаны
между собой линейной зависимостью _у = ал; + ^, однако значения
коэффициентов а и Ъ нам неизвестны и получаются в результате
эксперимента, в котором мы задаемся значениями х и измеряем
значения у. Будем для простоты считать, что значения х известны
созершенно точно, а степень точности в определении соответствую-
соответствующего значения у одна и та же при всех х. Обозначив через \ из-
измеренное значение х, а через г) измеренное значение у (£, г) — это
случайные величины), примем, что £ с равной вероятностью прини-
принимает все значения между —/ и /, т. е. соответствующая функция
распределения имеет вид
ф(*) = ( 2Г ('<*<')■ B9)
I о A*1 > 0-
Кроме того, примем, что при каждом значении 'Е. — х величина г)
распределена по нормальному закону вокруг значения ах-\-Ь с дис-
дисперсией Д2, не зависящей от х. (Предположение о нормальности
закона распределения естественно принять, если ошибка в опреде-
определении у складывается из большого числа независимых ошибок,
объясняющихся различными причинами.) Функцию распределения
величины г) при заданном значении £ = л: будем обозначать tyx(y),
так что
Обозначим, далее, через f(x, у) функцию совместного распреде-
распределения величин |, г); это значит, что вероятность одновременного
попадания % между х и x-\-dx, а т) — между у и y + dy равна
f(x, y)dxdy. Для подсчета функции f(x, у) заметим, что если
произведено большое число Af испытаний, то число случаев одно-
одновременного попадания | между х и x-\-dx, а т) — между у и y-\-dy
равно [f(x, y)dxdy]N. С другой стороны, можно рассуждать так:
при Af испытаниях число случаев, когда | попадет между х и x-\-dx,
равно N1 = [ф (л;) dx] N. Но из этих N1 случаев число случаев,
когда г) попадет между у и y-\-dy, равно
[гр, (у) dy] N, = гр, ДО <р (*) rfx dy. М
Приравнивая оба результата, получаем, что /(#, _у) = ф (дт) tyx(y)^
т. е. в наших предположениях
{
f(x, у)=\ 2/
I о

§ 9] КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ 503
Вычислим коэффициент корреляции г (|, т|). Из соображений
симметрии ясно, что £=0, r\=b. Среднее значение ^вычисля-
^вычисляется по общему правилу (сумма произведений значений случайной
величины на их вероятности), т. е. £г) = \ \ xyf(x, y)dxdy, или
I ОО /
-I -оо -/
;
Из формул B9) получаем А| = \ x2 -^r dx — — . Чтобы вычислить Av
—t *
найдем сначала функцию распределения гр (_у) величины т) (это не то
же самое, что tyx(y)l). Так как гр {у) dy есть вероятность того, что т)
окажется между _у и _y-)-dy, a | примет произвольное значение, то
00
гр (у) dy= \ [/ (х, у) dy] dx. Поэтому
— 00
оо ;
грО>)= {f{x,y)dx= Г L^e-nz-c^+W/aA2^
-оо _;
откуда
После перестановки порядка интегрирования и вычислений, которые
мы предоставляем читателю, получается Д^~Д2т|—г—. Отсюда на-
находим искомый коэффициент
1га "X
Хорошо видно, что \г\ < 1; при -г ► оо (например, при а = const ^= О,
/ = const, Д —у 0) будет г—*■ ± 1, т. е. корреляция экстремальна;
при -^г 1- 0 (например, при а = const, ft = const, Д—> оо) будет
г—у 0, корреляция теряется.
Пусть в результате эксперимента, после N замеров, мы полу-
получили при значениях x = xlt х2, ..., хА, соответствующие значения
y=yv у», ..., ,Удг. Если замеры независимы, то такой набор значе-
значений имеет функцию совместного распределения, равную в силу C0)
л)■/(*.>л)•...•/(■**. у*) ^

504 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
(Здесь суммирование 2 производится по i от 1 до N.) Если
нам известен результат эксперимента, и мы исходим из линей-
линейной зависимости у = ах -\-Ь, но коэффициенты а и Ь неизвестны,
то естественно их выбрать так, чтобы этот результат оказался
в зоне наибольшей возможной плотности распределения, т. е. чтобы
он был в определенном смысле наиболее вероятным. Это означает,
что коэффициенты а и Ъ подбираются из условия максимизации
правой части C1), т. е. минимизации суммы 2 (Л—(аЛ;/ + ^)]2- Мы
приходим к методу наименьших квадратов, уже разобранному в § II.3.
Итак, метод наименьших квадратов получает обоснование на основе
соображений теории вероятности.
После указанного эксперимента коэффициент корреляции можно
вычислить по формуле (заметим, что £г| — £г|=(£—£) (г) — х\):
— t) Ol — п) 2 (*/—*) (Уi —~У)IN
r=z
где х = ^Хр'1\1, _у = 2.y</N. Умножив на N числитель и 'знамена-
'знаменатель, полумаем
г —
N
*,-*)* 2
Если |гд.| получится малым, то может возникнуть подозрение,
чте на самом деле г = 0, а отличие гЛ. от нуля получилось из-за
естественного разброса экспериментальных значений. Можно дока-
доказать (мы этого делать не будем), что если истинное значение г = 0,
то при большом /V наблюдаемое значение rN приближенно подчи-
подчиняется нормальному закону со средним значением гЛ.= 0 и диспер-
дисперсией Дд' = т:—г. Рассуждая, как в § 3, получаем, что вероятность
неравенства |гЛ,|<в равна
4 =ф(е1/~Л/—Л).
Приравняв, например, правую часть 0,95, мы по таблице находим,
что с вероятностью 0,95 будет |гд,|<е, где ej//V—1 = 1,96 « 2.
2
Итак, если в результате эксперимента получится, что I rN ~~>-— ,
у N — 1
то с вероятностью, не меньшей 0,95, можно утверждать, что коэф-
коэффициент корреляции между изучаемыми физическими величинами
отличен от нуля, т. е. между этими величинами имеется определенная
корреляционная зависимость.
Подчеркнем ;\ заключение, что если коэффициент корреляции
оказывается равным нулю, то это еще не говорит об отсутствии

§ 10] О РАСПРЕДЕЛЕНИИ ПРОСТЫХ ЧИСЕЛ 505
зависимости, так как эта зависимость может оказаться нелиней-
нелинейной. Поэтому эмпирическое выявление зависимости у (х) всегда
надо начинать с нанесения результатов эксперимента на коор-
координатную плоскость х, у. При этом может оказаться, что эмпи-
эмпирические точки с достаточной точностью лягут на параболу или на
какую-либо иную простую линию; тогда эта линия определит функ-
функциональную зависимость у (х). И лишь если эмпирические точки
образуют «облако», то надо проводить их статистическую обра-
обработку, 'При этом применение понятия корреляции целесообразно,
если это «облако» напоминает линейную зависимость, как на рис. 12.
Нелинейную зависимость можно исследовать на небольших интер-
интервалах изменения х, приближенно полагая ее линейной' либо же
можно добиться линейности с помощью предварительного преобра-
преобразования переменных по методам § II.4.
§ 10. О распределении простых чисел
Приведем интересный пример применения теории вероятностей
к теории чисел. Рассмотрим -вопрос о распределении простых чисел
в натуральном ряде чисел. Этот вопрос очень сложный, и поэтому
наши рассуждения не будут вполне строгими, но они все же пра-
правильно передают общую картину.
Еще в древности было доказано, что не существует самого
большого простого числа, т. е. что простых чисел существует бес-
бесчисленное множество. Даже беглый взгляд на несколько первых
сотен чисел натурального ряда убеждает нас в том, что простые
числа распределены крайне неравномерно. Так, например, после
простого числа 113 идет 13 составных чисел, а четырнадцатое
число 127 — простое. Между 127 и следующим простым числом 131
находятся лишь три составных числа. Между соседними простыми
числами 131 и 137 имеется пять чисел, а после 137 через одно
число идет опять простое число 139.
Поэтому интересен такой вопрос. Сколько простых чисел имеется
между числами л и л-|-Д? Отношение числа простых чисел, ле-
лежащих между л !i п-\-А, к числу Д мы будем называть плот-
плотностью распределения простых чисел. Определению зависимости
плотности распределения простых чисел от л и посвящен этот
параграф.
Будем считать, что Д мало по сравнению с л, но значительно
больше 1. (Тем самым мы предполагаем, что л достаточно большое
число.) При этом предположении между л и л + Д имеется много
простых чисел. Обозначим плотность распределения простых чисел
через /(л). Тогда в промежутке от д до л + А содержится /(л)Д
простых чисел.
Можно составить список всех простых чисел, не превышающих
данного числа п, следующим образом.

506 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XII1
Напишем подряд все натуральные числа от 2 до л. Затем вы-
вычеркнем все числа, делящиеся на 2 (не считая самого числа 2),
после этого вычеркнем все числа, делящиеся на 3 (не считая
числа 3), затем все числа, делящиеся на 5 (не считая числа 5)
и т. д. В итоге все составные числа будут зачеркнуты и останутся
лишь простые числа. Этот способ известен под названием решето
Эратосфена.
Ясно, что 1/2 всех чисел от 2 до л делится на 2; на 3 делится
лишь 1/3 этих чисел; на 5 делится 1/5 часть и т. д. Таким обра-
образом, если мы рассматриваем натуральные числа от 2 до л, то
—-j-я часть их делится на простое число р. а ( 1 1-я часть не
Р J V Р 1
делится на р. При этом мы предполагаем, что р<^п.
Пусть даны два простых числа, р1 и рг. Возьмем любое нату-
натуральное число л. Оно может делиться на plt а может и не делиться
на него. Точно так же оно либо делится на р2, либо. нет. Будем
считать, что два события, первое из которых состоит в том, что л
не делится на ру, а второе в том, что л не делится на р2, являются
независимыми.
Среди чисел от 2 до л доля чисел, не делящихся на 2, равна
1—— ) , доля чисел, не делящихся на 3, равна ( 1—="), доля
1 Г 1\
чисел, не делящихся на 5, равна 1 =-) , вообще доля чисел,
не делящихся на простое число р, равна ( 1 j. Так как собы-
события, состоящие в том, что число не делится на различные меньшие
его простые числа, мы предполагаем независимыми, то по правилу
умножения вероятностей доля простых чисел, содержащихся между
2 и л, равна
(Мы приравняли эту долю плотности распределения простых чисел
/(л) на основании приближенного равенства F(п)/п»F' (л) при
больших F (л) и л.)
Если р> 1, то е р та 1 (мы пренебрегаем членами \/р2,
\/р3, ...). Поэтому j __L
1 ^ ^> tT
i_
1— -хе р,
Р

§ 10] О РАСПРЕДЕЛЕНИИ ПРОСТЫХ ЧИСЕЛ 507
1_ 1_ _1_
Формула C2) принимает вид/(/г) = е 2 -е '->...е ", откуда
= —jLj.- C3)
i
В промежутке от v до v-\-dv (где dv мало по сравнению с v)
имеется / (v) dv простых чисел. Ввиду того, что длина промежутка
невелика, можно считать, что все простые числа из этого проме-
промежутка приблизительно равны v, и поэтому — для этого промежутка
есть —. Тогда \\— для чисел из промежутка от v до v-\-dy при-
принимает вид— f(v)dv. Следовательно, для суммы V — , соответ-
ствующей промежутку от 2 до п, получаем
v
i ' ' ~а
Каковы пределы интегрирования в этом интеграле? Нас интере-
интересуют все простые числа, не превосходящие п. Поэтому верхний
предел интегрирования берем равным п. Заметим, что равенство
1 --
1 =е pi хорошо только при больших pt. Если pi невелико, то
последняя формула дает заметные ошибки. Так, например, для р = 1
получаем 1—— = 0,5; е 2 = 0,61 (ошибка более 20%). Замена
суммы интегралом тоже хороша лишь для тех промежутков, где pt
достаточно велико. Поэтому указать величину нижнего предела
интегрирования не представляется возможным. Оставим нижний
предел неопределенным. Формула C3) принимает вид
v. C4)
Возьмем производную от обеих частей этого равенства, получим
1 dftn) /(/?) .,
'=—L^-L . Мы получили уравнение с разделяющимися пе-
/ (п) dn n
ременными, которое нетрудно решить. Перепишем его так:
df (n) _ _dn
Проинтегрируем обе части от п0 до /г, получим
11пл + 1

508 теория вЕРОятностей [гл. хш
откуда
= тт—г — In /zo + ln /z = С-\-\х\ п,
/ (л) / («о)
где положено C—tj—т — 1п/г0.
/ (по)
Окончательно получаем
При больших /г постоянной С можно пренебречь по сравнению
с In п. Поэтому при весьма больших п будет
Пп) = ^п. C6)
Наш вывод был весьма груб, и легко указать некоторые его
неточности. Например, нужно ли испытывать, делится ли п на все
простые числа меньше /г? Конечно, нет. На самом деле достаточно испы-
испытать лишь те простые числа, которые не превосходят ]//г. Действи-
Действительно, пусть п не делится ни на одно простое число, меньшее |/ п. До-
Допустим, что п делится на простое число pY > У п. Тогда /z/p1 = &,
причем, так как ру > у п, то k <^У п. Заметим, что n=p1k, откуда
nlk=pl. Следовательно, п делится на k <Vn, что противоречит
условию.
Оказывается, что выражение C6) удовлетворяет (если отбросить
все члены, кроме главного) также и видоизмененному соотноше-
соотношению C4), в котором верхний предел п интеграла заменен на У п.
Исходя из совершенно иных идей, гораздо более сложным путем
показано, что точность формулы C6) при больших п весьма велика,
лучше, чем это могло бы следовать из наших рассуждений. В част-
частности, оказалось, что формула C5) дает наилучшее асимптотиче-
асимптотическое представление /(/г) именно при С=0.
Часто рассматривается вопрос не о плотности простых чисел,
а о числе А (/г) простых чисел, не превосходящих данного числа п.
п
Ясно, что А (п) = \ f(v) dv, где нижний предел интегрирования а
а
нам неизвестен. Итак,
Положим здесь v = ny, dv = n dy, тогда
i
Aln) = n \ d
j \nn-\-\ny'

§10] О РАСПРЕДЕЛЕНИИ ПРОСТЫХ ЧИСЕЛ 50У
Заметим, что при больших п
In n-\-ln у In n . In у In n |_ Inn ~r~ In2 n ■ ■ • J •
Поэтому
i
... n f Г. In у . In2 у 1 ,
A (n) = .— \ 1 — i—^ + т~ — . . . \ dy.
K ' Inn J |_ In n ' ln2n J s
a
n
Ограничиваясь первым членом разложения и заменяя — при боль-
больших п на 0, получаем отсюда
А (/г) = \h ■
Если взять большое число членов, то получим более точную
формулу. Например, ограничиваясь тремя членами разложения,
находим
„г 1 от
)• C8)
Оказывается, что ошибка любой из таких формул асимптоти-
асимптотически мала по сравнению с последним «точным» членом.
Упражнения
ч
1. Подсчитайте приближенно количество простых чисел, содержащихся
в промежутке от 3000 до 3100; от 3000 до 3200; от 3000 до 3500. Сравните
результат с истинным, подсчитав количество простых чисел в указанных про-
промежутках при помощи таблицы простых чисел.
2. Найдите количество простых чисел, меньших 4000, по формуле C7).
Затем уточните результат, удерживая в формуле C8) сперва член, содержа-
содержащий -. . а затем и член, содержащий -j — . Результат сравните с точным
подсчитав количество простых чисел, меньших 4000, по таблице простых чисел.
3. Подсчитайте количество простых чисел, содержащихся в промежутке
от 2000 до 5000. Выполните подсчет различными способами:
а) считая, что п = 2000, А = 3000;
б) находя разность между А E000) и А B000). Последние величины под-
подсчитайте сперва по формуле C7), а затем более точно, удерживая член, со-
содержащий -—.
* 1
*) При этом нам пришлось находить \ in у dy и \ Xrflydy, Оба интегра-
0 0
ла легко берутся интегрированием по частям. Следует учесть, что у In* y=0
при i/=0 для любого k.

510
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Таблица интеграла вероятности
е 2 dt
[ГЛ. ХШ
2 Г
Ф(х) = —4=
^2л J
X
0,00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Ф (X)
0,000
0,008
-0,016
",024
0,032
0,040
0,048
0,056
0,064
0,072
0,080
0,088
0,096
0,103
0,111
0,119
0,127
0,135
0,143
0,151
0,159
0,166
0,174
0,182
0,190
0,197
0,205
0,213
0,221
0,228
0,236
0,243
0,251
0,259
0,266
0,274
Л"
0,36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
Ф (х)
0,281
0,289
0,296
0,303
0,311
0,318
0,326
0,333
0,340
0,347
0,354
0,362
0,369
0,376
0,383
0,390
0,397
0,404
0,411
0,418
0,425
0,431
0,438
0,445
0,451
0,458
0,465
0,471
0,478
0,484
0,491
0,497
0,503
0,510
0,516
л:
0,71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
1,00
01
02
03
04
05
Ф (х)
0,522
0,528
0,535
0,541
0,547
0,553
0,559
0,565
0,570
0,576
0,582
0,588
0,593
0,599
0,605
0,610
0,616
0,621
0,627
0,632
0,637
0,642
0,648
0,653
0,658
0,663
0,668
0,673
0,678
0,683
0,687
0,692
0,697
0,702
0,706
X
1,06
07
08
09
10
11
Г2
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Ф (X)
0,711
0,715
0,720
0,724
0,729
0,733
0,737
0,742
0,746
0,750
0,754
0,758
0,762
0,766
0,770
0,774
0,778
0,781
0,785
0,789
0,792
0,796
0,799
0,803
0,806
0,810
0,813
0,816
0,820
0,823
0,826
0,829
0,832
0,835
0,838

ОТВЕТЫ И РЕШЕНИЯ
511
Продолжение
X
1,41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
Г.6
57
58
59
60
61
62
63
64
65
Ф(ЛГ)
0,841
0,844
0,847
0,850
0,853
0,856
0,858
0,861
0,864
0,866
0,869
0,871
0,874
0,876
0,879
0,881
0,884
0,886
0,888
0,890
0,893
0,895
0,897
0,899
0,901
X
1,66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
Ф(лО
0,903
0,905
0,907
0,909
0,911
0,913
0,915
0,916
0,918
0,920
0,922
0,923
0,925
0,927
0,928
0,930
0,931
0,933
0,934
0,936
0,937
0,939
0,940
0,941
0,943
X
1,91
92
93
94
95
96
97
98
99
2,00
05
10
15
20
25
30
35
40
45
50
Ф U)
0,944
0,945
0,946
0,948
0,949
0,950
0,951
0,952
0,953
0,954
0,960
0,964
0,968
0,972
0,976
0,979
0,981
0,984
0,986
0,988
2,55
60
65
70
80
90
3,00
10
20
30
40
3,50
3,9
4,4
4,9
5,3
Ф{х)
0,989
0,991
0,992
0,993
0,995 '
0,996
0,997
0,998
0,999
0,999
0,999
1—0,5-10-3
1 —10-*
1 —Ю-5
1 —10-е
1 —10 — 2
ОТВЕТЫ И РЕШЕНИЯ
§ 1
_9___J_. _4_ l_ _l_ _8_
36 ~ 4 ' 36 ~ 9 ' 36' 35'
§2
I 1 2 I- 1
1# 4 ' 8 ' 8 '
3. Вероятность появления черной грани равна
4 2
а вероятность появления белой грани
\_
3 #

512 ТЕОРИЯ ВЕРОЯТИОСТСИ [ГЛ. XIII
Так как w^ — wq-wh, to Ибб^тг- Аналогично
У
Вероятность того, что один раз появится белая грань, а другой раз—черная
(безразлично, в каком порядке), можно подсчитать по общей формуле
JfLa»p*. Получим-1.
2 4
4. Пользуясь общем формулой, находим -jr-, —.
5. 0,18. 6. 0,243; 0,027. 7. 0,29; 0,33.
§3
1. Пользуясь формулой C) и полагая в ней п = I 000, 6 = 0. а затем
п = !000, 6=10, получаем 0,025; 0,020.
2. Вероятность того, что выпадает какое-то количество гербов, не пре-
превосходящее 500, равна
U f2 + О
1 г ~J i Г
/2л J /2л J
+ 00 /2
-— 1 9
2 , J_ * I 2 J_
:л 1 J
0 0
Вероятность получить не меньше 500 гербов равна
Вероятность получить не больше 510 гербов F=10) равна
2
КГо t2 о,бз /2 , о /= о,бз /»
/2Тп
/2л J /2 И ^ J
4 - оо о
0,^63 ,2
= С e~~*dt = 0,5 + 4- -0,471 =0,74.
2Д J 2
о о
Поэтому вероятность получить число гербов не меньше 510 равна 1 —
— 0,74=0,26.
3. Полагая в (8) 6 = 0A0 попаданий), получаем w — 0,13; полагая 6=—2
(8 попаданий), получаем &j = 0,II.
4. Обозначим через 6 отклонение числа попаданий от наиболее вероятного
числа. Тогда вероятность того, что осуществится одно из событий, для кото-
которого 6 < 60, равна
60 м
е
— СО
Полагая здесь —■ =t, db=\rna$dt, получим & = ——=- ( е 2 dt,
/пар V 2п J
- ос
где положено /0= 2= . В рассматриваемом случае лг= 100; « = 0,1; р = 0,9.
/пар

OTBinhi и ri.ii!i;i:uii 513
Наиболее вероятное число попаданий есть па= 100-0.1 — 10. Подсчитаем, ка-
какова вероятность того, что число попаданий не Солее 8F=—2). Получим
dt 1=0,5 —0.15Ф (О Р7) = 0,25.
Следовательно, вероятность того, что число попаданий не меньше 8, равна
1—0,25 = 0,75.
Для двух других случаев вероятности соответственно равны 0,5 и 0,25.
5. 0,73; 0,37.
§5
£'„(«) _\\.me-v-(m — \)\ n
1. —j тт— , ,, . = —. Отсюда tt)u (m) > w.. (m— 1), пока
w(m— 1) m\nm-le-Y- т * ' <х 1 '
т < j.i, и to^ (m) < w^ (m— 1), когда m > |Л. Значит, если ц. не целое, то к.^ (т)
наибольшее, когда т равно целой части \i. Если же ^=1, 2, ... , то "наи-
"наибольшими являются w^ (ц—1)=ьу|1 ((.i).
2. Если проведено большое число N испытаний, то величина х приняла
p1N раз значение хх, p2N раз значение хг, ... , pnN раз значение хп. Поэтому
среднее ее.значение, в расчете на одно испытание, равно
1 + p,,V'X,+ ...+pn\'-xn_
-у — рхХ1-\-р.,Х.,-\- . . . -\-Р„Хп.
Для закона Пуассона это дает
где положено т—l=fc.
Система уравнений имеет вид
Эту систему надо решить при начальном условии ро(О) = 1, р,-@) = 0(£ Ф 0).
При применении метода последовательных приближений удобно сначала сде-
сделать замену переменных р(- = е-(«+<0" <?,-, откуда
-^ = @<7,-_, + а<7; + , (i = ... , —2, —1, 0, 1, 2, ...)-
Нулевое приближение:
<?п=1, прочие 9,- = 0.
Первое приближение:
17 Я- Б. Зельдович, А. Д. Мышкис

514 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. XIII
Второе приближение:
<7-2=-<г-' <7-i = a'< <7о:
92=—. прочие <7,- = 0
и т. д. Среднее значение номера состояния £ = (ш—a)t. Задача, разобранная
в основном тексте, получается при сс = О, ш=1.
§7
' Р2
■~ , если 0 < р < <7,
^-j (— 2p2-j-6p<7 — 3<72), если q < р < 2q,
1
9~5 (Р —6р<7 + 9<7 ), если 2q < р < Зд.
Если р < 0 и если р > 3q, то F3 (р) = 0. График функции F3 (р) при q = 1 см.
на рис. 191.
§8
I. I xF(x)dx = ^= Гх-
J A V2n J
— QO
Положим -rr=r — t, dx = Ay2dt. Тогда последний интеграл прини-
принимает вид
У л J
(х+А
*
— оо
Интеграл \ ^e-f Л = 0, потому что подынтегральная функция нечетная, так
— 00
что ее график симметричен относительно начала координат.
Для нахождения i (х—хJ ■ е 2А" dx выполним замену пере-
J А/2л
-00
меннон jr=r = t, dx = A ~\r2dt. Тогда исходный интеграл перейдет в такой:
+ 00
■ ~ \ t2e-li dt. Проинтегрируем по частям, полагая te~n dt = dg, t=f. Тогда
У л J
— оо
I
g= o~e • df = dt. Получаем

ОТВЕТЫ И РЕШЕНИЯ 515
2. Находим р1=-|-; A1=i-, поэтому
3 (р-5»)г /"-5— 3 (р-1
3. а) Так как рх = 1 кг, а рп = прх, то р20 = 2(Ы кг = 20 кг.
б) Воспользуемся результатом пункта а), полагая в выражении для
F (р; 20) величину q равной 2. Получим
40
• и-. --/— 2 )к Юл '
или
_3 (p-20)s
е
; 20)=О,
Вероятность того, что вес улова будет не больше 20 кг, есть ш=
20
= 0,154 I e-V?1 V-201' dp. Чтобы свести этот интеграл к табличной функции
о
Ф (*), noj
Поэтому
о
Ф (х), положим -2-*2=0,075 (р— 20J, откуда * = 0,387 (р—20), d* = 0,387 dp.
о 7,7 ,
'=0Т387 J в dx==0A ) е dx=0-
-7,7 0
Вероятность того, что вес улова окажется не больше 22 кг, равна
+ 0,77 _£_ /0 х*_ 0,77
И = 0,4 j e 2dx=0,4f J e~2dx+ $e
-7,7 V-7,7 0
= 0,4 ¥р [Ф G,7)+ Ф @,77)] =0,78.
Вероятность того, что вес улова будет не больше 25 кг, равна 0,98.
§ Ю
1. Приняв я = 3000, Д=100, 200, 500, получаем приближенные значения
12, 25, 62. Точные значения соответственно равны 12, 22, 59.
2. По формуле C7) А D000) = 482. По сокращенной формуле C8) Л =540.
По полной формуле C8) Л =554. Точное значение А D000) = 550.
3. Приняв я = 2000, Д = 3000, получаем количество ЛГ = 395. По фор-
формуле C7) УУ = 322. По сокращенной фориуле. C8) УУ = 358. Точное значе-
значение ./V = 366.

ГЛАВА XIV
ПРЕОБРАЗОВАНИЕ ФУРЬЕ*)
§ 1. Введение
В главах VII—VIII, при рассмотрении линейных дифференциаль-
дифференциальных ур~авнений с постоянными коэффициентами, а также систем таких
уравнений (другими словами, при рассмотрении линейных однород-
однородных во времени процессов с конечным числом степеней свободы),
мы видели, какую важную роль играет функция еР1. Дело в том,
что если подставить эту функцию в левую часть уравнения и про-
произвести все действия, то в результате получится эта же функция,
умноженная на некоторый постоянный множитель. Поэтому решение
однородного уравнения выражалось через функции вида е?*, через
них же выражалась функция Грина, да и решение неоднородного
уравнения имело наиболее простой вид, когда в правой части стояла
функция еР1. Мы включаем сюда как частный случай и функции
вида cos Ш или e^sincu^, которые по формуле Эйлера непосредст-
непосредственно выражаются через экспоненты егл с комплексным р (см. фор-
формулы C)).
Во многих задачах независимая переменная t, которой обычно
служит время, может принимать всевозможные значения, т. е.
— оо<^<оо, причем рассматриваемые решения, по смыслу задачи,
должны оставаться конечными как при конечных t, так и при
t~+±oo. Так как при р = у+гсо е^ = etf (cos cat-\-i s\n cat),
| cos at -j- i sin at | = 1, то при y>0 будет | epf | —<- oo, а при у<0
будет | epf I —>- oo. Значит, если требовать ограниченности экспо-
ненты е'А при t —<- ± оо, то должно быть у = 0, т. е. надо пользо-
пользоваться лишь «гармониками», функциями
еш = Cosco^+ islnat. A)
*) В этой главе нам потребуются сведения о комплексных числах
(§§ V.1—3) и о б-функции (§§ VI.1—3). В § 7 применяется понятие много-
многомерного векторного пространства (§ IX.6).

§ 1] введи tut i- 517
При наложении друг на друга гармоник с различными амплиту-
амплитудами и частотами, т. е. при рассмотрении сумм вида
могут получаться фуик"цип значительно более сложного вила. НаГюр
рассматриваемых здесь частот <Bft называется спектром функции/!/);
в данном случае мы имеем дискретный спектр*). Можно пользоваться
также суммами синусов или косинусов с различными чг.сютами и
амплитудами, так как по формуле A) можно перейти от зкс::онснт
к косинусам и синусам, а по формулам
coscot — "-z , sin со/= к~. ■ C)
—от косинусов п синусов к экспонентам. Мы будем для единооб-
единообразия в основном пользоваться экспонентами (ср. § V.5).
Еще более широкий класс функций/(г) получится, если вместо
суммы по отдельным частотам воспользоваться интегралом по всем
частотам, т. е. воспользоваться представлением вила
ОС
/U)= I F((_») e/to'rfco. D)
— х
Здесь мы имеем непрерывный спектр; он может занимать всю ось со,
но может занимать и некоторый интервал У этой осп, есл;: вне этого
интервала функция F (а) равна нулю, т. е. фактически интегриро-
интегрирование D) производится лишь по J (тогда J называется носителем
функции F(со)). Впрочем, в § VI.1 мы видели, что если функции F(и>)
представляет собой сумму дельтообразных слагаемых, то и весь
интеграф D) переходит в сумму (.2), т. е. спектр будет д;<с5-.т,сгиым
и будет состоять из набора тех значений со, в которых лельтсоб-
разные слагаемые имеют особенности. В общем случае спектр ;;ожет
обладать как непрерывной, так и дискретной частями.
Нетрудно понять смысл функции F (ы) в представлен;;:! D). Так
как в этом представлении на малый интервал частот от ы до (о-г ^
приходится слагаемое F (ц>) eiwt du> = [F [и>) da] eitttt, то, сравнивая
с B), мы видим, что F{(.o)dd)—это амплитуда, отвечающая указан-
указанному интервалу частот. Значит, F (со) можно рассматривать как «плот-
«плотность амплитуды», отвечающей малому интервалу частот и рассчи-
рассчитанной на единицу длины этого интервала. Поэтому функцию F(io)
называют спектральной плотностью функции f(t). Переход от суммы
B) к интегралу D) аналогичен переходу (ср. § ХИЛ) от дискретной
модели струны в виде упруго связанных друг с другом бусинок
к непрерывной модели, у которой масса «размазана» по всей длине
струны с определенной плотностью. Так и в представлении D)
*) От спектра функции, с которым мы будем иметь дело в этой главе,
надо отличать спектр краевом задачи (стр. 272).

518 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
амплитуда гармоник «размазана» по всему спектру частот с плот-
плотностью F(a).
В физических задачах мы в большинстве случаев встречаемся
с вещественными функциями / (t), например, когда/ (t) представляет
собой силу /, действующую на какую-то систему в зависимости от
времени t.
Условие вещественности / (t) можно записать так:
f(t) =/* (t), т. е. ^ F N еш da> = $ F* (со) е~ш dm.
— СО — 00
У величины со знак сопряжения мы не ставим, так как подразуме-
подразумевается, что со вещественно. Для того чтобы были равны суммы
гармоник при любых значениях t, нужно, чтобы были равны соот-
соответствующие амплитуды. Найдем множитель при еш°1; в левом ин-
интеграле это F (о)о). В правом интеграле из условия e~iu>t=eia°t найдем
@= —0H; значит, множитель при е'и»' в правом интеграле равен
F* (<в)=/:'* (— 0H). Итак, условие вещественности функции / (t) дает
/^(-со,,) =/=>„).
Это равенство относится к любому 0H, так что можно опустить
индекс «О» и записать
>•( —(D)=/?((D). E)
Функция F (со)—комплексная. Запишем в явном виде ее вещест-
вещественную и мнимую части с помощью двух вещественных функций
А (со) и В (со):
/=■(«)= А (со) + »5(со).
Условие вещественности исходной функции f(t), которое нам дало
формулу E), приводит к
А (—со) —*(—со)=Л (со) + »5(со),
т. 8.
А (—со)=Л (со), 5(—со) = —5(со). F)
Итак, вещественная часть Z7 есть четная функция со, а мнимая
часть F—нечетная функция со.
Теперь перейдем от представления с помощью е'ш* к представ-
представлению с помощью cos 0)^ и si
[t)= \ F (со) eiUit dm = \ [А (со) + iB (со)] [cos co^ + / sin co^] da) =
— CO
» + CO
А (со) cos cat did — ^ В (со) sin co^ Ao +
» —CO
+ 00 + CO
Л (со) sin со* Ao + * j 5 (со) cos co^ dm.

§ 1] ВВЕДЕНИЕ 519
Рассмотрим частный, но важный случай вещественной функции
f(t). Тогда условия F) приведут к обращению в нуль двух послед-
последних интегралов. В них входит произведение четной функции на
О оо +оо
нечетную, так что \kd(a = —J kda, ^ kdti> = 0, где k —
— 00 0 — 30
подынтегральная функция третьего или четвертого интегралов.
Напротив, в первых двух интегралах подынтегральное выражение
симметрично,
О со
л(со) = л(—со), ^ л (со) dco = ^ л (со) d(s>,
— 00 О
+ оо со
J л (со) dco = 2 J л (со) dco,
— ш О
так что окончательно
00 00
/ (Г) = 2 \ А (со) cos со* Ло—2 J 5 (со) sin со* dco. G)
о о
Итак, вещественная функция f (t) представляется в виде интеграла
от вещественных функций cos cat и sinatf, причем соответствующая
спектральная плотность Л (со) и В (со) тоже вещественна. Интегри-
Интегрирование в этом случае ведется только по положительным частотам
с со, меняющимся от 0 до оо.
Замечательно, что в форме D) оказывается возможным предста-
представить практически любую функцию f(t), остающуюся конечной при
^-»-±'оо. Это будет показано в § 2, где будет также дан ответ
на основной вопрос: как найти спектральную плотность F (со) задан-
заданной функции /@? Мы сейчас увидим, что вопрос имеет далеко не
только теоретический интерес.
Напомним простые факты из теории колебаний (§ VII.3,5; см.
также ВМ, гл. VI и VIII). Пусть рассматривается осциллятор с малым
затуханием, т. е. малым трением, если речь идет о механической
колебательной системе, или с малым сопротивлением, если это —
электрический колебательный контур, и т. д. Если такой осциллятор
испытывает гармоническое внешнее воздействие с частотой <вА, то
в нем возбуждаются гармонические вынужденные колебания с той
же частотой. Амплитуда этих колебаний тем больше, чем со ближе
к частоте 0H собственных колебаний осциллятора. Эта «избиратель-
«избирательность» осциллятора по отношению к частоте внешнего воздействия
тем резче выражена, чем затухание меньше. В пределе, когда рас-
рассматривается осциллятор без затухания, при (й = о)о наступает ре-
резонанс, т. е. амплитуда вынужденных колебаний возрастает неогра-
неограниченно.

520 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Пусть теперь гармоническое внешнее воздействие прилагается
к системе осцилляторов с малым затуханием, обладающих различ-
различными собственными частотами. Тогда на это воздействие «отзовется»
наиболее сильно тот осциллятор, собственная частота которого равна
частоте внешнего воздействия. Если, наконец, на такую систему
осцилляторов воздействует «смесь» гармоник, т. е. функция вида B),
то на их воздействие отзовутся те осцилляторы, собственная частота
которых совпадает с какой-либо из внешних частот ык. При этом
амплитуда вынужденных колебаний осциллятора с собственной ча-
частотой ы0 пропорциональна амплитуде воздействия, т. е. пропорци-
пропорциональна тому ak, для которого сок = ша. Таким образом, указанная
система осцилляторов осуществит «гармонический анализ» (говорят
также «спектральный анализ») внешнего воздействия, как бы разло-
разложит его на гармоники. Аналогичная картина получится при нало-
наложении внешнего воздействия вида D). Амплитуда осциллятора
с собственной частотой о)о пропорциональна F(u>a), где F—спект-
F—спектральная плотность (см. формулу D)). Точная формулировка условий,
необходимых для этого, будет дана ниже. Располагая набором ос-
осцилляторов со всевозможными значениями <в0, можно «прощупать»,
т. е. определить весь ход функции F (to).
Описанный гармонический анализ может быть реально осущест-
осуществлен. Например, в акустике пользуются системой «резонаторов»,
каждый из которых настроен на определенную частоту. Если на эту
систему воздействует акустическое (звуковое) колебание, которое
всегда можно представить как смесь «чистых звуков», т, е. гармо-
гармонических колебаний, то откликнутся те резонаторы, собственная
частота которых отвечает спектру этого воздействия. Определяя
амплитуду колебания резонаторов, мы тем самым осуществляем
гармонический анализ внешнего воздействия.
Упражнения
1. Чему должна быть равна функция F (со), чтобы интеграл D) перешел
в сумму B)?
2. При каком условии сумма B) будет периодической функцией п
§ 2. Формулы преобразования Фурье
Начнем с выяснения вопроса, который нам понадобится в даль-
дальнейшем: что будет, если амплитуда колебания равномерно «размазана»
по всей оси частот, другими словами, какая функция f (t) r фор-
формуле D) имеет спектральную плотность F(to)s^\? Это значит, что
нам надо исследовать интеграл
/(*) =

§ 2]
ФОГМУЛЫ ПРКОБРАЗОВАНИЯ ФУРЬЕ
521
Хотя этот интеграл и расходящийся (§ III.1), но его можно пред-
представить как предел интеграла по конечному промежутку
/(*)= lim IN(t),
N -*■ Ж
где
_
s\n(N
-N
(в последнем переходе мы пользовались второй формулой C)). По-
Полученный результат можно представить в виде
C)
Sin t
График функции Fl(t) показан на рис. 192. Можно показать
(см. решение упражнения 2 § III.6), что
^t. e.
Функция /^ имеет главный максимум при ^ = 0, F1@)=—; слева
и справа она, колеблясь, убывает (см. рис. 192).
F,
-ЗЛ
1/.Ч
4ft z
Из формул (8) мы видим, что IN{t), с точностью до постоянного
множителя 2л, получается из функции Fx (t) в результате того самого
преобразования, которое в § VI.1 привело к понятию дельта-функции.
Таким образом, переходя к пределу, мы получаем
du> = I{t) =
В этом выводе два пункта нуждаются в уточнении. Прежде всего,
при определении дельта-функцнн в § VI.1 мы пользовались в ка-
качестве примеров только функциями, не принимающими отрицатель-
отрицательных значений. Однако это условие, по существу, не использовалось,

522
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. XIV
так что отрицательные значения можно допускать. Во-вторых, что
более важно, функция F1 (t) не является быстро убывающей. В самом
деле, при большом TV график функции FN (t) = NFX (Nt) показан на
рис. 193; мы видим, что на любом конечном фиксированном интер-
интервале tlt t2, не содержащем точки ^=0, он часто колеблется, но
амплитуда колебаний не является малой, т. е. функция FN(t) не
близка к нулю, как в примерах
+ 00
§ VI.1. Если бы мы взяли ^\FN\dt,
— со
то такой интеграл расходился бы.
Рис. 193.
Рис. 194.
Однако и это несущественно, так как интеграл от функции FN(t)
при увеличении TV ведет себя следующим образом
t t
r? ,j.\ jj. P иг5'0 Nt ,,
FN(t)dt= j JV^rf/
— CO — CO
1
Nt
= \
sins
ds
0 (*<0),
1 (*>0).
График этого интеграла показан на рис. 194. Таким образом, при
больших N будет
FN @ dt « e @ (см. § VI.3), т. е. /^ @ « в' (t) = 6
Итак, дельтообразность функции FN(t) при больших N обеспечи-
обеспечивается не ее быстрым убыванием, а ее частыми колебаниями, из-за
которых она на конечном расстоянии от ^ = 0 при интегрировании
«все равно что тождественный нуль».
ТочЛэ такими же рассуждениями можно было бы показать, что
Q(t) FN(t—10) dt—±Q(t0) при N—»■ oo в соответствии со свой-
0
ствами дельта-функции. В таком интеграле вклад дает главный мак-
максимум FN при ^= t0, где /?Лг=Л^/л; «крылья», т. е. области t < tg — e
и ^>^0 + е, дают мало, потому что мал интеграл от знакоперемен-
знакопеременной функции.

§ 2] ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 523
С помощью формулы (9) легко рассмотреть случай спектральной
плотности, заданной выражением F (со) = Ае!шг (А = const, т= const):
подставляя в D), найдем
00
jj = 2лЛб (t + т).
Обратно, отсюда следует, что функции f(t) = ВЬ (t—т) соответствует
плотность F (а>) = ^— е~'шг.
Теперь можно перейти к случаю произвольной функции f{t)
в интеграле D). Как мы видели в § VI.2, каждую функцию f(t)
можно представить в виде суммы (более точно, интеграла) дельто-
дельтообразных функций
т
В силу только что доказанного каждому слагаемому отвечает
спектральная плотность -Ц^—е~'ш1; значит, всей сумме, т. е. функ-
функции f(t), отвечает спектральная плотность
Если вспомнить, что на самом деле это не сумма, а интеграл, и,
кроме того, обозначить переменную интегрирования через t, мы
приходим к формуле
Формулы A0) и D) называются формулами преобразования Фурье.
По ним мы переходим от любой функции f(t), конечной при t—»-±оо
(это нужно для того, чтобы интеграл A0) имел смысл), к ее спек-
спектральной плотности и, обратно, по спектральной плотности восста-
восстанавливаем функцию. Эти формулы удивительно симметричны, с точ-
1
ностыо до постоянного множителя ^— и знака в показателе.
Если f(t) стремится к нулю при t —> — сю и при t—»-+оо, то
интеграл A0) в принципе всегда можно вычислить, хотя бы численно.
Рассмотрим частный случай вещественной функции f(t). Запишем
e-iiot — cos qj^ — i s;n qj^
получим
OD OD
= hi) f {t) cos atdt~irlf{t) sin ^dt-

524 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Каждый из интегралов представляет собой вещественную функцию.
Вспомним, как мы писали F(a>) = А (со) -\- IB (со). Ясно, что
cos со* Л, |
+ СО
(И)
В (со) = — ^ f / (/) sin со*
-со J
Отсюда легко проверить свойства E) и F) плотности F(co) при
вещественной функции /(^).
Сравнивая G) и A1), убеждаемся, что коэффициент при cos со;1,
т. е. А (со), в свою очередь, выражается через интеграл от функ-
функции f(t), умноженной на cos соt\ аналогичное утверждение относится
к В (со).
Отметим два частных случая интеграла A0). Пусть/(^) = С = const.
Из формулы
пене, что для того, чтобы получить слева С, т. е.
нужно взять F(co) = С6 (со). По общему правилу
6 (со) i|) (со) d(s> = i|) @), \ 6 (о) e'w da> = e'Of нее
Аналогично разберем/(^) = De'@»'. В этом случае F(co) = D6((o — <в0),
что также легко проверить подстановкой в D). Те же результаты
можно получить и с помощью формулы (9):
+ 00 +00
^- Г e-i»>tdt = Cb( — со) = Сб(со), ^
—coo
Однако такие интегралы взять непосредственно нельзя, приходится
рассматривать незатухающую функцию С или DeIW°r как предел
затухающей, например Се~а1' или Del@«'-a!' I при ее—* 0. Получается
довольно длинная и сложная цепь рассуждений. Лучше получить
эти формулы как выше, из (9), и запомнить их.
Пусть на осциллятор без затухания с собственной частотой 0H
действует сила f(t), так что уравнение движения имеет вид
Предполагаем, что f(t) = 0 при ^ = —оо, и осциллятор покоился
в положении равновесия, лг = -тт = О. Легко построить решение за-
задачи (ср. § VH.5)
t
* = — \ sincoo(/ —т)/(т)<*т.

§ 2] ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 525
Это решение построено с помощью функции Грина этой задачи:
толчок, т. е. сила б (г1— т), подействовавший на покоящийся осцил-
осциллятор, придает ему скорость —, и начинаются свободные колеба-
колебания, х (t > т) = sin оH (t — т).
Пусть сила f(t) действует в течение ограниченного времени,
/=0 при t > Т. Как будет колебаться осциллятор по окончании
действия силы? Разложим
sin со0 (/— т) = sinco^ cos ы„ т — cos &at sin со0т,
получим
Г т т 1
If f
.v@ = — sinco,/ ) /(T)cosconTdT — cos co^ ] f(x) sinco0rdT .
T
Так как /(т) = 0 при t > Т, то можно вместо \/(t)cosсот Отписать
/ (т) cos сот dx; то же относится к интегралу с синусом. Вспоми-
О
ная формулы A1), получим для колебаний после окончания дей-
действия силы
х {t) = ~ [Л (со„) sin оу + В (оH) cos оу] при t > Т. A2)
Амплитуда незатухающих колебаний осциллятора с собственной
частотой со0 по окончании действия силы равна
Амплитуда зависит, следовательно, только от спектральной плотно-
плотности действующей силы F (со) при резонансной частоте, т. е. при
со = со0. Это и доказывает сделанные в § 1 утверждения.
В физике часто называют спектральной плотностью именно j /^ (со)|2,
а не F((i>). Если сила f(t) есть, например, давление в звуковой
волне или электрическое поле в электромагнитной волне, то | F (со) |2 dco
есть величина, пропорциональная энергии звуковых или электрома-
электромагнитных колебаний, приходящихся на участок спектра от со до co-f da.
После элементарных преобразований можно переписать A2) в виде
dx 'mM° \(t>T). (И)
^ = я [/=-()w' + /=■( )'w'] j
Погфобуем решить задачу о колебаниях осциллятора непосредственно

526 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
с помощью интеграла Фурье. Для этого запишем
+ 00
x(t)= J X (со) еш Ло A5)
— 00
и подставим это выражение в уравнение колебаний. Чтобы не за-
заботиться об условии покоя при t — —сю, рассмотрим осциллятор
с затуханием: ясно, что движение такого осциллятора не зависит
от того, что было в далеком прошлом.
Итак, мы рассматриваем уравнение
A6)
Подставляя х и / в виде Фурье-интегралов, получим
в +«
X (со) (—якоа + /ясо^ + м>й) е"°* Ло = $ Z7 М е'ш* Ло.
» —00
Отсюда сразу находим
A7)
т(соо — со2)+ icoA
Если затухание малб, то Х(со) особенно велико при тех значениях со,
при которых в знаменателе остается только малая величина кой.
Это происходит при cojj—со2 = 0, т. е. при со=;+; со0. Следовательно,
в Фурье-образе функции х (t) особенно велики X (со0) и Х(—со0).
В пределе при незатухающих колебаниях, т. е. при й—<■ 0, мето-
методами теории комплексного переменного можно получить из A5) и
A7) выражение A4). Подробнее мы на этом здесь не останавливаемся.
Последнее замечание, относящееся к спектральному анализу,
заключается в том, что приборы обычно регистрируют только ам-
амплитуду колебания различной частоты. Согласно A3) это значит,
что определяется только абсолютная величина *) (модуль) Фурье-
образа исследуемой силы |.F(co)|. Это относится к уху как реги-
регистратору звуковых колебаний, и к глазу, и к спектроскопу: ведь
в спектроскопе определяется только интенсивность света различной
частоты.
При этом мы теряем информацию, теряем сведения о фазе F((o).
Представим себе, например, две функции Fx (со) и Ft (со) такие,
что | Fx (со) | = \F^ (со) |, но сами Fx и Ft различны. Это значит, что
Fz (со) = F^ (со) е'ф 1Ш\ где ф — любая вещественная функция. Таким
двум Фурье-образам соответствуют различного вида Д (t) и /2 (t):
/г @ = S ^i М еШ ^, Л @ =
*) Напомним, что для вещественной силы F(—ш) = Г*(ш), так что
\F (—со) |ss \F (ш) |, знак со несуществен, достаточно рассмотреть со > 0.

§ 3] ПРИЧИННОСТЬ И ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ 527
Однако если f{t) есть давление воздуха в звуковой волне, то наш
слух воспримет одинаковые звуки, не сумеет отличить /х (t) и /2 (t).
Чтобы отличить /t от/2, кривую f(t) нужно записать быстродей-
быстродействующим манометром.} Лишь в последнее время начались энер-
энергичные поиски\пособов изучения фазы F(a)) в случае световых волн.
К вопросу о роли фазы мы вернемся в § 8.
Упражнения
1. Найдите спектральную плотность функции / (t) = e~a ' ' '(а > 0). Перейдя
к пределу при а—>• +0, получите спектральную плотность функции f(t)= 1.
Из формулы D) для этого примера выведите формулу A.1).
2. Получите в явной форме ограниченное при t—*■ ± оо решение урав-
уравнения A6).
§ 3. Причинность и дисперсионные соотношения
В § VII.5 мы видели, что решение уравнения A6) получается
из решения G(t, т) (так называемой функции Грина) аналогичного
уравнения со специальным неоднородным членом
по формуле
x(t)=
На основании § VI.2 подобный же вид имеет решение любой ли-
линейной задачи; при этом/(^) играет роль входного сигнала, a x(t) —
роль «отклика» рассматриваемой системы на этот сигнал. Функ-
Функция G(t; т) тогда представляет собой отклик на единичный мгно-
мгновенный импульс, подействовавший на систему в момент т.
В § VI.2 мы видели, что аналогичный вид имеет результат
воздействия на линейную систему и в случае, когда независимой
переменной служит пространственная координата (именно этот слу-
случай там разбирался более подробно). Оказывается, что если неза-
независимой переменной служит время с его специфической односто-
односторонней направленностью, то соответствующая функция Грина обладает
важными свойствами совершенно общего характера, к обсуждению
которых мы сейчас переходим.
Если параметры рассматриваемой линейной системы (например,
осциллятора), на которую воздействуют сигналы, не меняются с те-
течением времени, то все воздействия и соответствующие отклики
допускают произвольный сдвиг во времени. Это значит, что тогда
G=G(t—т) и потому
= S G(t— T)/(T)dT. A8)

;j28 преобразование фурье [гл. xiv
Введем в рассмотрение спектральные плотности функций x(t), /(/)
и 2nG(t) (множитель 2л поставлен для упрощения последующих
формул):
х (t) = [ X (со) е;в/ do\
, A9)
=■ (о) е;ы1 dco, 2л G (/) = ^ Z. (со) e/w/ dco,
все интегралы берутся от —оо до оо. Естественно, что при этом
мы будем считать все участвующие функции времени конечными
при t—>+оо, так как только для таких функций мы рассматри-
рассматриваем Фурье-представление. (Это требование конечности неявно
фигурировало и при построении решения A7), именно оно выделило
нужное нам решение уравнения A6) из двухпараметрического семей-
семейства всех его решений.) Подставляя A8) в A9) и меняя порядок
интегрирования, получим
^ X (со) еш dot = J [ G (t — т) J F (со) е;ит г/со] г/т =
= [^ G (t — т) F (со) eibn dvi di=^f И [ J G (^ —т) е"°т
Положив здесь /—
= ( F (со) е/ш' { J- Г [2яО (Ti)] е-'вт> йт,1 rfto = ( /=" (<о) Z. (со) е'°" г/ю.
Сравнивая последний интеграл с исходным, заключаем, что
X (со) = Z. (со) F (со).
Итак, Фурье-образы входного и выходного сигналов связаны
очень просто: второй получается из первого умножением на пере-
передаточную функцию L (со). Например, из формулы A7) видно, что
для простейшего линейного осциллятора передаточная функция
имеет вид
1 И '
Обратно, задаваясь передаточной функцией Z. (со) и вычисляя
функцию Грина G(t), можно перейти к формуле A8) для преобра-
преобразования сигналов. При этом возникает следующий интересный
вопрос. Пусть L (со) представляет собой передаточную функцию
реального преобразователя сигналов. Тогда должен выполняться
закон причинности, согласно которому отклик не должен возникнуть
раньше, чем был послан сигнал. Математически этот закон равно-
равносилен требованию, чтобы G(/ — т)г=0 при i < т, т. e. G(/)==0
при ^<0 (Поэтому верхний предел интеграла A8) для реальных

§ 3] причинность и дпспггспопньи; соотношения 529
систем равен не сю, a t, как мы и писали в § VII.5.) Каким требо-
требованиям должна удовлетворять функция L (со), чтобы выполнялся
закон причинности? Естественно, что такие требования надо поло-
положить в основу теории даже до вывода соответствующих уравнений.
Ограничимся для простоты случаем, когда L (со) имеет вид отно-
, . , Р (ш)
шеиия многочленов: L (со) = (}, ■. , причем степень знаменателя пре-
превосходит степень числителя по крайней мере на 2. (На самом деле
аналогичные рассмотрения можно провести для значительно более
широкого класса функций L (со).) Кроме того, будем считать, что Q (ш)
не имеет вещественных нулей. Тогда для вычисления и.пгеграла
со
О@= ^ J L (v) eie>'da
при i > 0 можно применить в точности тот самым прием, посред-
посредством которого мы вычислили интеграл (V.36), однако взамен комп-
комплексной плоскости z теперь надо рассматривать комплексную пло-
плоскость со. При этом «замыкающая» полуокружность проводится,
подобно рис. 67, в верхней полуплоскости со, так как при t > О
в этой полуплоскости будет | eiat | ^ 1 (тогда как в нижней полу-
полуплоскости | eial | принимает как угодно большие значения). На
основании общей теоремы (V.31) о вычетах получаем, что при ^>0
О@ = » 2 Вычш=(О(г{£(о))е'и/} (*>0), B1)
lltl (!) ^ > О
причем в правой части суммирование производится по всем особым
точкам (полюсам) функции L (со), т. е. нулям многочлена Q(io),
лежащим в верхней полуплоскости, Im со > 0.
Аналогично рассматривается случай t < 0. Тогда на рис. 67 надо
воспользоваться на верхней, а нижней полуокружностью, что даст
0@ = —/ 2 Вычм=@/;{1(со)е;и'} (*<0). B2)
Im cot < 0
Отсюда, в силу произвольности t, заключаем, что условием
выполнения закона причинности, т. е. G(/) = 0 при t < 0, является
отсутствие особых точек у передаточной функции L (со) в нижней
полуплоскости: Im со < 0. В частности, нетрудно проверить, что пере-
передаточная функция B0) удовлетворяет этому условию.
Полученное условие можно истолковать .еще следующим обра-
образом. Так как функция влияния G(t) при t^Q удовлетворяет одно-
однородному уравнению, то из формул B1) и B2) видно, что каждой
особой точке coft = aft-j-/|3ft передаточной функции отвечает слагае-
слагаемое вида е'ш*' = е~$к' е'а^1 в решениях однородного уравнения. Если
все &k находятся в верхней полуплоскости, то все |3fc > 0, и потому
все эти слагаемые затухают при t—*ao. Так и должно быть, если

530
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. XIV
система только преобразует сигналы и не имеет собственных источ-
источников энергии. Таким образом, физический эквивалент условия
о расположении особых точек передаточной функции состоит во
внутренней энергетической устойчивости системы, т. е. в затухании
возбуждающейся в ней энергии. (Отметим, что можно было бы рас-
рассматривать и линейные системы с внутренними источниками энергии,
т. е. неустойчивые; тогда для соблюдения закона причинности приш-
пришлось бы отказаться от требования ограниченности решений при t —>■ сю.)
Можно указать еще одно важное условие, равносильное выпол-
выполнению закона причинности. Для вы-
вывода его рассмотрим интеграл
B3)
распространенный по контуру рис.
195, где м0 — фиксированное ве-
вещественное значение и. Выполнение
закона причинности равносильно
отсутствию особых точек внутри (L), а потому, в силу произвольно-
произвольности (о0, условию /=0. Пусть теперь R—>• сю, а радиус малень-
маленькой окружности е—«-О. Тогда, рассуждая как в § V.9, получим,
что интеграл по большой окружности стремится к нулю. Интеграл
по горизонтальным отрезкам стремится к
,, f L(to)
—V.p \ ——
v J со — соо
B4)
где буквами V.p (от английского value principal, главное значение)
обозначено так называемое главное значение по Коми, т. е., по оп-
определению,
00 ГВо-Е 00 
V.p С JiM.d(o= lim Г + С .
K J со —со,, Е^о J J
— QD L_ — CO Q)o + £ -J
(Такое осложнение вызвано расход!шостью интеграла B4) при
(о = (о0 в обычном смысле § III. 1.) Наконец, интеграл по маленькой
полуокружности стремится к
Переходя в равенстве B3) к пределу при R—юо, е—►О, получаем
СО
00

§ 4] СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ 531
Представляя L (и) в виде Re L (и) + i Im L. (и) и отделяя в послед-
последнем равенстве вещественную часть от мнимой, получаем так назы-
называемые дисперсионные соотношения для передаточной функции
Rel (*>„) = _ — V.p
эквивалентные, как мы видим, закону причинности. Эти соотноше-
соотношения играют важную роль в квантовой механике. Они позволяют
получить полезные утверждения даже для систем, для которых
соответствующая теория еще не разработана, и потому вид урав-
уравнений неизвестен.
На законе причинности основана неосуществимость шуточного
приспособления, предложенного в статье Р. Хагедорна «Причинность
и дисперсионные соотношения» (Успехи физ. наук, 91 A967), стр. 151),
для фотографирования в полной темноте, когда источник света еще
не включен. Пусть в темноте произведена кратковременная вспышка.
Она описывается дельта-функцией, спектральное представление ко-
которой содержит гармоники вида е'ш', присутствующие во все моменты
времени. В статье предлагается установить фильтр, отсеивающий
все гармоники, кроме какой-то определенной, в результате чего мы
получим монохроматический свет, действующий не только после, но
и до вспышки1 Но это явно абсурдно, невозможность предлагаемого
фильтрования вытекает из закона причинности. Можно показать
и на основе дисперсионных соотношений, что фильтр, пропускаю-
пропускающий лишь одну частоту, невозможен. Закон пропускания всякого
фильтра таков, что сумма гармоник от любой вспышки должна тож-
тождественно равняться нулю до вспышки.
§ 4. Свойства преобразования Фурье
Будем называть функцию f(t) прообразом, а соответствующую
ей функцию F (и) — ее образом при преобразовании Фурье. Само
преобразование Фурье (иначе говорят оператор Фурье, ср. § VI.2)
определяется формулой A0), по ней мы переходим от прообраза
к образу. Формула D), по которой мы переходим от образа к про-
прообразу, определяет обратное преобразование Фурье.
Рассмотрим некоторые свойства преобразования Фурье. Прежде
всего оно линейно, т. е. при сложении прообразов складываются
и образы, при умножении прообраза на константу образ множится
на ту же константу. Это свойство сразу вытекает из аналогичных
свойств интеграла и было уже, по существу, применено нами в § 2,

532 ПРЕОБРАЗОВАНИИ ФУРЬЕ [ГЛ. XIV
когда мы воспользовались принципом суперпозиции при выводе
формулы A0). (Физически око вытекает из линейности рассматри-
рассматриваемых осцилляторов.) Естественно, что и обратное преобразование
также является линейным.
При «сдвиге» прообраза на постоянную а его образ умножается
на е~!а->. В самом деле, после сдвига получается функция f(t — а),
а ее спектральная плотность равна
~ J
(сделана подстановка t — а = т).
Эти свойство особенно ясно на отдельных гармониках: ведь если
гармонику el<oat сдвинуть на а, то получится e!"'°u~a) = e~iau><>eiwat,
т. е. она умножится на е~1аш"\ поэтому и ее образ, т. е б (со—оо0),
умножится на e~lawo или, что то же для этой функции, на е~!а'°.
А поскольку все эти образы получают одинаковый множитель, то и
их сумма, т. е. F(a), получит тот же множитель.
Аналогично проверяется, что если образ сдвинуть на а, то про-
прообраз умножится на elat. Именно это свойство инвариантности, с точ-
точностью до постоянного множителя, функции elu>t относительно сдви-
сдвигов, вместе с возможностью суперпозиции, и является причиной того,
что эта функция играет такую роль в преобразовании Фурье. Естест-
Естественно, что при изучении процессов, подчиняющихся линейным урав-
уравнениям, однородным во времени, надо опираться на функции, которые
сами допускают сдвиг во времени*).
Более подробно будем рассматривать преобразования семейства
решений поставленной задачи. Принято называть некоторую сово-
совокупность преобразований группой преобразований, если она вместе
с любыми двумя преобразованиял'и содержит преобразование, полу-
получающееся в результате их последовательного выполнения, и вместе
с каждым преобразованием содержит обратное преобразование.
Например, группу преобразований образует совокупность умножений
на константы, отличные от нуля (последнее нужно для существова-
существования обратного преобразования); при этом преобразовании каждая
функция f(t) переходит в Cf(t). Другим важным примером служит
группа сдвигов, при которых каждая функция /(/) переходит
*) При этом сами уравнения могут быть не только дифференциальными.
Типичное интегральное уравнение, однородное во времени:
/(/)= j k{t-x)f{r)dx.

§ 4] СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬР, 533
в/(? + т) (постоянная т<0 определяет сдзиг). Вели изучается ли-
линейная задача, однородная во времени, то ее общее решение (т. е.
семейство всех решений) должно быть инвариантным относительно
обеих этих групп преобразований. В линейной алгебре доказывается,
что это общее решение, включающее, вообще говоря, много пара-
параметров, можно представить в виде суммы однопараметрических
семейств решений, причем эти семейства также инвариантны отно-
относительно указанных групп преобразований (исключения будут ука-
указаны ниже).
Однако нетрудно проверить, что одмопараметрическое семейство
функций, обладающее такой инвариантностью, обязательно имеет
вид Се?1 (С произвольно, оно служит параметром внутри семейства,
р фиксировано, оно служит параметром самого семейства). В самом
деле, так как семейство однопараметрическое и инвариантное отно-
относительно умножения на постоянные, то оно исчерпывается функциями
р.ида С/(/), где С произвольное, а /(/)—какая-то одна функция
семейства. Но из инвариантности относительно сдвигов вытекает,
что f(t + T) = C.f(t), откуда
L т—> о т j
Обозначив предел, стоящий в квадратных скобках, буквой р, при-
приходим к дифференциальному уравнению /' (t) —pf (t), откуда fit) — е?1,
с точностью до постоянного множителя.
Отсюда получаем, что если семейство функций инвариантно
относительно обеих указанных групп преобразований и имеет, напри-
например, две степени свободы, то оно имеет вид C,e^'f-{- C,e''2*, где
С, и С2 — произвольные постоянные. Однако если изучаемая задача
содержит параметры и при некоторых значениях этих параметров
получится p1=p.i, то вид двухпараметрического семейства решений
. меняется. В этом случае аналогично § VII.3 можно показать, что
указанное семейство приобретает вид Cxefxt -f CjeP^. (При этом одно-
параметрическое семейство C2tePit само по себе не инвариантно
относительно сдвигов.) Если совпадают три значения рх=Рг = Р3, то
трехпараметрическое семейство решений приобретает вид СлеР^ -\-
-т- CJeP** + C3t2eP>t и т. д.
Из доказанных свойств следует, что при дифференцировании
функции /(t) ее Фурье-образ умножается иа ко. В самом деле, об-
образом функции !—-^ служит
Переходя к пределу при h—+0, получаем наше утверждение. Ана-
Аналогично проверяется, что при дифференцировании образа про-
прообраз умножается на —it. В этих свойствах можно убедиться и

534 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
непосредственно, составляя производную от интеграла по параметру,
^ = ~ С F (со) еш dt=\ /со F (со) e'w <ft
и также для обратного преобразования
Описанные свойства преобразования Фурье имеют замечательное
применение к решению линейных дифференциальных уравнений
с постоянными коэффициентами. Мы использовали их в § 2 при
рассмотрении задачи о вынужденных колебаниях осциллятора
с трением.
Интересно рассмотреть уравнение свободных колебаний, т. е.
уравнение A6) при/(^)==0. Совершая преобразование Фурье, по-
получаем
О, B5)
откуда А"(со) = О и x(t)=0. Мы получаем только тривиальное
(нулевое) решение. Решения, найденные нами в § VII.3, были не-
неограниченными (экспоненциально большими) при t—*—оо и потому
с помощью преобразования Фурье они не получаются; поэтому и в
§ 2 при решении уравнения A6) у нас получилось только одно
решение, не включающее произвольных постоянных. Пусть теперь
трение отсутствует, т. е. Л = 0. Тогда взамен B5) получаем
(—та2 + та1)Х(а) = 0, т. е. (со2—cog) Л" (со) = 0. B6)
Могло бы показаться, что отсюда тоже вытекает Л"(со)^О. Но на
самом деле уравнению B6) удовлетворяет функция
* (со) = (^6 (со — соо) + С26(со + соо), B7)
где Cj и С2— произвольные постоянные. Действительно (см. § VI. 1),
(со2-со2) \СХЬ (со-соо) + С2б (со + соо)] =
= Сх (со2 —со2о) б (со —соо) + С2 (со2 —со2) б (со + соо) =
= Ci(co2-co2) б(со-соо) + С2 [(-сооJ-со2] б(со + соо)=О.
Из B7) по формуле обращения D) получаем
ci6 (со —соо) +С2б (со + соо)] еш rfM = (?!е'
Мы приходим к решению, известному из § VII.3.
Рассмотрим теперь Фурье-образы некоторых функций, о которых
говорилось в § VI.3; при этом оператор Фурье будем обозначать
буквой JF. Формула (9) означает, что
-^; B8)
нетрудно проверить, что, и обратно, ¥ [ 1 ] = 6 (со).

§ 4]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
535
Чтобы вычислить JF [sign t] (см. § VI.3), заменим сначала в правой
части A0) пределы интегрирования на + N, где N велико. Мы
получим
N Г 0 N "I
2л J 2я I J J jxio)
-лг L _лг о -J
График этой функции, умноженной на /.показан на рис.196;при большом
Рис. 196.
N он часто осциллирует вокруг графика — . Поэтому на осно-
основании тех же соображений, что в § 2, естественно предположить, что
т. е.
И действительно, если понимать интеграл в смысле главного зна-
значения, то в справедливости последней формулы можно убедиться,
как в § 3.
Из формулы B9) вытекает Фурье-образ единичной функции
(/)] = <F [4 + 4 sign /] =4 б (со)
C0)
Эта формула находится в согласии с B8), так как из C0) вытекает, что

536 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Из числа других свойств преобразования Фурье остановимся на
асимптотическом поведении Фурье-образа мри со—>-±оо. Будем для
простоты считать, что функция f(t) отлична от нуля лишь на ко-
конечном интервале t или во всяком случае стремится к нулю при
t —>■ ± оо вместе со своими производными. Тогда не следует думать,
что и F((£>) обязательно обладает теми же свойствами при со—>■+оо:
асимптотическое поведение ^((о) зависит совсем от другого.
Из формулы A0) сразу следует, что если f{t) = b{t —10), то
/^(со) = —е~'ш(о, откуда f(co) при со —>■ ± °о остается ограниченной,
но не стремится к нулю. Можно показать, что так будет всегда,
если /(t) содержит дельта-слагаемые.
Пусть теперь f(t) не имеет дельта-слагаемых, но обладает так
называемыми разрывами 1-го рода, т. е. точками t0, для которых
пределы f(t0—0) и /(^0 + 0) конечны, но не равны друг другу.
(Типичная функция с разрывом 1-го рода—это единичная функции,
показанная на рис. 72.) Тогда, как было показано в § VI.3, f'(t)
будет обладать дельта-слагаемыми. Но в силу стр. 533 функция f (t)
имеет спектральную плотность /со/7 (со), и -потому согласно предыду-
предыдущему получаем, что /со/7(со) при со—>■ + оо ограничена, но не стре-
стремится к нулю. Значит, в рассматриваемых предположениях F (со)
при со —>■ ± оо стремится к нулю со скоростью —.
Если сама функция f(t) непрерывна, но ее производная имеет
разрывы 1-го рода (это значит, что график функции f(t) имеет
изломы, как на рис. 76), то аналогично получаем, что ^(со) при
со —>■ ± оо имеет порядок — и т. д. Наконец, если производные лю-
любого порядка от f(t) непрерывны, то F{(£>) при со —>■ + оо стремится
к нулю быстрее любой отрицательной степени |со|; так будет, на-
например, для f(t) = (см. формулу (V.40), в правой части кото-
которой при со < 0 надо со заменить на |со|), e~at' (см. § 5) и т. д.
Интеграл Фурье при большом со — это интеграл от быстроколеб-
лющейся функции. Подобные интегралы мы рассматривали в § III.4,
и теперь можно лучше понять, почему там в асимптотических фор-
формулах участвовали значения подынтегральной функции и ее произ-
производных только на концах интервала интегрирования. В самом деле,
там рассматривались интегралы типа
ft.
/ (t) eia>* dt
a
при со—>■ + оо. Однако такой интеграл можно переписать в виде

§ 4] свойства преобразования фурье 537
где функция f(t) получается из f(t) продолжением вне отрезка
<^.t^b тождественным нулем. Таким образом, мы получаем
1
с точностью до несущественного знака у со и коэффициента -~-
Фурье-образ функции f(t). Но эта функция и ее производные имеют
скачки при t = a и t=b, где /(() сменяется на тождественный нуль;
в силу сказанного выше этими особенностями и определяются коэф-
коэффициенты в асимптотических формулах, если сама функция f(t) до-
достаточно гладкая, Ясно также, что если функция f{t) или ее про-
производные имеют разрывы между а п Ь, то и эти разрывы скажутся
на асимптотических формулах, о чем мы упоминали в § III.4.
С другой стороны, методика интегрирования по частям, на ко-
которой был основан § III.4, приносит пользу в теории преобразо-
преобразования Фурье, так как дает возможность не только выяснить порядок
Фурье-образа при со —>■+оо, но и получить соответствующие асимп-
асимптотические формулы."
Рассмотрим, например, Фурье-образ функции f(t)~-. . ... :
Здесь функция fit) имеет особенность (излом) при ^ = 0. Интегриро-
Интегрирование по частям дает
-'1"'
, d\t\ I/ I „
где sign^ = -j—i = J—!■ . Значит,
— QO
Здесь подынтегральная функция уже имеет скачок при ^ = 0, рав-
равный 2, поэтому вторичное интегрирование по частям дает дельта-
слагаемое, которое порождает главный член асимптотической фор-
формулы
Так как последний интеграл при со—>± оо стремится к нулво, то

538
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. XIV
мы получаем асимптотическое выражение
1
F{a)
ям31
C2)
которое является более точным, чем общее утверждение, что F{a>)
при со—»■ ± °о должно иметь порядок —.
Выражение C2) можно уточнить с помощью повторного интегри-
интегрирования по частям последнего интеграла в правой части C1). Вычис-
Вычисления, которые мы предоставляем читателю, дают
'
Г
что приводит к асимптотическому выражению
1 / 1 6
[
более точному, чем C2). Этот процесс можно продолжать.
— со
Остановимся еще на следующем вопросе. В § 5 будет показано,
что Фурье-образом функции f(t) = e~'2 служит функция F(a) =
= ■ г—е~ш'/*. Здесь f(t) и ее производные совсем не имеют осо-
2i у JX
бенностей, поэтому и получилось, что F{a>) при со—>■ ±: оо стремится
к нулю быстрее любой отрицательной степени |со|. В то же время,
в силу сказанного выше, при как угодно большом фиксированном N
функция
N
-N
аппроксимирующая F (a) = FW (со), при со—»-±оо имеет поря-
порядок | со \~г.
Как это согласовать?
Дело здесь в том, что при больших N коэффициенты разложе-
разложения функции FN(a) по отрицательным степеням со становятся весьма

§ 5] ПРЕОБРАЗОВАНИЕ КОЛОКОЛА И ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 539
малыми, так что члены с со, со~2 и т. д. в пределе пропадают.
Это разложение легко получить с помощью интегрирования по
частям, оно начинается с членов
Например, уже при N=5 коэффициент при со имеет порядок 10~12,
т. е. весьма мал. Графики функций F(a) и FN(a>) схематически
показаны на рис. 197. Различие в характере их «крыльев» при боль-
больших (V практически не играет роли, так как сами значения полу-
получаются очень малыми.
Упражнения
1. Докажите, что если образом функции / (/) служит F (со), то образом
функции f (at) (a = const) служит -.—-. F f — ).
2. Пользуясь упражнением 1 к § 2, найдите Фурье-образы функ-
§ 5. Преобразование колокола и принцип неопределенности
Интересный пример преобразования Фурье дает функция
/(^) = Ce-a'2 (С, a = const>0) C3)
(график ее имеет вид колокола, см. рис. 187). Формула A0) дает
=-~ f Се-а'ге-шсИ = ~ f е-а'г~ш dt.
— 00 — 00
Преобразуя показатель по формуле
и обозначая }^а (t + к-) — z> получаем
где (L)—прямая в комплексной плоскости z, параллельная вещест-
вещественной оси и проходящая через точку z = —7r=i=vi.
2 у а
Сейчас мы покажем, что интеграл
\ I y C5)
(L)

540
ПРК.ПВРАЗОПЛНПЕ ФУРЬЕ
[ГЛ. XIV
на самом деле не зависит от у. Для этого продифференцируем /у
по параметру у (см. § 111.6), получим
-,> +,,»'- iix =—2i \ e-(^ + '".vJ (x-f iy) dx.
— GO
Однако последний интеграл берется, т. е.
<:/«
1= — СО
= 0
(полученная после интегрирования функция обращается в нуль на
обоях пределах). Итак, /у = const =/у|й=0 . Полагая _у = 0 в C5), мы
приводим к известному интегралу (§ IV.7), т. е.
-г2 dz =
Подставляя найденное значение в C4), находим спектральную
плотность «колокола» C3):
^'h. C6)
2 у ;ш
Мы видим, что зависимость плотности от ш получилась аналогичная,
колоколообразная, но с другими коэффициентами.
Из формул C3) и C6) вытекает важное следствие. Колоколо-
Колоколообразная функция ни при каком значении переменной не обращается
точно в нуль. Тем не менее можно разумно определить ширину колокола
(ср. § 111.2). Например, если принять за ширину колокола тот его
участок, на котором его высота понижается в е раз от максималь-
максимальной, то ширина колокола C3) равна At=2/ya, тогда как ширина
преобразованного колокола C6) равна Дсо=4|/^а. Таким образом,
ес.^и менять а, то один из колоколов становится уже, а другой —
во столько же раз шире, так что
А* Дсо—8 = const. C7)
Можно показать, что аналогичное правило справедливо при любой
форме преобразуемых функций. Этот результат имеет принципиаль-
принципиальное значение. Допустим, что мы рассматриваем, как в § 2, воздей-
воздействие силы /(/) на систему осцилляторов с различными собственными
частотами. Мы видим, что чем более «локализована» (сжата) внеш-
внешняя сила во времени, тем более «размазан» ее спектр, т. е. тем
большее число осцилляторов с различными частотами эта сила возбу-
возбудит с примерно одинаковой амплитудой. Обратно, увеличивая эту
избирательность, т. е. сокращая спектр, мы вынуждены размазывать
внешнее воздействие во времени. Эта невозможность одновременно

§ 5] ПРЕОБРАЗОВАНИЕ КОЛОКОЛА И ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 541
и локализовать внешнее воздействие во времени и усилить избира-
избирательность этого воздействия—одно из проявлений так называемого
принципа неопределенности, играющего фундаментальную роль в со-
современной физике.
Из принципа неопределенности вытекает, в частности, что если
некоторая система колеблется с переменной частотой, то бессмыс-
бессмысленно говорить о значении частоты в данный момент времени: напри-
например, в акустике нельзя говорить о точной высоте звука в данный
момент времени и т. п. Интервал времени, на протяжении которого
определяется эта частота, нельзя брать значительно меньшим периода
колебаний, звук определенной высоты не может продолжаться слиш-
слишком мало времени!
В квантовой механике энергия частицы связана с частотой вол-
волновой функции. Волновая функция г|з частицы с определенной энер-
энергией Е пропорциональна е~'Е1^, где &= 1,05-10~27 эрг-сек—по-
эрг-сек—постоянная Планка (сам Плаик ввел в физику величину /г = 6,6х
X 10~27 эрг^ сек; удобнее писать формулы с Й-=/г/2я). Если частица
наблюдается в течение малого интервала времени At, то, как следует
из предыдущего, частоту ее волновой функции, т. е. величину Е/п,
можно узнать лишь с малой точностью. Получается соотношение
AE-At имеет порядок %,
Аналогично у частицы с определенным количеством движения по
оси х, p = mvx, волновая функция пропорциональна eipx/^. Если
известно, что частица находится в определенном промежутке между
х и х-{-Ах, то волновая функция частицы отлична от нуля только
в этом промежутке. Раскладывая волновую функцию в интеграл
Фурье, мы придем к выводу, что количество движения частицы
известно лишь с определенной точностью Ар: в интеграле Фурье
будут велики члены с e'Px/h, где р1 < р <р1+ Ар. Из сказанного
следует, что Ар-Ах имеет порядок А.
Из формул C3) и C6) на основании описанных в § 4 свойств
преобразования Фурье вытекает, что
если f(t) = Ce-at' + lu><>1, то
=e .
2 у па
Вещественная часть функции /(t) и функция ^(со) показаны на
рис. 198. Ширина At «волнового пакета» (определяемая аналогично
тому, как для функции C3)) и ширина Дсо соответствующего спектра
связаны соотношением неопределенности C7), независимо от час-
частоты оH колебаний. От этой частоты зависит сдвиг спектра по оси
частот.
Отметим замечательное приложение преобразования колокола
к выводу нормального закона теории вероятностей (§ Х111.8). Пусть
случайные величины |lt §,,..., |„ независимы, но распределены по
одному и тому же закону с плотностью распределения ф (л;); для

542
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. XIV
простоты будем считать, что среднее значение ^ = 0. Рассмотрим
случайную величину х\к = -^е-шЬг где со —заданная вещественная
постоянная. Так как величина r\k принимает значения ^-е~Шх с плот-
плотностью вероятности ф (дг), то ее среднее значение
т. е. это как раз Фурье-образ функции ф (х).
Рис. 198.
Обозначив буквой г\ произведение величин r\k, получим
О"е * = Bп)"е '
1 • • • +1П. Отсюда
~
где обозначено | =
т. е. в силу предыдущего абзаца среднее значение величины
Bxt)"-iri служит Фурье-образом функции распределения я>_ (*) вели-
величины |.
В § XIII.7 мы видели, что при умножении независимых случай-
случайных величин их средние значения также перемножаются. Значит,
Легко проверить, что функция ф(со) при со = 0 имеет максимум.
В самом деле,

§ 5] ПРЕОБРЛЗОВаПИЕ КОЛОКОЛА И ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 543
тогда как при прочих со
со
ф (со) | = 7— \ е~'юх re i
dx
Однако на стр. 76—77 мы видели, что в этом случае функцию
[Ф(со)]л при больших п можно приближенно заменить на Ле~сш2,
где А = еп^°\ с = — 1 т|/' @), t|> (со) = 1п Ф (со).
В нашем примере получаем
Ф@) = -1, Ф'@) = 0,
(Д2 — дисперсия величины с1} см. § XIII.8), откуда
и потому
Bя)-ЧФ И]" « Bn)-i*n 1П « е~Т "Агш! = JL е-ТпД!ма.
В силу сказанного выше, получился Фурье-образ функции ф„(лг).
Как видим, он имеет вид колокола. Согласно формулам C3) и C6)
С 1 1 лД2 1 1 ч
в которых 7=- =о-> :г = -о— > откуда а = ?г^г7. С= ; —
получаем функцию распределения величины |:
Мы пришли к нормальному закону (XIII.25).
Упражнения
1. Докажите принцип неопределенности для функции /(/), постоянной и
отличной от нуля лишь на конечном интервале.
2. Установите связь принципа неопределенности с результатом упражне-
упражнения 1 к § 4.

544 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
§ 6. Спектральный анализ периодической функции
Пусть внешнее воздействие /(/) представляет собой периоди-
периодическую функцию с некоторым периодом Т>0, т. е.
f(t+T)^/(t). C8)
Тогда в ее разложении D) по гармоникам будут участвовать только
гармоники еиа, обладающие тем же свойством C8). Отсюда
(см. § V.4), и мы получаем, что частота со может принимать зна-
значения только
co = o)ft=^? (*=..., —2, —1, О, 1, 2, ...). C9)
Таким образом, периодическая функция имеет дискретный спектр,
а потому дельюобразную спектральную плотность
Подставляя в D), находим
Это — так называемый ряд Фурье, в который разлагается периоди-
периодическая функция.
Для вычисления коэффициентов ряда D0) возьмем средние зна-
значения обеих частей формулы D0). В силу периодичности функции
/{() среднее значение левой части равно
т
13 правой части среднее значение каждой гармоники равно нулю,
так как и при со ^ 0
N
1 elmi 'v sin co.'V
1 С
2,V 3
2Л/ но
!=-N Л'ш
"~7i *" 0-
Однако одно слагаемое в правой части D0) при k = 0 просто равно
постоянной ап, и его среднее значение, конечно, тоже равно а0.
If
Поэтому из D0) получаем /== у- \/(t) dt= ай.
it
Для нахождения коэффициента ak надо обе части D0) помно-
жить на е ' (при некотором фиксированном k), после чего

§ 6] СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 545
взять средние значения обеих частей. Рассуждая, как в пцедыду-
щем абзаце, получим
4=f{t)e T = -f\f(t)e T dt D1)
о
(k = 0, ±1, ±2, ...)•
Если функция /(/) вещественная, то часто пользуются другой,
вещественной формой ряда Фурье. Для этого в разложении D0)
объединяют симметричные члены
a-k) cos -^Г * + l (ak— e-Aism-jr- г1 [ =
sinfL0- D2)
При этом коэффициенты, в силу D1), равны
т
(*=1, 2, ...), D3)
г т
(*=1, 2, ...).
В правых частях D2) все величины вещественные.
Приведем пример разложения в ряд D2). Рассмотрим «периоди-
«периодическую ступеньку», показанную на рис. 199 жирными линиями.
— м
Здесь ао=/=у. По формулам D3)
т
2/гл . 2Л1 Г . 2/гл
т_
2
= 0,
2 f ., . 2Ал . .. 2.М Г
2
Я. Б. Зельдович, А. Д. Мышкис

546
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
[ГЛ. XIV
Отсюда
В1 = -^, Я2 = 0, В3 =
Ш
2М
т. е. мы получаем разложение
М 2М / 1 . 2л/ , 1 . 6л/ , 1
10л/
Вторая частная сумма S2 (t) и третья частная сумма S3 (t) этого
ряда показаны на рис. 199 пунктиром, причем для простоты Они
М
-Г
7
Т
Рис. 199.
показаны только на периоде, по обе стороны они продолжаются
периодически. Интересно, что в точках разрыва сумма ряда оказы-
оказывается равной среднему арифметическому (т. е. полусумме) предель-
предельных значений функции /(t) слева и справа*).
Так как периоду колебаний Т отвечает частота со = ^-=со,
(см. C9)), то из формул C9) и D0) (или D2)) мы видим, что общее,
негармоническое колебание с частотой со = со1 получается в резуль-
результате сложения гармонических колебаний с частотами coj, 0J = 2@!,
0K = 3@! и т. д. Первая частота, т. е. (Oj, являющаяся частотой
самого колебания, называется основной, и соответствующая ей гар-
гармоника также называется основной; остальные частоты и гармоники
называются верхними.
Полученные результаты имеют важное значение, в частности,
в акустике. Хорошо известно, что высота звука соответствует час-
частоте колебаний воздуха: например, ноте «ля» так называемой пер-
первой октавы отвечает частота 440 гц, т. е. 440 колебаний в секунду.
Однако известно также, что одна и та же нота, взятая на различ-
различных инструментах, имеет различный тембр, т. е. «окраску». От
чего же зависит этот тембр? Оказывается, что от верхних гармо-
*) Обратите также внимание, что частные суммы Sn (t) для функции / (/)
(рис. 199) на границе ступенек довольно сильно «выскакивают» из них. Это
общее свойство Sn (t) называется целением Гиббса.

§ 6] СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ 547
ник, наложенных на основную. Каждая из них входит в колебание
с определенной амплитудой, и если менять пропорции между этими
амплитудами, то будет изменяться и тембр.
Из наших результатов получается еще одно интересное след-
следствие. Мы знаем, что если осциллятор с собственной частотой со0
возбуждать внешней силой с частотой со, то при со=со0 наступает
резонанс.
Однако на практике оказывается, что резонанс наступает и при
со = y > "^ > ~£ и т- Д- При этом существенно, чтобы возбуждаю-
возбуждающая сила, будучи периодической, не была гармонической! Сила
/=cos^- не возбуждает осциллятора с собственной частотой со0.
Но возьмем другой типичный пример. Пусть осциллятор с частотой
со0 возбуждается отдельными толчками; лучший способ—давать по
одному толчку на каждом колебании. Лучший момент, когда л: = 0,
-г > 0, -г максимально, будет максимальна и работа силы (мы пред-
предполагаем, что сила действует в сторону увеличения л;). Ясно, что
если сила действует по одному разу в каждом периоде, то частота
силы совпадает с частотой со0 колебаний.
Теперь изменим действие силы. Пусть сила действует «через
раз», например каждое нечетное колебание. Ясно, что и при таком
способе действий колебания будут неограниченно усиливаться, будет
иметь место резонанс, хотя со = со0/2. Здесь дело в том, что сила
f=^6(t — пТ) (п — целое), состоящая из отдельных толчков, опре-
определенных интервалом Т, особенно богата обертонами. В первом
™ 2л гг п 2л 2л
случае Т =— ; во втором случае редких толчков 7=2—.= —,
частота силы со=со0/2, но и во втором случае в разложение f(t)
входит член с е'и»' = е'2И'. Это объясняется как раз наличием верх-
верхних частот. Если же сила действует с частотой -^> т0 она состоит
из смеси гармоник с частотами -^, 2-^, 3-^, 4-^ и т. д. Из них
о о о о
третья с частотой 3-^ = со0 как раз и возбуждает резонанс.
Напротив, периодическая внешняя сила с частотой 2со0, Зсо0,... не
вызывает резонанса, а возбуждает в рассматриваемом осцилляторе
только верхние гармоники.
Упражнение
Разложите в ряд Фурье функцию: а) А \ sin at |; б) периодическую с перио-
00
дом Г и равную hi при 0 < t < Т; в) 2 Ад((— 2пТ).
18*

548 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
§ 7. Пространство Гильберта
Разложения, указанные в § 6, имеют замечательное геометри-
геометрическое истолкование. Мы уже указывали в § IX.6, что любую сово-
совокупность объектов, в которой можно производить линейные дейст-
действия (сложение этих объектов и умножение их на скаляры, т. е.
числа)-, можно истолковать как многомерное векторное пространство.
Но ведь над функциями f(t), рассматриваемыми на некотором интер-
интервале оси t (этот интервал может быть конечным или бесконечным
и, в частности, может совпадать со всей осью, но он должен быть
одним и тем же для всех рассматриваемых функций), такие дейст-
действия возможно производить! Значит, эти функции можно рассматри-
рассматривать как векторы, они образуют векторное пространство. Однако
характерной особенностью пространства функций является его бес-
бесконечномерность: ведь при выборе произвольной функции/ имеется
бесконечное число степеней свободы, так как если, например, ука-
указать любое конечное число значений f(tk), то эту функцию еще
можно выбрать многими способами при остальных значениях t.
Будем сначала считать, что рассматриваемые функции принимают
вещественные значения.
В пространстве функций можно ввести скалярное произведение
по формуле
ь
Ф (')<«. D4)
где а и Ъ — начало и конец того интервала оси t, на котором рас-
рассматриваются функции. Естественность этой формулы вытекает из
следующих соображений. Выберем п значений независимой пере-
переменной
* = *Ц *21 • • • I *п
и будем рассматривать значения любой функции / только в этих
точках f{tx), /(г'г), ..., f{tn). Тогда мы будем иметь п степеней
свободы, т. е. такие функции образуют л-мерное векторное про-
пространство, в котором согласно § IX.6 скалярное произведение можно
ввести по формуле
п
(/, ф)=2/('*)ф('*)- D5)
k-i
При «сгущении» узловых значений tk л-мерное пространство пере-
переходит в бесконечномерное, а сумма D5), естественно, заменяется
на интеграл D4).
Согласно формуле D4) и правилам векторной алгебры вводится
«модуль вектора /», называемый нормой функции / и обозначаемый

§ 7] пространство гильберта 549
[|/||, по формуле
b
ii5lw- D6)
Пространство функций со скалярным произведением D4) и, стало
быть, с нормой D6) называется гильбертовым пространством (более
полно, вещественным гильбертовым пространством функций на за-
заданном интервале с концами а, Ь). В него входят как непрерывные,
так и разрывные и даже неограниченные функции. Однако так как
каждый вектор должен иметь конечный модуль, то в пространство
включаются только функции, для которых интеграл D6) либо
«собственный», либо несобственный сходящийся (см. § ИМ), т. е.
обязательно имеет конечное значение. В частности, дельта-функция
в пространство Гильберта не входит, так как интеграл от ее квад-
квадрата равен бесконечности (почему?). В дальнейшем мы ограничимся
функциями с конечной нормой.
В гильбертовом пространстве естественно вводится понятие орто-
ортогональности: две функции gl (t) и g2 (t) ортогональны друг другу
(на интервале с концами а, Ь), если их скалярное произведение равно
нулю, т. е. если
ъ .
ft(flft(*)<«=0. D7)
Две ортогональные функции подобны двум перпендикулярным друг
другу векторам. Если имеется ортогональная система функций, т. ё.
совокупность попарно ортогональных функций
ft @, ft @, •■■ . ft, @, ••• . D8)
то '.^сто возникает задача о разложении любой заданной функции
f(t) по этим функциям, т. е. о разложении f(t) в ряд вида
D9)
k=\
В гл. IX мы рассматривали задачу о разложении вектора в обыч-
обычном (трехмерном) пространстве по ортогональным, т. е. перпендику-
перпендикулярным векторам. Если этих ортогональных векторов три, то по ним
можно разложить любой вектор; такая тройка векторов называется
полной, как говорят, ее можно принять за базис в пространстве.
Если же ортогональных векторов два, то по ним можно разложить
не любой вектор, а только такие, которые лежат в плоскости этих
двух векторов; такая пара векторов в трехмерном пространстве не
является полной, она становится полной только после присоедине-
присоединения к ней третьего вектора.

550 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Подобно этому ортогональная система функций D8) называется
полной, если по ней можно разложить любую функцию f(t) в ряд
вида D9); любая такая система функции образует базис в простран-
пространстве Гильберта. Если же система D8) неполна, то по ней можно
разложить не все функции, а только функции, удовлетворяющие
определенным соотношениям; оказывается, что любую ортогональную
неполную систему функций можно «расширить» до ортогональной
полной системы, присоединив к исходной системе некоторое (быть
может, бесконечное!) количество функций.
В конечномерном векторном пространстве полнота или неполнота
системы ортогональных векторов выясняется очень просто: если число
векторов в системе равно размерности пространства, то система
полная, а если это число меньше размерности пространства, то си-
система неполная. В отличие от этого в бесконечномерном пространстве
и неполная система может содержать бесконечное количество век-
векторов, так что только по этому количеству установить полноту
системы нельзя. Обычно установить полноту системы D8) бывает
далеко не просто.
Если все же полнота системы функций D8) так или иначе уста-
установлена, то найти коэффициенты разложения заданной функции / (х)
в ряд D9) очень легко. Для этого надо обе части равенства
/ @ = *i*i @ + ад V) + ад3 @ + • • • E0)
скалярно помножить на одну из функций gk(t). При этом в правой
части равенства E0) в силу соотношения ортогональности все члены
обратятся в нуль, кроме одного, в котором функция множится сама
на себя. Мы получим равенство (/, gk) = ak(gk, gk), т. е.
ъ
$ g\ @ dt
(ср. формулу (IX.28)).
Важный пример ортогональной полной системы функций на ко-
конечном интервале О^^^Тдает система
, 2л . . 2л , 4л . . 4я , 6л . . 6л . ._„.
1, cos^t, sin у-г1, cos -jrt, sinyt, cos-jrt, sm-j-t, ... E2)
Ортогональность этой системы можно получить с помощью непосред-
непосредственного вычисления интегралов вида D7) (см. упражнение 1).
Полнота этой системы, по существу, показана в § 5, так как раз-
разложение по системе E2)—это не что иное, как разложение D2), а
мы видели, что оно возможно для любой функции f (t) (ведь перио-
периодическая с периодом Т функция может при 0 < t < Т принимать

§ 7] ПРОСТРАНСТВО ГИЛЬБЕРТА 551
совершенно произвольные значения). Если же вычислить коэффи-
коэффициенты разложения по системе E2) с помощью общей формулы E1)
и легко проверяемых равенств
0 0
(k=\, 2, ...),
то мы получим как раз формулы D3).
Интересное обобщение теоремы Пифагора на пространство Гиль-
Гильберта получится, если левую, а также правую части равенства E0)
скалярно помножить саму на себя. При этом в правой части все
попарные скалярные произведения равны нулю в силу соотношения
ортогональности, а останутся только скалярные квадраты всех сла-
слагаемых и мы получим
т. е.
II/ II2 = а\ || ft ||2 + а\ || ft ||« + а\ || g3||« + ... E3)
Здесь слева стоит квадрат модуля вектора /, а справа — сумма квад-
квадратов его проекций на базисные векторы ft, g,lt ...
Если рассматривается комплексное гильбертово пространство, т. е.
рассматриваемые функции от вещественного аргумента могут прини-
принимать комплексные значения, то формула для скалярного произведе-
произведения, взамен D4), будет иметь вид
ь
где звездочкой обозначена комплексно сопряженная величина (см.
§ V.2 и IX.6). Поэтому и формула для нормы изменится:
ь ъ
II/1|2 = (/,/) = $/ @ [/ {*)]*<" = J |/ @|" dt.
а а
Аналогичные изменения получат и дальнейшие формулы. Важным
примером полной ортогональной системы функций в комплексном
гильбертовом пространстве на интервале 0 ^ t ^ T служит совокуп-
совокупность функций
4nl 2nl_ 2я/_ Ш_ 2Ш
ете~т\етет е т (ZA\
Разложение по этой системе функций — это как раз разложение D0)
из § 6.

552 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Такой геометрический подход к совокупности функций дает воз-
возможность получить многие важные и интересные следствия, лежащие,
однако, за пределами данной книги.
В заключение остановимся немного на развитии понятия функции,
В XVIII веке, когда это понятие возникло, функция мыслилась за-
заданной обязательно с помощью формулы. Поэтому пример разложения
в ряд Фурье функции, заданной различными формулами на различ-
различных участках изменения аргумента (см, § 6), на некоторое время
постазил математиков в затруднение: одна это функция (ведь ряд
один, он образован по вполне определенному закону) или несколько?
Анализ подобных примероз привел в XIX веке к принятому сейчас
в математике определению функции как произвольного закона соот-
соответствия между зависимыми и независимыми переменными. Такой
подход оказался полезным для логического обоснования математики.
Однако с точки зрения приложений такое определение является
слишком аморфным, расплывчатым; право на существование получили
такие функции, как например, функция Дирихле, равная 0 для ирра-
иррациональных и 1 для рациональных значений независимого перемен-
переменного (попробуйте представить себе ее график!), и другие подобные
функции, которым трудно придать другой смысл, кроме формально
логического. В приложениях функция должна образовывать не дез-
дезорганизованную толпу значений, а рабочий организм. Сейчас стала
особенно ясной роль функций, заданных формулами, более точно —
аналитических функций (гл. V).
Но логический анализ понятия функции, проведенный в XIX веке,
не прошел и для приложений бесследно. Так, функции, заданные
несколькими формулами (кусочно аналитические функции), часто
встречаются в приложениях и более не вызывают замешательства
(простейший пример—единичная функция е (х) из § VI.3). Их место
стало еще более ясным после открытия в XX веке обобщенных функ-
функций—б-функции Дирака и связанных с ней функций (математиче-
(математическая строгая теория обобщенных функций была развита в 1936 г.
С. Л. Соболевым). Например, функцию /(х), равную /г(х)
при х < а и /2 (х) при х > а, можно записать единой формулой:
f(x)=f1 (х) е (а—х) +/, (х) е (х—а).
По-видимому, сейчас в приложениях индивидуальное («персональное»)
значение имеют только аналитические, кусочно аналитические и
простые обобщенные функции. (В теории случайных процессов типа
броуновского движения важную роль играют непрерывные, нигде не
дифференцируемые — и потому не аналитические — функции, описы-
описывающие траектории частиц; однако эти функции невоспронзводимы,
а потому имеют только вероятностное, а не индивидуальное значение.)
Роль особенностей функции—в частности, возникающих при
«сшивании» ее из различных формул—проявляется при переходе
к комплексным значениям независимого переменного. Рассмотрим,

§ 8] МОДУЛЬ й ФАЗА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ 553
например, функцию
(— оо<*< 0),
;
показанную на рис. 200. Две части /(х) «сшиты» при лг = О с со-
соблюдением непрерывности производной. Эту функцию можно прибли-
приближенно представить в виде
/ \Х) = 1 _|_ g-CtJC >
где а весьма велико. Однако если допустить, чтобы независимое
переменное принимало комплексные значения, то правая часть будет
иметь полюсы при \ -^е~ах = 0, т. е.
B*+1)« (k = 0, ±1, ±2, ...).
Эти полюсы при а—* оо заполняют мни-
мнимую ось, которая и разграничивает обла-
области действия обеих формул для функции.
Как мы видели в § 4, «сшивание»
проявляется и при спектральном анализе
исследуемой функции в асимптотическом Рис 2оо.
поведении ее Фурье-образа.
Для XX века характере» еще один подход к понятию функции,
именно как к элементу функционального пространства—например
пространства Гильберта, т. е. как к члену функционального кол-
коллектива. Такой подход имеет во многих задачах разнообразные
теоретические и прикладные преимущества, на которых здесь мы не
имеем возможности остановиться.
Упражнения
1. Докажите, что система функций E2) является ортогональной на интер-
Т
вале 0</<Г; та же система на интервале 0</<-=- неортогоиальная; та
же система на интервале 0</<2Г ортогональная, но неполная.
2. Докажите, что система функций E4) ортогональна на интер
§ 8. Модуль и фаза спектральной плотности
Выше, в § 2, было отмечено, что простейшие приемники колеба-
колебаний (в том числе ухо, глаз, фотопластинка) регистрируют только
абсолютную величину амплитуды; показания этих приемников не
зависят от фазы колебаний. Такой подход к колебаниям характерен
для XIX века с его интересом к энергетике, так как энергия колеба-
колебаний определяется только модулем амплитуды, точнее, модулем спект-
спектральной плотности. Если колебание описывается вещественной функ-
функцией f(t), то поток энергии дли различных типов колебаний

554 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
пропорционален [/(г1)]2 или [/'(г1)]2, так что полная энергия колебаний,
протекшая за все время —оо < t < оо, выражается через интегралы
/0 или
— 00 — 00
Однако эти интегралы легко выражаются через квадрат модуля
спектральной плотности. Чтобы получить это выражение для /0,
возведем обе части равенства D) в квадрат, после чего объединим
в правой части два интеграла в один:
Теперь проинтегрируем обе части по t и воспользуемся формулами
(9), (VI.4) и E):
/0 =
/0
dt = J J J F К)
= 2я ^ ^ (»i) ^ (®а) S К + <oa)
Аналогично, так как Фурье-образом функции/' (t) служит ко/7(о), то
/х = ^ [/' (г1)]2 ^ = 2я J | ко/7(«) |2 d(n = 2я
Соответствующие формулы для периодических функций с перио-
периодом Т были, по существу, выведены в § 7 (см. E3)):
где afc — коэффициенты разложения функции f(t) в ряд Фурье D0).
Здесь достаточно найти энергию за время одного периода, а вместо
интеграла по частоте входит сумма. Выражение для /t имеет анало-
аналогичный вид.
Два выражения для / — через интеграл по времени или интеграл
(сумму) по частотам—можно представить себе как выражение квад-
квадрата модуля вектора по теореме Пифагора в виде суммы квадратов
его компонент (ср. истолкование формулы E3) в § 7). При этом
разные выражения получаются потому, что мы пользуемся различ-
различными системами координат: в одной координатами являются значе-
значения функции в различных точках, т. е./(г'1), f(tlJrht), ..., в дру-
другой— коэффициенты Фурье. Равенство двух выражений для / пока-
показывает, что каждое из них является полным, ни одна из компонент
вектора не забыта.

§ 8]
МОДУЛЬ И ФАЗА СПЕКТРАЛЬНОЙ ПЛОСКОСТИ
555
Таким образом, выражение энергии не зависит от фазы колеба-
колебаний: заменяя F(«) на F (a) eia Ua\ где а («) —вещественная функция,
мы не меняем интеграл /. Остается неизменной не только полная
энергия, но и энергия, полученная осциллятором, настроенным на
ту или иную частоту. При энергетическом подходе фаза колебаний
несущественна.
В нашем XX веке и особенно в его второй половине огромное
значение приобрела передача информации, начиная от радиовещания
и телевидения и кончая кибернетическими системами управления
и исследовательскими задачами. Ясно, что, отказываясь от регистра-
регистрации фазы, мы теряем часть информации: если одинаковому по \F\2
спектру с разными фазами отвечают разные f(t), то при неизвест-
неизвестной фазе нельзя воспроизвести f(t), зная лишь \F\2. Записывая
fit)
Рис. 201.
Рис. 202.
\F\ и фазу, мы получили бы, грубо говоря, вдвое больше сведений,
вдвое больше информации от заданной волны. Более того, оказы-
оказывается возможным передавать информацию именно за счет измене-
изменения фазы колебаний, при постоянной их амплитуде.
В радиотехнике известны два способа передачи информации:
с помощью амплитудной модуляции
f(t) = a(t)cosa0t
(рис. 201) или с помощью частотной модуляции
/(*) = в0 COS (<D,< + C $&(<)<«)
(рис. 202). Информация, которую необходимо передать, в первом
случае заключена в функции a(t), а во втором — в функции b(t).
С точки зрения гармонического анализа, т. е. разложения /(t)
в интеграл Фурье, в обоих случаях мы имеем дело со спектром,
в котором F(w>) отлично от нуля в окрестности «0 — величины, назы-
называемой несущей частотой.
В случае амплитудной модуляции, чтобы определить спектр,
разложим a(t):
a(t) = ^A (а) еш da.

556 ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
Очевидно, что если A (t) отлично от нуля лишь в полосе —Л < а> < Л,
то разложение f(t) будет сосредоточено в полосе частот той же
ширины, т. е. F(a>)^0 при «„ — Л <«<&)„ +Л (конечно, и при
— «0—Л < со <—&H + Л, что в силу соотношения E) не дает для
частот ничего нового). Эта ширина не зависит от абсолютного зна-
значения амплитуды.
В случае частотной модуляции мгновенное значение частоты
равно производной от фазы:
">(t)=4t [<***+с §b(f)dt\=<i>0+cb(t).
Однако, согласно принципу неопределенности (§ 5), мы должны
иметь достаточный интервал времени т, для того чтобы частота
изменилась существенно и это изменение можно было бы зарегист-
зарегистрировать:
т> {cb(t))-\
где b надо понимать как F2I/2. Соответствующее время изменения
самой функции b (t) зависит от частоты передаваемого сигнала; это
время равно т=1/Д. Таким образом, если сй(/)/Д>1, то ширина
полосы, используемой для передачи, т. е. ширина спектра F(F)
функции f(t), равна cb(t) и больше ширины частоты сигнала Д.
В определенных условиях большая ширина передаваемого радио-
радиосигнала оказывается выгодной и позволяет уменьшить помехи.
Рисунки 201 и 202 показывают, в частности, что две функции
f (t) с похожим спектром, с похожей зависимостью, ^(оо)!2 могут
выглядеть совершенно по-разному. Это различие проистекает из-за
различия фаз, т. е. функции <р (о) в выражении F («) = |/1F («) |
ОТВЕТЫ И РЕШЕНИЯ
2. Так будет, если все (о^ соизмеримы, т. е. ы^ — п^а, где а не зависит
от k, а все п^—целые. Тогда все слагаемые, а потому и сумма имеют период
а
§2
— со
О со
^д+г^ = _L f_I.
2л V J J У 2л \<х— № ^- а—ко

ОТВЕТЫ И РЕШР.НИЯ 557
Если обозначить а = —, мы получим как раз один из примеров, из которых
в § VI.1 при т ■—>■ оо (т. е. а—>-+0) была получена дельта-функция; зна-
значит, для / (/) s 1 будет F (<о) = 6 (<о). Формула D) дает
t г*
Я I ~ ~
т. е.
00
a cos 1а> , _~ | / 1
С а cos
\ —j-;
При а=1 получаем формулу A.1) в других обозначениях.
2. Из A7) получаем
— 00
где
Заменяя в последнем интеграле обозначение переменной интегрирования i
на т, подставляя этот интеграл в первый и меняя порядок интегрирования,
получаем после преобразований
Внутренний интеграл можно вычислить по методам § V.9. Подынтегральная
функция имеет простые полюсы при
оба эти значения находятся в верхней полуплоскости. При / > т, пользуясь
верхней полуокружностью |<о| = Д —«- оо, получаем, что внутренний интеграл
равен
—о г^;Н—о г^т: =—е-т«-ч sin<o°(/—т).
При t < х надо пользоваться нижней полуокружностью, что приводит к ра-
равенству интеграла нулю. Таким образом,
t
x(t) = —- V e-T('--
— 00
§ 4
1. Образом функции /(а/) служит
to" (/— T
-on -аоо
(сделана подстановка a/^/t) при a > 0; при а < 0 надо переставить пределы

558 ' ПРЕОБРАЗОВАНИЕ ФУРЬЕ [ГЛ. XIV
интегрирования, что даст
л «2 +(со РJ' а
я <х3 + (со— РJ' а а2+ со3"
§5
1. Так как на соотношение неопределенности сдвиг по оси / не влияет,
то положим f(t) = C(\ х\ < h), f(t) = O (\x\ > h), так что M = 2h. Тогда по
формуле A0) F (ш)=С т—• Примем за ширину полученной функции ши-
ширину среднего «горба», т. е. расстояние между ее соседними нулями. Тогда
Аш = -г , откуда Д/ До = 2Л-^-=2я = const.
2. Если как-то определена ширина Д/ функции / (t) и ширина До ее
плотности F (со), то ширина функции / (at) равна -.—-, а ширина ее плот-
плотности -j—г-F ( — J равна |а|Дсо. При этом j—-. • \ а \ Дсо = Д/ До, т. е. не
зависит от а.
§ 6.
2А -^ 4А cos 2kat _
(—1)" . 2Ш
j_|ifsinT-;
со
в) '27r + r^j cos-jr . Период k-A гармоники равен —^- ,
§7
1. При ы Ф п будет
г т
f 2mit . 2пл , ,, 1 С Г 2(т + я)я, , 2(т—п)п 1 .
\ cos -^-/-cos —Ы/ = Т \ cos T / + cos v ' t\ dt =
2(т + я)я^ Г Ejn 2(m—a
При этом может быть и m = 0, тогда cos—-~t = \. Аналогично проверяется
ортогональность друг другу синусов, а также синуса — косинусу. Если ин-
Т
теграл берется от 0 до -^-, то синусы косинусам уже не ортогональны (интеграл
оказывается отличным от нуля). Для интервала 0^/<2Г интегралы тоже
равны нулю, но так так все функции E2) периодичны с периодом Т, то и
разлагать по ним можно только функцию, значения которой на части
Т ^ t < 2Г в точности повторяют ее значения на части 0Г
2. При пг ф п будет
I (m-n) nl 2 (т-п) nl T
Г ldt== 1 е Г '
" 2(т—п)лГ
= 0.

ГЛАВА XV
ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
Наше изложение будет неполным, если не сказать, хотя бы
совсем немного, об ЭЦВМ — электронных цифровых вычислительных
машинах, которые произвели переворот в современной прикладной
математике, да и не только в ней.
Простейшие вычислительные средства — логарифмическая линей-
линейка, конторские счеты, арифмометр, таблицы уже давно внедрены
в практику и широко известны. Однако для потребностей современ-
современной науки, техники, экономики эти средства недостаточны. Многие
важные задачи, в принципе разрешимые, требуют столь большой
вычислительной работы, что их решение с помощью указанных
средств невозможно получить в практически приемлемые сроки. Для
получения решения часто приходилось не принимать во внимание
многие существенные факторы, что приводило к количественным,
а иногда и к принципиальным ошибкам.
Поиски более эффективных вычислительных средств и достиже-
достижения современной техники привели к созданию ЭЦВМ, скорость дей-
действия которых на много порядков превосходит скорость дей-
действия «классических» средств. Хотя идея конструкции таких машин
была высказана еще в XIX в., но лишь достижения современной
электроники сделали возможной ее реализацию. Первая ЭЦВМ бы-
была построена в США в 1943 г., а в 1946 г. американский матема-
математик Дж. Нейман A903—1957) сформулировал основные идеи и
принципы построения таких машин. Интенсивное внедрение ЭЦВМ
в практику позволило успешно разрешить ряд важных задач и зна-
значительно увеличить количество областей человеческой деятельности,
в которых применение математики и примыкающей к ней новой ди-
дисциплины— кибернетики приводит к полезным результатам. Несом-
Несомненно, что дальнейшее развитие и особенно расширение круга
применений современной вычислительной техники приведут уже при
жизни нашего поколения к значительной перестройке организации
научных исследований, технических работ, экономических расчетов,
управления, обслуживания и т. д.

560 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ |ГЛ. XV
§ 1. Моделирующие вычислительные машины
Допустим, что какая-либо задача свелась к решению некоторого
математического уравнения. Тогда мы будем для краткости называть
величины, входящие в уравнение, математическими (хотя они могут,
конечно, иметь определенный физический смысл, который и привел
к рассматриваемому уравнению).
Имеются два основных способа представления (фиксации) мате-
математических величин, над которыми надо производить вычисления.
По одному способу такие величины непосредственно изображаются
теми пли иными физическими величинами—длинами, углами, электри-
электрическими напряжениями и т. д., причем независимо от того, какой смысл
имела исходная физическая задача; после этого подбирается физиче-
физическая схема, в которой физические величины преобразуются по тому
же закону, по которому должны преобразовываться математические
величины. Вычислительные машины, основанные на таком принципе,
называются аналоговыми или моделирующими. Простейшим аналого-
аналоговым прибором является логарифмическая линейка, в которой сложе-
сложение математических величин (логарифмов сомножителей) моделиру-
моделируется сложением длин. Другой пример: для вычисления интеграла
можно моделировать подынтегральную функцию законом открывания
крана для воды, тогда сам интеграл будет отвечать общему объе-
объему воды, который нетрудно измерить. Наиболее распространены мо-
моделирующие машины, основанные на электрических аналогиях.
По второму способу с помощью какой-либо конструкции изобра-
изображается цифровая запись рассматриваемых математических вели-
величин, а действия над ними заменяются арифметическими действиями над
цифрами. Вычислительные машины, основанные на этом принципе,
называются цифровыми; к ним относятся, в частности, конторские
счеты и арифмометр. Наибольшие достижения, о которых говорилось
выше, относятся к цифровым машинам, однако здесь мы для полноты
немного поговорим о моделирующих машинах.
Мы не будем подробно останавливаться на работе моделирующих
вычислительных машин, отметим только некоторые их особенности.
Прежде всего, входные параметры, т. е. величины, над которыми
производятся действия, здесь обычно могут непрерывно изменяться
в определенных диапазонах; поэтому данный класс машин называют
также вычислительными машинами непрерывного действия. Конечно,
может быть, например, что входные параметры реализуются в виде
электрических сопротивлений, которые меняются дискретно с по-
помощью «магазина сопротивлений»; но эта дискретность будет тогда
конструктивной, непринципиальной, тогда как цифровые машины
принципиально являются машинами дискретного действия.
Далее, ясно, что точность ввода параметров и получения резуль-
результатов для моделирующих машин невелика; и действительно, она
обычно бывает порядка процентов, в лучшем случае десятых долей

§ 2] ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ 661
процентов. Это, конечно, ограничивает возможности моделирования
громоздких вычислений. Кроме того, моделирующие машины обычно
являются сравнительно узко специализированными, т. е. приспособ-
приспособленными лишь для решения задач определенного узкого класса.
Но если такие специализированные задачи приходится решать часто
и особой точности не требуется, то применение моделирующих машин
и приборов оказывается очень эффективным. Например, довольно ши-
широко применяются электрические интеграторы, предназначенные для
решения систем обыкновенных дифференциальных уравнений.
Часто бывает, что одну и ту же взаимосвязь величин можно
осуществить на различных физических схемах. Это дает осно-
основание для моделирования физических процессов: чтобы в некоторой
физической схеме найти какую-либо величину S, которую трудно
замерить или подсчитать непосредственно, создают новую схему,
иной физической природы, но в которой между участвующими вели-
величинами имеет место такая же функциональная взаимосвязь; после
этого в новой схеме замеряют величину, соответствующую 6". При
этом, если математическая эквивалентность двух физических схем
установлена, то математическое решение задачи оказывается излиш-
излишним, так что никаких вычислений, если они не нужны для чего-либо
иного, можно не производить; по существу, здесь используется подо-
подобие явлений по определенным характеристикам (§ VIII.10) с размер-
размерным коэффициентом подобия. В последние годы такое аналоговое
решение задач на основе электромеханических, оптико-механических,
электродиффузионных и т. д. аналогий получило широкое развитие.
Если изучается течение некоторого процесса и по физическому
смыслу задачи независимой переменной является время t, то часто
и решение на моделирующей машине получается как функция
того же t. Тогда говорят, что задача решается в реальном масшта-
масштабе времени, а решение можно непосредственно, минуя человека, пере-
передавать в изучаемую схему для использования; на этом принципе
основаны многие приспособления для автоматического регулирова-
регулирования. Применение реального масштаба времени дает также возмож-
возможность при испытании сложных конструкций заменять отдельные до-
дорогостоящие агрегаты вычислительными машинами. Например, авто-
автопилот можно испытывать не в полете, что дорого и опасно, а на
стенде, заменив самолет моделирующей машиной, которая по своей
реакции на работу автопилота полностью тождественна самолету.
§ 2. Цифровые вычислительные машины
Перейдем теперь к цифровым вычислительным машинам. Мы не
станем останавливаться на широко распространенных сейчас малых
счетных машинах — усовершенствованных арифмометрах, произво-
производящих четыре арифметических действия. Эти машины чрезвычайно
полезны, но, конечно, не могут действовать очень быстро как иэ-эа

562
ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
У i 1
Устройство
Ввода
Устройства
вывода
ЗУ
(памят$
<—
i
УУ
i
i
АУ
Рис. 203.
невысокой скорости самого вычисления, так и из-за того, что
входные данные для каждого арифметического действия вводят-
вводятся человеком—вычислителем. Оба этих недостатка преодолены
'в ЭЦВМ.
Структурная схема (блок-схема) ЭЦВМ, т. е. основные ее блоки
и их взаимосвязь, показана на рис. 203, где каналы информации
обозначены сплошными стрелками, а каналы управления — пунктир-
пунктирными стрелками. В запоминающем устройстве (ЗУ) имеется опреде-
определенное количество, например 512, ячеек, каждая из которых слу-
служит для записи одного числа или одной «команды» (предписания).
Запись команды, как мы
увидим в § 3, по внешней
форме ничем не отличается
от записи числа. Некото-
Некоторые из этих ячеек запол-
заполняются от устройства ввода,
тогда как другие запол-
заполняются по мере работы,
причем в процессе работы
содержание ячеек может
многократно заменяться, а
часть ячеек не использует-
используется. Руководствуясь запи-
записанными командами, устройство, управления (УУ) направляет
числа (или команды) из ЗУ в арифметическое устройство (АУ), кото-
которое их преобразует в соответствии с этими командами и возвращает
в ЗУ. По мере получения требуемых результатов они по сиг-
сигналам УУ автоматически печатаются, а после окончания вычисле-
вычислений УУ останавливает машину.
С помощью дополнительного приспособления ЭЦВМ может вы-
выдавать результат в форме графика, приближенно построенного по
вычисленным координатам точек, и даже мультфильма, показываю-
показывающего изменение такого графика.
На универсальной ЭЦВМ можно решать любую математическую
задачу, для которой указан алгоритм, т. е. четкое предписание,
определяющее вычислительный процесс, которое, исходя из вводных
данных, обязательно приводит к требуемому результату. Однако
и нематематические задачи, для которых можно указать аналогич-
аналогичный алгоритм решения, разрешимы на таких машинах. Например,
цифровая машина может управлять станком при обработке детали
как угодно сложного профиля; при этом вводные данные характе-
характеризуют профиль, а результаты вычисления преобразуются в сигналы
устройству управления станком. Аналогично работают устройства,
управляющие полетом самолета или технологическим процессом,
причем в случае отклонения от первоначально заданной программы
ыашина может принимать наивыгоднейшие решения, сравнивая воз-

§ 3] ЗАПИСЬ ЧИСЕЛ И КОМАНД В ЭЦВМ 563
можные варианты, а также контролировать результат. Широкое
применение получили ЭЦВМ для прогноза погоды, планирования
перевозок и т. д. Впрочем, в таких применениях более эффектив-
эффективными оказываются не универсальные, а специализированные ЭЦВМ,
приспособленные для решения определенного круга задач.
§ 3. Запись чисел и команд в ЭЦВМ
Десятичная система счисления, которую мы изучаем в школе
и постоянно применяем в жизни, неудобна для использования в ра-
работе ЭЦВМ. Для записи чисел в машине применяется двоичная
система счисления, в которой имеются лишь две цифры, 0 и 1
(тогда как в десятичной системе имеется десять цифр), и все числа
записываются в виде комбинаций этих цифр. Для этого принимают, что
записи 10, 100 и т. д. означают не степени десятки, а степени двойки,
т. е. числа два, четыре и т. д. Это можно записать так:
11о=12. 210=102, 310=112, 41р=1002, 510=1012 и т. д.,
где индекс указывает на принятую систему счисления.
Любое целое число можно записать в двоичной системе счисле-
счисления; для этого из данного числа надо выделять степени двойки,
начиная со старшей. Например, в десятичной записи
1971 = 1-1024+ 1-512+ 1-256+1-128 + 0-64+1-32+Ы6 +
+ 0-8 + 0-4+1-2 + Ы,
т. е.' 197110=11110П0011г.
Аналогично составляются двоичные дроби взамен десятичных.
Например, число 10,1011а в десятичной записи означает 2 + -=- +
1 1 43
+ +
g g g 0. Любое нецелое число можно записать в виде
конечной или бесконечной двоичной дроби; естественно, что в реаль-
реальных вычислениях дроби округляются.
Таблицы сложения и умножения в двоичной системе крайне просты:
0 + 0 = 0, 1+0 = 0 + 1=0, 1 + 1 = 10, A)
0-0 = 0, 1-0 = 0-1=0, 1-1 = 1. B)
Пользуясь этими таблицами, возможно производить арифметические
действия над числами, записанными в двоичной системе, совершенно
аналогично тому, как это делается в школе для десятичной системы.
Не следует думать, что сам вычислитель при работе на машине
должен пользоваться двоичной системой! Нет, при составлении про-
программы пользуются десятичной записью, а переход к двоичной
осуществляется внутри машины по специальной команде, на чем мы
для простоты не будем останавливаться, равно как и на восьмеричной
и двоично-десятичной системах, которыми при этом приходится поль-

564
ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
зоваться. Результаты вычислений также печатаются машиной в деся-
десятичной записи.
При записи чисел в ЗУ (§ 2) под каждое число отводится
ячейка, причем все эти ячейки имеют одинаковую длину, т. е. одно
и то же число разрядов, каждый из которых содержит 0 или 1.
В наших ЭЦВМ принята запись с плавающей запятой; это означает,
что выписываются число, заключенное между —1 и 1, и показатель
степени двойки, на которую (степень) надо это число умножить.
При этом под показатель степени, включая его знак, отводится
некоторое вполне определенное число разрядов, например, в конце
ячейки.
Пусть, например, этих разрядов шесть, всего в ячейке 30 раз-
разрядов, знак« + »изображается в виде 0, а«—»в виде 1. Тогда
набор цифр в ячейке
знак
числа
1-
дробные разряды числа
знак
показателя
| разряды
показателя
1
1
0
1
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
означает число
C)
= —21,51в.
Наибольшее число, которое можно записать таким способом, имеет вид
D)
и равно A—3) 231 = 231 — 28 яй 231, тогда как наименьшее поло-
положительное число имеет вид
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
000000000000000000000001111111 E)
и равно 2~23-2~31 = 2~54 (продумайте это!).
Фактическая «запись» цифр для разных конструкций машин
производится различными способами. Для ввода чисел во вводное
устройство машины (§ 2) они пробиваются на специальной ленте —
перфоленте или на наборе специальных карточек—перфокарт; для
определенности будем говорить только о перфокартах. Здесь каждой
ячейке отвечает строка на карточке, причем длина строки соответ-
соответствует числу разрядов в ячейке, пробитое отверстие соответствует
цифре 1, а непробитое — цифре 0. Например, если бы числа, запи-
записанные в формулах C), D) и E), следовали одно за другим во
вводной программе, то соответствующая перфокарта имела бы участок
вида, изображенного на рис. 204 (проверьте!). Эти отверстия про-
пробиваются перед запуском машины на специальном перфораторе, не

§ 3]
ЗАПИСЬ ЧИСЕЛ И КОМАНД В ЭЦВМ
565
связанном с машиной и внешне напоминающем кассовый аппарат
в магазинах.
Обширная программа записывается на целой колоде перфокарт,
причем если обнаружена ошибка в программе или если входные дан-
данные изменились, то карты нетрудно заменить.
Для хранения (и преобразования по мере вычислений) чисел в ЗУ
внутри машины каждая ячейка ЗУ реализуется в виде набора эле-
элементов, каждый из которых может находиться в одном из двух
состояний; число элементов в наборе равно числу разрядов в ячейке,
а каждое из состояний элемента отвечает значению 0 и 1 в соот-
соответствующем разряде. Применяются различные типы таких элементов,
II
1
■г
1 1 1 1 1 1 1 Ш II:
IDDDDDDDDDDDDDDDDDDDDDDDIDDDDD
I
1
■ Т 1 IBiSill
Рис. 204.
причем от них всегда требуется безынерцаонность, т. е. мгновенный
переход из одного состояния в другое, и устойчивость, т. е. неопре-
неопределенно долгое сохранение состояния при отсутствии переходного
сигнала. Элементами могут служить магнитные ферритовые сердеч-
сердечники, меняющие направление магнитного поля при прохождении тока
по обмотке; намагниченные и ненаыагниченные участки на магнитном
барабане или магнитной ленте, действующих по принципу магнито-
магнитофона, и т. д.
Передача числа из ячейки ЗУ в АУ и обратно производится
по системе каналов, число которых может доходить до числа раз-
разрядов в ячейке (машины параллельного действия).
Чем больше ячеек в ЗУ, тем больше данных можно ввести в
машину, тем большей гибкостью в работе она обладает. Поэтому
для расширения объема памяти многим машинам придается внешнее ЗУ,
обычно оформляемое в виде магнитной ленты, с которой специаль-
специальное устройство по заранее предусмотренным командам может вводить
записанные там числа во внутреннее, оперативное ЗУ; возможен,
конечно, и обратный процесс. Если число ячеек в оперативном ЗУ
измеряется тысячами, то число ячеек на магнитной ленте может
доходить до миллионов; однако считывание чисел с ленты и запись
их "обратно на ленту осуществляются не так быстро, как внутри
оперативного ЗУ, так как требуется определенное время на пере-
перемещение ленты.
Если машина перерабатывает не числа, а какую-либо иную инфор-
информацию, например словесную, то эта информация должна быть закоди-
закодирована (зашифрована) с помощью двоичных чисел. Тогда можно

566 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ, XV
предусмотреть устройство, которое бы после окончания действий раско-
раскодировало результат, т, е, перевело его в форму, естественную для
данного вида информации.
Машина производит действия над числами, хранящимися в ЗУ,
только по командам, которые также вводятся перед началом работы
в ЗУ и по внешней записи не отличаются от чисел. Мы будем рас-
рассматривать только так называемые трехадресные команды. Каждая
такая команда представляет собой ячейку, мысленно разделенную
на четыре части вполне определенной длины, например в 3, 9, 9 и 9
разрядов. Эти части отведены под:
1) условную запись (код) действия, которое надо произвести;
2) адрес (номер ячейки) первого из чисел, участвующих в действии;
3) адрес второго из чисел, участвующих в действии;
4) адрес, по которому надо отправить результат действия.
При этом все ячейки нумеруются в естественном порядке. На-
Например, если в ЗУ имеется 512 ячеек, то девяти двоичных разрядов
как раз достаточно для указания адреса (почему?). Пусть кодом
операции сложения служит число 1. Тогда, если требуется сложить
числа, находящиеся в 271-й и 59-й ячейках, а результат поместить
в 422-ю ячейку, то при принятом выше разделении ячейки соответ-
соответствующая команда должна иметь вид (проверьте!)
001 100001111 000111011 110100110. F)
части: 1-я 2-я 3-я 4-я
После выполнения этой команды во всех ячейках ЗУ, включая 271-ю
и 59-ю, останется то же, что и было, за исключением 422-й, в ко-
которой взамен того, что в ней было, появится сумма чисел, стоящих
по адресам 271 и 59.
Команда F) пробивается на перфокарте и хранится в одной из
ячеек ЗУ в точности так же, как если бы это было число
0,01100001111000111011П4-210*. Различие проявляется лишь во
время работы машины, так как если программа работы составлена
правильно, то в УУ в качестве команд поступают сигналы только
от тех ячеек, которые и были предусмотрены как команды.
Вся работа машины и, в частности, выполнение действий по
командам обеспечиваются электронными схемами, которые осущест-
осуществляют преобразование электрических сигналов по необходимым пра-
правилам. Первоначально эти схемы были основаны на применении
электронных вакуумных ламп (триодов и пентодов), позже — на при-
применении полупроводников и интегральных схем. Основные виды пре-
преобразователей сигналов показаны на рис. 205. Первый обеспечивает
возникновение сигнала (положительного напряжения достаточно вы-
высокого уровня) на выходе В тогда и только тогда, когда сигнал на
входе А отсутствует. Второй обеспечивает сигнал на выходе С тогда
и только тогда, когда на оба входа А и В поданы сигналы, а тре-
третий— когда по крайней мере на один вход подан сигнал. Более

§ 3]
ЗАПИСЬ ЧИСЕЛ И КОМАНД В ЭЦВМ
567
сложные преобразователи получаются в результате комбинации этих
простейших. Проверьте, например, что схема, приведенная на рис. 206,
реализует таблицу сложения A), если наличие сигнала соответствует
единице, а отсутствие его — нулю. Таблицу умножения B) реализует
простейшая схема «и».
Порядок работы машины таков. В самом начале работы в ЗУ с
перфокарт вводится программа работы, т. е. определенная последо-
последовательность команд, и исходные данные, т. е. числовой массив, над
которым производятся действия. Затем УУ воспринимает содержимое
первой ячейки в качестве команды,
и в соответствии с этой командой 1-е слагаемое 2-е слагаемое
АУ выполняет предписанные дей-
действия. Далее УУ воспринимает
Число двоен
Рис. 206.
I
Число единиц
содержимое второй ячейки в качестве команды и т. д., за исключе-
исключением особых команд «передачи управления», о которых мы скажем
в § 4 и после выполнения которых УУ переходит не к очередной
ячейке, а к ячейке, номер которой указан в команде. Некоторые
команды предписывают печатание содержимого какой-либо ячейки,
но и после выполнения такой команды УУ переходит к следующей
ячейке. (Правда, если печатать приходится часто, то темп работы
замедляется, так как печатание производится медленнее, чем ариф-
арифметические операции.) И так продолжается до тех пор, пока УУ не
дойдет до команды, означающей останов машины, после чего работа
прекращается. Машина останавливается (аварийный останов) и в том
случае, если действие, предусмотренное программой, невыполнимо,
например, если по ходу вычислений получится столь большое число,
что оно не может быть записано в ячейке (переполнение ячеек). Спе-
Специальное устройство дает возможность с пульта управления машиной
в любой момент работы выяснить содержимое любой ячейки, а также
ввести дополнительные данные.
Упражнения
1. Запишите в двоичной системе счисления числа 9999; —1/3; 2,75.
2. Запишите те же числа по образцу формулы C}.

568 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [?Л. XV
§ 4. Программирование
Приведем несколько простых примеров, на которых можно понять
некоторые принципы составления программ, т. е. программирования;
впрочем, отметим, что составление серьезной программы является
очень ответственным делом, часто занимает много времени и требует
навыков работы. Мы будем для простоты записывать вместо кода
операции знак действия, например знак« + » вместо кода сложения.
Пусть требуется подсчитать решение системы уравнений первой
степени (VIII.6), причем будем считать значения чисел а,-, b;, di за-
заданными. Как известно, решение получается по формулам (VIII.7).
Будем размещать команды в ячейках с номерами 1, 2, ...; мы
пока не знаем, сколько потребуется команд. Шесть входных пара-
параметров аи bv at, b2, dlt йг разместим соответственно в ячейках
с номерами а+1, а+2, а + 3, а+4, а + 5, а + 6; значение а мы
уточним позже. Несколько дальнейших ячеек будут использованы
в качестве рабочих ячеек для хранения промежуточных результатов;
состояние этих ячеек к началу работы несущественно, так как при
любой записи в ячейке предыдущая запись в ней автоматически
стирается. Остальные ячейки ЗУ при составлении и работе программы
не используются. Начнем с подсчета значения dlbt—b±dv Чтобы
вычислить d$v требуется команда
1) х а + 5 а+4 а + 7;
при этом мы перед командой для ориентировки пишем ее номер,
который фактически нигде не пробивается. После исполнения этой
команды в ячейке (а + 7) появится число d^b^. Следующая команда
пусть имеет вид
2) X а + 2 а + 6 а + 8;
после ее исполнения в ячейке (а + 8) появится число b^dv Далее
надо из числа dj)^ (ячейка (а + 7)) вычесть число bldt (ячейка (а + 8)).
Так как эти числа больше не понадобятся, то результат можно запи-
записать в ячейке (а + 7) с помощью команды
3) — а + 7 а + 8 а + 7;
конечно, здесь можно было использовать и ячейку (а+ 9), но в более
сложных программах часто приходится экономить ячейки.
Аналогично находим знаменатель, т. е. агЬг—&1йа:
4) х а+1 а + 4 а + 8,
5) х а + 2 а + 3 а + 9,
6)— а + 8 а + 9 а + 8.
Теперь надо числитель, хранящийся в ячейке (а + 7), разделить
на знаменатель, хранящийся в ячейке (а + 8), и результат отпечатать:
7) : а + 7 а + 8 а + 7,
8) печ. а + 7;

§ 4J ПРОГРАММИРОВАНИЕ ' '569
по последней команде машина печатает содержимое ячейки, т. е.
значен! е л:, и переходит к исполнению следующей команды. Ана-
Аналогично вычисляем у, имея в виду, что знаменатель для у уже вы-
вычислен и хранится в ячейке (a-j-8):
a + I a + 6 a + 7,
a + 5 a + 3 a + 9,
a+7 a+9 a+ 7,
a + 7 a+8 a + 7,
a + 7,
14) ост.
По 14-й команде машина останавливается. Итак, в нашей про-
программе содержится 14 команд и потому можно принять а=14. Тогда
вся программа будет занимать 20 ячеек и иметь такой вид:
9)
10)
И)
12)
13)
X
X
—
:
печ.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
И)
12)
13)
14)
15)
16)
17)
18)
19)
20)
X
X
—
X
X
—
печ.
X
X
—
печ.
ост.,
ак
bv
at,
*..
d' -
19
16
21
15
16
22
21
21,
15
19
21
21
21,
18
20
22
18
17
23
22
20
17
23
22
21,
22,
21,
22,
23,
22,
21,
21,
23,
21,
21,
Итак, все промежуточные результаты в нашей программе требуют
трех рабочих ячеек (№№ 21, 22 и 23). Теперь остается только
пробить эту программу и пустить машину в ход. (На самом деле
требуются еще некоторые команды, не имеющие для нас принци-
принципиального значения, например команда ввода программы с перфокарт
в ЗУ и т. д.)
В разобранном примере число команд в программе равнялось
числу действий. Однако современные ЭЦВМ создавались в основном
для вычислений, требующих миллионов действий. Ясно, что в этом
случае писать отдельную команду на каждое действие невозможно.

570 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
К счастью, при большой массе вычислений обычно многие промежу-
промежуточные вычисления проводятся по одной и той же схеме несколько
раз; а тогда в программе можно предусмотреть образование циклов,
при которых УУ проходит один и тот же участок программы по
нескольку раз. Циклы образуются с помощью команды условной
передачи управления, которая имеет вид
ПУ Nt N2 N3
(ПУ означает «передачу управления»; конечно, на самом деле надо
указать код этой операции). Имеются различные варианты реализа-
реализации этой команды. Мы будем для определенности считать, что по
ней машина сравнивает содержимое (N,)' ячейки Л^ и содержимое
(Л^)' ячейки Nt; если (Л^)' < (N2)', то УУ переходит к исполнению
очередной команды; если же (Л^)' ^ (М,)', то УУ переходит к ис-
исполнению команды, содержащейся в ячейке с номером Ns, причем
в обоих случаях содержимое ячеек не меняется. В частности,
команда
ПУ 1 1 Л/,
означает, что УУ после ее прочтения обязательно переходит к испол-
исполнению команды, содержащейся в ячейке Ns; такую команду можно
считать командой безусловной передачи управления.
Составим для примера программу для напечатания таблицы
обратных величин к 500 натуральным числам, скажем, от 2001 до
2500; без команды ПУ программа заняла бы очень большой объем,
на деле же она получится очень маленькой. Поместим в ячейке
(а+1) число 2000, в ячейке (а+ 2) число 1, а в ячейке (а + 3)
число 2499 (мы вскоре увидим, зачем это нужно). Пусть первая
команда имеет вид
1) + а+1 а + 2 а+1.
После ее выполнения в ячейке (а+1) взамен числа 2000 появится
число 2001, для которого мы вычислим обратное и результат на-
напечатаем:
2) : 'а + 2 а+1 а+4,
3) печ. а+4.
Сравним число, стоящее в ячейке (а+1), с 2499 и, поскольку
оно еще не превзошло 2499, перейдем вновь к первой команде:
4) ПУ а + 3 а+1 1.
Так как в данном случае (а + 3)'= 2499, (а + 1)' = 2001, то, прочтя
четвертую команду, УУ переходит к первой команде. После ее вы-
выполнения в ячейке (а+1) взамен 2001 появится 2002; по следую-
следующим двум командам будет подсчитано и напечатано обратное число
к 2002. По четвертой команде машина сравнит 2499 с 2002 и вновь

§ 4] ПРОГРАММИРОВАНИЕ 571
перейдет к исполнению первой команды и т. д., и только когда
после очередного прибавления единицы в ячейке (а-J-l) появится
число 2500 и обратная величина к 2500 будет отпечатана, четвер-
четвертая команда «пропустит» УУ вперед, так как тогда будет (a-f-3)' =
= 2499, (« +1)'= 2500. Тогда остается остановить машину:
5) ост.,
так как все результаты уже отпечатаны.
Итак, можно принять a = 5, и полная программа будет иметь
вид
1) + 6 7 6,
2) : 7 6 9,
3) печ. 9,
4) ПУ 8 6 1,
5) ост.,
6) 2000,
7) 1,
8) 2499.
Для хранения промежуточных результатов нам понадобилась
всего одна рабочая ячейка (№ 9); однако по мере работы содержи-
содержимое шестой ячейки менялось от 2000 до 2500 через 1.
Приведем вариант, в котором к концу работы рассматриваемые
обратные величины оказываются не отпечатанными, а размещенными
в ячейках ЗУ с номерами от 10 до 509 (эти величины могут пона-
понадобиться для каких-либо дальнейших вычислений):
1) + 6 7 6,
2) +' 3 9 3,
3) : 7 6 9,
4) ПУ 8 6 1,
5) ост.,
6) 2000,
7) 1,
8) 2499,
9) A в последнем разряде ячейки, остальные 0).
Здесь в девятую ячейку программы засылается вспомогательное
число, не имеющее количественного значения, а служащее для пре-
преобразования команд, что является принципиально новым действием.
Именно, после первого выполнения второй команды третья команда,
.воспринятая АУ как число, примет вид: 7 6 10. (Заметим, что сло-
сложения по командам 1) и 2) выполняются по различным правилам,
что мы отметили штрихом; продумайте это!) Поэтому после выпол-
выполнения третьей команды число 1:2001 отправится в 10-ю ячейку.
После вторичного выполнения второй команды третья примет вид:
7 6 11, и потому после вторичного выполнения третьей команды

572 электронные цифровые вычислительные машины |;.ч: xv
число 1:2002 отправится в 11-ю ячейку и т. д. Эта операция из-
изменения адреса в команде называется переадресацией.
Таким образом, с командами можно совершать действия, автома-
автоматически преобразуя их по мере работы машины. Это открывает
дополнительные возможности в применении ЭЦВМ.
Команда условной ПУ применяется и без циклов в тех случаях,
когда требуется организовать разветвление программы, т. е. про-
производить различные последовательности действий в зависимости от
неизвестных заранее обстоятельств. Пусть, например, в процессе
вычислений в определенной ячейке с номером N должно получиться
число а и мы должны оставить его без изменения, если а^О, или
возвести в квадрат и результат оставить в ячейке N, если а < 0.
Так как в ячейке с номером 0 обычно помещается число 0, то тре-
требуемое действие можно осуществить, поместив в соответствующем
месте следующие команды:
k) ПУ N 0 k+2,
k+\) X N N N.
При этом разветвление осуществится автоматически, так что мы
даже не будем знать, какой вариант был реализован, если не пре-
предусмотреть особо информацию об этом.
Покажем, наконец, пример программы, в которой общее число
действий заранее не устанавливается. Пусть требуется решить
кубическое уравнение
л:=0,1л:3+1
методом итераций (§ 1.3) с точностью до 0,001, начиная от значе-
значения л:0 = 0. Для этого разместим число 0 в ячейке (а+1) (соот-
(соответствующая строка перфокарты просто не пробивается), число
0,1—в ячейке (а + 2), число 1—в ячейке (а + 3) и число 0,001 в
ячейке (а+ 4). Последовательные приближения будем помещать в
ячейке (а+1). Вычисление последующего приближения по преды-
предыдущему осуществляется по командам:
1) х а+1 а + 1 а+5,
2) X а + 5 а+1 а + 5,
3) X а + 2 а + 5 а + 5,
4) + а + 5 а + 3 а + 5.
Итак, последующее приближение помещено в ячейку (а + 5).
Его надо сравнить с предыдущим, содержащимся в ячейке (а+1),
и если они не совпадают с точностью до 0,001, то поместить по-
последующее приближение в ячейку (а+1) и повторить итерацию;
если же приближения отличаются менее чем на величину 0,001, то
надо отпечатать результат. Это можно сделать, например, по коман-
командам (проверьте!):
5) | —| а + 1 а + 5 а+1

§ 4| ПРОГРАММИРОВАНИЕ .573
(по этой команде число | (ос + 1)' — (а + 5)'| засылается в ячейку
(ос+1)),
6) ПУ 0 а+1 9,
7) + а + 5 0 а+1,
8) ПУ 1 1 1,
9) печ. а-)-5,
10) ост.
Итак, можно положить а= 10 и выписать всю программу, зани-
занимающую 14 ячеек. По этой программе машина будет совершать
итерации до тех пор, пока последующее приближение не совпадет
с предыдущим с указанной точностью, после чего она напечатает
результат и остановится.
Отметим, что если процесс итераций не сходится, то произой-
произойдет либо переполнение ячеек, либо зацикливание, при котором ма-
машина сама не может остановиться и для ее останова требуется
вмешательство извне с пульта управления.
Программы для более сложных задач могут занимать большой
объем; однако они нередко включают в себя более простые, часто
повторяющиеся задачи, например вычисление значения синуса от
участвующих величин и т. п.
Решение этих более простых задач осуществляется с помощью
стандартных подпрограмм, т. е. набора команд, которые составляют-
составляются заранее и хранятся в определенных ячейках оперативного ЗУ
или во внешнем ЗУ; тогда при составлении программы для более
сложной задачи обращение к стандартной подпрограмме производит-
производится по одной команде.
Для облегчения программирования в последние годы разработано
несколько универсальных машинных языков, на которых программа
расписывается в более привычных математических терминах, чем это
было описано выше. Программа на таком языке не зависит от типа
применяемой машины и печатается на устройстве, аналогичном пишу-
пишущей машинке; затем специальный транслятор автоматически пере-
переводит эту программу в программу той машины, которая будет
применяться.
Наиболее известны языки АЛГОЛ и ФОРТРАН (от английского
«algorithmic language»—алгоритмический язык и «formula translator»—
преобразователь формул), освоение которых делает применение ЭЦВМ
значительно более доступным.
Упражнения
1. Составьте программу для вычисления таблицы квадратов натуральных
чисел от 1 до 1000 включительно, причем в этой таблице значения п и п*
должны чередоваться: 1, 1, 2, 4, 3, 9, ... _
2. Составьте программу для вычисления суммы V~5-\- V~&-\-... + 1^ 100
(об этой сумме говорилось в § 1.2); при этом извлечение квадратного корня
примите за самостоятельное действие с кодом У~,

574 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
1
3, Составьте программу для вычисления интеграла \ по формуле
J 1 +■*
о
Симпсона (§ I.I) с разбиением промежутка интегрирования на 100 частей; на
1000 частей.
4. Составьте программу для интегрирования дифференциального уравнения
у'=хг—у2 на интервале —1<л:<0 с начальным условием у (—1) = 0 по
методу пересчета, описанному в § VIII.7 (ср. таблицу 5), взяв значение 0,001 за
шаг интегрирования и печатая результат через 0,1; воспользуйтесь операцией
{ } выделения дробной части числа ({ 5,3 } = 0,3; {—5,3} = 0,7; { 5 } = 0).
§ 5. Пользуйтесь ЭЦВМ!
Из § 4 вы могли увидеть, что составление программ для ЭЦВМ
в простых случаях не вызывает затруднений. И действительно, этому
сейчас успешно обучают рядовых школьников. В то же время при-
применение ЭЦВМ во многих случаях оказывается весьма полезным, на
несколько порядков повышая точность и скорость вычислений, а в
более сложных задачах — впервые делая возможными сами эти вы-
вычисления. (Для ориентировки укажем, что малые ЭЦВМ выполняют
в среднем несколько тысяч арифметических операций в секунду,
средние — несколько десятков тысяч и большие, как БЭСМ-6,—
миллион операций в секунду.)
Сейчас широкому внедрению ЭЦВМ препятствует в основном
психологический барьер. Грубо говоря, пока еще многие исследо-
исследователи боятся ЭЦВМ, так же как наши предки боялись «неберу-
щихся» интегралов, трансцендентных конечных уравнений, диффе-
дифференциальных уравнений, не разрешимых в квадратурах, и т. п. Вместо
того чтобы принципиально изменить подход к таким интегралам и
уравнениям, ученые упорно пытались найти новые случаи интегри-
интегрируемости, что существенно ограничивало возможности приложений
математики. Аналогичная ситуация возникла и сейчас в связи с ЭЦВМ.
Конечно, не следует впадать в другую крайность и думать, что
применение ЭЦВМ делает излишним получение аналитических (точ-
(точных, приближенных, асимптотических) формул и методов, «ручной»
счет с помощью электрического арифмометра, логарифмической ли-
линейки и простого карандаша! Аналитические решения, когда они
возможны, часто обладают неоценимым преимуществом из-за своей
компактности, особенно если задача включает параметры или реше-
решение получается как функция нескольких независимых переменных.
Асимптотические формулы действуют в случаях, когда применение
численных методов вообще становится затруднительным. «Ручной»
счет из-за своей мобильности наиболее приспособлен к выполнению
прикидочных расчетов, которые следует производить как можно
чаще, в том числе и при подготовке более объемных вычислений.
Таким образом, применение ЭЦВМ призвано не заменить другие
плодотворные математические методы, а сочетаться с ними,
существенно расширяя возможности приложения математики.

§ 5] пользуйтесь эцвм! 575
При решении иа ЭЦВМ задачи, уже сформулированной матема-
математически, обычно наиболее ответственным пунктом является подго-
подготовка задачи к программированию. Бывает не так-то просто выбрать
метод, чтобы он давал надежный результат и был посилен ЭЦВМ,
имеющейся в Вашем распоряжении,— а ведь ЭЦВМ мощны, по ла-
леко не всесильны! При такой подготовке зачастую приходится
значительно перестраивать «математическую психологию», воспи-
воспитанную на «ручных» методах.
Например, в «домашинную» эру считалось само собой разумею-
разумеющимся, что если в нелинейном дифференциальном уравнении воз-
возможно с помощью некоторой подстановки понизить порядок, то это
следует сделать. Например, для решения уравнения
У=/{У,У) (У=УМ) G)
рекомендовалась такая процедура: рассматривать зависимость у'=р
„ du' dp du dp ,r,\
от у, откуда у =-^-= ■— j- = P -f , и уравнение G) принимает вид
^ (8)
т. е. получается уравнение 1-го порядка. Если нам удастся его про-
проинтегрировать, т. е. найти общее решение p = ty(y, Сг), то дальше
пишем
откуда
Такая процедура иногда приводит к цели, особенно при анали-
аналитическом исследовании решения, однако для численного решения,
особенно на ЭЦВМ, она обычно оказывается нецелесообразной.
В самом деле, нам придется численно решать уравнение (8) (а*§сли
оно будет решено, в квадратурах, то вычислять соответствующие
интегралы), затем вычислять интеграл (9) и, наконец, обращать
полученную зависимость х(у). Но гораздо проще — как для состав-
составления таблицы значений частного решения, так и для сводных
таблиц общего решения — непосредственно численно инте-
интегрировать уравнение G), без понижения его порядка. Так и надо
поступать при работе на ЭЦВМ.
Таким образом, надо уметь хотя бы совсем грубо оценивать
объем вычислительной работы, необходимой для доведения решения
задачи до конца.
Другой пример. Сама постановка задачи §§ 1.2 и III.4 о при-
приближенном вычислении сумм с помощью интегралов была, конечно,
вызвана потребностями «ручного» счета. При таком счете приведен-
приведенные приближенные формулы и методы их уточнения оказываются

576 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ |ГЛ. XV
весьма полезными. Однако при применении ЭЦВМ в большинстве
случаев более эффективным оказывается непосредственное сумми-
суммирование членов.
Но и здесь нельзя действовать вслепую! Допустим, что мы
хотим вычислить сумму бесконечного ряда
Уверовав во всесилие ЭЦВМ, можно было бы попытаться подсчи-
подсчитывать и складывать члены ряда, пока они не обратятся в машинный
нуль, т. е. не станут равными нулю после округления, необходимого
для записи числа в ячейке, после чего частные суммы ряда пере-
перестанут возрастать. Однако при условных параметрах ЭЦВМ, при-
приведенных в § 3 (см. D), E)), это будет при
1<2~55, т.е. я>227'5«2.108.
Ошибка при этом, как видно из § III.4, будет близка к 1/л, т. е.
будет на восемь порядков выше последних слагаемых. Так как
добавление члена ряда к частной сумме требует нескольких опера-
операций, то при быстродействии ЭЦВМ 20 000 операций в секунду
вычисление займет около 5 часов, Вы истратите около 300 рублей
государственных денег и заслужите волчьи взгляды коллег, осо-
особенно если они узнают, что Вы вычисляли. (А если принять длину
ячейки не в 30, а в 40 разрядов, что ближе к реальным числам,
то срок вычисления и его стоимость повысятся в 32 раза.)
Конечно, так вычислять нельзя. Результат получится гораздо
быстрее и точнее, например, если просуммировать 1000 первых
членов ряда (это займет менее одной секунды), а остаток заменить
на интеграл по методу § 111.4; при этом точность результата можно
установить, повторив вычисление для 2000 членов. А еще лучше
посмотреть сначала справочник И. С. Градштейна и И. М. Рыжика,
где вы найдете, что 5г=л4/6, а значение п2 можно с большой
точностью найти из таблиц. (Конечно, тут нам просто повезло, так
как числовые ряды редко «сворачиваются» в конечные выражения
через известные константы.)
Вычисления на ЭЦВМ в принципе дискретны. Поэтому при ориен-
ориентировке на ЭЦВМ надо, формулируя задачу в виде дифференциаль-
дифференциального или интегрального уравнения, думать о том, как выглядит эта
задача и метод ее решения на дискретном языке. Для уравнений
с более чем одним независимым переменным это вызывает разно-
разнообразные осложнения, многие из которых еще не преодолены.
Особого внимания требуют задачи, содержащие параметры.
Пусть, например, мы хотим составить таблицу, по которой можно
было бы решать полное кубическое уравнение
ах* + Ьхг + сх + d - 0. A0)

§ 5] пользуйтесь эцвм! 577
Если допустить, что каждый из параметров а, Ь, с, d может при-
принимать 50 значений — а это не так уж много, — то всего получится
504«6-10в комбинаций этих значений. Средней ЭЦВМ для выдачи
результатов потребуется около месяца непрерывной работы (основ-
(основное время будет уходить на печать), после чего Вы будете иметь
набор рулонов лент общей длиной в 200 километров, весом в 2 тонны
и проклянете тот час, когда Вам пришла в голову идея заняться
этой задачей.
Вообще, характерной чертой многих людей, только что освоив-
освоивших технику работы на ЭЦВМ и пораженных их мощностью,
является стремление получить как можно большее количество
численных результатов, на основе наивного принципа «чем больше
результатов, тем больше информации, т. е. тем больше пользы».
Но часто эти люди оказываются потом подавленными морем цифр,
причем проблема извлечения полезного вывода из этого моря может
оказаться более сложной, чем исходная задача. Положение здесь
напоминает известную средневековую легенду об ученике волшеб-
волшебника, который в отсутствие учителя вызвал джина и велел ему
носить воду, но не смог его остановить вовремя и в результате
чуть не утонул. Поэтому весьма актуальным является один из ос-
основных тезисов, неоднократно подчеркиваемый известным американ-
американским вычислителем Р. Хсммингом в его книге «Численные методы»
(русский перевод, Физматлит, М., 1968):
«Прежде чем решать задачу, подумай, что делать с ее решением»,
Вернемся к уравнению A0). На самом деле положение не так
уж печально. Прежде всего поделим обе части урапнения на а:
Затем сделаем подстановку х = у-\-а, подобрав а так, чтобы унич-
уничтожить член с неизвестной во второй степени. Это даст а=—s~ .
и мы приходим к уравнению (проверьте!)
где ,=£_£, ,_
Сделаем, наконец, подстановку j/ = |32; это даст
O, т.е. 2* +
Выбрав P=f/<7> мы приходим к уравнению
■г8 + г*-И = 0, где г=Р9/3< (И)
Идея этих преобразований ясна: мы последовательно уменьшали
число параметров в уравнении, дойдя в итоге до уравнения A1)
с единственным параметром г, представляющим собой комбинацию
19 Я. Б. Зельдович, А. Д, Мышкио

578 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
исходных параметров. Для вычисления значения г по этим парамет-
параметрам требуются простые арифметические действия и таблица куби-
кубических корней. Таблицу значений решений уравнения A1) в зави-
зависимости от единственного параметра г уже нетрудно составить
с помощью ЭЦВМ, даже если этому параметру придать не 50, а
5000 значений. По решению z легко найти решение х:
х =f>z^-а = [B7 a3d — 9abc + 2b3)l^z—b]/3a.
Как видим, решение получится в виде двух таблиц с одним
входом каждая (таблиц кубических корней и z (г)), что, конечно,
несравненно проще, чем одна таблица с четырьмя входами.
Проблема уменьшения числа параметров может возникнуть и при
решении дифференциального уравнения, содержащего параметры.
Один из таких примеров был рассмотрен в § VIII.10, где задача о
решении уравнения (VIII.69) с начальными условиями (VIII.70), со-
содержащая пять параметров (если учесть, что само решение пред-
представляет собой функцию t, то получаем, что для представления
этого решения требуется таблица с шестью входами!), была с по-
помощью преобразований подобия сведена к задаче (VIII.71) с двумя
параметрами (VIII.72).
В качестве другого примера рассмотрим решение уравнения G)
без параметров при произвольных начальных данных
У(хо)=Уо, У' (хо)=Уо-
Здесь, по первому впечатлении^ для представления решения тре-
требуется таблица с четырьмя входами, так как параметры ха, уа, у'а
и независимое переменное х могут принимать произвольные значе-
значения. Однако число входов легко уменьшить до трех. В самом деле,
уравнение G) не содержит х, т. е. инвариантно относительно пре-
преобразования х—► лг-|~ const. Поэтому наряду с решением y = g(x)
уравнение G) при любом С имеет решение y = g(x-\-C). Но это
значит, что решение у зависит не от х и ха в отдельности, а от
комбинации х—х0:
y = ty(x—x0; y0, у'о). A2)
Таким образом, достаточно составить таблицу с тремя входами
y=ty(x; у0, у'о) для решения уравнения G) при хд = 0; после этого
при любом ха можно найти решение по формуле A2).
В последнем примере уменьшение числа входов в полной таб-
таблице решения получилось в результате указания группы преобразо-
преобразований х —*■ х + С, относительно которой рассматриваемое уравнение
остается инвариантным (о понятии группы преобразований см. в
§ XIV.4). Это означает также, что совокупность графиков всех
решений инвариантна относительно переносов вдоль оси х: каждый
такой график после переноса перейдет в график какого-либо иного
решения; интересно, что к этому выводу мы приходим на основании
анализа самого уравнения, не зная решений!

§ 5] пользуйтесь эцвм! 579
Оказывается, что знание непрерывной группы преобразований
(т. е. преобразований, зависящих от одного или нескольких непре-
непрерывных параметров), оставляющих заданное дифференциальное
уравнение инвариантным, всегда дает возможность понизить число
входов в полной таблице его решения. К сожалению, такие группы
удается обнаружить далеко не всегда, однако иногда они подска-
подсказываются физическими соображениями (как группа сдвигов во вре-
времени для автономной системы).
Не жалейте времени на уменьшение числа параметров в задаче!
Прежде всего это уменьшает объем вычислительной работы и делает
результаты вычисления более обозримыми: например, если параметр
принимает 20 значений, то избавление от него означает уменьшение
вычислительной работы и объема итоговых таблиц в 20 раз. Во-вто-
Во-вторых, получающиеся после преобразования задачи комбинации пара-
параметров часто имеют глубокий смысл, связанный с физической кар-
картиной явления.
Иногда при применении ЭЦВМ оказывается целесообразным
принципиально менять известную ранее методику решения задач.
Например, при вычислении интеграла
/=$ f(M)dQ
B)
по области (Q) высокой размерности и сложной формы оказывается
полезным не применение квадратурных формул типа формулы Симп-
сона (§ 1.1), а следущий метод, основанный на подходе к интегралу
как к среднему арифметическому значению функции. Именно, в об-
области (Q) наугад выбираются точки Mlt М2, ... , М^ (для этого
в ЭЦВМ имеются датчики случайных чисел, принимаемых за коор-
координаты этих точек), после чего полагается
При большом N—а ЭЦВМ может это обеспечить — точность этой
формулы оказывается практически приемлемой. Этот метод является
одним из простейших проявлений общего специфически машинного
метода Монте-Карло*), в котором искомая величина представляется
в виде среднего значения некоторой случайной величины (§ XIII.7),
а это среднее значение заменяется средним арифметическим реали-
реализаций этой величины при большом числе независимых испытаний.
Вопросом принципиальной важности при работе на ЭЦВМ ока-
оказывается влияние ошибок округления. Когда в длинных цепочках
вычислений последующие выкладки все время опираются на резуль-
результаты предыдущих, ошибки округления могут разрастаться до такой
*) Назван по имени города, печально знаменитого СЕоей рулеткой—уч-
рулеткой—учреждением, деятельность которого полностью основана на независимых
случайных испытаниях.
19*

580 ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
степени, что начиная с некоторого момента мы будем иметь дело с
одними лишь ошибками.
Приведем яркий пример такого эффекта, заимствованный из ин-
интересной книги И. Бабушки, Э. Витасека и М. Прагера «Численные
процессы решения дифференциальных уравнений» (русский перевод,
«Мир», М., 1969). При вычислении интеграла
1
In=j§x»e*dx (л = 0, 1, 2, ...) A3)
о
легко с помощью интегрирования по частям установить, что
/„=1-/1/,., (п=\, 2, 3, ...). A4)
Кроме того,
-ы
r = —(в—1)=1 — — = 0,632. A5)
Формулы A4) и A5) дают возможность последовательно вычислять
/, = 1 —1/0, /2=1—2/j и т.д. Приведем соответствующие резуль-
результаты l\ вычисления этих значений с тремя знаками после запятой:
П01234567 8
1\ 0,632 0,368 0,264 0,208 0,168 0,160 0,040 0,720 —4,760
Результаты становятся явно нелепыми, так как из A3) непосредст-
непосредственно видно, что /0 > 1Х > /2 >... > 0.
Причины ошибки здесь ясны: при вычислении l\ первоначальная
погрешность округления /0 множится на 1-2-3 ... п, а так как
точное значение /„ ограничено (и даже стремится к нулю при
п—*■ оо), то относительная погрешность стремительно возрастает.
Вычисления с большим числом знаков, свойственные ЭЦВМ, не-
несколько помогают, но ненадолго: так, при вычислениях с девятью
значащими цифрами результаты становятся нелепыми, начиная с
л=14. Пользой повторного счета, с другим числом десятичных
знаков, является то, что мы узнаем, насколько надежными были
наши вычисления.
В то же время вычисления нетрудно перестроить так, чтобы
погрешности не разрастались, а уменьшались. Для этого достаточно
соотношение A4), заменив п на л+1, переписать в виде
после чего вычислять /„ от ббльших п к меньшим, положив неко-
некоторое «отправное» /„ просто равным нулю. Так, положив /10 = 0, мы
получим значения
П98765432 10
/'' 0,100 0,100 0,112 0,127 0,146 0,171 0,207 0,264 0,368 0,632

ОТВЕТЫ И РЕШЕНИЯ
581
Более точные вычисления показывают, что /, = 0,092, /8 = 0,101,
тогда как все остальные цифры верные.
При вычислении интегралов и решении дифференциальных урав-
уравнений из-за влияния ошибок округления порой получается парадокс:
с целью увеличить точность результата мы измельчаем шаги, но если
применяемый метод неустойчив, то нз-за увеличения числа действий
ошибки округления начинают сказываться сильнее и итоговая по-
погрешность возрастает. Об этом необходимо помнить при работе
на ЭЦВМ.
Итак, пользуйтесь ЭЦВМ! Проводите вычисления по своим за-
задачам сами, не поручайте это другим*). Вычислитель, недостаточно
знакомый со спецификой задачи (если только он не является равно-
равноправным соавтором), будет проводить много лишней работы, не
сможет вовремя перестроиться, сойти с неправильного пути, приме-
применить физическую интуицию и грубые прикидки, что неизбежно
скажется на результате.
И наконец, помните еще одни основной тезис, подчеркиваемый
Р. Хеммннгом в его книге, указанной на стр. 577:
«Цель расчетов — понимание, а не числа».
Все результаты вычислений должны быть физически осмыслены, они
должны выявить тенденции, влияния, а венцом работы должно быть
создание ннтерполяцнонной приближенной теории с коэффициен-
коэффициентами, полученными из точных расчетов. Пусть этот идеал не
всегда достнжнм, но давайте стремиться к идеалу!
Упражнение
Укажите группу преобразований, оставляющих инвариантным уравнение
(/'"=/ (х, у"), и число входов, необходимых при составлении таблицы его
общего решения.
ОТВЕТЫ И РЕШЕНИЯ
§з
1. 10011100001111; —1/11=—0,010101...; 10,11.
2.
0
1
0
1
1
1
0
0
0
0
1
1
1
0
1
1
1
0
1
0
0
0
1
0
0
о 1 о
0
1
0
0
0
0
1
1
0
1
0
0
1
1
0
1
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
о
1
0
0
1
0
0
0
0
1
0
0
1
0
0
1
0
1
0
1
0
*) Как говорилось в популярной в свое время песке, надо
«Задачи решать самому,
И это серьезное дело
Нельзя поручать никому».
Там это было сказано по поводу любви, но не в меньшей степени это отно-
относится к вычислительной работе по реальным задачам.

582 9ЛЕКТР0ННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XV
§4
1. Здесь и далее указывается только один из возможных вариантов:
1) +
2) печ.
3) X
4) печ. ]
5) ПУ
6) ост.,
7) 1,
8) 999,
9) 0.
2. 1) +
2) V~
3) + 1
4) ПУ
5) печ. 1
6) ост.,
7) 1,
8)99,
9) 4,
10) 0.
3. 1) +
2 :
3) +
4) +
5) :
6) +
7 ПУ
8) -
9) X
10) X
11) +
12) +
135 Т
14) печ.
15) ост.,
16) 2,
17) 4,
18) 1,
19) 1,
20) 0,
21) 0,
22) 1,5,
23) 0,01,
24) 1,99,
25) 300.
Во втором
9
9,
9
ю,
8
9
7 9
)
9 10,
9 1
7
9 11,
10 11
8
ю,
18
19
20
18
19
21
24
21
21
20
22
22
22
22
1
i
9
23
18
26
23
18
26
18
26
16
17
21
20
25
1
)
9,
ю,
1,
18,
26,
20,
18,
26,
21,
1,
21,
21,
20,
22,
22,
22,
варианте
последних исходных параметра надо заменить
соответственно на 0,001, 1,999 и 3000; остальное сделает сама машина! Нетрудно
написать и Еариант программы, в котором при замене шага потребовалась бы
замена лишь одного исходного параметра.
4. 1) печ. 22,
2) печ. 23,
3) X 23 23 29,
4) — 24 29 29,
5) X 29 25 30,
6 + 23 30 30,

ОТВЕТЫ Н РЕШЕНИЯ 583
7) -1- 22 25 22,
8) X 22 22 24,
9) — 30 30 30,
10) — 24 30 30,
11) + 29 30 29,
12) X 29 26 29.
13) + 23 29 23,
14) X 22 27 29,
15) { } 29 29
16) ПУ 0 29 18,
17) ПУ 0 0 3,
18) печ. 22,
19) печ. 23,
20) ПУ 28 22 3,
21) ост.,
22) -1,
23) О,
24) 1,
25) 0,001,
26) 0,0005,
27) 10,
28) -0,1.
§5.
Двухпараметрическая группа (/->-(/+С,* + Cg. Если г = ф(д:; х0, г0) — ре-
решение уравнения г' = )'(х, г) при начальном условии г(хо) — го, то решение
заданного уравнения при начальных условиях у(хо)=уо, у'{хо) = у'о, у"(хо) = у1
имеет вид
У = Уо +Уп U—*о)+ [ ds ^ ф (а; х0, у"9) do —уа + у\ (х — х0) + у (х; х0, у),
т. е. достаточна таблица с тремя входами для ^.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно сходящийся ряд 86
Аварийный останов 567
Автономная система дифференциаль-
дифференциальных уравнений 247
Автономный процесс 247
Адамса метод 264
Адиабатический инвариант 260
Адиабатическое изменение 259
Адрес 566
Аксиальный вектор 372
Алгоритм 562
Амплитудная модуляция 555
Аналитическая функция 164
Аналоговая вычислительная машина
560
Аналоговое решение задачи 561
Антикоммутативность 350
Антисимметрический тензор 370
Античастица 185, 372
Аргумент комплексного числа 145
Арифметическое устройство 562
Архимеда закон 343
Асимптотическая формула 62
Асимптотически устойчивое по Ляпу-
Ляпунову решение 231, 249
Базис 285, 301
Безвихревое поле 382, 396
Безусловный экстремум 425
Бернулли интеграл 344
Бесконечномерное пространство 301
Бесселя формула 40
Бесциркуляционное поле 383
Бетатрон 395
Биения 229
Био—Савара закон 392
Блок-схема ЭЦВМ 562
Больцмана постоянная 54, 481
Быстроколеблющиеся функции, инте-
интегрирование 79—82, 536
Быстроменяющиеся функции, интегри-
интегрирование 69—77
Вариационное исчисление 402, 409
Вариационный принцип 438
Вариация функции 410
— функционала 411
Вектор 282
— аксиальный 372
— вихревой 377
— единичный 285, 301
— истинный 372
—, компоненты 285
—. модуль 282
—, момент 354
— обобщенный 301
— площадки 318, 342
— полярный 372
—, производная 289
— скользящий 353
— угловой скорости 353
Векторная линия 315, 332
Вскторно-векторное произведение 352
Векторное поле 306, 332
— — центральное 356
— произведение 350, 370, 372—373
— пространство 303—307
Векторно-скалярное произведение 352
Векторы линейно зависимые 284
Вероятностей интеграл 474, 510
— теория 459—509
Вероятность 459
Вес 48
Ветвления точка 171
Вещественная часть !44
Вещественное линейное пространство
302
Вихревая линия 381, 388
Вихревой вектор 377
Вихрь 377
Влияния функция 189
Внешнее ЗУ 565
Внешний интеграл 133
Внутренний интеграл 133
Возмущений метод 30
Возмущенное решение 32, 231
Волновой пакет 541

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
585
Волчек 365
Вспомогательное число 571
Вторая разделенная разность 406
— разность 37
Входные параметры 560
Вынужденные колебания 217. 224
Вычет 176
Вычислительные машины 560
Гамильтона оператор 379
Гармоническая функция 166, 340, 384
Гармонические колебания 157, 215
Гармонический анализ 520
— ряд 85
Гаусса теорема 323
Геометрическая прогрессия 83
Гиббса явление 546
Гильбертово пространство 549
Гиперболическая точка 126
Гиперплоскость 301
Гироскоп 365
Главная нормаль 293—294
Главное значение интеграла 530
Главные оси тензора 368
Градиент 308
Графический способ подбора формул
51—56
Грина функция 189
Группа преобразований 532, 579
Групповая скорость 444
Давление 342
Даламбера признак 84
Движение финитное (инфинитное) 358
Двоичная система счисления 563
Двойной интеграл 131
Действие 446
Декартова система координат 285
Декартовы коэффициенты вектора 285
Дельта-функция 185, 197
Детерминант 243
Диагональный вид тензора 368
Дивергенция 333, 335
Дидо задача 429
Диполь 197, 330
—, момент 197, 330
Дирака дельта-функция 185
Дирихле функция 552
Дискретный спектр 517
Дисперсионные соотношения Б31
Дисперсия 493
Дифференциал массы 129
— полный 101
Дифференциальное уравнение 201
— —, асимптотически устойчивое по
Ляпунову решение 231, 249
Дифференциальное уравнение, возму-
возмущенное решение 231
— — второго порядка 212, 267
линейное 205—230
— —, невозмущеиное решение 231
— — обыкновенное 201
, особая точка 237
первого порядка 201
— —, приближенное решение 250
— — Риккати 265
— — с разделяющимися переменными
204
— — с частными производными 201
, частное решение 203
, численное решение 261—268
Дифференциальных уравнений сиггема
239, 246
— замкнутая 242
Дифференцирование функций, задан-
заданных таблично 41—45
Евклидово пространство 301
Единица мнимая 144
Единичная функция 193
Единичный вектор 285. 301
— тензор 367
Зависимость корреляционная 500
Задача Дидо 429
— Коши 271
Закон Архимеда 343
— Био—Савара 392
— Кулона 320, 359
— линейности 191
— причинности 529
— сохранения четности 372
Законы Кеплера 356, 360, 361
— Кирхгофа 160
— Ньютона 315, 354, 355, 359
Замкнутая система дифференциальных
уравнений 242
Запоминающее устройство 562
Знакочередующаяся сумма 21
Знакочередующийся ряд 85
Изоклина 204
— бесконечностей 204
— пулей 204
Изолированная точка 127
Изопериметрическая задача 42Э
Изотропия 302
Импеданс 161
Инвариант адиабатическмл 260
Интеграл Бернулли 344

586
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Интеграл вероятностей 474, 510
— двойной 131
— кратный 131
— криволинейный 131
— линейный 311, 373
— несобственный 61—69
— —, главное значение 530
— — правильно сходящийся 94
равномерно сходящийся 94
, численное интегрирование 67
— объемный 129
— от функции комплексного перемен-
переменного 168—172
— ошибок 12
— первый 241
— по мере 198
— расходящийся 62, 63, 66, 95
— Римана 199
— собственный 61
— Стилтьеса 198
— сходящийся 62, 66
— тройной 131
— Фурье 228, 536
Интегралы, зависящие от параметра
93—96
Интегральная линия 202
— сумма 129
Интегральное уравнение 250
Интегральный признак Коши 84
— синус 12
Интегратор 561
Интегрирование функций, заданных
таблично 41—45
— численное 12—17
Интерполяционная задача 14
— формула Бесселя 40
— — Ньютона 39
Интерполяция 36, 54
— квадратичная 39
— линейная 38
Инфинитное движение 358
Истинны» вектор 372
Источник векторных линий 330. 332
Исходные данные 567
Исчисление вариационное 402. 409
Итераций метод 27, 251
Кавитация 346
Кажущееся сопротивление 161
Кардано формула 27
Квадратичная интерполяция 39
— форма 124
Квадратичный функционал 410
Кеплера законы 356, 360, 361
Кеплерово движение 361
Кинетическая энергия 293, 369
Кинетический момент 356
Кирхгофа законы 160
Код 566
Колебаний уравнение 212, 217. 234
Колебания вынужденные 217, 224
— гармонические 157, 215
— свободные (собственные) 163, 212—■
216
Количество векторных линий 318, 332
Команда 566
Коммутативность 350
Комплексное линейное пространство
302
— число 144
, аргумент 145
, извлечение корня 154
— —, модуль 145
— —, показательная форма 152
— — сопряженное 147
, тригонометрическая форма 145
Компонента вектора 285
Конвективная скорость 104
Конденсатор 329
Конечное уравнение 25
Концевой экстремум 436
Координаты обобщенные 138
Корень из комплексного числа 154
— кратный 156
Корреляции коэффициент 501
Корреляционная зависимость 500
Коши задача 271
— интегральный признак 84
— теорема 169
Коши—Римана условия 165
Коэффициент корреляции 501
Краевая задача 270
Краевое условие 270
Кратный интеграл 131
— корень 156
Кривизна 294
Криволинейный интеграл 131
Критерии подобия 278
Кронекера символ 366
Круговая подстановка 372, 376
Кулона закон 320, 359
Лаграпжа множитель 427
— функция 446
Лапласа оператор 339
— уравнение 166. 339, 384
Лейбница признак 85
Ленца правило 394
Линейная зависимость (независимость)
векторов 284
— интерполяция 38
— комбинация 213, 284
Линейное дифференциальное уравне-
уравнение 205—230

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
587
Линейное отображение 297
— пространство 301
вещественное 302
комплексное 302
Линейности закон 191
Линейные действия 283
Линейный интеграл 311, 373
— функционал 410
Линия векторная 315. 332
— вихревая 381, 388
—, изолированная точка 127
— интегральная 202
—, обыкновенная точка 127
— ориентированная 311
—, особая точка 127
— силовая 167, 315
— тока 316
—, точка самопересечения 126
— уровня 107, 309
— цепная 421
Логарифм комплексного числа 154
Локальная скорость изменения поля
104
— флуктуация 479
Лорана ряд 176
Магнитное поле 389
Мажорируемость 94
Максвелла уравнения 393—396
Малого параметра метод 30, 254
Массовая скорость 317, 337
Машинный нуль 576
Медленно меняющаяся величина 258
Мембрана 424, 447
Метод Адамса 264
— возмущений 30
— итераций 27, 251
— касательных 26
— малого параметра 30, 254
— Монте-Карло 579
— наименьших квадратов 47
— неопределенных коэффициентов 253
— Ньютона 26
— последовательных приближении 27
— Ритца (Ритца — Галеркина) 450
— трапеций 13
— Эйлера 261
— Эмткена 29
Минимакс 124
Мнимая единица 144
— степень 151
— часть 144
Мнимое число 148
Многозначная функция 171
Многомерное векторное пространство
300—303
Многомерное многообразие 138
— пространство 138
Многообразие 6-мерное 138
Множитель Лагранжа 427
Моделирование 279, 561
Моделирующая вычислительная маши-
машина 560
Модуль вектора 282
— комплексного числа 145
Модуляция 555
Момент вектора 354
— вращения 356
— диполя 330
— инерции 364
— кинетический 356
Монте-Карло метод 579
Набла-оператор 379
Наименьшего действия принцип 446
Наименьших квадратов метод 47
Напряженность магнитного поля 389
Начальная задача 269
Начальное условие 203, 216, 269
Неабсолютно сходящийся ряд 86
Неасимптотически устойчивое реше-
решение 231
Невозмущенное решение 31, 231
Независимые события 463
Нелинейный функционал 410
Немой индекс 296
Необратимый процесс 481
Неоднородное линейное дифференци-
дифференциальное уравнение 206, 217, 224, 273
Неодносвязная область 397
Неопределенности принцип 541
Неопределенных коэффициентов ме-
метод 253
Непрерывный спектр 517
Неразрывности уравнение 337
Несобственный интеграл 61—69
правильно сходящийся 94
равномерно сходящийся 94
, численное интегрирование 67
Неустановившееся поле 306
Неустойчивость вычислений 581
Неявная функция 109
— —, производная 113
Норма функции 548
Нормаль главная 293, 294
Нормальный закон 499
Нормировка 315
Нулевое приближение 25
Куль машинный 576
Нуль-вектор 284
Ньютона законы 315, 354, 355, 359
— метод 26
— формула 39

588
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Обильность источника 333
Область 128
—, мера 131
— неодносвязная 397
— односвязная 397
Обобщенные координаты 138
— функции 553
Обобщенный вектор 301
Образ 191, 531
Объемный интеграл 129
Обыкновенное дифференциальное урав-
уравнение 201
Огибающая 119
Однородное линейное дифференциаль-
дифференциальной уравнение 205, 212
Односвязная область 397
Оперативное ЗУ 565
Оператор 191
— Гамил-тона 379
— Лапласа 339
— Фурье 531
Определитель 243
— системы 243
Оптическая плотность 439
Ориентированная линия 311
— поверхность 317
Ортогональная система функций 649
полная 550
Особая точка дифференциального урав-
уравнения 237
линии 127
Особенности интеграла 61
Останов 567
Остроградского формула 333
Отображение линейное 297
Параболическая точка 126
Параллельность действия 565
Параметр 93, 112
Параметра малого метод 30
Параметрический резонанс 261
Параметрическое задание функции 112
Первая разность 37
Первого приближения система 248
Первое приближение 26
Первый интеграл 241
Переадресация 572
Передаточная функция 528
Передача управления 570
Переполнение ячеек 567
Перестановка круговая (циклическая)
372, 376
Пересчет 263
Переходный период 223
Перфокарта 564
Перфолента 564
Перфоратор 564
Плавающая запятая 564
Планка постоянная 260, 448, 481
Плоское поле 307
Плоскопараллельное поле 307
Плоскость соприкасающаяся 294
Плотность спектральная 517, 525
Поверхность ориентированная 317
— уровня 309
Пограничный слой 275
Подобие явлений 276
Поле 306
— безвихревое 382, 396
— бесциркуляционное 383
— векторное 306, 332
— магнитное 389
— нестационарное (неустановившееся)
306
— плоское 307
— плоскопараллельное 307
— потенциальное 382
— силовое 311
— скалярное 306
— скорости 316, 336, 386
— соленоидальное 391
— стационарное (установившееся) 104,
306
— электрическое 320, 339
— электромагнитное 392
— электростатическое 320
Полная ортогональная система функ-
функций 550
— производная 103
— энергия 314, 357
Полный дифференциал 101
«Полуцелые» значения аргумента 37
Полюс 175
Полярный вектор 372
Последовательных приближений ме-
метод 27
Постоянная Больцмана 54, 481
— Планка 260, 448, 481
— Эйлера 90
Поступательный перенос 283
Потенциал 315, 321, 382, 396
— центробежный 358
— эффективный 359
Потенциальная энергия 313
Потенциальное поле 382
Поток вектора 317, 332
Правило Ленца 394
— параллелограмма 283
— правого винта 349
Правильно сходящийся несобственный
интеграл 94
Правый пинт 349
Преобразование команды 571
— Фурье 523

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
589
Прецессионное движение 365
Приближение нулевое 25
— первое 26
Приближенные методы решения диф-
дифференциальных уравнений 250—258
Признак Даламбера 84
— Лейбница 85
Признаки сходимости рядов 83—85
Принцип вариационный 438
— наименьшего действия 446
— неопределенности 541
— сохранения четности 372
— суперпозиции 191
— Ферма 439
Причинности закон 528
Программа 567
Программирование 568
Прогрессия геометрическая 83
Проекция вектора 285
Произведение векторно-векторное 352
— векторное 350, 370, 372, 373
— векторно-скалярное 352
— скалярное 287, 548
— смешанное 352
— тензорное 298
Производная вектора 289
— неявной функции 113
— полная 103
— функции, заданной параметрически
112
— частная 101
второго порядка 104
— — смешанная 105
Прообраз 191, 531
Пространство бесконечномерное 301
— векторное 300—303
— вещественное 302
— Гильберта 549
— евклидово 301
— ^-мерное 138
— комплексное 302
— линейное 301
— —, размерность 302
— псевдоевклидово 302
Процесс автономный 247
— сходящийся 28
Прямые методы вариационного исчи-
исчисления 449
Псевдовектор 372
Псевдоевклидово пространство 302
Псевдоскаляр 373
Пуассона распределение 485, 487
— уравнение 339
Рабочая ячейка 568
Равномерно сходящийся несобствен-
несобственный интеграл 94
Радиоактивный распад 483
Радиолампа 116—118
—, внутреннее сопротивление 116
—, коэффициент усиления 117
—, крутизна характеристики 116
Разветвление программы 572
Разложение вектора 284
Размерность пространства 301
Разность вторая 37
разделенная 406
— первая 37
— первого порядка 37
— центральная 37
Разрез 172
Разрыв 1-го рода 536
Разряд 564
Ранг тензора 298
Распределение вероятностей нормаль-
нормальное 499
— простых чисел 505
— Пуассона 485, 487
Расходимость (дивергенция) 333
Расходящийся интеграл 62, 63, 66, 95
— процесс 29
— ряд 83
Резонанс 230
— параметрический 261
Решение асимптотически устойчивое
231, 249
— неасимптотическй устойчивое 231
— невозмущенное 31, 231
Риккати уравнение 265
Римана интеграл 199
Ритца (Ритца — Галеркина) метод 450
Ротор 377, 387
Ряд абсолютно сходящийся 86
— гармонический 85
— знакочередующийся 85
— Лорана 176
— неабсолютно сходящийся 86
— расходящийся 83
— сходящийся 83
— Тейлора 120
— Фурье 544
— числовой 82
Свободные колебания 163, 212, 234
Связи уравнение 426
Сдвиговое течение 387
Седло (особая точка) 238
Седловина 124
Сила тока комплексная 158
Силовая линия 167, 315
Силовое поле 311
Символ Кронекера 366
Симметрический тензор 368

590
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Снмпсопа формула 15
Синус интегральный 12
Система автономная 247
— дифференциальных уравнений 239,
246
— — — замкнутая 242
— укороченная (первого приближе-
приближения) 248
Скаляр 282
Скалярное поле 306
— —, градиент 308
— —, линии уровня 309
— —, поверхности уровня 309
— произведение 287, 548
Скользящий вектор 353
Скорость изменения поля 104
— — — конвективная (переносная)
104
местная (локальная) 104
След тензора 371
Сложение векторов 283
Слой пограничный 275
Случайная величина 478, 492
Случайные числа 579
Смешанное произведение 352
Собственные колебания 163, 212
Собственный интеграл 61
События независимые 463
Соленоидальное поле 391
Соприкасающаяся плоскость 294
Сопротивление кажущееся 161
Сопряженные гармонические функции
166
— комплексные числа 147
Составляющая вектора 285
Спектр дискретный 517
— задачи 272
— непрерывный 517
— функции 517
Спектральная плотность 525
Спектральный анализ 520, 544—547
Специализированная ЭЦВМ 563
Среднее значение функции 130
— квадратичное уклонение 495
Стандартная подпрограмма 572
Статистический массив 478
Стационарное значение 403
— поле 104, 306
Степени свободы 138
Степень мнимая 151
Стилтьеса интеграл 198
Стирлинга форм\ла 78
Сток 333
Стокса формула 378
Структурная схема ЭЦВМ 562
Струна 405
Сумма знакочередующаяся 21
Сумма интегральная 129
— частная 82
Суперпозиции принцип 191
Схема с пересчетом 263
Сходящийся интеграл 62, 66
— процесс 28
— ряд 83
Тангенциальная составляющая 294
Тейлора ряд 323
Температура 482
Тензор 298
— антисимметрический 370
—, диагональный вид 368
— единичный 367
— инерции 366
— симметрический 368
— упругих напряжений 369
Тензорное произведение 298
Теорема Гаусса 323
— Коши 169
Теория вероятностей 459—509
Теплосодержание 40
Ток смещения 393
Тока линия 316
— трубка 345
Точка ветвления 171
— воздействия 189
— линии изолированная 127
— — обыкновенная 127
особая 127
— наблюдения 189
— особая дифференциального уравне-
уравнения 237
— поверхности гиперболическая 126
— — параболическая 126
эллиптическая 126
— самопересечения линии 126
Транслятор 572
Трапеций способ 13
Трехадресная команда 566
Тригонометрическая форма комплекс-
комплексного числа 145
Тройной интеграл 131
Трубка тока 345
Узел (особая точка) 238
Умножение вектора на скаляр 284
Умножения вероятностей правило 462
Универсальная ЭЦВМ 562
Универсальный машинный язык 572
Уравнение дифференциальное 201
— интегральное 250
— колебаний 212, 217, 234
— конечное 25
— Лапласа 166, 339, 384

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
591
Уравнение неразрывности 337
— Пуассона 339
— Риккати 265
— с частными производными 201
— связи 426
— характеристическое 213, 246
— Эйлера 416, 424
Уравнения Максвелла 393—396
Уровня линия 107, 309
— поверхность 309
Условие краевое 270
— начальное 203, 216, 269
Условия Коши — Римана 165
Условный экстремум 425, 428
Установившееся поле 306
Устойчивое асимптотически решение
231, 249
— неасимптотически решение 231
Устойчивость 247, 272
— по Ляпунову 248
— — — асимптотическая 231, 249
Устройство управления 562
Фазовая диаграмма 160
— скорость 443
Ферма принцип 439
Финитное движение 358
Флуктуация локальная 479
Фокус 239
Форма квадратичная 124
Формула Бесселя 40
— Кардано 27
— Ньютона 39
— Остроградского 333
— Симпсона 15
— Стирлинга 78
— Стокса 378
— Эйлера 151
Функции ортогональные 549
Функционал 409
—, вариация 411
— линейный 410
— нелинейный (квадратичный) 410
—, экстремум 411
Функция аналитическая 164
— влияния (Грина) 189
— гармоническая 166, 340, 384
— Грина 189
— Дирихле 552
— единичная 193
— Лаграижа 446
— многозначная 171
— неявная 109
— —, производная 113
—, параметрическое задание 112
— распределения вероятностей 461,
488
Функция совместного распределения
—, среднее значение 130
— точки 306
—, экстремум 122
Функция-образ 191
Функция-прообраз 191
Фурье интеграл 228, 536
— оператор 531
— преобразование 523
— ряд 544
Характеристическое уравнение 213,
246
Характерное время 276
«Целые» значения аргумента 36
Центр масс 355
— (особая точка) 238
Центральная разность 37
Центральное векторное поле 356
Центрально-симметричное поле 310,
319, 334, 340
Центробежный потенциал 358
Цепная линия 421
Цикл 570
Циклическая перестановка 372, 376
Циклоида 418
Циркуляция 312, 313, 374
Цифровая вычислительная машина 560
Частная производная 101
— — второго порядка 104
смешанная 105
— сумма 82
Частное решение 203
Частотная модуляция 555
Численное интегрирование 12—17
— — быстроменяющихся функций
69-77
— — несобственных интегралов 67
— решение дифференциальных урав-
уравнений 261—268
конечных уравнений 25—33
Число комплексное 144
— степеней свободы 138
Числовой ряд 82
Чисто мнимое число 148
Шаг таС-лицы 37
Эйлера метод 261
■— постоянная 90

592
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Эйлера уравнение 416, 424
— формула 151
Зйткена метод 29
Экстраполяция 36, 54
Экстремум концевой 436
— с ограничениями 436—438
— условный 425, 428
— функции 122
— функционала 411
Электрическое поле 320, 339
Электромагнитное поле 392
Электростатическое поле 320
Элемент ЗУ 565
— массы 129
Элемент объема 129
Эллиптическая точка 126
Эмпирическая формула 46
Энергия кинетическая 293, 369
— полная 314, 357
— потенциальная 313
Энтальпия 40
Энтропия 479
Эффективный потенциал 359
ЭЦВМ 559
Явление Гиббса 546
Ячейка 562