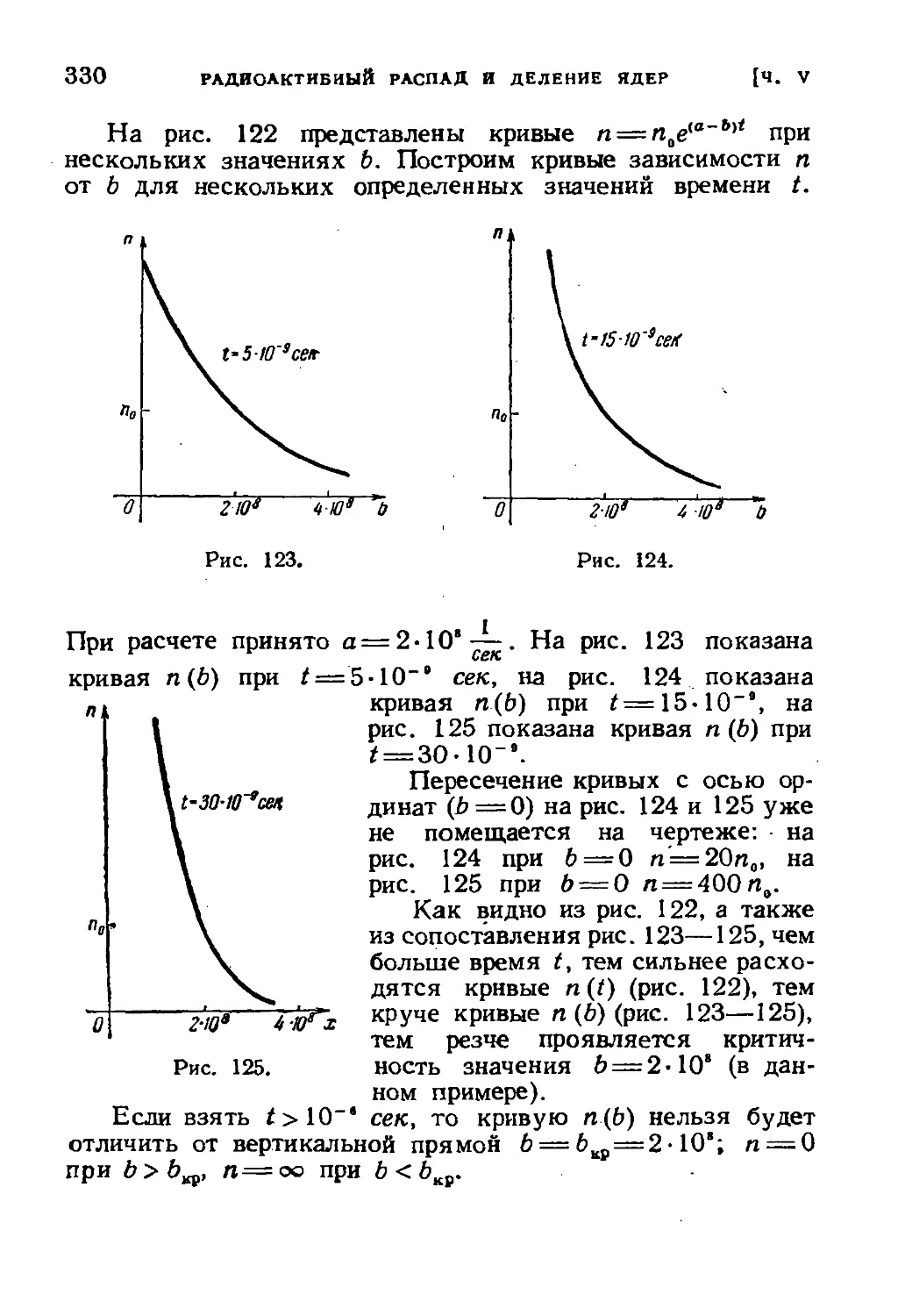
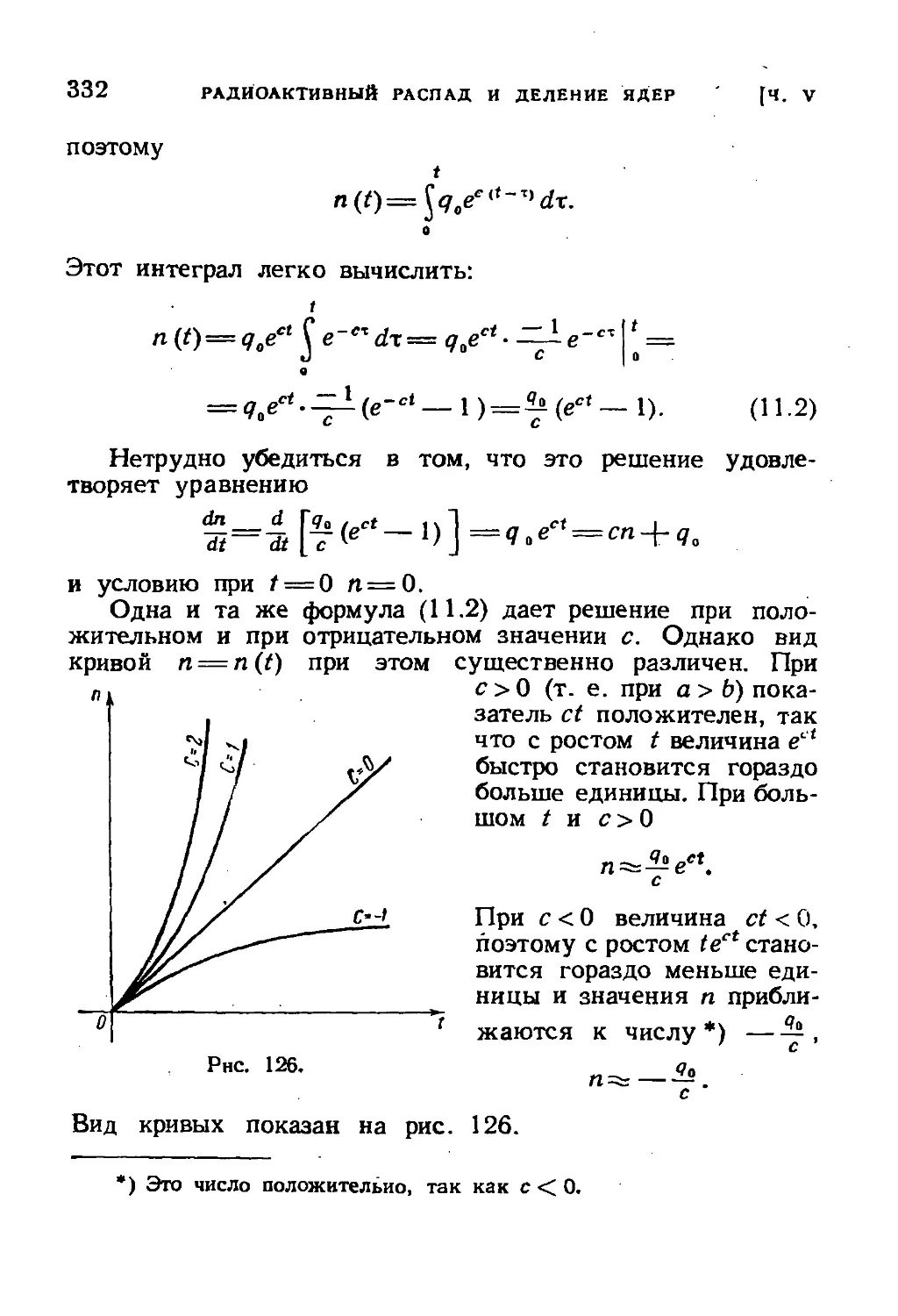
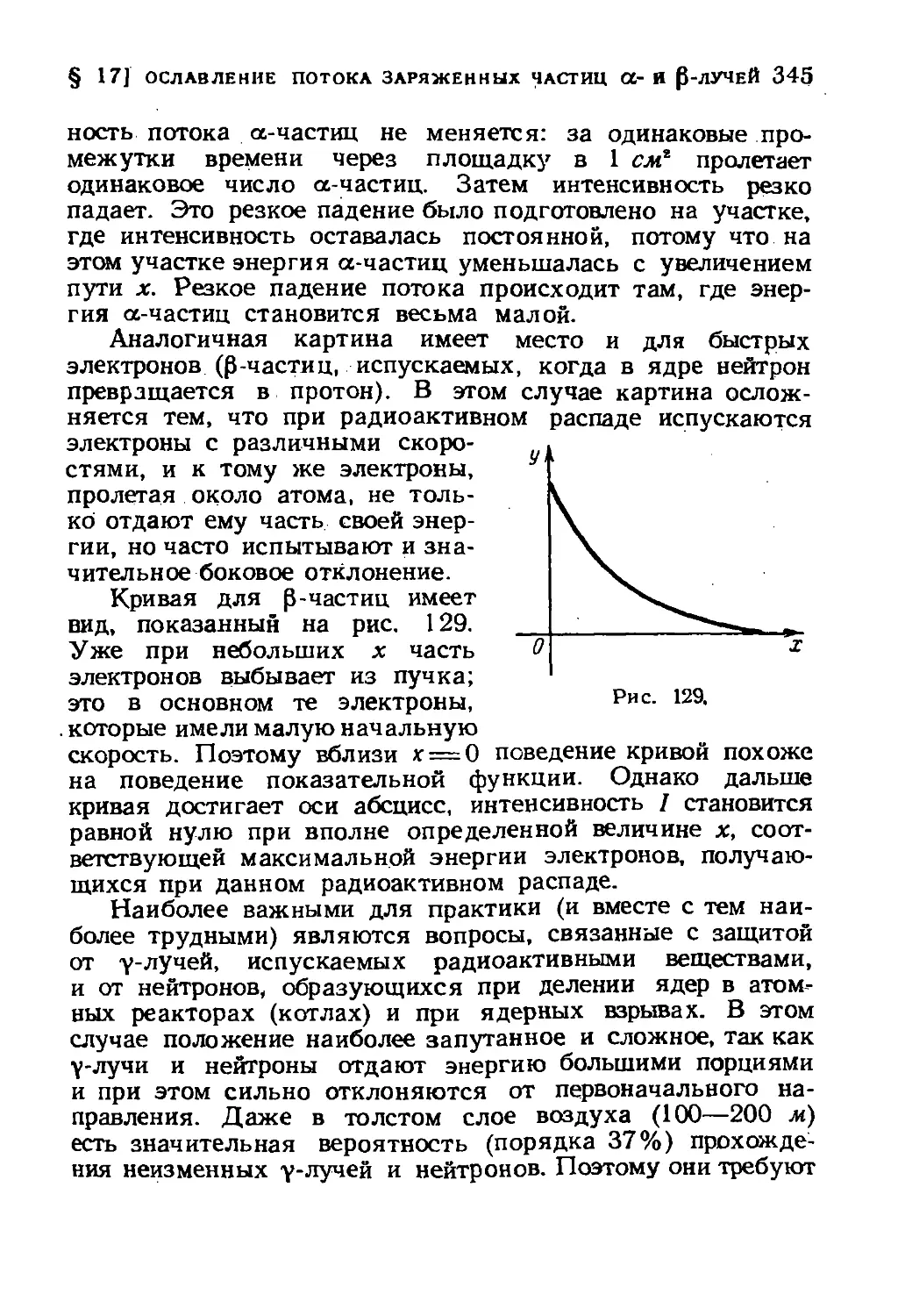
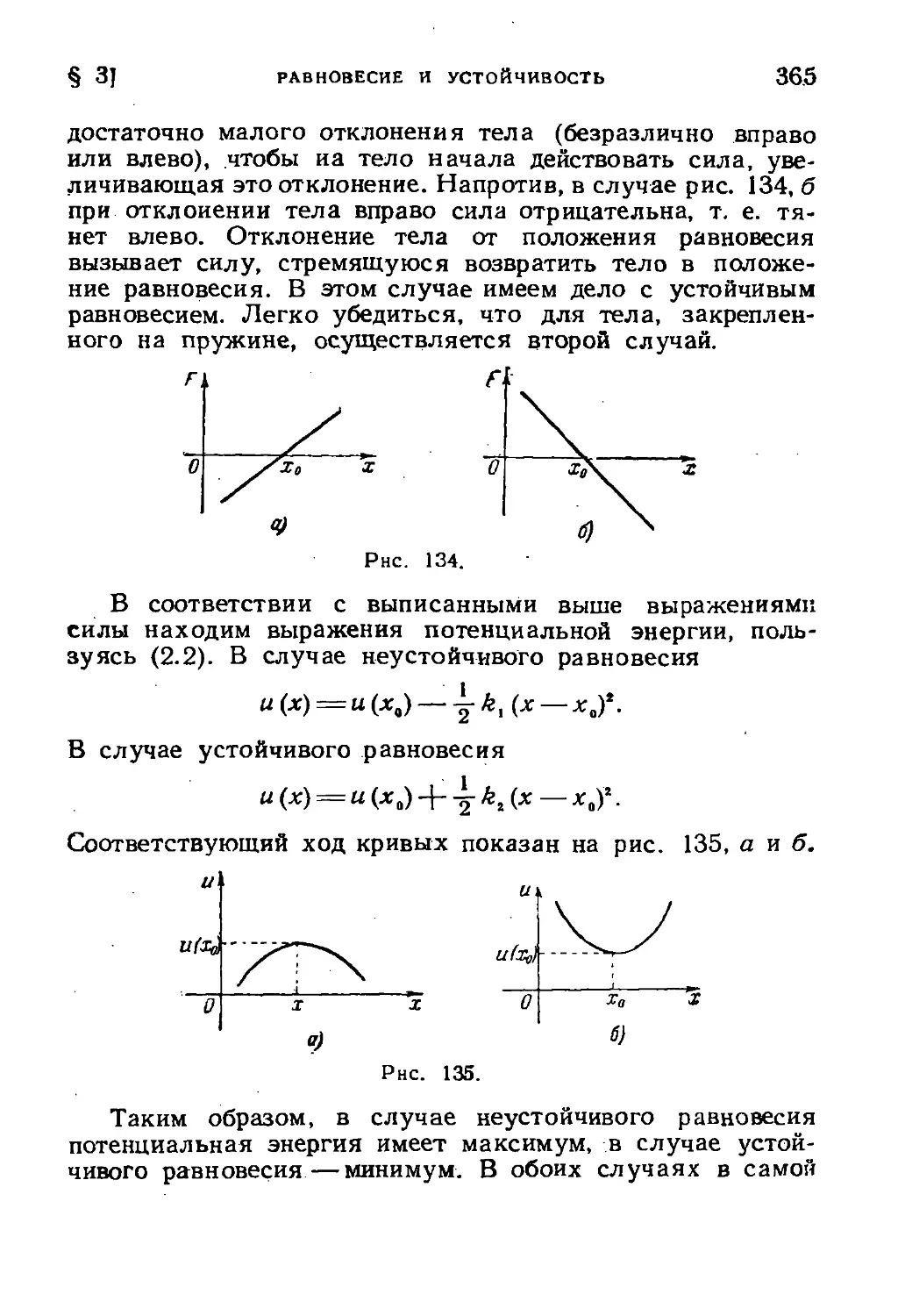
Author: Зельдович Я.Б.
Tags: физика математика математическая физика высшая математика прикладная математика интегральные исчисления
Year: 1963
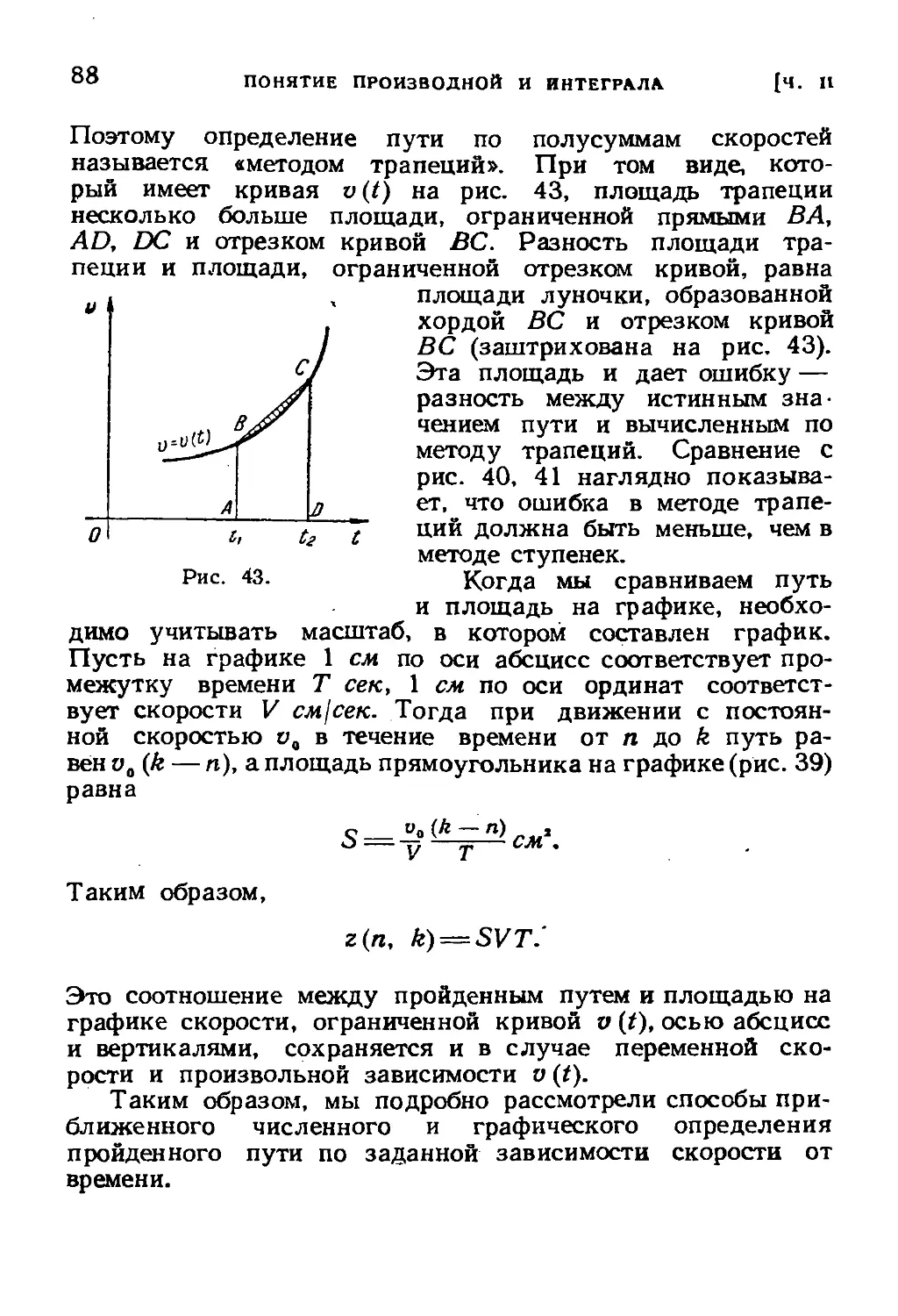
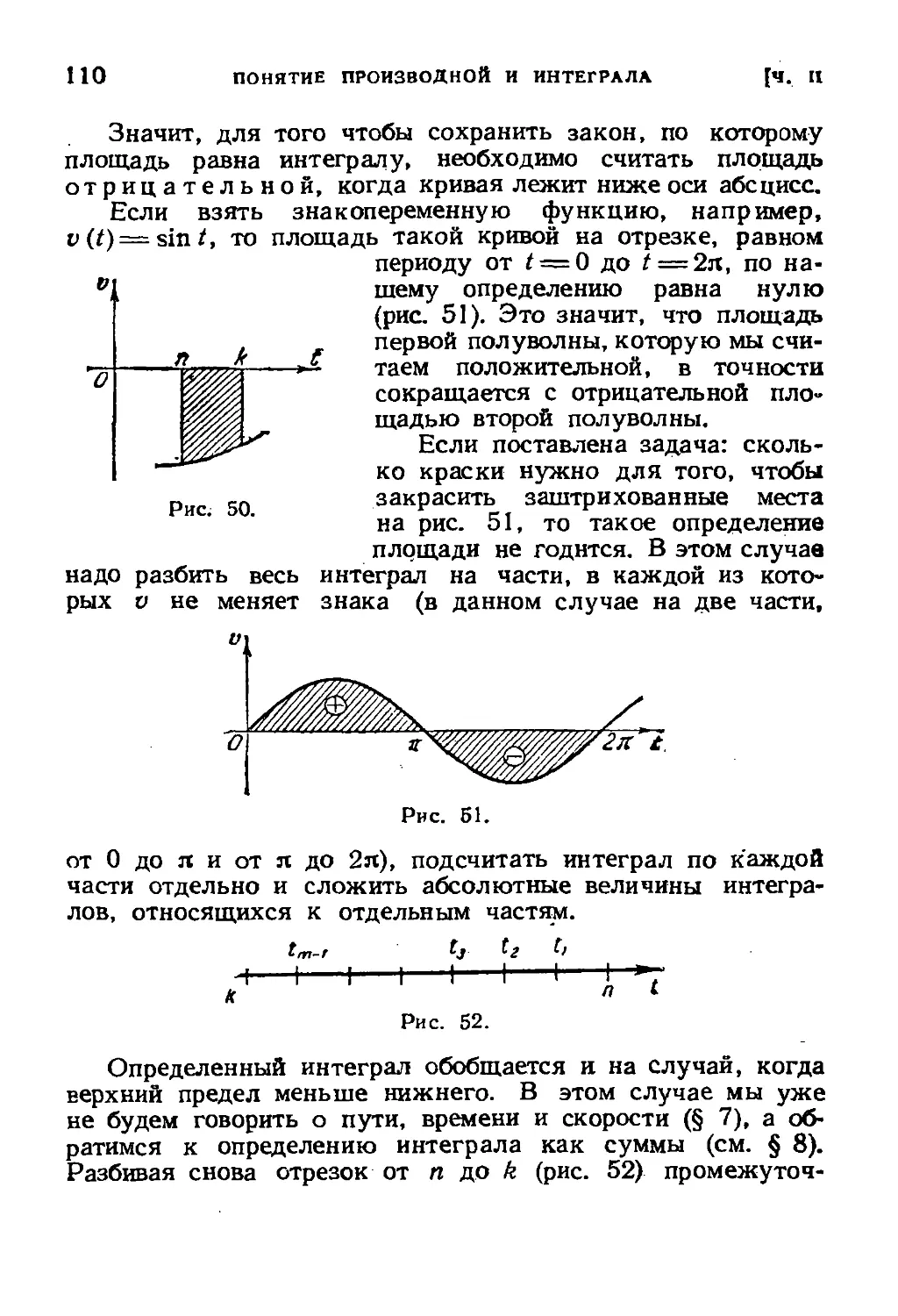
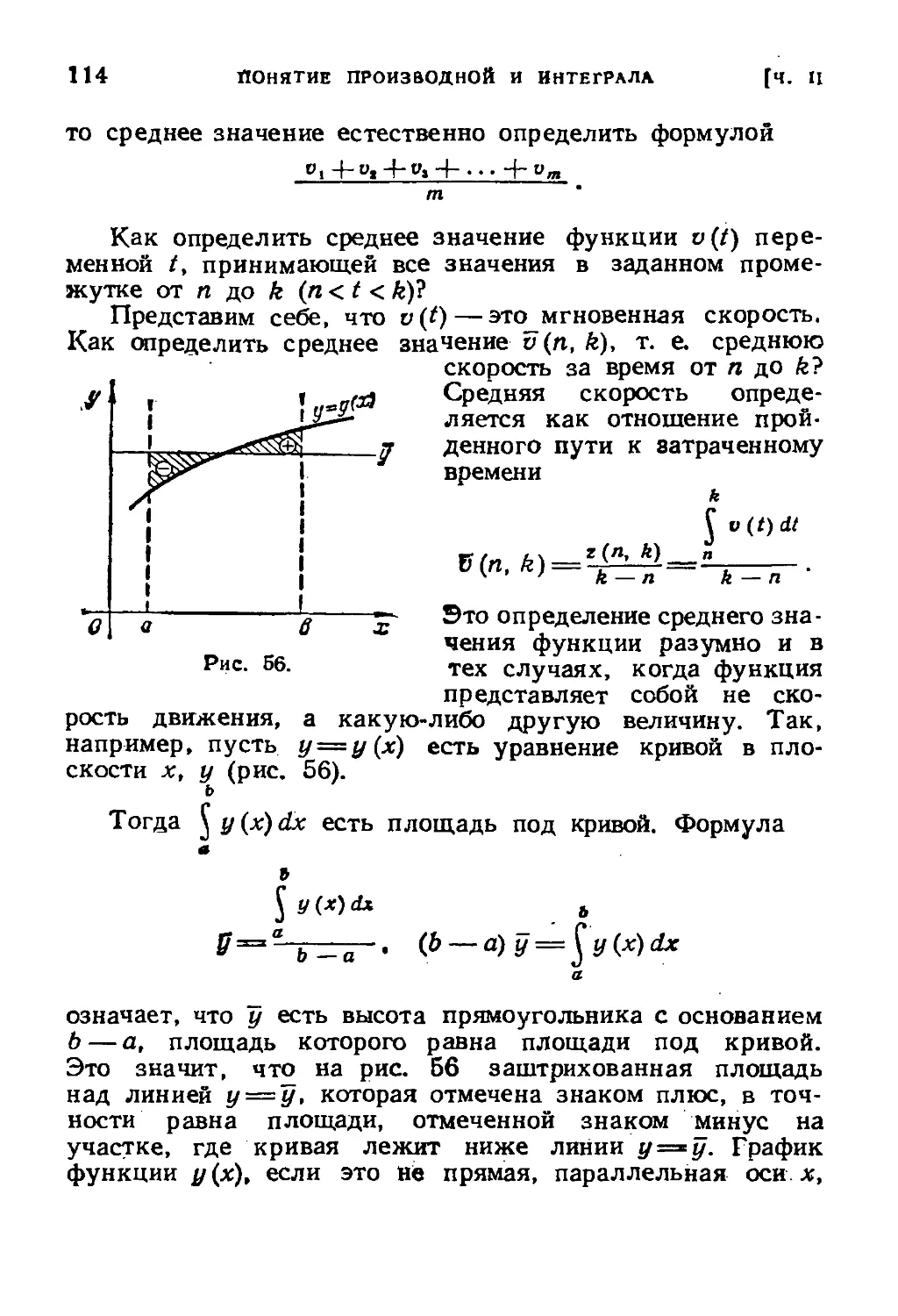
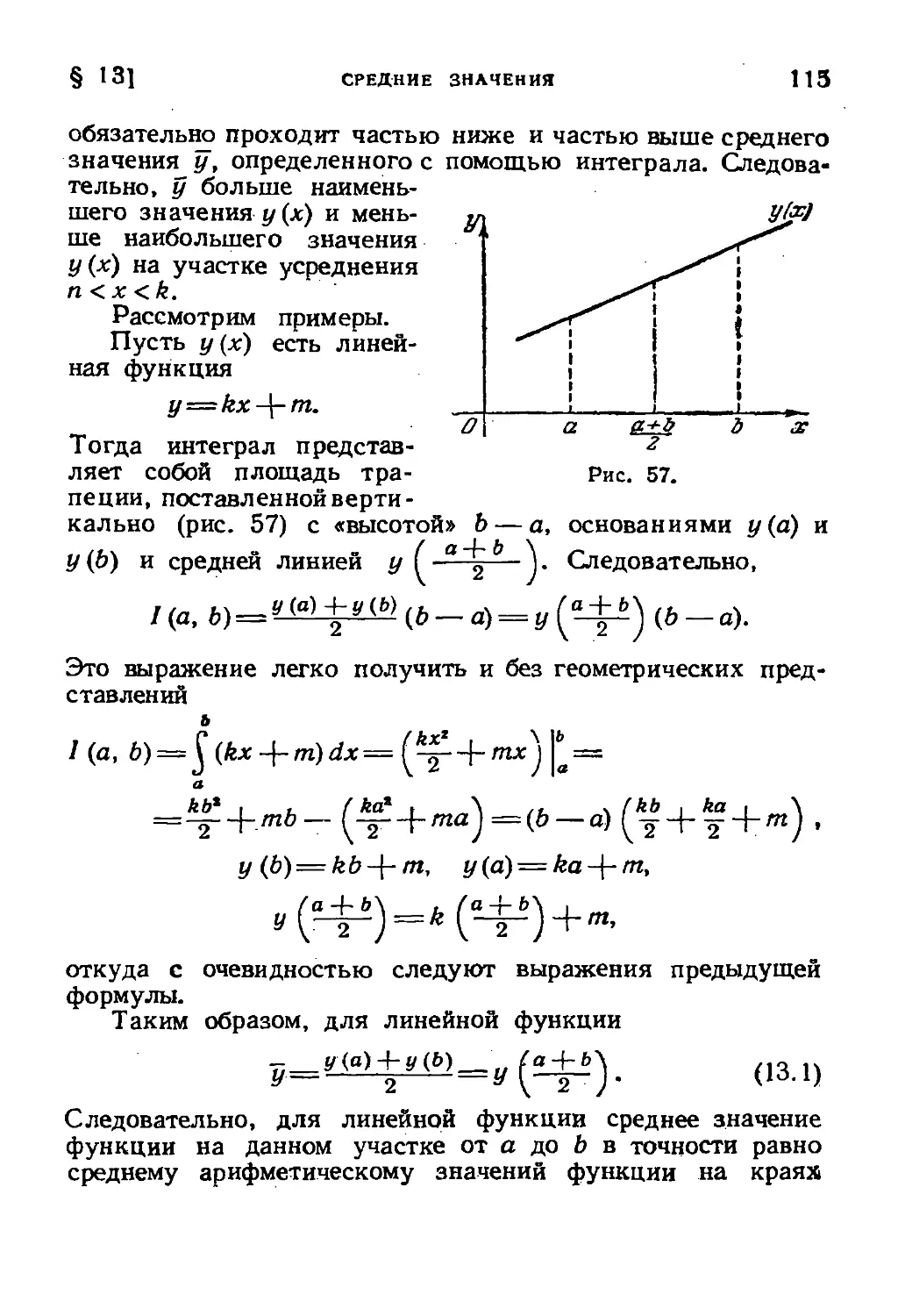
Text
Я. Б. ЗЕЛЬДОВИЧ
ВЫСШАЯ
МАТЕМАТИКА
для
НАЧИНАЮЩИХ
И ЕЕ ПРИЛОЖЕНИЯ
К ФИЗИКЕ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1963
517
3 50
ПРИ РЕДАКЦИОННОМ УЧАСТИИ
К. А. СЕМЕНДЯЕВА
АННОТАЦИЯ
Книга «Высшая математика для начинающих и
ее приложения к физике», написанная физиком-тео-
ретиком академиком Я. Б. Зельдовичем, рассчита-
на на школьников старших классов, учащихся тех-
никумов и лиц, занимающихся самообразованием,
она может быть полезна и студентам 1-го курса
вузов и втузов.
В книге в наиболее простой, наглядной и до-
ступной форме объясняются основные понятия диф-
ференциального и интегрального исчисления. Да-
лее даются сведения, необходимые для практиче-
ского применения высшей математики к задачам
физики и техники. На основе высшей математики
рассмотрено большое число физических вопросов:
радиоактивный распад, ядерная цепная реакция,
законы механики, в частности, реактивное движе-
ние и космическая скорость, молекулярное движе-
ние. Рассмотрены электрические явления и, в част-
ности, теория колебаний, лежащая в основе радио-
техники. Наряду с математическим исследованием
очень подробно изложена физическая сущность
рассматриваемых явлений.
Зельдович Яков Борисович.
Высшая математика для начинающих
и ее приложении к физике.
М.. Физматгнз. 1963 г., 560.стр. с илл.
Редактор С. Б. Норкин.
Техн. редактор А. П. Колесникова. Корректор В. В. Кузнецова.
Сдано в набор 5/IX 1962 г. Подписано к печати 13/XII 1962 г. Бумага
84X108/32. Фнз. печ. л. 17,5. Условн. печ. л. 28,7. Уч-изд. л. 28.42.
Тираж 150 000 экз. T-I506I. Цена книги 95 коп. Заказ № 3344.
Государственное издательство физико-математической литературы.
Москва, B-7I, Ленинский проспект. 15. '
Первая Образцовая типография имени А. А. Жданова Московского совнархоза.
Москва, Ж-54, Балован, 28.
СОДЕ РЖАНИЕ
Предисловие 7
Часть I. Функции и графики 11
§ 1. Функциональная зависимость 11
§ 2. Координаты 14
§ 3. Геометрические величины, выраженные через коорди-
наты 17
§ 4. Графическое изображение функций. Уравнение прямой 22
§ 5. Парабола 27
§ 6. Кубическая парабола, гипербола, круг 35
§ 7. Изменение масштабов кривой 38
§ 8. Параметрическое задание кривой 46
Заключение 48
Ответы и решения 49
Часть II. Понятие производной и интеграла 50
§ 1. Движение, путь и скорость 50
§ 2. Производная функции—предел отношения приращений 57
§ 3. Обозначения производной. Производная степенной
функции 60
§ 4. Приближенное вычисление функции с помощью произ-
водной 66
§ 5. Касательная к кривой 69
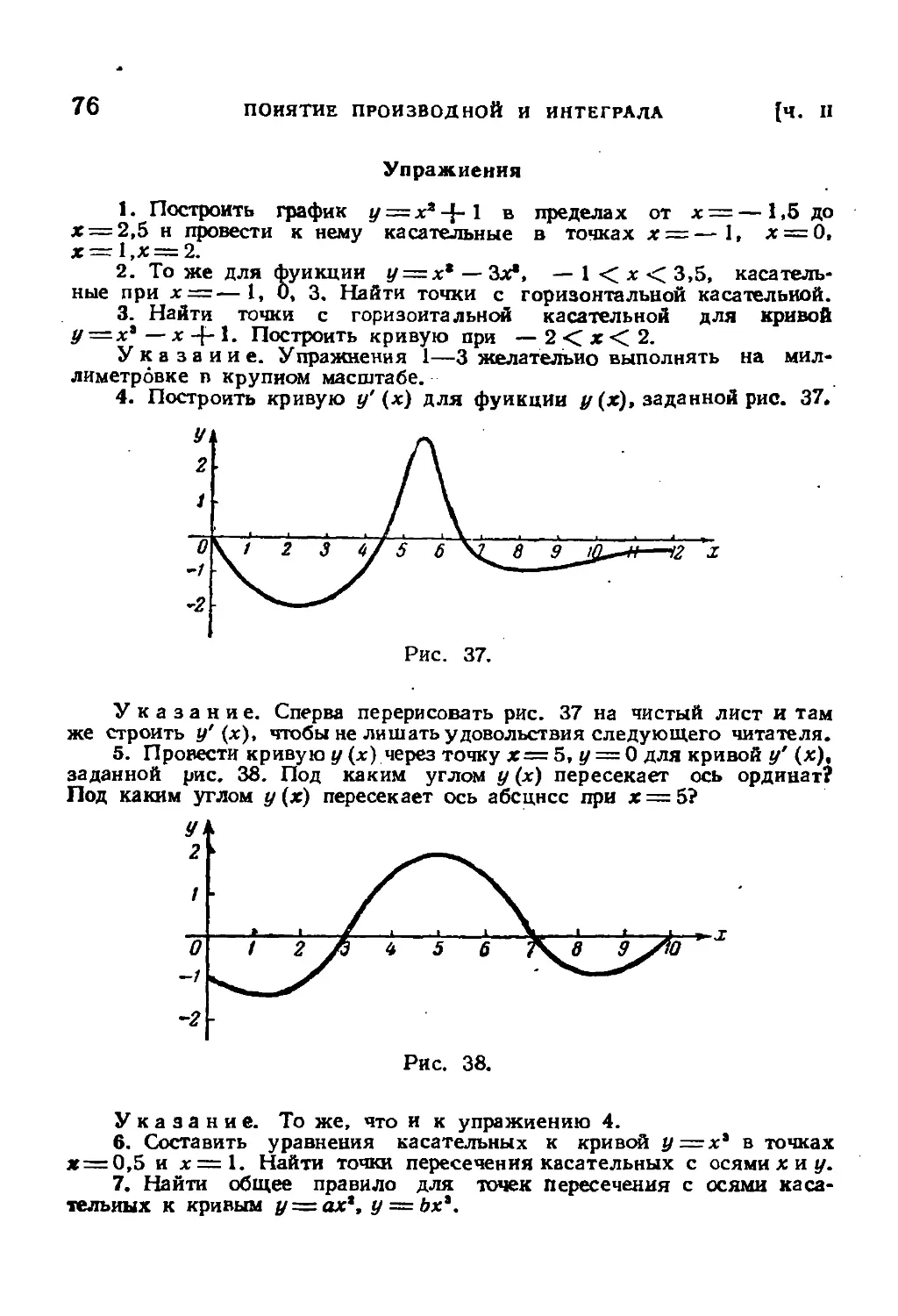
§ 6. Рост и убывание, максимум и минимум функций ... 77
§ 7. Определение пути по скорости движения и площадь
под кривой 82
§ 8. Определенный интеграл 89
§ 9. Связь между интегралом и производной 96
§ 10. Интеграл от производной 98
§ 11. Неопределенный интеграл 100
§ 12. Свойства интегралов 108
§ 13. Средние значения 113
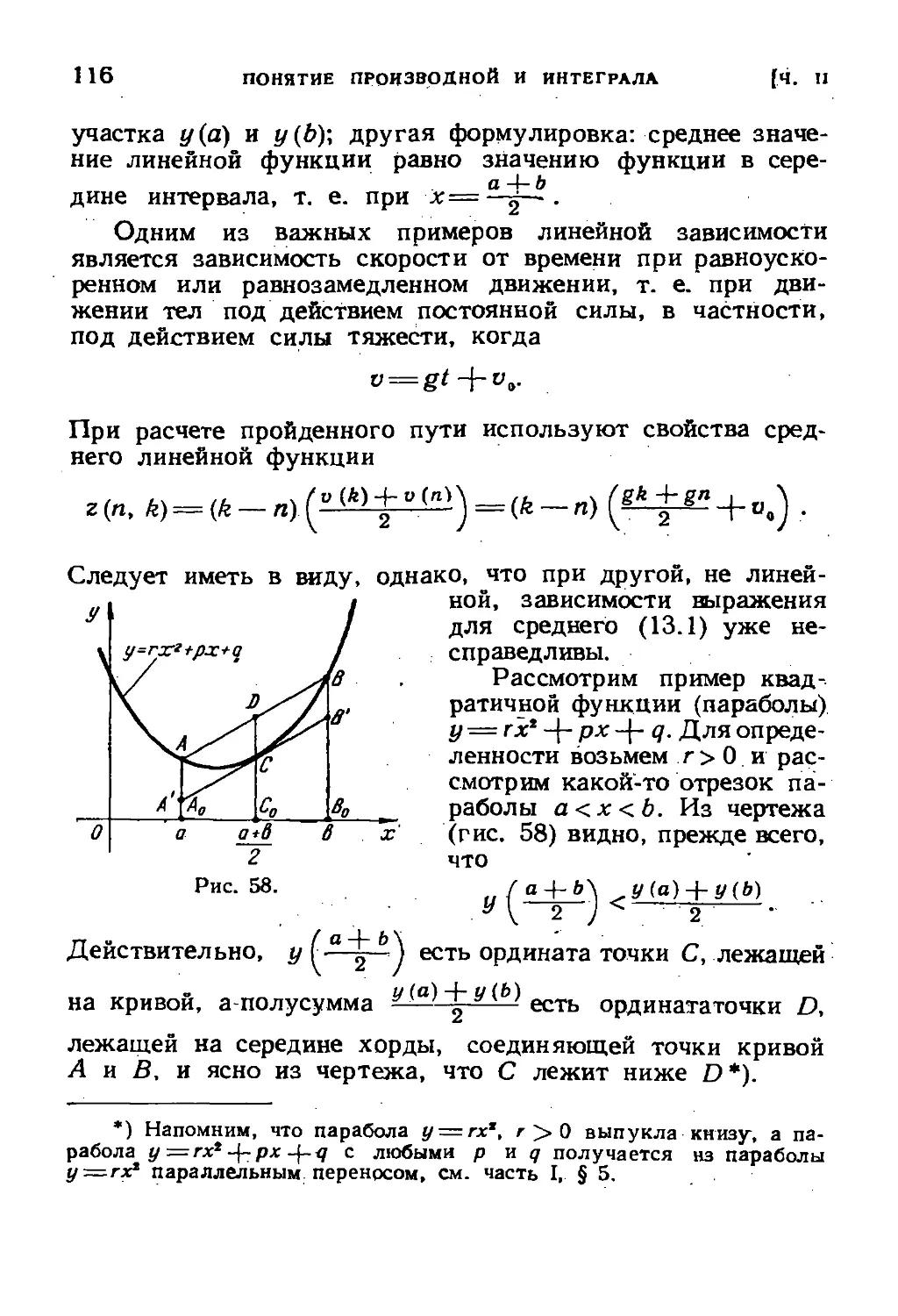
§ 14. Различные примеры производных и интегралов . . .118
Заключение 126
Ответы и решения 126
Часть III. Вычисление производных и интегралов 130
§ 1. Знак дифференциала. Производная суммы функций . 130
§ 2. Производная обратной функции 132
*
4 СОДЕРЖАНИЕ
§ 3. Сложная функция 134
§ 4. Производная произведения функций 137
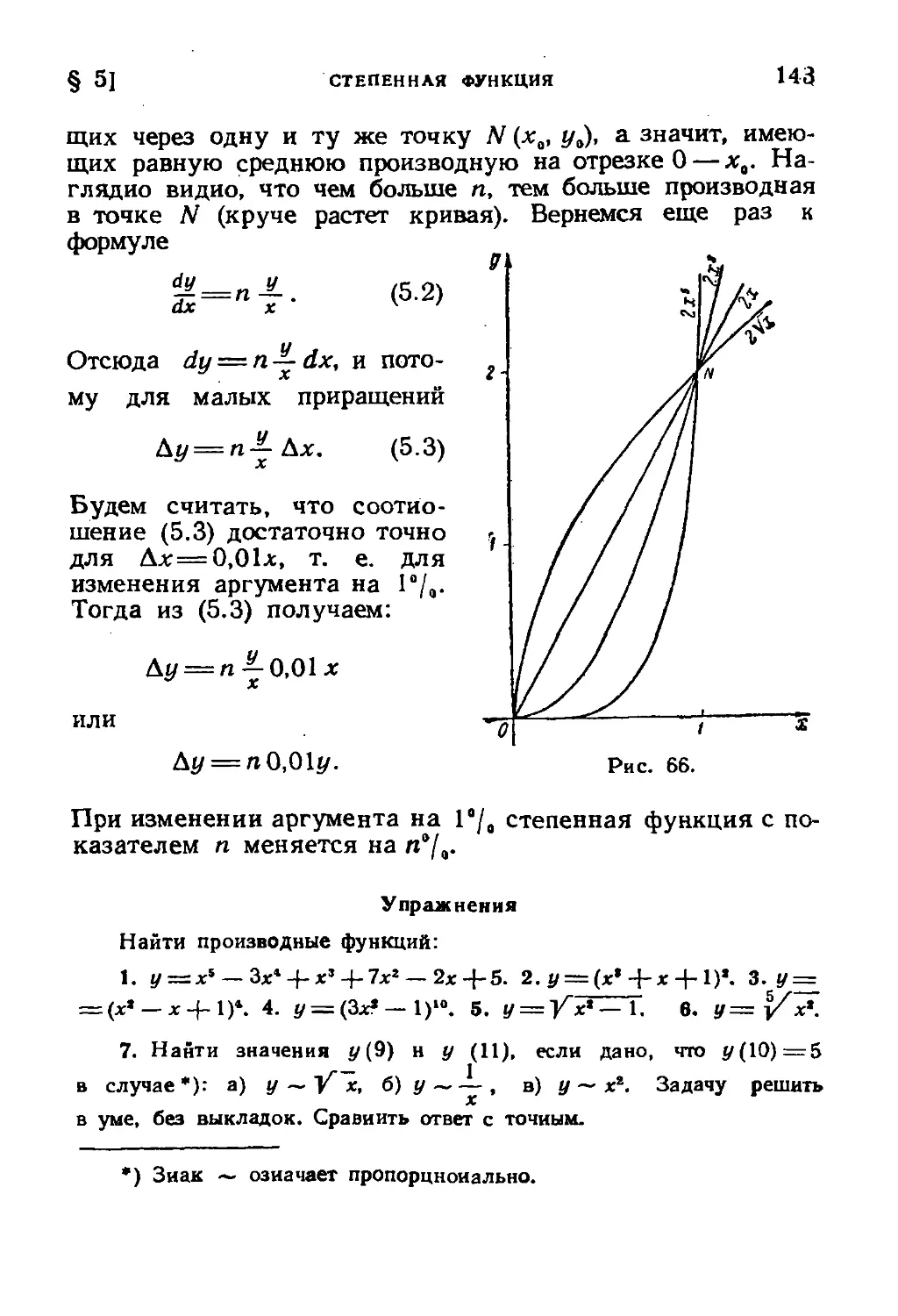
§ 5. Степенная функция 140
§ 6. Производные алгебраических функций с постоянными
показателями 144
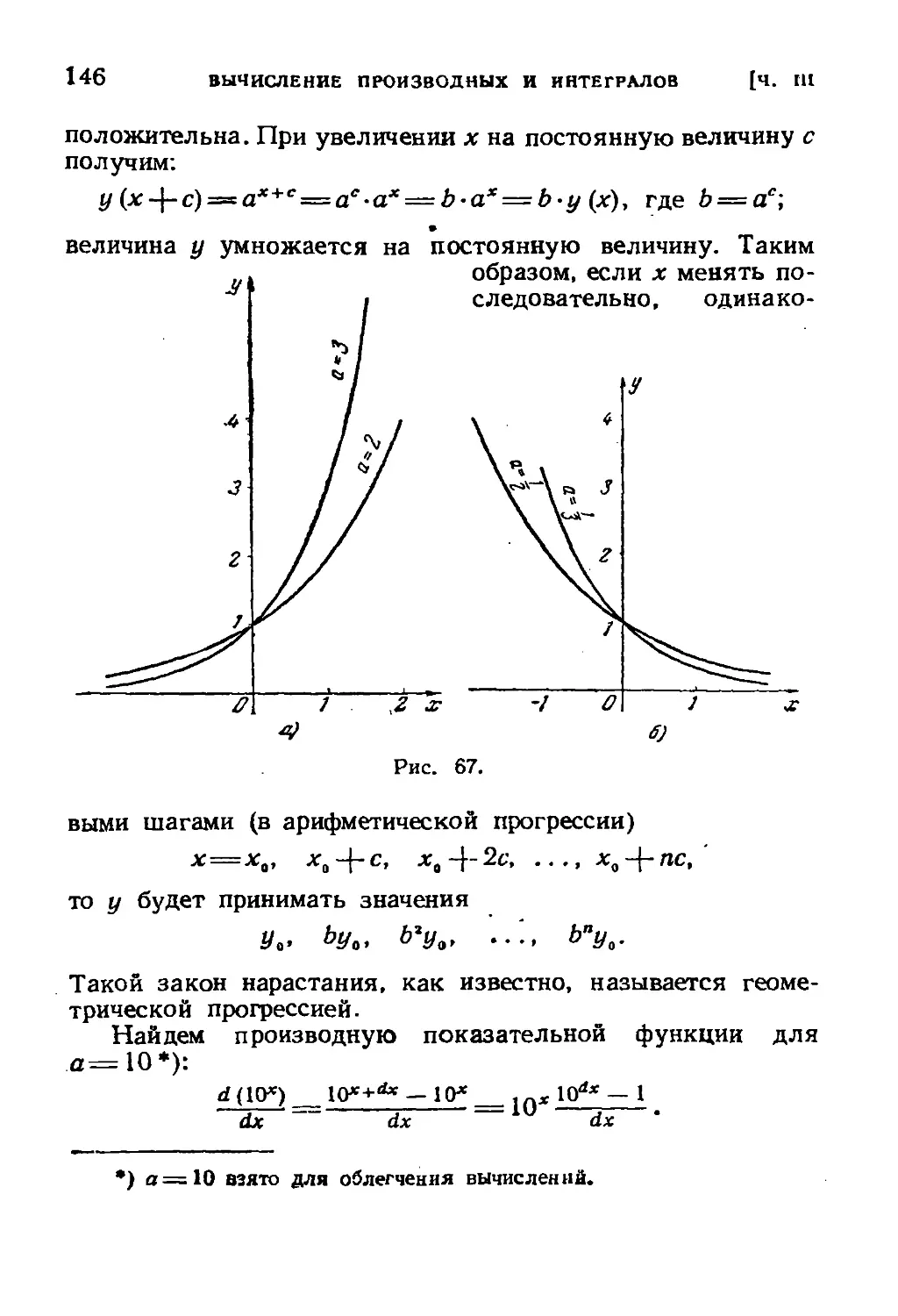
§ 7. Показательная функция 143
§ 8. Число е 148
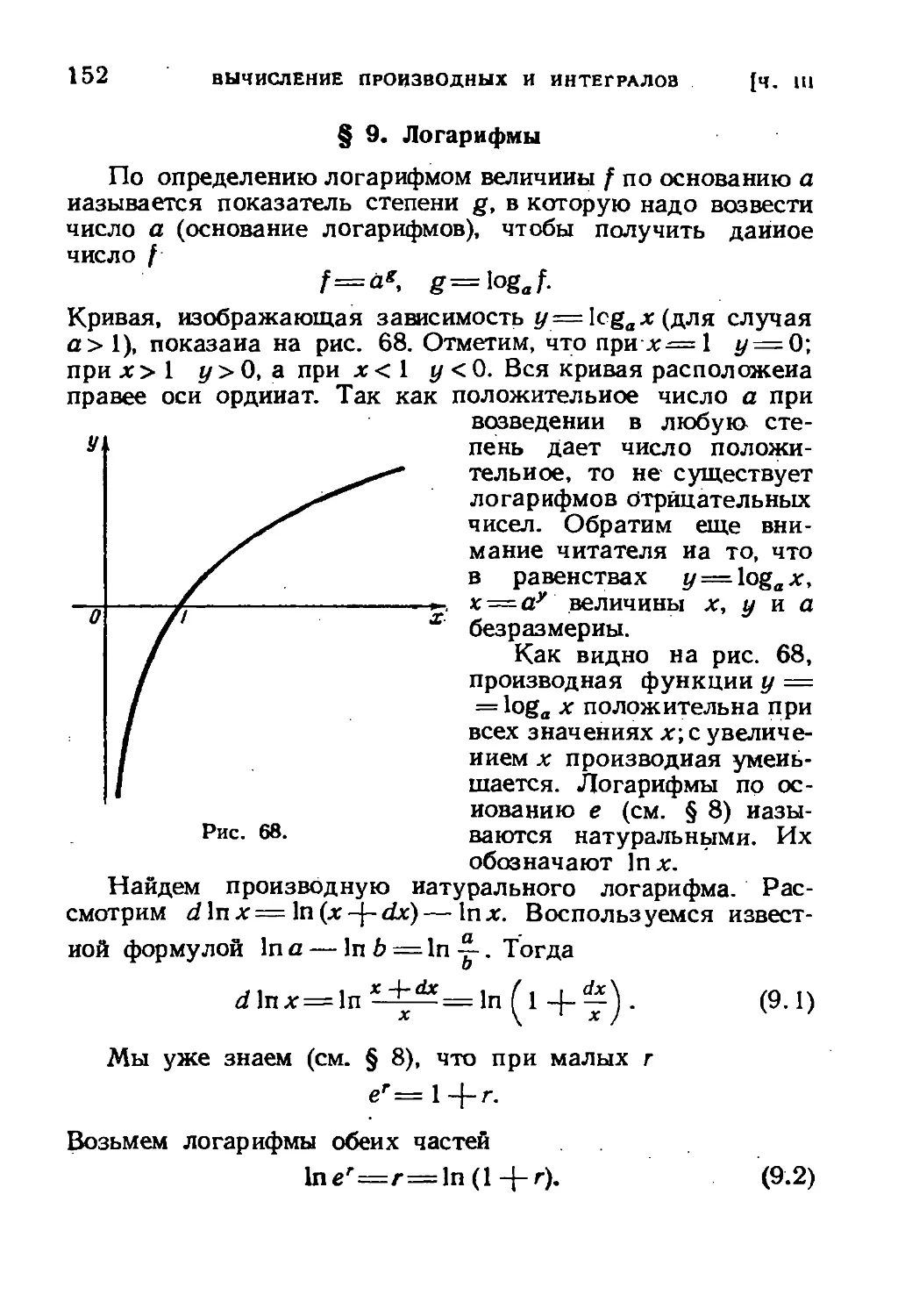
§ 9. Логарифмы ... 152
§ 10. Тригонометрические функции 155
§ 11. Обратные тригонометрические функции 160
§ 12. Производная функции, заданной неявно 163
§ 13. Интеграл. Постановка задачи 166
§ 14. Простейшие интегралы 168
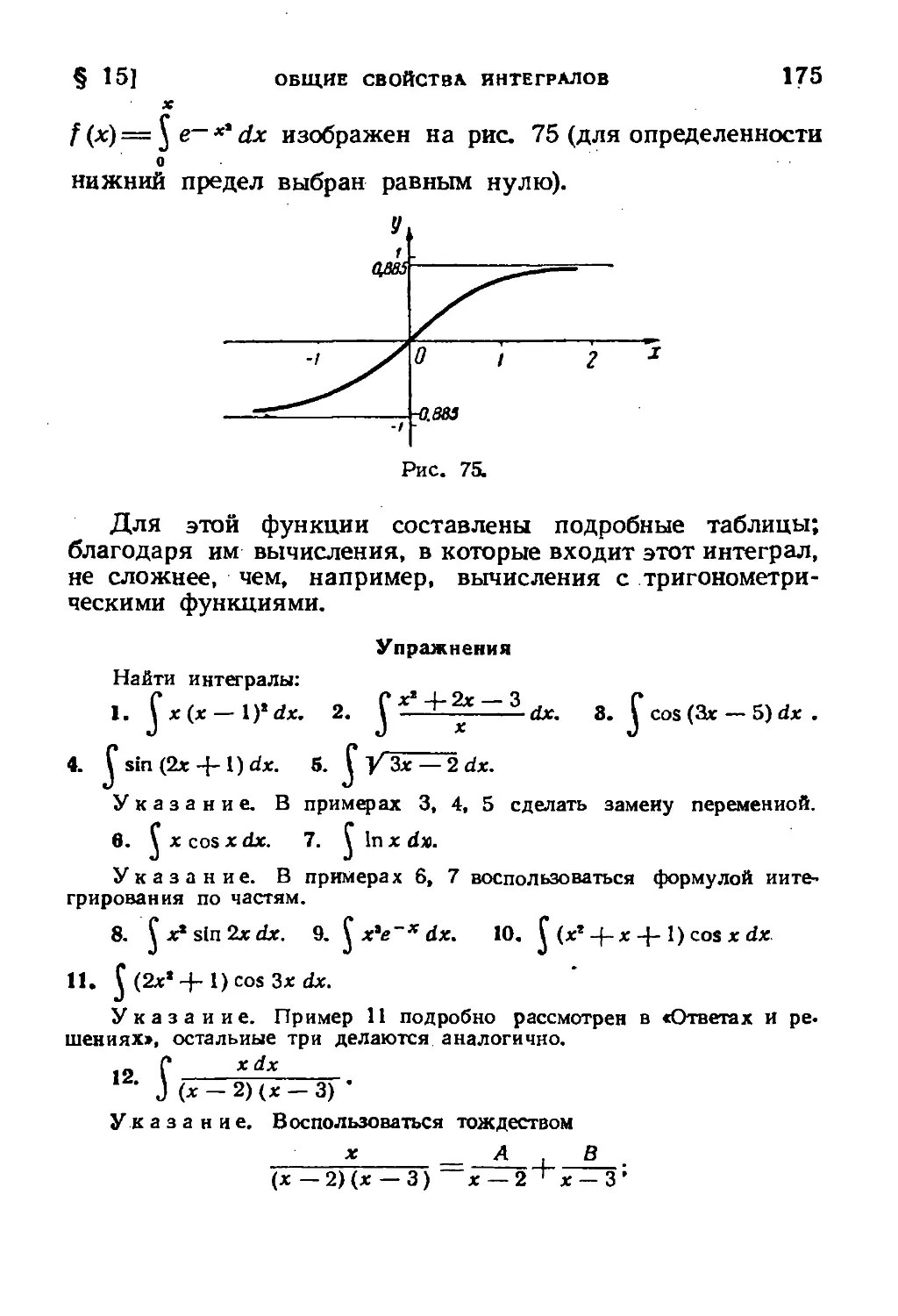
§ 15. Общие свойства интегралов 169
§ 16. Замена переменной в определенном интеграле . . .176
§ 17. Ряды 182
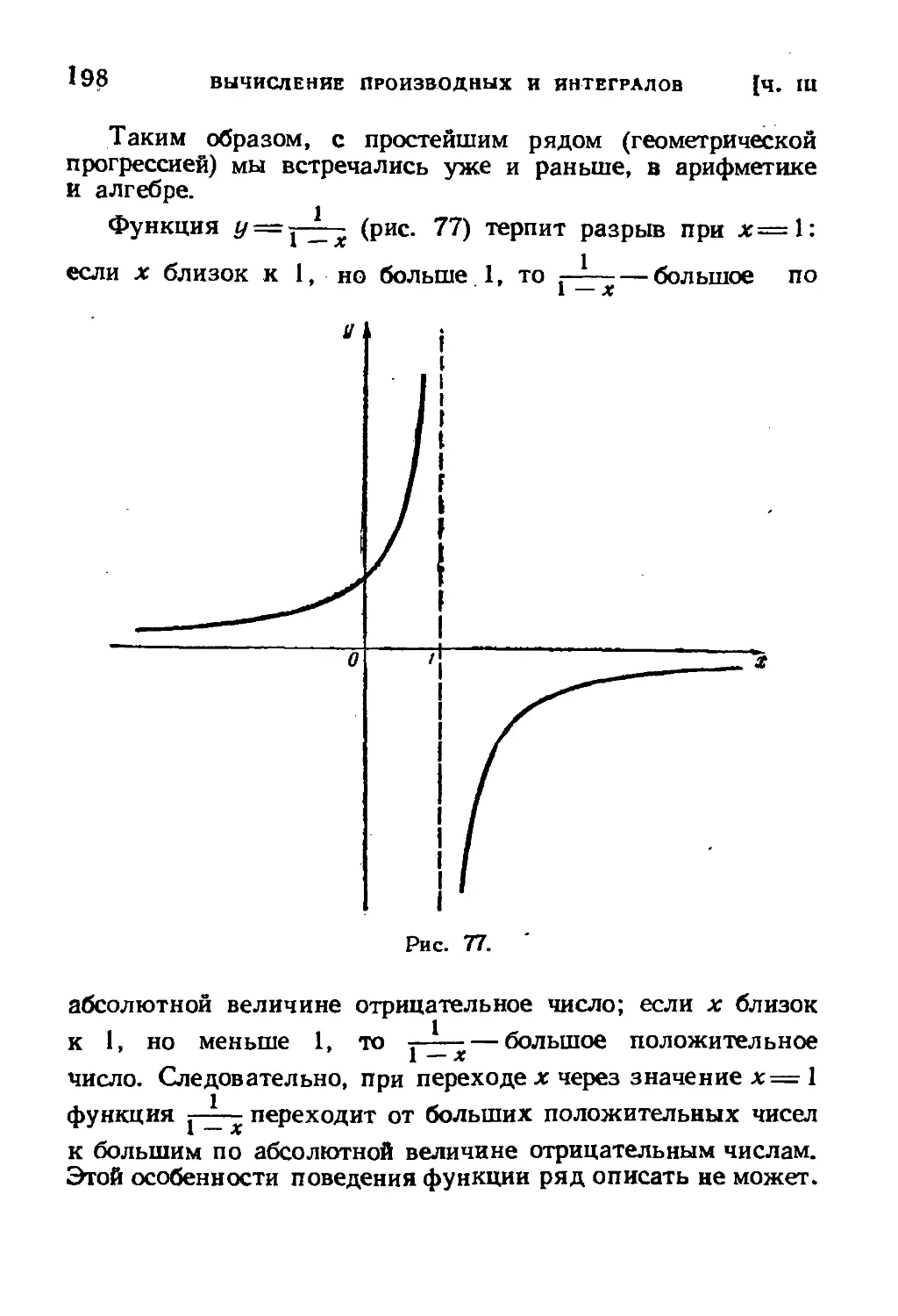
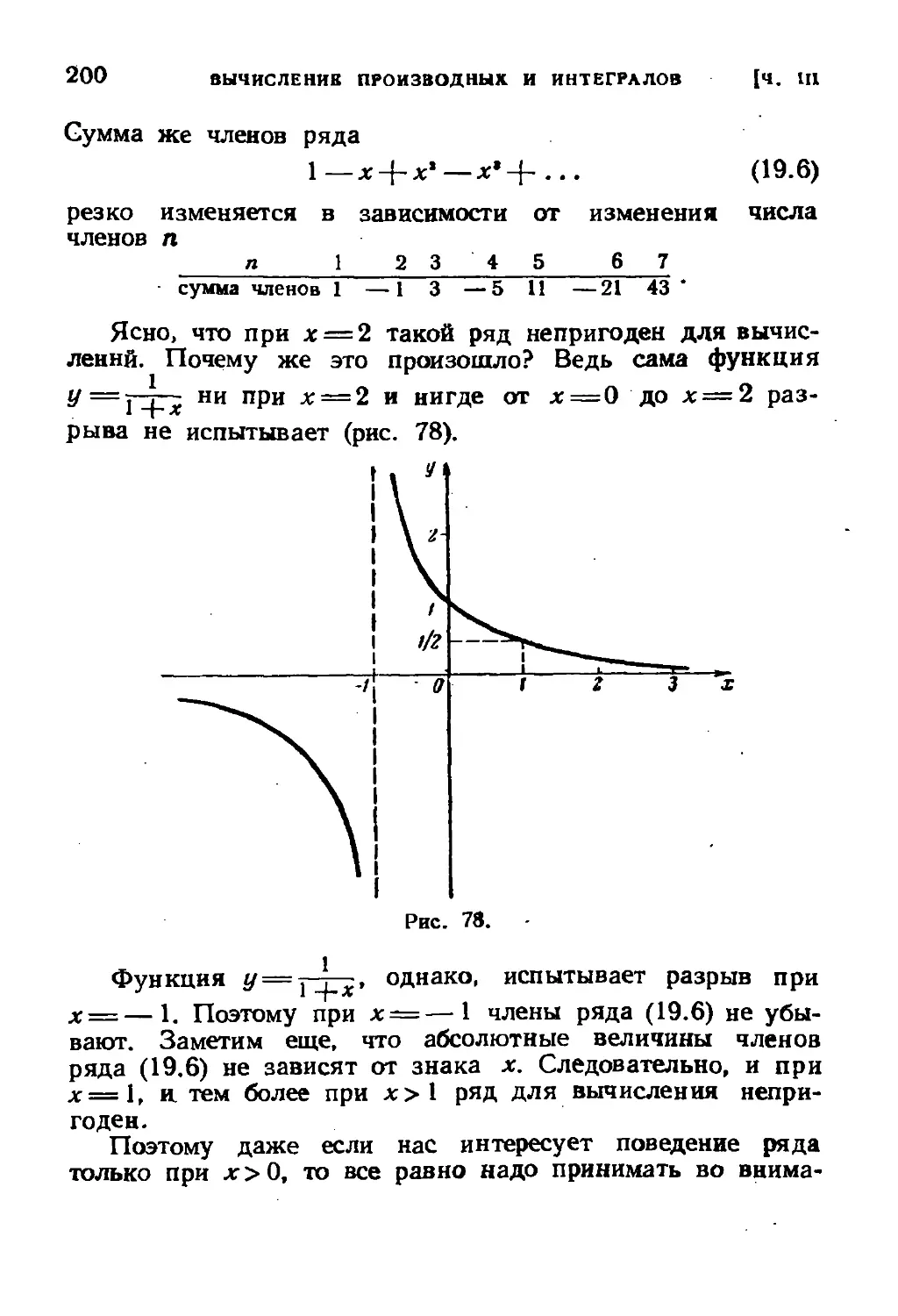
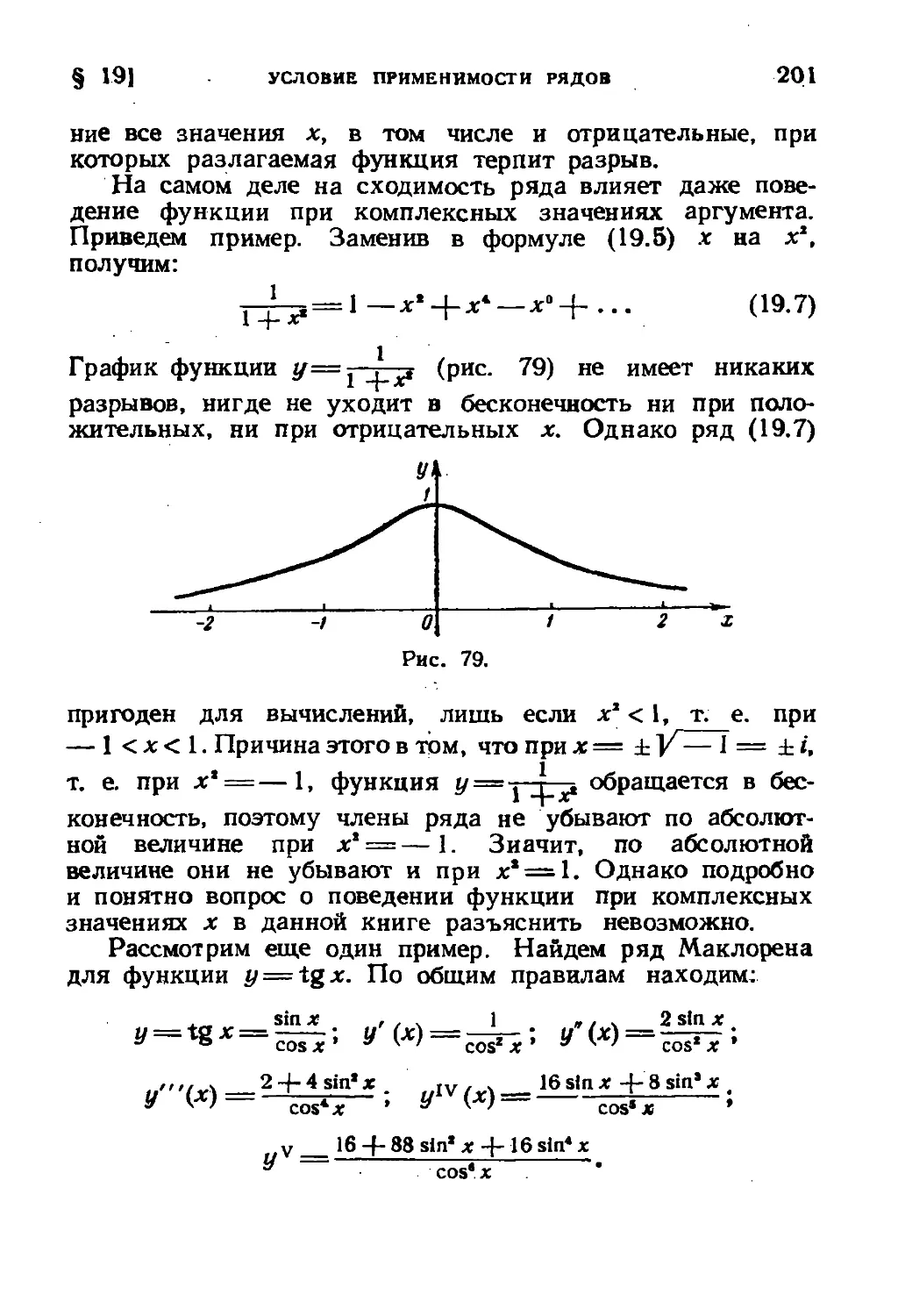
§ 18. Вычисление значений функций при помощи рядов . 190
§ 19. Условие применимости рядов. Геометрическая про-
грессия 195
§ 20. Бином Ньютона для целых и дробных показателей . . ?03
§ 21. Порядок возрастания и убывания функций 206
Ответы и решения 212
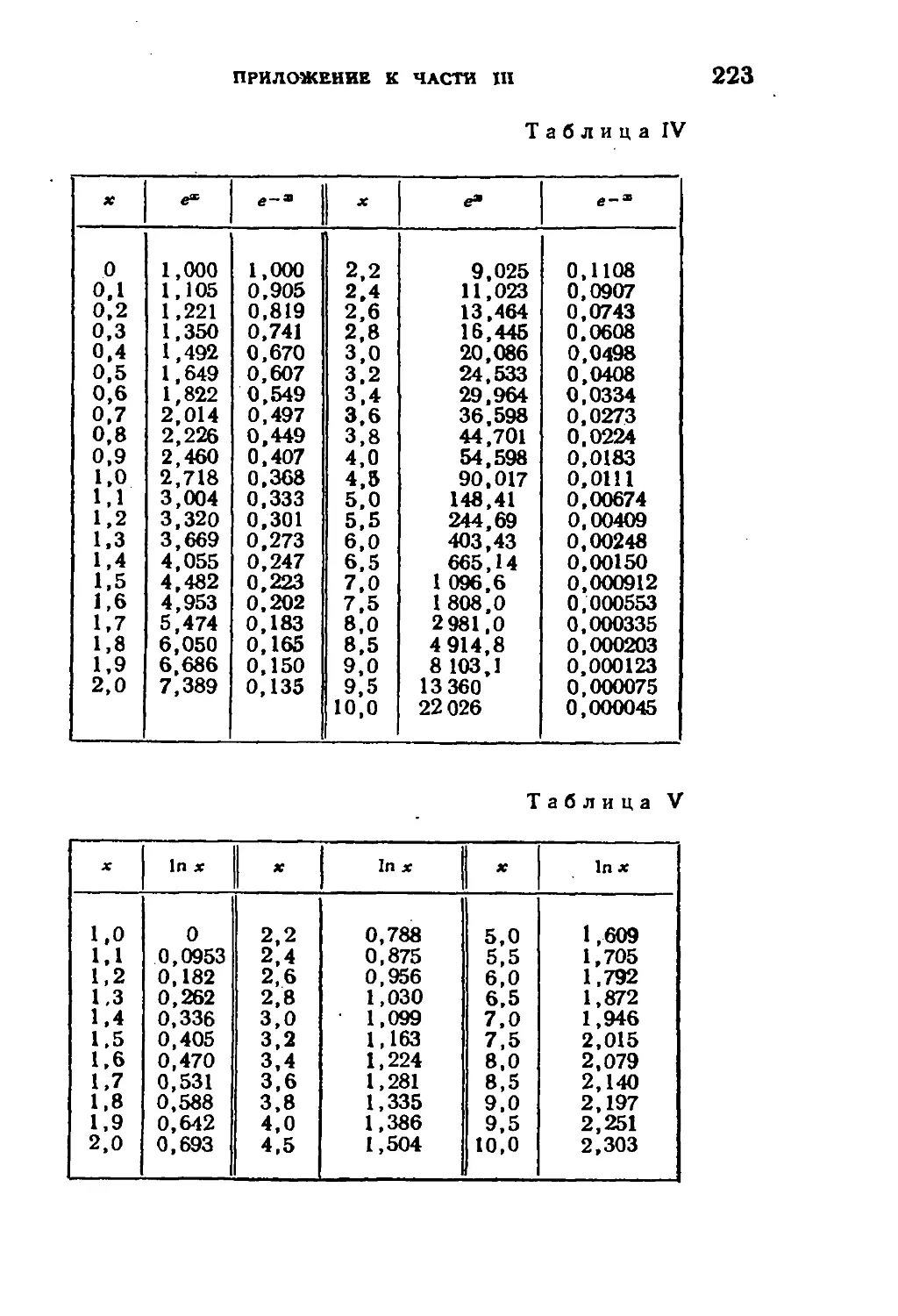
Приложение к части III 218
Часть IV. Приложения дифференциального и интегрального
исчисления к исследованию функций и геометрии .... 225
§ 1. Касательная, нормаль и ряд Тейлора 225
§ 2. Кривизна и касающийся круг ; 228
§ 3. Исследование максимумов и минимумов функций при
помощи второй производной 237
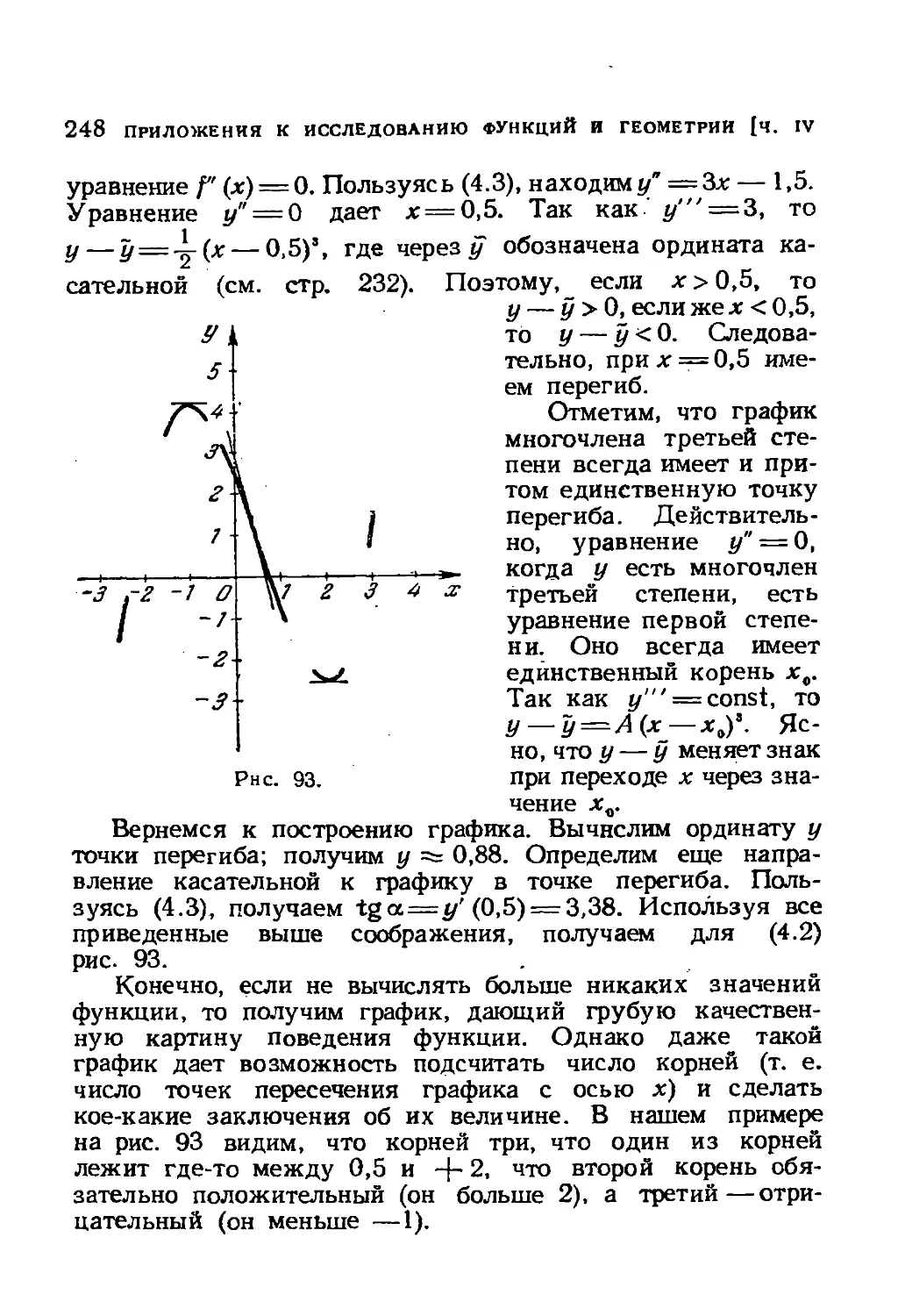
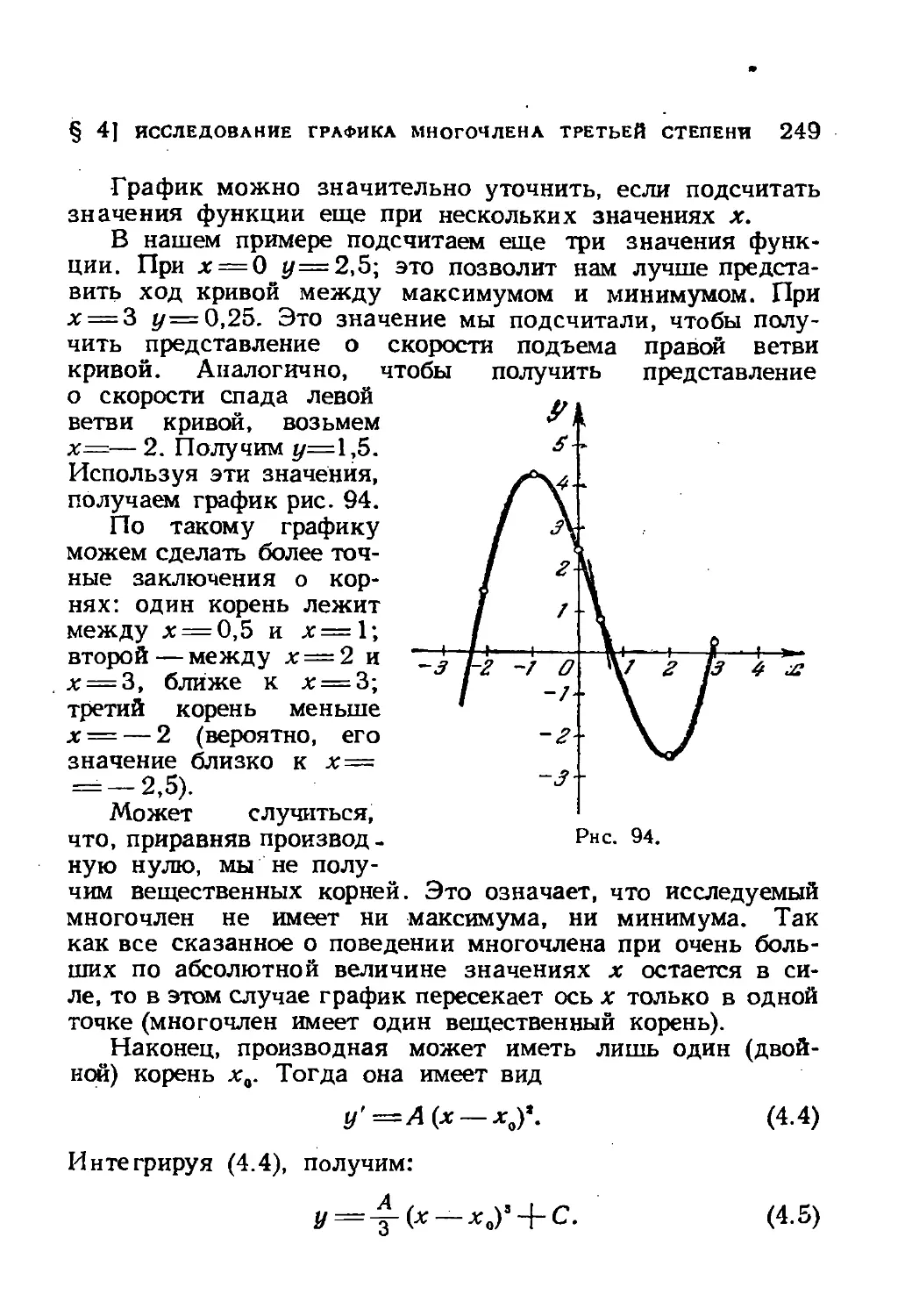
§ 4. Исследование графика многочлена третьей степени . 247
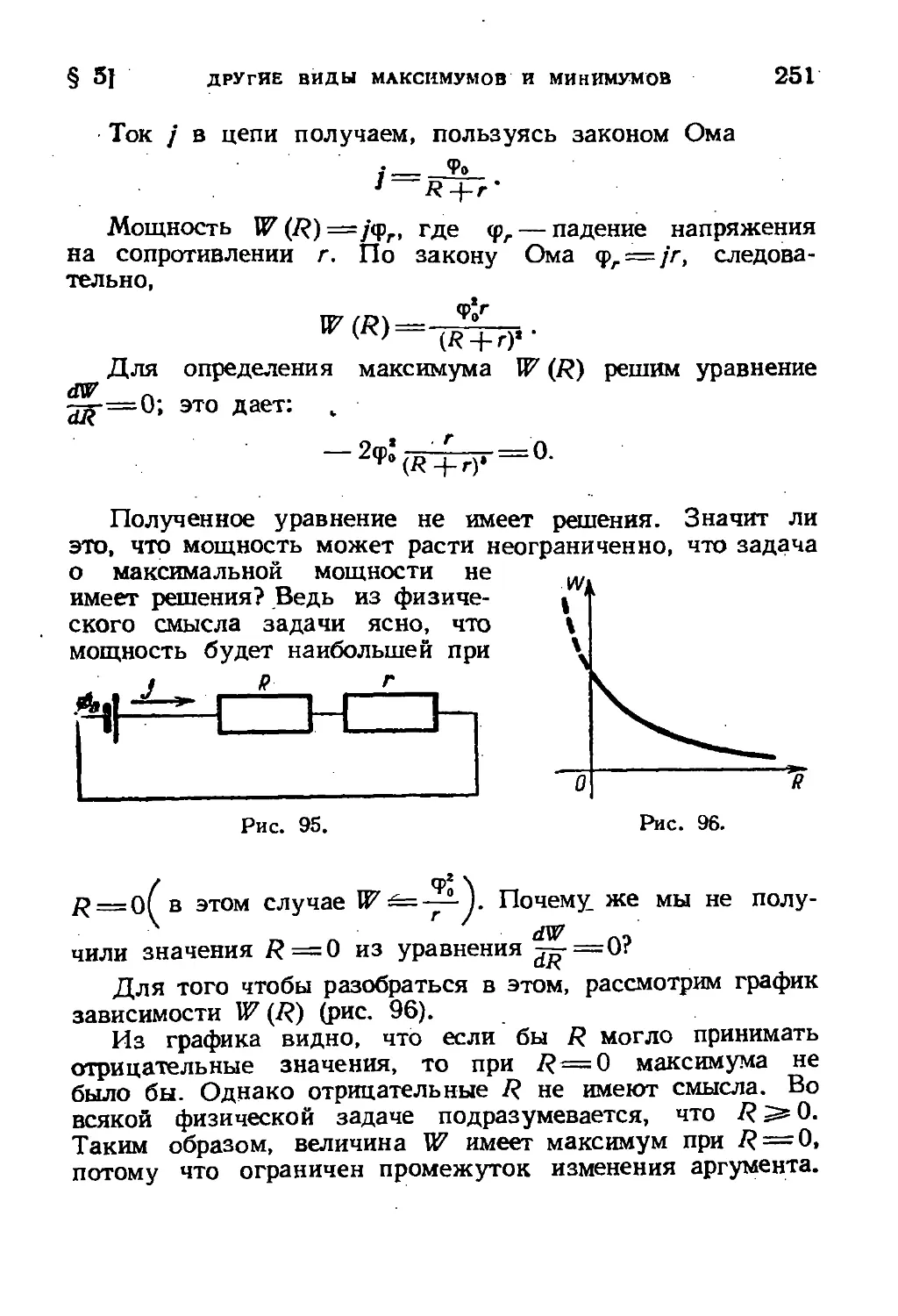
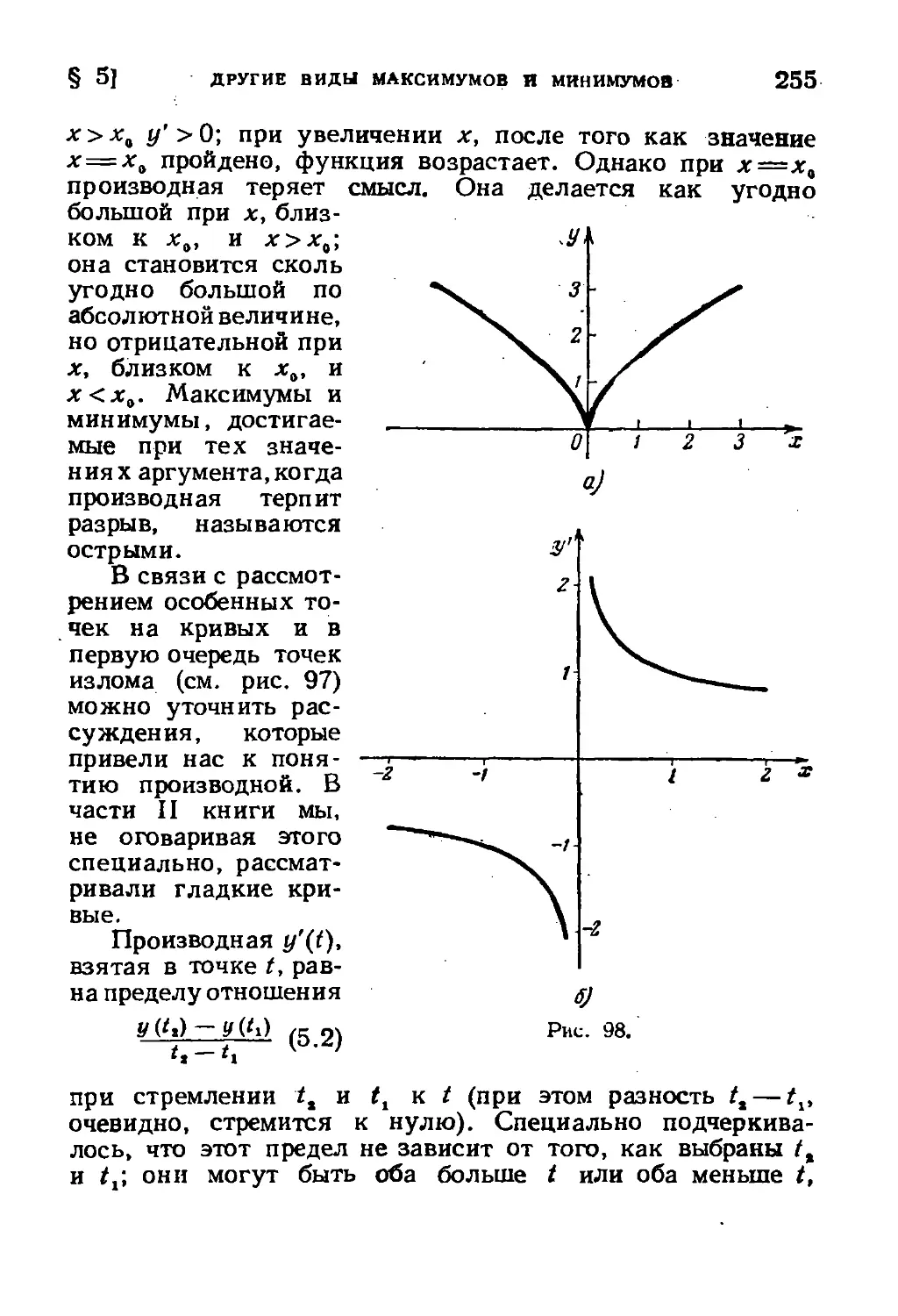
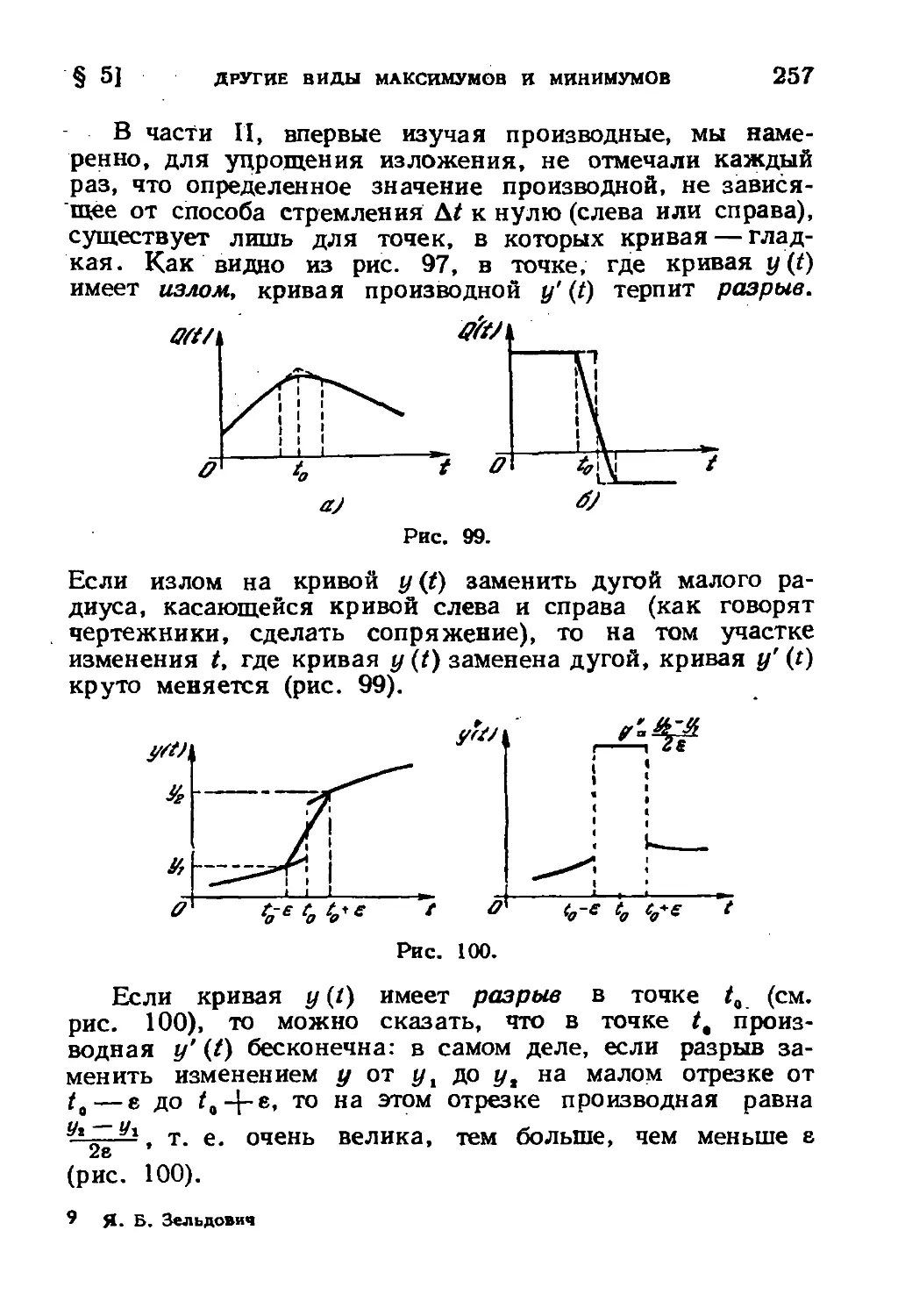
§ 5. Другие виды максимумов и минимумов. Изломы и
разрывы 250
§ 6. Эллипс 259
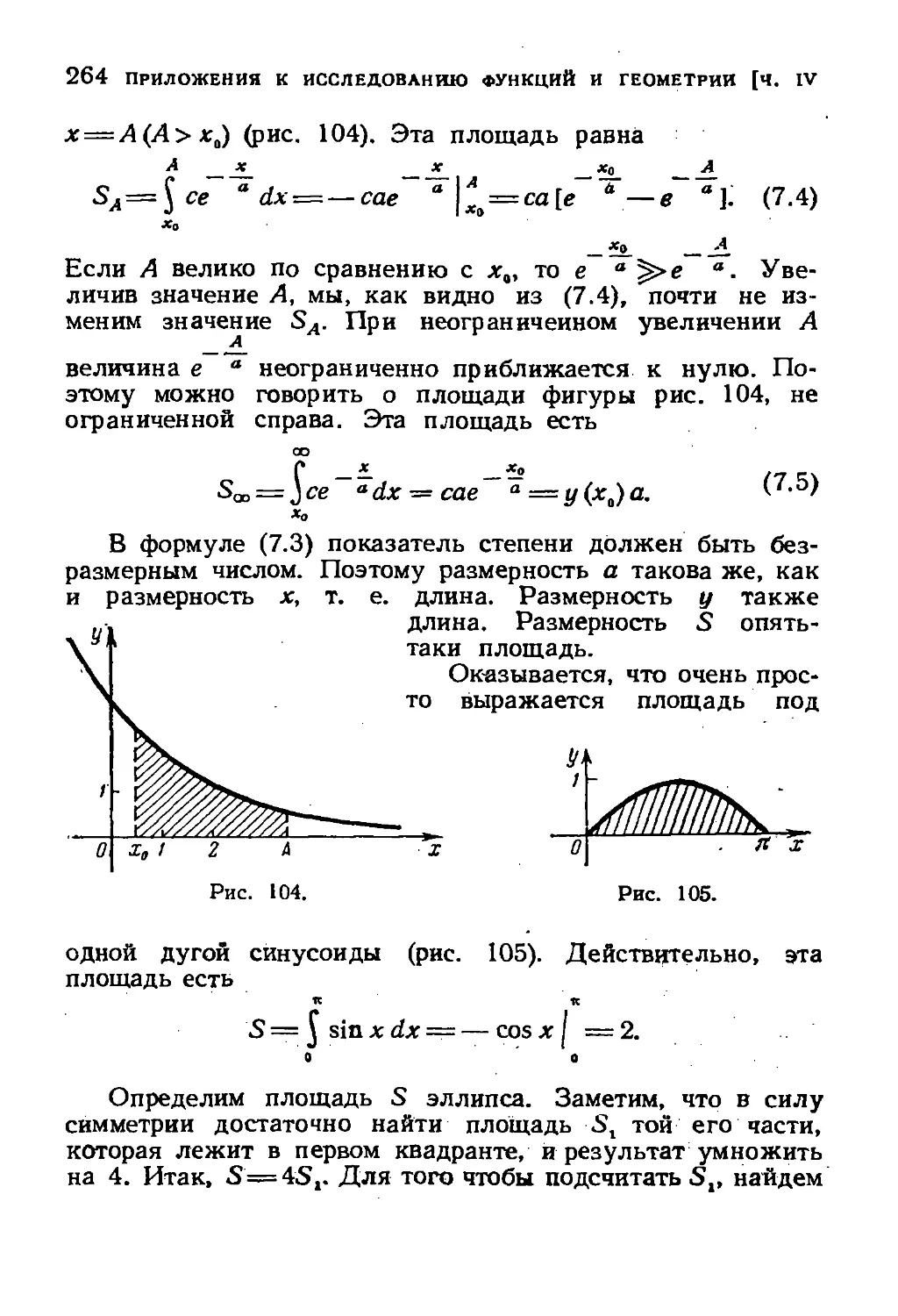
§ 7. Вычисление площадей 262
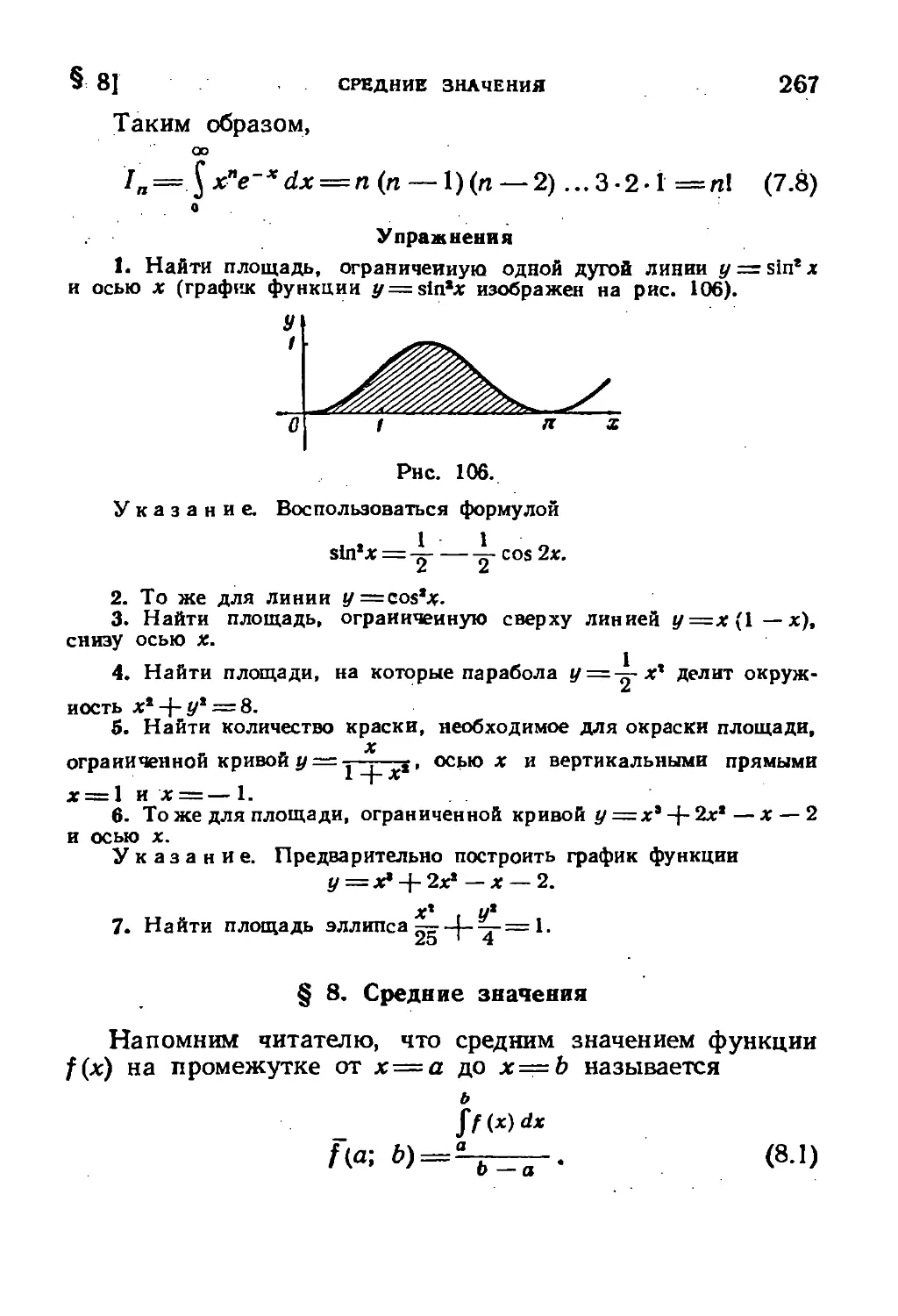
§ 8. Средние значения 267
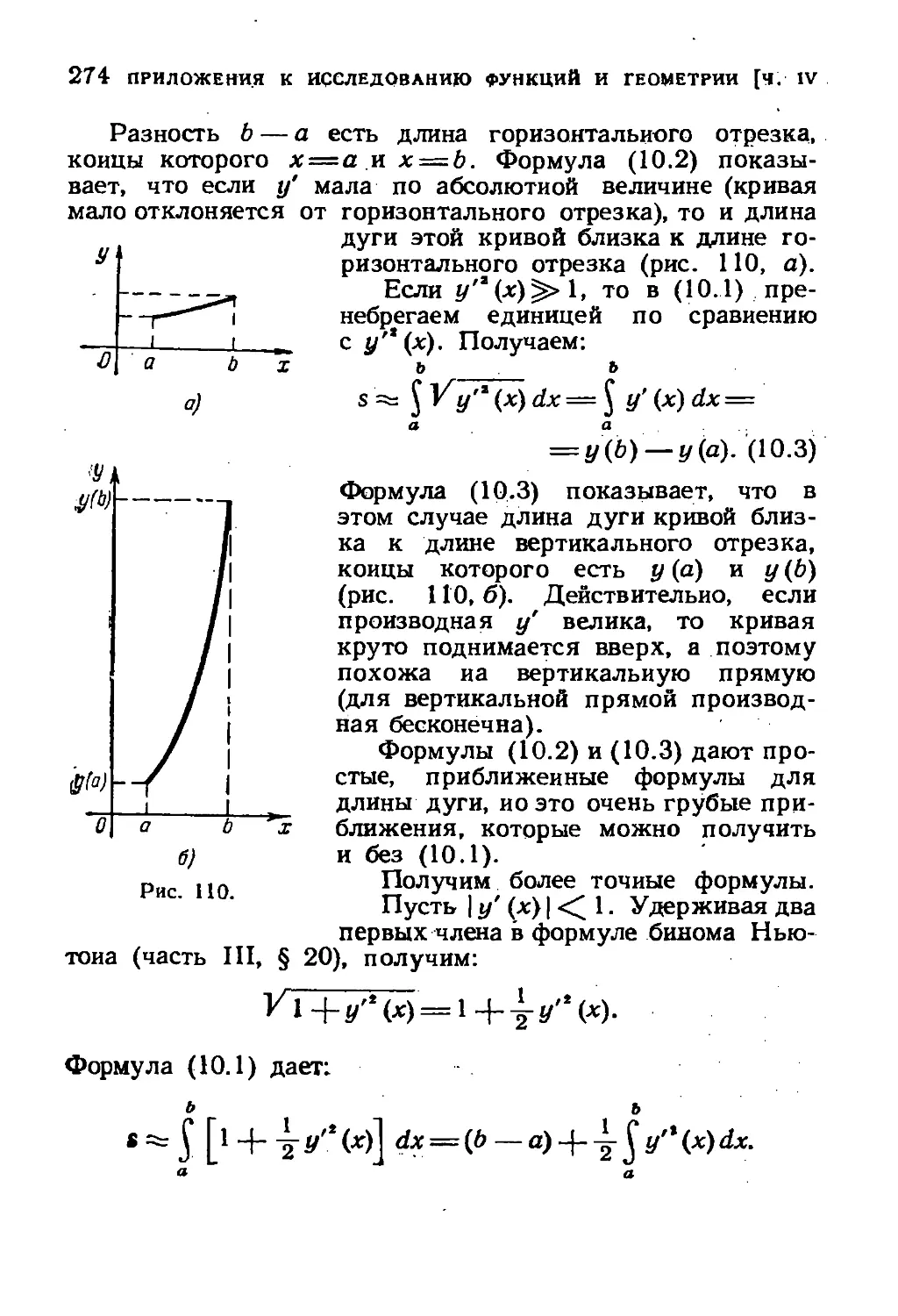
§ 9. Длина дуги кривой и кривизна 270
§ Ю. Приближенное вычисление длины дуги 273
§ 11. Вычисление объемов. Объем и поверхность тела вра-
щения ' 279
Отвгты и решения 283
Часть V. Вытекание воды. Радиоактивный распад и деление
ядер. Поглощение света 289
§ 1. Вытекание воды из сосуда. Постановка задачи . . . 289
§ 2. Решение уравнения в случае, когда производная за-
висит от искомой функции 293
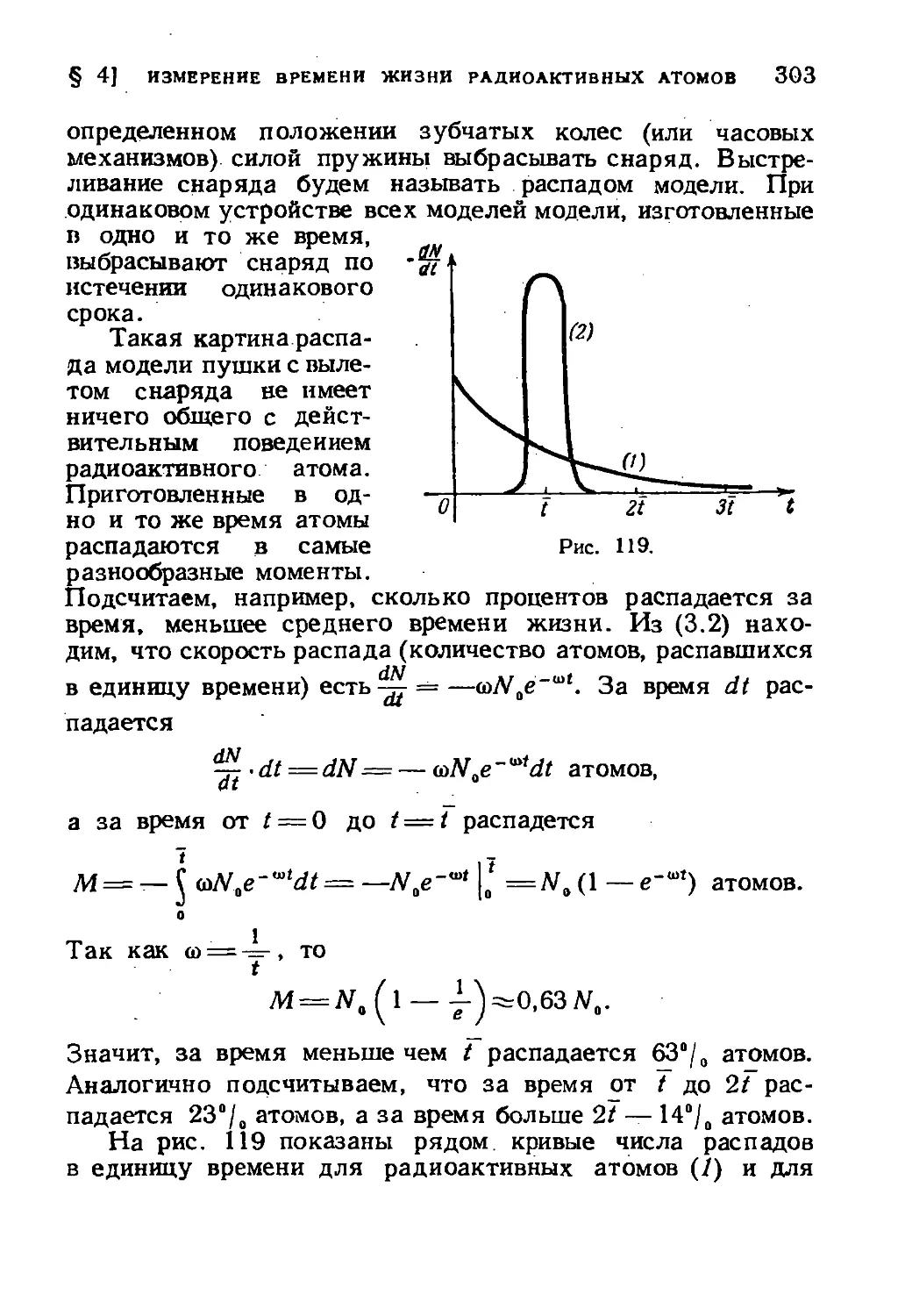
§ 3. Радиоактивный распад 296
| 4. Измерение среднего времени жизни радиоактивных
атомов 300
СОДЕРЖАНИЕ .5
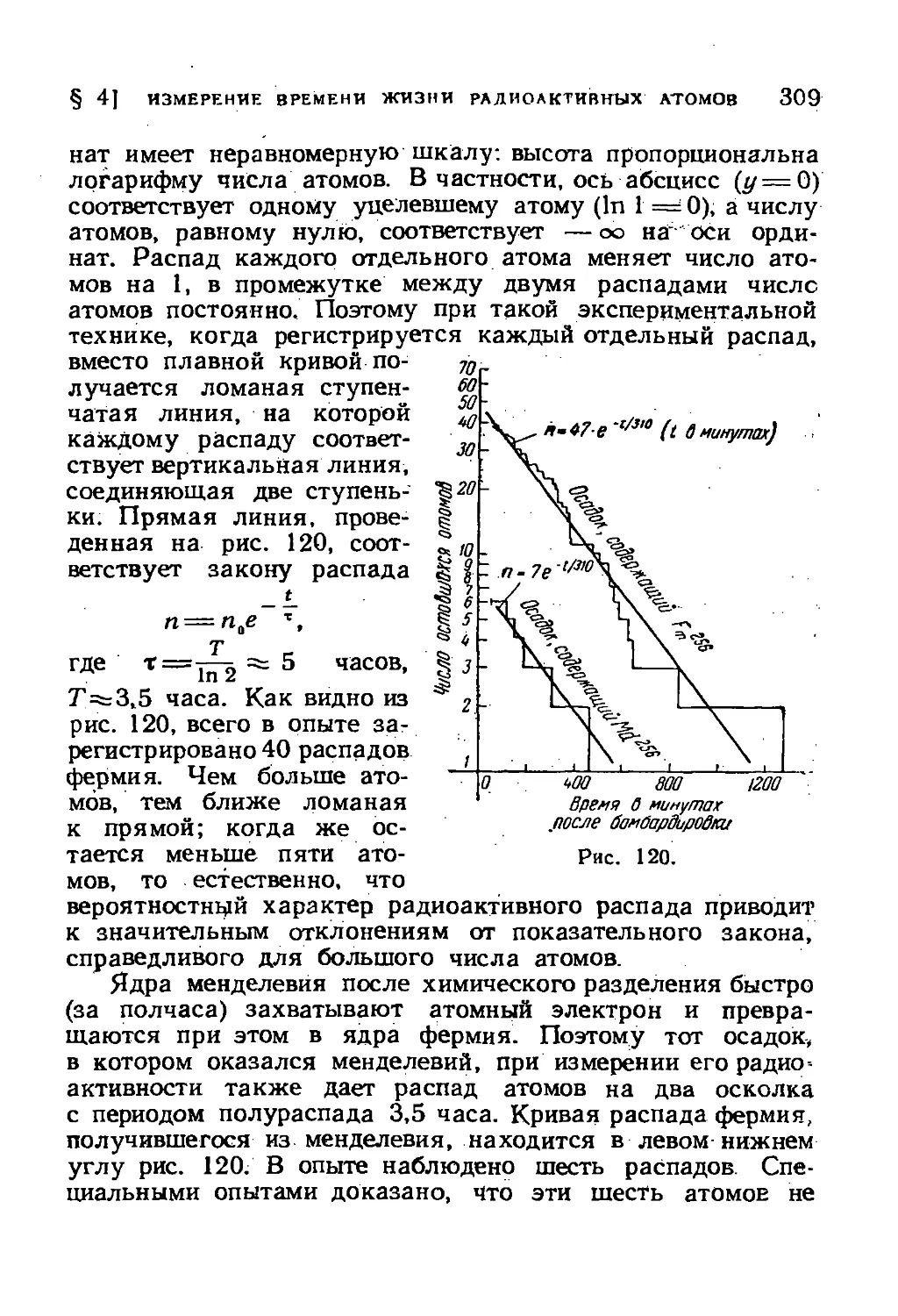
§ 5. Последовательный распад (радиоактивное семейство) 310
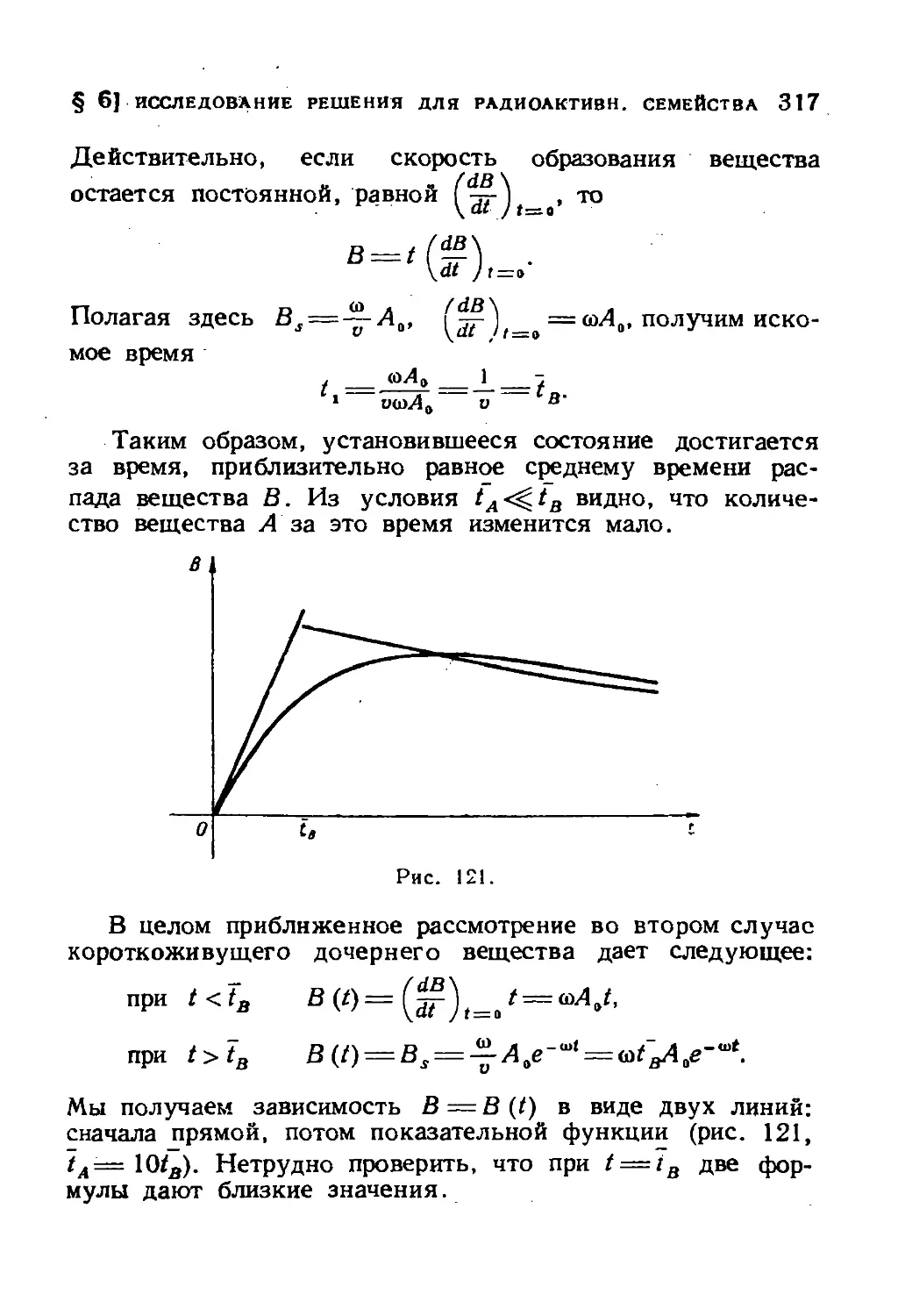
§ 6. Исследование решения для радиоактивного семейства 314
§ 7. Цепная реакция деления ураиа 320
§ 8. Размножение нейтронов в большой массе 322
§ 9. Вылет нейтронов 325
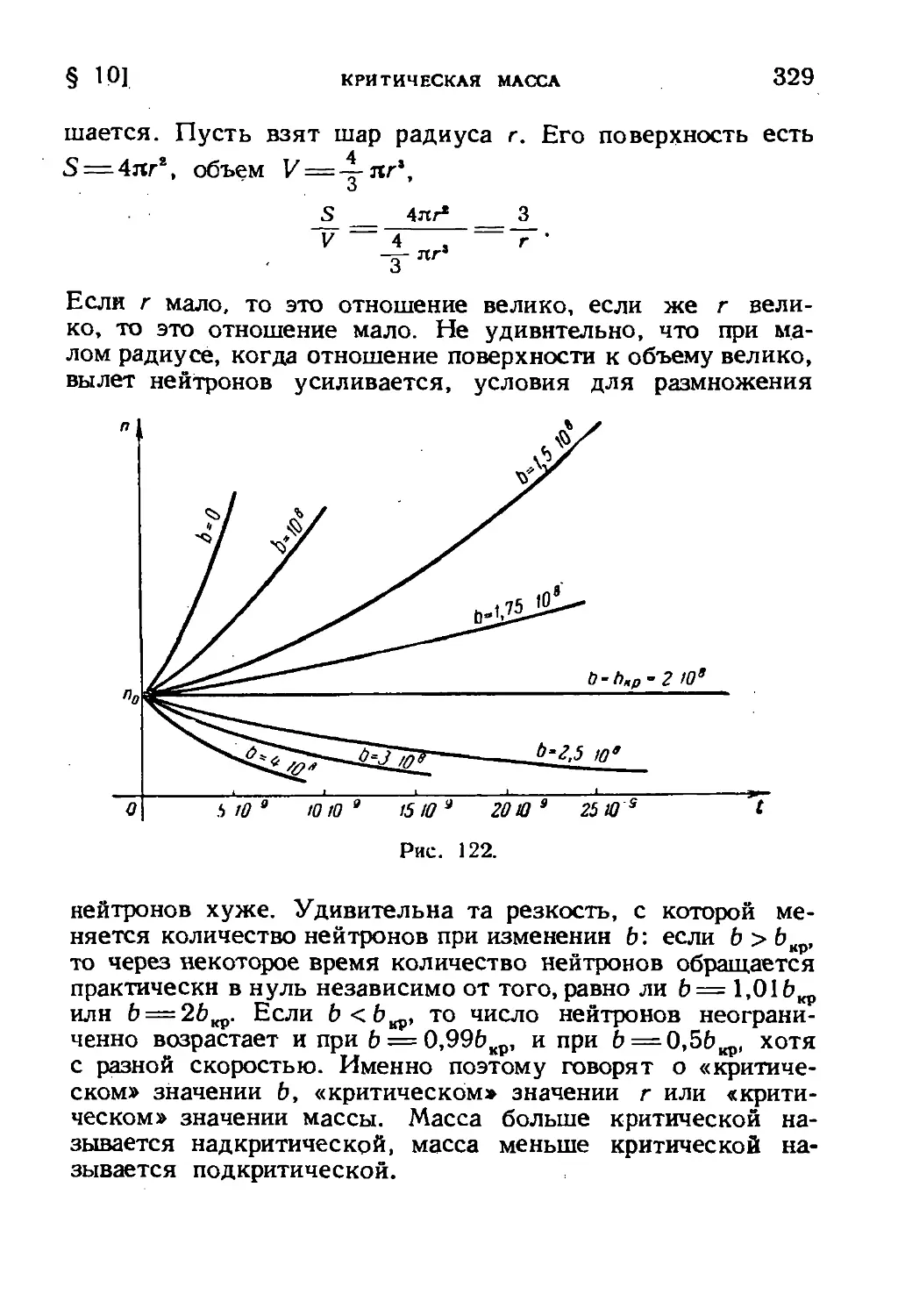
| 10. Критическая масса 327
§11. Подкритическая и надкритическая масса при непре-
рывном источнике нейтронов 331
6 12. Величина критической массы 334
§ 13. Поглощение света. Постановка задачи и грубая
оценка 335
14. Уравнение поглощения и его решение 338
15. Соотношение между точным и грубым расчетом . . 339
16. Эффективное сечение 341
17. Ослабление потока заряженных частиц—а- и 0-лучей 343
Ответы и решения 346
Часть VI. Механика 347
1. Сила, работа, мощность 347
2. Энергия . . ' 356
3. Равновесие и устойчивость 364
4. Второй закон Ньютона 372
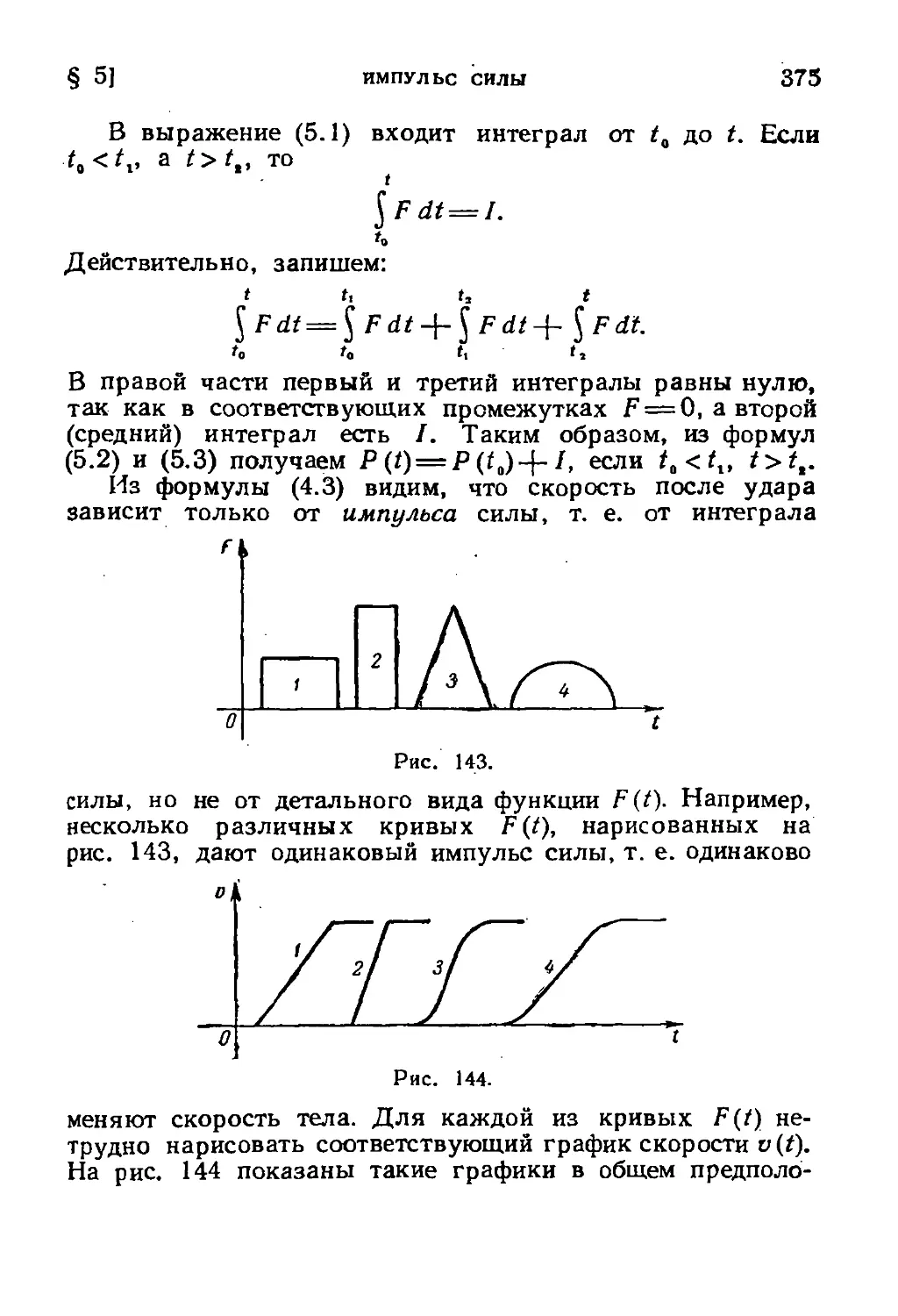
§ 5. Импульс силы 374
§ 6. Кинетическая энергия 378
§ 7. Движение под действием силы, зависящей только от
скорости 383
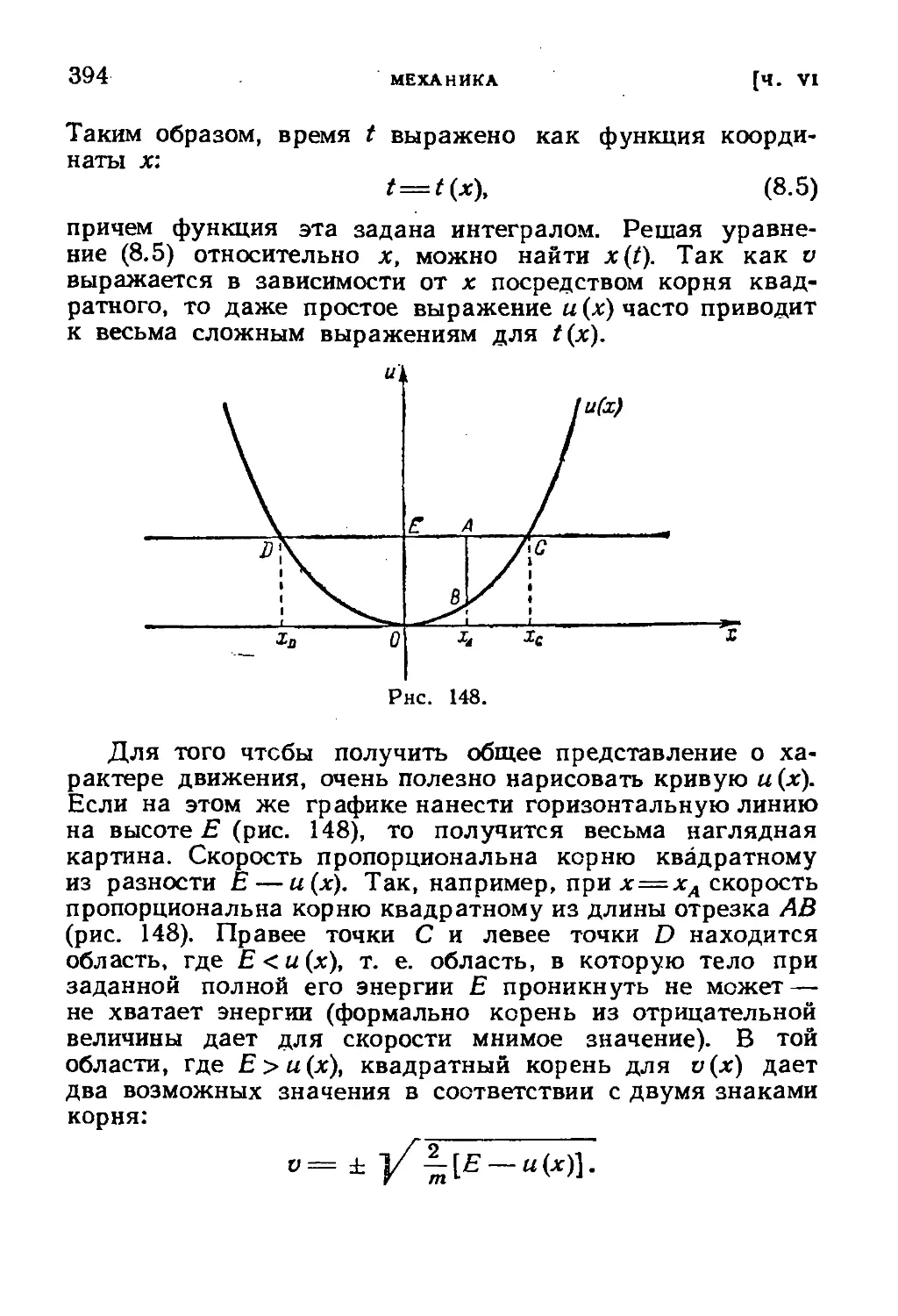
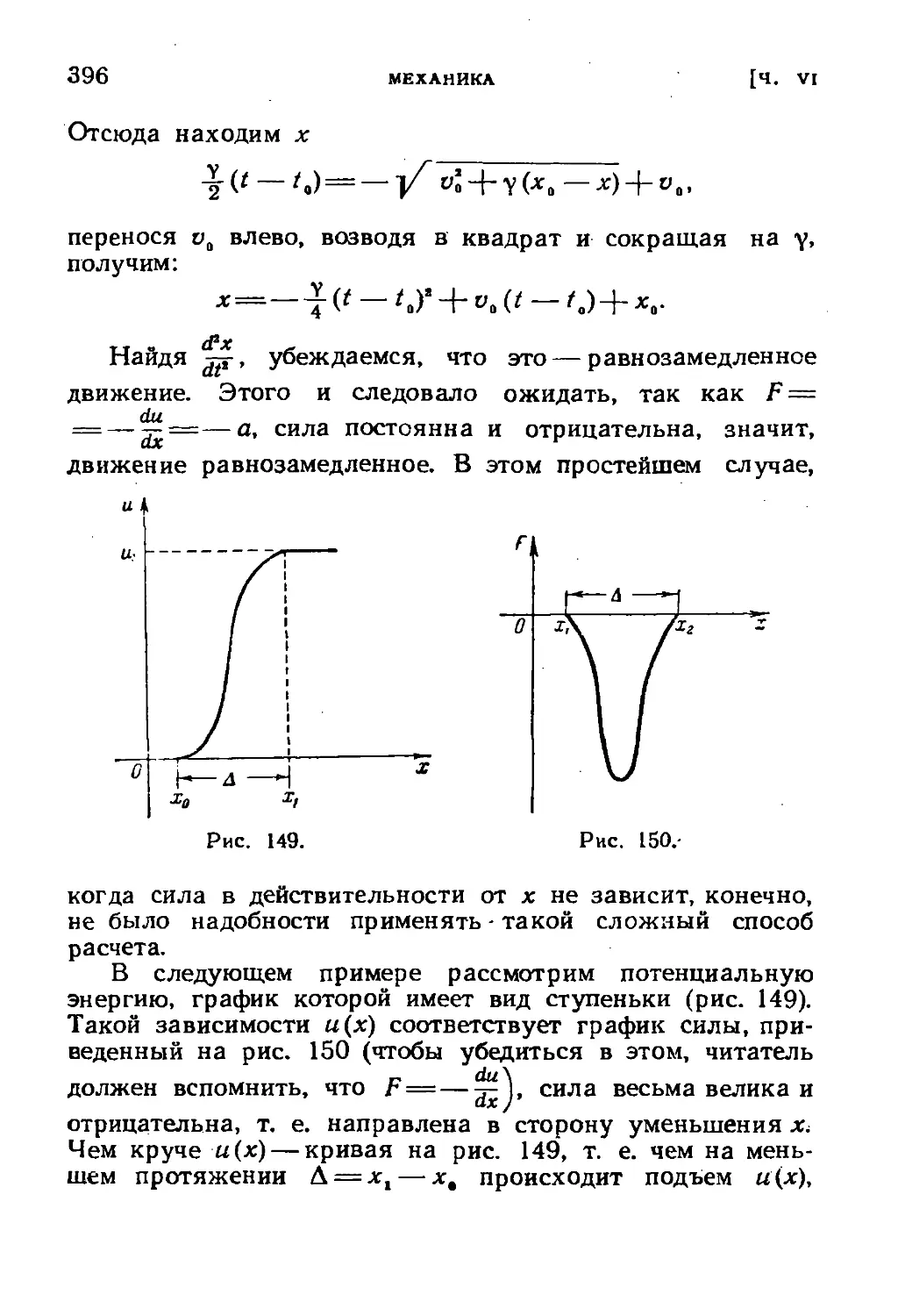
§ 8. Движение под действием упругой силы 391
§ 9. Колебания 398
§ 10. Энергия колебаний. Затухающие колебания .... 405
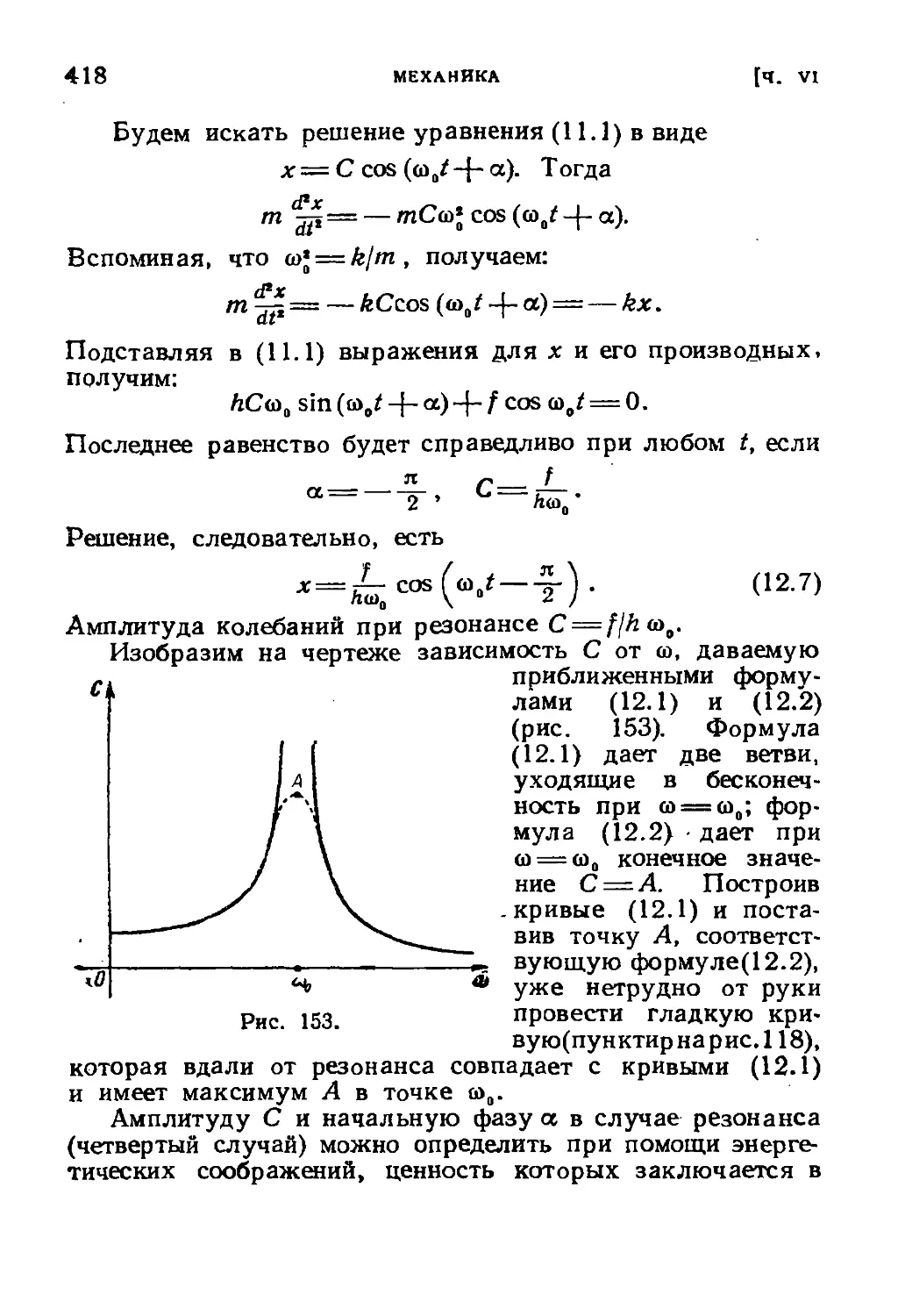
§ 11. Вынужденные колебания и резонанс 410
§ 12. О точных и приближенных решениях физических
задач 413
§ 13. Реактивное движение и формула К- Э. Циолковского 421
§ 14. Траектория снаряда 432
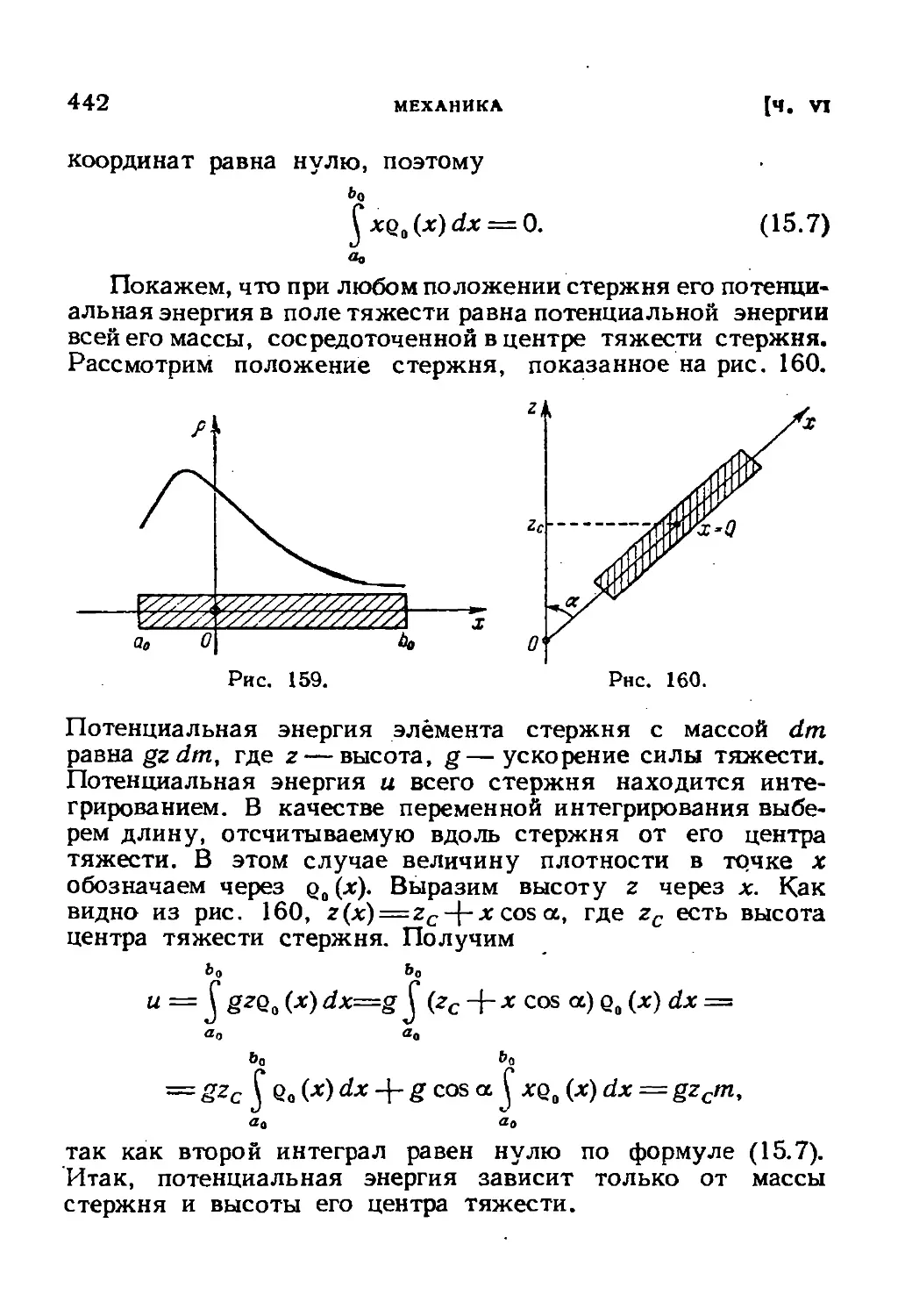
§ 15. Масса, центр тяжести и момент инерции стержня . 437
§ 16. Колебания подвешенного стержня 446
Ответы и решения 448
Часть VII. Тепловое движение молекул и распределение плот-
ности воздуха в атмосфере 458
§ 1. Условие равновесия в атмосфере 458
§ 2. Связь между плотностью и давлением 460
§ 3. Распределение плотности 462
§ 4. Молекулярно-кинетическая теория распределения плот-
ности 465
§ 5. Броуновское движение и распределение молекул по
кинетической энергии 470
§ 6. Скорости химических реакций 473
§ 7. Испарение. Ток эмиссии катода 475
Ответы и решения 479
6 СОДЕРЖАНИЕ
Часть VIII. Электрические цепи и колебательные явления
в них 480
§ 1. Основные понятия и единицы измерения 480
§ 2. Разряд емкости через сопротивление 490
§ 3. Колебания в цепи емкости с искровым промежутком 494
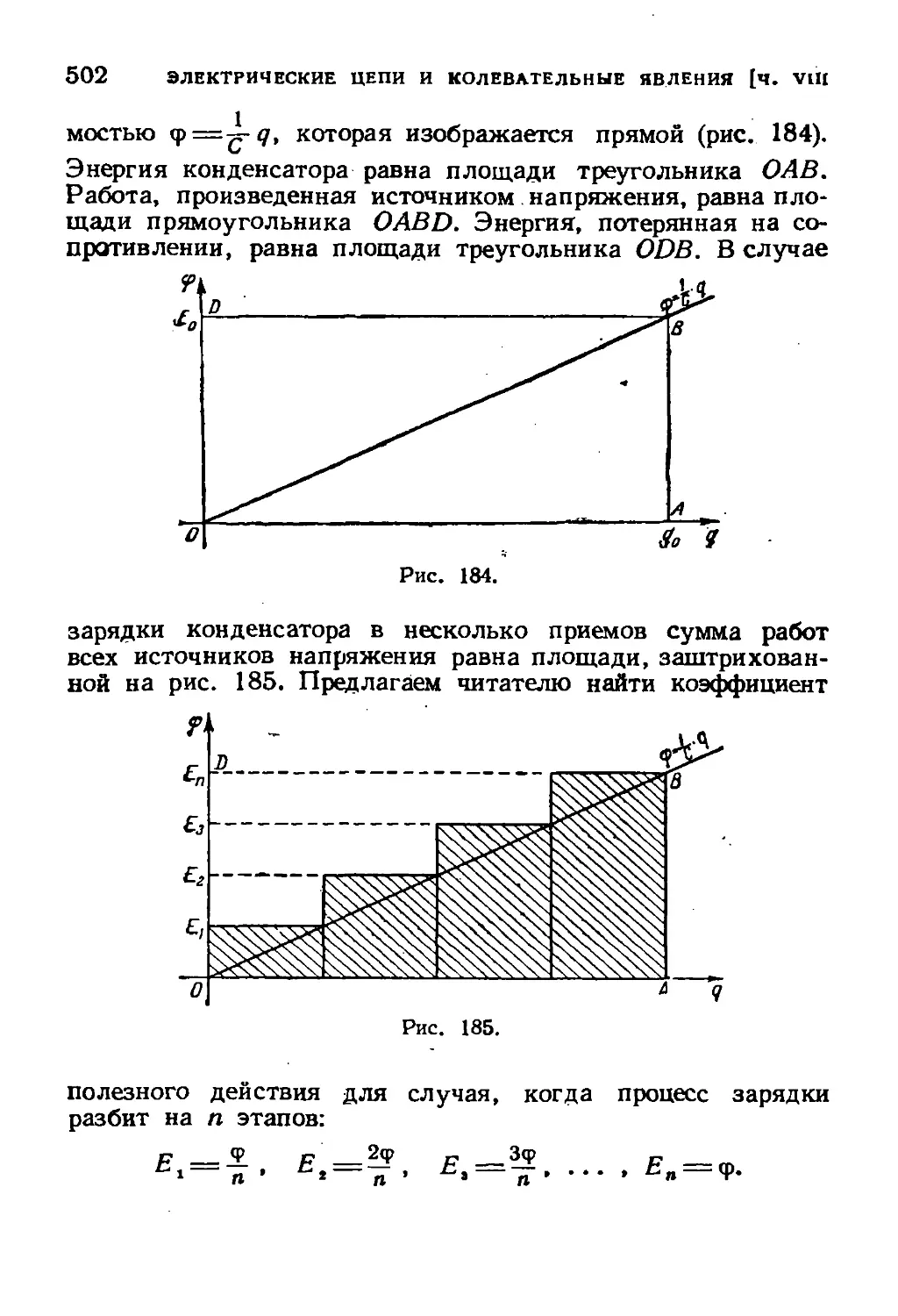
§ 4. Энергия конденсатора 498
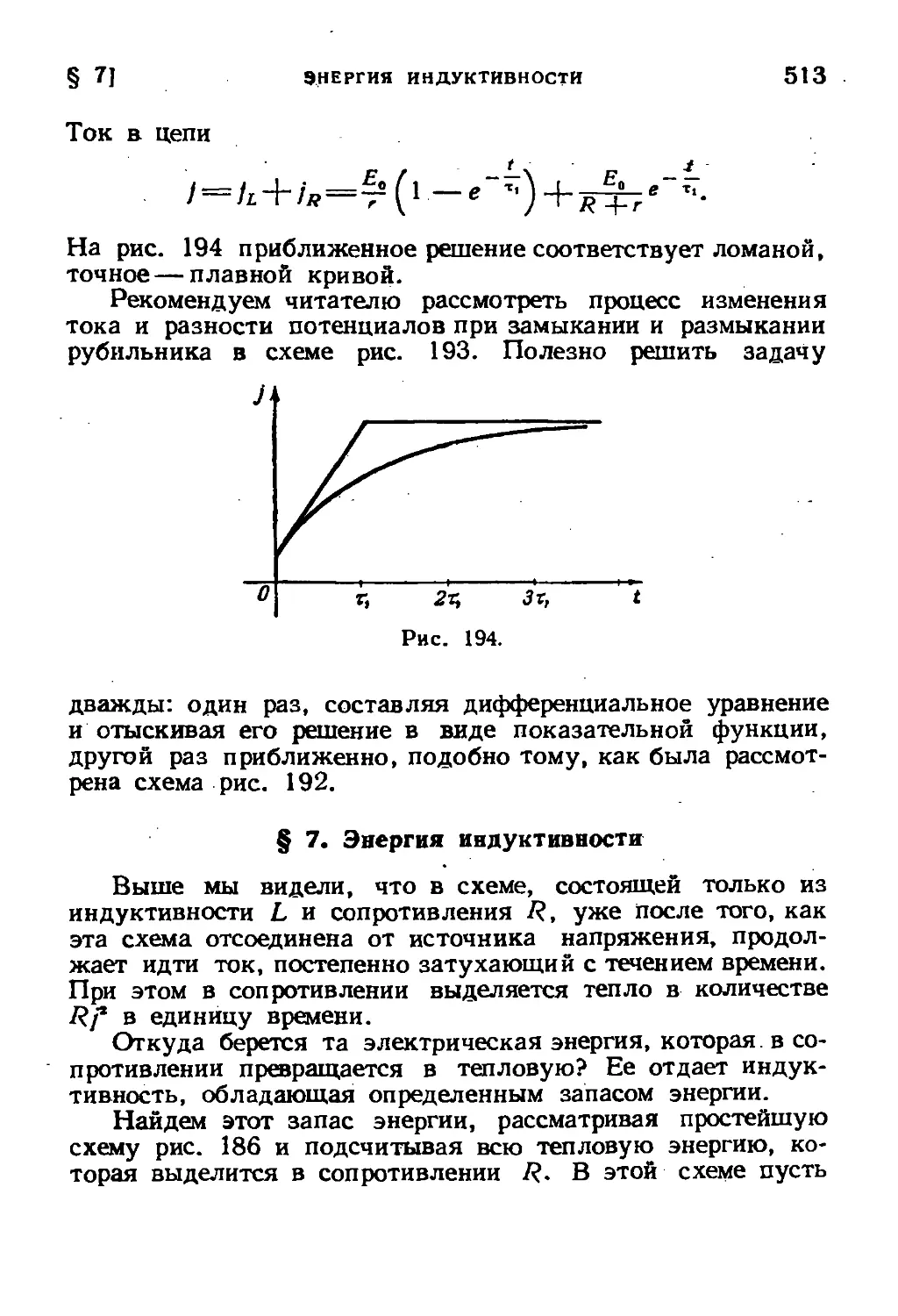
§ 5. Цепь с индуктивностью 505
§ 6. Размыкание цепи с индуктивностью 509
§ 7. Энергия индуктивности 513
§ 8. Колебательный контур 520
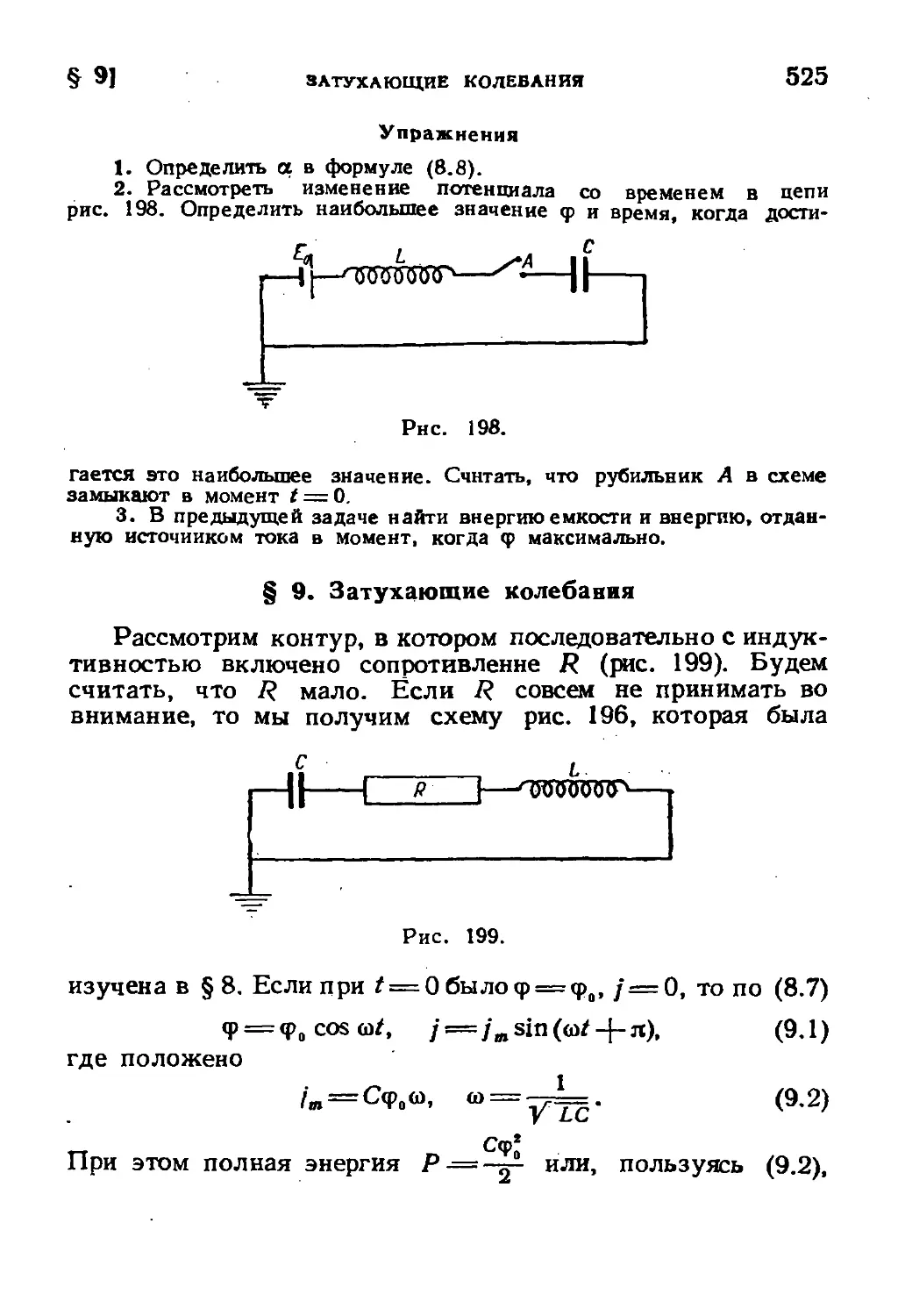
§ 9. Затухающие колебания 525
§ 10. Случай большого сопротивления 529
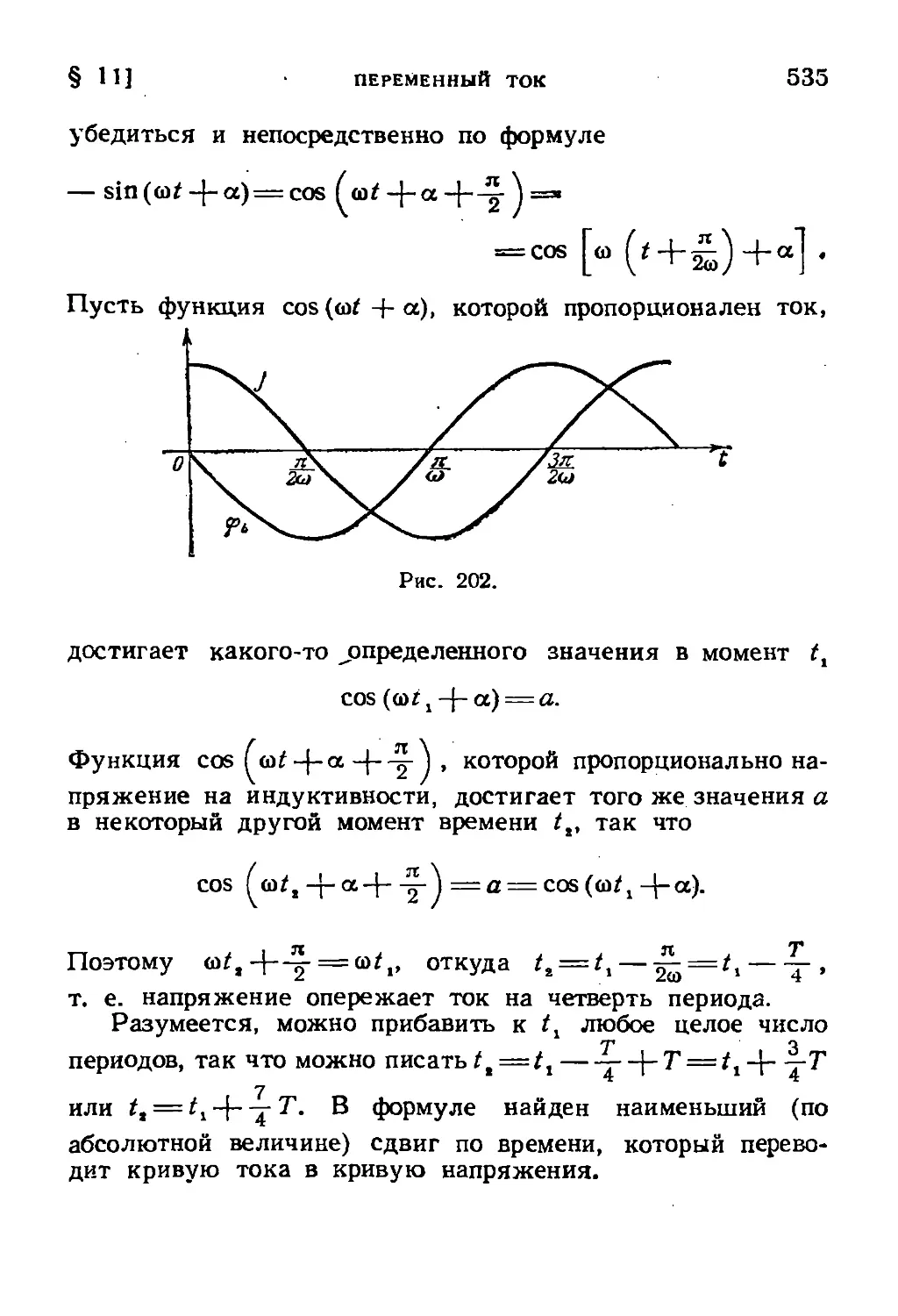
§ 11. Переменный ток 532
§ 12. Средние величины, мощность и сдвиг фазы .... 538
§ 13. Колебательный контур в цепи переменного тока.
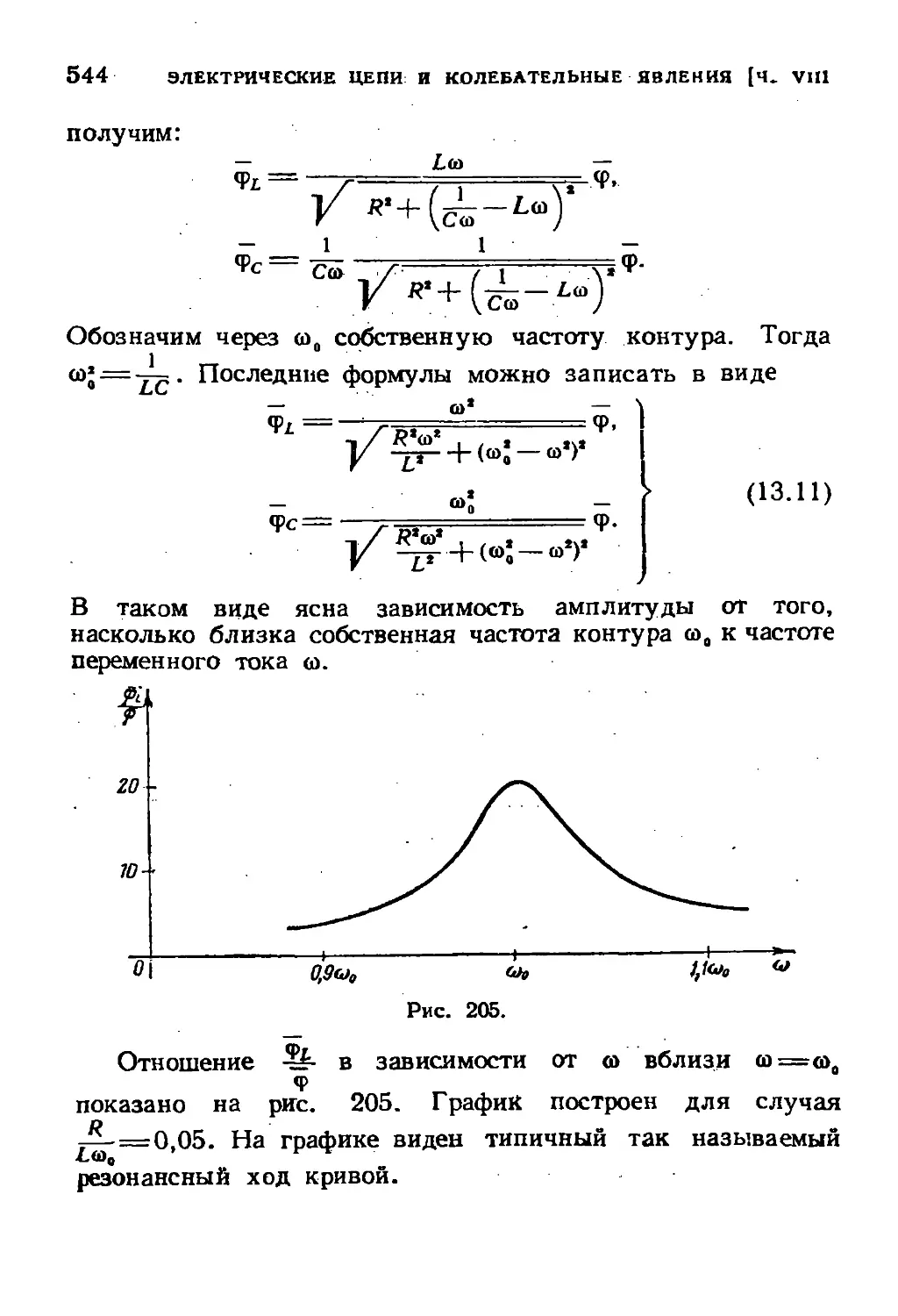
Резонанс напряжений 541
§ 14. Параллельное включение индуктивности и емкости.
Резонанс токов 545
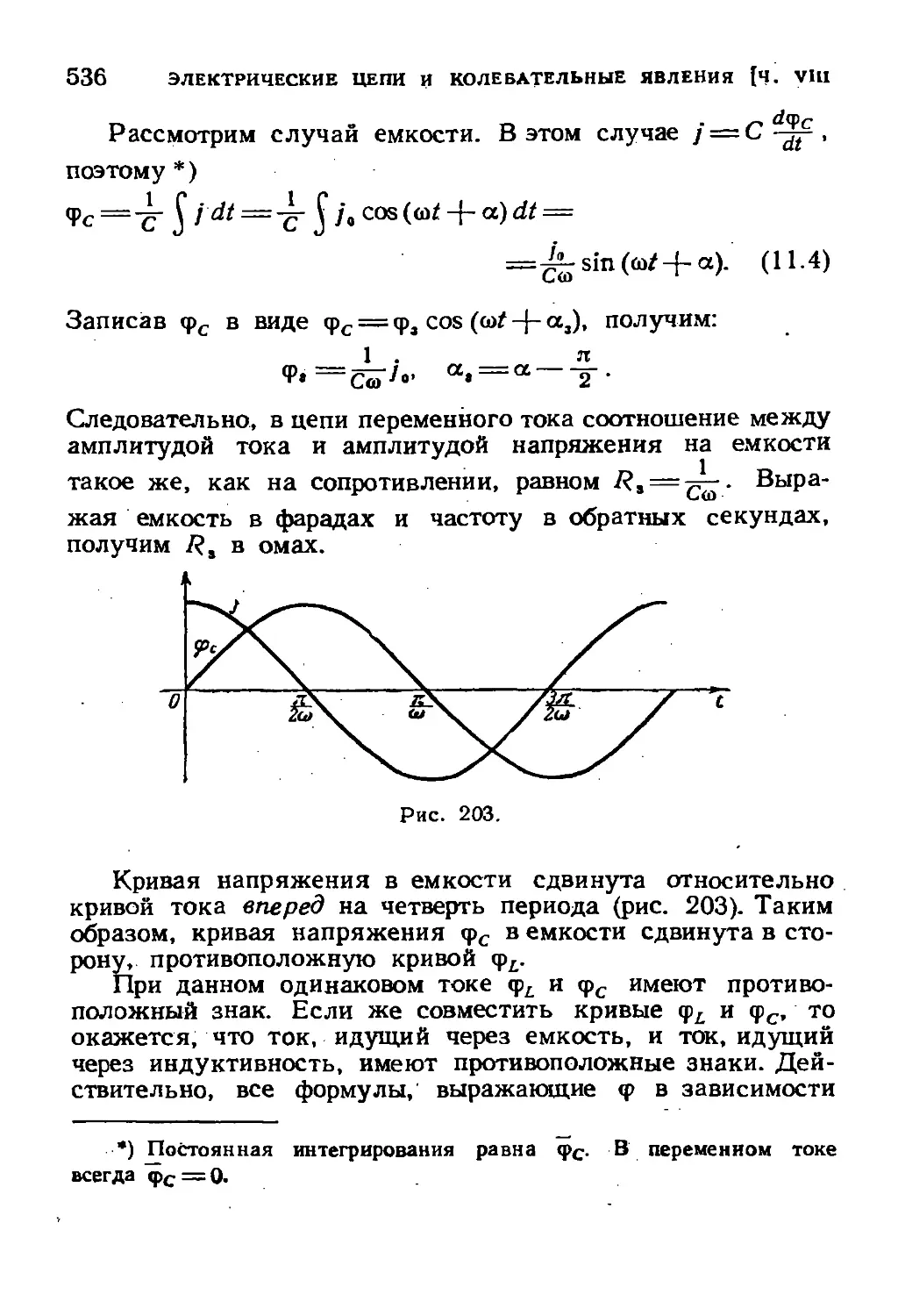
§ 15. Ток смещения и электромагнитная теория света . . . 549
§ 16. Нелинейное сопротивление и туннельный диод . . . 551
Ответы и решения 557
Приложение. Латинский алфавит. Греческий алфавит . . 560
ПРЕДИСЛОВИЕ
Высшей математикой называют дифференциальное и ин-
тегральное исчисление в отличие от алгебры, геометрии и
тригонометрии, изучение которых заканчивается в средней
школе.
Основные понятия высшей математики — производная и
интеграл — необходимы для описания физических явлений,
для точной формулировки законов природы.
Эти основные понятия уже давно стали необходимой
частью знаний каждого культурного человека наряду, напри-
мер, с пониманием того, что неизвестную величину можно
обозначать буквой х и производить с этой буквой алгебраи-
ческие действия. Понятия высшей математики необходимы
везде, где мы имеем дело с изменяющимися величинами,
с функциональной зависимостью одних величин от других.
В настоящее время существует большое число учебников
высшей математики. Естественно возникает вопрос о том,
каково отличие предлагаемой книги от изданных ранее,
какие новые цели ставил перед собой автор. Таким общим
отличием является иное отношение к читателю. Можно
представить себе читателя «упирающегося», требующего точ-
ного и строгого доказательства всех положений, которые
дает ему автор, выискивающего возражения и исключения.
Для такого читателя предмет следует излагать в виде стро-
гой и стройной цепи доказательств и теорем, заставляя этого
читателя признать правильность теорем. Многие учебники
построены именно таким образом.
Предлагаемая книга рассчитана на совершенно другого
читателя — читателя, который хочет понять, что такое выс-
шая математика, и научиться ее применению, т. е. читателя,
который не упирается, а сам тянется вперед. Такого чита-
теля не надо «подталкивать», с ним можно идти рядом и
дружески беседовать.
8 ПРЕДИСЛОВИЕ
Основной упор в книге сделан не на доказательства, а
на пояснения при помощи примеров. Сначала на наглядных
примерах выяснены смысл наиболее трудных понятий, спо-
соб их применения, их полезность и значение. Уже после
этого даются более строгие и точные формулировки.
Для чтения книги достаточно знания основ алгебры,
геометрии и тригонометрии в объеме, значительно меньшем
программ средней школы. Поэтому книга вполне доступна
для школьников 9—11 классов и для лиц, не имеющих
законченного среднего образования.
В предлагаемом втором издании книги в первой части
даны краткие сведения по графикам функций и аналитиче-
ской геометрии. Эта часть в значительной мере повторяет
материал, содержащийся в школьных учебниках алгебры.
Однако представляется, что читателю будет удобно повто-
рить этот материал, не обращаясь к другим книгам.
Вторая часть книги целиком посвящена выяснению
смысла понятий производной и интеграла и способов их
применения. Так же как в начале изучения алгебры учатся
составлению уравнений, так и во второй части книги на не-
скольких примерах показано, как при помощи понятий
высшей математики формулируются соотношения между
скоростью движения и пройденным путем, между уравне-
нием кривой и ограниченной этой кривой площадью и т. п.
Вторая часть требует минимальной подготовки, не выхо-
дящей за пределы самых простых понятий алгебры и гео-
метрии. Во втором издании в этой части изложение
приблизилось к традиционному по сравнению с первым
изданием, но по-прежнему отсутствует формальная- теория
пределов.
Третья часть представляет собой в основном изложение
правил дифференцирования и интегрирования и примене-
ние этих правил к нахождению производных и интегра-
лов от различных функций. В этой части дается техника
практической работы с понятиями высшей математики.
Следующие части — от четвертой до восьмой включи-
тельно— представляют собой простые применения высшей
математики.
В части четвертой рассматриваются применения к мате-
матическим вопросам — нахождение максимума и минимума
функций, вычисление площадей и объемов.
ПРЕДИСЛОВИЕ 9
Части пятая — восьмая посвящены применениям высшей
математики к физике. Они написаны не как примеры, ил-
люстрирующие определенные математические методы, а
екорее как главы курса физики.
Когда учащемуся известны основы высшей математики,
изложение физики можно существенно изменить по сравне-
нию с обычным школьным курсом.
В этих частях рассмотрены вопросы механики, электри-
чества, молекулярного движения, радиоактивного распада.
Наряду с решением различных физических задач много
внимания уделено физической сущности рассматриваемых
явлений и физическим следствиям из полученных формул.
Переработка в связи с выпуском второго издания в этих
частях сводилась к отдельным исправлениям и дополне-
ниям, перечислять которые нет необходимости.
Первое издание было выпущено тиражом 75 000 экзем-
пляров и быстро разошлось. Выпуск второго издания по-
казывает интерес к высшей математике в широких кругах
читателей, не имеющих высшего физико-математического
или технического образования. Этот круг читателей нуж-
дается в учебнике, упрощенном по сравнению с обычными
курсами для вузов и втузов.
Введение 11-летнего образования должно привести
к пересмотру школьных программ и включению элементов
высшей математики в курс средней школы при некотором
сокращении традиционных курсов арифметики, алгебры,
геометрии и тригонометрии. Предлагаемая книга (с неболь-
шими сокращениями) в первых четырех частях дает пред-
ставление о желательном объеме курса высшей математики
в средней школе: во всяком случае следует дать оба тесно
связанных понятия — производную и интеграл. Остальные
четыре части показывают, как можно было бы формули-
ровать физические законы и разбирать такие явления, как
колебания, резонанс и др., если физика читается парал-
лельно с высшей математикой.
Выпуск второго издания не является доказательством
правильности всех методических идей, заложенных в пер-
вом издании. При обсуждении книги на секции препода-
вателей втузов Московского математического общества и в
частном порядке справедливо указывалось на необходи-
мость более точной формулировки понятий производной и
10 ПРЕДИСЛОВИЕ
интеграла. В связи с этим начало книги было существенно
переработано.
В создании книги большая роль принадлежит В. Л. Ма-
нуйлову, подготовившему рукопись первого издания к пе-
чати и составившему упражнения и задачи, а также почти
всю четвертую часть, и К. А. Семендяеву, внимательно
просмотревшему рукопись и сделавшему много ценных за-
мечаний. Пользуюсь случаем выразить искреннюю благо-
дарность всем лицам, принимавшим участие в обсуждении
первого издания книги, и в особенности Н. А. Дмитриеву,
Н. Н. Мейману, Р. С. Гутеру и Л. Я. Цлафу за принци-
пиальные критические замечания.
С благодарностью приняты и использованы при пере-
работке замечания читателей Е. Ф.Давыдова, П. П. Скля-
рова, А. Г. Соколова.
Практическую помощь в подготовке второго издания
оказал X. Г. Цванг.
Академик Я- Б. Зельдович
ЧАСТЬ I
ФУНКЦИИ И ГРАФИКИ
§ 1. Функциональная зависимость
В природе, в технике, в математике мы чрезвычайно
часто встречаемся с функциональными зависимостями.
Функциональная зависимость одной величины (у) от дру-
гой (х) означает, что каждому значению х соответствует
определенное значение у.
Величина х при этом называется независимой перемен-
ной, у—функцией этой переменной. Иногда х называют
аргументом функции.
Приведем несколько примеров из геометрии и физики:
1) Объем шара V является функцией его радиуса г
2) Объем V конуса с данной высотой h зависит от
радиуса его основания г
3) Путь г, пройденный свободно падающим телом, за-
висит от времени t, протекшего с момента, когда началось
падение,
г — 8*
4) С»ла тока / по закону Ома зависит от сопротивле-
ния проводника R при данной разности потенциалов и
i==Jk- 0.1)
Можно было бы привести еще множество примеров такого
рода.
12
ФУНКЦИИ И ГРАФИКИ
Гч. i
Характерно, что в природе и в технике в большинстве
случаев интересующая нас величина (функция) зависит от
нескольких величин. Так, например, в последнем примере
сила тока зависит от двух величин: от разности потенциа-
лов и и от сопротивления проводника R. Объем конуса
зависит от его высоты ft и от радиуса основания г.
Считая заданными и постоянными все величины, кроме
одной, мы изучаем зависимость функции от одной пере-
менной; в данной книге мы в основном ограничиваемся
функциями одной переменной.
Так, например, взяв данную аккумуляторную батарею
с определенной разностью потенциалов и, будем менять
сопротивление проводника R и измерять силу тока /;
в такой постановке опыта сила тока зависит только от
сопротивления, величину и в формуле A.1) следует рас-
сматривать как постоянный коэффициент.
В математике функциональная зависимость чаще всего
задается формулами, например,
у = 3х' — х* — х, A.2)
В этих формулах очевидно, что мы имеем дело с функ-
циями одной переменной и формула дает способ вычисле-
ния значений функции при каждом заданном значении
независимой переменной.
Зная формулу, дающую зависимость у от х, легко со-
ставить таблицу значений у для нескольких произвольно
заданных значений х.
Составим, например, такую таблицу для третьей функ-
ции из A.2). В верхней строке даны выбранные нами зна-
чения х, в нижней строке под каждым данным х дано
соответствующее значение у.
У-
X
= Зх' — х*
— X
— 3
— 87
2
— 26
1
— 3
0
0
т
1
1
а
б л и
2
18
ца 1
3
69
§ .1]
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
13
Понятно, что по данной формуле можно составить и
более подробную таблицу, задавая, например, значения
х = 0; 0,1; 0,2; ... и т. д. Таким образом, формула
«сильнее» любой таблицы. Формула содержит не только
те сведения, которые позволяют составить данную таблицу,
но позволяет также найти значения функции при значе-
ниях независимой переменной, не содержащихся в данной
таблице. С другой стороны, таблица удобнее, так как
с ее помощью можно быстрее найти значение у при дан-
ном х — если это х есть в таблице,— поскольку вычисле-
ния по формуле уже были проделаны при составлении
таблицы.
В природе и в технике, когда уже установлен закон
интересующего нас явления, этот закон выражается фор-
мулой. Однако бывает и такое положение, когда теории
явления нет и физик (или химик, биолог, техник) может
дать только результаты проделанных им опытов — зависи-
мость исследуемой величины от величины, задаваемой при
постановке опыта. Так обстоит дело, например, при иссле-
довании зависимости сопротивления проводника от его
температуры. В этом случае функциональная зависимость
может быть задана только в виде таблицы, содержащей
результаты опыта.
Из опыта известно, что для данного проводника (из
данного материала, данного сечения и данной длины)
электрическое сопротивление зависит от температуры про-
водника. При каждом значении температуры Т проводник
имеет определенное сопротивление R, так что можно гово-
рить о функциональной зависимости R от Т, о том, что
сопротивление R есть функция температуры Т.
Проводя измерения, можно найти значения R при раз-
личных Т и таким образом найти зависимость R (Т); при
этом результатом опытов является таблица, в которой
даны значения R при различных Т, например:
Таблица 2
Т (градусы
Цельсия)
R (омы)
0°
112,0
25°
118,4
50°
124,6
75°
130,3
100°
135,2
14
ФУНКЦИИ И ГРАФИКИ
[Ч. 1
Если нас интересуют значения R при других темпера-
турах, не входящих в таблицу, то в принципе нужны
дополнительные измерения, так как точная формула, даю-
щая зависимость R(T), неизвестна. Практически можно
подобрать приближенную формулу, которая хорошо согла*
совалась бы с опытом при тех температурах, при которых
приведены измерения; возьмем, например, формулу
R = 112,0 -f 0,2727* — 0,0004Т*
и составим таблицу по этой формуле:
Таблица 3
т
R (по формуле)
0
112,0
25
118,55
50
124,6
75
130,15
100
135,2
Формула дает значения R, очень близкие к опыту, при
тех температурах, при которых проделаны измерения;
поэтому законно предположение, что и при промежуточ*
ных температурах (например, при \0я или при 80я и 90°)
формула также правильно описывает функциональную
зависимость R (Т). Однако пользование формулой за пре-
делами исследованного интервала (например, при —200°С
или -f-500° С) может привести к ошибкам, поскольку нет
оснований для того, чтобы R(T) выражалось квадратным
трехчленом.
Такие формулы, полученные не из теории, а подбором,
называют эмпирическими (т. е. опытными, основанными
на опыте).
§ 2. Координаты
Для наглядного изображения функциональной зависи»
мости с помощью рисунка (графика) пользуются коорди-
натами. Проведем на плоскости две перпендикулярные
прямые. Горизонтальная прямая называется «ось х» (ось
икс) или, иначе, «ось абсцисс»; вертикальная прямая —
«ось у» (ось игреков) или «ось ординат». Точка пересечения
2]
КООРДИНАТЫ
15
У
С
О
в
Рис. 1.
прямых называется «начало координат» (точка О на рис. 1).
Обычно представляют себе, что плоскость, на которой
проведены оси х и у, не лежит на столе, а поставлена
перед читателем вертикально, как стена, против которой
Вы сидите. При этом стрелка на оси х показывает слева
направо, а стрелка на оси у — снизу вверх.
Определенная пара значений х и у, например х = 2,
t/ = 4, изображается на графике одной точкой (точка А).
Положение этой точки определяется следующими усло-
виями: перпендикуляр АВ, опущенный из точки А на
ось х, отсекает на этой оси отрезок ОВ,
равный двум единицам длины; отрезок
ОВ от начала координат О до основания
перпендикуляра В считается положи-
тельным и соответствует положительно-
му значению х, когда точка В лежит
правее точки О.
Перпендикуляр АС, опущенный из
точки А на ось у, отсекает на оси отре-
зок ОС, длина которого равна 4. На оси у
положительные значения у соответству-
ют основанию перпендикуляра С, ле-
жащему выше начала координат О. Принято положитель-
ное направление оси отмечать стрелкой и около нее ставить
букву, обозначающую название оси. Представляя себе, что
плоскость вертикальна, говорят «чем больше у, тем выше
лежит точка», отрицательные у лежат ниже положи-
тельных. Практически удобно находить точки и строить
графики с помощью миллиметровой бумаги, на которой
уже заранее проведена сетка перпендикуляров.
Важный практический совет заключается в том, что
надо приучаться сразу ставить на чертеже точку А,
соответствующую заданным значениям хну. Не следует
ставить на чертеже точки В и С и проводить пунктирные
линии (перпендикуляры) АВ и АС: всю эту работу следует
проводить в уме и не загромождать чертеж лишними ли-
ниями и обозначениями.
Отрицательные значения х отсчитываются влево от О,
отрицательные значения у отсчитываются вниз от О. На
рис. 2 приведено несколько примеров точек, для которых
хну разного знака. Читатель должен проследить, согла-
ФУНКЦИИ И ГРАФИКИ
сен ли он с тем, как поставлены эти точки, и, таким
образом, проверить, полностью ли он понял предыдущее.
Точки на рис. 2 следующие:
А: х — 2, у — 4; D:
Е:
х = —2,
= 3;
F: х = — 1, у = —
У
D(-2.3J
9
Координаты точек иногда указывают сокращенно, в скоб-
ках после названия точки, при-
чем на первом месте ставится
значение х (абсцисса точки), на
втором месте — значение у (ор-
дината точки). Для перечислен-
ных четырех точек A, D, E, F
такие обозначения приведены на
рис. 2.
Оси координат делят пло-
скость рисунка на четыре ча-
сти— четверти; четверти перену-
мерованы на рис. 3. В каждой
четверти х и у имеют опреде-
ленный знак: в I четверти х>0,
г/>0, т. е. х я у положительны; во II четверти х<0,
у>0, т. е. х отрицателен, у положителен; в III четверти
х<0, у<0, т. е. х иг/ отрицательны; в IV четверти д:>0,
о
¦—А
?C.-2}
Рис- 2-
У
ш
у\
К(-ЗО)
G@.3l
0@.0) 4B01
ш-п
Рис. 3.
Рис. 4.
у<0, т. е. х положителен, у отрицателен. Знаки х и у в
каждой четверти показаны также на рис. 3. Сравните их
со знаками координат точек A, D, E, F на рис. 2.
Если для точки G (рис. 4) задано, что лс = О, то такая
точка лежит на оси у, при этом как раз перпендикуляр
§ 3] ГЕОМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ 17
из G на ось х совпадает с осью у. Значит, основание
перпендикуляра совпадает с началом координат О, так
что расстояние от основания перпендикуляра до начала
координат равно нулю, поэтому и можно сказать, что
равна нулю абсцисса точки G, лежащей на оси у. Если
для точки F задано, что у = 0, то такая точка лежит на
оси х; при этом перпендикуляр из точки F, опущенный
на ось у, совпадает с осью х, а его основание—с началом
координат О.
Примеры таких точек показаны на рис. 4:
G(* = 0, у=3), F(x = 2, y = 0),
Н(х = 0, у = —1), К(х = —3, у = 0).
Наконец, точка, у которой х = 0, у=0, есть не что иное,
как начало координат О.
Выше мы специально советовали не наносить на чер-
теж основания перпендикуляров, т. е. поступать не так,
как это было сделано на рис. 1 и 2.
На рис. 1 необходимо было поставить точку
А(х=2, у = 4), точки В я С были вспомогательными,
служили только для построения точки А; они были по-
лезны, когда мы только делали первый шаг, впервые
определяли понятие координат. Потом следует научиться
прямо ставить точку А: если на чертеже нанесены точки
В и С, то можно принять их за заданные точки, можно
подумать, что нам было задано построить три точки:
А B, 4), В B, 0) и С @, 4).
Читатель должен потренироваться в том, чтобы быстро
ставить на графике любые точки, с положительными,
отрицательными и нулевыми значениями лт и у, а также
быстро называть хотя бы приближенно, но с правильными
знаками х и у для точки, поставленной на чертеже.
§ 3. Геометрические величины, выраженные
через координаты
Задание двух чисел — значений х и у — определяет
положение точки на плоскости. Поэтому и все геометри-
ческие величины, относящиеся к этой точке, можно выра-
зить через координаты точки.
18
ФУНКЦИИ И ГРАФИКИ
[Ч. I
Я/я.!/}
Найдем расстояние г точки А с координатами х и у
от начала координат, т. е. длину отрезка г прямой ОА,
соединяющей начало координат О с точкой А (рис. 5),
а также угол а (а — «альфа» — первая
буква греческого алфавита) *) между
прямой ОА и осью абсцисс.
Проводим вспомогательные линии
АВ и АС. Длина ОВ равна х, длина АВ
равна длине ОС, т. е. равна у. Из пря-
моугольного треугольника ОАВ по тео-
реме Пифагора
Рис. б.
Далее по определению тангенса угла имеем:
Так, например, пусть дс=2, у=3 (рис. 5). Тогда
г = 1/13^=3,6,
Заметим, что угол а всегда отсчитывается от положитель-
ного направления оси х, поэтому, например, если у = 2,
О
Рис. 6.
Рис. 7.
лг = — 2 (рис 6), то угол а— тупой, tga=-^-r = —1,
a=135°. ~~
*) Греческий алфавит и названия греческих букв даны в конце
книги, на стр. 560.
§ 31
ГЕОМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ
19
У
Когда точка лежит ниже оси х, то принято отсчиты-
вать угол а вниз от оси, считая при этом а отрицатель-
ным. На рис. 7 показаны два примера: точка А(х = 2,
у = — 2), для нееа = — 45°, и точка В(х = — 3, у =— 3),
для нее угол а =—135°. Таким образом, угол а для
любой точки лежит в пределах от — 180° до -f- 180q.
Легко решить и обратную задачу: пусть дано, что
точка А находится на заданном расстоянии г от начала
координат О и отрезок ОА образует угол а с осью х (под-
разумевается — с положительной,
правой частью оси х). Требуется
найти координаты точки А. Гля-
дя на рис. 5, получим:
х = г cos a, y = r sin а.
Эти формулы правильны без ис-
ключений, для любых положи-
тельных и отрицательных углов
а, правильно дают знаки хну
в любой четверти.
Перейдем к задачам с дву-
мя точками, А, и Аг; коорди-
наты первой точки обозначим хх, уг, координаты второй
точки хг, уг (рис. 8). Найдем расстояние гхг между этими
точками и угол а12 между отрезком АхАг и осью л:*).
Удобно провести через точку Ах прямую, параллель-
ную оси х, а через точку Аг — прямую, параллельную
оси у, на рис. 8 они проведены пунктиром, а точка их
пересечения обозначена В. При этом в треугольнике АхАгВ
а
Рис. 8.
*) Значки снизу у букв называются индексами. По-латынн
индекс значит «указатель». Их ие надо путать с показателями. Чи-
тается такое выражение: х1 — икс-однн, Аг — а-два. Одинаковые буквы
с разными индексами ((/„, ух, у%, уа, уь) применяют вместо разных
букв, для того чтобы показать, что речь идет о похожих (но в то же
время разных) величинах. Так, например хх и хг—обе эти величины
откладываются по оси х, обе являются «иксами», абсциссами. В то
же время оии относятся к разным точкам. Величины, обозначаемые
разными буквами, но с одинаковым индексом, относятся к одной
и той же точке: А1—обозначение некоторой точки, х, —ее абсцисса,
ух — ее ордината. Иногда ставят и два индекса, например г12 (читать:
эр-один-два, а не эр-двенадцать) — расстояние между точкой первой
(A) и второй (At).
20
ФУНКЦИИ И ГРАФИКИ
[Ч. I
отрезок AtB равен хг—л^, отрезок АгВ равен у,—ух. Все
построение треугольника AxAtB подобно построению рис. 5.
. По теореме Пифагора получим:
C.1)
Угол а12 находится из условия
__ Ух —
Читатель должен убедиться, что формулы правильны
при любых знаках всех четырех
величин х,, уи xt, уг и при
любых соотношениях xx>xt или
х\ < xv У\ > Уг или
Т
v У\ Уг УхУг
Так, например, на рис. 9 по-
казан случай дс, < 0, х2> 0, коорди-
наты А, (^ = — 2, *Л = 1).
х Ах{хг=^2>у у2=3). В этом случае
длина отрезка АХВ равна сумме
абсолютных величин*) |;е1| = 2,
|д:,| = 3. Но это как раз и соответствует общей формуле
АгВ = хг — xt = 3 — ( — 2) = 3 + 2 = 5.
Следовательно, правильны и выражения для rlt и tga,,.
Рассмотрим теперь задачи, относящиеся к трем точкам:
Л,, At, Аг. Как выяснить без построения, путем вычисле-
ния по значениям координат точек, лежат ли эти три
точки на одной прямой? Очевидно, что когда угол а,2
отрезка А^Аг с осью х равен углу ais отрезка А,Аг
с осью х, то это значит, что отрезки АХАЯ и Л,Л, лежат
на одной прямой. На рис. 10 показан случай, когда
ais > aIt, точка Л, лежит выше продолжения прямой AtAt, но
из этого же рисунка видно, что если бы a,s было равно а12,
•> Прямые черточки заменяют слова «абсолютная величина». Таким
образом, для положительной величины этот знак ничего не меняет,
|3| = 3, | 0,1 1=0,1. Отрицательная величина, поставленная между
прямыми черточками, равна положительной величине, получающейся
умножением данной величины на —1; так, например, |—3\=3,
)—0,1 |г=0,1. Иначе говорят иногда «модуль:»: |—3| — это модуль
минус трех равен плюс трем.
ГЕОМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ
21
то точка At лежала бы на прямой, продолжающей отре-
зок АХАХ.
Из выражения тангенса угла C.1) следует, что при
aia = als между координатами точек имеет место соотно-
шение
Ух — У\ У г — Уу ,о оч
z ~—„ „ • \°-^)
*» — х\ хг — х\
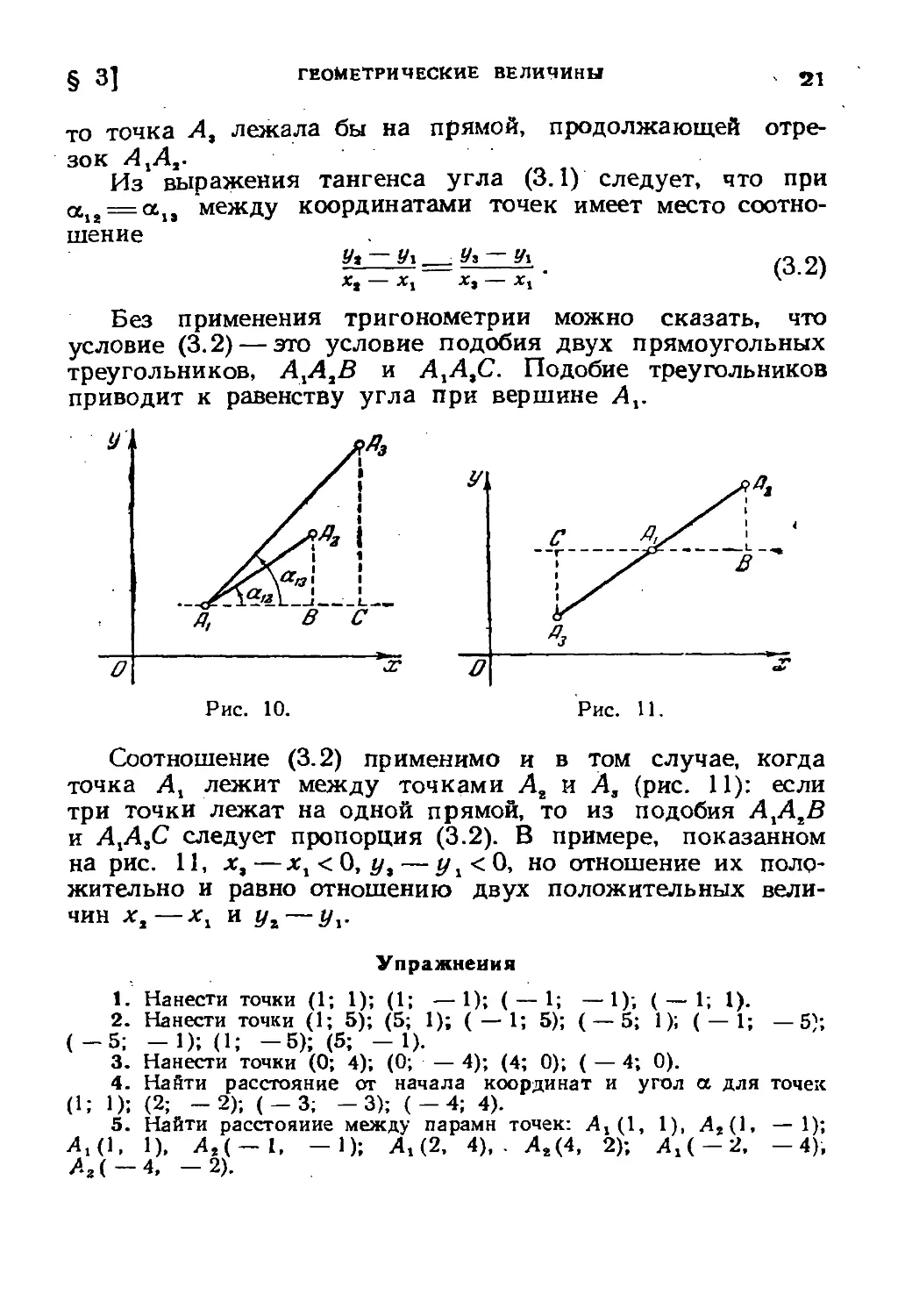
Без применения тригонометрии можно сказать, что
условие C.2) — это условие подобия двух прямоугольных
треугольников, AtA2B и АхАгС. Подобие треугольников
приводит к равенству угла при вершине Ах.
У'1
О
о
Рис. 10.
Рис. 11.
Соотношение C.2) применимо и в том случае, когда
точка Л, лежит между точками Аг и А, (рис. 11): если
три точки лежат на одной прямой, то из подобия AxAtB
и j4,j43C следует пропорция C.2). В примере, показанном
на рис. 11, х%—хх < 0, уг — ух<0, но отношение их поло-
жительно и равно отношению двух положительных вели-
чин х2—хх и уг — ух.
Упражнения
1. Нанести точки A; 1); A; —1); ( — 1; —1); ( — 1; 1).
2. Нанести точки A; 5); E; 1); ( — 1; 5); ( — 5; 1); ( — 1; —5);
(-5; -1); A; -5); E; -1).
3. Нанести точки @; 4); @; — 4); D; 0); ( — 4; 0).
4. Найти расстояние от начала координат и угол а для точек
A; 1); B; -2); (-3; - 3); ( - 4; 4).
5. Найти расстояние между парами точек: Л,A, 1), АгA, — 1);
А, (\, 1), А,( — 1. -1); Л, B, 4),. ЛгD, 2); Ах(-Ъ -4),
АА-4, -2).
22 функции и графики [ч. i
6. Выяснить, лежат ли на одной прямой тройки точек: Л, @, 0),
АгB, 3), .4,D,6); Л, @, 0), Лг B, 3), Л, ( - 2, -3); А, @. 0),
ЛгB. 3), Л,(-2, 3).
7. Выписать координаты вершин квадрата со стороной а, если
диагонали квадрата совпадают с осями хну.
8. Выписать координаты вершин правильного шестиугольника со
стороной а, если одна из его диагоналей совпадает с осью х, а центр
лежит в начале координат.
9. а) Выписать координаты вершин равностороннего треугольника
со стороной а, с основанием, лежащим на оси х, н вершиной противо-
лежащего угла на оси у. б) То же для случая, когда основание лежит
на оси х и вершина одного из углов совпадает с началом координат.
10. Дана точка Ах с координатами xlt у.. Выписать координаты
точки Ait расположенной симметрично Ах относительно оси х; то же
для Аа, расположенной симметрично Лг относительно осн у; то же
для Av расположенной симметрично Ах относительно начала коор-
динат.
§ 4. Графическое изображение функций.
Уравнение прямой
В § 2 было показано, как каждой паре значений х, у
соответствует определенная точка в плоскости.
Если задано, что у есть определенная функция х, то
это значит, что каждому значению х отвечает определен-
ное значение у; следовательно, задаваясь многими различ-
ными значениями х, мы найдем различные соответствую-
щие им у, и эти пары значений дадут много точек на
плоскости. Если увеличивать число отдельных значений х,
беря их все более близкими между собой, то, в конце
концов, точки сливаются в сплошную кривую. Эта кривая
называется графиком функции. В действительности- обычно
достаточно нанести на график несколько точек, а проме-
жуточные точки и весь график функций можно получить,
соединяя плавной линией нанесенные точки. Однако для
того чтобы при этом не сделать грубых ошибок, нужно
иметь общее представление о виде кривых, изображающих
различные функции. Мы начнем с изучения нескольких
типичных и наиболее важных функций.
Рассмотрим так называемую линейную зависимость
Пусть, например,
§ 4] ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИЙ. УРАВНЕНИЕ ПРЯМОЙ 23
Построим несколько точек, для которых х и у даиы
в таблице:
Таблица 4
X
У
0
1
1
3
2
5
3
7
Нанесем эти точки на график (рис. 12). Бросается в глаза,
что эти точки лежат на одной пря-
мой. В таком случае, проводя эту пря- У,
мую линию (отсюда название «линей-
ная зависимость», «линейная функция»),
получим полный график функции, для
любого х соответствующая точка (х, у)
лежит на прямой.
Как доказать для любой функции
вида y = kx-\-b при любых k и Ь, что
все точки ее графика лежат на одной
прямой? Для этого проверим, что усло-
вие, выведенное в конце § 3, выполняет-
ся для любой тройки точек графика.
В самом деле, рассмотрим две точ-
ки А(хх,ух) и В(х2,у2), координаты
которых удовлетворяют уравнению у = kx -\- Ь. Тогда
Уг — Ух = кхг -f- Ъ — (kxx -J- Ь) = k (лг2 — jc,),
откуда
Уш — jfi А
V
Рис. 12.
Отношение оказалось не зависящим от х1 и xt. Следо-
вательно, и для любой другой пары точек графика, и в
частности для пары точек A(xt, yx) и С(х3, у3), получим
также
Значит, для любых трех точек графика A(xt, yj,
(хг, у2) и С(хг, уа) имеет место соотношение
Уг — i/i _ Уз — Ух
24 ФУНКЦИИ И ГРАФИКИ [Ч. I
т. е. любые три точки лежат на одной прямой, а следо-
вательно, все точки графика функции у = kx -f- 6 лежат
на одной прямой. Значит, графиком функции 1/ = &лг-|-6
является прямая линия.
Уравнение у = kx -f- 6 называют уравнением прямой.
Коэффициент k определяет угол между прямой и осью х.
Подставляя в уравнение х = 0, получим у = Ь. Значит,
одна из точек прямой — это точка (О, 6); эта точка лежит
на оси у на высоте 6 над началом координат (если 6 < О,
то точка лежит под началом координат). Таким образом,
6 есть ордината точки пересечения прямой с осью у,
| 6 | — длина отрезка, отсекаемого прямой на оси ординат
(на рис. 12, 6=1).
Для того чтобы построить прямую, соответствующую
данному уравнению, не нужно вычислять координаты боль-
шого числа точек и наносить их на график: ясно, что если
построены две точки, то тем самым полностью определена
прямая, проходящая через эти две точки.
Можно, например, всегда брать две точки: при лг=О,
у = Ь и при х—\, y = b-{-k, и приводить прямую по
этим точкам. Можно в качестве второй точки брать точку
пересечения прямой с осью лг (* = *„, у = 0). Из условия
y=ikxo-irb = O найдем хо = -^ .
Полезно так поупражняться в построении графиков,
чтобы сразу, с одного взгляда на уравнение, примерно
представлять себе ход и положение соответствующей линии.
Для линейной функции, графиком которой является
прямая линия, это совсем легко. Ведь на самом деле ход
прямой зависит только от двух величин k и 6, входящих
в уравнение прямой. Таким образом, нужно разобрать не
так уж много вариантов: k может быть положительно или
отрицательно, k может быть большим или малым по абсо-
лютной величине (больше 1 или меньше 1), Ъ может быть
положительным или отрицательным.
Покажем, как проводится такое исследование.
Начнем со случая 6=0, т. е. с уравнения y = kx.
Соответствующая прямая, очевидно, проходит через начало
координат, т. е. через точку х=0, у = 0. На рис. 13 по-
казано несколько прямых с различными k: k = Q, 1; k=l;
k= 10; k = — 0,1; k = —1; fe = —10. Значения k обо-
§ 4] ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИЙ. УРАВНЕНИЕ ПРЯМОЙ 25
W
*=/
значены на обоих концах каждой прямой. Проверьте пра-
вильность проведения каждой прямой, и тогда Вы убеди-
тесь в правильности сле-
дующих общих выводов:
1) если k > 0, то пря-
мая лежит в I и III
четверти, если k < 0, пря-
мая лежит во II и IV
четверти.
2) При k= 1, со-
гласно предыдущему,
прямая лежит в I и III
четверти. Часть прямой,
лежащая в I четверти,
образует угол а =Ч45° с
осью х, т. е. делит по-
полам угол между осью
х и осью у; напомним,
что под словами «угол
с осью х» подразумевается угол с положительным направле-
нием оси х, показанным стрелкой. Продолжение прямой,
лежащее в III четверти, образует с осью х угол сс = — 135°
(на рис. 13 углы не показаны).
3) При k = — 1 часть прямой, лежащая во 11 четверти,
образует угол а= 135° с осью х, а продолжение прямой
в IV четверти — угол а = — 45°.
4) Если |fe|<^l, прямая идет полого, т. е. идет ближе
к оси х, чем к оси у< и тем более полого, чем меньше \k\.
Если |fe|^>l, прямая идет
круто, ближе к оси t/, чем
к оси х, тем круче, чем боль-
ше \k\.
Теперь, когда это усво-
ено, разберем общий случай
прямой с Ь, отличным от нуля.
Пусть на графике нарисо-
вана прямая с 6 = 0, напри-
рис 14. меР У== 0,5л: (Рис- 14). Чем
отличаются от нее прямые
с 6=7^=0, но с тем же k, т. е., например, прямая у =
= 0,5лг-{-2? Для удобства будем обозначать г/0 = 0,5д;
26 ФУНКЦИИ И ГРАФИКИ [Ч. I
и г/2 —0,5*-}-2 *). При каждом данном х уг на две едини-
цы больше уп. Значит, точки прямой ух получатся из точек
прямой у0 с тем же х путем подъема на две единицы. Зна-
чит, прямая уг параллельна прямой уа и лежит выше нее
на две единицы. Очевидно, что такое правило справедливо
при любом Ъ (если 6<^0, то прямая лежит ниже начала
координат, ниже соответствующей прямой y — kx).
Усвоив, как идут прямые с уравнениями y=kx при
различных k, мы теперь легко представим себе общий ход
прямой y = kx-\-b с любыми k и Ь. Упражнения для
тренировки даны в конце параграфа.
Величину k в уравнении у = kx -f- b называют угловым
коэффициентом прямой; короче и нагляднее можно на-
звать k «крутизной прямой», так как от этой величины
зависит наклон прямой. В частном случае fe = O полу-
чается уравнение у = Ь (подразумевается у = Ь при любых
значениях х), чему соответствует горизонтальная прямая,
крутизна которой равна нулю. Можно представить себе
пешехода, идущего по прямой слева направо, в сторону
возрастающих значений х. Если &^>0, то пешеход
поднимается в гору (крутизна положительная), если k <^ О,
пешеход идет под гору (отрицательная крутизна).
Величина k дает отношение изменения функции к из-
менению ее аргумента: в самом деле,
Ьхг + Ь — (kxx -\- Ь) __ ^
хг — хх хг — х,
Такое отношение мы уже вычисляли выше, когда доказы-
вали, что линейная функция на графике изображается
прямой линией.
В дальнейшем в общем случае произвольной функции
мы будем рассматривать величину ¦ *' — У(х\) ^ равную
Х2 Х1
тангенсу угла между отрезком, соединяющим две точки
xi> y(xi) и *». У (хг)> и осью абсцисс. Линейная функция
отличается тем, что для нее такая величина одинакова
*) Здесь мы пользуемся индексами несколько иначе, чем раньше.
у0 относится к целой прямой, это не ордината определенной точки,
а ордината произвольной точки на прямой с данным Аи й = 0; уг —
это ордината произвольной точки на прямой с данным Аи Ь = 2,
т. е. уа это ие число, а функция х, г/0 (х), и соответственно уг есть
Уг (х)> Другая функция х.
§ 5]
ПАРАБОЛА
27
для любой пары точек, не зависит ни от хг, ни от хх,
поэтому и получается, что все точки у линейной функции
лежат на одной прямой.
Упражнения
Построить прямые: у = Зх, у—Ъх-\-2, у = Ъх—1, у = 2— ж,
у = 2 — 0,5*. у = — х — 3.
§ 5. Парабола
Рассмотрим функции
=\
с различными значениями а. Так, например, при а
составим таблицу:
Таблица 5
X
у = *
— 2
j
+ 1
0
0
+ 1
+ 1
+ 2
+ 4
Какие общие свойства этой функции?
^0 >0
при
х и
толь-
1) Всегда у^>0, как при х>0, так и
Значит, кривая вся расположена выше оси
ко в начале координат соприка-
сается с осью х. У
2) Наименьшее значение (ми-
нимум) у достигается при д; = 0.
Минимум у равен 0. На гра-
фике минимум изображается
наиболее низкой точкой кривой.
3) При двух одинаковых по
абсолютной величине и проти-
воположных по знаку значе-
ниях х получаются одинаковые
как по знаку, так и по величи-
не значения у. Значит, кривая
симметрична относительно оси у.
Кривая показана на рис. 15. Такая кривая называется
параболой (при любом значении а).
q
Рис. 15.
28
ФУНКЦИИ И ГРАФИКИ
[Ч. I
При любом положительном а уравнение у = ахг имеет
те же свойства, которые указаны выше для t/ = je*.
Что будет, если а<^0? Рассмотрим пример а = — 2,
у = — 2х*. Составляем таблицу:
Таблица 6
X
У
— 2
— 8
— 1
— 2
0
0
1
— 2
2
— 8
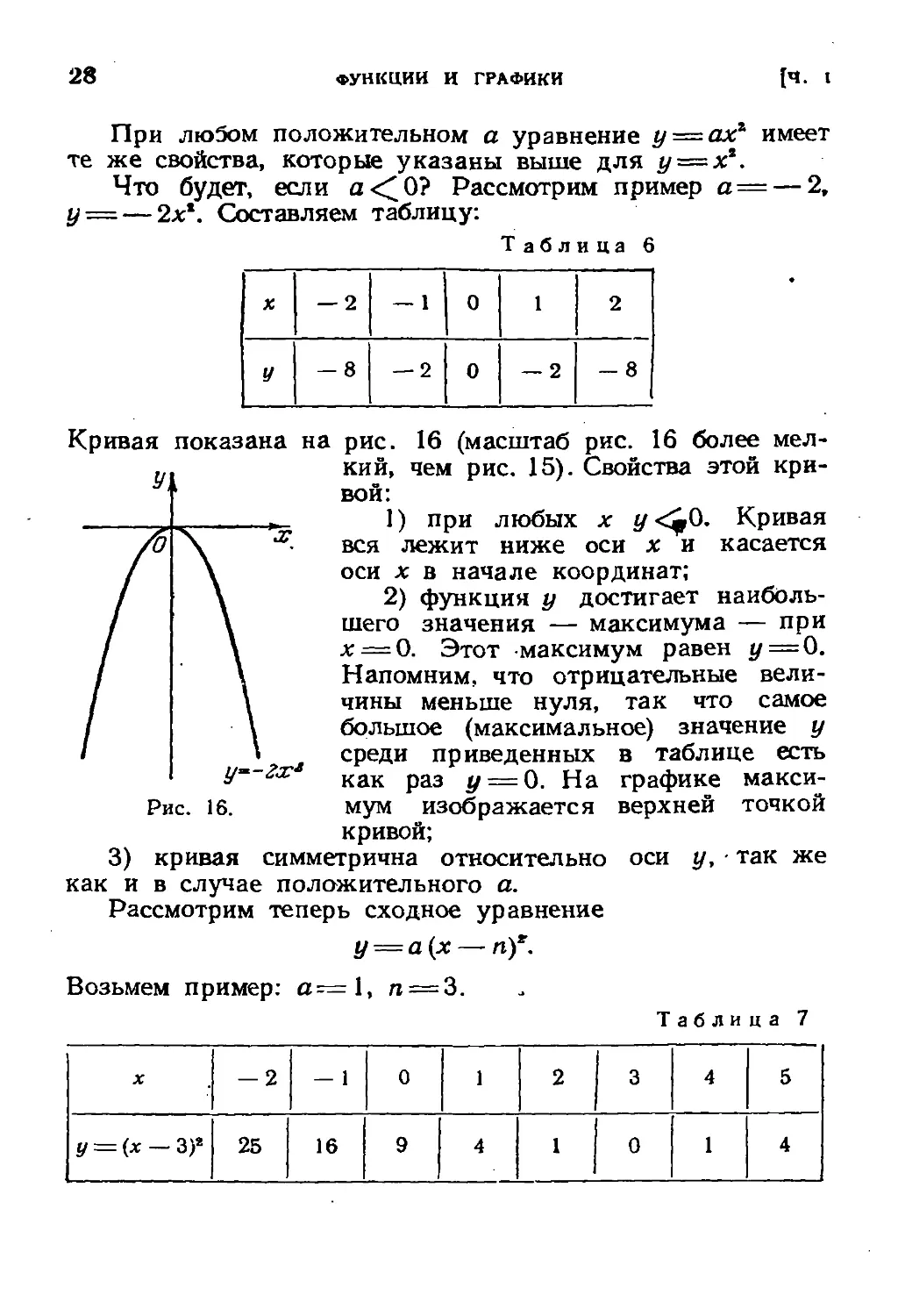
Кривая показана на рис. 16 (масштаб рис. 16 более мел-
кий, чем рис. 15). Свойства этой кри-
вой:
1) при любых х у<^0. Кривая
вся лежит ниже оси х и касается
оси х в начале координат;
2) функция у достигает наиболь-
шего значения — максимума — при
х = 0. Этот максимум равен у = 0.
Напомним, что отрицательные вели-
чины меньше нуля, так что самое
большое (максимальное) значение у
среди приведенных в таблице есть
как раз у = 0. На графике макси-
мум изображается верхней точкой
кривой;
3) кривая симметрична относительно оси у, ¦ так же
как и в случае положительного а.
Рассмотрим теперь сходное уравнение
Возьмем пример: а=1, п = 3.
X
у = (х-г)*
-2
25
— 1
16
0
9
1
4
2
1
Т
3
0
а б л и
4
1
ц a 7
5
4
§5]
ПАРАБОЛА
29
f{x)=x\ f( — x) = x\
О
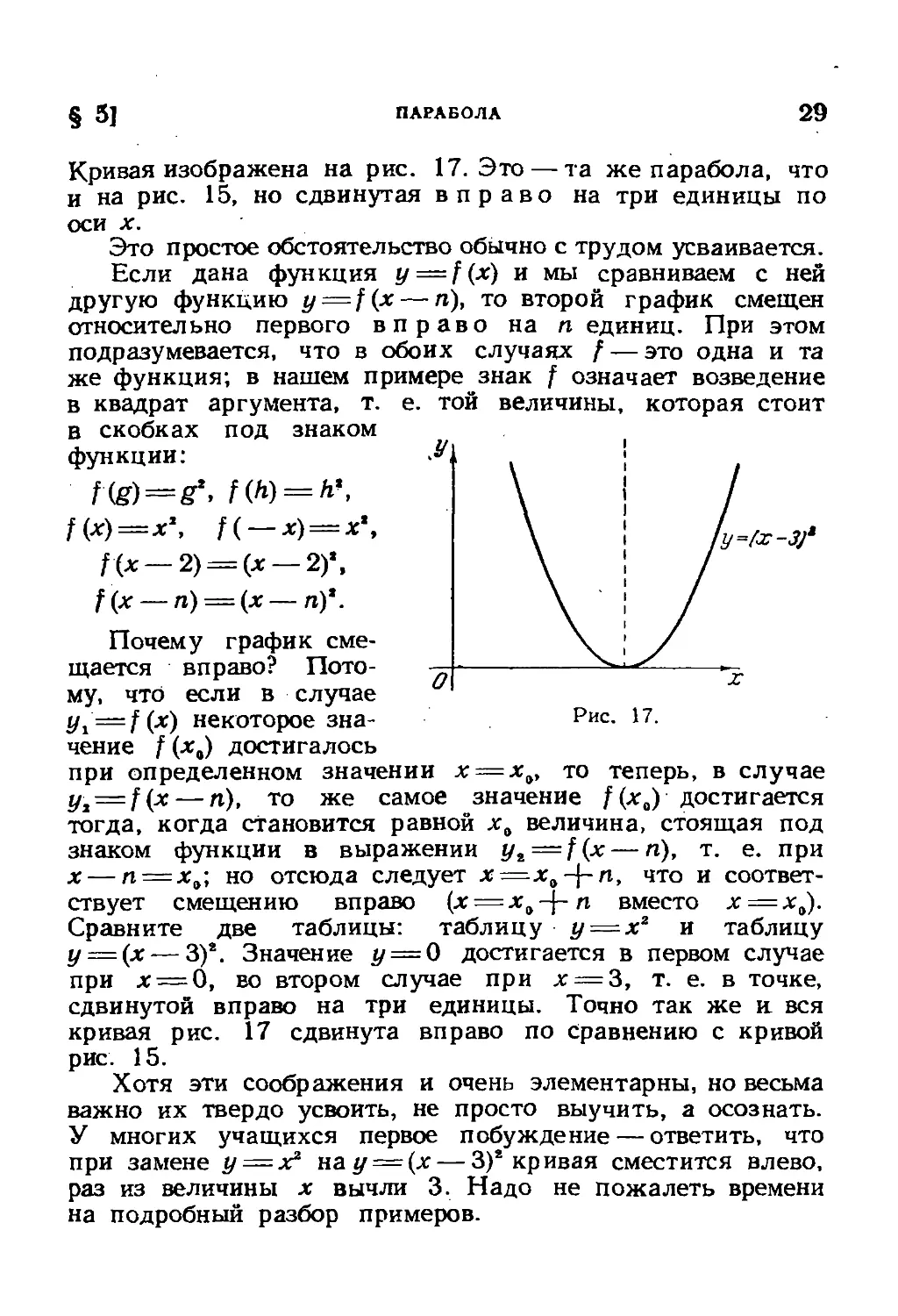
Кривая изображена на рис. 17. Это — та же парабола, что
и на рис. 15, но сдвинутая вправо на три единицы по
оси х.
Это простое обстоятельство обычно с трудом усваивается.
Если дана функция y = f(x) и мы сравниваем с ней
другую функцию y = f{x — п), то второй график смещен
относительно первого вправо на п единиц. При этом
подразумевается, что в обоих случаях / — это одна и та
же функция; в нашем примере знак / означает возведение
в квадрат аргумента, т. е. той величины, которая стоит
в скобках под знаком
функции:
fy-fx-Sf
Почему график сме-
щается вправо? Пото-
му, что если в случае
yx = f (x) некоторое зна-
чение / (дс0) достигалось
при определенном значении х = ха, то теперь, в случае
yt = f(x — n), то же самое значение f(xa) достигается
тогда, когда становится равной ха величина, стоящая под
знаком функции в выражении y2=f(x — п), т. е. при
х — п = ха; но отсюда следует x=xa-jrn, что и соответ-
ствует смещению вправо (х = ха-\- п вместо * = *„).
Сравните две таблицы: таблицу г/ = дсг и таблицу
у = (х — 3)г. Значение г/ = 0 достигается в первом случае
при дс = О, во втором случае при х = 3, т. е. в точке,
сдвинутой вправо на три единицы. Точно так же и. вся
кривая рис. 17 сдвинута вправо по сравнению с кривой
рис. 15.
Хотя эти соображения и очень элементарны, но весьма
важно их твердо усвоить, не просто выучить, а осознать.
У многих учащихся первое побуждение — ответить, что
при замене у = х* нау = (х — 3)* кривая сместится влево,
раз из величины х вычли 3. Надо не пожалеть времени
на подробный разбор примеров.
Рис. 17.
30
функции и графики
Теперь можно сформулировать общие правила:
1) Кривая у—а(х — tif имеет в качестве оси сим-
метрии вертикальную прямую х = п.
2) Эта кривая при а>0 лежит выше оси х и имеет
минимум у = 0 при х — п. При а<0 кривая лежит ниже
оси х и имеет максимум у = 0 при х = п.
Наконец, есть еще одно видоизменение уравнения,
которое не меняет формы кривой: рассмотрим функцию
у = а{х — п)*-\-т.
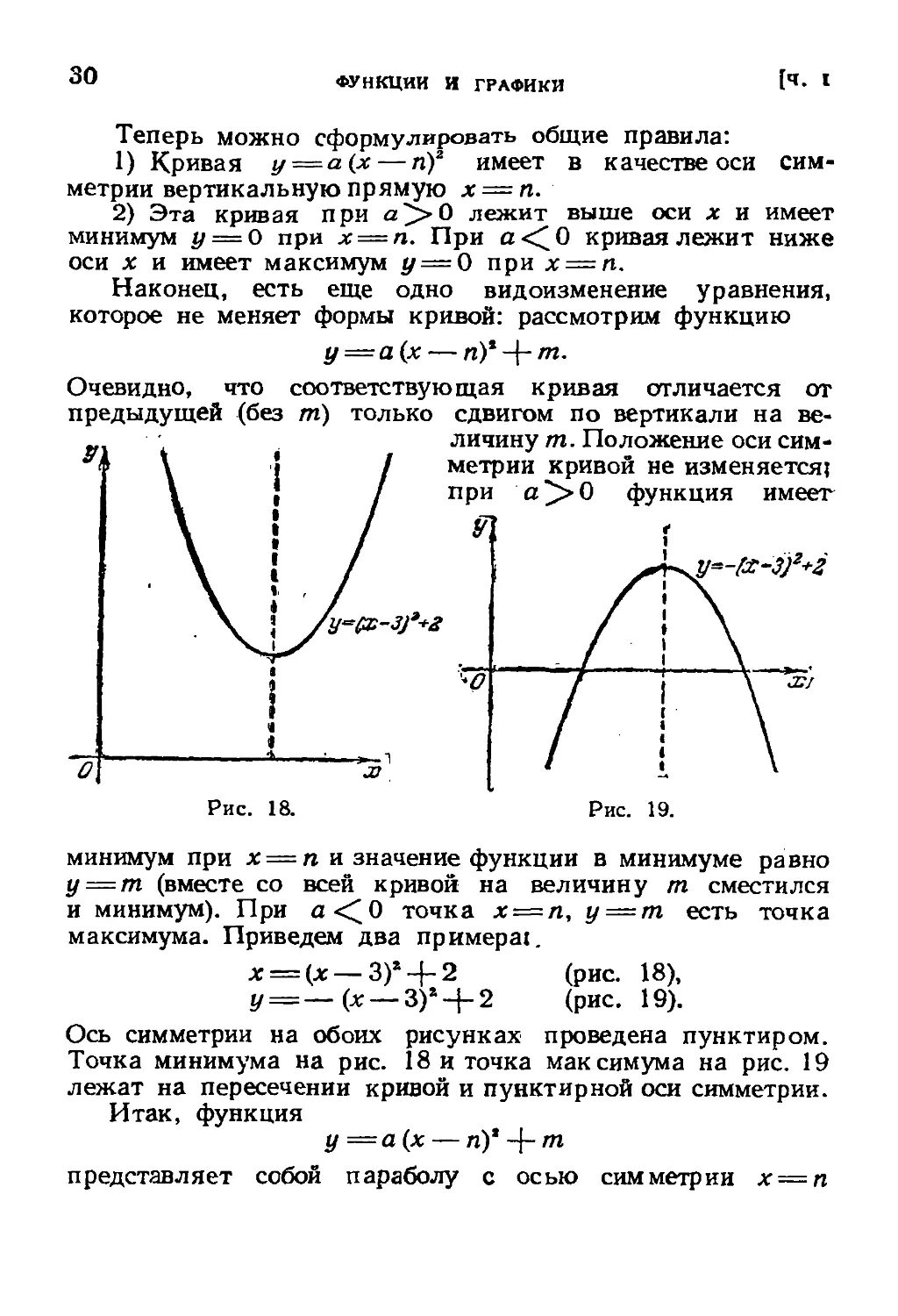
Очевидно, что соответствующая кривая отличается от
предыдущей (без т) только сдвигом по вертикали на ве-
личину т. Положение оси сим-
метрии кривой не изменяется}
при а^>0 функция имеет
Рис. 18.
Рис. 19.
минимум при х = п и значение функции в минимуме равно
у = т (вместе со всей кривой на величину т сместился
и минимум). При а«<0 точка х = п, у = т есть точка
максимума. Приведем два примера!.
х = (х — 3)* + 2 (рис. 18),
у = — (х — 3)*-f2 (рис 19).
Ось симметрии на обоих рисунках проведена пунктиром.
Точка минимума на рис. 18 и точка максимума на рис. 19
лежат на пересечении кривой и пунктирной оси симметрии.
Итак, функция
представляет собой параболу с осью симметрии
§ 5] ПАРАБОЛА 31
и минимумом у (если а^>0) в точке х = п, у = щ. При
а<ГО та же точка представляет собой максимум у.
t{a графике минимальное (в переводе на русский — на-
именьшее) значение у соответствует точке кривой, располо-
женной ниже всех других точек, т. е. точке кривой, у
которой у меньше, чем у других точек. Максимум функции
у(х) (наибольшее значение функции) на графике соответст-
вует точке, расположенной выше других точек. Вместо
того, чтобы говорить о точке на графике, соответствующей
минимуму или максимуму функции, мы кратко называем
эту точку точкой минимума или максимума на кривой.
Раскрывая скобки у выражений у = а(х— пJ-\-т,
запишем:
у = ах* — 2апх ~\- an* -\- т.
Это выражение есть полино_м__второй- степени. Обычный
способ записи самого"'общего"полинома второй степени
у = а1хх-\-Ьх-\-с.
Выбирая подходящие значения а, п, т. в предыдущем
выражении, можно всегда сделать его тождественным
с последним выражением. Для этого сравним соответственно
члены с Xх, с х и без х:
ахх* = ах*; — 2апх = Ьх; ап2 -\-т=с.
Из первого выражения следует ах =а.
Из второго — 2ап= Ь; п=—~- .
ьг
Из третьего an*-j-m = c; т = с—ап2=с — ^ .
Следовательно, можно написать тождество
С помощью графика параболы можно разобраться
в решении квадратного уравнения и в различных случаях,
которые при этом возникают. К решению квадратного
уравнения
ах*-\-Ьх-{-с = 0
можно подойти так: рассмотрим всю кривую
32
ФУНКЦИИ И ГРАФИКИ
и найдем точки пересечения этой кривой с осью л:. В этих
точках у = 0, следовательно, значения х, соответствующие
точкам пересечения, это и есть корни квадратного уравнения.
Но мы знаем, что кривая у = ах* -j- Ъх -j- с есть пара-
бола. Нам известно, что у этой параболы есть ось симмет-
Ь ^
рии — вертикаль х = — ^ , что при а^>0 парабола имеет
точку минимума на оси и высота этого минимума равна
У = с — ^- (мы смотрим на вторую часть последней формулы,
имеющую привычный вид
а (х — тг)г -j- m). «Рога» пара-
болы при а ^> 0 обращены
вверх.
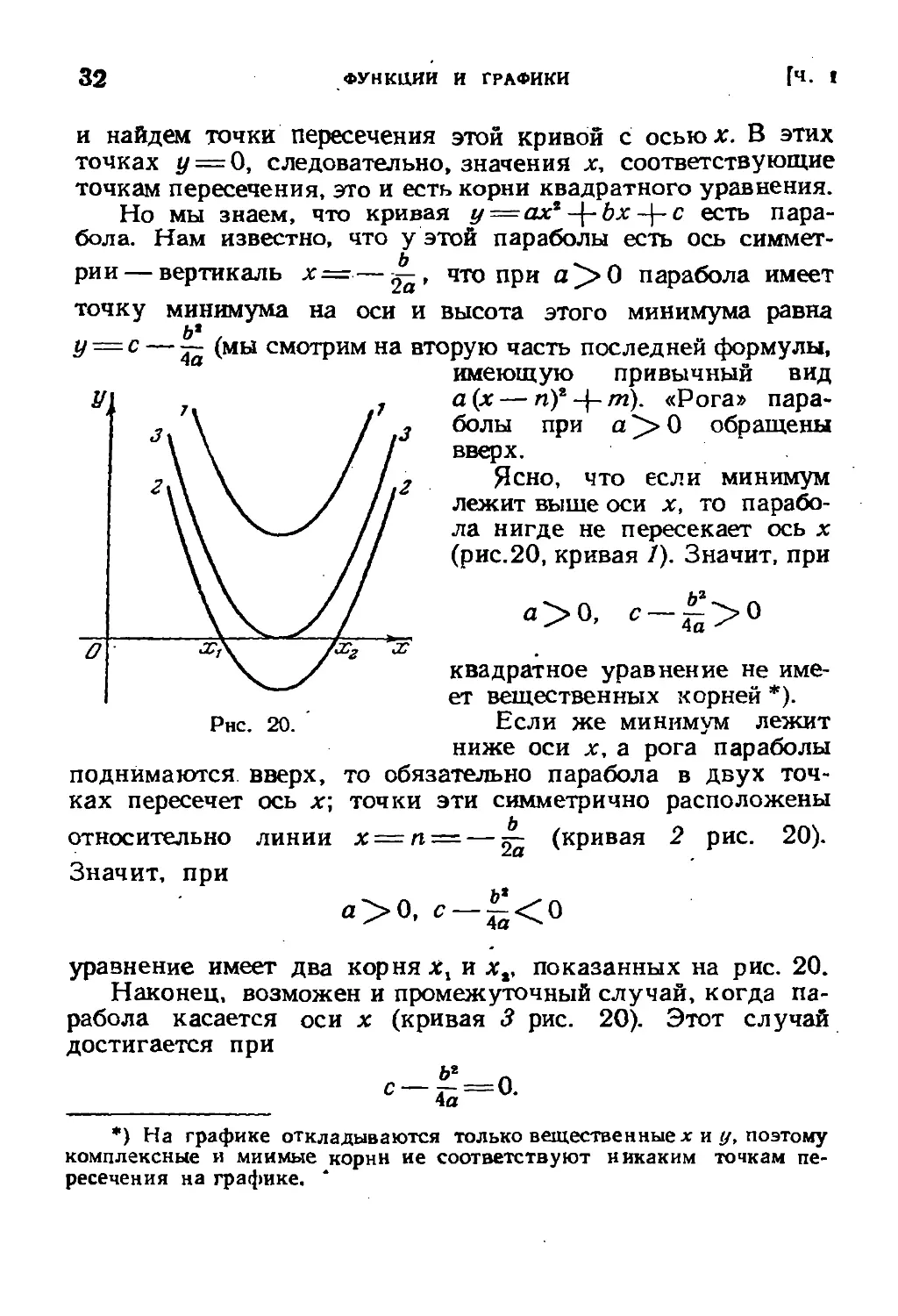
Ясно, что если минимум
лежит выше оси х, то парабо-
ла нигде не пересекает ось х
(рис.20, кривая /). Значит, при
а>0,
¦г>о
квадратное уравнение не име-
ет вещественных корней *).
Рнс. 20. Если же минимум лежит
ниже оси х, а рога параболы
поднимаются вверх, то обязательно парабола в двух точ-
ках пересечет ось х; точки эти симметрично расположены
относительно линии jc = n = — ^~ (кривая 2 рис. 20).
Значит, при
уравнение имеет два корня хх и xv показанных на рис. 20.
Наконец, возможен и промежуточный случай, когда па-
рабола касается оси х (кривая 3 рис. 20). Этот случай
достигается при
*) На графике откладываются только вещественные х и у, поэтому
комплексные и мнимые корнн ие соответствуют никаким точкам пе-
ресечения на графике. *
К 5] • ПАРАБОЛА 33
Если постепенно переходить от кривой 2 к кривой 3,
поднимая параболу, то, очевидно, два корня дс, и хг будут
сближаться, пока они не сольются в момент касания. По-
этому в случае с — 4а = 0 говорят не об одном корне,
а о двух равных (слившихся) корнях уравнения.
Таким же способом рассматривается случай а <^0, когда
кривая имеет максимум, а рога ее обращены вниз. Пред-
лагаем читателю самому нарисовать кривые и проверить,
что при:
с—4^с<С0 —нет вещественных корней,
^>0 —два вещественных корня.
с — — =0 —касание, два равных корня.
Обычная формула корней квадратного уравнения
— Aac
t1-* ~2~R
Уравнение имеет два вещественных корня в том случае,
если можно извлечь \^Ьг — 4ас, т. е. если
Ьг — 4а
Запишем это выражение так:
Условие Ь1 — 4ас^>0 выполняется в двух случаях:
2) а<0, С-?>0.
Это и есть те два случая существования двух корней,
которые были получены выше из рассмотрения кривых
у = ах* -j- bx -j- с.
Заметим, наконец, что в зависимости от знака коэф-
фициента а при х* в уравнении параболы кривая распо-
ложена выпуклостью вниз (при а > 0) или выпуклостью
2 Я. Б. Зельдович
34
ФУНКЦИИ И ГРАФИКИ
О
вверх (при а<0). Это свойство не зависит от значений
и знаков Ъ и с в уравнении параболы у = ах* -j- bx -f- с.
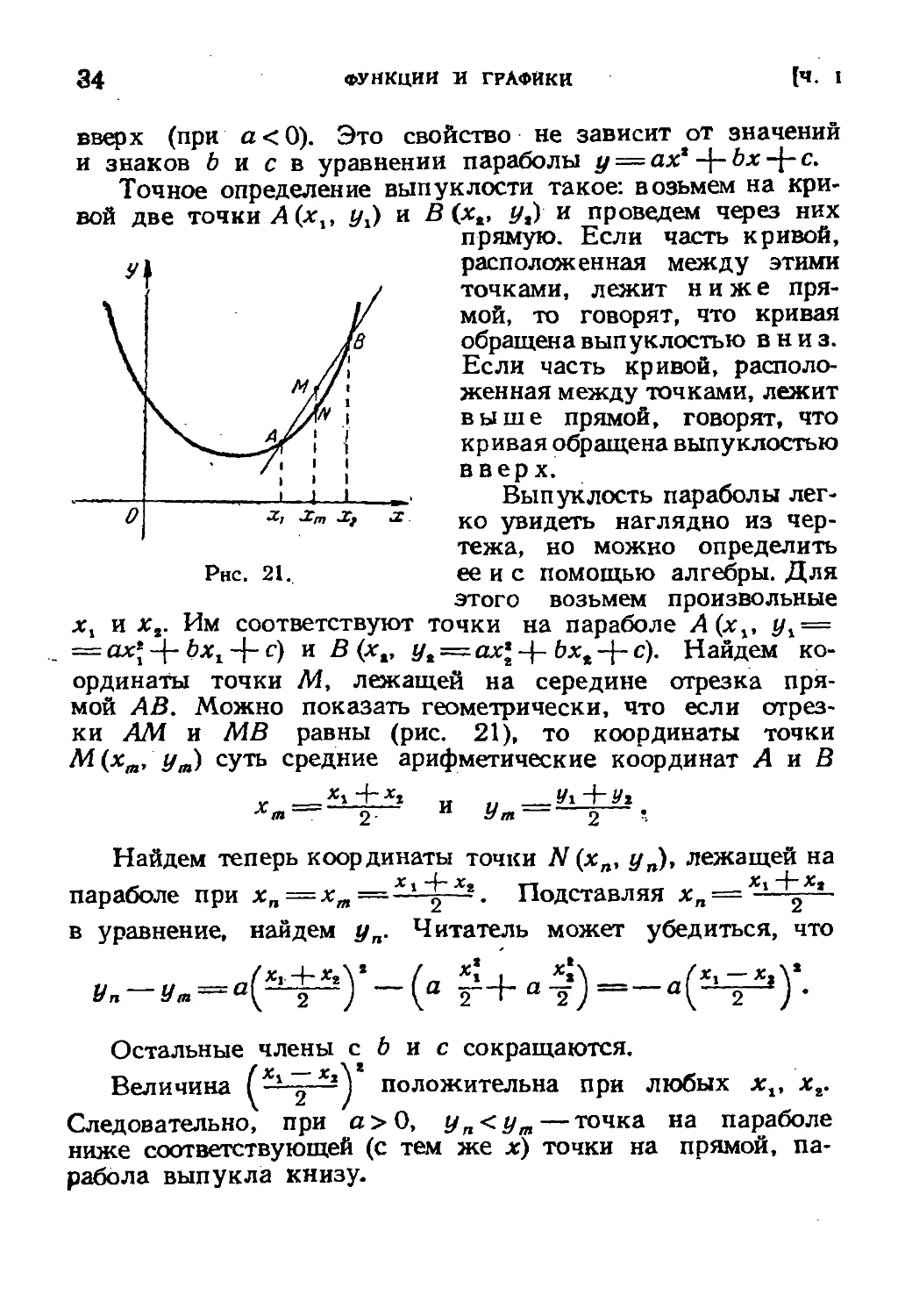
Точное определение выпуклости такое: возьмем на кри-
вой две точки Л (л:,, ух) и В (х„ у„) и проведем через них
прямую. Если часть кривой,
расположенная между этими
точками, лежит ниже пря-
\ I/ мой, то говорят, что кривая
\ /в обращена выпуклостью вниз.
\ /1\ Если часть кривой, располо-
^ м*'' женная между точками, лежит
выше прямой, говорят, что
кривая обращена выпуклостью
вверх.
Выпуклость параболы лег-
ко увидеть наглядно из чер-
тежа, но можно определить
ее и с помощью алгебры. Для
этого возьмем произвольные
хх и а:,. Им соответствуют точки на параболе А(хх, у^ —
= ах\-\- bxx -f-с) и В (хк, ул = ах\-\- Ьхг-\-с). Найдем ко-
ординаты точки М, лежащей на середине отрезка пря-
мой АВ. Можно показать геометрически, что если отрез-
ки AM и MB равны (рис. 21), то координаты точки
М(хт, ут) суть средние арифметические координат А и В
х *i+*t „ Ух+Ух
хт <f "т 2 '-
Найдем теперь координаты точки N (хп, уп), лежащей на
параболе при хп==хт==^-^~*. Подставляя х„ = *' „ * ¦
в уравнение, найдем уп. Читатель может убедиться, что
Рнс. 21.
Остальные члены с Ь и с сокращаются.
Величина ( -^—Ч положительна при любых xt, хг.
Следовательно, при а>0, Уп<у„ — точка на параболе
ниже соответствующей (с тем же х) точки на прямой, па-
рабола выпукла книзу.
§.61
КУБИЧЕСКАЯ ПАРАБОЛА, ГИПЕРБОЛА, КРУГ
35
§ в. Кубическая парабола, гипербола, круг
Рассмотрим коротко еще несколько примеров кривых,
изображающих простые функции.
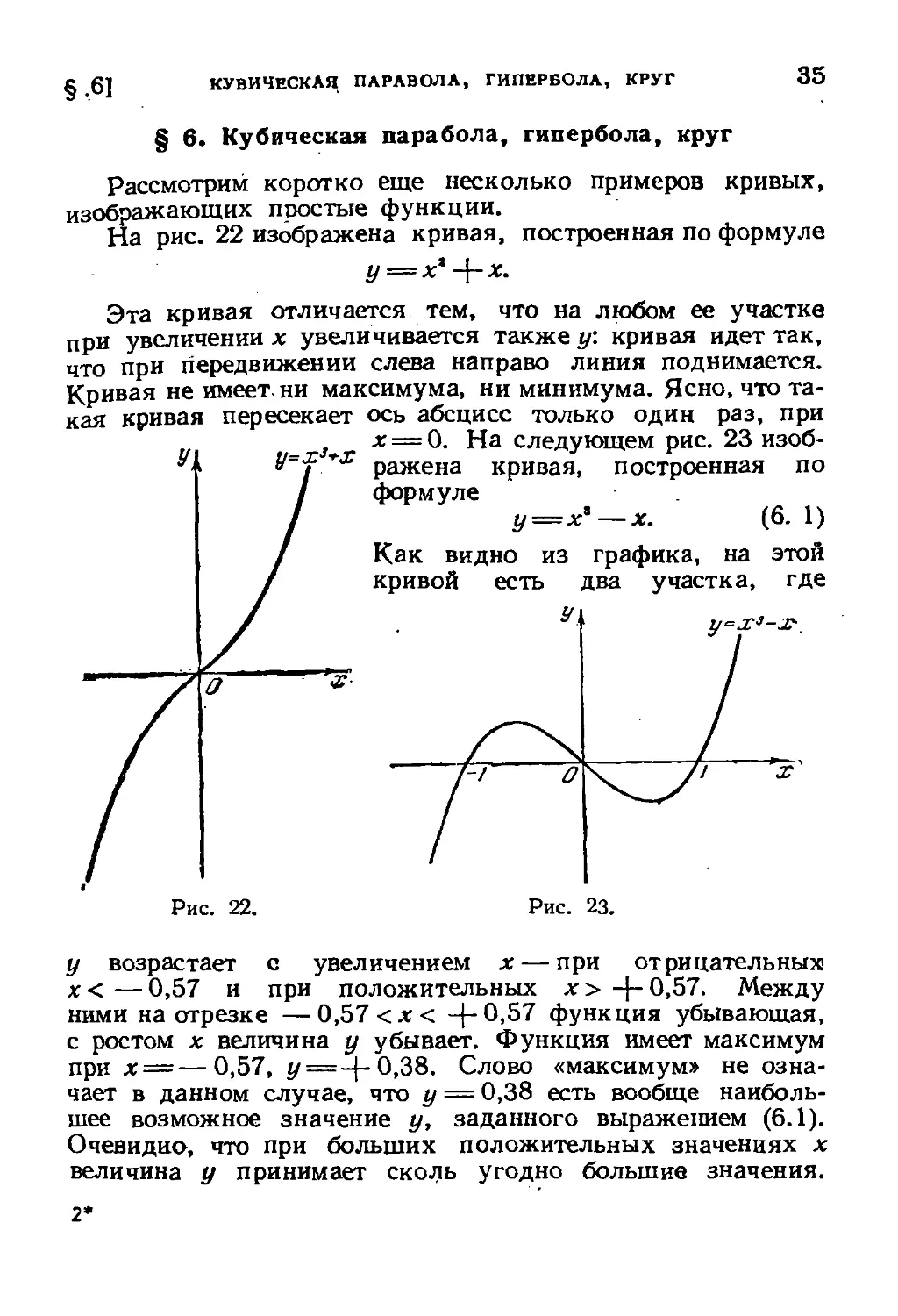
На рис. 22 изображена кривая, построенная по формуле
у = х*-{-х.
Эта кривая отличается тем, что на любом ее участке
при увеличении х увеличивается также у: кривая идет так,
что при передвижении слева направо линия поднимается.
Кривая не имеет, ни максимума, ни минимума. Ясно, что та-
кая кривая пересекает ось абсцисс только один раз, при
3 х = 0. На следующем рис. 23 изоб-
у=х *х разкеда кривая, построенная по
формуле
у = х'-Х. F.1)
Как видно из графика, на этой
кривой есть два участка, где
У1
X
Рис. 22.
Рис. 23.
у возрастает с увеличением х — при отрицательных
х< —0,57 и при положительных х> +0,57. Между
ними на отрезке —0,57 <х< -{-0,57 функция убывающая,
с ростом х величина у убывает. Функция имеет максимум
при х = —0,57, у = -\- 0,38. Слово «максимум» не озна-
чает в данном случае, что у = 0,38 есть вообще наиболь-
шее возможное значение у, заданного выражением F.1).
Очевидио, что при больших положительных значениях х
величина у принимает сколь угодно большие значения.
36
ФУНКЦИИ И ГРАФИКИ
Чем же выделяется точка максимума (х =— 0,57,
у = + 0,38)?
Как видно из графика, в этой точке у больше, чем
в соседних точках. Точка максимума отделяет участок,
где функция является ра-
стущей (слева от максиму-
ма), от участка, где функ-
ция убывает (справа от мак-
симума).
В точке je = -j-0,57,
у = — 0,38 функция имеет
минимум.
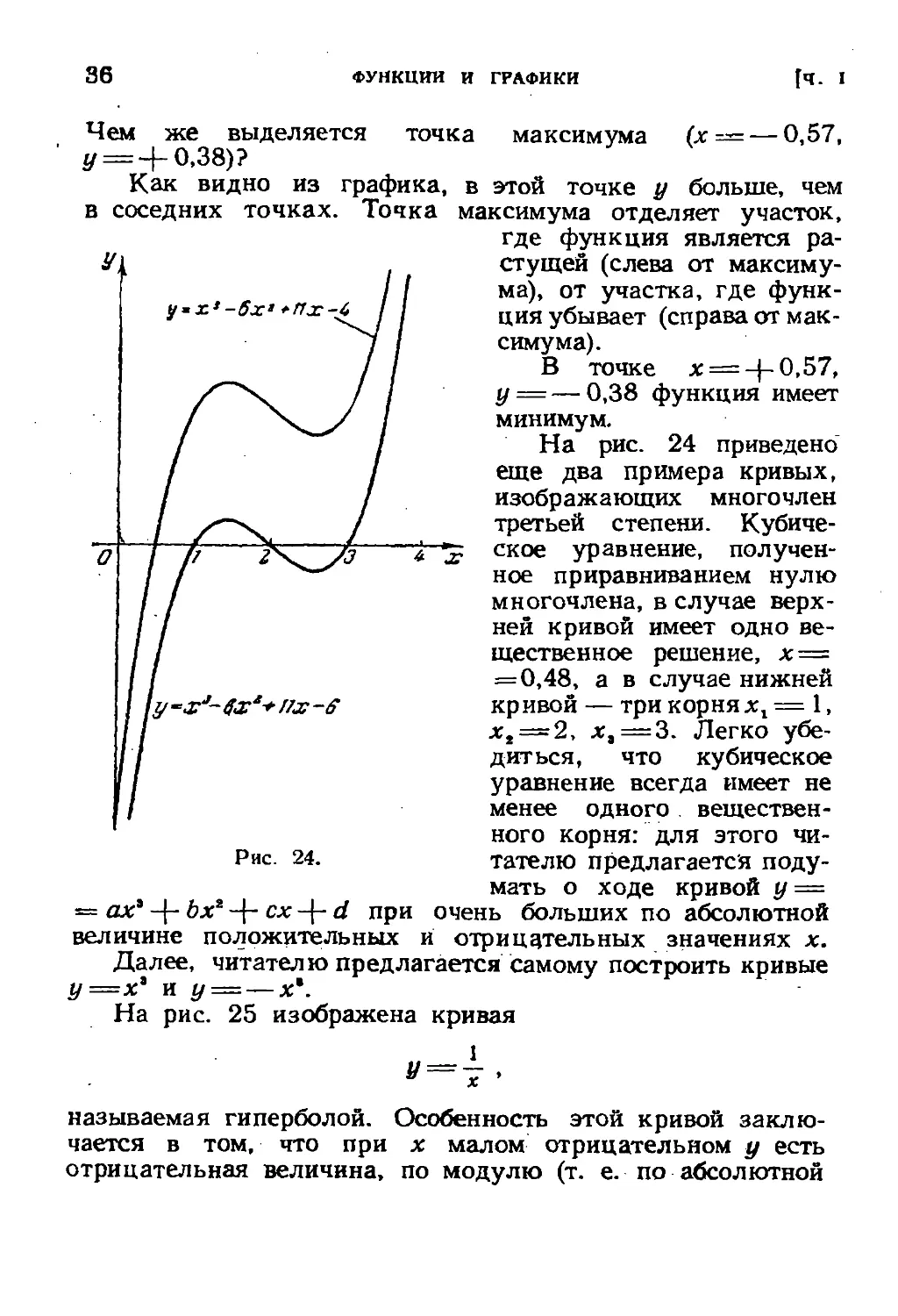
На рис. 24 приведено
еще два примера кривых,
изображающих многочлен
третьей степени. Кубиче-
ское уравнение, получен-
ное приравниванием нулю
многочлена, в случае верх-
ней кривой имеет одно ве-
щественное решение, х =
= 0,48, а в случае нижней
кривой — три корня хх = 1,
xt = 2, лг,=3. Легко убе-
диться, что кубическое
уравнение всегда имеет не
менее одного веществен-
ного корня: для этого чи-
тателю предлагается поду-
мать о ходе кривой у =
= ах* -\- Ьхг -\-cx-\-d при очень больших по абсолютной
величине положительных и отрицательных значениях х.
Далее, читателю предлагается самому построить кривые
у=х* и у = — х*.
На рис. 25 изображена кривая
Рис 24.
называемая гиперболой. Особенность этой кривой заклю-
чается в том, что при х малом отрицательном у есть
отрицательная величина, по модулю (т. е. по абсолютной
§ 6]
КУБИЧЕСКАЯ ПАРАБОЛА, ГИПЕРВОЛА, КРУГ
37
величине) очень большая, а при малом положительном х
у есть очень большая положительная величина — см. табл. 8.
X
У
— 1
1
— 0.1
— 10
— 0,01
— 100
— 0,001
— 1000
0.001
1000
0,01
100
Т а бл
0,1
10
и ца 8
1
1
Поэтому говорят, что значение у при х = 0 есть ± оо,
т. е. плюс бесконечность или минус бесконечность, в за-
висимости от того, с какой сторо-
ны мы подходим к х = 0.
Как видно из рис. 25, кривая
состоит из двух ветвей, при х < 0
и при х > 0, не соединенных меж-
ду собой.
До сих пор мы задавали у как
функцию х и строили соответству-
ющую кривую. Теперь на примере
круга решим обратную задачу: за-
дадим кривую и найдем, какой
функциональной зависимости у от
х соответствует эта кривая. Рассмотрим круг радиуса г
с центром в начале координат. Точки круга находятся
на расстоянии г от начала координат. По теореме Пифа-
гора это значит, что
У
о
К
—
Рис. 25.
Если выразить явно у как функцию х, получим:
Когда мы рассматриваем круг как график функции у(х)г
то из графика видно, что функция неоднозначна: при'
каждом значении х (при |д:|<г) есть две точки на кри-
вой— на верхней и на нижней полуокружности. Этим
двум точкам соответствуют два знака квадратного корня.
Функции у = -\-\/Ггг—хг соответствует верхняя полу-
окружность, функции у = — ]/"г* — ^соответствует ниж-
няя полуокружность.
38 функции и графики Гч. i
Составим теперь уравнение круга с центром в точке
(а, 6). Поступим формально: мы знаем, что если заменить
в выражении функции х на х— а, то график функции
смещается на а единиц вправо. Значит,
есть уравнение круга, смещенного вправо на а единиц,
т. е. с центром в точке (х = а, у=0) на оси х.
Далее, если ко всем значениям у добавить одну и ту
же величину Ъ, то весь график поднимется на b единиц *).
Значит, искомое уравнение круга с центром в точке (а, 6)
у=±У(х— а)* + г*-И.
В данном случае проще было вывести уравнение
непосредственно геометрически из выражения расстояния
между точками (х, у) и (а, 6)
г* = (х — а)г-\-(у — Ь)\
Мы нарочно поступили более формально для того, чтобы
еще на одном примере показать, как замена х на х — а
иг/ на (/ — Ь сдвигает кривую.
§ 7. Изменение масштабов кривой
Из предыдущего параграфа мы знаем, как надо изме-
нить уравнение кривой, чтобы кривая сместилась, т. е.
чтобы произошел параллельный перенос кривой. При за-
мене х на х-\-а в выражении, связывающем у и .х, соот-
ветствующая кривая смещается на а единиц влево, при
замене «/на у-\-Ь кривая смещается на Ь единиц вниз.
Для того чтобы сместить кривую на g единиц вправо,
надо заменить х на х — g, чтобы поднять кривую на
h единиц вверх, надо заменить у иа у — А.
Уравнение круга радиуса г с центром в начале коорди-
нат хх-\-у* = г*. Уравнение круга такого же радиуса
*' Можно было бы и здесь сказать, что график поднимается на Ь
единиц, когда у заменяют на у — Ь, так что получится:
что равносильно уравнению в тексте.
§ 7] ИЗМЕНЕНИЕ МАСШТАБОВ КРИВОЙ 39
с центром в точке xc = g, yc = h, т. е. смещенного на
g единиц вправо и на А единиц вверх (исходное положе-
ние— центр в начале), есть
Для произвольной кривой, уравнение которой записано
в виде y = f(x), для смещения вправо на g и вверх на
h единиц напишем:
y — h = f(x — g) или y = h-{-f(x— g).
Для кривой, уравнение которой записано в виде F (х, у) =
= 0, для такого же переноса надо заменить уравнение на
Fix — gy y — h) = O.
Теперь поставим вопрос: как изменить уравнение кри-
вой, чтобы увеличить в С раз *) все вертикальные размеры?
Очевидно, надо вместо уравнения ya = f (х) взять урав-
нение y1=Cf(x), тогда при том же х величина ух в С раз
больше, чем прежде, т. е. в С раз больше уа.
В качестве примера вспомним уравнения прямых, про-
ходящих через начало координат. Уравнение прямой, про-
ходящей под углом 45° в I четверти,
$/„ = *•
Уравнение
соответствует прямой, идущей более круто, у которой при
заданном х ордината больше в 10 раз (см. рис. 13).
Закон перехода от yt — f(x) к y1=Cf(x) можно запи-
сать и так: в. уравнении кривой yo=f(x) заменяем уа на
-^-, т. е. пишем -^- = f(x). Тогда зависимость ух от х
характеризуется тем, что кривая ух (х) вытянута в С раз по
вертикали по сравнению с кривой уа(х).
На первый взгляд кажется, что не стоит тратить слов
на две разные формулировки, тождественность которых
•) В дальнейшем для простоты изложения будем полагать, что
С>1; ведь увеличить в 2 раза какую-нибудь величину — это значит
умножить ее на 2, но увеличить в 0,3 раза значит умножить на 0,3,
т. е. в действительности уменьшить.
40
ФУНКЦИИ И ГРАФИКИ
[ч.
-^
настолько очевидна,
«Что в лоб, что по лбу».
Но вторая формулировка с заменойyt на -^-удобна для
случая, когда кривая задана уравнением, не разрешенным
относительно у, т. е. уравнением
вида F(x, y) = 0.
Так, например, уравнение ок-
ружности радиуса 1 удобно запи-
сать в виде
Как написать уравнение кри-
вой, вытянутой в 3 раза по верти-
кали (рис. 26, кривая, обозначен-
ная ух(х))?
По правилу, которое мы толь-
ко что сформулировали, для этого
в уравнении окружности заменим
уа на -^-. Получим:
<¦+(*)'¦
1=0.
Эта кривая называется «эллип-
сом». Она обладает замечательными
геометрическими свойствами и по-
дробно рассматривается в § 6 части IV.
В данном примере уравнения легко решаются:
и наглядно видно, что г/, = Зг/0 при равных х. Но пра-
вило, что замена у на ~?- приводит к вытягиванию кри-
вой в С раз по вертикали, справедливо и для кривых,
заданных таким сложным уравнением F(x, y) = Q, которое
не решается алгебраически относительно у, например,
§ л
ИЗМЕНЕНИЕ МАСШТАБОВ КРИВОЙ
41
Формулировка о замене у на — легко переносится и
С*
на координату х. При замене ха на ^ в уравнении кри-
вой кривая растягивается по оси х в С раз, т. е. при рав-
ном у значение хх в С раз больше значения д:0.
Начнем не с доказательства, а с примеров:
у=х, и у = ^=0,1*,
(см. рис. 13). Первая прямая идет под углом 45° к оси х,
вторая идет более полого.
Второй пример:
'—1=0, (^
1=0.
Первое уравнение соответствует окружности радиуса 1,
второе уравнение — это уравнение кривой, вытянутой по
оси х в 2 раза. В самом
деле, легко убедиться, что,
например, пересечение кри-
вой с осью х происходит
в точках
Х?= ± 2
(рис. 27).
Для доказательства мож-
но уравнение решить относи-
тельно х: если y = f(xn),
-2\ -А о
Х'Хо(У)
1/ J2 х
Рис. 27.
=f^-J, то, решая, получим:
где ф есть функция, как говорят, обратная функции f.
Важно то, что в верхней строчке f это одна и та же
функция в формулах с х9 и с хх. Поэтому ер тоже одина-
ковое для ха и хх. Переписывая второе равенство
42 функции и графики [ч. i
получим:
что и соответствует формулировке: при замене х -на -gr
кривая растягивается в С раз по оси х.
Приведем пример:
Функцией, обратной степени, является логарифм
Как быть, если в уравнении у =f(x) производится замена
х на kx? Для того чтобы воспользоваться сформулирован-
ным выше правилом, вспомним правило деления на дробь:
умножение на k — это то же самое, что деление на -г-
« »
Значит, -?- играет роль величины С из предыдущих
формул.
Если, например, Л=^", то -^- = 2, т. е. С = 2; зна-
чит, замена хя на 0,5jc, есть замена х0 на ^ и приводит
к растяжению кривой по оси х в 2 раза.
Если fe = 3, то-т-=-к-, т. е. С = -^-. Таким образом,
замена х на Ъх, есть замена л: на у Что это значит гео-
метрически?
До сих пор мы рассматривали только случай положи-
тельных и больших единицы значений С, С~^> 1, и форму-
лировали результат так: при замене у—>--?- в уравнении
кривой кривая в С раз растягивается по высоте, при замене
х—> -?- кривая в С раз растягивается в горизонтальном
направлении.
§. 7] ИЗМЕНЕНИЕ МАСШТАБОВ КРИВОЙ 43
Если С положительно, но меньше единицы,
что соответствует k^> 1, то при замене у —<- ^- вертикаль-
ные размеры изменяются в С раз; но так как С<4, то
изменение в С раз теперь представляет собой сжатие; так,
например, при С = 0,5 изменение размера в С раз озна-
чает умножение высоты на 0,5, т. е. уменьшение ее вдвое.
sin3x
Рис. 28.
То же самое относится и к замене х на-^-:
такая замена приводит к сжатию кривой.
Приведем еще один пример. На рис. 28 представлены
две кривые
У второй кривой горизонтальные размеры меньше вЗ раза.
Зависимость y = sinx — периодическая: придс = 2я=6,3
(что соответствует углу 360" в градусном измерении) синус
имеет такое же значение, как и при л: = 0. добавление 2л
к любому углу не меняет значения синуса. Функция у =
= sin3x тоже периодическая, но у нее период меньше
в 3 раза: достаточно, чтобы х изменилось на -у = 2,1 ра-
диана, тогда Зх (тот угол, синус которого мы откладываем
по оси ординат) меняется на 2я и sin3x возвращается к
тому же значению,
Продумайте на этом примере общее утверждение, что
замена х на kx в уравнении кривой приводит к тому, что
все горизонтальные размеры умножаются иа -^ . В данном
44
ФУНКЦИИ И ГРАФИКИ
К
примере k = 3, горизонтальные размеры и, в частности, рас-
стояние по оси х между точками, где у = 0, умножаются
на -q-, т. е. уменьшаются в 3 раза.
Для периодической функции при замене х на kx в k
раз уменьшается период, зато в k раз увеличивается
частота, т. е. число периодов на единице длины.
Как ни просты, «арифметичны» эти соображения, на-
чинающие (к которым адресована эта книга) в них часто
ошибаются.
Рассмотрим, наконец, что будет при замене у на -^~
или х на ^- при отрицательном С. Можно провести такую
замену в два приема: напишем С== —\-Ь, где Ъ положи-
тельно, и сделаем две замены
ff-x,-yho
о
х
*° ь —\.ь ь •
Первая операция — замена
ул на j-, где Ь > 0, — уже
разбиралась, она приводит к из-
менению вертикальных размеров
в b раз. Остается рассмотреть,
к чему приводит изменение зна-
ка у, т. е. замена у на —у.
Для отдельных точек этот во-
прос уже рассматривался в § 1.
Приводим для кривых ответ без
доказательства: изменение знака у приводит к отражению
кривой в оси х, изменение знака х приводит к отражению
в оси у.
Возьмем пример:
F (х, ^) = (х — 3)* —{— («/ — 5)* — 4 = 0.
Это уравнение окружности радиуса 2 с центром в точке
с координатами х = 3, у = 5.
На рис. 29 приведены кривые
Рис. 29.
F(— x, t/) = ( —
F( — x, — у) = ( —
— 5у-~ 4 = 0,
— у — 5У — 4 = 0.
§ 7J ИЗМЕНЕНИЕ МАСШТАБОВ КРИВОЙ 45
Как видно из формул, знак F во всех случаях пред-
ставляет собой одну и ту же функцию (проследите за этим
внимательно, рассматривая первую часть формул). Просле-
дите, что происходит с кривой (окружностью) при замене
л; на —х, у на —у и одновременной замене х—*¦ — х,
у—> — у. Ясное понимание изложенных правил позволит
Вам, построив и разобрав одну какую-то кривую,
y = f{x) или F(x, y) = 0,
представить себе, как идут кривые для всех сходных функ-
ций
с любыми значениями четырех постоянных а, Ь, сх, сх.
Упражнения
1. Построить кривые Х1 + ? - 1 = 0. <*±*1* + (У ~ ^
— 1 = 0, (х3) + {у + 5?—1=0, зная, что *• + »•-1=0
представляет собой уравнение окружности. При построении кривых
рекомендуется на чертеже ставить центр, верхнюю и нижнюю точки,
крайнюю правую и крайнюю левую точки, а затем соединять эти
точки плавной кривой от руки.
2. Построить кривую y = alnx подробно, взяв, например, х от
— л до +я с интервалом 0,25л. Подразумевается, что х — угол
выражен в радианной мере, поэтому удобно брать определенные доля
я, так как тогда углы, выраженные в градусах, будут целыми:
0,25л =45°; 0,5л = 90° и т. д.
Можно воспользоваться таблицами в конце части III, где дан
синус в зависимости от угла, выраженного в радианной мере. По
оси абсцисс во всех случаях откладывать х в радианах.
Построить кривые:
а) у = 2 sin x;
б) y=sinO,5x;
в) y =
г) # =
Указание. Воспользоваться тригонометрическим тождеством
сое* = eta
д) y = Y"
46 ФУНКЦИИ И ГРАФИКИ [Ч.
е) y=cos»x = -l + lco
ж) y=sln»x=l —-i-il
Все эти кривые от а) до ж) построить, передвигая, растягивая
или сжимая кривую ^ = sinx.
3. Построить по точкам кривые:
или в симметричном виде у* — х* -f-1 = 0, задаваясь х от — 5 до
-4-5 с интервалом 0,5. Если у получается мнимым, при соответст-
вующих х кривой нет;
б) у =2 ± У(л:-1L- 1;
в) y=±Vxx+l.
Указание. Преобразовав к виду х* — у* -\- 1 = О, заметить,
что в) получается из а) перестановкой хну.
г) 4
Указание. Записать уравнение в виде
н получить кривую, передвигая н сжимая кривую а).
§ 8. Параметрическое задание кривой
Пусть каждая из величин х и у задана как функция
времени t, т. е. заданы две функции x(t) и у it), на-
пример:
Эти зависимости можно изобразить графически в виде
двух кривых, откладывая на одном чертеже по оси
абсцисс t, а по оси ординат х, а на другом чертеже по
оси абсцисс t, а по оси ординат у.
Но возможна и другая постановка вопроса: представим
себе, что х и у — это координаты точки, каждому значению
t отвечает определенное положение точки; спрашивается,
какую кривую опишет точка в плоскости х, у при изме-
нении /?
§- 87
ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ КРИВОЙ
47
Для ответа на этот вопрос можно из двух уравнений,
дающих x=^x(t) и y=y(t), исключить величину t;
тогда мы получим выражение, в которое будут входить
только у я х, т. е. либо у — у(х), либо F (х, у) = 0. После
этого будем строить кривую, как обычно, задаваясь раз-
личными х и находя соответствующие у.
Так, в приведенном примере найдем:
хх -j- у* = cos*/ -f sin* / = 1;
#= ± |Л — JC* ИЛИ д;*-{-у»— 1=0,
так что в плоскости х, у кривая представляет собой ок-
ружность.
Однако часто даже сравнительно простые выражения
x(t) и y(t) приводят при попытке исключения t к таким
сложным формулам, что нет смысла этим заниматься. Так,
например, если
то для исключения t нужно решать уравнение четвертой
степени, что приводит к очень громоздким выражениям.
Между тем построить кривую в плоскости х, у можно,
не исключая /: достаточно задаваться различными значе-
ниями t, для каждого из них находить х и у. Приводим
такую таблицу для первого примера.
Таблица 9
t
x=cos t
у = sin t
0
1
0
я
т
0.7
0,7
я
~2
0
1
Зя
4
— 0.7
0,7
я
— 1
0
5л
4
— 0.7
— 0.7
Зп
2
0
1
7л
4
0.7
-0.7
2л
1
0
Очевидно, брать t больше 2я нет надобности, значения
х и у будут повторяться. Теперь с помощью этой таблицы
строим точки кривой. При этом мы пользуемся только
48 ФУНКЦИИ И ГРАФИКИ [Ч. I
значениями х и у. Те значения t. при которых эти х и у
вычислены, при построении точек не используются. «Мавр
сделал свое дело, мавр может уйти».
Такой способ задания кривой, или, что то же самое,
функциональной зависимости у (х), называется параметри-
ческим, а величина t называется параметром.
Упражнения
1. Построить кривую, заданную уравнением
x = cost, y — sin2t.
То же для '
*=cos/, y = sin3t.
Укааание. Так как sin3f меняется быстро, нужно брать зна-
чения t достаточно часто, например: 0; 0,1; 0,2; . . .
2. Задача-шутка: построить кривые
а) * = cos3/, y = sia3t;
б) х = cos Ef -f-1), у = sin Et + 1).
3. Нешуточная задача: построить кривую
* = cos/, y=cos (t + ~p )-
4. Построить кривую
x = cost, у = cost.
(Это — прямая {/=zx, ио не вся прямая, а только ее отрезок от
х= — 1, у = —1 до *= 4- 1. У= -М-)
б. Построить кривую, по которой движется точка А, лежащая
на окружности диска радиусом 1 см, катящегося по оси х со скоро-
стью 1 см/сек. В начальный момент центр круга Q лежит на оси у,
а рассматриваемая точка А — в начале координат. Через время t
координаты центра Q<(tf, 1), круг повернулся на угол —t радиан.
Кривая называется циклоидой.
ЗАКЛЮЧЕНИЕ
Мы ограничиваемся здесь лишь малыми сведениями из
аналитической геометрии — учения о графиках функций
и о применении координат и алгебраических методов к
геометрическим вопросам.
Не прибегая к высшей математике, можно получить еще
много интересных и поучительных результатов, относя-
ОТВЕТЫ И РЕШЕНИЯ 49
щихся к графикам функций и к уравнениям кривых
с определенными геометрическими свойствами.
Однако, по нашему мнению, лучше перейти к понятиям
производной и интеграла и уже потом снова вернуться
к вопросам геометрии в части IV книги.
ОТВЕТЫ И РЕШЕНИЯ
§§2иЗ. 4. r=V~2, а = 45°; г=2У~2, а= -45°; г==ЗУХ
а= — 135°; r=4V. а=135°. 5. 2; 2 У~2\ 2У~2; 2VT.
6. /1,@, 0), Л,B, 3), Л, D, 6) лежат на одной прямой; Д @, 0),
AtB, 3), /1,( — 2. —3) лежат на одной прямой; /4, @, 0), АгB, 3),
А,( — 2, 3) не лежат на одной прямой. 7. @, ); ( ¦ 0);
}а_ аУГ) (а_ аУ*\(а аУ Ъ \
V 2 ' 2 У 1 ' ;> V 2 ' 2/^2' 2 )'
9. а) Два случая: (~|, о), (|. q), (о, Ц1); ( - ± , о) .
^-J-, о), ^0, — ~^-)- б) Четыре случая: @, 0), (а, 0),
(f- eJrI): @- °>- (а> 0)- (т- -Чг
10. ^,(х,, —г/,), /1,( — ж,, г/,), Л4(— ж,, — 1Л).
§ 8. 5. Указание. Параметрические уравнения кривой
х = t — sin t, у = 1 — cos t.
ЧАСТЬ П
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
§ 1. Движение, путь и скорость
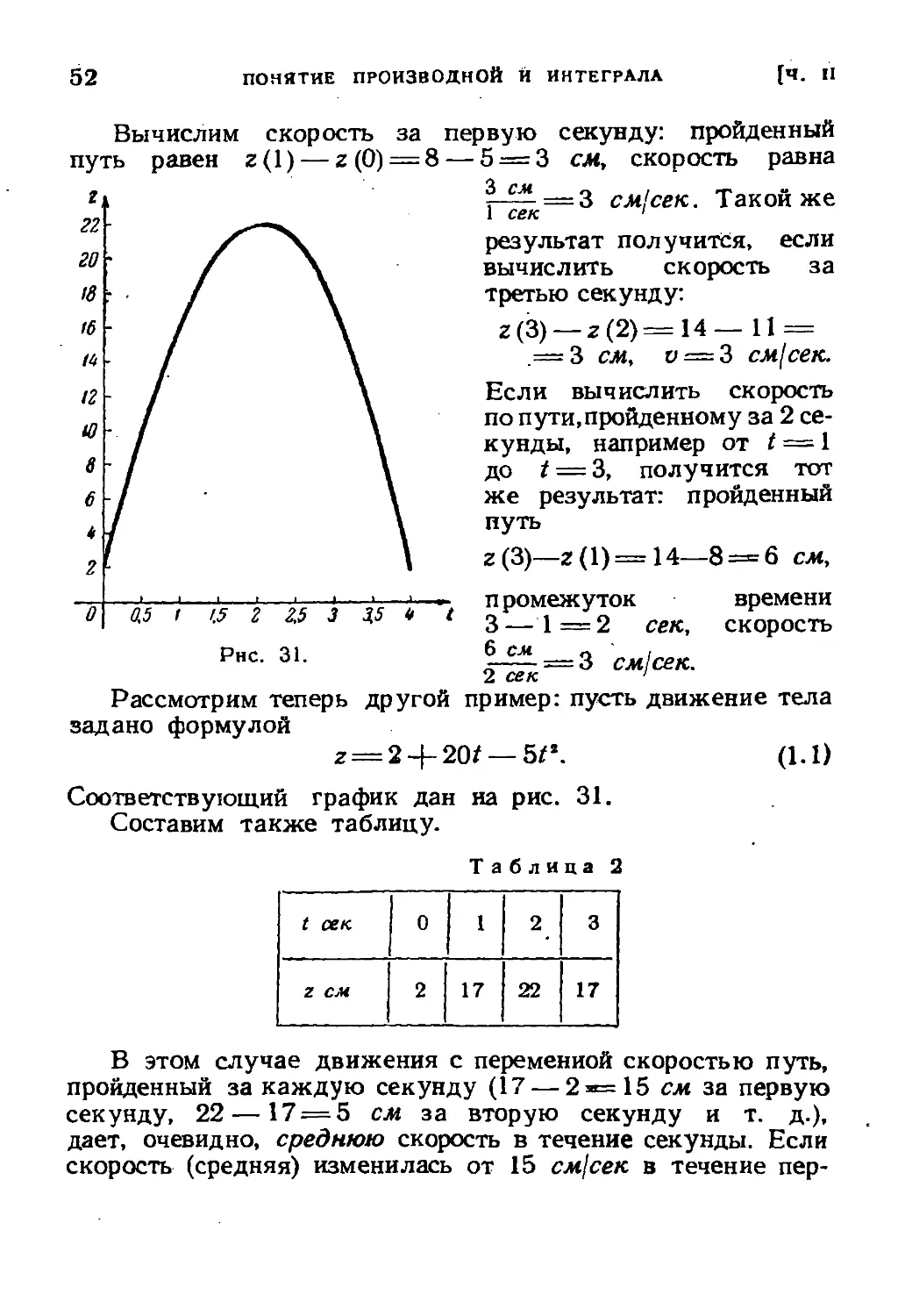
Рассмотрим поступательное движение тела вдоль неко-
торой прямой линии; расстояние определенной точки тела
от определенной точки на этой прямой обозначим 2, при-
чем в,одну сторону это расстояние будем считать положи-
тельным, а в другую — отрицательным. Пусть, например,
прямая, вдоль которой движется тело, расположена верти-
кально, точки выше О соответствуют положительным г,
точки ниже О — отрицательным г.
При движении координата z зависит от времени (мы
будем сокращенно говорить: «координата г» вместо «рассто-
яние определенной точки тела от определенной точки на
прямой»). Движение тела определяется зависимостью г от
времени t, т. е. заданием функции z(t). Зная функцию
г (t), можно найти положение тела в любой момент времени.
Функцию г (t) можно изобразить графически, отклады-
вая по оси абсцисс время (ось /), а по оси ординат—ве-
личину г, характеризующую положение тела.
При равномерном движении с постоянной скоростью v
путь s, пройденный за время t, равен произведению s = vt.
Обозначим г0 координату тела в момент * = 0. Путь,
пройденный за время t, равен разности г (/) — га. Значит,
2@ =
Следовательно, при равномерном движении зависимость
координаты от времени дается линейной функцией. График
зависимости z (/) при равномерном движении представляет
собой прямую линию на координатной плоскости, у кото-
рой по оси абсцисс (горизонтальной) отложено время t, a
по оси ординат (вертикальной) отложена координата 2.
§ 1]
ДВИЖЕНИЕ, ПУТЬ И СКОРОСТЬ
51
При неравномерном движении зависимость z{t) выра-
жается более сложными формулами и соответствующий
график представляет собой ту или иную кривую.
Разберем подробно следующую задачу: задана функция
z(t), т. е. зависимость координаты тела от времени, нужно
найти скорость движения тела v. В общем случае нерав-
номерного движения ско-
рость не остается посто-
янной, она меняется с
течением времени. Зна-
чит, скорость v есть так-
же функция времени
v(_t), и задача заклю-
чается в том, чтобы вы-
разить v {t) через извест-
ную функцию z(t).
Эту задачу мы сперва
будем решать даже не
алгебраически, а с по-
мощью арифметики, для рис> до
того, чтобы лучше осво-
иться с новыми понятиями, которые появляются в связи с
задачей.
В частном случае равномерного движения (с постоянной
скоростью) все просто. Скорость определяется как путь,
пройденный за единицу времени. Так как скорость посто-
янна, то безразлично, какой именно участок пути и какой
промежуток времени выбран для определения скорости.
Приведем пример. Пусть
2 = 54-3*.
причем г выражено в сантиметрах, t — в секундах (рис. 30).
Составим таблицу.
Таблица 1
2,
24
го
16
12
в
0
•
1 2 3 <
/
III у
t 5 6 t
t сек
г см
0
5
1
8
2
11
3
14
52
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Вычислим скорость за первую секунду: пройденный
путь равен z(l) — z@) = 8 — 5 = 3 см, скорость равна
L^. = 3 см/сек. Такой же
результат получится, если
вычислить скорость за
третью секунду:
zC) —zB)=14—11 =
= 3 см, 0 = 3 см[сек.
Если вычислить скорость
по пути,пройденному за 2 се-
кунды, например от t=1
до t = 3, получится тот
же результат: пройденный
путь
zC)—z(l) = 14—8 = 6 см,
промежуток
3 — 1=2 сек,
6 СМ о '
3 С
времени
скорость
Рассмотрим теперь другой пример: пусть движение тела
задано формулой
-5Г. A.1)
Соответствующий график дан на рис. 31.
Составим также таблицу.
Таблица 2
t сек
г см
0
2
1
17
2
22
3
17
В этом случае движения с переменной скоростью путь,
пройденный за каждую секунду A7 — 2 = 15 см за первую
секунду, 22 —17 = 5 см за вторую секунду и т. д.),
дает, очевидно, среднюю скорость в течение секунды. Если
скорость (средняя) изменилась от 15 см\сек в течение пер-
§ 1]
ДВИЖЕНИЕ, ПУТЬ И СКОРОСТЬ
53
вой секунды до 5 см/сек в течение второй секунды, то,
значит, скорость менялась и в самом промежутке времени
от /=0 до 7 = 1 сек во время первой секунды.
Скорость в момент t = 1 уже не та, что скорость в мо-
мент / = 0, поэтому, когда путь, пройденный за время от
/ = 0 до /=1 сек, делим на время прохождения этого
пути A сек), то полученную величину A5 см'сек) мы на-
зываем средней скоростью за промежуток времени от / = 0
до / = 1.
Как же найти мгновенную скорость?
Скорость меняется постепенно, -поэтому чем меньше
промежуток времени, в течение которого производится
измерение пройденного пути, тем меньше успеет измениться
скорость, тем ближе будет средняя скорость к ее мгновен-
ному значению.
Вычислим для примера мгновенную скорость в момент
/ = 1. Попробуем подсчитать среднюю скорость за 0,2 сек,
т. е. за время от / = 1 до /=1,2, потом за 0,1 сек (от
/ = 1 до / = 1,1), за 0,01 сек (от / = 1 до / = 1,01).
t
г
сек
см
1
17
1
17
Т а б л
.01
,0995
1
17
и ца
,1
.95
1
18
2а
,2
,8
Табл. 2 для этого слишком груба, и мы вычислим нужные
значения г по формуле A.1); они приведены в табл. 2а.
Интересующие нас средние скорости равны соответст-
венно:
за. от 1 до 1,1 „=
за , от 1 до 1,01- „_"L~-pJ7-e.ee?.
Закономерность видна чрезвычайно ясно: чем меньше
промежуток времени, тем ближе значение скорости к
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
10 см/сек. Значит, можно предположить, что мгновенная
скорость в момент t = \ равна именно 10 см\сек.
Найдем еще мгновенную скорость в момент времени
7 = 1,5. Нужные значения z приведены в табл. 26. Поль-
зуясь ими, получим:
за. от 1,5 до 1,7
за t от 1,5 до 1,6
за t от 1,5 до 1,51
-20'75
=4,95 с-^ .
СвК
Естественно считать, что мгновенная скорость в момент
/ = 1,5 равна 5 см\сек.
Таблица 26
t
2
1.5
20,75
1,51
20,7995
1.6
21,2
1,7
21,55
Мы видим, что в различные моменты времени t мгно-
венная скорость v имеет различные значения. Поэтому
мгновенная скорость есть функция времени t:
Для определения мгновенной скорости в момент t=l
можно было и по-другому выбирать промежуток времени:
0,2 сек от 0,8 до 1 сек; 0,1 сек от 0,9 до 1 сек; 0,01 сек
от 0,99 до 1 сек. Поступая совершенно так же (табл. 2в),
Таблица 2в
t
2
0
14
,8
,8
0
15
.9
.95
0
16,
,99
8995
1.0
17
% \] ДВИЖЕНИЕ, ПУТЬ И СКОРОСТЬ 55
найдем, что средние скорости соответственно равны:
за. от 0,8 до 1 о = !Ц^
за t от 0,9 до 1
за * от 0,99 до 1 v = l?- "¦"*«= ю,05
Снова мы убеждаемся в том, что чем короче промежу-
ток времени, тем ближе скорость к 10 см.\сек, убеждаемся
в правильности догадки, что мгновенная скорость в момент
t = \ равна 10 см/сек.
Внимательный читатель, может быть, уже догадался,
что лучше выбирать для расчета промежутки времени так,
чтобы интересующий нас момент t = \ был в середине
промежутка. Пользуясь табл. 2а и 2в, получим:
за t от 0.8 «о 1.2 в_!Ь^!_ю?.
за /ОТ 0.9 до 1,1 » = "*%"¦» - 10g ,
за < от 0.99 до 1,01 р^^«*>5-16,8995^,
В этом случае мы сразу получаем правильный ответ!
Что же, значит, не надо заботиться о том, чтобы брать
промежуток времени поменьше? Нет, такой вывод был бы
неправилен. Точное равенство средней скорости за какой-то
промежуток (например, t от 0,8 до 1,2) мгновенному зна-
чению в середине промежутка (при 7=1) есть специаль-
ное свойство движения по формуле вида A.2), когда z есть
квадратный трехчлен *). В других случаях такого точного
равенства может и не быть.
Разберем еще пример. Пусть тело движется по закону
z = *\ A.2)
График — см. рис. 32. Составим таблицу (табл. 3) так,
чтобы в ней были все данные для вычисления мгновенной
скорости в момент /= 1. Для средних скоростей по разным
*) Случай так называемого равноускоренного или равнозамедлен-
иого движения.
56
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
промежуткам дадим сразу таблички, опуская арифметиче-
ские действия.
Из табл. За, 36, За видно, что мгновенная скорость в
момент t = 1 равна 3 смjсек.
Таблица 3
t
Z
0
0
0,8
0,512
0,9
0,729
0,99
0,9703
1
1
1,01
1 ,0303
1.1
1,331
1,2
1,727
Таблица За
Таблица 36
Таблица За
Промежуток t
от
1
1
1
До
1.2
1.1
1 ,01
Ско-
рость
3,64
3,31
3,0301
Промежуток t
от
0,8
0,9
0,99
До
1
1
1
Ско-
рость
2.44
2,71
2,9701
Промежуток t
от
0.8
0,9
0,99
До
1,2
1.1
1,01
Ско-
рость
3,04
3,01
3,0001
к
ДИМ,
г
в
7
6
5
4
3
2
I
этому значению v = 3 см/сек мы неизменно прихо-
как бы мы ни выбирали промежуток времени (от
t = 1 до большего времени или от
меньшего времени до t = \, или
так, чтобы t = 1 было в середине
промежутка). Расчет с t = 1 в се-
редине при равном промежутке
времени точнее; получаются значе-
ния, более близкие к 3. Но и в этом
случае, чем -точнее мы хотим по-
дойти к истинному значению
t> = 3, тем меньше надо брать про-
межуток. Однако считать такой
способ обязательным нет оснований:
выбирая промежуток от t = 1 до
большего и уменьшая его, тоже
можно получить любую точность.
Так, например, в промежутке от
0,5 w i,5 2fl t5~t
Рис. 32.
рр ру
=1 до /=1,000001 скорость равна 3,000003000001.
§ 2) ПРОИЗВОДНАЯ ФУНКЦИИ ПРЕДЕЛ ОТНОШЕНИЯ ПРИРАЩЕНИЙ 57
Упражнения
1. Найти мгновенную скорость в момент f = 0, t=l, t — 2
в движении, заданном формулой A.1). По этим данным построить
график зависимости мгновенной скорости от времени.
2. То же для движения по формуле A.2).
3. Рассмотреть движение, заданное формулой г= — . Найти
мгновенную скорость в моменты t = \, t=2, t = 3. Обратить внима-
ние на знак скорости.
§ 2. Производная функции — предел отношения
приращений
В предыдущем параграфе в связи с задачей о мгно-
венной скорости мы пришли к рассмотрению отношений
вида
при очень близких между собой значениях tt и ?,.
Выражение «очень близкие» является неопределенным,
нестрогим. Точная формулировка такова: необходимо найти
предел, к которому стремится отношение
z(/,) 2 n
при tx, стремящемся к /г.
Удобно переменить обозначения: назовем tl = t, tt =
= t-{-At, так что разность /, — *,, т. е. промежуток вре-
мени, обозначена Д/. Подобно этому обозначим Дг раз-
ность
В этих обозначениях средняя скорость vcp в интервале Д/
от / до t -\- Д/ равна
Отметим, что Д — это не множитель, а знак, заменяющий
слово «приращение», так что сокращать Д в числителе и
знаменателе дроби нельзя»
53
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч, И
Сам знак Д — это прописная буква «дельта» греческого
алфавита, так что Д* читается «дельта тэ», Дг — «дельта
зет»; часто читают At— «приращение времени», Дг —
«приращение пути».
В формуле B.2) величины At и Az зависимы: можно
выбрать любой промежуток времени At, но после того,
как промежуток времени At, стоящий в знаменателе,
выбран, подразумевается, что Дг в числителе не любой
отрезок пути, а именно тот, который соответствует про-
межутку времени At. В формуле B.1) это было очевидно
из самого написания аргументов функции z(tt), z(tt) в
числителе, формула B.2) есть просто другая запись фор-
мулы B.1).
Интересующая нас величина мгновенной скорости v(t)
в момент t есть предел отношения -^ при At, стремящемся
к нулю. Очевидно, стремление At к нулю равносильно
стремлению t2 к /,, поскольку At — tt — tt. Приведенная
формулировка записывается так:
Буквы lim (начальные буквы латинского слова limes —
лимес — предел) обозначают «предел»; внизу записано, о ка-
ком именно пределе идет речь — при At, стремящемся к
нулю, стрелка заменяет слово «стремится», в скобках ука-
зана та величина -т-т-, предел которой ищется.
Что значит «предел», «стремление к пределу»? Те ариф-
метические расчеты, которые мы производили в предыду-
щем параграфе, как раз и служили наглядным пояснением
этих понятий. В самом деле, из этих расчетов следует,
например, что для функции z=?2-\-20t— Ы* при t=\
и различных Д/ соответствующее отношение меняется так:
д/
Дг
Д/
0,2
9
0,1
9,5
0,01
9,95
(см. вычисления скорости, следующие за табл. 2а).
§ 2] ПРОИЗВОДНАЯ ФУНКЦИИ ПРЕДЕЛ ОТНОШЕНИЯ ПРИРАЩЕНИЙ 59
Из этой таблицы был сделан вывод, который мы теперь
запишем так:
при t=\ lira -?f = Ю-
сек
На численном примере было выяснено, что к тому же
пределу мы приходим и в том случае, когда по другому
выбираем /х и tx. Так, в примере, которому соответствует
табл. 2в, /, все время одно и то же и равно tx = \, a f,
мы берем чсе ближе к /г, так что - вычисляется величина
- ~ д/ * ~—- • Предел, к которому стремится эта вели-
чина, тоже равен мгновенной скорости в момент t = \,
и, как видно из численного примера, при таком расчете
получился такой же предел, lira -^- = 10-^-.
д*-». о л' сек
Итак, отношение
At tt— t,
стремится к определенному пределу, когда At = tt — tt
стремится к нулю; при At, стремящемся к нулю, /, и tl
неограниченно сближаются между собой, и общую их
величину мы обозначаем (когда At—>-0) tt = tl = t.
Предел отношения, т. е. мгновенная скорость v, есть
определенная функция t,
"«о'
Так, например, если рассмотреть первое упражнение § 1 и
найти (путем уменьшения промежутка времени) мгновенную
скорость при t = 0, получим v = 20 см\сек, а при t = 2
о = 0 (напомним, что при ? = 1 с; =10 см/сек).
Почему при вычислении скорости по заданной формуле
z(t) приходится проводить такой длинный расчет, находить-
Дг для различных Д/ и затем только находить предел
lim ~- ? Нельзя ли сразу взять значение Д/ = 0? При
этом мы получили бы Az = 0, так как At = tt — tlt и если
tt = tx, то и z(ti)=z(tl) и Az = z(tt)—z(*x) = 0. Значит,
при таком бездумном способе действий мы получили
60 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
бы -д^-=-о"! т- е- не получили бы никакого определенного
ответа.
При вычислении скорости вся суть заключается в том,
чтобы брать малые At и соответствующие им малые Аг.
При этом получается каждый раз вполне определенное
отношение -^-; когда At уменьшается, стремится к нулю,
то Дг уменьшается приблизительно пропорционально вели-
чине At, а поэтому отношение остается приблизительно
постоянным.
Отношение -—- стремится к определенному пределу
при стремлении At к нулю.
Величина этого предела — мгновенная скорость v (t)
в случае движения или в общем случае производная
функции z(t) — зависит от вида функции z{t) и от значе-
ния переменной t. В следующем параграфе мы проведем
алгебраически вычисление производной нескольких простей-
ших функций и для них найдем точное значение предела,
т. е. производной, которую до сих пор мы находили
опытным путем, как бы на ощупь.
§ 3. Обозначения производной. Производная
степенной функции
Предел отношения приращения функции к приращению
независимой переменной при стремлении к нулю прираще-
ния независимой переменной имеет первостепенное значение
и для высшей математики и для ее приложений: выше мы
видели, например, что такое важнейшее понятие, как
мгновенная скорость движения, находится именное помощью
предела такого отношения. Поэтому предел этого отношения
имеет специальное название: «производная функция» или,
короче, «производная». Первое название связано с тем, что
если z есть функция t, z{t), то и предел отношения
lim -j— = v также есть функция (другая) v (/) перемен-
ной t — зависит от значения t, к которому стремятся tx
и /,, или, как иначе говорят, v зависит от значения t,
«при котором берется производная z».
Для производной имеются специальные обозначения.
§ 3] • ОБОЗНАЧЕНИЯ ПРОИЗВОДНОЙ 61
Один способ обозначения
dz .. Az
При этом величина -^- (читается: «де — зет по де — тэ»)
рассматривается не как дробь, а просто как сокращенная
запись предела, стоящего справа. Величина -?г записана
в форме дроби для того, чтобы напоминать, что эта вели-
чина получена из дроби -А- путем перехода к пределу.
Другое обозначение производной — с помощью штриха,
v = z'(t), или, например, для функции у (х)
В механике иногда производные по времени обозначают
точкой сверху, -^-=х, но мы такими обозначениями
пользоваться не будем.
Иногда вместо знака функции подставляют ее выраже-
ние: так, например, если z = at* ~\-b, то можно писать
dz d(at*-i-b) . ,t i u\r
вместо -дт- прямо \ ^—- или (at -\- о) .
Найдем алгебраически производную от функции
Для этого составим отношение
b.t At
Раскроем в числителе скобки:
+ ДО' — *' = *" 4- 2/ • А* + (М)г — Г = 2/ • A/ -f (ДО2-
Составим отношение
Az 2
Al
Теперь легко найти предел: очевидно, что если вели-
чина представляет собой сумму слагаемого, не зависящего
62 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
от Д^ (в данном случае 2t), и самого Д/, то при стремле-
нии Д/ к нулю останется просто слагаемое, не зависящее
от At:
*=*-?>=» Ига -?г = lira Bf-fc-AQ = 2/.
dt dt if^0 At ^^/ ^
Рассмотрим еще пример:
Az = (/ +А/I—*•=*•+ 3*'Д
В этих примерах предел можно было легко найти,
так как при вычислении отношения -~ величина Д/ со-
кращалась. Рассмотрим более сложный пример!
J_.
Z t '
J. \2f-f Al
t ' At At
Можно ли пренебречь величиной At в первой дроби,
в выражении , . ., когда мы перейдем к пределу? Нет,
потому что еще не проведено сокращение с величиной Д/
в знаменателе. Заменяя , на -г при малом At, мы
совершаем малую ошибку в одном из слагаемых числителя
дроби -дх • Однако у этой дроби малы и числитель и
знаменатель, если мало At. Поэтому малая ошибка в чи-
слителе недопустима.
Покажем правильный способ действия:
А 1 1 * —(/4- At) At
+ At t *(/-!-Af) t(t-t-At)'
Аг 1
At t{t-\-At)'
Теперь можно найти предел (производную), опуская
§ 3] ОБОЗНАЧЕНИЯ ПРОИЗВОДНОЙ 63
в знаменателе,
* 44) ,. r
dt lim
Г \ 1=_J-
L <(<h-aoJ ? •
На этих примерах можно увидеть очень важное, основное
свойство предела. При уменьшении величины At разность
между значением отношения -гт- и пределом этого отно-
шения (равным производной) lim —-==—. можно сделать,
как говорится, «сколь угодно малой», т. е. меньше любого
заданного числа.
Поясним это примером. Для z=—,
j? _ _
dt i* ' &t t
Возьмем, например, t = 2, -уг = —0,25. Можно ли
выбрать такое Д?, чтобы -дт- отличалось от своего предела
меньше чем на 0,0025? Это значит, что Д^ нужно выбрать
так, чтобы -—¦ лежало в пределах между — 0,25 +
+ 0,0025 = —0,2475 и — 0,25 — 0,0025 = — 0,2525. Под-
ставляя выражение -^- при t = 2, найдем, что At должно
быть по абсолютной величине меньше 0,02.
Точно так же обстоит дело и для других функций:
стремление к пределу при Д/—»-0 означает возможность
выбора Д/, при котором достигается любая степень при-
ближения к пределу.
Особенно просто находится производная в частном слу-
чае z=/: очевидно, при этом &z = At, -д|- = 1 — отно-
шение равно 1 для любых (больших и малых) Д^, а зна-
чит, и в пределе. Итак,
z=a='« dt dt l'
Наконец, постоянную величину z=C тоже можно
рассматривать как частный случай функции, но в этом
64 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
случае, очевидно, Дг = 0 при любых Д*, следовательно,
имеет место
Если функцию умножить на постоянный множитель,
то на такой, же множитель умножится и ее производная,
например
о,а. dz _dCf) dt' о 9t M
В общем виде, если
то ±. =
Очевидно также, что производная суммы двух функций
равна сумме .производных этих двух функций:
Используя оба эти правила, получим, что производная
суммы нескольких функций, взятых с постоянными
(но, вообще говоря, различными) коэффициентами, равна
сумме производных этих функций с теми же коэффициен-
тами:
dt —а dt r° dt -\~c dt ¦
Каждое из этих правил легко доказать, составляя
Az = z(t-{-At) — z(t); эти правила, которые справедливы
для -?- при любом Д/, справедливы и для предела, т. е.
для *L.
Теперь легко найти производную от многочлена. Пред-
варительно выпишем рядом все найденные выше произ-
водные:
В § 1 мы рассматривали
2@ = 2-^-20^ —
§ 3] ОБОЗНАЧЕНИЯ ПРОИЗВОДНОЙ 65
Найдем:
= 20— юг.
Легко убедиться, что значение скорости при ^=1,
о=10; которое мы нашли численно, получается из фор-
мулы. Точно так же и для функции z*=t* мы нашли
численно -д~ = 3 при *=1, что согласуется с формулой
-sr=3t •
Техника нахождения производных (или, как говорят
иначе, дифференцирования функций) подробно изложена
в начале следующей части.
Забегая вперед, можно отметить, что дифференцирова-
ние функций, заданных формулами, оказывается сравни-
тельно простым и легким делом, более легким, например,
чем решение алгебраических уравнений. Формулы для
производных никогда не получаются более сложными
(более сложного типа), чем формулы для самих функций;
так, например, если функция является многочленом
у = а + Ьх + сх* + lx* + fx\
то производная ее тоже является многочленом
(это относится к многочленам любой степени). Если функ-
ция является алгебраической дробью, то и производная
является дробью. Если функция содержит корни или
дробные степени, то и производная содержит их. Произ-
водные от тригонометрических функций также являются
тригонометрическими функциями. А в некоторых случаях,
например для логарифмической функции, производная
оказывается функцией даже более простого типа (в данном
случае алгебраической дробью).
Для нахождения производных не надо остроумия или
выдумки, задача всегда решается аккуратным, последо-
вательным применением простых правил, которые будут
изложены в части III.
3 Я. В. Зельдович
66 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. Ц
Производные различных более сложных функций рас-
сматриваются в следующей части книги.
Ввиду важности данного параграфа повторим основные
выводы.
1) Производная функция определяется как предел от-
ношения приращения функции к приращению независимой
переменной при стремлении к нулю приращения независи-
мой переменной!
dy ,.
¦37= hm
2) Мгновенная скорость движения тела равна произ-
водной координаты тела по времени. По аналогии говорят,
что производная ~ дает скорость изменения функции у
при изменении переменной (аргумента) х и в тех случаях,
когда х не является временем, а у не является координатой.
Упражнения
1. Найти алгебраически производную функций: a) z = /* н
б) г = ta, задаваясь ty = t ~- , ^» = ^~(~"o~J пРи этом момент t,
для которого находится производная, при любом t лежит в середине
промежутка времени от tx до tt (см. численные расчеты в конце § 1).
Найти производные для функций:
2. у = х*. 3. у=(х + \)г. 4. У = ^хт- S. у = а + ^ .
Указание к задаче 6. Умножить числитель и 8'наменатель
выражения
на сумму Ух -f- A* + У^сГ
jr
§ 4. Приближенное вычисление функции с помощью
производной
__ йг
Производная -^ определяется как предел отношения
приращений —¦ при Д?—>¦ 0. При Д/ не равном нулю
отношение приращений -дг не равно производной -тг , но
§ 4] ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ФУНКЦИИ 67
это отношение приближенно равно -^ и приближение тем
лучше, чем меньше Д/.
Поэтому приближенно напишем *):
-Ti^4t=z'^ Лг = ^-Д/ = г'(/)Д/. D.1)
Отсюда найдем и приближенное значение функции г (/ -f- ДО
Обратите внимание на то, что в формуле D.2) первый
знак равенства точный по определению Дг, второй — при-
ближенный.
Вернемся к обозначениям tt=t-{-At, t1 = t, которыми
мы пользовались раньше. Получим:
Таким образом, при малой разности tt — tlt т. е. при
tt близком к tt, функция z (tt) может быть выражена при-
ближенной формулой, в которую входят значение функ-
ции г(/г) и ее производной z' (tx) при t = it. Отметим,
что в эту формулу tt входит в первой степени или, как
говорят еще, линейно.
Приведем пример. Пусть 2 = *' и нас интересуют зна-
чения z при / близком к 1. Выберем tx = \, тогда
z(tx)=^t\=l, г'(?1) = 3/? = 3 и приближенная формула
имеет вид
*(^t) = /:=S!14-3(f1—l) = 3/t —2.
•) Утверждение, что приближенное равенство
Az = г (х -f- Ьх) — г (х) я= г' (х) Дли
становится точным в пределе при Дх—»¦ 0, нуждается в разъяснении.
При Лх—>-0, очевидно, и Дг—>¦ 0. Поэтому приближенное равенство
гД^:а-Дд« при Ах—>-0 становится точным прн любом а, так как это
равенство даст 0 = 0. Но мы утверждаем больше: при конечном Ах
из Дг=г=2' (х) Ах следует, что -z-^- =аг' (х). Мы утверждаем, что и
это следствие из приближенного равенства Дг =а= z'(х) Дх тоже ста-
новится точным в пределе прн Ах—>-0. Это следует из определения
производной г' (х).
68 ПОНЯТИЕ ПРОИЗВОДНОЙ Й ИНТЕГРАЛА [Ч. II
Сравним точное и приближенное выражения.
Таблица 4
3/, — 2
1
1
1
1
1
I
.01
,0303
.03
1
1
I
,02
,0612
,06
1
1
1
.05
,1576
.15
1
1
1
,1
,3310
,30
1
3
2
,5
,375
,50
2
8
4.
0
Приведем еще пример z=\/rt. Найдем значения функ-
ции при t близком к 4. В этом случае zD) = }/~4 = 2.
Производная z' (/) =—j= (см. упражнение 6 к § 3).
Поэтому г' D)= —-—= -у и приближенная формула
имеет вид
24-0,25(/t —4)= 1 + 0,25/,.
Сравним и в этом случае приближенное и точное вы-
ражения.
Таблица 4а
УХ
1+0,25*,
4
2
2
5
2,24
2,25
6
2,45
2,50
7
2,65
' 2,75
8
2,83
3,0
9
3
3,25
Представим себе, что At есть промежуток времени,
г'{t) — мгновенная скорость, Дг — приращение пути, т. е.
путь, пройденный за время А/. Формула
Az = z'(t)At D.4)
означает, что путь равен произведению мгновенной ско-
рости на промежуток времени. Но ведь мгновенная ско-
§5] КАСАТЕЛЬНАЯ К КРИВОЙ 69
рость сама меняется со временем. Поэтому D.4) верно
лишь в том случае, когда мгновенная скорость не успела
заметно измениться за время Д/. Следовательно, чем
быстрее меняется величина z' (t), тем меньше Д/ можно
брать в формуле D.4). И наоборот, чем медленнее меняется
z' (t), тем больше можно брать At, т. е. величина прира-
щения Д/, для которого формула D.4) дает еще малую
ошибку, зависит от скорости изменения производной на
промежутке Д/.
Рассмотренные примеры подтверждают этот вывод.
В первом примере при изменении /от 1 до 2 (Д/=1)
производная z'(/) = 3/* изменяется от 3 до 12 (т. е.
в 4 раза). Во втором примере при изменении / от 4 до 9
производная z'(t) = —у=. изменяется от 0,25 до 0,167
(т. е. примерно на 30°/0). Поэтому во втором случае фор-
мула Дает хороший результат при больших значениях Д/.
Подробно вопрос о границах применения формулы (при
заданной требуемой точности) и о возможности ее уточне-
ния разобран в последних параграфах третьей части.
Все сказанное в равной мере относится и к положи-
тельным и к отрицательным приращениям; пример с от-
рицательными приращениями дан в упражнениях.
Упражнения
1. Найти A,2)*, A,1)*, A,05)*, A.01J, пользуясь формулой D.3).
Сравнить полученные результаты с точными.
2. Для функции г (t) = 2 -\-20t—5<* найти при помощи произ-
водной z(l,l), гA,05), г@,98). Сравнить с точными значениями.
Указание. В последнем случае взять t=\, ht = —0,02.
§ 5. Касательная к кривой
С помощью производной можно решить важную задачу
аналитической геометрии — задачу о нахождении касатель-
ной к кривой, заданной уравнением y — f(x). Координаты точ-
ки касания А считаются заданными: х = х0, y=ya = f (xt).
Найти касательную — это значит найти ее уравнение.
Очевидно, что уравнение касательной — это уравнение
прямой, проходящей через точку касания. Уравнение лю-
бой прямой, проходящей через заданную точку A (xt, yt).
70
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
а,уа)
можно написать в виде
Для того чтобы найти уравнение касательной, остается опреде-
лить величину k—угло-
вой коэффициент каса-
тельной (ее «крутизну»).
Для этого сперва найдем
угловой коэффициент
прямой, проходящей через
две заданные точки А,
В рассматриваемой кри-
вой (рис. 33); такую пря-
мую называют секущей.
Когда эти две точки
"? кривой сближаются, то
прямая приближается к
Рис- 33. касательной. На рис. 33
показаны две секущие
через точки А и В и через А и В', причем В' лежит
ближе к Л по сравнению с В.
Чем ближе вторая точка к точке А, тем ближе секу-
щая к касательной. Поэтому угловой коэффициент каса-
тельной равен пределу, к которому стремится угловой
коэффициент секущей при
стремлении к нулю расстоя- i
ния между двумя точками пе-
ресечения секущей с кривой.
Угловой коэффициент се-
кущей легко выразить через
значения функции в точках
пересечения.
Возьмем в качестве одной
из точек пересечения секущей
с кривой точку А(хп, у0), в
Рис< 34>
которой мы хотим провести 0 я
касательную к кривой, коор-
динаты второй точки пересе-
чения В обозначим лг,, ух.
Так как эти точки лежат на кривой, уравнение кото-
рой есть y = f(x), то у0 =/(*,) и y1=f(x1). Как видно
§ 5] КАСАТЕЛЬНАЯ К КРИВОЙ
из рис. 34, угловой коэффициент секущей kc равен
С О V* V V*
Напомним, что выражение углового коэффициента
прямой, проходящей через две данные точки, рассматрива-
лось раньше, в §§ 3 и 4 части, I.
Чтобы получить угловой коэффициент касательной
в точке х=хп, нужно брать точку В все ближе к А
т. е. нужно, чтобы хх стремилось к ха. Следовательно,
угловой коэффициент касательной k равен пределу kc
при xt, стремящемся к ха:
Обозначим Ах разность ху—ха, xl = xa-\-Ax и соот-
ветственно
Af=/(*,) —/(*.)=/(*. +Л*) —f(*,).
В этих обозначениях угловые коэффициенты секущей kc
и касательной k выразятся формулами
Следовательно, угловой коэффициент касательной есть
производная функции / (х)
Мы знаем, что производная функции f(x) сама является
функцией х. Так как мы искали угловой коэффициент
касательной в точке А(ха, уа), то при вычислении предела
~ мы считали закрепленным значение х = ха. Поэтому в
окончательной формуле и стоит /' (д;0), значение производ-
ной при х = ха.
Рассмотрим пример параболы, у = хх, т. е. /(дс) = дг*.
Составим уравнение касательной в точке х0 = 2,
?/« = /(*«) = 4.
Мы знаем производную
72
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Следовательно, в интересующей нас точке угловой коэф-
фициент касательной
Уравнение касательной
У — У„=^(х — х0),
— 4 = 4(х— 2), у = 4х — 4.
Без помощи производных трудно провести касательную
к кривой, заданной уравнением y=f(x): нужно вычислить
большое число точек кривой, с помощью лекала провести
кривую по этим точкам и потом на глаз приставлять ли-
нейку к кривой в заданной точке, внимательно следя за
тем, чтобы не пересечь кривую вблизи точки касания.
С помощью производных мы находим уравнение касатель-
ной, по этому уравнению находим две
точки, лежащие на прямой, заданной
этим уравнением, и проводим прямую
(касательную) с помощью линейки по
этим двум точкам. В качестве одной
точки естественно взять саму точку ка-
сания А(ха, уа), вторую точку С на
прямой можно взять далеко от А, тогда
с большой точностью определится наклон
и положение касательной как прямой,
проходящей через две точки Л и С.
Так, например, выше мы нашли урав-
нение прямой, касающейся параболы
у=х* в точке ха = 2, уа = 4. Это урав-
нение имеет вид у = 4х — 4. Найдем ко-
ординаты двух точек на этой прямой:
при х = 2 найдем у = 4-2—4 = 4; это
есть сама точка ' касания А B, 4), ее ко-
ординаты можно было и не вычислять, касательная обязана
пройти через нее. В качестве второй точки (С) выберем
точку пересечения касательной с осью у: положим х = 0,
найдем у = — 4, так что С @, —4) (рис. 35).
Отметим любопытное обстоятельство: при х = 0, у = — уа
точка С пересечения касательной с осью у лежит ниже
оси х на столько же, на сколько сама точка касания ле-
жит выше оси х. Это не случайно, такое правило спра-
ведливо для всех касательных к квадратичным параболам
Рис. 35.
§ 5J КАСАТЕЛЬНАЯ К КРИВОЙ 73
с уравнением (/=шса. В самом деле, если касательная про-
ведена в точке А(ха, t/o=flutj), то ее уравнение есть
У — У о = 2аха (х — ха),
и при дг = О получаем:
Таким образом, касательная проходит через точки
А(ха, уа = ах1) и С @, у = — уа = — axl).
При построении кривой по точкам трудно точно про-
вести кривую, если вычислено мало точек. С помощью про-
изводных можно заранее провести касательные к кривой
в этих точках; после этого легче и точнее можно про-
вести саму кривую.
Наглядно ясно, что в точках максимума и минимума
кривой касательная горизонтальна. Уравнение горизонталь-
ной прямой ?/ = const, угловой коэффициент горизонталь-
ной прямой k = 0. В точках максимума и минимума кри-
вой, следовательно, равна нулю производная функции
y = f(x), графиком которой является кривая (подробно об
этом в следующем параграфе). Таким образом, с помощью
условия /'(*) = О можно находить координату х точек ми-
нимумов и максимумов кривой; координату у при этом
легко найти, подставляя х в уравнение кривой. Очевидно,
что, зная координаты точек максимума и минимума, можно
точнее провести саму кривую.
Полезно в порядке упражнения, нарисовав от руки
кривую у (х), хотя бы приблизительно, но быстро провести
кривую у' (х), обращая внимание на знак у' (х) и на точки,
где у' (х) обращается в нуль. Такой пример показан на
рис. 36, а (график у {х)) и 36, б (график производной!/' (х)).
Точки обращения в нуль самой функции у (х) для про-
изводной у (х) ничем не замечательны. Если кривую у(х)
поднять параллельно самой себе (верхняя кривая, рис. 36, а),
то кривая у' (х) от этого никак не изменится: при парал-
лельном переносе все наклоны остаются одинаковыми, на-
пример, при х = х0 касательные к кривой у(х) (точка А)
и к смещенной кривой (точка В) параллельны, углы оди-
наковы. Этот результат соответствует свойству производ-
ных: прибавление к функции константы (соответствующее
74
понятие производной и Интеграла
1ч. н
параллельному переносу по вертикали на графике) не ме-
няет производной.
Можно заниматься и другой математической игрой: нари-
совав от руки график производной, приблизительно постро-
ить график функции. При этом нужно произвольно задать
одну точку (хп, у (*„)) и от нее вести кривую вверх или
вниз (в соответствии со знаком производной).
В заключение заметим, что до сих пор предполагалось
равенство масштабов по оси у и по оси х, т. е. что одна
в)
Рис. 36.
единица измерения х и одна единица измерения у выра-
жаются на графике отрезками равной длины. Тогда дей-
ствительно 1%,а=%*
При построении графиков часто пользуются разными
масштабами, в особенности когда у и х суть величины
разной размерности. Пусть, например, у есть путь, а х —
время и откладывается график положения тела в зависи-
мости от времени у(х). По оси ординат (у) будем откла-
дывать у в масштабе 1 м пути= 1 см на чертеже. По оси
абсцисс (я) будем откладывать время в масштабе 1 сек
времени =1 см. на чертеже. Тогда действительно скорость
движения v, выраженная в метрах в секунду и равная
производной ¦—, равна tg а, тангенсу угла касательной на
графике. Но если мы выберем другой масштаб для шкалы х,
§ 5] касательная к кривой 75
например 1 сек = / см = 5 см на чертеже, то получим:
te а =-*? —L *Z = 1 *И. — JL „ _fl
/d / d* 5 <*х—Ъ сек'
В общем случае, если одна единица х на чертеже от-
кладывается в масштабе / см, а одна единица у отклады-
вается в масштабе п см, то
Когда г/ и jc — именованные (размерные) величины, на-
пример, у— метры, х — секунды или у — килограммы,
х — месяцы (зависимость веса ребенка от времени), произ-
¦ du du
водная -# тоже имеет размерность: в первом случае -~ = v
— это скорость движения, размерность —, во втором
случае^ — это скорость увеличения веса, кг\месяц.
Тригонометрическая функция tga безразмерна (она
равна отношению длин двух отрезков). Поэтому и не мо-
жет быть простого равенства tg a = ~-, так как в нем ле-
вая часть и правая часть имеют разные размерности. Мас-
штабные множители 2илв формуле tg a = -^- • ^ как раз
и делают равенство правильным с точки зрения размер-
ности. Так, во втором примере/ имеет размерность см/месяц
A см на графике на 1 месяц возраста), п имеет размер-
ность см!кг A см на графике на 1 кг веса), так что -у • ^
безразмерно. В формуле
п (—
( см \
\ месяц )
месяц
все размерности сокращаются.
Об этом следует помнить при сравнении производной
и наклона кривой.
76
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Упражнения
пределах от х = — 1,5 до
в точках х = — 1, х = О,
1. Построить график у = ха -J- 1 в
х = 2,5 н провести к нему касательные
х=1,х==2.
2. То же для функции у = х* — Ъх*. — 1 < х < 3,5, касатель-
ные при х = —1, 0, 3. Найти точки с горизонтальной касательной.
3. Найти точки с горизонтальной касательной для кривой
у =х* — х -f- 1. Построить кривую при — 2 < х < 2.
Указание. Упражнения 1—3 желательно выполнять на мил-
лиметровке п крупном масштабе.
4. Построить кривую у' (х) для функции у(х), заданной рис. 37.
У
2
О
-1
-2
5 6
Рис. 37.
-12 х
Указание. Сперва перерисовать рис. 37 на чистый лист и там
же строить у'(х), чтобы не лишать удовольствия следующего читателя.
5. Провести кривую у (х) через точку х= 5, у = 0 для кривой у' (х),
заданной рис. 38. Под каким углом у (х) пересекает ось ординат?
Под каким углом у(х) пересекает ось абсцисс при х = 5?
У'
2
1
0
-1
-2
а> i м
1 2 Л
' \
' ' 'л ' ' J » X
4 5 6 7\в 9/iQ
Рис. 38.
Указание. То же, что и к упражнению 4.
6. Составить уравнения касательных к кривой у=ха в точках
« = 0,5 и х=1. Найти точки пересечения касательных с осями х и у.
7. Найти общее правило для точек Пересечения с осями каса-
тельных к кривым y = axx, y = bxa.
§ 6] РОСТ И УБЫВАНИЕ, МАКСИМУМ И МИНИМУМ ФУНКЦИЙ 77
§ 6. Рост и убывание, максимум и минимум функций
Пусть нам задана зависимость какой-нибудь физиче-
ской величины, например температуры, от времени.
Итак, z — это температура, t — время, и дана формула
для функции z(t). Как определить, растет или падает
температура в данный момент /? Как определить, в ка-
кой момент температура достигает максимума или минимума?
Не зная производных, ответ на первый вопрос нужно
искать численно: иайти температуру в данный момент t,
затем взять какой-то следующий момент tt и посмотреть,
выросла температура или упала? Очевидно, что такой спо-
соб ненадежен: если z(tj и больше чем z(t), то ведь не
исключено, что в момент t температура падала, вскоре
(после /, но до г,) достигла минимума, а уже после этого
стала расти и к моменту tt стала выше z{t).
С помощью производных вопрос решается точно: надо
найти производную -4. Если -r=z' (t) при заданном t есть
положительная величина, то z(t) есть растущая функция:
при увеличении t на малую величину Д^ температура
изменится на малую величину Az = z'(t)-At (как было
выяснено раньше, чем меньше At, тем точнее это равен-
ство). Мы рассматриваем Д/ > О — увеличение времени.
Если z'(t)>0, Д/>0, то и Дг>0, т. е. с течением вре-
мени температура растет. Если z' (t) < О, At > 0, то Дг < О,
т. е. температура в следующий момент z (t-\-At) будет
ниже температуры z(t) в данный момент.
Таким образом, положительная производная указывает
на то, что функция является растущей, а отрицательная
производная — на то, что функция падающая.
Выражения «растущая функция» и «падающая функ-
ция» применяются не только к зависимости от времени, но
и к любой функции у(х); при этом растущей функцией
называется такая, у которой у увеличивается при увели-
чении независимой переменной х.
Производная ^ как раз и дает скорость роста, т. е.
отношение изменения у к изменению х. Отрицательная
скорость роста означает падение, уменьшение у при уве-
du I du\
личении х, и если ^<0. то ( — j-) есть скорость падения.
78 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
Выражение «величина у имеет большую отрицательную
производную по хъ обозначает, что у быстро падает с уве-
личением х. Положительная производная-^ означает, что у
растет с ростом х.
Физики и математики, в особенности будущие физики
и математики, только что узнавшие, что такое производ-
ная, часто применяют это понятие и в повседневной жизни:
«производная от моего настроения по времени положи-
тельна» — вместо «мое настроение улучшается».
Решите задачу-шутку: какой знак имеет производная
от настроения по расстоянию до кресла зубного врача?
Настроение ухудшается, «уменьшается», становится «отри-
цательным» по мере уменьшения расстояния, значит, про-
изводная положительна.
Может быть, писатели будут сетовать на засорение
языка, но на самом деле такое вольное шуточное употреб-
ление математических понятий — это хорошая тренировка
для будущих серьезных применений.
Есть функции, имеющие один и тот же знак производ-
ной при любых значениях переменной: таким свойством об-
ладает, например, линейная функция y = kx-\-b, у кото-
рой -ж. = к — постоянная величина. Позже мы увидим, что
у показательной функции у = ах производная имеет по-
стоянный знак (хотя и не постоянна по величине) при лю-
бых х. Однако постоянный знак производной, конечно,
совершенно не обязателен; знак производной данной функ-
ции может быть различным при различных значениях не-
зависимой переменной.
Представим себе функцию у (х), производная которой у' {х)
положительна при х<ха и отрицательна при х > дг0: кратко,
у'(х)>0, х<хп) у'(х)<0, х>ха.
Что можно сказать о такой функции? Начнем с х < ха.
При увеличении х до хп. у будет расти; при дальнейшем
увеличении х у падает. Отсюда вывод: при х = хп функ-
ция у(х) имеет максимум.
Рассмотрим противоположный случай:
у' (х) <0, х<ха; у' (х) > 0, х > х9.
Рассуждая таким же способом, придем к выводу, что
в этом случае при х — хп у{х) имеет минимум.
§ 6J РОСТ И УБЫВАНИЕ, МАКСИМУМ И МИНИМУМ ФУНКЦИЙ 79
Если функция у (х) задана формулой, которой соответ-
ствует плавная кривая, так что и у' (х) плавно изменя-
ется при изменении х, то разный знак у' (х) при х < ха и х> х„
в обоих случаях обозначает, что при х=-хп #(л;0) = 0.
Таким образом, приравнивая нулю производную, мы можем
найти те значения независимой переменной, при которых
функция имеет максимум или минимум. Об исключениях
из этого правила для негладких кривых поговорим позже,
в части IV.
Приведем численный пример. В § 1 части I была со-
ставлена таблица функции у = Ъх*— х* — х, см. стр. 12.
Судя по этой таблице, можно было бы думать, что функ-
ция является растущей при всех значениях х, так как каж-
дое увеличение х на единицу вызывало увеличением/.
Составим производную
Взяв дг = О, получим у' @) = —1<0. Значит, при х = 0
функция — падающая; это опровергает предположение, что
функция везде растущая, полученное из рассмотрения таб-
лицы.
Приравняем у' (х) нулю. Решая уравнение
9хг — 2х— 1=0,
найдем два корня:
^ = —0,24; хг = + 0.46.
Составим более подробную таблицу,
ные точки максимума и минимума.
включая найден-
Таблица 5
X
У
— 2
— 26
— 1
— 3
— 0,30
+ 0,129
— 0,24
+ 0,140
— 0,18
+ 0,131
X
У
0
0
0,40
— 0,372
0,46
— 0,381
0,52
— 0,370
1
2
+ 18
80 понятие производной и интеграла [ч. п
Мы видим, что, действительно, на участке от х==— 0,24
до * = 4-0,46 функция у падает от +0,14 до —0,38.
Сравнение значений у (—0,24) с соседними у (—0,30) и
у(—0,18) подтверждает, что при * = —0,24 у достигает
максимума, соседние у меньше.
Здесь же мы видим, что слово максимум надо понимать
не в смысле наибольшего из всех возможных вообще зна-
чений у. В самом деле, в точке максимума у{—0,24) = -[-0,14,
а при х=\ у=\, при х = 2 у = -\г\8, при х= 10
# = 269, и т. д., при неограниченном увеличении х у
также неограниченно растет. Чем же отличается най-
денная нами точка максимума*) хтях = — 0,24, # = 0,14?
Отличие ее в том, что при близких соседних значениях х,
как больших #max, так и меньших хтлх у меньше, чем
Утах = У (Хтах)- Эта ОСОбеННОСТЬ Хтлх НЭГЛЯДНО ВИДНЭ
в таблице (сравните у(—0,30), у (—0,24) и у (—0,18)).
Такие же соображения относятся и к минимуму: при
*mln = 0,46 #min = — 0,381; при больших по абсолют-
ной величине отрицательных х у неограниченно умень-
шается и становится меньше утщ., но xmin, Утш отличается
тем, что ymin меньше значении у при х, близких к хт\п-
Условие равенства нулю производной дает возможность
найти именно такие максимумы и минимумы.
Определение максимумов и минимумов арифметическим
путем, вычислением и сравнением значений функции при
различных значениях аргумента, является во много раз
более трудоемким и менее точным. Высшая математика
является не только замечательным идейным достижением.
Практические, конкретные вычислительные задачи также
гораздо легче решаются методами высшей математики.
Остановимся в заключение данного параграфа
на вопросе о том, как отличить максимум от минимума,
когда мы пользуемся условием у'(х) = 0. Это условие вы-
полняется и в максимуме и в минимуме, разница же за-
ключается в знаке у' (х) при х<ха и при х>ха.
Как определить знак у' (х) при х, близком к ха, не вы-
числяя непосредственно у' для других значений х? В первом
*) Значок max при х — сокращение латинского слова maximum —
максимум, читается: «икс — макс» или «икс — максимум»; значок
min — minimum — минимум.
§ 6J РОСТ И УБЫВАНИЕ, МАКСИМУМ И МИНИМУМ ФУНКЦИЙ 8}
случае мы видели, что функция у (х) имеет максимум,
когда у'(х)>0 при х<ха и у'(х)<0 при х>хп. Следова-
тельно, в этом случае производная у' (х) сама представ-
ляет собой падающую функцию: по мере роста х про-
изводная, которая сначала была положительной (прилс<х0),
обращается в нуль (при х = ха) и, продолжая падать, ста-
новится отрицательной при дох,. Но мы уже знаем, как
отличить падающую функцию: ее производная отрицательна.
Следовательно, в первом случае при том значении х = хтгх,
при котором у имеет максимум, у' (ха) = 0, а производная
от производной отрицательна. Такая величина—производ-
ная от производной,— которую можно по общим правилам
трехэтажно записать
ЧУ J\dx)
Ах dx '
имеет свое название — «вторая производная». Ее обозна-
чают также у" {х) или ~г.
Итак, условие максимума
у'(х) = О, у"(х)<0.
Таким же способом можно проверить, что при том ху
для которого
у'(х) = 0, у"(х)>0,
функция у (х) имеет минимум.
Обратимся к примеру, рассмотренному выше,
у = 3х'— х1— х, у' = 9х* — 2х—1.
Взяв производную от у', найдем:
у"=\8х — 2.
При х = — 0,24 #' = 0, у" = — 6,3<0, и действитель-
но, дг = — 0,24, е/ = 0,14 есть максимум. При х = ~\-0,4&
у' =0, #" = +6,3>0, ПрИ х = о,46 у = — 0,38, у имеет
минимум.
Упражнения
Найти значения х, при которых достигается максимум или ми-
нимум нижеследующих функций. В каждом случае выяснить, имеем
ли мы дело с минимумом нли с максимумом. В функциях, в которые
82 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
входит постоянная, заданная буквой а, дать ответ для а > 0 н
для а < 0.
\.у = ахх. 2. у=х-\ . 3.у=х-\~—. 4. # = xs —х.
Дь X
§ 7. Определение пути по скорости движения
и площадь под кривой
Задача об определении мгновенной скорости движения
v (t) по заданной зависимости положения тела от времени
z{t) привела нас к понятию производной
Обратная задача заключается в определении положения
тела и пути, пройденного телом за данный отрезок време-
ни, когда задана мгновенная скорость v (/) как функция
времени. Эта задача приводит ко второму важнейшему
понятию высшей математики — понятию интеграла.
Условимся об удобных обозначениях. Рассматриваем
путь, пройденный за время от /, до tt. Чтобы не писать
индексов, назовем начало рассматриваемого промежутка
времени одной буквой п («эн»—начало), t1 = n, и конец
этого промежутка k («ка» — конец), tx = k. Пройденный
путь обозначим z(n, k). Запомним, что когда в скобках
под знаком функции г стоят две величины п и k, то
z(n, k) есть длина пути, пройденного за время от п
до k, тогда как z (t) с одной величиной в скобках есть
положение (координата) тела в заданный момент t. Между
этими величинами есть простая связь:
z(k) = z(n) + z(n, k), \
г(п, k) = z(k) — z(n). I U- >
Путь, пройденный за время от п до k, равен разности
координаты в конце рассматриваемого промежутка вре-
мени z(k) и в начале этого промежутка z (n).
Теперь обратимся к вычислению z (n, k).
В простейшем случае, если скорость постоянна
р(*) = const = »„ G.2)
§ 7]
ОПРЕДЕЛЕНИЕ ПУТИ ПО СКОРОСТИ ДВИЖЕНИЯ
83
пройденный путь, очевидно, равен просто произведению
времени движения на скорость
г(п, k) = (k — n)va. G.3)
Если воспользоваться графиком зависимости скорости от
времени, то на таком графике постоянной скорости соот-
ветствует горизонтальная прямая (рис. 39). Пройденный
путь, очевидно, равен за-
штрихованной площади, по-
тому что площадь прямо-
угольника равна произве-
дению основания (k — п)
на высоту (о0).
Как быть в общем слу-
чае, когда мгновенная ско-
рость не постоянна? Рнс. 39.
Рассмотрим подробно
один численный пример. Пусть скорость движения задана
формулой*) v = t2. Найдем путь за время от * = л=1
до t = k = 2.
• Разобьем весь промежуток от п до k на десять частей
и составим таблицу скорости (табл. 6). Сокращенно назо-
вем At малые промежутки времени по 0,1 сек, на которые
мы разбили весь промежуток от t=n до t=k.
Таблица 6
t
V
1,0
1,0
1,1
1,21
1,2
1,44
1,3
1,69
1,4
1,96
1,5
2,25
1,6
2,56
1,7
2,89
1,8
3,24
1,9
3,61
2,0
4,0
В чем трудность вычисления пути при скорости v(t)
заданной формулой? Очевидно, все дело в том, что ско-
рость переменна, для постоянной скорости ответ элемен-
тарен. В рассматриваемом примере во всем промежутке
времени от ?=1 до ? = 2 скорость меняется в 4 раза.
*) Скорость v выражена в см/сек, I — в сек; чтобы соблюдались
требования размерности, напишем и = а<*, где а имеет размерность
см/сек*. Рассматриваем частный случай, когда коэффициент а численно
равен 1 см/сек*.
84 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
Однако после того как этот промежуток разбит на 10
частей, в каждом маленьком промежутке времени дли-
тельностью 0,1 сек скорость меняется меньше—всего на
10—20%. Следовательно, в маленьких промежутках ско-
рость можно приближенно считать постоянной и рассчи-
тывать путь в течение малого промежутка времени как
произведение этого промежутка времени на скорость.
Для вычисления пути в каждом промежутке At,
составляющем 0,1 сек, используем начальную скорость
в этом At: 1 см /сек в At от 1 до 1,1 сек, 1,21 см j сек
в Д* от 1,1 до 1,2 сек и т. д.; наконец, 3,61 см\сек
в последнем Д^ от 1,9 до 2,0 сек. Полный пройденный
путь за промежуток времени от ?=1 до * = 2 при этом
способе подсчета окажется равным
z(l; 2) = 0,1 + 0,121+0,144+...+0,361=2,185 см.
Очевидно, в таком расчете мы преуменьшили пройден-
ный путь: скорость в данном примере с течением времени
растет, поэтому скорость в начале каждого At меньше
средней скорости. Каждое из десяти слагаемых, на кото-
рые разбит весь путь, несколько занижено, следовательно,
занижен и весь результат.
Теперь подсчитаем путь по-другому, а именно, в каж-
дом At будем брать значение скорости в конце проме-
жутка At. Для первого At суг 1 до 1,1 сек эта скорость
равна 1,21 см\сек, для последнего от 1,9 до 2 сек ско-
рость равна 4 см/сек. Тогда для пройденного пути
получим:
z(l; 2) = 0,121+0,144+...+0,400 = 2,485 см.
Такой расчет, очевидно, дает преувеличенное значение
*A; 2). Значит, истинное значение' лежит в пределах
между 2,185 и 2,485 см. Различие между 2,185 и 2,485
составляет около 15%. Округляя границы для г, получаем:
2,18<z<2,49.
Проделанный расчет можно пояснить графически.
Построим график (рис. 40), на котором по оси абсцисс
отложено время, а по оси ординат — скорость. Для того
чтобы ступеньки были хорошо видны, на чертеже проме-
жуток времени разбит на пять частей (а не на десять
§ 7]
ОПРЕДЕЛЕНИЕ ПУТИ ПО СКОРОСТИ ДВИЖЕНИЯ
85
частей, как в таблице). Каждое слагаемое в первой сумме
представляет собой площадь узенького прямоугольника,
основанием которого является соответствующий интервал
Д/, а высотой—скорость в начале интервала. Следова-
тельно, сумма представляет собой площадь под ломаной
(ступенчатой) линией, заштрихованную на рис. 40. Вторая
сумма, в которой в каждом интервале бралась скорость
в конце промежутка, соответствует площади, заштрихо-
ванной на рис. 41.
2 X
О
Рис. 40.
Рис. 41.
Как точнее подсчитать путь, пройденный за данное
время, от t = п = 1 сек до t = k = 2 сек?
Различие между нижней и верхней оценкой, т. е.
разность между величинами 2,18 и 2,49, зависит от изме-
нения скорости в пределах каждого интервала Д7.
Для того чтобы найти более точное значение гA; 2),
надо разбить весь промежуток времени от 1 до 2 сек на
большее число промежутков меньшей длины. Так, напри-
мер, если разбить промежуток от 1 до 2 сек на 20 про-
межутков Д? по 0,05 сек, то такой же расчет даст по
начальным скоростям в каждом At
z(l; 2) = 0,05+ 0,05-1,1025+...+0,05-3,8025 = 2,25875,
а по конечным скоростям
z(l; 2)=0,05-1,1025+0,05-1,21 +.. . + 0,05-4 = 2,40875.
86
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Различие между 2,25875 и 2,40875 составляет около 7%.
Пределы, в которых заключено гA; 2), сузились. Округ-
ленно
2,26 < г A; 2) < 2,41.
При уменьшении Д* результат приближается к истин-
ному значению пути, которое будет вычислено в дальней-
шем и окажется равным
A j 2.) —— Z -TJ- = 2,, ооЗ...
При уменьшении At уменьшается различие между
начальной и конечной скоростями в каждом малом проме-
жутке At, следовательно, уменьшается относительная
ошибка в каждом слагаемом; поэтому и вся сумма путей за все
At, т. е. величина гA; 2), опре-
деляется тем точнее, чем меньше
At (число малых промежутков,
равное Tj-, при этом увели-
чивается).
Геометрически очевидно, что
при увеличении числа проме-
жутков Д* и уменьшении длины
каждого промежутка уменьша-
ются размеры каждой ступень-
ки на рис. типа 40, 41 и, сле-
довательно, ступенчатая линия
¦*? становится все ближе к кривой
v(t).
Таким образом, мы при-
ходим к- выводу, что путь,
пройденный за время от t = n до t = k при произвольной
зависимости мгновенной скорости от времени v (t), равен
площади ограниченной кривой v(t), вертикалями t = n и
t = k и осью t (рис. 42).
Этот вывод дает способ практического вычисления
пути: можно построить график на миллиметровке и опре-
делить заштрихованную площадь либо подсчетом клето-
чек, либо, например, вырезав эту площадь из бумаги,
взвесив вырезанный листочек и сравнив его вес с весом
О
Рис. 42.
§ 7] ОПРЕДЕЛЕНИЕ ПУТИ ПО СКОРОСТИ ДВИЖЕНИЯ 87
вырезанного из той же бумаги прямоугольника или
квадрата с известной площадью.
Такой способ удобен и вполне оправдан, когда ско-
рость известна не точно, задана в виде таблицы или гра-
фика, полученных из опыта. Но мы не остановимся на
этих приближенных способах и выясним дальше, как
выразить формулой пройденный путь, когда скорость
задана формулой.
Можно уточнить и численный метод определения пути
по сравнению с теми вычислениями, которые были приве-
дены выше: для этого путь в каждом малом промежутке
времени будем определять по среднему арифметическому
(т. е. полусумме) начальной и конечной скорости в данном
промежутке. При таком способе, при разбивке на десять
промежутков, скорость в первом промежутке от 1 до 1,1 сек
примем равной ^ ' = 1,105 см\сек и путь за этот
промежуток времени 0,1105 см, путь за второй промежу-
ток 0,1 •——~JT ' =0,1325 см и т. д. Складывая их,
получим таким способом путь, пройденный за все время
от л=1 сек до k = 2 сек, равным
гA; 2) = 0,1105+0,1325 + ...=2,335 см.
При разбивке на 20 промежутков получим таким же спосо-
бом (по полусумме скоростей)
гA; 2) =^2,33375 см.
Эти значения гораздо ближе к истинной величине
2,3333 см, чем вычисленные по начальному или конечному
значению скорости при том же числе промежутков: при
десяти промежутках ошибка равна 0,07"/0 вместо 15°/0
в прежнем способе, при 20 промежутках ошибка 0,02°/0
вместо 7°/0.
Такой способ также можно наглядно пояснить на гра-
фике. Произведение полусуммы скоростей в начале и
в конце промежутка на величину промежутка времени
есть площадь трапеции ABCD (рис. 43): ее основания АВ и
DC, высота AD, площадь
ЛД-f-DC
2
88
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
Поэтому определение пути по полусуммам скоростей
называется «методом трапеций». При том виде, кото-
рый имеет кривая v (t) на рис. 43, площадь трапеции
несколько больше площади, ограниченной прямыми ВА,
AD, DC и отрезком кривой ВС. Разность площади тра-
пеции и площади, ограниченной отрезком кривой, равна
площади луночки, образованной
хордой ВС и отрезком кривой
ВС (заштрихована на рис. 43).
Эта площадь и дает ошибку —
разность между истинным зна-
чением пути и вычисленным по
методу трапеций. Сравнение с
рис. 40, 41 наглядно показыва-
ет, что ошибка в методе трапе-
ций должна быть меньше, чем в
методе ступенек.
Рис- 43. Когда мы сравниваем путь
и площадь на графике, необхо-
димо учитывать масштаб, в котором составлен график.
Пусть на графике 1 см по оси абсцисс соответствует про-
межутку времени Т сек, 1 см по оси ординат соответст-
вует скорости V см\сек. Тогда при движении с постоян-
ной скоростью vn в течение времени от п до k путь ра-
вен v0 {k — п), а площадь прямоугольника на графике (рис. 39)
равна
С "о F — ") „,.г
Таким образом,
z(n, k) = SVT.'
Это соотношение между пройденным путем и площадью на
графике скорости, ограниченной кривой v (t), осью абсцисс
и вертикалями, сохраняется и в случае переменной ско-
рости и произвольной зависимости v (t).
Таким образом, мы подробно рассмотрели способы при-
ближенного численного и графического определения
пройденного пути по заданной зависимости скорости от
времени.
§ 8] " ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 89
§ 8. Определенный интеграл
В предыдущем параграфе две задачи: задача определе-
ния пройденного пути и равносильная ей задача опреде-
ления площади под кривой — привели к рассмотрению
сумм особого вида с большим числом малых слагаемых.
Постановка этих задач приводит к понятию интеграла.
Величина пути z(n, k), найденная по заданной скоро-
сти v(t), называется «определенным интегралом функции
v (t) — скорости по переменной t — времени, взятым от п
до k».
Дадим математическое определение интеграла, соответ-
ствующее тем идеям, которые были иллюстрированы числен-
ным примером предыдущего параграфа. Это определение
останется верным и в том случае, если рассматриваются
не скорость и путь, а какие-либо другие физические или
математические величины.
п н
to tt tj tj t4 t,., t, tm
-+^—h—н—i—у н—.
Рис. 44.
Итак, пусть дана функция v(t). Для нахождения ее
интеграла от п до k разбиваем промежуток от п до k на
большое число т. малых промежутков. Значения аргу-
мента t на границах малых промежутков обозначим /0,
tx, tx, ..., tm_lt tm. При этом, очевидно, tu = n и
Последнее tm = k (рис. 44).
Длины малых промежутков времени Д* равны разности
соседних значений t *).
Номер промежутка соответствует номеру аргумента
в конце промежутка (рис. 44). Таким образом, для
*) Если разбивать промежуток от п до k специально на от рав-
ных частей, то каждый промежуток Д* = . Однако для даль-
нейшего не обязательно, чтобы все части, на которые разбит проме-
жуток, были равны между собой, нужно только, чтобы каждый про-
межуток Д? был мал. Читатель может убедиться в этом, продумав
пример путь — скорость из § 7.
90 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
какого-нибудь произвольного I
Atl=tl—tl_l.
Значки снизу у величин t и At представляют собой не
множители, а номера, или, как' их иначе называют,
«индексы» (см. стр. 19).
Приближенное значение интеграла z(n, k) дается фор-
мулой
г {п. k)*J%v(tt_x)&tt. (8.1)
Знак 2 есть прописная греческая буква 2 (читается:
«сигма»). Буква 2 в греческом алфавите соответствует
букве S латинского алфавита — первой букве слова сумма.
2 означает, что выражение, стоящее справа от этого знака и
/=i
зависящее от индекса /, надо взять при всех значениях
/ от 1 до т и все эти выражения надо сложить. Так,
например, если т=\0, то
f.-f °('»)А'. + ••• + » С.) А',.-
В примере § 7 в табл. 6 /0=1, /,=^=1,1, /,= 1,2, ...,
z(l; 2) = г (я, ft)W2°*'-iA*,= 2,185.
В приближенном выражении (8.1) в каждом промежутке
значение функции v (t) бралось в начале промежутка —
в точке t[_l. Другое приближенное выражение получим,
беря в каждом промежутке значение функции в конце
промежутка
г (я, 6) ~'1> О1,) Дг,. (8.2)
В примере § 7 при т=10 эта сумма равнялась 2,485.
Определенным интегралом функции v (/), взятым от
п до к, называется предел, к которому стремятся суммы
(8.1) и (8.2) при стремлении к нулю всех промежутков At.
§ 8] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 91
Интеграл записывается в виде *)
k
z(n, k) = \v(t)dt. (8.3)
Знак ^ (интеграл) происходит также от латинской буквы
5 (первой буквы слова «сумма»), он получился растягива-
нием этой буквы.
Знак dt в отличие от At означает, что для получения
точного значения интеграла необходимо перейти к пре-
делу, когда все промежутки At стремятся к нулю. Фор-
мулы (8.1) и (8.2) с конечными At дают только прибли-
женные значения интеграла. Напомним, что в § 2, рас-
сматривая производную, мы также заменяли конечные
отрезки Дг и At дифференциалами dz и dt.
Когда малые промежутки At становятся все мельче и
мельче, то уже становится безразличным, брать ли зна-
чение функции v в начале, в конце или где-нибудь
внутри промежутка, т. е. безразлично, исходить из (8.1)
или из (8.2), н в формуле (8.3) стоит просто v (t) — зна-
чение функции в промежутке dt, без указания того,
берется значение v (t) в начале или в конце проме-
жутка.
Следующее отличие интеграла (8.3) от сумм (8.1) и (8.2),
которые дают приближенно значения интеграла, заклю-
чается в том, что при уменьшении величин At и при
увеличении числа малых промежутков мы отказываемся
от того, чтобы нумероаать их. Поэтому у интеграла ука-
зываются только пределы изменения t от п до k.
Величина п ставится снизу и называется нижним пре-
делом интегрирования, величина k стоит у верхнего кон-
ца знака интеграла и называется верхним пределом **).
*) Читается: «зет от эн, ка равняется интегралу от эн до ка
вэ от тэ де тэ».
**) В этом параграфе слово «предел» употребляется в двух смыс-
лах: интеграл есть предел суммы в том же смысле, в котором
производная есть предел отношения. Здесь слово «предел» соответст-
вует знаку lim. Кроме того, мы говорим о пределах изменения t от
п до к, о пределах интегрирования я и Л. Здесь слово «предел» имеет
другой смысл. Внимательный читатель не запутается в этих двух значе-
ниях слова «предел».
92
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Промежуток изменения t от п до k называется проме-
жутком интегрирования, функцию v (t) в выражении
интеграла называют «подынтегральная функция», t — «пе-
ременная интегрирования».
Таким образом, интеграл определяется как предел,
к которому стремится сумма произведений значений функ-
ции на разность значений аргументов при стремлении
к нулю всех разностей аргументов:
lira
1—т
У v(tl)Atl= Km У v(tl_1)Ati=\v(t)dt. (8.4)
л
Хотя первая и вторая суммы в равенстве (8.4) при
конечном числе малых промежутков различны, пределы
их при неограниченном уменьшении всех промежутков Д/
одинаковы.
Понятие предела суммы можно пояснить численным
примером предыдущего параграфа для § t'dt. В таблице
1
в верхней строке указано число интервалов т, во второй
строке — длина каждого интервала At, в третьей строке —
сумма, в которой функция берется в начале промежутка,
в четвертой строке — сумма, в которой функция берется
в конце промежутка. Стремление этих двух сумм к оди-
наковому пределу наглядно видно.
т.
М
2<'-.д<
2 *ы
10
0,1
2,18
2,49
20
0,05
2,26
2,41
50
0,02
2,30
2,37
00
0
2,33
2,33
Заметим, что в данном случае суммы выражаются
сравнительно простыми точными формулами, справедли-
выми при любом числе равных интервалов т и соответ-
§" 8] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 93
ствующей величине Af = * ~ ' = —:
tn tn
Вывод формул (8.5) и (8.6) для понимания дальнейшего
знать необязательно*). В этих формулах предел при Д*.
стремящемся к нулю, находим непосредственно **): пола-
гаем Д? = 0, получаем предел 7/3 = 2,333...
При стремлении Д^ к нулю каждое отдельное слагае-
мое стремится к нулю, но зато возрастает, стремится
к бесконечности, число членов суммы. Сама сумма стре-
мится к вполне определенному пределу, являющемуся
решением задачи и называемому «интеграл». Этот предел,
*) Эти формулы получаются с помощью элементарной алгебры.
Задачу можно свести к нахождению суммы квадратов натуральных
чисел. Легко видеть, что </=—'—; обозначим m-\~l = k. Первая
сумма равна —j( 2 **— 2 **)• вторая сумма равна
rrs" ( 2 ** — 2 **)• Для нахождения суммы квадратов 2 **
(k -t- 1)' — ft' . 1 „
используем тождество k* = -—!—^ я ^-. Суммируя, полу-
^^
чнм 2 я1== "о" (i -f- l)s — 5] ^ — "Т • ^° Формуле суммы членов
арифметической прогрессии 2 * == о • Отсюда окончательно
k = n j
2 **=: "с" п (п -f-1) Bn -(- 1). С помощью этих формул, подставляя
т = —•, получим приведенные в тексте выражения.
*•) Заметим, что путь, найденный методом трапеций, при данном
числе интервалов равен полусумме путей, найденных по начальной
и по конечной скорости в каждом интервале. Таким образом, для
метода трапеций путь равен -я-+ -ц-(&0г, предел при Д< -+ 0, есте-
ственно, тот же самый.
94
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. U
т. е. интеграл функции, равен пройденному пути, если
функция представляет собой мгновенную скорость.
Поскольку переменная интегрирования может прини-
мать значения п и k, то ясно, что пределы интегриро-
вания имеют размерность и их размерность равна размер-
ности переменной интегрирования (в примере путь—ско-
рость пределы интегрирования имеют размерность
времени). Размерность интеграла легко получить из фор-
мулы (8.1). Действительно, размерность суммы равна раз-
мерности отдельных слагаемых. Отдельные слагаемые
суммы (8.1) имеют размерность, равную произведению
размерности подынтегральной функции на размерность
переменной интегрирования. В примере путь — скорость
размерность интеграла есть см\сек-сек=см..
Заметим, что величина определенного интеграла зави-
сит от значений стоящей под знаком интеграла функции
лишь внутри промежутка интегрирования. Значения
функции вне промежутка интегрирования на величину
интеграла никак не влияют. Это станет совершенно
ясным, если вспомнить пример путь — скорость. Пройден-
ный путь зависит, конечно, от скорости (р (t)), но зависит
лишь от ее значений внут-
ри промежутка интегриро-
вания. Пройденный путь
z (n, k) совершенно не за-
висит от того, какова была
скорость до момента ? = я
(от которого мы начали рас»
сматривать движение) и
какова она стала после мо-
мента t = k.
В § 7 отмечалось, что
путь можно определить,
вычислив площадь на графике зависимости скорости от вре-
мени. Задача нахождения площади S, ограниченной сверху
кривой с заданным уравнением у (х), снизу — осью абсцисс
(осью х), с боков — линиями х=а и х = Ь (рис. 45),
также сводится к вычислению интеграла
ь
b b+Jb з?
Рис. 45.
§ 8] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 95
Для пояснения нужно вернуться к рис. 40 и 41; пред-
ставим себе, что по оси ординат откладываются значения
какой-то функции у(х), по оси абсцисс—независимая
переменная х, причем у (х) не имеет отношения к движе-
нию и скорости; вместо п и k подставим буквы а и Ь.
Сумма площадей прямоугольников, заштрихованных
на рис. 40, равна 2 l/fo-i) A*f a такая же сумма
на рис. 41 равна У у (xt) • Ахе. В пределе при Ахе—*0 эти
суммы по определению равны интегралу, а сумма площа-
дей прямоугольников стремится к площади ограниченной
кривой у(х), так как чем меньше все Д^, тем ближе
к кривой ломаная (зубчатая) линия, ограничивающая
пр ямоугольники.
В заключение отметим, что определенный интеграл
зависит от подынтегральной функции и пределов интегри-
рования, но не зависит от обозначения переменной интег-
рирования. Поясним сказанное. Пусть дана, например,
подынтегральная функция
»(*)==3*' + 5.
Подставив значение t = x, получим:
При вычислении же интеграла безразлично, как называ-
лась переменная интегрирования, важно только, в каких
пределах она менялась, каковы были значения функции.
Поэтому
к к
z (n, k) = J v (t) dt=\)v {x) dx.
п п
Переменную интегрирования можно называть как угодно.
Переменная, которая не входит в окончательный
результат, подобно переменной интегрирования, назы-
вается немой переменной. Переменную интегрирования
можно заменить под интегралом любой буквой, не нару-
шая справедливости формул. Обычную, не немую, пере-
менную можно заменять другой буквой только во всех
частях формулы: например, в формуле (х-\- \)г=хг-\-2х-\-\
96 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
нельзя написать (t-\-\y=x2~\-2x-X-\, а в интегралах
можно писать
к к
\ v @ dt = J v (х) dx.
п п
Упражнение
Рассмотреть случай v = at-\~b (равноускоренное движение).
Найтн путь за время от п до k, разбивая это время на т равных
интервалов; воспользоваться тем, что слагаемые сумм образуют
арифметическую прогрессию. Найти предел суммы при т -*-оо. Срав-
нить полученное выражение с площадью трапеции на плоскости
v, t, равной пройденному пути.
§ 9. Связь между интегралом и производной
Будем считать заданной и известной зависимость от
времени мгновенной скорости v(t). Будем считать
постоянным момент tJ = n начала пути. Рассмотрим путь,
пройденный за время от tl = n до tt = k, как функцию
конечного момента k. Мы знаем, что
z(&, n)=z(k) — г (л).
Возьмем производную от левой и правой частей; при
этом п рассматривается как постоянная величина, следо-
вательно, и г (п) есть постоянная величина. Получим:
dz(k, n) dz (k)
dk dk '
Но мы знаем, что производная от координаты тела по
времени есть не что иное, как мгновенная скорость тела
значит, и
Подставим сюда выражение г(п, К) в виде интеграла.
ПОЛУЧИМ1
§ 9], СВЯЗЬ МЕЖДУ ИНТЕГРАЛОМ И ПРОИЗВОДНОЙ 97
Это равенство является важнейшим общим свойством
определенного интеграла. Это равенство в таком виде
является общей математической теоремой; его правиль-
ность не зависит от того, является ли v (t) скоростью
(а интеграл — путем) или v (t) есть какая-то другая вели-
чина. Для любой функции, например у(х), имеем:
y{b). (9.2)
Формулировка теоремы: производная от определен-
ного интеграла по его верхнему пределу равна значению
подынтегральной функции на верхнем пределе.
Ввиду важности теоремы дадим другой вывод ее, ос-
нованный на рассмотрении площади. Производную будем
вычислять по всем правилам, как предел отношения прира-
щения функции к приращению независимой переменной.
Рассматриваем . ,
Этот интеграл есть площадь, ограниченная сверху кри-
вой у {х), снизу осью х, слева — вертикалью х =а, справа —
вертикалью х = Ь (см. рис. 45).
Как найти приращение интеграла? По общим правилам
Д/ = / (a, b -f- Д6) — / (а, Ь). Площадь, равная интегра-
лу / (а, Ь-\- Д6), отличается от площади / (а, Ь) тем, что
правая вертикаль сместилась еще вправо на Д6 (см. рис. 45).
Следовательно, приращение Д/ есть разность двух
площадей: площади от а до Ь-\-АЬ и площади от а до Ь.
Очевидно, Д/ есть площадь полоски, заштрихованной на
рис. 45. Основанием этой полоски на оси х является отре-
зок длиной Д6. Искомая производная равна пределу
Д/
Очевидно, что при стремлении Д6 к нулю площадь по-
лоски приближается к у(Ь)АЬ, а отношение дг — к вели-
чине у(Ь). Таким способом мы снова наглядно доказали
4 Я. Б. Зельдович
98 ПОНЯТИЕ ПРОИЗВОДНОЙ К ИНТЕГРАЛА [Ч. II
теорему
ft
?(§y(x)dx)=y(b). (9.2)
а.
Определенный интеграл известной функции у (х) или v (t)
есть функция пределов интегрирования а, Ъ или п, k.
Определение интеграла как предела суммы, которое было
дано в предыдущем параграфе, объясняет нам, какую роль
играет понятие интеграла в решении физических задач: в
вычислении пройденного пути при переменной скорости v (t),
в определении площади, ограниченной кривой, заданной
уравнением у = у (х). Но это определение не дает удобного
общего способа вычисления интеграла, не дает удобного
способа нахождения интеграла в виде формулы, как функ-
ции пределов интегрирования *).
Способ нахождения такой формулы следует из дока-
занной выше теоремы о производной от интеграла. При
этом, кроме свойства производной от интеграла, исполь-
зуется еще второе свойство определенного интеграла: опре-
деленный интеграл равен нулю, когда верхний и нижний
пределы его совпадают
z(n, fe = n)= J v(t)dt = O.
n
Это свойство вполне очевидно: путь равен нулю, если
время пути k—п=п—п = 0.
Сама формула, дающая значение интеграла как функ-
ции пределов интегрирования, будет выведена таким спо-
собом в § 12. Предварительно в § 11 мы дадим более
простой вывод.
§ 10. Интеграл от производной
Пусть подынтегральная функция v(t) равна производ-
ной известной функции f(t),
2
*) Лишь в редких случаях и с трудом удается провести сумми-
рование произвольного числа малых слагаемых так, как это сделано
для v = tx в формулах (8.5) и (8.6) и для v = at-\-b а упражне-
ниях к § 8.
§ 10] интеграл от производной 99
В этом случае можно найти точное значение интеграла
следующим образом. Вспомним приближенное выражение
приращения функции / (§ 4)
Д/ =s= /' (/) M = v (О Д/. A0.2)
Величина, стоящая в правой части равенства, представ-
ляет собой как раз одно из тех слагаемых, сумма которых
равна интегралу. Значит, можно написать приближенно
i — Q. A0.3)
Как уже говорилось раньше, равенство A0.2) является
приближенным и оно тем точнее, чем меньше приращение
п
t0 t, t2 tj ?* t5 t
Рис. 46.
Д/, т. е. чем меньше разность tl+l — tt. Но при умень-
шении разности tl+l — tt, т. е. при сближении t[+1 и tlt
уменьшается и различие между v(tt+l) и v (?,); поэтому
в правой части формулы A0.3) с одинаковым правом,
с одинаковой степенью точности можно ставить и v(t[+l)
и v (t(), как это и сделано выше. Напишем формулы та-
кого вида, как A0.3), для всех промежутков, на которые
разбита область интегрирования, т. е. интервал от п до k.
Пусть, например, интервал разбит на пять промежутков
(рис. 46), так что ?e = n, tt~=k. He поленимся и выпи-
шем все пять равенств:
- / (О = о С.) С. — О * о (О С. — О-
Сложим все эти пять равенств. В левой части сократятся
все значения функции / при промежуточных значениях t,
100 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. It
останется только
В правой части получатся как раз такие суммы, с по-
мощью которых мы приближенно выражали интеграл
в предыдущем параграфе, выражали путь z (n, k) при
данной скорости v (t). Итак,
f(k) — / (л) = 2 о См-.) (*!+. — '/)=* 2о (О Ci+i — *t) =*=
sfez(«,fe)=Jo@* при 0@ = 27-
п
Чем меньше каждое приращение At, т. е. величина
*/+1 — tt, тем точнее выражение A0.3) приращения /; но
при уменьшении разностей t[+l — tt суммы стремятся
к интегралу.
Поэтому равенство
к
(f)dt при »(*)=!? A0.4)
в действительности является точным.
Формула A0.4) устанавливает связь между задачами
об интеграле и о производной. Из этой формулы следует,
что если удалось найти такую функцию /, производная
которой равна подынтегральной функции v, то задача вы-
числения интеграла решена — остается подставить значе-
ния f(k) и f (п) и найти разность f (k) — /(«).
Ввиду огромной важности этой формулы в следующих
параграфах мы дадим другой вывод формулы A0.4) на
основе более подробного рассмотрения свойств интеграла
(см. конец § 9) и функции /.
§ 11. Неопределенный интеграл
В предыдущих параграфах мы ввели понятие опреде-
ленного интеграла как предела суммы большого числа
малых слагаемых. В § 9 было выяснено главное свойство
определенного интеграла: производная определенного ин-
теграла по верхнему пределу равна подынтегральной
§ 11] НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 101
функции:
г (п. k) =
Теперь мы хотим воспользоваться этим свойством для вы-
числения определенного интеграла.
Итак, будем искать функцию k, производная которой
есть известная функция v (fe). Обозначим эту функцию f(k).
Тогда, по определению,
^ °<*)- (П.2)
Уравнение A1.2) не полностью определяет функцию
/ (k). Мы знаем, что прибавление любой константы к функ-
ции / (k) не меняет производную функции. Следовательно,
если f (k) удовлетворяет уравнению A1.2), то и функция
g(k) = f (k) -\- С удовлетворяет тому же уравнению.
Функцию f(k), удовлетворяющую уравнению A1.2),
называют «неопределенным интегралом функции v (fe)».
В этом названии отражаются два свойства f (k): производ-
ная / (k) такая же, как у определенного интеграла z (n, k) *),
поэтому / (k) называют интегралом. К функции f (k),
удовлетворяющей A1.2), можно прибавить любую постоян-
ную величину,— отсюда прилагательное «неопределенный».
Любое решение A1.2) может отличаться от какого-ни-
будь решения f(k) только на ту или иную постоянную
величину. В самом деле, если есть другое решение A1.2),
которое мы обозначим g{k), то для их разности получим:
Но только производная постоянной равна нулю при лю-
бых значениях аргумента.
Определенный интеграл z{n, k) согласно A1.1) тоже
является одним из решений A1.2). Значит, и z(n, k) можно
представить в виде
, A1.3)
где f(k) — какое-то решение A1.2), В—постоянная, и
*) Сравните формулы A1.1) и A1.2).
102 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
остается только ее определить. Для этого воспользуемся
вторым свойством определенного интеграла: он равен
нулю, когда верхний и нижний пределы совпадают,
z(n, k=^n) = z(n, n)=0. A1.4)
Подставляя k = n в A1.3), получим, используя A1.4):
Отсюда следует окончательно:
г(п, k) = f(k)—f(n). A1.5)
Отметим, что «неопределенность» функции f (k) ничуть
не мешает вычислению с ее помощью определенного ин-
теграла по формуле A1.5). В самом деле, возьмем вместо
f(k) какое-нибудь другое решение уравнения A1.2), на-
пример g(k), отличающееся от f (k) на постоянную вели-
чину
Будем вычислять определенный интеграл по формуле
вида A1.5), только взяв g вместо /.
z(n, k)=g(k)—g(n)=f(k)-{-C—lf(n)+C] =
Получили результат, совпадающий с A1.5).
Удобно обозначить неопределенный интеграл той же
буквой г, которой мы обозначаем определенный интеграл.
При данной подынтегральной функции v (t) опреде-
ленный интеграл зависит от верхнего и от нижнего пре-
дела, т. е. является функцией двух переменных z(n, k).
Неопределенный интеграл есть функция одной перемен-
ной. Обозначим ее /. Итак, неопределенный интеграл г (t)
есть функция, удовлетворяющая уравнению
z'(t) = t±P=v(l). A1.6)
С помощью этой функции определенный интеграл z(n, k)
функции v (t) находится по формуле
к
z(n, k)=$v(t)dt = z(k) — z(n). A1.7)
§ 11] НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 103
Принята следующая краткая запись разности значений
одной и той же функции при двух различных значениях
переменной
к
z(t)\ = z(k) — z(n). A1.8)
п
В этой записи слева стоит функция немой переменной t,
справа от нее ставится вертикальная черта, сверху — то
значение переменной, при котором мы хотим взять функ-
цию с плюсом, снизу — то значение, при котором функция
берется с минусом.
Подставляя в A1.7) под интеграл v(t), выраженное
через z(t) согласно A1.6), а в правую часть — выражение
A1.8), получим тождество
к
A1.9)
Обратите внимание на одинаковое расположение п и k
слева и справа, облегчающее запоминание формулы.
Пора перейти к примерам.
Рассмотрим задачу о пути, пройденном за время от п
до k при скорости движения, равной v (t) =. t*. Этот путь
равен определенному интегралу
к
г{п, k)=\ t'dt.
В этой задаче неопределенный интеграл z (t) получается
решением уравнения
-ЗГ = о@='".
Но мы знаем, что-—; = 3^*, значит,—^-^-=-^C^*)= ^*.
Следовательно, уравнению удовлетворяет
104 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
Подставим это решение в формулу A1.9)
к к
at— з | — з з •
Частный случай п ¦=*= 1, k = 2 дает:
Таким образом, с помощью неопределенного интеграла
мы на нескольких строчках получили точно результат,
к которому мы мучительно приближались в § 9 числен-
ными расчетами.
Определенный интеграл есть предел суммы вида.
при стремлении к нулю каждого слагаемого и соответст-
вующем увеличении числа слагаемых; для его прибли-
женного вычисления нужно разбить область интегрирова-
ния на несколько интервалов, найти приближенное значение
пути vAt в каждом интервале и сложить их. Чтобы по-
лучить хорошую точность, нужно сделать много арифме-
тических операций. Но если известен неопределенный
интеграл z(t), т. е. известна функция, производная кото-
рой равна подынтегральной функции v(t), то любой опре-
деленный интеграл ]v(t)dt получается немедленно по
формуле 111.9). Умение находить' функции с заданной
производной (неопределенные интегралы) «неожиданно»
дает мощный способ вычисления сумм (определенных ин-
тегралов).
Неопределенный интеграл иногда называют «первооб-
разной функцией». Этот термин применяется в учебниках
в тех случаях, когда задачу о нахождении функции по
известной ее производной решают раньше, чем рассмотрены
определенные интегралы. Мы этот термин применять не
будем.
§ 11] НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 105
Неопределенный интеграл всегда можно выразить через
определенный интеграл t
t
z(t) = C-\-lv(x)dx. A1.10)
а
Применяя правило о производной определенного интеграла
по верхнему пределу, легко проверить, что z (t), заданное
уравнением A1.10), удовлетворяет уравнению A1.6) при
любых постоянных Сна.
Во всех задачах в ответ всегда входит разность зна-
чений z (fe)—z(n), которая не зависит от С и а. Поэтому
A1.10) можно писать короче:
t
Наконец, часто пишут еще короче:
z(t)=$v(t)dt. A1.11)
Этот способ весьма употребителен, и мы тоже будем им
пользоваться, но надо иметь в виду, что такой способ
записи, в сущности неправилен. Его можно сравнить
с теми грамматически неправильными выражениями, кото-
рые широко применяются в разговорной речи и всем (кроме
детей и педантов-придир) понятны, вроде«съесть тарелочку».
В записи A1.11) нарушено правило, по которому не-
мая переменная интегрирования не входит в результат.
Следовательно, употребляя краткую запись A1.11), надо
всегда помнить, что это лишь условное сокращение точ-
ного выражения A1.10).
Известные нам формулы для производных дают таб-
лицу неопределенных интегралов:
Для того чтобы проверить любую из этих формул, доста-
точно найти производную от правой части. Если при этом
*) См. упражнение 6 к § 3.
106 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
получится функция, стоящая под интегралом, то формула
верна. Подробно способы нахождения неопределенных
интегралов от различных функций рассматриваются
в части III. Благодаря связи между интегралом и произ-
водной удается найти интегралы большого числа функций.
Задача интегрирования является технически более
сложной, чем задача нахождения производных. Эта слож-
ность проявляется, в частности, в том, что при интегри-
ровании рациональных (не содержащих корней) алгебраи-
ческих выражений в ответе появляются логарифмы и
обратные тригонометрические функции; при интегрирова-
нии алгебраических выражений с корнями результат иногда
выражается только при помощи новых, не элементарных
функций, которые не могут быть выражены конечным
числом действий над алгебраическими, степенными и триго-
нометрическими функциями.
Однако трудности выражения интегралов формулами
не должны заслонять принципиальную простоту и ясность
понятия интеграла. Если нельзя (или трудно) подсчитать
интеграл по формуле A1.9), та его всегда можно подсчи-
тать приближенно при помощи трудоемких, но в прин-
ципе весьма простых расчетов.
Упражнения
Найти величину интегралов:
1 1,1 2
X.^dt. 2. j«-c«. 3.^. 4.
5. Найти площадь прямоугольного треугольника с основанием Ь
я высотой А при помощи интеграла. Поместить начало координат
в острый угол, прямой угол поместить иа ссь_ абсцисс в точке х = Ь,
у = 0 (рис. 47, а), найти уравнение гипотенузы в этой системе коор-
динат и найти площадь как интеграл. Воспользоваться при интегри-
х dx = -=¦ .
Замечание. Не возмущайтесь тем, что приходится с трудом
находить хорошо известный ответ S = -~- bh, потому что метод ин-
тегрирования будет применим там, где элементарные методы не дают
ответа.
6. Найти площадь того же треугольника, помещая прямой угол
в начало координат и острый угол в точку х=Ь, у = 0 (рис. 47,6).
При интегрировании использовать очевидное свойство интеграла суммы
§ 11]
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
107
двух членов \ (f -{- g) dx =i= S. f dx-^-\ g dx при любых fug, посто-
янных или функциях х, положительных и отрицательных.
0
Ал
¦
о)
Ж
1
I
/Г
b 'i
о
Рнс. 47.
б)
Замечание. То же, что к упражнению 1.
7. Найти площадь под параболой у = Ах*, проходящей через
точку x = xe, y = ya, ограниченную вертикалью х = х0 и осью абсцисс;
выразить площадь через ха, уа (рис. 48, а).
108 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. Н
8. То же для параболы, проходящей через начало координат,
с горизонтальной касательной в точке (л;,,, уа) (рис. 48,6).
Указание 1. Ответ можно получить. немедленно, пользуясь
результатом предыдущего упражнения.
Указание 2. Тем не менее не поленитесь и сделайте все
по порядку, без применении остроумия. Уравнение параболы искать
в виде у = кх* -\~пх -\~т, величины к, га, т.- иайти из условий про-
хождения через точки (ха, у0) и начало координат и из условия
горизонтальной касательной в точке х = ха, у = уа- Площадь выразить
через х0, у0.
Указание 3. Если не можете выполнить указание 1, то
сперва выполните указание 2, результат сам подскажет, как выпол-
нять указание 1.
9. Написать выражение площади полукруга радиуса г (рис. 4S, в)
в виде определенного интеграла.
Указание. Из чертежа по теореме Пифагора
это и есть уравнение окружиссти (см. § 6 части I).
Г dx
10. Найти величину интеграла \ -^ , ^ по формуле трапеций,
а
взяв т = 5 и т=10. Вычисления вести с четырьмя знаками после
запятой.
Замечание. Точное значение этого интеграла есть — . При-
ближенный подсчет интеграла лает возможность получить приближен-
нее значение числа я.
§ 12. Свойства интегралов
Мы рассматривали выше наиболее простой случай опре-
деленного интеграла, с положительной подынтегральной
функцией и верхним пределом, который больше нижнего
к
г(п, k)= J v{t)dt, v>0, k>n.
п
В этом случае интеграл, очевидно, положителен, так как
интеграл равен пределу суммы положительных членов.
Интеграл имеет простой физический смысл пройденного
пути (v (t) — скорость) или площади (v = v (t) — уравнение
кривой).
Каков знак интеграла от отрицательной функции, т. е.
в случае v (t) < 0?
СВОЙСТВА ИНТЕГРАЛОВ
109
Оставим пока в силе условие k > п. В выражении
суммы (переходящей в пределе в интеграл) в каждом члене
множитель Д/ положителен, множитель v(t) отрицателен,
каждое слагаемое отрицательно, сумма отрицательна, ин-
теграл также отрицателен. Итак, если v(t)<0 при
п< t <k, так что k>n, то
J v @ dt < 0.
п
В случае движения смысл ответа прост: отрицательное зна-
чение v означает, что движение происходит в сторону, про-
тивоположную положительному направлению, т. е. направ-
лению возрастания координаты z. Путь, пройденный в отрица-
тельном направлении, мы всегда считаем отрицательным.
При таком движении z уменьшается, z (k) < z (n). Так как
v dt в этом случае отрицателен, то остается в силе об-
щая формула
= z(n)~\-z(k, n) =
v dt.
В случае знакопеременной скорости может случиться,
в частности, что Sivdt = O, хотя k > п, k=^n; это про-
п
изойдет, если часть времени от п до k тело двигалось
в одну сторону, а другую часть вре-
мени — в противоположную и в ре-
зультате к моменту k вернулось в то
положение, в котором,оно находилось
в момент п.
Обратимся к задаче о площади
кривой. При k > п и v (t) > 0 интеграл
равен площади, ограниченной кривой
v(t), осью t и вертикалями t = n,
t = k (рис. 49). При v <0, k> n ^ v dt <0. В этом случае
п
кривая лежит ниже оси абсцисс (рис. 50).
по
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[ч. и
Значит, для того чтобы сохранить закон, по которому
площадь равна интегралу, необходимо считать площадь
отрицательной, когда кривая лежит ниже оси абсцисс.
Если взять знакопеременную функцию, например,
v(t) = sint, то площадь такой кривой на отрезке, равном
периоду от / = 0 до ? = 2я, по на-
шему определению равна нулю
(рис. 51). Это значит, что площадь
первой полуволны, которую мы счи-
— таем положительной, в точности
сокращается с отрицательной пло-
щадью второй полуволны.
Если поставлена задача: сколь-
ко краски нужно для того, чтобы
закрасить заштрихованные места
на рис. 51, то такое определение
площади не годится. В этом случав
надо разбить весь интеграл на части, в каждой из кото-
рых v не меняет знака (в данном случае на две части.
О
Рис. 50.
Рис. 61.
от 0 до я и от я до 2я), подсчитать интеграл по каждой
части отдельно и сложить абсолютные величины интегра-
лов, относящихся к отдельным частям.
tm.r tj t2 С,
Л 1 I 1 1 1 1
t
Рис. 52.
Определенный интеграл обобщается и на случай, когда
верхний предел меньше нижнего. В этом случае мы уже
не будем говорить о пути, времени и скорости (§ 7), а об-
ратимся к определению интеграла как суммы (см. § 8).
Разбивая снова отрезок от п до k (рис. 52) промежуточ-
§ 12] СВОЙСТВА ИНТЕГРАЛОВ 111
ными значениями tt, tt, ..., tm_l, убедимся, что все Д?
теперь отрицательны. Легко убедиться теперь, что
к
к п
п
= —\v(t)dt, A2.1)
k
так как при любом разбиении отрезка [п, k] соответствую-
щие суммы будут отличаться знаками всех А/ во всех
слагаемых.
л р л
Рис. 53.
t
Существенное свойство интеграла состоит в том, что об-
ласть интегрирования можно разбить на части: путь прой-
денный за время от п (начала) до ft (конца), можно представить
как сумму пути, пройденного за время от п до р (проме-
жуточного момента) и от р до k (рис. 53)
(t)dt. A2.2)
При помощи соотношения A2.1) можно распространить
формулу A2.2) и на случай, когда р не лежит внутри
промежутка [п, ft].
i ' ' t
п А /г
Рис. 54.
Пусть р> k> n (рис. 54). Тогда, очевидно,
) v(t)dt= J v(t)dt-\-\ v(t)dt. A2.3)
п п к
Перенесем последнее слагаемое налево и воспользуемся
A2.1)
р р р к к
\vdt — \ vdt = \ v(t)dt-\-'l v(t)dt=$vdt. A2.4)
п к п р п
112
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
!ч. и
Таким образом, мы получили равенство A2.4), в точ-
ности совпадающее с A2.2).
Аналогично можно рассмотреть случаи другого распо-
ложения чисел п, р, k (их всего шесть вариантов). Чита-
тель легко может рассмотреть их сам и убедиться, что
формула A2.2) оказывается верной во всех этих случаях,
т. е. независимо от взаимного расположения чисел п, р, k.
Все эти свойства определенных интегралов мы вывели,
по существу, из определения интеграла как предела суммы.
Эти свойства следуют также из выражения определен-
ного интеграла через неопределенный интеграл. В самом
деле, пусть неопределенный интеграл
Тогда
Основной закон о том, что производная от интеграла
равна подынтегральной функции, относится к производ-
ной по верхнему пределу.
Если определенный интеграл рассматривать как функ-
цию его нижнего предела при закрепленном (постоянном)
верхнем пределе, мы получим от-
вет с противоположным знаком:
. =-v(n). A2.5)
n л+Лл к ~~h~ Знак минус в этой формуле легко
рис 55. понять, рассматривая интеграл как
площадь: приращение п, оче-
видно, уменьшает площадь (рис. 55)*). Формально
тот же результат можно получить, переставив пределы
*) Площадь, ограниченная вертикальными прямыми n-f-An, к,
кривой и осью х, меньше, чем площадь, ограниченная вертикаль-
ными прямыми л, к, кривой и осью х.
§ 13] СРЕДНИЕ ЗНАЧЕНИЯ - 113
(при этом войдет минус) и применяя известный закон
о производной по верхнему пределу
В связи с вопросом о знаке интеграла отметим при-
мер, часто вызывающий недоумение у начинающих. Рас-
смотрим
J$—i. 02.6,
Это равенство вытекает из найденного ранее значения
производной
Правилен ли знак у интеграла? Может ли быть отри-
цательным интеграл ст положительной функции -^ ? Не
противоречит ли этот знак сделанным выше утвержде-
ниям?
В действительности все утверждения о знаке относи-
лись к определенному интегралу. Возьмем
— \ — т) — \к—-)—-—ь— аЬ .
а
При Ь > а интеграл положителен, как и должно быть,
т. е. формула A2.6) правильна, приводит к правильному
результату для определенного интеграла.
§ 13. Средние значения
С помощью интеграла можно дать точное определение
среднего для величины, являющейся функцией какой-то
переменной.
Если мы имеем величину, принимающую ряд отдель-
ных значений, например m значений
at, vt, vt, .... vm,
114 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
то среднее значение естественно определить формулой
Как определить среднее значение функции v{t) пере-
менной /, принимающей все значения в заданном проме-
жутке от п до k (n<t <k)?
Представим себе, что v(t) — этомгновенная скорость.
Как определить среднее значение v (л, k), т. е. среднюю
скорость за время от л до k?
Средняя скорость опреде-
ляется как отношение прой-
денного пути к ватраченному
времени
k
р (О dt
if I
1
ь 1
0 а
V |
в
а
X
(П. k) — -feZr^—
Это определение среднего зна-
чения функции разумно и в
Рис. 66. тех случаях, когда функция
представляет собой не ско-
рость движения, а какую-либо другую величину. Так,
например, пусть у = у(х) есть уравнение кривой в пло-
скости х, у (рис. 56).
ь
Тогда ^ y(x)dx есть площадь под кривой. Формула
b_a .
-=\y(x)dx
а
означает, что у есть высота прямоугольника с основанием
Ь — а, площадь которого равна площади под кривой.
Это значит, что на рис. 66 заштрихованная площадь
над линией у = У> которая отмечена знаком плюс, в точ-
ности равна площади, отмеченной знаком минус на
участке, где кривая лежит ниже линии у = у. График
функции у{х), если это не прямая, параллельная оси х,
СРЕДНИЕ ЗНАЧЕНИЯ
115
обязательно проходит частью ниже и частью выше среднего
значения у, определенного с помощью интеграла. Следова-
тельно, у больше наимень-
шего значения у{х) и мень- у
ше наибольшего значения
у(х) на участке усреднения
п <х <k.
Рассмотрим примеры.
Пусть у (х) есть линей-
ная функция
y=kx-\-m.
Тогда интеграл представ-
ляет собой площадь тра- Рис. 57.
пеции, поставленной верти-
кально (рис. 57) с «высотой» Ь — а, основаниями у (а) и
У (Ь) и средней линией у (¦ а ^—J. Следовательно,
О
а
Это выражение легко получить и без геометрических пред-
ставлений
/(a, 6) =
= kb-\-m, y(a) =
откуда с очевидностью следуют выражения предыдущей
формулы.
Таким образом, для линейной функции
У—
—у{ 2 ;•
A3.1)
Следовательно, для линейной функции среднее значение
функции на данном участке от а до Ь в точности равно
среднему арифметическому значений функции на краях
116
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
участка у (а) и уф)\ другая формулировка: среднее значе-
ние линейной функции равно значению функции в сере-
аЛ-Ь
дине интервала, т. е. при х=—^—.
Одним из важных примеров линейной зависимости
является зависимость скорости от времени при равноуско-
ренном или равнозамедленном движении, т. е. при дви-
жении тел под действием постоянной силы, в частности,
под действием силы тяжести, когда
v = gt-\rva.
При расчете пройденного пути используют свойства сред-
него линейной функции
Следует иметь в виду, однако, что при другой, не линей-
ной, зависимости выражения
для среднего A3.1) уже не-
справедливы.
Рассмотрим пример квад-
ратичной функции (параболы)
у = rx* -f- px -f- q. Для опреде-
ленности возьмем г> 0 и рас-
смотрим какой-то отрезок па-
раболы а<х<Ь. Из чертежа
(гис. 58) видно, прежде всего,
что
Действительно, у (•—§—) есть ордината точки С, лежащей
на кривой, а-полусумма
и (а) + v (Ъ\
есть ординататочки D,
лежащей на середине хорды, соединяющей точки кривой
А и В, и ясно из чертежа, что С лежит ниже D *).
*) Напомним, что парабола у = гх*, г > 0 выпукла книзу, а па-
рабола у = rx* -f- px -f-<7 с любыми р и q получается нз параболы
у=^гх* параллельным переносом, см. часть I, § 5.
§ 13] СРЕДНИЕ ЗНАЧЕНИЯ 117
ь
Обратимся теперь к интегралу ^ у (х) dx, т. е. к вы-
а
числению площади под кривой. Очевидно, что эта пло-
щадь меньше площади трапеции с основаниями АаА и
В0В. С другой стороны, если через точку С провести
касательную к кривой, то эта касательная пересечет вер-
тикали в точках А' и В' и образует трапецию со средней
линией С0С; площадь этой трапеции, очевидно, меньше
площади под кривой. Таким образом, в случае параболы
с г>0
Соответственно получаются неравенства для среднего зна-
чения ~у в промежутке от а до Ь:
g-f-ft
2
Для квадратичной функции имеет место точная фор-
мула (приводим ее без вывода, см. упражнение 4), справед-
ливая при любом знаке г:
77 2
у
A3.2)
Это выражение является хорошей приближенной формулой
для расчета площади под любой плавной кривой (см. упраж-
нения 6 и 7). Пользование средними практически очень
удобно, часто даже удобнее пользования интегралами.
По существу, эти величины равноценны, — зная
ь
интеграл / = \ у dx, находим среднее как у = ь__а . а вы-
а
числив среднее, так же легко находим интеграл
Г = (Ь — а)у.
Удобство среднего заключается в том, что это вели-
чина у той же размерности, что и у, и, очевидно, того
118 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
же порядка величины, что и значения у на исследуемом
участке. Поэтому труднее пропустить ошибку в 10 раз
в значении ~у, чем такую же ошибку в значении интеграла.
Обычно предполагается, что изучающие высшую мате-
матику в совершенстве знают арифметику и алгебру и
никогда не ошибаются в 10 раз или в знаке. Опыт пока-
зывает, что это не так! Поэтому и расчеты всегда надо
вести так, чтобы уменьшить вероятность незамеченной
ошибки.
Упражнения
1. Найти среднее значение у = х? на участке от 0 до 2.
2. Сравнить это среднее значение со средним арифметическим
значений функции на краях и со значением в середине промежутка.
3. Проверить формулу A3.2) для среднего по данным упраж-
нения 1.
4. Проверить формулу для среднего A3.2) в общем виде для
параболы у = гх* + рх -\- q.
5. Сила тяжести убывает с расстоянием от центра Земли как
,F = —j-. Найти с помощью интеграла среднее значение силы тяже-
сти на участке от поверхности Земли (радиус R) до расстояния R от
поверхности Земли, т. е. 2R от центра Земли.
6. Сравнить точное значение среднего в предыдущем упражне-
нии со средним арифметическим на краях участка.
7. Сравнить точное значение среднего в упражнении 5 со сред-
ним по формуле A3.2), относящейся к параболе.
§ 14. Различные примеры производных и интегралов
В предыдущих параграфах мы рассматривали .соотно-
шение между путем и скоростью, соотношение между
уравнением кривой и площадью под этой кривой. Эти
соотношения представляют собой конкретные вопросы, на
почве которых исторически сложились дифференциальное
и интегральное исчисления. Но понятия интеграла и про-
изводной применимы, конечно, не только к перечисленным
вопросам, а к чрезвычайно широкому кругу явлений,
к самым различным областям науки, техники, жизни.
В сущности говоря, интеграл и производная представляют
собой определенный язык, наиболее приспособленный для
описания природы.
Учащийся, начинающий изучение иностранного языка,
чтобы привыкнуть к нему, повторяет похожие простые
§ 14] РАЗЛИЧНЫЕ ПРИМЕРЫ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ Н9
фразы: «на столе стоит стакан», «на столе стоит хлеб»,
«на полу сидит кошка», «на полу сидит мышка». Вот
так же в начале изучения высшей математики надо на
многих похожих примерах повторять соотношения между
производной и интегралом. Сперва надо научиться ино-
странному языку, а уже потом высказывать на этом языке
определенные мысли, желания, утверждения. Так и мы
сперва научимся выражать хорошо известные соотношения
и формулировать задачи на языке высшей математики,
а уже потом будем решать эти задачи и получать новые
результаты.
Приведем несколько типичных примеров.
А) Производные по времени
1. Представим себе сосуд произвольной формы, из
которого вытекает жидкость (рис. 59). Масса жидкости,
находящейся в данный момент в сосуде, равна М. Эта
величина есть функция времени М (t). Жидкость соби-
рается в другом сосуде, количество ее
во втором сосуде т (t). Количество
жидкости, вытекающей из сосуда в
единицу времени, обозначим W (t). Эта
величина имеет размерность г]сек. Ве-
личины т, М и W связаны между
собой соотношениями.
dt
A4.1)
Те же соотношения можно напи-
сать в интегральном виде. При этом
зададимся тем, что в некоторый на- Рис. 59.
чальный момент ta в первом сосуде
количество жидкости равнялось М (ta) = Ma, а второй со-
суд был пуст m(tn) = 0. Тогда
Л
m{tx)=[W{t)dt,
t,
i-lW(t)dt.
to
A4.2)
120 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. И
Обращаем внимание на то, что если нас интересует коли-
чество жидкости в определенный момент tlt то оно вы-
ражается через интеграл, в котором переменная интегри-
рования t пробегает все значения от tn до /х.
Если мы хотим написать выражения для т (t) и М (t),
то для большей ясности удобно было бы переименовать
переменную интегрирования (пользуясь тем, что она не-
мая), назвав ее, например, т (т—тау — греческая буква,
соответствующая латинской t — тэ). Тогда
A4.3)
Обычно же пишут просто
t
w(t)dt, A4.4)
но надо помнить, что t, стоящее под интегралом, имеет
другой смысл, чем аргумент / в М (/) и т (/), который
совпадает с t на верхнем пределе. В этом отношении за-
пись A4.2) и A4.3) точнее, чем A4.4).
Написанные выше формулы соответствуют опыту, в ко-
тором в различные моменты времени измеряется М и по-
ток жидкости "П^.
Часто задача ставится так: W — расход жидкости —
зависит известным образом от ее давления, т. е. от вы-
соты столба жидкости А. В свою очередь при данной
форме сосуда величина h зависит от М. Таким образом,
известен расход W как функция от количества жидкости,
находящейся в сосуде,
Тогда равенство A4.1) приобретает вид
§ 14] РАЗЛИЧНЫЕ ПРИМЕРЫ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ 121
Это есть дифференциальное уравнение. Решение таких
уравнений будет рассмотрено в части V. Формул вида
A4.2) — A4.4) в этом случае уже писать нельзя, так как
W как функция времени не задана.
2. Рассмотрим конденсатор (рис. 60). Накопленный
в нем заряд (количество электричества) обозначим q.
В технической системе единиц q измеряется в кулонах.
Электрический ток /, протекающий по проводу, представ-
ляет собой количество электричества, протекающее в еди-
ницу времени, измеряется в технической системе в ампе-
рах. Один ампер есть ток в * j ^
один кулон в одну секунду. -,U i—-—1 ..С
Заряд конденсатора *) и I 'I I 1 '•
ток связаны между собой ра-
венством
f = / A4.5)
(положительное направление Рис. 60.
тока показано стрелкой).
Если задано или известно в результате измерения, как
изменяется ток в зависимости от времени, то можно на-
писать интегральное соотношение
t
Если дана емкость конденсатора С, то падение на-
пряжения на конденсаторе можно выразить через q:
Фс = -?-. Падение напряжения на сопротивлении R
равно
Ф/? = ?. — Фс=^о — -g- .
где Еа — напряжение батареи. По закону Ома ток через
сопротивление равен/ = — (Е9 — -Д-). и> пользуясь A4.5).
*) Зарядом конденсатора будем называть количество положи-
тельного электричества на левой пластине конденсатора С на рис. 60,
выраженное в кулонах.
122 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
получаем дифференциальное уравнение
dt~~ R V ° С
Подробно задачи с конденсатором рассмотрены в части VIII.
3. Понятие ускорения. Выше мы рассматривали
скорость движения как производную от координаты по
времени. Но после того как мгновенная скорость v най-
дена и известна зависимость мгновенной скорости от вре-
мени v (О. можно поставить вопрос о том, как с течением
времени меняется скорость.
Производная скорости по времени называется ускоре-
нием
^ = а A4.6)
и обозначается обычно a (acceleration — ускорение по-
французски; сравни название «акселератор» педали, регу-
лирующей подачу воздуха в автомобильный двигатель).
Так как размерность скорости см]сек или м]сек, то
размерность ускорения см\сек* или л/сек*.
Если известно ускорение как функция времени, то
мгновенное значение скорости можно записать в виде
интеграла
t
a(t)dt. A4.7)
Например, в случае движения под действием земного
тяготения а= —g, где g = 9,8 м1сек* (знак минус связан
с тем, что положительным считаем направление вверх).
Полагая в A4.7) а= —g, получаем:.
t
о@ = v(t.) —^gdt = v(ta) — (t- tt)g.
Запишем скорость в виде производной отпути повремени
° = 57 и п°дставим в A4.6). Тогда
d (dz\
a = 4t[dt)-
Такая величина — производная от производной — назы-
§ 14] РАЗЛИЧНЫЕ ПРИМЕРЫ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ 123
вается второй производной и обозначается
a = d~?
и читается: «де-два-зет по де-тэ-квадрат».
Заметим, как разумно поставлены показатели (двойки)
d2z т. г
в выражении тт» • Размерность ускорения именно -тг ;
отбрасывая безразмерные знаки d, получаем правильную
размерность второй производной.
Б) Производные по координате
4. Мысленно выделим в атмосфере вертикальный -столб
воздуха с постоянным сечением 5 см*. Плотность возду-
ха *) (зг/см* зависит от высоты h над поверхностью Зем-
ли. Объем тонкого слоя, заключенного между h и h-\-dh
(рис. 61), равен Sdh. Внутри этого
тонкого слоя плотность q(A) мож-
но считать неизменной — именно
для этого слой и брался тонким.
В данном примере dh можно
представить себе в 1 м или
10 м, даже (с несколько мень-
шей точностью) как 100 м, по-
скольку при изменении высоты
на 1 км плотность воздуха ме-
няется на 12—14%.
Масса воздуха в слое dh
равна dm==QSdh. Масса возду-
ха в столбе, простирающемся от
hx до ht, определяется интегра-
лом
а,
Рис. 61.
dh
$
А.
*) q — греческая буква, читается: сро». Часто применяемое в
школьной физике обозначение d (происходящее от французского
densite—плотность) весьма неудобно, так как его можно было бы
перепутать со знаком дифференциала.
124
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[ч. п
Масса воздуха в столбе от поверхности Земли (А = 0) до
высоты h
h
m @, К) =S J Q(h)dh.
о
Масса воздуха, находящегося выше заданной высоты /г,
равна
Давление Р на некоторой высоте А, умноженное на пло-
щадь 5, равно силе, с которой притягивается к земле.весь
столб воздуха, находящийся выше высоты А. Сила тяго-
тения равна массе, по-
множенной на ускорение
силы тяжести g, откуда
Рис. 62.
Пользуясь формулой
A2.5), получим отсюда:
dP ...
gQ(A)
Эту формулу можно было бы написать и сразу, рассмат-
ривая равновесие тонкого слоя dh, на который снизу дей-
ствует давление Р(А), сверху давление P(h-\-dh), равно-
действующая этих двух сил уравновешивает притяжение
к земле массы, заключенной в слое.
5. Выразим в виде интеграла объем тела (рис. 62).
Разобьем тело плоскостями х= const на тонкие слои.
Объем dV тонкого слоя равен произведению площади се-
чения 5 на толщину слоя dx. Таким образом, если известна
площадь сечения тела вертикальной плоскостью в зави-
*) Знак оо на верхнем пределе заменяет очень большое число А,
такое, что при его дальнейшем увеличении величина интеграла пра-
ктически не меняется.
§ 14J РАЗЛИЧНЫЕ ПРИМЕРЫ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ 125
симости от координаты сечения х, то объем тела может
быть вычислен по формуле z
A4.8)
Применим эту формулу к правиль-
ной четырехугольной пирамиде. Поста-
вим ее на вершину в начале коор-
динат с осью симметрии, направлен-
ной по оси z (рис. 63). Пусть высота пи-
рамиды ft, основание ее (оказавшееся
сверху) представляет собой квадрат
со стороной а. Из геометрии извест-
но, что сечение пирамиды горизонтальной плоскостью
на высоте г представляет собой также квадрат, сторона Ь
которого относится к а, как z к h,
Рис. 63.
-** h •
Следовательно, площадь сечения
S(z) = Ь' = ? г\
Объем пирамиды
О О
Воспользуемся результатом § 11
Тогда получим выражение объема пирамиды
Объем пирамиды равен одной трети произведения площади
основания на высоту пирамиды. Вывод этой формулы в
стереометрии без применения интегралов значительно
сложнее.
126 ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА [Ч. II
Упражнение
Вывести формулу для объема произвольной пирамиды, исполь-
зуя свойства параллельных сечений.
ЗАКЛЮЧЕНИЕ
В части II рассмотрены понятия производной и
интеграла, некоторые их самые простые свойства и связь
между интегралом и производной. Вопросы практического
вычисления производных и интегралов от различных
функций отнесены в часть III книги. В части II дано
только несколько самых простых примеров.
Хочется посоветовать учащемуся не измерять трудность
и значение того или иного раздела числом формул, их
сложностью и громоздкостью. В действительности самое
важное и трудное — именно математическая формулировка
задачи в виде алгебраического уравнения или интеграла
или дифференциального уравнения. Именно на это надо
обратить особое внимание.
Если последние три параграфа показались читателю
трудными, целесообразно еще раз перечесть всю часть II.
По собственному опыту автор знает, что те работы, ко-
торые ему не удалось сделать (которые тем временем были
сделаны другими!), не были им сделаны потому, что, огра-
ничиваясь общим размышлением, автор не находил смелости
писать уравнения, математически формулировать вадачу;
вычислительные трудности в четко поставленной задаче
с ясным физическим содержанием всегда преодолеваются,
если не точным расчетом, то приближенными методами.
ОТВЕТЫ И РЕШЕНИЯ
§ 1. 1. Найдем мгновенную скорость в момент / = 0. Рассмотрим
промежуток от f = 0 до / = 0,1. Из формулы z = 2-f-20/— St*
получаем z@) = 2, z @,1) =3,95; отсюда
, = 3,86-2 .«
0,1 сек
Рассмотрим еще промежуток от / = 0 до / = 0,01. z @,01) = 2,1995;
поэтому
2l*b2 м_
сек
0,01 сек
ОТВЕТЫ И РЕШЕНИЯ
127
Л€
Отсюда ясно, что и@)=20 —. Аналогично получим: иA) = 10,
сзк
v B) = 0 (рис. 64). 2. u@)=0, o(l)=3, о B) =12 (рис. 65).
dt '
л z (&t)x dz »,
-—=№4--——, -гг = 3г. Результаты совпадают с вычислением
at ' 4 at
ч Ш)
10
I 2\ 3 t
Рис. 64.
б
4
г
'о
1
/
/
1
/ 2 \
Рис. 65.
в § 3; обратите внимание на то, что в случае z=-t* отношение — не
вависит от Д^, а в случае z = t* отношение -г-содержит только (Д^)*.
в сравните с численными расчетами в§1.2. у' =4ха. 3. у'=2х-{-2.
§ 4. 1. Найдем A,2)*. Рассмотрим функцию г=Р; пусть t = l
в Д* = 0.2; z'=2t; z'(l) = 2; поэтому Д2 = 2-0,2 = 0.4; A,2)*= 1* +
-[-0,4=1,4. Точное значение A,2)'= 1,44. Ошибка составляет при-
мерно 3°/о- A,1)*= 1.2; точное значение 1,21. Ошибка примерно 1°/0.
A,05)*= 1,1; точное значение 1,1025. Ошибка примерно О,2°/о- A,01)* =
= 1,02; точное значение 1,0201. Ошибка примерно 0,01 %• 2. См. табл. 7.
128
ПОНЯТИЕ ПРОИЗВОДНОЙ И ИНТЕГРАЛА
[Ч. II
Т а бли ца 7
1
1
0
,1
.05
,98
18
17
16
t>
,0
.5
,8
17
17
16
ист
5
4875
798
Ошибка в •/„
округленно
0.3
0,07
0,01
§ 5. 3.
( Уз ;
: !-К
-д- ) • I _/-=- ' 1 :
)•
з Уз7 ' V Уз" ' " з Уъ )' ' ~~
= Т*-Т' (Т-0)' @,-\);у = Зх-2, (§-. О). @,-2).
7. Для кривой у = ах* касательная в точке (х0, уа) пересекает оси
координат в точках f^-.O] и @, — уа) (см. стр. 73). Для кривой
у=ах' уравнение касательной в точке (л:,,, уа) у = 3axJ х — 2у9. Точки
пересечения касательной с осями координат ( -~-хл, 0), @, —2i
§ 6. 1. х = 0, минимум при а > 0, максимум при а < 0. 2. х = — 1
максимум, х=1 минимум. 3. х =—"V~u(a > 0) максимум, х =
= уг*Г(а>0) минимум. При а <С 0 нет ни минимума, ни максимума.
4. х — т=- максимум, х = -= минимум. 5. а) a > 0, х = 0 мини-
> з уз
мум; б) а=0. х = 0 минимум; в) а < 0, х = 0 максимум, х =
у; )
= — I/ —Y"
минимум,
)
минимум.
§11. 1.4-• 2.0,11033... 3. 4-- 4. 2(УЗ~—1). 5. S =
где у=у(х) — уравнение гипотенузы. Возьмем произвольную точку А
с координатами х, у на гипотенузе. Через эту точку проведем верти-
кальную прямую (см. рис. 47, а). Из подобия треугольников
4~ = 4: ¦ Отсюда у = -?-X.
о ft о
10. 0.7837 для
^-i-x^,. 8. S = |-
. 9. S
/n = 5; 0,7850 для /n=10.
ОТВЕТЫ И РЕШЕНИЯ 129
а
13. 1. y=x* =
I A.
ь
±-уB)=1±±.4=1,33. 4.
-Srq{b-a) = (b~a) [1 г (й* + аЬ + а1) +\р{Ь + а)
По формуле A3.2) должно быть
ь
Подставляя у (а), //(—^С—J и у (Ь) и сравнивая с полученным выше
выражением, убеждаемся в том, что они тождественны.
2/г 2/?
^4(
Среднее значение силы на этом участке вдвое меньше силы на по-
верхности Земли, F = 0,5F0. 6. F(R) = F0, ^
1 2 4 11 1П9
6" F° +1" " "9 F» + ' Tf • = 2T6 Fl> = °>505 ''•• Ошибка
ЧАСТЬ III
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
§ 1. Знак дифференциала. Производная суммы функций
Удобные наглядные способы записи соотношений и про-
стые правила, позволяющие механически, без размышлений
и без ошибок, проводить вычисления, имеют очень большое
значение и для обучения и для самого развития математики.
В части II был разобран смысл понятия производной.
Задачей части III является изложение правил нахождения
производных от различных функций: многочленов, рацио-
нальных функции, в которые входят отношения многочле-
нов, корней и вообще дробных степеней, показательной
функции, тригонометрических функций и др. Нужно найти
общие правила для производных различных сочетаний
функций: суммы функций, произведения функций, слож-
ной функции. В конце части III (стр. 218) приведена таблица
производных для ряда функций, подытоживающая ниже-
следующие §§ 1 —12.
Из определения производной следует такой способ
действия: в каждом случае нужно задаться каким-то зна-
чением х и приращением А*; найти f(x) и f(x-{-Ax), найти
приращение Д/; составить отношение ~ и после этого
перейти к пределу Ах—> ().
Однако формула, дающая общее выражение д? при
произвольном Ах (не стремящемся к нулю), как правило,
бывает сложнее формулы для предела, lim ir=zr> т- е-
Лх -* а лх ах
производной. Поэтому в дальнейшем мы часто будем писать
такие формулы, которые справедливы только в пределе.
§ 1] ЗНАК ДИФФЕРЕНЦИАЛА. ПРОИЗВОДНАЯ СУММЫ ФУНКЦИЙ 131
при приращении, стремящемся к нулю, и в этом случае
вместо Ау, Ах будем писать dy, dx. Нужно выработать
такие правила действий с величинами dy, dx, чтобы имело
место основное равенство
т. е. чтобы отношение дифференциалов тождественно ра-
внялось производной. Раньше мы писали приближенное
выражение для приращения функции
у (х + Ах) — у (х)=Ау=^у' (х) • Ах.
Это выражение становится точным в пределе при Ах —»¦ О*).
Для дифференциалов будем писать точное равенство
dy = y'(x)dx.
Слова о пределе при Ах—> 0, которые нужно было добав-
лять к приближенному равенству Ay^sy' (х)-Ах, уже не
нужны при написании второй формулы: они подразумева-
ются при пользовании дифференциалами dy, dx.
Правила пользования дифференциалами должны быть
такими, чтобы отношение дифференциалов равнялось про-
изводной; для этого в формулах нужно сразу отбрасывать
члены, пропорциональные (dx)* и более высоким степеням dx.
Рассмотрим простейший пример у—х*, и на этом при-
мере сравним технику работы с приращениями и с диффе-
ренциалами: раньше мы писали
Ау = (х + Axf — х1 = 2х • Ах -\- (Ах)\
*У=2х-{-Ах; y'=\im ?=2х.
С помощью дифференциалов запишем:
dy=(x-\- dxI— x* = 2xdx.
Член (dx)* в правой части мы сразу отбросили!
В качестве второго примера рассмотрим сумму двух
функций, взятых с постоянными коэффициентами
*) См. сноску на стр. 67.
132 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
С помощью дифференциалов запишем:
= С df-\- E dg = Cf -dx + Eg'dx,
Читатель легко может получить такую же формулу,
пользуясь приращениями и пределами.
Написание dx, dy (читается: дифференциал икс, диф-
ференциал игрек) заменяет слова о пределе и упрощает
вид формул. Общее правило заключается в том, что при
написании формул с дифференциалами можно (и должно)
выкидывать члены, пропорциональные (dx)*, (dx)* и т. д.
В остальном же с дифференциалами можно обращаться
как с обычными алгебраическими величинами.
Мы будем пользоваться дифференциалом той или иной
переменной dx, dt и т. п., дифференциалом функции df, диф-
ференциалом какого-либо сложного выражения, составлен-
ного из нескольких функций, например d I — \ . Отноше-
df
ние —- по определению есть производная функция от f(x).
§ 2. Производная обратной функции
Задание у как функции х означает, что каждому х
соответствует определенное значение у. Значит, и обратно,
можно сказать, что каждому определенному у соответ-
ствует свое х. Таким образом, задание у (х) дает также
функциональную зависимость х(у). Эту зависимость назы-
вают обратной функцией.
Приведем несколько примеров: слева дано у(х), справа
написана обратная функция х от у:
§ 2] ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ 133
Во многих случаях обратная функция имеет более про-
стой вид, чем прямая функция: например, если прямая
функция у=1/х—1 содержит кубичный корень, то
обратная функция х = уа-\-\ есть степенная функция,
проще прямой. В этом случае найти производную обратной
функции, -j-, оказывается проще и легче, чем найти произ-
водную прямой функции, -^. Нельзя ли в этом случае
производную прямой функции как-то выразить через про-
изводную обратной функции?
Для прямой функции у(х) имеем:
Отсюда получим ответ для производной х' (у) обратной
функции х(у):
Отсюд получ
функции х(у):
В правой части B.1) стоит выражение, записанное в виде
функции х, а именно, с помощью у' (х). Но если обратная
функция х(у) известна, то это выражение можно предста-
вить как функцию у.
Поясним сказанное примерами. Первый пример (линей-
ная функция) слишком прост. Начнем со второго примера
B-2)
Подставляем в выражение B.2) обратную функцию х^=
dx_d(Vy)_\ _ 1 ,
dy dy 2x K
Раньше, в части II, этот результат был получен более
сложным путем.
Третий пример:
— d — 3
1 __ 1 . n~f
dy — 3*» — зуп-=1?~~ 3^ l) '
134 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
Такой способ пригодится нам и позже. Когда мы изучим
показательную функцию а*, то можно будет рассматри-
вать логарифмическую функцию как обратную; когда мы
изучим производные тригонометрических функций, sin*,
cos л:, tgx, то можно будет найти производные обратных
тригонометрических функций — arcsinx, arccosx, arctg*.
§ 3. Сложная функция
Пусть z задано как функция у, например z = —, а у
есть функция х, например у=х*-\-Ь. Очевидно, каждому
х соответствует определенное у, а так как каждому у соот-
ветствует определенное г, то в конце концов каждому х
соответствует определенное г, z есть функция х. Всегда
можно, подставляя выражение у через х, выписать непо-
средственно z (л:), в данном примере г = ^ ^.
Но для наших целей как раз выгоднее все функции
свести к сочетаниям самых простых функций; в отдель-
ности каждая из зависимостей z = — uy=x*-\-5 проще,
чем z = ¦
+
Сводя все функции к самым простым функциям, мы
сумеем обойтись правилами нахождения производных этих
простых функций.
Найдем дифференциал сложной функции г [у (х)\. Рас-
сматривая г как функцию у, напишем:
dzdy
Но у есть функция х; поэтому
Подставляя, получим:
**=%-%**¦ C-D
Поделив обе части C.1) на dx, получим правило определе-
§ 3] СЛОЖНАЯ ФУНКЦИЯ 135
C.2)
ния производной сложной функции *)
dz dz dy
dx dy "dx'
Вид формулы вполне соответствует тому, что было
сказано о возможности обращения с дифференциалами как
с обычными алгебраическими величинами: в произведении
-г- • ?¦ можно сократить dy.
Напомним, что г задано как функция у, поэтому ^
также является функцией у. Но так как само у есть функ-
ция х, то, подставляя у=у(х) в выражение —, получим
-т- как функцию х, а следовательно, и ^ как функцию х.
Проделаем расчет для случая, который понадобится в
дальнейшем. Пусть
Мы знаем, что при г = — -т- =— -f. Значит,
и
dz 1 dy
dx — — ^'di'
Так, например, если у = х*-{-5, z= t, 5 , то
Л 1 d {х* -f S) 2х
dx~ (х* + Ь)* ' dx (х*-\-5У
dz
•) Раньше для обозначения производной наряду с записью -у^мы
употребляли запись г'. Однако обозначение производной штрихом
может привести к неясностям: если написать г', неясно, что имеется
в виду: -г- или -т- . Поэтому в тех случаях, где может возникнуть со-
мнение, мы штрих употреблять не будем.
.136 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Это правило составления производной сложной функции
сохраняется и при многоступенчатой зависимости
z = z(y), y = y(x), x = x{t), t = t(w), ]
dw dy ' dx ' dt ' dw' I
Если функция задана параметрически (см. часть I, § 8),
то такое задание можно рассматривать как частный случай
сложной функции. В самом деле, если дано
x=f(t), y =
то первое из этих уравнений можно рассматривать как
уравнение, решение которого даст t (x); подставляя это t (х)
во второе уравнение, получим:
y
Следовательно,
dy dy dt_
dx. dt dx'
Но для применения этой формулы не обязательно вы-
ражать / как функцию х (если бы мы это сделали, то
избавились бы от параметра, а это не всегда возможно).
Достаточно знать х = f(t). Эта функция является обратной
по отношению к функции t (x). Значит,
d* 1 1
dx d[ dx'
dt dt
Таким образом,
dy
dy dt_
dx~ dx ' .
dt
Эта формула дает еще один пример того, что с диффе-
ренциалами можно обращаться как с обычными алгебраи-
ческими величинами: величина dt в правой части сокра-
щается.
Приводим пример:
Ш — zt^Tl* dx 2t-lm
§ 4J ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ 137
Таким образом, когда мы будем вычислять таблицу
для построения графика и, задаваясь t, находить х и у,
мы сможем в любой точке находить и значение производ-
ной -^, дающее наклон касательной в этой точке.
Упражнения
1. Найти производную от г=(ах-{-Ь)г как сложной функции
y = ax-\~tr. Раскрыть скобки и найти ту же производную.
2. Найти производную
1 1 1
— ах + Ь1 ' — (ах + Ь)*' 1+1'
х
§ 4. Производная произведения функций
Найдем производную произведения двух функций: g(x)
и h(x). Положим
f(x)=g(x)h(x),
df = f(x-\-dx)—f(x)=g(x-\-dx)h(x-\-dx) — g(x)h{x).
Но
Поэтому
df = \g (x) + dg] [h (x)-\-dh]—g (x) h (x) =
= g{x)dh-\-h{x
Заметим, что
dg = g'(x)dx,
dh = h'(x)dx,
откуда
dhdg=g'{x)h'{x){dxf.
Величина dh dg пропорциональна (dx)', поэтому произве-
дением dhdg в выражении df пренебрегаем. Окончательно
получаем:
df=g (x) dh + h (лг) dg. D.1)
138 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Разделив все члены D.1) на dx, получим:
Это выражение надо запомнить так: производная произведе-
ния gh равна сумме производной, взятой в предположении,
что зависит от х только h, a g постоянно ( член g -г- ] ,
и производной, взятой в предположении, что h постоянно,
а от х зависит только g (член h -^- ]. При этом, естест-
dh
венно, само постоянное значение g в члене g-^ берется
при том х, при котором ищется значение производной.
То же относится и к А во втором члене.
Как бы мы действовали старым способом? Простая
алгебра дает точное равенство
Д/ == g (х) • Ah + h (х) •
Поделим обе части на Ах:
Л/ , > ДЛ
Заметим, что в последнем члене для удобства мы умно-
жили и разделили на Д*. До сих пор все равенства яв-
ляются точными, справедливыми при любых значениях Дх.
Теперь переходим к пределу при Ах—»0. При этом
lim ?? =
и в силу D.3)
Последний член в формуле D.3) при переходе к пре-
делу исчез, так как первые два множителя в пределе
дают произведение h'-f, а Ах мы устремили к нулю.
С помощью приращений и перехода к пределу получен
тот же результат, что и с помощью дифференциалов, но
несколько более долгим способом. Это не удивительно,
так как в случае дифференциалов мы отбросили df-dg
механически, на основании ранее заученного правила,
согласно которому надо отбрасывать члены с (<?*)*, {dx)'
§ 4] ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ 139
и т. д., а значит, и любые произведения двух, трех и
большего числа дифференциалов.
При расчете с помощью приращений мы, в сущности,
по ходу дела доказали это правило еще раз для примера
произведения функций.
Последовательные действия с помощью приращений
нужны для обоснования правил и понимания их. Но, после
того как понимание достигнуто, пользование дифферен-
циалами быстрее ведет к цели, является более деловым;
было бы смешно каждый раз танцевать от печки, каждый
раз решая конкретную задачу, выписывать, что производ-
ная есть предел отношения, и т. д.
Пример. /=-BдгЧ-5)(Злг + 4).
Найти /' (х) и, в частности, /' B). Здесь
_^ = B-4-f5)-34-C-2-f4)-4-2 =
= 394-80=119.
*=»
Правило для нахождения производной произведения
обобщается на случай нескольких множителей. Например,
для произведения четырех функций f (x), g(x), h(x), k(x)
получаем:
- D-4)
Производную частного (отношения) двух функций най-
дем, записав f = — в виде произведения
Тогда
Г = * (¦*)'+*'Т-
140 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Производную функции — находим, пользуясь формулой
(з.з), е
Подставляя это в D.5), получим:
или
(лу=*?=,*«:. D.6)
Правило, согласно которому производную произведения
нескольких функций можно найти как сумму производных,
вычисленных в предположении, что каждый раз меняется
только одна функция, в действительности применимо не
только к произведению функций, но и к другим выраже-
ниям. Легко убедиться, что формула для производной
суммы функций также согласуется с этой формулировкой.
Позже мы увидим, что та же формулировка применима
и к таким случаям, как, например, g (x)hl*\ где функция g
возводится в степень h, зависящую от х.
Упражнения
1. Найти производную функции у=х*. записав х* =
Найти производные функций:
§ 5. Степенная функция
Рассмотрим производную степенной функции
где п есть постоянное число. При п целом положительном
х" есть произведение п одинаковых множителей
п. раз
у = Х-Х'Х . . . X,
п раз
g = Ь>-1 -f I .je"-r-f ... -f 1 .др«
§ 5] СТЕПЕННАЯ ФУНКЦИЯ 141
(по формуле типа D.4)), откуда*)
Покажем, что эта формула имеет место при любом п
(дробном, отрицательном).
При дробном п запишем п = —, где числа т и р —
т
целые. Получим у = хР, или
ур = хт. E.1)
Выражение у? в левой части E.1) является сложной функ-
цией от х, так как у зависит от х. Поэтому, вычисляя
производную от обеих частей равенства E.1), получим:
Отсюда
dy т хт~1 т хт~х т хт~х wi J~x
1 ~P ?L~l> X
dx p yf~' P f TL
Учитывая, что — = n, получаем окончательно:
При отрицательном показателе запишем л = — к, где
k — положительное число,
j
По правилу определения производной сложной функции
у = -г, f = xk найдем:
dx f* dx x**
•) Для целого я эту формулу можно получить прн помощи би-
нома Ньютона. Однако производная легко находится и без бинома,
его знание не обязательно.
142 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ 1ч. III
Подставляя обратно k== — п, получим и для отрицатель-
ного п
Зх~ ~х пх •
Таким образом, формула производной от степени при-
менима при любом рациональном показателе п. Она рас-
пространяется и на случай иррационального показателя
степени.
Формула эта имеет важнейшее значение. При всей ее
простоте эту формулу полезно записать еще в другом виде:
„_«*¦, ?-«*. E.2,
Этот результат надо глубоко прочувствовать. При поло-
жительных п степенная функция обладает очевидным свой-
ством, что при *=0 у также равно 0. Кривую у = сх"
при данном п ^> 0 можно провести через любую точку
(*<>' У*)—достаточно выбрать c = yjx". Пусть кривая про-
ходит через начало координат и через точку (ха, уа). Най-
дем среднее значение производной на участке кривой от
начала координат до точки (х0, у0). Согласно определению
среднего (см. выше, часть II, § 13)
y'{x)dx
откуда, пользуясь формулой A1.9) из части И, получаем
В самом деле, при изменении х от 0 до ха у растет
от 0 до у0. Значит, средняя скорость роста у (т. е. сред-
нее значение производной) равна yjx9, это очевидно и без
интегралов!
Как видно из формулы E.2), значение производной в
точке (ха, уа) в п раз (п — показатель степени) отличается от
среднего значения производной. На рис. 66 показано не-
сколько кривых с различными я: п = — , 1, 2, 5, проходя-
§ 5]
СТЕПЕННАЯ ФУНКЦИЯ
щих через одну и ту же точку N (ха, уа), а значит, имею-
щих равную среднюю производную на отрезке 0 — хл. На-
глядно видно, что чем больше п, тем больше производная
в точке N (круче растет кривая). Вернемся еще раз к
формуле
V
dy у_
dx х '
E.2)
Отсюда
= n-j-dx, и пото-
му для малых приращений
Ау = п — Ах.
3 х
E.3)
Будем считать, что соотно-
шение E.3) достаточно точно
для Ах = 0,01л, т. е. для
изменения аргумента на 1°/„.
Тогда из E.3) получаем:
или
= п0,0\у.
Рис. 66.
При изменении аргумента на 1°/0 степенная функция с по-
казателем п меняется на па[9.
Упражнения
Найти производные функций:
1. // = х5 — Зх*4-*'4-7*г — 2х+5. 2.у = (х*+х->г1
= (х* — x-f-1)*. 4. у = C**— II0. 5. у = Ух*— 1. в.
7. Найти значения у(9) н у A1), если дано, что уA0) =5
в случае*): а) у ~ V х, б) у
(
L
в) у ~ хг. Задачу решить
в уме, без выкладок. Сравнить ответ с точным.
•) Знак ~ означает пропорционально.
144 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ш
§ 6. Производные алгебраических функций
с постоянными показателями
Совокупность правил §§ 1—5 позволяет найти произ-
водную любой функции, составленной путем сложения и
вычитания, умножения и деления, возведения в степень
(постоянную), в том числе дробную (корни).
Покажем иа одном примере, как это удобнее всего де-
лать практически. Найдем производную функции
Ответ следует писать сразу, т. е. не вводя каких-либо
новых обозначений (вродз у/х* — 1 = у). Производную бе-
рут как бы отдельно по каждому месту, где стоит х, при-
говаривая для памяти примерно следующее (буквы «а», «б»,
«в», . . . показывают, к каким местам выражения производ-
ной, написанного внизу, относятся слова): производная (а)
по х, стоящему перед корнем, плюс (б) производная по
у/хх—1, умноженная на (в) производную от]/хг—1
по хг — 1, умноженная иа (г) производную от х* — 1
(а) (б) (в) (г)
I I i i I I I 1
3 х1 —
2х.
Имеет смысл сразу приучаться к такому деловому спо-
собу, без лишнего чистописания, пользуясь следующими
принципами:
а) правило дифференцирования сложной функции [§ 3,
формулы C.2), C,4)];
б) если выражение составлено из нескольких функций,
то его производная равна сумме производных, вычисленных
в предположении, что каждый раз лишь одна из функций
предполагается переменной, а остальные постоянны [§ 4,
формулы D.2), D.4), D.6I-
Формулу для производной степени удобно применять
в виде
„_*.. *=.„*,
как это сделано выше, в примере — см. выражение (в).
§ 7J ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ 145
Для того чтобы приобрести навык, нужно проделать
10—20 упражнений только на технику безотносительно
к физическим задачам.
Упражнения
Найти производные функций:
1. у=х*(х* — I)'. 2. у = х3 Vx*+x. 3- y = xi У*— !(** —
— 2х)Т. 4. y=(x + -f=_\Vxi^2. 5. // =
14. t, =
20 x-f-x-Hj/J+T
*2
22. у= 1/ **+* + 1 . 23. // = ;
x + I
24. -=f,+^=J^ 2в.„=?^.
§ 7. Показательная функция
Рассмотрим функцию
где число а больше 1. График функции у изображен на
рис. 67, а. При х=0 «/=1 при любом а.
Функция у при всех х положительна и растет с
увеличением х, так что и производная ее также везде
146
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. Ill
положительна. При увеличении х на постоянную величину с
получим:
y(x-{-c) = ax+c=ac-ax = b-ax = b-y(x), где Ь = ас;
9
величина у умножается на постоянную величину. Таким
образом, если х менять по-
следовательно, одинако-
выми шагами (в арифметической прогрессии)
х=ха, хл-\~с, ха-\-2с, .. ., х„-f-пс,
то у будет принимать значения
У„, Ьу0, Ь2у0, .."., Ьпуй.
Такой закон нарастания, как известно, называется геоме-
трической прогрессией.
Найдем производную показательной функции для
а=10*):
d A0х) lO*** 10х ^к/*—1
dx dx dx
•) a =10 взято для облегчения вычислений.
§ 7] ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ 147
Что представляет собой величина
10*-* — ! .
dx f
jq4x I
Это есть предел отношения —-^— при Длг—»0. Найдем
этот предел численно, «арифметически». Пользуясь четы-
рехзначной таблицей логарифмов, находим:
10е'1 =1,2586, Ю^-1^
1 А0,01 1
10°'01= 1,0233, QQ~ =2,33,
10°-°01 = 1,0023, ^^=-' =2,3.
Таким образом, получаем:
Следовательно, производная
^ 10*. 2,3.
Производную 10х мы нашли, так сказать, опытным путем,
при помощи таблиц. Для любой другой показательной
функции задачу теперь легко свести к предыдущей: поль-
зуясь понятием логарифма, запишем:
По правилу нахождения производной сложной функции
получим:
^ ax-2,3-lgfl!. G.1)
Замечательная особеиность показательной функции за-
ключается в том, что ее производная прямо пропорцио-
нальна самой функции. В этом главное свойство геометри-
ческой прогрессии: чем больше сама величина, тем быст-
рее она растет. Свойства геометрической прогрессии, необы-
чайно сильное ее возрастание — любимая тема популярных
книжек, например «Занимательной алгебры» и «Живой ма-
тематики» Перельмана.
148 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Если в показательной функции 0<а<1, то график
функции имеет вид рис. 67, б, при увеличении х в ариф-
метической прогрессии у уменьшается в геометрической
прогрессии. Формула G.1) по-прежнему применима. В этой
формуле lg а отрицателен при а < 1 и, следовательно, про-
изводная, будучи пропорциональна функции, имеет проти-
воположный знак.
В части V мы приведем несколько примеров, в которых
та или иная величина уменьшается с течением времени,
притом так, что скорость уменьшения пропорциональна
самой оставшейся на данный момент величине
Как видно из предыдущего, в этом случае решением за-
дачи явится показательная функция
у=уаа*(а<1).
Подробно об этих задачах будет рассказано в части V.
Упражнения
Найти производные функций:
1. //=10 . 2. у = 2*. 3. у==5х + \ 4. y=^
§ 8. Число е
Найдем такое основание, для которого формула произ-
водной показательной функции имела бы наиболее' простой
вид, а именно, чтобы в выражении производной коэффи-
циент равнялся единице, так что его можно было бы
не писать. Обозначим это число буквой е. Таким образом,
При помощи формулы G.1) число это легко найти:
23lgel lge
откуда по таблице логарифмов
§ 8] число е 149
Такой практический подход не соответствует историческому
ходу развития науки и принципиально не удовлетворителен.
Мы пользовались числами, заимствованными из таблицы
логарифмов, не задумываясь над тем, как они вычислены *).
Найдем число е, основываясь только на формуле (8.1).
По общему свойству показательных функций е°=1. Рас-
смотрим функцию у—е*. Тогда у@)=1. Из формулы
(8.1) t/'@)=l..
Возьмем малое Адг = г и подсчитаем приращение функ-
ции у = ех при переходе от х = 0 к х = г. Ау = у'Ах.
Поэтому Д(/ = 1-Дх = г; у(х) = у(О)-\-Ау, откуда
er=l-fr. (8.2)
Запишем малое число г как дробь с большим знаменателем:
г = -^-, если г<1, то л>1 **). Тогда из (8.2)
- 1 ( 1
еп=\-\-—, откуда e=fl-f- —
Это выражение тем точнее, чем больше п, так что строгое
определение числа е пишется так:
/ 1 ^п
(читается: е есть предел выражения f I -j ] при л,
стремящемся к бесконечности).
Однако не надо бояться слов «предел», «бесконечность».
1 -{-wjq) =2,705, что довольно
мало отличается от точного значения. Советуем читателю
f 1 \ *
самому найти f I -f- -g-) • Мы получили, что при малом г
ег=\-\-г ***),
и это тем точнее, чем меньше г. Проверим это на числах.
*) Точность, с которой дано здесь число в, также больше той
точности, которую можно получить, определяя производную 10* при
помощи четырехзначной таблицы логарифмов.
**) Запись г <^ 1 означает, что число г значительно меньше 1.
•**) Для функции «/ = в* составлены подробные таблицы.
150
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. Ш
Из табл. 1 *) видим, что даже при г = ±0,3 ошибка
не превышает 6"/а. Для расчетов полезно запомнить не
Таблица 1
г
-0,5
— 0,4
-0,3
— 0,2
-0,1
— 0,01
14- г
0,5
0,6
0,7
0,8
0,9
0,99
ег
0,6065
0,6703
0,7408
0,8187
0,9048
0,9900
г
0
+ 0,01
0,1
0,2
0,3
0,4
0,5
1
1,01
1,1
1,2
1,3
1.4
1,5
(Г
1.0101
1,1052
1,2214
1,3499
1,4918
1,6487
только е = 2,718, но и приближенные значения е* = 7,4,
е' = 20, е*=55, es=150. Краткая таблица ех и е~* дана
в приложении к части III, стр. 223, таблица IV.
При помощи числа е упрощается решение задач на гео-
метрические прогрессии и сложные проценты. Рассмотрим
пример: во сколько раз вырастет производство за 50 лет
при ежегодном росте на 2°/0? Нужно вычислить 1,02".
Применение числа е заключается в том, что приближенно
мы заменяем 1,02 = е0'", откуда l,02S0 = e°iOt"" = e = 2,72.
Общая формула
(\-)rr)m = emr (г<^1). (8.3)
Для применимости этой формулы достаточно, чтобы
было мало г; т и тг могут и не быть малыми. Если тг
тоже мало, то етг= 1 -\- тг, получаем известную ранее
формулу (I -\-г)т=. 1 -{-тг, однако при больших тг ею
пользоваться нельзя, тогда как выражение (8.3) остается
справедливым.
Так, для примера, приведенного выше, точное значе-
ние 1,02s0 = 2,693, приближенно 1,02" = е1== 2,718, по
формуле A-{-г)т = 1-{-тг получим 1 -f- 50 X 0,2 = 2.
Расчет с помощью числа е дал ошибку около 1%, тогда
) Значения вх взяты из четырехзначных таблиц.
§ 8j . число е \Ъ\
как расчет по формуле A -\-г)т= 1 -\-тг в этом случае
дал ошибку около 25 %. В общем виде оценка точности
формулы дана в § 17, упражнение 5.
В соответствии с первоначальным определением числа е
формулой (8.1) производные от показательных функций
имеют особенно простой вид, когда возводится в степень
число е. Эти производные удобно выражаются через самую
функцию. Приведем ряд формул
*У — demx)_ e-w dm (х)_u
их— dx —e dx —y
Вывод. Итак, можно дать три различных определе-
ния числа е: 1) из условия (ех)' = ех, 2) из условия
1-f- —J прип—*<х>.
Для закрепления этого очень важного раздела читатель
должен, отложив книгу, сам показать, как из каждого
определения следуют два другие, рассматриваемые как
свойства е.
У числа е есть и другие замечательные определения
и свойства. В частности, ряд, с помощью которого удоб-
но вычисляется е, дан ниже на стр. 191 (формула A8.2)).
Далее, есть формула е^^Т = cos Ф+У — 1 sintp; при ма-
лом ф справедливость этой формулы следует из 2-го опре-
деления е и из того, что соеф=1, sin ф=ф при
Упражнения
Найти производные функций;
5. о = 5ех — егх.
152
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[ч. ш
§ 9. Логарифмы
По определению логарифмом величины f по основанию а
называется показатель степени g, в которую надо возвести
число а (основание логарифмов), чтобы получить данное
число f
f=a*, g=logaf.
Кривая, изображающая зависимость y=\cgax (для случая
а> 1), показана на рис. 68. Отметим, что при х=\ t/ = 0;
при х > 1 у > О, а при х < 1 у < 0. Вся кривая расположена
правее оси ординат. Так как положительное число а при
возведении в любую сте-
пень дает число положи-
тельное, то не существует
логарифмов бтрйцательных
чисел. Обратим еще вни-
мание читателя на то, что
в равенствах y=-logax,
^, х = ау величины
х безразмерны.
Как видно на рис. 68,
производная функции у =
= loge х положительна при
всех значениях х\ с увеличе-
нием х производная умень-
шается. Логарифмы по ос-
нованию е (см. § 8) назы-
х, у
a
и
а
Рис. 68.
Их
ваются натуральными.
обозначают ]пх.
Найдем производную натурального логарифма. Рас-
смотрим d\nдг= \n{x-\-dx)—1пдс. Воспользуемся извест-
ной формулой In а — In b = In —. Тогда
(9.1)
Мы уже знаем (см. § 8), что при малых г
ет=\-\-г.
Возьмем логарифмы обеих частей
lner=/-=ln(l-l-r).
(9.2)
§ 9] ЛОГАРИФМЫ 153
Пользуясь (9.2), получаем из (9.1)
dln*=In(l+?)=?•
Поэтому
*%? (9.3)
х
Производную натурального логарифма можно найти
также, пользуясь тем, что логарифм и показательная функ-
ция— обратные функции. Запишем:
. „ ', dx d(e?) y dy I 1 1
у = 1пх, х = еУ% х =-Ту=-^- = еУ, ^ = -р = ^ = т.
Когда х меняется в геометрической прогрессии, \пх ме-
няется в арифметической прогрессии:
x — ab™ \пх = \па-\-т\п Ъ.
Поэтому чем больше х, тем медленнее растет \пх, тем
меньше производная.
Выведем формулу, связывающую логарифмы одного
и того же числа по разным основаниям. Пусть
/ = logoft, af=h. _ (9.4)
Прологарифмируем обе части второго равенства (9.4) по
основанию b: flogba = logbh, откуда /=^р^.Принимая
во внимание (9.4), получаем:
Пользуясь (9.5), можно получить производную лога-
рифма по любому основанию. Пусть у = logax. Тогда
и — ^ и ^——Ll!iL? _LJL ,да\
У In а и dx In а dx —In ах" K">
В формуле (9.5) положим 6 = еи/1 = е, получим: logae =
= ]j^i и формулу (9.6) перепишем в виде
d\ogax_\ogae ,q?v
dx —~T~- (У/>
Из формул (9.3), (9.6), (9.7) самая простая (9.3). Она
получается, если логарифмы взяты по основанию е.
154 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ Н ИНТЕГРАЛОВ [Ч. III
Поэтому они и называются натуральными, т. е. природны-
ми, естественными. Полезно запомнить для грубых расчетов
в уме: 1п 2 = 0,69, 1п 3=1,1, 1п 10 = 2,3 = 7-^ • Краткая
таблица натуральных логарифмов дана в приложении к
части III на стр. 223, таблица V.
Если под знаком логарифма стоит какая-нибудь функ-
ция f(x), то производную находим по правилу дифферен-
цирования сложных функций (§ 3)
d\nf(x)_ I df(x) . ~
dx —f{Z)'~dir' Фл>
Заметим, что, пользуясь понятием логарифма, легко
найти производную функции у-=а1С при любом а. Дейст-
вительно, \пу=х\па, поэтому t/ = e*lno, откуда
= у \па.
Формула (9.8) дает возможность находить производные
выражений вида f(x)h(X>, т. е. содержащих переменную
и в основании и в показателе степени. Пусть
y = f(x)hiX\ (9.9)
Прологарифмируем (9.9) (логарифмы можно брать по лю-
бому основанию; возьмем натуральные)
\ny = h(x)\nfix). (9.10)
Возьмем производную от обеих частей (9.10), при этом
учтем, что 1пу есть сложная функция х [так же как 1п / (х)]
i-у' = h' (х) In / (x) -f h (x)f-^g,
откуда
y'=i
или, пользуясь (9.9),
y' = f (*)*<*>/»' (x) In f{x)-\-h (x) f (*)Aw" 7' (*)• (9-11)
Рассмотрим формулу (9.11). Справа в ней стоит сумма
двух членов: первый член f{x)h{X)h' (x) \nf{x) есть произ-
водная выражения /А, вычисленная в предположении, что
переменной является лишь h, а / — постоянная; второй
§ 10] ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 155
член h(x)f(x)h(X)~1f'(x) — это производная выражения fh,
вычисленная в предположении, что/ — переменная, a h —
постоянная. Подтверждаегся общий принцип, высказанный
в конце § 4.
Упражнения
1. Вспомнив In 10, иайти In 100.
2. Пользуясь формулой (9.5), иайти log5 15.
3. Пользуясь тем, что In (u-v) = ln и -+- In v, и дифференцируя
обе части, получить формулу для производной произведения.
4. Исходя из соотношения In — = In и — In v, получить формулу
для производной частного.
Найти производные функций:
5. у = \п2х. 6. p=ln(jc-f-3). 7. // = 1пЗх. 8. у = \п(х*-{-1).
9. у = 1п(Зх«-х-}-1). Ю. у = \п~\. U. у=\п^~. 12. у =
= х\пх. 13. у = я*\п(х + 1). 14. у = х*. 15. у =
§ 10. Тригонометрические функции
Тригонометрические функции определяются как отно-
шения отрезков и, следовательно, безразмерны. Они зави-
сят от безразмерной величины — угла.
В пределах углов от нуля до прямого угла тригоно-
метрические функции можно определять как отношения
отрезков в прямоугольном треугольнике (сииус угла равен
отношению противолежащего углу катета к гипотенузе
и т. д.). Нам, однако, важно определить функции любых
углов'—и больших прямого, и отрицательных,— поэтому
тригонометрические функции будем рассматривать в круге.
Единственной мерой угла, употребляемой в высшей
математике, является радиан. Краткие таблицы тригоно-
метрических функций в зависимости от угла, выражен-
ного в радианной мере, приведены в приложении к час-
ти III на стр. 224, таблица VI.
Чтобы не говорить все время об отношении линии
синуса к радиусу круга или об угле как отношении длины
дуги к радиусу, будем рассматривать круг с радиусом,
равным 1. При этом кратко будем говорить, что синус
равен длине линии синуса в таком круге, угол равен
длине дуги и т. д.
156
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. III
Однако читатель должен помнить, что и тригонометри-
ческие функции и углы измеряются не единицами длины
(сантиметрами, дюймами или метрами), а они безразмерны.
Синус равен длине линии сину-
са (в сантиметрах), деленной на
длину радиуса (в сантиметрах),
и при г=\ см численно равен
длине линии синуса. Линии си-
нуса и косинуса показаны на
рис. 69.
Напомним вид графиков си-
нуса и косинуса в зависимости
от угла (рис. 70). Период сину-
са, так же как период косину-
са, равен 2я = 6,28, соответст-
Рис. 69 вует полному обороту радиуса
окружности. Найдем производ-
ные синуса и косинуса геометрически. На рис. 71 конец
Рис. 70.
9
О В' А1
Рис. 71.
радиуса, проведенного под углом <р, обозначен А; ко-
нец радиуса, проведенного под углом <p-f-^(p> обозначен
§ 10] ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 157
В. Таким образом, длина дуги АВ равна dtp. Проводим
из А перпендикуляр АС на линию синуса угла <p-{-dq>
ВВ'. Как видно из рис. 71,
АА'= siny, BB' = sin
и
ВС = sin (ф -\- dtp) — sin ф = d (sin ф).
Далее,
ОА' = cos ф, O?'=:cosfa-f-<fcp)
и
Л'В' = ЛС= cos ф — cos (ф 4~ Лр) = — d (cos ф).
Так как угол d<p мал, то длина дуги АВ не отличается
от длины хорды АВ и угол ABC, образованный хордой
АВ и вертикалью ВСВ', равен ф *).
Из рассмотрения Д ABC найдем ВС = АВ cos ф,
AC=^ABs'mq>. Таким образом,
d (sin ф) = cos ф dtp, d (cos ф) = — sin ф dq>
и, следовательно,
d(coscp)
_iJL==COsq,; =
Дадим другой способ вычисления производной втф и
cos ф без использования чертежа. Согласно общим формулам
Д sinq> = sin(9-f- Дф) — БШф. Вспомним формулу синуса
суммы двух углов
sin (a -f- Р) = sin а cos p -f- cos а sin p
и применим ее к sin (ф-f-Дф). Получим
sin (ф 4~ Дф) = sin Ф- cos Дф-}-cos ф • sin Дф,
откуда
Д sin ф = sin ф - cos Дф -f- cos ф • sin Дф — sin ф.
Составим отношение приращений, его можно записать так:
1 — cos Дф
dip
*) Точное значение угла равно ф-f--^-, но треугольник ABC
мал (АВ = dф), поэтому, пренебрегая d<p в выражении угла ABC,
мы в величинах ВС и АС совершаем ошибки, пропорциональные (dqpJ-
158 ВЫЧИСЛЕВИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Теперь нужно перейти к пределу Д<р—>-(Х Известно,
что при углах а или Д<р, стремящихся к 0, синус равен
дуге sina=a, sinA<p=A<p. Другими словами,
,. sin Дф ,
hm —т—- = 1.
Второй член надо сперва преобразовать: по известной
формуле
cos 2a = 1 — 2 sin* a, 1 — cos 2a = 2 sin* a,
В этой формуле при малом Д<р заменим sin (-j^ ) = -jp.
\ z j j.
Получим тогда
2fV
I — cos A<p \ 2 / Аф
Дф Дф ~2~ "
Следовательно, в пределе при Дф—>-0 второй член про-
.. I — COS Дф п ^-.
падает: hm т -г = 0. Отсюда
ДФ
Д sin ф d sin
Соотношения A0.1) справедливы для любых углов,
а не только в I четверти. Полезно также, глядя на график
функций sinx и cosat, проверить, что формула A0.1) пра-
вильно дает знаки производных при любом х, а не только
в I четверти.
Проверим еще формулы A0.1) при малых углах. При
малом ф геометрически очевидно,. что
sin<p=5=<p, cos<p=t:l.
Первая формула —Д^—^ = cos<p при малом ф дает -—-= 1.
г, , d cos ф d cos ф п п
Вторая формула даст —~^ = — ф, ¦ ж = 0 при ф = 0;
равенство нулю производной соответствует тому, что ко-
синус имеет максимум при ф = 0.
Зная производные функций y=sinx и y=cosx, легко
найти производные всех остальных тригонометрических
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
159
функций, используя соотношения, связывающие тригоно-
метрические функции.
Так, например, известно, что tgx = . Поэтому
d tg x cos* x — sin x ( — sin x)
dx cos*x
по формуле дифференцирования дроби. Отсюда
_ tg X COS* X -f- Sin* X 1
_____
COS* X
" COS* X '
A0.2)
Из рис. 72, на котором изображен график tgx, видно,
что функция у = tg х
при любых х имеет по-
ложительную производ-
ную. Вблизи точек разры- •
производная неограни-
ченно возрастает. Оба
эти вывода вполне со-
гласуются с формулой
A0. 2).
Совершенно анало-
гичным приемом нахо-
дим:
d (ctg x)
dx
1
sin* х
-f
f
P
Рис. 72.
cos Р —
cos
Производные тангенса и котангенса можно найти и не-
посредственно. Заметим, что
•» •»" cos a cosji
Отсюда
cos а cos
sin (ос — р
'cos а•cos I
sin Дф
A0.3)
Имея в виду (см. стр. 158), что
,. sin Дф ,
hm —-—-!¦ = 1,
'60 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
из A0.3) получим:
1
COS2 ф "
Упражнения
Найти производные функций:
1. у = sin Bx-f-3). 2. y = cos(x—1). 3. y = cos(x* — х -f- !)•
4. y = sin*x. 5. у = sin 3x cos* x. 6. y=(sin2x)x. 7. y = xtgx.
8. у = в'в«. 9. y = ctg?-.
§ 11. Обратные тригонометрические функции
Новые очень интересные результаты получаются при
рассмотрении обратных тригонометрических функций. На-
помним читателю определения этих функций. Функция
y = Acrsinx A11)
представляет собой угол такой, что
siny—x. A1.2)
Равенство A1.1) означает то же самое, что и A1.2). Ана-
логично функция
означает угол у такой, что
Аналогично определяются функции у = Arccos х (х = cos у)
и t/ = Arcctgjc(x==ctg у). Заметим, что функция у =
= ArcsinA; имеет смысл только при значениях х, удовле-
творяющих неравенству —lsS*^l, что видно из A1.2).
Функция t/ = ArctgA: имеет смысл при всех значениях х.
Рассмотрим подробнее функцию y = Arcsin*. Пусть,
например, х = -^, t/ = Arcsinу. Можем взять t/=^-, так
как sin -jr- = -~ , однако можем взять и у = -^ , так как
. 5я 1 ,. 13п 17л
sin -g- тоже равен -^. Можно взять у=.— , у = ~^- и т. д.
§ 11]
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИЯ
161
2~ «^ у
Мы видим, что одному значению х отвечает бесчисленное
множество значений у. Все эти свойства функции
i/ = Arcsinje видны на графике (рис. 73).
Будем рассматривать отрезок кривой, для которого
2 -й- • Эта часть кривой называется главным
значением функции t/ = Arcsin* и обозначается t/=arcsinjc
(пишется с малым а). Если ограничиться с
рассмотрением y = arcsin^, то каждому х >J\\
отвечает только одно значение у. Главное
значение арктангенса определяется анало-
гично
Найдем производную функции
y = arcsinx. Воспользуемся тем, что арк-
синус есть функция, обратная синусу:
A1.3)
~
. . dy 1
Kx) -aZ ТПТл
1
(у) cos у'
Однако аргументом мы считаем х, поэтому
-? следует выразить через х, а не через у,
как в A1.3). Воспользуемся известной фор-
мулой sin* у -\- cos* y=\, откуда cos у =
= ± V 1 —sin*у. Так как мы рассматриваем главное зна-
чение арксинуса, то F^^^IT' cosy^O, поэтому
перед корнем берем знак плюс: cos г/= 1^1—sin* у. Так
как smy = x согласно A1.2), то
ставляя это в (П.З), находим:
dy
dx~
или
= |A—х*- Под-
A1.4)
Я- Б. Зельдович
162
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. III
Формулой A1.4) можно пользоваться не только для
главного значения, но и для других участков кривой,
выбирая соответственно знак у корня. Действительно, при
одном и том же значении х на различных участках кри-
вой производная имеет разные знаки; так, в точках А и С
(рис. 73) производная положительна, а в точках В и D
отрицательна
Найдем теперь производную 1^ • Если у = arctg х,
¦у то x = tgy. Отсюда, анало-
гично
дим:
., , ч dx \
предыдущему, нахо-
dy cos' у'
A1.5)
Из тригонометрии известно,
что
поэтому
Пользуясь A1.5), получаем окончательно:
dy d (arctg x) 1
dx dx 1 +X2'
A1.6)
Для любой другой ветви арктангенса (рис. 74) остается
справедливой формула A1.6), так как любая другая ветвь
получается из основной параллельным переносом, а это
не изменяет величины производной.
Упражнения
1. Найти производные функции y = arccosx и « = arcctgx.
о о d(«*) -х d(lnx)
2. Зная, что ' =е*, найти v пользуясь тем, что из
равенства у = 1 п х следует х = еу.
Найти производные функций:
3. y = aTcsin2x. 4. у = arctg (Зх-f-l). б. у = arctg (х*—х).
6. у-
§ 12] ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО 163
§ 12. Производная функции, заданной неявно
Неявное задание функции у (х) — это задание ее выра-
жением вида
F(x, y) = 0. A2.1)
Если соответствующее уравнение можно решить отно-
сительно х или у, то мы вернемся к обычному заданию
функции.. Однако иногда такое решение приводит к слож-
ным формулам, а иногда его и вовсе нельзя найти. Так,
например, уравнение окружности в форме
х1-\-уг—\=0 A2.2)
проще, чем следующее из него выражение
у=±У\ —х\ A2.3)
Если в A2.1) левая часть — произвольный многочлен, со-
держащий х и у в степени выше четвертой, то в общем
случае это уравнение нельзя разрешить соответственно
относительно х или у. Также не разрешается, например,
простое с виду уравнение
F(x, y)=xs'mx-{-ysmy— я = 0. A2.4)
Однако и в тех случаях, когда нет решения в виде
формулы, прямо дающей способ вычисления у для дан-
ного х, все равно у есть определенная функция х, при
каждом х можно, решая уравнение численно, найти соот-
ветствующее у, можно построить кривую в плоскости х, у.
Возможно, что кривая будет существовать не при всех х
(в случае окружности, например, лишь при х между — г
и -\-г, где г — радиус окружности), при данном х может
быть больше одного значения у (в случае окружности,
например, два значения, в соответствии со знаком ± у
корня квадратного). Однако эти осложнения не отменяют
основного факта: F (x, y) = Q определяет у как функцию х.
Как найти производную ^? Можно ли это сделать,
не решив уравнение, т. е. не выразив у(х) явно?
Это было сделано еще Ньютоном. Пусть х, у удовлет-
воряют уравнению
F(x, y) = 0. A2.1)
164 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ш
Возьмем соседние значения х-{-Ах, у-\-Ау, также удо-
влетворяющие уравнению
F{x + Ax, у-\-Ау) = О. A2.5)
Запишем, пользуясь A2.1):
F(x+Ax, y-\-Ay) = F{x + Ax, у + Ау) —
— F(x-{-Ax, y)-lrF(x + Ax, y) — F(x, у). A2.6)
Разность F (х -f- Ах, у) — F (х, у) представляет собой при-
ращение функции F (х, у), рассматриваемой как функция
одной переменной х при неизменном у. Это приращение,
как мы знаем, в пределе *) может быть выражено так:
• Дх
у=const
Мы отмечаем здесь, что при вычислении производной по х
функции двух переменных х и у мы считаем у постоянным.
Вычисленную таким образом производную называют част-
ной производной и в ее обозначении вместо прямой буквы d
пишут круглую д:
F(x + Ax,y) — F(x,y) = ?F-?J?-Ax;
dF(x,y) д1}т F(x4-As,y) — Fjx. у)
дх ах-*о Л*
Аналогично для первой разности в A2.6) можно написать:
F(x-{-Ax, y-{-Ay)-F(x-{-Ax,y) = dP^ + ^x'y)Ay.
Условие A2.5) дает:
дх ' ду .
или
dF (х, у)
Aj/ дх
Л^ dF (х -\- Ь.хГу)'
ду
Переходя к пределу при Длг—>-0, получим слева производ-
*) Выражение «равно в пределе» при малом Дх или Ау разъяснено
подробно в § 4 часть II, где рассматривается выражение приращения
функции с помощью производной.
§ 12] производили функции, заданной неявно 165
ную, а справа при этом можно будет отбросить Д*. Окон-
чательно
(х. у)
дх
=
dx dF (%, у)'
ду
Обратите внимание на знак минус в A2.7) и на то, что
в данном случае нельзя просто «сократить» dF(x,y) в чи-
слителе и знаменателе.
Покажем применение A2.7) на примере уравнения A2.2).
Имеем F(x, у)=х*-\-у*— 1;
dF(x,y)_C) dF(x,y)
дх —гХл ду~~~~ У>
? = -? = --• A2-8)
dx 2у у v '
Легко убедиться, что этот результат совпадает с тем, что
получится, если вычислить производную A2.3).
Найдем производную в случае A2.4)
ду sin x-\-x cos x
дх sin у -\- у cos у '
Таким образом, в выражение производной неявной функ-
ции входят обе величины, х и у. Чтобы найти ее численно,
нужно при заданном х найти численно у. Но если бы мы
не имели формулы A2.7), то для нахождения производной
нам пришлось бы находить численно два значения yt и ух
при двух соседних хх и хх и находить отношение у*~Ух .
хх хх
При этом чем ближе хг и хх, тем точнее пришлось бы вы-
числять ух и ух, а это часто затруднительно.
Заметим, наконец, что если F(x, у) = 0 приводит к не-
однозначной кривой, т. е. при одном значении х есть два
или больше значений у (несколько ветвей кривой), то выра-
жение A2.7) при данном х при подстановке разных у дает
значения производной в соответствующих точках. Читателю
предлагается проверить это на примере уравнения окруж-
ности A2.2), для которого производная дана форму-
лой A2.8). -
166 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
Для нахождения производной функции, заданной неявно,
нам пришлось ввести новое понятие — понятие частной про-
изводной. Это понятие имеет большое значение и необхо-
димо для функций нескольких переменных, которые мы
в этой книге не изучаем. По существу, мы уже неявно
пользовались понятием частной производной даже в таких
элементарных вопросах, как производная произведения не-
скольких функций у =sh(x) g (х) или, например, производная
степени у = Л (*)«<*> (см. стр. 138, 154), когда мы говорили,
что у' складывается из члена, получающегося при взятии
производной по х, стоящему в h (х), и по х, стоящему
в выражении g (x). С помощью частных производных мы
запишем это правило так: если
то
, dy dF dg.itf dh_
У —dx— dg ' dx~r~dh ' dx'
Упражнения
1. Найти производную —¦ функции', заданной-уравнением A2.4)
я п _ ял
в точке х = -^-, у==—. То же а точке х== ^- , у=-^-.
2. Найти производную —¦ функции, заданной уравнением
лг1 -\- Ъх -f-уа4- Ъу — 8 = 0, в точке х = у=1.
§ 13. Интеграл. Постановка задачи
В части II мы познакомились с понятием интеграла.
При этом была выяснена тесная связь между двумя различ-
ными на первый взгляд задачами. Эти задачи суть:
1) нахождение суммы большого числа малых слагаемых,
когда эти слагаемые можно представить как v(t)dt;
2) нахождение функции z (t), производная которой равна
данной функции v(t)
Советуем читателю перед чтением дальнейшего мате-
риала повторить §§ 7—12 части II.
§ 13] ИНТЕГРАЛ. ПОСТАНОВКА ЗАДАЧИ 167
Задачи физики, математики, химии по большей части
возникают как задачи вычисления суммы. Эта постановка
задачи более наглядна; сам вопрос уже подсказывает про-
стой, хотя и приближенный путь для вычисления интере-
сующей величины. Однако этот путь не дает общих формул.
Вторая постановка задачи является более искусственной.
Однако у этой постановки задачи есть свои преимущества.
Нахождение производных оказалось простым делом, сводя-
щимся к четырем-пяти формулам (производная *", ех, In x,
sinx, cos*) и двум-трем правилам. Поэтому легко можно
найти производные большого числа функций. Каждый раз,
когда найдена производная какой-либо функции ~Ti==LVi
можно зарегистрировать, что для этого v известен интег-
рал z (см. § 14). Таким образом, можно набрать много
отдельных частных случаев, в которых удается решить
задачу о нахождении интеграла. При помощи тождествен-
ных алгебраических преобразований удалось для нескольких
простых типов функций v найти правила нахождения инте-
грала (см. § 15).
Этого не удается, однако, сделать для всех элементар-
ных функций, так что интегрирование труднее, чем нахож-
дение производных. Тем не менее формулы, полученные для
некоторых интегралов во второй постановке задачи, очень
важны. Если уж удалось для данной v найти интеграл
(неопределенный интеграл или первообразную функцию),
то тогда все задачи в первой постановке, все суммы, т. е.
ь
все определенные интегралы j v (?) dt, оказываются выра-
а
женными простыми формулами посредством функции г:
ь
)v(t) dt=z(b)—z(a). Такой результат является гораздо более
а
полным, более точным и ценным по сравнению с результатом
каждого отдельного численного расчета суммы, т. е. определен-
ь
ного интеграла \ v (t) dt в определенных пределах от а до Ь.
а
Поэтому нашей целью в первую очередь будет именно
решение задачи во второй постановке.
168 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. П1
§ 14. Простейшие интегралы
Выпишем формулы для производных, найденные в пре-
дыдущих параграфах, и соответствующие им интегралы:
-г- (sin kx) = k cos kx, k С cos kx dx = sin kx -f- C;
^ (cos kx)=— k sin иле, — A? \ sin fe* Лс= cos kx -\- C;
a; = arctg x + C.
Проделаем небольшие преобразования. В первом инте"
грале обозначим п— 1=т (тогда п=т-\-1) и перепишем
его так:
Очевидно, что формула справедлива при всех т, кроме
т = —1; при т = —1 знаменатель обращается в нуль,
хт+1==х'= 1, получается непригодное для расчетов выра-
жение -zr-\-C. Однако как раз в случае т=—1, т. е.
для \ —dx, имеет место формула
Эта формула справедлива лишь для положительных значе-
§ 15] ОВЩИЕ СВОЙСТВА ИНТЕГРАЛОВ 169
ний х, так как In л; имеет смысл лишь для х^>0. При
JC<d 0 \пх не имеет смысла, но имеет смысл 1п (—х). Так
как
d In (— x) J_ 1
dx — хК l)—Т'
Jdx
— = 1п(—л:) + С, если *<0. Обе формулы для
dx
— могут быть объединены в одну
J? A4.1)
J
Этой формулой можно пользоваться для любого проме-
жутка интегрирования, не содержащего х = 0.
Интеграл от показательной функции запишется так:
Аналогично получаем для синуса и косинуса
\sinkxdx=— -?-cos kx-\-C,
coskxdx = -? sinfex-f-C.
§ 15. Общие свойства интегралов
Выше, в §§ 1—3, были установлены свойства производной
суммы функций, производной сложной функции и производ-
ной произведения функций. Каждому из этих свойств со-
ответствует определенное свойство, относящееся к интег-
ралам.
Для интегралов имеет место равенство
J [Cf(x) + Eg(x)] dx = C J / (*) dx + E J g(x)dx. A5.1)
Для доказательства надо взять производную выраже-
ния, стоящего справа; если равенство верно, то получим
подынтегральную функцию. Дифференцируя, имеем:
'*= Cf(x) -f- Eg(x).
170 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. 1П
Таким образом, равенство A5.1) доказано. Оно показывает,
что интеграл суммы нескольких слагаемых разбивается на
сумму интегралов отдельных слагаемых, а постоянные мно-
жители можно выносить за знак интеграла.
Под знаком интеграла можно делать замену переменной,
переходить к новой, более удобной переменной. Рассмотрим
несколько простых примеров.
1. Найти ^(ax-\-b)ndx(n=? — 1).
Здесь в качестве новой переменной введем величину,
стоящую в скобке. Назовем ее г,
ах-\-Ъ=г. A5.2)
При этом надо также от дифференциала dx перейти
к дифференциалу dz.
Из выражения A5.2) получаем:
Таким образом,
dx=—.
В правильности результата легко убедиться, вычисляя про-
изводную правой части,
dx[ а(я+1) ~T~^]—dxl в (л
2. Аналогично выполняется замена переменной в инте-
грале
1 * = *х+Ь, dz=adx, dx = %,
-\~b
На практике в таких, очень несложных, примерах пре-
образования делают менее торжественно, не вводя отдель-
ных обозначений для новых, промежуточных переменных.
§ 15J ОБЩИЕ СВОЙСТВА ИНТЕГРАЛОВ 171
Пишут, например:
С (ах + Ь)п dx = J (ax -f- b)" ~ d (ax -f b) =
Пусть f(x) и g(*)—две различные функции перемен-
ной х. Правило нахождения производной произведения дает:
Равенство A5.3) дает возможность написать:
g«k. 05-4)
В справедливости A5.4) убеждаемся, составляя производ-
ную от его левой и правой частей. При этом получим вер-
ное равенство A5.3).
Перепишем A5.4) в виде
Сокращенно это равенство пишут так:
A5.5)
В чем смысл формулы A5.5)? При вычислении инте-
грала нет правила, выражающего интеграл произведения
двух функций через интегралы каждого из сомножителей.
Однако если в произведении двух функций fw интеграл
одного из сомножителей известен
то удается выразить интеграл \ fw dx через интеграл, в ко-
торый входит производная -?¦ При помощи w перепи-
шем A5.5) в виде
?fwdx=f (\wdx) — U§wdx\i[-xdx. A5.6)
Так как f wdx=g, то последний интеграл в A5.6) есть
172 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
g 4- dx\ он иногда бывает проще исходного интеграла
\fwdx или сводится к известному интегралу. В частно-
сти, если / — степенная функция, то ^ имеет степень на
единицу ниже, чем f. Формула A5.5) или A5.6) называется
формулой интегрирования по частям.
Приведем примеры.
1. Найти \ хех dx.
Положим f = x; тогда w=^=ex, e* dx=dg,
g=\e*dx = ex, df = dx. По формуле A5.5)
J xe* dx = xex — J e* dx = хе* — ех = ех (х — 1) -f С.
2. Найти С х*е* dx.
Положим f=x*\ тогда w=?=ex, e*dx = dg,
g=<\exdx = ex, df = 2xdx. Пользуясь A5.5), получа-
ем С х*ех dx = х*е* — 2 \ хе* dx; пользуясь результатом
первого примера, получаем:
хгех dx= xxex — 2хе* + 2ех-\-С = (х* —2х-\-2)ех-\-С.
Для нахождения ^ Рп (х) ekx dx, где Рп (х) — многочлен
степени л, придется л раз выполнить интегрирование по
частям. При этом в ответе получится Qn(x)ekx, где (?„(;*:) —
многочлен степени л. Зная это, можно не выполнять п раз
интегрирование по частям, а прямо находить коэффициенты
многочлена Qn (x).
Рассмотрим тот же пример. Найти \ х*ех dx. Напишем
равенство с неизвестными пока коэффициентами много-
члена Qn(x)
x = (atx'-\- alX-\-an) e*-\-C. A5.7)
Составим производную от обеих частей равенства A5.7)
х>е* = [^а, + х Bа, + а,) + (а, + а0)] в*.
§ 15] ОБЩИЕ СВОЙСТВА ИНТЕГРАЛОВ 173
Приравняем коэффициенты при одинаковых степенях х
в многочлене справа и слева. Получим:
«. = 1;
2at -\- а1 == О, откуда ах = — 2;
а,+ао = 0' откуда ао = 2;
окончательно получим, как и раньше,
J хгех dx = (х* — 2х -f 2) е* -f С.
Аналогичным приемом можно находить интегралы от функ-
ций Рп (х) cos kx и Рп (х) sin kx, где Р„ (х) — многочлен.
В обоих случаях ответ имеет вид
<2„ (*) cos kx -f- Я „ (д:) sin fex,
где Qn(x) и Я„(д;) — многочлены, степень которых равная
(или меньше л). Примеры такого рода приведены в упражне-
ниях.
Приведем пример интеграла, который удается привести
к известным нам интегралам посредством алгебраических
преобразований.
Рассмотрим интеграл \ ; г- гг.
J I* — а) (х — о)
Заметим, что справедливо тождество
_J 1 _ а — Ъ
х — а х — Ь ~ (х — а) (х — Ь) '
При его помощи получим:
1 1 г 1!
!_
(х — а) (х — Ь) ~ а — Ь 1х — а х — Ь
Поэтому
— a х — Ь
Существуют приемы, позволяющие интеграл любой алге-
браической дроби с целыми степенями переменной выразить
при помощи элементарных функций. При этом, однако,
в ответе появляются не только алгебраические функции,
174 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. 1П
но и логарифмы и обратные тригонометрические функции
(арктангенсы). Общая теория нахождения таких интегра-
лов слишком сложна для нашей книги.
Интегрирование многих функций, содержащих корни и
тригонометрические функции, может быть при помощи над-
лежащей замены переменной сведено к интегрированию
многочленов или алгебраических дробей с целыми степе-
нями. Рассмотрим один пример.
Найти j хУх-\-\ dx. Сделаем замену переменной:
z=j/jt+~T, x-f- I =z*. Отсюда 2zdz = dx. Переходя к но-
вой переменной в интеграле, получаем:
J х Vx~+Adx= J {г* — I)z2z dz = 2 J (z* — z1) dz=
Еще несколько примеров такого рода приведено в упраж-
нениях.
Наконец, приведем пример интеграла, который не может
быть представлен при помощи конечного числа элементар-
ных функций,
Доказательство того, что его нельзя выразить при помощи
конечного числа элементарных функций, весьма сложно, и
мы его приводить не будем.
Этот интеграл является функцией, свойства которой
можно изучить. Из определения fix) следует, что
Так как е~**>0 при любом х, то f(x) — возрастающая
функция. Производная максимальна при лг=О, значит,
f(x) имеет максимальный угол касательной с осью х при
х=0. При х больших по абсолютной величине (положи-
df
тельных и отрицательных) производная ^ очень мала,
значит, функция почти постоянна. График функции
§ 151
ОБЩИЕ СВОЙСТВА ИНТЕГРАЛОВ
175
f (х) = ^ е~ х* dx изображен на рис 75 (для определенности
о
нижний предел выбран равным нулю).
0883
-0.В83
Рис. 75.
Для этой функции составлены подробные таблицы;
благодаря им вычисления, в которые входит этот интеграл,
не сложнее, чем, например, вычисления с тригонометри-
ческими функциями.
Найти интегралы:
1. Jx(x-l)»dx.
2.
Упражнения
— 3
f
dx. 8. \ cos (Зх — 5) dx .
4. f sinBx-f-l)dx. 5. Г У Зх — 2 dx.
Указание. В примерах 3, 4, 5 сделать замену переменной.
в. V х cos х dx. 7. V In x d».
Указание. В примерах 6, 7 воспользоваться формулой инте-
грирован ия по частям.
8. С х* sin 2x dx. 9.
11.
10
. f (x*-f-x -f- l)cos x
dx
Указание. Пример 11 подробно рассмотрен в «Ответах и ре.
шениях», остальные три делаются аналогично.
12 Г Xdx
1 ' J(*-2)(x-3)'
Указание. Воспользоваться тождеством
х А , В
(х — 2)(х — 3) х — 2^х — 3'
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [ч. III
числа А и В находятся приравниванием коэффициентов при одинако-
вых степенях х после освобождения от знаменателя.
х +1 dx и Г dx ,ч Г xdx
Указание. Сделать замену переменной по формуле У~х = г .
xdx
Г
Указание. Сделать замену переменной х*— 5 = z.
17. f sin* x cos xdx.
Указание. Сделать замену переменной cosx=z.
18. \ . . dx.
J 3in*x
Указание. Сделать замену переменной sinx = г.
19. Jtgxdx. 20. J^.
Указание. Сделать замену переменной х = at.
21. i х -. 22. farcsinxdx. 23. farctgxdx.
J V*-x* J J
24. ^ «*x sin 3x dx. 25. С г* cos 2x dx.
Указание. В примерах 22—25 применить интегрирование по
частям.
Общее замечание. Пользуясь различными приемами, иногда полу-
чают для одного и того же интеграла различные выражения. Это не
должно смущать читателя. Если вычисления сделаны верно, такие
выражения должны отличаться лишь на постоянную. При нахожде-
нии определенного интеграла результаты окажутся одинаковыми.
Проверьте это замечание на примере 17, применив замену
sin х = 2.
§ 16. Замена переменной в определенном интеграле
Рассмотрим пример. Пусть требуется вычислить
к
\{ax-\-b)xdx.
п
Можно поступить следующим образом: вычислить сначала
неопределенный интеграл \{ax-\-b)*dx, а затем составить
разность его значений при x = k и при д; = л.
§ 16] ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 177
Для вычисления ^ (ах-{-b)* dx сделаем замену пере-
менной по формуле z — ax-\-b. Тогда dz = adx и
Поэтому
Можно, однако, действовать иначе. Выясним, как будет
изменяться г, когда х изменяется от п до k. Так как z
и х связаны формулой z=ax~\-b, то при изменении х
от п до k z будет меняться от ап-\-Ь до ak-\-b. Следо-
вательно,
* ак+Ь
an-\-b
При нахождении интегралов удобно поступать именно
так, т. е., выполняя замену переменной, одновременно
находить и новые пределы интегрирования. Тогда в выра-
жении неопределенного интеграла не придется возвра-
щаться назад, к старой переменной.
Рассмотрим примеры.
1
1. Подсчитаем величину интеграла \ ^ &• Заметим
J \4 — х)
о
сразу же, что функция -^ г, при изменении х от 0 до 1
1
Jdx л
lo \i> 0>
(/. х)
о
вместе с тем знаменатель в этом промежутке не обра-
щается в нуль, так что подынтегральная функция во всем
промежутке конечна. Сделаем замену переменной 2 — х=у,
dx = — dy. Тогда при дс = О t/ = 2, прид;=1 t/=l и
О 1
В правой части A6.1) пределы интегрирования даны уже
для у.
178 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
Читателя может смутить знак минус в последнем равен-
стве. Действительно, справа и слева стоят интегралы от
положительных функций, почему же положительна правая
часть A6.1)? Все дело в том, что в интеграле справа
нижний предел больше верхнего. Так как при перемене
пределов интегрирования интеграл меняет знак, то равен-
ство A6.1) можно записать так:
Г dx С dy
J B-х)» —J у* '
о 1
Теперь в интеграле справа верхний предел больше нижнего
и ясно, что интеграл справа положителен. Вычисления
легко довести до конца
С dy__ 1_ « _}_ | _L=i_
J ^ 2^ , 8 ~i~ 2 8 •
х
2. В § 15 мы рассматривали функцию f(x)=^e~xtdx.
Часто приходится иметь дело с функцией <р (а) = J e kxi dxf
о
а
о
где k — постоянное число. Покажем, что между функ-
циями <р и f существует простая зависимость.
В выражении для <р(а) сделаем замену переменной по
формуле kx* = t*. Отсюда находим yk t х
dx = ~)r=dt. При д;==0 Г = 0, при д; = а t = aVk. По-
У *
этому получаем:
Итак, q>(a) — -y=f(a\fk). Следовательно, для любого зна-
чения независимой переменной х
§ 16} ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 179
Имея таблицу функции f(x), можно найти также интег-
рал ф(х) при любом значении к.
3. В части II мы видели, что определенный интеграл
имеет размерность в случае, если имеют размерность
подынтегральная функция и пределы интегрирования.
Часто, однако, бывает удобно приводить интеграл к без-
размерному виду, вынося все множители, имеющие раз-
мерность., за знак интеграла. Покажем, как это можно
сделать.
ь
Пусть дан §f(x)dx. Обозначим через /тах наибольшее
а
значение функции f(x) на промежутке интегрирования
^ 06.2)
Ясно, что в последнем интеграле подынтегральная функ-
ция ~J- безразмерна, так как fix) и /тах имеют одинако-
/тах
вую размерность. Перейдем к безразмерным пределам
интегрирования. Для этого выполним замену переменной
по формуле
z=g^~, или д;=а + гF — а). A6.3)
Из A6.3) видно, что z — безразмерная величина. Так как
dx~(b — a)dz, а при х=а г = 0, при x = b z—\, то
интеграл в формуле A6.2) принимает вид
J
^ = Fа) (; rfz. A6.4)
/max /
а
Положим
/ma
тогда из A6.4)
180 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
окончательно
Ь 1
$ $ (г)Лг. A6.5)
В формуле A6.5) ^ф(г)^г есть безразмерная величина.
о
Если f (x) мало изменяется на промежутке интегриро-
вания, то 4^1=1, поэтому
(max
1 I
<p(z)=l и ]ф(г)^25=Ь^г=1.
о о
Таким образом, в этом случае безразмерный множитель
1
J cp(z)dz есть число порядка 1 и величина интеграла опре-
0
деляется главным образом произведением
Рассмотрим элементарный пример: свободное падение
тела в течение времени ?0. Путь есть ]v(t)dt. Скорость
о
тела равна v=gt, и максимальная скорость достигается
к моменту /„: vmaX=gtl).
Заметим, что здесь максимум обусловлен ни уменьше-
нием скорости после f = /0, а просто тем, что времена,
большие tn, не входят в промежуток, по которому ведется
интегрирование, 0<t<t9. Вводим -
t__ . . v gt_ t_
Рассмотрим в заключение пример, показывающий необ-
ходимость внимательного рассмотрения функции и опас-
§ 16] ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 181
Ь
С dx
ность формального подхода. Вычислим / = \ -р- • Неопре-
а
деленный интеграл Г-^- = f-C, поэтому
Ъ — а
Так как подынтегральная функция положительна,
результат должен быть положителен, если Ь> а. Ответ по
формуле A6.6) действительно положителен при Ь>а,
-И
если а и Ь одного знака. Однако для интеграла \
— 1
формула A6.6) дает явно нелепый результат / = — 2!
Причина заключается в том, что подынтегральная функ-
ция обращается в бесконечность внутри промежутка ин-
тегрирования при д;==0 и в этом же месте терпит беско-
нечный разрыв функция ( J, являющаяся неопреде-
ленным интегралом функции -р-.
Чтобы разобраться в положении, необходимо исключить
из всего интервала — 1 < х < -j- 1 малую область около
особой точки х = 0: —е1<лг<е, (е^ и е, — малые поло-
жительные числа), и рассмотреть
По формуле A6.6) получим:
Ясно, что при ех и е„ стремящихся к нулю, К—»оо.
В других случаях интеграл с подынтегральной функ-
цией, обращающейся в бесконечность на интервале интег-
рирования, может давать вполне определенный конечный
1
результат. Так, например, I —^ = 2. Для доказательства
J V х
182 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
1
вычислим \-yL-=2 — 2]/е; при е—»-0 интеграл стре-
Я
мится к 2.
Такого рода рассмотрение необходимо всегда при обра-
щении подынтегральной функции в бесконечность.
§ 17. Ряды
Поставим себе задачу построить простое и удобное
приближенное выражение функции у (х) (заданной точно
какой-либо формулой) на небольшом промежутке измене-
ния аргумента х, например при значениях х, близких к а.
Определение производной, которое было дано в части II,
можно записать в следующем виде:
х — а
Из этого определения следует, что в пределе, т. е. тем
точнее, чем меньше разность (х— а), можно написать:
-а)у'(а). A7.1)
Эта формула соответствует смыслу производной как ско-
рости изменения функции. Если известно значение функции
в данной точке у (а) и скорость изменения функции в этой
_ =у'(а), то при х, близком к а, когда аргу-
dy
точке fx
х=а
мент изменился на величину (х — а) по сравнению с на-
чальным значением а, функция изменяется на(х>—а) у' (а).
Выражение A7.1) является приближенным, и точность его
тем меньше, чем больше промежуток (х — а). Действи-
тельно, при расчете изменения, функции по формуле
(х— а)у' (а) мы пользовались значением скорости изменения
функции у' (а) в начале промежутка от а др х. Между тем
на этом промежутке сама скорость у' также меняется.
Точная формула имеет вид
X
y{x)=y{a)-\-[y'{t)dt. A7.2)
а
Применим формулу A7.1) к производной у' (х). Тогда
у' (х)=*у' (а) + (* — а)у" (а). A7.3)
§ 17] ряды 183
Прежде чем идти дальше, напомним читателю, что
у"(х) — вторая производная функция у по х, обозначаемая
сРи
также — , есть производная по х от у' (х)
»•<*>-?.
так что у" связана с у' таким же образом, как у' связана
с у. Аналогично определяется у'" — третья производная,
у — dx '
ylv — четвертая производная, yv—пятая производная
и т. д. Производная п-го порядка, которая получается
в результате п-кратного последовательного взятия произ-
водной функции у (х), обозначается у(п) (х) или ^р. В обо-
значении ут значок п ставится в скобки, чтобы отличить
его от показателя степени.
Вернемся к задаче приближенного выражения функ-
ции. Формула A7.3) для производной есть не что иное,
как формула A7.1), в которую вместо у(х) подставлена
функция у' (х). Подставим выражение производной A7.3)
в формулу A7.2). Тогда
г (а) + (/ — а)у"(a)]dt =
^^у"(а). A7.4)
Эта формула точнее выражения A7.1). При выводе A7.1)
предполагается (в первом приближении), что скорость изме-
нения функции у> т. е. ее производная и', постоянна
и равна значению производной при х=а. При этом полу-
чилась линейная зависимость у от х*). При выводе фор-
мулы A7.4) учтено, что производная у' (х) непостоянна,
но изменение у' (х) учтено лишь приближенно: формула
*) В выражение для у A7.1) х входит только в первой степени.
Иначе говоря, у есть многочлен первой степени от х. Такая зави-
симость называется линейной, потому что графически она изобра-
жается прямой линией (см. ч. I, § 4).
184 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
A7.3), которой мы пользовались в ходе вывода формулы
A7.4), подразумевает постоянство у" (х), что и приводит
к линейной зависимости у' от х\ при этом для у(х) полу-
чается квадратичная зависимость.
Уточним еще формулу A7.4). Для этого следует
учесть, что и у" непостоянна. Воспользуемся формулой
X
y'{x)=y'{,a)+\y"(t)dt. A7.5)
а
Она получается из A7.2) заменой у на у'. Заметим также,
что эту формулу (как и A7.2)) легко проверить, подсчи-
тав входящий в нее интеграл. Запишем теперь у" (х) по
формуле типа A7.1), примененной к у" (х),
У" {х) = У" (а) + (х—а)у'" (а). A7.6)
Тогда из формул A7.5) и A7.6) получим:
или
2 -y (a)- A7.7)
Заметим, что формула A7.7) есть формула типа A7.4),
записанная для у' (х).
Выражение для у'(х) из A7.7) подставим в A7.2):
= у(а) + J [у' (а) + у" (a)(t
Теперь легко представить себе, какой вид будут иметь
формулы для у(х), если еще продолжать процесс уточне-
ния: если учесть, что у'" непостоянна, то в формулу
войдет ylv (а); выражение для у (х) будет содержать
(х—а)*. Каждый следующий шаг по уточнению у (х) дает
дополнительный член с более высокой степенью (х — а).
§ 17] ряды 185
Этот закон проявляется со всей очевидностью, если
сравнить уже полученные нами выражения. В самом гру-
бом приближении, если х— а мало, можно считать
у(х) = у{а)\ для этого не нужно знать высшей матема-
тики. Назовем это равенство «нулевым приближением»,
выражение A7.1) — «первым приближением», выражение
A7.4) — «вторым приближением», выражение A7.8) —
«третьим приближением» и выпишем упомянутые формулы
рядом:
У(х)—у(а) (нулевое приближение),
у(х) = у (а) -\-(х — а) у' (а) (первое приближение),
У{х) = У (а) -\-(* — а)у'(а)-\-(х ~ g)* у" (а) (второе при-
ближение),
У" (а) + {1^гУ'" (а) (третье прибли-
жение).
Легко догадаться, какой вид будет иметь результат,
если все дальше уточнять формулы. Каждое следующее
приближение содержит на одно слагаемое больше, чем
предыдущее приближение, т. е. чем больше степеней (х — а)
входит в формулу, тем она точнее.
Формулу такого вида можно получить и несколько
другим способом.
Возьмем точное равенство A7.2) и проинтегрируем его
по частям, заменив *) сперва под интегралом dt на d (t — х):
' (t)dt =y(a) + l yr (t)d(t —x) =
а
х
A7.9)
*) При интегрировании t есть переменная (немая), х рассматри-
вается как постоянная, поэтому dt=d(t—х) и замена допустима.
186
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ В ИНТЕГРАЛОВ
[Ч. !П
Проводя интегрирование по частям п раз, мы получим
точное выражение для у (х), состоящее из п~\-2 членов.
Первые п-\-\ членов совпадают с п-и приближением
предыдущего вывода. Последний член дает выражение
остатка в виде интеграла от (п-\-\)-& производной функ-
ции у(х)
— 0"
t. A7.10)
Без последнего члена с интегралом формула является
приближенной. В общем случае произвольной функции
у(х) никакое конечное число степеней (х — а) не даст
абсолютно точной формулы *). Точную формулу может
дать только выражение, содержащее бесчисленное множе-
ство степеней (х—а):
— a)-\-ct{x — a)*-\- ...
A7.11)
Выражение такого вида называется бесконечным рядом.
Обычно слово «бесконечный» опускают и говорят просто
«ряд».
Коэффициенты е0, elf ..., сп, ... различны для различ-
ных функций. Они зависят также от значения величины а.
Эта коэффициенты можно найти более быстрым (по сравне-
нию с приведенным выводом) способом. Для этого посту-
пим следующим образом. Запишем равенство A7.11)
и вычислим первую, вторую и ... п-ю производные от
обеих его частей:
У(х) = сй + с1(х — a)-h с, (дс —а)'+ «?.(* — «)* + •• •
...-\-псп(х —
*) Кроме случая многочлена, см. конец § 18.
§ 17] ряды 187
у" (x) = 2ct + 3-2c,(x-a) -f- . . . n(n-l)cn(x — a)n-' + ....
...3.2cn+1(x — a
Каждое из написанных выше равенств позволяет опреде-
лить один из коэффициентов с(. Действительно, положим
в каждом из этих равенств справа и слева х = а. При
этом все члены, содержащие множители (х — а), обратятся
в нуль и мы получим уравнения для определения коэффи-
циентов:
у(а) = са, откуда с9 = у(а),
у'(а) = с1, Cl = y'(a),
у'" (а) =
Таким образом, получаем:
Первые п членов этой формулы и формулы A7.10) совпа-
дают. Отметим еще частный случай формулы, когда а = 0,
(О)х+^х' + ^х'+... A7.13)
Для произведения последовательных натуральных чисел
п(п—1) ... 3-2 есть удобное обозначение п\ (читается
эн-факториал, по-латыни фактор — сомножитель). Таким
образом, например, 3!=3-2=б; 41 = 4.3-2=24; 5!= 120.
Принято при определении факториала приписывать в числе
188 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
сомножителей еще 1:
п! = п(л —1) ... 3-2-1;
от этого, очевидно, произведение не меняется, зато удоб-
нее запомнить: п\ есть произведение п последовательных
натуральных чисел от п до 1. Например, 3! есть произ-
ведение трех множителей, 3-2-1, от 3 до 1. При этом
определении, естественно, получим 1! = 1. При помощи
таких обозначений запишем формулы A7.12) и A7.13)
в удобной сжатой форме:
л=оо
q«> (*_«,)-, (i7.i4)
y-^x". A7.15)
Формулы A7.14) и A7.15) дают разложение функции у (х)
в ряд по целым степеням х — а (или х). Формула A7.14)
называется рядом Тейлора, A7.15) называется рядом
Маклорена. Пусть, например, у(х) — ех. Тогда
У — с , у — е , . . ., у — с , . • •
Воспользуемся формулой A7.15) ряда Маклорена. В нашем
случае
Подставляя в A7.15), получим разложение функции у=ех
в ряд по степеням х:
Рассмотрим формулу, которая получается из ряда Тей-
лора, если ограничиться, например, тремя членами,
Раскроем в правой части скобки и расположим результат
§ 17] ряды 189
по степеням х-.
-\-\у"(а)х\ A7.16)
Справа в A7.16) стоит многочлен второй степени. Обра-
щаем внимание читателя на то, что это выражение не сов-
падает с тем, что получится, если взять три члена в ряде
Маклорена,
у(х) = у@) + у'@)х + ?рх\ A7.17)
Это станет понятным, если вспомнить, что формула A7.16)
дает хороший результат, если х близко к а, а формула
A7.17) хороша, если х близко к нулю.
В части И было дано определение производной как
предела отношения приращения функции к приращению
независимой переменной.
Теперь, после того как построено выражение функции
в виде ряда, можно дать общий ответ на вопрос о том,
Ду ^ du
как, по какому закону отношение -г| приближается к ^
при стремлении Ах к нулю.
Возьмем ряд Тейлора и обозначим (х — а) = Ах. При
этом у(х)—у{а) = Ау. Получим:
При малых Ах второй член с Ах больше третьего члена
с (Ах)*. Пренебрегая последним, придем к выводу, что
Ау
отличие отношения -^ от значения производной на краю
промежутка пропорционально величине промежутка Ах
и второй производной у" (а). При этом мы сравниваем
отношение приращения на участке от дс= а до х = а-\- Ах
с производной на краю участка у' (а).
Производную можно вычислять и иначе: возьмем при-
ращение при изменении х от а ^ до а-\--~- и, поделив
на Ах, сравним это отношение с производной у' (а), т. е. с
190 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. И1
производной в середине участка. Получим:
-/<«>-?Г Мн4 (?) Т W -т (т)>" «*
^Г' «О-
Такой способ гораздо точнее: разность между отношением
приращений и производной пропорциональна (АхJ, а не
(А*), и к тому же содержит коэффициент ^ (на стр.
55—56 на конкретном примере показано преимущество
этого способа вычисления производной).
Упражнения
1. Разложить полином третьей степени у = ах1 -\- Ьхг -f- ex -f- d
в ряд по х — х„. Сравнить первые два, три, четыре члена с поли-
номом.
2. Разложить в ряд Маклореиа функцию у = хе*\ проверить, что
ее разложение можно получить из разложения е*.
3. Разложить функцию е* в ряд Тейлора по степеням (х — 1).
4. Найти численно производную функции е* при х=0, зада-
ваясь интервалом Ах=1; -=-; -г-; -5-.
Z 4 о
5. Выяснить точность формулы A -f- г)т = етг. Для этого запи-
сать ее левую часть в виде A -\-г)т = ет 1пA+'> и разложить
In A -+- г) в ряд.
§ 18. Вычисление значений функций при помощи рядов
Остановимся вкратце на принципах, положенных в
основу формул § 17. В начале изучения высшей матема-
тики мы считали известным понятие функции и исходили
из того, что можем вычислить значение функции при лю-
бом значении аргумента. Поэтому при рассмотрении произ-
водных мы находили их непосредственно, так сказать,
опытным путем, вычисляя значения функции при близких
значениях аргумента. Потом мы научились находить про-
изводные по формулам, и оказалось, что составление фор-
§ 18] ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ ПРИ ПОМОЩИ РЯДОВ 191
мул для производных — довольно простое дело. Поэтому
вычисление значений функций при помощи формулы, в ко-
торую входят производные, оказывается часто даже более
простым, чем прямое вычисление функции.
Так как только в случае многочлена ряд Тейлора об-
рывается, содержит конечное число членов, то любая функ-
ция, отличная от многочлена, будет представлена беско-
нечным рядом. Практическая ценность такого ряда для
вычислений связана с возможностью ограничиться двумя-
тремя членами ряда и получить достаточно точный резуль-
тат. Для этого необходимо, чтобы отброшенные члены
ряда не были велики.
Рассмотрим несколько простейших примеров. Пусть
у=ех. В предыдущем параграфе была получена формула
в*=1+* + ¦? + !.+ ...+?_+... A8.1)
В частности, подставляя х=1, получим выражение чис-
ла е в виде ряда
в=1 + 1+|+4-+...+^ + ... A8.2)
Эта формула позволяет быстро и с большой точностью
вычислять ех, что можно видеть из табл. 2.
Таблица 2
*
0,10
0,25
0,50
0,75
1,00
1,25
1,50
2,00
1,1052
1,2840
1,6487
2,1170
2,7183
3,4903
4,4817
7,3891
1+Х
1.10
1,25
1.50
1,75
2,00
2.25
2,50
3,00
I-M + ?
1,1050
1,2812
1,6250
2,0312
2,5000
3,0312
3,6250
5.0000
1.1052
1.2838
1,6458
2,1015
2,6667
3.3568
4.1876
6,3333
Xя Я* X1
1+*+-+—+—
1,1052
1.2840
1,6484
2,1147
2.7083
3.4585
4.3986
7.0000
Первые два члена формулы дают точность 0,5°/0 при
дс«=0,1.
Первые три члена формулы дают точность 1,4е/, при
д:=0.5.
192
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. III
Первые четыре члена формулы дают точность 1,8°/,, при
х = 1,0.
Такая хорошая точность связана, очевидно, с тем, что
члены, ряда быстро убывают. Каждый следующий член
ряда меньше предыдущего, прежде всего, потому, что зна-
менатель (n-f-l)-ro члена в п раз больше знаменателя
предыдущего п-го члена. Если х < 1, то к этому добавляется
еще тот факт, что х" тем меньше, чем больше п.
Но даже при х> \ в далеких членах ряда увеличение
знаменателя обязательно пересиливает увеличение числи-
теля. Как видно из таблицы, при х~2 сумма пяти чле-
нов ряда дает ошибку б0/», если же добавить шестой член
ш)' то ПОлУчим 7> 3500. Ошибка составляет 0,57„-
X
0
л
20
л
То
Зя
20
4я
20
Бя
20
бя
20
7я
2П
8я
20
?л\3
9л
20
я
*) Ф-
?¦)
0°
9°
18°
27°
36°
45°
54°
63°
72°
81°
90°
sin х
0,0000
0,1564
0,3090
0,4540
0,5878
0,7071
0,8090
0,8910
0,9510
0,9877
1,0000
X
0.0000
0,1571
0,3142
0,4712
0,6283
0,7854
0,9425
1,0996
1,2566
1,4137
1,5708
— угол, соответствующий дс, но ¦
*-т
0,0000
0,1564
0,3090
0,4538
0,5869
0,7046
0,8029
0,8780
0,9258
0,9427
0,9248
шраженный
'аб л и ца 3
*-Т+775
0,0000
0,1564
0,3090
0,4540
0,5878
• 0,7071
0,8091
0,8914
0,9519
0,9898
1,0045
в градусах.
§ 18]; вычисление значений функций при помощи рядов 193
Построим формулы такого же типа для тригонометри-
ческих функций
y(x) = sinx; y'(x)==cosx\ у" (х) = — sin*;
у'" (х)= — cosx; ylv (x) — sin x.
Закон для последующих производных очевиден.
Таблица За
X
0
Я
20
я
10
Зя
27)
4я
20
5л
25
6л
20
7я
20
8я
20
9я
20
л
т
<р
0°
9°
18°
27°
36°
45°
54°
63°
72°
81°
90°
cos х
1,0000
0,9877
0,9510
0,8910
0,8090
0,7071
0,5878
0,4540
0,3080
0,1564
0,0000
ж*
1
1,0000
0,9877
0,9506
0,8890
0,8026
0,6916
0,5558
0,3954
0,2105
0,0007
— 0,2337
,-*:+«!
1,0000
0,9877
0,9510
0,8911
0,8091
0,7075
0,5887
0,4563
0,3144
0,1672
0,0200
г 'i* if
1,0000
0,9877
0,9510
0,8910
0,8090
0,7071.
0,5877
0,4539
0,3089
0,1561
— 0,0009
Подставляя х=0, получим:
t,@) = 0, yf@)=
Следовательно,
l,
Аналогично получим формулу
08.4)
7 Я- В. Зельдович
194
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[ч. ш
На рис. 76, а и б показаны графики синуса, косинуса, а
также графики многочленов, которые получаются, если
брать один, два или три члена соответствующего ряда.
Видно, как улучшается точность по мере того, как мы
берем все большее число членов ряда.
Рис. 76.
В табл. 3 и За приведены численные результаты. Как
видно из таблиц, достаточно двух-трех членов ряда, чтобы
получить прекрасную точность в промежутке от 0 до -j- .
Таким образом, степенной ряд дает очень удобный прак-
§ 19] УСЛОВИЕ ПРИМЕНИМОСТИ РЯДОВ 195
тический способ вычисления значений тригонометрических
функций. Заметим, что по абсолютной величине не рав-
ные нулю члены ряда для синуса и косинуса в точности
равны соответствующим членам ряда функции е*. Поэтому
все сказанное об убывании членов с высокими степенями
х в формуле A8.1) для ех относится и к рядам для си-
нуса и косинуса A8.3) и A8.4).
Заметим, что если подставить в выражение A8.1)
x=y\f—1, а в выражениях A8.3) и A8.4) заменить х на<р,
то получится соотношение e'v^T= cos<р-\-У — 1 simq>,
упомянутое на стр. 151.
Если функция у (х) есть многочлен степени п, то у'(х)
есть многочлен степени (п—1), у" (х} — многочлен степени
(п — 2), ..., tfny(x) — постоянная величина, а у(п+1}(х) и
все производные более высокого порядка — нули. Поэтому
для многочлена ряд Тейлора A7.14) обрьюается, он состоит
из конечного числа членов. Мы получаем многочлен, рас-
положенный по степеням (х — а). При этом для много-
членов п-й степени сумма первых п -f-1 членов ряда
Тейлора дает точное равенство, верное при любых х, а
не только при х, близких к а.
§ 19. Условие применимости рядов.
Геометрическая прогрессия
Формулы, в которых функции представляются как
суммы ряда степеней х с постоянными коэффициентами,
были составлены в предыдущем параграфе для трех функ-
ций: е*. sin* и cos*. В этих трех случаях оказалось, что
при любом х каждый следующий член ряда, исключая,
может быть, несколько первых членов, меньше предыду-
щего и чем больше номер члена, тем ближе этот член
к нулю. В этих примерах при любом х можно вычислить
значение функции при помощи ряда, если взять достаточ-
ное число членов ряда, так чтобы отброшенные члены
практически не влияли на результат.
Напомним, что мы начинали g задачи о приближенном
выражении функции в малой области изменения перемен-
ной и строили все более точные формулы с учетом первой,
второй, третьей н т. д. производных. Точность каждой
196 вычисление производных и интегралов [ч. in
формулы
у(х)=у(а), @)
у(х)=у(а) + (х — а)у'(а), (I)
у(х)=у(а) + (х-а)у'(а) + {±^у"(а) (II)
тем больше, чем меньше величина (х — а). С другой сто-
роны, при данном (х — а) формула (I) точнее формулы @),
формула (II) точнее формулы (I) и т. д. Значит, увеличе-
ние числа членов ряда позволяет увеличивать величину
(х — а), сохраняя заданную точность.
Вопрос заключается в том, всегда ли можно будет
достичь заданной точности при любом значении (х — а)
путем увеличения числа членов ряда. На очень важном
примере мы убедимся сейчас, что это не так. Степенной
ряд, построенный так, чтобы дать хорошее приближение
в малой области изменения х, при любых (х — а) может
иметь естественный предел применимости, предел допусти-
мого увеличения (х — а) (не зависящий от числа взятых
членов ряда), хотя этого и не было в примерах предыду-
щего параграфа.
Рассмотрим функцию
Вычисляя последовательно производные, найдем:
1-2 ,„, п\
">,
_ к)* ' * " * ' * A — x)n
+t
Подставляя х = 0, получим:
у@)=1; у'@)=1; 4Г(О) = 2; ...; у<п>@) = п\.
Таким образом, получим ряд .
^=-1+* + *• + *•+...+*"+... A9.1)
Пример функции ¦= замечателен не только необы-
чайно простым видом получившегося степенного ряда (все
коэффициенты равны 1). В этом случае нетрудно дать
точную формулу для суммы п первых членов ряда A9.1)
A9.2)
§ 19) УСЛОВИЕ ПРИМЕНИМОСТИ РЯДОВ 197
В справедливости этой формулы убедимся, умножая
обе части A9.2) на A —х). Формулу A9.3) можно пере-
писать так:
1+* + д-+...+*—= T-L-_r?-j. A9.3)
хп
Сравнивая A9.3) с формулой A9.1), видим, что -^zr есть та
величина, которой мы пренебрегаем, если ограничиваемся
первыми п членами ряда
l+* + xt + x1+...+;t'I + ... A9.4)
Если — 1 <*< 1, то хп тем ближе к нулю, чем больше п,
и следовательно, взяв достаточно много членов ряда, мы
отбрасываем малую величину. Заметим, что чем ближе х
к 1, тем больше членов ряда приходится брать для по-
лучения заданной точности.
Вся картина изменится, если взять х~^>\. В этом
случае каждый следующий член ряда A9.4) больше пре-
дыдущего. Формула A9.3) остается в силе, однако при
*>1 / иеограииченно растет вместе с ростом п и поэтому
дробью \*_ х пренебрегать никак нельзя. Формула A9.1)
в этом случае неверна. Нет даже никакого качественного
сходства между суммой положительных слагаемых A9.4)
и отр ицательной (так как х *> 1) величиной ? . Из фор-
мулы A9.3) видим, что при х^> 1 сумма ряда A9.4) не-
ограниченно увеличивается при увеличении п. Такие ряды
называются расходящимися.
Члены ряда A9.4) образуют геометрическую прогрес-
сию. Мы установили, что сумма членов бесконечной геомет-
рической прогрессии равна . _¦ , если |лг|<1. Если же
х^> 1, то бесконечная геометрическая прогрессия не имеет
конечной суммы.
Отметим еще, что любая периодическая дробь представ-
ляет собой сумму членов геометрической прогрессии,
например,
1, A) = 1,111... = 1 +0,1 +0,01 +0,001 + .. • =
,,1,1 ,1i 1 1 ю _ , 1
1 +1
198
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[ч. ш
Таким образом, с простейшим рядом (геометрической
прогрессией) мы встречались уже и раньше, в арифметике
и алгебре.
Функция у — ——- (рис. 77) терпит разрыв при х=\:
если х близок к 1, но больше 1, то г— большое
по
Рис. 77.
абсолютной величине отрицательное число; если х близок
к 1, но меньше 1, то -г-^ большое положительное
число. Следовательно, при переходе х через значение х= 1
функция _ переходит от больших положительных чисел
к большим по абсолютной величине отрицательным числам.
Этой особенности поведения функции ряд описать не может.
§ 19] УСЛОВИЕ ПРИМЕНИМОСТИ РЯДОВ 199
Отметим еще следующее обстоятельство: при х=\
функция у———- обращается в бесконечность (чем
ближе х к 1, тем больше у по абсолютной величине), и
при этом же х= 1 члены ряда A9.4) перестают убывать.
Ряд может быть пригоден для вычислений, лишь если
его члены убывают по абсолютной, величине *). При х=\
ряд для вычислений непригоден, так как его члены не
убывают. Значит, ряд непригоден для вычисления значе-
ний функции и при х==—1 (так как при х=—1 его
члены тоже не убывают по абсолютной величине), хотя
сама функция при х = — 1 разрыва не испытывает и равна
1 1
1 —<—1>~" 2 *
Как бы мы ни выбирали коэффициенты многочлена,
его график всегда будет сплошной, непрерывной, линией.
Значений аргумента, при которых многочлен терпит раз-
рыв, нет. Поэтому если некоторая функция f(x) терпит
разрыв при х=ха (в примере с 1 _ , дсо=1), то при
значении х=хп ряд, составленный для f(x), заведомо
непригоден для вычислений. Так как любой член
ряда спхп тем больше по абсолютной величине, чем больше
абсолютная величина х, то при любом х, по абсолютной
величине большем, чем хй, ряд также непригоден для
вычислений.
Таким образом, при наличии разрыва f(x) можно зара-
нее указать такое xt, что при всех х, больших хл по
абсолютной величине, ряд будет непригоден для вычис-
лений.
Рассмотрим функцию У — yzг^- Применяя формулу
A7.13), найдем:
_»_==1_jC_{_jC._jC.+ ... A9.5)
Возьмем, например, jc=2. Тогда
1
1+х|х=, 1+2 3 *
*) Конечно, если один-два или несколько первых членов ряда
возрастают, это не составляет беды, если следующие дальше члены
ряда быстро убывают; см. пример с е* при х = 2, табл. 2.
200
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
[Ч. Ill
Сумма же членов ряда
l—x + x'—x' -}-...
в зависимости от изменения
15 6 7
резко изменяется
членов п
л
A9.6)
числа
1
2 3
43
сумма членов 1 —1 3 —5 И —21
Ясно, что при х = 2 такой ряд непригоден для вычис-
лений. Почему же это произошло? Ведь сама функция
y=Y+n ни ПРИ х = 2 и нигде от х=0 до х = 2 раз-
рыва не испытывает (рис. 78).
г-
Рис. 78. -
Функция У — fzтг:ё» однако, испытывает разрыв при
х = —1. Поэтому при х — —1 члены ряда A9.6) не убы-
вают. Заметим еще, что абсолютные величины членов
ряда A9.6) не зависят от знака х. Следовательно, и при
х=1, я. тем более при х> 1 ряд для вычисления непри-
годен.
Поэтому даже если нас интересует поведение ряда
только при х>0, то все равно надо принимать во внима-
§ 19]
УСЛОВИЕ ПРИМЕНИМОСТИ РЯДОВ
201
ние все значения х, в том числе и отрицательные, при
которых разлагаемая функция терпит разрыв.
На самом деле на сходимость ряда влияет даже пове-
дение функции при комплексных значениях аргумента.
Приведем пример. Заменив в формуле A9.5) х на х1,
получим:
T±-?=l—xt-\-x^—ха-{-... A9.7)
График функции У=х ¦ ^ (рис. 79) не имеет никаких
разрывов, нигде не уходит в бесконечность ни при поло-
жительных, ни при отрицательных х. Однако ряд A9.7)
пригоден для вычислении, лишь если х1 < 1, т. е. при
— 1 < х < 1. Причина этого в том, что при х = ± У— I == ± i,
т. е. при х* = —1, функция у==. l. обращается в бес-
конечность, поэтому члены ряда не убывают по абсолют-
ной величине при х* = —1. Значит, по абсолютной
величине они не убывают и при х* = 1. Однако подробно
и понятно вопрос о поведении функции при комплексных
значениях х в данной книге разъяснить невозможно.
Рассмотрим еще один пример. Найдем ряд Маклорена
для функции y = tgx. По общим правилам находим;
sin х
2 sin д;
и'"(х\ 2 + 4sin»x. i
16sinх +8 sin'*.
. 16 + 88 sin* x + 16 sin4 x
COS* X
202 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ш
Отсюда
0; ?/' @) = 1;
Поэтому
Таким образом,
.. „ . ..1 1 А ..I I '.71 °^
2835
s
В последнем выражении коэффициенты при х1 и х* могут
быть получены так же, как получены в тексте коэф*
фициенты при х, х1, х*.
Что можно сказать об области применимости ряда A9.8)?
Глядя на график тангенса (см. рис. 72), легко сообразить,
что ряд A9.8) может быть пригоден для вычислений лишь
при |*|<-^-, так как при дс = -^- функция tgx ведет себя
так же плохо, как функция | при х=1.
к — А?
х1 2
Глядя на сам ряд х-\~~т-~\~ ]КХ*~\~ •••» было бы не-
легко сказать, при каком значении х этот ряд нельзя
будет применять, потому что закон, которому подчиняются
коэффициенты ряда, не простой, в отличие от рассмотрен-
ного выше ряда 1 -f- x -\- х* -{- ...
Упражнения
х А- 1
1. Написать ряд Маклорена для функции у = -.—!—.
1 Л
2. Написать ряд Маклорена для функции у= In (I -f-x).
3. Написать ряд Тейлора для функции у=\пх по степеням
(х—1). Какова область применимости рядов, полученных в зада-
чах 1—3?
4. Получить первые три члена разложения в ряд по степеням х
произведения функции f(x)g(x). Построить тот же ряд перемноже-
нием ряда для /(*) и ряда для ?(*).
§ 20] ВИНОМ НЬЮТОНА ДЛЯ ЦЕЛЫХ И ДРОВНЫХ ПОКАЗАТЕЛЕЙ 203
§ 20. Бином Ньютона для целых и дробных показателей
Составим разложение в ряд Маклорена произвольной
степени т двучлена (а-\-х): у = (а~\-х)т.
По общему правилу найдем сперва производные
у'=т(а-\-х)т-\ у" =
уЮ = т(т—\).. .{т — п-]-\)(а-\-х)т-п, Г B0Л)
и значения функции и производных при х=0
Л
Uo.2)
у(п)(Р) = т(т— \)...{т — п-\-1)ат~п, ... J
Отсюда получим ряд Маклорена
Если показатель степени т есть положительное целое
число, то {а-\~х)т есть многочлен степени т, так что
в этом случае ряд B0.3) будет конечным: производная
(т-\~ 1)-го порядка функции (а-\-х)т, а значит, и все
более высокие ее производные равны нулю. Формулы B0.1),
B0.2), B0.3) отражают это обстоятельство; в самом деле,
при п = т-\-\ множитель (т — п-\-1) обращается в нуль;
при п > т -j- 1 где-то в последовательности множителей
т(т — 1) ... найдется множитель, равный нулю, и, сле-
довательно, произведение равно нулю.
При целом положительном т произведение в числи-
теле можно записать в более удобной форме:
т(т— 1). . .(т — п~\- 1) =
т(т— l)...(m — п-\- 1) (т — п) (т—п— 1)...3-2-1 ml
"~ (т—я)(т —я —1)... 3-2-1 (т — л) I '
204 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. 1П
Таким образом, при целом положительном т получим
окончательно:
В формуле B0.4) справа и слева написаны многочлены
степени т. Таким образом, для случая целого положи-
тельного т мы получаем точное равенство, справедливое
при любых значениях х. Формула B0.4) симметрична
относительно х и а: коэффициенты при членах ап~"хп и
а"хп ~п равны. Это понятно, так как (х -j- a)m не зависит
от порядка слагаемых в скобке
Формула B0.4) называется биномом Ньютона. Ее можно
получить, не пользуясь высшей математикой и про-
изводными. Для этого нужно взять произведение
(a -f- х) (а -f- х)... (а -\- х), вып олнить умножение и привести
m раз
подобные члены. Однако при т, заданном в общем виде
буквой, а не числом, приведение подобных членов стано-
вится довольно трудным, и в целом вывод бинома Ньютона
при помощи ряда Маклорена оказывается проще.
Отметим, что Ныотои получил общую формулу B0.3),
т. е. разложение (х-\-а)т, в случае любых показателей т.
Поэтому правильнее было бы именно формулу B0.3)
называть формулой бинома Ньютона, а не B0.4), которая
представляет собой простой частный случай формулы B0.3).
Вернемся к общей формуле B0.3). Пусть т не целое
положительное. В ряде Маклорена B0.3) степени перемен-
ной х, т. е. числа п, целые положительные. Значит,
в B0.3), если т не положительное целое, числитель
не обращается в нуль ни при каком п, формула B0.3)
дает бесконечный ряд. В частности, для пг = — 1 этот
§ 20] ВИНОМ НЬЮТОНА ДЛЯ ЦЕЛЫХ И ДРОВНЫХ ПОКАЗАТЕЛЕЙ 205
ряд имеет вид
;nb=4-?+?- ?+••• B05)
Заметим, что при а=\ формула B0.5) переходит в уже
знакомую нам формулу
Из формулы B0.5) находим также
1 = 1 I * 1 ** I ** I
а — х а 1^ а* ' а* ' о* ' *
Для т=-2 получим:
Y ' 2 YH 8 а уН ~1~ 16 а» ^
5 х* [ 7 ** 21 *" .
В разложении (а-\-х)т при любом т все члены имеют
одинаковую сумму степеней а и х, каждый следующий
член отличается от предыдущего множителем (— J и
коэффициентом. Физик сказал бы, что а и х в фор-
муле B0.3) должны быть одинаковой размерности, значит,
— безразмерно. Можно было с самого начала вынести
за скобку а
f X \ X
и разлагать ( 1 +—)" по степеням —.
Оказывается, что при всех т (отрицательных и дроб-
ных положительных) ряд B0.3) пригоден лишь при
-j < 1, т. е. при |х|<|а|. При ? S* 1 ряд B0.3) —
расходящийся. Исключение представляют целые положи-
тельные т, потому что в этом случае формула B0.3)
содержит конечное число членов.
206 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Формула B0.6) дает хороший способ вычисления кор-
ней. При этом чем меньше МИ» тем меньше членов
можно брать в B0.6) для достижения заданной точности.
Упражнения
1. Путем разложения в ряд иайти V 1,1 и У' 1,5 как У 1 -f-x
при * = 0,1 и прн ж = 0,5, удерживая б разложении два, три и
четыре члена. Сравнить с табличными значениями.
2. Показать, что при | х |< 1 справедлива приближенная фор-
мула y/i+*=l-f , которая тем точнее, чем меньше х.
3. Найти по формуле предыдущего упражнения ?/" 1,2, у^\,\,
?/ 1,05. Сравнить с табличными значениями.
4. Найти У 6 с тремя верными знаками после запятой. _
Указание. Воспользоваться тем, что 6 = 4+2, У^4 = 2, и
применить формулу B0.6).
5. Почему нельзя разложять y = Y~x по формуле Маклорена?
§ 21. Порядок возрастания я убывания функций
Разложение функций в ряд дает общий способ приве-
дения различных функций к одинаковому виду и позво-
ляет сравнивать между собой различные функции. Такой
способ сравнения нужен, например, в тех случаях, когда
рассматривается отношение двух функций -J?L пРитаком
значении аргумента х, при котором значения обеих функ-
ций близки к нулю.
На примере вычисления производных было показано,
что отношение двух очень близких к нулю величин мо-
жет быть вполне определенным числом. В некоторых
случаях это отношение может быть равным нулю или
бесконечности. Приведем несколько примеров. Для
простоты записи возьмем примеры, в которых интересую-
щее нас значение х равно нулю.
При малом х функции sinx и tgx также малы.
Функции е* и cosx близки к 1, а следовательно, е*—1
и 1—cosjf малы. Прн этом значения функций sinx,
tg*. e*—1, 1-— cos* тем ближе к нулю, чем меньше l*j.
§ 21] ПОРЯДОК ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
207
Сравним эти функции с величиной х. Для этого на-
пишем их разложения в ряд Маклорейа:
sin.*r=x
Отсюда находим:
sin х
B1.1)
Следовательно,
sin*
•
X X
1 или hm =1.
X
Аналогично из B1.1) находим:
^*_1 I X*
х ' 3
1 — COS X X Xs
х 4"
1 — cos x 1 х*
х* Y 24~
е* —1 , . х ,
ж ->• о
О,
»2 '
1.
Можно найти и более сложные соотношения. Напри-
мер, из
sinx = .r—
следует:
tg x — sin л: = -=- х* + -g- x5 + ...
208 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
и
tg х — sin x 1
Можно построить шкалу порядка убывания различных
функций при стремлении х к нулю; порядком убывания
назовем степень х, которая убывает так же быстро, как
рассматриваемая величина. Если функция f(x) имеет ?-й
порядок убывания при малых х, это значит, что она убы-
вает как х", т. е. отношение ^~ имеет пределом при
х—»0 конечное, не равное нулю, число.
Таким образом, sinx, tgx, ex—1 убывают по первому
порядку, 1 — cos х убывает по второму порядку, tg х — sin x
убывает по третьему порядку при малых х.
В некоторых конкретных случаях порядок убывания
можно определить и без разложения в ряд. Например,
начертив линии синуса и косинуса, убедимся из чертежа,
что sin*=a:jc, tgx=^x при малых х, т. е. sin* и tgx
имеют первый порядок убывания. Справедлива формула
1 — cos х = 2 sin* y • и так как s*n \ первого порядка, то
отсюда вндим, что 1 — cos* имеет второй порядок убы-
вания. Функцию tgjc — sin* можно записать как
sin к . sin х ,, ч гг.
sinj: = A—cos л:). Так как для малых х cos*
COS Ж COS X
близок к 1, sin х первого порядка, 1 — cos x. второго
порядка, то ясно, что tgjt — sin* третьего порядка. Однако
эти конкретные приемы требуют больше остроумия, и
именно поэтому полезен простой безотказный общий
метод.
Такое соотношение между остроумным решением от-
дельных задач и общими методами наблюдается везде:
свойства касательных к параболе, площадь круга, объем
пирамиды, объем шара известны были древним грекам, но
только дифференциальное и интегральное исчисления дали
общие, простые способы решения всех задач такого типа.
При помощи рядов можно находить не только отно-
шения функции к степени х, но и отношение одной функ-
ции к другой.
§21] ПОРЯДОК ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ 209
Приводим примеры:
. X* . Xs
е*-1=*+-2- + -6-
sin х х* ,
1
»
Х-4- — -А- 14- —
1— COS* _ДС^ _fl_i ^.___^Lj_ Х-+й
2 24 "+"••• 2 24 "*"¦••
e*-\ * + -2~+---
* oo.
0.
Коэффициенты рядов Маклорена выражаются через
производные. Поэтому можно сформулировать результаты,
получаемые при помощи рядов, в виде правил, относя-
щихся к производным. Если f(O) = g(O) = O, то из фор-
мул
и
получаем:
и -
g(x
Отсюда
f.
210 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
тт.
Таким образом, вместо того чтобы рассматривать отноше-
ние двух функций, значения которых близки к нулю
(так как обе функции обращаются в иуль при одинаковом
значении аргумента, вблизи которого рассматривается
отношение), можно рассматривать отношение их производ-
ных. Этот результат называется правилом Лопиталя.
После изучения рядов удобнее не запоминать некое
особое правило, а при малых х пользоваться рядами,
в которых функция разложена по степеням х. Всюду
там, где стоит сумма различных степеней х, при переходе
к малым х оставляем только член с наименьшей степенью.
Точно так же как рассматривается порядок убывания
при малых х функций, равных нулю при х=0, можно
рассматривать поведение функций при неограниченном
возрастании х, т. е. при х—юо. Если мы имеем дело
с многочленом, то очевидно, что при большом х важен
только член с наиболее высокой степенью х; можно го-
ворить о порядке возрастания как х, как х* и т. д.
Важнейший факт заключается в том, что функция ех
возрастает быстрее любой степени х" при неограниченном
возрастании х. Для доказательства используем выраже-
ние е* в виде ряда, справедливое, как это выяснено
в § 19, при любых х. Получим:
При заданном п и при достаточно, большом х дробь —д-
станет сколь угодно большой за счет членов с положи-
тельными степенями х в формуле B1.2). Очевидно, тоже
самое относится к функции е** с положительным k:
обозначая kx=y, найдем, что
Лх Joe лг
~ У".ГТ~ B1.3)
Остается заметить, что если 󗻦 с», то и х—>-оо.
Рассмотрение дробного п ничего не изменит в результате.
§ 21] ПОРЯДОК ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
211
Таким образом, показательная функция при стремле-
нии аргумента к со растет быстрее любой степенной
функции.
Показательная функция с отрицательным показателем
в пределе при стремлении х к оо убывает быстрее любой
отрицательной степени. Это утверждение записывается
так: при любом п
— *•
*—>-0 при х—>-оо.
Пользоваться для доказательства разложением е~х по сте-
пеням х при большом х нельзя, потому что это разложе-
ние знакопеременное. Поэтому рассмотрим обратную
величину
1
' хп<
ОО.
Согласно B1.3) при любом п-^—>-оо при х
Из того, что -j—>-оо, следует, что /—»-0, что и требо-
валось доказать.
Таким образом, в пределе, при больших абсолютных
значениях аргумента, стоящего в показателе, показатель-
ная функция (экспонента) зависит от х сильнее, чем
любая постоянная степень х; ех возрастает быстрее хп,
е~* убывает быстрее х~п. Ниже в таблице это наглядно
видно на примере х* и е*.
X
Xs
е*
1
1
2,72
0,37
3
32
20
1.6
5
3125
150
21
10
10»
210*
5
20
3-10'
4-10»
0,01
50
310»
5-10"
10~"
100
1010
10*»
10"м
212 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. III
Упражнения
Найти следующие пределы:
X -*¦ О * Х-*- 0 "
. ,. в*—1 —tgx _ ,, е"—1 _ ,. slnx — х
4. lim г—-—. 5. Um —: . 6. lim —
ОТВЕТЫ И РЕШЕНИЯ
§ 3. 1. Найдем производную т = (ах —f— 6)*, раскрыв предвари-
тельно скобки: z = <Ае* -+- 2а6* -f- Ь*. г' = 2о*х -+- 2аЬ = 2а (а* -(- &)-
Найдем теперь эту же производную по правилу нахождения производ-
ной сложной функции *=у*, y=a*-f-fc, —- = ¦? -— = Чуа = Чау=
. 2. Z'=_
§4. 1. у = *• = *•*•; у' =
у
§5. 1. у' = 5х*- 12х'-|-За*+14* — 2. 2. у' =2 (х* + * + 1)Х
XCx*-f-l). 3. у'=4(х*— *+ 1)'Bд:— 1). 4. у' = 10(Зх* — 1)» 6х.
5. ^ = - . 6. Удобно записать i/ при помощи дробной сте-
V дс* — 1
пени у = х*1'. Теперь находим по общей формуле для производной
^xU
степени: ^'=яе =^ — х ". 7. а) Если * изменяется на 1%. то
Д0 = л-О,О1у; поэтому прн изменении * на А°/о будет Ду = л-0,01-^-А.
В данном случае * изменяется на Ю°/о> &?/•=¦» л-0,1 у. Так как « = -»- ,
то A^=-^-'°-1i' = 0'05j'- Поэтому (/A1) = i/A0)-f 0.05-5 = 5,25;
/() = i/A0) — 0,05-5 = 4,75. Получим точное решение. Обозначим
коэффициент пропорциональности через А; ^гргда у = 1гУ~~х. Так как
при *=10 должно быть «/ = 5, то 5^ft"V^10, откуда ft = l,58 (вы-
числения ведем с двумя знаками после запятой). Поэтому у = 1,58 уг~х;
i/(ll) = 1,58 УТТ = 5,24; //(9)=4,74 . б) Приближенные значения
(/A1) = 4,50; у(9) = 5,50. Точные значения j/(ll) = 4,54; j/(9) = 5,56.
в) Приближенные значения уA1) = 6,00; p(9)=z4,00. Точные зна-
чения 1/(П)=6,05; t/(9)=4,05.
ОТВЕТЫ И РЕШЕНИЯ
§6. 1. у'=3х*(х*— \yJrxs-2(xx— 1J* =
2. p' = 3*aV*'4-*4-B*.^ti^- 3.1/' =
3/xi _ i
213
1 — 1) Gдг* — 3).
ХГ?
- 2)
У*
У
1 -х1
X
3C*— 1)
.. 11. у'= —
2х*
Xя
:. 12. {/'=
14. ^ =
/
2х*
2Ух —
— 2дс«-х4-9
О /— _ 1 \t I/ Ov , О
О ^Л ^^ if у хл —'~ О
Ах* — Юле* — 22* — 11
3 (дг — 2I
: . 18. «/' =
19. у'
21. J^:
±i 1
х-Цх+iy
(Xм + 1)* Ух* — 1
20. и' =
У
22 у* =
214 вычисление производных я интегралов [ч. ш
з /¦— з/— зх— з/—
йч ..'—3К лС 1 i/*-2* _1 -б/х«-4л:)/У
§ 7. 1. ^=2,310Гж —!7=.2.i/'=2>31g2-2*.3.i/'=2,31g5-5*+1.
2 у х
4. y'=-2,3\g^y
§8. 1. у'= — е~х. 2. у'=2хех*. 3. у' = C** — 3)
§ 9. 1. 2,3026; 4,6052. 2. log515 = у-у= 1.6825. 3. Дифферен-
цируя обе части, находим -—- = 1 . Отсюда (uv)' = u'v -f- шз'.
В. у' = — B*)' = —. Этот же результат можно получить и так:
; у'= (In 2)'+ (In *)'=-j . 6. /=
-j. 14. Для нахожде-
ния производной возьмем логарифмы от обеих частей равенства (осно-
вание логарифмов можно брать любым, будем брать натуральные лога-
рифмы) \пу=.х\пх. Теперь возьмем производную от обеих частей
этого равенства, учитывая, что у есть функция от х и \пу, следова-
тельно, сложная функция: —у' = 1пд;-(- 1. Отсюда находим
у'= у {\пх-\-\), или окончательно у1 =дс*Aлх-(- 1). Аналогично
/ ""\
делается следующий пример
у (( )
Ух» _х / х In х У""**—1\
. 15. i/ =*- 1 -| )-
\ У дс*— 1 * /
У
§ 10. 1. у' = 2cos Bх + 3). 2. 1/'=— sin(*— 1).
= — Bх— 1) sin (Xs— *-f-l). 4. ^'=
5. у' = 3 cos Зх cos1 x — 2 cos дг sin x sin Зх. в. y' = (sin 2x)* In sin 2x +
\ (см- решение примера 14 из § 9). 7. i/'= tgx + ^-^ .
: cos 2x~\
~* sin2x
cos* 2х • - » — 2 . , * "
sln т
ОТВЕТЫ И РЕШЕНИЯ 215
1 . ~ ... 1 - , 2
A4-*)
§ 12. 1. — 1; 1. 2. — 1.
§ 15. 1. Для выполнения интегрирования раскроем скобки; полу-
чим интеграл от многочлена \дс(х — \)*dx=\ х(х* — 2х 4- 1) d* =
Jjc* 2 1
(*•— 2х* 4- х) dx = -j 5- дс* 4" "о" ** + ^* 2* Запишем подынте-
гральную функцию так: —^ = х4~2 . Теперь интегри-
X X
J^t I 2^ з х*
—— dx = -=--\-2x — 31пд;4-<3»
3. Сделаем замену переменной Зх — 5 = t; dt = Ъйх, \ cosCx — 5)dx =
IP 1 1
= у \ cos<<# = -g-sin*4-C=-g-sinCx — 5) 4-С. 4. Решается анало-
гично предыдущему. Получаем — -=- cos Bдс 4- 1) 4" О.
5. -| l/"C* — 2I 4- С. в. cos х 4-хsin x 4-С. 7. дг Aпдг — 1) 4-0.
Примеры 8—11 можно делать при помощи формулы интегриро-
вания по частям. Однако удобнее применить способ неопределенных
коэффициентов. 8. -=- xsin 2х — (-=- х* -г) cos 2x -{- О.
9. (— х* — Зх* — 6х — в)е-* + С. 10. B*4-l)cosx4-(**4-*— OX
Xsinx + C. П. f Bxt+l)cos3xdx = (a1xt-j-b1x-{-c1)cos3x-\-(atx2-{-
4- b^c 4- cj sin 3*. Возьмем производную от обеих частей равенства:
Bх* 4" 1) cos Здг = Bа,х 4-*i) cos Зд; — (З^дс* 4~ З^х 4- Зс,) sin 3*4"
4- BajX 4- *i) sin Зх 4- Cajx* 4- Зй,х 4~ Зся) cos Зх, или так: Bх*4-1)Х
X cos Зх = (— З^х* — З^х — Зс, 4- 2а»* 4" *»)sln Зх + (За1^ + 3*i* +
4- Зся 4- 2а1дг 4- &i) cos Здг. Поэтому должно быть 2х* -+¦ 1 = За,*1 -[-
4- 3V 4- Зс, 4- 2ахх 4- *i, 0 = — З^х* — Зй,дс — Зсх 4- 2at* 4~ *»•
Для того чтобы были равны два многочлена, надо, чтобы были равны
их коэффициенты при одинаковых степенях х. Приравнивая коэффи-
циенты, получим: Ъаг = 2, ЪЬг -\- 1ах = 0, Зс2-)-Ь1=\, — Зах = О,
— 36,4-204 = 0, — 3^4- *, = 0. Из этой системы находим а, = 0,
*. = 0, с,=0, ая = ^, Ьх = ±. ct = ^j. Поэтому J Bх« 4" 1) X
216 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. Ill
X cos Зх dx = ± х cos Зх + (-| х« + А) sln3x+C. 12. (ТГ5ПГ=3) =
= -) . Приводя к общему знаменателю и отбрасывая его.
получаем: А(х— 3)+В (х— 2)=х нли х (А + В) — ЗЛ — 2В=х.
Приравнивая коэффициенты при одинаковых степенях х, получим
А + В = 1, — ЗЛ - 2В = 0, откуда А =—2, Д = 3; J (х_^_3) =
=J { i^+db} ^=-21п (* - 2> +31п <^ ~
V(x -1Нх - 2) =Т=Г\ +х=2' А^х^ +
-\-В(х — 1)=х+1. В последнем равенстве положим х =2, получим
Д = 3; затем положим х = 1, получим Л =—2, \^_»,2dAC =
= -21n(x-l)+31n(x-2)+C. 14. — ln(x-l) + ln(x-2)+C.
15. Положим У~~х = г. Тогда х = г* и dj: = 2zdz; ( —* _ =
+V~x) +C
+C = x - 2
h-C. 19. — In cos я 4-C. 20. — arctg —+ C. 21. arcsin—+ C.
22. xarcsin x-f-Vl — x'+C. 23. x arctgx —-^In (x' + l)+C. 24. Вы-
полним интегрирование по частям, полагая f=sln3x, dg=e?xdx.
Получим \ в** sin Зх dx = -=- е*х sin Зх д" \ *** cos3x dx. В. последнем
интеграле опять вьшолним интефирование по частям, полагая /= cos3x,
С 1 3/1
dg = e*xdx. Получим V e**sin3xdx = -2-ff**sin Зх =-(-^-«"cosSx +
3 Г \
-|—д- V e*xsin3xdx 1 . Рассматривая последнее равенство как уравне-
р ._ . _ . (•.,.,. e*xBsin3x — ЗсозЗх)
для \ rx sin Зх ах, находим V erx sin3x dx = —* r^ .
ние
„ в* (cos 2x + 2 sin 2r )
*** g
о
§17. I. y = a \
-{- Caxa + й) (x — x»)* + a (x — x,,I. Следующие члены все равны
нулю. Сумма выписанных четырех членов равна многочлену.
2. ?@) =0. *'@) 1 "@) 2^»)@) +»f
217
) = e[l -\-(x-\) +
1(х—1)*_|_.1.(х-l)»_|_...j . 4. Первый способ; ^@) = 1,
ОТВЕТЫ И РЕШЕНИЯ
=***. 3.
ьу
Ь.х
i
2,7183
1,718
I
2
1.6487
1,297
i
4
1,2840
1,136
1
8
1,1331
1,065
Л(х)-*0
I+AW
1
Второй способ:
= у(-?) —у( ^
/ Дх\
( Дх\
A»
л*
Дх
i
1.6487
0,6065
1.042
1,042
l
2
1.2840
0.7788
0,5052
1,010
I
4
1,1331
0,8825
0,2506
1.002
i
в
1.064494
0,939412
0,125082
1,0006
Ax
1
u • d\n(l+r) 1 d4n(l+r)
5. Находим производные: .—'—-= -—j— , -j-j-!—'- =
or 1 -+- r an
1 d»ln(l+r) 2 o
= —t;—;—r«, \. —^-=^.——:—r^, ... Значения этих производных
A ~т~ f) 0.1 A ~r~'*)
при г = 0 равны соответственно: 1; —1; 2; ... Формула Маклорена
дает ln(l+r)=r-~r* + ±r.2r* + ...=r— ^-+-?+•¦•.
em\r\{\+r)==emr g 2 3 . при малом r gmr отличается от
нети и кого значения множителем в 2 . В примере § 8 на стр. 150
218 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ (Ч. Ш
/п = 50, г=0,02; в 2 = в»01 =0,99; ошибка 1%; т может быть
любым большим числом, лишь бы было мало тг*, при этом малость
тг*, тг*, ... обеспечена.
§ 19. 1. у — ^^х= 1-1г2х+2х*-\-2х*+2ял+...
ТТТ
-}--5-(дс—1)* — — (х — 1 )*-(-... В первом и втором примерах ряды
пригодны для вычислений, если | к \ < 1; в третьем, если 0 < дс< 2.
4. ±
+
+ 2/' @) g' @) +g?(O)f @)] *• + ...
§20. 1. 1. 2. —-j. 3. — . 4. со. 5. 1. в. -g-.
ПРИЛОЖЕНИЕ К ЧАСТИ III
Таблица I. Таблица производных
2- У = х %=1.
4. у = <*
5. у=а*
6. у=
I. y=iogax dx —
dv
8. у = sin * Щ = cos д?.
9. t/=cosje й^
,0. „_Ц, |=
ПРИЛОЖЕНИЕ К ЧАСТИ III
219
И. y =
12. u = arcsin* -r-=-
1 — хж
13. f/ = arccosje ^ = — .
14. */=
15. i/ =
Таблица II. Интегралы от некоторых функций
2.
3. J^ =
6.
7.
— -^- f x—l
le**
e**dx
9. С ekx sinavcfj: = yg, д> ('fe sin ax — a cos ax) -f-С
10. ^ ekx cos ax dx = ^ц-^ (k cos ax-{-a sin ax)-{-С.
с l
11. \ sin kx dx——-^ cos kx -j- С
12. С
si
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ [Ч. 111
С 11
15. \smxkxdx=Yx — ^sin2kx -\-C.
16. С cos1 kxdx = Y*~\-jksin2kx-\-c-
17. \xnsinkxdx = — ^cos kx -\- ^- \ x"~x cos kx dx.
18. Г jc" cos kxdx = ^-sinkx — ^\x"~% s*n *^dx.
19. ^sin^sin/^^!1^!^-^^!^^^ если
|Л|=И=|/| (если |jfe| = |/|, см. № 15).
20. $coskxcoslxcb = ^^ + ^±^ + C, если
|*|=И=|/| (если |jfe|=|Z|, см. № 16).
21. J '
если
22. {\gkxdx = — -^-In cos Л
23.
24.
25. f
J
26. J^^= aradn
27. J* K^R ^c 2 ^ -
28. §V a2 — x* dx = \(xVa* —x* -{-a*
29.
30.
ПРИЛОЖЕНИЕ К ЧАСТИ III
221
81. J
32.
33.
dx
In
34. \-
35.
36.
37. j
dx
x = Vxt — ая — aarccos-j+C.
arctg г У ¦.. -f- С, если
4oc—6a>0,
38
' J (^
ax* -f-ftx -\-c"
dx
b + Vb*— 4ac
если Aac—b*
¦ ^
(n — 1) Dac — b») (ax1 -f- bx
Bn — 3) 2g f»dx
(n— l)Dac — b") J
(см. № 37).
Г <** 1 . x1 6 f
* J x(ax»+*x+^K*=2cinax»-f-bx+c 2c J
-f-в
(см. № 37).
41 Г <** —
J >:in(acs-f-fcx-f-c)'1 (да —
—Э)а f
dx
*-!-tx-f-c)"
(m-l)c
(п + ш-2)Г
(m-l)c J je*-»
42.
222 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ Я ИНТЕГРАЛОВ [Ч. III
А1 Г d* П (Я*"+" *) * 1 Г>
J Л'вхЧ-Ь (га—Wa г/ох -4- Ь
44. j In лсс?дс=лгInjc — jc-f-C.
46. f arcsin -?- Л»:=x arcsin -J+Va* — x*~\-C.
47.
48. J arctg ^dx = x arctg -J- — ~ In (as + л:1) + С.
49. J arcctg -J dx = x arcctg -J + -| In (a1 + ^) -f C.
Таблица III. Некоторые разложения в ряды
1. ^^
2. sinA: = A: —^-f|l —7Т+-•• (jc —любое).
3. coe*«-l—^+if —|f+--- (* —любое).
4. tg*-=
5. e-=l4-J+^ + |f + ^+... (д:-любое).
6. 1пA+*)=д: —^ + Т —Т+--- (~1<^^0-
7. 1пA —*)= —х —|—^ —^-... (—
9.
ПРИЛОЖЕНИЕ К ЧАСТИ Ш
223
Таблица IV
0
0.1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1.0
1.1
1.2
1.3
1.4
1.5
1,6
1.7
1,8
1.9
2,0
1,000
1,105
1,221
1.350
1,492
1,649
1,822
2,014
2,226
2,460
2,718
3,004
3,320
3,669
4,055
4,482
4,953
5,474
6,050
6.686
7,389
е-»
1,000
0,905
0,819
0,741
0,670
0,607
0,549
0,497
0,449
0,407
0.368
0.333
0,301
0,273
0,247
0,223
0.202
0,183
0,165
0.150
0,135
X
2,2
2.4
2,6
2,8
3,0
3.2
3.4
3.6
3,8
4,0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
8.0
8.5
9,0
9,5
10,0
9.025
11.023
13.464
16.445
20.086
24.533
29.964
36,598
44,701
54,598
90,017
148,41
244,69
403,43
665,14
1 096,6
1808,0
2981.0
4 914.8
8 103,1
13 360
22026
е-'
0,1108
0,0907
0.0743
0.0608
0,0498
0,0408
0,0334
0,0273
0.0224
0,0183
0,0111
0,00674
0.00409
0,00248
0.00150
0.000912
0.000553
0.000335
0,000203
0,000123
0,000075
0,000045
Таблица V
X
1,0
1.1
1,2
1,3
1,4
1.5
1,6
1.7
1,8
1,9
2,0
In х
0
0,0953
0,182
0,262
0,336
0,405
0,470
0,531
0,588
0,642
0,693
ж
2.2
24
2.6
2.8
3,0
3.2
3,4
3.6
3.8
4.0
4.5
In*
0,788
0,875
0,956
1,030
1.099
1.163
1,224
1,281
1,335
1,386
1,504
X
5,0
5,5
6,0
6,5
7,0
7,5
8.0
8,5
9,0
9,5
10,0
In х
1,609
1,705
1,792
1,872
1,946
2,015
2,079
2,140
2,197
2,251
2,303
¦ооооооооо
IS!
ел сл о «j ор оо (р(р^о<
<оооооV)
W<0&00
Ш00Ц00Ц00Ш
ooooooooooooooo»—
ooooopoo*- — >-
»— h-h-p—»OOOOOOOO
O)
*"— ""^ *0 ^^ 00
о><о*^осл
to "^ ^0 ф СЛ (О № № О 00
Ш О СО Q ^J &> СЛ l О ^
соовюк>
^ &Р (О **^
Ю О О О
>со(осоо
tt)
H
— o«3oeVib>cn*. wto—
ooooooooooooooo>—oooooooooooooo
СП СЛСЛ СП
— отоооо
>->oooooooooooooooo
ooooooooooooooo
o ^
со
OO^^^MtO»— S«-"OC7I«
oi *¦
C5 c»
и~ 00
ooooooooo>->->»mww>»o(i»*«Mi->
О5СЛСЛ»-(
00*.
|-oooooooo
)>—О
>t5ооо*.оо
< 5
Ч АСТЬ IV
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО
И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ
§ 1. Касательная, нормаль и ряд Тейлора
В части II мы нашли уравнение касательной. По-
скольку в дальнейшем нас будет интересовать одновре-
менно и уравнение кривой и уравнение прямой, касающейся
этой кривой, изменим несколько обозначения: будем обоз-
начать по-прежнему уравнение кривой
Уравнение прямой (касательной) запишем в виде
y = kx-\-b.
Координаты точки касания обозначим ха, уа; очевидно,
*/о = /(*о)- При х=ха, y = ya=zf(xa) = y(xa), однако при
х=/=хл ордината касательной, очевидно, не совпадает с ор-
динатой кривой, (/(*)=?/(*).
Уравнение касательной имеет вид (см. часть II, § 5)
У— Уа=Г (ха)(х — ха)
или
?=/(*.)+/'(*.)(*—¦*.)• 0-1)
Сравним это выражение с рядом Тейлора функции fix)
вблизи х = ха:
8 Я- Б. Зельдович
226 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Правая часть уравнения касательной представляет собой
первые два члена ряда Тейлора функции. Касательная
к линии y=f(x) — это та прямая, которая наиболее близка
к кривой y = f(x) при х, близ-
ких к ха.
П-ример. Составим уравне-
ние касательной к линии
О
J
У=е' A.2)
в точке Р с абсциссой х=ха
(здесь а — постоянное число).
Дифференцируя A.2), полу-
чим:
/и I 2 М 3
откуда
Рис. 80. у'(ха) = — ё~*.
Подставляя это в A.1), получаем уравнение касательной
ё-е°=±е° (х~ха). A.3)
Найдем точку пересечения N касательной с осью х (на
рис. 80 а ==2, ха = 2,Ъ). В точке N у~0, поэтому, пола-
гая в A.3) у = 0, получим
еа = — еа {х — л:,,), откуда
¦а.
Найдем длину отрезка NM (М — проекция точки Р на
ось х)
NM==xa — (ха — а) = а.
Касательная в любой точке отсекает на оси х отрезок
длины а. Это дает простой геометрический способ построе-
ния касательной к рассматриваемой кривой. Из точки ка-
сания Р опускаем перпендикуляр РМ на ось абсцисс.
От основания перпендикуляра М откладываем отрезок MN
данной длины а. Точку N соединяем с точкой Р (точка
касания). Это по доказанному и есть касательная.
§ п
КАСАТЕЛЬНАЯ, НОРМАЛЬ И РЯД ТЕЙЛОРА
227
Нормалью к кривой называется прямая, перпендику-
лярная к касательной и проходящая через точку касания.
Она показана на рис. 81 пунктиром и отмечена буквой N.
Для того чтобы найти уравнение нормали, заметим, что
угол р, образованный нор-
малью с осью х, равен-»-~Ь"а»
где а — угол, образованный
касательной с осью х.
Известно, что
Так как tga=/'(x0), то
У
\
0
к
ч
ч
\
\
\ у
У
/Аш
(Хо.уо)
s<=^0 •„
s X
Рис. 81.
Уравнение прямой с таким
угловым коэффициентом, проходящей через точку М (ха, уа)
В качестве примера рассмотрим круг радиусом г с цент-
ром в начале координат. Его уравнение
Найдем производную. По правилу дифференцирования
функции, заданной неявно (см. часть III, § 12), имеем:
F(x, У) = хл + уг — г\
dF(x, у)__о„ dF(x, у)_р„
di —l?x' Ту ~Zy'
~dx
В точке М(ха, у0)
Таким образом, уравнение касательной к кругу
8*
228 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Уравнение нормали
Раскрывая скобки, получим:
Уравнение нормали к кругу представляет собой пря-
мую, проходящую через центр круга — через начало коор-
динат. Этот результат известен из элементарной геометрии:
радиус круга в точке касания перпендикулярен к каса-
тельной.
Упражнения
1. Составить уравнение касательной н нормали к кривой у = хп
в точке х = ха.
2. Составить уравнения касательных и нормалей к кривой г/ —х3
в точках х = 1, х = —2, х = 0.
3. То же для кривой у=2хх— х -f-1 в точках х=1, х = 0.
4. То же для окружности с центром в начале координат и ра-
диусом /?=2 в точке х = 1.
Указание к №4. Решить эту задачу двумя способами:
а) найти у как функцию от х из уравнения окружности хг -j-y2 = /?'
и, пользуясь этим, определить у' A);
б) найти у' по правилу дифференцирования функции, заданной
неявно.
Указание ко всем задачам. Рекомендуется построить
на миллиметровой бумаге кривые и касательные и нормали к ним.
§ 2. Кривизна и касающийся круг
Умение составлять уравнение касательной к кривой
дает возможность установить геометрический смысл знака
второй производной.
Вспомним, что первая производная показывает скорость
изменения функции. Следовательно, вторая производная
показывает скорость изменения первой производной, иначе
говоря, скорость изменения тангенса угла наклона каса-
тельной к оси х. Значит, вторая производная характери-
зует скорость изменения направления касательной. На-
правление касательной к кривой меняется тем быстрее,
чем сильнее изогнута кривая, т. е. вторая производная
связана с кривизной кривой.
§ 2] кривизна и касающийся круг 229
Можно записать выражение второй производной таким
образом, чтобы непосредственно была видна связь между
кривизной линии и второй производной функции у"=-г!к •
Для этого составим приближенное выражение произ-
водной как отношения разности значений функции к
разности значений аргумента. Для краткости нигде не
будем писать знаки предела и приближенного равенства.
На самом деле мы знаем, что следует либо говорить о том,
что производная есть предел этого отношения при стре-
мящемся к нулю приращении х, либо при конечном прира-
щении следует говорить о приближенном равенстве.
Итак, не останавливаясь на этих тонкостях, запишем,
что вторая производная у" есть производная от первой
производной у'(х), а следовательно,
, / , &.х\ , ( Ах
В свою очередь значение первой производной можно
записать как отношение приращений
Подставим эти выражения в предыдущую формулу.
Получим:
,.» (х\ У (х -f- Ах) — 2у (х)+у(х — As) B 34
Заметим, что при выводе этой формулы мы пользовались
наиболее точным из рассмотренных выше выражений
производной: отношение разности значений функции к
разности значений аргумента равно значению производной
в середине интервала, т. е. при значении аргумента, рав-
ном полусумме двух рассматриваемых значений, х равно
полусумме х-\-~ и х ~, х-{--? равно полусумме х и
х-{-Ах и т. д. Выражения B.1) и B.2) точнее, чем
,.Чу\ У (X + &Х) — У (X)
230 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Окончательная формула B.3), дающая выражение вто-
рой производной через значения функции в трех точках,
имеет большое значение. Выведем ее еще другим спосо-
бом, с помощью ряда Тейлора.
Составим ряды:
у(х+ Ах) = у{х)-\- Ay' (*)-f-^V (*)+ • • -. B-4)
= у(х)— Аху' (х)~\-(-^-у"(х)+ ... B.5)
Считая у (х -{- Ах), у (х), у(х — Ах) и само Ах извест-
ными, найдем из B.4) и B.5) величину у" (х). Для этого
сложим B.4) и B.5), получим *):
— Ах) = 2у (х) + (Ах)' у" (х),
откуда сразу следует B.3).
Формулу B.3) можно переписать так:
или, обозначая х-\- Ax=xlt х — Ах =
У
Какой наглядный смысл имеет выражение в квадратных
скобках в B.6)?
Дробь у(*')+у(*») есть среднее арифметическое значе-
ние функции у в двух точках, на двух концах интервала.
Величина, которую мы вычитаем, есть значение функции
в середине интервала, при дс =-*-?—?, т. е. при аргументе,
равном среднему арифметическому значений аргумента на
краях интервала хх и хг.
Для линейной функции у — ах-{-Ь обе величины сов-
падают, как и следовало ожидать, так как в этом случае
*) При этом члены с (\х)*-у"' сократятся, так что при выводе в
действителиности мы пренебрегаем только членами с (Ax)*i/iv и более
высокими, хотя разложения B.4) и B.5) доведены только до (Д*)' у".
§ 2]
КРИВИЗНА И КАСАЮЩИЙСЯ КРУГ
231
у" = 0. Для функции, изображаемой кривой, дробь
——2—— представляет собой ординату середины хорды,
проведенной между двумя точками хх, y(xt) и хж, у(хг).
Величина, которую мы вычитаем, есть ордината точки на
кривой при среднем значении х = ?1^*'. Таким образом,
величина в квадратных скобках формулы B.6) представ-
ляет собой длину отрезка на вертикальной линии х =
X •] • X
— 2 •'» заключенного между кривой и вышеупомянутой
хордой. Этот отрезок мы уже рассматривали в связи
с вопросом о выпуклости кривой — см. рис. 21 ¦
Отметим еще, что выражение B.3) или B.6) имеет
такую структуру: в числителе — величина, линейно состав-
ленная из значений у при разных значениях х; в знаме-
нателе— квадрат разности (А*)* или (xt — хг)г. Обратите
внимание на соответствие между такой структурой и сим-
волом 2р ( в числителе — у в первой степени, в знамена-
теле dx в квадрате).
В данной точке х=х0 кривую называют выпуклой,
если вблизи этого значения х точки кривой лежат ниже
касательной в точке дс0 (рис. 82). Если же точки кривой
лежат выше точек касательной, то кривая называется во-
гнутой в данной точке (рис. 83). Вогнутую кривую часто
называют выпуклой вниз.
Точки кривой, подобные точке М на рис. 84, в кото-
рых кривая переходит с одной стороны касательной на
другую, называются «точками перегиба»: с одной стороны
232 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
от точки М кривая выпуклая, с другой — вогнутая, в
точке М кривая «перегибается».
Для того чтобы решить, является данная кривая i/ =
= f(x) при х = ха выпуклой или вогнутой, или имеет
точку перегиба, составим уравнение касательной в точке
-г. f (г ) = Г (х ) (х х ) B 7)
где через у обозначена ордината касательной, соответст-
вующая абсциссе х (через у будем
"' • . обозначать ординату кривой). Вы-
числим у — у; знак этой разности
и решает вопрос о выпуклости или
вогнутости кривой в рассматривае-
мой точке. Если у — у ^> 0, т. е.
У^>У> т0 точки кривой лежат выше
точек касательной, получаем во-
гнутость. Если же У<С.У* получаем
выпуклость.
Как упоминалось в § 1, удержав
*х в разложении функции y=f(x) в
ряд Тейлора только первые два
члена, получим уравнение касатель-
ной в точке х = ха. Мы хотим рассмотреть отклонение
графика функции от касательной, поэтому нам теперь нельзя
уже ограничиться двумя членами разложения. Но так как
нас интересуют точки, близкие к ха, то мы можем записать
*/ = /(*) в виде ряда Тейлора, взяв только три члена:
О
Рис. 84.
Г(х.).(х — *.)л- B-8)
„ Пользуясь B.7) и B.8), получаем:
= y/"(*.)•(* — *.)¦• B-9)
Из B.9) видим, что если /" (*0) > 0, то и у — у "> 0, кри-
вая вогнута. Если же f (ха) <^ 0, то у — у < 0, кривая
выпукла.
Может случиться, что /"(*0) = 0. В этом случае для
установления характера поведения кривой при х=^ха
§ 2]
КРИВИЗНА И КАСАЮЩИЙСЯ КРУГ
233
(выпуклость, вогнутость, перегиб) нельзя ограничиваться
только тремя членами ряда Тейлора. Рассмотрим два при-
мера.
1) Кривая y=casx, у" — —cos*. Возьмем точку х =
==у, у = 0. Ясно, что t/"fyj=O, значит, третий член
ряда Тейлора обращается в нуль. Найдем следующий член;
у'" (х) = sin х, поэтому у'" ( ^Л = 1. Удержав в ряде Тей-
лора четыре члена, получим для у — у выражение
у—у="ъ{* — тI- BЛ0)
Из B.10) видно, что у — у <^0 при дг<^^-, а при х^>~
величина у — у"^>0. Поэтому для значений х, расположен-
ных левее значения *=—, точки кривой лежат ниже то-
чек касательной, а для значений х, расположенных правее
*=-=-? точки кривой лежат выше „,
точек касательной. Следовательно,
'y-2*fx-iy
В точке х = 1 кривая имеет
горизонтальную касательную t/= 2.
Так как (х — 1 )* > 0 при х =? 1, то
у~^>2 при х^=\, а это и означает,
что при х = 1 кривая вогнута
(рис. 85).
Итак, знак второй производной
указывает, выпукла или вогнута кривая. Случай обраще-
ния второй производной в нуль требует дополнительного
исследования, на котором мы не останавливаемся.
Мы выяснили, что величина f"{x) связана с кривизной
кривой—она показывает, насколько изогнута кривая. По-
стараемся теперь уточнить эти соображения. Для этого
построим окружность, которая касается данной кривой
y = f(x) в точке М (ха; f(xa)). Заметим, однако, что таких
= ^г кривая y—cosx имеет
перегиб.
2) у = 2-{-(х— 1)*. Ясно, что
"
2' 3
Рис. 85.
234 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
окружностей можно построить сколько угодно: достаточно
брать центр окружности на прямой, проходящей через
точку М, перпендикулярно касательной к кривой в этой
точке (рис. 86).
Выберем из этих окружностей ту, которая наиболее
близка к кривой y = f(x) вблизи значения х = х„. Окруж-
ность и кривая проходят
через точку М и каса-
ются в этой точке. По-
этому если уравнение
окружности есть у =
==ц>(х), то q>(xe) = /(xe)
и Ф'(*,) = /'(*.)• Стре-
буем еще, чтобы было
ф"(*„) = Г (*.)• Тогда
окружность и кривая
будут одинаково изогну-
ты вблизи точки М.
Естественно считать,
что окружность, удов-
летворяющая последне-
му требованию, будет
наиболее близкой к кри-
вой y = f(x). Она называется окружностью кривизны*);
ее радиус R называется радиусом кривизны кривой у=
= f(x) в точке М, а величина /С=1Г носит название
к
кривизны кривой. Действительно, ясно, что чем больше R,
тем менее изогнута кривая, чем меньше R, тем сильнее
изогнута кривая.
Из сказанного ясно, что если г/=<р(лг) есть уравнение
окружности кривизны, то
Рис. 86.
Получим формулу для радиуса кривизны. Предвари-
тельно заметим, что если центр окружности О имеет
•) В математической литературе часто встречается термин «круг
кривизны».
§ 21
КРИВИЗНА И КАСАЮЩИЙСЯ КРУГ
235
координаты х = a, y = b,a радиус окружности равен R, то
уравнение такой окружности есть (х — o)* + (t/ — b)x = R2.
Действительно, пусть Р (х; у) — любая точка на окруж-
ности. Тогда (рис. 87) ОК° +Я/С5 = ОР* или (х— а)ш+
~\~{.У — ^y = RX' Поэтому
уравнение окружности кри- у
визны имеет вид
B.12)
и первое из условий B.11) b
дает:
B.13)
Рис. 87.
Возьмем производную
от обеих частей равенства B.12), получим 2(х—а)-\~
-\-2(у — Ь)у'~0, откуда
B-14)
^
Следовательно, второе условие B.11) можно записать
в виде
^5- BЛ5)
Дифференцируя B.14), получим для круга
V \ I 9 (у _ Ьу.
Следовательно, третье из условий B.11), с учетом пер-
вых двух, дает:
г ,„ ч / (х0) — ь-Г (х0) (ха - а)
' Iх*'— (/(ха)-Ь)*
или в силу B.15)
236 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Из уравнений B.15) и B.16) нетрудно выразить хл— а
и / (х0) — Ь. Подставляя
в B.16), получим:
и, далее,
Формула B.13) дает:
R = V (*. - а)' + (/ (*.) - Ь)* = i1 + {f?W ' . B.17)
Поэтому кривизна кривой в данной точке определяется
формулой
Как расположен касающийся круг относительно кривой,
которой он касается?
На этот вопрос легко дать ответ с помощью ряда Тей-
лора.
Вспомним, как был найден ответ на аналогичный во-
прос в случае касательной прямой: у функции у\ описы-
вающей касательную прямую, значения функции и первой
производной в точке касания совпадают со значениями
функции и первой производной для функции y = f(x),
описывающей кривую. Различие начинается со второй
производной (у прямой у" = 0, у кривой в общем случае
f (ха)=^=0). Значит, в ряде Тейлора разности у — у первый
член есть -^ f (*0) (х — хо)г; этот член имеет одинаковый
знак при х <^х0 и х~^>х0, обе ветви кривой, слева и справа
от точки касания, лежат с одной стороны прямой — сверху
при /" (х0) > 0, снизу при f (ха) < 0. Когда соприкасается
круг (у = уя (х)) и кривая, то у них равны в точке каса-
ния значения функции, первой и второй производных.
§ 3J ИССЛЕДОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ ФУНКЦИЙ 237
Различие начинается с третьей производной, так что
у (х) — ук (х) = | (х — хйK [/'" (лг0) — у'к" (*,)] + . ..
Значит, в общем случае значения разности у(х) — Ук(х)
имеют разные знаки при х<^ха и д;^>лг0, кривая пересе-
кает касательный круг, как показано на рис. 86 (слева,
х<^ха— кривая ниже и снаружи круга, справа — выше и
внутри круга). Эти правила могут нарушаться в особых
точках, где касание более высокого порядка — например,
когда круг касается параболы у=х* в точке * = 0 — на
оси симметрии, где у'" = у'ь" = 0. В этом случае без вся-
ких расчетов, из симметрии картины, ясно, что касатель-
ный круг с обеих сторон точки касания идет выше пара-
болы. С точки зрения рассуждений, проведенных выше,
это объясняется тем, что различие начинается с члена с
четвертой производной у по х.
Упражнения
1. Выпукла или вогнута кривая у = х*—**-|-* + 2 при x=rl?
2. Найти точки перегиба кривой у = х*-\-2х3— 12x*-f- 12* — 12.
3. Является ли точка х=1 для кривой у = х* — 4х3 + 6х' —
— Ах -(- 1 точкой выпуклости, вогнутости или точкой перегиба?
4. Найти радиус кривизны кривой у = хг при * = 0 и при х =
= ~2 '
5. Найти выражение для радиуса кривизны кривой у = ех.
§ 3. Исследование максимумов и мвввмумов функций
при помощи второй производной
Задача о нахождении того значения х, при котором
данная функция y=f(x) достигает максимума или мини-
мума, не разрешима в общем виде средствами элементар-
ной алгебры.
В части II мы установили, что в точках, где функция
достигает максимума или минимума, ее производная равна
нулю. Там же было показано, как, пользуясь производ-
ной у', установить, что имеет функция в данной точке
ха — максимум, минимум или перегиб. Для этого прихо-
дилось вычислять значения у' при значениях х, близких
к ха, справа и слева от ха.
238 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
В данном параграфе мы дадим другой способ, при ко-
тором к исследованию привлекается вторая производная у",
но нужно знать ее значение только при х = ха.
Покажем, что если в точке x = xt
/'(*.)=о, П*.)<о.
то в рассматриваемой точке функция f (x) имеет максимум.
Действительно, из условия /' (ха) = 0 следует, что каса-
тельная в точке х = х„ горизонтальна. Из неравенства
/" (*») <С 0 следует, что точка х = ха является точкой вы-
пуклости, т. е. график вблизи х = х„ расположен под ка-
сательной, а эти два факта и означают, что функция f{x)
в точке х = ха имеет максимум.
Точно такими же рассуждениями легко убедиться, что
если в точке * = *,
/'(*,) = 0, /"(*,)> О,
то в рассматриваемой точке функция f (x) имеет минимум.
Эти выводы получаются также при рассмотрении ряда
Тейлора
nx)=f(x.) + f'(x.)-(x —х.) + ± Г (*.)•(* —*У + ~ C-1)
Пусть f (ха) ф- 0. Например, пусть f (х0) ^> 0. При х,
близких к ха, величинами (х — ха)*, (х — хаK, ... можно
пренебречь по сравнению с (х — ха). Получаем:
или
/(*) — /(*.)=/'(*.)•(* — *.)- . C.2)
Из C.2) видим, что при х > ха f (х) — /(дс0) > 0, т. е.
f(x)>f (х0). Если же х < ха, то f (x) < f (xj. Поэтому при
х=ха нет ни максимума, ни минимума. Аналогично ни
максимума, ни минимума нет, если /' (ха) < 0. Если же
/'(хо) = 0, то пренебречь членом с (л: — лг0)* уже нельзя.
Пренебрегая членами с (х — л:,)', (х — д;0)* и т. д. по
сравнению с (х — *„)*, получаем из C.1)
f(x) = f (xj + ^ Г (ха) (х —
Отсюда видим, что при f(xa)>Q f(x)>f(xa) независимо
от того, будет х < ха или х > х9. Значит, f(xa) меньше
всех соседних значений / (я) и поэтому / (х„) — минималь-
§ 3J ИССЛЕДОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ ФУНКЦИЙ 239
ное значение функции. Если /" (хя) < О, то f(x)<f (x0) и
/(*0) — максимальное значение функции.
Может случиться, однако, что и f.{xa) = Q. Как в этом
случае исследовать значение функции при х=ха? Нужно
обратиться к следующим производным функции f{x). Если
V" (ха) ф О, то, пренебрегая величинами (х — *„)* и т. д.
по сравнению с (х — xtK, получим из C.1)
f(x) = f(xo) + ^-f'" (х„)(х-хау.
Разность f(x) — /(*„) меняет знак в зависимости от
того, будет х>ха или х<ха. При х—ха не имеем ни мак-
симума, ни минимума.
Если же и /'"(*„)= 0, a /Iv (xa)^0, то
±pv(xa) (х-ха)\
Знак выражения f(x) — / (хл) одинаков при х < х,. и при
х>ха, он определяется знаком /Iv (х0). Если Р^О
то имеем минимум, если
/IV (*„) < 0, то максимум.
Внимательный читатель,
вероятно, уже догадался,
что если при лг=лг0 первая
не равная нулю производ-
ная нечетного порядка (пер-
вая, третья, пятая и т. д.),
то ни максимума, ни мини-
мума нет. Если же первая
не равная нулю производ-
ная четного порядка (вто-
рая, четвертая и т. д.), то
имеем либо максимум, ли-
бо минимум, в зависимости
от знака этой производной.
Рассмотрим примеры.
1) Из квадратного жестяного листа, сторона которого
равна 2 а, требуется сделать открытый сверху ящик воз-
можно большего объема, вырезая равные квадраты по
углам, удаляя их и затем загибая жесть, чтобы образо-
вать бока ящика (рис. 88). Какова должна быть длина
стороны у вырезаемых квадратов?
1
1
1
1
!
— 2о
t
ы
\
Рис. 88.
240 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Пусть стороны вырезаемых квадратов равны х. Объем
ящика зависит от того, какой квадрат мы вырезаем, поэто-
му его естественно обозначить V(x). Подсчитаем этот объем
V(дг) = Bс — 2х)а х=4(а — ху х.
Найдем теперь производную этой функции
V {х) = — 8 (с — лг) х + 4 (с — х)\
Решим уравнение V (х)=0:
— 8(с — х)х-\-Ь(а — xf=0 или (а — х)(а — Зл:) = 0,
откуда' х1 = а, xt = -^ .
Заметим сразу же, что значение хх = а нас не инте-
ресует, так как при таком способе разрезания листа ни-
какого ящика не получится. Остается х = -^-. При этом
3 J * 9 3 27' ^
V (x) = 8x — 8 (a — x) — 8 (a —
= 2Ax— 16c;
Следовательно, функция V{x) при * = -^ имеет максимум.
Итак, наибольшее значение получается при х = -%- ,
о
т. е. надо вырезать квадратики, стороны которых состав-
ляют ~ стороны исходного квадрата.
Подсчитаем V(x) при нескольких х, близких к -?-.
О
Результаты подсчетов сведены в таблицу.
0
0
0
X
,25а
,30а
,33а
0
0
0
V (х)
,562as
,588а3
,592а»
0
0
X
,40а
,45а
V
0,
0,
576а3
540а°
Из таблицы видно, что малые изменения х вблизи х =
= -у, т. е. около значения х, которому соответствует
§ 3] ИССЛЕДОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ ФУНКЦИЙ 24!
максимум функции, вызывают весьма малые изменения V.
Функция вблизи максимума изменяется очень медленно.
Это же видно из формулы Тейлора C.1). Так как в
точке максимума f'(xa) = 0, то C.1) принимает вид
Ряд не содержит (х — хп). Наименьшая степень (х — *„)*,
а она весьма мала при х, близком к ха. В нашем примере
изменение д; на 9% (от 0,33а до 0,30с) вызывает измене-
ние V меньше чем на 1 %, а изменение х на 24 % вызы-
вает изменение К на 5%.
Поэтому если нас интересует максимальное значение
функции, а при нахождении ха из уравнения f'(x)=0 мы
допустили небольшую ошибку, на-
пример, решили это уравнение при-
ближенно, то это очень мало по-
влияет на величину максимального
значения функции. Значение функ-
ции при х, близких к х0, будут
очень близкими к ее значению при
х=ха.
2) у = А-\-В{х — а)'. Найти —
максимумы и минимумы функции
у' = ЗВ(х— а)\ у'(а) = 0,
у" = 6В(х — а), г/"(а) = О,
1 2 3
Первой не равной нулю оказа-
лась производная третьего порядка.
В точке х = а нет ни максимума, Рнс. 89.
ни минимума, а есть перегиб. Это
наглядно видно на графике, изображенном на рис. 89.
(Он построен для случая Л = 2, В=1, а=\.)
3) у = А-\-В(х — а)*. Исследовать функцию на мак-
симум и минимум
У' = 4В(х — аK, 1/'(а) = 0,
'" = 24В(х—а),
242 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Первой не равной нулю оказалась производная чет-
вертого порядка. Если В > 0, то она положительна, имеем
минимум; если В < О, имеем максимум.
Этот вывод легко было сделать и непосредственно.
Действительно, при В < О В (х — а)*" отрицательно при
всех х=^=а, при х = а — это нуль. Поэтому из А всегда
вычитается какая-то положительная величина, а при х=а
ничего не вычитается. Значит, при х=а максимум.
Аналогично, если В > 0, то при х = а минимум. На
рис. 85 изображен график этой функции для случая А = 2,
В = 1, а=1.
4) Из имеющихся досок можно сделать забор дли-
ной / м. Как этим забором огородить прямоугольный двор
наибольшей площади, исполь-
//////////////////////////. Зуя в качестве одной стороны
стенку прилежащего здания
(рис. 90)?
Пусть две стороны имеют
длину по х м. Тогда третья
Рис- 90- сторона имеет длину / — 2х.
Площадь двора S (х) = (/ —
—2х)х = — 2x*-\-lx, S' (х) = — 4х-{-1. Решая уравне-
ние 5'(д;) = 0, получаем x = -j , S" (х) = — 4<0. При
х=-т S(x) имеет максимум.
Запишем S(x) по формуле C.1), полагая xa=-j ,
C.3)
Так как S(x) есть многочлен второй степени, то C.3) —
точное равенство (см. § 17 части III). Из него сразу
видно, что S(x) имеет максимум при д:==— .
Равенство C.3) можно получить, и не прибегая к ме-
тодам высшей математики. Действительно, пусть нужно
отыскать максимум (или минимум) многочлена второй
степени
. C.4)
§ 3J ИССЛЕДОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ ФУККЦИЙ
Преобразуем многочлен следующим образом:
243
6*
Итак,
Замечая, что
C.5)
ПРИ ВСех ^ причем равенство
нулю имеет место лишь при х — — -~i, получаем из C.5),
что у имеет максимум, если а < 0, и этот максимум полу-
чается при х==—2^; у имеет минимум, если а>0, и этот
минимум получается при дг = — —.
Значение х = —^- мы получили, проделав специаль-
ные искусственные преобразования с многочленом C.4).
находим х=—гп автомати-
2а
Пользуясь производной,
чески. Действительно,
приравняв нулю произ-
водную от C.4), получа-
ем 2ах -{-6 = 0, откуда
х = — 2~. Вторая произ-
водная от C.4): t/" = 2a.
Поэтому вопрос о том,
имеется максимум или ми-
нимум, решается в зави-
симости от знака числа а.
5) Пешеходу из пунк-
та А требуется подойти
к реке (прямая AfiJ, а затем прийти в пункт В. Как про-
делать этот путь, пройдя наименьшее расстояние (рис. 91)?
Итак, ЛЛг=а, SB1 = 6, A1Bl = c; числа а, Ь, с даны.
Пусть путь пешехода изображается ломаной АМВ. Нужно
узнать, при каком положении точки М на прямой А1В1
этот путь будет наименьшим. Для того чтобы определить
Рис. 91.
244 приложения к исследованию функций и геометрии [ч. iv
положение точки М, достаточно задать расстояние М от
точки Ах, лежащей в основании перпендикуляра, опущен-
ного из А на прямую, изображающую реку. Обозначим
это расстояние АХМ через х. Тогда
= Уа*-\-х2; МВ = У Ь* -f (с —jcI.
Путь, пройденный пешеходом, обозначим s (л:),
s(x) = V^+^+Vb'-{-(c-x)\ C.6)
Находим:
S' (Х\ = * _
с~х
Приравнивая s' (д;) нулю, получим:
I. C.7)
Это уравнение нетрудно решить. Возведя обе части
в квадрат, получим:
я* (с — х)*
ИЛИ
+ a;s(c — xf=a* (с —х)*
Извлекая из обеих частей корень, находим:
откуда
ас ас
Y = • Y
Подставляя значения хх и хг в исходное уравнение C.7),
видим, что второй корень не удовлетворяет уравнению.
Это посторонний корень, получившийся из-за возведения
в квадрат. Итак, * = дТ (,-
Однако можно, не решая уравнения, дать наглядную
геометрическую картину, позволяющую получить ответ.
Условие C.7) перепишем так:
§ 3] ИССЛЕДОВАНИЕ МАКСИМУМОВ И МИНИМУМОВ ФУНКЦИЙ 245
Но -д^- = cos AlMA=s'm а. Аналогично -^ = cos В ХМВ =
= sinp*. Условие C.8) дает:
sina = sinp. C.9)
Но а и р — углы острые. Поэтому из C.9) получаем:
в
Таким образом, пешеход должен двигаться так, как дви-
жется луч света: угол падения равен углу отражения.
Для полного решения задачи остается показать, что
при таком положении точки М путь действительно бу-
дет минимальным (а не
максимальным). Это мож-
но сделать, вычислив
вторую производную от
C.6).
Можно, однако, ис-
пользовать другие сооб-
ражения. Из выражения
C.6) для s(x) видим, что
при любом х s(x) — по-
ложительная величина.
При этом s (х) неограни-
ченно возрастает вместе
с ростом абсолютной ве-
личины х, независимо от
того, будет х>0 или
х < 0. А так как s' (x)
обращается в нуль лишь
при одном значении х,
то ясно, что при этом
значении х функция s(x)
имеет минимум. Если в интересующем нас промежутке пер-
вая производная имеет лишь один корень, то наглядные
соображения часто позволяют избежать формального ис-
следования при помощи второй производной.
Задачу 5) можно решить чисто геометрически, не при-
бегая к методам высшей математики. На продолжении
отрезка АА1 (рис. 92) отложим AtA' =ААЛ и точку А'
соединим с В. Тогда ЛМ=Л'М, так как ДЛ/4,Л1 =
= АА1А'М. Поэтому АМ-\-МВ=А'М-\-МВ=А'В. Для
Рис. 92.
246 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
любой другой точки D яа отрезке АХВ^ будет AD-{~DB =
=A'D~\-DB и A'D-\-DB> А'В, так как ломаная длиннее
отрезка прямой. Искомая точка М есть, следовательно,
точка пересечения прямых А'В и АХВХ. Отсюда следует
Два последних примера показывают, что некоторые
задачи на нахождение максимума и минимума можно
решить средствами элементарной математики. Однако,
во-первых, далеко не все задачи можно осилить, не при-
бегая к высшей математике, во-вторых, решение элемен-
тарными средствами требует смекалки и остроумия; выс-
шая математика дает стандартный способ решения таких
задач.
Это не значит, что в высшей математике не нужны
смекалка и остроумие! Но теперь они пригодятся для
более трудных вопросов.
Упражнения
1. Из прямоугольного жестяного листа со сторонами а и Ь- делают
ящик, вырезая равные квадраты по углам. Какова должна быть сто-
рона у вырезанных квадратов, чтобы ящнк имел максимальный
объем?
2. В остроугольный треугольник с основанием а и высотой Н
вписать прямоугольник, две вершины которого лежат на основании
треугольника, имеющий наибольшую площадь из всех прямоуголь-
ников такого вида.
3. Определить наибольшую площадь прямоугольника, вписан-
ного в круг радиуса R.
4. При каком радиусе основания и при какой высоте закрытая
цилиндрическая банка данного объема V будет иметь наименьшую
полную поверхность?
5. Два тела двигаются по сторонам прямого угла с постоянными
скоростями vx и и2 (м(сек) по направлению к вершине, от которой
в начале движения первое находилось на расстоянии а м, второе — иа
расстоянии Ь м. Через сколько секунд после начала движения рас-
стояние между телами будет наименьшим?
6. Доказать, что произведение двух положительных чисел, сумма
которых постоянна, имеет наибольшее значение при равенстве сомно-
жителей.
7. Прямой / плоскость разделена на две части (среды I и II).
Тело движется в среде I со скоростью и,, а в среде II со скоростью
v2. По какому пути должна двигаться точка, чтобы возможно скорее
попасть из данной точки А среды I в данную точку В среды II?
§ 4J ИССЛЕДОВАНИЕ ГРАФИКА. МНОГОЧЛЕНА ТРЕТЬЕЙ СТЕПЕНИ 247
§ 4. Исследование графика многочлена третьей степени
Покажем, что рассмотренные в § 3 приемы позволяют
легко исследовать график любого многочлена третьей сте-
пени, т. е. график функции
у = ах*-\-Ьх*-\- cx + d, - D.1)
и найти его замечательные точки — максимум» минимум,
перегиб.
Знание графика позволяет получить о функции ряд
важных сведений, например, число вещественных корней,
промежутки, в которых располагаются корни, и т. д.
Построим, например, график функции
у = 0,5*' — 0,75л;* — 3* + 2>5- D-2)
Найдем, прежде всего, максимумы и минимумы. Прирав-
нивая нулю производную от D.2), получим:
у> = \,Ъхг — \,Ъх — 3 = 0, D.3)
откуда находим хх = — 1, xt = 2.
Исследуем каждое из этих значений в отдельности.
Для этого найдем у": у" = 3х—1,5, у" (— 1)=—4,5 <0.
Значит, при xl = —1 функция имеет максимум
Утах = — 0,5— 0,75 + 3 + 2,5 = 4,25;
у" B) = 6—1,5 = 4,5 >0. Поэтому при xt—2 функция
дает минимум
Ут\п=— 2,5.
Теперь посмотрим, как будет вести себя многочлен
при очень больших по абсолютной величине значениях х.
Заметим, что при очень больших х член, содержащий х*,
будет значительно превосходить по абсолютной величине
остальные члены. Поэтому знак многочлена D.1) опреде-
ляется знаком выражения ах3.
Если а > 0, то ах3 > 0 при х > 0, правая Еетвь графика
уходит вверх; при *<0a*:'<0, левая ветвь графика ухо-
дит вниз. Ясно, что при а < 0 левая ветвь уходит вверх,
а правая — вниз.
Найдем точки перегиба. Из сказанного в § 2 ясно,
что для нахождения точек перегиба следует решить
248 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
а:
уравнение /" (х) = 0. Пользуясь D.3), находим у" =3* — 1,5.
Уравнение у" = 0 дает х = 0,5. Так как' г/'"=3, то
у—у — ^-(х — 0,5K, где через у обозначена ордината ка-
сательной (см. стр. 232). Поэтому, если дг>0,5, то
у — у > О, если же х < 0,5,
то у — у < 0. Следова-
тельно, при* = 0,5 име-
ем перегиб.
Отметим, что график
многочлена третьей сте-
пени всегда имеет и при-
том единственную точку
перегиба. Действитель-
но, уравнение у" = 0,
когда у есть многочлен
третьей степени, есть
уравнение первой степе-
ни. Оно всегда имеет
единственный корень х0.
Так как у'" = const, то
У — у = А(х — ха)\ Яс-
но, что у — у меняет знак
Рнс. 93. при переходе х через зна-
чение дсо.
Вернемся к построению графика. Вычислим ординату у
точки перегиба; получим у = 0,88. Определим еще напра-
вление касательной к графику в точке перегиба. Поль-
зуясь D.3), получаем tg<x=y' @,5) = 3,38. Используя все
приведенные выше соображения, получаем для D.2)
рис. 93.
Конечно, если не вычислять больше никаких значений
функции, то получим график, дающий грубую качествен-
ную картину поведения функции. Однако даже такой
график дает возможность подсчитать число корней (т. е.
число точек пересечения графика с осью х) и сделать
кое-какие заключения об их величине. В нашем примере
на рис. 93 видим, что корней три, что один из корней
лежит где-то между 0,5 и -f- 2, что второй корень обя-
зательно положительный (он больше 2), а третий—отри-
цательный (он меньше —1).
представление
§ 4] ИССЛЕДОВАНИЕ ГРАФИКА МНОГОЧЛЕНА ТРЕТЬЕЙ СТЕПЕНИ 249
График можно значительно уточнить, если подсчитать
значения функции еще при нескольких значениях х.
В нашем примере подсчитаем еще три значения функ-
ции. При х = 0 у =2,5; это позволит нам лучше предста-
вить ход кривой между максимумом и минимумом. При
х = 3 у =0,25. Это значение мы подсчитали, чтобы полу-
чить представление о скорости подъема правой ветви
кривой. Аналогично, чтобы получить
о скорости спада левой
ветви кривой, возьмем
х=—2. Получим у=1,5.
Используя эти значения,
получаем график рис. 94.
По такому графику
можем сделать более точ-
ные заключения о кор-
нях: один корень лежит
между х = 0,5 и х=\\
второй — между х = 2 и
* = 3, ближе к х = 3;
третий корень меньше
х = — 2 (вероятно, его
значение близко к х=
= — 2,5).
Может случиться,
что, приравняв производ- Рнс. 94.
ную нулю, мы не полу-
чим вещественных корней. Это означает, что исследуемый
многочлен не имеет ни максимума, ни минимума. Так
как все сказанное о поведении многочлена при очень боль-
ших по абсолютной величине значениях х остается в си-
ле, то в этом случае график пересекает ось х только в одной
точке (многочлен имеет один вещественный корень).
Наконец, производная может иметь лишь один (двой-
ной) корень хп. Тогда она имеет вид
у'=А(х — хо)\ D.4)
Интегрируя D.4), получим:
D.5)
250 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Мы видим из D.5), что в этом случае многочлен лишь
постоянным слагаемым отличается от полного куба. Из
D.5) заключаем, что ни максимума, ни минимума у не
имеет (см. пример 2) § 3). График пересекает ось х в одной
точке. Эту точку находим, приравнивая в D.5) у нулю,
зс
зс
Нахождение максимума и минимума многочлена третьей
степени, а значит, и исследование его графика всегда можно
Довести до конца, потому что, приравняв производную
нулю, получим квадратное уравнение, корни которого
найти нетрудно.
Упражнения
Найты максимумы и минимумы следующих функций и построить
их графики:
Определить число вещественных корней уравнений:
4. 2хг — Зх2 — 12х + 15 = 0. 5. 4х3+ \5х* — 18х — 2 = 0.
6. 2х* — х? — 4дг + 3=0. 7. х3 — х*4-2 = 0.
§ 5. Другие виды максимумов я минимумов.
Изломы я разрывы
До сих пор мы говорили, что максимумы и минимумы
функции бывают при таких значениях х, при которых
первая производная обращается в нуль. Однако максиму-
мы (и минимумы) могут быть и при таких значениях аргу-
мента, которые ке обращают в нуль первую производную.
Рассмотрим следующую задачу. Определить, при ка-
ком значении сопротивления R, включенного последова-
тельно с интересующим нас сопротивлением г, на г выде-
ляется максимальная мощность (рис. 95). При этом
сопротивление г и напряжение батареи <р0 считаем посто-
янными.
§ 51
ДРУГИЕ ВИДЫ МАКСИМУМОВ И МИНИМУМОВ
251
Ток / в цепи получаем, пользуясь законом Ома
Мощность W(R)=jq>r, где <рг — падение напряжения
на сопротивлении г. По закону Ома yr = jr, следова-
тельно,
dW
Для определения максимума W (R) решим уравнение
=0; это дает:
, г
лГ = 0.
Полученное уравнение не имеет решения. Значит ли
это, что мощность может расти неограниченно, что задача
о максимальной мощности не
имеет решения? Ведь из физиче-
ского смысла задачи ясно, что
мощность будет наибольшей при
f Р г
Рис. 95.
Рис. 96.
в этом случае W ?=—- ). Почему: же мы не полу-
чили значения /?=0 из уравнения yb-=0?
Для того чтобы разобраться в этом, рассмотрим график
зависимости W (R) (рис. 96).
Из графика видно, что если бы R могло принимать
отрицательные значения, то при R^=0 максимума не
было бы. Однако отрицательные R не имеют смысла. Во
всякой физической задаче подразумевается, что R^*0.
Таким образом, величина W имеет максимум при R = 0,
потому что ограничен промежуток изменения аргумента.
252 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Значит, если промежуток изменения аргумента ограничен,
то при исследовании на максимум и минимум надо при-
нимать во внимание граничные значения аргумента.
В случае, когда максимум (минимум) достигается на
краю промежутка изменения аргумента, ряд
может начинаться не с (х — *„)*, а с (х — ха). Поэтому
если максимум функции получается при х=ха, а мы
несколько отступили от х9, то при определении величины
максимума мы можем совершить значительную ошибку.
Эта ошибка пропорциональна (х — лг0), а не (х — хд)г, как
было в § 3. Значит, даже незначительный отход от зна-
чения аргумента, доставляющего максимальное значение,
в этом случае нежелателен.
В рассмотренном случае подразумевается, что функция
/ (.t) определена формулой и при х < хп, но значения функ-
ции при х<х„ в данной конкретной задаче нас не инте-
ресуют (не имеют физического смысла).
Может случиться, что / (х) просто не имеет смысла
при некоторых значениях аргумента. Так, например, если
функция содержит корень четной степени, например
квадратный, то промежуток изменения аргумента, как
правило, бывает ограничен (подкоренное выражение не
может быть отрицательным). Следовательно, граничными
являются значения аргумента, обращающие подкоренное
выражение в нуль. При исследовании на максимум они
должны быть рассмотрены специально.
Рассмотрим пример. Пусть
Хотя у' и не обращается в нуль, исследование не закон-
чено. Значение х = Ь обращает в нуль подкоренное
выражение. Из E.1) видим, что при х = Ь у=а; если же
х<Ь, то у<а, так как из а вычитается положительное
число*). Поэтому у имеет максимум при х=Ь.
•) Мы считаем, что J^b — х понимается как положительное
(арифметическое) значение корня.
§ 5] ДРУГИЕ ВИДЫ МАКСИМУМОВ И МИНИМУМОВ - - 253
Максимум (или минимум) может быть и во внутренних
точках, где производная не обращается в нуль, если кри-
вая имеет излом, угловую точку. Такие точки встреча-
ются, в частности, когда кривая состоит из двух частей,
описываемых различными формулами при х<ха и при
х > х9. Приведем пример физической зядачи такого рода.
Пусть на электроплитке постоянной мощности нагревается
чайник. Определить момент времени, когда чайник обла-
дает наибольшим количеством теплоты. Для простоты
будем считать, что коэффициент полезного действия
плитки 100°/0, т. е. она все тепло отдает чайнику. Пусть
мы поставили чайник на плитку в момент времени * = 0.
В этот момент чайник обладал q калориями теплоты*).
Количество теплоты, выделенное плиткой, дается формулой
где / — сила тока в амперах, R—сопротивление в омах,
t — время в секундах; при этом Q получается в калориях.
Таким образом, в момент t количество теплоты в чай-
нике
Q = <7+ 0,2APRt.
В некоторый момент t = ta чайник закипает. В этот
момент в нем накопилось q -\-0,241 !!Rta теплоты.
Когда чайник закипел, вода начинает превращаться
в. пар **) (выкипать). При этом на образование одного
грамма пара уходит 539 кал. Поэтому, обозначая через
dm количество воды, выкипевшее за время dt, получим:
0,
ат—
539
Следовательно, за 1 сек выкипает ¦?¦ = ¦ 'goQ—г воды.
at эоУ
Количество воды, выкипевшее в 1 сек, уносит из
чайника
«Я кал.
Поэтому к моменту времени t (t > ta) выкипевшая вода
унесет из чайника Qt = 0,041 PR (t — ?0) кал.
*) За нуль принимается тепловая энергия воды при 0° С.
*•) Парообразование происходит и при температуре меньше 100° С,
но мы им пренебрегаем.
254 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Следовательно, количество теплоты в чайнике выра-
жается так:
f
если t s^ /e (до начала кипения);
Q = q -f 0,24/*/? f. — 0,04 \PR (t — 10) =
= <7-f/*/? @,281*0 —0,041/),
если * s* f 0 (после того, как чайник закипел). График
Q(t) изображен на рис. 97, а. Из рисунка ясно, что Q(t)
имеет максимум при t = t9, хотя производная при этом
значении t не обращается в нуль.
о
Рис. 97.
Производная при t = t9 терпит разрыв. Действитель-
но Q' @ = 0,24/*/?, если t<ta\ Q' (/) = — 0,041/*/?, если
t>ta. График производной приведен на рис. 97, б.
Последний пример показывает, что максимум может
быть в случае, если производная разрывна, т. е. на
графике кривая образует угол. Соответствующая точка
кривой называется угловой точкой..
Наконец, из рис. 98, а*) видно, что минимум (или
максимум) может быть при тех значениях аргумента хах
где производная терпит бесконечный разрыв. Соответст-
вующая точка кривой называется острием. График произ-
водной для этого случая изображен на рис. 98,6. Здесь,
как и в случае обычного минимума, при х < хп у' < 0;
при приближении к х = хл слева функция убывает. При
*) На графике изображена функция у = х8 =
§ 51
ДРУГИЕ ВИДЫ МАКСИМУМОВ Я МИНИМУМОВ
255
х > хп у' > 0; при увеличении х, после того как значение
*=*„ пройдено, функция возрастает. Однако при х=ха
производная теряет смысл. Она делается как угодно
большой при х, близ-
ком к ха, и x>xt;
она становится сколь
угодно большой по
абсолютной величине,
но отрицательной при
х, близком к ха, и
х<ха. Максимумы и
минимумы, достигае-
мые при тех значе-
ниях аргумента, когда
производная терпит
разрыв, называются
острыми.
В связи с рассмот-
рением особенных то-
чек на кривых и в
первую очередь точек
излома (см. рис. 97)
можно уточнить рас-
суждения, которые
привели нас к поня-
тию производной. В
части II книги мы,
не оговаривая этого
специально, рассмат-
ривали гладкие кри-
вые.
Производная y'(t),
взятая в точке t, рав-
на пределу отношения
E.2)
2/''
Z
-2
-I
-1
б)
Рис. 98.
при стремлении tx и tx к t (при этом разность tx — tlt
очевидно, стремится к нулю). Специально подчеркива-
лось, что этот предел не зависит от того, как выбраны tt
и *,; они могут быть оба больше t или оба меньше t,
256 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
или один из них больше, а другой меньше t, или один
из них равен t, а другой больше или меньше t. В самом
деле, когда мы берем
КО и Д*>0,
то это выражение соответствует случаю, когда в E.2)
ty = t, tt = t-\~At>t. Когда мы берем
то это соответствует в формуле E.2) tx = t— At<t,
tt = t. Наконец, мы вычисляли также производную как
предел отношения
Д/ '
, . At . , , ¦ Д/ ,
что соответствует t1 = t 2~ » '*== ' ~2>*-
В случае гладкой кривой все три выражения дают
один и тот же предел, равный производной в данной
точке. В случае кривой с изломом положение меняется.
В самом деле, если обозначить через ta значение t, при
котором имеет место излом, то, взяв
А*
получим при Д?, положительном и стремящемся к нулю,
определенную величину — в примере на стр. 254 эта ве-
личина равна —0,041/*/?; такую величину называют
«производная справа». Взяв
Дх
получим при Ддг, положительном и стремящемся к нулю,
другой предел, равный в упомянутом примере -f-0,24/*./?.
Эта величина называется «производная слева».
Взяв tx и tt с разных сторон ta, можно получить
в пределе tt—<- tt, tx—>-10 разные значения отношения
E.2). Таким образом, в самой точке излома производная
не имеет определенного значения, но можно определить
«производную слева» и «производную справа».
§ 5]
ДРУГИЕ ВИДЫ МАКСИМУМОВ И МИНИМУМОВ
257
В части II, впервые изучая производные, мы наме-
ренно, для упрощения изложения, не отмечали каждый
раз, что определенное значение производной, не завися-
щее от способа стремления А* к нулю (слева или справа),
существует лишь для точек, в которых кривая — глад-
кая. Как видно из рис. 97, в точке, где кривая у (t)
имеет излом, кривая производной у' (/) терпит разрыв.
Oft/i
Рис. 99.
Если излом на кривой у (t) заменить дугой малого ра-
диуса, касающейся кривой слева и справа (как говорят
чертежники, сделать сопряжение), то на том участке
изменения t, где кривая у (t) заменена дугой, кривая у' (t)
круто меняется (рис. 99).
У*
Гд-?Гд^е t О
Рис. 100.
Если кривая у (V) имеет разрыв в точке tn (см.
рис. 100), то можно сказать, что в точке t% произ-
водная у' (t) бесконечна: в самом деле, если разрыв за-
менить изменением у от ух до yt на малом отрезке от
ta—е до tn-\-e, то на этом отрезке производная равна
у'~Ух, т. е. очень велика, тем больше, чем меньше s
(рис. 100).
Я. Б. Зельдович
258 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
ь
Как обстоит дело с интегралом \y{t) dtt если функ-
а
ция у (х) не гладкая?
Если функция имеет излом, то при вычислении пло-
щади, ограниченной кривой у (t), никаких новых вопро-
сов не возникает. В § 10 части II мы разбивали опреде-
ленный интеграл — площадь — на сумму площадей пря-
моугольных полосок вида
У ('»)('«+, — '.) или y(tn+1)(tn+l-tn).
В пределе, при уменьшении величин интервалов, т. е.
разностей (tn+1— tn), становится безразлично, брать y(tn)
или y(tn+l), как в случае гладкой кривой «/(/), так и
в случае кривой у (t) с изломом.
Если кривая y(t) терпит разрыв в точке t=^t0, но
остается ограниченной, то для интервала, внутри кото-
рого находится разрыв (/„ < /0 <*„+,), величины y(tn)
и y(tn+1) остаются различными, как бы мы ни сближа-
ли tn и tn+l. Таким образом, в выражении интеграла
как суммы величина одного из слагаемых в этом случае
зависит от того, как берется сумма — по формуле (8.1)
или (8.2) из части II. Однако при стремлении к нулю
величины интервала хп+1 — хп само слагаемое стремится
к нулю, поэтому предел суммы, т. е. интеграл, имеет
вполне определенное значение (не зависящее от спо-
соба вычисления суммы) и в том случае, когда подынте-
гральная функция имеет разрыв в области, интегри-
рования.
Сохраняется и соотношение между интегралом и про-
изводной.
В частности, можно снова обратиться к рис. 97: на-
зовем теперь функцию Q' (t), график которой дан на
рис. 97,6, Q'{t)=f(t). Тогда функция Q(t), график
которой дан на рис. 97, а, представляет собой неопреде-
ленный интеграл: Q(t) — ^f(t)dt. На этом примере мы
видим, что разрыв подынтегральной функции f (t) приво-
дит к излому в интеграле этой функции Q(t).
Определенный интеграл функции с конечным разры-
вом может быть найден с помощью неопределенного
§ 6J эллипс 259
интеграла по общему правилу
Можно пойти и дальше: рассматривая рис. 100,
можно сказать, что для функции, стремящейся к бесконеч-
ности, на интервале, стремящемся к нулю (рис. 100 справа),
интеграл является разрывной функцией (рис. 100 слева).
Однако при этом надо уточнять закон стремления к бес-
конечности функции и к нулю интервала,— на этом мы
останавливаться не будем.
Упражнения
1. Найти наименьшее значение функции у = х*— 2л:+ 3 При
изменении х от 2 до 10.
Найти острый максимум функций!
2. у = (х-Ь
3. 0= 1 - V**.
§ в. Эллипс
Эллипс—это кривая, с которой часто приходится
иметь дело в математике и физике. Напомним читателю,
что, например, планеты солнечной системы движутся по
эллипсам.
Эллипсом называется геометрическое место точек
плоскости, сумма расстояний которых от двух данных
точек есть величина постоянная. Эти данные точки носят
название фокусов эллипса. Эллипс легко построить сле-
дующим образом: в фокусы эллипса воткнем булавки, на
которых закрепим концы нити. Вставим в нее карандаш
и отодвинем его от линии, соединяющей фокусы, так,
чтобы нить натянулась. Теперь будем двигать карандаш,
следя чтобы нитка все время оставалась натянутой. При
этом конец карандаша начертит эллипс. Длина нити,
т. е. сумма отрезков FJW-\-MFlt—это и есть постоянная
величина, которая фигурирует в определении эллипса.
Эллипс изображен на рис. 101.
9*
260 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
§
Выведем уравнение эллипса, т. е. уравнение, кото-
рому должны удовлетворять координаты любой точки
эллипса. Для этого выберем такую систему координат:
ось х направим по прямой,
соединяющей фокусы Fx
и Fx, а начало координат вы-
берем в середине отрезка
FlF1. Расстояние FXFX обоз-
начим 2с*).
Возьмем любую точку М
на эллипсе. Пусть ее коор-
динаты (л; у). MFl-{-MFx
есть постоянная величина.
Рис. 101. Обозначим ее 2а. Заметим,
что 2а>2с, так как в
7Х сумма двух сторон больше третьей. Итак,
Из чертежа (рис. 101), пользуясь теоремой Пифагора,
получаем**):
MFX = У(с — х)г-\-уг, MFX = У(х-\-с)*-\-у*
и из F.1)
У(х~\-су+у*~\- У(с — х)*-{-уг = 2а. F.2)
Перенося в F.2) один из корней вправо, возводя обе
части в квадрат и сокращая на 4, получаем:
а У(с—х)*-\-у* = а* — сх.
Еще раз возводя в квадрат, получим:
= а*(а* — с1), F.3)
Так как а>с, то а* — с*>0. Обозначим а* — с* = Ь*.
Тогда из F.3)
•) Множитель 2 введен для удобства в дальнейших выкладках.
••) Читатель проверит, что формулы для MF^ и MFX справед-
ливы для любой точки М эллипса и учитывают знак числа х (аб-
сциссы точки М). На рис. 101 х < 0.
§ 6J эллипс 261
Разделив все члены на а%Ьл, получим:
Это и есть уравнение эллипса.
Из уравнения F.4) видно, что эллипс симметричен
относительно обеих координатных осей. Действительно,
пусть точка (х9; уа) лежит на эллипсе. Это значит, что
х* и*
— 4-——1
Точка, симметричная (ха; у9) относительно оси Ох, имеет
координаты (х0; —уа). Но
*• i (-У.)'_*> , уг _,
поэтому точка (дг0; —уа) также лежит на эллипсе. Точка
(—ха; г/0) симметрична точке (ха; уа) относительно оси у,
а точка (—xt; —уа) симметрична относительно начала
координат. Совершенно аналогично предыдущему уста-
навливаем, что обе эти точки также лежат на эллипсе.
Итак, эллипс имеет две оси симметрии (ось х и ось у)
и центр симметрии (начало координат). Числа а и Ъ
в уравнении F.4) имеют простой геометрический смысл.
Найдем точки пересечения эллипса с осью х. Для этого
в F.4) положим у=0. Получим д^ = а*, х, = а, xt=—а.
Точки пересечения с осью у будут иметь ординаты
yi==b, yt = —Ь. Поэтому числа а и Ь суть длины поло-
вин осей симметрии эллипса.
Окружность является частным случаем эллипса. Она
получается, если a = b = r (сравни уравнение на стр. 37).
Рассмотрим эллипс F.4) и окружность радиуса а
с центром в начале координат. Уравнение такой окруж-
ности есть
х1 + уг = а'. F.5)
Точки пересечения эллипса F.4) с осью Ох имеют коор-
динаты xt = — а, хх = а, В этих же точках окружность
F.5) пересекает ось Ох. Возьмем какое-нибудь х=хй
и найдем соответствующие значения у из уравнений F.4)
262 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
и F.5). Из F.4) у, =-| 1/а" — х\ из F.5) Уа = Уа1^х\
Поэтому
В соответствии со сказанным в части I, § 7 эллипс
может быть получен из окружности радиуса а путем
растяжения Г если — >1] или сжатия Гесли — <1)всех
вертикальных размеров. У эллипса, фокусы которого
расположены на оси х, всегда Ь<а, так как Ь* = а* —
— с* <а*. Поэтому эллипс сжат по оси у. Сравнивая
эллипс с вписанной в него окружностью радиуса Ь,
можно сказать, что эллипс получается из такой окруж-
ности растяжением по оси х в -— раз.
Упражнения
1. Провести (от руки) эллипс, уравнение которого ос ~Ь-т~= 1 •
2. Составить уравнение касательной к эллипсу —-\-уг=\
в точке х = 1; у = -^—.
Xх ы*
3. Доказать, что уравнение касательной к эллипсу —s + ^r7^!
в точке (*„; уа) можно представить в виде —?
§ 7. Вычисление площадей
В части II было показано, что величина определен-
ь
ного интеграла }j{x)dx дает площадь, ограниченную
а
сверху линией y=f(x), снизу осью х и по бокам верти-
кальными прямыми х = а и х = Ь (рис. 102). Поэтому
умение находить определенные интегралы дает возмож-
ность вычислять стандартными приемами различные пло-
щади, в то время как элементарная математика позволяет
находить только площади прямолинейных фигур и круга.
§ 7]
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
263
Найдем площадь, ограниченную сверху кривой у = схп
(л>0), снизу осью х и справа прямой х=х (на рис. 103
л = 2, с = 0,25):
G.1)
Формулу G.1) перепишем так:
с 1 rrnr
или так как сх" = у (ха), то получаем:
5= 1 и (х )х .
Величины у и х имеют размерность длины. Из G.2) ви-
дим, что S действительно измеряется в единицах пло-
щади. Мы видим, что по
порядку величин площадь
есть у (ха)-ха; от этого
y-ffx)
Рис. 102.
произведения величина площади отличается только мно-
жителем , . , который по порядку близок к единице
при не слишком больших п.
В качестве следующего примера найдем площадь,
ограниченную сверху линией
снизу осью х, слева прямой х = хЛ и справа прямой
264 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
: = А(А>ха) (рис. 104). Эта площадь равна
Ах х
dx = — сае
Xq
ха
= са[е а—в а\. G.4)
_ Ха_ А_
Если А велико по сравнению с лс„ то е ^*^>е а. Уве-
личив значение А, мы, как видно из G.4), почти не из-
меним значение SA. При неограниченном увеличении А
А
величина е а неограниченно приближается к нулю. По-
этому можно говорить о площади фигуры рис. 104, не
ограниченной справа. Эта площадь есть
се adx — cae a==
У(хл)а.
G.5)
В формуле G.3) показатель степени должен быть без-
размерным числом. Поэтому размерность а такова же, как
и размерность х, т. е. длина. Размерность у также
»•• длина. Размерность S опять-
\ '' таки площадь.
\ Оказывается, что очень прос-
^ то выражается площадь под
2 А
Рис. 104.
Я *х
Рис. 105.
одной дугой синусоиды (рис. 105). Действительно, эта
площадь есть
S = j sin х dx = — cos x\ =2.
о о
Определим площадь S эллипса. Заметим, что в силу
симметрии достаточно найти площадь 5г той его части,
которая лежит в первом квадранте, и результат умножить
на 4. Итак, 5=4S,. Для того чтобы подсчитать Sv найдем
§ 7] ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ 265
у из уравнения эллипса F.4)
з -^ а ' '
так как в первом квадранте у^>0, то берем
, Ь_ у д д
Поэтому
~l?dx. G.6)
Величину интеграла G.6) легко найти, выполнив замену
переменной по формуле x=as'mt. Получим:
*— x*dx = \ a V\ — sinV a cos t dt= \ a*cos*t dt
Пользуясь G.7), получаем из G.6) Sx = -|-^
Площадь всего эллипса S=nab. Если a=6 = r, то по-
лучаем S = nr' (площадь круга) в полном соответствии
с тем, что при a=6 = r эллипс переходит в окружность.
Отметим одно важное обстоятельство. Еще в части II
мы отметили, что площадь (интеграл) может быть как
числом положительным, так и отрицательным. Ввиду этого
при нахождении площади нужна некоторая осторожность.
Пусть, например, нас интересует количество краски, необ-
ходимое для того, чтобы покрасить площадку, ограничен-
ную двумя дугами синусоиды и осью х (см. рис. 51), если
на окраску единицы площади требуется а граммов краски.
Как показано на стр. ПО, в этом случае нельзя сразу
вычислять всю площадь одним интегралом. Приходится
отдельно брать интегралы по отрезкам от 0 до я и от я
до 2я.
Вообще, если подынтегральная функция y = f (x) меняет
знак, то для решения задачи о расходе краски нужно
промежуток интегрирования разбить на части, в которых
266 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
/(л) знака не меняет, и считать интеграл по отдельным
частям, после чего взять сумму абсолютных величин по-
лученных интегралов.
Найдем еще площадь фигуры, ограниченной сверху
линией у — х"е~х (п — целое положительное число), снизу
осью х при х ^ О (справа фигура не ограничена).
Эта площадь выражается интегралом
CD
~* dx.
М
Для вычисления этого интеграла применим интегрирование
по частям, полагая
e-*dx=dg, x"=/.
Тогда
g=—e-*, df—nx"-1 dx,
\хпе-х dx — — xne-x-\-\nxn-xe-*dxl
Поэтому
CD 00
J x"e-xdx=[— xne-*'F-\-lnxn-*e-xdx.
0 ° 0
В § 21 части III было установлено, что х"е~х=
=^ -О. Так какл^е-* —Опри дс=О, то [—х"е-х\° = О,
следовательно,
CD ОО
xdx= J nx*-xe-*dx.
а
Обозначим J x"e~*dx = I„. Тогда /„ = «/„_х.
о
Применив интегрирование по частям к /„_,, получим
точно так же /п_1 = (п—1)/„_, и т. д. Поэтому
а
со
/п=п(„—1)(п —2)...3-2/0.
ОО
Но /„= ^ e~xdx. Величину этого интеграла мы получим,
положив в G.5) с=\, а—\, xt = 0. Тогда Та = е°=1.
§ 8] СРЕДНИЕ ЗНАЧЕНИЯ 267
Таким образом,
CD
/„= \xne-xdx = n{yi — l)(n — 2) ...3-2-1 =n! G.8)
о
Упражнения
1. Найти площадь, ограниченную одной дугой линии у = sin* x
и осью х (график функции t/=slnxx изображен на рис. 106).
У
I
( я х
Рнс. 106.
Указание. Воспользоваться формулой
sin'* = -= =- cos 2х.
2. То же для линии у =cos*x.
3. Найти площадь, ограниченную сверху линией у=х{\ —х),
снизу осью х.
4. Найти площади, на которые парабола // = -=-** делит окруж-
иость х* + уг = 8.
5. Найти количество краски, необходимое для окраски площади,
ограниченной кривой у = ¦=—j-—j, осью х и вертикальными прямыми
х = 1 и х = — 1.
6. То же для площади, ограниченной кривой у =ха + 2дс* — х — 2
и осью х.
Указание. Предварительно построить график функции
— х — 2.
х* и*
7. Найти площадь эллипса ==¦ -4-^- = 1.
§ 8. Средние значения
Напомним читателю, что средним значением функции
f(x) на промежутке от х=а до х = Ь называется
ь
___. (8.1)
268 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Отметим два простых факта, относящихся к средним
значениям.
1. Среднее значение постоянной величины на любом
промежутке есть сама эта постоянная. Это ясно физически:
действительно, если мгновенная скорость ие изменяется,
то средняя скорость за промежуток равна этому постоян-
ному значению мгновенной скорости.
Совсем просто получить это и из формулы (8.1)
2. Среднее значение суммы двух функций равно сумме
средних значений слагаемых
Действительно,
а
ь ь
* W dx + V=rb IУ ¦ W dx = ^ + У*
Найдем среднее значение функции y=*=sinx на проме-
жутке от х = 0 до х = л
к
J* sin х dx
Среднее значение функции ^ = sinx на промежутке от
х=0 до х = Ь
ь
J* sin х dx
Что будет, если неограниченно увеличивать число Ь, т. е.
неограниченно увеличивать промежуток?
§ 81 СРЕДНИЕ ЗНАЧЕНИЯ 269
Числитель (8.2) при любом Ь не больше двух (он ра-
вен двум, если cos 6 = — 1, т. е. при 6 = я, Зя, 5я, 7я,...).
Знаменатель (8.2) будет неограниченно увеличиваться, по-
этому вся дробь будет неограниченно приближаться к нулю.
Поэтому чем больше промежуток, тем ближе к нулю сред-
нее значение sin^c.
Покажем, что среднее значение функции i/ = cos* на
бесконечном промежутке также равно нулю. Действительно,
J* cos х dx
Если теперь неограниченно увеличивать число Ь, то знаме-
натель (8.3) неограниченно увеличивается, а числитель
остается не больше единицы. Следовательно, вся дробь
стремится к нулю: # @; оо)=0.
Буквально так же получим, что среднее значение функ-
ции y=ca&kx на бесконечном промежутке тоже равно
нулю.
Найдем среднее значение функции y — sm*x на беско-
нечном промежутке от jf = O до дг = оо.
По известной формуле тригонометрии
Отсюда
Воспользовавшись формулой sin*jt-f-cos*x=\, полу-
чаем среднее значение cos'x на том же промежутке
Упражнения
1. Найти среднее значение функции у = х? на промежутке от
дг = О до * = *„. "
2. Найти среднее значение функции у = Се** на промежутке,
в котором у меняется at у = п до у=хт, выразить это среднее зна-
чение через пит, исключая С и ft из ответа. Исследовать полу-
ченное выражение при т, близком к n:m=n-\-v, v^n.
270 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV"
3. Найти средние значения функций у = sin* х и у = cos* х на про-
межутке: а) от х = 0 до х=л; б)отл: = Одох = —.
4
4. Определить период функции // = sin (a>t -j-a), где о», a — по-
стоянные числа. Найти среднее значение функции у1 за ее период.
§ 9. Длина дуги кривой и кривизна
Поставим задачу найти длину дуги s кривой y = f(x)
от точки х=а до точки х=Ъ (рис. 107).
Длину малого отрезка линии АС заменяем длиной от-
резка прямой, соединяющей точки А и С. Мы рассматри-
ваем только кривые без
разрывов и изломов. По
теореме Пифагора получим:
0
Рис. 107.
Отсюда
?) • (91>
Д«/
Переходим в (9.1) к пределу, Ад:—>-0; при этом ^
превращается в производную y'=f'(x), где y = f(x) —
уравнение линии; получаем*):
ds = V\-\-f'\x) dx.
Вся искомая длина дуги есть
ь
(9.2)
Из-за наличия корня под знаком интеграла в (9.2)
интеграл редко удается легко взять.
Приведем несколько примеров, когда выкладки не-
трудно довести до конца.
•) Отличие длины дуги от длины -отрезка прямой порядка (Дх)*
и при переходе к пределу (к дифференциалам) им законно можно
пренебречь.
§9]
длина дуги, кривой и кривизна
271
1. Длина окружности. Будем искать длину
окружности хг-\-у* — #г. При этом найдем длину s чет-
верти окружности, лежащей в первом квадранте, и резуль-
тат умножим на 4. Из уравнения окружности
У R1 — хг
По формуле (9.2)
R
(9.3)
_ о а
Введем новую переменную t по формуле
x=R sin t;
тогда dx = R cos / dt и из (9.3) получаем*):
откуда получаем длину окружности
2. Цепная линия. Это—
кривая, уравнение которой
), (9.4)
где а — постоянное число. На-
звание «цепная линия» происхо-
дит от того, что такую форму
принимает гибкая и нерастяжи-
мая тяжелая нить (например,
цепь), подвешенная за оба кон-
ца. График цепной линии при- Рис. 108.
веден на рис. 108 (для а = 2).
Найдем длину дуги цепной линии от точки х=0 до
точки х=хл.
•) См. § 16 части 111.
272 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
зе_ х_
еа е~ <Г
Из (9.4) у' = 2 ; поэтому
X JC
X — — — ^ ЛЧо
С^-Ьв» 1 Г* *1 _ , *«
Сеа +е а. 1 Г fL _*| д / *«. - ^-\
==J 2^ -rfx=Ta[ea_e eJe==^^a_e -j.
С длиной дуги связано определение кривизны, отлич-
ное от рассмотренного в § 2. Возьмем малый участок
кривой (рис. 109) длиной ds и найдем угол между каса-
тельными к кривой в концах этого участка. Этот угол
Рис. 109.
можно рассматривать как приращение da. угла а наклона
касательной к оси х. Проведем в двух соседних точках
нормали (перпендикуляры к касательным). Угол между
нормалями равен углу da. между касательными, сргласно
известной геометрической теореме. Отсюда можно найти
расстояние R точки пересечения нормалей от кривой.
Будем рассматривать малый участок кривой как дугу
окружности.
Нормаль к окружности, очевидно, представляет собой
радиус. Точка пересечения нормалей есть центр окруж-
ности. Если бы кривая была окружностью, то ds=Rda
§ 10] ПРИВЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ 273
da 1
или ^=^-; эта величина постоянна для любого участка
дуги окружности. Для произвольной кривой эта величина
^j для бесконечно малого участка кривой может служить
определением кривизны в данной точке. Пользуясь фор-
мулой для ds и тем, что a = arctgt/', можно убедиться,
что вычисленная таким образом кривизна совпадает с кри-
визной, определенной в § 2. Действительно,
da
ds ,
1
A+4
Упра;
dy'
dx
кнения
1. Записать в виде интеграла длину дуги параболы у—х* от
точки @; 0) до точки A; 1).
2. Записать в виде интеграла длину дуги линии «/ = е* отточки
х = 0 до точки х = 1.
3. Записать в виде интеграла длину эллипса.
4. Довести до конца задачу 2, выполнив в интеграле замену
переменной 1 -|-etx = z2.
§ 10. Приближенное вычисление длины дуги
В § 9 мы получили формулу для вычисления длины
дуги кривой
ь
s=\V\+y'x(x)dx. (ЮЛ)
а
Там же было отмечено, что чаще всего функцию
У \-\-у'г (х) проинтегрировать в элементарных функциях
трудно (или даже невозможно) из-за наличия корня.
Поэтому большой интерес представляют приближенные
формулы для вычисления длины дуги.
Предположим, что величина у' (х) мала по сравнению
с единицей: | у' {х) | <^ 1. Тогда, пренебрегая в (ЮЛ) у'* (х),
получим:
ь
$dx = b — a. A0.2)
274 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
Разность Ь — а есть длина горизонтального отрезка,
концы которого х=а и х = Ь. Формула A0.2) показы-
вает, что если у' мала по абсолютной величине (кривая
мало отклоняется от горизонтального отрезка), то и длина
дуги этой кривой близка к длине го-
ризонтального отрезка (рис. 110, а).
Если у'2(х)^\, то в A0.1) пре-
небрегаем единицей по сравнению
__ с у'*{х). Получаем:
X Ь Ь
s =* J Vy"(x) dx=\y' (x) dx =
а а
= У(Ь) — у{а). A0.3)
тоиа (часть III, § 20), получим:
Формула A0.3) показывает, что в
этом случае длина дуги кривой близ-
ка к длине вертикального отрезка,
концы которого есть у (а) и у (Ь)
(рис. 110,6). Действительно, если
производная у' велика, то кривая
круто поднимается вверх, а поэтому
похожа на вертикальную прямую
(для вертикальной прямой производ-
ная бесконечна).
Формулы A0.2) и A0.3) дают про-
стые, приближенные формулы для
длины дуги, но это очень грубые при-
ближения, которые можно получить
и без A0.1).
Получим более точные формулы.
Пусть | у' (х) | <^ 1. Удерживая два
первых члена в формуле бинома Нью-
Формула A0.1) дает:
ь
§ 10J ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ 275
Если \yf (х)\^> I, то
Vl+y"(x)=y' (х) /"l-f^ ;
к последнему корню применим формулу бинома Ньютона,
так как—-—<Г1,
у
==«' w. [i + ^]=у
Подставляя последнее в A0.1), получаем:
[ V
а
а
Итак, мы получили приближенные формулы:
ь
</*(x)dx, если \у
ь
а
-,. . , если
а
(Ю.4)
Входящие сюда интегралы проще, чем интеграл в
A0.1), поэтому по этим формулам гораздо проще считать,
чем по формуле A0.1). Однако эти формулы прибли-
женные.
Какую же ошибку делаем мы, пользуясь ими? Первая
из формул тем лучше, чем меньше | у' |, а вторая тем
лучше, чем больше \у J; обе формулы дают наиболее
плохой результат при \у'\=.\. Поэтому для оценки по-
грешности рассмотрим самый невыгодный случай у' (х)=1 *).
•) Если у' (х)—1, то у{х) = х-\-с, график этой функции —пря-
мая линия.
276 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
По точной формуле A0.1)
ь
s=J]/T+T^c = j/2F— a). A0.5)
а
По первой из формул A0.4)
ь
йх = \{Ъ — а). (Ш.б)
Вторая формула A0.4) дает то же самое: s==yF—а).
Сравнивая A0.5) и A0.6Х видим, что наибольшая по-
грешность приближенной формулы 6°/0.
При вычислении длины дуги кривую следует разбивать
на участки, на которых либо | у' | =sS 1, либо | у' | s* 1.
Тогда ошибка будет во всяком случае не больше б°/0.
А так как у'*(х) принимает значение, равное 1, лишь
в отдельных точках кривой, то при правильном разбиении
линии на участки ошибка будет меньше 6°/0. Длины прямо-
линейных отрезков, конечно, находить по приближенной
формуле незачем.
Рассмотрим примеры.
1. Найти длину дуги параболы у=х* между точками
с абсциссами лс = О и х = 2*).
Найдем производную у' = 2х. Она равна 1 при дс = 0,5
и больше 1 при х>0,5. Поэтому длину дуги (s^, соот-
ветствующую изменению л; от 0 до 0,5, найдем по первой
формуле A0.4), а длину дуги (st), соответствующую изме-
нению х от 0,5 до 2,— по второй формуле:
0.5
s1==@,5 —0)+0,5f 4x^ = 0,
о
1
st=4-0,25+0,5 С ^ =3,75+0,25 (In 2 —In 0,5)=4,10.
о,»
Искомая длина дуги
s = Sl + st = 0,58-{-4,10=4,68.
*) В этих примерах вычисления проведены с двумя знаками
после запятой.
§ 10J приближенное вычисление длины дуги 277
Подсчитаем точное значение длины дуги по формуле
A0.1):
о
Сделав замену 2х = г, по формуле 33 (стр. 221) по-
лучим:
= 1 [ху to* + 1 + i- In Bх -{-У to* + 1)]. A0.7)
Недоверчивый читатель может убедиться в справедли-
вости формулы, взяв производную правой части A0.7).
Пользуясь A0.7), получаем:
s =-1 [2VT7 +1 In D + KT7)] =4,65.
Ошибка при подсчете по формулам A0.4) составила
около 0,7%.
2. Найти длину дуги кривой у = ех между точками
с абсциссами х = 0 и х = 1.
В этом случае у' = ех, и при изменении х от 0 до 1
производная растет от 1 до е. Поэтому используем вторую
формулу A0.4)
s = ex~ e* 4-0,5 \ ^ =2,72 — 1—0,J
= 2,04.
Точная формула дает для длины дуги значение (см.
задачи 2 и 4 из § 9)
-!¦„ ^1=2.00.
Ошибка приближенной формулы 2%.
Иногда для приближенного вычисления длины дуги
подынтегральную функцию в A0.1) разлагают в ряд по
степеням лг. При этом, удерживая надлежащее число
278 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
членов разложения, можно получить значение длины
дуги с любой степенью точности.
Рассмотрим пример. Определим длину окружности.
При этом будем искать длину s дуги окружности, соот-
ветствующую центральному углу в 30° (рис. 111). Дли-
на окружности C = 12s. Ясно, что мы получим такой
. же интеграл, как и в (9.3), но с
'^ с другим верхним пределом
ол
Заметим, что ОЛ = ./? sin 30° =
-y-R- Поэтому
•г*
Рис. 111.
ч-
Rdx
A0.8)
Подынтегральное выражение преобразуется следующим
образом:
R R 1
Но
A0.9)
Выражение A0.9) разложим в ряд по формуле бинома
Ньютона *). Для этого положим (^\ ==t. Получим:
•) См. часть III, формула B0.3).
§' П J ' вычисление объемов 279
Подставляя A0.10) в A0.8) и интегрируя, получим:
Видно, что члены ряда A0.11) убывают довольно
быстро. Поэтому для получения s достаточно взять
несколько первых членов ряда. Взяв один член ряда,
получим s = -^R, откуда длина всей окружности C=6i?.
Взяв два члена, получим ,5 = 0,5217?, С = 6,2527?. Три
члена ряда дают s = 0,523/?, С=6,276 # и т. д.
Мы знаем, что длина окружности С = 2я/?. Сравнивая
это с полученными намн результатами, находим прибли-
женные значения числа я:
3, 3,126, 3,138, ...
Чем больше членов ряда A0.11) взять, тем точнее полу-
чим значение я. Значение числа я с семью верными
десятичными знаками 3,1415926.
Упражнения
1. Найтн, пользуясь приближенными формулами, длину дуги
цепной линии между точками х = 0 и *=2(a=l). Сравнить
с точным значением длины дуги.
2. Найти длину дуги гиперболы ху = —1 между точками * = 0,5
и х= 1.
Замечание. В этом случае точного решения получить нельзя,
так как интеграл в A0.1) не может быть выражен с помощью эле-
ментарных функций.
3. Получить приближенные значения числа п, исходя из подсчета
длины дуги окружности с центральным углом в 45° (удержать три,
четыре и пять членов ряда).
§ 11. Вычисление объемов. Объем и поверхность
тела вращения
В части II (§ 14) была получена формула
V = §S(x)dx, A1.1)
где S(x) — площадь сечения тела плоскостью, перпенди-
280 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
кулярной к оси х и проходящей через точку х (советуем
читателю повторить вывод этой формулы).
При помощи этой формулы было получено выражение
для объема пирамиды. Буквально так же получается объем
конуса. Возьмем начало коорди-
нат в центре круга, лежащего в
основании конуса, а ось х на-
правим по высоте конуса
(рис. 112). Пусть S(x) — пло-
щадь сечения конуса плоско-
стью, перпендикулярной к вы-
соте и отстоящей от основания
конуса на расстоянии х. Сечение
это есть круг радиуса гх. Из
подобных треугольников
гх Н — х
Т~~ТГ~ '
Рнс. 112.
где г — радиус основания, Н —
высота конуса. Отсюда '"х=тз- (Н — х), а следовательно,
и
н
пг*(Н -*)'
Н1 3
н
пг*Н
Для получения объема шара поместим начало коорди-
нат в центр большого круга, а ось х направим по диа-
метру шара, перпендикулярному к плоскости этого боль-
шого круга.
Сечение плоскостью, перпендикулярной к оси х и
отстоящей на расстоянии х от начала координат, есть
круг радиуса R^. При этом Rx=
реме Пифагора. Поэтому
1 — хж по тео-
V=
L
§ 11]
ВЫЧИСЛЕНИЕ ОБЪЕМОВ
281
Из формулы A1.1) следует принцип Кавальери *):
пусть между двумя параллельными плоскостями Р и Q
расположены два тела; если в сечении этих тел всякой
плоскостью, параллельной Р и Q, получаются равновели-
кие фигуры (равны подынтегральные функции S(x)), то
и объемы этих тел равны.
Пусть тело получено вращением фигуры, изображенной
на рис. 113, вокруг оси х (фигуру такого вида называют
криволинейной трапецией). В
этом случае сечение есть круг
радиуса y = f(x)inS(x)=siy1.
Пользуясь A1.1), находим:
A1.2)
Найдем, например, объем
тела, получаемого при вра-
щении верхней половины эллипса ^--{-^=1 вокруг
оси х. Тело это называется эллипсоидом вращения.
Из уравнения эллипса У = — Vcf—х*, а из A1.2)
__?- =4яа6а
0
а
Ь х
Рис. 113.
При a = b = R получаем объем шара радиуса R.
Выведем теперь формулу для поверхности тела вра-
щения (рис. 114). Рассмотрим тело, ограниченное сече-
ниями, проходящими через точки х и x-\-dx. Обозначим
через dF боковую поверхность этого тела. Считая его
усеченным конусом, получим:
dF=п[у (х) + У (х + dx)] ds,
где ds — длина малого участка кривой, причем
ds = V\+y'\x)dx (см. § 9). Сумму y(x)+y(x-{-dx)
*) Кавальери —математик первой половины XVII века. Упомянутый
принцип был сформулирован (по существу без доказательства) в его
книге «Геометрия неделимых» A635 г.).
282 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
можно заменить на 2у(х), пренебрегая величиной y'(x)dx
по сравнению с у (х) *).
Поэтому
dF = 2лу (х)У\-{-у"(х) dx.
Вся площадь поверхности вращения есть
ь
F=2л j у (х) Vl-\-y"(*) dx. (И.3)
При помощи этой формулы легко находим поверхность
шара. Действительно, шар получается вращением верхней
Рнс. 114.
полуокружности вокруг оси х. Уравнение окружности
хх-\-уг = а1, откуда
i/-? -г- ... — х
I uA
Подставляя в A1.3), получаем:
= 2« f Va'—
: = 2ztax
a* —
•) Заметим, что в выражении dF сумма y{x)-\-tf(x-\-dx) мно-
жится на ds, так что величина, которой мы пренебрегаем, порядка
dx-ds^dx*.
ОТВЕТЫ И РЕШЕНИЯ
283
Упражнения
1. Найти объем цилиндрического отрезка, т. е. тела, отсекаемого
от прямого кругового цилиндра радиуса R плоскостью, проведенной
через диаметр основания цилиндра под углом а (рис. 115).
Рис. 115.
2. Найтн объем конуса, пользуясь тем, что конус — это тело,
получаемое при вращении прямоугольного треугольника вокруг одного
из катетов.
3. Найти объем, тела, полученного при вращении фигуры, огра-
ниченной сверху линией # = Ух, снизу осью х, справа вертикальной
прямой х = 2.
ОТВЕТЫ И РЕШЕНИЯ
§ I. 1. у — уо = пха"~1(х — ха), у — уй = —(х—ха).
0+8=— ^
; у = 0, х = 0. 3. у-2 = 3(х-1), у-2 =
= j(x—l); y—\=—x, д—\=х.
4. На данной окружности, ее уравнение х*-|~#* = 4, имеются
две точки, у которых х = 1. У одной из них у = У~3, у другой
у=. —У^З. Поэтому задача имеет два решения. Определим у'{О
двумя способами", а) из уравнения окружности у = ±7^4 — х1, причем
анак плюс следует брать для точек верхней полуокружности,
а знак минус для точек нижней полуокружности. Следо-
вательно, для верхней полуокружности у' = , поэтому
У 4 — *'
284 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
для точки A; У~3) получаем у' A)= = . Уравнение касательной
^3
в этой точке у — УЗ = — — (дг — 1), нормали у — УЗ = УЗ(х — 1).
Для нижней полуокружности у = — У4 — х\ у' = ——Х . Для
точки A; — УЗ) получаем у' A) = -—. Уравнение касательной
УЗ
в этой точке у + УЗ z=-—(x— 1), нормали у + У3"=—У3~(х — 1).
Уз
б) По правилу дифференцирования функций, заданных неявно, на-
ходим (см. стр. 165) у' = — . Поэтому для точки A; УЗ) получаем
у' A) = —17=» а Для точки A; —УЗ~) получаем у'A) = -у=..
§ 2. 1. Вогнута. 2. Точки перегиба при х, = — 2, х,= 1.
3. При д:=1 точка перегиба. 4. Из уравнения кривой у = х* нахо-
—— —, откуда при х = О
получаем /? = —; при х =-$- получаем
2х, у" —2. Поэтому /?=
§з. 1.<=
5 „----„ g
2. Пусть основание треугольника А С = а,
высота ВН = h, пусть DEFG — искомый
прямоугольник. Из подобия (рис. 116)
ТЛЕ? D ff
-Тр=-^т>; обозначая DE — х, получаем
дг h—HxH „ „
= ^_> откуда «,//=,
Площадь прямоугольника S(x) = xh ( 1 — ) = hx х*. Ре-
шая уравнение S'(x)=O, находим *=-=-; тогда НХН= — .
3. Искомым прямоугольником является квадрат,
*. ¦. Радиус
основания банки r=y kz, высота ее // = 2г. 5. t= » , , .
7. Время движения 7* = — У~а* -\-х* -) У^1
(рис. 117). Условие -г— = 0 дает -
— xf, где с = A jfl,
с — х
Замечая, что
sin a v
ОТВЕТЫ И РЕШЕНИЯ
с — х
;=r sin а,
285
= stnP, находим
— . Это—закон Снелля, т. е. точка должна двигаться так,
А
Я/
как движется через границу двух сред световой луч. Для доказа-
тельства того, что мы действительно получаем минимум Т, доста-
точно выписать -7-$- . Легко убедиться, что прн всех х будет
§ 4. 1. Ушах = 2 ПРН -« = 0, ymin = — 2 при х=2. 2. Максиму-
мов я минимумов нет. Кривая пересекает ось х в точке * =
= 1 -f- у^14 =: 3,4, а ось у в точке «/ = — 15. 3. Максимумов н мини-
мумов нет. Кривая пересекает ось х между точками х = 0 и х =—1,
а ось у в точке у = 3. 4. Три корня, б. Три корня. 6. Два корня.
7. Один корень.
§ 5. 1. Ут\а = 3. 2. При х = 0 f/max=0. 3. При х = 0 {^,= 1.
§6. 1. Для данного эллипса длины полуосей а =5, й = 2.
2. Из уравнения эллипса у^=.—— , откуда р' = —
. Уравнение касательной у — ~- = уп.(х — 1)
2 V 3
„t .л
\. Из уравнения эллипса
Ь х
a Y& -х* ' h
Так как точка (х„;
лежит на эллипсе, то -т-г-гг*=1> откуда
t— У а* х1' поэтому у' (х0) = ^--i . Уравнение касательной
286 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
х Ь*
У — У а = — ?• ^ (* — *о) или ууоа* — у\а* = — х^сЬ* -\- х\Ь*. Разделим
Х1
1
все члены уравнения на а*Ьг, получим ^г—}Т — 5^ + ^ или
^ + ^r-=^-+^i- Остается заметить, что #д
§ 7. 1. %- . 2. -^ . 3. i-. 4. 2я +4- и 6л — 4- • 5. a In 2,
Z ^ о о о
где а — количество краски, идущее на окраску единицы площади.
в. у? а. 7. 10 я.
я л*
= n(l +2^)= —5"— • '• a) (->6a средних значения равны -^- ;
б)— ^и-^--| . 4. Если Т — период, то должно быть
sin [со (t -\- Т) 4- «1= sin (со* -f-а), откуда со (/ ¦+¦ Т) + а = со* -f- а + 2я,
соТ"=2я, Т1 = — . Но период функции у* равен — = —. Следо-
Си & О
вательно, надо найти среднее значение функции у = sin2 (со* -(- а)
на промежутке от * = 0 до / = —.
(О
. 2. S={y \ + e**dx.
3. S =
= — \ у а1 + -1 _ -1 dx* *• Выполняя указанную замену пере-
0
о С ггйг „ . Г 2*dz f* zzdz
с, получим S = V -j р- . Найдем \ я _ • \ я . =
менных,
ОТВЕТЫ И РЕШЕНИЯ 287
интеграле запишем подынтегральную функцию так:
1 ._ 1 А В
ZS — I (Z— 1) (Z -f- 1) 2— 1 ^2+1 •
Числа Л и В найдем, выполнив приведение к общему знаменателю
н приравняв числители A (z-\-\)-\-В (г—1) = 1, откуда А = -^-,
В =— -у . Окончательно \ ¦-, = г -\- -^- In Z ~ , поэтому S =
§ 10. 1. Разбивая на участки от х = 0 до дс = 0,9 и от х = 0,9 до
х = 2, находим Si = 1,043, S,^=—— -^ (-
2
]р 2
-| \ -^ =^j dx. В последнем интеграле можно положить ех = t.
0,9
Окончательно получим St = 2,624, S = S, ~\-St= 3,667. По точной
фзрмуле находим S = 3,627. Ошибка составляет 1%. 2. S= 1,146.
3. Длина дуги окружности, о которой идет речь, есть
Vf
Rdx
VT
= R V2 V + 12 + Тбб + 896 + 78432~+ *'' }'
Соответственно для числа я получаем:
а) я="^
б)
288 ПРИЛОЖЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ГЕОМЕТРИИ [Ч. IV
§ 11. 1. Примем диаметр А В за ось х, точку А за начало
координат. Сечение, перпендикулярное к диаметру АВ, есть прямо-
угольный треугольник PQR, его площадь (см/ рис 115) S(x) =
= —PQ-QR = ~PQitga. Но по известной теореме геометрии
= AP-PB = x (IR — x). Поэтому S (х) — ~ х BR — ж) tga.
(Ar)dr=y/?'tga. 3. У = 2я.
ЧАСТЬ V
ВЫТЕКАНИЕ ВОДЫ. РАДИОАКТИВНЫЙ РАСПАД
И ДЕЛЕНИЕ ЯДЕР. ПОГЛОЩЕНИЕ СВЕТА
§ 1. Вытекание воды из сосуда. Постановка задачи
Рассмотрим вытекание воды из сосуда, в котором
внизу имеется отверстие или тонкая трубка. В сосуд мо-
жет также поступать вода из внешнего источника. Эта
задача очень проста и наглядна по своей постановке.
Вместе с тем те математические методы, которые нужны
для описания вытекания воды, применяются и в более
сложных и интересных задачах.
Представим себе сосуд, в который втекает (или из
которого вытекает) вода. Объем воды, находящейся в со-
суде, обозначим через V (см3). Этот объем со временем
меняется, т. е. V есть функция времени t(cek). Каков смысл
величины j-?
Ясно, что dV = V (t -\- dt) — V (t) есть количество воды,
поступившее в сосуд за время dt. Поэтому -тт есть ко-
личество воды, поступившее в сосуд за единицу времени,
т. е. скорость изменения количества воды в сосуде. Эта
величина носит специальное название «поток воды». Бу-
дем обозначать поток через q (t). Если q > 0, то вода
поступает в сосуд, если же q < 0, то вода вытекает из
сосуда, количество воды в сосуде уменьшается.
Если зависимость потока воды от времени известна,
т. е. известна функция q (t), то
? = *(')• (LI)
В этом случае задача нахождения V подобна задаче
Ю я. Б. Зельдович
290 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
определения пути по заданной скорости, к еще в части I
было выяснено, что такая задача решается интегрированием.
Для того чтобы задача имела вполне определенное ре-
шение, нужно, чтобы было задано количество воды Vt,
которое находилось в сосуде в определенный начальный
момент времени /„. Условие, что V = V9 при t = t9 на-
зывается начальным условием.
Количество воды, которое втекло в сосуд за время
и . .
от ta до tt, есть \q(t)dt. Отсюда количество воды в
К
сосуде в момент tx
t,
(t)dt. A.2)
Это выражение справедливо для любого момента вре-
мени tt и, следовательно, полностью определяет иско-
мую зависимость V от tt. Заметим, в частности, что при
t, = ta интеграл в формуле A.2) равен нулю и V (ta) = Va.
Таким образом, решение A.2) действительно удовлетво-
ряет поставленному условию относительно количества
воды в момент /0 (начальному условию).
Отметим, что формулой A.2) можно пользоваться и
при /,<fe. Однако смысл формулы A.2) при /,<?, и
tt >ta различный. При tl>ta величина V(tj) есть коли-
чество воды, которое будет в сосуде в момент tit
если в момент ta в нем было количество воды. Va и по-
ток воды задан функцией q (t). При tl< tn величина
V (tt) есть то количество воды, которое должно находиться
в сосуде в момент tl для того, чтобы в более позднее
время, к моменту ta, в нем было количество воды Va
при потоке, заданном функцией q(t).
Вместо обозначения tx можно писать просто t. Тогда
формула A.2) принимает вид
V (t) = Vn+\q(t)dt. A.3)
К
Строго говоря, при этом буква t обозначает верхний
предел интегрирования и таким образом «занята». Поэтому
переменную интегрирования следовало бы обозначить
§ 1J ВЫТЕКАНИЕ ВОДЫ ИЗ СОСУДА. ПОСТАНОВКА ЗАДАЧИ 291
какой-нибудь другой буквой, например т, и писать A.3)
в виде
t
что совпадает с A.2), если в A.2) заменить tx на t и t
на т. Однако обычно этого не делают и пишут формулу
в виде A.3). При этом недоразумений не возникает. Надо
только помнить, что в A.3) q(t) это не значение q на
верхнем пределе, а функция переменной интегрирования,
пробегающей все значения от tt до t.
Формулу A.3), дающую решение задачи о вытекании
воды, если задан поток q (/) и количество воды в началь-
ный момент t = tn, можно получить при помощи несколько
иных рассуждений. Из A.1) в силу определения неопределен-
ного интеграла следует, что
Предположим, что неопределенный интеграл от функ-
ции q (t) каким-либо образом найден. Обозначим его / (t).
Тогда
где С — постоянная интегрирования. Отсюда
V @ =*/(*) +С. A.4)
Для определения постоянной интегрирования воспользу-
емся начальным условием, т. е. потребуем, чтобы при
t = t<i было V = Vn. Подставляя в A.4) t = ta, получим:
откуда
C — V9 —
Подставляя значение С в A.4), находим:
Это совпадает с формулой A.3), так как
t ...
f
10*
292
РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР
[Ч. V
Формулу A.4) можно назвать общим решением урав-
нения A.1). Выбирая то или иное значение С, из фор-
мулы A.4) можно получить различные частные решения,
соответствующие различным начальным условиям.
Однако обычно поток как функция времени не известен.
Чаще известен физический закон, характеризующий выте-
кание воды, который дает зависи-
мость потока от напора воды, т. е.
от высоты уровня воды z (рис. 118).
Так, например, при вытекании
воды через тонкую длинную трубку
где коэффициент k — положитель-
ное постоянное число, знак минус
означает, что вода вытекает. При
вытекании воды из отверстия в
тонкой стенке
<7= —d\/'z.
Рис. 118.
В каждом из этих случаев, пока
не решена задача, не известна за-
висимость от времени уровня воды в сосуде z(t), а значит,
не известен и поток. Поэтому задачу определения V из
уравнения
% A.5)
нельзя свести к предыдущей задаче. Мы сформулировали
здесь задачу в общем случае для произвольной зависимости
потока q от уровня z.
В уравнение A.5) входят две неизвестные величины:
количество (объем) воды V и уровень воды г. Очевидно,
эти величины не являются независимыми. Определенному
уровню воды соответствует вполне определенное количе-
ство воды, так что V есть известная функция *) от z, V(z).
*) Вид этой функция определяется формой сосуда. Так, напри-
мер, для цилиндрического сосуда
§ 2] РЕШЕНИЕ УРАВНЕНИЯ 293
Подставляя V(z) в уравнение A.5), найдем:
dt — dz dt —q(Z)'
Производная объема по высоте равна площади сечения на
высоте z (см. формулу A4.8) части II). Обозначим эту
производную через S(z)
Окончательно получим уравнение
^ A.6)
Способ решения этого уравнения рассмотрен в следующем
параграфе.
§ 2. Решение уравнения в случае, когда производная
зависит от искомой функции
Задача о вытекании воды свелась к определению функ-
ции z(t) из уравнения, в котором производная gj- задана
как функция г
S(z)?=q(z). A.6)
Перепишем уравнение A.6) в виде
dt S(zy ¦
Обозначим W\==ftz)' тогда окончательно
?B-D
Для конического сосуда (см. рис. 118) V =—S(z)z, где S есть
о
площадь сечения сосуда на высоте z, 5 = ягг(г), где r(z) есть радиус
сечения на уровне z. Из подобия треугольников найдем r(z) = ra—,
где г0 — радиус верхнего основания крнуса, h— полная высота, так
что У=^г>.
294 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Уравнения, содержащие искомую функцию и ее про-
изводные, называются дифференциальными уравнениями.
Если уравнение содержит лишь первую производную, то
оно называется уравнением первого порядка. С простей-
шими дифференциальными уравнениями вида
?-№>
мы уже имели дело. Решить такое уравнение — значит
найти функцию по ее производной. Эта задача решается
интегрированием.
Рассмотрим уравнение B.1). Перепишем его в виде
L
dz
Такая запись соответствует тому, что мы в ходе реше-
ния задачи временно будем рассматривать t как функцию z,
т. е. будем искать обратную функцию t(z) (см. часть III,
§ 2, в частности формулу B.3)), а уже найдя ее, выра-
зим г через t.
Проинтегрируем левую и правую части B.2)
*0
откуда
B-3)
Мы получили решение задачи: справа стоит функция
от z, слева — время t. Такое равенство позволяет при
каждом значении t найти соответствующее z. Реше-
ние B.3) удовлетворяет начальному условию при t = tal
z = z0 (в начальный момент t = ta задан уровень води
в сосуде г0).
В заключение этого параграфа рассмотрим два примера.
§ 2] РЕШЕНИЕ УРАВНЕНИЯ 295
1. Вода вытекает из конического сосуда по тонкой
трубке:
dV
*i\x dz_ q(z) kzh* kh* 1
— htz, dt —щ^- _^_____^_,
.
В этом примере не представляет труда выразить г как
функцию t
f —/.). B-4)
Эта формула полностью решает задачу. Легко проверить,
что
dz_ kh* 1 kk*
dt л,
так что z действительно удовлетворяет уравнению. Оче-
видно также, что при t = taz = zv Выражение B.4) позво-
ляет найти момент, когда закончится опорожнение сосуда:
1 2
пгл г.
г=0 при t=ta~\-j?^..
2. Цилиндрический сосуд с трубкой. В этом случае
,,. . з dV i dz .
V(z) = nrcz, -йТ=ягаЖ = —kz.
Отсюда
— nrl(lnz—lnza)= —nrlln— = nrl\n^=k(t — ta).B.
296 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Из B.5) нетрудно выразить z через t. Действительно,
lnz = lnzo г U — К)- Отсюда
2 = za e
Рассмотрим два момента времени t и t -j- At и найдем
отношение X.—-
ш
Мы видим, что это отношение зависит только от At и не
зависит от t. Поэтому за равные промежутки времени
уровень воды г падает в равном отношении.
Интересное качественное отличие второго примера от
первого заключается в том, что во втором решении нет
такого момента, когда г обращалось бы точно в нуль.
С течением времени z уменьшается, но к нулю стремится
только при t —»¦ оо .
§ 3. Радиоактивный распад
Основной закон радиоактивного распада состоит в том,
что отношение числа распавшихся за единицу времени
атомов к общему числу атомов является постоянной вели-
чиной, зависящей только от вида атомов. При этом под-
разумевается, что общее число атомов весьма велико.
Эта величина называется вероятностью распада. Обо-
значим количество атомов, которые еще не распались к
моменту времени t, через W@- В момент времени t-\-dt
нераспавшихся атомов будет N(t -f- dt). Поэтому за время
dt (от t до t-{-dt) распадается N(t) — N(t-{~dt)=—dN
атомов. Вероятность распада «=—щ-. Отсюда
?=-аМ. C.1)
dN
Из этого соотношения, вспоминая, что размерность —т-
§ 3J РАДИОАКТИВНЫЙ РАСПАД 297
N
такая же, что и отношения-^-, видим, что вероятность
распада <о имеет размерность-^-*).
Начальное условие состоит в задании числа атомов в
начальный момент времени: при / = 0 N = Na.
Решая уравнение C.1) способом, изложенным в пре-
дыдущем параграфе, и пользуясь начальным условием,
находим:
Щ1) = Мае-шг C.2)
(советуем читателю проделать все выкладки). Однако в
случае, когда производная пропорциональна искомой
функции, можно предложить более простой способ реше-
ния уравнения.
В части III мы выяснили, что производная от показа-
тельной функции пропорциональна самой функции
дх' = const ax,
в частности,
если С и k — постоянные. Вспомнив это свойство показа-
тельной функции, предположим, что решение уравнения
C.1) имеет вид
N = CeM, C.3)
и постараемся подобрать С и k так, чтобы удовлетворя-
лись уравнение и начальное условие. Дифференцируя C.3).
•) Следовательно, вероятность здесь понимается не в том смысле,
как в утверждении, что при бросании монеты вероятность того, что
монета упадет вверх гербом, равна половине. Определение вероят-
ности распада как отношения числа распадов в единицу времени к
начальному числу атомов справедливо только в том случае, если
число распадов в единицу времени (например, секунду) составляет
малую долю числа атомов. Точное определение вероятности распада
. . 1 dN
дается именно формулой <о = —~КГ ~лТ < т- е- вероятность распада
равна отношению числа распадов за малый промежуток времени к
общему числу атомов и к величине промежутка времени.
298 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
получим:
dt 1 '
подставим это в C.1): kN = —coN, откуда &== —со. Пола-
гая в C.3) ? = 0 и пользуясь начальным условием, полу-
чаем C = Nn. Итак, N=Nae-o>t.
Величина — со/, стоящая в показателе степени, безраз-
мерна, как и должно быть.
Радиоактивные атомы характеризуются периодом полу-
распада Т, который представляет собой время, в течение
которого число атомов N вследствие распада уменьшается
вдвое по сравнению с начальным.
Определим период полураспада Т. Из формулы C.2)
N (T) — Nae~u>T. С другой стороны, по определению
N(Т) = -^ N^. Поэтому Лгое~а)Т=-2-Лг4; e~WT=-^, откуда
In О Г\ CQ
— ©Г = —1п 2, Т=—як——. C.4)
Период полураспада обратно пропорционален вероятности
распада.
Каждый атом, прежде чем распасться-, существует не-
которое время, это время называется временем жизни
атома.
Найдем среднее время жизни t атома данного радио-
активного элемента. Пусть в начальный момент t = 0, когда
атомы были изготовлены, было Na атомов. За время от t
до t-\-dt распадается количество атомов
Все атомы этой группы прожили примерно поровну, их
время жизни есть t. Среди взятых в начальный момент
атомов имеются группы атомов, которым предстоит про-
жить различное время от общего для всех атомов момента
изготовления до различного для разных атомов момента
распада. Чтобы найти среднее время жизни, надо умно-
жить время жизни каждой группы на число атомов в этой
группе, сложить эти величины для всех групп и поделить
на общее число атомов во всех группах.
§ 3] РАДИОАКТИВНЫЙ РАСПАД 299
Так как будет складываться весьма большое количе-
ство слагаемых, то вместо суммы появится интеграл:
поэтому
^ t-<oN dt
't • C.5)
\ (oNdt
Подставим сюда выражение для N из C.2). Знамена-
тель
I/O ОО ОО
01
о
чего и следовало ожидать, так как интеграл в знаменателе
дает общее число всех распавшихся атомов, которое,
очевидно, равно числу атомов в начальный момент времени.
Интеграл, стоящий в числителе C.5), берем интегриро-
ванием по частям, полагая t = f, е~ы*(И = кц. Получаем:
Из формулы C.5) получим теперь
<о
Пользуясь этим, можно основное уравнение C.1) и его
решение C.2) записать так:
_
N = Nae T. C.8)
При этом надо помнить, что время t есть независимая
переменная, число атомов зависит Ът t. Величина же 7 есть
постоянная, характеризующая данный тип радиоактивных
атомов.
300 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [ч. V
Из формулы C.8) видно, что за время / = f число ато-
N
мов уменьшается от Nt до Nae~1 = —-, в е раз, т. е.
приблизительно в 2,72 раза.
По формуле C.7) начальная скорость распада такова,
что если бы число атомов, распадающихся за единицу
времени, не уменьшалось, то все атомы распались бы за
время t. Действительно, при t = 0 было N атомов и ско-
N
==~. При такой скорости для пол-
рость распада —
dt t=a t
ного распада нужно время, равное i. Из формулы C.4)
in 2
со = -уг-, поэтому
Величиной 1 в расчетах пользоваться удобнее, чем перио-
дом полураспада Т.
Упражнения
1. Среднее время жизни радия 2400 лет. Определить период по-
лураспада радия.
2. Вначале было 200 г радия. Сколько его останется через
300 лет?
3. За 500 лет распалось Юг радия. Сколько его было в началь-
ный момент?
4. Определить, через сколько времени распадается 1%, 10%,
90%, 99% от первоначального запаса радия.
5. Содержание радия на Земле в различных породах в среднем
около jzrft (по атомам). Каково было содержание радия 10 000 лет
назад, 10° лет назад, 5-10" лет назад E-Ю9 лет — возраст Земли)?
§ 4. Измерение среднего времени жизни
радиоактивных атомов
Среднее время жизни t различных радиоактивных ато-
мов весьма различно. Так, например, известно несколько
изотопов урана. Один из них, уран с атомным весом
238 (Uss0), имеет среднее время жизни 7 = 7-10* лет.
Другой изотоп (U*") имеет среднее время жизни 7= 10* лет
(получение атомной энергии на атомных электростанциях
§ 4] ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ РАДИОАКТИВНЫ* АТОМОВ 301
при делении урана происходит в основном за счет US3S).
Среднее время жизни радия 2400 лет *).
Однако не надо думать, что среднее время жизни всех
радиоактивных атомов исчисляется тысячелетиями. Среди
радиоактивных веществ, встречающихся в природе и изу-
ченных еще супругами Кюри и Эрнестом Резерфордом,
имеется полоний со средним временем жизни около 200
дней, радий А со средним временем жизни 4 минуты и ра-
дий С со средним временем жизни 2-10~* секунды.
В- последние 20 лет в связи с развитием ядерной фи-
зики и использованием атомной энергии открыто огромное
количество (более 400) различных радиоактивных веществ
с самым различным средним временем жизни.
Если в момент времени t имеется N (t) нераспавшихся
атомов, то в единицу времени распадается n(t)=(dN(t)
атомов. Величина п (t) есть скорость распада атомов.
Умножим обе части равенства C.2) на о. Получим:
или
л@ = ».@*—'. D-1)
где «0@ — скорость распада в начальный момент времени.
Если элемент имеет большое среднее время жизни, то
проверить формулу C.2) на опыте ие удается. Пусть взят
уран-238. Современная техника измерений позволяет обна-
ружить каждый случай распада радиоактивного атома.
Оказывается, что в одном грамме Utsi каждую секунду
происходит 1,2-10* распадов. Один грамм U"* содержит
2,5-10" атомов. Поэтому
Пользуясь C.6), находим / = 7*2-10* =2-10" сек = 7-10ш
лет. Пусть мы наблюдаем за распадом урана 10 лет. За
это время в одном грамме распадается около 4-10" ато-
мов. Обнаружить, что вместо 2,5-1 О*1 атомов осталось
B,5-10*1—4-Ю1*), было бы очень трудно.
•) Отметим, что в физических справочниках часто приводят
д полураспада Т = 0,69 t, см. § 3.
302 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Однако, проводя опыты с радиоактивными веществами,
имеющими не очень большое среднее время жизни (от
нескольких минут до нескольких дней), удается с большой
точностью проверить формулу D.1), а тем самым под-
твердить формулы C.1) и C.2). Для этого можно посту-
пить следующим образом. Будем подсчитывать число рас-
падов за небольшие промежутки времени. Поделив число
распадов на длину промежутка времени, получим скорость
распада в различные моменты времени.
Построим график зависимости скорости распада от
времени. Получим кривую линию. Как убедиться в том,
что эта кривая есть график показательной функции? Для
этого подсчитаем логарифмы полученных значений скоро-
сти распада и по этим данным построим график зависимо-
сти величины In n от времени /. В результате должна полу-
читься прямая линия, а это нетрудно проверить на глаз.
Многочисленные эксперименты действительно дают прямую.
Таким образом, 1л п (t) есть линейная функция от вре-
мени, т. е.
D.2)
А это значит, что n(t)'=ea+bt = eaebt = cebi. На графиках
величина Ь получается отрицательной: Ь = — о, где
ш — вероятность распада. Следовательно, опыт подтверж-
дает основной результат предыдущего параграфа и дает
возможность определить о, подсчитав тангенс угла на-
клона прямой D.2) к оси t.
Надо подчеркнуть, что этот результат, по существу,
чрезвычайно удивителен. Представим себе Nn радиоактив-
ных атомов, приготовленных одновременно в начальный
момент t = 0. Все они приготовлены одинаковым способом
и одновременно. Мы знаем, что радиоактивные атомы не-
устойчивы, способны распадаться. Можно допустить, что
распад атомов требует определенного времени. Представим
себе, что после приготовления атомы должны как-то со-
зреть до распада. Но в таком случае мы должны были
бы ожидать, что все атомы будут, не распадаясь, созре-
вать одно и то же время, а по истечении этого времени,
созрев, одновременно распадутся. Представим себе какие-
то модели пушек с натянутыми пружинами и зубчатыми
колесами (или часовыми механизмами), способные при
§ 4J ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ РАДИОАКТИВНЫХ АТОМОВ 303
определенном положении зубчатых колес (или часовых
механизмов) силой пружины выбрасывать снаряд. Выстре-
ливание снаряда будем называть распадом модели. При
одинаковом устройстве всех моделей модели, изготовленные
п одно и то же время,
выбрасывают снаряд по •%¦
истечении одинакового
срока.
Такая картина распа-
да модели пушки с выле-
том снаряда не имеет
ничего общего с дейст-
вительным поведением
радиоактивного атома.
Приготовленные в од-
но и то же время атомы
распадаются в самые
разнообразные моменты.
Подсчитаем, например, сколько процентов распадается за
время, меньшее среднего времени жизни. Из C.2) нахо-
дим, что скорость распада (количество атомов, распавшихся
dN
в единицу времени) есть -^ = —(aNae
падается
dt
dt
= dN = — a>Nae ~
. За время dt pac-
атомов,
М
а за время от /==0 до t = i распадется
= _ J (oN.e-^dt = —Nae-Wt \'a =Na(\— е~шг) атомов.
о
Так как ш = —, то
m=nJi —
Значит, за время меньше чем t распадается 63°/ 0 атомов.
Аналогично подсчитываем, что за время от / до 2/ рас-
падается 23°/О атомов, а за время больше 21—14°/0 атомов.
На рис. 119 показаны рядом кривые числа распадов
в единицу времени для радиоактивных атомов (/) и для
304 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
моделей пушек B). При этом кривая для моделей имеет
ширину. Можно представить себе, что модели изготовлены
не совсем точно и поэтому стреляют не совсем одновре-
менно. Чем точнее выполнены модели, тем уже кривая
на рис. 119.
Площадь под кривой представляет собой общее число
всех распавшихся атомов для одной кривой и общее число
всех моделей для второй кривой. Можно взять число
моделей, равное числу атомов. Тогда обе кривые будут
иметь одинаковую площадь.
Абсцисса центра тяжести обеих кривых также одина-
кова *); это значит, что рассматриваются такие модели,
у которых среднее время жизни (до выстрела) такое же,
как среднее время жизни рассматриваемых радиоактивных
атомов.
Таким образом, мы сделали все, что было в наших
силах, чтобы добиться сходства кривых: взяли столько
моделей и с таким механизмом, чтобы общее число моде-
лей и атомов и среднее время жизни моделей и атомов
были одинаковы. И тем не менее получились кривые,
необычайно резко отличающиеся по форме! Эксперимент
с радиоактивными ядрами с абсолютной неопровержи-
мостью отбрасывает тот тип кривой, который получается
для моделей. Чем точнее ставятся опыты, тем с большей
точностью подтверждается именно закон C.2).
Сравнение с моделями нам понадобилось для того,
чтобы не принимать как должную и естественную зави-
симость C.2) для радиоактивного распада, чтобы вызвать
чувство удивления и любопытства, вызвать вопрос: «А по-
чему же, в самом деле, радиоактивный распад идет таким
образом?»
Каков физический смысл величины вероятности рас-
пада? В далеком прошлом, в начале века, иногда выска-
зывались предположения, что радиоактивный распад тре-
бует еще какого-то внешнего воздействия, например по-
падания извне какой-то частицы. В этом случае можно
было бы себе представить, что один атом распался раньше,
а другой позже в зависимости от того, в который атом
*) Как будет показано в § 15 части VI, это следует из фор-
мулы C.5).
§ 4J ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ РАДИОАКТИВНЫХ АТОМОВ 303
раньше попала частица. Но эта гипотеза не соответствует
фактам, радиоактивный распад идет с одинаковой ско-
ростью в самых различных условиях, не зависит от тем-
пературы и столкновений атомов между собой, не зависит
от действия космических лучей; при радиоактивном рас-
паде в точности сохраняется энергия, что также опровер-
гает представление о каком-нибудь внешнем воздействии
при распаде.
Вторая возможная гипотеза заключается в предположе-
нии, что в действительности в начальный момент приго-
товления радиоактивных атомов они уже были не совсем
одинаковы и именно поэтому распались в различное время.
Это предположение соответствует картине моделей, кото-
рые выпускаются с часовыми механизмами, установлен-
ными на различное время. Эта гипотеза предполагает, что
точное знание состояния каждого атома полностью опре-
деляет всю его дальнейшую историю и, в частности, точно
определяет, когда именно распадается данный атом. Если
атомы распадаются через разное время после их приго-
товления, значит, так каждому из них и было на роду
написано: при изготовлении разные атомы одного и того же
радиоактивного вещества были изготовлены неодина-
ковыми и это разное время было предопределено при из-
готовлении.
Такая точка зрения также не выдерживает критики.
С этой точки зрения при каждом конкретном способе по-
лучения атомов радиоактивного элемента должна полу-
чаться своя зависимость скорости распада от времени.
Опыт опровергает такое предположение.
Один и тот же вид радиоактивных атомов часто можно
получить различными способами: например, атомы Мо0,
(молибден с атомным весом 99) получаются в атомных
котлах при делении урана. Такие же атомы раньше были
получены при действии ядер тяжелого водорода (дейтерия)
на атомы обычного, встречающегося в природе, нерадио-
активного молибдена. В настоящее время известно мно-
жество таких примеров, в которых один и тот же вид
радиоактивных атомов получается различными способами.
Опыт показывает, что независимо от способа получения
атомов всегда скорость распада дается формулой C.2)
с постоянным значением ш, характеризующим данный вид
306 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [ч- V
атомов. Следовательно, опыт доказывает именно основное
уравнение
В этом уравнении заключено очень большое содержа-
ние: все радиоактивные атомы в точности одинаковы.
Вероятность распада не зависит от того, как и когда они
были получены. Свежеполученные 100 атомов распадаются
совершенно так же, как в том случае, если приготовить
10° атомов, выждать время, нужное для того, чтобы уцеле-
ли 100 атомов, и рассмотреть эти 100 уцелевших атомов*).
Что же удивительного в том, что 100 атомов с данным
атомным весом и числом электронов всегда одинаковы?
Если бы это были нерадиоактивные атомы, то и, в самом
деле, удивляться было бы нечему. Но для радиоактивных
атомов этому надо удивляться, вспоминая, что из 100 ато-
мов 63 распадается за время t, а остальные 37 — после
t, т. е. надо удивляться тому, что у атомов время рас-
пада различно, хотя атомы одинаковы.
Это удивление небесплодно. В явлении радиоактивного
распада уже проявляются особенности законов движения
атомных и ядерных частиц, отличающиеся от законов
движения тел, с которыми мы встречаемся в повседневной
жизни. Эти особенности изучаются в квантовой механике.
Понятно, что в этой книге мы не будем ее касаться.
Нашей целью является более скромная задача: показать,
что постановка вопроса о необходимости выработки новых
представлений, отличающихся от обычной механики, сле-
дует из очень простых, известных школьнику фактов
о радиоактивности. Чтобы понять, что старых представ-
•) Характерной особенностью показательной функции является
именно тот факт, что часть кривой подобна всей кривой. Действи-
тельно, пусть N =Ы,?~Ш*. В момент t = t^ N =Ni =/V0e""lot«. Нач-
нем новый отсчет времени с момента *,, время, отсчитанное с этого
момента, обозначим т, x = t — tlt t = tl-{-t. Тогда Лг = Лгов~ш' =
= Nlte-u*tt+-z> = Noe-*'t'e-w'' = N1e-u'\ Рассматриваем распад Na
частиц, приготовленных в момент /=0. Интересуемся той частью
процесса, которая протекает после t = tx. Для этой части процесса
получаем N = УУов~ш'«-в~шт:^Л/1в~шт, гдет — время, отсчитанное от /,.
Таким образом, закон распада оставшихся от предыдущего распада
частиц в числе N1=Noe~wt> совершенно такой же, как закон распада
свежеполученных Nt частиц. Именно это утверждение и сделано в тексте.
§ 4] ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ РАДИОАКТИВНЫХ АТОМОВ 307
лений не достаточно, надо только суметь задуматься,
суметь удивиться.
В своей автобиографии Альберт Эйнштейн — величай-
ший физик XX века — подчеркивает свое удивление, ощу-
щение чуда, которое он испытал, когда впервые увидел
компас, увидел таинственное действие магнитной силы,
проникающей через бумагу, дерево, землю и воздействую-
щей на стрелку компаса без прямого соприкосновения.
Он пишет о том, что такое удивление является сильней-
шим побудительным мотивом для исследования. Он пишет
о любознательности, «которую современные методы обу-
чения почти совсем удушили». Сам Эйнштейн показал
исключительную способность удивляться и черпать вдох-
новение и побуждение к созданию теорий из самых обще-
известных фактов. Так, в основе гениальной общей теории
относительности лежит удивление перед фактом падения
различных тел с одинаковым ускорением.
Понятно, что одного удивления, одной постановки во-
проса не достаточно, и Эйнштейн соединил способность
ставить вопрос с умением решить его, с владением всей
нужной математической техникой. И все же среди многих
замечательных ученых именно умение удивиться и поста-
вить вопрос там, где другие не видели ничего замечатель-
ного,— вот что сделало Эйнштейна наиболее выдающимся
физиком XX века.
Может быть, рассмотренный выше разбор радиоактив-
ного распада послужит читателю примером того, какие
глубины можно увидеть за простыми фактами и форму-
лами.
В заключение приведем в качестве примера кривые
радиоактивного распада, полученные экспериментально
в 1955 г. в работе Сиборга и его сотрудников (США),
в которой впервые был наблюден 101-й элемент периоди-
ческой системы, названный авторами менделевием (хими-
ческий символ Md) в честь великого русского химика
Д. И. Менделеева.
В этой работе 98-й элемент, калифорний, с атомным
весом 252, облучался нейтронами в котле; при этом об-
разовывался калифорний-253. Калифорний-253 испускает
электрон и превращается в 99-й_элемент — эйнштейний, Еп,
с тем же атомным весом 253.
308 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР 14. V
Около 10' атомов эйнштейния (т. е. 4-10"" г) осадили
на золотую пластинку и подвергли в циклотроне бомбар-
дировке ос-частицами, т. е. ядрами гелия. При этом обра-
зуется элемент с номером 100 — фермий, Fm, по реакции
и менделевий по реакции
В этой записи у каждого химического символа внизу
поставлен номер в периодической системе Менделеева,
т. е. число протонов в ядре. Число справа сверху указы-
вает атомный вес, округленный до целого числа, т. е.
сумму числа нейтронов и протонов в ядре. Не* — это ядро
гелия, т. е. а-частица, р\ — ядро атома водорода — про-
тон, п\ — нейтрон. При ядерной реакции сумма нижних
чисел слева и справа одинакова, а также одинакова
и сумма верхних чисел, так как при ядерных реакциях
происходит только обмен нейтронами и протонами между
ядрами. После бомбардировки а-частицами золотая пла-
стинка вместе с образовавшимися фермием и менделевием
растворялась в кислоте, и фермий и менделевий выделя-
лись химически. Именно периодический закон Менделеева,
как пишет Сиборг, позволяет предвидеть заранее хими-
ческие свойства элемента, никогда ранее в природе не
существовавшего, никогда ранее не исследованного. После
химического разделения производились измерения радио-
активного распада. Фермий с атомным весом 256 радиоактив-
но распадается с периодом полураспада около 3,5 часа. Он
распадается на два ядра-осколка примерно равной массы,
т. е. самопроизвольно делится (о делении см. ниже, § 5).
Верхняя кривая на рис. 120 показывает зависимость
числа ядер фермия от времени в опыте. По оси абсцисс
отложено время в минутах. По оси ординат отложено
число атомов, имеющихся на данный момент*). Ось орди-
*) Число атомов, имеющихся в даииый момент, непосредст-
венно в этот момент подсчитать не удается. На опыте регистрируются
распады атомов. Число атомов N в момент t подсчитывается по окон-
чании опыта, когда все N атомов уже распались.
§ 4] ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ РАДИОАКТИВНЫХ АТОМОВ 309
нат имеет неравномерную шкалу, высота пропорциональна
логарифму числа атомов. В частности, ось абсцисс (у = 0)
соответствует одному уцелевшему атому (In 1=0), а числу
атомов, равному нулю, соответствует — оо на" оси орди-
нат. Распад каждого отдельного атома меняет число ато-
мов на 1, в промежутке между двумя распадами числе
атомов постоянно. Поэтому при такой экспериментальной
технике, когда регистрируется каждый отдельный распад,
вместо плавной кривой по-
лучается ломаная ступен-
чатая линия, на которой
каждому распаду соответ-
ствует вертикальная линия,
соединяющая две ступень-
ки. Прямая линия, прове-
денная на рис. 120, соот-
ветствует закону распада
11.47-е -ф"> (t в минутах)
п-
пае
800 1200
Время 0 минутах
после бомбардировки
Рис. 120.
где т = 1^~2 ^ ^ часов,
Т=^3%5 часа. Как видно из
рис. 120, всего в опыте за-
регистрировано 40 распадов
фермия. Чем больше ато-
мов, тем ближе ломаная
к прямой; когда же ос-
тается меньше пяти ато-
мов, то естественно, что
вероятностный характер радиоактивного распада приводит
к значительным отклонениям от показательного закона,
справедливого для большого числа атомов.
Ядра менделевия после химического разделения быстро
(за полчаса) захватывают атомный электрон и превра-
щаются при этом в ядра фермия. Поэтому тот осадок,
в котором оказался менделевий, при измерении его радио-
активности также дает распад атомов на два осколка
с периодом полураспада 3,5 часа. Кривая распада фермия,
получившегося из менделевия, находится в левом нижнем
углу рис. 120. В опыте наблюдено шесть распадов Спе-
циальными опытами доказано, что эти шесть этомое не
310 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
могли попасть в измеряемый осадок в качестве загрязне-
ния фермием, а именно образовались из менделевия.
Всего в нескольких опытах Сиборг и его сотрудники
наблюдали 17 атомов менделевия.
Приведенный выше пример не очень хорош для иллю-
страции точности выполнения показательного закона при
радиоактивном распаде. Опыты, доказывающие показатель-
ный закон, успешно ставились с более распространенными
радиоактивными веществами. Зато пример менделевия
и фермия показывает замечательное экспериментальное
искусство современных физиков, синтезирующих новые эле-
менты и регистрирующих распад каждого отдельного атома.
В опытах Сиборга счетчик распадов менделевия был
включен через усилитель в радиотрансляционную сеть
института, и при каждом распаде все сотрудники инсти-
тута, работающие в разных лабораториях, на разных
этажах, оповещались об успехе — о рождении (точнее,
о зарегистрированной смерти) каждого атома нового эле-
мента, созданного человеком (впрочем, еще раньше, чем
была закончена работа, вмешалась пожарная охрана
и оповещение было прекращено).
§ 5. Последовательный распад (радиоактивное семейство)
В ряде случаев радиоактивный распад приводит к обра-
зованию атомов, которые также радиоактивны, так что
осуществляется цепочка распадов: атом вещества А прев-
ращается в атом вещества В, атом вещества В в свою
очередь превращается в атом вещества Сит. д.. Рассмот-
рим математическую задачу об определении зависимости
от времени количества веществ А, В, С и способы ее ре-
шения. Количество атомов веществ А, В, С, не распав-
шихся к моменту времени t, будем обозначать теми же
буквами А, В, С.
Пусть вероятности распада вещества А, В, С равны
соответственно <о, v, и. Тогда
(Л называют материнским веществом). Напишем уравнение
для вещества В. За единицу времени распадается vB
атомов вещества В. С другой стороны, за это же время
§ 5] ПОСЛЕДОВАТЕЛЬНЫЙ РАСПАД (РАДИОАКТИВНОЕ СЕМЕЙСТВО) 311
происходит (оА распадов вещества А, а так как при каж-
дом распаде атома вещества А образуется атом вещества
В, то за единицу времени образуется а>А атомов вещества
В. Поэтому
? E.2)
Аналогичные рассуждения дают:
§ = -uC + vB. E.3)
Уравнения E.1) — E,3) образуют систему дифферен-
циальных уравнений. В данном случае эти уравнения
можно решать одно за другим, имея каждый раз дело
только с одним уравнением и одним неизвестным. Дей-
ствительно, в уравнение E.1) В и С не входят. По-
этому из него определяем A(t) = Atle~'*t; здесь Аа — коли-
чество атомов вещества А в начальный момент ^ = 0.
Подставляя выражение для A(t) в уравнение E.2),
получим уравнение, содержащее только одну неизвестную
функцию В,
™=—vB + <uA(t). E.4)
Как решить такое уравнение? Решение такого уравне-
ния можно найти, если рассмотреть сперва судьбу группы
атомов вещества В, образовавшихся в один и тот же про-
межуток времени — от т до т -{- Дт. Будем рассматривать
число атомов этой группы ДВ, оставшихся «в живых»,
т. е. не распавшихся к моменту t, в зависимости от вре-
мени t. Для того чтобы не смешать между собой момент t,
когда мы измеряем число атомов, и момент образования
группы, обозначаем эти моменты разными буквами: /ит
соответственно. В момент т скорость образования атомов
вещества В была и>А (т). За малый промежуток времени
Дт образовалось ДВ0 = шЛ(т)Дт атомов вещества В.
Как зависит число атомов в интересующей нас группе
от времени t? При t < т оно равно нулю: интересующие
нас атомы еще не образовались, так как ие образовалась
еще сама группа, Дб = 0. Пусть t>r. Заметим, что с мо-
мента образования группы уже прошло время t — т.
312 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Вероятность распада вещества В есть v. Поэтому по исте-
чении времени t — т с момента образования группы
число аераспавшихся атомов будет:
Для того чтобы найти полное число атомов вещества В
в момент времени /, надо сложить число атомов во всех
группах, образовавшихся до момента /. Если брать Дт
(а значит, и ДВ) весьма малыми, то сумма превратится
в интеграл
t t
t
B(t)= J AB(x)dx=
Отметим, что переменная интегрирования обозначена
здесь через т. Аргумент /, от которого зависит В, входит
в интеграл в двух местах: как верхний предел и в выра-
жении подынтегральной функции. При интегрировании по
т величину t следует рассматривать как постоянную.
Поэтому можно записать
и вынести ae~vt из-под интеграла как множитель, не за-
висящий от т. Сделав это, получим
(r)ez"dx. E.5)
Легко проверить, не вычисляя интеграла, что решение E.5)
удовлетворяет исходному уравнению E.4) при любой зави-
симости А (т). Действительно, найдем производную .' ' .
По правилу дифференцирования произведения получим:
Так как по свойству производной от интеграла (см. ч. II, §9)
§ 5J ПОСЛЕДОВАТЕЛЬНЫЙ РАСПАД (РАДИОАКТИВНОЕ СЕМЕЙСТВО) 318
ТО
Если же мы положим Л(т) = Лвв"о>т, то получим конкрет-
ное решение
Решение можно было найти, и не прибегая к рассмот-
рению отдельных групп атомов. Теперь, когда решение
найдено, уже легко угадать математический прием, веду-
щий к цели. Решение E.5) имеет вид
B(t)==e-vtI(t\, E.6)
где I (t) обозначает интеграл, зависящий от t. Будем искать
решение в виде произведения e~vt на неизвестную функ-
цию / и составим уравнение для /
w=^e~vtI>>—ve~vtI+e~vtii' E-7)
Подставляя выражения E.7) н E.6) в уравнение E.4),
получим:
или
% = <**>1 A(t). E.8)
По условию в начальный момент / = О, В = 0, а зна-
чит, и / = 0.
Решение уравнения E.8) с этим начальным условием
имеет вид
t
и окончательно
t
В @ = e~*7 (t) = e-vt J «>A(x)eVTdT.
314 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
В этой формуле существенно, во избежание ошибок,
сохранять более строгие обозначения и не обозначать пе-
ременную интегрирования т той же буквой, которой обо-
значен предел интегрирования t.
§ 6. Исследование решения для радиоактивного семейства
В предыдущем параграфе мы довели до конца реше-
ние задачи в случае двух радиоактивных веществ. Иссле-
дуем это решение для двух частных случаев:
1) короткож и в ущее материнское вещество Л, долго-
живущее дочернее вещество В;
2) долгоживущее материнское вещество А, коротко-
живущее дочернее вещество В,
Ниже мы будем наряду с вероятностями распада а> и
v пользоваться средними временами жизни tA = — ,
tB=—. В первом случае характер решения легко понять
без расчетов и формул. Весь процесс распадается на две
стадии. Сперва, при / порядка tA (при этом по условию
'л^'в» поэтому и / <^ tB в первой стадии), происходит
превращение Л в В; распада вещества В за это время
практически не происходит. В этом периоде количество В
равно разности начального количества Аа и количества А,
уцелевшего к моменту t,
В конце этого периода практически все вещество Л
превратилось в В, количество В становится равным на-
чальному количеству материнского вещества Аа. После
этого медленно, длительно происходит распад В
Покажем, как эти выражения получаются из точной
формулы. Для случая двух радиоактивных веществ А н
В мы получили в предыдущем параграфе формулу
В нашем случае tA<^tB, ш^>о, поэтому удобнее переме-
§ 6] ИССЛЕДОВАНИЕ РЕШЕНИЯ ДЛЯ РАДИОАКТИВН. СЕМЕЙСТВА 315
нить знаки, чтобы иметь дело с положительными вели-
чинами в скобках и в знаменателе дроби. Тогда
D lf\ Я СО (/* — У* />""U)*'l (fi 1 ^
Так как 0<g>, то^*-?=1.
Выражение e~vt — е~ш* рассмотрим для двух последо-
вательных стадий. Сначала, при /<^/в = —, будет и/<^1.
При этом e~vt =x 1. Так как / может быть величиной по-
рядка tA, a ©/, следовательно, порядка единицы, то ве-
личину е~т* надо вычислять точно. Из формулы F.1)
получаем:
Во второй стадии, при t^>tA — —, будет <о/^> 1. В этой
стадии можно пренебречь е~ш1. При этом е~ш* мало не
только по сравнению с единицей, но и по сравнению
с e~vt, так как v<^<o. Получим:
Таким образом, действительно, точная формула дает
те результаты, которые были получены из простых качест-
венных соображений.
Обратимся ко второму случаю долгоживущего мате-
ринского вещества А и короткоживущего дочернего ве-
щества В
Рассмотрим период, когда со времени начала процесса
прошло время /, значительно превышающее tB. В таком
случае то вещество В, которое образовалось в начале
процесса, к моменту / уже полностью распалось. Так
как В распадается быстро, за малое время, то в каждый
данный момент в наличии находится вещество В, образо-
вавшееся недавно. В рассматриваемом случае имеет место
установившееся состояние или, как его иначе называют,
стационарное состояние: вещество В образуется из А и
тут же распадается, вещество В при этом не накапли-
вается (потому что оно быстро распадается), но и не
316 РАДИОАКТИВНЫЙ РАСПАД К ДЕЛЕНИЕ ЯДЕР [Ч. V
исчезает совсем (потому что из вещества А все время полу-
чается новое вещество В). В установившемся состоянии
в единицу времени распадается столько атомов В, сколько
образуется атомов В из А. Математически это условие
записывается так:
vB
Отсюда
В установившемся состоянии мгновенное количество В
пропорционально количеству А и составляет всегда одну
и ту же малую долю А. Эта доля мала потому, что
в рассматриваемом втором случае tB<^tA и, значит,
=?- <^ 1, а иначе не было бы и самого установившегося
СОСТОЯНИЯ.
Как получается уравнение для установившегося со-
стояния из точного дифференциального уравнения
-у- — — иВ-\-<пА? Очевидно, если считать, что ^- мало по
сравнению с каждым из двух членов, стоящих в правой
части, то приближенно как раз и получим, заменяя
dB _
-di на °-
0 = — vB-{-<?>A, vB=<nA.
Рассмотрим теперь начало процесса. При t==Q А — Аа,
5 = 0. Значит в начальный момент мы имеем дело не
с установившимся состоянием, так как по формулам уста-
новившегося состояния должно быть вначале
(значок s у буквы В означает установившееся стационар-
ное состояние). В момент t =0 вещество В образуется
со скоростью ^ = шЛв, а распада В в начальный момент.
вовсе не происходит, так как 5 = 0.
Можно определить, за какое время t1 при начальной
скорости нарастания В будет достигнуто количество Bs.
§ 6] ИССЛЕДОВАНИЕ РЕШЕНИЯ ДЛЯ РАДИОАКТИВН. СЕМЕЙСТВА 317
Действительно, если скорость образования вещества
остается постоянной, равной (-п-) _ , то
Полагая здесь Bs = -
мое время
i)
_ = (оЛ0, получим иско-
Таким образом, установившееся состояние достигается
за время, приблизительно равное среднему времени рас-
пада вещества В. Из условия tA<^.tB видно, что количе-
ство вещества А за это время изменится мало.
Рис. 121.
В целом приближенное рассмотрение во втором случае
короткоживущего дочернего вещества дает следующее:
при t <ТВ В (t) =
при t>tB
,-wt
Мы получаем зависимость В = В (t) в виде двух линий:
сначала прямой, потом показательной функции (рис. 121,
7Д= 10/в). Нетрудно проверить, что при t = iB две фор-
мулы дают близкие значения.
318 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Посмотрим, что дает точное решение уравнения
В = А9^(е-">*-е-**) F.1)
в рассматриваемом случае, когда v^xa, lB<^.iA. Прене-
брегаем со по сравнению с v в знаменателе. При vt^>l
пренебрегаем е~ы в скобке. Получим:
т. е. как раз установившееся решение.
Приближение решения к установившемуся определяем
тем, насколько быстро убывает e~vt. При совсем малом t,
когда vt < 1, так что a>t и подавно мало, получим, разла-
гая в ряд е~ы и е~ш* и ограничиваясь двумя первыми
членами,
что также совпадает с приближенным результатом. Однако
в действительности точная формула дает на графике одну
плавную кривую, без разрывов и изломов (она показана
на рис. 121). Приближение этой кривой к установивше-
муся решению зависит от того, насколько быстро умень-
шается e~vt. Так, для того чтобы e~vt давало поправку по-
рядка 107„, нужно, чтобы было ttf=2,3, ?=2,3~» 2,3?в.
При этом нз-за малости (at считаем, что е~ш* =г= 1. Таким
образом, действительно, переход от стадии начального
нарастания к стадии, когда решение с достаточной точ-
ностью равно установившемуся, происходит за время по-
рядка времени распада Гв.
Пример радиоактивного семейства очень поучителен
в том отношении, что получение общего точного решения
никоим образом нельзя считать концом работы над зада-
чей. Построение приближенных теорий для различных
предельных случаев есть совершенно необходимая часть
работы, и наличие точной формулы вовсе не заменяет
приближенной теории. Приближенные, но ясные и нагляд-
ные представления служат для проверки точной формулы.
Приближенные теории дают нам такие важные новые
качественные понятия, как понятие установившегося
§ 6J ИССЛЕДОВАНИЕ РЕШЕНИЯ ДЛЯ РАДИОАКТИВН. СЕМЕЙСТВА 319
состояния. Такие понятия и лучше запоминаются, и об-
ладают более широкой областью применимости, чем точ-
ные формулы. Так, например, в случае радиоактивного
семейства, состоящего из нескольких поколений А —•• В —>•
—-С—»-D, точная формула весьма громоздка. Однако
если 1Л больше всех других времен, то все результаты,
относящиеся к установившемуся состоянию, получаются
так же просто, как и в случае двух веществ А и В.
Часто наиболее легкий путь состоит в том, чтобы
получить точное решение, справедливое для любых
v и со (в нашем примере), из которого затем при v<^.a>
или 0§>(о путем математических преобразований полу-
чаются более простые приближенные формулы для двух
крайних случаев. На этом нельзя успокаиваться! Если
простая приближенная формула получилась хотя и лег-
ким, но длинным путем через общее решение, то рядом
должен быть другой, простой путь получения прибли-
женной формулы. Нужно обязательно тренироваться
в нахождении простых путей, потому что будут встре-
чаться задачи, в которых путь, приводящий к точному
решению, непреодолимо сложен, и только простой прибли-
женный путь позволит продвинуть вперед решение вопроса.
В практической работе точные формулы встречаются
так же редко, как уравнения, решения которых выра-
жаются целыми числами, хотя в учебниках большинство
задач приводят к точным формулам подобно тому, как
в задачниках младших классов уравнения всегда решаются
в целых числах.
Отметим, что представления о радиоактивных семей-
ствах объясняют странный результат, получившийся
в упражнении § 3 относительно количества радия в прош-
лом: радий является потомком (правда, не прямым,
а через несколько промежуточных веществ) урана-238.
Поэтому нельзя считать имеющееся в настоящее время
количество радия результатом распада первоначального
радия. В действительности радий находится в установив-
шемся состоянии с ураном. Из уравнения
В = ^-А
V
найдем, что содержание радия В = 10~11 соответствует
320 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
содержанию урана
Мы нашли приближенно современное количество урана-238
в горных породах. Начальное содержание 5-10* лет назад
было вдвое больше, порядка б-10~°. Такие величины
вполне правдоподобны в отличие от результатов упраж-
нения § 3.
§ 7. Цепная реакция деления урана
В 1938 г. Хан и Штрассман в Германии и супруги
Жолио-Кюри во Франции показали, что при попадании
нейтрона в ядро урана происходит деление ядра, при ко-
тором оно распадается на два больших осколка и, кроме
того, испускает два-три новых нейтрона. Особенно активно
делится уран с атомным весом 235 (коротко уран-235),
содержащийся в количестве около 0,7°],, в природном
уране, 99,3е/,, атомов которого имеют атомный вес 238*).
«Осколки» представляют собой ядра среднего атомного
веса — от 75 до 160; заряд этих ядер лежит в пределах
от 35 до 57, при этом сумма зарядов двух осколков
всегда равна заряду ядра урана, т. е. 92 элементарным
зарядам; сумма атомных весов двух осколков равна
235 —(— 1—v, где 235 — атомный вес урана, 1—атомный
вес нейтрона, вызвавшего деление, v—число нейтронов,
*) Вслед за этим в 1939 г. в лаборатории И. В. Курчатова в
Ленинграде советские ученые К. А. Флеров и Г. Н. Петржак пока-
зали, что уран-238 способен делиться самопроизвольно, без попада-
ния в него нейтрона, хотя вероятность этого весьма мала. Вероят-
ность радиоактивного распада (с испусканием а-частицы) урана-238,
соответствующая периоду полураспада 4,5-10" лет, равна
со =5-10 ~" \\сек, а вероятность самопроизвольного деления урана-238
в 10* раз меньше, т. е. равна 5-10"" \\сек. Таким образом, в I кг
урана, содержащем примерно 2,5-10" атомов, в 1 сек происходит
примерно 107 актов радиоактивного распада и всего 10 самопроиз-
вольных делений.
Однако в самых тяжелых элементах самопроизвольное деление
становится уже главным, наиболее вероятным процессом распада
(см. конец § 4, где приведена кривая распада менделевия). В рас-
сматриваемом ниже вопросе о цепной реакции самопроизвольное
деление роли не играет.
§ f\ ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ УРАНА 321
образовавшихся при делении. При делении выделяется
большая энергия — 6«1017 эрг\г (на грамм разделившегося
урана). Благодаря этой энергии осколки летят в противо-
положные стороны со скоростью около 10° см\сек.
Источником этой энергии является электрическое от-
талкивание двух одноименно заряженных осколков. Пока
ядро не разделилось на две части, ядерные силы между
частицами, из которых состоит ядро, уравновешивают
электрическое отталкивание. Как только ядро раздели-
лось на два отдельных осколка, отталкивание этих двух
осколков уже ничем не уравновешивается и приводит
к тому, что они разлетаются с большой скоростью. В плот-
ном веществе осколки очень быстро останавливаются.
Время их движения составляет от 10" " до 10" " сек.
При этом они проходят от 10"* до 10"' см. Кинетическая
энергия осколков переходит в тепло. Нейтроны, образую-
щиеся при делении, имеют скорость того же порядка, что
и осколки (около 2-10* см/сек).
Для практического использования энергии деления
ядер решающее значение имеет тот факт, что при деле-
нии, вызванном одним нейтроном, получается больше
одного нейтрона. Ясно что если нейтроны не будут ухо-
дить из. системы, то число их будет нарастать в геомет-
рической прогрессии с течением времени, т. е. по закону
показательной функции. По такому же закону, пропор-
ционально числу нейтронов, будет нарастать скорость
выделения энергии. При этом если даже в начале про-
цесса было мало нейтронов, то очень скоро число нх
возрастает настолько, что энергия будет выделяться со
скоростью, удобной для практического использования
(например, в качестве источника энергии атомной электро-
станции или ледокола), еще через совсем небольшое время
выделение энергии возрастет настолько, что произойдет
атомный взрыв. В действительности часть нейтронов выхо-
дит из системы, часть нейтронов может захватываться
другими ядрами, не вызывая деления; пользуясь этим,
можно регулировать число нейтронов; в частности, можно
добиться установившегося состояния системы, при кото-
ром число образующихся в единицу времени нейтронов
равно числу исчезающих нейтронов, так что число ней-
тронов, находящихся в системе, с течением времени не
11 Я. Б. Зельдович
322 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
изменяется, выделение энергии происходит с постоянной
скоростью. Для использования атомной энергии в мирных
целях нужен именно такой режим работы.
Наша ближайшая задача — составить и исследовать
уравнение, описывающее зависимость числа нейтронов
в системе от времени.
§ 8. Размножение нейтронов в большой массе
Получим сперва уравнение для изменения числа ней-
тронов со временем в очень большой системе (например,
в большом слитке урана-235), когда выход нейтронов
наружу можно не учитывать *). Скорость всех нейтронов
приближенно можно считать одинаковой; обозначим" ее
через v.
Деление ядра происходит приблизительно в половине
всех случаев, когда нейтрон попадает в ядро урана-235. Во
второй половине случаев нейтрон вылетает обратно, оставляя
ядро в прежнем состоянии, и при этом число нейтронов
не меняется. Ядро урана представляет собой шарик ра-
диуса R порядка 10~м см.
Как часто нейтрон, летящий внутри металла, попадает
в ядро урана?
За малое время dt нейтрон проходит путь vdt. Пред-
ставим себе цилиндр, осью которого является путь, прой-
денный нейтроном, радиус цилиндра равен радиусу ядра
урана R. Нейтрон сталкивается с теми ядрами, центр
которых находится внутри цилиндра; если центр ядра
находится внутри цилиндра, значит, путь нейтрона прохо-
дит на расстоянии меньше R от центра ядра, поэтому
нейтрон задевает ядро, попадает в него. Объем цилиндра
равен nR2vdt.
В металлическом уране в единице объема содержится N
атомов и, следовательно, .Л/ ядер (размерность N есть—,)
Поэтому в интересующем нас объеме nR*vdt имеется
NnR*vdt ядер. Столько же будет попаданий нейтрона
в ядро за малый промежуток времени dt. He всякое попа-
дание нейтрона в ядро вызывает деление ядра. Пусть ос
*) Мы будем рассматривать самый простой случай металлического
ураиа-235, без графитового замедлителя и т. п.
§ 8] РАЗМНОЖЕНИЕ НЕЙТРОНОВ В БОЛЬШОЙ МАССЕ 323
есть доля тех случаев попадания нейтрона в ядро, когда
это попадание вызвало деление (в случае урана-235
а =5= y J. Тогда число делений за время dt равно
NautR'vdt.
Величина autR*, имеющая размерность площади, так
как а и я безразмерны, называется сечением деления
я обозначается of*).
Если внутри массы металлического урана находятся п
нейтронов, то число делений за время dt равно
При каждом делении образуется v нейтронов, но за счет
поглощения одного нейтрона. Таким образом, изменение
числа нейтронов при каждом делении равно (v — 1). На-
писанному выше числу делений соответствует изменение
числа нейтронов
dn = nN (v—l)o,udt. (8.1)
Таким образом, из (8.1) получаем:
Положим
N(v — \)ар = а; (8.2)
тогда
dn
dt=an-
Как мы уже знаем, решением такого уравнения является
n(t) = n,eat, (8.3)
где п„ — число нейтронов в системе при ? = 0.
Таким образом, если число нейтронов в системе
меняется только по причине деления, то число нейтронов
растет в геометрической прогрессии, если время растет
в арифметической прогрессии.
*) а — греческая буква «сигма». Индекс / есть перьая буква
английского слова fission (деление ядер).
11*
324 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Действительно, если взять несколько равноотстоящих
моментов времени
то соответствующее число нейтронов равно
л, = п,вв'-, /л„ fnx, f*nx, где / = е«Ч
Отметим, что такой способ описания процесса — «рост
в геометрической прогрессии» — часто встречается в попу-
лярной литературе. Специалисты физики и техники поль-
зуются им редко и говорят об экспоненциальном, т. е.
показательном законе возрастания. Показательный закон
характеризуется скоростью роста а [формула (8.3)].
Найдем размерность а. В формуле (8.3) at стоит в пока-
зателе степени. Поэтому at безразмерная величина и, сле-
довательно, размерность а есть \\сек. Этот же результат
можно получить, припомнив, что
Найдем приближенное значение постоянной величины а.
Плотность урана приблизительно равна 18 г}см*. Число
ядер в 1 см* N подсчитаем, вспоминая число Авогадро;
1 грамм-атом любого вещества содержит 6-10" атомов.
Следовательно, 235 г урана-235 содержат 6-10" атомов,
т. е. 610" ядер. В 1 см* содержится ^g-6-Ю" =зв 4-10"
ядер, N = 4-10** l/cAts. Подставим среднее значение
v^2,5, v = 2-109 см\сек, af=\ яA0-11)"=1,6- 10-"слс".
Получим a = 4-1011-l,5-l,6.J0-14-2.10i = 2-l0il/ce»c;
-1 = 5-10-' сек.
Таким образом, если нейтроны не вылетают из си-
стемы, то количество нейтронов возрастает в е раз за
5-10-* сек.
При такой скорости возрастания за одну микросекунду,
т. е. за 10 ~* сек, количество нейтронов возрастает в
т е в iOo,4« .оо^ю" раз.
Одна тонна урана-235 содержит 2,5-10" ядер. Поэтому
§ 9J вылет нейтронов 325
если нейтроны не выходят из системы, то это количество
урана разделится меньше чем за одну микросекунду.
Такой процесс представляет собой взрыв.
Для энергетического использования деления такая
скорость нарастания процесса недопустима. Необходимо,
чтобы вылет нейтронов из системы уменьшил скорость
нарастания количества нейтронов.
§ 9. Вылет нейтронов
Представим себе массу урана-235 в виде шара радиуса г.
Мы должны составить уравнение для числа п нейтронов,
находящихся внутри этого шара. Предположим для про-
стоты, что шар закреплен на какой-то тонкой подставке, так
что вокруг него полная пустота, нейтрон, покинувший
шар, уже никогда не возвращается обратно.
Как определить поток нейтронов, т. е. число нейтро-
нов, выходящих за пределы шара в единицу времени?
Сделаем грубый подсчет. Рассмотрим малый промежуток
времени dt. За это время каждый нейтрон проходит путь
длиной vdt. Где находятся те нейтроны, которые покинут
шар за время dt? Очевидно, они должны находиться
внутри шара в тонком слое, прилегающем к поверхности
шара, но на расстоянии не более vdt от поверхности,
иначе за время dt они не успеют дойти до поверхности,
пересечь ее и выйти наружу. Но и те нейтроны, которые
находятся внутри слоя толщиной vdt, тоже не все успеют
выйти за время dt, так как не у всех нейтронов внутри
слоя скорость направлена по радиусу наружу; при самом
грубом подсчете мы не будем учитывать последнее обсто-
ятельство.
Как найти число нейтронов в слое? Во всем шаре
находится п нейтронов. Объем шара V = 4- лг'« объем ин-
тересующего нас тонкого слоя у поверхности приближенно
равен Svdt, если vdt мало. Здесь 5 = 4ял* (поверхность
шара).
Средняя плотность нейтронов, т. е. число нейтронов
в единице объема, равна С = -^-. Предположим, что в
тонком слое у поверхности плотность не отличается о г
326 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
средней. Тогда число нейтронов в этом слое равно
vdt
Поэтому поток (число нейтронов, выходящих в единицу
времени) есть
nS п-Апг* 3d
В действительности у поверхности плотность нейтро-
нов меньше средней плотности, к тому же, как отмеча-
лось выше, скорости нейтронов имеют различные направ
ления. Поэтому в действительности поток нейтронов
меньше, чем мы получили
3kv ,_ ,.
<7=—л, (9.1)
где k — численный коэффициент, k<\. Ниже, в § 12,
путем сопоставления с опытом будет показано, что к
близко к 0,3. Если внутри шара не происходит деления
ядер и не рождаются новые нейтроны, то для числа ней-
dn
тронов внутри шара получается уравнение ^7 =—q или,
пользуясь (9.1),
dn 3kv
ш=—гп-
Обозначая
^ = 6. ' (9.2)
получим:
S = — bn-
Решение такого уравнения нам хорошо известно
n = noe-bt. (9.3)
Среднее время пребывания нейтронов внутри шара
согласно (9.3) равно
J J_ __ Г
Ь 3kv"
§ 10J КРИТИЧЕСКАЯ МАССА 327
Заметим, что 7 = —. Поэтому среднее время прибли-
зительно равно времени, за которое нейтрон, движущийся
со скоростью v, проходит путь, равный радиусу шара г.
Точное рассмотрение вылета нейтронов требует весьма
трудоемких расчетов. Очень важно с первых шагов обу«
чения привыкнуть приближенно определять все интересу*
ющие нас величины. Точный расчет часто бывает действи-
тельно очень труден и требует совсем другого объема
знаний, иногда требует коллективного труда нескольких
человек с использованием счетных машин и т. д. Значит
ли это, что учащийся, занимающийся самообразованием
где-нибудь далеко от Москвы, далеко от высших учебных
заведений, не может и помышлять о рассмотрении воп-
роса? Всегда есть простые, хотя и грубые (вроде приве-
денного выше) способы приближенного подхода к вопросу.
Не произвести приближенного расчета и ссылаться на то,
что точный расчет труден, значит просто прикрывать та-
кой ссылкой свою нерешительность и робость. Чаще
всего именно робость мешает начинающим ученым и
изобретателям!
§ 10. Критическая масса
До сих пор мы рассматривали отдельно два процесса:
размножение нейтронов без учета их вылета и вылет ней-
тронов без учета их размножения.
Рассмотрим теперь систему, в которой нейтроны и раз-
множаются и могут уходить из системы. В единицу вре-
мени в системе, как мы знаем, образуются an нейтронов
и Ьп нейтронов вылетают из системы. Так как изменение
числа нейтронов в единицу времени есть -^ , то
dn
или
A0.1)
где с = а—Ь. При данном начальном количестве нейтро-
нов па уравнение A0.1) имеет решение
п = п„ес\ A0.2)
328 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР (Ч. V
Это решение приводит к совершенно различным резуль-
татам при положительном и отрицательном с. Действи-
тельно, из A0.2) видно, что при с<0 число нейтронов п
тем меньше, чем больше t, т. е. с течением времени п
стремится к нулю. Если же с>0, то п тем больше, чем
больше t, т. е. п неограниченно растет с течением вре-
мени. Только вмешательство новых физических факторов,
не учтенных в , уравнении, может приостановить рост п.
Таким образом, значение с = 0 есть «критическое зна-
чение»,— это значение разделяет решения разного типа
с растущим и уменьшающимся количеством нейтронов.
Так как с = а — Ь, то при данном а можно говорить о
критическом значении b: &Кр = а, так как при b<bKf = a
с=а — Ъ > 0, а при b> bKV= а с=а — Ь <0. Величина а
определяется свойствами делящегося вещества: согласно
формуле (8.2) a = Nvaf(\—1). Величина Ь зависит от
количества взятого делящегося вещества
Ь-' (9.2)
Поэтому вводят понятие критического значения ради-
уса гкр, при котором & = 6кр = а. Из формул (8.2) и (9.2)
следует, что —- = Nvof(y — 1), откуда
3k
— 1) *
Масса шара, радиус которого равен гкр, называется кри-
тической массой m^. Ясно, что
ткр=-|яг'вкре, A0.3)
где q — плотность делящегося вещества*).
При г>глХ> (это то же, что m>mKV) будет с>0 — имеет
место размножение нейтронов. При г < г^ (пг < т^) будет
с < 0 — первоначально взятое количество нейтронов умень-
*) Мы по-прежнему считаем, что рассматривается масса деляще-
гося вещества (например, урана), имеющая форму шара.
§ 10]
КРИТИЧЕСКАЯ МАССА
329
шается. Пусть взят шар радиуса г. Его поверхность есть
S = 4nr*, объем V = -^-nr\
лг'
Если г мало, то это отношение велико, если же г вели-
ко, то это отношение мало. Не удивительно, что при ма-
лом радиусе, когда отношение поверхности к объему велико,
вылет нейтронов усиливается, условия для размножения
п
"о
0
А
1
/
ю ю '
1510 я
•У
ъ-ья,
. ь-г,5 ю"
20 Ю9 2510 s
•2
10'
Рис. 122.
нейтронов хуже. Удивительна та резкость, с которой ме-
няется количество нейтронов при изменении Ь: если Ь > 6кр,
то через некоторое время количество нейтронов обращается
практически в нуль независимо от того, равно ли Ь= 1,016^,
или Ь = 2Ькр. Если &<&нр, то число нейтронов неограни-
ченно возрастает и при 6 = 0,99&кР, и при & = 0,5&кр> хотя
с разной скоростью. Именно поэтому говорят о «критиче-
ском» значении Ь, «критическом» значении г или «крити-
ческом» значении массы. Масса больше критической на-
зывается надкритической, масса меньше критической на-
зывается подкритической.
330
РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР
[Ч. V
На рис. 122 представлены кривые n = naela~b)t при
нескольких значениях 6. Построим кривые зависимости п
от 6 для нескольких определенных значений времени /.
t'5iO'sceit
210s
Рис. 123.
t-tSW'ceX
г-ю'4 ю" ь
Рис. 124.
При расчете принято а=2-10* —. На рис. 123 показана
кривая л F) при / = 5-10~' сек, на рис. 124 показана
кривая п(Ь) при /=15-10"", на
рис. 125 показана кривая п F) при
п,
Пересечение кривых с осью ор-
, t-30-i0~*ceit динат (Ь =0) на рис. 124 и 125 уже
не помещается на чертеже: на
рис. 124 при 6 = 0 п'=20л0, на
рис. 125 при 6 = 0 п = 400па.
Как видно из рис. 122, а также
из сопоставления рис. 123—125, чем
больше время t, тем сильнее расхо-
дятся кривые n(t) (рис. 122), тем
круче кривые п F) (рис. 123—125),
тем резче проявляется критич-
Рис. 125. ность значения 6 = 2-10* (в дан-
ном примере).
Если взять *>10~* сек, то кривую п(Ь) нельзя будет
отличить от вертикальной прямой 6 = 6кр = 2-10"; п = 0
при 6>6кр, л=оо при 6<6кр.
4-ХГх
§ 11] ПОДКРИТИЧЕСКЛЯ И НАДКРИТИЧЕСКАЯ МАССА 331
§ 11. Подкритическая и надкритическая масса
при непрерывном источнике нейтронов
В предыдущем параграфе была рассмотрена задача об
изменении со временем числа нейтронов при данном на-
чальном числе нейтронов па. Поставим теперь несколько
иную задачу. Пусть в начальный момент / = 0 число ней-
тронов равно нулю и в этот момент включен источник
нейтронов, испускающий q0 нейтронов в единицу времени.
Эта задача приводит к уравнению
ft = cn + qa, A1.1)
где с = а — Ь. Мы ищем решение этого уравнения с на-
чальным условием: при ?=0, п = 0.
Способ решения похожей задачи был изложен в § 5.
Вкратце повторим ход рассуждений. Ищем количество
нейтронов в момент t. Весь промежуток времени от 0 до t
разбиваем на отдельные промежутки Дт. Рассмотрим один
такой промежуток времени от т до т-{-Лт. Источник дал
за это время количество нейтронов qatsx. Если бы источ-
ник действовал только в течение одного промежутка вре-
мени Дт, то мы имели бы дело с задачей предыдущего
параграфа с начальным количеством нейтронов nt = qaAr;
единственная разница была бы в том, что эти нейтроны
выделились в момент t = r, а не t = 0. Поэтому вместо
решения n = naect мы получили бы решение
n = neec <'-т> = <7„Дтес <'-т>
(это решение относится к t>x; при /<т л —0), так как
ясно, что изменение количества нейтронов зависит имен-
но от времени, которое прошло после того момента, когда
было задано начальное количество их, т. е. от величины
t — тв данном случае.
На самом деле источник действует непрерывно в тече-
ние всего времени от 0 до t. Значит, надо сложить вклад
всех нейтронов, испущенных источником в различные про-
межутки времени Дт, причем в сумме эти промежутки
времени покрывают весь промежуток времени от 0 до t.
Такая сумма при малых Дт представляет собой интеграл,
332 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР
поэтому
[Ч. V
Этот интеграл легко вычислить:
t
A1.2)
Нетрудно убедиться в том, что это решение удовле-
творяет уравнению
$-*[*(^-о] =*.«*=
и условию при / = 0 л=0.
Одна и та же формула A1.2) дает решение при поло-
жительном и при отрицательном значении с. Однако вид
кривой n = n(t) при этом существенно различен. При
„. о 0 (т. е. при а > Ь) пока-
затель ct положителен, так
^| о что с ростом t величина ect
^i t"-/ -ЛУ быстро становится гораздо
больше единицы. При боль-
шом t и о О
При с < 0 величина ct < О,
поэтому с ростом tect стано-
вится гораздо меньше еди-
ницы и значения п прибли-
жаются к числу *) — -у ,
Рнс. 126.
Вид кривых показан на рис. 126.
*) Это число положительно, так как с < 0.
§ П] ПОДКРИТИЧЕСКАЯ И НАДКРИТИЧЕСКАЯ МАССА 333
Отметим любопытный частный случай с = 0. Если
с=0, то формулой A1.2) непосредственно пользоваться
нельзя.
Разложим есХ в ряд
Подставляя в формулу A1.2), получим:
Этой формулой можно пользоваться при с=0, по-
лучаем:
n(t) = qj. A1.3)
Последний результат нетрудно получить и из уравне-
ния A1.1). Действительно, при с=0 A1.1) имеет вид
-^ — qa. Отсюда n(t) = qat-\-А, где А— постоянная ин-
тегрирования. При ? = 0 должно быть я = 0, поэтому
А = 0. Получаем A1.3).
Как было показано выше, при с<0 концентрация ней-
тронов с течением времени достигает постоянного значения
— — или, что то же самое, -—j-. Чем меньше I с | (чем мы
с \с\
ближе к критическому состоянию), тем больше это посто-
янное значение. Таким образом, даже при очень слабом
источнике (малом q0) масса, близкая к критической, может
давать любое большое число нейтронов, большое число деле-
ний, большое выделение энергии. В принципе режим ра-
боты атомных котлов именно такой.
Поддержание такого режима является нелегкой зада-
чей, так как малые изменения Ъ и с очень резко меняют
величину — , когда с близко к нулю, а работа при с, близ-
ких к нулю, необходима, когда надо получать большую
мощность при малом qa. Однако при помощи автоматиче-
ского регулирования эту техническую задачу удается
решить: когда п выходит из заданных пределов, си-
стема регулирования меняет величины а или Ь. К тому
же есть природные факторы, облегчающие регулирование:
334 РАДИОАКТИВНЫЙ РАСПАД И ДелЕНИЕ ЯДЕР ' [Ч. V
так, например, при увеличении п повышается температура
активного вещества и при этом оказывается, что с умень-
шается, так что в известных пределах система как бы
саморегулируется.
§ 12. Величина критической массы
Мы знаем теперь, насколько сильно меняются свойства
системы в зависимости от того, имеем ли мы дело с над*
критической или подкритической массой. Рассмотрим под-
робнее само условие критичности
3fe
r
Подставим числа для урана-235: аг= 1,6-10~14, v = 2,5,
№ = 4-10". Получим:
4.10t»-1.6-10-«*-l,S
см-
Коэффициент k мы не умеем определять, знаем только,
что он меньше единицы. Найдем этот коэффициент, сопо-
ставляя формулу с опытом. Опыт показывает, что крити-
ческая масса урана-235 около 50 кг. Урановый шар весом
50 кг имеет радиус около 8,5 см. Следовательно, в дан-
ном случае
85
Остановимся на физическом смысле формулы для кри-
тического радиуса. В выражении гкР скорость нейтронов-
сократилась. Значит, формулу для гкр можно получить,
не рассматривая хода процесса во времени, не рассматри-
вая скорости размножения нейтронов и скорости ухода
нейтронов из системы.
Если пренебречь безразмерным множителем 3k (он по-
рядка единицы), то формула для критического радиуса
принимает вид
rjfo/^^rr- A2-1)
Что за величина стоит в левой части формулы A2.1)? гкра/
есть объем цилиндра длиной, равной радиусу, и с пло-
щадью основания, равной аг Напомним, что если нейтрон
§ 13J ПОГЛОЩЕНИЕ СВЕТА. ПОСТАНОВКА ЗАДАЧИ 335
движется по оси такого цилиндра, то он вызывает деле-
ние тех ядер урана-235, центры которых находятся внутри
цилиндра. N есть число ядер в единице объема. Следова-
тельно, NrKVaf есть среднее число ядер в объеме цилиндра.
Теперь можем дать другую формулировку условию
критичности. Мы выяснили раньше, что средний путь, ко-
торый проходит внутри делящегося вещества нейтрон, ро-
дившийся внутри вещества (в результате деления), порядка
радиуса г. После того как нейтрон прошел путь около г,
он выходит за пределы делящегося вещества и для про-
цесса потерян. Условие критичности заключается в том,
что в среднем на этом пути нейтрон должен до ухода из си-
стемы родить один нейтрон. При делении образуется v — 1
новых нейтронов. Значит, нужно, чтобы до вылета ней-
трон вызвал примерно _ делений, т. е. чтобы в объеме
цилиндра тог было примерно _ ядер. Это условие и
приводит к формуле A2.1).
Понятно, что такие рассуждения не строги, но они
нужны для понимания физики дела и здесь их нельзя
заменить никакими расчетами, даже самыми точными вычис-
лениями на современных электронных машинах. Такие
расчеты на машинах не заменяют, а дополняют ясное по-
нимание качественной, физической стороны дела. В част-
ности, читатель должен обратить внимание на принцип,
который был высказан в начале параграфа: если какая-то
величина (и) входила в вывод формулы, но в окончатель-
ном результате эта величина сократилась, значит, есть
вывод формулы, в котором данная величина вообще не
рассматривается. Нужно всегда находить такой, болег
простой вывод формулы, потому что другой вывод фор-
мулы— это и другой, новый взгляд на исследуемый
процесс.
§ 13. Поглощение света. Постановка задачи
и грубая оценка
Рассмотрим поглощение света в воздухе, содержащем
черные пылинки сажи. Пусть в единице объема содер-
жится N пылинок. Площадь сечения одной пылинки плос-
костью, перпендикулярной к лучу света, обозначим через а.
336 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
Коротко будем называть <т «сечением». Так, например, для
пылинки, представляющей собой шар радиуса г, а есть
площадь сечения, проходящего через центр шара, т. е.
а=пг**).
Будем считать, что свет, попадающий на поверхность
пылинки, полностью поглощается. Задача заключается
в определении зависимости доли поглощенного света и
доли прошедшего света от величин N, а и длины пути х,
которую луч света прошел через воздух, содержащий
пыль.
Начнем с самой грубой оценки того пути, на котором
происходит поглощение значительной доли света. Эту длину
обозначим через L. Что именно обозначает многозначи-
тельное выражение «значительная доля света» — в этом мы
разберемся позже, в следующих параграфах. Не будем
смущаться нечеткой постановкой вопроса.
Рассмотрим цилиндр с площадью основания 5 и дли-
ной L. Потребуем, чтобы сумма сечений всех пылинок, нахо-
дящихся в этом цилиндре, равнялась 5.
В объеме цилиндра SL содержится NSL пылинок,
сумма их сечений равна oNSL, значит, мы требуем, чтобы
было
откуда
Проверим размерность в A3.1): а есть площадь, ее раз-
мерность см*; N есть число пылинок в единице объема,
размерность —,. Следовательно, [L] = — = aw, как
СЛ€ т % 1
СМ*
и должно быть.
Каков физический смысл поставленного условия? Если
бы можно было разместить пылинки так, чтобы закрытые
разными пылинками площади не перекрывались, то при
помощи пылинок, находящихся в цилиндре с длиной L и
площадью основания 5, можно было бы закрыть все осно-
*) Для пылинок сложной формы точное определение сечения о
таково: а есть средняя площадь тени, отбрасываемой пылинкой на
поверхность, перпендикулярную к лучу света.
§ 13] ПОГЛОЩЕНИЕ СВЕТА. ПОСТАНОВКА ЗАДАЧИ 337
ванне цилиндра и достичь полного поглощения всего света.
При х < L полное поглощение света заведомо невозможно:
как ни располагай пылинки, общая площадь их сечений
не достаточна для того, чтобы закрыть все основание ци-
линдра.
Ясно, что и при x--=L и даже при x>L в действи-
тельности полного поглощения не будет. При случай-
ном расположении пылинок при любом х будут оставать-
ся такие направления, вдоль которых не окажется ни
одной пылинки, и лучи света пройдут по этим направ-
лениям.
Энергия, которую свет переносит через какую-нибудь
площадку за 1 сек, называется потоком энергии света.
Пусть / есть поток энергии света через площадку 1 см*.
Эта величина называется плотностью потока энергий, ее
размерность —эрг г . Ниже мы будем рассматривать плот-
ность потока световой энергии / (х) в зависимости от тол-
щины слоя х. Ясно, что
l(x) = lj(x). A3.2)
где /0 есть энергия падающего света, f (х) — искомая
функция, характеризующая ослабление света.
Что можно сказать о свойствах функции f(x)? Если
х = 0, то ослабления света еще не произошло, /@)=/0,
поэтому / @) = 1. Если х > 0, то происходит ослабление
света, / (х) < /0, поэтому / (х) < 1.
Ясно, что с увеличением х функция f (х) уменьшается,
приближаясь к нулю, т. е. / (х) — убывающая функция.
Значит, ее производная отрицательна
Мы говорили, что полного поглощения не будет ни при
x — L, ни при х> L, поэтому мы не ждем, чтобы f(x)
обратилась в нуль при х = L. Однако можно предполагать,
что величина x = L является характерной длиной. Это
значит, что при прохождении светом пути x<gtL доля
поглощенного света весьма мала по сравнению с долей про-
шедшего света; при прохождении пути х =s L поглощает-
ся заметная часть света, а при прохождении пути х ^> L
338 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
большая часть света поглощается, проходит только весьма
малая часть света.
Функция f(x), как видно из формулы A3.2), безраз-
мерна. Можно предполагать, что если ввести безразмерную
переменную -|-, то функция / (т") будет всегда одинакова
для любых пылинок, любых N и а. Эти предположения бу-
дут подтверждены и уточнены в следующих параграфах.
§ 14. Уравнение поглощения и его решение
Рассмотрим тонкий слой воздуха между х и x-\-dx.
Все расчеты ведем для столба воздуха в виде цилиндра
с площадью основания 1 см* (в предыдущем параграфе,
когда рассматривался цилиндр с площадью основания
5 см*, величина 5 все равно сократилась).
Пучок света состоит из параллельных лучей и характе-
ризуется плотностью потока энергии /. Если бы не было
поглощения света пылинками, величина / была бы постоянна.
В рассматриваемом слое содержится N dx пылинок,
которые перекрывают площадь oN dx из полной площади
основания слоя 1 см*. Следовательно, в слое поглощается
доля aN dx энергии, падающей слева на слой. Поэтому
dQ = INadx. При прохождении светом слоя dx поток
энергии света уменьшается на величину, равную количеству
поглощенной энергии dQ. До входа в слой плотность по-
тока энергии была / (х), после выхода из слоя стала
I(x-\-dx), поэтому
=IoN dx. A4.1)
Замечая, что I(x-{-dx) — I(x)=dl, получаем из A4.1)
f = -INa.
dx
Решение этого уравнения
I = Iae-°Nx. A4.2)
Это решение получается совершенно таким же способом,
как и решение Ы—Мое~ы при рассмотрении радиоактив-
ного распада (см. § 3). Здесь /0 есть значение величины
/ при х = 0.
§ 15] СООТНОШЕНИЕ МЕЖДУ ТОЧНЫМ И ГРУБЫМ РАСЧЕТАМИ 339
При увеличении толщины слоя в арифметической про-
грессии х,=а, хг = 2а, дс, = 3а и т. д. сила света умень-
шается в геометрической прогрессии. В самом деле, обо-
значая e~"Na = a. (тогда а< 1), найдем, пользуясь A4.2),
/ (хг) = /,<х, / (х.) = /,«', / (дс.) = /оа' и т. д.
§ 15. Соотношение между точным и грубым расчетами
Весьма поучительно теперь, располагая и точным ре-
шением (§ 14) и грубой оценкой (§ 13), сравнить их. Такое
сравнение помогает пользоваться грубыми оценками в слож-
ных задачах, где точное решение найти трудно; сравнение
помогает понять границы применимости грубого решения.
При грубом решении мы нашли длину, на которой
происходит значительное поглощение,
При помощи величины L точное решение A4.2) можно вы-
разить так:
/ = /§в-Г. A5.1)
Значит, полностью подтверждается предположение, что
найденная грубым рассуждением величина L входит в точ-
ное решение.
Точное решение действительно имеет вид
Из точного решения A5.1) находим конкретный вид функ-
ции / ( "X ) • Действительно, / (-^- 1 = е L .
Рассмотрим длину x = L. Грубое рассуждение давало
на этой длине полное поглощение света. На самом деле
из точного решения A5.1), полагая в нем x = L, находим
/= /0е"'=0,37 /0, т. е. проходит 37°/0 света, а погло-
щается, следовательно, 63"/0. При малых у- выразим
г L по формуле Маклорена, ограничиваясь двумя
340
РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР
[Ч. V
членами. Получим:
X
т
A5.2)
х
Рнс. 127.
Геометрически это соответствует замене кривой на каса-
тельную к кривой при х = 0 (рис. 127). Как видно из
A5.2), касательная пересекает ось х при x — L. Поэтому
если бы поглощение происходило с одинаковой скоростью,
т. е. так, что на каждой единице длины поглощалось бы
одинаковое количество света, то
весь свет был бы поглощен на
длине x = L.
Таким образом, величина L,
полученная грубым рассужде-
нием, действительно, имеет важ-
нейшее значение и в точном
решении.
Вопрос о грубых решениях
очень важен в практической
работе, и надо всячески развивать умение быстро на-
ходить грубые решения, тренироваться в их нахожде-
нии и понимании; это гораздо важнее и плодотворнее зло-
радного подчеркивания недостатков грубых решений. Бу-
дем радоваться тому, что грубое решение дает 100°/0
поглощения там, где точное решение дает 63° /0 поглоще-
ния— ошибка всего в 1,5 раза. Грубое решение дает при
x=^L 0°/0 прохождения света вместо точного значения
37°/0; но это не беда, так как заранее было понятно, что
здесь от грубого решения нельзя ждать хорошей точности.
Если установлено, что задача не имеет точного реше-
ния в виде явной формулы, то. на этом никак нельзя
останавливаться. Надо отыскивать хотя бы очень грубое
решение задачи. Однако при пользовании им всегда сле-
дует помнить, что это не точное, а только грубое, при-
ближенное решение.
Остановимся еще на вопроса о размерностях. Размер-
ность величины L=-rj- мы проверили и установили, что
это длина. Часто оказывается возможным найти приближен-
ное выражение интересующей нас величины, зная только
ее размерность и размерность исходных величин, входя-
§ 16] ЭФФЕКТИВНОЕ СЕЧЕНИЕ 341
щих в условие задачи. Однако в данном случае это не-
возможно. Действительно, величину, имеющую размер-
ность длины, можно построить, исходя из одной только
концентрации N (—г):/ =т- . Величина /. представ-
шем / у N
ляет собой среднее расстояние между частицами. Величину,
имеющую размерность длины, можно построить также из
сечения a(cM*):lt = yro; величина 1Х характеризует размер
частицы. Очевидно, что величина la = i\ 1\~л при любом
значении показателя степени а также имеет размерность
длины. В частности, интересующая нас величина L полу-
чается при а = 3. Таким образом, в рассмотренной задаче
теория размерности не приводит к определенному ответу.
Для того чтобы найти L, т. е. величину размерности дли-
ны, входящую в точное решение, оказывается необходи-
мым найти именно грубое решение задачи. Формальное
применение теории размерности здесь не приводит к цели,
не дает однозначного ответа. Но даже в тех случаях,
когда соображения размерности дают единственный ответ
на вопрос, желательно также найти грубое решение за-
дачи, чтобы яснее представить картину явления.
§ 16. Эффективное сечение
В задаче об ослаблении света, проходящего через
воздух с пылью, величина а имеет простой геометриче-
ский смысл площади тени одной пылинки. Закон ослаб-
ления света A4.2) одинаков для света различной длины
волны (т. е. разного цвета), так как величина а от длины
волны не зависит.
При поглощении света отдельными молекулами и ато-
мами наблюдается сильная зависимость закона ослабле-
ния света от длины волны света. Так, например, в чистом
воздухе видимый свет практически совершенно не ослаб-
ляется (ослабление составляет меньше 1°/0 на пути в 1 км,
соответственно ослабление в е раз происходит на пути
около 100 км). Ультрафиолетовые лучи с длиной волны
1800-10" * см = 1,8-10"s сл=1800А*) ослабляются ве
•) А—ангстрем, lA=10~s см.
342 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
раз на пути Z. = 0,1 см. Еще более короткие ультрафио-
летовые лучи, с длиной волны 1,1-10"' си= 1100 А,
ослабляются в е раз на пути L = 0,01 см.
Следовательно, поглощение света воздухом не похоже
на поглощение света черной пылинкой, одинаково погло-
щающей свет с любой длиной волны.
Количество световой энергии q, поглощаемое одним
атомом в единицу времени, пропорционально плотности
потока световой энергии / в том месте, где находится
атом,
<7 = <т/. A6.1)
Здесь а есть коэффициент пропорциональности. Определим
размерность а. Размерность q есть эрг\сек. Размерность
потока энергии / есть эрг'\смг сек. Следовательно, размер-
ность а есть см*. Величина о называется эффективным
сечением. Для черной пылинки коэффициент а совпадает
с геометрической величиной — площадью тени. Для мо-
лекул и атомов а сильно зависит от длины волны
света.
Грубо можно так представить себе причину этой зави-
симости. Количество поглощаемой атомом энергии при
воздействии на него света оказывается особенно большим,
когда частота световых колебаний совпадает с частотой
движения электронов в атоме. При этом имеет место
явление резонанса, электрон колеблется особенно сильно
и поглощает особенно много световой энергии.
Такой резонанс достигается, например, при поглощении
атомами натрия (в парообразном состоянии) желтого света
с длиной волны 5890 А = 5,89- 10~s см. Точно такой же
желтый свет испускают атомы натрия. при более высокой
температуре, когда колебание электронов вызывается силь-
ными столкновениями атомов между собой.
При резонансе величина а достигает 10~10 см*. Размеры
атомов и молекул порядка 10~*—10~7 см, что соответ-
ствует сечениям порядка 10~"—Ю'1* см*.
Таким образом, максимальные эффективные сечения во
много раз больше истинных площадей сечений атомов и
молекул. С другой стороны, для света, частота которого
не соответствует собственной частоте атома, эффективное
сечение мало, гораздо меньше площади сечения атома.
§ 17] ОСЛАБЛЕНИЕ ПОТОКА ЗАРЯЖЕННЫХ ЧАСТИЦ а- И 0-ЛУЧЕЙ 343
§ 17. Ослабление потока заряженных частиц а- и ft-лучей
Показательный закон убывания потока частиц в зави-
симости от пройденного пути;
/ = /в"Г- A7.1)
основан на очень общем предположении, что ослабление
потока на малом пути dx пропорционально самой интен-
сивности потока
=—т'- <17-2>
где коэффициент пропорциональности у- есть постоянное
число, зависящее только от вида частиц.
Решение уравнения A7.2) есть
Поэтому формулы A7.1) и A7.2) равноценны, одна сле-
дует из другой.
Опыты показывают, что в некоторых случаях показа-
тельный закон A7.1) является вполне точным, а иногда
от него наблюдаются отклонения. Рассмотрим внимательно
те причины, которые могут вызвать отклонение от фор-
мулы A7.1) или (что то же самое) от формулы A7.2).
Легко ответить на вопрос о смысле отклонении от фор-
мулы A7.2). Формула A7.2) подразумевает, что при изме-
нении х и изменении / рассматриваемый свет (или другое
какое-нибудь излучение) качественно не изменяется, иначе
изменялось бы число L. Перепишем A7.2) в виде
J_d/ j_
/ dx— L '
Отсюда видно, что величина -j-jz постоянна. Если ока-
жется, что в различных точках пространства величина
1 di
-j-j- различна, значит, в этих точках различна не только
интенсивность излучения, но различно и его физическое
содержание, например свет разного цвета, т. е. с неоди-
наковой средней длиной волны.
344 РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР [Ч. V
При рассмотрении вопросов защиты от радиоактивных
излучений и вопросов прохождения а-, р*- и у-лучей
и нейтронов через различные вещества мы встречаемся
с другой причиной отклонений от простого закона A7.2).
В применении к процессу поглощения света закон
A7.2) означает следующее: если свет встретил на своем
пути пылинку, то часть света проходит мимо этой пылинки,
совсем не изменяясь, а другая часть света целиком по-
глощается пылинкой. В случае радиоактивных излучений
дело обстоит сложнее: а-частица представляет собой ядро
атома гелия, вылетающее из радиоактивного «родитель-
ского» ядра с большой скоростью, порядка 0,07 с (где
с — скорость света), т. е. со скоростью около 2-10° см\сек.
Пролетая через атом, а-частица отдает электронам малую
часть своей энергии. После примерно 50 000 столкновений
с атомами а-частица потеряет половину своей энергии.
При этом она не перестанет существовать, не исчезнет,
но энергия и скорость ее изменятся. После 100 000 столк-
новений а-частица останавливается, перестает сталкиваться
с атомами и выбивать из них
электроны. Такое число столк-
новений а-частица испытывает
в воздухе на пути в несколь-
ко сантиметров.
_ В действительности на
х этом пути различные а-части-
Рнс 128. - цы (одинаковой начальной
энергии) испытывают разное
число столкновений, не обязательно в точности 100000.
Однако, так как 100 000 — это большое число, то на данной
длине пути отклонения числа столкновений отдельных а-ча-
стиц от среднего A00 000) невелики (порядка 300, т. е. около
0,3% среднего числа столкновений). Поэтому а-частицы
одинаковой энергии всегда теряют всю свою энергию при-
близительно на одинаковом пути. Величина этого пути
зависит от начальной энергии а-частицы. Если поток
а-частиц одинаковой энергии летит вдоль оси х, то зави-
симость между интенсивностью потока и величиной прой-
денного пути х изображается кривой рис. 128. Кривая
эта совершенно не похожа на график показательной функ-
ции. На протяжении значительной части пути интенсив-
§ 17] ОСЛАВЛЕНИЕ ПОТОКА ЗАРЯЖЕННЫХ ЧАСТИЦ CL- Я Р"ЛУЧЕЙ 345
ность потока а-частиц не меняется: за одинаковые про-
межутки времени через площадку в 1 смг пролетает
одинаковое число а-частиц. Затем интенсивность резко
падает. Это резкое падение было подготовлено на участке,
где интенсивность оставалась постоянной, потому что на
этом участке энергия а-частиц уменьшалась с увеличением
пути х. Резкое падение потока происходит там, где энер-
гия а-частиц становится весьма малой.
Аналогичная картина имеет место и для быстрых
электронов (р-частиц, испускаемых, когда в ядре нейтрон
превращается в протон). В этом случае картина ослож-
няется тем, что при радиоактивном распаде испускаются
электроны с различными скоро-
стями, и к тому же электроны,
пролетая около атома, не толь-
ко отдают ему часть своей энер-
гии, но часто испытывают и зна-
чительное боковое отклонение.
Кривая для р-частиц имеет
вид, показанный на рис. 129.
Уже при небольших х часть
электронов выбывает из пучка;
это в основном те электроны, Рис- 129>
. которые имели малую начальную
скорость. Поэтому вблизи * = 0 поведение кривой похоже
на поведение показательной функции. Однако дальше
кривая достигает оси абсцисс, интенсивность / становится
равной нулю при вполне определенной величине х, соот-
ветствующей максимальной энергии электронов, получаю-
щихся при данном радиоактивном распаде.
Наиболее важными для практики (и вместе с тем наи-
более трудными) являются вопросы, связанные с защитой
от у-лучей, испускаемых радиоактивными веществами,
и от нейтронов, образующихся при делении ядер в атом-
ных реакторах (котлах) и при ядерных взрывах. В этом
случае положение наиболее запутанное и сложное, так как
Y-лучи и нейтроны отдают энергию большими порциями
и при этом сильно отклоняются от первоначального на-
правления. Даже в толстом слое воздуха A00—200 м)
есть значительная вероятность (порядка 37%) прохожде-
ния неизменных у-лу^й и нейтронов. Поэтому они требуют
346 РАДИОАКТИВНЫЙ РАСПАД Я ДЕЛЕНИЕ ЯДЕР [Ч. V
толстых защитных слоев. Поток у"лУче^ и нейтронов не
обращается в нуль при определенной толщине слоя, как
это имеет место для а- и 0-лучей; при большой толщине
защитного слоя, как показывают опыт и сложные расчеты,
поток у-лучей и нейтронов убывает приблизительно по
показательному закону.
ОТВЕТЫ И РЕШЕНИЯ
§ 3. 1. 2"^: 1660 лет. 2. 176,5 г. 3. 53,3 г. 4. Мы знаем, что
N (t) = N# *, где Na — количество вещества в начальный момент
/ = 0. Нас интересует момент времени /,, к которому осталось
A00- 1)%=99% вещества: ЛГ (*,) = "^ЛГ0. Поэтому ^^оЯ= Noe *.
- - 100 —
Отсюда находим tx == t\n -=¦. Для радня t = 2400 лет, поэтому
100
<i = 2400 In-qq- = 24 (года). Аналогично в трех других случаях на-
ходим tt ^s 250 лет, tt =n 5500 лет, tt =i. 11 000 лет. S. Пусть в началь-
ный момент времени/ = 0 количество атомов в 10'* атомов породы Nc,
10000
в момент /=10 000 это количество равно 1. Поэтому l=Nbe 0,
откуда •/V0 = e4=%:65. Аналогично находим, что 10' лет назад
ЛГ0 = в*17 =s; 101И. Получился явно нелепый результат: в Ю1* атомов
породы содержалось 101*1 атомов радия1 Еще более нелепый результат
получится, если подсчитывать содержание радия 5-10* лет назад.
Нелепость результата доказывает неправильность исходного предполо-
жения о том, что имеющееся в настоящее время количество радня
можно рассматривать как остаток от распада радия, входившего
в состав Земли в момент ее образования.
ЧАСТЬ VI
МЕХАНИКА
§ 1. Сила, работа, мощность
Соотношения между важнейшими величинами механики
можно точно сформулировать только при помощи интегра-
лов и производных. В части II мы уже рассматривали
соотношение между пройденным путем (или положением)
тела, его скоростью, а также между скоростью и ускоре-
нием. Не повторяя этого, рассмотрим теперь соотношения
между такими величинами, как сила, работа, энергия,
мощность. Рассмотрим прямолинейное движение тела вдоль
оси х. Пусть сила F, действующая на тело, также на-
правлена вдоль оси х. В элементарной физике работа А,
совершенная силой, определяется как произведение силы F
на пройденный телом путь l = xk— хп, где хп — началь-
ное положение тела, хк — конечное положение тела
A = Fl=F(xk-xn).
Очевидно, здесь имеет место такое же положение, как
и в случае соотношения между скоростью и путем: про-
стая формула — работа равна произведению силы на
путь — имеет место лишь в том случае, когда сила по-
стоянна. Если же-сила меняется на протяжении процесса
перемещения, тогда надо весь процесс перемещения раз-
бить на отдельные малые промежутки так, чтобы на
протяжении каждого малого промежутка силу можно было
считать постоянной. Тогда для малого промежутка
Значит, в общем случае переменной силы работа выра-
348 МЕХАНИКА [Ч. VI
жается не произведением, а интегралом
Хк
А=[ Fdx.
Мы считаем известным движение тела, которое задается
известной функцией x=x(t). Перемещение тела за малое
время dt равно произведению мгновенной скорости v на
время dt
dx = vdt = 21 dt.
Поэтому выражение работы можно написать и так:
<* tk
A = §F,%dt = $Fvdt. A.1)
tn и
Произведение Fv, которое входит в эту формулу, есть
работа, произведенная в единицу времени; оно называется
мощностью силы. Действительно, в случае постоянных
скорости и силы путь равен x = vt, работа равна
A = Fx — Fvt и отношение работы к протекшему времени
равно -r- = Fv. Обозначая мощность через W, Fv = W,
можно написать:
A=l Wdt.
tn
Напомним, что в технической системе единиц сила
измеряется килограммами*) (т. е. за единицу силы прини-
мается сила, с которой масса в I кг притягивается
к Земле), длина — метрами, единица работы — килограммо-
метрами (кгм), единица мощности — килограммометрами
в секунду {кгм\сек)\ часто пользуются также другой
единицей мощности — так называемой лошадиной силой,
равной 75 кгм/сек.
В физической системе единиц сила измеряется в динах
(сила, придающая массе 1 г ускорение 1 см]сек2), работа —
в эргах A эрг = \ дин-\ см), мощность — в эрг\сек, и вво-
дят также единицу работы—джоуль, равную 107 эрг,
и единицу мощности — ватт, равную дж\сек= 107 эрг[сек.
•) Обозначается кГ.
§ 1] СИЛА, РАБОТА, МОЩНОСТЬ 349
На тело могут действовать несколько сил, например,
F, и Ft; тогда можно говорить о работе, которую совер-
шила первая сила (Л,) и вторая сила (А,) за то время,
когда тело переместилось из начального положения хп
в конечное положение xk. Считая, что силы F1 и Fx — по-
стоянные, получим:
Обратим внимание на знаки величин, входящих в эти
выражения. Сила считается положительной, когда она
действует в сторону возрастания х, т. е. в сторону, пока-
занную стрелкой на оси х
(рис. 130) вправо. Сила, дей- К??Д г »
ствующая в противоположную ЕЩШ х
сторону — влево, считается .г<0 г>0-
отрицательной.
Если тело перемещается Рис 130.
в ту же сторону, в которую
действует сила, то работа силы положительна. Предста-
вим себе, что тело движется в направлении, противопо-
ложном направлению силы, так что F, и (хк — хп) имеют
разные знаки; тогда работа
силы А, окажется отрица-
тельной. Представим себе,
например, что на тело дей-
ствуют две силы (рис.
131, а): сила растянутой
пружины F1 н сила натя-
жения веревки F,, которую
ВЫ) читатель> натягиваете
рукой. F, тянет влево,
F1<0; вы тянете вправо,
Рнс. 131. Ft>0. Если вы тянете силь-
нее пружины *), то тело
будет перемещаться слева направо. На рис. 131, а показано
начальное положение тела, а на рис. 131, б — его конеч-
ное положение: (xk—*n)>0, F,<0. Работа Ах, совершен-
ная над телом силой натяжения пружины, или, короче,
*) Математически это означает, что абсолютная величина силы,
с которой вы тянете, большг абсолютной величины силы, с которой
тянет тело влево пружина: \Ft\>\Fl\.
350
МЕХАНИКА
[Ч. VI
х ,
х,
работа пружины, при этом перемещении отрицательна.
В этом случае работа, которую вы произвели, положитель-
на, Аг>0. Полная работа, совершенная над телом, А—
—Ал-\-Ах, также положительна. Но Л<Л,, так как Л,<0.
Это значит, что только часть произведенной вами работы
(А) воспринята телом, другая часть (\АХ\) пошла на рас-
тяжение пружины. Отметим, что сила трения о непо-
движную поверхность направлена всегда в сторону, проти-
воположную скорости движения тела; поэтому работа силы
трения о неподвижную поверхность всегда отрицательна
независимо от направления движения тела.
Сила F,, действующая на тело со стороны пружины,
другой конец которой закреплен, отличается весьма важ-
ным свойством: эта сила зависит исключительно от поло-
жения тела. Вовсе не все силы обладают таким свойством;
например, сила трения о неподвижную поверхность
всегда тормозит движение тела, направлена влево, если
тело движется вправо, и направ-
лена вправо, если тело движется
- влево. Поэтому направление силы
трения зависит от направления
движения тела. Кроме того, сила
трения может зависеть от величи-
ны скорости тела. Следовательно,
сила трения зависит от величины
и направления скорости тела.
Сила Fx, с которой вы тянете веревку в примере
рис. 131, а и б, может меняться любым образом, по ваше-
му произволу. В частности, тело может двигаться сначала
направо, а потом налево. При этом тело дважды будет про-
ходить одно и то же положение: первый раз на пути впе-
ред в момент tt, второй раз на обратном пути в момент t2.
Возможный график движения тела, т. е. зависимость
координаты к от времени t, показан для этого случая на
рис. 132. В нашей воле в момент tx тянуть тело вправо,
Ft{tx)>0, а в момент t2 отпустить трос, так что /г,('2) = 0,
или даже толкать тело влево, так что Ft (tt) < 0. Но
x(ti) = x(tt) = xl, значит, произвольную силу Ft нельзя,
вообще говоря, рассматривать как функцию координаты х.
Приведенные примеры силы трения и силы, прило-
женной человеком, действующим по своей воле, служат
Рис. 132.
§ 1] СИЛА, РАБОТА, МОЩНОСТЬ 351
для того, чтобы показать, что зависимость силы только
от положения, тела Fl = Fl(x), характерная для силы /•",,
с которой пружина действует на тело, не есть общее
свойство любых сил, а есть частное свойство, связанное
с упругостью пружины.
Для того чтобы найти работу данной силы Ft по одной
из формул А[=^ Ftdx; At=^ Fp dt, нужно знать две
хп 'л
вещи: 1) как двигалось тело, т. е. зависимость коорди-
наты тела от времени x(t), и 2) выражение силы Fit ко-
торая в общем случае зависит от х, t, v.
Зная зависимости x(t) и v(t) и подставляя их в вы-
ражение Fi(x; t; v), получим выражение для Ft в виде
функции времени и сможем записать работу как интеграл
по времени.
Пример. Пусть сила F(x) = —kx, а движение тела
задано уравнением x = b sin (at; тогда
v = -Л = ba> cos <nt, F (x (t)) = — kx(t) = -— kb sin tat,
A{ = — b*k(i> f sin at cos <ot dt = ~ ^ft(u f sin 2eo/ dt =
tn tn
cos 2(at |* = —-
A.2)
В этом случае, когда сила зависит только от коорди-
наты, гораздо проще и удобнее пользоваться выражением
работы как интеграла по х
Хк
• - — ~xk
— kx* Хк kx\ kx\
2 •
Подставляя сюда x = b sin©^, легко получить и выражение
работы в течение заданного промежутка времени от tn до th
л —2 2 ' \*--л)
Легко убедиться в том, что это выражение в точности
352 МЕХАНИКА • [Ч. VI
совпадает с предыдущим, так как
cos 2@/ = cos* (at — sin' tat =-1 — 2 sin* a>t,
cos 2a>tk— cos2(o/n= 1 -^2 sin* artft — A —2sin1(o/n) =
= 2 (sin* (atn — sin1 (i>tk).
Подставляя это тождество в A.2), получим A.3).
При пользовании выражением работы как интеграла
по координате х в общем случае силы F (х, v, t), завися-
щей от х, v, t, нужна большая осторожность. В самом
деле, в принципе, если задано движение, x = x(t), то
это уравнение можно решить относительно t и определить
t (x). Однако надо иметь в виду, что t может быть не-
однозначной функцией х, одно и то же положение х
возможно в два различных момента времени, т. е. для
одного и того же значения х получаем два различных
значения t (см. рис. 132). Тогда все движение надо раз-
бить на отдельные периоды, во время которых скорость
не меняет своего знака и t является однозначной функ-
цией х. Однако для разных периодов / вйражается раз-
личными функциями х. Пусть, например, тело движется
по закону x = bsin<ot, как и в предыдущем примере, но
сила задана как функция времени F = f cos a>t. При этом
сила не является однозначной функцией положения х.
Действительно, пусть, например, t = 0. Тогда х = 0,
F=f. Если положить / = -^-, то снова х = 0, но при
втом F = -—/, так что в различные моменты времени (t = 0
и t = — ] тело находится в одинаковом положении х = О,
но сила при этом различна. При интегрировании по вре-
мени этой трудности нет: каждому моменту t отвечает
одно определенное значение координаты х, силы F и всех
других величин.
Легко найти работу, интегрируя по времени,
А = ^ Fv dt =с ^ / cos (at Ьы cos (at dt = fb® ^ cos* a>t dt.
Воспользуемся приведенной выше тригонометрической
формулой
cos 2ф = 2 cos* q> — 1.
§ 1] СИЛА, РАБОТА, МОЩНОСТЬ 35&
Отсюда
¦ 1 , cos 2ш
Cos4 = -2-+~2~^'
поэтому
fk
)dt =
fk
/ 1 г cos2<oA
= -^fba>{tk—t^-\- — (sin2(D^— sin2u>*n). A-4)
С течением времени работа неограниченно возрастает, как
видно из формулы A.4). Это объясняется тем, что сила
и колебания находятся в резонансе (подробно явление
резонанса будет рассмотрено в § 11).
Движение по закону x=bsina)t представляет собой
колебание тела; рассмотрим работу силы за один полу-
период, выбрав начальный момент tn = О, хп = 0 и конеч-
ный момент tk=- —, sin a)/ft = sin я = 0, xk = 0. Тогда
в A.4) sin 2a)^ft = sin 2(о?„ = 0 и работа равна
Тело вернулось в исходное состояние, а работа, про-
изведенная силой, не равна нулю, имеет вполне опреде-
ленную величину. Как понять этот результат с точки
зрения первой формулы A = ^Fdx? На первый взгляд,
если подставить xn = xk = 0, получим:
В действительности мы должны рассмотреть отдельно про-
цесс нарастания х от 0 до xmax = b и процесс убывания
х от xmaX = b до 0. В процессе нарастания каждому
значению х соответствует определенное значение силы F,
которое обозначим /•",,
Ft=f cos vt = f V\ —sin1 v>t =
12 Я. Б. Зельдович
354 МЕХАНИКА [Ч. VI
Во время убывания л: тем же положительным значениям л:
соответствует отрицательное значение силы *). Эту силу
обозначим Ft:
Таким образом, интеграл с путем х в качестве переменной
интегрирования распадается на два:
ь о
Mdx + \Ft{x)dx. A.6)
Ь
Эти два интеграла нельзя сложить по формуле
с с
<$ dx -\-^ у dx = } q) dx,
ba
так как подынтегральная функция в двух интегралах
в A.6) хотя и имеет одинаковый смысл (сила), но выра-
жается разными формулами. Получается это потому, что
F задана как функция t, a t выражается через х различ-
ными формулами при возрастании х от 0 до Ь и при
убывании х от Ь до 0. В данном случае F1(x)=* — Fx{x).
Подставляя выражения для F х(х) н Ft(x) в A.6), получим:
Во втором интеграле можно переставить пределы инте-
грирования, причем меняется зндк, поэтому получим:
A.7)
•) Равенство cos* a>? -f- sin" oof = 1 правильно при любых значе-
ниях tot. Из него следует cosa>t= ± Vl —sin1 at, а вот знак перед
корнем зависит от того, какова величина tot. Легко убедиться, что
при at < -=- надо брать плюс, а при -=- < at < -=- надо брать
минус, что и сделано выше.
§ 1] СИЛА, РАБОТА, МОЩНОСТЬ 355
Обозначая г = 4-, dx = bdz, найдем:
1
Интеграл /= I ]/l —гг dz ==~ (площадь четверти круга
а
радиуса 1). Поэтому из A.7) получаем:
что совпадает с формулой A.5), полученной интегриро-
ванием по времени.
Таким образом, в случае силы, зависящей от времени
и могущей принимать разные значения при одинаковом
значении х, работа А также не является однозначной
функцией х. В приведенном примере колебательного дви-
жения F = f cos u>t, x = bs\x\(?>t с течением времени х
снова и снова проходит одни и те же значения, а работа,
произведенная силой, все увеличивается и увеличивается
(при положительном /).
Если сила зависит от скорости (как это имеет место
для силы трения), положение будет похожим: тело может
вернуться в исходное положение, но работа силы не
равна нулю. В случае силы трения работа отрицательна
(см. упражнения).
Упражнения
1. Найтн выражение в виде интеграла для работы силы трения,
пропорциональной скорости движения тела и направленной в проти-
воположную сторону F = — hv, h > 0. Показать, что работа отри-
цательна.
2. Сила трення постоянна по величине и направлена в сторону,
противоположную скорости, т. е.
— h, если v > 0,
-f- К если v < 0.
Тело движется по закону x = b sin at. Найти работу силы трения за
время от t = 0 до 11= — .
3. Сила, действующая на тело, задана формулой F = Д, sin a>at,
fa — постоянная. Ввиду того, что на тело действуют также и другие
12*
. (
356 МЕХАНИКА [Ч. VI
силы, оно движется по закону x = b sin <й^. Определить работу силы F
за время от t = 0 до t=^tk. Рассмотреть случаи со0 = со,.
at*
4. Тело падает по закону х = ?=- (ось х направлена вниз). Найти
v*
формулу для работы силы сопротивления воздуха F =—aSQ -^ , где
а — коэффициент пропорциональности, зависящий от формы тела (он
может изменяться от 0,1 до 1), S — площадь поперечного сечения
тела в см*, q— плотность воздуха A,3-10~" г/см*), v — скорость
падения тела в см сек. Найти также формулу для работы силы
тяжести F^=mg, m — масса тела.
Произвести вычисления и сравнить результаты для деревянного
шарика диаметром 1 см, а = 0,8 и для стальной пули длиной 3 см,
диаметром 0,7 см, а =0,2, для *=1 сек, 10 сек, 100 сек.
Замечание. Смысл расчета состоит в том, что мы предпола-
гаем, что сила сопротивления воздуха мала по сравнению с силой
тяжести и заметно не меняет закон свободного падения тела. Под-
считывая работу силы сопротивления воздуха и сравнивая ее с рабо-
той силы тяжести, проверяем правильность исходного предположения
о малой роли силы сопротивления воздуха. Точное решение задачи
о падении тела с учетом сопротивления воздуха будет дано в § 7.
5. Ветер, дующий со скоростью va, действует на парус с силой,
равной
— — при v < va,
(vu — v)*
2 ПрИ " > °»
где v—скорость движения судиа, 5 — площадь паруса, q—плот-
ность воздуха, а — безразмерный коэффициент (для паруса, постав-
ленного перпендикулярно к направлению ветра, a=sl). Найти работу
силы ветра при перемещении судна на Ь метров. Найти мощность
силы ветра. Движение судна считать равномерным с постоянной ско-
ростью v. Выяснить зависимость работы и мощности от величины о.
Найти максимальную мощность при ио = ЗО м(сек, а = 1, S = 10X10 м*
и выразить ее в лошадиных силах.
6. Тело движется по закону х =с. cos (ш/ +а) П°Д действием
силы F = f cos bit. Найти работу силы за время от t^=tn до t=tk.
Получить работу силы за один период ее действия (от <=0 до
t =—J . Найти среднюю мощность силы.
§ 2. Энергия
Рассмотрим случай силы, которая зависит только от
положения (координаты) тела, F=F(x). Как отмечалось
выше, примером силы такого рода является сила, с кото-
рой на тело действует пружина, второй конец которой
§ 2] энергия 357
закреплен неподвижно*). В таком случае выражение
Fdx можно применять без каких-либо осложнений
п
(сравните с предыдущим параграфом). В частности, в этом
случае, если тело двигалось сперва в одну сторону от хп
до хт, а потом в противоположную и вернулось в началь-
ное положение, то хк = хп, полная работа силы действи-
тельно равна нулю
¦** = *)|
А= J F(x)dx = 0.
х„
Разбиение пути на участки только подтверждает этот
вывод
*щ ¦** хт хт
Fdx+l Fdx=[ Fdx~\ Fdx,
и при xk = xn Л = 0.
В механике потенциальная энергия определяется как
способность произвести работу. Пружина обладает опре-
деленным запасом потенциальной энергии, зависящим от
того, насколько она растянута или сжата. При неподвиж-
ном положении одного закрепленного конца потенциаль-
ная энергия пружины зависит от положения тела, к ко-
торому прикреплен подвижной конец пружины. Таким
образом, потенциальная энергия и = и(х) есть функция
координаты х. Если в начальном положении потенциаль-
ная энергия равна и(хп), то после перемещения тела
в положение xk, когда пружина совершила работу А,
равную
Л = J F{x)dx,
хп
оставшаяся потенциальная энергия равна и(хп) — А.
*) Если второй конец пружины может перемещаться по произ-
волу, то сила, действующая на тело, будет зависеть не только от
положения тела, но и от положения второго конца пружины, а сле-
довательно, не удовлетворяет сформулированному условию.
358 МЕХАНИКА [Ч. VI
Таким образом,
и (xk) = и (*„),— А = и (хп) — J F (х) dx. B.1)
Надо полностью прочувствовать знак при А в этом выраже-
нии: если пружина совершает работ у, то запас способ-
ности пружины совершать работу при этом уменьшается 1
Произведенная пружиной работа черпается из запаса
потенциальной энергии. Поэтому произведенная работа
(то, что отдала пружина) равна разности начальной энер-
гии минус конечная энергия пружины:
Во все формулы входит разность величин потенциальной
энергии в двух положениях тела. Поэтому если заменить
и(х) на и(х)-\-С, где С — любая постоянная величина,
то это ничего не изменит в физических результатах. Дей-
ствительно,
[и (хп) + С] — [и (хк) -f С] = и (хп) — и (хк).
Значение и(х) в какой-то данной точке—обозначим
ее ха — можно выбрать произвольно. Обозначим его иа.
После этого в любой другой точке х значение функции
и(х) определяется по формуле B.1), если в ней положить
7 (х\ Нг (9 9\
Таким образом решается задача об определении потен-
циальной энергии по заданной силе.
Можно поставить обратную задачу: зная потенциаль-
ную энергию как функцию х, и(х), найти силу F(x). Для
решения этой задачи возьмем производную от обеих
частей равенства B.2). Производная от интеграла равна
подынтегральной функции, так что
dx
Знак минус здесь весьма существен. Сила положи-
тельна, направлена в сторону увеличения х в том случае,
§ 2] энергия 359
du
если ^ отрицательна, т. е. если при увеличении х потен-
циальная энергия и уменьшается. Сила отрицательна
(направлена в сторону уменьшения х), если ^>0, т. е. в
том случае, когда при увеличении х энергия и увеличи-
вается; в этом случае, очевидно, при уменьшении х энер-
гия и также уменьшается.
Значит, сила направлена всег-
да в ту сторону, при движе-
нии в которую потенциальная
энергия уменьшается.
Рассмотрим подробнее
пример пружины. Пусть в не-
натянутом состоянии пружины тело находится в начале
координат (рис. 13S). При оттягивании тела вправо сила
пропорциональна тому расстоянию, на которое оттянуто
тело, и направлена влево
F=—kx, k>0.
Положим при ха = 0 ао = О, т. е. примем потенциальную
энергию ненатянутой пружины за нуль. Получим:
X X
= — \ F dx = k \ х dx = k3^-.
Легко убедиться, что этому и(х) соответствует по фор-
муле F = — jjj сила F = — ^ (л т)=~ кх'
Рассмотрим второй пример: силу тяжести. Направим
ось z вверх. Сила тяжести, действующая вниз, равна
— mg, где g — ускорение силы тяжести. Она не зависит
от высоты z, но ведь постоянная величина есть частный
случай функции. Важно то, что сила тяжести не зависит
от времени и скорости. Поэтому можно применить полу-
ченные выше формулы. Примем за нуль потенциальную
энергию тела на уровне Земли при z = 0. Тогда
B.3)
Потенциальная энергия линейно растет с увеличением
высоты тела иад поверхностью Земли.
360 МЕХАНИКА [Ч. VI
В предыдущее примере мы предполагали, что расстоя-
ние z мало по сравнению с радиусом Земли. Будем
теперь рассматривать снова силу притяжения, считая,
что расстояния могут быть сколь угодно большими. По
закону тяготения Ньютона сила притяжения обратно
пропорциональна квадрату расстояния от притягивающей
массы. Известно, что для тела, находящегося над поверх-
ностью Земли, сила притяжения ко всему земному шару
равна силе притяжения к массе, равной массе Земли
и сосредоточенной в центре Земли *). Удобно поэтому
расстояние отсчитывать от центра Земли. Обозначим
его г. Итак, сила, действующая на тело, равна
'=-?•
Подразумевается, что константа С положительна. Сила
отрицательна, так как она направлена к центру Земли, а
координата г растет при удалении от Земли — сила дей-
ствует в сторону уменьшения г.
Константу С легко определить из того условия, что
сила, действующая на поверхности Земли (г=^га —
= 6400 /ш = 6,4-10* см), нам хорошо известна
/•"(/¦„) =— mg = -, C = mgt\, B.4)
где g есть ускорение силы тяжести именно на поверх-
ности Земли, g1 = 981 см/сек*. Окончательно
Примем снова за нуль потенциальную энергию тела
на уровне Земли. Тогда
r0 r0
= mgrf(r—r,). B.5)
*) Для тела, находящегося внутри Земли, это несправедливо.
В этом случае при расчете силы надо учитывать только ту часть
массы, которая ближе к центру Земли, чем рассматриваемое тело.
§ 2] ЭНЕРГИЯ 361
При малой высоте г=г—гп<^.г„, г-± мало отличается от
единицы и приблизительно
и (г) = mg{r — ra) = mgz,
что совпадает с формулой B.3), полученной раньше.
Однако при увеличении г, как видно из формулы B.5),
потенциальная энергия не растет неограниченно, как
это было бы по приближенной формуле B.3), а стре-
мится к определенному пределу
Таким образом, с учетом ослабления притяжения с рас-
стоянием энергия тела на бесконечном расстоянии такая
же, как по приближенной формуле на расстоянии га от
поверхности Земли, т. е. на расстоянии 2г0 от центра
Земли.
В этой задаче мы встречаемся с физическим вопро-
сом, в котором рассматривается бесконечное расстояние.
По этому поводу нужно иметь в виду, что в физической
задаче нас интересуют всегда конечные величины, ко-
нечные расстояния. Так, например, если рассматриваются
движение тела н энергия тела, зависящие от притяжения
Земли, то непосредственно может интересовать достиже-
ние Луны, Марса или других планет или даже других
звезд, т. е. достижение расстояний больших или очень
больших по сравнению с радиусом Земли, но все же
конечных!
Пусть рассматривается вопрос о запуске ракеты на
большую высоту, на большое расстояние от Земли. Инте-
ресуют необходимая энергия и время полета. Рассмотрим
два случая:
1) ракета должна пролететь расстояние R=\0ra, где
г0 — радиус Земли,
2) ракета должна пролететь расстояние R = \00ra.
Время полета приблизительно пропорционально рас-
стоянию. Поэтому во втором случае ракете придется ле-
теть примерно в 10 раз дольше, чем в первом. Измене-
ние R существенно изменяет время полета. Поэтому при
рассмотрении времени полета заменять R бесконечностью
никак нельзя.
Зб2 МЕХАНИКА [ч. VI
Работа, необходимая для того, чтобы, оторвавшись
от Земли, пройти на расстояние R от центра Земли,
равна
Вспоминая, что /-„ = 6,4-10* см, получаем в первом
случае A1 = mg -5,76 • 10", а во втором случае Аг =
= mg.6,34.108.
Изменение расстояния в 10 раз незначительно повли-
яло на величину необходимой энергии. Если бы мы за-
менили R бесконечностью, то получили бы
Л*, = mg-6,4.10е.
Л, отличается от А^ на 10°/e, At — на 1°/0- Поэтому при
подсчете работы R можно заменить бесконечностью.
Таким образом, одна и та же величина R в одной
и той же задаче при рассмотрении разных сторон воп-
роса либо может заменяться на бесконечность, либо не
должна заменяться на бесконечность. Возможность та-
кой замены зависит не только от самой величины R (и
ее сравнения с другими входящими в формулы величи-
нами той же размерности, в данном случае г0). Возмож-
ность замены зависит от строения самой той формулы,
в которой производится замена.
Возвращаясь к вопросу о потенциальной энергии
тела, притягиваемого к Земле, найдем численное значе-
ние и(оо) на единицу массы: в физической системе еди-
ниц оно равно gro = 981-6,4.1O8 ^6,28-Ю11 эрг\г, в тех-
нической системе gr0 = 6,28-10° килограммометров на
килограмм. Любопытно перевести эту величину в тепло-
вые единицы: 1 килокалория равна 427 кем, так что
и(оо)= 15-10* килокалорий на килограмм. Эта вели-
чина в 30 раз больше теплоты испарения воды и
в 10 раз больше химической энергии взрывчатых ве-
ществ.
В задачах небесной механики и в физике целесооб-
разно выбирать за нуль потенциальную энергию тела,
находящегося на бесконечном расстоянии от притягива-
ющей его массы. Тогда для потенциальной энергии тела
§ 2] ЭНЕРГИЯ 363
на расстоянии г получим:
где С — константа в выражении силы (f = — ~.Л; она
определяется по формуле B.4), если известно ускорение
силы тяжести на поверхности Земли g и радиус Земли г0.
Можно получить другое выражение для С. Действи-
тельно, по закону тяготения Ньютона F = — х^?-, где
т — масса тела, притягиваемого к Земле, М — масса
Земли, г — расстояние до центра Земли, х — гравита-
ционная постоянная, равная 6,7-10~* дин-см*1гг =
= 6,7-10~8 см*\г-сек*. Поэтому С = хтМ. Пользуясь этой
формулой, легко определить С, зная х и М.
Задача о потенциальной энергии двух электрических
зарядов е, и et совершенно аналогична предыдущей. Сила
взаимодействия между ними равна
F = ke-?. B.6)
При этом, если заряды выражены в электростатической си-
стеме единиц (единица заряда равна ~ ,., кулона! ,
а сила — в динах, то в формуле B.6) k = \. В формуле
нет знака минус, который стоит в выражении для силы
тяготения. Действительно, если е, и et одноименные (оба
положительны или оба отрицательны), то произведение
егег положительно. Но в этом случае заряды отталкива-
ются, т. е. сила F положительна.
Определяя снова и (г) так, чтобы ц(оо) = 0, получим:
, . е1ег
Потенциальная энергия двух одноименных зарядов на
конечном расстоянии положительна: они отталкиваются
и, расходясь с расстояния г до оо, могут совершить ра-
боту, равную
и (г) — и (оо) = и (г).
Потенциальная энергия двух разноименных зарядов от-
рицательна. Действительно, е1е1<0, если e,>0, et<0;
364 МЕХАНИКА [Ч. VI
это ясно и физически: так как разноименные заряды
притягиваются, то нужно затратить энергию для того,
чтобы растащить их один от другого на бесконечное
расстояние.
Отметим, что благодаря закону сохранения энергии
потенциальную энергию можно определить не только как
способность производить работу, но и как работу, кото-
рую нужно было затратить для приведения системы
в данное состояние. Растянутая пружина способна про-
извести определенную работу, возвращаясь в нерастя-
нутое состояние. Очевидно, именно такую же работу
надо было затратить для того, чтобы растянуть пружину.
Аналогичные утверждения можно высказать в случае
тела, поднятого на определенную высоту над Землей,
или для системы двух зарядов.
§ 3. Равновесие и устойчивость
Рассмотрим тело, могущее двигаться без трения вдоль
какой-то прямой, которую примем за координатную ось х.
Пусть на тело действует сила, направленная вдоль этой
оси и зависящая от координаты х. Можно снова пред-
ставить себе, например пружину. Ниже мы разберем и
другие примеры.
Положением равновесия называется такое положение,
когда сила равна нулю и тело может оставаться в по-
кое. Точку, в которой имеет место равновесие, назовем
х0, так что F(xa) = Q. Разлагая функцию ^(д;). в ряд
Тейлора и пренебрегая всеми степенями (х — ха), кроме
первой, видим, что может быть два варианта зависи-
мости F(x) в окрестности точки ха (при условии F(xa) = 0):
Р{х) = кг(х—х„), F(x) = — kt(x — ха). В обеих формулах
подразумевается, что kl и kx — положительные величины.
Первый случай показан на рис. 134, а, второй — на
рис. 134, б.
Этим двум случаям соответствует совершенно различ-
ный характер равновесия. В самом деле, в случае
рис. 134, а, если тело находится несколько правее точки
ха, то на него действует положительная сила, т. е. сила,
которая тяиет его дальше вправо. Таким образом, в слу-
чае рис. 134, а равновесие в точке х = ха неустойчивое:
§ 31
РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ
365
достаточно малого отклонения тела (безразлично вправо
или влево), чтобы иа тело начала действовать сила, уве-
личивающая это отклонение. Напротив, в случае рис. 134, б
при отклонении тела вправо сила отрицательна, т. е. тя-
нет влево. Отклонение тела от положения равновесия
вызывает силу, стремящуюся возвратить тело в положе-
ние равновесия. В этом случае имеем дело с устойчивым
равновесием. Легко убедиться, что для тела, закреплен-
ного на пружине, осуществляется второй случай.
Рнс. 134.
В соответствии с выписанными выше выражениями
силы находим выражения потенциальной энергии, поль-
зуясь B.2). В случае неустойчивого равновесия
и(х) = и (х9) — Lkx(x — xaf.
В случае устойчивого равновесия
« (х) = и (*о) -\~ ~2 &г (х хлТ ¦
Соответствующий ход кривых показан на рис. 135, а и б.
и
б)
Рнс. 135.
Таким образом, в случае неустойчивого равновесия
потенциальная энергия имеет максимум, в случае устой-
чивого равновесия—минимум. В обоих случаях в самой
366 МЕХАНИКА [q. VI
точке максимума или минимума F = — ^1 _ =0, сила
равна нулю. х~'*"
Результат является вполне естественным. Если тело
находится в состоянии максимума потенциальной энер-
гии, то при перемещении в обоих направлениях выде-
ляется энергия, которая может пойти на преодоление
инерции, превращаясь в кинетическую энергию. Если же
тело находится в состоянии минимума энергии, то для
перемещения его в любое другое положение нужно за-
тратить энергию извне; вта энергия пойдет на увеличение
потенциальной энергии; затратив малую энергию, можно
будет лишь незначительно сместить тело. Такие свойства
тела, находящегося в положении минимума потенциаль-
ной энергии, полностью соответствуют понятию устой-
чивого равновесия.
При действии силы тяжести вблизи поверхности Земли
потенциальная энергия равна mgz, где z есть высота над
поверхностью Земли. Кривые, изображающие зависи-
мость и{х), можно представить себе как кривые, изобра-
жающие высоту положения тела в зависимости от гори-
зонтальной координаты х. Надо представить себе тело,
которое движется вдоль кривой линии как бусина, нани-
занная на жесткую проволоку. Кривая и(х) соответствует
форме проволоки, если плоскость чертежа расположить
вертикально. Тогда очевидно, что максимум и(х) пред-
ставляет собой (рис. 135, а) точку проволоки, с которой
бусины при малейшем толчке скатываются вниз, мини-
мум и{х) (рис. 135,6) — ниж-
нюю точку, в которой' бусины
а находятся в устойчивом поло-
"г.—¦*' _ жении и.куда они сами скаты-
* ваются с соседних участков.
Таким образом, по графику
и(х) можно наглядно предста-
Рис. 136. вить себе направление сил и ха-
рактер равновесия.
Рассмотрим несколько примеров.
1. Пусть заряженное тело движется по прямой (при-
мем ее за ось х), на которой закреплены неподвижно
два одинаковых заряда симметрично относительно начала
координат на расстоянии 2а друг от друга (рис. 136).
о
§ 3]
РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ
867
Ясно, что в начале координат тело находится в поло-
жении равновесия. Действительно, в этом случае силы,
действующие на тело со стороны неподвижных зарядов,
равны по величине и противоположны по направлению,
так что они уравновешиваются, т. е. их равнодействую-
щая равна нулю.
Потенциальная энергия тела складывается из двух
членов
где е — заряд тела, е, — величина неподвижного заряда,
г' — расстояние от тела до щ
левого заряда, г" —* рас-
стояние от тела до правого
заряда,
г'=х-\-а, г"=а—х,
поэтому
eef>Q
C.1)
Соответствующие кри-
вые изображены на рис.
137. Верхняя кривая со-
ответствует е1е>0, т. е.
случаю одноименного заря-
да тела и неподвижных Рис* •
зарядов, нижняя кривая соответствует случаю е,е<0, т. е.
случаю, когда тело имеет заряд, знак которого противо-
положен знаку неподвижных зарядов.
В случае е,е<0 равновесие в начале координат не-
устойчивое. Действительно, тело притягивается и к левому
и к правому заряду, в начале координат силы протяжения
к двум зарядам уравновешивают друг друга. Однако
если тело немного сдвинется, например, вправо, то при-
тяжение к правому заряду окажется сильнее и тело будет
продолжать двигаться в ту же сторону.
Найдем -Л . Пользуясь C.1), получаем:
ах x^z. о
I L
)» Me —
C.2)
363 . МЕХАНИКА [Ч. VI
Полагая в формуле C.2) х = 0, находим:
Ж?
Следовательно, при х = 0 j4->0, если е,е>0. В этом
случае и (х) имеет минимум при х = 0, равновесие устой-
чиво. Если же ехе<0, то -т-% _ < О, и(х) имеет макси-
мум при дг = О, равновесие неустойчиво.
2. Аналогично рассмотрим случай, когда заряды рас-
положены на том же расстоянии от начала координат.
но иа прямой, перпендикулярной к
линии (оси абсцисс), по которой дви-
жется заряженное тело (рис. 138).
В этом случае потенциальная энергия
5 равна
У\
е,
е,
е.е
Рис. 138.
(график потенциальной энергии при
a=l, |el(?|:=l изображен на рис. 139). В примере 2
при е1е>0 равновесие в начале координат неустойчиво.
При заряде тела другого знака по сравнению с непо-
движными зарядами (е,е<0) равновесие устойчиво.
е,е<-0
Рис. 139.
Это нетрудно установить, рассматривая силу, дей-
ствующую на подвижный заряд (рис. 140). Пусть еле>0.
Сместим тело вправо от положения равновесия. Тогда
равнодействующая сил отталкивания направлена тоже
вправо, в сторону дальнейшего увеличения отклонения.
§ 3]
РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ
369
Равновесие неустойчивое. В случае е,е<0 равнодействую-
щая направлена в сторону уменьшения отклонения.
Равновесие устойчивое.
К этим результатам также нетрудно прийти, рассмат-
ривая -^
е,е=.О
как по рис
как по рис
Рис. 140.
Обратим внимание, что при е^е > 0, когда в примере 1
(рис. 136) была устойчивость, в примере 2 (рис. 138)
равновесие неустойчиво. При ete<0 (разноименные за-
ряды) положение обратное:
равновесие неустойчиво
при расположении зарядов
в соответствии с рис. 136
и устойчиво при располо- -•—i
жении их, как на рис. 138. е/
Повернув рис. 138 на
90°, мы заметим, что ои, в
сущности, относится к то-
му же начальному распре- Рис. иь
делению зарядов в положе-
нии равновесия, что и рис. 136. Можно сказать, что
рис. 136 и 138 относятся к одинаковому начальному
распределению зарядов, но рассматриваются различ-
ные направления движения (рис. 141). При этом
всегда (при любых знаках зарядов) в том или ином на-
правлении движения равновесие оказывается неустой-
чивым.
В электростатике доказывается, что этот результат
является совершенно общим: в пространстве между внеш-
ними закрепленными зарядами нигде нет точки равнове-
870 МЕХАНИКА [Ч. VI
сия такой, чтобы равновесие было устойчивым относи-
тельно перемещении в любом направлении.
Приведенное ниже общее доказательство этого факта
может показаться читателю довольно сложным. Его можно
пропустить без ущерба для понимания дальнейшего
материала.
Для доказательства в общем виде заметим, что потен-
циальная энергия заряда е, находящегося в точке (х, у, г),
в зависимости от его расстояния г от неподвижного за-
ряда elt помещенного в точку (лгг, ух, гг), дается фор-
мулой
Рассмотрим движение по оси х и найдем -? при по-
стоянных у и z; такая величина обозначается р-. Затем
6Ри дги
аналогично найдем з-j и -з-g-, относящиеся соответственно
аут oz"
к движению по осям у и г. Оказывается *), что при лю-
бых х, у, 2, хх, ух, 2г сумма вторых производных по
трем перпендикулярным осям равна нулю!
дги ¦ дги I ^ы «
дх1 'V ' йг*
Очевидно, это свойство сохранится и для суммы
любого числа членов вида —, где ек—неподвижный за-
ряд в точке (хк, yk, zk), a rk есть расстояние заряда е от
этой тачки. Следовательно, при любом распределении
неподвижных зарядов в пространстве между ними имеет
место формула
+ 0 <33>
в частности, и в той точке, где имеет место равновесие
заряда е. Для равновесия необходимо, чтобы силы' по
*) Читателю следует самому в этом убедиться.
§ 3] равновесие и устойчивость 371
любой оси равнялись нулю. Для этого нужно, чтобы
¦ <?и п ди п ди
Если равны нулю силы по трем перпендикулярным осям,
то равна нулю и сила в любом направлении*).
Для того чтобы равновесие было устойчивым относи-
тельно движения по всем трем перпендикулярным на-
правлениям, нужно, чтобы было
Однако это противоречит уравнению C.3), так как сумма
трех положительных величин не может равняться нулю.
В последнее время (с 1956 г.) вопрос о том, можно
ли устойчиво удерживать заряженные частицы, действуя
на них неподвижными зарядами, привлек большое
внимание. Для получения ядерной энергии при сжи-
гании дейтерия нужно удерживать заряженные ядра в
пространстве, не допуская столкновения их со стенками
сосуда. По доказанному выше этого нельзя достичь, рас-
полагая на стенках сосуда заряды, как бы ни были по-
добраны эти заряды. Таким образом, это направление
изобретательства можно сразу назвать безнадежным.
Известно, что положительное решение задачи в прин-
ципе может дать предложенный советскими академиками
А. Д. Сахаровым и И. Е. Таммом способ применения
магнитного поля.
Упражнения
1. Заряд е движется по прямой, на которой закреплены непо-
движно два положительных заряда ег и et = 4ei на расстоянии 2а
один от другого. Найти ту точку на прямой, в которой возможно
равновесие заряда, и установить характер равновесия. Рассмотреть
два случая: е>0 и е<0.
2. Решить задачу 1, изменив знак заряда et.
*) Если имеется отличная от нуля сила F, действующая в каком-
либо направлении, то вдоль каждой оси будет действовать сила,
равная проекции силы f на эту ось.
372 МЕХАНИКА [Ч. VI
§ 4. Второй закон Ньютона
Сформулированный Ньютоном второй закон движения
заключается в том, что произведение массы на ускорение
равно действующей силе*). Ускорение а есть производная
скорости v по времени; в свою очередь скорость есть
производная от координаты тела) по времени. Таким
образом,
та — m-^j- = F, D.1)
или
m^=F. D.2)
Начнем со случая, когда сила задана как функция
времени F=F(t). Это означает, что производная -ц за-
дана как функция времени. В таком случае легко найти
из закона Ньютона D.1) скорость в любой заданный мо-
мент; кроме действующей силы, при этом надо задать
также скорость в какой-то момент ta. Тогда
t
-L§ F{t)dt. D.3)
Зная скорость в зависимости от времени v (-/) и началь-
ное положение тела x(ta), найдем положение тела в лю-
бой момент
t
v(t)dt, ' D.4)
где v(t) дано предыдущей формулбй.
Соотношение между скоростью и путем" подробно
с примерами рассматривалось в части П.
В целом формулы D.3) и D.4) решают задачу нахож-
дения x{t) из уравнения D.2). Соотношение D.2) — это
*) Первый закон Ньютона — закон инерции — заключается в том,
что тело, на которое не действуют никакие силы, движется прямоли-
нейно и равномерно. Это значит, что у такого тела ускорение равно
нулю при равной нулю силе. Следовательно, первый закон Ньютона
содержится во втором законе, является его частным случаем.
§ 4] ВТОРОЙ ЗАКОН НЬЮТОНА 373
дифференциальное уравнение второго порядка, в него вхо-
дит вторая производная неизвестной функции x(t). В от-
вет входит не только заданная функция F{t), но и две
постоянные величины, определяемые из начальных усло-
вий: положение тела и скорость тела в заданный момент
времени ta.
Если задан или экспериментально найден закон дви-
жения тела, т. е. задана функция x{t), то нахождение
силы, действующей на тело, не представляет никакого
труда: надо найти вторую производную функции x(t) и
умножить ее на т [формула D.2)].
Упражнения
1. Найти закон движения тела под действием постоянной силы F,
если в момент времени / =0 тело покоилось в начале координат
(х = 0).
2. То же при условии, что при /= 0 х = 0, v = va.
3. То же при условии, что при / = 0 х=ха, о = о0.
4. Тело массой в 20 кг начинает двигаться под действием силы
1 кГ из начала координат без начальной скорости. Какой путь пройдет
оно за 10 сек?
5. Шарик свободно, т. е. с начальной скоростью, равной нулю,
падает с высоты 100 м. Через сколько времени он достигнет земли?
(Сопротивлением воздуха пренебречь.)
6. В условиях предыдущей задачи шарик начинает падение со ско-
ростью va = Юм/сек. Разобрать два случая: а) начальная скорость
шарика 1>„ направлена вниз, б) начальная скорость шарика va на-
правлена вверх. Определить, через сколько времени шарик достигнет
земли. Какова его скорость в момент приземления. Проверить, что
в случаях а) и б) скорость приземления одинакова.
7. На тело действует сила, пропорциональная времени, протек-
шему с начала движения (коэффициент пропорциональности равен k).
Найти закон движения тела, если известно, что тело начинает дви-
жение из точки х = 0 с начальной скоростью v0.
8. На тело действует сила, периодически меняющаяся со време-
нем F = fcoswt (f, (о — постоянные числа).
а) Найти закон движения тела при условии, что прн t = 0 x = 0,
v — 0. Установить, что такое движение является колебательным. Опре-
делить период колебания, наибольшее значение х (/)> наибольшее
значение скорости.
б) То же для силы F = fsinatt, прн t = 0 x = 0, v = 0.
9. Тело движется под действием постоянной силы F. В момент
времени t^=ta тело было в точке х=х0. Найти, какую скорость
должно иметь тело при / = t0, чтобы в момент времени / = tx попасть
в точку х = хх.
374 МЕХАНИКА [Ч. VI
§ 5. Импульс силы
Задача нахождения закона движения тела при задан-
ной зависимости силы от времени в принципе решена
в предыдущем параграфе. Здесь мы рассмотрим свойства
этого решения и некоторые новые понятия, связанные
с решением.
Произведение P = mv массы на скорость называется
«количеством движения». Величина
t
\F{t)dt E.1)
называется «импульсом силы» за время от ta до t.
Формула D.3) может быть записана так:
t
P{t) — P(to)=[Fdt. E.2)
и
Словесная формулировка результата E.2): изменение ко-
личества движения равно импульсу силы.
Часто встречается случай силы, действующей только
в течение краткого промежутка времени: примером яв-
ляется удар молотком, отскакива-
ющим после удара от тела. И до
и после удара сила равна ну-
лю. При отсутствии других сил,
кроме краткой силы удара, оче-
» видно, что до удара -тело дви-
с' l'- t ' жется с постоянной скоростью,
Рис. 142. а после удара тело движется с дру-
гой, тоже постоянной скоростью.
Пусть F(t) отлично от нуля только в промежутке
от tl до tt (рис. 142). Рассмотрим интеграл
и
E.3)
о
Эту величину можно назвать полным импульсом силы —
полным в том смысле, что. интеграл берется по всему
промежутку времени, когда сила фактически действует.
§ 5]
импульс силы
375
В выражение E.1) входит интеграл от tn до t. Если
*г, a t>tt, то
Действительно, запишем:
t t, и t
J F dt = 5 F dt + 5 F dt -f- J F dt.
to U t, fj
В правой части первый и третий интегралы равны нулю,
так как в соответствующих промежутках F = 0, а второй
(средний) интеграл есть /. Таким образом, из формул
E.2) и E.3) получаем Р(t) = P(ta)~\-1, если /0<*г, t>tt.
Из формулы D.3) видим, что скорость после удара
зависит только от импульса силы, т. е. от интеграла
Рис. 143.
силы, но не от детального вида функции F(t). Например,
несколько различных кривых F(t), нарисованных на
рис. 143, дают одинаковый импульс силы, т. е. одинаково
Рис. 144.
меняют скорость тела. Для каждой из кривых F(t) не-
трудно нарисовать соответствующий график скорости v(t).
На рис. 144 показаны такие графики в общем предполо-
376
МЕХАНИКА
[Ч. VI
жении, что начальная скорость равна нулю. Общим для
всех кривых рис. 144 является конечное значение скоро-
сти, все кривые переходят справа в горизонтальную пря-
мую на высоте v = —.
Каждую из кривых F(t) рис. 143 можно сжимать по
оси времени и пропорционально растягивать по оси силы.
Площадь под кривой F, -т. е. § F dt, полный импульс силы,
при этом не изменяется. Именно так получена, например,
кривая 2 на рис. 143 из кривой /.
Чем короче время действия силы, тем меньше время,
в течение которого скорость тела меняется от начального
значения va = Q до конечного значения vk=— (рис. 144).
m
и
0
i
1
i
t
Рис. 145.
Таким образом, в пределе, при очень большой- силе, дей-
ствующей в течение очень малого времени, график ско-
рости приобретает вид ступеньки (рис. 145). При этом
становится несущественным, какую из кривых рис. 143
мы сжимали: ступенька характеризуется только одной
величиной vk=— , а эта величина для всех кривых оди-
накова.
Если до действия силы тело покоилось в точке ха, то
после кратковременного действия большой силы тело
начинает двигаться с постоянной скоростью, равной — .
Если сила действовала в момент tx (промежуток времени
от tx до /, считаем малым и не различаем tt и ?г), то
§ 5] импульс силы 377
положение тела в зависимости от времени дается формулами
t>t1.
Соответствующий график показан на рис 146. Отметим,
что x(t) удовлетворяет уравнению
Напомним, что на графике (х; t) первая производная
2У связана с наклоном касательной к кривой. Вторая
производная характеризует скорость изменения первой
производной, т. е. вто-
рая производная свя-
зана с кривизной ли-
нии x(t).
На рис. 146 линия
х (t) имеет излом в точке
t — tx, х = ха. Излом
можно представить себе
как точку, в которой
кривизна бесконечна,
так что наличие изло-
ма соответствует рас-
смотрению очень боль-
шой (в пределе — беско-
нечной) силы. Однако до и после излома производная
-^ конечна; значит, очень большая сила действовала очень
малое время, так что импульс силы конечен. Импульс
легко определить по графику (рис. 146), вычисляя ско-
рость после действия силы и используя формулу E.2).
Напомним читателю, что по третьему закону Ньютона
при взаимодействии двух тел сила, с которой второе тело
действует на первое (/\)*), равна по величине и противо-
положна по направлению силе, с которой первое тело
о
Рис. 146.
*) Значок у буквы F ставим так, чтобы он показывал, на какое
тело действует сила F, значок у буквы Р также означает номер
тела, к которому относится количество движения.
378 МЕХАНИКА [Ч. VI
действует на второе (Ft),
F1(t) = -Fl(t).
Формула E.2) в применении к первому телу и силе Fx
дает:
Эта же формула в применении ко второму телу и силе Ft
дает:
t
Так как F2 = —Ft по третьему закону Ньютона, то
Поэтому E.5) принимает вид
t
Л@—Л('.)=—J^, Л- E-6)
Сопоставляя E.4) и E.6), находим:
J\@ —-Р.('.)=-Р.('.) —-Р.(').
Отсюда
Последняя формула показывает, что действие тел друг
на друга не меняет суммы количеств движения этих тел.
§ в. Кинетическая энергия
Рассмотрим тело, движущееся под действием известной
силы Fit), и найдем связь между работой, произведенной
этой силой, и скоростью движения тела.
Из основного уравнения m-n = F(t), умножая обе
части на скорость v, получим:
^ . F.1)
§ 6] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ 379
Имеет место тождество
справедливое, какова бы ни была зависимость v(t). Поль-
зуясь им, перепишем F.1) в виде
а так как т — постоянная величина, то
Вводя обозначение
? = К. F.2)
получим окончательно:
'§ = F(t)v. F.3)
Пользуясь выражением для работы A.1), получим:
откуда
A=K(t1)-K(ta). F.4)
Величина К. есть кинетическая энергия тела. Формула
F.4) выражает закон сохранения энергии: изменение
кинетической энергии тела равно работе, произведенной
силой. Формула F.3) выражает закон: скорость измене-
ния кинетической энергии равна мощности, которую раз-
вивает сила.
Когда сила задана определенной функцией времени,
то импульс силы и, следовательно, вызванное данной
силой изменение количества движения тела не зави-
сят ни от массы тела, ни от его начальной скорости,
так как импульс силы и изменение количества движения
t,
есть f F dt.
L
380 МЕХАНИКА [Ч. VI
Напротив, работа силы и изменение кинетической
энергии тела под действием силы, как видно из формул
F.2), F.3), F.4), существенно зависят не только от самой
силы, но и от массы тела и его начальной скорости.
Действительно, действуя заданной силой в течение опре-
деленного времени на тяжелое тело, покоившееся в на-
чале движения, мы придадим ему лишь малую скорость,
перемещение тела будет мало и работа силы также будет
мала. Легкое тело заберет на себя большую работу, при-
обретет большую энергию. Если до начала действия силы
тело двигалось в сторону, противоположную направле-
нию действия силы, то сила может уменьшить его энергию.
Представим себе тело, участвующее одновременно
в двух движениях. Например, человек ходит по каюте
парохода, а пароход движется, или в каюте падает бро-
шенный мяч. Предположим, что одно из этих движений
(в нашем примере это — движение парохода) равномерное;
Возникает вопрос: можно ли, наблюдая падение мяча
в каюте либо движение в ней какого-нибудь тела под
действием приложенной силы, установить, движется паро-
ход или нет? Иначе говоря, влияет ли равномерное дви-
жение парохода на характер движения предметов на самом
пароходе? Оказывается, что нет, никак не влияет. Опыты
показали, что отсутствие влияния равномерного движения
на физические явления относится не только к механике,
но и к процессу распространения света, к электрическим
и магнитным явлениям. Из этого факта Эйнштейн сумел
сделать выводы огромной важности, развивая теорию
относительности *).
В механике отмеченную независимость от равномер-
ного движения установить нетрудно. Действительно, пусть
тело движется в поезде со скоростью v, а сам поезд дви-
жется по рельсам с постоянной скоростью va. Тогда по
отношению к наблюдателю, стоящему на рельсах, тело
движется со скоростью v1=^v-\-va. При этом ускорение
тела одинаково и для наблюдателя, стоящего на рельсах,
и для наблюдателя, едущего в поезде,
dv, d , , . dv , dvn dv
•) В нашей кинге теория относительности ие излагается.
§ 6] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ 381
Таким образом, постоянное слагаемое в выражении для
скорости не меняет ускорения. Поэтому и сила, дейст-
вующая на тело, не меняется: F=ztna.1 = ma. Разность
скоростей тела до и после действия силы тоже одинакова
для наблюдателя, находящегося на рельсах, и для наблю-
дателя, стоящего в поезде. Действительно, пусть скорость
по отношению к наблюдателю, стоящему в поезде, до
действия силы есть v', после действия силы и"; для наблю-
дателя, стоящего на путях, соответствующие скорости —
v'x и v'[. Тогда v[ = v' -\-va, v\ = v" + o0. Поэтому
v\ — v[ = v" + va— v' — va=v"— v'.
Сложнее обстоит дело с кинетической энергией *): не
только сама кинетическая энергия, но даже и разности
кинетических энергий различны для различных наблюда-
телей. Для наблюдателя, стоящего на путях,
m
2
т (хГ)г т
1
= К"—К' -\-mo0(v' — v').
В этой формуле /Ci и К[ — конечная и начальная кинети-
ческая энергия, вычисленная наблюдателем на путях, а К"
а К' — соответствующая кинетическая энергия, вычислен-
ная наблюдателем в поезде.
Работа силы и мощность для различных наблюдателей
также различны, так как хотя сила одна и та же, но
пройденный путь и скорость различны для наблюдателя,
стоящего на путях, и для наблюдателя, едущего в поезде.
Однако закон равенства изменения кинетической энер-
гии и работы силы выполняется для любого наблюда-
теля, хотя каждая из этих величин в отдельности не-
одинакова для разных наблюдателей. (Примеры, под-
тверждающие это обстоятельство, имеются в упражнениях.)
Отметим замечательную формулу, которая имеет место,
если тело движется под действием одной только данной
*) Нижеследующее в первом чтении можно пропустить.
382 МЕХАНИКА [Ч. VI
силы F(t),
i]F{t)dt.
Таким образом, в этом случае скорость v(t) можно вы-
нести из-под интеграла, заменяя ее средним арифмети-
ческим начальной и конечной скоростей движения.
Этот вывод справедлив только в том случае, если v(t)
есть скорость, полученная телом _в результате действия
лишь одной силы F(t). Если же на тело действует не-
сколько сил: У7,, Ft, F3, то работа, произведенная всеми
силами, равна произведению средней скорости на сумму
импульсов всех сил:
Однако работа каждой из сил (например, F,) в отдель-
ности не равна соответствующему слагаемому ¦"" ^ °г \ F2dt
в формуле F.5), так как сила Fz, действуя .отдельно,
сообщила бы телу скорость, отличную от v(t)*).
Упражнения.
1. Найтн формулу для кинетической энергии тела, движущегося
под действием постоянной силы F (в начальный момент времени ско-
рость была равна нулю) в зависимости от времени, а также в зависи-
мости от пройденного пути.
2. Тело движется под действием силы F = f cos <ot, при < = 0
и = 0. Найти выражение для кинетической энергии тела. Определить
максимум кинетической энергии.
3. Тело движется по закону x(t)=A cos(<ot-\-a), (A, <o, а —
постоянные числа). Определить среднюю кинетическую энергию при
условии, что t неограниченно растет от значения f = 0.
*) См, ниже задачу № 6.
§ 7] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ 883
4. Шарик падает с высоты Н из состояния покоя. Показать,
что кинетическая энергия шарика K = mg(H — Л), где А — высота
шарика над землей в данный момент времени.
б. Поезд весом 500 т вышел со станции и, пройдя за 3 мин
1,5 км, развил скорость 45 км/час. Определить: а) работу и среднюю
мощность паровоза, предполагая, что трения о рельсы нет; б) эти же
величины, но с учетом треиия. Коэффициент трения k =0,004. (Сила
трения равна силе притяжения поезда к Земле, т. е. его весу, умно-
женной на k).
6. На тело действуют две силы: F1=^at и Ft = a{u— t).
Импульсы этих сил за время от 0 до в одинаковы. В момент вре-
мени < = 0 тело имело скорость va = 0. Найти работу каждой силы
за время от 0 до 9 н сравнить ее в произведением импульса иа
среднюю скорость.
7. Человек, стоя неподвижно на земле, действует на данную
массу т силой F в течение времени t. В результате этого масса, на-
Ft
ходившаяся раньше в покор, приобрела скорость v.=— и кинети-
т
mv\
ческую энергию g ' • равную работе, произведенной человеком.
Рассмотреть такой же опыт, проделанный в поезде, движущемся
со скоростью va. Масса m имела до опыта скорость иа, а после опыта
ua-\-vl. Найти изменение кинетической энергии массы т. Какую
работу произвел человек? Считая, что человек твердо опирается
о стенки вагона и скорость его о0 ие меняется-, найти работу силы,
произведенной поездом (паровозом) во время опыта.
8. Человек массы М, стоя на коньках на льду (трением о лед
пренебрегаем), действует силой F на массу т в течение времени t.
Какую кинетическую энергию приобретет масса т? Какую кинети-
ческую энергию приобретет человек? Чему равна полная работа,
произведенная силой иад массой т и над человеком? Почему она
больше, чем в задаче № 7?
9. Тот же опыт, что и в предыдущей задаче, производит чело-
век, который в начальный момент катился со скоростью о. вместе
Ft
с массой т. Скорость массы m после действия силы равна о0 -\ ,
скорость человека v0—vj- • Найти изменение кинетической энергии
массы т и человека в результате действия силы. Найти работу силы,
равную изменению суммарной кинетической энергии, и сравнить ее
с результатом предыдущей задачи.
§ 7. Движение под действием силы, зависящей
только от скорости
Всякое тело испытывает при движении противодействие
со стороны той среды, в которой происходит движение.
Если сопротивление невелико, то зачастую его можно
384 МЕХАНИКА [Ч. VI
не принимать во внимание. Однако в ряде случаев такой
подход неудовлетворителен, с сопротивлением среды при-
ходится считаться. Установлено, что если тело движется
в жидкости или газе, скорость движения невелика и тело
имеет малые размеры, то сила сопротивления пропорцио-
нальна скорости движения
—kv(t). G.1)
Здесь коэффициент пропорциональности k > О, а знак
минус в G.1) показывает, что сила сопротивления направ-
лена противоположно скорости движения тела. Число k
зависит от свойств среды, оно пропорционально вязко-
сти среды. Кроме того, k зависит от формы и размеров
тела. Например, для случая шара радиуса R формула G.1)
принимает вид
F = — 6nRr)v @*), G.2)
где т] — вязкость среды. Для воздуха т] = 1,8 -10"*, для
воды Ti = 0,01 (при 20° С), [т|] = _^**).
Рассмотрим задачу о торможении тела. Пусть некото-
рая сила сообщила телу скорость, а затем в момент вре-
мени t = ta перестала действовать. Тело продолжает дви-
гаться и на него действует только сила сопротивления.
*) Формула G.2) справедлива при—- < 5, где q — плотность
среды. Читатель легко убедится, что величина —- безразмерна.
Эта величина называется числом Рейнольдса.
**) Вязкость 1\ можег быть определена следующим образом.
Пусть жидкость (или газ) движется в направлении оси х, но вели-
чина скорости различных частиц различна, зависит от координаты у.
Ясно, что твердое тело не могло бы так двигаться — оно разруши-
лось бы. В жидкости или газе при этом между соседними слоями
возникает сила трения, которая будет пропорциональна разности
dv
скоростей соседних слоев, т. е. производной -г-. Коэффициент про-
порциональности в выражении для силы, приходящейся на 1 см*
горизонтальной поверхности, и называется вязкостью
, дин dv
§ 7] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ 385
Из второго закона Ньютона
dv ,
mTt = — kv.
Разделив обе части на т и обозначив — = а (а > 0),
получим:
dv
Решение этого уравнения есть (см. часть IV)
v{t) = vue—it-™. G.3)
Здесь va есть значение скорости в момент t = tt. Так как
а>0, то при t>tt показатель степени в G.3) отрицатель-
ный, е-а<'-'«><1 и, следовательно, v(t)<v0, т. е. ско-
рость убывает с течением времени. Среда тормозит дви-
жение тела.
Найдем выражение для пути, пройденного телом.
Из G.3) получаем:
ИЛИ
dx = vae~° «-W dt. G.4)
Пусть в начальный момент времени (при t=t0) тело на-
ходилось в начале координат: д;(^0) = 0. Интегрируя G.4),
получим:
откуда
X(t) = ^[l—e — (*-«.)]. G.5)
Пользуясь формулой G.5), можно получить весь путь,
который пройдет тело после момента ta, т. е. после того,
как сила перестала действовать на тело. Для этого заме-
тим, что при очень больших t величина е-я(*-М весьма
мала и ею можно пренебречь по сравнению с единицей.
Поэтому весь путь, который пройдет тело, есть —.
13 Я. Б. Зельдович
386 МЕХАНИКА [Ч. VI
Рассмотрим падение тела в воздухе. Направим ось х
вниз к земле, начало координат поместим на высоте Н
от земли (на земле х = Н). Пусть движение начинается
при t = Q со скоростью о0. Тогда д:@) = 0, v(O)=va.
Тело находится под действием двух сил: силы тяжести
(она способствует движению) и силы сопротивления воз-
духа (она препятствует движению).
Второй закон Ньютона дает:
Разделив все члены G.6) на т, получим (так как — = а)
щ=е—°»- G-7)
Справа в G.7) вынесем а за скобку
?=«(?-»)• <7-8>
Установим размерность величины —. Так как а==—,
a k = , то а имеет размерность 1/сесс. Размерность
¦?- есть см • секjсек* = смIсек, т. е. -^ имеет размерность
скорости *).
Обозначим -^-=ог. Уравнение G.8) принимает вид
* = a(Ol-o). - G.9)
Допустим, что va <vt. Тогда правая часть G.9) в начале
движения положительна, значит,' и левая часть положи-
тельна, ^г>0> поэтому скорость v{t) растет. При этом
а
*) Сделанный здесь подсчет размерности — есть проверка. Раз-
а
мерность — видна из формулы G.8). Так как вычитать можно только
а
величины одной размерности, то — должна иметь размерность ско-
рости.
§ 7]
ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ
dv
387
чем ближе значение v к vt, тем ближе -г к нулю, тем,
следовательно, медленнее растет v. Если бы в некоторый
момент времени tx оказалось v{tx)=-vx, то тогда v оста-
лось бы постоянным, так как v=lvv является решением
уравнения G.9) о начальным условием v(t1)=v1. Ана-
логично если в начале движения v > о„ то v прибли-
жается к vt, но в этом случае v убывает. Поэтому че-
рез некоторое время
после начала движения °(*)
тело падает практически
с постоянной скоростью
о. =— независимо от
1 ос
того, какую скорость
оно имело в начале па-
дения. График скорости
для случая va = 0 име-
ет вид, показанный на
рис. 147.
Проведенные рассу-
ждения показывают, что
ряд свойств v (t) можно обнаружить, даже не решая уравне-
ния G.9). Теперь решим это уравнение. Положим vx — v = z.
Тогда зт- = — зт, и уравнение G.9) перепишется так:
dz_
dt aZ>
причем при tf = 0 должно быть z = vx — va. Искомое
решение есть z(t) = (vx — va)e~at. Переходя к функции
v(t), получаем:
Рис. 147.
откуда
vx)e
—K
G.10)
Рассматривая формулу G.10), нетрудно сделать те же
выводы, которые мы уже сделали на пальцах, глядя на
уравнение G.9). Во-первых, если va > vx, то v(t)> vlt так как
(у0—vx)e-**' > 0. Если же v,<vlt то (va — t;1)e~at<0 и
поэтому v(t)<vx. Во-вторых, каково бы ни было v0, все
~л*
равно при достаточно больших t величина е~л* мала и
практически
13*
388 МЕХАНИКА [Ч. VI
Найдем, пользуясь G.10), выражение пути в зависи-
мости от времени
откуда, припоминая, что лг(О) = О,
Если скорость тела велика или тело больших разме-
ров, то сила сопротивления пропорциональна квадрату
скорости. Из опытов установлено, что в этом случае *)
где 5 — площадь сечения тела, q — плотность среды. От
вязкости среды при этом сила сопротивления практически
не зависит. Коэффициент k в этой формуле есть безраз-
мерное число; его величина зависит от формы тела (для
хорошо обтекаемых тел величина k может опуститься
до 0,03 — 0,05, для плохо обтекаемых тел величина k
достигает 1,0—1,5). Обозначая -^ = х, получим:
F(t) = — xv'(t). G-11)
Ясно, что х имеет размерность г\см.
Решим задачу о торможении для силы сопротивления
G.11). Соответствующее уравнение имеет вид
dv_ я
Разделив обе части на т и положив — = 0 ф > 0),
получим:
*) Эта формула справедлива при числе Рейнольдса —-> 100.
Смысл формулы, приведенной в тексте, заключается в том, что при
движении большого тела энергия, затрачиваемая в связи с сопротив-
лением среды, расходуется ие иа трение одних слоев жидкости отно-
сительно других, а иа кинетическую энергию жидкости, вынужден-
ной двигаться, для того чтобы расступиться и пропустить тело. По-
лучите отсюда сами формулу для силы.
§ 7] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ 389
¦о
Отсюда j^- = —fidt. Проинтегрировав, получим
t
= — Р^ , где va — скорость тела в момент времени t = 10.
__ 1,1
Поэтому 1 =- — р {t — t ), откуда
р- 1+РМ*-*.)- GЛ2)
Из формулы р = — получаем, что р имеет размер-
ность \/см.
Найдем формулу для пути. Пользуясь G.12), получаем:
откуда
{+р,*,_ц*. G.13)
Считая, что тело начинает движение из начала координат
(л:(/о) = О), получаем из G.13)
дс(9 = -р-In [1+р».(*-/,)]. G.14)
Легко убедиться, что формуле G.14) соответствует экспо-
ненциальная зависимость скорости от пройденного пути:
v = vae~$x. Если теперь мы захотим найти весь путь, ко-
торый пройдет тело после того, как сила, сообщившая
ему скорость, перестала действовать, то обнаружим, что
этот путь [формула G.14)] тем больше, чем больше
время t *). На самом деле это не так. Дело в том, что,
когда скорость тела станет малой, соотношение G.11)
перестанет быть верным. Надо переходить к формуле G.1)
и соответственно для подсчета пути к G.5).
Рассмотрим задачу о падении тела в воздухе в случае,
когда сопротивление воздуха пропорционально квадрату
скорости. Совершенно аналогично случаю, когда сопро-
тивление пропорционально скорости, получаем уравнение
g^g-po-. G.15)
*) По формуле G.14) х—*¦ оо при t—>¦ оо.
390 МЕХАНИКА [Ч. VI
Пусть тело начало падать из начала координат, имея
начальную скорость va. Уравнение G.15) перепишем в виде
Нетрудно установить, что V g/fi имеет размерность ско-
рости; обозначим Vgj$ = vl, g/P =v\. Тогда
JJH = P(O;—о'). G.16)
Точное решение дано в ответах к упражнению 1. Рас-
смотрим общие свойства решения. Рассуждениями, совер-
шенно аналогичными тем, которые были проведены для
уравнения G.9), показываем, что в этом случае должна
установиться скорость движения vt =Yg/p. Покажем,
что через достаточно большое время после начала паде-
ния справедлива формула
и — о1=Св-'Рв«*, G.17)
где С — постоянная величина. Уравнение G.16) перепишем
так:
^РК + сОК-»). G.18)
При больших t о*»,, поэтому в G.18) заменим vx~\-u
на 2vx. Если заменить v на о, в разности vx—v, полу-
чим 27 = 0, откуда c/ = const = u1. Так как нас интересует
именно малое различие между о и о, (закон приближения
v к о,), то пренебрегать разностью v—vt нельзя. Итак,
из G.18) получим:
? = 2pOl(Ol-o). G.19)
Положим vl — v = z, зг = — зг . Уравнение G.19) при-
нимает вид
Его решение есть
г — у-е р >¦. (/.ли)
что совпадает с G.17).
§ 8J ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ УПРУГОЙ СИЛЫ 391
Значение С в формуле G.20) нельзя определять из
начального условия v@)--=va (т. e. z@) = o1 — va), потому
что уравнение G.19) справедливо только при достаточно
больших t (вблизи ? = 0 заменять v-{-v1 на 2о, нельзя).
Заметим еще, что формула F(t)== — xv2(t) справедлива
лишь для случая, когда v > 0. Действительно, если v < 0,
то должно быть F(t) = xv1(t), так как сила сопротивления
направлена противоположно скорости и, следовательно,
положительна, если скорость отрицательна. Оба случая
(v > 0 и v < 0) охватываются формулой
= -y.v(t)\v(t)\.
Упражнения
1. Найти выражение скорости в зависимости от времени из урав-
нения 777 —P(yi —f*) при* начальном условии о@) = у„. Из формулы
для v показать, что происходит установление скорости, равной
vx = 1/ -§-. Показать, что для формулы G.20) С = 2"'-^"° "' .
2. В задаче о падении тела (сила сопротивления пропорциональна
скорости) учесть, что на тело действует выталкивающая сила по
закону Архимеда.
3. Применив результат предыдущей «задачи к шару и учитывая,
что для шара k = &jiRi\, где R — радиус шара, т) — вязкость среды,
показать, что устанавливается (при больших t) скорость падения
2/?V(Q — Q') ,
шара v = 2-нЬ—^ (здесь q — плотность материала, из которого
сделан шар, q — плотность среды).
§ 8. Движение под действием упругой силы
Рассмотрим случай, когда сила, действующая на тело,
зависит только от его положения: F=F(x). Выше мы
подробно рассматривали работу такой силы и выяснили,
что в этом случае система имеет определенную потен-
циальную энергию и (х), с которой сила связана соотно-
шением
F(x) = —
du(x)
dx '
Обратимся к задаче о движении тела под действием такой
392 МЕХАНИКА [Ч. VI
силы. Основное уравнение имеет вид
m?=F(x). (8.1)
Так как в уравнение входит производная по времени,
а сила задана как функция координаты х, то непосред-
ственно это уравнение решить нельзя. Естественно для
решения задачи искать интересующие нас величины как
функции координаты х. Будем искать, в частности, зави-
симость скорости от координаты, т. е. v{x). Производную
dv
по времени -гт мы тогда представим как производную
сложной функции, так как сама координата х зависит
от времени
dv [х (Q1 dv \х (t)] dx (t)
dt dx dt •
Ho -jr есть не что иное, как скорость v(x). Таким обра-
dv dv
зом, ^ = 03i' откуда
dv dv d fmvi
Подставляя последнее в уравнение движения (8.1), по-
лучим:
d
Интегрируя, находим:
ИЛИ
2 2~== ) (Х^
Физический смысл этого выражения совершенно ясен: изме-
нение кинетической энергии равно работе силы.
При помощи потенциальной энергии запишем (8.2)
в виде
— f^.\ ^И
dx\ 2 J dx
§ 8] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ УПРУГОЙ СИЛЫ 393
или
d /лш* , , \ „
d~x \~~2~~T~U{X>) •
Если производная какого-нибудь выражения тождест-
венно равна нулю, то само это выражение есть постоянная
величина. Поэтому
^+ «(*) = const. (8.3)
В таком виде формула (8.3) выражает закон сохранения
энергии: при движении тела под действием силы, зави-
сящей только от координаты, остается постоянной сумма
кинетической энергии тела ^§- и его потенциальной энер-
гии и(х). Эта сумма называется полной энергией тела.
Здесь и в предыдущем параграфе мы привели эти довольно
длинные преобразования с целью показать, что закон со-
хранения энергии (применительно к механике) есть след-
ствие закона Ньютона. Также следствием закона Ньютона
является тот факт, что кинетическая энергия тела есть
именно у, а не какая-нибудь другая функция скорости
тела.
Как решать дальше задачу о движении тела? По зна-
чениям скорости v0 и координаты тела xQ в начальный
момент времени находим полную энергию тела Е — вели-
чину, остающуюся постоянной на протяжении всего дви-
mv*
жения —jp-+ «(*„) = ?• ПРИ помощи формулы (8.3),
зная Е, находим скорость тела в зависимости от х
v (х) = ]/-| [?-«(*)]. (8.4)
Остается найти связь между х и t Из (8.4) получим:
отсюда
394
МЕХАНИКА
[Ч. VI
Таким образом, время t выражено как функция коорди-
наты х:
t = t(x), (8.5)
причем функция эта задана интегралом. Решая уравне-
ние (8.5) относительно х, можно найти x(t). Так как v
выражается в зависимости от х посредством корня квад-
ратного, то даже простое выражение и (х) часто приводит
к весьма сложным выражениям для t(x).
и
\
1 \_
Хд 0
А
1 /
j
/
С
xd хс
1и(х)
Z
Рнс. 148.
Для того чтсбы получить общее представление о ха-
рактере движения, очень полезно нарисовать кривую и (х).
Если на этом же графике нанести горизонтальную линию
на высоте Е (рис. 148), то получится весьма наглядная
картина. Скорость пропорциональна корню квадратному
из разности ? — и(х). Так, например, при х = хА скорость
пропорциональна корню квадратному из длины отрезка АВ
(рис. 148). Правее точки С и левее точки D находится
область, где ? < и (х), т. е. область, в которую тело при
заданной полной его энергии ? проникнуть не может —
не хватает энергии (формально корень из отрицательной
величины дает для скорости мнимое значение). В той
области, где Е>и(х), квадратный корень для v(x) дает
два возможных значения в соответствии с двумя знаками
корня:
§ 8J ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ УПРУГОЙ СИЛЫ 395
В начальный момент как величина, так и знак иа опре-
деляются начальными условиями. Дальше движение про-
исходит в направлении, заданном знаком начальной
скорости va. Очевидно, что при v^O знак скорости не
может внезапно измениться. Так, если в начальный мо-
мент тело находится в точке x=xt*) и va > О, то тело дой-
дет до крайней допустимой точки хс. В этой точке, где
скорость тела обращается в нуль, произойдет переход
/~~2
от формулы v= у — [?—и(х)] к формуле
v = — у —[Е — и(х)] . Так как в этой точке v = 0, то
изменение знака совершается без скачка (разрыва) ско-
рости. Аналогичная картина будет в точке x — xD. Таким
образом, в случае, изображенном на рис. 148, движение
тела будет представлять собой колебания между двумя
крайними положениями хс и Хд-
Рассмотрим другой пример. Потенциальная энергия тела
дается функцией и = ах (а>0). Найти закон движения
тела.
Пусть в начальный момент времени ta х=ха, v = va.
Тогда полная энергия Е = '0^± -\-аха. Пользуясь (8.4),
получаем:
где y = —. Зная v(x), находим время
, — X)
В интеграле сделаем замену v\-\-y{xa — х)=гг, 2zdz =
= — у dx. Получим:
у °\
"а
•) Точка д?! на рис. 148 не показана, она может находиться в
любом месте между хц н хс.
396
Отсюда находим х
МЕХАНИКА
[Ч. VI
перенося va влево, возводя в квадрат и сокращая на у,
получим:
у ,, .а .
Найдя ^-, убеждаемся, что это — равнозамедленное
движение. Этого и следовало ожидать, так как F =
du
— ~~te——а« сила постоянна и отрицательна, значит,
движение равнозамедленное. В этом простейшем случае,
U I
Рис. 149.
Рис. 150.
когда сила в действительности от х не зависит, конечно,
не было надобности применять - такой сложный способ
расчета.
В следующем примере рассмотрим потенциальную
энергию, график которой имеет вид ступеньки (рис. 149).
Такой зависимости и(х) соответствует график силы, при-
веденный на рис. 150 (чтобы убедиться в этом, читатель
должен вспомнить, что F = — ^V сила весьма велика и
отрицательна, т. е. направлена в сторону уменьшения х.
Чем круче и(х) — кривая на рис. 149, т. е. чем на мень-
шем протяжении Д —*, — хш происходит подъем и(х).
§ 8] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ УПРУГОЙ СИЛЫ 397
тем больше по абсолютной величине сила. Там, где и(х)
постоянна (слева от точки хл и справа от точки *,), сила
равна нулю.
Пусть тело начало движение от точки хл (рис. 149) со
скоростью va. Пусть полная энергия тела равна Е. При
каких значениях Е тело может попасть в точку л:,? Так
как и(ха) = 0, то ? = ^1. С другой стороны, Е= ^--\-
-\-и1Г где vt-—скорость тела в точке хх, а ил — потен-
циальная энергия при х = хх. Поэтому
^ = E-uv (8.6)
Из формулы (8.6) видно, что если Е<их, то тело не
может попасть в точку х,, так как в этом случае полу-
чаем v\ < 0, а этого быть не может. Поэтому тело может
попасть в точку х=.хх, только если E~s&ux.
Определим для этого случая работу силы F при переме-
щении тела из точки дс0 в хг
mv* nw*
Пользуясь (8.6), находим:
А =Е — их —Е = — и,.
При дальнейшем движении тела вправо от точки хх сила
F работы не совершает, так как F=0 при х>хх.
Упражнения
Ах*
1. Потенциальная энергия дана формулой и = -=- (А > 0). По-
строив график, показать, что соответствующее движение — колеба-
тельное.
2. Потенциальная энергия дана формулой
1( 0, если х
2х, если
2, если хЗг 1.
В начальный момент времени тело массой в 1 г выходит из начала
координат и движется вправо со скоростью va (см/сек): а) ио=1,
б) о0=1,9, в) о„ = 2,1. Для каждого случая указать, сможет ли тело
398 МЕХАНИКА [Ч. VI
неограниченно двигаться вправо. Если не может, найти точку оста-
новки.
3. и(х) = — х*-{-4хл. В начальный момент времени тело массой
в 2г выходит из точки ха и движется со скоростью va (см/сек):
а) Хо=1, о„ = 1, б) хо= —2, о,= 1, в) х„ = — 2, уо=—1. В каж-
дом случае исследовать характер движения (точки остановки, области,
в которые тело не может попасть). В случаях, когда есть точки оста-
новки, указать, хотя бы грубо, их координаты.
X1
4. Авалогичвые вопросы для и (х) = ,, т = 2: а) хо = О,
ио = 2, б) ха=-^-, ио = -2". Выразить время / в зависимости от я
через интеграл.
§ 9. Колебания
Рассмотрим тело, на которое действует сила
/=•=— kx.
Как мы знаем, такой силе соответствует потенциальная
энергия
Начало координат является положением устойчивого рав-
новесия. Кривая потенциальной энергии (парабола) имеет
вид, показанный на рис. 148.
Движение тела под действием такой силы представляет
собой колебания влево и вправо от положения равнове-
сия. Можно представить себе шарик, который скатывается
с одной ветки параболы, набирая скорость, по инерции
забирается на вторую ветвь, скатывается с нее и т. п.
Согласно второму закону Ньютона уравнение этих коле-
баний имеет вид
m^ = —kx. (9.1)
Мы не будем решать его общим, но довольно сложным
способом предыдущего параграфа, а вместо этого «угада-
ем» вид решения и сосредоточим внимание на исследова-
нии свойств этого решения.
Итак, предположим, что
х = a cos (at. (9.2)
§ 9] КОЛЕБАНИЯ 399
Такой вид решения выбран потому, что косинус является
одной из простейших периодических функций.
Подставим выражение (9.2) в основное уравнение
(9.1); так как
» = ^ = — асо sin©/, ~Ж* — — aco*cosu)f,
то
— maco* cos tat = — ka cos tat. (9.3)
Соотношение (9.3) будет справедливо при любом t, если
mv? = k. Поэтому функция (9.2) действительно удовлет-
воряет уравнению, если mco1=k, -откуда со=Т/ —.
Тогда
( /T) (9.4)
Отметим, что квадратный корень в выражении со не при-
водит к двум решениям, так как cos at = cos (—tat).
Найдем период колебаний, т. е. время, через которое
тело возвращается в исходное положение с исходной ско-
ростью. Функция cos ф возвращается к начальному значе-
нию, когда угол ф делает полный оборот, т. е. меняется
на 2л. Значит, в выражении acoscof величина (at за один
период Т также должна меняться на 2я. Поэтому Т на-
ходим из условия
Отсюда
соГ = 2л, г = ^ = 2я]/|". (9.5)
Величина v = ^- дает число колебаний в единицу вре-
мени и называется частотой колебаний. Размерность ее
\\сек (словами: обратная секунда). Единица частоты —
одно колебание в секунду имеет специальное название
герц в честь немецкого физика Генриха Герца. Из фор-
мулы (9.5) видно, что v = ^. Однако во всех формулах
удобнее иметь дело именно с со, а не с v, иначе повсюду
400 механика [ч. vi
появятся коэффициенты 2я и 4я*. Величина (о = -= назы-
вается круговой частотой *).
Константу а из уравнения (9.1) определить нельзя,
потому что уравнение удовлетворяется при любом а (в
обеих частях (9.3) а можно сократить).
Скорость тела v = -r =—acosincof. Из соотношения
cos*Go/l-f-sin*(o? = l следует, что при cosgo?=±1 будет
sino)? = 0. Следовательно, в те моменты времени, когда
отклонение тела в ту или другую сторону достигает своей
наибольшей величины (х = а илилг = —а), скорость v равна
нулю. Представим себе, что при t < 0 тело помещено
в точку х = а и удерживалось в этой точке в покое при
помощи другой посторонней силы (например, каким-нибудь
крючком) до момента t = О, когда крючок отпускает тело.
В этот момент тело было в покое и под действием силы
F = — kx начались колебания. В этом случае зависимость
координаты тела х от времени t дается формулой х =
= а cos (at. Так как абсолютная величина cos a>t не превос-
ходит 1, то а есть наибольшее значение величины х, т. е.
наибольшее отклонение тела от положения равновесия.
Число а называется амплитудой колебаний. Таким образом,
амплитуда колебаний равна начальному отклонению тела,
если в момент начала колебаний тело покоилось**).
•) Чтобы понять происхождение этого названия, рассмотрим от-
резок длин ой а, вращающийся против часовой стрелки. Сходство между
вращением и колебанием легко обнаружить: вращающаяся стрелка
после каждого оборота возвращается в исходное положение точно так
же, как колеблющееся тело по истечении одного периода возвращается
в свое исходное положение. При этом координата х конца вращающейся
стрелки меняется по закону х= a cos со*, если стрелка вращается с
угловой скоростью со. В случае вращения, если Т есть период одного
оборота, то v = =- есть число оборотов в единицу времени, со = 2яу
есть угловая скорость вращения, выраженная в радианах в секунду.
Так как радиан есть величина безразмерная, то со имеет размерность
1/сек. В связи с таким простым смыслом со при движении по кругу
величина со в задачах о колебаниях получила название круговой
частоты.
**) Мы определили амплитуду, как половину полного размаха
колебаний. На пути от крайней левой точки, х = — а, до крайней
правой точки, х =-\-а, тело проходит расстояние 1а, равное удвоен-
ной амплитуде.
§ 9] КОЛЕБАНИЯ 401
Отметим попутно, что, вообще, если A (t) = L cas<ot
(или A (t)-==-L sin at), то L есть наибольшее значение ве-
личины A (i), оно называется амплитудой величины А (/).
Отметим еще, что частота колебаний со не зависит от
их амплитуды а.
Пусть x = xx(t) есть решение уравнения (9.1), т. е.
справедливо равенство т-^- = —kxz. Рассмотрим функ-
цию xt B) = Сх,(*), где С — постоянная величина. Под-
ставляя в уравнение (9.1) значение дс, и -^, получим
d*x
тС-тт?=—kCx^{t) или, сокращая на С,
Итак, если x = xi(t) удовлетворяет уравнению (9.1), то
и xt(t) = Cxl(t) также удовлетворяет этому уравнению.
Легко убедиться, что уравнение (9.1) имеет и другое
решение х (t) = b sin (at. Действительно, —^"<°
= — о2 sin о/. Подставляя значение х и его второй произ-
водной в (9.1) и сокращая на since/, получим со = 1/ —,
т. е. то же самое значение, что и раньше*). Поэтому
*(*)=& sin (f )/?). (9.6)
Так же как и в предыдущем случае, & из уравнения (9.1)
определить нельзя. Оно определяется из начальных ус-
ловий. Пусть в начальный момент ? = 0тело находилось
в точке х = 0и получило определенную начальную ско-
рость va в результате кратковременного действия какой-то
внешней силы, например удара. Тогда, так как v(t) =
= Ьо cos tat, то при t=0
va = b(d, (9.7)
/~~k
*) Здесь также ш = — / — не дает нового решения, так как
г т
Ь sin ( — 1/ — 0 == — bsinf ~l/ — t у, знак минус у корня, вы-
ражающего to, соответствует тому же виду функции, что и раньше,
при другом значении константы Ь.
402 МЕХАНИКА [Ч. VI
откуда Ъ =3-. Следовательно, амплитуда в этом случае
определяется начальной скоростью.
Соотношение (9.7) дает практически удобный способ
измерения импульса силы и скорости, широко применяе-
мый в механике под названием баллистического маятника:
если тело подвешено в виде маятника или удерживается
в положении равновесия пружинами и частота его коле-
баний известна, то начальную скорость после удара можно
определить по амплитуде колебаний, вызванных ударом.
Покажем, что приближенно формулу (9.7) можно по-
лучить из общих элементарных соображений. Размерность
амплитуды — см, размерность скорости — CMJceK, а раз-
мерность времени — сек. Поэтому из соображении размер-
ности амплитуда должна быть величиной такого же по-
рядка, как произведение начальной скорости на некоторую
долю периода. Так как движение от момента удара до
максимального отклонения продолжается четверть периода
и v < va, потому что движение замедленное, то 6<о0Г/4.
Если бы движение было с постоянным замедлением, то
средняя скорость равнялась бы половине начальной и,
следовательно, 6=*=о0Г/8. В действительности, как следует
из формул (9.7) и (9.5),
и ^о <? ??_
и <о 2я 6,28-
Важно то, что благодаря независимости периода колеба-
ний от амплитуды последняя прямо пропорциональна на-
чальной скорости.
Мы проверили, что две различные функции (9.4) и
(9.6) удовлетворяют уравнению т^-=—kx. Пусть мы
хотим решить задачу о движении тела с заданным на-
чальным положением и данной начальной скоростью: при
/ = 0 дс = л;0, v — va (причем значения ха и va — любые,
каждое из них может не равняться нулю). Такую зада-
чу назовем общей. До сих пор в отличие от общей зада-
чи мы рассматривали лишь частные задачи. В одной из
них было при ? = 0 v = 0, х = хл, а в другой — при ? = 0
v = va, x = 0.
Допустим, что мы взяли решение x = acas<ut. Пола-
гая f = 0, получим ха=а; значит, x = jc0coso>?. Но тогда
§ 9] КОЛЕБАНИЯ 403
dx
v =57 = — ха со sin ©Л так что при ? = 0 v = 0, а не va. По-
этому при помощи решения х = а cos att мы не можем решить
общей задачи, а можем решить лишь задачу с нулевой
скоростью.
Попробуем взять решение x = bs'm<xit. В этом случае
v =-^ = &(ocos(of, при t = 0 получаем va = b<o, b=^,
откуда х= —s'm<ot. Однако при ?=0 х = 0, а не х9.
Следовательно, и при помощи этого решения мы не можем
решить общую задачу.
Легко убедиться, что сумма
х = a cos at -f- b sin at (9.8)
также является решением уравнения (9.1) при любых аи
b [читатель сам проверит это, находя вторую производную
от суммы (9.8) и подставляя ее в (9.1)]. Таким образом,
мы располагаем решением с двумя произвольными посто-
янными: х = a cos at-\-b sin t&t. Соответствующая скорость
v = — а<а sin (at ~\- Ьы cos tat.
При помощи (9.8) можно решить общую задачу о дви-
жении тела с произвольным положением и произвольной
скоростью в начальный момент: при /=0 х = ха, v = va.
Пользуясь начальными данными, находим из (9.8)а = лс0,
Ъ = ^-. Поэтому
х=хл cos at -J-— sin (at.
Из всего этого следует, что решения x — acos<ut,
x = 6sin(o? дают возможность решить не общую задачу
о движении, а лишь частные задачи со специальными на-
чальными условиями. Поэтому эти решения называются
частными. Решение же х = а cos tat ~f- b sin Ы позволяет
решить общую задачу о движении, задачу с любыми на-
чальными условиями. Поэтому это решение называется
общим решением.
Общее решение с двумя произвольными постоянными
можно получить и из других соображений. В уравнении
(9.1) вместо независимой переменной t введем новую неза-
висимую переменную т по формуле
г = * + /\ (9.9)
404 МЕХАНИКА [Ч. VI
где Г — постоянная. Тогда j~==~Ttj- = ~Tt> так как из
(9.9) видно, что т-=1. Аналогично j^ = j4- Уравнение
(9.1) принимает вид
d*x .
m kx
Нам известно его реление х = С cos от, где С — постоян-
ная, о = у —. Возвращаясь к переменной t, получим
x = Ccos <u(t-\-t') = Ccos(<dt ~{-Ш'). Положим (йГ^а.,
тогда
x = Ccos(utf + a). (9.10)
Используя формулу cos (a -f- P) = cosa cos{3 — sina sinp\
сравним решения (9.10) и (9.8)
С cos (att -f- a) = С cos a cos of — С sin a sinatf =
= a
Следовательно, чтобы оба решения описывали одно и
то же движение, нужно удовлетворить условиям
а = С cos a, b = — С sin a.
Поскольку а и Ь легко выражаются через начальное
положение и начальную скорость, полезно уметь решать
обратную задачу: находить С и а, зная а и 6. Для этого
составим выражения
откуда
C = Vc? + b', (9.11)
Ь sin a ' . / b \
= = tga, a = arctg .
a cos a s ' & \ a J
Если решение записано в форме (9.10), то ясно, что
амплитуда колебаний равна С. Следовательно, если реше-
ние имеет вид (9.8), то амплитуда равна У а2 ~\- Ь*. Пусть
при ^ = 0 х = х0 v = va, тогда а = ха, 6=^-, поэтому
амплитуда колебаний равна 1/ х\ -}- -А
§ 101 ЭНЕРГИЯ КОЛЕБАНИЙ. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 405
Упражнения
1. Тело колеблется по закону -пг= — х. Найти зависимость х (t)
и определить период колебаний для следующих случаев: а) при t = 0
х = 0, о = 2 см/сек; б) при t =0 x=l, v = 0; в) при 2 = 0 х = 1,
и = 2 см1сек. В случае в) записать решение как в виде (9.8), так и
в виде (9.10).
§ 10. Энергия колебаний. Затухающие колебания
Запишем общее решение уравнения (9.1) в виде
х = С cos (Ш + а). (9.10)
Потенциальная энергия тела в каждый момент равна
и (х @) = ^^ = ~ cos1 (at -f a),
а кинетическая энергия
Д' (t)= -q- =-q [ — Cat sin (go/ -j- c)J*== —s— sin* («^ 4~ a)«
Частота колебаний, как мы уже знаем, определяется фор-
мулой со* = —. Подставляя ю1 в выражение кинетической
энергии, получим:
К (t) = -g— sin* (ш/ -f- a).
Таким образом, множитель перед тригонометрической
функцией в выражении потенциальной энергии и в вы-
ражении кинетической энергии одинаков. Сами функции
я/2 " t
Рис. 151.
и sin1 (о/ -f- a) очень похожи одна на другую,
одна может быть получена из другой смещением по оси
времени на Д/ = ^- (рис. 151). Каждая из величин и и
406 МЕХАНИКА [Ч. VI
К колеблется от максимального значения до нуля, причем,
когда одна величина максимальна, другая равна нулю.
Отметим, что функции cos*(<at~\-a.) и sin1 (со?-f-а) описы-
вают колебания вокруг среднего значения, равного поло-
вине максимального. Это обстоятельство легко усмотреть
как из рис. 151, так и из известных формул
cos» р = i-A + cos 2р) = у + у cos 2 J3,
sin1 p =1 A — cos 20) = 1 — \ cos 2 p.
Здесь ясно, что величина у cos 2 р колеблется, становясь
то положительной, то отрицательной, а у представляет
собой среднее значение.
Сумма потенциальной и кинетической энергии, т. е.
полная энергия системы
? = /С + и = ^ [cos1 («в/ + а) + sin1 (tot + а)] = ~
постоянна, как и следовало ожидать.
Отметим, что если бы мы задались движением с час-
тотой, не удовлетворяющей формуле ш== 1/ — , то при
таком движении сумма потенциальной и кинетической
энергии не была бы постоянна, максимальная кинетиче-
ская энергия не равнялась бы максимальной потенциаль-
ной энергии. Это не удивительно, так как колебания с
частотой, отличающейся от о = у —, не удовлетворяют
основному уравнению движения; следовательно, для того
чтобы такие колебания осуществлялись, необходимо,
чтобы, кроме силы F = — kx *), на тело действовали еще
какие-то другие, внешние силы; за счет работы внешних
сил полная энергия (-тг~f~ ~йг ) У5146 не сохраняется.
Обратимся к вопросу о затухании колебаний. Пусть,
кроме силы пружины F= — kx, на тело действует сила
трения. Предположим, что сила трения сравнительно
мала, так что на протяжении одного периода колебаний
*) Этой силе соответствует потенциал и (*).
§ 10] ЭНЕРГИЯ КОЛЕБАНИЙ. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 407
работа силы трения мала по сравнению с энергией коле-
баний; тогда приближенно можно считать, что колебания
происходят так же, как и в отсутствие силы трения
Энергия колебаний равна ~^-. При наличии силы трения
энергия колебаний с течением времени уменьшается. Сле-
довательно, треиие приведет к тому, что коэффициент С
при cos(a)^-f~a) будет не постоянной, а медленно убы-
вающей величиной. Закон убывания С определится усло-
вием, что уменьшение энергии равно работе силы трения.
Относя обе величины к единице времени, получим:
df—}
dE_ \ 2 J_kCdC_F w
dt — dt — dt— ' — »'
где F1— сила трения, v — скорость тела, W1— мощность
силы трения. Скорость v, так же как и сила F,, в про-
цессе колебаний периодически меняется. Произведение
Fxv все время остается отрицательным. В интересующем
нас случае малого трения, т. е. медленного затухания
колебаний, можем считать, что изменение амплитуды С (t)
за время нескольких колебаний мало.
Под произведением F^v надо понимать среднее значе-
ние этого произведения за период. Формула A0.1) спра-
ведлива только для промежутков времени, превышающих
период колебаний.
Рассмотрим в качестве примера силу трения, пропор-
циональную скорости движения тела:
Подставив t; = — Cat sin (a>t-\- а), получим:
Ftv = — ЛС'со' sin1 (со/ -j- a).
Заметим, что среднее значение sin1 (at -j- а) за период равно
у (см. упражнения к § 8 части IV, а также формулы на
предыдущей странице). Пользуясь A0.1), получаем окон-
чательно:
йс -^ —— пс (о 2 ,
408 МЕХАНИКА [Ч. VI
откуда
dC Лео*
Tt~~~ 2FC'
Вспоминая, что о' = —, получим более простое выраже-
ние:
d?_ h_r
dt 2m
Решение этого уравнения есть
А
Здесь Со определяется из начальных условий. Умножая
обе части A0.2) на cos (со/-f-а) и пользуясь (9.10), полу-
чаем:
—— t fin "x\
х(/) = Сое tm cos(<ot-\-a), \iv-o)
где со= 1/ —. Это — приближенная формула, получен-
ная в предположении, что сила трения невелика и про-
порциональна скорости.
В случае, когда сила трения пропорциональна ско-
рости, задача имеет точное решение. На тело действуют
в этом случае две силы: — kx и ft^. В силу второго за-
кона Ньютона
d*x , . dx
Решение x(t) будем искать в таком же виде, как оно было
получено для малой силы трения,
Ar(/) = C0*?-T*cas(<D1/+a)- A0.5)
Тогда
^ ~^ cos (mj -\- а) — C0to1e~T'sin(aI/ -f-a),
g- = угСае-« cos К/ + a) + yCw* sin (to,/ + «
Подставляя выражение для х, -г; , гттг в A0.4) и сокращая
§ 101 ЭНЕРГИЯ КОЛЕБАНИЙ. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 409
на Сое~т', получим:
туг cos («,/ -{-ct)-\-tny<oi sin(u),/-|-aL-
г sin(co1/ 4~a) — ma)S cos (at J -4-a) =
или
[my* — mo*] cos (и,/ -{-a)-{-2mywi sin(aI/4~a)^
= — fk — hy] cos («/ + a) 4- ftot sin («/ + a). A0.6)
Равенство A0.6) будет выполнено при любом t, если
ту* — то' = — k-\-hy, \
О II. Г A07)
Из второго уравнения A0.7), сократив на cOj, получим:
Тогда из первого уравнения
Следовательно,
(Ю.Ю)
В случае, когда трение мало, т. е. число h мало по сравне-
нию с k, можно под корнем пренебречь членом —г по сравне-
нию с — . При этом формула A0.10) переходит в A0.3).
Счедовательно, в приближенном рассмотрении мы верно
получили закон уменьшения амплитуды, но не заметили
малого изменения частоты колебания, вызванного силой
трения.
Если трение велико, то подкоренное выражение может
стать отрицательным, формулы теряют смысл. Это озна-
чает, что при сильном трении движение уже не имеет
колебательного характера. В этом случае решение надо
искать в виде х = Се"т'. Подставив в уравнения, получим
два значения у. Сумма двух решений, соответствующих
этим у, даст нам общее решение, позволит решить задачу
410 МЕХАНИКА [Ч. VI
с любыми начальными данными. Подробно этот случай
рассмотрен в связи с электрическими колебаниями в § 10
части VIII.
Упражнения
1. Найтн закон затухания колебаний при силе трения, пропор-
циональной квадрату скорости (такое трение характерно для быстрого
движения тела в жидкости с малой вязкостью). Показать, что по
истечении большого промежутка времени амплитуда С (t)=l/bt, где
Ь — постоянное число, не зависящее от Со — значения амплитуды в
начальный момент времени.
2. Найти закон затухания колебаний для силы трения, не зави-
сящей от скорости (такая сила трения характерна для трения сухих
твердых поверхностей одна о другую). Определить время, по истече-
нии которого колебания прекратятся.
3. Получить уравнение малых колебаний маятника, т. е. мате-
риальной точки, подвешенной иа нити длины /. Малыми колебаниями
мы будем называть отклонения на небольшой угол, иначе говоря,
такие колебания, что величина отклонения по горизонтали х мала по
сравнению с I. Найтн период колебаний.
Ука зание. Воспользоваться тем, что сумма кинетической и
потенциальной энергии есть величина постоянная.
§ 11. Вынужденные колебания и резонанс
Рассмотрим тело, на которое действует упругая сила
F = — kx. Мы установили, что под действием этой силы
тело колеблется с определенной частотой а>=^у k\tn,
так называемой частотой свободных колебаний или соб-
ственной частотой. В дальнейшем будем обозначать соб-
ственную частоту через со0, так что а>0 = "|/?/т..
Пусть на тело действует, кроме упругой силы, еще и
периодическая внешняя сила с частотой а>. Тогда оказы-
вается, что амплитуда колебаний, вызванных внешней
силой, весьма сильно зависит от того, насколько частота
внешней силы ш близка к частоте свободных колебаний.
Это явление носит название резонанса и имеет очень
большое практическое значение. Явление это относится
к любым системам, в которых возможны колебания. В ме-
ханических системах (станках, моторах) такие колебания
могут приводить к опасным деформациям и разрушению.
Иногда резонанс сознательно используют для того,
чтобы малой силой вызвать колебания рабочего инстру-
мента с большой амплитудой.
§ 11] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ И РЕЗОНАНС 411
В электрических системах резонанс дает возможность
при действии нескольких периодических сил с разной
частотой (например, нескольких передающих радиостан-
ций) добиться того, чтобы колебания в нашей системе
зависели только от одной из периодических сил — той,
частота которой близка к собственной частоте системы.
Благодаря этому можно настраивать радиоприемник на
определенную станцию.
Составим уравнение колебаний
m^-=— kx — ft^ + fcoseo*. A1.1)
В этом уравнении f cos at есть внешняя сила.
Поделим обе части A1.1) на m и обозначим теперь
— = юЦ в соответствии с тем, что с такой частотой про-
исходят собственные колебания тела (в отсутствие трения);
отношение— обозначим 2у [см. предыдущий параграф,
формулы A0.8) и A0.9)]. Получаем:
Естественно ожидать, что под действием силы с часто-
той о тело будет совершать колебания стой же частотой.
Поэтому ищем решение в виде
x=acos<ot-\-b sin©/. A1.2)
Подставляя выражения для х и его производных в урав-
нение A1.1), получим:
— со' cos (at — 6<os sin (at = — a(a\ cos (at — 6oJ sin <at ~f-
-f- 2уат sin (at — 2y b(a cos (at -\- — cos (at.
Для того чтобы это равенство было верно при любых /,
должны быть равны между собой в отдельности члены с
cos (at и sin (at. Приравнивая эти члены, получаем:
— аыг = — аа>* — 2\Ьы -4- — ,
т \ Л1 '
412
МЕХАНИКА
[Ч. VI
Из второго уравнения A1.3) находим:
со* —(о»
а.
Подставляя это в первое уравнение A1.3), находим:
со»-со»
Тогда
I
2усо
т (Ш« _
A1.4)
A1.5)
Переходя к виду х = С cos (<ot -{-у) и вспоминая, что
С = 1/а14-61, (9.11)
получаем амплитуду С колебаний, вызванных внешней
силой,
/
у (со'-
A1.6)
Отсюда видно, что С тем больше, чем ближе со к а>0.
Кривая зависимости С от со при данном соо изображена
на рис. 152 при двух
значениях у. Принято
Wt Л / 1 1 тт
^=1, «0 = 1. Чем мень-
ше трение, тем резче
выражен подъем ампли-
туды колебаний при ра-
венстве частоты внеш-
. ней силы и собственной
% частоты.
Нетрудно убедиться,
что сумма решения
A0.5) уравнения A0.4)
и общего решения A1.2) уравнения A1.1)
х== a cos Ш -f- b sin art -f- Coe~T* cos (<в0* + а), A1.7)
где а и Ъ даются формулами A1.4) и A1.Б), также яв-
ляется решением уравнения A1.1). При помощи этого
решения можно решить задачу с любыми начальными дан-
0,10,2
Рис. 152.
§ 12] О ТОЧНЫХ И ПРИБЛИЖЕННЫХ РЕШЕНИЯХ ЗАДАЧ 413
ными, выбирая соответственно Со и а. Действительно,
пусть при / = 0, х = ха, и = иа. Тогда, пользуясь A1.7),
находим:
xa = a-{-Cacosa., \
va = b<o — C0(y cos a-f-©! sin a). J '
Из этой системы уравнений можно определить Со и а
(см. упражнения). Таким образом, A1.7) есть общее ре-
шение задачи о колебаниях тела под действием упругой
силы и периодической внешней силы. Это общее решение
подтверждает сделанное в начале параграфа предполо-
жение о том, что при длительном воздействии внешней
силы с частотой ш тело будет колебаться с той же часто-
той (о. В самом деле, каковы бы ни были начальные
условия, они влияют только на значения Са и а, т. е.
только на последнее слагаемое решения A1.7). Однако
с течением времени это слагаемое, имеющее частоту (о0,
становится сколь угодно близким к нулю за счет множи-
теля е* и им можно пренебречь при больших t. Остав-
шиеся слагаемые описывают колебания с частотой со, ко-
торые не затухают с течением времени, потому что они
поддерживаются действием внешней силы.
Упражнения
1. Определить С, и а из системы A1.8).
2. Благодаря наличию трения максимальная амплитуда С полу-
чается при со^ах > несколько отклоняющемся от со'#
Найти отклонение to^,ax/coj от 1 в зависимости от у.
Указан ие. Исследовать на минимум подкоренное выражение
в A1.6), обозначив to1 = г.
§ 12. О точных и приближеивых решениях
физических задач
В предыдущем параграфе нам посчастливилось сравни-
тельно просто найти точное решение задачи о колебаниях
тела под действием периодической внешней силы при
наличии возвращающей силы (— kx) и силы трения
(— h ^-J . Располагая этим точным решением, можно
легко найти ряд важных предельных случаев.
414 механика [ч. vi
1) Частота внешней силы а> весьма мала по сравнению
с со0, где <о* =—. Пренебрегая в формуле A1.6) о по
f f
сравнению с та, получаем С = —*— = -^-.
т<о0 я
2) Частота внешней силы о весьма велика и значи-
тельно больше ©.. Тогда С = — —~==? . Но
(трение не очень велико); пренебрегая членом 4у1<о*, по-
лучаем С = ^г.
3) Сила трения мала. Пренебрегая членом, содержа-
щим у» получаем:
Мы берем абсолютную величину, так как рассматриваем
положительное значение корня в формуле A1.6).
4) Явление точного резонанса: частота внешней силы
в точности равна собственной частоте, т. е. (о = а>0.
Тогда
С L. — X ^ /1 о о\
т 2у<л А(о Л(о0 ' \1*-*)
Совокупность этих предельных случаев, в сущности,
составляет больше 90°/0 содержания всех полученных
результатов. Получив общий результат, всегда необходимо
его упростить, рассматривая различные предельные слу-
чаи, как мы это сделали выше. Простые формулы, отно-
сящиеся к предельным случаям, легче запоминаются и
чаще используются на практике. Лишь изредка прихо-
дится прибегать к общим формулам. Зная предельные
случаи, мы знаем хотя и не все, но почти все, что со-
держится в более сложной точной формуле.
Возникает вопрос, нельзя ли было эти предельные
формулы получить прямо, производя упрощение в самом
уравнении. Решать точно сложное уравнение и потом
упрощать решение так же неразумно, как при помощи
сложных машин аккуратно упаковывать вместе и заво-
рачивать в изящную обертку несколько предметов, а
потом руками рвать эту обертку и пользоваться этими
предметами в отдельности.
§ 12] о точных и приближенных решениях задач 415
Прямое получение предельных (приближенных) выра-
жений особенно важно еще потому, что точное решение
очень чувствительно к малейшим изменениям постановки
задачи. Достаточно немного усложнить задачу, и точное
решение уже не удается найти. Приближенное решение
более грубо, но и более устойчиво относительно измене-
ния задачи.
Особенно важны для учащегося те случаи, когда пред-
ставляется возможным получить и сравнить между собой
оба решения — точное и приближенное. Именно на таких
случаях можно приобрести опыт правильного выбора
приближений и уверенность в результатах.
Вернемся к первому случаю: частота внешней силы
мала. Очевидно, мы имеем дело с медленным движением.
Поэтому в исходном уравнении
dt
A1.1)
опустим члены, связанные е движением т. -^ и h -^ .
Получим:
O = — kx-\-f cos со/,
откуда
* = ?^ = Ccoearf,C=4.
Таким образом, при малой частоте в каждый момент
приложенная внешняя сила уравновешивается силой упру-
гости. Ясно, что этот результат является весьма общим:
он относится к любому движению с малой частотой.
Такой предельный случай называется статическим.
В частности, сила упругости может быть любой функцией
координаты [F(x)], внешняя сила может быть любой
функцией времени [Fx (t)]. Уравнение колебаний принимает
вид
Точное решение этого уравнения можно получить не всегда,
но приближенный подход сохраняется. Действительно,
пренебрегая в случае медленного движения членами
416 МЕХАНИКА [Ч. VI
со скоростью и ускорением, получаем из A2.3)
Отсюда находим x(t)— приближенную зависимость между
х и t. Подставляя это x(t) в точное уравнение A2.3),
можно найти, какого порядка ошибку мы допустили,
пренебрегая членами т^ н/г^.
Обратимся ко второму предельному случаю — очень
большой частоты о. При большой частоте время действия
внешней силы, а следовательно, и импульс силы за каж-
дый полупериод (пока сила действует в одном направле-
нии) малы, потому что мала длительность полупериода.
Значит, при данной амплитуде силы /, чем больше со,
тем меньше скорость, которую может набрать тело, и тем
меньше перемещение тела. Пренебрегая в уравнении чле-
нами kx и hj-, получим уравнение движения свободного
тела, на которое не действуют никакие силы, кроме внеш-
ней силы,
^ >/. A2.4)
Будем искать решение уравнения A2.4) в виде
л; = С cos ш/.
Тогда
Подставляя в A2.4), получаем:
— Ста* cos <ot = f cos a»tt
откуда
" т<йг'
Поэтому
S^ «*«**. A2.5)
В стандартном виде х = С cos (<ot -\- а) решение A2.5)
можно записать так, чтобы С было положительным,
§ 12] О ТОЧНЫХ И ПРИБЛИЖЕННЫХ РЕШЕНИЯХ ЗАДАЧ 417
При этом упругая сила есть
— kx = —Ц cos о/ = —J- / cos mt.
Сила трения
, dx hf .
При сравнении сил, периодически зависящих от вре-
мени, нужно сравнивать не мгновенные их значения, а
амплитуды. Отношение внешней силы к упругой, силе
(отношение амплитуд) равно
Это отношение тем больше, чем больше ю. Аналогично и
отношение внешней силы к силе трения неограниченно
растет с ростом со. Поэтому при больших <о внешняя
сила значительно превосходит как упругую силу, так и
силу трения. Этим подтверждается возможность прибли-
женного рассмотрения движения под действием одной
только внешней силы *).
Третий предельный случай — пренебрежение трением—
легко получается непосредственно
)/ = — m(u\x-\-fcos<i>t. A2.6)
Решение уравнения A2.6) ищем в виде х=С cos((at-\-a.).
Подставляя в уравнение выражения для х и -^, получаем:
а = 0, т (о' — шг) С cos tat =¦ f cos mt,
откуда
c_ f
m (coj — cos)
Рассмотрим четвертый случай — частота внешней силы
в точности равна собственной частоте колебаний, <й = (о0.
*) Существенно, что рассмотренная выше сила трения тем ближе
к нулю, чем ближе скорость к нулю. При сухом трении (сила трения
не зависит от скорости) внешняя сила меньшая, чем сила трения,
не вызовет колебаний нн при какой частоте.
14 я. Б. Зельдович
418
МЕХАНИКА
[Ч. VI
Будем искать решение уравнения A1.1) в виде
х = С cos(oH/-j-ct)- Тогда
(Рх
т ^р= — тСшI cos (a>at-{- а).
Вспоминая, что coJ = Aj/m, получаем:
m^= — kCcos(<aJ-\-a) =— kx.
Подставляя в A1.1) выражения для х и его производных,
получим:
sini
Последнее равенство будет справедливо при любом t, если
а= 2"'
Решение, следовательно, есть
Амплитуда колебаний при резонансе С = //йй>0.
Изобразим на чертеже зависимость С от ш, даваемую
приближенными форму-
лами A2.1) и A2.2)
(рис. 153). Формула
A2.1) дает две ветви,
уходящие в бесконеч-
ность при а> = (о0; фор-
мула A2.2) • дает при
(о = (о0 конечное значе-
ние С = А Построив
-кривые A2.1) и поста-
вив точку А, соответст-
вующую формулеA2.2),
уже нетрудно от руки
провести гладкую кри-
вую(пунктирнарис.118),
которая вдали от резонанса совпадает с кривыми A2.1)
и имеет максимум А в точке со0.
Амплитуду С и начальную фазу се в случае резонанса
(четвертый случай) можно определить при помощи энерге-
тических соображений, ценность которых заключается в
кО
Рис. 153.
§ 12] О ТОЧНЫХ И ПРИБЛИЖЕННЫХ РЕШЕНИЯХ ЗАДАЧ 419
том, что они позволяют приближенно решить также и не-
которые задачи, не имеющие точного решения.
Мощность, развиваемая внешней силой /cos со/ при
движении, заданном выражением х= С cos (<o/~f-а), есть
Wm=f cosait-jj — — /Со cos <ot sin (<ot -f- a).
Определим среднюю мощность внешней силы за большой
(точнее говоря, за бесконечный) промежуток времени
Wm = — fCm cos (at sin ((at -j- a).
Заметим, что
cos (at sin ((at -f- a) = -5- sin 2a>/ cos a -f- cos* at sin a,
поэтому
cos «/ sin ((ot-\-a.) = -? sin 2(o/ cos a -{-cos1 o/sina = -^ sin a.
Следовательно,
или
^BB = ^-cos(a + ^-). A2.8)
Теперь определим среднюю мощность силы трения. Так
как /7тр = — hv, то
WTV =—Лог=—Ш\ A2.9)
Но
Поэтому A2.9) дает:
тр
Так как работа внешней силы идет на преодоление
трения, то средние мощности внешней силы и силы трения
должны быть равны по абсолютной величине:
14*
420 МЕХАНИКА [Ч. VI
т. в.
fC<o
2
или
/|cos (ос+^- )| =
откуда
Максимальная возможная амплитуда (явление резонанса)
получается, как видно из A2.11), при cos (a+f ) = 1. т. е.
при а = — \ При этом ш = (о0 и C = J—. Следовательно,
решение в случае резонанса есть
Мы опять получили формулу A2.7).
Вернемся- к формуле A2.8). Из нее видно, что при
резонансе IFBH имеет наибольшее значение, так как при
резонансе cos (a-f--^-j = 1. Поэтому в случае резонанса
внешняя сила развивает наибольшую среднюю мощность
и, следовательно, производит наибольшую работу.
Приведенные энергетические соображения позволяют
определить амплитуду при резонансе и в случае более
сложной зависимости силы трения от скорости. Пусть
сила трения дана формулой
FTP = — hv\v\n-\ A2.12)
При и > 0 A2.12) дает /7тр= — hvn, при и<0 получим
Frp= h\v\". Поэтому A2.12) при любом знаке скоро-
сти v дает силу трения, направленную противоположно
скорости. Средняя мощность внешней силы по-прежнему
дается формулой A2.8). Определим W^. Мгновенное зна-
чение WTV=F v= — hv*\u\n~1; так как v* = |o|1, то
lF h\\ подставляя сюда значение v, находим:
o/4-a)jn + 1. A2.13)
ие WTV=F v
= — h\v\
§ 13J РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 421
Пользуясь A2.13), получаем:
где положено А = | sin (o0* -f- а) ln+* *). УсловиеA2.10) дает:
Отсюда
Максимальная амплитуда, достигаемая при резонансе,
равна
Частным случаем формулы A2.14) прип=1 (сила трения
пропорциональна скорости) является найденная раньше
формула
рр
формула
С=
со„А
§ 13. Реактивное движение и формула
К. Э. Циолковского
При движении в безвоздушном пространстве единствен-
ный способ управления полетом (изменения скорости и
направления) заключается в отбрасывании части массы
самого летящего тела, т. е. в применении реактивного
принципа движения.
Русский ученый К. Э. Циолковский первый полностью
осознал значение реактивного принципа и исследовал
основные закономерности реактивного движения. От него,
через его учеников и последователей, советских ученых
и конструкторов, идет та научная традиция, воплощением
*) Приведем для справки значения А для нескольких п: п—>-0,
—» — = 0,64; л=1, Л = 0,5; п = 2, А = ~ = 0,42; л=3, А =
4 = 0,375.
422 МЕХАНИКА [Ч.
о.
которой явились советские искусственные спутники оемли,
искусственные планеты и космические корабли с космо-
навтами на борту.
Выведем основное уравнение прямолинейного движения
ракеты. Топливо ракеты — будь то порох или смесь го-
рючего (спирта, бензина) и окислителя (кислорода, азот-
ной кислоты) — обладает определенным запасом Q хими-
ческой энергии на единицу массы (Q порядка 1000 ккал\кг
для бездымного пороха и 2500 ккал/кг для бензина
с кислородом *)). При сгорании эта химическая энергия
превращается в тепловую энергию продуктов горения.
Затем продукты горения вытекают через сопло; при этом
тепловая энергия их превращается в кинетическую энергию
движения.
Когда реактивный двигатель закреплен на испытатель-
ном стенде, продукты горения вытекают с определенной
скоростью иа. При этом кинетическая энергия их на еди-
ницу массы составляет определенную долю химической
энергии топлива
!T=aQ, A3.1)
где а — безразмерное число — коэффициент полезного дей-
ствия процессов горения и истечения газов**).В дальней-
шем будем считать скорость истечения и„ известной,
заданной величиной. Она составляет около 2 км\сек для
пороха и около 3 км\сек для жидкого топлива. Легко
убедиться, что этим величинам соответствуют, значения
а=ь:0,5 (к. п. д. порядка 50°/0).
До горения топливо покоилось. Пусть сгорела и вы-
текла из сопла масса dm топлива. При этом она приобрела
количество движения uodm. Очевидно, что импульс силы
dl, с которой ракета действует на эту массу, равен
*) Теплотворная способность бензина около 10 000 ккал/кг,однако
для сжигания 1 кг бензина (СНХ) нужно израсходовать еще 3,4 кг
кислорода. В ракете, летящей в безвоздушном пространстве, кислород
надо везти с собой и энергию надо относить к сумме веса топлива
и окислителя.
**)В формуле A3.1) нужно Q выразить в механических единицах
(эрг/г), тогда иа получится в см/сек. При этом 1 ккал/кг =\кал\г =
= 4,18-107 эрг/г.
§ 131 РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 423
количеству движения, приобретенному массой dm *),
По закону равенства действия и противодействия импульс
силы, с которой масса dm продуктов горения действует
на ракету, равен той же величине с обратным знаком.
Пусть, например, скорость истечения иа направлена в сто-
рону убывания х. Тогда ис отрицательно, ио = — |ы„|.
Для импульса силы, действующей на ракету, имеем:
A3.2)
Величина
/' = Ж = 1"о1 03.3)
есть импульс силы, приходящейся на единицу массы, так
называемый единичный импульс. Эта величина равна
скорости истечения газов из покоящейся ракеты.
Проверим размерность в формуле A3.3). Сила F имеет
размерность г-см/сек* (дина), импульс силы / — это про-
изведение силы на время, поэтому его размерность г-см/сек.
Размерность -з— есть г • см/сек • г = см/сек — это размер-
ность скорости. Для пороховых газов иа = 2- 10s = 2 км/сек,
для жидкого топлива иа = 3 км/сек. В технической системе
единиц единичный импульс выражается в кГ-сек!кг, где
кГ обозначает силу, а кг—массу. Сила в 1 кГ равна
силе, выраженной в динах, деленной на 1000 g", где g" —
ускорение силы тяжести; масса в 1 кг равна массе, выра-
женной в граммах, деленной на 1000. Поэтому /', выра-
женный в кГ-сек!кг, численно равен ¦ |[Q0Q — = -f-.
Считая округленно g^=1000 см\секг, получим 200 кГ-сек\кг
для пороховых газов и 300кГ-сек/кг для жидкого топлива.
Сила, действующая на ракету, по формуле A3.2) есть
Р I , dm
tv — I"о \~dF'
Она пропорциональна количеству газов, вытекающему
в единицу времени.
*) Обозначение dl связано с тем, что рассматривается малая
масса dm.
424 МЕХАНИКА [Ч. VI
Обратимся теперь к выводу формулы для скорости
движения ракеты. Если ракета сама движется с какой-то
скоростью и, то скорость истечения газов отлична от иа
и равна u-f-uo = «—\иа\ (напомним, что в покоящейся
ракете скорость истечения газов равнялась — | иа |). Оче-
видно, что такие величины, как разность скоростей
пороха до горения и вытекших пороховых газов и сила,
с которой на ракету действуют пороховые газы, не зависят
от того, движется или покоится ракета.
Обозначим начальную массу ракеты вместе с порохомМа.
Массу вытекших пороховых газов обозначим т. Величи-
на т есть функция времени, т = /л(/). Обозначение т
находится в соответствии с тем, что малую вытекшую
массу мы обозначали dm, количество пороховых газов,
вытекающее в единицу времени, —-гг. Масса ракеты с по-
рохом в момент / равна
Ma — m(t). A3.4)
Уравнение движения (второй закон Ньютона)
**d« r- i , dm
Это уравнение можно записать так:
М du = 1 и01 dm
или, пользуясь A3.4)
(К->п)^ = \"Л 03.5)
Возможность сократить dt физически означает, что (при
отсутствии других сил, действующих на ракету) скорость
ракеты зависит только от количества вытекших пороховых
газов (при фиксированной величине иа). К моменту, ко-
гда из сопла вытекло данное количество пороховых газов
т, ракета приобретает определенную скорость и, неза-
висимо от того, за какое время произошло вытекание
данного количества пороховых газов.
§ 13] РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 425
Нетрудно решить уравнение A3.5). В начальный момент,
при т = 0, и = 0. Поэтому получаем:
Итак,
" = К|1п-^- A3.6)
Эта формула впервые была получена К. Э. Циолковским и
носит его имя.
Если нас интересует конечная скорость ик к моменту
окончания горения всего топлива, то надо в формулу A3.6)
подставить вместо М величину Мк—конечную массу
ракеты после сгорания всего топлива: МК = М„ — тп, где
та — полная масса всего топлива. Получим:
«K = |ujln-^-. A3.7)
При помощи этой формулы легко решается и обратная
задача: какой нужно взять начальную массу ракеты для
того, чтобы данной конечной массе Мк придать опреде-
ленную скорость ик
откуда
Ма = МкеТ^. A3.8)
Для того чтобы тело вращалось вокруг Земли в виде
спутника, нужно, чтобы его центробежная сила уравно-
вешивала силу притяжения Земли. Соответствующая
скорость ы, называется первой космической скоростью.
Для ее определения получаем:
MB4 = MKg, A39>
где R — радиус орбиты. Он приблизительно равен
426 МЕХАНИКА [Ч. VI
радиусу Земли, поэтому в правой части A3.9) в качестве
силы притяжения взята сила тяжести на поверхности
Земли. Из формулы A3.9) находим:
Для спутника, летящего на расстоянии г от центра
Земли, значительно отличающемся от г0, надо учесть,
что с изменением высоты меняется величина ускорения
силы тяжести, равная g на поверхности Земли. Действи-
тельно, по закону тяготения Ньютона тело, отстоящее
на расстоянии г от центра Земли, притягивается к Земле
с силой /7=х^Ц- , где т — масса тела, М — масса Земли.
С другой стороны, по второму закону Ньютона F = ma,
где а — ускорение силы тяжести на расстоянии г от центра
Земли. Сравнивая два выражения для F, находим
а=-^-. Если г = г0, то a = g, поэтому g — —-, откуда
о
я = —хр" • Окончательно получаем a = g —5- . В этом случае
равенство центробежной силы и силы тяжести дает:
откуда скорость спутника на орбите
Чем больше расстояние г, тем меньше скорость и,
необходимая для того, чтобы спутник вращался на со-
ответствующей орбите. Однако это вовсе не означает,
что легче запустить спутник на орбиту с весьма боль-
шим г, чем на орбиту с г, близким к /у. ведь для вывода
спутника на орбиту с большим г надо затратить большую
энергию на преодоление силы тяжести на пути от зем-
ной поверхности до орбиты.
Рассмотрим теперь следующую по трудности осуще-
ствления задачу. Для того чтобы тело могло уйти из
области действия земного притяжения, нужно, чтобы его
начальная кинетическая энергия была не меньше разности
§ 13J РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 427
потенциальной энергии удаленного тела и тела на по-
верхности Земли. Эту величину мы нашли в § 2 (фор-
мула B.5)]. При этом предполагается, что сгорание топ-
лива и приобретение скорости происходят быстро на
участке пути, малом по сравнению с радиусом Земли,
так что изменением потенциальной энергии на этом
участке пути можно пренебречь. Это значит, что во время
горения топлива реактивная сила весьма велика, и действием
силы тяжести в это время также можно пренебречь.
Доказано, что быстро сжигать топливо выгоднее (меньше
потребуется топлива), нежели растягивать процесс горе-
ния на время, необходимое для прохождения пути по-
рядка радиуса Земли *).
Начальная скорость, которую должно иметь тело для
того, чтобы уйти из области земного притяжения, назы-
вается второй космической скоростью. Найдем ее.
По формуле B.5) начальная энергия, необходимая
для достижения расстояния г от центра Земли телом,
первоначально находившимся на поверхности (г0), равна
/C0=mg —(г—г0). В нашем случае г значительно боль-
ше г0, поэтому г — го^=г, что дает Ka=mgrn. Приравня-
ем этой величине кинетическую энергию ракеты
отсюда
и2 =V2gro^=ll,2 км.\сек.
Наконец, начальная скорость, которой должно обла-
дать тело для того, чтобы уйти из поля тяготения Солн-
ца, т. е. за пределы солнечной планетной системы, назы-
вается третьей космической скоростью и,. Найдем ее,
пользуясь тем, что скорость vx вращения Земли вокруг
Солнца известна, а именно, Oj = 30 км\сек.
По закону тяготения Ньютона сила притяжения тела
массы m к Солнцу есть F = — k—§^-, где Mq—масса
*) Лишь на том участке пути, где еще велики плотность атмо-
сферы и сопротивление воздуха, невыгодно двигаться с большой
скоростью. Однако толщина атмосферы мала по сравнению с радиу-
сом Земли (см. часть VII), и мы ее учитывать не будем.
428 МЕХАНИКА [Ч. VI
Солнца*), г—расстояние от центра Солнца до тела, k —
постоянный коэффициент. Потенциальная энергия тела,
удаленного на расстояние г от центра Солнца, равна
и(г) = — Уу^т. A3.10)
При этом за нуль принято значение потенциальной
энергии на бесконечности (см. § 2).
Величину потенциальной энергии тела, находящегося
на радиусе земной орбиты, легко выразить через скорость
движения Земли по орбите. В самом деле, на орбите
Земли сила притяжения Земли к Солнцу уравновешивается
центробежной силой
где vy —скорость вращения Земли вокруг Солнца, а г,— ра-
диус земной орбиты 150 млн. км= 1,5-10" см. Отсюда
kMo=v\rl,
и формула A3.10) принимает вид
u(r1)= — vim.
Для того чтобы тело, находившееся на расстоянии г,
от Солнца, ушло из поля тяготения Солнца, нужно, чтобы
на этом расстоянии сумма его кинетической и потенци-
альной энергии была неотрицательна. Это приводит к
условию
Здесь vt — искомая скорость, необходимая для ухода
из солнечной системы, vx — известная скорость движения
Земли.
С таким положением мы уже встречались при рас-
смотрении движения тела в поле тяготения Земли:
скорости, необходимой для ухода тела из поля земного
тяготения; соответствует кинетическая энергия, вдвое
большая, чем кинетическая энергия, соответствующая ско-
рости, необходимой для вращения тела в виде спутника.
•) Значком О астрономы обозначают Солнце. Численно
2-l0" г.
§ 131 РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 429
Из последнего соотношения находим минимальную
необходимую скорость
vt = v i У 2 =*= 42 км/сек.
Итак, для того чтобы уйти из солнечной системы, необ-
ходимо на орбите Земли иметь начальную скорость
(относительно Солнца) 42 км/сек. При этом оказывается,
что тело со скоростью больше 42 км/сек уйдет из сол-
нечной системы независимо от того, куда направлена
эта скорость — прямо по
радиусу от Солнца [/] или
по касательной к орбите
Земли [2\, [3\, или даже
в сторону Солнца [4] (но
все же под некоторым уг-
лом, чтобы не попасть на
поверхность Солнца). От
направления начальной
скорости зависит только
форма траектории (рис.
154), цифры в скобках
соответствуют номерам
траекторий на рис. 154.
Ясно, что для запуска ракеты с Земли наиболее
выгодна траектория [2\: сама Земля движется со ско-
ростью 30 км/сек, поэтому для получения скорости
42 км/сек в этом же направлении достаточно, чтобы
относительно Земли ракета двигалась со скоростью
?^ = 12 км/сек. Эту скорость v'x ракета должна иметь
после того, как она выйдет из поля тяготения Земли,
т. е. удалится от Земли на расстояние, большое по срав-
нению с радиусом Земли, но малое по сравнению с ра-
диусом земной орбиты.
Какую же для этого надо иметь начальную скорость
на поверхности Земли? Именно эта скорость и называется
третьей космической скоростью иа. Определим ее из соот-
ношения t x
-^-. A3.11)
Здесь первый член справа есть энергия, необходимая для
430 МЕХАНИКА [Ч. VI
преодоления притяжения Земли, второй член — это энер-
гия, которая должна остаться после этого, чтобы ракета
имела (в сумме со скоростью движения Земли) скорость
vt, необходимую для ухода из солнечной системы. Фор-
мула A3.11) дает:
и\ = 2gfa -f v? =u\-\- о,,
откуда
иг = y^u'l-^v,' = 1/11,2*+ 12* ^=16,4 км [сек.
Заметим, что для того, чтобы приблизиться к Солнцу
или попасть, например, на Меркурий или Венеру, второй
космической скорости недостаточно. Действительно, при
наличии этой скорости ракета отделится от Земли и будет
двигаться по орбите со скоростью, равной скорости Зем-
ли, т. е. 30 км\сек.
Хотя потенциальная энергия и уменьшается при при-
ближении к Солнцу, но ракета не может приблизиться
к Солнцу, так как этому мешает центробежная сила ее
движения по орбите. Для того чтобы проникнуть в глубь
солнечной системы, необходимо уменьшить скорость ра-
кеты относительно Солнца, а это так же трудно, как и
увеличить ее. В частности, для попадания в Солнце нуж-
но ракету остановить, т. е. нужно, чтобы она имела ско-
рость 30 KMJceK относительно Земли (после выхода из
поля тяжести). Для этого нужна на поверхности Земли
начальная скорость
их = У 30* -f 11.2* = 32 км1сек. ¦
Попасть в Солнце труднее, чем уйти от него! Более
выгодные варианты можно получить, используя изменение
скорости ракеты под влиянием других планет. На этом
вопросе мы останавливаться не будем.
м
Найдем величины отношения -г~- , при которых дости-
гаются скорости их, ut, ил. Для пороха ]«0| = 2 км/сек.
Пользуясь формулой A3.8), получаем: для ы,=8 км/сек
-^°-= <?*== 54; для «,= 11,2 км\сек ~^- =е1'* =270;
для и. = 16,4 кмIсек 1~ = ев'г = 3641. В случае жидкого
§ 13] РЕАКТИВНОЕ ДВИЖЕНИЕ И ФОРМУЛА ЦИОЛКОВСКОГО 431
топлива | иа | = 3 KMJceK. Аналогичные подсчеты дают:
Jib. = 14,5,- -^а-= 42, Jis- = 245. Из подсчетов видно,
/VI к( 'wKi "Яка
что величина-гт2- сильно зависит от скорости истечения
газов (иа). Для того чтобы оценить трудности задачи по
запуску ракеты, следует иметь в виду, что Мк включает
в себя вес баков для топлива и т. п.
Найдем к.п.д. ракеты как целого. Определим эту
величину как отношение кинетической энергии ракеты
и
после сгорания топлива Мк-?- к химической энергии сго-
ревшего топлива mQ = (Ma — MK)Q. Коэффициент полез-
ного действия
Подставив в A3.12) выражение для ик из A3.7) и выразив и\
из A3.1), окончательно получим:
К-п.д. оказывается произведением «внутреннего к.п.д.» а,
характеризующего полноту сгорания топлива и преобразо-
вания тепловой энергии в кинетическую энергию газов,
и второго множителя, зависящего только от выбора со-
отношения между массой горючего та и массой полезного
груза Мк. Обозначим -^- = г. Тогда Ма =Мк-\-та =
1 -\~z) и к. п. д.
Мл (у My, -f- /п„\* 1
На первый взгляд может показаться, что к.п.д. очень
велик при малых z за счет дроби —. В действительности
при малых z имеет место In (I -j-z)=^z, поэтому
Tj=t:a — z* = az.
К.п.д. пропорционален z и, следовательно, он мал при
малом 2- При малом z ракета движется медленно, почти
всю энергию уносят газы. При очень больших z к.п.д.
432 МЕХАНИКА [Ч. VI
снова падает из-за уменьшения полезной массы*). Так как
окончательная скорость ракеты также зависит только от
z, то можно сказать, что к.п.д. ракеты определяется тре-
буемой скоростью. При малой скорости к.п.д. ракеты мал,
поэтому невыгодно применение ракет в автомобилях и в
других случаях сравнительно медленного движения. При
большой скорости энергетический к.п.д. ракеты снова
уменьшается, но применение ракет тем не менее оправдано,
так как мы не располагаем другими способами ускорения
тел до больших скоростей.
Упражнения
1. Найти значение г, дающее максимум коэффициенту полезного
действия ц. Найти величину этого максимума.
2. Найти радиус орбиты, на которой время обращения спутника
равно 24 часам. Спутник, запущенный иа такую орбиту в плоскости
экватора, внсит иад одной точкой земной поверхности.
§ 14. Траектория снаряда
Рассмотрим задачу о полете снаряда, выброшенного
из орудия с начальной скоростью va. Примем точку вы-
лета снаряда из ствола за начало координат, ось у на-
правим вертикально вверх. Для простоты силу сопротив-
ления воздуха не будем принимать во внимание, учет
этой силы значительно усложняет задачу.
По второму закону Ньютона
Этот закон мы применяли раньше только для прямолиней-
ного движения. Однако в задаче' о траектории направле-
ние v меняется с течением времени (скорость всегда на-
правлена по касательной к траектории полета снаряда).
Поэтому поступим следующим образом. Силу F разложим
на составляющие в направлении оси х и в направлении
оси у. Эти составляющие обозначим соответственно через
Fx и Fy. To же самое проделаем со скоростью и.
*) При большом z величина [In (I -\-z)\* растет медленнее, чем г.
Действительно, обозначая у=\п A -j-z), получим г = еУ— 1, а функ-
ция еУ растет быстрее любой степени у (см. ч. III).
§ 14] ТРАЕКТОРИЯ СНАРЯДА 433
Всякое движение в плоскости х, у можно рассматри-
вать как результат сложения двух движений: одного,
происходящего вдоль оси х под действием силы Fx со
скоростью vx, и другого вдоль оси у под действием силы
Fy со скоростью vy. Применив к каждому из этих движе-
ний в отдельности второй закон Ньютона, получим:
Мы получили два уравнения A4.1), однако в каждом из
этих уравнений сила и скорость направлены вдоль одной
прямой (вдоль оси х в первом уравнении и вдоль оси у
во втором).
Обозначим через <р угол ствола орудия с горизонталь-
ным направлением; <р. называют углом бросания. Так как
мы рассматриваем простейший случай, когда в процессе
полета на снаряд действует только сила тяжести, напра-
вленная к земле, то FX = Q, Fy = — mg. Поэтому уравне-
ния A4.1) в этом случае имеют вид
dvx n \
mf=0- I (H.2)
Поставим начальные условия для функций vx(t) и vy(t).
В момент вылета снаряда нз орудия ? = 0
vx@)=zvacosy,
Первое из уравнений A4.2) дает -^ = 0> откуда следует,
что vx постоянна, а поэтому
Второе уравнение A4.2) дает -yf = — g* откуда, интегри-
руя от 0 до t, находим:
»,@ — vy@) = — gt
или
. A4.4)
434 МЕХАНИКА [Ч. VI
Для определения перемещений х и у вдоль коорди-
натных осей воспользуемся очевидными соотношениями
dt — vy
Пользуясь формулами A4.3) и A4.4), получаем из A4.5)
dx
rnr=Va COS ф,
Л ° ' A4.6)
В начальный момент времени снаряд был в начале коор-
динат, поэтому
при * = 0 х = 0, у = 0. A4.7)
Интегрируя уравнения A4.6) от 0 до t и пользуясь на-
чальными условиями A4.7), находим:
A4.8)
Формулы A4.8) дают возможность определить положение
снаряда в любой момент времени t.
Беря различные значения t, можем найти по форму-
лам A4.8) положение снаряда в различные моменты вре-
мени и построить график полета снаряда (траекторию
снаряда). Таким образом, уравнения A4.8) дают кривую
на плоскости х, у. Задание кривой при помощи двух
уравнений
называется параметрическим заданием кривой. Число t
называется параметром.
Из уравнений A4.8) нетрудно исключить t и получить
уравнение траектории в обычном виде, в виде зависи-
мости у от х. Действительно, первое уравнение A4.8)
§ hi
ТРАЕКТОРИЯ СНАРЯДА
435
дает t= , после этого из второго уравнения A4.8)
находим:
2о* cos* i
A4.9)
Из A4.9) видим, что у есть многочлен второй степени от
х, график такого многочлена — парабола. Поэтому траек-
тория снаряда (если не учитывать сопротивление воздуха)
есть парабола. На рис. 155 изображена траектория A4.9)
для случая vа== 80 м[сек*), <р = 45°.
а
100'
50
0
50
100
гоо
300
400
500
600 х
Рис. 155.
Из A4.9) видно, что прн одном и том же va форма
траектории зависит от угла бросания <р. Найдем наиболь-
шую высоту подъема снаряда и дальность стрельбы при
данном ф и vQ. Для определения наибольшей высоты
подъема составим уравнение Щ = 0. Получаем:
S
о? cos'
= 0,
откуда
и* sin ф cos ф uj sin 2ф
При этом значении х высота у имеет максимум (физи-
чески ясно, что это именно максимум; впрочем, этот
*) При небольшой начальной скорости роль сопротнвлення воздуха
действительно невелика. Однако если взять начальную скорость va =
= 800 л/сея, то для снаряда калибром (диаметром) 305 мм при угле
бросания ф = 55° сопротивление воздуха уменьшает дальность с 61
до 22,2 км.
436 МЕХАНИКА [Ч. VI
факт легко проверить по зр). Подставляя найденное х
в A4.9), получаем:
v\ sin* ф
Утах == 2g "
Для определения дальности полета достаточно опреде-
лить то значение х, при котором {/ = 0 (см. рис. 155),
х tg <р — хх — = 0.
1v\ cos' ф
Отбрасывая не интересующее нас решение лг=О, находим:
= -^^. A4.10)
Дальность стрельбы зависит от начальной скорости и от
угла бросания.
При каком же угле бросания (начальная скорость v0
не меняется) дальность стрельбы наибольшая? Ясно, что
это будет тогда, когда sin2q>=l, т. е. при <р = 45°.
Определим время, в течение которого снаряд подни-
мается вверх. Для этого достаточно решить уравнение
-? = 0, потому что в тот момент t, когда у достигает
своего наибольшего значения, снаряд перестает подни-
маться и начинает падать. Условие ^ = 0 дает va sin <p —
— g/ = 0, откуда
f=o.sin9> '. A4.11)
Полное время полета ta определим, исходя из того,
что полет прекращается в тот момент, когда х =
Пользуясь A4.8) и A4.10), находим:
v* sin 2ф
t =
откуда
ta = 2o°sin4> . A4.12)
Сравнивая A4.12) и A4.11), видим, что полное полетное
§ 15] МАССА, ЦЕНТР ТЯЖЕСТИ, МОМЕНТ ИНЕРЦИИ СТЕРЖНЯ 437.
время ta в 2 раза больше времени подъема. Время подъ-
ема снаряда равно времени его падения.
Отметим в заключение, что реальные траектории сна-
рядов не являются в точности параболами, они несколько
искажены, так как в действительности снаряд испытывает
сопротивление воздуха. При этом дальность стрельбы,
высота подъема снаряда, полетное время и т. п. зависят
от веса снаряда, его формы и плотности воздуха.
Упражнения
1. Снаряд вылетает из орудия со скоростью 80 м/сек. Определить
дальность стрельбы н максимальную высоту подъема снаряда, если
угол бросания ф = 30°; 45°; 60°.
2. Определить наибольшую высоту, на которой снаряд с началь-
ной скоростью о0 —80 м/сек может поразить цель, расположенную на
расстоянии 500 м от местонахождения орудия.
§ 15. Масса, центр тяжести и момент инерции-стержня
Рассмотрим тонкий стержень. Направим ось х вдоль
стержня, обозначим q массу, приходящуюся на единицу
длины стержня. Таким образом, на отрезке dx между х
и x-\-dx расположена масса
dm = q dx.
Стержень может быть сделан из материала, плотность
которого зависит от х, или может иметь переменное по
длине, т. е. зависящее от х, сечение. Поэтому q является
функцией координаты х. Величина Q есть произведение
объемной плотности материала й(г\см*) и сечения стержня
5(cV):
q (г\см) = Sd.
Величину q следует назвать плотностью на единицу длины.
Однако так как настоящая плотность d (объемная) нигде
дальше не входит, то сокращенно будем называть q плот-
ностью, толщину стержня считаем малой и изображаем
его просто линией—отрезком оси х. Масса стержня, оче-
видно, равна
ь
(x)dx, A5.1)
где а и b — координаты концов стержня.
438
МЕХАНИКА
[Ч. VI
Пусть стержень закреплен на оси х; ось х располо-
жена горизонтально, ось у направлена вертикально вверх,
сила тяжести действует на стержень, как показано стрел-
кой, стремясь опустить стержень (рис. 156).
Представим себе, что ось х — это коромысло весов.
На рисунке схематически показана призма, на которую
в начале координат опирается ось х. Таким образом, ось
х может поворачиваться вокруг оси, перпендикулярной к
плоскости чертежа. Найдем, какой груз р, расположен-
ный слева на расстоянии R, нужен для того, чтобы
уравновесить находящийся справа стержень.
dm
х x+dx
Т71 1
Рис. 156.
По законам рычага элемент массы dm, находящийся
на расстоянии х справа от оси, уравновешивается эле-
ментом массы dp, находящейся слева, если массы отно-
сятся обратно пропорционально расстояниям, т. е. если
dfx х
dm R
ИЛИ
= x dm.
A5.2)
Элемент массы dm равен, как было выяснено раньше,
Q dx. Для того чтобы уравновесить весь стержень, нужна
масса р, удовлетворяющая равенству
ь
Rp='\) XQ(x)dx. A5.3)
а
Это равенство получено интегрированием левой и пра-
вой частей A5.2). При этом на правой стороне оси раз-
личные элементы массы dm находятся на разном рас-
стоянии х от опоры, поэтому величина х вошла под знак
§ 15J МАССА, ЦЕНТР ТЯЖЕСТИ, МОМЕНТ ИНЕРЦИИ СТЕРЖНЯ 439
интеграла. Слева на оси все элементы массы d\i (уравно-
вешивающие различные элементы dm стержня) собраны
на одном и том же расстоянии R от опоры. R есть по-
стоянная величина и поэтому
О
Как видно из сравнения A5.3) и A5.1), интеграл, от
которого зависит масса ц, уравновешивающая стержень,
отличается от интегра-
ла, выражающего массу
стержня.
Поставим вопрос: если
всю массу стержня сосре-
доточить в одной точке,
то на каком расстоянии хс Рис 157.
должна быть эта точка от
опоры (от начала координат), чтобы уравновешивать ту
же массу (i на расстоянии R, которую уравновешивает
стержень (рис. 157). Найдем
ь
R[x=xcm= \ xqdx, A5.4)
а
откуда
ь
ь V xgdx
A5.5)
Величина хс есть координата центра тяжести или, как
его иначе называют, центра массы стержня. Очень важно,
что точка хс есть действительно вполне определенная
точка стержня: если весь стержень как целое переместить
вдоль оси х, например вправо на расстояние / (рис. 158),
то при этом и хс увеличится на ту же величину /, так
что точка с координатой jc = jcc для данного стержня
всегда находится на вполне определенных расстояниях
от концов стержня.
440
МЕХАНИКА
[Ч. VI
Рассмотрим стержень, смещенный на расстояние /
вправо по ' сравнению с первоначальным положением
(рис. 158, низ). Величины, относящиеся к новому (сме-
щенному) положению, будем обозначать теми же буквами,
что и соответствующие величины, относящиеся к перво-
начальному положению, но с индексом 1. При этом
Следует особо обратить внимание на знак минус в по-
следней формуле. Действительно, из рис. 158 видно, что
У////////////////////,
V//////////////////77,
'////////У7///////УУХЛ
Рис. 158.
каждому значению х в новом положении стержня (ниж-
ний рисунок) соответствует такая же величина плотности,
как значению х — /в первоначальном положении стержня
(верхний рисунок). По формуле A5.5)
ь,
xq (х) dx
(*) dx
~> *с=ьТ
A5.6)
dx
б. (х) dx
а,
§ 15] МАССА, ЦЕНТР ТЯЖЕСТИ, МОМЕНТ ИНЕРЦИИ СТЕРЖНЯ 441
В интегралах, входящих в формулу для хс, сделаем за-
мену переменных по формуле z = x — / или x = z-\~l,
откуда dx = dz. Тогда q1(x) = q(x—1) — q(z). При х==
= а1=а-\-1 получим г = а\ при x = bv = b-\-1 полу-
чим z = b. Поэтому
Ь, Ь
\ Qt (x) dx = \ q B) dz = т.
Это означает, что масса стержня не зависит от того, в
каком положении находится стержень.
Обратимся к интегралу, стоящему в числителе,
ь, ь ь ь
Cxq, (x)dx = \ (zJrl)q(z)dz= ^ZQ(z)dz-{-l Г Q(z)dz.
at a a a
Заметим, что из формулы A5.4)
ь ь
\ zq B) dz=\xq (x) dx = хст.
а а
Поэтому
\ xq , (х) dx = хст -\- 1т.
а,
Теперь находим, пользуясь A5.6),
Хст -f- lm i .
Этот результат был очевиден заранее, однако проделан-
ные формальные преобразования являются полезными уп-
ражнениями на замену переменных в определенном инте-
грале.
Наиболее удобно выбирать систему координат с нача-
лом координат, помещенным в центре тяжести стержня
(рис. 159). Величины в этой системе координат отметим
индексом 0. Ясно, что
ь.
а„
Координата центра тяжести хСа в такой системе
442 МЕХАНИКА
координат равна нулю, поэтому
[Ч. VI
A5.7)
а.
Покажем, что при любом положении стержня его потенци-
альная энергия в поле тяжести равна потенциальной энергии
всей его массы, сосредоточенной в центре тяжести стержня.
Рассмотрим положение стержня, показанное на рис. 160.
-Q
Рис. 159.
Рнс. 160.
Потенциальная энергия элемента стержня с массой dm
равна gz dm, где z— высота, g—ускорение силы тяжести.
Потенциальная энергия и всего стержня находится инте-
грированием. В качестве переменной интегрирования выбе-
рем длину, отсчитываемую вдоль стержня от его центра
тяжести. В этом случае величину плотности в точке х
обозначаем через Qa(x). Выразим высоту z через х. Как
видно из рис. 160, z{x) = zc-\-x cos а, где zc есть высота
центра тяжести стержня. Получим
"
) dx=g J (zc + x cos a) q0 (x) dx =
gzc
(*)
60
cos a J XQa (x) dx = gzcm,
а„
так как второй интеграл равен нулю по формуле A5.7).
Итак, потенциальная энергия зависит только от массы
стержня и высоты его центра тяжести.
§ 15] МАССА, ЦЕНТР ТЯЖЕСТИ, МОМЕНТ ИНЕРЦИИ СТЕРЖНЯ 443
Рассмотрим теперь так называемый момент инерции.
Это понятие появляется при рассмотрении вращательного
движения стержня. Пусть стержень вращается вокруг оси,
перпендикулярной к плоскости чертежа и проходящей че-
рез начало координат. При таком вращении каждая точка
стержня описывает окруж- чч
ность, радиус которой ра-
вен абсциссе данной точки
х в начальном (горизон-
тальном) положении стер-
жня (рис. 161). Обозначим
to угловую скорость вра-
щения, выраженную в ра-
дианах в секунду. Это зна-
чит, что за время dt ось
х поворачивается на угол
dq> = <?>dt. Длина дуги, которую проходит произвольно
выбранная точка с абсциссой х, равна
dl=x d<p = ха> dt;
следовательно, линейная скорость движения каждой точки
окружности равна
, . dl
Найдем кинетическую энергию вращательного движе-
ния всего стержня. Элемент массы dm, находящийся на
расстоянии х от начала координат (в отрезке dx от х до
x-\-dx), имеет кинетическую энергию
-s-cfm=-K- dm=-x-Q(x)dx.
?t ?t Zi
Следовательно, кинетическая энергия всего стержня равна
ь
Интеграл в последней формуле носит название момента
инерции стержня относительно оси, проходящей через
начало, и обозначается /,
444 МЕХАНИКА [Ч. VI
Таким образом,
Е — /ш>
Кинетическая энергия вращения выражается через момент
инерции и угловую скорость совершенно так же, как ки-
нетическая энергия поступательного движения выражается
через массу и линейную скорость,
Обратимся к вычислению /. Для стержня, центр тя-
жести которого находится в начале координат, момент
инерции принимает значение /0,
J*4 (*)<**• A5.8)
Заметим, что величина /0 положительная, так как поло-
жительна подынтегральная функция в A5.8).
Определим момент инерции стержня для случая, когда
его центр тяжести находится на расстоянии / справа от
начала координат, так что хс, = 1- В этом случае
b = bt-\-l, Q(x) = Qa(x — l),
ь
а
Положим z = x — /, тогда x = z-\-l, dx = dz. При изме-
нении х от а до Ь величина z изменяется от а0 до Ьа.
Поэтому
/ = ?(*+04. (*)<**=
^^iU^dz. A5.9)
Заметим, что \Qa(z)dz = m, а второй интеграл справа в
а.
§ 151 масса, центр тяжести, момент инерции стержня 445
A5.9) равен нулю по формуле A5.7), наконец, третий ин-
теграл есть /0 согласно A5.8). Таким образом, формула
A5.9) принимает вид
/ = /?!/¦ +/.. A5.10)
Величина ml* есть, очевидно, момент инерции точечной
массы, находящейся на расстоянии / от оси вращения
(от начала координат). Таким образом, момент инерции
стержня относительно вращения вокруг произвольной оси,
перпендикулярной к стержню, равен сумме момента инер-
ции стержня относительно вращения вокруг центра тяжести
и момента инерции массы, равной массе стержня, нахо-
дящейся на расстоянии от оси, равном расстоянию центра
тяжести стержня от оси.
Рис. 162.
Наглядно можно представить себе стержень, закреп-
ленный в центре тяжести на шарнире. Тогда вращение
оси может не сопровождаться вращением самого стержня,
возможно движение, последовательные стадии которого
Показаны на рис. 162. Кинетическая энергия такого дви-
жения равна E'=-^mv1cl, где ос,—скорость центра тя-
жести стержня. Но 0с1=ю/, так что E' =^ ml*.
Движение, которое мы рассматривали раньше (рис. 161),
отличается от рис. 162 тем, что там сам стержень также вра-
щается с угловой скоростью ш вокруг своего центра тяже-
сти. Поэтому кинетическая энергия вращения рис. 161 оказы-
вается равной сумме энергии вращения по Типу рис. 162 и
энергии вращения вокруг центра тяжести, равной /0 ^ .
446 МЕХАНИКА [Ч. VI
Из вывода формулы видно, что такое простое .сложе-
ние энергий при сложении двух движений получается
только тогда, когда рассматривается движение центра тя-
жести; только в этом случае получается равенство нулю
интеграла A5.7).
Упражнения
1. Найти момент инерции относительно центра тяжести стержня
длины / с равномерно распределенной массой.
2. Стержень составлен из двух кусков: первый кусок длины /,
имеет постоянную плотность q,, второй кусок длины 1г имеет также
постоянную, ио другую плотность о,. Найтн положение центра тя-
жестн стержня.
3. Найти положение центра тяжести и величину момента инерции
относительно центра тяжести для стержня, имеющего форму тонкого
треугольника длины L. Выразить их через длину L и массу стержня т.
Указание. Если направить ось х по медиане, а начало коор-
динат выбрать в вершине треугольника, то q(x) = ox, где а—по-
стоянная.
§ 16. Колебания подвешенного стержня
Рассмотрим стержень, подвешенный в точке А (рис. 163).
Пусть центр тяжести находится ниже точки подвеса, при-
чем расстояние между точкой подвеса и центром тяжести
равно /. Такой стержень представляет со-
бой маятник. Определим период его коле-
баний.
Если маятник отклонен от положения
равновесия на малый угол ф, то его по-
тенциальная энергия равна
и = — mgl cos ф.
Разложим cos ф в ряд и ввиду малости
Ф ограничимся первыми двумя членами:
созф=1 — ^-. Поэтому
Рис. 163. U=-
Таким образом, увеличение потенциальной энергии при
отклонении маятника на угол ф от положения равновесия
(ф = 0) есть Аи = mgl ^-.
§ 16J КОЛЕБАНИЯ ПОДВЕШЕННОГО СТЕРЖНЯ 447
Кинетическая энергия вращения стержня вокруг оси
равна
Р /«' , 1 /dq>\«
Согласно формуле A5.10) I = ml* -f- /0, поэтому
где /0 — момент инерции маятника относительно центра
тяжести.
Предположим, что стержень совершает гармонические
колебания, т. е. <p==acos<ot. По закону сохранения энер-
гии Дитах = ?тах- Так как
dffi
^f = — a
то
откуда
что дает
период колебаний
гр 2л
to
В частности, если вся масса стержня сосредоточена в его
центре тяжести, то /0 = 0. В этом случае мы получаем
обычные формулы для частоты и периода колебаний так
называемого математического маятника
Из полученных формул следует, что чем больше /0, тем
меньше частота колебаний, соответственно тем больше пе-
риод.
448 МЕХАНИКА [Ч. VI
В случае, если /,=?0, имеется определенное положение
точки подвеса, при котором частота колебаний максимальна.
Так как положение точки подвеса характеризуется вели-
чиной /, то для отыскания интересующего нас положения
решим уравнение ^=0. Это дает
mg (ml* + /„) — mgl • 2ml = 0,
откуда получаем:
Для стержня длины L с равномерно распределенной
массой А> = -Г9~ (см- упражнения к § 15), поэтому /тах =
= ^0,32..
Упражнения
1. Маятник имеет вид тонкой треугольной полоски из листового
материала (жесть, картон) (рис. 164). Определить период колебаний,
если маятвик подвешен: а) за острый конец А, б) за середину
Рис. 164.
основания В. В обоих случаях определить, как надо сместить точку
подвеса, чтобы получить минимальный период колебаний.
ОТВЕТЫ И РЕШЕНИЯ
t
§ 1. 1. Л (О = — h\v*dt, величина А отрицательна, так как
S* • 2л
u*d<>0. 2. Движение тела периодическое с периодом Т=—.
Требуется определить работу за полпериода. Заметим, что в течение
первой четверти периода скорость положительна, а потому F = — А;
во второй четверти периода скорость отрицательна, поэтому F=-\-h.
В каждом из этих промежутков времени сила постоянна, а потому
работа разна произведению силы на путь, пройденный телом за это
время. Для первой четверти периода Al = —hb. Для второй четверти
ОТВЕТЫ И РЕШЕНИЯ 449
периода At=h(—ft) = — hb (скорость отрицательна!). Поэтому ра-
1к
бота за полпериода А = Ax-\-At =—2hb. 3. A = bfoa>1*\ sin coo* X
о
X cos со! t dt. Этот интеграл легко взять следующим способом. Запи-
шем известные формулы
Sin (C00f -f- COjf) = sin <Oat COS С0г* -f- COS C0e t Sin CO,*,
Sin ( COof — С0г* ) = Sin С0„* COS COj/ — COS (Oat Sin С0г/.
Сложив правые н левые части, получим:
Sin COof COS СО^ = -^- [Sin (©„ -f- С0г) t -f- Sin (CO,, — CO!) t].
bf со Л
Поэтому A = '" \ [sin (coo -f-coj / -(- sin (со,, — со,) t] dt =
о
1 , 1 cos (coo -f- cot) tk cos (coo — cot) tk~\
t -f- <*>i ш0 — tOi coo -f- to, coo — co4 I
В случае coi>==cu1 пользоваться конечной формулой нельзя. Однако
а этом случае &1па>а tcosa>1t =-^-sin2a)at, откуда
tk
А = - ° "• \ sin 2a>atdt = -j^ A —cos2co0/ft).
0
4. Работа силы сопротивлевия воздуха Ах (t) = 5=-**. Работа
о
силы тяжести Аг (t) = —^- ?. Для шарика: .4,A)=—0,00965,
Ах A0) = —96,5, Ах A00) = —965-10», Аг A) =0,0177, Аг{Щ = 1,77,
Л,A00)=177; для пули: Л, A) =— 1,18- Ю, Лг A0) = —11,8,
Л, A00) = —118-10», Л,A) = 0,435, ЛгA0) = 43,5, i4, A00) = 4350
, () , ,() ,, г() ,, ,()
(работа выражена в джоулях). 5. А = g *———. Мощность W
определяем, пользуясь формулой W = Fv, W = — о — •
Определим, при какой скорости v (при данном va) мощвость будет
dW
максимальной. Для этого решим уравнение—j—:^0. Получим о1=о,
и и, = -тг. Ясно, что значение w = w0 нас не интересует, так как оно
о
и
обращает мощность в вуль. Интересующее нас значение "есть v=-?
I d*W\
I читатель может произвести полное исследование по знаку -jet J •
\ аи j
15 я. Б. Зельдович
450 МЕХАНИКА [Ч. VI
При var= 30 м/сек, v= 10 м/сек Wmax = 2,6.10s кгм/сек = 35ОО л. с.
6. Работа силы за период A = cnf sin a, W= ^sina.
§ 3. 1. Прямую, на которой расположены заряды, примем за
ось х; точку, в которой расположен заряд ех, примем за начало
координат. Заряд в, пусть расположен в точке х=-\-2а. Равновесие
возможно лишь в тех точках х, где F — — — =0. Пусть х —коср-
днната заряда е. Тогда F=-\— -р:—-—д , если 0 <х <2а, т. е. если
хг {?а х)
заряд е расположен между зарядами е1 н еъ, F=—^f- — т~—-—г,, если
XT \Za X)
о о Ар р
х <0, и F = -р + па — хУ ' еслНдс>2а- В первом случае уравне-
ние F = 0 дает х, = 2а/3, xt = — 2а. Второй корень xt отбра-
сываем, так как должво быть х > 0. В случаях х < 0 и х > 2а
уравневие F = 0 решевий не имеет. Следовательно, имеется одно
положение равновесия xl=2a/3. Исследуем точку x^=2a/3. Для
этого подсчитаем -т-х в этой точке. Произведя подсчет, убеждаемся,
сРи
что если е > 0, то -j-у > 0, равновесие устойчиво; если же е < 0, то
равновесие неустойчиво. 2. Имеется одно положение равновесия х,
вне зарядов. Если система координат выбрана так же, как в реше-
нии задачи 1, то xt= — 2а. Если eex > О, то равновесие устойчивое;
если ехе < 0, то равновесие неустойчивое.
§ 4. 1. уравнение движения m — = F; пользуясь тем, что при
f=0 и = 0, находим v = — /. Поэтому —=—t, dx=—t dt,
m dt tn m
x t
откуда I dx = — \ tdt, так как при f = 0 x = 0. Окончательно
о а
х = 27к1'- 2- Х = ^ + ЙЛ •¦ж = х- + ^ + ^А 4- 24'5"-
do nt*
5. Уравнение движения есть m-7r = mg; отсюда находим •х==%~ >
t = у — ^4,5 сек при х = 100л. 6. а) t = 3,6 сек, б) / = 5,6 сек.
Определим в каждом из случаев скорость в момент приземления.
В случае а) и = gt -\-v0. Пусть vn есть скорость в момент приземле-
ния, тогда v1J = gta-{-va, где tn—время приземления. Из уравнения
v = gt -\-va находим x = vot +%-• Пусть шарик падает с высоты Я;
тогда х = Н при t = tn, поэтому 2H = 2v0tn-{-gt^, откуда tn =
ОТВЕТЫ И РЕШЕНИЯ 451
, поэтому un = g*n-f-o0= \/~ v\-\-2gH.
В случае б) v = gt — va, остальное аналогично; конечвая скорость
к f
получается такая же, как в а). 7. х = ^— t3 -\- vat. 8. а) х = ^—jcosco/,
^~~ г л ' ТПЭХ "*" "" .ъ. 9 * ШЭХ ~" • w f Л -"¦ — ь a olU UJt . дв 1 1VL1D
Cl) /7Z0) /71C0 fTlCO fTICO
искомая скорость есть w0. Тогда закон движения тела х = ха4-
-\-va(t — ta)-\~n~ С — 'оI- ^Рн ' = 'i *:=*i. поэтому х! = хо-|-
+ «о Ci — ^о) +2^ d ~ 'о)*' откУДа
б) Л=7-10*кги«, U7 = 520 л. с. 6. Определим работу каждой из сил
в отдельности. Для этого предварительно определим скорость тела.
Из уравнения т -гг = at -f-a (8 — t)=aO находим v=va-\ 1. Работа
силы Fl есть Л,= 4 arluo-j t \dt = —^ \--*— . Аналогично на-
о
ходим А.— работу свлы Ft. А.=—^ \--*—. Составим произведе-
2 от
ние импульса на среднюю скорость:
о-=2 , = «^ + ё"-
В в дно, что (/i + ^)u = j4i"I"^!> хотя /tw ?t А1г Itv Ф Л„ как и бы-
ло отмечено в § 6. 7. В начале опыта масса т имела скорость vc
(она двигалась вместе с поездом) и кинетическую энергию Kt= -j— .
15*
452 МЕХАНИКА [Ч. VI
После действия человека скорость массы стала ц, 4- v., Kt =
m(wo-f-w)* Ft
— 5 « где wi=—• Изменение кинетической энергии
т (v0 -\- wj* mv\
AK=Kt—Кх = g s~ • Это есть работа, произведенная
над массой поездом и человеком вместе. Для того чтобы определить
работу, произведенную над массой т человеком, заметим, что ско-
рость массы по отношению к человеку, едущему в том же поезде,
была равной нулю до опыта н стала раввой vx после опыта. Поэтому
то\ тт)\ F*t*
работа человека Л, =-« 0 = ——- = ——. Теперь легко опреде-
^ J. Ztn
лить работу паровоза At: Л, = Д/С — Л, = mo0o, = vaFt. Последний
результат легко получить и из других соображений. Действительно,
работа паровоза Л, = \ vF dt. Так как скорость v = v0 постоянна,
t
то At = va \ F dt ^^v^Ft. 8. До начала опыта скорость массы т
о
и скорость человека равны нулю. После опыта масса т приобрела
скорость о у, человек приобрел скорость о,. Определим эти скорости
из уравнений m^± = F и М-?* = — F, так как если человек дей-
01 at
ствует на массу т силой F, то масса т действует на человека
Ft Ft
силой—/7. Находим vz =—, vt = ——-. Работа, произведенная
т М
силой F над массой от и над человеком, есть Л = К, +К«. где
mv\ F*t*
К i = ~2~==~2 измевение кинетической энергии массы т,
Mv\ F4*
Кг = —g-- == 2M изменение киветической энергии человека. Отсюда
. РЧг(М+т) п ..
А = ятгг -. 9. Изменение кинетической энергии массы т
mv\ F
АК в> =/яо0о1 -(—н-, где Vy=—t; изменение кинетической энергии
Mv\ F F*t* (M -f- m)
человека ЛКЛ = -g— + Mvavx, где vt = — -^-1, A=
§ 7. 1. Запишем уравнение так: —= , откуда (учи-
dv P (и? — Vх)
V
тывая начальное услопне w @) = w0) находим^ ^^-д I — .Для того
V О v, — о*
чтобы выполнить интегрирование, надо записать подынтегральную
ОТВЕТЫ И РЕШЕНИЯ 453
функцию в виде = —- 1 . и определить числа
v\ U* Wj V Uj -f- V
а и. b (см. упражнения к § 15 части III), после чего интеграл легко
взять. Получим In "' *~ " = In А + 200^, где А = "* _ °°. Потенци-
руя, найдем ' ' = He*3V, откуда v — v. ; . При очень
*>i — v А&$°г -+- 1
больших t величина e*9"t'^l, поэтому для таких t будет о*»,.
Перепишем решение уравнения в виде v = vx ; вычитая
А Ле~*?°11
из обеих частей по v., получим v — v. =— 2v. .. При весьма
1 1f4-r-e-«?V
больших t в знаменателе можно пренебречь е *Р"«* по сравнению с А.
Поэтому при весьма больших t v—t\= — 2ох—-z— или v — vx ¦=
t. Сравнивая это с G.20), находим С = 2°l(~"l) .
()
i + vо v\ \ o
2. Для случая сопротивления, пропорционального скорости, уравне-
ние движения примет вид -тг= е v , где А—выталки-
at mm.
вающая сила. В этом случае происходит установление скорости
а та.
§ 8. 2. а) Точка остановки хо = —. б) Точка остановки х»= 0,9.
в) Точек остановки нет. 3. Прежде всего определим положение мак-
симума и (х). Получаем Ujnax^^'JJ при х„ = 8/3. Замечая, что левая
ветвь графика уходит вверх, а правая — яниз, можем построить
очень грубый график и(х). Однако для решения задачи достаточно
располагать таким графиком, а) Две точки остановки. Это — значения
наименьших корней ураввенвя —дс* -f- 4дс* = 6. Такое уравнение
можно решить либо графически, либо при помощи одного из числен-
ных методов. Получим х^—1,09, х, = 1,57. Тело совершает коле-
бания между точками хх и хш. б) Одна точка остановки x=s= — 2,04.
Однако эта точка остановки расположена левее точки, из которой
выходит тело в начальный момевт времени. Так как вачальная ско-
рость направлена вправо, то тело уйдет вправо, не побывав в точке
остановки, в) Одва точка остановки x=s — 2,04. В этом случае тело
пройдет влево до точки остановки, а затем уйдет вправо. 4. а) Точек
остановки нет. Тело уйдет вправо, б) Две точки остановки
jc, = -f- >^9/11, xt = —V9/11. Движение тела — колебание между
точками X! и хг. Для a) t=ta+ Г |/ ^j~ae ^' Для б) t = '•"+"
о
, ? , /20 +20хг . Г -ш /0 +
+ \ У 9-11*** АЛЯ *<Х» ' = <>-) У Э-
0,5 X,
454 МЕХАНИКА ' [Ч. VI
*i < х < *,, где /( — время достижения хх, и т. д. Следует заметить,
что интегралы остаются конечными, хотя в точках остановки подын-
тегральная функция обращается а бесконечность.
§ 9. 1. a) x = 2sln.tr б) x = cos/, в) х =cost -\-2sint. Это ре-
шение можно записать в виде х=С cos(t -)-а.)г где С = \П>, а =
= arctg(—2)=s=— 1,11, т. е. * = y5~eos (/— 1,11). Во всех трех
случаях Г = 2я.
§ 10. 1. Будем считать, что колебания происходят по закову
х = С cos (со/ -j- а); тогда v = —Ceo sin (со/+ а)- Воспользуемся соот-
dC
ношением kC-j? =F{o, где
Fx = — hv | v |, Fxv = — Аи* | v | = — AC*co* | sin1 (со/ -|- а) | .
Поэтому kC-^ = — ЛС*соМ, где положено А = j sin" (со/ -f- a) |. За-
метим, что sin (со/ -f- ex) сохраняет знак при изменения / от tx =
л — а ' . Т „
До /»= , причем rt — /j = -^-. Поэтому
sin» {tot +a)dt -jj-
l=- _ =— Г sin' (со/ -f- a) dt.
a
ш
Полагая в последнем интеграле cos (со/-f~a)== •*» получим
_ dC ЛСаш'4 r^, Лш'4 . dC '
Поэтому -jj- = о—г- .Обозначим^—г- = *> тогда -ц- = оСж, от-
куда -j?r==—Гг5 • Решением этого уравнения является
Выражая С через t, находим С = , . ° . Здесь
через С„ обозначено значение амплитуды в начальный момент вре-
мени f=0; оно определяется из начальных условий. Отметим, что
такой же закон мы получили для затухания скорости в случае
сопротивления, пропорционального квадрату скорости [см. формулу
G.12)]. 2. В этом случае работа за четверть периода равна — fC,
4 2a»
поэтому средняя мощность есть — /С-=-=—/С—. Получаем урав ение
.rdC 2fCco dC 2f<a _ а r г 2/со
*С5Г = - я ' откуда Ж=~1^- Огсюда с = Св-АНЛ
ОТВЕТЫ И РЕШЕНИЯ
455
Колебавия прекратятся в момент tlt когда станет С = 0, поэтому
*i = ¦¦?. (предполагается, что tx ^> Г). 3. Пусть маятник при х = 0
(положение равновесия) имеет потенциальную энергию иа, кинети-
ческая энергия в этот момент равна нулю. Отклоним маятник на
некоторый угол; в результате этого по горизонтали он отклонится на
величину х (рис. 165). В этом поло-
жении потенциальная энергия
где z = I — У?—х
ШШ/Ш
'dx\
кинетическая энергия равна -у ( зг ) •
В процессе колебаний сумма кинети-
ческой н потенциальной энергии ие
"о+"»«(' —
изменяется, поэтому
т
воспользуемся тем, что х
ла
ния малые), т. е. -j-^1.
или
А
Теперь
J (колеба-
Благодаря
Рис. 165.
этому у 1г — хг можно записать при помощи ряда Маклореиа:
У1* — х* = / у 1 — ( у- ) ^5=/ Г 1 — о/? ) ='*'~ Ш ^МЫ УдеРжали
fdx\*
два члева ряда). Уравнение колебаний принимает вид [ ут ) —
х*
= g —. Возьмем от обеих частей производную по t, получим
dx d?x x dx d*x &
Ж ' tit*'==^& ~l~Ж"' откУДа jTi == ~7" x- ^TO и есть уравнение малых
колебаний маятника.
§ 11. 1. Из первого уравнения системы получаем C0cosa = .*0 — а.
Пользуясь этим, из второго уравнения нетрудно найтн Cesina =
= Ь •— у — . Возведя полученные соотношения в квадрат,
со, со! ' со, '
получим С? = ( Ь — — v " а 1 -4- (х. — аJ; извлекая корень,
9 ^ со, со, ' со, ) ' v °
со,
находим С„; tga =
§ 13. 1. Задача сводится к определевию г из уравнения
2z
In A -\-г) =. _|_ • Решим это уравнение графически. Для этого
определим на графике точку пересечения линий y=ln(l-f-z)
2г
и у = , . Из графика рис. 166 видно, что z=u:4. Поэтому
Лтах = 0,65а. 2. г =s 30 000 км.
456
МЕХАНИКА
[ч. vi
§ 14. 1. Для ф = 30° хтах=565л, упгл = 81,5м; для <р = 45°
= 650 ¦*, А'тах= 163 ¦*: Для ф = 60° хтах = 565 м, утах — 244 м.
2. Уравнение траекгорни имеет вид у = х tg ф — хг . Прн за-
2v% c*
cos*
давном х = 500 м ищем ф, при котором у достигает максимума. Для
этого решаем уравнение -^=0. Получаем tgф=—- . Пользуясь
тождеством
= tg8 Ф "г" Ь получаем
1
cos* ф"
Поль-
COS* ф
зуясь этим из уравнения траектории, находим утах =-^—-~^
Полагая va = 80 м/сек, х=500м, находим #шах=135 м.
У
г
1
0
/ 2
3 « 5 г
Рис. 166.
§ 15. 1. Поместив начало координат в центр тяжести стержвя,
получаем:
/„ —•
= Q
= Q i2":
так как m = Ql, то результат можно записать так: /а = т-г^.
2. Поместим начало координат в точку стыка кусков различной плотно-
сти, так что для первого куска х < 0, а для второго х > 0. Тогда
3- Выбрав систему координат согласно указанию,
получаем хс = -~- •
момент инерция относительно начала
L
Г
= \
ОТВЕТЫ И РЕШЕНИЯ 457
... -~ _ aL1 Ъп
\(х) ах = —^-. Так как т= — , то a = js-; поэтому
— —2~ • Но /0 = / — /л/*, где lx=-^- L; отсюда /0 = -г-^-.
§ 16. 1. а) Обозначим через Z. длину маятника. Мы знаем, что
/те I 2 , mL*
г* , причем в нашем случае l = -^L, 1=—=- (см. уп-
ражвенвя к § 15). Поэтому
Значение /, которому соответствует максимальная частота, опреде-
ляется по формуле /тах= Л/ —2-. Так как в вашем случае
/0=—— , ТО /тах = -^==. Поэтому С0тах = Л/ —277" • Знаяштах»
находим Tmtn=—-—. б) В этом случае / = -^-L, / = /0-f- ml* =
«
max
mi8 ,1 ,. m/-1 -i/~1g „
= ^j—- 4- -jr "i^- — —a~ » «>= 1/ -v-. Минимальный период здесь
получится тот же, что и в случае а), для другой точки подвески,
с тем же значением /ща^.
ЧАСТЬ VII
ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ И РАСПРЕДЕЛЕНИЕ
ПЛОТНОСТИ ВОЗДУХА В АТМОСФЕРЕ
§ 1. Условие равновесия в атмосфере
Рассмотрим вопрос о законе распределения плотности
воздуха в атмосфере по высоте. Хорошо известно, что на
большой высоте воздух менее плотен, давление воздуха
меньше, чем на уровне моря. Причина зависимости дав-
ления от высоты очевидна: выделим мысленно цилиндриче-
ский объем (высота ДА, площадь основания
«S, объем SAh). Воздух, находящийся в
этом объеме (средняя плотность q, масса
т =q AhS), притягивается к земле, т. е. ис-
пытывает силу тяготения, направленную
вниз и равную mg = qAhSg. Однако этот
объем не падает, а находится в покое благо-
даря тому, что на него снизу на высоте А дей-
ствует давление p{h) большее, чем давле-
ние сверху на высоте A-j-ДЛ, равное
p(h-\-Ah) (рис. 167). Сила давления на
нижнее основание - цилиндра равна Sp(h);
это давленне уравновешивает сумму силы
давления на верхнее основание и силы
тяжести
A.1)
A.2)
Рис- 167-
Формулу A.1) можно записать так:
р (Л) — р (А + ДА) == qA hg.
Будем считать, что ДА весьма мало. Тогда нет надобности
§ 11 УСЛОВИЕ РАВНОВЕСИЯ В АТМОСФЕРЕ 459
говорить о средней плотности q, так как высоты h и
h~\-Ah весьма близки и q весьма мало отличается от
Q(h). Поэтому A.5) принимает вид
dp=_ A з)
Мы получили дифференциальное уравнение для зависи-
мости p{h). При этом в уравнение вошла плотность воз-
духа Q.
Величины р и q связаны между собой законом Бойля-
Мариотта. Мы будем предполагать, что температура атмо-
сферы одинакова на всех высотах. На самом деле темпе-
ратура воздуха зависит от притока тепла от солнца н
отвода тепла в основном за счет излучения тепла в ми-
ровое пространство воздухом или, точнее, водяными па-
рами и углекислотой, содержащимися в воздухе. Неболь-
шая часть лучей солнечного спектра поглощается верхними,
очень разреженными слоями воздуха. Большая часть
энергии солнечного света доходит до поверхности земли,
поглощается почвой, а уже от почвы нагревается воздух.
Поэтому в действительности в атмосфере получается до-
вольно сложное распределение температуры: на уровне
землн температура, как мы хорошо знаем, колеблется
примерно от —40° до -|~40°С в зависимости от геогра-
фического положения и времени года, на высоте около 15 км
температура минимальна — около — 80° С — и примерно
одинакова зимой и летом на всем земном шаре; на боль-
ших высотах температура возрастает, достигая -f-60°C —
+ 75° С на высоте 50—60 км.
Измерения, проделанные уже в самое последнее время
при помощи искусственных спутников Земли, показывают,
что на высоте 300—1000 км плотность воздуха хотя и
мала, но все же значительно больше, чем предполагалось
раньше. Как мы увидим ниже, большая плотность воз-
духа указывает на то, что в этих высоких слоях темпе-
ратура воздуха весьма высока. К тому же значительная
часть молекул кислорода и азота распадается на этой
высоте на атомы, ионы и электроны.
Если бы не было притока тепла извне и отвода тепла,
т. е. если рассматривать теплоизолированный столб воз-
духа, то с течением времени температура во всем столбе
460 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
должна была бы выровняться. Ниже мы будем рассмат-
ривать именно такой идеализированный случай полного
равновесия, теплового и механического. Тепловое равно-
весие заключается в том, что температура везде одина-
кова, следовательно, нет потоков тепла (если бы в раз-
личных точках воздушного столба температура была раз-
лична, то от более нагретых точек потекло бы тепло
к менее нагретым, т. е. возникли бы потоки тепла). Меха-
ническое равновесие заключается в том, что равнодейст-
вующая всех сил на любой объем воздуха, выделенный
в атмосфере, равна нулю; при этом надо рассматривать
силу тяжести воздуха в объеме и силу давления на всю
поверхность, ограничивающую данный объем.
При том распределении давления, которое удовлетво-
ряет уравнению A.3), атмосфера может находиться в состоя-
нии покоя.
Так как мы рассматриваем высоты h, малые по срав-
нению с радиусом Земли, то g" — ускорение силы тяжести—
можно считать постоянной величиной.
§ 2. Связь между плотностью и давлением
По закону Бойля-Мариотта произведение давления газа
на занимаемый им объем постоянно для данной массы
та газа и при данной температуре
pvz=a,
где а — постоянная величина. Обозначая плотность газа
через q, получим ma = vQ. Следовательно, v = mjQ, а так
как p = alv, то
P = bQ, B.1)
где положено b = alma. Таким образом, давление газа прямо
пропорционально его плотности.
Коэффициент пропорциональности для воздуха ком-
натной температуры легко найти. Известно, что атмосфер-
ное давление на уровне моря ра приблизительно равно
1 кг/см1 = 10' дин/см*. Плотность воздуха q0 при давлении ра
равна примерно 1,3-10""* г\см*. Эту величину легко найти
экспериментально при помощи взвешивания. Берут сосуд
известного объема с герметичным краном и сначала взве-
шивают его с воздухом, а потом без воздуха, откачав
§ 2] СВЯЗЬ МЕЖДУ ПЛОТНОСТЬЮ И ДАВЛЕНИЕМ 461
воздух из сосуда вакуумным насосом. Подставляя р0 и q0
в формулу B.1), получим po=bQo, откуда
Отметим, что по размерности величина b есть квадрат ско-
рости. В действительности эта величина тесно связана со
скоростью молекул и со скоростью звука: квадрат скорости
звука равен 1,4 Ь (выводить это соотношение не будем).
Для дальнейшего нам нужно не только численное зна-
чение b для воздуха комнатной температуры, но и общее
выражение постоянной Ъ для любого газа н при любой
температуре. Для этого воспользуемся законом Клапейрона
pV = RT, B.2)
где V — объем, занимаемый одной грамм-молекулой *) газа,
Т — абсолютная температура (отсчитываемая от абсолют-
ного нуля, соответствующего —273° С**)), R есть так на-
зываемая универсальная газовая постоянная. Известно, что
при температуре 0° С, равной 273° абсолютных, при атмо-
сферном давлении, т. е. при ро = 10" дин(смг, одна грамм-
молекула газа занимает объем, равный 22,4 л = 2,24-10* см*
(закон Авогадро)***). Отсюда 10'-2,24-10* = /?-273. Тогда
# = 8.3-107—динсм* д==8,3-107 1^— .
моль см* град град-моль
Обозначим молекулярный вес газа через М. Для водо-
рода Ht М=2, для гелия Не М = 4, для азота Nt
М =28, для воздуха среднее значение М = 29,4. По опре-
делению V содержит М граммов газа. Значит, плотность q
связана с V соотношением
М ,, М
Q=^T или 1/ = "У *
Подставляя это выражение для V в B.2), получаем:
р* <23>
•) Одна грамм-молекула газа сокращенно называется «один моль».
•*) Иногда абсолютную температуру отмечают буквой «К», по
имени английского ученого Кельвина, например, 20° С = 293° К,
читается «20 градусов Цельсия равны 293 градусам Кельвина».
*••) При этом мы пренебрегаем малыми различиями между 1 атмо-
сферой н 1 kTjcm* н между 1 кГ и 10' дин.
46 2 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
Сравнивая формулы B.3) и B.1), находим:
Ь=%. B.4)
Наконец, выразим давление через число молекул п,
содержащихся в единице объема газа. Известно, что одна
грамм-молекула любого вещества содержит б-10" молекул.
Величина б-10" называется числом Авогадро и обозна-
чается А. Таким образом, масса одной молекулы
т м- <2-5>
Если одна грамм-молекула занимает объем V, то число
молекул в единице объема п есть л = -р-. Плотность газа
Q = nm. Закон Клапейрона B.2) дает:
где k — постоянная Больцмана,
и # 8.3- Ю7 .од 1ri-i
Величина R относится к условно выбранному количе-
ству вещества — одной грамм-молекуле, поэтому в размер-
ность /? входит «моль». Величина k относится к одной
молекуле, поэтому k имеет размерность эрг/град. Вели-
чина kT имеет размерность энергии (эрг). В § 4 будет
показано, что в атмосфере величина kT равна средней
потенциальной энергии одной молекулы в поле тяжести
при температуре Т. Средняя кинетическая энергия посту-
Q
пательного движения одной молекулы равна -nkT.
§ 3. Распределение плотности
Из формулы B.1) находим Q = -^ . Подставляя это
в дифференциальное уравнение для плотности воздуха A.3),
получим:
§ 3] РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ 463
Решение этого уравнения есть р = Се ь , где С
определяется, из начального условия. Пусть при h = 0
Р = Ра> тогда
p = poe~^h. C.1)
Поделив равенство C.1) на Ь, получим:
e = Qoe~?A, C.2)
где Qa — плотность воздуха при fc = 0 (т. е. на уровне
моря). Из формулы C.1) видно, что на высоте Н=— над
уровнем моря давление воздуха уменьшается в е раз.
Получим формулу, связывающую величину Н с вели-
чиной kT: // = — ; пользуясь формулами B.4) и B.5), на-
ходим H = j^, откуда
//=?. C.3)
Подсчитаем величину Н, пользуясь формулой Н=—,
н 7,7-10» сл^/сек -„ . п5 7 7
Я— 10' ^/«vc* =7-7-Ю см = 7,7 км.
При помощи величины Я формулы C.1) и C.2) можно
записать так:
С увеличением высоты в арифметической прогрессии
давление и плотность падают в геометрической прогрессии:
если А = 0, то р = ра, Q = Qa; если h = Hy то р = ^ =
= 0,368 -р„ q = 0,368q0; если А = 2Я, то Р = § =0,135 ра,
e = 0,135Q(>; если h = 3H, то р=^=0,05р0, о^О.Обд,,.
Зная зависимость плотности от высоты, можно выра-
зить через q0 и Н полную массу воздуха та в столбе
464 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
с площадью основания 1 см*. Действительно,
оо оо ^
та== ] qdh = $ Qoe "dh.
а а
Сделаем замену переменной z = -tt; тогда dz=-rr dh,
При помощи соотношения ma = QaH подсчитаем (для
контроля) еще раз величину Н. Так как атмосферное дав-
ление равно 1 кг\смгу то масса воздуха в столбе с основа-
нием 1 см* как раз и равна 1 кг. Таким образом, та= 1 кг1см'=
= 1000 г\см*. Зная qo=1,3-1O~1 г\см*, отсюда получим:
tf=^ = __121^ = 7,7-10*™
в соответствии с прежним расчетом.
Найдем среднюю высоту, на которой находится воз-
дух, т. е. высоту центра тяжестн вертикального цилиндри-
ческого столба воздуха. Чтобы не вводить лишних величин,
рассматриваем столб воздуха с основанием 1 смг, однако
ясно, что высота центра тяжести от площади основания
цилиндра не зависит. На высоте h между h и h~\-dh
находится масса dm — qdh. Средняя высота равна
оо оо
\hdm \hQ(h)dh
h = •
\Q(h)dh
Найдем интеграл, стоящий в числителе. Пользуясь фор-
мулой C.3), получаем
оо со д оо
hQ(h)dh = l hQae~~»dh = QoH2 J ге~гdz = q0H*
о
со
ze z dz = 1, см. формулу G.8) части IV). Окончательно
§ 4] МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ 465
находим:
$?=*• C4)
Таким образом, та высота Н, на которой плотность и дав-
ление воздуха убывают в е раз, одновременно является и
средней высотой, на которой находится воздух.
Аналогичный результат получился раньше при рассмо-
трении радиоактивного распада (§ 3 части V): если вероят-
ность распада равна со —, -? = —от, « = /z0e~orf, то за
время Т = — количество радиоактивного вещества убывает
в е раз; при этом среднее время жизни радиоактивного
атома оказалось равным той же величине t = T=— .
Напомним, что простая зависимость C.3) плотности и
давления от высоты относится к случаю постоянной тем-
пературы. В действительности распределение плотности и
давления несколько отличается от формулы C.3) и зависит
от времени года и т. п.
Упражнения
1. Найти давление воздуха в шахте на глубине 1 км, 3 км, 10 км.
2. Найти зависимость давления воздуха от высоты при темпера-
туре воздуха — 40° С, то же для -f- 40° С.
3. Пусть температура воздуха меняется при изменении высоты
по закону -ir = — &Та, где Та— температура воздуха на поверхности
земли, а.— постоянный коэффициент. Найти зависимость давления
воздуха от высоты.
4. Известно, что в условиях задачи 3 величина а. =^0,07-10~* см~*.
Определить, пользуясь результатом задачи 3, давление воздуха в шахте
на глубине 1 км, 3 км, 10 км. Считать, что на поверхности земли
температура равна нулю. Сравнить результаты с результатами задачи 1.
§ 4. Молекулярно-кинетическая теория
распределения плотности
В предыдущих параграфах было найдено распределение
плотности воздуха по высоте при действии силы тяжести
в состоянии равновесия. При этом мы рассматривали воздух
как сплошную среду с данной зависимостью давления от
плотности.
466 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
Подойдем теперь к полученному результату с иной
точки зрения, а именно с точки зрения молекулярной тео-
рии. Будем рассматривать отдельные молекулы и их дви-
жение. Представление о том, что вещество состоит из
отдельных атомов, было высказано еще в Древней Греции.
Однако движение молекул и связь его с теплотой впервые
стал рассматривать великий русский ученый М. В. Ломо-
носов, который является, таким образом, основателем
молекулярно-кинетической теории.
Газовое состояние отличается от жидкого и твердого
состояний тем, что в газе молекулы можно рассматривать
как независимые, не взаимодействующие между собой.
Движение молекул газа представляет собой свободный
полет по инерции. Время от времени молекулы газа стал-
киваются между собой. В обычных условиях столкновения
молекул между собой происходят чрезвычайно часто, уча-
стки пути, которые молекулы пролетают от одного столкно-
вения до другого, весьма малы.
При атмосферном давлении и температуре 0°С в 22,4 л
газа содержится 1 грамм-молекула, т. е. 6-10" молекул;
б- ю8*
в 1 см3 содержится и = 2 24 1Q4 = 2,7-10" молекул.
Грубо будем рассматривать молекулы как шарики ра-
диусом около 2-Ю~* см*). Тогда для того, чтобы прои-
зошло столкновение двух молекул, надо, чтобы траектория
центра одной молекулы попала в мишень радиусом 4-10~* см
вокруг центра другой молекулы. Площадь такой мишени
а = лг2=^5- 10~ls см1. Значит, на пути в I см данная моле-
кула сталкивается со всеми теми молекулами, центры кото-
рых находятся в цилиндре с площадью основания 5 • 10~ls см*
и длиной 1 см. Объем такого цилиндра равен а см", и число
молекул в нем равно па, где я — число молекул в 1 см".
Таким образом, на пути в 1 см молекула испытывает па
столкновении. Поэтому среднее расстояние свободного по-
лета от одного столкновения до другого
I = ± = 0.7.10-см.
Эта величина называется длиной свободного пробега.
*) В действительности двухатомные молекулы, например моле-
кулы кислорода и азота, более похожи на пары слепленных шаров,
вроде арахиса с двумя ядрами в одной скорлупке.
§ 4] МОЛЕкУЛЯРНО-КИНЕТИЧЕСКЛЯ ТЕОРИЯ 467
Вследствие столкновений молекула летит не по прямой,
а по ломаной линии; однако объем цилиндра, образован-
ного ломаными, не отличается от объема прямого цилиндра,
поэтому расчет остается правильным.
На самом деле надо еще учесть, что движется не только
рассматриваемая молекула, но и те молекулы, с которыми
она сталкивается. Можно доказать, что это обстоятельство
мало меняет длину свободного пробега, а именно, умень-
шает ее всего в 1,5 раза.
Скорости молекул порядка 300—500 м/сек. Следова-
тельно, время свободного пробега, т. е. среднее время от
одного столкновения до другого, порядка
0.5.ю-«_ 1Л_10
4-10*
Ю-10 сек.
На первый взгляд величины 1=.IO~S см и т=5;10все«
очень малы. Однако их надо сравнить с размером моле-
кулы, радиус которой г^=2-10~* см, и с длительностью
самого столкновения, которая меньше ~=^\0~11 сек. После
такого сравнения видно, что молекулы газа редко сталки-
ваются друг с другом. Молекулы при атмосферном давлении
99,9% времени проводят в полете и лишь 0,1% времени
находятся в состоянии столкновения.
Столкновения молекул между собой в газе не влияют
на давление газа и не влияют на закон распределения
плотности газа в атмосфере. Подтверждение этого заклю-
чается в законах Бойля-Мариотта и Клапейрона. В § 2
этн законы были записаны в виде p = nkT.
Давление газа зависит от числа молекул в единице
объема, но радиус молекул г н их сечение а не входят
в формулу. Значит, величины г и о не могут войти н
в формулу распределения плотности по высоте.
Перепишем формулу распределения плотности C.2),
выразив Ь через молекулярные величины. Так как Ь = -гт-=-
AkT kT
= -; = , ТО
Am m
gft mgh
<41>
468 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VU
Разделим обе части формулы D.1) на т, где т обозна-
чает массу одной молекулы. Заметим, что — = п— число
т
молекул в единице объема на высоте h, ¦?*¦ = п„—число
молекул в единице объема на уровне моря. Формула D.1)
принимает вид
mgh
П
kT
D.2)
Величина mgh есть потенциальная энергия молекулы,
масса которой равна гп, находящейся на высоте А, если за
нуль принять потенциальную энергию молекулы на уровне
моря. Потенциальную энергию молекулы и (О) на уровне
моря можно выбрать произвольно (см. § 2 части VI). Тогда
u(h) = u@)~\-mgh,
откуда
mgh = u(h) — и @).
Формулу D.2) можем записать в виде
и (Л)-и @)
n(h) = n(Q)e kT
Это — закон распределения числа молекул по высоте. Ему
можно придать следующий вид:
n(h)=Be kT ,
где В есть константа, определяемая по значению плотно-
сти на уровне моря (А = 0)
а @)
n@)=Be .kT .
Замечательно то обстоятельство, что плотность молекул
на той или иной высоте зависит только от потенциальной
энергии молекул в данном месте: масса молекулы гп, уско-
рение силы тяжести g и высота h вошли в формулу D.2)
как раз в том сочетании (mgh), в котором они входят
в выражение для потенциальной энергии и.
Найдем среднее значение потенциальной энергии моле-
кулы и = mgh =mgh = mgH [см. формулу C.4)]. Пользуясь
§ 4] МОЛЕКУЛЯРНО-КИНЕТИЧЕСКЛЯ ТЕОРИЯ
формулой C.3), получаем:
469
S
Итак, средняя потенциальная энергия одной молекулы
равна kT.
Мы • установили, что распределение молекул воздуха
в атмосфере зависит от температуры и потенциальной энер-
гии молекул. Однако при данной средней потенциальной
энергии, равной kT, получаем определенное распределение
молекул по потенциальной энергии. Часть молекул — те,
которые находятся ниже высоты Н,— имеет потенциальную
энергию меньше kT. Найдем отношение числа таких моле-
кул к общему числу молекул. Это отношение есть
Н Н mgh
ndh пй\ е kT dh
ndh.
па
mgh
dh
Подсчитаем входящие сюда интегралы:
н
dh=— — e kT
mg
(
оо
J'
mgh
kT ,
e
mgh
mg
mg'
Поэтому
н
f ndh —A — e)
= 1
ndh
hT
—
mg
Таким образом, 63% всех молекул имеют потенциальную
энергию меньше средней, а 37% имеют потенциальную
энергию больше средней. При этом нетрудно подсчитать,
что потенциальную энергию больше 2kT имеют 14% всех
ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VU
молекул, а больше 2>kT — 5 % всех молекул, и т. Д.
Вообще, доля молекул, имеющих потенциальную энергию
а
больше данной величины и, равна е **\
§ 5. Броуновское движение и распределение молекул
по кинетической энергии
Более ста лет назад английский ботаник Броун заме-
тил, что мельчайшие, видимые в микроскоп пылинки нахо-
дятся в непрерывном движении. Эйнштейн высказал пред-
положение, что это движение пылинок представляет собой
их тепловое движение. Отсюда, в частности, следовал
вывод, что пылинки не будут все лежать на дне сосуда,
а будут распределены по высоте по такому же закону, по
которому распределены молекулы.
Если пылинка имеет форму шара диаметром
d — Ъ- 10~s см, то ее объем равен ^—=&6,5- 10~14сл1', и при
плотности Q=l г} см* масса пылинки равна 6,5-10"* г.
При комнатной температуре Т= 17° С = 290° К такие
пылинки распределены по высоте [согласно формуле D.2)]
по закону
_ и.»• ю-"-urn
П = Пле "o-i.u-ie-"
или л = яое-1-в 1О'Л. Таким образом, число пылинок в еди-
нице объема уменьшается в е раз при увеличении высоты
на величину y-gTio* см = 0,62- 10"* см.
Наблюдая распределение по высоте пылинок известного
размера и плотности, можно получить значение постоян-
ной Больцмана k. С другой стороны, закон Клапейрона
дает величину R=kA, после чего можно найти число
Авогадро. Эта работа, проведенная Эйнштейном и Пер-
реном в 1903—1907 гг., явилась важнейшим эксперимен-
тальным подтверждением всей атомно-молекулярной теории
и сыграла огромную роль в развитии физики.
При движении молекул под действием силы тяжести
все время происходит превращение энергии: если молекула
в данный момент движется вниз, то потенциальная энергия
переходит в кинетическую; если же молекула движется
§ 5] - - БРОУНОВСКОЕ ДВИЖЕНИИ 471
вверх, то кинетическая энергия переходит в потенциальную.
Когда газ находится в состоянии равновесия, т. е. давле-
ние газа уравновешивает силу тяжести, то в действитель-
ности молекулы газа движутся хаотически с большими
скоростями. Однако если мысленно выделить в газе какую-
нибудь горизонтальную плоскость, то число молекул,
проходящих за единицу времени через эту плоскость снизу
вверх, равно числу молекул, проходящих за то же время
сверху вниз, так что в среднем газ покоится. В состоянии
равновесия переход кинетической энергии в потенциальную
и переход потенциальной энергии в кинетическую взаимно
уравновешены, так как
число молекул, двигаю-
щихся вверх, равно чис- г ' 2 ' О
лу молекул, двигаю- О—- СО О
щихся вниз. . ¦
Отметим, что при X «
хаотическом движении ") у о) о)
отдельные (одинаковые)
молекулы имеют раз- Рис- 168-
личную скорость, т. е.
различную кинетическую энергию. Действительно, если
сталкиваются между собой два шарика, скорости которых
равны по величине, но направлены под углом одна к дру-
гой, то после столкновения скорости шариков могут быть
различны. На рис. 168 показан пример столкновения, после
которого один шарик, лежащий слева, останавливается,
а другой, двигавшийся снизу, движется с удвоенной энер-
гией [положения на рис. 168: а) до столкновения, б) момент
столкновения, в) после столкновения]. Обратите внимание
на то, как расположены шарики в момент столкновения;
если бы второй шарик во время столкновения был располо-
жен ниже первого, то он остановился бы, отдав всю энер-
гию первому шарику.
Так как при движении молекул происходит взаимное
превращение кинетической и потенциальной энергий, то
естественно предположить, что распределение молекул по
кинетической энергии похоже на их распределение по
потенциальной энергии.
Приведем без доказательства результат расчетов, проде-
ланных в конце XIX века Максвеллом и Больцманом.
472 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
Число молекул, имеющих составляющие скорости
по оси х между vx и vx~\-dvx,
по оси у между vy и vy -\-dvy,
по оси 2 между vz и vz-\-dvz,
равно
dn= ^—-е "т dvxdvydvz, E.1)
\ т ;
где п0 — полное число молекул, т — масса одной молекулы.
Отметим, что v*x-\- v* ~\- v\ = v*, где v — величина скорости
молекулы. Поэтому E.1) в показателе степени содержит
величину -2- : kT, т. е. отношение кинетической энергии
к потенциальной. Средняя кинетическая энергия, подсыи-
Q
тайная согласно закону E.1), оказалась равной -^kT. Для
числа молекул п, кинетическая энергия которых больше
заданной величины Е, получилась довольно сложная зави-
симость. Однако эта сложная зависимость приближенно
может быть описана простой формулой
п==пуш E.2)
Из закона E.2) получается неверное значение средней
кинетической энергии молекул
оо
ndE оо
С" 0
•-• кин ~
вместо -q-kT. Этот закон дает заметные отклонения от
истинного, если Е есть величина порядка kT. Однако при
E^>kT расхождение между точным и приближенным зако-
нами становится несущественным.
Отметим, что при равной температуре молекулы с раз-
личной массой имеют равные средние кинетические энергии
§ 6] СКОРОСТИ ХИМИЧЕСКИХ РЕАКЦИЙ 473
и одинаково распределены по величине кинетической энер-
гии, так как средняя скорость молекулы пропорцио-
нальна —~ , где т — масса молекулы.
Рассматривая столкновения молекул со стенками сосуда,
можно найти давление газа; оно оказывается равным
р = -^па Екин .
з
Полагая здесь ЕКин = -~ kT, получим закон Клапейрона
При столкновении молекул между собой происходит не
только обмен кинетической энергией между молекулами,
но и превращение кинетической энергии движения молекул
в энергию вращения молекулы, а также в энергию колеба-
ний атомов в молекуле, т. е. во внутреннюю энергию
молекулы. Возможен и обратный процесс, когда при столк-
новении часть внутренней энергии молекул переходит в кине-
тическую энергию. Поэтому естественно, что и распределение
молекул по величине их внутренней энергии W также
_w_
подчиняется закону пропорциональности величине е kT .
Показательная зависимость числа частиц, обладающих той
или иной энергией, от величины энергии является всеобъем-
лющим универсальным законом природы.
§ 6. Скорости химических реакций
Для чего нужен закон распределения молекул по кине-
тической энергии? Такие важные характеристики газа, как
его давление на стенки сосуда, теплоемкость, общий запас
энергии в объеме газа, определяются средними величинами.
Поэтому они определяются той наибольшей частью моле-
кул, энергия которых близка к среднему значению энергии.
Для чего же нам нужно знать, например, что есть ничтож-
ная доля (порядка 0,01%) молекул, кинетическая энергия
которых больше 17 kT? Ведь эти отдельные молекулы
с очень большой энергией на величину давления и на общий
запас энергии газа практически не влияют.
474 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
Картина, однако, резко меняется, если рассматривать
химические реакции. Оказывается, что именно эти редкие
молекулы с большой энергией полностью определяют ход
химических реакций. Загадка химических реакций заклю-
чается в том, что молекулы, вступающие в реакцию, стал-
киваются между собой каждые 10* сек, между тем реак-
ция часто требует нескольких минут (а иногда и часов)
для своего завершения. Значит, только редчайшая часть
всех столкновений приводит к химической реакции.
Высказывались предположения, что у молекул есть
какое-то очень маленькое «чувствительное место», в которое
нужно попасть, чтобы произошла реакция. Эта точка зре-
ния похожа на легенду о греческом герое Ахиллесе, кото-
рый был неуязвим везде, кроме пятки.
Однако правильное объяснение, которое дал в конце
XIX века шведский ученый Сванте Аррениус, заключается
в том, что к реакции приводит только столкновение моле-
кул, энергия которых превышает определенное значение,
так называемую энергию активации ЕА.
Когда, например, сталкиваются молекулы водорода и
йода и образуются две молекулы йодистого водорода HJ,
то нужно, чтобы энергия сталкивающихся молекул была
больше 3'10~1г эрг. Для сравнения отметим, что при О4С
величина kT = 1,38-Ю0-273 = 3,8-10""эрг. Таким об-
разом, при комнатной температуре нужной энергией обла-
дает лишь ничтожная часть молекул а = е~\ где
v = 3-10-lt/3,8-10-14=!= 80, откуда получим a = -^jg.
Время реакции получим, умножая время между двумя
столкновениями (оно порядка 100 сек) на то среднее число
столкновений, среди которых встретится одно столкновение
с нужной энергией. Это среднее число столкновений по-
рядка — =10". Получим время реакции при 0аС порядка
10" сек = 3-10" лет. Этот результат согласуется с тем
фактом, что при 0°С реакция Ht-f~J» = 2HJ практически
ненаблюдаема.
Из приведенных соображений следует, что в зависимости
от температуры время реакции выражается формулой
Ел
t = re"T .
§ 7] испарение, ток эмиссии катода 475
где т — время между двумя столкновениями, ЕА — энергия
активации. Эта формула правильно описывает зависимость
скорости химических реакций от температуры. Характерная
особенность формулы — крайне резкое уменьшение времени
реакции и увеличение скорости реакции при небольшом
изменении температуры.
Часто, однако, в химических реакциях дело обстоит
гораздо сложнее, потому что реакции могут идти через
различные промежуточные стадии. Советскому ученому
академику Н. Н. Семенову принадлежит заслуга всесторон-
него исследования сложных (цепных) химических реакций,
выяснения законов протекания таких реакций и общих
причин, приводящих к протеканию реакции по сложной схеме.
В качестве примера рассмотрим реакцию
Эта реакция идет не путем столкновений молекулы водо-
рода с молекулой хлора, а по схеме
В результате для -фактически наблюдаемой скорости
реакции получаются сложные зависимости. Однако для
каждой отдельной реакции, например для
Cl + Ht = HCl-fH (в реакции Ht -f-Clt = 2HCl),
имеет место закон Аррениуса, скорость реакции пропорцио-
-Ел
нальна е кТ , причем величина энергии активации ЕА имеет
различное значение для каждой реакции.
§ 7. Испарение. Ток эмиссии катода
Идея Сванте Аррениуса, о роли относительно малого
числа молекул, энергия которых намного превосходит сред-
нее значение энергии, помогает разобраться не только
в химических реакциях, но и в ряде других явлений.
К таким явлениям относится испарение жидкости.
Для испарения жидкости нужно затратить значитель-
ную энергию. Так, например, для испарения 1 г воды при
476 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
100°С нужно затратить*) около 540 калорий. На одну
молекулу это составляет**)Q = — - ', '— =7- 10~1J эрг,
при Г = 0°С = 273°К, ^Г=3,8.10-14; поэтому ^=20.
Оторваться от - поверхности жидкости и испариться могут
лишь те молекулы, энергия которых превышает теплоту
__?
испарения Q; доля таких молекул равна е кт. Поэтому и
_о_
скорость испарения пропорциональна е kT. Заметим, что
для удобства расчетов принято умножать числитель и зна-
менатель выражения ^ на число Авогадро А
Q_ J}A_ QA
kT kAl RT '
Величина QA есть теплота испарения б- 10е* молекул, т. е.
теплота испарения одной грамм-молекулы. Величина kA = R
есть универсальная газовая постоянная. В тепловых едини-
цах (малые калории на грамм-моль)
Р 8,3-Ю7 о кал
К 4,18-10' ^ г граЭмоль'
Теплота испарения одного моля воды равна
Qm = 18 - 540 = 10 000 кал\моль.
Таким образом, скорость испарения воды пропорциональна
Рассмотрим насыщенный пар над поверхностью воды.
Если пар является насыщенным, то число молекул воды,
испаряющихся в единицу времени, равно числу молекул,
находившихся в паре и прилипающих к поверхности воды
(конденсирующихся) в единицу времени. Скорость испаре-
•) Теплота испарения мало зависит от температуры: для воды
Q = 540 кал/г прн 100° С и 600 кал\г при 0° С. В дальнейшем этой
зависимостью пренебрегаем.
**) Молекулярный вес воды —18, число Авогадро —6-10*',
1 4,18107 эрг.
§ 7) ИСПАРЕНИЕ. ТОК ЭМИССИИ КАТОДА 477
ния равна
От
Се *т ,
где С — постоянная величина, пропорциональная площади
поверхности воды. Скорость конденсации пропорциональна
давлению паров воды и также пропорциональна площади
поверхности воды. Следовательно, в случае насыщенного
пара, когда скорости испарения и конденсации равны,
Dp = Ce «т,
где D и С — величины, пропорциональные площади по-
верхности, слабо зависящие от температуры и вовсе не
зависящие от давления, откуда
где постоянная F не зависит от величины площади поверх-
ности воды. Таким образом, устанавливается связь между
давлением насыщенного пара и. теплотой испарения.
Рассмотрим еще один процесс, похожий на испарение,—
испускание электронов нагретой поверхностью. Этот процесс
осуществляется на катоде радиоламп. Холодный катод
в пустоте не испускает электронов *). Однако при высокой
температуре катод испускает электроны. При этом если на
анод подан достаточно высокий положительный потенциал,
то анод притягивает электроны и каждый электрон, отор-
вавшийся от поверхности катода, попадает на анод. Элек-
трический ток, протекающий в цепи через радиолампу,
равен произведению числа электронов, испускаемых катодом
в единицу времени, на величину заряда одного электрона.
Опыт показывает, что в этих условиях имеет место сле-
дующая зависимость силы тока от температуры:
о_
*) Мы здесь не рассматриваем случай очень сильного электриче-
ского поля A0* в/см и больше), способного вырывать электроны
даже из холодного катода. Не рассматривается также выбивание элек-
тронов из катода действием света или бомбардировкой катода элек-
тронами, ионами или другими частицами.
478 ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ [Ч. VII
Величина Q для различных катодов различна. Напри-
мер, для катода из чистого вольфрама -^- = 55 000°, для
катода из окиси бария -^- = 30 000", и, следовательно, та-
кой катод может работать при более низкой температуре.
По зависимости / от Г можно определить величину -—- .
При этом величина Q, которая входит в последнюю фор-
мулу, совпадает с энергией, необходимой для того, чтобы
вырвать электрон из катода*).
Радиолампа дает замечательный способ измерения рас-
пределения электронов, вылетающих с поверхности катода,
по скоростям при данной температуре. Для этого при на-
гретом катоде дадим на анод небольшой отрицательный
потенциал <р. При таком потенциале анод отталкивает
электроны, испускаемые катодом. Поэтому большая часть
электронов, не долетев до анода, повернет назад и упадет
обратно на катод. Однако будут и такие электроны, кото-
рые все-таки попадут на анод, преодолев его отталкивание.
Для этого нужно, чтобы кинетическая энергия электрона,
вылетевшего с катода, превосходила разность потенциаль-
ной энергии у анода и у катода, т. е. величину е<р. Доля
— ду
таких электронов равна г кт . Таким образом, при отри-
цательном потенциале анода <р ток равен ]=jte kT , где
/„ есть ток при положительном потенциале. При осущест-
влении опыта необходимо, чтобы расстояние между катодом
и анодом было мало, для того чтобы количество электро-
нов между ними не было велико и взаимное отталкивание
электронов не повлияло на результат опыта.
Советский ученый академик А. Ф. Иоффе предложил
использовать это явление для прямого превращения тепло-
вой энергии в электрическую. Если электроны идут с ка-
тода на отрицательно заряженный анод, то в целом такая
система является источником напряжения: во внешней цепи
между отрицательно заряженным анодом и положительным
катодом ток имеет такое направление, что он совершает
*) Энергия, необходимая для вырывания электрона, может быть
определева другими способами.
ОТВЕТЫ И РЕШЕНИЯ 479
работу. Такой способ получения электрического тока заме-
чателен отсутствием каких бы то ии было движущихся частей,
принципиальной простотой схемы. В этом отношении та-
кой способ похож на получение электроэнергии при по-
мощи термоэлементов, также осуществленное академиком
А. Ф. Иоффе. В настоящее время во всем мире широко ве-
дутся работы по практическому применению нового способа.
ОТВЕТЫ И РЕШЕНИЯ
§ 3. 1. р=1,13рв, 0 = 1,48?,,, р = 3,67р0, где р„— давление воз-
духа на поверхности земли. 2. Зависимость давления от высоты дается
-— RT
формулой р=р^е ь , где Ь = -гт . Для температуры —40° С
Т = 273 — 40 = 233, Ь = ,!q а = 6'6-10* см%1сек*- в ^°м СЛУ"
чае Я = — = 6,6 км. Для температуры -f-40°C 7" = 313, 6=8,8Х
X Ю* смх1сек?, //=8,8 км. 3. Из уравнения -тг = —а^"о находим
7"= — аТ0А -(- С. Постоянную С определим из условия, что при
Л = 0 7* = Т0. Получим С = Т0, поэтому Г=Г0A—аЛ). Основное
уравнение для определения плотности -jx=—go. Воспользуемся урав-
ап
RT
неяием Клапейрона p = Q—-; подставляя сюда выражение для Т,
RTa(\ —ah) _ RTa
находим p = Q— ' ^. Положим -гт^ =^ ft», тогда р =
= оЬаA —otA), откуда о = г—тг^ тг • Дифференциальное- уравне-
но A —ал)
ние принимает вид зт = — gr—тт^- г: - Перепишем его так:
— = — -—т^ гт • Возьмем интегралы от обеих частей 1пр =
g
= г^-1пA —ah)-\-C. Потенцируя, получаем р = A—ал) ь°аеС. Так
g
как при Л=0 р = р0, то eCrrrpj, поэтому р = р0 A — аА) ь°в .
4. р=р„ A -0,037- 10-sA)»'4e. р= 1,13р0, р = 1,44р0, рв = 2,
ЧАСТЬ VIII
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ В НИХ
§ 1. Основные понятия и единицы измерения
В части VIII рассматриваются явления, происходящие
в электрических цепях. Основными элементами электриче-
ской цепи являются сопротивления, емкости, индуктивности,
источники тока (напряжения).
Так же как и в других частях, посвященных примене-
нию математики к физическим вопросам, наше изложение
не предназначено для замены учебника физики, а скорее
является дополнением, развитием и уточнением тех знаний,
которые дает школьный учебник физики. Поэтому здесь мы
только вкратце напомним определения сопротивления, емко-
сти и т: п. и единицы их измерения, считая, что в школь-
ном объеме основные понятия известны читателю.
Количество электричества определяется как разность
количества положительных зарядов и количества отрица-
тельных зарядов. Обозначаем его q. Пользуемся практиче-
ской системой единиц, так что единицей количества электри-
чества является -кулон (сокращенно — к). Элементарный за-
ряд— заряд протона — равен ер= 1,6-10~19 к, заряд элек-
трона равен ее = —1,6-10' к:
Сила тока (или кратко ток) определяется как количе-
ство электричества, протекающее в единицу времени через
поперечное сечение проводника. Силу тока будем обозначать
через /. В практической системе единиц за единицу силы
тока принимается такая сила тока, при которой через попе-
речное сечение проводника за одну секунду протекает 1 к.
Эта единица носит специальное название ампер (сокра-
щенно — а)
ампер = кулон/секунда.
§ 1] ОСНОВНЫЕ ПОНЯТИЯ И ЕДИНИЦЫ ИЗМЕРЕНИЯ 481
Направлением тока называется направление, в котором
должны были бы двигаться положительные заряды для
того, чтобы создать данный ток. В действительности в метал-
лических проводниках положительные заряды неподвижны,
а ток течет благодаря движению электронов. Тело, заряжен-
ное положительно,— это, как правило, тело, которое поте-
ряло часть своих электронов (только в редких случаях
положительный заряд есть результат того, что тело приоб-
рело положительные заряды). Отрицательно заряженное
тело — это тело, которое приобрело избыточные электроны.
Направление тока есть направление, противоположное тому
направлению, в котором в проводнике движутся электроны.
Электрическим потенциалом данной точки называется
потенциальная энергия, которой обладает положительный
заряд в 1 к, помещенный в данную точку. При этом счи-
тается, что электрический потенциал земли равен нулю.
Следовательно, равен нулю потенциал той точки схемы,
которая соединена с землей металлическим проводом («за-
землена»). Единицей потенциала в практической системе
единиц служит вольт. Потенциал точки равен 1 вольту A в),
если заряд в 1 к, помещенный в эту точку, обладает потен-
циальной энергией в 1 джоуль. Джоуль равен 107 эрг.
Потенциальная энергия и заряда q, помещенного в точку,
где потенциал равен <р, есть
и (джоуль) = q (кулон)-ф (вольт). A.1)
При этом надо представлять себе, что q мало, так как если
поместить в данную точку большой заряд (например, 1 к),
то от этого изменится сам потенциал <р. Поэтому лучше
сказать, что потенциал — это коэффициент при q в фор-
муле A.1).
Работа А, которую совершит заряд, переходя из точки,
где потенциал равен <p,, в точку, в которой потенциал
равен ф„ есть
А=и1 — ut = q (Фг — ф,).
Так же как во все физические результаты в механике
входит только разность потенциальных энергий, так в уче-
нии об электричестве в формулы входит всегда разность
потенциалов. Ко всем потенциалам во всех точках можно
прибавить одинаковое слагаемое,— разность потенциалов от
16 Я. В. Зельдович
482 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [ч. VIU
этого не изменяется. Поэтому потенциал в какой-нибудь
одной точке схемы или аппарата всегда можно выбрать
произвольно, например положить равным нулю. Однако
после этого потенциалы всех других точек становятся
вполне определенными. Именно это обстоятельство позволило
нам принять за нуль потенциал земли.
Рассмотрим конденсатор (рис. 169), состоящий из двух
параллельных пластин. Одна из пластин (левая) может быть
соединена с каким-либо источником напряжения. Количе-
ство электричества на левой пла-
стине прямо пропорционально раз-
ности потенциалов пластин конден-
~т сатора <рс
Рис. 169. ^ = Сфс,
причем разность потенциалов определяется как потенциал
девой пластины минус потенциал правой пластины. Так
как на рис. 169 правая пластина заземлена, то фс в этом
блучае равно потенциалу левой пластины.
Коэффициент пропорциональности С называется ем-
костью конденсатора. За единицу емкости принимается
фарада (сокращенно — ф). Это емкость конденсатора,
у которого разность потенциалов пластин 1 в при
заряде 1 к. Ю~'ф называется микрофарада, \0~*ф — на-
нофарада, 10~1*ф — п икофарада.
На правой пластине конденсатора скапливается равное
по величине и противоположное по знаку количество
электричества. Обозначая одну пластину кодденсатора
через А, другую через В, получим:
Электрический заряд есть сохраняющаяся величина,
ни при каких процессах не возникают и не исчезают
электрические заряды одного знака *). Изменение заряда
пластины конденсатора А связано с тем, что заряд с
пластины уходит куда-то в другое место, например в точку
D, по проволоке AD (рис. 170).
*) Прн возникновении или исчезновении двух противоположно
заряженных частиц с равным по абсолютной величине зарядом пол-
ный электрический заряд системы не изменяется.
§ IJ ОСНОВНЫЕ ПОНЯТИЯ И ЕДИНИЦЫ ИЗМЕРЕНИЯ 483
Если в направлении от D к А (слева направо) течет
ток /, то за время dt через поперечное сечение провод-
ника пройдет количество электричества jdt, поэтому
dq ,
ИЛИ -rp=xi.
Рассмотрим теперь, от чего зависит сила тока, текущего
по проводнику. По закону Ома сила тока пропорциональна
разности потенциалов на концах проводника, причем ток
течет от большего потенциала к меньшему. Таким
образом,
/ *() A-2)
Величина k положительна и называется проводимостью.
1 г
Рис. 170.
Величину <pD—фл обозначим через <рд. Это есть раз-
ность потенциалов на сопротивлении R, причем величина
Фя определяется (как и фс) как потенциал слева минус
потенциал справа.
Обратная величина -г- называется сопротивлением про-
водника и обозначается через R. Единица сопротивления
называется ом. Это сопротивление проводника, по которому
течет ток в 1 а при разности потенциалов на концах про-
водника в 1 в. Закон Ома A.2) можно записать так:
2S
или Фд = */. A.3)
Источником напряжения в цепи может быть, напри-
мер, гальванический элемент. На полюсах элемента имеется
определенная разность потенциалов. Приближенно можно
считать, что эта разность потенциалов не зависит от тока,
протекающего через элемент. В частности, в элементе ток
может течь в сторону от более низкого потенциала к более
высокому потенциалу. Через сопротивление ток всегда
течет от более высокого потенциала к более низкому,
16*
484 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
подобно тому как по трубе, соединяющей два сосуда,
вода течет из сосуда, в котором уровень воды выше,
в сосуд, в котором уровень воды ниже.
Элемент подобен насосу, кагорый может забирать воду
в нижнем сосуде и поднимать ее в верхний сосуд, т. е.
заставлять воду передвигаться снизу вверх. Для работы
насоса необходим какой-то внешний источник энергии,
приводящий насос в движение. Точно так же, когда через
элемент проходит ток от более низкого к более высокому
потенциалу, в элементе происходят химические реакции.
Энергия этих химических реакций в элементе превращается
в электрическую энергию.
Рнс. 171.
Разность потенциалов, которую дает элемент, называет-
ся электродвижущей силой или, коротко, э. д. с.
Разность потенциалов на элементе, взятая как потен-
циал слева минус потенциал справа (рис. 171), равна минус
э. д. с. элемента
Ф, — Ф, = — Е.
В действительности э. д. с. несколько зависит от силы тока,
протекающего через элемент. Когда ток течет (на рис. 171
слева направо) в направлении от более низкого потенциала
к более высокому (т. е. в нормальном режиме работы
элемента, когда он производит электрическую энергию),
э. д. с. Е уменьшается с увеличением силы тока. Прибли-
женно можно считать э. д. с. постоянной, но более точно
Е = а — Ъ\. A.4)
Элемент, э. д. с. которого не зависит от силы тока /, будем
называть идеальным элементом.
Рассмотрим последовательное соединение идеального
элемента с э. д. с., равной а, и сопротивления Ь (рис. 171).
Тогда
ф? = Ф, — Ф, = — а> Фь = Ф, —Ф. = &//
§ 1J ОСНОВНЫЕ ПОНЯТИЯ И ЕДИНИЦЫ ИЗМЕРЕНИЯ 485
поэтому
<Pi — Ф» = (Ф1-^Ф,) + (Ф, — Ф,) = — a-\-bj =
= — (a — bj) = —E.
Величину Ъ в формуле A.4) называют поэтому «внутрен-
нее сопротивление» элемента: реальный элемент, с которым
мы имеем дело, с э. д. с, удовлетворяющей формуле A.4),
дает такую же зависимость Е от у, как соединенные по-
следовательно идеальный элемент и сопротивление Ъ.
За величиной а сохраняют название э. д. с. реального эле-
мента, имея в виду, что при у' = 0 ? = а, а падение э. д. с.
при /=7^0 характеризуется величиной Ь*).
В дальнейшем при рассмотрении электрических цепей,
в которые входит источник тока, например элемент и раз-
личные сопротивления, можно представить себе, что имеем
дело с идеальным элементом с постоянной, не зависящей
от тока э. д. с, а внутреннее сопротивление Ъ объединить
с внешним сопротивлением R.. Таким образом, реальный
элемент с внутренним сопротивлением Ь, включенный
последовательно с сопротивлением R, эквивалентен иде-
альному элементу, включенному ^
последовательно с сопротивлением , * ?
Я (* + *) 1 Q \
Я, ( + )
Следует еще раз обратить осо-
бое внимание на различие между Рис. 172.
сопротивлением и источником на-
пряжения. Если в какой-то цепи на сопротивлении имеется
разность потенциалов такая, что «p.xpi (рис. 172), то, по
нашему определению, ф#= q>i—Ф, < 0, т. е. <рЛ отрицательно;
следовательно, по формуле A.3) и ток отрицателен. Зна-
чит, ток течет справа налево, от 2 к ). Теперь пусть
разность потенциалов такого же знака имеется на концах
источника напряжения, причем зависимость Е от у дается
формулой A.4) (рис. 171). Пусть при этом ф,>ф,, но
Ф,— ц>х<а. Тогда 6/^ф, —ф, + а = а —(ф, —фг)>0,
т. е. у>0. Поэтому ток течет слева направо, несмотря на
то, что потенциал ф, слева меньше, чем потенциал срл
справа. Таким образом, источник напряжения способен
*) Так как при разомкнутой цепи ток равен нулю, то э. д. с. можно
определить как разность потенциалов разомкнутого элемента.
486 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VUI
преодолевать разность напряжений и давать положитель-
ный ток (слева направо) при отрицательной разности
потенциалов ((<рх — <р,) < 0), если только эта отрицательная
разность потенциалов по абсолютной величине не превы-
шает э. д. с. источника. Между тем сопротивление при
отрицательной разности потенциалов всегда дает отрица*
тельный ток.
В частном случае (рис. 173), если элемент имеет внут-
реннее сопротивление Ь, а во внешней цепи последова-
тельно включено сопротив-
— , ление У?, ток определяется
формулой /=„,-.
Рассмотрим теперь индук-
тивность. Явление индуктив-
Рис„ 173. ности связано с магнитным
полем, возникающим в про-
странстве, окружающем проводник, когда по проводнику
течет ток. Это магнитное поле особенно велико, если
проводник имеет вид катушки с большим числом витков.
Поле еще больше увеличивается, если катушка намотана
на железный сердечник.
В свою очередь магнитное поле вызывает электриче-
ские явления. Известно, что каждый виток (и даже каждая
часть витка) катушки при наличии переменного магнит-
ного поля становится источником напряжения, становится
подобным гальваническому элементу. В катушке, в которой
витки намотаны так, что ток обходит сердечник, катушки
в одном и том же направлении на всем протяжении
катушки, все эти источники напряжения соединены после-
довательно, так что напряжения складываются.
В целом катушка эквивалентна источнику напряжения
с разностью потенциалов, пропорциональной скорости
изменения магнитного поля. Но магнитное поле в катушке
пропорционально силе тока в катушке *). Поэтому скорость
*) Мы не будем рассматривать случай, когда на одном сердечнике
намотаны две катушки, т. е. трансформатор, связывающий между
собой две электрические цепи, в которых текут разные токи.
Не рассматриваются также случаи более сложной зависимости
магнитного поля от тока, когда в катушку вставлен железный сер-
дечник и сила тока так велика, что железо «насыщается».
§ 1J ОСНОВНЫЕ ПОНЯТИЯ И ЕДИНИЦЫ ИЗМЕРЕНИЯ 487
изменения магнитного поля пропорциональна скорости
изменения тока, т. е. производной ^-. Окончательно в
катушке (рис. 174)
ф2.=ф1-_ф1 = ?^, A.5)
причем за положительное направление тока принято на-
правление от / к 2 внутри катушки, а величина ф^ есть
разность потенциалов , ^_
на катушке. Она опре- ; /ОООООООООЧ 2
деляется как потенциал 00000000 ¦ *
Ф, слева минус потенци-
ал ф» справа. Рассмат- Рис. 174.
ривая подробно направ-
ление магнитного поля и э. д. с, индуцируемую при его
изменении, можно доказать, что коэффициент L в этой
формуле (так называемая индуктивность) всегда положи-
телен.
Из формулы A.5) следует, что если ^у < 0, то ф,—фа < О,
т. е. ф, > <рх. Таким образом, если ток положителен (течет
от / к 2) и по величине уменьшается, то катушка играет
роль элемента, поддерживающего в цепи положительный
ток, несмотря на то, что q>L<Q. Если же ток положителен
и увеличивается, то jz>O> поэтому ф?>0. В этом случае
катушка играет роль добавочного сопротивления, так как
в этом случае на катушке разность потенциалов положи-
тельна при положительном токе [сравните с A.3)].
Существенное отличие катушки от источника напря-
жения и от сопротивления заключается в том, что вели-
чина ф, зависит не от величины тока /, а от скорости его
изменения ^.
Коэффициент L в уравнении носит название «индук-
тивность катушки» (раньше употреблялось выражение
«самоиндукция »).
Единица индуктивности называется генри. Если индук-
тивность катушки равна 1 генри, то это значит, что при
скорости изменения тока, равной 1 а\сек, в катушке
возникает разность потенциалов в 1 в. Размерность
488
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
индуктивности получаем из формулы A.5)
вольт-секунда
генри = i-=- .
г ампер
Часто для краткости говорят просто «индуктивность L»>
вместо того чтобы сказать «катушка, индуктивность кото^
рой равна Z.». Говорят также «емкость С» вместо «кон-
денсатор, емкость которого равна С». Точно так же гово-
рят об э. д. с. ?0, вместо того чтобы говорить о гальвани-
ческом элементе или источнике напряжения.
Из сказанного видно, что индуктивность влияет на
ток в цепи, подобно тому как инертная масса (маховик)
влияет на скорость движения: индуктивность препятствует
изменению тока, масса — по второму закону Ньютона —
препятствует изменению скорости. Подробнее это сходство
будет рассмотрено в § 4 этой части.
С точки зрения дальнейших расчетов емкость, сопро-
тивление, э. д. с. и индуктивность имеют между собой
общее свойство — в схеме все они присоединяются двумя
проводами (в отличие, например, от трансформатора,
имеющего четыре вывода, или радиолампы, имеющей три
вывода — анод, катод, управляющая сетка). Приборы,
которые включены в схему при помощи двух проводов,
носят название двух-
полюсников. Приборы,
включаемые при помощи
четырех проводов, назы-
ваются четырехполюс-
никами. В схеме каж-
дый элемент — емкость,
сопротивление, э. д. с. и
индуктивность — харак-
теризуются в каждый
данный момент времени
определенным током,
который проходит через этот элемент, и определенной раз-
ностью потенциалов на входе и выходе.
Можно представить себе закрытый ящик Я (рис. 175)
с двумя торчащими из него проводами А и В. Внутри
ящика может быть что угодно: R, E, L, С. Подключим
к ящику амперметр А и вольтметр V. При включении,
Рис. 175.
§ I] ОСНОВНЫЕ ПОНЯТИЯ И ЕДИНИЦЫ ИЗМЕРЕНИЯ 489
показанном на рис. 175 (значки «-{-» и «—» соответст-
вуют надписям на клеммах амперметра и вольтметра),
амперметр показывает ток /, идущий в направлении от
А к В. Вольтметр показывает разность потенциалов
фя = Фл — фд- От того, что находится внутри ящика,
зависит связь между <ря и /:
в случае сопротивления фя = ./?/, A-6)
в случае э. д. с. *) Еа фя =—?„, A.7)
в случае индуктивности L фя = ?-^, A.8)
t
в случае емкости**) С фя =(фяH +^- § J dt A.9)
(или % = ±j). A.9а)
В некоторых случаях осуществляются и более сложные
зависимости. Так, например, выпрямитель тока (двухэлек-
тродная лампа или полупроводниковый диод) не подходит
ни под одну из формул A.6)—-A.9). Однако в большом
числе важных вопросов можно ограничиться рассмо-
трением элементов схем, для которых с хорошей точ-
ностью выполняются формулы A.6) — A-9). Ниже будем
рассматривать именно такие схемы, кроме последнего
§ 16, где специально рассматриваются свойства контура,
в который включено устройство со сложной зависимостью
тока от разности потенциалов.
Рассмотрим схему, изображенную на рис. 176. Выпи-
шем падение напряжения на отдельных элементах схемы:
ТС тгА г. ' ВСУ
= Флв — Фвя. \
•) Внутреннее сопротивление э.д.с. не учитываем.
dq йфя \
••) g ==С<ря, -т?~и откуда -—¦ = -^/. Если в начальный
t
момент времени t = tQ, <ря = (фя)(„ то фя =(фяH -f-— \ jdt.
t
490 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIU
Заметим еще, что <рв = фд „, Фд = фд , ц>в = фд ; по-
этому, сложив почленно все равенства A.10), получим:
Фс 4" Фд + Vl + Фя = Ч>ас — Фвя-
Если цепь рис. 176 замкнута, то ф. =фэ . В этом случае,
следовательно,
©то общее равенство вместе с выражениями A.6) — A.9)
l_hr—ryoooooo°ov-s—г
Be V
Рис. 176.
прлностью определяет все процессы в цепи. Ниже будем,
пользуясь этим равенством, рассматривать различные цепн,
начиная с самых простых, состоящих только из двух
элементов.
§ 2. Разряд емкости через сопротивление
Рассмотрим процесс, происходящий в цепи из емкости С
и сопротивления R (рис. 177). Потенциал точки А обозна-
чим ф (противоположная пластина пусть заземлена).
Вначале пусть ф = фв. Соот-
ветствующее количество элек-
тричества на пластине А,
Можно ли говорить о то-
ке, идущем через емкость?
В конденсаторе две пластины
разделены изолятором (на-
Рис' 177- пример, воздухом), так что
в действительности электрон
не может пройти через емкость, т. е. попасть из Л в В.
Однако если на пластину А попадает положительный
заряд, то пластина В заряжается отрицательно, так что
С пластины В по проводу уходит положительный заряд
§ 2] РАЗРЯД ЕМКОСТИ ЧЕРЕЗ СОПРОТИВЛЕНИЕ 491
(ток также идет слева направо). Два амперметра А, и А4, один
из которых измеряет силу тока в проводе, присоединенном
к пластине А, другой — в проводе, присоединенном к плас-
тине В, дают одинаковые показания. Что именно, поло-
жительные заряды или электроны, проходят в различных
частях электрической цепи, нас не интересует, также как
не интересует, пройдут ли через Ах те же самые электроны,
которые ранее прошли через Ах, или другие. Поэтому
везде в дальнейшем будем говорить просто о токе, идущем
через конденсатор, имея при этом в виду ток, проходящий
по проводам, присоединенным к пластинам конденсатора.
В электрической цепи о токе, идущем через конденсатор,
можно говорить так же, как о токе через сопротивление
или индуктивность; отличие заключается в другом виде
связи между током и разностью потенциалов, что выра-
жено формулами A.9) и A.9а).
При замыкании рубильника Р (рис. 177) по сопротив-
лению R пойдет ток
По формуле A.11) ф-|-фя = О, откуда ф/? = —ф, поэтому
/ = — ^-Ф- B-1)
Так как положительным мы называем ток, текущий слева
направо, то при ф>0, как видно из формулы B.1), ток
отрицателен, течет справа налево, конденсатор разряжается*).
Вспоминая,» что / = -^ (ток через конденсатор), a q = C<p,
находим:
Сравнивая B.1) и B.2), находим:
*) Заметим, что во всех схемах (рис. 176 и далее), имеющих
вид прямоугольника, мы говорим о направлении тока в верхней сто-
роне прямоугольника; в нижней стороне, замыкающей цепь, ток
имеет, очевидно, противоположное направление.
492 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Такое уравнение мы решали в связи с задачей о радио-
активном распаде. Если при 7 = 0 <р = ф0, то
Отсюда
1@=-^
г pi ом вольт __ вольт секунда .
ампер кулон '
Из формулы B.3) видно, что величина RC имеет раз-
мерность времени. Проверим это:
г#~, кулон
1С] — ~вБл!т~-
Отсюда
, г,^-., вольт-секунда
' кулон
За время t = RC заряд конденсатора q, а также сила
тока / уменьшаются в е раз.
J-
кулон
— = секунда.
вольт J
Рнс. 178.
Процесс разряда конденсатора легко проследить на
опыте. В магазинах радиодеталей продаются конденсаторы
с емкостью С = 20 микрофарад = 20-10"" ф и сопротив-
ления У? = 20 мегом = 20 -10° ом. Для схемы с такими R.
и С получим RC = 400 сек, очень удобное для наблюде-
ния время.
Величина JRC называется постоянной времени контура,
состоящего из емкости и сопротивления (напомним, что
в случае радиоактивного распада аналогичная величина
называлась средним временем жизни).
Рассмотрим задачу зарядки емкости через сопротив-
ление. Схема показана на рис. 178. Если рубильник Р
замкнут, то согласно A.11) ф^;-{-ф/?-{-ф = 0, где ф — по-
тенциал незаземленной пластины конденсатора. Так как
§ 2J
РАЗРЯД ЕМКОСТИ ЧЕРЕЗ СОПРОТИВЛЕНИЕ
493
Фл = —?,. Ф/?=Я/. то — ?
конденсатор /=^ = С ^, поэтому
= 0. Ток через
или
5Г = -^«Р-
Для того чтобы найти, как меняется <р с течением
времени^ удобно ввести новую переменную z по формуле
2 = ф — Ей\ тогда dz = dy. Уравнение B.5) перепишется
в виде
dt
_
RC '
Его решение есть
f 7 p RC
B.6)
где z0 — значение z в начальный момент времени.
Найдем решение для случая, когда в начальный момент
времени конденсатор не заряжен, при t = 0 <р = 0. Тогда
zo = —Еа. Из B.6) получаем z = — Еле у?с,
t
= — Eae
B.7)
График зависимости ф от / изображен на рис. 179. Кривая
соответствует формуле B.7),
пунктирная горизонтальная
прямая представляет собой
то значение <р = ?0, к кото-
рому с течением времени
приближается решение. Be-
личина z имеет геометри-
ческий смысл расстояния
по вертикали от кривой до
пунктирной линии. Это расстояние с течением времени
убывает по показательному закону.
За время, равное RC, заряд конденсатора достигает
63°/,, своего конечного значения, за время 2RC — 8б°/0 и
за время 3RC — 950/0 конечного значения.
Рис- 17Э*
494 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Из формул B.4) и B.7) видно, что разрядка и зарядка
конденсатора происходят тем быстрее, чем меньше сопро-
тивление R.
Упражнения
1. В схеме рис. 177 С=10"" ф, /?=107 ом, /?=10» ом,
R= 10* ом. Для каждого из этих случаев определить, через сколько
времени ток, текший в начальный момент через конденсатор, умень-
шится на 10°/0; уменьшится вдвое.
2. Рассмотреть процесс выравнивания потенциала через сопротив-
ление R при последовательном соединении двух конденсаторов С,
и Сг, один из которых в начальный момент / = 0 заряжен до разности
потенциалов <рс @) = а, а другой не заряжен, вовсе, т. в. <рСа@) = 0
(рис. 180).
С, J - Сг
^1\
Рис. 180.
3. Определить изменение постоянной времени контура в схеме
рис. 177, если все линейные размеры схемы увеличить в п раз (кон-
денсатор считать плоским).
Замечание 1. Условие задачи надо понимать так: увеличя-
ваются как размеры конденсатора, так и размеры сопротивления, но
материалы, из которых изготовлены конденсатор и сопротивление,
не меняются.
Замечание 2. Из физики известна формула дли емкости
плоского конденсатора C = eS/4nd, где S—площадь пластины кон-
денсатора, d—расстояние между пластинами, е—постоянная вели-
чина, зависящая от материала между пластинами (диэлектрическая
постоянная). Величина проволочного сопротивления находится по
формуле R=q—, где I — длина, а—площадь поперечного сечения#
q — постоянная, зависящая от материала проволоки.
§ 3. Колебания в цепи емкости с искровым промежутком
Типичная схема использования конденсатора показана
на рис. 181. В цепь включен источник напряжения о
э. д. с. Е и сопротивлением R (роль R может играть
внутреннее сопротивление источника напряжения). Ниже
§ 3J КОЛЕБАНИЯ В ЦЕПИ ЕМКОСТИ С ИСКРОВЫМ ПРОМЕЖУТКОМ 495
находится искровой промежуток; при разности потенциа-
лов меньше определенного значения <р, искровой проме-
жуток является изолятором. При q> = <p1 проскакивает
искра, между проводами воздух накаляется до высокой
температуры и становится хорошим проводником. Сум-
марное сопротивление подводящих проводов и накален-
ного воздуха обозначим через г. Величина г мала и ос-
тается малой до тех пор, пока идет ток, поддерживающий
J—о o-
Рис. 181.
высокую температуру воздуха. При определенном малом
значении тока /, воздух остывает и искровой промежуток
снова становится изолятором. Этому значению тока соот-
ветствует разность потенциалов <p2=/sr. При этом q>, > q>,:
нужно большее напряжение для того, чтобы зажечь
искру, чем для того, чтобы поддерживать ее горение.
На рис. 182 показана зависимость фот / для такой
схемы. На участке О А происходит зарядка емкости, ток
не идет через искровой про-
межуток. В этом случае спра-
ведлива формула B.6)
Р\
Е
C.1)
В точке А в момент времени
t-=m.tA разность потенциалов
Рг
А..-'
t
Рис. 182.
достигает значения q>lt иск-
ровой промежуток начинает
проводить ток, идет разрядка конденсатора. Так как при
этом R^>r, то током, идущим от источника напряжения,
можно пренебречь по сравнению с током, идущим через
496 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
искровой промежуток. Поэтому для <р получаем уравне-
ние
d<p <р
И 7с'
причем при t = tA <р = ф1. Отсюда находим:
Ф = Ф,е гс . C.2)
В момент времени t = tB (в точке В) ф^гф,, при этом
искровой промежуток опять становится изолятором, снова
начинается зарядка (участок ВС).
Определим время tB — tA, в течение которого проис-
ходила разрядка емкости. Для этого воспользуемся тем,
что при t = tB ф^^ф,. Полагая в C.2) Ф = ф1, t = tB,
получим:
'в-* а
откуда
На участке ВС (зарядка) справедлива зависимость
C.1), сдвинутая по времени на величину т (на рис. 182
величина т изображается отрезком АаВ). Поэтому
- *в~*
Полагая здесь t = tg, получим:
Ф1==?A—
Аналогично, полагая t=^tCJ находим:
(
<f1 = E\\ — е Rc
Из последних двух формул
^J=^ ^и tc-tB = RC ln%=%.
§ 3J КОЛЕБАНИЯ В ЦЕПИ ЕМКОСТИ С ИСКРОВЫМ ПРОМЕЖУТКОМ 497
Полный период процесса (зарядка — разрядка) есть
Обычно сопротивление в цепи источника напряжения
R во много раз больше сопротивления искрового проме-
жутка, поэтому время зарядки гораздо больше времени
разряда. Зато ток разрядки оказывается во много раз
больше, чем ток зарядки, больше, чем тот максимальный
ток, который можно было бы получить от источника на-
пряжения (при наличии внутрен- ¦>
него сопротивления Rx источник 11
напряжения не дает ток больше 11
Е \
чем j~-J. Схема (рис. 181) преобра-
зует длительный малый ток, вы-
зываемый источником напряжения,
в сильный ток, который, однако,
течет не все время, а в течение
кратких промежутков времени ~-~-~-Л
(как принято говорить «короткие U >~-~-" >—»
импульсы» тока). г-) '-"-' -' |~|
Действие схемы подобно систе-
ме, в которой маленькая струйка
воды постепенно наполняет сосуд
(рис. 183). Сосуд закреплен так, Рис. 183.
что когда накопится достаточное
количество воды, то он опрокидывается, вода выливается,
после чего сосуд снова принимает вертикальное положе-
ние, и процесс начинается сначала. На рисунке сосуд
закреплен на горизонтальной оси 00' ниже середины.
Внизу к сосуду прикреплен груз, так что центр тяжести
пустого сосуда лежит ниже оси. Однако когда сосуд за-
полняется водой, то центр тяжести полного сосуда оказы-
вается выше оси и сосуд опрокидывается.
Вернемся к схемам рис. 177 и 178. В таких схемах,
состоящих из емкостей, сопротивлений и э. д. с, по ис-
течении некоторого промежутка времени потенциалы
практически выравниваются. Действительно, в схеме
рис. 177 устанавливается <р = 0, в схеме рис. 178 ц> = Еа
1см. формулы B.4) и B.7)]. Совершенно другую картину
17 Я. В. Зельдович
498 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
наблюдаем в случае схемы с искровым промежутком.
Здесь происходят незатухающие колебания величины <р
(правда, они очень непохожи на те колебания, которые
мы изучали раньше). Эти колебания связаны с особыми
свойствами искрового промежутка, в частности с тем фак-
том, что до достижения определенного потенциала (так
называемого потенциала пробоя <рх) ток через искровой
промежуток совсем не идет.
О свойствах разряда через воздух в искровом проме-
жутке написаны большие книги; мы привели только ми-
нимум сведений, необходимых для понимания действия
схемы рис. 181. Сведения, которые мы дали, недостаточны
для ответа на простой вопрос: что произойдет, если соеди-
нить искровой промежуток с источником напряжения без
конденсатора?
Действительно, если, ток не идет, то на искровом про-
межутке будет напряжение Еп. Так как Еа > <plt то должен
произойти пробой. Но если бы произошел пробой, то со-
противление искрового промежутка стало бы малым,
равным г. Тогда на искровом промежутке возникла бы
разность потенциалов, равная Еа • - \ р-, и ток / = —A~s ¦
Если R велико, то ток / мал—меньше /,, разность по-
тенциалов на искровом промежутке мала — меньше <pt.
Но в таком случае воздух не нагревается и сопротивление
искрового промежутка не станет малой величиной г, а
значит, разность потенциалов будет велика, равна Е.
Мы получили противоречие.
На самом деле в этих условиях получается электри-
ческий разряд другого типа, так называемый тлеющий
разряд (малый ток без нагрева воздуха), а не искра с
накаленным воздухом.
§ 4. Энергия конденсатора
Заряженный конденсатор обладает определенным за-
пасом энергии; этот запас энергии может быть отдан очень
быстро, если конденсатор разряжается на малое сопро-
тивление.
Найдем запас энергии конденсатора емкости С, одна
пластина которого заземлена, а другая имеет потенциал
<р0. Тогда количество электричества <70 = С
§ 4] ЭНЕРГИЯ КОНДЕНСАТОРА 499
На первый взгляд энергия равна произведению qaq>a.
В действительности это выражение хотя по порядку ве-
личины и правильно, но не точно; оно вдвое отличается от
истинного. Рассмотрим процесс зарядки конденсатора.
В момент, когда его потенциал равен <р, а заряд q, до-
бавка малого количества электричества dq увеличивает
энергию на
dW = <pdq. D.1)
Существенно то, что по мере зарядки сам потенциал <р
меняется, так как <p = ^q. Подставляя это значение ф
в D.1), получим:
±-qdq. D.2)
Проинтегрируем D.2) от q — О (незаряженный конденса-
тор) до q~qa; получим:
±^ ± { D.3)
Таким образом, точный расчет дает коэффициенту.
Рассмотрим процесс зарядки конденсатора от источника
напряжения через сопротивление (см. § 2, схема рис. 178).
Источник напряжения имеет постоянную э. д. с. Еа. По-
этому, когда протекает количество электричества dq, ис-
точник напряжения совершает работу Eodq (эта работа
совершается за счет соответствующего уменьшения хими-
ческой энергии источника напряжения). Следовательно,
полная работа, совершаемая источником напряжения, равна
Eaqa, где qa — полное протекшее количество электричества.
При зарядке конденсатора процесс заканчивается, когда
станет <р = ?0. При этом источник напряжения произведет
работу
Каким запасом энергии будет обладать конденсатор? Это
легко подсчитать по формуле D.3)
17*
500 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Куда же делась половина работы, совершенной источни-
ком? Покажем, что она пошла на нагревание сопротивле-
ния R. Для этого вспомним, что если через сопротивление
протекло количество электричества dq, то при этом выде-
лилась энергия
dA = q>Jfdq, D.4)
где <fR — разность потенциалов иа концах сопротивления.
Пользуясь тем, что dq = jdt, / = 5? можем D.4) преоб-
разовать к хорошо известному виду
Величина }*R = ^-p- представляет собой количество энер-
гии, выделяющейся на сопротивлении в единицу времени,
т. е. тепловую мощность.
Зависимость j(t) в случае зарядки конденсатора через
сопротивление была найдена в § 2
Поэтому
Е* ——
-?e *cdt.
Г xt
Энергия, выделившаяся за время t, есть
A(t) = -rr
Отсюда
A(t) = —
**
**
D.5)
Мы знаем, что при неограниченном возрастании величины
промежутка времени t потенциал <р неограниченно прибли-
жается к значению Ео. При этом, как видно из D.5), ве-
личина А неограниченно приближается к -=¦ СЕ%. Поэтому
§ 4] ЭНЕРГИЯ КОНДЕНСАТОРА 501
полная энергия, выделившаяся на сопротивлении,
A=-jCEl. D.6)
Таким образом, расчет подтверждает, что при зарядке
конденсатора половина энергии теряется на сопротивлении.
Коэффициент полезного действия зарядки всего 50%. За-
метим, что если прямо присоединить провод от источника
напряжения к конденсатору, то ничего не изменится, все
равно к. п. д. будет 50%, роль сопротивления /? возьмет
на себя внутреннее сопротивление источника напряжения,
который будет при этом нагреваться. Из формулы D.6)
видно, что энергия, бесполезно теряемая на сопротивлении
при зарядке конденсатора, не зависит от величины сопро-
тивления R, а следовательно, не зависит от того, насколько
быстро происходит зарядка.
Поскольку величина R не вошла в D.6), то эту фор-
мулу можно получить, не вводя R в промежуточные пре-
образования. Действительно, для схемы рис. 178 Фд-f-
+ Ф/?+Фс = 0' откуда фЛ = — фл — фс = Е, — ?. Поэто-
му dA = (Еа — ?- ] dq. Интегрируя это выражение от q = 0
до q = qa = EnC, получим:
Последний вывод справедлив и для случая, когда сопро-
тивление R меняется со временем. Предыдущий же вывод
был справедлив лишь для R = const, так как только в
этом случае можно применять формулы § 2.
Для того чтобы уменьшить потери при зарядке емкости,
нужно было бы поступать так: сначала взять источник
напряжения с малой э. д. с. Е1 и зарядить конденсатор до
потенциала ?,, затем первый источник напряжения отклю-
чить и присоединить второй источник с большей э. д. с. Ег.
Зарядив емкость до потенциала Et, отключить второй ис-
точник и подключить третий с э. д. с. Еа, и т. д. Выигрыш,
который при этом получается, легко видеть графически:
будем по оси абсцисс откладывать заряд конденсатора q,
по оси ординат — его потенциал ф. Они связаны зависи-
502 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [ч. VIII
мостью <р=?-<7, которая изображается прямой (рис. 184).
Энергия конденсатора равна площади треугольника ОАВ.
Работа, произведенная источником напряжения, равна пло-
щади прямоугольника 0ABD. Энергия, потерянная на со-
противлении, равна площади треугольника 0DB. В случае
Рис. 184.
зарядки конденсатора в несколько приемов сумма работ
всех источников напряжения равна площади, заштрихован-
ной на рис. 185. Предлагаем читателю найти коэффициент
Рис. 185.
полезного действия для случая, когда процесс зарядки
разбит на п этапов:
п
§ 4] ЭНЕРГИЯ КОНДЕНСАТОРА 603
Выше рассматривался конденсатор, одна пластина кото-
рого была заземлена, находилась при потенциале <px==0.
При этом энергия конденсатора зависит от потенциала вто-
рой пластины ф, W =~Сц>1 . Если ни одна из пластин
ие заземлена, то энергия конденсатора зависит от разности
потенциалов на пластинах <рс
Действительно, мы знаем, что заряд q на каждой плас-
тине конденсатора зависит от разности потенциалов, при
этом заряды на пластинах равны по величине и противо-
положны по знаку
Gл = Сфс, qB = — Сфс = — qA> dqA = —dqB.
При расчете изменения энергии в процессе зарядки надо
учесть изменение заряда обеих пластин. Пусть потенциал
пластины А равен ф1( потенциал пластины В равен <р,,
Фх — ф,==фс. Тогда
d W = ф1 dqA + ф, dqB — ф1 dqA — ф, dqA =
= (Фх — Ф,) dqA = фс dqA.
Так как фс = ^ , то
dW=±qAdqA. D.7)
Интегрируя D.7) от 0 до qA, получим:
Зная выражение энергии заряженного конденсатора в
зависимости от емкости, можно найти механические силы,
действующие между пластинами конденсатора. Представим
себе, что пластины конденсатора соединены механически
с каким-то рычагом и емкость С зависит от положения
рычага. Если положение рычага характеризуется значением
координаты х, то емкость есть С (*). При определенном по-
ложении рычага ха емкость конденсатора С(ха) = Са. Если
в этом положении конденсатор заряжен до потенциала ф0,
504 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
то заряд на пластинах qa = Caq>a, энергия конденсатора
2 2С„-
Отсоединим конденсатор от источника напряжения и будем
передвигать рычаг. Тогда заряд сохраняется постоянным
(потенциал меняется обратно пропорционально емкости),
энергия меняется
Электрическая энергия заряженного конденсатора подобна
упругой энергии пружины. Увеличение W(x) происходит
в том случае, если внешняя сила, приложенная к рычагу,
совершает работу. При этом внешняя сила преодолевает
силы, действующие на рычаг со стороны пластин конден-
сатора. Напротив, при уменьшении W (х) рычаг передви-
гается, совершая работу против внешних приложенных
сил. Можно сделать вывод, что сила, действующая на
рычаг со стороны пластин конденсатора, равна
F_ dw _ d ( <& \_ q\ dc (х) _
Г dx dx\2C(x)J 2[С(х)]*' dx
— ~2~ dx • У O)
Сила направлена в сторону увеличения емкости. Так,
например, если конденсатор состоит из двух равных па-
раллельных пластин, то емкость обратно пропорциональна
расстоянию между пластинами. Значит, емкость увеличи-
вается при сближении пластин. Действительно, при заря-
женном конденсаторе на пластинах находятся заряды
противоположных знаков, и пластины притягивают друг
друга тем сильнее, чем меньше расстояние между ними.
Формула D.8) позволяет найти силу и в более сложных
случаях, например в случае переменного конденсатора,
в котором одна пластина может перемещаться в зазоре
между двумя неподвижными.
dW
Важно обратить внимание на то, что производную —г-
мы брали при заданном постоянном заряде q. Однако
§ 3J цепь с индуктивностью 505
-г-
нельзя при нахождении силы по формуле г= -г- брать
производную огВ7 = —^ -, считая <р постоянным и учи-
тывая только, что С зависит от х. При этом мы получили
бы неправильный знак силы. Действительно, если конден-
сатор отсоединен от источника напряжения, то <р непосто-
янно, ф = Д-, С = С(лс). Если конденсатор присоединен к
С*
источнику напряжения, то при изменении емкости <р оста-
ется постоянным. Однако при этом меняется заряд q,
значит, через источник напряжения течет ток, т. е. источ-
ник напряжения совершает (при увеличении С) работу,
равную ydq. Следовательно, при постоянном <р при изме-
нении емкости, применяя закон сохранения энергии, надо
учитывать не только изменение энергии конденсатора и ра-
боту силы, но и работу, совершаемую источником напря-
жения.
§ 5. Цепь с индуктивностью
Рассмотрим цепь, состоящую из сопротивления R и ин-
дуктивности L (рис. 186). По формуле A.11)
<P* + <Pl = O. E.1)
Так как <рЛ = Rj, a q>L = Ljf , то, пользуясь E.1), находим:
Таким образом, ток » цепи (рис. 186) удовлетворяет урав-
L
нению г
-| R | г~00о0000
at L
Решение этого уравнения
/(/) = yte "г~*. E.3)
Таким образом, в цепи (рис. Рис. 186.
186) сила тока уменьшается
по показательному закону. Уменьшение силы тока в е раз
506 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. V11I
происходит за время
1 —W
Проверим размерность величины -5-. L измеряется в ген-
вольт-секунда _. вольт „
РИ' Т- е- В ампер ' ^-В 0Мах' Т- е- В Щц- П°"
этому размерность L есть «"»¦ секунда вольт_
3 v v R а*»пер ампер J '
? j 1 так что действительно -^
R, \-^ ооооол 'g-j имеет размерность времени.
Величину ^- будем назы-
вать временем нарастания.
Рис. 187. В схеме рис. 186, в кото-
рой нет источника напря-
жения, ток с течением времени стремится к нулю. Вопрос
о том, как в такой схеме создать начальное значение тока
/0, рассмотрим немного позже.
Сейчас рассмотрим схему, состоящую из источника с
э, д. с, равной Ео, сопротивления R и индуктивности L
(рис. 187). Из условия
вспоминая, что <ря=—?0, находим:
— Et + Rj + L% = 0. E.4)
Перепишем это уравнение так:
d\ _ R (Ей
Это уравнение аналогично уравнению B.5) из § 2 и ре-
шается точно таким же приемом. Получаем:
/@ = 1* + ^"^. E-5)
где значение А определяется из начального условия.
Пусть в начальный момент времени t = Q замкнули ру-
бильник, размыкающий цепь до этого момента. При этом
/@) = 0, потому что при разомкнутом рубильнике ток
§ 5]
ЦЕПЬ С ИНДУКТИВНОСТЬЮ
607
по цепи не шел. При таком условии находим Л
и E.5) принимает вид
С течением времени ток приближается к значению
/(~)=f. E.7)
Это значение тока не зависит от индуктивности L и про-
сто получается из закона Ома в цепи с э.д.с. Ел и со-
противлением R. Однако такое значение тока устанавли-
вается не сразу, а постепенно, и от индуктивности L за-
висит время установления тока: через время — ток
3b
Рис. 188.
Рис. 189
равен 0,63 /(оо), через время 2-^-ток равен 0,86/(оо),
через время 3 -^ ток равен 0,95 /(оо) и т. д. (рис. 188).
Согласно основному уравнению E.4) сумма разности
потенциалов на сопротивлении ./?/ и на индуктивности
L jj- равна э.д.с. ?0. Интересно проследить за каждым
членом в отдельности. Они показаны на рис. 189. В на-
чальный момент / = 0, Rj = 0, Ea<=L~; как говорят,
«напряжение целиком садится на индуктивность». С те-
чением времени ток приближается к постоянному значе-
нию, ^-стремится к нулю, «напряжение садится на со-
противление».
508
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIU
Интересно сопоставить решения, даваемые формулой
E.6) для одинакового Ео и разных /? и L. Пусть /?, ма-
ло, /?, велико, L, мало, L, велико. При разных комби-
нациях R и L получим четыре кривые зависимости тока
от времени, показанные на рис. 190. Конечный ток /(оо)
зависит только от R, он одинаков для /?,, L1 и для /?,,
Lt; j(<x>) одинаков также для пары кривых Rt, L, и
i?t, Lt. Начальная скорость нарастания тока зависит
Рис. 190.
только от индуктивности L и не зависит от сопротив-
ления.
Из соображений размерности очевидно, что установив-
шийся ток пропорционален начальной скорости нарастания
тока и времени нарастания. При нашем определении вре-
мени нарастания получается правильная формула, без ка-
ких-либо добавочных коэффициентов. Действительно, на-
dj Ев'
чальная скорость нарастания тока -г _ равна -?, время
нарастания
ток
= -q-, откуда и получается установившийся
__
R L
Как осуществить начальный ток /„ в схеме, с рассмо-
трения которой мы начали (рис. 186)? Для этого можно
взять схему рис. 191. Сначала замкнем рубильник А при
разомкнутом рубильнике В. Тогда в цепи пойдет ток, ко-
торый вскоре достигнет значения
согласно форму-
§ 6J РАЗМЫКАНИЕ ЦЕПИ С ИНДУКТИВНОСТЬЮ 509
ле E.7). Выберем Ео так, чтобы было R,9R =/0- Дож-
демся установившегося состояния, когда в схеме с зам-
кнутым А и разомкнутым В ток равен /0. В этом состоянии
замкнем рубильник В и разомкнем А. Получим схему
рис. 186, причем в начальный момент времени (в момент
замыкания В) в ней идет ток /„. Потенциал в точке / до
замыкания (р, = 0, так как в установившемся состоянии,
при постоянном /0, падение напряжения на индуктивности L
равно нулю. Потенциал в точке 2 до замыкания равен
L
С
I
УЗ.
Рис. 191.
<pt = /?/„. При замыкаиии рубильника В точка 2 оказывается
соединенной с «землей», потенциал в точке 2 <pt=0. Со-
ответственно перестраивается и потенциал в других точках
цепи. В частности, в точке/ потенциал теперь равен q>i=—R}'
§ 6. Размыкание цепи с индуктивностью
Выше был рассмотрен процесс установления тока в цепи
рис. 187, состоящей из источника напряжения, сопротив-
ления R, индуктивности L и рубильника. На рис. 188 по-
казана кривая нарастания тока, получающаяся при замы-
кании рубильника в момент ? = 0. С течением времени ток
р
достигает значения /, = ps- Что произойдет, если теперь
внезапно выключить рубильник В? Если ток прекратился
за очень малое время т, то производная тока по времени
gf ^ ~~ ' =—Ц-> т- е- производная по абсолютной
величине будет очень большой, если т очень мало. При
этом возникает очень большой по абсолютной величине
отрицательный потенциал в точке А: фд = ?^-=г=—L^-.
Разность потенциалов на сопротивлении R, равная Rj, и
510 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч.
э.д.с. источника при размыкании меняются мало. Поэтому
большая разность потенциалов, которая получается на ин-
дуктивности L, при размыкании почти целиком «садится»
на рубильник, т. е. разность потенциалов разомкнутых
пластин рубильника оказывается очень большой, порядка
L^-и может во много раз превосходить э.д.с. источника
тока Ев. При большой разности потенциалов происходит
L электрический пробой
воздушного промежутка
между разомкнутыми
пластинами рубильника
и между ними проскаки-
вает искра.
Задача об изменении
Рис- 192. тока в цепи при размы-
кании рубильника ока-
зывается очень сложной, так как сложны законы элек-
трического разряда в воздухе между пластинами. В са-
мом деле, до пробоя при ф < ф„ ток не идет; однако,
когда пробой произошел, сопротивление искры резко
падает, идет большой ток при разности потенциалов,
значительно меньшей фп. Отметим здесь только основной
факт: в цепи с индуктивностью при размыкании возникают
большие разности потенциалов; при замыкании такой цепи
г-1 1 Г |
В
L
—' (ГООООО""—|
Рис. 193.
разность потенциалов нигде не превышает Еа (э.д.с. источ-
ника).
Проследить количественно явление кратковременного
повышения разности потенциалов можно на примере двух
схем рис. 192 и 193. Отличие этих схем от схемы
рис. 187 заключается в том, что ток по индуктив-
ности L может идти и при разомкнутом рубильнике В,
§ 6] РАЗМЫКАНИЕ ЦЕПИ С ИНДУКТИВНОСТЬЮ 611
так что размыкание происходит без искры. Однако если
сопротивление /? гораздо больше сопротивления г, то при
размыкании возникает большая разность потенциалов на
индуктивности.
Рассмотрим, например, схему рис. 192. Будем считать,
что R^>r. Если рубильник замкнут, то в произвольный
момент времени ток в левой части цепи (г; Е) равен сумме
токов в параллельно соединенных R и L
При этом всегда <р? = фЛ. Пусть рубильник включен в мо-
мент t = 0. В этот момент весь ток идет через сопротив-
р
ление R, так что jro=fRo = R—Z— по закону Ома. При этом
E Ф«о = ?о г?т?; следовательно,^! =§ =х0==
= —¦ , р. По истечении достаточного времени после за-
мыкания в цепи установится постоянная сила тока.
В установившемся состоянии весь ток идет через индук-
тивность. Действительно, если ток / со временем не изме-
няется, то ^-=0, поэтому ф? = 0, а следовательно, <pJ? = 0,
откуда jR=0.
В установившемся состоянии <prOO=?'0, угао=/?ао = у.
Отсюда нетрудно получить порядок времени установления
тока т,
или
откуда
_L(R+r)^ L
1— rR — г '
Рассмотрим теперь размыкание цепи, произведенное че-
рез время t^>xt после замыкания, т. е. после того, как
в цепи установилось постоянное значение тока /оо =—•
Когда цепь разомкнута, j/. = je = O и /л + /? = °» откуда
512 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
}я=—jL, т. а весь ток, проходящий через L, должен
пройти через R в обратном направлении. По-прежнему, ко-
нечно, <pt = qv Поэтому ф/г=/?/д=—RjL или фл = —RjL.
Так как q>L — L-?j, то
L dt Wl'
Мы получили уравнение E.2), что вполне естественно, так
как правая часть схемы рис. 192 (после размыкания ру-
бильника) не отличается от схемы рис. 186.
Ток уменьшится в е раз за время ta = 3". При этом
т.^tj, так как R^>r. В момент размыкания ток имеет
Е
значение /?а0 = —^. После того как размыкание произошло,
но раньше, чем ток успел заметно уменьшиться, т. е. при
t размыкания <т,, получим:
Ф/г=<Pi = — RJloo — — Е о — •
Таким образом, при размыкании можно получить раз-
ность потенциалов, во много раз превышающую э.д.с.
источника напряжения. Этот принцип широко используется
в технике, в частности в системе зажигания двигателей
внутреннего сгорания. Отметим, что эта большая разность
потенциалов имеет место в течение весьма малого проме-
жутка времени.
Мы привели приближенное рассмотрение задачи — без
производных и высшей математики. Точное рассмотрение
задачи о замыкании рубильника в схеме рис. 192 дает сле-
дующее. Исходя из соотношений
получаем дифференциальное уравнение
dt i
EaR
dt
a
В начальный момент времени f = 0 ток через индуктив-
ность равен нулю, т. е. /L = 0 при f = 0. Поэтому
§ 7]
Ток в цепи
энергия индуктивности
513
На рис. 194 приближенное решение соответствует ломаной,
точное — плавной кривой.
Рекомендуем читателю рассмотреть процесс изменения
тока и разности потенциалов при замыкании и размыкании
рубильника в схеме рис. 193. Полезно решить задачу
г, 2t, Зг,
Рис. 194.
дважды: один раз, составляя дифференциальное уравнение
и отыскивая его решение в виде показательной функции,
другой раз приближенно, подобно тому, как была рассмот-
рена схема рис. 192.
§ 7. Энергия индуктивности
Выше мы видели, что в схеме, состоящей только из
индуктивности L и сопротивления R, уже после того, как
эта схема отсоединена от источника напряжения, продол-
жает идти ток, постепенно затухающий с течением времени.
При этом в сопротивлении выделяется тепло в количестве
Rj1 в единицу времени.
Откуда берется та электрическая энергия, которая, в со-
противлении превращается в тепловую? Ее отдает индук-
тивность, обладающая определенным запасом энергии.
Найдем этот запас энергии, рассматривая простейшую
схему рис. 186 и подсчитывая всю тепловую энергию, ко-
торая выделится в сопротивлении R. В этой схеме пусть
514 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
в начальный момент ? = 0 ток равен /0. С течением вре-
мени ток убывает по закону
= /.« Х. E-3)
Количество энергии, выделяющееся на сопротивлении R
в единицу времени, т. е. скорость выделения энергии, есть
мгновенная тепловая мощность h. Пользуясь E.3), находим:
Зная А, нетрудно найти полное количество тепла, выде-
лившееся за время от начального момента t = 0 до беско-
нечности (до полного затухания тока). Для этого доста-
точно проинтегрировать G.1) от / = 0 до? = оо. Получим:
iU L dt = Rjl§e- Ldt = Rjl± = ^. G.2)
о о
Это тепло равно запасу энергии индуктивности, по которой
идет ток /0. Запас энергии не зависит от величины сопро-
тивления R. Индуктивность L с током j0 имеет определен-
ный запас энергии, который, в конце концов, весь превра-
щается в тепло, независимо от величины сопротивления R.
От R зависит только скорость превращения энергии в тепло,
но не общее количество энергии.
Формулу G.2) можно также получить, рассматривая
процесс нарастания тока в индуктивности. Действительно,
мощность тока (работа в единицу времени) равна <р/. Эта
работа, совершаемая внешними источниками тока, тратится
на увеличение энергии индуктивности W
Л = ^ = Ф/. G.3)
Пользуясь тем, что q> = L~-, получим из G.3)
dW TidI l I d(/1) G 4)
Будем считать, что при t = Q / = 0, W = 0, при t = ta
j=ja, W'=Wii. Тогда, интегрируя G.4) от t=* 0 до t*=ta.
§ 7] ЭНЕРГИЯ ИНДУКТИВНОСТИ 515
получим:
л? _L / ;*
Для конкретности можно представить себе схему рис. 187
(ф = фд) и для нее произвести подробный расчет нараста-
ния энергии индуктивности. В установившемся режиме,
когда ток достиг постоянного значения /„, <рл = 0, энергия
индуктивности не меняется, однако источник э.д.с. для
поддержания постоянного тока /в должен продолжать рас-
ходовать энергию, которая выделяется в виде тепла в
сопротивлении R.
Энергия индуктивности W пропорциональна квадрату
силы тока, т. е. пропорциональна квадрату скорости дви-
odt
Рис. 195.
жения электронов. Поэтому по внешнему виду W напо-
минает кинетическую энергию. Не есть ли W кине-
тическая энергия электронов? Сравним порядок величины W
и энергии электронов. Располагая медной проволокой
длиной 100 л«=10* см и диаметром 0,35 мм (сечение
10~* смг), можно намотать катушку, индуктивность кото-
рой составит 0,02 гн. При токе 1 а в такой катушке
W = 0,02 -Г -0,5 =10~* дж — \0* эрг. Найдем кинетическую
энергию электронов. Будем считать, что на каждый атом
меди приходится один электрон, участвующий в про-
хождении тока («электрон проводимости»). Атомный вес
меди около 63, так что на 63 г приходится 6-10" элект-
ронов проводимости, или примерно 10" электронов в од-
ном грамме. Удельный вес меди около 8 г1см*, поэтому
в 1 сма содержится примерно п = 8-10" электронов про-
водимости. Можно представить себе кусок проволоки дли-
ной v dt и сечением S слева от сечения О (рис. 195). Если
516 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
скорость электронов *) равна v см/сек, то через площадь Scm*
за время dt проходит электронов («штук») Snudt. За вре-
мя dt электроны, находившиеся в сечении А, перейдут
в сечение О, значит, за это время через О пройдут все
электроны, которые находились в объеме между О и Л,
т. е. в объеме цилиндра длиной v dt н с основанием 5.
Обозначим через е заряд одного электрона в кулонах,
е = —1,б«10~10к. Количество электричества, которое пе-
реносят за время dt эти Sn v dt электронов, равно току в ам-
перах, умноженному на время dt. Поэтому Snvedt = jdt,
откуда j = Snue или и=^- Подставим j=\a, S=
= 10"' см, п = 8-10", е = — 1,6-10-"; найдем:
Найдем теперь кинетическую энергию электронов. Масса
электрона т = 9-10~**г. Общее число электронов, движу-
щихся в проволоке, равно
10* см-10-» см1-8-10" —,=s 10".
Кинетическая энергия равна
Т = ~ =9-l0-"-l0t*.^^^3-l0-t эрг.
Таким образом, кинетическая энергия электронов составляет
ничтожную долю энергии индуктивности, хотя она и за-
висит от силы тока по тому же закону (пропорциональна /*),
что и энергия индуктивности. Физическая энергия' индук-
тивности есть энергия того магнитного поля, которое появ-
ляется в катушке, когда по ней течет ток.
Отметим сходство и различие между емкостью и индук-
тивностью. Как емкость, так и индуктивность могут слу-
жить резервуарами, хранилищами энергии. При помощи
индуктивности, так же как и при помощи емкости, можно
накопить электрическую энергию от слабого, маломощного
первичного источника тока и затем быстро ее выделить
в нужном месте в нужный момент.
*) Имеется в виду средняя скорость их движения в направлении
тока, а не скорость хаотического теплового движения-
§ 7] энергия индуктивности 517
Конденсатор можно заряжать малым током /, в течение
большого времени tx\ быстро разряжая его через малое со-
противление, за малое время tt можно получить большой
ток j^-j1. Разность потенциалов конденсатора не превы-
шает при этом э.д.с. первичного источника. Конденсатор
позволяет увеличить ток, но не напряжение.
Через индуктивность можно пропускать большой ток
при малом напряжении (малой э.д.с.) Еа первичного источ-
ника. Для этого нужно только, чтобы сопротивление ин-
дуктивности и первичного источника тока было бы доста-
точно мало. При этом большой ток в индуктивности уста-
навливается не сразу, а за сравнительно большое время ta.
При замыкании индуктивности на большое сопротивление
удается получить большую разность потенциалов <р на ма-
лое время ?4, причем ф=^Е„т2-. Индуктивность позволяет
увеличить напряжение, но не ток.
Существенное практическое отличие емкости от индук-
тивности заключается в том, что конденсатор, отсоединен-
ный от источника тока, может очень долго, часами и даже
сутками, сохранять запасенную в нем энергию. Время раз-
рядки конденсатора равно RC, где С — емкость конденса-
тора, R — так называемое сопротивление утечки. Применяя
хорошие изоляторы, удается получать огромные значения R,
т. е. очень большое время разрядки. Индуктивность, вы-
полненная в виде катушки и замкнутая накоротко, т. е.
с минимальным возможным сопротивлением, при наличии
в ней электрического тока сохраняет энергию лишь на про-
тяжении долей секунды.
Время затухания тока имеет порядок-н-, но, даже при-
меняя наилучшие проводники (медь, серебро), нельзя сде-
лать -=- больше нескольких секунд для катушки лаборатор-
ных размеров. Заметим, что при увеличении числа витков
катушки в данном объеме за счет применения более тон-
кой проволоки увеличивается L, но увеличивается и R, их
отношение по порядку величины не изменяется. Поэтому
в лабораторных условиях индуктивность удобно применять
для повышения напряжения, но не для длительного хра-
нения энергии.
518 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VII]
В схемах, использующих емкости и индуктивности,
удается накапливать энергию от батареи карманного фонаря.
Такая батарея дает несколько вольт при внутреннем сопро-
тивлении в несколько ом, так что максимальная мощность
ее порядка 1—2 вт. При помощи вышеупомянутых схем
удается получать мощность в сотни киловатт. Однако та-
кая мощность действует в течение времени порядка 10"* сек.
Выше было отмечено, что в индуктивности электриче-
ская энергия быстро превращается в тепло за счет сопро-
тивления. Это утверждение справедливо для катушек обыч-
ного «комнатного», лабораторного, масштаба и в случае
обычных, нормальных, температур. Однако в двух крайних
случаях это утверждение оказывается неверным.
1. При очень низкой температуре, порядка — 260QC и
ниже, до абсолютного нуля (— 273" С), многие металлы
(например, свинец, ртуть, но не медь) переходят в так на-
зываемое сверхпроводящее состояние. Их удельное сопро-
тивление становится в точности равным нулю.
Голландский ученый Каммерлинг-Онес, открывший
это явление в 1911 г., наблюдал в кольце из сверхпрово-
дящего материала постоянный ток, который не ослабевал
в течение многих суток. Наличие тока в таком кольце об-
наруживается по магнитному полю этого тока.
Возможности практического применения сверхпроводни-
ков ограничиваются не только трудностью получения низ-
кой температуры. Сильное магнитное поле переводит сверх-
проводник в нормальное состояние (с конечным сопротив-
лением). Поэтому через сверхпроводник нельзя пропускать
большие токи *).
2. Соотношение между индуктивностью и сопротивле-
нием и условия затухания тока очень сильно изменяются
при увеличении всех размеров катушки и особенно при
переходе к астрономическим явлениям**).
Представим себе две геометрически подобные катушки,
одна из которых в п раз больше другой. При этом число
витков в обеих катушках одинаково. В большой катушке
*) В 1961 г. открыт сплав редкого элемента ниобия с оловом,
в котором ток до 100 000 а\см* и магнитное поле до 250 000 гс еще не
разрушают сверхпроводимости.
•*) Сравните с задачей 3 к § 2: для емкости с сопротивлением
время разрядки не изменяется при изменении всех размеров.
§ 7J энергия индуктивности 519
в п раз больше диаметр катушки, но во столько же раз
больше и высота катушки и диаметр проволоки, из кото-
рой сделана катушка. Пусть катушки изготовлены из
одинакового материала. Будем обозначать величины, отно-
сящиеся к меньшей катушке, индексом 1, а величины,
относящиеся к большей катушке, индексом 2. Подсчитаем
отношение сопротивлений катушек
где q—удельное сопротивление материала катушки, / —
длина проволоки, S — площадь ее поперечного сечения.
Геометрически ясно, что
и, следовательно,
Сопротивление обратно пропорционально п, т. е. обратно
пропорционально размеру.
Можно доказать, что индуктивность большой катушки
ровно в п раз больше индуктивности малой катушки,
т. е. при увеличении линейных размеров катушки в п раз
ее индуктивность увеличивается также в п раз. Время
затухания тока т имеет порядок -=>-, следовательно,
1 % t 1 I
Таким образом, время затухания тока пропорционально
квадрату размера. Если бы земной шар состоял из медн,
то время затухания тока в нем было бы порядка
10"— 101в сек, т. е. 10" лет.
Проводимость ионизованных газов того же порядка,
что и проводимость меди, поэтому в астрономических
явлениях время затухания тока оказывается огромным.
Это значит, что сопротивление, закон Ома, не играют
никакой роли в этих явлениях: напомним рис. 190, ток
520 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
на начальном участке кривой зависит только от L, но не
от R; в астрономии мы всегда находимся на «начальном
участке».
Земной магнетизм представляет собой магнитное поле
токов, протекающих в вязкой расплавленной массе цен-
трального ядра Земли. Медленные движения этой рас-
плавленной массы в самом этом магнитном поле поддер-
живают эти токи, как движение якоря динамо-машины
в магнитном поле поддерживает ток в обмотке якоря
и в обмотке электромагнита.
§ 8. Колебательный коитур
Рассмотрим контур, состоящий из емкости С и индук-
тивности L (рис. 196). Пусть точка В контура заземлена.
По формуле A.11) фс-|~ф? = 0. Здесь ф? = L -^, фс = ^-.
с __ Падение напряжения на ем-
11 /1 ОППУДСТДУ4 кости фс будем обозначать
11 д П ппосто ш. Тогда
Н:
Фс
просто ф. Тогда
Заметим, что / = ^. По-
с. 196. dj d?q т,
этому •^=5р-. Так как
=С-трг, то, пользуясь соотношением (8.1), находим:
или
^ L
dtt — LC
Аналогичное уравнение мы рассматривали в части V
при изучении механических колебаний. Там было уста-
новлено, что решением (8.2) являются функции ф=Л sin о/
и cp = ?cosW при любых Л и В и надлежащим образом
подобранном со. Проверим это, например, для y = As'm<iit
и попутно определим о. Для этого фи^ подставляем
в (8.2).
§ 3] КОЛЕБАТЕЛЬНЫЙ контур 521
Получим
— ALCvf sin (at =-- — A sin arf
или, сокращая на —A sin (at,
Отсюда находим:
(8-3>
Следовательно, решением уравнения (8.2) являются функ-
ции, описывающие колебания с круговой частотой . ;
период таких колебаний равен
Т = ^ = 2яУт. (8.4)
Проверим размерность (8.4): размерность емкости-—
гу-,, . кулон ампер-секунда
[С] = фарада = -^_= j^f , размерность индук-
ГТ , вольт вольт-секунда
тивности - [L] = генри = ампер/секунда = амперУ . так
что действительно V^LC имеет размерность секунда.
Обратимся к подробному рассмотрению решения урав-
нения (8.2). Решения <p = .<4sin(o/ и <p=»?Jcos(orf по суще-
ству не отличаются одно от другого, так как кривая
синуса получается из кривой косинуса сдвигом по оси t.
Поэтому рассмотрим одно из решений, например
Ф = В cos (at.
Амплитуда В может быть любой. При заданном
найдем зависимость тока от времени
/=С ^ = — СВ со sin at.
1 at
Найдем энергию емкости и энергию индуктивности
w Сф2 СВ1 t . m Lj1 L&B'a* . t .
W(~=^-=-Y-cost(xit, WL=-?- = —^ sin'orf.
Подставляя сюда выражение о (8.3), получим:
522 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Полная энергия, как и следовало ожидать, от времени не
зависит; действительно,
Р =WC + WL=^ (cos* orf+ sin*
Таким образом, движение зарядов контура, составлен-
ного из емкости и индуктивности, похоже на движение
массы, закрепленной на пружине. Энергию заряженного
конденсатора можно уподобить упругой энергии пружины,
которая максимальна в момент, когда масса находится
в крайнем положении, на максимальном расстоянии от
положения равновесия. Энергию индуктивности можно
уподобить кинетической энергии движущей массы. В мо-
мент, когда заряд емкости равен нулю, ток достигает
максимального значения (по абсолютной величине); в этот
момент энергия емкости равна нулю, а энергия индук-
тивности равна полной энергии (cos* (at = O, 8Ш*<о/=1).
Точно так же при колебаниях массы на пружине в мо-
мент, когда масса проходит через положение равновесия,
потенциальная энергия равна нулю, а кинетическая энер-
гия равна полной энергии колебаний.
Назовем общей задачей задачу о нахождении потен-
циала в контуре при условии, что в начальный момент
времени ? = 0 /=/„, ф = ф0. Ни решение <p = j4sinorf, ни
решение <p = Bcoso)f не дают нам возможности решить
общую задачу. Для решения общей задачи образуем
сумму
Ф = A sin <ot -\- В cos Ы. . (8.5)
Легко проверить, что эта сумма является решением урав-
нения (8.2).
При этом
p t — CB(osit\(ot. (8.6)
Полагая / = 0 в формуле (8.5) и (8.6), получим:
откуда найдем решение с заданными ф0 и /0
Ф= ^-sim (ot-\-<$a cascot, /.==/„ cos©* — Сф0со sin co?. (8.7)
§ 8] КОЛЕБАТЕЛЬНЫЙ КОНТУР 623
Предлагаем читателю проверить, что при таких колеба-
ниях полная энергия постоянна и равна начальной
энергии
Выражение (8.7) для <р можно записать в виде
<p = <pOTcos(orf-|-a) (8.8)
с амплитудой фя. В момент, когда cos(W-f-a)= ± 1,
вся энергия есть энергия емкости, т. е. —^. Ввиду
Сф*
того, что полная энергия сохраняется, находим —^р- =
= -2i + -si, откуда <pm= у ф? -\--q-j\. Из выражения
(8.8) находим: / = —С<рт<й sin (Ш-{-а.)=С<рт(д sin (at-j-a,) =
= fmsim(<ot-{-a.1), где «, = «4-», ]m = C<pm(o. Закон
сохранения энергии дает:
откуда
/„= V л+f Ф»-
Конечно, значения фя и \т можно получить и без
энергетических соображений, пользуясь формулами три-
гонометрии.
Схема для осуществления колебаний показана на
рис. 197. В схеме имеется источник напряжения Ей.
Если замкнуть А при разомкнутом В, то по истечении про-
межутка времени x^>RC после замыкания емкость будет
заряжена до потенциала Еа. Разомкнем А и после этого
в момент ? = 0 замкнем В. Тогда в цепи, состоящей из
L и С, начнутся колебания с ф = фо = ?о, / = 0 в момент
f = 0. Отметим, что при этих колебаниях разность потен-
циалов на пластинах разомкнутого рубильника А будет
периодически меняться от 0 до 2Е0.
524
ЭЛЕКТРИЧЕСКИЕ ЦЕПН И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Возможен другой вариант возбуждений колебаний
в схеме рис. 197. Сперва замыкаются оба рубильника А
и В. Тогда в цепи устанавливается ток /0 = -н8. Затем
в момент ?=0 размыкается рубильник А. При этом
в контуре, состоящем из! иС, начинаются колебания,
Рис. 197.
причем в начальный момент <р„=0 /0 = ^?. При этих
колебаниях максимальная амплитуда потенциала достигает
Напомним, что в схеме без емкости при размыкании
цепи, содержащей индуктивность L, на рубильнике раз-
вивается тем большая разность потенциалов, чем больше
сопротивление воздушного промежутка между пластинами
рубильника. При размыкании такой цепи (без емкости)
между пластинами рубильника обязательно возникает
разряд в воздушном промежутке. При наличии емкости
максимальная разность потенциалов между пластинами
рубильника А не превышает определенного значения
(Е0~\-<рт). Если это значение меньше того, которое необ-
ходимо для зажигания разряда в воздушном промежутке
рубильника, то разряда не будет: говорят, что включе-
ние емкости С «гасит» разряд при размыкании цепи
с индуктивностью. Отметим, что величина -р~ К "с может
быть больше единицы. Тогда, размыкая рубильник В
через четверть периода после размыкания А, получим на
емкости С потенциал более высокий, чем потенциал источ-
ника тока Еп.
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
525
Упражнения
1. Определить а в формуле (8.8).
^•Рассмотреть изменение потенциала со временем в цепи
рис. 198. Определить наибольшее значение <р и время, когда дости-
Рнс. 198.
гается это наибольшее значение. Считать, что рубильник А в схеме
замыкают в момент t = 0.
3. В предыдущей задаче найти внергию емкости и внергпю, отдан-
ную источником тока в момент, когда ф максимально.
§ 9. Затухающие колебания
Рассмотрим контур, в котором последовательно с индук-
тивностью включено сопротивление R (рис. 199). Будем
считать, что R мало. Если R совсем не принимать во
внимание, то мы получим схему рис. 196, которая была
ооооооо^
Рис. 199.
изучена в § 8. Если при г = Обылоф = ф0, /=0, то по (8.7)
Ф = ф0 cos оЛ / = jm sin (а/ + я), (9.1)
где положено
/» = Сф0со, ш = ^==. (9.2)
При этом полная энергия Р — -^- или, пользуясь (9.2),
526 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VUI
можно записать также:
При наличии сопротивления происходит превращение
электрической энергии в тепловую. Тепловая мощность h
равна
h=Rjt= Rj*m sin*((o^ + л) = Rjl sin* at =
= ^A— cos2(ot). (9.4)
Тепловая мощность при электрических колебаниях не
остается постоянной, на протяжении каждого периода h
дважды достигает максимума и дважды обращается
в нуль *). Найдем среднее значение h за период. Из фор-
j^
мулы (9.4) находим h = ~^{\—cos 2atf)l вспоминая, что
среднее значение косинуса за период равно нулю, полу-
чаем;
Выделение тепла на сопротивлении R может происходить
только за счет уменьшения электрической энергии Р.
Поэтому
~ = -h. (9.5)
Мы предположили, что R мало, значит, и h мало.
Энергия колебаний убывает медленно, значительное изме-
нение энергии заметно лишь по истечении нескольких
периодов. Рассматривая промежутки времени, большие по
сравнению с периодом колебаний Т, заменим в правой
части (9.5) h на h
Поскольку энергия Р медленно меняется, то из (9.3) ви-
*) Знак ее, конечно, не изменяется.
§ 9J ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 527
дим, что и fm есть медленно меняющаяся величина. Вы-
разив /„ из (9.3), получим:
U = |/^? . (9.7)
Пользуясь (9.7), получаем из (9.6)
dP J*_p
dt L
Решение этого уравнения есть
Р = Я е~~*-*
где Яо— это значение Р при t = 0. Поэтому согласно (9.7)
Тогда
/= |/^0e~2Tsin(^-l-jt). (9.8)
Вспоминая, что <p = <p0cos a>t, а фо = ^-, получаем*
t. (9.9)
Формулы (9.8) и (9.9) показывают, что при наличии не-
большого сопротивления электрические колебания зату-
хают по показательному закону.
Выписанное выше решение получено при помощи при-
ближенного расчета. Заметим, что в этом приближенном
решении не удовлетворяется соотношение ]'==CdT' хотЯ
оно выполнено тем точнее, чем меньше R. Постараемся
теперь решить задачу точно. Для схемы рис. 199 имеем
соотношение ф-{-ф/?-{-ф?==О' откуда
,p_|_#/-f_Lfy = 0, (9.10)
dt
причем ] = С-~-. Подставляя в (9.10) выражение для /
528 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
и ^» находим!
?. (9.11)
Будем искать решение уравнения (9.11) в том же виде,
который мы получили в приближенном рассмотрении, т. е.
4> = Ae-ktcos<ott (9.12)
где к, ш, А — постоянные числа, которые надо определить.
Выражения для <р и его производных подставим в урав-
нение (9.11) и сократим все члены на общий множитель
Ае~и. Получим:
LCK* cos <ot -{- 2?СА.ш sin <ot — LC<o* cos <ot =
= — 4cos at -f- RCk cos (ot -f- RC<u sin att.
Для того чтобы это равенство имело место при любом t,
нужно, чтобы были равны справа и слева коэффициенты
при cos (at и при sin ш/ в отдельности
LOS— LCa>* = RCX— I, (9.13)
(9.14)
Условие (9.14) дает ^=~т-, после чего из (9.13) получаем:
ш =
Постоянная А из уравнения (9.11) не определилась.
Величина этой постоянной определяется из начального
условия: при ? = 0 <р = <р0. Наконец, зная <р@» легко
найдем/=С^. Получим:
/ = — САе~и(ы sin at-{-к cos at). (9.16)
Сравнивая точное решение с приближенным, отметим
следующее: 1) в приближенном рассмотрении задачи мы
правильно определили число А., характеризующее скорость
затухания колебаний. Однако приближенное решение не
дает зависимости частоты со от величины сопротивления R;
2) формула для тока несколько отличается от той, кото-
рая была получена приближенно.
¦ случай большого сопротивления
529
Точно таким же способом можно показать, что урав-
нение (9.11) имеет еще одно решение
<р = Ве~и sin <ot, (9.17)
причем о и А. те же самые. Соответствующая сила тока
j = CBe~u(to cos (ot — X sin <at). (9.18)
Сумма решений (9.12) и (9.17) также является реше-
нием уравнения (9.11). Только при помощи этой суммы
можно решить общую задачу: найти решение уравнения
(9.11) с начальным условием при ? = 0 Ф = ф0, / = у0-
Действительно, тогда для коэффициентов А и В получаем
уравнения
откуда
- /„
Ссо
Упражнения
1. Найти j(t) в схеме рис. 199, если C=l, L = \, Я =.-0,1;
0,5; 1. При < = 0ф=1, / = 0.
2. Тот же вопрос, если при / = 0 <р = 0, /=1.
тпяяпяяг
Рис. 200.
3. Приближенным методом найти скорость затухания колебаний Л
в схеме рис. 200, считая, что R весьма велико.
§ 10. Случай большого сопротивления
Рассматриваемый здесь случай большого сопротивления
представляет главным образом математический интерес
и не связан с дальнейшим материалом. Поэтому в первом
чтении этот параграф может быть пропущен.
18 Я. Б. Зельдович
530 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Решение уравнения (9.11), полученное в предыдущем
параграфе, справедливо лишь для не слишком больших У?.
Действительно, из (9.15) видно, что если R>2 у q-* то
о смысла не имеет, так как под корнем получается отри-
цательное число. В этом случае уравнение (9.11) имеет
решение другого вида. Будем искать решение в виде
Ф = Ле~Р* (соответственно / = — АС$е~$*). Подставляя
в (9.11) выражения для <р и его производных и сокращая
все члены на Ае~?*, получим:
Это — квадратное уравнение для р. Решая его, найдем:
Подкоренное выражение в A0.1) отличается знаком от
подкоренного выражения в формуле (9.15) для со. Следо-
вательно, как раз в тех случаях, когда нельзя найти ш,
можно найти р. Формула A0.1) дает два различных зна-
чения р, поэтому можно составить два решения уравне-
ния (9.11)
А№ и
Решением будет и их сумма:
Ч> = Ае-Ы-\-Ве-М. (Ю.2)
Соответственно
/ = — ЛСР.в-fM — ВСр,е-М. (Ю.З)
Если при * = 0 ф = ф0, /=/„, то, полагая f = 6 в A0.2)
и A0.3), получим:
Из этой системы уравнений можно найти А и В.
Рассмотрим более подробно выражение для р. Пусть
Y\ Yw-Tc=& Y I-We можно
We
разложить по формуле бинома Ньютона. Ограничимся
двумя членами
R T/\ AL R_f. 1_ 41^\ R_ 1_
2L V R*C 2L\ 2 R*C) 2Z. RC *
§ Ю] случай большого сопротивления 531
Поэтому
Pl~~2L I 2Z. RC—L -RC ~Г'
так как R велико,
R _R_ __Я| 1_ J_
Р« 2Z. 2Z. ' ЯС RC '
Эти значения pt и р знакомы нам из §§ 1—5. Действи-
тельно, Pj соответствует затуханию тока по закону е L ,
т. е. как в цепи, составленной только из индуктивности
и сопротивления (см. § 5). Второй корень {$2 соответствует
затуханию тока по закону е RC, т. е. как в цепи, со-
стоящей только из емкости и сопротивления (см. § 2).
Представляет математический интерес частный случай,
когда подкоренное выражение в A0.1) точно равно нулю
R*___L
AL1 LC '
так что оба корня р, и р, совпадают. Мы получаем
только одно решение уравнения (9.11). Однако для того
чтобы решить задачу с начальными условиями при*=0,
ф = Ф0, / = /0, нам надо два решения.
Как найти второе решение? Предположим, чтор\=?р\,
но Pi — ps — малая величина. Тогда мы имеем два реше-
ния: е~м и е~Р*'. Их разность также является решением.
Запишем это решение так:
е - Pi' е ~ Р*' -= е - Р»' [е<Р* - &»>' — 1 ].
Так как Р8—р, мало, то*) е«"«-*>*=& 1+(?• —Pi)'»
откуда
Последнее выражение наводит на мысль, что в случае
р2 = Р, = Р надо второе решение брать в виде <p = Bte-P'.
Подставляя это <р в уравнение (9.11) и учитывая, что
*) В ряде Тейлора можно удержать только два члена.
18*
532 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
о
Р = 2? > увидим, что уравнение действительно удовлетво-
ряется. Итак, в случае p\ = pt = p надо брать <р в виде
Такое ф (и соответствующее j) позволяет решить задачу
с любыми начальными <р0 и /0.
Упражнения
1. Найти ф (О при / = 0, фо = 1, /„ = 0 для L=;l, C=l,
# = 2; 6; 10.
2. Найти ф (t) для L = l, C=\, R = 2; 4 при условии, что
при *=0 <ро=1, /„=1.
§ 11. Переменный ток
В отличие от рассматривавшихся ранее схем теперь
будем рассматривать схемы, в которых источник напря-
жения имеет э. д. с, периодически меняющуюся со вре-
менем, с определенной заданной частотой о. Эти задачи
имеют большое значение для радиосхем. Частота перг-
менного тока совершенно по-разному влияет на прохож-
дение тока чергз индуктивность и емкость. Чем больше
частота, тем быстрее меняется ток, тем «труднее» он
проходит через индуктивность, тем больше разность потен-
циалов, создаваемая током данной силы. Напротив, на
пластинах конденсатора разность потенциалов тем меньше,
чем больше частота. При увеличении частоты уменьшается
период и, следовательно, уменьшается время, в течение
которого ток, сохраняя свое направление, заряжает кон-
денсатор. Поэтому с увеличением частоты уменьшается
заряд конденсатора, уменьшается, разность потенциалов
на его пластинах.
Мы уже отмечали в § 8, что движение зарядов в кон-
туре, состоящем из индуктивности и емкости (контур L, С),
можно уподобить колебанию тела, подвешенного на пру-
жине: если при колебании тела периодически меняются
его расстояние от начала координат и скорость, то в кон-
туре периодически изменяются потенциал и сила тока.
Частота, с которой колеблется тело под действием
упругой силы пружины (при отсутствии всяких других
сил), называется собственной частотой колебаний. Подобно
§ II]
ПЕРЕМЕННЫЙ ТОК
533
этому частота колебаний потенциала в контуре L, С
называется собственной частотой этого контура.
Развивая эту аналогию дальше, можно предположить,
что если контур включен в цепь переменного тока, т. е.
периодически меняется подаваемый на контур потенци-
ал, то будет иметь место явление резонанса. Оно состо-
ит в том, что амплитуда колебаний максимальна при ча-
стоте тока ш, равной собственной частоте контура «0.
Амплитуда очень резко возрастает при приближении
(ш — (о0) к нулю. Явление резонанса на самом деле имеет
место, оно будет рассмотрено в § 13.
Для каждого двухполюсника (см. стр.' 488, рис. 175),
включенного в цепь переменного тока, есть определенное соот-
ношение между разностью потенциалов и силой тока.
Найдем это соотношение сперва для наиболее простого
случая отдельных элементов R, L, С, с тем чтобы потом
(в §§ 13 и 14) выяснить, как находить это соотношение
для более сложных схем.
Будем рассматривать переменный ток определенной
частоты о; как и раньше, частота о связана с периодом
соотношением
2л
у.
Так, например, в СССР
широко применяется
50-периодный ток: Т =
= ^ сек, ш = 2я-50 =
= 314 —.
сек
Представим себе схе-
му, показанную на рис. Рис. 201.
201. В цепь включены
амперметр А, показывающий силу тока /, и вольт-
метр V, измеряющий напряжение (разность потенциа-
лов). Допустим, что амперметр и вольтметр настолько
безынерционные, быстродействующие, что они позволяют
измерять мгновенное значение тока в каждый момент, и,
следовательно, показания их изменяются с периодом,
равным периоду тока. Практически такой опыт проводится
с помощью осциллографа, так называемого шлейфового
со
534 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VUI
осциллографа с двумя шлейфами, или с помощью катод-
ного осциллографа с двумя лучами. Положительное на-
правление тока показано стрелкой. Вольтметр V измеряет
величину ф = фд—фд. Включая тот или иной рубильник,
исследуем прохождение тока через сопротивление, индук-
тивность или емкость.
Пусть ток меняется со временем по закону
/ = /. сов («/ + <*). A1.1)
Если этот ток идет по сопротивлению R, то по закону
Ома
Фя== Rj = Rja cos (ш* + а). A1.2)
Для общности запишем это равенство так:
где ф1==Я/„ «=06,.
Пусть ток A1.1) идет через индуктивность L. Тогда
Фй = L -§- = — L(o/O sin (со* + а).
Положим
а,). (П.З)
Тогда ф1 = ?<в/0, oit=oi-\~-~. Действительно, известно,
что при любом р
cos (р+-5-)==-sin р,
поэтому
cos
Таким образом, в случае переменного тока соотноше-
ние между амплитудой тока / и амплитудой напряжения ф±
в индуктивности такое же, как в сопротивлении, равном
Rt = L(o. При этом если L выражено в генри, ш в обрат-
ных секундах, то Rt выражено в омах.
Отличие индуктивности от сопротивления проявляется
в том, что кривая напряжения сдвинута относительно
кривой тока на четверть периода (рис. 202). В этом можно
535
§11] ¦ ПЕРЕМЕННЫЙ ТОК
убедиться и непосредственно по формуле
— sin((o?-{-a) = cos f(otf-{-a-{--2-j=»
= cos о (t -\- ?
Пусть функция cos {(at + а), которой пропорционален ток,
Рис. 202.
достигает какого-то ^определенного значения в момент tx
cos(u>r1-|-a) = a.
Функция cos ((dt~\-a. -{--тг ) » которой пропорционально на-
пряжение на индуктивности, достигает того же значения а
в некоторый другой момент времени tt, так что
cos
Поэтому
-TJ- = e>'i. откуда ti = t1 — -^ = t1 —^
т. е. напряжение опережает ток на четверть периода.
Разумеется, можно прибавить к tx любое целое число
Т 3
периодов, так что можно писать tx=t1 ---\-T = tl-\- -^T
или tt = t1-\--^T. В формуле найден наименьший (по
абсолютной величине) сдвиг по времени, который перево-
дит кривую тока в кривую напряжения.
536
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Рассмотрим случай емкости. В этом случае / = С-^,
поэтому *)
sin
ос).
Записав фс в виде <рс = ф, cos ((of -j- а,), получим:
1
¦ CL-
я
"-
Следовательно, в цепи переменного тока соотношение между
амплитудой тока и амплитудой напряжения на емкости
такое же, как на сопротивлении, равном 7?, = ^—. Выра-
жая емкость в фарадах и частоту в обратных секундах,
получим У?, в омах.
Рис. 203.
Кривая напряжения в емкости сдвинута относительно
кривой тока вперед на четверть периода (рис. 203). Таким
образом, кривая напряжения фс в емкости сдвинута в сто-
рону, противоположную кривой ф^.
При данном одинаковом токе ф? и фс имеют противо-
положный знак. Если же совместить кривые ф^ и фс, то
окажется, что ток, идущий через емкость, и ток, идущий
через индуктивность, имеют противоположные знаки. Дей-
ствительно, все формулы, выражающие ф в зависимости
•) Постоянная интегрирования равна <рс. В переменном токе
всегда <рс = Q.
§ 11]
ПЕРЕМЕННЫЙ ТОК
537
от /, легко обратить, т. е. выразить / в зависимости от
Напишем их рядом:
/=/0 cos (o)*-f~a)« ф = ф0 cos (att -{- a),
ф/? = Я/о cos ((o^ + a), /„ = ^rcos
= gj сое
0 cos
Z.a>/e sin ((ot -f- а).
с=ФоС&) cos
= — ФОС« sin ((at -{- а).
Противоположный сдвиг фазы и противоположные
знаки в формулах, относящиеся к индуктивности и емкости,
имеют решающее значение при рассмотрении L и С, вклю-
ченных вместе.
В опытах с переменным током часто пользуются
однолучевым катодным осциллографом. При этом на одну
пару отклоняющих пластин (отклонение по оси х) подают
напряжение, пропорциональное силе тока. На другую пару
пластин (отклонение по оси у) подают напряжение.
Луч движется по линии, уравнение которой имеет вид
коэффициенты а и Ь зависят от чувствительности осцил-
лографа. Так как / и ф суть периодические функции вре-
мени, то луч прочерчивает на экране все время одну и ту
же линию. При частоте 50 периодов в секунду глаз не
замечает движения луча, а видит сплошную светящуюся
линию.
Если на пластинки вертикального отклонения осцилло-
графа подается разность потенциалов с сопротивления, ф^,
то луч описывает прямую: в самом деле,
х = а/ = а/в cos (<ot -\- а), у = b<pR = bRjn cos (<ot -\- a),
исключая t, найдем У = -г^х. Если же на эти пластин-
ок
ки подается разность потенциалов с емкости, ф-с, то
538 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
получается эллипс:
х = aj\ cos {att + а), у — Ъ ^ /0 sin (со/ -f- а).
Точно так же эллипс получается при включении ф^. При
включении Фд + ф^ или ф/у + Фс оси симметрии эллипса
уже не совпадают с осями х и у. Таким образом, по форме
осциллограммы можно судить, что включено в цепь (С, L
или R), чем «начинен ящик» (стр. 488, рис. 175).
§ 12. Средине величины, мощность и сдвиг фазы
В предыдущем параграфе ток и напряжение рассматри-
вались как функции времени. Однако во многих вопросах
достаточно знать средние значения этих величин.
Как простейший пример рассмотрим нагревательный при-
бор с сопротивлением R. Мы знаем, что в цепи постоян-
ного тока мощность (т. е. количество энергии, выделяю-
щейся в единицу времени) равна
В цепи переменного тока мгновенная мощность равна
а @ = ф (О i (О=Я U ОГ =[-^.
Поэтому
А (*) = /?/! cos1 («0D-а). A2.1)
На протяжении одного периода h (/) дважды обращается
в нуль и дважды достигает максимального значения, рав-
ного Rjl. При рассмотрении нагревательных приборов нас
обычно интересует количество тепла, выделившееся за
время t, во много раз превышающее период переменного
тока Т. Поэтому найдем среднее значение мощности за
большой промежуток времени t. В силу A2.1)
А= Rj\ cos1 (at -\-a) = /?/: cos2 (<af + a) =±Rj\, A2.2)
§ 12] СРЕДНИЕ ВЕЛИЧИНЫ, МОЩНОСТЬ И СДВИГ ФАЗЫ 539
причем последнее равенство приближенное, и оно тем точ-
нее, чем больше t.
Принято определять среднее значение силы переменного
тока у как силу постоянного тока, выделяющего равную
мощность на сопротивлении R,
Из A2.3) находим:
T=J?-/, = 0,71/0. A2.4)
У 2
Точно так же среднее значение напряжения <р определяется
из условия
и Ф5 _фо
Приборы, измеряющие переменный ток,— амперметры, вольт-
метры— градуированы так, что стрелки показывают на
шкале именно среднее значение у, <р.
Из формул A2.4) и A2.5) следует, что максимальные
значения силы тока и напряжения, достигаемые в цепи
переменного тока, в \^2 раз больше средних. Так, напри-
мер, в цепи со средним напряжением 220 в максимальное
мгновенное напряжение достигает ±310 в.
Из соотношений A2.2), A2.4), A2.5) и формулы ф0 = Rja
следует, что
4> = Rj и h = q>f,
так что закон Ома и связь между мощностью, током
и напряжением на сопротивлении справедливы для средних
значений.
При прохождении переменного тока через емкость и ин-
дуктивность мы встретились с тем, что сила тока и напря-
жение меняются по кривым, которые сдвинуты одна отно-
сительно другой, хотя частота их одинакова. Рассмотрим
мощность в общем случае произвольного сдвига фазы.
540 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VUI
Пусть
/•==/„ cos
ф = фв cos (at -j- P + а)-
Тогда
Л@=/вфв cos (wf + Р) cos (of + Р +<*)•
Воспользуемся известной формулой тригонометрии
cos ((of 4- Р 4~ а)= cos (ш' + Р)cos а — sin (ш* + Р)sin a-
Подставляя, получим:
cos ((of 4" Р) cos (of 4- Р 4- а) =
= cos а cos* (<и/ 4" Р) — s*n а cos (ш' ~Ь Р) s*n № ~f" P)-
Так как
cos (cof 4~ Р) sin (<Df 4- Р) =4"sin ^2ш^ ~Ь 2^ = Of
то
h = /офо cos а - -у = /ф cos а.
Таким образом, среднее значение мощности в общем слу-
чае, при наличии сдвига фаз а, пропорционально cos a.
В частном случае сопротивления а = 0, cos се =1 мы воз-
вращаемся к формуле A2.2).
В случае емкости а = ^-, cosa = 0, в случае индук-
тивности a = 4--у, cos a = 0. Таким образом, в общих
случаях средняя мощность равна нулю. Этот результат
вполне понятен физически. В емкости и индуктивности
электрическая энергия не превращается в тепло, а только
может запасаться. В цепи переменного тока на протяжении
одной части периода емкость забирает из цепи электриче-
скую энергию и запасает ее, во время другой части периода
емкость отдает обратно свою энергию, работает на цепь.
То же самое относится и к индуктивности, включенной
в цепь переменного тока.
§ 13] КОЛЕБАТЕЛЬНЫЙ КОНТУР В ЦЕНИ ПЕРЕМЕННОГО ТОКА 541
§13. Колебательный контур в цепи переменного тока.
Резонанс напряжений
Рассмотрим теперь включенные последовательно в цепь
переменного тока сопротивление, индуктивность и емкость
(рис. 204). Очевидно, что в этой системе ток, идущий
Рис. 204.
через R, L, С, одинаков. Запишем его в виде
/=/0cos((o*-{-a). A3.1)
Разность потенциалов в цепи
Припоминая формулы A1.2) — A1.4), получим:
Ф = Rja cos (ait -\- a) — Z.(o/O sin (at -f- «) -f" -^ sin (ait -J- a) =
= Rj9 cos (ait -f~oc) ~\~jt I p; Z.(o sin(a>^—j— a). A3.2)
Из этой формулы видно, что разности потенциалов на
индуктивности и на емкости имеют разные знаки, благо-
даря чему коэффициент при sin (ait -\- a) есть разность двух
членов. Запишем ф в виде
A3.3)
Тогда b есть амплитуда разности потенциалов, т. е. наи-
большее значение разности потенциалов (напряжения). Для
того чтобы найти Ь, перепишем A3.3) так:
Ф = b cos p cos (<ot -j- a) — b sin f$ sin (<ot -f- a).
Сравнивая последнее выражение с A3.2), находим:
6 cos Р =/?/». ^
6 sin в = /«
542 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
Возводя равенства A3.4) в квадрат и складывая, получим:
откуда
Из формулы A3.5) видно, что при данном значении амп-
литуды тока /0 амплитуда напряжения b минимальна при
1
S5 03.6)
Записав A3.5) в виде /,== ¦ — . видим,
что при данном значении амплитуды напряжения ам-
плитуда тока максимальна, если выполнено условие A3.6).
Условие A3.6) можно записать так:
1
VTc
= -^= есть как раз собственная частота контура
с данными L, С. Поэтому условие A3.6) есть условие
резонанса, условие совпадения собственной частоты контура
с частотой того переменного тока, который мы подаем.
Отметим, что при резонансе напряжение в цепи равно
Ф = Я/0 cos (at-{-a). A3.7)
Пользуясь A3.1), находим, что при резонансе
Ф = Я/. A3.8)
Перейдем к средним значениям. Средние значения величин
тока и разности потенциалов определяем в соответствии
сформулами A2.4) и A2.5). Из формулы ф? = L©/0 sin(o* -{-a)
находим:
фй = ?,«7 = ^ф. A3.9)
Аналогично из формулы фс=^/0 sin (со/-f-а) получим:
§ 13] КОЛЕБАТЕЛЬНЫЙ КОНТУР В ЦЕПИ ПЕРЕМЕННОГО ТОКА 543
Формулы A3.7) — A3.10) имеют место только в случае
резонанса, т.. е. при ш = ,.—:. Подставляя это значение о>
в формулы A3.9) и A3.10), получим:
Поэтому в случае резонанса напряжение на индуктивности
ii на емкости тем больше, чем меньше сопротивление R.
Ф^ и фс могут во много раз превышать напряжение источ-
ника переменного тока ф~
При последовательном соединении складываются сопро-
тивления. Но «сопротивления» емкости и индуктивности
имеют противоположный знак и по-разному зависят от
частоты. При резонансной частоте они равны по абсолют-
ной величине и, следовательно, взаимно уничтожаются.
Таким образом, система из последовательно включенных
R, L, С имеет при резонансе, <» = (оо, минимальное со-
противление, пропускает наибольший ток при данной
амплитуде переменного напряжения по сравнению с то-
ком при той же амплитуде, но частоте не в резонансе,
Интересно исследовать подробно, как меняются ампли-
туда напряжения и амплитуда силы тока, если мы отходим
от точного резонанса, т. е. если мы рассматриваем <о=^=—р= .
Для того чтобы сделать это, поступим следующим обра-
зом. Пользуясь формулой A3.3), найдем что ф = —^ ,
откуда Ь =У~2 ф. Подставляя это значение в A3.5), получаем:
но -?===/, поэтому
Находя отсюда j и подставляя его в A3.9) и A3.10),
544 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
получим:
Обозначим через «0 собственную частоту контура. Тогда
o>i = j?- Последние формулы можно записать в виде
О)"
:ф.
фс =
ф-
A3.11)
В таком виде ясна зависимость амплитуды от того,
насколько близка собственная частота контура <о0 к частоте
переменного тока о.
20
70--
0,9ы0
Рис. 205.
Отношение ~k- в зависимости от ш вблизи а>=г<л
Ф
показано на рис. 205. График построен для случая
а
-—=0,05. На графике виден типичный так называемый
резонансный ход кривой.
§ 14] ПАРАЛЛЕЛЬНОЕ ЗКЛЮЧЕНИЕ ИНДУКТИВНОСТИ И ЕМКОСТИ 545
Если -^ <^ 1, то зависимость ^- и ^ от <о определя-
ется главным образом вторым членом подкоренного выра-
жения, т. е величиной (о* — ш*)!. При ш = ш0 этот член
обращается в нуль, и при сделанном предположении
(^•^ 1 } знаменатель имеет минимум, а величина ампли-
туды максимальна. Амплитуда составляет 70°/0 максималь-
ной при («J — ш*)* = -у^-, т. е. при
откуда
То изменение частоты, при котором квадрат амплитуды
падает вдвое по сравнению со своим максимальным зна-
чением, называется шириной резонанса. Если амплитуда
составляет 70°/0, т. е. 0,7 от максимальной, то квадрат
амплитуды составляет 0,7*=&0,5 от максимального. Поэтому
ширина резонансной кривой ш — «0 есть -^т, т. е. ши-
рина равна величине, характеризующей скорость затухания
колебаний в таком контуре (см. § 9).
Следовательно, чем меньше сопротивление R, тем
меньше ширина резонанса, тем круче идет кривая вблизи
<й = <йп. Из формул A3.11) видно, что величина максимума
— тем больше, чем меньше R. Поэтому явление резонанса
Ф
особенно сильно, если R мало.
§ 14. Параллельное включение индуктивности и емкости.
Резонанс токов
Рассмотрим схему рис. 206, отличающуюся от схемы
рис. 204 тем, что L и С включены параллельно. Сопро-
тивление цепи считаем весьма малым и пренебрегаем им.
В этом случае фс и <pL одинаковы и равны напряжению
в цепи (т. ё. в источнике переменного тока) (р, а ток /
в цепи складывается из тока jc, текущего через С, н
546 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [ч. VIII
тока }L, текущего через L. Пусть
ф? = Фс=Ф = Фо cos
Пользуясь формулами § 11, найдем:
1с=—
Поэтому
Отсюда
или _ _
где положено соо = .
В этом случае также проявляется типичная резонансная
зависимость: при данной силе тока / напряжение <р тем
больше, чем ближе со к со0. Легко убедиться, что при со,
I——г
Рис. 206.
близком к со0, jL и /с гораздо больше, чем / цепи, т. е.,
по существу, в контуре, состоящем из L и С, происходят
сильные колебания. При этом достаточно малого внешнего
тока для того, чтобы поддерживать гор аздо более силь-
ные токи в контуре.
При параллельном соединении, как известно, склады-
ваются проводимости, т. е. величины, обратные сопротив-
лениям,
-L—_L_4—L _i__L _i_
R — Я, ^ R. ^ R, ^ т''
«Проводимости» (т. е. отношения тока к разности по-
тенциалов) у емкости и индуктивности имеют противопо-
§ 14] ПАРАЛЛЕЛЬНОЕ ВКЛЮЧЕНИЕ ИНДУКТИВНОСТИ И ЕМКОСТИ 547
ложный знак и по-разному зависят от частоты. При
резонансе (со —(о0) они взаимно уничтожаются и общая
проводимость системы наименьшая, т. е. ток наименьший
при данной разности потенциалов, а следовательно, раз-
ность потенциалов Фав наибольшая при данном токе во
внешней цепи.
В упрощенной схеме без сопротивления амплитуда
колебании неограниченно растет при приближении со к соо.
В действительности включенное в схему сопротивление
приводит к тому, что
амплитуда конечна при
Если включить R Г~*
параллельно L и С, то }___
все расчеты становятся
очень похожими на Рис. 207.
расчеты предыдущего
параграфа. Но этот случай редко встречается в практике.
В действительности индуктивность обычно имеет заметнее
сопротивление, поэтому типичной является схема рис. 207.
В этом случае расчеты несколько более длинны, чем
в предыдущем параграфе, и мы не будем приводить' их
в подробностях. Результат расчетов (при со, близком
R \
к сов, и при малом т—-J дает:
1l . 1с =
Таким образом, оказывается, что усиление тока при ре-
зонансе в цепи с параллельным включением подчиняется
тому же закону, что и усиление напряжения при после-
довательном включении, рассмотренное в предыдущем
параграфе.
В предыдущем параграфе мы получили формулу для
ширины резонанса
которая показывает, что чем медленнее затухают колебания,
548 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
тем меньше ширина резонанса. Этот факт имеет место
не только для электрических колебаний. Рассмотрим любую
систему, в которой могут происходить колебания. Пусть
некоторая внешняя сила вызвала колебания в такой системе
и после перестала действовать. Система оказалась предо-
ставленной самой себе. После этого колебания начинают
затухать. При этом если амплитуда колебаний пропорцио-
нальна е~*', то скорость затухания можно характеризо-
вать величиной у. Эта величина имеет размерность \\сек.
За время т=— амплитуда убывает ве раз, т. е. на 63е/0.
Теперь рассмотрим раскачку такой системы периоди-
ческой внешней силой. Амплитуда колебаний в данный
момент есть сумма амплитуд, приобретенных за все время
раскачки. При наличии затухания амплитуда, приобретен-
ная давно, слишком рано успевает затухнуть, не играет
роли, не вносит заметного вклада в амплитуду колебаний
в данный момент.
Время затухания, очевидно, равно —,— за это время
амплитуда свободных колебаний успевает уменьшиться
в е -раз, т. е. на 630/»- Следовательно, дажг в том случае,
когда раскачивающая сила действует непрерывно, от t=—оо,
все равно амплитуда колебаний определяется лишь интер-
валом времени от t до t, где t — момент наблюде-
ния; действие силы в более ранний период успевает
затухнуть.
Для того чтобы сильно проявилось различие- между
двумя периодическими силами с несколько различными
периодами, /-"„sin о>0г и /^sino?, нужно такое время наблю-
дения Т, за которое их фазы разойдутся приблизительно
на я единиц
так что
Следовательно, если колебания системы «помнят» только
действие силы за время Т=—, то у такой системы раз-
§ 15] ТОК СМЕЩЕНИЯ И ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ СВЕТА 549
личие в частотах возбуждающей силы, меньшее
мало повлияет на амплитуду.
Отсюда видно, что ширина резонансной кривой пропор-
циональна затуханию у.
С другой стороны, так как система «помнит» и собирает
воздействие силы за время —, то сама амплитуда в ре-
зонансе— а значит, и высота резонансной кривой — обратно
пропорциональна затуханию у. Наши расчеты подтверждают
эти соображения.
§ 15. Ток смещения и электромагнитная теория света
Выше везде мы почти без оговорок рассматривали ток,
идущий через конденсатор. Действительно, если включить
конденсатор в цепь переменного тока последовательно
с амперметром, то амперметр покажет вполне определенную
силу тока / =Соир. С другой стороны, через конденсатор
ток не идет: пластины конденсатора разделены изолятором
(например, между ними пустота), поэтому те индивидуаль-
ные носители электричества — электроны, которые находятся
в левом проводе и на левой пластине, никогда не попадут
на правую пластину и правый провод. Следовательно,
в пространстве между пластинами не движутся заряжен-
ные частицы, т. е. нет электрического тока в том смысле,
как мы понимали ток до сих пор.- В этом пространстве
есть только электрическое поле, которое изменяется, когда
меняется заряд пластин, т. е. когда в левом и правом
проводниках течет ток.
Теперь возникают две возможности:
1) либо надо извиниться перед читателем, сказав, что
везде, где говорилось 6 токе через емкость, мы выража-
лись неточно, на самом деле тока нет, ток течет только
в проводах слева и справа;
2) вторая возможность заключается в следующем.
Когда в проводах слева и справа течет ток, то в простран-
стве между пластинами обязательно меняется электрическое
поле. Значит, переменное электрическое поле нужно рас-
650 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
сматривать наравне с обычным током — движением заряжен-
ных частиц. Максвелл, высказавший эту точку зрения,
сумел из нее получить грандиозные следствия.
Давно было известно, что электрический ток, т. е.
движение заряженных частиц, вызывает появление маг-
нитного поля. Но если переменное электрическое поле
подобно электрическому току, то переменное электрическое
поле в пустоте тоже должно создавать магнитное поле.
Эта гипотеза Максвелла привела к замечательной сим-
метрии между электрическим и магнитным полями. Фара-
дей экспериментально открыл индукцию, т. е. тот факт,
что изменение магнитного поля вызывает появление
электрического поля. Максвелл умозрительно пришел
к предположению о существовании аналогичного явления,
при котором изменение электрического поля вызывает
появление магнитного поля. Только после этого предпо-
ложения теория электрических и магнитных полей приоб-
рела современный вид.
Математически теория Максвелла записывается в виде
дифференциальных уравнений, которые слишком сложны
для нашей книги, и мы их приводить не будем. Решения
этих уравнений описывают распространение в пустоте
электрических и магнитных полей. При этом обязательно
должны иметь место оба поля: изменение электрического
поля вызывает магнитное поле, изменение магнитного
поля вызывает электрическое поле.
Ко времени, когда работал Максвелл, уже были сделаны
опыты Фарадея, известна была связь между переменным
магнитным полем и индуцируемой им э.д.с. Известно было
магнитное поле тока. Наконец, известна была связь между
зарядом конденсатора и электрическим полем между его
пластинами. Этих данных достаточно для того, чтобы
написать уравнения для полей в пустоте.
Максвелл нашел скорость распространения полей
в пустоте. Эта скорость оказалась равной скорости света!
Отсюда, естественно, следовало предположение, что свет
и есть не что иное, как электромагнитные колебания.
Далее теория предсказывала возможность существования
электромагнитных колебаний любой длины волны, в том
числе и рентгеновых лучей (длина которых в тысячи раз
меньше длины световой волны) и радиоволн с большой
§ 16J НЕЛИНЕЙНОЕ СОПРОТИВЛЕНИЕ И ТУННЕЛЬНЫЙ ДИОД 551
длиной волны. Так работы Фарадея и Максвелла начали
тот путь, который завершился открытием радиоволн Герцем
и изобретением радио как средства связи нашим соотече-
ственником А. С. Поповым.
§ 16. Нелинейное сопротивление и туннельный диод
Рассмотрим двухполюсник — «ящик», похожий на сопро-
тивление в том отношении, что сила тока, проходящего
через ящик, зависит только от мгновенного значения раз-
ности потенциалов. В этом отношении ящик не похож ни
dj
на индуктивность, где <р зависит от з:, ни на емкость,
где ф зависит от ^ jdt. Однако от обычного сопротивления
ящик отличается тем, что зависимость / (ф) отличается от за-
кона Ома, / = -^-; у «ящика» зависимость ;' (ф) более слож-
ная. Эта функция j (ф) называется характеристикой ящика.
Единственное общее утверждение, которое можно сде-
лать про у'(ф), что ф и / не могут быть разного знака,
если внутри «ящика» не спрятаны батареи или другие
источники энергии. Если ф и / одного знака, то при про-
хождении тока энергия внутри «ящика» поглощается,
«ящик» отбирает электрическую энергию от той цепи,
в которую он включен; в «ящике» эта энергия превраща-
ется в тепловую и рассеивается. Так как ф непрерывно
и ф < 0 при у < 0 и ф > 0 при / > 0, то *
при /==0 ф = 0. В остальном зависи-
мость /(ф) может быть любой. Напри-
мер, в качестве выпрямителей тока
применяются «ящики», характеристика
которых показана на рис. 208: в
одну сторону ток течет легко, при Рис 208.
малой разности потенциалов, в дру-
гую сторону ток почти не идет; как видно из гра-
фика, даже при большой отрицательной разности потен-
циалов ток мал. Такими свойствами обладают так
называемые диоды, изготовляемые из двух полупроводни-
ков. В 1958 г. в Японии удалось сделать из специально
подобранных полупроводников «ящик», так называемый
туннельный диод (в действительности этот «ящик»
I
552
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБЛГЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
представляет собой миниатюрный цилиндрик, диаметр и
высота которого несколько миллиметров), с необычной
кривой / (ф) с минимумом (см. рис. 209, на котором даны
типичные значения ф и /). Такая кривая не противоречит
высказанному принципу, знак ф везде тот же, что и
знак /', так что <ящик» только поглощает энергию. Мы
не будем входить в рассмотрение
физических причин такой стран-
ной кривой, но зато рассмотрим
следствия для цепи, в которую
включен туннельный диод. Для
краткости будем называть его и
дальше просто «ящик».
Начнем с наиболее простой
__ цепи, состоящей из трех частей:
9 батарея с э.д.с. Е — сопротив-
ление R (обычное, подчиняю-
щееся закону Ома)—«ящик»
Рнс 209. (рис 210). Внутреннее сопротив-
ление батареи включим в R.
Уравнение, определяющее ток и распределение потен-
циала в цепи, имеет вид
6тА
tmA
O.OW
где ф — разность потенциалов на ящике, /(<р) есть функ-
ция, определяемая свойствами «ящика» (см. рис. 209).
Ток через R равен току через «ящик»,
поэтому фя = Rj = Rj (ф).
Это уравнение удобно решить гра- I '*
фически. Запишем его так: - I '
Ф = ? — /?/(ф), Рис- 21°
н построим в плоскости ф, / прямую у = Е— Rj. Эту пря-
мую можно назвать «нагрузочной линией» системы батарея —
сопротивление. Решение задачи дается пересечением прямой
Ф=?—Rj Г при / = Е ,ГУ) с линией/ (ф)—характеристикой
«ящика». На рис. 211 показано такое графическое решение
задачи, притом для одной батареи и трех разных сопро-
тивлений: малого Rlt среднего R% и большого Rt.
§ 18] НЕЛИНЕЙНОЕ СОПРОТИВЛЕНИЕ И ТУННЕЛЬНЫЙ ДИОД 553
j
Из графика видно, что при достаточно большом Е
можно подобрать такое У? — не слишком малое и не слиш-
ком большое, при котором есть три точки пересечения А,
В, С — три решения!
Необходимое условие для существования трех решений —
наличие падающего участ-
ка кривой / (ф). Ясно, что ли-
ния, на которой везде-Д- > О,
например рис. 208, может
только один раз пересечься
с нагрузочной прямой, ка-
ковы бы ни были Е и R.
(всегда R>0).
Рассмотрим теперь не-
сколько усложненную схе-
му с емкостью, включен-
ной параллельно «ящику»
(рис. 212). Для такой схе-
мы получим, что ток через
«ящик» /(ф) и Ток через
емкость С -? в сумме равны току через сопротивление
?-9
Я
Рис. 211.
Отсюда
Точки пересечения характеристики «ящика» /(<р) с нагру-
6 R Я
нис. 4V1.
зочной линией —jr^- соответствуют решениям
Ф = const, -j~ =0.
Посмотрим знак —ц- около этих точек. Легко убедиться.
554 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
глядя на рис. 211, что
при 4f
dfV л
при ФА<ф<Фа ЧГ<0'
dm л
при фа < ф < фс -?- > О,
при ф>Фс -fj2. <0.
На рис. 213 показано стрелками направление измене-
ния ф со временем. Следовательно, среднее решение В
Рис. 213.
неустойчиво: стоит от него немного отойти влево или
dtp
вправо — и появляется -~ такого знака, что отклонение
Ф от фв увеличивается!
Л и С представляют собой два устойчивых решения,
которым соответствуют устойчивые состояния системы.
Наличие двух устойчивых состояний позволяет при-
менять такие «ящики» в математических машинах как
ячейки памяти: сделав много таких цепей и переводя
внешним воздействием одни в состояние А, другие в сос-
тояние С, мы можем «записать», «запомнить» какое угодно
число или другую информацию. С помощью таких систем
любую информацию мы записываем шифром вида А АС А
С АС С С ..., где каждая
5 а я буква А или С означает со-
стояние, в котором находится
соответствующая система A-я
в Л, 2-я в А, 3-я в С, 4-я в
Рис. 214. Лит. д.).
Рассмотрим теперь систе-
му (рис. 214), состоящую из
индуктивности и емкости, включенных параллельно «ящи-
ку». Снова обозначаем ф разность потенциалов на «ящике»,
гН| Г г-т-{=Ь-1
16] НЕЛИНЕЙНОЕ СОПРОТИВЛЕНИЕ И ТУННЕЛЬНЫЙ ДИОД 555
/(ф) его характеристику; ток, текущий через L и С, обо-
значим /j
СЧГ=!" Ф-Фс = Ф,= ^.
Рассмотрим процесс в контуре, когда ток и потенциал
в «ящике» близки к средней точке пересечения В.
Пусть
/ = У (Фв) + / •% |„=»а = / (Ф
где k есть сокращенное обозначение производной -р- при
Ф = фа. Силу тока мы представили первыми двумя членами
ряда Тейлора, средний потенциал емкости равен ц>в, при-
чем фа и / (фа) удовлетворяют условию
Подставляя эти выражения в уравнения, получим после
сокращений:
где
Из
этих
уравнении
1 1
г R
получим
1
t" R
'•
df
1 dm
Из уравнений A6.1), найдем:
d<* d/ d< dt С '»•
556 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. V11I
и окончательно
чр-+~т ~ш~ + тс" i •=°-
Последнее уравнение представляет собой обычное урав-
нение колебательного контура с емкостью С, индуктив-
ностью L и сопротивлением г.
Сопротивление г соответствует тому, что емкость и
индуктивность замкнуты параллельно двумя цепями: цепью
батареи с сопротивлением R и «ящиком» с сопротивлением
1 d<p -^
-г- = -р- . Так как эти две цепи включены параллельно,
то складываются проводимости, т. е. величины, обратные
сопротивлениям, откуда и следует выражение для г.
Токи и потенциалы в системе распадаются на сумму
двух слагаемых: постоянного слагаемого <рв, /(фв) и коле-
бательного слагаемого /, (t), f(t), g(t). При этом для ко-
лебательного слагаемого роль сопротивления «ящика» играет
производная -р- , взятая по характеристике «ящика».
Будь в ящике обычное омическое сопротивление, <р = ./?/
( -р-= Rj, производная и равнялась бы величине сопротив-
ления.
К чему приводит необычная характеристика / (<р) «ящи-
ка»— туннельного диода (см. рис. 211)? В точке В про-
изводная -Лг < 0, т. е. по отношению к колебаниям
«ящик» имеет отрицательное сопротивление! Более того, из
рис. 211 видно, что в точке пересечения
dtp
>
R
так как -= это как раз угловой коэффициент нагрузоч-
ной прямой /=¦—р-?, пересекающей характеристику в
точке В. Следовательно, суммарное сопротивление коле-
бательного контура
1
Уравнение для колебательного контура с L, С, г при
г>0 давало затухающие колебания. При г<0 это уравне-
ОТВЕТЫ И РЕШЕНИЯ 557
ние даст раскачивающиеся, усиливающиеся с течением
времени колебания.
Таким образом, с помощью туннельного диода можно
генерировать (возбуждать) в контуре колебания.
Способность к возбуждению колебаний является след-
ствием неустойчивости точки В. Энергия колебаний чер-
пается от батареи. Амплитуда колебаний растет со временем
по показательному закону лишь до тех пор, пока можно
считать ее малой и пользоваться разложением в ряд
Тейлора характеристики / (<р) около точки В. Максималь-
ная амплитуда, грубо говоря, ограничивается точками А
и С рис. 211. В настоящее время A961 г.) испытаны гене-
раторы с к.п.д. до 25°/0 при мощности 0,5 милливатта
при частоте 7500 мегациклов (длина волны 4 см). Для нас
цепи с туннельным диодом интересны с точки зрения ма-
тематического рассмотрения нелинейной задачи, вопросов
устойчивости решений и представления токов в системе
как наложения постоянного решения и колебаний.
ОТВЕТЫ И РЕШЕНИЯ
t__
§ 2. 1. Ток в схеме убывает по закону / = /ое /?с. В интересую-
щнй нас момент времени tx / = —j/0, поэтому 7^/о=/ов *с, отку-
- —
да — = е ^с. Логарифмируя последнее равенство, находим
In у!г = — -рТТ» откуда tx = RC ln-^^rO,105 ЯС. Пользуясь этой
формулой, находим для У? —107 ом t1 = \ сек; для /? = 10° ом
/,= 10,5 сек; для /? = 10е ом /, = 105 сек. Момент tt, когда ток
упадет вдвое, определяем аналогично: 0,5/0=/вв . откуда
tt = 0,693RC. При R = \O1 ом tt = 6,93 сек; при R = 10° ом
tt = 69,3 сек; прн # = 10* сш tt =693 сек. 2. Воспользуемся
формулой A.11), получим фС( -(- Фя -+- фСа — °» откуда
Ф^ = —(Фс,-г" Фс5)« Ток в цепи всюду одинаков, поэтому
/ = Сг -^- = С2 -^- = ^- = — Фс' ~t Фс' . Получаем уравнения
at at К К
-#- = — TSr- <фс, + Фс). Щт3 = —Ъг~ (Фс.+Фс,)- Сложив эти урав-
558 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И КОЛЕБАТЕЛЬНЫЕ ЯВЛЕНИЯ [Ч. VIII
нення,.получим d (*<-.+*<:,)_ Фс, + Фс, ^ ^ положено с== с.с«
иГ /\С С] -j— Cg
(величина С есть емкость двух последовательно соединенных конден-
саторов с емкостями Сх и Ся). Так как <рс -\-уСл = а при t = 0, то
нз последнего уравнения находим фг -f-фс =ае ^с. Ясно, что
d<P(~ <^Фс d
Ci -^Г2- — С» -^ = ° или ~аГ (ci9Cl — С1Фса) = 0. Поэтому
Cj9C]—С,фСа = Л, где Л — постоянная. Пользуясь начальным усло-
вием фс==а, фСа = о при / = 0, находим A=Cta. Итак,
фс,-Н Фс, = ^ ^С> С1Фс2 — с«Фс, = ci°- Отсюда находим
2
3. Величины, относящиеся к контуру до увеличения всех линейных
размеров, отметим индексом 1, после увеличения размеров—инде-
ксом 2. Тогда Г.^ад, Га = Я,С„ С, = ?§-=«-|^-= яС,.
Л.= Q"^-. /?* = Q-^-=Q-^=T- Поэтому Г1 = Л1С,=^пС1 =
= /?,С, = Т1. Постоянная времени не изменилась.
§ 8. 1. cosa= / ^" Г1УСТЬ разность потенцна-
лов на пластинах конденсатора равна ф. Для схемы рис. 198
Фе + ф? 4-Фс = ° или, учитывая, что фЕ = —Еа, L -^- + ф=?0.
Так как j=C—~, то Z.C—т^-4-Ф = ^о- Запишем это уравнение
в виде LC —г^- z=—(ф — EQ). Положим г = ф — Ео; тогда уравне-
dxz
нне принимает вид LC ¦=—г. Его решение есть г = A cos wtf -f-
-f--Bslnco<, где ш =—= . Поэтому ф = A cos со/ -f- В sin co< -f- Ea.
Прн < = 0 ф = 0, /=0. Пользуясь этим, находим Л = — ?0, В = 0.
Окончательно ф = ?0A—coswt). Максимальное значение ф полу-
чается при cos ш/ =—1, т. е. при t=. = -=- (через половину
периода колебаний), фмакс:=2.Е0. 3. Энергия емкости W = —g— ==
4С?!
= —^—=2СЕ\. Энергия, отданная источником напряжения,
Р = дЕ0 = С<рЕ0 = 2СЕ\.
ОТВЕТЫ И РЕШЕНИЯ 559
§9. 1. /(*) = _ J^-e-«sIn со*, гдеХ = -^-, Ш. = _!__Х..
Для трех заданных случаев получим: /(*) =—1,0025"Mst sin *•
i(t)=~ 1,03 le'»' sin 0,97*; / @ = —1.15e"M* eta 0,87*.
2. /(*) = /„( cos со* sin со* J e"**, формулы для Я, и со см. 1.
Для заданных случаев
/(*)=«-»>»«'(— cos* -f- 0,05 sin*);
/ (*) =*-•¦*** (— cos 0,97* -f-0,26 sin 0,97*);
/ (*)=«-»•*' (— cos 0,86* 4- 0,58 sin 0,86*).
3. Если R велико, то ток через сопротивление мал, т. е. в основном
ток идет через индуктивность. Поэтому, чем больше R, тем ближе
эта схема к схеме рнс. 196. В схеме рис. 196 <р = ф0 cos (со* -f-a).
Если R велико, то можно считать, что в схеме рис. 200 <р имеет
такой же вид, но ф0 есть медленно меняющаяся со временем вели-
чина. Воспользуемся соотношением —гг- = — А- Но h = Rj*t где /,
Ф
есть ток, текущий через сопротивление R, /,=-^-. Поэтому
ф* cos1 (со* + а)
= Сф0 -^ = —-^-. Отсюда
§10. 1. ф(*)=е-'4-*е-'; ф (*)=— О.
ПРИЛОЖЕНИЕ
ЛАТИНСКИЙ АЛФАВИТ
Буквы
А а
В Ь
С с
D d
Е е
F t
G в
Название
а
бэ
ЦЭ
ДЭ
э
эф
гэ (жэ)
Буквы
н л
/ i
J i
К k
L I
M m
Название
ха (аш)
и
йот (жн)
ка
ЭЛЬ
эм
Буквы
JV п
0 о
р р
Q Я
R г
S s
Т t
Назваике
Эн
О
пэ
ку
эр
эс
тэ
Буквы
U и
V v
W w
X х
У у
Z z
Название
У
вэ
дубль-вэ
икс
игрек
зэт
ГРЕЧЕСКИЙ АЛФАВИТ
Буквы
А
В
Г
Д
Е
Z
а
Р
Y
б
е
Название
альфа
бета
гамма
дельта
эпсилон
дзета
(зёта)
Буквы
Н л
вед
11
К х
Л К
М A
Название
эта
тэта
ибта
калпа
ламбда
ми (мю)
Вуквы
N
2
О
П
Р
S
V
6
о
я
Q
О
Название
ни (ню)
кси
омикрон
пи
ро
сигма
Вуквы
т
Г
Ф
X
ft
т
¦о
ф
х
Ф
Название
тау
ипсилон
[юпсилон]
фи
хи
пси
омёга